Upload folder using huggingface_hub
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- .gitattributes +55 -55
- __pycache__/click.cpython-312.pyc +0 -0
- problem.py +60 -0
- problems/1000.txt +54 -0
- problems/10000.txt +88 -0
- problems/10001.txt +91 -0
- problems/10002.txt +159 -0
- problems/10003.txt +138 -0
- problems/10004.txt +92 -0
- problems/10005.txt +103 -0
- problems/10006.txt +98 -0
- problems/10007.txt +87 -0
- problems/10008.txt +148 -0
- problems/10009.txt +112 -0
- problems/1001.txt +298 -0
- problems/10010.txt +137 -0
- problems/10011.txt +45 -0
- problems/10012.txt +138 -0
- problems/10013.txt +71 -0
- problems/10014.txt +125 -0
- problems/10015.txt +184 -0
- problems/10016.txt +77 -0
- problems/10017.txt +404 -0
- problems/1002.txt +41 -0
- problems/10024.txt +71 -0
- problems/10025.txt +81 -0
- problems/10026.txt +95 -0
- problems/10027.txt +90 -0
- problems/10028.txt +51 -0
- problems/10029.txt +62 -0
- problems/1003.txt +73 -0
- problems/10030.txt +66 -0
- problems/10031.txt +52 -0
- problems/10032.txt +69 -0
- problems/10033.txt +81 -0
- problems/10034.txt +81 -0
- problems/10035.txt +112 -0
- problems/10036.txt +142 -0
- problems/10037.txt +151 -0
- problems/10038.txt +187 -0
- problems/10039.txt +74 -0
- problems/1004.txt +49 -0
- problems/10040.txt +44 -0
- problems/10041.txt +54 -0
- problems/10042.txt +67 -0
- problems/10043.txt +51 -0
- problems/10044.txt +78 -0
- problems/10045.txt +56 -0
- problems/10046.txt +39 -0
- problems/10047.txt +95 -0
.gitattributes
CHANGED
|
@@ -1,55 +1,55 @@
|
|
| 1 |
-
*.7z filter=lfs diff=lfs merge=lfs -text
|
| 2 |
-
*.arrow filter=lfs diff=lfs merge=lfs -text
|
| 3 |
-
*.bin filter=lfs diff=lfs merge=lfs -text
|
| 4 |
-
*.bz2 filter=lfs diff=lfs merge=lfs -text
|
| 5 |
-
*.ckpt filter=lfs diff=lfs merge=lfs -text
|
| 6 |
-
*.ftz filter=lfs diff=lfs merge=lfs -text
|
| 7 |
-
*.gz filter=lfs diff=lfs merge=lfs -text
|
| 8 |
-
*.h5 filter=lfs diff=lfs merge=lfs -text
|
| 9 |
-
*.joblib filter=lfs diff=lfs merge=lfs -text
|
| 10 |
-
*.lfs.* filter=lfs diff=lfs merge=lfs -text
|
| 11 |
-
*.lz4 filter=lfs diff=lfs merge=lfs -text
|
| 12 |
-
*.mlmodel filter=lfs diff=lfs merge=lfs -text
|
| 13 |
-
*.model filter=lfs diff=lfs merge=lfs -text
|
| 14 |
-
*.msgpack filter=lfs diff=lfs merge=lfs -text
|
| 15 |
-
*.npy filter=lfs diff=lfs merge=lfs -text
|
| 16 |
-
*.npz filter=lfs diff=lfs merge=lfs -text
|
| 17 |
-
*.onnx filter=lfs diff=lfs merge=lfs -text
|
| 18 |
-
*.ot filter=lfs diff=lfs merge=lfs -text
|
| 19 |
-
*.parquet filter=lfs diff=lfs merge=lfs -text
|
| 20 |
-
*.pb filter=lfs diff=lfs merge=lfs -text
|
| 21 |
-
*.pickle filter=lfs diff=lfs merge=lfs -text
|
| 22 |
-
*.pkl filter=lfs diff=lfs merge=lfs -text
|
| 23 |
-
*.pt filter=lfs diff=lfs merge=lfs -text
|
| 24 |
-
*.pth filter=lfs diff=lfs merge=lfs -text
|
| 25 |
-
*.rar filter=lfs diff=lfs merge=lfs -text
|
| 26 |
-
*.safetensors filter=lfs diff=lfs merge=lfs -text
|
| 27 |
-
saved_model/**/* filter=lfs diff=lfs merge=lfs -text
|
| 28 |
-
*.tar.* filter=lfs diff=lfs merge=lfs -text
|
| 29 |
-
*.tar filter=lfs diff=lfs merge=lfs -text
|
| 30 |
-
*.tflite filter=lfs diff=lfs merge=lfs -text
|
| 31 |
-
*.tgz filter=lfs diff=lfs merge=lfs -text
|
| 32 |
-
*.wasm filter=lfs diff=lfs merge=lfs -text
|
| 33 |
-
*.xz filter=lfs diff=lfs merge=lfs -text
|
| 34 |
-
*.zip filter=lfs diff=lfs merge=lfs -text
|
| 35 |
-
*.zst filter=lfs diff=lfs merge=lfs -text
|
| 36 |
-
*tfevents* filter=lfs diff=lfs merge=lfs -text
|
| 37 |
-
# Audio files - uncompressed
|
| 38 |
-
*.pcm filter=lfs diff=lfs merge=lfs -text
|
| 39 |
-
*.sam filter=lfs diff=lfs merge=lfs -text
|
| 40 |
-
*.raw filter=lfs diff=lfs merge=lfs -text
|
| 41 |
-
# Audio files - compressed
|
| 42 |
-
*.aac filter=lfs diff=lfs merge=lfs -text
|
| 43 |
-
*.flac filter=lfs diff=lfs merge=lfs -text
|
| 44 |
-
*.mp3 filter=lfs diff=lfs merge=lfs -text
|
| 45 |
-
*.ogg filter=lfs diff=lfs merge=lfs -text
|
| 46 |
-
*.wav filter=lfs diff=lfs merge=lfs -text
|
| 47 |
-
# Image files - uncompressed
|
| 48 |
-
*.bmp filter=lfs diff=lfs merge=lfs -text
|
| 49 |
-
*.gif filter=lfs diff=lfs merge=lfs -text
|
| 50 |
-
*.png filter=lfs diff=lfs merge=lfs -text
|
| 51 |
-
*.tiff filter=lfs diff=lfs merge=lfs -text
|
| 52 |
-
# Image files - compressed
|
| 53 |
-
*.jpg filter=lfs diff=lfs merge=lfs -text
|
| 54 |
-
*.jpeg filter=lfs diff=lfs merge=lfs -text
|
| 55 |
-
*.webp filter=lfs diff=lfs merge=lfs -text
|
|
|
|
| 1 |
+
*.7z filter=lfs diff=lfs merge=lfs -text
|
| 2 |
+
*.arrow filter=lfs diff=lfs merge=lfs -text
|
| 3 |
+
*.bin filter=lfs diff=lfs merge=lfs -text
|
| 4 |
+
*.bz2 filter=lfs diff=lfs merge=lfs -text
|
| 5 |
+
*.ckpt filter=lfs diff=lfs merge=lfs -text
|
| 6 |
+
*.ftz filter=lfs diff=lfs merge=lfs -text
|
| 7 |
+
*.gz filter=lfs diff=lfs merge=lfs -text
|
| 8 |
+
*.h5 filter=lfs diff=lfs merge=lfs -text
|
| 9 |
+
*.joblib filter=lfs diff=lfs merge=lfs -text
|
| 10 |
+
*.lfs.* filter=lfs diff=lfs merge=lfs -text
|
| 11 |
+
*.lz4 filter=lfs diff=lfs merge=lfs -text
|
| 12 |
+
*.mlmodel filter=lfs diff=lfs merge=lfs -text
|
| 13 |
+
*.model filter=lfs diff=lfs merge=lfs -text
|
| 14 |
+
*.msgpack filter=lfs diff=lfs merge=lfs -text
|
| 15 |
+
*.npy filter=lfs diff=lfs merge=lfs -text
|
| 16 |
+
*.npz filter=lfs diff=lfs merge=lfs -text
|
| 17 |
+
*.onnx filter=lfs diff=lfs merge=lfs -text
|
| 18 |
+
*.ot filter=lfs diff=lfs merge=lfs -text
|
| 19 |
+
*.parquet filter=lfs diff=lfs merge=lfs -text
|
| 20 |
+
*.pb filter=lfs diff=lfs merge=lfs -text
|
| 21 |
+
*.pickle filter=lfs diff=lfs merge=lfs -text
|
| 22 |
+
*.pkl filter=lfs diff=lfs merge=lfs -text
|
| 23 |
+
*.pt filter=lfs diff=lfs merge=lfs -text
|
| 24 |
+
*.pth filter=lfs diff=lfs merge=lfs -text
|
| 25 |
+
*.rar filter=lfs diff=lfs merge=lfs -text
|
| 26 |
+
*.safetensors filter=lfs diff=lfs merge=lfs -text
|
| 27 |
+
saved_model/**/* filter=lfs diff=lfs merge=lfs -text
|
| 28 |
+
*.tar.* filter=lfs diff=lfs merge=lfs -text
|
| 29 |
+
*.tar filter=lfs diff=lfs merge=lfs -text
|
| 30 |
+
*.tflite filter=lfs diff=lfs merge=lfs -text
|
| 31 |
+
*.tgz filter=lfs diff=lfs merge=lfs -text
|
| 32 |
+
*.wasm filter=lfs diff=lfs merge=lfs -text
|
| 33 |
+
*.xz filter=lfs diff=lfs merge=lfs -text
|
| 34 |
+
*.zip filter=lfs diff=lfs merge=lfs -text
|
| 35 |
+
*.zst filter=lfs diff=lfs merge=lfs -text
|
| 36 |
+
*tfevents* filter=lfs diff=lfs merge=lfs -text
|
| 37 |
+
# Audio files - uncompressed
|
| 38 |
+
*.pcm filter=lfs diff=lfs merge=lfs -text
|
| 39 |
+
*.sam filter=lfs diff=lfs merge=lfs -text
|
| 40 |
+
*.raw filter=lfs diff=lfs merge=lfs -text
|
| 41 |
+
# Audio files - compressed
|
| 42 |
+
*.aac filter=lfs diff=lfs merge=lfs -text
|
| 43 |
+
*.flac filter=lfs diff=lfs merge=lfs -text
|
| 44 |
+
*.mp3 filter=lfs diff=lfs merge=lfs -text
|
| 45 |
+
*.ogg filter=lfs diff=lfs merge=lfs -text
|
| 46 |
+
*.wav filter=lfs diff=lfs merge=lfs -text
|
| 47 |
+
# Image files - uncompressed
|
| 48 |
+
*.bmp filter=lfs diff=lfs merge=lfs -text
|
| 49 |
+
*.gif filter=lfs diff=lfs merge=lfs -text
|
| 50 |
+
*.png filter=lfs diff=lfs merge=lfs -text
|
| 51 |
+
*.tiff filter=lfs diff=lfs merge=lfs -text
|
| 52 |
+
# Image files - compressed
|
| 53 |
+
*.jpg filter=lfs diff=lfs merge=lfs -text
|
| 54 |
+
*.jpeg filter=lfs diff=lfs merge=lfs -text
|
| 55 |
+
*.webp filter=lfs diff=lfs merge=lfs -text
|
__pycache__/click.cpython-312.pyc
ADDED
|
Binary file (332 Bytes). View file
|
|
|
problem.py
ADDED
|
@@ -0,0 +1,60 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
from selenium import webdriver
|
| 2 |
+
from selenium.webdriver.chrome.service import Service
|
| 3 |
+
from selenium.webdriver.common.by import By
|
| 4 |
+
from selenium import webdriver
|
| 5 |
+
from selenium.webdriver.chrome.service import Service
|
| 6 |
+
from selenium.webdriver.common.by import By
|
| 7 |
+
from selenium.webdriver.chrome.options import Options
|
| 8 |
+
from selenium.webdriver.common.keys import Keys
|
| 9 |
+
from selenium.webdriver.support.ui import WebDriverWait
|
| 10 |
+
from selenium.webdriver.support import expected_conditions as EC
|
| 11 |
+
from selenium.webdriver.chrome.options import Options
|
| 12 |
+
from selenium.webdriver.common.keys import Keys
|
| 13 |
+
from selenium import webdriver
|
| 14 |
+
from selenium.webdriver.chrome.service import Service
|
| 15 |
+
from selenium.webdriver.chrome.options import Options
|
| 16 |
+
import pyperclip
|
| 17 |
+
import time
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
def get_problem(problemId: int):
|
| 21 |
+
baseURL = "https://www.luogu.com.cn/problem/P"
|
| 22 |
+
reqURL = baseURL + str(problemId)
|
| 23 |
+
|
| 24 |
+
try:
|
| 25 |
+
driver = webdriver.Chrome()
|
| 26 |
+
driver.minimize_window()
|
| 27 |
+
driver.get(reqURL)
|
| 28 |
+
|
| 29 |
+
# Wait for the button to be clickable
|
| 30 |
+
button = WebDriverWait(driver, 10).until(
|
| 31 |
+
EC.element_to_be_clickable(
|
| 32 |
+
(
|
| 33 |
+
By.XPATH,
|
| 34 |
+
'//*[@id="app"]/div[2]/main/div/section[2]/section/div/div[1]/a[1]',
|
| 35 |
+
)
|
| 36 |
+
)
|
| 37 |
+
)
|
| 38 |
+
|
| 39 |
+
# Click the button
|
| 40 |
+
button.click()
|
| 41 |
+
|
| 42 |
+
# Wait for a short time for the text to be copied (adjust as needed)
|
| 43 |
+
time.sleep(2)
|
| 44 |
+
|
| 45 |
+
# Use pyperclip to get the clipboard content (simulated)
|
| 46 |
+
clipboard_text = pyperclip.paste()
|
| 47 |
+
driver.quit()
|
| 48 |
+
|
| 49 |
+
# Write down to the file
|
| 50 |
+
file_name = str(problemId) + ".txt"
|
| 51 |
+
with open(file_name, "w", encoding="utf-8") as file:
|
| 52 |
+
file.write(clipboard_text)
|
| 53 |
+
|
| 54 |
+
except Exception as e:
|
| 55 |
+
print(f"An error occurred: {e}")
|
| 56 |
+
|
| 57 |
+
|
| 58 |
+
for i in range(8346, 10100):
|
| 59 |
+
get_problem(i)
|
| 60 |
+
time.sleep(30)
|
problems/1000.txt
ADDED
|
@@ -0,0 +1,54 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 超级玛丽游戏
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
本题是洛谷的试机题目,可以帮助了解洛谷的使用。
|
| 6 |
+
|
| 7 |
+
建议完成本题目后继续尝试 [P1001](/problem/P1001)、[P1008](/problem/P1008)。
|
| 8 |
+
|
| 9 |
+
另外强烈推荐[新用户必读贴](/discuss/show/241461)
|
| 10 |
+
|
| 11 |
+
## 题目描述
|
| 12 |
+
|
| 13 |
+
超级玛丽是一个非常经典的游戏。请你用字符画的形式输出超级玛丽中的一个场景。
|
| 14 |
+
|
| 15 |
+
```
|
| 16 |
+
********
|
| 17 |
+
************
|
| 18 |
+
####....#.
|
| 19 |
+
#..###.....##....
|
| 20 |
+
###.......###### ### ###
|
| 21 |
+
........... #...# #...#
|
| 22 |
+
##*####### #.#.# #.#.#
|
| 23 |
+
####*******###### #.#.# #.#.#
|
| 24 |
+
...#***.****.*###.... #...# #...#
|
| 25 |
+
....**********##..... ### ###
|
| 26 |
+
....**** *****....
|
| 27 |
+
#### ####
|
| 28 |
+
###### ######
|
| 29 |
+
##############################################################
|
| 30 |
+
#...#......#.##...#......#.##...#......#.##------------------#
|
| 31 |
+
###########################################------------------#
|
| 32 |
+
#..#....#....##..#....#....##..#....#....#####################
|
| 33 |
+
########################################## #----------#
|
| 34 |
+
#.....#......##.....#......##.....#......# #----------#
|
| 35 |
+
########################################## #----------#
|
| 36 |
+
#.#..#....#..##.#..#....#..##.#..#....#..# #----------#
|
| 37 |
+
########################################## ############
|
| 38 |
+
```
|
| 39 |
+
|
| 40 |
+
## 输入格式
|
| 41 |
+
|
| 42 |
+
无
|
| 43 |
+
|
| 44 |
+
## 输出格式
|
| 45 |
+
|
| 46 |
+
如描述
|
| 47 |
+
|
| 48 |
+
## 提示
|
| 49 |
+
|
| 50 |
+
**广告**
|
| 51 |
+
|
| 52 |
+
洛谷出品的算法教材,帮助您更简单的学习基础算法。[【官方网店绝赞热卖中!】>>>](https://item.taobao.com/item.htm?id=637730514783)
|
| 53 |
+
|
| 54 |
+
[](https://item.taobao.com/item.htm?id=637730514783)
|
problems/10000.txt
ADDED
|
@@ -0,0 +1,88 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 矩阵快速幂
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
请注意:**本题不是矩阵快速幂模板题**。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
给定一张 $n$ 个点 $m$ 条边的边带权有向图,可能有重边和自环。求从 $1$ 出发到每个点恰好走 $k$ 条边的路径权值的最小值 **对 $998244353$ 取模后的结果**。若路径不存在则输出 $-1$。多组数据。
|
| 10 |
+
|
| 11 |
+
路径权值的定义是路径上所有边的权值之和。
|
| 12 |
+
|
| 13 |
+
## 输入格式
|
| 14 |
+
|
| 15 |
+
第一行一个整数 $S$ 表示子任务编号。
|
| 16 |
+
|
| 17 |
+
第二行一个整数 $T$ 表示数据组数。
|
| 18 |
+
|
| 19 |
+
对于每组数据:
|
| 20 |
+
|
| 21 |
+
- 第一行三个整数 $n, m, k$。
|
| 22 |
+
- 接下来 $m$ 行,每行三个整数 $u, v, w$ 表示一条有向边。
|
| 23 |
+
|
| 24 |
+
## 输出格式
|
| 25 |
+
|
| 26 |
+
对于每组数据,输出一行 $n$ 个由空格隔开的整数表示答案。
|
| 27 |
+
|
| 28 |
+
## 样例 #1
|
| 29 |
+
|
| 30 |
+
### 样例输入 #1
|
| 31 |
+
|
| 32 |
+
```
|
| 33 |
+
1
|
| 34 |
+
1
|
| 35 |
+
5 5 101
|
| 36 |
+
1 2 1
|
| 37 |
+
2 3 100
|
| 38 |
+
3 4 10000
|
| 39 |
+
4 2 1000000
|
| 40 |
+
2 5 10
|
| 41 |
+
```
|
| 42 |
+
|
| 43 |
+
### 样例输出 #1
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
-1 -1 33333401 -1 33333311
|
| 47 |
+
```
|
| 48 |
+
|
| 49 |
+
## 样例 #2
|
| 50 |
+
|
| 51 |
+
### 样例输入 #2
|
| 52 |
+
|
| 53 |
+
```
|
| 54 |
+
见下发文件 ex_matrix1.in
|
| 55 |
+
```
|
| 56 |
+
|
| 57 |
+
### 样例输出 #2
|
| 58 |
+
|
| 59 |
+
```
|
| 60 |
+
见下发文件 ex_matrix1.ans
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
## 样例 #3
|
| 64 |
+
|
| 65 |
+
### 样例输入 #3
|
| 66 |
+
|
| 67 |
+
```
|
| 68 |
+
见下发文件 ex_matrix2.in
|
| 69 |
+
```
|
| 70 |
+
|
| 71 |
+
### 样例输出 #3
|
| 72 |
+
|
| 73 |
+
```
|
| 74 |
+
见下发文件 ex_matrix2.ans
|
| 75 |
+
```
|
| 76 |
+
|
| 77 |
+
## 提示
|
| 78 |
+
|
| 79 |
+
- Subtask #1($10$ 分):$\sum n ^ 3\leq 10 ^ 6$,$k\leq 10 ^ {18}$。
|
| 80 |
+
- Subtask #2($15$ 分):$m = 2n - 2$,且对任意 $1\leq i < n$,存在权值相等的 $(i, i + 1)$ 和 $(i + 1, i)$。
|
| 81 |
+
- Subtask #3($20$ 分):$m\geq 2n - 2$,且对任意 $(u, v)$,存在权值相等的 $(v, u)$,注意 $u$ 可以等于 $v$。依赖于 Subtask #2。
|
| 82 |
+
- Subtask #4($15$ 分):$\sum n ^ 3\leq 10 ^ 6$,依赖于 Subtask #1。
|
| 83 |
+
- Subtask #5($15$ 分):$k\leq 10 ^ {18}$,依赖于 Subtask #1。
|
| 84 |
+
- Subtask #6($25$ 分):无特殊性质。依赖于 Subtask #3,#4,#5。
|
| 85 |
+
|
| 86 |
+
对于所有数据,$1\leq S\leq 6$,$1\leq T\leq 10 ^ 4$,$2\leq n\leq 300$,$1\leq m\leq 2n$,$1\leq k\leq 10 ^ {64}$,$1\leq u, v\leq n$,$1\leq w\leq 10 ^ {18}$。保证 $\sum n \leq 2\times 10 ^ 5$ 且 $\sum n ^ 3 \leq 2.7 \times 10 ^ 7$。
|
| 87 |
+
|
| 88 |
+
题解在附件 `paper.pdf` 中。
|
problems/10001.txt
ADDED
|
@@ -0,0 +1,91 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 优惠购物
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
小 C 要购买 $n$ 个物品,这些物品有前置关系,必须**依次**购买(即在购买了第 $i$ 个后才能购买第 $i+1$ 个)。
|
| 6 |
+
|
| 7 |
+
他初始有 $m$ 张优惠劵和无穷多个金币。每个物品有两个属性,价格 $a_i$ 和优惠劵的使用上限 $b_i(0\le b_i\le a_i)$。
|
| 8 |
+
|
| 9 |
+
购买一个物品的流程如下:
|
| 10 |
+
|
| 11 |
+
- 选择使用 $x(0\le x\le b_i)$ 张优惠券,付出 $a_i-x$ 个金币和 $x$ 张优惠券。
|
| 12 |
+
- 购买完后可得到 $\lfloor \frac{a_i-x}{c} \rfloor$ 张优惠券(即一次购买中,每付出 $c$ 个金币可以得到一张优惠券,$c$ 为给定常数)
|
| 13 |
+
|
| 14 |
+
小 C 想求出最少花费多少个金币能购买全部物品。
|
| 15 |
+
|
| 16 |
+
## 输入格式
|
| 17 |
+
|
| 18 |
+
本题包含多组数据,第一行包含一个整数 $T$,表示数据组数。
|
| 19 |
+
|
| 20 |
+
对于每组数据:
|
| 21 |
+
|
| 22 |
+
- 第一行包含三个整数 $n,m,c$。
|
| 23 |
+
- 第二行包含 $n$ 个整数 $a_1,a_2,...,a_n$ 表示每个物品的价格。
|
| 24 |
+
- 第三行包含 $n$ 个整数 $b_1,b_2,...,b_n$ 表示优惠劵的使用上限。
|
| 25 |
+
|
| 26 |
+
## 输出格式
|
| 27 |
+
|
| 28 |
+
对于每组数据输出一行:
|
| 29 |
+
|
| 30 |
+
- 第一行输出一个整数,表示最少需要的金币数量。
|
| 31 |
+
|
| 32 |
+
## 样例 #1
|
| 33 |
+
|
| 34 |
+
### 样例输入 #1
|
| 35 |
+
|
| 36 |
+
```
|
| 37 |
+
4
|
| 38 |
+
6 16 2
|
| 39 |
+
17 14 13 5 13 4
|
| 40 |
+
12 5 5 2 10 2
|
| 41 |
+
6 4 2
|
| 42 |
+
8 1 20 10 4 10
|
| 43 |
+
8 1 15 3 4 6
|
| 44 |
+
5 40 7
|
| 45 |
+
21 47 7 25 47
|
| 46 |
+
9 26 4 4 39
|
| 47 |
+
5 151 10
|
| 48 |
+
86 84 164 158 160
|
| 49 |
+
43 42 82 79 80
|
| 50 |
+
```
|
| 51 |
+
|
| 52 |
+
### 样例输出 #1
|
| 53 |
+
|
| 54 |
+
```
|
| 55 |
+
34
|
| 56 |
+
34
|
| 57 |
+
95
|
| 58 |
+
463
|
| 59 |
+
```
|
| 60 |
+
|
| 61 |
+
## 样例 #2
|
| 62 |
+
|
| 63 |
+
### 样例输入 #2
|
| 64 |
+
|
| 65 |
+
```
|
| 66 |
+
见附件 ex_shop2.in。
|
| 67 |
+
```
|
| 68 |
+
|
| 69 |
+
### 样例输出 #2
|
| 70 |
+
|
| 71 |
+
```
|
| 72 |
+
见附件 ex_shop2.out。
|
| 73 |
+
```
|
| 74 |
+
|
| 75 |
+
## 提示
|
| 76 |
+
|
| 77 |
+
对于所有数据,$1\le \sum n\le 10^6,0\le m,a_i,b_i\le 10^9,2\le c\le 10^9$。
|
| 78 |
+
|
| 79 |
+
- Subtask 1 (5 pts):$1\le T\le 5,1\le n\le 10,1\le m,\sum a_i,\sum b_i\le 10$
|
| 80 |
+
- Subtask 2 (10 pts):$a_i=b_i$
|
| 81 |
+
- Subtask 3 (10 pts):$1\le \sum n\le 500,1\le \sum m,\sum a_i,\sum b_i\le 500$
|
| 82 |
+
- Subtask 4 (10 pts):$1\le \sum n\le 6000,1\le \sum m,\sum a_i,\sum b_i\le 6000$
|
| 83 |
+
- Subtask 5 (10 pts):$1\le \sum n\le 6000$
|
| 84 |
+
- Subtask 6 (15 pts):$1\le \sum n\le 2\times 10^5,2\le c\le 20$
|
| 85 |
+
- Subtask 7 (10 pts):$1\le \sum n\le 1\times 10^6,2\le c\le 20$
|
| 86 |
+
- Subtask 8 (15 pts):$1\le \sum n\le 2\times 10^5$
|
| 87 |
+
- Subtask 9 (15 pts):$1\le \sum n\le 1\times 10^6$
|
| 88 |
+
|
| 89 |
+
时间限制:$\texttt{1s}$
|
| 90 |
+
|
| 91 |
+
空间限制:$\texttt{2048MB}$
|
problems/10002.txt
ADDED
|
@@ -0,0 +1,159 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 树哈希
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
这是一道 [模板题](https://uoj.ac/problem/763)。
|
| 6 |
+
|
| 7 |
+
给定正整数 $n,q,mod$。保证 $mod$ 是质数。
|
| 8 |
+
|
| 9 |
+
对于一棵以点 $1$ 为根的有根树 $T$,设 $s(T)$ 为这棵树中最多能选出多少个互不同构的子树(也就是这颗树本质不同的子树个数),那么这个树的权值 $w(T) = q^{s(T)}$。
|
| 10 |
+
|
| 11 |
+
对于所有 $1 \le m \le n$,输出所有大小为 $m$,根为 $1$ 的有标号树的权值之和对 $mod$ 取模后的值。
|
| 12 |
+
|
| 13 |
+
两棵有根树 $T_1$、$T_2$ 同构当且仅当他们的大小相等,且存在一个顶点排列 $\sigma$ 使得在 $T_1$ 中 $i$ 是 $j$ 的祖先当且仅当在 $T_2$ 中 $\sigma(i)$ 是 $\sigma(j)$ 的祖先。
|
| 14 |
+
|
| 15 |
+
## 输入格式
|
| 16 |
+
|
| 17 |
+
一行两个整数,表示 $n,q,mod$。
|
| 18 |
+
|
| 19 |
+
## 输出格式
|
| 20 |
+
|
| 21 |
+
输出 $n$ 行,第 $m$ 行表示 $m$ 个点的答案。
|
| 22 |
+
|
| 23 |
+
## 样例 #1
|
| 24 |
+
|
| 25 |
+
### 样例输入 #1
|
| 26 |
+
|
| 27 |
+
```
|
| 28 |
+
3 2 998244353
|
| 29 |
+
```
|
| 30 |
+
|
| 31 |
+
### 样例输出 #1
|
| 32 |
+
|
| 33 |
+
```
|
| 34 |
+
2
|
| 35 |
+
4
|
| 36 |
+
20
|
| 37 |
+
```
|
| 38 |
+
|
| 39 |
+
## 样例 #2
|
| 40 |
+
|
| 41 |
+
### 样例输入 #2
|
| 42 |
+
|
| 43 |
+
```
|
| 44 |
+
11 4514 998244353
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
### 样例输出 #2
|
| 48 |
+
|
| 49 |
+
```
|
| 50 |
+
4514
|
| 51 |
+
20376196
|
| 52 |
+
299712732
|
| 53 |
+
706663250
|
| 54 |
+
721357660
|
| 55 |
+
977589073
|
| 56 |
+
794002114
|
| 57 |
+
369586566
|
| 58 |
+
663682963
|
| 59 |
+
347458730
|
| 60 |
+
524354925
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
## 样例 #3
|
| 64 |
+
|
| 65 |
+
### 样例输入 #3
|
| 66 |
+
|
| 67 |
+
```
|
| 68 |
+
40 787788 998244853
|
| 69 |
+
```
|
| 70 |
+
|
| 71 |
+
### 样例输出 #3
|
| 72 |
+
|
| 73 |
+
```
|
| 74 |
+
787788
|
| 75 |
+
699879231
|
| 76 |
+
445785131
|
| 77 |
+
857102003
|
| 78 |
+
759492151
|
| 79 |
+
898159394
|
| 80 |
+
575712517
|
| 81 |
+
634469464
|
| 82 |
+
412999753
|
| 83 |
+
814233648
|
| 84 |
+
333451903
|
| 85 |
+
852329440
|
| 86 |
+
584109489
|
| 87 |
+
270769240
|
| 88 |
+
532457985
|
| 89 |
+
79235443
|
| 90 |
+
2228568
|
| 91 |
+
266810999
|
| 92 |
+
310877128
|
| 93 |
+
614605839
|
| 94 |
+
485785485
|
| 95 |
+
338520973
|
| 96 |
+
113751992
|
| 97 |
+
692026056
|
| 98 |
+
664258393
|
| 99 |
+
650448721
|
| 100 |
+
505881810
|
| 101 |
+
237159658
|
| 102 |
+
107178163
|
| 103 |
+
629910112
|
| 104 |
+
513627947
|
| 105 |
+
915509519
|
| 106 |
+
737809847
|
| 107 |
+
921731327
|
| 108 |
+
233492829
|
| 109 |
+
202989716
|
| 110 |
+
728903945
|
| 111 |
+
776060784
|
| 112 |
+
105388817
|
| 113 |
+
121481849
|
| 114 |
+
```
|
| 115 |
+
|
| 116 |
+
## 提示
|
| 117 |
+
|
| 118 |
+
#### 样例解释 1
|
| 119 |
+
|
| 120 |
+
$n=3,q=2,mod=998244353$ 时,有三颗不同三个点的根为 $1$ 的有标号树,其中两颗满足 $w(T)=2^3$,另一颗满足 $w(T)=2^2$。因此答案为 $(2 \times 2^3+2^2) \bmod 998244353 = 20$。
|
| 121 |
+
|
| 122 |
+
#### 限制与约定
|
| 123 |
+
|
| 124 |
+
对于所有测试数据,保证 $n = 100, 10^8 \le mod \le 1.01 \times 10^9, 1 \le q < mod$,且 $mod$ 是质数。
|
| 125 |
+
|
| 126 |
+
本题共 $1$ 个子任务,每个子任务 $100$ 分。你在每个子任务中的得分为该子任务所有测试点的得分的最小值。
|
| 127 |
+
|
| 128 |
+
**你必须按照输出格式输出 $n$ 个数,但是你可以输出错误的答案**。如果你输出了 $c$ 个正确的答案,那么你获得的分数按照如下方式计算:
|
| 129 |
+
|
| 130 |
+
- 对于 $0 \le c \le 20$,你的得分为 $2c$ 分;
|
| 131 |
+
- 对于 $21 \le c \le 60$,你的得分为 $c + 20 $ 分。
|
| 132 |
+
- 对于 $61 \le c \le 100$,你的得分为 $\lfloor \frac{c}{2}\rfloor + 50$ 分。
|
| 133 |
+
|
| 134 |
+
时间限制:$\texttt{4s}$。
|
| 135 |
+
空间限制:$\texttt{2048MB}$。
|
| 136 |
+
|
| 137 |
+
你可以使用下面的代码来加速你的取模。
|
| 138 |
+
|
| 139 |
+
```cpp
|
| 140 |
+
struct fastmod {
|
| 141 |
+
typedef unsigned long long u64;
|
| 142 |
+
typedef __uint128_t u128;
|
| 143 |
+
|
| 144 |
+
int m;
|
| 145 |
+
u64 b;
|
| 146 |
+
|
| 147 |
+
fastmod(int m) : m(m), b(((u128)1 << 64) / m) {}
|
| 148 |
+
int reduce(u64 a) {
|
| 149 |
+
u64 q = ((u128)a * b) >> 64;
|
| 150 |
+
int r = a - q * m;
|
| 151 |
+
return r < m ? r : r - m;
|
| 152 |
+
}
|
| 153 |
+
} z(2);
|
| 154 |
+
void solve() {
|
| 155 |
+
long long mod = 998244353, qwq = 1e9;
|
| 156 |
+
z = fastmod(mod);
|
| 157 |
+
cout << z.reduce(qwq) << ' ' << qwq % mod << '\n';
|
| 158 |
+
}
|
| 159 |
+
```
|
problems/10003.txt
ADDED
|
@@ -0,0 +1,138 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 傅里叶与交通系统
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
傅里叶荣升巴黎市交通部长。新官上任三把火,傅里叶决定重构巴黎市的交通系统。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
巴黎市的地图可以看成一个无限大的二维平面。傅里叶在上面修建了 $n$ 条传送带:第 $i$ 条传送带修建于 $x\in[p_{i-1},p_i),y\in\mathbb R$ 的区域中。对于 $x<p_0$ 或者 $x\geq p_n$ 的部分,傅里叶没有修建传送带。
|
| 10 |
+
|
| 11 |
+
当一个人处于第 $i$ 个传送带的区域内时,他会受传送带影响强制以 $v_i$ 单位长度每秒的速度向 $y$ 坐标增加的方向移动。$v_i$ 可能为负,此时其 $y$ 坐标会以相应的速度减小。
|
| 12 |
+
|
| 13 |
+
在位于未修建传送带的区域上时,$y$ 坐标不会受到传送带的影响。
|
| 14 |
+
|
| 15 |
+
除了受传送带带动以外,这个人自己也可以移动。为了避免在速度不同的传送带间移动时出现跌倒事故,傅里叶委托麦克斯韦设计了脚底附有钢板的鞋子,并且在传送带上安装了强力磁铁。穿上这种鞋子后,你将只能 **沿着与某条坐标轴平行,可能与坐标轴同向或反向** 的方向,以不超过 $V$ 单位长度每秒的速度移动。有了这种鞋子,**在从一个传送带移动到另一个传送带时,先前的速度不会被继承,这个人将立刻按照新传送带的移动速度来移动**(自然,自身的移动还是可以同步进行的)。
|
| 16 |
+
|
| 17 |
+
**个人的运动与传送带的运动是叠加的**。
|
| 18 |
+
|
| 19 |
+
**在任意时刻,这个人都可以自由调整其运动的速率、方向;可以通过不断在极小间隔内切换方向以达到近似斜向移动的效果,甚至动态调整速率、方向达成近似曲线运动的效果;但是其任意时刻都只能有平行于坐标轴、不超过 $V$ 的瞬时速率。**
|
| 20 |
+
|
| 21 |
+
**就算在没有铺设传送带的位置上,这个人仍然可以靠他的自由意志移动,不过还是只能沿坐标轴方向以不超过 $V$ 单位长度每秒移动**(问就是麦克斯韦的靴子已经成为概念级装备了)。
|
| 22 |
+
|
| 23 |
+
现在,傅里叶想知道他的交通系统究竟有多么伟大。因此,他向你提出了 $q$ 组询问,每次询问如果有一个人要从 $(x_1,y_1)$ 走到 $(x_2,y_2)$,最少需要多少时间。因为傅里叶是唯一真神,所以他当然不会设计一个有缺陷的交通系统,因此所有的 $v_i$ 的绝对值均严格小于 $V$,进而总是可以从一个位置走到另一处。(虽然这将会导致就算在最优情况下,通过传送带系统到达目的地的时间也无法小于原本的一半,更多的时候反倒更慢了,但是谁让他是交通部长,而你只是他手下的一个雇员呢?)
|
| 24 |
+
|
| 25 |
+
## 输入格式
|
| 26 |
+
|
| 27 |
+
第一行三个整数 $n,q,V$,表示传送带数目、询问个数以及人的移动速度。
|
| 28 |
+
|
| 29 |
+
下一行 $n+1$ 个整数 $p_0,p_1,\dots,p_n$,表示传送带的边界信息。
|
| 30 |
+
|
| 31 |
+
下一行 $n$ 个整数 $v_1,v_2,\dots,v_n$,表示每个传送带的速率。
|
| 32 |
+
|
| 33 |
+
接下来 $q$ 行,每行四个整数 $x_1,y_1,x_2,y_2$,表示此次询问的起讫点。
|
| 34 |
+
|
| 35 |
+
## 输出格式
|
| 36 |
+
|
| 37 |
+
对于每次询问,输出一行一个实数,表示此次移动所需的最小时长,单位为秒。你需要保证输出与标准答案的相对或绝对误差不超过 $10^{-5}$。
|
| 38 |
+
|
| 39 |
+
- 如果你怀疑你的代码中出现了较大的精度误差,可以尝试使用更多整数和分数以规避浮点数运算,从而减少误差。
|
| 40 |
+
|
| 41 |
+
## 样例 #1
|
| 42 |
+
|
| 43 |
+
### 样例输入 #1
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
1 2 10
|
| 47 |
+
-5 5
|
| 48 |
+
5
|
| 49 |
+
-10 -20 10 20
|
| 50 |
+
10 20 -10 -20
|
| 51 |
+
```
|
| 52 |
+
|
| 53 |
+
### 样例输出 #1
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
4.3333333333
|
| 57 |
+
6.5
|
| 58 |
+
```
|
| 59 |
+
|
| 60 |
+
## 样例 #2
|
| 61 |
+
|
| 62 |
+
### 样例输入 #2
|
| 63 |
+
|
| 64 |
+
```
|
| 65 |
+
1 4 10
|
| 66 |
+
-5 5
|
| 67 |
+
5
|
| 68 |
+
10 -10 10 10
|
| 69 |
+
10 10 10 -10
|
| 70 |
+
10 -50 10 50
|
| 71 |
+
10 50 10 -50
|
| 72 |
+
```
|
| 73 |
+
|
| 74 |
+
### 样例输出 #2
|
| 75 |
+
|
| 76 |
+
```
|
| 77 |
+
2
|
| 78 |
+
2
|
| 79 |
+
7.6666666667
|
| 80 |
+
10
|
| 81 |
+
```
|
| 82 |
+
|
| 83 |
+
## 样例 #3
|
| 84 |
+
|
| 85 |
+
### 样例输入 #3
|
| 86 |
+
|
| 87 |
+
```
|
| 88 |
+
5 5 10
|
| 89 |
+
-10 -5 0 5 10 15
|
| 90 |
+
9 -4 7 -6 2
|
| 91 |
+
-1 0 -9 -100
|
| 92 |
+
-7 0 7 10
|
| 93 |
+
9 0 -3 20
|
| 94 |
+
12 0 -17 -30
|
| 95 |
+
2 0 19 39
|
| 96 |
+
```
|
| 97 |
+
|
| 98 |
+
### 样例输出 #3
|
| 99 |
+
|
| 100 |
+
```
|
| 101 |
+
8.085714
|
| 102 |
+
1.815789
|
| 103 |
+
2.382353
|
| 104 |
+
4.987500
|
| 105 |
+
3.988235
|
| 106 |
+
```
|
| 107 |
+
|
| 108 |
+
## 提示
|
| 109 |
+
|
| 110 |
+
样例 #4,#5 详见附件。
|
| 111 |
+
|
| 112 |
+
------------
|
| 113 |
+
|
| 114 |
+
样例 #1 的解释:
|
| 115 |
+
|
| 116 |
+
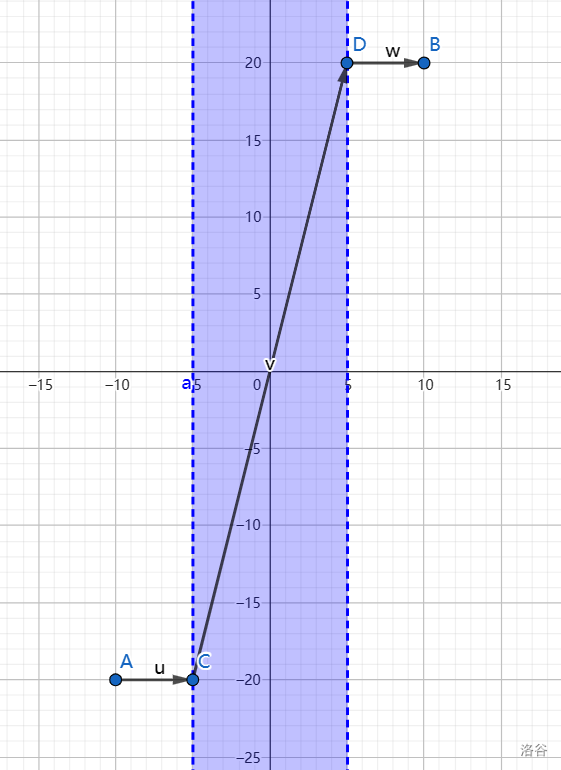
|
| 117 |
+
|
| 118 |
+
第一问中,上图是一种极优的行走方式。蓝色区域是传送带所在区域,在其上时我们以 $(3,12)$ 每秒的速度移动(其中自身移动的速度是 $(3,7)$,也即可以看作是三成时间沿着 $x$ 轴正方向、七成时间沿着 $y$ 轴正方向移动;在极短时间内不停切换,可以达成如上图中斜线行走的效果;$(3,7)$ 的自身行走与 $(0,5)$ 的传送带运转叠加成为 $(3,12)$ 的速度向量)。
|
| 119 |
+
|
| 120 |
+
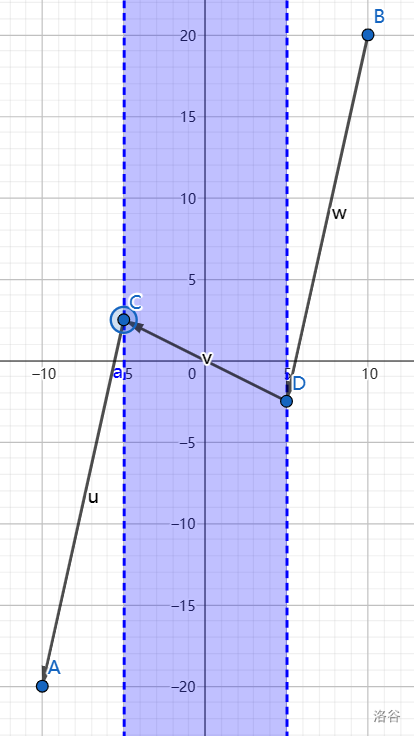
|
| 121 |
+
|
| 122 |
+
第二问中,上图是一种极优的行走方案。
|
| 123 |
+
|
| 124 |
+
需要注意的是,这两问中能达成最少时间的行走方案不止图中给出的两种。
|
| 125 |
+
|
| 126 |
+
对于所有数据,均满足 $n,q\leq1.5\times10^5$,$-5\times10^5\leq p_0<p_1<p_2<\dots<p_n\leq5\times10^5$,$ |x_1|,|y_1|,|x_2|,|y_2|\leq5\times10^5$,$0\leq|v_i|<V\leq5\times10^5$。
|
| 127 |
+
|
| 128 |
+
------------
|
| 129 |
+
|
| 130 |
+
- Subtask 1(5 分):保证 $n=0$。
|
| 131 |
+
- Subtask 2(10 分):保证 $n,q\leq1000$。
|
| 132 |
+
- Subtask 3(10 分):保证对于所有询问,$x_1=p_0,x_2=p_n$。
|
| 133 |
+
- Subtask 4(10 分):保证所有询问的 $x_1$ 全都相等,所有询问的 $x_2$ 全都相等(但不保证 $x_1=x_2$)。
|
| 134 |
+
- Subtask 5(15 分):保证 $v_i$ 单调不降,且询问的 $x_1\leq x_2$。
|
| 135 |
+
- Subtask 6(15 分):保证存在 $i$ 使得 $p_i=x_1=x_2$。(但并不保证所有询问的 $i$ 都相同)
|
| 136 |
+
- Subtask 7(15 分):保证除 $n,q,V$ 外,其它值都在合法范围内独立随机得到($p$ 的随机方式是随机 $n+1$ 个不等的 $[-5\times10^5,5\times10^5]$ 中的值并排序)。
|
| 137 |
+
- Subtask 8(15 分):保证 $n,q\leq5\times10^4$。
|
| 138 |
+
- Subtask 9(10 分):无特殊限制。
|
problems/10004.txt
ADDED
|
@@ -0,0 +1,92 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] Permutation Counting 2
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定 $n$,对于每组 $x,y\in [0,n)$ 求出有多少个 $1\sim n$ 的排列 $p$ 满足以下条件:
|
| 6 |
+
|
| 7 |
+
- $\sum\limits_{i=1}^{n-1}[p_i<p_{i+1}]=x$。
|
| 8 |
+
|
| 9 |
+
- $\sum\limits_{i=1}^{n-1}[p^{-1}_i<p^{-1}_{i+1}]=y$。
|
| 10 |
+
|
| 11 |
+
其中 $p^{-1}$ 表示 $p$ 的逆排列,满足 $p^{-1}_{p_i}=i$。
|
| 12 |
+
|
| 13 |
+
答案对给定的质数 $MOD$ 取模。
|
| 14 |
+
|
| 15 |
+
## 输入格式
|
| 16 |
+
|
| 17 |
+
共一行,两个整数,表示 $n,MOD$。
|
| 18 |
+
|
| 19 |
+
## 输出格式
|
| 20 |
+
|
| 21 |
+
共 $n$ 行,每行共 $n$ 个整数,第 $i$ 行第 $j$ 列的数表示 $x=i-1,y=j-1$ 时的答案。
|
| 22 |
+
|
| 23 |
+
## 样例 #1
|
| 24 |
+
|
| 25 |
+
### 样例输入 #1
|
| 26 |
+
|
| 27 |
+
```
|
| 28 |
+
3 1000000007
|
| 29 |
+
```
|
| 30 |
+
|
| 31 |
+
### 样例输出 #1
|
| 32 |
+
|
| 33 |
+
```
|
| 34 |
+
1 0 0
|
| 35 |
+
0 4 0
|
| 36 |
+
0 0 1
|
| 37 |
+
```
|
| 38 |
+
|
| 39 |
+
## 样例 #2
|
| 40 |
+
|
| 41 |
+
### 样例输入 #2
|
| 42 |
+
|
| 43 |
+
```
|
| 44 |
+
5 1000000007
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
### 样例输出 #2
|
| 48 |
+
|
| 49 |
+
```
|
| 50 |
+
1 0 0 0 0
|
| 51 |
+
0 20 6 0 0
|
| 52 |
+
0 6 54 6 0
|
| 53 |
+
0 0 6 20 0
|
| 54 |
+
0 0 0 0 1
|
| 55 |
+
```
|
| 56 |
+
|
| 57 |
+
## 样例 #3
|
| 58 |
+
|
| 59 |
+
### 样例输入 #3
|
| 60 |
+
|
| 61 |
+
```
|
| 62 |
+
10 1000000007
|
| 63 |
+
```
|
| 64 |
+
|
| 65 |
+
### 样例输出 #3
|
| 66 |
+
|
| 67 |
+
```
|
| 68 |
+
1 0 0 0 0 0 0 0 0 0
|
| 69 |
+
0 165 462 330 55 1 0 0 0 0
|
| 70 |
+
0 462 9273 22023 13750 2266 66 0 0 0
|
| 71 |
+
0 330 22023 147301 203610 75306 6556 66 0 0
|
| 72 |
+
0 55 13750 203610 592130 423236 75306 2266 1 0
|
| 73 |
+
0 1 2266 75306 423236 592130 203610 13750 55 0
|
| 74 |
+
0 0 66 6556 75306 203610 147301 22023 330 0
|
| 75 |
+
0 0 0 66 2266 13750 22023 9273 462 0
|
| 76 |
+
0 0 0 0 1 55 330 462 165 0
|
| 77 |
+
0 0 0 0 0 0 0 0 0 1
|
| 78 |
+
```
|
| 79 |
+
|
| 80 |
+
## 提示
|
| 81 |
+
|
| 82 |
+
对于 $100\%$ 数据,$1\le n\le 500$,$10^9\le MOD\le 1.01\times 10^9$,保证 $MOD$ 为质数。
|
| 83 |
+
|
| 84 |
+
$\operatorname{Subtask} 1(10\%):n\le 8$。
|
| 85 |
+
|
| 86 |
+
$\operatorname{Subtask} 2(15\%):n\le 16$。
|
| 87 |
+
|
| 88 |
+
$\operatorname{Subtask} 3(25\%):n\le 40$。
|
| 89 |
+
|
| 90 |
+
$\operatorname{Subtask} 4(25\%):n\le 100$。
|
| 91 |
+
|
| 92 |
+
$\operatorname{Subtask} 5(25\%):$ 无特殊限制。
|
problems/10005.txt
ADDED
|
@@ -0,0 +1,103 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 基础寄术练习题
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
对于长度为 $n$ 的序列 $a$,定义 $f(a)=\dfrac{1}{\prod\limits_{i=k}^ns_i}$,其中 $s_i$ 为 $\{a_n\}$ 的前缀和数组,**$k$ 是给定的常数且 $1\le k\le 2$**。
|
| 6 |
+
|
| 7 |
+
考虑所有满足以下三个条件的序列 $a$:
|
| 8 |
+
|
| 9 |
+
- $a$ 的长度为 $n$。
|
| 10 |
+
- $\forall i,j$,$a_i\ne a_j$。
|
| 11 |
+
- $1\le a_i\le m$。
|
| 12 |
+
|
| 13 |
+
求它们的 $f(a)$ 之和,答案对 $p$ 取模。保证 $p$ 是一个质数。
|
| 14 |
+
|
| 15 |
+
## 输入格式
|
| 16 |
+
|
| 17 |
+
第一行三个整数 $n,m,k,p$,分别代表序列长度,序列元素的上界和模数。
|
| 18 |
+
|
| 19 |
+
## 输出格式
|
| 20 |
+
|
| 21 |
+
一行一个整数表示答案对 $p$ 取模后的结果。
|
| 22 |
+
|
| 23 |
+
## 样例 #1
|
| 24 |
+
|
| 25 |
+
### 样例输入 #1
|
| 26 |
+
|
| 27 |
+
```
|
| 28 |
+
2 3 2 1000000007
|
| 29 |
+
```
|
| 30 |
+
|
| 31 |
+
### 样例输出 #1
|
| 32 |
+
|
| 33 |
+
```
|
| 34 |
+
966666675
|
| 35 |
+
```
|
| 36 |
+
|
| 37 |
+
## 样例 #2
|
| 38 |
+
|
| 39 |
+
### 样例输入 #2
|
| 40 |
+
|
| 41 |
+
```
|
| 42 |
+
3 5 2 998244353
|
| 43 |
+
```
|
| 44 |
+
|
| 45 |
+
### 样例输出 #2
|
| 46 |
+
|
| 47 |
+
```
|
| 48 |
+
148276980
|
| 49 |
+
```
|
| 50 |
+
|
| 51 |
+
## 样例 #3
|
| 52 |
+
|
| 53 |
+
### 样例输入 #3
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
6 10 2 1004535809
|
| 57 |
+
```
|
| 58 |
+
|
| 59 |
+
### 样例输出 #3
|
| 60 |
+
|
| 61 |
+
```
|
| 62 |
+
622165218
|
| 63 |
+
```
|
| 64 |
+
|
| 65 |
+
## 样例 #4
|
| 66 |
+
|
| 67 |
+
### 样例输入 #4
|
| 68 |
+
|
| 69 |
+
```
|
| 70 |
+
15 20 2 1064822107
|
| 71 |
+
```
|
| 72 |
+
|
| 73 |
+
### 样例输出 #4
|
| 74 |
+
|
| 75 |
+
```
|
| 76 |
+
53789887
|
| 77 |
+
```
|
| 78 |
+
|
| 79 |
+
## 样例 #5
|
| 80 |
+
|
| 81 |
+
### 样例输入 #5
|
| 82 |
+
|
| 83 |
+
```
|
| 84 |
+
30 40 1 265371653
|
| 85 |
+
```
|
| 86 |
+
|
| 87 |
+
### 样例输出 #5
|
| 88 |
+
|
| 89 |
+
```
|
| 90 |
+
179937201
|
| 91 |
+
```
|
| 92 |
+
|
| 93 |
+
## 提示
|
| 94 |
+
|
| 95 |
+
对于所有数据,保证 $2\le n\le m\le 100$,$10^8<p<1.07\times 10^9$ 且 $p$ 为质数,$1\le k\le 2$。
|
| 96 |
+
|
| 97 |
+
- Subtask 1 (10 pts):$m\le 20$。
|
| 98 |
+
- Subtask 2 (25 pts):$k=1$。
|
| 99 |
+
- Subtask 3 (15 pts):$n=m\le 30$。
|
| 100 |
+
- Subtask 4 (10 pts):$m\le 30$。
|
| 101 |
+
- Subtask 5 (15 pts):$m\le 40$。
|
| 102 |
+
- Subtask 6 (10 pts):$m\le 70$。
|
| 103 |
+
- Subtask 7 (15 pts):$m\le 100$。
|
problems/10006.txt
ADDED
|
@@ -0,0 +1,98 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 超现实树
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
Alek 喜欢打信息竞赛,尤其喜欢超现实树。超现实树,顾名思义,就是树上的超现实数。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
Alek 认为,对于常数 $k$,一个字符串被称为「$k$-超现实数串」,如果其只包含字符 $\texttt{\{}, \texttt{|}, \texttt{\}}$,且:
|
| 10 |
+
|
| 11 |
+
- 空串为 $k$-超现实数串;
|
| 12 |
+
- 如果 $s, t$ 为 $k$-超现实数串,那么 $s + t$ 为 $k$-超现实数串;
|
| 13 |
+
- 如果 $k + 1$ 个字符串 $s_1, s_2, \cdots, s_{k + 1}$ 都是 $k$-超现实数串,那么 $\texttt{\{} + s_1 + \texttt{|} + s_2 + \texttt{|} + \cdots + \texttt{|} + s_{k + 1} + \texttt{\}}$ 为 $k$-超现实数串;
|
| 14 |
+
- $k$-超现实数串仅限于此。
|
| 15 |
+
|
| 16 |
+
给定一棵 $n$ 个点的无根树,节点编号为 $1 \sim n$。每个点 $i$ 上有一个字符 $a_i \in \{\texttt{\{}, \texttt{|}, \texttt{\}}\}$。
|
| 17 |
+
|
| 18 |
+
给定整数 $m$,Alek 希望你对 $k = 0, 1, \cdots, m$ 分别求出:有多少有序对 $(x, y)$,$1 \leq x, y \leq n$,使得树上从点 $x$ 到点 $y$ 的唯一简单路径上的字符依次拼接所得字符串是 $k$-超现实数串。
|
| 19 |
+
|
| 20 |
+
## 输入格式
|
| 21 |
+
|
| 22 |
+
第一行两个整数 $n, m$,分别表示树的节点数,和需要求答案的 $k$ 的上限。
|
| 23 |
+
|
| 24 |
+
第二行一个字符串 $a$,$a$ 的第 $i$ 个字符表示点 $i$ 上的字符。
|
| 25 |
+
|
| 26 |
+
接下来 $n - 1$ 行,每行两个整数 $x, y$,表示存在一条连接点 $x$ 和点 $y$ 的边。
|
| 27 |
+
|
| 28 |
+
## 输出格式
|
| 29 |
+
|
| 30 |
+
输出一行 $m + 1$ 个整数,分别表示 $k = 0, 1, \cdots, m$ 时的答案。
|
| 31 |
+
|
| 32 |
+
## 样例 #1
|
| 33 |
+
|
| 34 |
+
### 样例输入 #1
|
| 35 |
+
|
| 36 |
+
```
|
| 37 |
+
5 3
|
| 38 |
+
|{}}}
|
| 39 |
+
2 1
|
| 40 |
+
3 2
|
| 41 |
+
4 1
|
| 42 |
+
5 1
|
| 43 |
+
```
|
| 44 |
+
|
| 45 |
+
### 样例输出 #1
|
| 46 |
+
|
| 47 |
+
```
|
| 48 |
+
1 2 0 0
|
| 49 |
+
```
|
| 50 |
+
|
| 51 |
+
## 样例 #2
|
| 52 |
+
|
| 53 |
+
### 样例输入 #2
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
10 8
|
| 57 |
+
|}||}{|{{{
|
| 58 |
+
2 1
|
| 59 |
+
3 1
|
| 60 |
+
4 3
|
| 61 |
+
5 2
|
| 62 |
+
6 5
|
| 63 |
+
7 5
|
| 64 |
+
8 4
|
| 65 |
+
9 2
|
| 66 |
+
10 3
|
| 67 |
+
```
|
| 68 |
+
|
| 69 |
+
### 样例输出 #2
|
| 70 |
+
|
| 71 |
+
```
|
| 72 |
+
2 0 1 1 0 0 0 0 0
|
| 73 |
+
```
|
| 74 |
+
|
| 75 |
+
## 样例 #3
|
| 76 |
+
|
| 77 |
+
### 样例输入 #3
|
| 78 |
+
|
| 79 |
+
```
|
| 80 |
+
见附加文件 ex_surreal3.in。
|
| 81 |
+
```
|
| 82 |
+
|
| 83 |
+
### 样例输出 #3
|
| 84 |
+
|
| 85 |
+
```
|
| 86 |
+
见附加文件 ex_surreal3.ans。
|
| 87 |
+
```
|
| 88 |
+
|
| 89 |
+
## 提示
|
| 90 |
+
|
| 91 |
+
对于所有数据,有 $2 \leq n \leq 10^5$,$0 \leq m \leq n - 2$,$a_i \in \{\texttt{\{}, \texttt{|}, \texttt{\}}\}$。
|
| 92 |
+
|
| 93 |
+
- **Subtask 1**(5 分):$n \leq 4601$;
|
| 94 |
+
- **Subtask 2**(20 分):对每条边 $(x, y)$ 有 $y = x + 1$;
|
| 95 |
+
- **Subtask 3**(5 分):$a_i \neq \texttt{|}$, $m = 0$;
|
| 96 |
+
- **Subtask 4**(15 分,依赖 Subtask 3):$m \leq 3$;
|
| 97 |
+
- **Subtask 5**(25 分,依赖 Subtask 1):$n \leq 5 \times 10^4$;
|
| 98 |
+
- **Subtask 6**(30 分,依赖 Subtask 1, 2, 3, 4, 5):无特殊限制。
|
problems/10007.txt
ADDED
|
@@ -0,0 +1,87 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 童话
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
童话只美在真实却从不续写。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
泠珞最近学习了前缀和算法,她写出了以下程序:
|
| 10 |
+
|
| 11 |
+
```cpp
|
| 12 |
+
read(n),read(a);
|
| 13 |
+
for(int i=0;i<=n;i++)read(f[i]);
|
| 14 |
+
for(int t=1;t<=n;t++){
|
| 15 |
+
for(int i=1;i<=n;i++)f[i]=f[i]+a*f[i-1];
|
| 16 |
+
ans[t]=f[t];
|
| 17 |
+
}
|
| 18 |
+
```
|
| 19 |
+
|
| 20 |
+
她发现这个程序在 $n$ 比较大的时候会运行超时,请你帮忙写一个程序帮她计算出 $\text{ans}_1,\text{ans}_2,\cdots,\text{ans}_n$,由于答案数值过大,你只需告诉她每个数除以 $998244353$ 的余数。
|
| 21 |
+
|
| 22 |
+
## 输入格式
|
| 23 |
+
|
| 24 |
+
第一行两个正整数 $n,a$。
|
| 25 |
+
|
| 26 |
+
接下来一行 $n+1$ 个非负整数,表示 $f_0,f_1,\cdots,f_n$。
|
| 27 |
+
|
| 28 |
+
## 输出格式
|
| 29 |
+
|
| 30 |
+
$n$ 个非负整数,表示 $\text{ans}_1,\text{ans}_2,\cdots,\text{ans}_n$。
|
| 31 |
+
|
| 32 |
+
## 样例 #1
|
| 33 |
+
|
| 34 |
+
### 样例输入 #1
|
| 35 |
+
|
| 36 |
+
```
|
| 37 |
+
2 1
|
| 38 |
+
1 2 0
|
| 39 |
+
```
|
| 40 |
+
|
| 41 |
+
### 样例输出 #1
|
| 42 |
+
|
| 43 |
+
```
|
| 44 |
+
3 7
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
## 样例 #2
|
| 48 |
+
|
| 49 |
+
### 样例输入 #2
|
| 50 |
+
|
| 51 |
+
```
|
| 52 |
+
10 10
|
| 53 |
+
5 9 7 8 0 6 3 2 4 10 1
|
| 54 |
+
```
|
| 55 |
+
|
| 56 |
+
### 样例输出 #2
|
| 57 |
+
|
| 58 |
+
```
|
| 59 |
+
59 1687 55618 1937320 69557006 549579657 621247830 250099579 483510144 968467040
|
| 60 |
+
```
|
| 61 |
+
|
| 62 |
+
## 提示
|
| 63 |
+
|
| 64 |
+
数据范围:
|
| 65 |
+
|
| 66 |
+
对于 $100\%$ 的数据,保证 $2\leqslant n\leqslant 10^6,0\leqslant f_i<998244353,1\leqslant a<998244353$。
|
| 67 |
+
|
| 68 |
+
| 子任务编号 | $n\leqslant$ | 特殊性质 | 分值 |
|
| 69 |
+
| :--------: | :------------: | :------: | :--: |
|
| 70 |
+
| $1$ | $2000$ | | $5$ |
|
| 71 |
+
| $2$ | $10^5$ | A | $5$ |
|
| 72 |
+
| $3$ | $10^5$ | BC | $5$ |
|
| 73 |
+
| $4$ | $10^5$ | BD | $10$ |
|
| 74 |
+
| $5$ | $10^5$ | C | $10$ |
|
| 75 |
+
| $6$ | $5\times10^4$ | | $10$ |
|
| 76 |
+
| $7$ | $10^5$ | | $10$ |
|
| 77 |
+
| $8$ | $2\times 10^5$ | | $15$ |
|
| 78 |
+
| $9$ | $5\times 10^5$ | | $15$ |
|
| 79 |
+
| $10$ | $10^6$ | | $15$ |
|
| 80 |
+
|
| 81 |
+
特殊性质 A:保证 $f_i\ne 0$ 的 $i$ 数量不超过 $100$。
|
| 82 |
+
|
| 83 |
+
特殊性质 B:保证 $a=1$。
|
| 84 |
+
|
| 85 |
+
特殊性质 C:保证对于所有 $i\in[0,n]$,都满足 $f_i=1$。
|
| 86 |
+
|
| 87 |
+
特殊性质 D:保证对于所有 $i\in[0,n]$,都满足 $f_i={i+2\choose 2}=\frac{(i+2)(i+1)}{2}$。
|
problems/10008.txt
ADDED
|
@@ -0,0 +1,148 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2022] Range Minimum Element
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
有一个长度为 $n$,值域为 $[1,c]$ 的正整数序列 $a$。给定 $m$ 个区间 $[l_i,r_i]$,设长度为 $m$ 的序列 $b$ 满足 $\forall i\in [1,m],b_i=\min\limits_{j=l_i}^{r_i}\{a_j\}$。求出 $a$ 在范围内任意取的情况下共能得到多少种不同的 $b$。答案对 $998244353$ 取模。
|
| 6 |
+
|
| 7 |
+
## 输入格式
|
| 8 |
+
|
| 9 |
+
第一行,三个数,依次表示 $n,m,c$。
|
| 10 |
+
|
| 11 |
+
接下来 $m$ 行,每行两个数 $l_i,r_i$ 表示一个给定的区间。
|
| 12 |
+
|
| 13 |
+
## 输出格式
|
| 14 |
+
|
| 15 |
+
共一行,一个数,表示答案。
|
| 16 |
+
|
| 17 |
+
## 样例 #1
|
| 18 |
+
|
| 19 |
+
### 样例输入 #1
|
| 20 |
+
|
| 21 |
+
```
|
| 22 |
+
3 2 2
|
| 23 |
+
1 2
|
| 24 |
+
2 3
|
| 25 |
+
```
|
| 26 |
+
|
| 27 |
+
### 样例输出 #1
|
| 28 |
+
|
| 29 |
+
```
|
| 30 |
+
4
|
| 31 |
+
```
|
| 32 |
+
|
| 33 |
+
## 样例 #2
|
| 34 |
+
|
| 35 |
+
### 样例输入 #2
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
10 11 2
|
| 39 |
+
1 10
|
| 40 |
+
2 2
|
| 41 |
+
3 3
|
| 42 |
+
5 5
|
| 43 |
+
6 10
|
| 44 |
+
6 7
|
| 45 |
+
6 6
|
| 46 |
+
7 7
|
| 47 |
+
8 10
|
| 48 |
+
8 9
|
| 49 |
+
10 10
|
| 50 |
+
```
|
| 51 |
+
|
| 52 |
+
### 样例输出 #2
|
| 53 |
+
|
| 54 |
+
```
|
| 55 |
+
129
|
| 56 |
+
```
|
| 57 |
+
|
| 58 |
+
## 样例 #3
|
| 59 |
+
|
| 60 |
+
### 样例输入 #3
|
| 61 |
+
|
| 62 |
+
```
|
| 63 |
+
40 40 40
|
| 64 |
+
31 34
|
| 65 |
+
9 34
|
| 66 |
+
4 25
|
| 67 |
+
36 38
|
| 68 |
+
8 29
|
| 69 |
+
8 30
|
| 70 |
+
6 26
|
| 71 |
+
17 19
|
| 72 |
+
6 23
|
| 73 |
+
36 39
|
| 74 |
+
11 39
|
| 75 |
+
2 10
|
| 76 |
+
32 37
|
| 77 |
+
32 33
|
| 78 |
+
33 35
|
| 79 |
+
17 21
|
| 80 |
+
8 35
|
| 81 |
+
31 40
|
| 82 |
+
11 25
|
| 83 |
+
11 20
|
| 84 |
+
8 37
|
| 85 |
+
26 36
|
| 86 |
+
22 34
|
| 87 |
+
17 39
|
| 88 |
+
28 38
|
| 89 |
+
26 28
|
| 90 |
+
11 12
|
| 91 |
+
12 15
|
| 92 |
+
12 37
|
| 93 |
+
1 9
|
| 94 |
+
11 23
|
| 95 |
+
5 26
|
| 96 |
+
8 11
|
| 97 |
+
1 23
|
| 98 |
+
12 32
|
| 99 |
+
7 19
|
| 100 |
+
22 28
|
| 101 |
+
20 27
|
| 102 |
+
8 40
|
| 103 |
+
19 40
|
| 104 |
+
```
|
| 105 |
+
|
| 106 |
+
### 样例输出 #3
|
| 107 |
+
|
| 108 |
+
```
|
| 109 |
+
567581188
|
| 110 |
+
```
|
| 111 |
+
|
| 112 |
+
## 提示
|
| 113 |
+
|
| 114 |
+
对于 $100\%$ 的数据,$1\le n\le 100,1\le m\le\dfrac{n(n+1)}{2},1\le c<998244353,\forall i\in [1,m],1\le l_i\le r_i\le n$。保证给定的 $m$ 个区间两两不同。
|
| 115 |
+
|
| 116 |
+
$\operatorname{Subtask}1(5\%):n,c\le 5$。
|
| 117 |
+
|
| 118 |
+
$\operatorname{Subtask}2(10\%):c\le 100$,且对于任意两个有交点的区间一定存在其中一个包含另一个。
|
| 119 |
+
|
| 120 |
+
$\operatorname{Subtask}3(15\%):m\le 18,c=2$。
|
| 121 |
+
|
| 122 |
+
$\operatorname{Subtask}4(20\%):c=2$。
|
| 123 |
+
|
| 124 |
+
$\operatorname{Subtask}5(15\%):n,c\le 40$。
|
| 125 |
+
|
| 126 |
+
$\operatorname{Subtask}6(15\%):c\le 100$。
|
| 127 |
+
|
| 128 |
+
$\operatorname{Subtask}7(20\%):$ 无特殊限制。
|
| 129 |
+
|
| 130 |
+
#### 样例说明 1
|
| 131 |
+
|
| 132 |
+
当 $a=(1,1,1)$ 时,$b=(1,1)$。
|
| 133 |
+
|
| 134 |
+
当 $a=(1,1,2)$ 时,$b=(1,1)$。
|
| 135 |
+
|
| 136 |
+
当 $a=(1,2,1)$ 时,$b=(1,1)$。
|
| 137 |
+
|
| 138 |
+
当 $a=(1,2,2)$ 时,$b=(1,2)$。
|
| 139 |
+
|
| 140 |
+
当 $a=(2,1,1)$ 时,$b=(1,1)$。
|
| 141 |
+
|
| 142 |
+
当 $a=(2,1,2)$ 时,$b=(1,1)$。
|
| 143 |
+
|
| 144 |
+
当 $a=(2,2,1)$ 时,$b=(2,1)$。
|
| 145 |
+
|
| 146 |
+
当 $a=(2,2,2)$ 时,$b=(2,2)$。
|
| 147 |
+
|
| 148 |
+
因此共能得到 $[1,1],[1,2],[2,1],[2,2]$ 这 $4$ 种不同的 $b$。
|
problems/10009.txt
ADDED
|
@@ -0,0 +1,112 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2022] 线段树
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
请注意:**本题不是线段树模板题**。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
给定一个长度为 $n$ 的序列 $a_1,a_2,\cdots a_n$。你需要进行共 $q$ 次下面两种操作:
|
| 10 |
+
|
| 11 |
+
- `1 l r`:将 $a_{l\sim r}$ 替换为它的异或差分。形式化地说,令 $b_i := a_i \text{ xor } a_{i-1}$($l<i\leq r$),然后对于每个 $l<i\leq r$,将 $a_i$ 替换为 $b_i$。
|
| 12 |
+
|
| 13 |
+
- `2 pos`:查询 $a_{pos}$ 的值。
|
| 14 |
+
|
| 15 |
+
操作执行完后,你还需要回答最终的 $a$ 序列。
|
| 16 |
+
|
| 17 |
+
## 输入格式
|
| 18 |
+
|
| 19 |
+
第一行包含一个整数 $T$,表示该数据满足第 $T$ 个子任务的限制。
|
| 20 |
+
|
| 21 |
+
第二行包含两个整数 $n,q$,分别表示序列的长度和操作的个数。
|
| 22 |
+
|
| 23 |
+
第三行包含 $n$ 个整数 $a_1,a_2,\cdots,a_n$。
|
| 24 |
+
|
| 25 |
+
接下来 $q$ 行,每行若干个数,表示一个操作。若操作为第一种操作,则此行包含三个数 `1 l r` 。若操作为第二种操作,则此行包含两个数 `2 pos`。
|
| 26 |
+
|
| 27 |
+
## 输出格式
|
| 28 |
+
|
| 29 |
+
设共有 $q_2$ 个第二种操作,则输出共包含 $q_2+n$ 行。
|
| 30 |
+
|
| 31 |
+
前 $q_2$ 行,每行输出一个整数,表示该操作的答案。
|
| 32 |
+
|
| 33 |
+
接下来 $n$ 行,每行输出一个整数,表示最终的 $a$
|
| 34 |
+
序列。
|
| 35 |
+
|
| 36 |
+
## 样例 #1
|
| 37 |
+
|
| 38 |
+
### 样例输入 #1
|
| 39 |
+
|
| 40 |
+
```
|
| 41 |
+
1
|
| 42 |
+
6 6
|
| 43 |
+
1 1 5 1 9 4
|
| 44 |
+
2 5
|
| 45 |
+
1 2 5
|
| 46 |
+
2 4
|
| 47 |
+
1 3 6
|
| 48 |
+
2 6
|
| 49 |
+
1 1 6
|
| 50 |
+
```
|
| 51 |
+
|
| 52 |
+
### 样例输出 #1
|
| 53 |
+
|
| 54 |
+
```
|
| 55 |
+
9
|
| 56 |
+
4
|
| 57 |
+
12
|
| 58 |
+
1
|
| 59 |
+
0
|
| 60 |
+
5
|
| 61 |
+
4
|
| 62 |
+
12
|
| 63 |
+
0
|
| 64 |
+
```
|
| 65 |
+
|
| 66 |
+
## 提示
|
| 67 |
+
|
| 68 |
+
**更多样例见下发文件**。对于第 $i + 1$ 个样例,$T = i$。
|
| 69 |
+
|
| 70 |
+
### 样例 1 解释
|
| 71 |
+
|
| 72 |
+
初始时 $a=[1,1,5,1,9,4]$。
|
| 73 |
+
|
| 74 |
+
第一个操作要求输出 $a_5$,此时 $a_5=9$,故输出 $9$。
|
| 75 |
+
|
| 76 |
+
第二个操作要求将 $a_{2\sim 5}$ 替换为它的异或差分,$a_{2\sim 5}$ 为 $[1,5,1,9]$,它的异或差分为 $[1,4,4,8]$,故操作执行完后,$a$ 序列变为 $[1,1,4,4,8,4]$
|
| 77 |
+
。
|
| 78 |
+
|
| 79 |
+
第三个操作要求输出 $a_4$,此时 $a_4=4$,故输出 $4$。
|
| 80 |
+
|
| 81 |
+
第四个操作要求将 $a_{3\sim 6}$ 替换为它的异或差分, $a_{3\sim 6}$ 为 $[4,4,8,4]$,它的异或差分为 $[4,0,12,12]$,故操作执行完后, $a$ 序列变为 $[1,1,4,0,12,12]$。
|
| 82 |
+
|
| 83 |
+
第五个操作要求输出 $a_6$,此时 $a_6=12$,故输出 $12$。
|
| 84 |
+
|
| 85 |
+
第六个操作要求将 $a_{1\sim 6}$ 替换为它的异或差分, $a_{1\sim 6}$ 为 $[1,1,4,0,12,12]$,它的异或差分为 $[1,0,5,4,12,0]$,故操作执行完后,$a$ 序列变为 $[1,0,5,4,12,0]$。
|
| 86 |
+
|
| 87 |
+
最终的 $a$ 序列为 $[1,0,5,4,12,0]$。
|
| 88 |
+
|
| 89 |
+
### 数据范围与约定
|
| 90 |
+
|
| 91 |
+
对于所有数据,保证 $1\leq n\leq 2.5\times 10^5$,$1\leq q\leq 10^5$,$0\leq a_i< 2^{30}$,$1\leq l\leq r\leq n$,$1\leq pos\leq n$。
|
| 92 |
+
|
| 93 |
+
| 子任务编号 | $n\leq$ | $q\leq$ | 特殊性质 | 分值 | 子任务依赖 |
|
| 94 |
+
| :--------: | :--------------: | :------------: | :------: | :--: | :-------------: |
|
| 95 |
+
| $1$ | $2\times 10^3$ | $2\times 10^3$ | 无 | $8$ | 无 |
|
| 96 |
+
| $2$ | $2.5\times 10^5$ | $10^5$ | A | $4$ | 无 |
|
| 97 |
+
| $3$ | $2.5\times 10^5$ | $10^5$ | B | $7$ | 无 |
|
| 98 |
+
| $4$ | $2.5\times 10^5$ | $10^5$ | CD | $13$ | 无 |
|
| 99 |
+
| $5$ | $2.5\times 10^5$ | $10^5$ | DE | $12$ | 无 |
|
| 100 |
+
| $6$ | $2.5\times 10^5$ | $10^5$ | D | $16$ | $5$ |
|
| 101 |
+
| $7$ | $2.5\times 10^5$ | $10^5$ | E | $11$ | $5$ |
|
| 102 |
+
| $8$ | $2.5\times 10^5$ | $10^5$ | 无 | $29$ | $1,2,3,4,5,6,7$ |
|
| 103 |
+
|
| 104 |
+
特殊性质 A:$\forall i\geq 2, a_i=0$。
|
| 105 |
+
|
| 106 |
+
特殊性质 B:$0\leq a_i\leq 1$。
|
| 107 |
+
|
| 108 |
+
特殊性质 C:记序列 $a$ 中非零位置个数为 $c$,则 $c\leq 100$。
|
| 109 |
+
|
| 110 |
+
特殊性质 D:操作 $1$ 满足 $l=1$,$r=n$。
|
| 111 |
+
|
| 112 |
+
特殊性质 E:没有操作 $2$。
|
problems/1001.txt
ADDED
|
@@ -0,0 +1,298 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# A+B Problem
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
强烈推荐[新用户必读帖](/discuss/show/241461)。
|
| 6 |
+
|
| 7 |
+
**不熟悉算法竞赛的选手请看这里:**
|
| 8 |
+
|
| 9 |
+
算法竞赛中要求的输出格式中,**不能有多余的内容**,**这也包括了“请输入整数 $\bm a$ 和 $\bm b$” 这一类的提示用户输入信息的内容**。若包含了这些内容,将会被认为是 `Wrong Answer`,即洛谷上的 `WA`。在对比代码输出和标准输出时,系统将忽略每一行结尾的空格,以及最后一行之后多余的换行符。
|
| 10 |
+
|
| 11 |
+
若因此类问题出现本机似乎输出了正确的结果,但是实际提交结果为错误的现象,请勿认为是洛谷评测机出了问题,而是你的代码中可能存在多余的输出信息。用户可以参考在题目末尾提供的代码。
|
| 12 |
+
|
| 13 |
+
此外,**请善用应用中的在线 IDE 功能**,以避免不同平台的评测产生差异。
|
| 14 |
+
|
| 15 |
+
最后,请不要在对应的题目讨论区中发布自己的题解,请发布到题解区域中,否则将处以删除或禁言的处罚。若发现无法提交题解则表明本题题解数量过多,仍不应发布讨论。若您的做法确实与其他所有题解均不一样,请联系管理员添加题解。
|
| 16 |
+
|
| 17 |
+
## 题目描述
|
| 18 |
+
|
| 19 |
+
输入两个整数 $a, b$,输出它们的和($|a|,|b| \le {10}^9$)。
|
| 20 |
+
|
| 21 |
+
注意
|
| 22 |
+
|
| 23 |
+
1. Pascal 使用 `integer` 会爆掉哦!
|
| 24 |
+
2. 有负数哦!
|
| 25 |
+
3. C/C++ 的 main 函数必须是 `int` 类型,而且 C 最后要 `return 0`。这不仅对洛谷其他题目有效,而且也是 NOIP/CSP/NOI 比赛的要求!
|
| 26 |
+
|
| 27 |
+
好吧,同志们,我们就从这一题开始,向着大牛的路进发。
|
| 28 |
+
|
| 29 |
+
> 任何一个伟大的思想,都有一个微不足道的开始。
|
| 30 |
+
|
| 31 |
+
## 输入格式
|
| 32 |
+
|
| 33 |
+
两个以空格分开的整数。
|
| 34 |
+
|
| 35 |
+
## 输出格式
|
| 36 |
+
|
| 37 |
+
一个整数。
|
| 38 |
+
|
| 39 |
+
## 样例 #1
|
| 40 |
+
|
| 41 |
+
### 样例输入 #1
|
| 42 |
+
|
| 43 |
+
```
|
| 44 |
+
20 30
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
### 样例输出 #1
|
| 48 |
+
|
| 49 |
+
```
|
| 50 |
+
50
|
| 51 |
+
```
|
| 52 |
+
|
| 53 |
+
## 提示
|
| 54 |
+
|
| 55 |
+
**广告**
|
| 56 |
+
|
| 57 |
+
洛谷出品的算法教材,帮助您更简单的学习基础算法。[【官方网店绝赞热卖中!】>>>](https://item.taobao.com/item.htm?id=637730514783)
|
| 58 |
+
|
| 59 |
+
[](https://item.taobao.com/item.htm?id=637730514783)
|
| 60 |
+
|
| 61 |
+
**本题各种语言的程序范例:**
|
| 62 |
+
|
| 63 |
+
C
|
| 64 |
+
```c
|
| 65 |
+
#include <stdio.h>
|
| 66 |
+
|
| 67 |
+
int main()
|
| 68 |
+
{
|
| 69 |
+
int a,b;
|
| 70 |
+
scanf("%d%d",&a,&b);
|
| 71 |
+
printf("%d\n", a+b);
|
| 72 |
+
return 0;
|
| 73 |
+
}
|
| 74 |
+
```
|
| 75 |
+
----------------
|
| 76 |
+
|
| 77 |
+
C++
|
| 78 |
+
```cpp
|
| 79 |
+
#include <iostream>
|
| 80 |
+
#include <cstdio>
|
| 81 |
+
|
| 82 |
+
using namespace std;
|
| 83 |
+
|
| 84 |
+
int main()
|
| 85 |
+
{
|
| 86 |
+
int a,b;
|
| 87 |
+
cin >> a >> b;
|
| 88 |
+
cout << a+b << endl;
|
| 89 |
+
return 0;
|
| 90 |
+
}
|
| 91 |
+
```
|
| 92 |
+
----------------
|
| 93 |
+
|
| 94 |
+
Pascal
|
| 95 |
+
```cpp
|
| 96 |
+
var a, b: longint;
|
| 97 |
+
begin
|
| 98 |
+
readln(a,b);
|
| 99 |
+
writeln(a+b);
|
| 100 |
+
end.
|
| 101 |
+
```
|
| 102 |
+
-----------------
|
| 103 |
+
|
| 104 |
+
Python2
|
| 105 |
+
|
| 106 |
+
```cpp
|
| 107 |
+
s = raw_input().split()
|
| 108 |
+
print int(s[0]) + int(s[1])
|
| 109 |
+
```
|
| 110 |
+
-----------------
|
| 111 |
+
|
| 112 |
+
Python3
|
| 113 |
+
|
| 114 |
+
```cpp
|
| 115 |
+
s = input().split()
|
| 116 |
+
print(int(s[0]) + int(s[1]))
|
| 117 |
+
```
|
| 118 |
+
-----------------
|
| 119 |
+
|
| 120 |
+
Java
|
| 121 |
+
```java
|
| 122 |
+
import java.io.*;
|
| 123 |
+
import java.util.*;
|
| 124 |
+
public class Main {
|
| 125 |
+
public static void main(String args[]) throws Exception {
|
| 126 |
+
Scanner cin=new Scanner(System.in);
|
| 127 |
+
int a = cin.nextInt(), b = cin.nextInt();
|
| 128 |
+
System.out.println(a+b);
|
| 129 |
+
}
|
| 130 |
+
}
|
| 131 |
+
```
|
| 132 |
+
-----------------
|
| 133 |
+
|
| 134 |
+
JavaScript (Node.js)
|
| 135 |
+
|
| 136 |
+
```javascript
|
| 137 |
+
const fs = require('fs')
|
| 138 |
+
const data = fs.readFileSync('/dev/stdin')
|
| 139 |
+
const result = data.toString('ascii').trim().split(' ').map(x => parseInt(x)).reduce((a, b) => a + b, 0)
|
| 140 |
+
console.log(result)
|
| 141 |
+
process.exit() // 请注意必须在出口点处加入此行
|
| 142 |
+
```
|
| 143 |
+
|
| 144 |
+
-----------------
|
| 145 |
+
|
| 146 |
+
Ruby
|
| 147 |
+
|
| 148 |
+
```ruby
|
| 149 |
+
a, b = gets.split.map(&:to_i)
|
| 150 |
+
print a+b
|
| 151 |
+
```
|
| 152 |
+
|
| 153 |
+
-----------------
|
| 154 |
+
|
| 155 |
+
PHP
|
| 156 |
+
|
| 157 |
+
```php
|
| 158 |
+
<?php
|
| 159 |
+
$input = trim(file_get_contents("php://stdin"));
|
| 160 |
+
list($a, $b) = explode(' ', $input);
|
| 161 |
+
echo $a + $b;
|
| 162 |
+
```
|
| 163 |
+
|
| 164 |
+
-----------------
|
| 165 |
+
|
| 166 |
+
Rust
|
| 167 |
+
|
| 168 |
+
```rust
|
| 169 |
+
use std::io;
|
| 170 |
+
|
| 171 |
+
fn main(){
|
| 172 |
+
let mut input=String::new();
|
| 173 |
+
io::stdin().read_line(&mut input).unwrap();
|
| 174 |
+
let mut s=input.trim().split(' ');
|
| 175 |
+
|
| 176 |
+
let a:i32=s.next().unwrap()
|
| 177 |
+
.parse().unwrap();
|
| 178 |
+
let b:i32=s.next().unwrap()
|
| 179 |
+
.parse().unwrap();
|
| 180 |
+
println!("{}",a+b);
|
| 181 |
+
}
|
| 182 |
+
```
|
| 183 |
+
|
| 184 |
+
-----------------
|
| 185 |
+
|
| 186 |
+
Go
|
| 187 |
+
|
| 188 |
+
```go
|
| 189 |
+
package main
|
| 190 |
+
|
| 191 |
+
import "fmt"
|
| 192 |
+
|
| 193 |
+
func main() {
|
| 194 |
+
var a, b int
|
| 195 |
+
fmt.Scanf("%d%d", &a, &b)
|
| 196 |
+
fmt.Println(a+b)
|
| 197 |
+
}
|
| 198 |
+
```
|
| 199 |
+
|
| 200 |
+
-----------------
|
| 201 |
+
|
| 202 |
+
C# Mono
|
| 203 |
+
|
| 204 |
+
```cs
|
| 205 |
+
using System;
|
| 206 |
+
|
| 207 |
+
public class APlusB{
|
| 208 |
+
private static void Main(){
|
| 209 |
+
string[] input = Console.ReadLine().Split(' ');
|
| 210 |
+
Console.WriteLine(int.Parse(input[0]) + int.Parse(input[1]));
|
| 211 |
+
}
|
| 212 |
+
}
|
| 213 |
+
```
|
| 214 |
+
|
| 215 |
+
------------------
|
| 216 |
+
|
| 217 |
+
Visual Basic Mono
|
| 218 |
+
|
| 219 |
+
```vb
|
| 220 |
+
Imports System
|
| 221 |
+
|
| 222 |
+
Module APlusB
|
| 223 |
+
Sub Main()
|
| 224 |
+
Dim ins As String() = Console.ReadLine().Split(New Char(){" "c})
|
| 225 |
+
Console.WriteLine(Int(ins(0))+Int(ins(1)))
|
| 226 |
+
End Sub
|
| 227 |
+
End Module
|
| 228 |
+
```
|
| 229 |
+
|
| 230 |
+
------------------
|
| 231 |
+
|
| 232 |
+
Kotlin
|
| 233 |
+
|
| 234 |
+
```kotlin
|
| 235 |
+
fun main(args: Array<String>) {
|
| 236 |
+
val (a, b) = readLine()!!.split(' ').map(String::toInt)
|
| 237 |
+
println(a + b)
|
| 238 |
+
}
|
| 239 |
+
```
|
| 240 |
+
|
| 241 |
+
------------------
|
| 242 |
+
|
| 243 |
+
Haskell
|
| 244 |
+
|
| 245 |
+
```haskell
|
| 246 |
+
main = do
|
| 247 |
+
[a, b] <- (map read . words) `fmap` getLine
|
| 248 |
+
print (a+b)
|
| 249 |
+
```
|
| 250 |
+
|
| 251 |
+
------------------
|
| 252 |
+
|
| 253 |
+
Lua
|
| 254 |
+
|
| 255 |
+
```lua
|
| 256 |
+
a = io.read('*n')
|
| 257 |
+
b = io.read('*n')
|
| 258 |
+
print(a + b)
|
| 259 |
+
```
|
| 260 |
+
|
| 261 |
+
------------------
|
| 262 |
+
|
| 263 |
+
OCaml
|
| 264 |
+
|
| 265 |
+
```ocaml
|
| 266 |
+
Scanf.scanf "%i %i\n" (fun a b -> print_int (a + b))
|
| 267 |
+
```
|
| 268 |
+
|
| 269 |
+
------------------
|
| 270 |
+
|
| 271 |
+
Julia
|
| 272 |
+
|
| 273 |
+
```julia
|
| 274 |
+
nums = map(x -> parse(Int, x), split(readline(), " "))
|
| 275 |
+
println(nums[1] + nums[2])
|
| 276 |
+
```
|
| 277 |
+
|
| 278 |
+
------------------
|
| 279 |
+
|
| 280 |
+
Scala
|
| 281 |
+
|
| 282 |
+
```scala
|
| 283 |
+
object Main extends App {
|
| 284 |
+
println(scala.io.StdIn.readLine().split(" ").map(_.toInt).sum)
|
| 285 |
+
}
|
| 286 |
+
```
|
| 287 |
+
|
| 288 |
+
------------------
|
| 289 |
+
|
| 290 |
+
Perl
|
| 291 |
+
|
| 292 |
+
```perl
|
| 293 |
+
my $in = <STDIN>;
|
| 294 |
+
chomp $in;
|
| 295 |
+
$in = [split /[\s,]+/, $in];
|
| 296 |
+
my $c = $in->[0] + $in->[1];
|
| 297 |
+
print "$c\n";
|
| 298 |
+
```
|
problems/10010.txt
ADDED
|
@@ -0,0 +1,137 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] Grievous Lady
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
对立从那灰暗的塔楼进入,逐步踏入这个扭曲的迷宫深处。
|
| 6 |
+
|
| 7 |
+
对立的心突然绞痛起来。
|
| 8 |
+
|
| 9 |
+
对立后退了一步,扑腾了一下便跪倒下来。
|
| 10 |
+
|
| 11 |
+
未及碰到,灰黑的地板就突然崩裂瓦解,先一步向下坠落。
|
| 12 |
+
|
| 13 |
+
先前收集的纷争碎片,连同塔楼本身,一同化作了一场倾盆大雨,包围在对立四周。
|
| 14 |
+
|
| 15 |
+
异象骤起,对立的思维也陷入一片混乱。
|
| 16 |
+
|
| 17 |
+
塔楼落入了先前的由光芒碎片组成的欢乐海洋,但对立却被纷争碎片紧紧地包裹着。
|
| 18 |
+
|
| 19 |
+
在那由光芒和纷争碎片交错的风暴之中,对立所见的只有那些令人厌恶的纷争碎片。
|
| 20 |
+
|
| 21 |
+
那枚世界尽头的记忆映入了对立的视野。
|
| 22 |
+
|
| 23 |
+
面对着世界一点点地走向终结的景象,对立的理性在碎裂。
|
| 24 |
+
|
| 25 |
+
对立意识到,一切美好的记忆不过是须臾,最终都会走向破灭。
|
| 26 |
+
|
| 27 |
+
四周的碎片依旧在飞旋,对立试图看清那些玻璃碎片的变换。
|
| 28 |
+
|
| 29 |
+
对立意识到,现在围绕着的那些碎片,正以最恐怖的方式运转。
|
| 30 |
+
|
| 31 |
+
这个碎片风暴所带来的「忧郁度」,可以被简单地描述为外侧碎片的旋转速度之和乘上内侧碎片的旋转速度之和。
|
| 32 |
+
|
| 33 |
+
一片玻璃碎片在外侧总是以一种速度正旋,而在内侧总是以另一种速度逆旋。
|
| 34 |
+
|
| 35 |
+
每片碎片都是是来自不同世界的刹那记忆,故而其转速总可以认为是独立随机指定的。
|
| 36 |
+
|
| 37 |
+
在残存无几的希望将尽未尽之时,对立只想知道,现在的碎片风暴的忧郁度,也就是最大可能的忧郁度,究竟是多少。
|
| 38 |
+
|
| 39 |
+
## 题目描述
|
| 40 |
+
|
| 41 |
+
共有 $n$ 个元素,标号 $1\sim n$,每个元素 $j$ 有两个正整数权值 $a_j,b_j$。
|
| 42 |
+
|
| 43 |
+
你要确定一个 $[1,n]\cap\mathbb N$ 的子集 $S$,从而最大化
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
(\sum_{k=1}^na_k[k\in S])(\sum_{k=1}^nb_k[k\notin S])
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
这个问题显然不可做,因此**保证每个 $a_j,b_j$ 分别在 $[1,A]\cap\mathbb N,[1,B]\cap\mathbb N$ 内独立均匀随机生成**。
|
| 50 |
+
|
| 51 |
+
现在给定 $n,A,B$ 和每个元素的两个权值 $(a_j,b_j)$,请求出这个最大的答案。
|
| 52 |
+
|
| 53 |
+
## 输入格式
|
| 54 |
+
|
| 55 |
+
本题每个测试点中有多组测试数据。
|
| 56 |
+
|
| 57 |
+
第一行四个整数,$T,n,A,B$,$T$ 表示该组数据内的数据组数,$n,A,B$ 表示该测试点内的所有数据均对应此 $n,A,B$。
|
| 58 |
+
|
| 59 |
+
接下来每组数据占 $n$ 行,其中第 $j$ 行两个整数 $a_j,b_j$。
|
| 60 |
+
|
| 61 |
+
保证 $a_j,b_j$ 在对应范围内独立均匀随机生成。
|
| 62 |
+
|
| 63 |
+
## 输出格式
|
| 64 |
+
|
| 65 |
+
对于每组数据输出一行一个整数,表示其答案。
|
| 66 |
+
|
| 67 |
+
注意这个答案可能很大,你可能需要使用 `__int128` 类型来进行中间存储与运算,并最后输出。注意你可能需要使用一些正确的输出方式。
|
| 68 |
+
|
| 69 |
+
## 提示
|
| 70 |
+
|
| 71 |
+
#### 输入输出样例
|
| 72 |
+
|
| 73 |
+
**因为本题数据规模太大,直接提交评测会对评测机带来很大压力,本题将提供很多大样例;请尽量减少本题的提交次数。**
|
| 74 |
+
|
| 75 |
+
请参见下发文件 `grievouslady*.in/ans`,共 $50$ 组,基本按照部分分的方法造。
|
| 76 |
+
|
| 77 |
+
由于本题保证数据随机,不提供手搓样例。
|
| 78 |
+
|
| 79 |
+
#### 数据范围与提示
|
| 80 |
+
|
| 81 |
+
对于所有的数据,保证 $10\le n\le3000$,$10^4\le A,B\le10^{12}$,$1\le T\le50$。
|
| 82 |
+
|
| 83 |
+
~~本题设置子任务,各子任务~~共 $100$ 个测试点。具体的测试点分布可以见下表。
|
| 84 |
+
|
| 85 |
+
**本题在洛谷上的版本不设置子任务**。
|
| 86 |
+
|
| 87 |
+
(**由于表格比较宽,洛谷上较难完整显示,你可能要使用题目页面的“展开”功能**)
|
| 88 |
+
|
| 89 |
+
|测试点编号|$n$|$A$|$B$|测试点编号|$n$|$A$|$B$|测试点编号|$n$|$A$|$B$|
|
| 90 |
+
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|
| 91 |
+
|$1\sim2$|$=10$|$=10^4$|$=10^4$|$33\sim34$|$=100$|$=10^4$|$=10^4$|$67\sim68$|$=1000$|$=10^5$|$=10^{12}$|
|
| 92 |
+
|$3\sim4$|$=10$|$=10^9$|$=10^9$|$35\sim36$|$=100$|$=10^5$|$=10^5$|$69\sim70$|$=1000$|$=10^9$|$=10^9$|
|
| 93 |
+
|$5\sim6$|$=10$|$=10^{12}$|$=10^{12}$|$37\sim38$|$=100$|$=10^5$|$=10^9$|$71\sim72$|$=1000$|$=10^{12}$|$=10^{12}$|
|
| 94 |
+
|$7\sim8$|$=20$|$=10^4$|$=10^4$|$39\sim40$|$=100$|$=10^9$|$=10^9$|$73\sim74$|$=1500$|$=10^5$|$=10^{12}$|
|
| 95 |
+
|$9\sim10$|$=20$|$=10^9$|$=10^9$|$41\sim42$|$=100$|$=10^{12}$|$=10^{12}$|$75\sim76$|$=1500$|$=10^9$|$=10^9$|
|
| 96 |
+
|$11\sim12$|$=20$|$=10^{12}$|$=10^{12}$|$43\sim44$|$=200$|$=10^5$|$=10^{12}$|$77\sim78$|$=1500$|$=10^{12}$|$=10^{12}$|
|
| 97 |
+
|$13\sim14$|$=30$|$=10^4$|$=10^4$|$45\sim46$|$=200$|$=10^9$|$=10^9$|$79\sim80$|$=2000$|$=10^5$|$=10^{12}$|
|
| 98 |
+
|$15\sim16$|$=30$|$=10^9$|$=10^9$|$47\sim48$|$=200$|$=10^{12}$|$=10^{12}$|$81\sim82$|$=2000$|$=10^9$|$=10^9$|
|
| 99 |
+
|$17\sim18$|$=30$|$=10^{12}$|$=10^{12}$|$49\sim50$|$=300$|$=10^5$|$=10^{12}$|$83\sim84$|$=2000$|$=10^{12}$|$=10^{12}$|
|
| 100 |
+
|$19\sim20$|$=40$|$=10^4$|$=10^4$|$51\sim52$|$=300$|$=10^9$|$=10^9$|$85\sim86$|$=2500$|$=10^4$|$=10^9$|
|
| 101 |
+
|$21\sim22$|$=40$|$=10^9$|$=10^9$|$53\sim54$|$=300$|$=10^{12}$|$=10^{12}$|$87\sim88$|$=2500$|$=10^5$|$=10^{12}$|
|
| 102 |
+
|$23\sim24$|$=40$|$=10^{12}$|$=10^{12}$|$55\sim56$|$=500$|$=10^5$|$=10^{12}$|$89\sim90$|$=2500$|$=10^9$|$=10^9$|
|
| 103 |
+
|$25\sim26$|$=50$|$=10^4$|$=10^4$|$57\sim58$|$=500$|$=10^9$|$=10^9$|$91\sim92$|$=2500$|$=10^{12}$|$=10^{12}$|
|
| 104 |
+
|$27\sim28$|$=50$|$=10^4$|$=10^9$|$59\sim60$|$=500$|$=10^{12}$|$=10^{12}$|$93\sim94$|$=3000$|$=10^4$|$=10^9$|
|
| 105 |
+
|$29\sim30$|$=50$|$=10^9$|$=10^9$|$61\sim62$|$=800$|$=10^5$|$=10^{12}$|$95\sim96$|$=3000$|$=10^5$|$=10^{12}$|
|
| 106 |
+
|$31\sim32$|$=50$|$=10^{12}$|$=10^{12}$|$63\sim64$|$=800$|$=10^9$|$=10^9$|$97\sim98$|$=3000$|$=10^9$|$=10^9$|
|
| 107 |
+
|||||$65\sim66$|$=800$|$=10^{12}$|$=10^{12}$|$99\sim100$|$=3000$|$=10^{12}$|$=10^{12}$|
|
| 108 |
+
|
| 109 |
+
~~我们按如下方式布局各测试点~~:
|
| 110 |
+
* ~~subtask $1$:$1\sim12$,占 $\rm12pts$~~。
|
| 111 |
+
* ~~subtask $2$:$13\sim32$,占 $\rm20pts$~~。
|
| 112 |
+
* ~~subtask $3$:$33\sim36$,占 $\rm4pts$~~。
|
| 113 |
+
* ~~subtask $4$:$37\sim48$,占 $\rm12pts$~~。
|
| 114 |
+
* ~~subtask $5$:$49\sim50$,占 $\rm2pts$~~。
|
| 115 |
+
* ~~subtask $6$:$51\sim60$,占 $\rm10pts$~~。
|
| 116 |
+
* ~~subtask $7$:$61\sim72$,占 $\rm12pts$~~。
|
| 117 |
+
* ~~subtask $8$:$73\sim84$,占 $\rm12pts$~~。
|
| 118 |
+
* ~~subtask $9$:$85\sim92$,占 $\rm8pts$~~。
|
| 119 |
+
* ~~subtask $10$:$93\sim100$,占 $\rm8pts$~~。
|
| 120 |
+
|
| 121 |
+
~~**本题不设置子任务依赖,因此请确保经样例测试后你的算法正确后再提交,以免卡评测机**。~~
|
| 122 |
+
|
| 123 |
+
#### 后记
|
| 124 |
+
|
| 125 |
+
这个世界——一切——都源于过去。过去的影像,哪怕是欢乐的记忆,就像是白昼过后的黑夜,渐渐导致了这份世界末日。
|
| 126 |
+
|
| 127 |
+
泪水盈眶。对立的眼神转为一片黑暗。
|
| 128 |
+
|
| 129 |
+
对立与这些玻璃起了共鸣,围绕于四周的回忆之壳开始崩裂。
|
| 130 |
+
|
| 131 |
+
对立就身处其中,站在那炫目的光芒前方,已经没有任何情感了。
|
| 132 |
+
|
| 133 |
+
扭曲的迷宫,也在对立的力量下,悉数损毁……
|
| 134 |
+
|
| 135 |
+
时光逝去,对立变了。不再激情地收集回忆,而是近乎无意识地走在这世界之中,并不再抱有任何雄心壮志。
|
| 136 |
+
|
| 137 |
+
如今,对立正在一个破旧坍塌的建筑旁行走着,旋转着某天在废墟中找到的太阳伞。
|
problems/10011.txt
ADDED
|
@@ -0,0 +1,45 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 网格图最大流计数
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定 $n,m,k$,和两个正整数序列 $a_{1...n},b_{1...m}$,以及一个 $k\times k$ 的 $01$ 矩阵 $s_{1...k,1...k}$。
|
| 6 |
+
|
| 7 |
+
考虑一张有向图 $G=(V,E)$,其中 $V=\{S,T\}\cup(\{0,1\}\times ([1,k]\cap\mathbb{Z})^2)$,而 $E=E_1\cup E_2\cup E_3$ 由三部分组成:
|
| 8 |
+
|
| 9 |
+
- $E_1=\{(S,(0,1,a_i)) \mid 1\le i\le n\}\cup\{((1,k,b_i),T)\mid 1\le i\le m\}$
|
| 10 |
+
- $E_2=\{((1,i,j),(0,i+1,j))\mid1\le i<k,1\le j\le k\}\cup \{(1,i,j),(0,i,j+1))\mid1\le i\le k,1\le j<k\}$
|
| 11 |
+
- $E_3=\{((0,i,j),(1,i,j))\mid 1\le i,j\le k,s_{i,j}=1\}$
|
| 12 |
+
|
| 13 |
+
简单来说,你可以看成每个格子 $(i,j),1\le i,j\le k$ 被拆成了一个入点 $(0,i,j)$ 和一个出点 $(1,i,j)$。$E_1$ 描述了 $S,T$ 与这些点之间的边,由 $a,b$ 决定;$E_2$ 描述了每个格子的出点连向它上方和右方格子的入点的边;$E_3$ 描述了每个格子的入点连向出点的边,由 $s$ 决定。
|
| 14 |
+
|
| 15 |
+
现在我们将 $G$ 看成一个网络,每条边的容量是 $1$。你需要求出以 $S$ 为源点,以 $T$ 为汇点的最大流,以及最大流的数量(两个流被认为是不同的,当且仅当存在一条边在两个流中的流量不同)。
|
| 16 |
+
|
| 17 |
+
## 输入格式
|
| 18 |
+
|
| 19 |
+
第一行三个正整数 $n,m,k$。
|
| 20 |
+
|
| 21 |
+
第二行 $n$ 个正整数 $1\le a_1<a_2<...<a_n\le k$。
|
| 22 |
+
|
| 23 |
+
第三行 $m$ 个正整数 $1\le b_1<b_2<...<b_m\le k$。
|
| 24 |
+
|
| 25 |
+
接下来 $k$ 行,每行一个长度为 $k$ 的 01 字符串,表示矩阵 $s$。
|
| 26 |
+
|
| 27 |
+
## 输出格式
|
| 28 |
+
|
| 29 |
+
输出一行两个非负整数,分别表示最大流和最大流的数量,后者对 $10^9+7$ 取模。
|
| 30 |
+
|
| 31 |
+
## 提示
|
| 32 |
+
|
| 33 |
+
样例见下发文件。
|
| 34 |
+
|
| 35 |
+
对于全部数据,$1\le n,m\le k\le400$。
|
| 36 |
+
|
| 37 |
+
| 子任务编号 | $n\le$ | $k\le$ | 特殊性质 | 子任务分值 |
|
| 38 |
+
| :--------: | :----: | :----: | :------------------: | :--------: |
|
| 39 |
+
| $1$ | $7$ | $7$ | 无 | $5$ |
|
| 40 |
+
| $2$ | $18$ | $18$ | 无 | $5$ |
|
| 41 |
+
| $3$ | $10$ | $400$ | 无 | $10$ |
|
| 42 |
+
| $4$ | $100$ | $400$ | 无 | $25$ |
|
| 43 |
+
| $5$ | $400$ | $400$ | $n=m$ 且最大流为 $n$ | $10$ |
|
| 44 |
+
| $6$ | $400$ | $400$ | 最大流为 $n$ | $25$ |
|
| 45 |
+
| $7$ | $400$ | $400$ | 无 | $20$ |
|
problems/10012.txt
ADDED
|
@@ -0,0 +1,138 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 落日珊瑚
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给一个长度为 $n$、包含方括号和圆括号的括号串,定义一个串 $S$ 合法,当且仅当以下几种情况之一:
|
| 6 |
+
|
| 7 |
+
1. $S$ 为空串;
|
| 8 |
+
1. $S= [T]$ 且 $T$ 合法;
|
| 9 |
+
1. $S= (T)$ 且 $T$ 合法;
|
| 10 |
+
1. $S=TU$ 且 $T, U$ 合法。
|
| 11 |
+
|
| 12 |
+
比如 ```()```,```[()]``` 都是一个合法的括号串,但 ```[()]())``` 不是。
|
| 13 |
+
|
| 14 |
+
定义一个操作叫选择一个区间 $[l, r]$,并把所有在区间里的字符从方括号变圆括号,从圆括号变方括号。
|
| 15 |
+
|
| 16 |
+
定义一个括号串的权值 $val(S)$ 为:如果这个括号串能通过操作变成合法,就是最小的操作次数;否则是 $0$。
|
| 17 |
+
|
| 18 |
+
给出 $q$ 次修改查询,有以下两种可能。
|
| 19 |
+
|
| 20 |
+
1. 修改,给出一个区间 $[l, r]$ 把所有在区间里的字符从方括号变圆括号,从圆括号变方括号。
|
| 21 |
+
2. 查询,给出一个区间 $[l, r]$,求 $\sum_{[l', r'] \in [l, r]} val(s[l', r'])$。
|
| 22 |
+
|
| 23 |
+
## 输入格式
|
| 24 |
+
|
| 25 |
+
第一行四个整数 $n, q, T, subtaskid$,分别表示字符串长度,操作次数,强制在线的参数,子任务编号。
|
| 26 |
+
|
| 27 |
+
接下来一行一个长度为 $n$ 的字符串。
|
| 28 |
+
|
| 29 |
+
接下来 $q$ 行,每行三个数 $opt, L, R$,表示一次操作。
|
| 30 |
+
|
| 31 |
+
强制在线,真实的 $l = \min((L + T \cdot lastans) \bmod n + 1, (R + T \cdot lastans) \bmod n + 1)$,$r = \max((L + T \cdot lastans) \bmod n + 1, (R + T \cdot lastans) \bmod n + 1)$ 其中 $lastans$ 是上一次询问的答案,如果没有上次询问则为 $0$。
|
| 32 |
+
|
| 33 |
+
**请注意,即使是离线的部分分,也有可能 $L \neq l$,$R \neq r$**。
|
| 34 |
+
|
| 35 |
+
## 输出格式
|
| 36 |
+
|
| 37 |
+
若干行,每次询问输出一个答案。
|
| 38 |
+
|
| 39 |
+
## 样例 #1
|
| 40 |
+
|
| 41 |
+
### 样例输入 #1
|
| 42 |
+
|
| 43 |
+
```
|
| 44 |
+
10 10 0 0
|
| 45 |
+
[)]]((()][
|
| 46 |
+
2 10 6
|
| 47 |
+
1 6 6
|
| 48 |
+
1 3 6
|
| 49 |
+
2 5 7
|
| 50 |
+
2 3 3
|
| 51 |
+
2 10 4
|
| 52 |
+
1 7 1
|
| 53 |
+
2 4 4
|
| 54 |
+
2 4 2
|
| 55 |
+
1 5 5
|
| 56 |
+
```
|
| 57 |
+
|
| 58 |
+
### 样例输出 #1
|
| 59 |
+
|
| 60 |
+
```
|
| 61 |
+
1
|
| 62 |
+
0
|
| 63 |
+
0
|
| 64 |
+
1
|
| 65 |
+
0
|
| 66 |
+
0
|
| 67 |
+
```
|
| 68 |
+
|
| 69 |
+
## 样例 #2
|
| 70 |
+
|
| 71 |
+
### 样例输入 #2
|
| 72 |
+
|
| 73 |
+
```
|
| 74 |
+
20 20 0 0
|
| 75 |
+
[)])[)[](()((]]([[)[
|
| 76 |
+
2 9 3
|
| 77 |
+
2 8 10
|
| 78 |
+
1 4 15
|
| 79 |
+
1 5 9
|
| 80 |
+
1 16 10
|
| 81 |
+
1 18 20
|
| 82 |
+
1 1 8
|
| 83 |
+
2 8 9
|
| 84 |
+
1 2 16
|
| 85 |
+
1 10 13
|
| 86 |
+
1 16 9
|
| 87 |
+
1 8 1
|
| 88 |
+
2 20 7
|
| 89 |
+
2 14 11
|
| 90 |
+
1 3 16
|
| 91 |
+
1 15 18
|
| 92 |
+
1 6 4
|
| 93 |
+
2 10 7
|
| 94 |
+
2 2 4
|
| 95 |
+
2 13 2
|
| 96 |
+
```
|
| 97 |
+
|
| 98 |
+
### 样例输出 #2
|
| 99 |
+
|
| 100 |
+
```
|
| 101 |
+
2
|
| 102 |
+
0
|
| 103 |
+
0
|
| 104 |
+
1
|
| 105 |
+
2
|
| 106 |
+
1
|
| 107 |
+
0
|
| 108 |
+
4
|
| 109 |
+
```
|
| 110 |
+
|
| 111 |
+
## 提示
|
| 112 |
+
|
| 113 |
+
对于所有数据,$1 \le n, q \le 5\cdot 10^5$,$0 \le T \le 10^9$,$1 \le l, r \le n$,$1 \le opt \le 2$。
|
| 114 |
+
|
| 115 |
+
| 子任务编号 | $n, q \le $ | 特殊性质 | 分值 |
|
| 116 |
+
| :--------: | :-----------: | :------: | :--: |
|
| 117 |
+
| 1 | $100$ | E | 5 |
|
| 118 |
+
| 2 | $6000$ | E | 5 |
|
| 119 |
+
| 3 | $10^5$ | AE | 5 |
|
| 120 |
+
| 4 | $2\cdot 10^5$ | BE | 5 |
|
| 121 |
+
| 5 | $2\cdot 10^5$ | CDE | 5 |
|
| 122 |
+
| 6 | $2\cdot 10^5$ | CE | 10 |
|
| 123 |
+
| 7 | $2\cdot 10^5$ | DE | 10 |
|
| 124 |
+
| 8 | $2\cdot 10^5$ | E | 10 |
|
| 125 |
+
| 9 | $2\cdot 10^5$ | 无 | 20 |
|
| 126 |
+
| 10 | $5\cdot 10^5$ | 无 | 25 |
|
| 127 |
+
|
| 128 |
+
|
| 129 |
+
|
| 130 |
+
A 性质:每个位置有 $\frac{1}{4}$ 的概率为方圆左右括号。
|
| 131 |
+
|
| 132 |
+
B 性质:保证没有修改。
|
| 133 |
+
|
| 134 |
+
C 性质:保证修改为单点修改。
|
| 135 |
+
|
| 136 |
+
D 性质:保证查询区间 $[l, r]$ 满足 $S[l, r]$ 经过若干次操作可以变成合法串,且不存在另一个 $k \in [l, r)$,使得 $S[l, k]$ 可以经过若干次操作变成合法串。
|
| 137 |
+
|
| 138 |
+
E 性质:保证 $T = 0$,即可以离线。
|
problems/10013.txt
ADDED
|
@@ -0,0 +1,71 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] Tree Topological Order Counting
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一颗 $n$ 个点的有根树,$1$ 是根,记 $u$ 的父亲是 $fa_u$。另给出一长度为 $n$ 的权值序列 $b$。
|
| 6 |
+
|
| 7 |
+
称一个长度为 $n$ 的排列 $a$ 为这颗树的合法拓扑序,当且仅当 $\forall 2 \le u \le n,a_u > a_{fa_u}$。
|
| 8 |
+
|
| 9 |
+
对每个点 $u$,定义 $f(u)$ 为,在所有这颗树的合法拓扑序中,$b_{a_u}$ 之和。
|
| 10 |
+
|
| 11 |
+
现在对 $1 \le u \le n$,求 $f(u) \bmod 10^9+7$。
|
| 12 |
+
|
| 13 |
+
## 输入格式
|
| 14 |
+
|
| 15 |
+
第一行一个整数 $n$ 表示树的点数。
|
| 16 |
+
|
| 17 |
+
第二行 $n-1$ 个整数,第 $i$ 个表示 $fa_{i+1}$,描述树的结构。
|
| 18 |
+
|
| 19 |
+
第三行 $n$ 个整数,第 $i$ 个表示 $b_i$,描述权值序列。
|
| 20 |
+
|
| 21 |
+
## 输出格式
|
| 22 |
+
|
| 23 |
+
一行 $n$ 个整数,第 $i$ 个表示 $f(i) \bmod 10^9+7$。
|
| 24 |
+
|
| 25 |
+
## 样例 #1
|
| 26 |
+
|
| 27 |
+
### 样例输入 #1
|
| 28 |
+
|
| 29 |
+
```
|
| 30 |
+
5
|
| 31 |
+
1 1 3 2
|
| 32 |
+
3 5 4 4 1
|
| 33 |
+
```
|
| 34 |
+
|
| 35 |
+
### 样例输出 #1
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
18 27 27 15 15
|
| 39 |
+
```
|
| 40 |
+
|
| 41 |
+
## 样例 #2
|
| 42 |
+
|
| 43 |
+
### 样例输入 #2
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
5
|
| 47 |
+
1 1 3 1
|
| 48 |
+
1 2 3 4 5
|
| 49 |
+
```
|
| 50 |
+
|
| 51 |
+
### 样例输出 #2
|
| 52 |
+
|
| 53 |
+
```
|
| 54 |
+
12 42 32 52 42
|
| 55 |
+
```
|
| 56 |
+
|
| 57 |
+
## 提示
|
| 58 |
+
|
| 59 |
+
| Subtask | $n \le$ | 特殊限制 | 分值 |
|
| 60 |
+
| :-----: | :-----: | :------: | :--: |
|
| 61 |
+
| $1$ | $10$ | 无 | $5$ |
|
| 62 |
+
| $2$ | $20$ | 无 | $10$ |
|
| 63 |
+
| $3$ | $100$ | 无 | $15$ |
|
| 64 |
+
| $4$ | $350$ | 无 | $15$ |
|
| 65 |
+
| $5$ | $3000$ | A | $15$ |
|
| 66 |
+
| $6$ | $3000$ | 无 | $20$ |
|
| 67 |
+
| $7$ | $5000$ | 无 | $20$ |
|
| 68 |
+
|
| 69 |
+
特殊限制 A:$\forall 1 \le i \le n,b_i=i$。
|
| 70 |
+
|
| 71 |
+
对于所有数据:$2 \le n \le 5000$,$1 \le fa_i < i$,$0 \le b_i < 10^9+7$。
|
problems/10014.txt
ADDED
|
@@ -0,0 +1,125 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 茧
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
Lily 是一个有趣的女孩子。她经常和 Kaguya 玩一些奇怪的游戏。
|
| 6 |
+
|
| 7 |
+
今天她们在玩一个名为 nim 的游戏。具体地,nim 游戏的规则如下:
|
| 8 |
+
|
| 9 |
+
- 有若干排数目已知的棋子,两人轮流从任意一排移除任意正整数枚棋子。
|
| 10 |
+
- Lily 先手,无法操作者负,即移除最后一枚棋子者获胜。
|
| 11 |
+
|
| 12 |
+
因为其最优策略非常简单,所以几局过后,她们就开始感到无趣了。于是,她们在原有规则的基础上增加了一条规则:
|
| 13 |
+
|
| 14 |
+
- 在一排 $x$ 枚棋子中可以移除 $y$ 枚,当且仅当 $y^k \le x$。
|
| 15 |
+
|
| 16 |
+
这下游戏变得有趣了。不过,由于策略比较复杂,Lily 在计算的时候常常感到力不从心。
|
| 17 |
+
|
| 18 |
+
可以证明,这个游戏的任意一个局面都满足:要么 Lily 有必胜策略,要么 Kaguya 有必胜策略。
|
| 19 |
+
|
| 20 |
+
于是,Lily 想请你编写一个程序来计算某个局面下谁有必胜策略(Lily 总是先手),以便复盘时分析哪次操作失误了。
|
| 21 |
+
|
| 22 |
+
由于求知欲旺盛的 Lily 可能会对局面进行比较细致的分析,所以你需要回答她的多次询问。
|
| 23 |
+
|
| 24 |
+
由于所有局面都是复盘同一局游戏时衍生出来的,所以所有询问的参数 $k$ 都相同。
|
| 25 |
+
|
| 26 |
+
**本题询问的局面形式比较特殊,详见输入格式。**
|
| 27 |
+
|
| 28 |
+
## 输入格式
|
| 29 |
+
|
| 30 |
+
输入的第一行包含两个整数 $t, k$,分别表示询问次数和操作中的参数。
|
| 31 |
+
|
| 32 |
+
接下来依次输入每次询问,对于每次询问:
|
| 33 |
+
|
| 34 |
+
输入的第一行包含一个整数 $n$。
|
| 35 |
+
|
| 36 |
+
输入的第二行包含 $n$ 个整数 $a_1, \dots, a_n$。
|
| 37 |
+
|
| 38 |
+
$(n, a_{1 \dots n})$ 表示有 $\sum a_i$ 排棋子,各排所含棋子数分别为 $1 \dots a_1, 1 \dots a_2, \dots, 1 \dots a_n$。
|
| 39 |
+
|
| 40 |
+
如果你对博弈论比较熟悉的话,不难发现题意可以转化为:
|
| 41 |
+
|
| 42 |
+
- 记一排 $x$ 个棋子的 [Grundy value](https://en.wikipedia.org/wiki/Sprague%E2%80%93Grundy_theorem) 为 $g(x)$,设 $h(x)$ 为 $g(x)$ 的前缀异或和,求 $h(a_1) \dots h(a_n)$ 的异或和是否为 $0$。
|
| 43 |
+
|
| 44 |
+
## 输出格式
|
| 45 |
+
|
| 46 |
+
对于每次询问输出一行一个字符串。
|
| 47 |
+
|
| 48 |
+
- 若 Lily 有必胜策略,输出 `Lily`;
|
| 49 |
+
- 若 Kaguya 有必胜策略,输出 `Kaguya`。
|
| 50 |
+
|
| 51 |
+
## 样例 #1
|
| 52 |
+
|
| 53 |
+
### 样例输入 #1
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
3 1
|
| 57 |
+
2
|
| 58 |
+
1 5
|
| 59 |
+
3
|
| 60 |
+
1 2 3
|
| 61 |
+
1
|
| 62 |
+
3
|
| 63 |
+
```
|
| 64 |
+
|
| 65 |
+
### 样例输出 #1
|
| 66 |
+
|
| 67 |
+
```
|
| 68 |
+
Kaguya
|
| 69 |
+
Lily
|
| 70 |
+
Kaguya
|
| 71 |
+
```
|
| 72 |
+
|
| 73 |
+
## 样例 #2
|
| 74 |
+
|
| 75 |
+
### 样例输入 #2
|
| 76 |
+
|
| 77 |
+
```
|
| 78 |
+
4 2
|
| 79 |
+
2
|
| 80 |
+
1 2
|
| 81 |
+
2
|
| 82 |
+
1 3
|
| 83 |
+
3
|
| 84 |
+
5 6 7
|
| 85 |
+
1
|
| 86 |
+
3
|
| 87 |
+
```
|
| 88 |
+
|
| 89 |
+
### 样例输出 #2
|
| 90 |
+
|
| 91 |
+
```
|
| 92 |
+
Kaguya
|
| 93 |
+
Lily
|
| 94 |
+
Kaguya
|
| 95 |
+
Kaguya
|
| 96 |
+
```
|
| 97 |
+
|
| 98 |
+
## 提示
|
| 99 |
+
|
| 100 |
+
样例三、四、五见下发文件。
|
| 101 |
+
|
| 102 |
+
对于所有测试数据保证:$1 \le k \le 5$,$1 \le n, \sum n \le 10^5$,$1 \le a_i \lt 2^{60}$。
|
| 103 |
+
|
| 104 |
+
每个子任务的具体限制见下表:
|
| 105 |
+
|
| 106 |
+
| 子任务编号 | $n$ | $k$ | $a_i$ | 特殊性质 | 分值 |
|
| 107 |
+
| ---------- | -------------------------- | --------------- | -------------- | -------- | ---- |
|
| 108 |
+
| 1 | $\sum n \le 10^5$ | $k = 1$ | $a_i < 2^{60}$ | | $5$ |
|
| 109 |
+
| 2 | $\sum n \le 10^5$ | $2 \le k \le 5$ | $a_i < 2^{16}$ | | $5$ |
|
| 110 |
+
| 3 | $\sum n \le 10^5$ | $2 \le k \le 5$ | $a_i < 2^{22}$ | | $10$ |
|
| 111 |
+
| 4 | $\sum n \le 10^3$,$n = 2$ | $2 \le k \le 3$ | $a_i < 2^{32}$ | A | $10$ |
|
| 112 |
+
| 5 | $\sum n \le 10^3$ | $2 \le k \le 5$ | $a_i < 2^{32}$ | A | $10$ |
|
| 113 |
+
| 6 | $\sum n \le 10^5$ | $k = 2$ | $a_i < 2^{60}$ | A | $10$ |
|
| 114 |
+
| 7 | $\sum n \le 10^5$ | $k = 3$ | $a_i < 2^{60}$ | A | $10$ |
|
| 115 |
+
| 8 | $\sum n \le 10^3$ | $k = 2$ | $a_i < 2^{32}$ | | $10$ |
|
| 116 |
+
| 9 | $\sum n \le 10^3$ | $k = 3$ | $a_i < 2^{32}$ | | $10$ |
|
| 117 |
+
| 10 | $\sum n \le 10^5$ | $1 \le k \le 5$ | $a_i < 2^{60}$ | | $20$ |
|
| 118 |
+
|
| 119 |
+
特殊性质 A:保证 $2 \mid n$,且 $a_{2k - 1} = a_{2k} - 1 \pod{1 \le k \le \frac n 2}$。
|
| 120 |
+
|
| 121 |
+
提示:如果你得到了预期之外的 TLE,你或许可以尝试优化你的时间复杂度。
|
| 122 |
+
|
| 123 |
+
> 微调了题面里的几处用词()
|
| 124 |
+
>
|
| 125 |
+
> 原题面请以 QOJ 为准()
|
problems/10015.txt
ADDED
|
@@ -0,0 +1,184 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 左蓝右红
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
小 S 是一个喜欢音游的女孩子。
|
| 6 |
+
|
| 7 |
+
2077 年 7 月 7 日,某三维立体音乐游戏的 20.7.7 版本更新了一个塞满直角蛇的谱面 Tnemitnep [Beyond 18+]。但是当小 S 开始游玩这个谱面之后发现,由于游戏 bug,所有的蛇的色彩指示都没了……
|
| 8 |
+
|
| 9 |
+
但是小 S 作为 ptt 20.77 的 18 星高端玩家,首个理论值这首曲目的位置她势在必得,因此她不想等游戏开发者修复 bug。她决定:通过这个游戏的机制自行计算出所有蛇原本的颜色!
|
| 10 |
+
|
| 11 |
+
不幸的是,小 S 经过一些简单的推理,发现这个游戏的机制并不足以唯一确定所有蛇的颜色。因此小 S 首先希望通过这个游戏的“左蓝右红”规则计算出一种反手尽量少的染色可能性;同时计算出不同的染色方案数,以获知自己在最坏情况下需要尝试多少次才能正确地接住所有蛇。
|
| 12 |
+
|
| 13 |
+
小 S 将这个问题抽象成了一个 OI 问题,可是小 S 并不是很会 OI,于是她找到了即将参加 IOI 2024 的你。你能帮助小 S 在别人都还在莫名其妙红蛇 Track Lost 的时候拿下 Tnemitnep BYD 的首杀吗?
|
| 14 |
+
|
| 15 |
+
## 题目描述
|
| 16 |
+
|
| 17 |
+
在平面直角坐标系上给定 $n$ 个矩形,形成若干个交点,每个矩形的所有边都平行于坐标轴。**保证没有两个矩形的两条边共线。**
|
| 18 |
+
|
| 19 |
+
矩形之间会形成若干个交点,每一个矩形都被它上面的交点分成若干段。定义属于一个矩形上的**一段**是该矩形上相邻的两个交点之间的部分。也就是说一个矩形上如果有 $n$ 个交点,就会被划分成 $n$ 段。
|
| 20 |
+
|
| 21 |
+
现在将每一个矩形上的每一段染色为蓝色或红色。要求:
|
| 22 |
+
|
| 23 |
+
- 与同一个交点相邻的**同属于一个矩形的**两段不同色;
|
| 24 |
+
- 所有红线形成若干互不相交的封闭曲线;
|
| 25 |
+
- 所有蓝线形成若干互不相交的封闭曲线。
|
| 26 |
+
|
| 27 |
+
定义两个图形 $R,B$:
|
| 28 |
+
|
| 29 |
+
- $R$ 为删去所有蓝线后,所有被**奇数个**红色封闭曲线包含的点组成的集合;
|
| 30 |
+
- $B$ 为删去所有红线后,所有被**奇数个**蓝色封闭曲线包含的点组成的集合。
|
| 31 |
+
|
| 32 |
+
一个方案合法当且仅当它满足上述所有条件,并且**使得 $R\cap B$ 里面只有有限个点**。
|
| 33 |
+
|
| 34 |
+
**如果无法理解上述定义,可以参考样例解释。**
|
| 35 |
+
|
| 36 |
+
你需要分别求出:
|
| 37 |
+
|
| 38 |
+
- 字典序最小的合法染色方案(字典序在输出格式里面有定义)。
|
| 39 |
+
- 合法染色方案数,对 $20,051,131$(质数)取模。两个染色方案不同当且仅当存在一段,在一种方案中被染成红色,在另一种方案中被染成蓝色。
|
| 40 |
+
|
| 41 |
+
## 输入格式
|
| 42 |
+
|
| 43 |
+
第一行一个整数 $n$。
|
| 44 |
+
|
| 45 |
+
接下来 $n$ 行,第 $i$ 行 4 个整数 $x_{1,i},y_{1,i},x_{2,i},y_{2,i}$,前两个表示左下角坐标,后两个表示右上角坐标。
|
| 46 |
+
|
| 47 |
+
## 输出格式
|
| 48 |
+
|
| 49 |
+
第一行输出字典序最小的合法方案:如果无解,输出一行 `-1`;否则输出一个长度为 $n$ 的 0/1 串。如果在你的方案中,按输入顺序给出的第 $i$ 个矩形的左下角是红色,则你输出的第 $i$ 个整数应该是 $0$;否则应该是 $1$。可以证明给定这些数之后能够唯一确定整个染色方案。如果有多解,你输出的解必须使得**上面描述的 01 序列字典序最小**。
|
| 50 |
+
|
| 51 |
+
第二行输出合法染色方案数,对 $20,051,131$ 取模。无解时应输出 $0$。
|
| 52 |
+
|
| 53 |
+
## 样例 #1
|
| 54 |
+
|
| 55 |
+
### 样例输入 #1
|
| 56 |
+
|
| 57 |
+
```
|
| 58 |
+
2
|
| 59 |
+
1 2 3 3
|
| 60 |
+
2 1 4 4
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
### 样例输出 #1
|
| 64 |
+
|
| 65 |
+
```
|
| 66 |
+
01
|
| 67 |
+
2
|
| 68 |
+
```
|
| 69 |
+
|
| 70 |
+
## 样例 #2
|
| 71 |
+
|
| 72 |
+
### 样例输入 #2
|
| 73 |
+
|
| 74 |
+
```
|
| 75 |
+
4
|
| 76 |
+
1 1 5 5
|
| 77 |
+
2 2 6 6
|
| 78 |
+
3 3 7 7
|
| 79 |
+
4 4 8 8
|
| 80 |
+
```
|
| 81 |
+
|
| 82 |
+
### 样例输出 #2
|
| 83 |
+
|
| 84 |
+
```
|
| 85 |
+
0000
|
| 86 |
+
2
|
| 87 |
+
```
|
| 88 |
+
|
| 89 |
+
## 样例 #3
|
| 90 |
+
|
| 91 |
+
### 样例输入 #3
|
| 92 |
+
|
| 93 |
+
```
|
| 94 |
+
2
|
| 95 |
+
1 1 4 4
|
| 96 |
+
2 2 3 3
|
| 97 |
+
```
|
| 98 |
+
|
| 99 |
+
### 样例输出 #3
|
| 100 |
+
|
| 101 |
+
```
|
| 102 |
+
00
|
| 103 |
+
2
|
| 104 |
+
```
|
| 105 |
+
|
| 106 |
+
## 样例 #4
|
| 107 |
+
|
| 108 |
+
### 样例输入 #4
|
| 109 |
+
|
| 110 |
+
```
|
| 111 |
+
3
|
| 112 |
+
1 2 4 5
|
| 113 |
+
2 3 5 6
|
| 114 |
+
3 1 6 4
|
| 115 |
+
```
|
| 116 |
+
|
| 117 |
+
### 样例输出 #4
|
| 118 |
+
|
| 119 |
+
```
|
| 120 |
+
-1
|
| 121 |
+
0
|
| 122 |
+
```
|
| 123 |
+
|
| 124 |
+
## 提示
|
| 125 |
+
|
| 126 |
+
样例 5、6、7 见附件。
|
| 127 |
+
|
| 128 |
+
---
|
| 129 |
+
|
| 130 |
+
样例 1 解释:
|
| 131 |
+
|
| 132 |
+

|
| 133 |
+
|
| 134 |
+
如图是给定的矩形在平面直角坐标系上的形态。
|
| 135 |
+
|
| 136 |
+

|
| 137 |
+
|
| 138 |
+
如图,标出颜色的地方是属于第 1 个矩形的两段。
|
| 139 |
+
|
| 140 |
+

|
| 141 |
+
|
| 142 |
+
如图,标出颜色的地方是属于第 2 个矩形的两段。按照上述图片给出的颜色进行染色可以得到样例输出中给出的合法方案:
|
| 143 |
+
|
| 144 |
+

|
| 145 |
+
|
| 146 |
+
如下图,左侧方案��不合法的,因为与用圈标出的交点相邻的同属于一个矩形的两段同色;右侧方案也是不合法的,因为 $R$ 与 $B$ 交在图中的紫色正方形内,$R\cap B$ 包含无限多个点。
|
| 147 |
+
|
| 148 |
+

|
| 149 |
+
|
| 150 |
+
如下方案是合法的,但是对应字符串 `10` 不是字典序最小的。
|
| 151 |
+
|
| 152 |
+

|
| 153 |
+
|
| 154 |
+
---
|
| 155 |
+
|
| 156 |
+
样例 2 解释:
|
| 157 |
+
|
| 158 |
+

|
| 159 |
+
|
| 160 |
+
左侧的图为给定的所有矩形。
|
| 161 |
+
|
| 162 |
+
中间的图表示对应的染色方案。每一个矩形都包含 $6$ 段,并且满足与任何一个交点相邻的同属于一个矩形的两段不同色。
|
| 163 |
+
|
| 164 |
+
右侧的图中,用红色区域标出 $R$ 的范围,蓝色区域标出 $B$ 的范围。两图形的交只包含 $12$ 个点。
|
| 165 |
+
|
| 166 |
+
---
|
| 167 |
+
|
| 168 |
+
样例 3 解释:
|
| 169 |
+
|
| 170 |
+

|
| 171 |
+
|
| 172 |
+
如图,该样例中,因为环内部的部分被 $2$ 条红色封闭曲线包含,$2$ 是偶数,所以环内部不属于 $R$,$R$ 形成一个环。
|
| 173 |
+
|
| 174 |
+
---
|
| 175 |
+
|
| 176 |
+
数据范围:
|
| 177 |
+
|
| 178 |
+
对于 $100\%$ 的数据,保证 $1\leq n\leq 2\times 10^5$,$x_{1,i}<x_{2,i}$,$y_{1,i}<y_{2,i}$,$\{x_{i,j}|1\leq i\leq 2,1\leq j\leq n\}=\{y_{i,j}|1\leq i\leq 2,1\leq j\leq n\}=\{1,2,3,\cdots,2n\}$。
|
| 179 |
+
|
| 180 |
+
- Subtask 1(5 pts):矩形之间互不相交。
|
| 181 |
+
- Subtask 2(20 pts):$n\leq 13$。
|
| 182 |
+
- Subtask 3(20 pts):$n\leq 200$。
|
| 183 |
+
- Subtask 4(25 pts):$n\leq 2000$。
|
| 184 |
+
- Subtask 5(30 pts):无特殊限制。
|
problems/10016.txt
ADDED
|
@@ -0,0 +1,77 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] 虹
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一棵 $n$ 个点的树。
|
| 6 |
+
|
| 7 |
+
- 称点集 $S$ **连通**,当且仅当 $\forall u,v \in S$,所有 $u$ 到 $v$ 的简单路径上的点均在 $S$ 中。
|
| 8 |
+
- 称点集 $S$ 是 $[l,r]$ 的**虹**,当且仅当 $S$ **连通**,且 $S$ 包含 $[l,r]$ 中的所有点。
|
| 9 |
+
- 称点集 $S_0$ 是 $[l,r]$ 的**最小虹**,当且仅当 $S_0$ 是 $[l,r]$ 的所有**虹**中大小最小的。可以证明,$S_0$ 是唯一的。
|
| 10 |
+
|
| 11 |
+
点带权,点 $u$ 的权值为 $w_u$,初始所有点权均为 $0$。同时,给定序列 $\{z_1,z_2,\cdots,z_n\}$。
|
| 12 |
+
|
| 13 |
+
给定 $q$ 次命令,每次命令形如以下两类之一:
|
| 14 |
+
|
| 15 |
+
- `1 l r`:令 $S_0$ 为 $[l,r]$ 的**最小虹**,$\forall u \in S_0$,将 $w_u$ 加 $1$。
|
| 16 |
+
- `2 l r u`:求 $\left(\sum_{i=l}^r 19901991^{z_{\gcd(i,u)} w_i} \right) \bmod {20242024}$ 的值。
|
| 17 |
+
|
| 18 |
+
## 输入格式
|
| 19 |
+
|
| 20 |
+
第一行两个正整数 $n,q$。
|
| 21 |
+
|
| 22 |
+
第二行 $n$ 个非负整数,依次表示 $z_1,z_2,\cdots,z_n$。
|
| 23 |
+
|
| 24 |
+
接下来 $n-1$ 行,每行两个正整数 $u,v$,描述一条树上从 $u$ 到 $v$ 的边。
|
| 25 |
+
|
| 26 |
+
最后 $q$ 行,每行 $3$ 或 $4$ 个正整数,描述一次命令。
|
| 27 |
+
|
| 28 |
+
**注意:本题输入文件行末有 `\r`,请选手自行过滤。**
|
| 29 |
+
|
| 30 |
+
## 输出格式
|
| 31 |
+
|
| 32 |
+
对于每次询问(即第二类命令)输出答案。
|
| 33 |
+
|
| 34 |
+
## 样例 #1
|
| 35 |
+
|
| 36 |
+
### 样例输入 #1
|
| 37 |
+
|
| 38 |
+
```
|
| 39 |
+
5 4
|
| 40 |
+
1 0 0 0 1
|
| 41 |
+
1 2
|
| 42 |
+
1 3
|
| 43 |
+
3 4
|
| 44 |
+
3 5
|
| 45 |
+
1 2 3
|
| 46 |
+
2 1 3 3
|
| 47 |
+
1 4 5
|
| 48 |
+
2 3 5 3
|
| 49 |
+
```
|
| 50 |
+
|
| 51 |
+
### 样例输出 #1
|
| 52 |
+
|
| 53 |
+
```
|
| 54 |
+
19561959
|
| 55 |
+
19561959
|
| 56 |
+
```
|
| 57 |
+
|
| 58 |
+
## 提示
|
| 59 |
+
|
| 60 |
+
**本题采用捆绑测试**。
|
| 61 |
+
|
| 62 |
+
对于所有测试数据保证:$1 \le n, q \le 8 \times 10^4,0 \le z_i \le 10^9$,所有命令满足 $1 \le l \le r \le n, 1 \le u \le n$,**保证第一类命令的 $(l,r)$ 随机生成**。随机生成方式如下:
|
| 63 |
+
- 在 $[1,n] \cap \mathrm{Z}$ 中等概率随机生成 $l$。
|
| 64 |
+
- 在 $[1,n] \cap \mathrm{Z}$ 中等概率随机生成 $r$。
|
| 65 |
+
- 若 $l>r$,则交换 $l,r$。
|
| 66 |
+
|
| 67 |
+
| 子任务编号 | 分值 | $n \le$ | $q \le$ | 特殊性质 | 子任务依赖 |
|
| 68 |
+
| :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :----------: |
|
| 69 |
+
| $1$ | $10$ | $10^3$ | $10^3$ | 无 | 无 |
|
| 70 |
+
| $2$ | $20$ | $65536$ | $65536$ | A, B | 无 |
|
| 71 |
+
| $3$ | $20$ | $65536$ | $65536$ | A | 依赖于子任务 $2$ |
|
| 72 |
+
| $4$ | $30$ | $65536$ | $65536$ | 无 | 依赖于子任务 $1,2,3$ |
|
| 73 |
+
| $5$ | $20$ | $80000$ | $80000$ | 无 | 依赖于子任务 $1,2,3,4$ |
|
| 74 |
+
|
| 75 |
+
特殊性质 A:保证所有第二类命令均在所有第一类命令之后。
|
| 76 |
+
|
| 77 |
+
特殊性质 B:保证第二类命令次数 $\le 20$。
|
problems/10017.txt
ADDED
|
@@ -0,0 +1,404 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [集训队互测 2023] Axium Crisis
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
在那灰暗的塔楼前,对立见到了些许光芒碎片。
|
| 6 |
+
|
| 7 |
+
那些光芒碎片萦绕在对立身旁,宛如繁花点缀。
|
| 8 |
+
|
| 9 |
+
步入那扭曲的迷宫,对立试图收集其中的纷争碎片,并尝试摧毁这个迷宫。
|
| 10 |
+
|
| 11 |
+
对立的身旁充斥着光芒和纷争碎片,交错纷飞。
|
| 12 |
+
|
| 13 |
+
终于,对立来到了那迷宫的最深处。
|
| 14 |
+
|
| 15 |
+
在那片形状极其古怪的记忆残片上,反射的,是一个世界走向灭亡的回忆。
|
| 16 |
+
|
| 17 |
+
末日来临,天空撕裂,大地崩坠。
|
| 18 |
+
|
| 19 |
+
由于这块残片上所承载的「能量」实在过于巨大,对立试图使用其身旁的光芒和纷争碎片来缓和这份巨大的精神上的冲击。
|
| 20 |
+
|
| 21 |
+
具体的,这块扭曲的残片形成一个「树」的结构,对立将在树的每条边上放上一片光芒或者纷争碎片。
|
| 22 |
+
|
| 23 |
+
对立将会把这颗树上的边切割成若干条链,使得最终每条边恰好属于其中的某一条链。由于残片的特殊结构,树上的一个节点可以同时属于多条链。
|
| 24 |
+
|
| 25 |
+
对立会取出一部分链,将放置碎片相同的前缀段进行合并,最后形成一颗新的树,也就是所谓的「Trie 树」。
|
| 26 |
+
|
| 27 |
+
这颗新的树上的节点越多,就越能缓和对立的情绪,让其冷静下来。
|
| 28 |
+
|
| 29 |
+
在疯狂中,对立已经给残片上的某些边放上了光芒碎片或者纷争碎片。
|
| 30 |
+
|
| 31 |
+
一刹那的清醒间,对立意识到了些许不对。因此对立还可以往剩下的边上任意选择光芒或者纷争碎片。
|
| 32 |
+
|
| 33 |
+
在恍惚间,对立发现自己并不知道如何放置并切割是最优的。
|
| 34 |
+
|
| 35 |
+
思绪飞快地运转起来。怎样是最优的呢?
|
| 36 |
+
|
| 37 |
+
相信你已有答案。
|
| 38 |
+
|
| 39 |
+
## 题目描述
|
| 40 |
+
|
| 41 |
+
给定一颗 $n$ 个节点的树,节点编号 $0\sim n-1$。
|
| 42 |
+
|
| 43 |
+
边有边权,边权一般为 $0$ 或者 $1$;但有的边的边权还未确定。
|
| 44 |
+
|
| 45 |
+
你要给每条未被确定边权的边确定一个 $0$ 或者 $1$ 的边权,然后从树上取出若干条有向路径,使得这些链两两之间满足**边不相交**。
|
| 46 |
+
|
| 47 |
+
然后你会把这些路径插入一颗 0/1-Trie,你希望最大化这颗 0/1-Trie 上的节点数。(0/1-Trie 定义略)
|
| 48 |
+
|
| 49 |
+
你可能需要构造具体的选择方案。
|
| 50 |
+
|
| 51 |
+
## 输入格式
|
| 52 |
+
|
| 53 |
+
本题每个测试点中有多组测试数据。
|
| 54 |
+
|
| 55 |
+
第一行两个整数 $T,o$,其中 $T$ 表示测试数据组数,$o$ 表示该测试点的一些特殊性质(请参见「数据范围与提示」一节的描述)。
|
| 56 |
+
|
| 57 |
+
接下来有 $T$ 组测试数据。
|
| 58 |
+
|
| 59 |
+
每组数据第一行一个整数 $n$,表示点的个数。
|
| 60 |
+
|
| 61 |
+
接下来 $n-1$ 行,每行三个整数 $u,v,w$,表示一条连接点 $u,v$ 的边。当 $0\le w\le 1$ 时,表示这条边边权为 $w$;否则总有 $w=2$,表示这条边的边权还未确定。
|
| 62 |
+
|
| 63 |
+
保证这些边形成一颗点集为 $0\sim n-1$ 的树。
|
| 64 |
+
|
| 65 |
+
## 输出格式
|
| 66 |
+
|
| 67 |
+
开头应当输出一个数 $c$($c\in\{0,1\}$),表示你是否选择在该测试点输出方案,我们会使用 Special Judge 来校验你的输出是否正确。**注意这将影响你在该测试点的得分上限,详见「数据范围与提示」一节的描述**。
|
| 68 |
+
|
| 69 |
+
对于每组测试数据,首先输出一行一个数 $A$,表示该组数据的答案。
|
| 70 |
+
|
| 71 |
+
当 $c=1$ 时,还需要继续按如下格式输出你所构造的方案:
|
| 72 |
+
* 先输出一行一个数 $m$,表示你构造的方案中路径的数目。
|
| 73 |
+
* 接下来一行 $n-1$ 个数,每个数为 $0$ 或者 $1$,表示按输入顺序各边的边权。**对于边权本身已经确定的边,请原样输出。**
|
| 74 |
+
* 接下来 $m$ 行,每行两个数 $u,v$,表示树上一条从 $u$ 到 $v$ 的路径。要求 $u\neq v$,且路径两两**边不相交**。
|
| 75 |
+
|
| 76 |
+
## 样例 #1
|
| 77 |
+
|
| 78 |
+
### 样例输入 #1
|
| 79 |
+
|
| 80 |
+
```
|
| 81 |
+
9 0
|
| 82 |
+
9
|
| 83 |
+
1 2 1
|
| 84 |
+
3 4 1
|
| 85 |
+
5 6 1
|
| 86 |
+
7 8 1
|
| 87 |
+
2 0 0
|
| 88 |
+
4 0 0
|
| 89 |
+
6 0 0
|
| 90 |
+
8 0 0
|
| 91 |
+
9
|
| 92 |
+
1 2 2
|
| 93 |
+
3 4 1
|
| 94 |
+
5 6 1
|
| 95 |
+
7 8 1
|
| 96 |
+
2 0 0
|
| 97 |
+
4 0 0
|
| 98 |
+
6 0 0
|
| 99 |
+
8 0 0
|
| 100 |
+
5
|
| 101 |
+
1 2 2
|
| 102 |
+
3 4 1
|
| 103 |
+
0 3 1
|
| 104 |
+
2 3 0
|
| 105 |
+
17
|
| 106 |
+
1 2 1
|
| 107 |
+
2 3 0
|
| 108 |
+
3 4 1
|
| 109 |
+
4 0 0
|
| 110 |
+
5 6 1
|
| 111 |
+
6 7 0
|
| 112 |
+
7 8 1
|
| 113 |
+
8 0 0
|
| 114 |
+
9 10 1
|
| 115 |
+
10 11 0
|
| 116 |
+
11 12 1
|
| 117 |
+
12 0 0
|
| 118 |
+
13 14 1
|
| 119 |
+
14 15 0
|
| 120 |
+
15 16 1
|
| 121 |
+
16 0 0
|
| 122 |
+
17
|
| 123 |
+
1 2 1
|
| 124 |
+
2 0 0
|
| 125 |
+
3 4 1
|
| 126 |
+
4 0 0
|
| 127 |
+
5 6 1
|
| 128 |
+
6 0 0
|
| 129 |
+
7 8 1
|
| 130 |
+
8 0 0
|
| 131 |
+
9 10 1
|
| 132 |
+
10 11 0
|
| 133 |
+
11 12 1
|
| 134 |
+
12 0 0
|
| 135 |
+
13 14 1
|
| 136 |
+
14 15 0
|
| 137 |
+
15 16 1
|
| 138 |
+
16 0 0
|
| 139 |
+
17
|
| 140 |
+
1 2 2
|
| 141 |
+
2 0 2
|
| 142 |
+
3 4 2
|
| 143 |
+
4 0 2
|
| 144 |
+
5 6 2
|
| 145 |
+
6 0 2
|
| 146 |
+
7 8 2
|
| 147 |
+
8 0 2
|
| 148 |
+
9 10 2
|
| 149 |
+
10 11 2
|
| 150 |
+
11 12 2
|
| 151 |
+
12 0 2
|
| 152 |
+
13 14 2
|
| 153 |
+
14 15 2
|
| 154 |
+
15 16 2
|
| 155 |
+
16 0 2
|
| 156 |
+
18
|
| 157 |
+
1 2 1
|
| 158 |
+
2 0 0
|
| 159 |
+
3 4 1
|
| 160 |
+
4 0 0
|
| 161 |
+
5 6 1
|
| 162 |
+
6 0 0
|
| 163 |
+
7 8 1
|
| 164 |
+
8 0 0
|
| 165 |
+
9 10 1
|
| 166 |
+
10 11 0
|
| 167 |
+
11 12 1
|
| 168 |
+
12 0 0
|
| 169 |
+
13 14 1
|
| 170 |
+
14 15 0
|
| 171 |
+
15 16 1
|
| 172 |
+
16 0 0
|
| 173 |
+
0 17 2
|
| 174 |
+
18
|
| 175 |
+
1 2 2
|
| 176 |
+
2 0 2
|
| 177 |
+
3 4 2
|
| 178 |
+
4 0 2
|
| 179 |
+
5 6 2
|
| 180 |
+
6 0 2
|
| 181 |
+
7 8 2
|
| 182 |
+
8 0 2
|
| 183 |
+
9 10 2
|
| 184 |
+
10 11 2
|
| 185 |
+
11 12 2
|
| 186 |
+
12 0 2
|
| 187 |
+
13 14 2
|
| 188 |
+
14 15 2
|
| 189 |
+
15 16 2
|
| 190 |
+
16 0 2
|
| 191 |
+
17 0 2
|
| 192 |
+
18
|
| 193 |
+
1 2 2
|
| 194 |
+
2 3 2
|
| 195 |
+
3 4 2
|
| 196 |
+
4 5 2
|
| 197 |
+
5 6 2
|
| 198 |
+
6 7 2
|
| 199 |
+
7 8 2
|
| 200 |
+
8 9 2
|
| 201 |
+
9 10 2
|
| 202 |
+
10 11 2
|
| 203 |
+
11 12 2
|
| 204 |
+
12 13 2
|
| 205 |
+
13 14 2
|
| 206 |
+
14 15 2
|
| 207 |
+
15 16 2
|
| 208 |
+
16 17 2
|
| 209 |
+
17 0 2
|
| 210 |
+
```
|
| 211 |
+
|
| 212 |
+
### 样例输出 #1
|
| 213 |
+
|
| 214 |
+
```
|
| 215 |
+
1
|
| 216 |
+
8
|
| 217 |
+
3
|
| 218 |
+
1 1 1 1 0 0 0 0
|
| 219 |
+
1 3
|
| 220 |
+
5 6
|
| 221 |
+
6 7
|
| 222 |
+
9
|
| 223 |
+
2
|
| 224 |
+
0 1 1 1 0 0 0 0
|
| 225 |
+
3 5
|
| 226 |
+
1 7
|
| 227 |
+
5
|
| 228 |
+
2
|
| 229 |
+
0 1 1 0
|
| 230 |
+
4 3
|
| 231 |
+
1 0
|
| 232 |
+
16
|
| 233 |
+
3
|
| 234 |
+
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
|
| 235 |
+
5 1
|
| 236 |
+
13 14
|
| 237 |
+
14 9
|
| 238 |
+
14
|
| 239 |
+
5
|
| 240 |
+
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
|
| 241 |
+
3 1
|
| 242 |
+
5 6
|
| 243 |
+
14 13
|
| 244 |
+
14 7
|
| 245 |
+
6 9
|
| 246 |
+
16
|
| 247 |
+
3
|
| 248 |
+
0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0
|
| 249 |
+
7 5
|
| 250 |
+
1 3
|
| 251 |
+
13 9
|
| 252 |
+
15
|
| 253 |
+
4
|
| 254 |
+
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0
|
| 255 |
+
13 3
|
| 256 |
+
1 7
|
| 257 |
+
0 5
|
| 258 |
+
17 9
|
| 259 |
+
16
|
| 260 |
+
4
|
| 261 |
+
1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1
|
| 262 |
+
1 7
|
| 263 |
+
17 0
|
| 264 |
+
5 3
|
| 265 |
+
13 9
|
| 266 |
+
18
|
| 267 |
+
1
|
| 268 |
+
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
|
| 269 |
+
1 0
|
| 270 |
+
```
|
| 271 |
+
|
| 272 |
+
## 提示
|
| 273 |
+
|
| 274 |
+
#### 样例解释
|
| 275 |
+
|
| 276 |
+
这组样例对应的答案文件为:
|
| 277 |
+
|
| 278 |
+
```plain
|
| 279 |
+
8
|
| 280 |
+
9
|
| 281 |
+
5
|
| 282 |
+
16
|
| 283 |
+
14
|
| 284 |
+
16
|
| 285 |
+
15
|
| 286 |
+
16
|
| 287 |
+
18
|
| 288 |
+
```
|
| 289 |
+
|
| 290 |
+
样例输出即 `.out` 文件,也就是你要输出的结果,在 $c=1$ 时需要构造一组合法方案。
|
| 291 |
+
|
| 292 |
+
样例答案即 `.ans` 文件,该文件中仅会给出每组数据的答案,不会给出构造方案。
|
| 293 |
+
|
| 294 |
+
接下来依次附上这 $9$ 组样例的图示(选择边权前 / 后各一张)。
|
| 295 |
+
|
| 296 |
+
|
| 297 |
+
|
| 298 |
+
|
| 299 |
+
|
| 300 |
+
|
| 301 |
+
|
| 302 |
+
|
| 303 |
+
|
| 304 |
+
|
| 305 |
+
|
| 306 |
+
|
| 307 |
+
|
| 308 |
+
|
| 309 |
+
|
| 310 |
+
|
| 311 |
+
|
| 312 |
+
|
| 313 |
+
|
| 314 |
+
#### 更多样例
|
| 315 |
+
|
| 316 |
+
**因为本题数据规模太大,直接提交评测会对评测机带来很大压力,本题将提供很多大样例;请尽量减少本题的提交次数。**
|
| 317 |
+
|
| 318 |
+
更多样例请参见下发文件 `axiumcrisis*.in/ans`,共 $20$ 组,基本按照部分分的方法造。
|
| 319 |
+
|
| 320 |
+
注意下发的答案文件中**没有给出构造方案**,仅会给出每组数据的答案。
|
| 321 |
+
|
| 322 |
+
下发了一个 `checker.cpp`,你可以自行编译并在终端运行校验合法性。具体使用方法请参考「数据范围与提示」一节的描述。正式测评时使用的 Special Judge 与其并不相同。
|
| 323 |
+
|
| 324 |
+
为了方便你更好地理解题意,此处额外附一个手搓的样例,这份样例未被放入下发文件。
|
| 325 |
+
|
| 326 |
+
**建议使用该组样例及样例解释校验你对题意的理解,以免误读**。
|
| 327 |
+
|
| 328 |
+
#### 数据范围与提示
|
| 329 |
+
|
| 330 |
+
与[互测实际使用的版本](https://qoj.ac/problem/7769)不同,本题此处将采用数据范围更大的版本。
|
| 331 |
+
|
| 332 |
+
对于所有的数据,保证 $2\le n\le18$,$1\le T\le3000$。
|
| 333 |
+
|
| 334 |
+
具体的数据规模分布可以见下表,**各子任务等分,即满分均为 $\rm5pts$**。其中形如 $(l,r)$ 的一列对应的数据表示 $l\le n\le r$ 的数据组数,「无限制」表示无额外限制。
|
| 335 |
+
|
| 336 |
+
各子任务**捆绑评测**,其分数为该子任务各测试点分数最小值。子任务依赖意味着只有所依赖的子任务分数均非 $0$ 才会评测当前子任务,且分数与所依赖的子任务也取最小值。$o$ 的含义将在之后注明。
|
| 337 |
+
|
| 338 |
+
|子任务|$(2,4)$|$(5,6)$|$(7,8)$|$(9,11)$|$(12,14)$|$(15,17)$|$(18,18)$|$o$|子任务依赖|
|
| 339 |
+
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|
| 340 |
+
|$1$|$\le1000$|$=0$|$=0$|$=0$|$=0$|$=0$|$=0$|$=0$|无|
|
| 341 |
+
|$2$|无限制|$\le15$|$=0$|$=0$|$=0$|$=0$|$=0$|$=0$|$1$|
|
| 342 |
+
|$3$|无限制|$\le500$|$\le10$|$=0$|$=0$|$=0$|$=0$|$=0$|$2$|
|
| 343 |
+
|$4$|无限制|$\le1000$|$\le50$|$\le10$|$=0$|$=0$|$=0$|$=2$|无|
|
| 344 |
+
|$5$|无限制|$\le1000$|$\le50$|$\le10$|$=0$|$=0$|$=0$|$=3$|无|
|
| 345 |
+
|$6$|无限制|$\le1000$|$\le50$|$\le10$|$=0$|$=0$|$=0$|$=4$|$4$|
|
| 346 |
+
|$7$|无限制|$\le1000$|$\le50$|$\le10$|$=0$|$=0$|$=0$|$=0$|$3,5,6$|
|
| 347 |
+
|$8$|无限制|无限制|$\le1000$|$\le60$|$\le10$|$=0$|$=0$|$=2$|$4$|
|
| 348 |
+
|$9$|无限制|无限制|$\le1000$|$\le60$|$\le10$|$=0$|$=0$|$=3$|$5$|
|
| 349 |
+
|$10$|无限制|无限制|$\le1000$|$\le60$|$\le10$|$=0$|$=0$|$=4$|$6,8$|
|
| 350 |
+
|$11$|无限制|无限制|$\le1000$|$\le60$|$\le10$|$=0$|$=0$|$=0$|$7,9,10$|
|
| 351 |
+
|$12$|无限制|无限制|无限制|$\le300$|$\le30$|$\le10$|$=0$|$=2$|$8$|
|
| 352 |
+
|$13$|无限制|无限制|无限制|$\le300$|$\le30$|$\le10$|$=0$|$=3$|$9$|
|
| 353 |
+
|$14$|无限制|无限制|无限制|$\le300$|$\le30$|$\le10$|$=0$|$=4$|$10,12$|
|
| 354 |
+
|$15$|无限制|无限制|无限制|$\le300$|$\le30$|$\le10$|$=0$|$=0$|$11,13,14$|
|
| 355 |
+
|$16$|无限制|无限制|无限制|$\le500$|$\le60$|$\le20$|$\le10$|$=1$|无|
|
| 356 |
+
|$17$|无限制|无限制|无限制|$\le500$|$\le60$|$\le20$|$\le10$|$=2$|$12$|
|
| 357 |
+
|$18$|无限制|无限制|无限制|$\le500$|$\le60$|$\le20$|$\le10$|$=3$|$13,16$|
|
| 358 |
+
|$19$|无限制|无限制|无限制|$\le500$|$\le60$|$\le20$|$\le10$|$=4$|$14,16,17$|
|
| 359 |
+
|$20$|无限制|无限制|无限制|$\le500$|$\le60$|$\le20$|$\le10$|$=0$|$15,18,19$|
|
| 360 |
+
|
| 361 |
+
接下来阐述关于 $o$ 的特殊性质。
|
| 362 |
+
* $o=0$ 时,不保证特殊性质。
|
| 363 |
+
* $o=1$ 时,保证输入中 $w=0$。
|
| 364 |
+
* $o=2$ 时,保证输入中 $w=2$。
|
| 365 |
+
* $o=3$ 时,保证输入中 $w=0$ 或 $w=1$。
|
| 366 |
+
* $o=4$ 时,保证输入中 $w=0$ 或 $w=2$。
|
| 367 |
+
|
| 368 |
+
接下来阐述是否输出方案对答案带来的影响。
|
| 369 |
+
* 如果选择了 $c=0$,则答案正确时,你将获得该测试点 $80\%$ 的分数,否则该测试点不得分。
|
| 370 |
+
* 如果选择了 $c=1$,则答案和构造方案**均正确**时,你将获得该测试点的全部分数,**否则该测试点不得分**。
|
| 371 |
+
|
| 372 |
+
因此如果你的输出方案可能写错,请慎重考虑是否改为不输出方案。
|
| 373 |
+
|
| 374 |
+
接下来介绍 `checker.cpp` 使用方法。
|
| 375 |
+
|
| 376 |
+
`checker.cpp` 使用类似于 Testlib 的命令行格式,但是并不基于 Testlib,因此**不需要 `testlib.h` 文件**;同时**兼容 Lemon 格式**。具体的,你可以这么使用:
|
| 377 |
+
|
| 378 |
+
打开终端,进入 `checker.cpp` 所在文件夹后,首先使用 `g++ checker.cpp -o checker` 命令生成可执行文件(需要本地默认采用 C++11 及以上标准)。
|
| 379 |
+
|
| 380 |
+
假设输入文件为 `data.in`,输出文件为 `data.out`,标准答案文件为 `data.ans`,则你需要将可执行文件 `checker` 和 `data.in/out/ans` 文件放置于同一文件夹下,然后在终端中输入如下命令执行:
|
| 381 |
+
* 如果你使用 Windows 操作系统,请在 cmd 中使用 `checker data.in data.out data.ans 5` 执行。
|
| 382 |
+
* 如果你使用 Linux 操作系统,请在 bash 中使用 `./checker data.in data.out data.ans 5` 执行。
|
| 383 |
+
|
| 384 |
+
如命令中去掉最后的这个 `5` 将认为 $c=0$ 时也为 AC。
|
| 385 |
+
|
| 386 |
+
稍等片刻即会返回提示信息。
|
| 387 |
+
|
| 388 |
+
如果你使用 Lemon 来进行本地评测,可以把 `checker.cpp` 的可执行文件直接作为 Lemon 中的「自定义校验器」使用。
|
| 389 |
+
|
| 390 |
+
#### 后记
|
| 391 |
+
|
| 392 |
+
透过指缝观看着那世界末日之景。对立咽了口口水,靠着那股不知名的勇气,将手从自己的脸上移开。
|
| 393 |
+
|
| 394 |
+
对立伸出了手,把那世界尽头收入了自己所搜集的无数回忆之中。
|
| 395 |
+
|
| 396 |
+
其余的悲惨记忆,在这枚残片的映衬下显得不足一提。
|
| 397 |
+
|
| 398 |
+
对立确信自己已经变得足够强大,理所当然地想立刻把一切都摧毁。
|
| 399 |
+
|
| 400 |
+
就这样,伴随着那抹真诚的微笑与疲惫的笑声,对立从天空中降落到了地面上。
|
| 401 |
+
|
| 402 |
+
那座古老的塔楼在这般力量驱使下逐渐陨落。
|
| 403 |
+
|
| 404 |
+
而对立则怀抱着英雄般的信念,坚定不移地迈步向前。
|
problems/1002.txt
ADDED
|
@@ -0,0 +1,41 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [NOIP2002 普及组] 过河卒
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
棋盘上 $A$ 点有一个过河卒,需要走到目标 $B$ 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
|
| 6 |
+
|
| 7 |
+
棋盘用坐标表示,$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$,同样马的位置坐标是需要给出的。
|
| 8 |
+
|
| 9 |
+
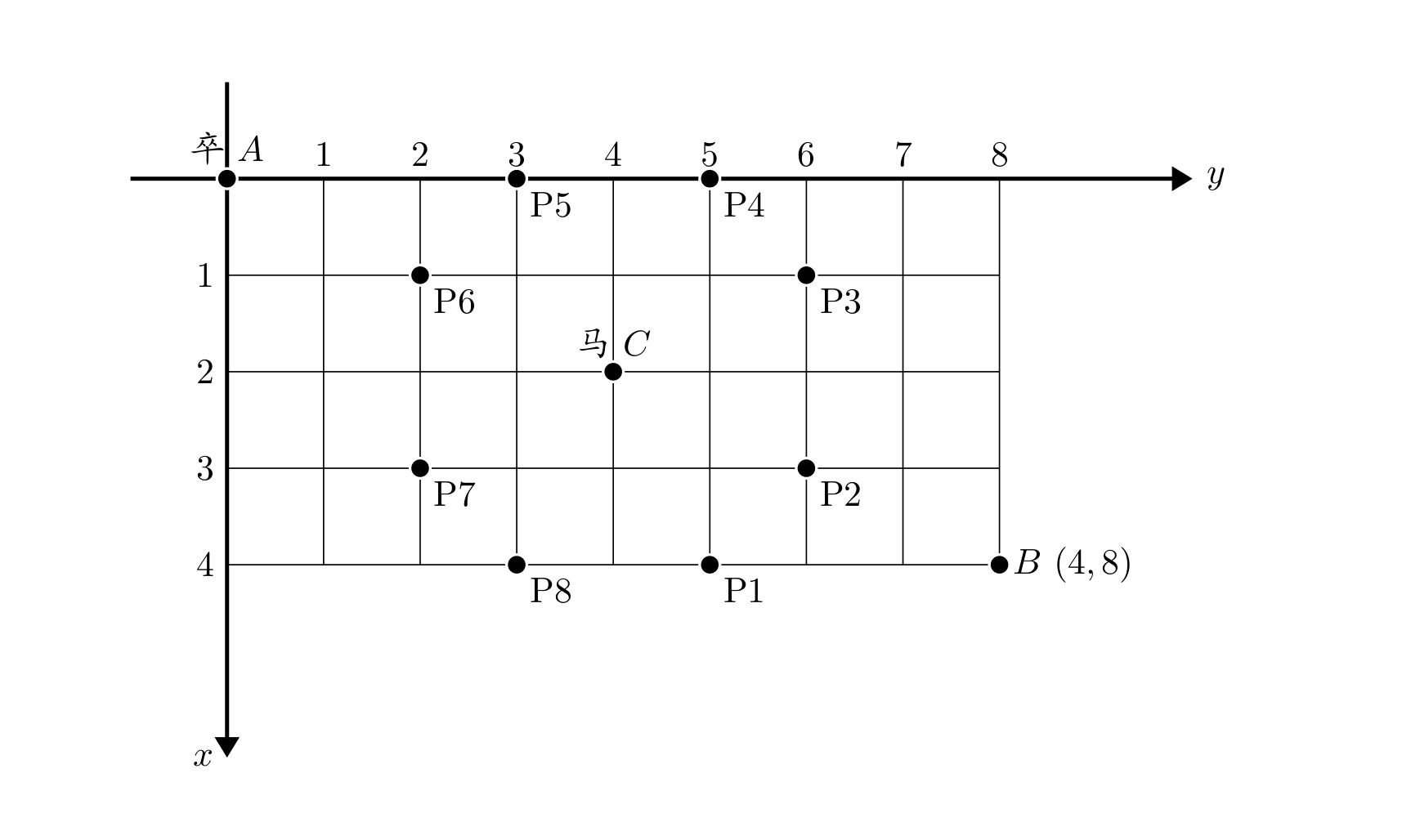
|
| 10 |
+
|
| 11 |
+
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
|
| 12 |
+
|
| 13 |
+
## 输入格式
|
| 14 |
+
|
| 15 |
+
一行四个正整数,分别表示 $B$ 点坐标和马的坐标。
|
| 16 |
+
|
| 17 |
+
## 输出格式
|
| 18 |
+
|
| 19 |
+
一个整数,表示所有的路径条数。
|
| 20 |
+
|
| 21 |
+
## 样例 #1
|
| 22 |
+
|
| 23 |
+
### 样例输入 #1
|
| 24 |
+
|
| 25 |
+
```
|
| 26 |
+
6 6 3 3
|
| 27 |
+
```
|
| 28 |
+
|
| 29 |
+
### 样例输出 #1
|
| 30 |
+
|
| 31 |
+
```
|
| 32 |
+
6
|
| 33 |
+
```
|
| 34 |
+
|
| 35 |
+
## 提示
|
| 36 |
+
|
| 37 |
+
对于 $100 \%$ 的数据,$1 \le n, m \le 20$,$0 \le$ 马的坐标 $\le 20$。
|
| 38 |
+
|
| 39 |
+
**【题目来源】**
|
| 40 |
+
|
| 41 |
+
NOIP 2002 普及组第四题
|
problems/10024.txt
ADDED
|
@@ -0,0 +1,71 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「HCOI-R1」报名人数
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
在一个电子展牌上,对于十进制数 $P$,从右到左,从 $P$ 的低位到高位,我们对每一位按照如下的方式进行显示:
|
| 6 |
+
|
| 7 |
+

|
| 8 |
+
|
| 9 |
+
所以,对于数位分别取 $0\sim 9$,该数位对应所用的短竖线数量分别是 $6, 2, 5, 5, 4, 5, 6, 3, 7, 6$。
|
| 10 |
+
|
| 11 |
+
## 题目描述
|
| 12 |
+
|
| 13 |
+
小 R 的家中有一个大型的电子展牌,上面记录着 HCOI-R1 的报名人数。
|
| 14 |
+
|
| 15 |
+
在小 R 布置完成的时候,HCOI-R1 的报名人数为 $l$。而现在,HCOI-R1 最终的报名人数为 $r$。
|
| 16 |
+
|
| 17 |
+
小 R 觉得这样的整数数对 $(i, j)$ 是**幸运**的,当且仅当在报名过程中,存在人数为 $i, i + 1, \dots, j$ 的时刻(也即 $l \leq i \leq j \leq r$),且在 **不含前导 $\bm 0$** 的情况下,表示 $i, i + 1 \dots j$ 这些数字所用的短竖线数量相同。
|
| 18 |
+
|
| 19 |
+
小 R 想知道,对于所有的幸运数对 $(i, j)$,其中 $j - i + 1$,也即数字个数——最大为多少。
|
| 20 |
+
|
| 21 |
+
## 输入格式
|
| 22 |
+
|
| 23 |
+
仅一行,两个整数 $l, r$,表示初始报名人数和最终报名人数。
|
| 24 |
+
|
| 25 |
+
## 输出格式
|
| 26 |
+
|
| 27 |
+
一行一个整数,表示所有数对 $(i, j)$ 中,$j - i + 1$ 的最大值。
|
| 28 |
+
|
| 29 |
+
## 样例 #1
|
| 30 |
+
|
| 31 |
+
### 样例输入 #1
|
| 32 |
+
|
| 33 |
+
```
|
| 34 |
+
2 5
|
| 35 |
+
```
|
| 36 |
+
|
| 37 |
+
### 样例输出 #1
|
| 38 |
+
|
| 39 |
+
```
|
| 40 |
+
2
|
| 41 |
+
```
|
| 42 |
+
|
| 43 |
+
## 样例 #2
|
| 44 |
+
|
| 45 |
+
### 样例输入 #2
|
| 46 |
+
|
| 47 |
+
```
|
| 48 |
+
114514 114514
|
| 49 |
+
```
|
| 50 |
+
|
| 51 |
+
### 样例输出 #2
|
| 52 |
+
|
| 53 |
+
```
|
| 54 |
+
1
|
| 55 |
+
```
|
| 56 |
+
|
| 57 |
+
## 提示
|
| 58 |
+
|
| 59 |
+
### 样例解释 1
|
| 60 |
+
|
| 61 |
+
存在幸运数对 $(2, 3)$,表示它们均需要 $5$ 条短竖线。
|
| 62 |
+
|
| 63 |
+
### 数据规模与约定
|
| 64 |
+
|
| 65 |
+
**本题采用捆绑测试。**
|
| 66 |
+
|
| 67 |
+
+ Subtask 0(19 pts):$r \leq 10^3$。
|
| 68 |
+
+ Subtask 1(33 pts):$r \leq 10^6$。
|
| 69 |
+
+ Subtask 2(48 pts):无特殊限制。
|
| 70 |
+
|
| 71 |
+
对于所有数据,保证 $1 \leq l \leq r \leq 10^{18}$。
|
problems/10025.txt
ADDED
|
@@ -0,0 +1,81 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「HCOI-R1」孤独的 sxz
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
sxz 不擅长与人交往,于是他平常都喜欢找偏僻的地方坐着。今天,sxz 来到了食堂,他依旧想找一个偏僻的地方坐着,让他与其他所有人的曼哈顿距离之和最大。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
食堂的座位可以看成一个被划分为 $n\times m$ 的格子的矩形,长为 $n$,宽为 $m$,矩形内的每一个格子 $(i, j)(i \in [1, n], j \in [1, m])$ $(i,j$ 为整数$)$ 都是一个座位。
|
| 10 |
+
|
| 11 |
+
现在,食堂里已经有了 $k$ 个人,其中第 $i(1 \leq i \leq k)$ 个人坐在 $(x_i, y_i)$ 处。sxz 想要找到一个座位,使得该座位与 $k$ 个人的曼哈顿距离之和最大。请你帮他找到这个最大值,剩下的就交给 sxz 吧!
|
| 12 |
+
|
| 13 |
+
假设 sxz 坐在点 $(a,b)$,那么他和 $k$ 个人的曼哈顿距离之和是 $\sum_{i=1}^{k}|a-x_i|+|b-y_i|$。
|
| 14 |
+
|
| 15 |
+
**很显然,sxz 不能和 $\bm k$ 个人中的任何一个人坐在同一个地方**。
|
| 16 |
+
|
| 17 |
+
## 输入格式
|
| 18 |
+
|
| 19 |
+
第一行包含三个整数 $n, m, k$。
|
| 20 |
+
|
| 21 |
+
接下来 $k$ 行,第 $i$ 行两个整数描述 $x_i, y_i$。
|
| 22 |
+
|
| 23 |
+
## 输出格式
|
| 24 |
+
|
| 25 |
+
仅一行一个整数,描述这个值。注意它可能很大。
|
| 26 |
+
|
| 27 |
+
## 样例 #1
|
| 28 |
+
|
| 29 |
+
### 样例输入 #1
|
| 30 |
+
|
| 31 |
+
```
|
| 32 |
+
2 5 3
|
| 33 |
+
1 1
|
| 34 |
+
1 3
|
| 35 |
+
1 4
|
| 36 |
+
```
|
| 37 |
+
|
| 38 |
+
### 样例输出 #1
|
| 39 |
+
|
| 40 |
+
```
|
| 41 |
+
10
|
| 42 |
+
```
|
| 43 |
+
|
| 44 |
+
## 样例 #2
|
| 45 |
+
|
| 46 |
+
### 样例输入 #2
|
| 47 |
+
|
| 48 |
+
```
|
| 49 |
+
7 4 9
|
| 50 |
+
1 4
|
| 51 |
+
2 3
|
| 52 |
+
4 1
|
| 53 |
+
6 2
|
| 54 |
+
7 1
|
| 55 |
+
5 2
|
| 56 |
+
3 4
|
| 57 |
+
1 1
|
| 58 |
+
7 4
|
| 59 |
+
```
|
| 60 |
+
|
| 61 |
+
### 样例输出 #2
|
| 62 |
+
|
| 63 |
+
```
|
| 64 |
+
38
|
| 65 |
+
```
|
| 66 |
+
|
| 67 |
+
## 提示
|
| 68 |
+
|
| 69 |
+
### 样例解释 1
|
| 70 |
+
|
| 71 |
+
最佳位置为 $(2,5)$,对于 $3$ 个人的曼哈顿距离分别为 $5, 3, 2$。
|
| 72 |
+
|
| 73 |
+
### 数据规模与约定
|
| 74 |
+
|
| 75 |
+
**本题采用捆绑测试。**
|
| 76 |
+
+ Subtask 0(15 pts):$n, m \leq 100$。
|
| 77 |
+
+ Subtask 1(25 pts):$n, m \leq 10000$。
|
| 78 |
+
+ Subtask 2(20 pts):$k = 3$。
|
| 79 |
+
+ Subtask 3(40 pts):无特殊限制。
|
| 80 |
+
|
| 81 |
+
对于所有数据,$1 \leq n, m \leq 10^9$,$1\leq k \leq \min\{4 \times 10^5, n\times m-1\}$,$1 \leq x_i \leq n$,$1 \leq y_i \leq m$,保证所有 $(x_i, y_i)$ 互不相同。
|
problems/10026.txt
ADDED
|
@@ -0,0 +1,95 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「HCOI-R1」哀之变化
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
哀喜欢数字。
|
| 6 |
+
|
| 7 |
+
她还喜欢变化。
|
| 8 |
+
|
| 9 |
+
## 题目描述
|
| 10 |
+
|
| 11 |
+
有一整数 $a$ 初始为 $1$。
|
| 12 |
+
|
| 13 |
+
哀想让 $a$ 进行恰好 $k$ 次变化,每次从以下两种变化中选择一个:
|
| 14 |
+
|
| 15 |
+
- $a\gets a - 1$;
|
| 16 |
+
- $a\gets a \times 2$。
|
| 17 |
+
|
| 18 |
+
哀很好奇,经过 **恰好** $k$ 次变化后 $a$ 能否变成 $n$。
|
| 19 |
+
|
| 20 |
+
## 输入格式
|
| 21 |
+
|
| 22 |
+
**本题有多组测试数据。**
|
| 23 |
+
|
| 24 |
+
第一行,一个正整数 $T$,表示测试数据组数。
|
| 25 |
+
|
| 26 |
+
接下来 $T$ 行,每行两个整数,依次为 $k$ 和 $n$,表示哀的一次询问。
|
| 27 |
+
|
| 28 |
+
## 输出格式
|
| 29 |
+
|
| 30 |
+
共 $T$ 行,对于每次询问,若 $a$ 可以变成 $n$,输出 `Yes`,否则输出 `No`。
|
| 31 |
+
|
| 32 |
+
## 样例 #1
|
| 33 |
+
|
| 34 |
+
### 样例输入 #1
|
| 35 |
+
|
| 36 |
+
```
|
| 37 |
+
3
|
| 38 |
+
2 5
|
| 39 |
+
2 4
|
| 40 |
+
3 3
|
| 41 |
+
```
|
| 42 |
+
|
| 43 |
+
### 样例输出 #1
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
No
|
| 47 |
+
Yes
|
| 48 |
+
Yes
|
| 49 |
+
```
|
| 50 |
+
|
| 51 |
+
## 样例 #2
|
| 52 |
+
|
| 53 |
+
### 样例输入 #2
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
5
|
| 57 |
+
4 869
|
| 58 |
+
48 69
|
| 59 |
+
8 328
|
| 60 |
+
66 114514
|
| 61 |
+
168 1919810
|
| 62 |
+
```
|
| 63 |
+
|
| 64 |
+
### 样例输出 #2
|
| 65 |
+
|
| 66 |
+
```
|
| 67 |
+
No
|
| 68 |
+
Yes
|
| 69 |
+
No
|
| 70 |
+
Yes
|
| 71 |
+
Yes
|
| 72 |
+
```
|
| 73 |
+
|
| 74 |
+
## 提示
|
| 75 |
+
|
| 76 |
+
### 样例解释 1
|
| 77 |
+
|
| 78 |
+
+ 若 $k = 2$,$n = 5$,可以证明无解。
|
| 79 |
+
+ 若 $k = 2$,$n = 4$,一种可能的操作方式如下:
|
| 80 |
+
+ 第一步,$a \gets a\times 2 = 2$;
|
| 81 |
+
+ 第二步,$a \gets a\times 2 = 4$。
|
| 82 |
+
+ 若 $k = 3$,$n = 3$,一种可能的操作方式如下:
|
| 83 |
+
+ 第一步,$a \gets a\times 2 = 2$;
|
| 84 |
+
+ 第二步,$a \gets a\times 2 = 4$。
|
| 85 |
+
+ 第三步,$a \gets a-1 = 3$。
|
| 86 |
+
|
| 87 |
+
### 数据规模与约定
|
| 88 |
+
|
| 89 |
+
**本题采用捆绑测试。**
|
| 90 |
+
|
| 91 |
+
+ Subtask 0(10 pts):$T \leq 10$,$k \leq 15$。
|
| 92 |
+
+ Subtask 1(25 pts):$n, k \leq 2\times 10^3$。
|
| 93 |
+
+ Subtask 2(65 pts):无特殊限制。
|
| 94 |
+
|
| 95 |
+
对于所有数据,$1 \leq T \leq 10^5$,$0 \leq n, k \leq 10^{18}$。
|
problems/10027.txt
ADDED
|
@@ -0,0 +1,90 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 梦境世界
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
哆来咪爱旅行。
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
有一个长为 $n$ 宽为 $m$ 的网格,其左上角编号为位置 $(1, 1)$ 而右下角编号为位置 $(n, m)$。哆来咪想要从左上角走到右下角,每次她可以往右或向下走一格,但不能超出 $n\times m$ 的网格边界。除此之外,有 $s$ 个禁止点是哆来咪无法走到的。
|
| 10 |
+
|
| 11 |
+
哆来咪有 $k$ 个神奇药水,喝药水可以撤销之前最后一次没有被撤销的行走操作,但移动序列并不会删去最后一个元素。当然,在 $(1, 1)$ 位置时不能使用药水,且 **药水不会撤销上一个药水的操作**。例如:从 $A$ 到 $B$ 后,在 $B$ 处喝了药水,则移动序列为 $A \to B \to A$;从 $A$ 走到 $B$ 再走到 $C$,连续喝下两次药水,移动序列为 $A \to B \to C \to B \to A$。
|
| 12 |
+
|
| 13 |
+
哆来咪认为一次 **旅行** 是指一次最终走到 $(n, m)$ 的行走路线。哆来咪想要求本质不同的 **旅行** 个数,答案对给定 $p$ 取模。哆来咪认为两次 **旅行** 不同,当且仅当两次旅行记录的移动序列不同。
|
| 14 |
+
|
| 15 |
+
## 输入格式
|
| 16 |
+
|
| 17 |
+
第一行五个整数 $n, m, k, p, s$,意义见题目描述。
|
| 18 |
+
|
| 19 |
+
接下来 $s$ 行,第 $i$ 行包含两个整数 $(x_i, y_i)$,表示不能经过网格中编号为 $(x_i, y_i)$ 的点。
|
| 20 |
+
|
| 21 |
+
## 输出格式
|
| 22 |
+
|
| 23 |
+
输出一行一个整数,表示答案对 $p$ 取模后的结果。
|
| 24 |
+
|
| 25 |
+
## 样例 #1
|
| 26 |
+
|
| 27 |
+
### 样例输入 #1
|
| 28 |
+
|
| 29 |
+
```
|
| 30 |
+
2 2 2 998244353 1
|
| 31 |
+
1 2
|
| 32 |
+
```
|
| 33 |
+
|
| 34 |
+
### 样例输出 #1
|
| 35 |
+
|
| 36 |
+
```
|
| 37 |
+
7
|
| 38 |
+
```
|
| 39 |
+
|
| 40 |
+
## 样例 #2
|
| 41 |
+
|
| 42 |
+
### 样例输入 #2
|
| 43 |
+
|
| 44 |
+
```
|
| 45 |
+
5 5 0 114514 0
|
| 46 |
+
```
|
| 47 |
+
|
| 48 |
+
### 样例输出 #2
|
| 49 |
+
|
| 50 |
+
```
|
| 51 |
+
70
|
| 52 |
+
```
|
| 53 |
+
|
| 54 |
+
## 样例 #3
|
| 55 |
+
|
| 56 |
+
### 样例输入 #3
|
| 57 |
+
|
| 58 |
+
```
|
| 59 |
+
5 5 3 998244353 3
|
| 60 |
+
3 4
|
| 61 |
+
2 5
|
| 62 |
+
4 4
|
| 63 |
+
```
|
| 64 |
+
|
| 65 |
+
### 样例输出 #3
|
| 66 |
+
|
| 67 |
+
```
|
| 68 |
+
13782
|
| 69 |
+
```
|
| 70 |
+
|
| 71 |
+
## 提示
|
| 72 |
+
|
| 73 |
+
### 样例解释 1
|
| 74 |
+
|
| 75 |
+
七种路线如下:
|
| 76 |
+
|
| 77 |
+

|
| 78 |
+
|
| 79 |
+
### 数据规模与约定
|
| 80 |
+
|
| 81 |
+
**本题采用捆绑测试。**
|
| 82 |
+
|
| 83 |
+
- Subtask 0(10pts):$1 \le n, m \le 100$,$k=0$。
|
| 84 |
+
- Subtask 1(15pts):$1 \le n, m \le 10$,$k=1$。
|
| 85 |
+
- Subtask 2(15pts):$n=1$,$m \le 100$,$k \le 100$。
|
| 86 |
+
- Subtask 3(25pts):$1 \le n, m \le 100$,$k \le 10$。
|
| 87 |
+
- Subtask 4(35pts):无特殊限制。
|
| 88 |
+
|
| 89 |
+
|
| 90 |
+
对于所有数据,保证 $1 \le n, m \le 100$,$0 \le k \le 100$,$2 \le p \le 10^9 + 9$,$0 \le s \le n \times m$,$1 \le x_i \le n$,$1 \le y_i \le m$,且 $(x_i, y_i)$ 互不相同。
|
problems/10028.txt
ADDED
|
@@ -0,0 +1,51 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [Ynoi2000] pri
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定 $1,\dots,n$ 的排列 $a_1,\dots,a_n$ ;
|
| 6 |
+
|
| 7 |
+
共 $m$ 次操作,每次操作给出 $x$ ,首先进行修改,将 $a_1,a_2,\dots,a_x$ 翻转为 $a_x,\dots,a_2,a_1$ ,然后查询有多少组不同的 $(i,j)$ ,满足 $1\le i<j\le x$ 使得 $a_i<a_j$ 。
|
| 8 |
+
|
| 9 |
+
## 输入格式
|
| 10 |
+
|
| 11 |
+
第一行两个整数 $n,m$ ;
|
| 12 |
+
|
| 13 |
+
第二行 $n$ 个整数依次表示 $a_1,\dots,a_n$ ;
|
| 14 |
+
|
| 15 |
+
接下来 $m$ 行,每行一个整数 $x$ ,表示一次操作。
|
| 16 |
+
|
| 17 |
+
## 输出格式
|
| 18 |
+
|
| 19 |
+
共 $m$ 行,每行一个整数,依次表示每次操作的查询的答案。
|
| 20 |
+
|
| 21 |
+
## 样例 #1
|
| 22 |
+
|
| 23 |
+
### 样例输入 #1
|
| 24 |
+
|
| 25 |
+
```
|
| 26 |
+
6 5
|
| 27 |
+
5 4 2 3 1 6
|
| 28 |
+
3
|
| 29 |
+
5
|
| 30 |
+
6
|
| 31 |
+
3
|
| 32 |
+
6
|
| 33 |
+
```
|
| 34 |
+
|
| 35 |
+
### 样例输出 #1
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
3
|
| 39 |
+
6
|
| 40 |
+
4
|
| 41 |
+
2
|
| 42 |
+
10
|
| 43 |
+
```
|
| 44 |
+
|
| 45 |
+
## 提示
|
| 46 |
+
|
| 47 |
+
Idea:ccz181078,Solution:ccz181078,Code:ccz181078,Data:ccz181078
|
| 48 |
+
|
| 49 |
+
所有数值为整数。
|
| 50 |
+
|
| 51 |
+
对于 $100\%$ 的数据,满足 $1\le a_i\le n$,$1\le x\le n$,$1\le n\le 2\times 10^5,\;1\le m\le 5\times 10^4$。
|
problems/10029.txt
ADDED
|
@@ -0,0 +1,62 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「Cfz Round 3」Battle
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
Alice 和 Bob 正在进行一个游戏,游戏的规则如下:
|
| 6 |
+
|
| 7 |
+
- Alice 初始时拥有一个整数 $n$,Bob 初始时拥有一个整数 $m$;
|
| 8 |
+
- 从 Alice 开始,两人轮流对**对方拥有的整数**进行操作:设对方此时拥有的整数为 $h$,使 $h$ 的值**减去** $h \bmod p$,其中 $\bmod$ 表示**取模**运算,$p$ 是给定的一个定值;
|
| 9 |
+
- 两人中率先使对方拥有的整数变为 $0$ 的人获得胜利,若在两人分别进行 $10^{10^{9961}}$ 次操作后仍无人获得胜利,则认为游戏平局。
|
| 10 |
+
|
| 11 |
+
你需要判断谁将会获得胜利,或报告游戏将会平局。
|
| 12 |
+
|
| 13 |
+
## 输入格式
|
| 14 |
+
|
| 15 |
+
**本题有多组测试数据。**
|
| 16 |
+
|
| 17 |
+
第一行输入一个整数 $T$,表示测试数据组数。
|
| 18 |
+
|
| 19 |
+
接下来依次输入每组测试数据。对于每组测试数据,输入三个整数 $n,m,p$。
|
| 20 |
+
|
| 21 |
+
## 输出格式
|
| 22 |
+
|
| 23 |
+
对于每组数据,一行一个字符串表示答案:
|
| 24 |
+
|
| 25 |
+
- 若 Alice 将会获得胜利,则输出 `Alice`;
|
| 26 |
+
- 若 Bob 将会获得胜利,则输出 `Bob`;
|
| 27 |
+
- 若游戏将会平局,则输出 `Lasting Battle`。
|
| 28 |
+
|
| 29 |
+
## 样例 #1
|
| 30 |
+
|
| 31 |
+
### 样例输入 #1
|
| 32 |
+
|
| 33 |
+
```
|
| 34 |
+
3
|
| 35 |
+
1 2 10
|
| 36 |
+
9 11 11
|
| 37 |
+
55 15 14
|
| 38 |
+
```
|
| 39 |
+
|
| 40 |
+
### 样例输出 #1
|
| 41 |
+
|
| 42 |
+
```
|
| 43 |
+
Alice
|
| 44 |
+
Bob
|
| 45 |
+
Lasting Battle
|
| 46 |
+
```
|
| 47 |
+
|
| 48 |
+
## 提示
|
| 49 |
+
|
| 50 |
+
#### 「样例解释 #1」
|
| 51 |
+
|
| 52 |
+
对于第 $1$ 组数据,Alice 在第一次操作中就会将 Bob 拥有的整数从 $2$ 变为 $2-(2\bmod 10)$ 即 $0$,所以 Alice 将会获得胜利。
|
| 53 |
+
|
| 54 |
+
对于第 $2$ 组数据,Alice 在第一次操作中会将 Bob 拥有的整数从 $11$ 变为 $11-(11\bmod 11)$ 即 $11$,而 Bob 在第一次操作中会将 Alice 拥有的整数从 $9$ 变为 $9-(9 \bmod 11)$ 即 $0$,所以 Bob 将会获得胜利。
|
| 55 |
+
|
| 56 |
+
对于第 $3$ 组数据,可以证明游戏将会平局。
|
| 57 |
+
|
| 58 |
+
#### 「数据范围」
|
| 59 |
+
|
| 60 |
+
对于所有数据,$1 \leq T \leq 5000$,$1 \leq n, m, p \leq 2\times 10^9$。
|
| 61 |
+
|
| 62 |
+
**只有你通过本题的所有测试点,你才能获得本题的分数。**
|
problems/1003.txt
ADDED
|
@@ -0,0 +1,73 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [NOIP2011 提高组] 铺地毯
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有 $n$ 张地毯,编号从 $1$ 到 $n$。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。
|
| 6 |
+
|
| 7 |
+
地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
|
| 8 |
+
|
| 9 |
+
## 输入格式
|
| 10 |
+
|
| 11 |
+
输入共 $n + 2$ 行。
|
| 12 |
+
|
| 13 |
+
第一行,一个整数 $n$,表示总共有 $n$ 张地毯。
|
| 14 |
+
|
| 15 |
+
接下来的 $n$ 行中,第 $i+1$ 行表示编号 $i$ 的地毯的信息,包含四个整数 $a ,b ,g ,k$,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标 $(a, b)$ 以及地毯在 $x$ 轴和 $y$ 轴方向的长度。
|
| 16 |
+
|
| 17 |
+
第 $n + 2$ 行包含两个整数 $x$ 和 $y$,表示所求的地面的点的坐标 $(x, y)$。
|
| 18 |
+
|
| 19 |
+
## 输出格式
|
| 20 |
+
|
| 21 |
+
输出共 $1$ 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出 `-1`。
|
| 22 |
+
|
| 23 |
+
## 样例 #1
|
| 24 |
+
|
| 25 |
+
### 样例输入 #1
|
| 26 |
+
|
| 27 |
+
```
|
| 28 |
+
3
|
| 29 |
+
1 0 2 3
|
| 30 |
+
0 2 3 3
|
| 31 |
+
2 1 3 3
|
| 32 |
+
2 2
|
| 33 |
+
```
|
| 34 |
+
|
| 35 |
+
### 样例输出 #1
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
3
|
| 39 |
+
```
|
| 40 |
+
|
| 41 |
+
## 样例 #2
|
| 42 |
+
|
| 43 |
+
### 样例输入 #2
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
3
|
| 47 |
+
1 0 2 3
|
| 48 |
+
0 2 3 3
|
| 49 |
+
2 1 3 3
|
| 50 |
+
4 5
|
| 51 |
+
```
|
| 52 |
+
|
| 53 |
+
### 样例输出 #2
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
-1
|
| 57 |
+
```
|
| 58 |
+
|
| 59 |
+
## 提示
|
| 60 |
+
|
| 61 |
+
【样例解释 1】
|
| 62 |
+
|
| 63 |
+
如下图,$1$ 号地毯用实线表示,$2$ 号地毯用虚线表示,$3$ 号用双实线表示,覆盖点 $(2,2)$ 的最上面一张地毯是 $3$ 号地毯。
|
| 64 |
+
|
| 65 |
+
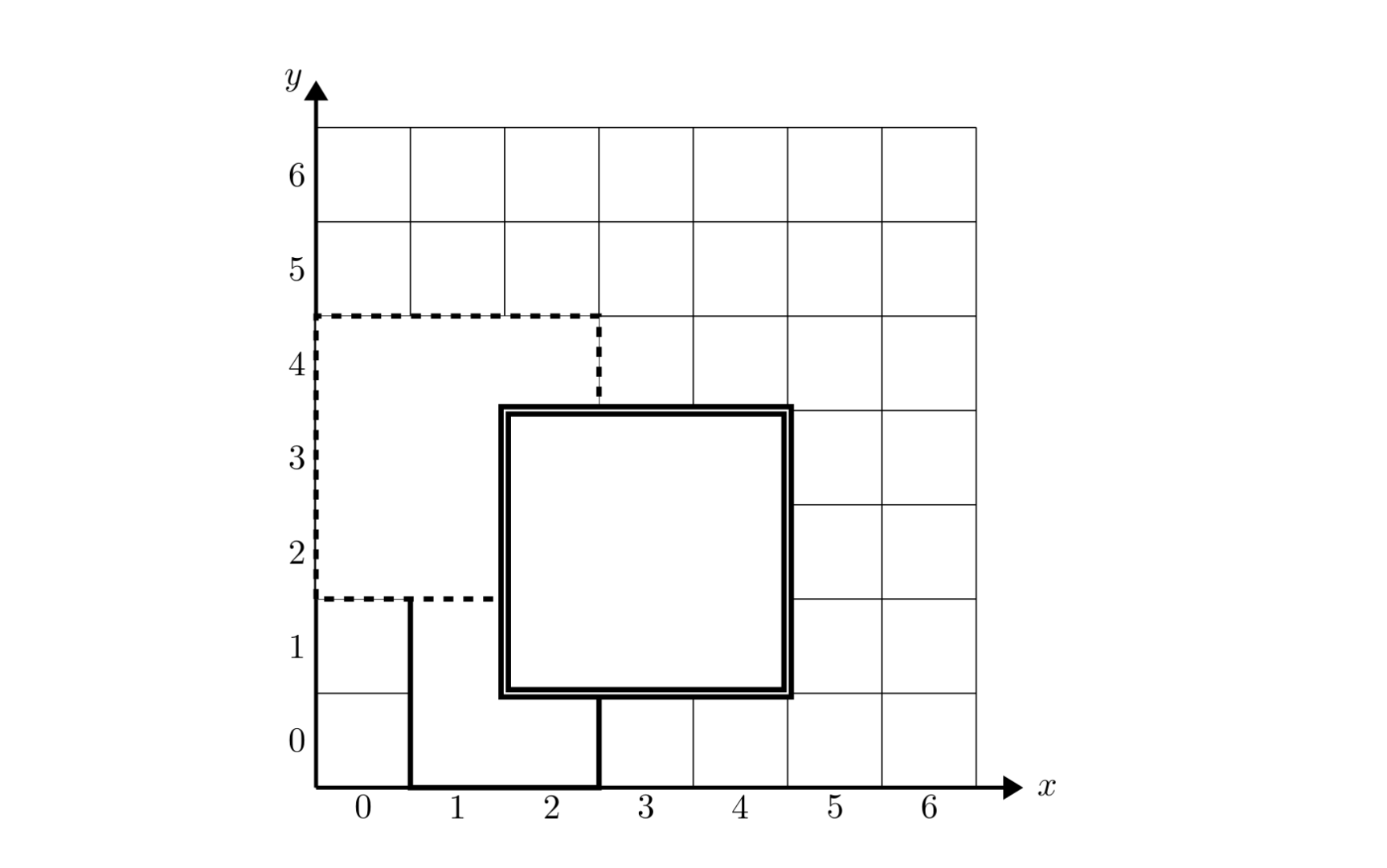
|
| 66 |
+
|
| 67 |
+
【数据范围】
|
| 68 |
+
|
| 69 |
+
对于 $30\%$ 的数据,有 $n \le 2$。
|
| 70 |
+
对于 $50\%$ 的数据,$0 \le a, b, g, k \le 100$。
|
| 71 |
+
对于 $100\%$ 的数据,有 $0 \le n \le 10^4$, $0 \le a, b, g, k \le {10}^5$。
|
| 72 |
+
|
| 73 |
+
noip2011 提高组 day1 第 $1$ 题。
|
problems/10030.txt
ADDED
|
@@ -0,0 +1,66 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「Cfz Round 3」Change
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一个质数 $p$ 和三个整数 $a,b,c$,你需要对一个初始为 $0$ 的整数 $x$ 进行操作,每次操作可以进行如下的两种之一:
|
| 6 |
+
|
| 7 |
+
- 第一种操作:令 $x$ 的值变为 $(x \times a) \bmod p$。
|
| 8 |
+
- 第二种操作:令 $x$ 的值变为 $(x+b) \bmod p$。
|
| 9 |
+
|
| 10 |
+
其中,$\bmod$ 表示**取模**运算。
|
| 11 |
+
|
| 12 |
+
你需要求出能否在**正整数次**操作后得到 $c$,若能则输出 `Yes`,否则输出 `No`。
|
| 13 |
+
|
| 14 |
+
本题中字符串大小写不敏感,即 `yes`、`yeS`、`yEs`、`Yes`、`YEs`、`YeS`、`yES`、`Yes` 都被认为是 `Yes`,`No` 同理。
|
| 15 |
+
|
| 16 |
+
## 输入格式
|
| 17 |
+
|
| 18 |
+
**本题有多组测试数据。**
|
| 19 |
+
|
| 20 |
+
第一行输入一个整数 $T$,表示测试数据组数。
|
| 21 |
+
|
| 22 |
+
接下来依次输入每组测试数据。对于每组测试数据,输入一行四个整数 $p,a,b,c$。
|
| 23 |
+
|
| 24 |
+
## 输出格式
|
| 25 |
+
|
| 26 |
+
对于每组测试数据,输出一行:
|
| 27 |
+
|
| 28 |
+
- 若能在正整数次操作后得到 $c$,则输出 `Yes`;
|
| 29 |
+
- 若不能在正整数次操作后得到 $c$,则输出 `No`。
|
| 30 |
+
|
| 31 |
+
本题中字符串大小写不敏感,即 `yes`、`yeS`、`yEs`、`Yes`、`YEs`、`YeS`、`yES`、`Yes` 都被认为是 `Yes`,`No` 同理。
|
| 32 |
+
|
| 33 |
+
## 样例 #1
|
| 34 |
+
|
| 35 |
+
### 样例输入 #1
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
3
|
| 39 |
+
5 2 1 4
|
| 40 |
+
3 2 2 1
|
| 41 |
+
7 2 0 3
|
| 42 |
+
```
|
| 43 |
+
|
| 44 |
+
### 样例输出 #1
|
| 45 |
+
|
| 46 |
+
```
|
| 47 |
+
Yes
|
| 48 |
+
Yes
|
| 49 |
+
No
|
| 50 |
+
```
|
| 51 |
+
|
| 52 |
+
## 提示
|
| 53 |
+
|
| 54 |
+
#### 「样例解释 #1」
|
| 55 |
+
|
| 56 |
+
对于第 $1$ 组数据,进行 $1$ 次第二种操作后进行 $2$ 次第一种操作即可。
|
| 57 |
+
|
| 58 |
+
对于第 $2$ 组数据,进行 $1$ 次第二种操作后进行 $1$ 次第一种操作即可。
|
| 59 |
+
|
| 60 |
+
对于第 $3$ 组数据,可以证明无论如何操作都无法得到 $3$。
|
| 61 |
+
|
| 62 |
+
#### 「数据范围」
|
| 63 |
+
|
| 64 |
+
对于所有数据,$1\le T \le 100$,$0\le a,b,c < p \le 10^9$,保证 $p$ 是质数。
|
| 65 |
+
|
| 66 |
+
**只有你通过本题的所有测试点,你才能获得本题的分数。**
|
problems/10031.txt
ADDED
|
@@ -0,0 +1,52 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「Cfz Round 3」Xor with Gcd
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一个整数 $n$。
|
| 6 |
+
|
| 7 |
+
你需要求出 $\bigoplus\limits_{i=1}^{n} \gcd(i,n)$,即 $\gcd(1,n) \oplus \gcd(2,n) \oplus \cdots \oplus \gcd(n,n)$ 的值。其中 $\gcd(a,b)$ 表示 $a$ 和 $b$ 的**最大公约数**,$\bigoplus$ 表示**按位异或**,即 C++ 中的 `^`。
|
| 8 |
+
|
| 9 |
+
## 输入格式
|
| 10 |
+
|
| 11 |
+
**本题有多组测试数据。**
|
| 12 |
+
|
| 13 |
+
第一行输入一个整数 $T$,表示测试数据组数。
|
| 14 |
+
|
| 15 |
+
接下来依次输入每组测试数据。对于每组测试数据,输入一行一个整数 $n$。
|
| 16 |
+
|
| 17 |
+
## 输出格式
|
| 18 |
+
|
| 19 |
+
对于每组测试数据,输出一行一个整数,表示 $\bigoplus\limits_{i=1}^{n} \gcd(i,n)$ 的值。
|
| 20 |
+
|
| 21 |
+
## 样例 #1
|
| 22 |
+
|
| 23 |
+
### 样例输入 #1
|
| 24 |
+
|
| 25 |
+
```
|
| 26 |
+
3
|
| 27 |
+
2
|
| 28 |
+
3
|
| 29 |
+
6
|
| 30 |
+
```
|
| 31 |
+
|
| 32 |
+
### 样例输出 #1
|
| 33 |
+
|
| 34 |
+
```
|
| 35 |
+
3
|
| 36 |
+
3
|
| 37 |
+
5
|
| 38 |
+
```
|
| 39 |
+
|
| 40 |
+
## 提示
|
| 41 |
+
|
| 42 |
+
#### 「样例解释 #1」
|
| 43 |
+
|
| 44 |
+
对于第 $1$ 组数据,$\bigoplus\limits_{i=1}^{2} \gcd(i,2)=\gcd(1,2)\oplus\gcd(2,2)=1\oplus2=3$。
|
| 45 |
+
|
| 46 |
+
对于第 $2$ 组数据,$\bigoplus\limits_{i=1}^{3} \gcd(i,3)=\gcd(1,3)\oplus\gcd(2,3)\oplus\gcd(3,3)=1\oplus1\oplus3=3$。
|
| 47 |
+
|
| 48 |
+
#### 「数据范围」
|
| 49 |
+
|
| 50 |
+
对于所有数据,$1 \le T \le 100$,$1 \le n \le 10^{18}$。
|
| 51 |
+
|
| 52 |
+
**只有你通过本题的所有测试点,你才能获得本题的分数。**
|
problems/10032.txt
ADDED
|
@@ -0,0 +1,69 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「Cfz Round 3」Mex of Sequence
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一个长度为 $n$ 的序列 $a$ 和一个整数 $m$。
|
| 6 |
+
|
| 7 |
+
我们定义一次操作为,**同时**将序列 $a$ 中的**每个**元素 $a_i$ 替换为序列 $a$ 中除 $a_i$ 以外的所有元素的 $\operatorname{mex}$。
|
| 8 |
+
|
| 9 |
+
你需要求出进行 $m$ 次操作后的序列 $a$。
|
| 10 |
+
|
| 11 |
+
其中,一个序列的 $\operatorname{mex}$ 为该序列中**未出现过的最小自然数**,例如:
|
| 12 |
+
|
| 13 |
+
- $\operatorname{mex}\{1,2,3\}=0$;
|
| 14 |
+
- $\operatorname{mex}\{0\}=1$;
|
| 15 |
+
- $\operatorname{mex}\{1,0,2,4\}=3$;
|
| 16 |
+
- $\operatorname{mex}\{2,1,3,0,2\}=4$。
|
| 17 |
+
|
| 18 |
+
特别地,当序列为空时,该序列的 $\operatorname{mex}$ 为 $0$。
|
| 19 |
+
|
| 20 |
+
## 输入格式
|
| 21 |
+
|
| 22 |
+
**本题有多组测试数据。**
|
| 23 |
+
|
| 24 |
+
第一行输入一个整数 $T$,表示测试数据组数。
|
| 25 |
+
|
| 26 |
+
接下来依次输入每组测试数据。对于每组测试数据:
|
| 27 |
+
|
| 28 |
+
- 第一行输入两个整数 $n,m$。
|
| 29 |
+
- 第二行输入 $n$ 个整数,表示给定的序列 $a$。
|
| 30 |
+
|
| 31 |
+
## 输出格式
|
| 32 |
+
|
| 33 |
+
对于每组测试数据,输出一行,包含用空格分隔的 $n$ 个整数,表示进行 $m$ 次操作后的序列 $a$。
|
| 34 |
+
|
| 35 |
+
## 样例 #1
|
| 36 |
+
|
| 37 |
+
### 样例输入 #1
|
| 38 |
+
|
| 39 |
+
```
|
| 40 |
+
3
|
| 41 |
+
4 1
|
| 42 |
+
1 0 1 2
|
| 43 |
+
4 5
|
| 44 |
+
9 9 6 1
|
| 45 |
+
3 5
|
| 46 |
+
1 3 0
|
| 47 |
+
```
|
| 48 |
+
|
| 49 |
+
### 样例输出 #1
|
| 50 |
+
|
| 51 |
+
```
|
| 52 |
+
3 0 3 2
|
| 53 |
+
0 0 0 0
|
| 54 |
+
1 2 0
|
| 55 |
+
```
|
| 56 |
+
|
| 57 |
+
## 提示
|
| 58 |
+
|
| 59 |
+
#### 「样例解释 #1」
|
| 60 |
+
|
| 61 |
+
对于第 $1$ 组数据,因为 $\operatorname{mex}\{0,1,2\}=3$,$\operatorname{mex}\{1,1,2\}=0$,$\operatorname{mex}\{1,0,2\}=3$,$\operatorname{mex}\{1,0,1\}=2$,所以进行 $1$ 次操作后的序列 $a$ 为 $\{3,0,3,2\}$。
|
| 62 |
+
|
| 63 |
+
#### 「数据范围」
|
| 64 |
+
|
| 65 |
+
设 $\sum n$ 表示单个测试点中 $n$ 的和。
|
| 66 |
+
|
| 67 |
+
对于所有数据,$1 \le T \le 1000$,$1 \le n \le 10^6$,$1 \le m \le 10^9$,$0 \le a_i \le 10^9$,$\sum n \le 10^6$。
|
| 68 |
+
|
| 69 |
+
**只有你通过本题的所有测试点,你才能获得本题的分数。**
|
problems/10033.txt
ADDED
|
@@ -0,0 +1,81 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「Cfz Round 3」Sum of Permutation
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
**请注意本题特殊的时间限制。**
|
| 6 |
+
|
| 7 |
+
给定一个 $1\sim n$ 的排列 $p$。
|
| 8 |
+
|
| 9 |
+
你需要构造一个长度为 $n$ 的序列 $a$,满足:
|
| 10 |
+
|
| 11 |
+
- 序列 $a$ 中的每个元素均为不大于 $n$ 的正整数;
|
| 12 |
+
- 不存在有序整数二元组 $(l,r)$,满足 $1 \le l \le r \le n$ 且 $\sum\limits_{i=l}^r a_i=\sum\limits_{i=l}^r p_i$;
|
| 13 |
+
|
| 14 |
+
或报告无解。
|
| 15 |
+
|
| 16 |
+
其中,$1\sim n$ 的排列指满足所有不大于 $n$ 的正整数恰好出现一次的序列。
|
| 17 |
+
|
| 18 |
+
## 输入格式
|
| 19 |
+
|
| 20 |
+
**本题有多组测试数据。**
|
| 21 |
+
|
| 22 |
+
第一行输入一个整数 $T$,表示测试数据组数。
|
| 23 |
+
|
| 24 |
+
接下来依次输入每组测试数据。对于每组测试数据:
|
| 25 |
+
|
| 26 |
+
- 第一行输入一个整数 $n$。
|
| 27 |
+
- 第二行输入 $n$ 个整数,表示给定的排列 $p$。
|
| 28 |
+
|
| 29 |
+
## 输出格式
|
| 30 |
+
|
| 31 |
+
对于每组数据,输出一行:
|
| 32 |
+
|
| 33 |
+
- 若存在满足条件的序列 $a$,则输出用空格分隔的 $n$ 个整数,表示你构造的序列 $a$;
|
| 34 |
+
- 若不存在满足条件的序列 $a$,则输出 $-1$。
|
| 35 |
+
|
| 36 |
+
**所有满足要求的输出均可通过。**
|
| 37 |
+
|
| 38 |
+
## 样例 #1
|
| 39 |
+
|
| 40 |
+
### 样例输入 #1
|
| 41 |
+
|
| 42 |
+
```
|
| 43 |
+
4
|
| 44 |
+
3
|
| 45 |
+
3 2 1
|
| 46 |
+
2
|
| 47 |
+
1 2
|
| 48 |
+
5
|
| 49 |
+
4 2 1 5 3
|
| 50 |
+
7
|
| 51 |
+
5 7 3 1 2 4 6
|
| 52 |
+
```
|
| 53 |
+
|
| 54 |
+
### 样例输出 #1
|
| 55 |
+
|
| 56 |
+
```
|
| 57 |
+
1 3 3
|
| 58 |
+
-1
|
| 59 |
+
5 3 2 1 1
|
| 60 |
+
2 3 5 4 6 3 1
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
## 提示
|
| 64 |
+
|
| 65 |
+
#### 「样例解释 #1」
|
| 66 |
+
|
| 67 |
+
对于第 $1$ 组数据,$\{1,3,3\}$ 和 $\{1,1,3\}$ 均为满足条件的序列 $a$。
|
| 68 |
+
|
| 69 |
+
对于第 $2$ 组数据,可以证明不存在满足条件的序列 $a$。
|
| 70 |
+
|
| 71 |
+
对于第 $3$ 组数据,除 $\{5,3,2,1,1 \}$ 外,$\{3,4,5,3,2 \}$、$\{1,4,5,3,4 \}$、$\{5,3,3,4,5\}$ 等均为满足条件的序列 $a$。
|
| 72 |
+
|
| 73 |
+
#### 「数据范围」
|
| 74 |
+
|
| 75 |
+
设 $\sum n$ 表示单个测试点中 $n$ 的和。
|
| 76 |
+
|
| 77 |
+
对于所有数据,$1 \le T \le 5000$,$2 \le n \le 10^6$,$\sum n \le 10^6$,保证 $p$ 是 $1\sim n$ 的排列。
|
| 78 |
+
|
| 79 |
+
**只有你通过本题的所有测试点,你才能获得本题的分数。**
|
| 80 |
+
|
| 81 |
+
**本题输入输出量较大,请使用较快的输入输出方式。**
|
problems/10034.txt
ADDED
|
@@ -0,0 +1,81 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「Cfz Round 3」Circle
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一个长度为 $n$ 的 $\tt{01}$ 串 $S$ 和一个非负整数 $l$。
|
| 6 |
+
|
| 7 |
+
我们定义,对于一个 $1\sim n$ 的排列 $t$ 和非负整数 $k$:
|
| 8 |
+
|
| 9 |
+
$$f_{t,k}(i)=\begin{cases}i & k=0\\f_{t,k-1}(t_i) & k \neq 0\end{cases}$$
|
| 10 |
+
|
| 11 |
+
你需要构造一个 $1\sim n$ 的排列 $p$,满足:
|
| 12 |
+
|
| 13 |
+
- 对于任意一个不大于 $n$ 的正整数 $i$,都满足 $p_i \neq i$;
|
| 14 |
+
- 若 $S_i$ 为 $\tt1$,则 $f_{p,l}(i)=i$(若 $S_i$ 为 $\tt0$ 则没有限制);
|
| 15 |
+
|
| 16 |
+
或报告无解。
|
| 17 |
+
|
| 18 |
+
其中,$1\sim n$ 的排列指满足所有不大于 $n$ 的正整数恰好出现一次的序列。
|
| 19 |
+
|
| 20 |
+
## 输入格式
|
| 21 |
+
|
| 22 |
+
**本题有多组测试数据。**
|
| 23 |
+
|
| 24 |
+
第一行输入一个整数 $T$,表示测试数据组数。
|
| 25 |
+
|
| 26 |
+
接下来依次输入每组测试数据。对于每组测试数据:
|
| 27 |
+
|
| 28 |
+
- 第一行输入两个整数 $n,l$。
|
| 29 |
+
- 第二行输入一个长度为 $n$ 的 $\tt{01}$ 串表示 $S$。
|
| 30 |
+
|
| 31 |
+
## 输出格式
|
| 32 |
+
|
| 33 |
+
对于每组数据,输出一行:
|
| 34 |
+
|
| 35 |
+
- 若存在满足条件的排列 $p$,则输出用空格分隔的 $n$ 个整数,表示你构造的排列 $p$;
|
| 36 |
+
- 若不存在满足条件的排列 $p$,则输出 $-1$。
|
| 37 |
+
|
| 38 |
+
**所有满足要求的输出均可通过。**
|
| 39 |
+
|
| 40 |
+
## 样例 #1
|
| 41 |
+
|
| 42 |
+
### 样例输入 #1
|
| 43 |
+
|
| 44 |
+
```
|
| 45 |
+
4
|
| 46 |
+
5 3
|
| 47 |
+
10011
|
| 48 |
+
4 5
|
| 49 |
+
1000
|
| 50 |
+
5 6
|
| 51 |
+
11111
|
| 52 |
+
9 6
|
| 53 |
+
011111011
|
| 54 |
+
```
|
| 55 |
+
|
| 56 |
+
### 样例输出 #1
|
| 57 |
+
|
| 58 |
+
```
|
| 59 |
+
4 3 2 5 1
|
| 60 |
+
-1
|
| 61 |
+
5 4 2 3 1
|
| 62 |
+
3 1 2 6 4 5 9 7 8
|
| 63 |
+
```
|
| 64 |
+
|
| 65 |
+
## 提示
|
| 66 |
+
|
| 67 |
+
#### 「样例解释 #1」
|
| 68 |
+
|
| 69 |
+
对于第 $1$ 组数据,$f_{p,3}(1)=f_{p,2}(4)=f_{p,1}(5)=f_{p,0}(1)=1$,其余数同理,所以 $p$ 为 $\{4,3,2,5,1\}$ 时满足条件。
|
| 70 |
+
|
| 71 |
+
对于第 $2$ 组数据,可以证明不存在满足条件的排列 $p$。
|
| 72 |
+
|
| 73 |
+
对于第 $3$ 组数据,$\{2,1,4,5,3\}$ 等也为满足条件的排列 $p$。
|
| 74 |
+
|
| 75 |
+
#### 「数据范围」
|
| 76 |
+
|
| 77 |
+
设 $\sum n$ 表示单个测试点中 $n$ 的和。
|
| 78 |
+
|
| 79 |
+
对于所有数据,$1 \le T \le 100$,$2 \le n \le 5\times 10^5$,$0 \le l \le 10^{18}$,$\sum n \le 5\times 10^5$,保证 $S$ 中只包含 $\tt{0}$ 和 $\tt{1}$。
|
| 80 |
+
|
| 81 |
+
**只有你通过本题的所有测试点,你才能获得本题的分数。**
|
problems/10035.txt
ADDED
|
@@ -0,0 +1,112 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「FAOI-R2」Paint (A)
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
小 Y 是一个胖子,他最爱下楼梯了,因为下楼梯很省力气,但是他却有强迫症。
|
| 6 |
+
|
| 7 |
+
由于刷漆工人 HG 的油漆不够,每一层台阶都只刷了一半——左边或右边,好让小 Y 下楼时不踩到油漆。(~~众人:这是什么逻辑?~~)
|
| 8 |
+
|
| 9 |
+
## 题目描述
|
| 10 |
+
|
| 11 |
+
整个楼梯共 $3^N$ 级台阶。
|
| 12 |
+
|
| 13 |
+
HG 刷漆的规律是:对于**从上到下**第 $I$ 级台阶,若 $V_3(I)$ 是奇数,则刷在左边,否则刷在右边。**$V_3(I)$ 的定义请见提示。**
|
| 14 |
+
|
| 15 |
+
小 Y 因为强迫症,要求自己不能踩到油漆。
|
| 16 |
+
|
| 17 |
+
现在他来求助你,他最少会踩到油漆多少次?
|
| 18 |
+
|
| 19 |
+
- 一次只能下一级台阶。
|
| 20 |
+
- 如果小 Y 站在当前台阶的左边,则他必须站在下一级台阶的右边,反之亦然。
|
| 21 |
+
- 如果油漆在当前台阶左边,那么需要站在当前台阶右边才算没踩到油漆,反之亦然。
|
| 22 |
+
- 小 Y 唯一可以控制的是:他在第 $1$ 级台阶上站在哪边。也就是说,小 Y 只有 $2$ 种下楼梯的方案供选择。
|
| 23 |
+
|
| 24 |
+
答案对 $10^9+7$ 取模。
|
| 25 |
+
|
| 26 |
+
### 形式化题意
|
| 27 |
+
|
| 28 |
+
给定三个 01 串 $A,B,C$,长度均为 $3^N$。字符串下标从 $1$ 开始。
|
| 29 |
+
|
| 30 |
+
其中:
|
| 31 |
+
|
| 32 |
+
- $A=\texttt{101010101\ldots101}$;
|
| 33 |
+
- $B=\texttt{010101010\ldots010}$;
|
| 34 |
+
- $C=\texttt{001001000\ldots}$;具体来说,第 $I$ 个字符为 $V_3(I) \bmod 2$。**$V_3(I)$ 的定义请见提示。**
|
| 35 |
+
|
| 36 |
+
记 $\operatorname{mc}(X,Y)$ 为字符串 $X$ 和 $Y$ 中匹配的字符的个数。
|
| 37 |
+
|
| 38 |
+
试求:
|
| 39 |
+
|
| 40 |
+
$$\min\{\operatorname{mc}(A,C),\operatorname{mc}(B,C)\}$$
|
| 41 |
+
|
| 42 |
+
答案对 $10^9+7$ 取模。
|
| 43 |
+
|
| 44 |
+
## 输入格式
|
| 45 |
+
|
| 46 |
+
**本题有多组数据。**
|
| 47 |
+
|
| 48 |
+
第一行,一个正整数 $T$,代表数据组数。
|
| 49 |
+
|
| 50 |
+
下面 $T$ 行,每行一个正整数 $N$。
|
| 51 |
+
|
| 52 |
+
## 输出格式
|
| 53 |
+
|
| 54 |
+
每组数据一行,输出踩到油漆的最少次数,即 $\min\{\operatorname{mc}(A,C),\operatorname{mc}(B,C)\}$。
|
| 55 |
+
|
| 56 |
+
**答案对 $10^9+7$ 取模。**
|
| 57 |
+
|
| 58 |
+
## 样例 #1
|
| 59 |
+
|
| 60 |
+
### 样例输入 #1
|
| 61 |
+
|
| 62 |
+
```
|
| 63 |
+
1
|
| 64 |
+
1
|
| 65 |
+
```
|
| 66 |
+
|
| 67 |
+
### 样例输出 #1
|
| 68 |
+
|
| 69 |
+
```
|
| 70 |
+
1
|
| 71 |
+
```
|
| 72 |
+
|
| 73 |
+
## 样例 #2
|
| 74 |
+
|
| 75 |
+
### 样例输入 #2
|
| 76 |
+
|
| 77 |
+
```
|
| 78 |
+
3
|
| 79 |
+
494699
|
| 80 |
+
494699494699
|
| 81 |
+
494699494699494699
|
| 82 |
+
```
|
| 83 |
+
|
| 84 |
+
### 样例输出 #2
|
| 85 |
+
|
| 86 |
+
```
|
| 87 |
+
994161775
|
| 88 |
+
899186285
|
| 89 |
+
348815909
|
| 90 |
+
```
|
| 91 |
+
|
| 92 |
+
## 提示
|
| 93 |
+
|
| 94 |
+
样例 $1$ 解释:
|
| 95 |
+
|
| 96 |
+
- $A=\texttt{101}$;
|
| 97 |
+
- $B=\texttt{010}$;
|
| 98 |
+
- $C=\texttt{001}$;
|
| 99 |
+
- $\operatorname{mc}(A,C)=2$;
|
| 100 |
+
- $\operatorname{mc}(B,C)=1$;
|
| 101 |
+
- $\min\{\operatorname{mc}(A,C),\operatorname{mc}(B,C)\}=1$。
|
| 102 |
+
|
| 103 |
+
------------
|
| 104 |
+
|
| 105 |
+
| 测试点编号 | $T \le$ | $N \le$ | 分值 |
|
| 106 |
+
| :-: | :-: | :-: | :-: |
|
| 107 |
+
| $1$ | $10$ | $10$ | $50$ |
|
| 108 |
+
| $2$ | $10^5$ | $10^{18}$ | $50$ |
|
| 109 |
+
|
| 110 |
+
对于 $100\%$ 的数据,$1 \le T \le 10^{5}$,$1 \le N \le 10^{18}$。
|
| 111 |
+
|
| 112 |
+
> **提示:** $V_3(X)$ 指 $X$ 中质因数 $3$ 的个数。例如,$V_3(14)=0$,$V_3(18)=2$。
|
problems/10036.txt
ADDED
|
@@ -0,0 +1,142 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「FAOI-R2」A trip to Macao (B)
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
这天,xhabc66 来到澳门旅游。一下飞机,他直奔赌场。
|
| 6 |
+
|
| 7 |
+
可是,今天的赌场格外热闹,不知发生了什么。
|
| 8 |
+
|
| 9 |
+
xhabc66 打开手机一看:啊,原来今天是 $12$ 月 $20$ 日!
|
| 10 |
+
|
| 11 |
+
因此,赌场在做活动!一年一度!机不可失!
|
| 12 |
+
|
| 13 |
+
xhabc66 径直走进了赌场。
|
| 14 |
+
|
| 15 |
+
## 题目描述
|
| 16 |
+
|
| 17 |
+
赌场贴出了如下规则(**你可以忽略没有加粗的内容**):
|
| 18 |
+
|
| 19 |
+
1. 所有玩家在注册后方可进行游戏。
|
| 20 |
+
2. 活动期间,**新注册的玩家可从抽奖盒内拿走一枚筹码。抽奖盒内共 $m$ 种筹码,面值分别为 $a_1,a_2,\ldots,a_m$ 澳元(均为正整数)**,每种一个,保证公平。
|
| 21 |
+
3. 本赌场仅提供一种游戏:猜拳。游戏开始时,双方各下注相同数量(以 $1$ 澳元为单位)的筹码;若猜拳分出胜负,则胜者拿走所有下注。
|
| 22 |
+
4. 根据上一条可知,**玩家一次游戏中赢得的筹码(正整数)不得超过自身所携带的筹码**。
|
| 23 |
+
5. 公平游戏,严禁作弊,违者严惩。
|
| 24 |
+
|
| 25 |
+
xhabc66 注册后,**连赢数局(可以是 $0$ 局,但没有输过,也没有平局过)**,最终带着 $n$ 澳元走出了赌场。
|
| 26 |
+
|
| 27 |
+
出赌场后,xhabc66 突然好奇他是怎么赢到这么多钱的。然而,他不记得他每局下了多少注,不记得他一共玩了多少局,甚至不记得他开始时拿走的筹码是什么面值。
|
| 28 |
+
|
| 29 |
+
**他想知道:他有多少种不同的赢钱方法。**
|
| 30 |
+
|
| 31 |
+
**答案对 $10^9+7$ 取模。**
|
| 32 |
+
|
| 33 |
+
> 两种赢钱方法在满足以下任何一个条件时,xhabc66 都会认为它们不同:
|
| 34 |
+
>
|
| 35 |
+
> - 他某一局的下注金额不同;
|
| 36 |
+
> - 他玩的局数不同;
|
| 37 |
+
> - 他开始时拿走的筹码的面值不同。
|
| 38 |
+
|
| 39 |
+
### 形式化题意
|
| 40 |
+
|
| 41 |
+
求有多少个数列 $\{b_k\}$ 满足:
|
| 42 |
+
|
| 43 |
+
1. $\forall i \in [1,k],b_i \in \mathbb{N^*}$;
|
| 44 |
+
2. $\forall i \in [2,k],b_i \in [b_{i-1}+1,b_{i-1} \times 2]$;
|
| 45 |
+
3. $b_1 \in\{a_m\}$;
|
| 46 |
+
4. $b_k=n$。
|
| 47 |
+
|
| 48 |
+
数列的长度 $k$ 可以是任何**正整数**。
|
| 49 |
+
|
| 50 |
+
答案对 $10^9+7$ 取模。
|
| 51 |
+
|
| 52 |
+
## 输入格式
|
| 53 |
+
|
| 54 |
+
两行。
|
| 55 |
+
|
| 56 |
+
第一行,两个正整数,$n,m$。
|
| 57 |
+
|
| 58 |
+
第二行,$m$ 个**从小到大排列**的正整数,$a_1 \sim a_m$。
|
| 59 |
+
|
| 60 |
+
## 输出格式
|
| 61 |
+
|
| 62 |
+
一行一个正整数,表示答案。
|
| 63 |
+
|
| 64 |
+
## 样例 #1
|
| 65 |
+
|
| 66 |
+
### 样例输入 #1
|
| 67 |
+
|
| 68 |
+
```
|
| 69 |
+
4 4
|
| 70 |
+
1 2 3 4
|
| 71 |
+
```
|
| 72 |
+
|
| 73 |
+
### 样例输出 #1
|
| 74 |
+
|
| 75 |
+
```
|
| 76 |
+
6
|
| 77 |
+
```
|
| 78 |
+
|
| 79 |
+
## 样例 #2
|
| 80 |
+
|
| 81 |
+
### 样例输入 #2
|
| 82 |
+
|
| 83 |
+
```
|
| 84 |
+
5 1
|
| 85 |
+
1
|
| 86 |
+
```
|
| 87 |
+
|
| 88 |
+
### 样例输出 #2
|
| 89 |
+
|
| 90 |
+
```
|
| 91 |
+
3
|
| 92 |
+
```
|
| 93 |
+
|
| 94 |
+
## 样例 #3
|
| 95 |
+
|
| 96 |
+
### 样例输入 #3
|
| 97 |
+
|
| 98 |
+
```
|
| 99 |
+
12345678 9
|
| 100 |
+
1 2 3 45 67 89 123 456 789
|
| 101 |
+
```
|
| 102 |
+
|
| 103 |
+
### 样例输出 #3
|
| 104 |
+
|
| 105 |
+
```
|
| 106 |
+
998899106
|
| 107 |
+
```
|
| 108 |
+
|
| 109 |
+
## 提示
|
| 110 |
+
|
| 111 |
+
样例 $1$ 解释:
|
| 112 |
+
|
| 113 |
+
```plain
|
| 114 |
+
1 2 3 4
|
| 115 |
+
1 2 4
|
| 116 |
+
2 3 4
|
| 117 |
+
2 4
|
| 118 |
+
3 4
|
| 119 |
+
4
|
| 120 |
+
```
|
| 121 |
+
|
| 122 |
+
样例 $2$ 解释:
|
| 123 |
+
|
| 124 |
+
```plain
|
| 125 |
+
1 2 3 4 5
|
| 126 |
+
1 2 3 5
|
| 127 |
+
1 2 4 5
|
| 128 |
+
```
|
| 129 |
+
|
| 130 |
+
----------
|
| 131 |
+
|
| 132 |
+
**本题采用捆绑测试。**
|
| 133 |
+
|
| 134 |
+
| Subtask 编号 | $m \le$ | $n \le$ | 分值 |
|
| 135 |
+
| :-: | :-: | :-: | :-: |
|
| 136 |
+
| $0$ | $3$ | $3$ | $20$ |
|
| 137 |
+
| $1$ | $10^5$ | $10^5$ | $40$ |
|
| 138 |
+
| $2$ | $10^6$ | $10^8$ | $40$ |
|
| 139 |
+
|
| 140 |
+
对于 $100\%$ 的数据,$1 \le m \le 10^6$,$1 \le a_1<a_2<\ldots<a_m \le n \le 10^8$,$m \le n$。
|
| 141 |
+
|
| 142 |
+
> **提示:** 请注意本题不同寻常的内存限制!
|
problems/10037.txt
ADDED
|
@@ -0,0 +1,151 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「FAOI-R2」梨花开 (C)
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
> 忽如一夜春风来,千树万树梨花开。
|
| 6 |
+
|
| 7 |
+
雪,覆盖了大漠上的一颗颗树,仿佛朵朵梨花盛开。但是令 krjt 意想不到的是,这些树居然真的是梨树!
|
| 8 |
+
|
| 9 |
+
## 题目描述
|
| 10 |
+
|
| 11 |
+
给你一颗以 $1$ 为根的树,初始时每个点都是白色,每个点有两个权值 $a_i,b_i$,初始时所有点的两个权值都为 $0$,但 $a_1=k$。
|
| 12 |
+
|
| 13 |
+
我们通过如下操作定义一个序列 $\{v_t\}$ 的权值:
|
| 14 |
+
- 从小到大度过 $1,2,3,\dots,t$ 这 $t$ 个时刻。
|
| 15 |
+
- 在第 $x$ 个时刻,对于 $i\in[1,n]$,执行 $b_i\gets b_i+v_x$。
|
| 16 |
+
- 对于父子 $(u,v)$,设 $u$ 为父亲,可以选定整数 $h\in[0,a_u]$ 执行操作 $a_u\gets a_u-h$,$a_v\gets a_v+h$,之后该时刻内形如 $(v,w)$ 且 $v$ 为父亲的父子不能操作。
|
| 17 |
+
- 若一个点 $i$ 满足 $a_i+b_i<0$,将 $i$ 以及 $i$ 的子树中的点染成黑色。
|
| 18 |
+
- 执行最优操作以最大化白点个数,该序列权值即为最大白点个数。
|
| 19 |
+
|
| 20 |
+
定义一个序列 $\{v_t\}$ 合法仅当 $\forall i\in[1,t]$,$\lvert v_i\rvert\in[0,m]$。给定 $t$,求出所有合法序列 $\{v_t\}$ 的权值之和对 $998244353$ 取模的值。
|
| 21 |
+
|
| 22 |
+
### 原题面
|
| 23 |
+
|
| 24 |
+
krjt 的目光注视在一棵以 $1$ 号结点为根的,$n$ 个结点的梨树上。
|
| 25 |
+
|
| 26 |
+
这颗梨树的每个点在每一刻都可以做**任意次**以下操作:将自己的**基本**热量提供**任意正整数量**给某个儿子。
|
| 27 |
+
|
| 28 |
+
**但需要注意的是,在同一个时刻里,只有当一个结点的所有儿子结束操作后,该结点才能操作。**
|
| 29 |
+
|
| 30 |
+
雪纷纷地下着,梨树在 $t$ 个时刻的冬天里,第 $i$ 天**所有操作完成后**每个结点的都会加上 $v_i$ 点**附加**热量,若**加上后**该结点的**总**热量仍然 $<0$ 则会连同它的子树一起冻死(自动与其祖先断开,掉到地上)。每个 $v_i$ 都是 $[-m,m]$ 中的一个不确定的整数值。
|
| 31 |
+
|
| 32 |
+
梨树定义一个序列 $\{v_t\}$ 的价值为它作为每时刻增加的热量时,梨树最多保留的结点数。
|
| 33 |
+
|
| 34 |
+
梨树不愿在这个冬天死去,希望求出所有方案的价值和,以保留尽量多的结点迎接春天,绽放花朵。因为在冬天前,它的根结点储蓄了 $k$ 点**基本**热量(和 $0$ 点附加热量,其他结点储蓄了 $0$ 点热量),这是自知活不过冬天的伙伴给它的。
|
| 35 |
+
|
| 36 |
+
而它伙伴在最后一点意识隐隐消失时,仿佛能够看到:一夜春风轻抚,冰雪消融,树林里朵朵梨花开……
|
| 37 |
+
|
| 38 |
+
答案对 $998244353$ 取模。
|
| 39 |
+
|
| 40 |
+
## 输入格式
|
| 41 |
+
|
| 42 |
+
第一行四个非负整数 $n,m,t,k$,分别表示树的结点个数,$v_i$ 的取值范围,冬天的时长,根结点原本存储的热量。
|
| 43 |
+
|
| 44 |
+
接下来 $n-1$ 行,每行两个正整数 $u,v$,表示 $u$ 号结点与 $v$ 号结点之间有一条边。
|
| 45 |
+
|
| 46 |
+
## 输出格式
|
| 47 |
+
|
| 48 |
+
输出所有 $(2m+1)^{t}$ 种情况的答案的**和对 $998244353$ 取模**后的结果。
|
| 49 |
+
|
| 50 |
+
## 样例 #1
|
| 51 |
+
|
| 52 |
+
### 样例输入 #1
|
| 53 |
+
|
| 54 |
+
```
|
| 55 |
+
1 1 1 1
|
| 56 |
+
```
|
| 57 |
+
|
| 58 |
+
### 样例输出 #1
|
| 59 |
+
|
| 60 |
+
```
|
| 61 |
+
3
|
| 62 |
+
```
|
| 63 |
+
|
| 64 |
+
## 样例 #2
|
| 65 |
+
|
| 66 |
+
### 样例输入 #2
|
| 67 |
+
|
| 68 |
+
```
|
| 69 |
+
3 1 2 2
|
| 70 |
+
1 2
|
| 71 |
+
1 3
|
| 72 |
+
```
|
| 73 |
+
|
| 74 |
+
### 样例输出 #2
|
| 75 |
+
|
| 76 |
+
```
|
| 77 |
+
22
|
| 78 |
+
```
|
| 79 |
+
|
| 80 |
+
## 样例 #3
|
| 81 |
+
|
| 82 |
+
### 样例输入 #3
|
| 83 |
+
|
| 84 |
+
```
|
| 85 |
+
5 2 3 5
|
| 86 |
+
1 2
|
| 87 |
+
2 3
|
| 88 |
+
2 4
|
| 89 |
+
4 5
|
| 90 |
+
```
|
| 91 |
+
|
| 92 |
+
### 样例输出 #3
|
| 93 |
+
|
| 94 |
+
```
|
| 95 |
+
407
|
| 96 |
+
```
|
| 97 |
+
|
| 98 |
+
## 样例 #4
|
| 99 |
+
|
| 100 |
+
### 样例输入 #4
|
| 101 |
+
|
| 102 |
+
```
|
| 103 |
+
10 5 6 44
|
| 104 |
+
1 2
|
| 105 |
+
1 3
|
| 106 |
+
2 5
|
| 107 |
+
2 6
|
| 108 |
+
3 4
|
| 109 |
+
6 7
|
| 110 |
+
6 8
|
| 111 |
+
4 9
|
| 112 |
+
9 10
|
| 113 |
+
```
|
| 114 |
+
|
| 115 |
+
### 样例输出 #4
|
| 116 |
+
|
| 117 |
+
```
|
| 118 |
+
10465095
|
| 119 |
+
```
|
| 120 |
+
|
| 121 |
+
## 提示
|
| 122 |
+
|
| 123 |
+
样例 $3$ 解释:
|
| 124 |
+
|
| 125 |
+
对于一种 $\{v_3\}=\{1,0,-2\}$ 的情况,一种最优操作如下:
|
| 126 |
+
- 第一个时刻,$1$ 号结点传递 $4$ 热量给 $2$ 号结点,操作完毕并增加 $v_1=1$ 后每个结点的热量分别为 $2,5,1,1,1$。
|
| 127 |
+
- 第二个时刻,$2$ 号结点传递 $2$ 热量给 $4$ 号结点,操作完毕并增加 $v_2=0$ 后每个结点的热量分别为 $2,3,1,3,1$。
|
| 128 |
+
- 第三个时刻,$2$ 号结点传递 $1$ 热量给 $3$ 号结点,$4$ 号结点传递 $1$ 热量给 $5$ 号结点,操作完毕并增加 $v_3=-2$ 后每个结点的热量分别为 $0,0,0,0,0$。
|
| 129 |
+
- 第四个时刻,冬天过去,$5$ 个结点全部存活。
|
| 130 |
+
|
| 131 |
+
样例 $4$ 解释:
|
| 132 |
+
|
| 133 |
+
对于一种 $\{v_{6}\}=\{1,2,1,2,1,2\}$ 的情况,一种最优操作如下:
|
| 134 |
+
- 每个时刻都不进行操作。
|
| 135 |
+
- 第 $7$ 个时刻,冬天过去,$5$ 个结点全部存活。
|
| 136 |
+
|
| 137 |
+
------------
|
| 138 |
+
|
| 139 |
+
**本题采用捆绑测试。**
|
| 140 |
+
|
| 141 |
+
| Subtask 编号 | $n \le$ | $m \le$ | $t \le$ | $k \le$ | 分值 |
|
| 142 |
+
| :----------: | :----------: | :----------: | :----------: | :----------: | :----------: |
|
| 143 |
+
| $0$ | $4$ | $4$ | $4$ | $40$ | $20$ |
|
| 144 |
+
| $\color{red}1$ | $\color{red}2 \times 10^5$ | $\color{red}20$ | $\color{red}20$ | $\color{red}1 \times 10^5$ | $\color{red}10$ |
|
| 145 |
+
| $2$ | $2 \times 10^5$ | $20$ | $20$ | $3 \times 10^5$ | $20$ |
|
| 146 |
+
| $3$ | $2 \times 10^5$ | $50$ | $100$ | $3 \times 10^5$ | $10$ |
|
| 147 |
+
| $4$ | $2 \times 10^5$ | $50$ | $500$ | $3 \times 10^5$ | $40$ |
|
| 148 |
+
|
| 149 |
+
**特殊性质:对于 Subtask 1,保证树的形态是菊花。**
|
| 150 |
+
|
| 151 |
+
对于 $100\%$ 的数据,$1\leq n\leq 2\times 10^5$,$1\leq k\leq 3\times 10^5$,$1\leq m\leq 50$,$1\leq t\leq 500$,保证输入构成一棵树。
|
problems/10038.txt
ADDED
|
@@ -0,0 +1,187 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 「FAOI-R2」Program of atom(x) 2027 (D)
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
这是来自 $2027$ 年的 FAOI 的一道题目,是一道带有 SPJ 的提交答案题,但也允许提交代码。
|
| 6 |
+
|
| 7 |
+
------------
|
| 8 |
+
|
| 9 |
+
自从 [krjt](https://www.luogu.com.cn/user/691537) 上次被 $160$ 人 [JC](https://www.luogu.com.cn/problem/T269289) 后,他换了一个「量子密码锁」,并用它锁上了自己的电脑包——打不开密码锁,就取不出包里的电脑。理论上,一旦 krjt 忘了密码,就连造这把锁的人也打不开。
|
| 10 |
+
|
| 11 |
+
然而,这把锁并非固若金汤。~~有一天,krjt 突然对化学产生了浓厚的兴趣。他拿起那把锁,放在酒精灯上加热,结果发现:~~ 在高温环境下,这把锁内的原子(严格来说是「离子」,下同)排布变得不稳定,这将导致它瘫痪。
|
| 12 |
+
|
| 13 |
+
## 题目描述
|
| 14 |
+
|
| 15 |
+
krjt 找来了密码锁的说明书:
|
| 16 |
+
|
| 17 |
+
> 在密码锁中,有一条长度为 $n$ 的链(不能更改,$n$ 的具体取值见密码锁铭牌),每个结点上可以存放至多一个原子。初始时,$1,2,\ldots,n$ 号原子以某个顺序(可以由用户自行调整)被存放在其中,每个结点存放一个原子。
|
| 18 |
+
>
|
| 19 |
+
> 定义 $i$ 号原子的电荷量为 $i!$。
|
| 20 |
+
>
|
| 21 |
+
> 现有一个计时器 $b$(单位为秒),其初值为 $0$。
|
| 22 |
+
>
|
| 23 |
+
> 密码锁被加热后,以下事件**依次循环发生**,直至达成停止条件:
|
| 24 |
+
>
|
| 25 |
+
> 1. 位于链两端的原子被移除(**这不会使链变短**),**不再对后续事件产生影响**;
|
| 26 |
+
> 2. 判定终止条件:
|
| 27 |
+
> - 若此时链中剩下不多于 $1$ 个原子(也可以是 $0$ 个),则**达成终止条件**,密码锁瘫痪(**此时计时器 $b$ 不会加 $1$**)。
|
| 28 |
+
> - 否则,将计时器 $b$ 的值加 $1$。
|
| 29 |
+
> 3. 给每个原子标定运动方向(**标定的运动方向是临时的,只生效一次,在下一次标定前会被重置**):
|
| 30 |
+
> - 计算它左边所有原子的电荷量之和为 $x$;
|
| 31 |
+
> - 计算它右边所有原子的电荷量之和为 $y$;
|
| 32 |
+
> - 如果 $x<y$,则标定方向为「向左」;
|
| 33 |
+
> - 如果 $x>y$,则标定方向为「向右」;
|
| 34 |
+
> - 可以证明,$x \ne y$。
|
| 35 |
+
> 4. 所有原子按照所标定的运动方向,移动一条边的距离,来到相邻的结点。
|
| 36 |
+
|
| 37 |
+
此外,krjt 从铭牌上读取到了 $n$ 的值。
|
| 38 |
+
|
| 39 |
+
krjt 定义,密码锁的瘫痪用时,为它瘫痪时 $b$ 的值。当然,krjt 希望密码锁尽量安全,因此他想**最大化密码锁的瘫痪用时**。
|
| 40 |
+
|
| 41 |
+
~~为了不让更多人再次 JC krjt~~,请问:他该如何排列密码锁中 $n$ 个原子的初始顺序?
|
| 42 |
+
|
| 43 |
+
## 输入格式
|
| 44 |
+
|
| 45 |
+
一行一个正整数,$n$。
|
| 46 |
+
|
| 47 |
+
## 输出格式
|
| 48 |
+
|
| 49 |
+
一行 $n$ 个正整数,一个 $1 \sim n$ 的排列,表示你给 krjt 规划的排列方案:从左到右(或者从右到左,可以证明它们的瘫痪用时相等)依次输出 $n$ 个原子的编号。
|
| 50 |
+
|
| 51 |
+
**答案可能有多个,输出一个即可。**
|
| 52 |
+
|
| 53 |
+
**请注意:和许多其他的提交答案题不同的是,本题不下发数据文件(请自行输入 $n=1,2,\ldots,100$),并且你的答案必须是最优解才能 AC,否则不能得分。**
|
| 54 |
+
|
| 55 |
+
## 样例 #1
|
| 56 |
+
|
| 57 |
+
### 样例输入 #1
|
| 58 |
+
|
| 59 |
+
```
|
| 60 |
+
1
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
### 样例输出 #1
|
| 64 |
+
|
| 65 |
+
```
|
| 66 |
+
1
|
| 67 |
+
```
|
| 68 |
+
|
| 69 |
+
## 样例 #2
|
| 70 |
+
|
| 71 |
+
### 样例输入 #2
|
| 72 |
+
|
| 73 |
+
```
|
| 74 |
+
2
|
| 75 |
+
```
|
| 76 |
+
|
| 77 |
+
### 样例输出 #2
|
| 78 |
+
|
| 79 |
+
```
|
| 80 |
+
1 2
|
| 81 |
+
```
|
| 82 |
+
|
| 83 |
+
## 样例 #3
|
| 84 |
+
|
| 85 |
+
### 样例输入 #3
|
| 86 |
+
|
| 87 |
+
```
|
| 88 |
+
3
|
| 89 |
+
```
|
| 90 |
+
|
| 91 |
+
### 样例输出 #3
|
| 92 |
+
|
| 93 |
+
```
|
| 94 |
+
2 1 3
|
| 95 |
+
```
|
| 96 |
+
|
| 97 |
+
## 样例 #4
|
| 98 |
+
|
| 99 |
+
### 样例输入 #4
|
| 100 |
+
|
| 101 |
+
```
|
| 102 |
+
4
|
| 103 |
+
```
|
| 104 |
+
|
| 105 |
+
### 样例输出 #4
|
| 106 |
+
|
| 107 |
+
```
|
| 108 |
+
4 2 3 1
|
| 109 |
+
```
|
| 110 |
+
|
| 111 |
+
## 样例 #5
|
| 112 |
+
|
| 113 |
+
### 样例输入 #5
|
| 114 |
+
|
| 115 |
+
```
|
| 116 |
+
5
|
| 117 |
+
```
|
| 118 |
+
|
| 119 |
+
### 样例输出 #5
|
| 120 |
+
|
| 121 |
+
```
|
| 122 |
+
5 4 1 2 3
|
| 123 |
+
```
|
| 124 |
+
|
| 125 |
+
## 样例 #6
|
| 126 |
+
|
| 127 |
+
### 样例输入 #6
|
| 128 |
+
|
| 129 |
+
```
|
| 130 |
+
6
|
| 131 |
+
```
|
| 132 |
+
|
| 133 |
+
### 样例输出 #6
|
| 134 |
+
|
| 135 |
+
```
|
| 136 |
+
2 4 5 1 6 3
|
| 137 |
+
```
|
| 138 |
+
|
| 139 |
+
## 提示
|
| 140 |
+
|
| 141 |
+
样例解释:
|
| 142 |
+
|
| 143 |
+
$6$ 个样例的瘫痪用时分别为 $0,0,0,1,1,2$ 秒。
|
| 144 |
+
|
| 145 |
+
实际上,枚举可知:当 $n \le 6$ 时,所有 $1 \sim n$ 的排列都是正确答案。
|
| 146 |
+
|
| 147 |
+
下面对样例 $6$ 进行模拟。在链的描述中:
|
| 148 |
+
|
| 149 |
+
- $0$ 表示该结点为空;
|
| 150 |
+
- $i$ 表示该结点上存放着 $i$ 号原子;
|
| 151 |
+
- $(x,y)$ 为计算结果。
|
| 152 |
+
|
| 153 |
+
1. **初始的链**为 $\color{blue}2-4-5-1-6-3$;
|
| 154 |
+
2. $b$ 初始为 $0$;
|
| 155 |
+
3. **位于两端的原子被移除**,链变为 $\color{blue}0-4-5-1-6-0$;
|
| 156 |
+
4. $b$ 增至 $1$;
|
| 157 |
+
5. **计算**,$4$ 个原子(从左向右)的结果分别为 $(\color{red}0\color{black},841),(\color{red}24\color{black},721),(\color{red}144\color{black},720),(145,\color{red}0\color{black})$;
|
| 158 |
+
6. 根据结果,左边 $3$ 个原子($4,5,1$)**向左运动**,最右边的原子($6$)**向右运动**,链变为 $\color{blue}4-5-1-0-0-6$;
|
| 159 |
+
7. **位于两端的原子被移除**,链变为 $\color{blue}0-5-1-0-0-0$;
|
| 160 |
+
8. $b$ 增至 $2$;
|
| 161 |
+
9. **计算**,$2$ 个原子(从左向右)的结果分别为 $(\color{red}0\color{black},1),(120,\color{red}0\color{black})$;
|
| 162 |
+
10. 根据结果,左边的原子($5$)**向左运动**,右边的原子($1$)**向右运动**,链变为 $\color{blue}5-0-0-1-0-0$;
|
| 163 |
+
11. **位于两端的原子被移除**,链变为 $\color{blue}0-0-0-1-0-0$;
|
| 164 |
+
11. 此时链中只剩下 $1$ 个原子($1$),**反应结束,密码锁瘫痪**。
|
| 165 |
+
|
| 166 |
+
综上,样例 $6$ 的瘫痪用时为 $2$ 秒。
|
| 167 |
+
|
| 168 |
+
|
| 169 |
+
------------
|
| 170 |
+
|
| 171 |
+
**本题允许提交答案。**
|
| 172 |
+
|
| 173 |
+
本题共 $100$ 个测试点,分别有 $n=1,2,\ldots,100$,每个 $1$ 分。
|
| 174 |
+
|
| 175 |
+
对于 $100\%$ 的数据,$1 \le n \le 100$。
|
| 176 |
+
|
| 177 |
+
> **提示 1:** 如果你 UKE 了,请联系出题人或管理员。
|
| 178 |
+
>
|
| 179 |
+
> **提示 2:** $n$ 的范围受到了洛谷的评测限制,否则它可以更大。
|
| 180 |
+
>
|
| 181 |
+
> **提示 3:** 提交答案时,$n$ 值应与测试点编号一致。
|
| 182 |
+
>
|
| 183 |
+
> **提示 4:** 本题可以当作传统题来做,提交答案只是为了方便打表。
|
| 184 |
+
>
|
| 185 |
+
> **提示 5:** 样例是手造的,不是 std 的运行结果。
|
| 186 |
+
>
|
| 187 |
+
> **提示 6:** 本题有 $6$ 分的样例分,一定要拿到哦!
|
problems/10039.txt
ADDED
|
@@ -0,0 +1,74 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 游戏
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
小 I 和小 J 又在玩游戏。
|
| 6 |
+
|
| 7 |
+
小 J 找来了一棵 $n$ 个点的树。树上的每条边有开启和关闭两个状态,初始树上每条边都是开启的。
|
| 8 |
+
|
| 9 |
+
初始树上有一颗棋子放在 $1$ 号节点。小 I 可以移动棋子,目标是将棋子移动到一个度数**恰好**为 $1$ 的节点上;小 J 可以关闭树上的边,目标是阻止小 I 将棋子移动到度数恰好为 $1$ 的节点上。
|
| 10 |
+
|
| 11 |
+
游戏分为若干轮,每轮有如下环节:
|
| 12 |
+
|
| 13 |
+
1. 小 I 任务判定:如果棋子在度数恰好为 $1$ 的节点上,小 I 获胜,否则进入第 2 步;
|
| 14 |
+
2. 小 J 行动:小 J 将一条目前开启的边,将这条边永久关闭,进入第 3 步,如果目前不存在开启的边则直接跳过行动进入第 3 步;
|
| 15 |
+
3. 小 I 行动:小 I 选择一条连接当前棋子所在节点且开启的边,将棋子移动到这条边的另一个节点上。如果没有这样的边,小 J 获胜,否则进入新的一轮,回到第 1 步。
|
| 16 |
+
|
| 17 |
+
小 J 想知道,如果小 I 和小 J 知道这棵树的形态且绝顶聪明,谁会获胜。
|
| 18 |
+
|
| 19 |
+
## 输入格式
|
| 20 |
+
|
| 21 |
+
第一行一个整数 $n (1 \le n \le 10^5)$ 表示树的节点数,接下来 $n-1$ 行每行两个整数 $u,v (1 \le u, v \le n)$,表示树上的一条边。
|
| 22 |
+
|
| 23 |
+
## 输出格式
|
| 24 |
+
|
| 25 |
+
如果小 I 获胜,输出 `You win, temporarily.`,否则输出 `Wasted.`。
|
| 26 |
+
|
| 27 |
+
## 样例 #1
|
| 28 |
+
|
| 29 |
+
### 样例输入 #1
|
| 30 |
+
|
| 31 |
+
```
|
| 32 |
+
6
|
| 33 |
+
1 2
|
| 34 |
+
2 3
|
| 35 |
+
2 4
|
| 36 |
+
1 5
|
| 37 |
+
5 6
|
| 38 |
+
```
|
| 39 |
+
|
| 40 |
+
### 样例输出 #1
|
| 41 |
+
|
| 42 |
+
```
|
| 43 |
+
Wasted.
|
| 44 |
+
```
|
| 45 |
+
|
| 46 |
+
## 样例 #2
|
| 47 |
+
|
| 48 |
+
### 样例输入 #2
|
| 49 |
+
|
| 50 |
+
```
|
| 51 |
+
7
|
| 52 |
+
1 2
|
| 53 |
+
2 3
|
| 54 |
+
2 4
|
| 55 |
+
1 5
|
| 56 |
+
5 6
|
| 57 |
+
5 7
|
| 58 |
+
```
|
| 59 |
+
|
| 60 |
+
### 样例输出 #2
|
| 61 |
+
|
| 62 |
+
```
|
| 63 |
+
You win, temporarily.
|
| 64 |
+
```
|
| 65 |
+
|
| 66 |
+
## 提示
|
| 67 |
+
|
| 68 |
+
【样例解释 1】
|
| 69 |
+
|
| 70 |
+
小 J 的策略如下:
|
| 71 |
+
|
| 72 |
+
- 小 J 将 $(1,2)$ 关闭,这样小 I 只能移动到 $5$;
|
| 73 |
+
- 小 J 将 $(5,6)$ 关闭,这样小 I 只得移动回 $1$;
|
| 74 |
+
- 小 J 将 $(1,5)$ 关闭,于是小 I 无法移动。
|
problems/1004.txt
ADDED
|
@@ -0,0 +1,49 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [NOIP2000 提高组] 方格取数
|
| 2 |
+
|
| 3 |
+
## 题目背景
|
| 4 |
+
|
| 5 |
+
NOIP 2000 提高组 T4
|
| 6 |
+
|
| 7 |
+
## 题目描述
|
| 8 |
+
|
| 9 |
+
设有 $N \times N$ 的方格图 $(N \le 9)$,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 $0$。如下图所示(见样例):
|
| 10 |
+
|
| 11 |
+
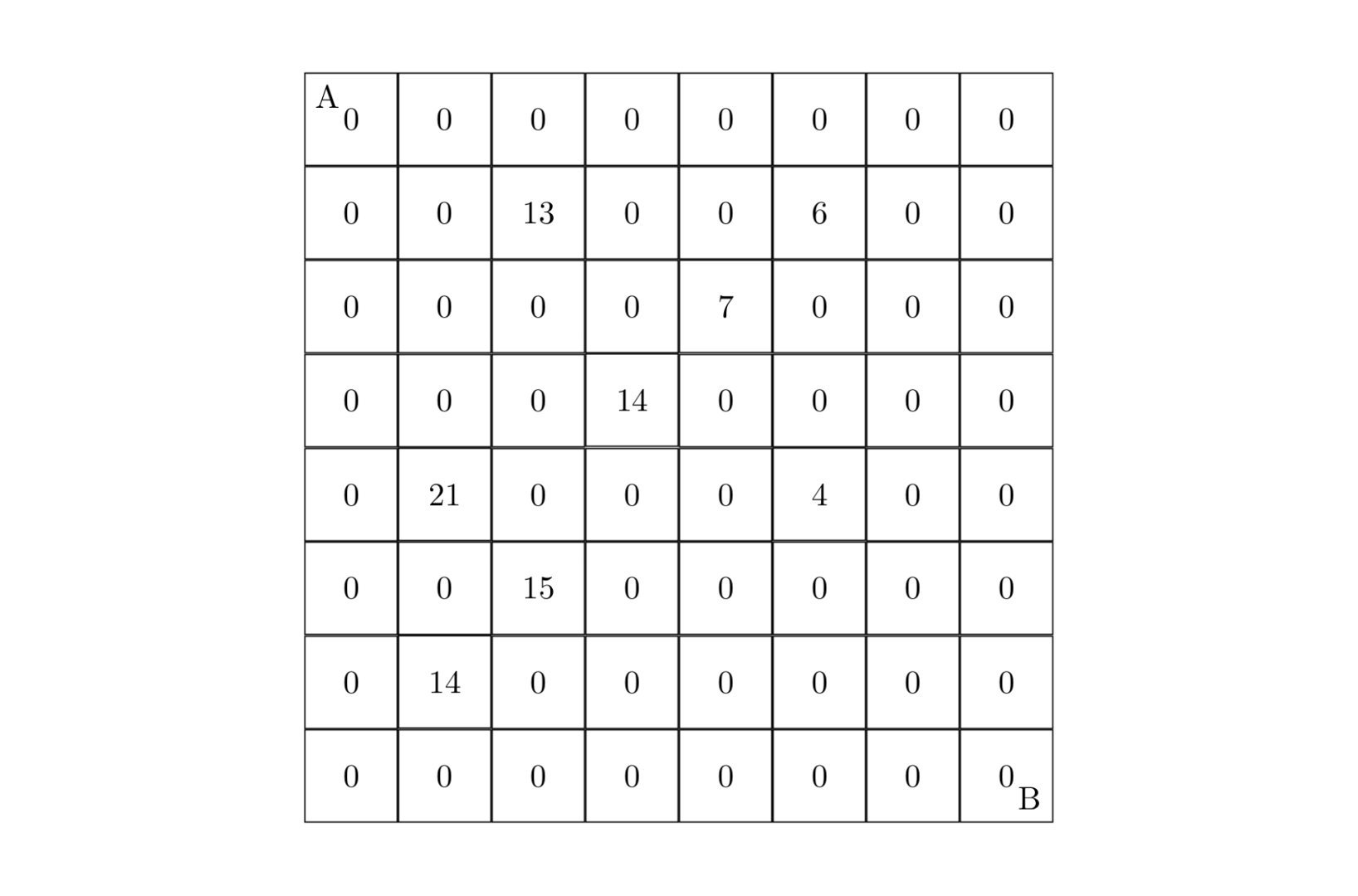
|
| 12 |
+
|
| 13 |
+
某人从图的左上角的 $A$ 点出发,可以向下行走,也可以向右走,直到到达右下角的 $B$ 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 $0$)。
|
| 14 |
+
此人从 $A$ 点到 $B$ 点共走两次,试找出 $2$ 条这样的路径,使得取得的数之和为最大。
|
| 15 |
+
|
| 16 |
+
## 输入格式
|
| 17 |
+
|
| 18 |
+
输入的第一行为一个整数 $N$(表示 $N \times N$ 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。
|
| 19 |
+
|
| 20 |
+
## 输出格式
|
| 21 |
+
|
| 22 |
+
只需输出一个整数,表示 $2$ 条路径上取得的最大的和。
|
| 23 |
+
|
| 24 |
+
## 样例 #1
|
| 25 |
+
|
| 26 |
+
### 样例输入 #1
|
| 27 |
+
|
| 28 |
+
```
|
| 29 |
+
8
|
| 30 |
+
2 3 13
|
| 31 |
+
2 6 6
|
| 32 |
+
3 5 7
|
| 33 |
+
4 4 14
|
| 34 |
+
5 2 21
|
| 35 |
+
5 6 4
|
| 36 |
+
6 3 15
|
| 37 |
+
7 2 14
|
| 38 |
+
0 0 0
|
| 39 |
+
```
|
| 40 |
+
|
| 41 |
+
### 样例输出 #1
|
| 42 |
+
|
| 43 |
+
```
|
| 44 |
+
67
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
## 提示
|
| 48 |
+
|
| 49 |
+
数据范围:$1\le N\le 9$。
|
problems/10040.txt
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 替换
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给定一个长度为 $n$、字符集为 `01?` 的字符串 $s_1s_2 \cdots s_n$。
|
| 6 |
+
|
| 7 |
+
对于任意 $k \in [1,n]$,考察字符串 $T_k = t_1 t_2 \cdots t_n$,其中对于 $1 \le i \le n$,
|
| 8 |
+
|
| 9 |
+
- 若 $s_i \ne$ `?`,则 $t_i = s_i$;
|
| 10 |
+
- 否则,若 $i \le k$,$t_i =$ `0`;
|
| 11 |
+
- 否则 $t_i = t_{i-k}$,你可以通过递归地算出 $t_{i-k}$ 得到 $t_i$。
|
| 12 |
+
|
| 13 |
+
容易发现 $T_k$ 的字符集为 `01`。你需要对所有 $k \in [1,n]$ 求出 $T_k$ 中 `1` 的个数。
|
| 14 |
+
|
| 15 |
+
## 输入格式
|
| 16 |
+
|
| 17 |
+
输入的第一行一个整数 $n (1 \le n \le 10^5)$ 表示字符串长度,第二行一个长度为 $n$、字符集为 `01?` 的字符串 $s_1s_2\cdots s_n$。
|
| 18 |
+
|
| 19 |
+
## 输出格式
|
| 20 |
+
|
| 21 |
+
输出 $n$ 行,第 $i$ 行一个整数表示 $T_i$ 中 `1` 的个数。
|
| 22 |
+
|
| 23 |
+
## 样例 #1
|
| 24 |
+
|
| 25 |
+
### 样例输入 #1
|
| 26 |
+
|
| 27 |
+
```
|
| 28 |
+
5
|
| 29 |
+
10?1?
|
| 30 |
+
```
|
| 31 |
+
|
| 32 |
+
### 样例输出 #1
|
| 33 |
+
|
| 34 |
+
```
|
| 35 |
+
3
|
| 36 |
+
4
|
| 37 |
+
2
|
| 38 |
+
3
|
| 39 |
+
2
|
| 40 |
+
```
|
| 41 |
+
|
| 42 |
+
## 提示
|
| 43 |
+
|
| 44 |
+
$T_1 =$ `10011`,$T_2 =$ `10111`,$T_3 =$ `10010`,$T_4 =$ `10011`,$T_5 =$ `10010`。
|
problems/10041.txt
ADDED
|
@@ -0,0 +1,54 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 史莱姆工厂
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
有 $n$ 个史莱姆排成一行,其中第 $i$ 个的颜色为 $c_i$,质量为 $m_i$。
|
| 6 |
+
|
| 7 |
+
你可以执行任意次把一个史莱姆的质量增加 $1$ 的操作,需要花费 $w$ 的价钱。
|
| 8 |
+
|
| 9 |
+
但是一旦史莱姆的质量达到 $k$ 或以上,就会变得不稳定而必须在下一次操作之前被卖掉。你只能卖出质量大于等于 $k$ 的史莱姆。根据市场价,卖掉一个质量为 $i$ 的史莱姆可以得到 $p_i$ 的收入。保证 $p_i-p_{i-1}<w$。但不保证 $p_i$ 单调不降。
|
| 10 |
+
|
| 11 |
+
卖掉一个史莱姆之后,它两边的史莱姆会被挤压继而靠在一起。如果这两个史莱姆颜色相同,那么就会互相融合成一个史莱姆,其质量是二者的质量之和。这个新的史莱姆也有可能需要被卖掉从而接着进行这个过程。
|
| 12 |
+
|
| 13 |
+
你想知道卖掉所有史莱姆最多可以净赚多少。
|
| 14 |
+
|
| 15 |
+
## 输入格式
|
| 16 |
+
|
| 17 |
+
第一行三个正整数 $n,k,w(1\le n\le 150, 2\le k\le 10, 1\le w\le 10^6)$。
|
| 18 |
+
|
| 19 |
+
第二行 $n$ 个正整数,其中第 $i$ 个表示 $c_i(1\le c_i\le n)$。保证 $c_i\not=c_{i-1}$。
|
| 20 |
+
|
| 21 |
+
第三行 $n$ 个正整数,其中第 $i$ 个表示 $m_i(1\le m_i<k)$。
|
| 22 |
+
|
| 23 |
+
第四行 $k-1$ 个整数,分别表示卖出质量为 $k$ 到 $2k-2$ 的史莱姆的收入,即 $p_k$ 到 $p_{2k-2}$,保证 $0\le p_i\le 10^9$,且 $p_i-p_{i-1}<w$。
|
| 24 |
+
|
| 25 |
+
保证相邻两个史莱姆的颜色不同。
|
| 26 |
+
|
| 27 |
+
## 输出格式
|
| 28 |
+
|
| 29 |
+
一行一个整数,表示卖出所有史莱姆最大的净利润。
|
| 30 |
+
|
| 31 |
+
## 样例 #1
|
| 32 |
+
|
| 33 |
+
### 样例输入 #1
|
| 34 |
+
|
| 35 |
+
```
|
| 36 |
+
4 5 6
|
| 37 |
+
2 1 2 3
|
| 38 |
+
3 3 3 4
|
| 39 |
+
5 7 9 11
|
| 40 |
+
```
|
| 41 |
+
|
| 42 |
+
### 样例输出 #1
|
| 43 |
+
|
| 44 |
+
```
|
| 45 |
+
-1
|
| 46 |
+
```
|
| 47 |
+
|
| 48 |
+
## 提示
|
| 49 |
+
|
| 50 |
+
先增加颜色为 $3$ 的史莱姆的质量。然后它被卖掉,获得 $5$ 的收入。
|
| 51 |
+
|
| 52 |
+
然后增加颜色为 $1$ 的史莱姆的质量两次。然后它被卖掉,获得 $5$ 的收入。接着两个颜色为 $2$ 的史莱姆融合在一起卖掉,获得 $7$ 的收入。
|
| 53 |
+
|
| 54 |
+
操作了三次需要 $18$ 的花费,所以净利润为 $-1$。可以证明不存在更好的方案。
|
problems/10042.txt
ADDED
|
@@ -0,0 +1,67 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 三染色
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
我有一个调色盘,总共 $n$ 行 $m$ 列,形成了 $n\times m$ 个格子,每个格子里要放一朵花。可以放置的花有 $3$ 种颜色可以选择,分别用 $0,1,2$ 表示。
|
| 6 |
+
|
| 7 |
+
花朵注视着它周围的花,并想要变成其他花朵的样子。如果在一个时刻,一朵颜色为 $c$ 的花的上、下、左、右之一,有至少一朵花的颜色为 $c-1$,那么这朵花在下一个时刻会变成颜色 $c-1$,否则它在下一个时刻的颜色仍然是 $c$。其中颜色 $\bmod 3$ 考虑。
|
| 8 |
+
|
| 9 |
+
对于一个初始的在调色盘中放花的方案,如果经过有限个时刻之后,所有花都变成同一颜色,我们称这个放花的方案是**美好的**。
|
| 10 |
+
|
| 11 |
+
不难看出,对于一个美好的放花方案,每朵花都有一个最早的时刻,它在这个时刻之后一直不变色。我们称这个时刻为这朵花的**稳定时刻**。
|
| 12 |
+
我们从第 $0$ 时刻开始计时,所以一朵花如果从未改变颜色,那么它的稳定时刻就是 $0$。
|
| 13 |
+
|
| 14 |
+
现在我已经在调色盘的一些格子中放置了花朵,也有一些格子是空的。我想知道,有多少种给剩余的格子放花的方案,使得这个方案是美好的?以及,对于这些美好的方案,位于第 1 行第 1 列格子中花朵的稳定时刻的总和是多少?
|
| 15 |
+
|
| 16 |
+
你只需要回答我这两个结果对 $998244353$ 取模的值。
|
| 17 |
+
|
| 18 |
+
## 输入格式
|
| 19 |
+
|
| 20 |
+
输入第一行为两个正整数 $n,m$($2 \le n \le 5$,$2 \le m \le 50$)。
|
| 21 |
+
|
| 22 |
+
接下来 $n$ 行,每一行 $m$ 个整数,第 $i$ 行第 $j$ 个整数 $a_{i,j}\in \{0,1,2,3\}$ 表示对应方格的状态。其中 $a_{i,j}\in \{0,1,2\}$ 表示有一朵花,以及这朵花的颜色,$a_{i,j}=3$ 表示没有花。
|
| 23 |
+
|
| 24 |
+
## 输出格式
|
| 25 |
+
|
| 26 |
+
输出一行两个整数,表示美好的方案数,和左上角格子中花朵稳定时刻的总和。
|
| 27 |
+
|
| 28 |
+
## 样例 #1
|
| 29 |
+
|
| 30 |
+
### 样例输入 #1
|
| 31 |
+
|
| 32 |
+
```
|
| 33 |
+
2 2
|
| 34 |
+
1 0
|
| 35 |
+
3 2
|
| 36 |
+
```
|
| 37 |
+
|
| 38 |
+
### 样例输出 #1
|
| 39 |
+
|
| 40 |
+
```
|
| 41 |
+
1 2
|
| 42 |
+
```
|
| 43 |
+
|
| 44 |
+
## 样例 #2
|
| 45 |
+
|
| 46 |
+
### 样例输入 #2
|
| 47 |
+
|
| 48 |
+
```
|
| 49 |
+
5 5
|
| 50 |
+
3 3 3 3 2
|
| 51 |
+
2 3 3 3 1
|
| 52 |
+
1 3 3 3 3
|
| 53 |
+
3 3 3 3 3
|
| 54 |
+
3 3 3 3 3
|
| 55 |
+
```
|
| 56 |
+
|
| 57 |
+
### 样例输出 #2
|
| 58 |
+
|
| 59 |
+
```
|
| 60 |
+
50830224 170059345
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
## 提示
|
| 64 |
+
|
| 65 |
+
**【样例解释 1】**
|
| 66 |
+
|
| 67 |
+
只有在未知格子放入花朵颜色为 $0$ 的时候会结束,并且在两个时刻之后所有花朵的颜色全部变为 $2$,此时左上角方格中的花朵颜色变成 $2$ 并不再改变,因此它的稳定时刻就是 $2$。
|
problems/10043.txt
ADDED
|
@@ -0,0 +1,51 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 广播
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
小 I 正在学习使用 Pytorch。这是一个非常热门的用于机器学习训练的 Python 库。
|
| 6 |
+
|
| 7 |
+
小 I 注意到,Pytorch 中对于张量运算有称作“广播”(broadcast)的机制。你可以认为张量是高维数组。对于一个 $k$ 维张量 $A$,我们用长度为 $k$ 的序列 $(a_1,a_2,\cdots,a_k)$ 表示其各个维度的长度,也就是说 $A$ 是一个 $a_1 \times a_2 \times \cdots \times a_k$ 的张量。
|
| 8 |
+
|
| 9 |
+
对于两个张量 $A$ 和 $B$,设它们的维度分别为 $(a_1,a_2,\cdots,a_m)$ 和 $(b_1,b_2,\cdots,b_n)$,称 $A$ 和 $B$ 是 **可广播的**,当且仅当以下性质成立:
|
| 10 |
+
|
| 11 |
+
- 对于任意整数 $0 \le i \le \min(n,m) - 1$,要么 $a_{m-i} = b_{n-i}$,要么 $a_{m-i}$ 和 $b_{n-i}$ 中至少有一个是 $1$。
|
| 12 |
+
|
| 13 |
+
现在小 I 有两个张量,它们的维度分别是 $(p_1,p_2,\cdots,p_m)$ 和 $(q_1,q_2,\cdots,q_n)$,它们不一定是可广播的。
|
| 14 |
+
|
| 15 |
+
为此,小 I 可以使用 Pytorch 内置的函数进行若干次操作(可以不做操作),每次操作对序列 $p$ 或 $q$ 进行以下修改:
|
| 16 |
+
|
| 17 |
+
- 选择 $p$ 或 $q$,在选定序列的任意一个位置插入一个 $1$。
|
| 18 |
+
|
| 19 |
+
小 I 想知道他最少要多少次操作才能让两个张量变为可广播的。
|
| 20 |
+
|
| 21 |
+
## 输入格式
|
| 22 |
+
|
| 23 |
+
输入的第一行两个整数 $m,n(1 \le m,n \le 2000)$ 表示两个张量的维度。
|
| 24 |
+
|
| 25 |
+
第二行 $m$ 个整数 $p_1,p_2,\cdots,p_m (1 \le p_i \le 2000)$ 描述第一个张量每个维度的长度。
|
| 26 |
+
|
| 27 |
+
第三行 $n$ 个整数 $q_1,q_2,\cdots,q_n (1 \le q_i \le 2000)$ 描述第二个张量每个维度的长度。
|
| 28 |
+
|
| 29 |
+
## 输出格式
|
| 30 |
+
|
| 31 |
+
输入一行一个整数表示最少的插入 $1$ 的数量使得两个张量变为可广播的。
|
| 32 |
+
|
| 33 |
+
## 样例 #1
|
| 34 |
+
|
| 35 |
+
### 样例输入 #1
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
4 2
|
| 39 |
+
2 1 3 2
|
| 40 |
+
4 2
|
| 41 |
+
```
|
| 42 |
+
|
| 43 |
+
### 样例输出 #1
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
1
|
| 47 |
+
```
|
| 48 |
+
|
| 49 |
+
## 提示
|
| 50 |
+
|
| 51 |
+
在序列 $q$ 的第二个位置之前插入一个 $1$(得到 `4 1 2`),两个张量就会变为可广播的。
|
problems/10044.txt
ADDED
|
@@ -0,0 +1,78 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 最小环
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
小 I 发明了 $O(n + m)$ 的有向图最小环,于是他想考考你。
|
| 6 |
+
|
| 7 |
+
给定一个 $n$ 个节点、$m$ 条边的有向图,每条边有正整数边权。你需要求出图上的一个环使得环上边的边权和最小。求出这个最小值,或者报告不存在环。
|
| 8 |
+
|
| 9 |
+
当然,由于你不会 $O(n + m)$ 的有向图最小环,于是小 I 放宽了条件:保证输入的图是弱连通的,且 $m-n$ 不会很大。一个图是弱连通的当且仅当将有向边换为无向边后图连通。
|
| 10 |
+
|
| 11 |
+
## 输入格式
|
| 12 |
+
|
| 13 |
+
第一行两个整数 $n,m (1 \le n \le 3 \times 10^5, -1 \le m-n \le 1500)$,表示图的点数和边数。
|
| 14 |
+
|
| 15 |
+
接下来 $m$ 行每行三个整数 $u_i,v_i,w_i (1 \le u_i,v_i \le n, 1 \le w_i \le 10^9)$,表示一条从 $u_i$ 到 $v_i$、边权为 $w_i$ 的有向边。保证图是弱连通的。
|
| 16 |
+
|
| 17 |
+
## 输出格式
|
| 18 |
+
|
| 19 |
+
如果图中不存在环,输出 `-1`,否则输出一个整数表示最小环的长度和。
|
| 20 |
+
|
| 21 |
+
## 样例 #1
|
| 22 |
+
|
| 23 |
+
### 样例输入 #1
|
| 24 |
+
|
| 25 |
+
```
|
| 26 |
+
4 6
|
| 27 |
+
1 2 1
|
| 28 |
+
4 3 3
|
| 29 |
+
4 1 9
|
| 30 |
+
2 4 1
|
| 31 |
+
3 1 2
|
| 32 |
+
3 2 6
|
| 33 |
+
```
|
| 34 |
+
|
| 35 |
+
### 样例输出 #1
|
| 36 |
+
|
| 37 |
+
```
|
| 38 |
+
7
|
| 39 |
+
```
|
| 40 |
+
|
| 41 |
+
## 样例 #2
|
| 42 |
+
|
| 43 |
+
### 样例输入 #2
|
| 44 |
+
|
| 45 |
+
```
|
| 46 |
+
1 0
|
| 47 |
+
```
|
| 48 |
+
|
| 49 |
+
### 样例输出 #2
|
| 50 |
+
|
| 51 |
+
```
|
| 52 |
+
-1
|
| 53 |
+
```
|
| 54 |
+
|
| 55 |
+
## 样例 #3
|
| 56 |
+
|
| 57 |
+
### 样例输入 #3
|
| 58 |
+
|
| 59 |
+
```
|
| 60 |
+
1 1
|
| 61 |
+
1 1 1
|
| 62 |
+
```
|
| 63 |
+
|
| 64 |
+
### 样例输出 #3
|
| 65 |
+
|
| 66 |
+
```
|
| 67 |
+
1
|
| 68 |
+
```
|
| 69 |
+
|
| 70 |
+
## 提示
|
| 71 |
+
|
| 72 |
+
**【样例解释 1】**
|
| 73 |
+
|
| 74 |
+
最小环为 $1 \to 2 \to 4 \to 3 \to 1$。
|
| 75 |
+
|
| 76 |
+
**【样例解释 3】**
|
| 77 |
+
|
| 78 |
+
最小环为 $1 \to 1$。
|
problems/10045.txt
ADDED
|
@@ -0,0 +1,56 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 线段树
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
有一个长度为 $n$ 的序列 $a_1,a_2,\cdots,a_n$,保证 $a_i$ 为**奇数**。
|
| 6 |
+
|
| 7 |
+
有两种操作:
|
| 8 |
+
|
| 9 |
+
1. 给定 $l,r,x$,将 $a_l,a_{l+1},\cdots,a_r$ 加上**偶数** $x$;
|
| 10 |
+
|
| 11 |
+
2. 给定 $l,r$,求 $a_l,a_{l+1},\cdots,a_r$ 的乘积,答案对 $2^{20}$ 取模;
|
| 12 |
+
|
| 13 |
+
## 输入格式
|
| 14 |
+
|
| 15 |
+
第一行两个正整数 $n,q$ 表示序列的长度和询问的个数. 保证 $1 \le n,q \le 2\times 10^5$。
|
| 16 |
+
|
| 17 |
+
第二行 $n$ 个**奇数** $a_1,a_2,\cdots,a_n$. 保证 $1 \le a_i < 2^{20}$。
|
| 18 |
+
|
| 19 |
+
接下来 $q$ 行,每一行表示一个操作,格式为以下两种之一:
|
| 20 |
+
|
| 21 |
+
- $1 ~ l ~ r ~ x$:表示进行第一种操作. 保证 $1 \le l \le r \le n$,$0 \le x < 2 ^ {20}$。
|
| 22 |
+
- $2 ~ l ~ r$:表示进行第二种操作. 保证 $1 \le l \le r \le n$。
|
| 23 |
+
|
| 24 |
+
## 输出格式
|
| 25 |
+
|
| 26 |
+
对于每一次 $2$ 操作,输出一行一个整数表示答案。
|
| 27 |
+
|
| 28 |
+
## 样例 #1
|
| 29 |
+
|
| 30 |
+
### 样例输入 #1
|
| 31 |
+
|
| 32 |
+
```
|
| 33 |
+
10 10
|
| 34 |
+
969575 741825 24903 1047319 450475 256145 1045323 479255 810659 768323
|
| 35 |
+
1 5 6 3034
|
| 36 |
+
2 1 10
|
| 37 |
+
2 1 9
|
| 38 |
+
2 1 4
|
| 39 |
+
1 3 6 126904
|
| 40 |
+
2 5 5
|
| 41 |
+
2 9 9
|
| 42 |
+
1 7 7 853094
|
| 43 |
+
1 4 9 1025178
|
| 44 |
+
2 5 8
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
### 样例输出 #1
|
| 48 |
+
|
| 49 |
+
```
|
| 50 |
+
1045541
|
| 51 |
+
1012343
|
| 52 |
+
558151
|
| 53 |
+
580413
|
| 54 |
+
810659
|
| 55 |
+
527353
|
| 56 |
+
```
|
problems/10046.txt
ADDED
|
@@ -0,0 +1,39 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 哈密顿
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
给出 $n$ 个二元组 $(a_i,b_i)$。
|
| 6 |
+
|
| 7 |
+
考虑 $n$ 个节点的带权有向完全图 $G$,其中从 $i (1 \le i \le n)$ 到 $j (1 \le j \le n)$ 的边边权为 $|a_i-b_j|$。
|
| 8 |
+
|
| 9 |
+
求 $G$ 的一条哈密顿回路使得其经过的边的边权和最大,并给出这个最大值。
|
| 10 |
+
|
| 11 |
+
## 输入格式
|
| 12 |
+
|
| 13 |
+
输入的第一行一个整数 $n(2 \le n \le 10^5)$ 表示二元组个数,接下来 $n$ 行每行两个整数 $a_i,b_i(0 \le a_i,b_i \le 10^9)$ 表示每个二元组。保证输入的 $n$ 个二元组中的总共 $2n$ 个数两两不同。
|
| 14 |
+
|
| 15 |
+
## 输出格式
|
| 16 |
+
|
| 17 |
+
输出一行一个整数表示最大的哈密顿回路边权和。
|
| 18 |
+
|
| 19 |
+
## 样例 #1
|
| 20 |
+
|
| 21 |
+
### 样例输入 #1
|
| 22 |
+
|
| 23 |
+
```
|
| 24 |
+
3
|
| 25 |
+
1 10
|
| 26 |
+
8 2
|
| 27 |
+
4 5
|
| 28 |
+
```
|
| 29 |
+
|
| 30 |
+
### 样例输出 #1
|
| 31 |
+
|
| 32 |
+
```
|
| 33 |
+
10
|
| 34 |
+
```
|
| 35 |
+
|
| 36 |
+
## 提示
|
| 37 |
+
|
| 38 |
+
考察哈密顿回路 $1 \to 2 \to 3 \to 1$,其边权和为 $|1-2| + |
|
| 39 |
+
8-5| + |4-10| = 10$。可以证明不存在哈密顿回路边权和超过 $10$,因此答案为 $10$。
|
problems/10047.txt
ADDED
|
@@ -0,0 +1,95 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# [CCPC 2023 北京市赛] 勿蹖宠物
|
| 2 |
+
|
| 3 |
+
## 题目描述
|
| 4 |
+
|
| 5 |
+
Ene 喜欢回文。
|
| 6 |
+
|
| 7 |
+
Ene 现在有一些单词。她想选出若干个单词并将它们首尾相连,形成长度恰好为 $L$ 的回文串。每个单词都可以选择多次,也可以不选。
|
| 8 |
+
|
| 9 |
+
Ene 想知道这样做的方案数。Ene 认为两个方案不同,当且仅当各单词出现次数不同或它们的排列顺序不同,注意多种不同的方案可能会得到同一个回文串。由于答案可能会很大,你需要将答案对 $1,000,000,007$ 取模。
|
| 10 |
+
|
| 11 |
+
## 输入格式
|
| 12 |
+
|
| 13 |
+
输入的第一行包含两个正整数 $N, L$,分别表示单词的数量和需要组成的回文串的长度。保证 $1\le N\le 333$,$1\le L\le 1000$。
|
| 14 |
+
|
| 15 |
+
接下来 $N$ 行,每行输入一个字符串 $s_i$,表示一个单词。保证 $1\le |s_i| \le L$,$\sum_{i=1}^N |s_i| \le 600$;输入的单词仅包含小写字符,且互不相同。
|
| 16 |
+
|
| 17 |
+
## 输出格式
|
| 18 |
+
|
| 19 |
+
输出一个非负整数,表示组成回文串的方案数对 $1,000,000,007$ 取模后的结果。
|
| 20 |
+
|
| 21 |
+
## 样例 #1
|
| 22 |
+
|
| 23 |
+
### 样例输入 #1
|
| 24 |
+
|
| 25 |
+
```
|
| 26 |
+
7 9
|
| 27 |
+
cats
|
| 28 |
+
eel
|
| 29 |
+
eve
|
| 30 |
+
evil
|
| 31 |
+
lee
|
| 32 |
+
olive
|
| 33 |
+
stack
|
| 34 |
+
```
|
| 35 |
+
|
| 36 |
+
### 样例输出 #1
|
| 37 |
+
|
| 38 |
+
```
|
| 39 |
+
5
|
| 40 |
+
```
|
| 41 |
+
|
| 42 |
+
## 样例 #2
|
| 43 |
+
|
| 44 |
+
### 样例输入 #2
|
| 45 |
+
|
| 46 |
+
```
|
| 47 |
+
2 2
|
| 48 |
+
a
|
| 49 |
+
aa
|
| 50 |
+
```
|
| 51 |
+
|
| 52 |
+
### 样例输出 #2
|
| 53 |
+
|
| 54 |
+
```
|
| 55 |
+
2
|
| 56 |
+
```
|
| 57 |
+
|
| 58 |
+
## 样例 #3
|
| 59 |
+
|
| 60 |
+
### 样例输入 #3
|
| 61 |
+
|
| 62 |
+
```
|
| 63 |
+
6 12
|
| 64 |
+
aa
|
| 65 |
+
aab
|
| 66 |
+
no
|
| 67 |
+
on
|
| 68 |
+
pets
|
| 69 |
+
step
|
| 70 |
+
```
|
| 71 |
+
|
| 72 |
+
### 样例输出 #3
|
| 73 |
+
|
| 74 |
+
```
|
| 75 |
+
43
|
| 76 |
+
```
|
| 77 |
+
|
| 78 |
+
## 提示
|
| 79 |
+
|
| 80 |
+
**【样例解释 1】**
|
| 81 |
+
|
| 82 |
+
有以下五种方案:
|
| 83 |
+
|
| 84 |
+
- `stack` `cats`
|
| 85 |
+
- `evil` `olive`
|
| 86 |
+
- `eel` `eve` `lee`
|
| 87 |
+
- `lee` `eve` `eel`
|
| 88 |
+
- `eve` `eve` `eve`
|
| 89 |
+
|
| 90 |
+
**【样例解释 2】**
|
| 91 |
+
|
| 92 |
+
有以下两种方案:
|
| 93 |
+
|
| 94 |
+
- `a` `a`
|
| 95 |
+
- `aa`
|