add segmented data for Nordic MO (1987 - 2024)
Browse files- Nordic_MO/download_script/download.py +77 -0
- Nordic_MO/md/en-1987-2011-sol.md +0 -0
- Nordic_MO/md/en-2012-sol.md +142 -0
- Nordic_MO/md/en-2013-sol.md +136 -0
- Nordic_MO/md/en-2014-sol.md +123 -0
- Nordic_MO/md/en-2015-sol.md +87 -0
- Nordic_MO/md/en-2016-sol.md +86 -0
- Nordic_MO/md/en-2017-sol.md +133 -0
- Nordic_MO/md/en-2018-sol.md +70 -0
- Nordic_MO/md/en-2019-sol.md +103 -0
- Nordic_MO/md/en-2021-sol.md +83 -0
- Nordic_MO/md/en-2022-sol.md +116 -0
- Nordic_MO/md/en-2024-sol.md +207 -0
- Nordic_MO/raw/en-1987-2011-sol.pdf +3 -0
- Nordic_MO/raw/en-2012-sol.pdf +3 -0
- Nordic_MO/raw/en-2013-sol.pdf +3 -0
- Nordic_MO/raw/en-2014-sol.pdf +3 -0
- Nordic_MO/raw/en-2015-sol.pdf +3 -0
- Nordic_MO/raw/en-2016-sol.pdf +3 -0
- Nordic_MO/raw/en-2017-sol.pdf +3 -0
- Nordic_MO/raw/en-2018-sol.pdf +3 -0
- Nordic_MO/raw/en-2019-sol.pdf +3 -0
- Nordic_MO/raw/en-2021-sol.pdf +3 -0
- Nordic_MO/raw/en-2022-sol.pdf +3 -0
- Nordic_MO/raw/en-2024-sol.pdf +3 -0
- Nordic_MO/segment_script/segment.py +157 -0
- Nordic_MO/segment_script/segment_1987_2011.py +158 -0
- Nordic_MO/segment_script/segment_2014.py +157 -0
- Nordic_MO/segmented/en-1987-2011-sol.jsonl +0 -0
- Nordic_MO/segmented/en-2012-sol.jsonl +6 -0
- Nordic_MO/segmented/en-2013-sol.jsonl +4 -0
- Nordic_MO/segmented/en-2014-sol.jsonl +4 -0
- Nordic_MO/segmented/en-2015-sol.jsonl +7 -0
- Nordic_MO/segmented/en-2016-sol.jsonl +4 -0
- Nordic_MO/segmented/en-2017-sol.jsonl +4 -0
- Nordic_MO/segmented/en-2019-sol.jsonl +4 -0
- Nordic_MO/segmented/en-2021-sol.jsonl +1 -0
- Nordic_MO/segmented/en-2022-sol.jsonl +5 -0
- Nordic_MO/segmented/en-2024-sol.jsonl +5 -0
Nordic_MO/download_script/download.py
ADDED
|
@@ -0,0 +1,77 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-12-18
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download script for Nordic MO
|
| 7 |
+
To run:
|
| 8 |
+
`python Nordic_MO/download_script/download.py`
|
| 9 |
+
'''
|
| 10 |
+
|
| 11 |
+
import requests
|
| 12 |
+
from bs4 import BeautifulSoup
|
| 13 |
+
from tqdm import tqdm
|
| 14 |
+
from pathlib import Path
|
| 15 |
+
from requests.adapters import HTTPAdapter
|
| 16 |
+
from urllib3.util.retry import Retry
|
| 17 |
+
from urllib.parse import urljoin
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
def build_session(
|
| 21 |
+
max_retries: int = 3,
|
| 22 |
+
backoff_factor: int = 2,
|
| 23 |
+
session: requests.Session = None
|
| 24 |
+
) -> requests.Session:
|
| 25 |
+
"""
|
| 26 |
+
Build a requests session with retries
|
| 27 |
+
|
| 28 |
+
Args:
|
| 29 |
+
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 30 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 31 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 32 |
+
"""
|
| 33 |
+
session = session or requests.Session()
|
| 34 |
+
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 35 |
+
session.mount("http://", adapter)
|
| 36 |
+
session.mount("https://", adapter)
|
| 37 |
+
session.headers.update({
|
| 38 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 39 |
+
})
|
| 40 |
+
|
| 41 |
+
return session
|
| 42 |
+
|
| 43 |
+
|
| 44 |
+
def main():
|
| 45 |
+
base_url = "https://www.georgmohr.dk/nmcperm/probl/"
|
| 46 |
+
req_session = build_session()
|
| 47 |
+
|
| 48 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 49 |
+
output_dir.mkdir(parents=True, exist_ok=True)
|
| 50 |
+
|
| 51 |
+
resp = req_session.get(base_url)
|
| 52 |
+
soup = BeautifulSoup(resp.text, 'html.parser')
|
| 53 |
+
|
| 54 |
+
sol_list = soup.find_all('a', href=lambda x: x and x.endswith('sol.pdf'))
|
| 55 |
+
sol_url = [ele["href"] for ele in sol_list]
|
| 56 |
+
|
| 57 |
+
for url in tqdm(sol_url):
|
| 58 |
+
if (not url.startswith("all")) and int(url.split('/')[0]) <= 2011:
|
| 59 |
+
continue
|
| 60 |
+
|
| 61 |
+
output_file = output_dir / f"en-{'-'.join(url.split('/')).replace('all+sol', '1987-2011-sol')}"
|
| 62 |
+
|
| 63 |
+
# Check if the file already exists
|
| 64 |
+
if output_file.exists():
|
| 65 |
+
continue
|
| 66 |
+
|
| 67 |
+
pdf_resp = req_session.get(urljoin(base_url, url))
|
| 68 |
+
|
| 69 |
+
if pdf_resp.status_code != 200:
|
| 70 |
+
print(f"Failed to download {url}")
|
| 71 |
+
continue
|
| 72 |
+
|
| 73 |
+
output_file.write_bytes(pdf_resp.content)
|
| 74 |
+
|
| 75 |
+
|
| 76 |
+
if __name__ == "__main__":
|
| 77 |
+
main()
|
Nordic_MO/md/en-1987-2011-sol.md
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
Nordic_MO/md/en-2012-sol.md
ADDED
|
@@ -0,0 +1,142 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 26th Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
Tuesday, 27 March 2012
|
| 4 |
+
|
| 5 |
+
## Solutions
|
| 6 |
+
|
| 7 |
+
Each problem is worth 5 points.
|
| 8 |
+
|
| 9 |
+
PROBLEM 1. The real numbers $a, b, c$ are such that $a^{2}+b^{2}=2 c^{2}$, and also such that $a \neq b, c \neq-a, c \neq-b$. Show that
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\frac{(a+b+2 c)\left(2 a^{2}-b^{2}-c^{2}\right)}{(a-b)(a+c)(b+c)}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
is an integer.
|
| 16 |
+
|
| 17 |
+
SolUTiON. Let us first note that
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\frac{a+b+2 c}{(a+c)(b+c)}=\frac{(a+c)+(b+c)}{(a+c)(b+c)}=\frac{1}{a+c}+\frac{1}{b+c}
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Further we have
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
2 a^{2}-b^{2}-c^{2}=2 a^{2}-\left(2 c^{2}-a^{2}\right)-c^{2}=3 a^{2}-3 c^{2}=3(a+c)(a-c)
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
and
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
2 a^{2}-b^{2}-c^{2}=2\left(2 c^{2}-b^{2}\right)-b^{2}-c^{2}=3 c^{2}-3 b^{2}=3(b+c)(c-b)
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
so that
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
\frac{(a+b+2 c)\left(2 a^{2}-b^{2}-c^{2}\right)}{(a-b)(a+c)(b+c)}=\frac{3(a-c)+3(c-b)}{a-b}=\frac{3(a-b)}{a-b}=3
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
an integer.
|
| 42 |
+
|
| 43 |
+
Problem 2. Given a triangle $A B C$, let $P$ lie on the circumcircle of the triangle and be the midpoint of the arc $B C$ which does not contain $A$. Draw a straight line $l$ through $P$ so that $l$ is parallel to $A B$. Denote by $k$ the circle which passes through $B$, and is tangent to $l$ at the point $P$. Let $Q$ be the second point of intersection of $k$ and the line $A B$ (if there is no second point of intersection, choose $Q=B)$. Prove that $A Q=A C$.
|
| 44 |
+
|
| 45 |
+
Solution I. There are three possibilities: $Q$ between $A$ and $B, Q=B$, and $B$ between $A$ and $Q$. If $Q=B$ we have that $\angle A B P$ is right, and $A P$ is a diameter
|
| 46 |
+
of the circumcircle. The triangles $A B P$ and $A C P$ are then congruent (they have $A P$ in common, $P B=P C$, and both have a right angle opposite to $A P$ ). Hence ir follows that $A B=A C$.
|
| 47 |
+
|
| 48 |
+
The solutions in the other two cases are very similar. We present the one in the case when $Q$ lies between $A$ and $B$.
|
| 49 |
+
|
| 50 |
+
The segment $A P$ is the angle bisector of the angle at $A$, since $P$ is the midpoint of the arc $B C$ of the circumcircle which does not contain $A$. Also, $P C=P B$. Since the segment $Q B$ is parallel to the tangent to $k$ at $P$, it is orthogonal to the diameter of $k$ through $P$. Thus this diameter cuts $Q B$ in halves, to form two congruent right triangles, and it follows that $P Q=P B$. We have (in the usual notation) $\angle P C B=\angle P B C=\frac{\alpha}{2}$, and
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\angle A Q P=180^{\circ}-\angle B Q P=180^{\circ}-\angle Q B P=180^{\circ}-\beta-\frac{\alpha}{2}=\frac{\alpha}{2}+\gamma=\angle A C P
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
Hence the triangles $A Q P$ and $A C P$ are congruent (two pairs of equal angles and one pair of equal corresponding sides), and it follows that $A C=A Q$.
|
| 57 |
+
|
| 58 |
+
Solution II. Again we consider the case when $Q$ is between $A$ and $B$. We shall use trigonometry. As above, we have $\angle A B P=\beta+\frac{\alpha}{2}$, and thus
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
Q B=2 P B \cos \left(\beta+\frac{\alpha}{2}\right)=2 P B \cos \left(\pi-\frac{\alpha}{2}-\gamma\right)
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
and
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
A Q=2 R \sin \gamma-4 R \sin \frac{\alpha}{2} \cos \left(\pi-\frac{\alpha}{2}-\gamma\right)
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Since $A C=2 R \cos \beta$, it remains to prove that
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
\sin \beta=\sin \gamma+2 \sin \frac{\alpha}{2} \cos \left(\frac{\alpha}{2}+\gamma\right)
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
which is easy, using standard trigonometry.
|
| 77 |
+
|
| 78 |
+
Problem 3. Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \ldots, x_{n}$ (not necessarily different), with $1 \leq x_{k} \leq n, 1 \leq k \leq n$, and such that
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}, \quad \text { and } \quad x_{1} x_{2} \cdots x_{n}=n!
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
but $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} \neq\{1,2, \ldots, n\}$.
|
| 85 |
+
|
| 86 |
+
Solution. If it is possible to find a set of numbers as required for some $n=k$, then it will also be possible for $n=k+1$ (choose $x_{1}, \ldots, x_{k}$ as for $n=k$, and
|
| 87 |
+
let $x_{k+1}=k+1$ ). Thus we have to find a positive integer $n$ such that a set as required exists, and prove that such a set does not exist for $n-1$.
|
| 88 |
+
|
| 89 |
+
For $n=9$ we have $8+6+3=9+4+4$, and $8 \cdot 6 \cdot 3=9 \cdot 4 \cdot 4$, so that a set of numbers as required will exist for all $n \geq 9$. It remains to eliminate $n=8$.
|
| 90 |
+
|
| 91 |
+
Assume $x_{1}, \ldots, x_{8}$ are numbers that satisfy the conditions of the problem. Since 5 and 7 are primes, and since $2 \cdot 5>8$ and $2 \cdot 7>8$, two of the $x$-numbers have to be equal to 5 and 7 ; without loss of generality we can assume that $x_{1}=5, x_{2}=7$. For the remaining numbers we have $x_{3} x_{4} \cdots x_{8}=2^{7} \cdot 3^{2}$, and $x_{3}+x_{4}+\cdots+x_{8}=36-12=24$. Since $3^{2}=9>8$, it follows that exactly two of the numbers $x_{3}, \ldots, x_{8}$ are divisible by 3 , and the rest of the numbers are powers of 2. There are three possible cases to consider: two of the numbers are equal to 3 ; two of the numbers are equal to 6 ; one number is equal to 3 and another one is equal to 6 .
|
| 92 |
+
|
| 93 |
+
Case 1. $x_{3}=x_{4}=3$
|
| 94 |
+
|
| 95 |
+
We then have $x_{5}+x_{6}+x_{7}+x_{8}=18$, and $x_{5} x_{6} x_{7} x_{8}=2^{7}$. The possible powers of 2 with sum 18 are $(1,1,8,8)$ and $(2,4,4,8)$, none of them gives the product $2^{7}$.
|
| 96 |
+
|
| 97 |
+
Case 2. $x_{3}=3, x_{4}=6$
|
| 98 |
+
|
| 99 |
+
We have $x_{5}+x_{6}+x_{7}+x_{8}=15$, and $x_{5} x_{6} x_{7} x_{8}=2^{6}$. It is immediate to check that the only possibility for the remaining numbers is $(1,2,4,8)$, which is not allowed, since it gives $\left\{x_{1}, x_{2}, \ldots, x_{8}\right\}=\{1,2, \ldots, 8\}$.
|
| 100 |
+
|
| 101 |
+
Case 3. $x_{3}=x_{4}=6$
|
| 102 |
+
|
| 103 |
+
Now we have $x_{5}+x_{6}+x_{7}+x_{8}=12$, and $x_{5} x_{6} x_{7} x_{8}=2^{5}$. The possible powers of 2 which give the correct sum are $(1,1,2,8)$ and $(2,2,4,4)$, but again, they do not give the desired product.
|
| 104 |
+
|
| 105 |
+
Thus the smallest positive integer with the required property is 9 .
|
| 106 |
+
|
| 107 |
+
Problem 4. The number 1 is written on the blackboard. After that a sequence of numbers is created as follows: at each step each number $a$ on the blackboard is replaced by the numbers $a-1$ and $a+1$; if the number 0 occurs, it is erased immediately; if a number occurs more than once, all its occurrences are left on the blackboard. Thus the blackboard will show 1 after 0 steps; 2 after 1 step; 1,3 after 2 steps; 2, 2, 4 after 3 steps, and so on. How many numbers will there be on the blackboard after $n$ steps?
|
| 108 |
+
|
| 109 |
+
Solution I. Let $S$ be a set of different numbers, all of them less than $2^{n-1}$, and create two new sets as follows: $S_{1}$, consisting of all the numbers in $S$ except
|
| 110 |
+
the smallest one, and $S_{2}$, with elements the smallest element of $S$ and all the numbers we get by adding $2^{n-1}$ to each number in $S$. Note that if the number of elements in $S$ is $a$, then $S_{1}$ has $a-1$ elements, and $S_{2}$ has $a+1$ elements. This corresponds to the operations we are allowed to perform on the blackboard, if we throw away all empty sets. If we now operate simultaneously on the sets and on the numbers, then after $n$ steps the number of sets will be exactly equal to the number of numbers on the blackboard.
|
| 111 |
+
|
| 112 |
+
Let us see what the set operations look like. We must start with a set, consisting only of the number 0 . Next we get an empty set (thrown away), and the set $\{0,1\}$; next the sets $\{1\}$ and $\{0,2,3\}$; next again (an empty set and) $\{1,5\},\{2,3\},\{0,4,6,7\}$, etc.
|
| 113 |
+
|
| 114 |
+
It is now fairly easy to prove by induction that after $n$ steps
|
| 115 |
+
|
| 116 |
+
(1) each number less than $2^{n}$ appears in exactly one set;
|
| 117 |
+
|
| 118 |
+
(2) the number of elements in the sets corresponds exactly to the numbers on the blackboard;
|
| 119 |
+
|
| 120 |
+
(3) if the numbers in each set are written in increasing order, then the difference between two neighbours is a power of 2 ; thus the binary representations of two neighbours differ in exactly one position (in the binary system the example above looks like this: $\{0\} ;\{0,1\} ;\{01\},\{00,10,11\} ;\{001,101\},\{010,011\}$, $\{000,100,110,111\}) ;$
|
| 121 |
+
|
| 122 |
+
(4) if $k$ is the number of ones in the binary code of the smallest number of a set, and $l$ the number of ones in the largest number of the same set, then $k+l=n$; (5) each set contains exactly one number with $\left\lfloor\frac{n}{2}\right\rfloor$ ones.
|
| 123 |
+
|
| 124 |
+
The last property tells us that the number of sets after $n$ steps is equal to the number of numbers such that their binary representation contains exactly $\left\lfloor\frac{n}{2}\right\rfloor$ ones out of $n$ digits, i.e. the number of numbers on the blackboard after $n$ steps will be equal to $\binom{n}{\left\lfloor\frac{n}{2}\right\rfloor}$.
|
| 125 |
+
|
| 126 |
+
SolUTION II. Denote by $\sigma_{n}$ the number of numbers on the blackboard after $n$ steps (thus $\sigma_{0}=\sigma_{1}=1, \sigma_{2}=2, \sigma_{3}=3, \ldots$ ). Regard all points in the plane with coordinates $(m, n)$, where $m, n$ are defined as follows: the number $n$ is written on the blackboard after $m$ steps ( $m, n$ are positive integers by the condition). At each node, i.e. each point with integer coordinates of the above type, write the number of occurrences of $n$ after $m$ steps. Thus the number written at $(3,2)$ will be the number of occurrences of 2 directly after step 3 , which is 2 . Observe that the number at each node is equal to the number of ways to reach this node from the point $(0,1)$, walking from one node to another one step at the time, from left to right and either up or down, without going down to the horizontal axis.
|
| 127 |
+
|
| 128 |
+
(Since all zeroes are erased, we can never reach the horizontal axis.) For each $m$ we want to find the total number of paths $\sigma_{m}$, reaching the vertical line $y=m$.
|
| 129 |
+
|
| 130 |
+
If we were to remove the constraint that we are not allowed to step on the horizontal axis (i.e. that all zeroes are erased), we would get Pascal's triangle, and the total number of paths would be $2^{m}$. The binomial coefficient at each node is then the total number of paths to reach this node, without constraint.
|
| 131 |
+
|
| 132 |
+
We need to find and subtract the number of paths from $A(0,1)$ to a point $B$ among the allowed nodes, which go down to the horizontal axis. Choose such a path, and find a new one by reflecting in the horizontal axis the part between the starting point $(0,1)$ and the path's first contact with the horizontal axis. The original path and the reflected one will end at the same point (among the allowed nodes); the reflected one will start at $A^{\prime}(0,-1)$. We have constructed a bijection between the original set of paths from $A$ to $B$ that reach down to the horizontal axis and the set of paths from $A^{\prime}$ to $B$. Observe that starting at $A^{\prime}$ we can get another copy of Pascal's triangle, which is the original one, translated two units down. It is easier to count the number of paths from $A^{\prime}$ to $B$, since they are not subject to any constraints. Thus the number of "positive" paths from $A$ to the points above the horizontal axis for $m=2 k$ will be
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
\begin{gathered}
|
| 136 |
+
\left(\binom{2 k}{2 k}+\binom{2 k}{2 k-1}+\cdots+\binom{2 k}{k+1}+\binom{2 k}{k}\right)- \\
|
| 137 |
+
-\left(\binom{2 k}{2 k}+\binom{2 k}{2 k-1}+\cdots+\binom{2 k}{k+1}\right)=\binom{2 k}{k}
|
| 138 |
+
\end{gathered}
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
In case $m$ is odd, a modification of the above argument gives the answer obtained in solution I.
|
| 142 |
+
|
Nordic_MO/md/en-2013-sol.md
ADDED
|
@@ -0,0 +1,136 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $27^{\text {th }}$ Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
Monday, 8 April 2013
|
| 4 |
+
|
| 5 |
+
## Solution
|
| 6 |
+
|
| 7 |
+
Each problem is worth 5 points.
|
| 8 |
+
|
| 9 |
+
PRoblem 1. Let $\left(a_{n}\right)_{n \geq 1}$ be a sequence with $a_{1}=1$ and
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
a_{n+1}=\left\lfloor a_{n}+\sqrt{a_{n}}+\frac{1}{2}\right\rfloor
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
for all $n \geq 1$, where $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$. Find all $n \leq 2013$ such that $a_{n}$ is a perfect square.
|
| 16 |
+
|
| 17 |
+
Solution. We will show by induction that $a_{n}=1+\left\lfloor\frac{n}{2}\right\rfloor\left\lfloor\frac{n+1}{2}\right\rfloor$, which is equivalent to $a_{2 m}=1+m^{2}$ and $a_{2 m+1}=1+m(m+1)$. Clearly this is true for $a_{1}$. If $a_{2 m+1}=1+m(m+1)$ then
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
a_{2 m+2}=\left\lfloor m^{2}+m+1+\sqrt{m^{2}+m+1}+\frac{1}{2}\right\rfloor
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
and since $m+\frac{1}{2}<\sqrt{m^{2}+m+1}<m+1$ (easily seen by squaring), we get $a_{2 m+2}=\left(m^{2}+m+1\right)+(m+1)=1+(m+1)^{2}$.
|
| 24 |
+
|
| 25 |
+
And if $a_{2 m}=1+m^{2}$ then
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
a_{2 m+1}=\left\lfloor m^{2}+1+\sqrt{m^{2}+1}+\frac{1}{2}\right\rfloor
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
and here $m<\sqrt{m^{2}+1}<m+\frac{1}{2}$, so $a_{2 m+1}=\left(m^{2}+1\right)+m=1+m(m+1)$.
|
| 32 |
+
|
| 33 |
+
If $m \geq 1$ then $m^{2}<1+m^{2}<(m+1)^{2}$ and $m^{2}<m^{2}+m+1<(m+1)^{2}$, so $a_{n}$ cannot be a perfect square if $n>1$. Therefore $a_{1}=1$ is the only perfect square in the sequence.
|
| 34 |
+
|
| 35 |
+
Problem 2. In a football tournament there are $n$ teams, with $n \geq 4$, and each pair of teams meets exactly once. Suppose that, at the end of the tournament, the final scores form an arithmetic sequence where each team scores 1 more point than the following team on the scoreboard. Determine the maximum possible score of the lowest scoring team, assuming usual scoring for football games (where the winner of a game gets 3 points, the loser 0 points, and if there is a tie both teams get 1 point).
|
| 36 |
+
|
| 37 |
+
Solution. Note that the total number of games equals the number of different pairings, that is, $n(n-1) / 2$. Suppose the lowest scoring team ends with $k$ points. Then the total score for all teams is
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
k+(k+1)+\cdots+(k+n-1)=n k+\frac{(n-1) n}{2}
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Some games must end in a tie, for otherwise, all team scores would be a multiple of 3 and cannot be 1 point apart. Since the total score of a tie is only 2 points compared to 3 points if one of the teams wins, we therefore know that
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
n k+\frac{(n-1) n}{2}<3 \cdot \frac{n(n-1)}{2}
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
so $n k<n(n-1)$, and hence $k<n-1$. It follows that the lowest scoring team can score no more than $n-2$ points.
|
| 50 |
+
|
| 51 |
+
We now show by induction that it is indeed possible for the lowest scoring team to score $n-2$ points.
|
| 52 |
+
|
| 53 |
+
The following scoreboard shows this is possible for $n=4$ :
|
| 54 |
+
|
| 55 |
+
| - | 3 | 1 | 1 | 5 |
|
| 56 |
+
| :---: | :---: | :---: | :---: | :---: |
|
| 57 |
+
| 0 | - | 1 | 3 | 4 |
|
| 58 |
+
| 1 | 1 | - | 1 | 3 |
|
| 59 |
+
| 1 | 0 | 1 | - | 2 |
|
| 60 |
+
|
| 61 |
+
Now suppose we have a scoreboard for $n$ teams labelled $T_{n-2}, \ldots, T_{2 n-3}$, where team $T_{i}$ scores $i$ points. Keep the results among these teams unchanged while adding one more team.
|
| 62 |
+
|
| 63 |
+
Write $n=3 q+r$ with $r \in\{1,-1,0\}$, and let the new team tie with just one of the original teams, lose against $q$ teams, and win against the rest of them. The new team thus wins $n-1-q$ games, and gets $1+3(n-1-q)=3 n-2-3 q=2 n-2+r$ points.
|
| 64 |
+
|
| 65 |
+
Moreover, we arrange for the $q$ teams which win against the new team to form an arithmetic sequence $T_{j}, T_{j+3}, \ldots, T_{j+3(q-1)}=T_{j+n-r-3}$, so that each of them, itself having gained three points, fills the slot vacated by the next one.
|
| 66 |
+
|
| 67 |
+
(i) If $r=1$, then let the new team tie with team $T_{n-2}$ and lose to each of the teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-5}$.
|
| 68 |
+
|
| 69 |
+
Team $T_{n-2}$ now has $n-1$ points and takes the place vacated by $T_{n-1}$. At the other end, $T_{2 n-5}$ now has $2 n-2$ points, just one more than the previous top team $T_{2 n-3}$. And the new team has $2 n-2+r=2 n-1$ points, becoming the new top team. The teams now have all scores from $n-1$ up to $2 n-1$.
|
| 70 |
+
|
| 71 |
+
(ii) If $r=-1$, then let the new team tie with team $T_{2 n-3}$ and lose to each of the teams $T_{n-2}, T_{n+1}, \ldots, T_{n-2+n-r-3}=T_{2 n-4}$.
|
| 72 |
+
|
| 73 |
+
The old top team $T_{2 n-3}$ now has $2 n-2$ points, and its former place is filled by the new team, which gets $2 n-2+r=2 n-3$ points. $T_{2 n-4}$ now has $2 n-1$ points and is the new top team. So again we have all scores ranging from $n-1$ up to $2 n-1$.
|
| 74 |
+
|
| 75 |
+
(iii) If $r=0$, then let the new team tie with team $T_{n-2}$ and lose to teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-4}$.
|
| 76 |
+
|
| 77 |
+
Team $T_{n-2}$ now has $n-1$ points and fills the slot vacated by $T_{n-1}$. At the top end, $T_{2 n-4}$ now has $2 n-1$ points, while the new team has $2 n-2+r=2 n-2$ points, and yet again we have all scores from $n-1$ to $2 n-1$.
|
| 78 |
+
|
| 79 |
+
This concludes the proof.
|
| 80 |
+
|
| 81 |
+
Problem 3. Define a sequence $\left(n_{k}\right)_{k \geq 0}$ by $n_{0}=n_{1}=1$, and $n_{2 k}=n_{k}+n_{k-1}$ and $n_{2 k+1}=n_{k}$ for $k \geq 1$. Let further $q_{k}=n_{k} / n_{k-1}$ for each $k \geq 1$. Show that every positive rational number is present exactly once in the sequence $\left(q_{k}\right)_{k \geq 1}$.
|
| 82 |
+
|
| 83 |
+
Solution. Clearly, all the numbers $n_{k}$ are positive integers. Moreover,
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
q_{2 k}=\frac{n_{2 k}}{n_{2 k-1}}=\frac{n_{k}+n_{k-1}}{n_{k-1}}=q_{k}+1
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
and similarly,
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\frac{1}{q_{2 k+1}}=\frac{n_{2 k}}{n_{2 k+1}}=\frac{n_{k}+n_{k-1}}{n_{k}}=\frac{1}{q_{k}}+1
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
In particular, $q_{k}>1$ when $k$ is even, and $q_{k}<1$ when $k \geq 3$ is odd.
|
| 96 |
+
|
| 97 |
+
We will show the following by induction on $t=2,3,4, \ldots$ :
|
| 98 |
+
|
| 99 |
+
Claim: Every rational number $r / s$ where $r$, s are positive integers with $\operatorname{gcd}(r, s)=$ 1 and $r+s \leq t$ occurs precisely once among the numbers $q_{k}$.
|
| 100 |
+
|
| 101 |
+
The claim is clearly true for $t=2$, since then $r / s=1 / 1=1$ is the only possibility, and $q_{1}$ is the only occurrence of 1 in the sequence.
|
| 102 |
+
|
| 103 |
+
Now, assume that $u \geq 3$ and that the claim holds for $t=u-1$. Let $r$ and $s$ be positive integers with $\operatorname{gcd}(r, s)=1$ and $r+s=u$.
|
| 104 |
+
|
| 105 |
+
First, assume that $r>s$. We know that $r / s=q_{m}$ is only possible if $m$ is even. But
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
\frac{r}{s}=q_{2 k} \Leftrightarrow \frac{r-s}{s}=q_{k}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
by (1), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(r-s, s)=1$ and $(r-s)+s=r \leq t$.
|
| 112 |
+
|
| 113 |
+
Next, assume that $r<s$. We know that $r / s=q_{m}$ is only possible if $m$ is odd. But
|
| 114 |
+
|
| 115 |
+
$$
|
| 116 |
+
\frac{r}{s}=q_{2 k+1} \Leftrightarrow \frac{s}{r}=\frac{1}{q_{2 k+1}} \Leftrightarrow \frac{s-r}{r}=\frac{1}{q_{k}}
|
| 117 |
+
$$
|
| 118 |
+
|
| 119 |
+
by (2), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(s-r, r)=1$ and $(s-r)+r=s \leq t$.
|
| 120 |
+
|
| 121 |
+
Problem 4. Let $A B C$ be an acute angled triangle, and $H$ a point in its interior. Let the reflections of $H$ through the sides $A B$ and $A C$ be called $H_{c}$ and $H_{b}$, respectively, and let the reflections of $H$ through the midpoints of these same sides be called $H_{c}^{\prime}$ and $H_{b}^{\prime}$, respectively. Show that the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if at least two of them coincide or $H$ lies on the altitude from $A$ in triangle $A B C$.
|
| 122 |
+
|
| 123 |
+
Solution. If at least two of the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ coincide, all four are obviously concyclic. Therefore we may assume that these four points are distinct.
|
| 124 |
+
|
| 125 |
+
Let $P_{b}$ denote the midpoint of segment $H H_{b}, P_{b}^{\prime}$ the midpoint of segment $H H_{b}^{\prime}, P_{c}$ the midpoint of segment $H H_{c}$, and $P_{c}^{\prime}$ the midpoint of segment $H H_{c}^{\prime}$.
|
| 126 |
+
|
| 127 |
+
The triangle $H H_{b} H_{b}^{\prime}$ being right-angled in $H_{b}$, it follows that the perpendicular bisector $\ell_{b}$ of the side $H_{b} H_{b}^{\prime}$ goes through the point $P_{b}^{\prime}$. Since the segments $P_{b} P_{b}^{\prime}$ and $H_{b} H_{b}^{\prime}$ are parallel and $P_{b}^{\prime}$ is the midpoint of the side $A C$, we then conclude that $\ell_{b}$ also goes through the circumcentre $O$ of triangle $A B C$.
|
| 128 |
+
|
| 129 |
+
Similarly the perpendicular bisector $\ell_{c}$ of the segment $H_{c} H_{c}^{\prime}$ also goes through $O$. Hence the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if also the perpendicular bisector $\ell$ of the segment $H_{b}^{\prime} H_{c}^{\prime}$ goes through the point $O$. Since $H_{b}^{\prime} H_{c}^{\prime}\left\|P_{b}^{\prime} P_{c}^{\prime}\right\| B C$, this is the case if and only if $\ell$ is the perpendicular bisector $m$ of the segment $B C$.
|
| 130 |
+
|
| 131 |
+
Let $k$ denote the perpendicular bisector of the segment $P_{b}^{\prime} P_{c}^{\prime}$. Since the lines $\ell$ and $m$ are obtained from $k$ by similarities of ratio 2 and centres $H$ and $A$, respectively, they coincide if and only if $H A$ is parallel to $m$. Thus $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if $H$ lies on the altitude from $A$ in triangle $A B C$.
|
| 132 |
+
|
| 133 |
+
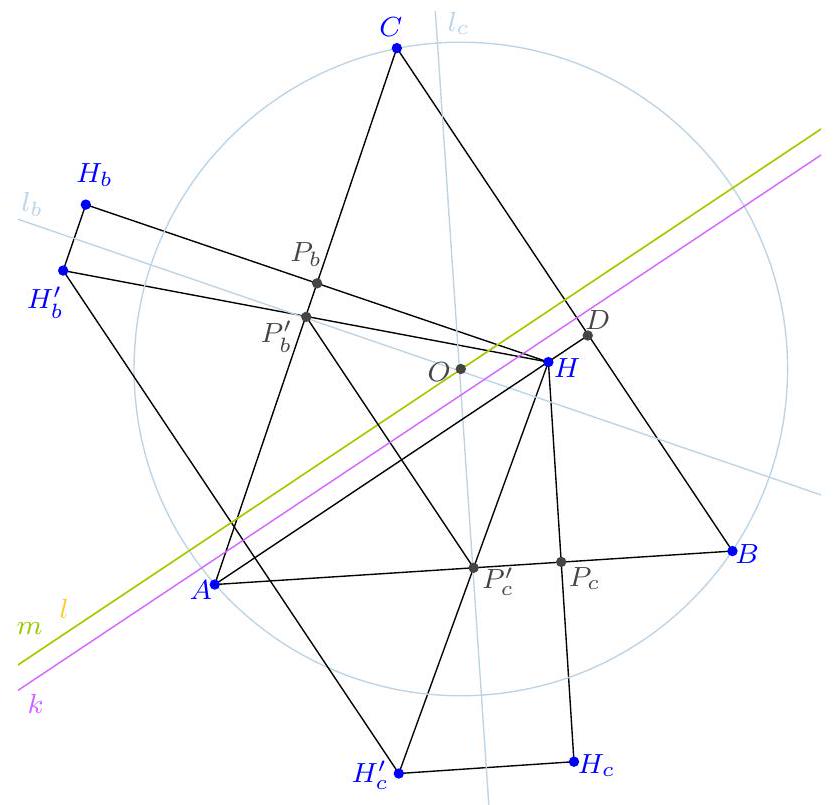
|
| 134 |
+
|
| 135 |
+
Click here to experiment with the figure in GeoGebra.
|
| 136 |
+
|
Nordic_MO/md/en-2014-sol.md
ADDED
|
@@ -0,0 +1,123 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 28th Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
Monday, 31 March 2014
|
| 4 |
+
|
| 5 |
+
Problem set with solutions
|
| 6 |
+
|
| 7 |
+
## The time allowed is 4 hours. Each problem is worth 5 points. The only permitted aids are writing and drawing tools.
|
| 8 |
+
|
| 9 |
+
## Problem 1
|
| 10 |
+
|
| 11 |
+
Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ (where $\mathbb{N}$ is the set of the natural numbers and is assumed to contain 0 ), such that
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
f\left(x^{2}\right)-f\left(y^{2}\right)=f(x+y) f(x-y)
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
for all $x, y \in \mathbb{N}$ with $x \geq y$.
|
| 18 |
+
|
| 19 |
+
## Problem 2
|
| 20 |
+
|
| 21 |
+
Given an equilateral triangle, find all points inside the triangle such that the distance from the point to one of the sides is equal to the geometric mean of the distances from the point to the other two sides of the triangle.
|
| 22 |
+
|
| 23 |
+
[The geometric mean of two numbers $x$ and $y$ equals $\sqrt{x y}$.]
|
| 24 |
+
|
| 25 |
+
## Problem 3
|
| 26 |
+
|
| 27 |
+
Find all nonnegative integers $a, b, c$, such that
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\sqrt{a}+\sqrt{b}+\sqrt{c}=\sqrt{2014}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
## Problem 4
|
| 34 |
+
|
| 35 |
+
A game is played on an $n \times n$ chessboard. At the beginning there are 99 stones on each square. Two players $A$ and $B$ take turns, where in each turn the player chooses either a row or a column and removes one stone from each square in the chosen row or column. They are only allowed to choose a row or a column, if it has least one stone on each square. The first player who cannot move, looses the game. Player $A$ takes the first turn. Determine all $n$ for which player $A$ has a winning strategy.
|
| 36 |
+
|
| 37 |
+
## SOLUTIONS
|
| 38 |
+
|
| 39 |
+
## Solution 1
|
| 40 |
+
|
| 41 |
+
It is easily seen that both $f(x)=x$ and $f \equiv 0$ solve the equation; we shall show that there are no other solutions.
|
| 42 |
+
|
| 43 |
+
Setting $x=y=0$ gives $f(0)=0$; if only $y=0$ we get $f\left(x^{2}\right)=(f(x))^{2}$, for all admissible $x$. For $x=1$ we now get $f(1)=0$, or $f(1)=1$.
|
| 44 |
+
|
| 45 |
+
Case 1. $f(1)=0$ : We have
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
f\left((x+1)^{2}\right)-f\left(x^{2}\right)=f(2 x+1) \cdot f(1)=0=(f(x+1))^{2}-(f(x))^{2}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
so that $f(x+1)=f(x)$ for all $x$, and it follows that $f \equiv 0$.
|
| 52 |
+
|
| 53 |
+
Case 2. $f(1)=1$ : Denote $f(2)=a$. We have
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
(f(2))^{2}-1=f\left(2^{2}\right)-f\left(1^{2}\right)=f(3) \cdot f(1)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
so that $f(3)=a^{2}-1$. Obviously $f(4)=a^{2}$, and $x=3, y=1$ now give
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\left(a^{2}-1\right)^{2}-1=a^{3}
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
so that $a=0$ or $a=2$, since $a$ cannot be negative. If $f(2)=0$, then $f(3)=0-1$, which is impossible. Thus we have $a=2$. The fact that $f(n)=n$ for all $n \in \mathbb{N}$ is now easy to establish using induction.
|
| 66 |
+
|
| 67 |
+
## Solution 2
|
| 68 |
+
|
| 69 |
+
Let $P$ be a point inside $\triangle A B C$. Denote its orthogonal projections on $A B, B C, C A$ by $X, Y, Z$, respectively. We have $\angle X P Z=\angle Y P X=120^{\circ}$.
|
| 70 |
+
|
| 71 |
+
Assume that $P X^{2}=P Y \cdot P Z$. Together with $\angle X P Z=\angle Y P X=120^{\circ}$, this gives $\triangle X P Z \sim \triangle Y P X$ (s-a-s). It means that $\angle P Z X=\angle P X Y$. The quadrilaterals $A X P Z$ and $B Y P X$ are circumscribed, and we get $\angle P A X=\angle P B Y$, so that $\angle P A B+\angle P B A=60^{\circ}$. We now have $\angle A P B=120^{\circ}$, meaning that $P$ lies on an arc inside the triangle, which is part of the circle through $A, B$, and the centre of the triangle.
|
| 72 |
+
|
| 73 |
+
The above argument can be reversed to see that all points on this arc satisfy the condition.
|
| 74 |
+
|
| 75 |
+
The set of all points as described is thus the union of three arcs, each of them passing through two of the vertices and through the centre of the triangle.
|
| 76 |
+
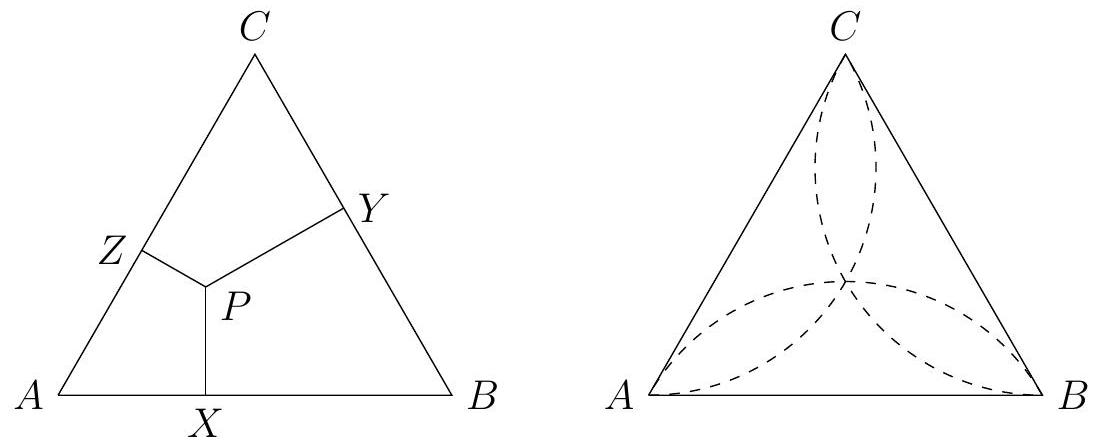
|
| 77 |
+
|
| 78 |
+
Remark: It is also possible to solve this by introducing a coordinate system and deriving equations for the locus of $P$.
|
| 79 |
+
|
| 80 |
+
## Solution 3
|
| 81 |
+
|
| 82 |
+
We start with a lemma:
|
| 83 |
+
|
| 84 |
+
Lemma. If $p, q$ are nonnegative integers and $\sqrt{p}+\sqrt{q}=r \in \mathbb{Q}$, then $p$ and $q$ are squares of integers.
|
| 85 |
+
|
| 86 |
+
Proof of lemma: If $r=0$, then $p=q=0$. For $r \neq 0$, take the square of both sides to get $p+q+2 \sqrt{p q}=r^{2}$, which means that $\sqrt{p q} \in \mathbb{Q}$, so that $p q$ must be the square of a rational number, and, being an integer, it must be the square of an integer. Denote $p q=s^{2}, s \geq 0$. Then $p=\frac{s^{2}}{q}$, and
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
r=\sqrt{p}+\sqrt{q}=\frac{s}{\sqrt{q}}+\sqrt{q}
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
which implies that $\sqrt{q}=\frac{s+q}{r} \in \mathbb{Q}$, and it follows that $q$ is a square. Then $p$ must also be a square.
|
| 93 |
+
|
| 94 |
+
Back to the problem: we can rewrite the equation as
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
a+b+2 \sqrt{a b}=2014+c-2 \sqrt{2014 c}
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
so that
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\sqrt{a b}+\sqrt{2014 c} \in \mathbb{Q}
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
The lemma now tells us that $a b$ and $2014 c$ need to be squares of integers. Since $2014=2 \cdot 19 \cdot 53$, we must have $c=2014 m^{2}$ for some nonnegative integer $m$. Similarly, $a=2014 k^{2}, b=2014 l^{2}$. The equation now implies
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
k+l+m=1
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
so that the only possibilities are $(2014,0,0),(0,2014,0),(0,0,2014)$.
|
| 113 |
+
|
| 114 |
+
## Solution 4
|
| 115 |
+
|
| 116 |
+
Player $A$ has a winning strategy if and only if $n$ is odd.
|
| 117 |
+
|
| 118 |
+
First we prove that no matter how they play, the play will not end before the board is empty. Let $(i, j)$ denote the square in row $i$ and column $j$, let $r_{i}$ denote the number of times row $i$ has been chosen when the game ends, and let $c_{j}$ denote the same for columns. Assume by contradiction that there is a none empty square $(a, b)$ when no more moves are possible. Hence there is an empty square in row $a$, let us say $(a, c)$, and an empty square in column $b$, let us say $(d, b)$. This shows that $r_{a}+c_{b}<99, r_{a}+c_{c}=99$ and $r_{d}+c_{b}=99$. But this leads to $r_{d}+c_{c}>99$ which is impossible since there are exactly 99 stones on square $(d, c)$ when the game begins.
|
| 119 |
+
|
| 120 |
+
This shows that the game will end after $\frac{n \times n \times 99}{99}=n \times n$ moves since each player removes 99 stones in each move. The number $n \times n$ has the same parity as $n$, and hence $A$ wins if $n$ is odd and $B$ wins if $n$ is even no matter how they play.
|
| 121 |
+
|
| 122 |
+
Remark: It can by shown that player $B$ has a winning strategy when $n$ is even in a very different way: If player $B$ copies the choice of $A$, i.e. when $A$ chooses row $m, B$ chooses row $n-m$, and the same for columns, then player $B$ wins when $n$ is even.
|
| 123 |
+
|
Nordic_MO/md/en-2015-sol.md
ADDED
|
@@ -0,0 +1,87 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 29th Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
Tuesday, March 24, 2015
|
| 4 |
+
|
| 5 |
+
Solutions
|
| 6 |
+
|
| 7 |
+
## Problem 1.
|
| 8 |
+
|
| 9 |
+
Let $A B C$ be a triangle and $\Gamma$ the circle with diameter $A B$. The bisectors of $\angle B A C$ and $\angle A B C$ intersect $\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.
|
| 10 |
+
|
| 11 |
+
Solution 1. Let the line $E D$ meet $A C$ at $G^{\prime}$ and $B C$ at $F^{\prime} . A D$ and $B E$ intersect at $I$, the incenter of $A B C$. As angles subtending the same arc $\widehat{B D}$, $\angle D A B=\angle D E B=\angle G^{\prime} E I$. But $\angle D A B=\angle C A D=$ $\angle G^{\prime} A I$. This means that $E, A, I$ and $G^{\prime}$ are concyclic, and $\angle A E I=\angle A G^{\prime} I$ as angles subtending the same chord $A I$. But $A B$ is a diameter of $\Gamma$, and so $\angle A E B=$ $\angle A E I$ is a right angle. So $I G^{\prime} \perp A C$, or $G^{\prime}$ is the foot of the perpendicular from $I$ to $A C$. This implies $G^{\prime}=G$. In a similar manner we prove that $F^{\prime}=F$, and the proof is complete.
|
| 12 |
+
|
| 13 |
+
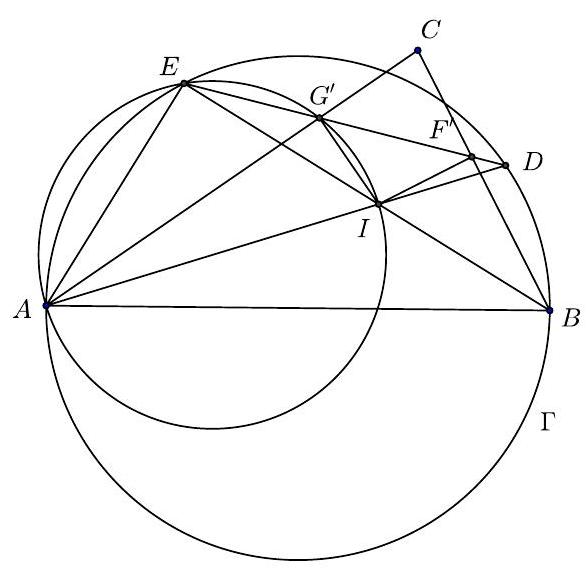
|
| 14 |
+
|
| 15 |
+
Solution 2. (Read the attached figure so that $F^{\prime}$ and $G^{\prime}$ are as $F$ and $G$ in the problem text.) The angles $\angle A E I=\angle A E B$ and $\angle A G I$ are right angles. This means that $A I G E$ is a cyclic quadrilateral. But then $\angle B E G=\angle I E G=\angle I A G=\angle D A C=\angle D A B=\angle B E D$, implying that $G$ and $D$ are on the same line through $E$. The same argument shows $F$ and $E$ are on the same line through $D$. So the points $G$ and $F$ are on the line $E D$.
|
| 16 |
+
|
| 17 |
+
## Problem 2.
|
| 18 |
+
|
| 19 |
+
Find the primes $p, q, r$, given that one of the numbers $p q r$ and $p+q+r$ is 101 times the other.
|
| 20 |
+
|
| 21 |
+
Solution. We may assume $r=\max \{p, q, r\}$. Then $p+q+r \leq 3 r$ and $p q r \geq 4 r$. So the sum of the three primes is always less than their product. The only relevant requirement thus is $p q r=101(p+q+r)$. We observe that 101 is a prime. So one of $p, q, r$ must be 101. Assume $r=101$. Then $p q=p+q+101$. This can be written as $(p-1)(q-1)=102$. Since $102=1 \cdot 102=2 \cdot 51=3 \cdot 34=6 \cdot 17$, the possibilities for $\{p, q\}$ are $\{2,103\},\{3,52\},\{4,35\},\{7,18\}$ The only case, where both the numbers are primes, is $\{2,103\}$. So the only solution to the problem is $\{p, q, r\}=\{2,101,103\}$.
|
| 22 |
+
|
| 23 |
+
## Problem 3.
|
| 24 |
+
|
| 25 |
+
Let $n>1$ and $p(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial with $n$ real roots (counted with multiplicity). Let the polynomial $q$ be defined by
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
q(x)=\prod_{j=1}^{2015} p(x+j)
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
We know that $p(2015)=2015$. Prove that $q$ has at least 1970 different roots $r_{1}, \ldots, r_{1970}$ such that $\left|r_{j}\right|<2015$ for all $j=1, \ldots, 1970$.
|
| 32 |
+
|
| 33 |
+
Solution. Let $h_{j}(x)=p(x+j)$. Consider $h_{2015}$. Like $p$, it has $n$ real roots $s_{1}, s_{2}, \ldots, s_{n}$, and $h_{2015}(0)=p(2015)=2015$. By Viète, the product $\left|s_{1} s_{2} \cdots s_{n}\right|$ equals 2015. Since $n \geq 2$, there is at least one $s_{j}$ such that $\left|s_{j}\right| \leq \sqrt{2015}<\sqrt{2025}=45$. Denote this $s_{j}$ by $m$. Now for all $j=0,1, \ldots, 2014, h_{2015-j}(m+j)=p(m+j+2015-j)=p(m+2015)=$ $h_{2015}(m)=0$. So $m, m+1, \ldots, m+2014$ are all roots of $q$. Since $0 \leq|m|<45$, the condition $|m+j|<2015$ is satisfied by at least 1970 different $j, 0 \leq j \leq 2014$, and we are done.
|
| 34 |
+
|
| 35 |
+
## Problem 4.
|
| 36 |
+
|
| 37 |
+
An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:
|
| 38 |
+
|
| 39 |
+
(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.
|
| 40 |
+
|
| 41 |
+
(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.
|
| 42 |
+
|
| 43 |
+
How many different permutations of the volumes can be obtained by using these two operations repeatedly?
|
| 44 |
+
|
| 45 |
+
Solution 1. (By the proposer.) Let the positions of the books in the stack be $1,2,3, \ldots, 2000$ from the top (and consider them modulo 2000). Notice that both operations fix the parity of the number of the book at a any given position. Operation (i) subtracts an even integer from the number of the book at each position. If $A$ is an operation of type (i), and $B$ is an operation of type (ii), then the operation $A^{-1} B A$ changes the order of the books in the positions $n+1$ to $n+m$ where $n$ is even and $m$ is odd. This is called turning the interval.
|
| 46 |
+
|
| 47 |
+
Now we prove that all the volumes in odd positions can be placed in the odd positions in every way we like: If the volume we want in position 1 is in position $m_{1}$, we turn the interval 1 to $m_{1}$. Now if the volume we want in position 3 is in position $m_{3}$, we turn the interval 3 to $m_{3}$, and so on. In this way we can permute the volumes in odd positions exactly as we want to.
|
| 48 |
+
|
| 49 |
+
Now we prove that we can permute the volumes in even positions exactly as we want without changing the positions of the volumes in the odd positions: We can make a transposition of the two volumes in position $2 n$ and $2 n+2 m$ by turning the interval $2 n+1$ to $2 n+2 m-1$, then turning the interval $2 n+2 m+1$ to $2 n-1$, then turning the interval $2 n+1$ to $2 n-1$, and finally adding $2 m$ to the number of the volume in each position.
|
| 50 |
+
|
| 51 |
+
Since there are 1000! permutations of the volumes in the odd positions, and 1000! permutations of the volumes in the even positions, altogether we have (1000!) ${ }^{2}$ different permutations.
|
| 52 |
+
|
| 53 |
+
Solution 2. We show that the volumes can be permuted so that the volumes with odd numbers are in an arbitrary order in the odd-numbered palaces and the volumes with even numbers are in an arbitrary order in the even-numbered places. The main idea is to construct two combinations of the allowed operations. The first one turns the volumes in a specified interval, starting and ending in an odd-numbered place, in the opposite order while keeping everything outside this interval fixed, or keeps everything fixed in an interval while turning the order of the volumes outside this interval in the opposite direction, when the counting starts below that interval and is continued from the top after reaching the bottom volume. The second combined operation just exchanges two volumes in evennumbered places while keeping everything else fixed. - It is clear that 2000 is not a special number, and it could be replaced by a generic even integer. However, we formulate the proof according to the problem text.
|
| 54 |
+
|
| 55 |
+
Let $E=\{1,2, \ldots, 2000\}$. We formulate the operations described in conditions (i) and (ii), depending on an even integer $n$ and odd integer $m$ as functions $f_{n}: E \rightarrow E$ and $g_{m}: E \rightarrow E$, defined by
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
f_{n}(p)=\left\{\begin{array}{ll}
|
| 59 |
+
2000+p-n & \text { for } p \geq n, \\
|
| 60 |
+
p-n & \text { for } n<p
|
| 61 |
+
\end{array} \quad \text { and } \quad g_{m}(p)= \begin{cases}m-p+1 & \text { for } p \leq m \\
|
| 62 |
+
p & \text { for } m<p\end{cases}\right.
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
We immediately see that $f_{n}$ and $g_{m}$ map even numbers into even numbers and odd numbers into odd numbers. So the volumes can never be permuted so that an odd-numbered volume would be in an even place or an even-numbered would be in an odd place. The observation $f([1, n])=[2000-(n+1), 2000]$ easily leads to $f_{n}^{-1}=f_{2000-n}$.
|
| 66 |
+
|
| 67 |
+
Now let $n$ be even and $m$ odd and $n+m<2000$. Consider the combined mapping $f_{n}^{-1} \circ g_{m} \circ f_{n}$. If $n<n+p \leq n+m$, then $f_{n}(n+p)=p \leq m, g_{m}(p)=m-p+1<2000-n$ and $f_{n}^{-1}(m-p+1)=f_{2000-n}(m-p+1)=2000+m-p+1-2000+n=n+m+1-p$. Because $f_{n}([n+1, n+m])=[1, m], f_{n}$ maps numbers $p$ outside the interval $[n+1, n+m]$ into numbers outside the interval $[1, m] ; g_{m}$ keeps these numbers fixed and $f_{n}^{-1}$ returns $f_{n}(p)$ into $p$. So we have shown that for any interval $[s, t] \subset E$ with $s$ and $t$ odd, there is a function $h_{s, t}$, combined of functions of the $f$ type and $g$ type such that $h_{s, t}$ reverses the order of numbers in the interval $[s, t]$ and is the identity function outside this interval.
|
| 68 |
+
|
| 69 |
+
The functions $h_{s, t}$ allow us to order the odd numbers in an arbitrary manner. If $p_{1}$ ought to be in position 1 , then apply (if needed) $h_{1, p_{1}}$; if the number $p_{2}$ which ought to be in position 3 now is in position $x$, the $x \geq 3$ and we may apply (if needed) $h_{3, x}$. Continuing this way, we eventually arrive at the desired order of the odd numbers.
|
| 70 |
+
|
| 71 |
+
To construct the second one of the desired operations, we have to obtain a counterpart for $h_{s, t}$ for $t<s$. To this end, consider $f_{n}^{-1} \circ g_{m} \circ f_{n}$ for $m+n>2000$. By the definition of $f_{n}$, $f_{n}(n+m-2000)=2000+(n+m-2000)-n=m$, and so $f_{n}[n+m-2000+1, n]=[m+$ 1, 2000] Consequently, $f_{n}^{-1} \circ g_{m} \circ f_{n}$ keeps numbers in the interval $[n+m-2000+1, n]$ (with even endpoints) fixed. Since $g_{m}$ turns the order around in $[1, m]$ and $f_{n}^{-1}=f_{2000-n}$ maps $[1, m]$ onto the complement of $[n+m-2000+1, n]$ in such a way that $f_{2000-1}(1)=n+1$, the
|
| 72 |
+
order of numbers in the complement is reversed in the desired manner. - We have shown that for odd $s$ and $t$ such that $t<s$ there exists a function $h_{s, t}$, combined of functions of the $f$ type and $g$ type such that $h_{s, t}$ is the identity on the interval $[t+1, s-1]$, but reverses the order of the numbers outside this interval, when counting is started from $s$ and continued through over 2000 and 1 over to $t$, in other words modulo 2000 .
|
| 73 |
+
|
| 74 |
+
To finish the proof, we show that two numbers in the even positions can be exchanged while everything else is fixed. This clearly allows us to put the even numbers in an arbitrary order without violating the order of the odd numbers. To achieve this, we take two even numbers $p$ and $q, p<q$, and consider the function $\phi_{p, q}=f_{2000+p-q} \circ h_{p+1, p-1} \circ h_{q+1, p-1} \circ h_{p+1, q-1}$. The innermost function $h_{p+1, q-1}$ reverses the order on $[p+1, q-1]$ and fixes everything else, the next function $h_{q+1, p-1}$ fixes numbers in $[p, q], h_{p+1, p-1}$ fixes $p$ and reverses the order $(\bmod 2000)$ in $E \backslash\{p\}$, and $f_{2000+p-q}(p)=q$. The two innermost components of $\phi_{p, q}$ fix $q, h_{p+1, p-1}$ takes $q$ to a position $x q-p$ steps ahead of $p(\bmod 2000)$ and $f_{2000+p-q}=f_{q-p}^{-1}$ moves $x q-p$ positions back, i.e. to $p$. If $p+k$ is between $p$ and $q$, then the innermost function maps it to $q-k$, the next one fixes $q-k$, the third function maps $q-k$ to $p-(q-k-p)=2 p-q+k(\bmod 2000)$, and $f_{q-p}^{-1}$ maps $2 p-q+k$ back to $p+k$. A similar reasoning shows that $\phi_{p, q}$ also fixes numbers in $E \backslash[p, q]$.
|
| 75 |
+
|
| 76 |
+
Since both even and odd numbers have 1000! different permutations, the volumes can be permuted into (1000!) $)^{2}$ different orders by using the given operations repeatedly.
|
| 77 |
+
|
| 78 |
+
Solution 3. We show by induction, that if in an ordered sequence one may exchange two consecutive elements without changing the places of any other element, then any two elements can be exchanged so that all other elements remain in place. We assume that this is true for elements which are at most $k$ steps away from each other in the sequence. Assuming that $a$ precedes $b$ by $k+1$ steps and that $c$ is immediately behind $a$, the following sequence of exchanges is allowed: $\ldots, a, c, \ldots, b, \ldots \rightarrow \ldots, a, b, \ldots, c, \ldots \rightarrow$ $\ldots, b, a, \ldots, c, \ldots \rightarrow \ldots, b, c, \ldots, a, \ldots .$. By assumption, all elements in the places indicated by three dots remain on their places, as does $c$.
|
| 79 |
+
|
| 80 |
+
If any two elements can be exchanged without violating the other elements, then the elements in the sequence can be arranged to any order. One just gets the desired first element to its place by (at most) one exchange, and if the first $k$ elements already are in their desired places, then the one wanted to be in place $k+1$ is not among the first $k$ elements, and it can be moved to its place by at most one exchange, no violating the order of the first $k$ elements.
|
| 81 |
+
|
| 82 |
+
We now show, that any two volumes in consecutive odd places can be exchanged. The volumes on top and in place 3 can be exchanged by operation (ii) applied to the three topmost volumes. The volumes in places $2 n+1$ and $2 n+3$ can be exchanged by first applying operation (i) to the $2 n$ topmost volumes, which moves them in the bottom but preserves their order, then applying (ii) to the three topmost volumes and finally operation (i) to the $2000-2 n$ topmost volumes. The last operation returns the $2 n$ volumes to top preserving the order and returns the remaining $2000-2 n$ volumes to the bottom, preserving the order, save the volumes in places $2 n+1$ and $2 n+3$, which have changed places. By the general remarks above, it is now clear that operations (i) and (ii) can be used to arrange the volumes in odd positions into any order while the volumes in even positions remain in their places.
|
| 83 |
+
|
| 84 |
+
We still need to show, that a similar procedure is possible for volumes in even positions. First of all, the volumes in positions 1 to 5 can be moved to order $5,4,3,2,1$ by performing operation (ii) to the five topmost volumes. Then it is possible to exchange the volumes in positions 1 and 5 without changing anything else. So the volumes in even positions closest to the top can be exchanged. For volumes on positions $2 n$ and $2 n+2$ one can first perform operation (i) to the $2 n-2$ topmost volumes. The volumes in places $2 n$ and $2 n+2$ will be taken to places 2 and 4 , and they can be exchanged. Performing operation (i) to the $2000-(2 n-1)$ topmost volumes then returns everything to their previous places, except that the volumes in positions $2 n$ and $2 n+2$ have changed places. So all volumes in even positions can be put into any order by using the operations (i) and (ii), and the total number of possible orderings is $(1000 \text { ! })^{2}$.
|
| 85 |
+
|
| 86 |
+
(We note that operation (ii) can be replaced by a weaker operation: "It is possible to turn the order around for the 3 and 5 topmost volumes.")
|
| 87 |
+
|
Nordic_MO/md/en-2016-sol.md
ADDED
|
@@ -0,0 +1,86 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 30th Nordic Mathematical Contest <br> Tuesday, April 5, 2016 <br> Solutions
|
| 2 |
+
|
| 3 |
+
## Problem 1
|
| 4 |
+
|
| 5 |
+
Determine all sequences of non-negative integers $a_{1}, \ldots, a_{2016}$ all less than or equal to 2016 satisfying $i+j \mid i a_{i}+j a_{j}$ for all $i, j \in\{1,2, \ldots, 2016\}$.
|
| 6 |
+
|
| 7 |
+
Solution Answer: All constant sequences of non-negative integers.
|
| 8 |
+
|
| 9 |
+
The condition rewrites to $i+j \mid i\left(a_{i}-a_{j}\right)$. Since $2 k-1$ and $k$ are coprime, we see that $2 k-1 \mid a_{k}-a_{k-1}$. Thus if $2 k-1>2016$, then $a_{k}=a_{k-1}$ since $a_{k}$ and $a_{k-1}$ are non-negative and at most 2016. All together $a_{1009}=a_{1010}=\cdots=a_{2016}$.
|
| 10 |
+
|
| 11 |
+
If $i<1009$ we know that $i$ is coprime to one of the number $2016,2015, \ldots, 2017-i$ say $j$. Then $i+j \mid a_{i}-a_{j}$ and since $i+j>2016$ we conclude as before that $a_{i}=a_{j}=a_{2016}$. So any such sequence is constant.
|
| 12 |
+
|
| 13 |
+
## Problem 2
|
| 14 |
+
|
| 15 |
+
Let $A B C D$ be a cyclic quadrilateral satisfying $A B=A D$ and $A B+B C=C D$.
|
| 16 |
+
|
| 17 |
+
Determine $\angle C D A$.
|
| 18 |
+
|
| 19 |
+
Solution 2 Answer: $\angle C D A=60^{\circ}$.
|
| 20 |
+
|
| 21 |
+
Choose the point $E$ on the segment $C D$ such that $D E=A D$. Then $C E=C D-A D=$ $C D-A B=B C$, and hence the triangle $C E B$ is isosceles.
|
| 22 |
+
|
| 23 |
+
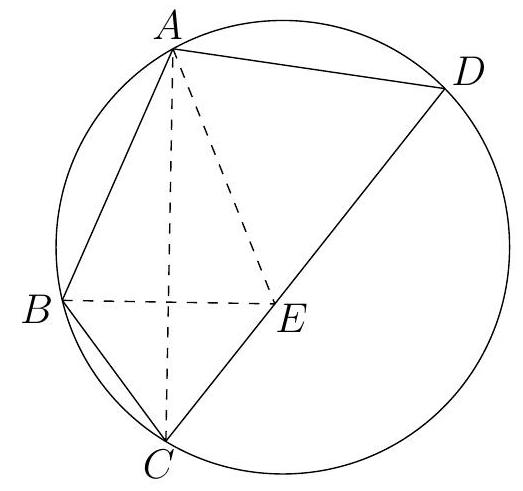
|
| 24 |
+
|
| 25 |
+
Now, since $A B=A D$ then $\angle B C A=\angle A C D$. This shows that $C A$ is the bisector of $\angle B C D=\angle B C E$. In an isosceles triangle, the bisector of the apex angle is also the perpendicular bisector of the base. Hence $A$ is on the perpendicular bisector of $B E$, and $A E=A B=A D=D E$. This shows that triangle $A E D$ is equilateral, and thus $\angle C D A=60^{\circ}$.
|
| 26 |
+
|
| 27 |
+
## Problem 3
|
| 28 |
+
|
| 29 |
+
Find all $a \in \mathbb{R}$ for which there exists a function $f: \mathbb{R} \rightarrow \mathbb{R}$, such that
|
| 30 |
+
|
| 31 |
+
(i) $f(f(x))=f(x)+x$, for all $x \in \mathbb{R}$,
|
| 32 |
+
|
| 33 |
+
(ii) $f(f(x)-x)=f(x)+$ ax, for all $x \in \mathbb{R}$.
|
| 34 |
+
|
| 35 |
+
Solution 3 Answer: $a=\frac{1 \pm \sqrt{5}}{2}$.
|
| 36 |
+
|
| 37 |
+
From (i) we get $f(f(f(x))-f(x))=f(x)$. On the other hand (ii) gives
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
f(f(f(x))-f(x))=f(f(x))+a f(x)
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Thus we have $(1-a) f(x)=f(f(x))$. Now it follows by (i) that $(1-a) f(x)=f(x)+x$, and hence $f(x)=-\frac{1}{a} x$, since $a=0$ obviously does not give a solution.
|
| 44 |
+
|
| 45 |
+
We now need to check whether (i) and (ii) hold for this function for some values of $a$ and all real $x$. We have
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
f(f(x))=-\frac{1}{a} f(x)=\frac{1}{a^{2}} x, \text { and } f(x)+x=-\frac{1}{a} x+x=\frac{a-1}{a} x
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Thus (i) will hold for all real $x$ iff $\frac{1}{a^{2}}=\frac{a-1}{a}$, i.e. iff $a=\frac{1 \pm \sqrt{5}}{2}$. For these values of $a$ we have
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
f(f(x)-x)=-\frac{1}{a}(f(x)-x)=-\frac{1}{a}\left(-\frac{1}{a} x-x\right)=\left(\frac{1}{a^{2}}+\frac{1}{a}\right) x=\frac{a+1}{a^{2}} x=x
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
and
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
f(x)+a x=-\frac{1}{a} x+a x=\frac{a^{2}-1}{a} x=x
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
so that for these two values of $a$ both (i) and (ii) hold for all real $x$. Thus the values of $a$ such that there exists a function $f$ with the desired properties are $a=\frac{1 \pm \sqrt{5}}{2}$.
|
| 64 |
+
|
| 65 |
+
## Problem 4
|
| 66 |
+
|
| 67 |
+
King George has decided to connect the 1680 islands in his kingdom by bridges. Unfortunately the rebel movement will destroy two bridges after all the bridges have been built, but not two bridges from the same island.
|
| 68 |
+
|
| 69 |
+
What is the minimal number of bridges the King has to build in order to make sure that it is still possible to travel by bridges between any two of the 1680 islands after the rebel movement has destroyed two bridges?
|
| 70 |
+
|
| 71 |
+
Solution 4 Answer: 2016
|
| 72 |
+
|
| 73 |
+
An island cannot be connected with just one bridge, since this bridge could be destroyed. Consider the case of two islands, each with only two bridges, connected by a bridge. (It is not possible that they are connected with two bridges, since then they would be isolated from the other islands no matter what.) If they are also connected to two separate islands, then they would be isolated if the rebel movement destroys the two bridges from these islands not connecting the two. So the two bridges not connecting them must go to the same island. That third island must have at least two other bridges, otherwise the rebel movement could cut off these three islands.
|
| 74 |
+
|
| 75 |
+
Suppose there is a pair of islands with exactly two bridges that are connected to each other. From the above it is easy to see that removing the pair (and the three bridges connected to them) must leave a set of islands with the same properties. Continue removing such pairs, until there are none left. (Note that the reduced set of islands could have a new such pair and that also needs to be removed.) Suppose we are left with $n$ islands and since two islands are removed at a time, $n$ must be an even number. And from the argument above it is clear that $n \geq 4$.
|
| 76 |
+
|
| 77 |
+
Consider the remaining set of islands and let $x$ be the number of islands with exactly two bridges (which now are not connected to each other). Then $n-x$ islands have at least three bridges each. Let $B^{\prime}$ be the number of bridges in the reduced set. Now $B^{\prime} \geq 2 x$ and $2 B^{\prime} \geq 2 x+3(n-x)=3 n-x$. Hence $2 B^{\prime} \geq \max (4 x, 3 n-x) \geq 4 \cdot \frac{3 n}{5}$, and thus $B^{\prime} \geq \frac{6 n}{5}$. Now let $B$ be the number of bridges in the original set. Then
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
B=B^{\prime}+3 \cdot \frac{1680-n}{2} \geq \frac{6 n}{5}+\frac{6(1680-n)}{4} \geq \frac{6 \cdot 1680}{5}=2016
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
It is possible to construct an example with exactly 2016 bridges: Take 672 of the islands and number them $0,1,2, \ldots 671$. Connect island number $i$ with the islands numbered $i-1$, $i+1$ and $i+336$ (modulo 672). This gives 1008 bridges. We now have a circular path of 672 bridges: $0-1-2-\cdots-671-0$. If one of these 672 bridges are destroyed, the 672 islands are still connected. If two of these bridges are destroyed, the path is broken into two parts. Let $i$ be an island on the shortest path (if they have the same length, just pick a random one). Then island $i+336$ (modulo 672) must be on the other part of the path, and the bridge connecting these two islands will connect the two paths. Hence no matter which two bridges the rebel movement destroys, it is possible to travel between any of the 672 islands.
|
| 84 |
+
|
| 85 |
+
Now for every of the 1008 bridges above, replace it with two bridges with a new island between the two. This increases the number of bridges to 2016 and the number of islands to $672+1008=1680$ completing the construction. Since the rebel movement does not destroy two bridges from the same island, the same argument as above shows that with this construction it is possible to travel between any of the 1680 islands after the destruction of the two bridges.
|
| 86 |
+
|
Nordic_MO/md/en-2017-sol.md
ADDED
|
@@ -0,0 +1,133 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 31st Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
## Monday, 3 April 2017
|
| 4 |
+
|
| 5 |
+
## Solutions
|
| 6 |
+
|
| 7 |
+
Problem 1 Let $n$ be a positive integer. Show that there exist positive integers $a$ and $b$ such that:
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
\frac{a^{2}+a+1}{b^{2}+b+1}=n^{2}+n+1
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
Solution 1 Let $P(x)=x^{2}+x+1$. We have $P(n) P(n+1)=\left(n^{2}+n+1\right)\left(n^{2}+3 n+3\right)=$ $n^{4}+4 n^{3}+7 n^{2}+6 n+3$. Also, $P\left((n+1)^{2}\right)=n^{4}+4 n^{3}+7 n^{2}+6 n+3$. By choosing $a=(n+1)^{2}$ and $b=n+1$ we get $P(a) / P(b)=P(n)$ as desired.
|
| 14 |
+
|
| 15 |
+
Problem 2 Let $a, b, \alpha, \beta$ be real numbers such that $0 \leq a, b \leq 1$, and $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. Show that if
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
a b \cos (\alpha-\beta) \leq \sqrt{\left(1-a^{2}\right)\left(1-b^{2}\right)}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
then
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
a \cos \alpha+b \sin \beta \leq 1+a b \sin (\beta-\alpha)
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
Solution 2 The condition can be rewritten as
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
a b \cos (\alpha-\beta)=a b \cos \alpha \cos \beta+a b \sin \alpha \sin \beta \leq \sqrt{\left(1-a^{2}\right)\left(1-b^{2}\right)}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Set $x=a \cos \alpha, y=b \sin \beta, z=b \cos \beta, t=a \sin \alpha$. We can now rewrite the condition as
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
x z+y t \leq \sqrt{\left(1-x^{2}-t^{2}\right)\left(1-y^{2}-z^{2}\right)}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
whereas the inequality we need to prove now looks like
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
x+y \leq 1+x y-z t
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Since $x, y, z, t \geq 0$, and $1+x y-z t=1+a b \sin (\beta-\alpha) \geq 0$, we can square both sides of both inequalities, and get equivalent ones. After a couple of cancelations the condition yields
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
2 x y z t \leq 1-x^{2}-y^{2}-z^{2}-t^{2}+x^{2} y^{2}+z^{2} t^{2}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
so that
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
x^{2}+y^{2}+z^{2}+t^{2} \leq(x y-z t)^{2}+1
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
which is equivalent to
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
x^{2}+y^{2}+z^{2}+t^{2}+2 x y-2 z t \leq(1+x y-z t)^{2}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
or
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
(x+y)^{2}+(z-t)^{2} \leq(1+x y-z t)^{2}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Since $(x+y)^{2} \leq(x+y)^{2}+(z-t)^{2}$, the desired inequality follows.
|
| 70 |
+
|
| 71 |
+
Problem 3 Let $M$ and $N$ be the midpoints of the sides $A C$ and $A B$, respectively, of an acute triangle $A B C, A B \neq A C$. Let $\omega_{B}$ be the circle centered at $M$ passing through $B$, and let $\omega_{C}$ be the circle centered at $N$ passing through $C$. Let the point $D$ be such that $A B C D$ is an isosceles trapezoid with $A D$ parallel to $B C$. Assume that $\omega_{B}$ and $\omega_{C}$ intersect in two distinct points $P$ and $Q$. Show that $D$ lies on the line $P Q$.
|
| 72 |
+
|
| 73 |
+
Solution 3 Let $E$ be such that $A B E C$ is a parallelogram with $A B \| C E$ and $A C \| B E$, and let $\omega$ be the circumscribed circle of $\triangle A B C$ with centre $O$.
|
| 74 |
+
|
| 75 |
+
It is known that the radical axis of two circles is perpendicular to the line connecting the two centres. Since $B E \perp M O$ and $C E \perp N O$, this means that $B E$ and $C E$ are the radical axes of $\omega$ and $\omega_{B}$, and of $\omega$ and $\omega_{C}$, respectively, so $E$ is the radical centre of $\omega$, $\omega_{B}$, and $\omega_{C}$.
|
| 76 |
+
|
| 77 |
+
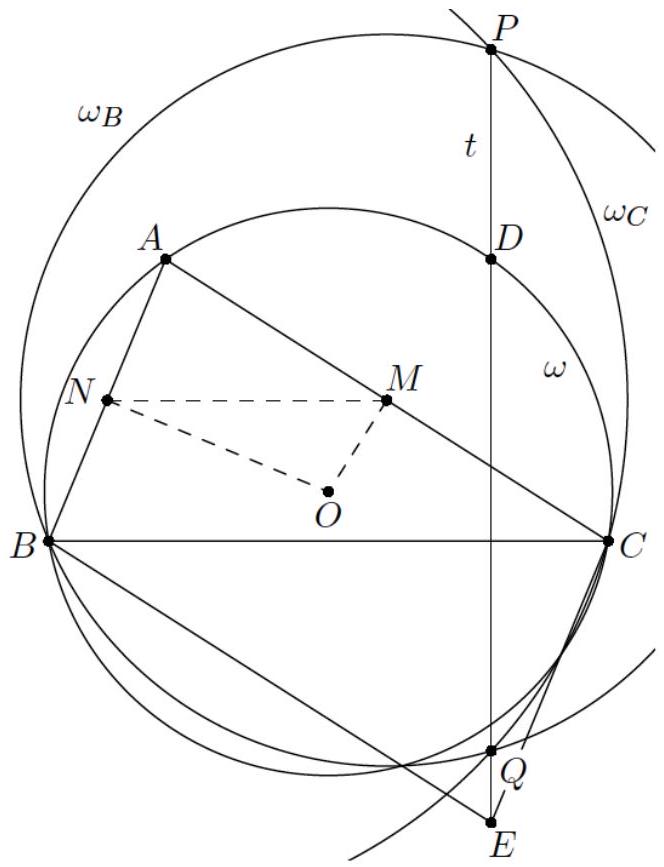
|
| 78 |
+
|
| 79 |
+
Now as $B E=A C=B D$ and $C E=A B=C D$ we find that $B C$ is the perpendicular bisector of $D E$. Most importantly we have $D E \perp B C$. Denote by $t$ the radical axis of $\omega_{B}$ and $\omega_{C}$, i.e. $t=P Q$. Then since $t \perp M N$ we find that $t$ and $D E$ are parallel. Therefore since $E$ lies on $t$ we get that $D$ also lies on $t$.
|
| 80 |
+
|
| 81 |
+
Alternative solution Reflect $B$ across $M$ to a point $B^{\prime}$ forming a parallelogram $A B C B^{\prime}$. Then $B^{\prime}$ lies on $\omega_{B}$ diagonally opposite $B$, and since $A B^{\prime} \| B C$ it lies on $A D$. Similarly reflect $C$ across $N$ to a point $C^{\prime}$, which satisfies analogous properties. Note that $C B^{\prime}=A B=C D$, so we find that triangle $C D B^{\prime}$ and similarly triangle $B D C^{\prime}$ are isosceles.
|
| 82 |
+
|
| 83 |
+
Let $B^{\prime \prime}$ and $C^{\prime \prime}$ be the orthogonal projections of $B$ and $C$ onto $A D$. Since $B B^{\prime}$ is a diameter of $\omega_{B}$ we get that $B^{\prime \prime}$ lies on $\omega_{B}$, and similarly $C^{\prime \prime}$ lies on $\omega_{C}$. Moreover $B B^{\prime \prime}$ is an altitude of the isosceles triangle $B D C^{\prime}$ with $B D=B C^{\prime}$, hence it coincides with the median from $B$, so $B^{\prime \prime}$ is in fact the midpoint of $D C^{\prime}$. Similarly $C^{\prime \prime}$ is the midpoint of $D B^{\prime}$. From this we get
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
2=\frac{D C^{\prime}}{D B^{\prime \prime}}=\frac{D B^{\prime}}{D C^{\prime \prime}}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
which rearranges as $D C^{\prime} \cdot D C^{\prime \prime}=D B^{\prime} \cdot D B^{\prime \prime}$. This means that $D$ has same the power with respect to $\omega_{B}$ and $\omega_{C}$, hence it lies on their radical axis $P Q$.
|
| 90 |
+
|
| 91 |
+
Problem 4 Find all integers $n$ and $m, n>m>2$, and such that a regular $n$-sided polygon can be inscribed in a regular $m$-sided polygon so that all the vertices of the $n$-gon lie on the sides of the $m$-gon.
|
| 92 |
+
|
| 93 |
+
Solution 4 It works only for $n=2 m$, and for $m=3$ and $n=4$.
|
| 94 |
+
|
| 95 |
+
To begin with let's see why it works for $n=2 m$. For a $2 m$-gon we can choose two points on each side, symmetrically, so that the distance between the two of them is equal to the distance between two close points on adjacent sides.
|
| 96 |
+
|
| 97 |
+
For $n=4$ and $m=3$ we need to inscribe a square in an equilateral triangle, by choosing two vertices of the square symmetrically on one of the sides of the triangle. It is easy to calculate the side length of the square so that its remaining two vertices lie on the remaining two sides of the triangle.
|
| 98 |
+
|
| 99 |
+
We need to show that it cannot be done in any other way. One side of the $m$-gon can contain at most two of the vertices of the $n$-gon, so that $n \leq 2 m$. For $n \geq m+2$ at least two of the sides of the $m$-gon must contain two of the vertices of the $n$-gon each. By symmetry the midpoints, and thus the perpendicular bisectors, of such a side of the $m$-gon and of the side of the $n$-gon it contains must coincide. If two such sides of the $m$-gon are not opposite to each other the corresponding perpendicular bisectors will intersect, and we can deduce that the centres of the circumscribed circles of the $m$-gon and of the $n$-gon must coincide. If two such sides are opposite, then the centres of the circumscribed circles will coincide with the midpoint of the segment between the midpoints of the sides, and thus the two circumscribed circles will once again have the same centre.
|
| 100 |
+
|
| 101 |
+
Denote the radii of the two circumscribed circles by $R$ and $r$, where $R>r$. The smaller circle intersects the sides of the $m$-gon at $2 m$ points, among which are the possible vertices for the $n$-gon. Denote these points by $P_{1}, P_{2}, \ldots, P_{2 m}$ clockwise, where $P_{1}$ and $P_{2}$
|
| 102 |
+
are vertices of the $n$-gon. If the side length of the $n$-gon is $s$, we now have $\left|P_{1} P_{2}\right|=s$, and thus $\left|P_{3} P_{4}\right|=s$. If only one of the points $P_{3}$ and $P_{4}$ is a vertex in the $n$-gon, it would have to be $P_{4}$, but the distance between $P_{2}$ and $P_{4}$ is greater than $s$, which means $P_{2} P_{4}$ cannot be a side. We can now deduce that both $P_{3}$ and $P_{4}$ are vertices of the $n$-gon, and by symmetry all the $2 m$ points of intersection will be vertices of the $n$-gon, so that $n=2 m$.
|
| 103 |
+
|
| 104 |
+
We now need to handle the case $n=m+1>4$. Denote the vertices of the $m$-gon by $Q_{1}, Q_{2}, \ldots, Q_{m}$ clockwise. Now only one of the sides of the $m$-gon contains two of the vertices of the $n$-gon, let this side be $Q_{m} Q_{1}$. Denote the vertices of the $(m+1)$-gon by $P_{1}, P_{2}, \ldots, P_{m+1}$ clockwise, where $P_{1}$ and $P_{m+1}$ lie on the side $Q_{m} Q_{1}$ of the $m$-gon. Let $\alpha=\pi-2 \pi /(m+1)$, and $\beta=\pi-2 \pi / m$ be the angles of the $n$-gon and the $m$ gon, respectively. We now get a number of triangles $P_{1} Q_{1} P_{2}, P_{2} Q_{2} P_{3}, \ldots P_{m} Q_{m} P_{m+1}$. We begin by establishing a connection between the sizes of the angles. To begin with we have $\angle Q_{1} P_{1} P_{2}=\pi-\alpha$, and $\angle P_{1} Q_{1} P_{2}=\beta$, so that $\angle P_{1} P_{2} Q_{1}=\alpha-\beta$. We now proceed to get $\angle Q_{2} P_{2} P_{3}=\pi-\alpha-(\alpha-\beta)$, and $\angle P_{2} Q_{2} P_{3}=\beta$, which gives $\angle P_{2} P_{3} Q_{2}=2(\alpha-\beta)$, and so on. If now $\gamma=\alpha-\beta=2 \pi / m(m+1)$, we have $\angle P_{k} P_{k+1} Q_{k}=k \gamma$, and $\angle Q_{k} P_{k} P_{k+1}=$ $(m+1-k) \gamma$ for $k=1,2, \ldots, m$.
|
| 105 |
+
|
| 106 |
+
Since $s$ is the side length of the $n$-gon, i.e. $s=\left|P_{1} P_{2}\right|=\left|P_{1} P_{2}\right|=\cdots=\left|P_{m+1} P_{1}\right|$, according to the law of sines we get
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
\frac{s}{\sin \beta}=\frac{\left|P_{k} Q_{k}\right|}{\sin \left(P_{k} P_{k+1} Q_{k}\right)}=\frac{\left|Q_{k} P_{k+1}\right|}{\sin \left(Q_{k} P_{k} P_{k+1}\right)}
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
i.e.
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
\frac{s}{\sin \beta}=\frac{\left|P_{k} Q_{k}\right|}{\sin (k \gamma)}=\frac{\left|Q_{k} P_{k+1}\right|}{\sin ((m+1-k) \gamma)}
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
Since $\left|Q_{k} Q_{k+1}\right|=\left|Q_{k} P_{k+1}\right|+\left|P_{k+1} Q_{k+1}\right|$, we get
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
\sin ((k+1) \gamma)+\sin ((m+1-k) \gamma)=\frac{\sigma \sin \beta}{s}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
where $\sigma=\left|Q_{1} Q_{2}\right|=\left|Q_{2} Q_{3}\right|=\cdots=\left|Q_{m} Q_{1}\right|$ is the side length of the $m$-gon.
|
| 125 |
+
|
| 126 |
+
Using the above for $k=1$ and $k=2$, we get
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
\sin 2 \gamma+\sin m \gamma=\sin 3 \gamma+\sin (m-1) \gamma
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
For $m \geq 4$ the angles $3 \gamma$ and $(m-1) \gamma$ are both in the interval between $2 \gamma$ and $m \gamma$, which means we can't have equality as the sine function is concave (convex from above) in the interval $[0, \pi / 2]$. We therefore deduce that it is impossible to inscribe an $(m+1)$-gon in an $m$-gon for $m \geq 4$.
|
| 133 |
+
|
Nordic_MO/md/en-2018-sol.md
ADDED
|
@@ -0,0 +1,70 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Solutions NMC 2018
|
| 2 |
+
|
| 3 |
+
## Solution to problem 1
|
| 4 |
+
|
| 5 |
+
It is clear that $2 k$ lines do not suffice, as the two rays parallel to any fixed line intersect a total of $2 k-1$ lines, so one intersects at most $k-1$. We shall show that $2 k+1$ lines are sufficient.
|
| 6 |
+
|
| 7 |
+
Let $P$ be at the origin. Given an angle $v$, let $s(v)$ denote the ray from $P$ that intersects the unit circle at the point $(\cos v, \sin v)$. For each angle $v_{i}$ and each $\epsilon>0$, by drawing two "almost parallel" lines on each side of $P$ guarantee that all rays from $P$ that are not $s(v)$ for some $v_{i} \leq v \leq v_{i}+\epsilon$ intersect at least one of these two lines. If we for example choose $v_{i}=2 i \epsilon$ and $\epsilon$ sufficiently small, we may see that $\left[v_{i}, v_{i}+\epsilon\right], i \in\{1, \ldots, k\}$ are pairwise disjoint and $0<v_{i}<\pi-\epsilon$. We then have $2 k$ lines with the property that each $s(v), 0<v<\pi$, intersects at least $k-1$ lines and each $s(v), \pi \leq v \leq 2 \pi$, intersects $k$ lines. Now add the line that is tangent to the unit circle at $(0,1)$ and we have $2 k+1$ lines with the required properties.
|
| 8 |
+
|
| 9 |
+
An alternative description is as follows. Pick any line that does not go through $P$, and call it $\ell$. Then choose points $Q_{1}, Q_{2}, \ldots, Q_{2 k}$ on $\ell$ so that they appear in this order. For each $1 \leq j \leq k$, choose a point $S_{j}$ so that the triangle $Q_{2 j-1} Q_{2 j} S_{j}$ contains $P$ in its interior. Our remaining $k$ lines are then going to be $Q_{2 j-1} S_{j}$ and $Q_{2 j} S_{j}$ with $1 \leq j \leq k$. Note that for any ray $s$ from $P$ and index $j$, the ray $s$ intersects at least one of the lines $Q_{2 j-1} S_{j}$ and $Q_{2 j} S_{j}$ unless it intersects the segment $Q_{2 j-1} Q_{2 j}$. Since these segments are pairwise disjoint, this may happen at most once, in which case $\ell$ provides the $k$-th intersection.
|
| 10 |
+
|
| 11 |
+
## Solution to problem 2
|
| 12 |
+
|
| 13 |
+
First we prove that $p_{n+2} \leq \max \left(p_{n}, p_{n}+1\right)+2020$ for all positive integers $n$. Assume that $p_{n}, p_{n+1}>2$. Then $p_{n}+p_{n+1}+2018$ is even, og and hence
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
p_{n+2} \leq \frac{p_{n}+p_{n+1}}{2}+1009 \leq \max \left(p_{n}, p_{n+1}\right)+2020
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
If $p_{n}$ or $p_{n+1}$ is 2 , then
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
p_{n+2} \leq p_{n}+p_{n+1}+2018=\max \left(p_{n}, p_{n+1}\right)+2020
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Choose $m$ such that $M=m \cdot 2021$ ! is greater than both $p_{1}$ and $p_{2}$. Now $M+2, M+3, \ldots, M+2021$ are 2020 consecutive integers and none of which are primes. By induction it follows that all primes of the sequnce are less than or equal to $M+1$ :
|
| 26 |
+
|
| 27 |
+
By construction $p_{1}$ and $p_{2}$ are less than $M+1$. Assume that $p_{1}, p_{2}, \ldots, p_{n+1}$ all are less than or equal to $M+1$ for some $n \geq 1$. Then
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
p_{n+2} \leq \max \left(p_{n}, p_{n}+1\right)+2020 \leq M+2021
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Since $p_{n+2}$ is a prime, and none of the integers $M+2, M+3, \ldots, M+2021$ are primes, we conclude $p_{n+2} \leq M+1$.
|
| 34 |
+
|
| 35 |
+
Hence the sequence only contains finitely many primes.
|
| 36 |
+
|
| 37 |
+
## Solution to problem 3
|
| 38 |
+
|
| 39 |
+
Let the point $A^{\prime}$ be such that $A B A^{\prime} C$ is a parallelogram with $A B \| A^{\prime} C$ and $A C \| A^{\prime} B$. Denote $\alpha=\angle B A C=\angle C A^{\prime} B$.
|
| 40 |
+
|
| 41 |
+
Since $C D=A B=C A^{\prime}$, we find that $C D A^{\prime}$ is an isosceles triangle. As $\angle D C A^{\prime}=180^{\circ}-\alpha$, we deduce that $\angle A^{\prime} D C=\angle C A^{\prime} D=\frac{\alpha}{2}$, so that $D$ lies on the angle bisector $\ell$ of $\angle C A^{\prime} B$. Similarly $E$ lies on $\ell$.
|
| 42 |
+
|
| 43 |
+
Next notice that $\angle C B H=90^{\circ}-\angle B C I=90^{\circ}-\frac{1}{2} \angle B C A=90^{\circ}-\frac{1}{2} \angle A^{\prime} B C$, so $B H$ is the exterior angle bisector of $\angle A^{\prime} B C$. Similarly $C H$ is the exterior angle bisector of $\angle A^{\prime} C B$, so $H$ is in fact the excenter of triangle $A^{\prime} B C$ opposite $A^{\prime}$. Therefore we conclude that $D, E$, and $H$ all lie on $\ell$.
|
| 44 |
+
|
| 45 |
+
|
| 46 |
+
|
| 47 |
+
## Solution to problem 4
|
| 48 |
+
|
| 49 |
+
Introducing new variables $X=x-y, Y=y-z$, we may write $f$ as $A_{1}(X, Y, z) X+$ $B_{1}(X, Y, z) Y+c(z)$. To see this, note that this transformation is invertible, i.e., we can express the original variables as polynomials of the new ones: $x=X+Y+z$ and $y=Y+z$, and plugging in yields a polynomial in the three variables $X, Y, z$. Then we group the terms in the new expression with those having a factor $X$ in the first group, among the remaining ones, those containing a factor $Y$ in the second, and the rest in the third group. This yields the desired expression (note that we have some freedom as to where we want to put terms with factor XY).
|
| 50 |
+
|
| 51 |
+
Alternatively, we may consider $f$ as a polynomial in one variable, $x$, and with $y, z$ as parameters. Then performing a polynomial division with $x-y$, we obtain $f(x, y, z)=g(x, y, z) \cdot(x-y)+r(x, y, z)$. Note that $r$ has to have degree zero as a polynomial in $x$, so in fact $r(x, y, z)=r(y, z)$. Now repeat this with $r$ as a polynomial in $y$ with parameter $z$, divided by $y-z$. This yields the same result as the above approach.
|
| 52 |
+
|
| 53 |
+
Thus $f=A_{2}(x, y, z)(x-y)+B_{2}(x, y, z)(y-z)+c(z)$. Since $f(w, w, w)=0$, we obtain $c(w)=0$ for all $w$, that is $c(z)=0$. Let $C(x, y, z)=-\frac{A_{2}+B_{2}}{3}, A=$ $A_{2}+C, B=B_{2}+C$. Then $A+B+C=A_{2}+B_{2}+3 C=A_{2}+B_{2}-\left(A_{2}+B_{2}\right)=0$, and
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
f=(A-C)(x-y)+(B-C)(y-z)=A(x-y)+B(y-z)+C(z-x)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
The representation is never unique. To show this, it is by additivity enough to show that the representation is not unique for the zero polynomial. Let
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\begin{aligned}
|
| 63 |
+
& A=2 z-x-y=(z-x)-(y-z) \\
|
| 64 |
+
& B=2 x-y-z=(x-y)-(z-x) \\
|
| 65 |
+
& C=2 y-x-z=(y-z)-(x-y)
|
| 66 |
+
\end{aligned}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
where $A+B+C=A \cdot(x-y)+B \cdot(y-z)+C \cdot(z-x)=0$, showing that 0 has two different representations (the other being the trivial one).
|
| 70 |
+
|
Nordic_MO/md/en-2019-sol.md
ADDED
|
@@ -0,0 +1,103 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 33rd Nordic Mathematical Contest <br> Monday, April 1st, 2019 <br> English version
|
| 2 |
+
|
| 3 |
+
Time allowed: 4 hours. Each problem is worth 7 points.
|
| 4 |
+
|
| 5 |
+
Only writing and drawing tools are allowed.
|
| 6 |
+
|
| 7 |
+
Problem 1 A set of different positive integers is called meaningful if for any finite nonempty subset the corresponding arithmetic and geometric means are both integers.
|
| 8 |
+
|
| 9 |
+
a) Does there exist a meaningful set which consists of 2019 numbers?
|
| 10 |
+
|
| 11 |
+
b) Does there exist an infinite meaningful set?
|
| 12 |
+
|
| 13 |
+
Note: The geometric mean of the non-negative numbers $a_{1}, a_{2}, \ldots, a_{n}$ is defined as $\sqrt[n]{a_{1} a_{2} \cdots a_{n}}$
|
| 14 |
+
|
| 15 |
+
Problem 2 Let $a, b, c$ be the side lengths of a right angled triangle with $c>a, b$.
|
| 16 |
+
|
| 17 |
+
Show that
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
3<\frac{c^{3}-a^{3}-b^{3}}{c(c-a)(c-b)} \leq \sqrt{2}+2
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Problem 3 The quadrilateral $A B C D$ satisfies $\angle A C D=2 \angle C A B, \angle A C B=2 \angle C A D$ and $C B=C D$.
|
| 24 |
+
|
| 25 |
+
Show that $\angle C A B=\angle C A D$.
|
| 26 |
+
|
| 27 |
+
Problem 4 Let $n$ be an integer with $n \geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.
|
| 28 |
+
|
| 29 |
+
Solution 1 a) Notice that $\left\{2019!\cdot 1^{2019!}, 2019!\cdot 2^{2019!}, \ldots, 2019!\cdot 2019^{2019!}\right\}$ is such a set. Observe that if all the elements are divisible by 2019! then the arithmetic means will be integer for all the subsets. Also, if $A$ is a set such that the geometric means are integer for all non-empty subsets and the set $B$ is obtained from the set $A$ by multiplying each element with with a given integer $c$ then all the non-empty subsets of $B$ will have an integer geometric mean, since
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\sqrt[k]{c a_{i_{1}} c a_{i_{2}} \cdots c a_{i_{k}}}=c \sqrt[k]{a_{i_{1}} a_{i_{2}} \cdots a_{i_{k}}}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
It is thus sufficient to find a set of 2019 positive integers such that the geometric mean of every non-empty subset in an integer. Now, for an integer $a$ the number $\sqrt[k]{a^{2019!}}=a^{\frac{2019!}{k}}$ for all integers $1 \leq k \leq 2019$ so $\left\{1^{2019!}, 2^{2019!}, \ldots, 2019^{2019!}\right\}$ is a set such that the geometric mean of every non-empty subset is an integer.
|
| 36 |
+
|
| 37 |
+
b) Assume there exist such a set $A$ and let $n, m, a_{1}, a_{2}, \ldots, a_{m-1}$ be distinct elements in $A$ with $n<m$. Then $\frac{n+a_{1}+a_{2}+\cdots+a_{m-1}}{m}$ and $\frac{m+a_{1}+a_{2}+\cdots+a_{m-1}}{m}$ are integers and also their difference
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\frac{m+a_{1}+a_{2}+\cdots+a_{m-1}}{m}-\frac{n+a_{1}+a_{2}+\cdots+a_{m-1}}{m}=\frac{m-n}{m}
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Therefore, we have $\frac{n}{m}$ is an integer and since $m$ and $n$ are positive integers we have $m \leq n$ which is a contradiction.
|
| 44 |
+
|
| 45 |
+
Solution 2 Observe that
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\begin{gathered}
|
| 49 |
+
c^{3}-a^{3}-b^{3}=c a^{2}+c b^{2}-a^{3}-b^{3}=a^{2}(c-a)+b^{2}(c-b)= \\
|
| 50 |
+
\left(c^{2}-b^{2}\right)(c-a)+\left(c^{2}-b^{2}\right)(c-b)=(c-a)(c-b)(c+a+c+b)
|
| 51 |
+
\end{gathered}
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Therefore, it is equivalent to prove that
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
c<a+b \leq \sqrt{2} c
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
The left inequality we get from the triangle inequality and the right inequality we get from
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
a+b \leq \sqrt{2} c \Leftrightarrow(a+b)^{2} \leq 2 c^{2}=2 a^{2}+2 b^{2} \Leftrightarrow 0 \leq(a-b)^{2}
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
Solution 3 Let the angle bisectors from angle $C$ in triangle $A C B$ and $A C D$ intersect $A B$ and $A D$ in points $E$ and $F$ respectively. From $\angle A C E=\angle C A D$ it follows that $C E$ and $A D$ are parallel. Similarly $C F$ and $A B$ are parallel. Hence $A E C F$ is a parallelogram. From this it follows that $\angle B E C=\angle B A D=\angle C F D$.
|
| 67 |
+
|
| 68 |
+
|
| 69 |
+
|
| 70 |
+
The angle bisector theorem yields
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
\frac{B E}{C F}=\frac{B E}{A E}=\frac{C B}{C A}=\frac{C D}{C A}=\frac{D F}{A F}=\frac{D F}{C E}
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
which gives
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
|B E| \cdot|C E|=|D F| \cdot|C F| \text {. }
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
By the sine area formula we obtain that $B C E$ have $D C F$ have equal area. Hence triangles $B C A$ and $D C A$ also have equal areal. By the sine area formula we now get
|
| 83 |
+
|
| 84 |
+
$$
|
| 85 |
+
\sin (\angle A C B)=\sin (\angle D C A)
|
| 86 |
+
$$
|
| 87 |
+
|
| 88 |
+
Since $A B C D$ is a quadrilateral, $\angle A C B+\angle D C A \neq 180$ and hence we conclude from the above that $\angle C A B=\angle C A D$.
|
| 89 |
+
|
| 90 |
+
Solution 4 Assume that it is possible to color $2 n$ of the vertices of a $4 n+1$-gon such that there are no three colored vertices forming an isosceles triangle. Enumerate the vertices consecutively as $H_{-2 n}, H_{-2 n+1}, \ldots, H_{0}, H_{1}, H_{2}, \ldots, H_{2 n}$ and consider first the case where there are two colored neighboring vertices. Assume wlog that the vertices $H_{0}$ and $H_{1}$ are colored. Then at most one of the vertices $H_{-i}$ and $H_{i}$ are colored for all $i=1,2, \ldots, 2 n$ since these form an isosceles triangle with $H_{0}$. Similarly at most one of $H_{-i}$ and $H_{i+2}$ are colored for all $i=1,2, \ldots, 2 n-2$, and at most one of $H_{-(2 n-1)}$ and $H_{-2 n}$ are colored since these form an isosceles triangles with $H_{1}$. The three vertices $H_{0}, H_{1}, H_{i}, i=2,-1,-2 n$ also form isoceles triangles and hence $H_{-1}, H_{2}, H_{-2 n}$ are not colored. It follows that no consecutive vertices in the two strings
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
\begin{array}{r}
|
| 94 |
+
H_{-2}-H_{4}-H_{-4}-H_{6}-\ldots-H_{2 n-2}-H_{-(2 n-2)}-H_{2 n} \\
|
| 95 |
+
H_{3}-H_{-3}-H_{5}-H_{-5}-\ldots-H_{2 n-1}-H_{-(2 n-1)}
|
| 96 |
+
\end{array}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
are colored. Since each string contains an even amount of vertices, at most half of each string are colored and this is obtained only when every second vertex is colored in each string. By counting we see that each string contains $2 n-2$ vertices and we conclude that every second vertex is colored in each string. Because $n \geq 3$ at least one of the isoceles
|
| 100 |
+
triangles $H_{0} H_{-2} H_{-4}, H_{1} H_{3} H_{5}$ or $H_{2 n-2} H_{2 n} H_{-(2 n-1)}$ must be colored. Hence there are no colored neighboring vertices.
|
| 101 |
+
|
| 102 |
+
If there are no colored neighboring vertices we can assume wlog that $H_{i}$ is colored for all odd $i$, but then $H_{1} H_{3} H_{5}$ is an isosceles colored triangle. Hence we have a contradiction, showing that there must neccesarily exists 3 colored vertices forming an isosceles triangle.
|
| 103 |
+
|
Nordic_MO/md/en-2021-sol.md
ADDED
|
@@ -0,0 +1,83 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 35th Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
Friday, 16 April 2021
|
| 4 |
+
|
| 5 |
+
Time allowed: 4 hours. Each problem is worth 7 points.<br>Only writing and drawing tools are allowed.
|
| 6 |
+
|
| 7 |
+
Problem 1. On a blackboard a finite number of integers greater than one are written. Every minute, Nordi additionally writes on the blackboard the smallest positive integer greater than every other integer on the blackboard and not divisible by any of the numbers on the blackboard. Show that from some point onwards Nordi only writes primes on the blackboard.
|
| 8 |
+
|
| 9 |
+
Problem 2. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying that for every $x \in \mathbb{R}$,
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
f(x(1+|x|)) \leq x \leq f(x)(1+|f(x)|)
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Problem 3. Let $n$ be a positive integer. Alice and Bob play the following game. First, Alice picks $n+1$ subsets $A_{1}, \ldots, A_{n+1}$ of $\left\{1, \ldots, 2^{n}\right\}$ each of size $2^{n-1}$. Second, Bob picks $n+1$ arbitrary integers $a_{1}, \ldots, a_{n+1}$. Finally, Alice picks an integer $t$. Bob wins if there exists an integer $1 \leq i \leq n+1$ and $s \in A_{i}$ such that $s+a_{i} \equiv t\left(\bmod 2^{n}\right)$. Otherwise, Alice wins.
|
| 16 |
+
|
| 17 |
+
Find all values of $n$ where Alice has a winning strategy.
|
| 18 |
+
|
| 19 |
+
Problem 4. Let $A, B, C$ and $D$ be points on the circle $\omega$ such that $A B C D$ is a convex quadrilateral. Suppose that $A B$ and $C D$ intersect at a point $E$ such that $A$ is between $B$ and $E$ and that $B D$ and $A C$ intersect at a point $F$. Let $X \neq D$ be the point on $\omega$ such that $D X$ and $E F$ are parallel. Let $Y$ be the reflection of $D$ through $E F$ and suppose that $Y$ is inside the circle $\omega$.
|
| 20 |
+
|
| 21 |
+
Show that $A, X$, and $Y$ are collinear.
|
| 22 |
+
|
| 23 |
+
## Solutions
|
| 24 |
+
|
| 25 |
+
Problem 1. Let $a$ be the largest integer initially written on the blackboard. Furthermore, denote by $a_{n}$ the integer written by Nordi on the blackboard after $n$ minutes.
|
| 26 |
+
|
| 27 |
+
Suppose that $p>a$ is prime. If Nordi never writes $p$ on the blackboard, there exist $a_{n}<p<a_{n+1}$ since $a_{1}, a_{2}, \ldots$ is a strictly increasing sequence of positive integers. However, $p$ is a prime greater than $a_{n}$, so $p$ is not divisible by any of the integers written on the blackboard after $n$ minutes. This contradicts that $a_{n+1}$ is the smallest integer greater than $a_{n}$ which is not divisible by any of the integers on the blackboard after $n$ minutes. It follows that every prime greater than $a$ is written on the blackboard.
|
| 28 |
+
|
| 29 |
+
It follows that every non-prime written on the blackboard contains only prime factors less than or equal to $a$. Assume for contradiction that Nordi writes infinitely many integers on the blackboard that are not integer. Let $b_{1}, b_{2}, \ldots$ be these integers, and let $p_{1}, \ldots, p_{r}$ be the primes less than or equal to $a$. It follows that for every $n \in \mathbb{N}$, we can write
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
b_{n}=p_{1}^{e_{n, 1}} p_{2}^{e_{n, 2}} \cdots p_{r}^{e_{n, r}}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
where $e_{n, 1}, \ldots, e_{n, r}$ are non-negative integers.
|
| 36 |
+
|
| 37 |
+
Note that for any infinite sequence of non-negative integers, we may find an infinite subsequence that is weakly increasing: If the sequence is bounded, some integer occurs infinitely many times, otherwise we may find an infinite strictly increasing subsequence.
|
| 38 |
+
|
| 39 |
+
Consider now the sequence
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\left(e_{1,1}, e_{1,2}, \ldots, e_{1, r}\right),\left(e_{2,1}, e_{2,2}, \ldots, e_{2, r}\right), \ldots
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
For the first coordinate, we may find an infinite weakly increasing subsequence $e_{n_{1}, 1}, e_{n_{2}, 1}, \ldots, e_{n_{i}, 1}, \ldots$. Considering the sequence $e_{n_{1}, 2}, e_{n_{2}, 2}, \ldots$, we may now again find a weakly increasing subsequence $e_{n_{1}^{\prime}, 2}, e_{n_{2}^{\prime}, 2}, \ldots$. In this manner, we may find indices $m_{1}<m_{2}<\ldots$ such that for every $1 \leq i \leq r, e_{m_{1}, i}, e_{m_{2}, i}, \ldots$ is a weakly increasing sequence. However, then $b_{m_{1}}\left|b_{m_{2}}\right| b_{m_{3}} \mid \ldots$ A contradiction. Thus, Nordi only writes finitely many integers on the blackboard that are not primes.
|
| 46 |
+
|
| 47 |
+
Problem 2. With $g(x)=x(1+|x|)$ we want that $f(g(x)) \leq x \leq g(f(x))$ for all $x$. The solution only uses that $g$ is strictly increasing and surjective with an inverse which is also strictly increasing.
|
| 48 |
+
|
| 49 |
+
Notice that the inverse function to such $g$ gives a solution $f=g^{-1}$ since $x \leq x \leq x$ is true for all $x \in \mathbb{R}$.
|
| 50 |
+
|
| 51 |
+
For uniqueness take any $x$ and let $y=g^{-1}(x)$. Then $g(f(x)) \geq x$. On the other hand $f(g(y)) \leq y$ and hence $g(f(x))=g(f(g(y))) \leq g(y)=x$ where we used that $g$ is increasing in the inequality. In other words $g(f(x))=x$ for all $x$ and hence $f(x)=g^{-1}(x)$.
|
| 52 |
+
|
| 53 |
+
Solving $y(1+|y|)=x$ we get explicitly for $f$ that
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
f(x)=\left\{\begin{array}{l}
|
| 57 |
+
\frac{-1+\sqrt{1+4 x}}{\frac{2}{1-4 x}}, x \geq 0 \\
|
| 58 |
+
\frac{1-\sqrt{1}}{2}, x \leq 0
|
| 59 |
+
\end{array}\right.
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
Problem 3. Bob has a winning strategy for every $n \in \mathbb{N}$. Initially, note that Bob wins if and only if he can "shift" the sets $A_{1}, \ldots, A_{n+1}$ modulo $2^{n}$ such that they together cover every residue class. For a set of integers $C \subset \mathbb{Z}$ and $r \in \mathbb{N}$, let $C+r$ be the set $\{c+r \mid c \in C\}$, and let $(C \bmod r)$ denote the subset of $\{0,1, \ldots, r-1\}$ corresponding to the residue classes modulo $r$ represented by the members of $C$.
|
| 63 |
+
|
| 64 |
+
Let $A_{1}, \ldots, A_{n+1}$ be the subsets of $\left\{1, \ldots, 2^{n}\right\}$ chosen by Alice. Bob now proceeds as follows. Suppose some choice of $a_{1}, \ldots, a_{n+1}$ is given, let $B_{0}=$ $\left\{0,1,2, \ldots, 2^{n}-1\right\}$, and for $1 \leq i \leq n+1$, let $B_{i}=B_{i-1} \backslash\left(\left(A_{i}+a_{i}\right) \bmod 2^{n}\right)$. Note that if Alice chooses $t$ such that the residue class of $t$ modulo $2^{n}$ is not contained in $B_{j}$ for some $1 \leq j \leq n+1$, then Bob can choose an $i \leq j$ and find $s \in A_{i}$ such that $s+a_{i} \equiv t\left(\bmod 2^{n}\right)$. Thus, Bob wins if he can ensure that $B_{n+1}=\emptyset$.
|
| 65 |
+
|
| 66 |
+
To that end, we show that Bob can choose $a_{1}, \ldots, a_{n+1}$ such that $\left|B_{i}\right| \leq$ $\left|B_{i-1}\right| / 2$ for every $1 \leq i \leq n$. If this holds, $\left|B_{n+1}\right| \leq 2^{n-(n+1)}=1 / 2$, and the conclusion follows. Consider some $1 \leq i \leq n+1$. We wish to find $a_{i}$ such that $\left(A_{i}+a_{i}\right) \bmod 2^{n}$ contains at least half of the elements of $B_{i-1}$. Note that $\left(A_{i}+b\right) \bmod 2^{n}$ contains $2^{n-1}$ elements and consider the sum
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
S:=\sum_{a=0}^{2^{n}-1}\left|\left(\left(A_{i}+a\right) \quad \bmod 2^{n}\right) \cap B_{i-1}\right|
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
For each $b \in B_{i-1}$, there are exactly $2^{n-1}$ choices of $0 \leq a<2^{n}$ such that $b$ is contained in $\left(\left(A_{i}+a\right) \bmod 2^{n}\right)$, one for each element of $A_{i}$. It follows that $S=2^{n-1} \cdot\left|B_{i-1}\right|$. Since there are only $2^{n}$ summands in $S$, at least one must have magnitude at least $\left|B_{i-1}\right| / 2$. Thus, there is some $0 \leq a<2^{n}$ with $\left|\left(\left(A_{i}+a\right) \bmod 2^{n}\right) \cap B_{i-1}\right| \geq\left|B_{i-1}\right| / 2$, so choosing $a_{i}=a$, Bob ensures that
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\left|B_{i}\right|=\left|B_{i-1} \backslash\left(\left(A_{i}+a_{i}\right) \quad \bmod 2^{n}\right)\right| \leq\left|B_{i-1}\right| / 2
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Problem 4. It can be difficult to find out what to do, but the key is to show that $A Y F E$ is cyclic. The motivation for this is that we want to show that $\angle B A Y=\angle B A X$. But $\angle B A X=\angle B D X$ since $B X D A$ is cyclic, and $\angle B D X=$ $\angle F D X=\angle D F E$ since $D X$ and $E F$ are parallel, and $\angle D F E=\angle E F Y$ since $Y$ is the reflection of $D$ through $E F$, so $\angle B A X=\angle E F Y$. Hence we only need to show that $\angle B A Y=180^{\circ}-\angle E A Y=\angle E F Y$, and this is true if and only if $A Y F E$ is cyclic. The trick is to show that $A Y F E$ is cyclic in a different way, i.e. by showing that $\angle E A F=\angle E Y F$. This follows from $A B C D$ being cyclic since then $\angle E A F=180^{\circ}-\angle C A B=180^{\circ}-\angle C D B=\angle F D E=\angle E Y F$. The last equality follows from $Y$ being a reflection.
|
| 79 |
+
|
| 80 |
+
Note: We have shown the claim for just one configuration, the one in the sketch. The other cases follow from the same idea, but one need to chase angles in a different way. Using oriented angles one can take case of all possibilities.
|
| 81 |
+
|
| 82 |
+
|
| 83 |
+
|
Nordic_MO/md/en-2022-sol.md
ADDED
|
@@ -0,0 +1,116 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The 36th Nordic Mathematical Contest
|
| 2 |
+
|
| 3 |
+
Monday, 4 April 2022
|
| 4 |
+
|
| 5 |
+
## Solutions
|
| 6 |
+
|
| 7 |
+
## Problem 1
|
| 8 |
+
|
| 9 |
+
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
f(f(x) f(1-x))=f(x) \quad \text { and } \quad f(f(x))=1-f(x)
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
for all real $x$.
|
| 16 |
+
|
| 17 |
+
Solution 1. Notice that $f(f(f(x)))=^{2} 1-f(f(x))={ }^{2} f(x)$. This is equation 3 . By substituting $f(x)$ for $x$ in the first equation we get:
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
f(\underline{f(x)})={ }^{1} f(f(\underline{f(x)}) f(1-\underline{f(x)}))={ }^{2} f(f(f(x)) f(f(f(x))))={ }^{3} f(f(f(x)) f(x))
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Again we substitute $f(x)$ for $x$ above:
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
f(f(\underline{f(x)}))=f(f(f(\underline{f(x)})) f(\underline{f(x)}))
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
Equation 3 applied on both sides gives us:
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
f(x)=f(f(x) f(f(x)))
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
But this is the same as what we started with so
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
f(x)=f(f(x) f(f(x)))=f(f(x))={ }^{2} 1-f(x)
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
Therefore $f(x)=\frac{1}{2}$, which is a solution.
|
| 42 |
+
|
| 43 |
+
Solution 2. Let first $c$ be a fix point of $f$, that is $f(c)=c$. Then from the second equation we have
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
c=1-c \Rightarrow c=\frac{1}{2}
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
The substitution $y=1-x$ in the first equation shows that $f(1-x)=f(x)$ for any $x$. Now, using this and applying $f$ to the second equation we get
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
f(f(f(x)))=f(1-f(x)))=f(f(x))
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
thus $f(f(x))$ is a fix point and therefore $f(f(x))=\frac{1}{2}$. Now the second equation gives $f(x)=\frac{1}{2}$. It is easy to check that this is a solution.
|
| 56 |
+
|
| 57 |
+
## Problem 2
|
| 58 |
+
|
| 59 |
+
In Wonderland, the towns are connected by roads, and whenever there is a direct road between two towns there is also a route between these two towns that does not use that road. (There is at most one direct road between any two towns.) The Queen
|
| 60 |
+
of Hearts ordered the Spades to provide a list of all "even" subsystems of the system of roads, that is, systems formed by subsets of the set of roads, where each town is connected to an even number of roads (possibly none). For each such subsystem they should list its roads. If there are totally $n$ roads in Wonderland and $x$ subsystems on the Spades' list, what is the number of roads on their list when each road is counted as many times as it is listed?
|
| 61 |
+
|
| 62 |
+
Solution. The answer is $\frac{1}{2} n x$.
|
| 63 |
+
|
| 64 |
+
Proof: We reformulate the problem in terms of graph theory with the towns being vertices and the roads being edges of a graph $G=(V, E)$. The given information implies that every edge $e \in E$ is part of a cycle. The subgraphs to be counted are those with every valence even, briefly the even subgraphs. Let $N$ be the sum of the numbers of edges in those subgraphs. We can calculate this number by counting for each edge $e \in E$ the even subgraphs of $G$ containing $e$. If $S(e)$ is the set of these graphs, then $N=\sum_{e \in E}|S(e)|$. Now consider for a given $e \in E$ some cycle $c(e)$ containing $e$. For every even subgraph $H$ of $G$ one can define the graph $H^{\prime}$ obtained from $H$ by replacing the set of edges in $H$ that are also edges in $c(e)$ by the set of edges in $c(e)$ that are not edges in $H$. For a given vertex $v \in V$ the following possibilities exist. (i) $c(e)$ does not pass through $v$. (ii) Both edges in $c(e)$ adjacent to $v$ are in $H$. They are then absent from $H^{\prime}$. (iii) None of the edges in $c(e)$ adjacent to $v$ are in $H$. They are then both in $H^{\prime}$. (iv) Exactly one of the edges in $c(e)$ adjacent to $v$ are in $H$. It is then not in $H^{\prime}$ while the other one belongs to $H^{\prime}$. In every case any edge adjacent to $v$ that is not in $c(e)$ is in either none or both of $H$ and $H^{\prime}$. It follows that $H^{\prime}$ is an even subgraph of $G$. Since evidently $H^{\prime \prime}=H$, the total set of even subgraphs of $G$ is thus the union of disjoint pairs $\left\{H, H^{\prime}\right\}$. Exactly one member of each pair belongs to $S(e)$, so $|S(e)|=x / 2$, and $N=\frac{1}{2} n x$.
|
| 65 |
+
|
| 66 |
+
## Problem 3
|
| 67 |
+
|
| 68 |
+
Anton and Britta play a game with the set $M=\{1,2,3, \ldots, n-1\}$ where $n \geq 5$ is an odd integer. In each step Anton removes a number from $M$ and puts it in his set $A$, and Britta removes a number from $M$ and puts it in her set $B$ (both $A$ and $B$ are empty to begin with). When $M$ is empty, Anton picks two distinct numbers $x_{1}, x_{2}$ from $A$ and shows them to Britta. Britta then picks two distinct numbers $y_{1}, y_{2}$ from $B$. Britta wins if
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
\left(x_{1} x_{2}\left(x_{1}-y_{1}\right)\left(x_{2}-y_{2}\right)\right)^{\frac{n-1}{2}} \equiv 1 \quad \bmod n
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
otherwise Anton wins. Find all $n$ for which Britta has a winning strategy.
|
| 75 |
+
|
| 76 |
+
Solution. Britta wins if and only if $n$ is prime.
|
| 77 |
+
|
| 78 |
+
If $n$ is not prime, then Anton can add any prime divisor $p<n$ of $n$ to his set $A$ in the first round and choose $x_{1}=p$ which means that the product $\left(x_{1} x_{2}\left(x_{1}-y_{1}\right)\left(x_{2}-y_{2}\right)\right)^{\frac{n-1}{2}}$ is divisible by $p$ and is not $1 \bmod n$ no matter what Britta chooses. And so Britta loses.
|
| 79 |
+
|
| 80 |
+
If $n$ is prime, then $x_{1} x_{2} \not \equiv 0 \bmod n$, and there exists a number $\alpha$ such that $x^{2} \equiv \alpha$ $\bmod n$ has no solution. Then Britta can always add the number $Y \in M, Y \equiv \alpha X^{-1}$ to $B$, if Anton adds the number $X$ to $A$ in each round. Notice that Anton can never have chosen the number $Y$ beforehand, since $Y \equiv \alpha X^{-1} \Longleftrightarrow X \equiv \alpha Y^{-1}$ and $X \neq Y$ (as $X^{2} \equiv \alpha \bmod n$ is not possible). This means that Britta can always choose the
|
| 81 |
+
numbers $y_{1}=\alpha x_{2}^{-1}, y_{2}=\alpha x_{1}^{-1}$ from $B$. This will result in
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\begin{aligned}
|
| 85 |
+
\left(x_{1} x_{2}\left(x_{1}-y_{1}\right)\left(x_{2}-y_{2}\right)\right)^{\frac{n-1}{2}} & \equiv\left(\left(x_{1} x_{2}-x_{2} y_{1}\right)\left(x_{1} x_{2}-x_{1} y_{2}\right)\right)^{\frac{n-1}{2}} \\
|
| 86 |
+
& \equiv\left(\left(x_{1} x_{2}-\alpha\right)\left(x_{1} x_{2}-\alpha\right)\right)^{\frac{n-1}{2}} \\
|
| 87 |
+
& \equiv\left(x_{1} x_{2}-\alpha\right)^{n-1} \\
|
| 88 |
+
& \equiv 1 \quad \bmod n
|
| 89 |
+
\end{aligned}
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
The last equation is true by Fermat's little theorem, because $n$ is prime and $x_{1} x_{2}-\alpha \not \equiv$ $0 \bmod n\left(\right.$ since $x_{1} \not \equiv y_{1}=\alpha x_{2}^{-1}$ ).
|
| 93 |
+
|
| 94 |
+
Alternative strategy for Britta is to choose $n-a$ when Anton pick up $a$, which is always possible because $n$ is an odd number and if one of the numbers $a, n-a$ was already chosen before the same is true for the second one. At the end Britta chooses $y_{i}=-x_{i}$ and gets
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
\left(x_{1} x_{2}\left(x_{1}-y_{1}\right)\left(x_{2}-y_{2}\right)\right)^{\frac{n-1}{2}}=\left(\left(2 x_{1}\right)^{2}\left(2 x_{2}\right)^{2}\right)^{\frac{n-1}{2}} \equiv 1 \quad \bmod n
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
## Problem 4
|
| 101 |
+
|
| 102 |
+
Let $A B C$ be an acute-angled triangle with circumscribed circle $k$ and centre of the circumscribed circle $O$. A line through $O$ intersects the sides $A B$ and $A C$ at $D$ and $E$. Denote by $B^{\prime}$ and $C^{\prime}$ the reflections of $B$ and $C$ over $O$, respectively. Prove that the circumscribed circles of $O D C^{\prime}$ and $O E B^{\prime}$ concur on $k$.
|
| 103 |
+
|
| 104 |
+
Solution. Let $P$ be the intersection of the circles $k$ and the circumscribed circle of triangle $A D E^{1}$. Let $C_{1}$ be the second intersection of the circumscribed circle of $\triangle D O P$ with $k$. We will prove that $C_{1}=C^{\prime}$, i.e. the reflection of $C$ over $O$. We know that $\left|O C_{1}\right|=|O P|$, and hence $\measuredangle C_{1} P O=\measuredangle O C_{1} P$, furthermore $\measuredangle O C_{1} P=\measuredangle O D P=$ $\measuredangle E D P$, since the quadrilateral $C_{1} P O D$ by assumption is inscribed and the points $O, D$ and $E$ are collinear. Now, since $P$ is the centre of spiral similarity sending $D E$ to $B C$ the triangles $P D E$ and $P B C$ are similar, and we have $\measuredangle E D P=\measuredangle C B P$, and finally, from the inscribed angle theorem we have
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\measuredangle O P C=90^{\circ}-\frac{\measuredangle C O P}{2}=90^{\circ}-\measuredangle C B P=90^{\circ}-\measuredangle C_{1} P O
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
The conclusion follows, since $90^{\circ}=\measuredangle C_{1} P O+\measuredangle O P C$, and since $C_{1}$ is by assumption on $k$, it must be the antipodal point of $C$ with respect to $k$.
|
| 111 |
+
|
| 112 |
+
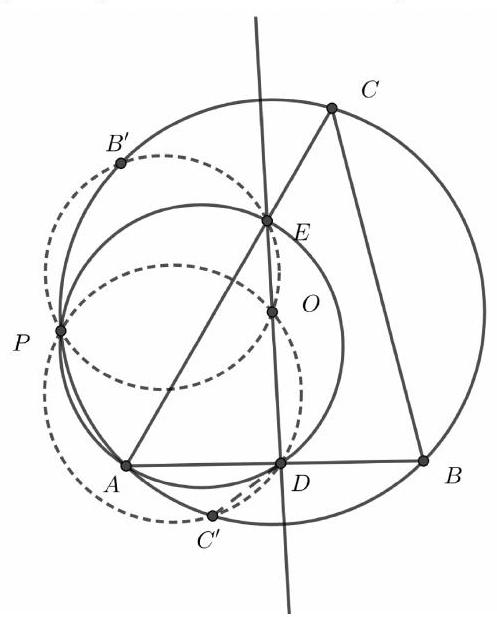[^0]
|
| 113 |
+
|
| 114 |
+
|
| 115 |
+
[^0]: ${ }^{1}$ That is, the Miquel point of quadrilateral BCED.
|
| 116 |
+
|
Nordic_MO/md/en-2024-sol.md
ADDED
|
@@ -0,0 +1,207 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
The Fanatical Mathematical Syndicate of the Far North
|
| 2 |
+
|
| 3 |
+
## The 38th Nordic Mathematical Contest Solutions
|
| 4 |
+
|
| 5 |
+
## Problem 1
|
| 6 |
+
|
| 7 |
+
Let $T(a)$ be the sum of digits of $a$. For which positive integers $R$ does there exist a positive integer $n$ such that $\frac{T\left(n^{2}\right)}{T(n)}=R$ ?
|
| 8 |
+
|
| 9 |
+
## Solution
|
| 10 |
+
|
| 11 |
+
All positive integers $R$.
|
| 12 |
+
Let $R$ be a positive integer and consider the number
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
N=\sum_{k=0}^{R-1} 10^{2^{k}}
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
We see that $T(N)=R$. Now
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
\begin{aligned}
|
| 22 |
+
N^{2} & =\left(\sum_{k=0}^{R-1} 10^{2^{k}}\right)^{2} \\
|
| 23 |
+
& =\sum_{0 \leq a, b<R} 10^{2^{a}+2^{b}},
|
| 24 |
+
\end{aligned}
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
and since $2^{a}+2^{b}=2^{c}+2^{d}$ if and only if $(a, b)=(c, d)$ or $(a, b)=(d, c)$, there is never a carry in the summation $\sum_{0 \leq a, b<R} 10^{2^{a}+2^{b}}$, and we can write
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\begin{aligned}
|
| 31 |
+
T\left(N^{2}\right) & =\sum_{0 \leq a, b<R} T\left(10^{2^{a}+2^{b}}\right) \\
|
| 32 |
+
& =R^{2}
|
| 33 |
+
\end{aligned}
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
So $\frac{T\left(n^{2}\right)}{T(n)}=R$.
|
| 37 |
+
|
| 38 |
+
## Problem 2
|
| 39 |
+
|
| 40 |
+
Let $\mathcal{Q}_{1}$ be a quadrilateral such that the midpoints of its sides lie on a circle. Prove that there exists a cyclic quadrilateral $\mathcal{Q}_{2}$ with the same sidelengths as $\mathcal{Q}_{1}$, such that two of the angles in $\mathcal{Q}_{2}$ are equal.
|
| 41 |
+
|
| 42 |
+
## Solution
|
| 43 |
+
|
| 44 |
+
Let $A, B, C$ and $D$ be the vertices of $\mathcal{Q}_{1}$, and $K, L, M$ and $N$ be the midpoints of the sides $A B, B C, C D$ and $D A$, respectively.
|
| 45 |
+
We have $K L\|A C\| M N$ and $L M\|B D\| N K$, and thus $K L M N$ is a parallelogram. From the problem condition it is known that $K L M N$ is cyclic, and thus, from the inscribed angle theorem, $K L M N$ must be a rectangle. Hence, $A C \perp B D$. Now, let $P$ denote the intersections of the diagonals of $A B C D$.
|
| 46 |
+
|
| 47 |
+
|
| 48 |
+
Applying Pythagoras' theorem repeatedly therefore yields
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
|A B|^{2}+|C D|^{2}=|A P|^{2}+|B P|^{2}+|C P|^{2}+|D P|^{2}=|A D|^{2}+|B C|^{2} .
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Thus, we can construct the quadrilateral $\mathcal{Q}_{2}$ with a segment $A^{\prime} C^{\prime}$ satisfying $\left|A^{\prime} C^{\prime}\right|^{2}=|A B|^{2}+$ $|C D|^{2}$, and then place $B^{\prime}, D^{\prime}$ on the circle with diameter $A^{\prime} C^{\prime}$ on opposite sides of $A^{\prime} C^{\prime}$ such that $\left|A^{\prime} B^{\prime}\right|=|A B|$ and $\left|A^{\prime} D^{\prime}\right|=|A D|$.
|
| 55 |
+
From the previous computation, we then obtain $\left|C^{\prime} B^{\prime}\right|=|C D|$ and $\left|C^{\prime} D^{\prime}\right|=|B C|$. Hence, $\mathcal{Q}_{2}$ and $\mathcal{Q}_{1}$ has the same set of sidelengths. Finally, $A^{\prime} B^{\prime} \perp B^{\prime} C^{\prime}$ and $A^{\prime} D^{\prime} \perp D^{\prime} C^{\prime}$, so $\mathcal{Q}_{2}$ has two identical right angels.
|
| 56 |
+
|
| 57 |
+
## Problem 3
|
| 58 |
+
|
| 59 |
+
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
f(f(x) f(y)+y)=f(x) y+f(y-x+1)
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
for all $x, y \in \mathbb{R}$.
|
| 66 |
+
|
| 67 |
+
## Solution
|
| 68 |
+
|
| 69 |
+
First note that $f$ satisfies the functional equation if and only if $-f$ does as well. We can therefore assume that $f(0) \geq 0$. We consider two cases, depending on whether $f$ is injective or not.
|
| 70 |
+
|
| 71 |
+
1. First assume that $f$ is not injective. Then there exist $a, t \in \mathbb{R}, t \neq 0$ such that $f(a+t)=$ $f(a)$. Apply the substitutions $x \mapsto a, y \mapsto y$ and $x \mapsto a+t, y \mapsto y$ to the functional equation (3.1). This gives:
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
f(y-a+1)=f(f(a) f(y)+y)-f(a) y
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
and
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
f(y-a-t+1)=f(f(a+t) f(y)+y)-f(a+t) y
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
As $f(a+t)=f(a)$ the right hand sides of the equations are equal to one another. Hence
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
f(y-a+1)=f(y-a-t+1) .
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Applying the substitution $y \mapsto x+a+t-1$ to equation (3.2) yields:
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
f(x+t)=f(x) .
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
In other words $f$ is $t$-periodic. Perform the substitution $x \mapsto x$ and $y \mapsto y+t$ to equation (3.1). The result is
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
f(f(x) f(y+t)+y+t)=f(x)(y+t)=f(y+t-x+1) .
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
As $f$ is $t$-periodic we have $f(y+t)=f(y), f(f(x) f(y)+y+t)=f(f(x) f(y)+y)$ and $f(y+t-x+1)=f(y-x+1)$. As a result equation (3.4) simplifies to
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
f(f(x) f(y)+y)=f(x)(y+t)+f(y-x+1)
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
By comparing equation (3.5) with the given equation (3.1) we get
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
f(x) y=f(x)(y+t)
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
As $t \neq 0$ it follows that $f(x)=0$. That is $f$ is the zero function.
|
| 114 |
+
2. Next assume that $f$ is injective. Apply the substitution $x \mapsto x$ and $y \mapsto 0$ to the functional equation (3.1). This gives
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
f(f(x) f(0))=f(-x+1)
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
As $f$ injective, the arguments must equate, that is
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
f(x) f(0)=1-x
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
Evaluation this equation at $x=0$ gives $(f(0))^{2}=1$, that is $f(0)=1$ as we assumed that $f(0) \geq 0$. Equation (3.6) simplifies to
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
f(x)=1-x
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
It remains to verify that the candidates $f(x)=0$ and $f(x)=1-x$ are in fact solution to the functional equation. Routine calculation show that this is the case. We have hence found that the complete collection of solutions to the functional equation is
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
f: \mathbb{R} \longrightarrow \mathbb{R}, x \longmapsto 0, f: \mathbb{R} \longrightarrow \mathbb{R}, x \longmapsto x-1 \quad \text { and } \quad f: \mathbb{R} \longrightarrow \mathbb{R}, x \longmapsto 1-x .
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
## Problem 4
|
| 139 |
+
|
| 140 |
+
Alice and Bob are playing a game. First, Alice chooses a partition $\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\mathcal{C}$. Then Bob does the following operation a finite number of times.
|
| 141 |
+
Choose a set $S \in \mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \backslash S$ (possibly the empty set) to $\mathcal{C}$.
|
| 142 |
+
Bob wins if there are two equal sets in $\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.
|
| 143 |
+
|
| 144 |
+
Answer: Alice has a winning strategy.
|
| 145 |
+
|
| 146 |
+
## Solution 1
|
| 147 |
+
|
| 148 |
+
We will use the following notation. If $S \subseteq \mathbb{Z}^{+}$is a subset of the positive integers and $D$ is defined as in the problem statement, define $d(S)=D \backslash S$. In addition, the $d$-sequence of $S$, written $\left\{d^{S}\right\}_{n \in \mathbb{Z}^{+}}$, is defined recursively as $d_{0}^{S}=S$, and $d_{n+1}^{S}=d\left(d_{n}^{S}\right)$ for each $n \in \mathbb{Z}^{+}$.
|
| 149 |
+
Let $p_{1}, p_{2}, \ldots$ be an enumeration of all the prime numbers. Alice chooses the sets
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
A=\left\{p_{m}^{n} \mid n \equiv m \quad \bmod 3,0<n \leq m\right\}, \quad B=\left\{p_{m}^{n} \mid n \equiv m-1 \quad \bmod 3,0<n \leq m-1\right\}
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
and
|
| 156 |
+
|
| 157 |
+
$$
|
| 158 |
+
C=\mathbb{Z}^{+} \backslash(A \cup B)
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
It is clear that each positive integer belongs to exactly on of the sets $A, B$ or $C$. By induction we readily get that
|
| 162 |
+
|
| 163 |
+
$$
|
| 164 |
+
d^{k}(A)=\left\{\begin{array}{ll}
|
| 165 |
+
\left\{p_{m}^{n} \mid n \equiv m\right. & \bmod 3, n \leq m-3 k / 2\} \\
|
| 166 |
+
\left\{p_{m}^{n} \mid n \not \equiv m\right. & \bmod 3, n \leq m-1-3(k-1) / 2\}
|
| 167 |
+
\end{array} \quad \text { if } k \text { is even and } k \neq 0\right.
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
and
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
d^{k}(B)=\left\{\begin{array}{lll}
|
| 174 |
+
\left\{p_{m}^{n} \mid n \equiv m-1\right. & \bmod 3, n \leq m-1-3 k / 2\} & \text { if } k \text { is even and } k \neq 0 \\
|
| 175 |
+
\left\{p_{m}^{n} \mid n \not \equiv m-1\right. & \bmod 3, n \leq m-2-3(k-1) / 2\} & \text { if } k \text { is odd. }
|
| 176 |
+
\end{array}\right.
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
If $m \in \mathbb{Z}^{+}$then $6 m$ is definitely in $C$ as $6 m$ is not a power of a prime. This means that all positive integers divide at least one number in $C$. It follows that
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
d(C)=\mathbb{Z}^{+} \backslash C=\mathbb{Z}^{+} \backslash\left(\mathbb{Z}^{+} \backslash(A \cup B)\right)=A \cup B=\left\{p_{m}^{n} \mid n \not \equiv m-2 \bmod 3,0<n \leq m\right\}
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
By induction it follows that
|
| 186 |
+
|
| 187 |
+
From this it is clear that all of the sets $d^{k}(M)$ are all distinct. Hence Bob can never create the same set in two different ways.
|
| 188 |
+
|
| 189 |
+
Remark. In fact Alice has to partition the positive integers in at least three parts if she wishes to beat Bob. It is clear that selecting a singe set, namely $\mathbb{Z}^{+}$will not do as $d\left(\mathbb{Z}^{+}\right)=\emptyset$ and $d(\emptyset)=\emptyset$. Next assume Alice has partitioned the positive integers in two sets $A$ and $B$. It can be assumed that $d(A) \neq B$ and $d(B) \neq A$ as Bob would win either case. As $d(A)$ is disjoint from $A$ and $B$ is the complement of $A$ this means that $d(A)$ is a strict subset of $B$. Hence there is some $b$ in $B$ that does not belong to $d(A)$. The implication is that $b$ does not divide any number in $A$. Similarly there exists a number $a$ in $A$ that does not divide any number in $B$. Their product $a b$ belongs to either of the sets $A$ or $B$ and is divisible by both $a$ and $b$. This contradicts the existence of said numbers, $a$ and $b$. In fact we have proven for any subset $A$ of $\mathbb{Z}^{+}$that $d(A)=\mathbb{Z}^{+} \backslash A$ or $d\left(\mathbb{Z}^{+} \backslash A\right)=A$.
|
| 190 |
+
|
| 191 |
+
## Solution 2
|
| 192 |
+
|
| 193 |
+
Use the same notation as in solution 1 . We wish to construct a partition $\bigcup_{i \in \mathbb{Z}^{+}} A_{i}$ of the positive integers, such that no two sets among all sets in $\left\{d^{A_{1}}\right\}_{n \in \mathbb{Z}^{+}},\left\{d^{A_{2}}\right\}_{n \in \mathbb{Z}^{+}}, \ldots$ are equal.
|
| 194 |
+
To begin with, consider a partition $\bigcup_{i \in \mathbb{Z}^{+}} P_{i}$ of the primes, such that each $P_{i}=\left\{p_{i 1}, p_{i 2}, \ldots\right\}$ is infinite. We may assume each set is infinite since the set of primes and $\mathbb{Z}^{+} \times \mathbb{Z}^{+}$both are countable, so there exists a bijection between them. Define the sets
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
Q_{i}=\left\{p_{i 1}, p_{i 2}^{2}, p_{i 3}, p_{i 3}^{3}, p_{i 4}^{2}, p_{i 4}^{4}, p_{i 5}, p_{i 5}^{3}, p_{i 5}^{5}, \ldots\right\}
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
consisting of $p_{i j}^{j}, p_{i j}^{j-2}, \ldots, p_{i j}^{(1,2)}$ for each $p_{i j} \in P_{i}$. By the exponent $(1,2)$ we indicate that the last power is 1 when $j$ is odd and 2 when it is even.
|
| 201 |
+
We will include the remaining integers $\left\{r_{1}, r_{2}, \ldots\right\}=\mathbb{Z}^{+} \backslash\left(\bigcup_{i \in \mathbb{Z}^{+}} Q_{i}\right)$ to the partition as follows. First, add $r_{1}$ to some set $Q_{i_{1}}$, such that $\operatorname{gcd}\left(r_{1}, q\right)=1$ for each $q \in Q_{i_{1}}$. Then, for each $k \in \mathbb{Z}^{+}$, add $r_{k+1}$ to a set $Q_{i_{k+1}}$ where $i_{k+1}>i_{k}$, such that $\operatorname{gcd}\left(r_{k+1}, q\right)=1$ for each $q \in Q_{i_{k+1}}$. Note that such an $i_{k+1}$ always exists, since there always is an infinite amount of prime divisors among $Q_{i_{k}+1}, Q_{i_{k}+2}, \ldots$, and $r_{k+1}$ only has a finite amount of prime divisors.
|
| 202 |
+
The collection of $Q_{i}$ now forms a partition of $\mathbb{Z}^{+}$. What remains is to show that it satisfies Alice's winning condition.
|
| 203 |
+
We first see that we may ignore all the $r_{k}$. By definition, no divisor of $r_{k}$ coincides with any divisor of $Q_{i_{k}}$, and their contributions in the $d$-sequence will therefore be completely disjoint. As $d\left(d\left(\left\{r_{k}\right\}\right)\right)=\emptyset$, the $d$-sequence will show no trace of the $r_{k}$ after the second element. Hence, we will work with the original $Q_{i}$.
|
| 204 |
+
We observe that $d\left(Q_{i}\right)=\left\{1, p_{i 2}, p_{i 3}^{2}, p_{i 4}, p_{i 4}^{3}, p_{i 5}^{2}, p_{i 5}^{4}, p_{i 6}, p_{i 6}^{3}, p_{i 6}^{5}, \ldots\right\}$. This is simply $Q_{i}$ with the indices shifted by 1 and with an added 1 . As this set essentially is on the same form as $Q_{i}$, we see that $\left\{d^{Q_{i}}\right\}_{n}$ consists of every possible shift in indices of the first set $Q_{i}$ (except the element 1 appearing in every other set). It is therefore obvious that the sets in the sequence are pairwise distinct. Additionally, the set of primes dividing some element in some set of $\left\{d^{Q_{i}}\right\}_{n}$ is $P_{i}$. Since the $P_{i}$ partition the primes, it is clear that all the sets in all the $d$-sequences of the $Q_{i}$ are distinct, which is what we wanted.
|
| 205 |
+
|
| 206 |
+
Remark. The main idea of the problem is to construct a single set $S$, such that the sets in the $d$-sequence of $S$ are pairwise distinct. Any set with similar properties to the $Q_{i}$ should give a valid initial collection $\mathcal{C}$ such that Alice wins.
|
| 207 |
+
|
Nordic_MO/raw/en-1987-2011-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:a62f6d9749a40d6ba14f0661358e3e371c725b8026757db9b1a45116ec4e8b3f
|
| 3 |
+
size 567880
|
Nordic_MO/raw/en-2012-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:b55ec062a6b17f3292d8ca7812d12a5f9f985b67ce324f36d1d1ba2a907fdc75
|
| 3 |
+
size 77219
|
Nordic_MO/raw/en-2013-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:15ba78ea4f02800675740fdaf08c73c3ff5cdcadd3562490a3e333f389d5bdff
|
| 3 |
+
size 180540
|
Nordic_MO/raw/en-2014-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:b783bc8453f7ecf34dd046d084b3aca11655cfe193a44d0b0f27bd2cd227833f
|
| 3 |
+
size 161645
|
Nordic_MO/raw/en-2015-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:24e7e298df1c2d8a45440b8de6aafb84646cb4c2bc0eda2270e3652476639fba
|
| 3 |
+
size 87255
|
Nordic_MO/raw/en-2016-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:a8a44a7934b73511dbcd9aea83bf311d78632c2b503a1d1fac6137d560b996f9
|
| 3 |
+
size 157369
|
Nordic_MO/raw/en-2017-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:373e5ae3a0908b4175df52244f7129356f82ad9ed848f47382cee21884677d52
|
| 3 |
+
size 159614
|
Nordic_MO/raw/en-2018-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:f2d7febddbce4bcc5046848087b735dee45ca022a839f0c4c21c824c8ad1a8f2
|
| 3 |
+
size 142186
|
Nordic_MO/raw/en-2019-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:d7c1571ca4ce5385ff19d28f53763be8f5d0eeb8bfe7bbfebe7fb9a2445448b7
|
| 3 |
+
size 168795
|
Nordic_MO/raw/en-2021-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3adcf24f6ada1ba0d589c2cfdeae93406317956cb83ddc2216bd7d27e2b15acb
|
| 3 |
+
size 226224
|
Nordic_MO/raw/en-2022-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:4bc7ed82bacfd1ee0a5cc0f69a2c25c879bb01b7ee9efb010a1b6dcf989d7812
|
| 3 |
+
size 481532
|
Nordic_MO/raw/en-2024-sol.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:bc4b698e73f2e6026aca1ce71e751e2b2ce438e87ad63ae3e508cafcb87635ee
|
| 3 |
+
size 225600
|
Nordic_MO/segment_script/segment.py
ADDED
|
@@ -0,0 +1,157 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
project_root = Path(__file__).parent.parent.parent
|
| 12 |
+
|
| 13 |
+
problem_tag = 'Problem'
|
| 14 |
+
solution_tag = 'Solution'
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
def find_problem_with_solution(
|
| 18 |
+
text: str,
|
| 19 |
+
problem_parttern: re.Pattern,
|
| 20 |
+
solution_pattern: re.Pattern
|
| 21 |
+
) -> int:
|
| 22 |
+
"""
|
| 23 |
+
Find the problem with solution start position in the text.
|
| 24 |
+
|
| 25 |
+
Args:
|
| 26 |
+
text (str): The text to search.
|
| 27 |
+
|
| 28 |
+
Returns:
|
| 29 |
+
int: The start position of the problem with solution.
|
| 30 |
+
"""
|
| 31 |
+
matchs = list(problem_parttern.finditer(text))
|
| 32 |
+
|
| 33 |
+
for index, match in enumerate(matchs):
|
| 34 |
+
section_end_position = matchs[index + 1].start() if index + 1 < len(matchs) else len(text)
|
| 35 |
+
if solution_pattern.search(text[match.start():section_end_position]) and index != len(matchs) - 1:
|
| 36 |
+
return match.start()
|
| 37 |
+
|
| 38 |
+
|
| 39 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 40 |
+
"""
|
| 41 |
+
Analyze the text and return the tags and problem number.
|
| 42 |
+
Args:
|
| 43 |
+
text (str): The markdown text to analyze.
|
| 44 |
+
Returns:
|
| 45 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 46 |
+
"""
|
| 47 |
+
problem_pattern = re.compile(r'(?:\n|\n\#*\s*)Problem (\d+)\.?', re.IGNORECASE)
|
| 48 |
+
solution_pattern = re.compile(r'(?:\n|\n\#*\s*)(?:Solution \d+|Solution I{1,3}|Solution)\.?', re.IGNORECASE)
|
| 49 |
+
|
| 50 |
+
start_position = find_problem_with_solution(text, problem_pattern, solution_pattern) or 0
|
| 51 |
+
|
| 52 |
+
tags = []
|
| 53 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text, start_position)])
|
| 54 |
+
problem_num = len(tags)
|
| 55 |
+
|
| 56 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text, start_position)])
|
| 57 |
+
solution_num = len(tags) - problem_num
|
| 58 |
+
|
| 59 |
+
tags.sort(key=lambda x: x[0].start())
|
| 60 |
+
return tags, problem_num, solution_num
|
| 61 |
+
|
| 62 |
+
|
| 63 |
+
def segment(text: str, tags):
|
| 64 |
+
starts = []
|
| 65 |
+
ends = []
|
| 66 |
+
|
| 67 |
+
for i in range(len(tags)):
|
| 68 |
+
starts.append(tags[i][0].end())
|
| 69 |
+
if i + 1 < len(tags):
|
| 70 |
+
ends.append(tags[i + 1][0].start())
|
| 71 |
+
else:
|
| 72 |
+
ends.append(len(text))
|
| 73 |
+
|
| 74 |
+
return [text[start:end].strip() for start, end in zip(starts, ends)]
|
| 75 |
+
|
| 76 |
+
|
| 77 |
+
def join(tags, segments):
|
| 78 |
+
problem, solution = '', ''
|
| 79 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 80 |
+
pairs = []
|
| 81 |
+
|
| 82 |
+
for tag, segment in zip(tags, segments):
|
| 83 |
+
if tag[1] == problem_tag:
|
| 84 |
+
problem = segment
|
| 85 |
+
problem_match = tag[0].group(0)
|
| 86 |
+
problem_label = tag[0].group(1)
|
| 87 |
+
else:
|
| 88 |
+
solution = segment
|
| 89 |
+
if solution.strip() == '':
|
| 90 |
+
continue
|
| 91 |
+
|
| 92 |
+
solution_match = tag[0].group(0)
|
| 93 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 94 |
+
|
| 95 |
+
return pairs
|
| 96 |
+
|
| 97 |
+
|
| 98 |
+
def write_pairs(output_file: Path, pairs):
|
| 99 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 100 |
+
|
| 101 |
+
output_jsonl_text = ""
|
| 102 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 103 |
+
output_jsonl_text += json.dumps(
|
| 104 |
+
{
|
| 105 |
+
'year': year,
|
| 106 |
+
'tier': "T2",
|
| 107 |
+
'problem_label': problem_label,
|
| 108 |
+
'problem_type': None,
|
| 109 |
+
'problem': problem,
|
| 110 |
+
'solution': solution,
|
| 111 |
+
'metadata': {
|
| 112 |
+
'resource_path': output_file.relative_to(project_root).as_posix(),
|
| 113 |
+
'problem_match': problem_match,
|
| 114 |
+
'solution_match': solution_match
|
| 115 |
+
}
|
| 116 |
+
},
|
| 117 |
+
ensure_ascii=False
|
| 118 |
+
) + '\n'
|
| 119 |
+
|
| 120 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 121 |
+
|
| 122 |
+
|
| 123 |
+
def main():
|
| 124 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 125 |
+
compet_md_path = compet_base_path / "md"
|
| 126 |
+
seg_output_path = compet_base_path / "segmented"
|
| 127 |
+
|
| 128 |
+
total_problem_count = 0
|
| 129 |
+
total_solution_count = 0
|
| 130 |
+
|
| 131 |
+
for nmo_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 132 |
+
if nmo_md.stem == "en-1987-2011-sol" or nmo_md.stem == "en-2014-sol":
|
| 133 |
+
continue
|
| 134 |
+
|
| 135 |
+
output_file = seg_output_path / nmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 136 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 137 |
+
|
| 138 |
+
text = '\n' + nmo_md.read_text(encoding="utf-8")
|
| 139 |
+
|
| 140 |
+
tags, problem_num, solution_num = analyze(text)
|
| 141 |
+
|
| 142 |
+
segments = segment(text, tags)
|
| 143 |
+
pairs = join(tags, segments)
|
| 144 |
+
if pairs and problem_num > 0:
|
| 145 |
+
write_pairs(output_file, pairs)
|
| 146 |
+
|
| 147 |
+
total_problem_count += problem_num
|
| 148 |
+
total_solution_count += len(pairs)
|
| 149 |
+
else:
|
| 150 |
+
logger.warning(f"No problem found in {nmo_md}")
|
| 151 |
+
|
| 152 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 153 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 154 |
+
|
| 155 |
+
|
| 156 |
+
if __name__ == '__main__':
|
| 157 |
+
main()
|
Nordic_MO/segment_script/segment_1987_2011.py
ADDED
|
@@ -0,0 +1,158 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
project_root = Path(__file__).parent.parent.parent
|
| 12 |
+
|
| 13 |
+
problem_tag = 'Problem'
|
| 14 |
+
solution_tag = 'Solution'
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
def find_problem_with_solution(
|
| 18 |
+
text: str,
|
| 19 |
+
problem_parttern: re.Pattern,
|
| 20 |
+
solution_pattern: re.Pattern
|
| 21 |
+
) -> int:
|
| 22 |
+
"""
|
| 23 |
+
Find the problem with solution start position in the text.
|
| 24 |
+
|
| 25 |
+
Args:
|
| 26 |
+
text (str): The text to search.
|
| 27 |
+
|
| 28 |
+
Returns:
|
| 29 |
+
int: The start position of the problem with solution.
|
| 30 |
+
"""
|
| 31 |
+
matchs = list(problem_parttern.finditer(text))
|
| 32 |
+
|
| 33 |
+
for index, match in enumerate(matchs):
|
| 34 |
+
section_end_position = matchs[index + 1].start() if index + 1 < len(matchs) else len(text)
|
| 35 |
+
if solution_pattern.search(text[match.start():section_end_position]) and index != len(matchs) - 1:
|
| 36 |
+
return match.start()
|
| 37 |
+
|
| 38 |
+
|
| 39 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 40 |
+
"""
|
| 41 |
+
Analyze the text and return the tags and problem number.
|
| 42 |
+
Args:
|
| 43 |
+
text (str): The markdown text to analyze.
|
| 44 |
+
Returns:
|
| 45 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 46 |
+
"""
|
| 47 |
+
problem_pattern = re.compile(r'\n(\d+\.\d+)\.\s+', re.IGNORECASE)
|
| 48 |
+
solution_pattern = re.compile(r'\n(?:Solution \d+|Solution)\.?\s+', re.IGNORECASE)
|
| 49 |
+
# year_pattern = re.compile(r'\n\#+\s*NMC\s*\d+.+(\d{4})\s*\n')
|
| 50 |
+
|
| 51 |
+
start_position = find_problem_with_solution(text, problem_pattern, solution_pattern) or 0
|
| 52 |
+
|
| 53 |
+
tags = []
|
| 54 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text, start_position)])
|
| 55 |
+
problem_num = len(tags)
|
| 56 |
+
|
| 57 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text, start_position)])
|
| 58 |
+
solution_num = len(tags) - problem_num
|
| 59 |
+
|
| 60 |
+
tags.sort(key=lambda x: x[0].start())
|
| 61 |
+
return tags, problem_num, solution_num
|
| 62 |
+
|
| 63 |
+
|
| 64 |
+
def segment(text: str, tags):
|
| 65 |
+
starts = []
|
| 66 |
+
ends = []
|
| 67 |
+
|
| 68 |
+
for i in range(len(tags)):
|
| 69 |
+
starts.append(tags[i][0].end())
|
| 70 |
+
if i + 1 < len(tags):
|
| 71 |
+
ends.append(tags[i + 1][0].start())
|
| 72 |
+
else:
|
| 73 |
+
ends.append(len(text))
|
| 74 |
+
|
| 75 |
+
return [text[start:end].strip() for start, end in zip(starts, ends)]
|
| 76 |
+
|
| 77 |
+
|
| 78 |
+
def join(tags, segments):
|
| 79 |
+
problem, solution = '', ''
|
| 80 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 81 |
+
pairs = []
|
| 82 |
+
|
| 83 |
+
for tag, segment in zip(tags, segments):
|
| 84 |
+
if tag[1] == problem_tag:
|
| 85 |
+
problem = segment
|
| 86 |
+
problem_match = tag[0].group(0)
|
| 87 |
+
problem_label = tag[0].group(1)
|
| 88 |
+
else:
|
| 89 |
+
solution = segment
|
| 90 |
+
if solution.strip() == '':
|
| 91 |
+
continue
|
| 92 |
+
|
| 93 |
+
solution_match = tag[0].group(0)
|
| 94 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 95 |
+
|
| 96 |
+
return pairs
|
| 97 |
+
|
| 98 |
+
|
| 99 |
+
def write_pairs(output_file: Path, pairs):
|
| 100 |
+
output_jsonl_text = ""
|
| 101 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 102 |
+
subyear = int(problem_label.split('.')[0])
|
| 103 |
+
year = f"{1900 + subyear}" if subyear > 50 else f"{2000 + subyear}"
|
| 104 |
+
output_jsonl_text += json.dumps(
|
| 105 |
+
{
|
| 106 |
+
'year': year,
|
| 107 |
+
'tier': "T2",
|
| 108 |
+
'problem_label': problem_label,
|
| 109 |
+
'problem_type': None,
|
| 110 |
+
'problem': problem,
|
| 111 |
+
'solution': solution,
|
| 112 |
+
'metadata': {
|
| 113 |
+
'resource_path': output_file.relative_to(project_root).as_posix(),
|
| 114 |
+
'problem_match': problem_match,
|
| 115 |
+
'solution_match': solution_match
|
| 116 |
+
}
|
| 117 |
+
},
|
| 118 |
+
ensure_ascii=False
|
| 119 |
+
) + '\n'
|
| 120 |
+
|
| 121 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 122 |
+
|
| 123 |
+
|
| 124 |
+
def main():
|
| 125 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 126 |
+
compet_md_path = compet_base_path / "md"
|
| 127 |
+
seg_output_path = compet_base_path / "segmented"
|
| 128 |
+
|
| 129 |
+
total_problem_count = 0
|
| 130 |
+
total_solution_count = 0
|
| 131 |
+
|
| 132 |
+
for nmo_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 133 |
+
if nmo_md.stem != "en-1987-2011-sol":
|
| 134 |
+
continue
|
| 135 |
+
|
| 136 |
+
output_file = seg_output_path / nmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 137 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 138 |
+
|
| 139 |
+
text = '\n' + nmo_md.read_text(encoding="utf-8")
|
| 140 |
+
|
| 141 |
+
tags, problem_num, solution_num = analyze(text)
|
| 142 |
+
|
| 143 |
+
segments = segment(text, tags)
|
| 144 |
+
pairs = join(tags, segments)
|
| 145 |
+
if pairs and problem_num > 0:
|
| 146 |
+
write_pairs(output_file, pairs)
|
| 147 |
+
|
| 148 |
+
total_problem_count += problem_num
|
| 149 |
+
total_solution_count += len(pairs)
|
| 150 |
+
else:
|
| 151 |
+
logger.warning(f"No problem found in {nmo_md}")
|
| 152 |
+
|
| 153 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 154 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 155 |
+
|
| 156 |
+
|
| 157 |
+
if __name__ == '__main__':
|
| 158 |
+
main()
|
Nordic_MO/segment_script/segment_2014.py
ADDED
|
@@ -0,0 +1,157 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
project_root = Path(__file__).parent.parent.parent
|
| 12 |
+
|
| 13 |
+
problem_tag = 'Problem'
|
| 14 |
+
solution_tag = 'Solution'
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
def find_problem_with_solution(
|
| 18 |
+
text: str,
|
| 19 |
+
problem_parttern: re.Pattern,
|
| 20 |
+
solution_pattern: re.Pattern
|
| 21 |
+
) -> int:
|
| 22 |
+
"""
|
| 23 |
+
Find the problem with solution start position in the text.
|
| 24 |
+
|
| 25 |
+
Args:
|
| 26 |
+
text (str): The text to search.
|
| 27 |
+
|
| 28 |
+
Returns:
|
| 29 |
+
int: The start position of the problem with solution.
|
| 30 |
+
"""
|
| 31 |
+
matchs = list(problem_parttern.finditer(text))
|
| 32 |
+
|
| 33 |
+
for index, match in enumerate(matchs):
|
| 34 |
+
section_end_position = matchs[index + 1].start() if index + 1 < len(matchs) else len(text)
|
| 35 |
+
if solution_pattern.search(text[match.start():section_end_position]) and index != len(matchs) - 1:
|
| 36 |
+
return match.start()
|
| 37 |
+
|
| 38 |
+
|
| 39 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 40 |
+
"""
|
| 41 |
+
Analyze the text and return the tags and problem number.
|
| 42 |
+
Args:
|
| 43 |
+
text (str): The markdown text to analyze.
|
| 44 |
+
Returns:
|
| 45 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 46 |
+
"""
|
| 47 |
+
problem_pattern = re.compile(r'(?:\n|\n\#*\s*)Problem (\d+)\.?', re.IGNORECASE)
|
| 48 |
+
solution_pattern = re.compile(r'(?:\n|\n\#*\s*)(?:Solution (\d+)|Solution I{1,3}|Solution)\.?', re.IGNORECASE)
|
| 49 |
+
|
| 50 |
+
start_position = find_problem_with_solution(text, problem_pattern, solution_pattern) or 0
|
| 51 |
+
|
| 52 |
+
tags = []
|
| 53 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text, start_position)])
|
| 54 |
+
problem_num = len(tags)
|
| 55 |
+
|
| 56 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text, start_position)])
|
| 57 |
+
solution_num = len(tags) - problem_num
|
| 58 |
+
|
| 59 |
+
tags.sort(key=lambda x: x[0].start())
|
| 60 |
+
return tags, problem_num, solution_num
|
| 61 |
+
|
| 62 |
+
|
| 63 |
+
def segment(text: str, tags):
|
| 64 |
+
starts = []
|
| 65 |
+
ends = []
|
| 66 |
+
|
| 67 |
+
for i in range(len(tags)):
|
| 68 |
+
starts.append(tags[i][0].end())
|
| 69 |
+
if i + 1 < len(tags):
|
| 70 |
+
ends.append(tags[i + 1][0].start())
|
| 71 |
+
else:
|
| 72 |
+
ends.append(len(text))
|
| 73 |
+
|
| 74 |
+
return [text[start:end].strip() for start, end in zip(starts, ends)]
|
| 75 |
+
|
| 76 |
+
|
| 77 |
+
def join(tags, segments):
|
| 78 |
+
problem, solution = '', ''
|
| 79 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 80 |
+
pairs = []
|
| 81 |
+
|
| 82 |
+
seem = {}
|
| 83 |
+
for tag, segment in zip(tags, segments):
|
| 84 |
+
if tag[0].group(1) not in seem:
|
| 85 |
+
seem[tag[0].group(1)] = (tag, segment)
|
| 86 |
+
else:
|
| 87 |
+
problem_tag, problem = seem[tag[0].group(1)]
|
| 88 |
+
problem_match = problem_tag[0].group(0)
|
| 89 |
+
problem_label = problem_tag[0].group(1)
|
| 90 |
+
|
| 91 |
+
solution = segment
|
| 92 |
+
solution_match = tag[0].group(1)
|
| 93 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 94 |
+
|
| 95 |
+
return pairs
|
| 96 |
+
|
| 97 |
+
|
| 98 |
+
def write_pairs(output_file: Path, pairs):
|
| 99 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 100 |
+
|
| 101 |
+
output_jsonl_text = ""
|
| 102 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 103 |
+
output_jsonl_text += json.dumps(
|
| 104 |
+
{
|
| 105 |
+
'year': year,
|
| 106 |
+
'tier': "T2",
|
| 107 |
+
'problem_label': problem_label,
|
| 108 |
+
'problem_type': None,
|
| 109 |
+
'problem': problem,
|
| 110 |
+
'solution': solution,
|
| 111 |
+
'metadata': {
|
| 112 |
+
'resource_path': output_file.relative_to(project_root).as_posix(),
|
| 113 |
+
'problem_match': problem_match,
|
| 114 |
+
'solution_match': solution_match
|
| 115 |
+
}
|
| 116 |
+
},
|
| 117 |
+
ensure_ascii=False
|
| 118 |
+
) + '\n'
|
| 119 |
+
|
| 120 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 121 |
+
|
| 122 |
+
|
| 123 |
+
def main():
|
| 124 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 125 |
+
compet_md_path = compet_base_path / "md"
|
| 126 |
+
seg_output_path = compet_base_path / "segmented"
|
| 127 |
+
|
| 128 |
+
total_problem_count = 0
|
| 129 |
+
total_solution_count = 0
|
| 130 |
+
|
| 131 |
+
for nmo_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 132 |
+
if nmo_md.stem != "en-2014-sol":
|
| 133 |
+
continue
|
| 134 |
+
|
| 135 |
+
output_file = seg_output_path / nmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 136 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 137 |
+
|
| 138 |
+
text = '\n' + nmo_md.read_text(encoding="utf-8")
|
| 139 |
+
|
| 140 |
+
tags, problem_num, solution_num = analyze(text)
|
| 141 |
+
|
| 142 |
+
segments = segment(text, tags)
|
| 143 |
+
pairs = join(tags, segments)
|
| 144 |
+
if pairs and problem_num > 0:
|
| 145 |
+
write_pairs(output_file, pairs)
|
| 146 |
+
|
| 147 |
+
total_problem_count += problem_num
|
| 148 |
+
total_solution_count += len(pairs)
|
| 149 |
+
else:
|
| 150 |
+
logger.warning(f"No problem found in {nmo_md}")
|
| 151 |
+
|
| 152 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 153 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 154 |
+
|
| 155 |
+
|
| 156 |
+
if __name__ == '__main__':
|
| 157 |
+
main()
|
Nordic_MO/segmented/en-1987-2011-sol.jsonl
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
Nordic_MO/segmented/en-2012-sol.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "The real numbers $a, b, c$ are such that $a^{2}+b^{2}=2 c^{2}$, and also such that $a \\neq b, c \\neq-a, c \\neq-b$. Show that\n\n$$\n\\frac{(a+b+2 c)\\left(2 a^{2}-b^{2}-c^{2}\\right)}{(a-b)(a+c)(b+c)}\n$$\n\nis an integer.", "solution": "Let us first note that\n\n$$\n\\frac{a+b+2 c}{(a+c)(b+c)}=\\frac{(a+c)+(b+c)}{(a+c)(b+c)}=\\frac{1}{a+c}+\\frac{1}{b+c}\n$$\n\nFurther we have\n\n$$\n2 a^{2}-b^{2}-c^{2}=2 a^{2}-\\left(2 c^{2}-a^{2}\\right)-c^{2}=3 a^{2}-3 c^{2}=3(a+c)(a-c)\n$$\n\nand\n\n$$\n2 a^{2}-b^{2}-c^{2}=2\\left(2 c^{2}-b^{2}\\right)-b^{2}-c^{2}=3 c^{2}-3 b^{2}=3(b+c)(c-b)\n$$\n\nso that\n\n$$\n\\frac{(a+b+2 c)\\left(2 a^{2}-b^{2}-c^{2}\\right)}{(a-b)(a+c)(b+c)}=\\frac{3(a-c)+3(c-b)}{a-b}=\\frac{3(a-b)}{a-b}=3\n$$\n\nan integer.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl", "problem_match": "\n\nPROBLEM 1.", "solution_match": "\n\nSolUTiON."}}
|
| 2 |
+
{"year": "2012", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Given a triangle $A B C$, let $P$ lie on the circumcircle of the triangle and be the midpoint of the arc $B C$ which does not contain $A$. Draw a straight line $l$ through $P$ so that $l$ is parallel to $A B$. Denote by $k$ the circle which passes through $B$, and is tangent to $l$ at the point $P$. Let $Q$ be the second point of intersection of $k$ and the line $A B$ (if there is no second point of intersection, choose $Q=B)$. Prove that $A Q=A C$.", "solution": "There are three possibilities: $Q$ between $A$ and $B, Q=B$, and $B$ between $A$ and $Q$. If $Q=B$ we have that $\\angle A B P$ is right, and $A P$ is a diameter\nof the circumcircle. The triangles $A B P$ and $A C P$ are then congruent (they have $A P$ in common, $P B=P C$, and both have a right angle opposite to $A P$ ). Hence ir follows that $A B=A C$.\n\nThe solutions in the other two cases are very similar. We present the one in the case when $Q$ lies between $A$ and $B$.\n\nThe segment $A P$ is the angle bisector of the angle at $A$, since $P$ is the midpoint of the arc $B C$ of the circumcircle which does not contain $A$. Also, $P C=P B$. Since the segment $Q B$ is parallel to the tangent to $k$ at $P$, it is orthogonal to the diameter of $k$ through $P$. Thus this diameter cuts $Q B$ in halves, to form two congruent right triangles, and it follows that $P Q=P B$. We have (in the usual notation) $\\angle P C B=\\angle P B C=\\frac{\\alpha}{2}$, and\n\n$$\n\\angle A Q P=180^{\\circ}-\\angle B Q P=180^{\\circ}-\\angle Q B P=180^{\\circ}-\\beta-\\frac{\\alpha}{2}=\\frac{\\alpha}{2}+\\gamma=\\angle A C P\n$$\n\nHence the triangles $A Q P$ and $A C P$ are congruent (two pairs of equal angles and one pair of equal corresponding sides), and it follows that $A C=A Q$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl", "problem_match": "\n\nProblem 2.", "solution_match": "\n\nSolution I."}}
|
| 3 |
+
{"year": "2012", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Given a triangle $A B C$, let $P$ lie on the circumcircle of the triangle and be the midpoint of the arc $B C$ which does not contain $A$. Draw a straight line $l$ through $P$ so that $l$ is parallel to $A B$. Denote by $k$ the circle which passes through $B$, and is tangent to $l$ at the point $P$. Let $Q$ be the second point of intersection of $k$ and the line $A B$ (if there is no second point of intersection, choose $Q=B)$. Prove that $A Q=A C$.", "solution": "Again we consider the case when $Q$ is between $A$ and $B$. We shall use trigonometry. As above, we have $\\angle A B P=\\beta+\\frac{\\alpha}{2}$, and thus\n\n$$\nQ B=2 P B \\cos \\left(\\beta+\\frac{\\alpha}{2}\\right)=2 P B \\cos \\left(\\pi-\\frac{\\alpha}{2}-\\gamma\\right)\n$$\n\nand\n\n$$\nA Q=2 R \\sin \\gamma-4 R \\sin \\frac{\\alpha}{2} \\cos \\left(\\pi-\\frac{\\alpha}{2}-\\gamma\\right)\n$$\n\nSince $A C=2 R \\cos \\beta$, it remains to prove that\n\n$$\n\\sin \\beta=\\sin \\gamma+2 \\sin \\frac{\\alpha}{2} \\cos \\left(\\frac{\\alpha}{2}+\\gamma\\right)\n$$\n\nwhich is easy, using standard trigonometry.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl", "problem_match": "\n\nProblem 2.", "solution_match": "\n\nSolution II."}}
|
| 4 |
+
{"year": "2012", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \\ldots, x_{n}$ (not necessarily different), with $1 \\leq x_{k} \\leq n, 1 \\leq k \\leq n$, and such that\n\n$$\nx_{1}+x_{2}+\\cdots+x_{n}=\\frac{n(n+1)}{2}, \\quad \\text { and } \\quad x_{1} x_{2} \\cdots x_{n}=n!\n$$\n\nbut $\\left\\{x_{1}, x_{2}, \\ldots, x_{n}\\right\\} \\neq\\{1,2, \\ldots, n\\}$.", "solution": "If it is possible to find a set of numbers as required for some $n=k$, then it will also be possible for $n=k+1$ (choose $x_{1}, \\ldots, x_{k}$ as for $n=k$, and\nlet $x_{k+1}=k+1$ ). Thus we have to find a positive integer $n$ such that a set as required exists, and prove that such a set does not exist for $n-1$.\n\nFor $n=9$ we have $8+6+3=9+4+4$, and $8 \\cdot 6 \\cdot 3=9 \\cdot 4 \\cdot 4$, so that a set of numbers as required will exist for all $n \\geq 9$. It remains to eliminate $n=8$.\n\nAssume $x_{1}, \\ldots, x_{8}$ are numbers that satisfy the conditions of the problem. Since 5 and 7 are primes, and since $2 \\cdot 5>8$ and $2 \\cdot 7>8$, two of the $x$-numbers have to be equal to 5 and 7 ; without loss of generality we can assume that $x_{1}=5, x_{2}=7$. For the remaining numbers we have $x_{3} x_{4} \\cdots x_{8}=2^{7} \\cdot 3^{2}$, and $x_{3}+x_{4}+\\cdots+x_{8}=36-12=24$. Since $3^{2}=9>8$, it follows that exactly two of the numbers $x_{3}, \\ldots, x_{8}$ are divisible by 3 , and the rest of the numbers are powers of 2. There are three possible cases to consider: two of the numbers are equal to 3 ; two of the numbers are equal to 6 ; one number is equal to 3 and another one is equal to 6 .\n\nCase 1. $x_{3}=x_{4}=3$\n\nWe then have $x_{5}+x_{6}+x_{7}+x_{8}=18$, and $x_{5} x_{6} x_{7} x_{8}=2^{7}$. The possible powers of 2 with sum 18 are $(1,1,8,8)$ and $(2,4,4,8)$, none of them gives the product $2^{7}$.\n\nCase 2. $x_{3}=3, x_{4}=6$\n\nWe have $x_{5}+x_{6}+x_{7}+x_{8}=15$, and $x_{5} x_{6} x_{7} x_{8}=2^{6}$. It is immediate to check that the only possibility for the remaining numbers is $(1,2,4,8)$, which is not allowed, since it gives $\\left\\{x_{1}, x_{2}, \\ldots, x_{8}\\right\\}=\\{1,2, \\ldots, 8\\}$.\n\nCase 3. $x_{3}=x_{4}=6$\n\nNow we have $x_{5}+x_{6}+x_{7}+x_{8}=12$, and $x_{5} x_{6} x_{7} x_{8}=2^{5}$. The possible powers of 2 which give the correct sum are $(1,1,2,8)$ and $(2,2,4,4)$, but again, they do not give the desired product.\n\nThus the smallest positive integer with the required property is 9 .", "metadata": {"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl", "problem_match": "\n\nProblem 3.", "solution_match": "\n\nSolution."}}
|
| 5 |
+
{"year": "2012", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "The number 1 is written on the blackboard. After that a sequence of numbers is created as follows: at each step each number $a$ on the blackboard is replaced by the numbers $a-1$ and $a+1$; if the number 0 occurs, it is erased immediately; if a number occurs more than once, all its occurrences are left on the blackboard. Thus the blackboard will show 1 after 0 steps; 2 after 1 step; 1,3 after 2 steps; 2, 2, 4 after 3 steps, and so on. How many numbers will there be on the blackboard after $n$ steps?", "solution": "Let $S$ be a set of different numbers, all of them less than $2^{n-1}$, and create two new sets as follows: $S_{1}$, consisting of all the numbers in $S$ except\nthe smallest one, and $S_{2}$, with elements the smallest element of $S$ and all the numbers we get by adding $2^{n-1}$ to each number in $S$. Note that if the number of elements in $S$ is $a$, then $S_{1}$ has $a-1$ elements, and $S_{2}$ has $a+1$ elements. This corresponds to the operations we are allowed to perform on the blackboard, if we throw away all empty sets. If we now operate simultaneously on the sets and on the numbers, then after $n$ steps the number of sets will be exactly equal to the number of numbers on the blackboard.\n\nLet us see what the set operations look like. We must start with a set, consisting only of the number 0 . Next we get an empty set (thrown away), and the set $\\{0,1\\}$; next the sets $\\{1\\}$ and $\\{0,2,3\\}$; next again (an empty set and) $\\{1,5\\},\\{2,3\\},\\{0,4,6,7\\}$, etc.\n\nIt is now fairly easy to prove by induction that after $n$ steps\n\n(1) each number less than $2^{n}$ appears in exactly one set;\n\n(2) the number of elements in the sets corresponds exactly to the numbers on the blackboard;\n\n(3) if the numbers in each set are written in increasing order, then the difference between two neighbours is a power of 2 ; thus the binary representations of two neighbours differ in exactly one position (in the binary system the example above looks like this: $\\{0\\} ;\\{0,1\\} ;\\{01\\},\\{00,10,11\\} ;\\{001,101\\},\\{010,011\\}$, $\\{000,100,110,111\\}) ;$\n\n(4) if $k$ is the number of ones in the binary code of the smallest number of a set, and $l$ the number of ones in the largest number of the same set, then $k+l=n$; (5) each set contains exactly one number with $\\left\\lfloor\\frac{n}{2}\\right\\rfloor$ ones.\n\nThe last property tells us that the number of sets after $n$ steps is equal to the number of numbers such that their binary representation contains exactly $\\left\\lfloor\\frac{n}{2}\\right\\rfloor$ ones out of $n$ digits, i.e. the number of numbers on the blackboard after $n$ steps will be equal to $\\binom{n}{\\left\\lfloor\\frac{n}{2}\\right\\rfloor}$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl", "problem_match": "\n\nProblem 4.", "solution_match": "\n\nSolution I."}}
|
| 6 |
+
{"year": "2012", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "The number 1 is written on the blackboard. After that a sequence of numbers is created as follows: at each step each number $a$ on the blackboard is replaced by the numbers $a-1$ and $a+1$; if the number 0 occurs, it is erased immediately; if a number occurs more than once, all its occurrences are left on the blackboard. Thus the blackboard will show 1 after 0 steps; 2 after 1 step; 1,3 after 2 steps; 2, 2, 4 after 3 steps, and so on. How many numbers will there be on the blackboard after $n$ steps?", "solution": "Denote by $\\sigma_{n}$ the number of numbers on the blackboard after $n$ steps (thus $\\sigma_{0}=\\sigma_{1}=1, \\sigma_{2}=2, \\sigma_{3}=3, \\ldots$ ). Regard all points in the plane with coordinates $(m, n)$, where $m, n$ are defined as follows: the number $n$ is written on the blackboard after $m$ steps ( $m, n$ are positive integers by the condition). At each node, i.e. each point with integer coordinates of the above type, write the number of occurrences of $n$ after $m$ steps. Thus the number written at $(3,2)$ will be the number of occurrences of 2 directly after step 3 , which is 2 . Observe that the number at each node is equal to the number of ways to reach this node from the point $(0,1)$, walking from one node to another one step at the time, from left to right and either up or down, without going down to the horizontal axis.\n\n(Since all zeroes are erased, we can never reach the horizontal axis.) For each $m$ we want to find the total number of paths $\\sigma_{m}$, reaching the vertical line $y=m$.\n\nIf we were to remove the constraint that we are not allowed to step on the horizontal axis (i.e. that all zeroes are erased), we would get Pascal's triangle, and the total number of paths would be $2^{m}$. The binomial coefficient at each node is then the total number of paths to reach this node, without constraint.\n\nWe need to find and subtract the number of paths from $A(0,1)$ to a point $B$ among the allowed nodes, which go down to the horizontal axis. Choose such a path, and find a new one by reflecting in the horizontal axis the part between the starting point $(0,1)$ and the path's first contact with the horizontal axis. The original path and the reflected one will end at the same point (among the allowed nodes); the reflected one will start at $A^{\\prime}(0,-1)$. We have constructed a bijection between the original set of paths from $A$ to $B$ that reach down to the horizontal axis and the set of paths from $A^{\\prime}$ to $B$. Observe that starting at $A^{\\prime}$ we can get another copy of Pascal's triangle, which is the original one, translated two units down. It is easier to count the number of paths from $A^{\\prime}$ to $B$, since they are not subject to any constraints. Thus the number of \"positive\" paths from $A$ to the points above the horizontal axis for $m=2 k$ will be\n\n$$\n\\begin{gathered}\n\\left(\\binom{2 k}{2 k}+\\binom{2 k}{2 k-1}+\\cdots+\\binom{2 k}{k+1}+\\binom{2 k}{k}\\right)- \\\\\n-\\left(\\binom{2 k}{2 k}+\\binom{2 k}{2 k-1}+\\cdots+\\binom{2 k}{k+1}\\right)=\\binom{2 k}{k}\n\\end{gathered}\n$$\n\nIn case $m$ is odd, a modification of the above argument gives the answer obtained in solution I.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl", "problem_match": "\n\nProblem 4.", "solution_match": "\n\nSolUTION II."}}
|
Nordic_MO/segmented/en-2013-sol.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Let $\\left(a_{n}\\right)_{n \\geq 1}$ be a sequence with $a_{1}=1$ and\n\n$$\na_{n+1}=\\left\\lfloor a_{n}+\\sqrt{a_{n}}+\\frac{1}{2}\\right\\rfloor\n$$\n\nfor all $n \\geq 1$, where $\\lfloor x\\rfloor$ denotes the greatest integer less than or equal to $x$. Find all $n \\leq 2013$ such that $a_{n}$ is a perfect square.", "solution": "We will show by induction that $a_{n}=1+\\left\\lfloor\\frac{n}{2}\\right\\rfloor\\left\\lfloor\\frac{n+1}{2}\\right\\rfloor$, which is equivalent to $a_{2 m}=1+m^{2}$ and $a_{2 m+1}=1+m(m+1)$. Clearly this is true for $a_{1}$. If $a_{2 m+1}=1+m(m+1)$ then\n\n$$\na_{2 m+2}=\\left\\lfloor m^{2}+m+1+\\sqrt{m^{2}+m+1}+\\frac{1}{2}\\right\\rfloor\n$$\n\nand since $m+\\frac{1}{2}<\\sqrt{m^{2}+m+1}<m+1$ (easily seen by squaring), we get $a_{2 m+2}=\\left(m^{2}+m+1\\right)+(m+1)=1+(m+1)^{2}$.\n\nAnd if $a_{2 m}=1+m^{2}$ then\n\n$$\na_{2 m+1}=\\left\\lfloor m^{2}+1+\\sqrt{m^{2}+1}+\\frac{1}{2}\\right\\rfloor\n$$\n\nand here $m<\\sqrt{m^{2}+1}<m+\\frac{1}{2}$, so $a_{2 m+1}=\\left(m^{2}+1\\right)+m=1+m(m+1)$.\n\nIf $m \\geq 1$ then $m^{2}<1+m^{2}<(m+1)^{2}$ and $m^{2}<m^{2}+m+1<(m+1)^{2}$, so $a_{n}$ cannot be a perfect square if $n>1$. Therefore $a_{1}=1$ is the only perfect square in the sequence.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl", "problem_match": "\n\nPRoblem 1.", "solution_match": "\n\nSolution."}}
|
| 2 |
+
{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "In a football tournament there are $n$ teams, with $n \\geq 4$, and each pair of teams meets exactly once. Suppose that, at the end of the tournament, the final scores form an arithmetic sequence where each team scores 1 more point than the following team on the scoreboard. Determine the maximum possible score of the lowest scoring team, assuming usual scoring for football games (where the winner of a game gets 3 points, the loser 0 points, and if there is a tie both teams get 1 point).", "solution": "Note that the total number of games equals the number of different pairings, that is, $n(n-1) / 2$. Suppose the lowest scoring team ends with $k$ points. Then the total score for all teams is\n\n$$\nk+(k+1)+\\cdots+(k+n-1)=n k+\\frac{(n-1) n}{2}\n$$\n\nSome games must end in a tie, for otherwise, all team scores would be a multiple of 3 and cannot be 1 point apart. Since the total score of a tie is only 2 points compared to 3 points if one of the teams wins, we therefore know that\n\n$$\nn k+\\frac{(n-1) n}{2}<3 \\cdot \\frac{n(n-1)}{2}\n$$\n\nso $n k<n(n-1)$, and hence $k<n-1$. It follows that the lowest scoring team can score no more than $n-2$ points.\n\nWe now show by induction that it is indeed possible for the lowest scoring team to score $n-2$ points.\n\nThe following scoreboard shows this is possible for $n=4$ :\n\n| - | 3 | 1 | 1 | 5 |\n| :---: | :---: | :---: | :---: | :---: |\n| 0 | - | 1 | 3 | 4 |\n| 1 | 1 | - | 1 | 3 |\n| 1 | 0 | 1 | - | 2 |\n\nNow suppose we have a scoreboard for $n$ teams labelled $T_{n-2}, \\ldots, T_{2 n-3}$, where team $T_{i}$ scores $i$ points. Keep the results among these teams unchanged while adding one more team.\n\nWrite $n=3 q+r$ with $r \\in\\{1,-1,0\\}$, and let the new team tie with just one of the original teams, lose against $q$ teams, and win against the rest of them. The new team thus wins $n-1-q$ games, and gets $1+3(n-1-q)=3 n-2-3 q=2 n-2+r$ points.\n\nMoreover, we arrange for the $q$ teams which win against the new team to form an arithmetic sequence $T_{j}, T_{j+3}, \\ldots, T_{j+3(q-1)}=T_{j+n-r-3}$, so that each of them, itself having gained three points, fills the slot vacated by the next one.\n\n(i) If $r=1$, then let the new team tie with team $T_{n-2}$ and lose to each of the teams $T_{n-1}, T_{n+2}, \\ldots, T_{n-1+n-r-3}=T_{2 n-5}$.\n\nTeam $T_{n-2}$ now has $n-1$ points and takes the place vacated by $T_{n-1}$. At the other end, $T_{2 n-5}$ now has $2 n-2$ points, just one more than the previous top team $T_{2 n-3}$. And the new team has $2 n-2+r=2 n-1$ points, becoming the new top team. The teams now have all scores from $n-1$ up to $2 n-1$.\n\n(ii) If $r=-1$, then let the new team tie with team $T_{2 n-3}$ and lose to each of the teams $T_{n-2}, T_{n+1}, \\ldots, T_{n-2+n-r-3}=T_{2 n-4}$.\n\nThe old top team $T_{2 n-3}$ now has $2 n-2$ points, and its former place is filled by the new team, which gets $2 n-2+r=2 n-3$ points. $T_{2 n-4}$ now has $2 n-1$ points and is the new top team. So again we have all scores ranging from $n-1$ up to $2 n-1$.\n\n(iii) If $r=0$, then let the new team tie with team $T_{n-2}$ and lose to teams $T_{n-1}, T_{n+2}, \\ldots, T_{n-1+n-r-3}=T_{2 n-4}$.\n\nTeam $T_{n-2}$ now has $n-1$ points and fills the slot vacated by $T_{n-1}$. At the top end, $T_{2 n-4}$ now has $2 n-1$ points, while the new team has $2 n-2+r=2 n-2$ points, and yet again we have all scores from $n-1$ to $2 n-1$.\n\nThis concludes the proof.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl", "problem_match": "\n\nProblem 2.", "solution_match": "\n\nSolution."}}
|
| 3 |
+
{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Define a sequence $\\left(n_{k}\\right)_{k \\geq 0}$ by $n_{0}=n_{1}=1$, and $n_{2 k}=n_{k}+n_{k-1}$ and $n_{2 k+1}=n_{k}$ for $k \\geq 1$. Let further $q_{k}=n_{k} / n_{k-1}$ for each $k \\geq 1$. Show that every positive rational number is present exactly once in the sequence $\\left(q_{k}\\right)_{k \\geq 1}$.", "solution": "Clearly, all the numbers $n_{k}$ are positive integers. Moreover,\n\n$$\nq_{2 k}=\\frac{n_{2 k}}{n_{2 k-1}}=\\frac{n_{k}+n_{k-1}}{n_{k-1}}=q_{k}+1\n$$\n\nand similarly,\n\n$$\n\\frac{1}{q_{2 k+1}}=\\frac{n_{2 k}}{n_{2 k+1}}=\\frac{n_{k}+n_{k-1}}{n_{k}}=\\frac{1}{q_{k}}+1\n$$\n\nIn particular, $q_{k}>1$ when $k$ is even, and $q_{k}<1$ when $k \\geq 3$ is odd.\n\nWe will show the following by induction on $t=2,3,4, \\ldots$ :\n\nClaim: Every rational number $r / s$ where $r$, s are positive integers with $\\operatorname{gcd}(r, s)=$ 1 and $r+s \\leq t$ occurs precisely once among the numbers $q_{k}$.\n\nThe claim is clearly true for $t=2$, since then $r / s=1 / 1=1$ is the only possibility, and $q_{1}$ is the only occurrence of 1 in the sequence.\n\nNow, assume that $u \\geq 3$ and that the claim holds for $t=u-1$. Let $r$ and $s$ be positive integers with $\\operatorname{gcd}(r, s)=1$ and $r+s=u$.\n\nFirst, assume that $r>s$. We know that $r / s=q_{m}$ is only possible if $m$ is even. But\n\n$$\n\\frac{r}{s}=q_{2 k} \\Leftrightarrow \\frac{r-s}{s}=q_{k}\n$$\n\nby (1), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\\operatorname{gcd}(r-s, s)=1$ and $(r-s)+s=r \\leq t$.\n\nNext, assume that $r<s$. We know that $r / s=q_{m}$ is only possible if $m$ is odd. But\n\n$$\n\\frac{r}{s}=q_{2 k+1} \\Leftrightarrow \\frac{s}{r}=\\frac{1}{q_{2 k+1}} \\Leftrightarrow \\frac{s-r}{r}=\\frac{1}{q_{k}}\n$$\n\nby (2), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\\operatorname{gcd}(s-r, r)=1$ and $(s-r)+r=s \\leq t$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl", "problem_match": "\n\nProblem 3.", "solution_match": "\n\nSolution."}}
|
| 4 |
+
{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $A B C$ be an acute angled triangle, and $H$ a point in its interior. Let the reflections of $H$ through the sides $A B$ and $A C$ be called $H_{c}$ and $H_{b}$, respectively, and let the reflections of $H$ through the midpoints of these same sides be called $H_{c}^{\\prime}$ and $H_{b}^{\\prime}$, respectively. Show that the four points $H_{b}, H_{b}^{\\prime}, H_{c}$, and $H_{c}^{\\prime}$ are concyclic if and only if at least two of them coincide or $H$ lies on the altitude from $A$ in triangle $A B C$.", "solution": "If at least two of the four points $H_{b}, H_{b}^{\\prime}, H_{c}$, and $H_{c}^{\\prime}$ coincide, all four are obviously concyclic. Therefore we may assume that these four points are distinct.\n\nLet $P_{b}$ denote the midpoint of segment $H H_{b}, P_{b}^{\\prime}$ the midpoint of segment $H H_{b}^{\\prime}, P_{c}$ the midpoint of segment $H H_{c}$, and $P_{c}^{\\prime}$ the midpoint of segment $H H_{c}^{\\prime}$.\n\nThe triangle $H H_{b} H_{b}^{\\prime}$ being right-angled in $H_{b}$, it follows that the perpendicular bisector $\\ell_{b}$ of the side $H_{b} H_{b}^{\\prime}$ goes through the point $P_{b}^{\\prime}$. Since the segments $P_{b} P_{b}^{\\prime}$ and $H_{b} H_{b}^{\\prime}$ are parallel and $P_{b}^{\\prime}$ is the midpoint of the side $A C$, we then conclude that $\\ell_{b}$ also goes through the circumcentre $O$ of triangle $A B C$.\n\nSimilarly the perpendicular bisector $\\ell_{c}$ of the segment $H_{c} H_{c}^{\\prime}$ also goes through $O$. Hence the four points $H_{b}, H_{b}^{\\prime}, H_{c}$, and $H_{c}^{\\prime}$ are concyclic if and only if also the perpendicular bisector $\\ell$ of the segment $H_{b}^{\\prime} H_{c}^{\\prime}$ goes through the point $O$. Since $H_{b}^{\\prime} H_{c}^{\\prime}\\left\\|P_{b}^{\\prime} P_{c}^{\\prime}\\right\\| B C$, this is the case if and only if $\\ell$ is the perpendicular bisector $m$ of the segment $B C$.\n\nLet $k$ denote the perpendicular bisector of the segment $P_{b}^{\\prime} P_{c}^{\\prime}$. Since the lines $\\ell$ and $m$ are obtained from $k$ by similarities of ratio 2 and centres $H$ and $A$, respectively, they coincide if and only if $H A$ is parallel to $m$. Thus $H_{b}, H_{b}^{\\prime}, H_{c}$, and $H_{c}^{\\prime}$ are concyclic if and only if $H$ lies on the altitude from $A$ in triangle $A B C$.\n\n\n\nClick here to experiment with the figure in GeoGebra.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl", "problem_match": "\n\nProblem 4.", "solution_match": "\n\nSolution."}}
|
Nordic_MO/segmented/en-2014-sol.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ (where $\\mathbb{N}$ is the set of the natural numbers and is assumed to contain 0 ), such that\n\n$$\nf\\left(x^{2}\\right)-f\\left(y^{2}\\right)=f(x+y) f(x-y)\n$$\n\nfor all $x, y \\in \\mathbb{N}$ with $x \\geq y$.", "solution": "It is easily seen that both $f(x)=x$ and $f \\equiv 0$ solve the equation; we shall show that there are no other solutions.\n\nSetting $x=y=0$ gives $f(0)=0$; if only $y=0$ we get $f\\left(x^{2}\\right)=(f(x))^{2}$, for all admissible $x$. For $x=1$ we now get $f(1)=0$, or $f(1)=1$.\n\nCase 1. $f(1)=0$ : We have\n\n$$\nf\\left((x+1)^{2}\\right)-f\\left(x^{2}\\right)=f(2 x+1) \\cdot f(1)=0=(f(x+1))^{2}-(f(x))^{2}\n$$\n\nso that $f(x+1)=f(x)$ for all $x$, and it follows that $f \\equiv 0$.\n\nCase 2. $f(1)=1$ : Denote $f(2)=a$. We have\n\n$$\n(f(2))^{2}-1=f\\left(2^{2}\\right)-f\\left(1^{2}\\right)=f(3) \\cdot f(1)\n$$\n\nso that $f(3)=a^{2}-1$. Obviously $f(4)=a^{2}$, and $x=3, y=1$ now give\n\n$$\n\\left(a^{2}-1\\right)^{2}-1=a^{3}\n$$\n\nso that $a=0$ or $a=2$, since $a$ cannot be negative. If $f(2)=0$, then $f(3)=0-1$, which is impossible. Thus we have $a=2$. The fact that $f(n)=n$ for all $n \\in \\mathbb{N}$ is now easy to establish using induction.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2014-sol.jsonl", "problem_match": "\n## Problem 1", "solution_match": "1"}}
|
| 2 |
+
{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Given an equilateral triangle, find all points inside the triangle such that the distance from the point to one of the sides is equal to the geometric mean of the distances from the point to the other two sides of the triangle.\n\n[The geometric mean of two numbers $x$ and $y$ equals $\\sqrt{x y}$.]", "solution": "Let $P$ be a point inside $\\triangle A B C$. Denote its orthogonal projections on $A B, B C, C A$ by $X, Y, Z$, respectively. We have $\\angle X P Z=\\angle Y P X=120^{\\circ}$.\n\nAssume that $P X^{2}=P Y \\cdot P Z$. Together with $\\angle X P Z=\\angle Y P X=120^{\\circ}$, this gives $\\triangle X P Z \\sim \\triangle Y P X$ (s-a-s). It means that $\\angle P Z X=\\angle P X Y$. The quadrilaterals $A X P Z$ and $B Y P X$ are circumscribed, and we get $\\angle P A X=\\angle P B Y$, so that $\\angle P A B+\\angle P B A=60^{\\circ}$. We now have $\\angle A P B=120^{\\circ}$, meaning that $P$ lies on an arc inside the triangle, which is part of the circle through $A, B$, and the centre of the triangle.\n\nThe above argument can be reversed to see that all points on this arc satisfy the condition.\n\nThe set of all points as described is thus the union of three arcs, each of them passing through two of the vertices and through the centre of the triangle.\n\n\nRemark: It is also possible to solve this by introducing a coordinate system and deriving equations for the locus of $P$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2014-sol.jsonl", "problem_match": "\n## Problem 2", "solution_match": "2"}}
|
| 3 |
+
{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Find all nonnegative integers $a, b, c$, such that\n\n$$\n\\sqrt{a}+\\sqrt{b}+\\sqrt{c}=\\sqrt{2014}\n$$", "solution": "We start with a lemma:\n\nLemma. If $p, q$ are nonnegative integers and $\\sqrt{p}+\\sqrt{q}=r \\in \\mathbb{Q}$, then $p$ and $q$ are squares of integers.\n\nProof of lemma: If $r=0$, then $p=q=0$. For $r \\neq 0$, take the square of both sides to get $p+q+2 \\sqrt{p q}=r^{2}$, which means that $\\sqrt{p q} \\in \\mathbb{Q}$, so that $p q$ must be the square of a rational number, and, being an integer, it must be the square of an integer. Denote $p q=s^{2}, s \\geq 0$. Then $p=\\frac{s^{2}}{q}$, and\n\n$$\nr=\\sqrt{p}+\\sqrt{q}=\\frac{s}{\\sqrt{q}}+\\sqrt{q}\n$$\n\nwhich implies that $\\sqrt{q}=\\frac{s+q}{r} \\in \\mathbb{Q}$, and it follows that $q$ is a square. Then $p$ must also be a square.\n\nBack to the problem: we can rewrite the equation as\n\n$$\na+b+2 \\sqrt{a b}=2014+c-2 \\sqrt{2014 c}\n$$\n\nso that\n\n$$\n\\sqrt{a b}+\\sqrt{2014 c} \\in \\mathbb{Q}\n$$\n\nThe lemma now tells us that $a b$ and $2014 c$ need to be squares of integers. Since $2014=2 \\cdot 19 \\cdot 53$, we must have $c=2014 m^{2}$ for some nonnegative integer $m$. Similarly, $a=2014 k^{2}, b=2014 l^{2}$. The equation now implies\n\n$$\nk+l+m=1\n$$\n\nso that the only possibilities are $(2014,0,0),(0,2014,0),(0,0,2014)$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2014-sol.jsonl", "problem_match": "\n## Problem 3", "solution_match": "3"}}
|
| 4 |
+
{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "A game is played on an $n \\times n$ chessboard. At the beginning there are 99 stones on each square. Two players $A$ and $B$ take turns, where in each turn the player chooses either a row or a column and removes one stone from each square in the chosen row or column. They are only allowed to choose a row or a column, if it has least one stone on each square. The first player who cannot move, looses the game. Player $A$ takes the first turn. Determine all $n$ for which player $A$ has a winning strategy.", "solution": "Player $A$ has a winning strategy if and only if $n$ is odd.\n\nFirst we prove that no matter how they play, the play will not end before the board is empty. Let $(i, j)$ denote the square in row $i$ and column $j$, let $r_{i}$ denote the number of times row $i$ has been chosen when the game ends, and let $c_{j}$ denote the same for columns. Assume by contradiction that there is a none empty square $(a, b)$ when no more moves are possible. Hence there is an empty square in row $a$, let us say $(a, c)$, and an empty square in column $b$, let us say $(d, b)$. This shows that $r_{a}+c_{b}<99, r_{a}+c_{c}=99$ and $r_{d}+c_{b}=99$. But this leads to $r_{d}+c_{c}>99$ which is impossible since there are exactly 99 stones on square $(d, c)$ when the game begins.\n\nThis shows that the game will end after $\\frac{n \\times n \\times 99}{99}=n \\times n$ moves since each player removes 99 stones in each move. The number $n \\times n$ has the same parity as $n$, and hence $A$ wins if $n$ is odd and $B$ wins if $n$ is even no matter how they play.\n\nRemark: It can by shown that player $B$ has a winning strategy when $n$ is even in a very different way: If player $B$ copies the choice of $A$, i.e. when $A$ chooses row $m, B$ chooses row $n-m$, and the same for columns, then player $B$ wins when $n$ is even.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2014-sol.jsonl", "problem_match": "\n## Problem 4", "solution_match": "4"}}
|
Nordic_MO/segmented/en-2015-sol.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle and $\\Gamma$ the circle with diameter $A B$. The bisectors of $\\angle B A C$ and $\\angle A B C$ intersect $\\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.", "solution": "Let the line $E D$ meet $A C$ at $G^{\\prime}$ and $B C$ at $F^{\\prime} . A D$ and $B E$ intersect at $I$, the incenter of $A B C$. As angles subtending the same arc $\\widehat{B D}$, $\\angle D A B=\\angle D E B=\\angle G^{\\prime} E I$. But $\\angle D A B=\\angle C A D=$ $\\angle G^{\\prime} A I$. This means that $E, A, I$ and $G^{\\prime}$ are concyclic, and $\\angle A E I=\\angle A G^{\\prime} I$ as angles subtending the same chord $A I$. But $A B$ is a diameter of $\\Gamma$, and so $\\angle A E B=$ $\\angle A E I$ is a right angle. So $I G^{\\prime} \\perp A C$, or $G^{\\prime}$ is the foot of the perpendicular from $I$ to $A C$. This implies $G^{\\prime}=G$. In a similar manner we prove that $F^{\\prime}=F$, and the proof is complete.\n\n", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 1.", "solution_match": "\n\nSolution 1."}}
|
| 2 |
+
{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle and $\\Gamma$ the circle with diameter $A B$. The bisectors of $\\angle B A C$ and $\\angle A B C$ intersect $\\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.", "solution": "(Read the attached figure so that $F^{\\prime}$ and $G^{\\prime}$ are as $F$ and $G$ in the problem text.) The angles $\\angle A E I=\\angle A E B$ and $\\angle A G I$ are right angles. This means that $A I G E$ is a cyclic quadrilateral. But then $\\angle B E G=\\angle I E G=\\angle I A G=\\angle D A C=\\angle D A B=\\angle B E D$, implying that $G$ and $D$ are on the same line through $E$. The same argument shows $F$ and $E$ are on the same line through $D$. So the points $G$ and $F$ are on the line $E D$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 1.", "solution_match": "\n\nSolution 2."}}
|
| 3 |
+
{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Find the primes $p, q, r$, given that one of the numbers $p q r$ and $p+q+r$ is 101 times the other.", "solution": "We may assume $r=\\max \\{p, q, r\\}$. Then $p+q+r \\leq 3 r$ and $p q r \\geq 4 r$. So the sum of the three primes is always less than their product. The only relevant requirement thus is $p q r=101(p+q+r)$. We observe that 101 is a prime. So one of $p, q, r$ must be 101. Assume $r=101$. Then $p q=p+q+101$. This can be written as $(p-1)(q-1)=102$. Since $102=1 \\cdot 102=2 \\cdot 51=3 \\cdot 34=6 \\cdot 17$, the possibilities for $\\{p, q\\}$ are $\\{2,103\\},\\{3,52\\},\\{4,35\\},\\{7,18\\}$ The only case, where both the numbers are primes, is $\\{2,103\\}$. So the only solution to the problem is $\\{p, q, r\\}=\\{2,101,103\\}$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 2.", "solution_match": "\n\nSolution."}}
|
| 4 |
+
{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Let $n>1$ and $p(x)=x^{n}+a_{n-1} x^{n-1}+\\cdots+a_{0}$ be a polynomial with $n$ real roots (counted with multiplicity). Let the polynomial $q$ be defined by\n\n$$\nq(x)=\\prod_{j=1}^{2015} p(x+j)\n$$\n\nWe know that $p(2015)=2015$. Prove that $q$ has at least 1970 different roots $r_{1}, \\ldots, r_{1970}$ such that $\\left|r_{j}\\right|<2015$ for all $j=1, \\ldots, 1970$.", "solution": "Let $h_{j}(x)=p(x+j)$. Consider $h_{2015}$. Like $p$, it has $n$ real roots $s_{1}, s_{2}, \\ldots, s_{n}$, and $h_{2015}(0)=p(2015)=2015$. By Viète, the product $\\left|s_{1} s_{2} \\cdots s_{n}\\right|$ equals 2015. Since $n \\geq 2$, there is at least one $s_{j}$ such that $\\left|s_{j}\\right| \\leq \\sqrt{2015}<\\sqrt{2025}=45$. Denote this $s_{j}$ by $m$. Now for all $j=0,1, \\ldots, 2014, h_{2015-j}(m+j)=p(m+j+2015-j)=p(m+2015)=$ $h_{2015}(m)=0$. So $m, m+1, \\ldots, m+2014$ are all roots of $q$. Since $0 \\leq|m|<45$, the condition $|m+j|<2015$ is satisfied by at least 1970 different $j, 0 \\leq j \\leq 2014$, and we are done.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 3.", "solution_match": "\n\nSolution."}}
|
| 5 |
+
{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:\n\n(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.\n\n(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.\n\nHow many different permutations of the volumes can be obtained by using these two operations repeatedly?", "solution": "(By the proposer.) Let the positions of the books in the stack be $1,2,3, \\ldots, 2000$ from the top (and consider them modulo 2000). Notice that both operations fix the parity of the number of the book at a any given position. Operation (i) subtracts an even integer from the number of the book at each position. If $A$ is an operation of type (i), and $B$ is an operation of type (ii), then the operation $A^{-1} B A$ changes the order of the books in the positions $n+1$ to $n+m$ where $n$ is even and $m$ is odd. This is called turning the interval.\n\nNow we prove that all the volumes in odd positions can be placed in the odd positions in every way we like: If the volume we want in position 1 is in position $m_{1}$, we turn the interval 1 to $m_{1}$. Now if the volume we want in position 3 is in position $m_{3}$, we turn the interval 3 to $m_{3}$, and so on. In this way we can permute the volumes in odd positions exactly as we want to.\n\nNow we prove that we can permute the volumes in even positions exactly as we want without changing the positions of the volumes in the odd positions: We can make a transposition of the two volumes in position $2 n$ and $2 n+2 m$ by turning the interval $2 n+1$ to $2 n+2 m-1$, then turning the interval $2 n+2 m+1$ to $2 n-1$, then turning the interval $2 n+1$ to $2 n-1$, and finally adding $2 m$ to the number of the volume in each position.\n\nSince there are 1000! permutations of the volumes in the odd positions, and 1000! permutations of the volumes in the even positions, altogether we have (1000!) ${ }^{2}$ different permutations.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 4.", "solution_match": "\n\nSolution 1."}}
|
| 6 |
+
{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:\n\n(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.\n\n(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.\n\nHow many different permutations of the volumes can be obtained by using these two operations repeatedly?", "solution": "We show that the volumes can be permuted so that the volumes with odd numbers are in an arbitrary order in the odd-numbered palaces and the volumes with even numbers are in an arbitrary order in the even-numbered places. The main idea is to construct two combinations of the allowed operations. The first one turns the volumes in a specified interval, starting and ending in an odd-numbered place, in the opposite order while keeping everything outside this interval fixed, or keeps everything fixed in an interval while turning the order of the volumes outside this interval in the opposite direction, when the counting starts below that interval and is continued from the top after reaching the bottom volume. The second combined operation just exchanges two volumes in evennumbered places while keeping everything else fixed. - It is clear that 2000 is not a special number, and it could be replaced by a generic even integer. However, we formulate the proof according to the problem text.\n\nLet $E=\\{1,2, \\ldots, 2000\\}$. We formulate the operations described in conditions (i) and (ii), depending on an even integer $n$ and odd integer $m$ as functions $f_{n}: E \\rightarrow E$ and $g_{m}: E \\rightarrow E$, defined by\n\n$$\nf_{n}(p)=\\left\\{\\begin{array}{ll}\n2000+p-n & \\text { for } p \\geq n, \\\\\np-n & \\text { for } n<p\n\\end{array} \\quad \\text { and } \\quad g_{m}(p)= \\begin{cases}m-p+1 & \\text { for } p \\leq m \\\\\np & \\text { for } m<p\\end{cases}\\right.\n$$\n\nWe immediately see that $f_{n}$ and $g_{m}$ map even numbers into even numbers and odd numbers into odd numbers. So the volumes can never be permuted so that an odd-numbered volume would be in an even place or an even-numbered would be in an odd place. The observation $f([1, n])=[2000-(n+1), 2000]$ easily leads to $f_{n}^{-1}=f_{2000-n}$.\n\nNow let $n$ be even and $m$ odd and $n+m<2000$. Consider the combined mapping $f_{n}^{-1} \\circ g_{m} \\circ f_{n}$. If $n<n+p \\leq n+m$, then $f_{n}(n+p)=p \\leq m, g_{m}(p)=m-p+1<2000-n$ and $f_{n}^{-1}(m-p+1)=f_{2000-n}(m-p+1)=2000+m-p+1-2000+n=n+m+1-p$. Because $f_{n}([n+1, n+m])=[1, m], f_{n}$ maps numbers $p$ outside the interval $[n+1, n+m]$ into numbers outside the interval $[1, m] ; g_{m}$ keeps these numbers fixed and $f_{n}^{-1}$ returns $f_{n}(p)$ into $p$. So we have shown that for any interval $[s, t] \\subset E$ with $s$ and $t$ odd, there is a function $h_{s, t}$, combined of functions of the $f$ type and $g$ type such that $h_{s, t}$ reverses the order of numbers in the interval $[s, t]$ and is the identity function outside this interval.\n\nThe functions $h_{s, t}$ allow us to order the odd numbers in an arbitrary manner. If $p_{1}$ ought to be in position 1 , then apply (if needed) $h_{1, p_{1}}$; if the number $p_{2}$ which ought to be in position 3 now is in position $x$, the $x \\geq 3$ and we may apply (if needed) $h_{3, x}$. Continuing this way, we eventually arrive at the desired order of the odd numbers.\n\nTo construct the second one of the desired operations, we have to obtain a counterpart for $h_{s, t}$ for $t<s$. To this end, consider $f_{n}^{-1} \\circ g_{m} \\circ f_{n}$ for $m+n>2000$. By the definition of $f_{n}$, $f_{n}(n+m-2000)=2000+(n+m-2000)-n=m$, and so $f_{n}[n+m-2000+1, n]=[m+$ 1, 2000] Consequently, $f_{n}^{-1} \\circ g_{m} \\circ f_{n}$ keeps numbers in the interval $[n+m-2000+1, n]$ (with even endpoints) fixed. Since $g_{m}$ turns the order around in $[1, m]$ and $f_{n}^{-1}=f_{2000-n}$ maps $[1, m]$ onto the complement of $[n+m-2000+1, n]$ in such a way that $f_{2000-1}(1)=n+1$, the\norder of numbers in the complement is reversed in the desired manner. - We have shown that for odd $s$ and $t$ such that $t<s$ there exists a function $h_{s, t}$, combined of functions of the $f$ type and $g$ type such that $h_{s, t}$ is the identity on the interval $[t+1, s-1]$, but reverses the order of the numbers outside this interval, when counting is started from $s$ and continued through over 2000 and 1 over to $t$, in other words modulo 2000 .\n\nTo finish the proof, we show that two numbers in the even positions can be exchanged while everything else is fixed. This clearly allows us to put the even numbers in an arbitrary order without violating the order of the odd numbers. To achieve this, we take two even numbers $p$ and $q, p<q$, and consider the function $\\phi_{p, q}=f_{2000+p-q} \\circ h_{p+1, p-1} \\circ h_{q+1, p-1} \\circ h_{p+1, q-1}$. The innermost function $h_{p+1, q-1}$ reverses the order on $[p+1, q-1]$ and fixes everything else, the next function $h_{q+1, p-1}$ fixes numbers in $[p, q], h_{p+1, p-1}$ fixes $p$ and reverses the order $(\\bmod 2000)$ in $E \\backslash\\{p\\}$, and $f_{2000+p-q}(p)=q$. The two innermost components of $\\phi_{p, q}$ fix $q, h_{p+1, p-1}$ takes $q$ to a position $x q-p$ steps ahead of $p(\\bmod 2000)$ and $f_{2000+p-q}=f_{q-p}^{-1}$ moves $x q-p$ positions back, i.e. to $p$. If $p+k$ is between $p$ and $q$, then the innermost function maps it to $q-k$, the next one fixes $q-k$, the third function maps $q-k$ to $p-(q-k-p)=2 p-q+k(\\bmod 2000)$, and $f_{q-p}^{-1}$ maps $2 p-q+k$ back to $p+k$. A similar reasoning shows that $\\phi_{p, q}$ also fixes numbers in $E \\backslash[p, q]$.\n\nSince both even and odd numbers have 1000! different permutations, the volumes can be permuted into (1000!) $)^{2}$ different orders by using the given operations repeatedly.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 4.", "solution_match": "\n\nSolution 2."}}
|
| 7 |
+
{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:\n\n(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.\n\n(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.\n\nHow many different permutations of the volumes can be obtained by using these two operations repeatedly?", "solution": "We show by induction, that if in an ordered sequence one may exchange two consecutive elements without changing the places of any other element, then any two elements can be exchanged so that all other elements remain in place. We assume that this is true for elements which are at most $k$ steps away from each other in the sequence. Assuming that $a$ precedes $b$ by $k+1$ steps and that $c$ is immediately behind $a$, the following sequence of exchanges is allowed: $\\ldots, a, c, \\ldots, b, \\ldots \\rightarrow \\ldots, a, b, \\ldots, c, \\ldots \\rightarrow$ $\\ldots, b, a, \\ldots, c, \\ldots \\rightarrow \\ldots, b, c, \\ldots, a, \\ldots .$. By assumption, all elements in the places indicated by three dots remain on their places, as does $c$.\n\nIf any two elements can be exchanged without violating the other elements, then the elements in the sequence can be arranged to any order. One just gets the desired first element to its place by (at most) one exchange, and if the first $k$ elements already are in their desired places, then the one wanted to be in place $k+1$ is not among the first $k$ elements, and it can be moved to its place by at most one exchange, no violating the order of the first $k$ elements.\n\nWe now show, that any two volumes in consecutive odd places can be exchanged. The volumes on top and in place 3 can be exchanged by operation (ii) applied to the three topmost volumes. The volumes in places $2 n+1$ and $2 n+3$ can be exchanged by first applying operation (i) to the $2 n$ topmost volumes, which moves them in the bottom but preserves their order, then applying (ii) to the three topmost volumes and finally operation (i) to the $2000-2 n$ topmost volumes. The last operation returns the $2 n$ volumes to top preserving the order and returns the remaining $2000-2 n$ volumes to the bottom, preserving the order, save the volumes in places $2 n+1$ and $2 n+3$, which have changed places. By the general remarks above, it is now clear that operations (i) and (ii) can be used to arrange the volumes in odd positions into any order while the volumes in even positions remain in their places.\n\nWe still need to show, that a similar procedure is possible for volumes in even positions. First of all, the volumes in positions 1 to 5 can be moved to order $5,4,3,2,1$ by performing operation (ii) to the five topmost volumes. Then it is possible to exchange the volumes in positions 1 and 5 without changing anything else. So the volumes in even positions closest to the top can be exchanged. For volumes on positions $2 n$ and $2 n+2$ one can first perform operation (i) to the $2 n-2$ topmost volumes. The volumes in places $2 n$ and $2 n+2$ will be taken to places 2 and 4 , and they can be exchanged. Performing operation (i) to the $2000-(2 n-1)$ topmost volumes then returns everything to their previous places, except that the volumes in positions $2 n$ and $2 n+2$ have changed places. So all volumes in even positions can be put into any order by using the operations (i) and (ii), and the total number of possible orderings is $(1000 \\text { ! })^{2}$.\n\n(We note that operation (ii) can be replaced by a weaker operation: \"It is possible to turn the order around for the 3 and 5 topmost volumes.\")", "metadata": {"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl", "problem_match": "\n## Problem 4.", "solution_match": "\n\nSolution 3."}}
|
Nordic_MO/segmented/en-2016-sol.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Determine all sequences of non-negative integers $a_{1}, \\ldots, a_{2016}$ all less than or equal to 2016 satisfying $i+j \\mid i a_{i}+j a_{j}$ for all $i, j \\in\\{1,2, \\ldots, 2016\\}$.", "solution": "Answer: All constant sequences of non-negative integers.\n\nThe condition rewrites to $i+j \\mid i\\left(a_{i}-a_{j}\\right)$. Since $2 k-1$ and $k$ are coprime, we see that $2 k-1 \\mid a_{k}-a_{k-1}$. Thus if $2 k-1>2016$, then $a_{k}=a_{k-1}$ since $a_{k}$ and $a_{k-1}$ are non-negative and at most 2016. All together $a_{1009}=a_{1010}=\\cdots=a_{2016}$.\n\nIf $i<1009$ we know that $i$ is coprime to one of the number $2016,2015, \\ldots, 2017-i$ say $j$. Then $i+j \\mid a_{i}-a_{j}$ and since $i+j>2016$ we conclude as before that $a_{i}=a_{j}=a_{2016}$. So any such sequence is constant.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2016-sol.jsonl", "problem_match": "\n## Problem 1", "solution_match": "\n\nSolution"}}
|
| 2 |
+
{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Let $A B C D$ be a cyclic quadrilateral satisfying $A B=A D$ and $A B+B C=C D$.\n\nDetermine $\\angle C D A$.", "solution": "Answer: $\\angle C D A=60^{\\circ}$.\n\nChoose the point $E$ on the segment $C D$ such that $D E=A D$. Then $C E=C D-A D=$ $C D-A B=B C$, and hence the triangle $C E B$ is isosceles.\n\n\n\nNow, since $A B=A D$ then $\\angle B C A=\\angle A C D$. This shows that $C A$ is the bisector of $\\angle B C D=\\angle B C E$. In an isosceles triangle, the bisector of the apex angle is also the perpendicular bisector of the base. Hence $A$ is on the perpendicular bisector of $B E$, and $A E=A B=A D=D E$. This shows that triangle $A E D$ is equilateral, and thus $\\angle C D A=60^{\\circ}$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2016-sol.jsonl", "problem_match": "\n## Problem 2", "solution_match": "\n\nSolution 2"}}
|
| 3 |
+
{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Find all $a \\in \\mathbb{R}$ for which there exists a function $f: \\mathbb{R} \\rightarrow \\mathbb{R}$, such that\n\n(i) $f(f(x))=f(x)+x$, for all $x \\in \\mathbb{R}$,\n\n(ii) $f(f(x)-x)=f(x)+$ ax, for all $x \\in \\mathbb{R}$.", "solution": "Answer: $a=\\frac{1 \\pm \\sqrt{5}}{2}$.\n\nFrom (i) we get $f(f(f(x))-f(x))=f(x)$. On the other hand (ii) gives\n\n$$\nf(f(f(x))-f(x))=f(f(x))+a f(x)\n$$\n\nThus we have $(1-a) f(x)=f(f(x))$. Now it follows by (i) that $(1-a) f(x)=f(x)+x$, and hence $f(x)=-\\frac{1}{a} x$, since $a=0$ obviously does not give a solution.\n\nWe now need to check whether (i) and (ii) hold for this function for some values of $a$ and all real $x$. We have\n\n$$\nf(f(x))=-\\frac{1}{a} f(x)=\\frac{1}{a^{2}} x, \\text { and } f(x)+x=-\\frac{1}{a} x+x=\\frac{a-1}{a} x\n$$\n\nThus (i) will hold for all real $x$ iff $\\frac{1}{a^{2}}=\\frac{a-1}{a}$, i.e. iff $a=\\frac{1 \\pm \\sqrt{5}}{2}$. For these values of $a$ we have\n\n$$\nf(f(x)-x)=-\\frac{1}{a}(f(x)-x)=-\\frac{1}{a}\\left(-\\frac{1}{a} x-x\\right)=\\left(\\frac{1}{a^{2}}+\\frac{1}{a}\\right) x=\\frac{a+1}{a^{2}} x=x\n$$\n\nand\n\n$$\nf(x)+a x=-\\frac{1}{a} x+a x=\\frac{a^{2}-1}{a} x=x\n$$\n\nso that for these two values of $a$ both (i) and (ii) hold for all real $x$. Thus the values of $a$ such that there exists a function $f$ with the desired properties are $a=\\frac{1 \\pm \\sqrt{5}}{2}$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2016-sol.jsonl", "problem_match": "\n## Problem 3", "solution_match": "\n\nSolution 3"}}
|
| 4 |
+
{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "King George has decided to connect the 1680 islands in his kingdom by bridges. Unfortunately the rebel movement will destroy two bridges after all the bridges have been built, but not two bridges from the same island.\n\nWhat is the minimal number of bridges the King has to build in order to make sure that it is still possible to travel by bridges between any two of the 1680 islands after the rebel movement has destroyed two bridges?", "solution": "Answer: 2016\n\nAn island cannot be connected with just one bridge, since this bridge could be destroyed. Consider the case of two islands, each with only two bridges, connected by a bridge. (It is not possible that they are connected with two bridges, since then they would be isolated from the other islands no matter what.) If they are also connected to two separate islands, then they would be isolated if the rebel movement destroys the two bridges from these islands not connecting the two. So the two bridges not connecting them must go to the same island. That third island must have at least two other bridges, otherwise the rebel movement could cut off these three islands.\n\nSuppose there is a pair of islands with exactly two bridges that are connected to each other. From the above it is easy to see that removing the pair (and the three bridges connected to them) must leave a set of islands with the same properties. Continue removing such pairs, until there are none left. (Note that the reduced set of islands could have a new such pair and that also needs to be removed.) Suppose we are left with $n$ islands and since two islands are removed at a time, $n$ must be an even number. And from the argument above it is clear that $n \\geq 4$.\n\nConsider the remaining set of islands and let $x$ be the number of islands with exactly two bridges (which now are not connected to each other). Then $n-x$ islands have at least three bridges each. Let $B^{\\prime}$ be the number of bridges in the reduced set. Now $B^{\\prime} \\geq 2 x$ and $2 B^{\\prime} \\geq 2 x+3(n-x)=3 n-x$. Hence $2 B^{\\prime} \\geq \\max (4 x, 3 n-x) \\geq 4 \\cdot \\frac{3 n}{5}$, and thus $B^{\\prime} \\geq \\frac{6 n}{5}$. Now let $B$ be the number of bridges in the original set. Then\n\n$$\nB=B^{\\prime}+3 \\cdot \\frac{1680-n}{2} \\geq \\frac{6 n}{5}+\\frac{6(1680-n)}{4} \\geq \\frac{6 \\cdot 1680}{5}=2016\n$$\n\nIt is possible to construct an example with exactly 2016 bridges: Take 672 of the islands and number them $0,1,2, \\ldots 671$. Connect island number $i$ with the islands numbered $i-1$, $i+1$ and $i+336$ (modulo 672). This gives 1008 bridges. We now have a circular path of 672 bridges: $0-1-2-\\cdots-671-0$. If one of these 672 bridges are destroyed, the 672 islands are still connected. If two of these bridges are destroyed, the path is broken into two parts. Let $i$ be an island on the shortest path (if they have the same length, just pick a random one). Then island $i+336$ (modulo 672) must be on the other part of the path, and the bridge connecting these two islands will connect the two paths. Hence no matter which two bridges the rebel movement destroys, it is possible to travel between any of the 672 islands.\n\nNow for every of the 1008 bridges above, replace it with two bridges with a new island between the two. This increases the number of bridges to 2016 and the number of islands to $672+1008=1680$ completing the construction. Since the rebel movement does not destroy two bridges from the same island, the same argument as above shows that with this construction it is possible to travel between any of the 1680 islands after the destruction of the two bridges.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2016-sol.jsonl", "problem_match": "\n## Problem 4", "solution_match": "\n\nSolution 4"}}
|
Nordic_MO/segmented/en-2017-sol.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Let $n$ be a positive integer. Show that there exist positive integers $a$ and $b$ such that:\n\n$$\n\\frac{a^{2}+a+1}{b^{2}+b+1}=n^{2}+n+1\n$$", "solution": "Let $P(x)=x^{2}+x+1$. We have $P(n) P(n+1)=\\left(n^{2}+n+1\\right)\\left(n^{2}+3 n+3\\right)=$ $n^{4}+4 n^{3}+7 n^{2}+6 n+3$. Also, $P\\left((n+1)^{2}\\right)=n^{4}+4 n^{3}+7 n^{2}+6 n+3$. By choosing $a=(n+1)^{2}$ and $b=n+1$ we get $P(a) / P(b)=P(n)$ as desired.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl", "problem_match": "\n\nProblem 1", "solution_match": "\n\nSolution 1"}}
|
| 2 |
+
{"year": "2017", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Let $a, b, \\alpha, \\beta$ be real numbers such that $0 \\leq a, b \\leq 1$, and $0 \\leq \\alpha, \\beta \\leq \\frac{\\pi}{2}$. Show that if\n\n$$\na b \\cos (\\alpha-\\beta) \\leq \\sqrt{\\left(1-a^{2}\\right)\\left(1-b^{2}\\right)}\n$$\n\nthen\n\n$$\na \\cos \\alpha+b \\sin \\beta \\leq 1+a b \\sin (\\beta-\\alpha)\n$$", "solution": "The condition can be rewritten as\n\n$$\na b \\cos (\\alpha-\\beta)=a b \\cos \\alpha \\cos \\beta+a b \\sin \\alpha \\sin \\beta \\leq \\sqrt{\\left(1-a^{2}\\right)\\left(1-b^{2}\\right)}\n$$\n\nSet $x=a \\cos \\alpha, y=b \\sin \\beta, z=b \\cos \\beta, t=a \\sin \\alpha$. We can now rewrite the condition as\n\n$$\nx z+y t \\leq \\sqrt{\\left(1-x^{2}-t^{2}\\right)\\left(1-y^{2}-z^{2}\\right)}\n$$\n\nwhereas the inequality we need to prove now looks like\n\n$$\nx+y \\leq 1+x y-z t\n$$\n\nSince $x, y, z, t \\geq 0$, and $1+x y-z t=1+a b \\sin (\\beta-\\alpha) \\geq 0$, we can square both sides of both inequalities, and get equivalent ones. After a couple of cancelations the condition yields\n\n$$\n2 x y z t \\leq 1-x^{2}-y^{2}-z^{2}-t^{2}+x^{2} y^{2}+z^{2} t^{2}\n$$\n\nso that\n\n$$\nx^{2}+y^{2}+z^{2}+t^{2} \\leq(x y-z t)^{2}+1\n$$\n\nwhich is equivalent to\n\n$$\nx^{2}+y^{2}+z^{2}+t^{2}+2 x y-2 z t \\leq(1+x y-z t)^{2}\n$$\n\nor\n\n$$\n(x+y)^{2}+(z-t)^{2} \\leq(1+x y-z t)^{2}\n$$\n\nSince $(x+y)^{2} \\leq(x+y)^{2}+(z-t)^{2}$, the desired inequality follows.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl", "problem_match": "\n\nProblem 2", "solution_match": "\n\nSolution 2"}}
|
| 3 |
+
{"year": "2017", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Let $M$ and $N$ be the midpoints of the sides $A C$ and $A B$, respectively, of an acute triangle $A B C, A B \\neq A C$. Let $\\omega_{B}$ be the circle centered at $M$ passing through $B$, and let $\\omega_{C}$ be the circle centered at $N$ passing through $C$. Let the point $D$ be such that $A B C D$ is an isosceles trapezoid with $A D$ parallel to $B C$. Assume that $\\omega_{B}$ and $\\omega_{C}$ intersect in two distinct points $P$ and $Q$. Show that $D$ lies on the line $P Q$.", "solution": "Let $E$ be such that $A B E C$ is a parallelogram with $A B \\| C E$ and $A C \\| B E$, and let $\\omega$ be the circumscribed circle of $\\triangle A B C$ with centre $O$.\n\nIt is known that the radical axis of two circles is perpendicular to the line connecting the two centres. Since $B E \\perp M O$ and $C E \\perp N O$, this means that $B E$ and $C E$ are the radical axes of $\\omega$ and $\\omega_{B}$, and of $\\omega$ and $\\omega_{C}$, respectively, so $E$ is the radical centre of $\\omega$, $\\omega_{B}$, and $\\omega_{C}$.\n\n\n\nNow as $B E=A C=B D$ and $C E=A B=C D$ we find that $B C$ is the perpendicular bisector of $D E$. Most importantly we have $D E \\perp B C$. Denote by $t$ the radical axis of $\\omega_{B}$ and $\\omega_{C}$, i.e. $t=P Q$. Then since $t \\perp M N$ we find that $t$ and $D E$ are parallel. Therefore since $E$ lies on $t$ we get that $D$ also lies on $t$.\n\nAlternative solution Reflect $B$ across $M$ to a point $B^{\\prime}$ forming a parallelogram $A B C B^{\\prime}$. Then $B^{\\prime}$ lies on $\\omega_{B}$ diagonally opposite $B$, and since $A B^{\\prime} \\| B C$ it lies on $A D$. Similarly reflect $C$ across $N$ to a point $C^{\\prime}$, which satisfies analogous properties. Note that $C B^{\\prime}=A B=C D$, so we find that triangle $C D B^{\\prime}$ and similarly triangle $B D C^{\\prime}$ are isosceles.\n\nLet $B^{\\prime \\prime}$ and $C^{\\prime \\prime}$ be the orthogonal projections of $B$ and $C$ onto $A D$. Since $B B^{\\prime}$ is a diameter of $\\omega_{B}$ we get that $B^{\\prime \\prime}$ lies on $\\omega_{B}$, and similarly $C^{\\prime \\prime}$ lies on $\\omega_{C}$. Moreover $B B^{\\prime \\prime}$ is an altitude of the isosceles triangle $B D C^{\\prime}$ with $B D=B C^{\\prime}$, hence it coincides with the median from $B$, so $B^{\\prime \\prime}$ is in fact the midpoint of $D C^{\\prime}$. Similarly $C^{\\prime \\prime}$ is the midpoint of $D B^{\\prime}$. From this we get\n\n$$\n2=\\frac{D C^{\\prime}}{D B^{\\prime \\prime}}=\\frac{D B^{\\prime}}{D C^{\\prime \\prime}}\n$$\n\nwhich rearranges as $D C^{\\prime} \\cdot D C^{\\prime \\prime}=D B^{\\prime} \\cdot D B^{\\prime \\prime}$. This means that $D$ has same the power with respect to $\\omega_{B}$ and $\\omega_{C}$, hence it lies on their radical axis $P Q$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl", "problem_match": "\n\nProblem 3", "solution_match": "\n\nSolution 3"}}
|
| 4 |
+
{"year": "2017", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Find all integers $n$ and $m, n>m>2$, and such that a regular $n$-sided polygon can be inscribed in a regular $m$-sided polygon so that all the vertices of the $n$-gon lie on the sides of the $m$-gon.", "solution": "It works only for $n=2 m$, and for $m=3$ and $n=4$.\n\nTo begin with let's see why it works for $n=2 m$. For a $2 m$-gon we can choose two points on each side, symmetrically, so that the distance between the two of them is equal to the distance between two close points on adjacent sides.\n\nFor $n=4$ and $m=3$ we need to inscribe a square in an equilateral triangle, by choosing two vertices of the square symmetrically on one of the sides of the triangle. It is easy to calculate the side length of the square so that its remaining two vertices lie on the remaining two sides of the triangle.\n\nWe need to show that it cannot be done in any other way. One side of the $m$-gon can contain at most two of the vertices of the $n$-gon, so that $n \\leq 2 m$. For $n \\geq m+2$ at least two of the sides of the $m$-gon must contain two of the vertices of the $n$-gon each. By symmetry the midpoints, and thus the perpendicular bisectors, of such a side of the $m$-gon and of the side of the $n$-gon it contains must coincide. If two such sides of the $m$-gon are not opposite to each other the corresponding perpendicular bisectors will intersect, and we can deduce that the centres of the circumscribed circles of the $m$-gon and of the $n$-gon must coincide. If two such sides are opposite, then the centres of the circumscribed circles will coincide with the midpoint of the segment between the midpoints of the sides, and thus the two circumscribed circles will once again have the same centre.\n\nDenote the radii of the two circumscribed circles by $R$ and $r$, where $R>r$. The smaller circle intersects the sides of the $m$-gon at $2 m$ points, among which are the possible vertices for the $n$-gon. Denote these points by $P_{1}, P_{2}, \\ldots, P_{2 m}$ clockwise, where $P_{1}$ and $P_{2}$\nare vertices of the $n$-gon. If the side length of the $n$-gon is $s$, we now have $\\left|P_{1} P_{2}\\right|=s$, and thus $\\left|P_{3} P_{4}\\right|=s$. If only one of the points $P_{3}$ and $P_{4}$ is a vertex in the $n$-gon, it would have to be $P_{4}$, but the distance between $P_{2}$ and $P_{4}$ is greater than $s$, which means $P_{2} P_{4}$ cannot be a side. We can now deduce that both $P_{3}$ and $P_{4}$ are vertices of the $n$-gon, and by symmetry all the $2 m$ points of intersection will be vertices of the $n$-gon, so that $n=2 m$.\n\nWe now need to handle the case $n=m+1>4$. Denote the vertices of the $m$-gon by $Q_{1}, Q_{2}, \\ldots, Q_{m}$ clockwise. Now only one of the sides of the $m$-gon contains two of the vertices of the $n$-gon, let this side be $Q_{m} Q_{1}$. Denote the vertices of the $(m+1)$-gon by $P_{1}, P_{2}, \\ldots, P_{m+1}$ clockwise, where $P_{1}$ and $P_{m+1}$ lie on the side $Q_{m} Q_{1}$ of the $m$-gon. Let $\\alpha=\\pi-2 \\pi /(m+1)$, and $\\beta=\\pi-2 \\pi / m$ be the angles of the $n$-gon and the $m$ gon, respectively. We now get a number of triangles $P_{1} Q_{1} P_{2}, P_{2} Q_{2} P_{3}, \\ldots P_{m} Q_{m} P_{m+1}$. We begin by establishing a connection between the sizes of the angles. To begin with we have $\\angle Q_{1} P_{1} P_{2}=\\pi-\\alpha$, and $\\angle P_{1} Q_{1} P_{2}=\\beta$, so that $\\angle P_{1} P_{2} Q_{1}=\\alpha-\\beta$. We now proceed to get $\\angle Q_{2} P_{2} P_{3}=\\pi-\\alpha-(\\alpha-\\beta)$, and $\\angle P_{2} Q_{2} P_{3}=\\beta$, which gives $\\angle P_{2} P_{3} Q_{2}=2(\\alpha-\\beta)$, and so on. If now $\\gamma=\\alpha-\\beta=2 \\pi / m(m+1)$, we have $\\angle P_{k} P_{k+1} Q_{k}=k \\gamma$, and $\\angle Q_{k} P_{k} P_{k+1}=$ $(m+1-k) \\gamma$ for $k=1,2, \\ldots, m$.\n\nSince $s$ is the side length of the $n$-gon, i.e. $s=\\left|P_{1} P_{2}\\right|=\\left|P_{1} P_{2}\\right|=\\cdots=\\left|P_{m+1} P_{1}\\right|$, according to the law of sines we get\n\n$$\n\\frac{s}{\\sin \\beta}=\\frac{\\left|P_{k} Q_{k}\\right|}{\\sin \\left(P_{k} P_{k+1} Q_{k}\\right)}=\\frac{\\left|Q_{k} P_{k+1}\\right|}{\\sin \\left(Q_{k} P_{k} P_{k+1}\\right)}\n$$\n\ni.e.\n\n$$\n\\frac{s}{\\sin \\beta}=\\frac{\\left|P_{k} Q_{k}\\right|}{\\sin (k \\gamma)}=\\frac{\\left|Q_{k} P_{k+1}\\right|}{\\sin ((m+1-k) \\gamma)}\n$$\n\nSince $\\left|Q_{k} Q_{k+1}\\right|=\\left|Q_{k} P_{k+1}\\right|+\\left|P_{k+1} Q_{k+1}\\right|$, we get\n\n$$\n\\sin ((k+1) \\gamma)+\\sin ((m+1-k) \\gamma)=\\frac{\\sigma \\sin \\beta}{s}\n$$\n\nwhere $\\sigma=\\left|Q_{1} Q_{2}\\right|=\\left|Q_{2} Q_{3}\\right|=\\cdots=\\left|Q_{m} Q_{1}\\right|$ is the side length of the $m$-gon.\n\nUsing the above for $k=1$ and $k=2$, we get\n\n$$\n\\sin 2 \\gamma+\\sin m \\gamma=\\sin 3 \\gamma+\\sin (m-1) \\gamma\n$$\n\nFor $m \\geq 4$ the angles $3 \\gamma$ and $(m-1) \\gamma$ are both in the interval between $2 \\gamma$ and $m \\gamma$, which means we can't have equality as the sine function is concave (convex from above) in the interval $[0, \\pi / 2]$. We therefore deduce that it is impossible to inscribe an $(m+1)$-gon in an $m$-gon for $m \\geq 4$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl", "problem_match": "\n\nProblem 4", "solution_match": "\n\nSolution 4"}}
|
Nordic_MO/segmented/en-2019-sol.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $n$ be an integer with $n \\geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.", "solution": "a) Notice that $\\left\\{2019!\\cdot 1^{2019!}, 2019!\\cdot 2^{2019!}, \\ldots, 2019!\\cdot 2019^{2019!}\\right\\}$ is such a set. Observe that if all the elements are divisible by 2019! then the arithmetic means will be integer for all the subsets. Also, if $A$ is a set such that the geometric means are integer for all non-empty subsets and the set $B$ is obtained from the set $A$ by multiplying each element with with a given integer $c$ then all the non-empty subsets of $B$ will have an integer geometric mean, since\n\n$$\n\\sqrt[k]{c a_{i_{1}} c a_{i_{2}} \\cdots c a_{i_{k}}}=c \\sqrt[k]{a_{i_{1}} a_{i_{2}} \\cdots a_{i_{k}}}\n$$\n\nIt is thus sufficient to find a set of 2019 positive integers such that the geometric mean of every non-empty subset in an integer. Now, for an integer $a$ the number $\\sqrt[k]{a^{2019!}}=a^{\\frac{2019!}{k}}$ for all integers $1 \\leq k \\leq 2019$ so $\\left\\{1^{2019!}, 2^{2019!}, \\ldots, 2019^{2019!}\\right\\}$ is a set such that the geometric mean of every non-empty subset is an integer.\n\nb) Assume there exist such a set $A$ and let $n, m, a_{1}, a_{2}, \\ldots, a_{m-1}$ be distinct elements in $A$ with $n<m$. Then $\\frac{n+a_{1}+a_{2}+\\cdots+a_{m-1}}{m}$ and $\\frac{m+a_{1}+a_{2}+\\cdots+a_{m-1}}{m}$ are integers and also their difference\n\n$$\n\\frac{m+a_{1}+a_{2}+\\cdots+a_{m-1}}{m}-\\frac{n+a_{1}+a_{2}+\\cdots+a_{m-1}}{m}=\\frac{m-n}{m}\n$$\n\nTherefore, we have $\\frac{n}{m}$ is an integer and since $m$ and $n$ are positive integers we have $m \\leq n$ which is a contradiction.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2019-sol.jsonl", "problem_match": "\n\nProblem 4", "solution_match": "\n\nSolution 1"}}
|
| 2 |
+
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $n$ be an integer with $n \\geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.", "solution": "Observe that\n\n$$\n\\begin{gathered}\nc^{3}-a^{3}-b^{3}=c a^{2}+c b^{2}-a^{3}-b^{3}=a^{2}(c-a)+b^{2}(c-b)= \\\\\n\\left(c^{2}-b^{2}\\right)(c-a)+\\left(c^{2}-b^{2}\\right)(c-b)=(c-a)(c-b)(c+a+c+b)\n\\end{gathered}\n$$\n\nTherefore, it is equivalent to prove that\n\n$$\nc<a+b \\leq \\sqrt{2} c\n$$\n\nThe left inequality we get from the triangle inequality and the right inequality we get from\n\n$$\na+b \\leq \\sqrt{2} c \\Leftrightarrow(a+b)^{2} \\leq 2 c^{2}=2 a^{2}+2 b^{2} \\Leftrightarrow 0 \\leq(a-b)^{2}\n$$", "metadata": {"resource_path": "Nordic_MO/segmented/en-2019-sol.jsonl", "problem_match": "\n\nProblem 4", "solution_match": "\n\nSolution 2"}}
|
| 3 |
+
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $n$ be an integer with $n \\geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.", "solution": "Let the angle bisectors from angle $C$ in triangle $A C B$ and $A C D$ intersect $A B$ and $A D$ in points $E$ and $F$ respectively. From $\\angle A C E=\\angle C A D$ it follows that $C E$ and $A D$ are parallel. Similarly $C F$ and $A B$ are parallel. Hence $A E C F$ is a parallelogram. From this it follows that $\\angle B E C=\\angle B A D=\\angle C F D$.\n\n\n\nThe angle bisector theorem yields\n\n$$\n\\frac{B E}{C F}=\\frac{B E}{A E}=\\frac{C B}{C A}=\\frac{C D}{C A}=\\frac{D F}{A F}=\\frac{D F}{C E}\n$$\n\nwhich gives\n\n$$\n|B E| \\cdot|C E|=|D F| \\cdot|C F| \\text {. }\n$$\n\nBy the sine area formula we obtain that $B C E$ have $D C F$ have equal area. Hence triangles $B C A$ and $D C A$ also have equal areal. By the sine area formula we now get\n\n$$\n\\sin (\\angle A C B)=\\sin (\\angle D C A)\n$$\n\nSince $A B C D$ is a quadrilateral, $\\angle A C B+\\angle D C A \\neq 180$ and hence we conclude from the above that $\\angle C A B=\\angle C A D$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2019-sol.jsonl", "problem_match": "\n\nProblem 4", "solution_match": "\n\nSolution 3"}}
|
| 4 |
+
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $n$ be an integer with $n \\geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.", "solution": "Assume that it is possible to color $2 n$ of the vertices of a $4 n+1$-gon such that there are no three colored vertices forming an isosceles triangle. Enumerate the vertices consecutively as $H_{-2 n}, H_{-2 n+1}, \\ldots, H_{0}, H_{1}, H_{2}, \\ldots, H_{2 n}$ and consider first the case where there are two colored neighboring vertices. Assume wlog that the vertices $H_{0}$ and $H_{1}$ are colored. Then at most one of the vertices $H_{-i}$ and $H_{i}$ are colored for all $i=1,2, \\ldots, 2 n$ since these form an isosceles triangle with $H_{0}$. Similarly at most one of $H_{-i}$ and $H_{i+2}$ are colored for all $i=1,2, \\ldots, 2 n-2$, and at most one of $H_{-(2 n-1)}$ and $H_{-2 n}$ are colored since these form an isosceles triangles with $H_{1}$. The three vertices $H_{0}, H_{1}, H_{i}, i=2,-1,-2 n$ also form isoceles triangles and hence $H_{-1}, H_{2}, H_{-2 n}$ are not colored. It follows that no consecutive vertices in the two strings\n\n$$\n\\begin{array}{r}\nH_{-2}-H_{4}-H_{-4}-H_{6}-\\ldots-H_{2 n-2}-H_{-(2 n-2)}-H_{2 n} \\\\\nH_{3}-H_{-3}-H_{5}-H_{-5}-\\ldots-H_{2 n-1}-H_{-(2 n-1)}\n\\end{array}\n$$\n\nare colored. Since each string contains an even amount of vertices, at most half of each string are colored and this is obtained only when every second vertex is colored in each string. By counting we see that each string contains $2 n-2$ vertices and we conclude that every second vertex is colored in each string. Because $n \\geq 3$ at least one of the isoceles\ntriangles $H_{0} H_{-2} H_{-4}, H_{1} H_{3} H_{5}$ or $H_{2 n-2} H_{2 n} H_{-(2 n-1)}$ must be colored. Hence there are no colored neighboring vertices.\n\nIf there are no colored neighboring vertices we can assume wlog that $H_{i}$ is colored for all odd $i$, but then $H_{1} H_{3} H_{5}$ is an isosceles colored triangle. Hence we have a contradiction, showing that there must neccesarily exists 3 colored vertices forming an isosceles triangle.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2019-sol.jsonl", "problem_match": "\n\nProblem 4", "solution_match": "\n\nSolution 4"}}
|
Nordic_MO/segmented/en-2021-sol.jsonl
ADDED
|
@@ -0,0 +1 @@
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $A, B, C$ and $D$ be points on the circle $\\omega$ such that $A B C D$ is a convex quadrilateral. Suppose that $A B$ and $C D$ intersect at a point $E$ such that $A$ is between $B$ and $E$ and that $B D$ and $A C$ intersect at a point $F$. Let $X \\neq D$ be the point on $\\omega$ such that $D X$ and $E F$ are parallel. Let $Y$ be the reflection of $D$ through $E F$ and suppose that $Y$ is inside the circle $\\omega$.\n\nShow that $A, X$, and $Y$ are collinear.", "solution": "s", "metadata": {"resource_path": "Nordic_MO/segmented/en-2021-sol.jsonl", "problem_match": "\n\nProblem 4.", "solution_match": "\n## Solution"}}
|
Nordic_MO/segmented/en-2022-sol.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2022", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Find all functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf(f(x) f(1-x))=f(x) \\quad \\text { and } \\quad f(f(x))=1-f(x)\n$$\n\nfor all real $x$.", "solution": "Notice that $f(f(f(x)))=^{2} 1-f(f(x))={ }^{2} f(x)$. This is equation 3 . By substituting $f(x)$ for $x$ in the first equation we get:\n\n$$\nf(\\underline{f(x)})={ }^{1} f(f(\\underline{f(x)}) f(1-\\underline{f(x)}))={ }^{2} f(f(f(x)) f(f(f(x))))={ }^{3} f(f(f(x)) f(x))\n$$\n\nAgain we substitute $f(x)$ for $x$ above:\n\n$$\nf(f(\\underline{f(x)}))=f(f(f(\\underline{f(x)})) f(\\underline{f(x)}))\n$$\n\nEquation 3 applied on both sides gives us:\n\n$$\nf(x)=f(f(x) f(f(x)))\n$$\n\nBut this is the same as what we started with so\n\n$$\nf(x)=f(f(x) f(f(x)))=f(f(x))={ }^{2} 1-f(x)\n$$\n\nTherefore $f(x)=\\frac{1}{2}$, which is a solution.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl", "problem_match": "\n## Problem 1", "solution_match": "\n\nSolution 1."}}
|
| 2 |
+
{"year": "2022", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Find all functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf(f(x) f(1-x))=f(x) \\quad \\text { and } \\quad f(f(x))=1-f(x)\n$$\n\nfor all real $x$.", "solution": "Let first $c$ be a fix point of $f$, that is $f(c)=c$. Then from the second equation we have\n\n$$\nc=1-c \\Rightarrow c=\\frac{1}{2}\n$$\n\nThe substitution $y=1-x$ in the first equation shows that $f(1-x)=f(x)$ for any $x$. Now, using this and applying $f$ to the second equation we get\n\n$$\nf(f(f(x)))=f(1-f(x)))=f(f(x))\n$$\n\nthus $f(f(x))$ is a fix point and therefore $f(f(x))=\\frac{1}{2}$. Now the second equation gives $f(x)=\\frac{1}{2}$. It is easy to check that this is a solution.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl", "problem_match": "\n## Problem 1", "solution_match": "\n\nSolution 2."}}
|
| 3 |
+
{"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "In Wonderland, the towns are connected by roads, and whenever there is a direct road between two towns there is also a route between these two towns that does not use that road. (There is at most one direct road between any two towns.) The Queen\nof Hearts ordered the Spades to provide a list of all \"even\" subsystems of the system of roads, that is, systems formed by subsets of the set of roads, where each town is connected to an even number of roads (possibly none). For each such subsystem they should list its roads. If there are totally $n$ roads in Wonderland and $x$ subsystems on the Spades' list, what is the number of roads on their list when each road is counted as many times as it is listed?", "solution": "The answer is $\\frac{1}{2} n x$.\n\nProof: We reformulate the problem in terms of graph theory with the towns being vertices and the roads being edges of a graph $G=(V, E)$. The given information implies that every edge $e \\in E$ is part of a cycle. The subgraphs to be counted are those with every valence even, briefly the even subgraphs. Let $N$ be the sum of the numbers of edges in those subgraphs. We can calculate this number by counting for each edge $e \\in E$ the even subgraphs of $G$ containing $e$. If $S(e)$ is the set of these graphs, then $N=\\sum_{e \\in E}|S(e)|$. Now consider for a given $e \\in E$ some cycle $c(e)$ containing $e$. For every even subgraph $H$ of $G$ one can define the graph $H^{\\prime}$ obtained from $H$ by replacing the set of edges in $H$ that are also edges in $c(e)$ by the set of edges in $c(e)$ that are not edges in $H$. For a given vertex $v \\in V$ the following possibilities exist. (i) $c(e)$ does not pass through $v$. (ii) Both edges in $c(e)$ adjacent to $v$ are in $H$. They are then absent from $H^{\\prime}$. (iii) None of the edges in $c(e)$ adjacent to $v$ are in $H$. They are then both in $H^{\\prime}$. (iv) Exactly one of the edges in $c(e)$ adjacent to $v$ are in $H$. It is then not in $H^{\\prime}$ while the other one belongs to $H^{\\prime}$. In every case any edge adjacent to $v$ that is not in $c(e)$ is in either none or both of $H$ and $H^{\\prime}$. It follows that $H^{\\prime}$ is an even subgraph of $G$. Since evidently $H^{\\prime \\prime}=H$, the total set of even subgraphs of $G$ is thus the union of disjoint pairs $\\left\\{H, H^{\\prime}\\right\\}$. Exactly one member of each pair belongs to $S(e)$, so $|S(e)|=x / 2$, and $N=\\frac{1}{2} n x$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl", "problem_match": "\n## Problem 2", "solution_match": "\n\nSolution."}}
|
| 4 |
+
{"year": "2022", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Anton and Britta play a game with the set $M=\\{1,2,3, \\ldots, n-1\\}$ where $n \\geq 5$ is an odd integer. In each step Anton removes a number from $M$ and puts it in his set $A$, and Britta removes a number from $M$ and puts it in her set $B$ (both $A$ and $B$ are empty to begin with). When $M$ is empty, Anton picks two distinct numbers $x_{1}, x_{2}$ from $A$ and shows them to Britta. Britta then picks two distinct numbers $y_{1}, y_{2}$ from $B$. Britta wins if\n\n$$\n\\left(x_{1} x_{2}\\left(x_{1}-y_{1}\\right)\\left(x_{2}-y_{2}\\right)\\right)^{\\frac{n-1}{2}} \\equiv 1 \\quad \\bmod n\n$$\n\notherwise Anton wins. Find all $n$ for which Britta has a winning strategy.", "solution": "Britta wins if and only if $n$ is prime.\n\nIf $n$ is not prime, then Anton can add any prime divisor $p<n$ of $n$ to his set $A$ in the first round and choose $x_{1}=p$ which means that the product $\\left(x_{1} x_{2}\\left(x_{1}-y_{1}\\right)\\left(x_{2}-y_{2}\\right)\\right)^{\\frac{n-1}{2}}$ is divisible by $p$ and is not $1 \\bmod n$ no matter what Britta chooses. And so Britta loses.\n\nIf $n$ is prime, then $x_{1} x_{2} \\not \\equiv 0 \\bmod n$, and there exists a number $\\alpha$ such that $x^{2} \\equiv \\alpha$ $\\bmod n$ has no solution. Then Britta can always add the number $Y \\in M, Y \\equiv \\alpha X^{-1}$ to $B$, if Anton adds the number $X$ to $A$ in each round. Notice that Anton can never have chosen the number $Y$ beforehand, since $Y \\equiv \\alpha X^{-1} \\Longleftrightarrow X \\equiv \\alpha Y^{-1}$ and $X \\neq Y$ (as $X^{2} \\equiv \\alpha \\bmod n$ is not possible). This means that Britta can always choose the\nnumbers $y_{1}=\\alpha x_{2}^{-1}, y_{2}=\\alpha x_{1}^{-1}$ from $B$. This will result in\n\n$$\n\\begin{aligned}\n\\left(x_{1} x_{2}\\left(x_{1}-y_{1}\\right)\\left(x_{2}-y_{2}\\right)\\right)^{\\frac{n-1}{2}} & \\equiv\\left(\\left(x_{1} x_{2}-x_{2} y_{1}\\right)\\left(x_{1} x_{2}-x_{1} y_{2}\\right)\\right)^{\\frac{n-1}{2}} \\\\\n& \\equiv\\left(\\left(x_{1} x_{2}-\\alpha\\right)\\left(x_{1} x_{2}-\\alpha\\right)\\right)^{\\frac{n-1}{2}} \\\\\n& \\equiv\\left(x_{1} x_{2}-\\alpha\\right)^{n-1} \\\\\n& \\equiv 1 \\quad \\bmod n\n\\end{aligned}\n$$\n\nThe last equation is true by Fermat's little theorem, because $n$ is prime and $x_{1} x_{2}-\\alpha \\not \\equiv$ $0 \\bmod n\\left(\\right.$ since $x_{1} \\not \\equiv y_{1}=\\alpha x_{2}^{-1}$ ).\n\nAlternative strategy for Britta is to choose $n-a$ when Anton pick up $a$, which is always possible because $n$ is an odd number and if one of the numbers $a, n-a$ was already chosen before the same is true for the second one. At the end Britta chooses $y_{i}=-x_{i}$ and gets\n\n$$\n\\left(x_{1} x_{2}\\left(x_{1}-y_{1}\\right)\\left(x_{2}-y_{2}\\right)\\right)^{\\frac{n-1}{2}}=\\left(\\left(2 x_{1}\\right)^{2}\\left(2 x_{2}\\right)^{2}\\right)^{\\frac{n-1}{2}} \\equiv 1 \\quad \\bmod n\n$$", "metadata": {"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl", "problem_match": "\n## Problem 3", "solution_match": "\n\nSolution."}}
|
| 5 |
+
{"year": "2022", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Let $A B C$ be an acute-angled triangle with circumscribed circle $k$ and centre of the circumscribed circle $O$. A line through $O$ intersects the sides $A B$ and $A C$ at $D$ and $E$. Denote by $B^{\\prime}$ and $C^{\\prime}$ the reflections of $B$ and $C$ over $O$, respectively. Prove that the circumscribed circles of $O D C^{\\prime}$ and $O E B^{\\prime}$ concur on $k$.", "solution": "Let $P$ be the intersection of the circles $k$ and the circumscribed circle of triangle $A D E^{1}$. Let $C_{1}$ be the second intersection of the circumscribed circle of $\\triangle D O P$ with $k$. We will prove that $C_{1}=C^{\\prime}$, i.e. the reflection of $C$ over $O$. We know that $\\left|O C_{1}\\right|=|O P|$, and hence $\\measuredangle C_{1} P O=\\measuredangle O C_{1} P$, furthermore $\\measuredangle O C_{1} P=\\measuredangle O D P=$ $\\measuredangle E D P$, since the quadrilateral $C_{1} P O D$ by assumption is inscribed and the points $O, D$ and $E$ are collinear. Now, since $P$ is the centre of spiral similarity sending $D E$ to $B C$ the triangles $P D E$ and $P B C$ are similar, and we have $\\measuredangle E D P=\\measuredangle C B P$, and finally, from the inscribed angle theorem we have\n\n$$\n\\measuredangle O P C=90^{\\circ}-\\frac{\\measuredangle C O P}{2}=90^{\\circ}-\\measuredangle C B P=90^{\\circ}-\\measuredangle C_{1} P O\n$$\n\nThe conclusion follows, since $90^{\\circ}=\\measuredangle C_{1} P O+\\measuredangle O P C$, and since $C_{1}$ is by assumption on $k$, it must be the antipodal point of $C$ with respect to $k$.\n\n[^0]\n\n\n[^0]: ${ }^{1}$ That is, the Miquel point of quadrilateral BCED.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl", "problem_match": "\n## Problem 4", "solution_match": "\n\nSolution."}}
|
Nordic_MO/segmented/en-2024-sol.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Let $T(a)$ be the sum of digits of $a$. For which positive integers $R$ does there exist a positive integer $n$ such that $\\frac{T\\left(n^{2}\\right)}{T(n)}=R$ ?", "solution": "All positive integers $R$.\nLet $R$ be a positive integer and consider the number\n\n$$\nN=\\sum_{k=0}^{R-1} 10^{2^{k}}\n$$\n\nWe see that $T(N)=R$. Now\n\n$$\n\\begin{aligned}\nN^{2} & =\\left(\\sum_{k=0}^{R-1} 10^{2^{k}}\\right)^{2} \\\\\n& =\\sum_{0 \\leq a, b<R} 10^{2^{a}+2^{b}},\n\\end{aligned}\n$$\n\nand since $2^{a}+2^{b}=2^{c}+2^{d}$ if and only if $(a, b)=(c, d)$ or $(a, b)=(d, c)$, there is never a carry in the summation $\\sum_{0 \\leq a, b<R} 10^{2^{a}+2^{b}}$, and we can write\n\n$$\n\\begin{aligned}\nT\\left(N^{2}\\right) & =\\sum_{0 \\leq a, b<R} T\\left(10^{2^{a}+2^{b}}\\right) \\\\\n& =R^{2}\n\\end{aligned}\n$$\n\nSo $\\frac{T\\left(n^{2}\\right)}{T(n)}=R$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl", "problem_match": "\n## Problem 1", "solution_match": "\n## Solution"}}
|
| 2 |
+
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Let $\\mathcal{Q}_{1}$ be a quadrilateral such that the midpoints of its sides lie on a circle. Prove that there exists a cyclic quadrilateral $\\mathcal{Q}_{2}$ with the same sidelengths as $\\mathcal{Q}_{1}$, such that two of the angles in $\\mathcal{Q}_{2}$ are equal.", "solution": "Let $A, B, C$ and $D$ be the vertices of $\\mathcal{Q}_{1}$, and $K, L, M$ and $N$ be the midpoints of the sides $A B, B C, C D$ and $D A$, respectively.\nWe have $K L\\|A C\\| M N$ and $L M\\|B D\\| N K$, and thus $K L M N$ is a parallelogram. From the problem condition it is known that $K L M N$ is cyclic, and thus, from the inscribed angle theorem, $K L M N$ must be a rectangle. Hence, $A C \\perp B D$. Now, let $P$ denote the intersections of the diagonals of $A B C D$.\n\n\nApplying Pythagoras' theorem repeatedly therefore yields\n\n$$\n|A B|^{2}+|C D|^{2}=|A P|^{2}+|B P|^{2}+|C P|^{2}+|D P|^{2}=|A D|^{2}+|B C|^{2} .\n$$\n\nThus, we can construct the quadrilateral $\\mathcal{Q}_{2}$ with a segment $A^{\\prime} C^{\\prime}$ satisfying $\\left|A^{\\prime} C^{\\prime}\\right|^{2}=|A B|^{2}+$ $|C D|^{2}$, and then place $B^{\\prime}, D^{\\prime}$ on the circle with diameter $A^{\\prime} C^{\\prime}$ on opposite sides of $A^{\\prime} C^{\\prime}$ such that $\\left|A^{\\prime} B^{\\prime}\\right|=|A B|$ and $\\left|A^{\\prime} D^{\\prime}\\right|=|A D|$.\nFrom the previous computation, we then obtain $\\left|C^{\\prime} B^{\\prime}\\right|=|C D|$ and $\\left|C^{\\prime} D^{\\prime}\\right|=|B C|$. Hence, $\\mathcal{Q}_{2}$ and $\\mathcal{Q}_{1}$ has the same set of sidelengths. Finally, $A^{\\prime} B^{\\prime} \\perp B^{\\prime} C^{\\prime}$ and $A^{\\prime} D^{\\prime} \\perp D^{\\prime} C^{\\prime}$, so $\\mathcal{Q}_{2}$ has two identical right angels.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl", "problem_match": "\n## Problem 2", "solution_match": "\n## Solution"}}
|
| 3 |
+
{"year": "2024", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Find all functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf(f(x) f(y)+y)=f(x) y+f(y-x+1)\n$$\n\nfor all $x, y \\in \\mathbb{R}$.", "solution": "First note that $f$ satisfies the functional equation if and only if $-f$ does as well. We can therefore assume that $f(0) \\geq 0$. We consider two cases, depending on whether $f$ is injective or not.\n\n1. First assume that $f$ is not injective. Then there exist $a, t \\in \\mathbb{R}, t \\neq 0$ such that $f(a+t)=$ $f(a)$. Apply the substitutions $x \\mapsto a, y \\mapsto y$ and $x \\mapsto a+t, y \\mapsto y$ to the functional equation (3.1). This gives:\n\n$$\nf(y-a+1)=f(f(a) f(y)+y)-f(a) y\n$$\n\nand\n\n$$\nf(y-a-t+1)=f(f(a+t) f(y)+y)-f(a+t) y\n$$\n\nAs $f(a+t)=f(a)$ the right hand sides of the equations are equal to one another. Hence\n\n$$\nf(y-a+1)=f(y-a-t+1) .\n$$\n\nApplying the substitution $y \\mapsto x+a+t-1$ to equation (3.2) yields:\n\n$$\nf(x+t)=f(x) .\n$$\n\nIn other words $f$ is $t$-periodic. Perform the substitution $x \\mapsto x$ and $y \\mapsto y+t$ to equation (3.1). The result is\n\n$$\nf(f(x) f(y+t)+y+t)=f(x)(y+t)=f(y+t-x+1) .\n$$\n\nAs $f$ is $t$-periodic we have $f(y+t)=f(y), f(f(x) f(y)+y+t)=f(f(x) f(y)+y)$ and $f(y+t-x+1)=f(y-x+1)$. As a result equation (3.4) simplifies to\n\n$$\nf(f(x) f(y)+y)=f(x)(y+t)+f(y-x+1)\n$$\n\nBy comparing equation (3.5) with the given equation (3.1) we get\n\n$$\nf(x) y=f(x)(y+t)\n$$\n\nAs $t \\neq 0$ it follows that $f(x)=0$. That is $f$ is the zero function.\n2. Next assume that $f$ is injective. Apply the substitution $x \\mapsto x$ and $y \\mapsto 0$ to the functional equation (3.1). This gives\n\n$$\nf(f(x) f(0))=f(-x+1)\n$$\n\nAs $f$ injective, the arguments must equate, that is\n\n$$\nf(x) f(0)=1-x\n$$\n\nEvaluation this equation at $x=0$ gives $(f(0))^{2}=1$, that is $f(0)=1$ as we assumed that $f(0) \\geq 0$. Equation (3.6) simplifies to\n\n$$\nf(x)=1-x\n$$\n\nIt remains to verify that the candidates $f(x)=0$ and $f(x)=1-x$ are in fact solution to the functional equation. Routine calculation show that this is the case. We have hence found that the complete collection of solutions to the functional equation is\n\n$$\nf: \\mathbb{R} \\longrightarrow \\mathbb{R}, x \\longmapsto 0, f: \\mathbb{R} \\longrightarrow \\mathbb{R}, x \\longmapsto x-1 \\quad \\text { and } \\quad f: \\mathbb{R} \\longrightarrow \\mathbb{R}, x \\longmapsto 1-x .\n$$", "metadata": {"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl", "problem_match": "\n## Problem 3", "solution_match": "\n## Solution"}}
|
| 4 |
+
{"year": "2024", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Alice and Bob are playing a game. First, Alice chooses a partition $\\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\\mathcal{C}$. Then Bob does the following operation a finite number of times.\nChoose a set $S \\in \\mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \\backslash S$ (possibly the empty set) to $\\mathcal{C}$.\nBob wins if there are two equal sets in $\\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.\n\nAnswer: Alice has a winning strategy.", "solution": "We will use the following notation. If $S \\subseteq \\mathbb{Z}^{+}$is a subset of the positive integers and $D$ is defined as in the problem statement, define $d(S)=D \\backslash S$. In addition, the $d$-sequence of $S$, written $\\left\\{d^{S}\\right\\}_{n \\in \\mathbb{Z}^{+}}$, is defined recursively as $d_{0}^{S}=S$, and $d_{n+1}^{S}=d\\left(d_{n}^{S}\\right)$ for each $n \\in \\mathbb{Z}^{+}$.\nLet $p_{1}, p_{2}, \\ldots$ be an enumeration of all the prime numbers. Alice chooses the sets\n\n$$\nA=\\left\\{p_{m}^{n} \\mid n \\equiv m \\quad \\bmod 3,0<n \\leq m\\right\\}, \\quad B=\\left\\{p_{m}^{n} \\mid n \\equiv m-1 \\quad \\bmod 3,0<n \\leq m-1\\right\\}\n$$\n\nand\n\n$$\nC=\\mathbb{Z}^{+} \\backslash(A \\cup B)\n$$\n\nIt is clear that each positive integer belongs to exactly on of the sets $A, B$ or $C$. By induction we readily get that\n\n$$\nd^{k}(A)=\\left\\{\\begin{array}{ll}\n\\left\\{p_{m}^{n} \\mid n \\equiv m\\right. & \\bmod 3, n \\leq m-3 k / 2\\} \\\\\n\\left\\{p_{m}^{n} \\mid n \\not \\equiv m\\right. & \\bmod 3, n \\leq m-1-3(k-1) / 2\\}\n\\end{array} \\quad \\text { if } k \\text { is even and } k \\neq 0\\right.\n$$\n\nand\n\n$$\nd^{k}(B)=\\left\\{\\begin{array}{lll}\n\\left\\{p_{m}^{n} \\mid n \\equiv m-1\\right. & \\bmod 3, n \\leq m-1-3 k / 2\\} & \\text { if } k \\text { is even and } k \\neq 0 \\\\\n\\left\\{p_{m}^{n} \\mid n \\not \\equiv m-1\\right. & \\bmod 3, n \\leq m-2-3(k-1) / 2\\} & \\text { if } k \\text { is odd. }\n\\end{array}\\right.\n$$\n\nIf $m \\in \\mathbb{Z}^{+}$then $6 m$ is definitely in $C$ as $6 m$ is not a power of a prime. This means that all positive integers divide at least one number in $C$. It follows that\n\n$$\nd(C)=\\mathbb{Z}^{+} \\backslash C=\\mathbb{Z}^{+} \\backslash\\left(\\mathbb{Z}^{+} \\backslash(A \\cup B)\\right)=A \\cup B=\\left\\{p_{m}^{n} \\mid n \\not \\equiv m-2 \\bmod 3,0<n \\leq m\\right\\}\n$$\n\nBy induction it follows that\n\nFrom this it is clear that all of the sets $d^{k}(M)$ are all distinct. Hence Bob can never create the same set in two different ways.\n\nRemark. In fact Alice has to partition the positive integers in at least three parts if she wishes to beat Bob. It is clear that selecting a singe set, namely $\\mathbb{Z}^{+}$will not do as $d\\left(\\mathbb{Z}^{+}\\right)=\\emptyset$ and $d(\\emptyset)=\\emptyset$. Next assume Alice has partitioned the positive integers in two sets $A$ and $B$. It can be assumed that $d(A) \\neq B$ and $d(B) \\neq A$ as Bob would win either case. As $d(A)$ is disjoint from $A$ and $B$ is the complement of $A$ this means that $d(A)$ is a strict subset of $B$. Hence there is some $b$ in $B$ that does not belong to $d(A)$. The implication is that $b$ does not divide any number in $A$. Similarly there exists a number $a$ in $A$ that does not divide any number in $B$. Their product $a b$ belongs to either of the sets $A$ or $B$ and is divisible by both $a$ and $b$. This contradicts the existence of said numbers, $a$ and $b$. In fact we have proven for any subset $A$ of $\\mathbb{Z}^{+}$that $d(A)=\\mathbb{Z}^{+} \\backslash A$ or $d\\left(\\mathbb{Z}^{+} \\backslash A\\right)=A$.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl", "problem_match": "\n## Problem 4", "solution_match": "\n## Solution 1"}}
|
| 5 |
+
{"year": "2024", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Alice and Bob are playing a game. First, Alice chooses a partition $\\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\\mathcal{C}$. Then Bob does the following operation a finite number of times.\nChoose a set $S \\in \\mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \\backslash S$ (possibly the empty set) to $\\mathcal{C}$.\nBob wins if there are two equal sets in $\\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.\n\nAnswer: Alice has a winning strategy.", "solution": "Use the same notation as in solution 1 . We wish to construct a partition $\\bigcup_{i \\in \\mathbb{Z}^{+}} A_{i}$ of the positive integers, such that no two sets among all sets in $\\left\\{d^{A_{1}}\\right\\}_{n \\in \\mathbb{Z}^{+}},\\left\\{d^{A_{2}}\\right\\}_{n \\in \\mathbb{Z}^{+}}, \\ldots$ are equal.\nTo begin with, consider a partition $\\bigcup_{i \\in \\mathbb{Z}^{+}} P_{i}$ of the primes, such that each $P_{i}=\\left\\{p_{i 1}, p_{i 2}, \\ldots\\right\\}$ is infinite. We may assume each set is infinite since the set of primes and $\\mathbb{Z}^{+} \\times \\mathbb{Z}^{+}$both are countable, so there exists a bijection between them. Define the sets\n\n$$\nQ_{i}=\\left\\{p_{i 1}, p_{i 2}^{2}, p_{i 3}, p_{i 3}^{3}, p_{i 4}^{2}, p_{i 4}^{4}, p_{i 5}, p_{i 5}^{3}, p_{i 5}^{5}, \\ldots\\right\\}\n$$\n\nconsisting of $p_{i j}^{j}, p_{i j}^{j-2}, \\ldots, p_{i j}^{(1,2)}$ for each $p_{i j} \\in P_{i}$. By the exponent $(1,2)$ we indicate that the last power is 1 when $j$ is odd and 2 when it is even.\nWe will include the remaining integers $\\left\\{r_{1}, r_{2}, \\ldots\\right\\}=\\mathbb{Z}^{+} \\backslash\\left(\\bigcup_{i \\in \\mathbb{Z}^{+}} Q_{i}\\right)$ to the partition as follows. First, add $r_{1}$ to some set $Q_{i_{1}}$, such that $\\operatorname{gcd}\\left(r_{1}, q\\right)=1$ for each $q \\in Q_{i_{1}}$. Then, for each $k \\in \\mathbb{Z}^{+}$, add $r_{k+1}$ to a set $Q_{i_{k+1}}$ where $i_{k+1}>i_{k}$, such that $\\operatorname{gcd}\\left(r_{k+1}, q\\right)=1$ for each $q \\in Q_{i_{k+1}}$. Note that such an $i_{k+1}$ always exists, since there always is an infinite amount of prime divisors among $Q_{i_{k}+1}, Q_{i_{k}+2}, \\ldots$, and $r_{k+1}$ only has a finite amount of prime divisors.\nThe collection of $Q_{i}$ now forms a partition of $\\mathbb{Z}^{+}$. What remains is to show that it satisfies Alice's winning condition.\nWe first see that we may ignore all the $r_{k}$. By definition, no divisor of $r_{k}$ coincides with any divisor of $Q_{i_{k}}$, and their contributions in the $d$-sequence will therefore be completely disjoint. As $d\\left(d\\left(\\left\\{r_{k}\\right\\}\\right)\\right)=\\emptyset$, the $d$-sequence will show no trace of the $r_{k}$ after the second element. Hence, we will work with the original $Q_{i}$.\nWe observe that $d\\left(Q_{i}\\right)=\\left\\{1, p_{i 2}, p_{i 3}^{2}, p_{i 4}, p_{i 4}^{3}, p_{i 5}^{2}, p_{i 5}^{4}, p_{i 6}, p_{i 6}^{3}, p_{i 6}^{5}, \\ldots\\right\\}$. This is simply $Q_{i}$ with the indices shifted by 1 and with an added 1 . As this set essentially is on the same form as $Q_{i}$, we see that $\\left\\{d^{Q_{i}}\\right\\}_{n}$ consists of every possible shift in indices of the first set $Q_{i}$ (except the element 1 appearing in every other set). It is therefore obvious that the sets in the sequence are pairwise distinct. Additionally, the set of primes dividing some element in some set of $\\left\\{d^{Q_{i}}\\right\\}_{n}$ is $P_{i}$. Since the $P_{i}$ partition the primes, it is clear that all the sets in all the $d$-sequences of the $Q_{i}$ are distinct, which is what we wanted.\n\nRemark. The main idea of the problem is to construct a single set $S$, such that the sets in the $d$-sequence of $S$ are pairwise distinct. Any set with similar properties to the $Q_{i}$ should give a valid initial collection $\\mathcal{C}$ such that Alice wins.", "metadata": {"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl", "problem_match": "\n## Problem 4", "solution_match": "\n## Solution 2"}}
|