add segmented data for HarvardMIT
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- HarvardMIT/md/en-102-2007-feb-alg-solutions.md +120 -0
- HarvardMIT/md/en-102-2007-feb-calc-solutions.md +130 -0
- HarvardMIT/md/en-102-2007-feb-comb-solutions.md +75 -0
- HarvardMIT/md/en-102-2007-feb-gen1-solutions.md +36 -0
- HarvardMIT/md/en-102-2007-feb-gen2-solutions.md +61 -0
- HarvardMIT/md/en-102-2007-feb-geo-solutions.md +55 -0
- HarvardMIT/md/en-102-2007-feb-guts-solutions.md +391 -0
- HarvardMIT/md/en-102-2007-feb-team1-solutions.md +291 -0
- HarvardMIT/md/en-102-2007-feb-team2-solutions.md +219 -0
- HarvardMIT/md/en-112-2008-feb-alg-solutions.md +151 -0
- HarvardMIT/md/en-112-2008-feb-calc-solutions.md +127 -0
- HarvardMIT/md/en-112-2008-feb-comb-solutions.md +88 -0
- HarvardMIT/md/en-112-2008-feb-gen1-solutions.md +46 -0
- HarvardMIT/md/en-112-2008-feb-gen2-solutions.md +40 -0
- HarvardMIT/md/en-112-2008-feb-geo-solutions.md +91 -0
- HarvardMIT/md/en-112-2008-feb-guts-solutions.md +359 -0
- HarvardMIT/md/en-112-2008-feb-team1-solutions.md +170 -0
- HarvardMIT/md/en-112-2008-feb-team2-solutions.md +239 -0
- HarvardMIT/md/en-12-1998-feb-adv-solutions.md +126 -0
- HarvardMIT/md/en-12-1998-feb-alg-solutions.md +115 -0
- HarvardMIT/md/en-12-1998-feb-calc-solutions.md +72 -0
- HarvardMIT/md/en-12-1998-feb-geo-solutions.md +14 -0
- HarvardMIT/md/en-12-1998-feb-team-solutions.md +79 -0
- HarvardMIT/md/en-121-2008-nov-gen1-solutions.md +67 -0
- HarvardMIT/md/en-121-2008-nov-gen2-solutions.md +44 -0
- HarvardMIT/md/en-121-2008-nov-guts-solutions.md +224 -0
- HarvardMIT/md/en-121-2008-nov-team-solutions.md +111 -0
- HarvardMIT/md/en-122-2009-feb-alg-solutions.md +111 -0
- HarvardMIT/md/en-122-2009-feb-calc-solutions.md +135 -0
- HarvardMIT/md/en-122-2009-feb-comb-solutions.md +77 -0
- HarvardMIT/md/en-122-2009-feb-gen1-solutions.md +87 -0
- HarvardMIT/md/en-122-2009-feb-gen2-solutions.md +47 -0
- HarvardMIT/md/en-122-2009-feb-geo-solutions.md +124 -0
- HarvardMIT/md/en-122-2009-feb-guts-solutions.md +282 -0
- HarvardMIT/md/en-122-2009-feb-team1-solutions.md +66 -0
- HarvardMIT/md/en-122-2009-feb-team2-solutions.md +31 -0
- HarvardMIT/md/en-131-2009-nov-gen1-solutions.md +47 -0
- HarvardMIT/md/en-131-2009-nov-gen2-solutions.md +61 -0
- HarvardMIT/md/en-131-2009-nov-guts-solutions.md +212 -0
- HarvardMIT/md/en-131-2009-nov-team-solutions.md +55 -0
- HarvardMIT/md/en-132-2010-feb-alg-solutions.md +147 -0
- HarvardMIT/md/en-132-2010-feb-calc-solutions.md +113 -0
- HarvardMIT/md/en-132-2010-feb-comb-solutions.md +107 -0
- HarvardMIT/md/en-132-2010-feb-gen1-solutions.md +131 -0
- HarvardMIT/md/en-132-2010-feb-gen2-solutions.md +126 -0
- HarvardMIT/md/en-132-2010-feb-geo-solutions.md +157 -0
- HarvardMIT/md/en-132-2010-feb-guts-solutions.md +443 -0
- HarvardMIT/md/en-132-2010-feb-team1-solutions.md +125 -0
- HarvardMIT/md/en-132-2010-feb-team2-solutions.md +95 -0
- HarvardMIT/md/en-141-2010-nov-gen1-solutions.md +91 -0
HarvardMIT/md/en-102-2007-feb-alg-solutions.md
ADDED
|
@@ -0,0 +1,120 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
## Individual Round: Algebra Test
|
| 4 |
+
|
| 5 |
+
1. [3] Compute
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
(Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
| 12 |
+
Answer: 2006. We have
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor=\left\lfloor\frac{\left(2007 \cdot 2006+\frac{1}{2005}\right) \cdot 2005!}{(2006+1) \cdot 2005!}\right\rfloor=\left\lfloor\frac{2007 \cdot 2006+\frac{1}{2005}}{2007}\right\rfloor=\left\lfloor 2006+\frac{1}{2005 \cdot 2007}\right\rfloor
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
2. [3] Two reals $x$ and $y$ are such that $x-y=4$ and $x^{3}-y^{3}=28$. Compute $x y$.
|
| 19 |
+
|
| 20 |
+
Answer: $-\mathbf{3}$. We have $28=x^{3}-y^{3}=(x-y)\left(x^{2}+x y+y^{2}\right)=(x-y)\left((x-y)^{2}+3 x y\right)=4 \cdot(16+3 x y)$, from which $x y=-3$.
|
| 21 |
+
3. [4] Three real numbers $x, y$, and $z$ are such that $(x+4) / 2=(y+9) /(z-3)=(x+5) /(z-5)$. Determine the value of $x / y$.
|
| 22 |
+
Answer: 1/2. Because the first and third fractions are equal, adding their numerators and denominators produces another fraction equal to the others: $((x+4)+(x+5)) /(2+(z-5))=(2 x+9) /(z-3)$. Then $y+9=2 x+9$, etc.
|
| 23 |
+
4. [4] Compute
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\frac{2^{3}-1}{2^{3}+1} \cdot \frac{3^{3}-1}{3^{3}+1} \cdot \frac{4^{3}-1}{4^{3}+1} \cdot \frac{5^{3}-1}{5^{3}+1} \cdot \frac{6^{3}-1}{6^{3}+1}
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
Answer: $\frac{\mathbf{4 3} \text {. }}{63}$ Use the factorizations $n^{3}-1=(n-1)\left(n^{2}+n+1\right)$ and $n^{3}+1=(n+1)\left(n^{2}-n+1\right)$ to write
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\frac{1 \cdot 7}{3 \cdot 3} \cdot \frac{2 \cdot 13}{4 \cdot 7} \cdot \frac{3 \cdot 21}{5 \cdot 13} \cdot \frac{4 \cdot 31}{6 \cdot 21} \cdot \frac{5 \cdot 43}{7 \cdot 31}=\frac{1 \cdot 2 \cdot 43}{3 \cdot 6 \cdot 7}=\frac{43}{63}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
5. [5] A convex quadrilateral is determined by the points of intersection of the curves $x^{4}+y^{4}=100$ and $x y=4$; determine its area.
|
| 36 |
+
Answer: $\mathbf{4 \sqrt { 1 7 }}$. By symmetry, the quadrilateral is a rectangle having $x=y$ and $x=-y$ as axes of symmetry. Let $(a, b)$ with $a>b>0$ be one of the vertices. Then the desired area is
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
(\sqrt{2}(a-b)) \cdot(\sqrt{2}(a+b))=2\left(a^{2}-b^{2}\right)=2 \sqrt{a^{4}-2 a^{2} b^{2}+b^{4}}=2 \sqrt{100-2 \cdot 4^{2}}=4 \sqrt{17}
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
6. [5] Consider the polynomial $P(x)=x^{3}+x^{2}-x+2$. Determine all real numbers $r$ for which there exists a complex number $z$ not in the reals such that $P(z)=r$.
|
| 43 |
+
Answer: $\mathbf{r}>\mathbf{3}, \mathbf{r}<\frac{\mathbf{4 9}}{\mathbf{2 7}}$. Because such roots to polynomial equations come in conjugate pairs, we seek the values $r$ such that $P(x)=r$ has just one real root $x$. Considering the shape of a cubic, we are interested in the boundary values $r$ such that $P(x)-r$ has a repeated zero. Thus, we write
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
P(x)-r=x^{3}+x^{2}-x+(2-r)=(x-p)^{2}(x-q)=x^{3}-(2 p+q) x^{2}+p(p+2 q) x-p^{2} q
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Then $q=-2 p-1$ and $1=p(p+2 q)=p(-3 p-2)$ so that $p=1 / 3$ or $p=-1$. It follows that the graph of $P(x)$ is horizontal at $x=1 / 3$ (a maximum) and $x=-1$ (a minimum), so the desired values $r$ are $r>P(-1)=3$ and $r<P(1 / 3)=1 / 27+1 / 9-1 / 3+2=49 / 27$.
|
| 50 |
+
7. [5] An infinite sequence of positive real numbers is defined by $a_{0}=1$ and $a_{n+2}=6 a_{n}-a_{n+1}$ for $n=0,1,2, \cdots$ Find the possible value(s) of $a_{2007}$.
|
| 51 |
+
Answer: $\mathbf{2}^{\mathbf{2 0 0 7}}$. The characteristic equation of the linear homogeneous equation is $m^{2}+m-6=$ $(m+3)(m-2)=0$ with solutions $m=-3$ and $m=2$. Hence the general solution is given by $a_{n}=A(2)^{n}+B(-3)^{n}$ where $A$ and $B$ are constants to be determined. Then we have $a_{n}>0$ for $n \geq 0$, so necessarily $B=0$, and $a_{0}=1 \Rightarrow A=1$. Therefore, the unique solution to the recurrence is $a_{n}=2^{n}$ for all n .
|
| 52 |
+
8. [6] Let $A:=\mathbb{Q} \backslash\{0,1\}$ denote the set of all rationals other than 0 and 1. A function $f: A \rightarrow \mathbb{R}$ has the property that for all $x \in A$,
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
f(x)+f\left(1-\frac{1}{x}\right)=\log |x|
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Compute the value of $f(2007)$.
|
| 59 |
+
Answer: $\log (\mathbf{2 0 0 7} / \mathbf{2 0 0 6})$. Let $g: A \rightarrow A$ be defined by $g(x):=1-1 / x$; the key property is that
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
g(g(g(x)))=1-\frac{1}{1-\frac{1}{1-\frac{1}{x}}}=x
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
The given equation rewrites as $f(x)+f(g(x))=\log |x|$. Substituting $x=g(y)$ and $x=g(g(z))$ gives the further equations $f(g(y))+f(g(g(y)))=\log |g(x)|$ and $f(g(g(z)))+f(z)=\log |g(g(x))|$. Setting $y$ and $z$ to $x$ and solving the system of three equations for $f(x)$ gives
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
f(x)=\frac{1}{2} \cdot(\log |x|-\log |g(x)|+\log |g(g(x))|)
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
For $x=2007$, we have $g(x)=\frac{2006}{2007}$ and $g(g(x))=\frac{-1}{2006}$, so that
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
f(2007)=\frac{\log |2007|-\log \left|\frac{2006}{2007}\right|+\log \left|\frac{-1}{2006}\right|}{2}=\log (2007 / 2006)
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
9. [7] The complex numbers $\alpha_{1}, \alpha_{2}, \alpha_{3}$, and $\alpha_{4}$ are the four distinct roots of the equation $x^{4}+2 x^{3}+2=0$. Determine the unordered set
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
\left\{\alpha_{1} \alpha_{2}+\alpha_{3} \alpha_{4}, \alpha_{1} \alpha_{3}+\alpha_{2} \alpha_{4}, \alpha_{1} \alpha_{4}+\alpha_{2} \alpha_{3}\right\} .
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
Answer: $\{\mathbf{1} \pm \sqrt{\mathbf{5}}, \mathbf{- 2}\}$. Employing the elementary symmetric polynomials $\left(s_{1}=\alpha_{1}+\alpha_{2}+\alpha_{3}+\alpha_{4}=\right.$ $-2, s_{2}=\alpha_{1} \alpha_{2}+\alpha_{1} \alpha_{3}+\alpha_{1} \alpha_{4}+\alpha_{2} \alpha_{3}+\alpha_{2} \alpha_{4}+\alpha_{3} \alpha_{4}=0, s_{3}=\alpha_{1} \alpha_{2} \alpha_{3}+\alpha_{2} \alpha_{3} \alpha_{4}+\alpha_{3} \alpha_{4} \alpha_{1}+\alpha_{4} \alpha_{1} \alpha_{2}=0$, and $s_{4}=\alpha_{1} \alpha_{2} \alpha_{3} \alpha_{4}=2$ ) we consider the polynomial
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
P(x)=\left(x-\left(\alpha_{1} \alpha_{2}+\alpha_{3} \alpha_{4}\right)\right)\left(x-\left(\alpha_{1} \alpha_{3}+\alpha_{2} \alpha_{4}\right)\right)\left(x-\left(\alpha_{1} \alpha_{4}+\alpha_{2} \alpha_{3}\right)\right)
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Because $P$ is symmetric with respect to $\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}$, we can express the coefficients of its expanded form in terms of the elementary symmetric polynomials. We compute
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\begin{aligned}
|
| 93 |
+
P(x) & =x^{3}-s_{2} x^{2}+\left(s_{3} s_{1}-4 s_{4}\right) x+\left(-s_{3}^{2}-s_{4} s_{1}^{2}+s_{4} s_{2}\right) \\
|
| 94 |
+
& =x^{3}-8 x-8 \\
|
| 95 |
+
& =(x+2)\left(x^{2}-2 x-4\right)
|
| 96 |
+
\end{aligned}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
The roots of $P(x)$ are -2 and $1 \pm \sqrt{5}$, so the answer is $\{1 \pm \sqrt{5},-2\}$.
|
| 100 |
+
Remarks. It is easy to find the coefficients of $x^{2}$ and $x$ by expansion, and the constant term can be computed without the complete expansion and decomposition of $\left(\alpha_{1} \alpha_{2}+\alpha_{3} \alpha_{4}\right)\left(\alpha_{1} \alpha_{3}+\alpha_{2} \alpha_{4}\right)\left(\alpha_{1} \alpha_{4}+\right.$ $\alpha_{2} \alpha_{3}$ ) by noting that the only nonzero 6 th degree expressions in $s_{1}, s_{2}, s_{3}$, and $s_{4}$ are $s_{1}^{6}$ and $s_{4} s_{1}^{2}$. The general polynomial $P$ constructed here is called the cubic resolvent and arises in Galois theory.
|
| 101 |
+
10. [8] The polynomial $f(x)=x^{2007}+17 x^{2006}+1$ has distinct zeroes $r_{1}, \ldots, r_{2007}$. A polynomial $P$ of degree 2007 has the property that $P\left(r_{j}+\frac{1}{r_{j}}\right)=0$ for $j=1, \ldots, 2007$. Determine the value of $P(1) / P(-1)$.
|
| 102 |
+
|
| 103 |
+
Answer: | $\mathbf{2 8 9}$. |
|
| 104 |
+
| :---: |
|
| 105 |
+
| For some constant $k$, we have |
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
P(z)=k \prod_{j=1}^{2007}\left(z-\left(r_{j}+\frac{1}{r_{j}}\right)\right)
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
Now writing $\omega^{3}=1$ with $\omega \neq 1$, we have $\omega^{2}+\omega=-1$. Then
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
\begin{gathered}
|
| 115 |
+
P(1) / P(-1)=\frac{k \prod_{j=1}^{2007}\left(1-\left(r_{j}+\frac{1}{r_{j}}\right)\right)}{k \prod_{j=1}^{2007}\left(-1-\left(r_{j}+\frac{1}{r_{j}}\right)\right)}=\prod_{j=1}^{2007} \frac{r_{j}^{2}-r_{j}+1}{r_{j}^{2}+r_{j}+1}=\prod_{j=1}^{2007} \frac{\left(-\omega-r_{j}\right)\left(-\omega^{2}-r_{j}\right)}{\left(\omega-r_{j}\right)\left(\omega^{2}-r_{j}\right)} \\
|
| 116 |
+
=\frac{f(-\omega) f\left(-\omega^{2}\right)}{f(\omega) f\left(\omega^{2}\right)}=\frac{\left(-\omega^{2007}+17 \omega^{2006}+1\right)\left(-\left(\omega^{2}\right)^{2007}+17\left(\omega^{2}\right)^{2006}+1\right)}{\left(\omega^{2007}+17 \omega^{2006}+1\right)\left(\left(\omega^{2}\right)^{2007}+17\left(\omega^{2}\right)^{2006}+1\right)}=\frac{\left(17 \omega^{2}\right)(17 \omega)}{\left(2+17 \omega^{2}\right)(2+17 \omega)} \\
|
| 117 |
+
=\frac{289}{4+34\left(\omega+\omega^{2}\right)+289}=\frac{289}{259} .
|
| 118 |
+
\end{gathered}
|
| 119 |
+
$$
|
| 120 |
+
|
HarvardMIT/md/en-102-2007-feb-calc-solutions.md
ADDED
|
@@ -0,0 +1,130 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
Individual Round: Calculus Test
|
| 4 |
+
|
| 5 |
+
1. [3] Compute:
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
\lim _{x \rightarrow 0} \frac{x^{2}}{1-\cos (x)}
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
Answer: 2. Since $\sin ^{2}(x)=1-\cos ^{2}(x)$, we multiply the numerator and denominator by $1+\cos (x)$ and use the fact that $x / \sin (x) \rightarrow 1$, obtaining
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
\lim _{x \rightarrow 0} \frac{x^{2}}{1-\cos (x)}=\lim _{x \rightarrow 0} \frac{x^{2}(1+\cos (x))}{1-\cos ^{2}(x)}=\lim _{x \rightarrow 0}\left(\frac{x}{\sin (x)}\right)^{2} \cdot 2=2
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
Remarks. Another solution, using L'Hôpital's rule, is possible: $\lim _{x \rightarrow 0} \frac{x^{2}}{1-\cos (x)}=\lim _{x \rightarrow 0} \frac{2 x}{\sin (x)}=2$.
|
| 18 |
+
2. [3] Determine the real number $a$ having the property that $f(a)=a$ is a relative minimum of $f(x)=$ $x^{4}-x^{3}-x^{2}+a x+1$.
|
| 19 |
+
Answer: 1. Being a relative minimum, we have $0=f^{\prime}(a)=4 a^{3}-3 a^{2}-2 a+a=a(4 a+1)(a-1)$. Then $a=0,1,-1 / 4$ are the only possibilities. However, it is easily seen that $a=1$ is the only value satisfying $f(a)=a$.
|
| 20 |
+
3. [4] Let $a$ be a positive real number. Find the value of $a$ such that the definite integral
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\int_{a}^{a^{2}} \frac{\mathrm{~d} x}{x+\sqrt{x}}
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
achieves its smallest possible value.
|
| 27 |
+
Answer: $\sqrt[{3-2 \sqrt{2}}]{ }$ Let $F(a)$ denote the given definite integral. Then
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
F^{\prime}(a)=\frac{\mathrm{d}}{\mathrm{~d} a} \int_{a}^{a^{2}} \frac{\mathrm{~d} x}{x+\sqrt{x}}=2 a \cdot \frac{1}{a^{2}+\sqrt{a^{2}}}-\frac{1}{a+\sqrt{a}} .
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Setting $F^{\prime}(a)=0$, we find that $2 a+2 \sqrt{a}=a+1$ or $(\sqrt{a}+1)^{2}=2$. We find $\sqrt{a}= \pm \sqrt{2}-1$, and because $\sqrt{a}>0, a=(\sqrt{2}-1)^{2}=3-2 \sqrt{2}$.
|
| 34 |
+
4. [4] Find the real number $\alpha$ such that the curve $f(x)=e^{x}$ is tangent to the curve $g(x)=\alpha x^{2}$.
|
| 35 |
+
|
| 36 |
+
Answer: $\mathbf{e}^{\mathbf{2} / 4}$. Suppose tangency occurs at $x=x_{0}$. Then $e^{x_{0}}=\alpha x_{0}^{2}$ and $f^{\prime}\left(x_{0}\right)=2 \alpha x_{0}$. On the other hand, $f^{\prime}(x)=f(x)$, so $\alpha x_{0}^{2}=2 \alpha x_{0}$. Clearly, $\alpha=0$ and $x_{0}=0$ are impossible, so it must be that $x_{0}=2$. Then $\alpha=e^{x_{0}} /\left(x_{0}^{2}\right)=e^{2} / 4$.
|
| 37 |
+
5. [5] The function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies $f\left(x^{2}\right) f^{\prime \prime}(x)=f^{\prime}(x) f^{\prime}\left(x^{2}\right)$ for all real $x$. Given that $f(1)=1$ and $f^{\prime \prime \prime}(1)=8$, determine $f^{\prime}(1)+f^{\prime \prime}(1)$.
|
| 38 |
+
Answer: 6. Let $f^{\prime}(1)=a$ and $f^{\prime \prime}(1)=b$. Then setting $x=1$ in the given equation, $b=a^{2}$. Differentiating the given yields
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
2 x f^{\prime}\left(x^{2}\right) f^{\prime \prime}(x)+f\left(x^{2}\right) f^{\prime \prime \prime}(x)=f^{\prime \prime}(x) f^{\prime}\left(x^{2}\right)+2 x f^{\prime}(x) f^{\prime \prime}\left(x^{2}\right)
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Plugging $x=1$ into this equation gives $2 a b+8=a b+2 a b$, or $a b=8$. Then because $a$ and $b$ are real, we obtain the solution $(a, b)=(2,4)$.
|
| 45 |
+
Remarks. A priori, the function needn't exist, but one possibility is $f(x)=e^{2 x-2}$.
|
| 46 |
+
6. [5] The elliptic curve $y^{2}=x^{3}+1$ is tangent to a circle centered at $(4,0)$ at the point $\left(x_{0}, y_{0}\right)$. Determine the sum of all possible values of $x_{0}$.
|
| 47 |
+
Answer: $\frac{\mathbf{1}}{\mathbf{3}}$. Note that $y^{2} \geq 0$, so $x^{3} \geq-1$ and $x \geq-1$. Let the circle be defined by $(x-4)^{2}+y^{2}=c$ for some $c \geq 0$. Now differentiate the equations with respect to $x$, obtaining $2 y \frac{\mathrm{~d} y}{\mathrm{~d} x}=3 x^{2}$ from the given and $2 y \frac{\mathrm{~d} y}{\mathrm{~d} x}=-2 x+8$ from the circle. For tangency, the two expressions $\frac{\mathrm{d} y}{\mathrm{~d} x}$ must be equal if they are well-defined, and this is almost always the case. Thus, $-2 x_{0}+8=3 x_{0}^{2}$ so $x_{0}=-2$ or $x_{0}=4 / 3$, but only the latter corresponds to a point on $y^{2}=x^{3}+1$. Otherwise, $y_{0}=0$, and this gives the trivial solution $x_{0}=-1$.
|
| 48 |
+
7. [5] Compute
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\sum_{n=1}^{\infty} \frac{1}{n \cdot(n+1) \cdot(n+1)!}
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Answer: 3-e. We write
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
\begin{gathered}
|
| 58 |
+
\sum_{n=1}^{\infty} \frac{1}{n \cdot(n+1) \cdot(n+1)!}=\sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n+1}\right) \frac{1}{(n+1)!}=\sum_{n=1}^{\infty} \frac{1}{n \cdot(n+1)!}-\sum_{n=1}^{\infty} \frac{1}{(n+1) \cdot(n+1)!} \\
|
| 59 |
+
\frac{1}{2}+\sum_{n=2}^{\infty} \frac{1}{n \cdot(n+1)!}-\sum_{n=1}^{\infty} \frac{1}{(n+1) \cdot(n+1)!}=\frac{1}{2}+\sum_{n=1}^{\infty} \frac{1}{(n+1) \cdot(n+2)!}-\frac{1}{(n+1) \cdot(n+1)!} \\
|
| 60 |
+
\frac{1}{2}+\sum_{n=1}^{\infty} \frac{1-(n+2)}{(n+1) \cdot(n+2)!}=\frac{1}{2}-\left(\frac{1}{3!}+\frac{1}{4!}+\cdots\right)=3-\left(\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots\right)=3-e .
|
| 61 |
+
\end{gathered}
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Alternatively, but with considerably less motivation, we can induce telescoping by adding and subtracting $e-2=1 / 2!+1 / 3!+\cdots$, obtaining
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
\begin{aligned}
|
| 68 |
+
2-e & +\sum_{n=1}^{\infty} \frac{n(n+1)+1}{n \cdot(n+1) \cdot(n+1)!}=2-e+\sum_{n=1}^{\infty} \frac{(n+1)^{2}-n}{n \cdot(n+1) \cdot(n+1)!} \\
|
| 69 |
+
2 & -e+\sum_{n=1}^{\infty} \frac{1}{n \cdot n!}-\frac{1}{(n+1) \cdot(n+1)!}=3-e
|
| 70 |
+
\end{aligned}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
8. [6] Suppose that $\omega$ is a primitive $2007^{\text {th }}$ root of unity. Find $\left(2^{2007}-1\right) \sum_{j=1}^{2006} \frac{1}{2-\omega^{j}}$.
|
| 74 |
+
|
| 75 |
+
For this problem only, you may express your answer in the form $m \cdot n^{k}+p$, where $m, n, k$, and $p$ are positive integers. Note that a number $z$ is a primitive $n^{\text {th }}$ root of unity if $z^{n}=1$ and $n$ is the smallest number amongst $k=1,2, \ldots, n$ such that $z^{k}=1$.
|
| 76 |
+
Answer: $2005 \cdot \mathbf{2}^{2006}+1$. Note that
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
\begin{aligned}
|
| 80 |
+
& \frac{1}{z-\omega}+\cdots+\frac{1}{z-\omega^{2006}}=\frac{\sum_{j=1}^{2006} \prod_{i \neq j}\left(z-\omega^{i}\right)}{(z-\omega) \cdots\left(z-\omega^{2006}\right)} \\
|
| 81 |
+
& \quad=\frac{\frac{\mathrm{d}}{\mathrm{~d} z}\left[z^{2006}+z^{2005}+\cdots+1\right]}{z^{2006}+z^{2005}+\cdots+1}=\frac{2006 z^{2005}+2005 z^{2004}+\cdots+1}{z^{2006}+z^{2005}+\cdots+1} \cdot \frac{z-1}{z-1} \\
|
| 82 |
+
& \quad=\frac{2006 z^{2006}-z^{2005}-z^{2004}-\cdots-1}{z^{2007}-1} \cdot \frac{z-1}{z-1}=\frac{2006 z^{2007}-2007 z^{2006}+1}{\left(z^{2007}-1\right)(z-1)} .
|
| 83 |
+
\end{aligned}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
Plugging in $z=2$ gives $\frac{2005 \cdot 2^{2006}+1}{2^{2007}-1}$; whence the answer.
|
| 87 |
+
9. $[7] g$ is a twice differentiable function over the positive reals such that
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\begin{aligned}
|
| 91 |
+
g(x)+2 x^{3} g^{\prime}(x)+x^{4} g^{\prime \prime}(x) & =0 \quad \text { for all positive reals } x . \\
|
| 92 |
+
\lim _{x \rightarrow \infty} x g(x) & =1
|
| 93 |
+
\end{aligned}
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
Find the real number $\alpha>1$ such that $g(\alpha)=1 / 2$.
|
| 97 |
+
Answer: $\frac{6}{\pi}$. In the first equation, we can convert the expression $2 x^{3} g^{\prime}(x)+x^{4} g^{\prime \prime}(x)$ into the derivative of a product, and in fact a second derivative, by writing $y=1 / x$. Specifically,
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\begin{aligned}
|
| 101 |
+
0=g(x)+2 x^{3} g^{\prime}(x)+x^{4} g^{\prime \prime}(x) & =g\left(\frac{1}{y}\right)+2 y^{-3} g^{\prime}\left(\frac{1}{y}\right)+y^{-4} g^{\prime \prime}\left(\frac{1}{y}\right) \\
|
| 102 |
+
& =g\left(\frac{1}{y}\right)+\frac{\mathrm{d}}{\mathrm{~d} y}\left[-y^{-2} g^{\prime}\left(\frac{1}{y}\right)\right] \\
|
| 103 |
+
& =g\left(\frac{1}{y}\right)+\frac{\mathrm{d}^{2}}{\mathrm{~d} y^{2}}\left[g\left(\frac{1}{y}\right)\right]
|
| 104 |
+
\end{aligned}
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
Thus $g\left(\frac{1}{y}\right)=c_{1} \cos (y)+c_{2} \sin (y)$ or $g(x)=c_{1} \cos (1 / x)+c_{2} \sin (1 / x)$. Now the second condition gives
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
1=\lim _{x \rightarrow \infty} c_{1} x+c_{2} \cdot \frac{\sin (1 / x)}{1 / x}=c_{2}+\lim _{x \rightarrow \infty} c_{1} x
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
It must be that $c_{1}=0, c_{2}=1$. Now since $0<1 / \alpha<1$, the value of $\alpha$ such that $g(\alpha)=\sin (1 / \alpha)=1 / 2$ is given by $1 / \alpha=\pi / 6$ and so $\alpha=6 / \pi$.
|
| 114 |
+
10. [8] Compute
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\int_{0}^{\infty} \frac{e^{-x} \sin (x)}{x} d x
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
Answer: $\frac{\pi}{4}$. We can compute the integral by introducing a parameter and exchanging the order of integration:
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
\begin{aligned}
|
| 124 |
+
\int_{0}^{\infty} e^{-x}\left(\frac{\sin (x)}{x}\right) \mathrm{d} x & =\int_{0}^{\infty} e^{-x}\left(\int_{0}^{1} \cos (a x) \mathrm{d} a\right) \mathrm{d} x=\int_{0}^{1}\left(\int_{0}^{\infty} e^{-x} \cos (a x) \mathrm{d} x\right) \mathrm{d} a \\
|
| 125 |
+
& =\int_{0}^{1} \operatorname{Re}\left[\int_{0}^{\infty} e^{(-1+a i) x} \mathrm{~d} x\right] \mathrm{d} a=\int_{0}^{1} \operatorname{Re}\left[\left.\frac{e^{(-1+a i) x}}{-1+a i}\right|_{x=0} ^{\infty}\right] \mathrm{d} a \\
|
| 126 |
+
& =\int_{0}^{1} \operatorname{Re}\left[\frac{1}{1-a i}\right] \mathrm{d} a=\int_{0}^{1} \operatorname{Re}\left[\frac{1+a i}{1+a^{2}}\right] \mathrm{d} a \\
|
| 127 |
+
& =\int_{0}^{1} \frac{1}{1+a^{2}} \mathrm{~d} a=\left.\tan ^{-1}(a)\right|_{a=0} ^{1}=\frac{\pi}{4}
|
| 128 |
+
\end{aligned}
|
| 129 |
+
$$
|
| 130 |
+
|
HarvardMIT/md/en-102-2007-feb-comb-solutions.md
ADDED
|
@@ -0,0 +1,75 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> <br> Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
<br> <br> Saturday 24 February 2007}
|
| 4 |
+
|
| 5 |
+
## Individual Round: Combinatorics Test
|
| 6 |
+
|
| 7 |
+
1. [3] A committee of 5 is to be chosen from a group of 9 people. How many ways can it be chosen, if Biff and Jacob must serve together or not at all, and Alice and Jane refuse to serve with each other?
|
| 8 |
+
Answer: 41. If Biff and Jacob are on the committee, there are $\binom{7}{3}=35$ ways for the other members to be chosen. Amongst these 35 possibilities, we reject the $\binom{5}{1}=5$ choices where both Alice and Jane are also serving. If Biff and Jacob are not serving, then there are $\binom{7}{5}=21$ ways to choose the remaining 5 members. Again, we reject the $\binom{5}{3}=10$ instances where Alice and Jane are chosen, so the total is $(35-5)+(21-10)=41$.
|
| 9 |
+
2. [3] How many 5-digit numbers $\overline{a b c d e}$ exist such that digits $b$ and $d$ are each the sum of the digits to their immediate left and right? (That is, $b=a+c$ and $d=c+e$.)
|
| 10 |
+
Answer: 330. Note that $a>0$, so that $b>c$, and $e \geq 0$ so that $d \geq c$. Conversely, for each choice of $(b, c, d)$ with $b>c$ and $d \geq c$, there exists a unique pair $(a, e)$ such that $\overline{a b c d e}$ is a number having the desired property. Thus, we compute
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
\sum_{c=0}^{9}(9-c)(10-c)=\sum_{c=0}^{9} c^{2}-19 c+90=330
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
3. [4] Jack, Jill, and John play a game in which each randomly picks and then replaces a card from a standard 52 card deck, until a spades card is drawn. What is the probability that Jill draws the spade? (Jack, Jill, and John draw in that order, and the game repeats if no spade is drawn.)
|
| 17 |
+
Answer: $\frac{\mathbf{1 2}}{\mathbf{3 7}}$. The desired probability is the relative probability that Jill draws the spade. In the first round, Jack, Jill, and John draw a spade with probability $1 / 4,3 / 4 \cdot 1 / 4$, and $(3 / 4)^{2} \cdot 1 / 4$ respectively. Thus, the probability that Jill draws the spade is
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\frac{3 / 4 \cdot 1 / 4}{1 / 4+3 / 4 \cdot 1 / 4+(3 / 4)^{2} \cdot 1 / 4}=\frac{12}{37}
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
4. [4] On the Cartesian grid, Johnny wants to travel from $(0,0)$ to $(5,1)$, and he wants to pass through all twelve points in the set $S=\{(i, j) \mid 0 \leq i \leq 1,0 \leq j \leq 5, i, j \in \mathbb{Z}\}$. Each step, Johnny may go from one point in $S$ to another point in $S$ by a line segment connecting the two points. How many ways are there for Johnny to start at $(0,0)$ and end at $(5,1)$ so that he never crosses his own path?
|
| 24 |
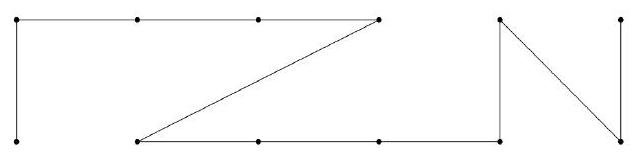
+
|
| 25 |
+
|
| 26 |
+
Answer: 252. Observe that Johnny needs to pass through the points $(0,0),(1,0),(2,0), \ldots,(5,0)$ in that order, and he needs to pass through $(0,1),(1,1),(2,1), \ldots,(5,1)$ in that order, or else he will intersect his own path. Then, the problem is equivalent to interlacing those two sequence together, so that the first term is $(0,0)$ and the final term is $(5,1)$. To do this, we need to select 5 positions out of 10 to have points with $x$-coordinate 0 . Hence the answer is $\binom{10}{5}=252$.
|
| 27 |
+
5. [5] Determine the number of ways to select a positive number of squares on an $8 \times 8$ chessboard such that no two lie in the same row or the same column and no chosen square lies to the left of and below another chosen square.
|
| 28 |
+
|
| 29 |
+
Answer: $12869=\binom{16}{8}$ - 1. If $k$ is the number of squares chosen, then there are $\binom{8}{k}$ ways to choose $k$ columns, and $\binom{8}{k}$ ways to choose $k$ rows, and this would uniquely determine the set of squares selected. Thus the answer is
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\sum_{k=1}^{8}\binom{8}{k}\binom{8}{k}=-1+\sum_{k=0}^{8}\binom{8}{k}\binom{8}{k}=-1+\binom{16}{8}=12869
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
6. [5] Kevin has four red marbles and eight blue marbles. He arranges these twelve marbles randomly, in a ring. Determine the probability that no two red marbles are adjacent.
|
| 36 |
+
Answer: $\frac{7}{\mathbf{7 3}}$. Select any blue marble and consider the remaining eleven marbles, arranged in a line. The proportion of arrangement for which no two red marbles are adjacent will be the same as for the original twelve marbles, arranged in a ring. The total number of ways of arranging 4 red marbles out of 11 is $\binom{11}{4}=330$. To count the number of arrangements such that no two red marbles are adjacent, there must be one red marble between each two would-be adjacent red marbles. Having fixed the positions of three blue marbles we have four blue marbles to play with. So that we can arrange the remaining four marbles is $\binom{8}{4}=70$ ways. This yields a probability of $70 / 330=7 / 33$ as our final answer.
|
| 37 |
+
7. [5] Forty two cards are labeled with the natural numbers 1 through 42 and randomly shuffled into a stack. One by one, cards are taken off of the top of the stack until a card labeled with a prime number is removed. How many cards are removed on average?
|
| 38 |
+
Answer: $\frac{\mathbf{4 3}}{\mathbf{1 4}}$. Note that there are 13 prime numbers amongst the cards. We may view these as separating the remaining 29 cards into 14 groups of nonprimes - those appearing before the first prime, between the first and second, etc. Each of these groups is equally likely to appear first, so 29/14 nonprimes are removed on average. We are done since exactly one prime is always drawn.
|
| 39 |
+
8. [6] A set of six edges of a regular octahedron is called Hamiltonian cycle if the edges in some order constitute a single continuous loop that visits each vertex exactly once. How many ways are there to partition the twelve edges into two Hamiltonian cycles?
|
| 40 |
+

|
| 41 |
+
|
| 42 |
+
Answer: 6. Call the octahedron $A B C D E F$, where $A, B$, and $C$ are opposite $D, E$, and $F$, respectively. Note that each Hamiltonian cycle can be described in terms of the order it visits vertices in exactly 12 different ways. Conversely, listing the six vertices in some order determines a Hamiltonian cycle precisely when no pair of opposite vertices are listed consecutively or first-and-last. Suppose we begin with $A B$. If $D$ is listed third, then the final three letters are $C E F$ or $F E C$. Otherwise, $C$ or $F$ is listed next, and each gives three possibilities for the final three. For example $A B C$ is be followed by $D E F, D F E$, or $E D F$. Thus, there are $6 \cdot 4 \cdot(2+3+3)=192$ listings. These correspond to $192 / 12=16$ Hamiltonian cycles. Finally, the complement of all but four Hamiltonian cycles is a Hamiltonian cycle. For, each vertex has degree four, so is an endpoint of two edges in the complement of a Hamiltonian cycle, so is also a Hamiltonian cycle unless it describes two opposite faces. It follows that there are six pairs of disjoint Hamiltonian cycles.
|
| 43 |
+
9. [7] Let $S$ denote the set of all triples $(i, j, k)$ of positive integers where $i+j+k=17$. Compute
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
\sum_{(i, j, k) \in S} i j k .
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Answer: $11628=\binom{\mathbf{1 9}}{\mathbf{5}}$. We view choosing five objects from a row of 19 objects in an unual way. First, remove two of the chosen objects, the second and fourth, which are not adjacent nor at either end, forming three nonempty groups of consecutive objects. We then have $i, j$, and $k$ choices for the first, third, and fifth objects. Because this is a reversible process taking a triple $(i, j, k)$ to $i j k$ choices, the answer is $\binom{19}{5}=11628$.
|
| 50 |
+
A simple generating functions argument is also possible. Let $s_{n}=\sum_{i+j+k=n} i j k$. Then
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\sum_{n \geq 0} s_{n} x^{n}=\left(\sum_{n \geq 0} n x^{n}\right)^{3}=\left(\frac{x}{(1-x)^{2}}\right)^{3}=\frac{x^{3}}{(1-x)^{6}}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
and so $s_{n}=\left(\binom{6}{n-3}\right)=\binom{n+2}{5}$, yielding $s_{17}=\binom{19}{5}$.
|
| 57 |
+
10. [8] A subset $S$ of the nonnegative integers is called supported if it contains 0 , and $k+8, k+9 \in S$ for all $k \in S$. How many supported sets are there?
|
| 58 |
+
Answer: 1430. Note that every supported set $S$ contains $0,8,9,16,17,18,24-27,32-36,40-45$, $48-54$, and all $n \geq 55$. Now define $\bar{S}:=\mathbb{Z}^{+} \backslash S$, which is a subset of $\{1-7,10-15,19-23,28-$ $31,37,38,39,46,47,55\}$ satisfying the opposite property that $k \in \bar{S} \Longrightarrow k-8, k-9 \in \bar{S}$.
|
| 59 |
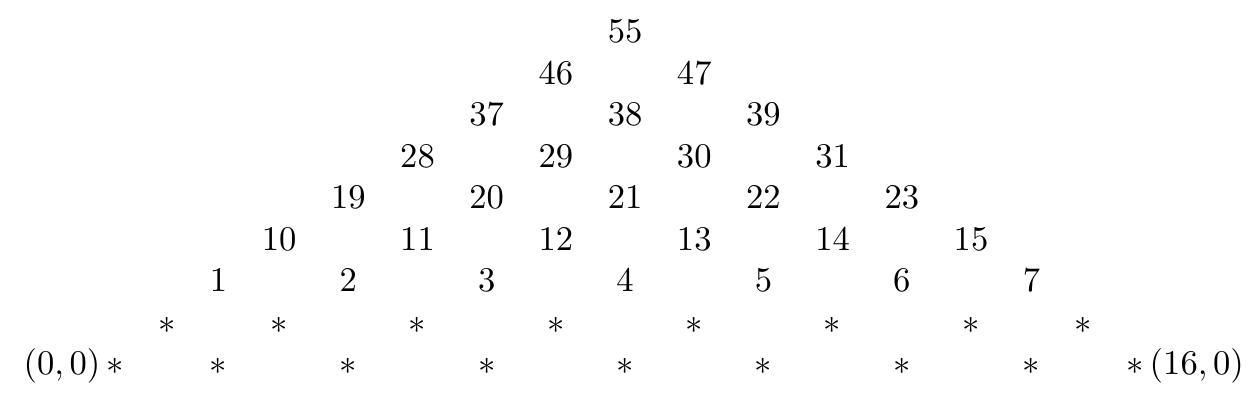
+
|
| 60 |
+
|
| 61 |
+
Consider the above arrangement after removing the numbers not in $\bar{S}$. The condition that $S$ be supported ensures that sets $\bar{S}$ are in bijective correspondence with paths from $(0,0)$ to $(16,0)$ consisting of discrete steps of $\langle 1,1\rangle$ and $\langle 1,-1\rangle$ and lying above the $x$-axis: from the modified version of the above diagram, a unique path passes through the top items left in each column. The number of such paths is the 8th Catalan number, so the answer is $C_{8}=\frac{1}{8+1}\binom{8 \cdot 2}{8}=\frac{12870}{9}=1430$. (Incidentally, 16 choose 8 was computed in an earlier problem.) Without the explicit formula for Catalan numbers, the answer can be computed recursively by filling in the number of ways a path can reach $(16,0)$ from each position in the figure. One works right to left, obtaining the following:
|
| 62 |
+
|
| 63 |
+
| | | | | | | | | 1 | | | | | | | |
|
| 64 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 65 |
+
| | | | | | | | 8 | | 1 | | | | | | |
|
| 66 |
+
| | | | | | | 35 | | 7 | | 1 | | | | | |
|
| 67 |
+
| | | | | | 110 | | 27 | | 6 | | 1 | | | | |
|
| 68 |
+
| | | | | 275 | | 75 | | 20 | | 5 | | 1 | | | |
|
| 69 |
+
| | | | 572 | | 165 | | 48 | | 14 | | 4 | | 1 | | |
|
| 70 |
+
| | | 1001 | | 297 | | 90 | | 28 | | 9 | | 3 | | 1 | |
|
| 71 |
+
| | 1430 | | 429 | | 132 | | 42 | | 14 | | 5 | | 2 | | 1 |
|
| 72 |
+
| 1430 | | 429 | | 132 | | 42 | | 14 | | 5 | | 2 | | 1 | |
|
| 73 |
+
|
| 74 |
+
One can exploit symmetry and, having determined the middle column, sum the squares: $1^{2}+7^{2}+$ $20^{2}+28^{2}+14^{2}=1430$.
|
| 75 |
+
|
HarvardMIT/md/en-102-2007-feb-gen1-solutions.md
ADDED
|
@@ -0,0 +1,36 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
Individual Round: General Test, Part 1
|
| 4 |
+
|
| 5 |
+
1. [2] Michael has 16 white socks, 3 blue socks, and 6 red socks in a drawer. Ever the lazy college student, he has overslept and is late for his favorite team's season-opener. Because he is now in such a rush to get from Harvard to Foxborough, he randomly takes socks from the drawer (one at a time) until he has a pair of the same color. What is the largest number of socks he could possibly withdraw in this fashion?
|
| 6 |
+
Answer: 4. It is possible for him to begin with three socks of different colors, but an instance of the Pigeon Hole Principle is that among any four objects of three types some two are the same type.
|
| 7 |
+
2. [2] Rectangle $A B C D$ has side lengths $A B=12$ and $B C=5$. Let $P$ and $Q$ denote the midpoints of segments $A B$ and $D P$, respectively. Determine the area of triangle $C D Q$.
|
| 8 |
+
Answer: 15. Note that $[C D P]=\frac{1}{2} \cdot 5 \cdot 12=30$, while the area of triangle $C D Q$ is half of the area of triangle $C D P$.
|
| 9 |
+
3. $[3] A, B, C$, and $D$ are points on a circle, and segments $\overline{A C}$ and $\overline{B D}$ intersect at $P$, such that $A P=8$, $P C=1$, and $B D=6$. Find $B P$, given that $B P<D P$.
|
| 10 |
+
Answer: 2. Same as Geometry \#2.
|
| 11 |
+
4. [3] Let $a$ and $b$ be integer solutions to $17 a+6 b=13$. What is the smallest possible positive value for $a-b$ ?
|
| 12 |
+
Answer: 17. First group as $17(a-b)+23 b=13$. Taking this equation modulo 23, we get $-6(a-b) \equiv$ $-10(\bmod 23)$. Since -4 is an inverse of -6 modulo 23 , then we multiply to get $(a-b) \equiv 17(\bmod 23)$. Therefore, the smallest possible positive value for $(a-b)$ is 17 . This can be satisfied by $a=5, b=-12$.
|
| 13 |
+
5. [4] Find the smallest positive integer that is twice a perfect square and three times a perfect cube.
|
| 14 |
+
|
| 15 |
+
Answer: 648. Let $n$ be such a number. If $n$ is divisible by 2 and 3 exactly $e_{2}$ and $e_{3}$ times, then $e_{2}$ is odd and a multiple of three, and $e_{3}$ is even and one more than a multiple of three. The smallest possible exponents are $n_{2}=3$ and $n_{3}=4$. The answer is then $2^{3} \cdot 3^{4}=648$.
|
| 16 |
+
6. [4] The positive integer $n$ is such that the numbers $2^{n}$ and $5^{n}$ start with the same digit when written in decimal notation; determine this common leading digit.
|
| 17 |
+
Answer: 3. Note $1=1^{2}<2^{2}<3^{2}<10<4^{2}<\cdots<9^{2}<10^{2}=100$. Divide $2^{n}$ and $5^{n}$ by 10 repeatedly until each is reduced to a decimal number less than 10 but at least 1 ; call the resulting numbers $x$ and $y$. Since $\left(5^{n}\right)\left(2^{n}\right)=10^{n}$, either $x y=1$ or $x y=10$. Because $2^{n}$ and $5^{n}$ begin with the same digit, $x$ and $y$ are bounded by the same pair of adjacent integers. It follows that either $x=y=1$ or $3 \leq x, y<4$. Because $n$ is positive, neither $2^{n}$ nor $5^{n}$ is a perfect power of 10 , so the former is impossible.
|
| 18 |
+
7. [4] Jack, Jill, and John play a game in which each randomly picks and then replaces a card from a standard 52 card deck, until a spades card is drawn. What is the probability that Jill draws the spade? (Jack, Jill, and John draw in that order, and the game repeats if no spade is drawn.)
|
| 19 |
+
Answer: $\frac{\mathbf{1 2}}{\mathbf{3 7}}$. Same as Combo \#3.
|
| 20 |
+
8. [5] Determine the largest positive integer $n$ such that there exist positive integers $x, y, z$ so that
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
n^{2}=x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x+3 x+3 y+3 z-6
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
Answer: 8. The given equation rewrites as $n^{2}=(x+y+z+1)^{2}+(x+y+z+1)-8$. Writing $r=x+y+z+1$, we have $n^{2}=r^{2}+r-8$. Clearly, one possibility is $n=r=8$, which is realized by $x=y=1, z=6$. On the other hand, for $r>8$, we have $r^{2}<r^{2}+r-8<(r+1)^{2}$.
|
| 27 |
+
9. [6] I have four distinct rings that I want to wear on my right hand hand (five distinct fingers.) One of these rings is a Canadian ring that must be worn on a finger by itself, the rest I can arrange however I want. If I have two or more rings on the same finger, then I consider different orders of rings along the same finger to be different arrangements. How many different ways can I wear the rings on my fingers?
|
| 28 |
+
Answer: 600. First we pick the finger for the Canadian ring. This gives a multiplicative factor of 5 . For distributing the remaining 3 rings among 4 fingers, they can either be all on the same finger ( $4 \cdot 3$ ! ways), all on different fingers $\left(\binom{4}{3} \cdot 3\right.$ ! ways), or two on one finger and one on another $\left(4 \cdot\binom{3}{2} \cdot 2!\cdot 3\right.$ ways.) Therefore, I have $5 \cdot(24+24+72)=600$ choices.
|
| 29 |
+
10. [7] $\alpha_{1}, \alpha_{2}, \alpha_{3}$, and $\alpha_{4}$ are the complex roots of the equation $x^{4}+2 x^{3}+2=0$. Determine the unordered set
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\left\{\alpha_{1} \alpha_{2}+\alpha_{3} \alpha_{4}, \alpha_{1} \alpha_{3}+\alpha_{2} \alpha_{4}, \alpha_{1} \alpha_{4}+\alpha_{2} \alpha_{3}\right\}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
Answer: $\{\mathbf{1} \pm \sqrt{\mathbf{5}}, \mathbf{- 2}\}$. Same as Algebra $\# 9$.
|
| 36 |
+
|
HarvardMIT/md/en-102-2007-feb-gen2-solutions.md
ADDED
|
@@ -0,0 +1,61 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
## Individual Round: General Test, Part 2
|
| 4 |
+
|
| 5 |
+
1. [2] A cube of edge length $s>0$ has the property that its surface area is equal to the sum of its volume and five times its edge length. Compute all possible values of $s$.
|
| 6 |
+
Answer: 1,5. Same as Geometry \#1.
|
| 7 |
+
2. [2] A parallelogram has 3 of its vertices at $(1,2),(3,8)$, and $(4,1)$. Compute the sum of all possible $x$ coordinates of the 4th vertex.
|
| 8 |
+
Answer: 8. There are three possibilities: the 4th vertex must be opposite one of the three given vertices. These three possibilities have as a medial triangle the three given vertices, so the sum of their $x$ coordinates is the same as the sum of the $x$ coordinates of the given triangle.
|
| 9 |
+
3. [3] Compute
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
(Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
| 16 |
+
Answer: 2006. Same as Algebra \#1.
|
| 17 |
+
4. [3] Three brothers Abel, Banach, and Gauss each have portable music players that can share music with each other. Initially, Abel has 9 songs, Banach has 6 songs, and Gauss has 3 songs, and none of these songs are the same. One day, Abel flips a coin to randomly choose one of his brothers and he adds all of that brother's songs to his collection. The next day, Banach flips a coin to randomly choose one of his brothers and he adds all of that brother's collection of songs to his collection. Finally, each brother randomly plays a song from his collection with each song in his collection being equally likely to be chosen. What is the probability that they all play the same song?
|
| 18 |
+
Answer: $\frac{\mathbf{1}}{\mathbf{2 8 8}}$. If Abel copies Banach's songs, this can never happen. Therefore, we consider only the cases where Abel copies Gauss's songs. Since all brothers have Gauss's set of songs, the probability that they play the same song is equivalent to the probability that they independently match whichever song Gauss chooses. Case 1: Abel copies Gauss and Banach copies Gauss (1/4 chance) - The probability of songs matching is then $1 / 12 \cdot 1 / 9$. Case 2: Abel copies Gauss and Banach copies Abel ( $1 / 4$ probability) - The probability of songs matching is then $1 / 12 \cdot 1 / 18$. We add the two probabilities together to get $1 / 4 \cdot 1 / 12 \cdot(1 / 9+1 / 18)=1 / 288$.
|
| 19 |
+
5. [4] A best of 9 series is to be played between two teams. That is, the first team to win 5 games is the winner. One of the teams, the Mathletes, has a $2 / 3$ chance of winning any given game. What is the probability that the winner is determined in the 7th game?
|
| 20 |
+
|
| 21 |
+
Answer: | $\mathbf{2 0}$ |
|
| 22 |
+
| :---: |
|
| 23 |
+
| $\mathbf{8 1}$ | . If the Mathletes are the winners, they must win the 7 th game and have won exactly four of the previous 6 games. The probability of this occurring is
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\left((2 / 3)^{4} \cdot(1 / 3)^{2} \cdot\binom{6}{2}\right) \cdot(2 / 3)
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
Analogously, the other team wins with probability $\left((1 / 3)^{4} \cdot(2 / 3)^{2} \cdot\binom{6}{2}\right) \cdot(1 / 3)$. Summing, the probability is
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\frac{\binom{6}{2} \cdot 2^{2} \cdot\left(2^{3} \cdot 1^{2}+1^{5}\right)}{3^{7}}=\frac{5 \cdot 4}{3^{4}}=\frac{20}{81}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
6. [4] Circle $\omega$ has radius 5 and is centered at $O$. Point $A$ lies outside $\omega$ such that $O A=13$. The two tangents to $\omega$ passing through $A$ are drawn, and points $B$ and $C$ are chosen on them (one on each
|
| 36 |
+
tangent), such that line $B C$ is tangent to $\omega$ and $\omega$ lies outside triangle $A B C$. Compute $A B+A C$ given that $B C=7$.
|
| 37 |
+
Answer: 17. Same as Geometry \#4.
|
| 38 |
+
7. [4] My friend and I are playing a game with the following rules: If one of us says an integer $n$, the opponent then says an integer of their choice between $2 n$ and $3 n$, inclusive. Whoever first says 2007 or greater loses the game, and their opponent wins. I must begin the game by saying a positive integer less than 10 . With how many of them can I guarantee a win?
|
| 39 |
+
Answer: 6. We assume optimal play and begin working backward. I win if I say any number between 1004 and 2006. Thus, by saying such a number, my friend can force a win for himself if I ever say a number between 335 and 1003. Then I win if I say any number between 168 and 334 , because my friend must then say one of the losing numbers just considered. Similarly, I lose by saying 56 through 167 , win by saying 28 through 55 , lose with 10 through 17 , win with 5 through 9 , lose with 2 through 4 , and win with 1 .
|
| 40 |
+
8. [5] Compute the number of sequences of numbers $a_{1}, a_{2}, \ldots, a_{10}$ such that
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\begin{aligned}
|
| 44 |
+
& \text { I. } a_{i}=0 \text { or } 1 \text { for all } i \\
|
| 45 |
+
& \text { II. } a_{i} \cdot a_{i+1}=0 \text { for } i=1,2, \ldots, 9 \\
|
| 46 |
+
& \text { III. } a_{i} \cdot a_{i+2}=0 \text { for } i=1,2, \ldots, 8
|
| 47 |
+
\end{aligned}
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Answer: 60. Call such a sequence "good," and let $A_{n}$ be the number of good sequences of length $n$. Let $a_{1}, a_{2}, \ldots, a_{n}$ be a good sequence. If $a_{1}=0$, then $a_{1}, a_{2}, \ldots, a_{n}$ is a good sequence if and only if $a_{2}, \ldots, a_{n}$ is a good sequence, so there are $A_{n-1}$ of them. If $a_{1}=1$, then we must have $a_{2}=a_{3}=0$, and in this case, $a_{1}, a_{2}, \ldots, a_{n}$ is a good sequence if and only if $a_{4}, a_{5}, \ldots, a_{n}$ is a good sequence, so there are $A_{n-3}$ of them. We thus obtain the recursive relation $A_{n}=A_{n-1}+A_{n-3}$. Note that $A_{1}=2, A_{2}=3, A_{3}=4$. Plugging these into the recursion eventually yields $A_{10}=60$.
|
| 51 |
+
9. [6] Let $A:=\mathbb{Q} \backslash\{0,1\}$ denote the set of all rationals other than 0 and 1. A function $f: A \rightarrow \mathbb{R}$ has the property that for all $x \in A$,
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
f(x)+f\left(1-\frac{1}{x}\right)=\log |x|
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Compute the value of $f(2007)$.
|
| 58 |
+
Answer: $\log (\mathbf{2 0 0 7} / \mathbf{2 0 0 6})$. Same as Algebra \#8.
|
| 59 |
+
10. [7] $A B C D$ is a convex quadrilateral such that $A B=2, B C=3, C D=7$, and $A D=6$. It also has an incircle. Given that $\angle A B C$ is right, determine the radius of this incircle.
|
| 60 |
+
Answer: $\frac{1+\sqrt{13}}{3}$. Same as Geometry $\# 10$.
|
| 61 |
+
|
HarvardMIT/md/en-102-2007-feb-geo-solutions.md
ADDED
|
@@ -0,0 +1,55 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
## Individual Round: Geometry Test
|
| 4 |
+
|
| 5 |
+
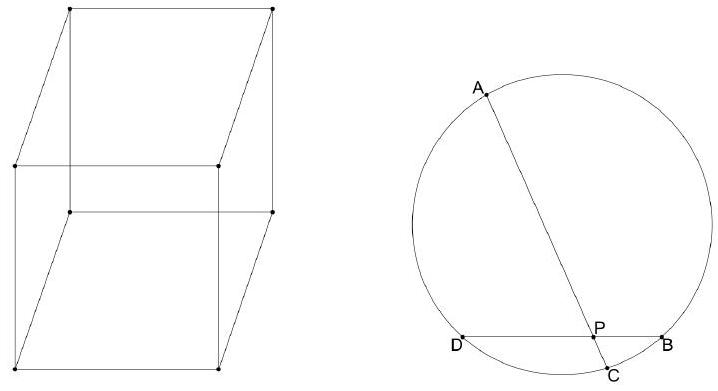
1. [3] A cube of edge length $s>0$ has the property that its surface area is equal to the sum of its volume and five times its edge length. Compute all possible values of $s$.
|
| 6 |
+
Answer: 1,5. The volume of the cube is $s^{3}$ and its surface area is $6 s^{2}$, so we have $6 s^{2}=s^{3}+5 s$, or $0=s^{3}-6 s^{2}+5 s=s(s-1)(s-5)$.
|
| 7 |
+
|
| 8 |
+
2. [3] $A, B, C$, and $D$ are points on a circle, and segments $\overline{A C}$ and $\overline{B D}$ intersect at $P$, such that $A P=8$, $P C=1$, and $B D=6$. Find $B P$, given that $B P<D P$.
|
| 9 |
+
Answer: 2. Writing $B P=x$ and $P D=6-x$, we have that $B P<3$. Power of a point at $P$ gives $A P \cdot P C=B P \cdot P D$ or $8=x(6-x)$. This can be solved for $x=2$ and $x=4$, and we discard the latter.
|
| 10 |
+
3. [4] Circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ are centered at $M, N$, and $O$, respectively. The points of tangency between $\omega_{2}$ and $\omega_{3}, \omega_{3}$ and $\omega_{1}$, and $\omega_{1}$ and $\omega_{2}$ are tangent at $A, B$, and $C$, respectively. Line $M O$ intersects $\omega_{3}$ and $\omega_{1}$ again at $P$ and $Q$ respectively, and line $A P$ intersects $\omega_{2}$ again at $R$. Given that $A B C$ is an equilateral triangle of side length 1 , compute the area of $P Q R$.
|
| 11 |
+
Answer: $\mathbf{2 \sqrt { 3 }}$. Note that $O N M$ is an equilateral triangle of side length 2, so $m \angle B P A=m \angle B O A / 2=$ $\pi / 6$. Now $B P A$ is a $30-60-90$ triangle with short side length 1 , so $A P=\sqrt{3}$. Now $A$ and $B$ are the midpoints of segments $P R$ and $P Q$, so $[P Q R]=\frac{P R}{P A} \cdot \frac{P Q}{P B}[P B A]=2 \cdot 2[P B A]=2 \sqrt{3}$.
|
| 12 |
+

|
| 13 |
+
4. [4] Circle $\omega$ has radius 5 and is centered at $O$. Point $A$ lies outside $\omega$ such that $O A=13$. The two tangents to $\omega$ passing through $A$ are drawn, and points $B$ and $C$ are chosen on them (one on each tangent), such that line $B C$ is tangent to $\omega$ and $\omega$ lies outside triangle $A B C$. Compute $A B+A C$ given that $B C=7$.
|
| 14 |
+
|
| 15 |
+
Answer: 17. Let $T_{1}, T_{2}$, and $T_{3}$ denote the points of tangency of $A B, A C$, and $B C$ with $\omega$, respectively. Then $7=B C=B T_{3}+T_{3} C=B T_{1}+C T_{2}$. By Pythagoras, $A T_{1}=A T_{2}=\sqrt{13^{2}-5^{2}}=12$. Now note that $24=A T_{1}+A T_{2}=A B+B T_{1}+A C+C T_{2}=A B+A C+7$.
|
| 16 |
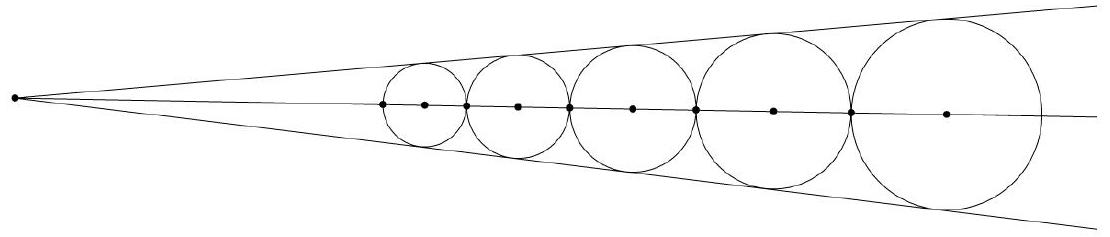
+
5. [5] Five marbles of various sizes are placed in a conical funnel. Each marble is in contact with the adjacent marble(s). Also, each marble is in contact all around the funnel wall. The smallest marble has a radius of 8 , and the largest marble has a radius of 18 . What is the radius of the middle marble?
|
| 17 |
+
Answer: 12. One can either go through all of the algebra, find the slope of the funnel wall and go from there to figure out the radius of the middle marble. Or one can notice that the answer will just be the geometric mean of 18 and 8 which is 12 .
|
| 18 |
+
|
| 19 |
+
6. [5] Triangle $A B C$ has $\angle A=90^{\circ}$, side $B C=25, A B>A C$, and area 150. Circle $\omega$ is inscribed in $A B C$, with $M$ its point of tangency on $A C$. Line $B M$ meets $\omega$ a second time at point $L$. Find the length of segment $B L$.
|
| 20 |
+
|
| 21 |
+
Answer: $4 \mathbf{4 5} \sqrt{\mathbf{1 7} / 17}$. Let $D$ be the foot of the altitude from $A$ to side $B C$. The length of $A D$ is $2 \cdot 150 / 25=12$. Triangles $A D C$ and $B D A$ are similar, so $C D \cdot D B=A D^{2}=144 \Rightarrow B D=16$ and $C D=9 \Rightarrow A B=20$ and $A C=15$. Using equal tangents or the formula inradius as area divided by semiperimeter, we can find the radius of $\omega$ to be 5 . Now, let $N$ be the tangency point of $\omega$ on $A B$. By power of a point, we have $B L \cdot B M=B N^{2}$. Since the center of $\omega$ together with $M, A$, and $N$ determines a square, $B N=15$ and $B M=5 \sqrt{17}$, and we have $B L=45 \sqrt{17} / 17$.
|
| 22 |
+

|
| 23 |
+
7. [5] Convex quadrilateral $A B C D$ has sides $A B=B C=7, C D=5$, and $A D=3$. Given additionally that $m \angle A B C=60^{\circ}$, find $B D$.
|
| 24 |
+
Answer: 8. Triangle $A B C$ is equilateral, so $A C=7$ as well. Now the law of cosines shows that $m \angle C D A=120^{\circ}$; i.e., $A B C D$ is cyclic. Ptolemy's theorem now gives $A C \cdot B D=A B \cdot C D+A D \cdot B C$, or simply $B D=C D+A D=8$.
|
| 25 |
+
8. [6] $A B C D$ is a convex quadrilateral such that $A B<A D$. The diagonal $\overline{A C}$ bisects $\angle B A D$, and $m \angle A B D=130^{\circ}$. Let $E$ be a point on the interior of $\overline{A D}$, and $m \angle B A D=40^{\circ}$. Given that $B C=$ $C D=D E$, determine $m \angle A C E$ in degrees.
|
| 26 |
+
|
| 27 |
+
Answer: 55 ${ }^{\circ}$. First, we check that $A B C D$ is cyclic. Reflect $B$ over $\overline{A C}$ to $B^{\prime}$ on $\overline{A D}$, and note that $B^{\prime} C=C D$. Therefore, $m \angle A D C=m \angle B^{\prime} D C=m \angle C B^{\prime} D=180^{\circ}-m \angle A B^{\prime} C=180^{\circ}-m \angle C B A$. Now $m \angle C B D=m \angle C A D=20^{\circ}$ and $m \angle A D C=180^{\circ}-m \angle C B A=30^{\circ}$. Triangle $C D E$ is isosceles, so $m \angle C E D=75^{\circ}$ and $m \angle A E C=105^{\circ}$. It follows that $m \angle E C A=180^{\circ}-m \angle A E C-m \angle C A E=55^{\circ}$.
|
| 28 |
+
|
| 29 |
+
9. [7] $\triangle A B C$ is right angled at $A . D$ is a point on $A B$ such that $C D=1 . A E$ is the altitude from $A$ to $B C$. If $B D=B E=1$, what is the length of $A D$ ?
|
| 30 |
+
Answer: $\sqrt[3]{2}-1$. Let $A D=x$, angle $A B C=t$. We also have $\angle B C A=90-t$ and $\angle D C A=90-2 t$ so that $\angle A D C=2 t$. Considering triangles $A B E$ and $A D C$, we obtain, respectively,
|
| 31 |
+
$\cos (t)=1 /(1+x)$ and $\cos (2 t)=x$. By the double angle formula we get, $(1+x)^{3}=2$.
|
| 32 |
+
Alternatively, construct $M$, the midpoint of segment $B C$, and note that triangles $A B C, E B A$, and $M B D$ are similar. Thus, $A B^{2}=B C \cdot B E=B C$. In particular,
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
A B=\frac{B C}{A B}=\frac{A B}{B E}=\frac{B D}{B M}=\frac{2 B D}{B C}=\frac{2}{A B^{2}}
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
from which $A B=\sqrt[3]{2}$ and $A D=\sqrt[3]{2}-1$.
|
| 39 |
+
10. [8] $A B C D$ is a convex quadrilateral such that $A B=2, B C=3, C D=7$, and $A D=6$. It also has an incircle. Given that $\angle A B C$ is right, determine the radius of this incircle.
|
| 40 |
+

|
| 41 |
+
|
| 42 |
+
Answer: $\frac{1+\sqrt{13}}{\mathbf{3}}$. Note that $A C^{2}=A B^{2}+B C^{2}=13=C D^{2}-D A^{2}$. It follows that $\angle D A C$ is right, and so
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
[A B C D]=[A B C]+[D A C]=2 \cdot 3 / 2+6 \cdot \sqrt{13} / 2=3+3 \sqrt{13}
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
On the other hand, if $I$ denotes the incenter and $r$ denotes the inradius,
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
[A B C D]=[A I B]+[B I C]+[C I D]+[D I A]=A B \cdot r / 2+B C \cdot r / 2+C D \cdot r / 2+D A \cdot r / 2=9 r
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Therefore, $r=(3+3 \sqrt{13}) / 9=\frac{1+\sqrt{13}}{3}$.
|
| 55 |
+
|
HarvardMIT/md/en-102-2007-feb-guts-solutions.md
ADDED
|
@@ -0,0 +1,391 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
Guts Round
|
| 4 |
+
|
| 5 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 6 |
+
Note that there are just 36 problems in the Guts round this year.
|
| 7 |
+
|
| 8 |
+
1. [5] Define the sequence of positive integers $a_{n}$ recursively by $a_{1}=7$ and $a_{n}=7^{a_{n-1}}$ for all $n \geq 2$. Determine the last two digits of $a_{2007}$.
|
| 9 |
+
Answer: 43. Note that the last two digits of $7^{4}$ are 01. Also, $a_{2006}=7^{a_{2005}}=(-1)^{a_{2005}}=-1=3$ $(\bmod 4)$ since $a_{2005}$ is odd. Therefore, $a_{2007}=7^{a_{2006}}=7^{3}=43(\bmod 100)$.
|
| 10 |
+
2. [5] A candy company makes 5 colors of jellybeans, which come in equal proportions. If I grab a random sample of 5 jellybeans, what is the probability that I get exactly 2 distinct colors?
|
| 11 |
+
Answer: $\frac{\mathbf{1 2}}{\mathbf{1 2 5}}$. There are $\binom{5}{2}=10$ possible pairs of colors. Each pair of colors contributes $2^{5}-2=30$ sequences of beans that use both colors. Thus, the answer is $10 \cdot 30 / 5^{5}=12 / 125$.
|
| 12 |
+
3. [5] The equation $x^{2}+2 x=i$ has two complex solutions. Determine the product of their real parts.
|
| 13 |
+
|
| 14 |
+
Answer: $\frac{1-\sqrt{2}}{\mathbf{2}}$. Complete the square by adding 1 to each side. Then $(x+1)^{2}=1+i=e^{\frac{i \pi}{4}} \sqrt{2}$, so $x+1= \pm e^{\frac{i \pi}{8}} \sqrt[4]{2}$. The desired product is then
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
\left(-1+\cos \left(\frac{\pi}{8}\right) \sqrt[4]{2}\right)\left(-1-\cos \left(\frac{\pi}{8}\right) \sqrt[4]{2}\right)=1-\cos ^{2}\left(\frac{\pi}{8}\right) \sqrt{2}=1-\frac{\left(1+\cos \left(\frac{\pi}{4}\right)\right)}{2} \sqrt{2}=\frac{1-\sqrt{2}}{2}
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 21 |
+
4. [6] A sequence consists of the digits $122333444455555 \ldots$ such that the each positive integer $n$ is repeated $n$ times, in increasing order. Find the sum of the 4501 st and 4052 nd digits of this sequence.
|
| 22 |
+
Answer: 13. Note that $n$ contributes $n \cdot d(n)$ digits, where $d(n)$ is the number of digits of $n$. Then because $1+\cdots+99=4950$, we know that the digits of interest appear amongst copies of two digit numbers. Now for $10 \leq n \leq 99$, the number of digits in the subsequence up to the last copy of $n$ is
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
1+2+3+\cdots+9+2 \cdot(10+\cdots+n)=2 \cdot(1+\cdots+n)-45=n^{2}+n-45
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
Since $67^{2}+67-45=4511$, the two digits are 6 and 7 in some order, so have sum 13 .
|
| 29 |
+
5. [6] Compute the largest positive integer such that $\frac{2007!}{2007^{n}}$ is an integer.
|
| 30 |
+
|
| 31 |
+
Answer: 9. Note that $2007=3^{2} \cdot 223$. Using the fact that the number of times a prime $p$ divides $n$ ! is given by
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\left\lfloor\frac{n}{p^{3}}\right\rfloor+\cdots
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
it follows that the answer is 9 .
|
| 38 |
+
6. [6] There are three video game systems: the Paystation, the WHAT, and the ZBoz2 $\pi$, and none of these systems will play games for the other systems. Uncle Riemann has three nephews: Bernoulli, Galois, and Dirac. Bernoulli owns a Paystation and a WHAT, Galois owns a WHAT and a ZBoz2r, and Dirac owns a ZBoz2 $\pi$ and a Paystation. A store sells 4 different games for the Paystation, 6 different games for the WHAT, and 10 different games for the ZBoz2 $\pi$. Uncle Riemann does not understand the
|
| 39 |
+
difference between the systems, so he walks into the store and buys 3 random games (not necessarily distinct) and randomly hands them to his nephews. What is the probability that each nephew receives a game he can play?
|
| 40 |
+
Answer: $\frac{\mathbf{7}}{\mathbf{2 5}}$. Since the games are not necessarily distinct, probabilities are independent. Multiplying the odds that each nephew receives a game he can play, we get $10 / 20 \cdot 14 / 20 \cdot 16 / 20=7 / 25$.
|
| 41 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 42 |
+
7. [7] A student at Harvard named Kevin
|
| 43 |
+
|
| 44 |
+
Was counting his stones by 11
|
| 45 |
+
He messed up $n$ times
|
| 46 |
+
And instead counted 9s
|
| 47 |
+
And wound up at 2007.
|
| 48 |
+
|
| 49 |
+
How many values of $n$ could make this limerick true?
|
| 50 |
+
Answer: 21. The mathematical content is that $9 n+11 k=2007$, for some nonnegative integers $n$ and $k$. As $2007=9 \cdot 223, k$ must be divisible by 9 . Using modulo 11 , we see that $n$ is 3 more than a multiple of 11 . Thus, the possibilities are $n=223,212,201, \ldots, 3$, which are 21 in number.
|
| 51 |
+
8. [7] A circle inscribed in a square,
|
| 52 |
+
|
| 53 |
+
Has two chords as shown in a pair.
|
| 54 |
+
It has radius 2,
|
| 55 |
+
And $P$ bisects $T U$.
|
| 56 |
+
The chords' intersection is where?
|
| 57 |
+
|
| 58 |
+
|
| 59 |
+
Answer the question by giving the distance of the point of intersection from the center of the circle.
|
| 60 |
+
Answer: $\sqrt[2]{\mathbf{2} \sqrt{\mathbf{2}}-\mathbf{2} .}$ Let $O B$ intersect the circle at $X$ and $Y$, and the chord $P M$ at $Q$, such that $O$ lies between $X$ and $Q$. Then $M N X Q$ is a parallelogram. For, $O B \| N M$ by homothety at $C$ and $P M \| N X$ because $M N X P$ is an isoceles trapezoid. It follows that $Q X=M N$. Considering that the center of the circle together with points $M, C$, and $N$ determines a square of side length 2 , it follows that $M N=2 \sqrt{2}$, so the answer is $2 \sqrt{2}-2$.
|
| 61 |
+
9. [7] I ponder some numbers in bed,
|
| 62 |
+
|
| 63 |
+
All products of three primes I've said,
|
| 64 |
+
Apply $\phi$ they're still fun:
|
| 65 |
+
now Elev'n cubed plus one.
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
\begin{gathered}
|
| 69 |
+
n=37^{2} \cdot 3 \ldots \\
|
| 70 |
+
\phi(n)= \\
|
| 71 |
+
11^{3}+1 ?
|
| 72 |
+
\end{gathered}
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
What numbers could be in my head?
|
| 76 |
+
Answer: 2007, 2738,3122. The numbers expressible as a product of three primes are each of the form $p^{3}, p^{2} q$, or $p q r$, where $p, q$, and $r$ are distinct primes. Now, $\phi\left(p^{3}\right)=p^{2}(p-1), \phi\left(p^{2} q\right)=$ $p(p-1)(q-1)$, and $\phi(p q r)=(p-1)(q-1)(r-1)$. We require $11^{3}+1=12 \cdot 111=2^{2} 3^{2} 37$. The first case is easy to rule out, since necessarily $p=2$ or $p=3$, which both fail. The second case requires $p=2, p=3$, or $p=37$. These give $q=667,223$, and 2 , respectively. As $667=23 \cdot 29$, we reject $2^{2} \cdot 667$, but $3^{2} 233=2007$ and $37^{2} 2=2738$. In the third case, exactly one of the primes is 2 , since all other primes are odd. So say $p=2$. There are three possibilities for $(q, r):\left(2 \cdot 1+1,2 \cdot 3^{2} \cdot 37+1\right),(2 \cdot 3+1,2 \cdot 3 \cdot 37+1)$, and $\left(2 \cdot 3^{2}+1,2 \cdot 37+1\right)$. Those are $(3,667),(7,223)$, and $(19,75)$, respectively, of which only $(7,223)$ is a pair of primes. So the third and final possibility is $2 \cdot 7 \cdot 223=3122$.
|
| 77 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 78 |
+
10. [8] Let $A_{12}$ denote the answer to problem 12. There exists a unique triple of digits $(B, C, D)$ such that $10>A_{12}>B>C>D>0$ and
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\overline{A_{12} B C D}-\overline{D C B A_{12}}=\overline{B D A_{12} C}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
where $\overline{A_{12} B C D}$ denotes the four digit base 10 integer. Compute $B+C+D$.
|
| 85 |
+
Answer: 11. Since $D<A_{12}$, when $A$ is subtracted from $D$ we must carry over from $C$. Thus, $D+10-\overline{A_{12}}=C$. Next, since $C-1<C<B$, we must carry over from the tens digit, so that $(C-1+10)-B=A_{12}$. Now $B>C$ so $B-1 \geq C$, and $(B-1)-C=D$. Similarly, $A_{12}-D=B$. Solving this system of four equations produces $\left(A_{12}, B, C, D\right)=(7,6,4,1)$.
|
| 86 |
+
11. [8] Let $A_{10}$ denote the answer to problem 10. Two circles lie in the plane; denote the lengths of the internal and external tangents between these two circles by $x$ and $y$, respectively. Given that the product of the radii of these two circles is $15 / 2$, and that the distance between their centers is $A_{10}$, determine $y^{2}-x^{2}$.
|
| 87 |
+
Answer: 30. Suppose the circles have radii $r_{1}$ and $r_{2}$. Then using the tangents to build right triangles, we have $x^{2}+\left(r_{1}+r_{2}\right)^{2}=A_{10}^{2}=y^{2}+\left(r_{1}-r_{2}\right)^{2}$. Thus, $y^{2}-x^{2}=\left(r_{1}+r_{2}\right)^{2}-\left(r_{1}-r_{2}\right)^{2}=$ $4 r_{1} r_{2}=30$.
|
| 88 |
+
|
| 89 |
+
12. [8] Let $A_{11}$ denote the answer to problem 11. Determine the smallest prime $p$ such that the arithmetic sequence $p, p+A_{11}, p+2 A_{11}, \ldots$ begins with the largest possible number of primes.
|
| 90 |
+
Answer: 7. First, note that the maximal number of initial primes is bounded above by the smallest prime not dividing $A_{11}$, with equality possible only if $p$ is this prime. For, if $q$ is the smallest prime not dividing $A_{11}$, then the first $q$ terms of the arithmetic sequence determine a complete residue class modulo $q$, and the multiple of $q$ is nonprime unless it equals $q$. If $q<A_{11}$, then $q$ must appear first in the sequence, and thus divide the $(q+1)$ st term. If $q>A_{11}$, then $A_{11}=2$ and $q=3$ by Bertrand's postulate, so $q$ must appear first by inspection.
|
| 91 |
+
Now since $A_{11}=30$, the bound is 7 . In fact, $7,37,67,97,127$, and 157 are prime, but 187 is not. Then on the one hand, our bound of seven initial primes is not realizable. On the other hand, this implies an upper bound of six, and this bound is achieved by $p=7$. Smaller primes $p$ yield only one initial prime, so 7 is the answer.
|
| 92 |
+
|
| 93 |
+
Remarks. A number of famous theorems are concerned with the distribution of prime numbers. For two relatively prime positive integers $a$ and $b$, the arithmetic progression $a, a+b, a+2 b, \ldots$ contains infinitely many primes, a result known as Dirichlet's theorem. It was shown recently (c. 2004) that there exist arbitrarily long arithmetic progressions consisting of primes only. Bertrand's postulate states that for any positive integer $n$, there exists a prime $p$ such that $n<p \leq 2 n$. This is an unfortunate misnomer, as the statement is known to be true. As with many theorems concerning the distributions of primes, these results are easily stated in elementary terms, concealing elaborate proofs.
|
| 94 |
+
|
| 95 |
+
There is just one triple of possible $\left(A_{10}, A_{11}, A_{12}\right)$ of answers to these three problems. Your team will receive credit only for answers matching these. (So, for example, submitting a wrong answer for problem 11 will not alter the correctness of your answer to problem 12.)
|
| 96 |
+
13. [9] Determine the largest integer $n$ such that $7^{2048}-1$ is divisible by $2^{n}$.
|
| 97 |
+
|
| 98 |
+
Answer: 14. We have
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
7^{2048}-1=(7-1)(7+1)\left(7^{2}+1\right)\left(7^{4}+1\right) \cdots\left(7^{1024}+1\right)
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
In the expansion, the eleven terms other than $7+1$ are divisible by 2 exactly once, as can be checked easily with modulo 4 .
|
| 105 |
+
14. [9] We are given some similar triangles. Their areas are $1^{2}, 3^{2}, 5^{2} \ldots$, and $49^{2}$. If the smallest triangle has a perimeter of 4 , what is the sum of all the triangles' perimeters?
|
| 106 |
+
Answer: 2500. Because the triangles are all similar, they all have the same ratio of perimeter squared to area, or, equivalently, the same ratio of perimeter to the square root of area. Because the latter ratio is 4 for the smallest triangle, it is 4 for all the triangles, and thus their perimeters are $4 \cdot 1,4 \cdot 3,4 \cdot 5, \ldots, 4 \cdot 49$, and the sum of these numbers is $\left[4(1+3+5+\cdots+49)=4\left(25^{2}\right)=2500\right.$.
|
| 107 |
+
15. [9] Points $A, B$, and $C$ lie in that order on line $\ell$, such that $A B=3$ and $B C=2$. Point $H$ is such that $C H$ is perpendicular to $\ell$. Determine the length $C H$ such that $\angle A H B$ is as large as possible.
|
| 108 |
+
|
| 109 |
+
|
| 110 |
+
Answer: $\sqrt{\sqrt{\mathbf{1 0}}}$. Let $\omega$ denote the circumcircle of triangle $A B H$. Since $A B$ is fixed, the smaller the radius of $\omega$, the bigger the angle $A H B$. If $\omega$ crosses the line $C H$ in more than one point, then there exists a smaller circle that goes through $A$ and $B$ that crosses $C H$ at a point $H^{\prime}$. But angle $A H^{\prime} B$ is greater than $A H B$, contradicting our assumption that $H$ is the optimal spot. Thus the circle $\omega$ crosses the line $C H$ at exactly one spot: ie, $\omega$ is tangent to $C H$ at $H$. By Power of a Point, $C H^{2}=C A C B=5 \cdot 2=10$, so $C H=\sqrt{10}$.
|
| 111 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 112 |
+
16. [10] Let $A B C$ be a triangle with $A B=7, B C=9$, and $C A=4$. Let $D$ be the point such that $A B \| C D$ and $C A \| B D$. Let $R$ be a point within triangle $B C D$. Lines $\ell$ and $m$ going through $R$ are parallel to $C A$ and $A B$ respectively. Line $\ell$ meets $A B$ and $B C$ at $P$ and $P^{\prime}$ respectively, and $m$ meets $C A$ and $B C$ at $Q$ and $Q^{\prime}$ respectively. If $S$ denotes the largest possible sum of the areas of triangles $B P P^{\prime}, R P^{\prime} Q^{\prime}$, and $C Q Q^{\prime}$, determine the value of $S^{2}$.
|
| 113 |
+
|
| 114 |
+
|
| 115 |
+
Answer: 180. Let $R^{\prime}$ denote the intersection of the lines through $Q^{\prime}$ and $P^{\prime}$ parallel to $\ell$ and $m$ respectively. Then $\left[R P^{\prime} Q^{\prime}\right]=\left[R^{\prime} P^{\prime} Q^{\prime}\right]$. Triangles $B P P^{\prime}, R^{\prime} P^{\prime} Q^{\prime}$, and $C Q Q^{\prime}$ lie in $A B C$ without overlap, so that on the one hand, $S \leq A B C$. On the other, this bound is realizable by taking $R$ to be a vertex of triangle $B C D$. We compute the square of the area of $A B C$ to be $10 \cdot(10-9) \cdot(10-7) \cdot(10-4)=$ 180.
|
| 116 |
+
17. [10] During the regular season, Washington Redskins achieve a record of 10 wins and 6 losses. Compute the probability that their wins came in three streaks of consecutive wins, assuming that all possible arrangements of wins and losses are equally likely. (For example, the record LLWWWWWLWWLWWWLL contains three winning streaks, while WWWWWWWLLLLLLWWW has just two.)
|
| 117 |
+
|
| 118 |
+
Answer: \( \frac{45}{286} \). Suppose the winning streaks consist of \( w_1, w_2, \) and \( w_3 \) wins, in chronological order, where the first winning streak is preceded by $l_{0}$ consecutive losses and the $i$ winning streak is immediately succeeded by $l_{i}$ losses. Then $w_{1}, w_{2}, w_{3}, l_{1}, l_{2}>0$ are positive and $l_{0}, l_{3} \geq 0$ are nonnegative. The equations
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
w_{1}+w_{2}+w_{3}=10 \quad \text { and } \quad\left(l_{0}+1\right)+l_{1}+l_{2}+\left(l_{3}+1\right)=8
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
are independent, and have $\binom{9}{2}$ and $\binom{7}{3}$ solutions, respectively. It follows that the answer is
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\frac{\binom{9}{2}\binom{7}{3}}{\binom{16}{6}}=\frac{315}{2002}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
18. [10] Convex quadrilateral $A B C D$ has right angles $\angle A$ and $\angle C$ and is such that $A B=B C$ and $A D=C D$. The diagonals $A C$ and $B D$ intersect at point $M$. Points $P$ and $Q$ lie on the circumcircle of triangle $A M B$ and segment $C D$, respectively, such that points $P, M$, and $Q$ are collinear. Suppose that $m \angle A B C=160^{\circ}$ and $m \angle Q M C=40^{\circ}$. Find $M P \cdot M Q$, given that $M C=6$.
|
| 131 |
+
|
| 132 |
+
|
| 133 |
+
Answer: 36. Note that $m \angle Q P B=m \angle M P B=m \angle M A B=m \angle C A B=\angle B C A=\angle C D B$. Thus, $M P \cdot M Q=M B \cdot M D$. On the other hand, segment $C M$ is an altitude of right triangle $B C D$, so $M B \cdot M D=M C^{2}=36$.
|
| 134 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 135 |
+
19. [10] Define $x \star y=\frac{\sqrt{x^{2}+3 x y+y^{2}-2 x-2 y+4}}{x y+4}$. Compute
|
| 136 |
+
|
| 137 |
+
$$
|
| 138 |
+
((\cdots((2007 \star 2006) \star 2005) \star \cdots) \star 1) .
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
Answer: $\frac{\sqrt{\mathbf{1 5}}}{\mathbf{9}}$. Note that $x \star 2=\frac{\sqrt{x^{2}+6 x+4-2 x-4+4}}{2 x+4}=\frac{\sqrt{(x+2)^{2}}}{2(x+2)}=\frac{1}{2}$ for $x>-2$. Because $x \star y>0$ if $x, y>0$, we need only compute $\frac{1}{2} \star 1=\frac{\sqrt{\frac{1}{4}+\frac{3}{2}+1-3+4}}{\frac{1}{2}+4}=\frac{\sqrt{15}}{9}$.
|
| 142 |
+
20. [10] For $a$ a positive real number, let $x_{1}, x_{2}, x_{3}$ be the roots of the equation $x^{3}-a x^{2}+a x-a=0$. Determine the smallest possible value of $x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}$.
|
| 143 |
+
Answer: -4 . Note that $x_{1}+x_{2}+x_{3}=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a$. Then
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
\begin{aligned}
|
| 147 |
+
& x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}=\left(x_{1}+x_{2}+x_{3}\right)\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)\right) \\
|
| 148 |
+
& \quad=\left(x_{1}+x_{2}+x_{3}\right)\left(\left(x_{1}+x_{2}+x_{3}\right)^{2}-3\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)\right)=a \cdot\left(a^{2}-3 a\right)=a^{3}-3 a^{2}
|
| 149 |
+
\end{aligned}
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
The expression is negative only where $0<a<3$, so we need only consider these values of $a$. Finally, AM-GM gives $\sqrt[3]{(6-2 a)(a)(a)} \leq \frac{(6-2 a)+a+a}{3}=2$, with equality where $a=2$, and this rewrites as $(a-3) a^{2} \geq-4$.
|
| 153 |
+
21. [10] Bob the bomb-defuser has stumbled upon an active bomb. He opens it up, and finds the red and green wires conveniently located for him to cut. Being a seasoned member of the bomb-squad, Bob quickly determines that it is the green wire that he should cut, and puts his wirecutters on the green wire. But just before he starts to cut, the bomb starts to count down, ticking every second. Each time the bomb ticks, starting at time $t=15$ seconds, Bob panics and has a certain chance to move his wirecutters to the other wire. However, he is a rational man even when panicking, and has a $\frac{1}{2 t^{2}}$ chance of switching wires at time $t$, regardless of which wire he is about to cut. When the bomb ticks at $t=1$, Bob cuts whatever wire his wirecutters are on, without switching wires. What is the probability that Bob cuts the green wire?
|
| 154 |
+
Answer: $\frac{\mathbf{2 3}}{\mathbf{3 0}}$. Suppose Bob makes $n$ independent decisions, with probabilities of switching $p_{1}, p_{2}, \ldots, p_{n}$. Then in the expansion of the product
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
P(x)=\left(p_{1}+\left(1-p_{1}\right) x\right)\left(p_{2}+\left(1-p_{2}\right) x\right) \cdots\left(p_{n}+\left(1-p_{n}\right) x\right)
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
the sum of the coefficients of even powers of $x$ gives the probability that Bob makes his original decision. This is just $(P(1)+P(-1)) / 2$, so the probability is just
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
\frac{1+\left(1-\frac{1}{1515}\right)\left(1-\frac{1}{1414}\right) \cdots\left(1-\frac{1}{22}\right)}{2}=\frac{1+\frac{1416 \frac{1315}{1515} 1414}{\cdots \frac{13}{22}}}{2}=\frac{1+\frac{8}{15}}{2}=\frac{23}{30} .
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 167 |
+
22. [12] The sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined by $a_{n+2}=7 a_{n+1}-a_{n}$ for positive integers $n$ with initial values $a_{1}=1$ and $a_{2}=8$. Another sequence, $\left\{b_{n}\right\}$, is defined by the rule $b_{n+2}=3 b_{n+1}-b_{n}$ for positive integers $n$ together with the values $b_{1}=1$ and $b_{2}=2$. Find $\operatorname{gcd}\left(a_{5000}, b_{501}\right)$.
|
| 168 |
+
Answer: 89. We show by induction that $a_{n}=F_{4 n-2}$ and $b_{n}=F_{2 n-1}$, where $F_{k}$ is the $k$ th Fibonacci number. The base cases are clear. As for the inductive steps, note that
|
| 169 |
+
|
| 170 |
+
$$
|
| 171 |
+
F_{k+2}=F_{k+1}+F_{k}=2 F_{k}+F_{k-1}=3 F_{k}-F_{k-2}
|
| 172 |
+
$$
|
| 173 |
+
|
| 174 |
+
and
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
F_{k+4}=3 F_{k+2}-F_{k}=8 F_{k}+3 F_{k-2}=7 F_{k}-F_{k-4}
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
We wish to compute the greatest common denominator of $F_{19998}$ and $F_{1001}$. The Fibonacci numbers satisfy the property that $\operatorname{gcd}\left(F_{m}, F_{n}\right)=F_{\operatorname{gcd}(m, n)}$, which can be proven by noting that they are periodic modulo any positive integer. So since $\operatorname{gcd}(19998,1001)=11$, the answer is $F_{11}=89$.
|
| 181 |
+
23. [12] In triangle $A B C, \angle A B C$ is obtuse. Point $D$ lies on side $A C$ such that $\angle A B D$ is right, and point $E$ lies on side $A C$ between $A$ and $D$ such that $B D$ bisects $\angle E B C$. Find $C E$, given that $A C=35, B C=7$, and $B E=5$.
|
| 182 |
+

|
| 183 |
+
|
| 184 |
+
Answer: 10. Reflect $A$ and $E$ over $B D$ to $A^{\prime}$ and $E^{\prime}$ respectively. Note that the angle conditions show that $A^{\prime}$ and $E^{\prime}$ lie on $A B$ and $B C$ respectively. $B$ is the midpoint of segment $A A^{\prime}$ and $C E^{\prime}=$ $B C-B E^{\prime}=2$. Menelaus' theorem now gives
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
\frac{C D}{D A} \cdot \frac{A A^{\prime}}{A^{\prime} B} \cdot \frac{B E^{\prime}}{E^{\prime} C}=1
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
from which $D A=5 C D$ or $C D=A C / 6$. By the angle bisector theorem, $D E=5 C D / 7$, so that $C E=12 C D / 7=10$.
|
| 191 |
+
24. [12] Let $x, y, n$ be positive integers with $n>1$. How many ordered triples $(x, y, n)$ of solutions are there to the equation $x^{n}-y^{n}=2^{100}$ ?
|
| 192 |
+
Answer: 49. Break all possible values of $n$ into the four cases: $n=2, n=4, n>4$ and $n$ odd. By Fermat's theorem, no solutions exist for the $n=4$ case because we may write $y^{4}+\left(2^{25}\right)^{4}=x^{4}$.
|
| 193 |
+
We show that for $n$ odd, no solutions exist to the more general equation $x^{n}-y^{n}=2^{k}$ where $k$ is a positive integer. Assume otherwise for contradiction's sake, and suppose on the grounds of well ordering that $k$ is the least exponent for which a solution exists. Clearly $x$ and $y$ must both be even or both odd. If both are odd, we have $(x-y)\left(x^{n-1}+\ldots+y^{n-1}\right)$. The right factor of this expression contains an odd number of odd terms whose sum is an odd number greater than 1 , impossible. Similarly if $x$ and $y$ are even, write $x=2 u$ and $y=2 v$. The equation becomes $u^{n}-v^{n}=2^{k-n}$. If $k-n$ is greater than 0 , then our choice $k$ could not have been minimal. Otherwise, $k-n=0$, so that two consecutive positive integers are perfect $n$th powers, which is also absurd.
|
| 194 |
+
For the case that $n$ is even and greater than 4, consider the same generalization and hypotheses. Writing $n=2 m$, we find $\left(x^{m}-y^{m}\right)\left(x^{m}+y^{m}\right)=2^{k}$. Then $x^{m}-y^{m}=2^{a}<2^{k}$. By our previous work, we see that $m$ cannot be an odd integer greater than 1 . But then $m$ must also be even, contrary to the minimality of $k$.
|
| 195 |
+
Finally, for $n=2$ we get $x^{2}-y^{2}=2^{100}$. Factoring the left hand side gives $x-y=2^{a}$ and $x+y=2^{b}$, where implicit is $a<b$. Solving, we get $x=2^{b-1}+2^{a-1}$ and $y=2^{b-1}-2^{a-1}$, for a total of 49 solutions. Namely, those corresponding to $(a, b)=(1,99),(2,98), \cdots,(49,51)$.
|
| 196 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 197 |
+
25. [12] Two real numbers $x$ and $y$ are such that $8 y^{4}+4 x^{2} y^{2}+4 x y^{2}+2 x^{3}+2 y^{2}+2 x=x^{2}+1$. Find all possible values of $x+2 y^{2}$.
|
| 198 |
+
Answer: $\frac{\mathbf{1}}{\mathbf{2}}$. Writing $a=x+2 y^{2}$, the given quickly becomes $4 y^{2} a+2 x^{2} a+a+x=x^{2}+1$. We can rewrite $4 y^{2} a$ for further reduction to $a(2 a-2 x)+2 x^{2} a+a+x=x^{2}+1$, or
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
2 a^{2}+\left(2 x^{2}-2 x+1\right) a+\left(-x^{2}+x-1\right)=0
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
The quadratic formula produces the discriminant
|
| 205 |
+
|
| 206 |
+
$$
|
| 207 |
+
\left(2 x^{2}-2 x+1\right)^{2}+8\left(x^{2}-x+1\right)=\left(2 x^{2}-2 x+3\right)^{2},
|
| 208 |
+
$$
|
| 209 |
+
|
| 210 |
+
an identity that can be treated with the difference of squares, so that $a=\frac{-2 x^{2}+2 x-1 \pm\left(2 x^{2}-2 x+3\right)}{4}=$ $\frac{1}{2},-x^{2}+x-1$. Now $a$ was constructed from $x$ and $y$, so is not free. Indeed, the second expression flies in the face of the trivial inequality: $a=-x^{2}+x-1<-x^{2}+x \leq x+2 y^{2}=a$. On the other hand, $a=1 / 2$ is a bona fide solution to $\left(^{*}\right)$, which is identical to the original equation.
|
| 211 |
+
26. [12] $A B C D$ is a cyclic quadrilateral in which $A B=4, B C=3, C D=2$, and $A D=5$. Diagonals $A C$ and $B D$ intersect at $X$. A circle $\omega$ passes through $A$ and is tangent to $B D$ at $X$. $\omega$ intersects $A B$ and $A D$ at $Y$ and $Z$ respectively. Compute $Y Z / B D$.
|
| 212 |
+
|
| 213 |
+
|
| 214 |
+
Answer: $\frac{\mathbf{1 1 5}}{\mathbf{1 4 3}}$. Denote the lengths $A B, B C, C D$, and $D A$ by $a, b, c$, and $d$ respectively. Because $A B C D$ is cyclic, $\triangle A B X \sim \triangle D C X$ and $\triangle A D X \sim \triangle B C X$. It follows that $\frac{A X}{D X}=\frac{B X}{C X}=\frac{a}{c}$ and $\frac{A X}{B X}=\frac{D X}{C X}=\frac{d}{b}$. Therefore we may write $A X=a d k, B X=a b k, C X=b c k$, and $D X=c d k$ for some $k$. Now, $\angle X D C=\angle B A X=\angle Y X B$ and $\angle D C X=\angle X B Y$, so $\triangle B X Y \sim \triangle C D X$. Thus, $X Y=$ $D X \cdot \frac{B X}{C D}=c d k \cdot \frac{a b k}{c}=a b d k^{2}$. Analogously, $X Y=a c d k^{2}$. Note that $X Y / X Z=C B / C D$. Since $\angle Y X Z=\pi-\angle Z A \stackrel{c}{Y}=\angle B C D$, we have that $\triangle X Y Z \sim \triangle C B D$. Thus, $Y Z / B D=X Y / C B=a d k^{2}$.
|
| 215 |
+
Finally, Ptolemy's theorem applied to $A B C D$ gives
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
(a d+b c) k \cdot(a b+c d) k=a c+b d
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
It follows that the answer is
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
\frac{a d(a c+b d)}{(a b+c d)(a d+b c)}=\frac{20 \cdot 23}{22 \cdot 26}=\frac{115}{143}
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
27. [12] Find the number of 7 -tuples $\left(n_{1}, \ldots, n_{7}\right)$ of integers such that
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
\sum_{i=1}^{7} n_{i}^{6}=96957
|
| 231 |
+
$$
|
| 232 |
+
|
| 233 |
+
Answer: 2688. Consider the equation in modulo 9. All perfect 6 th powers are either 0 or 1 . Since 9 divides 96957 , it must be that each $n_{i}$ is a multiple of 3 . Writing $3 a_{i}=n_{i}$ and dividing both sides by $3^{6}$, we have $a_{1}^{6}+\cdots+a_{7}^{6}=133$. Since sixth powers are nonnegative, $\left|a_{i}\right| \leq 2$. Again considering modulo 9 , we see that $a_{i} \neq 0$. Thus, $a_{i}^{6} \in\{1,64\}$. The only possibility is $133=64+64+1+1+1+1+1$, so $\left|a_{1}\right|, \ldots,\left|a_{7}\right|$ consists of 22 's and 51 's. It follows that the answer is $\binom{7}{2} \cdot 2^{7}=2688$.
|
| 234 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 235 |
+
28. [15] Compute the circumradius of cyclic hexagon $A B C D E F$, which has side lengths $A B=B C=$ $2, C D=D E=9$, and $E F=F A=12$.
|
| 236 |
+
|
| 237 |
+
|
| 238 |
+
Answer: 8. Construct point $E^{\prime}$ on the circumcircle of $A B C D E F$ such that $D E^{\prime}=E F=12$ and $E^{\prime} F=D E=9$; then $\overline{B E^{\prime}}$ is a diameter. Let $B E^{\prime}=d$. Then $C E^{\prime}=\sqrt{B E^{\prime 2}-B C^{2}}=\sqrt{d^{2}-4}$ and $B D=\sqrt{B E^{\prime 2}-D E^{\prime 2}}=\sqrt{d^{2}-144}$. Applying Ptolemy's theorem to $B C D E^{\prime}$ now yields
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
9 \cdot d+2 \cdot 12=\sqrt{\left(d^{2}-4\right)\left(d^{2}-144\right)}
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
Squaring and rearranging, we find $0=d^{4}-229 d^{2}-432 d=d(d-16)\left(d^{2}+16 d+27\right)$. Since $d$ is a positive real number, $d=16$, and the circumradius is 8 .
|
| 245 |
+
29. [15] A sequence $\left\{a_{n}\right\}_{n \geq 1}$ of positive reals is defined by the rule $a_{n+1} a_{n-1}^{5}=a_{n}^{4} a_{n-2}^{2}$ for integers $n>2$ together with the initial values $a_{1}=8$ and $a_{2}=64$ and $a_{3}=1024$. Compute
|
| 246 |
+
|
| 247 |
+
$$
|
| 248 |
+
\sqrt{a_{1}+\sqrt{a_{2}+\sqrt{a_{3}+\cdots}}}
|
| 249 |
+
$$
|
| 250 |
+
|
| 251 |
+
Answer: $\mathbf{3} \sqrt{\mathbf{2}}$. Taking the base- $2 \log$ of the sequence $\left\{a_{n}\right\}$ converts the multiplicative rule to a more familiar additive rule: $\log _{2}\left(a_{n+1}\right)-4 \log _{2}\left(a_{n}\right)+5 \log _{2}\left(a_{n-1}\right)-2 \log _{2}\left(a_{n-2}\right)=0$. The characteristic equation is $0=x^{3}-4 x^{2}+5 x-2=(x-1)^{2}(x-2)$, so $\log _{2}\left(a_{n}\right)$ is of the form $a \cdot n+b+c \cdot 2^{n}$ and we find $a_{n}=2^{2 n+2^{n-1}}$. Now,
|
| 252 |
+
|
| 253 |
+
$$
|
| 254 |
+
\sqrt{a_{1}+\sqrt{a_{2}+\sqrt{a_{3}+\cdots}}}=\sqrt{2} \cdot \sqrt{4+\sqrt{16+\sqrt{64+\cdots}}}
|
| 255 |
+
$$
|
| 256 |
+
|
| 257 |
+
We can estimate the new nested radical expression as 3 , which expands thus
|
| 258 |
+
|
| 259 |
+
$$
|
| 260 |
+
3=\sqrt{4+5}=\sqrt{4+\sqrt{16+9}}=\sqrt{4+\sqrt{16+\sqrt{64+17}}}=\cdots
|
| 261 |
+
$$
|
| 262 |
+
|
| 263 |
+
As a rigorous confirmation, we have $2^{k}+1=\sqrt{4^{k}+\left(2^{k+1}+1\right)}$, as desired. It follows that the answer is $3 \sqrt{2}$.
|
| 264 |
+
30. [15] $A B C D$ is a cyclic quadrilateral in which $A B=3, B C=5, C D=6$, and $A D=10 . M, I$, and $T$ are the feet of the perpendiculars from $D$ to lines $A B, A C$, and $B C$ respectively. Determine the value of $M I / I T$.
|
| 265 |
+
|
| 266 |
+
|
| 267 |
+
Answer: $\frac{\mathbf{2 5}}{\mathbf{9}}$. Quadrilaterals $A M I D$ and $D I C T$ are cyclic, having right angles $\angle A M D, \angle A I D$, and $\angle C I D, \angle C T D$ respectively. We see that $M, I$, and $T$ are collinear. For, $m \angle M I D=\pi-m \angle D A M=$ $\pi-m \angle D A B=m \angle B C D=\pi-m \angle D C T=\pi-m \angle D I T$. Therefore, Menelaus' theorem applied to triangle $M T B$ and line $I C A$ gives
|
| 268 |
+
|
| 269 |
+
$$
|
| 270 |
+
\frac{M I}{I T} \cdot \frac{T C}{C B} \cdot \frac{B A}{A M}=1
|
| 271 |
+
$$
|
| 272 |
+
|
| 273 |
+
On the other hand, triangle $A D M$ is similar to triangle $C D T$ since $\angle A M D \cong \angle C T D$ and $\angle D A M \cong$ $\angle D C T$ and thus $A M / C T=A D / C D$. It follows that
|
| 274 |
+
|
| 275 |
+
$$
|
| 276 |
+
\frac{M I}{I T}=\frac{B C \cdot A M}{A B \cdot C T}=\frac{B C \cdot A D}{A B \cdot C D}=\frac{5 \cdot 10}{3 \cdot 6}=\frac{25}{9}
|
| 277 |
+
$$
|
| 278 |
+
|
| 279 |
+
Remarks. The line MIT, constructed in this problem by taking perpendiculars from a point on the circumcircle of $A B C$, is known as the Simson line. It is often helpful for us to use directed angles while angle chasing to avoid supplementary configuration issues, such as those arising while establishing the collinearity of $M, I$, and $T$.
|
| 280 |
+
|
| 281 |
+
## $10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 282 |
+
|
| 283 |
+
31. [18] A sequence $\left\{a_{n}\right\}_{n \geq 0}$ of real numbers satisfies the recursion $a_{n+1}=a_{n}^{3}-3 a_{n}^{2}+3$ for all positive integers $n$. For how many values of $a_{0}$ does $a_{2007}=a_{0}$ ?
|
| 284 |
+
Answer: $\mathbf{3}^{\mathbf{2 0 0 7}}$. If $x$ appears in the sequence, the next term $x^{3}-3 x^{2}+3$ is the same if and only if $0=x^{3}-3 x^{2}-x+3=(x-3)(x-1)(x+1)$. Moreover, that next term is strictly larger if $x>3$ and strictly smaller if $x<-1$. It follows that no values of $a_{0}$ with $\left|a_{0}-1\right|>2$ yield $a_{0}=a_{2007}$.
|
| 285 |
+
Now suppose $a_{0}=a_{2007}$ and write $a_{0}=1+e^{\alpha i}+e^{-\alpha i}$; the values $a_{0}$ we seek will be in bijective correspondence with solutions $\alpha$ where $0 \leq \alpha \leq \pi$. Then
|
| 286 |
+
|
| 287 |
+
$$
|
| 288 |
+
a_{1}=\left(a_{0}-1\right)^{3}-3 a_{0}+4=e^{3 \alpha i}+3 e^{\alpha i}+3 e^{-\alpha i}+e^{-3 \alpha i}-3 e^{\alpha i}-3 e^{-\alpha i}-3+4=e^{3 \alpha i}+e^{-3 \alpha i}+1
|
| 289 |
+
$$
|
| 290 |
+
|
| 291 |
+
and an easy inductive argument gives $a_{2007}=e^{3^{2007} \alpha i}+e^{-3^{2007} \alpha i}+1$. It follows that $a_{0}=a_{2007}$ is equivalent to $\cos (\alpha)=\cos \left(3^{2007} \alpha\right)$. Now,
|
| 292 |
+
|
| 293 |
+
$$
|
| 294 |
+
\cos \left(3^{2007} \alpha\right)-\cos (\alpha)=2 \sin \left(\left(\frac{3^{2007}+1}{2}\right) \alpha\right) \sin \left(\left(\frac{3^{2007}-1}{2}\right) \alpha\right)
|
| 295 |
+
$$
|
| 296 |
+
|
| 297 |
+
so $\operatorname{since} \sin (k x)=0$ for a positive integer $k$ if and only if $x$ is a multiple of $\frac{\pi}{k}$, the solutions $\alpha$ are $\left\{0, \frac{2 \pi}{3^{2007}-1}, \frac{4 \pi}{3^{2007}-1}, \ldots, \pi\right\} \cup\left\{0, \frac{2 \pi}{3^{2007}+1}, \ldots, \pi\right\}$. Because our values $k$ are consecutive, these sets overlap only at 0 and $\pi$, so there are $3^{2007}$ distinct $\alpha$.
|
| 298 |
+
32. [18] Triangle $A B C$ has $A B=4, B C=6$, and $A C=5$. Let $O$ denote the circumcenter of $A B C$. The circle $\Gamma$ is tangent to and surrounds the circumcircles of triangles $A O B, B O C$, and $A O C$. Determine the diameter of $\Gamma$.
|
| 299 |
+
Answer: $\frac{\mathbf{2 5 6} \sqrt{\mathbf{7}}}{\mathbf{1 7}}$. Denote by $\omega, \Gamma_{1}, \Gamma_{2}$, and $\Gamma_{3}$ the circumcenters of triangles $A B C, B O C, C O A$, and $A O B$, respectively. An inversion about $\omega$ interchanges $\Gamma_{1}$ and line $B C, \Gamma_{2}$ and line $C A$, and $\Gamma_{3}$ and line $A B$. This inversion also preserves tangency between generalized circles, so the image of $\Gamma$ is a circle tangent to $A B, B C$, and $C A$. It is the incircle of $A B C$ because it is closer to $O$ than these lines and $A B C$ is acute.
|
| 300 |
+
Now we run a few standard calculations. Where $s, r$, and $R$ denote the semiperimeter, inradius, and circumradius of $A B C$, respectively, we have the following:
|
| 301 |
+
|
| 302 |
+
$$
|
| 303 |
+
\begin{aligned}
|
| 304 |
+
& {[A B C]=\sqrt{s(s-a)(s-b)(s-c)}=\frac{15 \sqrt{7}}{4}} \\
|
| 305 |
+
& r=[A B C] / s=\sqrt{7} / 2 \\
|
| 306 |
+
& R=\frac{a b c}{4[A B C]}=\frac{8}{\sqrt{7}} \\
|
| 307 |
+
& O I^{2}=R(R-2 r)=\frac{8}{7}
|
| 308 |
+
\end{aligned}
|
| 309 |
+
$$
|
| 310 |
+
|
| 311 |
+
Let $O I$ intersect the incircle of $A B C$ at $P$ and $Q$, with $I$ between $P$ and $O$. Then $O P=r+O I$ and $O Q=r-O I$, and $\overline{P Q}$ is a diameter. Under the inversion, $P$ and $Q$ map to $P^{\prime}$ and $Q^{\prime}$ respectively. Because $P, I, O$, and $Q$ are collinear in that order, $P^{\prime}$ and $Q^{\prime}$ are diametrically opposed on $\Gamma$. It follows that the diameter of $\Gamma$ is
|
| 312 |
+
|
| 313 |
+
$$
|
| 314 |
+
P^{\prime} Q^{\prime}=O P^{\prime}+O Q^{\prime}=\frac{R^{2}}{O P}+\frac{R^{2}}{O Q}=R^{2}\left(\frac{1}{r+O I}+\frac{1}{r-O I}\right)=\frac{2 r R^{2}}{r^{2}-O I^{2}} .
|
| 315 |
+
$$
|
| 316 |
+
|
| 317 |
+
We plug in the values found above to arrive at $\frac{256 \sqrt{7}}{17}$.
|
| 318 |
+
|
| 319 |
+
33. [18] Compute
|
| 320 |
+
|
| 321 |
+
$$
|
| 322 |
+
\int_{1}^{2} \frac{9 x+4}{x^{5}+3 x^{2}+x} d x
|
| 323 |
+
$$
|
| 324 |
+
|
| 325 |
+
(No, your TI-89 doesn't know how to do this one. Yes, the end is near.)
|
| 326 |
+
Answer: $\ln \frac{\mathbf{8 0}}{\mathbf{2 3}}$. We break the given integral into two pieces:
|
| 327 |
+
|
| 328 |
+
$$
|
| 329 |
+
\int_{1}^{2} \frac{9 x+4}{x^{5}+3 x^{2}+x} d x=5 \int_{1}^{2} \frac{x^{4}+3 x+1}{x^{5}+3 x^{2}+x} d x-\int_{1}^{2} \frac{5 x^{4}+6 x+1}{x^{5}+3 x^{2}+x} d x
|
| 330 |
+
$$
|
| 331 |
+
|
| 332 |
+
These two new integrals are easily computed; for, the first integrand reduces to $1 / x$ and the second is of the form $f^{\prime}(x) / f(x)$. We obtain
|
| 333 |
+
|
| 334 |
+
$$
|
| 335 |
+
\left[5 \ln |x|-\ln \left|x^{5}+3 x^{2}+x\right|\right]_{1}^{2}=\ln 32-\ln 46+\ln 5=\ln \frac{80}{23}
|
| 336 |
+
$$
|
| 337 |
+
|
| 338 |
+
Motivation. Writing $f(x)=9 x+4$ and $g(x)=x^{5}+3 x^{2}+x=x\left(x^{4}+3 x+1\right)$, we wish to find the antiderivative of $f(x) / g(x)$. It makes sense to consider other rational functions with denominator $g(x)$ that have an exact antiderivative. Clearly, if the numerator were $f_{1}(x)=x^{4}+3 x+1$ or a constant multiple, then we can integrate the function. Another trivial case is if the numerator were $f_{2}(x)=g^{\prime}(x)=5 x^{4}+6 x+1$ or a constant multiple. Guessing that $f(x)$ is a linear combination of $f_{1}(x)$ and $f_{2}(x)$, we easily find that $f(x)=9 x+4=5 f_{1}(x)-f_{2}(x)$.
|
| 339 |
+
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
| 340 |
+
34. [?] The Game. Eric and Greg are watching their new favorite TV show, The Price is Right. Bob Barker recently raised the intellectual level of his program, and he begins the latest installment with bidding on following question: How many Carmichael numbers are there less than 100,000?
|
| 341 |
+
Each team is to list one nonnegative integer not greater than 100,000. Let $X$ denote the answer to Bob's question. The teams listing $N$, a maximal bid (of those submitted) not greater than $X$, will receive $N$ points, and all other teams will neither receive nor lose points. (A Carmichael number is an odd composite integer $n$ such that $n$ divides $a^{n-1}-1$ for all integers $a$ relatively prime to $n$ with $1<a<n$.)
|
| 342 |
+
Answer: 16? There are 16 such numbers: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, $29341,41041,46657,52633,62745,63973$, and 75361 . The next, 101101 , is too large to be counted. Their distribution is considerably more subtle than that of the primes, and it was only recently proven that there are infinitely many Carmichael numbers. For sufficiently large $n, C(n)>n^{2 / 7}$, although this bound has been subsequently improved. (For details, see Alford, W. R.; Granville, A.; and Pomerance, C. "There are Infinitely Many Carmichael Numbers." Annals of Mathematics. 139 (1994), 703-722.) The expectation is that teams are unable to determine that $X=16$; otherwise, the obvious dominant play is listing 16. The Problem Czar, anticipating that teams will attempt to deduce $X$ by considering the point values of the other problems in the triplet, has chosen a value $X$ that is considerably lower. Teams may of course speculate whether this action has been taken, and to what extent, etc... On the actual TV show, many contestants win by guessing prices of 1 , or other numbers dramatically lower than the actual price. This strategy is enhanced because of the show's ordered bidding, and will be more difficult here. It will be interesting to see the submissions.
|
| 343 |
+
35. [ $\leq \mathbf{2 5}]$ The Algorithm. There are thirteen broken computers situated at the following set $S$ of thirteen points in the plane:
|
| 344 |
+
|
| 345 |
+
$$
|
| 346 |
+
\begin{array}{lll}
|
| 347 |
+
A=(1,10) & B=(976,9) & C=(666,87) \\
|
| 348 |
+
D=(377,422) & E=(535,488) & F=(775,488) \\
|
| 349 |
+
G=(941,500) & H=(225,583) & I=(388,696) \\
|
| 350 |
+
J=(3,713) & K=(504,872) & L=(560,934) \\
|
| 351 |
+
& M=(22,997) &
|
| 352 |
+
\end{array}
|
| 353 |
+
$$
|
| 354 |
+
|
| 355 |
+
At time $t=0$, a repairman begins moving from one computer to the next, traveling continuously in straight lines at unit speed. Assuming the repairman begins and $A$ and fixes computers instantly, what path does he take to minimize the total downtime of the computers? List the points he visits in order. Your score will be $\left\lfloor\frac{N}{40}\right\rfloor$, where
|
| 356 |
+
|
| 357 |
+
$$
|
| 358 |
+
N=1000+\lfloor\text { the optimal downtime }\rfloor-\lfloor\text { your downtime }\rfloor,
|
| 359 |
+
$$
|
| 360 |
+
|
| 361 |
+
or 0 , whichever is greater. By total downtime we mean the sum
|
| 362 |
+
|
| 363 |
+
$$
|
| 364 |
+
\sum_{P \in S} t_{P}
|
| 365 |
+
$$
|
| 366 |
+
|
| 367 |
+
where $t_{P}$ is the time at which the repairman reaches $P$.
|
| 368 |
+
Answer: ADHIKLEFGBCJM. This is an instance of the minimum-latency problem, which is at least NP-hard. There is an easy $O(n!)$ algorithm, but this is unavailable to teams on computational grounds ( 100 MHz calculators used to seem fast...) The best strategy may be drawing an accurate picture and exercising geometric intuition. The distribution of the points somewhat resembles a short, four-pronged fork with its outermost prongs bent apart; it is plausible to assume that the optimal order respects this shape. The optimal downtime is 24113.147907 , realized by ADHIKLEFGBCJM, though a number of others also receive positive marks.
|
| 369 |
+
36. [25] The Marathon. Let $\omega$ denote the incircle of triangle $A B C$. The segments $B C, C A$, and $A B$ are tangent to $\omega$ at $D, E$, and $F$, respectively. Point $P$ lies on $E F$ such that segment $P D$ is perpendicular to $B C$. The line $A P$ intersects $B C$ at $Q$. The circles $\omega_{1}$ and $\omega_{2}$ pass through $B$ and $C$, respectively, and are tangent to $A Q$ at $Q$; the former meets $A B$ again at $X$, and the latter meets $A C$ again at $Y$. The line $X Y$ intersects $B C$ at $Z$. Given that $A B=15, B C=14$, and $C A=13$, find $\lfloor X Z \cdot Y Z\rfloor$.
|
| 370 |
+
|
| 371 |
+
|
| 372 |
+
Answer: 101. Construct $D^{\prime}$ diametrically opposed to $D$, so that $\angle D F D^{\prime}$ and $\angle D E D^{\prime}$ are right, and note that $P$ lies on $D D^{\prime}$. By standard angle chasing, $m \angle F D D^{\prime}=\beta$ (half angle $B$ ) and $m \angle D^{\prime} D E=\gamma$. Thus, $m \angle D D^{\prime} F=90^{\circ}-\beta$ and $m \angle E D^{\prime} D=90^{\circ}-\gamma$. Then by the law of sines, $D E: E D^{\prime}: D^{\prime} F$ : $F D=\cos (\gamma): \sin (\gamma): \sin (\beta): \sin (\gamma)$. Now using $\triangle D E P \sim \triangle F D^{\prime} P$ and $\triangle D F P \sim \triangle E D^{\prime} P$, we have
|
| 373 |
+
|
| 374 |
+
$$
|
| 375 |
+
\frac{E P}{P F}=\frac{E D \cdot E D^{\prime}}{F D \cdot F D^{\prime}}=\frac{\sin (\gamma) \cos (\gamma)}{\sin (\beta) \sin (\beta)}=\frac{c}{b}
|
| 376 |
+
$$
|
| 377 |
+
|
| 378 |
+
Let the dilation centered at $A$ sending $E$ to $C$ map $P$ and $F$ to $P^{\prime}$ and $F^{\prime}$, respectively. Note that $A F^{\prime}=A C$ as $A E$ and $A F$ are equal tangents, and $C P^{\prime}: P^{\prime} F^{\prime}=E P: P F=c: b$ by similarity. Then by Menelaus' theorem,
|
| 379 |
+
|
| 380 |
+
$$
|
| 381 |
+
1=\frac{B Q}{Q C} \frac{C P^{\prime}}{P^{\prime} F^{\prime}} \frac{F^{\prime} A}{A B}=\frac{B Q}{Q C} \frac{c}{b} \frac{b}{c}
|
| 382 |
+
$$
|
| 383 |
+
|
| 384 |
+
so that $B Q=Q C$ and $A Q$ is actually a median. So, $A Q^{2}=\frac{1}{4}\left(2 b^{2}+2 c^{2}-a^{2}\right)=148$. Now by Power of a Point, $A B \cdot A X=A Q^{2}=A C \cdot A Y$, so $A X=148 / 15$ and $A Y=148 / 13$. Moreover, $B X C Y$ is cyclic as $\triangle A B C \sim \triangle A Y X$. Thus, $X Z \cdot Y Z=B Z \cdot C Z$, and it suffices to compute $B Z / C Z$. Menelaus once more gives
|
| 385 |
+
|
| 386 |
+
$$
|
| 387 |
+
1=\frac{B Z}{Z C} \frac{C Y}{Y A} \frac{A X}{X B}
|
| 388 |
+
$$
|
| 389 |
+
|
| 390 |
+
whence, $B Z / C Z=(A Y / A X)(B X / C Y)=(15 / 13)((77 \cdot 13) /(21 \cdot 15))=11 / 3$. We write $C Z=3 d$ and $B Z=11 d$. Because $A X<A B$ and $A Y<A C, Z$ does not lie on segment $B C$. Given the configuration information, $B C=8 d=14$, so $d=7 / 4$, and finally $\lfloor B Z \cdot C Z\rfloor=\left\lfloor 33 d^{2}\right\rfloor=\left\lfloor\frac{1617}{16}\right\rfloor=101$.
|
| 391 |
+
|
HarvardMIT/md/en-102-2007-feb-team1-solutions.md
ADDED
|
@@ -0,0 +1,291 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> <br> Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
<br> <br> Saturday 24 February 2007}
|
| 4 |
+
|
| 5 |
+
Team Round: A Division<br>$\Sigma, \tau$, and You: Fun at Fraternities? [270]
|
| 6 |
+
|
| 7 |
+
A number theoretic function is a function whose domain is the set of positive integers. A multiplicative number theoretic function is a number theoretic function $f$ such that $f(m n)=f(m) f(n)$ for all pairs of relatively prime positive integers $m$ and $n$. Examples of multiplicative number theoretic functions include $\sigma, \tau, \phi$, and $\mu$, defined as follows. For each positive integer $n$,
|
| 8 |
+
|
| 9 |
+
- The sum-of-divisors function, $\sigma(n)$, is the sum of all positive integer divisors of $n$. If $p_{1}, \ldots, p_{i}$ are distinct primes and $e_{1}, \ldots, e_{i}$ are positive integers,
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\sigma\left(p_{1}^{e_{1}} \cdots p_{i}^{e_{i}}\right)=\prod_{k=1}^{i}\left(1+p_{k}+\cdots+p_{k}^{e_{k}}\right)=\prod_{k=1}^{i} \frac{p_{k}^{e_{k}+1}-1}{p_{k}-1}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
- The divisor function, $\tau(n)$, is the number of positive integer divisors of $n$. It can be computed by the formula
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
\tau\left(p_{1}^{e_{1}} \cdots p_{i}^{e_{i}}\right)=\left(e_{1}+1\right) \cdots\left(e_{i}+1\right)
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
where $p_{1}, \ldots, p_{i}$ and $e_{1}, \ldots, e_{i}$ are as above.
|
| 22 |
+
|
| 23 |
+
- Euler's totient function, $\phi(n)$, is the number of positive integers $k \leq n$ such that $k$ and $n$ are relatively prime. For $p_{1}, \ldots, p_{i}$ and $e_{1}, \ldots, e_{i}$ as above, the phi function satisfies
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\phi\left(p_{1}^{e_{1}} \cdots p_{i}^{e_{i}}\right)=\prod_{k=1}^{i} p_{k}^{e_{k}-1}\left(p_{k}-1\right)
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
- The Möbius function, $\mu(n)$, is equal to either $1,-1$, or 0 . An integer is called square-free if it is not divisible by the square of any prime. If $n$ is a square-free positive integer having an even number of distinct prime divisors, $\mu(n)=1$. If $n$ is a square-free positive integer having an odd number of distinct prime divisors, $\mu(n)=-1$. Otherwise, $\mu(n)=0$.
|
| 30 |
+
|
| 31 |
+
The Möbius function has a number of peculiar properties. For example, if $f$ and $g$ are number theoretic functions such that
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
g(n)=\sum_{d \mid n} f(d)
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
for all positive integers $n$, then
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
f(n)=\sum_{d \mid n} g(d) \mu\left(\frac{n}{d}\right)
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
This is known as Möbius inversion. In proving the following problems, you may use any of the preceding assertions without proving them. You may also cite the results of previous problems, even if you were unable to prove them.
|
| 44 |
+
|
| 45 |
+
1. [15] Evaluate the functions $\phi(n), \sigma(n)$, and $\tau(n)$ for $n=12, n=2007$, and $n=2^{2007}$.
|
| 46 |
+
|
| 47 |
+
Solution. For $n=12=2^{2} \cdot 3^{1}$,
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\phi(12)=2(2-1)(3-1)=4, \quad \sigma(12)=(1+2+4)(1+3)=28, \quad \tau(12)=(2+1)(1+1)=6
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
for $n=2007=3^{2} \cdot 223$,
|
| 54 |
+
$\phi(2007)=3(3-1)(223-1)=1332, \quad \sigma(2007)=(1+3+9)(1+223)=2912, \quad \tau(2007)=(2+1)(1+1)=6 ;$
|
| 55 |
+
and for $n=2^{2007}$,
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\phi\left(2^{2007}\right)=2^{2006}, \quad \sigma\left(2^{2007}\right)=\left(1+2+\cdots+2^{2007}\right)=2^{2008}-1, \quad \tau\left(2^{2007}\right)=2007+1=2008
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
2. [20] Solve for the positive integer(s) $n$ such that $\phi\left(n^{2}\right)=1000 \phi(n)$.
|
| 62 |
+
|
| 63 |
+
Answer: 1000.
|
| 64 |
+
Solution. The unique solution is $n=1000$. For, $\phi(p n)=p \phi(n)$ for every prime $p$ dividing $n$, so that $\phi\left(n^{2}\right)=n \phi(n)$ for all positive integers $n$.
|
| 65 |
+
3. [25] Prove that for every integer $n$ greater than 1 ,
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
\sigma(n) \phi(n) \leq n^{2}-1
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
When does equality hold?
|
| 72 |
+
Solution. Note that
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\sigma(m n) \phi(m n)=\sigma(m) \phi(m) \sigma(n) \phi(n) \leq\left(m^{2}-1\right)\left(n^{2}-1\right)=(m n)^{2}-\left(m^{2}+n^{2}-1\right)<(m n)^{2}-1
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
for any pair of relatively prime positive integers $(m, n)$ other than $(1,1)$. Now, for $p$ a prime and $k$ a positive integer, $\sigma\left(p^{k}\right)=1+p+\cdots+p^{k}=\frac{p^{k+1}-1}{p-1}$ and $\phi\left(p^{k}\right)=p^{k}-\frac{1}{p} \cdot p^{k}=(p-1) p^{k-1}$. Thus,
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\sigma\left(p^{k}\right) \phi\left(p^{k}\right)=\frac{p^{k+1}-1}{p-1} \cdot(p-1) p^{k-1}=\left(p^{k+1}-1\right) p^{k-1}=p^{2 k}-p^{k-1} \leq p^{2 k}-1
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
with equality where $k=1$. It follows that equality holds in the given inequality if and only if $n$ is prime.
|
| 85 |
+
4. [25] Let $F$ and $G$ be two multiplicative functions, and define for positive integers $n$,
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
H(n)=\sum_{d \mid n} F(d) G\left(\frac{n}{d}\right)
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
The number theoretic function $H$ is called the convolution of $F$ and $G$. Prove that $H$ is multiplicative. Solution. Let $m$ and $n$ be relatively prime positive integers. We have
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
\begin{aligned}
|
| 95 |
+
& H(m) H(n)=\left(\sum_{d \mid m} F(d) G\left(\frac{m}{d}\right)\right)\left(\sum_{d^{\prime} \mid n} F\left(d^{\prime}\right) G\left(\frac{n}{d^{\prime}}\right)\right) \\
|
| 96 |
+
& \quad=\sum_{d\left|m, d^{\prime}\right| n} F(d) F\left(d^{\prime}\right) G\left(\frac{m}{d^{\prime}}\right) G\left(\frac{n}{d}\right)=\sum_{d\left|m, d^{\prime}\right| n} F\left(d d^{\prime}\right) G\left(\frac{m n}{d d^{\prime}}\right) \\
|
| 97 |
+
& \quad=\sum_{d \mid m n} F(d) G\left(\frac{m n}{d}\right)=H(m n)
|
| 98 |
+
\end{aligned}
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
5. [30] Prove the identity
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
\sum_{d \mid n} \tau(d)^{3}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
Solution. Note that $\tau^{3}$ is multiplicative; in light of the convolution property just shown, it follows that both sides of the posed equality are multiplicative. Thus, it would suffice to prove the claim for $n$ a power of a prime. So, write $n=p^{k}$ where $p$ is a prime and $k$ is a nonnegative integer. Then
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\begin{aligned}
|
| 111 |
+
& \sum_{d \mid n} \tau(d)^{3}=\sum_{i=0}^{k} \tau\left(p^{i}\right)^{3}=\sum_{i=0}^{k}(i+1)^{3} \\
|
| 112 |
+
& \quad=1^{3}+\cdots+(k+1)^{3}=\frac{(k+1)^{2}(k+2)^{2}}{4}=\left(\frac{(k+1)(k+2)}{2}\right)^{2} \\
|
| 113 |
+
& \quad=\left(\sum_{i=0}^{k} \tau\left(p^{i}\right)\right)^{2}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
|
| 114 |
+
\end{aligned}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
as required.
|
| 118 |
+
6. [25] Show that for positive integers $n$,
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
\sum_{d \mid n} \phi(d)=n
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
Solution. Both sides are multiplicative functions of $n$, the right side trivially and the left because for relatively prime positive integers $n$ and $n^{\prime}$,
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\left(\sum_{d \mid n} \phi(d)\right)\left(\sum_{d^{\prime} \mid n^{\prime}} \phi\left(d^{\prime}\right)\right)=\sum_{d\left|n, d^{\prime}\right| n^{\prime}} \phi(d) \phi\left(d^{\prime}\right),
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
and $\phi(d) \phi\left(d^{\prime}\right)=\phi\left(d d^{\prime}\right)$. The identity is then easy to check; since $\phi\left(p^{k}\right)=p^{k-1}(p-1)$ for positive integers $k$ and $\phi(1)=1$, we have $\phi(1)+\phi(p)+\cdots+\phi\left(p^{k}\right)=1+(p-1)+\left(p^{2}-p\right)+\cdots+\left(p^{k}-p^{k-1}\right)=p^{k}$, as desired.
|
| 131 |
+
7. [25] Show that for positive integers $n$,
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\sum_{d \mid n} \frac{\mu(d)}{d}=\frac{\phi(n)}{n}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
Solution. On the grounds of the previous problem, Möbius inversion with $f(k)=\phi(k)$ and $g(k)=k$ gives:
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
\phi(n)=f(n)=\sum_{d \mid n} g(d) \mu\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} g\left(\frac{n}{d^{\prime}}\right) \mu\left(d^{\prime}\right)=\sum_{d^{\prime} \mid n} \frac{n}{d^{\prime}} \mu\left(d^{\prime}\right)
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
Alternatively, one uses the convolution of the functions $f(k)=n$ and $g(k)=\frac{\mu(d)}{d}$. The strategy is the same as the previous convolution proof. For $n=p^{k}$ with $k$ a positive integer, we have $\phi(n)=p^{k}-p^{k-1}$, while the series reduces to $p^{k} \cdot \mu(1)+p^{k} \cdot \mu(p) / p=p^{k}-p^{k-1}$.
|
| 144 |
+
8. [30] Determine with proof, a simple closed form expression for
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
\sum_{d \mid n} \phi(d) \tau\left(\frac{n}{d}\right)
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
Solution. We claim the series reduces to $\sigma(n)$. The series counts the ordered triples $(d, x, y)$ with $d|n ; x| d ; 0<y \leq n / d ;$ and $(y, n / d)=1$. To see this, write
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
\sum_{d \mid n} \phi(d) \tau\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} \phi\left(\frac{n}{d^{\prime}}\right) \tau\left(d^{\prime}\right)
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
so that for a given $d^{\prime} \mid n$ we may choose $x$ and $y$ as described above. On the other hand, we can count these triples by groups sharing a given $x$. Fixing $x$ as a divisor of $n$ fixes an integer $\frac{n}{x}$. Then $d$ varies such that $\frac{n}{d}$ is a divisor of $\frac{n}{x}$. For each divisor $\frac{n}{d}$ of $\frac{n}{x}$ there are precisely $\phi\left(\frac{n}{d}\right)$ choices $y$, so that by the lemma from the previous problem, there are $\frac{n}{x}$ triples $(d, x, y)$ for a given $x$. It follows that there are precisely $\sigma(n)$ such triples $(d, x, y)$.
|
| 157 |
+
Again, an alternative is to use the multiplicativity of the convolution, although it is now a little more difficult. Write $n=p^{k}$ so that
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\begin{aligned}
|
| 161 |
+
\sum_{d \mid n} & \phi(d) \tau\left(\frac{n}{d}\right)=\sum_{m=0}^{k} \phi\left(p^{m}\right) \tau\left(p^{k-m}\right)=k+1+\sum_{m=1}^{k} p^{m-1}(p-1)(k-m+1) \\
|
| 162 |
+
& =k+1+\left(\sum_{m=1}^{k} p^{m}(k-m+1)\right)-\left(\sum_{m=1}^{k} p^{m-1}(k-m+1)\right)=k+1+p^{k}-k+\sum_{m^{\prime}=1}^{k-1} p^{m^{\prime}} \\
|
| 163 |
+
& =1+p+\cdots+p^{k}=\sigma\left(p^{k}\right)
|
| 164 |
+
\end{aligned}
|
| 165 |
+
$$
|
| 166 |
+
|
| 167 |
+
9. [35] Find all positive integers $n$ such that
|
| 168 |
+
|
| 169 |
+
$$
|
| 170 |
+
\sum_{k=1}^{n} \phi(k)=\frac{3 n^{2}+5}{8}
|
| 171 |
+
$$
|
| 172 |
+
|
| 173 |
+
Answer: 1, 3,5.
|
| 174 |
+
Solution. We contend that the proper relation is
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
\sum_{k=1}^{n} \phi(k) \leq \frac{3 n^{2}+5}{8}
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
Let $\Phi(k)$ denote the left hand side of $(*)$. It is trivial to see that for $n \leq 7$ the posed inequality holds, has equality where $n=1,3,5$, and holds strictly for $n=7$. Note that $\phi(2 k) \leq k$ and $\phi(2 k+1) \leq 2 k$, the former because $2,4, \ldots, 2 k$ share a common divisor. It follows that $\phi(2 k)+\phi(2 k+1) \leq 3 k$. Suppose for the sake of induction that $\Phi(2 k-1)<\frac{3(2 k-1)^{2}+5}{8}$. Then
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
\Phi(2 k+1)=\Phi(2 k-1)+\phi(2 k)+\phi(2 k+1)<\frac{3(2 k-1)^{2}+5}{8}+3 k=\frac{3(2 k+1)^{2}+5}{8}
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
To complete the proof, it is enough to note that for a positive integer $k$,
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
\frac{3(2 k-1)^{2}+5}{8}+k<\frac{3(2 k)^{2}+5}{8}
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
10. [40] Find all pairs $(n, k)$ of positive integers such that
|
| 193 |
+
|
| 194 |
+
$$
|
| 195 |
+
\sigma(n) \phi(n)=\frac{n^{2}}{k}
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
Answer: (1, 1).
|
| 199 |
+
Solution. It is clear that for a given integer $n$, there is at most one integer $k$ for which the equation holds. For $n=1$ this is $k=1$. But, for $n>1$, problem 1 asserts that $\sigma(n) \phi(n) \leq n^{2}-1<n^{2}$, so that $k \geq 2$. We now claim that $2>\frac{n^{2}}{\sigma(n) \phi(n)}$. Write $n=p_{1}^{e_{1}} \cdots p_{k}^{e_{k}}$, where the $p_{i}$ are distinct primes and $e_{i} \geq 1$ for all $i$, and let $q_{1}<q_{2}<\cdots$ be the primes in ascending order. Then
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
\begin{aligned}
|
| 203 |
+
& \frac{n^{2}}{\sigma(n) \phi(n)}=\prod_{i=1}^{k} \frac{p_{i}^{2 e_{i}}}{\frac{p_{i}^{e_{i}+1}-1}{p_{i}-1} \cdot\left(p_{i}-1\right) p_{i}^{e_{i}-1}}=\prod_{i=1}^{k} \frac{p_{i}^{2 e_{i}}}{p_{i}^{2 e_{i}}-p_{i}^{e_{i}-1}} \\
|
| 204 |
+
& \quad=\prod_{i=1}^{k} \frac{1}{1-p_{i}^{-1-e_{i}}} \leq \prod_{i=1}^{k} \frac{1}{1-p_{i}^{-2}}<\prod_{i=1}^{\infty} \frac{1}{1-q_{i}^{-2}} \\
|
| 205 |
+
& \quad=\prod_{i=1}^{\infty}\left(\sum_{j=0}^{\infty} \frac{1}{q_{i}^{2 j}}\right)=\sum_{n=1}^{\infty} \frac{1}{n^{2}} \\
|
| 206 |
+
& \quad<1+\sum_{n=2}^{\infty} \frac{1}{n^{2}-1}=1+\frac{1}{2}\left(\left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\cdots\right)=\frac{7}{4}<2 .
|
| 207 |
+
\end{aligned}
|
| 208 |
+
$$
|
| 209 |
+
|
| 210 |
+
It follows that there can be no solutions to $k=\frac{n^{2}}{\sigma(n) \phi(n)}$ other than $n=k=1$.
|
| 211 |
+
|
| 212 |
+
## Grab Bag - Miscellaneous Problems [130]
|
| 213 |
+
|
| 214 |
+
11. $[30]$ Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
\begin{aligned}
|
| 218 |
+
f(x) f(y) & =f(x)+f(y)-f(x y) \\
|
| 219 |
+
1+f(x+y) & =f(x y)+f(x) f(y)
|
| 220 |
+
\end{aligned}
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
for all rational numbers $x, y$.
|
| 224 |
+
Answer: $\mathbf{f}(\mathbf{x})=\mathbf{1} \forall \mathbf{x}$, and $\mathbf{f}(\mathbf{x})=\mathbf{1}-\mathbf{x} \forall \mathbf{x}$.
|
| 225 |
+
Solution. Considering the first equation, either side of the second equation is equal to $f(x)+f(y)$. Now write $g(x)=1-f(x)$, so that
|
| 226 |
+
|
| 227 |
+
$$
|
| 228 |
+
\begin{aligned}
|
| 229 |
+
& g(x y)=1-f(x y)=1-f(x)-f(y)+f(x) f(y)=(1-f(x))(1-f(y))=g(x) g(y) \\
|
| 230 |
+
& g(x+y)=1-f(x+y)=1-f(x)+1-f(y)=g(x)+g(y)
|
| 231 |
+
\end{aligned}
|
| 232 |
+
$$
|
| 233 |
+
|
| 234 |
+
By induction, $g(n x)=n g(x)$ for all integers $n$, so that $g(p / q)=(p / q) g(1)$ for integers $p$ and $q$ with $q$ nonzero; i.e., $g(x)=x g(1)$. As $g$ is multiplicative, $g(1)=g(1)^{2}$, so the only possibilities are $g(1)=1$ and $g(1)=0$. These give $g(x)=x$ and $g(x)=0$, or $f(x)=1-x$ and $f(x)=1$, respectively. One easily checks that these functions are satisfactory.
|
| 235 |
+
12. [30] Let $A B C D$ be a cyclic quadrilateral, and let $P$ be the intersection of its two diagonals. Points $R, S, T$, and $U$ are feet of the perpendiculars from $P$ to sides $A B, B C, C D$, and $A D$, respectively. Show that quadrilateral $R S T U$ is bicentric if and only if $A C \perp B D$. (Note that a quadrilateral is called inscriptible if it has an incircle; a quadrilateral is called bicentric if it is both cyclic and inscriptible.)
|
| 236 |
+
|
| 237 |
+
|
| 238 |
+
Solution. First we show that $R S T U$ is always inscriptible. Note that in addition to $A B C D$, we have cyclic quadrilaterals $A R P U$ and $B S P R$. Thus,
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
\angle P R U=\angle P A U=\angle C A D=\angle C B D=\angle S B P=\angle S R P
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
and it follows that $P$ lies on the bisector of $\angle S R U$. Analogously, $P$ lies on the bisectors of $\angle T S R$ and $\angle U T S$, so is equidistant from lines $U R, R S, S T$, and $T U$, and $R S T U$ is inscriptible having incenter $P$. Now we show that $R S T U$ is cyclic if and only if the diagonals of $A B C D$ are orthogonal. We have
|
| 245 |
+
|
| 246 |
+
$$
|
| 247 |
+
\begin{aligned}
|
| 248 |
+
& \angle A P B=\pi-\angle B A P-\angle P B A=\pi-\angle R A P-\angle P B R=\pi-\angle R U P-\angle P S R \\
|
| 249 |
+
& \quad=\pi-\frac{1}{2}(\angle R U T+\angle T S R)
|
| 250 |
+
\end{aligned}
|
| 251 |
+
$$
|
| 252 |
+
|
| 253 |
+
It follows that $\angle A P B=\frac{\pi}{2}$ if and only if $\angle R U T+\angle T S R=\pi$, as desired.
|
| 254 |
+
13. [30] Find all nonconstant polynomials $P(x)$, with real coefficients and having only real zeros, such that $P(x+1) P\left(x^{2}-x+1\right)=P\left(x^{3}+1\right)$ for all real numbers $x$.
|
| 255 |
+
|
| 256 |
+
Answer: $\left\{\mathbf{P}(\mathbf{x})=\mathbf{x}^{\mathbf{k}} \mid \mathbf{k} \in \mathbb{Z}^{+}\right\}$.
|
| 257 |
+
Solution. Note that if $P(\alpha)=0$, then by setting $x=\alpha-1$ in the given equation, we find $0=P\left(x^{3}+\right.$ $1)=P\left(\alpha^{3}-3 \alpha^{2}+3 \alpha\right)$. Because $P$ is nonconstant, it has at least one zero. Because $P$ has finite degree, there exist minimal and maximal roots of $P$. Writing $\alpha^{3}-3 \alpha^{2}+3 \alpha \geq \alpha \Longleftrightarrow \alpha(\alpha-1)(\alpha-2) \geq 0$, we see that the largest zero of $P$ cannot exceed 2 . Likewise, the smallest zero cannot be negative, so all of the zeroes of $P$ lie in [0,2]. Moreover, if $\alpha \notin\{0,1,2\}$ is a zero of $P$, then $\alpha^{\prime}=\alpha^{3}-3 \alpha^{2}+3 \alpha$ is another zero of $P$ that lies strictly between $\alpha$ and 1. Because $P$ has only finitely many zeroes, all of its zeroes must lie in $\{0,1,2\}$. Now write $P(x)=k x^{p}(x-1)^{q}(x-2)^{r}$ for nonnegative integers $p, q$ and $r$ having a positive sum. The given equation becomes
|
| 258 |
+
|
| 259 |
+
$$
|
| 260 |
+
\begin{aligned}
|
| 261 |
+
& k^{2}(x+1)^{p} x^{q}(x-1)^{r}\left(x^{2}-x+1\right)^{p}\left(x^{2}-x\right)^{q}\left(x^{2}-x-1\right)^{r}=P(x+1) P\left(x^{2}-x+1\right) \\
|
| 262 |
+
& \quad=P\left(x^{3}+1\right)=k\left(x^{3}+1\right)^{p} x^{3 q}\left(x^{3}-1\right)^{r}
|
| 263 |
+
\end{aligned}
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
For the leading coefficients to agree, we require $k=k^{2}$. Because the leading coefficient is nonzero, $P$ must be monic. In $(*), r$ must be zero lest $P\left(x^{3}+1\right)=0$ have complex roots. Then $q$ must be zero as well. For, if $q$ is positive, then $P\left(x^{2}-x+1\right)=0$ has 1 as a root while $P\left(x^{3}+1\right)$ does not. Finally, the remaining possibilities are $P(x)=x^{p}$ for $p$ an arbitrary positive integer. It is easily seen that these polynomials are satisfactory.
|
| 267 |
+
14. [40] Find an explicit, closed form formula for
|
| 268 |
+
|
| 269 |
+
$$
|
| 270 |
+
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}
|
| 271 |
+
$$
|
| 272 |
+
|
| 273 |
+
Answer: $\frac{-\mathbf{1}}{\binom{2 \mathbf{1}+1}{\mathbf{n}}}$ or $-\frac{\mathbf{n}!(\mathbf{n}+\mathbf{1})!}{(\mathbf{2 n}+\mathbf{1})!}$ or obvious equivalent.
|
| 274 |
+
Solution. Consider the interpolation of the polynomial $P(x)=x \cdot n!$ at $x=0,1, \ldots, n$. We obtain the identity
|
| 275 |
+
|
| 276 |
+
$$
|
| 277 |
+
\begin{aligned}
|
| 278 |
+
P(x) & =x \cdot n!=\sum_{k=0}^{n} k \cdot n!\prod_{j \neq k} \frac{x-j}{k-j} \\
|
| 279 |
+
& =\sum_{k=0}^{n} k \cdot n!\cdot \frac{x(x-1) \cdots(x-k+1)(x-k-1) \cdots(x-n)}{k!(n-k)!(-1)^{n-k}} \\
|
| 280 |
+
& =\sum_{k=1}^{n} k \cdot(-1)^{n-k} \cdot\binom{n}{k} \cdot x(x-1) \cdots(x-k+1)(x-k-1) \cdots(x-n)
|
| 281 |
+
\end{aligned}
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
This identity is valid for all complex numbers $x$, but, to extract a factor $\frac{1}{n+k+1}$ from the valid product of each summand, we set $x=-n-1$, so that
|
| 285 |
+
$-(n+1)!=\sum_{k=1}^{n} k(-1)^{n-k}\binom{n}{k}(-n-1) \cdots(-n-k)(-n-k-2) \cdots(-2 n-1)=\sum_{k=1}^{n} \frac{k(-1)^{k}\binom{n}{k}(2 n+1)!}{n!(n+k+1)}$.
|
| 286 |
+
Finally,
|
| 287 |
+
|
| 288 |
+
$$
|
| 289 |
+
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}=\frac{-n!(n+1)!}{(2 n+1)!}=\frac{-1}{\binom{2 n+1}{n}} \cdot \square
|
| 290 |
+
$$
|
| 291 |
+
|
HarvardMIT/md/en-102-2007-feb-team2-solutions.md
ADDED
|
@@ -0,0 +1,219 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $10^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> <br> Saturday 24 February 2007
|
| 2 |
+
|
| 3 |
+
<br> <br> Saturday 24 February 2007}
|
| 4 |
+
|
| 5 |
+
Team Round: B Division
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
\text { Compute }(x-a)(x-b) \cdots(x-z) \text { - Short Answer [200] }
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
For this section, your team should give only the anwers to the problems.
|
| 12 |
+
|
| 13 |
+
1. [20] Find the sum of the positive integer divisors of $2^{2007}$.
|
| 14 |
+
|
| 15 |
+
Answer: $\mathbf{2}^{\mathbf{2 0 0 8}}-\mathbf{1}$. The divisors are the powers of two not exceeding $2^{2007}$. So the sum is
|
| 16 |
+
$1+2+2^{2}+\cdots+2^{2007}=-1+2+2+2^{2}+\cdots+2^{2007}=-1+2^{2}+2^{2}+\cdots+2^{2007}=\cdots=-1+2^{2008}$.
|
| 17 |
+
2. [20] The four sides of quadrilateral $A B C D$ are equal in length. Determine the perimeter of $A B C D$ given that it has area 120 and $A C=10$.
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
Answer: 52. Let $M$ be the midpoint of $A C$. Then triangles $A M B, B M C, C M D$, and $D M A$ are all right triangles having legs 5 and $h$ for some $h$. The area of $A B C D$ is 120 , but also $4 \cdot\left(\frac{1}{2} \cdot 5 \cdot h\right)=10 h$, so $h=12$. Then $A B=B C=C D=D A=\sqrt{12^{2}+5^{2}}=13$, and the perimeter of $A B C D$ is 52 .
|
| 21 |
+
3. [20] Five people are crowding into a booth against a wall at a noisy restaurant. If at most three can fit on one side, how many seating arrangements accomodate them all?
|
| 22 |
+
Answer: 240. Three people will sit on one side and two sit on the other, giving a factor of two. Then there are 5 ! ways to permute the people.
|
| 23 |
+
4. [20] Thomas and Michael are just two people in a large pool of well qualified candidates for appointment to a problem writing committee for a prestigious college math contest. It is 40 times more likely that both will serve if the size of the committee is increased from its traditional 3 members to a whopping $n$ members. Determine $n$. (Each person in the pool is equally likely to be chosen.)
|
| 24 |
+
Answer: 16. Suppose there are $k$ candidates. Then the probability that both serve on a 3 membered committee is $(k-2) /\binom{k}{3}$, and the odds that both serve on an $n$ membered committee are $\binom{k-2}{n-2} /\binom{k}{n}$. The ratio of the latter to the former is
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
\frac{\binom{k}{3}\binom{k-2}{n-2}}{(k-2)\binom{k}{n}}=\frac{k!(k-2)!1!(k-3)!n!(k-n)!}{k!(k-2)!(n-2)!(k-n)!3!(k-3)!}=\frac{n \cdot(n-1)}{3!}
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
Solving $n \cdot(n-1)=240$ produces $n=16,-15$, and we discard the latter.
|
| 31 |
+
5. [20] The curves $y=x^{2}(x-3)^{2}$ and $y=\left(x^{2}-1\right)(x-2)$ intersect at a number of points in the real plane. Determine the sum of the $x$-coordinates of these points of intersection.
|
| 32 |
+
Answer: 7. Because the first curve touches the $x$-axis at $x=0$ and $x=3$ while the second curve crosses the $x$-axis at $x= \pm 1$ and $x=2$, there are four points of intersection. In particular, the points of intersection have $x$-coordinates determined by the difference of the two curves:
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
0=x^{2}(x-3)^{2}-\left(x^{2}-1\right)(x-2)=\left(x^{4}-6 x^{3}+\cdots\right)-\left(x^{3}+\cdots\right)=x^{4}-7 x^{3}+\cdots
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
We need only the first two coefficients to determine $x_{1}+x_{2}+x_{3}+x_{4}=-\left(\frac{-7}{1}\right)=7$.
|
| 39 |
+
6. [20] Andrew has a fair six sided die labeled with 1 through 6 as usual. He tosses it repeatedly, and on every third roll writes down the number facing up as long as it is not the 6 . He stops as soon as the last two numbers he has written down are squares or one is a prime and the other is a square. What is the probability that he stops after writing squares consecutively?
|
| 40 |
+
Answer: $4 / \mathbf{2 5}$. We can safely ignore all of the rolls he doesn't record. The probability that he stops after writing two squares consecutively is the same as the probability that he never rolls a prime. For, as soon as the first prime is written, either it must have been preceded by a square or it will be followed by a nonnegative number of additional primes and then a square. So we want the probability that two numbers chosen uniformly with replacement from $\{1,2,3,4,5\}$ are both squares, which is $(2 / 5)^{2}$.
|
| 41 |
+
7. [20] Three positive reals $x, y$, and $z$ are such that
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
\begin{aligned}
|
| 45 |
+
x^{2}+2(y-1)(z-1) & =85 \\
|
| 46 |
+
y^{2}+2(z-1)(x-1) & =84 \\
|
| 47 |
+
z^{2}+2(x-1)(y-1) & =89
|
| 48 |
+
\end{aligned}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Compute $x+y+z$.
|
| 52 |
+
Answer: 18. Add the three equations to obtain
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x-4 x-4 y-4 z+6=258
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
which rewrites as $(x+y+z-2)^{2}=256$. Evidently, $x+y+z=2 \pm 16$. Since $x, y$, and $z$ are positive, $x+y+z>0$ so $x+y+z=2+16=18$.
|
| 59 |
+
8. [20] Find the positive real number(s) $x$ such that $\frac{1}{2}\left(3 x^{2}-1\right)=\left(x^{2}-50 x-10\right)\left(x^{2}+25 x+5\right)$.
|
| 60 |
+
|
| 61 |
+
Answer: $\mathbf{2 5}+\mathbf{2} \sqrt{\mathbf{1 5 9}}$. Write $a=x^{2}-50 x-10$ and $b=x^{2}+25 x+5$; the given becomes $\frac{a+2 b-1}{2}=a b$, so $0=2 a b-a-2 b+1=(a-1)(2 b-1)$. Then $a-1=x^{2}-50 x-11=0$ or $2 b-1=2 x^{2}+50 x+9=0$. The former has a positive root, $x=25+2 \sqrt{159}$, while the latter cannot, for obvious reasons.
|
| 62 |
+
9. [20] Cyclic quadrilateral $A B C D$ has side lengths $A B=1, B C=2, C D=3$, and $A D=4$. Determine $A C / B D$.
|
| 63 |
+
|
| 64 |
+
|
| 65 |
+
Answer: 5/7. Let the diagonals intersect at $P$. Note that triangles $A B P$ and $D C P$ are similar, so that $3 A P=D P$ and $3 B P=C P$. Additionally, triangles $B C P$ and $A D P$ are similar, so that $2 B P=A P$. It follows that
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
\frac{A C}{B D}=\frac{A P+P C}{B P+P D}=\frac{2 B P+3 B P}{B P+6 B P}=\frac{5}{7}
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
10. [20] A positive real number $x$ is such that
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
\sqrt[3]{1-x^{3}}+\sqrt[3]{1+x^{3}}=1
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
Find $x^{2}$.
|
| 78 |
+
Answer: $\frac{\sqrt[3]{28}}{\mathbf{3}}$. Cubing the given equation yields
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
1=\left(1-x^{3}\right)+3 \sqrt[3]{\left(1-x^{3}\right)\left(1+x^{3}\right)}\left(\sqrt[3]{1-x^{3}}+\sqrt[3]{1+x^{3}}\right)+\left(1+x^{3}\right)=2+3 \sqrt[3]{1-x^{6}}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Then $\frac{-1}{3}=\sqrt[3]{1-x^{6}}$, so $\frac{-1}{27}=1-x^{6}$ and $x^{6}=\frac{28}{27}$ and $x^{2}=\frac{\sqrt[3]{28}}{3}$.
|
| 85 |
+
|
| 86 |
+
## Adult Acorns - Gee, I'm a Tree! [200]
|
| 87 |
+
|
| 88 |
+
In this section of the team round, your team will derive some basic results concerning tangential quadrilaterals. Tangential quadrilaterals have an incircle, or a circle lying within them that is tangent to all four sides. If a quadrilateral has an incircle, then the center of this circle is the incenter of the quadrilateral. As you shall see, tangential quadrilaterals are related to cyclic quadrilaterals. For reference, a review of cyclic quadrilaterals is given at the end of this section.
|
| 89 |
+
|
| 90 |
+
Your answers for this section of the team test should be proofs. Note that you may use any standard facts about cyclic quadrilaterals, such as those listed at the end of this test, without proving them. Additionally, you may cite the results of previous problems, even if you were unable to prove them.
|
| 91 |
+
|
| 92 |
+
For these problems, $A B C D$ is a tangential quadrilateral having incenter $I$. For the first three problems, the point $P$ is constructed such that triangle $P A B$ is similar to triangle $I D C$ and lies outside $A B C D$.
|
| 93 |
+
|
| 94 |
+
1. $[\mathbf{3 0}]$ Show that $P A I B$ is cyclic by proving that $\angle I A P$ is supplementary to $\angle P B I$.
|
| 95 |
+
|
| 96 |
+
Solution. Note that $I$ lies on the angle bisectors of the angles of quadrilateral $A B C D$. So writing $\angle D A B=2 \alpha, \angle A B C=2 \beta, \angle B C D=2 \gamma$, and $\angle C D A=2 \delta$, we have
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\begin{aligned}
|
| 100 |
+
\angle I A P+\angle P B I & =\angle I A B+\angle B A P+\angle P B A+\angle A B I \\
|
| 101 |
+
& =\angle I A B+\angle C D I+\angle I C D+\angle A B I \\
|
| 102 |
+
& =\alpha+\beta+\gamma+\delta .
|
| 103 |
+
\end{aligned}
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
We are done because the angles in quadrilateral $A B C D$ add up to $360^{\circ}$.
|
| 107 |
+

|
| 108 |
+
2. [40] Show that triangle $P A I$ is similar to triangle $B I C$. Then conclude that
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
P A=\frac{P I}{B C} \cdot B I
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Solution. We have $\angle I B C=\angle A B I$ because $I$ lies on the angle bisector, and $\angle A B I=\angle A P I$ because $P A I B$ is cyclic. Additionally,
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\angle B C I=\angle I C D=\angle P B A=\angle P I A
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
by the angle bisector $C I$, that triangles $P A B$ and $I D C$ are similar, and the fact that $P A I B$ is cyclic, respectively. It follows that triangles $P A I$ and $B I C$ are similar. In particular, it follows that $I P / P A=B C / B I$, as required.
|
| 121 |
+
3. [25] Deduce from the above that
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
\frac{B C}{A D} \cdot \frac{A I}{B I} \cdot \frac{D I}{C I}=1
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
Solution. Exchanging the roles of $A$ and $D$ with $B$ and $C$, respectively, converts the formula from problem 2 into another formula:
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
P B=\frac{P I}{A D} \cdot A D
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
Then one the one hand, dividing the two gives $P A / P B=(A D \cdot B I) /(B C \cdot A I)$. On the other hand, $P A / P B=D I / C I$ because triangles $P A B$ and $I D C$ are similar. Clearing the denominators in the equation
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\frac{D I}{C I}=\frac{A D \cdot B I}{B C \cdot A I}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
yields the desired form.
|
| 140 |
+
4. [25] Show that $A B+C D=A D+B C$. Use the above to conclude that for some positive number $\alpha$,
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
\begin{array}{ll}
|
| 144 |
+
A B=\alpha \cdot\left(\frac{A I}{C I}+\frac{B I}{D I}\right) & B C=\alpha \cdot\left(\frac{B I}{D I}+\frac{C I}{A I}\right) \\
|
| 145 |
+
C D=\alpha \cdot\left(\frac{C I}{A I}+\frac{D I}{B I}\right) & D A=\alpha \cdot\left(\frac{D I}{B I}+\frac{A I}{C I}\right) .
|
| 146 |
+
\end{array}
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
Solution. Draw in the points of tangency $P, Q, R$, and $S$, of the incircle with sides $A B, B C, C D$, and $A D$, as shown. Then we have equal tangents $A P=A S, B P=B Q, C Q=C R$, and $D R=D S$. Then
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
A B+C D=A P+B P+C R+D R=A S+(B Q+C Q)+D S=B C+A D
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
Using the result of problem 3, we set $B C=x \cdot B I \cdot C I$ and $A D=x \cdot A I \cdot D I$ for some $x$, and $A B=y \cdot A I \cdot B I$ and $C D=y \cdot C I \cdot D I$ for some $y$. Now because $A B+C D=B C+A D$, we obtain
|
| 156 |
+
|
| 157 |
+
$$
|
| 158 |
+
y(A I \cdot B I+C I \cdot D I)=x(B I \cdot C I+A I \cdot D I)
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
So it follows that the ratio $A B: B C: C D: D A$ is uniquely determined. One easily checks that the posed ratio satisfies the three required relations.
|
| 162 |
+
|
| 163 |
+
5. [40] Show that
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
A B \cdot B C=B I^{2}+\frac{A I \cdot B I \cdot C I}{D I}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
Solution. Returning to the original set up, Ptolemy's theorem applied to quadrilateral $P A I B$ gives $A B \cdot P I=P A \cdot B I+P B \cdot A I$. Substituting equation $P A=\frac{P I}{B C} \cdot B I$ from problem 2 and its cousin $P B=\frac{P I}{A D} \cdot A I$ allows us to write
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
A B \cdot P I=\frac{P I}{B C} \cdot B I^{2}+\frac{P I}{A D} \cdot A I^{2}
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
or
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
A B \cdot B C=B I^{2}+\frac{B C}{A D} \cdot A I^{2}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
Substituting the formula $B C / A D=\frac{B I \cdot C I}{A I \cdot D I}$ from problem 3 finishes the problem.
|
| 182 |
+
6. [40] Let the incircle of $A B C D$ be tangent to sides $A B, B C, C D$, and $A D$ at points $P, Q, R$, and $S$, respectively. Show that $A B C D$ is cyclic if and only if $P R \perp Q S$.
|
| 183 |
+
Solution. Let the diagonals of $P Q R S$ intersect at $T$. Because $\overline{A P}$ and $\overline{A S}$ are tangent to $\omega$ at $P$ and $S$, we may write $\alpha=\angle A S P=\angle S P A=\angle S Q P$ and $\beta=\angle C Q R=\angle Q R C=\angle Q P R$. Then $\angle P T Q=\pi-\alpha-\beta$. On the other hand, $\angle P A S=\pi-2 \alpha$ and $\angle R C Q=\pi-2 \beta$, so that $A B C D$ is cyclic if and only if
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
\pi=\angle B A D+\angle D C B=2 \pi-2 \alpha-2 \beta
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
or simply
|
| 190 |
+
|
| 191 |
+
$$
|
| 192 |
+
\pi / 2=\pi-\alpha-\beta=\angle P T Q
|
| 193 |
+
$$
|
| 194 |
+
|
| 195 |
+
as desired.
|
| 196 |
+
|
| 197 |
+
A brief review of cyclic Quadrilaterals.
|
| 198 |
+
|
| 199 |
+
The following discussion of cyclic quadrilaterals is included for reference. Any of the results given here may be cited without proof in your writeups.
|
| 200 |
+
A cyclic quadrilateral is a quadrilateral whose four vertices lie on a circle called the circumcircle (the circle is unique if it exists.) If a quadrilateral has a circumcircle, then the center of this circumcircle is called the circumcenter of the quadrilateral. For a convex quadrilateral $A B C D$, the following are equivalent:
|
| 201 |
+
|
| 202 |
+
- Quadrilateral $A B C D$ is cyclic;
|
| 203 |
+
- $\angle A B D=\angle A C D$ (or $\angle B C A=\angle B D A$, etc.);
|
| 204 |
+
- Angles $\angle A B C$ and $\angle C D A$ are supplementary, that is, $m \angle A B C+m \angle C D A=180^{\circ}$ (or angles $\angle B C D$ and $\angle B A D$ are supplementary);
|
| 205 |
+
|
| 206 |
+
Cyclic quadrilaterals have a number of interesting properties. A cyclic quadrilateral $A B C D$ satisfies
|
| 207 |
+
|
| 208 |
+
$$
|
| 209 |
+
A C \cdot B D=A B \cdot C D+A D \cdot B C
|
| 210 |
+
$$
|
| 211 |
+
|
| 212 |
+
a result known as Ptolemy's theorem. Another result, typically called Power of a Point, asserts that given a circle $\omega$, a point $P$ anywhere in the plane of $\omega$, and a line $\ell$ through $P$ intersecting $\omega$ at points $A$ and $B$, the value of $A P \cdot B P$ is independent of $\ell$; i.e., if a second line $\ell^{\prime}$ through $P$ intersects $\omega$ at $A^{\prime}$ and $B^{\prime}$, then $A P \cdot B P=A^{\prime} P \cdot B^{\prime} P$. This second theorem is proved via similar triangles. Say $P$ lies outside of $\omega$, that $\ell$ and $\ell^{\prime}$ are as before and that $A$ and $A^{\prime}$ lie on segments $B P$ and $B^{\prime} P$ respectively. Then triangle $A A^{\prime} P$ is similar to triangle $B^{\prime} B P$ because the triangles share an angle at $P$ and we have
|
| 213 |
+
|
| 214 |
+
$$
|
| 215 |
+
m \angle A A^{\prime} P=180^{\circ}-m \angle B^{\prime} A^{\prime} A=m \angle A B B^{\prime}=m \angle P B B^{\prime}
|
| 216 |
+
$$
|
| 217 |
+
|
| 218 |
+
The case where $A=B$ is valid and describes the tangents to $\omega$. A similar proof works for $P$ inside $\omega$.
|
| 219 |
+
|
HarvardMIT/md/en-112-2008-feb-alg-solutions.md
ADDED
|
@@ -0,0 +1,151 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
## Individual Round: Algebra Test
|
| 6 |
+
|
| 7 |
+
1. [3] Positive real numbers $x, y$ satisfy the equations $x^{2}+y^{2}=1$ and $x^{4}+y^{4}=\frac{17}{18}$. Find $x y$.
|
| 8 |
+
|
| 9 |
+
Answer: $\sqrt[\frac{1}{6}]{ }$ We have $2 x^{2} y^{2}=\left(x^{2}+y^{2}\right)^{2}-\left(x^{4}+y^{4}\right)=\frac{1}{18}$, so $x y=\frac{1}{6}$.
|
| 10 |
+
2. [3] Let $f(n)$ be the number of times you have to hit the $\sqrt{ }$ key on a calculator to get a number less than 2 starting from $n$. For instance, $f(2)=1, f(5)=2$. For how many $1<m<2008$ is $f(m)$ odd?
|
| 11 |
+
Answer: 242 This is $\left[2^{1}, 2^{2}\right) \cup\left[2^{4}, 2^{8}\right) \cup\left[2^{16}, 2^{32}\right) \ldots$, and $2^{8}<2008<2^{16}$ so we have exactly the first two intervals.
|
| 12 |
+
3. [4] Determine all real numbers $a$ such that the inequality $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution in $x$.
|
| 13 |
+
Answer: 1,2 Let $f(x)=x^{2}+2 a x+3 a$. Note that $f(-3 / 2)=9 / 4$, so the graph of $f$ is a parabola that goes through $(-3 / 2,9 / 4)$. Then, the condition that $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution means that the parabola has exactly one point in the strip $-1 \leq y \leq 1$, which is possible if and only if the parabola is tangent to $y=1$. That is, $x^{2}+2 a x+3 a=2$ has exactly one solution. Then, the discriminant $\Delta=4 a^{2}-4(3 a-2)=4 a^{2}-12 a+8$ must be zero. Solving the equation yields $a=1,2$.
|
| 14 |
+
4. [4] The function $f$ satisfies
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
f(x)+f(2 x+y)+5 x y=f(3 x-y)+2 x^{2}+1
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
for all real numbers $x, y$. Determine the value of $f(10)$.
|
| 21 |
+
Answer: $\quad-49$ Setting $x=10$ and $y=5$ gives $f(10)+f(25)+250=f(25)+200+1$, from which we get $f(10)=-49$.
|
| 22 |
+
|
| 23 |
+
Remark: By setting $y=\frac{x}{2}$, we see that the function is $f(x)=-\frac{1}{2} x^{2}+1$, and it can be checked that this function indeed satisfies the given equation.
|
| 24 |
+
5. [5] Let $f(x)=x^{3}+x+1$. Suppose $g$ is a cubic polynomial such that $g(0)=-1$, and the roots of $g$ are the squares of the roots of $f$. Find $g(9)$.
|
| 25 |
+
Answer: 899 Let $a, b, c$ be the zeros of $f$. Then $f(x)=(x-a)(x-b)(x-c)$. Then, the roots of $g$ are $a^{2}, b^{2}, c^{2}$, so $g(x)=k\left(x-a^{2}\right)\left(x-b^{2}\right)\left(x-c^{2}\right)$ for some constant $k$. Since $a b c=-f(0)=-1$, we have $k=k a^{2} b^{2} c^{2}=-g(0)=1$. Thus,
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
g\left(x^{2}\right)=\left(x^{2}-a^{2}\right)\left(x^{2}-b^{2}\right)\left(x^{2}-c^{2}\right)=(x-a)(x-b)(x-c)(x+a)(x+b)(x+c)=-f(x) f(-x)
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Setting $x=3$ gives $g(9)=-f(3) f(-3)=-(31)(-29)=899$.
|
| 32 |
+
6. [5] A root of unity is a complex number that is a solution to $z^{n}=1$ for some positive integer $n$. Determine the number of roots of unity that are also roots of $z^{2}+a z+b=0$ for some integers $a$ and $b$.
|
| 33 |
+
Answer: 8 The only real roots of unity are 1 and -1 . If $\zeta$ is a complex root of unity that is also a root of the equation $z^{2}+a z+b$, then its conjugate $\bar{\zeta}$ must also be a root. In this case, $|a|=|\zeta+\bar{\zeta}| \leq|\zeta|+|\bar{\zeta}|=$ 2 and $b=\zeta \bar{\zeta}=1$. So we only need to check the quadratics $z^{2}+2 z+1, z^{2}+z+1, z^{2}+1, z^{2}-z+1, z^{2}-2 z+1$. We find 8 roots of unity: $\pm 1, \pm i, \frac{1}{2}( \pm 1 \pm \sqrt{3} i)$.
|
| 34 |
+
7. [5] Compute $\sum_{n=1}^{\infty} \sum_{k=1}^{n-1} \frac{k}{2^{n+k}}$.
|
| 35 |
+
|
| 36 |
+
Answer: $\frac{4}{9}$ We change the order of summation:
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
\sum_{n=1}^{\infty} \sum_{k=1}^{n-1} \frac{k}{2^{n+k}}=\sum_{k=1}^{\infty} \frac{k}{2^{k}} \sum_{n=k+1}^{\infty} \frac{1}{2^{n}}=\sum_{k=1}^{\infty} \frac{k}{4^{k}}=\frac{4}{9} .
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
(The last two steps involve the summation of an infinite geometric series, and what is sometimes called an infinite arithmetico-geometric series. These summations are quite standard, and thus we omit the details here.)
|
| 43 |
+
8. [6] Compute $\arctan \left(\tan 65^{\circ}-2 \tan 40^{\circ}\right)$. (Express your answer in degrees as an angle between $0^{\circ}$ and $180^{\circ}$.)
|
| 44 |
+
Answer: $25^{\circ}$ First Solution: We have
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
\tan 65^{\circ}-2 \tan 40^{\circ}=\cot 25^{\circ}-2 \cot 50^{\circ}=\cot 25^{\circ}-\frac{\cot ^{2} 25^{\circ}-1}{\cot 25^{\circ}}=\frac{1}{\cot 25^{\circ}}=\tan 25^{\circ} .
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Therefore, the answer is $25^{\circ}$.
|
| 51 |
+
Second Solution: We have
|
| 52 |
+
$\tan 65^{\circ}-2 \tan 40^{\circ}=\frac{1+\tan 20^{\circ}}{1-\tan 20^{\circ}}-\frac{4 \tan 20^{\circ}}{1-\tan ^{2} 20^{\circ}}=\frac{\left(1-\tan 20^{\circ}\right)^{2}}{\left(1-\tan 20^{\circ}\right)\left(1+\tan 20^{\circ}\right)}=\tan \left(45^{\circ}-20^{\circ}\right)=\tan 25^{\circ}$.
|
| 53 |
+
Again, the answer is $25^{\circ}$.
|
| 54 |
+
9. [7] Let $S$ be the set of points $(a, b)$ with $0 \leq a, b \leq 1$ such that the equation
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
x^{4}+a x^{3}-b x^{2}+a x+1=0
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
has at least one real root. Determine the area of the graph of $S$.
|
| 61 |
+
Answer: $\frac{1}{4}$ After dividing the equation by $x^{2}$, we can rearrange it as
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\left(x+\frac{1}{x}\right)^{2}+a\left(x+\frac{1}{x}\right)-b-2=0
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Let $y=x+\frac{1}{x}$. We can check that the range of $x+\frac{1}{x}$ as $x$ varies over the nonzero reals is $(-\infty,-2] \cup[2, \infty)$. Thus, the following equation needs to have a real root:
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
y^{2}+a y-b-2=0 .
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
Its discriminant, $a^{2}+4(b+2)$, is always positive since $a, b \geq 0$. Then, the maximum absolute value of the two roots is
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\frac{a+\sqrt{a^{2}+4(b+2)}}{2} .
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
We need this value to be at least 2 . This is equivalent to
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\sqrt{a^{2}+4(b+2)} \geq 4-a .
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
We can square both sides and simplify to obtain
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
2 a \geq 2-b
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
This equation defines the region inside $[0,1] \times[0,1]$ that is occupied by $S$, from which we deduce that the desired area is $1 / 4$.
|
| 92 |
+
10. [8] Evaluate the infinite sum
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\sum_{n=0}^{\infty}\binom{2 n}{n} \frac{1}{5^{n}}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
Answer: $\sqrt{5}$ First Solution: Note that
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\begin{aligned}
|
| 102 |
+
\binom{2 n}{n} & =\frac{(2 n)!}{n!\cdot n!}=\frac{(2 n)(2 n-2)(2 n-4) \cdots(2)}{n!} \cdot \frac{(2 n-1)(2 n-3)(2 n-5) \cdots(1)}{n!} \\
|
| 103 |
+
& =2^{n} \cdot \frac{(-2)^{n}}{n!}\left(-\frac{1}{2}\right)\left(-\frac{1}{2}-1\right)\left(-\frac{1}{2}-2\right) \cdots\left(-\frac{1}{2}-n+1\right) \\
|
| 104 |
+
& =(-4)^{n}\binom{-\frac{1}{2}}{n}
|
| 105 |
+
\end{aligned}
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Then, by the binomial theorem, for any real $x$ with $|x|<\frac{1}{4}$, we have
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
(1-4 x)^{-1 / 2}=\sum_{n=0}^{\infty}\binom{-\frac{1}{2}}{n}(-4 x)^{n}=\sum_{n=0}^{\infty}\binom{2 n}{n} x^{n} .
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Therefore,
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\sum_{n=0}^{\infty}\binom{2 n}{n}\left(\frac{1}{5}\right)^{n}=\frac{1}{\sqrt{1-\frac{4}{5}}}=\sqrt{5}
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
Second Solution: Consider the generating function
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
f(x)=\sum_{n=0}^{\infty}\binom{2 n}{n} x^{n}
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
It has formal integral given by
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
g(x)=I(f(x))=\sum_{n=0}^{\infty} \frac{1}{n+1}\binom{2 n}{n} x^{n+1}=\sum_{n=0}^{\infty} C_{n} x^{n+1}=x \sum_{n=0}^{\infty} C_{n} x^{n}
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
where $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$ is the $n$th Catalan number. Let $h(x)=\sum_{n=0}^{\infty} C_{n} x^{n}$; it suffices to compute this generating function. Note that
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
1+x h(x)^{2}=1+x \sum_{i, j \geq 0} C_{i} C_{j} x^{i+j}=1+x \sum_{k \geq 0}\left(\sum_{i=0}^{k} C_{i} C_{k-i}\right) x^{k}=1+\sum_{k \geq 0} C_{k+1} x^{k+1}=h(x)
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
where we've used the recurrence relation for the Catalan numbers. We now solve for $h(x)$ with the quadratic equation to obtain
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
h(x)=\frac{1 / x \pm \sqrt{1 / x^{2}-4 / x}}{2}=\frac{1 \pm \sqrt{1-4 x}}{2 x}
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
Note that we must choose the - sign in the $\pm$, since the + would lead to a leading term of $\frac{1}{x}$ for $h$ (by expanding $\sqrt{1-4 x}$ into a power series). Therefore, we see that
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
f(x)=D(g(x))=D(x h(x))=D\left(\frac{1-\sqrt{1-4 x}}{2}\right)=\frac{1}{\sqrt{1-4 x}}
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
and our answer is hence $f(1 / 5)=\sqrt{5}$.
|
| 151 |
+
|
HarvardMIT/md/en-112-2008-feb-calc-solutions.md
ADDED
|
@@ -0,0 +1,127 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
## Individual Round: Calculus Test
|
| 6 |
+
|
| 7 |
+
1. [3] Let $f(x)=1+x+x^{2}+\cdots+x^{100}$. Find $f^{\prime}(1)$.
|
| 8 |
+
|
| 9 |
+
Answer: 5050 Note that $f^{\prime}(x)=1+2 x+3 x^{2}+\cdots+100 x^{99}$, so $f^{\prime}(1)=1+2+\cdots+100=\frac{100 \cdot 101}{2}=$ 5050.
|
| 10 |
+
2. [3] Let $\ell$ be the line through $(0,0)$ and tangent to the curve $y=x^{3}+x+16$. Find the slope of $\ell$.
|
| 11 |
+
|
| 12 |
+
Answer: 13 Let the point of tangency be $\left(t, t^{3}+t+16\right)$, then the slope of $\ell$ is $\left(t^{3}+t+16\right) / t$. On the other hand, since $d y / d x=3 x^{2}+1$, the slope of $\ell$ is $3 t^{2}+1$. Therefore,
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\frac{t^{3}+t+16}{t}=3 t^{2}+1
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
Simplifying, we get $t^{3}=8$, so $t=2$. It follows that the slope is $3(2)^{2}+1=13$.
|
| 19 |
+
3. [4] Find all $y>1$ satisfying $\int_{1}^{y} x \ln x d x=\frac{1}{4}$.
|
| 20 |
+
|
| 21 |
+
Answer: $\sqrt{\sqrt{e}}$ Applying integration by parts with $u=\ln x$ and $v=\frac{1}{2} x^{2}$, we get
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\int_{1}^{y} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{1} ^{y}-\frac{1}{2} \int_{1}^{y} x d x=\frac{1}{2} y^{2} \ln y-\frac{1}{4} y^{2}+\frac{1}{4}
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
So $y^{2} \ln y=\frac{1}{2} y^{2}$. Since $y>1$, we obtain $\ln y=\frac{1}{2}$, and thus $y=\sqrt{e}$.
|
| 28 |
+
4. [4] Let $a, b$ be constants such that $\lim _{x \rightarrow 1} \frac{(\ln (2-x))^{2}}{x^{2}+a x+b}=1$. Determine the pair $(a, b)$.
|
| 29 |
+
|
| 30 |
+
Answer: $(-2,1)$ When $x=1$, the numerator is 0 , so the denominator must be zero as well, so $1+a+b=0$. Using l'Hôpital's rule, we must have
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
1=\lim _{x \rightarrow 1} \frac{(\ln (2-x))^{2}}{x^{2}+a x+b}=\lim _{x \rightarrow 1} \frac{2 \ln (2-x)}{(x-2)(2 x+a)}
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
and by the same argument we find that $2+a=0$. Thus, $a=-2$ and $b=1$. This is indeed a solution, as can be seen by finishing the computation.
|
| 37 |
+
5. [4] Let $f(x)=\sin ^{6}\left(\frac{x}{4}\right)+\cos ^{6}\left(\frac{x}{4}\right)$ for all real numbers $x$. Determine $f^{(2008)}(0)$ (i.e., $f$ differentiated 2008 times and then evaluated at $x=0$ ).
|
| 38 |
+
|
| 39 |
+
Answer: | $\frac{3}{8}$ |
|
| 40 |
+
| :---: |
|
| 41 |
+
| We have |
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
\begin{aligned}
|
| 45 |
+
\sin ^{6} x+\cos ^{6} x & =\left(\sin ^{2} x+\cos ^{2} x\right)^{3}-3 \sin ^{2} x \cos ^{2} x\left(\sin ^{2} x+\cos ^{2} x\right) \\
|
| 46 |
+
& =1-3 \sin ^{2} x \cos ^{2} x=1-\frac{3}{4} \sin ^{2} 2 x=1-\frac{3}{4}\left(\frac{1-\cos 4 x}{2}\right) \\
|
| 47 |
+
& =\frac{5}{8}+\frac{3}{8} \cos 4 x
|
| 48 |
+
\end{aligned}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
It follows that $f(x)=\frac{5}{8}+\frac{3}{8} \cos x$. Thus $f^{(2008)}(x)=\frac{3}{8} \cos x$. Evaluating at $x=0$ gives $\frac{3}{8}$.
|
| 52 |
+
6. [5] Determine the value of $\lim _{n \rightarrow \infty} \sum_{k=0}^{n}\binom{n}{k}^{-1}$.
|
| 53 |
+
|
| 54 |
+
Answer: 2 Let $S_{n}$ denote the sum in the limit. For $n \geq 1$, we have $S_{n} \geq\binom{ n}{0}^{-1}+\binom{n}{n}^{-1}=2$. On the other hand, for $n \geq 3$, we have
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
S_{n}=\binom{n}{0}^{-1}+\binom{n}{1}^{-1}+\binom{n}{n-1}^{-1}+\binom{n}{n}^{-1}+\sum_{k=2}^{n-2}\binom{n}{k}^{-1} \leq 2+\frac{2}{n}+(n-3)\binom{n}{2}^{-1}
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
which goes to 2 as $n \rightarrow \infty$. Therefore, $S_{n} \rightarrow 2$.
|
| 61 |
+
7. [5] Find $p$ so that $\lim _{x \rightarrow \infty} x^{p}(\sqrt[3]{x+1}+\sqrt[3]{x-1}-2 \sqrt[3]{x})$ is some non-zero real number.
|
| 62 |
+
|
| 63 |
+
Answer: $\sqrt{\frac{5}{3}}$ Make the substitution $t=\frac{1}{x}$. Then the limit equals to
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\lim _{t \rightarrow 0} t^{-p}\left(\sqrt[3]{\frac{1}{t}+1}+\sqrt[3]{\frac{1}{t}-1}-2 \sqrt[3]{\frac{1}{t}}\right)=\lim _{t \rightarrow 0} t^{-p-\frac{1}{3}}(\sqrt[3]{1+t}+\sqrt[3]{1-t}-2)
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
We need the degree of the first nonzero term in the MacLaurin expansion of $\sqrt[3]{1+t}+\sqrt[3]{1-t}-2$. We have
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
\sqrt[3]{1+t}=1+\frac{1}{3} t-\frac{1}{9} t^{2}+o\left(t^{2}\right), \quad \sqrt[3]{1-t}=1-\frac{1}{3} t-\frac{1}{9} t^{2}+o\left(t^{2}\right)
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
It follows that $\sqrt[3]{1+t}+\sqrt[3]{1-t}-2=-\frac{2}{9} t^{2}+o\left(t^{2}\right)$. By consider the degree of the leading term, it follows that $-p-\frac{1}{3}=-2$. So $p=\frac{5}{3}$.
|
| 76 |
+
8. $[7]$ Let $T=\int_{0}^{\ln 2} \frac{2 e^{3 x}+e^{2 x}-1}{e^{3 x}+e^{2 x}-e^{x}+1} d x$. Evaluate $e^{T}$.
|
| 77 |
+
|
| 78 |
+
Answer: $\frac{11}{4}$ Divide the top and bottom by $e^{x}$ to obtain that
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
T=\int_{0}^{\ln 2} \frac{2 e^{2 x}+e^{x}-e^{-x}}{e^{2 x}+e^{x}-1+e^{-x}} d x
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Notice that $2 e^{2 x}+e^{x}-e^{-x}$ is the derivative of $e^{2 x}+e^{x}-1+e^{-x}$, and so
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
T=\left[\ln \left|e^{2 x}+e^{x}-1+e^{-x}\right|\right]_{0}^{\ln 2}=\ln \left(4+2-1+\frac{1}{2}\right)-\ln 2=\ln \left(\frac{11}{4}\right)
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Therefore, $e^{T}=\frac{11}{4}$.
|
| 91 |
+
9. [7] Evaluate the limit $\lim _{n \rightarrow \infty} n^{-\frac{1}{2}\left(1+\frac{1}{n}\right)}\left(1^{1} \cdot 2^{2} \cdots \cdots n^{n}\right)^{\frac{1}{n^{2}}}$.
|
| 92 |
+
|
| 93 |
+
Answer: $e^{-1 / 4}$ Taking the logarithm of the expression inside the limit, we find that it is
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
-\frac{1}{2}\left(1+\frac{1}{n}\right) \ln n+\frac{1}{n^{2}} \sum_{k=1}^{n} k \ln k=\frac{1}{n} \sum_{k=1}^{n} \frac{k}{n} \ln \left(\frac{k}{n}\right)
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
We can recognize this as the as Riemann sum expansion for the integral $\int_{0}^{1} x \ln x d x$, and thus the limit of the above sum as $n \rightarrow \infty$ equals to the value of this integral. Evaluating this integral using integration by parts, we find that
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
\int_{0}^{1} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{0} ^{1}-\int_{0}^{1} \frac{x}{2} d x=-\frac{1}{4}
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
Therefore, the original limit is $e^{-1 / 4}$.
|
| 106 |
+
10. [8] Evaluate the integral $\int_{0}^{1} \ln x \ln (1-x) d x$.
|
| 107 |
+
|
| 108 |
+
Answer: $2-\frac{\pi^{2}}{6}$ We have the MacLaurin expansion $\ln (1-x)=-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\cdots$. So
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
\int_{0}^{1} \ln x \ln (1-x) d x=-\int_{0}^{1} \ln x \sum_{n=1}^{\infty} \frac{x^{n}}{n} d x=-\sum_{n=1}^{\infty} \frac{1}{n} \int_{0}^{1} x^{n} \ln x d x
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Using integration by parts, we get
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\int_{0}^{1} x^{n} \ln x d x=\left.\frac{x^{n+1} \ln x}{n+1}\right|_{0} ^{1}-\int_{0}^{1} \frac{x^{n}}{n+1} d x=-\frac{1}{(n+1)^{2}}
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
(We used the fact that $\lim _{x \rightarrow 0} x^{n} \ln x=0$ for $n>0$, which can be proven using l'Hôpital's rule.) Therefore, the original integral equals to
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
\sum_{n=1}^{\infty} \frac{1}{n(n+1)^{2}}=\sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n+1}-\frac{1}{(n+1)^{2}}\right)
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
Telescoping the sum and using the well-known identity $\sum_{n=0}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6}$, we see that the above sum is equal to $2-\frac{\pi^{2}}{6}$.
|
| 127 |
+
|
HarvardMIT/md/en-112-2008-feb-comb-solutions.md
ADDED
|
@@ -0,0 +1,88 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
Individual Round: Combinatorics Test
|
| 6 |
+
|
| 7 |
+
1. [3] A $3 \times 3 \times 3$ cube composed of 27 unit cubes rests on a horizontal plane. Determine the number of ways of selecting two distinct unit cubes from a $3 \times 3 \times 1$ block (the order is irrelevant) with the property that the line joining the centers of the two cubes makes a $45^{\circ}$ angle with the horizontal plane.
|
| 8 |
+
Answer: 60 There are 6 such slices, and each slice gives 10 valid pairs (with no overcounting). Therefore, there are 60 such pairs.
|
| 9 |
+
2. [3] Let $S=\{1,2, \ldots, 2008\}$. For any nonempty subset $A \subset S$, define $m(A)$ to be the median of $A$ (when $A$ has an even number of elements, $m(A)$ is the average of the middle two elements). Determine the average of $m(A)$, when $A$ is taken over all nonempty subsets of $S$.
|
| 10 |
+
|
| 11 |
+
Answer: $\frac{-2009}{2}$ For any subset $A$, we can define the "reflected subset" $A^{\prime}=\{i \mid 2009-i \in A\}$. Then $m(A)=2009-m\left(A^{\prime}\right)$. Note that as $A$ is taken over all nonempty subsets of $S, A^{\prime}$ goes through all the nonempty subsets of $S$ as well. Thus, the average of $m(A)$ is equal to the average of $\frac{m(A)+m\left(A^{\prime}\right)}{2}$, which is the constant $\frac{2009}{2}$.
|
| 12 |
+
|
| 13 |
+
Remark: : This argument is very analogous to the famous argument that Gauss used to sum the series $1+2+\cdots+100$.
|
| 14 |
+
3. [4] Farmer John has 5 cows, 4 pigs, and 7 horses. How many ways can he pair up the animals so that every pair consists of animals of different species? Assume that all animals are distinguishable from each other. (Please write your answer as an integer, without any incomplete computations.)
|
| 15 |
+
Answer: 100800 Since there are 9 cow and pigs combined and 7 horses, there must be a pair with 1 cow and 1 pig, and all the other pairs must contain a horse. There are $4 \times 5$ ways of selecting the cow-pig pair, and 7! ways to select the partners for the horses. It follows that the answer is $4 \times 5 \times 7!=100800$.
|
| 16 |
+
4. [4] Kermit the frog enjoys hopping around the infinite square grid in his backyard. It takes him 1 Joule of energy to hop one step north or one step south, and 1 Joule of energy to hop one step east or one step west. He wakes up one morning on the grid with 100 Joules of energy, and hops till he falls asleep with 0 energy. How many different places could he have gone to sleep?
|
| 17 |
+
Answer: 10201
|
| 18 |
+
It is easy to see that the coordinates of the frog's final position must have the same parity. Suppose that the frog went to sleep at $(x, y)$. Then, we have that $-100 \leq y \leq 100$ and $|x| \leq 100-|y|$, so $x$ can take on the values $-100+|y|,-98+|y|, \ldots, 100-|y|$. There are $101-|y|$ such values, so the total number of such locations is
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
\sum_{y=-100}^{100} 101-|y|=201 \cdot 101-2 \cdot \frac{100(100+1)}{2}=101^{2}=10201
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
5. [5] Let $S$ be the smallest subset of the integers with the property that $0 \in S$ and for any $x \in S$, we have $3 x \in S$ and $3 x+1 \in S$. Determine the number of non-negative integers in $S$ less than 2008.
|
| 25 |
+
Answer: 128 Write the elements of $S$ in their ternary expansion (i.e. base 3). Then the second condition translates into, if $\overline{d_{1} d_{2} \cdots d_{k}} \in S$, then $\overline{d_{1} d_{2} \cdots d_{k} 0}$ and $\overline{d_{1} d_{2} \cdots d_{k} 1}$ are also in $S$. It follows that $S$ is the set of nonnegative integers whose tertiary representation contains only the digits 0 and 1. Since $2 \cdot 3^{6}<2008<3^{7}$, there are $2^{7}=128$ such elements less than 2008 . Therefore, there are 128 such non-negative elements.
|
| 26 |
+
6. [5] A Sudoku matrix is defined as a $9 \times 9$ array with entries from $\{1,2, \ldots, 9\}$ and with the constraint that each row, each column, and each of the nine $3 \times 3$ boxes that tile the array contains each digit from 1 to 9 exactly once. A Sudoku matrix is chosen at random (so that every Sudoku matrix has equal probability of being chosen). We know two of squares in this matrix, as shown. What is the probability that the square marked by? contains the digit 3 ?
|
| 27 |
+
|
| 28 |
+
|
| 29 |
+
Answer: $\quad \frac{2}{21}$ The third row must contain the digit 1, and it cannot appear in the leftmost three squares. Therefore, the digit 1 must fall into one of the six squares shown below that are marked with $\star$. By symmetry, each starred square has an equal probability of containing the digit 1 (To see this more precisely, note that swapping columns 4 and 5 gives another Sudoku matrix, so the probability that the 4 th column $\star$ has the 1 is the same as the probability that the 5 th column $\star$ has the 1 . Similarly, switching the 4-5-6th columns with the 7-8-9th columns yields another Sudoku matrix, which implies in particular that the probability that the 4 th column $\star$ has the 1 is the same as the probability that the 7 th column $\star$ has the 1 . The rest of the argument follows analogously.) Therefore, the probability that the ? square contains 1 is $1 / 6$.
|
| 30 |
+
|
| 31 |
+
|
| 32 |
+
Similarly the probability that the digit 2 appears at? is also $1 / 6$. By symmetry, the square ? has equal probability of containing the digits $3,4,5,6,7,8,9$. It follows that this probability is $\left(1-\frac{1}{6}-\frac{1}{6}\right) / 7=$ $\frac{2}{21}$.
|
| 33 |
+
7. [6] Let $P_{1}, P_{2}, \ldots, P_{8}$ be 8 distinct points on a circle. Determine the number of possible configurations made by drawing a set of line segments connecting pairs of these 8 points, such that: (1) each $P_{i}$ is the endpoint of at most one segment and (2) two no segments intersect. (The configuration with no edges drawn is allowed. An example of a valid configuration is shown below.)
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
Answer: 323 Let $f(n)$ denote the number of valid configurations when there are $n$ points on the circle. Let $P$ be one of the points. If $P$ is not the end point of an edge, then there are $f(n-1)$ ways to connect the remaining $n-1$ points. If $P$ belongs to an edge that separates the circle so that there are $k$ points on one side and $n-k-2$ points on the other side, then there are $f(k) f(n-k-2)$ ways of finishing the configuration. Thus, $f(n)$ satisfies the recurrence relation
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
f(n)=f(n-1)+f(0) f(n-2)+f(1) f(n-3)+f(2) f(n-4)+\cdots+f(n-2) f(0), n \geq 2
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
The initial conditions are $f(0)=f(1)=1$. Using the recursion, we find that $f(2)=2, f(3)=4, f(4)=$ $9, f(5)=21, f(6)=51, f(7)=127, f(8)=323$.
|
| 43 |
+
|
| 44 |
+
Remark: These numbers are known as the Motzkin numbers. This is sequence A001006 in the On-Line Encyclopedia of Integer Sequences (http://www.research.att.com/~njas/sequences/A001006). In
|
| 45 |
+
|
| 46 |
+
Richard Stanley's Enumerative Combinatorics Volume 2, one can find 13 different interpretations of Motzkin numbers in exercise 6.38.
|
| 47 |
+
8. [6] Determine the number of ways to select a sequence of 8 sets $A_{1}, A_{2}, \ldots, A_{8}$, such that each is a subset (possibly empty) of $\{1,2\}$, and $A_{m}$ contains $A_{n}$ if $m$ divides $n$.
|
| 48 |
+
Answer: 2025 Consider an arbitrary $x \in\{1,2\}$, and let us consider the number of ways for $x$ to be in some of the sets so that the constraints are satisfied. We divide into a few cases:
|
| 49 |
+
|
| 50 |
+
- Case: $x \notin A_{1}$. Then $x$ cannot be in any of the sets. So there is one possibility.
|
| 51 |
+
- Case: $x \in A_{1}$ but $x \notin A_{2}$. Then the only other sets that $x$ could be in are $A_{3}, A_{5}, A_{7}$, and $x$ could be in some collection of them. There are 8 possibilities in this case.
|
| 52 |
+
- Case: $x \in A_{2}$. Then $x \in A_{1}$ automatically. There are 4 independent choices to be make here: (1) whether $x \in A_{5} ;(2)$ whether $x \in A_{7}$; (3) whether $x \in A_{3}$, and if yes, whether $x \in A_{6}$; (4) whether $x \in A_{4}$, and if yes, whether $x \in A_{8}$. There are $2 \times 2 \times 3 \times 3=36$ choices here.
|
| 53 |
+
|
| 54 |
+
Therefore, there are $1+8+36=45$ ways to place $x$ into some of the sets. Since the choices for $x=1$ and $x=2$ are made independently, we see that the total number of possibilities is $45^{2}=2025$.
|
| 55 |
+
|
| 56 |
+
Remark: The solution could be guided by the following diagram. Set $A$ is above $B$ and connected to $B$ if and only if $A \subset B$. Such diagrams are known as Hasse diagrams, which are used to depict partially ordered sets.
|
| 57 |
+
|
| 58 |
+
9. [7] On an infinite chessboard (whose squares are labeled by $(x, y)$, where $x$ and $y$ range over all integers), a king is placed at $(0,0)$. On each turn, it has probability of 0.1 of moving to each of the four edgeneighboring squares, and a probability of 0.05 of moving to each of the four diagonally-neighboring squares, and a probability of 0.4 of not moving. After 2008 turns, determine the probability that the king is on a square with both coordinates even. An exact answer is required.
|
| 59 |
+
|
| 60 |
+
Answer: | $\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}$ |
|
| 61 |
+
| :---: |
|
| 62 |
+
| Since only the parity of the coordinates are relevant, it is equivalent to | consider a situation where the king moves $(1,0)$ with probability 0.2 , moves $(0,1)$ with probability 0.2 , moves $(1,1)$ with probability 0.2 , and stays put with probability 0.4 . This can be analyzed using the generating function
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
f(x, y)=(0.4+2 \times 0.1 x+2 \times 0.1 y+4 \times 0.05 x y)^{2008}=\frac{(2+x+y+x y)^{2008}}{5^{2008}} .
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
We wish to find the sum of the coefficients of the terms $x^{a} y^{b}$, where both $a$ and $b$ are even. This is simply equal to $\frac{1}{4}(f(1,1)+f(1,-1)+f(-1,1)+f(-1,-1))$. We have $f(1,1)=1$ and $f(1,-1)=$ $f(-1,1)=f(-1,-1)=1 / 5^{2008}$. Therefore, the answer is
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
\frac{1}{4}(f(1,1)+f(1,-1)+f(-1,1)+f(-1,-1))=\frac{1}{4}\left(1+\frac{3}{5^{2008}}\right)=\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
10. [7] Determine the number of 8-tuples of nonnegative integers $\left(a_{1}, a_{2}, a_{3}, a_{4}, b_{1}, b_{2}, b_{3}, b_{4}\right)$ satisfying $0 \leq$ $a_{k} \leq k$, for each $k=1,2,3,4$, and $a_{1}+a_{2}+a_{3}+a_{4}+2 b_{1}+3 b_{2}+4 b_{3}+5 b_{4}=19$.
|
| 75 |
+
Answer: 1540 For each $k=1,2,3,4$, note that set of pairs $\left(a_{k}, b_{k}\right)$ with $0 \leq a_{k} \leq k$ maps bijectively to the set of nonnegative integers through the map $\left(a_{k}, b_{k}\right) \mapsto a_{k}+(k+1) b_{k}$, as $a_{k}$ is simply the remainder of $a_{k}+(k+1) b_{k}$ upon division by $k+1$. By letting $x_{k}=a_{k}+(k+1) b_{k}$, we see that the problem is equivalent to finding the number of quadruples of nonnegative integers $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ such that $x_{1}+x_{2}+x_{3}+x_{4}=19$. This is the same as finding the number of quadruples of positive integers $\left(x_{1}+1, x_{2}+1, x_{3}+1, x_{4}+1\right)$ such that $x_{1}+x_{2}+x_{3}+x_{4}=23$. By a standard "dots and bars" argument, we see that the answer is $\binom{22}{3}=1540$.
|
| 76 |
+
A generating functions solution is also available. It's not hard to see that the answer is the coefficient of $x^{19}$ in
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
\begin{aligned}
|
| 80 |
+
& (1+x)\left(1+x+x^{2}\right)\left(1+x+x^{2}+x^{3}\right)\left(1+x+x^{2}+x^{3}+x^{4}\right) \\
|
| 81 |
+
& \quad\left(1+x^{2}+x^{4}+\cdots\right)\left(1+x^{3}+x^{6}+\cdots\right)\left(1+x^{4}+x^{8}+\cdots\right)\left(1+x^{5}+x^{10}+\cdots\right) \\
|
| 82 |
+
= & \left(\frac{1-x^{2}}{1-x}\right)\left(\frac{1-x^{3}}{1-x}\right)\left(\frac{1-x^{4}}{1-x}\right)\left(\frac{1-x^{5}}{1-x}\right)\left(\frac{1}{1-x^{2}}\right)\left(\frac{1}{1-x^{3}}\right)\left(\frac{1}{1-x^{4}}\right)\left(\frac{1}{1-x^{5}}\right) \\
|
| 83 |
+
= & \frac{1}{(1-x)^{4}}=(1-x)^{-4} .
|
| 84 |
+
\end{aligned}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Using binomial theorem, we find that the coefficient of $x^{19}$ in $(1-x)^{-4}$ is $(-1)^{19}\binom{-4}{19}=\binom{22}{19}=1540$.
|
| 88 |
+
|
HarvardMIT/md/en-112-2008-feb-gen1-solutions.md
ADDED
|
@@ -0,0 +1,46 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
## Individual Round: General Test, Part 1
|
| 6 |
+
|
| 7 |
+
1. [2] Let $A B C D$ be a unit square (that is, the labels $A, B, C, D$ appear in that order around the square). Let $X$ be a point outside of the square such that the distance from $X$ to $A C$ is equal to the distance from $X$ to $B D$, and also that $A X=\frac{\sqrt{2}}{2}$. Determine the value of $C X^{2}$.
|
| 8 |
+
Answer: $\quad \frac{5}{2}$
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
Since $X$ is equidistant from $A C$ and $B D$, it must lie on either the perpendicular bisector of $A B$ or the perpendicular bisector of $A D$. It turns that the two cases yield the same answer, so we will just assume the first case. Let $M$ be the midpoint of $A B$ and $N$ the midpoint of $C D$. Then, $X M$ is perpendicular to $A B$, so $X M=\frac{1}{2}$ and thus $X N=\frac{3}{2}, N C=\frac{1}{2}$. By the Pythagorean Theorem we find $X C=\frac{\sqrt{10}}{2}$ and the answer follows.
|
| 12 |
+
2. [3] Find the smallest positive integer $n$ such that $107 n$ has the same last two digits as $n$.
|
| 13 |
+
|
| 14 |
+
Answer: 50 The two numbers have the same last two digits if and only if 100 divides their difference $106 n$, which happens if and only if 50 divides $n$.
|
| 15 |
+
3. [3] There are 5 dogs, 4 cats, and 7 bowls of milk at an animal gathering. Dogs and cats are distinguishable, but all bowls of milk are the same. In how many ways can every dog and cat be paired with either a member of the other species or a bowl of milk such that all the bowls of milk are taken?
|
| 16 |
+
Answer: 20 Since there are 9 dogs and cats combined and 7 bowls of milk, there can only be one dog-cat pair, and all the other pairs must contain a bowl of milk. There are $4 \times 5$ ways of selecting the dog-cat pair, and only one way of picking the other pairs, since the bowls of milk are indistinguishable, so the answer is $4 \times 5=20$.
|
| 17 |
+
4. [3] Positive real numbers $x, y$ satisfy the equations $x^{2}+y^{2}=1$ and $x^{4}+y^{4}=\frac{17}{18}$. Find $x y$.
|
| 18 |
+
|
| 19 |
+
Answer: $\frac{1}{6}$ Same as Algebra Test problem 1.
|
| 20 |
+
5. [4] The function $f$ satisfies
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
f(x)+f(2 x+y)+5 x y=f(3 x-y)+2 x^{2}+1
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
for all real numbers $x, y$. Determine the value of $f(10)$.
|
| 27 |
+
Answer: $\quad-49$ Same as Algebra Test problem 4.
|
| 28 |
+
6. [4] In a triangle $A B C$, take point $D$ on $B C$ such that $D B=14, D A=13, D C=4$, and the circumcircle of $A D B$ is congruent to the circumcircle of $A D C$. What is the area of triangle $A B C$ ?
|
| 29 |
+
Answer: 108 Same as Geometry Test problem 4.
|
| 30 |
+
7. [5] The equation $x^{3}-9 x^{2}+8 x+2=0$ has three real roots $p, q, r$. Find $\frac{1}{p^{2}}+\frac{1}{q^{2}}+\frac{1}{r^{2}}$.
|
| 31 |
+
|
| 32 |
+
Answer: 25 From Vieta's relations, we have $p+q+r=9, p q+q r+p r=8$ and $p q r=-2$. So
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
\frac{1}{p^{2}}+\frac{1}{q^{2}}+\frac{1}{r^{2}}=\frac{(p q+q r+r p)^{2}-2(p+q+r)(p q r)}{(p q r)^{2}}=\frac{8^{2}-2 \cdot 9 \cdot(-2)}{(-2)^{2}}=25
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
8. [5] Let $S$ be the smallest subset of the integers with the property that $0 \in S$ and for any $x \in S$, we have $3 x \in S$ and $3 x+1 \in S$. Determine the number of positive integers in $S$ less than 2008.
|
| 39 |
+
Answer: 127 Same as Combinatorics Problem 5.
|
| 40 |
+
9. [5] A Sudoku matrix is defined as a $9 \times 9$ array with entries from $\{1,2, \ldots, 9\}$ and with the constraint that each row, each column, and each of the nine $3 \times 3$ boxes that tile the array contains each digit from 1 to 9 exactly once. A Sudoku matrix is chosen at random (so that every Sudoku matrix has equal probability of being chosen). We know two of squares in this matrix, as shown. What is the probability that the square marked by ? contains the digit 3 ?
|
| 41 |
+
|
| 42 |
+
|
| 43 |
+
Answer: $\frac{2}{21}$ Same as Combinatorics Test problem 6.
|
| 44 |
+
10. [6] Let $A B C$ be an equilateral triangle with side length 2 , and let $\Gamma$ be a circle with radius $\frac{1}{2}$ centered at the center of the equilateral triangle. Determine the length of the shortest path that starts somewhere on $\Gamma$, visits all three sides of $A B C$, and ends somewhere on $\Gamma$ (not necessarily at the starting point). Express your answer in the form of $\sqrt{p}-q$, where $p$ and $q$ are rational numbers written as reduced fractions.
|
| 45 |
+
Answer: $\sqrt{\frac{28}{3}}-1$ Same as Geometry Test problem 8.
|
| 46 |
+
|
HarvardMIT/md/en-112-2008-feb-gen2-solutions.md
ADDED
|
@@ -0,0 +1,40 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
## Individual Round: General Test, Part 2
|
| 6 |
+
|
| 7 |
+
1. [2] Four students from Harvard, one of them named Jack, and five students from MIT, one of them named Jill, are going to see a Boston Celtics game. However, they found out that only 5 tickets remain, so 4 of them must go back. Suppose that at least one student from each school must go see the game, and at least one of Jack and Jill must go see the game, how many ways are there of choosing which 5 people can see the game?
|
| 8 |
+
Answer: 104 Let us count the number of way of distributing the tickets so that one of the conditions is violated. There is 1 way to give all the tickets to MIT students, and $\binom{7}{5}$ ways to give all the tickets to the 7 students other than Jack and Jill. Therefore, the total number of valid ways is $\binom{9}{5}-1-\binom{7}{5}=104$.
|
| 9 |
+
2. [2] Let $A B C$ be an equilateral triangle. Let $\Omega$ be a circle inscribed in $A B C$ and let $\omega$ be a circle tangent externally to $\Omega$ as well as to sides $A B$ and $A C$. Determine the ratio of the radius of $\Omega$ to the radius of $\omega$.
|
| 10 |
+
Answer: 3 Same as Geometry Test problem 2.
|
| 11 |
+
3. [3] A $3 \times 3 \times 3$ cube composed of 27 unit cubes rests on a horizontal plane. Determine the number of ways of selecting two distinct unit cubes (order is irrelevant) from a $3 \times 3 \times 1$ block with the property that the line joining the centers of the two cubes makes a $45^{\circ}$ angle with the horizontal plane.
|
| 12 |
+
Answer: 60 Same as Combinatorics Test problem 1.
|
| 13 |
+
4. [3] Suppose that $a, b, c, d$ are real numbers satisfying $a \geq b \geq c \geq d \geq 0, a^{2}+d^{2}=1, b^{2}+c^{2}=1$, and $a c+b d=1 / 3$. Find the value of $a b-c d$.
|
| 14 |
+
|
| 15 |
+
Answer: $\frac{2 \sqrt{2}}{3}$ We have
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
(a b-c d)^{2}=\left(a^{2}+d^{2}\right)\left(b^{2}+c^{2}\right)-(a c+b d)^{2}=(1)(1)-\left(\frac{1}{3}\right)^{2}=\frac{8}{9}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Since $a \geq b \geq c \geq d \geq 0, a b-c d \geq 0$, so $a b-c d=\frac{2 \sqrt{2}}{3}$.
|
| 22 |
+
Comment: Another way to solve this problem is to use the trigonometric substitutions $a=\sin \theta$, $b=\sin \phi, c=\cos \phi, d=\cos \theta$.
|
| 23 |
+
5. [4] Kermit the frog enjoys hopping around the infinite square grid in his backyard. It takes him 1 Joule of energy to hop one step north or one step south, and 1 Joule of energy to hop one step east or one step west. He wakes up one morning on the grid with 100 Joules of energy, and hops till he falls asleep with 0 energy. How many different places could he have gone to sleep?
|
| 24 |
+
Answer: 10201 Same as Combinatorics Test problem 4.
|
| 25 |
+
6. [4] Determine all real numbers $a$ such that the inequality $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution in $x$.
|
| 26 |
+
Answer: 1,2 Same as Algebra Test problem 3.
|
| 27 |
+
7. [5] A root of unity is a complex number that is a solution to $z^{n}=1$ for some positive integer $n$. Determine the number of roots of unity that are also roots of $z^{2}+a z+b=0$ for some integers $a$ and $b$.
|
| 28 |
+
Answer: 8 Same as Algebra Test problem 6.
|
| 29 |
+
8. [5] A piece of paper is folded in half. A second fold is made such that the angle marked below has measure $\phi\left(0^{\circ}<\phi<90^{\circ}\right)$, and a cut is made as shown below.
|
| 30 |
+
|
| 31 |
+
|
| 32 |
+
When the piece of paper is unfolded, the resulting hole is a polygon. Let $O$ be one of its vertices. Suppose that all the other vertices of the hole lie on a circle centered at $O$, and also that $\angle X O Y=144^{\circ}$, where $X$ and $Y$ are the the vertices of the hole adjacent to $O$. Find the value(s) of $\phi$ (in degrees).
|
| 33 |
+
|
| 34 |
+
Answer: $81^{\circ}$ Same as Geometry Test problem 5.
|
| 35 |
+
9. [6] Let $A B C$ be a triangle, and $I$ its incenter. Let the incircle of $A B C$ touch side $B C$ at $D$, and let lines $B I$ and $C I$ meet the circle with diameter $A I$ at points $P$ and $Q$, respectively. Given $B I=$ $6, C I=5, D I=3$, determine the value of $(D P / D Q)^{2}$.
|
| 36 |
+
|
| 37 |
+
Answer: $\frac{75}{64}$ Same as Geometry Test problem 9.
|
| 38 |
+
10. [6] Determine the number of 8-tuples of nonnegative integers ( $a_{1}, a_{2}, a_{3}, a_{4}, b_{1}, b_{2}, b_{3}, b_{4}$ ) satisfying $0 \leq$ $a_{k} \leq k$, for each $k=1,2,3,4$, and $a_{1}+a_{2}+a_{3}+a_{4}+2 b_{1}+3 b_{2}+4 b_{3}+5 b_{4}=19$.
|
| 39 |
+
Answer: 1540 Same as Combinatorics Test problem 10.
|
| 40 |
+
|
HarvardMIT/md/en-112-2008-feb-geo-solutions.md
ADDED
|
@@ -0,0 +1,91 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
## Individual Round: Geometry Test
|
| 6 |
+
|
| 7 |
+
1. [3] How many different values can $\angle A B C$ take, where $A, B, C$ are distinct vertices of a cube?
|
| 8 |
+
|
| 9 |
+
Answer: 5 . In a unit cube, there are 3 types of triangles, with side lengths $(1,1, \sqrt{2}),(1, \sqrt{2}, \sqrt{3})$ and $(\sqrt{2}, \sqrt{2}, \sqrt{2})$. Together they generate 5 different angle values.
|
| 10 |
+
2. [3] Let $A B C$ be an equilateral triangle. Let $\Omega$ be its incircle (circle inscribed in the triangle) and let $\omega$ be a circle tangent externally to $\Omega$ as well as to sides $A B$ and $A C$. Determine the ratio of the radius of $\Omega$ to the radius of $\omega$.
|
| 11 |
+
Answer: $\quad 3$ Label the diagram as shown below, where $\Omega$ and $\omega$ also denote the center of the corresponding circles. Note that $A M$ is a median and $\Omega$ is the centroid of the equilateral triangle. So $A M=3 M \Omega$. Since $M \Omega=N \Omega$, it follows that $A M / A N=3$, and triangle $A B C$ is the image of triangle $A B^{\prime} C^{\prime}$ after a scaling by a factor of 3 , and so the two incircles must also be related by a scale factor of 3 .
|
| 12 |
+
|
| 13 |
+
3. [4] Let $A B C$ be a triangle with $\angle B A C=90^{\circ}$. A circle is tangent to the sides $A B$ and $A C$ at $X$ and $Y$ respectively, such that the points on the circle diametrically opposite $X$ and $Y$ both lie on the side $B C$. Given that $A B=6$, find the area of the portion of the circle that lies outside the triangle.
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
Answer: $\pi-2$ Let $O$ be the center of the circle, and $r$ its radius, and let $X^{\prime}$ and $Y^{\prime}$ be the points diametrically opposite $X$ and $Y$, respectively. We have $O X^{\prime}=O Y^{\prime}=r$, and $\angle X^{\prime} O Y^{\prime}=90^{\circ}$. Since triangles $X^{\prime} O Y^{\prime}$ and $B A C$ are similar, we see that $A B=A C$. Let $X^{\prime \prime}$ be the projection of $Y^{\prime}$ onto $A B$. Since $X^{\prime \prime} B Y^{\prime}$ is similar to $A B C$, and $X^{\prime \prime} Y^{\prime}=r$, we have $X^{\prime \prime} B=r$. It follows that $A B=3 r$, so $r=2$.
|
| 17 |
+
|
| 18 |
+
|
| 19 |
+
Then, the desired area is the area of the quarter circle minus that of the triangle $X^{\prime} O Y^{\prime}$. And the answer is $\frac{1}{4} \pi r^{2}-\frac{1}{2} r^{2}=\pi-2$.
|
| 20 |
+
4. [4] In a triangle $A B C$, take point $D$ on $B C$ such that $D B=14, D A=13, D C=4$, and the circumcircle of $A D B$ is congruent to the circumcircle of $A D C$. What is the area of triangle $A B C$ ?
|
| 21 |
+
Answer: 108
|
| 22 |
+
|
| 23 |
+
|
| 24 |
+
The fact that the two circumcircles are congruent means that the chord $A D$ must subtend the same angle in both circles. That is, $\angle A B C=\angle A C B$, so $A B C$ is isosceles. Drop the perpendicular $M$ from $A$ to $B C$; we know $M C=9$ and so $M D=5$ and by Pythagoras on $A M D, A M=12$. Therefore, the area of $A B C$ is $\frac{1}{2}(A M)(B C)=\frac{1}{2}(12)(18)=108$.
|
| 25 |
+
5. [5] A piece of paper is folded in half. A second fold is made such that the angle marked below has measure $\phi\left(0^{\circ}<\phi<90^{\circ}\right)$, and a cut is made as shown below.
|
| 26 |
+
|
| 27 |
+
|
| 28 |
+
When the piece of paper is unfolded, the resulting hole is a polygon. Let $O$ be one of its vertices. Suppose that all the other vertices of the hole lie on a circle centered at $O$, and also that $\angle X O Y=144^{\circ}$, where $X$ and $Y$ are the the vertices of the hole adjacent to $O$. Find the value(s) of $\phi$ (in degrees).
|
| 29 |
+
|
| 30 |
+
Answer: $81^{\circ}$ Try actually folding a piece of paper. We see that the cut out area is a kite, as shown below. The fold was made on $A C$, and then $B E$ and $D E$. Since $D C$ was folded onto $D A$, we have $\angle A D E=\angle C D E$.
|
| 31 |
+

|
| 32 |
+
|
| 33 |
+
Either $A$ or $C$ is the center of the circle. If it's $A$, then $\angle B A D=144^{\circ}$, so $\angle C A D=72^{\circ}$. Using $C A=D A$, we see that $\angle A C D=\angle A D C=54^{\circ}$. So $\angle E D A=27^{\circ}$, and thus $\phi=72^{\circ}+27^{\circ}=99^{\circ}$, which is inadmissible, as $\phi<90^{\circ}$.
|
| 34 |
+
So $C$ is the center of the circle. Then, $\angle C A D=\angle C D A=54^{\circ}, \angle A D E=27^{\circ}$, and $\phi=54^{\circ}+27^{\circ}=81^{\circ}$.
|
| 35 |
+
6. [5] Let $A B C$ be a triangle with $\angle A=45^{\circ}$. Let $P$ be a point on side $B C$ with $P B=3$ and $P C=5$. Let $O$ be the circumcenter of $A B C$. Determine the length $O P$.
|
| 36 |
+
|
| 37 |
+
Answer: $\sqrt{\sqrt{17}}$ Using extended Sine law, we find the circumradius of $A B C$ to be $R=\frac{B C}{2 \sin A}=4 \sqrt{2}$. By considering the power of point $P$, we find that $R^{2}-O P^{2}=P B \cdot P C=15$. So $O P=\sqrt{R^{2}-15}=$ $\sqrt{16 \cdot 2-15}=\sqrt{17}$.
|
| 38 |
+
7. [6] Let $C_{1}$ and $C_{2}$ be externally tangent circles with radius 2 and 3 , respectively. Let $C_{3}$ be a circle internally tangent to both $C_{1}$ and $C_{2}$ at points $A$ and $B$, respectively. The tangents to $C_{3}$ at $A$ and $B$ meet at $T$, and $T A=4$. Determine the radius of $C_{3}$.
|
| 39 |
+
Answer: 8 Let $D$ be the point of tangency between $C_{1}$ and $C_{2}$. We see that $T$ is the radical center of the three circles, and so it must lie on the radical axis of $C_{1}$ and $C_{2}$, which happens to be their common tangent $T D$. So $T D=4$.
|
| 40 |
+
|
| 41 |
+
|
| 42 |
+
We have
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
\tan \frac{\angle A T D}{2}=\frac{2}{T D}=\frac{1}{2}, \quad \text { and } \quad \tan \frac{\angle B T D}{2}=\frac{3}{T D}=\frac{3}{4} .
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
Thus, the radius of $C_{3}$ equals to
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\begin{aligned}
|
| 52 |
+
T A \tan \frac{\angle A T B}{2} & =4 \tan \left(\frac{\angle A T D+\angle B T D}{2}\right) \\
|
| 53 |
+
& =4 \cdot \frac{\tan \frac{\angle A T D}{2}+\tan \frac{\angle B T D}{2}}{1-\tan \frac{\angle A T D}{2} \tan \frac{\angle B T D}{2}} \\
|
| 54 |
+
& =4 \cdot \frac{\frac{1}{2}+\frac{3}{4}}{1-\frac{1}{2} \cdot \frac{3}{4}} \\
|
| 55 |
+
& =8 .
|
| 56 |
+
\end{aligned}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
8. [6] Let $A B C$ be an equilateral triangle with side length 2 , and let $\Gamma$ be a circle with radius $\frac{1}{2}$ centered at the center of the equilateral triangle. Determine the length of the shortest path that starts somewhere on $\Gamma$, visits all three sides of $A B C$, and ends somewhere on $\Gamma$ (not necessarily at the starting point). Express your answer in the form of $\sqrt{p}-q$, where $p$ and $q$ are rational numbers written as reduced fractions.
|
| 60 |
+
Answer: $\sqrt{\frac{28}{3}}-1$ Suppose that the path visits sides $A B, B C, C A$ in this order. Construct points $A^{\prime}, B^{\prime}, C^{\prime}$ so that $C^{\prime}$ is the reflection of $C$ across $A B, A^{\prime}$ is the reflection of $A$ across $B C^{\prime}$, and $B^{\prime}$ is the reflection of $B$ across $A^{\prime} C^{\prime}$. Finally, let $\Gamma^{\prime}$ be the circle with radius $\frac{1}{2}$ centered at the center of $A^{\prime} B^{\prime} C^{\prime}$. Note that $\Gamma^{\prime}$ is the image of $\Gamma$ after the three reflections: $A B, B C^{\prime}, C^{\prime} A^{\prime}$.
|
| 61 |
+
|
| 62 |
+
|
| 63 |
+
When the path hits $A B$, let us reflect the rest of the path across $A B$ and follow this reflected path. When we hit $B C^{\prime}$, let us reflect the rest of the path across $B C^{\prime}$, and follow the new path. And when we hit $A^{\prime} C^{\prime}$, reflect the rest of the path across $A^{\prime} C^{\prime}$ and follow the new path. We must eventually end up at $\Gamma^{\prime}$.
|
| 64 |
+
It is easy to see that the shortest path connecting some point on $\Gamma$ to some point on $\Gamma^{\prime}$ lies on the line connecting the centers of the two circles. We can easily find the distance between the two centers to be $\sqrt{3^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}}=\sqrt{\frac{28}{3}}$. Therefore, the length of the shortest path connecting $\Gamma$ to $\Gamma^{\prime}$ has length $\sqrt{\frac{28}{3}}-1$. By reflecting this path three times back into $A B C$, we get a path that satisfies our conditions.
|
| 65 |
+
9. [7] Let $A B C$ be a triangle, and $I$ its incenter. Let the incircle of $A B C$ touch side $B C$ at $D$, and let lines $B I$ and $C I$ meet the circle with diameter $A I$ at points $P$ and $Q$, respectively. Given $B I=$ $6, C I=5, D I=3$, determine the value of $(D P / D Q)^{2}$.
|
| 66 |
+
|
| 67 |
+
## Answer: <br> $\qquad$
|
| 68 |
+
|
| 69 |
+
|
| 70 |
+
|
| 71 |
+
Let the incircle touch sides $A C$ and $A B$ at $E$ and $F$ respectively. Note that $E$ and $F$ both lie on the circle with diameter $A I$ since $\angle A E I=\angle A F I=90^{\circ}$. The key observation is that $D, E, P$ are collinear. To prove this, suppose that $P$ lies outside the triangle (the other case is analogous), then $\angle P E A=\angle P I A=\angle I B A+\angle I A B=\frac{1}{2}(\angle B+\angle A)=90^{\circ}-\frac{1}{2} \angle C=\angle D E C$, which implies that $D, E, P$ are collinear. Similarly $D, F, Q$ are collinear. Then, by Power of a Point, $D E \cdot D P=D F \cdot D Q$. So $D P / D Q=D F / D E$.
|
| 72 |
+
Now we compute $D F / D E$. Note that $D F=2 D B \sin \angle D B I=2 \sqrt{6^{2}-3^{2}}\left(\frac{3}{6}\right)=3 \sqrt{3}$, and $D E=$ $2 D C \sin \angle D C I=2 \sqrt{5^{2}-3^{2}}\left(\frac{3}{5}\right)=\frac{24}{5}$. Therefore, $D F / D E=\frac{5 \sqrt{3}}{8}$.
|
| 73 |
+
10. [7] Let $A B C$ be a triangle with $B C=2007, C A=2008, A B=2009$. Let $\omega$ be an excircle of $A B C$ that touches the line segment $B C$ at $D$, and touches extensions of lines $A C$ and $A B$ at $E$ and $F$, respectively (so that $C$ lies on segment $A E$ and $B$ lies on segment $A F$ ). Let $O$ be the center of $\omega$. Let $\ell$ be the line through $O$ perpendicular to $A D$. Let $\ell$ meet line $E F$ at $G$. Compute the length $D G$.
|
| 74 |
+
Answer: 2014024 Let line $A D$ meet $\omega$ again at $H$. Since $A F$ and $A E$ are tangents to $\omega$ and $A D H$ is a secant, we see that $D E H F$ is a harmonic quadrilateral. This implies that the pole of $A D$ with respect to $\omega$ lies on $E F$. Since $\ell \perp A D$, the pole of $A D$ lies on $\ell$. It follows that the pole of $A D$ is $G$.
|
| 75 |
+
|
| 76 |
+
|
| 77 |
+
Thus, $G$ must lie on the tangent to $\omega$ at $D$, so $C, D, B, G$ are collinear. Furthermore, since the pencil of lines $(A E, A F ; A D, A G)$ is harmonic, by intersecting it with the line $B C$, we see that $(C, B ; D, G)$ is harmonic as well. This means that
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
\frac{B D}{D C} \cdot \frac{C G}{G B}=-1
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
(where the lengths are directed.) The semiperimeter of $A B C$ is $s=\frac{1}{2}(2007+2008+2009)=3012$. So $B D=s-2009=1003$ and $C D=s-2008=1004$. Let $x=D G$, then the above equations gives
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
\frac{1003}{1004} \cdot \frac{x+1004}{x-1003}=1
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Solving gives $x=2014024$.
|
| 90 |
+
Remark: If you are interested to learn about projective geometry, check out the last chapter of Geometry Revisited by Coxeter and Greitzer or Geometric Transformations III by Yaglom.
|
| 91 |
+
|
HarvardMIT/md/en-112-2008-feb-guts-solutions.md
ADDED
|
@@ -0,0 +1,359 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 23 February 2008
|
| 4 |
+
|
| 5 |
+
## Guts Round
|
| 6 |
+
|
| 7 |
+
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 8 |
+
|
| 9 |
+
1. [5] Determine all pairs $(a, b)$ of real numbers such that $10, a, b, a b$ is an arithmetic progression.
|
| 10 |
+
|
| 11 |
+
Answer: $(4,-2),\left(\frac{5}{2},-5\right)$ Since $10, a, b$ is an arithmetic progression, we have $a=\frac{1}{2}(10+b)$. Also, we have $a+a b=2 b$, and so $a(1+b)=2 b$. Substituting the expression for $a$ gives $(10+b)(1+b)=4 b$. Solving this quadratic equation gives the solutions $b=-2$ and $b=-5$. The corresponding values for $a$ can be found by $a=\frac{1}{2}(10+b)$.
|
| 12 |
+
2. [5] Given right triangle $A B C$, with $A B=4, B C=3$, and $C A=5$. Circle $\omega$ passes through $A$ and is tangent to $B C$ at $C$. What is the radius of $\omega$ ?
|
| 13 |
+
Answer: $\quad \frac{25}{8}$ Let $O$ be the center of $\omega$, and let $M$ be the midpoint of $A C$. Since $O A=O C$, $O M \perp A C$. Also, $\angle O C M=\angle B A C$, and so triangles $A B C$ and $C M O$ are similar. Then, $C O / C M=$ $A C / A B$, from which we obtain that the radius of $\omega$ is $C O=\frac{25}{8}$.
|
| 14 |
+
3. [5] How many ways can you color the squares of a $2 \times 2008$ grid in 3 colors such that no two squares of the same color share an edge?
|
| 15 |
+
Answer: $2 \cdot 3^{2008}$ Denote the colors $A, B, C$. The left-most column can be colored in 6 ways. For each subsequent column, if the $k$ th column is colored with $A B$, then the $(k+1)$ th column can only be colored with one of $B A, B C, C A$. That is, if we have colored the first $k$ columns, then there are 3 ways to color the $(k+1)$ th column. It follows that the number of ways of coloring the board is $6 \times 3^{2007}$.
|
| 16 |
+
|
| 17 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 18 |
+
|
| 19 |
+
4. [6] Find the real solution(s) to the equation $(x+y)^{2}=(x+1)(y-1)$.
|
| 20 |
+
|
| 21 |
+
Answer: $(-1,1)$ Set $p=x+1$ and $q=y-1$, then we get $(p+q)^{2}=p q$, which simplifies to $p^{2}+p q+q^{2}=0$. Then we have $\left(p+\frac{q}{2}\right)^{2}+\frac{3 q^{2}}{4}$, and so $p=q=0$. Thus $(x, y)=(-1,1)$.
|
| 22 |
+
5. [6] A Vandal and a Moderator are editing a Wikipedia article. The article originally is error-free. Each day, the Vandal introduces one new error into the Wikipedia article. At the end of the day, the moderator checks the article and has a $2 / 3$ chance of catching each individual error still in the article. After 3 days, what is the probability that the article is error-free?
|
| 23 |
+
Answer: $\frac{416}{729}$ Consider the error that was introduced on day 1. The probability that the Moderator misses this error on all three checks is $1 / 3^{3}$, so the probability that this error gets removed is $1-\frac{1}{3^{3}}$. Similarly, the probability that the moderator misses the other two errors are $1-\frac{1}{3^{2}}$ and $1-\frac{1}{3}$. So the probability that the article is error-free is
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\left(1-\frac{1}{3^{3}}\right)\left(1-\frac{1}{3^{2}}\right)\left(1-\frac{1}{3}\right)=\frac{416}{729}
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
6. [6] Determine the number of non-degenerate rectangles whose edges lie completely on the grid lines of the following figure.
|
| 30 |
+

|
| 31 |
+
|
| 32 |
+
Answer: 297 First, let us count the total number of rectangles in the grid without the hole in the middle. There are $\binom{7}{2}=21$ ways to choose the two vertical boundaries of the rectangle, and there are 21 ways to choose the two horizontal boundaries of the rectangles. This makes $21^{2}=441$ rectangles. However, we must exclude those rectangles whose boundary passes through the center point. We can count these rectangles as follows: the number of rectangles with the center of the grid lying in the interior of its south edge is $3 \times 3 \times 3=27$ (there are three choices for each of the three other edges); the number of rectangles whose south-west vertex coincides with the center is $3 \times 3=9$. Summing over all 4 orientations, we see that the total number of rectangles to exclude is $4(27+9)=144$. Therefore, the answer is $441-144=297$.
|
| 33 |
+
|
| 34 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 35 |
+
|
| 36 |
+
7. [6] Given that $x+\sin y=2008$ and $x+2008 \cos y=2007$, where $0 \leq y \leq \pi / 2$, find the value of $x+y$.
|
| 37 |
+
Answer: $2007+\frac{\pi}{2}$ Subtracting the two equations gives $\sin y-2008 \cos y=1$. But since $0 \leq y \leq \pi / 2$, the maximum of $\sin y$ is 1 and the minimum of $\cos y$ is 0 , so we must have $\sin y=1$, so $y=\pi / 2$ and $x+y=2007+\frac{\pi}{2}$.
|
| 38 |
+
8. [6] Trodgor the dragon is burning down a village consisting of 90 cottages. At time $t=0$ an angry peasant arises from each cottage, and every 8 minutes ( 480 seconds) thereafter another angry peasant spontaneously generates from each non-burned cottage. It takes Trodgor 5 seconds to either burn a peasant or to burn a cottage, but Trodgor cannot begin burning cottages until all the peasants around him have been burned. How many seconds does it take Trodgor to burn down the entire village?
|
| 39 |
+
Answer: 1920 We look at the number of cottages after each wave of peasants. Let $A_{n}$ be the number of cottages remaining after $8 n$ minutes. During each 8 minute interval, Trodgor burns a total of $480 / 5=96$ peasants and cottages. Trodgor first burns $A_{n}$ peasants and spends the remaining time burning $96-A_{n}$ cottages. Therefore, as long as we do not reach negative cottages, we have the recurrence relation $A_{n+1}=A_{n}-\left(96-A_{n}\right)$, which is equivalent to $A_{n+1}=2 A_{n}-96$. Computing the first few terms of the series, we get that $A_{1}=84, A_{2}=72, A_{3}=48$, and $A_{4}=0$. Therefore, it takes Trodgor 32 minutes, which is 1920 seconds.
|
| 40 |
+
9. [6] Consider a circular cone with vertex $V$, and let $A B C$ be a triangle inscribed in the base of the cone, such that $A B$ is a diameter and $A C=B C$. Let $L$ be a point on $B V$ such that the volume of the cone is 4 times the volume of the tetrahedron $A B C L$. Find the value of $B L / L V$.
|
| 41 |
+
Answer: $\sqrt{\frac{\pi}{4-\pi}}$ Let $R$ be the radius of the base, $H$ the height of the cone, $h$ the height of the pyramid and let $B L / L V=x / y$. Let [•] denote volume. Then [cone] $=\frac{1}{3} \pi R^{2} H$ and $[A B C L]=\frac{1}{3} \pi R^{2} h$ and $h=\frac{x}{x+y} H$. We are given that $[$ cone $]=4[A B C L]$, so $x / y=\frac{\pi}{4-\pi}$.
|
| 42 |
+
|
| 43 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 44 |
+
|
| 45 |
+
10. [7] Find the number of subsets $S$ of $\{1,2, \ldots 63\}$ the sum of whose elements is 2008 .
|
| 46 |
+
|
| 47 |
+
Answer: 6 Note that $1+2+\cdots+63=2016$. So the problem is equivalent to finding the number of subsets of $\{1,2, \cdots 63\}$ whose sum of elements is 8 . We can count this by hand: $\{8\},\{1,7\},\{2,6\}$, $\{3,5\},\{1,2,5\},\{1,3,4\}$.
|
| 48 |
+
11. [7] Let $f(r)=\sum_{j=2}^{2008} \frac{1}{j^{r}}=\frac{1}{2^{r}}+\frac{1}{3^{r}}+\cdots+\frac{1}{2008^{r}}$. Find $\sum_{k=2}^{\infty} f(k)$.
|
| 49 |
+
|
| 50 |
+
Answer: $\frac{2007}{2008}$ We change the order of summation:
|
| 51 |
+
$$
|
| 52 |
+
\sum_{k=2}^{\infty} \sum_{j=2}^{2008} \frac{1}{j^{k}}=\sum_{j=2}^{2008} \sum_{k=2}^{\infty} \frac{1}{j^{k}}=\sum_{j=2}^{2008} \frac{1}{j^{2}\left(1-\frac{1}{j}\right)}=\sum_{j=2}^{2008} \frac{1}{j(j-1)}=\sum_{j=2}^{2008}\left(\frac{1}{j-1}-\frac{1}{j}\right)=1-\frac{1}{2008}=\frac{2007}{2008}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
12. [7] Suppose we have an (infinite) cone $\mathcal{C}$ with apex $A$ and a plane $\pi$. The intersection of $\pi$ and $\mathcal{C}$ is an ellipse $\mathcal{E}$ with major axis $B C$, such that $B$ is closer to $A$ than $C$, and $B C=4, A C=5, A B=3$. Suppose we inscribe a sphere in each part of $\mathcal{C}$ cut up by $\mathcal{E}$ with both spheres tangent to $\mathcal{E}$. What is the ratio of the radii of the spheres (smaller to larger)?
|
| 56 |
+
Answer: $\sqrt{\frac{1}{3}}$ It can be seen that the points of tangency of the spheres with $E$ must lie on its major axis due to symmetry. Hence, we consider the two-dimensional cross-section with plane $A B C$. Then the two spheres become the incentre and the excentre of the triangle $A B C$, and we are looking for the ratio of the inradius to the exradius. Let $s, r, r_{a}$ denote the semiperimeter, inradius, and exradius (opposite to $A$ ) of the triangle $A B C$. We know that the area of $A B C$ can be expressed as both $r s$ and $r_{a}(s-|B C|)$, and so $\frac{r}{r_{a}}=\frac{s-|B C|}{s}$. For the given triangle, $s=6$ and $a=4$, so the required ratio is $\frac{1}{3}$.
|
| 57 |
+
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 58 |
+
13. [8] Let $P(x)$ be a polynomial with degree 2008 and leading coefficient 1 such that
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
P(0)=2007, P(1)=2006, P(2)=2005, \ldots, P(2007)=0 .
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Determine the value of $P(2008)$. You may use factorials in your answer.
|
| 65 |
+
Answer: $2008!-1$ Consider the polynomial $Q(x)=P(x)+x-2007$. The given conditions
|
| 66 |
+
 we know that $Q(x)$ is also a polynomial with degree 2008 and leading coefficient 1 . It follows that $Q(x)=x(x-1)(x-2)(x-3) \cdots(x-2007)$. Thus
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
P(x)=x(x-1)(x-2)(x-3) \cdots(x-2007)-x+2007 .
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Setting $x=2008$ gives the answer.
|
| 73 |
+
14. [8] Evaluate the infinite sum $\sum_{n=1}^{\infty} \frac{n}{n^{4}+4}$.
|
| 74 |
+
|
| 75 |
+
Answer: | $\frac{3}{8}$ |
|
| 76 |
+
| :---: |
|
| 77 |
+
| We have |
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
\begin{aligned}
|
| 81 |
+
\sum_{n=1}^{\infty} \frac{n}{n^{4}+4} & =\sum_{n=1}^{\infty} \frac{n}{\left(n^{2}+2 n+2\right)\left(n^{2}-2 n+2\right)} \\
|
| 82 |
+
& =\frac{1}{4} \sum_{n=1}^{\infty}\left(\frac{1}{n^{2}-2 n+2}-\frac{1}{n^{2}+2 n+2}\right) \\
|
| 83 |
+
& =\frac{1}{4} \sum_{n=1}^{\infty}\left(\frac{1}{(n-1)^{2}+1}-\frac{1}{(n+1)^{2}+1}\right)
|
| 84 |
+
\end{aligned}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Observe that the sum telescopes. From this we find that the answer is $\frac{1}{4}\left(\frac{1}{0^{2}+1}+\frac{1}{1^{2}+1}\right)=\frac{3}{8}$.
|
| 88 |
+
15. [8] In a game show, Bob is faced with 7 doors, 2 of which hide prizes. After he chooses a door, the host opens three other doors, of which one is hiding a prize. Bob chooses to switch to another door. What is the probability that his new door is hiding a prize?
|
| 89 |
+
|
| 90 |
+
Answer: | $\frac{5}{21}$ | If Bob initially chooses a door with a prize, then he will not find a prize by switching. |
|
| 91 |
+
| :---: | :---: | :---: | With probability $5 / 7$ his original door does not hide the prize. After the host opens the three doors, the remaining three doors have equal probability of hiding the prize. Therefore, the probability that Bob finds the prize is $\frac{5}{7} \times \frac{1}{3}=\frac{5}{21}$.
|
| 92 |
+
|
| 93 |
+
Remark: This problem can be easily recognized as a variation of the classic Monty Hall problem.
|
| 94 |
+
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 95 |
+
16. [9] Point $A$ lies at $(0,4)$ and point $B$ lies at $(3,8)$. Find the $x$-coordinate of the point $X$ on the $x$-axis maximizing $\angle A X B$.
|
| 96 |
+
Answer: $\quad 5 \sqrt{2}-3$ Let $X$ be a point on the $x$-axis and let $\theta=\angle A X B$. We can easily see that the circle with diameter $A B$ does not meet the $x$-axis, so $\theta \leq \pi$. Thus, maximizing $\theta$ is equivalent to maximizing $\sin \theta$. By the Law of Sines, this in turn is equivalent to minimizing the circumradius of triangle $A B X$. This will occur when the circumcircle of $A B X$ is the smaller of the two circles through $A$ and $B$ tangent to the $x$-axis. So let $X$ now be this point of tangency. Extend line $A B$ to meet the $x$-axis at $C=(-3,0)$; by Power of a Point $C X^{2}=C A \cdot C B=50$ so $C X=5 \sqrt{2}$. Clearly $X$ has larger $x$-coordinate than $C$, so the $x$-coordinate of $X$ is $5 \sqrt{2}-3$.
|
| 97 |
+
17. [9] Solve the equation
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\sqrt{x+\sqrt{4 x+\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}}}-\sqrt{x}=1
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Express your answer as a reduced fraction with the numerator and denominator written in their prime factorization.
|
| 104 |
+
Answer: $\frac{1}{2^{4016}}$ Rewrite the equation to get
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\sqrt{x+\sqrt{4 x+\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}}}=\sqrt{x}+1
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Squaring both sides yields
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
\sqrt{4 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}=2 \sqrt{x}+1
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
Squaring again yields
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}=4 \sqrt{x}+1
|
| 120 |
+
$$
|
| 121 |
+
|
| 122 |
+
One can see that by continuing this process one gets
|
| 123 |
+
|
| 124 |
+
$$
|
| 125 |
+
\sqrt{4^{2008} x+3}=2^{2008} \sqrt{x}+1
|
| 126 |
+
$$
|
| 127 |
+
|
| 128 |
+
so that $2 \cdot 2^{2008} \sqrt{x}=2$. Hence $x=4^{-2008}$. It is also easy to check that this is indeed a solution to the original equation.
|
| 129 |
+
18. [9] Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. Let $D$ be the midpoint of $A B$ and let $E$ be a point on segment $A C$ such that $A D=A E$. Let $B E$ meet $C D$ at $F$. If $\angle B F C=135^{\circ}$, determine $B C / A B$.
|
| 130 |
+
Answer: $\frac{\sqrt{13}}{2}$ Let $\alpha=\angle A D C$ and $\beta=\angle A B E$. By exterior angle theorem, $\alpha=\angle B F D+\beta=$ $45^{\circ}+\beta$. Also, note that $\tan \beta=A E / A B=A D / A B=1 / 2$. Thus,
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
1=\tan 45^{\circ}=\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}=\frac{\tan \alpha-\frac{1}{2}}{1+\frac{1}{2} \tan \alpha}
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
Solving for $\tan \alpha$ gives $\tan \alpha=3$. Therefore, $A C=3 A D=\frac{3}{2} A B$. Using Pythagorean Theorem, we find that $B C=\frac{\sqrt{13}}{2} A B$. So the answer is $\frac{\sqrt{13}}{2}$.
|
| 137 |
+
|
| 138 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 139 |
+
|
| 140 |
+
19. [10] Let $A B C D$ be a regular tetrahedron, and let $O$ be the centroid of triangle $B C D$. Consider the point $P$ on $A O$ such that $P$ minimizes $P A+2(P B+P C+P D)$. Find $\sin \angle P B O$.
|
| 141 |
+
|
| 142 |
+
Answer: | $\frac{1}{6}$ |
|
| 143 |
+
| :---: |
|
| 144 |
+
| We translate the problem into one about 2-D geometry. Consider the right triangle | $A B O$, and $P$ is some point on $A O$. Then, the choice of $P$ minimizes $P A+6 P B$. Construct the line $\ell$ through $A$ but outside the triangle $A B O$ so that $\sin \angle(A O, \ell)=\frac{1}{6}$. For whichever $P$ chosen, let $Q$ be the projection of $P$ onto $\ell$, then $P Q=\frac{1}{6} A P$. Then, since $P A+6 P B=6(P Q+P B)$, it is equivalent to minimize $P Q+P B$. Observe that this sum is minimized when $B, P, Q$ are collinear and the line through them is perpendicular to $\ell$ (so that $P Q+P B$ is simply the distance from $B$ to $\ell$ ). Then, $\angle A Q B=90^{\circ}$, and since $\angle A O B=90^{\circ}$ as well, we see that $A, Q, P, B$ are concyclic. Therefore, $\angle P B O=\angle O P A=\angle(A O, \ell)$, and the sine of this angle is therefore $\frac{1}{6}$.
|
| 145 |
+
|
| 146 |
+
20. [10] For how many ordered triples $(a, b, c)$ of positive integers are the equations $a b c+9=a b+b c+c a$ and $a+b+c=10$ satisfied?
|
| 147 |
+
Answer: 21 Subtracting the first equation from the second, we obtain $1-a-b-c+a b+b c+c a-a b c=$ $(1-a)(1-b)(1-c)=0$. Since $a, b$, and $c$ are positive integers, at least one must equal 1 . Note that $a=b=c=1$ is not a valid triple, so it suffices to consider the cases where exactly two or one of $a, b, c$ are equal to 1 . If $a=b=1$, we obtain $c=8$ and similarly for the other two cases, so this gives 3 ordered triples. If $a=1$, then we need $b+c=9$, which has 6 solutions for $b, c \neq 1$; a similar argument for $b$ and $c$ gives a total of 18 such solutions. It is easy to check that all the solutions we found are actually solutions to the original equations. Adding, we find $18+3=21$ total triples.
|
| 148 |
+
21. [10] Let $A B C$ be a triangle with $A B=5, B C=4$ and $A C=3$. Let $\mathcal{P}$ and $\mathcal{Q}$ be squares inside $A B C$ with disjoint interiors such that they both have one side lying on $A B$. Also, the two squares each have an edge lying on a common line perpendicular to $A B$, and $\mathcal{P}$ has one vertex on $A C$ and $\mathcal{Q}$ has one vertex on $B C$. Determine the minimum value of the sum of the areas of the two squares.
|
| 149 |
+
|
| 150 |
+
|
| 151 |
+
Answer: $\frac{144}{49}$ Let the side lengths of $\mathcal{P}$ and $\mathcal{Q}$ be $a$ and $b$, respectively. Label two of the vertices of $\mathcal{P}$ as $D$ and $E$ so that $D$ lies on $A B$ and $E$ lies on $A C$, and so that $D E$ is perpendicular to $A B$. The triangle $A D E$ is similar to $A C B$. So $A D=\frac{3}{4} a$. Using similar arguments, we find that
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
\frac{3 a}{4}+a+b+\frac{4 b}{3}=A B=5
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
so
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\frac{a}{4}+\frac{b}{3}=\frac{5}{7}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
Using Cauchy-Schwarz inequality, we get
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
\left(a^{2}+b^{2}\right)\left(\frac{1}{4^{2}}+\frac{1}{3^{2}}\right) \geq\left(\frac{a}{4}+\frac{b}{3}\right)^{2}=\frac{25}{49}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
It follows that
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
a^{2}+b^{2} \geq \frac{144}{49}
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
Equality occurs at $a=\frac{36}{35}$ and $b=\frac{48}{35}$.
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
11^{\text {th }} \text { HARVARD-MIT MATHEMATICS TOURNAMENT, } 23 \text { FEBRUARY } 2008 \text { - GUTS ROUND }
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
22. [10] For a positive integer $n$, let $\theta(n)$ denote the number of integers $0 \leq x<2010$ such that $x^{2}-n$ is divisible by 2010. Determine the remainder when $\sum_{n=0}^{2009} n \cdot \theta(n)$ is divided by 2010.
|
| 182 |
+
Answer: 335 Let us consider the sum $\sum_{n=0}^{2009} n \cdot \theta(n)(\bmod 2010)$ in a another way. Consider the sum $0^{2}+1^{2}+2^{2}+\cdots+2007^{2}(\bmod 2010)$. For each $0 \leq n<2010$, in the latter sum, the term $n$ appears $\theta(n)$ times, so the sum is congruent to $\sum_{n=0}^{2009} n \cdot \theta(n)$. In other words,
|
| 183 |
+
|
| 184 |
+
$$
|
| 185 |
+
\sum_{n=0}^{2009} n \cdot \theta(n)=\sum_{n=0}^{2009} n^{2}=\frac{(2009)(2009+1)(2 \cdot 2009+1)}{6} \equiv(-1) \cdot \frac{2010}{6} \cdot(-1)=335 \quad(\bmod 2010)
|
| 186 |
+
$$
|
| 187 |
+
|
| 188 |
+
23. [10] Two mathematicians, Kelly and Jason, play a cooperative game. The computer selects some secret positive integer $n<60$ (both Kelly and Jason know that $n<60$, but that they don't know what the value of $n$ is). The computer tells Kelly the unit digit of $n$, and it tells Jason the number of divisors of $n$. Then, Kelly and Jason have the following dialogue:
|
| 189 |
+
Kelly: I don't know what $n$ is, and I'm sure that you don't know either. However, I know that $n$ is divisible by at least two different primes.
|
| 190 |
+
Jason: Oh, then I know what the value of $n$ is.
|
| 191 |
+
Kelly: Now I also know what $n$ is.
|
| 192 |
+
Assuming that both Kelly and Jason speak truthfully and to the best of their knowledge, what are all the possible values of $n$ ?
|
| 193 |
+
Answer: 10 The only way in which Kelly can know that $n$ is divisible by at least two different primes is if she is given 0 as the unit digit of $n$, since if she received anything else, then there is some number with that unit digit and not divisible by two primes (i.e., $1,2,3,4,5,16,7,8,9$ ). Then, after Kelly says the first line, Jason too knows that $n$ is divisible by 10 .
|
| 194 |
+
The number of divisors of $10,20,30,40,50$ are $4,6,8,8,6$, respectively. So unless Jason received 4 , he cannot otherwise be certain of what $n$ is. It follows that Jason received 4 , and thus $n=10$.
|
| 195 |
+
24. [10] Suppose that $A B C$ is an isosceles triangle with $A B=A C$. Let $P$ be the point on side $A C$ so that $A P=2 C P$. Given that $B P=1$, determine the maximum possible area of $A B C$.
|
| 196 |
+
Answer: $\sqrt{\frac{9}{10}}$ Let $Q$ be the point on $A B$ so that $A Q=2 B Q$, and let $X$ be the intersection of $B P$ and $C Q$. The key observation that, as we will show, $B X$ and $C X$ are fixed lengths, and the ratio of areas $[A B C] /[B C X]$ is constant. So, to maximize $[A B C]$, it is equivalent to maximize $[B C X]$.
|
| 197 |
+
Using Menelaus' theorem on $A B P$, we have
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
\frac{B X \cdot P C \cdot A Q}{X P \cdot C A \cdot Q B}=1
|
| 201 |
+
$$
|
| 202 |
+
|
| 203 |
+
Since $P C / C A=1 / 3$ and $A Q / Q B=2$, we get $B X / X P=3 / 2$. It follows that $B X=3 / 5$. By symmetry, $C X=3 / 5$.
|
| 204 |
+
Also, we have
|
| 205 |
+
|
| 206 |
+
$$
|
| 207 |
+
[A B C]=3[B P C]=3 \cdot \frac{5}{3}[B X C]=5[B X C]
|
| 208 |
+
$$
|
| 209 |
+
|
| 210 |
+
Note that $[B X C]$ is maximized when $\angle B X C=90^{\circ}$ (one can check that this configuration is indeed possible). Thus, the maximum value of $[B X C]$ is $\frac{1}{2} B X \cdot C X=\frac{1}{2}\left(\frac{3}{5}\right)^{2}=\frac{9}{50}$. It follows that the maximum value of $[A B C]$ is $\frac{9}{10}$.
|
| 211 |
+
|
| 212 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 213 |
+
|
| 214 |
+
25. [12] Alice and the Cheshire Cat play a game. At each step, Alice either (1) gives the cat a penny, which causes the cat to change the number of (magic) beans that Alice has from $n$ to $5 n$ or (2) gives the cat a nickel, which causes the cat to give Alice another bean. Alice wins (and the cat disappears) as soon as the number of beans Alice has is greater than 2008 and has last two digits 42 . What is the minimum number of cents Alice can spend to win the game, assuming she starts with 0 beans?
|
| 215 |
+
Answer: 35 Consider the number of beans Alice has in base 5 . Note that $2008=31013_{5}, 42=132_{5}$, and $100=400_{5}$. Now, suppose Alice has $d_{k} \cdots d_{2} d_{1}$ beans when she wins; the conditions for winning mean that these digits must satisfy $d_{2} d_{1}=32, d_{k} \cdots d_{3} \geq 310$, and $d_{k} \cdots d_{3}=4 i+1$ for some $i$. To gain these $d_{k} \cdots d_{2} d_{1}$ beans, Alice must spend at least $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1$ cents (5 cents to get each bean in the "units digit" and $k-1$ cents to promote all the beans). We now must have $k \geq 5$ because $d_{k} \cdots d_{2} d_{1}>2008$. If $k=5$, then $d_{k} \geq 3$ since $d_{k} \cdots d_{3} \geq 3100$; otherwise, we have $d_{k} \geq 1$. Therefore, if $k=5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 44>36$; if $k>5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 30+k-1 \geq 35$. But we can attain 36 cents by taking $d_{k} \cdots d_{3}=1000$, so this is indeed the minimum.
|
| 216 |
+
26. [12] Let $\mathcal{P}$ be a parabola, and let $V_{1}$ and $F_{1}$ be its vertex and focus, respectively. Let $A$ and $B$ be points on $\mathcal{P}$ so that $\angle A V_{1} B=90^{\circ}$. Let $\mathcal{Q}$ be the locus of the midpoint of $A B$. It turns out that $\mathcal{Q}$ is also a parabola, and let $V_{2}$ and $F_{2}$ denote its vertex and focus, respectively. Determine the ratio $F_{1} F_{2} / V_{1} V_{2}$.
|
| 217 |
+
Answer: $\frac{7}{8}$ Since all parabolas are similar, we may assume that $\mathcal{P}$ is the curve $y=x^{2}$. Then, if $A=\left(a, a^{2}\right)$ and $B=\left(b, b^{2}\right)$, the condition that $\angle A V_{1} B=90^{\circ}$ gives $a b+a^{2} b^{2}=0$, or $a b=-1$. Then, the midpoint of $A B$ is
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
\frac{A+B}{2}=\left(\frac{a+b}{2}, \frac{a^{2}+b^{2}}{2}\right)=\left(\frac{a+b}{2}, \frac{(a+b)^{2}-2 a b}{2}\right)=\left(\frac{a+b}{2}, \frac{(a+b)^{2}}{2}+1\right) .
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
(Note that $a+b$ can range over all real numbers under the constraint $a b=-1$.) It follows that the locus of the midpoint of $A B$ is the curve $y=2 x^{2}+1$.
|
| 224 |
+
Recall that the focus of $y=a x^{2}$ is $\left(0, \frac{1}{4 a}\right)$. We find that $V_{1}=(0,0), V_{2}=(0,1), F_{1}=\left(0, \frac{1}{4}\right)$, $F_{2}=\left(0,1+\frac{1}{8}\right)$. Therefore, $F_{1} F_{2} / V_{1} V_{2}=\frac{7}{8}$.
|
| 225 |
+
27. [12] Cyclic pentagon $A B C D E$ has a right angle $\angle A B C=90^{\circ}$ and side lengths $A B=15$ and $B C=20$. Supposing that $A B=D E=E A$, find $C D$.
|
| 226 |
+
Answer: 7 By Pythagoras, $A C=25$. Since $\overline{A C}$ is a diameter, angles $\angle A D C$ and $\angle A E C$ are also right, so that $C E=20$ and $A D^{2}+C D^{2}=A C^{2}$ as well. Beginning with Ptolemy's theorem,
|
| 227 |
+
|
| 228 |
+
$$
|
| 229 |
+
\begin{aligned}
|
| 230 |
+
& (A E \cdot C D+A C \cdot D E)^{2}=A D^{2} \cdot E C^{2}=\left(A C^{2}-C D^{2}\right) E C^{2} \\
|
| 231 |
+
& \quad \Longrightarrow C D^{2}\left(A E^{2}+E C^{2}\right)+2 \cdot C D \cdot A E^{2} \cdot A C+A C^{2}\left(D E^{2}-E C^{2}\right)=0 \\
|
| 232 |
+
& \quad \Longrightarrow C D^{2}+2 C D\left(\frac{A E^{2}}{A C}\right)+D E^{2}-E C^{2}=0
|
| 233 |
+
\end{aligned}
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
It follows that $C D^{2}+18 C D-175=0$, from which $C D=7$.
|
| 237 |
+
Remark: A simple trigonometric solution is possible. One writes $\alpha=\angle A C E=\angle E C D \Longrightarrow \angle D A C=$ $90^{\circ}-2 \alpha$ and applies double angle formula.
|
| 238 |
+
|
| 239 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 240 |
+
|
| 241 |
+
28. [15] Let $P$ be a polyhedron where every face is a regular polygon, and every edge has length 1. Each vertex of $P$ is incident to two regular hexagons and one square. Choose a vertex $V$ of the polyhedron. Find the volume of the set of all points contained in $P$ that are closer to $V$ than to any other vertex.
|
| 242 |
+
Answer: $\quad \frac{\sqrt{2}}{3}$ Observe that $P$ is a truncated octahedron, formed by cutting off the corners from a regular octahedron with edge length 3 . So, to compute the value of $P$, we can find the volume of the octahedron, and then subtract off the volume of truncated corners. Given a square pyramid where each triangular face an equilateral triangle, and whose side length is $s$, the height of the pyramid is $\frac{\sqrt{2}}{2} s$, and thus the volume is $\frac{1}{3} \cdot s^{2} \cdot \frac{\sqrt{2}}{2} s=\frac{\sqrt{2}}{6} s^{3}$. The side length of the octahedron is 3 , and noting that the octahedron is made up of two square pyramids, its volume must be is $2 \cdot \frac{\sqrt{2}(3)^{3}}{6}=9 \sqrt{2}$. The six "corners" that we remove are all square pyramids, each with volume $\frac{\sqrt{2}}{6}$, and so the resulting polyhedron $P$ has volume $9 \sqrt{2}-6 \cdot \frac{\sqrt{2}}{6}=8 \sqrt{2}$.
|
| 243 |
+
Finally, to find the volume of all points closer to one particular vertex than any other vertex, note that due to symmetry, every point in $P$ (except for a set with zero volume), is closest to one of the 24 vertices. Due to symmetry, it doesn't matter which $V$ is picked, so we can just divide the volume of $P$ by 24 to obtain the answer $\frac{\sqrt{2}}{3}$.
|
| 244 |
+
29. [15] Let $(x, y)$ be a pair of real numbers satisfying
|
| 245 |
+
|
| 246 |
+
$$
|
| 247 |
+
56 x+33 y=\frac{-y}{x^{2}+y^{2}}, \quad \text { and } \quad 33 x-56 y=\frac{x}{x^{2}+y^{2}}
|
| 248 |
+
$$
|
| 249 |
+
|
| 250 |
+
Determine the value of $|x|+|y|$.
|
| 251 |
+
Answer: $\frac{11}{65}$ Observe that
|
| 252 |
+
|
| 253 |
+
$$
|
| 254 |
+
\frac{1}{x+y i}=\frac{x-y i}{x^{2}+y^{2}}=33 x-56 y+(56 x+33 y) i=(33+56 i)(x+y i)
|
| 255 |
+
$$
|
| 256 |
+
|
| 257 |
+
So
|
| 258 |
+
|
| 259 |
+
$$
|
| 260 |
+
(x+y i)^{2}=\frac{1}{33+56 i}=\frac{1}{(7+4 i)^{2}}=\left(\frac{7-4 i}{65}\right)^{2}
|
| 261 |
+
$$
|
| 262 |
+
|
| 263 |
+
It follows that $(x, y)= \pm\left(\frac{7}{65},-\frac{4}{65}\right)$.
|
| 264 |
+
30. [15] Triangle $A B C$ obeys $A B=2 A C$ and $\angle B A C=120^{\circ}$. Points $P$ and $Q$ lie on segment $B C$ such that
|
| 265 |
+
|
| 266 |
+
$$
|
| 267 |
+
\begin{aligned}
|
| 268 |
+
A B^{2}+B C \cdot C P & =B C^{2} \\
|
| 269 |
+
3 A C^{2}+2 B C \cdot C Q & =B C^{2}
|
| 270 |
+
\end{aligned}
|
| 271 |
+
$$
|
| 272 |
+
|
| 273 |
+
Find $\angle P A Q$ in degrees.
|
| 274 |
+
Answer: $40^{\circ}$ We have $A B^{2}=B C(B C-C P)=B C \cdot B P$, so triangle $A B C$ is similar to triangle $P B A$. Also, $A B^{2}=B C(B C-2 C Q)+A C^{2}=(B C-C Q)^{2}-C Q^{2}+A C^{2}$, which rewrites as $A B^{2}+C Q^{2}=$ $B Q^{2}+A C^{2}$. We deduce that $Q$ is the foot of the altitude from $A$. Thus, $\angle P A Q=90^{\circ}-\angle Q P A=90^{\circ}-$ $\angle A B P-\angle B A P$. Using the similar triangles, $\angle P A Q=90^{\circ}-\angle A B C-\angle B C A=\angle B A C-90^{\circ}=40^{\circ}$.
|
| 275 |
+
|
| 276 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 277 |
+
|
| 278 |
+
31. [18] Let $\mathcal{C}$ be the hyperbola $y^{2}-x^{2}=1$. Given a point $P_{0}$ on the $x$-axis, we construct a sequence of points $\left(P_{n}\right)$ on the $x$-axis in the following manner: let $\ell_{n}$ be the line with slope 1 passing passing
|
| 279 |
+
through $P_{n}$, then $P_{n+1}$ is the orthogonal projection of the point of intersection of $\ell_{n}$ and $\mathcal{C}$ onto the $x$-axis. (If $P_{n}=0$, then the sequence simply terminates.)
|
| 280 |
+
Let $N$ be the number of starting positions $P_{0}$ on the $x$-axis such that $P_{0}=P_{2008}$. Determine the remainder of $N$ when divided by 2008.
|
| 281 |
+
Answer: 254 Let $P_{n}=\left(x_{n}, 0\right)$. Then the $\ell_{n}$ meet $\mathcal{C}$ at $\left(x_{n+1}, x_{n+1}-x_{n}\right)$. Since this point lies on the hyperbola, we have $\left(x_{n+1}-x_{n}\right)^{2}-x_{n+1}^{2}=1$. Rearranging this equation gives
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
x_{n+1}=\frac{x_{n}^{2}-1}{2 x_{n}}
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
Choose a $\theta_{0} \in(0, \pi)$ with $\cot \theta_{0}=x_{0}$, and define $\theta_{n}=2^{n} \theta_{0}$. Using the double-angle formula, we have
|
| 288 |
+
|
| 289 |
+
$$
|
| 290 |
+
\cot \theta_{n+1}=\cot \left(2 \theta_{n}\right)=\frac{\cot ^{2} \theta_{n}-1}{2 \cot \theta_{n}}
|
| 291 |
+
$$
|
| 292 |
+
|
| 293 |
+
It follows by induction that $x_{n}=\cot \theta_{n}$. Then, $P_{0}=P_{2008}$ corresponds to $\cot \theta_{0}=\cot \left(2^{2008} \theta_{0}\right)$ (assuming that $P_{0}$ is never at the origin, or equivalently, $2^{n} \theta$ is never an integer multiple of $\pi$ ). So, we need to find the number of $\theta_{0} \in(0, \pi)$ with the property that $2^{2008} \theta_{0}-\theta_{0}=k \pi$ for some integer $k$. We have $\theta_{0}=\frac{k \pi}{2^{2008}-1}$, so $k$ can be any integer between 1 and $2^{2008}-2$ inclusive (and note that since the denominator is odd, the sequence never terminates). It follows that the number of starting positions is $N=2^{2008}-2$.
|
| 294 |
+
Finally, we need to compute the remainder when $N$ is divided by 2008 . We have $2008=2^{3} \times 251$. Using Fermat's Little Theorem with 251 , we get $2^{2008} \equiv\left(2^{250}\right)^{4} \cdot 256 \equiv 1^{4} \cdot 5=5(\bmod 251)$. So we have $N \equiv 3(\bmod 251)$ and $N \equiv-2(\bmod 8)$. Using Chinese Remainder Theorem, we get $N \equiv 254$ $(\bmod 2008)$.
|
| 295 |
+
32. [18] Cyclic pentagon $A B C D E$ has side lengths $A B=B C=5, C D=D E=12$, and $A E=14$. Determine the radius of its circumcircle.
|
| 296 |
+
Answer: $\frac{225 \sqrt{11}}{88}$ Let $C^{\prime}$ be the point on minor arc $B C D$ such that $B C^{\prime}=12$ and $C^{\prime} D=5$, and write $A C^{\prime}=B D=C^{\prime} E=x, A D=y$, and $B D=z$. Ptolemy applied to quadrilaterals $A B C^{\prime} D, B C^{\prime} D E$, and $A B D E$ gives
|
| 297 |
+
|
| 298 |
+
$$
|
| 299 |
+
\begin{aligned}
|
| 300 |
+
& x^{2}=12 y+5^{2} \\
|
| 301 |
+
& x^{2}=5 z+12^{2} \\
|
| 302 |
+
& y z=14 x+5 \cdot 12
|
| 303 |
+
\end{aligned}
|
| 304 |
+
$$
|
| 305 |
+
|
| 306 |
+
Then
|
| 307 |
+
|
| 308 |
+
$$
|
| 309 |
+
\left(x^{2}-5^{2}\right)\left(x^{2}-12^{2}\right)=5 \cdot 12 y z=5 \cdot 12 \cdot 14 x+5^{2} \cdot 12^{2}
|
| 310 |
+
$$
|
| 311 |
+
|
| 312 |
+
from which $x^{3}-169 x-5 \cdot 12 \cdot 14=0$. Noting that $x>13$, the rational root theorem leads quickly to the root $x=15$. Then triangle $B C D$ has area $\sqrt{16 \cdot 1 \cdot 4 \cdot 11}=8 \sqrt{11}$ and circumradius $R=\frac{5 \cdot 12 \cdot 15}{4 \cdot 8 \sqrt{11}}=$ $\frac{225 \sqrt{11}}{88}$.
|
| 313 |
+
33. [18] Let $a, b, c$ be nonzero real numbers such that $a+b+c=0$ and $a^{3}+b^{3}+c^{3}=a^{5}+b^{5}+c^{5}$. Find the value of $a^{2}+b^{2}+c^{2}$.
|
| 314 |
+
Answer: $\quad \frac{6}{5}$ Let $\sigma_{1}=a+b+c, \sigma_{2}=a b+b c+c a$ and $\sigma_{3}=a b c$ be the three elementary symmetric polynomials. Since $a^{3}+b^{3}+c^{3}$ is a symmetric polynomial, it can be written as a polynomial in $\sigma_{1}, \sigma_{2}$ and $\sigma_{3}$. Now, observe that $\sigma_{1}=0$, and so we only need to worry about the terms not containing $\sigma_{1}$. By considering the degrees of the terms, we see that the only possibility is $\sigma_{3}$. That is, $a^{3}+b^{3}+c^{3}=k \sigma_{3}$ for some constant $k$. By setting $a=b=1, c=-2$, we see that $k=3$.
|
| 315 |
+
By similar reasoning, we find that $a^{5}+b^{5}+c^{5}=h \sigma_{2} \sigma_{3}$ for some constant $h$. By setting $a=b=1$ and $c=-2$, we get $h=-5$.
|
| 316 |
+
|
| 317 |
+
So, we now know that $a+b+c=0$ implies
|
| 318 |
+
|
| 319 |
+
$$
|
| 320 |
+
a^{3}+b^{3}+c^{3}=3 a b c \quad \text { and } \quad a^{5}+b^{5}+c^{5}=-5 a b c(a b+b c+c a)
|
| 321 |
+
$$
|
| 322 |
+
|
| 323 |
+
Then $a^{3}+b^{3}+c^{3}=a^{5}+b^{5}+c^{5}$ implies that $3 a b c=-5 a b c(a b+b c+c a)$. Given that $a, b, c$ are nonzero, we get $a b+b c+c a=-\frac{3}{5}$. Then, $a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=\frac{6}{5}$.
|
| 324 |
+
|
| 325 |
+
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
| 326 |
+
|
| 327 |
+
34. Who Wants to Be a Millionaire. In 2000, the Clay Mathematics Institute named seven Millennium Prize Problems, with each carrying a prize of $\$ 1$ Million for its solution. Write down the name of ONE of the seven Clay Millennium Problems. If your submission is incorrect or misspelled, then your submission is disqualified. If another team wrote down the same Millennium Problem as you, then you get 0 points, otherwise you get 20 points.
|
| 328 |
+
|
| 329 |
+
Solution: The seven Millennium Prize Problems are:
|
| 330 |
+
(a) Birch and Swinnerton-Dyer Conjecture
|
| 331 |
+
(b) Hodge Conjecture
|
| 332 |
+
(c) Navier-Stokes Equations
|
| 333 |
+
(d) P vs NP
|
| 334 |
+
(e) Poincaré Conjecture
|
| 335 |
+
(f) Riemann Hypothesis
|
| 336 |
+
(g) Yang-Mills Theory
|
| 337 |
+
|
| 338 |
+
More information can be found on its official website http://www.claymath.org/millennium/.
|
| 339 |
+
As far as this as an HMMT problem goes, it's probably a good idea to submit something that you think is least likely for another team to think of (or to spell correctly). Though, this may easily turn into a contest of who can still remember the names of the user ranks from the Art of Problem Solving forum.
|
| 340 |
+
35. NUMB3RS. The RSA Factoring Challenge, which ended in 2007, challenged computational mathematicians to factor extremely large numbers that were the product of two prime numbers. The largest number successfully factored in this challenge was RSA-640, which has 193 decimal digits and carried a prize of $\$ 20,000$. The next challenge number carried prize of $\$ 30,000$, and contains $N$ decimal digits. Your task is to submit a guess for $N$. Only the team(s) that have the closest guess(es) receives points. If $k$ teams all have the closest guesses, then each of them receives $\left\lceil\frac{20}{k}\right\rceil$ points.
|
| 341 |
+
Answer: 212 For more information, see the Wikipedia entry at http://en.wikipedia.org/wiki/ RSA_Factoring_Challenge.
|
| 342 |
+
RSA-640 was factored in November 2005, and the effort took approximately 302.2 GHz -Opteron-CPU years over five months of calendar time.
|
| 343 |
+
36. The History Channel. Below is a list of famous mathematicians. Your task is to list a subset of them in the chronological order of their birth dates. Your submission should be a sequence of letters. If your sequence is not in the correct order, then you get 0 points. Otherwise your score will be $\min \{\max \{5(N-4), 0\}, 25\}$, where $N$ is the number of letters in your sequence.
|
| 344 |
+
(A) Niels Abel (B) Arthur Cayley (C) Augustus De Morgan (D) Gustav Dirichlet (E) Leonhard Euler (F) Joseph Fourier (G) Évariste Galois (H) Carl Friedrich Gauss (I) Marie-Sophie Germain (J) Joseph Louis Lagrange (K) Pierre-Simon Laplace (L) Henri Poincaré (N) Bernhard Riemann
|
| 345 |
+
Answer: any subsequence of EJKFIHADCGBNL The corresponding birth dates are listed below:
|
| 346 |
+
(A) Niels Abel (1802-1829)
|
| 347 |
+
(B) Arthur Cayley (1821-1895)
|
| 348 |
+
(C) Augustus De Morgan (1806-1871)
|
| 349 |
+
(D) Gustav Dirichlet (1805-1859)
|
| 350 |
+
(E) Leonhard Euler (1707-1783)
|
| 351 |
+
(F) Joseph Fourier (1768-1830)
|
| 352 |
+
(G) Évariste Galois (1811-1832)
|
| 353 |
+
(H) Carl Friedrich Gauss (1777-1855)
|
| 354 |
+
(I) Marie-Sophie Germain (1776-1831)
|
| 355 |
+
(J) Joseph Louis Lagrange (1736-1813)
|
| 356 |
+
(K) Pierre-Simon Laplace (1749-1827)
|
| 357 |
+
(L) Henri Poincaré (1854-1912)
|
| 358 |
+
(N) Bernhard Riemann (1826-1866)
|
| 359 |
+
|
HarvardMIT/md/en-112-2008-feb-team1-solutions.md
ADDED
|
@@ -0,0 +1,170 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 23 February 2008
|
| 2 |
+
|
| 3 |
+
## Team Round: A Division
|
| 4 |
+
|
| 5 |
+
## Lattice Walks [90]
|
| 6 |
+
|
| 7 |
+
1. [20] Determine the number of ways of walking from $(0,0)$ to $(5,5)$ using only up and right unit steps such that the path does not pass through any of the following points: $(1,1),(1,4),(4,1),(4,4)$.
|
| 8 |
+

|
| 9 |
+
|
| 10 |
+
Answer: 34
|
| 11 |
+
Solution: In the following figure, each lattice point (with the bottom-left-most point $(0,0)$ ) is labeled with the number of ways of reaching there from $(0,0)$. With the exception of the forbidden points, the labels satisfy the recursion formula $f(x, y)=f(x-1, y)+f(x, y-1)$. We see from the diagram that there are 34 ways to reach $(5,5)$.
|
| 12 |
+
|
| 13 |
+
| 1 | 1 | 5 | 17 | 17 | 34 |
|
| 14 |
+
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
|
| 15 |
+
| 1 | 0 | 4 | 12 | 0 | 17 |
|
| 16 |
+
| 1 | 2 | 4 | 8 | 12 | 17 |
|
| 17 |
+
| 1 | 1 | 2 | 4 | 4 | 5 |
|
| 18 |
+
| 1 | 0 | 1 | 2 | 0 | 1 |
|
| 19 |
+
| 1 | 1 | 1 | 1 | 1 | 1 |
|
| 20 |
+
|
| 21 |
+
2. [20] Let $n>2$ be a positive integer. Prove that there are $\frac{1}{2}(n-2)(n+1)$ ways to walk from $(0,0)$ to $(n, 2)$ using only up and right unit steps such that the walk never visits the line $y=x$ after it leaves the origin.
|
| 22 |
+
|
| 23 |
+
Solution: The first two steps can only go to the right. Then we need to compute the number of ways of walking from $(2,0)$ to $(n, 2)$ which does not pass through the point $(2,2)$. There are $\binom{n}{2}$ ways to walk from $(2,0)$ to $(n, 2)$, and exactly one of those paths passes through the point (2,2). So the number of valid paths is $\binom{n}{2}-1=\frac{1}{2} n(n-1)-1=\frac{1}{2}(n-2)(n+1)$.
|
| 24 |
+
|
| 25 |
+
Remark: We used the well-known fact that there are $\binom{a+b}{a}$ ways to walk from $(0,0)$ to $(a, b)$ using only up and right unit steps. This is true because there are $a+b$ steps, and we need to choose $a$ of them to be right steps, and the rest up steps.
|
| 26 |
+
3. [20] Let $n>4$ be a positive integer. Determine the number of ways to walk from $(0,0)$ to $(n, 2)$ using only up and right unit steps such that the path does not meet the lines $y=x$ or $y=x-n+2$ except at the start and at the end.
|
| 27 |
+
|
| 28 |
+
Answer: $\frac{1}{2}\left(n^{2}-5 n+2\right)$
|
| 29 |
+
Solution: It is easy to see the the first two steps and the last two steps must all be right steps. So we need to compute the number of walks from $(2,0)$ to $(n-2,0)$ that does not pass through $(2,2)$ and $(n-2,0)$. There are $\binom{n-2}{2}$ paths from $(2,0)$ to $(n-2,0)$, and exactly two of them are invalid. So the answer is $\binom{n-2}{2}-2=\frac{1}{2}(n-2)(n-3)-2=\frac{1}{2}\left(n^{2}-5 n+2\right)$.
|
| 30 |
+
4. [30] Let $n>6$ be a positive integer. Determine the number of ways to walk from $(0,0)$ to $(n, 3)$ using only up and right unit steps such that the path does not meet the lines $y=x$ or $y=x-n+3$ except at the start and at the end.
|
| 31 |
+
Answer: $\quad \frac{1}{6}(n-6)(n-1)(n+1)$ Consider the first point of the path that lies on $x=3$. There are two possibilities for this point: $(3,0)$ and $(3,1)$, and there is exactly one valid way of getting to each point from the origin. Similarly, consider the last point of the path that lies on $x=n-3$. There are two possibilities: $(n-3,2)$ and $(n-3,3)$, and there is exactly one valid way of getting to the destination from each of the two points. Now we count the number of valid paths from each of $(3,0)$ and $(3,1)$, to each of $(n-3,2)$ and $(n-3,3)$, and the answer will be the sum.
|
| 32 |
+
|
| 33 |
+
- From $(3,1)$ to $(n-3,2)$ : there are no forbidden points along the way, so there are $n-5$ ways.
|
| 34 |
+
- From $(3,0)$ to $(n-3,2)$ : the path must not pass through $(n-3,0)$, and there is exactly one invalid path. So there are $\binom{n-4}{2}-1$ ways.
|
| 35 |
+
- From $(3,1)$ to $(n-3,3)$ : the path must not pass through $(3,3)$, and there is exactly one invalid path. So there are $\binom{n-4}{2}-1$ ways.
|
| 36 |
+
- From $(3,0)$ to $(n-3,3)$ : the path must not pass through $(n-3,0)$ and $(3,3)$, and there are exactly two invalid paths. So there are $\binom{n-3}{3}-2$ ways.
|
| 37 |
+
|
| 38 |
+
Summing, we obtain the answer:
|
| 39 |
+
$n-5+\binom{n-4}{2}-1+\binom{n-4}{2}-1+\binom{n-3}{3}-2=\frac{n^{3}-6 n^{2}-n+6}{6}=\frac{(n-6)(n-1)(n+1)}{6}$.
|
| 40 |
+
|
| 41 |
+
## Lattice and Centroids [130]
|
| 42 |
+
|
| 43 |
+
A d-dimensional lattice point is a point of the form $\left(x_{1}, x_{2}, \ldots, x_{d}\right)$ where $x_{1}, x_{2}, \ldots, x_{d}$ are all integers. For a set of $d$-dimensional points, their centroid is the point found by taking the coordinatewise average of the given set of points.
|
| 44 |
+
Let $f(n, d)$ denote the minimal number $f$ such that any set of $f$ lattice points in the $d$-dimensional Euclidean space contains a subset of size $n$ whose centroid is also a lattice point.
|
| 45 |
+
5. [10] Let $S$ be a set of 5 points in the 2 -dimensional lattice. Show that we can always choose a pair of points in $S$ whose midpoint is also a lattice point.
|
| 46 |
+
|
| 47 |
+
Solution: Consider the parities of the coordinates. There are four possibilities: (odd, odd), (odd, even), (even, odd), (even, even). By the pigeonhole principle, two of the points must have the same parity in both coordinates (i.e., they are congruent in mod 2). Then, the midpoint of these two points must be a lattice point.
|
| 48 |
+
6. [10] Construct a set of $2^{d} d$-dimensional lattice points so that for any two chosen points $A, B$, the line segment $A B$ does not pass through any other lattice point.
|
| 49 |
+
|
| 50 |
+
Solution: The simplest example is the set of $2^{d}$ points of the form $\left(a_{1}, a_{2}, \ldots, a_{d}\right)$, where $a_{k} \in\{0,1\}$ for each $k$. This is the set of vertices of a $d$-dimensional cube.
|
| 51 |
+
7. [35] Show that for positive integers $n$ and $d$,
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
(n-1) 2^{d}+1 \leq f(n, d) \leq(n-1) n^{d}+1 .
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Solution: Note that taking the set of points to be a multiset does not affect $f(n, d)$ as adding multiples of $n$ to any of the coordinate values does not change the result. The lower bound is obtained by considering the multiset consisting of $n-1$ copies of each of the $2^{d}$ 0,1 -vectors of length $d$, as it contains no submultiset of size $n$ whose centroid is also a lattice point. By the pigeonhole principle, any multiset of $(n-1) n^{d}+1$ lattice points must contain $n$ points whose coordinates are congruent modulo $n$. The centroid of these $n$ points is also a lattice point, thus proving the upper bound.
|
| 58 |
+
8. [40] Show that for positive integers $n_{1}, n_{2}$ and $d$,
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
f\left(n_{1} n_{2}, d\right) \leq f\left(n_{1}, d\right)+n_{1}\left(f\left(n_{2}, d\right)-1\right)
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Solution: Given a multiset of $f\left(n_{1}, d\right)+n_{1}\left(f\left(n_{2}, d\right)-1\right)$ lattice points, we may select $l=f\left(n_{2}, d\right)$ pairwise disjoint submultisets $S_{1}, S_{2}, \ldots, S_{l}$, each consisting of $n_{1}$ points, whose centroid is a lattice point. Let $\varphi$ map each multiset $S_{i}$ to its centroid $g_{i}$. By the definition of $f\left(n_{2}, d\right)$, there exists a submultiset $T \subset\left\{g_{1}, g_{2}, \ldots, g_{l}\right\}$ satisfying $|T|=n_{2}$ whose centroid is a lattice point. Then $\bigcup_{i \in T} \varphi^{-1}\left(g_{i}\right)$ is a multiset of $n_{1} n_{2}$ lattice points whose centroid is also a lattice point.
|
| 65 |
+
9. [35] Determine, with proof, a simple closed-form expression for $f\left(2^{a}, d\right)$.
|
| 66 |
+
|
| 67 |
+
Answer: $\left(2^{a}-1\right) 2^{d}+1$
|
| 68 |
+
Solution: From Problem ??, $f\left(2^{a}, d\right) \geq\left(2^{a}-1\right) 2^{d}+1$. We prove by induction on $a$ that $f\left(2^{a}, d\right) \leq\left(2^{a}-1\right) 2^{d}+1$. When $a=1$, Problem ?? shows that $f(2, d) \leq 2^{d}+1$. Fix $a>1$ and suppose that the assertion holds for smaller values of $a$. Using Problem ??,
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
\begin{aligned}
|
| 72 |
+
f\left(2^{a}, d\right) & \leq f(2, d)+2\left(f\left(2^{a-1}, d\right)-1\right) \\
|
| 73 |
+
& \leq 2^{d}+1+2 \cdot\left(2^{a-1}-1\right) 2^{d} \\
|
| 74 |
+
& =\left(2^{a}-1\right) 2^{d}+1 .
|
| 75 |
+
\end{aligned}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Thus $f\left(2^{a}, d\right)=\left(2^{a}-1\right) 2^{d}+1$.
|
| 79 |
+
|
| 80 |
+
## Incircles [180]
|
| 81 |
+
|
| 82 |
+
In the following problems, $A B C$ is a triangle with incenter $I$. Let $D, E, F$ denote the points where the incircle of $A B C$ touches sides $B C, C A, A B$, respectively.
|
| 83 |
+
|
| 84 |
+
|
| 85 |
+
At the end of this section you can find some terminology and theorems that may be helpful to you.
|
| 86 |
+
10. On the circumcircle of $A B C$, let $A^{\prime}$ be the midpoint of arc $B C$ (not containing $A$ ).
|
| 87 |
+
(a) $[\mathbf{1 0}]$ Show that $A, I, A^{\prime}$ are collinear.
|
| 88 |
+
(b) $[\mathbf{2 0}]$ Show that $A^{\prime}$ is the circumcenter of BIC.
|
| 89 |
+
|
| 90 |
+
## Solution:
|
| 91 |
+
|
| 92 |
+
|
| 93 |
+
(a) Since $A^{\prime}$ bisectors the arc $B C$, the two arcs $A^{\prime} B$ and $A^{\prime} C$ are equal, and so $\angle B A A^{\prime}=$ $\angle C A A^{\prime}$. Thus, $A^{\prime}$ lies on the angle bisector of $B A C$. Since $I$ also lies on the angle bisector of $B A C$, we see that $A, I, A^{\prime}$ are collinear.
|
| 94 |
+
(b) We have
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
\angle C I A^{\prime}=\angle A^{\prime} A C+\angle I C A=\angle A^{\prime} A B+\angle I C B=\angle A^{\prime} C B+\angle I C B=\angle I C A^{\prime} .
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
Therefore, $A^{\prime} I=A^{\prime} C$. By similar arguments, $A^{\prime} I=A^{\prime} B$. So, $A^{\prime}$ is equidistant from $B, I, C$, and thus is its circumcenter.
|
| 101 |
+
11. [30] Let lines $B I$ and $E F$ meet at $K$. Show that $I, K, E, C, D$ are concyclic.
|
| 102 |
+
|
| 103 |
+
Solution: First, note that there are two possible configurations, as $K$ could lie inside segment $E F$, or on its extension. The following proof works for both cases. We have
|
| 104 |
+
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\angle K I C=\angle I B C+\angle I C B=\frac{1}{2} \angle A B C+\frac{1}{2} \angle A C B=90^{\circ}-\frac{1}{2} \angle B A C=\angle A E F .
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
It follows that $I, K, E, C$ are concyclic. The point $D$ also lies on this circle because $\angle I D C=$ $\angle I E C=90^{\circ}$. Thus, all five points are concyclic.
|
| 111 |
+
12. [40] Let $K$ be as in the previous problem. Let $M$ be the midpoint of $B C$ and $N$ the midpoint of $A C$. Show that $K$ lies on line $M N$.
|
| 112 |
+
|
| 113 |
+
Solution: Since $I, K, E, C$ are concyclic, we have $\angle I K C=\angle I E C=90^{\circ}$. Let $C^{\prime}$ be the reflection of $C$ across $B I$, then $C^{\prime}$ must lie on $A B$. Then, $K$ is the midpoint of $C C^{\prime}$. Consider a dilation centered at $C$ with factor $\frac{1}{2}$. Since $C^{\prime}$ lies on $A B$, it follows that $K$ lies on $M N$.
|
| 114 |
+
|
| 115 |
+
13. [40] Let $M$ be the midpoint of $B C$, and $T$ diametrically opposite to $D$ on the incircle of $A B C$. Show that $D T, A M, E F$ are concurrent.
|
| 116 |
+
|
| 117 |
+
Solution: If $A B=A C$, then the result is clear as $A M$ and $D T$ coincide. So, assume that $A B \neq A C$.
|
| 118 |
+
|
| 119 |
+
|
| 120 |
+
Let lines $D T$ and $E F$ meet at $Z$. Construct a line through $Z$ parallel to $B C$, and let it meet $A B$ and $A C$ at $X$ and $Y$, respectively. We have $\angle X Z I=90^{\circ}$, and $\angle X F I=90^{\circ}$. Therefore, $F, Z, I, X$ are concyclic, and thus $\angle I X Z=\angle I F Z$. By similar arguments, we also have $\angle I Y Z=\angle I E Z$. Thus, triangles $I F E$ and $I X Y$ are similar. Since $I E=I F$, we must also have $I X=I Y$. Since $I Z$ is an altitude of the isosceles triangle $I X Y, Z$ is the midpoint of $X Y$.
|
| 121 |
+
|
| 122 |
+
Since $X Y$ and $B C$ are parallel, there is a dilation centered at $A$ that sends $X Y$ to $B C$. So it must send the midpoint $Z$ to the midpoint $M$. Therefore, $A, Z, M$ are collinear. It follows that $D T, A M, E F$ are concurrent.
|
| 123 |
+
14. [40] Let $P$ be a point inside the incircle of $A B C$. Let lines $D P, E P, F P$ meet the incircle again at $D^{\prime}, E^{\prime}, F^{\prime}$. Show that $A D^{\prime}, B E^{\prime}, C F^{\prime}$ are concurrent.
|
| 124 |
+
|
| 125 |
+
Solution: Using the trigonometric version of Ceva's theorem, it suffices to prove that
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
\frac{\sin \angle B A D^{\prime}}{\sin \angle D^{\prime} A C} \cdot \frac{\sin \angle C B E^{\prime}}{\sin \angle E^{\prime} B A} \cdot \frac{\sin \angle A C F^{\prime}}{\sin \angle F^{\prime} C B}=1 .
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
|
| 132 |
+
|
| 133 |
+
Using sine law, we have
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\sin \angle B A D^{\prime}=\frac{F D^{\prime}}{A D^{\prime}} \cdot \sin \angle A F D^{\prime}=\frac{F D^{\prime}}{A D^{\prime}} \cdot \sin \angle F D D^{\prime}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Let $r$ be the inradius of $A B C$. Using the extended sine law, we have $F D^{\prime}=2 r \sin \angle F D D^{\prime}$. Therefore,
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
\sin \angle B A D^{\prime}=\frac{2 r}{A D^{\prime}} \cdot \sin ^{2} \angle F D D^{\prime}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
Do this for all the factors in ( $\dagger$ ), and we get
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\frac{\sin \angle B A D^{\prime}}{\sin \angle D^{\prime} A C} \cdot \frac{\sin \angle C B E^{\prime}}{\sin \angle E^{\prime} B A} \cdot \frac{\sin \angle A C F^{\prime}}{\sin \angle F^{\prime} C B}=\left(\frac{\sin \angle F D D^{\prime}}{\sin \angle D^{\prime} D E} \cdot \frac{\sin \angle D E E^{\prime}}{\sin \angle E^{\prime} E F} \cdot \frac{\sin \angle E F F^{\prime}}{\sin \angle F^{\prime} F D}\right)^{2}
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
Since $D D^{\prime}, E E^{\prime}, F F^{\prime}$ are concurrent, the above expression equals to 1 by using trig Ceva on triangle $D E F$. The result follows.
|
| 152 |
+
|
| 153 |
+
Remark: This result is known as Steinbart Theorem. Beware that its converse is not completely true. For more information and discussion, see Darij Grinberg's paper "Variations of the Steinbart Theorem" at http://de.geocities.com/darij_grinberg/.
|
| 154 |
+
|
| 155 |
+
## Glossary and some possibly useful facts
|
| 156 |
+
|
| 157 |
+
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point. A set of points are concyclic if they lie on a common circle.
|
| 158 |
+
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
|
| 159 |
+
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
- "Trig" Ceva states that given $A B C$ a triangle, and points $X, Y, Z$ inside the triangle, the lines $A X, B Y, C Z$ are concurrent if and only if
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\frac{\sin \angle B A X}{\sin \angle X A C} \cdot \frac{\sin \angle C B Y}{\sin \angle Y B A} \cdot \frac{\sin \angle A C Z}{\sin \angle Z C B}=1 .
|
| 169 |
+
$$
|
| 170 |
+
|
HarvardMIT/md/en-112-2008-feb-team2-solutions.md
ADDED
|
@@ -0,0 +1,239 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $11^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 23 February 2008
|
| 2 |
+
|
| 3 |
+
Team Round: B Division
|
| 4 |
+
Tropical Mathematics [95]
|
| 5 |
+
|
| 6 |
+
For real numbers $x$ and $y$, let us consider the two operations $\oplus$ and $\odot$ defined by
|
| 7 |
+
|
| 8 |
+
$$
|
| 9 |
+
x \oplus y=\min (x, y) \quad \text { and } \quad x \odot y=x+y .
|
| 10 |
+
$$
|
| 11 |
+
|
| 12 |
+
We also include $\infty$ in our set, and it satisfies $x \oplus \infty=x$ and $x \odot \infty=\infty$ for all $x$. When unspecified, $\odot$ precedes $\oplus$ in the order of operations.
|
| 13 |
+
|
| 14 |
+
1. [10] (Distributive law) Prove that $(x \oplus y) \odot z=x \odot z \oplus y \odot z$ for all $x, y, z \in \mathbb{R} \cup\{\infty\}$.
|
| 15 |
+
|
| 16 |
+
Solution: This is equivalent to proving that
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\min (x, y)+z=\min (x+z, y+z) .
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Consider two cases. If $x \leq y$, then $L H S=x+z$ and $R H S=x+z$. If $x>y$, then $L H S=y+z$ and $R H S=y+z$. It follows that $L H S=R H S$.
|
| 23 |
+
2. [10] (Freshman's Dream) Let $z^{n}$ denote $z \odot z \odot z \odot \cdots \odot z$ with $z$ appearing $n$ times. Prove that $(x \oplus y)^{n}=x^{n} \oplus y^{n}$ for all $x, y \in \mathbb{R} \cup\{\infty\}$ and positive integer $n$.
|
| 24 |
+
|
| 25 |
+
Solution: Without loss of generality, suppose that $x \leq y$, then $L H S=\min (x, y)^{n}=x^{n}=$ $n x$, and RHS $=\min \left(x^{n}, y^{n}\right)=\min (n x, n y)=n x$.
|
| 26 |
+
3. [35] By a tropical polynomial we mean a function of the form
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
where exponentiation is as defined in the previous problem.
|
| 33 |
+
Let $p$ be a tropical polynomial. Prove that
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
p\left(\frac{x+y}{2}\right) \geq \frac{p(x)+p(y)}{2}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
for all $x, y \in \mathbb{R} \cup\{\infty\}$. (This means that all tropical polynomials are concave.)
|
| 40 |
+
Solution: First, note that for any $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$, we have
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\min \left\{x_{1}+y_{1}, x_{2}+y_{2}, \ldots, x_{n}+y_{n}\right\} \geq \min \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}+\min \left\{y_{1}, y_{2}, \ldots, y_{n}\right\} .
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Indeed, suppose that $x_{m}+y_{m}=\min _{i}\left\{x_{i}+y_{i}\right\}$, then $x_{m} \geq \min _{i} x_{i}$ and $y_{m} \geq \min _{i} y_{i}$, and so $\min _{i}\left\{x_{i}+y_{i}\right\}=x_{m}+y_{m} \geq \min _{i} x_{i}+\min _{i} y_{i}$.
|
| 47 |
+
Now, let us write a tropical polynomial in a more familiar notation. We have
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
So
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
\begin{aligned}
|
| 57 |
+
p\left(\frac{x+y}{2}\right) & =\min _{0 \leq k \leq n}\left\{a_{k}+k\left(\frac{x+y}{2}\right)\right\} \\
|
| 58 |
+
& =\frac{1}{2} \min _{0 \leq k \leq n}\left\{\left(a_{k}+k x\right)+\left(a_{k}+k y\right)\right\} \\
|
| 59 |
+
& \geq \frac{1}{2}\left(\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\}+\min _{0 \leq k \leq n}\left\{a_{k}+k y\right\}\right) \\
|
| 60 |
+
& =\frac{1}{2}(p(x)+p(y)) .
|
| 61 |
+
\end{aligned}
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
4. [40] (Fundamental Theorem of Algebra) Let $p$ be a tropical polynomial:
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}, \quad a_{n} \neq \infty
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Prove that we can find $r_{1}, r_{2}, \ldots, r_{n} \in \mathbb{R} \cup\{\infty\}$ so that
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
p(x)=a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right)
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
for all $x$.
|
| 77 |
+
Solution: Again, we have
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
So the graph of $y=p(x)$ can be drawn as follows: first, draw all the lines $y=a_{k}+k x$, $k=0,1, \ldots, n$, then trace out the lowest broken line, which then is the graph of $y=p(x)$.
|
| 84 |
+
So $p(x)$ is piecewise linear and continuous, and has slopes from the set $\{0,1,2, \ldots, n\}$. We know from the previous problem that $p(x)$ is concave, and so its slope must be decreasing (this can also be observed simply from the drawing of the graph of $y=p(x)$ ). Then, let $r_{k}$ denote the $x$-coordinate of the leftmost kink such that the slope of the graph is less than $k$ to the right of this kink. Then, $r_{n} \leq r_{n-1} \leq \cdots \leq r_{1}$, and for $r_{k-1} \leq x \leq r_{k}$, the graph of $p$ is linear with slope $k$. Note that is if possible that $r_{k-1}=r_{k}$, if no segment of $p$ has slope $k$. Also, since $a_{n} \neq \infty$, the leftmost piece of $p(x)$ must have slope $n$, and thus $r_{n}$ exists, and thus all $r_{i}$ exist.
|
| 85 |
+
Now, compare $p(x)$ with
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
\begin{aligned}
|
| 89 |
+
q(x) & =a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right) \\
|
| 90 |
+
& =a_{n}+\min \left(x, r_{1}\right)+\min \left(x, r_{2}\right)+\cdots+\min \left(x, r_{n}\right) .
|
| 91 |
+
\end{aligned}
|
| 92 |
+
$$
|
| 93 |
+
|
| 94 |
+
For $r_{k-1} \leq x \leq r_{k}$, the slope of $q(x)$ is $k$, and for $x \leq r_{n}$ the slope of $q$ is $n$ and for $x \geq r_{1}$ the slope of $q$ is 0 . So $q$ is piecewise linear, and of course it is continuous. It follows that the graph of $q$ coincides with that of $p$ up to a translation. By taking any $x<r_{n}$, we see that $q(x)=a_{n}+n x=p(x)$, we see that the graphs of $p$ and $q$ coincide, and thus they must be the same function.
|
| 95 |
+
|
| 96 |
+
## Juggling [125]
|
| 97 |
+
|
| 98 |
+
A juggling sequence of length $n$ is a sequence $j(\cdot)$ of $n$ nonnegative integers, usually written as a string
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
j(0) j(1) \ldots j(n-1)
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
such that the mapping $f: \mathbb{Z} \rightarrow \mathbb{Z}$ defined by
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
f(t)=t+j(\bar{t})
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
is a permutation of the integers. Here $\bar{t}$ denotes the remainder of $t$ when divided by $n$. In this case, we say that $f$ is the corresponding juggling pattern.
|
| 111 |
+
For a juggling pattern $f$ (or its corresponding juggling sequence), we say that it has $b$ balls if the permutation induces $b$ infinite orbits on the set of integers. Equivalently, $b$ is the maximum number such that we can find a set of $b$ integers $\left\{t_{1}, t_{2}, \ldots, t_{b}\right\}$ so that the sets $\left\{t_{i}, f\left(t_{i}\right), f\left(f\left(t_{i}\right)\right), f\left(f\left(f\left(t_{i}\right)\right)\right), \ldots\right\}$ are all infinite and mutually disjoint (i.e. non-overlapping) for $i=1,2, \ldots, b$. (This definition will become clear in a second.)
|
| 112 |
+
|
| 113 |
+
Now is probably a good time to pause and think about what all this has to do with juggling. Imagine that we are juggling a number of balls, and at time $t$, we toss a ball from our hand up to a height $j(\bar{t})$. This ball stays up in the air for $j(\bar{t})$ units of time, so that it comes back to our hand at time $f(t)=t+j(\bar{t})$. Then, the juggling pattern presents a simplified model of how balls are juggled (for instance, we ignore information such as which hand we use to toss the ball). A throw height of 0 (i.e., $j(\bar{t})=0$ and $f(t)=t$ ) represents that no thrown takes place at time $t$, which could correspond to an empty hand. Then, $b$ is simply the minimum number of balls needed to carry out the juggling.
|
| 114 |
+
|
| 115 |
+
The following graphical representation may be helpful to you. On a horizontal line, an curve is drawn from $t$ to $f(t)$. For instance, the following diagram depicts the juggling sequence 441 (or the juggling sequences 414 and 144). Then $b$ is simply the number of contiguous "paths" drawn, which is 3 in this case.
|
| 116 |
+
|
| 117 |
+
|
| 118 |
+
Figure 1: Juggling diagram of 441.
|
| 119 |
+
5. [10] Prove that 572 is not a juggling sequence.
|
| 120 |
+
|
| 121 |
+
Solution: We are given $j(0)=5, j(1)=7$ and $j(2)=2$. So $f(3)=3+j(0)=8$ and $f(1)=1+j(1)=8$. Thus $f(3)=f(1)$ and so $f$ is not a permutation of $\mathbb{Z}$, and hence 572 is not a juggling pattern. (In other words, there is a "collision" at times $t \equiv 2(\bmod 3)$.)
|
| 122 |
+
6. [40] Suppose that $j(0) j(1) \cdots j(n-1)$ is a valid juggling sequence. For $i=0,1, \ldots, n-1$, Let $a_{i}$ denote the remainder of $j(i)+i$ when divided by $n$. Prove that $\left(a_{0}, a_{1}, \ldots, a_{n-1}\right)$ is a permutation of $(0,1, \ldots, n-1)$.
|
| 123 |
+
|
| 124 |
+
Solution: Suppose that $a_{i}=j(i)+i-b_{i} n$, where $b_{i}$ is an integer. Note that $f\left(i-b_{i} n\right)=$ $i-b_{i} n+j(i)=a_{i}$. Since $\left\{i-b_{i} n \mid i=0,1, \ldots, n-1\right\}$ contains $n$ distinct integers (as their residue $\bmod n$ are all distinct), and $f$ is a permutation, we see that after applying the map $f$, the resulting set $\left\{a_{0}, a_{1}, \ldots, a_{n-1}\right\}$ is a set of $n$ distinct integers. Since $0 \leq a_{i}<n$ from definition, we see that ( $a_{0}, a_{1}, \ldots, a_{n-1}$ ) is a permutation of $(0,1, \ldots, n-1)$.
|
| 125 |
+
7. [30] Determine the number of juggling sequences of length $n$ with exactly 1 ball.
|
| 126 |
+
|
| 127 |
+
Answer: $2^{n}-1$. Solution: With 1 ball, we simply need to decide at times should the ball land in our hand. That is, we need to choose a non-empty subset of $\{0,1,2, \ldots, n-1\}$ where the ball lands. It follows that the answer is $2^{n}-1$.
|
| 128 |
+
8. [40] Prove that the number of balls $b$ in a juggling sequence $j(0) j(1) \cdots j(n-1)$ is simply the average
|
| 129 |
+
|
| 130 |
+
$$
|
| 131 |
+
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n} .
|
| 132 |
+
$$
|
| 133 |
+
|
| 134 |
+
Solution: Consider the corresponding juggling diagram. Say the length of an curve from $t$ to $f(t)$ is $f(t)-t$. Let us draw only the curves whose left endpoint lies inside $[0, M n-1]$. For every single ball, the sum of the lengths of the arrows drawn corresponding to that ball is between $M n-J$ and $M n+J$, where $J=\max \{j(0), j(1), \ldots, j(n-1)\}$. It follows that the sum of the lengths of the arrows drawn is between $b(M n-J)$ and $b(M n+J)$. Since the arrow drawn at $t$ has length $j(\bar{t})$, the sum of the lengths of the arrows drawn is $M(j(0)+j(1)+\cdots+j(n-1))$. It follows that
|
| 135 |
+
|
| 136 |
+
$$
|
| 137 |
+
b(M n-J) \leq M(j(0)+j(1)+\cdots+j(n-1)) \leq b(M n+J)
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
Dividing by $M n$, we get
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
b\left(1-\frac{J}{n M}\right) \leq \frac{j(0)+j(1)+\cdots+j(n-1)}{n} \leq b\left(1+\frac{J}{n M}\right)
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
Since we can take $M$ to be arbitrarily large, we must have
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n}
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
as desired.
|
| 153 |
+
9. [5] Show that the converse of the previous statement is false by providing a non-juggling sequence $j(0) j(1) j(2)$ of length 3 where the average $\frac{1}{3}(j(0)+j(1)+j(2))$ is an integer. Show that your example works.
|
| 154 |
+
|
| 155 |
+
Solution: One such example is 210 . This is not a juggling sequence since $f(0)=f(1)=2$.
|
| 156 |
+
|
| 157 |
+
## Incircles [180]
|
| 158 |
+
|
| 159 |
+
In the following problems, $A B C$ is a triangle with incenter $I$. Let $D, E, F$ denote the points where the incircle of $A B C$ touches sides $B C, C A, A B$, respectively.
|
| 160 |
+
|
| 161 |
+
|
| 162 |
+
At the end of this section you can find some terminology and theorems that may be helpful to you.
|
| 163 |
+
10. [15] Let $a, b, c$ denote the side lengths of $B C, C A, A B$. Find the lengths of $A E, B F, C D$ in terms of $a, b, c$.
|
| 164 |
+
|
| 165 |
+
Solution: Let $x=A E=A F, y=B D=B F, z=C D=C E$. Since $B C=B D+C D$, we have $a=x+y$. Similarly with the other sides, we arrive at the following system of equations:
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
a=y+z, \quad b=x+z, \quad c=x+y .
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
Solving this system gives us
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
\begin{aligned}
|
| 175 |
+
& A E=x=\frac{b+c-a}{2}, \\
|
| 176 |
+
& B F=y=\frac{a+c-b}{2}, \\
|
| 177 |
+
& C D=z=\frac{a+b-c}{2}
|
| 178 |
+
\end{aligned}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
11. [15] Show that lines $A D, B E, C F$ pass through a common point.
|
| 182 |
+
|
| 183 |
+
Solution: Using Ceva's theorem on triangle $A B C$, we see that it suffices to show that
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
\frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B}=1
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
Since $A F=A E, B D=B F$, and $C D=C E$ (due to equal tangents), we see that the LHS is indeed 1.
|
| 190 |
+
|
| 191 |
+
Remark: The point of concurrency is known as the Gergonne point.
|
| 192 |
+
12. [35] Show that the incenter of triangle $A E F$ lies on the incircle of $A B C$.
|
| 193 |
+
|
| 194 |
+
Solution: Let segment $A I$ meet the incircle at $A_{1}$. Let us show that $A_{1}$ is the incenter of $A E F$.
|
| 195 |
+
|
| 196 |
+
|
| 197 |
+
Since $A E=A F$ and $A A^{\prime}$ is the angle bisector of $\angle E A F$, we find that $A_{1} E=A_{1} F$. Using tangent-chord, we see that $\angle A F A_{1}=\angle A_{1} E F=\angle A_{1} F E$. Therefore, $A_{1}$ lies on the angle bisector of $\angle A F E$. Since $A_{1}$ also lies on the angle bisector of $\angle E A F, A_{1}$ must be the incenter of $A E F$, as desired.
|
| 198 |
+
13. [35] Let $A_{1}, B_{1}, C_{1}$ be the incenters of triangle $A E F, B D F, C D E$, respectively. Show that $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
| 199 |
+
|
| 200 |
+
Solution: Using the result from the previous problem, we see that $A_{1}, B_{1}, C_{1}$ are respectively the midpoints of the $\operatorname{arc} F E, F D, D F$ of the incircle. We have
|
| 201 |
+
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\begin{aligned}
|
| 205 |
+
\angle D A_{1} C_{1}+\angle B_{1} C_{1} A_{1} & =\frac{1}{2} \angle D I C_{1}+\frac{1}{2} \angle B_{1} I F+\frac{1}{2} \angle F I A_{1} \\
|
| 206 |
+
& =\frac{1}{4}(\angle E I D+\angle D I F+\angle F I E) \\
|
| 207 |
+
& =\frac{1}{4} \cdot 360^{\circ} \\
|
| 208 |
+
& =90^{\circ} .
|
| 209 |
+
\end{aligned}
|
| 210 |
+
$$
|
| 211 |
+
|
| 212 |
+
It follows that $A_{1} D$ is perpendicular to $B_{1} C_{1}$, and thus $A_{1} D$ passes through the orthocenter of $A_{1} B_{1} C_{1}$. Similarly, $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
| 213 |
+
14. [40] Let $X$ be the point on side $B C$ such that $B X=C D$. Show that the excircle $A B C$ opposite of vertex $A$ touches segment $B C$ at $X$.
|
| 214 |
+
|
| 215 |
+
Solution: Let the excircle touch lines $B C, A C$ and $A B$ at $X^{\prime}, Y$ and $Z$, respectively. Using the equal tangent property repeatedly, we have
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
B X^{\prime}-X^{\prime} C=B Z-C Y=(E Y-C Y)-(F Z-B Z)=C E-B F=C D-B D .
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
It follows that $B X^{\prime}=C D$, and thus $X^{\prime}=X$. So the excircle touches $B C$ at $X$.
|
| 222 |
+
|
| 223 |
+
15. [40] Let $X$ be as in the previous problem. Let $T$ be the point diametrically opposite to $D$ on on the incircle of $A B C$. Show that $A, T, X$ are collinear.
|
| 224 |
+
|
| 225 |
+
Solution: Consider a dilation centered at $A$ that carries the incircle to the excircle. This dilation must send the diameter $D T$ to some the diameter of excircle that is perpendicular to $B C$. The only such diameter is the one goes through $X$. It follows that $T$ gets carried to $X$. Therefore, $A, T, X$ are collinear.
|
| 226 |
+
|
| 227 |
+
## Glossary and some possibly useful facts
|
| 228 |
+
|
| 229 |
+
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point.
|
| 230 |
+
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
|
| 231 |
+
- The excircles of a triangle $A B C$ are the three circles on the exterior the triangle but tangent to all three lines $A B, B C, C A$.
|
| 232 |
+
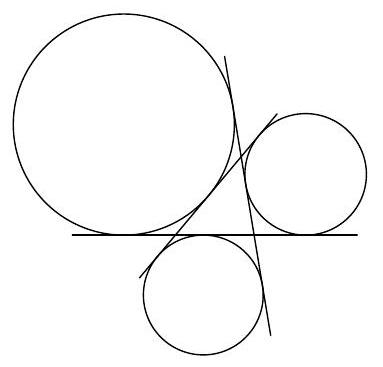
|
| 233 |
+
- The orthocenter of a triangle is the point of concurrency of the three altitudes.
|
| 234 |
+
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
|
| 235 |
+
|
| 236 |
+
$$
|
| 237 |
+
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
|
| 238 |
+
$$
|
| 239 |
+
|
HarvardMIT/md/en-12-1998-feb-adv-solutions.md
ADDED
|
@@ -0,0 +1,126 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Advanced Topics
|
| 2 |
+
|
| 3 |
+
1. Evaluate
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
Answer: $-\frac{1}{4}$. We have $\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)=\sin \left(2235^{\circ}\right) \sin \left(345^{\circ}\right)=\sin \left(75^{\circ}\right) \sin \left(-15^{\circ}\right)=$ $-\sin \left(75^{\circ}\right) \sin \left(15^{\circ}\right)=-\sin \left(15^{\circ}\right) \cos \left(15^{\circ}\right)=-\frac{\sin \left(30^{\circ}\right)}{2}=-\frac{1}{4}$.
|
| 10 |
+
2. How many values of $x,-19<x<98$, satisfy
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
\cos ^{2} x+2 \sin ^{2} x=1 ?
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
Answer: 38. For any $x, \sin ^{2} x+\cos ^{2} x=1$. Subtracting this from the given equation gives $\sin ^{2} x=0$, or $\sin x=0$. Thus $x$ must be a multiple of $\pi$, so $-19<k \pi<98$ for some integer $k$, or approximately $-6.1<k<31.2$. There are 32 values of $k$ that satisfy this, so there are 38 values of $x$ that satisfy $\cos ^{2} x+2 \sin ^{2} x=1$.
|
| 17 |
+
3. Find the sum of the infinite series
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
1+2\left(\frac{1}{1998}\right)+3\left(\frac{1}{1998}\right)^{2}+4\left(\frac{1}{1998}\right)^{3}+\ldots
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Answer: $\left(\frac{1998}{1997}\right)^{2}$ or $\frac{3992004}{3988009}$. We can rewrite the sum as
|
| 24 |
+
$\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)+\left(\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\left(\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\ldots$.
|
| 25 |
+
Evaluating each of the infinite sums gives
|
| 26 |
+
$\frac{1}{1-\frac{1}{1998}}+\frac{\frac{1}{1998}}{1-\frac{1}{1998}}+\frac{\left(\frac{1}{1998}\right)^{2}}{1-\frac{1}{1998}}+\ldots=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)$,
|
| 27 |
+
which is equal to $\left(\frac{1998}{1997}\right)^{2}$, or $\frac{3992004}{3988009}$, as desired.
|
| 28 |
+
4. Find the range of
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
f(A)=\frac{(\sin A)\left(3 \cos ^{2} A+\cos ^{4} A+3 \sin ^{2} A+\left(\sin ^{2} A\right)\left(\cos ^{2} A\right)\right)}{(\tan A)(\sec A-(\sin A)(\tan A))}
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
if $A \neq \frac{n \pi}{2}$.
|
| 35 |
+
Answer: $(3,4)$. We factor the numerator and write the denominator in term of fractions to get
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
\frac{(\sin A)\left(3+\cos ^{2} A\right)\left(\sin ^{2} A+\cos ^{2} A\right)}{\left(\frac{\sin A}{\cos A}\right)\left(\frac{1}{\cos A}-\frac{\sin ^{2} A}{\cos A}\right)}=\frac{(\sin A)\left(3+\cos ^{2} A\right)\left(\sin ^{2} A+\cos ^{2} A\right)}{\frac{(\sin A)\left(1-\sin ^{2} A\right)}{\cos ^{2} A}} .
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
Because $\sin ^{2} A+\cos ^{2} A=1,1-\sin ^{2} A=\cos ^{2} A$, so the expression is simply equal to $3+\cos ^{2} A$. The range of $\cos ^{2} A$ is $(0,1)$ ( 0 and 1 are not included because $A \neq \frac{n \pi}{2}$, so the range of $3+\cos ^{2} A$ is $(3,4)$.
|
| 42 |
+
5. How many positive integers less than 1998 are relatively prime to 1547 ? (Two integers are relatively prime if they have no common factors besides 1.)
|
| 43 |
+
Answer: 1487. The factorization of 1547 is $7 \cdot 13 \cdot 17$, so we wish to find the number of positive integers less than 1998 that are not divisible by 7,13 , or 17 . By the Principle of Inclusion-Exclusion, we first subtract the numbers that are divisible by one of 7,13 , and 17 , add back those that are divisible by two of 7,13 , and 17 , then subtract those divisible by three of them. That is,
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
1997-\left\lfloor\frac{1997}{7}\right\rfloor-\left\lfloor\frac{1997}{13}\right\rfloor-\left\lfloor\frac{1997}{17}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 13}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 17}\right\rfloor+\left\lfloor\frac{1997}{13 \cdot 17}\right\rfloor-\left\lfloor\frac{1997}{7 \cdot 13 \cdot 17}\right\rfloor,
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
or 1487.
|
| 50 |
+
6. In the diagram below, how many distinct paths are there from January 1 to December 31, moving from one adjacent dot to the next either to the right, down, or diagonally down to the right?
|
| 51 |
+
|
| 52 |
+
| Jan. $1->$ | * | * | * | * | * | * | * | * | * | * | |
|
| 53 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 54 |
+
| | * | * | | * | * | | * | * | | * | |
|
| 55 |
+
| | * | * | * | * | * | * | * | * | * | * | |
|
| 56 |
+
| | * | | | * | | | * | * | | * | |
|
| 57 |
+
| | * | * | * | * | * | * | * | * | * | * | <-Dec. 31 |
|
| 58 |
+
|
| 59 |
+
Answer: 372. For each dot in the diagram, we can count the number of paths from January 1 to it by adding the number of ways to get to the dots to the left of it, above it, and above and to the left of it, starting from the topmost leftmost dot. This yields the following numbers of paths:
|
| 60 |
+
|
| 61 |
+
| Jan. $1->$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ |
|
| 62 |
+
| ---: | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |$* 1$
|
| 63 |
+
|
| 64 |
+
So the number of paths from January 1 to December 31 is 372 .
|
| 65 |
+
7. The Houson Association of Mathematics Educators decides to hold a grand forum on mathematics education and invites a number of politicians from the United States to participate. Around lunch time the politicians decide to play a game. In this game, players can score 19 points for pegging the coordinator of the gathering with a spit ball, 9 points for downing an entire cup of the forum's interpretation of coffee, or 8 points for quoting more than three consecutive words from the speech Senator Bobbo delivered before lunch. What is the product of the two greatest scores that a player cannot score in this game?
|
| 66 |
+
Answer: 1209. Attainable scores are positive integers that can be written in the form $8 a+9 b+19 c$, where $a, b$, and $c$ are nonnegative integers. Consider attainable number of points modulo 8 .
|
| 67 |
+
Scores that are $0(\bmod 8)$ can be obtained with $8 a$ for positive $a$.
|
| 68 |
+
Scores that are $1(\bmod 8)$ greater than or equal to 9 can be obtained with $9+8 a$ for nonnegative $a$.
|
| 69 |
+
Scores that are $2(\bmod 8)$ greater than or equal to 18 can be obtained with $9 \cdot 2+8 a$.
|
| 70 |
+
Scores that are $3(\bmod 8)$ greater than or equal to 19 can be obtained with $19+8 a$.
|
| 71 |
+
Scores that are $4(\bmod 8)$ greater than or equal to $19+9=28$ can be obtained with $19+9+8 a$.
|
| 72 |
+
Scores that are $5(\bmod 8)$ greater than or equal to $19+9 \cdot 2=37$ can be obtained with $19+9 \cdot 2+8 a$.
|
| 73 |
+
Scores that are $6(\bmod 8)$ greater than or equal to $19 \cdot 2=38$ can be obtained with $19 \cdot 2+8 a$.
|
| 74 |
+
Scores that are $7(\bmod 8)$ greater than or equal to $19 \cdot 2+9=47$ can be obtained with $19 \cdot 2+9+8 a$.
|
| 75 |
+
So the largest two unachievable values are 39 and 31. Multiplying them gives 1209.
|
| 76 |
+
8. Given any two positive real numbers $x$ and $y$, then $x \diamond y$ is a positive real number defined in terms of $x$ and $y$ by some fixed rule. Suppose the operation $x \diamond y$ satisfies the equations $(x \cdot y) \diamond y=x(y \diamond y)$ and $(x \diamond 1) \diamond x=x \diamond 1$ for all $x, y>0$. Given that $1 \diamond 1=1$, find $19 \diamond 98$.
|
| 77 |
+
Answer: 19. Note first that $x \diamond 1=(x \cdot 1) \diamond 1=x \cdot(1 \diamond 1)=x \cdot 1=x$. Also, $x \diamond x=(x \diamond 1) \diamond x=x \diamond 1=x$. Now, we have $(x \cdot y) \diamond y=x \cdot(y \diamond y)=x \cdot y$. So $19 \diamond 98=\left(\frac{19}{98} \cdot 98\right) \diamond 98=\frac{19}{98} \cdot(98 \diamond 98)=\frac{19}{98} \cdot 98=19$.
|
| 78 |
+
9. Bob's Rice ID number has six digits, each a number from 1 to 9 , and any digit can be used any number of times. The ID number satisfies the following property: the first two digits is a number divisible by 2 , the first three digits is a number divisible by 3 , etc. so that the ID number itself is divisible by 6 . One ID number that satisfies this condition is 123252 . How many different possibilities are there for Bob's ID number?
|
| 79 |
+
Answer: 324 . We will count the number of possibilities for each digit in Bob's ID number, then multiply them to find the total number of possibilities for Bob's ID number. There are 3 possibilities for the first digit given any last 5 digits, because the entire number must be divisible by 3 , so the sum of the digits must be divisible by 3 . Because the first two digits are a number divisible by 2 , the second digit must be $2,4,6$, or 8 , which is 4 possibilities. Because the first five digits are a number divisible by 5 , the fifth digit must be a 5 . Now, if the fourth digit is a 2 , then the last digit has two choices, 2,8 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is a 4 , then the last digit must be a 6 , and the third digit has 4 choices, $2,4,6,8$. If the fourth digit is a 6 , then the last digit must be a 4 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is an 8 , then the last digit has two choices, 2,8 , and the third digit has 4 choices, $2,4,6,8$. So there are a total of $3 \cdot 4(2 \cdot 5+4+5+2 \cdot 4)=3 \cdot 4 \cdot 27=324$ possibilities for Bob's ID number.
|
| 80 |
+
10. In the fourth annual Swirled Series, the Oakland Alphas are playing the San Francisco Gammas. The first game is played in San Francisco and succeeding games alternate in location. San Francisco has a $50 \%$ chance of winning their home games, while Oakland has a probability of $60 \%$ of winning at home. Normally, the serios will stretch on forever until one team gets a three-game lead, in which case they are declared the winners. However, after each game in San Francisco there is a $50 \%$ chance of an earthquake, which will cause the series to end with the team that has won more games declared the winner. What is the probability that the Gammas will win?
|
| 81 |
+
|
| 82 |
+
Answer: | $\frac{34}{73} \cdot$ | Let $F(x)$ be the probability that the Gammas will win the series if they are ahead by |
|
| 83 |
+
| :--- | :--- | $x$ games and are about to play in San Francisco, and let $A(x)$ be the probability that the Gammas will win the series if they are ahead by $x$ games and are about to play in Oakland. Then we have
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
\begin{gathered}
|
| 87 |
+
F(2)=\frac{3}{4}+\frac{A(1)}{4} \\
|
| 88 |
+
A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10} \\
|
| 89 |
+
F(0)=\frac{1}{4}+\frac{A(1)}{4}+\frac{A(-1)}{4} \\
|
| 90 |
+
A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10} \\
|
| 91 |
+
F(-2)=\frac{A(-1)}{4}
|
| 92 |
+
\end{gathered}
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
Plugging $A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10}$ into $F(2)=\frac{3}{4}+\frac{A(1)}{4}$, we get
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
\begin{gathered}
|
| 99 |
+
F(2)=\frac{3}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right) \\
|
| 100 |
+
\frac{9 F(2)}{10}=\frac{3}{4}+\frac{6 F(0)}{40} \Leftrightarrow F(2)=\frac{5}{6}+\frac{F(0)}{6}
|
| 101 |
+
\end{gathered}
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Plugging $A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}$ into $F(-2)=\frac{A(-1)}{4}$, we get
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\frac{34 A(-1)}{40}=\frac{4 F(0)}{10} \Leftrightarrow F(-2)=\frac{2 F(0)}{17}
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Now,
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
F(0)=\frac{1}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right)+\frac{1}{4}\left(\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}\right)
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
This simplifies to $F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{F(2)}{10}+\frac{6 F(-2)}{40}$. Then, plugging our formulas in, we get
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
\begin{gathered}
|
| 120 |
+
F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{1}{10}\left(\frac{5}{6}+\frac{F(0)}{6}\right)+\frac{3 F(0)}{170} \\
|
| 121 |
+
\frac{73 F(0)}{102}=\frac{1}{3} \Leftrightarrow F(0)=\frac{34}{73}
|
| 122 |
+
\end{gathered}
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
Since $F(0)$ is the situation before the Series has started, the probability that the Gammas will win is $\frac{34}{73}$.
|
| 126 |
+
|
HarvardMIT/md/en-12-1998-feb-alg-solutions.md
ADDED
|
@@ -0,0 +1,115 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## HMMT 1998: Algebra Solutions
|
| 2 |
+
|
| 3 |
+
1. Problem: The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $\$ 23.50$. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $\$ 39.50$. What is the cost of 2 hamburgers, 2 milk shakes ,and 2 orders of fries at this restaurant?
|
| 4 |
+
|
| 5 |
+
Solution: Let $H=$ hamburger, $M=$ milk shake, and $F=$ order of fries. Then $3 H+5 M+F=\$ 23.50$. Multiplying the equation by 2 yields $6 H+10 M+2 F=\$ 47$. Also, it is given that $5 H+9 M+F=\$ 39.50$. Then subtracting the following equations
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
\begin{aligned}
|
| 9 |
+
& 6 H+10 M+2 F=\$ 47.00 \\
|
| 10 |
+
& 5 H+9 M+F=\$ 39.50
|
| 11 |
+
\end{aligned}
|
| 12 |
+
$$
|
| 13 |
+
|
| 14 |
+
yields $H+M+F=\$ 7.50$. Multiplying the equation by 2 yields $2 H+2 M+2 F=\$ 15$.
|
| 15 |
+
2. Problem: Bobbo starts swimming at 2 feet/s across a 100 foot wide river with a current of 5 feet/s. Bobbo doesn't know that there is a waterfall 175 feet from where he entered the river. He realizes his predicament midway across the river. What is the minimum speed that Bobbo must increase to make it to the other side of the river safely?
|
| 16 |
+
|
| 17 |
+
Solution: When Bobbo is midway across the river, he has travelled 50 feet. Going at a speed of 2 feet $/ \mathrm{s}$, this means that Bobbo has already been in the river for $\frac{50 \text { feet }}{20 \text { feet } / \mathrm{s}}=25 \mathrm{~s}$. Then he has traveled 5 feet $/ \mathrm{s} \cdot 25 \mathrm{~s}=125$ feet down the river. Then he has 175 feet- 125 feet $=50$ feet left to travel downstream before he hits the waterfall.
|
| 18 |
+
|
| 19 |
+
Bobbo travels at a rate of 5 feet/s downstream. Thus there are $\frac{50 \mathrm{feet}}{5 \text { feet } / \mathrm{s}}=10 \mathrm{~s}$ before he hits the waterfall. He still has to travel 50 feet horizontally across the river. Thus he must travel at a speed of $\frac{50 \text { feet }}{10 \mathrm{~s}}=5$ feet $/ \mathrm{s}$. This is a 3 feet/s difference from Bobbo's original speed of 2 feet $/ \mathrm{s}$.
|
| 20 |
+
3. Problem: Find the sum of every even positive integer less than 233 not divisible by 10 .
|
| 21 |
+
|
| 22 |
+
Solution: We find the sum of all positive even integers less than 233 and then subtract all the positive integers less than 233 that are divisible by 10 .
|
| 23 |
+
$2+4+\ldots+232=2(1+2+\ldots+116)=116 \cdot 117=13572$. The sum of all positive integers less than 233 that are divisible by 10 is $10+20+\ldots+230=10(1+2+\ldots+23)=2760$. Then our answer is $13572-2760=10812$.
|
| 24 |
+
4. Problem: Given that $r$ and $s$ are relatively prime positive integers such that $\frac{r}{s}=\frac{2(\sqrt{2}+\sqrt{10})}{5(\sqrt{3+\sqrt{5}})}$, find $r$ and $s$.
|
| 25 |
+
|
| 26 |
+
Solution: Squaring both sides of the given equation yields $\frac{r^{2}}{s^{2}}=\frac{4(12+4 \sqrt{5})}{25(3+\sqrt{5})}=\frac{16(3+\sqrt{5})}{25(3+\sqrt{5})}=\frac{16}{25}$. Because $r$ and $s$ are positive and relatively prime, then by inspection, $r=4$ and $s=5$.
|
| 27 |
+
5. Problem: A man named Juan has three rectangular solids, each having volume 128. Two of the faces of one solid have areas 4 and 32 . Two faces of another solid have areas 64 and 16 . Finally, two faces of the last solid have areas 8 and 32 . What is the minimum possible exposed surface area of the tallest tower Juan can construct by stacking his solids one on top of the other, face to face? (Assume that the base of the tower is not exposed).
|
| 28 |
+
|
| 29 |
+
Solution: Suppose that $x, y, z$ are the sides of the following solids. Then Volume $=x y z=128$. For the first solid, without loss of generality (with respect to assigning lengths to $x, y, z$ ), $x y=4$ and $y z=32$. Then $x y^{2} z=128$. Then $y=1$. Solving the remaining equations yields $x=4$ and $z=32$. Then the first solid has dimensions $4 \times 1 \times 32$.
|
| 30 |
+
|
| 31 |
+
For the second solid, without loss of generality, $x y=64$ and $y z=16$. Then $x y^{2} z=1024$. Then $y=8$. Solving the remaining equations yields $x=8$ and $z=2$. Then the second solid has dimensions $8 \times 8 \times 2$.
|
| 32 |
+
|
| 33 |
+
For the third solid, without loss of generality, $x y=8$ and $y z=32$. Then $y=2$. Solving the remaining equations yields $x=4$ and $z=16$. Then the third solid has dimensions $4 \times 2 \times 16$.
|
| 34 |
+
|
| 35 |
+
To obtain the tallest structure, Juan must stack the boxes such that the longest side of each solid is oriented vertically. Then for the first solid, the base must be $1 \times 4$, so that the side of length 32 can
|
| 36 |
+
contribute to the height of the structure. Similarly, for the second solid, the base must be $8 \times 2$, so that the side of length 8 can contribute to the height. Finally, for the third solid, the base must be $4 \times 2$. Thus the structure is stacked, from bottom to top: second solid, third solid, first solid. This order is necessary, so that the base of each solid will fit entirely on the top of the solid directly beneath it.
|
| 37 |
+
|
| 38 |
+
All the side faces of the solids contribute to the surface area of the final solid. The side faces of the bottom solid have area $8 \cdot(8+2+8+2)=160$. The side faces of the middle solid have area $16 \cdot(4+2+4+2)=192$. The sides faces of the top solid have area $32 \cdot(4+1+4+1)=320$.
|
| 39 |
+
|
| 40 |
+
Furthermore, the top faces of each of the solids are exposed. The top face of the bottom solid is partially obscured by the middle solid. Thus the total exposed area of the top face of the bottom solid is $8 \cdot 2-4 \cdot 2=8$. The top face of the middle solid is partially obscured by the top solid. Thus the total exposed area of the top face of the middle solid is $4 \cdot 2-4 \cdot 1=4$. The top face of the top solid is fully exposed. Thus the total exposed area of the top face of the top solid is $4 \cdot 1=4$.
|
| 41 |
+
|
| 42 |
+
Then the total surface area of the entire structure is $160+192+320+8+4+4=688$.
|
| 43 |
+
6. Problem: How many pairs of positive integers $(a, b)$ with $\leq b$ satisfy $\frac{1}{a}+\frac{1}{b}=\frac{1}{6}$ ?
|
| 44 |
+
|
| 45 |
+
Solution: $\frac{1}{a}+\frac{1}{b}=\frac{1}{6} \Rightarrow \frac{a+b}{a b}=\frac{1}{6} \Rightarrow a b=6 a+6 b \Rightarrow a b-6 a-6 b=0$. Factoring yields $(a-b)(b-6)-36=0$. Then $(a-6)(b-6)=36$. Because $a$ and $b$ are positive integers, only the factor pairs of 36 are possible values of $a-6$ and $b-6$. The possible pairs are:
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\begin{aligned}
|
| 49 |
+
& a-6=1, b-6=36 \\
|
| 50 |
+
& a-6=2, b-6=18 \\
|
| 51 |
+
& a-6=3, b-6=12 \\
|
| 52 |
+
& a-6=4, b-6=9 \\
|
| 53 |
+
& a-6=6, b-6=6
|
| 54 |
+
\end{aligned}
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Because $a \leq b$, the symmetric cases, such as $a-6=12, b-6=3$ are not applicable. Then there are 5 possible pairs.
|
| 58 |
+
7. Problem: Given that three roots of $f(x)=x^{4}+a x^{2}+b x+c$ are $2,-3$, and 5 , what is the value of $a+b+c$ ?
|
| 59 |
+
|
| 60 |
+
Solution: By definition, the coefficient of $x^{3}$ is negative the sum of the roots. In $f(x)$, the coefficient of $x^{3}$ is 0 . Thus the sum of the roots of $f(x)$ is 0 . Then the fourth root is -4 . Then $f(x)=(x-2)(x+3)(x-5)(x+4)$. Notice that $f(1)$ is $1+a+b+c$. Thus our answer is $f(1)-1=(1-2)(1+3)(1-5)(1+4)-1=79$.
|
| 61 |
+
8. Problem: Find the set of solutions for $x$ in the inequality $\frac{x+1}{x+2}>\frac{3 x+4}{2 x+9}$ when $x \neq-2, x \neq \frac{9}{2}$.
|
| 62 |
+
|
| 63 |
+
Solution: There are 3 possible cases of $x$ : 1) $\left.\left.-\frac{9}{2}<x, 2\right) \frac{9}{2} \leq x \leq-2,3\right)-2<x$. For the cases (1) and (3), $x+2$ and $2 x+9$ are both positive or negative, so the following operation can be carried out without changing the inequality sign:
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\begin{aligned}
|
| 67 |
+
\frac{x+1}{x+2} & >\frac{3 x+4}{2 x+9} \\
|
| 68 |
+
\Rightarrow 2 x^{2}+11 x+9 & >3 x^{2}+10 x+8 \\
|
| 69 |
+
\Rightarrow 0 & >x^{2}-x-1
|
| 70 |
+
\end{aligned}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
The inequality holds for all $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$. The initial conditions were $-\frac{9}{2}<x$ or $-2<x$. The intersection of these three conditions occurs when $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.
|
| 74 |
+
|
| 75 |
+
Case (2) is $\frac{9}{2} \leq x \leq-2$. For all $x$ satisfying these conditions, $x+2<0$ and $2 x+9>0$. Then the following operations will change the direction of the inequality:
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
\begin{aligned}
|
| 79 |
+
\frac{x+1}{x+2} & >\frac{3 x+4}{2 x+9} \\
|
| 80 |
+
\Rightarrow 2 x^{2}+11 x+9 & <3 x^{2}+10 x+8 \\
|
| 81 |
+
\Rightarrow 0 & <x^{2}-x-1
|
| 82 |
+
\end{aligned}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
The inequality holds for all $x<\frac{1-\sqrt{5}}{2}$ and $\frac{1+\sqrt{5}}{2}<x$. The initial condition was $\frac{-9}{2} \leq x \leq-2$. Hence the intersection of these conditions yields all $x$ such that $\frac{-9}{2} \leq x \leq-2$. Then all possible cases of $x$ are $\frac{-9}{2} \leq x \leq-2 \cup \frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.
|
| 86 |
+
9. Problem: Suppose $f(x)$ is a rational function such that $3 f\left(\frac{1}{x}\right)+\frac{2 f(x)}{x}=x^{2}$ for $x \neq 0$. Find $f(-2)$.
|
| 87 |
+
|
| 88 |
+
Solution: Let $x=\frac{-1}{2}$. Then
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
\begin{aligned}
|
| 92 |
+
& 3 f(-2)+\frac{2 f\left(\frac{-1}{2}\right)}{\frac{-1}{2}}=\frac{1}{4} \\
|
| 93 |
+
& \Rightarrow 3 f(-2)-4 f\left(\frac{-1}{2}\right)= \frac{1}{4}
|
| 94 |
+
\end{aligned}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Let $x=-2$. Then
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\begin{aligned}
|
| 101 |
+
& 3 f\left(\frac{-1}{2}\right)+\frac{2 f(-2)}{-2}=4 \\
|
| 102 |
+
\Rightarrow 3 f\left(\frac{-1}{2}\right)-f(-2) & =4
|
| 103 |
+
\end{aligned}
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
Solving this system of equations $\{(1),(2)\}$ for $f(-2)$ yields $f(-2)=\frac{67}{20}$.
|
| 107 |
+
10. Problem: G.H. Hardy once went to visit Srinivasa Ramanujan in the hospital, and he started the conversation with: "I came here in taxi-cab number 1729. That number seems dull to me, which I hope isn't a bad omen." "Nonsense," said Ramanujan. "The number isn't dull at all. It's quite interesting. It's the smallest number that can be expressed as the sum of two cubes in two different ways." Ramanujan had immediately seen that $1729=12^{3}+1^{3}=10^{3}+9^{3}$. What is the smallest positive integer representable as the sum of the cubes of three positive integers in two different ways?
|
| 108 |
+
|
| 109 |
+
Solution: Let this smallest positive integer be represented as $a^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. By inspection, a solution is not possible with the first 4 cubes. We prove that it is impossible to write the same number as two different sums of the first 5 cubes. Because we necessarily need to use the 5 th cube (otherwise, this proof would be for the first 4 cubes), we have $5^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. Without loss of generality, suppose $d=5$. By inspection, there is no solution to $b^{3}+c^{3}=e^{3}+f^{3}$, such that $b, c, e, f \leq 5$ and $b, c$ and $e, f$ are unique.
|
| 110 |
+
|
| 111 |
+
Then none of $d, e, f$ are 5 . Then at least two must be 4 , otherwise the RHS would be too small. Without loss of generality, suppose $d=e=4$. Then $b^{3}+c^{3}=3+f^{3}$. By inspection, there are no possible solutions if $b, c, f \leq 4$.
|
| 112 |
+
|
| 113 |
+
Thus if $a=5$, there are no solutions.
|
| 114 |
+
Suppose that there is a solution within the first 6 cubes. Then $a=6$. By the same analysis as above, $d=e=5$, otherwise the RHS would be too small. Then $b^{3}+c^{3}=34+f^{3}$. By inspection, we see that a possible solution is $b=3, c=2, f=1$. Then the desired integer is $6^{3}+3^{3}+2^{3}=251$.
|
| 115 |
+
|
HarvardMIT/md/en-12-1998-feb-calc-solutions.md
ADDED
|
@@ -0,0 +1,72 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## HMMT 1998: Calculus Solutions
|
| 2 |
+
|
| 3 |
+
1. Problem: Farmer Tim is lost in the densely-forested Cartesian plane. Starting from the origin he walks a sinusoidal path in search of home; that is, after $t$ minutes he is at position $(t, \sin t)$.
|
| 4 |
+
|
| 5 |
+
Five minutes after he sets out, Alex enters the forest at the origin and sets out in search of Tim. He walks in such a way that after he has been in the forest for $m$ minutes, his position is $(m, \cos t)$.
|
| 6 |
+
|
| 7 |
+
What is the greatest distance between Alex and Farmer Tim while they are walking in these paths?
|
| 8 |
+
Solution: At arbitrary time $t$, Farmer Tim is at position $(t, \sin t)$ and Alex is at position $(t-5, \cos t)$. Hence at time $t$, the distance, $d$, between Tim and Alex is $d=\sqrt{(\sin t-\cos t)^{2}+25}$. To find the maximum value of $d$, we solve for $t$ such that $\frac{d d}{d t}=0$.
|
| 9 |
+
$\frac{d d}{d t}=\frac{(\sin t-\cos t)(\cos t+\sin t)}{\sqrt{(\sin t-\cos t)^{2}+25}}$. Then $\frac{d d}{d t}=0 \Rightarrow \sin ^{2} t-\cos ^{2} t=0 \Rightarrow \sin ^{2} t=\cos ^{2} t$. Equality happens if $t$ is any constant multiple of $\frac{\pi}{4}$.
|
| 10 |
+
|
| 11 |
+
Notice that to maximize $d$, we need to maximize $(\sin t-\cos t)^{2}$. This is achieved when $\cos t=-\sin t$. Because we determined earlier that $t$ is a constant multiple of $\frac{\pi}{4}$, then with this new condition, we see that $t$ must be a constant multiple of $\frac{3 \pi}{4}$.
|
| 12 |
+
|
| 13 |
+
Then $(\sin t-\cos t)^{2}=2 \Rightarrow d=\sqrt{29}$.
|
| 14 |
+
2. Problem: A cube with sides 1 m in length is filled with water, and has a tiny hole through which the water drains into a cylinder of radius 1 m . If the water level in the cube is falling at a rate of $1 \mathrm{~cm} / \mathrm{s}$, at what rate is the water level in the cylinder rising?
|
| 15 |
+
|
| 16 |
+
Solution: The magnitude of the change in volume per unit time of the two solids is the same. The change in volume per unit time of the cube is $1 \mathrm{~cm} \cdot \mathrm{~m}^{2} / \mathrm{s}$. The change in volume per unit time of the cylinder is $\pi \cdot \frac{d h}{d t} \cdot m^{2}$, where $\frac{d h}{d t}$ is the rate at which the water level in the cylinder is rising.
|
| 17 |
+
|
| 18 |
+
Solving the equation $\pi \cdot \frac{d h}{d t} \cdot m^{2}=1 \mathrm{~cm} \cdot m^{2} / \mathrm{s}$ yields $\frac{1}{\pi} \mathrm{~cm} / \mathrm{s}$.
|
| 19 |
+
3. Problem: Find the area of the region bounded by the graphs of $y=x^{2}, y=x$, and $x=2$.
|
| 20 |
+
|
| 21 |
+
Solution: There are two regions to consider. First, there is the region bounded by $y=x^{2}$ and $y=x$, in the interval $[0,1]$. In this interval, the values of $y=x$ are greater than the values of $y=x^{2}$, thus the area is calculated by $\int_{0}^{1}\left(x-x^{2}\right) d x$.
|
| 22 |
+
|
| 23 |
+
Second, there is the region bounded by $y=x^{2}$ and $y=x$ and $x=2$, in the interval [1,2]. In this interval, the values of $y=x^{2}$ are greater than the values of $y=x$, thus the area is calculated by $\int_{1}^{2}\left(x^{2}-x\right) d x$. Then the total area of the region bounded by the three graphs is $\int_{0}^{1}\left(x-x^{2}\right) d x+\int_{1}^{2}\left(x^{2}-x\right) d x=1$.
|
| 24 |
+
4. Problem: Let $f(x)=1+\frac{x}{2}+\frac{x^{2}}{4}+\frac{x^{3}}{8}+\ldots$, for $-1 \leq x \leq 1$. Find $\sqrt{e^{\int_{0}^{1} f(x) d x}}$.
|
| 25 |
+
|
| 26 |
+
Solution: Observe that $f(x)$ is merely an infinite geometric series. Thus $f(x)=\frac{1}{1-\frac{x}{2}}=\frac{2}{2-x}$. Then $\int_{0}^{1} \frac{2}{2-x}=2 \ln 2$. Then $\sqrt{e^{2 \ln 2}}=\sqrt{2^{2}}=2$.
|
| 27 |
+
5. Problem: Evaluate $\lim _{x \rightarrow 1} x^{\frac{x}{\sin (1-x)}}$.
|
| 28 |
+
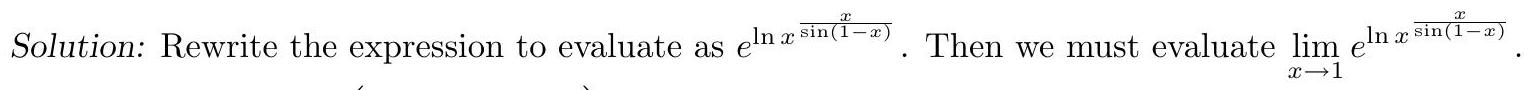
|
| 29 |
+
$\lim _{x \rightarrow 1} \ln x^{\frac{x}{\sin (1-x)}}=\lim _{x \rightarrow 1}\left(\frac{x}{\sin (1-x)} \ln x\right)$. Because direct calculation of the limit results in indeterminate form $\left(\frac{1}{0} \cdot 0\right)$, we can use L'Hopital's rule to evaluate the limit. By L'Hopital's rule, $\lim _{x \rightarrow 1}\left(\frac{x}{\sin (1-x)} \ln x\right)=$ $\lim _{x \rightarrow 1} \frac{\ln x+1}{-\cos (1-x)}$. This limit is simply -1.
|
| 30 |
+
|
| 31 |
+
Hence $\lim _{x \rightarrow 1} e^{\ln x^{\frac{x}{\sin (1-x)}}}=e^{-1}=\frac{1}{e}$.
|
| 32 |
+
6. Problem: Edward, the author of this test, had to escape from prison to work in the grading room today. He stopped to rest at a place 1,875 feet from the prison and was spotted by a guard with a crossbow. The guard fired an arrow with an initial velocity of $100 \mathrm{ft} / \mathrm{s}$. At the same time, Edward started running away with an acceleration of $1 \mathrm{ft} / \mathrm{s}^{2}$. Assuming that air resistance causes the arrow to decelerate at $1 \mathrm{ft} / \mathrm{s}^{2}$ and that it does hit Edward, how fast was the arrow moving at the moment of impact (in $\mathrm{ft} / \mathrm{s}$ )?
|
| 33 |
+
|
| 34 |
+
Solution: We use the formula for distance, $d=\frac{1}{2} a t^{2}+v t+d_{0}$. Then after $t$ seconds, Edward is at location $1875+\frac{1}{2}(1)\left(t^{2}\right)$ from the prison. After $t$ seconds, the arrow is at location $\frac{1}{2}(-1)\left(t^{2}\right)+100 t$ from the prison. When the arrow hits Edward, both objects are at the same distance away from the tower. Hence $1875+\frac{1}{2}(1)\left(t^{2}\right)=\frac{1}{2}(-1)\left(t^{2}\right)+100 t$. Solving for $t$ yields $t^{2}-100 t+1875=0 \Rightarrow t=25$ or $t=75$. Then it must be $t=25$, because after the arrow hits Edward, he will stop running.
|
| 35 |
+
|
| 36 |
+
After 25 seconds, the arrow is moving at a velocity of $100-25(1)=75 \mathrm{ft} / \mathrm{s}$.
|
| 37 |
+
7. Problem: A parabola is inscribed in equilateral triangle $A B C$ of side length 1 in the sense that $A C$ and $B C$ are tangent to the parabola at $A$ and $B$, respectively. Find the area between $A B$ and the parabola.
|
| 38 |
+
|
| 39 |
+
Solution: Suppose $A=(0,0), B=(1,0)$, and $C=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. Then the parabola in question goes through $(0,0)$ and $(1,0)$ and has tangents with slopes of $\sqrt{3}$ and $-\sqrt{3}$, respectively, at these points. Suppose the parabola has equation $y=a x^{2}+b x+c$. Then $\frac{d y}{d x}=2 a x+b$.
|
| 40 |
+
|
| 41 |
+
At point $(0,0), \frac{d y}{d x}=b$. Also the slope at $(0,0)$, as we determined earlier, is $\sqrt{3}$. Hence $b=\sqrt{3}$. Similarly, at point $(1,0), \frac{d y}{d x}=2 a+b$. The slope at $(1,0)$, as we determined earlier, is $-\sqrt{3}$. Then $a=-\sqrt{3}$.
|
| 42 |
+
|
| 43 |
+
Since the parabola goes through $(0,0), c=0$. Hence the equation of the parabola is $y=-\sqrt{3} x^{2}+\sqrt{3} x$. The desired area is simply the area under the parabolic curve in the interval $[0,1]$.
|
| 44 |
+
|
| 45 |
+
Hence $\int_{0}^{1}\left(-\sqrt{3} x^{2}+\sqrt{3} x\right) d x=\frac{\sqrt{3}}{6}$.
|
| 46 |
+
8. Problem: Find the slopes of all lines passing through the origin and tangent to the curve $y^{2}=x^{3}+39 x-35$.
|
| 47 |
+
|
| 48 |
+
Solution: Any line passing throug the origin has equation $y=m x$, where $m$ is the slope of the line. If a line is tangent to the given curve, then at the point of tangency, $(x, y), \frac{d y}{d x}=m$.
|
| 49 |
+
|
| 50 |
+
First, we calculate $\frac{d y}{d x}$ of the curve: $2 y d y=3 x^{2} d x+39 d x \Rightarrow \frac{d y}{d x}=\frac{3 x^{2}+39}{2 y}$. Substituting $m x$ for $y$, we get the following system of equations:
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\begin{aligned}
|
| 54 |
+
m^{2} x^{2} & =x^{3}+39 x-35 \\
|
| 55 |
+
m & =\frac{3 x^{2}+39}{2 m x}
|
| 56 |
+
\end{aligned}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Solving for $x$ yields the equation $x^{3}-39 x+70=0 \Rightarrow(x-2)(x+7)(x-5)=0 \Rightarrow x=2$ or $x=-7$ or $x=5$. These solutions indicate the $x$-coordinate of the points at which the desired lines are tangent to the curve. Solving for the slopes of these lines, we get $m= \pm \frac{\sqrt{51}}{2}$ for $x=2$, no real solutions for $x=-7$, and $m= \pm \frac{\sqrt{285}}{5}$ for $x=5$. Thus $m= \pm \frac{\sqrt{51}}{2}, \pm \frac{\sqrt{285}}{5}$.
|
| 60 |
+
9. Problem: Evaluate $\sum_{n=1}^{\infty} \frac{1}{n \cdot 2^{n-1}}$.
|
| 61 |
+
|
| 62 |
+
Solution: Note that if we take the integral of $f(x)$ in problem 4, we get the function $F(x)=x+\frac{x^{2}}{2 \cdot 2}+$ $\frac{x^{3}}{3 \cdot 2^{2}}+\ldots$. Evaluating this integral in the interval $[0,1]$, we get $1+\frac{1}{2 \cdot 2}+\frac{1}{3 \cdot 2^{2}}+\ldots$, which is the desired sum.
|
| 63 |
+
|
| 64 |
+
Hence $\int_{0}^{1} \frac{2}{2-x} d x=2 \ln 2$.
|
| 65 |
+
10. Problem: Let $S$ be the locus of all points $(x, y)$ in the first quadrant such that $\frac{x}{t}+\frac{y}{1-t}=1$ for some $t$ with $0<t<1$. Find the area of $S$.
|
| 66 |
+
|
| 67 |
+
Solution: Solving for $t$ in the given equation, we get $t^{2}+(y-x-1) t+x=0$. Using the quadratic equation, we get $t=\frac{(x+1-y) \pm \sqrt{(y-x-1)^{2}-4 x}}{2}$. For all valid combinations of $(x, y), t$ is positive and less than 1 (this is easy to see by inspection). All valid combinations of $(x, y)$ are those that make $(y-x-1)^{2}-4 x \geq 0$.
|
| 68 |
+
|
| 69 |
+
Solving for $y$ in the equation $(y-x-1)^{2}-4 x=0$ yields $y^{2}-(2 x+2) y+(x-1)^{2} \geq 0 \Rightarrow y=(x+1) \pm 2 \sqrt{x}$. In the original equation, it is given that $\frac{x}{t}+\frac{y}{1-t}=1$, and $0<t<1$. This implies that $x, y<1$. Then the only possible $y<1$ that satisfies $(y-x-1)^{2}-4 x=0$ is $y=x+1-2 \sqrt{x}$.
|
| 70 |
+
|
| 71 |
+
Then to satisfy the inequality $(y-x-1)^{2}-4 x \geq 0$, we must have $y \leq x+1-2 \sqrt{x}$. Recall that this is when $0<y<1$. Hence we integrate in the interval $[0,1]: \in_{0}^{1} x+1-2 \sqrt{x}=\frac{1}{6}$.
|
| 72 |
+
|
HarvardMIT/md/en-12-1998-feb-geo-solutions.md
ADDED
|
@@ -0,0 +1,14 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Geometry Solutions
|
| 2 |
+
|
| 3 |
+
Harvard-MIT Math Tournament<br>Written by Anders Kaseorg
|
| 4 |
+
|
| 5 |
+
1. $m \angle E D X=180^{\circ}-m \angle L A X-m \angle E L A=180^{\circ}-m \angle L A X-\left(180^{\circ}-m \angle A X E\right)=80^{\circ}$.
|
| 6 |
+
2. If the angle in radians is $\theta$, then Anne travels $R \theta$ and Lisa travels $(R-r)+r \theta+(R-r)$. Setting these equal yields $R(\theta-2)=r(\theta-2)$, so $\theta=2$ radians.
|
| 7 |
+
3. $m \angle M L D=\frac{1}{2} \overparen{A B}=45^{\circ}$.
|
| 8 |
+
4. The cylinder has a cross-sectional area $\pi$ times greater than the cube, so the water raises $\frac{1}{\pi}$ times as quickly in the cylinder as it lowers in the cube; that is, at $\frac{1}{\pi} \frac{\mathrm{~cm}}{\mathrm{~s}}$.
|
| 9 |
+
5. If the new circle has radius $r$, then the distance from its center to $E$ can be computed either as $1+r$ or $(2-r) \sqrt{2}$. Setting these equal yields $r=\frac{2 \sqrt{2}-1}{\sqrt{2}+1}=5-3 \sqrt{2}$.
|
| 10 |
+
6. The central circle has area $\pi\left(\frac{1}{2 \sqrt{3}}\right)^{2}=\frac{\pi}{12}$, and each of the three small triangles are copies of the entire figure dilated by $\frac{1}{3}$. Therefore, the total area is given by $K=\frac{\pi}{12}+3 \cdot\left(\frac{1}{3}\right)^{2} K \Longleftrightarrow$ $\frac{2}{3} K=\frac{\pi}{12} \Longleftrightarrow K=\frac{\pi}{8}$.
|
| 11 |
+
7. Let $E=(a, b, 0), A=(-c, b, 0), R=(-c,-d, 0), L=(a,-d, 0), Y=(0,0, h)$, and observe that $E Y^{2}+R Y^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2 h^{2}=A Y^{2}+L Y^{2}$, which can only be satisfied by $E Y=1, A Y=4, R Y=8, L Y=7$ (or the symmetric configurations). Since $E A$ is an integral side of a triangle whose other sides are 1 and 4 , we must have $E A=4$; similarly, $E L=7$. Therefore, the area of rectangle $E A R L$ is 28 . (Such a pyramid may be constructed by taking $a=\frac{1}{8}, b=\frac{1}{14}, c=\frac{31}{8}, d=\frac{97}{14}, h=\frac{\sqrt{3071}}{56}$.)
|
| 12 |
+
8. Since $O D \perp A C$ and $\triangle A O C$ is equilateral, we have $\angle A O D=30^{\circ}$. So $A E=\frac{1}{\sqrt{3}}$, and $B H=\sqrt{A B^{2}+A H^{2}}=\sqrt{2^{2}+\left(3-\frac{1}{\sqrt{3}}\right)^{2}}=\sqrt{\frac{40}{3}-2 \sqrt{3}} \approx 3.141533339$.
|
| 13 |
+
9. The dilation of ratio $-\frac{2}{3}$ about $T$ sends $C_{2}$ to $C_{1}, O_{2}$ to $O_{1}$, and $S$ to the other intersection of $s$ with $C_{1}$, which we shall call $U$. We can now compute $T R \cdot T S=\frac{3}{2} T R \cdot T U=\frac{3}{2} T P^{2}=$ $\frac{3}{2}\left(O_{1} T^{2}-O_{1} P^{2}\right)=\frac{3}{2}\left(\left(\frac{O_{1} O_{2}}{1+3 / 2}\right)^{2}-O_{1} P^{2}\right)=\frac{3}{2}\left(\left(\frac{20}{5 / 2}\right)^{2}-4^{2}\right)=72$.
|
| 14 |
+
10. Suppose that when the ball hits a side of the table, instead of reflecting the ball's path, we reflect the entire table over this side so that the path remains straight. If we repeatedly reflect the table over its sides in all possible ways, we get a triangular grid that tiles the plane. Whenever the path crosses $n$ lines in this grid parallel to $C T$, it will cross $\frac{7}{8} n$ lines parallel to $C H$ and $\frac{15}{8} n$ lines parallel to $H T$. After crosssing $8+7+15=30$ grid lines it will have crossed three lines simultaneously again, which means that the ball will have landed in a pocket after bouncing 27 times. By picturing the grid it is easy to see that the pocket in question is $H$. The distance the ball travels during the $\frac{1}{8}$ of its trip described in the problem is the third side of a triangle with an $120^{\circ}$ angle between two sides 16 and 14 , which is $\sqrt{16^{2}+14^{2}-2 \cdot 16 \cdot 14 \cos 120^{\circ}}=26$, so length of the entire trip is 208 .
|
HarvardMIT/md/en-12-1998-feb-team-solutions.md
ADDED
|
@@ -0,0 +1,79 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## 1998 Power Question Solutions
|
| 2 |
+
|
| 3 |
+
I. Graphs, total of 20 points
|
| 4 |
+
a. completely correct gets 1 point, total of 6 points
|
| 5 |
+
i. yes. vertices $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$, edges $\mathrm{AB}, \mathrm{AC}, \mathrm{AD}, \mathrm{BD}$
|
| 6 |
+
ii. no. $A$ and $B$ are connected twice
|
| 7 |
+
iii. yes. vertices $A, B, C$, edges $A B C$
|
| 8 |
+
iv. yes. vertices $A, B, C, D, E$, edges $A B, A D, A E, B E, C D, C E$
|
| 9 |
+
$v$. no. the edge from $B$ does not connect to another vertex
|
| 10 |
+
vi. no. E is connected to itself
|
| 11 |
+
b. completely correct gets 1 point, total of 2 points
|
| 12 |
+
i. BL,BE,BU,EL,EU
|
| 13 |
+
ii. $\mathrm{A} \leftrightarrow \mathrm{B}, \mathrm{B} \leftrightarrow \mathrm{L}, \mathrm{C} \leftrightarrow \mathrm{U}, \mathrm{D} \leftrightarrow \mathrm{E}$
|
| 14 |
+
c. 1 point each for i-iii, 3 for iv-vi, total of 12 points
|
| 15 |
+
i. no
|
| 16 |
+
ii. no
|
| 17 |
+
iii. no
|
| 18 |
+
iv. yes
|
| 19 |
+
v. no
|
| 20 |
+
vi. yes
|
| 21 |
+
note that the second graph in v has more vertices of degree 3 than the first
|
| 22 |
+
II. Planar Graphs, total of 60 points
|
| 23 |
+
a. 1 point each for $\mathrm{v}, \mathrm{e}, \mathrm{f}$, total of 6 points
|
| 24 |
+
i. $v=9, e=16, f=9$
|
| 25 |
+
ii. $v=7, e=14, f=9$
|
| 26 |
+
note that $\mathrm{v}-\mathrm{e}+\mathrm{f}=2$ by Euler's formula
|
| 27 |
+
b. 3 points each, total of 12 points
|
| 28 |
+
i. yes
|
| 29 |
+
ii. yes
|
| 30 |
+
iii. no
|
| 31 |
+
note that this is a planar drawing of ii:
|
| 32 |
+
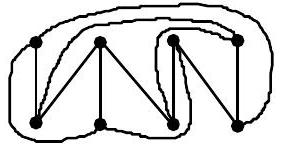
|
| 33 |
+
iv. yes
|
| 34 |
+
for iii, note that if we remove the two vertices of degree two and make the vertices they were adjacent to adjacent to each other then we get a graph isomorphic to the one in d.ii.
|
| 35 |
+
c. total of 15 points
|
| 36 |
+
partial credit: up to 5 for effort, 5 for insight, otherwise as described below [1 point] If $G$ has 3 vertices and two edges then the assertion is easy since $f=1$. [ 6 points] Otherwise each face is bounded by 3 or more edges, hence counting the number of edges bounding each faces and summing, then using the fact that we at most double counted [ -2 for asserting we exactly double counted] each face we get $3 \mathrm{f} \leq 2 \mathrm{e}$, thus proving the left inequality.
|
| 37 |
+
[ 8 points] Now $\mathrm{f} \leq(2 / 3) \mathrm{e}$ and we want to eliminate f , so we can add v-e to both sides to get $v-e+f \leq v-e+(2 / 3) e$, thus by Euler's formula $2 \leq v-e / 3$, and rearranging yields the right inequality.
|
| 38 |
+
d. 5 points for $i, 10$ for $i i$, total of 15 points
|
| 39 |
+
partial credit: if Jordan curve thm is used then 3 points for i, 5 for ii.
|
| 40 |
+
on part ii: 3 for effort, 3 for insight, otherwise as described
|
| 41 |
+
i. Assume it is planar. $v=5, e=10,3 \mathrm{v}-6=9<e$, contradicting c , thus nonplanar
|
| 42 |
+
ii. [1 point] Note that $v=6, e=9$, so $3 v-6=12>e$ is not a contradiction
|
| 43 |
+
[ 2 points] There are no triangles in this graph, thus every face is bordered by at least 4 edges. This will allow us to prove a better inequality as in c with the assumption the graph is planar, and that will provide the contradiction.
|
| 44 |
+
[ 2 points] Thus as in the proof of c we get $4 \mathrm{f} \leq 2 \mathrm{e}$.
|
| 45 |
+
[ 4 points] Hence $\mathrm{f} \leq e / 2$, and again we want to eliminate f so adding v -e to both sides and applying Euler's formula yields $2 \leq \mathrm{v}-\mathrm{e} / 2$. (or $\mathrm{e} \leq 2 \mathrm{v}-4$ )
|
| 46 |
+
[1 point] 6-9/2<2, contradicting the inequality just proved, thus the graph is not planar.
|
| 47 |
+
e. total of 12 points
|
| 48 |
+
partial credit: 4 for effort, 4 for insight, otherwise as described
|
| 49 |
+
[2 points] Without loss of generality we may assume the graph is connected.
|
| 50 |
+
[2 points] If the graph has fewer than 3 vertices then the assertion is obvious.
|
| 51 |
+
[5 points] Otherwise we can apply the inequality in c. First assume every vertex has degree at least 6 , then adding the degrees of each vertex double counts the edges so $6 \mathrm{v} \leq$ 2 e .
|
| 52 |
+
[3 points] Now by c. e $\leq 3 \mathrm{v}-6$, and combining these inequalities we get $6 \mathrm{v} \leq 6 \mathrm{v}-12$, a contradiction, thus the graph must have at least one vertex of degree 5 or less.
|
| 53 |
+
III. Coloring, total of 56 points
|
| 54 |
+
a. 3 points each, total of 12 points
|
| 55 |
+
i. 4
|
| 56 |
+
ii. 5
|
| 57 |
+
iii. 4
|
| 58 |
+
iv. 3
|
| 59 |
+
b. total of 14 points
|
| 60 |
+
partial credit: 5 for effort, 5 for insight, otherwise as described
|
| 61 |
+
[ 8 points] Number the colors used in $G 1,2, \ldots, \chi$. Let $\mathrm{v}_{1}$ be the number of vertices colored with color $1_{\underline{\chi}}$. Then since no pair of them are adjacent, the are all adjacent in the new graph and thus $\bar{\chi} \geq v_{1}$. Repeating this procedure for $v_{2}, \ldots, v_{\chi}$ and adding we get $\chi \bar{\chi}$ $\geq \mathrm{v}$.
|
| 62 |
+
[6 points] By the AM-GM inequality $\chi+\bar{\chi} \geq 2 \sqrt{\chi \bar{\chi}} \geq 2 \sqrt{\mathrm{v}}$.
|
| 63 |
+
c. 5 points for i and iii, 20 for ii, total of 30 points
|
| 64 |
+
partial credit: as described below
|
| 65 |
+
i. By II.e. $G$ must have a vertex of degree 5 or less
|
| 66 |
+
ii. [2 points] We want to remove the vertex V without decreasing the number of colors needed. In the cases where V has degree $<5$ this is obviously possible.
|
| 67 |
+
[10 points] In the case where V has degree 5 , color the adjacent vertices with colors 1, 2, $3,4,5$ in clockwise order. If the vertices colored 1 and 3 are not connected by a walk with all vertices colored 1 or 3 then change the vertex colored 3 to 1 , change any 1 vertices adjacent to it to 3 , then change any 3 vertices adjacent to those to 1 , and so on. This recoloring does not affect any of the other vertices adjacent to V and thus allows us to make V color 3, i.e. if a sixth color is needed for $G$ then it is still needed after we remove V.
|
| 68 |
+
[ 8 points] If the vertices colored 1 and 3 are connected by a walk of vertices colored 1 or 3 then look at the vertices colored 2 and 4 . If they are connected by a walk then by the Jordan Curve Theorem [-4 for not using this] this walk must cross the closed curve formed by the 1-3 walk and the edges from V to the vertices colored 1 and 3. The graph is planar, so we can assume it is drawn without edge crossings, thus the walk from the vertex colored 2 to the one colored 4 must cross this curve at a vertex, hence they are not connected by a walk with all vertices colored 2 or 4 , and by the previous argument we can change the vertex colored 2 to 4 and make V color 2, so it can be removed without removing the need for a sixth color.
|
| 69 |
+
iii. [4 points] We have shown that for any graph with $\chi>5$ we can find one with fewer vertices, and since the proof did not depend on the number of vertices we can keep doing this until we get a graph with 5 vertices, which can clearly be colored with only 5 colors, thus $G$ could not require more than 5 colors.
|
| 70 |
+
[1 points] To make this rigorous some mention should be made of the well-ordering principal or infinite descent.
|
| 71 |
+
|
| 72 |
+
Historical notes and inspiration for further study of the subject:
|
| 73 |
+
The Four Color theorem was first conjectured in 1852. Many "proofs" were given, including one in 1879 by A. B. Kempe that was believed to be correct until P. J. Heawood found a flaw in 1890. The proof of the Four Color theorem, given in 1976 by Haken and Appel, uses a similar technique to what we just used, but instead of using 6 possible subgraphs it uses 1482 . The way these theorems relate to coloring maps is that we can consider the dual graph, formed by putting a vertex in every face and connecting the vertices whose faces share an edge. Coloring the dual graph is the same as coloring the faces of the original graph in such a way that no two faces sharing an edge have the same color, which is what one does when coloring a map.
|
| 74 |
+
While it may seem that we used many definitions in this power question, there are many more that had to be omitted. Some of the other interesting definitions used in graph theory are expansion, which is what you get if you add vertices along an edge of a graph, and supergraph, which is what you get if you add new vertices anywhere and connect them arbitrarily to the other vertices. Kuratowski's Theorem states that every nonplanar graph is a supergraph of an expansion of one of the two graphs in II.d. A corollary of this is that a graph is nonplanar iff it is a supergraph of an expansion of one of those two graphs, thus we can classify planar and nonplanar graphs in terms of just two particular graphs.
|
| 75 |
+
|
| 76 |
+
A planar graph can alo be described as one that can be drawn on a sphere with no edge crossings. A torus is essentially the surface of a solid sphere with a hole drilled all the way through it. The genus $g$ of a graph is the minimum number of holes that must be drilled in a sphere in order to be able to draw it without edge crossings. In other words a graph of genus $g$ can be drawn on a $g$ holed torus without edge crossings, but not on a $g-1$ holed torus. The Heawood Coloring Theorem states that if $G$ has genus $g>0$ then $G$ can be colored with $\left[\frac{7+\sqrt{1+48 \mathrm{~g}}}{2}\right\rfloor$ colors. Note that plugging in $\mathrm{g}=0$ yields 4 , but no proof of this theorem is known that does not depend on the condition $g>0$ (of course we can combine the proof for $\mathrm{g}>0$ with the four color theorem to conclude that the result holds for all g , but it would be nice to have just one proof that works equally well for all g ).
|
| 77 |
+
Another thing we can study about graphs is what kind of walks exist in them. An eulerian walk, named after the great Swiss mathematician Leonhard Euler (1707-1783, pronounced Oiler), is one that uses every edge exactly once. A hamiltonian walk, named after the Irish mathematician Sir William Rowan Hamilton (1805-1865), is one that uses every vertex exactly once. Try to classify which graphs have such walks, with or without the condition that the starting and ending points must be the same (in the case of a hamiltonian walk the end vertex is thus counted twice and it is called a closed hamiltonian walk to distinguish from the open walk).
|
| 78 |
+
This power question was barely an introduction to graph theory. It is a very broad field of mathematics, closely related to topology and knot theory. I hope you enjoyed this test, learned something from it, and that you will continue your studies of mathematics for many years.
|
| 79 |
+
|
HarvardMIT/md/en-121-2008-nov-gen1-solutions.md
ADDED
|
@@ -0,0 +1,67 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $1^{\text {st }}$ Annual Harvard-MIT November Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 8 November 2008
|
| 4 |
+
|
| 5 |
+
## Individual Round
|
| 6 |
+
|
| 7 |
+
1. [2] Find the minimum of $x^{2}-2 x$ over all real numbers $x$.
|
| 8 |
+
|
| 9 |
+
Answer: -1 Write $x^{2}-2 x=x^{2}-2 x+1-1=(x-1)^{2}-1$. Since $(x-1)^{2} \geq 0$, it is clear that the minimum is -1 .
|
| 10 |
+
Alternate method: The graph of $y=x^{2}-2 x$ is a parabola that opens up. Therefore, the minimum occurs at its vertex, which is at $\frac{-b}{2 a}=\frac{-(-2)}{2}=1$. But $1^{2}-2 \cdot 1=-1$, so the minimum is -1 .
|
| 11 |
+
2. [3] What is the units digit of $7^{2009}$ ?
|
| 12 |
+
|
| 13 |
+
Answer: 7 Note that the units digits of $7^{1}, 7^{2}, 7^{3}, 7^{4}, 7^{5}, 7^{6}, \ldots$ follows the pattern $7,9,3,1,7,9,3,1, \ldots$. The 2009th term in this sequence should be 7 .
|
| 14 |
+
Alternate method: Note that the units digit of $7^{4}$ is equal to 1 , so the units digit of $\left(7^{4}\right)^{502}$ is also 1. But $\left(7^{4}\right)^{502}=7^{2008}$, so the units digit of $7^{2008}$ is 1 , and therefore the units digit of $7^{2009}$ is 7 .
|
| 15 |
+
3. [3] How many diagonals does a regular undecagon (11-sided polygon) have?
|
| 16 |
+
|
| 17 |
+
Answer: 44 There are 8 diagonals coming from the first vertex, 8 more from the next, 7 from the next, 6 from the next, 5 from the next, etc., and 1 from the last, for $8+8+7+6+5+4+3+2+1=44$ total.
|
| 18 |
+
|
| 19 |
+
Third method: Each vertex has 8 diagonals touching it. There are 11 vertices. Since each diagonal touches two vertices, this counts every diagonal twice, so there are $\frac{8 \cdot 11}{2}=44$ diagonals.
|
| 20 |
+
4. [4] How many numbers between 1 and $1,000,000$ are perfect squares but not perfect cubes?
|
| 21 |
+
|
| 22 |
+
Answer: $9901000000=1000^{2}=10^{6}$. A number is both a perfect square and a perfect cube if and only if it is exactly a perfect sixth power. So, the answer is the number of perfect squares, minus the number of perfect sixth powers, which is $1000-10=990$.
|
| 23 |
+
5. [5] Joe has a triangle with area $\sqrt{3}$. What's the smallest perimeter it could have?
|
| 24 |
+
|
| 25 |
+
Answer: 6 The minimum occurs for an equilateral triangle. The area of an equilateral triangle with side-length $s$ is $\frac{\sqrt{3}}{4} s^{2}$, so if the area is $\sqrt{3}$ then $s=\sqrt{\sqrt{3} \frac{4}{\sqrt{3}}}=2$. Multiplying by 3 to get the perimeter yields the answer.
|
| 26 |
+
6. [5] We say " $s$ grows to $r$ " if there exists some integer $n>0$ such that $s^{n}=r$. Call a real number $r$ "sparse" if there are only finitely many real numbers $s$ that grow to $r$. Find all real numbers that are sparse.
|
| 27 |
+
Answer: $-1,0,1$ For any number $x$, other than these $3, x, \sqrt[3]{x}, \sqrt[5]{x}, \sqrt[7]{x}, \ldots$ provide infinitely many possible values of $s$, so these are the only possible sparse numbers. On the other hand, -1 is the only possible value of $s$ for $r=-1,0$ is the only value for $r=0$, and -1 and 1 are the only values for $r=1$. Therefore, $-1,0$, and 1 are all sparse.
|
| 28 |
+
7. [6] Find all ordered pairs $(x, y)$ such that
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
(x-2 y)^{2}+(y-1)^{2}=0
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
Answer: $(2,1)$ The square of a real number is always at least 0 , so to have equality we must have $(x-2 y)^{2}=0$ and $(y-1)^{2}=0$. Then $y=1$ and $x=2 y=2$.
|
| 35 |
+
8. [7] How many integers between 2 and 100 inclusive cannot be written as $m \cdot n$, where $m$ and $n$ have no common factors and neither $m$ nor $n$ is equal to 1 ? Note that there are 25 primes less than 100 .
|
| 36 |
+
Answer: 35 A number cannot be written in the given form if and only if it is a power of a prime. We can see this by considering the prime factorization. Suppose that $k=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$, with $p_{1}, \ldots, p_{n}$ primes. Then we can write $m=p_{1}^{e_{1}}$ and $n=p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$. So, we want to find the powers of primes that are less than or equal to 100 . There are 25 primes, as given in the problem statement. The squares of primes are $2^{2}, 3^{2}, 5^{2}, 7^{2}$. The cubes of primes are $2^{3}, 3^{3}$. The fourth powers of primes are $2^{4}, 3^{4}$. The fifth powers of primes are $2^{5}$, The sixth powers of primes are $2^{6}$. There are no seventh or higher powers of primes between 2 and 100 . This adds 10 non-primes to the list, so that in total there are $10+25=35$ such integers.
|
| 37 |
+
9. [7] Find the product of all real $x$ for which
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
2^{3 x+1}-17 \cdot 2^{2 x}+2^{x+3}=0
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Answer: -3 We can re-write the equation as $2^{x}\left(2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8\right)=0$, or $2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8=0$. Make the substitution $y=2^{x}$. Then we have $2 y^{2}-17 y+8=0$, which has solutions (by the quadratic formula) $y=\frac{17 \pm \sqrt{289-64}}{4}=\frac{17 \pm 15}{4}=8, \frac{1}{2}$, so $2^{x}=8, \frac{1}{2}$ and $x=3,-1$. The product of these numbers is -3 .
|
| 44 |
+
10. [8] Find the largest positive integer $n$ such that $n^{3}+4 n^{2}-15 n-18$ is the cube of an integer.
|
| 45 |
+
|
| 46 |
+
Answer: 19 Note that the next cube after $n^{3}$ is $(n+1)^{3}=n^{3}+3 n^{2}+3 n+1$. After that, it is $(n+2)^{3}=n^{3}+6 n^{2}+12 n+8 . n^{3}+6 n^{3}+12 n+8$ is definitely bigger than $n^{3}+4 n^{2}-15 n-18$, so the largest cube that $n^{3}+4 n^{2}-15 n-18$ could be is $(n+1)^{3}$. On the other hand, for $n \geq 4, n^{3}+4 n^{2}-15 n-18$ is larger than $(n-2)^{3}=n^{3}-6 n^{2}+12 n-8$ (as $4 n^{2}-15 n-18>-6 n^{2}+12 n-8 \Longleftrightarrow 10 n^{2}-27 n-10>0$, which is true for $n \geq 4$ ).
|
| 47 |
+
So, we will check for all solutions to $n^{3}+4 n^{2}-15 n-18=(n-1)^{3}, n^{3},(n+1)^{3}$. The first case yields
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
n^{3}+4 n^{2}-15 n-18=n^{3}-3 n^{2}+3 n-1 \Longleftrightarrow 7 n^{2}-18 n-17=0
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
which has no integer solutions. The second case yields
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
n^{3}+4 n^{2}-15 n-18=n^{3} \Longleftrightarrow 4 n^{2}-15 n-18=0
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
which also has no integer solutions. The final case yields
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
n^{3}+4 n^{2}-15 n-18=n^{3}+3 n^{2}+3 n+1 \Longleftrightarrow n^{2}-18 n-19=0
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
which has integer solutions $n=-1,19$. So, the largest possible $n$ is 19 .
|
| 66 |
+
Remark: The easiest way to see that the first two polynomials have no integer solutions is using the Rational Root Theorem, which states that the rational solutions of a polynomial $a x^{n}+\ldots+b$ are all of the form $\pm \frac{b^{\prime}}{a^{\prime}}$, where $b^{\prime}$ divides $b$ and $a^{\prime}$ divides $a$.
|
| 67 |
+
|
HarvardMIT/md/en-121-2008-nov-gen2-solutions.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $1^{\text {st }}$ Annual Harvard-MIT November Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 8 November 2008
|
| 4 |
+
|
| 5 |
+
Theme Round
|
| 6 |
+
|
| 7 |
+
Triangular Areas [25]
|
| 8 |
+
|
| 9 |
+
Triangles have many properties. Calculate some things about their area.
|
| 10 |
+
|
| 11 |
+
1. [3] A triangle has sides of length 9,40 , and 41 . What is its area?
|
| 12 |
+
|
| 13 |
+
Answer: 180 Observe that $9^{2}+40^{2}=41^{2}$, so this triangle is right and therefore has area $\frac{1}{2} \cdot 9 \cdot 40=$ 180.
|
| 14 |
+
2. [4] Let $A B C$ be a triangle, and let $M$ be the midpoint of side $A B$. If $A B$ is 17 units long and $C M$ is 8 units long, find the maximum possible value of the area of $A B C$.
|
| 15 |
+
Answer: 68 Let $h$ be the length of the altitude from $C$ to $A B$. Observe that $K=\frac{1}{2} \cdot h \cdot A B \leq$ $\frac{1}{2} \cdot C M \cdot A B=68$ and that equality is achieved when $C M \perp A B$.
|
| 16 |
+
3. [5] Let $D E F$ be a triangle and $H$ the foot of the altitude from $D$ to $E F$. If $D E=60, D F=35$, and $D H=21$, what is the difference between the minimum and the maximum possible values for the area of $D E F$ ?
|
| 17 |
+
Answer: 588 Observe that the two possible configurations come from $D E F$ obtuse and $D E F$ acute. In either case, we have that $H F=\sqrt{35^{2}-21^{2}}=28$ and $E H=\sqrt{60^{2}-21^{2}}=9 \sqrt{39}$. This means that $H F-E H$, so in the two cases the values of $E F$ are $F H+E H$ and $E H-F H$. The difference in area is hence $\frac{1}{2} \cdot 2 \cdot F H \cdot D H=28 \cdot 21=588$.
|
| 18 |
+
4. [6] Right triangle $X Y Z$, with hypotenuse $Y Z$, has an incircle of radius $\frac{3}{8}$ and one leg of length 3. Find the area of the triangle.
|
| 19 |
+
|
| 20 |
+
Answer: $\quad \frac{21}{16}$ Let the other leg have length $x$. Then the tangents from $Y$ and $Z$ to the incircle have length $x-\frac{3}{8}$ and $3-\frac{3}{8}$. So the hypotenuse has length $x+\frac{9}{4}$, the semiperimeter of the triangle is $x+\frac{21}{8}$, and the area of the triangle is $\frac{3}{8}\left(x+\frac{21}{8}\right)$. But the area can also be calculated as $\frac{3 x}{2}$. Setting these expressions equal, we find $x=\frac{7}{8}$ and the area is $\frac{21}{16}$.
|
| 21 |
+
5. [7] A triangle has altitudes of length 15,21 , and 35 . Find its area.
|
| 22 |
+
|
| 23 |
+
Answer: $\quad 245 \sqrt{3}$ If $A$ is the area of the triangle, the sides are $\frac{2 A}{15}, \frac{2 A}{21}$, and $\frac{2 A}{35}$. So the triangle is similar to a $\frac{1}{15}, \frac{1}{21}, \frac{1}{35}$ triangle, which is similar to a $3,5,7$ triangle. Let the sides be $3 k, 5 k$, and $7 k$. Then the angle between the sides of length $3 k$ and $7 k$ is $120^{\circ}$, so the area is $\frac{15 \sqrt{3}}{4} k^{2}$. But the area can also be calculated as $\frac{(3 k)(35)}{2}=\frac{105 k}{2}$. Setting these values equal, $k=\frac{14 \sqrt{3}}{3}$ and the area is $245 \sqrt{3}$.
|
| 24 |
+
|
| 25 |
+
Chessboards [25]
|
| 26 |
+
|
| 27 |
+
Joe B. is playing with some chess pieces on a $6 \times 6$ chessboard. Help him find out some things.
|
| 28 |
+
|
| 29 |
+
1. [3] Joe B. first places the black king in one corner of the board. In how many of the 35 remaining squares can he place a white bishop so that it does not check the black king?
|
| 30 |
+
Answer: 30 Any square not on the diagonal containing the corner is a possible location, and there are $36-6=30$ such squares.
|
| 31 |
+
2. [4] Joe B. then places a white king in the opposite corner of the board. How many total ways can he place one black bishop and one white bishop so that neither checks the king of the opposite color?
|
| 32 |
+
Answer: 876 Observe that either both bishops are on the diagonal containing both kings or neither are. If both are on the diagonal, each of the $\binom{4}{2}=6$ choices of pairs of squares yields one possible configuration, so there are 6 possibilities in this case. Off the diagonal, any pair of locations works, giving $30 \cdot 29=870$ possibilities in this case. Summing, we obtain $870+6=876$ total possibilities.
|
| 33 |
+
3. [5] Joe B. now clears the board. How many ways can he place 3 white rooks and 3 black rooks on the board so that no two rooks of opposite color can attack each other?
|
| 34 |
+
Answer: 608 Consider first placing the white rooks. They will occupy either 3 columns and 1 row, 3 columns and 2 rows, 3 columns and 3 rows, 2 rows and 2 columns, 2 columns and 3 rows, or 1 column and 3 rows. First note that placing the black rooks is impossible in the second, third, and fifth cases. The first case can happen in 4.4 ways, and each leads to a unique way to place the black rooks. In the fourth case, we can choose the row with 2 rooks in 4 ways, place the rooks in $\binom{4}{2}$ ways, choose the column of the other rook in 2 ways, and place it in 3 ways, for a total of $4 \cdot\binom{4}{2} \cdot 2 \cdot 3=144$ ways to place the white rooks in this configuration; the black rooks can then be placed in any of 4 possible locations, and there are 4 ways to do this, leading to 576 possibilities in this case. Finally, the sixth case is analogous to the first, giving 16 possibilities. Summing, we find $16+576+16=608$ total placements.
|
| 35 |
+
4. [6] Joe B. is frustrated with chess. He breaks the board, leaving a $4 \times 4$ board, and throws 3 black knights and 3 white kings at the board. Miraculously, they all land in distinct squares! What is the expected number of checks in the resulting position? (Note that a knight can administer multiple checks and a king can be checked by multiple knights.)
|
| 36 |
+
Answer: $\quad \frac{9}{5}$ We first compute the expected number of checks between a single knight-king pair. If the king is located at any of the 4 corners, the knight has 2 possible checks. If the king is located in one of the 8 squares on the side of the board but not in the corner, the knight has 3 possible checks. If the king is located in any of the 4 central squares, the knight has 4 possible checks. Summing up, $4 \cdot 2+8 \cdot 3+4 \cdot 4=48$ of the $16 \cdot 15$ knight-king positions yield a single check, so each pair yields $\frac{48}{16 \cdot 15}=\frac{1}{5}$ expected checks. Now, note that each of the 9 knight-king pairs is in each of $16 \cdot 15$ possible positions with equal probability, so by linearity of expectation the answer is $9 \cdot \frac{1}{5}=\frac{9}{5}$.
|
| 37 |
+
5. [7] Suppose that at some point Joe B. has placed 2 black knights on the original board, but gets bored of chess. He now decides to cover the 34 remaining squares with 17 dominos so that no two overlap and the dominos cover the entire rest of the board. For how many initial arrangements of the two pieces is this possible?
|
| 38 |
+
Answer: 324 Color the squares of the board red and blue in a checkerboard pattern, and observe that any domino will cover exactly one red square and one blue square. Therefore, if the two knights cover squares of the same color, this is impossible. We now claim that it is always possible if they cover squares of opposite colors, which will give an answer of $18^{2}=324$. Consider the rectangle $R$ with the knights at its corners. Because the knights cover differently colored squares, $R$ must have one side length odd and one side length even. Therefore, the 4 lines bounding $R$ cut the original board into $R$ and up to 8 other rectangles, which can be put together into rectangles with at least one side even. These rectangles can be tiled, and it is easy to see that $R$ can be tiled, proving the claim.
|
| 39 |
+
|
| 40 |
+
- Bishop: This piece can move any number of squares diagonally if there are no other pieces along its path.
|
| 41 |
+
- Rook: This piece can move any number of squares either vertically or horizontally if there are no other pieces along its path
|
| 42 |
+
- Knight: This piece can move either two squares along a row and one square along a column or two squares along a column and one square along a row.
|
| 43 |
+
- King: This piece can move to any open adjacent square (including diagonally).
|
| 44 |
+
|
HarvardMIT/md/en-121-2008-nov-guts-solutions.md
ADDED
|
@@ -0,0 +1,224 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $1^{\text {st }}$ Annual Harvard-MIT November Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 8 November 2008
|
| 4 |
+
|
| 5 |
+
Guts Round
|
| 6 |
+
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 7 |
+
|
| 8 |
+
1. [5] Find the sum of all solutions for $x$ :
|
| 9 |
+
|
| 10 |
+
$$
|
| 11 |
+
\begin{aligned}
|
| 12 |
+
x y & =1 \\
|
| 13 |
+
x+y & =3
|
| 14 |
+
\end{aligned}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
Answer: 3 Substitute $3-x$ in for $y$ into the first equation:
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
x(3-x)=1 \Leftrightarrow x^{2}-3 x+1=0
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
This equation has two distinct roots, each of which corresponds to a possible solution $x$. The sum of the roots of the quadratic equation $a x^{2}+b x+c=0$ is $\frac{-b}{a}$, which in this case is 3 .
|
| 24 |
+
2. [5] Evaluate the sum
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
1-2+3-4+\cdots+2007-2008
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
Answer: -1004 Every odd integer term can be paired with the next even integer, and this pair sums to -1 . There are 1004 such pairs, so the total sum is -1004 .
|
| 31 |
+
3. [5] What is the largest $x$ such that $x^{2}$ divides $24 \cdot 35 \cdot 46 \cdot 57$ ?
|
| 32 |
+
|
| 33 |
+
Answer: 12 We factor the product as $2^{4} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 23$. If $x^{2}$ divides this product, $x$ can have at most 2 factors of 2,1 factor of 3 , and no factors of any other prime. So $2^{2} \cdot 3=12$ is the largest value of $x$.
|
| 34 |
+
|
| 35 |
+
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 36 |
+
|
| 37 |
+
4. [6] What is the smallest prime divisor of $5^{7^{10^{7^{10}}}}+1$ ?
|
| 38 |
+
|
| 39 |
+
Answer: 2 Notice that 5 to any power is odd, so this number is even. Then 2 is a prime divisor. It also happens to be the smallest prime.
|
| 40 |
+
5. [6] What is the sum of all integers $x$ such that $|x+2| \leq 10$ ?
|
| 41 |
+
|
| 42 |
+
Answer: $\quad-42$ The inequality $|x+2| \leq 10$ holds if and only if $x+2 \leq 10$ and $x+2 \geq-10$. So $x$ must be in the range $-12 \leq x \leq 8$. If we add up the integers in this range, each positive integer cancels with its additive inverse, so the sum is equal to $-12-11-10-9=-42$.
|
| 43 |
+
6. [6] Sarah is deciding whether to visit Russia or Washington, DC for the holidays. She makes her decision by rolling a regular 6 -sided die. If she gets a 1 or 2 , she goes to DC . If she rolls a 3,4 , or 5 , she goes to Russia. If she rolls a 6 , she rolls again. What is the probability that she goes to DC?
|
| 44 |
+
Answer: $\quad \frac{2}{5}$ On each roll, the probability that Sarah decides to go to Russia is $3 / 2$ times the probability she decides to go to DC. So, the total probability that she goes to Russia is $3 / 2$ times the total probability that she goes to DC. Since these probabilities sum to 1 (they are the only two eventual outcomes) Sarah goes to DC with probability $\frac{2}{5}$ and Russia with probability $\frac{3}{5}$.
|
| 45 |
+
|
| 46 |
+
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 47 |
+
|
| 48 |
+
7. [7] Compute $2009^{2}-2008^{2}$.
|
| 49 |
+
|
| 50 |
+
Answer: 4017 Factoring this product with difference of squares, we find it equals:
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
(2009+2008)(2009-2008)=(4017)(1)=4017
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
8. [7] Alice rolls two octahedral dice with the numbers $2,3,4,5,6,7,8,9$. What's the probability the two dice sum to 11 ?
|
| 57 |
+
Answer: $\frac{1}{8}$ No matter what comes up on the first die, there is exactly one number that could appear on the second die to make the sum 11 , because 2 can be paired with 9,3 with 8 , and so on. So, there is a $\frac{1}{8}$ chance of getting the correct number on the second die.
|
| 58 |
+
9. [7] Let $a_{0}=\frac{6}{7}$, and
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
a_{n+1}= \begin{cases}2 a_{n} & \text { if } a_{n}<\frac{1}{2} \\ 2 a_{n}-1 & \text { if } a_{n} \geq \frac{1}{2}\end{cases}
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Find $a_{2008}$.
|
| 65 |
+
Answer: $\sqrt{\frac{5}{7}}$ We calculate the first few $a_{i}$ :
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
a_{1}=\frac{5}{7}, a_{2}=\frac{3}{7}, a_{3}=\frac{6}{7}=a_{0}
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
So this sequence repeats every three terms, so $a_{2007}=a_{0}=\frac{6}{7}$. Then $a_{2008}=\frac{5}{7}$.
|
| 72 |
+
|
| 73 |
+
```
|
| 74 |
+
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 75 |
+
```
|
| 76 |
+
|
| 77 |
+
10. [8] Find the sum of all positive integers $n$ such that $n$ divides $n^{2}+n+2$.
|
| 78 |
+
|
| 79 |
+
Answer: 3 Since $n$ always divides $n^{2}+n$, the only $n$ that work are divisors of 2 , because if $n$ divides $a$ and $n$ divides $b$, then $n$ divides $a+b$. So the solutions are 1 and 2 which sum to 3 .
|
| 80 |
+
11. [8] Al has a rectangle of integer side lengths $a$ and $b$, and area 1000 . What is the smallest perimeter it could have?
|
| 81 |
+
Answer: 130 To minimize the sum of the side lengths, we need to keep the height and width as close as possible, because the square has the smallest perimeter of all rectangles with a fixed area. So, 40 and 25 multiply to 1000 and are as close as possible - the $40 \times 25$ rectangle has perimeter 130 .
|
| 82 |
+
12. [8] Solve the following system of equations for $w$.
|
| 83 |
+
|
| 84 |
+
$$
|
| 85 |
+
\begin{aligned}
|
| 86 |
+
& 2 w+x+y+z=1 \\
|
| 87 |
+
& w+2 x+y+z=2 \\
|
| 88 |
+
& w+x+2 y+z=2 \\
|
| 89 |
+
& w+x+y+2 z=1
|
| 90 |
+
\end{aligned}
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
Answer: $\quad \frac{-1}{5}$ Add all the equations together to find that $5 x+5 y+5 z+5 w=6$, or $x+y+z+w=\frac{6}{5}$. We can now subtract this equation from the first equation to see that $w=\frac{-1}{5}$.
|
| 94 |
+
13. [9] Find the number of distinct primes dividing $1 \cdot 2 \cdot 3 \cdots 9 \cdot 10$.
|
| 95 |
+
|
| 96 |
+
Answer: 4 A prime divides this product if and only if it divides one of the multiplicands, so prime divisors of this product must be less than 10 . There are 4 primes less than 10 , namely, $2,3,5$, and 7 .
|
| 97 |
+
14. [9] You have a $2 \times 3$ grid filled with integers between 1 and 9 . The numbers in each row and column are distinct, the first row sums to 23 , and the columns sum to 14,16 , and 17 respectively.
|
| 98 |
+
|
| 99 |
+
| | 14 | 16 | 17 |
|
| 100 |
+
| :---: | :---: | :---: | :---: |
|
| 101 |
+
| 23 | $a$ | $b$ | $c$ |
|
| 102 |
+
| | $x$ | $y$ | $z$ |
|
| 103 |
+
|
| 104 |
+
What is $x+2 y+3 z ?$
|
| 105 |
+
Answer: 49 The sum of all 6 numbers is $14+16+17=47$, so $x+y+z=47-23=24$. If three distinct digits sum to 24 , they must be 7,8 , and 9 , because any other triple of digits would have a smaller sum. So, we try placing these digits in for $x, y$, and $z$, and the only arrangement that does not force equal digits in any row or column is $x=8, y=7, z=9$. In this case, $x+2 y+3 z=49$.
|
| 106 |
+
15. [9] A cat is going up a stairwell with ten stairs. However, instead of walking up the stairs one at a time, the cat jumps, going either two or three stairs up at each step (though if necessary, it will just walk the last step). How many different ways can the cat go from the bottom to the top?
|
| 107 |
+
Answer: 12 The number of ways for the cat to get to the $i$ th step is the number of ways for the cat to get to step $i-2$ plus the number of ways to get to step $i-3$, because for each way to get to step $i$, we can undo the last move the cat made to go back to one of these two steps. The cat can get to step 1 in 0 ways, to step 2 in 1 way, and to step 3 in 1 way. Now we repeatedly use our formula for calculating the number of ways to get to the $i$ th step to see that the cat gets to:
|
| 108 |
+
|
| 109 |
+
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 110 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 111 |
+
| Number of ways | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 7 |
|
| 112 |
+
|
| 113 |
+
So our answer is $5+7=12$.
|
| 114 |
+
16. [10] If $p$ and $q$ are positive integers and $\frac{2008}{2009}<\frac{p}{q}<\frac{2009}{2010}$, what is the minimum value of $p$ ?
|
| 115 |
+
|
| 116 |
+
Answer: 4017 By multiplying out the fraction inequalities, we find that $2008 q+1 \leq 2009 p$ and $2010 p+\leq 2009 q$. Adding 2009 times the first inequality to 2008 times the second, we find that $2008 \cdot 2009 q+4017 \leq 2008 \cdot 2009 q+p$, or $p \geq 4017$. This minumum is attained when $\frac{p}{q}=\frac{4017}{4019}$.
|
| 117 |
+
17. [10] Determine the last two digits of $17^{17}$, written in base 10 .
|
| 118 |
+
|
| 119 |
+
Answer: 77 We are asked to find the remainder when $17^{17}$ is divided by 100 . Write the power as $(7+10)^{17}$ and expand with the binomial theorem:
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
(7+10)^{17}=7^{17}+17 \cdot 7^{16} \cdot 10+\ldots
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
We can ignore terms with more than one factor of 10 because these terms are divisible by 100 , so adding them does not change the last two digits. Now, $7^{4}=2401$, which has remainder $1 \bmod 100$, so $7^{17}$ has last two digits 07 and $7^{16} \cdot 10$ has last two digits 70 . We add these together.
|
| 126 |
+
18. [10] Find the coefficient of $x^{6}$ in the expansion of
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
(x+1)^{6} \cdot \sum_{i=0}^{6} x^{i}
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
Answer: 64 Each term of $(x+1)^{6}$ can be multiplied by a unique power $x^{i}, 0 \leq i \leq 6$ to get a sixth degree term. So the answer is the sum of the coefficients of the terms of $(x+1)^{6}$, which is the same as substituting $x=1$ into this power to get $2^{6}=64$.
|
| 133 |
+
|
| 134 |
+
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 135 |
+
|
| 136 |
+
19. [11] Let $P$ be a polynomial with $P(1)=P(2)=\cdots=P(2007)=0$ and $P(0)=2009$ !. $P(x)$ has leading coefficient 1 and degree 2008. Find the largest root of $P(x)$.
|
| 137 |
+
Answer: $4034072 P(0)$ is the constant term of $P(x)$, which is the product of all the roots of the polynomial, because its degree is even. So the product of all 2008 roots is 2009 ! and the product of the first 2007 is 2007!, which means the last root is $\frac{2009!}{2007!}=2009 \cdot 2008=4034072$.
|
| 138 |
+
20. [11] You have a die with faces labelled 1 through 6 . On each face, you draw an arrow to an adjacent face, such that if you start on a face and follow the arrows, after 6 steps you will have passed through every face once and will be back on your starting face. How many ways are there to draw the arrows so that this is true?
|
| 139 |
+
Answer: 32 There are 4 choices for where to go from face 1 . Consider the 4 faces adjacent to 1 . We can visit either 1,2 , or 3 of them before visiting the face opposite 1 . If we only visit one of these adjacent faces, we have 4 choices for which one, then we visit face 6 , opposite face 1 , then we visit the remaining 3 faces in one of two orders - for a total of 8 ways. If we visit 2 adjacent faces first, there is 8 choices for these two faces, then 2 choices for the path back from face 6 to face 1 . Lastly, there are 8 ways to visit three of the adjacent faces before visiting the opposite face. These choices give 32 total.
|
| 140 |
+
21. [11] Call a number overweight if it has at least three positive integer divisors (including 1 and the number), and call a number obese if it has at least four positive integer divisors (including 1 and the number). How many positive integers between 1 and 200 are overweight, but not obese?
|
| 141 |
+
Answer: 6 A positive integer is overweight, but not obese, if it has exactly 3 factors - this can only happen if that integer is the square of a prime. (If two primes, $p$ and $q$, divide the number, then $p, q$, $p q$, and 1 all divide it, making it at least obese). So, the integers less than 200 which are squares of a prime are the squares of $2,3,5,7,11$, and 13 .
|
| 142 |
+
|
| 143 |
+
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 144 |
+
|
| 145 |
+
22. [12] Sandra the Maverick has 5 pairs of shoes in a drawer, each pair a different color. Every day for 5 days, Sandra takes two shoes out and throws them out the window. If they are the same color, she treats herself to a practice problem from a past HMMT. What is the expected value (average number) of practice problems she gets to do?
|
| 146 |
+
Answer: $\quad \frac{5}{9}$ On any given day, there is a $\frac{1}{9}$ chance that the second shoe that Sandra chooses makes a pair with the first shoe she chose. Thus the average number of problems she does in a day is $\frac{1}{9}$, so, by the linearity of expectation, she does $\frac{5}{9}$ problems total, on average.
|
| 147 |
+
23. [12] If $x$ and $y$ are real numbers such that $\frac{(x-4)^{2}}{4}+\frac{y^{2}}{9}=1$, find the largest possible value of $\frac{x^{2}}{4}+\frac{y^{2}}{9}$.
|
| 148 |
+
|
| 149 |
+
Answer: 9 The first equation is an ellipse with major axis parallel to the y-axis. If the second expression is set equal to a certain value $c$, then it is also the equation of an ellipse with major axis parallel to the y-axis; further, it is similar to the first ellipse. So the largest value of $c$ occurs when both ellipse are tangent on the x-axis, at $x=6, y=0$, which gives 9 as the largest value of $c$.
|
| 150 |
+
24. [12] Let $f(x)=\frac{1}{1-x}$. Let $f^{k+1}(x)=f\left(f^{k}(x)\right)$, with $f^{1}(x)=f(x)$. What is $f^{2008}(2008)$ ?
|
| 151 |
+
|
| 152 |
+
Answer: $\frac{-1}{2007}$ Notice that, if $x \neq 0,1$, then $f^{2}(x)=\frac{1}{1-\frac{1}{1-x}}=\frac{x-1}{x}$, which means that $f^{3}(x)=$ $\frac{1}{1-\frac{x-1}{x}}=x$. So $f^{n}$ is periodic with period $n=3$, which means that $f^{2007}(x)=x$ so $f^{2008}(2008)=$ $f(2008)=\frac{-1}{2007}$.
|
| 153 |
+
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 154 |
+
25. [13] Evaluate the sum
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
\cos \left(\frac{2 \pi}{18}\right)+\cos \left(\frac{4 \pi}{18}\right)+\cdots+\cos \left(\frac{34 \pi}{18}\right)
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
Answer: -1 If $k<18$, then we can pair $\cos \left(\frac{k \pi}{18}\right)$ with $\cos \left(\frac{(18-k) \pi}{18}\right)$, and these two terms sum to 0 . If $k>18$, then the pair $\cos \left(\frac{k \pi}{18}\right)$ and $\cos \left(\frac{(36-k) \pi}{18}\right)$ also sums to 0 . So, the only term in this series that is left over is $\cos \left(\frac{18 \pi}{18}\right)=-1$.
|
| 161 |
+
26. [13] John M. is sitting at ( 0,0 ), looking across the aisle at his friends sitting at $(i, j)$ for each $1 \leq i \leq 10$ and $0 \leq j \leq 5$. Unfortunately, John can only see a friend if the line connecting them doesn't pass through any other friend. How many friends can John see?
|
| 162 |
+
Answer: 36 The simplest method is to draw a picture and count which friends he can see. John can see the friend on point $(i, j)$ if and only if $i$ and $j$ are relatively prime.
|
| 163 |
+
27. [13] $A B C D E$ is a regular pentagon inscribed in a circle of radius 1 . What is the area of the set of points inside the circle that are farther from $A$ than they are from any other vertex?
|
| 164 |
+
Answer: $\quad \frac{\pi}{5}$ Draw the perpendicular bisectors of all the sides and diagonals of the pentagon with one endpoint at $A$. These lines all intersect in the center of the circle, because they are the set of points equidistant from two points on the circle. Now, a given point is farther from $A$ than from point $X$ if it is on the $X$ side of the perpendicular bisector of segment $A X$. So, we want to find the area of the set of all points which are separated from $A$ by all of these perpendicular bisectors, which turns out to be a single $72^{\circ}$ sector of the circle, which has area $\frac{\pi}{5}$.
|
| 165 |
+
|
| 166 |
+
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 167 |
+
|
| 168 |
+
28. [14] Johnny the grad student is typing all the integers from 1 to $\infty$, in order. The 2 on his computer is broken however, so he just skips any number with a 2 . What's the 2008th number he types?
|
| 169 |
+
Answer: 3781 Write 2008 in base 9 as 2671, and interpret the result as a base 10 number such that the base 9 digits $2,3, \ldots 8$ correspond to the base 10 digits $3,4, \ldots 9$. This gives an answer of 3781 .
|
| 170 |
+
29. [14] Let $p(x)$ be the polynomial of degree 4 with roots $1,2,3,4$ and leading coefficient 1 . Let $q(x)$ be the polynomial of degree 4 with roots $1, \frac{1}{2}, \frac{1}{3}$, and $\frac{1}{4}$ and leading coefficient 1 . Find $\lim _{x \rightarrow 1} \frac{p(x)}{q(x)}$.
|
| 171 |
+
Answer: -24 Consider the polynomial $f(x)=x^{4} q\left(\frac{1}{1}\right)(x)$ - it has the same roots, 1, 2, 3, and 4, as $p(x)$. But this polynomial also has the same coefficients as $q(x)$, just in reverse order. Its leading coefficient is $q(0)=1 \cdot \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{4}=\frac{1}{24}$. So $f(x)$ is $p(x)$ scaled by $\frac{1}{24}$, which means that $p(x) / f(x)$ goes to 24 as $x$ goes to 1 , and $f(x) / q(x)$ goes to -1 .
|
| 172 |
+
30. [14] Alice has an equilateral triangle $A B C$ of area 1. Put $D$ on $B C, E$ on $C A$, and $F$ on $A B$, with $B D=D C, C E=2 E A$, and $2 A F=F B$. Note that $A D, B E$, and $C F$ pass through a single point $M$. What is the area of triangle $E M C$ ?
|
| 173 |
+
Answer: $\frac{1}{6}$ Triangles $A C F$ and $B C F$ share a height, so the ratio of their areas is $A F / B F=1 / 2$. By the same method, the ratio of the areas of $A M F$ and $B M F$ is $1 / 2$. So, the ratio of the areas of
|
| 174 |
+
$A C M$ and $B C M$ is also $1 / 2$. Similarly, the ratio of the areas of $A B M$ and $B C M$ is $1 / 2$. But the sum of the areas of $A C M, B C M$, and $A B M$ is 1 , so the area of $A C M$ is $\frac{1}{4}$. Then the area of $E M C$ is $2 / 3$ the area of $A C M$, because they share heights, so their areas are in the same ratio as their bases. The area of $E M C$ is then $\frac{2 \cdot 1}{3 \cdot 4}=\frac{1}{6}$.
|
| 175 |
+
|
| 176 |
+
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
| 177 |
+
|
| 178 |
+
31. [15] Find the sum of all primes $p$ for which there exists a prime $q$ such that $p^{2}+p q+q^{2}$ is a square.
|
| 179 |
+
|
| 180 |
+
Answer: 83 and 5 both work, because $3^{2}+3 \cdot 5+5^{2}=49$. Now, say $p^{2}+p q+q^{2}=k^{2}$, for a positive integer $k$. Then $(p+q)^{2}-k^{2}=p q$, or:
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
(p+q+k)(p+q-k)=p q
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
Since $p+q+k$ is a divisor of $p q$, and it is greater than $p$ and $q, p+q+k=p q$. Then $p+q-k=1$. So:
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
2 p+2 q=p q+1 \Leftrightarrow p q-2 p-2 q+4=3 \Leftrightarrow(p-2)(q-2)=3
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
This shows that one of $p$ and $q$ is 3 and the other is 5 .
|
| 193 |
+
32. [15] Pirate ships Somy and Lia are having a tough time. At the end of the year, they are both one pillage short of the minimum required for maintaining membership in the Pirate Guild, so they decide to pillage each other to bring their counts up. Somy by tradition only pillages $28 \cdot 3^{k}$ coins for integers $k$, and Lia by tradition only pillages $82 \cdot 3^{j}$ coins for integers $j$. Note that each pillage can have a different $k$ or $j$. Soma and Lia work out a system where Somy pillages Lia $n$ times, Lia pillages Somy $n$ times, and after both sets of pillages Somy and Lia are financially even.
|
| 194 |
+
What is the smallest $n$ can be?
|
| 195 |
+
Answer: 2 Clearly, $n=1$ cannot be acheived, because $28 \cdot 3^{k}$ is never a multiple of 82 . However, two pillages is enough: Somy pillages 28 and $28 \cdot 81$ from Lia, and Lia pillages 81 and $81 \cdot 27$ from Somy. As is easily checked, both pillage $28 \cdot 82$.
|
| 196 |
+
33. [15] The polynomial $a x^{2}-b x+c$ has two distinct roots $p$ and $q$, with $a, b$, and $c$ positive integers and with $0<p, q<1$. Find the minimum possible value of $a$.
|
| 197 |
+
Answer: 5 Let $x$ and $y$ be the roots. Then:
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
\begin{gathered}
|
| 201 |
+
\frac{b}{a}=x+y<2 \Rightarrow b<2 a \\
|
| 202 |
+
\frac{c}{a}=x y<1 \Rightarrow c<a \Rightarrow a>1 \\
|
| 203 |
+
b^{2}>4 a c>4 c^{2} \Rightarrow b>2 c
|
| 204 |
+
\end{gathered}
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
Evaluated at 1 , the polynomial must be greater than 0 , so $a+c>b$. Then:
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
\begin{gathered}
|
| 211 |
+
2 c<b<a+c \\
|
| 212 |
+
2 c+1 \leq b \leq a+c-1 \\
|
| 213 |
+
a \geq c+2 \geq 3
|
| 214 |
+
\end{gathered}
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
If $a=3$, then $c=1$ and $b=3$, by the above bounds, but this polynomial has complex roots. Similarly, if $a=4$, then $c=1$ and $b$ is forced to be either 3 or 4 , again giving either 0 or 1 distinct real roots. So $a \geq 5$. But the polynomial $5 x^{2}-5 x+1$ satisfies the condition, so 5 is the answer.
|
| 218 |
+
34. [20] How many hits did "math tournament" get on Google the morning of November 8, 2008? If you submit integer $N$, and the correct answer is $A$, you will receive $\left\lfloor 20 \cdot \min \left\{\frac{N}{A}, \frac{A}{N}\right\}\right\rfloor$ points for this problem.
|
| 219 |
+
35. [25] Find $\max \{\operatorname{Perimeter}(T)\}$ for $T$ a triangle contained in a regular septagon (7-sided figure) of unit edge length. Write your answer $N$ to 2 places after the decimal. If the correct answer rounded to 2 decimal places is $A$, you will receive 0 points if $N<A$ and $\lfloor\max \{0,25-50 \cdot(N-A)\}\rfloor$ points otherwise.
|
| 220 |
+
Answer: 5.85086 Let the septagon be $A_{0} A_{1} \ldots A_{6}$.
|
| 221 |
+
If $x$ is a point that can move along the x -axis, the distance from $x$ to a fixed point $p$ is a convex function in the x -coordinate. Therefore, the sum of the distances from $x$ to two other points is convex too, so if $x$ is constrained to lie on a closed line segment, its maximum value is attained at an endpoint. Therefore, the triangle of maximal perimeter has vertices at the vertices of the pentagon. The triangle with the largest such perimeter has almost evenly spaced vertices, so triangle $A_{0} A_{2} A_{4}$ has the maximal perimeter. It has area $5.85 \ldots$
|
| 222 |
+
36. [25] How many numbers less than $1,000,000$ are the product of exactly 2 distinct primes? You will receive $\left\lfloor 25-50 \cdot\left|\frac{N}{A}-1\right|\right\rfloor$ points, if you submit $N$ and the correct answer is $A$.
|
| 223 |
+
Answer: 209867 While it is difficult to compute this answer without writing a program or using a calculator, it can be approximated using the fact that the number of primes less than a positive integer $n$ is about $\frac{n}{\log n}$.
|
| 224 |
+
|
HarvardMIT/md/en-121-2008-nov-team-solutions.md
ADDED
|
@@ -0,0 +1,111 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $1^{\text {st }}$ Annual Harvard-MIT November Tournament <br> Saturday 8 November 2008
|
| 2 |
+
|
| 3 |
+
## Team Round
|
| 4 |
+
|
| 5 |
+
## Unit Fractions [100]
|
| 6 |
+
|
| 7 |
+
A unit fraction is a fraction of the form $\frac{1}{n}$, where $n$ is a positive integer. In this problem, you will find out how rational numbers can be expressed as sums of these unit fractions. Even if you do not solve a problem, you may apply its result to later problems.
|
| 8 |
+
|
| 9 |
+
We say we decompose a rational number $q$ into unit fractions if we write $q$ as a sum of 2 or more distinct unit fractions. In particular, if we write $q$ as a sum of $k$ distinct unit fractions, we say we have decomposed $q$ into $k$ fractions. As an example, we can decompose $\frac{2}{3}$ into 3 fractions: $\frac{2}{3}=\frac{1}{3}+\frac{1}{4}+\frac{1}{12}$.
|
| 10 |
+
|
| 11 |
+
1. (a) Decompose 1 into unit fractions.
|
| 12 |
+
|
| 13 |
+
Answer: $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$
|
| 14 |
+
(b) Decompose $\frac{1}{4}$ into unit fractions.
|
| 15 |
+
|
| 16 |
+
Answer: $\frac{1}{8}+\frac{1}{12}+\frac{1}{24}$
|
| 17 |
+
(c) Decompose $\frac{2}{5}$ into unit fractions.
|
| 18 |
+
|
| 19 |
+
Answer: $\frac{1}{5}+\frac{1}{10}+\frac{1}{15}+\frac{1}{30}$
|
| 20 |
+
2. Explain how any unit fraction $\frac{1}{n}$ can be decomposed into other unit fractions.
|
| 21 |
+
|
| 22 |
+
Answer: $\frac{1}{2 n}+\frac{1}{3 n}+\frac{1}{6 n}$
|
| 23 |
+
3. (a) Write 1 as a sum of 4 distinct unit fractions.
|
| 24 |
+
|
| 25 |
+
Answer: $\frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{42}$
|
| 26 |
+
(b) Write 1 as a sum of 5 distinct unit fractions.
|
| 27 |
+
|
| 28 |
+
Answer: $\frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{43}+\frac{1}{43 \cdot 42}$
|
| 29 |
+
(c) Show that, for any integer $k>3,1$ can be decomposed into $k$ unit fractions.
|
| 30 |
+
|
| 31 |
+
Solution: If we can do it for $k$ fractions, simply replace the last one (say $\frac{1}{n}$ ) with $\frac{1}{n+1}+\frac{1}{n(n+1)}$. Then we can do it for $k+1$ fractions. So, since we can do it for $k=3$, we can do it for any $k>3$.
|
| 32 |
+
4. Say that $\frac{a}{b}$ is a positive rational number in simplest form, with $a \neq 1$. Further, say that $n$ is an integer such that:
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
\frac{1}{n}>\frac{a}{b}>\frac{1}{n+1}
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
Show that when $\frac{a}{b}-\frac{1}{n+1}$ is written in simplest form, its numerator is smaller than $a$.
|
| 39 |
+
Solution: $\quad \frac{a}{b}-\frac{1}{n+1}=\frac{a(n+1)-b}{b(n+1)}$. Therefore, when we write it in simplest form, its numerator will be at most $a(n+1)-b$. We claim that $a(n+1)-b<a$. Indeed, this is the same as $a n-b<0 \Longleftrightarrow a n<b \Longleftrightarrow \frac{b}{a}>n$, which is given.
|
| 40 |
+
|
| 41 |
+
## 5. An aside: the sum of all the unit fractions
|
| 42 |
+
|
| 43 |
+
It is possible to show that, given any real M , there exists a positive integer $k$ large enough that:
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
\sum_{n=1}^{k} \frac{1}{n}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3} \ldots>M
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Note that this statement means that the infinite harmonic series, $\sum_{n=1}^{\infty} \frac{1}{n}$, grows without bound, or diverges. For the specific example $\mathrm{M}=5$, find a value of $k$, not necessarily the smallest, such that the inequality holds. Justify your answer.
|
| 50 |
+
|
| 51 |
+
Solution: Note that $\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{2 n}>\frac{1}{2 n}+\ldots+\frac{1}{2 n}=\frac{1}{2}$. Therefore, if we apply this to $n=1,2,4,8,16,32,64,128$, we get
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\left(\frac{1}{2}\right)+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)+\ldots+\left(\frac{1}{129}+\ldots+\frac{1}{256}\right)>\frac{1}{2}+\ldots+\frac{1}{2}=4
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
so, adding in $\frac{1}{1}$, we get
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\sum_{n=1}^{256} \frac{1}{n}>5
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
so $k=256$ will suffice.
|
| 64 |
+
6. Now, using information from problems 4 and 5 , prove that the following method to decompose any positive rational number will always terminate:
|
| 65 |
+
Step 1. Start with the fraction $\frac{a}{b}$. Let $t_{1}$ be the largest unit fraction $\frac{1}{n}$ which is less than or equal to $\frac{a}{b}$.
|
| 66 |
+
Step 2. If we have already chosen $t_{1}$ through $t_{k}$, and if $t_{1}+t_{2}+\ldots+t_{k}$ is still less than $\frac{a}{b}$, then let $t_{k+1}$ be the largest unit fraction less than both $t_{k}$ and $\frac{a}{b}$.
|
| 67 |
+
Step 3. If $t_{1}+\ldots+t_{k+1}$ equals $\frac{a}{b}$, the decomposition is found. Otherwise, repeat step 2 .
|
| 68 |
+
Why does this method never result in an infinite sequence of $t_{i}$ ?
|
| 69 |
+
Solution: Let $\frac{a_{k}}{b_{k}}=\frac{a}{b}-t_{1}-\ldots-t_{k}$, where $\frac{a_{k}}{b_{k}}$ is a fraction in simplest terms. Initially, this algorithm will have $t_{1}=1, t_{2}=\frac{1}{2}, t_{3}=\frac{1}{3}$, etc. until $\frac{a_{k}}{b_{k}}<\frac{1}{k+1}$. This will eventually happen by problem 5 , since there exists a $k$ such that $\frac{1}{1}+\ldots+\frac{1}{k+1}>\frac{a_{k}}{b_{k}}$. At that point, there is some $n$ with $\frac{1}{n}<t_{k}$ such that $\frac{1}{n}>\frac{a_{k}}{b_{k}}>\frac{1}{n+1}$. In this case, $t_{k+1}=\frac{1}{n+1}$.
|
| 70 |
+
Suppose that there exists $n_{k}$ such that $\frac{1}{n_{k}}>\frac{a_{k}}{b_{k}}>\frac{1}{n_{k}+1}$ for some $k$. Then we have $t_{k+1}=\frac{1}{n_{k}+1}$ and $\frac{a_{k+1}}{b_{k+1}}<\frac{1}{n_{k}\left(n_{k}+1\right)}$. This shows that once we have found $n_{k}$ such that $\frac{1}{n_{k}}>\frac{a_{k}}{b_{k}}>\frac{1}{n_{k}+1}$ and $\frac{1}{n_{k}} \leq t_{k}$, we no longer have to worry about $t_{k+1}$ being less than $t_{k}$, since $t_{k+1}=\frac{1}{n_{k}+1}<\frac{1}{n_{k}}<$ $t_{k}$, and also $n_{k+1} \geq n_{k}\left(n_{k}+1\right)$ while $\frac{1}{n_{k}\left(n_{k}+1\right)} \leq \frac{1}{n_{k}+1}=t_{k+1}$.
|
| 71 |
+
On the other hand, once we have found such an $n_{k}$, the sequence $\left\{a_{k}\right\}$ must be decreasing by problem 4. Since the $a_{k}$ are all integers, we eventually have to get to 0 (as there is no infinite decreasing sequence of positive integers). Therefore, after some finite number of steps the algorithm terminates with $a_{k+1}=0$, so $0=\frac{a_{k}}{b_{k}}=\frac{a}{b}-t_{1}-\ldots-t_{k}$, so $\frac{a}{b}=t_{1}+\ldots+t_{k}$, which is what we wanted.
|
| 72 |
+
|
| 73 |
+
## Juicy Numbers [100]
|
| 74 |
+
|
| 75 |
+
A juicy number is an integer $j>1$ for which there is a sequence $a_{1}<a_{2}<\ldots<a_{k}$ of positive integers such that $a_{k}=j$ and such that the sum of the reciprocals of all the $a_{i}$ is 1 . For example, 6 is a juicy number because $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$, but 2 is not juicy.
|
| 76 |
+
|
| 77 |
+
In this part, you will investigate some of the properties of juicy numbers. Remember that if you do not solve a question, you can still use its result on later questions.
|
| 78 |
+
|
| 79 |
+
1. Explain why 4 is not a juicy number.
|
| 80 |
+
|
| 81 |
+
Solution: If 4 were juicy, then we would have $1=\ldots+\frac{1}{4}$. The $\ldots$ can only possible contain $\frac{1}{2}$ and $\frac{1}{3}$, but it is clear that $\frac{1}{2}+\frac{1}{4}, \frac{1}{3}+\frac{1}{4}$, and $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ are all not equal to 1 .
|
| 82 |
+
2. It turns out that 6 is the smallest juicy integer. Find the next two smallest juicy numbers, and show a decomposition of 1 into unit fractions for each of these numbers. You do not need to prove that no smaller numbers are juicy.
|
| 83 |
+
Answer: 12 and $151=\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12}, 1=\frac{1}{2}+\frac{1}{3}+\frac{1}{10}+\frac{1}{15}$.
|
| 84 |
+
3. Let $p$ be a prime. Given a sequence of positive integers $b_{1}$ through $b_{n}$, exactly one of which is divisible by $p$, show that when
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\ldots+\frac{1}{b_{n}}
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
is written as a fraction in lowest terms, then its denominator is divisible by $p$. Use this fact to explain why no prime $p$ is ever juicy.
|
| 91 |
+
|
| 92 |
+
Solution: We can assume that $b_{n}$ is the term divisible by $p$ (i.e. $b_{n}=k p$ ) since the order of addition doesn't matter. We can then write
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\ldots+\frac{1}{b_{n-1}}=\frac{a}{b}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
where $b$ is not divisible by $p$ (since none of the $b_{i}$ are). But then $\frac{a}{b}+\frac{1}{k p}=\frac{k p a+b}{k p b}$. Since $b$ is not divisible by $p, k p a+b$ is not divisible by $p$, so we cannot remove the factor of $p$ from the denominator. In particular, $p$ cannot be juicy as 1 can be written as $\frac{1}{1}$, which has a denominator not divisible by $p$, whereas being juicy means we have a sum $\frac{1}{b_{1}}+\ldots+\frac{1}{b_{n}}=1$, where $b_{1}<b_{2}<\ldots<b_{n}=p$, and so in particular none of the $b_{i}$ with $i<n$ are divisible by p.
|
| 99 |
+
4. Show that if $j$ is a juicy integer, then $2 j$ is juicy as well.
|
| 100 |
+
|
| 101 |
+
Solution: Just replace $\frac{1}{b_{1}}+\ldots+\frac{1}{b_{n}}$ with $\frac{1}{2}+\frac{1}{2 b_{1}}+\frac{1}{2 b_{2}}+\ldots+\frac{1}{2 b_{n}}$. Since $n>1,2 b_{1}>2$.
|
| 102 |
+
5. Prove that the product of two juicy numbers (not necessarily distinct) is always a juicy number. Hint: if $j_{1}$ and $j_{2}$ are the two numbers, how can you change the decompositions of 1 ending in $\frac{1}{j_{1}}$ or $\frac{1}{j_{2}}$ to make them end in $\frac{1}{j_{1} j_{2}}$ ?
|
| 103 |
+
|
| 104 |
+
Solution: Let $1=\frac{1}{b_{1}}+\ldots+\frac{1}{b_{n}}=\frac{1}{c_{1}}+\ldots+\frac{1}{c_{m}}$, where $b_{n}=j_{1}$ and $c_{m}=j_{2}$. Then
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
1=\frac{1}{b_{1}}+\ldots+\frac{1}{b_{n-1}}+\left(\frac{1}{b_{n} c_{1}}+\frac{1}{b_{n} c_{2}}+\ldots+\frac{1}{b_{n} c_{m}}\right)
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
and so $j_{1} j_{2}$ is juicy.
|
| 111 |
+
|
HarvardMIT/md/en-122-2009-feb-alg-solutions.md
ADDED
|
@@ -0,0 +1,111 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Individual Round: Algebra Test
|
| 6 |
+
|
| 7 |
+
1. [3] If $a$ and $b$ are positive integers such that $a^{2}-b^{4}=2009$, find $a+b$.
|
| 8 |
+
|
| 9 |
+
Answer: 47
|
| 10 |
+
Solution: We can factor the equation as $\left(a-b^{2}\right)\left(a+b^{2}\right)=41 \cdot 49$, from which it is evident that $a=45$ and $b=2$ is a possible solution. By examining the factors of 2009 , one can see that there are no other solutions.
|
| 11 |
+
2. [3] Let $S$ be the sum of all the real coefficients of the expansion of $(1+i x)^{2009}$. What is $\log _{2}(S)$ ?
|
| 12 |
+
|
| 13 |
+
Answer: 1004
|
| 14 |
+
Solution: The sum of all the coefficients is $(1+i)^{2009}$, and the sum of the real coefficients is the real part of this, which is $\frac{1}{2}\left((1+i)^{2009}+(1-i)^{2009}\right)=2^{1004}$. Thus $\log _{2}(S)=1004$.
|
| 15 |
+
3. [4] If $\tan x+\tan y=4$ and $\cot x+\cot y=5$, compute $\tan (x+y)$.
|
| 16 |
+
|
| 17 |
+
Answer: 20
|
| 18 |
+
Solution: We have $\cot x+\cot y=\frac{\tan x+\tan y}{\tan x \tan y}$, so $\tan x \tan y=\frac{4}{5}$. Thus, by the tan sum formula, $\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=20$.
|
| 19 |
+
4. [4] Suppose $a, b$ and $c$ are integers such that the greatest common divisor of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x+1$ (in the ring of polynomials in $x$ with integer coefficients), and the least common multiple of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x^{3}-4 x^{2}+x+6$. Find $a+b+c$.
|
| 20 |
+
Answer: $\quad-6$
|
| 21 |
+
Solution: Since $x+1$ divides $x^{2}+a x+b$ and the constant term is $b$, we have $x^{2}+a x+b=(x+1)(x+b)$, and similarly $x^{2}+b x+c=(x+1)(x+c)$. Therefore, $a=b+1=c+2$. Furthermore, the least common multiple of the two polynomials is $(x+1)(x+b)(x+b-1)=x^{3}-4 x^{2}+x+6$, so $b=-2$. Thus $a=-1$ and $c=-3$, and $a+b+c=-6$.
|
| 22 |
+
5. [4] Let $a, b$, and $c$ be the 3 roots of $x^{3}-x+1=0$. Find $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}$.
|
| 23 |
+
|
| 24 |
+
Answer: $\quad-2$
|
| 25 |
+
Solution: We can substitute $x=y-1$ to obtain a polynomial having roots $a+1, b+1, c+1$, namely, $(y-1)^{3}-(y-1)+1=y^{3}-3 y^{2}+2 y+1$. The sum of the reciprocals of the roots of this polynomial is, by Viete's formulas, $\frac{2}{-1}=-2$.
|
| 26 |
+
6. [5] Let $x$ and $y$ be positive real numbers and $\theta$ an angle such that $\theta \neq \frac{\pi}{2} n$ for any integer $n$. Suppose
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
\frac{\sin \theta}{x}=\frac{\cos \theta}{y}
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
and
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
\frac{\cos ^{4} \theta}{x^{4}}+\frac{\sin ^{4} \theta}{y^{4}}=\frac{97 \sin 2 \theta}{x^{3} y+y^{3} x}
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
Compute $\frac{x}{y}+\frac{y}{x}$.
|
| 39 |
+
Answer: 4
|
| 40 |
+
Solution: From the first relation, there exists a real number $k$ such that $x=k \sin \theta$ and $y=k \cos \theta$. Then we have
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\frac{\cos ^{4} \theta}{\sin ^{4} \theta}+\frac{\sin ^{4} \theta}{\cos ^{4} \theta}=\frac{194 \sin \theta \cos \theta}{\sin \theta \cos \theta\left(\cos ^{2} \theta+\sin ^{2} \theta\right)}=194
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Notice that if $t=\frac{x}{y}+\frac{y}{x}$ then $\left(t^{2}-2\right)^{2}-2=\frac{\cos ^{4} \theta}{\sin ^{4} \theta}+\frac{\sin ^{4} \theta}{\cos ^{4} \theta}=194$ and so $t=4$.
|
| 47 |
+
7. [5] Simplify the product
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\prod_{m=1}^{100} \prod_{n=1}^{100} \frac{x^{n+m}+x^{n+m+2}+x^{2 n+1}+x^{2 m+1}}{x^{2 n}+2 x^{n+m}+x^{2 m}}
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
Express your answer in terms of $x$.
|
| 54 |
+
Answer: $x^{9900}\left(\frac{1+x^{100}}{2}\right)^{2}\left(\right.$ OR $\left.\frac{1}{4} x^{9900}+\frac{1}{2} x^{10000}+\frac{1}{4} x^{10100}\right)$
|
| 55 |
+
Solution: We notice that the numerator and denominator of each term factors, so the product is equal to
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\prod_{m=1}^{100} \prod_{n=1}^{100} \frac{\left(x^{m}+x^{n+1}\right)\left(x^{m+1}+x^{n}\right)}{\left(x^{m}+x^{n}\right)^{2}}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Each term of the numerator cancels with a term of the denominator except for those of the form $\left(x^{m}+x^{101}\right)$ and $\left(x^{101}+x^{n}\right)$ for $m, n=1, \ldots, 100$, and the terms in the denominator which remain are of the form $\left(x^{1}+x^{n}\right)$ and $\left(x^{1}+x^{m}\right)$ for $m, n=1, \ldots, 100$. Thus the product simplifies to
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\left(\prod_{m=1}^{100} \frac{x^{m}+x^{101}}{x^{1}+x^{m}}\right)^{2}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Reversing the order of the factors of the numerator, we find this is equal to
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\begin{aligned}
|
| 71 |
+
\left(\prod_{m=1}^{100} \frac{x^{101-m}+x^{101}}{x^{1}+x^{m}}\right)^{2} & =\left(\prod_{m=1}^{100} x^{100-m} \frac{x^{1}+x^{m+1}}{x^{1}+x^{m}}\right)^{2} \\
|
| 72 |
+
& =\left(\frac{x^{1}+x^{1} 01}{x^{1}+x^{1}} \prod_{m=1}^{100} x^{100-m}\right)^{2} \\
|
| 73 |
+
& =\left(x^{\frac{99 \cdot 100}{2}}\right)^{2}\left(\frac{1+x^{100}}{2}\right)^{2}
|
| 74 |
+
\end{aligned}
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
as desired.
|
| 78 |
+
8. [7] If $a, b, x$, and $y$ are real numbers such that $a x+b y=3, a x^{2}+b y^{2}=7, a x^{3}+b y^{3}=16$, and $a x^{4}+b y^{4}=42$, find $a x^{5}+b y^{5}$.
|
| 79 |
+
Answer: 20.
|
| 80 |
+
Solution: We have $a x^{3}+b y^{3}=16$, so $\left(a x^{3}+b y^{3}\right)(x+y)=16(x+y)$ and thus
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
a x^{4}+b y^{4}+x y\left(a x^{2}+b y^{2}\right)=16(x+y)
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
It follows that
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
42+7 x y=16(x+y)
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
From $a x^{2}+b y^{2}=7$, we have $\left(a x^{2}+b y^{2}\right)(x+y)=7(x+y)$ so $a x^{3}+b y^{3}+x y\left(a x^{2}+b y^{2}\right)=7(x+y)$. This simplifies to
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
16+3 x y=7(x+y)
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
We can now solve for $x+y$ and $x y$ from (1) and (2) to find $x+y=-14$ and $x y=-38$. Thus we have $\left(a x^{4}+b y^{4}\right)(x+y)=42(x+y)$, and so $a x^{5}+b y^{5}+x y\left(a x^{3}+b y^{3}\right)=42(x+y)$. Finally, it follows that $a x^{5}+b y^{5}=42(x+y)-16 x y=20$ as desired.
|
| 99 |
+
9. [7] Let $f(x)=x^{4}+14 x^{3}+52 x^{2}+56 x+16$. Let $z_{1}, z_{2}, z_{3}, z_{4}$ be the four roots of $f$. Find the smallest possible value of $\left|z_{a} z_{b}+z_{c} z_{d}\right|$ where $\{a, b, c, d\}=\{1,2,3,4\}$.
|
| 100 |
+
Answer: 8
|
| 101 |
+
Solution: Note that $\frac{1}{16} f(2 x)=x^{4}+7 x^{3}+13 x^{2}+7 x+1$. Because the coefficients of this polynomial are symmetric, if $r$ is a root of $f(x)$ then $\frac{4}{r}$ is as well. Further, $f(-1)=-1$ and $f(-2)=16$ so $f(x)$ has two distinct roots on $(-2,0)$ and two more roots on $(-\infty,-2)$. Now, if $\sigma$ is a permutation of $\{1,2,3,4\}$ :
|
| 102 |
+
$\left|z_{\sigma(1)} z_{\sigma(2)}+z_{\sigma(3)} z_{\sigma(4)}\right| \leq \frac{1}{2}\left(z_{\sigma(1)} z_{\sigma(2)}+z_{\sigma(3)} z_{\sigma(4)}+z_{\sigma(4)} z_{\sigma(3)}+z_{\sigma(2)} z_{\sigma(1)}\right)$
|
| 103 |
+
Let the roots be ordered $z_{1} \leq z_{2} \leq z_{3} \leq z_{4}$, then by rearrangement the last expression is at least:
|
| 104 |
+
$\frac{1}{2}\left(z_{1} z_{4}+z_{2} z_{3}+z_{3} z_{2}+z_{4} z_{1}\right)$
|
| 105 |
+
Since the roots come in pairs $z_{1} z_{4}=z_{2} z_{3}=4$, our expression is minimized when $\sigma(1)=1, \sigma(2)=$ $4, \sigma(3)=3, \sigma(4)=2$ and its minimum value is 8 .
|
| 106 |
+
10. [8] Let $f(x)=2 x^{3}-2 x$. For what positive values of $a$ do there exist distinct $b, c, d$ such that $(a, f(a))$, $(b, f(b)),(c, f(c)),(d, f(d))$ is a rectangle?
|
| 107 |
+
Answer: $\left[\frac{\sqrt{3}}{3}, 1\right]$
|
| 108 |
+
Solution: Say we have four points $(a, f(a)),(b, f(b)),(c, f(c)),(d, f(d))$ on the curve which form a rectangle. If we interpolate a cubic through these points, that cubic will be symmetric around the center of the rectangle. But the unique cubic through the four points is $f(x)$, and $f(x)$ has only one point of symmetry, the point $(0,0)$.
|
| 109 |
+
So every rectangle with all four points on $f(x)$ is of the form $(a, f(a)),(b, f(b)),(-a, f(-a)),(-b, f(-b))$, and without loss of generality we let $a, b>0$. Then for any choice of $a$ and $b$ these points form a parallelogram, which is a rectangle if and only if the distance from $(a, f(a))$ to $(0,0)$ is equal to the distance from $(b, f(b))$ to $(0,0)$. Let $g(x)=x^{2}+(f(x))^{2}=4 x^{6}-8 x^{4}+5 x^{2}$, and consider $g(x)$ restricted to $x \geq 0$. We are looking for all the values of $a$ such that $g(x)=g(a)$ has solutions other than $a$.
|
| 110 |
+
Note that $g(x)=h\left(x^{2}\right)$ where $h(x)=4 x^{3}-8 x^{2}+5 x$. This polynomial $h(x)$ has a relative maximum of 1 at $x=\frac{1}{2}$ and a relative minimum of $25 / 27$ at $x=\frac{5}{6}$. Thus the polynomial $h(x)-h(1 / 2)$ has the double root $1 / 2$ and factors as $\left(4 x^{2}-4 x+1\right)(x-1)$, the largest possible value of $a^{2}$ for which $h\left(x^{2}\right)=h\left(a^{2}\right)$ is $a^{2}=1$, or $a=1$. The smallest such value is that which evaluates to $25 / 27$ other than $5 / 6$, which is similarly found to be $a^{2}=1 / 3$, or $a=\frac{\sqrt{3}}{3}$. Thus, for $a$ in the range $\frac{\sqrt{3}}{3} \leq a \leq 1$ the equation $g(x)=g(a)$ has nontrivial solutions and hence an inscribed rectangle exists.
|
| 111 |
+
|
HarvardMIT/md/en-122-2009-feb-calc-solutions.md
ADDED
|
@@ -0,0 +1,135 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Individual Round: Calculus Test Solutions
|
| 6 |
+
|
| 7 |
+
1. [3] Let $f$ be a differentiable real-valued function defined on the positive real numbers. The tangent lines to the graph of $f$ always meet the $y$-axis 1 unit lower than where they meet the function. If $f(1)=0$, what is $f(2)$ ?
|
| 8 |
+
Answer: $\ln 2$
|
| 9 |
+
Solution: The tangent line to $f$ at $x$ meets the $y$-axis at $f(x)-1$ for any $x$, so the slope of the tangent line is $f^{\prime}(x)=\frac{1}{x}$, and so $f(x)=\ln (x)+C$ for some $a$. Since $f(1)=0$, we have $C=0$, and so $f(x)=\ln (x)$. Thus $f(2)=\ln (2)$.
|
| 10 |
+
2. [3] The differentiable function $F: \mathbb{R} \rightarrow \mathbb{R}$ satisfies $F(0)=-1$ and
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
\frac{d}{d x} F(x)=\sin (\sin (\sin (\sin (x)))) \cdot \cos (\sin (\sin (x))) \cdot \cos (\sin (x)) \cdot \cos (x)
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
Find $F(x)$ as a function of $x$.
|
| 17 |
+
Answer: $-\cos (\sin (\sin (\sin (x))))$
|
| 18 |
+
Solution: $\quad$ Substituting $u=\sin (\sin (\sin (x)))$, we find
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
F(x)=\int \sin (u) d u=-\cos (u)+C
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
for some $C$. Since $F(0)=1$ we find $C=0$.
|
| 25 |
+
3. [4] Compute $e^{A}$ where $A$ is defined as
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
\int_{3 / 4}^{4 / 3} \frac{2 x^{2}+x+1}{x^{3}+x^{2}+x+1} d x
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Answer: $\frac{16}{9}$
|
| 32 |
+
Solution: We can use partial fractions to decompose the integrand to $\frac{1}{x+1}+\frac{x}{x^{2}+1}$, and then integrate the addends separately by substituting $u=x+1$ for the former and $u=x^{2}+1$ for latter, to obtain $\ln (x+1)+\left.\frac{1}{2} \ln \left(x^{2}+1\right)\right|_{3 / 4} ^{4 / 3}=\left.\ln \left((x+1) \sqrt{x^{2}+1}\right)\right|_{3 / 4} ^{4 / 3}=\ln \frac{16}{9}$. Thus $e^{A}=16 / 9$.
|
| 33 |
+
Alternate solution: Substituting $u=1 / x$, we find
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
A=\int_{4 / 3}^{3 / 4} \frac{2 u+u^{2}+u^{3}}{1+u+u^{2}+u^{3}}\left(-\frac{1}{u^{2}}\right) d u=\int_{3 / 4}^{4 / 3} \frac{2 / u+1+u}{1+u+u^{2}+u^{3}} d u
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
Adding this to the original integral, we find
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
2 A=\int_{3 / 4}^{4 / 3} \frac{2 / u+2+2 u+2 u^{2}}{1+u+u^{2}+u^{3}} d u=\int_{3 / 4}^{4 / 3} \frac{2}{u} d u
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Thus $A=\ln \frac{16}{9}$ and $e^{A}=\frac{16}{9}$.
|
| 46 |
+
4. [4] Let $P$ be a fourth degree polynomial, with derivative $P^{\prime}$, such that $P(1)=P(3)=P(5)=P^{\prime}(7)=0$. Find the real number $x \neq 1,3,5$ such that $P(x)=0$.
|
| 47 |
+
Answer: $\frac{89}{11}$
|
| 48 |
+
Solution: Observe that 7 is not a root of $P$. If $r_{1}, r_{2}, r_{3}, r_{4}$ are the roots of $P$, then $\frac{P^{\prime}(7)}{P(7)}=$ $\sum_{i} \frac{1}{7-r_{i}}=0$. Thus $r_{4}=7-\left(\sum_{i \neq 4} \frac{1}{7-r_{i}}\right)^{-1}=7+\left(\frac{1}{6}+\frac{1}{4}+\frac{1}{2}\right)^{-1}=7+12 / 11=89 / 11$.
|
| 49 |
+
5. [4] Compute
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\lim _{h \rightarrow 0} \frac{\sin \left(\frac{\pi}{3}+4 h\right)-4 \sin \left(\frac{\pi}{3}+3 h\right)+6 \sin \left(\frac{\pi}{3}+2 h\right)-4 \sin \left(\frac{\pi}{3}+h\right)+\sin \left(\frac{\pi}{3}\right)}{h^{4}}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Answer: $\frac{\sqrt{3}}{2}$
|
| 56 |
+
Solution: The derivative of a function is defined as $f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$. Iterating this formula four times yields
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
f^{(4)}(x)=\lim _{h \rightarrow 0} \frac{f(x+4 h)-4 f(x+3 h)+6 f(x+2 h)-4 f(x+h)+f(x)}{h^{4}} .
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
Substituting $f=\sin$ and $x=\pi / 3$, the expression is equal to $\sin ^{(4)}(\pi / 3)=\sin (\pi / 3)=\frac{\sqrt{3}}{2}$.
|
| 63 |
+
6. [5] Let $p_{0}(x), p_{1}(x), p_{2}(x), \ldots$ be polynomials such that $p_{0}(x)=x$ and for all positive integers $n$, $\frac{d}{d x} p_{n}(x)=p_{n-1}(x)$. Define the function $p(x):[0, \infty) \rightarrow \mathbb{R} x$ by $p(x)=p_{n}(x)$ for all $x \in[n, n+1]$. Given that $p(x)$ is continuous on $[0, \infty)$, compute
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\sum_{n=0}^{\infty} p_{n}(2009)
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Answer: $e^{2010}-e^{2009}-1$
|
| 70 |
+
Solution: By writing out the first few polynomials, one can guess and then show by induction that $p_{n}(x)=\frac{1}{(n+1)!}(x+1)^{n+1}-\frac{1}{n!} x^{n}$. Thus the sum evaluates to $e^{2010}-e^{2009}-1$ by the series expansion of $e^{x}$.
|
| 71 |
+
7. [5] A line in the plane is called strange if it passes through $(a, 0)$ and $(0,10-a)$ for some $a$ in the interval $[0,10]$. A point in the plane is called charming if it lies in the first quadrant and also lies below some strange line. What is the area of the set of all charming points?
|
| 72 |
+
Answer: $50 / 3$
|
| 73 |
+
Solution: The strange lines form an envelope (set of tangent lines) of a curve $f(x)$, and we first find the equation for $f$ on $[0,10]$. Assuming the derivative $f^{\prime}$ is continuous, the point of tangency of the line $\ell$ through $(a, 0)$ and $(0, b)$ to $f$ is the limit of the intersection points of this line with the lines $\ell_{\epsilon}$ passing through $(a+\epsilon, 0)$ and $(0, b-\epsilon)$ as $\epsilon \rightarrow 0$. If these limits exist, then the derivative is indeed continuous and we can calculate the function from the points of tangency.
|
| 74 |
+
The intersection point of $\ell$ and $\ell_{\epsilon}$ can be calculated to have $x$-coordinate $\frac{a(a-\epsilon)}{a+b}$, so the tangent point of $\ell$ has $x$-coordinate $\lim _{\epsilon \rightarrow 0} \frac{a(a-\epsilon)}{a+b}=\frac{a^{2}}{a+b}=\frac{a^{2}}{10}$. Similarly, the $y$-coordinate is $\frac{b^{2}}{10}=\frac{(10-a)^{2}}{10}$. Thus,
|
| 75 |
+
solving for the $y$ coordinate in terms of the $x$ coordinate for $a \in[0,10]$, we find $f(x)=10-2 \sqrt{10} \sqrt{x}+x$, and so the area of the set of charming points is
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
\int_{0}^{10}(10-2 \sqrt{10} \sqrt{x}+x) d x=50 / 3
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
8. [7] Compute
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\int_{1}^{\sqrt{3}} x^{2 x^{2}+1}+\ln \left(x^{2 x^{2 x^{2}+1}}\right) d x
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Answer: 13
|
| 88 |
+
Solution: Using the fact that $x=e^{\ln (x)}$, we evaluate the integral as follows:
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
\begin{aligned}
|
| 92 |
+
\int x^{2 x^{2}+1}+\ln \left(x^{2 x^{2 x^{2}+1}}\right) d x & =\int x^{2 x^{2}+1}+x^{2 x^{2}+1} \ln \left(x^{2}\right) d x \\
|
| 93 |
+
& =\int e^{\ln (x)\left(2 x^{2}+1\right)}\left(1+\ln \left(x^{2}\right)\right) d x \\
|
| 94 |
+
& =\int x e^{x^{2} \ln \left(x^{2}\right)}\left(1+\ln \left(x^{2}\right)\right) d x
|
| 95 |
+
\end{aligned}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
Noticing that the derivative of $x^{2} \ln \left(x^{2}\right)$ is $2 x\left(1+\ln \left(x^{2}\right)\right)$, it follows that the integral evaluates to
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\frac{1}{2} e^{x^{2} \ln \left(x^{2}\right)}=\frac{1}{2} x^{2 x^{2}}
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Evaluating this from 1 to $\sqrt{3}$ we obtain the answer.
|
| 105 |
+
9. [7] let $\mathcal{R}$ be the region in the plane bounded by the graphs of $y=x$ and $y=x^{2}$. Compute the volume of the region formed by revolving $\mathcal{R}$ around the line $y=x$.
|
| 106 |
+
|
| 107 |
+
Answer: $\square$
|
| 108 |
+
Solution: We integrate from 0 to 1 using the method of washers. Fix $d$ between 0 and 1. Let the line $x=d$ intersect the graph of $y=x^{2}$ at $Q$, and let the line $x=d$ intersect the graph of $y=x$ at $P$. Then $P=(d, d)$, and $Q=\left(d, d^{2}\right)$. Now drop a perpendicular from $Q$ to the line $y=x$, and let $R$ be the foot of this perpendicular. Because $P Q R$ is a $45-45-90$ triangle, $Q R=\left(d-d^{2}\right) / \sqrt{2}$. So the differential washer has a radius of $\left(d-d^{2}\right) / \sqrt{2}$ and a height of $\sqrt{2} d x$. So we integrate (from 0 to 1 ) the expression $\left[\left(x-x^{2}\right) / \sqrt{2}\right]^{2} \sqrt{2} d x$, and the answer follows.
|
| 109 |
+
10. [8] Let $a$ and $b$ be real numbers satisfying $a>b>0$. Evaluate
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\int_{0}^{2 \pi} \frac{1}{a+b \cos (\theta)} d \theta
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Express your answer in terms of $a$ and $b$.
|
| 116 |
+
Answer: $\frac{2 \pi}{\sqrt{a^{2}-b^{2}}}$
|
| 117 |
+
|
| 118 |
+
Solution: Using the geometric series formula, we can expand the integral as follows:
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
\begin{aligned}
|
| 122 |
+
\int_{0}^{2 \pi} \frac{1}{a+b \cos (\theta)} d \theta & =\frac{1}{a} \int_{0}^{2 \pi} 1+\frac{b}{a} \cos (\theta)+\left(\frac{b}{a}\right)^{2} \cos ^{2}(\theta) d \theta \\
|
| 123 |
+
& =\frac{1}{a} \sum_{n=0}^{\infty} \int_{0}^{2 \pi}\left(\frac{b}{a}\right)^{n}\left(\frac{e^{i \theta}+e^{-i \theta}}{2}\right)^{n} d \theta \\
|
| 124 |
+
& =\frac{2 \pi}{a} \sum_{n=0}^{\infty}\left(\frac{b^{2}}{a^{2}}\right)^{n} \frac{\binom{2 n}{n}}{2^{2 n}} d \theta
|
| 125 |
+
\end{aligned}
|
| 126 |
+
$$
|
| 127 |
+
|
| 128 |
+
To evaluate this sum, recall that $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$ is the $n$th Catalan number. The generating function for the Catalan numbers is
|
| 129 |
+
|
| 130 |
+
$$
|
| 131 |
+
\sum_{n=0}^{\infty} C_{n} x^{n}=\frac{1-\sqrt{1-4 x}}{2 x}
|
| 132 |
+
$$
|
| 133 |
+
|
| 134 |
+
and taking the derivative of $x$ times this generating function yields $\sum\binom{2 n}{n} x^{n}=\frac{1}{\sqrt{1-4 x}}$. Thus the integral evaluates to $\frac{2 \pi}{\sqrt{a^{2}-b^{2}}}$, as desired.
|
| 135 |
+
|
HarvardMIT/md/en-122-2009-feb-comb-solutions.md
ADDED
|
@@ -0,0 +1,77 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
Individual Round: Combinatorics Test
|
| 6 |
+
|
| 7 |
+
1. [3] How many ways can the integers from -7 to 7 be arranged in a sequence such that the absolute value of the numbers in the sequence is nondecreasing?
|
| 8 |
+
Answer: 128
|
| 9 |
+
Solution: Each of the pairs $a,-a$ must occur in increasing order of $a$ for $a=1, \ldots, 7$, but $a$ can either occur before or after $-a$, for a total of $2^{7}=128$ possible sequences.
|
| 10 |
+
2. [3] Two jokers are added to a 52 card deck and the entire stack of 54 cards is shuffled randomly. What is the expected number of cards that will be between the two jokers?
|
| 11 |
+
Answer: $52 / 3$
|
| 12 |
+
Solution: Each card has an equal likelihood of being either on top of the jokers, in between them, or below the jokers. Thus, on average, $1 / 3$ of them will land between the two jokers.
|
| 13 |
+
3. [4] In how many ways can you rearrange the letters of "HMMTHMMT" such that the consecutive substring "HMMT" does not appear?
|
| 14 |
+
Answer: 361
|
| 15 |
+
Solution: There are $8!/(4!2!2!)=420$ ways to order the letters. If the permuted letters contain "HMMT", there are $5 \cdot 4!/ 2!=60$ ways to order the other letters, so we subtract these. However, we have subtracted "HMMTHMMT" twice, so we add it back once to obtain 361 possibilities.
|
| 16 |
+
4. [4] How many functions $f:\{1,2,3,4,5\} \rightarrow\{1,2,3,4,5\}$ satisfy $f(f(x))=f(x)$ for all $x \in\{1,2,3,4,5\}$ ?
|
| 17 |
+
|
| 18 |
+
Answer: 196
|
| 19 |
+
Solution: A fixed point of a function $f$ is an element $a$ such that $f(a)=a$. The condition is equivalent to the property that $f$ maps every number to a fixed point. Counting by the number of fixed points of $f$, the total number of such functions is
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
\begin{aligned}
|
| 23 |
+
\sum_{k=1}^{5}\binom{5}{k} k^{5-k} & =1 \cdot\left(5^{0}\right)+5 \cdot\left(1^{4}+4^{1}\right)+10 \cdot\left(2^{3}+3^{2}\right) \\
|
| 24 |
+
& =1+25+10 \cdot 17 \\
|
| 25 |
+
& =196
|
| 26 |
+
\end{aligned}
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
5. [4] Let $s(n)$ denote the number of 1's in the binary representation of $n$. Compute
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\frac{1}{255} \sum_{0 \leq n<16} 2^{n}(-1)^{s(n)}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
Answer: 45
|
| 36 |
+
Solution: Notice that if $n<8,(-1)^{s(n)}=(-1) \cdot(-1)^{s(n+8)}$ so the sum becomes $\frac{1}{255}\left(1-2^{8}\right) \sum_{0 \leq n<8} 2^{n}(-1)^{s(n)}=$ 45.
|
| 37 |
+
6. [5] How many sequences of 5 positive integers $(a, b, c, d, e)$ satisfy $a b c d e \leq a+b+c+d+e \leq 10$ ?
|
| 38 |
+
|
| 39 |
+
Answer: 116
|
| 40 |
+
Solution: We count based on how many 1's the sequence contains. If $a=b=c=d=e=1$ then this gives us 1 possibility. If $a=b=c=d=1$ and $e \neq 1$, $e$ can be $2,3,4,5,6$. Each such sequence $(1,1,1,1, e)$ can be arranged in 5 different ways, for a total of $5 \cdot 5=25$ ways in this case.
|
| 41 |
+
If three of the numbers are 1 , the last two can be $(2,2),(3,3),(2,3),(2,4)$, or $(2,5)$. Counting ordering, this gives a total of $2 \cdot 10+3 \cdot 20=80$ possibilities.
|
| 42 |
+
|
| 43 |
+
If two of the numbers are 1 , the other three must be equal to 2 for the product to be under 10 , and this yields 10 more possibilities.
|
| 44 |
+
Thus there are $1+25+80+10=116$ such sequences.
|
| 45 |
+
7. [7] Paul fills in a $7 \times 7$ grid with the numbers 1 through 49 in a random arrangement. He then erases his work and does the same thing again (to obtain two different random arrangements of the numbers in the grid). What is the expected number of pairs of numbers that occur in either the same row as each other or the same column as each other in both of the two arrangements?
|
| 46 |
+
Answer: $147 / 2$
|
| 47 |
+
Solution: Each of the $\binom{49}{2}$ pairs of numbers has a probability of $\frac{14 \cdot\binom{7}{2}}{\binom{49}{2}}=1 / 4$ of being in the same row or column in one of the arrangements, so the expected number that are in the same row or column in both arrangements is
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\binom{49}{2} \cdot(1 / 4)^{2}=\frac{147}{2}
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
8. [7] There are 5 students on a team for a math competition. The math competition has 5 subject tests. Each student on the team must choose 2 distinct tests, and each test must be taken by exactly two people. In how many ways can this be done?
|
| 54 |
+
Answer: 2040
|
| 55 |
+
Solution: We can model the situation as a bipartite graph on 10 vertices, with 5 nodes representing the students and the other 5 representing the tests. We now simply want to count the number of bipartite graphs on these two sets such that there are two edges incident on each vertex.
|
| 56 |
+
Notice that in such a graph, we can start at any vertex and follow one of the edges eminating from it, then follow the other edge eminating from the second vertex, etc, and in this manner we must eventually end up back at the starting vertex, so the graph is partitioned into even cycles. Since each vertex has degree two, we cannot have a 2 -cycle, so we must have either a 10 -cycle or a 4 -cycle and a 6 -cycle.
|
| 57 |
+
In the former case, starting with Person $A$, there are 5 ways to choose one of his tests. This test can be taken by one of 4 other people, who can take one of 4 other tests, which can be taken by one of 3 other people, etc, so the number of 10 -cycles we obtain in this way is $5!\cdot 4!$. However, it does not matter which of the first person's tests we choose first in a given 10 -cycle, so we overcounted by a factor of 2 . Thus there are $5!\cdot 4!/ 2=1440$ possibilities in this case.
|
| 58 |
+
In the latter case, there are $\binom{5}{3}^{2}=100$ ways to choose which three people and which three tests are in the 6 -cycle. After choosing this, a similar argument to that above shows there are $2!\cdot 1!/ 2$ possible 4 -cycles and $3!\cdot 2!/ 2$ possible 6 -cycles, for a total of $100 \cdot 1 \cdot 6=600$ possibilities in this case.
|
| 59 |
+
Thus there are a total of 2040 ways they can take the tests.
|
| 60 |
+
9. [5] The squares of a $3 \times 3$ grid are filled with positive integers such that 1 is the label of the upperleftmost square, 2009 is the label of the lower-rightmost square, and the label of each square divides the one directly to the right of it and the one directly below it. How many such labelings are possible?
|
| 61 |
+
Answer: 2448
|
| 62 |
+
Solution: We factor 2009 as $7^{2} \cdot 41$ and place the 41 's and the 7 's in the squares separately. The number of ways to fill the grid with 1 's and 41 's so that the divisibility property is satisfied is equal to the number of nondecreasing sequences $a_{1}, a_{2}, a_{3}$ where each $a_{i} \in\{0,1,2,3\}$ and the sequence is not $0,0,0$ and not $1,1,1$ (here $a_{i}$ corresponds to the number of 41 's in the $i$ th column.) Thus there are $\binom{3+4-1}{3}-2=18$ ways to choose which squares are divisible by 41 .
|
| 63 |
+
To count the arrangements of divisibility by 7 and 49 , we consider three cases.
|
| 64 |
+
If 49 divides the middle square, then each of the squares to the right and below it are divisible 49. The two squares in the top row (besides the upper left) can be $(1,1),(1,7),(1,49),(7,7),(7,49)$, or $(49,49)$ (in terms of the highest power of 7 dividing the square). The same is true, independently, for the two blank squares on the left column, for a total of $6^{2}=36$ possibilities in this case.
|
| 65 |
+
If 1 is the highest power of 7 dividing the middle square, there are also 36 possibilities by a similar argument.
|
| 66 |
+
If 7 is the highest power of 7 dividing the middle square, there are 8 possibilities for the upper right three squares. Thus there are 64 possibilities in this case.
|
| 67 |
+
Thus there are a total of 136 options for the divisibility of each number by 7 and $7^{2}$, and 18 options for the divisibility of the numbers by 41 . Since each number divides 2009 , this uniquely determines the numbers, and so there are a total of $18 \cdot 136=2448$ possibilities.
|
| 68 |
+
10. [8] Given a rearrangement of the numbers from 1 to $n$, each pair of consecutive elements $a$ and $b$ of the sequence can be either increasing (if $a<b$ ) or decreasing (if $b<a$ ). How many rearrangements of the numbers from 1 to $n$ have exactly two increasing pairs of consecutive elements?
|
| 69 |
+
Answer: $3^{n}-(n+1) \cdot 2^{n}+n(n+1) / 2$ or equivalent
|
| 70 |
+
Solution: Notice that each such permutation consists of 3 disjoint subsets of $\{1, \ldots, n\}$ whose union is $\{1, \ldots, n\}$, each arranged in decreasing order. For instance, if $n=6$, in the permutation 415326 (which has the two increasing pairs 15 and 26), the three sets are $\{4,1\},\{5,3,2\}$, and 6 . There are $3^{n}$ ways to choose which of the first, second, or third set each element is in. However, we have overcounted: some choices of these subsets result in permutations with 1 or 0 increasing pairs, such as $\{6,5,4\},\{3,2\},\{1\}$.
|
| 71 |
+
Thus, we must subtract the number of ordered partitions of $\{1,2, \ldots, n\}$ into 3 subsets for which the minimum value of the first is not less than the maximum of the second, or the minimum value of the second is not less than the maximum of the third.
|
| 72 |
+
We first prove that the number of permutations having exactly one increasing consecutive pair of elements is $2^{n}-(n+1)$. To do so, note that there are $2^{n}$ ways to choose which elements occur before the increasing pair, and upon choosing this set we must arrange them in decreasing order, followed by the remaining elements arranged in decreasing order. The resulting permutation will have either one increasing pair or none. There are exactly $n+1$ subsets for which the resulting permutation has none, namely, $\},\{n\},\{n, n-1\},\{n, n-1, n-2\}$, etc. Thus the total number of permutations having one increasing pair is $2^{n}-(n+1)$ as desired.
|
| 73 |
+
We now count the partitions of $\{1,2, \ldots, n\}$ whose associated permutation has exactly one increasing pair. For each of the $2^{n}-(n+1)$ permutations $p$ having exacly one increasing pair, there are $n+1$ partitions of $\{1,2, \ldots, n\}$ into 3 subsets whose associated permutation is $p$. This is because there are $n+1$ ways to choose the "breaking point" to split one of the subsets into two. Thus there are a total of $(n+1)\left(2^{n}-(n+1)\right)$ partitions whose associaated permutation has exactly one increasing pair.
|
| 74 |
+
Finally, we must count the number of partitions whose associated permutation is $n, n-1, \ldots, 3,2,1$, i.e. has no increasing pair. There are $\frac{n+2}{2}$ ways of placing two barriers between these elements to split the numbers into three subsets, and so there are $\frac{n+2}{2}$ such partitions of $\{1,2, \ldots, n\}$ into three subsets.
|
| 75 |
+
|
| 76 |
+
Thus, subtracting off the partitions we did not want to count, the answer is $3^{n}-(n+1)\left(2^{n}-(n+\right.$ 1) $)-\binom{n+2}{2}=3^{n}-(n+1) \cdot 2^{n}+n(n+1) / 2$.
|
| 77 |
+
|
HarvardMIT/md/en-122-2009-feb-gen1-solutions.md
ADDED
|
@@ -0,0 +1,87 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Individual Round: General Test, Part 1
|
| 6 |
+
|
| 7 |
+
1. [2] If $a$ and $b$ are positive integers such that $a^{2}-b^{4}=2009$, find $a+b$.
|
| 8 |
+
|
| 9 |
+
Answer: 47
|
| 10 |
+
Solution: We can factor the equation as $\left(a-b^{2}\right)\left(a+b^{2}\right)=41 \cdot 49$, from which it is evident that $a=45$ and $b=2$ is a possible solution. By examining the factors of 2009 , one can see that there are no other solutions.
|
| 11 |
+
2. [2] Suppose $N$ is a 6-digit number having base-10 representation $\underline{a} \underline{b} \underline{c} \underline{d} \underline{e} \underline{f}$. If $N$ is $6 / 7$ of the number having base-10 representation $\underline{d} \underline{e} \underline{f} \underline{a} \underline{b} \underline{c}$, find $N$.
|
| 12 |
+
Answer: 461538
|
| 13 |
+
Solution: We have $7(a b c d e f)_{10}=6(\text { defabc })_{10}$, so $699400 a+69940 b+6994 c=599300 d+59930 e+$ $5993 f$. We can factor this equation as $6994(100 a+10 b+c)=5993(100 d+10 e+f)$, which yields $538(a b c)_{10}=461(d e f)_{10}$. Since $\operatorname{gcd}(538,461)=1$, we must have $(a b c)_{10}=461$ and $(d e f)_{10}=538$.
|
| 14 |
+
3. [3] A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
Answer: $55 / 2$
|
| 18 |
+
Solution: Drawing the perpendiculars from the point of intersection of the corners to the bases of the trapezoid, we see that we have similar $3-4-5$ right triangles, and we can calculate that the length of the smaller base is 3 . Thus the area of the trapezoid is $\frac{8+3}{2} \cdot 5=55 / 2$.
|
| 19 |
+
4. [3] If $\tan x+\tan y=4$ and $\cot x+\cot y=5$, compute $\tan (x+y)$.
|
| 20 |
+
|
| 21 |
+
Answer: 20
|
| 22 |
+
Solution: We have $\cot x+\cot y=\frac{\tan x+\tan y}{\tan x \tan y}$, so $\tan x \tan y=\frac{4}{5}$. Thus, by the tan addition formula, $\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=20$.
|
| 23 |
+
5. [4] Two jokers are added to a 52 card deck and the entire stack of 54 cards is shuffled randomly. What is the expected number of cards that will be strictly between the two jokers?
|
| 24 |
+
Answer: $52 / 3$
|
| 25 |
+
|
| 26 |
+
Solution: Each card has an equal likelihood of being either on top of the jokers, in between them, or below the jokers. Thus, on average, $1 / 3$ of them will land between the two jokers.
|
| 27 |
+
6. [4] The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?
|
| 28 |
+
Answer: $2 \sqrt{3} / 3$
|
| 29 |
+
Solution: The major diagonal has a length of $\sqrt{3}$. The volume of the pyramid is $1 / 6$, and so its height $h$ satisfies $\frac{1}{3} \cdot h \cdot \frac{\sqrt{3}}{4}(\sqrt{2})^{2}=1 / 6$ since the freshly cut face is an equilateral triangle of side length $\sqrt{2}$. Thus $h=\sqrt{3} / 3$, and the answer follows.
|
| 30 |
+
7. [5] Let $s(n)$ denote the number of 1's in the binary representation of $n$. Compute
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
\frac{1}{255} \sum_{0 \leq n<16} 2^{n}(-1)^{s(n)}
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
## Answer: 45
|
| 37 |
+
|
| 38 |
+
Solution: Notice that if $n<8,(-1)^{s(n)}=(-1) \cdot(-1)^{s(n+8)}$ so the sum becomes $\frac{1}{255}\left(1-2^{8}\right) \sum_{0 \leq n<8} 2^{n}(-1)^{s(n)}=$ 45.
|
| 39 |
+
8. [5] Let $a, b$, and $c$ be the 3 roots of $x^{3}-x+1=0$. Find $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}$.
|
| 40 |
+
|
| 41 |
+
Answer: $\quad-2$
|
| 42 |
+
Solution: We can substitute $x=y-1$ to obtain a polynomial having roots $a+1, b+1, c+1$, namely, $(y-1)^{3}-(y-1)+1=y^{3}-3 y^{2}+2 y+1$. The sum of the reciprocals of the roots of this polynomial is, by Viete's formulas, $\frac{2}{-1}=-2$.
|
| 43 |
+
9. [6] How many functions $f:\{1,2,3,4,5\} \rightarrow\{1,2,3,4,5\}$ satisfy $f(f(x))=f(x)$ for all $x \in\{1,2,3,4,5\}$ ?
|
| 44 |
+
|
| 45 |
+
Answer: 196
|
| 46 |
+
Solution: A fixed point of a function $f$ is an element $a$ such that $f(a)=a$. The condition is equivalent to the property that $f$ maps every number to a fixed point. Counting by the number of fixed points of $f$, the total number of such functions is
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
\begin{aligned}
|
| 50 |
+
\sum_{k=1}^{5}\binom{5}{k} k^{5-k} & =1 \cdot\left(0^{5}+5^{0}\right)+5 \cdot\left(1^{4}+4^{1}\right)+10 \cdot\left(2^{3}+3^{2}\right) \\
|
| 51 |
+
& =1+25+10 \cdot 17 \\
|
| 52 |
+
& =196
|
| 53 |
+
\end{aligned}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
10. [6] A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\angle B=$ $\angle D=90^{\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\prime} C^{\prime} D^{\prime}$ that is similar to $A B C D$ and whose incircle is $\omega$. Let $N^{\prime}$ be the point of tangency of $B^{\prime} C^{\prime}$ to $\omega$. If $M N^{\prime} \| A C$, then what is the ratio of $A B: B C$ ?
|
| 57 |
+
|
| 58 |
+
Answer: $\frac{1+\sqrt{5}}{2}$
|
| 59 |
+
Solution: Let's focus on the right triangle $A B C$ and the semicircle inscribed in it since the situation is symmetric about $A C$. First we find the radius $a$ of circle $O$. Let $A B=x$ and $B C=y$. Drawing the radii $O M$ and $O N$, we see that $A M=x-a$ and $\triangle A M O \sim \triangle A B C$. In other words,
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\begin{aligned}
|
| 63 |
+
\frac{A M}{M O} & =\frac{A B}{B C} \\
|
| 64 |
+
\frac{x-a}{a} & =\frac{x}{y} \\
|
| 65 |
+
a & =\frac{x y}{x+y}
|
| 66 |
+
\end{aligned}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Now we notice that the situation is homothetic about $A$. In particular,
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
\triangle A M O \sim \triangle O N C \sim \triangle C N^{\prime} C^{\prime}
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
Also, $C B$ and $C N^{\prime}$ are both radii of circle $C$. Thus, when $M N^{\prime} \| A C^{\prime}$, we have
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
\begin{aligned}
|
| 79 |
+
A M & =C N^{\prime}=C B \\
|
| 80 |
+
x-a & =y \\
|
| 81 |
+
a=\frac{x y}{x+y} & =x-y \\
|
| 82 |
+
x^{2}-x y-y^{2} & =0 \\
|
| 83 |
+
x & =\frac{y}{2} \pm \sqrt{\frac{y^{2}}{4}+y^{2}} \\
|
| 84 |
+
\frac{A B}{B C}=\frac{x}{y} & =\frac{1+\sqrt{5}}{2} .
|
| 85 |
+
\end{aligned}
|
| 86 |
+
$$
|
| 87 |
+
|
HarvardMIT/md/en-122-2009-feb-gen2-solutions.md
ADDED
|
@@ -0,0 +1,47 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Individual Round: General Test, Part 2
|
| 6 |
+
|
| 7 |
+
1. [2] How many ways can the integers from -7 to 7 be arranged in a sequence such that the absolute values of the numbers in the sequence are nonincreasing?
|
| 8 |
+
Answer: 128
|
| 9 |
+
Solution: Each of the pairs $a,-a$ must occur in increasing order of $a$ for $a=1, \ldots, 7$, but $a$ can either occur before or after $-a$, for a total of $2^{7}=128$ possible sequences.
|
| 10 |
+
2. [2] How many ways can you tile the white squares of following $2 \times 24$ grid with dominoes? (A domino covers two adjacent squares, and a tiling is a non-overlapping arrangement of dominoes that covers every white square and does not intersect any black square.)
|
| 11 |
+

|
| 12 |
+
|
| 13 |
+
Answer: 27
|
| 14 |
+
Solution: Divide the rectangle into three $3 \times 8$ sub-rectangles. It is easy to count that there are 3 ways of tiling each of these sub-rectangles independently, for a total of $3^{3}=27$ possibilities.
|
| 15 |
+
3. [3] Let $S$ be the sum of all the real coefficients of the expansion of $(1+i x)^{2009}$. What is $\log _{2}(S)$ ?
|
| 16 |
+
|
| 17 |
+
Answer: 1004
|
| 18 |
+
Solution: The sum of all the coefficients is $(1+i)^{2009}$, and the sum of the real coefficients is the real part of this, which is $\frac{1}{2}\left((1+i)^{2009}+(1-i)^{2009}\right)=2^{1004}$. Thus $\log _{2}(S)=1004$.
|
| 19 |
+
4. [3] A torus (donut) having inner radius 2 and outer radius 4 sits on a flat table. What is the radius of the largest spherical ball that can be placed on top of the center torus so that the ball still touches the horizontal plane? (If the $x-y$ plane is the table, the torus is formed by revolving the circle in the $x-z$ plane centered at $(3,0,1)$ with radius 1 about the $z$ axis. The spherical ball has its center on the $z$-axis and rests on either the table or the donut.)
|
| 20 |
+
Answer: $9 / 4$
|
| 21 |
+
Solution: Let $r$ be the radius of the sphere. One can see that it satisfies $(r+1)^{2}=(r-1)^{2}+3^{2}$ by the Pythagorean Theorem, so $r=9 / 4$.
|
| 22 |
+
5. [4] Suppose $a, b$ and $c$ are integers such that the greatest common divisor of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x+1$ (in the set of polynomials in $x$ with integer coefficients), and the least common multiple of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x^{3}-4 x^{2}+x+6$. Find $a+b+c$.
|
| 23 |
+
Answer: $\quad-6$
|
| 24 |
+
Solution: Since $x+1$ divides $x^{2}+a x+b$ and the constant term is $b$, we have $x^{2}+a x+b=(x+1)(x+b)$, and similarly $x^{2}+b x+c=(x+1)(x+c)$. Therefore, $a=b+1=c+2$. Furthermore, the least common
|
| 25 |
+
multiple of the two polynomials is $(x+1)(x+b)(x+b-1)=x^{3}-4 x^{2}+x+6$, so $b=-2$. Thus $a=-1$ and $c=-3$, and $a+b+c=-6$.
|
| 26 |
+
6. [4] In how many ways can you rearrange the letters of "HMMTHMMT" such that the consecutive substring "HMMT" does not appear?
|
| 27 |
+
Answer: 361
|
| 28 |
+
Solution: There are $8!/(4!2!2!)=420$ ways to order the letters. If the permuted letters contain "HMMT", there are $5 \cdot 4!/ 2!=60$ ways to order the other letters, so we subtract these. However, we have subtracted "HMMTHMMT" twice, so we add it back once to obtain 361 possibilities.
|
| 29 |
+
7. [5] Let $F_{n}$ be the Fibonacci sequence, that is, $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$. Compute $\sum_{n=0}^{\infty} F_{n} / 10^{n}$.
|
| 30 |
+
Answer: $10 / 89$
|
| 31 |
+
Solution: Write $F(x)=\sum_{n=0}^{\infty} F_{n} x^{n}$. Then the Fibonacci recursion tells us that $F(x)-x F(x)-$ $x^{2} F(x)=x$, so $F(x)=x /\left(1-x-x^{2}\right)$. Plugging in $x=1 / 10$ gives the answer.
|
| 32 |
+
8. [5] The incircle $\omega$ of equilateral triangle $A B C$ has radius 1. Three smaller circles are inscribed tangent to $\omega$ and the sides of $A B C$, as shown. Three smaller circles are then inscribed tangent to the previous circles and to each of two sides of $A B C$. This process is repeated an infinite number of times. What is the total length of the circumferences of all the circles?
|
| 33 |
+
|
| 34 |
+
|
| 35 |
+
Answer: $5 \pi$
|
| 36 |
+
Solution: One can find using the Pythagorean Theorem that, in each iteration, the new circles have radius $1 / 3$ of that of the previously drawn circles. Thus the total circumference is $2 \pi+3 \cdot 2 \pi\left(\frac{1}{1-1 / 3}-1\right)=$ $5 \pi$.
|
| 37 |
+
9. [6] How many sequences of 5 positive integers $(a, b, c, d, e)$ satisfy $a b c d e \leq a+b+c+d+e \leq 10$ ?
|
| 38 |
+
|
| 39 |
+
Answer: 116
|
| 40 |
+
Solution: We count based on how many 1's the sequence contains. If $a=b=c=d=e=1$ then this gives us 1 possibility. If $a=b=c=d=1$ and $e \neq 1, e$ can be $2,3,4,5,6$. Each such sequence $(1,1,1,1, e)$ can be arranged in 5 different ways, for a total of $5 \cdot 5=25$ ways in this case.
|
| 41 |
+
If three of the numbers are 1 , the last two can be $(2,2),(3,3),(2,3),(2,4)$, or $(2,5)$. Counting ordering, this gives a total of $2 \cdot 10+3 \cdot 20=80$ possibilities.
|
| 42 |
+
If two of the numbers are 1 , the other three must be equal to 2 for the product to be under 10 , and this yields 10 more possibilities.
|
| 43 |
+
Thus there are $1+25+80+10=116$ such sequences.
|
| 44 |
+
10. [6] Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
| 45 |
+
Answer: $3 / 2$
|
| 46 |
+
Solution: The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.
|
| 47 |
+
|
HarvardMIT/md/en-122-2009-feb-geo-solutions.md
ADDED
|
@@ -0,0 +1,124 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Individual Round: Geometry Test
|
| 6 |
+
|
| 7 |
+
1. [3] A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.
|
| 8 |
+
|
| 9 |
+
|
| 10 |
+
Answer: $55 / 2$
|
| 11 |
+
Solution: Drawing the perpendiculars from the point of intersection of the corners to the bases of the trapezoid, we see that we have similar $3-4-5$ right triangles, and we can calculate that the length of the smaller base is 3 . Thus the area of the trapezoid is $\frac{8+3}{2} \cdot 5=55 / 2$.
|
| 12 |
+
2. [3] The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?
|
| 13 |
+
Answer: $2 \sqrt{3} / 3$
|
| 14 |
+
Solution: The major diagonal has a length of $\sqrt{3}$. The volume of the pyramid is $1 / 6$, and so its height $h$ satisfies $\frac{1}{3} \cdot h \cdot \frac{\sqrt{3}}{4}(\sqrt{2})^{2}=1 / 6$ since the freshly cut face is an equilateral triangle of side length $\sqrt{2}$. Thus $h=\sqrt{3} / 3$, and the answer follows.
|
| 15 |
+
3. [4] Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
| 16 |
+
Answer: $3 / 2$
|
| 17 |
+
Solution: The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.
|
| 18 |
+
4. [4] A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\angle B=$ $\angle D=90^{\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\prime} C^{\prime} D^{\prime}$ that is similar to $A B C D$ and whose incircle is $\omega$. Let $N^{\prime}$ be the point of tangency of $B^{\prime} C^{\prime}$ to $\omega$. If $M N^{\prime} \| A C$, then what is the ratio of $A B: B C$ ?
|
| 19 |
+
Answer: $\frac{1+\sqrt{5}}{2}$
|
| 20 |
+
|
| 21 |
+
Solution: Let's focus on the right triangle $A B C$ and the semicircle inscribed in it since the situation is symmetric about $A C$. First we find the radius $a$ of circle $O$. Let $A B=x$ and $B C=y$. Drawing the radii $O M$ and $O N$, we see that $A M=x-a$ and $\triangle A M O \sim \triangle A B C$. In other words,
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\begin{aligned}
|
| 25 |
+
\frac{A M}{M O} & =\frac{A B}{B C} \\
|
| 26 |
+
\frac{x-a}{a} & =\frac{x}{y} \\
|
| 27 |
+
a & =\frac{x y}{x+y} .
|
| 28 |
+
\end{aligned}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Now we notice that the situation is homothetic about $A$. In particular,
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\triangle A M O \sim \triangle O N C \sim \triangle C N^{\prime} C^{\prime}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Also, $C B$ and $C N^{\prime}$ are both radii of circle $C$. Thus, when $M N^{\prime} \| A C^{\prime}$, we have
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\begin{aligned}
|
| 41 |
+
A M & =C N^{\prime}=C B \\
|
| 42 |
+
x-a & =y \\
|
| 43 |
+
a=\frac{x y}{x+y} & =x-y \\
|
| 44 |
+
x^{2}-x y-y^{2} & =0 \\
|
| 45 |
+
x & =\frac{y}{2} \pm \sqrt{\frac{y^{2}}{4}+y^{2}} \\
|
| 46 |
+
\frac{A B}{B C}=\frac{x}{y} & =\frac{1+\sqrt{5}}{2} .
|
| 47 |
+
\end{aligned}
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
5. [4] Circle $B$ has radius $6 \sqrt{7}$. Circle $A$, centered at point $C$, has radius $\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.
|
| 51 |
+
Answer: $168 \pi$
|
| 52 |
+
Solution: The conditions imply that there exists a triangle such that $B$ is the circumcircle and $A$ is the incircle for the position of $A$. The distance between the circumcenter and incenter is given by $\sqrt{(R-2 r) R}$, where $R, r$ are the circumradius and inradius, respectively. Thus the locus of $C$ is a circle concentric to $B$ with radius $2 \sqrt{42}$. The conclusion follows.
|
| 53 |
+
6. [4] Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.
|
| 54 |
+
Answer: $1+5 \sqrt{2}+\sqrt{65}$
|
| 55 |
+
Solution: Let $a$ denote the area of the triangle, $r$ the inradius, and $p$ the perimeter. Then $a=r p / 2$, so $r=2 a / p>2 a / 17$. Notice that $a=h / 2$ where $h$ is the height of the triangle from $C$ to $A B$, and $h$ is an integer since the vertices are lattice points. Thus we first guess that the inradius is minimized when $h=1$ and the area is $1 / 2$. In this case, we can now assume WLOG that $A=(0,0), B=(1,0)$, and $C=(n+1,1)$ for some nonnegative integer $n$. The perimeter of $A B C$ is $\sqrt{n^{2}+2 n+2}+\sqrt{n^{2}+1}+1$. Since $n=8$ yields a perimeter greater than 17 , the required triangle has $n=7$ and inradius $r=1 / p=$ $\frac{1}{1+5 \sqrt{2}+\sqrt{65}}$ which yields the answer of $1 / r=1+5 \sqrt{2}+\sqrt{65}$. We can now verify that this is indeed
|
| 56 |
+
minimal over all $h$ by noting that its perimeter is greater than $17 / 2$, which is the upper bound in the case $h \geq 2$.
|
| 57 |
+
7. [5] In $\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.
|
| 58 |
+
Answer: $\frac{6 \sqrt{37}}{5}, \frac{21}{205} \sqrt{7585}$
|
| 59 |
+
Solution: There are two possibilities for the triangle $A B C$ based on whether $E$ is between $B$ and $C$ or not. We first consider the former case.
|
| 60 |
+
We find from the area and the Pythagorean theorem that $A E=12, A B=13$, and $A C=15$. We can then use Stewart's theorem to obtain $A D=2 \sqrt{37}$.
|
| 61 |
+
Since the area of $\triangle A D C$ is half that of $A B C$, we have $\frac{1}{2} A C \cdot D F=42$, so $D F=14 / 5$. Also, $D C=14 / 2=7$ so $E D=9-7=2$.
|
| 62 |
+
Notice that $A E D F$ is a cyclic quadrilateral. By Ptolemy's theorem, we have $E F \cdot 2 \sqrt{37}=(28 / 5) \cdot 12+$ $2 \cdot(54 / 5)$. Thus $E F=\frac{6 \sqrt{37}}{5}$ as desired.
|
| 63 |
+
The latter case is similar.
|
| 64 |
+
8. [7] Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.
|
| 65 |
+
Answer: 208
|
| 66 |
+
Solution: Note that $\angle A B C$ is right since
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
B C^{2}=160^{2}=50 \cdot 512=(A C-A B) \cdot(A C+A B)=A C^{2}-A B^{2}
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Construct point $B^{\prime}$ such that $A B C B^{\prime}$ is a rectangle, and construct $D^{\prime}$ on segment $B^{\prime} C$ such that $A D=A D^{\prime}$. Then
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
B^{\prime} D^{\prime 2}=A D^{\prime 2}-A B^{\prime 2}=A D^{2}-B C^{2}=(A D-B C)(A D+B C)=18 \cdot 338=78^{2}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
It follows that $C D^{\prime}=B^{\prime} C-B^{\prime} D^{\prime}=153=C D$; thus, points $D$ and $D^{\prime}$ coincide, and $A B \| C D$. Let $M$ denote the midpoint of segment $A D$, and denote the orthogonal projections $M$ to lines $A B$ and $B C$ by $P$ and $Q$ respectively. Then $Q$ is the midpoint of $B C$ and $A P=39$, so that $P B=A B-A P=192$ and
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
B M=P Q=\sqrt{80^{2}+192^{2}}=16 \sqrt{5^{2}+12^{2}}=208
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
9. [7] Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\angle A B C$ and $\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.
|
| 85 |
+
Answer: 14
|
| 86 |
+
Solution: As the incenter of triangle $A B C$, point $P$ has many properties. Extend $A P$ past $P$ to its intersection with the circumcircle of triangle $A B C$, and call this intersection $M$. Now observe that
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
\angle P B M=\angle P B C+\angle C B M=\angle P B C+\angle C A M=\beta+\alpha=90-\gamma
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
where $\alpha, \beta$, and $\gamma$ are the half-angles of triangle $A B C$. Since
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\angle B M P=\angle B M A=\angle B C A=2 \gamma
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
it follows that $B M=M P=C M$. Let $Q$ denote the intersection of $A M$ and $B C$, and observe that $\triangle A Q B \sim \triangle C Q M$ and $\triangle A Q C \sim \triangle B Q M$; some easy algebra gives
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
A M / B C=(A B \cdot A C+B M \cdot C M) /(A C \cdot C M+A B \cdot B M)
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Writing $(a, b, c, d, x)=(B C, A C, A B, M P, A P)$, this is $(x+d) / a=\left(b c+d^{2}\right) /((b+c) d)$. Ptolemy's theorem applied to $A B C D$ gives $a(d+x)=d(b+c)$. Multiplying the two gives $(d+x)^{2}=b c+d^{2}$. We easily solve for $d=\left(b c-x^{2}\right) /(2 x)=8$ and $a=d(b+c) /(d+x)=14$.
|
| 105 |
+
10. [8] Points $A$ and $B$ lie on circle $\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\ell$ passes through $P$ and is tangent to $\omega$. The tangents to $\omega$ at points $A$ and $B$ intersect $\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.
|
| 106 |
+
Answer: 9
|
| 107 |
+
Solution: Say that $\ell$ be tangent to $\omega$ at point $T$. Observing equal tangents, write
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
C D=C T+D T=B C+A D=5 .
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
Let the tangents to $\omega$ at $A$ and $B$ intersect each other at $Q$. Working from Menelaus applied to triangle $C D Q$ and line $A B$ gives
|
| 114 |
+
|
| 115 |
+
$$
|
| 116 |
+
\begin{aligned}
|
| 117 |
+
-1 & =\frac{D A}{A Q} \cdot \frac{Q B}{B C} \cdot \frac{C P}{P D} \\
|
| 118 |
+
& =\frac{D A}{B C} \cdot \frac{C P}{P C+C D} \\
|
| 119 |
+
& =\frac{3}{2} \cdot \frac{C P}{P C+5},
|
| 120 |
+
\end{aligned}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
from which $P C=10$. By power of a point, $P T^{2}=A P \cdot B P$, or $12^{2}=B P \cdot(B P+7)$, from which $B P=9$.
|
| 124 |
+
|
HarvardMIT/md/en-122-2009-feb-guts-solutions.md
ADDED
|
@@ -0,0 +1,282 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $12^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Guts Round
|
| 6 |
+
|
| 7 |
+
$12{ }^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 8 |
+
|
| 9 |
+
1. [5] Compute
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
1 \cdot 2^{2}+2 \cdot 3^{2}+3 \cdot 4^{2}+\cdots+19 \cdot 20^{2}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Answer: 41230 y Solution: We can write this as $\left(1^{3}+2^{3}+\cdots+20^{3}\right)-\left(1^{2}+2^{2}+\cdots+20^{2}\right)$, which is equal to $44100-2870=41230$.
|
| 16 |
+
2. [5] Given that $\sin A+\sin B=1$ and $\cos A+\cos B=3 / 2$, what is the value of $\cos (A-B)$ ?
|
| 17 |
+
|
| 18 |
+
Answer: $5 / 8$
|
| 19 |
+
Solution: Squaring both equations and add them together, one obtains $1+9 / 4=2+2(\cos (A) \cos (B)+$ $\sin (A) \sin (B))=2+2 \cos (A-B)$. Thus $\cos A-B=5 / 8$.
|
| 20 |
+
3. [5] Find all pairs of integer solutions $(n, m)$ to
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
2^{3^{n}}=3^{2^{m}}-1
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
Answer: $(0,0)$ and $(1,1)$
|
| 27 |
+
Solution: We find all solutions of $2^{x}=3^{y}-1$ for positive integers $x$ and $y$. If $x=1$, we obtain the solution $x=1, y=1$, which corresponds to $(n, m)=(0,0)$ in the original problem. If $x>1$, consider the equation modulo 4 . The left hand side is 0 , and the right hand side is $(-1)^{y}-1$, so $y$ is even. Thus we can write $y=2 z$ for some positive integer $z$, and so $2^{x}=\left(3^{z}-1\right)\left(3^{z}+1\right)$. Thus each of $3^{z}-1$ and $3^{z}+1$ is a power of 2 , but they differ by 2 , so they must equal 2 and 4 respectively. Therefore, the only other solution is $x=3$ and $y=2$, which corresponds to $(n, m)=(1,1)$ in the original problem.
|
| 28 |
+
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 29 |
+
4. [6] Simplify: $i^{0}+i^{1}+\cdots+i^{2009}$.
|
| 30 |
+
|
| 31 |
+
Answer: $1+i$
|
| 32 |
+
Solution: By the geometric series formula, the sum is equal to $\frac{i^{2010}-1}{i-1}=\frac{-2}{i-1}=1+i$.
|
| 33 |
+
5. [6] In how many distinct ways can you color each of the vertices of a tetrahedron either red, blue, or green such that no face has all three vertices the same color? (Two colorings are considered the same if one coloring can be rotated in three dimensions to obtain the other.)
|
| 34 |
+
Answer: 6
|
| 35 |
+
Solution: If only two colors are used, there is only one possible arrangement up to rotation, so this gives 3 possibilities. If all three colors are used, then one is used twice. There are 3 ways to choose the color that is used twice. Say this color is red. Then the red vertices are on a common edge, and the green and blue vertices are on another edge. We see that either choice of arrangement of the green and blue vertices is the same up to rotation. Thus there are 6 possibilities total.
|
| 36 |
+
6. [6] Let $A B C$ be a right triangle with hypotenuse $A C$. Let $B^{\prime}$ be the reflection of point $B$ across $A C$, and let $C^{\prime}$ be the reflection of $C$ across $A B^{\prime}$. Find the ratio of $\left[B C B^{\prime}\right]$ to $\left[B C^{\prime} B^{\prime}\right]$.
|
| 37 |
+
Answer: 1 Solution: Since $C, B^{\prime}$, and $C^{\prime}$ are collinear, it is evident that $\left[B C B^{\prime}\right]=\frac{1}{2}\left[B C C^{\prime}\right]$. It immediately follows that $\left[B C B^{\prime}\right]=\left[B C^{\prime} B^{\prime}\right]$. Thus, the ratio is 1 .
|
| 38 |
+
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 39 |
+
7. [6] How many perfect squares divide $2^{3} \cdot 3^{5} \cdot 5^{7} \cdot 7^{9}$ ?
|
| 40 |
+
|
| 41 |
+
Answer: 120
|
| 42 |
+
Solution: The number of such perfect squares is $2 \cdot 3 \cdot 4 \cdot 5$, since the exponent of each prime can be any nonnegative even number less than the given exponent.
|
| 43 |
+
8. [6] Which is greater, $\log _{2008}(2009)$ or $\log _{2009}(2010)$ ?
|
| 44 |
+
|
| 45 |
+
Answer: $\log _{2008} 2009$.
|
| 46 |
+
Solution: Let $f(x)=\log _{x}(x+1)$. Then $f^{\prime}(x)=\frac{x \ln x-(x+1) \ln (x+1)}{x(x+1) \ln ^{2} x}<0$ for any $x>1$, so $f$ is decreasing. Thus $\log _{2008}(2009)$ is greater.
|
| 47 |
+
9. [6] An icosidodecahedron is a convex polyhedron with 20 triangular faces and 12 pentagonal faces. How many vertices does it have?
|
| 48 |
+
Answer: 30
|
| 49 |
+
Solution: Since every edge is shared by exactly two faces, there are $(20 \cdot 3+12 \cdot 5) / 2=60$ edges. Using Euler's formula $v-e+f=2$, we see that there are 30 vertices.
|
| 50 |
+
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 51 |
+
10. [7] Let $a, b$, and $c$ be real numbers. Consider the system of simultaneous equations in variables $x$ and $y$ :
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\begin{aligned}
|
| 55 |
+
a x+b y & =c-1 \\
|
| 56 |
+
(a+5) x+(b+3) y & =c+1
|
| 57 |
+
\end{aligned}
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Determine the value(s) of $c$ in terms of $a$ such that the system always has a solution for any $a$ and $b$.
|
| 61 |
+
Answer:
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
2 a / 5+1 .\left(\text { or } \frac{2 a+5}{5}\right)
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Solution: We have to only consider when the determinant of $\left(\begin{array}{cc}a \\ a+5 & b \\ b+3\end{array}\right)$ is zero. That is, when $b=3 a / 5$. Plugging in $b=3 a / 5$, we find that $(a+5)(c-1)=a(c+1)$ or that $c=2 a / 5+1$.
|
| 68 |
+
11. [7] There are 2008 distinct points on a circle. If you connect two of these points to form a line and then connect another two points (distinct from the first two) to form another line, what is the probability that the two lines intersect inside the circle?
|
| 69 |
+
Answer: $1 / 3$
|
| 70 |
+
Solution: Given four of these points, there are 3 ways in which to connect two of them and then connect the other two, and of these possibilities exactly one will intersect inside the circle. Thus $1 / 3$ of all the ways to connect two lines and then connect two others have an intersection point inside the circle.
|
| 71 |
+
12. [7] Bob is writing a sequence of letters of the alphabet, each of which can be either uppercase or lowercase, according to the following two rules:
|
| 72 |
+
|
| 73 |
+
- If he had just written an uppercase letter, he can either write the same letter in lowercase after it, or the next letter of the alphabet in uppercase.
|
| 74 |
+
- If he had just written a lowercase letter, he can either write the same letter in uppercase after it, or the preceding letter of the alphabet in lowercase.
|
| 75 |
+
|
| 76 |
+
For instance, one such sequence is $a A a A B C D d c b B C$. How many sequences of 32 letters can he write that start at (lowercase) $a$ and end at (lowercase) $z$ ? (The alphabet contains 26 letters from $a$ to $z$.)
|
| 77 |
+
Answer: 376
|
| 78 |
+
Solution: The smallest possible sequence from $a$ to $z$ is $a A B C D \ldots Z z$, which has 28 letters. To insert 4 more letters, we can either switch two (not necessarily distinct) letters to lowercase and back again (as in $a A B C c C D E F f F G H \ldots Z z$ ), or we can insert a lowercase letter after its corresponding uppercase letter, insert the previous letter of the alphabet, switch back to uppercase, and continue the sequence (as in $a A B C c b B C D E \ldots Z z$ ). There are $\binom{27}{2}=13 \cdot 27$ sequences of the former type and 25 of the latter, for a total of 376 such sequences.
|
| 79 |
+
|
| 80 |
+
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 81 |
+
|
| 82 |
+
13. [8] How many ordered quadruples $(a, b, c, d)$ of four distinct numbers chosen from the set $\{1,2,3, \ldots, 9\}$ satisfy $b<a, b<c$, and $d<c$ ?
|
| 83 |
+
Answer: 630
|
| 84 |
+
Solution: Given any 4 elements $p<q<r<s$ of $\{1,2, \ldots, 9\}$, there are 5 ways of rearranging them to satisfy the inequality: prqs, psqr, qspr, qrps, and rspq. This gives a total of $\binom{9}{4} \cdot 5=630$ quadruples.
|
| 85 |
+
14. [8] Compute
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
\sum_{k=1}^{2009} k\left(\left\lfloor\frac{2009}{k}\right\rfloor-\left\lfloor\frac{2008}{k}\right\rfloor\right)
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Answer: 2394
|
| 92 |
+
Solution: The summand is equal to $k$ if $k$ divides 2009 and 0 otherwise. Thus the sum is equal to the sum of the divisors of 2009 , or 2394.
|
| 93 |
+
15. [8] Stan has a stack of 100 blocks and starts with a score of 0 , and plays a game in which he iterates the following two-step procedure:
|
| 94 |
+
(a) Stan picks a stack of blocks and splits it into 2 smaller stacks each with a positive number of blocks, say $a$ and $b$. (The order in which the new piles are placed does not matter.)
|
| 95 |
+
(b) Stan adds the product of the two piles' sizes, $a b$, to his score.
|
| 96 |
+
|
| 97 |
+
The game ends when there are only 1-block stacks left. What is the expected value of Stan's score at the end of the game?
|
| 98 |
+
Answer: 4950
|
| 99 |
+
Solution: Let $E(n)$ be the expected value of the score for an $n$-block game. It suffices to show that the score is invariant regardless of how the game is played. We proceed by induction. We have $E(1)=0$ and $E(2)=1$. We require that $E(n)=E(n-k)+E(k)+(n-k) k$ for all $k$. Setting $k=1$, we hypothesize that $E(n)=n(n-1) / 2$. This satisfies the recursion and base cases so $E(100)=100 \cdot 99 / 2=4950$.
|
| 100 |
+
16. [9] A spider is making a web between $n>1$ distinct leaves which are equally spaced around a circle. He chooses a leaf to start at, and to make the base layer he travels to each leaf one at a time, making a straight line of silk between each consecutive pair of leaves, such that no two of the lines of silk cross each other and he visits every leaf exactly once. In how many ways can the spider make the base layer of the web? Express your answer in terms of $n$.
|
| 101 |
+
|
| 102 |
+
Answer: $n 2^{n-2}$
|
| 103 |
+
Solution: There are $n$ ways to choose a starting vertex, and at each vertex he has only two choices for where to go next: the nearest untouched leaf in the clockwise direction, and the nearest untouched leaf in the counterclockwise direction. For, if the spider visited a leaf which is not nearest in some direction, there are two untouched leaves which are separated by this line of silk, and so the silk would eventually cross itself. Thus, for the first $n-2$ choices there are 2 possibilities, and the $(n-1)$ st choice is then determined.
|
| 104 |
+
|
| 105 |
+
Note: This formula can also be derived recursively.
|
| 106 |
+
17. [9] How many positive integers $n \leq 2009$ have the property that $\left\lfloor\log _{2}(n)\right\rfloor$ is odd?
|
| 107 |
+
|
| 108 |
+
Answer: 682
|
| 109 |
+
Solution: We wish to find $n$ such that there is some natural number $k$ for which $2 k-1 \leq \log _{2} n<$ $2 k$. Since $n \leq 2009$ we must have $k \leq 5$. This is equivalent to finding the number of positive integers $n \leq 2009$ satisfying $2^{2 k-1} \leq n<2^{2 k}$ for some $k \leq 5$, so the number of such integers is $2+2^{3}+2^{5}+2^{7}+2^{9}=682$.
|
| 110 |
+
18. [9] If $n$ is a positive integer such that $n^{3}+2 n^{2}+9 n+8$ is the cube of an integer, find $n$.
|
| 111 |
+
|
| 112 |
+
Answer: 7
|
| 113 |
+
Solution: Since $n^{3}<n^{3}+2 n^{2}+9 n+8<(n+2)^{3}$, we must have $n^{3}+2 n^{2}+9 n+8=(n+1)^{3}$. Thus $n^{2}=6 n+7$, so $n=7$.
|
| 114 |
+
$\qquad$
|
| 115 |
+
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 116 |
+
19. [10] Shelly writes down a vector $v=(a, b, c, d)$, where $0<a<b<c<d$ are integers. Let $\sigma(v)$ denote the set of 24 vectors whose coordinates are $a, b, c$, and $d$ in some order. For instance, $\sigma(v)$ contains $(b, c, d, a)$. Shelly notes that there are 3 vectors in $\sigma(v)$ whose sum is of the form $(s, s, s, s)$ for some $s$. What is the smallest possible value of $d$ ?
|
| 117 |
+
Answer: 6
|
| 118 |
+
Solution: If $k=a+b+c+d$, first you notice $4 \mid 3 k$, and $k \geq 10$. So we try $k=12$, which works with $a, b, c, d=1,2,3,6$ and not $1,2,4,5$.
|
| 119 |
+
20. [10] A positive integer is called jubilant if the number of 1's in its binary representation is even. For example, $6=110_{2}$ is a jubilant number. What is the 2009th smallest jubilant number?
|
| 120 |
+
Answer: 4018
|
| 121 |
+
Solution: Notice that for each pair of consecutive positive integers $2 k$ and $2 k+1$, their binary representation differs by exactly one 1 (in the units digit), so exactly one of 2 and 3 is jubilant, exactly one of 4 and 5 is jubilant, etc. It follows that there are exactly 2009 jubilant numbers less than or equal to 4019 . We now simply need to check whether 4018 or 4019 is jubilant. Since the binary representation of 4018 is 111110110010,4018 is the 2009 th jubilant number.
|
| 122 |
+
|
| 123 |
+
21. [10] Simplify
|
| 124 |
+
$$
|
| 125 |
+
2 \cos ^{2}(\ln (2009) i)+i \sin (\ln (4036081) i)
|
| 126 |
+
$$
|
| 127 |
+
|
| 128 |
+
Solution:
|
| 129 |
+
$$
|
| 130 |
+
\begin{aligned}
|
| 131 |
+
& \text { Answer: } \begin{aligned}
|
| 132 |
+
& \frac{4036082}{4036081} \text { Solution: We have } \\
|
| 133 |
+
& \begin{aligned}
|
| 134 |
+
2 \cos ^{2}(\ln (2009) i)+i \sin (\ln (4036081) i) & =1+\cos (2 \ln (2009) i)+i \sin (\ln (4036081) i) \\
|
| 135 |
+
& =1+\cos (\ln (4036081) i)+i \sin (\ln (4036081) i) \\
|
| 136 |
+
& =1+e^{i^{2} \ln (4036081)} \\
|
| 137 |
+
& =1+\frac{1}{4036081} \\
|
| 138 |
+
& =\frac{4036082}{4036081}
|
| 139 |
+
\end{aligned}
|
| 140 |
+
\end{aligned} . \begin{array}{l}
|
| 141 |
+
\\
|
| 142 |
+
\end{array}
|
| 143 |
+
\end{aligned}
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
as desired.
|
| 147 |
+
|
| 148 |
+
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 149 |
+
|
| 150 |
+
22. [10] A circle having radius $r_{1}$ centered at point $N$ is tangent to a circle of radius $r_{2}$ centered at $M$. Let $l$ and $j$ be the two common external tangent lines to the two circles. A circle centered at $P$ with radius $r_{2}$ is externally tangent to circle $N$ at the point at which $l$ coincides with circle $N$, and line $k$ is externally tangent to $P$ and $N$ such that points $M, N$, and $P$ all lie on the same side of $k$. For what ratio $r_{1} / r_{2}$ are $j$ and $k$ parallel?
|
| 151 |
+
Answer: 3
|
| 152 |
+
Solution: Suppose the lines are parallel. Draw the other tangent line to $N$ and $P$ - since $M$ and $P$ have the same radius, it is tangent to all three circles. Let $j$ and $k$ meet circle $N$ at $A$ and $B$, respectively. Then by symmetry we see that $\angle A N M=\angle M N P=\angle P N B=60^{\circ}$ since $A, N$, and $B$ are collinear (perpendicular to $j$ and $k$ ). Let $D$ be the foot of the perpendicular from $M$ to $A N$. In $\triangle M D N$, we have $M N=2 D N$, so $r_{1}+r_{2}=2\left(r_{1}-r_{2}\right)$, and so $r_{1} / r_{2}=3$.
|
| 153 |
+
23. [10] The roots of $z^{6}+z^{4}+z^{2}+1=0$ are the vertices of a convex polygon in the complex plane. Find the sum of the squares of the side lengths of the polygon.
|
| 154 |
+
Answer: $12-4 \sqrt{2}$
|
| 155 |
+
Solution: Factoring the polynomial as $\left(z^{4}+1\right)\left(z^{2}+1\right)=0$, we find that the 6 roots are $e^{ \pm i \pi / 4}$, $e^{ \pm i \pi / 2}, e^{ \pm i 3 \pi / 4}$. The calculation then follows from the Law of Cosines or the distance formula.
|
| 156 |
+
24. [10] Compute, in terms of $n$,
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
Note that whenever $s<t,\binom{s}{t}=0$.
|
| 163 |
+
Answer:
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
\frac{2 \cdot 2^{n}+(-1)^{n}}{3}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
Solution: Let $T_{n}=\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}$. From Pascal's recursion for binomial coefficients, we can find $T_{n}=2 T_{n-2}+T_{n-1}$, with $T_{0}=1$ and $T_{1}=1$. The characteristic polynomial of this recursion is $x^{2}-x-2=0$, which has roots 2 and -1 . Thus $T_{n}=a \cdot 2^{n}+b \cdot(-1)^{n}$ for some $a$ and $b$. From the initial conditions we have $a+b=1$ and $2 a-b=1$. It follows that $a=2 / 3$ and $b=1 / 3$, from which the conclusion follows.
|
| 170 |
+
25. [12] Four points, $A, B, C$, and $D$, are chosen randomly on the circumference of a circle with independent uniform probability. What is the expected number of sides of triangle $A B C$ for which the projection of $D$ onto the line containing the side lies between the two vertices?
|
| 171 |
+
Answer: $3 / 2$
|
| 172 |
+
Solution: By linearity of expectations, the answer is exactly 3 times the probability that the orthogonal projection of $D$ onto $A B$ lies interior to the segment. This happens exactly when either $\angle D A B$ or $\angle D B A$ is obtuse, which is equivalent to saying that $A$ and $B$ lie on the same side of the diameter through $D$. This happens with probability $1 / 2$. Therefore, desired answer is $3 / 2$.
|
| 173 |
+
26. [12] Define the sequence $\left\{x_{i}\right\}_{i \geq 0}$ by $x_{0}=2009$ and $x_{n}=-\frac{2009}{n} \sum_{k=0}^{n-1} x_{k}$ for all $n \geq 1$. Compute the value of $\sum_{n=0}^{2009} 2^{n} x_{n}$.
|
| 174 |
+
Answer: 2009
|
| 175 |
+
Solution: We have
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
-\frac{n x_{n}}{2009}=x_{n-1}+x_{n-2}+\ldots+x_{0}=x_{n-1}+\frac{(n-1) x_{n-1}}{2009}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
, which yields the recursion $x_{n}=\frac{n-2010}{n} x_{n-1}$. Unwinding this recursion, we find $x_{n}=(-1)^{n} \cdot 2009$. $\binom{2008}{n}$. Thus
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\begin{aligned}
|
| 185 |
+
\sum_{k=0}^{2009} 2^{n} x_{n} & =\sum_{k=0}^{2009}(-2)^{n} \cdot 2009 \cdot\binom{2008}{n} \\
|
| 186 |
+
& =2009 \sum_{k=0}^{2008}(-2)^{n}\binom{2008}{n} \\
|
| 187 |
+
& =2009(-2+1)^{2008}
|
| 188 |
+
\end{aligned}
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
as desired.
|
| 192 |
+
27. [12] Circle $\Omega$ has radius 5. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 6 . A unit circle $\omega$ is tangent to chord $A B$ at point $T$. Given that $\omega$ is also internally tangent to $\Omega$, find $A T \cdot B T$.
|
| 193 |
+
Answer: 2
|
| 194 |
+
Solution: Let $M$ be the midpoint of chord $A B$ and let $O$ be the center of $\Omega$. Since $A M=B M=3$, Pythagoras on triangle $A M O$ gives $O M=4$. Now let $\omega$ be centered at $P$ and say that $\omega$ and $\Omega$ are tangent at $Q$. Because the diameter of $\omega$ exceeds 1 , points $P$ and $Q$ lie on the same side of $A B$. By tangency, $O, P$, and $Q$ are collinear, so that $O P=O Q-P Q=4$. Let $H$ be the orthogonal projection of $P$ onto $O M$; then $O H=O M-H M=O M-P T=3$. Pythagoras on $O H P$ gives $H P^{2}=7$. Finally,
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
A T \cdot B T=A M^{2}-M T^{2}=A M^{2}-H P^{2}=9-7=2
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 201 |
+
28. [15] The vertices of a regular hexagon are labeled $\cos (\theta), \cos (2 \theta), \ldots, \cos (6 \theta)$. For every pair of vertices, Bob draws a blue line through the vertices if one of these functions can be expressed as a polynomial function of the other (that holds for all real $\theta$ ), and otherwise Roberta draws a red line through the
|
| 202 |
+
vertices. In the resulting graph, how many triangles whose vertices lie on the hexagon have at least one red and at least one blue edge?
|
| 203 |
+
Answer: 14 Solution: The existence of the Chebyshev polynomials, which express $\cos (n \theta)$ as a polynomial in $\cos (\theta)$, imply that Bob draws a blue line between $\cos (\theta)$ and each other vertex, and also between $\cos (2 \theta)$ and $\cos (4 \theta)$, between $\cos (2 \theta)$ and $\cos (6 \theta)$, and between $\cos (3 \theta)$ and $\cos (6 \theta)$ (by substituting $\theta^{\prime}=2 \theta$ or $3 \theta$ as necessary). We now show that Roberta draws a red line through each other pair of vertices.
|
| 204 |
+
Let $m$ and $n$ be positive integers. Notice that $\cos (n \theta)$ is a periodic function with period $\frac{2 \pi}{n}$, and $\cos (m \theta)$ is periodic with period $\frac{2 \pi}{m}$. Thus, any polynomial in $\cos (m \theta)$ is also periodic of period $\frac{2 \pi}{m}$. This may not be the minimum period of the polynomial, however, so the minimum period is $\frac{2 \pi}{m k}$ for some $k$. Therefore, if $\cos (n \theta)$ can be expressed as a polynomial in $\cos (m \theta)$ then $\frac{2 \pi}{n}=\frac{2 \pi}{m k}$ for some $k$, so $m \mid n$. This shows that there is a blue line between two vertices $\cos (a \theta)$ and $\cos (b \theta)$ if and only if one of $a$ or $b$ divides the other.
|
| 205 |
+
Drawing the graph, one can easily count that there are 3 triangles with all blue edges, 3 triangles with all red edges, and $\binom{6}{3}=20$ triangles total. Thus there are $20-3-3=14$ triangles having at least one red and at least one blue edge.
|
| 206 |
+
29. [15] The average of a set of distinct primes is 27 . What is the largest prime that can be in this set?
|
| 207 |
+
|
| 208 |
+
Answer: 139 Solution: Denote the set of these primes by $A$ and the number of elements in $A$ by
|
| 209 |
+
$n$. There are 9 primes smaller than 27 , namely $2,3,5,7,11,13,17,19$ and 23 . Since 27 is odd and all primes except 2 are odd, $2 \notin A$. Thus the largest prime $p$ is at most $27 \cdot 9-3-5-7-11-13-17-19-23=145$, so $p \leq 141$. When the primes are $3,5,7,11,13,17,19,23,29,31$ and 139 , their average is 27 . Therefore $p=139$.
|
| 210 |
+
30. [15] Let $f$ be a polynomial with integer coefficients such that the greatest common divisor of all its coefficients is 1 . For any $n \in \mathbb{N}, f(n)$ is a multiple of 85 . Find the smallest possible degree of $f$.
|
| 211 |
+
|
| 212 |
+
Answer: 17 Solution: Notice that, if $p$ is a prime and $g$ is a polynomial with integer coefficients
|
| 213 |
+
such that $g(n) \equiv 0(\bmod p)$ for some $n$, then $g(n+m p)$ is divisible by $p$ as well for any integer multiple $m p$ of $p$. Therefore, it suffices to find the smallest possible degree of a polynomial $f$ for which $f(0), f(1), f(2), \ldots, f(16)$ are divisible by 17 and by 5 .
|
| 214 |
+
There is a polynomial of degree 17 with integer coefficients having $f(0)=f(1)=\cdots=f(16)=0$, namely $f(x)=(x)(x-1)(x-2) \cdots(x-16)$. Thus the minimal degree is no larger than 17 .
|
| 215 |
+
Now, let $f$ be such a polynomial and consider $f$ modulo 17 . The polynomial has 17 roots, so it must be at least degree 17 when taken modulo 17 . Thus $f$ has degree at least 17 as well.
|
| 216 |
+
|
| 217 |
+
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 218 |
+
|
| 219 |
+
31. [18] How many ways are there to win tic-tac-toe in $\mathbb{R}^{n}$ ? (That is, how many lines pass through three of the lattice points $\left(a_{1}, \ldots, a_{n}\right)$ in $\mathbb{R}^{n}$ with each coordinate $a_{i}$ in $\{1,2,3\} ?$ ) Express your answer in terms of $n$.
|
| 220 |
+
Answer: $\quad\left(5^{n}-3^{n}\right) / 2$ Solution: A line consists of three points. Each coordinate can do one of three things passing from the first point to the last point: increase by 1 each time, stay the same, or decrease by 1 each time. There are three ways to stay the same (three coordinates), one way to increase by 1 , and one way to decrease by 1 , so there are $5^{n}$ possible types of behavior. Determining this behavior uniquely determines the end point and start point except that we have traced every line exactly twice (forwards and backwards) and incorrectly counted the $3^{n}$ "lines" where each coordinate stays the same, so we subtract $3^{n}$ and divide by 2 .
|
| 221 |
+
32. [18] Circle $\Omega$ has radius 13. Circle $\omega$ has radius 14 and its center $P$ lies on the boundary of circle $\Omega$. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 24 and is tangent to $\omega$ at point $T$. Find $A T \cdot B T$.
|
| 222 |
+
Answer: 56 Solution: Let $M$ be the midpoint of chord $A B$; then $A M=B M=12$ and Pythagoras on triangle $A M O$ gives $M O=5$. Note that $\angle A O M=\angle A O B / 2=\angle A P B=\angle A P T+\angle T P B$ or $\tan (\angle A O M)=\tan (\angle A P T+\angle T P B)$. Applying the tangent addition formula,
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
\begin{aligned}
|
| 226 |
+
\frac{A M}{M O} & =\frac{\frac{A T}{T P}+\frac{B T}{T P}}{1-\frac{A T}{T P} \cdot \frac{B T}{T P}} \\
|
| 227 |
+
& =\frac{A B \cdot T P}{T P^{2}-A T \cdot B T}
|
| 228 |
+
\end{aligned}
|
| 229 |
+
$$
|
| 230 |
+
|
| 231 |
+
from which $A T \cdot B T=T P^{2}-A B \cdot T P \cdot M O / A M=14^{2}-24 \cdot 14 \cdot 5 / 12=56$.
|
| 232 |
+
33. [18] Let $m$ be a positive integer. Let $d(n)$ denote the number of divisors of $n$, and define the function
|
| 233 |
+
|
| 234 |
+
$$
|
| 235 |
+
F(x)=\sum_{n=1}^{105^{m}} \frac{d(n)}{n^{x}}
|
| 236 |
+
$$
|
| 237 |
+
|
| 238 |
+
Define the numbers $a(n)$ to be the positive integers for which
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
F(x)^{2}=\sum_{n=1}^{105^{2 m}} \frac{a(n)}{n^{x}}
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
for all real $x$. Express $a\left(105^{m}\right)$ in terms of $m$.
|
| 245 |
+
Answer: $\left(\frac{m^{3}+6 m^{2}+11 m+6}{6}\right)^{3}$ OR $\binom{m+3}{3}^{3}$
|
| 246 |
+
(The expanded polynomial $\frac{1}{216}\left(216+1188 m+2826 m^{2}+3815 m^{3}+3222 m^{4}+1767 m^{5}+630 m^{6}+141 m^{7}+\right.$ $18 m^{8}+m^{9}$ ) is also an acceptable answer.)
|
| 247 |
+
|
| 248 |
+
Solution: The denominator of a term in the expansion of $F(x)^{2}$ is equal to $n^{x}$ if and only if it is a product of two terms of $F$ of the form $\frac{d(n / k)}{(n / k)^{x}}$ and $\frac{d(k)}{k^{x}}$ for some divisor $k$ of $n$. Thus $a\left(105^{m}\right)=$ $\sum_{k \mid 105^{m}} d(k) d\left(\frac{105^{m}}{k}\right)$. We can write $k=3^{a} 5^{b} 7^{c}$ with $a, b, c \leq m$ for any divisor $k$ of $105^{m}$, and in this case $d(k)=(a+1)(b+1)(c+1)$. Thus the sum becomes
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
\sum_{0 \leq a, b, c \leq m}(a+1)(b+1)(c+1)(m-a+1)(m-b+1)(m-c+1)
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
For a fixed $b$ and $c$, we can factor out $(b+1)(c+1)(m-b+1)(m-c+1)$ from the terms having this $b$ and $c$ and find that the sum is equal to
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
\begin{aligned}
|
| 258 |
+
a\left(105^{m}\right) & =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left(\sum_{a=1}^{m+1} a(m-a+2)\right) \\
|
| 259 |
+
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left((m+2) \frac{(m+1)(m+2)}{2}-\frac{(m+1)(m+2)(2 m+3)}{6}\right) \\
|
| 260 |
+
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left(\frac{(3 m+6-2 m-3)(m+1)(m+2)}{6}\right) \\
|
| 261 |
+
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\binom{m+3}{3}
|
| 262 |
+
\end{aligned}
|
| 263 |
+
$$
|
| 264 |
+
|
| 265 |
+
Fixing $c$ and factoring out terms again, we find by a similar argument that $a\left(105^{m}\right)=\binom{m+3}{3}^{3}$.
|
| 266 |
+
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
| 267 |
+
34. $[\leq \mathbf{2 5}]$ Descartes's Blackjack: How many integer lattice points (points of the form $(m, n)$ for integers $m$ and $n$ ) lie inside or on the boundary of the disk of radius 2009 centered at the origin?
|
| 268 |
+
|
| 269 |
+
If your answer is higher than the correct answer, you will receive 0 points. If your answer is $d$ less than the correct answer, your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$.
|
| 270 |
+
Answer: 12679605
|
| 271 |
+
35. $[\leq \mathbf{2 5}]$ Von Neumann's Poker: The first step in Von Neumann's game is selecting a random number on $[0,1]$. To generate this number, Chebby uses the factorial base: the number $0 . A_{1} A_{2} A_{3} A_{4} \ldots$ stands for $\sum_{n=0}^{\infty} \frac{A_{n}}{(n+1)!}$, where each $A_{n}$ is an integer between 0 and $n$, inclusive.
|
| 272 |
+
Chebby has an infinite number of cards labeled $\mathbf{0}, \mathbf{1}, \mathbf{2}, \ldots$. He begins by putting cards $\mathbf{0}$ and $\mathbf{1}$ into a hat and drawing randomly to determine $A_{1}$. The card assigned $A_{1}$ does not get reused. Chebby then adds in card 2 and draws for $A_{2}$, and continues in this manner to determine the random number. At each step, he only draws one card from two in the hat.
|
| 273 |
+
Unfortunately, this method does not result in a uniform distribution. What is the expected value of Chebby's final number?
|
| 274 |
+
|
| 275 |
+
Your score on this problem will be the larger of 0 and $\lfloor 25(1-d)\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
| 276 |
+
Answer: .57196
|
| 277 |
+
36. [ $\leq \mathbf{2 5}$ ] Euler's Bridge: The following figure is the graph of the city of Konigsburg in 1736 - vertices represent sections of the cities, edges are bridges. An Eulerian path through the graph is a path which moves from vertex to vertex, crossing each edge exactly once. How many ways could World War II bombers have knocked out some of the bridges of Konigsburg such that the Allied victory parade could trace an Eulerian path through the graph? (The order in which the bridges are destroyed matters.)
|
| 278 |
+
Your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
| 279 |
+
|
| 280 |
+
|
| 281 |
+
Answer: 13023
|
| 282 |
+
|
HarvardMIT/md/en-122-2009-feb-team1-solutions.md
ADDED
|
@@ -0,0 +1,66 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $12^{\text {th }}$ Annual Harvard-MIT Math Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Solutions: Team Round - Division A
|
| 6 |
+
|
| 7 |
+
1. [8] Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
|
| 8 |
+
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
| 9 |
+
|
| 10 |
+
Solution: We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3. Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an ( $n-1$ )-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
| 11 |
+
2. (a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
| 12 |
+
Answer: 2
|
| 13 |
+
Solution: At least two colors are needed in a good coloring of $P$. We show that two is sufficient. Write the positive integer $n$ as $p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}$, for distinct primes $p_{1}, p_{2}, \ldots p_{k}$, and let $f(n)=e_{1}+e_{2}+\ldots+e_{k}$. Notice that if $v_{a}$ and $v_{b}$ are connected, then $f(a)$ and $f(b)$ have opposite parity. So, if we color $v_{n}$ red if $f(n)$ is odd and blue otherwise, the two-coloring is good.
|
| 14 |
+
(b) [6] Let $T$ be a graph with one vertex $v_{n}$ for every integer $n$. An edge connects $v_{a}$ and $v_{b}$ if $|a-b|$ is a power of two. What is the chromatic number of $T$ ? Prove your answer.
|
| 15 |
+
Answer: 3
|
| 16 |
+
Solution: Since $v_{0}, v_{1}$, and $v_{2}$ are all connected to each other, three colors is necessary. Now, color $v_{n}$ red if $n \equiv 0(\bmod 3)$, blue if $n \equiv 1(\bmod 3)$, and green otherwise. Since $v_{a}$ and $v_{b}$ are the same color only if $3 \mid(a-b)$, no two connected vertices are the same color.
|
| 17 |
+
3. A graph is finite if it has a finite number of vertices.
|
| 18 |
+
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
| 19 |
+
|
| 20 |
+
Solution: We find a good coloring with $k+1$ colors. Order the vertices and color them one by one. Since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
|
| 21 |
+
(b) [10] In terms of $n$, what is the minimum number of edges a finite graph with chromatic number $n$ could have? Prove your answer.
|
| 22 |
+
Answer: $\frac{n(n-1)}{2}$
|
| 23 |
+
Solution: We prove this claim by induction - it holds for $n=1$. Now assume the claim holds for $n$, and consider a graph of chromatic number $n+1$. This graph must have at least one vertex of degree $n$, or else, by part a), it could be colored with only $n$ colors.
|
| 24 |
+
Now, if we remove this vertex, the remaining graph must have chromatic number $n$ or $n+1$ - if the chromatic number is $n-1$ or less, we can add the vertex back and give it a new color, creating a good coloring with only $n$ colors. By the inductive hypothesis, the new graph has at least $\frac{n(n-1)}{2}$ edges, so the original graph had at least $\frac{n(n-1)}{2}+n=\frac{n(n+1)}{2}$ edges.
|
| 25 |
+
The complete graph on $n+1$ vertices has exactly $\frac{n(n+1)}{2}$ edges, so the lower bound is tight and the inductive step is complete.
|
| 26 |
+
4. A $k$-clique of a graph is a set of $k$ vertices such that all pairs of vertices in the clique are adjacent.
|
| 27 |
+
(a) [4] Find a graph with chromatic number 3 that does not contain any 3 -cliques.
|
| 28 |
+
|
| 29 |
+
Solution: Consider a graph with 5 vertices arranged in a circle, with each vertex connected to its two neighbors. If only two colors are used, it is impossible to alternate colors to avoid using the same color on two adjacent vertices, so the chromatic number is 3 .
|
| 30 |
+
(b) [10] Prove that, for all $n>3$, there exists a graph with chromatic number $n$ that does not contain any $n$-cliques.
|
| 31 |
+
|
| 32 |
+
Solution: We prove the claim by induction on $n$. The case $n=3$ was adressed in (a). Let $n \geq 3$ and suppose $G$ is a graph with chromatic number $n$ containing no $n$-cliques. We produce a graph $G^{\prime}$ with chromatic number $n+1$ containing no $(n+1)$-cliques as follows. Add a vertex $v$ to $G$, and add an edge from $v$ to each vertex of $G$.
|
| 33 |
+
To see this graph has chromatic number $n+1$, observe that any coloring of the vertices of $G^{\prime}$ restricts to a valid coloring of the vertices of $G$. So at least $n$ distinct colors must be used among the vertices of $G$. In addition, another color must be used for $v$. By coloring $v$ a new color, we have constructed a coloring of $G^{\prime}$ having $n+1$ colors.
|
| 34 |
+
Lastly, any ( $n+1$ )-clique in $G^{\prime}$ must have at least $n$ vertices in $G$ which form an $n$-clique, which is impossible. Therefore, $G^{\prime}$ has no $(n+1)$-cliques.
|
| 35 |
+
5. The size of a finite graph is the number of vertices in the graph.
|
| 36 |
+
(a) [15] Show that, for any $n>2$, and any positive integer $N$, there are finite graphs with size at least $N$ and with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.
|
| 37 |
+
|
| 38 |
+
Solution: Let $k>1$ be an odd number, and let $G$ be a graph with $k$ vertices arranged in a circle, with each vertex connected to its two neighbors. If $n=3$, these graphs can be arbitrarily large, and are the graphs we need. If $n>3$, let $H$ be a complete graph on $n-3$ vertices, and let $J$ be the graph created by adding an edge from every vertex in $G$ to every vertex in $H$. Then $n-3$ colors are needed to color $H$ and another 3 are
|
| 39 |
+
needed to color $G$, so $n$ colors is both necessary and sufficient for a good coloring of $J$. Now, say a vertex is removed from $J$. There are two cases:
|
| 40 |
+
If the vertex was removed from $G$, then the remaining vertices in $G$ can be colored with 2 colors, because the cycle has been broken. A set of $n-3$ different colors can be used to color $H$, so only $n-1$ colors are needed to color the reduced graph. On the other hand, if the vertex was removed from $H$, then $n-4$ colors are used to color $H$ and 3 used to color $G$. So removing any vertex decreases the chromatic number of $J$.
|
| 41 |
+
(b) [15] Show that, for any positive integers $n$ and $r$, there exists a positive integer $N$ such that for any finite graph having size at least $N$ and chromatic number equal to $n$, it is possible to remove $r$ vertices (and all their incident edges) in such a way that the remaining vertices form a graph with chromatic number at least $n-1$.
|
| 42 |
+
|
| 43 |
+
Solution: We claim that $N=n r$ is large enough. Take a graph with at least $n r$ vertices and chromatic number $n$, and take a good $n$-coloring of the graph. Then by Pigeonhole, at least $r$ of the vertices are the same color, which means that no pair of these $r$ vertices is adjacent.
|
| 44 |
+
Remove this $r$ vertices. If the resulting graph can be colored with only $n-2$ colors, then we can add the $r$ vertices back in and color them with a new $(n-1)$ st color, creating a good coloring of the graph with only $n-1$ colors. Since the original graph has chromatic number $n$, it must be impossible to color the smaller graph with $n-2$ colors, so we have removed $r$ vertices without decreasing the chromatic number by 2 or more.
|
| 45 |
+
6. For any set of graphs $G_{1}, G_{2}, \ldots, G_{n}$ all having the same set of vertices $V$, define their overlap, denoted $G_{1} \cup G_{2} \cup \cdots \cup G_{n}$, to be the graph having vertex set $V$ for which two vertices are adjacent in the overlap if and only if they are adjacent in at least one of the graphs $G_{i}$.
|
| 46 |
+
(a) $[\mathbf{1 0}]$ Let $G$ and $H$ be graphs having the same vertex set and let $a$ be the chromatic number of $G$ and $b$ the chromatic number of $H$. Find, in terms of $a$ and $b$, the largest possible chromatic number of $G \cup H$. Prove your answer.
|
| 47 |
+
Answer: $a b$
|
| 48 |
+
Solution: First, we show that we can always color $G \cup H$ using $a b$ colors. Given a good coloring of $G$ in $a$ colors $c_{1}, \ldots, c_{a}$ and a good coloring of $H$ using $b$ colors $d_{1}, \ldots, d_{b}$, define $a b$ new colors to be the ordered pairs $\left(c_{i}, d_{j}\right)$. Label a vertex of $G \cup H$ with the color $\left(c_{i}, d_{j}\right)$ if it is colored $c_{i}$ in $G$ and $d_{i}$ in $H$. This gives a good coloring of $G \cup H$.
|
| 49 |
+
Now, it only remains to find graphs $G$ and $H$ such that $G \cup H$ has chromatic number $a b$. Consider the complete graph $K_{a b}$ having $a b$ vertices $v_{1}, \ldots, v_{a b}$ (every pair of vertices is adjacent). Let $G$ be the graph with vertices $v_{1}, \ldots, v_{a b}$ such that $v_{i}$ is connected to $v_{j}$ if and only if $i-j$ is a multiple of $a$. Also, let $H$ be the graph on $v_{1}, \ldots, v_{a b}$ such that two vertices are adjacent if and only if they are not adjacent in $G$. Then $G \cup H=K_{a b}$. Note that $G$ has chromatic number $a$ since it is the disjoint union of $b$ complete graphs on $a$ vertices. Also, $H$ has chromatic number $b$ since we can color each set of vertices $v_{i}$ with a color corresponding to $i$ modulo $b$ to obtain a good coloring. The chromatic number of $G \cup H$ is clearly $a b$, and so we have found such a pair of graphs.
|
| 50 |
+
(b) $[\mathbf{1 0}]$ Suppose $G$ is a graph with chromatic number $n$. Suppose there exist $k$ graphs $G_{1}, G_{2}, \ldots, G_{k}$ having the same vertex set as $G$ such that $G_{1} \cup G_{2} \cup \cdots \cup G_{k}=G$ and each $G_{i}$ has chromatic number at most 2. Show that $k \geq\left\lceil\log _{2}(n)\right\rceil$, and show that one can always find such a decomposition of $G$ into $\left\lceil\log _{2}(n)\right\rceil$ graphs.
|
| 51 |
+
|
| 52 |
+
Solution: [NOTE: This problem differs from the problem statement in the test as administered at the 2009 HMMT. The reader is encouraged to try it before reading the solution.]
|
| 53 |
+
The bound on $k$ follows from iterating part (a).
|
| 54 |
+
Let $G$ be a graph with chromatic number $n$. Consider a coloring of $G$ using $n$ colors labeled $1,2, \ldots, n$. For $i$ from 1 to $\left\lceil\log _{2}(n)\right\rceil$, define $G_{i}$ to be the graph on the vertices of $G$ for which two vertices are connected by an edge if and only if the $i$ th digit from the right in the binary expansions of their colors do not match. Clearly each of the graphs $G_{i}$ have chromatic number at most 2 , by coloring each node with the $i$ th digit of the binary expansion of their color in $G$. Moreover, each edge occurs in some $G_{i}$, since if two vertices match in every digit they are not connected by an edge. Therefore $G_{1} \cup G_{2} \cup \cdots \cup G_{\left\lceil\log _{2}(n)\right\rceil}=G$, and so we have found such a decomposition of $G$.
|
| 55 |
+
7. [20] Let $n$ be a positive integer. Let $V_{n}$ be the set of all sequences of 0 's and 1's of length $n$. Define $G_{n}$ to be the graph having vertex set $V_{n}$, such that two sequences are adjacent in $G_{n}$ if and only if they differ in either 1 or 2 places. For instance, if $n=3$, the sequences $(1,0,0)$, $(1,1,0)$, and $(1,1,1)$ are mutually adjacent, but $(1,0,0)$ is not adjacent to $(0,1,1)$.
|
| 56 |
+
Show that, if $n+1$ is not a power of 2 , then the chromatic number of $G_{n}$ is at least $n+2$.
|
| 57 |
+
Solution: We will assume that there is a coloring with $n+1$ colors and derive a contradiction. For each string $s$, let $T_{s}$ be the set consisting of all strings that differ from $s$ in at most 1 place. Thus $T_{s}$ has size $n+1$ and all vertices in $T_{s}$ are adjacent. In particular, if there is an $(n+1)$-coloring, then each color is used exactly once in $T_{s}$. Let $c$ be one of the colors that we used. We will determine how many vertices are colored with $c$. We will do this by counting in two ways.
|
| 58 |
+
Let $k$ be the number of vertices colored with color $c$. Each such vertex is part of $T_{s}$ for exactly $n+1$ values of $s$. On the other hand, each $T_{s}$ contains exactly one vertex with color $c$. It follows that $k(n+1)=2^{n}$. In particular, since $k$ is an integer, $n+1$ divides $2^{n}$. This is a contradiction since $n+1$ is now a power of 2 by assumption, so actually there can be no $n+1$-coloring, as claimed.
|
| 59 |
+
8. [30] Two colorings are distinct if there is no way to relabel the colors to transform one into the other. Equivalently, they are distinct if and only if there is some pair of vertices which are the same color in one coloring but different colors in the other. For what pairs $(n, k)$ of positive integers does there exist a finite graph with chromatic number $n$ which has exactly $k$ distinct good colorings using $n$ colors?
|
| 60 |
+
Answer: $(1,1),\left(2,2^{k}\right)$ for integers $k \geq 0$, and $(n, k)$ for $n>2, k>0$
|
| 61 |
+
Solution: If $n=1$, there is only one coloring. If $n=2$, then each connected component of the graph can be colored in two ways, because the color of any vertex in the graph determines the colors of all vertices connected to it. If the color scheme in one component is fixed, and there are $k$ components, then there are $2^{k-1}$ ways to finish the coloring.
|
| 62 |
+
Now say $n>2$. We construct a graph with $k$ different colorings. We begin with a complete graph $G$ on $n$ vertices, which can be colored in exactly one way. Let $v_{1}, v_{2}$, and $v_{3}$ be three vertices in the complete graph. If $k>1$, add to the graph a row of vertices $w_{1}, w_{2}, \ldots w_{k-1}$, such that $w_{i}$ is connected to $w_{i+1}$ for $1 \leq k-2$. Now, if $i \equiv 0(3)$, connect $w_{i}$ to all the
|
| 63 |
+
vertices in $G$ except $v_{1}$ and $v_{2}$. If $i \equiv 1(\bmod 3)$, connect $w_{i}$ to all the vertices in $G$ except $v_{2}$ and $v_{3}$, and if $i \equiv 2(\bmod 3)$, connect $w_{i}$ to all the vertices in $G$ except $v_{1}$ and $v_{3}$.
|
| 64 |
+
We need to show that this graph can be colored with $n$ colors in exactly $k$ different ways. Say that $v_{1}$ is colored red, $v_{2}$ blue, and $v_{3}$ green. Then each of the $w_{i}$ can be colored one of exactly two colors. Further, there is exactly one possible color that $w_{i}$ and $w_{i+1}$ could both be. Call the color $w_{i}$ and $w_{i+1}$ could both be $w_{i}$ 's leading color, and call $w_{i}$ 's other color its lagging color. Notice that $w_{i}$ 's lagging color is $w_{i+1}$ 's leading color. So, if any $w_{i}$ is colored with its lagging color, then all $w_{j}$ with $j>i$ are also colored with their lagging colors.
|
| 65 |
+
So one possibility is that all the $w_{i}$ are colored with their leading colors. Otherwise, some of them are colored with their lagging colors - these colorings are completely defined by which one of the $k-1 w_{i}$ is the first vertex colored with its lagging color. So there are $1+k-1$ or $k$ colorings of this graph, as needed.
|
| 66 |
+
|
HarvardMIT/md/en-122-2009-feb-team2-solutions.md
ADDED
|
@@ -0,0 +1,31 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $12^{\text {th }}$ Annual Harvard-MIT Math Tournament
|
| 2 |
+
|
| 3 |
+
## Saturday 21 February 2009
|
| 4 |
+
|
| 5 |
+
## Solutions: Team Round - Division B
|
| 6 |
+
|
| 7 |
+
1. [6] What are the chromatic numbers of each of the three graphs shown below? Draw a coloring having the minimum number of colors for each. Label the vertices with symbols to indicate the color of each vertex. (For example, you may mark a vertex "R" if you wish to indicate that it is colored red.)
|
| 8 |
+
|
| 9 |
+
|
| 10 |
+
Solution: The chromatic numbers of the three graphs are 3,5 , and 2 , respectively.
|
| 11 |
+
2. [6] In a connected graph, it is possible to reach any vertex from any other vertex by following the edges. A tree is a connected graph with $n$ vertices and $n-1$ edges for some positive integer $n$. Suppose $n \geq 2$. What is the chromatic number of a tree having $n$ vertices? Prove your answer.
|
| 12 |
+
|
| 13 |
+
Solution: The chromatic number of any tree is 2 . We show this by induction on the size of the tree. A tree with 2 nodes can clearly be 2 -colored. Now, suppose a tree of size $n-1$ can be colored in 2 colors. Given a tree of size $n$, choose any leaf (node with only one edge coming out of it), say $l$, of the tree, and color it red. The node it is adjacent to, say $x$, must be colored a different color, say blue. Using the inductive hypothesis, we can 2-color the tree formed by removing $l$, and we can choose the color of $x$ to be blue and the other color to be red. Thus the entire tree on $n$ vertices can be two-colored, completing the induction.
|
| 14 |
+
3. [8] Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
|
| 15 |
+
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
| 16 |
+
|
| 17 |
+
Solution: We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3 . Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an $n-1$-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
| 18 |
+
4. [10] Let $G$ be a finite graph in which every vertex has degree less than or equal to $k$. Prove that the chromatic number of $G$ is less than or equal to $k+1$.
|
| 19 |
+
|
| 20 |
+
Solution: Using a greedy algorithm we find a good coloring with $k+1$ colors. Order the vertices and color them one by one - since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
|
| 21 |
+
5. [10] A $k$-clique of a graph is a set of $k$ vertices such that all pairs of vertices in the clique are adjacent. The clique number of a graph is the size of the largest clique in the graph. Does there exist a graph which has a clique number smaller than its chromatic number?
|
| 22 |
+
|
| 23 |
+
Solution: Consider a graph with 5 vertices arranged in a circle, with each vertex connected to its two neighbors. If only two colors are used, it is impossible to alternate colors to avoid using the same color on two adjacent vertices, so the chromatic number is 3 . Its clique number is 2 , so we have found such a graph.
|
| 24 |
+
6. (a) [5] If a single vertex (and all its incident edges) is removed from a finite graph, show that the graph's chromatic number cannot decrease by more than 1.
|
| 25 |
+
|
| 26 |
+
Solution: Suppose the chromatic number of the graph was $C$, and removing a single vertex resulted in a graph with chromatic number at most $C-2$. Then we can color the remaining graph with at most $C-2$ colors. Replacing the vertex and its edges, we can then choose any color not already used to form a coloring of the original graph using at most $C-1$ colors, contradicting the fact that $C$ is the chromatic number of the graph.
|
| 27 |
+
(b) [15] Show that, for any $n>2$, there are infinitely many graphs with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.
|
| 28 |
+
|
| 29 |
+
Solution: Let $k>0$ be an odd number, and let $G$ be a graph with $k$ vertices arranged in a circle, with each vertex connected to its two neighbors. If $n=3$, these graphs can be arbitrarily large, and are the graphs we need. If $n>3$, let $H$ be a complete graph on $n-3$ vertices, and let $J$ be the graph created by adding an edge from every vertex in $G$ to every vertex in $H$. Then $n-3$ colors are needed to color $H$ and another 3 are needed to color $G$, so $n$ colors is both necessary and sufficient for a good coloring of $J$. Now, say a vertex is removed from $J$. There are two cases:
|
| 30 |
+
If the vertex was removed from $G$, then the remaining vertices in $G$ can be colored with 2 colors, because the cycle has been broken. A set of $n-3$ different colors can be used to color $H$, so only $n-1$ colors are needed to color the reduced graph. On the other hand, if the vertex was removed from $H$, then $n-4$ colors are used to color $H$ and 3 used to color $G$. So removing any vertex decreases the chromatic number of $J$.
|
| 31 |
+
|
HarvardMIT/md/en-131-2009-nov-gen1-solutions.md
ADDED
|
@@ -0,0 +1,47 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $2^{\text {nd }}$ Annual Harvard-MIT November Tournament Saturday 7 November 2009 <br> <br> General Test
|
| 2 |
+
|
| 3 |
+
<br> <br> General Test}
|
| 4 |
+
|
| 5 |
+
1. [2] Evaluate the sum:
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
11^{2}-1^{2}+12^{2}-2^{2}+13^{2}-3^{2}+\ldots+20^{2}-10^{2}
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
Answer: 2100 This sum can be written as $\sum_{a=1}^{10}(a+10)^{2}-a^{2}=\sum_{a=1}^{10} 10(2 a+10)=10 * 10 *$ $11+10 * 10 * 10=2100$.
|
| 12 |
+
2. [3] Given that $a+b+c=5$ and that $1 \leq a, b, c \leq 2$, what is the minimum possible value of $\frac{1}{a+b}+\frac{1}{b+c}$ ?
|
| 13 |
+
|
| 14 |
+
Answer: | $\frac{4}{7}$ | If $a>1$ and $b<2$, we can decrease the sum by decreasing $a$ and increasing $b$. You can |
|
| 15 |
+
| :---: | :---: | follow a similar procedure if $c>1$ and $b<2$. Therefore, the sum is minimized when $b=2$. We can then cross-multiply the two fractions and see that we are trying to minimize $\frac{a+c+4}{(a+2)(c+2)}=\frac{7}{(a+2)(c+2)}$. The product of two numbers with a fixed sum is maximized when those two numbers are equal, so $\frac{7}{(a+2)(c+2)}$ is minimized for $a=c=\frac{3}{2}$, which gives us an answer of $\frac{4}{7}$.
|
| 16 |
+
|
| 17 |
+
3. [3] What is the period of the function $f(x)=\cos (\cos (x))$ ?
|
| 18 |
+
|
| 19 |
+
Answer: $\pi$ Since $f(x)$ never equals $\cos (1)$ for $x \in(0, \pi)$ but $f(0)=\cos (1)$, the period is at least $\pi$. However, $\cos (x+\pi)=-\cos (x)$, so $\cos (\cos (x+\pi))=\cos (\cos (x))$.
|
| 20 |
+
4. [4] How many subsets $A$ of $\{1,2,3,4,5,6,7,8,9,10\}$ have the property that no two elements of $A$ sum to 11 ?
|
| 21 |
+
Answer: 243 For each element listed, there is exactly one other element such that the two elements sum to 11. Thus, we can list all the 10 numbers above as 5 pairs of numbers, such that each pair sums to 11. The problem then can be solved as follows: in any given subset with no two elements summing to 11 , at most one element from each pair can be present. Thus, there are 3 ways in which each pair can contribute to a given subset (no element, the first element in the pair, or the second element in the pair). Since there are 5 pairs, the total number of ways to construct a subset with no two elements summing to 11 is $3^{5}=243$.
|
| 22 |
+
5. [5] A polyhedron has faces that are all either triangles or squares. No two square faces share an edge, and no two triangular faces share an edge. What is the ratio of the number of triangular faces to the number of square faces?
|
| 23 |
+
|
| 24 |
+
Answer: | $\frac{4}{3}$ | Let $s$ be the number of square faces and $t$ be the number of triangular faces. Every |
|
| 25 |
+
| :---: | :---: | :---: | edge is adjacent to exactly one square face and one triangular face. Therefore, the number of edges is equal to $4 s$, and it is also equal to $3 t$. Thus $4 s=3 t$ and $\frac{t}{s}=\frac{4}{3}$
|
| 26 |
+
|
| 27 |
+
6. [5] Find the maximum value of $x+y$, given that $x^{2}+y^{2}-3 y-1=0$.
|
| 28 |
+
|
| 29 |
+
Answer: $\frac{\sqrt{26}+3}{2}$ We can rewrite $x^{2}+y^{2}-3 y-1=0$ as $x^{2}+\left(y-\frac{3}{2}\right)^{2}=\frac{13}{4}$. We then see that the set of solutions to $x^{2}-y^{2}-3 y-1=0$ is the circle of radius $\frac{\sqrt{13}}{2}$ and center $\left(0, \frac{3}{2}\right)$. This can be written as $x=\frac{\sqrt{13}}{2} \cos (\theta)$ and $y=\frac{\sqrt{13}}{2} \sin (\theta)+\frac{3}{2}$. Thus, $x+y=\frac{3}{2}+\frac{\sqrt{13}}{2}(\cos (\theta)+\sin (\theta))=\frac{3}{2}+\frac{\sqrt{13}}{2} \sqrt{2} \sin \left(\theta+45^{\circ}\right)$, which is maximized for $\theta=45^{\circ}$ and gives $\frac{\sqrt{26}+3}{2}$. (We could also solve this geometrically by noting that if $x+y$ attains a maximum value of $s$ then the line $x+y=s$ is tangent to the circle.)
|
| 30 |
+
7. [6] There are 15 stones placed in a line. In how many ways can you mark 5 of these stones so that there are an odd number of stones between any two of the stones you marked?
|
| 31 |
+
Answer: 77 Number the stones 1 through 15 in order. We note that the condition is equivalent to stipulating that the stones have either all odd numbers or all even numbers. There are $\binom{8}{5}$ ways to choose 5 odd-numbered stones, and $\binom{7}{5}$ ways to choose all even-numbered stones, so the total number
|
| 32 |
+
of ways to pick the stones is $\binom{8}{5}+\binom{7}{5}=77$. $\binom{n}{k}$ is the number of ways to choose $k$ out of $n$ items. It equals $\left.\frac{n!}{k!(n-k)!}\right)$.
|
| 33 |
+
8. [7] Let $\triangle A B C$ be an equilateral triangle with height 13 , and let $O$ be its center. Point $X$ is chosen at random from all points inside $\triangle A B C$. Given that the circle of radius 1 centered at $X$ lies entirely inside $\triangle A B C$, what is the probability that this circle contains $O$ ?
|
| 34 |
+
Answer: $\frac{\sqrt{3} \pi}{100}$ The set of points $X$ such that the circle of radius 1 centered at $X$ lies entirely inside $\triangle A B C$ is itself a triangle, $A^{\prime} B^{\prime} C^{\prime}$, such that $A B$ is parallel to $A^{\prime} B^{\prime}, B C$ is parallel to $B^{\prime} C^{\prime}$, and $C A$ is parallel to $C^{\prime} A^{\prime}$, and furthermore $A B$ and $A^{\prime} B^{\prime}, B C$ and $B^{\prime} C^{\prime}$, and $C A$ and $C^{\prime} A^{\prime}$ are all 1 unit apart. We can use this to calculate that $A^{\prime} B^{\prime} C^{\prime}$ is an equilateral triangle with height 10, and hence has area $\frac{100}{\sqrt{3}}$. On the other hand, the set of points $X$ such that the circle of radius 1 centered at $X$ contains $O$ is a circle of radius 1 , centered at $O$, and hence has area $\pi$. The probability that the circle centered at $X$ contains $O$ given that it also lies in $A B C$ is then the ratio of the two areas, that is, $\frac{\pi}{\frac{100}{\sqrt{3}}}=\frac{\sqrt{3} \pi}{100}$.
|
| 35 |
+
9. [7] A set of points is convex if the points are the vertices of a convex polygon (that is, a non-selfintersecting polygon with all angles less than or equal to $180^{\circ}$ ). Let $S$ be the set of points $(x, y)$ such that $x$ and $y$ are integers and $1 \leq x, y \leq 26$. Find the number of ways to choose a convex subset of $S$ that contains exactly 98 points.
|
| 36 |
+
Answer: 4958 For this problem, let $n=26$. A convex set may be divided into four subsets: a set of points with maximal $y$ coordinate, a set of points with minimal $y$ coordinate, the points to the left of one of these subsets, and the points to the right of one of these subsets (the left, top, right, and bottom of the corresponding convex polygon). Each of these four parts contains at most $n$ points. (All points in the top or bottom have distinct $x$ coordinates while all points in the left or right have distinct $y$ coordinates.) Moreover, there are four corners each of which is contained in two of these regions. This implies that at most $4 n-4$ distinct points are in any convex set. To find a set of size $4 n-6$ we can remove 2 additional points. Either exactly one of the top, bottom, left, or right contains exactly $n-2$ points or some two of them each contain exactly $n-1$ points.
|
| 37 |
+
Any of the $\binom{100}{98}=4950$ sets of 98 points with either $x$ or $y$ coordinate either 1 or 26 have this property. Suppose instead that some of the points have $x$ coordinate and $y$ coordinate both different from 1 and from 26. In this case we can check that it is impossible for one side to have $n-2$ points. If two opposite sides (top/bottom or left/right) have $n-1$ points, then we obtain all the points on the boundary of an $n-1$ by $n$ rectangle (of which there are four). If two adjacent sides (any of the other pairs) have $n-1$ points, then we obtain the points on the boundary of an $n$ by $n$ square with the points $(1,1),(1,2)$, $(2,1)$ missing and the point $(2,2)$ added (or one of its rotations). There are an additional 4 such sets, for a total of 4958.
|
| 38 |
+
10. [8] Compute
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
\prod_{n=0}^{\infty}\left(1-\left(\frac{1}{2}\right)^{3^{n}}+\left(\frac{1}{4}\right)^{3^{n}}\right)
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Answer: | $\frac{2}{3}$ |
|
| 45 |
+
| :---: |
|
| 46 |
+
| We can rewrite each term as $\frac{1+\left(\frac{1}{2}\right)^{3^{n+1}}}{1+\left(\frac{1}{2}\right)^{3^{n}}}$. In the infinite product, each term of the form | $1+\left(\frac{1}{2}\right)^{3^{n}}$ with $n>0$ appears once in the numerator and once in the denominator. The only remaining term is $1+\left(\frac{1}{2}\right)^{1}$ in the first denominator.
|
| 47 |
+
|
HarvardMIT/md/en-131-2009-nov-gen2-solutions.md
ADDED
|
@@ -0,0 +1,61 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $2^{\text {nd }}$ Annual Harvard-MIT November Tournament Saturday 7 November 2009 <br> Theme Round
|
| 2 |
+
|
| 3 |
+
## Shortest Paths
|
| 4 |
+
|
| 5 |
+
1. [3] Paul starts with the number 19. In one step, he can add 1 to his number, divide his number by 2 , or divide his number by 3 . What is the minimum number of steps Paul needs to get to 1 ?
|
| 6 |
+
Answer: 6 One possible path is $19 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 6 \rightarrow 2 \rightarrow 1$.
|
| 7 |
+
2. [4] You start with a number. Every second, you can add or subtract any number of the form $n$ ! to your current number to get a new number. In how many ways can you get from 0 to 100 in 4 seconds? ( $n!$ is defined as $n \times(n-1) \times(n-2) \times \cdots \times 2 \times 1$, so $1!=1,2!=2,3!=6,4!=24$, etc.)
|
| 8 |
+
Answer: 36 To get to 100 , you have to use one number which is at least $5!=120$, because $24 \times 4=96$, which is less than 100 . If you use $6!=720$ or anything larger, you need to get back from 720 to 100 (or further) in three seconds. Since $3 \cdot 5!<620$, there is no way to do this in 3 seconds. This means you have to use 5 ! at least once. The remaining numbers must get you from 120 to 100 . If you use three numbers all at most 3 !, you can move by at most $3 \cdot 3!=18<120-100$. This means you have to use 4 !. From $120-24=96$, there are two ways to get to 100: adding 6 then subtracting 2 , or adding 2 twice. So, to get to 100 from 0 in four seconds, you must either add 120 , subtract 24 , add 6 , and subtract 2 , or add 120 , subtract 24 , and add 2 twice. You can do these steps in any order, so the first sequence yields 24 paths and the second sequence yields 12 .
|
| 9 |
+
3. [5] Let $C$ be the circle of radius 12 centered at $(0,0)$. What is the length of the shortest path in the plane between $(8 \sqrt{3}, 0)$ and $(0,12 \sqrt{2})$ that does not pass through the interior of $C$ ?
|
| 10 |
+
Answer: $12+4 \sqrt{3}+\pi$ The shortest path consists of a tangent to the circle, a circular arc, and then another tangent. The first tangent, from $(8 \sqrt{3}, 0)$ to the circle, has length $4 \sqrt{3}$, because it is a leg of a 30-60-90 right triangle. The $15^{\circ}$ arc has length $\frac{15}{360}(24 \pi)$, or $\pi$, and the final tangent, to $(0,12 \sqrt{2})$, has length 12.
|
| 11 |
+
4. [6] You are given a $5 \times 6$ checkerboard with squares alternately shaded black and white. The bottomleft square is white. Each square has side length 1 unit. You can normally travel on this board at a speed of 2 units per second, but while you travel through the interior (not the boundary) of a black square, you are slowed down to 1 unit per second. What is the shortest time it takes to travel from the bottom-left corner to the top-right corner of the board?
|
| 12 |
+
Answer: $\frac{1+5 \sqrt{2}}{2}$ It is always faster to take a path around a black square than through it, since the length of the hypotenuse of any right triangle is greater than half the sum of the length of its legs. Therefore, an optimal path always stays on white squares or on boundaries, and the shortest such path has length $1+5 \sqrt{2}$.
|
| 13 |
+
5. [7] The following grid represents a mountain range; the number in each cell represents the height of the mountain located there. Moving from a mountain of height $a$ to a mountain of height $b$ takes $(b-a)^{2}$ time. Suppose that you start on the mountain of height 1 and that you can move up, down, left, or right to get from one mountain to the next. What is the minimum amount of time you need to get to the mountain of height 49 ?
|
| 14 |
+
|
| 15 |
+
| 1 | 3 | 6 | 10 | 15 | 21 | 28 |
|
| 16 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 17 |
+
| 2 | 5 | 9 | 14 | 20 | 27 | 34 |
|
| 18 |
+
| 4 | 8 | 13 | 19 | 26 | 33 | 39 |
|
| 19 |
+
| 7 | 12 | 18 | 25 | 32 | 38 | 43 |
|
| 20 |
+
| 11 | 17 | 24 | 31 | 37 | 42 | 46 |
|
| 21 |
+
| 16 | 23 | 30 | 36 | 41 | 45 | 48 |
|
| 22 |
+
| 22 | 29 | 35 | 40 | 44 | 47 | 49 |
|
| 23 |
+
|
| 24 |
+
Answer: 212 Consider the diagonals of the board running up and to the right - so the first diagonal is the square 1 , the second diagonal is the squares 2 and 3 , and so on. The $i$ th ascent is the largest step taken from a square in the $i$ th diagonal to a square in the $i+1$ st. Since you must climb from square 1 to square 49 , the sum of the ascents is at least 48 . Since there are 12 ascents, the average ascent is at least 4.
|
| 25 |
+
|
| 26 |
+
The 1 st and 12 th ascents are at most 2 , and the 2 nd and 11 th ascents are at most 3 . The 6 th and 7 th ascents are at least 6 , and the 5 th and 8 th ascents are at least 5 . Because $f(x)=x^{2}$ is convex, the sum of squares of the ascents is minimized when they are as close together as possible. One possible shortest path is then $1 \rightarrow 3 \rightarrow 6 \rightarrow 10 \rightarrow 14 \rightarrow 19 \rightarrow 25 \rightarrow 31 \rightarrow 36 \rightarrow 40 \rightarrow 44 \rightarrow 47 \rightarrow 49$, which has ascents of size $2,3,4,4,5,6,6,5,4,4,3$, and 2 . Thus, our answer is 212 , the sums of the squares of these ascents. There are other solutions to this problem. One alternative problem involves computing the shortest path to each square of the graph, recursively, starting from squares 2 and 3 .
|
| 27 |
+
|
| 28 |
+
## Five Guys
|
| 29 |
+
|
| 30 |
+
6. [3] There are five guys named Alan, Bob, Casey, Dan, and Eric. Each one either always tells the truth or always lies. You overhear the following discussion between them:
|
| 31 |
+
```
|
| 32 |
+
Alan: "All of us are truth-tellers."
|
| 33 |
+
Bob: "No, only Alan and I are truth-tellers."
|
| 34 |
+
Casey: "You are both liars."
|
| 35 |
+
Dan: "If Casey is a truth-teller, then Eric is too."
|
| 36 |
+
Eric: "An odd number of us are liars."
|
| 37 |
+
```
|
| 38 |
+
|
| 39 |
+
Who are the liars?
|
| 40 |
+
Answer: Alan, Bob, Dan, and Eric Alan and Bob each claim that both of them are telling the truth, but they disagree on the others. Therefore, they must both be liars, and Casey must be a truth-teller. If Dan is a truth-teller, then so is Eric, but then there would only be two truth-tellers, contradicting Eric's claim. Therefore, Dan is a liar, and so is Eric.
|
| 41 |
+
7. [4] Five guys are eating hamburgers. Each one puts a top half and a bottom half of a hamburger bun on the grill. When the buns are toasted, each guy randomly takes two pieces of bread off of the grill. What is the probability that each guy gets a top half and a bottom half?
|
| 42 |
+
Answer: $\frac{8}{63}$ Say a guy is content if he gets a top half and a bottom half. Suppose, without loss of generality, that the first guy's first piece of bread is a top. Then there is a $\frac{5}{9}$ chance that his second piece of bread is a bottom. By the same reasoning, given that the first guy is content, there is a $\frac{4}{7}$ chance that the second guy is content. Given that the first two guys are content, there is a $\frac{3}{5}$ chance that the third guy is content, and so on. Our final answer is $\frac{5}{9} \cdot \frac{4}{7} \cdot \frac{3}{5} \cdot \frac{2}{3} \cdot \frac{1}{1}=\frac{8}{63}$.
|
| 43 |
+
8. [5] A single burger is not enough to satisfy a guy's hunger. The five guys go to Five Guys' Restaurant, which has 20 different meals on the menu. Each meal costs a different integer dollar amount between $\$ 1$ and $\$ 20$. The five guys have $\$ 20$ to split between them, and they want to use all the money to order five different meals. How many sets of five meals can the guys choose?
|
| 44 |
+
Answer: 7 Suppose the meals, sorted in descending order, cost $5+x_{1}, 4+x_{2}, \ldots, 1+x_{5}$. To satisfy the conditions in the problem, the $x_{i}$ must be a non-increasing sequence of non-negative integers which sums to 5 . Therefore, there is exactly one order for each partition of 5 : order the elements of the partition from largest to smallest and use these parts as the $x_{i}$. For example, the partition $3+2$ corresponds to the order $5+3,4+2,3,2,1$. There are thus 7 orders, corresponding to the 7 partitions of 5 below.
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
1+1+1+1+1,1+1+1+2,1+2+2,1+1+3,2+3,1+4,5
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
These partitions yield the following seven orders:
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
(2,3,4,5,6),(1,3,4,5,7),(1,2,4,6,7),(1,2,3,5,7)
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
$(1,2,3,6,8),(1,2,3,5,9),(1,2,3,4,10)$
|
| 57 |
+
9. [6] Five guys each have a positive integer (the integers are not necessarily distinct). The greatest common divisor of any two guys' numbers is always more than 1 , but the greatest common divisor of all the numbers is 1 . What is the minimum possible value of the product of the numbers?
|
| 58 |
+
Answer: 32400 Let $\omega(n)$ be the number of distinct prime divisors of a number. Each of the guys' numbers must have $\omega(n) \geq 2$, since no prime divides all the numbers. Therefore, if the answer has prime factorization $p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}$, then $e_{1}+e_{2}+\ldots+e_{k} \geq 10$. If $p^{2}$ divided any of the guys' numbers, we could divide their number by $p$ to reduce the product. Therefore we may assume $e_{i} \leq 4$ for each $i$, so the smallest possible product is $2^{4} 3^{4} 5^{2}$. This bound is achievable: give the guys the numbers $10,6,6,6$, and 15 .
|
| 59 |
+
10. [7] Five guys join five girls for a night of bridge. Bridge games are always played by a team of two guys against a team of two girls. The guys and girls want to make sure that every guy and girl play against each other an equal number of times. Given that at least one game is played, what is the least number of games necessary to accomplish this?
|
| 60 |
+
Answer: 25 Suppose that each guy plays each girl $t$ times. Since each guy plays against two girls in one game, the total number of games each guy plays is $\frac{5 t}{2}$. Then the total number of games is $\frac{25 t}{4}$, which is a multiple of 25 and therefore at least 25 . To check that 25 games is enough, we arrange the guys and girls in two circles. A good pair of guys is a pair of guys who are adjacent in the circle; a good pair of girls is defined similarly. There are 5 good pairs of guys and girls - making each good pair of guys play each good pair of girls works.
|
| 61 |
+
|
HarvardMIT/md/en-131-2009-nov-guts-solutions.md
ADDED
|
@@ -0,0 +1,212 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $2^{\text {nd }}$ Annual Harvard-MIT November Tournament Saturday 7 November 2009
|
| 2 |
+
|
| 3 |
+
## Guts Round
|
| 4 |
+
|
| 5 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 6 |
+
|
| 7 |
+
1. [5] If $f(x)=x /(x+1)$, what is $f(f(f(f(2009))))$ ?
|
| 8 |
+
|
| 9 |
+
Answer: $\frac{2009}{8037} f(f(x))=\frac{(x /(x+1))}{(x /(x+1))+1}=x / 2 x+1, f(f(f(f(x))))=x / 4 x+1=\frac{2009}{8037}$
|
| 10 |
+
2. [5] A knight begins on the lower-left square of a standard chessboard. How many squares could the knight end up at after exactly 2009 legal knight's moves? (A knight's move is 2 squares either horizontally or vertically, followed by 1 square in a direction perpendicular to the first.)
|
| 11 |
+
Answer: 32 The knight goes from a black square to a white square on every move, or vice versa, so after 2009 moves he must be on a square whose color is opposite of what he started on. So he can only land on half the squares after 2009 moves. Note that he can access any of the 32 squares (there are no other parity issues) because any single jump can also be accomplished in 3 jumps, so with 2009 jumps, he can land on any of the squares of the right color.
|
| 12 |
+
3. [5] Consider a square, inside which is inscribed a circle, inside which is inscribed a square, inside which is inscribed a circle, and so on, with the outermost square having side length 1. Find the difference between the sum of the areas of the squares and the sum of the areas of the circles.
|
| 13 |
+
Answer: $2-\frac{\pi}{2}$
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
The ratio of the area of each square and the circle immediately inside it is $\frac{4}{\pi}$. The total sum of the areas of the squares is $1+\frac{1}{2}+\frac{1}{4}+\ldots=2$. Difference in area is then $2-2 \cdot \frac{4}{\pi}$.
|
| 17 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER $2009 —$ GUTS ROUND
|
| 18 |
+
4. [6] A cube has side length 1. Find the product of the lengths of the diagonals of this cube (a diagonal is a line between two vertices that is not an edge).
|
| 19 |
+
Answer: 576 There are 12 diagonals that go along a face and 4 that go through the center of the cube, so the answer is $\sqrt{2}^{12} \cdot \sqrt{3}^{4}=576$.
|
| 20 |
+
5. [6] Tanks has a pile of 5 blue cards and 5 red cards. Every morning, he takes a card and throws it down a well. What is the probability that the first card he throws down and the last card he throws down are the same color?
|
| 21 |
+
|
| 22 |
+
Answer: | $\frac{4}{9}$ | Once he has thrown the first card down the well, there are 9 remaining cards, and only |
|
| 23 |
+
| :---: | :---: | 4 have the same color as the card that was thrown down. Therefore, the probability that the last card he throws down has the same color is $\frac{4}{9}$.
|
| 24 |
+
|
| 25 |
+
6. [6] Find the last two digits of $1032^{1032}$. Express your answer as a two-digit number.
|
| 26 |
+
|
| 27 |
+
Answer: 76 The last two digits of $1032^{1032}$ is the same as the last two digits of $32^{1032}$. The last two digits of $32^{n}$ repeat with a period of four as $32,24,68,76,32,24,68,76, \ldots$.
|
| 28 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 29 |
+
7. [7] A computer program is a function that takes in 4 bits, where each bit is either a 0 or a 1 , and outputs TRUE or FALSE. How many computer programs are there?
|
| 30 |
+
Answer: 65536 The function has $2^{4}$ inputs and 2 outputs for each possible input, so the answer is $2^{2^{4}}=2^{16}=65536$.
|
| 31 |
+
8. [7] The angles of a convex $n$-sided polygon form an arithmetic progression whose common difference (in degrees) is a non-zero integer. Find the largest possible value of $n$ for which this is possible. (A polygon is convex if its interior angles are all less than $180^{\circ}$.)
|
| 32 |
+
Answer: 27 The exterior angles form an arithmetic sequence too (since they are each $180^{\circ}$ minus the corresponding interior angle). The sum of this sequence must be $360^{\circ}$. Let the smallest exterior angle be $x$ and the common difference be $d$. The sum of the exterior angles is then $x+(x+a)+(x+$ $2 a)+\ldots+(x+(n-1) a)=\frac{n(n-1)}{2} \cdot a+n x$. Setting this to 360 , and using $n x>0$, we get $n(n-1)<720$, so $n \leq 27$.
|
| 33 |
+
9. [7] Daniel wrote all the positive integers from 1 to $n$ inclusive on a piece of paper. After careful observation, he realized that the sum of all the digits that he wrote was exactly 10,000 . Find $n$.
|
| 34 |
+
Answer: 799 Let $S(n)$ denote the sum of the digits of $n$, and let $f(x)=\sum_{n=0}^{x} S(n)$. (We may add $n=0$ because $S(0)=0$.) Observe that:
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
f(99)=\sum_{a=0}^{9}\left(\sum_{b=0}^{9}(a+b)\right)=10 \sum_{b=0}^{9} b+10 \sum_{a=0}^{9} a=900
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
If $a$ is an integer between 1 and 9 inclusive, then:
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\sum_{n=100 a}^{100 a+99} S(n)=\sum_{n=100 a}^{100 a+99}(a+S(n-100 a))=100 a+f(99)=100 a+900
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Summing, we get:
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
f(100 a+99)=\sum_{n=0}^{a}(100 a+900)=900(a+1)+50 a(a+1)
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
This formula can be used to find benchmarks. However, it turns out that this formula alone will suffice, as things turn out rather nicely:
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\begin{aligned}
|
| 56 |
+
900(a+1)+50 a(a+1) & =10000 \\
|
| 57 |
+
50 a^{2}+950 a+900 & =10000 \\
|
| 58 |
+
50 a^{2}+950 a-9100 & =0 \\
|
| 59 |
+
50(a+26)(a-7) & =0 \\
|
| 60 |
+
a & =7
|
| 61 |
+
\end{aligned}
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Therefore $f(799)=10000$, and our answer is 799 .
|
| 65 |
+
|
| 66 |
+
## $2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 67 |
+
|
| 68 |
+
10. [8] Admiral Ackbar needs to send a 5-character message through hyperspace to the Rebels. Each character is a lowercase letter, and the same letter may appear more than once in a message. When the message is beamed through hyperspace, the characters come out in a random order. Ackbar chooses his message so that the Rebels have at least a $\frac{1}{2}$ chance of getting the same message he sent. How many distinct messages could he send?
|
| 69 |
+
Answer: 26 If there is more than one distinct letter sent in the message, then there will be at most a $1 / 5$ chance of transmitting the right message. So the message must consist of one letter repeated five times, so there are 26 possible messages.
|
| 70 |
+
11. [8] Lily and Sarah are playing a game. They each choose a real number at random between -1 and 1 . They then add the squares of their numbers together. If the result is greater than or equal to 1 , Lily wins, and if the result is less than 1, Sarah wins. What is the probability that Sarah wins?
|
| 71 |
+
Answer: $\frac{\pi}{4}$ If we let $x$ denote Lily's choice of number and $y$ denote Sarah's, then all possible outcomes are represented by the square with vertices $(-1,-1),(-1,1),(1,-1)$, and $(1,1)$. Sarah wins if $x^{2}+y^{2} \leq 1$, which is the area inside the unit circle. Since this has an area of $\pi$ and the entire square has an area of 4 , the probability that Sarah wins is $\frac{\pi}{4}$.
|
| 72 |
+
12. [8] Let $\omega$ be a circle of radius 1 centered at $O$. Let $B$ be a point on $\omega$, and let $l$ be the line tangent to $\omega$ at $B$. Let $A$ be on $l$ such that $\angle A O B=60^{\circ}$. Let $C$ be the foot of the perpendicular from $B$ to $O A$. Find the length of line segment $O C$.
|
| 73 |
+
Answer: $\frac{1}{2}$ We have $O C / O B=\cos \left(60^{\circ}\right)$. Since $O B=1, O C=\frac{1}{2}$.
|
| 74 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 75 |
+
13. [8] 8 students are practicing for a math contest, and they divide into pairs to take a practice test. In how many ways can they be split up?
|
| 76 |
+
Answer: 105 We create the pairs one at a time. The first person has 7 possible partners. Set this pair aside. Of the remaining six people, pick a person. He or she has 5 possible partners. Set this pair aside. Of the remaining four people, pick a person. He or she has 3 possible partners. Set this pair aside. Then the last two must be partners. So there are $7 \cdot 5 \cdot 3=105$ possible groupings. Alternatively, we can consider the 8 ! permutations of the students in a line, where the first two are a pair, the next two are a pair, etc. Given a grouping, there are 4 ! ways to arrange the four pairs in order, and in each pair, 2 ways to order the students. So our answer is $\frac{8!}{4!2^{4}}=7 \cdot 5 \cdot 3=105$.
|
| 77 |
+
14. [8] Let $f(x)=x^{4}+a x^{3}+b x^{2}+c x+d$ be a polynomial whose roots are all negative integers. If $a+b+c+d=2009$, find $d$.
|
| 78 |
+
Answer: 528 Call the roots $-x_{1},-x_{2},-x_{3}$, and $-x_{4}$. Then $f(x)$ must factor as $\left(x+x_{1}\right)\left(x+x_{2}\right)(x+$ $\left.x_{3}\right)\left(x+x_{4}\right)$. If we evaluate $f$ at 1 , we get $\left(1+x_{1}\right)\left(1+x_{2}\right)\left(1+x_{3}\right)\left(1+x_{4}\right)=a+b+c+d+1=$ $2009+1=2010$. $2010=2 \cdot 3 \cdot 5 \cdot 67$. $d$ is the product of the four roots, so $d=(-1) \cdot(-2) \cdot(-4) \cdot(-66)$.
|
| 79 |
+
15. [8] The curves $x^{2}+y^{2}=36$ and $y=x^{2}-7$ intersect at four points. Find the sum of the squares of the $x$-coordinates of these points.
|
| 80 |
+
Answer: 26 If we use the system of equations to solve for $y$, we get $y^{2}+y-29=0$ (since $x^{2}=y+7$ ). The sum of the roots of this equation is -1 . Combine this with $x^{2}=y+7$ to see that the sum of the square of the possible values of $x$ is $2 \cdot(-1+7 \cdot 2)=26$.
|
| 81 |
+
16. [9] Pick a random digit in the decimal expansion of $\frac{1}{99999}$. What is the probability that it is 0 ?
|
| 82 |
+
|
| 83 |
+
Answer: | $\frac{4}{5}$ |
|
| 84 |
+
| :---: |
|
| 85 |
+
| The decimal expansion of $\frac{1}{99999}$ | is $0 . \overline{00001}$.
|
| 86 |
+
|
| 87 |
+
17. [9] A circle passes through the points $(2,0)$ and $(4,0)$ and is tangent to the line $y=x$. Find the sum of all possible values for the $y$-coordinate of the center of the circle.
|
| 88 |
+
Answer: -6 First, we see that the x coordinate must be 3. Let the y coordinate be y. Now, we see that the radius is $r=\sqrt{1+y^{2}}$. The line from the center of the circle to the point of tangency with the line $x=y$ is perpendicular to the line $x=y$. Hence, the distance from the center of the circle to the line $x=y$ is $d=\sqrt{2}(3-y)$. Letting $r=d$ we see that the two possible values for y are 1 and -7 , which sum to -6 .
|
| 89 |
+
18. [9] Let $f$ be a function that takes in a triple of integers and outputs a real number. Suppose that $f$ satisfies the equations
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\begin{aligned}
|
| 93 |
+
f(a, b, c) & =\frac{f(a+1, b, c)+f(a-1, b, c)}{2} \\
|
| 94 |
+
f(a, b, c) & =\frac{f(a, b+1, c)+f(a, b-1, c)}{2} \\
|
| 95 |
+
f(a, b, c) & =\frac{f(a, b, c+1)+f(a, b, c-1)}{2}
|
| 96 |
+
\end{aligned}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
for all integers $a, b, c$. What is the minimum number of triples at which we need to evaluate $f$ in order to know its value everywhere?
|
| 100 |
+
Answer: 8 Note that if we have the value of $f$ at the 8 points: $(0,0,0),(1,0,0),(0,1,0),(0,0,1),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$, we can calculate the value for any triple of points because we have that $f(a+1, b, c)-(a, b, c)$ constant for any $a$, if $b$ and $c$ are fixed (and similarly for the other coordinates). To see why we cannot do this with less points, notice that we need to determine what the value of these 8 points anyways, and there is no "more efficient" way to determine them all in fewer evaluations.
|
| 101 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 102 |
+
19. [11] You are trapped in ancient Japan, and a giant enemy crab is approaching! You must defeat it by cutting off its two claws and six legs and attacking its weak point for massive damage. You cannot cut off any of its claws until you cut off at least three of its legs, and you cannot attack its weak point until you have cut off all of its claws and legs. In how many ways can you defeat the giant enemy crab? (Note that the legs are distinguishable, as are the claws.)
|
| 103 |
+
|
| 104 |
+
Answer: 14400 The answer is given by $6!2!\binom{5}{2}$, because we can cut off the claws and legs in any order and there are $\binom{5}{2}$ ways to decide when to cut off the two claws (since we can do it at any time among the last 5 cuts).
|
| 105 |
+
20. [11] Consider an equilateral triangle and a square both inscribed in a unit circle such that one side of the square is parallel to one side of the triangle. Compute the area of the convex heptagon formed by the vertices of both the triangle and the square.
|
| 106 |
+
Answer: $\frac{3+\sqrt{3}}{2}$
|
| 107 |
+
|
| 108 |
+
|
| 109 |
+
Consider the diagram above. We see that the shape is a square plus 3 triangles. The top and bottom triangles have base $\sqrt{2}$ and height $\frac{1}{2}(\sqrt{3}-\sqrt{2})$, and the triangle on the side has the same base and height $1-\frac{\sqrt{2}}{2}$ Adding their areas, we get the answer.
|
| 110 |
+
21. [11] Let $f(x)=x^{2}+2 x+1$. Let $g(x)=f(f(\cdots f(x)))$, where there are $2009 f \mathrm{~s}$ in the expression for $g(x)$. Then $g(x)$ can be written as
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
g(x)=x^{2^{2009}}+a_{2^{2009}-1} x^{2^{2009}-1}+\cdots+a_{1} x+a_{0}
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
where the $a_{i}$ are constants. Compute $a_{2^{2009}-1}$.
|
| 117 |
+
Answer: $2^{2009} f(x)=(x+1)^{2}$, so $f\left(x^{n}+c x^{n-1}+\ldots\right)=\left(x^{n}+c x^{n-1}+\ldots+1\right)^{2}=x^{2 n}+2 c x^{2 n-1}+\ldots$. Applying the preceding formula repeatedly shows us that the coefficient of the term of second highest degree in the polynomial doubles each time, so after 2009 applications of $f$ it is $2^{2009}$.
|
| 118 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 119 |
+
22. [12] Five cards labeled A, B, C, D, and E are placed consecutively in a row. How many ways can they be re-arranged so that no card is moved more than one position away from where it started? (Not moving the cards at all counts as a valid re-arrangement.)
|
| 120 |
+
Answer: 8 The only things we can do is leave cards where they are or switch them with adjacent cards. There is 1 way to leave them all where they are, 4 ways to switch just one adjacent pair, and 3 ways to switch two different adjacent pairs, for 8 possibilities total.
|
| 121 |
+
23. [12] Let $a_{0}, a_{1}, \ldots$ be a sequence such that $a_{0}=3, a_{1}=2$, and $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 0$. Find
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
\sum_{n=0}^{8} \frac{a_{n}}{a_{n+1} a_{n+2}}
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
Answer: $\frac{105}{212}$ We can re-write $\frac{a_{n}}{a_{n+1} a_{n+2}}$ as $\frac{a_{n+2}-a_{n+1}}{a_{n+1} a_{n+2}}=\frac{1}{a_{n+1}}-\frac{1}{a_{n+2}}$. We can thus re-write the sum as
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\left(\frac{1}{a_{1}}-\frac{1}{a_{2}}\right)+\left(\frac{1}{a_{2}}-\frac{1}{a_{3}}\right)+\left(\frac{1}{a_{4}}-\frac{1}{a_{3}}\right)+\ldots+\left(\frac{1}{a_{9}}-\frac{1}{a_{10}}\right)=\frac{1}{a_{1}}-\frac{1}{a_{10}}=\frac{1}{2}-\frac{1}{212}=\frac{105}{212} .
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
24. [12] Penta chooses 5 of the vertices of a unit cube. What is the maximum possible volume of the figure whose vertices are the 5 chosen points?
|
| 134 |
+
Answer: $\frac{1}{2}$ Label the vertices of the cube $A, B, C, D, E, F, G, H$, such that $A B C D$ is the top face of the cube, $E$ is directly below $A, F$ is directly below $B, G$ is directly below $C$, and $H$ is directly
|
| 135 |
+
below $D$. We can obtain a volume of $\frac{1}{2}$ by taking the vertices $A, B, C, F$, and $H$. To compute the volume of $A C B F H$, we will instead compute the volume of the parts of the cube that are not part of $A B C F H$. This is just the three tetrahedrons $C F G H, A E F H$, and $A C D H$, which each have volume $\frac{1}{6}$ (by using the $\frac{1}{3} b h$ formula for the area of a pyramid). Therefore, the volume not contained in $A C B F H$ is $3 \cdot \frac{1}{6}=\frac{1}{2}$, so the volume contained in $A C B F H$ is $1-\frac{1}{2}=\frac{1}{2}$.
|
| 136 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 137 |
+
25. [14] Find all solutions to $x^{4}+2 x^{3}+2 x^{2}+2 x+1=0$ (including non-real solutions).
|
| 138 |
+
|
| 139 |
+
Answer: $-1, i,-i$ We can factor the polynomial as $(x+1)^{2}\left(x^{2}+1\right)$.
|
| 140 |
+
26. [14] In how many ways can the positive integers from 1 to 100 be arranged in a circle such that the sum of every two integers placed opposite each other is the same? (Arrangements that are rotations of each other count as the same.) Express your answer in the form $a!\cdot b^{c}$.
|
| 141 |
+
Answer: $49!\cdot 2^{49}$ Split the integers up into pairs of the form $(x, 101-x)$. In the top half of the circle, exactly one element from each pair occurs, and there are thus 50 ! ways to arrange them. and also $2^{50}$ ways to decide whether the larger or smaller number in each pair occurs in the top half of the circle. We then need to divide by 100 since rotations are not considered distinct, so we get $\frac{50!2^{50}}{100}=49!\cdot 2^{49}$.
|
| 142 |
+
27. [14] $A B C D$ is a regular tetrahedron of volume 1. Maria glues regular tetrahedra $A^{\prime} B C D, A B^{\prime} C D$, $A B C^{\prime} D$, and $A B C D^{\prime}$ to the faces of $A B C D$. What is the volume of the tetrahedron $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ ?
|
| 143 |
+
Answer: $\frac{125}{27}$ Consider the tetrahedron with vertices at $W=(1,0,0), X=(0,1,0), Y=(0,0,1)$, and $Z=(1,1,1)$. This tetrahedron is similar to $A B C D$. It has center $O=\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right)$. We can construct a tetrahedron $W^{\prime} X^{\prime} Y^{\prime} Z^{\prime}$ in the same way that $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ was constructed by letting $W^{\prime}$ be the reflection of $W$ across $X Y Z$ and so forth. Then we see that $Z^{\prime}=\left(-\frac{1}{3},-\frac{1}{3},-\frac{1}{3}\right)$, so $O Z^{\prime}$ has length $\frac{5}{6} \sqrt{3}$, whereas $O Z$ has length $\frac{1}{2} \sqrt{3}$. We thus see that $W^{\prime} X^{\prime} Y^{\prime} Z^{\prime}$ has a side length $\frac{\frac{5}{6}}{\frac{1}{2}}=\frac{5}{3}$ that of $W X Y Z$, so by similarity the same is true of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ and $A B C D$. In particular, the volume of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is $\left(\frac{5}{3}\right)^{3}$ that of $A B C D$, so it is $\frac{125}{27}$.
|
| 144 |
+
|
| 145 |
+
## $2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 146 |
+
|
| 147 |
+
28. [17] Six men and their wives are sitting at a round table with 12 seats. These men and women are very jealous - no man will allow his wife to sit next to any man except for himself, and no woman will allow her husband to sit next to any woman except for herself. In how many distinct ways can these 12 people be seated such that these conditions are satisfied? (Rotations of a valid seating are considered distinct.)
|
| 148 |
+
|
| 149 |
+
Answer: 288000 Think of this problem in terms of "blocks" of men and women, that is, groups of men and women sitting together. Each block must contain at least two people; otherwise you have a man sitting next to two women (or vice-versa).
|
| 150 |
+
We will define the notation $\left[a_{1}, b_{1}, a_{2}, b_{2}, \ldots\right]$ to mean a seating arrangement consisting of, going in order, $a_{1}$ men, $b_{1}$ women, $a_{2}$ men, $b_{2}$ women, and so on.
|
| 151 |
+
|
| 152 |
+
Split the problem into three cases, each based on the number of blocks of men and women:
|
| 153 |
+
Case 1: One block of each, $[6,6]$.
|
| 154 |
+
There are 12 ways to choose the seats where the men sit, and $6!$ ways to arrange those men. The two women on either side of the men are uniquely determined by the men they sit next to. There are 4 ! ways to arrange the other four women. This gives $6!\cdot 288$ ways.
|
| 155 |
+
Case 2: Two blocks of each.
|
| 156 |
+
|
| 157 |
+
The arrangement is $[a, b, c, d]$, where $a+c=b+d=6$. There are five distinct block schematics: $[2,2,4,4],[2,3,4,3],[2,4,4,2],[3,2,3,4]$, and $[3,3,3,3]$. (The others are rotations of one of the above.) For each of these, there are 6 ! ways to arrange the men. In addition, four women are uniquely determined because they sit next to a man. There are 2 ways to arrange the other two women. Each of the first four possible block schematics gives 12 distinct rotations, while the fifth one gives 6 . This gives $6!(2)(12+12+12+12+6)=6!\cdot 108$ ways.
|
| 158 |
+
Case 3: Three blocks of each, $[2,2,2,2,2,2]$.
|
| 159 |
+
There are 4 ways to choose where the men sit and 6 ! ways to arrange those men. Each placement of men will uniquely determine the placement of each women. This gives $6!\cdot 4$ ways.
|
| 160 |
+
Then we have a grand total of $6!\cdot(288+108+4)=6!\cdot 400=288000$ seating arrangements.
|
| 161 |
+
29. [17] For how many integer values of $b$ does there exist a polynomial function with integer coefficients such that $f(2)=2010$ and $f(b)=8$ ?
|
| 162 |
+
Answer: 32 We can take $f(x)=-\frac{2002}{d}(x-b)+2010$ for all divisors $d$ of -2002 . To see that we can't get any others, note that $b-2$ must divide $f(b)-f(2)$, so $b-2$ divides -2002 (this is because $b-2$ divides $b^{n}-2^{n}$ and hence any sum of numbers of the form $b^{n}-2^{n}$ ).
|
| 163 |
+
30. [17] Regular hexagon $A B C D E F$ has side length 2. A laser beam is fired inside the hexagon from point $A$ and hits $\overline{B C}$ at point $G$. The laser then reflects off $\overline{B C}$ and hits the midpoint of $\overline{D E}$. Find $B G$.
|
| 164 |
+
Answer: $\frac{2}{5}$ Look at the diagram below, in which points $J, K, M, T$, and $X$ have been defined. $M$ is the midpoint of $\overline{D E}, B C J K$ is a rhombus with $J$ lying on the extension of $\overline{C D}, T$ is the intersection of lines $\overline{C D}$ and $\overline{G M}$ when extended, and $X$ is on $\overline{J T}$ such that $\overline{X M} \| \overline{J K}$.
|
| 165 |
+
|
| 166 |
+
|
| 167 |
+
It can be shown that $m \angle M D X=m \angle M X D=60^{\circ}$, so $\triangle D M X$ is equilateral, which yields $X M=1$. The diagram indicates that $J X=5$. One can show by angle-angle similarity that $\triangle T X M \sim \triangle T J K$, which yields $T X=5$.
|
| 168 |
+
One can also show by angle-angle similarity that $\triangle T J K \sim \triangle T C G$, which yields the proportion $\frac{T J}{J K}=\frac{T C}{C G}$. We know everything except $C G$, which we can solve for. This yields $C G=\frac{8}{5}$, so $B G=\frac{2}{5}$.
|
| 169 |
+
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
| 170 |
+
31. [20] There are two buildings facing each other, each 5 stories high. How many ways can Kevin string ziplines between the buildings so that:
|
| 171 |
+
(a) each zipline starts and ends in the middle of a floor.
|
| 172 |
+
(b) ziplines can go up, stay flat, or go down, but can't touch each other (this includes touching at their endpoints).
|
| 173 |
+
|
| 174 |
+
Note that you can't string a zipline between two floors of the same building.
|
| 175 |
+
Answer: 252 Associate with each configuration of ziplines a path in the plane as follows: Suppose there are $k$ ziplines. Let $a_{0}, \ldots, a_{k}$ be the distances between consecutive ziplines on the left building
|
| 176 |
+
( $a_{0}$ is the floor on which the first zipline starts, and $a_{k}$ is the distance from the last zipline to the top of the building). Define $b_{0}, \ldots, b_{k}$ analogously for the right building. The path in the plane consists of starting at $(0,0)$ and going a distance $a_{0}$ to the right, $b_{0}$ up, $a_{1}$ to the right, $b_{1}$ up, etc. We thus go from $(0,0)$ to $(5,5)$ while traveling only up and to the right between integer coordinates. We can check that there is exactly one configuration of ziplines for each such path, so the answer is the number of paths from $(0,0)$ to $(5,5)$ where you only travel up and to the right. This is equal to $\binom{10}{5}=252$, since there are 10 total steps to make, and we must choose which 5 of them go to the right.
|
| 177 |
+
32. [20] A circle $\omega_{1}$ of radius 15 intersects a circle $\omega_{2}$ of radius 13 at points $P$ and $Q$. Point $A$ is on line $P Q$ such that $P$ is between $A$ and $Q . R$ and $S$ are the points of tangency from $A$ to $\omega_{1}$ and $\omega_{2}$, respectively, such that the line $A S$ does not intersect $\omega_{1}$ and the line $A R$ does not intersect $\omega_{2}$. If $P Q=24$ and $\angle R A S$ has a measure of $90^{\circ}$, compute the length of $A R$.
|
| 178 |
+
Answer: $\sqrt[{14+\sqrt{97}}]{ }$ Let $O_{1}$ be the center of $\omega_{1}$ and $O_{2}$ be the center of $\omega_{2}$. Then $O_{1} O_{2}$ and $P Q$ are perpendicular. Let their point of intersection be $X$. Using the Pythagorean theorem, the fact that $P Q=24$, and our knowledge of the radii of the circles, we can compute that $O_{1} X=9$ and $O_{2} X=5$, so $O_{1} O_{2}=14$. Let $S O_{1}$ and $R O_{2}$ meet at $Y$. Then $S A R Y$ is a square, say of side length $s$. Then $O_{1} Y=s-15$ and $O_{2} Y=s-13$. So, $O_{1} O_{2} Y$ is a right triangle with sides $14, s-15$, and $s-13$. By the Pythagorean theorem, $(s-13)^{2}+(s-15)^{2}=14^{2}$. We can write this as $2 s^{2}-4 \cdot 14 s+198=0$, or $s^{2}-28 s+99=0$. The quadratic formula then gives $s=\frac{28 \pm \sqrt{388}}{2}=14 \pm \sqrt{97}$. Since $14-\sqrt{97}<15$ and $Y O_{1}>15$, we can discard the root of $14-\sqrt{97}$, and the answer is therefore $14+\sqrt{97}$.
|
| 179 |
+
33. [20] Compute
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
Note that $\binom{n}{k}$ is defined as $\frac{n!}{k!(n-k)!}$.
|
| 186 |
+
Answer: $\frac{2009}{2008}$ Observe that
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
\begin{aligned}
|
| 190 |
+
\frac{k+1}{k}\left(\frac{1}{\binom{n-1}{k}}-\frac{1}{\binom{n}{k}}\right) & =\frac{k+1}{k} \frac{\binom{n}{k}-\binom{n-1}{k}}{\binom{n}{k}\binom{n-1}{k}} \\
|
| 191 |
+
& =\frac{k+1}{k} \frac{\binom{n-1}{k-1}}{\binom{n}{k}\binom{n-1}{k}} \\
|
| 192 |
+
& =\frac{k+1}{k} \frac{(n-1)!k!k!(n-k-1)!(n-k)!}{n!(n-1)!(k-1)!(n-k)!} \\
|
| 193 |
+
& =\frac{k+1}{k} \frac{k \cdot k!(n-k-1)!}{n!} \\
|
| 194 |
+
& =\frac{(k+1)!(n-k-1)!}{n!} \\
|
| 195 |
+
& =\frac{1}{\binom{n}{k+1}}
|
| 196 |
+
\end{aligned}
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
Now apply this with $k=2008$ and sum across all $n$ from 2009 to $\infty$. We get
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}=\frac{2009}{2008} \sum_{n=2009}^{\infty} \frac{1}{\binom{n-1}{2008}}-\frac{1}{\binom{n}{2008}}
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
All terms from the sum on the right-hand-side cancel, except for the initial $\frac{1}{\binom{2008}{2008}}$, which is equal to 1 , so we get $\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}=\frac{2009}{2008}$.
|
| 206 |
+
34. [25] How many hits does "3.1415" get on Google? Quotes are for clarity only, and not part of the search phrase. Also note that Google does not search substrings, so a webpage with 3.14159 on it will not match 3.1415 . If $A$ is your answer, and $S$ is the correct answer, then you will get $\max (25-\mid \ln (A)-$ $\ln (S) \mid, 0)$ points, rounded to the nearest integer.
|
| 207 |
+
|
| 208 |
+
Answer: 422000
|
| 209 |
+
35. [25] Call an integer $n>1$ radical if $2^{n}-1$ is prime. What is the 20 th smallest radical number? If $A$ is your answer, and $S$ is the correct answer, you will get $\max \left(25\left(1-\frac{|A-S|}{S}\right), 0\right)$ points, rounded to the nearest integer.
|
| 210 |
+
Answer: 4423
|
| 211 |
+
36. [25] Write down a pair of integers $(a, b)$, where $-100000<a<b<100000$. You will get $\max (25, k)$ points, where $k$ is the number of other teams' pairs that you interleave. (Two pairs $(a, b)$ and $(c, d)$ of integers interleave each other if $a<c<b<d$ or $c<a<d<b$.)
|
| 212 |
+
|
HarvardMIT/md/en-131-2009-nov-team-solutions.md
ADDED
|
@@ -0,0 +1,55 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $2^{\text {nd }}$ Annual Harvard-MIT November Tournament <br> Saturday 7 November 2009 <br> Team Round <br> Down the Infinite Corridor
|
| 2 |
+
|
| 3 |
+
Consider an isosceles triangle $T$ with base 10 and height 12 . Define a sequence $\omega_{1}, \omega_{2}, \ldots$ of circles such that $\omega_{1}$ is the incircle of $T$ and $\omega_{i+1}$ is tangent to $\omega_{i}$ and both legs of the isosceles triangle for $i>1$.
|
| 4 |
+
|
| 5 |
+
1. [3] Find the radius of $\omega_{1}$.
|
| 6 |
+
|
| 7 |
+
Answer: $\frac{10}{3}$ Using the Pythagorean theorem, we see that the legs of $T$ each have length 13. Let $r$ be the radius of $\omega_{1}$. We can divide $T$ into three triangles, each with two vertices at vertices of $T$ and one vertex at the center of $\omega_{1}$. These triangles all have height $r$ and have bases 13,13 , and 10 . Thus their total area is $\frac{13 r}{2}+\frac{13 r}{2}+\frac{10 r}{2}=18 r$. However, $T$ has height 12 and base 10 , so its area is 60 . Thus $18 r=60$, so $r=\frac{10^{2}}{3}$.
|
| 8 |
+
2. [3] Find the ratio of the radius of $\omega_{i+1}$ to the radius of $\omega_{i}$.
|
| 9 |
+
3. [3] Find the total area contained in all the circles.
|
| 10 |
+
|
| 11 |
+
Answer: $\frac{180 \pi}{13}$ Using the notation from the previous solution, the area contained in the $i$ th circle is equal to $\pi r_{i}^{2}$. Since the radii form a geometric sequence, the areas do as well. Specifically, the areas form a sequence with initial term $\pi \cdot \frac{100}{9}$ and common ratio $\frac{16}{81}$, so their sum is then $\pi \cdot \frac{\frac{100}{9}}{\frac{95}{81}}=\frac{180 \pi}{13}$.
|
| 12 |
+
|
| 13 |
+
## Bouncy Balls
|
| 14 |
+
|
| 15 |
+
In the following problems, you will consider the trajectories of balls moving and bouncing off of the boundaries of various containers. The balls are small enough that you can treat them as points. Let us suppose that a ball starts at a point $X$, strikes a boundary (indicated by the line segment $A B$ ) at $Y$, and then continues, moving along the ray $Y Z$. Balls always bounce in such a way that $\angle X Y A=\angle B Y Z$. This is indicated in the above diagram.
|
| 16 |
+
|
| 17 |
+
|
| 18 |
+
Balls bounce off of boundaries in the same way light reflects off of mirrors - if the ball hits the boundary at point $P$, the trajectory after $P$ is the reflection of the trajectory before $P$ through the perpendicular to the boundary at $P$.
|
| 19 |
+
|
| 20 |
+
A ball inside a rectangular container of width 7 and height 12 is launched from the lower-left vertex of the container. It first strikes the right side of the container after traveling a distance of $\sqrt{53}$ (and strikes no other sides between its launch and its impact with the right side).
|
| 21 |
+
4. [2] Find the height at which the ball first contacts the right side.
|
| 22 |
+
|
| 23 |
+
Answer: 2 Let $h$ be this height. Then, using the Pythagorean theorem, we see that $h^{2}+7^{2}=53$, so $h=2$.
|
| 24 |
+
5. [3] How many times does the ball bounce before it returns to a vertex? (The final contact with a vertex does not count as a bounce.)
|
| 25 |
+
Answer: 5 Every segment the ball traverses between bounces takes it 7 units horizontally and 2 units up. Thus, after 5 bounces it has traveled up 10 units, and the final segment traversed takes it directly to the upper right vertex of the rectangle.
|
| 26 |
+
|
| 27 |
+
Now a ball is launched from a vertex of an equilateral triangle with side length 5 . It strikes the opposite side after traveling a distance of $\sqrt{19}$.
|
| 28 |
+
6. [4] Find the distance from the ball's point of first contact with a wall to the nearest vertex.
|
| 29 |
+
|
| 30 |
+
Answer: 2
|
| 31 |
+
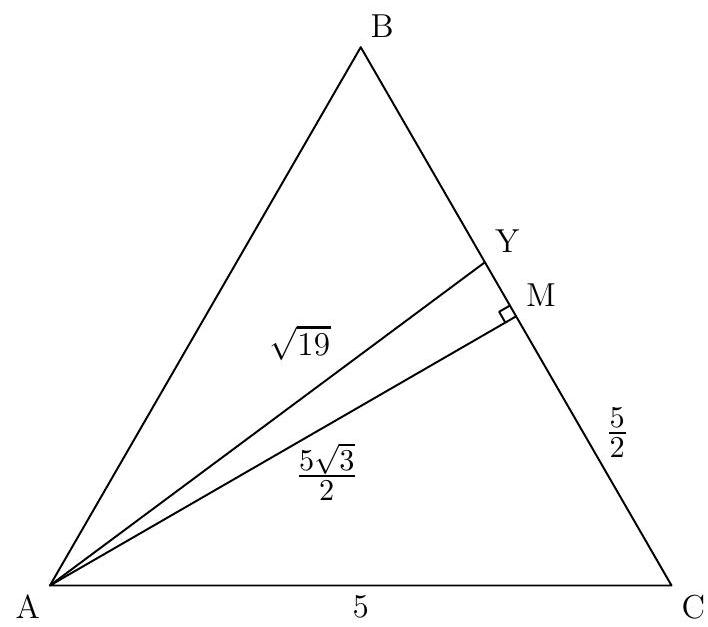
|
| 32 |
+
|
| 33 |
+
Consider the diagram above, where $M$ is the midpoint of $B C$. Then $A M$ is perpendicular to $B C$ since $A B C$ is equilateral, so by the Pythagorean theorem $A M=\frac{5 \sqrt{3}}{2}$. Then, using the Pythagorean theorem again, we see that $M Y=\frac{1}{2}$, so that $B Y=2$.
|
| 34 |
+
7. [4] How many times does the ball bounce before it returns to a vertex? (The final contact with a vertex does not count as a bounce.)
|
| 35 |
+
Answer: 7 The key idea is that, instead of reflecting the line $A Y$ off of $B C$, we will reflect $A B C$ about $B C$ and extend $A Y$ beyond $\triangle A B C$. We keep doing this until the extension of $A Y$ hits a vertex of one of our reflected triangles. This is illustrated in the diagram below:
|
| 36 |
+
|
| 37 |
+
|
| 38 |
+
We can calculate that the line $A Y$ has slope $\frac{\frac{3 \sqrt{3}}{\frac{2}{2}}}{\frac{7}{2}}=\frac{3 \sqrt{3}}{7}$, so that (as indicated in the diagram), $A Y$ first intersects a vertex at the point $\left(\frac{35}{2}, \frac{15 \sqrt{3}}{2}\right)^{2}$. To get there, it has to travel through 2 horizontal lines, 1 upward sloping line, and 4 downward sloping lines, so it bounces $2+1+4=7$ times total.
|
| 39 |
+
|
| 40 |
+
In this final problem, a ball is again launched from the vertex of an equilateral triangle with side length 5 .
|
| 41 |
+
8. [6] In how many ways can the ball be launched so that it will return again to a vertex for the first time after 2009 bounces?
|
| 42 |
+
Answer: 502 We will use the same idea as in the previous problem. We first note that every vertex of a triangle can be written uniquely in the form $a(5,0)+b\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)$, where $a$ and $b$ are non-negative integers. Furthermore, if a ball ends at $a(5,0)+b\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)$, then it bounches off of a wall $2(a+b)-3$ times. Therefore, the possible directions that you can launch the ball in correspond to solutions to $2(a+b)-3=2009$, or $a+b=1006$. However, if $a$ and $b$ have a common factor, say, $k$, then the ball will pass through the vertex corresponding to $\frac{a}{k}$ and $\frac{b}{k}$ before it passes through the vertex corresponding to $a$ and $b$. Therefore, we must discount all such pairs $a, b$. This corresponds to when $a$ is even or $a=503$, so after removing these we are left with 502 remaining possible values of $a$, hence 502 possible directions in which to launch the ball.
|
| 43 |
+
|
| 44 |
+
## Super Mario 64!
|
| 45 |
+
|
| 46 |
+
Mario is once again on a quest to save Princess Peach. Mario enters Peach's castle and finds himself in a room with 4 doors. This room is the first in a sequence of 2 indistinugishable rooms. In each room, 1 door leads to the next room in the sequence (or, for the second room, into Bowser's level), while the other 3 doors lead to the first room.
|
| 47 |
+
9. [3] Suppose that in every room, Mario randomly picks a door to walk through. What is the expected number of doors (not including Mario's initial entrance to the first room) through which Mario will pass before he reaches Bowser's level?
|
| 48 |
+
Answer: 20 Let $E_{i}$ be the expected number of doors through which Mario will pass in the future if he is currently in room $i$ for $i=1,2,3$ (we will set $E_{3}=0$ ). We claim that $E_{i}=1+\frac{3}{4} E_{1}+\frac{1}{4} E_{i+1}$. Indeed, the 1 at the beginning comes from the fact that we need to pass through a door to leave the room, the $\frac{3}{4} E_{1}$ comes from the fact that there is a $\frac{3}{4}$ chance of ending up in room 1 , and the $\frac{1}{4} E_{i+1}$ corresponds to the fact that there is a $\frac{1}{4}$ chance of ending up in $E_{i+1}$. Using this, we get $E_{1}=1+\frac{3}{4} E_{1}+\frac{1}{4} E_{2}$, or $E_{1}=4+E_{2}$. We also get $E_{2}=1+\frac{3}{4} E_{1}$. Solving this system of equations yields $E_{1}=20$.
|
| 49 |
+
10. [4] Suppose that instead there are 6 rooms with 4 doors. In each room, 1 door leads to the next room in the sequence (or, for the last room, Bowser's level), while the other 3 doors lead to the first room. Now what is the expected number of doors through which Mario will pass before he reaches Bowser's level?
|
| 50 |
+
|
| 51 |
+
Answer: 5460 This problem works in the same general way as the last problem, but it can be more succintly solved using the general formula, which is provided below in the solution to the next problem.
|
| 52 |
+
11. [5] In general, if there are $d$ doors in every room (but still only 1 correct door) and $r$ rooms, the last of which leads into Bowser's level, what is the expected number of doors through which Mario will pass before he reaches Bowser's level?
|
| 53 |
+
Answer: $\frac{d\left(d^{r}-1\right)}{d-1}$ Let $E_{i}$ be the expected number of doors through which Mario will pass in the future if he is currently in room $i$ for $i=1,2, \ldots, r+1$ (we will set $E_{r+1}=0$ ). We claim that $E_{i}=1+\frac{d-1}{d} E_{1}+\frac{1}{d} E_{i+1}$. This is because, as before, there is a $\frac{d-1}{d}$ chance of ending up in room 1, and a $\frac{1}{d}$ chance of ending up in room $i+1$. Note that we can re-write this equation as $d E_{i}=d+(d-1) E_{1}+E_{i+1}$.
|
| 54 |
+
We can solve this system of equation as follows: let $E_{1}=E_{i}+c_{i}$. Then we can re-write each equation as $d E_{1}-d \cdot c_{i}=d+(d-1) E_{1}+E_{1}-c_{i+1}$, so $c_{i+1}=d \cdot c_{i}+d$, and $c_{1}=0$. We can then see that $c_{i}=d \frac{d^{i-1}-1}{d-1}$ (either by finding the pattern or by using more advanced techniques, such as those given at http://en.wikipedia.org/wiki/Recurrence_relation). Solving for $E_{1}$ using $E_{1}=E_{r}+c_{r}$ and $E_{r}=1+\frac{d-1}{d} E_{1}$, we get $E_{1}=\frac{d\left(d^{r}-1\right)}{d-1}$.
|
| 55 |
+
|
HarvardMIT/md/en-132-2010-feb-alg-solutions.md
ADDED
|
@@ -0,0 +1,147 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament
|
| 2 |
+
|
| 3 |
+
Saturday 20 February 2010
|
| 4 |
+
Algebra Subject Test
|
| 5 |
+
|
| 6 |
+
1. [3] Suppose that $x$ and $y$ are positive reals such that
|
| 7 |
+
|
| 8 |
+
$$
|
| 9 |
+
x-y^{2}=3, \quad x^{2}+y^{4}=13
|
| 10 |
+
$$
|
| 11 |
+
|
| 12 |
+
Find $x$.
|
| 13 |
+
Answer: $\frac{3+\sqrt{17}}{2}$ Squaring both sides of $x-y^{2}=3$ gives $x^{2}+y^{4}-2 x y^{2}=9$. Subtract this equation from twice the second given to get $x^{2}+2 x y^{2}+y^{4}=17 \Longrightarrow x+y^{2}= \pm 17$. Combining this equation with the first given, we see that $x=\frac{3 \pm \sqrt{17}}{2}$. Since $x$ is a positive real, $x$ must be $\frac{3+\sqrt{17}}{2}$.
|
| 14 |
+
2. [3] The rank of a rational number $q$ is the unique $k$ for which $q=\frac{1}{a_{1}}+\cdots+\frac{1}{a_{k}}$, where each $a_{i}$ is the smallest positive integer such that $q \geq \frac{1}{a_{1}}+\cdots+\frac{1}{a_{i}}$. Let $q$ be the largest rational number less than $\frac{1}{4}$ with rank 3 , and suppose the expression for $q$ is $\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}$. Find the ordered triple $\left(a_{1}, a_{2}, a_{3}\right)$.
|
| 15 |
+
Answer: $(5,21,421)$ Suppose that $A$ and $B$ were rational numbers of rank 3 less than $\frac{1}{4}$, and let $a_{1}, a_{2}, a_{3}, b_{1}, b_{2}, b_{3}$ be positive integers so that $A=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}$ and $B=\frac{1}{b_{1}}+\frac{1}{b_{2}}+\frac{1}{b_{3}}$ are the expressions for $A$ and $B$ as stated in the problem. If $b_{1}<a_{1}$ then $A<\frac{1}{a_{1}-1} \leq \frac{1}{b_{1}}<B$. In other words, of all the rationals less than $\frac{1}{4}$ with rank 3 , those that have $a_{1}=5$ are greater than those that have $a_{1}=6,7,8, \ldots$ Therefore we can "build" $q$ greedily, adding the largest unit fraction that keeps $q$ less than $\frac{1}{4}$ :
|
| 16 |
+
$\frac{1}{5}$ is the largest unit fraction less than $\frac{1}{4}$, hence $a_{1}=5$;
|
| 17 |
+
$\frac{1}{27}$ is the largest unit fraction less than $\frac{1}{4}-\frac{1}{5}$, hence $a_{2}=21$;
|
| 18 |
+
$\frac{1}{421}$ is the largest unit fraction less than $\frac{1}{4}-\frac{1}{5}-\frac{1}{21}$, hence $a_{3}=421$.
|
| 19 |
+
3. [4] Let $S_{0}=0$ and let $S_{k}$ equal $a_{1}+2 a_{2}+\ldots+k a_{k}$ for $k \geq 1$. Define $a_{i}$ to be 1 if $S_{i-1}<i$ and -1 if $S_{i-1} \geq i$. What is the largest $k \leq 2010$ such that $S_{k}=0$ ?
|
| 20 |
+
Answer: 1092 Suppose that $S_{N}=0$ for some $N \geq 0$. Then $a_{N+1}=1$ because $N+1 \geq S_{N}$. The following table lists the values of $a_{k}$ and $S_{k}$ for a few $k \geq N$ :
|
| 21 |
+
|
| 22 |
+
| $k$ | $a_{k}$ | $S_{k}$ |
|
| 23 |
+
| :--- | ---: | :--- |
|
| 24 |
+
| $N$ | | 0 |
|
| 25 |
+
| $N+1$ | 1 | $N+1$ |
|
| 26 |
+
| $N+2$ | 1 | $2 N+3$ |
|
| 27 |
+
| $N+3$ | -1 | $N$ |
|
| 28 |
+
| $N+4$ | 1 | $2 N+4$ |
|
| 29 |
+
| $N+5$ | -1 | $N-1$ |
|
| 30 |
+
| $N+6$ | 1 | $2 N+5$ |
|
| 31 |
+
| $N+7$ | -1 | $N-2$ |
|
| 32 |
+
|
| 33 |
+
We see inductively that, for every $i \geq 1$,
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
S_{N+2 i}=2 N+2+i
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
and
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
S_{N+1+2 i}=N+1-i
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
thus $S_{3 N+3}=0$ is the next $k$ for which $S_{k}=0$. The values of $k$ for which $S_{k}=0$ satisfy the recurrence relation $p_{n+1}=3 p_{n}+3$, and we compute that the first terms of the sequence are $0,3,12,39,120,363,1092$; hence 1092 is our answer.
|
| 46 |
+
4. [4] Suppose that there exist nonzero complex numbers $a, b, c$, and $d$ such that $k$ is a root of both the equations $a x^{3}+b x^{2}+c x+d=0$ and $b x^{3}+c x^{2}+d x+a=0$. Find all possible values of $k$ (including complex values).
|
| 47 |
+
Answer: $1,-1, i,-i$ Let $k$ be a root of both polynomials. Multiplying the first polynomial by $k$ and subtracting the second, we have $a k^{4}-a=0$, which means that $k$ is either $1,-1, i$, or $-i$. If $a=b=c=d=1$, then $-1, i$, and $-i$ are roots of both polynomials. If $a=b=c=1$ and $d=-3$, then 1 is a root of both polynomials. So $k$ can be $1,-1, i$, and $-i$.
|
| 48 |
+
5. [5] Suppose that $x$ and $y$ are complex numbers such that $x+y=1$ and that $x^{20}+y^{20}=20$. Find the sum of all possible values of $x^{2}+y^{2}$.
|
| 49 |
+
Answer: -90 We have $x^{2}+y^{2}+2 x y=1$. Define $a=2 x y$ and $b=x^{2}+y^{2}$ for convenience. Then $a+b=1$ and $b-a=x^{2}+y^{2}-2 x y=(x-y)^{2}=2 b-1$ so that $x, y=\frac{\sqrt{2 b-1} \pm 1}{2}$. Then
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\begin{aligned}
|
| 53 |
+
x^{20}+y^{20} & =\left(\frac{\sqrt{2 b-1}+1}{2}\right)^{20}+\left(\frac{\sqrt{2 b-1}-1}{2}\right)^{20} \\
|
| 54 |
+
& =\frac{1}{2^{20}}\left[(\sqrt{2 b-1}+1)^{20}+(\sqrt{2 b-1}-1)^{20}\right] \\
|
| 55 |
+
& =\frac{2}{2^{20}}\left[(\sqrt{2 b-1})^{20}+\binom{20}{2}(\sqrt{2 b-1})^{18}+\binom{20}{4}(\sqrt{2 b-1})^{16}+\ldots\right] \\
|
| 56 |
+
& =\frac{2}{2^{20}}\left[(2 b-1)^{10}+\binom{20}{2}(2 b-1)^{9}+\binom{20}{4}(2 b-1)^{8}+\ldots\right] \\
|
| 57 |
+
& =20
|
| 58 |
+
\end{aligned}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
We want to find the sum of distinct roots of the above polynomial in $b$; we first prove that the original polynomial is square-free. The conditions $x+y=1$ and $x^{20}+y^{20}=20$ imply that $x^{20}+(1-x)^{20}-20=0$; let $p(x)=x^{20}+(1-x)^{20}-20 . p$ is square-free if and only if $G C D\left(p, p^{\prime}\right)=c$ for some constant $c$ :
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\begin{aligned}
|
| 65 |
+
\operatorname{GCD}\left(p, p^{\prime}\right) & =\operatorname{GCD}\left(x^{20}+(1-x)^{20}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
|
| 66 |
+
& =\operatorname{GCD}\left(x^{20}-x(1-x)^{19}+(1-x)^{19}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
|
| 67 |
+
& =G C D\left((1-x)^{19}-20, x^{19}-(1-x)^{19}\right) \\
|
| 68 |
+
& =G C D\left((1-x)^{19}-20, x^{19}-20\right)
|
| 69 |
+
\end{aligned}
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
The roots of $x^{19}-20$ are $\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$; the roots of $(1-x)^{19}-20$ are $1-\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$. If $x^{19}-20$ and $(1-x)^{19}-20$ share a common root, then there exist integers $m, n$ such that $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=1-\sqrt[19]{20^{n}} \exp \left(\frac{2 \pi i n}{19}\right)$; since the imaginary parts of both sides must be the same, we have $m=n$ and $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=\frac{1}{2} \Longrightarrow 20^{m}=\frac{1}{2^{19}}$, a contradiction. Thus we have proved that the polynomial in $x$ has no double roots. Since for each $b$ there exists a unique pair ( $x, y$ ) (up to permutations) that satisfies $x^{2}+y^{2}=b$ and $(x+y)^{2}=1$, the polynomial in $b$ has no double roots.
|
| 73 |
+
Let the coefficient of $b^{n}$ in the above equation be $\left[b^{n}\right]$. By Vieta's Formulas, the sum of all possible values of $b=x^{2}+y^{2}$ is equal to $-\frac{\left[b^{9}\right]}{\left[b^{0}\right]} .\left[b^{10}\right]=\frac{2}{2^{20}}\left(2^{10}\right)$ and $\left[b^{9}\right]=\frac{2}{2^{20}}\left(-\binom{10}{1} 2^{9}+\binom{20}{2} 2^{9}\right)$; thus $-\frac{\left[b^{9}\right]}{\left[b^{10}\right]}=-\frac{\binom{10}{1} 2^{9}-\binom{20}{2_{2}}^{9}}{2^{10}}=-90$.
|
| 74 |
+
6. [5] Suppose that a polynomial of the form $p(x)=x^{2010} \pm x^{2009} \pm \cdots \pm x \pm 1$ has no real roots. What is the maximum possible number of coefficients of -1 in $p$ ?
|
| 75 |
+
Answer: 1005 Let $p(x)$ be a polynomial with the maximum number of minus signs. $p(x)$ cannot have more than 1005 minus signs, otherwise $p(1)<0$ and $p(2) \geq 2^{2010}-2^{2009}-\ldots-2-1=$ 1 , which implies, by the Intermediate Value Theorem, that $p$ must have a root greater than 1 .
|
| 76 |
+
Let $p(x)=\frac{x^{2011}+1}{x+1}=x^{2010}-x^{2009}+x^{2008}-\ldots-x+1$. -1 is the only real root of $x^{2011}+1=0$ but $p(-1)=2011$; therefore $p$ has no real roots. Since $p$ has 1005 minus signs, it is the desired polynomial.
|
| 77 |
+
7. [5] Let $a, b, c, x, y$, and $z$ be complex numbers such that
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
a=\frac{b+c}{x-2}, \quad b=\frac{c+a}{y-2}, \quad c=\frac{a+b}{z-2} .
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
If $x y+y z+z x=67$ and $x+y+z=2010$, find the value of $x y z$.
|
| 84 |
+
Answer: -5892 Manipulate the equations to get a common denominator: $a=\frac{b+c}{x-2} \Longrightarrow x-2=$ $\frac{b+c}{a} \Longrightarrow x-1=\frac{a+b+c}{a} \Longrightarrow \frac{1}{x-1}=\frac{a}{a+b+c}$; similarly, $\frac{1}{y-1}=\frac{b}{a+b+c}$ and $\frac{1}{z-1}=\frac{c}{a+b+c}$. Thus
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\begin{aligned}
|
| 88 |
+
\frac{1}{x-1}+\frac{1}{y-1}+\frac{1}{z-1} & =1 \\
|
| 89 |
+
(y-1)(z-1)+(x-1)(z-1)+(x-1)(y-1) & =(x-1)(y-1)(z-1) \\
|
| 90 |
+
x y+y z+z x-2(x+y+z)+3 & =x y z-(x y+y z+z x)+(x+y+z)-1 \\
|
| 91 |
+
x y z-2(x y+y z+z x)+3(x+y+z)-4 & =0 \\
|
| 92 |
+
x y z-2(67)+3(2010)-4 & =0 \\
|
| 93 |
+
x y z & =-5892
|
| 94 |
+
\end{aligned}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
8. [6] How many polynomials of degree exactly 5 with real coefficients send the set $\{1,2,3,4,5,6\}$ to a permutation of itself?
|
| 98 |
+
Answer: 714 For every permutation $\sigma$ of $\{1,2,3,4,5,6\}$, Lagrange Interpolation ${ }^{1}$ gives a polynomial of degree at most 5 with $p(x)=\sigma(x)$ for every $x=1,2,3,4,5,6$. Additionally, this polynomial is unique: assume that there exist two polynomials $p, q$ of degree $\leq 5$ such that they map $\{1,2,3,4,5,6\}$ to the same permutation. Then $p-q$ is a nonzero polynomial of degree $\leq 5$ with 6 distinct roots, a contradiction. Thus an upper bound for the answer is $6!=720$ polynomials.
|
| 99 |
+
However, not every polynomial obtained by Lagrange interpolation is of degree 5 (for example, $p(x)=$ $x$ ). We can count the number of invalid polynomials using finite differences ${ }^{2}$ A polynomial has degree less than 5 if and only if the sequence of 5 th finite differences is 0 . The 5 th finite difference of $p(1), p(2), p(3), p(4), p(5), p(6)$ is $p(1)-5 p(2)+10 p(3)-10 p(4)+5 p(5)-p(6)$; thus we want to solve $p(1)-5 p(2)+10 p(3)-10 p(4)+5 p(5)-p(6)=0$ with $\{p(1), p(2), p(3), p(4), p(5), p(6)\}=\{1,2,3,4,5,6\}$.
|
| 100 |
+
Taking the above equation modulo 5 , we get $p(1)=p(6)(\bmod 5) \Longrightarrow\{p(1), p(6)\}=\{1,6\}$. Note that $1-5 p(2)+10 p(3)-10 p(4)+5 p(5)-6=0$ if and only if $6-5 p(5)+10 p(4)-10 p(3)+5 p(2)-1=0$, so we may assume that $p(1)=1$ and double our result later. Then we have $\{p(2), p(3), p(4), p(5)\}=\{2,3,4,5\}$ and
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
-p(2)+2 p(3)-2 p(4)+p(5)=1
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
The above equation taken modulo 2 implies that $p(2), p(5)$ are of opposite parity, so $p(3), p(4)$ are of opposite parity. We do casework on $\{p(2), p(5)\}$ :
|
| 107 |
+
(a) $p(2)=2, p(5)=3 ; 2 p(3)-2 p(4)=0$ is a contradiction
|
| 108 |
+
(b) $p(2)=2, p(5)=5 ; 2 p(3)-2 p(4)=-2 \Longrightarrow p(3)-p(4)=-1 \Longrightarrow p(3)=3, p(4)=4$
|
| 109 |
+
(c) $p(2)=3, p(5)=2 ; 2 p(3)-2 p(4)=-2 \Longrightarrow p(3)-p(4)=-1 \Longrightarrow p(3)=4, p(4)=5$
|
| 110 |
+
(d) $p(2)=3, p(5)=4 ; 2 p(3)-2 p(4)=0$ is a contradiction
|
| 111 |
+
(e) $p(2)=4, p(5)=3 ; 2 p(3)-2 p(4)=2 \Longrightarrow p(3)-p(4)=1$ but $\{p(3), p(4)\}=\{2,5\}$, contradiction
|
| 112 |
+
(f) $p(2)=4, p(5)=5 ; 2 p(3)-2 p(4)=0$ is a contradiction
|
| 113 |
+
(g) $p(2)=5, p(5)=2 ; 2 p(3)-2 p(4)=4 \Longrightarrow p(3)-p(4)=2$, contradiction
|
| 114 |
+
(h) $p(2)=5, p(5)=4 ; 2 p(3)-2 p(4)=2 \Longrightarrow p(3)-p(4)=1 \Longrightarrow p(3)=3, p(4)=2$
|
| 115 |
+
|
| 116 |
+
Hence there are a total of $720-2(3)=714$ polynomials.
|
| 117 |
+
|
| 118 |
+
9. [7] Let $f(x)=c x(x-1)$, where $c$ is a positive real number. We use $f^{n}(x)$ to denote the polynomial obtained by composing $f$ with itself $n$ times. For every positive integer $n$, all the roots of $f^{n}(x)$ are real. What is the smallest possible value of $c$ ?
|
| 119 |
+
Answer: 2 We first prove that all roots of $f^{n}(x)$ are greater than or equal to $-\frac{c}{4}$ and less than or equal to $1+\frac{c}{4}$. Suppose that $r$ is a root of $f^{n}(x)$. If $r=-\frac{c}{4}, f^{-1}(r)=\left\{\frac{1}{2}\right\}$ and $-\frac{c}{4}<\frac{1}{2}<1+\frac{c}{4}$ since $c$ is positive. Suppose $r \neq-\frac{c}{4}$; by the quadratic formula, there exist two complex numbers $r_{1}, r_{2}$ such that $r_{1}+r_{2}=1$ and $f\left(r_{1}\right)=f\left(r_{2}\right)=r$. Thus all the roots of $f^{n}(x)$ (except $\frac{1}{2}$ ) come in pairs that sum to 1 . No root $r$ of $f^{n}(x)$ can be less than $-\frac{c}{4}$, otherwise $f^{n+1}(x)$ has an imaginary root, $f^{-1}(r)$. Also, no root $r$ of $f^{n}(x)$ can be greater than $1+\frac{c}{4}$, otherwise its "conjugate" root will be less than $-\frac{c}{4}$.
|
| 120 |
+
Define $g(x)=\frac{1}{2}\left(1+\sqrt{1+\frac{4 x}{c}}\right)$, the larger inverse of $f(x)$. Note that $g^{n}(x)$ is the largest element of $f^{-n}(x)$ (which is a set). $g^{n}(0)$ should be less than or equal to $1+\frac{c}{4}$ for all $n$. Let $x_{0}$ be the nonzero real number such that $g\left(x_{0}\right)=x_{0}$; then $c x_{0}\left(x_{0}-1\right)=x_{0} \Longrightarrow x_{o}=1+\frac{1}{c}$. $x_{0}<g(x)<x$ if $x>x_{0}$ and $x<g(x)<x_{0}$ if $x<x_{0}$; it can be proved that $g^{n}$ converges to $x_{0}$. Hence we have the requirement that $x_{0}=1+\frac{1}{c} \leq 1+\frac{c}{4} \Longrightarrow c \geq 2$.
|
| 121 |
+
We verify that $c=2$ is possible. All the roots of $f^{-} n(x)$ will be real if $g(0) \leq 1+\frac{c}{4}=\frac{3}{2}$. We know that $0<\frac{3}{2} \Longrightarrow g(0)<\frac{3}{2}$, so $g^{2}(0)<\frac{3}{2}$ and $g^{n}(0)<g^{n+1}(0)<\frac{3}{2}$ for all $n$. Therefore all the roots of $f^{n}(x)$ are real.
|
| 122 |
+
10. [8] Let $p(x)$ and $q(x)$ be two cubic polynomials such that $p(0)=-24, q(0)=30$, and
|
| 123 |
+
$$
|
| 124 |
+
p(q(x))=q(p(x))
|
| 125 |
+
$$
|
| 126 |
+
for all real numbers $x$. Find the ordered pair $(p(3), q(6))$.
|
| 127 |
+
Answer: $(3,-24)$ Note that the polynomials $f(x)=a x^{3}$ and $g(x)=-a x^{3}$ commute under composition. Let $h(x)=x+b$ be a linear polynomial, and note that its inverse $h^{-1}(x)=x-b$ is also a linear polynomial. The composite polynomials $h^{-1} f h$ and $h^{-1} g h$ commute, since function composition is associative, and these polynomials are also cubic.
|
| 128 |
+
We solve for the $a$ and $b$ such that $\left(h^{-1} f h\right)(0)=-24$ and $\left(h^{-1} g h\right)(0)=30$. We must have:
|
| 129 |
+
$$
|
| 130 |
+
a b^{3}-b=-24,-a b^{3}-b=30 \Rightarrow a=1, b=-3
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
These values of $a$ and $b$ yield the polynomials $p(x)=(x-3)^{3}+3$ and $q(x)=-(x-3)^{3}+3$. The polynomials take on the values $p(3)=3$ and $q(6)=-24$.
|
| 134 |
+
Remark: The pair of polynomials found in the solution is not unique. There is, in fact, an entire family of commuting cubic polynomials with $p(0)=-24$ and $q(0)=30$. They are of the form
|
| 135 |
+
|
| 136 |
+
$$
|
| 137 |
+
p(x)=t x(x-3)(x-6)-24, q(x)=-t x(x-3)(x-6)+30
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
where $t$ is any real number. However, the values of $p(3)$ and $q(6)$ are the same for all polynomials in this family. In fact, if we give the initial conditions $p(0)=k_{1}$ and $q(0)=k_{2}$, then we get a general solution of
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
\begin{gathered}
|
| 144 |
+
p(x)=t\left(x^{3}-\frac{3}{2}\left(k_{1}+k_{2}\right) x^{2}+\frac{1}{2}\left(k_{1}+k_{2}\right)^{2} x\right)+\frac{k_{2}-k_{1}}{k_{2}+k_{1}} x+k_{1} \\
|
| 145 |
+
q(x)=-t\left(x^{3}-\frac{3}{2}\left(k_{1}+k_{2}\right) x^{2}+\frac{1}{2}\left(k_{1}+k_{2}\right)^{2} x\right)-\frac{k_{2}-k_{1}}{k_{2}+k_{1}} x+k_{2}
|
| 146 |
+
\end{gathered}
|
| 147 |
+
$$
|
HarvardMIT/md/en-132-2010-feb-calc-solutions.md
ADDED
|
@@ -0,0 +1,113 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 20 February 2010 <br> Calculus Subject Test
|
| 2 |
+
|
| 3 |
+
1. [3] Suppose that $p(x)$ is a polynomial and that $p(x)-p^{\prime}(x)=x^{2}+2 x+1$. Compute $p(5)$.
|
| 4 |
+
|
| 5 |
+
Answer: 50 Observe that $p(x)$ must be quadratic. Let $p(x)=a x^{2}+b x+c$. Comparing coefficients gives $a=1, b-2 a=2$, and $c-b=1$. So $b=4, c=5, p(x)=x^{2}+4 x+5$ and $p(5)=25+20+5=50$.
|
| 6 |
+
2. [3] Let $f$ be a function such that $f(0)=1, f^{\prime}(0)=2$, and
|
| 7 |
+
|
| 8 |
+
$$
|
| 9 |
+
f^{\prime \prime}(t)=4 f^{\prime}(t)-3 f(t)+1
|
| 10 |
+
$$
|
| 11 |
+
|
| 12 |
+
for all $t$. Compute the 4th derivative of $f$, evaluated at 0 .
|
| 13 |
+
Answer: 54 Putting $t=0$ gives $f^{\prime \prime}(0)=6$. By differentiating both sides, we get $f^{(3)}(t)=4 f^{\prime \prime}(t)-$ $3 f^{\prime}(t)$ and $f^{(3)}(0)=4 \cdot 6-3 \cdot 2=18$. Similarly, $f^{(4)}(t)=4 f^{(3)}(t)-3 f^{\prime \prime}(t)$ and $f^{(4)}(0)=4 \cdot 18-3 \cdot 6=54$.
|
| 14 |
+
3. [4] Let $p$ be a monic cubic polynomial such that $p(0)=1$ and such that all the zeros of $p^{\prime}(x)$ are also zeros of $p(x)$. Find $p$. Note: monic means that the leading coefficient is 1 .
|
| 15 |
+
Answer: $(x+1)^{3}$ A root of a polynomial $p$ will be a double root if and only if it is also a root of $p^{\prime}$. Let $a$ and $b$ be the roots of $p^{\prime}$. Since $a$ and $b$ are also roots of $p$, they are double roots of $p$. But $p$ can have only three roots, so $a=b$ and $a$ becomes a double root of $p^{\prime}$. This makes $p^{\prime}(x)=3 c(x-a)^{2}$ for some constant $3 c$, and thus $p(x)=c(x-a)^{3}+d$. Because $a$ is a root of $p$ and $p$ is monic, $d=0$ and $c=1$. From $p(0)=1$ we get $p(x)=(x+1)^{3}$.
|
| 16 |
+
4. [4] Compute $\lim _{n \rightarrow \infty} \frac{\sum_{k=1}^{n}|\cos (k)|}{n}$.
|
| 17 |
+
|
| 18 |
+
Answer: $\frac{2}{\pi}$ The main idea lies on the fact that positive integers are uniformly distributed modulo $\pi$. (In the other words, if each integer $n$ is written as $q \pi+r$ where $q$ is an integer and $0 \leq r<\pi$, the value of $r$ will distribute uniformly in the interval $[0, \pi]$.) Using this fact, the summation is equivalent to the average value (using the Riemann summation) of the function $|\cos (k)|$ over the interval $[0, \pi]$. Therefore, the answer is $\frac{1}{\pi} \int_{0}^{\pi}|\cos (k)|=\frac{2}{\pi}$.
|
| 19 |
+
5. [4] Let the functions $f(\alpha, x)$ and $g(\alpha)$ be defined as
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
f(\alpha, x)=\frac{\left(\frac{x}{2}\right)^{\alpha}}{x-1} \quad g(\alpha)=\left.\frac{d^{4} f}{d x^{4}}\right|_{x=2}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Then $g(\alpha)$ is a polynomial in $\alpha$. Find the leading coefficient of $g(\alpha)$.
|
| 26 |
+
Answer: $\frac{1}{16}$ Write the first equation as $(x-1) f=\left(\frac{x}{2}\right)^{\alpha}$. For now, treat $\alpha$ as a constant. From this equation, repeatedly applying derivative with respect to $x$ gives
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
\begin{aligned}
|
| 30 |
+
(x-1) f^{\prime}+f & =\left(\frac{\alpha}{2}\right)\left(\frac{x}{2}\right)^{\alpha-1} \\
|
| 31 |
+
(x-1) f^{\prime \prime}+2 f^{\prime} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{x}{2}\right)^{\alpha-2} \\
|
| 32 |
+
(x-1) f^{(3)}+3 f^{\prime \prime} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{x}{2}\right)^{\alpha-3} \\
|
| 33 |
+
(x-1) f^{(4)}+4 f^{(3)} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{\alpha-3}{2}\right)\left(\frac{x}{2}\right)^{\alpha-4}
|
| 34 |
+
\end{aligned}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Substituting $x=2$ to all equations gives $g(\alpha)=f^{(4)}(\alpha, 2)=\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{\alpha-3}{2}\right)-4 f^{(3)}(\alpha, 2)$. Because $f^{(3)}(\alpha, 2)$ is a cubic polynomial in $\alpha$, the leading coefficient of $g(\alpha)$ is $\frac{1}{16}$.
|
| 38 |
+
6. [5] Let $f(x)=x^{3}-x^{2}$. For a given value of $c$, the graph of $f(x)$, together with the graph of the line $c+x$, split the plane up into regions. Suppose that $c$ is such that exactly two of these regions have finite area. Find the value of $c$ that minimizes the sum of the areas of these two regions.
|
| 39 |
+
Answer: $-\frac{11}{27}$ Observe that $f(x)$ can be written as $\left(x-\frac{1}{3}\right)^{3}-\frac{1}{3}\left(x-\frac{1}{3}\right)-\frac{2}{27}$, which has $180^{\circ}$ symmetry around the point $\left(\frac{1}{3},-\frac{2}{27}\right)$. Suppose the graph of $f$ cuts the line $y=c+x$ into two segments of lengths $a$ and $b$. When we move the line toward point $P$ with a small distance $\Delta x$ (measured along the line perpendicular to $y=x+c)$, the sum of the enclosed areas will increase by $|a-b|(\Delta x)$. As long as the line $x+c$ does not passes through $P$, we can find a new line $x+c^{*}$ that increases the sum of the enclosed areas. Therefore, the sum of the areas reaches its maximum when the line passes through $P$. For that line, we can find that $c=y-x=-\frac{2}{27}-\frac{1}{3}=-\frac{11}{27}$.
|
| 40 |
+
7. [6] Let $a_{1}, a_{2}$, and $a_{3}$ be nonzero complex numbers with non-negative real and imaginary parts. Find the minimum possible value of
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\frac{\left|a_{1}+a_{2}+a_{3}\right|}{\sqrt[3]{\left|a_{1} a_{2} a_{3}\right|}}
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Answer: $\sqrt{3} \sqrt[3]{2}$ Write $a_{1}$ in its polar form $r e^{i \theta}$ where $0 \leq \theta \leq \frac{\pi}{2}$. Suppose $a_{2}, a_{3}$ and $r$ are fixed so that the denominator is constant. Write $a_{2}+a_{3}$ as $s e^{i \phi}$. Since $a_{2}$ and $a_{3}$ have non-negative real and imaginary parts, the angle $\phi$ lies between 0 and $\frac{\pi}{2}$. Consider the function
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
f(\theta)=\left|a_{1}+a_{2}+a_{3}\right|^{2}=\left|r e^{i \theta}+s e^{i \phi}\right|^{2}=r^{2}+2 r s \cos (\theta-\phi)+s^{2}
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Its second derivative is $\left.f^{\prime \prime}(\theta)=-2 \operatorname{rs}(\cos (\theta-\phi))\right)$. Since $-\frac{\pi}{2} \leq(\theta-\phi) \leq \frac{\pi}{2}$, we know that $f^{\prime \prime}(\theta)<0$ and $f$ is concave. Therefore, to minimize $f$, the angle $\theta$ must be either 0 or $\frac{\pi}{2}$. Similarly, each of $a_{1}, a_{2}$ and $a_{3}$ must be either purely real or purely imaginary to minimize $f$ and the original fraction.
|
| 53 |
+
By the AM-GM inequality, if $a_{1}, a_{2}$ and $a_{3}$ are all real or all imaginary, then the minimum value of the fraction is 3 . Now suppose only two of the $a_{i}$ 's, say, $a_{1}$ and $a_{2}$ are real. Since the fraction is homogenous, we may fix $a_{1}+a_{2}$ - let the sum be 2 . The term $a_{1} a_{2}$ in the denominator acheives its maximum only when $a_{1}$ and $a_{2}$ are equal, i.e. when $a_{1}=a_{2}=1$. Then, if $a_{3}=k i$ for some real number $k$, then the expression equals
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
\frac{\sqrt{k^{2}+4}}{\sqrt[3]{k}}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Squaring and taking the derivative, we find that the minimum value of the fraction is $\sqrt{3} \sqrt[3]{2}$, attained when $k=\sqrt{2}$. With similar reasoning, the case where only one of the $a_{i}$ 's is real yields the same minimum value.
|
| 60 |
+
8. [6] Let $f(n)=\sum_{k=2}^{\infty} \frac{1}{k^{n} \cdot k!}$. Calculate $\sum_{n=2}^{\infty} f(n)$.
|
| 61 |
+
|
| 62 |
+
Answer: $3-e$
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\begin{aligned}
|
| 66 |
+
\sum_{n=2}^{\infty} f(n) & =\sum_{k=2}^{\infty} \sum_{n=2}^{\infty} \frac{1}{k^{n} \cdot k!} \\
|
| 67 |
+
& =\sum_{k=2}^{\infty} \frac{1}{k!} \sum_{n=2}^{\infty} \frac{1}{k^{n}} \\
|
| 68 |
+
& =\sum_{k=2}^{\infty} \frac{1}{k!} \cdot \frac{1}{k(k-1)} \\
|
| 69 |
+
& =\sum_{k=2}^{\infty} \frac{1}{(k-1)!} \cdot \frac{1}{k^{2}(k-1)}
|
| 70 |
+
\end{aligned}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
\begin{aligned}
|
| 75 |
+
& =\sum_{k=2}^{\infty} \frac{1}{(k-1)!}\left(\frac{1}{k-1}-\frac{1}{k^{2}}-\frac{1}{k}\right) \\
|
| 76 |
+
& =\sum_{k=2}^{\infty}\left(\frac{1}{(k-1)(k-1)!}-\frac{1}{k \cdot k!}-\frac{1}{k!}\right) \\
|
| 77 |
+
& =\sum_{k=2}^{\infty}\left(\frac{1}{(k-1)(k-1)!}-\frac{1}{k \cdot k!}\right)-\sum_{k=2}^{\infty} \frac{1}{k!} \\
|
| 78 |
+
& =\frac{1}{1 \cdot 1!}-\left(e-\frac{1}{0!}-\frac{1}{1!}\right) \\
|
| 79 |
+
& =3-e
|
| 80 |
+
\end{aligned}
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
9. [7] Let $x(t)$ be a solution to the differential equation
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
\left(x+x^{\prime}\right)^{2}+x \cdot x^{\prime \prime}=\cos t
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
with $x(0)=x^{\prime}(0)=\sqrt{\frac{2}{5}}$. Compute $x\left(\frac{\pi}{4}\right)$.
|
| 90 |
+
Answer: $\frac{\sqrt[4]{450}}{5}$ Rewrite the equation as $x^{2}+2 x x^{\prime}+\left(x x^{\prime}\right)^{\prime}=\cos t$. Let $y=x^{2}$, so $y^{\prime}=2 x x^{\prime}$ and the equation becomes $y+y^{\prime}+\frac{1}{2} y^{\prime \prime}=\cos t$. The term $\cos t$ suggests that the particular solution should be in the form $A \sin t+B \cos t$. By substitution and coefficient comparison, we get $A=\frac{4}{5}$ and $B=\frac{2}{5}$. Since the function $y(t)=\frac{4}{5} \sin t+\frac{2}{5} \cos t$ already satisfies the initial conditions $y(0)=x(0)^{2}=\frac{2}{5}$ and $y^{\prime}(0)=2 x(0) x^{\prime}(0)=\frac{4}{5}$, the function $y$ also solves the initial value problem. Note that since $x$ is positive at $t=0$ and $y=x^{2}$ never reaches zero before $t$ reaches $\frac{\pi}{4}$, the value of $x\left(\frac{\pi}{4}\right)$ must be positive. Therefore, $x\left(\frac{\pi}{4}\right)=+\sqrt{y\left(\frac{\pi}{4}\right)}=\sqrt{\frac{6}{5} \cdot \frac{\sqrt{2}}{2}}=\frac{\sqrt[4]{450}}{5}$.
|
| 91 |
+
10. [8] Let $f(n)=\sum_{k=1}^{n} \frac{1}{k}$. Then there exists constants $\gamma, c$, and $d$ such that
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
f(n)=\ln (n)+\gamma+\frac{c}{n}+\frac{d}{n^{2}}+O\left(\frac{1}{n^{3}}\right)
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
where the $O\left(\frac{1}{n^{3}}\right)$ means terms of order $\frac{1}{n^{3}}$ or lower. Compute the ordered pair $(c, d)$.
|
| 98 |
+
Answer: $\left(\frac{1}{2},-\frac{1}{12}\right)$ From the given formula, we pull out the term $\frac{k}{n^{3}}$ from $O\left(\frac{1}{n^{4}}\right)$, making $f(n)=$ $\log (n)+\gamma+\frac{c}{n}+\frac{d}{n^{2}}+\frac{k}{n^{3}}+O\left(\frac{1}{n^{4}}\right)$. Therefore,
|
| 99 |
+
$f(n+1)-f(n)=\log \left(\frac{n+1}{n}\right)-c\left(\frac{1}{n}-\frac{1}{n+1}\right)-d\left(\frac{1}{n^{2}}-\frac{1}{(n+1)^{2}}\right)-k\left(\frac{1}{n^{3}}-\frac{1}{(n+1)^{3}}\right)+O\left(\frac{1}{n^{4}}\right)$.
|
| 100 |
+
For the left hand side, $f(n+1)-f(n)=\frac{1}{n+1}$. By substituting $x=\frac{1}{n}$, the formula above becomes
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\frac{x}{x+1}=\log (1+x)-c x^{2} \cdot \frac{1}{x+1}-d x^{3} \cdot \frac{x+2}{(x+1)^{2}}-k x^{4} \cdot \frac{x^{2}+3 x+3}{(x+1)^{3}}+O\left(x^{4}\right)
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
Because $x$ is on the order of $\frac{1}{n}, \frac{1}{(x+1)^{3}}$ is on the order of a constant. Therefore, all the terms in the expansion of $k x^{4} \cdot \frac{x^{2}+3 x+3}{(x+1)^{3}}$ are of order $x^{4}$ or higher, so we can collapse it into $O\left(x^{4}\right)$. Using the Taylor expansions, we get
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
x\left(1-x+x^{2}\right)+O\left(x^{4}\right)=\left(x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}\right)-c x^{2}(1-x)-d x^{3}(2)+O\left(x^{4}\right) .
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
Coefficient comparison gives $c=\frac{1}{2}$ and $d=-\frac{1}{12}$.
|
| 113 |
+
|
HarvardMIT/md/en-132-2010-feb-comb-solutions.md
ADDED
|
@@ -0,0 +1,107 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 20 February 2010
|
| 2 |
+
|
| 3 |
+
## Combinatorics Subject Test
|
| 4 |
+
|
| 5 |
+
1. [2] Let $S=\{1,2,3,4,5,6,7,8,9,10\}$. How many (potentially empty) subsets $T$ of $S$ are there such that, for all $x$, if $x$ is in $T$ and $2 x$ is in $S$ then $2 x$ is also in $T$ ?
|
| 6 |
+
Answer: 180 We partition the elements of $S$ into the following subsets: $\{1,2,4,8\},\{3,6\},\{5,10\}$, $\{7\},\{9\}$. Consider the first subset, $\{1,2,4,8\}$. Say 2 is an element of $T$. Because $2 \cdot 2=4$ is in $S, 4$ must also be in $T$. Furthermore, since $4 \cdot 2=8$ is in $S, 8$ must also be in $T$. So if $T$ contains 2 , it must also contain 4 and 8 . Similarly, if $T$ contains 1 , it must also contain 2,4 , and 8 . So $T$ can contain the following subsets of the subset $\{1,2,4,8\}$ : the empty set, $\{8\},\{4,8\},\{2,4,8\}$, or $\{1,2,4,8\}$. This gives 5 possibilities for the first subset. In general, we see that if $T$ contains an element $q$ of one of these subsets, it must also contain the elements in that subset that are larger than $q$, because we created the subsets for this to be true. So there are 3 possibilities for $\{3,6\}, 3$ for $\{5,10\}, 2$ for $\{7\}$, and 2 for $\{9\}$. This gives a total of $5 \cdot 3 \cdot 3 \cdot 2 \cdot 2=180$ possible subsets $T$.
|
| 7 |
+
2. [3] How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0! and 1! to be distinct.
|
| 8 |
+
Answer: 39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain 3 !, 4 !, 5 !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \cdot 2 \cdot 2 \cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.
|
| 9 |
+
3. [4] How many ways are there to choose 2010 functions $f_{1}, \ldots, f_{2010}$ from $\{0,1\}$ to $\{0,1\}$ such that $f_{2010} \circ f_{2009} \circ \cdots \circ f_{1}$ is constant? Note: a function $g$ is constant if $g(a)=g(b)$ for all $a, b$ in the domain of $g$.
|
| 10 |
+
Answer: $4^{2010}-2^{2010}$ If all 2010 functions are bijective ${ }^{1}$, then the composition $f_{2010} \circ f_{2009} \circ \cdots \circ f_{1}$ will be bijective also, and therefore not constant. If, however, one of $f_{1}, \ldots, f_{2010}$ is not bijective, say $f_{k}$, then $f_{k}(0)=f_{k}(1)=q$, so $f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1} \circ f_{k} \circ \cdots f_{1}(0)=f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1}(q)=$ $f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1} \circ f_{k} \circ \cdots f_{1}(1)$. So the composition will be constant unless all $f_{i}$ are bijective. Since there are 4 possible functions ${ }^{2}$ from $\{0,1\}$ to $\{0,1\}$ and 2 of them are bijective, we subtract the cases where all the functions are bijective from the total to get $4^{2010}-2^{2010}$.
|
| 11 |
+
4. [4] Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).
|
| 12 |
+
|
| 13 |
+
Answer: 3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13-1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=3384$.
|
| 14 |
+
5. [5] John needs to pay 2010 dollars for his dinner. He has an unlimited supply of 2, 5, and 10 dollar notes. In how many ways can he pay?
|
| 15 |
+
Answer: 20503
|
| 16 |
+
Let the number of 2,5 , and 10 dollar notes John can use be $x, y$, and $z$ respectively. We wish to find the number of nonnegative integer solutions to $2 x+5 y+10 z=2010$. Consider this equation $\bmod 2$. Because $2 x, 10 z$, and 2010 are even, $5 y$ must also be even, so $y$ must be even. Now consider the equation mod 5 . Because $5 y, 10 z$, and 2010 are divisible by $5,2 x$ must also be divisible by 5 , so $x$ must be divisible by 5 . So both $2 x$ and $5 y$ are divisible by 10 . So the equation is equivalent to $10 x^{\prime}+10 y^{\prime}+10 z=2010$, or $x^{\prime}+y^{\prime}+z=201$, with $x^{\prime}, y^{\prime}$, and $z$ nonnegative integers. There is a well-known bijection between solutions of this equation and picking 2 of 203 balls in a row on the table (explained in further detail below), so there are $\binom{203}{2}=20503$ ways.
|
| 17 |
+
The bijection between solutions of $x^{\prime}+y^{\prime}+z=201$ and arrangements of 203 balls in a row is as follows. Given a solution of the equation, we put $x^{\prime}$ white balls in a row, then a black ball, then $y^{\prime}$ white balls, then a black ball, then $z$ white balls. This is like having 203 balls in a row on a table and picking two of them to be black. To go from an arrangement of balls to a solution of the equation, we just read off $x^{\prime}, y^{\prime}$, and $z$ from the number of white balls in a row. There are $\binom{203}{2}$ ways to choose 2 of 203 balls to be black, so there are $\binom{203}{2}$ solutions to $x^{\prime}+y^{\prime}+z=201$.
|
| 18 |
+
6. [5] An ant starts out at $(0,0)$. Each second, if it is currently at the square $(x, y)$, it can move to $(x-1, y-1),(x-1, y+1),(x+1, y-1)$, or $(x+1, y+1)$. In how many ways can it end up at $(2010,2010)$ after 4020 seconds?
|
| 19 |
+
Answer: $\binom{4020}{1005}^{2}$ Note that each of the coordinates either increases or decreases the $x$ and $y$ coordinates by 1. In order to reach 2010 after 4020 steps, each of the coordinates must be increased 3015 times and decreased 1005 times. A permutation of 3015 plusses and 1005 minuses for each of $x$ and $y$ uniquely corresponds to a path the ant could take to $(2010,2010)$, because we can take ordered pairs from the two lists and match them up to a valid step the ant can take. So the number of ways the ant can end up at $(2010,2010)$ after 4020 seconds is equal to the number of ways to arrange plusses and minuses for both $x$ and $y$, or $\left(\binom{4020}{1005}\right)^{2}$.
|
| 20 |
+
7. [6] For each integer $x$ with $1 \leq x \leq 10$, a point is randomly placed at either $(x, 1)$ or $(x,-1)$ with equal probability. What is the expected area of the convex hull of these points? Note: the convex hull of a finite set is the smallest convex polygon containing it.
|
| 21 |
+
Answer: $\frac{1793}{\frac{1728}{128}}$ Let $n=10$. Given a random variable $X$, let $\mathbb{E}(X)$ denote its expected value. If all points are collinear, then the convex hull has area zero. This happens with probability $\frac{2}{2^{n}}$ (either all points are at $y=1$ or all points are at $y=-1$ ). Otherwise, the points form a trapezoid with height 2 (the trapezoid is possibly degenerate, but this won't matter for our calculation). Let $x_{1, l}$ be the $x$-coordinate of the left-most point at $y=1$ and $x_{1, r}$ be the $x$-coordinate of the right-most point at $y=1$. Define $x_{-1, l}$ and $x_{-1, r}$ similarly for $y=-1$. Then the area of the trapezoid is
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
2 \cdot \frac{\left(x_{1, r}-x_{1, l}\right)+\left(x_{-1, r}-x_{-1, l}\right)}{2}=x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l} .
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
The expected area of the convex hull (assuming the points are not all collinear) is then, by linearity of expectation,
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\mathbb{E}\left(x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l}\right)=\mathbb{E}\left(x_{1, r}\right)+\mathbb{E}\left(x_{-1, r}\right)-\mathbb{E}\left(x_{1, l}\right)-\mathbb{E}\left(x_{-1, l}\right) .
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
We need only compute the expected values given in the above equation. Note that $x_{1, r}$ is equal to $k$ with probability $\frac{2^{k-1}}{2^{n}-2}$, except that it is equal to $n$ with probability $\frac{2^{n-1}-1}{2^{n}-2}$ (the denominator is $2^{n}-2$ instead of $2^{n}$ because we need to exclude the case where all points are collinear). Therefore, the expected value of $x_{1, r}$ is equal to
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\begin{aligned}
|
| 37 |
+
& \frac{1}{2^{n}-2}\left(\left(\sum_{k=1}^{n} k \cdot 2^{k-1}\right)-n \cdot 1\right) \\
|
| 38 |
+
& \quad=\frac{1}{2^{n}-2}\left(\left(1+2+\cdots+2^{n-1}\right)+\left(2+4+\cdots+2^{n-1}\right)+\cdots+2^{n-1}-n\right) \\
|
| 39 |
+
& =\frac{1}{2^{n}-2}\left(\left(2^{n}-1\right)+\left(2^{n}-2\right)+\cdots+\left(2^{n}-2^{n-1}\right)-n\right) \\
|
| 40 |
+
& =\frac{1}{2^{n}-2}\left(n \cdot 2^{n}-\left(2^{n}-1\right)-n\right) \\
|
| 41 |
+
& \quad=(n-1) \frac{2^{n}-1}{2^{n}-2}
|
| 42 |
+
\end{aligned}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Similarly, the expected value of $x_{-1, r}$ is also $(n-1) \frac{2^{n}-1}{2^{n}-2}$. By symmetry, the expected value of both $x_{1, l}$ and $x_{-1, l}$ is $n+1-(n-1) \frac{\frac{2}{n}^{n}-1}{2^{n}-2}$. This says that if the points are not all collinear then the expected area is $2 \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right)$. So, the expected area is
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\begin{aligned}
|
| 49 |
+
\frac{2}{2^{n}} \cdot 0+(1- & \left.\frac{2}{2^{n}}\right) \cdot 2 \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right) \\
|
| 50 |
+
& =2 \cdot \frac{2^{n-1}-1}{2^{n-1}} \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right) \\
|
| 51 |
+
& =2 \cdot \frac{(n-1)\left(2^{n}-1\right)-(n+1)\left(2^{n-1}-1\right)}{2^{n-1}} \\
|
| 52 |
+
& =2 \cdot \frac{((2 n-2)-(n+1)) 2^{n-1}+2}{2^{n-1}} \\
|
| 53 |
+
& =2 n-6+\frac{1}{2^{n-3}}
|
| 54 |
+
\end{aligned}
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Plugging in $n=10$, we get $14+\frac{1}{128}=\frac{1793}{128}$.
|
| 58 |
+
8. [6] How many functions $f$ from $\{-1005, \ldots, 1005\}$ to $\{-2010, \ldots, 2010\}$ are there such that the following two conditions are satisfied?
|
| 59 |
+
|
| 60 |
+
- If $a<b$ then $f(a)<f(b)$.
|
| 61 |
+
- There is no $n$ in $\{-1005, \ldots, 1005\}$ such that $|f(n)|=|n|$.
|
| 62 |
+
|
| 63 |
+
Answer: $\cdots$ Note: the intended answer was $\binom{4019}{2011}$, but the original answer was incorrect. The correct answer is:
|
| 64 |
+
1173346782666677300072441773814388000553179587006710786401225043842699552460942166630860 5302966355504513409792805200762540756742811158611534813828022157596601875355477425764387 2333935841666957750009216404095352456877594554817419353494267665830087436353494075828446 0070506487793628698617665091500712606599653369601270652785265395252421526230453391663029 1476263072382369363170971857101590310272130771639046414860423440232291348986940615141526 0247281998288175423628757177754777309519630334406956881890655029018130367627043067425502 2334151384481231298380228052789795136259575164777156839054346649261636296328387580363485 2904329986459861362633348204891967272842242778625137520975558407856496002297523759366027
|
| 65 |
+
|
| 66 |
+
1506637984075036473724713869804364399766664507880042495122618597629613572449327653716600 6715747717529280910646607622693561789482959920478796128008380531607300324374576791477561 5881495035032334387221203759898494171708240222856256961757026746724252966598328065735933 6668742613422094179386207330487537984173936781232801614775355365060827617078032786368164 8860839124954588222610166915992867657815394480973063139752195206598739798365623873142903 28539769699667459275254643229234106717245366005816917271187760792
|
| 67 |
+
|
| 68 |
+
This obviously cannot be computed by hand, but there is a polynomial-time dynamic programming algorithm that will compute it.
|
| 69 |
+
9. [7] Rosencrantz and Guildenstern are playing a game where they repeatedly flip coins. Rosencrantz wins if 1 heads followed by 2009 tails appears. Guildenstern wins if 2010 heads come in a row. They will flip coins until someone wins. What is the probability that Rosencrantz wins?
|
| 70 |
+
Answer: $\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}$ We can assume the first throw is heads (because neither player can win starting from a string of only tails). Let $x$ be the probability that Rosencrantz wins. Let $y$ be the probability that Rosencrantz wins after HT.
|
| 71 |
+
|
| 72 |
+
Whenever there is a string of less than 2009 tails followed by a heads, the heads basically means the two are starting from the beginning, where Rosencrantz has probability $x$ of winning.
|
| 73 |
+
We also know that $x=y\left(1-\frac{1}{2^{2009}}\right)$. This is because from the initial heads there is a $\left(1-\frac{1}{2^{2009}}\right)$ chance Rosencrantz doesn't lose, and in this case the last two flips are HT, in which case Rosencrantz has probability $y$ of winning.
|
| 74 |
+
If the first two throws are HT, there is a $\frac{1}{2^{2008}}$ chance Rosencrantz wins; otherwise, there is eventually a heads, and so we are back in the case of starting from a heads, which corresponds to $x$. Therefore, $y=\frac{1}{2^{2008}}+x\left(1-\frac{1}{2^{2008}}\right)$. Putting this together with the previous equation, we get:
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\begin{aligned}
|
| 78 |
+
x & =\left(\frac{1}{2^{2008}}+x\left(1-\frac{1}{2^{2008}}\right)\right)\left(1-\frac{1}{2^{2009}}\right) \\
|
| 79 |
+
\Longrightarrow \quad x & =\left(\frac{1+2^{2008} x-x}{2^{2008}}\right)\left(\frac{2^{2009}-1}{\left.2^{2009}\right)}\right. \\
|
| 80 |
+
\Longrightarrow \quad 2^{4017} x & =x\left(2^{4017}-2^{2009}-2^{2008}+1\right)+2^{2009}-1 \\
|
| 81 |
+
\Longrightarrow \quad x & =\frac{2^{2009}-1}{2^{2009}+2^{2008}-1},
|
| 82 |
+
\end{aligned}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
so the answer is $\frac{2^{2009}-1}{2^{2009}+2^{2008}-1}=\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}$.
|
| 86 |
+
10. [8] In a $16 \times 16$ table of integers, each row and column contains at most 4 distinct integers. What is the maximum number of distinct integers that there can be in the whole table?
|
| 87 |
+
Answer: 49 First, we show that 50 is too big. Assume for sake of contradiction that a labeling with at least 50 distinct integers exists. By the Pigeonhole Principle, there must be at least one row, say the first row, with at least 4 distinct integers in it; in this case, that is exactly 4 , since that is the maximum number of distinct integers in one row. Then, in the remaining 15 rows there must be at least 46 distinct integers (these 46 will also be distinct from the 4 in the first row). Using Pigeonhole again, there will be another row, say the second row, with 4 distinct integers in it. Call the set of integers in the first and second rows $S$. Because the 4 distinct integers in the second row are distinct from the 4 in the first row, there are 8 distinct values in the first two rows, so $|S|=8$. Now consider the subcolumns containing the cells in rows 3 to 16 . In each subcolumn, there are at most 2 values not in $S$, because there are already two distinct values in that column from the cells in the first two rows. So, the maximum number of distinct values in the table is $16 \cdot 2+8=40$, a contradiction. So a valid labeling must have fewer than 50 distinct integers. Below, we show by example that 49 is attainable.
|
| 88 |
+
|
| 89 |
+
| 1 | 17 | 33 | - | - | - | - | - | - | - | - | - | - | - | - | - |
|
| 90 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 91 |
+
| - | 2 | 18 | 34 | - | - | - | - | - | - | - | - | - | - | - | - |
|
| 92 |
+
| - | - | 3 | 19 | 35 | - | - | - | - | - | - | - | - | - | - | - |
|
| 93 |
+
| - | - | - | 4 | 20 | 36 | - | - | - | - | - | - | - | - | - | - |
|
| 94 |
+
| - | - | - | - | 5 | 21 | 37 | - | - | - | - | - | - | - | - | - |
|
| 95 |
+
| - | - | - | - | - | 6 | 22 | 38 | - | - | - | - | - | - | - | - |
|
| 96 |
+
| - | - | - | - | - | - | 7 | 23 | 39 | - | - | - | - | - | - | - |
|
| 97 |
+
| - | - | - | - | - | - | - | 8 | 24 | 40 | - | - | - | - | - | - |
|
| 98 |
+
| - | - | - | - | - | - | - | - | 9 | 25 | 41 | - | - | - | - | - |
|
| 99 |
+
| - | - | - | - | - | - | - | - | - | 10 | 26 | 42 | - | - | - | - |
|
| 100 |
+
| - | - | - | - | - | - | - | - | - | - | 11 | 27 | 43 | - | - | - |
|
| 101 |
+
| - | - | - | - | - | - | - | - | - | - | - | 12 | 28 | 44 | - | - |
|
| 102 |
+
| - | - | - | - | - | - | - | - | - | - | - | - | 13 | 29 | 45 | - |
|
| 103 |
+
| - | - | - | - | - | - | - | - | - | - | - | - | - | 14 | 30 | 46 |
|
| 104 |
+
| 47 | - | - | - | - | - | - | - | - | - | - | - | - | - | 15 | 31 |
|
| 105 |
+
| 32 | 48 | - | - | - | - | - | - | - | - | - | - | - | - | - | 16 |
|
| 106 |
+
|
| 107 |
+
Cells that do not contain a number are colored with color 49 .
|
HarvardMIT/md/en-132-2010-feb-gen1-solutions.md
ADDED
|
@@ -0,0 +1,131 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 20 February 2010 <br> <br> General Test, Part 1
|
| 2 |
+
|
| 3 |
+
<br> <br> General Test, Part 1}
|
| 4 |
+
|
| 5 |
+
1. [3] Suppose that $x$ and $y$ are positive reals such that
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
x-y^{2}=3, \quad x^{2}+y^{4}=13
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
Find $x$.
|
| 12 |
+
Answer: $\frac{3+\sqrt{17}}{2}$ Squaring both sides of $x-y^{2}=3$ gives $x^{2}+y^{4}-2 x y^{2}=9$. Subtract this equation from twice the second given to get $x^{2}+2 x y^{2}+y^{4}=17 \Longrightarrow x+y^{2}= \pm 17$. Combining this equation with the first given, we see that $x=\frac{3 \pm \sqrt{17}}{2}$. Since $x$ is a positive real, $x$ must be $\frac{3+\sqrt{17}}{2}$.
|
| 13 |
+
2. [3] Let $S=\{1,2,3,4,5,6,7,8,9,10\}$. How many (potentially empty) subsets $T$ of $S$ are there such that, for all $x$, if $x$ is in $T$ and $2 x$ is in $S$ then $2 x$ is also in $T$ ?
|
| 14 |
+
Answer: 180 We partition the elements of $S$ into the following subsets: $\{1,2,4,8\},\{3,6\},\{5,10\}$, $\{7\},\{9\}$. Consider the first subset, $\{1,2,4,8\}$. Say 2 is an element of $T$. Because $2 \cdot 2=4$ is in $S, 4$ must also be in $T$. Furthermore, since $4 \cdot 2=8$ is in $S, 8$ must also be in $T$. So if $T$ contains 2 , it must also contain 4 and 8 . Similarly, if $T$ contains 1 , it must also contain 2,4 , and 8 . So $T$ can contain the following subsets of the subset $\{1,2,4,8\}$ : the empty set, $\{8\},\{4,8\},\{2,4,8\}$, or $\{1,2,4,8\}$. This gives 5 possibilities for the first subset. In general, we see that if $T$ contains an element $q$ of one of these subsets, it must also contain the elements in that subset that are larger than $q$, because we created the subsets for this to be true. So there are 3 possibilities for $\{3,6\}, 3$ for $\{5,10\}, 2$ for $\{7\}$, and 2 for $\{9\}$. This gives a total of $5 \cdot 3 \cdot 3 \cdot 2 \cdot 2=180$ possible subsets $T$.
|
| 15 |
+
3. [4] A rectangular piece of paper is folded along its diagonal (as depicted below) to form a non-convex pentagon that has an area of $\frac{7}{10}$ of the area of the original rectangle. Find the ratio of the longer side of the rectangle to the shorter side of the rectangle.
|
| 16 |
+
|
| 17 |
+
|
| 18 |
+
Answer: $\sqrt{5}$
|
| 19 |
+
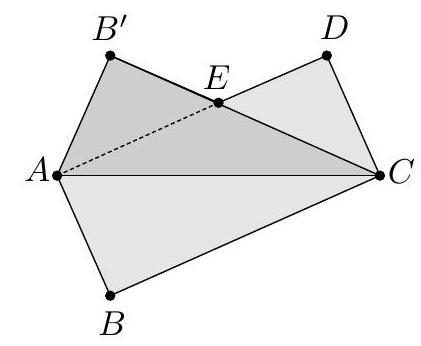
|
| 20 |
+
|
| 21 |
+
Given a polygon $P_{1} P_{2} \cdots P_{k}$, let $\left[P_{1} P_{2} \cdots P_{k}\right]$ denote its area. Let $A B C D$ be the rectangle. Suppose we fold $B$ across $\overline{A C}$, and let $E$ be the intersection of $\overline{A D}$ and $\overline{B^{\prime} C}$. Then we end up with the pentagon $A C D E B^{\prime}$, depicted above. Let's suppose, without loss of generality, that $A B C D$ has area 1. Then $\triangle A E C$ must have area $\frac{3}{10}$, since
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\begin{aligned}
|
| 25 |
+
{[A B C D] } & =[A B C]+[A C D] \\
|
| 26 |
+
& =\left[A B^{\prime} C\right]+[A C D] \\
|
| 27 |
+
& =\left[A B^{\prime} E\right]+2[A E C]+[E D C] \\
|
| 28 |
+
& =\left[A C D E B^{\prime}\right]+[A E C] \\
|
| 29 |
+
& =\frac{7}{10}[A B C D]+[A E C],
|
| 30 |
+
\end{aligned}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
That is, $[A E C]=\frac{3}{10}[A B C D]=\frac{3}{10}$.
|
| 34 |
+
Since $\triangle E C D$ is congruent to $\triangle E A B^{\prime}$, both triangles have area $\frac{1}{5}$. Note that $\triangle A B^{\prime} C, \triangle A B C$, and $\triangle C D A$ are all congruent, and all have area $\frac{1}{2}$. Since $\triangle A E C$ and $\triangle E D C$ share altitude $\overline{D C}$, $\frac{D E}{E A}=\frac{[D E C]}{[A E C]}=\frac{2}{3}$. Because $\triangle C A E$ is isosceles, $C E=E A$. Let $A E=3 x$. The $C E=3 x, D E=2 x$, and $C D=x \sqrt{9-4}=x \sqrt{5}$. Then $\frac{A D}{D C}=\frac{A E+E D}{D C}=\frac{3+2}{\sqrt{5}}=\sqrt{5}$.
|
| 35 |
+
4. [4] Let $S_{0}=0$ and let $S_{k}$ equal $a_{1}+2 a_{2}+\ldots+k a_{k}$ for $k \geq 1$. Define $a_{i}$ to be 1 if $S_{i-1}<i$ and -1 if $S_{i-1} \geq i$. What is the largest $k \leq 2010$ such that $S_{k}=0$ ?
|
| 36 |
+
Answer: 1092 Suppose that $S_{N}=0$ for some $N \geq 0$. Then $a_{N+1}=1$ because $N+1 \geq S_{N}$. The following table lists the values of $a_{k}$ and $S_{k}$ for a few $k \geq N$ :
|
| 37 |
+
|
| 38 |
+
| $k$ | $a_{k}$ | $S_{k}$ |
|
| 39 |
+
| :--- | ---: | :--- |
|
| 40 |
+
| $N$ | | 0 |
|
| 41 |
+
| $N+1$ | 1 | $N+1$ |
|
| 42 |
+
| $N+2$ | 1 | $2 N+3$ |
|
| 43 |
+
| $N+3$ | -1 | $N$ |
|
| 44 |
+
| $N+4$ | 1 | $2 N+4$ |
|
| 45 |
+
| $N+5$ | -1 | $N-1$ |
|
| 46 |
+
| $N+6$ | 1 | $2 N+5$ |
|
| 47 |
+
| $N+7$ | -1 | $N-2$ |
|
| 48 |
+
|
| 49 |
+
We see inductively that, for every $i \geq 1$,
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
S_{N+2 i}=2 N+2+i
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
and
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
S_{N+1+2 i}=N+1-i
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
thus $S_{3 N+3}=0$ is the next $k$ for which $S_{k}=0$. The values of $k$ for which $S_{k}=0$ satisfy the recurrence relation $p_{n+1}=3 p_{n}+3$, and we compute that the first terms of the sequence are $0,3,12,39,120,363,1092$; hence 1092 is our answer.
|
| 62 |
+
5. [4] Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).
|
| 63 |
+

|
| 64 |
+
|
| 65 |
+
Answer: 3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13-1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=3384$.
|
| 66 |
+
6. [5] John needs to pay 2010 dollars for his dinner. He has an unlimited supply of 2, 5, and 10 dollar notes. In how many ways can he pay?
|
| 67 |
+
|
| 68 |
+
## Answer: 20503
|
| 69 |
+
|
| 70 |
+
Let the number of 2,5 , and 10 dollar notes John can use be $x, y$, and $z$ respectively. We wish to find the number of nonnegative integer solutions to $2 x+5 y+10 z=2010$. Consider this equation $\bmod 2$. Because $2 x, 10 z$, and 2010 are even, $5 y$ must also be even, so $y$ must be even. Now consider the equation $\bmod 5$. Because $5 y, 10 z$, and 2010 are divisible by $5,2 x$ must also be divisible by 5 , so $x$ must be divisible by 5 . So both $2 x$ and $5 y$ are divisible by 10 . So the equation is equivalent to $10 x^{\prime}+10 y^{\prime}+10 z=2010$, or $x^{\prime}+y^{\prime}+z=201$, with $x^{\prime}, y^{\prime}$, and $z$ nonnegative integers. There is a well-known bijection between solutions of this equation and picking 2 of 203 balls in a row on the table (explained in further detail below), so there are $\binom{203}{2}=20503$ ways.
|
| 71 |
+
The bijection between solutions of $x^{\prime}+y^{\prime}+z=201$ and arrangements of 203 balls in a row is as follows. Given a solution of the equation, we put $x^{\prime}$ white balls in a row, then a black ball, then $y^{\prime}$ white balls, then a black ball, then $z$ white balls. This is like having 203 balls in a row on a table and picking two of them to be black. To go from an arrangement of balls to a solution of the equation, we just read off $x^{\prime}, y^{\prime}$, and $z$ from the number of white balls in a row. There are $\binom{203}{2}$ ways to choose 2 of 203 balls to be black, so there are $\binom{203}{2}$ solutions to $x^{\prime}+y^{\prime}+z=201$.
|
| 72 |
+
7. [6] Suppose that a polynomial of the form $p(x)=x^{2010} \pm x^{2009} \pm \cdots \pm x \pm 1$ has no real roots. What is the maximum possible number of coefficients of -1 in $p$ ?
|
| 73 |
+
Answer: 1005 Let $p(x)$ be a polynomial with the maximum number of minus signs.
|
| 74 |
+
$p(x)$ cannot have more than 1005 minus signs, otherwise $p(1)<0$ and $p(2) \geq 2^{2010}-2^{2009}-\ldots-2-1=$ 1 , which implies, by the Intermediate Value Theorem, that $p$ must have a root greater than 1.
|
| 75 |
+
Let $p(x)=\frac{x^{2011}+1}{x+1}=x^{2010}-x^{2009}+x^{2008}-\ldots-x+1 .-1$ is the only real root of $x^{2011}+1=0$ but $p(-1)=2011$; therefore $p$ has no real roots. Since $p$ has 1005 minus signs, it is the desired polynomial.
|
| 76 |
+
8. [6] A sphere is the set of points at a fixed positive distance $r$ from its center. Let $\mathcal{S}$ be a set of 2010dimensional spheres. Suppose that the number of points lying on every element of $\mathcal{S}$ is a finite number $n$. Find the maximum possible value of $n$.
|
| 77 |
+
Answer: 2 The answer is 2 for any number of dimensions. We prove this by induction on the dimension.
|
| 78 |
+
Note that 1-dimensional spheres are pairs of points, and 2-dimensional spheres are circles.
|
| 79 |
+
Base case, $d=2$ : The intersection of two circles is either a circle (if the original circles are identical, and in the same place), a pair of points, a single point (if the circles are tangent), or the empty set. Thus, in dimension 2 , the largest finite number of intersection points is 2 , because the number of pairwise intersection points is 0,1 , or 2 for distinct circles.
|
| 80 |
+
We now prove that the intersection of two $k$-dimensional spheres is either the empty set, a $(k-1)$ dimensional sphere, a $k$-dimensional sphere (which only occurs if the original spheres are identical and coincident). Consider two spheres in $k$-dimensional space, and impose a coordinate system such that the centers of the two spheres lie on one coordinate axis. Then the equations for the two spheres become identical in all but one coordinate:
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\begin{aligned}
|
| 84 |
+
& \left(x_{1}-a_{1}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{1}^{2} \\
|
| 85 |
+
& \left(x_{1}-a_{2}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{2}^{2}
|
| 86 |
+
\end{aligned}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
If $a_{1}=a_{2}$, the spheres are concentric, and so they are either nonintersecting or coincident, intersecting in a $k$-dimensional sphere. If $a_{1} \neq a_{2}$, then subtracting the equations and solving for $x_{1}$ yields $x_{1}=\frac{r_{1}^{2}-a_{1}^{2}-r_{2}^{2}+a_{2}^{2}}{2\left(a_{2}-a_{2}\right)}$. Plugging this in to either equation above yields a single equation equation that describes a $(k-1)$-dimensional sphere.
|
| 90 |
+
Assume we are in dimension $d$, and suppose for induction that for all $k$ less than $d$, any two distinct $k$-dimensional spheres intersecting in a finite number of points intersect in at most two points. Suppose we have a collection of $d$-dimensional spheres $s_{1}, s_{2}, \ldots, s_{m}$. Without loss of generality, suppose the $s_{i}$ are distinct. Let $t_{i}$ be the intersection of $s_{i}$ and $s_{i+1}$ for $1 \leq i<m$. If any $t_{i}$ are the empty set, then the intersection of the $t_{i}$ is empty. None of the $t_{i}$ is a $d$-dimensional sphere because the $s_{i}$ are distinct. Thus each of $t_{1}, t_{2}, \ldots, t_{m-1}$ is a $(d-1)$-dimensional sphere, and the intersection of all of them is the same as the intersection of the $d$-dimensional spheres. We can then apply the inductive hypothesis to find that $t_{1}, \ldots, t_{m-1}$ intersect in at most two points. Thus, by induction, a set of spheres in any dimension which intersect at only finitely many points intersect at at most two points.
|
| 91 |
+
We now exhibit a set of $2^{2009}$ 2010-dimensional spheres, and prove that their intersection contains exactly two points. Take the spheres with radii $\sqrt{2013}$ and centers $(0, \pm 1, \pm 1, \ldots, \pm 1)$, where the sign of each coordinate is independent from the sign of every other coordinate. Because of our choice of radius, all these spheres pass through the points $( \pm 2,0,0, \ldots 0)$. Then the intersection is the set of points $\left(x_{1}, x_{2}, \ldots, x_{2010}\right)$ which satisfy the equations $x_{1}^{2}+\left(x_{2} \pm 1\right)^{2}+\cdots+\left(x_{2010} \pm 1\right)^{2}=2013$. The only solutions to these equations are the points $( \pm 2,0,0, \ldots, 0)$ (since $\left(x_{i}+1\right)^{2}$ must be the same as $\left(x_{i}-1\right)^{2}$ for all $i>1$, because we may hold all but one of the $\pm$ choices constant, and change the remaining one).
|
| 92 |
+
9. [7] Three unit circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ in the plane have the property that each circle passes through the centers of the other two. A square $S$ surrounds the three circles in such a way that each of its four sides is tangent to at least one of $\omega_{1}, \omega_{2}$ and $\omega_{3}$. Find the side length of the square $S$.
|
| 93 |
+
Answer: $\frac{\sqrt{6}+\sqrt{2}+8}{4}$
|
| 94 |
+
|
| 95 |
+
|
| 96 |
+
By the Pigeonhole Principle, two of the sides must be tangent to the same circle, say $\omega_{1}$. Since $S$ surrounds the circles, these two sides must be adjacent, so we can let $A$ denote the common vertex of the two sides tangent to $\omega_{1}$. Let $B, C$, and $D$ be the other vertices of $S$ in clockwise order, and let $P, Q$, and $R$ be the centers of $\omega_{1}, \omega_{2}$, and $\omega_{3}$ respectively, and suppose WLOG that they are also in clockwise order. Then $A C$ passes through the center of $\omega_{1}$, and by symmetry ( since $A B=A D$ ) it
|
| 97 |
+
must also pass through the other intersection point of $\omega_{2}$ and $\omega_{3}$. That is, $A C$ is the radical axis of $\omega_{2}$ and $\omega_{3}$.
|
| 98 |
+
Now, let $M$ and $N$ be the feet of the perpendiculars from $P$ and $R$, respectively, to side $A D$. Let $E$ and $F$ be the feet of the perpendiculars from $P$ to $A B$ and from $R$ to $D C$, respectively. Then $P E A M$ and $N R F D$ are rectangles, and $P E$ and $R F$ are radii of $\omega_{1}$ and $\omega_{2}$ respectively. Thus $A M=E P=1$ and $N D=R F=1$. Finally, we have
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\begin{aligned}
|
| 102 |
+
M N & =P R \cdot \cos \left(180^{\circ}-\angle E P R\right) \\
|
| 103 |
+
& =\cos \left(180^{\circ}-E P Q-R P Q\right) \\
|
| 104 |
+
& =-\cos \left(\left(270^{\circ}-60^{\circ}\right) / 2+60^{\circ}\right) \\
|
| 105 |
+
& =-\cos \left(165^{\circ}\right) \\
|
| 106 |
+
& =\cos \left(15^{\circ}\right) \\
|
| 107 |
+
& =\frac{\sqrt{6}+\sqrt{2}}{4} .
|
| 108 |
+
\end{aligned}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
Thus $A D=A M+M N+N D=1+\frac{\sqrt{6}+\sqrt{2}}{4}+1=\frac{\sqrt{6}+\sqrt{2}+8}{4}$ as claimed.
|
| 112 |
+
10. [8] Let $a, b, c, x, y$, and $z$ be complex numbers such that
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
a=\frac{b+c}{x-2}, \quad b=\frac{c+a}{y-2}, \quad c=\frac{a+b}{z-2} .
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
If $x y+y z+z x=67$ and $x+y+z=2010$, find the value of $x y z$.
|
| 119 |
+
Answer: -5892 Manipulate the equations to get a common denominator: $a=\frac{b+c}{x-2} \Longrightarrow x-2=$ $\frac{b+c}{a} \Longrightarrow x-1=\frac{a+b+c}{a} \Longrightarrow \frac{1}{x-1}=\frac{a}{a+b+c}$; similarly, $\frac{1}{y-1}=\frac{b}{a+b+c}$ and $\frac{1}{z-1}=\frac{c}{a+b+c}$. Thus
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
\begin{aligned}
|
| 123 |
+
\frac{1}{x-1}+\frac{1}{y-1}+\frac{1}{z-1} & =1 \\
|
| 124 |
+
(y-1)(z-1)+(x-1)(z-1)+(x-1)(y-1) & =(x-1)(y-1)(z-1) \\
|
| 125 |
+
x y+y z+z x-2(x+y+z)+3 & =x y z-(x y+y z+z x)+(x+y+z)-1 \\
|
| 126 |
+
x y z-2(x y+y z+z x)+3(x+y+z)-4 & =0 \\
|
| 127 |
+
x y z-2(67)+3(2010)-4 & =0 \\
|
| 128 |
+
x y z & =-5892
|
| 129 |
+
\end{aligned}
|
| 130 |
+
$$
|
| 131 |
+
|
HarvardMIT/md/en-132-2010-feb-gen2-solutions.md
ADDED
|
@@ -0,0 +1,126 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 20 February 2010
|
| 2 |
+
|
| 3 |
+
## General Test, Part 2
|
| 4 |
+
|
| 5 |
+
1. [3] Below is pictured a regular seven-pointed star. Find the measure of angle $a$ in radians.
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
Answer: | $\frac{3 \pi}{7}$ |
|
| 9 |
+
| :---: | The measure of the interior angle of a point of the star is $\frac{\pi}{7}$ because it is an inscribed angle on the circumcircle which intercepts a seventh of the circle ${ }^{1}$
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
|
| 13 |
+
Consider the triangle shown above in bold. Because the sum of the angles in any triangle is $\pi$,
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
2 \varphi+3\left(\frac{\pi}{7}\right)=\pi=2 \varphi+a
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Canceling the $2 \varphi$ on the right-hand side and on the left-hand side, we obtain
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
a=\frac{3 \pi}{7} .
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
2. [3] The rank of a rational number $q$ is the unique $k$ for which $q=\frac{1}{a_{1}}+\cdots+\frac{1}{a_{k}}$, where each $a_{i}$ is the smallest positive integer such that $q \geq \frac{1}{a_{1}}+\cdots+\frac{1}{a_{i}}$. Let $q$ be the largest rational number less than $\frac{1}{4}$ with rank 3 , and suppose the expression for $q$ is $\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}$. Find the ordered triple $\left(a_{1}, a_{2}, a_{3}\right)$.
|
| 26 |
+
Answer: $(5,21,421)$ Suppose that $A$ and $B$ were rational numbers of rank 3 less than $\frac{1}{4}$, and let $a_{1}, a_{2}, a_{3}, b_{1}, b_{2}, b_{3}$ be positive integers so that $A=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}$ and $B=\frac{1}{b_{1}}+\frac{1}{b_{2}}+\frac{1}{b_{3}}$ are the expressions for $A$ and $B$ as stated in the problem. If $b_{1}<a_{1}$ then $A<\frac{1}{a_{1}-1} \leq \frac{1}{b_{1}}<B$. In other words, of all the rationals less than $\frac{1}{4}$ with rank 3 , those that have $a_{1}=5$ are greater than those that have $a_{1}=6,7,8, \ldots$ Therefore we can "build" $q$ greedily, adding the largest unit fraction that keeps $q$ less than $\frac{1}{4}$ :
|
| 27 |
+
$\frac{1}{5}$ is the largest unit fraction less than $\frac{1}{4}$, hence $a_{1}=5$;
|
| 28 |
+
$\frac{1}{27}$ is the largest unit fraction less than $\frac{1}{4}-\frac{1}{5}$, hence $a_{2}=21$;
|
| 29 |
+
$\frac{1}{421}$ is the largest unit fraction less than $\frac{1}{4}-\frac{1}{5}-\frac{1}{21}$, hence $a_{3}=421$.
|
| 30 |
+
|
| 31 |
+
3. [4] How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0 ! and 1 ! to be distinct.
|
| 32 |
+
Answer: 39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain $3!, 4!, 5$ !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \cdot 2 \cdot 2 \cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.
|
| 33 |
+
4. [4] For $0 \leq y \leq 2$, let $D_{y}$ be the half-disk of diameter 2 with one vertex at $(0, y)$, the other vertex on the positive $x$-axis, and the curved boundary further from the origin than the straight boundary. Find the area of the union of $D_{y}$ for all $0 \leq y \leq 2$.
|
| 34 |
+
Answer: $\pi$
|
| 35 |
+
|
| 36 |
+
|
| 37 |
+
From the picture above, we see that the union of the half-disks will be a quarter-circle with radius 2 , and therefore area $\pi$. To prove that this is the case, we first prove that the boundary of every half-disk intersects the quarter-circle with radius 2 , and then that the half-disk is internally tangent to the quarter-circle at that point. This is sufficient because it is clear from the diagram that we need not worry about covering the interior of the quarter-circle.
|
| 38 |
+
Let $O$ be the origin. For a given half-disk $D_{y}$, label the vertex on the $y$-axis $A$ and the vertex on the $x$-axis $B$. Let $M$ be the midpoint of line segment $\overline{A B}$. Draw segment $O M$, and extend it until it intersects the curved boundary of $D_{y}$. Label the intersection point $C$. This construction is shown in the diagram below.
|
| 39 |
+
|
| 40 |
+
|
| 41 |
+
We first prove that $C$ lies on the quarter-circle, centered at the origin, with radius 2 . Since $M$ is the midpoint of $\overline{A B}$, and $A$ is on the $y$-axis, $M$ is horizontally halfway between $B$ and the $y$-axis. Since
|
| 42 |
+
$O$ and $B$ are on the $x$-axis (which is perpendicular to the $y$-axis), segments $\overline{O M}$ and $\overline{M B}$ have the same length. Since $M$ is the midpoint of $\overline{A B}$, and $A B=2, O M=1$. Since $D_{y}$ is a half-disk with radius 1 , all points on its curved boundary are 1 away from its center, $M$. Then $C$ is 2 away from the origin, and the quarter-circle consists of all points which are 2 away from the origin. Thus, $C$ is an intersection of the half-disk $D_{y}$ with the positive quarter-circle of radius 2 .
|
| 43 |
+
It remains to show that the half-disk $D_{y}$ is internally tangent to the quarter-circle. Since $\overline{O C}$ is a radius of the quarter-circle, it is perpendicular to the tangent of the quarter-circle at $C$. Since $\overline{M C}$ is a radius of the half-disk, it is perpendicular to the tangent of the half-disk at $C$. Then the tangents lines of the half-disk and the quarter-circle coincide, and the half-disk is tangent to the quarter-circle. It is obvious from the diagram that the half-disk lies at least partially inside of the quarter-circle, the half-disk $D_{y}$ is internally tangent to the quarter-circle.
|
| 44 |
+
Then the union of the half-disks is be a quarter-circle with radius 2 , and has area $\pi$.
|
| 45 |
+
5. [5] Suppose that there exist nonzero complex numbers $a, b, c$, and $d$ such that $k$ is a root of both the equations $a x^{3}+b x^{2}+c x+d=0$ and $b x^{3}+c x^{2}+d x+a=0$. Find all possible values of $k$ (including complex values).
|
| 46 |
+
Answer: $1,-1, i,-i$ Let $k$ be a root of both polynomials. Multiplying the first polynomial by $k$ and subtracting the second, we have $a k^{4}-a=0$, which means that $k$ is either $1,-1, i$, or $-i$. If $a=b=c=d=1$, then $-1, i$, and $-i$ are roots of both polynomials. If $a=b=c=1$ and $d=-3$, then 1 is a root of both polynomials. So $k$ can be $1,-1, i$, and $-i$.
|
| 47 |
+
6. [5] Let $A B C D$ be an isosceles trapezoid such that $A B=10, B C=15, C D=28$, and $D A=15$. There is a point $E$ such that $\triangle A E D$ and $\triangle A E B$ have the same area and such that $E C$ is minimal. Find $E C$.
|
| 48 |
+
|
| 49 |
+
Answer: | $\frac{216}{\sqrt{145}}$ |
|
| 50 |
+
| :---: |
|
| 51 |
+
|
| 52 |
+
|
| 53 |
+
|
| 54 |
+
The locus of points $E$ such that $[A E D]=[A E B]$ forms a line, since area is a linear function of the coordinates of $E$; setting the areas equal gives a linear equation in the coordinates $E^{2}$. Note that $A$ and $M$, the midpoint of $\overline{D B}$, are on this line; $A$ because both areas are 0 , and $M$ because the triangles share an altitude, and bases $\overline{D M}$ and $\overline{M B}$ are equal in length. Then $\overline{A M}$ is the set of points satisfying the area condition. The point $E$, then, is such that $\triangle A E C$ is a right angle (to make the distance minimal) and $E$ lies on $\overline{A M}$.
|
| 55 |
+
Let $X$ be the point of intersection of $\overline{A M}$ and $\overline{C D}$. Then $\triangle A M B \sim \triangle X M D$, and since $M D=B M$, they are in fact congruent. Thus $D X=A B=10$, and $X C=18$. Similarly, $B X=15$, so $A B X D$ is a parallelogram. Let $Y$ be the foot of the perpendicular from $A$ to $\overline{D C}$, so that $D Y=\frac{D C-A B}{2}=9$. Then
|
| 56 |
+
|
| 57 |
+
[^1]$A Y=\sqrt{A D^{2}-D Y^{2}}=\sqrt{225-81}=12$. Then $Y X=D X-D Y=1$ and $A X=\sqrt{A Y^{2}+Y X^{2}}=$ $\sqrt{144+1}=\sqrt{145}$. Since both $\triangle A X Y$ and $\triangle C X E$ have a right angle, and $\angle E X C$ and $\angle Y X A$ are congruent because they are vertical angles, $\triangle A X Y \sim \triangle C X E$. Then $\frac{C E}{A Y}=\frac{C X}{A X}$, so $C E=12 \cdot \frac{18}{\sqrt{145}}=$ $\frac{216}{\sqrt{145}}$.
|
| 58 |
+
7. [5] Suppose that $x$ and $y$ are complex numbers such that $x+y=1$ and that $x^{20}+y^{20}=20$. Find the sum of all possible values of $x^{2}+y^{2}$.
|
| 59 |
+
Answer: -90 We have $x^{2}+y^{2}+2 x y=1$. Define $a=2 x y$ and $b=x^{2}+y^{2}$ for convenience. Then $a+b=1$ and $b-a=x^{2}+y^{2}-2 x y=(x-y)^{2}=2 b-1$ so that $x, y=\frac{\sqrt{2 b-1} \pm 1}{2}$. Then
|
| 60 |
+
\[
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
\begin{aligned}
|
| 64 |
+
x^{20}+y^{20} & =\left(\frac{\sqrt{2 b-1}+1}{2}\right)^{20}+\left(\frac{\sqrt{2 b-1}-1}{2}\right)^{20} \\
|
| 65 |
+
& =\frac{1}{2^{20}}\left[(\sqrt{2 b-1}+1)^{20}+(\sqrt{2 b-1}-1)^{20}\right] \\
|
| 66 |
+
& =\frac{2}{2^{20}}\left[(\sqrt{2 b-1})^{20}+\binom{20}{2}(\sqrt{2 b-1})^{18}+\binom{20}{4}(\sqrt{2 b-1})^{16}+\ldots\right] \\
|
| 67 |
+
& =\frac{2}{2^{20}}\left[(2 b-1)^{10}+\binom{20}{2}(2 b-1)^{9}+\binom{20}{4}(2 b-1)^{8}+\ldots\right] \\
|
| 68 |
+
& =20
|
| 69 |
+
\end{aligned}
|
| 70 |
+
$$
|
| 71 |
+
\]
|
| 72 |
+
|
| 73 |
+
We want to find the sum of distinct roots of the above polynomial in $b$; we first prove that the original polynomial is square-free. The conditions $x+y=1$ and $x^{20}+y^{20}=20$ imply that $x^{20}+(1-x)^{20}-20=0$; let $p(x)=x^{20}+(1-x)^{20}-20 . p$ is square-free if and only if $G C D\left(p, p^{\prime}\right)=c$ for some constant $c$ :
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\begin{aligned}
|
| 77 |
+
G C D\left(p, p^{\prime}\right) & =G C D\left(x^{20}+(1-x)^{20}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
|
| 78 |
+
& =G C D\left(x^{20}-x(1-x)^{19}+(1-x)^{19}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
|
| 79 |
+
& =G C D\left((1-x)^{19}-20, x^{19}-(1-x)^{19}\right) \\
|
| 80 |
+
& =G C D\left((1-x)^{19}-20, x^{19}-20\right)
|
| 81 |
+
\end{aligned}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
The roots of $x^{19}-20$ are $\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$; the roots of $(1-x)^{19}-20$ are $1-\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$. If $x^{19}-20$ and $(1-x)^{19}-20$ share a common root, then there exist integers $m$, $n$ such that $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=1-\sqrt[19]{20^{n}} \exp \left(\frac{2 \pi i n}{19}\right)$; since the imaginary parts of both sides must be the same, we have $m=n$ and $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=\frac{1}{2} \Longrightarrow 20^{m}=\frac{1}{2^{19}}$, a contradiction. Thus we have proved that the polynomial in $x$ has no double roots. Since for each $b$ there exists a unique pair $(x, y)$ (up to permutations) that satisfies $x^{2}+y^{2}=b$ and $(x+y)^{2}=1$, the polynomial in $b$ has no double roots.
|
| 85 |
+
Let the coefficient of $b^{n}$ in the above equation be $\left[b^{n}\right]$. By Vieta's Formulas, the sum of all possible values of $b=x^{2}+y^{2}$ is equal to $-\frac{\left[b^{9}\right]}{\left[b^{10}\right]} . \quad\left[b^{10}\right]=\frac{2}{2^{20}}\left(2^{10}\right)$ and $\left[b^{9}\right]=\frac{2}{2^{20}}\left(-\binom{10}{1} 2^{9}+\binom{20}{2} 2^{9}\right)$; thus $-\frac{\left[b^{9}\right]}{\left[b^{10}\right]}=-\frac{\binom{10}{1} 2^{9}-\binom{20}{2} 2^{9}}{2^{10}}=-90$.
|
| 86 |
+
8. [6] An ant starts out at $(0,0)$. Each second, if it is currently at the square $(x, y)$, it can move to $(x-1, y-1),(x-1, y+1),(x+1, y-1)$, or $(x+1, y+1)$. In how many ways can it end up at $(2010,2010)$ after 4020 seconds?
|
| 87 |
+
Answer: \( \binom{4020}{1005}^2 \). Note that each of the coordinates either increases or decreases the x and y- coordinates by 1. In order to reach 2010 after 4020 steps, each of the coordinates must be increased 3015 times and decreased 1005 times. A permutation of 3015 plusses and 1005 minuses for each of $x$ and $y$ uniquely corresponds to a path the ant could take to $(2010,2010)$, because we can take ordered pairs from the two lists and match them up to a valid step the ant can take. So the number of ways the ant can end up at $(2010,2010)$ after 4020 seconds is equal to the number of ways to arrange plusses and minuses for both $x$ and $y$, or $\left(\binom{4020}{1005}\right)^{2}$.
|
| 88 |
+
9. [7] You are standing in an infinitely long hallway with sides given by the lines $x=0$ and $x=6$. You start at $(3,0)$ and want to get to $(3,6)$. Furthermore, at each instant you want your distance to $(3,6)$ to either decrease or stay the same. What is the area of the set of points that you could pass through on your journey from $(3,0)$ to $(3,6)$ ?
|
| 89 |
+
Answer: $9 \sqrt{3}+\frac{21 \pi}{2}$
|
| 90 |
+
|
| 91 |
+
|
| 92 |
+
If you draw concentric circles around the destination point, the condition is equivalent to the restriction that you must always go inwards towards the destination. In the diagram above, the regions through which you might pass are shaded.
|
| 93 |
+
We find the areas of regions $\mathrm{A}, \mathrm{B}$, and C separately, and add them up (doubling the area of region A, because there are two of them).
|
| 94 |
+
The hypotenuse of triangle A is of length 6 , and the base is of length 3 , so it is a $\frac{\pi}{6}-\frac{\pi}{3}-\frac{\pi}{2}$ triangle (30-60-90 triangle) with area $\frac{9 \sqrt{3}}{2}$. Then the total area of the regions labeled A is $9 \sqrt{3}$.
|
| 95 |
+
Since the angle of triangle A nearest the center of the circle (the destination point) is $\frac{\pi}{3}$, sector B has central angle $\frac{\pi}{3}$. Then the area of sector B is $\frac{1}{2} r^{2} \theta=\frac{1}{2} \cdot 36 \cdot \frac{\pi}{3}=6 \pi$.
|
| 96 |
+
Region C is a half-disc of radius 3 , so its area is $\frac{9 \pi}{2}$.
|
| 97 |
+
Thus, the total area is $9 \sqrt{3}+\frac{21 \pi}{2}$.
|
| 98 |
+
10. [8] In a $16 \times 16$ table of integers, each row and column contains at most 4 distinct integers. What is the maximum number of distinct integers that there can be in the whole table?
|
| 99 |
+
Answer: 49 First, we show that 50 is too big. Assume for sake of contradiction that a labeling with at least 50 distinct integers exists. By the Pigeonhole Principle, there must be at least one row, say the first row, with at least 4 distinct integers in it; in this case, that is exactly 4 , since that is the maximum number of distinct integers in one row. Then, in the remaining 15 rows there must be at
|
| 100 |
+
least 46 distinct integers (these 46 will also be distinct from the 4 in the first row). Using Pigeonhole again, there will be another row, say the second row, with 4 distinct integers in it. Call the set of integers in the first and second rows $S$. Because the 4 distinct integers in the second row are distinct from the 4 in the first row, there are 8 distinct values in the first two rows, so $|S|=8$. Now consider the subcolumns containing the cells in rows 3 to 16 . In each subcolumn, there are at most 2 values not in $S$, because there are already two distinct values in that column from the cells in the first two rows. So, the maximum number of distinct values in the table is $16 \cdot 2+8=40$, a contradiction. So a valid labeling must have fewer than 50 distinct integers. Below, we show by example that 49 is attainable.
|
| 101 |
+
|
| 102 |
+
| 1 | 17 | 33 | - | - | - | - | - | - | - | - | - | - | - | - | - |
|
| 103 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 104 |
+
| - | 2 | 18 | 34 | - | - | - | - | - | - | - | - | - | - | - | - |
|
| 105 |
+
| - | - | 3 | 19 | 35 | - | - | - | - | - | - | - | - | - | - | - |
|
| 106 |
+
| - | - | - | 4 | 20 | 36 | - | - | - | - | - | - | - | - | - | - |
|
| 107 |
+
| - | - | - | - | 5 | 21 | 37 | - | - | - | - | - | - | - | - | - |
|
| 108 |
+
| - | - | - | - | - | 6 | 22 | 38 | - | - | - | - | - | - | - | - |
|
| 109 |
+
| - | - | - | - | - | - | 7 | 23 | 39 | - | - | - | - | - | - | - |
|
| 110 |
+
| - | - | - | - | - | - | - | 8 | 24 | 40 | - | - | - | - | - | - |
|
| 111 |
+
| - | - | - | - | - | - | - | - | 9 | 25 | 41 | - | - | - | - | - |
|
| 112 |
+
| - | - | - | - | - | - | - | - | - | 10 | 26 | 42 | - | - | - | - |
|
| 113 |
+
| - | - | - | - | - | - | - | - | - | - | 11 | 27 | 43 | - | - | - |
|
| 114 |
+
| - | - | - | - | - | - | - | - | - | - | - | 12 | 28 | 44 | - | - |
|
| 115 |
+
| - | - | - | - | - | - | - | - | - | - | - | - | 13 | 29 | 45 | - |
|
| 116 |
+
| - | - | - | - | - | - | - | - | - | - | - | - | - | 14 | 30 | 46 |
|
| 117 |
+
| 47 | - | - | - | - | - | - | - | - | - | - | - | - | - | 15 | 31 |
|
| 118 |
+
| 32 | 48 | - | - | - | - | - | - | - | - | - | - | - | - | - | 16 |
|
| 119 |
+
|
| 120 |
+
Cells that do not contain a number are colored with color 49 .
|
| 121 |
+
|
| 122 |
+
|
| 123 |
+
[^0]: 1/http://en.wikipedia.org/wiki/Inscribed_angle_theorem
|
| 124 |
+
|
| 125 |
+
[^1]: ${ }^{2}$ The notation $\left[A_{1} A_{2} \ldots A_{n}\right]$ means the area of polygon $A_{1} A_{2} \ldots A_{n}$.
|
| 126 |
+
|
HarvardMIT/md/en-132-2010-feb-geo-solutions.md
ADDED
|
@@ -0,0 +1,157 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 20 February 2010 <br> Geometry Subject Test
|
| 2 |
+
|
| 3 |
+
1. [3] Below is pictured a regular seven-pointed star. Find the measure of angle $a$ in radians.
|
| 4 |
+
|
| 5 |
+
|
| 6 |
+
Answer: | $3 \pi$ |
|
| 7 |
+
| :---: |
|
| 8 |
+
| 7 | The measure of the interior angle of a point of the star is $\frac{\pi}{7}$ because it is an inscribed angle on the circumcircle which intercepts a seventh of the circle ${ }^{1}$
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
Consider the triangle shown above in bold. Because the sum of the angles in any triangle is $\pi$,
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
2 \varphi+3\left(\frac{\pi}{7}\right)=\pi=2 \varphi+a
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
Canceling the $2 \varphi$ on the right-hand side and on the left-hand side, we obtain
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
a=\frac{3 \pi}{7} .
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
2. [3] A rectangular piece of paper is folded along its diagonal (as depicted below) to form a non-convex pentagon that has an area of $\frac{7}{10}$ of the area of the original rectangle. Find the ratio of the longer side of the rectangle to the shorter side of the rectangle.
|
| 25 |
+
|
| 26 |
+
|
| 27 |
+
Answer: $\sqrt{5}$
|
| 28 |
+
|
| 29 |
+
[^0]
|
| 30 |
+
|
| 31 |
+
Given a polygon $P_{1} P_{2} \cdots P_{k}$, let $\left[P_{1} P_{2} \cdots P_{k}\right]$ denote its area. Let $A B C D$ be the rectangle. Suppose we fold $B$ across $\overline{A C}$, and let $E$ be the intersection of $\overline{A D}$ and $\overline{B^{\prime} C}$. Then we end up with the pentagon $A C D E B^{\prime}$, depicted above. Let's suppose, without loss of generality, that $A B C D$ has area 1. Then $\triangle A E C$ must have area $\frac{3}{10}$, since
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\begin{aligned}
|
| 35 |
+
{[A B C D] } & =[A B C]+[A C D] \\
|
| 36 |
+
& =\left[A B^{\prime} C\right]+[A C D] \\
|
| 37 |
+
& =\left[A B^{\prime} E\right]+2[A E C]+[E D C] \\
|
| 38 |
+
& =\left[A C D E B^{\prime}\right]+[A E C] \\
|
| 39 |
+
& =\frac{7}{10}[A B C D]+[A E C]
|
| 40 |
+
\end{aligned}
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
That is, $[A E C]=\frac{3}{10}[A B C D]=\frac{3}{10}$.
|
| 44 |
+
Since $\triangle E C D$ is congruent to $\triangle E A B^{\prime}$, both triangles have area $\frac{1}{5}$. Note that $\triangle A B^{\prime} C, \triangle A B C$, and $\triangle C D A$ are all congruent, and all have area $\frac{1}{2}$. Since $\triangle A E C$ and $\triangle E D C$ share altitude $\overline{D C}$, $\frac{D E}{E A}=\frac{[D E C]}{[A E C]}=\frac{2}{3}$. Because $\triangle C A E$ is isosceles, $C E=E A$. Let $A E=3 x$. The $C E=3 x, D E=2 x$, and $C D=x \sqrt{9-4}=x \sqrt{5}$. Then $\frac{A D}{D C}=\frac{A E+E D}{D C}=\frac{3+2}{\sqrt{5}}=\sqrt{5}$.
|
| 45 |
+
3. [4] For $0 \leq y \leq 2$, let $D_{y}$ be the half-disk of diameter 2 with one vertex at $(0, y)$, the other vertex on the positive $x$-axis, and the curved boundary further from the origin than the straight boundary. Find the area of the union of $D_{y}$ for all $0 \leq y \leq 2$.
|
| 46 |
+
Answer: $\pi$
|
| 47 |
+
|
| 48 |
+
|
| 49 |
+
From the picture above, we see that the union of the half-disks will be a quarter-circle with radius 2 , and therefore area $\pi$. To prove that this is the case, we first prove that the boundary of every half-disk intersects the quarter-circle with radius 2 , and then that the half-disk is internally tangent to the quarter-circle at that point. This is sufficient because it is clear from the diagram that we need not worry about covering the interior of the quarter-circle.
|
| 50 |
+
|
| 51 |
+
Let $O$ be the origin. For a given half-disk $D_{y}$, label the vertex on the $y$-axis $A$ and the vertex on the $x$-axis $B$. Let $M$ be the midpoint of line segment $\overline{A B}$. Draw segment $O M$, and extend it until it intersects the curved boundary of $D_{y}$. Label the intersection point $C$. This construction is shown in the diagram below.
|
| 52 |
+
|
| 53 |
+
|
| 54 |
+
We first prove that $C$ lies on the quarter-circle, centered at the origin, with radius 2 . Since $M$ is the midpoint of $\overline{A B}$, and $A$ is on the $y$-axis, $M$ is horizontally halfway between $B$ and the $y$-axis. Since $O$ and $B$ are on the $x$-axis (which is perpendicular to the $y$-axis), segments $\overline{O M}$ and $\overline{M B}$ have the same length. Since $M$ is the midpoint of $\overline{A B}$, and $A B=2, O M=1$. Since $D_{y}$ is a half-disk with radius 1 , all points on its curved boundary are 1 away from its center, $M$. Then $C$ is 2 away from the origin, and the quarter-circle consists of all points which are 2 away from the origin. Thus, $C$ is an intersection of the half-disk $D_{y}$ with the positive quarter-circle of radius 2 .
|
| 55 |
+
It remains to show that the half-disk $D_{y}$ is internally tangent to the quarter-circle. Since $\overline{O C}$ is a radius of the quarter-circle, it is perpendicular to the tangent of the quarter-circle at $C$. Since $\overline{M C}$ is a radius of the half-disk, it is perpendicular to the tangent of the half-disk at $C$. Then the tangents lines of the half-disk and the quarter-circle coincide, and the half-disk is tangent to the quarter-circle. It is obvious from the diagram that the half-disk lies at least partially inside of the quarter-circle, the half-disk $D_{y}$ is internally tangent to the quarter-circle.
|
| 56 |
+
Then the union of the half-disks is be a quarter-circle with radius 2 , and has area $\pi$.
|
| 57 |
+
4. [4] Let $A B C D$ be an isosceles trapezoid such that $A B=10, B C=15, C D=28$, and $D A=15$. There is a point $E$ such that $\triangle A E D$ and $\triangle A E B$ have the same area and such that $E C$ is minimal. Find $E C$.
|
| 58 |
+
Answer: $\frac{216}{\sqrt{145}}$
|
| 59 |
+
|
| 60 |
+
|
| 61 |
+
Geometry Subject Test
|
| 62 |
+
|
| 63 |
+
The locus of points $E$ such that $[A E D]=[A E B]$ forms a line, since area is a linear function of the coordinates of $E$; setting the areas equal gives a linear equation in the coordinates $E^{2}$. Note that $A$ and $M$, the midpoint of $\overline{D B}$, are on this line; $A$ because both areas are 0 , and $M$ because the triangles share an altitude, and bases $\overline{D M}$ and $\overline{M B}$ are equal in length. Then $\overline{A M}$ is the set of points satisfying the area condition. The point $E$, then, is such that $\triangle A E C$ is a right angle (to make the distance minimal) and $E$ lies on $\overline{A M}$.
|
| 64 |
+
Let $X$ be the point of intersection of $\overline{A M}$ and $\overline{C D}$. Then $\triangle A M B \sim \triangle X M D$, and since $M D=B M$, they are in fact congruent. Thus $D X=A B=10$, and $X C=18$. Similarly, $B X=15$, so $A B X D$ is a parallelogram. Let $Y$ be the foot of the perpendicular from $A$ to $\overline{D C}$, so that $D Y=\frac{D C-A B}{2}=9$. Then $A Y=\sqrt{A D^{2}-D Y^{2}}=\sqrt{225-81}=12$. Then $Y X=D X-D Y=1$ and $A X=\sqrt{A Y^{2}+Y X^{2}}=$ $\sqrt{144+1}=\sqrt{145}$. Since both $\triangle A X Y$ and $\triangle C X E$ have a right angle, and $\angle E X C$ and $\angle Y X A$ are congruent because they are vertical angles, $\triangle A X Y \sim \triangle C X E$. Then $\frac{C E}{A Y}=\frac{C X}{A X}$, so $C E=12 \cdot \frac{18}{\sqrt{145}}=$ $\frac{216}{\sqrt{145}}$.
|
| 65 |
+
5. [4] A sphere is the set of points at a fixed positive distance $r$ from its center. Let $\mathcal{S}$ be a set of 2010dimensional spheres. Suppose that the number of points lying on every element of $\mathcal{S}$ is a finite number $n$. Find the maximum possible value of $n$.
|
| 66 |
+
Answer: 2 The answer is 2 for any number of dimensions. We prove this by induction on the dimension.
|
| 67 |
+
Note that 1-dimensional spheres are pairs of points, and 2-dimensional spheres are circles.
|
| 68 |
+
Base case, $d=2$ : The intersection of two circles is either a circle (if the original circles are identical, and in the same place), a pair of points, a single point (if the circles are tangent), or the empty set. Thus, in dimension 2, the largest finite number of intersection points is 2 , because the number of pairwise intersection points is 0,1 , or 2 for distinct circles.
|
| 69 |
+
We now prove that the intersection of two $k$-dimensional spheres is either the empty set, a $(k-1)$ dimensional sphere, a $k$-dimensional sphere (which only occurs if the original spheres are identical and coincident). Consider two spheres in $k$-dimensional space, and impose a coordinate system such that the centers of the two spheres lie on one coordinate axis. Then the equations for the two spheres become identical in all but one coordinate:
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
\begin{aligned}
|
| 73 |
+
& \left(x_{1}-a_{1}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{1}^{2} \\
|
| 74 |
+
& \left(x_{1}-a_{2}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{2}^{2}
|
| 75 |
+
\end{aligned}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
If $a_{1}=a_{2}$, the spheres are concentric, and so they are either nonintersecting or coincident, intersecting in a $k$-dimensional sphere. If $a_{1} \neq a_{2}$, then subtracting the equations and solving for $x_{1}$ yields $x_{1}=\frac{r_{1}^{2}-a_{1}^{2}-r_{2}^{2}+a_{2}^{2}}{2\left(a_{2}-a_{2}\right)}$. Plugging this in to either equation above yields a single equation equation that describes a $(k-1)$-dimensional sphere.
|
| 79 |
+
Assume we are in dimension $d$, and suppose for induction that for all $k$ less than $d$, any two distinct $k$-dimensional spheres intersecting in a finite number of points intersect in at most two points. Suppose we have a collection of $d$-dimensional spheres $s_{1}, s_{2}, \ldots, s_{m}$. Without loss of generality, suppose the $s_{i}$ are distinct. Let $t_{i}$ be the intersection of $s_{i}$ and $s_{i+1}$ for $1 \leq i<m$. If any $t_{i}$ are the empty set, then the intersection of the $t_{i}$ is empty. None of the $t_{i}$ is a $d$-dimensional sphere because the $s_{i}$ are distinct. Thus each of $t_{1}, t_{2}, \ldots, t_{m-1}$ is a $(d-1)$-dimensional sphere, and the intersection of all of them is the same as the intersection of the $d$-dimensional spheres. We can then apply the inductive hypothesis to find that $t_{1}, \ldots, t_{m-1}$ intersect in at most two points. Thus, by induction, a set of spheres in any dimension which intersect at only finitely many points intersect at at most two points.
|
| 80 |
+
We now exhibit a set of $2^{2009} 2010$-dimensional spheres, and prove that their intersection contains exactly two points. Take the spheres with radii $\sqrt{2013}$ and centers $(0, \pm 1, \pm 1, \ldots, \pm 1)$, where the sign of each coordinate is independent from the sign of every other coordinate. Because of our choice of radius, all these spheres pass through the points $( \pm 2,0,0, \ldots 0)$. Then the intersection is the set of
|
| 81 |
+
|
| 82 |
+
[^1]points $\left(x_{1}, x_{2}, \ldots, x_{2010}\right)$ which satisfy the equations $x_{1}^{2}+\left(x_{2} \pm 1\right)^{2}+\cdots+\left(x_{2010} \pm 1\right)^{2}=2013$. The only solutions to these equations are the points $( \pm 2,0,0, \ldots, 0)$ (since $\left(x_{i}+1\right)^{2}$ must be the same as $\left(x_{i}-1\right)^{2}$ for all $i>1$, because we may hold all but one of the $\pm$ choices constant, and change the remaining one).
|
| 83 |
+
6. [5] Three unit circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ in the plane have the property that each circle passes through the centers of the other two. A square $S$ surrounds the three circles in such a way that each of its four sides is tangent to at least one of $\omega_{1}, \omega_{2}$ and $\omega_{3}$. Find the side length of the square $S$.
|
| 84 |
+
Answer: $\frac{\sqrt{6}+\sqrt{2}+8}{4}$
|
| 85 |
+
|
| 86 |
+
|
| 87 |
+
By the Pigeonhole Principle, two of the sides must be tangent to the same circle, say $\omega_{1}$. Since $S$ surrounds the circles, these two sides must be adjacent, so we can let $A$ denote the common vertex of the two sides tangent to $\omega_{1}$. Let $B, C$, and $D$ be the other vertices of $S$ in clockwise order, and let $P, Q$, and $R$ be the centers of $\omega_{1}, \omega_{2}$, and $\omega_{3}$ respectively, and suppose WLOG that they are also in clockwise order. Then $A C$ passes through the center of $\omega_{1}$, and by symmetry (since $A B=A D$ ) it must also pass through the other intersection point of $\omega_{2}$ and $\omega_{3}$. That is, $A C$ is the radical axis of $\omega_{2}$ and $\omega_{3}$.
|
| 88 |
+
Now, let $M$ and $N$ be the feet of the perpendiculars from $P$ and $R$, respectively, to side $A D$. Let $E$ and $F$ be the feet of the perpendiculars from $P$ to $A B$ and from $R$ to $D C$, respectively. Then $P E A M$ and $N R F D$ are rectangles, and $P E$ and $R F$ are radii of $\omega_{1}$ and $\omega_{2}$ respectively. Thus $A M=E P=1$ and $N D=R F=1$. Finally, we have
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
\begin{aligned}
|
| 92 |
+
M N & =P R \cdot \cos \left(180^{\circ}-\angle E P R\right) \\
|
| 93 |
+
& =\cos \left(180^{\circ}-E P Q-R P Q\right) \\
|
| 94 |
+
& =-\cos \left(\left(270^{\circ}-60^{\circ}\right) / 2+60^{\circ}\right) \\
|
| 95 |
+
& =-\cos \left(165^{\circ}\right) \\
|
| 96 |
+
& =\cos \left(15^{\circ}\right) \\
|
| 97 |
+
& =\frac{\sqrt{6}+\sqrt{2}}{4}
|
| 98 |
+
\end{aligned}
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
Thus $A D=A M+M N+N D=1+\frac{\sqrt{6}+\sqrt{2}}{4}+1=\frac{\sqrt{6}+\sqrt{2}+8}{4}$ as claimed.
|
| 102 |
+
7. [6] You are standing in an infinitely long hallway with sides given by the lines $x=0$ and $x=6$. You start at $(3,0)$ and want to get to $(3,6)$. Furthermore, at each instant you want your distance to $(3,6)$ to either decrease or stay the same. What is the area of the set of points that you could pass through on your journey from $(3,0)$ to $(3,6)$ ?
|
| 103 |
+
Answer: $9 \sqrt{3}+\frac{21 \pi}{2}$
|
| 104 |
+
|
| 105 |
+
|
| 106 |
+
If you draw concentric circles around the destination point, the condition is equivalent to the restriction that you must always go inwards towards the destination. In the diagram above, the regions through which you might pass are shaded.
|
| 107 |
+
We find the areas of regions A, B, and C separately, and add them up (doubling the area of region A, because there are two of them).
|
| 108 |
+
The hypotenuse of triangle A is of length 6 , and the base is of length 3 , so it is a $\frac{\pi}{6}-\frac{\pi}{3}-\frac{\pi}{2}$ triangle (30-60-90 triangle) with area $\frac{9 \sqrt{3}}{2}$. Then the total area of the regions labeled A is $9 \sqrt{3}$.
|
| 109 |
+
Since the angle of triangle A nearest the center of the circle (the destination point) is $\frac{\pi}{3}$, sector B has central angle $\frac{\pi}{3}$. Then the area of sector B is $\frac{1}{2} r^{2} \theta=\frac{1}{2} \cdot 36 \cdot \frac{\pi}{3}=6 \pi$.
|
| 110 |
+
Region C is a half-disc of radius 3 , so its area is $\frac{9 \pi}{2}$.
|
| 111 |
+
Thus, the total area is $9 \sqrt{3}+\frac{21 \pi}{2}$.
|
| 112 |
+
8. [6] Let $O$ be the point $(0,0)$. Let $A, B, C$ be three points in the plane such that $A O=15, B O=15$, and $C O=7$, and such that the area of triangle $A B C$ is maximal. What is the length of the shortest side of $A B C$ ?
|
| 113 |
+
Answer: 20 We claim that $O$ should be the orthocenter of the triangle $A B C$. If $O$ is not on an altitude of $\triangle A B C$, suppose (without loss of generality) that $\overline{A O}$ is not perpendicular to $\overline{B C}$. We can
|
| 114 |
+
rotate $A$ around $O$, leaving $B$ and $C$ fixed, to make $\overline{A O}$ perpendicular to $\overline{B C}$, which strictly increases the area. Therefore, if $[A B C]$ is maximal then $\triangle A B C$ is an isosceles triangle with orthocenter $O$ and base $\overline{A B}$.
|
| 115 |
+
|
| 116 |
+
|
| 117 |
+
Let $F$ be the foot of the perpendicular from $C$ to $\overline{A B}$. Since $\angle F O A$ and $\angle C O E$ are vertical, $\angle F A O=$ $\angle O C E$. Then $\triangle F A O$ is similar to $\triangle F C B$, so we have $\frac{A F}{O F}=\frac{C F}{B F}=\frac{O F+7}{A F}$, so $A F^{2}=O F^{2}+7 \cdot O F$. Since $A F^{2}=225-O F^{2}, 2 \cdot O F^{2}+7 \cdot O F-225=0$, so $O F=9$. Then $A F=12$, so $A B=24$ and $B C=20$. Thus, the length of the shortest side of $\triangle A B C$ is 20 .
|
| 118 |
+
9. [7] Let $A B C D$ be a quadrilateral with an inscribed circle centered at $I$. Let $C I$ intersect $A B$ at $E$. If $\angle I D E=35^{\circ}, \angle A B C=70^{\circ}$, and $\angle B C D=60^{\circ}$, then what are all possible measures of $\angle C D A$ ?
|
| 119 |
+
Answer: $70^{\circ}$ and $160^{\circ}$
|
| 120 |
+
Arbitrarily defining $B$ and $C$ determines $I$ and $E$ up to reflections across $B C$. D lies on both the circle determined by $\angle E D I=35^{\circ}$ and the line through $C$ tangent to the circle (and on the opposite side of $B)$; since the intersection of a line and a circle has at most two points, there are only two cases for $A B C D$. The diagram below on the left shows the construction made in this solution, containing both cases. The diagram below on the right shows only the degenerate case.
|
| 121 |
+
|
| 122 |
+
|
| 123 |
+
Reflect $B$ across $E C$ to $B^{\prime}$; then $C B=C B^{\prime}$. Since $B A$ and $B C$ are tangent to the circle centered at $I, I B$ is the angle bisector of $\angle A B C$. Then $\angle I B E=\angle I B^{\prime} E=35^{\circ}$. If $B^{\prime}=D$, then $\angle A D C=$ $\angle E B^{\prime} C=70^{\circ}$. Otherwise, since $\angle I B^{\prime} E=35^{\circ}=\angle I D E$ (given), $E B^{\prime} D I$ is a cyclic quadrilateral. Then $\angle I E D=\angle I B^{\prime} D=35^{\circ}$ and $\angle B C I=\angle E C D=30^{\circ}$, so $\triangle C E D \sim \triangle C B I$.
|
| 124 |
+
Since $\angle C I D$ is exterior to $\triangle D I E, \angle C I D=\angle I D E+\angle D E I=70^{\circ}$. Then $\triangle C D I \sim \triangle C E B$. Because $E B^{\prime} D I$ is cyclic, $\angle I D C=\angle I E B^{\prime}=\angle I E B=180^{\circ}-70^{\circ}-30^{\circ}=80^{\circ}$. Then $\angle A D C=2 \angle I D C=160^{\circ}$.
|
| 125 |
+
Thus, the two possible measures are $70^{\circ}$ and $160^{\circ}$.
|
| 126 |
+
10. [8] Circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Segment $P Q$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$, and $A$ is closer to $P Q$ than $B$. Point $X$ is on $\omega_{1}$ such that $P X \| Q B$, and point $Y$ is on $\omega_{2}$ such that $Q Y \| P B$. Given that $\angle A P Q=30^{\circ}$ and $\angle P Q A=15^{\circ}$, find the ratio $A X / A Y$.
|
| 127 |
+
Answer: $2-\sqrt{3}$
|
| 128 |
+
|
| 129 |
+
|
| 130 |
+
Let $C$ be the fourth vertex of parallelogram $A P C Q$. The midpoint $M$ of $\overline{P Q}$ is the intersection of the diagonals of this parallelogram. Because $M$ has equal power ${ }^{3}$ with respect to the two circles $\omega_{1}$ and $\omega_{2}$, it lies on $\overleftrightarrow{A B}$, the circles' radical axis $4^{4}$. Therefore, $C$ lies on $\overleftrightarrow{A B}$ as well.
|
| 131 |
+
Using a series of parallel lines and inscribed arcs, we have:
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\angle A P C=\angle A P Q+\angle C P Q=\angle A P Q+\angle P Q A=\angle A B P+\angle Q B A=\angle P B Q=\angle X P B
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
where the last equality follows from the fact that $P X \| Q B$.
|
| 138 |
+
|
| 139 |
+
[^2]We also know that $\angle B X P=180^{\circ}-\angle P A B=\angle C A P$, so triangles $B X P$ and $C A P$ are similar. By the spiral similarity theorem triangles $B P C$ and $X P A$ are similar, too.
|
| 140 |
+
By analogous reasoning, triangles $B Q C$ and $Y Q A$ are similar. Then we have:
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
\frac{A X}{A Y}=\frac{A X / B C}{A Y / B C}=\frac{A P / C P}{A Q / C Q}=\frac{A P^{2}}{A Q^{2}}
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
where the last inequality holds because $A P C Q$ is a parallelogram. Using the Law of Sines, the last expression equals $\frac{\sin ^{2} 15^{\circ}}{\sin ^{2} 30^{\circ}}=2-\sqrt{3}$.
|
| 147 |
+
|
| 148 |
+
[^3]
|
| 149 |
+
[^0]: ${ }^{1}$ http://en.wikipedia.org/wiki/Inscribed_angle_theorem
|
| 150 |
+
|
| 151 |
+
[^1]: ${ }^{2}$ The notation $\left[A_{1} A_{2} \ldots A_{n}\right]$ means the area of polygon $A_{1} A_{2} \ldots A_{n}$.
|
| 152 |
+
|
| 153 |
+
[^2]: $\sqrt[3]{ }$ http://en.wikipedia.org/wiki/Power_of_a_point
|
| 154 |
+
4 http://en.wikipedia.org/wiki/Radical_axis
|
| 155 |
+
|
| 156 |
+
[^3]: ${ }^{5}$ This theorem states that if $\triangle P A B$ and $\triangle P X Y$ are similar and oriented the same way, then $\triangle P A X$ and $\triangle P B Y$ are similar too. It is true because the first similarity implies that $A P / B P=X P / Y P$ and $\angle A P B=\angle X P Y$, which proves the second similarity.
|
| 157 |
+
|
HarvardMIT/md/en-132-2010-feb-guts-solutions.md
ADDED
|
@@ -0,0 +1,443 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament Saturday 20 February 2010
|
| 2 |
+
|
| 3 |
+
Guts Round
|
| 4 |
+
|
| 5 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 6 |
+
|
| 7 |
+
1. [4] If $A=10^{9}-987654321$ and $B=\frac{123456789+1}{10}$, what is the value of $\sqrt{A B}$ ?
|
| 8 |
+
|
| 9 |
+
Answer: 12345679 Both $A$ and $B$ equal 12345679, so $\sqrt{A B}=12345679$ as well.
|
| 10 |
+
2. [4] Suppose that $x, y$, and $z$ are non-negative real numbers such that $x+y+z=1$. What is the maximum possible value of $x+y^{2}+z^{3}$ ?
|
| 11 |
+
Answer: 1 Since $0 \leq y, z \leq 1$, we have $y^{2} \leq y$ and $z^{3} \leq z$. Therefore $x+y^{2}+z^{3} \leq x+y+z=1$. We can get $x+y^{2}+z^{3}=1$ by setting $(x, y, z)=(1,0,0)$.
|
| 12 |
+
3. [4] In a group of people, there are 13 who like apples, 9 who like blueberries, 15 who like cantaloupe, and 6 who like dates. (A person can like more than 1 kind of fruit.) Each person who likes blueberries also likes exactly one of apples and cantaloupe. Each person who likes cantaloupe also likes exactly one of blueberries and dates. Find the minimum possible number of people in the group.
|
| 13 |
+
Answer: 22 Everyone who likes cantaloupe likes exactly one of blueberries and dates. However, there are 15 people who like cantaloupe, 9 who like blueberries, and 6 who like dates. Thus, everyone who likes blueberries or dates must also like cantaloupes (because if any of them didn't, we would end up with less than 15 people who like cantaloupe).
|
| 14 |
+
Since everyone who likes blueberries likes cantaloupes, none of them can like apples. However, the 6 people who like both cantaloupe and dates can also like apples. So, we could have a group where 7 people like apples alone, 9 like blueberries and cantaloupe, and 6 like apples, cantaloupe, and dates. This gives 22 people in the group, which is optimal.
|
| 15 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 16 |
+
4. [5] To set up for a Fourth of July party, David is making a string of red, white, and blue balloons. He places them according to the following rules:
|
| 17 |
+
|
| 18 |
+
- No red balloon is adjacent to another red balloon.
|
| 19 |
+
- White balloons appear in groups of exactly two, and groups of white balloons are separated by at least two non-white balloons.
|
| 20 |
+
- Blue balloons appear in groups of exactly three, and groups of blue balloons are separated by at least three non-blue balloons.
|
| 21 |
+
|
| 22 |
+
If David uses over 600 balloons, determine the smallest number of red balloons that he can use.
|
| 23 |
+
Answer: 99 It is possible to achieve 99 red balloons with the arrangement
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\text { WWBBBWW } \underbrace{\text { RBBBWWRBBBWW . . RBBBWW }}_{99 \text { RBBBWW's }},
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
which contains $99 \cdot 6+7=601$ balloons.
|
| 30 |
+
Now assume that one can construct a chain with 98 or fewer red balloons. Then there can be 99 blocks of non-red balloons, which in total must contain more than 502 balloons. The only valid combinations of white and blue balloons are WWBBB, BBBWW, and WWBBBWW (Any others contain the subsequence BBBWWBBB , which is invalid). The sequence ... WWR must be followed by BBBWW; otherwise two groups of white balloons would be too close. Similarly, the sequence
|
| 31 |
+
|
| 32 |
+
RWW . . . must be preceded by WWBBB. It follows that WWBBBWW can be used at most once in a valid sequence, meaning that there can be at most $98 \cdot 5+7=497$ non-red balloons. Contradiction. Therefore the minimum is 99 red balloons. (Better if the party's outdoors; then we'd have 99 red balloons floating in the summer sky. :-p)
|
| 33 |
+
5. [5] You have a length of string and 7 beads in the 7 colors of the rainbow. You place the beads on the string as follows - you randomly pick a bead that you haven't used yet, then randomly add it to either the left end or the right end of the string. What is the probability that, at the end, the colors of the beads are the colors of the rainbow in order? (The string cannot be flipped, so the red bead must appear on the left side and the violet bead on the right side.)
|
| 34 |
+
Answer: $\frac{1}{5040}$ The threading method does not depend on the colors of the beads, so at the end all configurations are equally likely. Since there are $7!=5040$ configurations in total, the probability of any particular configuration is $\frac{1}{5040}$.
|
| 35 |
+
6. [5] How many different numbers are obtainable from five 5 s by first concatenating some of the 5 s, then multiplying them together? For example, we could do $5 \cdot 55 \cdot 55,555 \cdot 55$, or 55555 , but not $5 \cdot 5$ or 2525 .
|
| 36 |
+
Answer: 7 If we do 55555 , then we're done.
|
| 37 |
+
Note that $5,55,555$, and 5555 all have completely distinguishable prime factorizations. This means that if we are given a product of them, we can obtain the individual terms. The number of 5555's is the exponent of 101 , the number of 555 's is the exponent of 37 , the number of 55 's is the exponent of 11 minus the exponent of 101 , and the number of 5 's is just whatever we need to get the proper exponent of 5 . Then the answer is the number of ways we can split the five 5 's into groups of at least one. This is the number of unordered partitions of 5 , which is 7 .
|
| 38 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 39 |
+
7. [6] What are the last 8 digits of
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
11 \times 101 \times 1001 \times 10001 \times 100001 \times 1000001 \times 111 ?
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Answer: 19754321 Multiply terms in a clever order.
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\begin{aligned}
|
| 49 |
+
11 \cdot 101 \cdot 10001 & =11,111,111 \\
|
| 50 |
+
111 \cdot 1001 \cdot 1000001 & =111,111,111,111
|
| 51 |
+
\end{aligned}
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
The last eight digits of $11,111,111 \cdot 111,111,111,111$ are 87654321 . We then just need to compute the last 8 digits of $87654321 \cdot 100001=87654321+\ldots 32100000$, which are 19754321 .
|
| 55 |
+
8. [6] Each square in the following hexomino has side length 1. Find the minimum area of any rectangle that contains the entire hexomino.
|
| 56 |
+
|
| 57 |
+
|
| 58 |
+
Answer: $\frac{21}{2}$ If a rectangle contains the entire hexomino, it must also contain its convex hull, which is an origin-symmetric hexagon. It is fairly clear that the smallest rectangle that contains such a hexagon must share one set of parallel sides with the hexagon. There are three such rectangles, and checking them all, we find that the one shown below is the smallest. It has area $\frac{21}{2}$.
|
| 59 |
+
|
| 60 |
+
9. [6] Indecisive Andy starts out at the midpoint of the 1-unit-long segment $\overline{H T}$. He flips 2010 coins. On each flip, if the coin is heads, he moves halfway towards endpoint $H$, and if the coin is tails, he moves halfway towards endpoint $T$. After his 2010 moves, what is the expected distance between Andy and the midpoint of $\overline{H T}$ ?
|
| 61 |
+
|
| 62 |
+
Answer: | $\frac{1}{4}$ |
|
| 63 |
+
| :---: |
|
| 64 |
+
| Let Andy's position be $x$ units from the H end after 2009 flips. If Any moves towards | the $H$ end, he ends up at $\frac{x}{2}$, a distance of $\frac{1-x}{2}$ from the midpoint. If Andy moves towards the $T$ end, he ends up at $\frac{1+x}{2}$, a distance of $\frac{x}{2}$ from the midpoint. His expected distance from the midpoint is then
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
\frac{\frac{1-x}{2}+\frac{x}{2}}{2}=\frac{1}{4} .
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Since this does not depend on $x, \frac{1}{4}$ is the answer.
|
| 71 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 — GUTS ROUND
|
| 72 |
+
10. [7] Let $A B C$ be a triangle with $A B=8, B C=15$, and $A C=17$. Point $X$ is chosen at random on line segment $A B$. Point $Y$ is chosen at random on line segment $B C$. Point $Z$ is chosen at random on line segment $C A$. What is the expected area of triangle $X Y Z$ ?
|
| 73 |
+
Answer: 15 Let $\mathbb{E}(X)$ denote the expected value of $X$, and let $[S]$ denote the area of $S$. Then
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\begin{aligned}
|
| 77 |
+
\mathbb{E}([\triangle X Y Z]) & =\mathbb{E}([\triangle A B C]-[\triangle X Y B]-[\triangle Z Y C]-[\triangle X B Z]) \\
|
| 78 |
+
& =[\triangle A B C]-\mathbb{E}([\triangle X Y B])-\mathbb{E}([\triangle Z Y C])-[\triangle X B Z])
|
| 79 |
+
\end{aligned}
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
where the last step follows from linearity of expectation ${ }^{1}$. But $[\triangle X Y B]=\frac{1}{2} \cdot B X \cdot B Y \cdot \sin (B)$. The $\frac{1}{2} \sin (B)$ term is constant, and $B X$ and $B Y$ are both independent with expected values $\frac{A B}{2}$ and $\frac{B C}{2}$, respectively. Thus $\mathbb{E}([\triangle X Y B])=\frac{1}{8} A B \cdot B C \cdot \sin (B)=\frac{1}{4}[\triangle A B C]$. Similarly, $\mathbb{E}([\triangle Z Y C])=$ $\mathbb{E}([\triangle Z B X])=\frac{1}{4}[\triangle A B C]$.
|
| 83 |
+
Then we have $\mathbb{E}([\triangle X Y Z])=\left(1-\frac{1}{4}-\frac{1}{4}-\frac{1}{4}\right)[\triangle A B C]=\frac{1}{4}[\triangle A B C]=15$.
|
| 84 |
+
Note: We can also solve this problem (and the more general case of polygons) by noting that the area of $X Y Z$ is linear in the coordinates of $X, Y$, and $Z$, so the expected area of $X Y Z$ is the same as the area of $X^{\prime} Y^{\prime} Z^{\prime}$, where $X^{\prime}$ is the expected location of $X, Y^{\prime}$ is the expected location of $Y$, and $Z^{\prime}$ is the expected location of $Z$. In our case, this corresponds to the midpoints of the three sides $A B$, $B C$, and $C A$.
|
| 85 |
+
|
| 86 |
+
11. [7] From the point $(x, y)$, a legal move is a move to $\left(\frac{x}{3}+u, \frac{y}{3}+v\right)$, where $u$ and $v$ are real numbers such that $u^{2}+v^{2} \leq 1$. What is the area of the set of points that can be reached from $(0,0)$ in a finite number of legal moves?
|
| 87 |
+
|
| 88 |
+
Answer: | $\frac{9 \pi}{4}$ |
|
| 89 |
+
| :---: |
|
| 90 |
+
| We claim that the set of points is the disc with radius $\frac{3}{2}$ centered at the origin, which | clearly has area $\frac{9 \pi}{4}$.
|
| 91 |
+
|
| 92 |
+
First, we show that the set is contained in this disc. This is because if we are currently at a distance of $r$ from the origin, then we can't end up at a distance of greater than $\frac{r}{3}+1$ from the origin after a single move. Since $\frac{r}{3}+1<\frac{3}{2}$ if $r<\frac{3}{2}$, we will always end up in the disc of radius $\frac{3}{2}$ if we start in it. Since the origin is inside this disc, any finite number of moves will leave us inside this disc.
|
| 93 |
+
|
| 94 |
+
Next, we show that all points in this disc can be reached in a finite number of moves. Indeed, after one move we can get all points within a distance of 1 . After two moves, we can get all points within a distance of $\frac{4}{3}$. After three moves, we can get all points within a distance of $\frac{13}{9}$. In general, after $n$ moves we can get all points within a distance of $\frac{3}{2}-\frac{1}{2 \cdot 3^{k-1}}$. This means that for any distance $d<\frac{3}{2}$, we will eventually get all points within a distance of $d$, so all points in the disc of radius $\frac{3}{2}$ can be reached after some number of moves.
|
| 95 |
+
12. [7] How many different collections of 9 letters are there? A letter can appear multiple times in a collection. Two collections are equal if each letter appears the same number of times in both collections.
|
| 96 |
+
Answer: $\left.\begin{array}{c}34 \\ 9\end{array}\right)$ We put these collections in bijections with binary strings of length 34 containing 9 zeroes and 25 ones. Take any such string - the 9 zeroes will correspond to the 9 letters in the collection. If there are $n$ ones before a zero, then that zero corresponds to the $(n+1)$ st letter of the alphabet. This scheme is an injective map from the binary strings to the collections, and it has an inverse, so the number of collections is $\binom{34}{9}$.
|
| 97 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 98 |
+
13. [8] A triangle in the $x y$-plane is such that when projected onto the $x$-axis, $y$-axis, and the line $y=x$, the results are line segments whose endpoints are $(1,0)$ and $(5,0),(0,8)$ and $(0,13)$, and $(5,5)$ and $(7.5,7.5)$, respectively. What is the triangle's area?
|
| 99 |
+
Answer: $\frac{17}{2}$ Sketch the lines $x=1, x=5, y=8, y=13, y=10-x$, and $y=15-x$. The triangle has to be contained in the hexagonal region contained in all these lines. If all the projections are correct, every other vertex of the hexagon must be a vertex of the triangle, which gives us two possibilities for the triangle. One of these triangles has vertices at $(2,8),(1,13)$, and $(5,10)$, and has an area of $\frac{17}{2}$. It is easy to check that the other triangle has the same area, so the answer is unique.
|
| 100 |
+
14. [8] In how many ways can you fill a $3 \times 3$ table with the numbers 1 through 9 (each used once) such that all pairs of adjacent numbers (sharing one side) are relatively prime?
|
| 101 |
+
|
| 102 |
+
Answer: 2016 The numbers can be separated into four sets. Numbers in the set $A=\{1,5,7\}$ can be placed next to anything. The next two sets are $B=\{2,4,8\}$ and $C=\{3,9\}$. The number 6 , which forms the final set $D$, can only be placed next to elements of $A$. The elements of each group can be interchanged without violating the condition, so without loss of generality, we can pretend we have three 1 's, three 2's, two 3 's, and one 6 , as long as we multiply our answer by $3!3!2$ ! at the end. The available arrangements are, grouped by the position of the 6 , are:
|
| 103 |
+
When 6 is in contact with three numbers:
|
| 104 |
+
|
| 105 |
+
| 1 | 2 | 3 |
|
| 106 |
+
| :--- | :--- | :--- |
|
| 107 |
+
| 6 | 1 | 2 |
|
| 108 |
+
| 1 | 2 | 3 |
|
| 109 |
+
|
| 110 |
+
When 6 is in contact with two numbers:
|
| 111 |
+
|
| 112 |
+
| 6 | 1 | 2 | | | |
|
| 113 |
+
| :--- | :--- | :--- | :--- | :--- | :--- |
|
| 114 |
+
| 1 | 2 | 3 | 6 1 2 <br> 1 1 3 <br> 2 3 1 | 2 | 3 |
|
| 115 |
+
|
| 116 |
+
The next two can be flipped diagonally to create different arrangements:
|
| 117 |
+
|
| 118 |
+
| 6 | 1 | 2 | | | |
|
| 119 |
+
| :--- | :--- | :--- | :--- | :--- | :--- |
|
| 120 |
+
| 1 | 2 | 3 | 6 1 | 2 | |
|
| 121 |
+
| 1 | 2 | 3 | | | |
|
| 122 |
+
| 1 | 3 | 2 | 3 | 1 | 2 |
|
| 123 |
+
|
| 124 |
+
Those seven arrangements can be rotated 90, 180, and 270 degrees about the center to generate a total of 28 arrangements. $28 \cdot 3!3!2!=2016$.
|
| 125 |
+
15. [8] Pick a random integer between 0 and 4095, inclusive. Write it in base 2 (without any leading zeroes). What is the expected number of consecutive digits that are not the same (that is, the expected number of occurrences of either 01 or 10 in the base 2 representation)?
|
| 126 |
+
Answer: $\frac{20481}{4096}$ Note that every number in the range can be written as a 12-digit binary string. For $i=1,2, \ldots 11$, let $R_{i}$ be a random variable which is 1 if the $i$ th and $(i+1)$ st digits differ in a randomly chosen number in the range. By linearity of expectation, $E\left(\sum_{i} R_{i}\right)=\sum E\left(R_{i}\right)$.
|
| 127 |
+
Since we choose every binary string of length 12 with equal probability, the sum of the expectations is $\frac{11}{2}$. However, this is not the expected number of 01 s and $10 s$ - we need to subtract the occasions where the leading digit is zero. There is a $\frac{1}{2}$ chance that the number starts with a 0 , in which case we must ignore the first digit change - unless the number was 0 , in which case there are no digit changes. Therefore, our answer is $\frac{11}{2}-\frac{1}{2}+\frac{1}{4096}=\frac{20481}{4096}$.
|
| 128 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 129 |
+
16. [9] Jessica has three marbles colored red, green, and blue. She randomly selects a non-empty subset of them (such that each subset is equally likely) and puts them in a bag. You then draw three marbles from the bag with replacement. The colors you see are red, blue, red. What is the probability that the only marbles in the bag are red and blue?
|
| 130 |
+
|
| 131 |
+
Answer: | $\frac{27}{35}$ |
|
| 132 |
+
| :---: |
|
| 133 |
+
| There are two possible sets of marbles in the bag, $\{$ red,blue\} and \{red,blue,green\}. | Initially, both these sets are equally likely to be in the bag. However, the probability of red, blue, red being drawn from a set $S$ of marbles is proportional to $|S|^{-3}$, as long as red and blue are both in $S$. By Bayes's Rule, we must weight the probability of these two sets by $|S|^{-3}$. The answer is $\frac{(1 / 2)^{3}}{(1 / 2)^{3}+(1 / 3)^{3}}$.
|
| 134 |
+
|
| 135 |
+
17. [9] An ant starts at the origin, facing in the positive $x$-direction. Each second, it moves 1 unit forward, then turns counterclockwise by $\sin ^{-1}\left(\frac{3}{5}\right)$ degrees. What is the least upper bound on the distance between the ant and the origin? (The least upper bound is the smallest real number $r$ that is at least as big as every distance that the ant ever is from the origin.)
|
| 136 |
+
Answer: $\sqrt{10}$ We claim that the points the ant visits lie on a circle of radius $\frac{\sqrt{10}}{2}$. We show this by saying that the ant stays a constant distance $\frac{\sqrt{10}}{2}$ from the point $\left(\frac{1}{2}, \frac{3}{2}\right)$.
|
| 137 |
+
Suppose the ant moves on a plane $P$. Consider a transformation of the plane $P^{\prime}$ such that after the first move, the ant is at the origin of $P^{\prime}$ and facing in the direction of the $x^{\prime}$ axis (on $P^{\prime}$ ). The transformation to get from $P$ to $P^{\prime}$ can be gotten by rotating $P$ about the origin counterclockwise through an angle $\sin ^{-1}\left(\frac{3}{5}\right)$ and then translating it 1 unit to the right. Observe that the point $\left(\frac{1}{2}, \frac{3}{2}\right)$ is fixed under this transformation, which can be shown through the expression $\left(\frac{1}{2}+\frac{3}{2} i\right)\left(\frac{4}{5}+\frac{3}{5} i\right)+1=\frac{1}{2}+\frac{3}{2} i$. It follows that at every point the ant stops, it will always be the same distance from $\left(\frac{1}{2}, \frac{3}{2}\right)$. Since it starts at $(0,0)$, this fixed distance is $\frac{\sqrt{10}}{2}$.
|
| 138 |
+

|
| 139 |
+
|
| 140 |
+
Since $\sin ^{-1}\left(\frac{3}{5}\right)$ is not a rational multiple of $\pi$, the points the ant stops at form a dense subset of the circle in question. As a result, the least upper bound on the distance between the ant and the origin is the diameter of the circle, which is $\sqrt{10}$.
|
| 141 |
+
18. [9] Find two lines of symmetry of the graph of the function $y=x+\frac{1}{x}$. Express your answer as two equations of the form $y=a x+b$.
|
| 142 |
+
Answer: $y=(1+\sqrt{2}) x$ and $y=(1-\sqrt{2}) x$ The graph of the function $y=x+\frac{1}{x}$ is a hyperbola. We can see this more clearly by writing it out in the standard form $x^{2}-x y+1=0$ or $\left(\frac{y}{2}\right)^{2}-\left(x-\frac{1}{2} y\right)^{2}=1$. The hyperbola has asymptotes given by $x=0$ and $y=x$, so the lines of symmetry will be the (interior and exterior) angle bisectors of these two lines. This means that they will be $y=\tan \left(67.5^{\circ}\right) x$ and $y=-\cot \left(67.5^{\circ}\right) x$, which, using the tangent half-angle formula $\tan \left(\frac{x}{2}\right)=\sqrt{\frac{1+\cos (x)}{1-\cos (x)}}$, gives the two lines $y=(1+\sqrt{2}) x$ and $y=(1-\sqrt{2}) x$.
|
| 143 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 144 |
+
19. [10] A 5-dimensional ant starts at one vertex of a 5 -dimensional hypercube of side length 1 . A move is when the ant travels from one vertex to another vertex at a distance of $\sqrt{2}$ away. How many ways can the ant make 5 moves and end up on the same vertex it started at?
|
| 145 |
+
Answer: 6240 We let the cube lie in $\mathbb{R}^{5}$ with each corner with coordinates 1 or 0 . Assume the ant starts at $(0,0,0,0,0)$. Every move the ant adds or subtracts 1 to two of the places. Note that this means the ant can only land on a vertex with the sum of its coordinates an even number. Every move the ant has $\binom{5}{2}=10$ choices.
|
| 146 |
+
From any vertex there are 10 two-move sequences that put the ant at the same vertex it started at.
|
| 147 |
+
There are 6 two-move sequences to move from one vertex to a different, chosen vertex. If your chosen vertex differs from your current vertex by 2 of the 5 coordinates, your first move corrects for one of these two. There are 2 ways to choose which coordinate to correct for on the first move, and there are 3 ways to choose the second coordinate you change, yielding 6 sequences. If your chosen vertex differs from your current vertex by 4 of the 5 coordinates, each move corrects for two of these four. This yields $\binom{4}{2}=6$ sequences.
|
| 148 |
+
Finally, there are 60 three-move sequences that put the ant at the same vertex it started at. There are 10 ways to choose the first move, and there are 6 ways to make two moves to return to your original position.
|
| 149 |
+
The motion of the ant can be split into two cases.
|
| 150 |
+
Case 1: After the 3rd move the ant is on the vertex it started at. There are $(60)(10)=600$ different possible paths.
|
| 151 |
+
Case 2: After the third move the ant is on a vertex different from the one it started on. There are $\left(10^{3}-60\right)(6)=(940)(6)=5640$ different possible paths.
|
| 152 |
+
So there are 6240 total possible paths.
|
| 153 |
+
20. [10] Find the volume of the set of points $(x, y, z)$ satisfying
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\begin{aligned}
|
| 157 |
+
x, y, z & \geq 0 \\
|
| 158 |
+
x+y & \leq 1 \\
|
| 159 |
+
y+z & \leq 1 \\
|
| 160 |
+
z+x & \leq 1
|
| 161 |
+
\end{aligned}
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
Answer: $\frac{1}{4}$ Without loss of generality, assume that $x \geq y$ - half the volume of the solid is on this side of the plane $x=y$. For each value of $c$ from 0 to $\frac{1}{2}$, the region of the intersection of this half of the solid with the plane $y=c$ is a trapezoid. The trapezoid has height $1-2 c$ and average base $\frac{1}{2}$, so it has an area of $\frac{1}{2}-c$.
|
| 165 |
+
The total volume of this region is $\frac{1}{2}$ times the average area of the trapezoids, which is $\frac{1}{2} \cdot \frac{1}{4}=\frac{1}{8}$. Double that to get the total volume, which is $\frac{1}{4}$.
|
| 166 |
+
21. [10] Let $\triangle A B C$ be a scalene triangle. Let $h_{a}$ be the locus of points $P$ such that $|P B-P C|=|A B-A C|$. Let $h_{b}$ be the locus of points $P$ such that $|P C-P A|=|B C-B A|$. Let $h_{c}$ be the locus of points $P$ such that $|P A-P B|=|C A-C B|$. In how many points do all of $h_{a}, h_{b}$, and $h_{c}$ concur?
|
| 167 |
+
Answer: 2 The idea is similar to the proof that the angle bisectors concur or that the perpendicular bisectors concur. Assume WLOG that $B C>A B>C A$. Note that $h_{a}$ and $h_{b}$ are both hyperbolas. Therefore, $h_{a}$ and $h_{b}$ intersect in four points (each branch of $h_{a}$ intersects exactly once with each branch of $h_{b}$ ). Note that the branches of $h_{a}$ correspond to the cases when $P B>P C$ and when $P B<P C$. Similarly, the branches of $h_{b}$ correspond to the cases when $P C>P A$ and $P C<P A$.
|
| 168 |
+
|
| 169 |
+
If either $P A<P B<P C$ or $P C<P B<P A$ (which each happens for exactly one point of intersection of $h_{a}$ and $h_{b}$ ), then $|P C-P A|=|P C-P B|+|P B-P A|=|A B-A C|+|B C-B A|=|B C-A C|$, and so $P$ also lies on $h_{c}$. So, exactly two of the four points of intersection of $h_{a}$ and $h_{b}$ lie on $h_{c}$, meaning that $h_{a}, h_{b}$, and $h_{c}$ concur in four points.
|
| 170 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 171 |
+
22. [12] You are the general of an army. You and the opposing general both have an equal number of troops to distribute among three battlefields. Whoever has more troops on a battlefield always wins (you win ties). An order is an ordered triple of non-negative real numbers $(x, y, z)$ such that $x+y+z=1$, and corresponds to sending a fraction $x$ of the troops to the first field, $y$ to the second, and $z$ to the third. Suppose that you give the order $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{2}\right)$ and that the other general issues an order chosen uniformly at random from all possible orders. What is the probability that you win two out of the three battles?
|
| 172 |
+
|
| 173 |
+
Answer: | $\frac{5}{8}$ |
|
| 174 |
+
| :---: |
|
| 175 |
+
| Let $x$ | be the portion of soldiers the opposing general sends to the first battlefield, and $y$ the portion he sends to the second. Then $1-x-y$ is the portion he sends to the third. Then $x \geq 0$, $y \geq 0$, and $x+y \leq 1$. Furthermore, you win if one of the three conditions is satisfied: $x \leq \frac{1}{4}$ and $y \leq \frac{1}{4}, x \leq \frac{1}{4}$ and $1-x-y \leq \frac{1}{2}$, or $y \leq \frac{1}{4}$ and $1-x-y \leq \frac{1}{2}$. This is illustrated in the picture below.
|
| 176 |
+
|
| 177 |
+
|
| 178 |
+
|
| 179 |
+
Guts Round
|
| 180 |
+
|
| 181 |
+
This triangle is a linear projection of the region of feasible orders, so it preserves area and probability ratios. The probability that you win, then is given by the portion of the triangle that satisfies one of the three above constraints - in other words, the area of the shaded region divided by the area of the entire triangle. We can easily calculate this to be $\frac{\frac{5}{16}}{\frac{1}{2}}=\frac{5}{8}$.
|
| 182 |
+
23. [12] In the country of Francisca, there are 2010 cities, some of which are connected by roads. Between any two cities, there is a unique path which runs along the roads and which does not pass through any city twice. What is the maximum possible number of cities in Francisca which have at least 3 roads running out of them?
|
| 183 |
+
Answer: 1004 The restrictions on how roads connect cities directly imply that the graph of the cities of Francisca with the roads as edges is a tree. Therefore the sum of the degrees of all the vertices is $2009 \cdot 2=4018$. Suppose that $b$ vertices have degree $\geq 3$. The other $2010-b$ vertices must have a degree of at least 1 , so $3 b+(2010-b) \leq 4018$ or $2 b \leq 2008$. So $b$ is at most 1004 . We can achieve $b=1004$ with the following graph:
|
| 184 |
+

|
| 185 |
+
24. [12] Define a sequence of polynomials as follows: let $a_{1}=3 x^{2}-x$, let $a_{2}=3 x^{2}-7 x+3$, and for $n \geq 1$, let $a_{n+2}=\frac{5}{2} a_{n+1}-a_{n}$. As $n$ tends to infinity, what is the limit of the sum of the roots of $a_{n}$ ?
|
| 186 |
+
Answer: $\frac{13}{3}$ By using standard methods for solving linear recurrences ${ }^{2}$, we see that this recurrence has a characteristic polynomial of $x^{2}-\frac{5}{2} x+1=\left(x-\frac{1}{2}\right)(x-2)$, hence $a_{n}(x)=c(x) \cdot 2^{n}+d(x) \cdot 2^{-n}$ for some polynomials $c$ and $d$. Plugging in $n=1$ and $n=2$ gives
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
2 c(x)+\frac{1}{2} d(x)=3 x^{2}-x
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
and
|
| 193 |
+
|
| 194 |
+
$$
|
| 195 |
+
4 c(x)+\frac{1}{4} d(x)=3 x^{2}-7 x+3
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
Subtracting the first equation from two times the second equation gives $6 c(x)=3 x^{2}-13 x+6$, so $c(x)=\frac{3 x^{2}-13 x+6}{6}$. As $n$ grows large, the $c(x) 2^{n}$ term dominates compared to the $d(x) 2^{-n}$ term, so the roots of $a_{n}(x)$ converge to the roots of $c(x)$. Thus the roots of $a_{n}(x)$ converge to the roots of $3 x^{2}-13 x+6$, which by Vieta's formula ${ }^{3}$ have a sum of $\frac{13}{3}$.
|
| 199 |
+
25. [15] How many functions $f:\{1,2,3,4,5\} \rightarrow\{1,2,3,4,5\}$ have the property that $f(\{1,2,3\})$ and $f(f(\{1,2,3\}))$ are disjoint?
|
| 200 |
+
Answer: 94 Let $f(\{1,2,3\})$ be $A$. Then $A \cap f(A)=\emptyset$, so $A$ must be a subset of $\{4,5\}$. If $B=\{4,5\}$, there are $2^{3}-2$ ways to assign each element in $\{1,2,3\}$ to a value in $\{4,5\}$, and 9 ways to assign each element of $\{4,5\}$ to a value in $\{1,2,3\}$, for a total of 54 choices of $f$. If $A=\{4\}$, there is 1 possible value for each element of $\{1,2,3\}, 4$ ways to assign $\{4\}$ with a value from $\{1,2,3,5\}$, and 5 ways to assign a value to $\{5\}$. Similarly, if $A=\{5\}$, there are $4 \cdot 5=20$ choices for $f$. In total, there are $54+20 \cdot 2=94$ possible functions.
|
| 201 |
+
|
| 202 |
+
[^1]26. [15] Express the following in closed form, as a function of $x$ :
|
| 203 |
+
$\sin ^{2}(x)+\sin ^{2}(2 x) \cos ^{2}(x)+\sin ^{2}(4 x) \cos ^{2}(2 x) \cos ^{2}(x)+\cdots+\sin ^{2}\left(2^{2010} x\right) \cos ^{2}\left(2^{2009} x\right) \cdots \cos ^{2}(2 x) \cos ^{2}(x)$.
|
| 204 |
+
Answer: $1-\frac{\sin ^{2}\left(2^{2011} x\right)}{4^{2011} \sin ^{2}(x)}$ Note that
|
| 205 |
+
\[
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
\begin{aligned}
|
| 209 |
+
& \sin ^{2}(x)+\sin ^{2}(2 x) \cos ^{2}(x)+\cdots+\sin ^{2}\left(2^{2010} x\right) \cos ^{2}\left(2^{2009} x\right) \cdots \cos ^{2}(2 x) \cos ^{2}(x) \\
|
| 210 |
+
& \quad=\left(1-\cos ^{2}(x)\right)+\left(1-\cos ^{2}(2 x)\right) \cos ^{2}(x)+\cdots+\left(1-\cos ^{2}\left(2^{2010} x\right)\right) \cos ^{2}\left(2^{2009} x\right) \cdots \cos ^{2}(x)
|
| 211 |
+
\end{aligned}
|
| 212 |
+
$$
|
| 213 |
+
\]
|
| 214 |
+
|
| 215 |
+
which telescopes to $1-\cos ^{2}(x) \cos ^{2}(2 x) \cos ^{2}(4 x) \cdots \cos ^{2}\left(2^{2010} x\right)$. To evaluate $\cos ^{2}(x) \cos ^{2}(2 x) \cdots \cos ^{2}\left(2^{2010} x\right)$, multiply and divide by $\sin ^{2}(x)$. We then get
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
1-\frac{\sin ^{2}(x) \cos ^{2}(x) \cos ^{2}(2 x) \cdots \cos ^{2}\left(2^{2010} x\right)}{\sin ^{2}(x)}
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
Using the double-angle formula for sin, we get that $\sin ^{2}(y) \cos ^{2}(y)=\frac{\sin ^{2}(2 y)}{4}$. Applying this 2011 times makes the above expression
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
1-\frac{\sin ^{2}\left(2^{2011} x\right)}{4^{2011} \sin ^{2}(x)}
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
which is in closed form.
|
| 228 |
+
27. [15] Suppose that there are real numbers $a, b, c \geq 1$ and that there are positive reals $x, y, z$ such that
|
| 229 |
+
|
| 230 |
+
$$
|
| 231 |
+
\begin{aligned}
|
| 232 |
+
a^{x}+b^{y}+c^{z} & =4 \\
|
| 233 |
+
x a^{x}+y b^{y}+z c^{z} & =6 \\
|
| 234 |
+
x^{2} a^{x}+y^{2} b^{y}+z^{2} c^{z} & =9
|
| 235 |
+
\end{aligned}
|
| 236 |
+
$$
|
| 237 |
+
|
| 238 |
+
What is the maximum possible value of $c$ ?
|
| 239 |
+
Answer: $\sqrt[3]{4}$ The Cauchy-Schwarz inequality states that given 2 sequences of $n$ real numbers $x_{1}, x_{2}, \ldots, x_{n}$ and $y_{1}, y_{2}, \ldots, y_{n}$, then $\left(x_{1}^{2}+x_{2}^{2}+\ldots+x_{n}^{2}\right)\left(y_{1}^{2}+y_{2}^{2}+\ldots+y_{n}^{2}\right) \geq\left(x_{1} y_{1}+x_{2} y_{2}+\ldots+x_{n} y_{n}\right)^{2}$ with equality holding if and only if $\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}=\ldots=\frac{x_{n}}{y_{n}}$. Applying this to $\left\{a^{x / 2}, b^{y / 2}, c^{z / 2}\right\}$ and $\left\{x a^{x / 2}, y b^{y / 2}, z c^{z / 2}\right\}$ yields $\left(a^{x}+b^{y}+c^{z}\right)\left(x^{2} a^{x}+y^{2} b^{y}+z^{2} c^{z}\right) \geq\left(x a^{x}+y b^{y}+z b^{z}\right)^{2}$ with equality holding if and only if $x=y=z$.
|
| 240 |
+
However, equality does hold (both sides evaluate to 36 ), so $x=y=z$. The second equation then becomes $x\left(a^{x}+b^{x}+c^{x}\right)=6$, which implies $x=\frac{3}{2}$. Then we have $a^{3 / 2}+b^{3 / 2}+c^{3 / 2}=4$. To maximize $c$, we minimize $a$ and $b$ by setting $a=b=1$. Then $c^{3 / 2}=2$ or $c=\sqrt[3]{4}$.
|
| 241 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 242 |
+
28. [18] Danielle Bellatrix Robinson is organizing a poker tournament with 9 people. The tournament will have 4 rounds, and in each round the 9 players are split into 3 groups of 3 . During the tournament, each player plays every other player exactly once. How many different ways can Danielle divide the 9 people into three groups in each round to satisfy these requirements?
|
| 243 |
+
Answer: 20160 We first split the 9 people up arbitrarily into groups of 3 . There are $\frac{\binom{9}{3}\binom{6}{3}\binom{3}{3}}{3!}=280$ ways of doing this. Without loss of generality, label the people 1 through 9 so that the first round groups are $\{1,2,3\},\{4,5,6\}$, and $\{7,8,9\}$. We will use this numbering to count the number of ways DBR can divide the 9 players in rounds 2,3 , and 4 .
|
| 244 |
+
|
| 245 |
+
In round 2 , because players 1,2 , and 3 are together in the first round, they must be in separate groups, and likewise for $\{4,5,6\}$ and $\{7,8,9\}$. Disregarding ordering of the three groups in a single round, we will first place 1,2 , and 3 into their groups, then count the number of ways to place $\{4,5,6\}$ and $\{7,8,9\}$ in the groups with them. We do this by placing one member from each of $\{4,5,6\}$ and $\{7,8,9\}$ into each group. There are $(3!)^{2}$ ways to do this. Now, because of symmetry, we can use the round 2 grouping $\{1,4,7\},\{2,5,8\},\{3,6,9\}$ to list out the remaining possibilities for round 3 and 4 groupings.
|
| 246 |
+
Casework shows that there are 2 ways to group the players in the remaining two rounds. We multiply $280 \cdot(3!)^{2} \cdot 2$ to get 20160.
|
| 247 |
+
29. [18] Compute the remainder when
|
| 248 |
+
|
| 249 |
+
$$
|
| 250 |
+
\sum_{k=1}^{30303} k^{k}
|
| 251 |
+
$$
|
| 252 |
+
|
| 253 |
+
is divided by 101 .
|
| 254 |
+
Answer: 29 The main idea is the following lemma:
|
| 255 |
+
Lemma. For any non-negative integer $n$ and prime $p, \sum_{k=n+1}^{n+p^{2}-p} k^{k} \equiv 1(\bmod p)$.
|
| 256 |
+
Proof. Note that $a^{b}$ depends only on the value of $a(\bmod p)$ and the value of $b(\bmod p-1)$. Since $p$ and $p-1$ are relatively prime, the Chinese Remainder Theorem ${ }^{4}$ implies that any $p^{2}-p$ consecutive integers will take on each possible pair of a residue $\bmod p$ and a residue $\bmod p-1$. In other words, if we let $(a, b)=(k(\bmod p), k(\bmod p-1))$, then as $k$ ranges through $p^{2}-p$ consecutive integers, $(a, b)$ will range through all $p^{2}-p$ ordered pairs of residues $\bmod p$ and residues mod $p-1$. This implies that
|
| 257 |
+
|
| 258 |
+
$$
|
| 259 |
+
\sum_{k=n+1}^{n+p^{2}-p} k^{k} \equiv \sum_{b=1}^{p-1} \sum_{a=1}^{p} a^{b} .
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
It is well-known that $\sum_{a=1}^{p} a^{b}=\left\{\begin{array}{rl}-1 & p-1 \mid b \\ 0 & p-1 \nmid b\end{array}\right.$. We will sketch a proof here. When $p-1 \mid b$, the result follows from Fermat's Little Theorem ${ }^{5}$. When $p-1 \nmid b$, it suffices to consider the case when $b \mid p-1$, since the $b$ th powers $\bmod p$ are the same as the $\operatorname{gcd}(b, p-1)$ th powers $\bmod p$, and there are an equal number of every non-zero $b$ th power. But in this case, the $b$ th powers are just the solutions to $x^{\frac{p-1}{b}}-1$, which add up to zero by Vieta's formulas.
|
| 263 |
+
Now, using the formula for $\sum a^{b}$, we get that
|
| 264 |
+
|
| 265 |
+
$$
|
| 266 |
+
\sum_{b=1}^{p-1} \sum_{a=1}^{p} a^{b} \equiv-1 \quad(\bmod p)
|
| 267 |
+
$$
|
| 268 |
+
|
| 269 |
+
which completes the lemma.
|
| 270 |
+
We now apply the lemma with $p=101$ and $n=3,10103$, and 20103 to get that $\sum_{k=1}^{30303} k^{k} \equiv$ $\left(\sum_{k=1}^{3} k^{k}\right)-3$. But $\sum_{k=1}^{3} k^{k}=1^{1}+2^{2}+3^{3}=1+4+27=32$, so the answer is $32-3=29$.
|
| 271 |
+
30. [18] A monomial term $x_{i_{1}} x_{i_{2}} \ldots x_{i_{k}}$ in the variables $x_{1}, x_{2}, \ldots x_{8}$ is square-free if $i_{1}, i_{2}, \ldots i_{k}$ are distinct. (A constant term such as 1 is considered square-free.) What is the sum of the coefficients of the squarefree terms in the following product?
|
| 272 |
+
|
| 273 |
+
$$
|
| 274 |
+
\prod_{1 \leq i<j \leq 8}\left(1+x_{i} x_{j}\right)
|
| 275 |
+
$$
|
| 276 |
+
|
| 277 |
+
Answer: 764 Let $a_{n}$ be the sum of the coefficients of the square-terms in the product $\prod_{1 \leq i<j \leq n}(1+$ $x_{i} x_{j}$ ). Square-free terms in this product come in two types: either they include $x_{n}$, or they do not. The sum of the coefficients of the terms that include $x_{n}$ is $(n-1) a_{n-2}$, since we can choose any of the $n-1$ other variables to be paired with $x_{n}$, and then choose any square-free term from the product taken over the other $n-2$ variables. The sum of the coefficients of the terms that do not include $x_{n}$ are $a_{n-1}$, because they all come from the product over the other $n-1$ variables. Therefore, $a_{n}=a_{n-1}+(n-1) a_{n-2}$.
|
| 278 |
+
We use this recursion to find $a_{8}$. As base cases, $a_{0}$ and $a_{1}$ are both 1 . Then $a_{2}=2, a_{3}=4, a_{4}=10$, $a_{5}=26, a_{6}=76, a_{7}=232$, and finally, $a_{8}=764$.
|
| 279 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 280 |
+
31. [21] In the Democratic Republic of Irun, 5 people are voting in an election among 5 candidates. If each person votes for a single candidate at random, what is the expected number of candidates that will be voted for?
|
| 281 |
+
|
| 282 |
+
Answer: | $\frac{2101}{625}$ |
|
| 283 |
+
| :---: |
|
| 284 |
+
| The probability that a chosen candidate will receive no votes at all is $\left(\frac{4}{5}\right)^{5}$, or the | probability that every person will vote for someone other than that one candidate. Then the probability that a chosen candidate will receive at least one vote is $1-\left(\frac{4}{5}\right)^{5}=\frac{2101}{3125}$. By linearity of expectations, the final answer is this probability times the number of candidates, or $5 \cdot \frac{2101}{3125}=\frac{2101}{625}$.
|
| 285 |
+
|
| 286 |
+
32. [21] There are 101 people participating in a Secret Santa gift exchange. As usual each person is randomly assigned another person for whom (s)he has to get a gift, such that each person gives and receives exactly one gift and no one gives a gift to themself. What is the probability that the first person neither gives gifts to or receives gifts from the second or third person? Express your answer as a decimal rounded to five decimal places.
|
| 287 |
+
Answer: 0.96039 Let $D_{k}$ denote the number of derangements of $\{1,2, \ldots, k\}$. (A derangement is a permutation in which no element appears in its original position.)
|
| 288 |
+
Call the first three people $A, B$, and $C$. Let $X \rightarrow Y$ denote that $X$ gives a gift to $Y$ and let $X \nrightarrow Y$ denote that $X$ gives a gift to anyone other than $Y$. We are fine unless we have $A \rightarrow B, B \rightarrow A$, $A \rightarrow C$, or $C \rightarrow A$. We will compute the number of ways for various things to occur, then combine it into what we want.
|
| 289 |
+
There are $D_{n-1}$ ways to have $A \rightarrow B \nrightarrow A$. This is because if $A \rightarrow B$, we can treat $A$ and $B$ as a single vertex, and since $B \nrightarrow A$, we have a derangement. Similarly, there are $D_{n-1}$ ways to have $B \rightarrow A \nrightarrow B$. Thirdly, there are $D_{n-2}$ ways to have $A \rightarrow B \rightarrow A$, since $D_{n-2}$ says how many ways the other $n-2$ people can exchange their gifts. So there are $2 D_{n-1}+D_{n-2}$ ways to have a conflict between $A$ and $B$.
|
| 290 |
+
|
| 291 |
+
Similarly, there are $2 D_{n-1}+D_{n-2}$ ways to have a conflict between $A$ and $C$.
|
| 292 |
+
Using similar arguments, we can show that there are $D_{n-2}$ ways for $B \rightarrow A \rightarrow C \nrightarrow B$ to occur and $D_{n-3}$ ways for $B \rightarrow A \rightarrow C \rightarrow B$ to occur. We get the same results when $B$ and $C$ are reversed. This gives $2 D_{n-2}+2 D_{n-3}$ ways for a conflict to occur within all three people.
|
| 293 |
+
By the Principle of Inclusion-Exclusion, the total number of ways to have a conflict is
|
| 294 |
+
(\# conflicts between $A$ and $B)+(\#$ conflicts between $A$ and $C)-(\#$ conflicts between $A, B$, and $C)$,
|
| 295 |
+
which evaluates to $4 D_{n-1}-2 D_{n-3}$.
|
| 296 |
+
Approximating $D_{n}$ as $\frac{n!}{e}$ (the actual formula is this quantity rounded to the nearest integer, so this is a great approximation), we find that the probability of no conflicts is
|
| 297 |
+
$1-\frac{4 D_{n-1}-2 D_{n-3}}{D_{n}} \approx 1-4\left(\frac{(n-1)!/ e}{n!/ e}\right)-2\left(\frac{(n-3)!/ e}{n!/ e}\right)=\frac{n(n-1)(n-2)-4(n-1)(n-2)-2}{n(n-1)(n-2)}$.
|
| 298 |
+
|
| 299 |
+
Substitute $m=n-1$ (this makes $m=100$, so the expression is easier to evaluate) to get a probability of
|
| 300 |
+
|
| 301 |
+
$$
|
| 302 |
+
\begin{gathered}
|
| 303 |
+
\frac{m^{3}-m-4 m^{2}+4 m-2}{m^{3}-m}=\frac{m^{3}-4 m^{2}+3 m-2}{m^{3}-m}=\frac{1,000,000-40,000+300-2}{100 \cdot 9999}=\frac{960298}{100 \cdot 9999} \\
|
| 304 |
+
=0.960208 \cdot(1.000100010001 \ldots)=0.960208+0.0000960208+\ldots=0.9603940 \ldots
|
| 305 |
+
\end{gathered}
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+
To five decimal places, the desired probability is 0.96039 .
|
| 309 |
+
33. [21] Let $a_{1}=3$, and for $n>1$, let $a_{n}$ be the largest real number such that
|
| 310 |
+
|
| 311 |
+
$$
|
| 312 |
+
4\left(a_{n-1}^{2}+a_{n}^{2}\right)=10 a_{n-1} a_{n}-9
|
| 313 |
+
$$
|
| 314 |
+
|
| 315 |
+
What is the largest positive integer less than $a_{8}$ ?
|
| 316 |
+
Answer: 335 Let $t_{n}$ be the larger real such that $a_{n}=t_{n}+\frac{1}{t_{n}}$. Then $t_{1}=\frac{3+\sqrt{5}}{2}$. We claim that $t_{n}=2 t_{n-1}$. Writing the recurrence as a quadratic polynomial in $a_{n}$, we have:
|
| 317 |
+
|
| 318 |
+
$$
|
| 319 |
+
4 a_{n}^{2}-10 a_{n-1} a_{n}+4 a_{n-1}^{2}+9=0
|
| 320 |
+
$$
|
| 321 |
+
|
| 322 |
+
Using the quadratic formula, we see that $a_{n}=\frac{5}{4} a_{n-1}+\frac{3}{4} \sqrt{a_{n-1}^{2}-4}$. (We ignore the negative square root, since $a_{n}$ is the largest real number satisfying the polynomial.) Substituting $t_{n-1}+\frac{1}{t_{n-1}}$ for $a_{n-1}$, we see that $\sqrt{a_{n-1}^{2}-4}=\sqrt{t_{n-1}^{2}-2+\frac{1}{t_{n-1}^{2}}}$, so we have:
|
| 323 |
+
|
| 324 |
+
$$
|
| 325 |
+
a_{n}=\frac{5}{4}\left(t_{n-1}+\frac{1}{t_{n-1}}\right)+\frac{3}{4} \sqrt{\left(t_{n-1}-\frac{1}{t_{n-1}}\right)^{2}}=2 t_{n-1}+\frac{1}{2 t_{n-1}}
|
| 326 |
+
$$
|
| 327 |
+
|
| 328 |
+
so $t_{n}=2 t_{n-1}$, as claimed. Then $a_{8}=\frac{128(3+\sqrt{5})}{2}+\frac{2}{128(3+\sqrt{5})}$. The second term is vanishingly small, so $\left\lfloor a_{8}\right\rfloor=\lfloor 64(3+\sqrt{5})\rfloor$. We approximate $\sqrt{5}$ to two decimal places as 2.24 , making this expression $\lfloor 335.36\rfloor=335$. Since our value of $\sqrt{5}$ is correct to within 0.005 , the decimal is correct to within 0.32 , which means the final answer is exact.
|
| 329 |
+
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
| 330 |
+
34. [25] 3000 people each go into one of three rooms randomly. What is the most likely value for the maximum number of people in any of the rooms? Your score for this problem will be 0 if you write down a number less than or equal to 1000 . Otherwise, it will be $25-27 \frac{|A-C|}{\min (A, C)-1000}$.
|
| 331 |
+
Answer: 1019 To get a rough approximation, we can use the fact that a sum of identical random variables converges to a Gaussian distribution ${ }^{6}$ in this case with a mean of 1000 and a variance of $3000 \cdot \frac{2}{9}=667$. Since $\sqrt{667} \approx 26,1026$ is a good guess, as Gaussians tend to differ from their mean by approximately their variance.
|
| 332 |
+
The actual answer was computed with the following python program:
|
| 333 |
+
|
| 334 |
+
```
|
| 335 |
+
facts = [0]*3001
|
| 336 |
+
facts[0]=1
|
| 337 |
+
for a in range(1,3001):
|
| 338 |
+
facts[a]=a*facts[a-1]
|
| 339 |
+
def binom(n,k):
|
| 340 |
+
return facts[n]/(facts[k]*facts[n-k])
|
| 341 |
+
```
|
| 342 |
+
|
| 343 |
+
[^3]```
|
| 344 |
+
maxes = [0]*3001
|
| 345 |
+
M = 1075
|
| 346 |
+
for a in range(0,3001):
|
| 347 |
+
for b in range(0,3001-a):
|
| 348 |
+
c = 3000-a-b
|
| 349 |
+
m = max (a,max (b,c))
|
| 350 |
+
if m < M:
|
| 351 |
+
maxes[m] += facts[3000]/(facts[a]*facts[b]*facts[c])
|
| 352 |
+
print [a,b]
|
| 353 |
+
best = 1000
|
| 354 |
+
for a in range(1000,1050):
|
| 355 |
+
print maxes[a],a
|
| 356 |
+
if maxes[best] <= maxes[a]:
|
| 357 |
+
best = a
|
| 358 |
+
print maxes[best]
|
| 359 |
+
print best
|
| 360 |
+
```
|
| 361 |
+
|
| 362 |
+
We can use arguments involving the Chernoff bound ${ }^{7}$ to show that the answer is necessarily less than 1075. Alternately, if we wanted to be really careful, we could just set $M=3001$, but then we'd have to wait a while for the script to finish.
|
| 363 |
+
35. [25] Call an positive integer almost-square if it can be written as $a \cdot b$, where $a$ and $b$ are integers and $a \leq b \leq \frac{4}{3} a$. How many almost-square positive integers are less than or equal to 1000000 ? Your score will be equal to $25-65 \frac{|A-C|}{\min (A, C)}$.
|
| 364 |
+
Answer: 130348 To get a good estimate for the number of almost-square integers, note that any number of the form $a \cdot b$, with $b \leq \frac{4}{3} a$, will be by definition almost-square. Let's assume that it's relatively unlikely that a number is almost-square in more than one way. Then the number of almostsquare numbers less than $n$ will be approximately
|
| 365 |
+
|
| 366 |
+
$$
|
| 367 |
+
\sum_{a=1}^{\sqrt{n}} \sum_{b=a}^{\frac{4}{3} a} 1=\frac{1}{3} \sum_{a=1}^{\sqrt{n}} a=\frac{1}{6} \sqrt{n}(\sqrt{n}+1)
|
| 368 |
+
$$
|
| 369 |
+
|
| 370 |
+
which is about $\frac{n}{6}$. So, $\frac{n}{6}$ will be a fairly good estimate for the number of almost-square numbers less than $n$, making 160000 a reasonable guess.
|
| 371 |
+
|
| 372 |
+
We can do better, though. For example, we summed $\frac{a}{3}$ all the way up to $\sqrt{n}$, but we are really overcounting here because when $a$ is close to $\sqrt{n}, a \cdot b$ will be less than $n$ only when $b \leq \frac{n}{a}$, as opposed to $b \leq \frac{4 a}{3}$. So we should really be taking the sum
|
| 373 |
+
|
| 374 |
+
[^4]\[
|
| 375 |
+
|
| 376 |
+
$$
|
| 377 |
+
\begin{aligned}
|
| 378 |
+
& \sum_{a=1}^{\sqrt{\frac{3 n}{4}}} \sum_{b=a}^{\frac{4 a}{3}} 1+\sum_{a=\sqrt{\frac{3 n}{4}}}^{\sqrt{n}} \sum_{b=a}^{\frac{n}{a}} 1 \\
|
| 379 |
+
& \quad=\sum_{a=1}^{\sqrt{\frac{3 n}{4}}} \frac{a}{3}+\sum_{a=\sqrt{\frac{3 n}{4}}}^{\sqrt{n}}\left(\frac{n}{a}-a\right) \\
|
| 380 |
+
& \quad \approx \frac{1}{6} \frac{3 n}{4}+n\left(\log (\sqrt{n})-\log \left(\sqrt{\frac{3 n}{4}}\right)\right)-\left(\frac{n}{2}-\frac{3 n}{8}\right) \\
|
| 381 |
+
& \quad=\frac{n}{8}+n \frac{\log (4)-\log (3)}{2}-\frac{n}{8} \\
|
| 382 |
+
& \quad=n \frac{\log (4)-\log (3)}{2}
|
| 383 |
+
\end{aligned}
|
| 384 |
+
$$
|
| 385 |
+
\]
|
| 386 |
+
|
| 387 |
+
In the process of taking the sum, we saw that we had something between $\frac{n}{8}$ and $\frac{n}{6}$, so we could also guess something between 166000 and 125000 , which would give us about 145000 , an even better answer. If we actually calculate $\frac{\log (4)-\log (3)}{2}$, we see that it's about 0.14384 , so 143840 would be the best guess if we were to use this strategy. In reality, we would want to round down a bit in both cases, since we are overcounting (because numbers could be square-free in multiple ways), so we should probably answer something like 140000 .
|
| 388 |
+
|
| 389 |
+
A final refinement to our calculation (and perhaps easier than the previous one), is to assume that the products $a \cdot b$ that we consider are randomly distributed between 1 and $n$, and to compute the expected number of distinct numbers we end up with. This is the same type of problem as number 31 on this contest, and we compute that if we randomly distribute $k$ numbers between 1 and $n$ then we expect to end up with $n\left(1-\left(1-\frac{1}{n}\right)^{k}\right)$ distinct numbers. When $k=n \frac{\log (4)-\log (3)}{2}$, we get that this equals
|
| 390 |
+
|
| 391 |
+
$$
|
| 392 |
+
\begin{aligned}
|
| 393 |
+
n\left(1-\left(\left(1-\frac{1}{n}\right)^{n}\right)^{\frac{\log (4)-\log (3)}{2}}\right) & =n\left(1-\sqrt{e^{\log (3)-\log (4)}}\right) \\
|
| 394 |
+
& =n\left(1-\sqrt{\frac{3}{4}}\right) \\
|
| 395 |
+
& =n\left(1-\frac{\sqrt{3}}{2}\right) \\
|
| 396 |
+
& \approx 0.134 n
|
| 397 |
+
\end{aligned}
|
| 398 |
+
$$
|
| 399 |
+
|
| 400 |
+
Giving us an answer of 134000 , which is very close to the correct answer.
|
| 401 |
+
The actual answer was found by computer, using the following $\mathrm{C}++$ program:
|
| 402 |
+
|
| 403 |
+
```
|
| 404 |
+
#include <stdio.h>
|
| 405 |
+
using namespace std;
|
| 406 |
+
bool isAlmostSquare(int n){
|
| 407 |
+
for(int k=1;k*k<=n;k++)
|
| 408 |
+
if(n%k==0 && 3*(n/k) <= 4*k) return true;
|
| 409 |
+
return false;
|
| 410 |
+
}
|
| 411 |
+
```
|
| 412 |
+
|
| 413 |
+
```
|
| 414 |
+
int main(){
|
| 415 |
+
int c = 0;
|
| 416 |
+
for(int n=1;n<=1000000;n++)
|
| 417 |
+
if(isAlmostSquare(n)) c++;
|
| 418 |
+
printf("%d\n",c);
|
| 419 |
+
return 0;
|
| 420 |
+
}
|
| 421 |
+
```
|
| 422 |
+
|
| 423 |
+
36. [25] Consider an infinite grid of unit squares. An $n$-omino is a subset of $n$ squares that is connected. Below are depicted examples of 8 -ominoes. Two $n$-ominoes are considered equivalent if one can be obtained from the other by translations and rotations. What is the number of distinct 15 -ominoes? Your score will be equal to $25-13|\ln (A)-\ln (C)|$.
|
| 424 |
+
|
| 425 |
+
|
| 426 |
+
Answer: 3426576 We claim that there are approximately $\frac{3^{n-1}}{4} n$-ominoes. First, we define an order on the squares in an $n$-omino, as follows: we order the squares from left to right, and within a column, we order the squares from top to bottom.
|
| 427 |
+
We construct an $n$-omino by starting with a single square and attaching squares, one by one, as close to order we just defined as possible. After the first square is placed, the next square can be attached to its bottom or right side. If the second square is right of the first, then the third square can be attached to the top, right, or bottom edges of the second. The third square cannot be attached to the first square, because the first column must be completed before the second is begun. If the second square is below the first, the third square can be attached to the bottom or right sides of the second square, or the right side of the first way. In either case, there are 3 choices for the third square.
|
| 428 |
+
Suppose that $m$ squares have been added, and that $k$ squares are in the right-most column right now. If $k=1$, then the next square can be attached to the top, right, or bottom side of this square. If $k>1$, then the next square can be added to the bottom or right side of the last square in this column. The next square can also be added to the right of the top square in this column, so there are still 3 choices for the next square. Therefore, there are $3^{n-1}$ ways to build up the entire $n$-omino.
|
| 429 |
+
Almost all $n$-omines have no rotational symmetry, so they can be built in 4 different ways by this method. This correction gives us our estimate of $\frac{3^{n-1}}{4}$ for the number of $n$-ominoes. This reasoning is not exactly correct, because some $n$-ominoes are highly non-convex, and do not admit an in-order traversal like the one described above. If some columns in the $n$-ominoes have gaps, they are not enumerated by this construction, so $\frac{3^{n-1}}{4}$ is an underestimate. We estimate that there are 1195742 15 -ominoes. The actual value of 3426576 , which can be found in the Sloane Encyclopedia of Integer Sequences, differes from the estimate by less than a factor of 3 .
|
| 430 |
+
|
| 431 |
+
|
| 432 |
+
[^0]: ${ }^{1}$ See http://www-math.mit.edu/~spielman/AdvComplexity/handout.ps for an introduction to linearity of expectation and other important tools in probability
|
| 433 |
+
|
| 434 |
+
[^1]: ${ }^{2}$ See the sections "Linear homogeneous recurrence relations with constant coefficients" and "Theorem" at http://en. wikipedia.org/wiki/Recurrence_relation
|
| 435 |
+
${ }^{3}$ See http://mathworld.wolfram.com/VietasFormulas.html
|
| 436 |
+
|
| 437 |
+
[^2]: ${ }^{4}$ See http://en.wikipedia.org/wiki/Chinese_remainder_theorem
|
| 438 |
+
${ }^{5}$ See http://en.wikipedia.org/wiki/Fermat's_little_theorem
|
| 439 |
+
|
| 440 |
+
[^3]: ${ }^{6}$ See http://en.wikipedia.org/wiki/Central_limit_theorem
|
| 441 |
+
|
| 442 |
+
[^4]: ${ }^{7}$ See http://en.wikipedia.org/wiki/Chernoff_bound
|
| 443 |
+
|
HarvardMIT/md/en-132-2010-feb-team1-solutions.md
ADDED
|
@@ -0,0 +1,125 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 20 February 2010 <br> <br> Team Round A
|
| 2 |
+
|
| 3 |
+
<br> <br> Team Round A}
|
| 4 |
+
|
| 5 |
+
1. You are trying to sink a submarine. Every second, you launch a missile at a point of your choosing on the $x$-axis. If the submarine is at that point at that time, you sink it. A firing sequence is a sequence of real numbers that specify where you will fire at each second. For example, the firing sequence $2,3,5,6, \ldots$ means that you will fire at 2 after one second, 3 after two seconds, 5 after three seconds, 6 after four seconds, and so on.
|
| 6 |
+
(a) [5] Suppose that the submarine starts at the origin and travels along the positive $x$-axis with an (unknown) positive integer velocity. Show that there is a firing sequence that is guaranteed to hit the submarine eventually.
|
| 7 |
+
Solution: The firing sequence $1,4,9, \ldots, n^{2}, \ldots$ works. If the velocity of the submarine is $v$, then after $v$ seconds it will be at $x=v^{2}$, the same location where the mine explodes at time $v$.
|
| 8 |
+
(b) [10] Suppose now that the submarine starts at an unknown integer point on the non-negative $x$-axis and again travels with an unknown positive integer velocity. Show that there is still a firing sequence that is guaranteed to hit the submarine eventually.
|
| 9 |
+
Solution: Represent the submarine's motion by an ordered pair ( $a, b$ ), where $a$ is the starting point of the submarine and $b$ is its velocity. We want to find a way to map each positive integer to a possible ordered pair so that every ordered pair is covered. This way, if we fire at $b_{n} n+a_{n}$ at time $n$, where $\left(a_{n}, b_{n}\right)$ is the point that $n$ maps to, then we will eventually hit the submarine. (Keep in mind that $b_{n} n+a_{n}$ would be the location of the submarine at time $n$.) There are many such ways to map the positive integers to possible points; here is one way:
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\begin{aligned}
|
| 13 |
+
& 1 \rightarrow(1,1), 2 \rightarrow(2,1), 3 \rightarrow(1,2), 4 \rightarrow(3,1), 5 \rightarrow(2,2), 6 \rightarrow(1,3), 7 \rightarrow(4,1), 8 \rightarrow(3,2), \\
|
| 14 |
+
& 9 \rightarrow(2,3), 10 \rightarrow(1,4), 11 \rightarrow(5,1), 12 \rightarrow(4,2), 13 \rightarrow(3,3), 14 \rightarrow(2,4), 15 \rightarrow(1,5), \ldots
|
| 15 |
+
\end{aligned}
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
(The path of points trace out diagonal lines that sweep every lattice point in the coordinate plane.) Since we cover every point, we will eventually hit the submarine.
|
| 19 |
+
Remark: The mapping shown above is known as a bijection between the positive integers and ordered pairs of integers $(a, b)$ where $b>0$.
|
| 20 |
+
2. [15] Consider the following two-player game. Player 1 starts with a number, $N$. He then subtracts a proper divisor of $N$ from $N$ and gives the result to player 2 (a proper divisor of $N$ is a positive divisor of $N$ that is not equal to 1 or $N)$. Player 2 does the same thing with the number she gets from player 1 , and gives the result back to player 1. The two players continue until a player is given a prime number or 1 , at which point that player loses. For which values of $N$ does player 1 have a winning strategy?
|
| 21 |
+
Answer: All even numbers except for odd powers of 2 . First we show that if you are stuck with an odd number, then you are guaranteed to lose. Suppose you have an odd number $a b$, where $a$ and $b$ are odd numbers, and you choose to subtract $a$. You pass your opponent the number $a(b-1)$. This cannot be a power of 2 (otherwise $a$ is a power of 2 and hence $a=1$, which is not allowed), so your opponent can find an odd proper divisor of $a(b-1)$, and you will have a smaller odd number. Eventually you will get to an odd prime and lose.
|
| 22 |
+
Now consider even numbers that aren't powers of 2. As with before, you can find an odd proper divisor of $N$ and pass your opponent an odd number, so you are guaranteed to win.
|
| 23 |
+
Finally consider powers of 2 . If you have the number $N=2^{k}$, it would be unwise to choose a proper divisor other than $2^{k-1}$; otherwise you would give your opponent an even number that isn't a power of 2 . Therefore if $k$ is odd, you will end up with 2 and lose. If $k$ is even, though, your opponent will end up with 2 and you will win.
|
| 24 |
+
Therefore player 1 has a winning strategy for all even numbers except for odd powers of 2.
|
| 25 |
+
3. [15] Call a positive integer in base $10 k$-good if we can split it into two integers y and z , such that y is all digits on the left and z is all digits on the right, and such that $y=k \cdot z$. For example, 2010 is 2 -good because we can split it into 20 and 10 and $20=2 \cdot 10.20010$ is also 2 -good, because we can split it into 20 and 010 . In addition, it is 20 -good, because we can split it into 200 and 10 .
|
| 26 |
+
Show that there exists a 48 -good perfect square.
|
| 27 |
+
Solution: We wish to find integers $a, z$ such that $48 z \cdot 10^{a}+z=z\left(48 \cdot 10^{a}+1\right)$ a perfect square, where $z<10^{a}$. This would prove that there exists a 48 -good perfect square because we are pulling off the last $a$ digits of the number and get two integers $48 z$ and $z$. To make $z$ small by keeping the product a perfect square, we'd like $48 \cdot 10^{a}+1$ to be divisible by some reasonably large square. Take $a=42=\varphi(49)$. By Euler's theorem, $10^{42} \equiv 1(\bmod 49)$, so $48 \cdot 10^{a}+1$ is a multiple of 49 . Then we can take $z=\frac{48 \cdot 10^{a}+1}{49}$. (Clearly $z<10^{a}$, so we're fine.) Then we have $z\left(48 \cdot 10^{a}+1\right)=\left(\frac{48 \cdot 10^{42}+1}{7}\right)^{2}$.
|
| 28 |
+
4. [20] Let
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
\begin{gathered}
|
| 32 |
+
e^{x}+e^{y}=A \\
|
| 33 |
+
x e^{x}+y e^{y}=B \\
|
| 34 |
+
x^{2} e^{x}+y^{2} e^{y}=C \\
|
| 35 |
+
x^{3} e^{x}+y^{3} e^{y}=D \\
|
| 36 |
+
x^{4} e^{x}+y^{4} e^{y}=E .
|
| 37 |
+
\end{gathered}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Prove that if $A, B, C$, and $D$ are all rational, then so is $E$.
|
| 41 |
+
Solution: We can express $x+y$ in two ways:
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
\begin{aligned}
|
| 45 |
+
& x+y=\frac{A D-B C}{A C-B^{2}} \\
|
| 46 |
+
& x+y=\frac{A E-C^{2}}{A D-B C}
|
| 47 |
+
\end{aligned}
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
(We have to be careful if $A C-B^{2}$ or $A D-B C$ is zero. We'll deal with that case later.) It is easy to check that these equations hold by substituting the expressions for $A, B, C, D$, and $E$. Setting these two expressions for $x+y$ equal to each other, we get
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\frac{A D-B C}{A C-B^{2}}=\frac{A E-C^{2}}{A D-B C}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
which we can easily solve for $E$ as a rational function of $A, B, C$, and $D$. Therefore if $A, B, C$, and $D$ are all rational, then $E$ will be rational as well.
|
| 57 |
+
Now, we have to check what happens if $A C-B^{2}=0$ or $A D-B C=0$. If $A C-B^{2}=0$, then writing down the expressions for $A, B$, and $C$ gives us that $(x-y)^{2} e^{x+y}=0$, meaning that $x=y$. If $x=y$, and $x \neq 0, A$ and $D$ are also non-zero, and $\frac{B}{A}=\frac{E}{D}=x$. Since $\frac{B}{A}$ is rational and $D$ is rational, this implies that $E$ is rational. If $x=y=0$, then $E=0$ and so is certainly rational.
|
| 58 |
+
We finally must check what happens if $A D-B C=0$. Since $A D-B C=(x+y)\left(A C-B^{2}\right)$, either $A C-B^{2}=0$ (a case we have already dealt with), or $x+y=0$. But if $x+y=0$ then $A E-C^{2}=0$, which implies that $E=\frac{C^{2}}{A}$ (we know that $A \neq 0$ because $e^{x}$ and $e^{y}$ are both positive). Since $A$ and $C$ are rational, this implies that $E$ is also rational.
|
| 59 |
+
So, we have shown $E$ to be rational in all cases, as desired.
|
| 60 |
+
5. [20] Show that, for every positive integer $n$, there exists a monic polynomial of degree $n$ with integer coefficients such that the coefficients are decreasing and the roots of the polynomial are all integers.
|
| 61 |
+
Solution: We claim we can find values $a$ and $b$ such that $p(x)=(x-a)(x+b)^{n}$ is a polynomial of degree $n+1$ that satisfies these constraints. We show that its coefficients are decreasing by finding a general formula for the coefficient of $x^{k}$.
|
| 62 |
+
|
| 63 |
+
The coefficient of $x^{k}$ is $b^{k}\binom{n}{k}-a b^{k-1}\binom{n}{k-1}$, which can be seen by expanding out $(x+b)^{n}$ and then multiplying by $(x-a)$. Then we must prove that
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
b^{k+1}\binom{n}{k+1}-a b^{k}\binom{n}{k}<b^{k}\binom{n}{k}-a b^{k-1}\binom{n}{k-1}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
or
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
a b^{k-1}\left(b\binom{n}{k}-\binom{n}{k-1}\right)>b^{k}\left(b\binom{n}{k+1}-\binom{n}{k}\right) .
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
Choose $b>\max \left(\frac{\binom{n}{k}}{\binom{n}{k-1}}\right)$ in order to make sure the right-hand term in each product on each side of the inequality sign is positive (we'll be dividing by it, so this makes things much easier), and choose $a>\max \left(\frac{b\left(b\binom{n}{k+1}-\binom{n}{k}\right)}{b\binom{n}{k}-\binom{n}{k-1}}\right)$ to make sure the inequality always holds. Since there are only finite values that $k$ can take on given a fixed $n$ (namely, integers between 0 and $n$ inclusive), we can always find values of $a$ and $b$ that satisfy these constraints.
|
| 76 |
+
6. [20] Let $S$ be a convex set in the plane with a finite area $a$. Prove that either $a=0$ or $S$ is bounded. Note: a set is bounded if it is contained in a circle of finite radius. Note: a set is convex if, whenever two points $A$ and $B$ are in the set, the line segment between them is also in the set.
|
| 77 |
+
Solution: If all points in $S$ lie on a straight line, then $a=0$.
|
| 78 |
+
Otherwise we may pick three points $A, B$, and $C$ that are not collinear. Let $\omega$ be the incircle of $\triangle A B C$, with $I$ its center and $r$ its radius. Since $S$ is convex, $S$ must contain $\omega$.
|
| 79 |
+

|
| 80 |
+
|
| 81 |
+
Suppose $S$ also contains a point $X$ at a distance $d$ from $I$, with $d>R$. We will show that $d \leq \sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$, which implies that the $S$ is bounded since all points are contained within the circle centered at $I$ of radius $\sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$.
|
| 82 |
+
Let $Y$ and $Z$ be on $\omega$ such that $\overline{X Y}$ and $\overline{X Z}$ are tangents to $\omega$. Because $S$ is convex, it must contain kite $I Y X Z$, whose area we can compute in terms of $d$ and $r$.
|
| 83 |
+
Let $M$ be the midpoint of $\overline{Y Z}$. Since $\triangle I Y X \sim \triangle I M Y$, we know that $\frac{I M}{I Y}=\frac{I Y}{I X}$, that is, $I M=$ $\frac{(I Y)^{2}}{I X}=\frac{r^{2}}{d}$. Then $M Y=\sqrt{r^{2}-\frac{r^{4}}{d^{2}}}=r \sqrt{1-\left(\frac{r}{d}\right)^{2}}=\frac{1}{2} Y Z$.
|
| 84 |
+
The area of $I Y X Z$ is $\frac{1}{2}(Y Z)(I X)=r d \sqrt{1-\left(\frac{r}{d}\right)^{2}}=r \sqrt{d^{2}-r^{2}}$. This must be less than or equal to $a$, the area of $S$. This yields $a^{2} \geq r^{2} d^{2}-r^{4}$ or $d^{2} \leq r^{2}+\frac{a^{2}}{r^{2}}$. It follows that $d \leq \sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$, as desired.
|
| 85 |
+
7. [25] Point $P$ lies inside a convex pentagon $A F Q D C$ such that $F P D Q$ is a parallelogram. Given that $\angle F A Q=\angle P A C=10^{\circ}$, and $\angle P F A=\angle P D C=15^{\circ}$. What is $\angle A Q C ?$
|
| 86 |
+
Answer: $\frac{\pi}{12}$ Let $C^{\prime}$ be the point such that there is a spiral similarity between $\triangle A F P$ and $\triangle A Q C^{\prime}$. In other words, one triangle can be formed from the other by dilating and rotating about one of the
|
| 87 |
+
triangle's vertices (in this case, $A$ ). We will show that $C^{\prime}$ is $C$, so our answer will be $\angle A Q C=$ $\angle A Q C^{\prime}=\angle A F P=15^{\circ}$. By the spiral similarity theorem, $\triangle A F Q \sim \triangle A P C^{\prime}$ (this is intuitive by looking at a diagram), so $\angle P A C=\angle F A Q=10^{\circ}$, so to show that $C^{\prime}$ is $C$, it is sufficient to show that $\angle P D C^{\prime}=15^{\circ}$.
|
| 88 |
+
|
| 89 |
+
|
| 90 |
+
Let $X$ be the fourth point of the parallelogram $F P C^{\prime} X$ (see the above diagram). The angle between lines $\overline{F P}$ and $\overline{F A}$ is $15^{\circ}$. Since $\overline{X C^{\prime}} \| \overline{F P}$, the angle between $\overline{F A}$ and $\overline{X C^{\prime}}$ is $15^{\circ}$ as well. In addition, the angle between $\overline{Q A}$ and $\overline{Q C^{\prime}}$ is $\angle A Q C^{\prime}=15^{\circ}$, so $\angle X C^{\prime} Q=\angle F A Q$. Further, because $F P C^{\prime} X$ is a parallelogram, $\frac{Q C^{\prime}}{X C^{\prime}}=\frac{Q C^{\prime}}{F P}$. By similar triangles $\triangle A F P$ and $\triangle A Q C^{\prime}, \frac{Q C^{\prime}}{F P}=\frac{Q A}{F A}$. By SAS similarity, there is a spiral similarity between $\triangle X C^{\prime} Q$ and $\triangle F A Q$, so $\angle F Q X=\angle A Q C^{\prime}=15^{\circ}$.
|
| 91 |
+
Note that the segments $\overline{F P}, \overline{X C^{\prime}}$, and $\overline{Q D}$ are all parallel and equal in length. Therefore, $\triangle F Q X \cong$ $\triangle P D C^{\prime}$ are congruent, and $\angle P D C^{\prime}=15^{\circ}$ as well. So $C^{\prime}$ is $C$, and $\angle A Q C=15^{\circ}$.
|
| 92 |
+
8. [30] A knight moves on a two-dimensional grid. From any square, it can move 2 units in one axisparallel direction, then move 1 unit in an orthogonal direction, the way a regular knight moves in a game of chess. The knight starts at the origin. As it moves, it keeps track of a number $t$, which is initially 0 . When the knight lands at the point $(a, b)$, the number is changed from $x$ to $a x+b$.
|
| 93 |
+
|
| 94 |
+
Show that, for any integers $a$ and $b$, it is possible for the knight to land at the points $(1, a)$ and $(-1, a)$ with $t$ equal to $b$.
|
| 95 |
+
Solution: For convenience, we will refer to $(a, b)$ as $[a x+b]$, the function it represents. This will make it easier to follow the trajectory of $t$ over a given sequence of moves.
|
| 96 |
+
Suppose we start at $[x+1]$ with $t=a$. Taking the path $[x+1] \rightarrow[-x] \rightarrow[x-1] \rightarrow[-x] \rightarrow[x+1]$ will yield $t=a+2$. So we can go from $t=a$ to $t=a+2$ at $[x+1]$.
|
| 97 |
+
We can also move until we get to $[-3]$, then go $[-3] \rightarrow[x-1]$ to end up with $t=-4$ at $[x-1]$. But going $[x-1] \rightarrow[3 x] \rightarrow[x-1]$ means we can go from $t=a$ to $t=3 a-1$ at $x-1$. Since we can start with $t=-4$, this means we can therefore get arbitrarily small even and odd numbers at $[x-1]$, hence also $[3 x]$, hence also at $[x+1]$.
|
| 98 |
+
This implies we can get any value of $t$ we want at $[x+1]$, so we can also get any value of $t$ we want at $[-x],[x-1],[-x-2],[x-3]$, etc., as well as $[-x+2],[x+3],[-x+4],[x+5]$, etc. We can do a similar thing starting at $[-x+1]$ to get from $t=a$ to $t=a+2$, and use the $[-x-1] \rightarrow[-3 x] \rightarrow[-x-1]$ loop to get arbitrarily small integers of both parities. So we can get any value of $t$ we want at all points of the form $[ \pm x+k]$ for any integer $k$.
|
| 99 |
+
9. [30] Let $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{0}$ be a polynomial with complex coefficients such that $a_{i} \neq 0$ for all $i$. Prove that $|r| \leq 2 \max _{i=0}^{n-1}\left|\frac{a_{i-1}}{a_{i}}\right|$ for all roots $r$ of all such polynomials $p$. Here we let $|z|$ denote the absolute value of the complex number $z$.
|
| 100 |
+
Solution: If $r$ is a root, then $-a_{n} r^{n}=a_{n-1} r^{n-1}+\ldots+a_{0}$. By the Triangle Inequality, $\left|-a_{n} r^{n}\right| \leq$ $\left|a_{n-1} r^{n-1}\right|+\ldots+\left|a_{0}\right|$. Rearranging this inequality yields $\left|a_{n} r^{n}\right|-\left|a_{n-1} r^{n-1}\right|-\ldots-\left|a_{0}\right| \leq 0$.
|
| 101 |
+
Now suppose $|r|=k \max \left|\frac{a_{i-1}}{a_{i}}\right|$. Applying this over values of $i$ ranging from $m+1$ to $n$ (assuming $m+1 \leq n$ ), we get $\left|a_{m} r^{m}\right| \leq \frac{\left|a_{n} r^{n}\right|}{k^{n-m}}$. This, along with the above equation, yields:
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
\left|a_{n} r^{n}\right| \cdot\left(1-\frac{1}{k}-\frac{1}{k^{2}}-\frac{1}{k^{3}}-\ldots-\frac{1}{k^{n}}\right)=0
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
This is only true when $a_{n}=0, r=0$, or $\left(1-\frac{1}{k}-\frac{1}{k^{2}}-\ldots\right)=0$. The first option is impossible by the constraints in the problem. The second option implies $k=0$. The third option implies that $k<2$; otherwise ( $1-\frac{1}{k}-\frac{1}{k^{2}}-\ldots-\frac{1}{k^{n}}$ ) would always remain positive. Either way, $|r| \leq 2 \max _{i=0}^{n-1}\left|\frac{a_{i-1}}{a_{i}}\right|$.
|
| 108 |
+
10. Call an $2 n$-digit base-10 number special if we can split its digits into two sets of size $n$ such that the sum of the numbers in the two sets is the same. Let $p_{n}$ be the probability that a randomly-chosen $2 n$-digit number is special. (We allow leading zeros in $2 n$-digit numbers).
|
| 109 |
+
(a) [20] The sequence $p_{n}$ converges to a constant $c$. Find $c$.
|
| 110 |
+
|
| 111 |
+
Answer: $\frac{1}{2}$ We first claim that if a $2 n$-digit number $x$ has at least eight 0 's and at least eight 1's and the sum of its digits is even, then $x$ is special.
|
| 112 |
+
Let $A$ be a set of eight 0 's and eight 1's and let $B$ be the set of all the other digits. We split $b$ arbitrily into two sets $Y$ and $Z$ of equal size. If $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right|>8$, then we swap the biggest element of the set with the bigger sum with the smallest element of the other set. This transposition always decreases the absolute value of the sum: in the worst case, a 9 from the bigger set is swapped for a 0 from the smaller set, which changes the difference by at most 18 . Therefore, after a finite number of steps, we will have $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right| \leq 8$.
|
| 113 |
+
Note that this absolute value is even, since the sum of all the digits is even. Without loss of generality, suppose that $\sum_{y \in Y} y-\sum_{z \in Z} z$ is $2 k$, where $0 \leq k \leq 4$. If we add $k 0$ 's and $8-k$ 's to $Y$, and we add the other elements of $A$ to $Z$, then the two sets will balance, so $x$ is special.
|
| 114 |
+
(b) [45] Let $q_{n}=p_{n}-c$. There exists a unique positive constant $r$ such that $\frac{q_{n}}{r^{n}}$ converges to a constant $d$. Find $r$ and $d$.
|
| 115 |
+
Answer: $r=\frac{1}{4}, d=-1$ To get the next asymptotic term after the constant term of $\frac{1}{2}$, we need to consider what happens when the digit sum is even; we want to find the probability that such a number isn't balanced. We claim that the configuration that contributes the vast majority of unbalanced numbers is when all numbers are even and the sum is $2 \bmod 4$, or such a configuration with all numbers increased by 1. Clearly this gives $q_{n}$ being asymptotic to $-\frac{1}{2} \cdot 2 \cdot\left(\frac{1}{2}\right)^{2 n}=-\left(\frac{1}{4}\right)^{n}$, so $r=\frac{1}{4}$ and $d=-1$.
|
| 116 |
+
To prove the claim, first note that the asymptotic probability that there are at most 4 digits that occur more than 10 times is asymptotically much smaller than $\left(\frac{1}{2}\right)^{n}$, so we can assume that there exist 5 digits that each occur at least 10 times. If any of those digits are consecutive, then the digit sum being even implies that the number is balanced (by an argument similar to part (a)).
|
| 117 |
+
So, we can assume that none of the numbers are consecutive. We would like to say that this implies that the numbers are either $0,2,4,6,8$ or $1,3,5,7,9$. However, we can't quite say this yet, as we need to rule out possibilities like $0,2,4,7,9$. In this case, though, we can just pair 0 and 7 up with 2 and 4 ; by using the same argument as in part (a), except using 0 and 7 both (to get a sum of 7 ) and 2 and 4 both (to get a sum of 6 ) to balance out the two sets at the end.
|
| 118 |
+
In general, if there is ever a gap of size 3 , consider the number right after it and the 3 numbers before it (so we have $k-4, k-2, k, k+3$ for some $k$ ), and pair them up such that one pair has a sum that's exactly one more than the other (i.e. pair $k-4$ with $k+3$ and $k-2$ with $k$ ). Since we again have pairs of numbers whose sums differ by 1 , we can use the technique from part (a) of balancing out the sets at the end.
|
| 119 |
+
So, we can assume there is no gap of size 3 , which together with the condition that no two numbers are adjacent implies that the 5 digits are either $0,2,4,6,8$ or $1,3,5,7,9$. For the remainder of the solution, we will deal with the $0,2,4,6,8$ case, since it is symmetric with the other case under the transformation $x \mapsto 9-x$.
|
| 120 |
+
If we can distribute the odd digits into two sets $S_{1}$ and $S_{2}$ such that (i) the differense in sums of $S_{1}$ and $S_{2}$ is small; and (ii) the difference in sums of $S_{1}$ and $S_{2}$, plus the sum of the even digits, is divisible by 4 , then the same argument as in part (a) implies that the number is good.
|
| 121 |
+
|
| 122 |
+
In fact, if there are any odd digits, then we can use them at the beginning to fix the parity mod 4 (by adding them all in such that the sums of the two sets remain close, and then potentially switching one with an even digit). Therefore, if there are any odd digits then the number is good.
|
| 123 |
+
Also, even if there are no odd digits, if the sum of the digits is divisible by 4 then the number is good.
|
| 124 |
+
So, we have shown that almost all non-good numbers come from having all numbers being even with a digit sum that is $2 \bmod 4$, or the analogous case under the mapping $x \mapsto 9-x$. This formalizes the claim we made in the first paragraph, so $r=\frac{1}{4}$ and $d=-1$, as claimed.
|
| 125 |
+
|
HarvardMIT/md/en-132-2010-feb-team2-solutions.md
ADDED
|
@@ -0,0 +1,95 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## $13^{\text {th }}$ Annual Harvard-MIT Mathematics Tournament <br> Saturday 20 February 2010 <br> Team Round B
|
| 2 |
+
|
| 3 |
+
1. [10] How many ways are there to place pawns on an $8 \times 8$ chessboard, so that there is at most 1 pawn in each horizontal row? Express your answer in the form $p_{1}^{e_{1}} \cdot p_{2}^{e_{2}} \cdots$, where the $p_{i}$ are distinct primes and the $e_{i}$ are positive integers.
|
| 4 |
+
Answer: $3^{16}$ If there is at most 1 pawn in each row, then each row of the chessboard may have either 0 or 1 pawn somewhere in the row. There is 1 case if there are no pawns in the row. There are 8 possible cases if there is 1 pawn in the row, one case for each square in the row. Hence for each row, there are 9 possible pawn arrangements. There are 8 rows, thus we have $9^{8}=3^{16}$.
|
| 5 |
+
2. [10] In the following figure, a regular hexagon of side length 1 is attached to a semicircle of diameter 1. What is the longest distance between any two points in the figure?
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
Answer: $\frac{1+\sqrt{13}}{2}$ Inspection shows that one point must be on the semicircle and the other must be on the side of the hexagon directly opposite the edge with the semicircle, the bottom edge of the hexagon in the above diagram. Let $O$ be the center of the semicircle and let $M$ be the midpoint of the bottom edge.
|
| 9 |
+
We will determine the longest distance between points in the figure by comparing the lengths of all the segments with one endpoint on the bottom edge and the other endpoint on the semicircle. Fix a point $A$ on the bottom edge of the hexagon. Suppose that $B$ is chosen on the semicircle such that $A B$ is as long as possible. Let $C$ be the circle centered at $A$ with radius $A B$. If $C$ is not tangent to the semicircle, then part of the semicircle is outside $C$, so we could pick a $B^{\prime}$ on the semicircle such that $A B^{\prime}$ is longer than $A B$. So $C$ must be tangent to the semicircle, and $A B$ must pass through $O$.
|
| 10 |
+
Then $O B$ is always $\frac{1}{2}$, no matter which $A$ we choose on the bottom edge. All that remains is maximizing $A O$. This length is the hypotenuse of a right triangle with the fixed height $M O$, so it is maximized when $A M$ is as large as possible - when $A$ is an endpoint of the bottom edge. Note that $M O=2 \cdot \frac{\sqrt{3}}{2}$, and that $A M$ can be at most $\frac{1}{2}$, so $A O$ can be at most $\frac{\sqrt{13}}{2}$. So the maximum distance between two points in the diagram is $A O+O B=\frac{1+\sqrt{13}}{2}$.
|
| 11 |
+
3. [15] Let $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{0}$, where each $a_{i}$ is either 1 or -1 . Let $r$ be a root of $p$. If $|r|>\frac{15}{8}$, what is the minimum possible value of $n$ ?
|
| 12 |
+
Answer: 4 We claim that $n=4$ is the answer. First, we show that $n>3$. Suppose that $n \leq 3$. Let $r$ be the root of the polynomial with $|r| \geq \frac{15}{8}$. Then, by the Triangle Inequality, we have:
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\begin{gathered}
|
| 16 |
+
\left|a_{n} r^{n}\right|=\left|a_{n-1} r^{n-1}+a_{n-2} r^{n-2}+\ldots+a_{0}\right| \leq\left|a_{n-1} r^{n-1}\right|+\left|a_{n-2} r^{n-2}\right|+\ldots+\left|a_{0}\right| \\
|
| 17 |
+
|r|^{n} \leq\left|r^{n-1}\right|+\left|r^{n-2}\right|+\ldots+|1|=\frac{|r|^{n}-1}{|r|-1} \\
|
| 18 |
+
|r|^{n+1}-2|r|^{n}+1 \leq 0 \Rightarrow 1 \leq|r|^{n}(2-|r|)
|
| 19 |
+
\end{gathered}
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
The right-hand side is increasing in $n$, for $|r|>1$, so it is bounded by $|r|^{3}(2-|r|)$. This expression is decreasing in $r$ for $r \geq \frac{3}{2}$. When $|r|=\frac{15}{8}$, then the right-hand side is less than 1 , which violates the inequalities. Therefore $n>3$. Now, we claim that there is a 4 th degree polynomial with a root $r$ with $|r| \geq \frac{15}{8}$. Let $p(x)=x^{4}-x^{3}-x^{2}-x-1$. Then $p\left(\frac{15}{8}\right)<0$ and $p(2)>2$. By the Intermediate Value Theorem, $p(x)$ has such a root $r$.
|
| 23 |
+
4. [20] Find all 4-digit integers of the form $a a b b$ (when written in base 10) that are perfect squares.
|
| 24 |
+
|
| 25 |
+
Answer: 7744 Let $x$ be an integer such that $x^{2}$ is of the desired form. Then $1100 a+11 b=x^{2}$. Then $x^{2}$ is divisible by 11 , which means $x$ is divisible by 11 . Then for some integer, $y, x=11 y$. Then $1100 a+11 b=11^{2} y^{2} \Rightarrow 100 a+b=11 y^{2}$. This means that $100 a+b \equiv 0(\bmod 11) \Rightarrow a+b \equiv 0(\bmod 11)$. Because $a$ and $b$ must be nonzero digits, we have $2 \leq a, b \leq 9$, so we can write $b=11-a$.
|
| 26 |
+
Replacing $b$ in the equation derived above, we obtain $99 a+11=11 y^{2} \Rightarrow 9 a+1=y^{2}$. We check the possible values of $a$ from 2 to 9 , and only $a=7$ yields a perfect square. When $a=7, b=4$, so the only perfect square of for $a a b b$ is 7744 .
|
| 27 |
+
5. [25] Compute
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\sum_{n=1}^{98} \frac{2}{\sqrt{n}+\sqrt{n+2}}+\frac{1}{\sqrt{n+1}+\sqrt{n+2}}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Answer: $\quad 3 \sqrt{11}-2 \sqrt{2}+19$ Rationalizing the denominator of both terms in the summation yields $\sqrt{n+2}-\sqrt{n}+\sqrt{n+2}-\sqrt{n+1}=2 \sqrt{n+2}-(\sqrt{n}+\sqrt{n+1})$. Then the sum $\sum_{n=1}^{98} 2 \sqrt{n+2}-(\sqrt{n}+\sqrt{n+1})$ telescopes. All terms cancel except for $-(\sqrt{1}+\sqrt{2})-\sqrt{2}+2 \sqrt{99}+2 \sqrt{100}-\sqrt{99}=3 \sqrt{11}-2 \sqrt{2}+19$.
|
| 34 |
+
6. [25] Into how many regions can a circle be cut by 10 parabolas?
|
| 35 |
+
|
| 36 |
+
Answer: 201 We will consider the general case of $n$ parabolas, for which the answer is $2 n^{2}+1$.
|
| 37 |
+
We will start with some rough intuition, then fill in the details afterwards. The intuition is that, if we make the parabolas steep enough, we can basically treat them as two parallel lines. Furthermore, the number of regions is given in terms of the number of intersections of the parabolas that occur within the circle, since every time two parabolas cross a new region is created. Since two pairs of parallel lines intersect in 4 points, and pairs of parabolas also intersect in 4 points, as long as we can always make all 4 points of intersection lie inside the circle, the parallel lines case is the best we can do.
|
| 38 |
+
In other words, the answer is the same as the answer if we were trying to add ten pairs of parallel lines. We can compute the answer for pairs of parallel lines as follows - when we add the $k$ th set of parallel lines, there are already $2 k-2$ lines that the two new lines can intersect, meaning that each of the lines adds $2 k-1$ new regions ${ }^{1}$. This means that we add $4 k-2$ regions when adding the $k$ th set of lines, making the answer $1+2+6+10+14+\cdots+(4 n-2)=1+2(1+3+5+7+\cdots+(2 n-1))=1+2 \cdot n^{2}=2 n^{2}+1$.
|
| 39 |
+
Now that we have sketched out the solution, we will fill in the details more rigorously. First, if there are $n$ parabolas inside the circle, and the they intersect in $K$ points total, then we claim that the number of regions the circle is divided into will be at most $K+n+r+1$, where $r$ is the number of parabolas that intersect the circle itself in exactly four points.
|
| 40 |
+
We will prove this by induction. In the base case of $n=0$, we are just saying that the circle itself consists of exactly one region.
|
| 41 |
+
To prove the inductive step, suppose that we have $n$ parabolas with $K$ points of intersection. We want to show that if we add an additional parabola, and this parabola intersects the other parabolas in $p$ points, then this new parabola adds either $p+1$ or $p+2$ regions to the circle, and that we get $p+2$ regions if and only if the parabola intersects the circle in exactly four points.
|
| 42 |
+
We will do this by considering how many regions the parabola cuts through, following its path from when it initially enters the circle to when it exits the circle for the last time. When it initially enters the circle, it cuts through one region, thereby increasing the number of regions by on ${ }^{2}$. Then, for each other parabola that this parabola crosses, we cut through one additional region. It is also possible for the parabola to leave and then re-enter the circle, which happens if and only if the parabola intersects
|
| 43 |
+
|
| 44 |
+
[^0]the circle in four points, and also adds one additional region. Therefore, the number of regions is either $p+1$ or $p+2$, and it is $p+2$ if and only if the parabola intersects the circle in four points. This completes the induction and proves the claim.
|
| 45 |
+
So, we are left with trying to maximize $K+n+r+1$. Since a pair of parabolas intersects in at most 4 points, and there are $\binom{n}{2}$ pairs of parabolas, we have $K \leq 4\binom{n}{2}=2 n^{2}-2 n$. Also, $r \leq n$, so $K+n+r+1 \leq 2 n^{2}+1$. On the other hand, as explained in the paragraphs giving the intuition, we can attain $2 n^{2}+1$ by making the parabolas sufficiently steep that they act like pairs of parallel lines. Therefore, the answer is $2 n^{2}+1$, as claimed.
|
| 46 |
+
7. [30] Evaluate
|
| 47 |
+
$$
|
| 48 |
+
\sum_{k=1}^{2010} \cos ^{2}(k)
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Answer: $1005+\frac{\sin (4021)-\sin (1)}{4 \sin (1)}$ We use the identity $\cos ^{2}(k)=\frac{1+\cos (2 x)}{2}$. Then our expression evalutes to $1005+\frac{(\cos (2)+\ldots+\cos (4020))}{2}$.
|
| 52 |
+
To evaluate $\cos (2)+\cdots+\cos (4020)$, let $y=\cos (2)+\cdots+\cos (4020) \Rightarrow y(\sin (1))=\cos (2) \sin (1)+$ $\ldots+\cos (4020) \sin (1)$. Observe that for any $x, \cos (x) \sin (1)=\frac{\sin (x+1)-\sin (x-1)}{2}$. Then $y(\sin (1))=$ $\frac{\sin (3)-\sin (1)}{2}+\frac{\sin (5)-\sin (3)}{2}+\ldots+\frac{\sin 4021-\sin (4019)}{2}$. This is clearly a telescoping sum; we get $y(\sin (1))=$ $\frac{\sin (4021)-\sin (1)}{2}$. Then we have the desired $y=\frac{\sin (4021)-\sin (1)}{2 \sin (1)}$. Then our original expression evaluates to $1005+\frac{\sin (4021)-\sin (1)}{4 \sin (1)}$.
|
| 53 |
+
8. [30] Consider the following two-player game. Player 1 starts with a number, $N$. He then subtracts a proper divisor of $N$ from $N$ and gives the result to player 2 (a proper divisor of $N$ is a positive divisor of $N$ that is not equal to 1 or $N)$. Player 2 does the same thing with the number she gets from player 1 , and gives the result back to player 1. The two players continue until a player is given a prime number, at which point that player loses. For how many values of $N$ between 2 and 100 inclusive does player 1 have a winning strategy?
|
| 54 |
+
Answer: 47 We claim that player 1 has a winning strategy if and only if $N$ is even and not an odd power of 2 .
|
| 55 |
+
First we show that if you are stuck with an odd number, then you are guaranteed to lose. Suppose you have an odd number $a b$, where $a$ and $b$ are odd numbers, and you choose to subtract $a$. You pass your opponent the number $a(b-1)$. This cannot be a power of 2 (otherwise $a$ is a power of 2 and hence $a=1$, which is not allowed), so your opponent can find an odd proper divisor of $a(b-1)$ (such as $a$ ), and you will have a smaller odd number. Eventually you will get to an odd prime and lose.
|
| 56 |
+
Now consider even numbers that aren't powers of 2. As with before, you can find an odd proper divisor of $N$ and pass your opponent an odd number, so you are guaranteed to win.
|
| 57 |
+
Finally consider powers of 2 . If you have the number $N=2^{k}$, it would be unwise to choose a proper divisor other than $2^{k-1}$; otherwise you would give your opponent an even number that isn't a power of 2 . Therefore if $k$ is odd, you will end up with 2 and lose. If $k$ is even, though, your opponent will end up with 2 and you will win.
|
| 58 |
+
Therefore player 1 has a winning strategy for all even numbers except for odd powers of 2 .
|
| 59 |
+
9. [35] Let $S$ be the set of ordered pairs of integers $(x, y)$ with $1 \leq x \leq 5$ and $1 \leq y \leq 3$. How many subsets $R$ of $S$ have the property that all the points of $R$ lie on the graph of a single cubic? A cubic is a polynomial of the form $y=a x^{3}+b x^{2}+c x+d$, where $a, b, c$, and $d$ are real numbers (meaning that $a$ is allowed to be 0 ).
|
| 60 |
+
Answer: 796 We observe that $R$ must contain at most 1 point from each column of $S$, because no function can contain more than 1 point with the same $x$-coordinate. Therefore, $|R| \leq 5(|R|$ denotes the number of elements of $R$ ). Note that 4 points determine a cubic, so if $R$ is any subset of points in distinct columns and $|R| \leq 4$, then $R$ has the desired property. There are $4^{5}$ ways to choose at most 1
|
| 61 |
+
point from each column and $3^{5}$ ways to choose exactly 1 point from each column. There are therefore $4^{5}-3^{5}=781$ subsets $R$ of $S$ such that $|R| \leq 4$ and all points of $R$ lie in distinct columns. As noted, these sets all automatically have the desired property.
|
| 62 |
+
Now we consider all sets $R$ of size 5 . As before, each point in $R$ must come from a different column. Let us shift our origin to $(3,2)$, and let $p$ be the polynomial containing all 5 points of $R$. Then $R=\{(-2, p(-2)),(-1, p(-1)),(0, p(0)),(1, p(1)),(2, p(2))\}$.
|
| 63 |
+
By the method of finite differences $3^{3}$ or alternately by Lagrange Interpolation there is a unique polynomial $p$ of degree less than 5 going through 5 specified points, and this polynomial is of degree less than 4 if and only if $p(-2)-4 p(-1)+6 p(0)-4 p(1)+p(2)=0$.
|
| 64 |
+
Then $p(-2)+p(2)+6 p(0)=4(p(-1)+p(1))$, where $p(-2)+p(2) \in\{-2-1,0,1,2\}, p(-1)+p(1) \in$ $\{-2,-1,0,1,2\}$, and $p(0) \in\{-1,0,1\}$. We know that $6 p(0)$ and $4(p(-1)+p(1))$ are necessarily even, thus we must have $p(-2)+p(2) \in\{-2,0,2\}$ in order for the equation to be satisfied.
|
| 65 |
+
Let $(a, b, c)=(p(-2)+p(2), 6 p(0), 4(p(-1)+p(1)))$. The possible values of $(a, b, c)$ that are solutions to $a+b=c$ are then $\{(-2,-6,-8),(-2,6,4),(0,0,0),(2,-6,-4),(2,6,8)\}$.
|
| 66 |
+
If $(a, b, c)=(-2,-6,-8)$, then we need $p(-2)+p(2)=-2, p(0)=-1, p(-1)+p(1)=-2$. There is only 1 possible solution to each of these equations: $(p(-2), p(2))=(-1,-1)$ for the first one, $p(0)=-1$ for the second, and $(p(1))=(-1,-1)$ for the third. Hence there is 1 possible subset $R$ for the case $(a, b, c)=(-2,-6,-8)$.
|
| 67 |
+
If $(a, b, c)=(-2,6,4)$, then there is again 1 possible solution to $p(-2)+p(2)=1$. There are two solutions to $p(-1)+p(1)=1:(p(-1), p(1))=(0,1),(1,0)$. Also, $p(0)$ can only be 1 , so there are 2 possible subsets for this case.
|
| 68 |
+
If $(a, b, c)=(0,0,0)$, then there there are 3 possible solutions to $p(-2)+p(2)=0:(p(-2), p(2))=$ $(-1,1),(0,0),(1,-1)$. Similarly, there are 3 possible solutions to $p(-1)+p(1)=0$. Also, $p(0)$ can only be 0 , so there are 9 possible subsets for this case.
|
| 69 |
+
If $(a, b, c)=(2,-6,-4)$, then there is 1 possible solution to $p(-2)+p(2)=2:(p(-2), p(2))=(1,1)$. There are 2 possible solutions to $p(-1)+p(1)=-1:(p(-1), p(1))=(0,-1),(-1,0)$. Also, $p(0)$ can only be -1 , so there are 2 possible subsets for this case.
|
| 70 |
+
If $(a, b, c)=(2,6,8)$, then there is 1 possible solution to $p(-2)+p(2)=2$, as shown above. There is 1 solution to $p(-1)+p(1)=2:(p(-1), p(1))=(1,1)$. Also, $p(0)$ can only be 1 , so there is 1 possible subset for this case.
|
| 71 |
+
Then there are $1+2+9+2+1=15$ total possible subsets of size 5 that can be fit to a polynomial of degree less than 4 . Hence there are $781+15=796$ possible subsets total.
|
| 72 |
+
10. Call an $2 n$-digit number special if we can split its digits into two sets of size $n$ such that the sum of the numbers in the two sets is the same. Let $p_{n}$ be the probability that a randomly-chosen $2 n$-digit number is special (we will allow leading zeros in the number).
|
| 73 |
+
(a) [25] The sequence $p_{n}$ converges to a constant $c$. Find $c$.
|
| 74 |
+
|
| 75 |
+
Answer: $\frac{1}{2}$ We first claim that if a $2 n$-digit number $x$ has at least eight 0 's and at least eight 1's and the sum of its digits is even, then $x$ is special.
|
| 76 |
+
Let $A$ be a set of eight 0 's and eight 1 's and let $B$ be the set of all the other digits. We split $b$ arbitrily into two sets $Y$ and $Z$ of equal size. If $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right|>8$, then we swap the biggest element of the set with the bigger sum with the smallest element of the other set. This transposition always decreases the absolute value of the sum: in the worst case, a 9 from the bigger set is swapped for a 0 from the smaller set, which changes the difference by at most 18 . Therefore, after a finite number of steps, we will have $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right| \leq 8$.
|
| 77 |
+
Note that this absolute value is even, since the sum of all the digits is even. Without loss of generality, suppose that $\sum_{y \in Y} y-\sum_{z \in Z} z$ is $2 k$, where $0 \leq k \leq 4$. If we add $k 0$ 's and $8-k$ 's to $Y$, and we add the other elements of $A$ to $Z$, then the two sets will balance, so $x$ is special.
|
| 78 |
+
|
| 79 |
+
[^1](b) $[\mathbf{3 0}]$ Let $q_{n}=p_{n}-c$. There exists a unique positive constant $r$ such that $\frac{q_{n}}{r^{n}}$ converges to a constant $d$. Find $r$ and $d$.
|
| 80 |
+
Answer: $\left(\frac{1}{4},-1\right)$ To get the next asymptotic term after the constant term of $\frac{1}{2}$, we need to consider what happens when the digit sum is even; we want to find the probability that such a number isn't balanced. We claim that the configuration that contributes the vast majority of unbalanced numbers is when all numbers are even and the sum is $2 \bmod 4$, or such a configuration with all numbers increased by 1. Clearly this gives $q_{n}$ being asymptotic to $-\frac{1}{2} \cdot 2 \cdot\left(\frac{1}{2}\right)^{2 n}=-\left(\frac{1}{4}\right)^{n}$, so $r=\frac{1}{4}$ and $d=-1$.
|
| 81 |
+
To prove the claim, first note that the asymptotic probability that there are at most 4 digits that occur more than 10 times is asymptotically much smaller than $\left(\frac{1}{2}\right)^{n}$, so we can assume that there exist 5 digits that each occur at least 10 times. If any of those digits are consecutive, then the digit sum being even implies that the number is balanced (by an argument similar to part (a)).
|
| 82 |
+
So, we can assume that none of the numbers are consecutive. We would like to say that this implies that the numbers are either $0,2,4,6,8$ or $1,3,5,7,9$. However, we can't quite say this yet, as we need to rule out possibilities like $0,2,4,7,9$. In this case, though, we can just pair 0 and 7 up with 2 and 4 ; by using the same argument as in part (a), except using 0 and 7 both (to get a sum of 7 ) and 2 and 4 both (to get a sum of 6 ) to balance out the two sets at the end.
|
| 83 |
+
In general, if there is ever a gap of size 3 , consider the number right after it and the 3 numbers before it (so we have $k-4, k-2, k, k+3$ for some $k$ ), and pair them up such that one pair has a sum that's exactly one more than the other (i.e. pair $k-4$ with $k+3$ and $k-2$ with $k$ ). Since we again have pairs of numbers whose sums differ by 1 , we can use the technique from part (a) of balancing out the sets at the end.
|
| 84 |
+
So, we can assume there is no gap of size 3 , which together with the condition that no two numbers are adjacent implies that the 5 digits are either $0,2,4,6,8$ or $1,3,5,7,9$. For the remainder of the solution, we will deal with the $0,2,4,6,8$ case, since it is symmetric with the other case under the transformation $x \mapsto 9-x$.
|
| 85 |
+
If we can distribute the odd digits into two sets $S_{1}$ and $S_{2}$ such that (i) the differense in sums of $S_{1}$ and $S_{2}$ is small; and (ii) the difference in sums of $S_{1}$ and $S_{2}$, plus the sum of the even digits, is divisible by 4 , then the same argument as in part (a) implies that the number is good.
|
| 86 |
+
In fact, if there are any odd digits, then we can use them at the beginning to fix the parity mod 4 (by adding them all in such that the sums of the two sets remain close, and then potentially switching one with an even digit). Therefore, if there are any odd digits then the number is good. Also, even if there are no odd digits, if the sum of the digits is divisible by 4 then the number is good.
|
| 87 |
+
So, we have shown that almost all non-good numbers come from having all numbers being even with a digit sum that is $2 \bmod 4$, or the analogous case under the mapping $x \mapsto 9-x$. This formalizes the claim we made in the first paragraph, so $r=\frac{1}{4}$ and $d=-1$, as claimed.
|
| 88 |
+
|
| 89 |
+
|
| 90 |
+
[^0]: ${ }^{1}$ This is the maximum possible number of new regions, but it's not too hard to see that this is always attainable.
|
| 91 |
+
${ }^{2}$ While the fact that a curve going through a region splits it into two new regions is intuitively obvious, it is actually very difficult to prove. The proof relies on some deep results from algebraic topology and is known as the Jordan Curve Theorem. If you are interested in learning more about this, see http://en.wikipedia.org/wiki/Jordan_curve_theorem
|
| 92 |
+
|
| 93 |
+
[^1]: ${ }^{3}$ See http://www.artofproblemsolving.com/Forum/weblog_entry.php?p=1263378
|
| 94 |
+
${ }^{4}$ See http://en.wikipedia.org/wiki/Lagrange_polynomial
|
| 95 |
+
|
HarvardMIT/md/en-141-2010-nov-gen1-solutions.md
ADDED
|
@@ -0,0 +1,91 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $3{ }^{\text {rd }}$ Annual Harvard-MIT November Tournament <br> Sunday 7 November 2010
|
| 2 |
+
|
| 3 |
+
## General Test
|
| 4 |
+
|
| 5 |
+
1. [2] Jacob flips five coins, exactly three of which land heads. What is the probability that the first two are both heads?
|
| 6 |
+
Answer: $\frac{3}{10}$ We can associate with each sequence of coin flips a unique word where $H$ represents heads, and T represents tails. For example, the word HHTTH would correspond to the coin flip sequence where the first two flips were heads, the next two were tails, and the last was heads. We are given that exactly three of the five coin flips came up heads, so our word must be some rearrangement of HHHTT. To calculate the total number of possibilities, any rearrangement corresponds to a choice of three spots to place the H flips, so there are $\binom{5}{3}=10$ possibilities. If the first two flips are both heads, then we can only rearrange the last three HTT flips, which corresponds to choosing one spot for the remaining $H$. This can be done in $\binom{3}{1}=3$ ways. Finally, the probability is the quotient of these two, so we get the answer of $\frac{3}{10}$. Alternatively, since the total number of possiblities is small, we can write out all rearrangements: HHHTT, HHTHT, HHTTH, HTHHT, HTHTH, HTTHH, THHHT, THHTH, THTHH, TTHHH. Of these ten, only in the first three do we flip heads the first two times, so we get the same answer of $\frac{3}{10}$.
|
| 7 |
+
2. [3] How many sequences $a_{1}, a_{2}, \ldots, a_{8}$ of zeroes and ones have $a_{1} a_{2}+a_{2} a_{3}+\cdots+a_{7} a_{8}=5$ ?
|
| 8 |
+
|
| 9 |
+
Answer: 9 First, note that we have seven terms in the left hand side, and each term can be either 0 or 1 , so we must have five terms equal to 1 and two terms equal to 0 . Thus, for $n \in\{1,2, \ldots, 8\}$, at least one of the $a_{n}$ must be equal to 0 . If we can find $i, j \in\{2,3, \ldots, 7\}$ such that $a_{i}=a_{j}=0$ and $i<j$, then the terms $a_{i-1} a_{i}, a_{i} a_{i+1}$, and $a_{j} a_{j+1}$ will all be equal to 0 . We did not count any term twice because $i-1<i<j$, so we would have three terms equal to 0 , which cannot happen because we can have only two. Thus, we can find at most one $n \in\{2,3, \ldots, 7\}$ such that $a_{n}=0$. We will do casework on which $n$ in this range have $a_{n}=0$.
|
| 10 |
+
If $n \in\{3,4,5,6\}$, then we know that the terms $a_{n-1} a_{n}=a_{n} a_{n+1}=0$, so all other terms must be 1 , so $a_{1} a_{2}=a_{2} a_{3}=\ldots=a_{n-2} a_{n-1}=1$ and $a_{n+1} a_{n+2}=\ldots=a_{7} a_{8}=1$. Because every $a_{i}$ appears in one of these equations for $i \neq n$, then we must have $a_{i}=1$ for all $i \neq n$, so we have 1 possibility for each choice of $n$ and thus 4 possibilities total for this case.
|
| 11 |
+
If $n=2$, then again we have $a_{1} a_{2}=a_{2} a_{3}=0$, so we must have $a_{3} a_{4}=a_{4} a_{5}=\ldots=a_{7} a_{8}=1$, so $a_{3}=a_{4}=\ldots=a_{8}=1$. However, this time $a_{1}$ is not fixed, and we see that regardless of our choice of $a_{1}$ the sum will still be equal to 5 . Thus, since there are 2 choices for $a_{1}$, then there are 2 possibilities total for this case. The case where $n=7$ is analogous, with $a_{8}$ having 2 possibilities, so we have another 2 possibilities.
|
| 12 |
+
Finally, if $a_{n}=1$ for $n \in\{2,3, \ldots, 7\}$, then we will have $a_{2} a_{3}=a_{3} a_{4}=\ldots=a_{6} a_{7}=1$. We already have five terms equal to 1 , so the remaining two terms $a_{1} a_{2}$ and $a_{7} a_{8}$ must be 0 . Since $a_{2}=1$, then we must have $a_{1}=0$, and since $a_{7}=1$ then $a_{8}=0$. Thus, there is only 1 possibility for this case.
|
| 13 |
+
Summing, we have $4+2+2+1=9$ total sequences.
|
| 14 |
+
3. [3] Triangle $A B C$ has $A B=5, B C=7$, and $C A=8$. New lines not containing but parallel to $A B$, $B C$, and $C A$ are drawn tangent to the incircle of $A B C$. What is the area of the hexagon formed by the sides of the original triangle and the newly drawn lines?
|
| 15 |
+
|
| 16 |
+
Answer: $\frac{31}{5} \sqrt{3}$
|
| 17 |
+
|
| 18 |
+
|
| 19 |
+
From the law of cosines we compute $\measuredangle A=\cos ^{-1}\left(\frac{5^{2}+8^{2}-7^{2}}{2(5)(8)}\right)=60^{\circ}$. Using brackets to denote the area of a region, we find that
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
[A B C]=\frac{1}{2} A B \cdot A C \cdot \sin 60^{\circ}=10 \sqrt{3}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
The radius of the incircle can be computed by the formula
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
r=\frac{2[A B C]}{A B+B C+C A}=\frac{20 \sqrt{3}}{20}=\sqrt{3}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Now the height from $A$ to $B C$ is $\frac{2[A B C]}{B C}=\frac{20 \sqrt{3}}{7}$. Then the height from $A$ to $D E$ is $\frac{20 \sqrt{3}}{7}-2 r=\frac{6 \sqrt{3}}{7}$. Then $[A D E]=\left(\frac{6 \sqrt{3} / 7}{20 \sqrt{3} / 7}\right)^{2}[A B C]=\frac{9}{100}[A B C]$. Here, we use the fact that $\triangle A B C$ and $\triangle A D E$ are similar.
|
| 32 |
+
Similarly, we compute that the height from $B$ to $C A$ is $\frac{2[A B C]}{C A}=\frac{20 \sqrt{3}}{8}=\frac{5 \sqrt{3}}{2}$. Then the height from $B$ to $H J$ is $\frac{5 \sqrt{3}}{2}-2 r=\frac{\sqrt{3}}{2}$. Then $[B H J]=\left(\frac{\sqrt{3} / 2}{5 \sqrt{3} / 2}\right)^{2}[A B C]=\frac{1}{25}[A B C]$.
|
| 33 |
+
Finally, we compute that the height from $C$ to $A B$ is $\frac{2[A B C]}{5}=\frac{20 \sqrt{3}}{5}=4 \sqrt{3}$. Then the height from $C$ to $F G$ is $4 \sqrt{3}-2 r=2 \sqrt{3}$. Then $[C F G]=\left(\frac{2 \sqrt{3}}{4 \sqrt{3}}\right)^{2}[A B C]=\frac{1}{4}[A B C]$.
|
| 34 |
+
Finally we can compute the area of hexagon $D E F G H J$. We have
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
\begin{gathered}
|
| 38 |
+
{[D E F G H J]=[A B C]-[A D E]-[B H J]-[C F G]=[A B C]\left(1-\frac{9}{100}-\frac{1}{25}-\frac{1}{4}\right)=[A B C]\left(\frac{31}{50}\right)=} \\
|
| 39 |
+
10 \sqrt{3}\left(\frac{31}{50}\right)=\frac{31}{5} \sqrt{3} .
|
| 40 |
+
\end{gathered}
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
4. [4] An ant starts at the point $(1,0)$. Each minute, it walks from its current position to one of the four adjacent lattice points until it reaches a point $(x, y)$ with $|x|+|y| \geq 2$. What is the probability that the ant ends at the point $(1,1)$ ?
|
| 44 |
+
Answer: $\frac{7}{24}$ From the starting point of $(1,0)$, there is a $\frac{1}{4}$ chance we will go directly to $(1,1)$, a $\frac{1}{2}$ chance we will end at $(2,0)$ or $(1,-1)$, and a $\frac{1}{4}$ chance we will go to $(0,0)$. Thus, if $p$ is the probability that we will reach $(1,1)$ from $(0,0)$, then the desired probability is equal to $\frac{1}{4}+\frac{1}{4} p$, so we need only calculate $p$. Note that we can replace the condition $|x|+|y| \geq 2$ by $|x|+|y|=2$, since in each iteration the quantity $|x|+|y|$ can increase by at most 1 . Thus, we only have to consider the eight points $(2,0),(1,1),(0,2),(-1,1),(-2,0),(-1,-1),(0,-2),(1,-1)$. Let $p_{1}, p_{2}, \ldots, p_{8}$ be the probability of
|
| 45 |
+
reaching each of these points from $(0,0)$, respectively. By symmetry, we see that $p_{1}=p_{3}=p_{5}=p_{7}$ and $p_{2}=p_{4}=p_{6}=p_{8}$. We also know that there are two paths from $(0,0)$ to $(1,1)$ and one path from $(0,0)$ to $(2,0)$, thus $p_{2}=2 p_{1}$. Because the sum of all probabilities is 1 , we have $p_{1}+p_{2}+\ldots+p_{8}=1$. Combining these equations, we see that $4 p_{1}+4 p_{2}=12 p_{1}=1$, so $p_{1}=\frac{1}{12}$ and $p_{2}=\frac{1}{6}$. Since $p=p_{2}=\frac{1}{6}$, then the final answer is $\frac{1}{4}+\frac{1}{4} \cdot \frac{1}{6}=\frac{7}{24}$
|
| 46 |
+
5. [5] A polynomial $P$ is of the form $\pm x^{6} \pm x^{5} \pm x^{4} \pm x^{3} \pm x^{2} \pm x \pm 1$. Given that $P(2)=27$, what is $P(3)$ ?
|
| 47 |
+
Answer: 439 We use the following lemma:
|
| 48 |
+
Lemma. The sign of $\pm 2^{n} \pm 2^{n-1} \pm \cdots \pm 2 \pm 1$ is the same as the sign of the $2^{n}$ term.
|
| 49 |
+
Proof. Without loss of generality, let $2^{n}$ be positive. (We can flip all signs.) Notice that $2^{n} \pm 2^{n-1} \pm$ $2^{n-2} \pm \cdots 2 \pm 1 \geq 2^{n}-2^{n-1}-2^{n-2}-\cdots-2-1=1$, which is positive.
|
| 50 |
+
We can use this lemma to uniquely determine the signs of $P$. Since our desired sum, 27, is positive, the coefficient of $x^{6}$ must be positive. Subtracting 64 , we now have that $\pm 2^{5} \pm 2^{4} \pm \ldots \pm 2 \pm 1=-37$, so the sign of $2^{5}$ must be negative. Continuing in this manner, we find that $P(x)=x^{6}-x^{5}-x^{4}+x^{3}+x^{2}-x+1$, so $P(3)=3^{6}-3^{5}-3^{4}+3^{3}+3^{2}-3+1=439$.
|
| 51 |
+
6. [5] What is the sum of the positive solutions to $2 x^{2}-x\lfloor x\rfloor=5$, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$ ?
|
| 52 |
+
Answer: $\frac{3+\sqrt{41}+2 \sqrt{11}}{4}$ We first note that $\lfloor x\rfloor \leq x$, so $2 x^{2}-x\lfloor x\rfloor \geq 2 x^{2}-x^{2}=x^{2}$. Since this function is increasing on the positive reals, all solutions must be at most $\sqrt{5}$. This gives us 3 possible values of $\lfloor x\rfloor: 0,1$, and 2 .
|
| 53 |
+
If $\lfloor x\rfloor=0$, then our equation becomes $2 x^{2}=5$, which has positive solution $x=\sqrt{\frac{5}{2}}$. This number is greater than 1 , so its floor is not 0 ; thus, there are no solutions in this case.
|
| 54 |
+
If $\lfloor x\rfloor=1$, then our equation becomes $2 x^{2}-x=5$. Using the quadratic formula, we find the positive solution $x=\frac{1+\sqrt{41}}{4}$. Since $3<\sqrt{41}<7$, this number is between 1 and 2 , so it satisfies the equation.
|
| 55 |
+
If $\lfloor x\rfloor=2$, then our equation becomes $2 x^{2}-2 x=5$. We find the positive solution $x=\frac{1+\sqrt{11}}{2}$. Since $3<\sqrt{11}<5$, this number is between 2 and 3 , so it satisfies the equation.
|
| 56 |
+
We then find that the sum of positive solutions is $\frac{1+\sqrt{41}}{4}+\frac{1+\sqrt{11}}{2}=\frac{3+\sqrt{41}+2 \sqrt{11}}{4}$.
|
| 57 |
+
7. [6] What is the remainder when $(1+x)^{2010}$ is divided by $1+x+x^{2}$ ?
|
| 58 |
+
|
| 59 |
+
Answer: 1 We use polynomial congruence $\bmod 1+x+x^{2}$ to find the desired remainder. Since $x^{2}+x+1 \mid x^{3}-1$, we have that $x^{3} \equiv 1\left(\bmod 1+x+x^{2}\right)$. Now:
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\begin{aligned}
|
| 63 |
+
(1+x)^{2010} & \equiv\left(-x^{2}\right)^{2010} \quad\left(\bmod 1+x+x^{2}\right) \\
|
| 64 |
+
& \equiv x^{4020} \quad\left(\bmod 1+x+x^{2}\right) \\
|
| 65 |
+
& \equiv\left(x^{3}\right)^{1340} \quad\left(\bmod 1+x+x^{2}\right) \\
|
| 66 |
+
& \equiv 1^{1340} \quad\left(\bmod 1+x+x^{2}\right) \\
|
| 67 |
+
& \equiv 1 \quad\left(\bmod 1+x+x^{2}\right)
|
| 68 |
+
\end{aligned}
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Thus, the answer is 1 .
|
| 72 |
+
8. [7] Two circles with radius one are drawn in the coordinate plane, one with center $(0,1)$ and the other with center $(2, y)$, for some real number $y$ between 0 and 1 . A third circle is drawn so as to be tangent to both of the other two circles as well as the $x$ axis. What is the smallest possible radius for this third circle?
|
| 73 |
+
Answer: $3-2 \sqrt{2}$ Suppose that the smaller circle has radius $r$. Call the three circles (in order from left to right) $O_{1}, O_{2}$, and $O_{3}$. The distance between the centers of $O_{1}$ and $O_{2}$ is $1+r$, and the distance in their $y$-coordinates is $1-r$. Therefore, by the Pythagorean theorem, the difference in $x$-coordinates
|
| 74 |
+
is $\sqrt{(1+r)^{2}-(1-r)^{2}}=2 \sqrt{r}$, which means that $O_{2}$ has a center at $(2 \sqrt{r}, r)$. But $O_{2}$ is also tangent to $O_{3}$, which means that the difference in $x$-coordinate from the right-most point of $O_{2}$ to the center of $O_{3}$ is at most 1. Therefore, the center of $O_{3}$ has an $x$-coordinate of at most $2 \sqrt{r}+r+1$, meaning that $2 \sqrt{r}+r+1 \leq 2$. We can use the quadratic formula to see that this implies that $\sqrt{r} \leq \sqrt{2}-1$, so $r \leq 3-2 \sqrt{2}$. We can achieve equality by placing the center of $O_{3}$ at $(2, r)$ (which in this case is $(2,3-2 \sqrt{2}))$.
|
| 75 |
+
9. [7] What is the sum of all numbers between 0 and 511 inclusive that have an even number of 1 s when written in binary?
|
| 76 |
+
Answer: 65408 Call a digit in the binary representation of a number a bit. We claim that for any given $i$ between 0 and 8 , there are 128 numbers with an even number of 1 s that have a 1 in the bit representing $2^{i}$. To prove this, we simply make that bit a 1 , then consider all possible configurations of the other bits, excluding the last bit (or the second-last bit if our given bit is already the last bit). The last bit will then be restricted to satisfy the parity condition on the number of 1 s . As there are 128 possible configurations of all the bits but two, we find 128 possible numbers, proving our claim.
|
| 77 |
+
|
| 78 |
+
Therefore, each bit is present as a 1 in 128 numbers in the sum, so the bit representing $2^{i}$ contributes $128 \cdot 2^{i}$ to our sum. Summing over all $0 \leq i \leq 8$, we find the answer to be $128(1+2+\ldots+128)=$ $128 \cdot 511=65408$.
|
| 79 |
+
10. [8] You are given two diameters $A B$ and $C D$ of circle $\Omega$ with radius 1. A circle is drawn in one of the smaller sectors formed such that it is tangent to $A B$ at $E$, tangent to $C D$ at $F$, and tangent to $\Omega$ at $P$. Lines $P E$ and $P F$ intersect $\Omega$ again at $X$ and $Y$. What is the length of $X Y$, given that $A C=\frac{2}{3}$ ?
|
| 80 |
+
Answer: \( \frac{4\sqrt{2}}{3} \). Let \( O \) denote the center of circle \( \Omega \). We first prove that \( OX \perp AB \) and \( OY \perp CD \). Consider the homothety about $P$ which maps the smaller circle to $\Omega$. This homothety takes $E$ to $X$ and also takes $A B$ to the line tangent to circle $\Omega$ parallel to $A B$. Therefore, $X$ is the midpoint of the arc $A B$, and so $O X \perp A B$. Similarly, $O Y \perp C D$.
|
| 81 |
+
Let $\theta=\angle A O C$. By the Law of Sines, we have $A C=2 \sin \frac{\theta}{2}$. Thus, $\sin \frac{\theta}{2}=\frac{1}{3}$, and $\cos \frac{\theta}{2}=\sqrt{1-\left(\frac{1}{3}\right)^{2}}=$ $\frac{2 \sqrt{2}}{3}$. Therefore,
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\begin{aligned}
|
| 85 |
+
X Y & =2 \sin \frac{\angle X O Y}{2} \\
|
| 86 |
+
& =2 \sin \left(90^{\circ}-\frac{\theta}{2}\right) \\
|
| 87 |
+
& =2 \cos \frac{\theta}{2} \\
|
| 88 |
+
& =\frac{4 \sqrt{2}}{3}
|
| 89 |
+
\end{aligned}
|
| 90 |
+
$$
|
| 91 |
+
|