Remove USA_TST_TST dirctory
Browse files- USA_TST_TST/md/en-sols-TSTST-2011.md +0 -321
- USA_TST_TST/md/en-sols-TSTST-2012.md +0 -454
- USA_TST_TST/md/en-sols-TSTST-2013.md +0 -437
- USA_TST_TST/md/en-sols-TSTST-2014.md +0 -254
- USA_TST_TST/md/en-sols-TSTST-2015.md +0 -304
- USA_TST_TST/md/en-sols-TSTST-2016.md +0 -278
- USA_TST_TST/md/en-sols-TSTST-2017.md +0 -571
- USA_TST_TST/md/en-sols-TSTST-2018.md +0 -678
- USA_TST_TST/md/en-sols-TSTST-2019.md +0 -764
- USA_TST_TST/md/en-sols-TSTST-2020.md +0 -535
- USA_TST_TST/md/en-sols-TSTST-2021.md +0 -1228
- USA_TST_TST/md/en-sols-TSTST-2022.md +0 -618
- USA_TST_TST/md/en-sols-TSTST-2023.md +0 -1241
- USA_TST_TST/segment_script/segment_usamo.py +0 -320
- USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl +0 -9
- USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl +0 -13
- USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl +0 -9
- USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl +0 -6
- USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl +0 -9
- USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl +0 -8
- USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl +0 -13
- USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl +0 -14
- USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl +0 -15
- USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl +0 -10
- USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl +0 -28
- USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl +0 -12
- USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl +0 -22
USA_TST_TST/md/en-sols-TSTST-2011.md
DELETED
|
@@ -1,321 +0,0 @@
|
|
| 1 |
-
# TSTST 2011 Solution Notes <br> Lincoln, Nebraska <br> \author{ Evan Chen《陳誼廷》
|
| 2 |
-
|
| 3 |
-
}
|
| 4 |
-
|
| 5 |
-
15 April 2024
|
| 6 |
-
|
| 7 |
-
This is a compilation of solutions for the 2011 TSTST. The ideas of the solution are a mix of my own work, the solutions provided by the competition organizers, and solutions found by the community. However, all the writing is maintained by me.
|
| 8 |
-
|
| 9 |
-
These notes will tend to be a bit more advanced and terse than the "official" solutions from the organizers. In particular, if a theorem or technique is not known to beginners but is still considered "standard", then I often prefer to use this theory anyways, rather than try to work around or conceal it. For example, in geometry problems I typically use directed angles without further comment, rather than awkwardly work around configuration issues. Similarly, sentences like "let $\mathbb{R}$ denote the set of real numbers" are typically omitted entirely.
|
| 10 |
-
|
| 11 |
-
Corrections and comments are welcome!
|
| 12 |
-
|
| 13 |
-
## Contents
|
| 14 |
-
|
| 15 |
-
0 Problems ..... 2
|
| 16 |
-
1 Solutions to Day 1 ..... 3
|
| 17 |
-
1.1 TSTST 2011/1 ..... 3
|
| 18 |
-
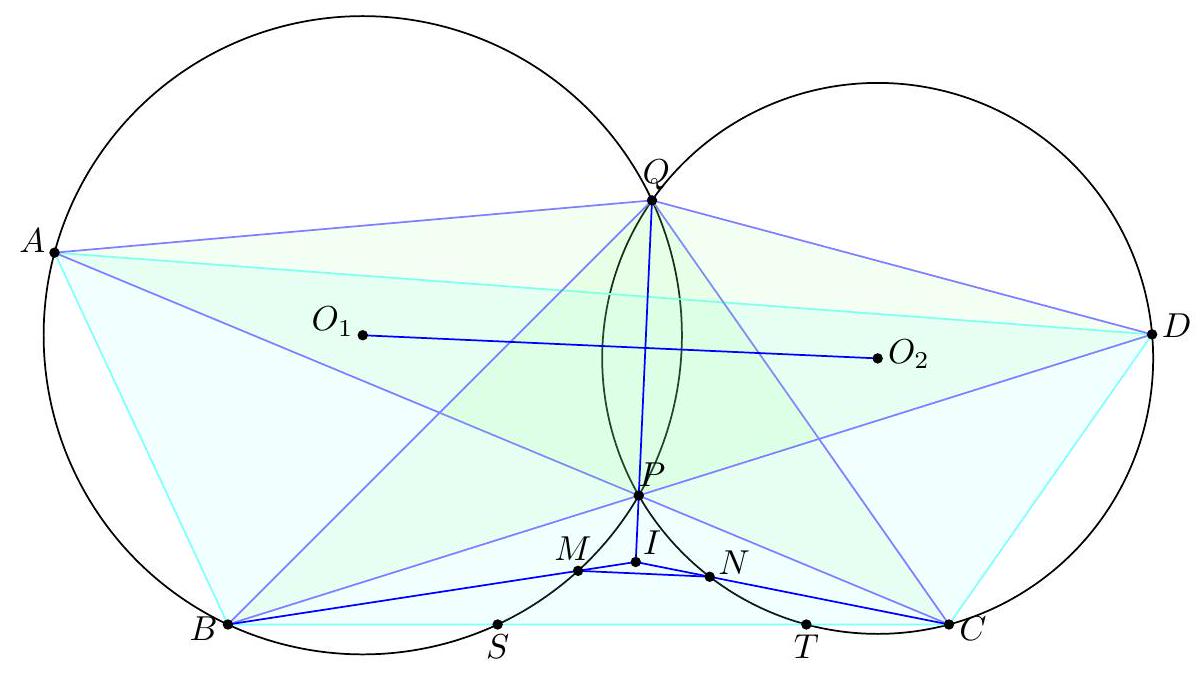
1.2 TSTST 2011/2 ..... 4
|
| 19 |
-
1.3 TSTST 2011/3 ..... 6
|
| 20 |
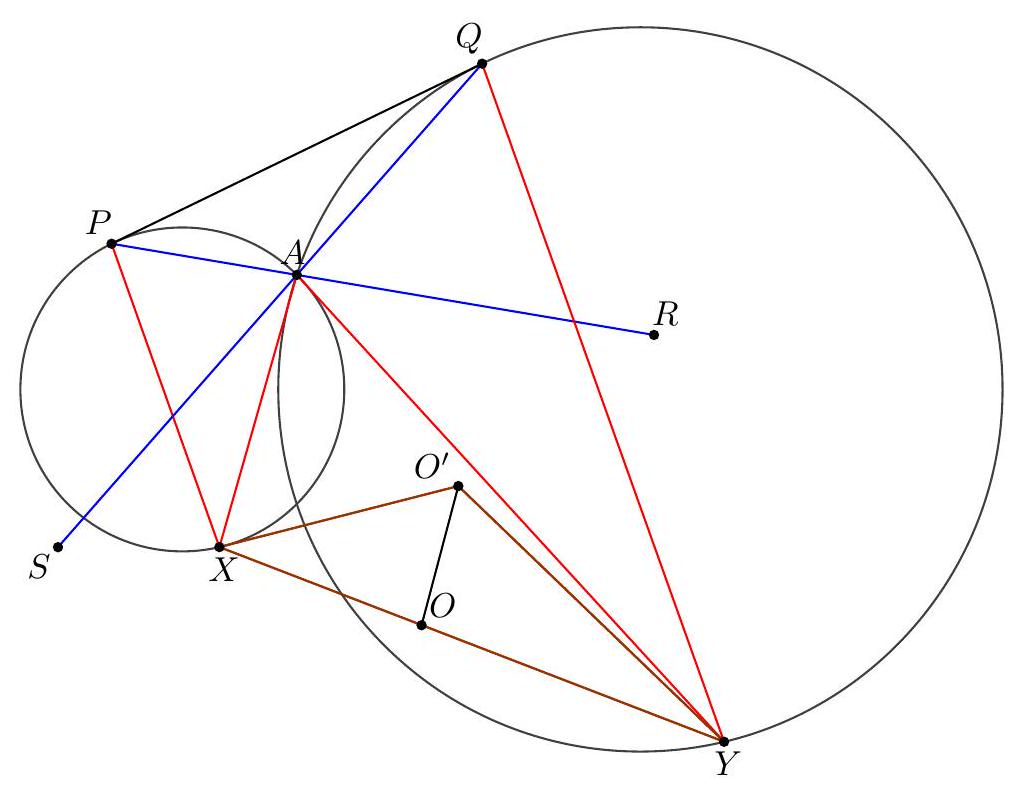
-
2 Solutions to Day 2 ..... 7
|
| 21 |
-
2.1 TSTST 2011/4 ..... 7
|
| 22 |
-
2.2 TSTST 2011/5 ..... 8
|
| 23 |
-
2.3 TSTST 2011/6 ..... 9
|
| 24 |
-
3 Solutions to Day 3 ..... 10
|
| 25 |
-
3.1 TSTST 2011/7 ..... 10
|
| 26 |
-
3.2 TSTST 2011/8 ..... 11
|
| 27 |
-
3.3 TSTST 2011/9 ..... 12
|
| 28 |
-
|
| 29 |
-
## §0 Problems
|
| 30 |
-
|
| 31 |
-
1. Find all real-valued functions $f$ defined on pairs of real numbers, having the following property: for all real numbers $a, b, c$, the median of $f(a, b), f(b, c), f(c, a)$ equals the median of $a, b, c$.
|
| 32 |
-
(The median of three real numbers, not necessarily distinct, is the number that is in the middle when the three numbers are arranged in nondecreasing order.)
|
| 33 |
-
2. Two circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Line $\ell$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$ so that $A$ is closer to $\ell$ than $B$. Let $X$ and $Y$ be points on major $\operatorname{arcs} \widehat{P A}\left(\right.$ on $\left.\omega_{1}\right)$ and $\overparen{A Q}$ (on $\left.\omega_{2}\right)$, respectively, such that $A X / P X=A Y / Q Y=c$. Extend segments $P A$ and $Q A$ through $A$ to $R$ and $S$, respectively, such that $A R=A S=c \cdot P Q$. Given that the circumcenter of triangle $A R S$ lies on line $X Y$, prove that $\angle X P A=\angle A Q Y$.
|
| 34 |
-
3. Prove that there exists a real constant $c$ such that for any pair $(x, y)$ of real numbers, there exist relatively prime integers $m$ and $n$ satisfying the relation
|
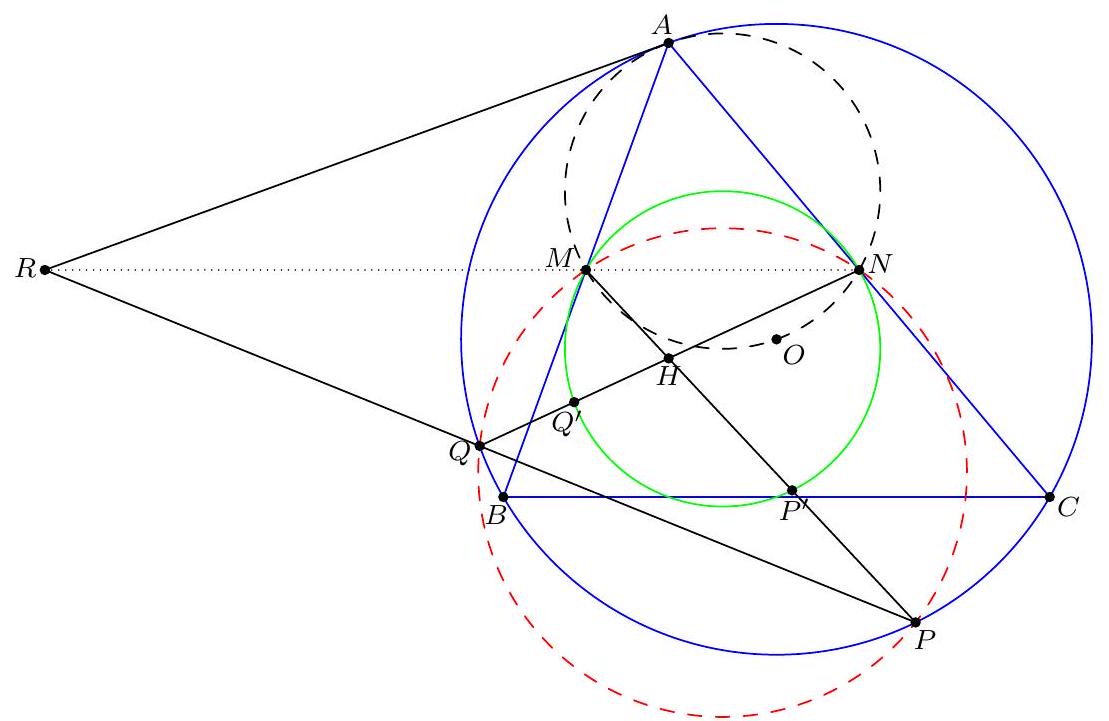
| 35 |
-
|
| 36 |
-
$$
|
| 37 |
-
\sqrt{(x-m)^{2}+(y-n)^{2}}<c \log \left(x^{2}+y^{2}+2\right) .
|
| 38 |
-
$$
|
| 39 |
-
|
| 40 |
-
4. Acute triangle $A B C$ is inscribed in circle $\omega$. Let $H$ and $O$ denote its orthocenter and circumcenter, respectively. Let $M$ and $N$ be the midpoints of sides $A B$ and $A C$, respectively. Rays $M H$ and $N H$ meet $\omega$ at $P$ and $Q$, respectively. Lines $M N$ and $P Q$ meet at $R$. Prove that $\overline{O A} \perp \overline{R A}$.
|
| 41 |
-
5. At a certain orphanage, every pair of orphans are either friends or enemies. For every three of an orphan's friends, an even number of pairs of them are enemies. Prove that it's possible to assign each orphan two parents such that every pair of friends shares exactly one parent, but no pair of enemies does, and no three parents are in a love triangle (where each pair of them has a child).
|
| 42 |
-
6. Let $a, b, c$ be real numbers in the interval $[0,1]$ with $a+b, b+c, c+a \geq 1$. Prove that
|
| 43 |
-
|
| 44 |
-
$$
|
| 45 |
-
1 \leq(1-a)^{2}+(1-b)^{2}+(1-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}}
|
| 46 |
-
$$
|
| 47 |
-
|
| 48 |
-
7. Let $A B C$ be a triangle. Its excircles touch sides $B C, C A, A B$ at $D, E, F$. Prove that the perimeter of triangle $A B C$ is at most twice that of triangle $D E F$.
|
| 49 |
-
8. Let $x_{0}, x_{1}, \ldots, x_{n_{0}-1}$ be integers, and let $d_{1}, d_{2}, \ldots, d_{k}$ be positive integers with $n_{0}=d_{1}>d_{2}>\cdots>d_{k}$ and $\operatorname{gcd}\left(d_{1}, d_{2}, \ldots, d_{k}\right)=1$. For every integer $n \geq n_{0}$, define
|
| 50 |
-
|
| 51 |
-
$$
|
| 52 |
-
x_{n}=\left\lfloor\frac{x_{n-d_{1}}+x_{n-d_{2}}+\cdots+x_{n-d_{k}}}{k}\right\rfloor .
|
| 53 |
-
$$
|
| 54 |
-
|
| 55 |
-
Show that the sequence $\left(x_{n}\right)$ is eventually constant.
|
| 56 |
-
9. Let $n$ be a positive integer. Suppose we are given $2^{n}+1$ distinct sets, each containing finitely many objects. Place each set into one of two categories, the red sets and the blue sets, so that there is at least one set in each category. We define the symmetric difference of two sets as the set of objects belonging to exactly one of the two sets. Prove that there are at least $2^{n}$ different sets which can be obtained as the symmetric difference of a red set and a blue set.
|
| 57 |
-
|
| 58 |
-
## §1 Solutions to Day 1
|
| 59 |
-
|
| 60 |
-
## §1.1 TSTST 2011/1
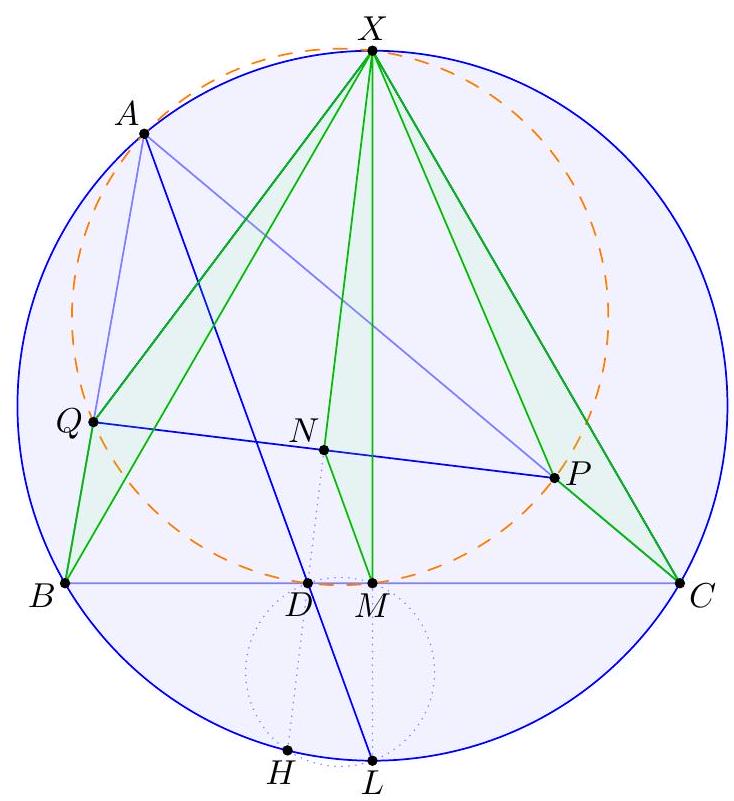
|
| 61 |
-
|
| 62 |
-
Available online at https://aops.com/community/p2374841.
|
| 63 |
-
|
| 64 |
-
## Problem statement
|
| 65 |
-
|
| 66 |
-
Find all real-valued functions $f$ defined on pairs of real numbers, having the following property: for all real numbers $a, b, c$, the median of $f(a, b), f(b, c), f(c, a)$ equals the median of $a, b, c$.
|
| 67 |
-
(The median of three real numbers, not necessarily distinct, is the number that is in the middle when the three numbers are arranged in nondecreasing order.)
|
| 68 |
-
|
| 69 |
-
The following solution is joint with Andrew He.
|
| 70 |
-
We prove the following main claim, from which repeated applications can deduce the problem.
|
| 71 |
-
|
| 72 |
-
Claim - Let $a<b<c$ be arbitrary. On $\{a, b, c\}^{2}, f$ takes one of the following two forms, where the column indicates the $x$-value and the row indicates the $y$-value.
|
| 73 |
-
|
| 74 |
-
| $f$ | $a$ | $b$ | $c$ |
|
| 75 |
-
| ---: | ---: | ---: | ---: |
|
| 76 |
-
| $a$ | $a$ | $b$ | $\geq c$ |
|
| 77 |
-
| $b$ | $\leq a$ | $b$ | $\geq c$ |
|
| 78 |
-
| $c$ | $\leq a$ | $b$ | $c$ |
|
| 79 |
-
|
| 80 |
-
or
|
| 81 |
-
|
| 82 |
-
| $f$ | $a$ | $b$ | $c$ |
|
| 83 |
-
| ---: | ---: | ---: | ---: |
|
| 84 |
-
| $a$ | $a$ | $\leq a$ | $\leq a$ |
|
| 85 |
-
| $b$ | $b$ | $b$ | $b$ |
|
| 86 |
-
| $c$ | $\geq c$ | $\geq c$ | $c$ |
|
| 87 |
-
|
| 88 |
-
Proof. First, we of course have $f(x, x)=x$ for all $x$. Now:
|
| 89 |
-
|
| 90 |
-
- By considering the assertion for $(a, a, c)$ and $(a, c, c)$ we see that one of $f(a, c)$ and $f(c, a)$ is $\geq c$ and the other is $\leq a$.
|
| 91 |
-
- Hence, by considering $(a, b, c)$ we find that one of $f(a, b)$ and $f(b, c)$ must be $b$, and similarly for $f(b, a)$ and $f(c, b)$.
|
| 92 |
-
- Now, WLOG $f(b, a)=b$; we prove we get the first case.
|
| 93 |
-
- By considering $(a, a, b)$ we deduce $f(a, b) \leq a$, so $f(b, c)=b$ and then $f(c, b) \geq c$.
|
| 94 |
-
- Finally, considering $(c, b, a)$ once again in conjunction with the first bullet, we arrive at the conclusion that $f(a, c) \leq a$; similarly $f(c, a) \geq c$.
|
| 95 |
-
|
| 96 |
-
From this it's easy to obtain that $f(x, y) \equiv x$ or $f(x, y) \equiv y$ are the only solutions.
|
| 97 |
-
|
| 98 |
-
## §1.2 TSTST 2011/2
|
| 99 |
-
|
| 100 |
-
Available online at https://aops.com/community/p2374843.
|
| 101 |
-
|
| 102 |
-
## Problem statement
|
| 103 |
-
|
| 104 |
-
Two circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Line $\ell$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$ so that $A$ is closer to $\ell$ than $B$. Let $X$ and $Y$ be points on major $\operatorname{arcs} \widehat{P A}\left(\right.$ on $\left.\omega_{1}\right)$ and $\widehat{A Q}\left(\right.$ on $\left.\omega_{2}\right)$, respectively, such that $A X / P X=A Y / Q Y=c$. Extend segments $P A$ and $Q A$ through $A$ to $R$ and $S$, respectively, such that $A R=A S=c \cdot P Q$. Given that the circumcenter of triangle $A R S$ lies on line $X Y$, prove that $\angle X P A=\angle A Q Y$.
|
| 105 |
-
|
| 106 |
-
We begin as follows:
|
| 107 |
-
Claim - There is a spiral similarity centered at $X$ mapping $A R$ to $P Q$. Similarly there is a spiral similarity centered at $Y$ mapping $S A$ to $P Q$.
|
| 108 |
-
|
| 109 |
-
Proof. Since $\measuredangle X A R=\measuredangle X A P=\measuredangle X P Q$, and $A R / A X=P Q / P X$ is given.
|
| 110 |
-
Now the composition of the two spiral similarities
|
| 111 |
-
|
| 112 |
-
$$
|
| 113 |
-
A R \stackrel{X}{\mapsto} P Q \stackrel{Y}{\mapsto} S A
|
| 114 |
-
$$
|
| 115 |
-
|
| 116 |
-
must be a rotation, since $A R=A S$. The center of this rotation must coincide with the circumcenter $O$ of $\triangle A R S$, which is known to lie on line $X Y$.
|
| 117 |
-
|
| 118 |
-
|
| 119 |
-
As $O$ is a fixed-point of the composed map above, we may let $O^{\prime}$ be the image of $O$ under the rotation at $X$, so that
|
| 120 |
-
|
| 121 |
-
$$
|
| 122 |
-
\triangle X P A \AA \triangle X O^{\prime} O, \quad \triangle Y Q A \AA \triangle Y O^{\prime} O .
|
| 123 |
-
$$
|
| 124 |
-
|
| 125 |
-
Because
|
| 126 |
-
|
| 127 |
-
$$
|
| 128 |
-
\frac{X O}{X O^{\prime}}=\frac{X A}{X P}=c \frac{Y Q}{Y A}=\frac{Y O}{Y O^{\prime}}
|
| 129 |
-
$$
|
| 130 |
-
|
| 131 |
-
it follows $\overline{O^{\prime} O}$ bisects $\angle X O^{\prime} Y$. Finally, we have
|
| 132 |
-
|
| 133 |
-
$$
|
| 134 |
-
\measuredangle X P A=\measuredangle X O^{\prime} O=\measuredangle O O^{\prime} Y=\measuredangle A Q Y
|
| 135 |
-
$$
|
| 136 |
-
|
| 137 |
-
Remark. Indeed, this also shows $\overline{X P} \| \overline{Y Q}$; so the positive homothety from $\omega_{1}$ to $\omega_{2}$ maps $P$ to $Q$ and $X$ to $Y$.
|
| 138 |
-
|
| 139 |
-
## §1.3 TSTST 2011/3
|
| 140 |
-
|
| 141 |
-
Available online at https://aops.com/community/p2374845.
|
| 142 |
-
|
| 143 |
-
## Problem statement
|
| 144 |
-
|
| 145 |
-
Prove that there exists a real constant $c$ such that for any pair $(x, y)$ of real numbers, there exist relatively prime integers $m$ and $n$ satisfying the relation
|
| 146 |
-
|
| 147 |
-
$$
|
| 148 |
-
\sqrt{(x-m)^{2}+(y-n)^{2}}<c \log \left(x^{2}+y^{2}+2\right)
|
| 149 |
-
$$
|
| 150 |
-
|
| 151 |
-
This is actually the same problem as USAMO 2014/6. Surprise!
|
| 152 |
-
|
| 153 |
-
## §2 Solutions to Day 2
|
| 154 |
-
|
| 155 |
-
## §2.1 TSTST 2011/4
|
| 156 |
-
|
| 157 |
-
Available online at https://aops.com/community/p2374848.
|
| 158 |
-
|
| 159 |
-
## Problem statement
|
| 160 |
-
|
| 161 |
-
Acute triangle $A B C$ is inscribed in circle $\omega$. Let $H$ and $O$ denote its orthocenter and circumcenter, respectively. Let $M$ and $N$ be the midpoints of sides $A B$ and $A C$, respectively. Rays $M H$ and $N H$ meet $\omega$ at $P$ and $Q$, respectively. Lines $M N$ and $P Q$ meet at $R$. Prove that $\overline{O A} \perp \overline{R A}$.
|
| 162 |
-
|
| 163 |
-
Let $M H$ and $N H$ meet the nine-point circle again at $P^{\prime}$ and $Q^{\prime}$, respectively. Recall that $H$ is the center of the homothety between the circumcircle and the nine-point circle. From this we can see that $P$ and $Q$ are the images of this homothety, meaning that
|
| 164 |
-
|
| 165 |
-
$$
|
| 166 |
-
H Q=2 H Q^{\prime} \quad \text { and } \quad H P=2 H P^{\prime}
|
| 167 |
-
$$
|
| 168 |
-
|
| 169 |
-
Since $M, P^{\prime}, Q^{\prime}, N$ are cyclic, Power of a Point gives us
|
| 170 |
-
|
| 171 |
-
$$
|
| 172 |
-
M H \cdot H P^{\prime}=H N \cdot H Q^{\prime}
|
| 173 |
-
$$
|
| 174 |
-
|
| 175 |
-
Multiplying both sides by two, we thus derive
|
| 176 |
-
|
| 177 |
-
$$
|
| 178 |
-
H M \cdot H P=H N \cdot H Q
|
| 179 |
-
$$
|
| 180 |
-
|
| 181 |
-
It follows that the points $M, N, P, Q$ are concyclic.
|
| 182 |
-
|
| 183 |
-
|
| 184 |
-
Let $\omega_{1}, \omega_{2}, \omega_{3}$ denote the circumcircles of $M N P Q, A M N$, and $A B C$, respectively. The radical axis of $\omega_{1}$ and $\omega_{2}$ is line $M N$, while the radical axis of $\omega_{1}$ and $\omega_{3}$ is line $P Q$. Hence the line $R$ lies on the radical axis of $\omega_{2}$ and $\omega_{3}$.
|
| 185 |
-
|
| 186 |
-
But we claim that $\omega_{2}$ and $\omega_{3}$ are internally tangent at $A$. This follows by noting the homothety at $A$ with ratio 2 sends $M$ to $B$ and $N$ to $C$. Hence the radical axis of $\omega_{2}$ and $\omega_{3}$ is a line tangent to both circles at $A$.
|
| 187 |
-
|
| 188 |
-
Hence $\overline{R A}$ is tangent to $\omega_{3}$. Therefore, $\overline{R A} \perp \overline{O A}$.
|
| 189 |
-
|
| 190 |
-
## §2.2 TSTST 2011/5
|
| 191 |
-
|
| 192 |
-
Available online at https://aops.com/community/p2374849.
|
| 193 |
-
|
| 194 |
-
## Problem statement
|
| 195 |
-
|
| 196 |
-
At a certain orphanage, every pair of orphans are either friends or enemies. For every three of an orphan's friends, an even number of pairs of them are enemies. Prove that it's possible to assign each orphan two parents such that every pair of friends shares exactly one parent, but no pair of enemies does, and no three parents are in a love triangle (where each pair of them has a child).
|
| 197 |
-
|
| 198 |
-
Of course, we consider the graph with vertices as children and edges as friendships. Consider all the maximal cliques in the graph (i.e. repeatedly remove maximal cliques until no edges remain; thus all edges are in some clique).
|
| 199 |
-
|
| 200 |
-
Claim - Every vertex is in at most two maximal cliques.
|
| 201 |
-
Proof. Indeed, consider a vertex $v$ adjacent to $w_{1}$ and $w_{2}$, but with $w_{1}$ not adjacent to $w_{2}$. Then by condition, any third vertex $u$ must be adjacent to exactly one of $w_{1}$ and $w_{2}$. Moreover, given vertices $u$ and $u^{\prime}$ adjacent to $w_{1}$, vertices $u$ and $u^{\prime}$ are adjacent too. This proves the claim.
|
| 202 |
-
|
| 203 |
-
Now, for every maximal clique we assign a particular parent to all vertices in that clique, adding in additional distinct parents if there are any deficient children. This satisfies the friendship/enemy condition. Moreover, one can readily check that there are no love triangles: given children $a, b, c$ such that $a$ and $b$ share a parent while $a$ and $c$ share another parent, according to the claim $b$ and $c$ can't share a third parent. This completes the problem.
|
| 204 |
-
|
| 205 |
-
Remark. This solution is highly motivated for the following reason: by experimenting with small cases, one quickly finds that given some vertices which form a clique, one must assign some particular parent to all vertices in that clique. That is, the requirements of the problem are sufficiently rigid that there is no room for freedom on our part, so we know a priori that an assignment based on cliques (as above) must work. From there we know exactly what to prove, and everything else follows through.
|
| 206 |
-
|
| 207 |
-
Ironically, the condition that there be no love triangle actually makes the problem easier, because it tells us exactly what to do!
|
| 208 |
-
|
| 209 |
-
## §2.3 TSTST 2011/6
|
| 210 |
-
|
| 211 |
-
Available online at https://aops.com/community/p2374852.
|
| 212 |
-
|
| 213 |
-
## Problem statement
|
| 214 |
-
|
| 215 |
-
Let $a, b, c$ be real numbers in the interval $[0,1]$ with $a+b, b+c, c+a \geq 1$. Prove that
|
| 216 |
-
|
| 217 |
-
$$
|
| 218 |
-
1 \leq(1-a)^{2}+(1-b)^{2}+(1-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}}
|
| 219 |
-
$$
|
| 220 |
-
|
| 221 |
-
The following approach is due to Ashwin Sah.
|
| 222 |
-
We will prove the inequality for any $a, b, c$ the sides of a possibly degenerate triangle (which is implied by the condition), ignoring the particular constant 1. Homogenizing, we instead prove the problem in the following form:
|
| 223 |
-
|
| 224 |
-
Claim - We have
|
| 225 |
-
|
| 226 |
-
$$
|
| 227 |
-
k^{2} \leq(k-a)^{2}+(k-b)^{2}+(k-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}}
|
| 228 |
-
$$
|
| 229 |
-
|
| 230 |
-
for any $a, b, c, k$ with $(a, b, c)$ the sides of a possibly degenerate triangle.
|
| 231 |
-
Proof. For any particular $(a, b, c)$ this is a quadratic in $k$ of the form $2 k^{2}-2(a+b+c) k+$ $C \geq 0$; thus we will verify it holds for $k=\frac{1}{2}(a+b+c)$.
|
| 232 |
-
|
| 233 |
-
Letting $x=\frac{1}{2}(b+c-a)$ as is usual, the problem rearranges to In that case, the problem amounts to
|
| 234 |
-
|
| 235 |
-
$$
|
| 236 |
-
(x+y+z)^{2} \leq x^{2}+y^{2}+z^{2}+\frac{2(x+y)(y+z)(z+x)}{\sqrt{x^{2}+y^{2}+z^{2}+x y+y z+z x}}
|
| 237 |
-
$$
|
| 238 |
-
|
| 239 |
-
or equivalently
|
| 240 |
-
|
| 241 |
-
$$
|
| 242 |
-
x^{2}+y^{2}+z^{2}+x y+y z+z x \leq\left(\frac{(x+y)(y+z)(z+x)}{x y+y z+z x}\right)^{2} .
|
| 243 |
-
$$
|
| 244 |
-
|
| 245 |
-
To show this, one may let $t=x y+y z+z x$, then using $(x+y)(x+z)=x^{2}+B$ this becomes
|
| 246 |
-
|
| 247 |
-
$$
|
| 248 |
-
t^{2}\left(x^{2}+y^{2}+z^{2}+t\right) \leq\left(x^{2}+t\right)\left(y^{2}+t\right)\left(z^{2}+t\right)
|
| 249 |
-
$$
|
| 250 |
-
|
| 251 |
-
which is obvious upon expansion.
|
| 252 |
-
Remark. The inequality holds actually for all real numbers $a, b$, $c$, with very disgusting proofs.
|
| 253 |
-
|
| 254 |
-
## §3 Solutions to Day 3
|
| 255 |
-
|
| 256 |
-
## §3.1 TSTST 2011/7
|
| 257 |
-
|
| 258 |
-
Available online at https://aops.com/community/p2374855.
|
| 259 |
-
|
| 260 |
-
## Problem statement
|
| 261 |
-
|
| 262 |
-
Let $A B C$ be a triangle. Its excircles touch sides $B C, C A, A B$ at $D, E, F$. Prove that the perimeter of triangle $A B C$ is at most twice that of triangle $D E F$.
|
| 263 |
-
|
| 264 |
-
Solution by August Chen: It turns out that it is enough to take the orthogonal projection of $E F$ onto side $B C$ (which has length $a-(s-a)(\cos B+\cos C)$ ) and sum cyclically:
|
| 265 |
-
|
| 266 |
-
$$
|
| 267 |
-
\begin{aligned}
|
| 268 |
-
-s+\sum_{\mathrm{cyc}} E F & \geq-s+\sum_{\mathrm{cyc}}[a-(s-a)(\cos B+\cos C)] \\
|
| 269 |
-
& =s-\sum_{\mathrm{cyc}} a \cos A=\sum_{\mathrm{cyc}} a\left(\frac{1}{2}-\cos A\right) \\
|
| 270 |
-
& =R \sum_{\mathrm{cyc}} \sin A(1-2 \cos A) \\
|
| 271 |
-
& =R \sum_{\mathrm{cyc}}(\sin A-\sin 2 A)
|
| 272 |
-
\end{aligned}
|
| 273 |
-
$$
|
| 274 |
-
|
| 275 |
-
Thus we're done upon noting that
|
| 276 |
-
|
| 277 |
-
$$
|
| 278 |
-
\frac{\sin 2 B+\sin 2 C}{2}=\sin (B+C) \cos (B-C)=\sin A \cos (B-C) \leq \sin A
|
| 279 |
-
$$
|
| 280 |
-
|
| 281 |
-
(Alternatively, one can avoid trigonometry by substituting $\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$ and doing some routine but long calculation.)
|
| 282 |
-
|
| 283 |
-
## §3.2 TSTST 2011/8
|
| 284 |
-
|
| 285 |
-
Available online at https://aops.com/community/p2374856.
|
| 286 |
-
|
| 287 |
-
## Problem statement
|
| 288 |
-
|
| 289 |
-
Let $x_{0}, x_{1}, \ldots, x_{n_{0}-1}$ be integers, and let $d_{1}, d_{2}, \ldots, d_{k}$ be positive integers with $n_{0}=d_{1}>d_{2}>\cdots>d_{k}$ and $\operatorname{gcd}\left(d_{1}, d_{2}, \ldots, d_{k}\right)=1$. For every integer $n \geq n_{0}$, define
|
| 290 |
-
|
| 291 |
-
$$
|
| 292 |
-
x_{n}=\left\lfloor\frac{x_{n-d_{1}}+x_{n-d_{2}}+\cdots+x_{n-d_{k}}}{k}\right\rfloor
|
| 293 |
-
$$
|
| 294 |
-
|
| 295 |
-
Show that the sequence $\left(x_{n}\right)$ is eventually constant.
|
| 296 |
-
|
| 297 |
-
Note that if the initial terms are contained in some interval $[A, B]$ then they will remain in that interval. Thus the sequence is eventually periodic. Discard initial terms and let the period be $T$; we will consider all indices modulo $T$ from now on.
|
| 298 |
-
|
| 299 |
-
Let $M$ be the maximal term in the sequence (which makes sense since the sequence is periodic). Note that if $x_{n}=M$, we must have $x_{n-d_{i}}=M$ for all $i$ as well. By taking a linear combination $\sum c_{i} d_{i} \equiv 1(\bmod T)($ possibly be Bezout's theorem, since $\operatorname{gcd}_{i}\left(d_{i}\right)=1$ ), we conclude $x_{n-1}=M$, as desired.
|
| 300 |
-
|
| 301 |
-
## §3.3 TSTST 2011/9
|
| 302 |
-
|
| 303 |
-
Available online at https://aops.com/community/p2374857.
|
| 304 |
-
|
| 305 |
-
## Problem statement
|
| 306 |
-
|
| 307 |
-
Let $n$ be a positive integer. Suppose we are given $2^{n}+1$ distinct sets, each containing finitely many objects. Place each set into one of two categories, the red sets and the blue sets, so that there is at least one set in each category. We define the symmetric difference of two sets as the set of objects belonging to exactly one of the two sets. Prove that there are at least $2^{n}$ different sets which can be obtained as the symmetric difference of a red set and a blue set.
|
| 308 |
-
|
| 309 |
-
We can interpret the problem as working with binary strings of length $\ell \geq n+1$, with $\ell$ the number of elements across all sets.
|
| 310 |
-
|
| 311 |
-
Let $F$ be a field of cardinality $2^{\ell}$, hence $F \cong \mathbb{F}_{2}^{\oplus \ell}$.
|
| 312 |
-
Then, we can think of red/blue as elements of $F$, so we have some $B \subseteq F$, and an $R \subseteq F$. We wish to prove that $|B+R| \geq 2^{n}$. Want $|B+R| \geq 2^{n}$.
|
| 313 |
-
|
| 314 |
-
Equivalently, any element of a set $X$ with $|X|=2^{n}-1$ should omit some element of $|B+R|$. To prove this: we know $|B|+|R|=2^{n}+1$, and define
|
| 315 |
-
|
| 316 |
-
$$
|
| 317 |
-
P(b, r)=\prod_{x \in X}(b+r-x)
|
| 318 |
-
$$
|
| 319 |
-
|
| 320 |
-
Consider $b^{|B|-1} r^{|R|-1}$. The coefficient of is $\binom{2^{n}-1}{|B|-1}$, which is odd (say by Lucas theorem), so the nullstellensatz applies.
|
| 321 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2012.md
DELETED
|
@@ -1,454 +0,0 @@
|
|
| 1 |
-
# TSTST 2012 Solution Notes <br> Lincoln, Nebraska <br> \author{ Evan Chen《陳誼廷》
|
| 2 |
-
|
| 3 |
-
}
|
| 4 |
-
|
| 5 |
-
15 April 2024
|
| 6 |
-
|
| 7 |
-
This is a compilation of solutions for the 2012 TSTST. The ideas of the solution are a mix of my own work, the solutions provided by the competition organizers, and solutions found by the community. However, all the writing is maintained by me.
|
| 8 |
-
|
| 9 |
-
These notes will tend to be a bit more advanced and terse than the "official" solutions from the organizers. In particular, if a theorem or technique is not known to beginners but is still considered "standard", then I often prefer to use this theory anyways, rather than try to work around or conceal it. For example, in geometry problems I typically use directed angles without further comment, rather than awkwardly work around configuration issues. Similarly, sentences like "let $\mathbb{R}$ denote the set of real numbers" are typically omitted entirely.
|
| 10 |
-
|
| 11 |
-
Corrections and comments are welcome!
|
| 12 |
-
|
| 13 |
-
## Contents
|
| 14 |
-
|
| 15 |
-
0 Problems ..... 2
|
| 16 |
-
1 Solutions to Day 1 ..... 4
|
| 17 |
-
1.1 TSTST 2012/1, proposed by Palmer Mebane ..... 4
|
| 18 |
-
1.2 TSTST 2012/2 ..... 5
|
| 19 |
-
1.3 TSTST 2012/3 ..... 6
|
| 20 |
-
2 Solutions to Day 2 ..... 8
|
| 21 |
-
2.1 TSTST 2012/4 ..... 8
|
| 22 |
-
2.2 TSTST 2012/5 ..... 9
|
| 23 |
-
2.3 TSTST 2012/6, proposed by Sung-Yoon Kim ..... 10
|
| 24 |
-
3 Solutions to Day 3 ..... 11
|
| 25 |
-
3.1 TSTST 2012/7 ..... 11
|
| 26 |
-
3.2 TSTST 2012/8, proposed by Palmer Mebane ..... 13
|
| 27 |
-
3.3 TSTST 2012/9, proposed by John Berman ..... 15
|
| 28 |
-
|
| 29 |
-
## §0 Problems
|
| 30 |
-
|
| 31 |
-
1. Determine all infinite strings of letters with the following properties:
|
| 32 |
-
(a) Each letter is either $T$ or $S$,
|
| 33 |
-
(b) If position $i$ and $j$ both have the letter $T$, then position $i+j$ has the letter $S$,
|
| 34 |
-
(c) There are infinitely many integers $k$ such that position $2 k-1$ has the $k$ th $T$.
|
| 35 |
-
2. Let $A B C D$ be a quadrilateral with $A C=B D$. Diagonals $A C$ and $B D$ meet at $P$. Let $\omega_{1}$ and $O_{1}$ denote the circumcircle and circumcenter of triangle $A B P$. Let $\omega_{2}$ and $O_{2}$ denote the circumcircle and circumcenter of triangle $C D P$. Segment $B C$ meets $\omega_{1}$ and $\omega_{2}$ again at $S$ and $T$ (other than $B$ and $C$ ), respectively. Let $M$ and $N$ be the midpoints of minor arcs $\widehat{S P}$ (not including $B$ ) and $\overparen{T P}$ (not including $C$ ). Prove that $\overline{M N} \| \overline{O_{1} O_{2}}$.
|
| 36 |
-
3. Let $\mathbb{N}$ be the set of positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function satisfying the following two conditions:
|
| 37 |
-
(a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime.
|
| 38 |
-
(b) $n \leq f(n) \leq n+2012$ for all $n$.
|
| 39 |
-
|
| 40 |
-
Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.
|
| 41 |
-
4. In scalene triangle $A B C$, let the feet of the perpendiculars from $A$ to $\overline{B C}, B$ to $\overline{C A}$, $C$ to $\overline{A B}$ be $A_{1}, B_{1}, C_{1}$, respectively. Denote by $A_{2}$ the intersection of lines $B C$ and $B_{1} C_{1}$. Define $B_{2}$ and $C_{2}$ analogously. Let $D, E, F$ be the respective midpoints of sides $\overline{B C}, \overline{C A}, \overline{A B}$. Show that the perpendiculars from $D$ to $\overline{A A_{2}}, E$ to $\overline{B B_{2}}$ and $F$ to $\overline{C C_{2}}$ are concurrent.
|
| 42 |
-
5. A rational number $x$ is given. Prove that there exists a sequence $x_{0}, x_{1}, x_{2}, \ldots$ of rational numbers with the following properties:
|
| 43 |
-
(a) $x_{0}=x$;
|
| 44 |
-
(b) for every $n \geq 1$, either $x_{n}=2 x_{n-1}$ or $x_{n}=2 x_{n-1}+\frac{1}{n}$;
|
| 45 |
-
(c) $x_{n}$ is an integer for some $n$.
|
| 46 |
-
6. Positive real numbers $x, y, z$ satisfy $x y z+x y+y z+z x=x+y+z+1$. Prove that
|
| 47 |
-
|
| 48 |
-
$$
|
| 49 |
-
\frac{1}{3}\left(\sqrt{\frac{1+x^{2}}{1+x}}+\sqrt{\frac{1+y^{2}}{1+y}}+\sqrt{\frac{1+z^{2}}{1+z}}\right) \leq\left(\frac{x+y+z}{3}\right)^{5 / 8} .
|
| 50 |
-
$$
|
| 51 |
-
|
| 52 |
-
7. Triangle $A B C$ is inscribed in circle $\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.
|
| 53 |
-
8. Let $n$ be a positive integer. Consider a triangular array of nonnegative integers as follows:
|
| 54 |
-

|
| 55 |
-
|
| 56 |
-
Call such a triangular array stable if for every $0 \leq i<j<k \leq n$ we have
|
| 57 |
-
|
| 58 |
-
$$
|
| 59 |
-
a_{i, j}+a_{j, k} \leq a_{i, k} \leq a_{i, j}+a_{j, k}+1
|
| 60 |
-
$$
|
| 61 |
-
|
| 62 |
-
For $s_{1}, \ldots, s_{n}$ any nondecreasing sequence of nonnegative integers, prove that there exists a unique stable triangular array such that the sum of all of the entries in row $k$ is equal to $s_{k}$.
|
| 63 |
-
9. Given a set $S$ of $n$ variables, a binary operation $\times$ on $S$ is called simple if it satisfies $(x \times y) \times z=x \times(y \times z)$ for all $x, y, z \in S$ and $x \times y \in\{x, y\}$ for all $x, y \in S$. Given a simple operation $\times$ on $S$, any string of elements in $S$ can be reduced to a single element, such as $x y z \rightarrow x \times(y \times z)$. A string of variables in $S$ is called full if it contains each variable in $S$ at least once, and two strings are equivalent if they evaluate to the same variable regardless of which simple $\times$ is chosen. For example $x x x, x x$, and $x$ are equivalent, but these are only full if $n=1$. Suppose $T$ is a set of full strings such that any full string is equivalent to exactly one element of $T$. Determine the number of elements of $T$.
|
| 64 |
-
|
| 65 |
-
## §1 Solutions to Day 1
|
| 66 |
-
|
| 67 |
-
## §1.1 TSTST 2012/1, proposed by Palmer Mebane
|
| 68 |
-
|
| 69 |
-
Available online at https://aops.com/community/p2745864.
|
| 70 |
-
|
| 71 |
-
## Problem statement
|
| 72 |
-
|
| 73 |
-
Determine all infinite strings of letters with the following properties:
|
| 74 |
-
(a) Each letter is either $T$ or $S$,
|
| 75 |
-
(b) If position $i$ and $j$ both have the letter $T$, then position $i+j$ has the letter $S$,
|
| 76 |
-
(c) There are infinitely many integers $k$ such that position $2 k-1$ has the $k$ th $T$.
|
| 77 |
-
|
| 78 |
-
We wish to find all infinite sequences $a_{1}, a_{2}, \ldots$ of positive integers satisfying the following properties:
|
| 79 |
-
(a) $a_{1}<a_{2}<a_{3}<\cdots$,
|
| 80 |
-
(b) there are no positive integers $i, j, k$, not necessarily distinct, such that $a_{i}+a_{j}=a_{k}$,
|
| 81 |
-
(c) there are infinitely many $k$ such that $a_{k}=2 k-1$.
|
| 82 |
-
|
| 83 |
-
If $a_{k}=2 k-1$ for some $k>1$, let $A_{k}=\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$. By (b) and symmetry, we have
|
| 84 |
-
|
| 85 |
-
$$
|
| 86 |
-
2 k-1 \geq \frac{\left|A_{k}-A_{k}\right|-1}{2}+\left|A_{k}\right| \geq \frac{2\left|A_{k}\right|-2}{2}+\left|A_{k}\right|=2 k-1 .
|
| 87 |
-
$$
|
| 88 |
-
|
| 89 |
-
But in order for $\left|A_{k}-A_{k}\right|=2\left|A_{k}\right|-1$, we must have $A_{k}$ an arithmetic progression, whence $a_{n}=2 n-1$ for all $n$ by taking $k$ arbitrarily large.
|
| 90 |
-
|
| 91 |
-
## §1.2 TSTST 2012/2
|
| 92 |
-
|
| 93 |
-
Available online at https://aops.com/community/p2745851.
|
| 94 |
-
|
| 95 |
-
## Problem statement
|
| 96 |
-
|
| 97 |
-
Let $A B C D$ be a quadrilateral with $A C=B D$. Diagonals $A C$ and $B D$ meet at $P$. Let $\omega_{1}$ and $O_{1}$ denote the circumcircle and circumcenter of triangle $A B P$. Let $\omega_{2}$ and $O_{2}$ denote the circumcircle and circumcenter of triangle $C D P$. Segment $B C$ meets $\omega_{1}$ and $\omega_{2}$ again at $S$ and $T$ (other than $B$ and $C$ ), respectively. Let $M$ and $N$ be the midpoints of minor arcs $\widehat{S P}$ (not including $B$ ) and $\widehat{T P}$ (not including $C$ ). Prove that $\overline{M N} \| \overline{O_{1} O_{2}}$.
|
| 98 |
-
|
| 99 |
-
Let $Q$ be the second intersection point of $\omega_{1}, \omega_{2}$. Suffice to show $\overline{Q P} \perp \overline{M N}$. Now $Q$ is the center of a spiral congruence which sends $\overline{A C} \mapsto \overline{B D}$. So $\triangle Q A B$ and $\triangle Q C D$ are similar isosceles. Now,
|
| 100 |
-
|
| 101 |
-
$$
|
| 102 |
-
\measuredangle Q P A=\measuredangle Q B A=\measuredangle D C Q=\measuredangle D P Q
|
| 103 |
-
$$
|
| 104 |
-
|
| 105 |
-
and so $\overline{Q P}$ is bisects $\angle B P C$.
|
| 106 |
-
|
| 107 |
-
|
| 108 |
-
Now, let $I=\overline{B M} \cap \overline{C N} \cap \overline{P Q}$ be the incenter of $\triangle P B C$. Then $I M \cdot I B=I P \cdot I Q=$ $I N \cdot I C$, so $B M N C$ is cyclic, meaning $\overline{M N}$ is antiparallel to $\overline{B C}$ through $\angle B I C$. Since $\overline{Q P I}$ passes through the circumcenter of $\triangle B I C$, it follows now $\overline{Q P I} \perp \overline{M N}$ as desired.
|
| 109 |
-
|
| 110 |
-
## §1.3 TSTST 2012/3
|
| 111 |
-
|
| 112 |
-
Available online at https://aops.com/community/p2745877.
|
| 113 |
-
|
| 114 |
-
## Problem statement
|
| 115 |
-
|
| 116 |
-
Let $\mathbb{N}$ be the set of positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function satisfying the following two conditions:
|
| 117 |
-
(a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime.
|
| 118 |
-
(b) $n \leq f(n) \leq n+2012$ for all $n$.
|
| 119 |
-
|
| 120 |
-
Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.
|
| 121 |
-
|
| 122 |
-
【 First short solution, by Jeffrey Kwan. Let $p_{0}, p_{1}, p_{2}, \ldots$ denote the sequence of all prime numbers, in any order. Pick any primes $q_{i}$ such that
|
| 123 |
-
|
| 124 |
-
$$
|
| 125 |
-
q_{0}\left|f\left(p_{0}\right), \quad q_{1}\right| f\left(p_{1}\right), \quad q_{2} \mid f\left(p_{2}\right), \text { etc. }
|
| 126 |
-
$$
|
| 127 |
-
|
| 128 |
-
This is possible since each $f$ value above exceeds 1 . Also, since by hypothesis the $f\left(p_{i}\right)$ are pairwise coprime, the primes $q_{i}$ are all pairwise distinct.
|
| 129 |
-
|
| 130 |
-
Claim - We must have $q_{i}=p_{i}$ for each $i$. (Therefore, $f\left(p_{i}\right)$ is a power of $p_{i}$ for each $i$.)
|
| 131 |
-
|
| 132 |
-
Proof. Assume to the contrary that $q_{0} \neq p_{0}$. By changing labels if necessary, assume $\min \left(p_{1}, p_{2}, \ldots, p_{2012}\right)>2012$. Then by Chinese remainder theorem we can choose an integer $m$ such that
|
| 133 |
-
|
| 134 |
-
$$
|
| 135 |
-
\begin{array}{rr}
|
| 136 |
-
m+i & \equiv 0 \\
|
| 137 |
-
m & \left(\bmod q_{i}\right) \\
|
| 138 |
-
m & \equiv{ }^{\prime} \\
|
| 139 |
-
\left(\bmod p_{i}\right)
|
| 140 |
-
\end{array}
|
| 141 |
-
$$
|
| 142 |
-
|
| 143 |
-
for $0 \leq i \leq 2012$. But now $f(m)$ should be coprime to all $f\left(p_{i}\right)$, ergo coprime to $q_{0} q_{1} \ldots q_{2012}$, violating $m \leq f(m) \leq m+2012$.
|
| 144 |
-
|
| 145 |
-
All that is left to do is note that whenever $p \nmid n$, we have $\operatorname{gcd}(f(p), f(n))=1$, hence $p \nmid f(n)$. This is the contrapositive of the problem statement.
|
| 146 |
-
|
| 147 |
-
【 Second solution with a grid. Fix $n$ and $p$, and assume for contradiction $p \nmid n$.
|
| 148 |
-
Claim - There exists a large integer $N$ with $f(N)=N$, that also satisfies $N \equiv 1$ $(\bmod n)$ and $N \equiv 0(\bmod p)$.
|
| 149 |
-
|
| 150 |
-
Proof. We'll need to pick both $N$ and an ancillary integer $M$. Here is how: pick $2012 \cdot 2013$ distinct primes $q_{i, j}>n+p+2013$ for every $i=1, \ldots, 2012$ and $j=0, \ldots, 2012$, and use
|
| 151 |
-
it to fill in the following table:
|
| 152 |
-
|
| 153 |
-
| | $N+1$ | $N+2$ | $\ldots$ | $N+2012$ |
|
| 154 |
-
| :---: | :---: | :---: | :---: | :---: |
|
| 155 |
-
| $M$ | $q_{0,1}$ | $q_{0,2}$ | $\ldots$ | $q_{0,2012}$ |
|
| 156 |
-
| $M+1$ | $q_{1,1}$ | $q_{1,2}$ | $\ldots$ | $q_{1,2012}$ |
|
| 157 |
-
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
|
| 158 |
-
| $M+2012$ | $q_{2012,1}$ | $q_{2012,2}$ | $\ldots$ | $q_{2012,2012}$ |.
|
| 159 |
-
|
| 160 |
-
By the Chinese Remainder Theorem, we can construct $N$ such that $N+1 \equiv 0\left(\bmod q_{i, 1}\right)$ for every $i$, and similarly for $N+2$, and so on. Moreover, we can also tack on the extra conditions $N \equiv 0(\bmod p)$ and $N \equiv 1(\bmod n)$ we wanted.
|
| 161 |
-
|
| 162 |
-
Notice that $N$ cannot be divisible by any of the $q_{i, j}$ 's, since the $q_{i, j}$ 's are greater than 2012.
|
| 163 |
-
|
| 164 |
-
After we've chosen $N$, we can pick $M$ such that $M \equiv 0\left(\bmod q_{0, j}\right)$ for every $j$, and similarly $M+1 \equiv 0\left(\bmod q_{1, j}\right)$, et cetera. Moreover, we can tack on the condition $M \equiv 1$ $(\bmod N)$, which ensures $\operatorname{gcd}(M, N)=1$.
|
| 165 |
-
|
| 166 |
-
What does this do? We claim that $f(N)=N$ now. Indeed $f(M)$ and $f(N)$ are relatively prime; but look at the table! The table tells us that $f(M)$ must have a common factor with each of $N+1, \ldots, N+2012$. So the only possibility is that $f(N)=N$.
|
| 167 |
-
|
| 168 |
-
Now we're basically done. Since $N \equiv 1(\bmod n)$, we have $\operatorname{gcd}(N, n)=1$ and hence $1=\operatorname{gcd}(f(N), f(n))=\operatorname{gcd}(N, f(n))$. But $p \mid N$ and $p \mid f(n)$, contradiction.
|
| 169 |
-
|
| 170 |
-
## §2 Solutions to Day 2
|
| 171 |
-
|
| 172 |
-
## §2.1 TSTST 2012/4
|
| 173 |
-
|
| 174 |
-
Available online at https://aops.com/community/p2745854.
|
| 175 |
-
|
| 176 |
-
## Problem statement
|
| 177 |
-
|
| 178 |
-
In scalene triangle $A B C$, let the feet of the perpendiculars from $A$ to $\overline{B C}, B$ to $\overline{C A}$, $C$ to $\overline{A B}$ be $A_{1}, B_{1}, C_{1}$, respectively. Denote by $A_{2}$ the intersection of lines $B C$ and $B_{1} C_{1}$. Define $B_{2}$ and $C_{2}$ analogously. Let $D, E, F$ be the respective midpoints of sides $\overline{B C}, \overline{C A}, \overline{A B}$. Show that the perpendiculars from $D$ to $\overline{A A_{2}}, E$ to $\overline{B B_{2}}$ and $F$ to $\overline{C C_{2}}$ are concurrent.
|
| 179 |
-
|
| 180 |
-
We claim that they pass through the orthocenter $H$. Indeed, consider the circle with diameter $\overline{B C}$, which circumscribes quadrilateral $B C B_{1} C_{1}$ and has center $D$. Then by Brokard theorem, $\overline{A A_{2}}$ is the polar of line $H$. Thus $\overline{D H} \perp \overline{A A_{2}}$.
|
| 181 |
-
|
| 182 |
-
## §2.2 TSTST 2012/5
|
| 183 |
-
|
| 184 |
-
Available online at https://aops.com/community/p2745867.
|
| 185 |
-
|
| 186 |
-
## Problem statement
|
| 187 |
-
|
| 188 |
-
A rational number $x$ is given. Prove that there exists a sequence $x_{0}, x_{1}, x_{2}, \ldots$ of rational numbers with the following properties:
|
| 189 |
-
(a) $x_{0}=x$;
|
| 190 |
-
(b) for every $n \geq 1$, either $x_{n}=2 x_{n-1}$ or $x_{n}=2 x_{n-1}+\frac{1}{n}$;
|
| 191 |
-
(c) $x_{n}$ is an integer for some $n$.
|
| 192 |
-
|
| 193 |
-
Think of the sequence as a process over time. We'll show that:
|
| 194 |
-
Claim - At any given time $t$, if the denominator of $x_{t}$ has some odd prime power $q=p^{e}$, then we can delete a factor of $p$ from the denominator, while only adding powers of two to the denominator.
|
| 195 |
-
(Thus we can just delete off all the odd primes one by one and then double appropriately many times.)
|
| 196 |
-
|
| 197 |
-
Proof. The idea is to add only fractions of the form $\left(2^{k} q\right)^{-1}$.
|
| 198 |
-
Indeed, let $n$ be large, and suppose $t<2^{r+1} q<2^{r+2} q<\cdots<2^{r+m} q<n$. For some binary variables $\varepsilon_{i} \in\{0,1\}$ we can have
|
| 199 |
-
|
| 200 |
-
$$
|
| 201 |
-
x_{n}=2^{n-t} x_{t}+c_{1} \cdot \frac{\varepsilon_{1}}{q}+c_{2} \cdot \frac{\varepsilon_{2}}{q} \cdots+c_{s} \cdot \frac{\varepsilon_{m}}{q}
|
| 202 |
-
$$
|
| 203 |
-
|
| 204 |
-
where $c_{i}$ is some power of 2 (to be exact, $c_{i}=\frac{2^{n-2^{r+i} q}}{2^{r+1}}$, but the exact value doesn't matter).
|
| 205 |
-
If $m$ is large enough the set $\left\{0, c_{1}\right\}+\left\{0, c_{2}\right\}+\cdots+\left\{0, c_{m}\right\}$ spans everything modulo p. (Actually, Cauchy-Davenport implies $m=p$ is enough, but one can also just use Pigeonhole to notice some residue appears more than $p$ times, for $m=O\left(p^{2}\right)$.) Thus we can eliminate one factor of $p$ from the denominator, as desired.
|
| 206 |
-
|
| 207 |
-
## §2.3 TSTST 2012/6, proposed by Sung-Yoon Kim
|
| 208 |
-
|
| 209 |
-
Available online at https://aops.com/community/p2745861.
|
| 210 |
-
|
| 211 |
-
## Problem statement
|
| 212 |
-
|
| 213 |
-
Positive real numbers $x, y, z$ satisfy $x y z+x y+y z+z x=x+y+z+1$. Prove that
|
| 214 |
-
|
| 215 |
-
$$
|
| 216 |
-
\frac{1}{3}\left(\sqrt{\frac{1+x^{2}}{1+x}}+\sqrt{\frac{1+y^{2}}{1+y}}+\sqrt{\frac{1+z^{2}}{1+z}}\right) \leq\left(\frac{x+y+z}{3}\right)^{5 / 8}
|
| 217 |
-
$$
|
| 218 |
-
|
| 219 |
-
The key is the identity
|
| 220 |
-
|
| 221 |
-
$$
|
| 222 |
-
\begin{aligned}
|
| 223 |
-
\frac{x^{2}+1}{x+1} & =\frac{\left(x^{2}+1\right)(y+1)(z+1)}{(x+1)(y+1)(z+1)} \\
|
| 224 |
-
& =\frac{x(x y z+x y+x z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\
|
| 225 |
-
& =\frac{x(x+y+z+1-y z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\
|
| 226 |
-
& =\frac{(x+y)(x+z)+x^{2}+(x-x y z+y+z+1)}{2(1+x+y+z)} \\
|
| 227 |
-
& =\frac{2(x+y)(x+z)}{2(1+x+y+z)} \\
|
| 228 |
-
& =\frac{(x+y)(x+z)}{1+x+y+z} .
|
| 229 |
-
\end{aligned}
|
| 230 |
-
$$
|
| 231 |
-
|
| 232 |
-
Remark. The "trick" can be rephrased as $\left(x^{2}+1\right)(y+1)(z+1)=2(x+y)(x+z)$.
|
| 233 |
-
After this, straight Cauchy in the obvious way will do it (reducing everything to an inequality in $s=x+y+z$ ). One writes
|
| 234 |
-
|
| 235 |
-
$$
|
| 236 |
-
\begin{aligned}
|
| 237 |
-
\left(\sum_{\mathrm{cyc}} \frac{\sqrt{(x+y)(x+z)}}{\sqrt{1+s}}\right)^{2} & \leq \frac{\left(\sum_{\mathrm{cyc}} x+y\right)\left(\sum_{\mathrm{cyc}} x+z\right)}{1+s} \\
|
| 238 |
-
& =\frac{4 s^{2}}{1+s}
|
| 239 |
-
\end{aligned}
|
| 240 |
-
$$
|
| 241 |
-
|
| 242 |
-
and so it suffices to check that $\frac{4 s^{2}}{1+s} \leq 9(s / 3)^{5 / 4}$, which is true because
|
| 243 |
-
|
| 244 |
-
$$
|
| 245 |
-
(s / 3)^{5} \cdot 9^{4} \cdot(1+s)^{4}-\left(4 s^{2}\right)^{4}=s^{5}(s-3)^{2}\left(27 s^{2}+14 s+3\right) \geq 0
|
| 246 |
-
$$
|
| 247 |
-
|
| 248 |
-
## §3 Solutions to Day 3
|
| 249 |
-
|
| 250 |
-
## §3.1 TSTST 2012/7
|
| 251 |
-
|
| 252 |
-
Available online at https://aops.com/community/p2745857.
|
| 253 |
-
|
| 254 |
-
## Problem statement
|
| 255 |
-
|
| 256 |
-
Triangle $A B C$ is inscribed in circle $\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.
|
| 257 |
-
|
| 258 |
-
By angle chasing, equivalent to show $\overline{M N} \| \overline{A D}$, so discard the point $H$. We now present a three solutions.
|
| 259 |
-
|
| 260 |
-
ब First solution using vectors. We first contend that:
|
| 261 |
-
Claim - We have $Q B=P C$.
|
| 262 |
-
|
| 263 |
-
Proof. Power of a Point gives $B M \cdot B D=A B \cdot Q B$. Then use the angle bisector theorem.
|
| 264 |
-
|
| 265 |
-
Now notice that the vector
|
| 266 |
-
|
| 267 |
-
$$
|
| 268 |
-
\overrightarrow{M N}=\frac{1}{2}(\overrightarrow{B Q}+\overrightarrow{C P})
|
| 269 |
-
$$
|
| 270 |
-
|
| 271 |
-
which must be parallel to the angle bisector since $\overrightarrow{B Q}$ and $\overrightarrow{C P}$ have the same magnitude.
|
| 272 |
-
『 Second solution using spiral similarity. let $X$ be the arc midpoint of $B A C$. Then $A D M X$ is cyclic with diameter $\overline{A M}$, and hence $X$ is the Miquel point $X$ of $Q B P C$ is the midpoint of arc $B A C$. Moreover $\overline{X N D}$ collinear (as $X P=X Q, D P=D Q)$ on $(A P Q)$.
|
| 273 |
-
|
| 274 |
-
|
| 275 |
-
Then $\triangle X N M \sim \triangle X P C$ spirally, and
|
| 276 |
-
|
| 277 |
-
$$
|
| 278 |
-
\measuredangle X M N=\measuredangle X C P=\measuredangle X C A=\measuredangle X L A
|
| 279 |
-
$$
|
| 280 |
-
|
| 281 |
-
thus done.
|
| 282 |
-
『 Third solution using barycentrics (mine). Once reduced to $\overline{M N} \| \overline{A B}$, straight bary will also work. By power of a point one obtains
|
| 283 |
-
|
| 284 |
-
$$
|
| 285 |
-
\begin{aligned}
|
| 286 |
-
P & =\left(a^{2}: 0: 2 b(b+c)-a^{2}\right) \\
|
| 287 |
-
Q & =\left(a^{2}: 2 c(b+c)-a^{2}: 0\right) \\
|
| 288 |
-
\Longrightarrow N & =\left(a^{2}(b+c): 2 b c(b+c)-b a^{2}: 2 b c(b+c)-c a^{2}\right) .
|
| 289 |
-
\end{aligned}
|
| 290 |
-
$$
|
| 291 |
-
|
| 292 |
-
Now the point at infinity along $\overline{A D}$ is $(-(b+c): b: c)$ and so we need only verify
|
| 293 |
-
|
| 294 |
-
$$
|
| 295 |
-
\operatorname{det}\left[\begin{array}{ccc}
|
| 296 |
-
a^{2}(b+c) & 2 b c(b+c)-b a^{2} & 2 b c(b+c)-c a^{2} \\
|
| 297 |
-
0 & 1 & 1 \\
|
| 298 |
-
-(b+c) & b & c
|
| 299 |
-
\end{array}\right]=0
|
| 300 |
-
$$
|
| 301 |
-
|
| 302 |
-
which follows since the first row is $-a^{2}$ times the third row plus $2 b c(b+c)$ times the second row.
|
| 303 |
-
|
| 304 |
-
## §3.2 TSTST 2012/8, proposed by Palmer Mebane
|
| 305 |
-
|
| 306 |
-
Available online at https://aops.com/community/p2745872.
|
| 307 |
-
|
| 308 |
-
## Problem statement
|
| 309 |
-
|
| 310 |
-
Let $n$ be a positive integer. Consider a triangular array of nonnegative integers as follows:
|
| 311 |
-
|
| 312 |
-
$$
|
| 313 |
-
\begin{array}{clllll}
|
| 314 |
-
\text { Row 1: } & & & a_{0,1} \\
|
| 315 |
-
\text { Row 2: } & & a_{0,2} & a_{1,2} & \\
|
| 316 |
-
& \vdots & \vdots & & \ddots & \\
|
| 317 |
-
\text { Row } n-1: & a_{0, n-1} & a_{1, n-1} & \ldots & a_{n-2, n-1} \\
|
| 318 |
-
\text { Row } n \text { : } & a_{0, n} \quad a_{1, n} \quad a_{2, n} & & \ldots & a_{n-1, n}
|
| 319 |
-
\end{array}
|
| 320 |
-
$$
|
| 321 |
-
|
| 322 |
-
Call such a triangular array stable if for every $0 \leq i<j<k \leq n$ we have
|
| 323 |
-
|
| 324 |
-
$$
|
| 325 |
-
a_{i, j}+a_{j, k} \leq a_{i, k} \leq a_{i, j}+a_{j, k}+1
|
| 326 |
-
$$
|
| 327 |
-
|
| 328 |
-
For $s_{1}, \ldots, s_{n}$ any nondecreasing sequence of nonnegative integers, prove that there exists a unique stable triangular array such that the sum of all of the entries in row $k$ is equal to $s_{k}$.
|
| 329 |
-
|
| 330 |
-
Firstly, here are illustrative examples showing the arrays for $\left(s_{1}, s_{2}, s_{3}, s_{4}\right)=(2,5,9, x)$ where $9 \leq x \leq 14$. (The array has been left justified.)
|
| 331 |
-
|
| 332 |
-
$$
|
| 333 |
-
\begin{aligned}
|
| 334 |
-
& {\left[\begin{array}{cccc}
|
| 335 |
-
2 & \swarrow & & \\
|
| 336 |
-
4 & 1 & \swarrow & \\
|
| 337 |
-
5 & 3 & 1 & \swarrow \\
|
| 338 |
-
5 & 3 & 1 & 0
|
| 339 |
-
\end{array}\right]\left[\begin{array}{llll}
|
| 340 |
-
2 & \swarrow & & \\
|
| 341 |
-
4 & 1 & \swarrow & \\
|
| 342 |
-
5 & 3 & 1 & \swarrow \\
|
| 343 |
-
6 & 3 & 1 & 0
|
| 344 |
-
\end{array}\right]\left[\begin{array}{llll}
|
| 345 |
-
2 & \swarrow & & \\
|
| 346 |
-
4 & 1 & \swarrow & \\
|
| 347 |
-
5 & 3 & 1 & \swarrow \\
|
| 348 |
-
6 & 3 & 2 & 0
|
| 349 |
-
\end{array}\right]} \\
|
| 350 |
-
& {\left[\begin{array}{cccc}
|
| 351 |
-
2 & \swarrow & & \\
|
| 352 |
-
4 & 1 & \swarrow & \swarrow \\
|
| 353 |
-
5 & 3 & 1 & \swarrow \\
|
| 354 |
-
6 & 4 & 2 & 0
|
| 355 |
-
\end{array}\right]\left[\begin{array}{llll}
|
| 356 |
-
2 & \swarrow & \\
|
| 357 |
-
4 & 1 & \swarrow & \\
|
| 358 |
-
5 & 3 & 1 & \swarrow \\
|
| 359 |
-
6 & 4 & 2 & 1
|
| 360 |
-
\end{array}\right]\left[\begin{array}{cccc}
|
| 361 |
-
2 & \swarrow & \\
|
| 362 |
-
4 & 1 & \swarrow & \\
|
| 363 |
-
5 & 3 & 1 & \swarrow \\
|
| 364 |
-
7 & 4 & 2 & 1
|
| 365 |
-
\end{array}\right]}
|
| 366 |
-
\end{aligned}
|
| 367 |
-
$$
|
| 368 |
-
|
| 369 |
-
Now we outline the proof. By induction on $n$, we may assume the first $n-1$ rows are fixed. Now, let $N=s_{n}$ vary. Now, we prove our result by (another) induction on $N \geq s_{n-1}$.
|
| 370 |
-
|
| 371 |
-
The base case $N=s_{n-1}$ is done by copying the $n-1$ st row and adding a zero at the end. This is also unique, since $a_{i, n} \geq a_{i-1, n}+a_{n-1, n}$ for all $i=0, \ldots, n-2$, whence $\sum a_{i, n} \geq s_{n-1}$ follows.
|
| 372 |
-
|
| 373 |
-
Now the inductive step is based on the following lemma, which illustrates the idea of a "unique increasable entry".
|
| 374 |
-
|
| 375 |
-
## Lemma
|
| 376 |
-
|
| 377 |
-
Fix a stable array Construct a tournament on the $n$ entries of the last row as follows: for $i<j$,
|
| 378 |
-
|
| 379 |
-
- $a_{i, n} \rightarrow a_{j, n}$ if $a_{i, n}=a_{i, j}+a_{j, n}$, and
|
| 380 |
-
- $a_{j, n} \rightarrow a_{i, n}$ if $a_{i, n}=a_{i, j}+a_{j, n}+1$.
|
| 381 |
-
|
| 382 |
-
Then this tournament is transitive. Also, except for $N=s_{n-1}$, a 0 entry is never a source.
|
| 383 |
-
|
| 384 |
-
Intuitively, $a_{i, n} \rightarrow a_{j, n}$ if $a_{i, n}$ blocks $a_{j, n}$ from increasing. For instance, in the example
|
| 385 |
-
|
| 386 |
-
$$
|
| 387 |
-
\left[\begin{array}{rrrr}
|
| 388 |
-
2 & \swarrow & & \\
|
| 389 |
-
4 & 1 & \swarrow & \\
|
| 390 |
-
5 & 3 & 1 & \swarrow \\
|
| 391 |
-
\mathbf{6} & 3 & 1 & 0
|
| 392 |
-
\end{array}\right]
|
| 393 |
-
$$
|
| 394 |
-
|
| 395 |
-
the tournament is $1 \rightarrow 3 \rightarrow 0 \rightarrow 6$.
|
| 396 |
-
Proof of lemma. Let $0 \leq i<j<k<n$ be indices. Let $x=a_{i, n}, y=a_{j, n}, z=a_{k, n}$, $p=a_{i, j}, s=a_{i, k}, q=a_{j, k}$. Picture:
|
| 397 |
-
|
| 398 |
-
$$
|
| 399 |
-
\left[\begin{array}{ccc}
|
| 400 |
-
p & \swarrow & \\
|
| 401 |
-
s & q & \swarrow \\
|
| 402 |
-
x & y & z
|
| 403 |
-
\end{array}\right]
|
| 404 |
-
$$
|
| 405 |
-
|
| 406 |
-
If $x \rightarrow y \rightarrow z \rightarrow x$ happens, that means $x=y+p, y=q+z, x=s+z+1$, which gives $s=p+q-1$, contradiction. Similarly if $x \leftarrow y \leftarrow z \leftarrow x$ then $x=y+p+1, y=q+z+1$, $x=s+z$, which gives $s=p+q+2$, also contradiction.
|
| 407 |
-
|
| 408 |
-
Now this allows us to perform our induction. Indeed, to show existence from $N$ to $N+1$ we take a source of the tournament above and increase it. Conversely, to show uniqueness for $N$, note that we can take the (nonzero) sink of the tournament and decrement it, which gives $N-1$; our uniqueness inductive hypothesis now finishes.
|
| 409 |
-
|
| 410 |
-
Remark. Colin Tang found a nice proof of uniqueness:
|
| 411 |
-
|
| 412 |
-
$$
|
| 413 |
-
s_{k}+\sum_{i=1}^{k-1} a_{0, i} \leq k a_{0, k} \leq s_{k}+\sum_{i=1}\left(a_{0, i}+1\right)
|
| 414 |
-
$$
|
| 415 |
-
|
| 416 |
-
and similarly for other entries.
|
| 417 |
-
|
| 418 |
-
## §3.3 TSTST 2012/9, proposed by John Berman
|
| 419 |
-
|
| 420 |
-
Available online at https://aops.com/community/p2745874.
|
| 421 |
-
|
| 422 |
-
## Problem statement
|
| 423 |
-
|
| 424 |
-
Given a set $S$ of $n$ variables, a binary operation $\times$ on $S$ is called simple if it satisfies $(x \times y) \times z=x \times(y \times z)$ for all $x, y, z \in S$ and $x \times y \in\{x, y\}$ for all $x, y \in S$. Given a simple operation $\times$ on $S$, any string of elements in $S$ can be reduced to a single element, such as $x y z \rightarrow x \times(y \times z)$. A string of variables in $S$ is called full if it contains each variable in $S$ at least once, and two strings are equivalent if they evaluate to the same variable regardless of which simple $\times$ is chosen. For example $x x x, x x$, and $x$ are equivalent, but these are only full if $n=1$. Suppose $T$ is a set of full strings such that any full string is equivalent to exactly one element of $T$. Determine the number of elements of $T$.
|
| 425 |
-
|
| 426 |
-
The answer is $(n!)^{2}$. In fact it is possible to essentially find all $x$ : one assigns a real number to each variable in $S$. Then $x \times y$ takes the larger of $\{x, y\}$, and in the event of a tie picks either "left" or "right", where the choice of side is fixed among elements of each size.
|
| 427 |
-
|
| 428 |
-
【 First solution (Steven Hao). The main trick is the two lemmas, which are not hard to show (and are motivated by our conjecture).
|
| 429 |
-
|
| 430 |
-
$$
|
| 431 |
-
\begin{aligned}
|
| 432 |
-
x x & =x \\
|
| 433 |
-
x y x z x & =x y z x .
|
| 434 |
-
\end{aligned}
|
| 435 |
-
$$
|
| 436 |
-
|
| 437 |
-
Consequently, define a double rainbow to be the concatenation of two full strings of length $n$, of which there are $(n!)^{2}$. We claim that these form equivalence classes for $T$.
|
| 438 |
-
|
| 439 |
-
To see that any string $s$ is equivalent to a double rainbow, note that $s=s s$, and hence using the second identity above repeatedly lets us reduce ss to a double rainbow.
|
| 440 |
-
|
| 441 |
-
To see two distinct double rainbows $R_{1}$ and $R_{2}$ aren't equivalent, one can use the construction mentioned in the beginning. Specifically, take two variables $a$ and $b$ which do not appear in the same order in $R_{1}$ and $R_{2}$. Then it's not hard to see that $a b a b, a b b a$, $b a a b, b a b a$ are pairwise non-equivalent by choosing "left" or "right" appropriately. Now construct $\times$ on the whole set by having $a$ and $b$ be the largest variables, so the rest of the variables don't matter in the evaluation of the string.
|
| 442 |
-
|
| 443 |
-
【 Second solution outline (Ankan Bhattacharya). We outline a proof of the characterization claimed earlier, which will also give the answer $(n!)^{2}$. We say $a \sim b$ if $a b \neq b a$. Also, say $a>b$ if $a b=b a=a$. The following are proved by finite casework, using the fact that $\{a b, b c, c a\}$ always has exactly two distinct elements for any different $a, b, c$.
|
| 444 |
-
|
| 445 |
-
- If $a>b$ and $b>c$ then $a>c$.
|
| 446 |
-
- If $a \sim b$ and $b \sim c$ then $a b=a$ if and only if $b c=b$.
|
| 447 |
-
- If $a \sim b$ and $b \sim c$ then $a \sim c$.
|
| 448 |
-
- If $a \sim b$ and $a>c$ then $b>c$.
|
| 449 |
-
- If $a \sim b$ and $c>a$ then $c>b$.
|
| 450 |
-
|
| 451 |
-
This gives us the total ordering on the elements and the equivalence classes by $\sim$. In this we way can check the claimed operations are the only ones.
|
| 452 |
-
|
| 453 |
-
We can then (as in the first solution) verify that every full string is equivalent to a unique double rainbow - but this time we prove it by simply considering all possible $\times$, because we have classified them all.
|
| 454 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2013.md
DELETED
|
@@ -1,437 +0,0 @@
|
|
| 1 |
-
# TSTST 2013 Solution Notes <br> Lincoln, Nebraska <br> \author{ Evan Chen《陳誼廷》
|
| 2 |
-
|
| 3 |
-
}
|
| 4 |
-
|
| 5 |
-
23 April 2024
|
| 6 |
-
|
| 7 |
-
This is a compilation of solutions for the 2013 TSTST. The ideas of the solution are a mix of my own work, the solutions provided by the competition organizers, and solutions found by the community. However, all the writing is maintained by me.
|
| 8 |
-
|
| 9 |
-
These notes will tend to be a bit more advanced and terse than the "official" solutions from the organizers. In particular, if a theorem or technique is not known to beginners but is still considered "standard", then I often prefer to use this theory anyways, rather than try to work around or conceal it. For example, in geometry problems I typically use directed angles without further comment, rather than awkwardly work around configuration issues. Similarly, sentences like "let $\mathbb{R}$ denote the set of real numbers" are typically omitted entirely.
|
| 10 |
-
|
| 11 |
-
Corrections and comments are welcome!
|
| 12 |
-
|
| 13 |
-
## Contents
|
| 14 |
-
|
| 15 |
-
0 Problems ..... 2
|
| 16 |
-
1 Solutions to Day 1 ..... 4
|
| 17 |
-
1.1 TSTST 2013/1 ..... 4
|
| 18 |
-
1.2 TSTST 2013/2 ..... 5
|
| 19 |
-
1.3 TSTST 2013/3 ..... 6
|
| 20 |
-
2 Solutions to Day 2 ..... 8
|
| 21 |
-
2.1 TSTST 2013/4 ..... 8
|
| 22 |
-
2.2 TSTST 2013/5 ..... 10
|
| 23 |
-
2.3 TSTST 2013/6 ..... 11
|
| 24 |
-
3 Solutions to Day 3 ..... 13
|
| 25 |
-
3.1 TSTST 2013/7 ..... 13
|
| 26 |
-
3.2 TSTST 2013/8 ..... 14
|
| 27 |
-
3.3 TSTST 2013/9 ..... 15
|
| 28 |
-
|
| 29 |
-
## §0 Problems
|
| 30 |
-
|
| 31 |
-
1. Let $A B C$ be a triangle and $D, E, F$ be the midpoints of $\operatorname{arcs} B C, C A, A B$ on the circumcircle. Line $\ell_{a}$ passes through the feet of the perpendiculars from $A$ to $\overline{D B}$ and $\overline{D C}$. Line $m_{a}$ passes through the feet of the perpendiculars from $D$ to $\overline{A B}$ and $\overline{A C}$. Let $A_{1}$ denote the intersection of lines $\ell_{a}$ and $m_{a}$. Define points $B_{1}$ and $C_{1}$ similarly. Prove that triangles $D E F$ and $A_{1} B_{1} C_{1}$ are similar to each other.
|
| 32 |
-
2. A finite sequence of integers $a_{1}, a_{2}, \ldots, a_{n}$ is called regular if there exists a real number $x$ satisfying
|
| 33 |
-
|
| 34 |
-
$$
|
| 35 |
-
\lfloor k x\rfloor=a_{k} \quad \text { for } 1 \leq k \leq n
|
| 36 |
-
$$
|
| 37 |
-
|
| 38 |
-
Given a regular sequence $a_{1}, a_{2}, \ldots, a_{n}$, for $1 \leq k \leq n$ we say that the term $a_{k}$ is forced if the following condition is satisfied: the sequence
|
| 39 |
-
|
| 40 |
-
$$
|
| 41 |
-
a_{1}, a_{2}, \ldots, a_{k-1}, b
|
| 42 |
-
$$
|
| 43 |
-
|
| 44 |
-
is regular if and only if $b=a_{k}$.
|
| 45 |
-
Find the maximum possible number of forced terms in a regular sequence with 1000 terms.
|
| 46 |
-
3. Divide the plane into an infinite square grid by drawing all the lines $x=m$ and $y=n$ for $m, n \in \mathbb{Z}$. Next, if a square's upper-right corner has both coordinates even, color it black; otherwise, color it white (in this way, exactly $1 / 4$ of the squares are black and no two black squares are adjacent). Let $r$ and $s$ be odd integers, and let $(x, y)$ be a point in the interior of any white square such that $r x-s y$ is irrational. Shoot a laser out of this point with slope $r / s$; lasers pass through white squares and reflect off black squares. Prove that the path of this laser will from a closed loop.
|
| 47 |
-
4. Circle $\omega$, centered at $X$, is internally tangent to circle $\Omega$, centered at $Y$, at $T$. Let $P$ and $S$ be variable points on $\Omega$ and $\omega$, respectively, such that line $P S$ is tangent to $\omega($ at $S)$. Determine the locus of $O$ - the circumcenter of triangle $P S T$.
|
| 48 |
-
5. Let $p$ be a prime. Prove that in a complete graph with $1000 p$ vertices whose edges are labelled with integers, one can find a cycle whose sum of labels is divisible by $p$.
|
| 49 |
-
6. Let $\mathbb{N}$ be the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ that satisfy the equation
|
| 50 |
-
|
| 51 |
-
$$
|
| 52 |
-
f^{a b c-a}(a b c)+f^{a b c-b}(a b c)+f^{a b c-c}(a b c)=a+b+c
|
| 53 |
-
$$
|
| 54 |
-
|
| 55 |
-
for all $a, b, c \geq 2$. (Here $f^{k}$ means $f$ applied $k$ times.)
|
| 56 |
-
7. A country has $n$ cities, labelled $1,2,3, \ldots, n$. It wants to build exactly $n-1$ roads between certain pairs of cities so that every city is reachable from every other city via some sequence of roads. However, it is not permitted to put roads between pairs of cities that have labels differing by exactly 1 , and it is also not permitted to put a road between cities 1 and $n$. Let $T_{n}$ be the total number of possible ways to build these roads.
|
| 57 |
-
(a) For all odd $n$, prove that $T_{n}$ is divisible by $n$.
|
| 58 |
-
(b) For all even $n$, prove that $T_{n}$ is divisible by $n / 2$.
|
| 59 |
-
8. Define a function $f: \mathbb{N} \rightarrow \mathbb{N}$ by $f(1)=1, f(n+1)=f(n)+2^{f(n)}$ for every positive integer $n$. Prove that $f(1), f(2), \ldots, f\left(3^{2013}\right)$ leave distinct remainders when divided by $3^{2013}$.
|
| 60 |
-
9. Let $r$ be a rational number in the interval $[-1,1]$ and let $\theta=\cos ^{-1} r$. Call a subset $S$ of the plane good if $S$ is unchanged upon rotation by $\theta$ around any point of $S$ (in both clockwise and counterclockwise directions). Determine all values of $r$ satisfying the following property: The midpoint of any two points in a good set also lies in the set.
|
| 61 |
-
|
| 62 |
-
## §1 Solutions to Day 1
|
| 63 |
-
|
| 64 |
-
## §1.1 TSTST 2013/1
|
| 65 |
-
|
| 66 |
-
Available online at https://aops.com/community/p3181479.
|
| 67 |
-
|
| 68 |
-
## Problem statement
|
| 69 |
-
|
| 70 |
-
Let $A B C$ be a triangle and $D, E, F$ be the midpoints of $\operatorname{arcs} B C, C A, A B$ on the circumcircle. Line $\ell_{a}$ passes through the feet of the perpendiculars from $A$ to $\overline{D B}$ and $\overline{D C}$. Line $m_{a}$ passes through the feet of the perpendiculars from $D$ to $\overline{A B}$ and $\overline{A C}$. Let $A_{1}$ denote the intersection of lines $\ell_{a}$ and $m_{a}$. Define points $B_{1}$ and $C_{1}$ similarly. Prove that triangles $D E F$ and $A_{1} B_{1} C_{1}$ are similar to each other.
|
| 71 |
-
|
| 72 |
-
In fact, it is true for any points $D, E, F$ on the circumcircle. More strongly we contend:
|
| 73 |
-
|
| 74 |
-
Claim - Point $A_{1}$ is the midpoint of $\overline{H D}$.
|
| 75 |
-
|
| 76 |
-
Proof. Lines $m_{a}$ and $\ell_{a}$ are Simson lines, so they both pass through the point $(a+b+$ $c+d) / 2$ in complex coordinates.
|
| 77 |
-
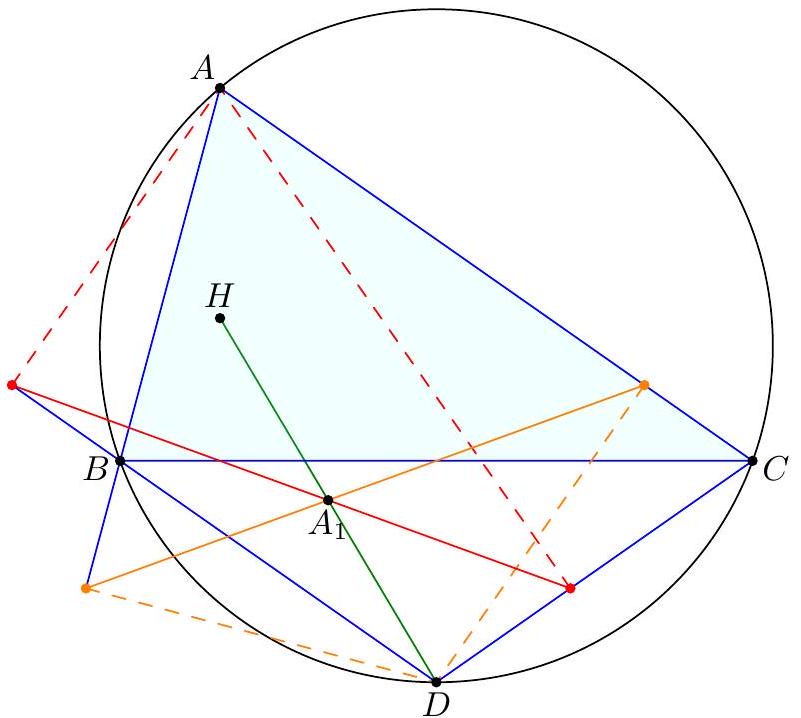
|
| 78 |
-
|
| 79 |
-
Hence $A_{1} B_{1} C_{1}$ is similar to $D E F$ through a homothety at $H$ with ratio $\frac{1}{2}$.
|
| 80 |
-
|
| 81 |
-
## §1.2 TSTST 2013/2
|
| 82 |
-
|
| 83 |
-
Available online at https://aops.com/community/p3181480.
|
| 84 |
-
|
| 85 |
-
## Problem statement
|
| 86 |
-
|
| 87 |
-
A finite sequence of integers $a_{1}, a_{2}, \ldots, a_{n}$ is called regular if there exists a real number $x$ satisfying
|
| 88 |
-
|
| 89 |
-
$$
|
| 90 |
-
\lfloor k x\rfloor=a_{k} \quad \text { for } 1 \leq k \leq n .
|
| 91 |
-
$$
|
| 92 |
-
|
| 93 |
-
Given a regular sequence $a_{1}, a_{2}, \ldots, a_{n}$, for $1 \leq k \leq n$ we say that the term $a_{k}$ is forced if the following condition is satisfied: the sequence
|
| 94 |
-
|
| 95 |
-
$$
|
| 96 |
-
a_{1}, a_{2}, \ldots, a_{k-1}, b
|
| 97 |
-
$$
|
| 98 |
-
|
| 99 |
-
is regular if and only if $b=a_{k}$.
|
| 100 |
-
Find the maximum possible number of forced terms in a regular sequence with 1000 terms.
|
| 101 |
-
|
| 102 |
-
The answer is 985 . WLOG, by shifting $a_{1}=0$ (clearly $a_{1}$ isn't forced). Now, we construct regular sequences inductively using the following procedure. Start with the inequality
|
| 103 |
-
|
| 104 |
-
$$
|
| 105 |
-
\frac{0}{1} \leq x<\frac{1}{1}
|
| 106 |
-
$$
|
| 107 |
-
|
| 108 |
-
Then for each $k=2,3, \ldots, 1000$ we perform the following procedure. If there is no fraction of the form $F=\frac{m}{k}$ in the interval $A \leq x<B$, then $a_{k}$ is forced, and the interval of possible $x$ values does not change. Otherwise, $a_{k}$ is not forced, and we pick a value of $a_{k}$ and update the interval accordingly.
|
| 109 |
-
|
| 110 |
-
The theory of Farey sequences tells us that when we have a stage $\frac{a}{b} \leq x<\frac{c}{d}$ then the next time we will find a fraction in that interval is exactly $\frac{a+c}{b+d}$ (at time $k=b+d$ ), and it will be the only such fraction.
|
| 111 |
-
|
| 112 |
-
So essentially, starting with $\frac{0}{1} \leq x<\frac{1}{1}$ we repeatedly replace one of the endpoints of the intervals with the mediant, until one of the denominators exceeds 1000; we are trying to minimize the number of non-forced terms, which is the number of denominators that appear in this process. It is not hard to see that this optimum occurs by always replacing the smaller of the denominators, so that the sequence is
|
| 113 |
-
$\frac{0}{1} \leq x<\frac{1}{1}$
|
| 114 |
-
$\frac{0}{1} \leq x<\frac{1}{2}$
|
| 115 |
-
$\frac{1}{3} \leq x<\frac{1}{2}$
|
| 116 |
-
$\frac{1}{3} \leq x<\frac{2}{5}$
|
| 117 |
-
$\frac{3}{8} \leq x<\frac{2}{5}$
|
| 118 |
-
$\frac{3}{8} \leq x<\frac{5}{13}$
|
| 119 |
-
and so on; we see that the non-forced terms in this optimal configuration are exactly the Fibonacci numbers. There are 15 Fibonacci numbers less than 1000, hence the answer $1000-15=985$.
|
| 120 |
-
|
| 121 |
-
## §1.3 TSTST 2013/3
|
| 122 |
-
|
| 123 |
-
Available online at https://aops.com/community/p3181481.
|
| 124 |
-
|
| 125 |
-
## Problem statement
|
| 126 |
-
|
| 127 |
-
Divide the plane into an infinite square grid by drawing all the lines $x=m$ and $y=n$ for $m, n \in \mathbb{Z}$. Next, if a square's upper-right corner has both coordinates even, color it black; otherwise, color it white (in this way, exactly $1 / 4$ of the squares are black and no two black squares are adjacent). Let $r$ and $s$ be odd integers, and let $(x, y)$ be a point in the interior of any white square such that $r x-s y$ is irrational. Shoot a laser out of this point with slope $r / s$; lasers pass through white squares and reflect off black squares. Prove that the path of this laser will from a closed loop.
|
| 128 |
-
|
| 129 |
-
Here is Sammy Luo's solution. Fix the speed of light at $\sqrt{r^{2}+s^{2}}$ units per second. We prove periodicity every six seconds.
|
| 130 |
-
|
| 131 |
-
We re-color the white squares as red, blue, or green according as to whether they have a black square directly to the left/right, above/below, or neither, as shown below. Finally, we fix time zero to be a moment just before the laser passes a horizontal (WLOG) lattice line (not necessarily a wall). Shown below is an example for $(r, s)=(3,5)$.
|
| 132 |
-
|
| 133 |
-
|
| 134 |
-
The main idea is to keep track of every time the laser passes a lattice line (again, not necessarily a wall). There are four possible types of events:
|
| 135 |
-
|
| 136 |
-
- A horizontal $h$ event where the laser switches from red to green (or vice-versa);
|
| 137 |
-
- A horizontal $h$ event where the laser rebounds off a wall, remaining in a blue square, but flips the $x$-component of its velocity;
|
| 138 |
-
- A vertical $v$ event where the laser switches from blue to green (or vice-versa)
|
| 139 |
-
- A vertical $v$ event where the laser rebounds off a wall, remaining in a red square, but flips the $y$-component of its velocity.
|
| 140 |
-
|
| 141 |
-
The first key observation is that:
|
| 142 |
-
Claim - In the first second, the laser will encounter exactly $r$ horizontal events
|
| 143 |
-
and $s$ vertical events. In every second after that, the same sequence of $r+s$ events occurs.
|
| 144 |
-
|
| 145 |
-
Proof. Bouncing off a wall doesn't change this as opposed to if the laser had passed through the wall.
|
| 146 |
-
|
| 147 |
-
We let the key-word be the sequence $w$ of $r+s$ letters corresponding to the sequence. For example, the picture above denotes an example with keyword $w=h v v h v v h v$; so no matter what, every second, the laser will encounter eight lattice lines, which are horizontal and vertical in that order.
|
| 148 |
-
|
| 149 |
-
Claim - Color is periodic every 3 seconds.
|
| 150 |
-
|
| 151 |
-
Proof. The free group generated by $h$ and $v$ acts on the set $\{R, G, B\}$ of colors in an obvious way; consider this right action. First we consider the color of the square after each second. Note that with respect to color, each letter is an involution; so as far as color changes are concerned, it's enough to work with the reduced word $w^{\prime}$ obtained by modding out by $h^{2}=1$ and $v^{2}=1$. (For example, $w^{\prime}=h v$ in our example.) In general, $w^{\prime}=(h v)^{k}$ or $w^{\prime}=(v h)^{k}$, for some odd integer $k($ since $k \equiv r \equiv s \equiv 1(\bmod 2))$. Now we see that the action of $h v$ on the set of colors is red $\mapsto$ blue $\mapsto$ green $\mapsto$ red, and similarly for $v h$ (being the inverse). This implies that the color is periodic every three seconds.
|
| 152 |
-
|
| 153 |
-
Now in a 3 -second period, consider the $3 r$ horizontal events and $3 s$ vertical events (both are odd). In order for the color to remain the same (as the only color changes are $R \leftrightarrow G$ for $h$ and $B \leftrightarrow G$ for $v$ ) there must have been an even number of color swaps for each orientation. Therefore there was an odd number of wall collisions of each orientation. So, the laser is pointing in the opposite direction at the end of 3 seconds.
|
| 154 |
-
|
| 155 |
-
Finally, let $x_{t}$ be the fractional part of the $x$ coordinate after $t$ seconds (the $y$-coordinate is always zero by our setup at these moments). Note that
|
| 156 |
-
|
| 157 |
-
$$
|
| 158 |
-
x_{t+1}= \begin{cases}x_{t} & \text { even number of vertical wall collisions } \\ 1-x_{t} & \text { odd numbers of vertical wall collisions }\end{cases}
|
| 159 |
-
$$
|
| 160 |
-
|
| 161 |
-
Since over the there seconds there were an odd number of vertical collisions; it follows $x_{3}=1-x_{0}$. Thus at the end of three seconds, the laser is in a symmetric position from the start; and in 6 seconds it will form a closed loop.
|
| 162 |
-
|
| 163 |
-
## §2 Solutions to Day 2
|
| 164 |
-
|
| 165 |
-
## §2.1 TSTST 2013/4
|
| 166 |
-
|
| 167 |
-
Available online at https://aops.com/community/p3181482.
|
| 168 |
-
|
| 169 |
-
## Problem statement
|
| 170 |
-
|
| 171 |
-
Circle $\omega$, centered at $X$, is internally tangent to circle $\Omega$, centered at $Y$, at $T$. Let $P$ and $S$ be variable points on $\Omega$ and $\omega$, respectively, such that line $P S$ is tangent to $\omega($ at $S)$. Determine the locus of $O$ - the circumcenter of triangle $P S T$.
|
| 172 |
-
|
| 173 |
-
The answer is a circle centered at $Y$ with radius $\sqrt{Y X \cdot Y T}$, minus the two points on line $X Y$ itself.
|
| 174 |
-
|
| 175 |
-
We let $P S$ meet $\Omega$ again at $P^{\prime}$, and let $O^{\prime}$ be the circumcenter of $\triangle T P S^{\prime}$. Note that $O^{\prime}, X, O$ are collinear on the perpendicular bisector of line $\overline{T S}$ Finally, we let $M$ denote the arc midpoint of $P P^{\prime}$ which lies on line $T S$ (by homothety).
|
| 176 |
-
|
| 177 |
-
|
| 178 |
-
By three applications of Salmon theorem, we have the following spiral similarities all centered at $T$ :
|
| 179 |
-
|
| 180 |
-
$$
|
| 181 |
-
\begin{aligned}
|
| 182 |
-
\triangle T S P & \stackrel{+}{\sim} \triangle T O^{\prime} Y \\
|
| 183 |
-
\triangle T P^{\prime} S & \stackrel{ }{\sim} \triangle T Y O \\
|
| 184 |
-
\triangle T P^{\prime} P & \stackrel{+}{\sim} \triangle T O^{\prime} O
|
| 185 |
-
\end{aligned}
|
| 186 |
-
$$
|
| 187 |
-
|
| 188 |
-
However, the shooting lemma also gives us two similarities:
|
| 189 |
-
|
| 190 |
-
$$
|
| 191 |
-
\begin{aligned}
|
| 192 |
-
& \triangle T P^{\prime} M \stackrel{ \pm}{\sim} \triangle T S P \\
|
| 193 |
-
& \triangle T M P \stackrel{ \pm}{\sim} \triangle T P^{\prime} S
|
| 194 |
-
\end{aligned}
|
| 195 |
-
$$
|
| 196 |
-
|
| 197 |
-
Putting everything together, we find that
|
| 198 |
-
|
| 199 |
-
$$
|
| 200 |
-
T P^{\prime} M P \stackrel{ \pm}{\sim} T O^{\prime} Y O
|
| 201 |
-
$$
|
| 202 |
-
|
| 203 |
-
Then by shooting lemma, $Y O^{\prime 2}=Y X \cdot Y T$, so $O$ indeed lies on the claimed circle.
|
| 204 |
-
As the line $\overline{O^{\prime} O}$ may be any line through $X$ other than line $X Y$ (one takes $S$ to be the reflection of $T$ across this line) one concludes the only two non-achievable points are the diametrically opposite ones on line $X Y$ of this circle (because this leads to the only degenerate situation where $S=T$ ).
|
| 205 |
-
|
| 206 |
-
## §2.2 TSTST 2013/5
|
| 207 |
-
|
| 208 |
-
Available online at https://aops.com/community/p3181483.
|
| 209 |
-
|
| 210 |
-
## Problem statement
|
| 211 |
-
|
| 212 |
-
Let $p$ be a prime. Prove that in a complete graph with $1000 p$ vertices whose edges are labelled with integers, one can find a cycle whose sum of labels is divisible by $p$.
|
| 213 |
-
|
| 214 |
-
Select $p-1$ disjoint triangles arbitrarily. If any of these triangles have 0 sum modulo $p$ we are done. Otherwise, we may label the vertices $u_{i}, x_{i}$, and $v_{i}$ (where $1 \leq i \leq p-1$ ) in such a way that $u_{i} x_{i}+x_{i} v_{i} \neq u_{i} v_{i}$.
|
| 215 |
-
|
| 216 |
-
Let $A_{i}=\left\{u_{i} x_{i}+x_{i} v_{i}, u_{i} v_{i}\right\}$. We can show that $\left|A_{1}+A_{2}+\cdots+A_{t}\right| \geq \min \{p, t+1\}$ for each $1 \leq t \leq p-1$, by using induction on $t$ alongside Cauchy-Davenport. So, $A_{1}+A_{2}+\cdots+A_{p-1}$ spans all of $\mathbb{Z}_{p}$. All that's left to do is join the triangles together to form a cycle, and then delete either $u_{i} x_{i}, x_{i} v_{i}$ or $u_{i} v_{i}$ from each triangle in such a way that the final sum is $0 \bmod p$.
|
| 217 |
-
|
| 218 |
-
## §2.3 TSTST 2013/6
|
| 219 |
-
|
| 220 |
-
Available online at https://aops.com/community/p3181484.
|
| 221 |
-
|
| 222 |
-
## Problem statement
|
| 223 |
-
|
| 224 |
-
Let $\mathbb{N}$ be the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ that satisfy the equation
|
| 225 |
-
|
| 226 |
-
$$
|
| 227 |
-
f^{a b c-a}(a b c)+f^{a b c-b}(a b c)+f^{a b c-c}(a b c)=a+b+c
|
| 228 |
-
$$
|
| 229 |
-
|
| 230 |
-
for all $a, b, c \geq 2$. (Here $f^{k}$ means $f$ applied $k$ times.)
|
| 231 |
-
|
| 232 |
-
The answer is $f(n)=n-1$ for $n \geq 3$ with $f(1)$ and $f(2)$ arbitrary; check these work.
|
| 233 |
-
|
| 234 |
-
## Lemma
|
| 235 |
-
|
| 236 |
-
We have $f^{t^{2}-t}\left(t^{2}\right)=t$ for all $t$.
|
| 237 |
-
Proof. We say $1 \leq k \leq 8$ is good if $f^{t^{9}-t^{k}}\left(t^{9}\right)=t^{k}$ for all $t$. First, we observe that
|
| 238 |
-
|
| 239 |
-
$$
|
| 240 |
-
f^{t^{9}-t^{3}}\left(t^{9}\right)=t^{3} \quad \text { and } \quad f^{t^{3}-t}\left(t^{3}\right)=t \Longrightarrow f^{t^{9}-t}\left(t^{9}\right)=t
|
| 241 |
-
$$
|
| 242 |
-
|
| 243 |
-
so $k=1$ and $k=3$ are good. Then taking $(a, b, c)=\left(t, t^{4}, t^{4}\right),(a, b, c)=\left(t^{2}, t^{3}, t^{4}\right)$ gives that $k=4$ and $k=2$ are good, respectively. The lemma follows from this $k=1$ and $k=2$ being good.
|
| 244 |
-
|
| 245 |
-
Now, letting $t=a b c$ we combine
|
| 246 |
-
|
| 247 |
-
$$
|
| 248 |
-
\begin{aligned}
|
| 249 |
-
f^{t-a}(a)+f^{t-b}(b)+f^{t-c}(c) & =a+b+c \\
|
| 250 |
-
f^{t^{2}-a b}\left(t^{2}\right)+f^{t^{2}-t}\left(t^{2}\right)+f^{t^{2}-c}\left(t^{2}\right) & =a b+t+c \\
|
| 251 |
-
\Longrightarrow\left[f^{t-a}(t)-a\right]+\left[f^{t-b}(t)-b\right] & =\left[f^{t-a b}(t)-a b\right]
|
| 252 |
-
\end{aligned}
|
| 253 |
-
$$
|
| 254 |
-
|
| 255 |
-
by subtracting and applying the lemma repeatedly. In other words, we have proven the second lemma:
|
| 256 |
-
|
| 257 |
-
## Lemma
|
| 258 |
-
|
| 259 |
-
Let $t$ be fixed, and define $g_{t}(n)=f^{t-n}(t)-n$ for $n<t$. If $a, b \geq 2$ and $a b \mid t, a b<t$, then $g_{t}(a)+g_{t}(b)=g_{t}(a b)$.
|
| 260 |
-
|
| 261 |
-
Now let $a, b \geq 2$ be arbitrary, and let $p>q>\max \{a, b\}$ be primes. Suppose $s=a^{p} b^{q}$ and $t=s^{2}$; then
|
| 262 |
-
|
| 263 |
-
$$
|
| 264 |
-
p g_{t}(a)+q g_{t}(b)=g_{t}\left(a^{p} b^{q}\right)=g_{t}(s)=f^{s^{2}-s}(s)-s=0
|
| 265 |
-
$$
|
| 266 |
-
|
| 267 |
-
Now
|
| 268 |
-
|
| 269 |
-
$$
|
| 270 |
-
q \mid g_{t}(a)>-a \quad \text { and } \quad p \mid g_{t}(b)>-b \Longrightarrow g_{t}(a)=g_{t}(b)=0
|
| 271 |
-
$$
|
| 272 |
-
|
| 273 |
-
and so we conclude $f^{t-a}(t)=a$ and $f^{t-b}(t)=b$ for $a, b \geq 2$.
|
| 274 |
-
In particular, if $a=n$ and $b=n+1$ then we deduce $f(n+1)=n$ for all $n \geq 2$, as desired.
|
| 275 |
-
|
| 276 |
-
Remark. If you let $c=(a b)^{2}$ after the first lemma, you recover the 2-variable version!
|
| 277 |
-
|
| 278 |
-
## §3 Solutions to Day 3
|
| 279 |
-
|
| 280 |
-
## §3.1 TSTST 2013/7
|
| 281 |
-
|
| 282 |
-
Available online at https://aops.com/community/p3181485.
|
| 283 |
-
|
| 284 |
-
## Problem statement
|
| 285 |
-
|
| 286 |
-
A country has $n$ cities, labelled $1,2,3, \ldots, n$. It wants to build exactly $n-1$ roads between certain pairs of cities so that every city is reachable from every other city via some sequence of roads. However, it is not permitted to put roads between pairs of cities that have labels differing by exactly 1 , and it is also not permitted to put a road between cities 1 and $n$. Let $T_{n}$ be the total number of possible ways to build these roads.
|
| 287 |
-
(a) For all odd $n$, prove that $T_{n}$ is divisible by $n$.
|
| 288 |
-
(b) For all even $n$, prove that $T_{n}$ is divisible by $n / 2$.
|
| 289 |
-
|
| 290 |
-
You can just spin the tree!
|
| 291 |
-
Fixing $n$, the group $G=\mathbb{Z} / n \mathbb{Z}$ acts on the set of trees by rotation (where we imagine placing $1,2, \ldots, n$ along a circle).
|
| 292 |
-
|
| 293 |
-
Claim - For odd $n$, all trees have trivial stabilizer.
|
| 294 |
-
Proof. One way to see this is to look at the degree sequence. Suppose $g^{e}$ fixes a tree $T$. Then so does $g^{k}$, for $k=\operatorname{gcd}(e, n)$. Then it follows that $n / k$ divides $\sum_{v} \operatorname{deg} v=2 n-2$. Since $\operatorname{gcd}(2 n-2, n)=1$ we must then have $k=n$.
|
| 295 |
-
|
| 296 |
-
The proof for even $n$ is identical except that $\operatorname{gcd}(2 n-2, n)=2$ and hence each tree either has stabilizer with size $\leq 2$.
|
| 297 |
-
|
| 298 |
-
There is also a proof using linear algebra, using Kirchoff's tree formula. (Overkill.)
|
| 299 |
-
|
| 300 |
-
## §3.2 TSTST 2013/8
|
| 301 |
-
|
| 302 |
-
Available online at https://aops.com/community/p3181486.
|
| 303 |
-
|
| 304 |
-
## Problem statement
|
| 305 |
-
|
| 306 |
-
Define a function $f: \mathbb{N} \rightarrow \mathbb{N}$ by $f(1)=1, f(n+1)=f(n)+2^{f(n)}$ for every positive integer $n$. Prove that $f(1), f(2), \ldots, f\left(3^{2013}\right)$ leave distinct remainders when divided by $3^{2013}$.
|
| 307 |
-
|
| 308 |
-
I'll prove by induction on $k \geq 1$ that any $3^{k}$ consecutive values of $f$ produce distinct residues modulo $3^{k}$. The base case $k=1$ is easily checked ( $f$ is always odd, hence $f$ cycles $1,0,2 \bmod 3)$.
|
| 309 |
-
|
| 310 |
-
For the inductive step, assume it's true up to $k$. Since $2^{\bullet}\left(\bmod 3^{k+1}\right)$ cycles every $2 \cdot 3^{k}$, and $f$ is always odd, it follows that
|
| 311 |
-
|
| 312 |
-
$$
|
| 313 |
-
\begin{aligned}
|
| 314 |
-
f\left(n+3^{k}\right)-f(n) & =2^{f(n)}+2^{f(n+1)}+\cdots+2^{f\left(n+3^{k}-1\right)} \quad\left(\bmod 3^{k+1}\right) \\
|
| 315 |
-
& \equiv 2^{1}+2^{3}+\cdots+2^{2 \cdot 3^{k}-1} \quad\left(\bmod 3^{k+1}\right) \\
|
| 316 |
-
& =2 \cdot \frac{4^{3^{k}}-1}{4-1}
|
| 317 |
-
\end{aligned}
|
| 318 |
-
$$
|
| 319 |
-
|
| 320 |
-
Hence
|
| 321 |
-
|
| 322 |
-
$$
|
| 323 |
-
f\left(n+3^{k}\right)-f(n) \equiv C \quad\left(\bmod 3^{k+1}\right) \quad \text { where } \quad C=2 \cdot \frac{4^{3^{k}}-1}{4-1}
|
| 324 |
-
$$
|
| 325 |
-
|
| 326 |
-
noting that $C$ does not depend on $n$. Exponent lifting gives $\nu_{3}(C)=k$ hence $f(n)$, $f\left(n+3^{k}\right), f\left(n+2 \cdot 3^{k}\right)$ differ mod $3^{k+1}$ for all $n$, and the inductive hypothesis now solves the problem.
|
| 327 |
-
|
| 328 |
-
## §3.3 TSTST 2013/9
|
| 329 |
-
|
| 330 |
-
Available online at https://aops.com/community/p3181487.
|
| 331 |
-
|
| 332 |
-
## Problem statement
|
| 333 |
-
|
| 334 |
-
Let $r$ be a rational number in the interval $[-1,1]$ and let $\theta=\cos ^{-1} r$. Call a subset $S$ of the plane good if $S$ is unchanged upon rotation by $\theta$ around any point of $S$ (in both clockwise and counterclockwise directions). Determine all values of $r$ satisfying the following property: The midpoint of any two points in a good set also lies in the set.
|
| 335 |
-
|
| 336 |
-
The answer is that $r$ has this property if and only if $r=\frac{4 n-1}{4 n}$ for some integer $n$.
|
| 337 |
-
Throughout the solution, we will let $r=\frac{a}{b}$ with $b>0$ and $\operatorname{gcd}(a, b)=1$. We also let
|
| 338 |
-
|
| 339 |
-
$$
|
| 340 |
-
\omega=e^{i \theta}=\frac{a}{b} \pm \frac{\sqrt{b^{2}-a^{2}}}{b} i
|
| 341 |
-
$$
|
| 342 |
-
|
| 343 |
-
This means we may work with complex multiplication in the usual way; the rotation of $z$ through center $c$ is given by $z \mapsto \omega(z-c)+c$.
|
| 344 |
-
|
| 345 |
-
For most of our proof, we start by constructing a good set as follows.
|
| 346 |
-
|
| 347 |
-
- Start by letting $S_{0}=\{0,1\}$.
|
| 348 |
-
- Let $S_{i}$ consist of $S_{i-1}$ plus all points that can be obtained by rotating a point of $S_{i-1}$ through a different point of $S_{i-1}$ (with scale factor $\omega$ ).
|
| 349 |
-
- Let $S_{\infty}=\bigcup_{i \geq 0} S_{i}$.
|
| 350 |
-
|
| 351 |
-
The set $S_{\infty}$ is the (minimal, by inclusion) good set containing 0 and 1 . We are going to show that for most values of $r$, we have $\frac{1}{2} \notin S_{\infty}$.
|
| 352 |
-
|
| 353 |
-
Claim - If $b$ is odd, then $\frac{1}{2} \notin S_{\infty}$.
|
| 354 |
-
Proof. Idea: denominators that appear are always odd.
|
| 355 |
-
Consider the ring
|
| 356 |
-
|
| 357 |
-
$$
|
| 358 |
-
A=\mathbb{Z}_{\{b\}}=\left\{\frac{s}{t}|s, t \in \mathbb{Z}, t| b^{\infty}\right\}
|
| 359 |
-
$$
|
| 360 |
-
|
| 361 |
-
which consists of all rational numbers whose denominators divide $b^{\infty}$. Then, $0,1, \omega \in$ $A\left[\sqrt{b^{2}-a^{2}}\right]$ and hence $S_{\infty} \subseteq A\left[\sqrt{b^{2}-a^{2}}\right]$ too. (This works even if $\sqrt{b^{2}-a^{2}} \in \mathbb{Z}$, in which case $S_{\infty} \subseteq A=A\left[\sqrt{b^{2}-a^{2}}\right]$.)
|
| 362 |
-
But $\frac{1}{2} \notin A\left[\sqrt{b^{2}-a^{2}}\right]$.
|
| 363 |
-
|
| 364 |
-
Claim - If $b$ is even and $|b-a| \neq 1$, then $\frac{1}{2} \notin S_{\infty}$.
|
| 365 |
-
Proof. Idea: take modulo a prime dividing $b-a$.
|
| 366 |
-
Let $D=b^{2}-a^{2} \equiv 3(\bmod 4)$. Let $p$ be a prime divisor of $b-a$. Because $\operatorname{gcd}(a, b)=1$, we have $p \neq 2$ and $p \nmid b$.
|
| 367 |
-
|
| 368 |
-
Consider the ring
|
| 369 |
-
|
| 370 |
-
$$
|
| 371 |
-
A=\mathbb{Z}_{(p)}=\left\{\left.\frac{s}{t} \right\rvert\, s, t \in \mathbb{Z}, p \perp t\right\}
|
| 372 |
-
$$
|
| 373 |
-
|
| 374 |
-
which consists of all rational numbers whose denominators are coprime to $p$. Then, $0,1, \omega \in A[\sqrt{-D}]$ and hence $S_{\infty} \subseteq A[\sqrt{-D}]$ too.
|
| 375 |
-
|
| 376 |
-
Now, there is a well-defined "mod- $p$ " ring homomorphism
|
| 377 |
-
|
| 378 |
-
$$
|
| 379 |
-
\Psi: A[\sqrt{-D}] \rightarrow \mathbb{F}_{p} \quad \text { by } \quad x+y \sqrt{-D} \mapsto x \bmod p
|
| 380 |
-
$$
|
| 381 |
-
|
| 382 |
-
which commutes with addition and multiplication (as $p \mid D$ ). Under this map,
|
| 383 |
-
|
| 384 |
-
$$
|
| 385 |
-
\omega \mapsto \frac{a}{b} \bmod p=1
|
| 386 |
-
$$
|
| 387 |
-
|
| 388 |
-
Consequently, the rotation $z \mapsto \omega(z-c)+c$ is just the identity map modulo $p$. In other words, the pre-image of any point in $S_{\infty}$ under $\Psi$ must be either $\Psi(0)=0$ or $\Psi(1)=1$.
|
| 389 |
-
|
| 390 |
-
However, $\Psi(1 / 2)=1 / 2$ is neither of these. So this point cannot be achieved.
|
| 391 |
-
|
| 392 |
-
Claim - Suppose $a=2 n-1$ and $b=2 n$ for $n$ an odd integer. Then $\frac{1}{2} \notin S_{\infty}$
|
| 393 |
-
|
| 394 |
-
Proof. Idea: $\omega$ is "algebraic integer" sans odd denominators.
|
| 395 |
-
This time, we define the ring
|
| 396 |
-
|
| 397 |
-
$$
|
| 398 |
-
B=\mathbb{Z}_{(2)}=\left\{\left.\frac{s}{t} \right\rvert\, s, t \in \mathbb{Z}, t \text { odd }\right\}
|
| 399 |
-
$$
|
| 400 |
-
|
| 401 |
-
of rational numbers with odd denominator. We carefully consider the ring $B[\omega]$ where
|
| 402 |
-
|
| 403 |
-
$$
|
| 404 |
-
\omega=\frac{2 n-1 \pm \sqrt{1-4 n}}{2 n}
|
| 405 |
-
$$
|
| 406 |
-
|
| 407 |
-
So $S_{\infty} \subseteq B[\omega]$ as $0,1, \omega \in B[\omega]$.
|
| 408 |
-
I claim that $B[\omega]$ is an integral extension of $B$; equivalently that $\omega$ is integral over $B$. Indeed, $\omega$ is the root of the monic polynomial
|
| 409 |
-
|
| 410 |
-
$$
|
| 411 |
-
(T-1)^{2}+\frac{1}{n}(T-1)-\frac{1}{n}=0
|
| 412 |
-
$$
|
| 413 |
-
|
| 414 |
-
where $\frac{1}{n} \in B$ makes sense as $n$ is odd.
|
| 415 |
-
On the other hand, $\frac{1}{2}$ is not integral over $B$ so it is not an element of $B[\omega]$.
|
| 416 |
-
It remains to show that if $r=\frac{4 n-1}{4 n}$, then goods sets satisfy the midpoint property. Again starting from the points $z_{0}=0, z_{1}=1$ construct the sequence
|
| 417 |
-
|
| 418 |
-
$$
|
| 419 |
-
\begin{aligned}
|
| 420 |
-
z_{2} & =\omega\left(z_{1}-z_{0}\right)+z_{0} \\
|
| 421 |
-
z_{3} & =\omega^{-1}\left(z_{0}-z_{2}\right)+z_{2} \\
|
| 422 |
-
z_{4} & =\omega^{-1}\left(z_{2}-z_{3}\right)+z_{3} \\
|
| 423 |
-
z_{5} & =\omega\left(z_{3}-z_{4}\right)+z_{4}
|
| 424 |
-
\end{aligned}
|
| 425 |
-
$$
|
| 426 |
-
|
| 427 |
-
as shown in the diagram below.
|
| 428 |
-
|
| 429 |
-
|
| 430 |
-
This construction shows that if we have the length-one segment $\{0,1\}$ then we can construct the length-one segment $\{2 r-2,2 r-1\}$. In other words, we can shift the segment to the left by
|
| 431 |
-
|
| 432 |
-
$$
|
| 433 |
-
1-(2 r-1)=2(1-r)=\frac{1}{2 n}
|
| 434 |
-
$$
|
| 435 |
-
|
| 436 |
-
Repeating this construction $n$ times gives the desired midpoint $\frac{1}{2}$.
|
| 437 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2014.md
DELETED
|
@@ -1,254 +0,0 @@
|
|
| 1 |
-
# TSTST 2014 Solution Notes
|
| 2 |
-
|
| 3 |
-
## Lincoln, Nebraska
|
| 4 |
-
|
| 5 |
-
## Evan Chen《陳誼廷》
|
| 6 |
-
|
| 7 |
-
15 April 2024
|
| 8 |
-
|
| 9 |
-
This is a compilation of solutions for the 2014 TSTST. The ideas of the solution are a mix of my own work, the solutions provided by the competition organizers, and solutions found by the community. However, all the writing is maintained by me.
|
| 10 |
-
|
| 11 |
-
These notes will tend to be a bit more advanced and terse than the "official" solutions from the organizers. In particular, if a theorem or technique is not known to beginners but is still considered "standard", then I often prefer to use this theory anyways, rather than try to work around or conceal it. For example, in geometry problems I typically use directed angles without further comment, rather than awkwardly work around configuration issues. Similarly, sentences like "let $\mathbb{R}$ denote the set of real numbers" are typically omitted entirely.
|
| 12 |
-
|
| 13 |
-
Corrections and comments are welcome!
|
| 14 |
-
|
| 15 |
-
## Contents
|
| 16 |
-
|
| 17 |
-
0 Problems ..... 2
|
| 18 |
-
1 Solutions to Day 1 ..... 3
|
| 19 |
-
1.1 TSTST 2014/1 ..... 3
|
| 20 |
-
1.2 TSTST 2014/2 ..... 4
|
| 21 |
-
1.3 TSTST 2014/3 ..... 5
|
| 22 |
-
2 Solutions to Day 2 ..... 6
|
| 23 |
-
2.1 TSTST 2014/4 ..... 6
|
| 24 |
-
2.2 TSTST 2014/5 ..... 7
|
| 25 |
-
2.3 TSTST 2014/6 ..... 8
|
| 26 |
-
|
| 27 |
-
## §0 Problems
|
| 28 |
-
|
| 29 |
-
1. Let $\leftarrow$ denote the left arrow key on a standard keyboard. If one opens a text editor and types the keys "ab $\leftarrow \mathrm{cd} \leftarrow \leftarrow \mathrm{e} \leftarrow \leftarrow \mathrm{f}$ ", the result is "faecdb". We say that a string $B$ is reachable from a string $A$ if it is possible to insert some amount of $\leftarrow$ 's in $A$, such that typing the resulting characters produces $B$. So, our example shows that "faecdb" is reachable from "abcdef".
|
| 30 |
-
|
| 31 |
-
Prove that for any two strings $A$ and $B, A$ is reachable from $B$ if and only if $B$ is reachable from $A$.
|
| 32 |
-
2. Consider a convex pentagon circumscribed about a circle. We name the lines that connect vertices of the pentagon with the opposite points of tangency with the circle gergonnians.
|
| 33 |
-
(a) Prove that if four gergonnians are concurrent, then all five of them are concurrent.
|
| 34 |
-
(b) Prove that if there is a triple of gergonnians that are concurrent, then there is another triple of gergonnians that are concurrent.
|
| 35 |
-
3. Find all polynomials $P(x)$ with real coefficients that satisfy
|
| 36 |
-
|
| 37 |
-
$$
|
| 38 |
-
P(x \sqrt{2})=P\left(x+\sqrt{1-x^{2}}\right)
|
| 39 |
-
$$
|
| 40 |
-
|
| 41 |
-
for all real numbers $x$ with $|x| \leq 1$.
|
| 42 |
-
4. Let $P(x)$ and $Q(x)$ be arbitrary polynomials with real coefficients, with $P \neq 0$, and let $d=\operatorname{deg} P$. Prove that there exist polynomials $A(x)$ and $B(x)$, not both zero, such that $\max \{\operatorname{deg} A, \operatorname{deg} B\} \leq d / 2$ and $P(x) \mid A(x)+Q(x) \cdot B(x)$.
|
| 43 |
-
5. Find the maximum number $E$ such that the following holds: there is an edge-colored graph with 60 vertices and $E$ edges, with each edge colored either red or blue, such that in that coloring, there is no monochromatic cycles of length 3 and no monochromatic cycles of length 5 .
|
| 44 |
-
6. Suppose we have distinct positive integers $a, b, c, d$ and an odd prime $p$ not dividing any of them, and an integer $M$ such that if one considers the infinite sequence
|
| 45 |
-
|
| 46 |
-
$$
|
| 47 |
-
\begin{gathered}
|
| 48 |
-
c a-d b \\
|
| 49 |
-
c a^{2}-d b^{2} \\
|
| 50 |
-
c a^{3}-d b^{3} \\
|
| 51 |
-
c a^{4}-d b^{4}
|
| 52 |
-
\end{gathered}
|
| 53 |
-
$$
|
| 54 |
-
|
| 55 |
-
and looks at the highest power of $p$ that divides each of them, these powers are not all zero, and are all at most $M$. Prove that there exists some $T$ (which may depend on $a, b, c, d, p, M)$ such that whenever $p$ divides an element of this sequence, the maximum power of $p$ that divides that element is exactly $p^{T}$.
|
| 56 |
-
|
| 57 |
-
## §1 Solutions to Day 1
|
| 58 |
-
|
| 59 |
-
## §1.1 TSTST 2014/1
|
| 60 |
-
|
| 61 |
-
Available online at https://aops.com/community/p3549404.
|
| 62 |
-
|
| 63 |
-
## Problem statement
|
| 64 |
-
|
| 65 |
-
Let $\leftarrow$ denote the left arrow key on a standard keyboard. If one opens a text editor and types the keys "ab $\leftarrow \mathrm{cd} \leftarrow \leftarrow \mathrm{e} \leftarrow \leftarrow \mathrm{f}$ ", the result is "faecdb". We say that a string $B$ is reachable from a string $A$ if it is possible to insert some amount of $\leftarrow$ 's in $A$, such that typing the resulting characters produces $B$. So, our example shows that "faecdb" is reachable from "abcdef".
|
| 66 |
-
|
| 67 |
-
Prove that for any two strings $A$ and $B, A$ is reachable from $B$ if and only if $B$ is reachable from $A$.
|
| 68 |
-
|
| 69 |
-
Obviously $A$ and $B$ should have the same multiset of characters, and we focus only on that situation.
|
| 70 |
-
|
| 71 |
-
Claim - If $A=123 \ldots n$ and $B=\sigma(1) \sigma(2) \ldots \sigma(n)$ is a permutation of $A$, then $B$ is reachable if and only if it is $\mathbf{2 1 3}$-avoiding, i.e. there are no indices $i<j<k$ such that $\sigma(j)<\sigma(i)<\sigma(k)$.
|
| 72 |
-
|
| 73 |
-
Proof. This is clearly necessary. To see its sufficient, one can just type $B$ inductively: after typing $k$, the only way to get stuck is if $k+1$ is to the right of $k$ and there is some character in the way; this gives a 213 pattern.
|
| 74 |
-
|
| 75 |
-
Claim - A permutation $\sigma$ on $\{1, \ldots, n\}$ is 213 -avoiding if and only if the inverse $\sigma^{-1}$ is.
|
| 76 |
-
|
| 77 |
-
Proof. Suppose $i<j<k$ and $\sigma(j)<\sigma(i)<\sigma(k)$. Let $i^{\prime}=\sigma(j), j^{\prime}=\sigma(i), k^{\prime}=\sigma(k)$; then $i^{\prime}<j^{\prime}<k^{\prime}$ and $\sigma^{-1}\left(j^{\prime}\right)<\sigma^{-1}\left(i^{\prime}\right)<\sigma^{-1}\left(k^{\prime}\right)$.
|
| 78 |
-
|
| 79 |
-
This essentially finishes the problem. Suppose $B$ is reachable from $A$. By using the typing pattern, we get some permutation $\sigma:\{1, \ldots, n\}$ such that the $i$ th character of $A$ is the $\sigma(i)$ th character of $B$, and which is 213 -avoiding by the claim. (The permutation is unique if $A$ has all distinct characters, but there could be multiple if $A$ has repeated ones.) Then $\sigma^{-1}$ is 213 -avoiding too and gives us a way to change $B$ into $A$.
|
| 80 |
-
|
| 81 |
-
## §1.2 TSTST 2014/2
|
| 82 |
-
|
| 83 |
-
Available online at https://aops.com/community/p3549405.
|
| 84 |
-
|
| 85 |
-
## Problem statement
|
| 86 |
-
|
| 87 |
-
Consider a convex pentagon circumscribed about a circle. We name the lines that connect vertices of the pentagon with the opposite points of tangency with the circle gergonnians.
|
| 88 |
-
(a) Prove that if four gergonnians are concurrent, then all five of them are concurrent.
|
| 89 |
-
(b) Prove that if there is a triple of gergonnians that are concurrent, then there is another triple of gergonnians that are concurrent.
|
| 90 |
-
|
| 91 |
-
This problem is insta-killed by taking a homography sending the concurrency point (in either part) to the center of the circle while fixing the incircle. Alternatively, one may send any four of the tangency points to a rectangle.
|
| 92 |
-
Here are the details. Let $A B C D E$ be a pentagon with gergonnians $\overline{A V}, \overline{B W}, \overline{C X}$, $\overline{D Y}, \overline{E Z}$. We prove the following lemma, which (up to a suitable permutation of point names) solves both parts (a) and (b).
|
| 93 |
-
|
| 94 |
-
## Lemma
|
| 95 |
-
|
| 96 |
-
The gergonnians $\overline{A V}, \overline{C X}, \overline{D Y}$ are concurrent if and only if the gergonnians $\overline{A V}$, $\overline{B W}, \overline{E Z}$ are concurrent.
|
| 97 |
-
|
| 98 |
-
Proof. We prove the first set implies the second (the converse direction being identical). Suppose $\overline{A V}, \overline{C X}, \overline{D Y}$ intersect at $P$ and take a homography fixing the circle and moving $P$ to its center.
|
| 99 |
-
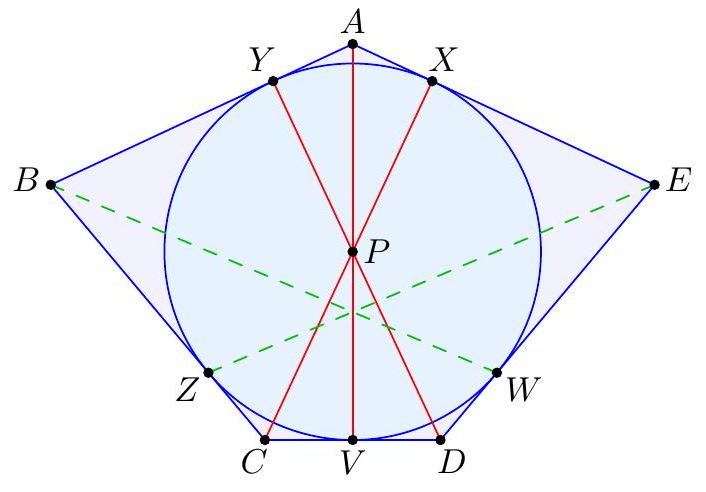
|
| 100 |
-
|
| 101 |
-
Then $X$ and $Y$ are symmetric around $\overline{A P V}$ by hypothesis. Since $D=\overline{V V} \cap \overline{P Y}$, $C=\overline{V V} \cap \overline{P X}$, it follows that $C$ and $D$, and hence $Z$ and $W$, are also symmetric around $\overline{A P V}$. Consequently $B$ and $E$ are symmetric too. So $\overline{B W}$ and $\overline{E Z}$ meet on $\overline{A V}$.
|
| 102 |
-
|
| 103 |
-
## §1.3 TSTST 2014/3
|
| 104 |
-
|
| 105 |
-
Available online at https://aops.com/community/p3549407.
|
| 106 |
-
|
| 107 |
-
## Problem statement
|
| 108 |
-
|
| 109 |
-
Find all polynomials $P(x)$ with real coefficients that satisfy
|
| 110 |
-
|
| 111 |
-
$$
|
| 112 |
-
P(x \sqrt{2})=P\left(x+\sqrt{1-x^{2}}\right)
|
| 113 |
-
$$
|
| 114 |
-
|
| 115 |
-
for all real numbers $x$ with $|x| \leq 1$.
|
| 116 |
-
|
| 117 |
-
The answer is any polynomial of the form $P(x)=f(U(x / \sqrt{2}))$, where $f \in \mathbb{R}[x]$ and $U$ is the unique polynomial satisfying $U(\cos \theta)=\cos (8 \theta)$.
|
| 118 |
-
|
| 119 |
-
Let $Q(x)=P(x \sqrt{2})$, then the condition reads
|
| 120 |
-
|
| 121 |
-
$$
|
| 122 |
-
Q(\cos \theta)=Q\left(\frac{1}{\sqrt{2}}(\cos \theta+\sin \theta)\right)=Q\left(\cos \left(\theta-45^{\circ}\right)\right) \quad \forall 0 \leq \theta \leq 180^{\circ} .
|
| 123 |
-
$$
|
| 124 |
-
|
| 125 |
-
We call a polynomial good if it satisfies this functional equation.
|
| 126 |
-
|
| 127 |
-
## Lemma
|
| 128 |
-
|
| 129 |
-
The minimal (by degree) good nonconstant polynomial is $U$.
|
| 130 |
-
|
| 131 |
-
Proof. Since $U$ works, it suffices to show that $\operatorname{deg} Q \geq 8$. Note that:
|
| 132 |
-
|
| 133 |
-
$$
|
| 134 |
-
\begin{aligned}
|
| 135 |
-
Q\left(\cos 136^{\circ}\right) & =Q\left(\cos 91^{\circ}\right)=Q\left(\cos 46^{\circ}\right)=Q\left(\cos 1^{\circ}\right)=Q\left(\cos -44^{\circ}\right) \\
|
| 136 |
-
& =Q\left(\cos 44^{\circ}\right)=Q\left(\cos 89^{\circ}\right)=Q\left(\cos 134^{\circ}\right)=Q\left(\cos 179^{\circ}\right)
|
| 137 |
-
\end{aligned}
|
| 138 |
-
$$
|
| 139 |
-
|
| 140 |
-
Hence $Q$ is equal at eight distinct values (not nine since $\cos -44^{\circ}=\cos 44^{\circ}$ is repeated), so $\operatorname{deg} Q \geq 8$ (unless $Q$ is constant).
|
| 141 |
-
|
| 142 |
-
Now, we claim $Q(x) \equiv f(U(x))$ for some $f \in \mathbb{R}[x]$. Indeed, if $Q$ is good, then by minimality the quotient $Q \bmod U$ must be constant, so $Q(x)=\widetilde{Q}(x) \cdot U(x)+c$ for some constant $c$, but then $\widetilde{Q}(x)$ is good too and we finish iteratively.
|
| 143 |
-
|
| 144 |
-
## §2 Solutions to Day 2
|
| 145 |
-
|
| 146 |
-
## §2.1 TSTST 2014/4
|
| 147 |
-
|
| 148 |
-
Available online at https://aops.com/community/p3549409.
|
| 149 |
-
|
| 150 |
-
## Problem statement
|
| 151 |
-
|
| 152 |
-
Let $P(x)$ and $Q(x)$ be arbitrary polynomials with real coefficients, with $P \neq 0$, and let $d=\operatorname{deg} P$. Prove that there exist polynomials $A(x)$ and $B(x)$, not both zero, such that $\max \{\operatorname{deg} A, \operatorname{deg} B\} \leq d / 2$ and $P(x) \mid A(x)+Q(x) \cdot B(x)$.
|
| 153 |
-
|
| 154 |
-
Let $V$ be the vector space of real polynomials with degree at most $d / 2$. Consider maps of linear spaces
|
| 155 |
-
|
| 156 |
-
$$
|
| 157 |
-
\begin{aligned}
|
| 158 |
-
V^{\oplus 2} & \rightarrow \mathbb{R}[x] /(P(x)) \\
|
| 159 |
-
\text { by } \quad(A, B) & \mapsto A+Q B \quad(\bmod P) .
|
| 160 |
-
\end{aligned}
|
| 161 |
-
$$
|
| 162 |
-
|
| 163 |
-
The domain has dimension
|
| 164 |
-
|
| 165 |
-
$$
|
| 166 |
-
2(\lfloor d / 2\rfloor+1)
|
| 167 |
-
$$
|
| 168 |
-
|
| 169 |
-
while the codomain has dimension $d$. For dimension reasons it has nontrivial kernel.
|
| 170 |
-
|
| 171 |
-
## §2.2 TSTST 2014/5
|
| 172 |
-
|
| 173 |
-
Available online at https://aops.com/community/p3549412.
|
| 174 |
-
|
| 175 |
-
## Problem statement
|
| 176 |
-
|
| 177 |
-
Find the maximum number $E$ such that the following holds: there is an edge-colored graph with 60 vertices and $E$ edges, with each edge colored either red or blue, such that in that coloring, there is no monochromatic cycles of length 3 and no monochromatic cycles of length 5 .
|
| 178 |
-
|
| 179 |
-
The answer is $E=30^{2}+2 \cdot 15^{2}=6 \cdot 15^{2}=1350$.
|
| 180 |
-
First, we prove $E \leq 1350$. Observe that:
|
| 181 |
-
Claim - $G$ contains no $K_{5}$.
|
| 182 |
-
Proof. It's a standard fact that the only triangle-free two-coloring of the edges of $K_{5}$ is the union of two monochromatic $C_{5}$ 's.
|
| 183 |
-
|
| 184 |
-
Hence by Turán theorem we have $E \leq\binom{ 4}{2} \cdot 15^{2}=1350$.
|
| 185 |
-
To show this is achievable, take a red $K_{30,30}$, and on each side draw a blue $K_{15,15}$. This graph has no monochromatic odd cycles at all as desired.
|
| 186 |
-
|
| 187 |
-
## §2.3 TSTST 2014/6
|
| 188 |
-
|
| 189 |
-
Available online at https://aops.com/community/p3549417.
|
| 190 |
-
|
| 191 |
-
## Problem statement
|
| 192 |
-
|
| 193 |
-
Suppose we have distinct positive integers $a, b, c, d$ and an odd prime $p$ not dividing any of them, and an integer $M$ such that if one considers the infinite sequence
|
| 194 |
-
|
| 195 |
-
$$
|
| 196 |
-
\begin{gathered}
|
| 197 |
-
c a-d b \\
|
| 198 |
-
c a^{2}-d b^{2} \\
|
| 199 |
-
c a^{3}-d b^{3} \\
|
| 200 |
-
c a^{4}-d b^{4}
|
| 201 |
-
\end{gathered}
|
| 202 |
-
$$
|
| 203 |
-
|
| 204 |
-
and looks at the highest power of $p$ that divides each of them, these powers are not all zero, and are all at most $M$. Prove that there exists some $T$ (which may depend on $a, b, c, d, p, M)$ such that whenever $p$ divides an element of this sequence, the maximum power of $p$ that divides that element is exactly $p^{T}$.
|
| 205 |
-
|
| 206 |
-
By orders, the indices of terms divisible by $p$ is an arithmetic subsequence of $\mathbb{N}$ : say they are $\kappa, \kappa+\lambda, \kappa+2 \lambda, \ldots$, where $\lambda$ is the order of $a / b$. That means we want
|
| 207 |
-
|
| 208 |
-
$$
|
| 209 |
-
\nu_{p}\left(c a^{\kappa+n \lambda}-d b^{\kappa+n \lambda}\right)=\nu_{p}\left(\left(\frac{a^{\lambda}}{b^{\lambda}}\right)^{n}-\frac{d a^{\kappa}}{c b^{\kappa}}\right)
|
| 210 |
-
$$
|
| 211 |
-
|
| 212 |
-
to be constant. Thus, we have reduced the problem to the following proposition:
|
| 213 |
-
|
| 214 |
-
## Proposition
|
| 215 |
-
|
| 216 |
-
Let $p$ be an odd prime. Let $x, y \in \mathbb{Q}_{>0}$ such that $x \equiv y \equiv 1(\bmod p)$. If the sequence $\nu_{p}\left(x^{n}-y\right)$ of positive integers is nonconstant, then it is unbounded.
|
| 217 |
-
|
| 218 |
-
For this it would be sufficient to prove the following claim.
|
| 219 |
-
Claim - Let $p$ be an odd prime. Let $x, y \in \mathbb{Q}>0$ such that $x \equiv y \equiv 1(\bmod p)$. Suppose $m$ and $n$ are positive integers such that
|
| 220 |
-
|
| 221 |
-
$$
|
| 222 |
-
d=\nu_{p}\left(x^{n}-y\right)<\nu_{p}\left(x^{m}-y\right)=e .
|
| 223 |
-
$$
|
| 224 |
-
|
| 225 |
-
Then there exists $\ell$ such that $\nu_{p}\left(x^{\ell}-y\right) \geq e+1$.
|
| 226 |
-
Proof. First, note that $\nu_{p}\left(x^{m}-x^{n}\right)=\nu_{p}\left(\left(x^{m}-y\right)-\left(x^{n}-y\right)\right)=d$ and so by exponent lifting we can find some $k$ such that
|
| 227 |
-
|
| 228 |
-
$$
|
| 229 |
-
\nu_{p}\left(x^{k}-1\right)=e
|
| 230 |
-
$$
|
| 231 |
-
|
| 232 |
-
namely $k=p^{e-d}|m-n|$. (In fact, one could also choose more carefully $k=p^{e-d} \cdot \operatorname{gcd}(m-$ $\left.n, p^{\infty}\right)$, so that $k$ is a power of $p$.)
|
| 233 |
-
|
| 234 |
-
Suppose we set $x^{k}=p^{e} u+1$ and $x^{m}=p^{e} v+y$ where $u, v \in \mathbb{Q}$ aren't divisible by $p$. Now for any integer $1 \leq r \leq p-1$ we consider
|
| 235 |
-
|
| 236 |
-
$$
|
| 237 |
-
\begin{aligned}
|
| 238 |
-
x^{k r+m}-y & =\left(p^{e} u+1\right)^{r} \cdot\left(p^{e} v+y\right)-y \\
|
| 239 |
-
& =p^{e}(v+y u \cdot r)+p^{2 e}(\ldots)
|
| 240 |
-
\end{aligned}
|
| 241 |
-
$$
|
| 242 |
-
|
| 243 |
-
By selecting $r$ with $r \equiv-v / u(\bmod p)$, we ensure $p^{e+1} \mid x^{k r+m}-y$, hence $\ell=k r+m$ is as desired.
|
| 244 |
-
|
| 245 |
-
Remark. One way to motivate the proof of the claim is as follows. Suppose we are given $\nu_{p}\left(x^{m}-y\right)=e$, and we wish to find $\ell$ such that $\nu_{p}\left(x^{\ell}-y\right)>e$. Then, it is necessary (albeit insufficient) that
|
| 246 |
-
|
| 247 |
-
$$
|
| 248 |
-
x^{\ell-m} \equiv 1 \quad\left(\bmod p^{e}\right) \text { but } x^{\ell-m} \not \equiv 1 \quad\left(\bmod p^{e+1}\right)
|
| 249 |
-
$$
|
| 250 |
-
|
| 251 |
-
In particular, we need $\nu_{p}\left(x^{\ell-m}-1\right)=e$ exactly. So the $k$ in the claim must exist if we are going to succeed.
|
| 252 |
-
|
| 253 |
-
On the other hand, if $k$ is some integer for which $\nu_{p}\left(x^{k}-1\right)=e$, then by choosing $\ell-m$ to be some multiple of $k$ with no extra factors of $p$, we hope that we can get $\nu_{p}\left(x^{\ell}-y\right)=e+1$. That's why we write $\ell=k r+m$ and see what happens when we expand.
|
| 254 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2015.md
DELETED
|
@@ -1,304 +0,0 @@
|
|
| 1 |
-
# TSTST 2015 Solution Notes
|
| 2 |
-
|
| 3 |
-
## Pittsburgh, PA
|
| 4 |
-
|
| 5 |
-
Evan Chen《陳誼廷》
|
| 6 |
-
|
| 7 |
-
15 April 2024
|
| 8 |
-
|
| 9 |
-
This is a compilation of solutions for the 2015 TSTST. The ideas of the solution are a mix of my own work, the solutions provided by the competition organizers, and solutions found by the community. However, all the writing is maintained by me.
|
| 10 |
-
|
| 11 |
-
These notes will tend to be a bit more advanced and terse than the "official" solutions from the organizers. In particular, if a theorem or technique is not known to beginners but is still considered "standard", then I often prefer to use this theory anyways, rather than try to work around or conceal it. For example, in geometry problems I typically use directed angles without further comment, rather than awkwardly work around configuration issues. Similarly, sentences like "let $\mathbb{R}$ denote the set of real numbers" are typically omitted entirely.
|
| 12 |
-
|
| 13 |
-
Corrections and comments are welcome!
|
| 14 |
-
|
| 15 |
-
## Contents
|
| 16 |
-
|
| 17 |
-
0 Problems ..... 2
|
| 18 |
-
1 Solutions to Day 1 ..... 3
|
| 19 |
-
1.1 TSTST 2015/1, proposed by Mark Sellke ..... 3
|
| 20 |
-
1.2 TSTST 2015/2, proposed by Ivan Borsenco
|
| 21 |
-
1.3 TSTST 2015/3, proposed by Alex Zhai
|
| 22 |
-
2 Solutions to Day 2 ..... 6
|
| 23 |
-
2.1 TSTST 2015/4, proposed by Alyazeed Basyoni ..... 6
|
| 24 |
-
2.2 TSTST 2015/5
|
| 25 |
-
2.3 TSTST 2015/6, proposed by Linus Hamilton
|
| 26 |
-
|
| 27 |
-
## §0 Problems
|
| 28 |
-
|
| 29 |
-
1. Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of real numbers, and let $m$ be a fixed positive integer less than $n$. We say an index $k$ with $1 \leq k \leq n$ is good if there exists some $\ell$ with $1 \leq \ell \leq m$ such that
|
| 30 |
-
|
| 31 |
-
$$
|
| 32 |
-
a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0
|
| 33 |
-
$$
|
| 34 |
-
|
| 35 |
-
where the indices are taken modulo $n$. Let $T$ be the set of all good indices. Prove that
|
| 36 |
-
|
| 37 |
-
$$
|
| 38 |
-
\sum_{k \in T} a_{k} \geq 0
|
| 39 |
-
$$
|
| 40 |
-
|
| 41 |
-
2. Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
| 42 |
-
3. Let $P$ be the set of all primes, and let $M$ be a non-empty subset of $P$. Suppose that for any non-empty subset $\left\{p_{1}, p_{2}, \ldots, p_{k}\right\}$ of $M$, all prime factors of $p_{1} p_{2} \ldots p_{k}+1$ are also in $M$. Prove that $M=P$.
|
| 43 |
-
4. Let $x, y, z$ be real numbers (not necessarily positive) such that $x^{4}+y^{4}+z^{4}+x y z=4$. Prove that $x \leq 2$ and
|
| 44 |
-
|
| 45 |
-
$$
|
| 46 |
-
\sqrt{2-x} \geq \frac{y+z}{2}
|
| 47 |
-
$$
|
| 48 |
-
|
| 49 |
-
5. Let $\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\varphi(n)=m$ has at least 2015 solutions in $n$.
|
| 50 |
-
6. A Nim-style game is defined as follows. Two positive integers $k$ and $n$ are specified, along with a finite set $S$ of $k$-tuples of integers (not necessarily positive). At the start of the game, the $k$-tuple $(~ n, 0,0, \ldots, 0)$ is written on the blackboard.
|
| 51 |
-
A legal move consists of erasing the tuple $\left(a_{1}, a_{2}, \ldots, a_{k}\right)$ which is written on the blackboard and replacing it with $\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{k}+b_{k}\right)$, where $\left(b_{1}, b_{2}, \ldots, b_{k}\right)$ is an element of the set $S$. Two players take turns making legal moves, and the first to write a negative integer loses. In the event that neither player is ever forced to write a negative integer, the game is a draw.
|
| 52 |
-
Prove that there is a choice of $k$ and $S$ with the following property: the first player has a winning strategy if $n$ is a power of 2 , and otherwise the second player has a winning strategy.
|
| 53 |
-
|
| 54 |
-
## §1 Solutions to Day 1
|
| 55 |
-
|
| 56 |
-
## §1.1 TSTST 2015/1, proposed by Mark Sellke
|
| 57 |
-
|
| 58 |
-
Available online at https://aops.com/community/p5017901.
|
| 59 |
-
|
| 60 |
-
## Problem statement
|
| 61 |
-
|
| 62 |
-
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of real numbers, and let $m$ be a fixed positive integer less than $n$. We say an index $k$ with $1 \leq k \leq n$ is good if there exists some $\ell$ with $1 \leq \ell \leq m$ such that
|
| 63 |
-
|
| 64 |
-
$$
|
| 65 |
-
a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0
|
| 66 |
-
$$
|
| 67 |
-
|
| 68 |
-
where the indices are taken modulo $n$. Let $T$ be the set of all good indices. Prove that
|
| 69 |
-
|
| 70 |
-
$$
|
| 71 |
-
\sum_{k \in T} a_{k} \geq 0
|
| 72 |
-
$$
|
| 73 |
-
|
| 74 |
-
First we prove the result if the indices are not taken modulo $n$. Call a number $\ell$-good if $\ell$ is the smallest number such that $a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0$, and $\ell \leq m$. Then if $a_{k}$ is $\ell$-good, the numbers $a_{k+1}, \ldots, a_{k+\ell-1}$ are good as well.
|
| 75 |
-
|
| 76 |
-
Then by greedy from left to right, we can group all the good numbers into blocks with nonnegative sums. Repeatedly take the first good number, if $\ell$-good, group it with the next $\ell$ numbers. An example for $m=3$ :
|
| 77 |
-
|
| 78 |
-
$$
|
| 79 |
-
\langle 4\rangle \quad \begin{array}{ccccccccc}
|
| 80 |
-
-1 & -2 & 6\rangle & -9 & -7 & \langle 3\rangle & \langle-2 & 4\rangle & \langle-1 .
|
| 81 |
-
\end{array}
|
| 82 |
-
$$
|
| 83 |
-
|
| 84 |
-
We can now return to the original problem. Let $N$ be a large integer; applying the algorithm to $N$ copies of the sequence, we deduce that
|
| 85 |
-
|
| 86 |
-
$$
|
| 87 |
-
N \sum_{k \in T} a_{k}+c_{N} \geq 0
|
| 88 |
-
$$
|
| 89 |
-
|
| 90 |
-
where $c_{N}$ represents some "error" from left-over terms. As $\left|c_{N}\right| \leq \sum\left|a_{i}\right|$, by taking $N$ large enough we deduce the problem.
|
| 91 |
-
|
| 92 |
-
Remark. This solution was motivated by looking at the case $m=1$, realizing how dumb it was, then looking at $m=2$, and realizing it was equally dumb.
|
| 93 |
-
|
| 94 |
-
## §1.2 TSTST 2015/2, proposed by Ivan Borsenco
|
| 95 |
-
|
| 96 |
-
Available online at https://aops.com/community/p5017915.
|
| 97 |
-
|
| 98 |
-
## Problem statement
|
| 99 |
-
|
| 100 |
-
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
| 101 |
-
|
| 102 |
-
The main content of the problem:
|
| 103 |
-
Claim - $\angle H X_{a} G=90^{\circ}$.
|
| 104 |
-
This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.)
|
| 105 |
-
In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$.
|
| 106 |
-
First proof by Brokard. To do this, it suffices to show that $M$ has the same power with respect to the circle with diameter $\overline{A H}$ and the circle with diameter $\overline{K L}$. In fact I claim both circles are orthogonal to the circle with diameter $\overline{B C}$ ! The former follows from Brokard's theorem, noting that $A$ is on the polar of $H$, and the latter follows from the harmonic bundle.
|
| 107 |
-
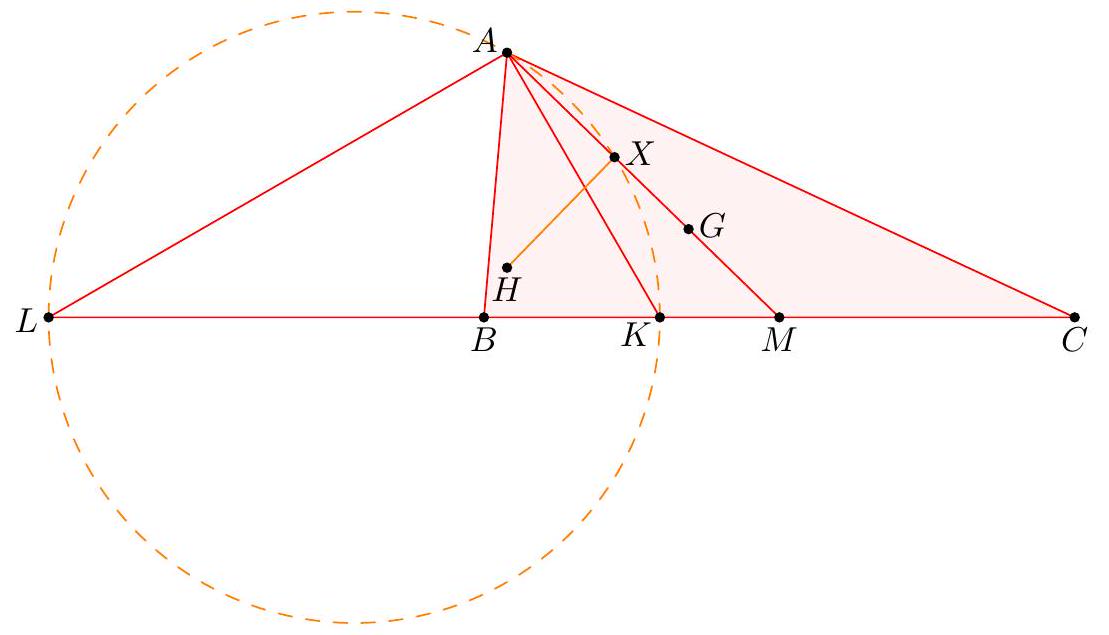
|
| 108 |
-
|
| 109 |
-
Then $\overline{A M}$ is the radical axis, so $X$ lies on both circles.
|
| 110 |
-
Second proof by orthocenter reflection, Bendit Chan. As before, we know $M X \cdot M A=$ $M K \cdot M L=M B \cdot M C$, but $X$ lies inside segment $A M$. Construct parallelogram $A B A^{\prime} C$. Then $M X \cdot M A^{\prime}=M B \cdot M C$, so $X B A^{\prime} C$ is concyclic.
|
| 111 |
-
|
| 112 |
-
However, it is well-known the circumcircle of $\triangle B A^{\prime} C$ (which is the reflection of $(A B C)$ across $\overline{B C}$ ) passes through $H$ and in fact has diameter $\overline{A^{\prime} H}$. So this gives $\angle H X A^{\prime}=90^{\circ}$ as needed.
|
| 113 |
-
Third proof by barycentric coordinates. Alternatively we may just compute $X=\left(a^{2}\right.$ : $\left.2 S_{A}: 2 S_{A}\right)$. Let $F=\left(0: S_{C}: S_{B}\right)$ be the foot from $H$. Then we check that $X H F M$ is cyclic, which is power of a point from $A$.
|
| 114 |
-
|
| 115 |
-
## §1.3 TSTST 2015/3, proposed by Alex Zhai
|
| 116 |
-
|
| 117 |
-
Available online at https://aops.com/community/p5017928.
|
| 118 |
-
|
| 119 |
-
## Problem statement
|
| 120 |
-
|
| 121 |
-
Let $P$ be the set of all primes, and let $M$ be a non-empty subset of $P$. Suppose that for any non-empty subset $\left\{p_{1}, p_{2}, \ldots, p_{k}\right\}$ of $M$, all prime factors of $p_{1} p_{2} \ldots p_{k}+1$ are also in $M$. Prove that $M=P$.
|
| 122 |
-
|
| 123 |
-
The following solution was found by user Aiscrim on AOPS.
|
| 124 |
-
Obviously $|M|=\infty$. Assume for contradiction $p \notin M$. We say a prime $q \in M$ is sparse if there are only finitely many elements of $M$ which are $q(\bmod p)$ (in particular there are finitely many sparse primes).
|
| 125 |
-
|
| 126 |
-
Now let $C$ be the product of all sparse primes (note $p \nmid C$ ). First, set $a_{0}=1$. For $k \geq 0$, consider then the prime factorization of the number
|
| 127 |
-
|
| 128 |
-
$$
|
| 129 |
-
C a_{k}+1
|
| 130 |
-
$$
|
| 131 |
-
|
| 132 |
-
No prime in its factorization is sparse, so consider the number $a_{k+1}$ obtained by replacing each prime in its factorization with some arbitrary representative of that prime's residue class. In this way we select a number $a_{k+1}$ such that
|
| 133 |
-
|
| 134 |
-
- $a_{k+1} \equiv C a_{k}+1(\bmod p)$, and
|
| 135 |
-
- $a_{k+1}$ is a product of distinct primes in $M$.
|
| 136 |
-
|
| 137 |
-
In particular, $a_{k} \equiv C^{k}+C^{k-1}+\cdots+1(\bmod p)$
|
| 138 |
-
But since $C \not \equiv 0(\bmod p)$, we can find a $k$ such that $a_{k} \equiv 0(\bmod p)($ namely, $k=p-1$ if $C \equiv 1$ and $k=p-2$ else) which is clearly impossible since $a_{k}$ is a product of primes in $M$ !
|
| 139 |
-
|
| 140 |
-
## §2 Solutions to Day 2
|
| 141 |
-
|
| 142 |
-
## §2.1 TSTST 2015/4, proposed by Alyazeed Basyoni
|
| 143 |
-
|
| 144 |
-
Available online at https://aops.com/community/p5017801.
|
| 145 |
-
|
| 146 |
-
## Problem statement
|
| 147 |
-
|
| 148 |
-
Let $x, y, z$ be real numbers (not necessarily positive) such that $x^{4}+y^{4}+z^{4}+x y z=4$. Prove that $x \leq 2$ and
|
| 149 |
-
|
| 150 |
-
$$
|
| 151 |
-
\sqrt{2-x} \geq \frac{y+z}{2}
|
| 152 |
-
$$
|
| 153 |
-
|
| 154 |
-
We prove that the condition $x^{4}+y^{4}+z^{4}+x y z=4$ implies
|
| 155 |
-
|
| 156 |
-
$$
|
| 157 |
-
\sqrt{2-x} \geq \frac{y+z}{2}
|
| 158 |
-
$$
|
| 159 |
-
|
| 160 |
-
We first prove the easy part.
|
| 161 |
-
Claim - We have $x \leq 2$.
|
| 162 |
-
Proof. Indeed, AM-GM gives that
|
| 163 |
-
|
| 164 |
-
$$
|
| 165 |
-
\begin{aligned}
|
| 166 |
-
5=x^{4}+y^{4}+\left(z^{4}+1\right)+x y z & =\frac{3 x^{4}}{4}+\left(\frac{x^{4}}{4}+y^{4}\right)+\left(z^{4}+1\right)+x y z \\
|
| 167 |
-
& \geq \frac{3 x^{4}}{4}+x^{2} y^{2}+2 z^{2}+x y z .
|
| 168 |
-
\end{aligned}
|
| 169 |
-
$$
|
| 170 |
-
|
| 171 |
-
We evidently have that $x^{2} y^{2}+2 z^{2}+x y z \geq 0$ because the quadratic form $a^{2}+a b+2 b^{2}$ is positive definite, so $x^{4} \leq \frac{20}{3} \Longrightarrow x \leq 2$.
|
| 172 |
-
|
| 173 |
-
Now, the desired statement is implied by its square, so it suffices to show that
|
| 174 |
-
|
| 175 |
-
$$
|
| 176 |
-
2-x \geq\left(\frac{y+z}{2}\right)^{2}
|
| 177 |
-
$$
|
| 178 |
-
|
| 179 |
-
We are going to proceed by contradiction (it seems that many solutions do this) and assume that
|
| 180 |
-
|
| 181 |
-
$$
|
| 182 |
-
2-x<\left(\frac{y+z}{2}\right)^{2} \Longleftrightarrow 4 x+y^{2}+2 y z+z^{2}>8
|
| 183 |
-
$$
|
| 184 |
-
|
| 185 |
-
By AM-GM,
|
| 186 |
-
|
| 187 |
-
$$
|
| 188 |
-
\begin{aligned}
|
| 189 |
-
x^{4}+3 & \geq 4 x \\
|
| 190 |
-
\frac{y^{4}+1}{2} & \geq y^{2} \\
|
| 191 |
-
\frac{z^{4}+1}{2} & \geq z^{2}
|
| 192 |
-
\end{aligned}
|
| 193 |
-
$$
|
| 194 |
-
|
| 195 |
-
which yields that
|
| 196 |
-
|
| 197 |
-
$$
|
| 198 |
-
x^{4}+\frac{y^{4}+z^{4}}{2}+2 y z+4>8
|
| 199 |
-
$$
|
| 200 |
-
|
| 201 |
-
If we replace $x^{4}=4-\left(y^{4}+z^{4}+x y z\right)$ now, this gives
|
| 202 |
-
|
| 203 |
-
$$
|
| 204 |
-
-\frac{y^{4}+z^{4}}{2}+(2-x) y z>0 \Longrightarrow(2-x) y z>\frac{y^{4}+z^{4}}{2}
|
| 205 |
-
$$
|
| 206 |
-
|
| 207 |
-
Since $2-x$ and the right-hand side are positive, we have $y z \geq 0$. Now
|
| 208 |
-
|
| 209 |
-
$$
|
| 210 |
-
\frac{y^{4}+z^{4}}{2 y z}<2-x<\left(\frac{y+z}{2}\right)^{2} \Longrightarrow 2 y^{4}+2 z^{4}<y z(y+z)^{2}=y^{3} z+2 y^{2} z^{2}+y z^{3}
|
| 211 |
-
$$
|
| 212 |
-
|
| 213 |
-
This is clearly false by AM-GM, so we have a contradiction.
|
| 214 |
-
|
| 215 |
-
## §2.2 TSTST 2015/5
|
| 216 |
-
|
| 217 |
-
Available online at https://aops.com/community/p5017821.
|
| 218 |
-
|
| 219 |
-
## Problem statement
|
| 220 |
-
|
| 221 |
-
Let $\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\varphi(n)=m$ has at least 2015 solutions in $n$.
|
| 222 |
-
|
| 223 |
-
Here are two explicit solutions.
|
| 224 |
-
『 First solution with ad-hoc subsets, by Evan Chen. I consider the following eleven prime numbers:
|
| 225 |
-
|
| 226 |
-
$$
|
| 227 |
-
S=\{11,13,17,19,29,31,37,41,43,61,71\}
|
| 228 |
-
$$
|
| 229 |
-
|
| 230 |
-
This has the property that for any $p \in S$, all prime factors of $p-1$ are one digit.
|
| 231 |
-
Let $N=(210)^{\text {billion }}$, and consider $M=\varphi(N)$. For any subset $T \subset S$, we have
|
| 232 |
-
|
| 233 |
-
$$
|
| 234 |
-
M=\varphi\left(\frac{N}{\prod_{p \in T}(p-1)} \prod_{p \in T} p\right)
|
| 235 |
-
$$
|
| 236 |
-
|
| 237 |
-
Since $2^{|S|}>2015$ we're done.
|
| 238 |
-
Remark. This solution is motivated by the deep fact that $\varphi(11 \cdot 1000)=\varphi(10 \cdot 1000)$, for example.
|
| 239 |
-
|
| 240 |
-
【 Second solution with smallest primes, by Yang Liu. Let $2=p_{1}<p_{2}<\cdots<p_{2015}$ be the smallest 2015 primes. Then the 2015 numbers
|
| 241 |
-
|
| 242 |
-
$$
|
| 243 |
-
\begin{aligned}
|
| 244 |
-
n_{1} & =\left(p_{1}-1\right) p_{2} \ldots p_{2015} \\
|
| 245 |
-
n_{2} & =p_{1}\left(p_{2}-1\right) \ldots p_{2015} \\
|
| 246 |
-
& \vdots \\
|
| 247 |
-
n_{2015} & =p_{1} p_{2} \ldots\left(p_{2015}-1\right)
|
| 248 |
-
\end{aligned}
|
| 249 |
-
$$
|
| 250 |
-
|
| 251 |
-
all have the same phi value, namely
|
| 252 |
-
|
| 253 |
-
$$
|
| 254 |
-
\varphi\left(p_{1} p_{2} \ldots p_{2015}\right)=\prod_{i=1}^{2015}\left(p_{i}-1\right)
|
| 255 |
-
$$
|
| 256 |
-
|
| 257 |
-
## §2.3 TSTST 2015/6, proposed by Linus Hamilton
|
| 258 |
-
|
| 259 |
-
Available online at https://aops.com/community/p5017871.
|
| 260 |
-
|
| 261 |
-
## Problem statement
|
| 262 |
-
|
| 263 |
-
A Nim-style game is defined as follows. Two positive integers $k$ and $n$ are specified, along with a finite set $S$ of $k$-tuples of integers (not necessarily positive). At the start of the game, the $k$-tuple $(n, 0,0, \ldots, 0)$ is written on the blackboard.
|
| 264 |
-
A legal move consists of erasing the tuple $\left(a_{1}, a_{2}, \ldots, a_{k}\right)$ which is written on the blackboard and replacing it with $\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{k}+b_{k}\right)$, where $\left(b_{1}, b_{2}, \ldots, b_{k}\right)$ is an element of the set $S$. Two players take turns making legal moves, and the first to write a negative integer loses. In the event that neither player is ever forced to write a negative integer, the game is a draw.
|
| 265 |
-
|
| 266 |
-
Prove that there is a choice of $k$ and $S$ with the following property: the first player has a winning strategy if $n$ is a power of 2 , and otherwise the second player has a winning strategy.
|
| 267 |
-
|
| 268 |
-
Here we present a solution with 14 registers and 22 moves. Initially $X=n$ and all other variables are zero.
|
| 269 |
-
|
| 270 |
-
|
| 271 |
-
Now, the "game" is played as follows. The mechanics are controlled by the turn counters $A$ and $B$.
|
| 272 |
-
|
| 273 |
-
Observe the game starts with Alice playing Init. Thereafter, we say that the game is
|
| 274 |
-
|
| 275 |
-
- In the main part if $A+B=1$, and no one has played Init a second time.
|
| 276 |
-
- In the death part otherwise.
|
| 277 |
-
|
| 278 |
-
Observe that in the main state, on Alice's turn we always have $(A, B)=(1,0)$ and on Bob's turn we always have $(A, B)=(0,1)$.
|
| 279 |
-
|
| 280 |
-
Claim - A player who plays Init a second time must lose. In particular, a player who makes a move when $A=B=0$ must lose.
|
| 281 |
-
|
| 282 |
-
Proof. Situations with $A+B \geq 2$ cannot occur during main part, so there are only a few possibilities.
|
| 283 |
-
|
| 284 |
-
- Suppose the offending player is in a situation where $A=B=0$. Then he/she must play Init. At this point, the opposing player can respond by playing Kill. Then the offending player must play Init again. The opposing player now responds with Kill'. This iteration continues until $X$ reaches a negative number and the offending player loses.
|
| 285 |
-
- Suppose Alice has $(A, B)=(1,0)$ but plays Init again anyways. Then Bob responds with PunB to punish her; he then wins as in the first case.
|
| 286 |
-
- Suppose Bob has $(A, B)=(0,1)$ but plays Init again anyways. Alice responds with PunA in the same way.
|
| 287 |
-
|
| 288 |
-
Thus we may assume that players avoid the death part at all costs. Hence the second moves consist of Bob playing Sleep, and then Alice playing Begin (thus restoring the value of $n$ in $X$ ), then Bob playing Sleep.
|
| 289 |
-
|
| 290 |
-
Now we return to analysis of the main part. We say the game is in state $S$ for $S \in$ $\left\{S_{X}^{0}, S_{X}, S_{X}^{\prime}, S_{Y}^{0}, S_{Y}, S_{Y}^{\prime}, \mathrm{Cl}\right\}$ if $S=1$ and all other variables are zero. By construction, this is always the case. From then on the main part is divided into several phases:
|
| 291 |
-
|
| 292 |
-
- An $X$-phase: this begins with Alice at $S_{X}^{0}$, and ends when the game is in a state other than $S_{X}$ and $S_{X}^{\prime}$. (She can never return to $S_{X}^{0}$ during an $X$-phase.)
|
| 293 |
-
- A $Y$-phase: this begins with Alice at $S_{Y}^{0}$, and ends when the game is in a state other than $S_{Y}$ and $S_{Y}^{\prime}$. (She can never return to $S_{Y}^{0}$ during a $Y$-phase.)
|
| 294 |
-
|
| 295 |
-
Claim - Consider an $X$-phase in which $(X, Y)=(x, 0), x>1$. Then Alice can complete the phase without losing if and only if $x$ is even; if so she begins a $Y$-phase with $(X, Y)=(0, x / 2)$.
|
| 296 |
-
|
| 297 |
-
Proof. As $x>1$, Alice cannot play ClaimX since Bob will respond with FakeX and win. Now by alternating between WorkX and WorkX', Alice can repeatedly deduct 2 from $X$ and add 1 to $Y$, leading to $(x-2, y+1),(x-4, y+2)$, and so on. (During this time, Bob can only play Sleep.) Eventually, she must stop this process by playing DoneX, which begins a $Y$-phase.
|
| 298 |
-
|
| 299 |
-
Now note that unless $X=0$, Bob now has a winning move WrongX. Conversely he may only play Sleep if $X=0$.
|
| 300 |
-
|
| 301 |
-
We have an analogous claim for $Y$-phases. Thus if $n$ is not a power of 2 , we see that Alice eventually loses.
|
| 302 |
-
|
| 303 |
-
Now suppose $n=2^{k}$; then Alice reaches $(X, Y)=\left(0,2^{k-1}\right),\left(2^{k-2}, 0\right), \ldots$ until either reaching $(1,0)$ or $(0,1)$. At this point she can play ClaimX or ClaimY, respectively; the game is now in state Cl. Bob cannot play either FakeX or FakeY, so he must play Sleep, and then Alice wins by playing Win. Thus Alice has a winning strategy when $n=2^{k}$.
|
| 304 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2016.md
DELETED
|
@@ -1,278 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2016 Solutions <br> United States of America - TST Selection Test <br> Evan Chen《陳誼廷》 <br> $58^{\text {th }}$ IMO 2017 Brazil and $6^{\text {th }}$ EGMO 2017 Switzerland
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 3
|
| 7 |
-
1.1 TSTST 2016/1, proposed by Victor Wang ..... 3
|
| 8 |
-
1.2 TSTST 2016/2, proposed by Evan Chen ..... 4
|
| 9 |
-
1.3 TSTST 2016/3, proposed by Yang Liu ..... 6
|
| 10 |
-
2 Solutions to Day 2 ..... 8
|
| 11 |
-
2.1 TSTST 2016/4, proposed by Linus Hamilton ..... 8
|
| 12 |
-
2.2 TSTST 2016/5, proposed by Linus Hamilton, Cynthia Stoner ..... 9
|
| 13 |
-
2.3 TSTST 2016/6, proposed by Danielle Wang ..... 10
|
| 14 |
-
|
| 15 |
-
## §0 Problems
|
| 16 |
-
|
| 17 |
-
1. Let $A=A(x, y)$ and $B=B(x, y)$ be two-variable polynomials with real coefficients. Suppose that $A(x, y) / B(x, y)$ is a polynomial in $x$ for infinitely many values of $y$, and a polynomial in $y$ for infinitely many values of $x$. Prove that $B$ divides $A$, meaning there exists a third polynomial $C$ with real coefficients such that $A=B \cdot C$.
|
| 18 |
-
2. Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose the circle $\gamma$ with diameter $\overline{A H}$ meets the circumcircle of $A B C$ at $G \neq A$, and meets line $\overline{A N}$ at $Q \neq A$. The tangent to $\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\triangle G N Q$ and $\triangle M B C$ intersect on $\overline{P N}$.
|
| 19 |
-
3. Decide whether or not there exists a nonconstant polynomial $Q(x)$ with integer coefficients with the following property: for every positive integer $n>2$, the numbers
|
| 20 |
-
|
| 21 |
-
$$
|
| 22 |
-
Q(0), Q(1), Q(2), \ldots, Q(n-1)
|
| 23 |
-
$$
|
| 24 |
-
|
| 25 |
-
produce at most $0.499 n$ distinct residues when taken modulo $n$.
|
| 26 |
-
4. Prove that if $n$ and $k$ are positive integers satisfying $\varphi^{k}(n)=1$, then $n \leq 3^{k}$. (Here $\varphi^{k}$ denotes $k$ applications of the Euler phi function.)
|
| 27 |
-
5. In the coordinate plane are finitely many walls, which are disjoint line segments, none of which are parallel to either axis. A bulldozer starts at an arbitrary point and moves in the $+x$ direction. Every time it hits a wall, it turns at a right angle to its path, away from the wall, and continues moving. (Thus the bulldozer always moves parallel to the axes.)
|
| 28 |
-
Prove that it is impossible for the bulldozer to hit both sides of every wall.
|
| 29 |
-
6. Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\overline{B C}, \overline{C A}$, $\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\overline{E F}$. Suppose that the circumcircle of $\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\triangle B B_{1} B_{2}$ and $\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\overline{D K}$.
|
| 30 |
-
|
| 31 |
-
## §1 Solutions to Day 1
|
| 32 |
-
|
| 33 |
-
## §1.1 TSTST 2016/1, proposed by Victor Wang
|
| 34 |
-
|
| 35 |
-
Available online at https://aops.com/community/p6575197.
|
| 36 |
-
|
| 37 |
-
## Problem statement
|
| 38 |
-
|
| 39 |
-
Let $A=A(x, y)$ and $B=B(x, y)$ be two-variable polynomials with real coefficients. Suppose that $A(x, y) / B(x, y)$ is a polynomial in $x$ for infinitely many values of $y$, and a polynomial in $y$ for infinitely many values of $x$. Prove that $B$ divides $A$, meaning there exists a third polynomial $C$ with real coefficients such that $A=B \cdot C$.
|
| 40 |
-
|
| 41 |
-
This is essentially an application of the division algorithm, but the details require significant care.
|
| 42 |
-
|
| 43 |
-
First, we claim that $A / B$ can be written as a polynomial in $x$ whose coefficients are rational functions in $y$. To see this, use the division algorithm to get
|
| 44 |
-
|
| 45 |
-
$$
|
| 46 |
-
A=Q \cdot B+R \quad Q, R \in(\mathbb{R}(y))[x]
|
| 47 |
-
$$
|
| 48 |
-
|
| 49 |
-
where $Q$ and $R$ are polynomials in $x$ whose coefficients are rational functions in $y$, and moreover $\operatorname{deg}_{x} B>\operatorname{deg}_{x} R$.
|
| 50 |
-
|
| 51 |
-
Now, we claim that $R \equiv 0$. Indeed, we have by hypothesis that for infinitely many values of $y_{0}$ that $B\left(x, y_{0}\right)$ divides $A\left(x, y_{0}\right)$, which means $B\left(x, y_{0}\right) \mid R\left(x, y_{0}\right)$ as polynomials in $\mathbb{R}[x]$. Now, we have $\operatorname{deg}_{x} B\left(x, y_{0}\right)>\operatorname{deg}_{x} R\left(x, y_{0}\right)$ outside of finitely many values of $y_{0}$ (but not all of them!); this means for infinitely many $y_{0}$ we have $R\left(x, y_{0}\right) \equiv 0$. So each coefficient of $x^{i}$ (in $\left.\mathbb{R}(y)\right)$ has infinitely many roots, hence is a zero polynomial.
|
| 52 |
-
|
| 53 |
-
Consequently, we are able to write $A / B=F(x, y) / M(y)$ where $F \in \mathbb{R}[x, y]$ and $M \in \mathbb{R}[y]$ are each polynomials. Repeating the same argument now gives
|
| 54 |
-
|
| 55 |
-
$$
|
| 56 |
-
\frac{A}{B}=\frac{F(x, y)}{M(y)}=\frac{G(x, y)}{N(x)}
|
| 57 |
-
$$
|
| 58 |
-
|
| 59 |
-
Now, by unique factorization of polynomials in $\mathbb{R}[x, y]$, we can discuss GCD's. So, we tacitly assume $\operatorname{gcd}(F, M)=\operatorname{gcd}(G, N)=(1)$. Also, we obviously have $\operatorname{gcd}(M, N)=(1)$. But $F \cdot N=G \cdot M$, so $M \mid F \cdot N$, thus we conclude $M$ is the constant polynomial. This implies the result.
|
| 60 |
-
|
| 61 |
-
Remark. This fact does not generalize to arbitrary functions that are separately polynomial: see e.g. http://aops.com/community/c6h523650p2978180.
|
| 62 |
-
|
| 63 |
-
## §1.2 TSTST 2016/2, proposed by Evan Chen
|
| 64 |
-
|
| 65 |
-
Available online at https://aops.com/community/p6575204.
|
| 66 |
-
|
| 67 |
-
## Problem statement
|
| 68 |
-
|
| 69 |
-
Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose the circle $\gamma$ with diameter $\overline{A H}$ meets the circumcircle of $A B C$ at $G \neq A$, and meets line $\overline{A N}$ at $Q \neq A$. The tangent to $\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\triangle G N Q$ and $\triangle M B C$ intersect on $\overline{P N}$.
|
| 70 |
-
|
| 71 |
-
We present two solutions, one using essentially only power of a point, and the other more involved.
|
| 72 |
-
|
| 73 |
-
【 First solution (found by contestants). Denote by $\triangle D E F$ the orthic triangle. Observe $\overline{P A}$ and $\overline{P G}$ are tangents to $\gamma$, since $\overline{O M}$ is the perpendicular bisector of $\overline{A G}$. Also note that $\overline{A G}, \overline{E F}, \overline{B C}$ are concurrent at some point $R$ by radical axis on $(A B C), \gamma$, (BFEC).
|
| 74 |
-
|
| 75 |
-
Now, consider circles (PAGM), (MFDNE), and (MBC). We already saw the point $R$ satisfies
|
| 76 |
-
|
| 77 |
-
$$
|
| 78 |
-
R A \cdot R G=R E \cdot R F=R B \cdot R C
|
| 79 |
-
$$
|
| 80 |
-
|
| 81 |
-
and hence has equal powers to all three circles; but since the circles at $M$ already, they must actually be coaxial. Assume they meet again at $T \in \overline{R M}$, say. Then $\angle P T M$ and $\angle M T N$ are both right angles, hence $T$ lies on $\overline{P N}$.
|
| 82 |
-
|
| 83 |
-
Finally $H$ is the orthocenter of $\triangle A R N$, and thus the circle with diameter $\overline{R N}$ passes through $G, Q, N$.
|
| 84 |
-
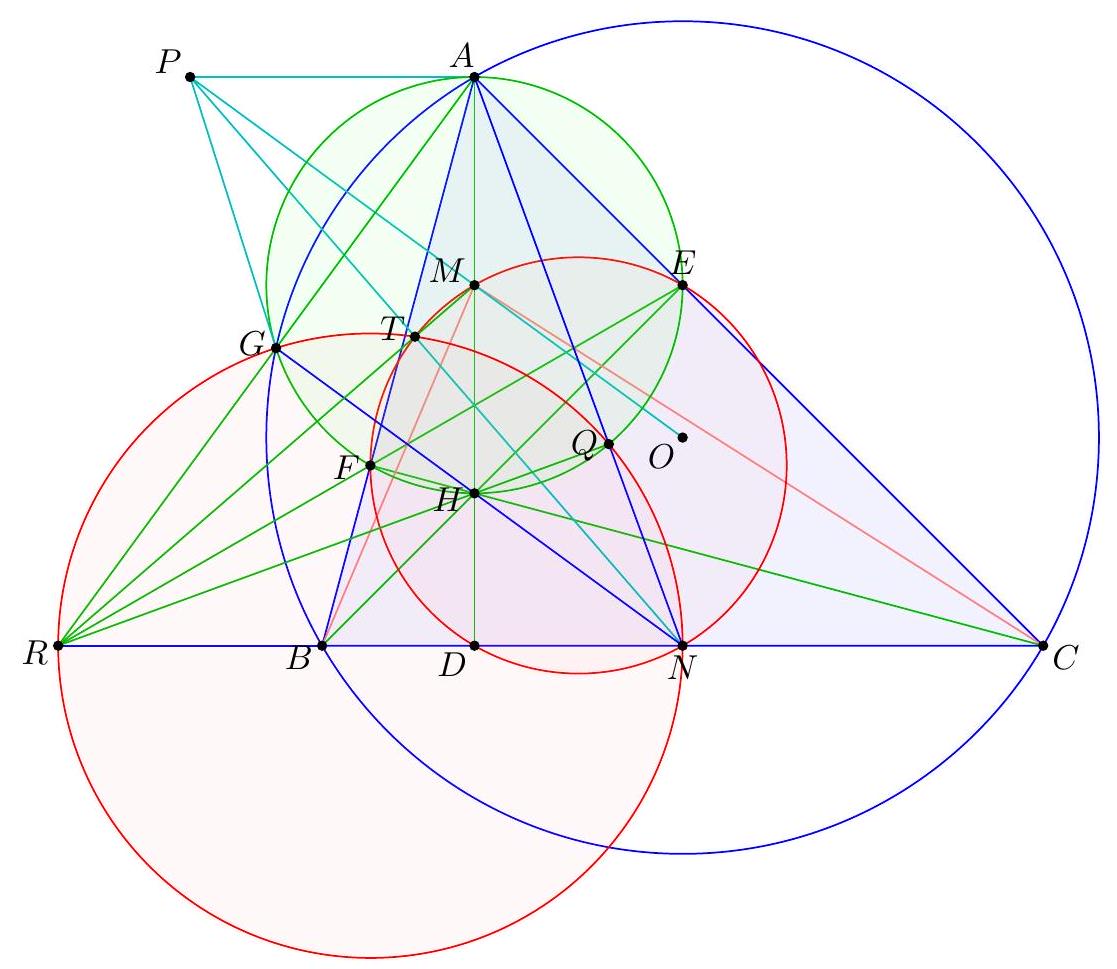
|
| 85 |
-
|
| 86 |
-
『 Alternate solution (by proposer). Let $L$ be diametrically opposite $A$ on the circumcircle. Denote by $\triangle D E F$ the orthic triangle. Let $X=\overline{A H} \cap \overline{E F}$. Finally, let $T$ be the second intersection of (MFDNE) and (MBC).
|
| 87 |
-
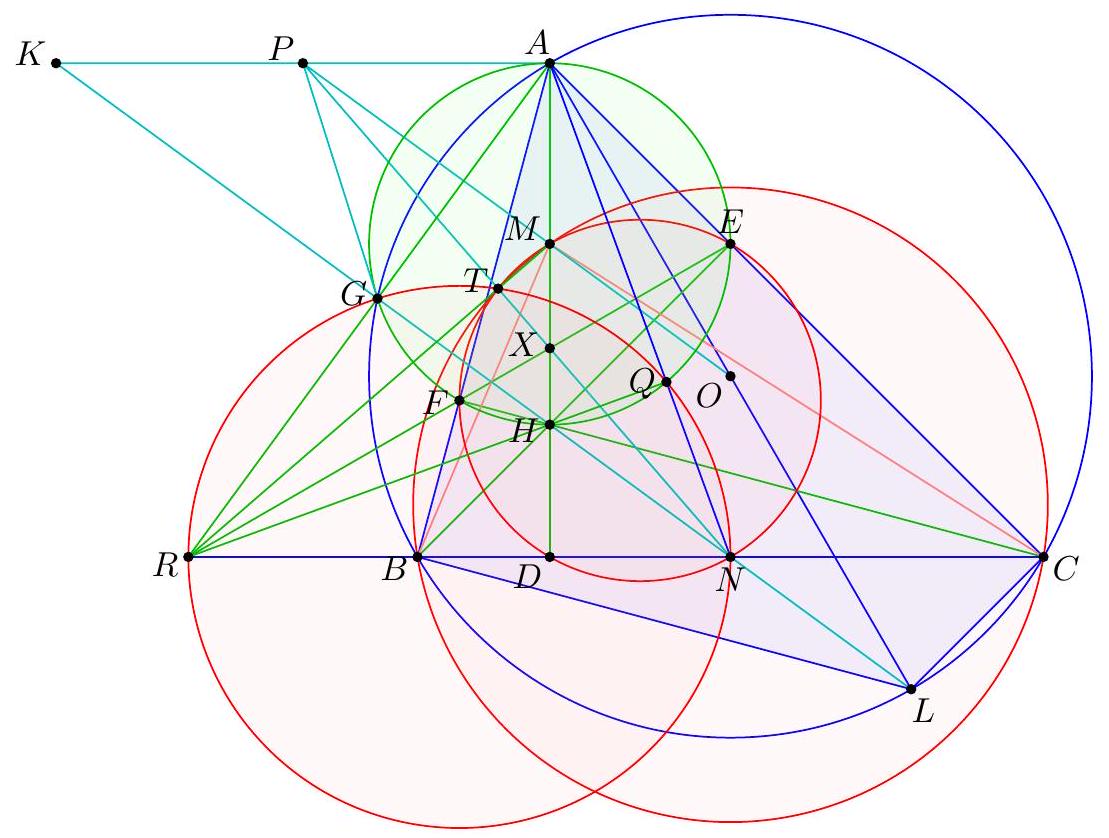
|
| 88 |
-
|
| 89 |
-
We begin with a few easy observations. First, points $H, G, N, L$ are collinear and $\angle A G L=90^{\circ}$. Also, $Q$ is the foot from $H$ to $\overline{A N}$. Consequently, lines $A G, E F, H Q$, $B C, T M$ concur at a point $R$ (radical axis). Moreover, we already know $\angle M T N=90^{\circ}$. This implies $T$ lies on the circle with diameter $\overline{R N}$, which is exactly the circumcircle of $\triangle G Q N$.
|
| 90 |
-
|
| 91 |
-
Note by Brokard's Theorem on $A F H E$, the point $X$ is the orthocenter of $\triangle M B C$. But $\angle M T N=90^{\circ}$ already, and $N$ is the midpoint of $\overline{B C}$. Consequently, points $T, X$, $N$ are collinear.
|
| 92 |
-
|
| 93 |
-
Finally, we claim $P, X, N$ are collinear, which solves the problem. Note $P=\overline{G G} \cap \overline{A A}$. Set $K=\overline{H N L} \cap \overline{A P}$. Then by noting
|
| 94 |
-
|
| 95 |
-
$$
|
| 96 |
-
-1=(D, X ; A, H) \stackrel{N}{=}(\infty, \overline{N X} \cap \overline{A K} ; A, K)
|
| 97 |
-
$$
|
| 98 |
-
|
| 99 |
-
we see that $\overline{N X}$ bisects segment $\overline{A K}$, as desired. (A more projective finish is to show that $\overline{P X N}$ is the polar of $R$ to $\gamma$ ).
|
| 100 |
-
|
| 101 |
-
Remark. The original problem proposal reads as follows:
|
| 102 |
-
Let $A B C$ be a triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose ray $O M$ meets the line parallel to $\overline{B C}$ through $A$ at $P$. Prove that the line through the circumcenter of $\triangle M B C$ and the midpoint of $\overline{O H}$ is parallel to $\overline{N P}$.
|
| 103 |
-
The points $G$ and $Q$ were added to the picture later to prevent the problem from being immediate by coordinates.
|
| 104 |
-
|
| 105 |
-
## §1.3 TSTST 2016/3, proposed by Yang Liu
|
| 106 |
-
|
| 107 |
-
Available online at https://aops.com/community/p6575217.
|
| 108 |
-
|
| 109 |
-
## Problem statement
|
| 110 |
-
|
| 111 |
-
Decide whether or not there exists a nonconstant polynomial $Q(x)$ with integer coefficients with the following property: for every positive integer $n>2$, the numbers
|
| 112 |
-
|
| 113 |
-
$$
|
| 114 |
-
Q(0), Q(1), Q(2), \ldots, Q(n-1)
|
| 115 |
-
$$
|
| 116 |
-
|
| 117 |
-
produce at most $0.499 n$ distinct residues when taken modulo $n$.
|
| 118 |
-
|
| 119 |
-
We claim that
|
| 120 |
-
|
| 121 |
-
$$
|
| 122 |
-
Q(x)=420\left(x^{2}-1\right)^{2}
|
| 123 |
-
$$
|
| 124 |
-
|
| 125 |
-
works. Clearly, it suffices to prove the result when $n=4$ and when $n$ is an odd prime $p$. The case $n=4$ is trivial, so assume now $n=p$ is an odd prime.
|
| 126 |
-
|
| 127 |
-
First, we prove the following easy claim.
|
| 128 |
-
Claim - For any odd prime $p$, there are at least $\frac{1}{2}(p-3)$ values of $a$ for which $\left(\frac{1-a^{2}}{p}\right)=+1$.
|
| 129 |
-
|
| 130 |
-
Proof. Note that if $k \neq 0$ and $k^{2} \neq-1$, then $a=\frac{1-k^{2}}{k^{2}+1}$ works.
|
| 131 |
-
Remark. The above identity comes from starting with the equation $1-a^{2}=b^{2}$, and writing it as $\left(\frac{1}{b}\right)^{2}-\left(\frac{a}{b}\right)^{2}=1$. Then solve $\frac{1}{b}-\frac{a}{b}=k$ and $\frac{1}{b}+\frac{a}{b}=1 / k$ for $a$.
|
| 132 |
-
|
| 133 |
-
Let $F(x)=\left(x^{2}-1\right)^{2}$. The range of $F$ modulo $p$ is contained within the $\frac{1}{2}(p+1)$ quadratic residues modulo $p$. On the other hand, if for some $t$ neither of $1 \pm t$ is a quadratic residue, then $t^{2}$ is omitted from the range of $F$ as well. Call such a value of $t$ useful, and let $N$ be the number of useful residues. We aim to show $N \geq \frac{1}{4} p-2$.
|
| 134 |
-
|
| 135 |
-
We compute a lower bound on the number $N$ of useful $t$ by writing
|
| 136 |
-
|
| 137 |
-
$$
|
| 138 |
-
\begin{aligned}
|
| 139 |
-
N & =\frac{1}{4}\left(\sum_{t}\left[\left(1-\left(\frac{1-t}{p}\right)\right)\left(1-\left(\frac{1+t}{p}\right)\right)\right]-\left(1-\left(\frac{2}{p}\right)\right)-\left(1-\left(\frac{-2}{p}\right)\right)\right) \\
|
| 140 |
-
& \geq \frac{1}{4} \sum_{t}\left[\left(1-\left(\frac{1-t}{p}\right)\right)\left(1-\left(\frac{1+t}{p}\right)\right)\right]-1 \\
|
| 141 |
-
& =\frac{1}{4}\left(p+\sum_{t}\left(\frac{1-t^{2}}{p}\right)\right)-1 \\
|
| 142 |
-
& \geq \frac{1}{4}\left(p+(+1) \cdot \frac{1}{2}(p-3)+0 \cdot 2+(-1) \cdot\left((p-2)-\frac{1}{2}(p-3)\right)\right)-1 \\
|
| 143 |
-
& \geq \frac{1}{4}(p-5) .
|
| 144 |
-
\end{aligned}
|
| 145 |
-
$$
|
| 146 |
-
|
| 147 |
-
Thus, the range of $F$ has size at most
|
| 148 |
-
|
| 149 |
-
$$
|
| 150 |
-
\frac{1}{2}(p+1)-\frac{1}{2} N \leq \frac{3}{8}(p+3) .
|
| 151 |
-
$$
|
| 152 |
-
|
| 153 |
-
This is less than $0.499 p$ for any $p \geq 11$.
|
| 154 |
-
|
| 155 |
-
Remark. In fact, the computation above is essentially an equality. There are only two points where terms are dropped: one, when $p \equiv 3(\bmod 4)$ there are no $k^{2}=-1$ in the lemma, and secondly, the terms $1-(2 / p)$ and $1-(-2 / p)$ are dropped in the initial estimate for $N$. With suitable modifications, one can show that in fact, the range of $F$ is exactly equal to
|
| 156 |
-
|
| 157 |
-
$$
|
| 158 |
-
\frac{1}{2}(p+1)-\frac{1}{2} N=\left\{\begin{array}{lll}
|
| 159 |
-
\frac{1}{8}(3 p+5) & p \equiv 1 & (\bmod 8) \\
|
| 160 |
-
\frac{1}{8}(3 p+7) & p \equiv 3 & (\bmod 8) \\
|
| 161 |
-
\frac{1}{8}(3 p+9) & p \equiv 5 & (\bmod 8) \\
|
| 162 |
-
\frac{1}{8}(3 p+3) & p \equiv 7 & (\bmod 8)
|
| 163 |
-
\end{array}\right.
|
| 164 |
-
$$
|
| 165 |
-
|
| 166 |
-
## §2 Solutions to Day 2
|
| 167 |
-
|
| 168 |
-
## §2.1 TSTST 2016/4, proposed by Linus Hamilton
|
| 169 |
-
|
| 170 |
-
Available online at https://aops.com/community/p6580534.
|
| 171 |
-
|
| 172 |
-
## Problem statement
|
| 173 |
-
|
| 174 |
-
Prove that if $n$ and $k$ are positive integers satisfying $\varphi^{k}(n)=1$, then $n \leq 3^{k}$. (Here $\varphi^{k}$ denotes $k$ applications of the Euler phi function.)
|
| 175 |
-
|
| 176 |
-
The main observation is that the exponent of 2 decreases by at most 1 with each application of $\varphi$. This will give us the desired estimate.
|
| 177 |
-
|
| 178 |
-
Define the weight function $w$ on positive integers as follows: it satisfies
|
| 179 |
-
|
| 180 |
-
$$
|
| 181 |
-
\begin{aligned}
|
| 182 |
-
w(a b) & =w(a)+w(b) \\
|
| 183 |
-
w(2) & =1 ; \quad \text { and } \\
|
| 184 |
-
w(p) & =w(p-1) \quad \text { for any prime } p>2
|
| 185 |
-
\end{aligned}
|
| 186 |
-
$$
|
| 187 |
-
|
| 188 |
-
By induction, we see that $w(n)$ counts the powers of 2 that are produced as $\varphi$ is repeatedly applied to $n$. In particular, $k \geq w(n)$.
|
| 189 |
-
|
| 190 |
-
From $w(2)=1$, it suffices to prove that $w(p) \geq \log _{3} p$ for every $p>2$. We use strong induction and note that
|
| 191 |
-
|
| 192 |
-
$$
|
| 193 |
-
w(p)=w(2)+w\left(\frac{p-1}{2}\right) \geq 1+\log _{3}(p-1)-\log _{3} 2 \geq \log _{3} p
|
| 194 |
-
$$
|
| 195 |
-
|
| 196 |
-
for any $p>2$. This solves the problem.
|
| 197 |
-
Remark. One can motivate this solution through small cases $2^{x} 3^{y}$ like $2^{x} 17^{w}, 2^{x} 3^{y} 7^{z}$, $2^{x} 11^{t}$ 。
|
| 198 |
-
|
| 199 |
-
Moreover, the stronger bound
|
| 200 |
-
|
| 201 |
-
$$
|
| 202 |
-
n \leq 2 \cdot 3^{k-1}
|
| 203 |
-
$$
|
| 204 |
-
|
| 205 |
-
is true and best possible.
|
| 206 |
-
|
| 207 |
-
## §2.2 TSTST 2016/5, proposed by Linus Hamilton, Cynthia Stoner
|
| 208 |
-
|
| 209 |
-
Available online at https://aops.com/community/p6580545.
|
| 210 |
-
|
| 211 |
-
## Problem statement
|
| 212 |
-
|
| 213 |
-
In the coordinate plane are finitely many walls, which are disjoint line segments, none of which are parallel to either axis. A bulldozer starts at an arbitrary point and moves in the $+x$ direction. Every time it hits a wall, it turns at a right angle to its path, away from the wall, and continues moving. (Thus the bulldozer always moves parallel to the axes.)
|
| 214 |
-
Prove that it is impossible for the bulldozer to hit both sides of every wall.
|
| 215 |
-
|
| 216 |
-
We say a wall $v$ is above another wall $w$ if some point on $v$ is directly above a point on $w$. (This relation is anti-symmetric, as walls do not intersect).
|
| 217 |
-
|
| 218 |
-
The critical claim is as follows:
|
| 219 |
-
Claim - There exists a lowest wall, i.e. a wall not above any other walls.
|
| 220 |
-
Proof. Assume not. Then we get a directed cycle of some length $n \geq 3$ : it's possible to construct a series of points $P_{i}, Q_{i}$, for $i=1, \ldots, n$ (indices modulo $n$ ), such that the point $Q_{i}$ is directly above $P_{i+1}$ for each $i$, the segment $\overline{Q_{i} P_{i+1}}$ does not intersect any wall in its interior, and finally each segment $\overline{P_{i} Q_{i}}$ is contained inside a wall. This gives us a broken line on $2 n$ vertices which is not self-intersecting.
|
| 221 |
-
Now consider the leftmost vertical segment $\overline{Q_{i} P_{i+1}}$ and the rightmost vertical segment $\overline{Q_{j} P_{j+1}}$. The broken line gives a path from $P_{i+1}$ to $Q_{j}$, as well as a path from $P_{j+1}$ to $Q_{i}$. These clearly must intersect, contradiction.
|
| 222 |
-
|
| 223 |
-
Remark. This claim is Iran TST 2010.
|
| 224 |
-
Thus if the bulldozer eventually moves upwards indefinitely, it may never hit the bottom side of the lowest wall. Similarly, if the bulldozer eventually moves downwards indefinitely, it may never hit the upper side of the highest wall.
|
| 225 |
-
|
| 226 |
-
## §2.3 TSTST 2016/6, proposed by Danielle Wang
|
| 227 |
-
|
| 228 |
-
Available online at https://aops.com/community/p6580553.
|
| 229 |
-
|
| 230 |
-
## Problem statement
|
| 231 |
-
|
| 232 |
-
Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\overline{B C}, \overline{C A}$, $\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\overline{E F}$. Suppose that the circumcircle of $\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\triangle B B_{1} B_{2}$ and $\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\overline{D K}$.
|
| 233 |
-
\I First solution (Allen Liu). Let $X, Y, Z$ be midpoints of $E F, F D, D E$, and let $G$ be the Gergonne point. By radical axis on $(A E I F),(D E F),(A I C)$ we see that $B_{1}$, $X, B_{2}$ are collinear. Likewise, $B_{1}, Z, B_{2}$ are collinear, so lines $B_{1} B_{2}$ and $X Z$ coincide. Similarly, lines $C_{1} C_{2}$ and $X Y$ coincide. In particular lines $B_{1} B_{2}$ and $C_{1} C_{2}$ meet at $X$.
|
| 234 |
-
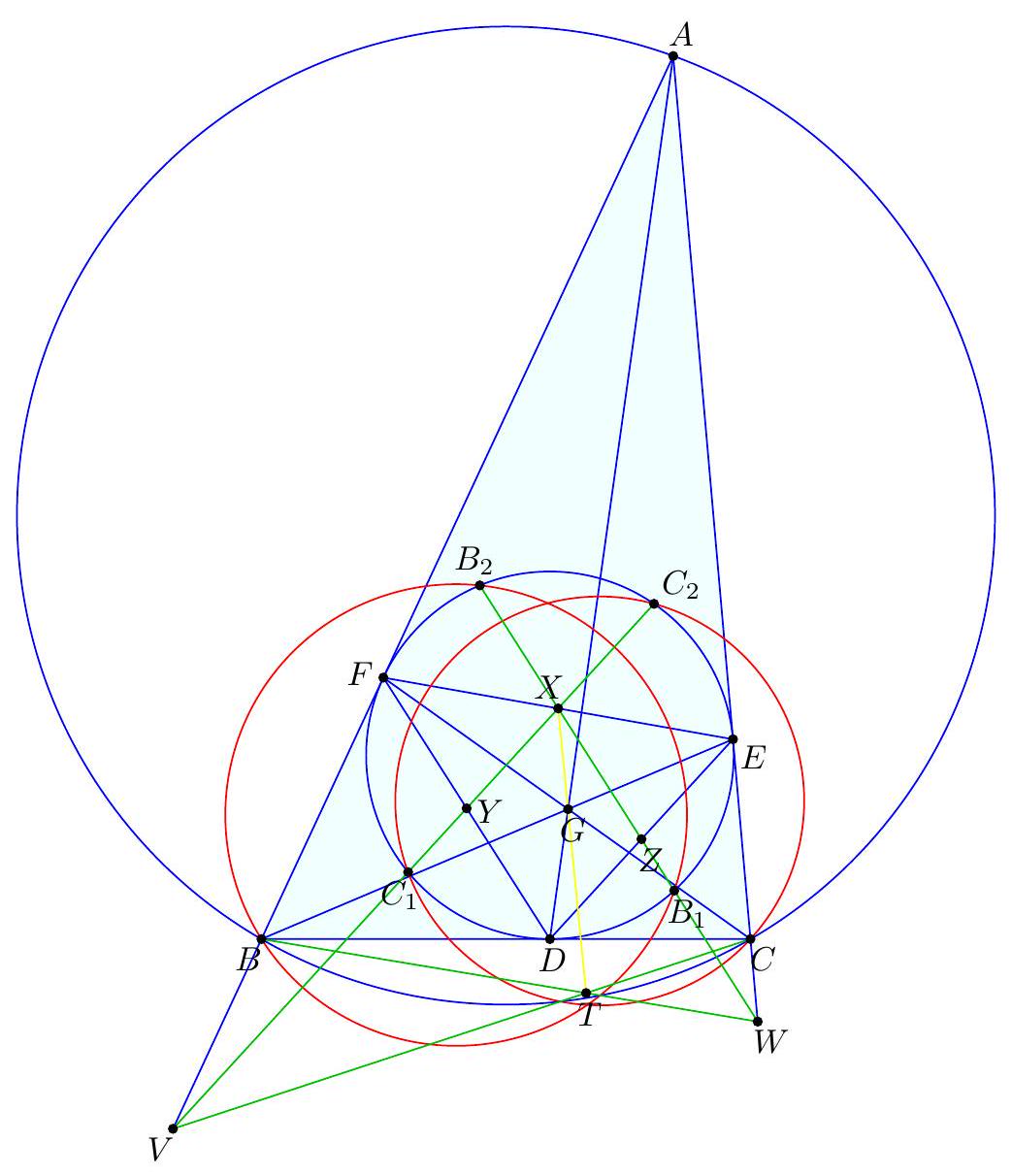
|
| 235 |
-
|
| 236 |
-
Note $G$ is the symmedian point of $D E F$, so it is well-known that $X G$ passes through the midpoint of $D K$. So we just have to prove $G$ lies on the radical axis.
|
| 237 |
-
|
| 238 |
-
First, note that $\triangle D E F$ is the cevian triangle of the Gergonne point $G$. Set $V=$ $\overline{X Y} \cap \overline{A B}, W=\overline{X Z} \cap \overline{A C}$, and $T=\overline{B W} \cap \overline{C V}$.
|
| 239 |
-
|
| 240 |
-
We begin with the following completely projective claim.
|
| 241 |
-
|
| 242 |
-
Claim - The points $X, G, T$ are collinear.
|
| 243 |
-
Proof. It suffices to view $\triangle X Y Z$ as any cevian triangle of $\triangle D E F$ (which is likewise any cevian triangle of $\triangle A B C)$. Then
|
| 244 |
-
|
| 245 |
-
- By Cevian Nest on $\triangle A B C$, it follows that $\overline{A X}, \overline{B Y}, \overline{C Z}$ are concurrent.
|
| 246 |
-
- Hence $\triangle B Y V$ and $\triangle C Z W$ are perspective.
|
| 247 |
-
- Hence $\triangle B Z W$ and $\triangle C Y V$ are perspective too.
|
| 248 |
-
- Hence we deduce by Desargues theorem that $T, X$, and $\overline{B Z} \cap \overline{C Y}$ are collinear.
|
| 249 |
-
- Finally, the Cevian Nest theorem applied on $\triangle G B C$ (which has cevian triangles $\triangle D F E, \triangle X Z Y$ ) we deduce $G, X$, and $\overline{B Z} \cap \overline{C Y}$, proving the claim.
|
| 250 |
-
|
| 251 |
-
One could also proceed by using barycentric coordinates on $\triangle D E F$.
|
| 252 |
-
|
| 253 |
-
Remark (Eric Shen). The first four bullets can be replaced by non-projective means: one can check that $\overline{B Z} \cap \overline{C Y}$ is the radical center of $(B I C),\left(B B_{1} B_{2}\right),\left(C C_{1} C_{2}\right)$ and therefore it lies on line $\overline{X T}$.
|
| 254 |
-
|
| 255 |
-
Now, we contend point $V$ is the radical center $\left(C C_{1} C_{2}\right),(A B C)$ and $(D E F)$. To see this, let $V^{\prime}=\overline{E D} \cap \overline{A B}$; then $\left(F V^{\prime} ; A B\right)$ is harmonic, and $V$ is the midpoint of $\overline{F V^{\prime}}$, and thus $V A \cdot V B=V F^{2}=V C_{1} \cdot V C_{2}$.
|
| 256 |
-
|
| 257 |
-
So in fact $\overline{C V}$ is the radical axis of $(A B C)$ and $\left(C C_{1} C_{2}\right)$.
|
| 258 |
-
Similarly, $\overline{B W}$ is the radical axis of $(A B C)$ and $\left(B B_{1} B_{2}\right)$. Thus $T$ is the radical center of $(A B C),\left(B B_{1} B_{2}\right),\left(C C_{1} C_{2}\right)$.
|
| 259 |
-
|
| 260 |
-
This completes the proof, as now $\overline{X T}$ is the desired radical axis.
|
| 261 |
-
『 Second solution (Evan Chen). As before, we just have to prove $G$ lies on the radical axis.
|
| 262 |
-
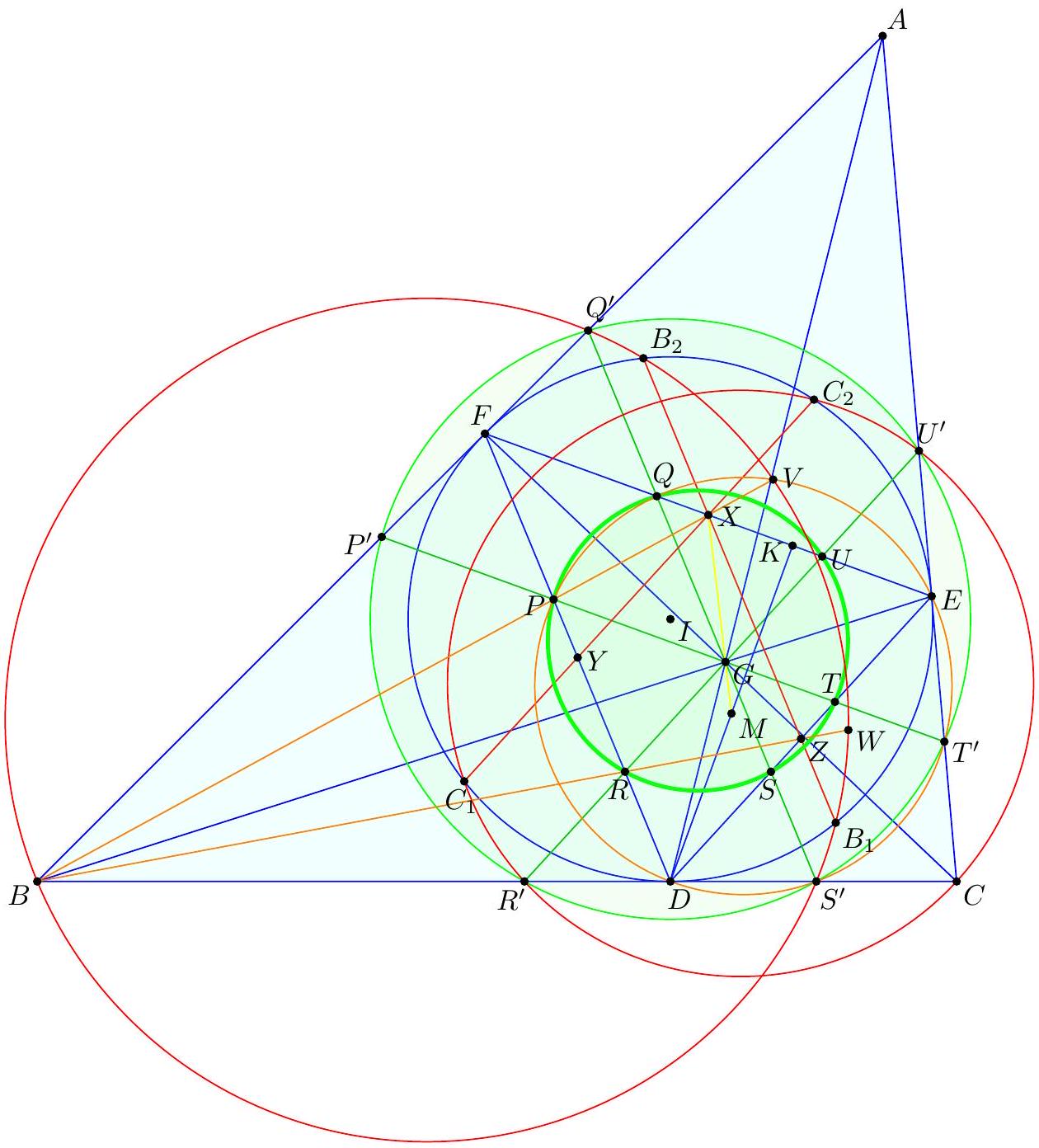
|
| 263 |
-
|
| 264 |
-
Construct parallelograms $G P F Q, G R D S, G T U E$ such that $P, R \in D F, S, T \in D E$, $Q, U \in E F$. As $F G$ bisects $P Q$ and is isogonal to $F Z$, we find $P Q E D$, hence $P Q R U$, is cyclic. Repeating the same logic and noticing $P R, S T, Q U$ not concurrent, all six points $P Q R S T U$ are cyclic. Moreover, since $P Q$ bisects $G F$, we see that a dilation with factor 2 at $G$ sends $P Q$ to $P^{\prime}, Q^{\prime} \in A B$, say, with $F$ the midpoint of $P^{\prime} Q^{\prime}$. Define $R^{\prime}, S^{\prime} \in B C$ similarly now and $T^{\prime}, U^{\prime} \in C A$.
|
| 265 |
-
|
| 266 |
-
Note that $E Q P D S^{\prime}$ is in cyclic too, as $\measuredangle D S^{\prime} Q=\measuredangle D R S=\measuredangle D E F$. By homothety through $B$, points $B, P, X$ are collinear; assume they meet ( $\left.E Q P D S^{\prime}\right)$ again at $V$. Thus $E V Q P D S^{\prime}$ is cyclic, and now
|
| 267 |
-
|
| 268 |
-
$$
|
| 269 |
-
\measuredangle B V S^{\prime}=\measuredangle P V S^{\prime}=\measuredangle P Q S=\measuredangle P T S=\measuredangle F E D=\measuredangle X E Z=\measuredangle X V Z
|
| 270 |
-
$$
|
| 271 |
-
|
| 272 |
-
hence $V$ lies on $\left(B Q^{\prime} S^{\prime}\right)$.
|
| 273 |
-
Since $F B \| Q P$, we get $E V F B$ is cyclic too, so $X V \cdot X B=X E \cdot X F$ now; thus $X$ lies on the radical axis of $\left(B S^{\prime} Q^{\prime}\right)$ and $(D E F)$. By the same argument with $W \in B Z$, we get $Z$ lies on the radical axis too. Thus the radical axis of $\left(B S^{\prime} Q^{\prime}\right)$ and ( $D E F$ ) must be line $X Z$, which coincides with $B_{1} B_{2}$; so $\left(B B_{1} B_{2}\right)=\left(B S^{\prime} Q^{\prime}\right)$.
|
| 274 |
-
|
| 275 |
-
Analogously, $\left(C C_{1} C_{2}\right)=\left(C R^{\prime} U^{\prime}\right)$. Since $G=Q^{\prime} S^{\prime} \cap R^{\prime} U^{\prime}$, we need only prove that $Q^{\prime} R^{\prime} S^{\prime} U^{\prime}$ is cyclic. But $Q R S U$ is cyclic, so we are done.
|
| 276 |
-
|
| 277 |
-
The circle ( $P Q R S T U$ ) is called the Lemoine circle of $A B C$.
|
| 278 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2017.md
DELETED
|
@@ -1,571 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2017 Solutions <br> United States of America - TST Selection Test <br> Evan Chen《陳誼廷》 <br> $59^{\text {th }}$ IMO 2018 Romania and $7^{\text {th }}$ EGMO 2018 Italy
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 3
|
| 7 |
-
1.1 TSTST 2017/1, proposed by Ray Li ..... 3
|
| 8 |
-
1.2 TSTST 2017/2, proposed by Kevin Sun ..... 5
|
| 9 |
-
1.3 TSTST 2017/3, proposed by Calvin Deng, Linus Hamilton ..... 7
|
| 10 |
-
2 Solutions to Day 2 ..... 9
|
| 11 |
-
2.1 TSTST 2017/4, proposed by Mark Sellke ..... 9
|
| 12 |
-
2.2 TSTST 2017/5, proposed by Ray Li ..... 10
|
| 13 |
-
2.3 TSTST 2017/6, proposed by Ivan Borsenco ..... 12
|
| 14 |
-
|
| 15 |
-
## §0 Problems
|
| 16 |
-
|
| 17 |
-
1. Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
| 18 |
-
2. Ana and Banana are playing a game. First Ana picks a word, which is defined to be a nonempty sequence of capital English letters. Then Banana picks a nonnegative integer $k$ and challenges Ana to supply a word with exactly $k$ subsequences which are equal to Ana's word. Ana wins if she is able to supply such a word, otherwise she loses. For example, if Ana picks the word "TST", and Banana chooses $k=4$, then Ana can supply the word "TSTST" which has 4 subsequences which are equal to Ana's word. Which words can Ana pick so that she can win no matter what value of $k$ Banana chooses?
|
| 19 |
-
3. Consider solutions to the equation
|
| 20 |
-
|
| 21 |
-
$$
|
| 22 |
-
x^{2}-c x+1=\frac{f(x)}{g(x)}
|
| 23 |
-
$$
|
| 24 |
-
|
| 25 |
-
where $f$ and $g$ are nonzero polynomials with nonnegative real coefficients. For each $c>0$, determine the minimum possible degree of $f$, or show that no such $f, g$ exist.
|
| 26 |
-
4. Find all nonnegative integer solutions to
|
| 27 |
-
|
| 28 |
-
$$
|
| 29 |
-
2^{a}+3^{b}+5^{c}=n!
|
| 30 |
-
$$
|
| 31 |
-
|
| 32 |
-
5. Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
| 33 |
-
6. A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
| 34 |
-
|
| 35 |
-
## §1 Solutions to Day 1
|
| 36 |
-
|
| 37 |
-
## §1.1 TSTST 2017/1, proposed by Ray Li
|
| 38 |
-
|
| 39 |
-
Available online at https://aops.com/community/p8526098.
|
| 40 |
-
|
| 41 |
-
## Problem statement
|
| 42 |
-
|
| 43 |
-
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
| 44 |
-
|
| 45 |
-
【 First solution (power of a point). Let $\gamma$ denote the nine-point circle of $A B C$.
|
| 46 |
-
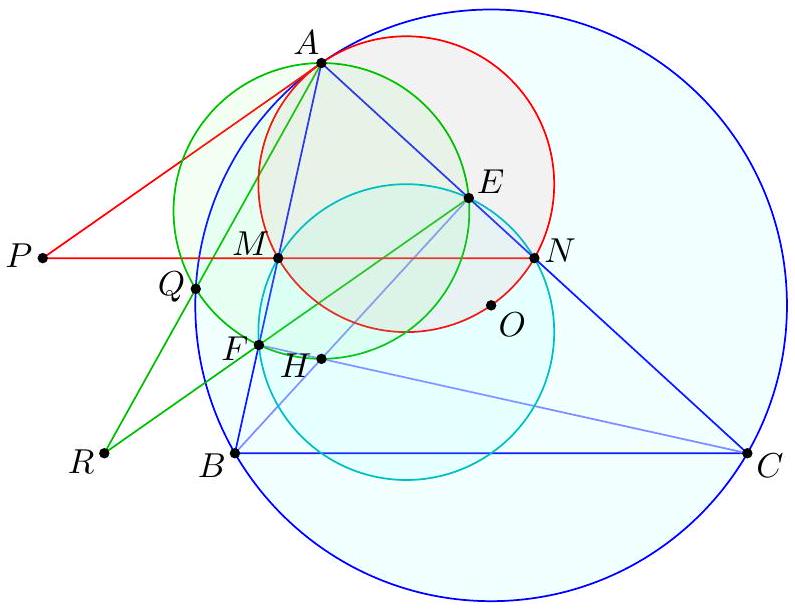
|
| 47 |
-
|
| 48 |
-
Note that
|
| 49 |
-
|
| 50 |
-
- $P A^{2}=P M \cdot P N$, so $P$ lies on the radical axis of $\Gamma$ and $\gamma$.
|
| 51 |
-
- $R A \cdot R Q=R E \cdot R F$, so $R$ lies on the radical axis of $\Gamma$ and $\gamma$.
|
| 52 |
-
|
| 53 |
-
Thus $\overline{P R}$ is the radical axis of $\Gamma$ and $\gamma$, which is evidently perpendicular to $\overline{O H}$.
|
| 54 |
-
Remark. In fact, by power of a point one may also observe that $R$ lies on $\overline{B C}$, since it is on the radical axis of $(A Q F H E),(B F E C),(A B C)$. Ironically, this fact is not used in the solution.
|
| 55 |
-
|
| 56 |
-
II Second solution (barycentric coordinates). Again note first $R \in \overline{B C}$ (although this can be avoided too). We compute the points in much the same way as before. Since $\overline{A P} \cap \overline{B C}=\left(0: b^{2}:-c^{2}\right)$ we have
|
| 57 |
-
|
| 58 |
-
$$
|
| 59 |
-
P=\left(b^{2}-c^{2}: b^{2}:-c^{2}\right)
|
| 60 |
-
$$
|
| 61 |
-
|
| 62 |
-
(since $x=y+z$ is the equation of line $\overline{M N}$ ). Now in Conway notation we have
|
| 63 |
-
|
| 64 |
-
$$
|
| 65 |
-
R=\overline{E F} \cap \overline{B C}=\left(0: S_{C}:-S_{B}\right)=\left(0: a^{2}+b^{2}-c^{2}:-a^{2}+b^{2}-c^{2}\right) .
|
| 66 |
-
$$
|
| 67 |
-
|
| 68 |
-
Hence
|
| 69 |
-
|
| 70 |
-
$$
|
| 71 |
-
\overrightarrow{P R}=\frac{1}{2\left(b^{2}-c^{2}\right)}\left(b^{2}-c^{2}, c^{2}-a^{2}, a^{2}-b^{2}\right)
|
| 72 |
-
$$
|
| 73 |
-
|
| 74 |
-
On the other hand, we have $\overrightarrow{O H}=\vec{A}+\vec{B}+\vec{C}$. So it suffices to check that
|
| 75 |
-
|
| 76 |
-
$$
|
| 77 |
-
\sum_{\mathrm{cyc}} a^{2}\left(\left(a^{2}-b^{2}\right)+\left(c^{2}-a^{2}\right)\right)=0
|
| 78 |
-
$$
|
| 79 |
-
|
| 80 |
-
which is immediate.
|
| 81 |
-
|
| 82 |
-
『 Third solution (complex numbers). Let $A B C$ be the unit circle. We first compute $P$ as the midpoint of $A$ and $\overline{A A} \cap \overline{B C}$ :
|
| 83 |
-
|
| 84 |
-
$$
|
| 85 |
-
\begin{aligned}
|
| 86 |
-
p & =\frac{1}{2}\left(a+\frac{a^{2}(b+c)-b c \cdot 2 a}{a^{2}-b c}\right) \\
|
| 87 |
-
& =\frac{a\left(a^{2}-b c\right)+a^{2}(b+c)-2 a b c}{2\left(a^{2}-b c\right)}
|
| 88 |
-
\end{aligned}
|
| 89 |
-
$$
|
| 90 |
-
|
| 91 |
-
Using the remark above, $R$ is the inverse of $D$ with respect to the circle with diameter $\overline{B C}$, which has radius $\left|\frac{1}{2}(b-c)\right|$. Thus
|
| 92 |
-
|
| 93 |
-
$$
|
| 94 |
-
\begin{aligned}
|
| 95 |
-
r-\frac{b+c}{2} & =\frac{\frac{1}{4}(b-c)\left(\frac{1}{b}-\frac{1}{c}\right)}{\frac{1}{2}\left(a-\frac{b c}{a}\right)} \\
|
| 96 |
-
r & =\frac{b+c}{2}+\frac{-\frac{1}{2} \frac{(b-c)^{2}}{b c}}{\frac{1}{a}-\frac{a}{b c}} \\
|
| 97 |
-
& =\frac{b+c}{2}+\frac{a(b-c)^{2}}{2\left(a^{2}-b c\right)} \\
|
| 98 |
-
& =\frac{a(b-c)^{2}+(b+c)\left(a^{2}-b c\right)}{2\left(a^{2}-b c\right)}
|
| 99 |
-
\end{aligned}
|
| 100 |
-
$$
|
| 101 |
-
|
| 102 |
-
Expanding and subtracting gives
|
| 103 |
-
|
| 104 |
-
$$
|
| 105 |
-
p-r=\frac{a^{3}-a b c-a b^{2}-a c^{2}+b^{2} c+b c^{2}}{2\left(a^{2}-b c\right)}=\frac{(a+b+c)(a-b)(a-c)}{2\left(a^{2}-b c\right)}
|
| 106 |
-
$$
|
| 107 |
-
|
| 108 |
-
which is visibly equal to the negation of its conjugate once the factor of $a+b+c$ is deleted.
|
| 109 |
-
(Actually, one can guess this factorization ahead of time by noting that if $A=B$, then $P=B=R$, so $a-b$ must be a factor; analogously $a-c$ must be as well.)
|
| 110 |
-
|
| 111 |
-
## §1.2 TSTST 2017/2, proposed by Kevin Sun
|
| 112 |
-
|
| 113 |
-
Available online at https://aops.com/community/p8526115.
|
| 114 |
-
|
| 115 |
-
## Problem statement
|
| 116 |
-
|
| 117 |
-
Ana and Banana are playing a game. First Ana picks a word, which is defined to be a nonempty sequence of capital English letters. Then Banana picks a nonnegative integer $k$ and challenges Ana to supply a word with exactly $k$ subsequences which are equal to Ana's word. Ana wins if she is able to supply such a word, otherwise she loses. For example, if Ana picks the word "TST", and Banana chooses $k=4$, then Ana can supply the word "TSTST" which has 4 subsequences which are equal to Ana's word. Which words can Ana pick so that she can win no matter what value of $k$ Banana chooses?
|
| 118 |
-
|
| 119 |
-
First we introduce some notation. Define a block of letters to be a maximal contiguous subsequence of consecutive letters. For example, the word $A A B B B C A A A$ has four blocks, namely $A A, B B B, C, A A A$. Throughout the solution, we fix the word $A$ that Ana picks, and introduce the following notation for its $m$ blocks:
|
| 120 |
-
|
| 121 |
-
$$
|
| 122 |
-
A=A_{1} A_{2} \ldots A_{m}=\underbrace{a_{1} \ldots a_{1}}_{x_{1}} \underbrace{a_{2} \ldots a_{2}}_{x_{2}} \cdots \underbrace{a_{m} \ldots a_{m}}_{x_{m}}
|
| 123 |
-
$$
|
| 124 |
-
|
| 125 |
-
A rainbow will be a subsequence equal to Ana's initial word $A$ (meaning Ana seeks words with exactly $k$ rainbows). Finally, for brevity, let $A_{i}=\underbrace{a_{i} \ldots a_{i}}_{x_{i}}$, so $A=A_{1} \ldots A_{m}$.
|
| 126 |
-
|
| 127 |
-
We prove two claims that resolve the problem.
|
| 128 |
-
Claim - If $x_{i}=1$ for some $i$, then for any $k \geq 1$, the word
|
| 129 |
-
|
| 130 |
-
$$
|
| 131 |
-
W=A_{1} \ldots A_{i-1} \underbrace{a_{i} \ldots a_{i}}_{k} A_{i+1} \ldots A_{m}
|
| 132 |
-
$$
|
| 133 |
-
|
| 134 |
-
obtained by repeating the $i$ th letter $k$ times has exactly $k$ rainbows.
|
| 135 |
-
Proof. Obviously there are at least $\binom{k}{k-1}=k$ rainbows, obtained by deleting $k-1$ choices of the letter $a_{i}$ in the repeated block. We show they are the only ones.
|
| 136 |
-
|
| 137 |
-
Given a rainbow, consider the location of this singleton block in $W$. It cannot occur within the first $\left|A_{1}\right|+\cdots+\left|A_{i-1}\right|$ letters, nor can it occur within the final $\left|A_{i+1}\right|+\cdots+\left|A_{m}\right|$ letters. So it must appear in the $i$ th block of $W$. That implies that all the other $a_{i}$ 's in the $i$ th block of $W$ must be deleted, as desired. (This last argument is actually nontrivial, and has some substance; many students failed to realize that the upper bound requires care.)
|
| 138 |
-
|
| 139 |
-
Claim - If $x_{i} \geq 2$ for all $i$, then no word $W$ has exactly two rainbows.
|
| 140 |
-
Proof. We prove if there are two rainbows of $W$, then we can construct at least three rainbows.
|
| 141 |
-
|
| 142 |
-
Let $W=w_{1} \ldots w_{n}$ and consider the two rainbows of $W$. Since they are not the same, there must be a block $A_{p}$ of the rainbow, of length $\ell \geq 2$, which do not occupy the same locations in $W$.
|
| 143 |
-
|
| 144 |
-
Assume the first rainbow uses $w_{i_{1}}, \ldots, w_{i_{\ell}}$ for this block and the second rainbow uses $w_{j_{1}}, \ldots, w_{j_{\ell}}$ for this block. Then among the letters $w_{q}$ for $\min \left(i_{1}, j_{1}\right) \leq q \leq \max \left(i_{\ell}, j_{\ell}\right)$, there must be at least $\ell+1$ copies of the letter $a_{p}$. Moreover, given a choice of $\ell$ copies of the letter $a_{p}$ in this range, one can complete the subsequence to a rainbow. So the number of rainbows is at least $\binom{\ell+1}{\ell} \geq \ell+1$.
|
| 145 |
-
|
| 146 |
-
Since $\ell \geq 2$, this proves $W$ has at least three rainbows.
|
| 147 |
-
In summary, Ana wins if and only if $x_{i}=1$ for some $i$, since she can duplicate the isolated letter $k$ times; but if $x_{i} \geq 2$ for all $i$ then Banana only needs to supply $k=2$.
|
| 148 |
-
|
| 149 |
-
## §1.3 TSTST 2017/3, proposed by Calvin Deng, Linus Hamilton
|
| 150 |
-
|
| 151 |
-
Available online at https://aops.com/community/p8526130.
|
| 152 |
-
|
| 153 |
-
## Problem statement
|
| 154 |
-
|
| 155 |
-
Consider solutions to the equation
|
| 156 |
-
|
| 157 |
-
$$
|
| 158 |
-
x^{2}-c x+1=\frac{f(x)}{g(x)}
|
| 159 |
-
$$
|
| 160 |
-
|
| 161 |
-
where $f$ and $g$ are nonzero polynomials with nonnegative real coefficients. For each $c>0$, determine the minimum possible degree of $f$, or show that no such $f, g$ exist.
|
| 162 |
-
|
| 163 |
-
First, if $c \geq 2$ then we claim no such $f$ and $g$ exist. Indeed, one simply takes $x=1$ to get $f(1) / g(1) \leq 0$, impossible.
|
| 164 |
-
|
| 165 |
-
For $c<2$, let $c=2 \cos \theta$, where $0<\theta<\pi$. We claim that $f$ exists and has minimum degree equal to $n$, where $n$ is defined as the smallest integer satisfying $\sin n \theta \leq 0$. In other words
|
| 166 |
-
|
| 167 |
-
$$
|
| 168 |
-
n=\left\lceil\frac{\pi}{\arccos (c / 2)}\right\rceil
|
| 169 |
-
$$
|
| 170 |
-
|
| 171 |
-
First we show that this is necessary. To see it, write explicitly
|
| 172 |
-
|
| 173 |
-
$$
|
| 174 |
-
g(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n-2} x^{n-2}
|
| 175 |
-
$$
|
| 176 |
-
|
| 177 |
-
with each $a_{i} \geq 0$, and $a_{n-2} \neq 0$. Assume that $n$ is such that $\sin (k \theta) \geq 0$ for $k=1, \ldots, n-1$. Then, we have the following system of inequalities:
|
| 178 |
-
|
| 179 |
-
$$
|
| 180 |
-
\begin{aligned}
|
| 181 |
-
& a_{1} \geq 2 \cos \theta \cdot a_{0} \\
|
| 182 |
-
& a_{0}+a_{2} \geq 2 \cos \theta \cdot a_{1} \\
|
| 183 |
-
& a_{1}+a_{3} \geq 2 \cos \theta \cdot a_{2} \\
|
| 184 |
-
& \vdots \\
|
| 185 |
-
& a_{n-5}+a_{n-3} \geq 2 \cos \theta \cdot a_{n-4} \\
|
| 186 |
-
& a_{n-4}+a_{n-2} \geq 2 \cos \theta \cdot a_{n-3} \\
|
| 187 |
-
& a_{n-3} \geq 2 \cos \theta \cdot a_{n-2} .
|
| 188 |
-
\end{aligned}
|
| 189 |
-
$$
|
| 190 |
-
|
| 191 |
-
Now, multiply the first equation by $\sin \theta$, the second equation by $\sin 2 \theta$, et cetera, up to $\sin ((n-1) \theta)$. This choice of weights is selected since we have
|
| 192 |
-
|
| 193 |
-
$$
|
| 194 |
-
\sin (k \theta)+\sin ((k+2) \theta)=2 \sin ((k+1) \theta) \cos \theta
|
| 195 |
-
$$
|
| 196 |
-
|
| 197 |
-
so that summing the entire expression cancels nearly all terms and leaves only
|
| 198 |
-
|
| 199 |
-
$$
|
| 200 |
-
\sin ((n-2) \theta) a_{n-2} \geq \sin ((n-1) \theta) \cdot 2 \cos \theta \cdot a_{n-2}
|
| 201 |
-
$$
|
| 202 |
-
|
| 203 |
-
and so by dividing by $a_{n-2}$ and using the same identity gives us $\sin (n \theta) \leq 0$, as claimed.
|
| 204 |
-
This bound is best possible, because the example
|
| 205 |
-
|
| 206 |
-
$$
|
| 207 |
-
a_{k}=\sin ((k+1) \theta) \geq 0
|
| 208 |
-
$$
|
| 209 |
-
|
| 210 |
-
makes all inequalities above sharp, hence giving a working pair $(f, g)$.
|
| 211 |
-
|
| 212 |
-
Remark. Calvin Deng points out that a cleaner proof of the lower bound is to take $\alpha=\cos \theta+i \sin \theta$. Then $f(\alpha)=0$, but by condition the imaginary part of $f(\alpha)$ is apparently strictly positive, contradiction.
|
| 213 |
-
|
| 214 |
-
Remark. Guessing that $c<2$ works at all (and realizing $c \geq 2$ fails) is the first part of the problem.
|
| 215 |
-
|
| 216 |
-
The introduction of trigonometry into the solution may seem magical, but is motivated in one of two ways:
|
| 217 |
-
|
| 218 |
-
- Calvin Deng points out that it's possible to guess the answer from small cases: For $c \leq 1$ we have $n=3$, tight at $\frac{x^{3}+1}{x+1}=x^{2}-x+1$, and essentially the "sharpest $n=3$ example". A similar example exists at $n=4$ with $\frac{x^{4}+1}{x^{2}+\sqrt{2} x+1}=x^{2}-\sqrt{2} x+1$ by the Sophie-Germain identity. In general, one can do long division to extract an optimal value of $c$ for any given $n$, although $c$ will be the root of some polynomial.
|
| 219 |
-
The thresholds $c \leq 1$ for $n=3, c \leq \sqrt{2}$ for $n=4, c \leq \frac{1+\sqrt{5}}{2}$ for $n=5$, and $c \leq 2$ for $n<\infty$ suggest the unusual form of the answer via trigonometry.
|
| 220 |
-
- One may imagine trying to construct a polynomial recursively / greedily by making all inequalities above hold (again the "sharpest situation" in which $f$ has few coefficients). If one sets $c=2 t$, then we have
|
| 221 |
-
|
| 222 |
-
$$
|
| 223 |
-
a_{0}=1, \quad a_{1}=2 t, \quad a_{2}=4 t^{2}-1, \quad a_{3}=8 t^{3}-4 t, \quad \ldots
|
| 224 |
-
$$
|
| 225 |
-
|
| 226 |
-
which are the Chebyshev polynomials of the second type. This means that trigonometry is essentially mandatory. (One may also run into this when by using standard linear recursion techniques, and noting that the characteristic polynomial has two conjugate complex roots.)
|
| 227 |
-
|
| 228 |
-
Remark. Mitchell Lee notes that an IMO longlist problem from 1997 shows that if $P(x)$ is any polynomial satisfying $P(x)>0$ for $x>0$, then $(x+1)^{n} P(x)$ has nonnegative coefficients for large enough $n$. This show that $f$ and $g$ at least exist for $c \leq 2$, but provides no way of finding the best possible $\operatorname{deg} f$.
|
| 229 |
-
|
| 230 |
-
Meghal Gupta also points out that showing $f$ and $g$ exist is possible in the following way:
|
| 231 |
-
|
| 232 |
-
$$
|
| 233 |
-
\left(x^{2}-1.99 x+1\right)\left(x^{2}+1.99 x+1\right)=\left(x^{4}-1.9601 x^{2}+1\right)
|
| 234 |
-
$$
|
| 235 |
-
|
| 236 |
-
and so on, repeatedly multiplying by the "conjugate" until all coefficients become positive. To my best knowledge, this also does not give any way of actually minimizing $\operatorname{deg} f$, although Ankan Bhattacharya points out that this construction is actually optimal in the case where $n$ is a power of 2 .
|
| 237 |
-
|
| 238 |
-
Remark. It's pointed out that Matematicheskoe Prosveshchenie, issue 1, 1997, page 194 contains a nearly analogous result, available at https://mccme.ru/free-books/matpros/ pdf/mp-01.pdf with solutions presented in https://mccme.ru/free-books/matpros/pdf/ mp-05.pdf, pages 221-223; and https://mccme.ru/free-books/matpros/pdf/mp-10.pdf, page 274.
|
| 239 |
-
|
| 240 |
-
## §2 Solutions to Day 2
|
| 241 |
-
|
| 242 |
-
## §2.1 TSTST 2017/4, proposed by Mark Sellke
|
| 243 |
-
|
| 244 |
-
Available online at https://aops.com/community/p8526131.
|
| 245 |
-
|
| 246 |
-
## Problem statement
|
| 247 |
-
|
| 248 |
-
Find all nonnegative integer solutions to
|
| 249 |
-
|
| 250 |
-
$$
|
| 251 |
-
2^{a}+3^{b}+5^{c}=n!
|
| 252 |
-
$$
|
| 253 |
-
|
| 254 |
-
For $n \leq 4$, one can check the only solutions are:
|
| 255 |
-
|
| 256 |
-
$$
|
| 257 |
-
\begin{aligned}
|
| 258 |
-
& 2^{2}+3^{0}+5^{0}=3! \\
|
| 259 |
-
& 2^{1}+3^{1}+5^{0}=3! \\
|
| 260 |
-
& 2^{4}+3^{1}+5^{1}=4!
|
| 261 |
-
\end{aligned}
|
| 262 |
-
$$
|
| 263 |
-
|
| 264 |
-
Now we prove there are no solutions for $n \geq 5$.
|
| 265 |
-
A tricky way to do this is to take modulo 120 , since
|
| 266 |
-
|
| 267 |
-
$$
|
| 268 |
-
\begin{aligned}
|
| 269 |
-
2^{a} \quad(\bmod 120) & \in\{1,2,4,8,16,32,64\} \\
|
| 270 |
-
3^{b} \quad(\bmod 120) & \in\{1,3,9,27,81\} \\
|
| 271 |
-
5^{c} \quad(\bmod 120) & \in\{1,5,25\}
|
| 272 |
-
\end{aligned}
|
| 273 |
-
$$
|
| 274 |
-
|
| 275 |
-
and by inspection one notes that no three elements have vanishing sum modulo 120 .
|
| 276 |
-
I expect most solutions to instead use casework. Here is one possible approach with cases (with $n \geq 5$ ). First, we analyze the cases where $a<3$ :
|
| 277 |
-
|
| 278 |
-
- $a=0$ : No solutions for parity reasons.
|
| 279 |
-
- $a=1$ : since $3^{b}+5^{c} \equiv 6(\bmod 8)$, we find $b$ even and $c$ odd (hence $\left.c \neq 0\right)$. Now looking modulo 5 gives that $3^{b}+5^{c} \equiv 3(\bmod 5)$,
|
| 280 |
-
- $a=2$ : From $3^{b}+5^{c} \equiv 4(\bmod 8)$, we find $b$ is odd and $c$ is even. Now looking modulo 5 gives a contradiction, even if $c=0$, since $3^{b} \in\{2,3(\bmod 5)\}$ but $3^{b}+5^{c} \equiv 1(\bmod 5)$.
|
| 281 |
-
|
| 282 |
-
Henceforth assume $a \geq 3$. Next, by taking modulo 8 we have $3^{b}+5^{c} \equiv 0(\bmod 8)$, which forces both $b$ and $c$ to be odd (in particular, $b, c>0$ ). We now have
|
| 283 |
-
|
| 284 |
-
$$
|
| 285 |
-
\begin{aligned}
|
| 286 |
-
& 2^{a}+5^{c} \equiv 0 \quad(\bmod 3) \\
|
| 287 |
-
& 2^{a}+3^{b} \equiv 0 \quad(\bmod 5) .
|
| 288 |
-
\end{aligned}
|
| 289 |
-
$$
|
| 290 |
-
|
| 291 |
-
The first equation implies $a$ is even, but the second equation requires $a$ to be odd, contradiction. Hence no solutions with $n \geq 5$.
|
| 292 |
-
|
| 293 |
-
## §2.2 TSTST 2017/5, proposed by Ray Li
|
| 294 |
-
|
| 295 |
-
Available online at https://aops.com/community/p8526136.
|
| 296 |
-
|
| 297 |
-
## Problem statement
|
| 298 |
-
|
| 299 |
-
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
| 300 |
-
|
| 301 |
-
『 First solution (homothety). Let $Z$ be the diametrically opposite point on the incircle. We claim this is the desired intersection.
|
| 302 |
-
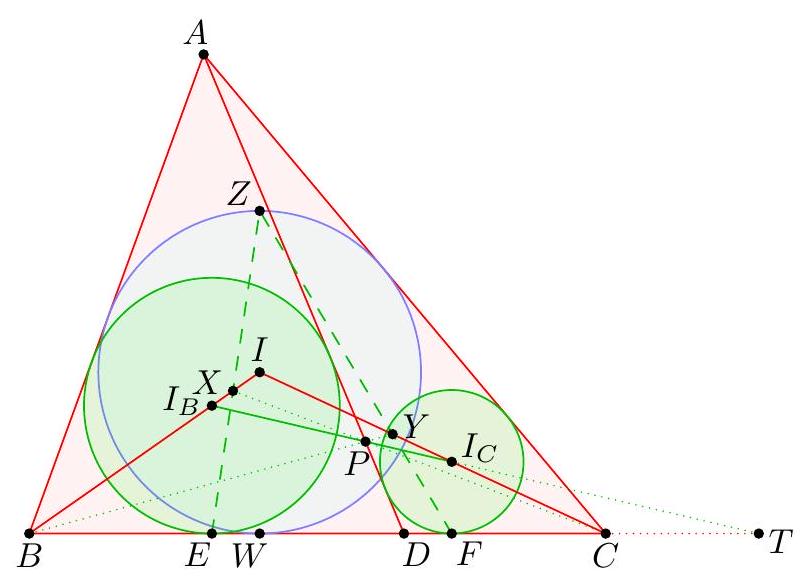
|
| 303 |
-
|
| 304 |
-
Note that:
|
| 305 |
-
|
| 306 |
-
- $P$ is the insimilicenter of $\omega_{B}$ and $\omega_{C}$
|
| 307 |
-
- $C$ is the exsimilicenter of $\omega$ and $\omega_{C}$.
|
| 308 |
-
|
| 309 |
-
Thus by Monge theorem, the insimilicenter of $\omega_{B}$ and $\omega$ lies on line $C P$.
|
| 310 |
-
This insimilicenter should also lie on the line joining the centers of $\omega$ and $\omega_{B}$, which is $\overline{B I}$, hence it coincides with the point $X$. So $X \in \overline{E Z}$ as desired.
|
| 311 |
-
|
| 312 |
-
【 Second solution (harmonic). Let $T=\overline{I_{B} I_{C}} \cap \overline{B C}$, and $W$ the foot from $I$ to $\overline{B C}$. Define $Z=\overline{F Y} \cap \overline{I W}$. Because $\angle I_{B} D I_{C}=90^{\circ}$, we have
|
| 313 |
-
|
| 314 |
-
$$
|
| 315 |
-
-1=\left(I_{B} I_{C} ; P T\right) \stackrel{B}{\stackrel{B}{2}}\left(I I_{C} ; Y C\right) \stackrel{F}{=}(I \infty ; Z W)
|
| 316 |
-
$$
|
| 317 |
-
|
| 318 |
-
So $I$ is the midpoint of $\overline{Z W}$ as desired.
|
| 319 |
-
【 Third solution (outline, barycentric, Andrew Gu). Let $A D=t, B D=x, C D=y$, so $a=x+y$ and by Stewart's theorem we have
|
| 320 |
-
|
| 321 |
-
$$
|
| 322 |
-
(x+y)\left(x y+t^{2}\right)=b^{2} x+c^{2} y
|
| 323 |
-
$$
|
| 324 |
-
|
| 325 |
-
We then have $D=(0: y: x)$ and so
|
| 326 |
-
|
| 327 |
-
$$
|
| 328 |
-
\overline{A I_{B}} \cap \overline{B C}=\left(0: y+\frac{t x}{c+t}: \frac{c x}{c+t}\right)
|
| 329 |
-
$$
|
| 330 |
-
|
| 331 |
-
hence intersection with $B I$ gives
|
| 332 |
-
|
| 333 |
-
$$
|
| 334 |
-
I_{B}=(a x: c y+a t: c x)
|
| 335 |
-
$$
|
| 336 |
-
|
| 337 |
-
Similarly,
|
| 338 |
-
|
| 339 |
-
$$
|
| 340 |
-
I_{C}=(a y: b y: b x+a t)
|
| 341 |
-
$$
|
| 342 |
-
|
| 343 |
-
Then, we can compute
|
| 344 |
-
|
| 345 |
-
$$
|
| 346 |
-
P=(2 a x y: y(a t+b x+c y): x(a t+b x+c y))
|
| 347 |
-
$$
|
| 348 |
-
|
| 349 |
-
since $P \in \overline{I_{B} I_{C}}$, and clearly $P \in \overline{A D}$. Intersection now gives
|
| 350 |
-
|
| 351 |
-
$$
|
| 352 |
-
\begin{aligned}
|
| 353 |
-
& X=(2 a x: a t+b x+c y: 2 c x) \\
|
| 354 |
-
& Y=(2 a y: 2 b y: a t+b x+c y)
|
| 355 |
-
\end{aligned}
|
| 356 |
-
$$
|
| 357 |
-
|
| 358 |
-
Finally, we have $B E=\frac{1}{2}(c+x-t)$, and similarly for $C F$. Now if we reflect $D=$ $\left(0, \frac{s-c}{a}, \frac{s-b}{a}\right)$ over $I=\left(\frac{a}{2 s}, \frac{b}{2 s}, \frac{c}{2 s}\right)$, we get the antipode
|
| 359 |
-
|
| 360 |
-
$$
|
| 361 |
-
Q:=\left(4 a^{2}:-a^{2}+2 a b-b^{2}+c^{2}:-a^{2}+2 a c-c^{2}+b^{2}\right) .
|
| 362 |
-
$$
|
| 363 |
-
|
| 364 |
-
We may then check $Q$ lies on each of lines $E X$ and $F Y$ (by checking $\operatorname{det}(Q, E, X)=0$ using the equation (1)).
|
| 365 |
-
|
| 366 |
-
## §2.3 TSTST 2017/6, proposed by Ivan Borsenco
|
| 367 |
-
|
| 368 |
-
Available online at https://aops.com/community/p8526142.
|
| 369 |
-
|
| 370 |
-
## Problem statement
|
| 371 |
-
|
| 372 |
-
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
| 373 |
-
|
| 374 |
-
Yes, it is possible. The following solutions were written for me by Kevin Sun and Mark Sellke. We let $F_{1}=F_{2}=1, F_{3}=2, F_{4}=3, F_{5}=5, \ldots$ denote the Fibonacci numbers.
|
| 375 |
-
|
| 376 |
-
【 First solution (Kevin Sun). We are going to appeal to the so-called Zeckendorf theorem:
|
| 377 |
-
|
| 378 |
-
Theorem (Zeckendorf)
|
| 379 |
-
Every positive integer can be uniquely expressed as the sum of nonconsecutive Fibonacci numbers.
|
| 380 |
-
|
| 381 |
-
This means every positive integer has a Zeckendorf ("Fibonacci-binary") representation where we put 1 in the $i$ th digit from the right if $F_{i+1}$ is used. The idea is then to take the following so-called Wythoff array:
|
| 382 |
-
|
| 383 |
-
- Row 1: 1, 2, 3, 5, ...
|
| 384 |
-
- Row 101: $1+3,2+5,3+8, \ldots$
|
| 385 |
-
- Row 1001: $1+5,2+8,3+13, \ldots$
|
| 386 |
-
- Row 10001: $1+8,2+13,3+21, \ldots$
|
| 387 |
-
- Row 10101: $1+3+8,2+5+13,3+8+21, \ldots$
|
| 388 |
-
- . . .et cetera.
|
| 389 |
-
|
| 390 |
-
More concretely, the array has the following rows to start:
|
| 391 |
-
|
| 392 |
-
| 1 | 2 | 3 | 5 | 8 | 13 | 21 | $\ldots$ |
|
| 393 |
-
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 394 |
-
| 4 | 7 | 11 | 18 | 29 | 47 | 76 | $\ldots$ |
|
| 395 |
-
| 6 | 10 | 16 | 26 | 42 | 68 | 110 | $\ldots$ |
|
| 396 |
-
| 9 | 15 | 24 | 39 | 63 | 102 | 165 | $\ldots$ |
|
| 397 |
-
| 12 | 20 | 32 | 52 | 84 | 136 | 220 | $\ldots$ |
|
| 398 |
-
| 14 | 23 | 37 | 60 | 97 | 157 | 254 | $\ldots$ |
|
| 399 |
-
| 17 | 28 | 45 | 73 | 118 | 191 | 309 | $\ldots$ |
|
| 400 |
-
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ |
|
| 401 |
-
|
| 402 |
-
Here are the full details.
|
| 403 |
-
We begin by outlining a proof of Zeckendorf's theorem, which implies the representation above is unique. Note that if $F_{k}$ is the greatest Fibonacci number at most $n$, then
|
| 404 |
-
|
| 405 |
-
$$
|
| 406 |
-
n-F_{k}<F_{k+1}-F_{k}=F_{k-1} .
|
| 407 |
-
$$
|
| 408 |
-
|
| 409 |
-
In particular, repeatedly subtracting off the largest $F_{k}$ from $n$ will produce one such representation with no two consecutive Fibonacci numbers. On the other hand, this $F_{k}$ must be used, as
|
| 410 |
-
|
| 411 |
-
$$
|
| 412 |
-
n \geq F_{k}>F_{k-1}+F_{k-3}+F_{k-5}+\cdots
|
| 413 |
-
$$
|
| 414 |
-
|
| 415 |
-
This shows, by a simple inductive argument, that such a representation exists and unique.
|
| 416 |
-
We write $n={\bar{a} k \ldots a_{1}}_{\text {Fib }}$ for the Zeckendorf representation as we described (where $a_{i}=1$ if $F_{i+1}$ is used). Now for each ${\bar{a} k \ldots a_{1}}^{\text {Fib }}$ with $a_{1}=1$, consider the sequence
|
| 417 |
-
|
| 418 |
-
$$
|
| 419 |
-
{\overline{a_{k} \ldots a_{1}}}_{\mathrm{Fib}},{\overline{a_{k} \ldots a_{1} 0}}_{\mathrm{Fib}},{\overline{a_{k} \ldots a_{1} 00}}_{\mathrm{Fib}}, \ldots
|
| 420 |
-
$$
|
| 421 |
-
|
| 422 |
-
These sequences are Fibonacci-type by definition, and partition the positive integers since each positive integer has exactly one Fibonacci base representation.
|
| 423 |
-
\I Second solution. Call an infinite set of integers $S$ sandwiched if there exist increasing sequences $\left\{a_{i}\right\}_{i=0}^{\infty},\left\{b_{i}\right\}_{i=0}^{\infty}$ such that the following are true:
|
| 424 |
-
|
| 425 |
-
- $a_{i}+a_{i+1}=a_{i+2}$ and $b_{i}+b_{i+1}=b_{i+2}$.
|
| 426 |
-
- The intervals $\left[a_{i}+1, b_{i}-1\right]$ are disjoint and are nondecreasing in length.
|
| 427 |
-
- $S=\bigcup_{i=0}^{\infty}\left[a_{i}+1, b_{i}-1\right]$.
|
| 428 |
-
|
| 429 |
-
We claim that if $S$ is any nonempty sandwiched set, then $S$ can be partitioned into a Fibonacci-type sequence (involving the smallest element of $S$ ) and two smaller sandwiched sets. If this claim is proven, then we can start with $\mathbb{N} \backslash\{1,2,3,5, \ldots\}$, which is a sandwiched set, and repeatedly perform this partition, which will eventually sort each natural number into a Fibonacci-type sequence.
|
| 430 |
-
|
| 431 |
-
Let $S$ be a sandwiched set given by $\left\{a_{i}\right\}_{i=0}^{\infty},\left\{b_{i}\right\}_{i=0}^{\infty}$, so the smallest element in $S$ is $x=a_{0}+1$. Note that $y=a_{1}+1$ is also in $S$ and $x<y$. Then consider the Fibonaccitype sequence given by $f_{0}=x, f_{1}=y$, and $f_{k+2}=f_{k+1}+f_{k}$. We can then see that $f_{i} \in\left[a_{i}+1, b_{i}-1\right]$, as the sum of numbers in the intervals $\left[a_{k}+1, b_{k}-1\right],\left[a_{k+1}+1, b_{k+1}-1\right]$ lies in the interval
|
| 432 |
-
|
| 433 |
-
$$
|
| 434 |
-
\left[a_{k}+a_{k+1}+2, b_{k}+b_{k+1}-2\right]=\left[a_{k+2}+2, b_{k+2}-2\right] \subset\left[a_{k+2}+1, b_{k+2}-1\right]
|
| 435 |
-
$$
|
| 436 |
-
|
| 437 |
-
Therefore, this gives a natural partition of $S$ into this sequence and two sets:
|
| 438 |
-
|
| 439 |
-
$$
|
| 440 |
-
\begin{aligned}
|
| 441 |
-
S_{1} & =\bigcup_{i=0}^{\infty}\left[a_{i}+1, f_{i}-1\right] \\
|
| 442 |
-
\text { and } S_{2} & =\bigcup_{i=0}^{\infty}\left[f_{i}+1, b_{i}-1\right] .
|
| 443 |
-
\end{aligned}
|
| 444 |
-
$$
|
| 445 |
-
|
| 446 |
-
(For convenience, $[x, x-1]$ will be treated as the empty set.)
|
| 447 |
-
We now show that $S_{1}$ and $S_{2}$ are sandwiched. Since $\left\{a_{i}\right\},\left\{f_{i}\right\}$, and $\left\{b_{i}\right\}$ satisfy the Fibonacci recurrence, it is enough to check that the intervals have nondecreasing lengths. For $S_{1}$, that is equivalent to $f_{k+1}-a_{k+1} \geq f_{k}-a_{k}$ for each $k$. Fortunately, for $k \geq 1$, the difference is $f_{k-1}-a_{k-1} \geq 0$, and for $k=0, f_{1}-a_{1}=1=f_{0}-a_{0}$. Similarly for $S_{2}$, checking $b_{k+1}-f_{k+1} \geq b_{k}-f_{k}$ is easy for $k \geq 1$ as $b_{k-1}-f_{k-1} \geq 0$, and
|
| 448 |
-
|
| 449 |
-
$$
|
| 450 |
-
\left(b_{1}-f_{1}\right)-\left(b_{0}-f_{0}\right)=\left(b_{1}-a_{1}\right)-\left(b_{0}-a_{0}\right)
|
| 451 |
-
$$
|
| 452 |
-
|
| 453 |
-
which is nonnegative since the lengths of intervals in $S$ are nondecreasing.
|
| 454 |
-
Therefore we have shown that $S_{1}$ and $S_{2}$ are sandwiched. (Note that some of the $\left[a_{i}+1, f_{i}-1\right]$ may be empty, which would shift some indices back.) Since this gives us a procedure to take a set $S$ and produce a Fibonacci-type sequence with its smallest element, along which two other sandwiched types, we can partition $\mathbb{N}$ into an infinite number of Fibonacci-type sequences.
|
| 455 |
-
\l Third solution. We add Fibonacci-type sequences one-by-one. At each step, let $x$ be the smallest number that has not been used in any previous sequence. We generate a new Fibonacci-type sequence as follows. Set $a_{0}=x$ and for $i \geq 1$, set
|
| 456 |
-
|
| 457 |
-
$$
|
| 458 |
-
a_{i}=\left\lfloor\varphi a_{i-1}+\frac{1}{2}\right\rfloor
|
| 459 |
-
$$
|
| 460 |
-
|
| 461 |
-
Equivalently, $a_{i}$ is the closest integer to $\varphi a_{i-1}$.
|
| 462 |
-
It suffices to show that this sequence is Fibonacci-type and that no two sequences generated in this way overlap. We first show that for a positive integer $n$,
|
| 463 |
-
|
| 464 |
-
$$
|
| 465 |
-
\left\lfloor\varphi\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor=n+\left\lfloor\varphi n+\frac{1}{2}\right\rfloor .
|
| 466 |
-
$$
|
| 467 |
-
|
| 468 |
-
Indeed,
|
| 469 |
-
|
| 470 |
-
$$
|
| 471 |
-
\begin{aligned}
|
| 472 |
-
\left\lfloor\varphi\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor & =\left\lfloor\left(1+\varphi^{-1}\right)\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor \\
|
| 473 |
-
& =\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\left\lfloor\varphi^{-1}\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor .
|
| 474 |
-
\end{aligned}
|
| 475 |
-
$$
|
| 476 |
-
|
| 477 |
-
Note that $\left\lfloor\varphi n+\frac{1}{2}\right\rfloor=\varphi n+c$ for some $|c| \leq \frac{1}{2}$; this implies that $\varphi^{-1}\left\lfloor\varphi n+\frac{1}{2}\right\rfloor$ is within $\varphi^{-1} \cdot \frac{1}{2}<\frac{1}{2}$ of $n$, so its closest integer is $n$, proving the claim.
|
| 478 |
-
|
| 479 |
-
Therefore these sequences are Fibonacci-type. Additionally, if $a \neq b$, then $|\varphi a-\varphi b| \geq$ $\varphi>1$. Then
|
| 480 |
-
|
| 481 |
-
$$
|
| 482 |
-
a \neq b \Longrightarrow\left\lfloor\varphi a+\frac{1}{2}\right\rfloor \neq\left\lfloor\varphi b+\frac{1}{2}\right\rfloor,
|
| 483 |
-
$$
|
| 484 |
-
|
| 485 |
-
and since the first term of each sequence is chosen to not overlap with any previous sequences, these sequences are disjoint.
|
| 486 |
-
|
| 487 |
-
Remark. Ankan Bhattacharya points out that the same sequence essentially appears in IMO 1993, Problem 5 - in other words, a strictly increasing function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ with $f(1)=2$, and $f(f(n))=f(n)+n$.
|
| 488 |
-
|
| 489 |
-
Nikolai Beluhov sent us an older reference from March 1977, where Martin Gardner wrote in his column about Wythoff's Nim. The relevant excerpt goes:
|
| 490 |
-
"Imagine that we go through the infinite sequence of safe pairs (in the manner of Eratosthenes' sieve for sifting out primes) and cross out the infinite set of all safe pairs that are pairs in the Fibonacci sequence. The smallest pair that is not crossed out is $4 / 7$. We can now cross out a second infinite set of safe pairs, starting with $4 / 7$, that are pairs in the Lucas sequence. An infinite number of safe pairs, of which the lowest is now $6 / 10$, remain. This pair too begins another infinite Fibonacci sequence, all of whose pairs are safe. The process continues forever. Robert Silber, a mathematician at North Carolina State University, calls a safe pair "primitive" if it is the first safe pair that generates a Fibonacci sequence."
|
| 491 |
-
|
| 492 |
-
The relevant article by Robert Silber is A Fibonacci Property of Wythoff Pairs, from The Fibonacci Quarterly 11/1976.
|
| 493 |
-
|
| 494 |
-
I Fourth solution (Mark Sellke). For later reference let
|
| 495 |
-
|
| 496 |
-
$$
|
| 497 |
-
f_{1}=0, f_{2}=1, f_{3}=1, \ldots
|
| 498 |
-
$$
|
| 499 |
-
|
| 500 |
-
denote the ordinary Fibonacci numbers. We will denote the Fibonacci-like sequences by $F^{i}$ and the elements with subscripts; hence $F_{1}^{2}$ is the first element of the second sequence. Our construction amounts to just iteratively add new sequences; hence the following claim is the whole problem.
|
| 501 |
-
|
| 502 |
-
## Lemma
|
| 503 |
-
|
| 504 |
-
For any disjoint collection of Fibonacci-like sequences $F^{1}, \ldots, F^{k}$ and any integer $m$ contained in none of them, there is a new Fibonacci-like sequence $F^{k+1}$ beginning with $F_{1}^{k+1}=m$ which is disjoint from the previous sequences.
|
| 505 |
-
|
| 506 |
-
Observe first that for each sequence $F^{j}$ there is $c^{j} \in \mathbb{R}^{n}$ such that
|
| 507 |
-
|
| 508 |
-
$$
|
| 509 |
-
F_{n}^{j}=c^{j} \phi^{n}+o(1)
|
| 510 |
-
$$
|
| 511 |
-
|
| 512 |
-
where
|
| 513 |
-
|
| 514 |
-
$$
|
| 515 |
-
\phi=\frac{1+\sqrt{5}}{2}
|
| 516 |
-
$$
|
| 517 |
-
|
| 518 |
-
Collapse the group $\left(\mathbb{R}^{+}, \times\right)$into the half-open interval $J=\{x \mid 1 \leq x<\phi\}$ by defining $T(x)=y$ for the unique $y \in J$ with $x=y \phi^{n}$ for some integer $n$.
|
| 519 |
-
|
| 520 |
-
Fix an interval $I=[a, b] \subseteq[1.2,1.3]$ (the last condition is to avoid wrap-around issues) which contains none of the $c^{j}$, and take $\varepsilon<0.001$ to be small enough that in fact each $c^{j}$ has distance at least $10 \varepsilon$ from $I$; this means any $c_{j}$ and element of $I$ differ by at least a $(1+10 \varepsilon)$ factor. The idea will be to take $F_{1}^{k+1}=m$ and $F_{2}^{k+1}$ to be a large such that the induced values of $F_{j}^{k+1}$ grow like $k \phi^{j}$ for $j \in T^{-1}(I)$, so that $F_{n}^{k+1}$ is separated from the $c^{j}$ after applying $T$. What's left to check is the convergence.
|
| 521 |
-
|
| 522 |
-
Now let
|
| 523 |
-
|
| 524 |
-
$$
|
| 525 |
-
c=\lim _{n \rightarrow \infty} \frac{f_{n}}{\phi^{n}}
|
| 526 |
-
$$
|
| 527 |
-
|
| 528 |
-
and take $M$ large enough that for $n>M$ we have
|
| 529 |
-
|
| 530 |
-
$$
|
| 531 |
-
\left|\frac{f_{n}}{c \phi^{n}}-1\right|<\varepsilon
|
| 532 |
-
$$
|
| 533 |
-
|
| 534 |
-
Now $\frac{T^{-1}(I)}{c}$ contains arbitrarily large integers, so there are infinitely many $N$ with $c N \in T^{-1}(I)$ with $N>\frac{10 m}{\varepsilon}$. We claim that for any such $N$, the sequence $F^{(N)}$ defined by
|
| 535 |
-
|
| 536 |
-
$$
|
| 537 |
-
F_{1}^{(N)}=m, F_{2}^{(N)}=N
|
| 538 |
-
$$
|
| 539 |
-
|
| 540 |
-
will be very multiplicatively similar to the normal Fibonacci numbers up to rescaling; indeed for $j=2, j=3$ we have $\frac{F_{2}^{(N)}}{f_{2}}=N, \frac{F_{3}^{(N)}}{f_{3}}=N+m$ and so by induction we will have
|
| 541 |
-
|
| 542 |
-
$$
|
| 543 |
-
\frac{F_{j}^{(N)}}{f_{j}} \in[N, N+m] \subseteq[N, N(1+\varepsilon)]
|
| 544 |
-
$$
|
| 545 |
-
|
| 546 |
-
for $j \geq 2$. Therefore, up to small multiplicative errors, we have
|
| 547 |
-
|
| 548 |
-
$$
|
| 549 |
-
F_{j}^{(N)} \approx N f_{j} \approx c N \phi^{j}
|
| 550 |
-
$$
|
| 551 |
-
|
| 552 |
-
From this we see that for $j>M$ we have
|
| 553 |
-
|
| 554 |
-
$$
|
| 555 |
-
T\left(F_{j}^{(N)}\right) \in T(c N) \cdot[1-2 \varepsilon, 1+2 \varepsilon]
|
| 556 |
-
$$
|
| 557 |
-
|
| 558 |
-
In particular, since $T(c N) \in I$ and $I$ is separated from each $c_{j}$ by a factor of $(1+10 \varepsilon)$, we get that $F_{j}^{(N)}$ is not in any of $F^{1}, F^{2}, \ldots, F^{k}$.
|
| 559 |
-
|
| 560 |
-
Finishing is easy, since we now have a uniform estimate on how many terms we need to check for a new element before the exponential growth takes over. We will just use pigeonhole to argue that there are few possible collisions among those early terms, so we can easily pick a value of $N$ which avoids them all. We write it out below.
|
| 561 |
-
|
| 562 |
-
For large $L$, the set
|
| 563 |
-
|
| 564 |
-
$$
|
| 565 |
-
S_{L}=\left(I \cdot \phi^{L}\right) \cap \mathbb{Z}
|
| 566 |
-
$$
|
| 567 |
-
|
| 568 |
-
contains at least $k_{I} \phi^{L}$ elements. As $N$ ranges over $S_{L}$, for each fixed $j$, the value of $F_{j}^{(N)}$ varies by at most a factor of 1.1 because we imposed $I \subseteq[1.2,1.3]$ and so this is true for the first two terms, hence for all subsequent terms by induction. Now suppose $L$ is very large, and consider a fixed pair $(i, j)$ with $i \leq k$ and $j \leq M$. We claim there is at most 1 possible value $k$ such that the term $F_{k}^{i}$ could equal $F_{j}^{(N)}$ for some $N \in S_{L}$; indeed, the terms of $F^{i}$ are growing at exponential rate with factor $\phi>1.1$, so at most one will be in a given interval of multiplicative width at most 1.1.
|
| 569 |
-
|
| 570 |
-
Hence, of these $k_{I} \phi^{L}$ values of $N$, at most $k M$ could cause problems, one for each pair $(i, j)$. However by monotonicity of $F_{j}^{(N)}$ in $N$, at most 1 value of $N$ causes a collision for each pair $(i, j)$. Hence for large $L$ so that $k_{I} \phi^{L}>10 k M$ we can find a suitable $N \in S_{L}$ by pigeonhole and the sequence $F^{(N)}$ defined by $(m, N, N+m, \ldots)$ works.
|
| 571 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2018.md
DELETED
|
@@ -1,678 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2018 Solutions <br> United States of America - TST Selection Test <br> Evan Chen《陳誼廷》 <br> $60^{\text {th }}$ IMO 2019 United Kingdom and $8^{\text {th }}$ EGMO 2019 Ukraine
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 4
|
| 7 |
-
1.1 TSTST 2018/1, proposed by Evan Chen, Yang Liu ..... 4
|
| 8 |
-
1.2 TSTST 2018/2, proposed by Victor Wang ..... 6
|
| 9 |
-
1.3 TSTST 2018/3, proposed by Yannick Yao, Evan Chen ..... 8
|
| 10 |
-
2 Solutions to Day 2 ..... 11
|
| 11 |
-
2.1 TSTST 2018/4, proposed by Ivan Borsenco ..... 11
|
| 12 |
-
2.2 TSTST 2018/5, proposed by Ankan Bhattacharya, Evan Chen ..... 13
|
| 13 |
-
2.3 TSTST 2018/6, proposed by Ray Li ..... 17
|
| 14 |
-
3 Solutions to Day 3 ..... 20
|
| 15 |
-
3.1 TSTST 2018/7, proposed by Ashwin Sah ..... 20
|
| 16 |
-
3.2 TSTST 2018/8, proposed by Ankan Bhattacharya, Evan Chen ..... 22
|
| 17 |
-
3.3 TSTST 2018/9, proposed by Linus Hamilton ..... 24
|
| 18 |
-
|
| 19 |
-
## §0 Problems
|
| 20 |
-
|
| 21 |
-
1. As usual, let $\mathbb{Z}[x]$ denote the set of single-variable polynomials in $x$ with integer coefficients. Find all functions $\theta: \mathbb{Z}[x] \rightarrow \mathbb{Z}$ such that for any polynomials $p, q \in$ $\mathbb{Z}[x]$,
|
| 22 |
-
|
| 23 |
-
- $\theta(p+1)=\theta(p)+1$, and
|
| 24 |
-
- if $\theta(p) \neq 0$ then $\theta(p)$ divides $\theta(p \cdot q)$.
|
| 25 |
-
|
| 26 |
-
2. In the nation of Onewaynia, certain pairs of cities are connected by one-way roads. Every road connects exactly two cities (roads are allowed to cross each other, e.g., via bridges), and each pair of cities has at most one road between them. Moreover, every city has exactly two roads leaving it and exactly two roads entering it.
|
| 27 |
-
We wish to close half the roads of Onewaynia in such a way that every city has exactly one road leaving it and exactly one road entering it. Show that the number of ways to do so is a power of 2 greater than 1 (i.e. of the form $2^{n}$ for some integer $n \geq 1$ ).
|
| 28 |
-
3. Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$.
|
| 29 |
-
|
| 30 |
-
Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
| 31 |
-
4. For an integer $n>0$, denote by $\mathcal{F}(n)$ the set of integers $m>0$ for which the polynomial $p(x)=x^{2}+m x+n$ has an integer root.
|
| 32 |
-
(a) Let $S$ denote the set of integers $n>0$ for which $\mathcal{F}(n)$ contains two consecutive integers. Show that $S$ is infinite but
|
| 33 |
-
|
| 34 |
-
$$
|
| 35 |
-
\sum_{n \in S} \frac{1}{n} \leq 1
|
| 36 |
-
$$
|
| 37 |
-
|
| 38 |
-
(b) Prove that there are infinitely many positive integers $n$ such that $\mathcal{F}(n)$ contains three consecutive integers.
|
| 39 |
-
5. Let $A B C$ be an acute triangle with circumcircle $\omega$, and let $H$ be the foot of the altitude from $A$ to $\overline{B C}$. Let $P$ and $Q$ be the points on $\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that the circumcircles of $\triangle A E_{1} F_{1}$ and $\triangle A E_{2} F_{2}$ are congruent, and the line through their centers is parallel to the tangent to $\omega$ at $A$.
|
| 40 |
-
6. Let $S=\{1, \ldots, 100\}$, and for every positive integer $n$ define
|
| 41 |
-
|
| 42 |
-
$$
|
| 43 |
-
T_{n}=\left\{\left(a_{1}, \ldots, a_{n}\right) \in S^{n} \mid a_{1}+\cdots+a_{n} \equiv 0 \quad(\bmod 100)\right\}
|
| 44 |
-
$$
|
| 45 |
-
|
| 46 |
-
Determine which $n$ have the following property: if we color any 75 elements of $S$ red, then at least half of the $n$-tuples in $T_{n}$ have an even number of coordinates with red elements.
|
| 47 |
-
7. Let $n$ be a positive integer. A frog starts on the number line at 0 . Suppose it makes a finite sequence of hops, subject to two conditions:
|
| 48 |
-
|
| 49 |
-
- The frog visits only points in $\left\{1,2, \ldots, 2^{n}-1\right\}$, each at most once.
|
| 50 |
-
- The length of each hop is in $\left\{2^{0}, 2^{1}, 2^{2}, \ldots\right\}$. (The hops may be either direction, left or right.)
|
| 51 |
-
|
| 52 |
-
Let $S$ be the sum of the (positive) lengths of all hops in the sequence. What is the maximum possible value of $S$ ?
|
| 53 |
-
8. For which positive integers $b>2$ do there exist infinitely many positive integers $n$ such that $n^{2}$ divides $b^{n}+1$ ?
|
| 54 |
-
9. Show that there is an absolute constant $c<1$ with the following property: whenever $\mathcal{P}$ is a polygon with area 1 in the plane, one can translate it by a distance of $\frac{1}{100}$ in some direction to obtain a polygon $\mathcal{Q}$, for which the intersection of the interiors of $\mathcal{P}$ and $\mathcal{Q}$ has total area at most $c$.
|
| 55 |
-
|
| 56 |
-
## §1 Solutions to Day 1
|
| 57 |
-
|
| 58 |
-
## §1.1 TSTST 2018/1, proposed by Evan Chen, Yang Liu
|
| 59 |
-
|
| 60 |
-
Available online at https://aops.com/community/p10570981.
|
| 61 |
-
|
| 62 |
-
## Problem statement
|
| 63 |
-
|
| 64 |
-
As usual, let $\mathbb{Z}[x]$ denote the set of single-variable polynomials in $x$ with integer coefficients. Find all functions $\theta: \mathbb{Z}[x] \rightarrow \mathbb{Z}$ such that for any polynomials $p, q \in \mathbb{Z}[x]$,
|
| 65 |
-
|
| 66 |
-
- $\theta(p+1)=\theta(p)+1$, and
|
| 67 |
-
- if $\theta(p) \neq 0$ then $\theta(p)$ divides $\theta(p \cdot q)$.
|
| 68 |
-
|
| 69 |
-
The answer is $\theta: p \mapsto p(c)$, for each choice of $c \in \mathbb{Z}$. Obviously these work, so we prove these are the only ones. In what follows, $x \in \mathbb{Z}[x]$ is the identity polynomial, and $c=\theta(x)$.
|
| 70 |
-
|
| 71 |
-
【 First solution (Merlijn Staps). Consider an integer $n \neq c$. Because $x-n \mid p(x)-p(n)$, we have
|
| 72 |
-
|
| 73 |
-
$$
|
| 74 |
-
\theta(x-n)|\theta(p(x)-p(n)) \Longrightarrow c-n| \theta(p(x))-p(n) .
|
| 75 |
-
$$
|
| 76 |
-
|
| 77 |
-
On the other hand, $c-n \mid p(c)-p(n)$. Combining the previous two gives $c-n \mid$ $\theta(p(x))-p(c)$, and by letting $n$ large we conclude $\theta(p(x))-p(c)=0$, so $\theta(p(x))=p(c)$.
|
| 78 |
-
|
| 79 |
-
II Second solution. First, we settle the case $\operatorname{deg} p=0$. In that case, from the second property, $\theta(m)=m+\theta(0)$ for every integer $m \in \mathbb{Z}$ (viewed as a constant polynomial). Thus $m+\theta(0) \mid 2 m+\theta(0)$, hence $m+\theta(0) \mid-\theta(0)$, so $\theta(0)=0$ by taking $m$ large. Thus $\theta(m)=m$ for $m \in \mathbb{Z}$.
|
| 80 |
-
|
| 81 |
-
Next, we address the case of $\operatorname{deg} p=1$. We know $\theta(x+b)=c+b$ for $b \in \mathbb{Z}$. Now for each particular $a \in \mathbb{Z}$, we have
|
| 82 |
-
|
| 83 |
-
$$
|
| 84 |
-
c+k|\theta(x+k)| \theta(a x+a k)=\theta(a x)+a k \Longrightarrow c+k \mid \theta(a x)-a c .
|
| 85 |
-
$$
|
| 86 |
-
|
| 87 |
-
for any $k \neq-c$. Since this is true for large enough $k$, we conclude $\theta(a x)=a c$. Thus $\theta(a x+b)=a c+b$.
|
| 88 |
-
|
| 89 |
-
We now proceed by induction on $\operatorname{deg} p$. Fix a polynomial $p$ and assume it's true for all $p$ of smaller degree. Choose a large integer $n$ (to be determined later) for which $p(n) \neq p(c)$. We then have
|
| 90 |
-
|
| 91 |
-
$$
|
| 92 |
-
\left.\frac{p(c)-p(n)}{c-n}=\theta\left(\frac{p-p(n)}{x-n}\right) \right\rvert\, \theta(p-p(n))=\theta(p)-p(n)
|
| 93 |
-
$$
|
| 94 |
-
|
| 95 |
-
Subtracting off $c-n$ times the left-hand side gives
|
| 96 |
-
|
| 97 |
-
$$
|
| 98 |
-
\left.\frac{p(c)-p(n)}{c-n} \right\rvert\, \theta(p)-p(c)
|
| 99 |
-
$$
|
| 100 |
-
|
| 101 |
-
The left-hand side can be made arbitrarily large by letting $n \rightarrow \infty$, since $\operatorname{deg} p \geq 2$. Thus $\theta(p)=p(c)$, concluding the proof.
|
| 102 |
-
\ Authorship comments. I will tell you a story about the creation of this problem. Yang Liu and I were looking over the drafts of December and January TST in October 2017, and both of us had the impression that the test was too difficult. This sparked a non-serious suggestion that we should try to come up with a problem now that would be easy enough to use. While we ended up just joking about changing the TST, we did get this problem out of it.
|
| 103 |
-
|
| 104 |
-
Our idea was to come up with a functional equation that was different from the usual fare: at first we tried $\mathbb{Z}[x] \rightarrow \mathbb{Z}[x]$, but then I suggested the idea of using $\mathbb{Z}[x] \rightarrow \mathbb{Z}$, with the answer being the "evaluation" map. Well, what properties does that satisfy? One answer was $a-b \mid p(a)-p(b)$; this didn't immediately lead to anything, but eventually we hit on the form of the problem above off this idea. At first we didn't require $\theta(p) \neq 0$ in the bullet, but without the condition the problem was too easy, since 0 divides only itself; and so the condition was added and we got the functional equation.
|
| 105 |
-
|
| 106 |
-
I proposed the problem to USAMO 2018, but it was rejected (unsurprisingly; I think the problem may be too abstract for novice contestants). Instead it was used for TSTST, which I thought fit better.
|
| 107 |
-
|
| 108 |
-
## §1.2 TSTST 2018/2, proposed by Victor Wang
|
| 109 |
-
|
| 110 |
-
Available online at https://aops.com/community/p10570985.
|
| 111 |
-
|
| 112 |
-
## Problem statement
|
| 113 |
-
|
| 114 |
-
In the nation of Onewaynia, certain pairs of cities are connected by one-way roads. Every road connects exactly two cities (roads are allowed to cross each other, e.g., via bridges), and each pair of cities has at most one road between them. Moreover, every city has exactly two roads leaving it and exactly two roads entering it.
|
| 115 |
-
|
| 116 |
-
We wish to close half the roads of Onewaynia in such a way that every city has exactly one road leaving it and exactly one road entering it. Show that the number of ways to do so is a power of 2 greater than 1 (i.e. of the form $2^{n}$ for some integer $n \geq 1$ ).
|
| 117 |
-
|
| 118 |
-
In the language of graph theory, we have a simple digraph $G$ which is 2 -regular and we seek the number of sub-digraphs which are 1-regular. We now present two solution paths.
|
| 119 |
-
|
| 120 |
-
『 First solution, combinatorial. We construct a simple undirected bipartite graph $\Gamma$ as follows:
|
| 121 |
-
|
| 122 |
-
- the vertex set consists of two copies of $V(G)$, say $V_{\text {out }}$ and $V_{\text {in }}$; and
|
| 123 |
-
- for $v \in V_{\text {out }}$ and $w \in V_{\text {in }}$ we have an undirected edge $v w \in E(\Gamma)$ if and only if the directed edge $v \rightarrow w$ is in $G$.
|
| 124 |
-
|
| 125 |
-
Moreover, the desired sub-digraphs of $H$ correspond exactly to perfect matchings of $\Gamma$.
|
| 126 |
-
However the graph $\Gamma$ is 2 -regular and hence consists of several disjoint (simple) cycles of even length. If there are $n$ such cycles, the number of perfect matchings is $2^{n}$, as desired.
|
| 127 |
-
|
| 128 |
-
Remark. The construction of $\Gamma$ is not as magical as it may first seem.
|
| 129 |
-
Suppose we pick a road $v_{1} \rightarrow v_{2}$ to use. Then, the other road $v_{3} \rightarrow v_{2}$ is certainly not used; hence some other road $v_{3} \rightarrow v_{4}$ must be used, etc. We thus get a cycle of forced decisions until we eventually return to the vertex $v_{1}$.
|
| 130 |
-
|
| 131 |
-
These cycles in the original graph $G$ (where the arrows alternate directions) correspond to the cycles we found in $\Gamma$. It's merely that phrasing the solution in terms of $\Gamma$ makes it cleaner in a linguistic sense, but not really in a mathematical sense.
|
| 132 |
-
|
| 133 |
-
【 Second solution by linear algebra over $\mathbb{F}_{2}$ (Brian Lawrence). This is actually not that different from the first solution. For each edge $e$, we create an indicator variable $x_{e}$. We then require for each vertex $v$ that:
|
| 134 |
-
|
| 135 |
-
- If $e_{1}$ and $e_{2}$ are the two edges leaving $v$, then we require $x_{e_{1}}+x_{e_{2}} \equiv 1(\bmod 2)$.
|
| 136 |
-
- If $e_{3}$ and $e_{4}$ are the two edges entering $v$, then we require $x_{e_{3}}+x_{e_{4}} \equiv 1(\bmod 2)$.
|
| 137 |
-
|
| 138 |
-
We thus get a large system of equations. Moreover, the solutions come in natural pairs $\vec{x}$ and $\vec{x}+\overrightarrow{1}$ and therefore the number of solutions is either zero, or a power of two. So we just have to prove there is at least one solution.
|
| 139 |
-
|
| 140 |
-
For linear algebra reasons, there can only be zero solutions if some nontrivial linear combination of the equations gives the sum $0 \equiv 1$. So suppose we added up some subset $S$
|
| 141 |
-
of the equations for which every variable appeared on the left-hand side an even number of times. Then every variable that did appear appeared exactly twice; and accordingly we see that the edges corresponding to these variables form one or more even cycles as in the previous solution. Of course, this means $|S|$ is even, so we really have $0 \equiv 0(\bmod 2)$ as needed.
|
| 142 |
-
|
| 143 |
-
Remark. The author's original proposal contained a second part asking to show that it was not always possible for the resulting $H$ to be connected, even if $G$ was strongly connected. This problem is related to IMO Shortlist 2002 C6, which gives an example of a strongly connected graph which does have a full directed Hamiltonian cycle.
|
| 144 |
-
|
| 145 |
-
## §1.3 TSTST 2018/3, proposed by Yannick Yao, Evan Chen
|
| 146 |
-
|
| 147 |
-
Available online at https://aops.com/community/p10570988.
|
| 148 |
-
|
| 149 |
-
## Problem statement
|
| 150 |
-
|
| 151 |
-
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$.
|
| 152 |
-
|
| 153 |
-
Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
| 154 |
-
|
| 155 |
-
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$.
|
| 156 |
-
|
| 157 |
-
Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put
|
| 158 |
-
|
| 159 |
-
$$
|
| 160 |
-
x=K A=L B=L C=L X=L Y=K X=K Y .
|
| 161 |
-
$$
|
| 162 |
-
|
| 163 |
-
Proof. By construction, $K A=L B=L C$. Also, $\overline{M O}$ is the perpendicular bisector of $\overline{K L}$ (since the chords $\overline{K L}, \overline{A B}$ of $\omega$ are parallel) and so $K X L Y$ is a rhombus as well.
|
| 164 |
-
|
| 165 |
-
Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since
|
| 166 |
-
|
| 167 |
-
$$
|
| 168 |
-
\measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C .
|
| 169 |
-
$$
|
| 170 |
-
|
| 171 |
-
|
| 172 |
-
|
| 173 |
-
Up to now we have not used the existence of $Q$; we henceforth do so.
|
| 174 |
-
|
| 175 |
-
Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$.
|
| 176 |
-
|
| 177 |
-
The main claim is now:
|
| 178 |
-
Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$.
|
| 179 |
-
|
| 180 |
-
First proof of Claim, communicated by Milan Haiman. Observe that $\triangle Q L C \sim \triangle L O C$ since both triangles are isosceles and share a base angle. Hence, $C L^{2}=C O \cdot C Q$.
|
| 181 |
-
|
| 182 |
-
Let $N$ be the midpoint of $\overline{A C}$, which lies on $(A M O Q)$. Then,
|
| 183 |
-
|
| 184 |
-
$$
|
| 185 |
-
x^{2}=C L^{2}=C O \cdot C Q=C N \cdot C A=\frac{1}{2} C A^{2}=\frac{1}{2} L K^{2}
|
| 186 |
-
$$
|
| 187 |
-
|
| 188 |
-
where we have also used the fact $A Q O N$ is cyclic. Thus $L K=\sqrt{2} x$ and so the rhombus $L X K Y$ is actually a square.
|
| 189 |
-
|
| 190 |
-
Second proof of Claim, Evan Chen. Observe that $Q$ lies on the circle with diameter $\overline{A C}$, centered at $N$, say. This means that $O$ lies on the radical axis of $\omega$ and $(N)$, hence $\overline{N L} \perp \overline{C O}$ implying
|
| 191 |
-
|
| 192 |
-
$$
|
| 193 |
-
\begin{aligned}
|
| 194 |
-
N O^{2}+C L^{2} & =N C^{2}+L O^{2}=N C^{2}+O C^{2}=N C^{2}+N O^{2}+N C^{2} \\
|
| 195 |
-
\Longrightarrow x^{2} & =2 N C^{2} \\
|
| 196 |
-
\Longrightarrow x & =\sqrt{2} N C=\frac{1}{\sqrt{2}} A C=\frac{1}{\sqrt{2}} L K
|
| 197 |
-
\end{aligned}
|
| 198 |
-
$$
|
| 199 |
-
|
| 200 |
-
So $L X K Y$ is a rhombus with $L K=\sqrt{2} x$. Hence it is a square.
|
| 201 |
-
Third proof of Claim. A solution by trig is also possible. As in the previous claims, it suffices to show that $A C=\sqrt{2} x$.
|
| 202 |
-
|
| 203 |
-
First, we compute the length $C Q$ in two ways; by angle chasing one can show $\angle C B Q=$ $180^{\circ}-(\angle B Q C+\angle Q C B)=\frac{1}{2} \angle A$, and so
|
| 204 |
-
|
| 205 |
-
$$
|
| 206 |
-
\begin{aligned}
|
| 207 |
-
A C \sin B=C Q & =\frac{B C}{\sin \left(90^{\circ}+\frac{1}{2} \angle A\right)} \cdot \sin \frac{1}{2} \angle A \\
|
| 208 |
-
\Longleftrightarrow \sin ^{2} B & =\frac{\sin A \cdot \sin \frac{1}{2} \angle A}{\cos \frac{1}{2} \angle A} \\
|
| 209 |
-
\Longleftrightarrow \sin ^{2} B & =2 \sin ^{2} \frac{1}{2} \angle A \\
|
| 210 |
-
\Longleftrightarrow \sin B & =\sqrt{2} \sin \frac{1}{2} \angle A \\
|
| 211 |
-
\Longleftrightarrow 2 R \sin B & =\sqrt{2}\left(2 R \sin \frac{1}{2} \angle A\right) \\
|
| 212 |
-
\Longleftrightarrow A C & =\sqrt{2} x
|
| 213 |
-
\end{aligned}
|
| 214 |
-
$$
|
| 215 |
-
|
| 216 |
-
as desired (we have here used the fact $\triangle A B C$ is acute to take square roots).
|
| 217 |
-
It is interesting to note that $\sin ^{2} B=2 \sin ^{2} \frac{1}{2} \angle A$ can be rewritten as
|
| 218 |
-
|
| 219 |
-
$$
|
| 220 |
-
\cos A=\cos ^{2} B
|
| 221 |
-
$$
|
| 222 |
-
|
| 223 |
-
since $\cos ^{2} B=1-\sin ^{2} B=1-2 \sin ^{2} \frac{1}{2} \angle A=\cos A$; this is the condition for the existence of the point $Q$.
|
| 224 |
-
|
| 225 |
-
We finish by proving that
|
| 226 |
-
|
| 227 |
-
$$
|
| 228 |
-
K D=K A
|
| 229 |
-
$$
|
| 230 |
-
|
| 231 |
-
and hence line $\overline{K D}$ is tangent to $\gamma$. Let $E=\overline{B C} \cap \overline{K L}$. Then
|
| 232 |
-
|
| 233 |
-
$$
|
| 234 |
-
L E \cdot L K=L C^{2}=L X^{2}=\frac{1}{2} L K^{2}
|
| 235 |
-
$$
|
| 236 |
-
|
| 237 |
-
and so $E$ is the midpoint of $\overline{L K}$. Thus $\overline{M X O Y}, \overline{B C}, \overline{K L}$ are concurrent at $E$. As $\overline{D L} \| \overline{K C}$, we find that $D L C K$ is a parallelogram, so $K D=C L=K A$ as well. Thus $\overline{K D}$ and $\overline{K A}$ are tangent to $\gamma$.
|
| 238 |
-
|
| 239 |
-
Remark. The condition $\angle A \neq 60^{\circ}$ cannot be dropped, since if $Q=O$ the problem is not true.
|
| 240 |
-
|
| 241 |
-
On the other hand, nearly all solutions begin by observing $Q \neq O$ and then obtaining $\angle A Q O=90^{\circ}$. This gives a way to construct the diagram by hand with ruler and compass. One draws an arbitrary chord $\overline{B C}$ of a circle $\omega$ centered at $L$, and constructs $O$ as the circumcenter of $\triangle B L C$ (hence obtaining $\Gamma$ ). Then $Q$ is defined as the intersection of ray $C O$ with $\omega$, and $A$ is defined by taking the perpendicular line through $Q$ on the circle $\Gamma$. In this way we can draw a triangle $A B C$ satisfying the problem conditions.
|
| 242 |
-
\ Authorship comments. In the notation of the present points, the question originally sent to me by Yannick Yao read:
|
| 243 |
-
|
| 244 |
-
Circles $(L)$ and $(O)$ are drawn, meeting at $B$ and $C$, with $L$ on $(O)$. Ray $C O$ meets $(L)$ at $Q$, and $A$ is on $(O)$ such that $\angle C Q A=90^{\circ}$. The angle bisector of $\angle A O B$ meets $(L)$ at $X$ and $Y$. Show that $\angle X L Y=90^{\circ}$.
|
| 245 |
-
|
| 246 |
-
Notice the points $M$ and $K$ are absent from the problem. I am told this was found as part of the computer game "Euclidea". Using this as the starting point, I constructed the TSTST problem by recognizing the significance of that special point $K$, which became the center of attention.
|
| 247 |
-
|
| 248 |
-
## §2 Solutions to Day 2
|
| 249 |
-
|
| 250 |
-
## §2.1 TSTST 2018/4, proposed by Ivan Borsenco
|
| 251 |
-
|
| 252 |
-
Available online at https://aops.com/community/p10570991.
|
| 253 |
-
|
| 254 |
-
## Problem statement
|
| 255 |
-
|
| 256 |
-
For an integer $n>0$, denote by $\mathcal{F}(n)$ the set of integers $m>0$ for which the polynomial $p(x)=x^{2}+m x+n$ has an integer root.
|
| 257 |
-
(a) Let $S$ denote the set of integers $n>0$ for which $\mathcal{F}(n)$ contains two consecutive integers. Show that $S$ is infinite but
|
| 258 |
-
|
| 259 |
-
$$
|
| 260 |
-
\sum_{n \in S} \frac{1}{n} \leq 1
|
| 261 |
-
$$
|
| 262 |
-
|
| 263 |
-
(b) Prove that there are infinitely many positive integers $n$ such that $\mathcal{F}(n)$ contains three consecutive integers.
|
| 264 |
-
|
| 265 |
-
We prove the following.
|
| 266 |
-
Claim - The set $S$ is given explicitly by $S=\{x(x+1) y(y+1) \mid x, y>0\}$.
|
| 267 |
-
|
| 268 |
-
Proof. Note that $m, m+1 \in \mathcal{F}(n)$ if and only if there exist integers $q>p \geq 0$ such that
|
| 269 |
-
|
| 270 |
-
$$
|
| 271 |
-
\begin{aligned}
|
| 272 |
-
m^{2}-4 n & =p^{2} \\
|
| 273 |
-
(m+1)^{2}-4 n & =q^{2}
|
| 274 |
-
\end{aligned}
|
| 275 |
-
$$
|
| 276 |
-
|
| 277 |
-
Subtraction gives $2 m+1=q^{2}-p^{2}$, so $p$ and $q$ are different parities. We can thus let $q-p=2 x+1, q+p=2 y+1$, where $y \geq x \geq 0$ are integers. It follows that
|
| 278 |
-
|
| 279 |
-
$$
|
| 280 |
-
\begin{aligned}
|
| 281 |
-
4 n & =m^{2}-p^{2} \\
|
| 282 |
-
& =\left(\frac{q^{2}-p^{2}-1}{2}\right)^{2}-p^{2}=\left(\frac{q^{2}-p^{2}-1}{2}-p\right)\left(\frac{q^{2}-p^{2}-1}{2}+p\right) \\
|
| 283 |
-
& =\frac{q^{2}-\left(p^{2}+2 p+1\right)}{2} \cdot \frac{q^{2}-\left(p^{2}-2 p+1\right)}{2} \\
|
| 284 |
-
& =\frac{1}{4}(q-p-1)(q-p+1)(q+p-1)(q+p+1)=\frac{1}{4}(2 x)(2 x+2)(2 y)(2 y+2) \\
|
| 285 |
-
\Longrightarrow n & =x(x+1) y(y+1) .
|
| 286 |
-
\end{aligned}
|
| 287 |
-
$$
|
| 288 |
-
|
| 289 |
-
Since $n>0$ we require $x, y>0$. Conversely, if $n=x(x+1) y(y+1)$ for positive $x$ and $y$ then $m=\sqrt{p^{2}+4 n}=\sqrt{(y-x)^{2}+4 n}=2 x y+x+y=x(y+1)+(x+1) y$ and $m+1=2 x y+x+y+1=x y+(x+1)(y+1)$. Thus we conclude the main claim.
|
| 290 |
-
|
| 291 |
-
From this, part (a) follows as
|
| 292 |
-
|
| 293 |
-
$$
|
| 294 |
-
\sum_{n \in S} n^{-1} \leq\left(\sum_{x \geq 1} \frac{1}{x(x+1)}\right)\left(\sum_{y \geq 1} \frac{1}{y(y+1)}\right)=1 \cdot 1=1
|
| 295 |
-
$$
|
| 296 |
-
|
| 297 |
-
As for (b), retain the notation in the proof of the claim. Now $m+2 \in S$ if and only if $(m+2)^{2}-4 n$ is a square, say $r^{2}$. Writing in terms of $p$ and $q$ as parameters we find
|
| 298 |
-
|
| 299 |
-
$$
|
| 300 |
-
\begin{aligned}
|
| 301 |
-
r^{2} & =(m+2)^{2}-4 n=m^{2}-4 n+4 m+4=p^{2}+2+2(2 m+1) \\
|
| 302 |
-
& =p^{2}+2\left(q^{2}-p^{2}\right)+2=2 q^{2}-p^{2}+2 \\
|
| 303 |
-
\Longleftrightarrow 2 q^{2}+2 & =p^{2}+r^{2} \quad(\dagger)
|
| 304 |
-
\end{aligned}
|
| 305 |
-
$$
|
| 306 |
-
|
| 307 |
-
with $q>p$ of different parity and $n=\frac{1}{16}(q-p-1)(q-p+1)(q+p-1)(q+p+1)$.
|
| 308 |
-
Note that (by taking modulo 8 ) we have $q \not \equiv p \equiv r(\bmod 2)$, and so there are no parity issues and we will always assume $p<q<r$ in ( $\dagger$ ). Now, for every $q$, the equation ( $\dagger$ ) has a canonical solution $(p, r)=(q-1, q+1)$, but this leaves $n=0$. Thus we want to show for infinitely many $q$ there is a third way to write $2 q^{2}+2$ as a sum of squares, which will give the desired $p$.
|
| 309 |
-
|
| 310 |
-
To do this, choose large integers $q$ such that $q^{2}+1$ is divisible by at least three distinct $1 \bmod 4$ primes. Since each such prime can be written as a sum of two squares, using Lagrange identity, we can deduce that $2 q^{2}+2$ can be written as a sum of two squares in at least three different ways, as desired.
|
| 311 |
-
|
| 312 |
-
Remark. We can see that $n=144$ is the smallest integer such that $\mathcal{F}(n)$ contains three consecutive integers and $n=15120$ is the smallest integer such that $\mathcal{F}(n)$ contains four consecutive integers. It would be interesting to determine whether the number of consecutive elements in $\mathcal{F}(n)$ can be arbitrarily large or is bounded.
|
| 313 |
-
|
| 314 |
-
## §2.2 TSTST 2018/5, proposed by Ankan Bhattacharya, Evan Chen
|
| 315 |
-
|
| 316 |
-
Available online at https://aops.com/community/p10571000.
|
| 317 |
-
|
| 318 |
-
## Problem statement
|
| 319 |
-
|
| 320 |
-
Let $A B C$ be an acute triangle with circumcircle $\omega$, and let $H$ be the foot of the altitude from $A$ to $\overline{B C}$. Let $P$ and $Q$ be the points on $\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that the circumcircles of $\triangle A E_{1} F_{1}$ and $\triangle A E_{2} F_{2}$ are congruent, and the line through their centers is parallel to the tangent to $\omega$ at $A$.
|
| 321 |
-
|
| 322 |
-
Let $O$ be the center of $\omega$, and let $M=\overline{P Q} \cap \overline{A B}$ and $N=\overline{P Q} \cap \overline{A C}$ be the midpoints of $\overline{A B}$ and $\overline{A C}$ respectively. Refer to the diagram below.
|
| 323 |
-
|
| 324 |
-
|
| 325 |
-
The main idea is to prove two key claims involving $O$, which imply the result:
|
| 326 |
-
(i) quadrilaterals $A O E_{1} F_{1}$ and $A O E_{2} F_{2}$ are cyclic (giving the radical axis is $\overline{A O}$ ),
|
| 327 |
-
(ii) $\triangle O E_{1} F_{1} \cong \triangle O E_{2} F_{2}$ (giving the congruence of the circles).
|
| 328 |
-
|
| 329 |
-
We first note that (i) and (ii) are equivalent. Indeed, because $O P=O Q$, (ii) is equivalent to just the similarity $\triangle O E_{1} F_{1} \sim \triangle O E_{2} F_{2}$, and then by the spiral similarity lemma (or even just angle chasing) we have (i) $\Longleftrightarrow$ (ii).
|
| 330 |
-
|
| 331 |
-
We now present five proofs, two of (i) and three of (ii). Thus, we are essentially presenting five different solutions.
|
| 332 |
-
|
| 333 |
-
II Proof of (i) by angle chasing. Note that
|
| 334 |
-
|
| 335 |
-
$$
|
| 336 |
-
\measuredangle F_{2} E_{2} O=\measuredangle Q E_{2} O=\measuredangle Q N O=\measuredangle M N O=\measuredangle M A O=\measuredangle F_{2} A O
|
| 337 |
-
$$
|
| 338 |
-
|
| 339 |
-
and hence $E_{2} O A F_{2}$ is cyclic. Similarly, $E_{1} O A F_{1}$ is cyclic.
|
| 340 |
-
|
| 341 |
-
I Proof of (i) by Simson lines. Since $P, M, N$ are collinear, we see that $\overline{P M N}$ is the Simson line of $O$ with respect to $\triangle A E_{1} F_{1}$.
|
| 342 |
-
|
| 343 |
-
I Proof of (ii) by butterfly theorem. By using the Butterfly Theorem on the three chords $\overline{A C}, \overline{P Q}, \overline{P Q}$ concurring at the midpoint $N$ of $\overline{A C}$, it follows that $E_{1} N=N E_{2}$ (since $E_{1}=\overline{P P} \cap \overline{A C}, E_{2}=\overline{Q Q} \cap \overline{A C}$ ). Thus
|
| 344 |
-
|
| 345 |
-
$$
|
| 346 |
-
E_{1} P=\sqrt{E_{1} A \cdot E_{1} C}=\sqrt{E_{2} A \cdot E_{2} C}=E_{2} P
|
| 347 |
-
$$
|
| 348 |
-
|
| 349 |
-
But also $O P=O Q$ and hence $\triangle O P E_{1} \cong \triangle O Q E_{2}$. Similarly for the other pair.
|
| 350 |
-
\ Proof of (ii) by projective geometry. Let $T=\overline{P P} \cap \overline{Q Q}$. Let $S$ be on $\overline{P Q}$ with $\overline{S T} \| \overline{A C}$; then $\overline{T S} \perp \overline{O N}$, and it follows $\overline{S T}$ is the polar of $N$ (it passes through $T$ by La Hire).
|
| 351 |
-
|
| 352 |
-
Now,
|
| 353 |
-
|
| 354 |
-
$$
|
| 355 |
-
-1=(P Q ; N S) \stackrel{T}{=}\left(E_{1} E_{2} ; N \infty\right)
|
| 356 |
-
$$
|
| 357 |
-
|
| 358 |
-
with $\infty=\overline{A C} \cap \overline{S T}$ the point at infinity. Hence $E_{1} N=N E_{2}$ and we can proceed as in the previous solution.
|
| 359 |
-
|
| 360 |
-
Remark. The assumption that $\triangle A B C$ is acute is not necessary; it is only present to ensure that $P$ lies on segment $E_{1} F_{1}$ and $Q$ lies on segment $E_{2} F_{2}$, which may be helpful for contestants. The argument presented above is valid in all configurations. When one of $\angle B$ and $\angle C$ is a right angle, some of the points $E_{1}, F_{1}, E_{2}, F_{2}$ lie at infinity; when one of them is obtuse, both $P$ and $Q$ lie outside segments $E_{1} F_{1}$ and $E_{2} F_{2}$ respectively.
|
| 361 |
-
|
| 362 |
-
I Proof of (ii) by complex numbers. We will give using complex numbers on $\triangle A B C$ a proof that $\left|E_{1} P\right|=\left|E_{2} Q\right|$.
|
| 363 |
-
|
| 364 |
-
We place $A P B C Q$ on the unit circle. Since $\overline{P Q} \| \overline{B C}$, we have $p q=b c$. Also, the midpoint of $\overline{A B}$ lies on $\overline{P Q}$, so
|
| 365 |
-
|
| 366 |
-
$$
|
| 367 |
-
\begin{aligned}
|
| 368 |
-
p+q & =\frac{a+b}{2}+\overline{\left(\frac{a+b}{2}\right)} \cdot p q \\
|
| 369 |
-
& =\frac{a+b}{2}+\frac{a+b}{2 a b} \cdot b c \\
|
| 370 |
-
& =\frac{a(a+b)}{2 a}+\frac{c(a+b)}{2 a} \\
|
| 371 |
-
& =\frac{(a+b)(a+c)}{2 a} .
|
| 372 |
-
\end{aligned}
|
| 373 |
-
$$
|
| 374 |
-
|
| 375 |
-
Now,
|
| 376 |
-
|
| 377 |
-
$$
|
| 378 |
-
\begin{aligned}
|
| 379 |
-
p-e_{1} & =p-\frac{p p(a+c)-a c(p+p)}{p p-a c} \\
|
| 380 |
-
& =\frac{p\left(p^{2}-p(a+c)+a c\right)}{p p-a c}=\frac{(p-a)(p-c)}{p^{2}-a c} \\
|
| 381 |
-
\left|P E_{1}\right|^{2} & =\left(p-e_{1}\right) \cdot \overline{p-e_{1}}=\frac{(p-a)(p-c)}{p^{2}-a c} \cdot \frac{\left(\frac{1}{p}-\frac{1}{a}\right)\left(\frac{1}{p}-\frac{1}{c}\right)}{\frac{1}{p^{2}}-\frac{1}{a c}} \\
|
| 382 |
-
& =-\frac{(p-a)^{2}(p-c)^{2}}{\left(p^{2}-a c\right)^{2}}
|
| 383 |
-
\end{aligned}
|
| 384 |
-
$$
|
| 385 |
-
|
| 386 |
-
Similarly,
|
| 387 |
-
|
| 388 |
-
$$
|
| 389 |
-
\left|Q E_{2}\right|^{2}=-\frac{(q-a)^{2}(q-c)^{2}}{\left(q^{2}-a c\right)^{2}}
|
| 390 |
-
$$
|
| 391 |
-
|
| 392 |
-
But actually, we claim that
|
| 393 |
-
|
| 394 |
-
$$
|
| 395 |
-
\frac{(p-a)(p-c)}{p^{2}-a c}=\frac{(q-a)(q-c)}{q^{2}-a c}
|
| 396 |
-
$$
|
| 397 |
-
|
| 398 |
-
One calculates
|
| 399 |
-
|
| 400 |
-
$$
|
| 401 |
-
(p-a)(p-c)\left(q^{2}-a c\right)=p^{2} q^{2}-p q^{2} a-p q^{2} c+q^{2} a c-p^{2} a c+p a^{2} c+p a c^{2}-(a c)^{2}
|
| 402 |
-
$$
|
| 403 |
-
|
| 404 |
-
Thus $(p-a)(p-c)\left(q^{2}-a c\right)-(q-a)(q-c)\left(p^{2}-a c\right)$ is equal to
|
| 405 |
-
|
| 406 |
-
$$
|
| 407 |
-
\begin{aligned}
|
| 408 |
-
-(a+c)(p q) & (q-p)+\left(q^{2}-p^{2}\right) a c-\left(p^{2}-q^{2}\right) a c+a c(a+c)(p-q) \\
|
| 409 |
-
& =(p-q)[(a+c) p q-2(p+q) a c+a c(a+c)] \\
|
| 410 |
-
& =(p-q)\left[(a+c) b c-2 \cdot \frac{(a+b)(a+c)}{2 a} \cdot a c+a c(a+c)\right] \\
|
| 411 |
-
& =(p-q)(a+c)[b c-c(a+b)+a c]=0
|
| 412 |
-
\end{aligned}
|
| 413 |
-
$$
|
| 414 |
-
|
| 415 |
-
This proves $\left|E_{1} P\right|=\left|E_{2} Q\right|$. Together with the similar $\left|F_{1} P\right|=\left|F_{2} Q\right|$, we have proved (ii).
|
| 416 |
-
|
| 417 |
-
【 Authorship comments. Ankan provides an extensive dialogue at https://aops.com/ community/c6h1664170p10571644 of how he came up with this problem, which at first was intended just to be an AMC-level question about an equilateral triangle. Here, we provide just the change-log of the versions of this problem.
|
| 418 |
-
0. (Original version) Let $A B C$ be an equilateral triangle with side 2 inscribed in circle $\omega$, and let $P$ be a point on small arc $A B$ of its circumcircle. The tangent line to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$. If $P E=P F$, find $E F$. (Answer: 4.)
|
| 419 |
-
|
| 420 |
-
1. (Generalize to isosceles triangle) Let $A B C$ be an isosceles triangle with $A B=A C$, and let $M$ be the midpoint of $\overline{B C}$. Let $P$ be a point on the circumcircle with $P A=P M$. The tangent to the circumcircle at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$, respectively. Show that $P E=P F$.
|
| 421 |
-
2. (Block coordinate bashes) Let $A B C$ be an isosceles triangle with $A B=A C$ and circumcircle $\omega$, and let $M$ be the midpoint of $\overline{B C}$. Let $P$ be a point on $\omega$ with $P A=P M$. The tangent to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$, respectively. Show that the circumcircle of $\triangle A E F$ passes through the center of $\omega$.
|
| 422 |
-
3. (Delete isosceles condition) Let $A B C$ be a triangle with circumcircle $\omega$, and let $H$ be the foot of the altitude from $A$ to $\overline{B C}$. Let $P$ be a point on $\omega$ with $P A=P H$. The tangent to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$, respectively. Show that the circumcircle of $\triangle A E F$ passes through the center of $\omega$.
|
| 423 |
-
4. (Add in both tangents) Let $A B C$ be an acute triangle with circumcircle $\omega$, and let $H$ be the foot of the altitude from $A$ to $\overline{B C}$. Let $P$ and $Q$ be the points on $\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that $E_{1} F_{1}=E_{2} F_{2}$.
|
| 424 |
-
5. (Merge v3 and v4) Let $A B C$ be an acute triangle with circumcircle $\omega$, and let $H$ be the foot of the altitude from $A$ to $\overline{B C}$. Let $P$ and $Q$ be the points on $\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that the circumcircles of $\triangle A E_{1} F_{1}$ and $\triangle A E_{2} F_{2}$ are congruent, and the line through their centers is parallel to the tangent to $\omega$ at $A$.
|
| 425 |
-
|
| 426 |
-
The problem bears Evan's name only because he suggested the changes v2 and v5.
|
| 427 |
-
|
| 428 |
-
## §2.3 TSTST 2018/6, proposed by Ray Li
|
| 429 |
-
|
| 430 |
-
Available online at https://aops.com/community/p10570994.
|
| 431 |
-
|
| 432 |
-
## Problem statement
|
| 433 |
-
|
| 434 |
-
Let $S=\{1, \ldots, 100\}$, and for every positive integer $n$ define
|
| 435 |
-
|
| 436 |
-
$$
|
| 437 |
-
T_{n}=\left\{\left(a_{1}, \ldots, a_{n}\right) \in S^{n} \mid a_{1}+\cdots+a_{n} \equiv 0 \quad(\bmod 100)\right\}
|
| 438 |
-
$$
|
| 439 |
-
|
| 440 |
-
Determine which $n$ have the following property: if we color any 75 elements of $S$ red, then at least half of the $n$-tuples in $T_{n}$ have an even number of coordinates with red elements.
|
| 441 |
-
|
| 442 |
-
We claim this holds exactly for $n$ even.
|
| 443 |
-
\I First solution by generating functions. Define
|
| 444 |
-
|
| 445 |
-
$$
|
| 446 |
-
R(x)=\sum_{s \text { red }} x^{s}, \quad B(x)=\sum_{s \text { blue }} x^{s} .
|
| 447 |
-
$$
|
| 448 |
-
|
| 449 |
-
(Here "blue" means "not-red", as always.) Then, the number of tuples in $T_{n}$ with exactly $k$ red coordinates is exactly equal to
|
| 450 |
-
|
| 451 |
-
$$
|
| 452 |
-
\binom{n}{k} \cdot \frac{1}{100} \sum_{\omega} R(\omega)^{k} B(\omega)^{n-k}
|
| 453 |
-
$$
|
| 454 |
-
|
| 455 |
-
where the sum is over all 100th roots of unity. So, we conclude the number of tuples in $T_{n}$ with an even (resp odd) number of red elements is exactly
|
| 456 |
-
|
| 457 |
-
$$
|
| 458 |
-
\begin{aligned}
|
| 459 |
-
X & =\frac{1}{100} \sum_{\omega} \sum_{k \text { even }}\binom{n}{k} R(\omega)^{k} B(\omega)^{n-k} \\
|
| 460 |
-
Y & =\frac{1}{100} \sum_{\omega} \sum_{k \text { odd }}\binom{n}{k} R(\omega)^{k} B(\omega)^{n-k} \\
|
| 461 |
-
\Longrightarrow X-Y & =\frac{1}{100} \sum_{\omega}(B(\omega)-R(\omega))^{n} \\
|
| 462 |
-
& =\frac{1}{100}\left[(B(1)-R(1))^{n}+\sum_{\omega \neq 1}(2 B(\omega))^{n}\right] \\
|
| 463 |
-
& =\frac{1}{100}\left[(B(1)-R(1))^{n}-(2 B(1))^{n}+2^{n} \sum_{\omega} B(\omega)^{n}\right] \\
|
| 464 |
-
& =\frac{1}{100}\left[(B(1)-R(1))^{n}-(2 B(1))^{n}\right]+2^{n} Z \\
|
| 465 |
-
& =\frac{1}{100}\left[(-50)^{n}-50^{n}\right]+2^{n} Z
|
| 466 |
-
\end{aligned}
|
| 467 |
-
$$
|
| 468 |
-
|
| 469 |
-
where
|
| 470 |
-
|
| 471 |
-
$$
|
| 472 |
-
Z:=\frac{1}{100} \sum_{\omega} B(\omega)^{n} \geq 0
|
| 473 |
-
$$
|
| 474 |
-
|
| 475 |
-
counts the number of tuples in $T_{n}$ which are all blue. Here we have used the fact that $B(\omega)+R(\omega)=0$ for $\omega \neq 1$.
|
| 476 |
-
|
| 477 |
-
We wish to show $X-Y \geq 0$ holds for $n$ even, but may fail when $n$ is odd. This follows from two remarks:
|
| 478 |
-
|
| 479 |
-
- If $n$ is even, then $X-Y=2^{n} Z \geq 0$.
|
| 480 |
-
- If $n$ is odd, then if we choose the coloring for which $s$ is red if and only if $s \not \equiv 2$ $(\bmod 4)$; we thus get $Z=0$. Then $X-Y=-\frac{2}{100} \cdot 50^{n}<0$.
|
| 481 |
-
|
| 482 |
-
『 Second solution by strengthened induction and random coloring. We again prove that $n$ even work. Let us define
|
| 483 |
-
|
| 484 |
-
$$
|
| 485 |
-
T_{n}(a)=\left\{\left(a_{1}, \ldots, a_{n}\right) \in S^{n} \mid a_{1}+\cdots+a_{n} \equiv a \quad(\bmod 100)\right\}
|
| 486 |
-
$$
|
| 487 |
-
|
| 488 |
-
Also, call an $n$-tuple good if it has an even number of red elements. We claim that $T_{n}(a)$ also has at least $50 \%$ good tuples, by induction.
|
| 489 |
-
|
| 490 |
-
This follows by induction on $n \geq 2$. Indeed, the base case $n=2$ can be checked by hand, since $T_{2}(a)=\{(x, a-x) \mid x \in S\}$. With the stronger claim, one can check the case $n=2$ manually and proceed by induction to go from $n-2$ to $n$, noting that
|
| 491 |
-
|
| 492 |
-
$$
|
| 493 |
-
T_{n}(a)=\bigsqcup_{b+c=a} T_{n-2}(b) \oplus T_{2}(c)
|
| 494 |
-
$$
|
| 495 |
-
|
| 496 |
-
where $\oplus$ denotes concatenation of tuples, applied set-wise. The concatenation of an $(n-2)$-tuple and 2-tuple is good if and only if both or neither are good. Thus for each $b$ and $c$, if the proportion of $T_{n-2}(b)$ which is good is $p \geq \frac{1}{2}$ and the proportion of $T_{2}(c)$ which is good is $q \geq \frac{1}{2}$, then the proportion of $T_{n-2}(b) \oplus T_{2}(c)$ which is good is $p q+(1-p)(1-q) \geq \frac{1}{2}$, as desired. Since each term in the union has at least half the tuples good, all of $T_{n}(a)$ has at least half the tuples good, as desired.
|
| 497 |
-
|
| 498 |
-
It remains to fail all odd $n$. We proceed by a suggestion of Yang Liu and Ankan Bhattacharya by showing that if we pick the 75 elements randomly, then any particular tuple in $S^{n}$ has strictly less than $50 \%$ chance of being good. This will imply (by linearity of expectation) that $T_{n}$ (or indeed any subset of $S^{n}$ ) will, for some coloring, have less than half good tuples.
|
| 499 |
-
|
| 500 |
-
Let $\left(a_{1}, \ldots, a_{n}\right)$ be such an $n$-tuple. If any element appears in the tuple more than once, keep discarding pairs of that element until there are zero or one; this has no effect on the good-ness of the tuple. If we do this, we obtain an $m$-tuple $\left(b_{1}, \ldots, b_{m}\right)$ with no duplicated elements where $m \equiv n \equiv 1(\bmod 2)$. Now, the probability that any element is red is $\frac{3}{4}$, so the probability of being good is
|
| 501 |
-
|
| 502 |
-
$$
|
| 503 |
-
\begin{aligned}
|
| 504 |
-
\sum_{k \text { even }}^{m}\binom{m}{k}\left(\frac{3}{4}\right)^{k}\left(-\frac{1}{4}\right)^{m-k} & =\frac{1}{2}\left[\left(\frac{3}{4}+\frac{1}{4}\right)^{m}-\left(\frac{3}{4}-\frac{1}{4}\right)^{m}\right] \\
|
| 505 |
-
& =\frac{1}{2}\left[1-\left(\frac{1}{2}\right)^{m}\right]<\frac{1}{2}
|
| 506 |
-
\end{aligned}
|
| 507 |
-
$$
|
| 508 |
-
|
| 509 |
-
Remark (Adam Hesterberg). Here is yet another proof that $n$ even works. Group elements of $T_{n}$ into equivalence classes according to the $n / 2$ sums of pairs of consecutive elements (first and second, third and fourth, ...). For each such pair sum, there are at least as many monochrome pairs with that sum as nonmonochrome ones, since every nonmonochrome pair uses one of the 25 non-reds. The monochromaticity of the pairs is independent.
|
| 510 |
-
|
| 511 |
-
If $p_{i} \leq \frac{1}{2}$ is the probability that the $i$ th pair is nonmonochrome, then the probability that $k$ pairs are nonmonochrome is the coefficient of $x^{k}$ in $f(x)=\prod_{i}\left(x p_{i}+\left(1-p_{i}\right)\right)$. Then the probability that evenly many pairs are nonmonochrome (and hence that evenly many coordinates are red) is the sum of the coefficients of even powers of $x$ in $f$, which is
|
| 512 |
-
|
| 513 |
-
$$
|
| 514 |
-
(f(1)+f(-1)) / 2=\left(1+\prod_{i}\left(1-2 p_{i}\right)\right) / 2 \geq \frac{1}{2}, \text { as desired. }
|
| 515 |
-
$$
|
| 516 |
-
|
| 517 |
-
## §3 Solutions to Day 3
|
| 518 |
-
|
| 519 |
-
## §3.1 TSTST 2018/7, proposed by Ashwin Sah
|
| 520 |
-
|
| 521 |
-
Available online at https://aops.com/community/p10570996.
|
| 522 |
-
|
| 523 |
-
## Problem statement
|
| 524 |
-
|
| 525 |
-
Let $n$ be a positive integer. A frog starts on the number line at 0 . Suppose it makes a finite sequence of hops, subject to two conditions:
|
| 526 |
-
|
| 527 |
-
- The frog visits only points in $\left\{1,2, \ldots, 2^{n}-1\right\}$, each at most once.
|
| 528 |
-
- The length of each hop is in $\left\{2^{0}, 2^{1}, 2^{2}, \ldots\right\}$. (The hops may be either direction, left or right.)
|
| 529 |
-
|
| 530 |
-
Let $S$ be the sum of the (positive) lengths of all hops in the sequence. What is the maximum possible value of $S$ ?
|
| 531 |
-
|
| 532 |
-
We claim the answer is $\frac{4^{n}-1}{3}$.
|
| 533 |
-
We first prove the bound. First notice that the hop sizes are in $\left\{2^{0}, 2^{1}, \ldots, 2^{n-1}\right\}$, since the frog must stay within bounds the whole time. Let $a_{i}$ be the number of hops of size $2^{i}$ the frog makes, for $0 \leq i \leq n-1$.
|
| 534 |
-
|
| 535 |
-
Claim - For any $k=1, \ldots, n$ we have
|
| 536 |
-
|
| 537 |
-
$$
|
| 538 |
-
a_{n-1}+\cdots+a_{n-k} \leq 2^{n}-2^{n-k}
|
| 539 |
-
$$
|
| 540 |
-
|
| 541 |
-
Proof. Let $m=n-k$ and look modulo $2^{m}$. Call a jump small if its length is at most $2^{m-1}$, and large if it is at least $2^{m}$; the former changes the residue class of the frog modulo $2^{m}$ while the latter does not.
|
| 542 |
-
|
| 543 |
-
Within each fixed residue modulo $2^{m}$, the frog can make at most $\frac{2^{n}}{2^{m}}-1$ large jumps. So the total number of large jumps is at most $2^{m}\left(\frac{2^{n}}{2^{m}}-1\right)=2^{n}-2^{m}$.
|
| 544 |
-
(As an example, when $n=3$ this means there are at most four hops of length 4 , at most six hops of length 2 or 4 , and at most seven hops total. Of course, if we want to max the length of the hops, we see that we want $a_{2}=4, a_{1}=2, a_{0}=1$, and in general equality is achieved when $a_{m}=2^{m}$ for any $m$.)
|
| 545 |
-
|
| 546 |
-
Now, the total distance the frog travels is
|
| 547 |
-
|
| 548 |
-
$$
|
| 549 |
-
S=a_{0}+2 a_{1}+4 a_{2}+\cdots+2^{n-1} a_{n-1}
|
| 550 |
-
$$
|
| 551 |
-
|
| 552 |
-
We rewrite using the so-called "summation by parts":
|
| 553 |
-
|
| 554 |
-
$$
|
| 555 |
-
\begin{array}{rrrr}
|
| 556 |
-
S & =a_{0}+a_{1}+a_{2}+ & a_{3}+\ldots+ & a_{n-1} \\
|
| 557 |
-
& + & a_{1}+a_{2}+a_{3}+\ldots+ & a_{n-1} \\
|
| 558 |
-
& + & 2 a_{2}+2 a_{3}+\ldots+ & 2 a_{n-1} \\
|
| 559 |
-
& + & 4 a_{3}+\ldots+ & 4 a_{n-1} \\
|
| 560 |
-
& \vdots & \ddots & \vdots \\
|
| 561 |
-
& & & \\
|
| 562 |
-
+ & & & 2^{n-2} a_{n-1}
|
| 563 |
-
\end{array}
|
| 564 |
-
$$
|
| 565 |
-
|
| 566 |
-
Hence
|
| 567 |
-
|
| 568 |
-
$$
|
| 569 |
-
\begin{aligned}
|
| 570 |
-
S & \leq\left(2^{n}-2^{0}\right)+\left(2^{n}-2^{1}\right)+2\left(2^{n}-2^{2}\right)+\cdots+2^{n-2}\left(2^{n}-2^{n-1}\right) \\
|
| 571 |
-
& =\frac{4^{n}-1}{3} .
|
| 572 |
-
\end{aligned}
|
| 573 |
-
$$
|
| 574 |
-
|
| 575 |
-
It remains to show that equality can hold. There are many such constructions but most are inductive. Here is one approach. We will construct two family of paths such that there are $2^{k}$ hops of size $2^{k}$, for every $0 \leq k \leq n-1$, and we visit each of $\left\{0, \ldots, 2^{n}-1\right\}$ once, starting on 0 and ending on $x$, for the two values $x \in\left\{1,2^{n}-1\right\}$.
|
| 576 |
-
|
| 577 |
-
The base case $n=1$ is clear. To take a path from 0 to $2^{n+1}-1$.
|
| 578 |
-
|
| 579 |
-
- Take a path on $\left\{0,2,4, \ldots, 2^{n+1}-2\right\}$ starting from 0 and ending on 2 (by inductive hypothesis).
|
| 580 |
-
- Take a path on $\left\{1,3,5, \ldots, 2^{n+1}-1\right\}$ starting from 1 and ending on $2^{n+1}-1$ (by inductive hypothesis).
|
| 581 |
-
- Link them together by adding a single jump $2 \rightarrow 1$.
|
| 582 |
-
|
| 583 |
-
The other case is similar, but we route $0 \rightarrow\left(2^{n+1}-2\right) \rightarrow\left(2^{n+1}-1\right) \rightarrow 1$ instead. (This can also be visualized as hopping along a hypercube of binary strings; each inductive step takes two copies of the hypercube and links them together by a single edge.)
|
| 584 |
-
|
| 585 |
-
Remark (Ashwin Sah). The problem can also be altered to ask for the minimum value of the sum of the reciprocals of the hop sizes, where further we stipulate that the frog must hit every point precisely once (to avoid triviality). With a nearly identical proof that also exploits the added condition $a_{0}+\cdots+a_{n-1}=2^{n}-1$, the answer is $n$. This yields a nicer form for the generalization. The natural generalization changes the above problem by replacing $2^{k}$ with $a_{k}$ where $a_{k} \mid a_{k+1}$, so that the interval covered by hops is of size $a_{n}$ and the hop sizes are restricted to the $a_{i}$, where $a_{0}=1$. In this case, similar bounding yields
|
| 586 |
-
|
| 587 |
-
$$
|
| 588 |
-
\sum_{i=1}^{2^{n}-1} \frac{1}{b_{k}} \geq \sum_{i=0}^{n-1}\left(\frac{a_{k+1}}{a_{k}}-1\right)
|
| 589 |
-
$$
|
| 590 |
-
|
| 591 |
-
Bounds for the total distance traveled happen in the same way as the solution above, and equality for both can be constructed in an analogous fashion.
|
| 592 |
-
|
| 593 |
-
## §3.2 TSTST 2018/8, proposed by Ankan Bhattacharya, Evan Chen
|
| 594 |
-
|
| 595 |
-
Available online at https://aops.com/community/p10570998.
|
| 596 |
-
|
| 597 |
-
## Problem statement
|
| 598 |
-
|
| 599 |
-
For which positive integers $b>2$ do there exist infinitely many positive integers $n$ such that $n^{2}$ divides $b^{n}+1$ ?
|
| 600 |
-
|
| 601 |
-
This problem is sort of the union of IMO 1990/3 and IMO 2000/5.
|
| 602 |
-
The answer is any $b$ such that $b+1$ is not a power of 2 . In the forwards direction, we first prove more carefully the following claim.
|
| 603 |
-
|
| 604 |
-
Claim - If $b+1$ is a power of 2 , then the only $n$ which is valid is $n=1$.
|
| 605 |
-
Proof. Assume $n>1$ and let $p$ be the smallest prime dividing $n$. We cannot have $p=2$, since then $4 \mid b^{n}+1 \equiv 2(\bmod 4)$. Thus,
|
| 606 |
-
|
| 607 |
-
$$
|
| 608 |
-
b^{2 n} \equiv 1 \quad(\bmod p)
|
| 609 |
-
$$
|
| 610 |
-
|
| 611 |
-
so the order of $b(\bmod p)$ divides $\operatorname{gcd}(2 n, p-1)=2$. Hence $p \mid b^{2}-1=(b-1)(b+1)$.
|
| 612 |
-
But since $b+1$ was a power of 2 , this forces $p \mid b-1$. Then $0 \equiv b^{n}+1 \equiv 2(\bmod p)$, contradiction.
|
| 613 |
-
|
| 614 |
-
On the other hand, suppose that $b+1$ is not a power of 2 (and that $b>2$ ). We will inductively construct an infinite sequence of distinct primes $p_{0}, p_{1}, \ldots$, such that the following two properties hold for each $k \geq 0$ :
|
| 615 |
-
|
| 616 |
-
- $p_{0}^{2} \ldots p_{k-1}^{2} p_{k} \mid b^{p_{0} \ldots p_{k-1}}+1$,
|
| 617 |
-
- and hence $p_{0}^{2} \ldots p_{k-1}^{2} p_{k}^{2} \mid b^{p_{0} \ldots p_{k-1} p_{k}}+1$ by exponent lifting lemma.
|
| 618 |
-
|
| 619 |
-
This will solve the problem.
|
| 620 |
-
Initially, let $p_{0}$ be any odd prime dividing $b+1$. For the inductive step, we contend there exists an odd prime $q \notin\left\{p_{0}, \ldots, p_{k}\right\}$ such that $q \mid b^{p_{0} \ldots p_{k}}+1$. Indeed, this follows immediately by Zsigmondy theorem since $p_{0} \ldots p_{k}$ divides $b^{p_{0} \ldots p_{k-1}}+1$. Since $\left(b^{p_{0} \ldots p_{k}}\right)^{q} \equiv b^{p_{0} \ldots p_{k}}(\bmod q)$, it follows we can then take $p_{k+1}=q$. This finishes the induction.
|
| 621 |
-
|
| 622 |
-
To avoid the use of Zsigmondy, one can instead argue as follows: let $p=p_{k}$ for brevity, and let $c=b^{p_{0} \ldots p_{k-1}}$. Then $\frac{\frac{c}{}^{p}+1}{c+1}=c^{p-1}-c^{p-2}+\cdots+1$ has GCD exactly $p$ with $c+1$. Moreover, this quotient is always odd. Thus as long as $c^{p}+1>p \cdot(c+1)$, there will be some new prime dividing $c^{p}+1$ but not $c+1$. This is true unless $p=3$ and $c=2$, but we assumed $b>2$ so this case does not appear.
|
| 623 |
-
|
| 624 |
-
Remark (On new primes). In going from $n^{2} \mid b^{n}+1$ to $(n q)^{2} \mid b^{n q}+1$, one does not necessarily need to pick a $q$ such that $q \nmid n$, as long as $\nu_{q}\left(n^{2}\right)<\nu_{q}\left(b^{n}+1\right)$. In other words it suffices to just check that $\frac{b^{n}+1}{n^{2}}$ is not a power of 2 in this process.
|
| 625 |
-
|
| 626 |
-
However, this calculation is a little more involved with this approach. One proceeds by noting that $n$ is odd, hence $\nu_{2}\left(b^{n}+1\right)=\nu_{2}(b+1)$, and thus $\frac{b^{n}+1}{n^{2}}=2^{\nu_{2}(b+1)} \leq b+1$, which is a little harder to bound than the analogous $c^{p}+1>p \cdot(c+1)$ from the previous solution.
|
| 627 |
-
\ Authorship comments. I came up with this problem by simply mixing together the main ideas of IMO 1990/3 and IMO 2000/5, late one night after a class. On the other hand, I do not consider it very original; it is an extremely "routine" number theory problem for experienced contestants, using highly standard methods. Thus it may not be that interesting, but is a good discriminator of understanding of fundamentals.
|
| 628 |
-
|
| 629 |
-
IMO 1990/3 shows that if $b=2$, then the only $n$ which work are $n=1$ and $n=3$. Thus $b=2$ is a special case and for this reason the problem explicitly requires $b>2$.
|
| 630 |
-
|
| 631 |
-
An alternate formulation of the problem is worth mentioning. Originally, the problem statement asked whether there existed $n$ with at least 3 (or 2018, etc.) prime divisors, thus preventing the approach in which one takes a prime $q$ dividing $\frac{b^{n}+1}{n^{2}}$. Ankan Bhattacharya suggested changing it to "infinitely many $n$ ", which is more natural.
|
| 632 |
-
|
| 633 |
-
These formulations are actually not so different though. Explicitly, suppose $k^{2} \mid b^{k}+1$ and $p \mid b^{k}+1$. Consider any $k \mid n$ with $n^{2} \mid b^{n}+1$, and let $p$ be an odd prime dividing $b^{k}+1$. Then $2 \nu_{p}(n) \leq \nu_{p}\left(b^{n}+1\right)=\nu_{p}(n / k)+\nu_{p}\left(b^{k}+1\right)$ and thus
|
| 634 |
-
|
| 635 |
-
$$
|
| 636 |
-
\nu_{p}(n / k) \leq \nu_{p}\left(\frac{b^{k}+1}{k^{2}}\right) .
|
| 637 |
-
$$
|
| 638 |
-
|
| 639 |
-
Effectively, this means we can only add each prime a certain number of times.
|
| 640 |
-
|
| 641 |
-
## §3.3 TSTST 2018/9, proposed by Linus Hamilton
|
| 642 |
-
|
| 643 |
-
Available online at https://aops.com/community/p10571003.
|
| 644 |
-
|
| 645 |
-
## Problem statement
|
| 646 |
-
|
| 647 |
-
Show that there is an absolute constant $c<1$ with the following property: whenever $\mathcal{P}$ is a polygon with area 1 in the plane, one can translate it by a distance of $\frac{1}{100}$ in some direction to obtain a polygon $\mathcal{Q}$, for which the intersection of the interiors of $\mathcal{P}$ and $\mathcal{Q}$ has total area at most $c$.
|
| 648 |
-
|
| 649 |
-
The following solution is due to Brian Lawrence. We will prove the result with the generality of any measurable set $\mathcal{P}$ (rather than a polygon). For a vector $v$ in the plane, write $\mathcal{P}+v$ for the translate of $\mathcal{P}$ by $v$.
|
| 650 |
-
|
| 651 |
-
Suppose $\mathcal{P}$ is a polygon of area 1 , and $\varepsilon>0$ is a constant, such that for any translate $\mathcal{Q}=\mathcal{P}+v$, where $v$ has length exactly $\frac{1}{100}$, the intersection of $\mathcal{P}$ and $\mathcal{Q}$ has area at least $1-\varepsilon$. The problem asks us to prove a lower bound on $\varepsilon$.
|
| 652 |
-
|
| 653 |
-
## Lemma
|
| 654 |
-
|
| 655 |
-
Fix a sequence of $n$ vectors $v_{1}, v_{2}, \ldots, v_{n}$, each of length $\frac{1}{100}$. A grasshopper starts at a random point $x$ of $\mathcal{P}$, and makes $n$ jumps to $x+v_{1}+\cdots+v_{n}$. Then it remains in $\mathcal{P}$ with probability at least $1-n \varepsilon$.
|
| 656 |
-
|
| 657 |
-
Proof. In order for the grasshopper to leave $\mathcal{P}$ at step $i$, the grasshopper's position before step $i$ must be inside the difference set $\mathcal{P} \backslash\left(\mathcal{P}-v_{i}\right)$. Since this difference set has area at most $\varepsilon$, the probability the grasshopper leaves $\mathcal{P}$ at step $i$ is at most $\varepsilon$. Summing over the $n$ steps, the probability that the grasshopper ever manages to leave $\mathcal{P}$ is at most $n \varepsilon$.
|
| 658 |
-
|
| 659 |
-
## Corollary
|
| 660 |
-
|
| 661 |
-
Fix a vector $w$ of length at most 8. A grasshopper starts at a random point $x$ of $\mathcal{P}$, and jumps to $x+w$. Then it remains in $\mathcal{P}$ with probability at least $1-800 \varepsilon$.
|
| 662 |
-
|
| 663 |
-
Proof. Apply the previous lemma with 800 jumps. Any vector $w$ of length at most 8 can be written as $w=v_{1}+v_{2}+\cdots+v_{800}$, where each $v_{i}$ has length exactly $\frac{1}{100}$.
|
| 664 |
-
|
| 665 |
-
Now consider the process where we select a random starting point $x \in \mathcal{P}$ for our grasshopper, and a random vector $w$ of length at most 8 (sampled uniformly from the closed disk of radius 8 ). Let $q$ denote the probability of staying inside $\mathcal{P}$ we will bound $q$ from above and below.
|
| 666 |
-
|
| 667 |
-
- On the one hand, suppose we pick $w$ first. By the previous corollary, $q \geq 1-800 \varepsilon$ (irrespective of the chosen $w$ ).
|
| 668 |
-
- On the other hand, suppose we pick $x$ first. Then the possible landing points $x+w$ are uniformly distributed over a closed disk of radius 8 , which has area $64 \pi$. The probability of landing in $\mathcal{P}$ is certainly at most $\frac{[\mathcal{P}]}{64 \pi}$.
|
| 669 |
-
|
| 670 |
-
Consequently, we deduce
|
| 671 |
-
|
| 672 |
-
$$
|
| 673 |
-
1-800 \varepsilon \leq q \leq \frac{[\mathcal{P}]}{64 \pi} \Longrightarrow \varepsilon>\frac{1-\frac{[\mathcal{P}]}{64 \pi}}{800}>0.001
|
| 674 |
-
$$
|
| 675 |
-
|
| 676 |
-
as desired.
|
| 677 |
-
Remark. The choice of 800 jumps is only for concreteness; any constant $n$ for which $\pi(n / 100)^{2}>1$ works. I think $n=98$ gives the best bound following this approach.
|
| 678 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2019.md
DELETED
|
@@ -1,764 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2019 Solutions <br> United States of America - TST Selection Test <br> Ankan Bhattacharya and Evan Chen <br> $61^{\text {st }}$ IMO 2020 Russia and $9^{\text {th }}$ EGMO 2020 Netherlands
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 3
|
| 7 |
-
1.1 TSTST 2019/1, proposed by Evan Chen ..... 3
|
| 8 |
-
1.2 TSTST 2019/2, proposed by Merlijn Staps ..... 6
|
| 9 |
-
1.3 TSTST 2019/3, proposed by Nikolai Beluhov ..... 9
|
| 10 |
-
2 Solutions to Day 2 ..... 11
|
| 11 |
-
2.1 TSTST 2019/4, proposed by Merlijn Staps ..... 11
|
| 12 |
-
2.2 TSTST 2019/5, proposed by Gunmay Handa ..... 13
|
| 13 |
-
2.3 TSTST 2019/6, proposed by Nikolai Beluhov ..... 19
|
| 14 |
-
3 Solutions to Day 3 ..... 21
|
| 15 |
-
3.1 TSTST 2019/7, proposed by Ankan Bhattacharya ..... 21
|
| 16 |
-
3.2 TSTST 2019/8, proposed by Ankan Bhattacharya ..... 23
|
| 17 |
-
3.3 TSTST 2019/9, proposed by Ankan Bhattacharya ..... 25
|
| 18 |
-
|
| 19 |
-
## §0 Problems
|
| 20 |
-
|
| 21 |
-
1. Find all binary operations $\diamond: \mathbb{R}_{>0} \times \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ (meaning $\diamond$ takes pairs of positive real numbers to positive real numbers) such that for any real numbers $a, b, c>0$,
|
| 22 |
-
|
| 23 |
-
- the equation $a \diamond(b \diamond c)=(a \diamond b) \cdot c$ holds; and
|
| 24 |
-
- if $a \geq 1$ then $a \diamond a \geq 1$.
|
| 25 |
-
|
| 26 |
-
2. Let $A B C$ be an acute triangle with circumcircle $\Omega$ and orthocenter $H$. Points $D$ and $E$ lie on segments $A B$ and $A C$ respectively, such that $A D=A E$. The lines through $B$ and $C$ parallel to $\overline{D E}$ intersect $\Omega$ again at $P$ and $Q$, respectively. Denote by $\omega$ the circumcircle of $\triangle A D E$.
|
| 27 |
-
(a) Show that lines $P E$ and $Q D$ meet on $\omega$.
|
| 28 |
-
(b) Prove that if $\omega$ passes through $H$, then lines $P D$ and $Q E$ meet on $\omega$ as well.
|
| 29 |
-
3. On an infinite square grid we place finitely many cars, which each occupy a single cell and face in one of the four cardinal directions. Cars may never occupy the same cell. It is given that the cell immediately in front of each car is empty, and moreover no two cars face towards each other (no right-facing car is to the left of a left-facing car within a row, etc.). In a move, one chooses a car and shifts it one cell forward to a vacant cell. Prove that there exists an infinite sequence of valid moves using each car infinitely many times.
|
| 30 |
-
4. Consider coins with positive real denominations not exceeding 1. Find the smallest $C>0$ such that the following holds: if we are given any 100 such coins with total value 50 , then we can always split them into two stacks of 50 coins each such that the absolute difference between the total values of the two stacks is at most $C$.
|
| 31 |
-
5. Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
| 32 |
-
6. Suppose $P$ is a polynomial with integer coefficients such that for every positive integer $n$, the sum of the decimal digits of $|P(n)|$ is not a Fibonacci number. Must $P$ be constant?
|
| 33 |
-
7. Let $f: \mathbb{Z} \rightarrow\left\{1,2, \ldots, 10^{100}\right\}$ be a function satisfying
|
| 34 |
-
|
| 35 |
-
$$
|
| 36 |
-
\operatorname{gcd}(f(x), f(y))=\operatorname{gcd}(f(x), x-y)
|
| 37 |
-
$$
|
| 38 |
-
|
| 39 |
-
for all integers $x$ and $y$. Show that there exist positive integers $m$ and $n$ such that $f(x)=\operatorname{gcd}(m+x, n)$ for all integers $x$.
|
| 40 |
-
8. Let $\mathcal{S}$ be a set of 16 points in the plane, no three collinear. Let $\chi(\mathcal{S})$ denote the number of ways to draw 8 line segments with endpoints in $\mathcal{S}$, such that no two drawn segments intersect, even at endpoints. Find the smallest possible value of $\chi(\mathcal{S})$ across all such $\mathcal{S}$.
|
| 41 |
-
9. Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\triangle A B K$ and $\triangle A B L$ are tangent at $P$, and the incircles of $\triangle A C K$ and $\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.
|
| 42 |
-
|
| 43 |
-
## §1 Solutions to Day 1
|
| 44 |
-
|
| 45 |
-
## §1.1 TSTST 2019/1, proposed by Evan Chen
|
| 46 |
-
|
| 47 |
-
Available online at https://aops.com/community/p12608849.
|
| 48 |
-
|
| 49 |
-
## Problem statement
|
| 50 |
-
|
| 51 |
-
Find all binary operations $\diamond: \mathbb{R}_{>0} \times \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ (meaning $\diamond$ takes pairs of positive real numbers to positive real numbers) such that for any real numbers $a, b, c>0$,
|
| 52 |
-
|
| 53 |
-
- the equation $a \diamond(b \diamond c)=(a \diamond b) \cdot c$ holds; and
|
| 54 |
-
- if $a \geq 1$ then $a \diamond a \geq 1$.
|
| 55 |
-
|
| 56 |
-
The answer is only multiplication and division, which both obviously work.
|
| 57 |
-
We present two approaches, one appealing to theorems on Cauchy's functional equation, and one which avoids it.
|
| 58 |
-
|
| 59 |
-
【 First solution using Cauchy FE. We prove:
|
| 60 |
-
Claim - We have $a \diamond b=a f(b)$ where $f$ is some involutive and totally multiplicative function. (In fact, this classifies all functions satisfying the first condition completely.)
|
| 61 |
-
|
| 62 |
-
Proof. Let $P(a, b, c)$ denote the assertion $a \diamond(b \diamond c)=(a \diamond b) \cdot c$.
|
| 63 |
-
|
| 64 |
-
- Note that for any $x$, the function $y \mapsto x \diamond y$ is injective, because if $x \diamond y_{1}=x \diamond y_{2}$ then take $P\left(1, x, y_{i}\right)$ to get $y_{1}=y_{2}$.
|
| 65 |
-
- Take $P(1, x, 1)$ and injectivity to get $x \diamond 1=x$.
|
| 66 |
-
- Take $P(1,1, y)$ to get $1 \diamond(1 \diamond y)=y$.
|
| 67 |
-
- Take $P(x, 1,1 \diamond y)$ to get
|
| 68 |
-
|
| 69 |
-
$$
|
| 70 |
-
x \diamond y=x \cdot(1 \diamond y)
|
| 71 |
-
$$
|
| 72 |
-
|
| 73 |
-
Henceforth let us define $f(y)=1 \diamond y$, so $f(1)=1, f$ is involutive and
|
| 74 |
-
|
| 75 |
-
$$
|
| 76 |
-
x \diamond y=x f(y)
|
| 77 |
-
$$
|
| 78 |
-
|
| 79 |
-
Plugging this into the original condition now gives $f(b f(c))=f(b) c$, which (since $f$ is an involution) gives $f$ completely multiplicative.
|
| 80 |
-
|
| 81 |
-
In particular, $f(1)=1$. We are now interested only in the second condition, which reads $f(x) \geq 1 / x$ for $x \geq 1$.
|
| 82 |
-
|
| 83 |
-
Define the function
|
| 84 |
-
|
| 85 |
-
$$
|
| 86 |
-
g(t)=\log f\left(e^{t}\right)
|
| 87 |
-
$$
|
| 88 |
-
|
| 89 |
-
so that $g$ is additive, and also $g(t) \geq-t$ for all $t \geq 0$. We appeal to the following theorem:
|
| 90 |
-
|
| 91 |
-
## Lemma
|
| 92 |
-
|
| 93 |
-
If $h: \mathbb{R} \rightarrow \mathbb{R}$ is an additive function which is not linear, then it is dense in the plane: for any point $\left(x_{0}, y_{0}\right)$ and $\varepsilon>0$ there exists $(x, y)$ such that $h(x)=y$ and $\sqrt{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}<\varepsilon$.
|
| 94 |
-
|
| 95 |
-
Applying this lemma with the fact that $g(t) \geq-t$ implies readily that $g$ is linear. In other words, $f$ is of the form $f(x)=x^{r}$ for some fixed real number $r$. It is easy to check $r= \pm 1$ which finishes.
|
| 96 |
-
|
| 97 |
-
【 Second solution manually. As before we arrive at $a \diamond b=a f(b)$, with $f$ an involutive and totally multiplicative function.
|
| 98 |
-
|
| 99 |
-
We prove that:
|
| 100 |
-
Claim - For any $a>0$, we have $f(a) \in\{1 / a, a\}$.
|
| 101 |
-
|
| 102 |
-
Proof. WLOG $b>1$, and suppose $f(b)=a \geq 1 / b$ hence $f(a)=b$.
|
| 103 |
-
Assume that $a b>1$; we show $a=b$. Note that for integers $m$ and $n$ with $a^{n} b^{m} \geq 1$, we must have
|
| 104 |
-
|
| 105 |
-
$$
|
| 106 |
-
a^{m} b^{n}=f(b)^{m} f(a)^{n}=f\left(a^{n} b^{m}\right) \geq \frac{1}{a^{n} b^{m}} \Longrightarrow(a b)^{m+n} \geq 1
|
| 107 |
-
$$
|
| 108 |
-
|
| 109 |
-
and thus we have arrived at the proposition
|
| 110 |
-
|
| 111 |
-
$$
|
| 112 |
-
m+n<0 \Longrightarrow n \log _{b} a+m<0
|
| 113 |
-
$$
|
| 114 |
-
|
| 115 |
-
for all integers $m$ and $n$. Due to the density of $\mathbb{Q}$ in the real numbers, this can only happen if $\log _{b} a=1$ or $a=b$.
|
| 116 |
-
|
| 117 |
-
Claim - The function $f$ is continuous.
|
| 118 |
-
|
| 119 |
-
Proof. Indeed, it's equivalent to show $g(t)=\log f\left(e^{t}\right)$ is continuous, and we have that
|
| 120 |
-
|
| 121 |
-
$$
|
| 122 |
-
|g(t)-g(s)|=\left|\log f\left(e^{t-s}\right)\right|=|t-s|
|
| 123 |
-
$$
|
| 124 |
-
|
| 125 |
-
since $f\left(e^{t-s}\right)=e^{ \pm|t-s|}$. Therefore $g$ is Lipschitz. Hence $g$ continuous, and $f$ is too.
|
| 126 |
-
Finally, we have from $f$ multiplicative that
|
| 127 |
-
|
| 128 |
-
$$
|
| 129 |
-
f\left(2^{q}\right)=f(2)^{q}
|
| 130 |
-
$$
|
| 131 |
-
|
| 132 |
-
for every rational number $q$, say. As $f$ is continuous this implies $f(x) \equiv x$ or $f(x) \equiv 1 / x$ identically (depending on whether $f(2)=2$ or $f(2)=1 / 2$, respectively).
|
| 133 |
-
|
| 134 |
-
Therefore, $a \diamond b=a b$ or $a \diamond b=a \div b$, as needed.
|
| 135 |
-
Remark. The Lipschitz condition is one of several other ways to proceed. The point is that if $f(2)=2$ (say), and $x / 2^{q}$ is close to 1 , then $f(x) / 2^{q}=f\left(x / 2^{q}\right)$ is close to 1 , which is enough to force $f(x)=x$ rather than $f(x)=1 / x$.
|
| 136 |
-
|
| 137 |
-
Remark. Compare to AMC 10A 2016 \#23, where the second condition is $a \diamond a=1$.
|
| 138 |
-
|
| 139 |
-
## §1.2 TSTST 2019/2, proposed by Merlijn Staps
|
| 140 |
-
|
| 141 |
-
Available online at https://aops.com/community/p12608478.
|
| 142 |
-
|
| 143 |
-
## Problem statement
|
| 144 |
-
|
| 145 |
-
Let $A B C$ be an acute triangle with circumcircle $\Omega$ and orthocenter $H$. Points $D$ and $E$ lie on segments $A B$ and $A C$ respectively, such that $A D=A E$. The lines through $B$ and $C$ parallel to $\overline{D E}$ intersect $\Omega$ again at $P$ and $Q$, respectively. Denote by $\omega$ the circumcircle of $\triangle A D E$.
|
| 146 |
-
(a) Show that lines $P E$ and $Q D$ meet on $\omega$.
|
| 147 |
-
(b) Prove that if $\omega$ passes through $H$, then lines $P D$ and $Q E$ meet on $\omega$ as well.
|
| 148 |
-
|
| 149 |
-
We will give one solution to (a), then several solutions to (b).
|
| 150 |
-
【 Solution to (a). Note that $\measuredangle A Q P=\measuredangle A B P=\measuredangle A D E$ and $\measuredangle A P Q=\measuredangle A C Q=$ $\measuredangle A E D$, so we have a spiral similarity $\triangle A D E \sim \triangle A Q P$. Therefore, lines $P E$ and $Q D$ meet at the second intersection of $\omega$ and $\Omega$ other than $A$. Call this point $X$.
|
| 151 |
-
|
| 152 |
-
【 Solution to (b) using angle chasing. Let $L$ be the reflection of $H$ across $\overline{A B}$, which lies on $\Omega$.
|
| 153 |
-
|
| 154 |
-
Claim - Points $L, D, P$ are collinear.
|
| 155 |
-
Proof. This is just angle chasing:
|
| 156 |
-
|
| 157 |
-
$$
|
| 158 |
-
\begin{aligned}
|
| 159 |
-
\measuredangle C L D & =\measuredangle D H L=\measuredangle D H A+\measuredangle A H L=\measuredangle D E A+\measuredangle A H C \\
|
| 160 |
-
& =\measuredangle A D E+\measuredangle C B A=\measuredangle A B P+\measuredangle C B A=\measuredangle C B P=\measuredangle C L P .
|
| 161 |
-
\end{aligned}
|
| 162 |
-
$$
|
| 163 |
-
|
| 164 |
-
|
| 165 |
-
|
| 166 |
-
Now let $K \in \omega$ such that $D H K E$ is an isosceles trapezoid, i.e. $\measuredangle B A H=\measuredangle K A E$.
|
| 167 |
-
|
| 168 |
-
Claim - Points $D, K, P$ are collinear.
|
| 169 |
-
|
| 170 |
-
Proof. Using the previous claim,
|
| 171 |
-
|
| 172 |
-
$$
|
| 173 |
-
\measuredangle K D E=\measuredangle K A E=\measuredangle B A H=\measuredangle L A B=\measuredangle L P B=\measuredangle D P B=\measuredangle P D E .
|
| 174 |
-
$$
|
| 175 |
-
|
| 176 |
-
By symmetry, $\overline{Q E}$ will then pass through the same $K$, as needed.
|
| 177 |
-
Remark. These two claims imply each other, so guessing one of them allows one to realize the other. It is likely the latter is easiest to guess from the diagram, since it does not need any additional points.
|
| 178 |
-
|
| 179 |
-
【 Solution to (b) by orthogonal circles (found by contestants). We define $K$ as in the previous solution, but do not claim that $K$ is the desired intersection. Instead, we note that:
|
| 180 |
-
|
| 181 |
-
Claim - Point $K$ is the orthocenter of isosceles triangle $A P Q$.
|
| 182 |
-
Proof. Notice that $A H=A K$ and $B C=P Q$. Moreover from $\overline{A H} \perp \overline{B C}$ we deduce $\overline{A K} \perp \overline{P Q}$ by reflection across the angle bisector.
|
| 183 |
-
|
| 184 |
-
In light of the formula " $A H^{2}=4 R^{2}-a^{2}$ ", this implies the conclusion.
|
| 185 |
-
Let $M$ be the midpoint of $\overline{P Q}$. Since $\triangle A P Q$ is isosceles,
|
| 186 |
-
|
| 187 |
-
$$
|
| 188 |
-
\overline{A K M} \perp \overline{P Q} \Longrightarrow M K \cdot M A=M P^{2}
|
| 189 |
-
$$
|
| 190 |
-
|
| 191 |
-
by orthocenter properties.
|
| 192 |
-
So to summarize
|
| 193 |
-
|
| 194 |
-
- The circle with diameter $\overline{P Q}$ is orthogonal to $\omega$. In other words, point $P$ lies on the polar of $Q$ with respect to $\omega$.
|
| 195 |
-
- The point $X=\overline{Q D} \cap \overline{P E}$ is on $\omega$.
|
| 196 |
-
|
| 197 |
-
On the other hand, if we let $K^{\prime}=\overline{Q E} \cap \omega$, then by Brokard theorem on $X D K^{\prime} E$, the polar of $Q=\overline{X D} \cap \overline{K^{\prime} E}$ pass through $\overline{D K^{\prime}} \cap \overline{X E}$; this point must therefore be $P$ and $K^{\prime}=K$ as desired.
|
| 198 |
-
|
| 199 |
-
『 S Solution to (b) by complex numbers (Yang Liu and Michael Ma). Let $M$ be the arc midpoint of $\widehat{B C}$. We use the standard arc midpoint configuration. We have that
|
| 200 |
-
|
| 201 |
-
$$
|
| 202 |
-
A=a^{2}, B=b^{2}, C=c^{2}, M=-b c, H=a^{2}+b^{2}+c^{2}, P=\frac{a^{2} c}{b}, Q=\frac{a^{2} b}{c}
|
| 203 |
-
$$
|
| 204 |
-
|
| 205 |
-
where $M$ is the arc midpoint of $\widehat{B C}$. By direct angle chasing we can verify that $\overline{M B} \| \overline{D H}$. Also, $D \in \overline{A B}$. Therefore, we can compute $D$ as follows.
|
| 206 |
-
|
| 207 |
-
$$
|
| 208 |
-
d+a^{2} b^{2} \bar{d}=a^{2}+b^{2} \text { and } \frac{d-h}{\bar{d}-\bar{h}}=-m b^{2}=b^{3} c \Longrightarrow d=\frac{a^{2}\left(a^{2} c+b^{2} c+c^{3}-b^{3}\right)}{c\left(b c+a^{2}\right)} .
|
| 209 |
-
$$
|
| 210 |
-
|
| 211 |
-
By symmetry, we have that
|
| 212 |
-
|
| 213 |
-
$$
|
| 214 |
-
e=\frac{a^{2}\left(a^{2} b+b c^{2}+b^{3}-c^{3}\right)}{b\left(b c+a^{2}\right)} .
|
| 215 |
-
$$
|
| 216 |
-
|
| 217 |
-
To finish, we want to show that the angle between $\overline{D P}$ and $\overline{E Q}$ is angle $A$. To show this, we compute $\frac{d-p}{e-q} / \overline{\frac{d-p}{e-q}}$. First, we compute
|
| 218 |
-
|
| 219 |
-
$$
|
| 220 |
-
\begin{aligned}
|
| 221 |
-
d-p & =\frac{a^{2}\left(a^{2} c+b^{2} c+c^{3}-b^{3}\right)}{c\left(b c+a^{2}\right)}-\frac{a^{2} c}{b} \\
|
| 222 |
-
& =a^{2}\left(\frac{a^{2} c+b^{2} c+c^{3}-b^{3}}{c\left(b c+a^{2}\right)}-\frac{c}{b}\right)=\frac{a^{2}\left(a^{2} c-b^{3}\right)(b-c)}{b c\left(b c+a^{2}\right)}
|
| 223 |
-
\end{aligned}
|
| 224 |
-
$$
|
| 225 |
-
|
| 226 |
-
By symmetry,
|
| 227 |
-
|
| 228 |
-
$$
|
| 229 |
-
\frac{d-p}{e-q}=-\frac{a^{2} c-b^{3}}{a^{2} b-c^{3}} \Longrightarrow \frac{d-p}{e-q} / \overline{\frac{d-p}{e-q}}=\frac{a^{2} b^{3} c}{a^{2} b c^{3}}=\frac{b^{2}}{c^{2}}
|
| 230 |
-
$$
|
| 231 |
-
|
| 232 |
-
as desired.
|
| 233 |
-
\I Solution to (b) using untethered moving points (Zack Chroman). We work in the real projective plane $\mathbb{R P}^{2}$, and animate $C$ linearly on a fixed line through $A$.
|
| 234 |
-
|
| 235 |
-
Recall:
|
| 236 |
-
|
| 237 |
-
## Lemma (Zack's lemma)
|
| 238 |
-
|
| 239 |
-
Suppose points $A, B$ have degree $d_{1}, d_{2}$, and there are $k$ values of $t$ for which $A=B$. Then line $A B$ has degree at most $d_{1}+d_{2}-k$. Similarly, if lines $\ell_{1}, \ell_{2}$ have degrees $d_{1}, d_{2}$, and there are $k$ values of $t$ for which $\ell_{1}=\ell_{2}$, then the intersection $\ell_{1} \cap \ell_{2}$ has degree at most $d_{1}+d_{2}-k$.
|
| 240 |
-
|
| 241 |
-
Now, note that $H$ moves linearly in $C$ on line $B H$. Furthermore, angles $\angle A H E$, $\angle A H F$ are fixed, we get that $D$ and $E$ have degree 2 . One way to see this is using the lemma; $D$ lies on line $A B$, which is fixed, and line $H D$ passes through a point at infinity which is a constant rotation of the point at infinity on line $A H$, and therefore has degree 1. Then $D, E$ have degree at most $1+1-0=2$.
|
| 242 |
-
|
| 243 |
-
Now, note that $P, Q$ move linearly in $C$. Both of these are because the circumcenter $O$ moves linearly in $C$, and $P, Q$ are reflections of $B, C$ in a line through $O$ with fixed direction, which also moves linearly.
|
| 244 |
-
|
| 245 |
-
So by the lemma, the lines $P D, Q E$ have degree at most 3 . I claim they actually have degree 2; to show this it suffices to give an example of a choice of $C$ for which $P=D$ and one for which $Q=E$. But an easy angle chase shows that in the unique case when $P=B$, we get $D=B$ as well and thus $P=D$. Similarly when $Q=C, E=C$. It follows from the lemma that lines $P D, Q E$ have degree at most 2 .
|
| 246 |
-
|
| 247 |
-
Let $\ell_{\infty}$ denote the line at infinity. I claim that the points $P_{1}=P D \cap \ell_{\infty}, P_{2}=Q E \cap \ell_{\infty}$ are projective in $C$. Since $\ell_{\infty}$ is fixed, it suffices to show by the lemma that there exists some value of $C$ for which $Q E=\ell_{\infty}$ and $P D=\ell_{\infty}$. But note that as $C \rightarrow \infty$, all four points $P, D, Q, E$ go to infinity. It follows that $P_{1}, P_{2}$ are projective in $C$.
|
| 248 |
-
|
| 249 |
-
Then to finish, recall that we want to show that $\angle(P D, Q E)$ is constant. It suffices then to show that there's a constant rotation sending $P_{1}$ to $P_{2}$. Since $P_{1}, P_{2}$ are projective, it suffices to verify this for 3 values of $C$.
|
| 250 |
-
|
| 251 |
-
We can take $C$ such that $\angle A B C=90, \angle A C B=90$, or $A B=A C$, and all three cases are easy to check.
|
| 252 |
-
|
| 253 |
-
## §1.3 TSTST 2019/3, proposed by Nikolai Beluhov
|
| 254 |
-
|
| 255 |
-
Available online at https://aops.com/community/p12608769.
|
| 256 |
-
|
| 257 |
-
## Problem statement
|
| 258 |
-
|
| 259 |
-
On an infinite square grid we place finitely many cars, which each occupy a single cell and face in one of the four cardinal directions. Cars may never occupy the same cell. It is given that the cell immediately in front of each car is empty, and moreover no two cars face towards each other (no right-facing car is to the left of a left-facing car within a row, etc.). In a move, one chooses a car and shifts it one cell forward to a vacant cell. Prove that there exists an infinite sequence of valid moves using each car infinitely many times.
|
| 260 |
-
|
| 261 |
-
Let $S$ be any rectangle containing all the cars. Partition $S$ into horizontal strips of height 1 , and color them red and green in an alternating fashion. It is enough to prove all the cars may exit $S$.
|
| 262 |
-
|
| 263 |
-
|
| 264 |
-
To do so, we outline a five-stage plan for the cars.
|
| 265 |
-
|
| 266 |
-
1. All vertical cars in a green cell may advance one cell into a red cell (or exit $S$ altogether), by the given condition. (This is the only place where the hypothesis about empty space is used!)
|
| 267 |
-
2. All horizontal cars on green cells may exit $S$, as no vertical cars occupy green cells.
|
| 268 |
-
3. All vertical cars in a red cell may advance one cell into a green cell (or exit $S$ altogether), as all green cells are empty.
|
| 269 |
-
4. All horizontal cars within red cells may exit $S$, as no vertical car occupy red cells.
|
| 270 |
-
5. The remaining cars exit $S$, as they are all vertical. The solution is complete.
|
| 271 |
-
|
| 272 |
-
Remark (Author's comments). The solution I've given for this problem is so short and simple that it might appear at first to be about IMO 1 difficulty. I don't believe that's true! There are very many approaches that look perfectly plausible at first, and then fall apart in this or that twisted special case.
|
| 273 |
-
|
| 274 |
-
Remark (Higher-dimensional generalization by author). The natural higher-dimensional generalization is true, and can be proved in largely the same fashion. For example, in three dimensions, one may let $S$ be a rectangular prism and partition $S$ into horizontal slabs and color them red and green in an alternating fashion. Stages 1, 3, and 5 generalize immediately, and stages 2 and 4 reduce to an application of the two-dimensional problem. In the same way, the general problem is handled by induction on the dimension.
|
| 275 |
-
|
| 276 |
-
Remark (Historical comments). For $k>1$, we could consider a variant of the problem where cars are $1 \times k$ rectangles (moving parallel to the longer edge) instead of occupying single cells. In that case, if there are $2 k-1$ empty spaces in front of each car, the above proof works (with the red and green strips having height $k$ instead). On the other hand, at least $k$ empty spaces are necessary. We don't know the best constant in this case.
|
| 277 |
-
|
| 278 |
-
## §2 Solutions to Day 2
|
| 279 |
-
|
| 280 |
-
## §2.1 TSTST 2019/4, proposed by Merlijn Staps
|
| 281 |
-
|
| 282 |
-
Available online at https://aops.com/community/p12608513.
|
| 283 |
-
|
| 284 |
-
## Problem statement
|
| 285 |
-
|
| 286 |
-
Consider coins with positive real denominations not exceeding 1. Find the smallest $C>0$ such that the following holds: if we are given any 100 such coins with total value 50 , then we can always split them into two stacks of 50 coins each such that the absolute difference between the total values of the two stacks is at most $C$.
|
| 287 |
-
|
| 288 |
-
The answer is $C=\frac{50}{51}$. The lower bound is obtained if we have 51 coins of value $\frac{1}{51}$ and 49 coins of value 1. (Alternatively, 51 coins of value $1-\frac{\varepsilon}{51}$ and 49 coins of value $\frac{\varepsilon}{49}$ works fine for $\varepsilon>0$.) We now present two (similar) proofs that this $C=\frac{50}{51}$ suffices.
|
| 289 |
-
|
| 290 |
-
【 First proof (original). Let $a_{1} \leq \cdots \leq a_{100}$ denote the values of the coins in ascending order. Since the 51 coins $a_{50}, \ldots, a_{100}$ are worth at least $51 a_{50}$, it follows that $a_{50} \leq \frac{50}{51}$; likewise $a_{51} \geq \frac{1}{51}$.
|
| 291 |
-
|
| 292 |
-
We claim that choosing the stacks with coin values
|
| 293 |
-
|
| 294 |
-
$$
|
| 295 |
-
a_{1}, a_{3}, \ldots, a_{49}, \quad a_{52}, a_{54}, \ldots, a_{100}
|
| 296 |
-
$$
|
| 297 |
-
|
| 298 |
-
and
|
| 299 |
-
|
| 300 |
-
$$
|
| 301 |
-
a_{2}, a_{4}, \ldots, a_{50}, \quad a_{51}, a_{53}, \ldots, a_{99}
|
| 302 |
-
$$
|
| 303 |
-
|
| 304 |
-
works. Let $D$ denote the (possibly negative) difference between the two total values. Then
|
| 305 |
-
|
| 306 |
-
$$
|
| 307 |
-
\begin{aligned}
|
| 308 |
-
D & =\left(a_{1}-a_{2}\right)+\cdots+\left(a_{49}-a_{50}\right)-a_{51}+\left(a_{52}-a_{53}\right)+\cdots+\left(a_{98}-a_{99}\right)+a_{100} \\
|
| 309 |
-
& \leq 25 \cdot 0-\frac{1}{51}+24 \cdot 0+1=\frac{50}{51}
|
| 310 |
-
\end{aligned}
|
| 311 |
-
$$
|
| 312 |
-
|
| 313 |
-
Similarly, we have
|
| 314 |
-
|
| 315 |
-
$$
|
| 316 |
-
\begin{aligned}
|
| 317 |
-
D & =a_{1}+\left(a_{3}-a_{2}\right)+\cdots+\left(a_{49}-a_{48}\right)-a_{50}+\left(a_{52}-a_{51}\right)+\cdots+\left(a_{100}-a_{99}\right) \\
|
| 318 |
-
& \geq 0+24 \cdot 0-\frac{50}{51}+25 \cdot 0=-\frac{50}{51}
|
| 319 |
-
\end{aligned}
|
| 320 |
-
$$
|
| 321 |
-
|
| 322 |
-
It follows that $|D| \leq \frac{50}{51}$, as required.
|
| 323 |
-
|
| 324 |
-
【 Second proof (Evan Chen). Again we sort the coins in increasing order $0<a_{1} \leq$ $a_{2} \leq \cdots \leq a_{100} \leq 1$. A large gap is an index $i \geq 2$ such that $a_{i}>a_{i-1}+\frac{50}{51}$; obviously there is at most one such large gap.
|
| 325 |
-
|
| 326 |
-
Claim - If there is a large gap, it must be $a_{51}>a_{50}+\frac{50}{51}$.
|
| 327 |
-
|
| 328 |
-
Proof. If $i<50$ then we get $a_{50}, \ldots, a_{100}>\frac{50}{51}$ and the sum $\sum_{1}^{100} a_{i}>50$ is too large. Conversely if $i>50$ then we get $a_{1}, \ldots, a_{i-1}<\frac{1}{51}$ and the sum $\sum_{1}^{100} a_{i}<1 / 51 \cdot 51+49$ is too small.
|
| 329 |
-
|
| 330 |
-
Now imagine starting with the coins $a_{1}, a_{3}, \ldots, a_{99}$, which have total value $S \leq 25$. We replace $a_{1}$ by $a_{2}$, then $a_{3}$ by $a_{4}$, and so on, until we replace $a_{99}$ by $a_{100}$. At the end of the process we have $S \geq 25$. Moreover, since we did not cross a large gap at any point, the quantity $S$ changed by at most $C=\frac{50}{51}$ at each step. So at some point in the process we need to have $25-C / 2 \leq S \leq 25+C / 2$, which proves $C$ works.
|
| 331 |
-
|
| 332 |
-
## §2.2 TSTST 2019/5, proposed by Gunmay Handa
|
| 333 |
-
|
| 334 |
-
Available online at https://aops.com/community/p12608496.
|
| 335 |
-
|
| 336 |
-
## Problem statement
|
| 337 |
-
|
| 338 |
-
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
| 339 |
-
|
| 340 |
-
We present several solutions. (There are more in the official packet; some are omitted here, which explains the numbering.)
|
| 341 |
-
|
| 342 |
-
『 First solution (Andrew Gu). We begin with the following two observations.
|
| 343 |
-
Claim - Point $K$ lies on the radical axis of $(B E H)$ and $(C F H)$.
|
| 344 |
-
Proof. Actually we claim $\overline{K E}$ and $\overline{K F}$ are tangents. Indeed,
|
| 345 |
-
|
| 346 |
-
$$
|
| 347 |
-
\measuredangle H E K=90^{\circ}-\measuredangle E A F=90^{\circ}-\measuredangle B A C=\measuredangle H B E
|
| 348 |
-
$$
|
| 349 |
-
|
| 350 |
-
implying the result. Since $K E=K F$, this implies the result.
|
| 351 |
-
|
| 352 |
-
Claim - The second intersection $M$ of $(B E H)$ and $(C F H)$ lies on $\Gamma$.
|
| 353 |
-
Proof. By Miquel's theorem on $\triangle A E F$ with $H \in \overline{E F}, B \in \overline{A E}, C \in \overline{A F}$.
|
| 354 |
-
|
| 355 |
-
|
| 356 |
-
In particular, $M, H, K$ are collinear. Let $X$ be on $\Gamma$ with $\overline{D X} \perp \overline{B C}$; we then wish to show $X$ lies on the line $M H K$ we found. This is angle chasing: compute
|
| 357 |
-
|
| 358 |
-
$$
|
| 359 |
-
\measuredangle X M B=\measuredangle X D B=90^{\circ}-\measuredangle D B C=90^{\circ}-\measuredangle D A C
|
| 360 |
-
$$
|
| 361 |
-
|
| 362 |
-
$$
|
| 363 |
-
=90^{\circ}-\measuredangle K A F=\measuredangle F E A=\measuredangle H E B=\measuredangle H M B
|
| 364 |
-
$$
|
| 365 |
-
|
| 366 |
-
as needed.
|
| 367 |
-
|
| 368 |
-
II Second solution (Ankan Bhattacharya). We let $D^{\prime}$ be the second intersection of $\overline{E F}$ with $(B H C)$ and redefine $D$ as the reflection of $D^{\prime}$ across $\overline{B C}$. We will first prove that this point $D$ coincides with the point $D$ given in the problem statement. The idea is that:
|
| 369 |
-
|
| 370 |
-
Claim - $A$ is the $D$-excenter of $\triangle D E F$.
|
| 371 |
-
|
| 372 |
-
Proof. We contend $B E D^{\prime} D$ is cyclic. This follows by angle chasing:
|
| 373 |
-
|
| 374 |
-
$$
|
| 375 |
-
\begin{aligned}
|
| 376 |
-
\measuredangle D^{\prime} D B & =\measuredangle B D^{\prime} D=\measuredangle D^{\prime} B C+90^{\circ}=\measuredangle D^{\prime} H C+90^{\circ} \\
|
| 377 |
-
& =\measuredangle D^{\prime} H C+\measuredangle(H C, A B)=\measuredangle\left(D^{\prime} H, A B\right)=\measuredangle D^{\prime} E B
|
| 378 |
-
\end{aligned}
|
| 379 |
-
$$
|
| 380 |
-
|
| 381 |
-
Now as $B D=B D^{\prime}$, we obtain $\overline{B E A}$ externally bisects $\angle D E D^{\prime} \cong \angle D E F$. Likewise $\overline{F A}$ externally bisects $\angle D F E$, so $A$ is the $D$-excenter of $\triangle D E F$.
|
| 382 |
-
|
| 383 |
-
Hence, by the so-called "Fact 5 ", point $K$ lies on $\overline{D A}$, so this point $D$ is the one given in the problem statement.
|
| 384 |
-
|
| 385 |
-
|
| 386 |
-
Now choose point $X$ on $(A B C)$ satisfying $\overline{D X} \perp \overline{B C}$.
|
| 387 |
-
Claim - Point $K$ lies on line $H X$.
|
| 388 |
-
|
| 389 |
-
Proof. Clearly $A H D^{\prime} X$ is a parallelogram. By Ptolemy on $D E K F$,
|
| 390 |
-
|
| 391 |
-
$$
|
| 392 |
-
\frac{K D}{K A}=\frac{K D}{K E}=\frac{D E+D F}{E F}
|
| 393 |
-
$$
|
| 394 |
-
|
| 395 |
-
On the other hand, if we let $r_{D}$ denote the $D$-exradius of $\triangle D E F$ then
|
| 396 |
-
|
| 397 |
-
$$
|
| 398 |
-
\frac{X D}{X D^{\prime}}=\frac{[D E X]+[D F X]}{[X E F]}=\frac{[D E X]+[D F X]}{[A E F]}=\frac{D E \cdot r_{D}+D F \cdot r_{D}}{E F \cdot r_{D}}=\frac{D E+D F}{E F}
|
| 399 |
-
$$
|
| 400 |
-
|
| 401 |
-
Thus
|
| 402 |
-
|
| 403 |
-
$$
|
| 404 |
-
[A K X]=\frac{K A}{K D} \cdot[D K X]=\frac{K A}{K D} \cdot \frac{X D}{X D^{\prime}} \cdot\left[K D^{\prime} X\right]=\left[D^{\prime} K X\right]
|
| 405 |
-
$$
|
| 406 |
-
|
| 407 |
-
This is sufficient to prove $K$ lies on $\overline{H X}$.
|
| 408 |
-
The solution is complete: $X$ is the desired concurrency point.
|
| 409 |
-
|
| 410 |
-
I Fourth solution, complex numbers with spiral similarity (Evan Chen). First if $\overline{A D} \perp \overline{B C}$ there is nothing to prove, so we assume this is not the case. Let $W$ be the antipode of $D$. Let $S$ denote the second intersection of $(A E F)$ and $(A B C)$. Consider the spiral similarity sending $\triangle S E F$ to $\triangle S B C$ :
|
| 411 |
-
|
| 412 |
-
- It maps $H$ to a point $G$ on line $B C$,
|
| 413 |
-
- It maps $K$ to $O$.
|
| 414 |
-
- It maps the $A$-antipode of $\triangle A E F$ to $D$.
|
| 415 |
-
- Hence (by previous two observations) it maps $A$ to $W$.
|
| 416 |
-
- Also, the image of line $A D$ is line $W O$, which does not coincide with line $B C$ (as $O$ does not lie on line $B C$ ).
|
| 417 |
-
|
| 418 |
-
Therefore, $K$ is the unique point on line $\overline{A D}$ for one can get a direct similarity
|
| 419 |
-
|
| 420 |
-
$$
|
| 421 |
-
\triangle A K H \sim \triangle W O G
|
| 422 |
-
$$
|
| 423 |
-
|
| 424 |
-
for some point $G$ lying on line $\overline{B C}$.
|
| 425 |
-
|
| 426 |
-
|
| 427 |
-
On the other hand, let us re-define $K$ as $\overline{X H} \cap \overline{A D}$. We will show that the corresponding $G$ making $(\triangle)$ true lies on line $B C$.
|
| 428 |
-
|
| 429 |
-
We apply complex numbers with $\Gamma$ the unit circle, with $a, b, c, d$ taking their usual meanings, $H=a+b+c, X=-b c / d$, and $W=-d$. Then point $K$ is supposed to satisfy
|
| 430 |
-
|
| 431 |
-
$$
|
| 432 |
-
k+a d \bar{k}=a+d
|
| 433 |
-
$$
|
| 434 |
-
|
| 435 |
-
$$
|
| 436 |
-
\begin{aligned}
|
| 437 |
-
\frac{k+\frac{b c}{d}}{a+b+c+\frac{b c}{d}} & =\frac{\bar{k}+\frac{d}{b c}}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}} \\
|
| 438 |
-
\Longleftrightarrow \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}}{a+b+c+\frac{b c}{d}}\left(k+\frac{b c}{d}\right) & =\bar{k}+\frac{d}{b c}
|
| 439 |
-
\end{aligned}
|
| 440 |
-
$$
|
| 441 |
-
|
| 442 |
-
Adding $a d$ times the last line to the first line and cancelling $a d \bar{k}$ now gives
|
| 443 |
-
|
| 444 |
-
$$
|
| 445 |
-
\left(a d \cdot \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}}{a+b+c+\frac{b c}{d}}+1\right) k=a+d+\frac{a d^{2}}{b c}-a b c \cdot \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}}{a+b+c+\frac{b c}{d}}
|
| 446 |
-
$$
|
| 447 |
-
|
| 448 |
-
or
|
| 449 |
-
|
| 450 |
-
$$
|
| 451 |
-
\begin{aligned}
|
| 452 |
-
\left(a d\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}\right)+a+b+c+\frac{b c}{d}\right) k & =\left(a+b+c+\frac{b c}{d}\right)\left(a+d+\frac{a d^{2}}{b c}\right) \\
|
| 453 |
-
& -a b c \cdot\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}\right) .
|
| 454 |
-
\end{aligned}
|
| 455 |
-
$$
|
| 456 |
-
|
| 457 |
-
We begin by simplifying the coefficient of $k$ :
|
| 458 |
-
|
| 459 |
-
$$
|
| 460 |
-
\begin{aligned}
|
| 461 |
-
a d\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}\right)+a+b+c+\frac{b c}{d} & =a+b+c+d+\frac{b c}{d}+\frac{a d}{b}+\frac{a d}{c}+\frac{a d^{2}}{b c} \\
|
| 462 |
-
& =a+\frac{b c}{d}+\left(1+\frac{a d}{b c}\right)(b+c+d) \\
|
| 463 |
-
& =\frac{a d+b c}{b c d}[b c+d(b+c+d)] \\
|
| 464 |
-
& =\frac{(a d+b c)(d+b)(d+c)}{b c d}
|
| 465 |
-
\end{aligned}
|
| 466 |
-
$$
|
| 467 |
-
|
| 468 |
-
Meanwhile, the right-hand side expands to
|
| 469 |
-
|
| 470 |
-
$$
|
| 471 |
-
\begin{aligned}
|
| 472 |
-
\mathrm{RHS}= & \left(a+b+c+\frac{b c}{d}\right)\left(a+d+\frac{a d^{2}}{b c}\right)-a b c \cdot\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{d}{b c}\right) \\
|
| 473 |
-
= & \left(a^{2}+a b+a c+\frac{a b c}{d}\right)+(d a+d b+d c+b c) \\
|
| 474 |
-
& +\left(\frac{a^{2} d^{2}}{b c}+\frac{a d^{2}}{c}+\frac{a d^{2}}{b}+a d\right)-(a b+b c+c a+a d) \\
|
| 475 |
-
= & a^{2}+d(a+b+c)+\frac{a b c}{d}+\frac{a^{2} d^{2}}{b c}+\frac{a d^{2}}{b}+\frac{a d^{2}}{c} \\
|
| 476 |
-
= & a^{2}+\frac{a b c}{d}+d(a+b+c) \cdot \frac{a d+b c}{b c} \\
|
| 477 |
-
= & \frac{a d+b c}{b c d}\left[a b c+d^{2}(a+b+c)\right] .
|
| 478 |
-
\end{aligned}
|
| 479 |
-
$$
|
| 480 |
-
|
| 481 |
-
Therefore, we get
|
| 482 |
-
|
| 483 |
-
$$
|
| 484 |
-
k=\frac{a b c+d^{2}(a+b+c)}{(d+b)(d+c)}
|
| 485 |
-
$$
|
| 486 |
-
|
| 487 |
-
In particular,
|
| 488 |
-
|
| 489 |
-
$$
|
| 490 |
-
\begin{aligned}
|
| 491 |
-
k-a & =\frac{a b c+d^{2}(a+b+c)-a(d+b)(d+c)}{(d+b)(d+c)} \\
|
| 492 |
-
& =\frac{d^{2}(b+c)-d a(b+c)}{(d+b)(d+c)}=\frac{d(b+c)(d-a)}{(d+b)(d+c)}
|
| 493 |
-
\end{aligned}
|
| 494 |
-
$$
|
| 495 |
-
|
| 496 |
-
Now the corresponding point $G$ obeying $(\Omega)$ satisfies
|
| 497 |
-
|
| 498 |
-
$$
|
| 499 |
-
\begin{aligned}
|
| 500 |
-
\frac{g-(-d)}{0-(-d)} & =\frac{(a+b+c)-a}{k-a} \\
|
| 501 |
-
\Longrightarrow g & =-d+\frac{d(b+c)}{k-a} \\
|
| 502 |
-
& =-d+\frac{(d+b)(d+c)}{d-a}=\frac{d b+d c+b c+a d}{d-a} . \\
|
| 503 |
-
\Longrightarrow b c \bar{g} & =\frac{b c \cdot \frac{a c+a b+a d+b c}{a b c d}}{\frac{a-d}{a d}}=-\frac{a b+a c+a d+b c}{d-a} . \\
|
| 504 |
-
\Longrightarrow g+b c \bar{g} & =\frac{(d-a)(b+c)}{d-a}=b+c .
|
| 505 |
-
\end{aligned}
|
| 506 |
-
$$
|
| 507 |
-
|
| 508 |
-
Hence $G$ lies on $B C$ and this completes the proof.
|
| 509 |
-
|
| 510 |
-
【 Seventh solution using moving points (Zack Chroman). We state the converse of the problem as follows:
|
| 511 |
-
|
| 512 |
-
Take a point $D$ on $\Gamma$, and let $G \in \Gamma$ such that $\overline{D G} \perp \overline{B C}$. Then define $K$ to lie on $\overline{G H}, \overline{A D}$, and take $L \in \overline{A D}$ such that $K$ is the midpoint of $\overline{A L}$. Then if we define $E$ and $F$ as the projections of $L$ onto $\overline{A B}$ and $\overline{A C}$ we want to show that $E, H, F$ are collinear.
|
| 513 |
-
|
| 514 |
-
It's clear that solving this problem will solve the original. In fact we will show later that each line $E F$ through $H$ corresponds bijectively to the point $D$.
|
| 515 |
-
|
| 516 |
-
We animate $D$ projectively on $\Gamma$ (hence $\operatorname{deg} D=2$ ). Since $D \mapsto G$ is a projective map $\Gamma \rightarrow \Gamma$, it follows $\operatorname{deg} G=2$. By Zack's lemma, $\operatorname{deg}(\overline{A D}) \leq 0+2-1=1$ (since $D$ can coincide with $A$ ), and $\operatorname{deg}(\overline{H G}) \leq 0+2-0=2$. So again by Zack's lemma, $\operatorname{deg} K \leq 1+2-1=2$, since lines $A D$ and $G H$ can coincide once if $D$ is the reflection of $H$ over $\overline{B C}$. It follows $\operatorname{deg} L=2$, since it is obtained by dilating $K$ by a factor of 2 across the fixed point $A$.
|
| 517 |
-
|
| 518 |
-
Let $\infty_{C}$ be the point at infinity on the line perpendicular to $A C$, and similarly $\infty_{B}$. Then
|
| 519 |
-
|
| 520 |
-
$$
|
| 521 |
-
F=\overline{A C} \cap \overline{\infty_{C} L}, \quad E=\overline{A B} \cap \overline{\infty_{B} L} .
|
| 522 |
-
$$
|
| 523 |
-
|
| 524 |
-
We want to use Zack's lemma again on line $\overline{\infty_{B} L}$. Consider the case $G=B$; we get $\overline{H G} \| \overline{A D}$, so $A D G H$ is a parallelogram, and then $K=L=\infty_{B}$. Thus there is at least one $t$ where $L=\infty_{B}$ and by Zack's lemma we get $\operatorname{deg}\left(\overline{\infty_{B} L}\right) \leq 0+2-1=1$. Again by Zack's lemma, we conclude $\operatorname{deg} E \leq 0+1-0=1$. Similarly, $\operatorname{deg} F \leq 1$.
|
| 525 |
-
|
| 526 |
-
We were aiming to show $E, F, H$ collinear which is a condition of degree at most $1+1+0=2$. So it suffices to verify the problem for three distinct choices of $D$.
|
| 527 |
-
|
| 528 |
-
- If $D=A$, then line $G H$ is line $A H$, and $L=\overline{A D} \cap \overline{A H}=A$. So $E=F=A$ and the statement is true.
|
| 529 |
-
- If $D=B, G$ is the antipode of $C$ on $\Gamma$. Then $K=\overline{H G} \cap \overline{A D}$ is the midpoint of $\overline{A B}$, so $L=B$. Then $E=B$ and $F$ is the projection of $B$ onto $A C$, so $E, H, F$ collinear.
|
| 530 |
-
- We finish similarly when $D=C$.
|
| 531 |
-
|
| 532 |
-
This completes the proof.
|
| 533 |
-
|
| 534 |
-
Remark. Less careful approaches are possible which give a worse bound on the degrees, requiring to check (say) five choices of $D$ instead. We present the most careful one showing $\operatorname{deg} D=2$ for instructional reasons, but the others may be easier to find.
|
| 535 |
-
|
| 536 |
-
## §2.3 TSTST 2019/6, proposed by Nikolai Beluhov
|
| 537 |
-
|
| 538 |
-
Available online at https://aops.com/community/p12608536.
|
| 539 |
-
|
| 540 |
-
## Problem statement
|
| 541 |
-
|
| 542 |
-
Suppose $P$ is a polynomial with integer coefficients such that for every positive integer $n$, the sum of the decimal digits of $|P(n)|$ is not a Fibonacci number. Must $P$ be constant?
|
| 543 |
-
|
| 544 |
-
The answer is yes, $P$ must be constant. By $S(n)$ we mean the sum of the decimal digits of $|n|$.
|
| 545 |
-
|
| 546 |
-
We need two claims.
|
| 547 |
-
Claim - If $P(x) \in \mathbb{Z}[x]$ is nonconstant with positive leading coefficient, then there exists an integer polynomial $F(x)$ such that all coefficients of $P \circ F$ are positive except for the second one, which is negative.
|
| 548 |
-
|
| 549 |
-
Proof. We will actually construct a cubic $F$. We call a polynomial good if it has the property.
|
| 550 |
-
|
| 551 |
-
First, consider $T_{0}(x)=x^{3}+x+1$. Observe that in $T_{0}^{\operatorname{deg} P}$, every coefficient is strictly positive, except for the second one, which is zero.
|
| 552 |
-
|
| 553 |
-
Then, let $T_{1}(x)=x^{3}-\frac{1}{D} x^{2}+x+1$. Using continuity as $D \rightarrow \infty$, it follows that if $D$ is large enough (in terms of $\operatorname{deg} P$ ), then $T_{1}^{\operatorname{deg} P}$ is good, with $-\frac{3}{D} x^{3 \operatorname{deg} P-1}$ being the only negative coefficient.
|
| 554 |
-
|
| 555 |
-
Finally, we can let $F(x)=C T_{1}(x)$ where $C$ is a sufficiently large multiple of $D$ (in terms of the coefficients of $P$ ); thus the coefficients of $\left(C T_{1}(x)\right)^{\operatorname{deg} P}$ dominate (and are integers), as needed.
|
| 556 |
-
|
| 557 |
-
Claim - There are infinitely many Fibonacci numbers in each residue class modulo 9.
|
| 558 |
-
|
| 559 |
-
Proof. Note the Fibonacci sequence is periodic modulo 9 (indeed it is periodic modulo any integer). Moreover (allowing negative indices),
|
| 560 |
-
|
| 561 |
-
$$
|
| 562 |
-
\begin{aligned}
|
| 563 |
-
F_{0}=0 & \equiv 0 \quad(\bmod 9) \\
|
| 564 |
-
F_{1}=1 & \equiv 1 \quad(\bmod 9) \\
|
| 565 |
-
F_{3}=2 & \equiv 2 \quad(\bmod 9) \\
|
| 566 |
-
F_{4}=3 & \equiv 3 \quad(\bmod 9) \\
|
| 567 |
-
F_{7}=13 & \equiv 4 \quad(\bmod 9) \\
|
| 568 |
-
F_{5}=5 & \equiv 5 \quad(\bmod 9) \\
|
| 569 |
-
F_{-4}=-3 & \equiv 6 \quad(\bmod 9) \\
|
| 570 |
-
F_{9}=34 & \equiv 7 \quad(\bmod 9) \\
|
| 571 |
-
F_{6}=8 & \equiv 8 \quad(\bmod 9) .
|
| 572 |
-
\end{aligned}
|
| 573 |
-
$$
|
| 574 |
-
|
| 575 |
-
We now show how to solve the problem with the two claims. WLOG $P$ satisfies the conditions of the first claim, and choose $F$ as above. Let
|
| 576 |
-
|
| 577 |
-
$$
|
| 578 |
-
P(F(x))=c_{N} x^{N}-c_{N-1} x^{N-1}+c_{N-2} x^{N-2}+\cdots+c_{0}
|
| 579 |
-
$$
|
| 580 |
-
|
| 581 |
-
where $c_{i}>0$ (and $N=3 \operatorname{deg} P$ ). Then if we select $x=10^{e}$ for $e$ large enough (say $\left.x>10 \max _{i} c_{i}\right)$, the decimal representation $P\left(F\left(10^{e}\right)\right)$ consists of the concatenation of
|
| 582 |
-
|
| 583 |
-
- the decimal representation of $c_{N}-1$,
|
| 584 |
-
- the decimal representation of $10^{e}-c_{N-1}$
|
| 585 |
-
- the decimal representation of $c_{N-2}$, with several leading zeros,
|
| 586 |
-
- the decimal representation of $c_{N-3}$, with several leading zeros,
|
| 587 |
-
- ...
|
| 588 |
-
- the decimal representation of $c_{0}$, with several leading zeros.
|
| 589 |
-
(For example, if $P(F(x))=15 x^{3}-7 x^{2}+4 x+19$, then $P(F(1000))=14,993,004,019$.) Thus, the sum of the digits of this expression is equal to
|
| 590 |
-
|
| 591 |
-
$$
|
| 592 |
-
S\left(P\left(F\left(10^{e}\right)\right)\right)=9 e+k
|
| 593 |
-
$$
|
| 594 |
-
|
| 595 |
-
for some constant $k$ depending only on $P$ and $F$, independent of $e$. But this will eventually hit a Fibonacci number by the second claim, contradiction.
|
| 596 |
-
|
| 597 |
-
Remark. It is important to control the number of negative coefficients in the created polynomial. If one tries to use this approach on a polynomial $P$ with $m>0$ negative coefficients, then one would require that the Fibonacci sequence is surjective modulo $9 m$ for any $m>1$, which is not true: for example the Fibonacci sequence avoids all numbers congruent to $4 \bmod 11($ and thus $4 \bmod 99)$.
|
| 598 |
-
|
| 599 |
-
In bases $b$ for which surjectivity modulo $b-1$ fails, the problem is false. For example, $P(x)=11 x+4$ will avoid all Fibonacci numbers if we take sum of digits in base 12, since that base-12 sum is necessarily $4(\bmod 11)$, hence not a Fibonacci number.
|
| 600 |
-
|
| 601 |
-
## §3 Solutions to Day 3
|
| 602 |
-
|
| 603 |
-
## §3.1 TSTST 2019/7, proposed by Ankan Bhattacharya
|
| 604 |
-
|
| 605 |
-
Available online at https://aops.com/community/p12608512.
|
| 606 |
-
|
| 607 |
-
## Problem statement
|
| 608 |
-
|
| 609 |
-
Let $f: \mathbb{Z} \rightarrow\left\{1,2, \ldots, 10^{100}\right\}$ be a function satisfying
|
| 610 |
-
|
| 611 |
-
$$
|
| 612 |
-
\operatorname{gcd}(f(x), f(y))=\operatorname{gcd}(f(x), x-y)
|
| 613 |
-
$$
|
| 614 |
-
|
| 615 |
-
for all integers $x$ and $y$. Show that there exist positive integers $m$ and $n$ such that $f(x)=\operatorname{gcd}(m+x, n)$ for all integers $x$.
|
| 616 |
-
|
| 617 |
-
Let $\mathcal{P}$ be the set of primes not exceeding $10^{100}$. For each $p \in \mathcal{P}$, let $e_{p}=\max _{x} \nu_{p}(f(x))$ and let $c_{p} \in \operatorname{argmax}_{x} \nu_{p}(f(x))$.
|
| 618 |
-
|
| 619 |
-
We show that this is good enough to compute all values of $x$, by looking at the exponent at each individual prime.
|
| 620 |
-
|
| 621 |
-
Claim - For any $p \in \mathcal{P}$, we have
|
| 622 |
-
|
| 623 |
-
$$
|
| 624 |
-
\nu_{p}(f(x))=\min \left(\nu_{p}\left(x-c_{p}\right), e_{p}\right)
|
| 625 |
-
$$
|
| 626 |
-
|
| 627 |
-
Proof. Note that for any $x$, we have
|
| 628 |
-
|
| 629 |
-
$$
|
| 630 |
-
\operatorname{gcd}\left(f\left(c_{p}\right), f(x)\right)=\operatorname{gcd}\left(f\left(c_{p}\right), x-c_{p}\right)
|
| 631 |
-
$$
|
| 632 |
-
|
| 633 |
-
We then take $\nu_{p}$ of both sides and recall $\nu_{p}(f(x)) \leq \nu_{p}\left(f\left(c_{p}\right)\right)=e_{p}$; this implies the result.
|
| 634 |
-
|
| 635 |
-
This essentially determines $f$, and so now we just follow through. Choose $n$ and $m$ such that
|
| 636 |
-
|
| 637 |
-
$$
|
| 638 |
-
\begin{aligned}
|
| 639 |
-
n & =\prod_{p \in \mathcal{P}} p^{e_{p}} \\
|
| 640 |
-
m & \equiv-c_{p} \quad\left(\bmod p^{e_{p}}\right) \quad \forall p \in \mathcal{P}
|
| 641 |
-
\end{aligned}
|
| 642 |
-
$$
|
| 643 |
-
|
| 644 |
-
the latter being possible by Chinese remainder theorem. Then, from the claim we have
|
| 645 |
-
|
| 646 |
-
$$
|
| 647 |
-
\begin{aligned}
|
| 648 |
-
f(x) & =\prod_{p \in \mathcal{P}} p^{\nu_{p}(f(x))}=\prod_{p \mid n} p^{\min \left(\nu_{p}\left(x-c_{p}\right), e_{p}\right)} \\
|
| 649 |
-
& =\prod_{p \mid n} p^{\min \left(\nu_{p}(x+m), \nu_{p}(n)\right)}=\operatorname{gcd}(x+m, n)
|
| 650 |
-
\end{aligned}
|
| 651 |
-
$$
|
| 652 |
-
|
| 653 |
-
for every $x \in \mathbb{Z}$, as desired.
|
| 654 |
-
Remark. The functions $f(x)=x$ and $f(x)=|2 x-1|$ are examples satisfying the gcd equation (the latter always being strictly positive). Hence the hypothesis $f$ bounded cannot be dropped.
|
| 655 |
-
|
| 656 |
-
Remark. The pair $(m, n)$ is essentially unique: every other pair is obtained by shifting $m$ by a multiple of $n$. Hence there is not really any choice in choosing $m$ and $n$.
|
| 657 |
-
|
| 658 |
-
## §3.2 TSTST 2019/8, proposed by Ankan Bhattacharya
|
| 659 |
-
|
| 660 |
-
Available online at https://aops.com/community/p12608780.
|
| 661 |
-
|
| 662 |
-
## Problem statement
|
| 663 |
-
|
| 664 |
-
Let $\mathcal{S}$ be a set of 16 points in the plane, no three collinear. Let $\chi(\mathcal{S})$ denote the number of ways to draw 8 line segments with endpoints in $\mathcal{S}$, such that no two drawn segments intersect, even at endpoints. Find the smallest possible value of $\chi(\mathcal{S})$ across all such $\mathcal{S}$.
|
| 665 |
-
|
| 666 |
-
The answer is 1430 . In general, we prove that with $2 n$ points the answer is the $n^{\text {th }}$ Catalan number $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$.
|
| 667 |
-
|
| 668 |
-
First of all, it is well-known that if $\mathcal{S}$ is a convex $2 n$-gon, then $\chi(\mathcal{S})=C_{n}$.
|
| 669 |
-
It remains to prove the lower bound. We proceed by (strong) induction on $n$, with the base case $n=0$ and $n=1$ clear. Suppose the statement is proven for $0,1, \ldots, n$ and consider a set $\mathcal{S}$ with $2(n+1)$ points.
|
| 670 |
-
|
| 671 |
-
Let $P$ be a point on the convex hull of $\mathcal{S}$, and label the other $2 n+1$ points $A_{1}, \ldots, A_{2 n+1}$ in order of angle from $P$.
|
| 672 |
-
|
| 673 |
-
Consider drawing a segment $\overline{P A_{2 k+1}}$. This splits the $2 n$ remaining points into two halves $\mathcal{U}$ and $\mathcal{V}$, with $2 k$ and $2(n-k)$ points respectively.
|
| 674 |
-
|
| 675 |
-
|
| 676 |
-
Note that by choice of $P$, no segment in $\mathcal{U}$ can intersect a segment in $\mathcal{V}$. By the inductive hypothesis,
|
| 677 |
-
|
| 678 |
-
$$
|
| 679 |
-
\chi(\mathcal{U}) \geq C_{k} \quad \text { and } \quad \chi(\mathcal{V}) \geq C_{n-k}
|
| 680 |
-
$$
|
| 681 |
-
|
| 682 |
-
Thus, drawing $\overline{P A_{2 k+1}}$, we have at least $C_{k} C_{n-k}$ ways to complete the drawing. Over all choices of $k$, we obtain
|
| 683 |
-
|
| 684 |
-
$$
|
| 685 |
-
\chi(\mathcal{S}) \geq C_{0} C_{n}+\cdots+C_{n} C_{0}=C_{n+1}
|
| 686 |
-
$$
|
| 687 |
-
|
| 688 |
-
as desired.
|
| 689 |
-
Remark. It is possible to show directly from the lower bound proof that convex $2 n$-gons achieve the minimum: indeed, every inequality is sharp, and no segment $\overline{P A_{2 k}}$ can be drawn (since this splits the rest of the points into two halves with an odd number of points, and no crossing segment can be drawn).
|
| 690 |
-
|
| 691 |
-
Bobby Shen points out that in the case of 6 points, a regular pentagon with its center also achieves equality, so this is not the only equality case.
|
| 692 |
-
|
| 693 |
-
Remark. The result that $\chi(S) \geq 1$ for all $S$ is known (consider the choice of 8 segments with smallest sum), and appeared on Putnam 1979. However, it does not seem that knowing this gives an advantage for this problem, since the answer is much larger than 1.
|
| 694 |
-
|
| 695 |
-
## §3.3 TSTST 2019/9, proposed by Ankan Bhattacharya
|
| 696 |
-
|
| 697 |
-
Available online at https://aops.com/community/p12608472.
|
| 698 |
-
|
| 699 |
-
## Problem statement
|
| 700 |
-
|
| 701 |
-
Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\triangle A B K$ and $\triangle A B L$ are tangent at $P$, and the incircles of $\triangle A C K$ and $\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.
|
| 702 |
-
|
| 703 |
-
We present two solutions.
|
| 704 |
-
【 First solution, mostly elementary (original). Let $I_{B}, J_{B}, I_{C}, J_{C}$ be the incenters of $\triangle A B K, \triangle A B L, \triangle A C K, \triangle A C L$ respectively.
|
| 705 |
-
|
| 706 |
-
|
| 707 |
-
We begin with the following claim which does not depend on the existence of tangency points $P$ and $Q$.
|
| 708 |
-
|
| 709 |
-
Claim - Lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at a point $R$ (possibly at infinity).
|
| 710 |
-
|
| 711 |
-
Proof. By rotating by $\frac{1}{2} \angle A$ we have the equality
|
| 712 |
-
|
| 713 |
-
$$
|
| 714 |
-
A\left(B I ; I_{B} J_{B}\right)=A\left(I C ; I_{C} J_{C}\right) .
|
| 715 |
-
$$
|
| 716 |
-
|
| 717 |
-
It follows $\left(B I ; I_{B} J_{B}\right)=\left(I C ; I_{C} J_{C}\right)=\left(C I ; J_{C} I_{C}\right)$. (One could also check directly that both cross ratios equal $\frac{\sin \angle B A K / 2}{\sin \angle C A K / 2} \div \frac{\sin \angle B A L / 2}{\sin \angle C A L / 2}$, rather than using rotation.)
|
| 718 |
-
|
| 719 |
-
Therefore, the concurrence follows from the so-called prism lemma on $\overline{I B I_{B} J_{B}}$ and $\overline{I C J_{C} I_{C}}$.
|
| 720 |
-
|
| 721 |
-
Remark (Nikolai Beluhov). This result is known; it appears as 4.5.32 in Akopyan's Geometry in Figures. The cross ratio is not necessary to prove this claim: it can be proven by length chasing with circumscribed quadrilaterals. (The generalization mentioned later also admits a trig-free proof for the analogous step.)
|
| 722 |
-
|
| 723 |
-
We now bring $P$ and $Q$ into the problem.
|
| 724 |
-
Claim - Line $P Q$ also passes through $R$.
|
| 725 |
-
|
| 726 |
-
Proof. Note $\left(B P ; I_{B} J_{B}\right)=-1=\left(C Q ; J_{C} I_{C}\right)$, so the conclusion again follows by prism lemma.
|
| 727 |
-
|
| 728 |
-
We are now ready to complete the proof. Point $R$ is the exsimilicenter of the incircles of $\triangle A B K$ and $\triangle A C L$, so $\frac{P I_{B}}{R I_{B}}=\frac{Q J_{C}}{R J_{C}}$. Now by Menelaus,
|
| 729 |
-
|
| 730 |
-
$$
|
| 731 |
-
\frac{I_{B} P}{P I} \cdot \frac{I Q}{Q J_{C}} \cdot \frac{J_{C} R}{R I_{B}}=-1 \Longrightarrow I P=I Q
|
| 732 |
-
$$
|
| 733 |
-
|
| 734 |
-
Remark (Author's comments on drawing the diagram). Drawing the diagram directly is quite difficult. If one draws $\triangle A B C$ first, they must locate both $K$ and $L$, which likely involves some trial and error due to the complex interplay between the two points.
|
| 735 |
-
|
| 736 |
-
There are alternative simpler ways. For example, one may draw $\triangle A K L$ first; then the remaining points $B$ and $C$ are not related and the task is much simpler (though some trial and error is still required).
|
| 737 |
-
|
| 738 |
-
In fact, by breaking symmetry, we may only require one application of guesswork. Start by drawing $\triangle A B K$ and its incircle; then the incircle of $\triangle A B L$ may be constructed, and so point $L$ may be drawn. Thus only the location of point $C$ needs to be guessed. I would be interested in a method to create a general diagram without any trial and error.
|
| 739 |
-
|
| 740 |
-
【 Second solution, inversion (Nikolai Beluhov). As above, the lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at some point $R$ (possibly at infinity). Let $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ be the incircles of $\triangle A B K$, $\triangle A C L, \triangle A B L$, and $\triangle A C K$.
|
| 741 |
-
|
| 742 |
-
Claim - There exists an inversion $\iota$ at $R$ swapping $\left\{\omega_{1}, \omega_{2}\right\}$ and $\left\{\omega_{3}, \omega_{4}\right\}$.
|
| 743 |
-
|
| 744 |
-
Proof. Consider the inversion at $R$ swapping $\omega_{1}$ and $\omega_{2}$. Since $\omega_{1}$ and $\omega_{3}$ are tangent, the image of $\omega_{3}$ is tangent to $\omega_{2}$ and is also tangent to $B C$. The circle $\omega_{4}$ is on the correct side of $\omega_{3}$ to be this image.
|
| 745 |
-
|
| 746 |
-
Claim - Circles $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ share a common radical center.
|
| 747 |
-
|
| 748 |
-
Proof. Let $\Omega$ be the circle with center $R$ fixed under $\iota$, and let $k$ be the circle through $P$ centered at the radical center of $\Omega, \omega_{1}, \omega_{3}$.
|
| 749 |
-
|
| 750 |
-
Then $k$ is actually orthogonal to $\Omega, \omega_{1}, \omega_{3}$, so $k$ is fixed under $\iota$ and $k$ is also orthogonal to $\omega_{2}$ and $\omega_{4}$. Thus the center of $k$ is the desired radical center.
|
| 751 |
-
|
| 752 |
-
The desired statement immediately follows. Indeed, letting $S$ be the radical center, it follows that $\overline{S P}$ and $\overline{S Q}$ are the common internal tangents to $\left\{\omega_{1}, \omega_{3}\right\}$ and $\left\{\omega_{2}, \omega_{4}\right\}$.
|
| 753 |
-
|
| 754 |
-
Since $S$ is the radical center, $S P=S Q$. In light of $\angle S P I=\angle S Q I=90^{\circ}$, it follows that $I P=I Q$, as desired.
|
| 755 |
-
|
| 756 |
-
Remark (Nikolai Beluhov). There exists a circle tangent to all four incircles, because circle $k$ is orthogonal to all four, and line $B C$ is tangent to all four; thus the inverse of line $B C$ in $k$ is a circle tangent to all four incircles.
|
| 757 |
-
|
| 758 |
-
The amusing thing here is that Casey's theorem is completely unhelpful for proving this fact: all it can tell us is that there is a line or circle tangent to these incircles, and line $B C$ already satisfies this property.
|
| 759 |
-
|
| 760 |
-
Remark (Generalization by Nikolai Beluhov). The following generalization holds:
|
| 761 |
-
Let $A B C D$ be a quadrilateral circumscribed about a circle with center $I$. A line through $A$ meets $\overrightarrow{B C}$ and $\overrightarrow{D C}$ at $K$ and $L$; another line through $A$ meets $\overrightarrow{B C}$ and $\overrightarrow{D C}$ at $M$ and $N$. Suppose that the incircles of $\triangle A B K$ and $\triangle A B M$ are tangent at $P$, and the incircles of $\triangle A C L$ and $\triangle A C N$ are tangent at $Q$. Prove that $I P=I Q$.
|
| 762 |
-
|
| 763 |
-
The first approach can be modified to the generalization. There is an extra initial step required: by Monge, the exsimilicenter of the incircles of $\triangle A B K$ and $\triangle A D N$ lies on line $B D$; likewise for the incircles of $\triangle A B L$ and $\triangle A D M$. Now one may prove using the same trig approach that these pairs of incircles have a common exsimilicenter, and the rest of the solution plays out similarly. The second approach can also be modified in the same way, once we obtain that a common exsimilicenter exists. (Thus in the generalization, it seems we also get there exists a circle tangent to all four incircles.)
|
| 764 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2020.md
DELETED
|
@@ -1,535 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2020 Solutions <br> United States of America - TST Selection Test <br> Ankan Bhattacharya and Evan Chen <br> 62 $2^{\text {nd }}$ IMO 2021 Russia and $10^{\text {th }}$ EGMO 2021 Georgia
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 4
|
| 7 |
-
1.1 TSTST 2020/1, proposed by Ankan Bhattacharya ..... 4
|
| 8 |
-
1.2 TSTST 2020/2, proposed by Zack Chroman, Daniel Liu ..... 6
|
| 9 |
-
1.3 TSTST 2020/3, proposed by Evan Chen, Danielle Wang ..... 8
|
| 10 |
-
2 Solutions to Day 2 ..... 10
|
| 11 |
-
2.1 TSTST 2020/4, proposed by Yang Liu ..... 10
|
| 12 |
-
2.2 TSTST 2020/5, proposed by Ashwin Sah, Mehtaab Sawhney ..... 12
|
| 13 |
-
2.3 TSTST 2020/6, proposed by Andrew Gu . ..... 14
|
| 14 |
-
3 Solutions to Day 3 ..... 16
|
| 15 |
-
3.1 TSTST 2020/7, proposed by Ankan Bhattacharya ..... 16
|
| 16 |
-
3.2 TSTST 2020/8, proposed by Ankan Bhattacharya ..... 18
|
| 17 |
-
3.3 TSTST 2020/9, proposed by Nikolai Beluhov ..... 20
|
| 18 |
-
|
| 19 |
-
## §0 Problems
|
| 20 |
-
|
| 21 |
-
1. Let $a, b, c$ be fixed positive integers. There are $a+b+c$ ducks sitting in a circle, one behind the other. Each duck picks either rock, paper, or scissors, with $a$ ducks picking rock, $b$ ducks picking paper, and $c$ ducks picking scissors.
|
| 22 |
-
|
| 23 |
-
A move consists of an operation of one of the following three forms:
|
| 24 |
-
|
| 25 |
-
- If a duck picking rock sits behind a duck picking scissors, they switch places.
|
| 26 |
-
- If a duck picking paper sits behind a duck picking rock, they switch places.
|
| 27 |
-
- If a duck picking scissors sits behind a duck picking paper, they switch places.
|
| 28 |
-
|
| 29 |
-
Determine, in terms of $a, b$, and $c$, the maximum number of moves which could take place, over all possible initial configurations.
|
| 30 |
-
2. Let $A B C$ be a scalene triangle with incenter $I$. The incircle of $A B C$ touches $\overline{B C}$, $\overline{C A}, \overline{A B}$ at points $D, E, F$, respectively. Let $P$ be the foot of the altitude from $D$ to $\overline{E F}$, and let $M$ be the midpoint of $\overline{B C}$. The rays $A P$ and $I P$ intersect the circumcircle of triangle $A B C$ again at points $G$ and $Q$, respectively. Show that the incenter of triangle $G Q M$ coincides with $D$.
|
| 31 |
-
3. We say a nondegenerate triangle whose angles have measures $\theta_{1}, \theta_{2}, \theta_{3}$ is quirky if there exists integers $r_{1}, r_{2}, r_{3}$, not all zero, such that
|
| 32 |
-
|
| 33 |
-
$$
|
| 34 |
-
r_{1} \theta_{1}+r_{2} \theta_{2}+r_{3} \theta_{3}=0
|
| 35 |
-
$$
|
| 36 |
-
|
| 37 |
-
Find all integers $n \geq 3$ for which a triangle with side lengths $n-1, n, n+1$ is quirky.
|
| 38 |
-
4. Find all pairs of positive integers $(a, b)$ satisfying the following conditions:
|
| 39 |
-
(i) $a$ divides $b^{4}+1$,
|
| 40 |
-
(ii) $b$ divides $a^{4}+1$,
|
| 41 |
-
(iii) $\lfloor\sqrt{a}\rfloor=\lfloor\sqrt{b}\rfloor$.
|
| 42 |
-
5. Let $\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ of $\mathbb{N}^{2}$ with both $x^{\prime} \leq x$ and $y^{\prime} \leq y$.
|
| 43 |
-
Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.
|
| 44 |
-
6. Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\triangle B C D, \triangle C A D$, $\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.
|
| 45 |
-
7. Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.
|
| 46 |
-
8. For every positive integer $N$, let $\sigma(N)$ denote the sum of the positive integer divisors of $N$. Find all integers $m \geq n \geq 2$ satisfying
|
| 47 |
-
|
| 48 |
-
$$
|
| 49 |
-
\frac{\sigma(m)-1}{m-1}=\frac{\sigma(n)-1}{n-1}=\frac{\sigma(m n)-1}{m n-1} .
|
| 50 |
-
$$
|
| 51 |
-
|
| 52 |
-
9. Ten million fireflies are glowing in $\mathbb{R}^{3}$ at midnight. Some of the fireflies are friends, and friendship is always mutual. Every second, one firefly moves to a new position so that its distance from each one of its friends is the same as it was before moving. This is the only way that the fireflies ever change their positions. No two fireflies may ever occupy the same point.
|
| 53 |
-
Initially, no two fireflies, friends or not, are more than a meter away. Following some finite number of seconds, all fireflies find themselves at least ten million meters away from their original positions. Given this information, find the greatest possible number of friendships between the fireflies.
|
| 54 |
-
|
| 55 |
-
## §1 Solutions to Day 1
|
| 56 |
-
|
| 57 |
-
## §1.1 TSTST 2020/1, proposed by Ankan Bhattacharya
|
| 58 |
-
|
| 59 |
-
Available online at https://aops.com/community/p18933796.
|
| 60 |
-
|
| 61 |
-
## Problem statement
|
| 62 |
-
|
| 63 |
-
Let $a, b, c$ be fixed positive integers. There are $a+b+c$ ducks sitting in a circle, one behind the other. Each duck picks either rock, paper, or scissors, with a ducks picking rock, $b$ ducks picking paper, and $c$ ducks picking scissors.
|
| 64 |
-
|
| 65 |
-
A move consists of an operation of one of the following three forms:
|
| 66 |
-
|
| 67 |
-
- If a duck picking rock sits behind a duck picking scissors, they switch places.
|
| 68 |
-
- If a duck picking paper sits behind a duck picking rock, they switch places.
|
| 69 |
-
- If a duck picking scissors sits behind a duck picking paper, they switch places.
|
| 70 |
-
|
| 71 |
-
Determine, in terms of $a, b$, and $c$, the maximum number of moves which could take place, over all possible initial configurations.
|
| 72 |
-
|
| 73 |
-
The maximum possible number of moves is $\max (a b, a c, b c)$.
|
| 74 |
-
First, we prove this is best possible. We define a feisty triplet to be an unordered triple of ducks, one of each of rock, paper, scissors, such that the paper duck is between the rock and scissors duck and facing the rock duck, as shown. (There may be other ducks not pictured, but the orders are irrelevant.)
|
| 75 |
-
|
| 76 |
-
|
| 77 |
-
Claim - The number of feisty triplets decreases by $c$ if a paper duck swaps places with a rock duck, and so on.
|
| 78 |
-
|
| 79 |
-
## Proof. Clear.
|
| 80 |
-
|
| 81 |
-
Obviously the number of feisty triples is at most $a b c$ to start. Thus at most $\max (a b, b c, c a)$ moves may occur, since the number of feisty triplets should always be nonnegative, at which point no moves are possible at all.
|
| 82 |
-
|
| 83 |
-
To see that this many moves is possible, assume WLOG $a=\min (a, b, c)$ and suppose we have $a$ rocks, $b$ papers, and $c$ scissors in that clockwise order.
|
| 84 |
-
|
| 85 |
-
|
| 86 |
-
Then, allow the scissors to filter through the papers while the rocks stay put. Each of the $b$ papers swaps with $c$ scissors, for a total of $b c=\max (a b, a c, b c)$ swaps.
|
| 87 |
-
|
| 88 |
-
Remark (Common errors). One small possible mistake: it is not quite kösher to say that "WLOG $a \leq b \leq c$ " because the condition is not symmetric, only cyclic. Therefore in this solution we only assume $a=\min (a, b, c)$.
|
| 89 |
-
|
| 90 |
-
It is true here that every pair of ducks swaps at most once, and some solutions make use of this fact. However, this fact implicitly uses the fact that $a, b, c>0$ and is false without this hypothesis.
|
| 91 |
-
|
| 92 |
-
## §1.2 TSTST 2020/2, proposed by Zack Chroman, Daniel Liu
|
| 93 |
-
|
| 94 |
-
Available online at https://aops.com/community/p18933557.
|
| 95 |
-
|
| 96 |
-
## Problem statement
|
| 97 |
-
|
| 98 |
-
Let $A B C$ be a scalene triangle with incenter $I$. The incircle of $A B C$ touches $\overline{B C}$, $\overline{C A}, \overline{A B}$ at points $D, E, F$, respectively. Let $P$ be the foot of the altitude from $D$ to $\overline{E F}$, and let $M$ be the midpoint of $\overline{B C}$. The rays $A P$ and $I P$ intersect the circumcircle of triangle $A B C$ again at points $G$ and $Q$, respectively. Show that the incenter of triangle $G Q M$ coincides with $D$.
|
| 99 |
-
|
| 100 |
-
Refer to the figure below.
|
| 101 |
-
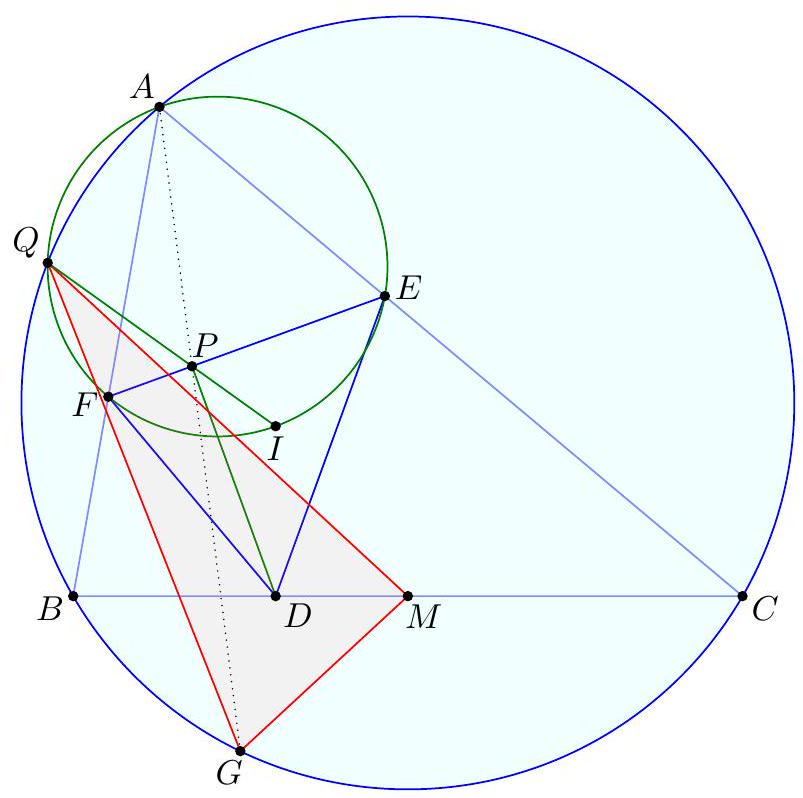
|
| 102 |
-
|
| 103 |
-
Claim - The point $Q$ is the Miquel point of $B F E C$. Also, $\overline{Q D}$ bisects $\angle B Q C$.
|
| 104 |
-
Proof. Inversion around the incircle maps line $E F$ to $(A I E F)$ and the nine-point circle of $\triangle D E F$ to the circumcircle of $\triangle A B C$ (as the midpoint of $\overline{E F}$ maps to $A$, etc.). This implies $P$ maps to $Q$; that is, $Q$ coincides with the second intersection of (AFIE) with $(A B C)$. This is the claimed Miquel point.
|
| 105 |
-
|
| 106 |
-
The spiral similarity mentioned then gives $\frac{Q B}{B F}=\frac{Q C}{C E}$, so $\overline{Q D}$ bisects $\angle B Q C$.
|
| 107 |
-
Remark. The point $Q$ and its properties mentioned in the first claim have appeared in other references. See for example Canada 2007/5, ELMO 2010/6, HMMT 2016 T-10, USA TST 2017/2, USA TST 2019/6 for a few examples.
|
| 108 |
-
|
| 109 |
-
Claim - We have $(Q G ; B C)=-1$, so in particular $\overline{G D}$ bisects $\angle B G C$.
|
| 110 |
-
Proof. Note that
|
| 111 |
-
|
| 112 |
-
$$
|
| 113 |
-
-1=(A I ; E F) \stackrel{Q}{=}(\overline{A Q} \cap \overline{E F}, P ; E, F) \stackrel{A}{=}(Q G ; B C)
|
| 114 |
-
$$
|
| 115 |
-
|
| 116 |
-
The last statement follows from Apollonian circle, or more bluntly $\frac{G B}{G C}=\frac{Q B}{Q C}=\frac{B D}{D C}$.
|
| 117 |
-
Hence $\overline{Q D}$ and $\overline{G D}$ are angle bisectors of $\angle B Q C$ and $\angle B G C$. However, $\overline{Q M}$ and $\overline{Q G}$ are isogonal in $\angle B Q C$ (as median and symmedian), and similarly for $\angle B G C$, as desired.
|
| 118 |
-
|
| 119 |
-
## §1.3 TSTST 2020/3, proposed by Evan Chen, Danielle Wang
|
| 120 |
-
|
| 121 |
-
Available online at https://aops.com/community/p18933954.
|
| 122 |
-
|
| 123 |
-
## Problem statement
|
| 124 |
-
|
| 125 |
-
We say a nondegenerate triangle whose angles have measures $\theta_{1}, \theta_{2}, \theta_{3}$ is quirky if there exists integers $r_{1}, r_{2}, r_{3}$, not all zero, such that
|
| 126 |
-
|
| 127 |
-
$$
|
| 128 |
-
r_{1} \theta_{1}+r_{2} \theta_{2}+r_{3} \theta_{3}=0
|
| 129 |
-
$$
|
| 130 |
-
|
| 131 |
-
Find all integers $n \geq 3$ for which a triangle with side lengths $n-1, n, n+1$ is quirky.
|
| 132 |
-
|
| 133 |
-
The answer is $n=3,4,5,7$.
|
| 134 |
-
We first introduce a variant of the $k$ th Chebyshev polynomials in the following lemma (which is standard, and easily shown by induction).
|
| 135 |
-
|
| 136 |
-
## Lemma
|
| 137 |
-
|
| 138 |
-
For each $k \geq 0$ there exists $P_{k}(X) \in \mathbb{Z}[X]$, monic for $k \geq 1$ and with degree $k$, such that
|
| 139 |
-
|
| 140 |
-
$$
|
| 141 |
-
P_{k}\left(X+X^{-1}\right) \equiv X^{k}+X^{-k} .
|
| 142 |
-
$$
|
| 143 |
-
|
| 144 |
-
The first few are $P_{0}(X) \equiv 2, P_{1}(X) \equiv X, P_{2}(X) \equiv X^{2}-2, P_{3}(X) \equiv X^{3}-3 X$.
|
| 145 |
-
Suppose the angles of the triangle are $\alpha<\beta<\gamma$, so the law of cosines implies that
|
| 146 |
-
|
| 147 |
-
$$
|
| 148 |
-
2 \cos \alpha=\frac{n+4}{n+1} \quad \text { and } \quad 2 \cos \gamma=\frac{n-4}{n-1}
|
| 149 |
-
$$
|
| 150 |
-
|
| 151 |
-
Claim - The triangle is quirky iff there exists $r, s \in \mathbb{Z}_{\geq 0}$ not both zero such that
|
| 152 |
-
|
| 153 |
-
$$
|
| 154 |
-
\cos (r \alpha)= \pm \cos (s \gamma) \quad \text { or equivalently } \quad P_{r}\left(\frac{n+4}{n+1}\right)= \pm P_{s}\left(\frac{n-4}{n-1}\right)
|
| 155 |
-
$$
|
| 156 |
-
|
| 157 |
-
Proof. If there are integers $x, y, z$ for which $x \alpha+y \beta+z \gamma=0$, then we have that $(x-y) \alpha=(y-z) \gamma-\pi y$, whence it follows that we may take $r=|x-y|$ and $s=|y-z|$ (noting $r=s=0$ implies the absurd $x=y=z$ ). Conversely, given such $r$ and $s$ with $\cos (r \alpha)= \pm \cos (s \gamma)$, then it follows that $r \alpha \pm s \gamma=k \pi=k(\alpha+\beta+\gamma)$ for some $k$, so the triangle is quirky.
|
| 158 |
-
|
| 159 |
-
If $r=0$, then by rational root theorem on $P_{s}(X) \pm 2$ it follows $\frac{n-4}{n-1}$ must be an integer which occurs only when $n=4$ (recall $n \geq 3$ ). Similarly we may discard the case $s=0$.
|
| 160 |
-
|
| 161 |
-
Thus in what follows assume $n \neq 4$ and $r, s>0$. Then, from the fact that $P_{r}$ and $P_{s}$ are nonconstant monic polynomials, we find
|
| 162 |
-
|
| 163 |
-
## Corollary
|
| 164 |
-
|
| 165 |
-
If $n \neq 4$ works, then when $\frac{n+4}{n+1}$ and $\frac{n-4}{n-1}$ are written as fractions in lowest terms, the denominators have the same set of prime factors.
|
| 166 |
-
|
| 167 |
-
But $\operatorname{gcd}(n+1, n-1)$ divides 2 , and $\operatorname{gcd}(n+4, n+1), \operatorname{gcd}(n-4, n-1)$ divide 3 . So we only have three possibilities:
|
| 168 |
-
|
| 169 |
-
- $n+1=2^{u}$ and $n-1=2^{v}$ for some $u, v \geq 0$. This is only possible if $n=3$. Here $2 \cos \alpha=\frac{7}{4}$ and $2 \cos \gamma=-\frac{1}{2}$, and indeed $P_{2}(-1 / 2)=-7 / 4$.
|
| 170 |
-
- $n+1=3 \cdot 2^{u}$ and $n-1=2^{v}$ for some $u, v \geq 0$, which implies $n=5$. Here $2 \cos \alpha=\frac{3}{2}$ and $2 \cos \gamma=\frac{1}{4}$, and indeed $P_{2}(3 / 2)=1 / 4$.
|
| 171 |
-
- $n+1=2^{u}$ and $n-1=3 \cdot 2^{v}$ for some $u, v \geq 0$, which implies $n=7$. Here $2 \cos \alpha=\frac{11}{8}$ and $2 \cos \gamma=\frac{1}{2}$, and indeed $P_{3}(1 / 2)=-11 / 8$.
|
| 172 |
-
|
| 173 |
-
Finally, $n=4$ works because the triangle is right, completing the solution.
|
| 174 |
-
Remark (Major generalization due to Luke Robitaille). In fact one may find all quirky triangles whose sides are integers in arithmetic progression.
|
| 175 |
-
|
| 176 |
-
Indeed, if the side lengths of the triangle are $x-y, x, x+y$ with $\operatorname{gcd}(x, y)=1$ then the problem becomes
|
| 177 |
-
|
| 178 |
-
$$
|
| 179 |
-
P_{r}\left(\frac{x+4 y}{x+y}\right)= \pm P_{s}\left(\frac{x-4 y}{x-y}\right)
|
| 180 |
-
$$
|
| 181 |
-
|
| 182 |
-
and so in the same way as before, we ought to have $x+y$ and $x-y$ are both of the form $3 \cdot 2^{*}$ unless $r s=0$. This time, when $r s=0$, we get the extra solutions $(1,0)$ and $(5,2)$.
|
| 183 |
-
|
| 184 |
-
For $r s \neq 0$, by triangle inequality, we have $x-y \leq x+y<3(x-y)$, and $\min \left(\nu_{2}(x-\right.$ $\left.y), \nu_{2}(x+y)\right) \leq 1$, so it follows one of $x-y$ or $x+y$ must be in $\{1,2,3,6\}$. An exhaustive check then leads to
|
| 185 |
-
|
| 186 |
-
$$
|
| 187 |
-
(x, y) \in\{(3,1),(5,1),(7,1),(11,5)\} \cup\{(1,0),(5,2),(4,1)\}
|
| 188 |
-
$$
|
| 189 |
-
|
| 190 |
-
as the solution set. And in fact they all work.
|
| 191 |
-
In conclusion the equilateral triangle, $3-5-7$ triangle (which has a $120^{\circ}$ angle) and $6-11-16$ triangle (which satisfies $B=3 A+4 C$ ) are exactly the new quirky triangles (up to similarity) whose sides are integers in arithmetic progression.
|
| 192 |
-
|
| 193 |
-
## §2 Solutions to Day 2
|
| 194 |
-
|
| 195 |
-
## §2.1 TSTST 2020/4, proposed by Yang Liu
|
| 196 |
-
|
| 197 |
-
Available online at https://aops.com/community/p19444614.
|
| 198 |
-
|
| 199 |
-
## Problem statement
|
| 200 |
-
|
| 201 |
-
Find all pairs of positive integers $(a, b)$ satisfying the following conditions:
|
| 202 |
-
(i) $a$ divides $b^{4}+1$,
|
| 203 |
-
(ii) $b$ divides $a^{4}+1$,
|
| 204 |
-
(iii) $\lfloor\sqrt{a}\rfloor=\lfloor\sqrt{b}\rfloor$.
|
| 205 |
-
|
| 206 |
-
The only solutions are $(1,1),(1,2)$, and $(2,1)$, which clearly work. Now we show there are no others.
|
| 207 |
-
|
| 208 |
-
Obviously, $\operatorname{gcd}(a, b)=1$, so the problem conditions imply
|
| 209 |
-
|
| 210 |
-
$$
|
| 211 |
-
a b \mid(a-b)^{4}+1
|
| 212 |
-
$$
|
| 213 |
-
|
| 214 |
-
since each of $a$ and $b$ divide the right-hand side. We define
|
| 215 |
-
|
| 216 |
-
$$
|
| 217 |
-
k \stackrel{\text { def }}{=} \frac{(b-a)^{4}+1}{a b} .
|
| 218 |
-
$$
|
| 219 |
-
|
| 220 |
-
Claim (Size estimate) — We must have $k \leq 16$.
|
| 221 |
-
|
| 222 |
-
Proof. Let $n=\lfloor\sqrt{a}\rfloor=\lfloor\sqrt{b}\rfloor$, so that $a, b \in\left[n^{2}, n^{2}+2 n\right]$. We have that
|
| 223 |
-
|
| 224 |
-
$$
|
| 225 |
-
\begin{aligned}
|
| 226 |
-
a b & \geq n^{2}\left(n^{2}+1\right) \geq n^{4}+1 \\
|
| 227 |
-
(b-a)^{4}+1 & \leq(2 n)^{4}+1=16 n^{4}+1
|
| 228 |
-
\end{aligned}
|
| 229 |
-
$$
|
| 230 |
-
|
| 231 |
-
which shows $k \leq 16$.
|
| 232 |
-
|
| 233 |
-
Claim (Orders argument) - In fact, $k=1$.
|
| 234 |
-
|
| 235 |
-
Proof. First of all, note that $k$ cannot be even: if it was, then $a, b$ have opposite parity, but then $4 \mid(b-a)^{4}+1$, contradiction.
|
| 236 |
-
|
| 237 |
-
Thus $k$ is odd. However, every odd prime divisor of $(b-a)^{4}+1$ is congruent to 1 $(\bmod 8)$ and is thus at least 17 , so $k=1$ or $k \geq 17$. It follows that $k=1$.
|
| 238 |
-
|
| 239 |
-
At this point, we have reduced to solving
|
| 240 |
-
|
| 241 |
-
$$
|
| 242 |
-
a b=(b-a)^{4}+1
|
| 243 |
-
$$
|
| 244 |
-
|
| 245 |
-
and we need to prove the claimed solutions are the only ones. Write $b=a+d$, and assume WLOG that $d \geq 0$ : then we have $a(a+d)=d^{4}+1$, or
|
| 246 |
-
|
| 247 |
-
$$
|
| 248 |
-
a^{2}-d a-\left(d^{4}+1\right)=0
|
| 249 |
-
$$
|
| 250 |
-
|
| 251 |
-
The discriminant $d^{2}+4\left(d^{4}+1\right)=4 d^{4}+d^{2}+4$ must be a perfect square.
|
| 252 |
-
|
| 253 |
-
- The cases $d=0$ and $d=1$ lead to pairs $(1,1)$ and $(1,2)$.
|
| 254 |
-
- If $d \geq 2$, then we can sandwich
|
| 255 |
-
|
| 256 |
-
$$
|
| 257 |
-
\left(2 d^{2}\right)^{2}<4 d^{4}+d^{2}+4<4 d^{4}+4 d^{2}+1=\left(2 d^{2}+1\right)^{2}
|
| 258 |
-
$$
|
| 259 |
-
|
| 260 |
-
so the discriminant is not a square.
|
| 261 |
-
The solution is complete.
|
| 262 |
-
Remark (Author remarks on origin). This comes from the problem of the existence of a pair of elliptic curves over $\mathbb{F}_{a}, \mathbb{F}_{b}$ respectively, such that the number of points on one is the field size of the other. The bound $n^{2} \leq a, b<(n+1)^{2}$ is the Hasse bound. The divisibility conditions correspond to asserting that the embedding degree of each curve is 8 , so that they are pairing friendly. In this way, the problem is essentially the key result of https://arxiv.org/pdf/1803.02067.pdf, shown in Proposition 3.
|
| 263 |
-
|
| 264 |
-
## §2.2 TSTST 2020/5, proposed by Ashwin Sah, Mehtaab Sawhney
|
| 265 |
-
|
| 266 |
-
Available online at https://aops.com/community/p19444403.
|
| 267 |
-
|
| 268 |
-
## Problem statement
|
| 269 |
-
|
| 270 |
-
Let $\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ of $\mathbb{N}^{2}$ with both $x^{\prime} \leq x$ and $y^{\prime} \leq y$.
|
| 271 |
-
Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.
|
| 272 |
-
|
| 273 |
-
The following inductive solution was given by Nikolai Beluhov. We proceed by induction on $|S|$, with $|S| \leq 1$ clear.
|
| 274 |
-
|
| 275 |
-
Suppose $|S| \geq 2$. For any $p \in S$, let $R(p)$ denote the stable rectangle with upper-right corner $p$. We say such $p$ is pivotal if $p+(1,1) \notin S$ and $|R(p)|$ is even.
|
| 276 |
-
|
| 277 |
-
|
| 278 |
-
Claim - If $|S| \geq 2$, then a pivotal $p$ always exists.
|
| 279 |
-
Proof. Consider the top row of $S$.
|
| 280 |
-
|
| 281 |
-
- If it has length at least 2 , one of the two rightmost points in it is pivotal.
|
| 282 |
-
- Otherwise, the top row has length 1. Now either the top point or the point below it (which exists as $|S| \geq 2$ ) is pivotal.
|
| 283 |
-
|
| 284 |
-
We describe how to complete the induction, given some pivotal $p \in S$. There is a partition
|
| 285 |
-
|
| 286 |
-
$$
|
| 287 |
-
S=R(p) \sqcup S_{1} \sqcup S_{2}
|
| 288 |
-
$$
|
| 289 |
-
|
| 290 |
-
where $S_{1}$ and $S_{2}$ are the sets of points in $S$ above and to the right of $p$ (possibly empty).
|
| 291 |
-
Claim - The desired inequality holds for stable subsets containing $p$.
|
| 292 |
-
Proof. Let $E_{1}$ denote the number of even stable subsets of $S_{1}$; denote $E_{2}, O_{1}, O_{2}$ analogously. The stable subsets containing $p$ are exactly $R(p) \sqcup T_{1} \sqcup T_{2}$, where $T_{1} \subseteq S_{1}$ and $T_{2} \subseteq S_{2}$ are stable.
|
| 293 |
-
|
| 294 |
-
Since $|R(p)|$ is even, exactly $E_{1} E_{2}+O_{1} O_{2}$ stable subsets containing $p$ are even, and exactly $E_{1} O_{2}+E_{2} O_{1}$ are odd. As $E_{1} \geq O_{1}$ and $E_{2} \geq O_{2}$ by inductive hypothesis, we obtain $E_{1} E_{2}+O_{1} O_{2} \geq E_{1} O_{2}+E_{2} O_{1}$ as desired.
|
| 295 |
-
|
| 296 |
-
By the inductive hypothesis, the desired inequality also holds for stable subsets not containing $p$, so we are done.
|
| 297 |
-
|
| 298 |
-
## §2.3 TSTST 2020/6, proposed by Andrew Gu
|
| 299 |
-
|
| 300 |
-
Available online at https://aops.com/community/p19444197.
|
| 301 |
-
|
| 302 |
-
## Problem statement
|
| 303 |
-
|
| 304 |
-
Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\triangle B C D, \triangle C A D$, $\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.
|
| 305 |
-
|
| 306 |
-
Let $T$ be the concurrency point, and let $H$ be the orthocenter of $\triangle A B C$.
|
| 307 |
-
|
| 308 |
-
|
| 309 |
-
Claim (Key claim) - $T$ is the midpoint of $\overline{A P}, \overline{B Q}, \overline{C R}, \overline{D H}$, and $D$ is the orthocenter of $\triangle P Q R$.
|
| 310 |
-
|
| 311 |
-
Proof. Note that $\overline{A Q} \| \overline{B P}$, as both are perpendicular to $\overline{C D}$. Since lines $A P$ and $B Q$ are distinct, lines $A Q$ and $B P$ are distinct.
|
| 312 |
-
By symmetric reasoning, we get that $A Q C P B R$ is a hexagon with opposite sides parallel and concurrent diagonals as $\overline{A P}, \overline{B Q}, \overline{C R}$ meet at $T$. This implies that the hexagon is centrally symmetric about $T$; indeed
|
| 313 |
-
|
| 314 |
-
$$
|
| 315 |
-
\frac{A T}{T P}=\frac{T Q}{B T}=\frac{C T}{T R}=\frac{T P}{A T}
|
| 316 |
-
$$
|
| 317 |
-
|
| 318 |
-
so all the ratios are equal to +1 .
|
| 319 |
-
Next, $\overline{P D} \perp \overline{B C} \| \overline{Q R}$, so by symmetry we get $D$ is the orthocenter of $\triangle P Q R$. This means that $T$ is the midpoint of $\overline{D H}$ as well.
|
| 320 |
-
|
| 321 |
-
## Corollary
|
| 322 |
-
|
| 323 |
-
The configuration is now symmetric: we have four points $A, B, C, D$, and their reflections in $T$ are four orthocenters $P, Q, R, H$.
|
| 324 |
-
|
| 325 |
-
Let $S$ be the centroid of $\{A, B, C, D\}$, and let $O$ be the reflection of $T$ in $S$. We are ready to conclude:
|
| 326 |
-
|
| 327 |
-
Claim - $A, B, C, D$ are equidistant from $O$.
|
| 328 |
-
Proof. Let $A^{\prime}, O^{\prime}, S^{\prime}, T^{\prime}, D^{\prime}$ be the projections of $A, O, S, T, D$ onto line $B C$.
|
| 329 |
-
Then $T^{\prime}$ is the midpoint of $\overline{A^{\prime} D^{\prime}}$, so $S^{\prime}=\frac{1}{4}\left(A^{\prime}+D^{\prime}+B+C\right)$ gives that $O^{\prime}$ is the midpoint of $\overline{B C}$.
|
| 330 |
-
|
| 331 |
-
Thus $O B=O C$ and we're done.
|
| 332 |
-
|
| 333 |
-
## §3 Solutions to Day 3
|
| 334 |
-
|
| 335 |
-
## §3.1 TSTST 2020/7, proposed by Ankan Bhattacharya
|
| 336 |
-
|
| 337 |
-
Available online at https://aops.com/community/p20020202.
|
| 338 |
-
|
| 339 |
-
## Problem statement
|
| 340 |
-
|
| 341 |
-
Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1 .
|
| 342 |
-
|
| 343 |
-
The answer is $P(x)$ should be a polynomial of the form $P(x)=\lambda x^{n}-\mu$ where $|\lambda|=|\mu|$ and $\operatorname{Re} \mu=-\frac{1}{2}$. One may check these all work; let's prove they are the only solutions.
|
| 344 |
-
\l First approach (Evan Chen). We introduce the following notations:
|
| 345 |
-
|
| 346 |
-
$$
|
| 347 |
-
\begin{aligned}
|
| 348 |
-
P(x) & =c_{n} x^{n}+c_{n-1} x^{n-1}+\cdots+c_{1} x+c_{0} \\
|
| 349 |
-
& =c_{n}\left(x+\alpha_{1}\right) \ldots\left(x+\alpha_{n}\right) \\
|
| 350 |
-
P(x)-1 & =c_{n}\left(x+\beta_{1}\right) \ldots\left(x+\beta_{n}\right)
|
| 351 |
-
\end{aligned}
|
| 352 |
-
$$
|
| 353 |
-
|
| 354 |
-
By taking conjugates,
|
| 355 |
-
|
| 356 |
-
$$
|
| 357 |
-
\begin{aligned}
|
| 358 |
-
\left(x+\alpha_{1}\right) \cdots\left(x+\alpha_{n}\right) & =\left(x+\beta_{1}\right) \cdots\left(x+\beta_{n}\right)+c_{n}^{-1} \\
|
| 359 |
-
\Longrightarrow\left(x+\frac{1}{\alpha_{1}}\right) \cdots\left(x+\frac{1}{\alpha_{n}}\right) & =\left(x+\frac{1}{\beta_{1}}\right) \cdots\left(x+\frac{1}{\beta_{n}}\right)+\left(\overline{c_{n}}\right)^{-1}
|
| 360 |
-
\end{aligned}
|
| 361 |
-
$$
|
| 362 |
-
|
| 363 |
-
The equation $(\boldsymbol{\oplus})$ is the main player:
|
| 364 |
-
Claim - We have $c_{k}=0$ for all $k=1, \ldots, n-1$.
|
| 365 |
-
|
| 366 |
-
Proof. By comparing coefficients of $x^{k}$ in ( $\left.\boldsymbol{\phi}\right)$ we obtain
|
| 367 |
-
|
| 368 |
-
$$
|
| 369 |
-
\frac{c_{n-k}}{\prod_{i} \alpha_{i}}=\frac{c_{n-k}}{\prod_{i} \beta_{i}}
|
| 370 |
-
$$
|
| 371 |
-
|
| 372 |
-
but $\prod_{i} \alpha_{i}-\prod_{i} \beta_{i}=\frac{1}{c_{n}} \neq 0$. Hence $c_{k}=0$.
|
| 373 |
-
It follows that $P(x)$ must be of the form $P(x)=\lambda x^{n}-\mu$, so that $P(x)=\lambda x^{n}-(\mu+1)$. This requires $|\mu|=|\mu+1|=|\lambda|$ which is equivalent to the stated part.
|
| 374 |
-
|
| 375 |
-
II Second approach (from the author). We let $A=P$ and $B=P-1$ to make the notation more symmetric. We will as before show that $A$ and $B$ have all coefficients equal to zero other than the leading and constant coefficient; the finish is the same.
|
| 376 |
-
|
| 377 |
-
First, we rule out double roots.
|
| 378 |
-
Claim - Neither $A$ nor $B$ have double roots.
|
| 379 |
-
|
| 380 |
-
Proof. Suppose that $b$ is a double root of $B$. By differentiating, we obtain $A^{\prime}=B^{\prime}$, so $A^{\prime}(b)=0$. However, by Gauss-Lucas, this forces $A(b)=0$, contradiction.
|
| 381 |
-
|
| 382 |
-
Let $\omega=e^{2 \pi i / n}$, let $a_{1}, \ldots, a_{n}$ be the roots of $A$, and let $b_{1}, \ldots, b_{n}$ be the roots of $B$. For each $k$, let $A_{k}$ and $B_{k}$ be the points in the complex plane corresponding to $a_{k}$ and $b_{k}$ 。
|
| 383 |
-
|
| 384 |
-
Claim (Main claim) - For any $i$ and $j, \frac{a_{i}}{a_{j}}$ is a power of $\omega$.
|
| 385 |
-
Proof. Note that
|
| 386 |
-
|
| 387 |
-
$$
|
| 388 |
-
\frac{a_{i}-b_{1}}{a_{j}-b_{1}} \cdots \frac{a_{i}-b_{n}}{a_{j}-b_{n}}=\frac{B\left(a_{i}\right)}{B\left(a_{j}\right)}=\frac{A\left(a_{i}\right)-1}{A\left(a_{j}\right)-1}=\frac{0-1}{0-1}=1
|
| 389 |
-
$$
|
| 390 |
-
|
| 391 |
-
Since the points $A_{i}, A_{j}, B_{k}$ all lie on the unit circle, interpreting the left-hand side geometrically gives
|
| 392 |
-
|
| 393 |
-
$$
|
| 394 |
-
\measuredangle A_{i} B_{1} A_{j}+\cdots+\measuredangle A_{i} B_{n} A_{j}=0 \Longrightarrow n \widehat{A_{i} A_{j}}=0
|
| 395 |
-
$$
|
| 396 |
-
|
| 397 |
-
where angles are directed modulo $180^{\circ}$ and arcs are directed modulo $360^{\circ}$. This implies that $\frac{a_{i}}{a_{j}}$ is a power of $\omega$.
|
| 398 |
-
|
| 399 |
-
Now the finish is easy: since $a_{1}, \ldots, a_{n}$ are all different, they must be $a_{1} \omega^{0}, \ldots, a_{1} \omega^{n-1}$ in some order; this shows that $A$ is a multiple of $x^{n}-a_{1}^{n}$, as needed.
|
| 400 |
-
|
| 401 |
-
## §3.2 TSTST 2020/8, proposed by Ankan Bhattacharya
|
| 402 |
-
|
| 403 |
-
Available online at https://aops.com/community/p20020195.
|
| 404 |
-
|
| 405 |
-
## Problem statement
|
| 406 |
-
|
| 407 |
-
For every positive integer $N$, let $\sigma(N)$ denote the sum of the positive integer divisors of $N$. Find all integers $m \geq n \geq 2$ satisfying
|
| 408 |
-
|
| 409 |
-
$$
|
| 410 |
-
\frac{\sigma(m)-1}{m-1}=\frac{\sigma(n)-1}{n-1}=\frac{\sigma(m n)-1}{m n-1}
|
| 411 |
-
$$
|
| 412 |
-
|
| 413 |
-
The answer is that $m$ and $n$ should be powers of the same prime number. These all work because for a prime power we have
|
| 414 |
-
|
| 415 |
-
$$
|
| 416 |
-
\frac{\sigma\left(p^{e}\right)-1}{p^{e}-1}=\frac{\left(1+p+\cdots+p^{e}\right)-1}{p^{e}-1}=\frac{p\left(1+\cdots+p^{e-1}\right)}{p^{e}-1}=\frac{p}{p-1}
|
| 417 |
-
$$
|
| 418 |
-
|
| 419 |
-
So we now prove these are the only ones. Let $\lambda$ be the common value of the three fractions.
|
| 420 |
-
|
| 421 |
-
Claim - Any solution $(m, n)$ should satisfy $d(m n)=d(m)+d(n)-1$.
|
| 422 |
-
Proof. The divisors of $m n$ include the divisors of $m$, plus $m$ times the divisors of $n$ (counting $m$ only once). Let $\lambda$ be the common value; then this gives
|
| 423 |
-
|
| 424 |
-
$$
|
| 425 |
-
\begin{aligned}
|
| 426 |
-
\sigma(m n) & \geq \sigma(m)+m \sigma(n)-m \\
|
| 427 |
-
& =(\lambda m-\lambda+1)+m(\lambda n-\lambda+1)-m \\
|
| 428 |
-
& =\lambda m n-\lambda+1
|
| 429 |
-
\end{aligned}
|
| 430 |
-
$$
|
| 431 |
-
|
| 432 |
-
and so equality holds. Thus these are all the divisors of $m n$, for a count of $d(m)+d(n)-$ 1.
|
| 433 |
-
|
| 434 |
-
Claim - If $d(m n)=d(m)+d(n)-1$ and $\min (m, n) \geq 2$, then $m$ and $n$ are powers of the same prime.
|
| 435 |
-
|
| 436 |
-
Proof. Let $A$ denote the set of divisors of $m$ and $B$ denote the set of divisors of $n$. Then $|A \cdot B|=|A|+|B|-1$ and $\min (|A|,|B|)>1$, so $|A|$ and $|B|$ are geometric progressions with the same ratio. It follows that $m$ and $n$ are powers of the same prime.
|
| 437 |
-
|
| 438 |
-
Remark (Nikolai Beluhov). Here is a completion not relying on $|A \cdot B|=|A|+|B|-1$. By the above arguments, we see that every divisor of $m n$ is either a divisor of $n$, or $n$ times a divisor of $m$.
|
| 439 |
-
|
| 440 |
-
Now suppose that some prime $p \mid m$ but $p \nmid n$. Then $p \mid m n$ but $p$ does not appear in the above classification, a contradiction. By symmetry, it follows that $m$ and $n$ have the same prime divisors.
|
| 441 |
-
|
| 442 |
-
Now suppose we have different primes $p \mid m$ and $q \mid n$. Write $\nu_{p}(m)=\alpha$ and $\nu_{p}(n)=\beta$. Then $p^{\alpha+\beta} \mid m n$, but it does not appear in the above characterization, a contradiction. Thus, $m$ and $n$ are powers of the same prime.
|
| 443 |
-
|
| 444 |
-
Remark (Comments on the function in the problem). Let $f(n)=\frac{\sigma(n)-1}{n-1}$. Then $f$ is not really injective even outside the above solution; for example, we have $f\left(6 \cdot 11^{k}\right)=\frac{11}{5}$ for all $k$, plus sporadic equivalences like $f(14)=f(404)$, as pointed out by one reviewer during test-solving. This means that both relations should be used at once, not independently.
|
| 445 |
-
|
| 446 |
-
Remark (Authorship remarks). Ankan gave the following story for how he came up with the problem while thinking about so-called almost perfect numbers.
|
| 447 |
-
|
| 448 |
-
I was in some boring talk when I recalled a conjecture that if $\sigma(n)=2 n-1$, then $n$ is a power of 2 . For some reason (divine intervention, maybe) I had the double idea of (1) seeing whether $m, n, m n$ all almost perfect implies $m, n$ powers of 2 , and (2) trying the naive divisor bound to resolve this. Through sheer dumb luck this happened to work out perfectly. I thought this was kinda cool but I felt that I hadn't really unlocked a lot of the potential this idea had: then I basically tried to find the "general situation" which allows for this manipulation, and was amazed that it led to such a striking statement.
|
| 449 |
-
|
| 450 |
-
## §3.3 TSTST 2020/9, proposed by Nikolai Beluhov
|
| 451 |
-
|
| 452 |
-
Available online at https://aops.com/community/p20020206.
|
| 453 |
-
|
| 454 |
-
## Problem statement
|
| 455 |
-
|
| 456 |
-
Ten million fireflies are glowing in $\mathbb{R}^{3}$ at midnight. Some of the fireflies are friends, and friendship is always mutual. Every second, one firefly moves to a new position so that its distance from each one of its friends is the same as it was before moving. This is the only way that the fireflies ever change their positions. No two fireflies may ever occupy the same point.
|
| 457 |
-
Initially, no two fireflies, friends or not, are more than a meter away. Following some finite number of seconds, all fireflies find themselves at least ten million meters away from their original positions. Given this information, find the greatest possible number of friendships between the fireflies.
|
| 458 |
-
|
| 459 |
-
In general, we show that when $n \geq 70$, the answer is $f(n)=\left\lfloor\frac{n^{2}}{3}\right\rfloor$.
|
| 460 |
-
Construction: Choose three pairwise parallel lines $\ell_{A}, \ell_{B}, \ell_{C}$ forming an infinite equilateral triangle prism (with side larger than 1). Split the $n$ fireflies among the lines as equally as possible, and say that two fireflies are friends iff they lie on different lines.
|
| 461 |
-
|
| 462 |
-
To see this works:
|
| 463 |
-
|
| 464 |
-
1. Reflect $\ell_{A}$ and all fireflies on $\ell_{A}$ in the plane containing $\ell_{B}$ and $\ell_{C}$.
|
| 465 |
-
2. Reflect $\ell_{B}$ and all fireflies on $\ell_{B}$ in the plane containing $\ell_{C}$ and $\ell_{A}$.
|
| 466 |
-
3. Reflect $\ell_{C}$ and all fireflies on $\ell_{C}$ in the plane containing $\ell_{A}$ and $\ell_{B}$.
|
| 467 |
-
|
| 468 |
-
Proof: Consider a valid configuration of fireflies. If there is no 4 -clique of friends, then by Turán's theorem, there are at most $f(n)$ pairs of friends.
|
| 469 |
-
Let $g(n)$ be the answer, given that there exist four pairwise friends (say $a, b, c, d$ ). Note that for a firefly to move, all its friends must be coplanar.
|
| 470 |
-
|
| 471 |
-
Claim (No coplanar $K_{4}$ ) — We can't have four coplanar fireflies which are pairwise friends.
|
| 472 |
-
|
| 473 |
-
Proof. If we did, none of them could move (unless three are collinear, in which case they can't move).
|
| 474 |
-
|
| 475 |
-
Claim (Key claim — tetrahedrons don't share faces often) — There are at most 12 fireflies $e$ which are friends with at least three of $a, b, c, d$.
|
| 476 |
-
|
| 477 |
-
Proof. First denote by $A, B, C, D$ the locations of fireflies $a, b, c, d$. These four positions change over time as fireflies move, but the tetrahedron $A B C D$ always has a fixed shape, and we will take this tetrahedron as our reference frame for the remainder of the proof.
|
| 478 |
-
|
| 479 |
-
WLOG, will assume that $e$ is friends with $a, b, c$. Then $e$ will always be located at one of two points $E_{1}$ and $E_{2}$ relative to $A B C$, such that $E_{1} A B C$ and $E_{2} A B C$ are two
|
| 480 |
-
congruent tetrahedrons with fixed shape. We note that points $D, E_{1}$, and $E_{2}$ are all different: clearly $D \neq E_{1}$ and $E_{1} \neq E_{2}$. (If $D=E_{2}$, then some fireflies won't be able to move.)
|
| 481 |
-
|
| 482 |
-
Consider the moment where firefly $a$ moves. Its friends must be coplanar at that time, so one of $E_{1}, E_{2}$ lies in plane $B C D$. Similar reasoning holds for planes $A C D$ and $A B D$.
|
| 483 |
-
|
| 484 |
-
So, WLOG $E_{1}$ lies on both planes $B C D$ and $A C D$. Then $E_{1}$ lies on line $C D$, and $E_{2}$ lies in plane $A B D$. This uniquely determines $\left(E_{1}, E_{2}\right)$ relative to $A B C D$ :
|
| 485 |
-
|
| 486 |
-
- $E_{1}$ is the intersection of line $C D$ with the reflection of plane $A B D$ in plane $A B C$.
|
| 487 |
-
- $E_{2}$ is the intersection of plane $A B D$ with the reflection of line $C D$ in plane $A B C$.
|
| 488 |
-
|
| 489 |
-
Accounting for WLOGs, there are at most 12 possibilities for the set $\left\{E_{1}, E_{2}\right\}$, and thus at most 12 possibilities for $E$. (It's not possible for both elements of one pair $\left\{E_{1}, E_{2}\right\}$ to be occupied, because then they couldn't move.)
|
| 490 |
-
|
| 491 |
-
Thus, the number of friendships involving exactly one of $a, b, c, d$ is at most $(n-16)$. $2+12 \cdot 3=2 n+4$, so removing these four fireflies gives
|
| 492 |
-
|
| 493 |
-
$$
|
| 494 |
-
g(n) \leq 6+(2 n+4)+\max \{f(n-4), g(n-4)\}
|
| 495 |
-
$$
|
| 496 |
-
|
| 497 |
-
The rest of the solution is bounding. When $n \geq 24$, we have $(2 n+10)+f(n-4) \leq f(n)$, so
|
| 498 |
-
|
| 499 |
-
$$
|
| 500 |
-
g(n) \leq \max \{f(n),(2 n+10)+g(n-4)\} \quad \forall n \geq 24
|
| 501 |
-
$$
|
| 502 |
-
|
| 503 |
-
By iterating the above inequality, we get
|
| 504 |
-
|
| 505 |
-
$$
|
| 506 |
-
\begin{aligned}
|
| 507 |
-
g(n) \leq \max \{f(n),(2 n+10) & +(2(n-4)+10) \\
|
| 508 |
-
& +\cdots+(2(n-4 r)+10)+g(n-4 r-4)\}
|
| 509 |
-
\end{aligned}
|
| 510 |
-
$$
|
| 511 |
-
|
| 512 |
-
where $r$ satisfies $n-4 r-4<24 \leq n-4 r$.
|
| 513 |
-
Now
|
| 514 |
-
|
| 515 |
-
$$
|
| 516 |
-
\begin{aligned}
|
| 517 |
-
& (2 n+10)+(2(n-4)+10)+\cdots+(2(n-4 r)+10)+g(n-4 r-4) \\
|
| 518 |
-
= & (r+1)(2 n-4 r+10)+g(n-4 r-4) \\
|
| 519 |
-
\leq & \left(\frac{n}{4}-5\right)(n+37)+\binom{24}{2} .
|
| 520 |
-
\end{aligned}
|
| 521 |
-
$$
|
| 522 |
-
|
| 523 |
-
This is less than $f(n)$ for $n \geq 70$, which concludes the solution.
|
| 524 |
-
Remark. There are positive integers $n$ such that it is possible to do better than $f(n)$ friendships. For instance, $f(5)=8$, whereas five fireflies $a, b, c, d$, and $e$ as in the proof of the Lemma ( $E_{1}$ being the intersection point of line $C D$ with the reflection of plane $(A B D)$ in plane $(A B C), E_{2}$ being the intersection point of plane $(A B D)$ with the reflection of line $C D$ in plane $(A B C)$, and tetrahedron $A B C D$ being sufficiently arbitrary that points $E_{1}$ and $E_{2}$ exist and points $D, E_{1}$, and $E_{2}$ are pairwise distinct) give a total of nine friendships.
|
| 525 |
-
|
| 526 |
-
Remark (Author comments). It is natural to approach the problem by looking at the two-dimensional version first. In two dimensions, the following arrangement suggests itself almost immediately: We distribute all fireflies as equally as possible among two parallel lines, and two fireflies are friends if and only if they are on different lines.
|
| 527 |
-
|
| 528 |
-
Similarly to the three-dimensional version, this attains the greatest possible number of friendships for all sufficiently large $n$, though not for all $n$. For instance, at least one friendlier arrangements exists for $n=4$, similarly to the above friendlier arrangement for $n=5$ in three dimensions.
|
| 529 |
-
|
| 530 |
-
This observation strongly suggests that in three dimensions we should distribute the fireflies as equally as possible among two parallel planes, and that two fireflies should be friends if and only if they are on different planes. It was a great surprise for me to discover that this arrangement does not in fact give the correct answer!
|
| 531 |
-
|
| 532 |
-
Remark. On the other hand, Ankan Bhattacharya gives the following reasoning as to why the answer should not be that surprising:
|
| 533 |
-
|
| 534 |
-
I think the answer $\left(10^{14}-1\right) / 3$ is quite natural if you realize that $(n / 2)^{2}$ is probably optimal in 2D and $\binom{n}{2}$ is optimal in super high dimensions (i.e. around $n$ ). So going from dimension 2 to 3 should increase the answer (and indeed it does).
|
| 535 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2021.md
DELETED
|
@@ -1,1228 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2021 Solutions <br> United States of America - TST Selection Test <br> Andrew Gu and Evan Chen <br> $63^{\text {rd }}$ IMO 2022 Norway and $11^{\text {th }}$ EGMO 2022 Hungary
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 3
|
| 7 |
-
1.1 TSTST 2021/1, proposed by Holden Mui ..... 3
|
| 8 |
-
1.2 TSTST 2021/2, proposed by Merlijn Staps ..... 7
|
| 9 |
-
1.3 TSTST 2021/3, proposed by Merlijn Staps ..... 11
|
| 10 |
-
2 Solutions to Day 2 ..... 13
|
| 11 |
-
2.1 TSTST 2021/4, proposed by Holden Mui ..... 13
|
| 12 |
-
2.2 TSTST 2021/5, proposed by Vincent Huang ..... 15
|
| 13 |
-
2.3 TSTST 2021/6, proposed by Nikolai Beluhov ..... 17
|
| 14 |
-
3 Solutions to Day 3 ..... 23
|
| 15 |
-
3.1 TSTST 2021/7, proposed by Ankit Bisain, Holden Mui ..... 23
|
| 16 |
-
3.2 TSTST 2021/8, proposed by Fedir Yudin ..... 25
|
| 17 |
-
3.3 TSTST 2021/9, proposed by Victor Wang ..... 28
|
| 18 |
-
|
| 19 |
-
## §0 Problems
|
| 20 |
-
|
| 21 |
-
1. Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
| 22 |
-
2. Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence
|
| 23 |
-
|
| 24 |
-
$$
|
| 25 |
-
\frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots
|
| 26 |
-
$$
|
| 27 |
-
|
| 28 |
-
3. Find all positive integers $k>1$ for which there exists a positive integer $n$ such that $\binom{n}{k}$ is divisible by $n$, and $\binom{n}{m}$ is not divisible by $n$ for $2 \leq m<k$.
|
| 29 |
-
4. Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.
|
| 30 |
-
5. Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
| 31 |
-
6. Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly.
|
| 32 |
-
(a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel.
|
| 33 |
-
(b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
| 34 |
-
7. Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
| 35 |
-
8. Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
| 36 |
-
9. Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\zeta=e^{\frac{2 \pi i}{q}}$. Find the least positive integer $n$ such that
|
| 37 |
-
|
| 38 |
-
$$
|
| 39 |
-
\sum_{\substack{1 \leq k \leq q \\ \operatorname{gcd}(k, p)=1}} \frac{1}{\left(1-\zeta^{k}\right)^{n}}
|
| 40 |
-
$$
|
| 41 |
-
|
| 42 |
-
is not an integer. (The sum is over all $1 \leq k \leq q$ with $p$ not dividing $k$.)
|
| 43 |
-
|
| 44 |
-
## §1 Solutions to Day 1
|
| 45 |
-
|
| 46 |
-
## §1.1 TSTST 2021/1, proposed by Holden Mui
|
| 47 |
-
|
| 48 |
-
Available online at https://aops.com/community/p23586650.
|
| 49 |
-
|
| 50 |
-
## Problem statement
|
| 51 |
-
|
| 52 |
-
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
| 53 |
-
|
| 54 |
-
We present many solutions.
|
| 55 |
-
|
| 56 |
-
『 First solution, angle chasing only (Ankit Bisain). Let lines $B Q$ and $D P$ meet $(A B C D)$ again at $D^{\prime}$ and $B^{\prime}$, respectively.
|
| 57 |
-
|
| 58 |
-
|
| 59 |
-
Then $B B^{\prime} \| P X$ and $D D^{\prime} \| Q Y$ by Reim's theorem. Segments $B B^{\prime}, D D^{\prime}$, and $P Q$ share a perpendicular bisector which passes through $O$, so $O P=O Q$.
|
| 60 |
-
|
| 61 |
-
【 Second solution via isosceles triangles (from contestants). Let $T=\overline{B Q} \cap \overline{D P}$.
|
| 62 |
-
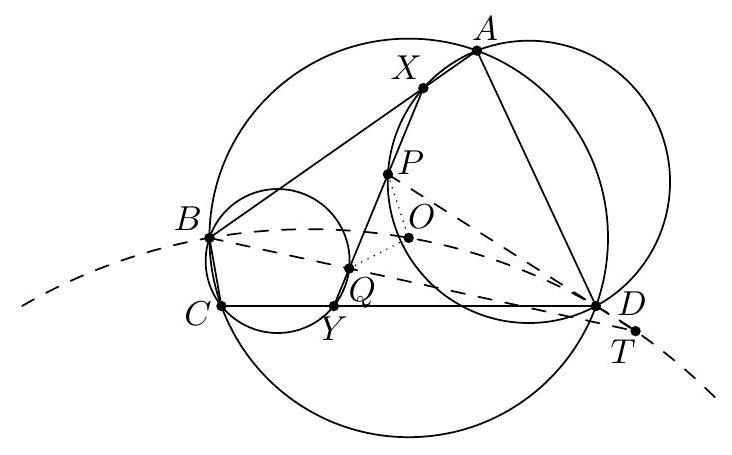
|
| 63 |
-
|
| 64 |
-
Note that $P Q T$ is isosceles because
|
| 65 |
-
|
| 66 |
-
$$
|
| 67 |
-
\measuredangle P Q T=\measuredangle Y Q B=\measuredangle B C D=\measuredangle B A D=\measuredangle X P D=\measuredangle T P Q
|
| 68 |
-
$$
|
| 69 |
-
|
| 70 |
-
Then $(B O D T)$ is cyclic because
|
| 71 |
-
|
| 72 |
-
$$
|
| 73 |
-
\measuredangle B O D=2 \measuredangle B C D=\measuredangle P Q T+\measuredangle T P Q=\measuredangle B T D .
|
| 74 |
-
$$
|
| 75 |
-
|
| 76 |
-
Since $B O=O D, \overline{T O}$ is an angle bisector of $\measuredangle B T D$. Since $\triangle P Q T$ is isosceles, $\overline{T O} \perp \overline{P Q}$, so $O P=O Q$.
|
| 77 |
-
|
| 78 |
-
ब Third solution using a parallelogram (from contestants). Let $(B C Y)$ meet $\overline{A B}$ again at $W$ and let $(A D X)$ meet $\overline{C D}$ again at $Z$. Additionally, let $O_{1}$ be the center of $(A D X)$ and $O_{2}$ be the center of $(B C Y)$.
|
| 79 |
-
|
| 80 |
-
|
| 81 |
-
Note that $(W X Y Z)$ is cyclic since
|
| 82 |
-
|
| 83 |
-
$$
|
| 84 |
-
\measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ}
|
| 85 |
-
$$
|
| 86 |
-
|
| 87 |
-
so let $O^{\prime}$ be the center of ( $W X Y Z$ ). Since $\overline{A D} \| \overline{W Y}$ and $\overline{B C} \| \overline{X Z}$ by Reim's theorem, $O O_{1} O^{\prime} O_{2}$ is a parallelogram.
|
| 88 |
-
|
| 89 |
-
To finish the problem, note that projecting $O_{1}, O_{2}$, and $O^{\prime}$ onto $\overline{X Y}$ gives the midpoints of $\overline{P X}, \overline{Q Y}$, and $\overline{X Y}$. Since $O O_{1} O^{\prime} O_{2}$ is a parallelogram, projecting $O$ onto $\overline{X Y}$ must give the midpoint of $\overline{P Q}$, so $O P=O Q$.
|
| 90 |
-
|
| 91 |
-
ब Fourth solution using congruent circles (from contestants). Let the angle bisector of $\measuredangle B O D$ meet $\overline{X Y}$ at $K$.
|
| 92 |
-
|
| 93 |
-
|
| 94 |
-
Then $(B Q O K)$ is cyclic because $\measuredangle K O D=\measuredangle B A D=\measuredangle K P D$, and $(D O P K)$ is cyclic similarly. By symmetry over $K O$, these circles have the same radius $r$, so
|
| 95 |
-
|
| 96 |
-
$$
|
| 97 |
-
O P=2 r \sin \angle O K P=2 r \sin \angle O K Q=O Q
|
| 98 |
-
$$
|
| 99 |
-
|
| 100 |
-
by the Law of Sines.
|
| 101 |
-
|
| 102 |
-
【 Fifth solution by ratio calculation (from contestants). Let $\overline{X Y}$ meet $(A B C D)$ at $X^{\prime}$ and $Y^{\prime}$.
|
| 103 |
-
|
| 104 |
-
|
| 105 |
-
Since $\measuredangle Y^{\prime} B D=\measuredangle P X^{\prime} D$ and $\measuredangle B Y^{\prime} D=\measuredangle B A D=\measuredangle X^{\prime} P D$,
|
| 106 |
-
|
| 107 |
-
$$
|
| 108 |
-
\triangle B Y^{\prime} D \sim \triangle X P^{\prime} D \Longrightarrow P X^{\prime}=B Y^{\prime} \cdot \frac{D X^{\prime}}{B D}
|
| 109 |
-
$$
|
| 110 |
-
|
| 111 |
-
Similarly,
|
| 112 |
-
|
| 113 |
-
$$
|
| 114 |
-
\triangle B X^{\prime} D \sim \triangle B Q Y^{\prime} \Longrightarrow Q Y^{\prime}=D X^{\prime} \cdot \frac{B Y^{\prime}}{B D}
|
| 115 |
-
$$
|
| 116 |
-
|
| 117 |
-
Thus $P X^{\prime}=Q Y^{\prime}$, which gives $O P=O Q$.
|
| 118 |
-
|
| 119 |
-
I Sixth solution using radical axis (from author). Without loss of generality, assume $\overline{A D} \nVdash \overline{B C}$, as this case holds by continuity. Let $(B C Y)$ meet $\overline{A B}$ again at $W$, let $(A D X)$ meet $\overline{C D}$ again at $Z$, and let $\overline{W Z}$ meet $(A D X)$ and $(B C Y)$ again at $R$ and $S$.
|
| 120 |
-
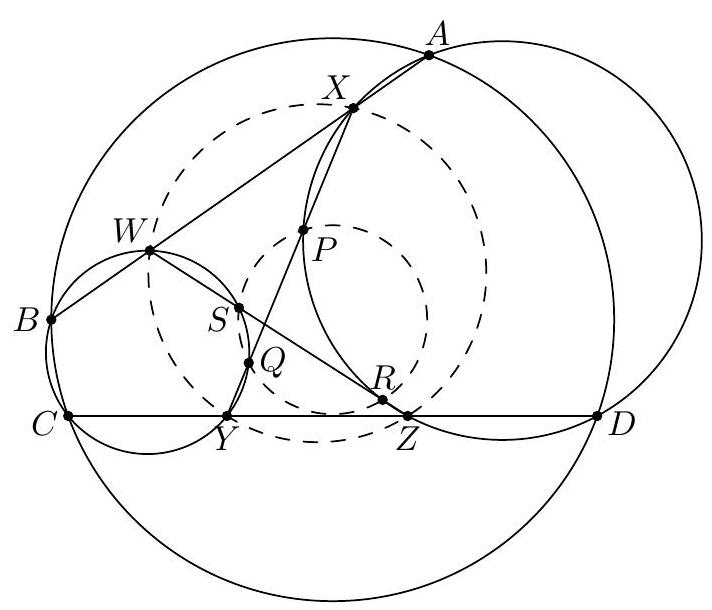
|
| 121 |
-
|
| 122 |
-
Note that $(W X Y Z)$ is cyclic since
|
| 123 |
-
|
| 124 |
-
$$
|
| 125 |
-
\measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ}
|
| 126 |
-
$$
|
| 127 |
-
|
| 128 |
-
and $(P Q R S)$ is cyclic since
|
| 129 |
-
|
| 130 |
-
$$
|
| 131 |
-
\measuredangle P Q S=\measuredangle Y Q S=\measuredangle Y W S=\measuredangle P X Z=\measuredangle P R Z=\measuredangle S R P
|
| 132 |
-
$$
|
| 133 |
-
|
| 134 |
-
Additionally, $\overline{A D} \| \overline{P R}$ since
|
| 135 |
-
|
| 136 |
-
$$
|
| 137 |
-
\measuredangle D A X+\measuredangle A X P+\measuredangle X P R=\measuredangle Y W X+\measuredangle W X Y+\measuredangle X Y W=0^{\circ},
|
| 138 |
-
$$
|
| 139 |
-
|
| 140 |
-
and $\overline{B C} \| \overline{S Q}$ similarly.
|
| 141 |
-
Lastly, $(A B C D)$ and $(P Q R S)$ are concentric; if not, using the radical axis theorem twice shows that their radical axis must be parallel to both $\overline{A D}$ and $\overline{B C}$, contradiction.
|
| 142 |
-
|
| 143 |
-
【 Seventh solution using Cayley-Bacharach (author). Define points $W, Z, R, S$ as in the previous solution.
|
| 144 |
-
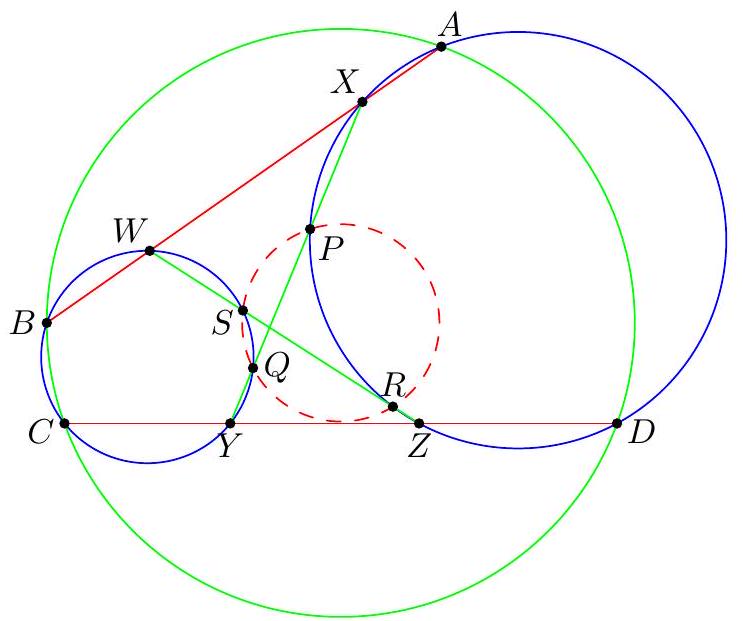
|
| 145 |
-
|
| 146 |
-
The quartics $(A D X Z) \cup(B C W Y)$ and $\overline{X Y} \cup \overline{W Z} \cup(A B C D)$ meet at the 16 points
|
| 147 |
-
|
| 148 |
-
$$
|
| 149 |
-
A, B, C, D, W, X, Y, Z, P, Q, R, S, I, I, J, J
|
| 150 |
-
$$
|
| 151 |
-
|
| 152 |
-
where $I$ and $J$ are the circular points at infinity. Since $\overline{A B} \cup \overline{C D} \cup(P Q R)$ contains the 13 points
|
| 153 |
-
|
| 154 |
-
$$
|
| 155 |
-
A, B, C, D, P, Q, R, W, X, Y, Z, I, J
|
| 156 |
-
$$
|
| 157 |
-
|
| 158 |
-
it must contain $S, I$, and $J$ as well, by quartic Cayley-Bacharach. Thus, $(P Q R S)$ is cyclic and intersects $(A B C D)$ at $I, I, J$, and $J$, implying that the two circles are concentric, as desired.
|
| 159 |
-
|
| 160 |
-
Remark (Author comments). Holden says he came up with this problem via the CayleyBacharach solution, by trying to get two quartics to intersect.
|
| 161 |
-
|
| 162 |
-
## §1.2 TSTST 2021/2, proposed by Merlijn Staps
|
| 163 |
-
|
| 164 |
-
Available online at https://aops.com/community/p23586635.
|
| 165 |
-
|
| 166 |
-
## Problem statement
|
| 167 |
-
|
| 168 |
-
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence
|
| 169 |
-
|
| 170 |
-
$$
|
| 171 |
-
\frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots
|
| 172 |
-
$$
|
| 173 |
-
|
| 174 |
-
We present three solutions.
|
| 175 |
-
【 Solution 1 (Merlijn Staps). We argue by contradiction, so suppose that for each $\lambda$ for which the set $S_{\lambda}=\left\{k: a_{k} / k=\lambda\right\}$ is non-empty, it contains at least two elements. Note that $S_{\lambda}$ is always a finite set because $a_{k}=k \lambda$ implies $k<1 / \lambda$.
|
| 176 |
-
Write $m_{\lambda}$ and $M_{\lambda}$ for the smallest and largest element of $S_{\lambda}$, respectively, and define $T_{\lambda}=\left\{m_{\lambda}, m_{\lambda}+1, \ldots, M_{\lambda}\right\}$ as the smallest set of consecutive positive integers that contains $S_{\lambda}$. Then all $T_{\lambda}$ are sets of at least two consecutive positive integers, and moreover the $T_{\lambda}$ cover $\mathbb{N}$. Additionally, each positive integer is covered finitely many times because there are only finitely many possible values of $m_{\lambda}$ smaller than any fixed integer.
|
| 177 |
-
|
| 178 |
-
Recall that if three intervals have a point in common then one of them is contained in the union of the other two. Thus, if any positive integer is covered more than twice by the sets $T_{\lambda}$, we may throw out one set while maintaining the property that the $T_{\lambda}$ cover $\mathbb{N}$. By using the fact that each positive integer is covered finitely many times, we can apply this process so that each positive integer is eventually covered at most twice.
|
| 179 |
-
|
| 180 |
-
Let $\Lambda$ denote the set of the $\lambda$-values for which $T_{\lambda}$ remains in our collection of sets; then $\bigcup_{\lambda \in \Lambda} T_{\lambda}=\mathbb{N}$ and each positive integer is contained in at most two sets $T_{\lambda}$.
|
| 181 |
-
We now obtain
|
| 182 |
-
|
| 183 |
-
$$
|
| 184 |
-
\sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \leq 2 \sum_{k \geq 1}\left(a_{k+1}-a_{k}\right) \leq 2
|
| 185 |
-
$$
|
| 186 |
-
|
| 187 |
-
On the other hand, because $a_{m_{\lambda}}=\lambda m_{\lambda}$ and $a_{M_{\lambda}}=\lambda M_{\lambda}$, we have
|
| 188 |
-
|
| 189 |
-
$$
|
| 190 |
-
\begin{aligned}
|
| 191 |
-
2 \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) & \geq 2 \sum_{m_{\lambda} \leq k<M_{\lambda}}\left(a_{k+1}-a_{k}\right)=2\left(a_{M_{\lambda}}-a_{m_{\lambda}}\right)=2\left(M_{\lambda}-m_{\lambda}\right) \lambda \\
|
| 192 |
-
& =2\left(M_{\lambda}-m_{\lambda}\right) \cdot \frac{a_{m_{\lambda}}}{m_{\lambda}} \geq\left(M_{\lambda}-m_{\lambda}+1\right) \cdot \frac{a_{1}}{m_{\lambda}} \geq a_{1} \cdot \sum_{k \in T_{\lambda}} \frac{1}{k} .
|
| 193 |
-
\end{aligned}
|
| 194 |
-
$$
|
| 195 |
-
|
| 196 |
-
Combining this with our first estimate, and using the fact that the $T_{\lambda}$ cover $\mathbb{N}$, we obtain
|
| 197 |
-
|
| 198 |
-
$$
|
| 199 |
-
4 \geq 2 \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \geq a_{1} \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}} \frac{1}{k} \geq a_{1} \sum_{k \geq 1} \frac{1}{k}
|
| 200 |
-
$$
|
| 201 |
-
|
| 202 |
-
contradicting the fact that the harmonic series diverges.
|
| 203 |
-
【 Solution 2 (Sanjana Das). Assume for the sake of contradiction that no number appears exactly once in the sequence. For every $i<j$ with $a_{i} / i=a_{j} / j$, draw an edge
|
| 204 |
-
between $i$ and $j$, so every $i$ has an edge (and being connected by an edge is a transitive property). Call $i$ good if it has an edge with some $j>i$.
|
| 205 |
-
|
| 206 |
-
First, each $i$ has finite degree - otherwise
|
| 207 |
-
|
| 208 |
-
$$
|
| 209 |
-
\frac{a_{x_{1}}}{x_{1}}=\frac{a_{x_{2}}}{x_{2}}=\cdots
|
| 210 |
-
$$
|
| 211 |
-
|
| 212 |
-
for an infinite increasing sequence of positive integers $x_{i}$, but then the $a_{x_{i}}$ are unbounded.
|
| 213 |
-
Now we use the following process to build a sequence of indices whose $a_{i}$ we can lower-bound:
|
| 214 |
-
|
| 215 |
-
- Start at $x_{1}=1$, which is good.
|
| 216 |
-
- If we're currently at good index $x_{i}$, then let $s_{i}$ be the largest positive integer such that $x_{i}$ has an edge to $x_{i}+s_{i}$. (This exists because the degrees are finite.)
|
| 217 |
-
- Let $t_{i}$ be the smallest positive integer for which $x_{i}+s_{i}+t_{i}$ is good, and let this be $x_{i+1}$. This exists because if all numbers $k \leq x \leq 2 k$ are bad, they must each connect to some number less than $k$ (if two connect to each other, the smaller one is good), but then two connect to the same number, and therefore to each other this is the idea we will use later to bound the $t_{i}$ as well.
|
| 218 |
-
|
| 219 |
-
Then $x_{i}=1+s_{1}+t_{1}+\cdots+s_{i-1}+t_{i-1}$, and we have
|
| 220 |
-
|
| 221 |
-
$$
|
| 222 |
-
a_{x_{i+1}}>a_{x_{i}+s_{i}}=\frac{x_{i}+s_{i}}{x_{i}} a_{x_{i}}=\frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} a_{x_{i}}
|
| 223 |
-
$$
|
| 224 |
-
|
| 225 |
-
This means
|
| 226 |
-
|
| 227 |
-
$$
|
| 228 |
-
c_{n}:=\frac{a_{x_{n}}}{a_{1}}>\prod_{i=1}^{n-1} \frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}
|
| 229 |
-
$$
|
| 230 |
-
|
| 231 |
-
## Lemma
|
| 232 |
-
|
| 233 |
-
$t_{1}+\cdots+t_{n} \leq s_{1}+\cdots+s_{n}$ for each $n$.
|
| 234 |
-
|
| 235 |
-
Proof. Consider $1 \leq i \leq n$. Note that for every $i$, the $t_{i}-1$ integers strictly between $x_{i}+s_{i}$ and $x_{i}+s_{i}+t_{i}$ are all bad, so each such index $x$ must have an edge to some $y<x$.
|
| 236 |
-
|
| 237 |
-
First we claim that if $x \in\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$, then $x$ cannot have an edge to $x_{j}$ for any $j \leq i$. This is because $x>x_{i}+s_{i} \geq x_{j}+s_{j}$, contradicting the fact that $x_{j}+s_{j}$ is the largest neighbor of $x_{j}$.
|
| 238 |
-
|
| 239 |
-
This also means $x$ doesn't have an edge to $x_{j}+s_{j}$ for any $j \leq i$, since if it did, it would have an edge to $x_{j}$.
|
| 240 |
-
|
| 241 |
-
Second, no two bad values of $x$ can have an edge, since then the smaller one is good. This also means no two bad $x$ can have an edge to the same $y$.
|
| 242 |
-
|
| 243 |
-
Then each of the $\sum\left(t_{i}-1\right)$ values in the intervals $\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$ for $1 \leq i \leq n$ must have an edge to an unique $y$ in one of the intervals $\left(x_{i}, x_{i}+s_{i}\right)$ (not necessarily with the same $i$ ). Therefore
|
| 244 |
-
|
| 245 |
-
$$
|
| 246 |
-
\sum\left(t_{i}-1\right) \leq \sum\left(s_{i}-1\right) \Longrightarrow \sum t_{i} \leq \sum s_{i}
|
| 247 |
-
$$
|
| 248 |
-
|
| 249 |
-
Now note that if $a>b$, then $\frac{a+x}{b+x}=1+\frac{a-b}{b+x}$ is decreasing in $x$. This means
|
| 250 |
-
|
| 251 |
-
$$
|
| 252 |
-
c_{n}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+2 s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}}
|
| 253 |
-
$$
|
| 254 |
-
|
| 255 |
-
By multiplying both products, we have a telescoping product, which results in
|
| 256 |
-
|
| 257 |
-
$$
|
| 258 |
-
c_{n}^{2} \geq 1+2 s_{1}+\cdots+2 s_{n}+2 s_{n+1}
|
| 259 |
-
$$
|
| 260 |
-
|
| 261 |
-
The right hand side is unbounded since the $s_{i}$ are positive integers, while $c_{n}=a_{x_{n}} / a_{1}<$ $1 / a_{1}$ is bounded, contradiction.
|
| 262 |
-
|
| 263 |
-
【 Solution 3 (Gopal Goel). Suppose for sake of contradiction that the problem is false. Call an index $i$ a pin if
|
| 264 |
-
|
| 265 |
-
$$
|
| 266 |
-
\frac{a_{j}}{j}=\frac{a_{i}}{i} \Longrightarrow j \geq i
|
| 267 |
-
$$
|
| 268 |
-
|
| 269 |
-
## Lemma
|
| 270 |
-
|
| 271 |
-
There exists $k$ such that if we have $\frac{a_{i}}{i}=\frac{a_{j}}{j}$ with $j>i \geq k$, then $j \leq 1.1 i$.
|
| 272 |
-
|
| 273 |
-
Proof. Note that for any $i$, there are only finitely many $j$ with $\frac{a_{j}}{j}=\frac{a_{i}}{i}$, otherwise $a_{j}=\frac{j a_{i}}{i}$ is unbounded. Thus it suffices to find $k$ for which $j \leq 1.1 i$ when $j>i \geq k$.
|
| 274 |
-
|
| 275 |
-
Suppose no such $k$ exists. Then, take a pair $j_{1}>i_{1}$ such that $\frac{a_{j_{1}}}{j_{1}}=\frac{a_{i_{1}}}{i_{1}}$ and $j_{1}>1.1 i_{1}$, or $a_{j_{1}}>1.1 a_{i_{1}}$. Now, since $k=j_{1}$ can't work, there exists a pair $j_{2}>i_{2} \geq i_{1}$ such that $\frac{a_{j_{2}}}{j_{2}}=\frac{a_{i_{2}}}{i_{2}}$ and $j_{2}>1.1 i_{2}$, or $a_{j_{2}}>1.1 a_{i_{2}}$. Continuing in this fashion, we see that
|
| 276 |
-
|
| 277 |
-
$$
|
| 278 |
-
a_{j_{\ell}}>1.1 a_{i_{\ell}}>1.1 a_{j_{\ell-1}}
|
| 279 |
-
$$
|
| 280 |
-
|
| 281 |
-
so we have that $a_{j_{\ell}}>1.1^{\ell} a_{i_{1}}$. Taking $\ell>\log _{1.1}\left(1 / a_{1}\right)$ gives the desired contradiction.
|
| 282 |
-
|
| 283 |
-
## Lemma
|
| 284 |
-
|
| 285 |
-
For $N>k^{2}$, there are at most $0.8 N$ pins in $[\sqrt{N}, N)$.
|
| 286 |
-
|
| 287 |
-
Proof. By the first lemma, we see that the number of pins in $\left[\sqrt{N}, \frac{N}{1.1}\right)$ is at most the number of non-pins in $[\sqrt{N}, N)$. Therefore, if the number of pins in $[\sqrt{N}, N)$ is $p$, then we have
|
| 288 |
-
|
| 289 |
-
$$
|
| 290 |
-
p-N\left(1-\frac{1}{1.1}\right) \leq N-p
|
| 291 |
-
$$
|
| 292 |
-
|
| 293 |
-
so $p \leq 0.8 N$, as desired.
|
| 294 |
-
We say that $i$ is the pin of $j$ if it is the smallest index such that $\frac{a_{i}}{i}=\frac{a_{j}}{j}$. The pin of $j$ is always a pin.
|
| 295 |
-
|
| 296 |
-
Given an index $i$, let $f(i)$ denote the largest index less than $i$ that is not a pin (we leave the function undefined when no such index exists, as we are only interested in the behavior for large $i$ ). Then $f$ is weakly increasing and unbounded by the first lemma. Let $N_{0}$ be a positive integer such that $f\left(\sqrt{N_{0}}\right)>k$.
|
| 297 |
-
|
| 298 |
-
Take any $N>N_{0}$ such that $N$ is not a pin. Let $b_{0}=N$, and $b_{1}$ be the pin of $b_{0}$. Recursively define $b_{2 i}=f\left(b_{2 i-1}\right)$, and $b_{2 i+1}$ to be the pin of $b_{2 i}$.
|
| 299 |
-
|
| 300 |
-
Let $\ell$ be the largest odd index such that $b_{\ell} \geq \sqrt{N}$. We first show that $b_{\ell} \leq 100 \sqrt{N}$. Since $N>N_{0}$, we have $b_{\ell+1}>k$. By the choice of $\ell$ we have $b_{\ell+2}<\sqrt{N}$, so
|
| 301 |
-
|
| 302 |
-
$$
|
| 303 |
-
b_{\ell+1}<1.1 b_{\ell+2}<1.1 \sqrt{N}
|
| 304 |
-
$$
|
| 305 |
-
|
| 306 |
-
by the first lemma. We see that all the indices from $b_{\ell+1}+1$ to $b_{\ell}$ must be pins, so we have at least $b_{\ell}-1.1 \sqrt{N}$ pins in $\left[\sqrt{N}, b_{\ell}\right)$. Combined with the second lemma, this shows that $b_{\ell} \leq 100 \sqrt{N}$.
|
| 307 |
-
Now, we have that $a_{b_{2 i}}=\frac{b_{2 i}}{b_{2 i+1}} a_{b_{2 i+1}}$ and $a_{b_{2 i+1}}>a_{b_{2 i+2}}$, so combining gives us
|
| 308 |
-
|
| 309 |
-
$$
|
| 310 |
-
\frac{a_{b_{0}}}{a_{b_{\ell}}}>\frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} .
|
| 311 |
-
$$
|
| 312 |
-
|
| 313 |
-
Note that there are at least
|
| 314 |
-
|
| 315 |
-
$$
|
| 316 |
-
\left(b_{1}-b_{2}\right)+\left(b_{3}-b_{4}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right)
|
| 317 |
-
$$
|
| 318 |
-
|
| 319 |
-
pins in $[\sqrt{N}, N)$, so by the second lemma, that sum is at most $0.8 N$. Thus,
|
| 320 |
-
|
| 321 |
-
$$
|
| 322 |
-
\begin{aligned}
|
| 323 |
-
\left(b_{0}-b_{1}\right)+\left(b_{2}-b_{3}\right)+\cdots+\left(b_{\ell-1}-b_{\ell}\right) & =b_{0}-\left[\left(b_{1}-b_{2}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right)\right]-b_{\ell} \\
|
| 324 |
-
& \geq 0.2 N-100 \sqrt{N} .
|
| 325 |
-
\end{aligned}
|
| 326 |
-
$$
|
| 327 |
-
|
| 328 |
-
Then
|
| 329 |
-
|
| 330 |
-
$$
|
| 331 |
-
\begin{aligned}
|
| 332 |
-
\frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} & \geq 1+\frac{b_{0}-b_{1}}{b_{1}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{\ell}} \\
|
| 333 |
-
& >1+\frac{b_{0}-b_{1}}{b_{0}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{0}} \\
|
| 334 |
-
& \geq 1+\frac{0.2 N-100 \sqrt{N}}{N}
|
| 335 |
-
\end{aligned}
|
| 336 |
-
$$
|
| 337 |
-
|
| 338 |
-
which is at least 1.01 if $N_{0}$ is large enough. Thus, we see that
|
| 339 |
-
|
| 340 |
-
$$
|
| 341 |
-
a_{N}>1.01 a_{b_{\ell}} \geq 1.01 a_{\lfloor\sqrt{N}\rfloor}
|
| 342 |
-
$$
|
| 343 |
-
|
| 344 |
-
if $N>N_{0}$ is not a pin. Since there are arbitrarily large non-pins, this implies that the sequence $\left(a_{n}\right)$ is unbounded, which is the desired contradiction.
|
| 345 |
-
|
| 346 |
-
## §1.3 TSTST 2021/3, proposed by Merlijn Staps
|
| 347 |
-
|
| 348 |
-
Available online at https://aops.com/community/p23586679.
|
| 349 |
-
|
| 350 |
-
## Problem statement
|
| 351 |
-
|
| 352 |
-
Find all positive integers $k>1$ for which there exists a positive integer $n$ such that $\binom{n}{k}$ is divisible by $n$, and $\binom{n}{m}$ is not divisible by $n$ for $2 \leq m<k$.
|
| 353 |
-
|
| 354 |
-
Such an $n$ exists for any $k$.
|
| 355 |
-
First, suppose $k$ is prime. We choose $n=(k-1)$ !. For $m<k$, it follows from $m!\mid n$ that
|
| 356 |
-
|
| 357 |
-
$$
|
| 358 |
-
\begin{aligned}
|
| 359 |
-
(n-1)(n-2) \cdots(n-m+1) & \equiv(-1)(-2) \cdots(-m+1) \\
|
| 360 |
-
& \equiv(-1)^{m-1}(m-1)! \\
|
| 361 |
-
& \not \equiv 0 \bmod m!
|
| 362 |
-
\end{aligned}
|
| 363 |
-
$$
|
| 364 |
-
|
| 365 |
-
We see that $\binom{n}{m}$ is not a multiple of $m$. For $m=k$, note that $\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}$. Because $k \nmid n$, we must have $k \left\lvert\,\binom{ n-1}{k-1}\right.$, and it follows that $n \left\lvert\,\binom{ n}{k}\right.$.
|
| 366 |
-
|
| 367 |
-
Now suppose $k$ is composite. We will choose $n$ to satisfy a number of congruence relations. For each prime $p \leq k$, let
|
| 368 |
-
|
| 369 |
-
$$
|
| 370 |
-
t_{p}=\nu_{p}(\operatorname{lcm}(1,2, \ldots, k-1))=\max \left(\nu_{p}(1), \nu_{p}(2), \ldots, \nu_{p}(k-1)\right)
|
| 371 |
-
$$
|
| 372 |
-
|
| 373 |
-
and choose $k_{p} \in\{1,2, \ldots, k-1\}$ as large as possible such that $\nu_{p}\left(k_{p}\right)=t_{p}$. We now require
|
| 374 |
-
|
| 375 |
-
$$
|
| 376 |
-
\begin{aligned}
|
| 377 |
-
n \equiv 0 \quad \bmod p^{t_{p}+1} & \text { if } p \nmid k \\
|
| 378 |
-
\nu_{p}\left(n-k_{p}\right)=t_{p}+\nu_{p}(k) & \text { if } p \mid k
|
| 379 |
-
\end{aligned}
|
| 380 |
-
$$
|
| 381 |
-
|
| 382 |
-
for all $p \leq k$. From the Chinese Remainder Theorem, we know that an $n$ exists that satisfies (1) and (2) (indeed, a sufficient condition for (2) is the congruence $n \equiv$ $\left.k_{p}+p^{t_{p}+\nu_{p}(k)} \bmod p^{t_{p}+\nu_{p}(k)+1}\right)$. We show that this $n$ has the required property.
|
| 383 |
-
|
| 384 |
-
We first will compute $\nu_{p}(n-i)$ for primes $p<k$ and $1 \leq i<k$.
|
| 385 |
-
|
| 386 |
-
- If $p \nmid k$, then we have $\nu_{p}(i), \nu_{p}(n-i) \leq t_{p}$ and $\nu_{p}(n)>t_{p}$, so $\nu_{p}(n-i)=\nu_{p}(i)$;
|
| 387 |
-
- If $p \mid k$ and $i \neq k_{p}$, then we have $\nu_{p}(i), \nu_{p}(n-i) \leq t_{p}$ and $\nu_{p}(n) \geq t_{p}$, so again $\nu_{p}(n-i)=\nu_{p}(i) ;$
|
| 388 |
-
- If $p \mid k$ and $i=k_{p}$, then we have $\nu_{p}(n-i)=\nu_{p}(i)+\nu_{p}(k)$ by (2).
|
| 389 |
-
|
| 390 |
-
We conclude that $\nu_{p}(n-i)=\nu_{p}(i)$ always holds, except when $i=k_{p}$, when we have $\nu_{p}(n-i)=\nu_{p}(i)+\nu_{p}(k)$ (this formula holds irrespective of whether $p \mid k$ or $\left.p \nmid k\right)$.
|
| 391 |
-
|
| 392 |
-
We can now show that $\binom{n}{k}$ is divisible by $n$, which amounts to showing that $k$ ! divides $(n-1)(n-2) \cdots(n-k+1)$. Indeed, for each prime $p \leq k$ we have
|
| 393 |
-
|
| 394 |
-
$$
|
| 395 |
-
\begin{aligned}
|
| 396 |
-
\nu_{p}((n-1)(n-2) \ldots(n-k+1)) & =\nu_{p}\left(n-k_{p}\right)+\sum_{i<k, i \neq k_{p}} \nu_{p}(n-i) \\
|
| 397 |
-
& =\nu_{p}\left(k_{p}\right)+\nu_{p}(k)+\sum_{i<k, i \neq k_{p}} \nu_{p}(i)
|
| 398 |
-
\end{aligned}
|
| 399 |
-
$$
|
| 400 |
-
|
| 401 |
-
$$
|
| 402 |
-
=\sum_{i=1}^{k} \nu_{p}(i)=\nu_{p}(k!)
|
| 403 |
-
$$
|
| 404 |
-
|
| 405 |
-
so it follows that $(n-1)(n-2) \cdots(n-k+1)$ is a multiple of $k$ !.
|
| 406 |
-
Finally, let $1<m<k$. We will show that $n$ does not divide $\binom{n}{m}$, which amounts to showing that $m$ ! does not divide $(n-1)(n-2) \cdots(n-m+1)$. First, suppose that $m$ has a prime divisor $q$ that does not divide $k$. Then we have
|
| 407 |
-
|
| 408 |
-
$$
|
| 409 |
-
\begin{aligned}
|
| 410 |
-
\nu_{q}((n-1)(n-2) \ldots(n-m+1)) & =\sum_{i=1}^{m-1} \nu_{q}(n-i) \\
|
| 411 |
-
& =\sum_{i=1}^{m-1} \nu_{q}(i) \\
|
| 412 |
-
& =\nu_{q}((m-1)!)<\nu_{q}(m!)
|
| 413 |
-
\end{aligned}
|
| 414 |
-
$$
|
| 415 |
-
|
| 416 |
-
as desired. Therefore, suppose that $m$ is only divisible by primes that divide $k$. If there is such a prime $p$ with $\nu_{p}(m)>\nu_{p}(k)$, then it follows that
|
| 417 |
-
|
| 418 |
-
$$
|
| 419 |
-
\begin{aligned}
|
| 420 |
-
\nu_{p}((n-1)(n-2) \ldots(n-m+1)) & =\nu_{p}(k)+\sum_{i=1}^{m-1} \nu_{p}(i) \\
|
| 421 |
-
& <\nu_{p}(m)+\sum_{i=1}^{m-1} \nu_{p}(i) \\
|
| 422 |
-
& =\nu_{p}(m!)
|
| 423 |
-
\end{aligned}
|
| 424 |
-
$$
|
| 425 |
-
|
| 426 |
-
so $m$ ! cannot divide $(n-1)(n-2) \ldots(n-m+1)$. On the other hand, suppose that $\nu_{p}(m) \leq \nu_{p}(k)$ for all $p \mid k$, which would mean that $m \mid k$ and hence $m \leq \frac{k}{2}$. Consider a prime $p$ dividing $m$. We have $k_{p} \geq \frac{k}{2}$, because otherwise $2 k_{p}$ could have been used instead of $k_{p}$. It follows that $m \leq \frac{k}{2} \leq k_{p}$. Therefore, we obtain
|
| 427 |
-
|
| 428 |
-
$$
|
| 429 |
-
\begin{aligned}
|
| 430 |
-
\nu_{p}((n-1)(n-2) \ldots(n-m+1)) & =\sum_{i=1}^{m-1} \nu_{p}(n-i) \\
|
| 431 |
-
& =\sum_{i=1}^{m-1} \nu_{p}(i) \\
|
| 432 |
-
& =\nu_{p}((m-1)!)<\nu_{p}(m!)
|
| 433 |
-
\end{aligned}
|
| 434 |
-
$$
|
| 435 |
-
|
| 436 |
-
showing that $(n-1)(n-2) \cdots(n-m+1)$ is not divisible by $m$ !. This shows that $\binom{n}{m}$ is not divisible by $n$ for $m<k$, and hence $n$ does have the required property.
|
| 437 |
-
|
| 438 |
-
## §2 Solutions to Day 2
|
| 439 |
-
|
| 440 |
-
## §2.1 TSTST 2021/4, proposed by Holden Mui
|
| 441 |
-
|
| 442 |
-
Available online at https://aops.com/community/p23864177.
|
| 443 |
-
|
| 444 |
-
## Problem statement
|
| 445 |
-
|
| 446 |
-
Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.
|
| 447 |
-
|
| 448 |
-
Treating $a$ and $b$ as fixed, we are given that there are infinitely many quadrpules $(m, n, r, s)$ which satisfy the system
|
| 449 |
-
|
| 450 |
-
$$
|
| 451 |
-
\begin{aligned}
|
| 452 |
-
m^{2}+a n+b & =(m+r)^{2} \\
|
| 453 |
-
n^{2}+a m+b & =(n+s)^{2}
|
| 454 |
-
\end{aligned}
|
| 455 |
-
$$
|
| 456 |
-
|
| 457 |
-
We say that $(r, s)$ is exceptional if there exists infinitely many $(m, n)$ that satisfy.
|
| 458 |
-
Claim - If $(r, s)$ is exceptional, then either
|
| 459 |
-
|
| 460 |
-
- $0<r<a / 2$, and $0<s<\frac{1}{4} a^{2}$; or
|
| 461 |
-
- $0<s<a / 2$, and $0<r<\frac{1}{4} a^{2}$; or
|
| 462 |
-
- $r^{2}+s^{2} \leq 2 b$.
|
| 463 |
-
|
| 464 |
-
In particular, finitely many pairs $(r, s)$ can be exceptional.
|
| 465 |
-
|
| 466 |
-
Proof. Sum the two equations to get:
|
| 467 |
-
|
| 468 |
-
$$
|
| 469 |
-
r^{2}+s^{2}-2 b=(a-2 r) m+(a-2 s) n
|
| 470 |
-
$$
|
| 471 |
-
|
| 472 |
-
If $0<r<a / 2$, then the idea is to use the bound $a n+b \geq 2 m+1$ to get $m \leq \frac{a n+b-1}{2}$. Consequently,
|
| 473 |
-
|
| 474 |
-
$$
|
| 475 |
-
(n+s)^{2}=n^{2}+a m+b \leq n^{2}+a \cdot \frac{a n+b-1}{2}+b
|
| 476 |
-
$$
|
| 477 |
-
|
| 478 |
-
For this to hold for infinitely many integers $n$, we need $2 s \leq \frac{a^{2}}{2}$, by comparing coefficients.
|
| 479 |
-
A similar case occurs when $0<s<a / 2$.
|
| 480 |
-
If $\min (r, s)>a / 2$, then $(\dagger)$ forces $r^{2}+s^{2} \leq 2 b$, giving the last case.
|
| 481 |
-
Hence, there exists some particular pair $(r, s)$ for which there are infinitely many solutions $(m, n)$. Simplifying the system gives
|
| 482 |
-
|
| 483 |
-
$$
|
| 484 |
-
\begin{aligned}
|
| 485 |
-
& a n=2 r m+r^{2}-b \\
|
| 486 |
-
& 2 s n=a m+b-s^{2}
|
| 487 |
-
\end{aligned}
|
| 488 |
-
$$
|
| 489 |
-
|
| 490 |
-
Since the system is linear, for there to be infinitely many solutions $(m, n)$ the system must be dependent. This gives
|
| 491 |
-
|
| 492 |
-
$$
|
| 493 |
-
\frac{a}{2 s}=\frac{2 r}{a}=\frac{r^{2}-b}{b-s^{2}}
|
| 494 |
-
$$
|
| 495 |
-
|
| 496 |
-
so $a=2 \sqrt{r s}$ and $b=\frac{s^{2} \sqrt{r}+r^{2} \sqrt{s}}{\sqrt{r}+\sqrt{s}}$. Since $r s$ must be square, we can reparametrize as $r=k x^{2}, s=k y^{2}$, and $\operatorname{gcd}(x, y)=1$. This gives
|
| 497 |
-
|
| 498 |
-
$$
|
| 499 |
-
\begin{aligned}
|
| 500 |
-
a & =2 k x y \\
|
| 501 |
-
b & =k^{2} x y\left(x^{2}-x y+y^{2}\right)
|
| 502 |
-
\end{aligned}
|
| 503 |
-
$$
|
| 504 |
-
|
| 505 |
-
Thus, $a \mid 2 b$, as desired.
|
| 506 |
-
|
| 507 |
-
## §2.2 TSTST 2021/5, proposed by Vincent Huang
|
| 508 |
-
|
| 509 |
-
Available online at https://aops.com/community/p23864182.
|
| 510 |
-
|
| 511 |
-
## Problem statement
|
| 512 |
-
|
| 513 |
-
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
| 514 |
-
|
| 515 |
-
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color.
|
| 516 |
-
|
| 517 |
-
## 【 Solution 1 (Ankan Bhattacharya, Jeffery Li).
|
| 518 |
-
|
| 519 |
-
## Lemma
|
| 520 |
-
|
| 521 |
-
If $S$ is an independent set of $T$, then
|
| 522 |
-
|
| 523 |
-
$$
|
| 524 |
-
\sum_{v \in S} \operatorname{deg}(v) \leq n-1
|
| 525 |
-
$$
|
| 526 |
-
|
| 527 |
-
Equality holds if and only if $S$ is one of the two components of the unique 2-coloring of $T$.
|
| 528 |
-
|
| 529 |
-
Proof. Each edge of $T$ is incident to at most one vertex of $S$, so we obtain the inequality by counting how many vertices of $S$ each edge is incident to. For equality to hold, each edge is incident to exactly one vertex of $S$, which implies the 2 -coloring.
|
| 530 |
-
|
| 531 |
-
We are given that there exists an independent set of at least $\frac{n+k-1}{2}$ vertices. By greedily choosing vertices of smallest degree, the sum of the degrees of these vertices is at least
|
| 532 |
-
|
| 533 |
-
$$
|
| 534 |
-
k+2 \cdot \frac{n-k-1}{2}=n-1
|
| 535 |
-
$$
|
| 536 |
-
|
| 537 |
-
Thus equality holds everywhere, which implies that the independent set contains every leaf and is one of the components of the 2 -coloring.
|
| 538 |
-
|
| 539 |
-
## 【 Solution 2 (Andrew Gu).
|
| 540 |
-
|
| 541 |
-
## Lemma
|
| 542 |
-
|
| 543 |
-
The vertices of $T$ can be partitioned into $k-1$ paths (i.e. the induced subgraph on each set of vertices is a path) such that all edges of $T$ which are not part of a path are incident to an endpoint of a path.
|
| 544 |
-
|
| 545 |
-
Proof. Repeatedly trim the tree by taking a leaf and removing the longest path containing that leaf such that the remaining graph is still a tree.
|
| 546 |
-
|
| 547 |
-
Now given a path of $a$ vertices, at most $\frac{a+1}{2}$ of those vertices can be in an independent set of $T$. By the lemma, $T$ can be partitioned into $k-1$ paths of $a_{1}, \ldots, a_{k-1}$ vertices, so the maximum size of an independent set of $T$ is
|
| 548 |
-
|
| 549 |
-
$$
|
| 550 |
-
\sum \frac{a_{i}+1}{2}=\frac{n+k-1}{2} .
|
| 551 |
-
$$
|
| 552 |
-
|
| 553 |
-
For equality to hold, each path in the partition must have an odd number of vertices, and has a unique 2 -coloring in red and blue where the endpoints are red. The unique independent set of $T$ of size $\frac{n+k-1}{2}$ is then the set of red vertices. By the lemma, the edges of $T$ which are not part of a path connect an endpoint of a path (which is colored red) to another vertex (which must be blue, because the red vertices are independent). Thus the coloring of the paths extends to the unique 2 -coloring of $T$. The leaves of $T$ are endpoints of paths, so they are all red.
|
| 554 |
-
|
| 555 |
-
## §2.3 TSTST 2021/6, proposed by Nikolai Beluhov
|
| 556 |
-
|
| 557 |
-
Available online at https://aops.com/community/p23864189.
|
| 558 |
-
|
| 559 |
-
## Problem statement
|
| 560 |
-
|
| 561 |
-
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly.
|
| 562 |
-
(a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel.
|
| 563 |
-
(b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
| 564 |
-
|
| 565 |
-
|
| 566 |
-
Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly.
|
| 567 |
-
|
| 568 |
-
I Part (a). All solutions to part (a) will prove the stronger claim that
|
| 569 |
-
|
| 570 |
-
$$
|
| 571 |
-
\left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right)
|
| 572 |
-
$$
|
| 573 |
-
|
| 574 |
-
The four lines will concur at the homothetic center of these figures (possibly at infinity).
|
| 575 |
-
Solution 1 (author) Let the second tangent to $\omega$ parallel to $E F$ meet lines $A B$ and $A C$ at $P$ and $Q$, respectively, and let the second tangent to $\omega$ parallel to $B C$ meet lines $D E$ and $D F$ at $R$ and $S$, respectively. Furthermore, let $\omega$ touch $P Q$ and $R S$ at $U$ and $V$, respectively.
|
| 576 |
-
|
| 577 |
-
Let $h$ be inversion with respect to $\omega$. Then $h$ maps $A, B$, and $C$ onto the midpoints of the sides of triangle $D_{1} E_{1} F_{1}$. So $h$ maps $k$ onto the Euler circle of triangle $D_{1} E_{1} F_{1}$.
|
| 578 |
-
Similarly, $h$ maps $k$ onto the Euler circle of triangle $A_{1} B_{1} C_{1}$. Therefore, triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$ share a common nine-point circle $\gamma$. Let $K$ be its center; its radius equals $\frac{1}{2} r$.
|
| 579 |
-
|
| 580 |
-
Let $H$ be the reflection of $I$ in $K$. Then $H$ is the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$.
|
| 581 |
-
|
| 582 |
-
Let $\gamma_{U}$ of center $K_{U}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $U E_{1} F_{1}$, and let $\gamma_{V}$ of center $K_{V}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $V B_{1} C_{1}$.
|
| 583 |
-
|
| 584 |
-
Let $H_{U}$ be the orthocenter of triangle $U E_{1} F_{1}$. Since quadrilateral $D_{1} E_{1} F_{1} U$ is cyclic, vectors $\overrightarrow{H H_{U}}$ and $\overrightarrow{D_{1} U}$ are equal. Consequently, $\overrightarrow{K K_{U}}=\frac{1}{2} \overrightarrow{D_{1} U}$. Similarly, $\overrightarrow{K K_{V}}=$ $\frac{1}{2} \overrightarrow{A_{1} V}$.
|
| 585 |
-
Since both of $A_{1} U$ and $D_{1} V$ are diameters in $\omega$, vectors $\overrightarrow{D_{1} U}$ and $\overrightarrow{A_{1} V}$ are equal. Therefore, $K_{U}$ and $K_{V}$ coincide, and so do $\gamma_{U}$ and $\gamma_{V}$.
|
| 586 |
-
|
| 587 |
-
As above, $h$ maps $\gamma_{U}$ onto the circumcircle of triangle $A P Q$ and $\gamma_{V}$ onto the circumcircle of triangle $D R S$. Therefore, triangles $A P Q$ and $D R S$ are inscribed inside the same circle $\Omega_{A D}$.
|
| 588 |
-
|
| 589 |
-
Since $E F$ and $P Q$ are parallel, triangles $\Delta_{A}$ and $A P Q$ are homothetic, and so are figures $\Omega_{A} \cup \omega_{A}$ and $\Omega_{A D} \cup \omega$. Consequently, we have
|
| 590 |
-
|
| 591 |
-
$$
|
| 592 |
-
\left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right),
|
| 593 |
-
$$
|
| 594 |
-
|
| 595 |
-
which solves part (a).
|
| 596 |
-
Solution 2 (Michael Ren) As in the previous solution, let the second tangent to $\omega$ parallel to $E F$ meet $A B$ and $A C$ at $P$ and $Q$, respectively. Let $(A P Q)$ meet $\Omega$ again at $D^{\prime}$, so that $D^{\prime}$ is the Miquel point of $\{A B, A C, B C, P Q\}$. Since the quadrilateral formed by these lines has incircle $\omega$, it is classical that $D^{\prime} I$ bisects $\angle P D^{\prime} C$ and $B D^{\prime} Q$ (e.g. by DDIT).
|
| 597 |
-
|
| 598 |
-
Let $\ell$ be the tangent to $\Omega$ at $D^{\prime}$ and $D^{\prime} I$ meet $\Omega$ again at $M$. We have
|
| 599 |
-
|
| 600 |
-
$$
|
| 601 |
-
\measuredangle\left(\ell, D^{\prime} B\right)=\measuredangle D^{\prime} C B=\measuredangle D^{\prime} Q P=\measuredangle\left(D^{\prime} Q, E F\right) .
|
| 602 |
-
$$
|
| 603 |
-
|
| 604 |
-
Therefore $D^{\prime} I$ also bisects the angle between $\ell$ and the line parallel to $E F$ through $D^{\prime}$. This means that $M$ is one of the arc midpoints of $E F$. Additionally, $D^{\prime}$ lies on $\operatorname{arc} B C$ not containing $A$, so $D^{\prime}=D$.
|
| 605 |
-
|
| 606 |
-
Similarly, letting the second tangent to $\omega$ parallel to $B C$ meet $D E$ and $D F$ again at $R$ and $S$, we have $A D R S$ cyclic.
|
| 607 |
-
|
| 608 |
-
## Lemma
|
| 609 |
-
|
| 610 |
-
There exists a circle $\Omega_{A D}$ tangent to $\Omega_{A}$ and $\Omega_{D}$ at $A$ and $D$, respectively.
|
| 611 |
-
|
| 612 |
-
Proof. (This step is due to Ankan Bhattacharya.) It is equivalent to have $\measuredangle O A O_{A}=$ $\measuredangle O_{D} D O$. Taking isogonals with respect to the shared angle of $\triangle A B C$ and $\Delta_{A}$, we see that
|
| 613 |
-
|
| 614 |
-
$$
|
| 615 |
-
\measuredangle O A O_{A}=\measuredangle(\perp E F, \perp B C)=\measuredangle(E F, B C) .
|
| 616 |
-
$$
|
| 617 |
-
|
| 618 |
-
(Here, $\perp E F$ means the direction perpendicular to $E F$.) By symmetry, this is equal to $\measuredangle O_{D} D O$.
|
| 619 |
-
|
| 620 |
-
The circle $(A D P Q)$ passes through $A$ and $D$, and is tangent to $\Omega_{A}$ by homothety. Therefore it coincides with $\Omega_{A D}$, as does ( $A D R S$ ). Like the previous solution, we finish with
|
| 621 |
-
|
| 622 |
-
$$
|
| 623 |
-
\left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) .
|
| 624 |
-
$$
|
| 625 |
-
|
| 626 |
-
Solution 3 (Andrew Gu) Construct triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$ (with positive ratio) which have the same circumcircle; it suffices to show that these copies have the same incircle as well. Let $O$ be the center of this common circumcircle, which we take to be the origin, and $M_{X Y}$ denote the point on the circle such that the tangent at that point is parallel to line $X Y$ (from the two possible choices, we make the choice that corresponds to the arc midpoint on $\Omega$, e.g. $M_{A B}$ should correspond to the arc midpoint on the internal angle bisector of $A C B$ ). The left diagram below shows the original triangles $A B C$ and $D E F$, while the right diagram shows the triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$.
|
| 627 |
-
|
| 628 |
-
|
| 629 |
-
Using the fact that the incenter is the orthocenter of the arc midpoints, the incenter of $\Delta_{A}$ in this reference frame is $M_{A B}+M_{A C}-M_{E F}$ and the incenter of $\Delta_{D}$ in this reference frame is $M_{D E}+M_{D F}-M_{B C}$. Since $A B C$ and $D E F$ share a common incenter, we have
|
| 630 |
-
|
| 631 |
-
$$
|
| 632 |
-
M_{A B}+M_{B C}+M_{C A}=M_{D E}+M_{E F}+M_{F D}
|
| 633 |
-
$$
|
| 634 |
-
|
| 635 |
-
Thus the copies of $\Delta_{A}$ and $\Delta_{D}$ have the same incenter, and therefore the same incircle as well (Euler's theorem determines the inradius).
|
| 636 |
-
|
| 637 |
-
【 Part (b). We present several solutions for this part of the problem. Solutions 3 and 4 require solving part (a) first, while the others do not. Solutions 1,4 , and 5 define $T_{A}$ solely as the exsimilicenter of $\omega_{A}$ and $\omega_{D}$, whereas solutions 2 and 3 define $T_{A}$ solely as the exsimilicenter of $\Omega_{A}$ and $\Omega_{D}$.
|
| 638 |
-
|
| 639 |
-
Solution 1 (author) By Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Therefore, $T_{A}=A D \cap I_{A} I_{D}$.
|
| 640 |
-
|
| 641 |
-
Let $p$ be pole-and-polar correspondence with respect to $\omega$. Then $p$ maps $A$ onto line $E_{1} F_{1}$ and $D$ onto line $B_{1} C_{1}$. Consequently, $p$ maps line $A D$ onto $X_{A}=B_{1} C_{1} \cap E_{1} F_{1}$.
|
| 642 |
-
|
| 643 |
-
Furthermore, $p$ maps the line that bisects the angle formed by lines $A B$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} F_{1}$. Similarly, $p$ maps the line that bisects the angle formed by lines $A C$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} E_{1}$. So $p$ maps $I_{A}$ onto the midline of triangle $A_{1} E_{1} F_{1}$ opposite $A_{1}$. Similarly, $p$ maps $I_{D}$ onto the midline of triangle $D_{1} B_{1} C_{1}$ opposite $D_{1}$. Consequently, $p$ maps line
|
| 644 |
-
$I_{A} I_{D}$ onto the intersection point $Y_{A}$ of this pair of midlines, and $p$ maps $T_{A}$ onto line $X_{A} Y_{A}$.
|
| 645 |
-
|
| 646 |
-
As in the solution to part (a), let $H$ be the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$. Let $H_{A}$ be the foot of the altitude from $A_{1}$ in triangle $A_{1} B_{1} C_{1}$ and let $H_{D}$ be the foot of the altitude from $D_{1}$ in triangle $D_{1} E_{1} F_{1}$. Furthermore, let $L_{A}=H A_{1} \cap E_{1} F_{1}$ and $L_{D}=H D_{1} \cap B_{1} C_{1}$.
|
| 647 |
-
|
| 648 |
-
Since the reflection of $H$ in line $B_{1} C_{1}$ lies on $\omega, A_{1} H \cdot H H_{A}$ equals half the power of $H$ with respect to $\omega$. Similarly, $D_{1} H \cdot H H_{D}$ equals half the power of $H$ with respect to $\omega$.
|
| 649 |
-
|
| 650 |
-
Then $A_{1} H \cdot H H_{A}=D_{1} H \cdot H H_{D}$ and $A_{1} H H_{D} \sim D_{1} H H_{A}$. Since $\angle H H_{D} L_{A}=90^{\circ}=$ $\angle H H_{A} L_{D}$, figures $A_{1} H H_{D} L_{A}$ and $D_{1} H H_{A} L_{D}$ are similar as well. Consequently,
|
| 651 |
-
|
| 652 |
-
$$
|
| 653 |
-
\frac{H L_{A}}{L_{A} A_{1}}=\frac{H L_{D}}{L_{D} D_{1}}=s
|
| 654 |
-
$$
|
| 655 |
-
|
| 656 |
-
as a signed ratio.
|
| 657 |
-
Let the line through $A_{1}$ parallel to $E_{1} F_{1}$ and the line through $D_{1}$ parallel to $B_{1} C_{1}$ meet at $Z_{A}$. Then $H X_{A} / X_{A} Z_{A}=s$ and $Y_{A}$ is the midpoint of segment $X_{A} Z_{A}$. Therefore, $H$ lies on line $X_{A} Y_{A}$. This means that $T_{A}$ lies on the polar of $H$ with respect to $\omega$, and by symmetry so do $T_{B}$ and $T_{C}$.
|
| 658 |
-
|
| 659 |
-
Solution 2 (author) As in the first solution to part (a), let $h$ be inversion with respect to $\omega$, let $\gamma$ of center $K$ be the common Euler circle of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$, and let $H$ be their common orthocenter.
|
| 660 |
-
|
| 661 |
-
Again as in the solution to part (a), $h$ maps $\Omega_{A}$ onto the nine-point circle $\gamma_{A}$ of triangle $A_{1} E_{1} F_{1}$ and $\Omega_{D}$ onto the nine-point circle $\gamma_{D}$ of triangle $D_{1} B_{1} C_{1}$.
|
| 662 |
-
|
| 663 |
-
Let $K_{A}$ and $K_{D}$ be the centers of $\gamma_{A}$ and $\gamma_{D}$, respectively, and let $\ell_{A}$ be the perpendicular bisector of segment $K_{A} K_{D}$. Since $\gamma_{A}$ and $\gamma_{D}$ are congruent (both of them are of radius $\left.\frac{1}{2} r\right)$, they are reflections of each other across $\ell_{A}$.
|
| 664 |
-
|
| 665 |
-
Inversion $h$ maps the two common external tangents of $\Omega_{A}$ and $\Omega_{D}$ onto the two circles $\alpha$ and $\beta$ through $I$ that are tangent to both of $\gamma_{A}$ and $\gamma_{D}$ in the same way. (That is, either internally to both or externally to both.) Consequently, $\alpha$ and $\beta$ are reflections of each other in $\ell_{A}$ and so their second point of intersection $S_{A}$, which $h$ maps $T_{A}$ onto, is the reflection of $I$ in $\ell_{A}$.
|
| 666 |
-
|
| 667 |
-
Define $\ell_{B}, \ell_{C}, S_{B}$, and $S_{C}$ similarly. Then $S_{B}$ is the reflection of $I$ in $\ell_{B}$ and $S_{C}$ is the reflection of $I$ in $\ell_{C}$.
|
| 668 |
-
|
| 669 |
-
As in the solution to part (a), $\overrightarrow{K K_{A}}=\frac{1}{2} \overrightarrow{D_{1} A_{1}}$ and $\overrightarrow{K K_{D}}=\frac{1}{2} \overrightarrow{A_{1} D_{1}}$. Consequently, $K$ is the midpoint of segment $K_{A} K_{D}$ and so $K$ lies on $\ell_{A}$. Similarly, $K$ lies on $\ell_{B}$ and $\ell_{C}$.
|
| 670 |
-
|
| 671 |
-
Therefore, all four points $I, S_{A}, S_{B}$, and $S_{C}$ lie on the circle of center $K$ that contains $I$. (This is also the circle on diameter $I H$.) Since points $S_{A}, S_{B}$, and $S_{C}$ are concyclic with $I$, their images $T_{A}, T_{B}$, and $T_{C}$ under $h$ are collinear, and the solution is complete.
|
| 672 |
-
|
| 673 |
-
Solution 3 (Ankan Bhattacharya) From either of the first two solutions to part (a), we know that there is a circle $\Omega_{A D}$ passing through $A$ and $D$ which is (internally) tangent to $\Omega_{A}$ and $\Omega_{D}$. By Monge's theorem applied to $\Omega_{A}, \Omega_{D}$, and $\Omega_{A D}$, it follows that $A, D$, and $T_{A}$ are collinear.
|
| 674 |
-
|
| 675 |
-
The inversion at $T_{A}$ swapping $\Omega_{A}$ with $\Omega_{D}$ also swaps $A$ with $D$ because $T_{A}$ lies on $A D$ and $A$ is not homologous to $D$. Let $\Omega_{A}$ and $\Omega_{D}$ meet $\Omega$ again at $L_{A}$ and $L_{D}$. Since $A D L_{A} L_{D}$ is cyclic, the same inversion at $T_{A}$ also swaps $L_{A}$ and $L_{D}$, so $T_{A}=A D \cap L_{A} L_{D}$.
|
| 676 |
-
|
| 677 |
-
By Taiwan TST 2014, $L_{A}$ and $L_{D}$ are the tangency points of the $A$-mixtilinear and $D$-mixtilinear incircles, respectively, with $\Omega$. Therefore $A L_{A} \cap D L_{D}$ is the exsimilicenter $X$ of $\Omega$ and $\omega$. Then $T_{A}, T_{B}$, and $T_{C}$ all lie on the polar of $X$ with respect to $\Omega$.
|
| 678 |
-
|
| 679 |
-
Solution 4 (Andrew Gu) We show that $T_{A}$ lies on the radical axis of the point circle at $I$ and $\Omega$, which will solve the problem. Let $I_{A}$ and $I_{D}$ be the centers of $\omega_{A}$ and $\omega_{D}$ respectively. By the Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Additionally, these other triples are collinear: $\left(A, I_{A}, I\right),\left(D, I_{D}, I\right),\left(I_{A}, I_{D}, T\right)$. By Menelaus's theorem, we have
|
| 680 |
-
|
| 681 |
-
$$
|
| 682 |
-
\frac{T_{A} D}{T_{A} A}=\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} .
|
| 683 |
-
$$
|
| 684 |
-
|
| 685 |
-
If $s$ is the length of the side opposite $A$ in $\Delta_{A}$, then we compute
|
| 686 |
-
|
| 687 |
-
$$
|
| 688 |
-
\begin{aligned}
|
| 689 |
-
\frac{I_{A} I}{I_{A} A} & =\frac{s / \cos (A / 2)}{r_{A} / \sin (A / 2)} \\
|
| 690 |
-
& =\frac{2 R_{A} \sin (A) \sin (A / 2)}{\cos (A / 2)} \\
|
| 691 |
-
& =\frac{4 R_{A} \sin ^{2}(A / 2)}{r_{A}} \\
|
| 692 |
-
& =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} .
|
| 693 |
-
\end{aligned}
|
| 694 |
-
$$
|
| 695 |
-
|
| 696 |
-
From part (a), we know that $\frac{R_{A}}{r_{A}}=\frac{R_{D}}{r_{D}}$. Therefore, doing a similar calculation for $\frac{I_{D} D}{I_{D} I}$, we get
|
| 697 |
-
|
| 698 |
-
$$
|
| 699 |
-
\begin{aligned}
|
| 700 |
-
\frac{T_{A} D}{T_{A} A} & =\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} \\
|
| 701 |
-
& =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} \cdot \frac{r_{D} D I^{2}}{4 R_{D} r^{2}} \\
|
| 702 |
-
& =\frac{D I^{2}}{A I^{2}}
|
| 703 |
-
\end{aligned}
|
| 704 |
-
$$
|
| 705 |
-
|
| 706 |
-
Thus $T_{A}$ is the point where the tangent to $(A I D)$ at $I$ meets $A D$ and $T_{A} I^{2}=T_{A} A \cdot T_{A} D$. This shows what we claimed at the start.
|
| 707 |
-
|
| 708 |
-
Solution 5 (Ankit Bisain) As in the previous solution, it suffices to show that $\frac{I_{A} I}{A I_{A}} \cdot \frac{D I_{D}}{I_{D} I}=\frac{D I^{2}}{A I^{2}}$. Let $A I$ and $D I$ meet $\Omega$ again at $M$ and $N$, respectively. Let $\ell$ be the line parallel to $B C$ and tangent to $\omega$ but different from $B C$. Then
|
| 709 |
-
|
| 710 |
-
$$
|
| 711 |
-
\frac{D I_{D}}{I_{D} I}=\frac{d(D, B C)}{d(B C, \ell)}=\frac{D B \cdot D C / 2 R}{2 r}=\frac{M I^{2}-M D^{2}}{4 R r}
|
| 712 |
-
$$
|
| 713 |
-
|
| 714 |
-
Since $I D M \sim I A N$, we have
|
| 715 |
-
|
| 716 |
-
$$
|
| 717 |
-
\frac{D I_{D}}{I_{D} I} \cdot \frac{I_{A} I}{A I_{A}}=\frac{M I^{2}-M D^{2}}{N I^{2}-N A^{2}}=\frac{D I^{2}}{A I^{2}}
|
| 718 |
-
$$
|
| 719 |
-
|
| 720 |
-
as desired.
|
| 721 |
-
Remark (Author comments on generalization of part (b) with a circumscribed hexagram). Let triangles $A B C$ and $D E F$ be circumscribed about the same circle $\omega$ so that they form a hexagram. However, we do not require anymore that they are inscribed in the same circle.
|
| 722 |
-
|
| 723 |
-
Define circles $\Omega_{A}, \omega_{A}, \ldots, \omega_{F}$ as in the problem. Let $T_{A}^{\text {Circ }}$ be the intersection point of the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$, and define points $T_{B}^{\text {Circ }}$ and $T_{C}^{\text {Circ }}$ similarly. Also let $T_{A}^{\text {In }}$ be the intersection point of the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$, and define points $T_{B}^{\mathrm{In}}$ and $T_{C}^{\mathrm{In}}$ similarly.
|
| 724 |
-
|
| 725 |
-
Then points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\mathrm{Circ}}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear.
|
| 726 |
-
|
| 727 |
-
The second solution to part (b) of the problem works also for the circumcircles part of the generalisation. To see that segments $K_{A} K_{D}, K_{B} K_{E}$, and $K_{C} K_{F}$ still have a common midpoint, let $M$ be the centroid of points $A, B, C, D, E$, and $F$. Then the midpoint of segment $K_{A} K_{D}$ divides segment $O M$ externally in ratio $3: 1$, and so do the other two midpoints as well.
|
| 728 |
-
|
| 729 |
-
For the incircles part of the generalisation, we start out as in the first solution to part (b) of the problem, and eventually we reduce everything to the following:
|
| 730 |
-
|
| 731 |
-
Let points $A_{1}, B_{1}, C_{1}, D_{1}, E_{1}$, and $F_{1}$ lie on circle $\omega$. Let lines $B_{1} C_{1}$ and $E_{1} F_{1}$ meet at point $X_{A}$, let the line through $A_{1}$ parallel to $B_{1} C_{1}$ and the line through $D_{1}$ parallel to $E_{1} F_{1}$ meet at point $Z_{A}$, and define points $X_{B}, Z_{B}, X_{C}$, and $Z_{C}$ similarly. Then lines $X_{A} Z_{A}$, $X_{B} Z_{B}$, and $X_{C} Z_{C}$ are concurrent.
|
| 732 |
-
|
| 733 |
-
Take $\omega$ as the unit circle and assign complex numbers $u, v, w, x, y$, and $z$ to points $A_{1}$, $F_{1}, B_{1}, D_{1}, C_{1}$, and $E_{1}$, respectively, so that when we permute $u, v, w, x, y$, and $z$ cyclically the configuration remains unchanged. Then by standard complex bash formulas we obtain that each two out of our three lines meet at $\varphi / \psi$, where
|
| 734 |
-
|
| 735 |
-
$$
|
| 736 |
-
\varphi=\sum_{\mathrm{Cyc}} u^{2} v w(w x-w y+x y)(y-z)
|
| 737 |
-
$$
|
| 738 |
-
|
| 739 |
-
and
|
| 740 |
-
|
| 741 |
-
$$
|
| 742 |
-
\psi=-u^{2} w^{2} y^{2}-v^{2} x^{2} z^{2}-4 u v w x y z+\sum_{\mathrm{Cyc}} u^{2}(v w x y-v w x z+v w y z-v x y z+w x y z)
|
| 743 |
-
$$
|
| 744 |
-
|
| 745 |
-
(But the calculations were too difficult for me to do by hand, so I used SymPy.)
|
| 746 |
-
|
| 747 |
-
Remark (Author comments on generalization of part (b) with an inscribed hexagram). Let triangles $A B C$ and $D E F$ be inscribed inside the same circle $\Omega$ so that they form a hexagram. However, we do not require anymore that they are circumscribed about the same circle.
|
| 748 |
-
|
| 749 |
-
Define points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}, \ldots, T_{C}^{\mathrm{In}}$ as in the previous remark. It looks like once again points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. However, I do not have proofs of these claims.
|
| 750 |
-
|
| 751 |
-
Remark (Further generalization from Andrew Gu). Let $A B C$ and $D E F$ be triangles which share an inconic, or equivalently share a circumconic. Define points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}, \ldots, T_{C}^{\mathrm{In}}$ as in the previous remarks. Then it is conjectured that points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. (Note that extraversion may be required depending on the configuration of points, e.g. excircles instead of incircles.) Additionally, it appears that the insimilicenters of the circumcircles lie on a line perpendicular to the line through $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$.
|
| 752 |
-
|
| 753 |
-
## §3 Solutions to Day 3
|
| 754 |
-
|
| 755 |
-
## §3.1 TSTST 2021/7, proposed by Ankit Bisain, Holden Mui
|
| 756 |
-
|
| 757 |
-
Available online at https://aops.com/community/p24130213.
|
| 758 |
-
|
| 759 |
-
## Problem statement
|
| 760 |
-
|
| 761 |
-
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
| 762 |
-
|
| 763 |
-
We present two approaches.
|
| 764 |
-
|
| 765 |
-
�� Solution 1. We prove the statement by induction on $n$. We use $n=0$ as a base case, where the statement follows from $1 \geq 2^{-|M|}$. For the inductive step, let $n>0$. There exists at least one mine-avoiding path, which must pass through either $(0,1)$ or $(1,0)$. We consider two cases:
|
| 766 |
-
|
| 767 |
-
Case 1: there exist mine-avoiding paths starting at both $(1,0)$ and $(0,1)$.
|
| 768 |
-
By the inductive hypothesis, there are at least $2^{n-1-|M|}$ mine-avoiding paths starting from each of $(1,0)$ and $(0,1)$. Then the total number of mine-avoiding paths is at least $2^{n-1-|M|}+2^{n-1-|M|}=2^{n-|M|}$.
|
| 769 |
-
|
| 770 |
-
Case 2: only one of $(1,0)$ and $(0,1)$ is on a mine-avoiding path.
|
| 771 |
-
Without loss of generality, suppose no mine-avoiding path starts at $(0,1)$. Then some element of $M$ must be of the form $(0, k)$ for $1 \leq k \leq n$ in order to block the path along the $y$-axis. This element can be ignored for any mine-avoiding path starting at (1,0). By the inductive hypothesis, there are at least $2^{n-1-(|M|-1)}=2^{n-|M|}$ mine-avoiding paths.
|
| 772 |
-
|
| 773 |
-
This completes the induction step, which solves the problem.
|
| 774 |
-
|
| 775 |
-
## 【 Solution 2.
|
| 776 |
-
|
| 777 |
-
## Lemma
|
| 778 |
-
|
| 779 |
-
If $|M|<n$, there is more than one mine-avoiding path.
|
| 780 |
-
|
| 781 |
-
Proof. Let $P_{0}, P_{1}, \ldots, P_{n}$ be a mine-avoiding path. Set $P_{i}=\left(x_{i}, y_{i}\right)$. For $0 \leq i<n$, define a path $Q_{i}$ as follows:
|
| 782 |
-
|
| 783 |
-
- Make the first $i+1$ points $P_{0}, P_{1}, \ldots, P_{i}$.
|
| 784 |
-
- If $P_{i} \rightarrow P_{i+1}$ is one unit up, go right until $\left(n-y_{i}, y_{i}\right)$.
|
| 785 |
-
- If $P_{i} \rightarrow P_{i+1}$ is one unit right, go up until $\left(x_{i}, n-x_{i}\right)$.
|
| 786 |
-
|
| 787 |
-
|
| 788 |
-
The diagram above is an example for $n=5$ with the new segments formed by the $Q_{i}$ in red, and the line $x+y=n$ in blue.
|
| 789 |
-
|
| 790 |
-
By definition, $M$ has less than $n$ points, none of which are in the original path. Since all $Q_{i}$ only intersect in the original path, each mine is in at most one of $Q_{0}, Q_{1}, \ldots, Q_{n-1}$. By the Pigeonhole Principle, one of the $Q_{i}$ is mine-avoiding.
|
| 791 |
-
|
| 792 |
-
Now, consider the following process:
|
| 793 |
-
|
| 794 |
-
- Start at $(0,0)$.
|
| 795 |
-
- If there is only one choice of next step that is part of a mine-avoiding path, make that choice.
|
| 796 |
-
- Repeat the above until at a point with two possible steps that are part of mineavoiding paths.
|
| 797 |
-
- Add a mine to the choice of next step with more mine-avoiding paths through it. If both have the same number of mine-avoiding paths through them, add a mine arbitrarily.
|
| 798 |
-
|
| 799 |
-
|
| 800 |
-
For instance, consider the above diagram for $n=4$. Lattice points are replaced with squares. Mines are black squares and each non-mine is labelled with the number of mine-avoiding paths passing through it. This process would start at $(0,0)$, go to $(1,0)$, then place a mine at $(1,1)$.
|
| 801 |
-
|
| 802 |
-
This path increases the size of $M$ by one, and reduces the number of mine-avoiding paths to a nonzero number at most half of the original. Repeat this process until there is only one path left. By our lemma, the number of mines must be at least $n$ by the end of the process, so the process was iterated at least $n-|M|$ times. By the halving property, there must have been at least $2^{n-|M|}$ mine-avoiding paths before the process, as desired.
|
| 803 |
-
|
| 804 |
-
## §3.2 TSTST 2021/8, proposed by Fedir Yudin
|
| 805 |
-
|
| 806 |
-
Available online at https://aops.com/community/p24130228.
|
| 807 |
-
|
| 808 |
-
## Problem statement
|
| 809 |
-
|
| 810 |
-
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
| 811 |
-
|
| 812 |
-
We give three solutions.
|
| 813 |
-
ब Solution 1 (author). We'll use the following lemma.
|
| 814 |
-
|
| 815 |
-
## Lemma
|
| 816 |
-
|
| 817 |
-
Suppose that $P Q R S$ is a convex quadrilateral with $\angle P=\angle R$. Then there is a point $T$ on $Q S$ such that $\angle Q P T=\angle S R P, \angle T R Q=\angle R P S$, and $P T=R T$.
|
| 818 |
-
|
| 819 |
-
Before proving the lemma, we will show how it solves the problem. The lemma applied for the quadrilateral $A B_{1} A_{1} C_{1}$ with $\angle A=\angle A_{1}$ shows that $\angle B_{1} A_{1} A_{2}=\angle C_{1} A A_{1}$. This implies that the point $A_{2}$ in $\triangle A_{1} B_{1} C_{1}$ corresponds to the point $A_{1}$ in $\triangle A B C$. Then $\triangle A_{2} B_{2} C_{2} \sim \triangle A_{1} B_{1} C_{1} \sim \triangle A B C$, as desired.
|
| 820 |
-
|
| 821 |
-
Additionally, $P T=R T$ is a corollary of the angle conditions because
|
| 822 |
-
|
| 823 |
-
$$
|
| 824 |
-
\measuredangle P R T=\measuredangle S R Q-\measuredangle T R Q-\measuredangle S R P=\measuredangle Q P S-\measuredangle R P S-\measuredangle Q P T=\measuredangle T P R
|
| 825 |
-
$$
|
| 826 |
-
|
| 827 |
-
Therefore we only need to prove the angle conditions.
|
| 828 |
-
Proof 1 of lemma Denote $X=P Q \cap R S$ and $Y=P S \cap R Q$. Note that $\angle X P Y=$ $\angle X R Y$, so $P R X Y$ is cyclic. Let $T$ be the point of intersection of tangents to this circle at $P$ and $R$. By Pascal's theorem for the degenerate hexagon $P P X R R Y$, we have $T \in Q S$ (alternatively, $Q, S$, and $T$ are collinear on the pole of $P R \cap X Y$ with respect to the circle). Also, $\measuredangle Q P T=\measuredangle X R P=\measuredangle S R P$ and similarly $\measuredangle T R Q=\measuredangle R P Y=\measuredangle R P S$, so we're done.
|
| 829 |
-
|
| 830 |
-
|
| 831 |
-
Proof 2 of lemma Let $P^{\prime}$ and $R^{\prime}$ be the reflections of $P$ and $R$ in $Q S$. Note that $P R^{\prime}$ and $R P^{\prime}$ intersect at a point $X$ on $Q S$. Let $T$ be the second intersection of the circumcircle of $\triangle P R X$ with $Q S$. Note that
|
| 832 |
-
|
| 833 |
-
$$
|
| 834 |
-
\begin{aligned}
|
| 835 |
-
\measuredangle P X T & =\measuredangle R^{\prime} P Q+\measuredangle P Q S \\
|
| 836 |
-
& =\measuredangle R^{\prime} S Q+\measuredangle P Q S \\
|
| 837 |
-
& =\measuredangle Q S R+\measuredangle P Q S \\
|
| 838 |
-
& =\measuredangle(P Q, S R) \\
|
| 839 |
-
& =\measuredangle Q P R+\measuredangle P R S .
|
| 840 |
-
\end{aligned}
|
| 841 |
-
$$
|
| 842 |
-
|
| 843 |
-
This means that
|
| 844 |
-
|
| 845 |
-
$$
|
| 846 |
-
\begin{aligned}
|
| 847 |
-
\measuredangle Q P T & =\measuredangle Q P R-\measuredangle T P R \\
|
| 848 |
-
& =\measuredangle Q P R-\measuredangle T X R \\
|
| 849 |
-
& =\measuredangle Q P R-\measuredangle P X T \\
|
| 850 |
-
& =\measuredangle Q P R-\measuredangle Q P R-\measuredangle P R S \\
|
| 851 |
-
& =\measuredangle S R P .
|
| 852 |
-
\end{aligned}
|
| 853 |
-
$$
|
| 854 |
-
|
| 855 |
-
Similarly, $\measuredangle Q R T=\measuredangle S P R$, so we're done.
|
| 856 |
-
|
| 857 |
-
|
| 858 |
-
Proof 3 of lemma Let $T$ be the point on $Q S$ such that $\angle Q P T=\angle S R P$. Then we have
|
| 859 |
-
|
| 860 |
-
$$
|
| 861 |
-
\frac{Q T}{T S}=\frac{\sin Q P T \cdot P T / \sin P Q T}{\sin T P S \cdot P T / \sin T S P}=\frac{P Q / \sin P R Q}{P S / \sin S R P}=\frac{R(\triangle P Q R)}{R(\triangle P R S)}
|
| 862 |
-
$$
|
| 863 |
-
|
| 864 |
-
which is symmetric in $P$ and $R$, so we're done.
|
| 865 |
-
|
| 866 |
-
Solution 2 (Ankan Bhattacharya). We prove the main claim $\frac{B_{1} A_{2}}{A_{2} C_{1}}=\frac{B A_{1}}{A_{1} C}$.
|
| 867 |
-
Let $\triangle A_{0} B_{0} C_{0}$ be the medial triangle of $\triangle A B C$. In addition, let $A_{1}^{\prime}$ be the reflection of $A_{1}$ over $\overline{B_{1} C_{1}}$, and let $X$ be the point satisfying $\triangle X B C \approx \triangle A B_{1} C_{1}$, so that we have a compound similarity
|
| 868 |
-
|
| 869 |
-
$$
|
| 870 |
-
\triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A .
|
| 871 |
-
$$
|
| 872 |
-
|
| 873 |
-
Finally, let $O_{A}$ be the circumcenter of $\triangle A_{1}^{\prime} B_{1} C_{1}$, and let $A_{2}^{*}$ be the point on $\overline{B_{1} C_{1}}$ satisfying $\frac{B_{1} A_{2}^{*}}{A_{2}^{*} C_{1}}=\frac{B A_{1}}{A_{1} C}$.
|
| 874 |
-
|
| 875 |
-
Recall that $O$ is the Miquel point of $\triangle A_{1} B_{1} C_{1}$, as well as its orthocenter.
|
| 876 |
-
|
| 877 |
-
Claim $-\overline{A A_{1}^{\prime}} \| \overline{B C}$.
|
| 878 |
-
Proof. We need to verify that the foot from $A_{1}$ to $\overline{B_{1} C_{1}}$ lies on the $A$-midline. This follows from the fact that $O$ is both the Miquel point and the orthocenter.
|
| 879 |
-
|
| 880 |
-
$$
|
| 881 |
-
\text { Claim }-\overline{A X} \| \overline{B_{1} C_{1}} .
|
| 882 |
-
$$
|
| 883 |
-
|
| 884 |
-
Proof. From the compound similarity,
|
| 885 |
-
|
| 886 |
-
$$
|
| 887 |
-
\measuredangle(\overline{B C}, \overline{A X})=\measuredangle\left(\overline{A A_{1}^{\prime}}, \overline{B_{1} C_{1}}\right) .
|
| 888 |
-
$$
|
| 889 |
-
|
| 890 |
-
As $\overline{A A_{1}^{\prime}} \| \overline{B C}$, we obtain $\overline{A X} \| \overline{B_{1} C_{1}}$.
|
| 891 |
-
|
| 892 |
-
$$
|
| 893 |
-
\text { Claim }-\overline{A X} \perp \overline{A_{1} O} .
|
| 894 |
-
$$
|
| 895 |
-
|
| 896 |
-
Proof. Because $O$ is the orthocenter of $\triangle A_{1} B_{1} C_{1}$.
|
| 897 |
-
|
| 898 |
-
$$
|
| 899 |
-
\text { Claim }-\overline{A A_{1}^{\prime}} \perp \overline{A_{2}^{*} O_{A}}
|
| 900 |
-
$$
|
| 901 |
-
|
| 902 |
-
Proof. Follows from $\overline{A X} \perp \overline{A_{1} O}$ after the similarity
|
| 903 |
-
|
| 904 |
-
$$
|
| 905 |
-
\triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A .
|
| 906 |
-
$$
|
| 907 |
-
|
| 908 |
-
Claim $-A A_{2}^{*}=A_{1}^{\prime} A_{2}$.
|
| 909 |
-
Proof. Since $\measuredangle C_{1} A B_{1}=\measuredangle C_{1} A_{1}^{\prime} B_{1}, A O_{A}=A_{1}^{\prime} O_{A}$, so $\overline{A A_{1}^{\prime}} \perp \overline{A_{2}^{*} O_{A}}$ implies $A A_{2}^{*}=$ $A_{1}^{\prime} A_{2}^{*}$.
|
| 910 |
-
|
| 911 |
-
Finally, $A_{1}^{\prime} A_{2}^{*}=A_{1} A_{2}^{*}$ by reflections, so $A A_{2}^{*}=A_{1} A_{2}^{*}$, and $A_{2}^{*}=A_{2}$.
|
| 912 |
-
|
| 913 |
-
## §3.3 TSTST 2021/9, proposed by Victor Wang
|
| 914 |
-
|
| 915 |
-
Available online at https://aops.com/community/p24130243.
|
| 916 |
-
|
| 917 |
-
## Problem statement
|
| 918 |
-
|
| 919 |
-
Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\zeta=e^{\frac{2 \pi i}{q}}$. Find the least positive integer $n$ such that
|
| 920 |
-
|
| 921 |
-
$$
|
| 922 |
-
\sum_{\substack{1 \leq k \leq q \\ \operatorname{gcd}(k, p)=1}} \frac{1}{\left(1-\zeta^{k}\right)^{n}}
|
| 923 |
-
$$
|
| 924 |
-
|
| 925 |
-
is not an integer. (The sum is over all $1 \leq k \leq q$ with $p$ not dividing $k$.)
|
| 926 |
-
|
| 927 |
-
Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ).
|
| 928 |
-
|
| 929 |
-
【 Solution 1 (author). Let $\zeta_{p}=e^{2 \pi i / p}$ be a fixed primitive $p$ th root of unity. Observe that the given sum is an integer for all $n \leq 0$ (e.g. because the sum is an integer symmetric polynomial in the primitive $q$ th roots of unity). By expanding polynomials in the basis $(1-x)^{k}$, it follows that if the sum in the problem statement is an integer for all $n<n_{0}$, then
|
| 930 |
-
|
| 931 |
-
$$
|
| 932 |
-
\sum_{\omega \in S_{q}} \frac{f(\omega)}{(1-\omega)^{n}} \in \mathbb{Z}
|
| 933 |
-
$$
|
| 934 |
-
|
| 935 |
-
for all $n<n_{0}$ and $f \in \mathbb{Z}[x]$, whereas for $n=n_{0}$ there is some $f \in \mathbb{Z}[x]$ for which the sum is not an integer (e.g. $f=1$ ).
|
| 936 |
-
Let $z_{q}=r \phi(q)-q / p=p^{r-1}[r(p-1)-1]$. We claim that the answer is $n=z_{q}+1$. We prove this by induction on $r$. First is the base case $r=1$.
|
| 937 |
-
|
| 938 |
-
## Lemma
|
| 939 |
-
|
| 940 |
-
There exist polynomials $u, v \in \mathbb{Z}[x]$ such that $(1-\omega)^{p-1} / p=u(\omega)$ and $p /(1-\omega)^{p-1}=$ $v(\omega)$ for all $\omega \in S_{p}$.
|
| 941 |
-
(What we are saying is that $p$ is $(1-\omega)^{p-1}$ times a unit (invertible algebraic integer), namely $v(\omega)$.)
|
| 942 |
-
|
| 943 |
-
Proof. Note that $p=(1-\omega) \cdots\left(1-\omega^{p-1}\right)$. Thus we can write
|
| 944 |
-
|
| 945 |
-
$$
|
| 946 |
-
\frac{p}{(1-\omega)^{p-1}}=\frac{1-\omega}{1-\omega} \cdot \frac{1-\omega^{2}}{1-\omega} \cdots \frac{1-\omega^{p-1}}{1-\omega}
|
| 947 |
-
$$
|
| 948 |
-
|
| 949 |
-
and take
|
| 950 |
-
|
| 951 |
-
$$
|
| 952 |
-
v(x)=\prod_{k=1}^{p-1} \frac{1-x^{k}}{1-x}
|
| 953 |
-
$$
|
| 954 |
-
|
| 955 |
-
Similarly, the polynomial $u$ is
|
| 956 |
-
|
| 957 |
-
$$
|
| 958 |
-
u(x)=\prod_{k=1}^{p-1} \frac{1-x^{k \ell_{k}}}{1-x^{k}}
|
| 959 |
-
$$
|
| 960 |
-
|
| 961 |
-
where $\ell_{k}$ is a multiplicative inverse of $k$ modulo $p$.
|
| 962 |
-
Now, the main idea: given $g \in \mathbb{Z}[x]$, observe that
|
| 963 |
-
|
| 964 |
-
$$
|
| 965 |
-
S=\sum_{\omega \in S_{p}}(1-\omega) g(\omega)
|
| 966 |
-
$$
|
| 967 |
-
|
| 968 |
-
is divisible by $1-\zeta_{p}^{k}$ (i.e. it is $1-\zeta_{p}^{k}$ times an algebraic integer) for every $k$ coprime to $p$. By symmetric sums, $S$ is an integer; since $S^{p-1}$ is divisible by $\left(1-\zeta_{p}\right) \cdots\left(1-\zeta_{p}^{p-1}\right)=p$, the integer $S$ must itself be divisible by $p$. (Alternatively, since $h(x):=(1-x) g(x)$ vanishes at $x=1$, one can interpret $S$ using a roots of unity filter: $S=p \cdot h\left(\left[x^{0}\right]+\left[x^{p}\right]+\cdots\right) \equiv 0$ $(\bmod p)$.$) Now write$
|
| 969 |
-
|
| 970 |
-
$$
|
| 971 |
-
\mathbb{Z} \ni \frac{S}{p}=\sum_{\omega \in S_{p}} \frac{(1-\omega)^{p-1}}{p} \frac{g(\omega)}{(1-\omega)^{p-2}}=\sum_{\omega \in S_{p}} u(\omega) \frac{g(\omega)}{(1-\omega)^{p-2}} .
|
| 972 |
-
$$
|
| 973 |
-
|
| 974 |
-
Taking $g=v \cdot(1-x)^{k}$ for $k \geq 0$, we see that the sum in the problem statement is an integer for any $n \leq p-2$.
|
| 975 |
-
|
| 976 |
-
Finally, we have
|
| 977 |
-
|
| 978 |
-
$$
|
| 979 |
-
\sum_{\omega \in S_{p}} \frac{u(\omega)}{(1-\omega)^{p-1}}=\sum_{\omega \in S_{p}} \frac{1}{p}=\frac{p-1}{p} \notin \mathbb{Z}
|
| 980 |
-
$$
|
| 981 |
-
|
| 982 |
-
so the sum is not an integer for $n=p-1$.
|
| 983 |
-
Now let $r \geq 2$ and assume the induction hypothesis for $r-1$.
|
| 984 |
-
|
| 985 |
-
## Lemma
|
| 986 |
-
|
| 987 |
-
There exist polynomials $U, V \in \mathbb{Z}[x]$ such that $(1-\omega)^{p} /\left(1-\omega^{p}\right)=U(\omega)$ and $\left(1-\omega^{p}\right) /(1-\omega)^{p}=V(\omega)$ for all $\omega \in S_{q}$. (Again, these are units.)
|
| 988 |
-
|
| 989 |
-
Proof. Similarly to the previous lemma, we write $1-\omega^{p}=\left(1-\omega \zeta_{p}^{0}\right) \cdots\left(1-\omega \zeta_{p}^{p-1}\right)$. The polynomials $U$ and $V$ are
|
| 990 |
-
|
| 991 |
-
$$
|
| 992 |
-
\begin{aligned}
|
| 993 |
-
U(x) & =\prod_{k=1}^{p-1} \frac{1-x^{(k q / p+1) \ell_{k}}}{1-x^{k q / p+1}} \\
|
| 994 |
-
V(x) & =\prod_{k=1}^{p-1} \frac{1-x^{k q / p+1}}{1-x}
|
| 995 |
-
\end{aligned}
|
| 996 |
-
$$
|
| 997 |
-
|
| 998 |
-
where $\ell_{k}$ is a multiplicative inverse of $k q / p+1$ modulo $q$.
|
| 999 |
-
|
| 1000 |
-
## Corollary
|
| 1001 |
-
|
| 1002 |
-
If $\omega \in S_{q}$, then $(1-\omega)^{\phi(q)} / p$ is a unit.
|
| 1003 |
-
|
| 1004 |
-
Proof. Induct on $r$. For $r=1$, this is the first lemma. For the inductive step, we are given that $\left(1-\omega^{p}\right)^{\phi(q / p)} / p$ is a unit. By the second lemma, $(1-\omega)^{\phi(q)} /\left(1-\omega^{p}\right)^{\phi(q / p)}$ is also a unit. Multiplying these together yields another unit.
|
| 1005 |
-
|
| 1006 |
-
Thus we have polynomials $A, B \in \mathbb{Z}[x]$ such that
|
| 1007 |
-
|
| 1008 |
-
$$
|
| 1009 |
-
\begin{aligned}
|
| 1010 |
-
& A(\omega)=\frac{p}{(1-\omega)^{\phi(q)}} V(\omega)^{z_{q / p}} \\
|
| 1011 |
-
& B(\omega)=\frac{(1-\omega)^{\phi(q)}}{p} U(\omega)^{z_{q / p}}
|
| 1012 |
-
\end{aligned}
|
| 1013 |
-
$$
|
| 1014 |
-
|
| 1015 |
-
for all $\omega \in S_{q}$.
|
| 1016 |
-
Given $g \in \mathbb{Z}[x]$, consider the $p$ th roots of unity filter
|
| 1017 |
-
|
| 1018 |
-
$$
|
| 1019 |
-
S(x):=\sum_{k=0}^{p-1} g\left(\zeta_{p}^{k} x\right)=p \cdot h\left(x^{p}\right)
|
| 1020 |
-
$$
|
| 1021 |
-
|
| 1022 |
-
where $h \in \mathbb{Z}[x]$. Then
|
| 1023 |
-
|
| 1024 |
-
$$
|
| 1025 |
-
p h(\eta)=S(\omega)=\sum_{\omega^{p}=\eta} g(\omega)
|
| 1026 |
-
$$
|
| 1027 |
-
|
| 1028 |
-
for all $\eta \in S_{q / p}$, so
|
| 1029 |
-
|
| 1030 |
-
$$
|
| 1031 |
-
\begin{aligned}
|
| 1032 |
-
\frac{h(\eta)}{(1-\eta)^{z_{q / p}}}=\frac{S(\omega)}{p(1-\eta)^{z_{q / p}}} & =\sum_{\omega^{p}=\eta} \frac{(1-\omega)^{p z_{q / p}}}{\left(1-\omega^{p}\right)^{z_{q / p}}} \frac{g(\omega)}{p(1-\omega)^{p z_{q / p}}} \\
|
| 1033 |
-
& =\sum_{\omega^{p}=\eta} U(\omega)^{z_{q / p}} \frac{(1-\omega)^{\phi(q)}}{p} \frac{g(\omega)}{(1-\omega)^{z_{q}}}
|
| 1034 |
-
\end{aligned}
|
| 1035 |
-
$$
|
| 1036 |
-
|
| 1037 |
-
(Implicit in the last line is $z_{q}=\phi(q)+p z_{q / p}$.) Since $U(\omega)$ and $(1-\omega)^{\phi(q)} / p$ are units, we can let $g=A \cdot f$ for arbitrary $f \in \mathbb{Z}[x]$, so that the expression in the summation simplifies to $f(\omega) /(1-\omega)^{z_{q}}$. From this we conclude that for any $f \in \mathbb{Z}[x]$, there exists $h \in \mathbb{Z}[x]$ such that
|
| 1038 |
-
|
| 1039 |
-
$$
|
| 1040 |
-
\begin{aligned}
|
| 1041 |
-
\sum_{\omega \in S_{q}} \frac{f(\omega)}{(1-\omega)^{z_{q}}} & =\sum_{\eta \in S_{q / p}} \sum_{\omega^{p}=\eta} \frac{f(\omega)}{(1-\omega)^{z_{q}}} \\
|
| 1042 |
-
& =\sum_{\eta \in S_{q / p}} \frac{h(\eta)}{(1-\eta)^{z_{q / p}}}
|
| 1043 |
-
\end{aligned}
|
| 1044 |
-
$$
|
| 1045 |
-
|
| 1046 |
-
By the inductive hypothesis, this is always an integer.
|
| 1047 |
-
In the other direction, for $\eta \in S_{q / p}$ we have
|
| 1048 |
-
|
| 1049 |
-
$$
|
| 1050 |
-
\begin{aligned}
|
| 1051 |
-
\sum_{\omega^{p}=\eta} \frac{B(\omega)}{(1-\omega)^{1+z_{q}}} & =\sum_{\omega^{p}=\eta} \frac{1}{p\left(1-\omega^{p}\right)^{z_{q / p}}(1-\omega)} \\
|
| 1052 |
-
& =\frac{1}{p(1-\eta)^{z_{q / p}}} \sum_{\omega^{p}=\eta} \frac{1}{1-\omega} \\
|
| 1053 |
-
& =\frac{1}{p(1-\eta)^{z_{q / p}}}\left[\frac{p x^{p-1}}{x^{p}-\eta}\right]_{x=1} \\
|
| 1054 |
-
& =\frac{1}{(1-\eta)^{1+z_{q / p}}}
|
| 1055 |
-
\end{aligned}
|
| 1056 |
-
$$
|
| 1057 |
-
|
| 1058 |
-
Summing over all $\eta \in S_{q / p}$, we conclude by the inductive hypothesis that
|
| 1059 |
-
|
| 1060 |
-
$$
|
| 1061 |
-
\sum_{\omega \in S_{q}} \frac{B(\omega)}{(1-\omega)^{1+z_{q}}}=\sum_{\eta \in S_{q / p}} \frac{1}{(1-\eta)^{1+z_{q / p}}}
|
| 1062 |
-
$$
|
| 1063 |
-
|
| 1064 |
-
is not an integer. This completes the solution.
|
| 1065 |
-
|
| 1066 |
-
Solution 2 (Nikolai Beluhov). Suppose that the complex numbers $\frac{1}{1-\omega}$ for $\omega \in S_{q}$ are the roots of
|
| 1067 |
-
|
| 1068 |
-
$$
|
| 1069 |
-
P(x)=x^{d}-c_{1} x^{d-1}+c_{2} x^{d-2}-\cdots \pm c_{d}
|
| 1070 |
-
$$
|
| 1071 |
-
|
| 1072 |
-
so that $c_{k}$ is their $k$-th elementary symmetric polynomial and $d=\phi(q)=(p-1) p^{r-1}$. Additionally denote
|
| 1073 |
-
|
| 1074 |
-
$$
|
| 1075 |
-
S_{n}=\sum_{\omega \in S_{q}} \frac{1}{(1-\omega)^{n}}
|
| 1076 |
-
$$
|
| 1077 |
-
|
| 1078 |
-
Then, by Newton's identities,
|
| 1079 |
-
|
| 1080 |
-
$$
|
| 1081 |
-
\begin{aligned}
|
| 1082 |
-
S_{1} & =c_{1} \\
|
| 1083 |
-
S_{2} & =c_{1} S_{1}-2 c_{2} \\
|
| 1084 |
-
S_{3} & =c_{1} S_{2}-c_{2} S_{1}+3 c_{3}
|
| 1085 |
-
\end{aligned}
|
| 1086 |
-
$$
|
| 1087 |
-
|
| 1088 |
-
and so on. The general pattern when $n \leq d$ is
|
| 1089 |
-
|
| 1090 |
-
$$
|
| 1091 |
-
S_{n}=\left[\sum_{j=1}^{n-1}(-1)^{j+1} c_{j} S_{n-j}\right]+(-1)^{n+1} n c_{n}
|
| 1092 |
-
$$
|
| 1093 |
-
|
| 1094 |
-
After that, when $n>d$, the pattern changes to
|
| 1095 |
-
|
| 1096 |
-
$$
|
| 1097 |
-
S_{n}=\sum_{j=1}^{d}(-1)^{j+1} c_{j} S_{n-j}
|
| 1098 |
-
$$
|
| 1099 |
-
|
| 1100 |
-
## Lemma
|
| 1101 |
-
|
| 1102 |
-
All of the $c_{i}$ are integers except for $c_{d}$. Furthermore, $c_{d}$ is $1 / p$ times an integer.
|
| 1103 |
-
|
| 1104 |
-
Proof. The $q$ th cyclotomic polynomial is
|
| 1105 |
-
|
| 1106 |
-
$$
|
| 1107 |
-
\Phi_{q}(x)=1+x^{p^{r-1}}+x^{2 p^{r-1}}+\cdots+x^{(p-1) p^{r-1}}
|
| 1108 |
-
$$
|
| 1109 |
-
|
| 1110 |
-
The polynomial
|
| 1111 |
-
|
| 1112 |
-
$$
|
| 1113 |
-
Q(x)=1+(1+x)^{p^{r-1}}+(1+x)^{2 p^{r-1}}+\cdots+(1+x)^{(p-1) p^{r-1}}
|
| 1114 |
-
$$
|
| 1115 |
-
|
| 1116 |
-
has roots $\omega-1$ for $\omega \in S_{q}$, so it is equal to $p(-x)^{d} P(-1 / x)$ by comparing constant coefficients. Comparing the remaining coefficients, we find that $c_{n}$ is $1 / p$ times the $x^{n}$ coefficient of $Q$.
|
| 1117 |
-
|
| 1118 |
-
Since $(x+y)^{p} \equiv x^{p}+y^{p}(\bmod p)$, we conclude that, modulo $p$,
|
| 1119 |
-
|
| 1120 |
-
$$
|
| 1121 |
-
\begin{aligned}
|
| 1122 |
-
Q(x) & \equiv 1+\left(1+x^{p^{r-1}}\right)+\left(1+x^{p^{r-1}}\right)^{2}+\cdots+\left(1+x^{p^{r-1}}\right)^{p-1} \\
|
| 1123 |
-
& \equiv\left[\left(1+x^{p^{r-1}}\right)^{p}-1\right] / x^{p^{r-1}}
|
| 1124 |
-
\end{aligned}
|
| 1125 |
-
$$
|
| 1126 |
-
|
| 1127 |
-
Since $\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, it follows that all coefficients of $Q(x)$ are multiples of $p$ save for the leading one. Therefore, $c_{n}$ is an integer when $n<d$, while $c_{d}$ is $1 / p$ times an integer.
|
| 1128 |
-
|
| 1129 |
-
By the recurrences above, $S_{n}$ is an integer for $n<d$. When $r=1$, we get that $d c_{d}$ is not an integer, so $S_{d}$ is not an integer, either. Thus the answer for $r=1$ is $n=p-1$.
|
| 1130 |
-
|
| 1131 |
-
Suppose now that $r \geq 2$. Then $d c_{d}$ does become an integer, so $S_{d}$ is an integer as well.
|
| 1132 |
-
|
| 1133 |
-
## Lemma
|
| 1134 |
-
|
| 1135 |
-
For all $n$ with $1 \leq n \leq d$, we have $\nu_{p}\left(n c_{n}\right) \geq r-2$. Furthermore, the smallest $n$ such that $\nu_{p}\left(n c_{n}\right)=r-2$ is $d-p^{r-1}+1$.
|
| 1136 |
-
|
| 1137 |
-
Proof. The value of $n c_{n}$ is $1 / p$ times the coefficient of $x^{n-1}$ in the derivative $Q^{\prime}(x)$. This derivative is
|
| 1138 |
-
|
| 1139 |
-
$$
|
| 1140 |
-
p^{r-1}(1+x)^{p^{r-1}-1}\left[\sum_{k=1}^{p-1} k(1+x)^{(k-1) p^{r-1}}\right] .
|
| 1141 |
-
$$
|
| 1142 |
-
|
| 1143 |
-
What we want to prove reduces to showing that all coefficients of the polynomial in the square brackets are multiples of $p$ except for the leading one.
|
| 1144 |
-
|
| 1145 |
-
Using the same trick $(x+y)^{p} \equiv x^{p}+y^{p}(\bmod p)$ as before and also writing $w$ for $x^{p^{r-1}}$, modulo $p$ the polynomial in the square brackets becomes
|
| 1146 |
-
|
| 1147 |
-
$$
|
| 1148 |
-
1+2(1+w)+3(1+w)^{2}+\cdots+(p-1)(1+w)^{p-2}
|
| 1149 |
-
$$
|
| 1150 |
-
|
| 1151 |
-
This is the derivative of
|
| 1152 |
-
|
| 1153 |
-
$$
|
| 1154 |
-
1+(1+w)+(1+w)^{2}+\cdots+(1+w)^{p-1}=\left[(1+w)^{p}-1\right] / w
|
| 1155 |
-
$$
|
| 1156 |
-
|
| 1157 |
-
and so, since $\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, we are done.
|
| 1158 |
-
Finally, we finish the problem with the following claim.
|
| 1159 |
-
|
| 1160 |
-
Claim - Let $m=d-p^{r-1}$. Then for all $k \geq 0$ and $1 \leq j \leq d$, we have
|
| 1161 |
-
|
| 1162 |
-
$$
|
| 1163 |
-
\begin{aligned}
|
| 1164 |
-
& \nu_{p}\left(S_{k d+m+1}\right)=r-2-k \\
|
| 1165 |
-
& \nu_{p}\left(S_{k d+m+j}\right) \geq r-2-k
|
| 1166 |
-
\end{aligned}
|
| 1167 |
-
$$
|
| 1168 |
-
|
| 1169 |
-
Proof. First, $S_{1}, S_{2}, \ldots, S_{m}$ are all divisible by $p^{r-1}$ by Newton's identities and the second lemma. Then $\nu_{p}\left(S_{m+1}\right)=r-2$ because
|
| 1170 |
-
|
| 1171 |
-
$$
|
| 1172 |
-
\nu_{p}\left((m+1) c_{m+1}\right)=r-2
|
| 1173 |
-
$$
|
| 1174 |
-
|
| 1175 |
-
and all other terms in the recurrence relation are divisible by $p^{r-1}$. We can similarly check that $\nu_{p}\left(S_{n}\right) \geq r-2$ for $m+1 \leq n \leq d$. Newton's identities combined with the first lemma now imply the following for $n>d$ :
|
| 1176 |
-
|
| 1177 |
-
- If $\nu_{p}\left(S_{n-j}\right) \geq \ell$ for all $1 \leq j \leq d$ and $\nu_{p}\left(S_{n-d}\right) \geq \ell+1$, then $\nu_{p}\left(S_{n}\right) \geq \ell$.
|
| 1178 |
-
- If $\nu_{p}\left(S_{n-j}\right) \geq \ell$ for all $1 \leq j \leq d$ and $\nu_{p}\left(S_{n-d}\right)=\ell$, then $\nu_{p}\left(S_{n}\right)=\ell-1$.
|
| 1179 |
-
|
| 1180 |
-
Together, these prove the claim by induction.
|
| 1181 |
-
By the claim, the smallest $n$ for which $\nu_{p}\left(S_{n}\right)<0$ (equivalent to $S_{n}$ not being an integer, by the recurrences) is
|
| 1182 |
-
|
| 1183 |
-
$$
|
| 1184 |
-
n=(r-1) d+m+1=((p-1) r-1) p^{r-1}+1
|
| 1185 |
-
$$
|
| 1186 |
-
|
| 1187 |
-
Remark. The original proposal was the following more general version:
|
| 1188 |
-
Let $n$ be an integer with prime power factorization $q_{1} \cdots q_{m}$. Let $S_{n}$ denote the set of primitive $n$th roots of unity. Find all tuples of nonnegative integers $\left(z_{1}, \ldots, z_{m}\right)$ such that
|
| 1189 |
-
|
| 1190 |
-
$$
|
| 1191 |
-
\sum_{\omega \in S_{n}} \frac{f(\omega)}{\left(1-\omega^{n / q_{1}}\right)^{z_{1}} \cdots\left(1-\omega^{n / q_{m}}\right)^{z_{m}}} \in \mathbb{Z}
|
| 1192 |
-
$$
|
| 1193 |
-
|
| 1194 |
-
for all polynomials $f \in \mathbb{Z}[x]$.
|
| 1195 |
-
The maximal $z_{i}$ are exponents in the prime ideal factorization of the different ideal of the cyclotomic extension $\mathbb{Q}\left(\zeta_{n}\right) / \mathbb{Q}$.
|
| 1196 |
-
|
| 1197 |
-
Remark. Let $F=\left(x^{p}-1\right) /(x-1)$ be the minimal polynomial of $\zeta_{p}=e^{2 \pi i / p}$ over $\mathbb{Q}$. A calculation of Euler shows that
|
| 1198 |
-
|
| 1199 |
-
$$
|
| 1200 |
-
\left(\mathbb{Z}\left[\zeta_{p}\right]\right)^{*}:=\left\{\alpha=g\left(\zeta_{p}\right) \in \mathbb{Q}\left[\zeta_{p}\right]: \sum_{\omega \in S_{p}} f(\omega) g(\omega) \in \mathbb{Z} \forall f \in \mathbb{Z}[x]\right\}=\frac{1}{F^{\prime}\left(\zeta_{p}\right)} \cdot \mathbb{Z}\left[\zeta_{p}\right],
|
| 1201 |
-
$$
|
| 1202 |
-
|
| 1203 |
-
where
|
| 1204 |
-
|
| 1205 |
-
$$
|
| 1206 |
-
F^{\prime}\left(\zeta_{p}\right)=\frac{p \zeta_{p}^{p-1}-\left[1+\zeta_{p}+\cdots+\zeta_{p}^{p-1}\right]}{1-\zeta_{p}}=p\left(1-\zeta_{p}\right)^{-1} \zeta_{p}^{p-1}
|
| 1207 |
-
$$
|
| 1208 |
-
|
| 1209 |
-
is $\left(1-\zeta_{p}\right)^{[p-1]-1}=\left(1-\zeta_{p}\right)^{p-2}$ times a unit of $\mathbb{Z}\left[\zeta_{p}\right]$. Here, $\left(\mathbb{Z}\left[\zeta_{p}\right]\right)^{*}$ is the dual lattice of $\mathbb{Z}\left[\zeta_{p}\right]$.
|
| 1210 |
-
|
| 1211 |
-
Remark. Let $K=\mathbb{Q}(\omega)$, so $(p)$ factors as $(1-\omega)^{p-1}$ in the ring of integers $\mathcal{O}_{K}$ (which, for cyclotomic fields, can be shown to be $\mathbb{Z}[\omega])$. In particular, the ramification index $e$ of $(1-\omega)$ over $p$ is the exponent, $p-1$. Since $e=p-1$ is not divisible by $p$, we have so-called tame ramification. Now by the ramification theory of Dedekind's different ideal, the exponent $z_{1}$ that works when $n=p$ is $e-1=p-2$.
|
| 1212 |
-
|
| 1213 |
-
Higher prime powers are more interesting because of wild ramification: $p$ divides $\phi\left(p^{r}\right)=$ $p^{r-1}(p-1)$ if and only if $r>1$. (This is a similar phenomena to how Hensel's lemma for $x^{2}-c$ is more interesting mod powers of 2 than mod odd prime powers.)
|
| 1214 |
-
|
| 1215 |
-
Remark. Let $F=\left(x^{q}-1\right) /\left(x^{q / p}-1\right)$ be the minimal polynomial of $\zeta_{q}=e^{2 \pi i / q}$ over $\mathbb{Q}$. The aforementioned calculation of Euler shows that
|
| 1216 |
-
|
| 1217 |
-
$$
|
| 1218 |
-
\left(\mathbb{Z}\left[\zeta_{q}\right]\right)^{*}:=\left\{\alpha=g\left(\zeta_{q}\right) \in \mathbb{Q}\left[\zeta_{q}\right]: \sum_{\omega \in S_{q}} f(\omega) g(\omega) \in \mathbb{Z} \forall f \in \mathbb{Z}[x]\right\}=\frac{1}{F^{\prime}\left(\zeta_{q}\right)} \cdot \mathbb{Z}\left[\zeta_{q}\right]
|
| 1219 |
-
$$
|
| 1220 |
-
|
| 1221 |
-
where the chain rule implies (using the computation from the prime case)
|
| 1222 |
-
|
| 1223 |
-
$$
|
| 1224 |
-
F^{\prime}\left(\zeta_{q}\right)=\left[p\left(1-\zeta_{p}\right)^{-1} \zeta_{p}^{p-1}\right] \cdot \frac{q}{p} \zeta_{q}^{(q / p)-1}=q\left(1-\zeta_{p}\right)^{-1} \zeta_{q}^{-1}
|
| 1225 |
-
$$
|
| 1226 |
-
|
| 1227 |
-
is $\left(1-\zeta_{q}\right)^{r \phi(q)-q / p}=\left(1-\zeta_{q}\right)^{z_{q}}$ times a unit of $\mathbb{Z}\left[\zeta_{q}\right]$.
|
| 1228 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2022.md
DELETED
|
@@ -1,618 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2022 Solutions <br> United States of America - TST Selection Test <br> Andrew Gu and Evan Chen <br> 64 ${ }^{\text {th }}$ IMO 2023 Japan and $12^{\text {th }}$ EGMO 2023 Slovenia
|
| 2 |
-
|
| 3 |
-
## Contents
|
| 4 |
-
|
| 5 |
-
0 Problems ..... 2
|
| 6 |
-
1 Solutions to Day 1 ..... 4
|
| 7 |
-
1.1 TSTST 2022/1, proposed by Holden Mui ..... 4
|
| 8 |
-
1.2 TSTST 2022/2, proposed by Hongzhou Lin ..... 7
|
| 9 |
-
1.3 TSTST 2022/3 ..... 9
|
| 10 |
-
2 Solutions to Day 2 ..... 11
|
| 11 |
-
2.1 TSTST 2022/4, proposed by Merlijn Staps ..... 11
|
| 12 |
-
2.2 TSTST 2022/5, proposed by Ray Li ..... 12
|
| 13 |
-
2.3 TSTST 2022/6, proposed by Hongzhou Lin ..... 14
|
| 14 |
-
3 Solutions to Day 3 ..... 17
|
| 15 |
-
3.1 TSTST 2022/7, proposed by Merlijn Staps ..... 17
|
| 16 |
-
3.2 TSTST 2022/8, proposed by Merlijn Staps ..... 18
|
| 17 |
-
3.3 TSTST 2022/9, proposed by Vincent Huang ..... 19
|
| 18 |
-
|
| 19 |
-
## §0 Problems
|
| 20 |
-
|
| 21 |
-
1. Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold:
|
| 22 |
-
|
| 23 |
-
- The sides of each rectangle are parallel to the sides of the unit square.
|
| 24 |
-
- Each point in $S$ is not in the interior of any rectangle.
|
| 25 |
-
- Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles.
|
| 26 |
-
(The interior of a polygon does not contain its boundary.)
|
| 27 |
-
|
| 28 |
-
2. Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which
|
| 29 |
-
|
| 30 |
-
$$
|
| 31 |
-
\theta<\frac{1}{2} \min (\angle A, \angle B, \angle C)
|
| 32 |
-
$$
|
| 33 |
-
|
| 34 |
-
Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$.
|
| 35 |
-
Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
| 36 |
-
3. Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\cdots$ satisfying the following properties:
|
| 37 |
-
|
| 38 |
-
- the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \ldots$ is periodic; and
|
| 39 |
-
- $s_{s_{n}}-s_{s_{n-1}} \leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.
|
| 40 |
-
|
| 41 |
-
4. A function $f: \mathbb{N} \rightarrow \mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers
|
| 42 |
-
|
| 43 |
-
$$
|
| 44 |
-
f(m+1), f(m+2), \ldots, f(m+f(n))
|
| 45 |
-
$$
|
| 46 |
-
|
| 47 |
-
is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.
|
| 48 |
-
5. Let $A_{1}, \ldots, A_{2022}$ be the vertices of a regular 2022 -gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.)
|
| 49 |
-
In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \ldots$, $\left.A_{2022}\right)$ and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \ldots, A_{2022}$ in $Q$ rounds?
|
| 50 |
-
6. Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$.
|
| 51 |
-
Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
| 52 |
-
7. Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that
|
| 53 |
-
|
| 54 |
-
$$
|
| 55 |
-
2 \angle A E B=\angle A D B+\angle A C B,
|
| 56 |
-
$$
|
| 57 |
-
|
| 58 |
-
and point $F$ lies on segment $B C$ such that
|
| 59 |
-
|
| 60 |
-
$$
|
| 61 |
-
2 \angle D F A=\angle D C A+\angle D B A .
|
| 62 |
-
$$
|
| 63 |
-
|
| 64 |
-
Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.
|
| 65 |
-
8. Find all functions $f: \mathbb{N} \rightarrow \mathbb{Z}$ such that
|
| 66 |
-
|
| 67 |
-
$$
|
| 68 |
-
\left\lfloor\frac{f(m n)}{n}\right\rfloor=f(m)
|
| 69 |
-
$$
|
| 70 |
-
|
| 71 |
-
for all positive integers $m, n$.
|
| 72 |
-
9. Let $k>1$ be a fixed positive integer. Prove that if $n$ is a sufficiently large positive integer, there exists a sequence of integers with the following properties:
|
| 73 |
-
|
| 74 |
-
- Each element of the sequence is between 1 and $n$, inclusive.
|
| 75 |
-
- For any two different contiguous subsequences of the sequence with length between 2 and $k$ inclusive, the multisets of values in those two subsequences is not the same.
|
| 76 |
-
- The sequence has length at least $0.499 n^{2}$.
|
| 77 |
-
|
| 78 |
-
|
| 79 |
-
## §1 Solutions to Day 1
|
| 80 |
-
|
| 81 |
-
## §1.1 TSTST 2022/1, proposed by Holden Mui
|
| 82 |
-
|
| 83 |
-
Available online at https://aops.com/community/p25516960.
|
| 84 |
-
|
| 85 |
-
## Problem statement
|
| 86 |
-
|
| 87 |
-
Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold:
|
| 88 |
-
|
| 89 |
-
- The sides of each rectangle are parallel to the sides of the unit square.
|
| 90 |
-
- Each point in $S$ is not in the interior of any rectangle.
|
| 91 |
-
- Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles.
|
| 92 |
-
(The interior of a polygon does not contain its boundary.)
|
| 93 |
-
|
| 94 |
-
We give the author's solution. In terms of $n$, we wish find the smallest integer $k$ for which $(0,1)^{2} \backslash S$ is always a union of $k$ open rectangles for every set $S \subset(0,1)^{2}$ of size $n$.
|
| 95 |
-
|
| 96 |
-
We claim the answer is $k=2 n+2$.
|
| 97 |
-
The lower bound is given by picking
|
| 98 |
-
|
| 99 |
-
$$
|
| 100 |
-
S=\left\{\left(s_{1}, s_{1}\right),\left(s_{2}, s_{2}\right), \ldots,\left(s_{n}, s_{n}\right)\right\}
|
| 101 |
-
$$
|
| 102 |
-
|
| 103 |
-
for some real numbers $0<s_{1}<s_{2}<\cdots<s_{n}<1$. Consider the $4 n$ points
|
| 104 |
-
|
| 105 |
-
$$
|
| 106 |
-
S^{\prime}=S+\{(\varepsilon, 0),(0, \varepsilon),(-\varepsilon, 0),(0,-\varepsilon)\} \subset(0,1)^{2}
|
| 107 |
-
$$
|
| 108 |
-
|
| 109 |
-
for some sufficiently small $\varepsilon>0$. The four rectangles covering each of
|
| 110 |
-
|
| 111 |
-
$$
|
| 112 |
-
\left(s_{1}-\varepsilon, s_{1}\right),\left(s_{1}, s_{1}-\varepsilon\right),\left(s_{n}+\varepsilon, s_{n}\right),\left(s_{n}, s_{n}+\varepsilon\right)
|
| 113 |
-
$$
|
| 114 |
-
|
| 115 |
-
cannot cover any other points in $S^{\prime}$; all other rectangles can only cover at most 2 points in $S^{\prime}$, giving a bound of
|
| 116 |
-
|
| 117 |
-
$$
|
| 118 |
-
k \geq 4+\frac{\left|S^{\prime}\right|-4}{2}=2 n+2
|
| 119 |
-
$$
|
| 120 |
-
|
| 121 |
-

|
| 122 |
-
|
| 123 |
-
To prove that $2 n+2$ rectangles are sufficient, assume that the number of distinct $y$-coordinates is at least the number of distinct $x$-coordinates. Let
|
| 124 |
-
|
| 125 |
-
$$
|
| 126 |
-
0=x_{0}<x_{1}<\cdots<x_{m}<x_{m+1}=1
|
| 127 |
-
$$
|
| 128 |
-
|
| 129 |
-
where $x_{1}, \ldots, x_{m}$ are the distinct $x$-coordinates of points in $S$, and let $Y_{i}$ be the set of $y$-coordinates of points with $x$-coordinate $x_{i}$. For each $1 \leq i \leq m$, include the $\left|Y_{i}\right|+1$ rectangles
|
| 130 |
-
|
| 131 |
-
$$
|
| 132 |
-
\left(x_{i-1}, x_{i+1}\right) \times\left((0,1) \backslash Y_{i}\right)
|
| 133 |
-
$$
|
| 134 |
-
|
| 135 |
-
in the union, and also include $\left(0, x_{1}\right) \times(0,1)$ and $\left(x_{m}, 1\right) \times(0,1)$; this uses $m+n+2$ rectangles.
|
| 136 |
-

|
| 137 |
-
|
| 138 |
-
All remaining uncovered points are between pairs of points with the same $y$-coordinate and adjacent $x$-coordinates $\left\{x_{i}, x_{i+1}\right\}$. There are at most $n-m$ such pairs by the initial assumption, so covering the points between each pair with
|
| 139 |
-
|
| 140 |
-
$$
|
| 141 |
-
\left(x_{i}, x_{i+1}\right) \times(y-\varepsilon, y+\varepsilon)
|
| 142 |
-
$$
|
| 143 |
-
|
| 144 |
-
for some sufficiently small $\varepsilon>0$ gives a total of
|
| 145 |
-
|
| 146 |
-
$$
|
| 147 |
-
(m+n+2)+(n-m)=2 n+2
|
| 148 |
-
$$
|
| 149 |
-
|
| 150 |
-
rectangles.
|
| 151 |
-
|
| 152 |
-
## §1.2 TSTST 2022/2, proposed by Hongzhou Lin
|
| 153 |
-
|
| 154 |
-
Available online at https://aops.com/community/p25516988.
|
| 155 |
-
|
| 156 |
-
## Problem statement
|
| 157 |
-
|
| 158 |
-
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which
|
| 159 |
-
|
| 160 |
-
$$
|
| 161 |
-
\theta<\frac{1}{2} \min (\angle A, \angle B, \angle C)
|
| 162 |
-
$$
|
| 163 |
-
|
| 164 |
-
Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$.
|
| 165 |
-
|
| 166 |
-
Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
| 167 |
-
|
| 168 |
-
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement.
|
| 169 |
-
|
| 170 |
-
【 First solution, by author. Let $X$ be the projection from $C$ to $A P_{A}, Y$ be the projection from $B$ to $A Q_{A}$.
|
| 171 |
-
|
| 172 |
-
|
| 173 |
-
Claim - Line $\ell_{A}$ passes through $M_{A}$, the midpoint of $B C$. Also, quadrilateral $P_{A} Q_{A} Y X$ is cyclic with circumcenter $M_{A}$.
|
| 174 |
-
|
| 175 |
-
Proof. Since
|
| 176 |
-
|
| 177 |
-
$$
|
| 178 |
-
A P_{A} \cdot A X=A B \cdot A C \cdot \cos \theta \cos (\angle A-\theta)=A Q_{A} \cdot A Y
|
| 179 |
-
$$
|
| 180 |
-
|
| 181 |
-
it follows that $P_{A}, Q_{A}, Y, X$ are concyclic by power of a point. Moreover, by projection, the perpendicular bisector of $P_{A} X$ passes through $M_{A}$, similar for $Q_{A} Y$, implying that $M_{A}$ is the center of $P_{A} Q_{A} Y X$. Hence $\ell_{A}$ passes through $M_{A}$.
|
| 182 |
-
|
| 183 |
-
$$
|
| 184 |
-
\text { Claim }-\measuredangle\left(M_{A} M_{C}, \ell_{A}\right)=\measuredangle Y P_{A} Q_{A}
|
| 185 |
-
$$
|
| 186 |
-
|
| 187 |
-
Proof. Indeed, $\ell_{A} \perp P_{A} Q_{A}$, and $M_{A} M_{C} \perp P_{A} Y$ (since $M_{A} P_{A}=M_{A} Y$ from $\left(P_{A} Q_{A} Y_{A} X\right)$ and $M_{C} P_{A}=M_{C} M_{A}=M_{C} Y$ from the circle with diameter $\left.A B\right)$. Hence $\measuredangle\left(M_{A} M_{C}, \ell_{A}\right)=$ $\measuredangle\left(P_{A} Y, P_{A} Q_{A}\right)=\measuredangle Y P_{A} Q_{A}$.
|
| 188 |
-
|
| 189 |
-
Therefore,
|
| 190 |
-
|
| 191 |
-
$$
|
| 192 |
-
\frac{\sin \angle\left(M_{A} M_{C}, \ell_{A}\right)}{\sin \angle\left(\ell_{A}, M_{A} M_{B}\right)}=\frac{\sin \angle Y P_{A} Q_{A}}{\sin \angle P_{A} Q_{A} X}=\frac{Y Q_{A}}{X P_{A}}=\frac{B C \sin (\angle C+\theta)}{B C \sin (\angle B+\theta)}=\frac{\sin (\angle C+\theta)}{\sin (\angle B+\theta)},
|
| 193 |
-
$$
|
| 194 |
-
|
| 195 |
-
and we conclude by trig Ceva theorem.
|
| 196 |
-
【 Second solution via Jacobi, by Maxim Li. Let $D$ be the foot of the $A$-altitude. Note that line $B C$ is the external angle bisector of $\angle P_{A} D Q_{A}$.
|
| 197 |
-
|
| 198 |
-
Claim - $\left(D P_{A} Q_{A}\right)$ passes through the midpoint $M_{A}$ of $B C$.
|
| 199 |
-
Proof. Perform $\sqrt{b c}$ inversion. Then the intersection of $B C$ and $\left(D P_{A} Q_{A}\right)$ maps to the second intersection of $(A B C)$ and $\left(A^{\prime} P_{A} Q_{A}\right)$, where $A^{\prime}$ is the antipode to $A$ on $(A B C)$, i.e. the center of spiral similarity from $B C$ to $P_{A} Q_{A}$. Since $B P_{A}: C Q_{A}=A B: A C$, we see the center of spiral similarity is the intersection of the $A$-symmedian with $(A B C)$, which is the image of $M_{A}$ in the inversion.
|
| 200 |
-
|
| 201 |
-
It follows that $M_{A}$ lies on $\ell_{A}$; we need to identify a second point. We'll use the circumcenter $O_{A}$ of $\left(D P_{A} Q_{A}\right)$. The perpendicular bisector of $D P_{A}$ passes through $M_{C}$; indeed, we can easily show the angle it makes with $M_{C} M_{A}$ is $90^{\circ}-\theta-C$, so $\angle O_{A} M_{C} M_{A}=90-\theta-C$, and then by analogous angle-chasing we can finish with Jacobi's theorem on $\triangle M_{A} M_{B} M_{C}$.
|
| 202 |
-
|
| 203 |
-
## §1.3 TSTST 2022/3
|
| 204 |
-
|
| 205 |
-
Available online at https://aops.com/community/p25517008.
|
| 206 |
-
|
| 207 |
-
## Problem statement
|
| 208 |
-
|
| 209 |
-
Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\cdots$ satisfying the following properties:
|
| 210 |
-
|
| 211 |
-
- the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \ldots$ is periodic; and
|
| 212 |
-
- $s_{s_{n}}-s_{s_{n-1}} \leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.
|
| 213 |
-
|
| 214 |
-
【 Answer. All $N$ such that $t^{2} \leq N<t^{2}+t$ for some positive integer $t$.
|
| 215 |
-
Solution 1 (local). If $t^{2} \leq N<t^{2}+t$ then the sequence $s_{n}=t n+1$ satisfies both conditions. It remains to show that no other values of $N$ work.
|
| 216 |
-
|
| 217 |
-
Define $a_{n}:=s_{n}-s_{n-1}$, and let $p$ be the minimal period of $\left\{a_{n}\right\}$. For each $k \in \mathbb{Z}_{\geq 0}$, let $f(k)$ be the integer such that
|
| 218 |
-
|
| 219 |
-
$$
|
| 220 |
-
s_{f(k)}-s_{k} \leq N<s_{f(k)+1}-s_{k}
|
| 221 |
-
$$
|
| 222 |
-
|
| 223 |
-
Note that $f\left(s_{n-1}\right)=s_{n}$ for all $n$. Since $\left\{a_{n}\right\}$ is periodic with period $p, f(k+p)=f(k)+p$ for all $k$, so $k \mapsto f(k)-k$ is periodic with period $p$. We also note that $f$ is nondecreasing: if $k<k^{\prime}$ but $f\left(k^{\prime}\right)<f(k)$ then
|
| 224 |
-
|
| 225 |
-
$$
|
| 226 |
-
N<s_{f\left(k^{\prime}\right)+1}-s_{k^{\prime}}<s_{f(k)}-s_{k} \leq N
|
| 227 |
-
$$
|
| 228 |
-
|
| 229 |
-
which is absurd. We now claim that
|
| 230 |
-
|
| 231 |
-
$$
|
| 232 |
-
\max _{k}(f(k)-k)<p+\min _{k}(f(k)-k)
|
| 233 |
-
$$
|
| 234 |
-
|
| 235 |
-
Indeed, if $f\left(k^{\prime}\right)-k^{\prime} \geq p+f(k)-k$ then we can shift $k$ and $k^{\prime}$ so that $0 \leq k-k^{\prime}<p$, and it follows that $k \leq k^{\prime} \leq f\left(k^{\prime}\right)<f(k)$, violating the fact that $f$ is nondecreasing. Therefore $\max _{k}(f(k)-k)<p+\min _{k}(f(k)-k)$, so $f(k)-k$ is uniquely determined by its value modulo $p$. In particular, since $a_{n}=f\left(s_{n-1}\right)-s_{n-1}, a_{n}$ is also uniquely determined by its value modulo $p$, so $\left\{a_{n} \bmod p\right\}$ also has minimal period $p$.
|
| 236 |
-
Now work in $\mathbb{Z} / p \mathbb{Z}$ and consider the sequence $s_{0}, f\left(s_{0}\right), f\left(f\left(s_{0}\right)\right), \ldots$. This sequence must be eventually periodic; suppose it has minimal period $p^{\prime}$, which must be at most $p$. Then, since
|
| 237 |
-
|
| 238 |
-
$$
|
| 239 |
-
f^{n}\left(s_{0}\right)-f^{n-1}\left(s_{0}\right)=s_{n}-s_{n-1}=a_{n}
|
| 240 |
-
$$
|
| 241 |
-
|
| 242 |
-
and $\left\{a_{n} \bmod p\right\}$ has minimal period $p$, we must have $p^{\prime}=p$. Therefore the directed graph $G$ on $\mathbb{Z} / p \mathbb{Z}$ given by the edges $k \rightarrow f(k)$ is simply a $p$-cycle, which implies that the map $k \mapsto f(k)$ is a bijection on $\mathbb{Z} / p \mathbb{Z}$. Therefore, $f(k+1) \neq f(k)$ for all $k$ (unless $p=1$, but in this case the following holds anyways), hence
|
| 243 |
-
|
| 244 |
-
$$
|
| 245 |
-
f(k)<f(k+1)<\cdots<f(k+p)=f(k)+p
|
| 246 |
-
$$
|
| 247 |
-
|
| 248 |
-
This implies $f(k+1)=f(k)+1$ for all $k$, so $f(k)-k$ is constant, therefore $a_{n}=$ $f\left(s_{n-1}\right)-s_{n-1}$ is also constant. Let $a_{n} \equiv t$. It follows that $t^{2} \leq N<t^{2}+t$ as we wanted.
|
| 249 |
-
|
| 250 |
-
【 Solution 2 (global). Define $\left\{a_{n}\right\}$ and $f$ as in the previous solution. We first show that $s_{i} \not \equiv s_{j}(\bmod p)$ for all $i<j<i+p$. Suppose the contrary, i.e. that $s_{i} \equiv s_{j}$ $(\bmod p)$ for some $i, j$ with $i<j<i+p$. Then $a_{s_{i}+k}=a_{s_{j}+k}$ for all $k \geq 0$, therefore $s_{s_{i}+k}-s_{s_{i}}=s_{s_{j}+k}-s_{s_{j}}$ for all $k \geq 0$, therefore
|
| 251 |
-
|
| 252 |
-
$$
|
| 253 |
-
a_{i+1}=f\left(s_{i}\right)-s_{i}=f\left(s_{j}\right)-s_{j}=a_{j+1} \quad \text { and } \quad s_{i+1}=f\left(s_{i}\right) \equiv f\left(s_{j}\right)=s_{j+1} \quad(\bmod p)
|
| 254 |
-
$$
|
| 255 |
-
|
| 256 |
-
Continuing this inductively, we obtain $a_{i+k}=a_{j+k}$ for all $k$, so $\left\{a_{n}\right\}$ has period $j-i<p$, which is a contradiction. Therefore $s_{i} \not \equiv s_{j}(\bmod p)$ for all $i<j<i+p$, and this implies that $\left\{s_{i}, \ldots, s_{i+p-1}\right\}$ forms a complete residue system modulo $p$ for all $i$. Consequently we must have $s_{i+p} \equiv s_{i}(\bmod p)$ for all $i$.
|
| 257 |
-
|
| 258 |
-
Let $T=s_{p}-s_{0}=a_{1}+\cdots+a_{p}$. Since $\left\{a_{n}\right\}$ is periodic with period $p$, and $\{i+1, \ldots, i+k p\}$ contains exactly $k$ values of each residue class modulo $p$,
|
| 259 |
-
|
| 260 |
-
$$
|
| 261 |
-
s_{i+k p}-s_{i}=a_{i+1}+\cdots+a_{i+k p}=k T
|
| 262 |
-
$$
|
| 263 |
-
|
| 264 |
-
for all $i, k$. Since $p \mid T$, it follows that $s_{s_{p}}-s_{s_{0}}=\frac{T}{p} \cdot T=\frac{T^{2}}{p}$. Summing up the inequalities
|
| 265 |
-
|
| 266 |
-
$$
|
| 267 |
-
s_{s_{n}}-s_{s_{n-1}} \leq N<s_{s_{n}+1}-s_{s_{n-1}}=s_{s_{n}}-s_{s_{n-1}}+a_{s_{n}+1}
|
| 268 |
-
$$
|
| 269 |
-
|
| 270 |
-
for $n \in\{1, \ldots, p\}$ then implies
|
| 271 |
-
|
| 272 |
-
$$
|
| 273 |
-
\frac{T^{2}}{p}=s_{s_{p}}-s_{s_{0}} \leq N p<\frac{T^{2}}{p}+a_{s_{1}+1}+a_{s_{2}+1}+\cdots+a_{s_{p}+1}=\frac{T^{2}}{p}+T
|
| 274 |
-
$$
|
| 275 |
-
|
| 276 |
-
where the last equality holds because $\left\{s_{1}+1, \ldots, s_{p}+1\right\}$ is a complete residue system modulo $p$. Dividing this by $p$ yields $t^{2} \leq N<t^{2}+t$ for $t:=\frac{T}{p} \in \mathbb{Z}^{+}$.
|
| 277 |
-
|
| 278 |
-
Remark (Author comments). There are some similarities between this problem and IMO 2009/3, mainly that they both involve terms of the form $s_{s_{n}}$ and $s_{s_{n}+1}$ and the sequence $s_{0}, s_{1}, \ldots$ turns out to be an arithmetic progression. Other than this, I don't think knowing about IMO 2009/3 will be that useful on this problem, since in this problem the fact that $\left\{s_{n+1}-s_{n}\right\}$ is periodic is fundamentally important.
|
| 279 |
-
|
| 280 |
-
The motivation for this problem comes from the following scenario: assume we have boxes that can hold some things of total size $\leq N$, and a sequence of things of size $a_{1}, a_{2}, \ldots$ (where $a_{i}:=s_{i+1}-s_{i}$ ). We then greedily pack the things in a sequence of boxes, 'closing' each box when it cannot fit the next thing. The number of things we put in each box gives a sequence $b_{1}, b_{2}, \ldots$. This problem asks when we can have $\left\{a_{n}\right\}=\left\{b_{n}\right\}$, assuming that we start with a sequence $\left\{a_{n}\right\}$ that is periodic.
|
| 281 |
-
(Extra motivation: I first thought about this scenario when I was pasting some text repeatedly into the Notes app and noticed that the word at the end of lines are also (eventually) periodic.)
|
| 282 |
-
|
| 283 |
-
## §2 Solutions to Day 2
|
| 284 |
-
|
| 285 |
-
## §2.1 TSTST 2022/4, proposed by Merlijn Staps
|
| 286 |
-
|
| 287 |
-
Available online at https://aops.com/community/p25517031.
|
| 288 |
-
|
| 289 |
-
## Problem statement
|
| 290 |
-
|
| 291 |
-
A function $f: \mathbb{N} \rightarrow \mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers
|
| 292 |
-
|
| 293 |
-
$$
|
| 294 |
-
f(m+1), f(m+2), \ldots, f(m+f(n))
|
| 295 |
-
$$
|
| 296 |
-
|
| 297 |
-
is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.
|
| 298 |
-
|
| 299 |
-
We start with the following claim:
|
| 300 |
-
|
| 301 |
-
$$
|
| 302 |
-
\text { Claim - If } a \mid b \text { then } f(a) \mid f(b)
|
| 303 |
-
$$
|
| 304 |
-
|
| 305 |
-
Proof. From applying the condition with $n=a$, we find that the set $S_{a}=\{n \geq 2$ : $a \mid f(n)\}$ is an arithmetic progression with common difference $f(a)$. Similarly, the set $S_{b}=\{n \geq 2: b \mid f(n)\}$ is an arithmetic progression with common difference $f(b)$. From $a \mid b$ it follows that $S_{b} \subseteq S_{a}$. Because an arithmetic progression with common difference $x$ can only be contained in an arithmetic progression with common difference $y$ if $y \mid x$, we conclude $f(a) \mid f(b)$.
|
| 306 |
-
|
| 307 |
-
In what follows, let $a \geq 2$ be any positive integer. Because $f(a)$ and $f(2 a)$ are both divisible by $f(a)$, there are $a+1$ consecutive values of $f$ of which at least two divisible by $f(a)$. It follows that $f(f(a)) \leq a$.
|
| 308 |
-
|
| 309 |
-
However, we also know that exactly one of $f(2), f(3), \ldots, f(1+f(a))$ is divisible by $a$; let this be $f(t)$. Then we have $S_{a}=\{t, t+f(a), t+2 f(a), \ldots\}$. Because $a|f(t)| f(2 t)$, we know that $2 t \in S_{a}$, so $t$ is a multiple of $f(a)$. Because $2 \leq t \leq 1+f(a)$, and $f(a) \geq 2$ for $a \geq 2$, we conclude that we must have $t=f(a)$, so $f(f(a))$ is a multiple of $a$. Together with $f(f(a)) \leq a$, this yields $f(f(a))=a$. Because $f(f(a))=a$ also holds for $a=1$ (from the given condition for $n=1$ it immediately follows that $f(1)=1$ ), we conclude that $f(f(a))=a$ for all $a$, and hence $f$ is a bijection.
|
| 310 |
-
|
| 311 |
-
Moreover, we now have that $f(a) \mid f(b)$ implies $f(f(a)) \mid f(f(b))$, i.e. $a \mid b$, so $a \mid b$ if and only if $f(a) \mid f(b)$. Together with the fact that $f$ is a bijection, this implies that $f(n)$ has the same number of divisors of $n$. Let $p$ be a prime. Then $f(p)=q$ must be a prime as well. If $q \neq p$, then from $f(p) \mid f(p q)$ and $f(q) \mid f(p q)$ it follows that $p q \mid f(p q)$, so $f(p q)=p q$ because $f(p q)$ and $p q$ must have the same number of divisors. Therefore, for every prime number $p$ we either have that $f(p)=p$ or $f(p f(p))=p f(p)$. From here, it is easy to see that $f(n)=n$ for infinitely many $n$.
|
| 312 |
-
|
| 313 |
-
## §2.2 TSTST 2022/5, proposed by Ray Li
|
| 314 |
-
|
| 315 |
-
Available online at https://aops.com/community/p25517063.
|
| 316 |
-
|
| 317 |
-
## Problem statement
|
| 318 |
-
|
| 319 |
-
Let $A_{1}, \ldots, A_{2022}$ be the vertices of a regular 2022-gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.)
|
| 320 |
-
|
| 321 |
-
In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \ldots$, $A_{2022}$ ) and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \ldots, A_{2022}$ in $Q$ rounds?
|
| 322 |
-
|
| 323 |
-
The answer is 22 . To prove the lower bound, note that there are $2022 \cdot 2021+2>2^{21}$ possible colorings. If Bob makes less than 22 queries, then he can only output $2^{21}$ possible colorings, which means he is wrong on some coloring.
|
| 324 |
-
|
| 325 |
-
Now we show Bob can always win in 22 queries. A key observation is that the set of red points is convex, as is the set of blue points, so if a set of points is all the same color, then their convex hull is all the same color.
|
| 326 |
-
|
| 327 |
-
## Lemma
|
| 328 |
-
|
| 329 |
-
Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}$ and $B_{k+1}$ differ and are known. Then it is possible to determine the colors of $B_{1}$, $\ldots, B_{k}$ in $\left\lceil\log _{2} k\right\rceil$ queries.
|
| 330 |
-
|
| 331 |
-
Proof. There exists some $0 \leq i \leq k$ such that $B_{0}, \ldots, B_{i}$ are the same color and $B_{i+1}$, $\ldots, B_{k+1}$ are the same color. (If $i<j$ and $B_{0}$ and $B_{j}$ were red and $B_{i}$ and $B_{k+1}$ were blue, then segment $B_{0} B_{j}$ is red and segment $B_{i} B_{k+1}$ is blue, but they intersect). Therefore we can binary search.
|
| 332 |
-
|
| 333 |
-
## Lemma
|
| 334 |
-
|
| 335 |
-
Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}, B_{\lceil k / 2\rceil}, B_{k+1}$ are both red and are known. Then at least one of the following holds: all of $B_{1}, \ldots, B_{\lceil k / 2\rceil}$ are red or all of $B_{\lceil k / 2\rceil}, \ldots, B_{k}$ are red. Furthermore, in one query we can determine which one of the cases holds.
|
| 336 |
-
|
| 337 |
-
Proof. The existence part holds for similar reason to previous lemma. To figure out which case, choose a point $P$ such that all of $B_{0}, \ldots, B_{k+1}$ lie between rays $P B_{0}$ and $P B_{\lceil k / 2\rceil}$, and such that $B_{1}, \ldots, B_{\lceil k / 2\rceil-1}$ lie inside triangle $P B_{0} B_{\lceil k / 2\rceil}$ and such that $B_{\lceil k / 2\rceil+1}, \ldots, B_{k+1}$ lie outside (this point should always exist by looking around the intersections of lines $B_{0} B_{1}$ and $\left.B_{\lceil k / 2\rceil-1} B_{\lceil k / 2\rceil}\right)$. Then if $P$ is red, all the inside points are red because they lie in the convex hull of red points $P, B_{0}, B_{\lceil k / 2\rceil}$. If $P$ is blue, then all the outside points are red: if $B_{i}$ were blue for $i>\lceil k / 2\rceil$, then the segment $P B_{i}$ is blue and intersect the segment $B_{0} B_{\lceil k / 2\rceil}$, which is red, contradiction.
|
| 338 |
-
|
| 339 |
-
Now the strategy is: Bob picks $A_{1}$. WLOG it is red. Now suppose Bob does not know the colors of $\leq 2^{k}-1$ points $A_{i}, \ldots, A_{j}$ with $j-i+1 \leq 2^{k}-1$ and knows the rest are red. I claim Bob can win in $2 k-1$ queries. First, if $k=1$, there is one point and he wins by querying the point, so the base case holds, so assume $k>1$. Bob queries $A_{i+\lceil(j-i+1) / 2\rceil}$. If it is blue, he finishes in $2 \log _{2}\lceil(j-i+1) / 2\rceil \leq 2(k-1)$ queries by the first lemma, for a total of $2 k-1$ queries. If it is red, he can query one more point and learn some half of $A_{i}, \ldots, A_{j}$ that are red by the second lemma, and then he has reduced it to the case with $\leq 2^{k-1}-1$ points in two queries, at which point we induct.
|
| 340 |
-
|
| 341 |
-
## §2.3 TSTST 2022/6, proposed by Hongzhou Lin
|
| 342 |
-
|
| 343 |
-
Available online at https://aops.com/community/p25516957.
|
| 344 |
-
|
| 345 |
-
## Problem statement
|
| 346 |
-
|
| 347 |
-
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$.
|
| 348 |
-
Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
| 349 |
-
|
| 350 |
-
We present several approaches.
|
| 351 |
-
\ First solution, by author. Let $\odot O X_{A} Y_{A}$ intersects $A B, A C$ again at $U, V$. Then by Reim's theorem $U V C B$ are concyclic. Hence the radical axis of $\odot O X_{A} Y_{A}, \odot O B C$ and $\odot(U V C B)$ are concurrent, i.e. $O K_{A}, B C, U V$ are concurrent, Denote the intersection as $K_{A}^{*}$, which is indeed the inversion of $K_{A}$ with respect to $\odot O$. (The inversion sends $\odot O B C$ to the line $B C$ ).
|
| 352 |
-
Let $P_{A}, P_{B}, P_{C}$ be the circumcenters of $\triangle O B C, \triangle O C A, \triangle O A B$ respectively.
|
| 353 |
-
Claim $-K_{A}^{*}$ coincides with the intersection of $P_{B} P_{C}$ and $B C$.
|
| 354 |
-
Proof. Note that $d(O, B C)=1 / 2 A H=d\left(A, X_{A} Y_{A}\right)$. This means the midpoint $M_{C}$ of $A B$ is equal distance to $X_{A} Y_{A}$ and the line through $O$ parallel to $B C$. Together with $O M_{C} \perp A B$ implies that $\angle M_{C} X_{A} O=\angle B$. Hence $\angle U V O=\angle B=\angle A V U$. Similarly $\angle V U O=\angle A U V$, hence $\triangle A U V \simeq \triangle O U V$. In other words, $U V$ is the perpendicular bisector of $A O$, which pass through $P_{B}, P_{C}$. Hence $K_{A}^{*}$ is indeed $P_{B} P_{C} \cap B C$.
|
| 355 |
-
|
| 356 |
-
Finally by Desargue's theorem, it suffices to show that $A P_{A}, B P_{B}, C P_{C}$ are concurrent. Note that
|
| 357 |
-
|
| 358 |
-
$$
|
| 359 |
-
\begin{aligned}
|
| 360 |
-
& d\left(P_{A}, A B\right)=P_{A} B \sin \left(90^{\circ}+\angle C-\angle A\right) \\
|
| 361 |
-
& d\left(P_{A}, A C\right)=P_{A} C \sin \left(90^{\circ}+\angle B-\angle A\right)
|
| 362 |
-
\end{aligned}
|
| 363 |
-
$$
|
| 364 |
-
|
| 365 |
-
Hence the symmetric product and trig Ceva finishes the proof.
|
| 366 |
-
|
| 367 |
-
|
| 368 |
-
I Second solution, from Jeffrey Kwan. Let $O_{A}$ be the circumcenter of $\triangle A X_{A} Y_{A}$. The key claim is that:
|
| 369 |
-
|
| 370 |
-
Claim $-O_{A} X_{A} Y_{A} O$ is cyclic.
|
| 371 |
-
|
| 372 |
-
Proof. Let $D E F$ be the orthic triangle; we will show that $\triangle O X_{A} Y_{A} \sim \triangle D E F$. Indeed, since $A O$ and $A D$ are isogonal, it suffices to note that
|
| 373 |
-
|
| 374 |
-
$$
|
| 375 |
-
\frac{A X_{A}}{A B}=\frac{A H / 2}{A D}=\frac{R \cos A}{A D}
|
| 376 |
-
$$
|
| 377 |
-
|
| 378 |
-
and so
|
| 379 |
-
|
| 380 |
-
$$
|
| 381 |
-
\frac{A O}{A D}=R \cdot \frac{A X_{A}}{A B \cdot R \cos A}=\frac{A X_{A}}{A E}=\frac{A Y_{A}}{A F}
|
| 382 |
-
$$
|
| 383 |
-
|
| 384 |
-
Hence $\angle X_{A} O Y_{A}=180^{\circ}-2 \angle A=180^{\circ}-\angle X_{A} O_{A} Y_{A}$, which proves the claim.
|
| 385 |
-
Let $P_{A}$ be the circumcenter of $\triangle O B C$, and define $P_{B}, P_{C}$ similarly. By the claim, $A$ is the exsimilicenter of $\left(O X_{A} Y_{A}\right)$ and $(O B C)$, so $A P_{A}$ is the line between their two centers. In particular, $A P_{A}$ is the perpendicular bisector of $O K_{A}$.
|
| 386 |
-
|
| 387 |
-
|
| 388 |
-
Claim $-A P_{A}, B P_{B}, C P_{C}$ concur at $T$.
|
| 389 |
-
Proof. The key observation is that $O$ is the incenter of $\triangle P_{A} P_{B} P_{C}$, and that $A, B, C$ are the reflections of $O$ across the sides of $\triangle P_{A} P_{B} P_{C}$. Hence $P_{A} A, P_{B} B, P_{C} C$ concur by Jacobi.
|
| 390 |
-
|
| 391 |
-
Now $T$ lies on the perpendicular bisectors of $O K_{A}, O K_{B}$, and $O K_{C}$. Hence $O K_{A} K_{B} K_{C}$ is cyclic with center $T$, as desired.
|
| 392 |
-
|
| 393 |
-
## §3 Solutions to Day 3
|
| 394 |
-
|
| 395 |
-
## §3.1 TSTST 2022/7, proposed by Merlijn Staps
|
| 396 |
-
|
| 397 |
-
Available online at https://aops.com/community/p25516961.
|
| 398 |
-
|
| 399 |
-
## Problem statement
|
| 400 |
-
|
| 401 |
-
Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that
|
| 402 |
-
|
| 403 |
-
$$
|
| 404 |
-
2 \angle A E B=\angle A D B+\angle A C B,
|
| 405 |
-
$$
|
| 406 |
-
|
| 407 |
-
and point $F$ lies on segment $B C$ such that
|
| 408 |
-
|
| 409 |
-
$$
|
| 410 |
-
2 \angle D F A=\angle D C A+\angle D B A .
|
| 411 |
-
$$
|
| 412 |
-
|
| 413 |
-
Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.
|
| 414 |
-
|
| 415 |
-
Let the circle through $A, B$, and $E$ intersect $C D$ again at $E^{\prime}$, and let the circle through $D$, $A$, and $F$ intersect $B C$ again at $F^{\prime}$. Now $A B E E^{\prime}$ and $D A F^{\prime} F$ are cyclic quadrilaterals with two parallel sides, so they are isosceles trapezoids. From $K A=K B$, it now follows that $K E=K E^{\prime}$, whereas from $K A=K D$ it follows that $K F=K F^{\prime}$.
|
| 416 |
-
|
| 417 |
-
Next, let the circle through $A, B$, and $E$ intersect $A C$ again at $S$. Then
|
| 418 |
-
|
| 419 |
-
$$
|
| 420 |
-
\angle A S B=\angle A E B=\frac{1}{2}(\angle A D B+\angle A C B)=\frac{1}{2}(\angle A D B+\angle D A C)=\frac{1}{2} \angle A M B,
|
| 421 |
-
$$
|
| 422 |
-
|
| 423 |
-
where $M$ is the intersection of $A C$ and $B D$. From $\angle A S B=\frac{1}{2} \angle A M B$, it follows that $M S=M B$, so $S$ is the point on $M C$ such that $M S=M B=M D$. By symmetry, the circle through $A, D$, and $F$ also passes through $S$, and it follows that the line $A S$ is the radical axis of the circles $(A B E)$ and $(A D F)$.
|
| 424 |
-
|
| 425 |
-
By power of a point, we now obtain
|
| 426 |
-
|
| 427 |
-
$$
|
| 428 |
-
C E \cdot C E^{\prime}=C S \cdot C A=C F \cdot C F^{\prime},
|
| 429 |
-
$$
|
| 430 |
-
|
| 431 |
-
from which it follows that $E, F, E^{\prime}$, and $F^{\prime}$ are concyclic. The segments $E E^{\prime}$ and $F F^{\prime}$ are not parallel, so their perpendicular bisectors only meet at one point, which is $K$. Hence $K E=K F$.
|
| 432 |
-
|
| 433 |
-
## §3.2 TSTST 2022/8, proposed by Merlijn Staps
|
| 434 |
-
|
| 435 |
-
Available online at https://aops.com/community/p25516968.
|
| 436 |
-
|
| 437 |
-
## Problem statement
|
| 438 |
-
|
| 439 |
-
Find all functions $f: \mathbb{N} \rightarrow \mathbb{Z}$ such that
|
| 440 |
-
|
| 441 |
-
$$
|
| 442 |
-
\left\lfloor\frac{f(m n)}{n}\right\rfloor=f(m)
|
| 443 |
-
$$
|
| 444 |
-
|
| 445 |
-
for all positive integers $m, n$.
|
| 446 |
-
|
| 447 |
-
There are two families of functions that work: for each $\alpha \in \mathbb{R}$ the function $f(n)=\lfloor\alpha n\rfloor$, and for each $\alpha \in \mathbb{R}$ the function $f(n)=\lceil\alpha n\rceil-1$. (For irrational $\alpha$ these two functions coincide.) It is straightforward to check that these functions indeed work; essentially, this follows from the identity
|
| 448 |
-
|
| 449 |
-
$$
|
| 450 |
-
\left\lfloor\frac{\lfloor x n\rfloor}{n}\right\rfloor=\lfloor x\rfloor
|
| 451 |
-
$$
|
| 452 |
-
|
| 453 |
-
which holds for all positive integers $n$ and real numbers $x$.
|
| 454 |
-
We now show that every function that works must be of one of the above forms. Let $f$ be a function that works, and define the sequence $a_{1}, a_{2}, \ldots$ by $a_{n}=f(n!) / n!$. Applying the give condition with $(n!, n+1)$ yields $a_{n+1} \in\left[a_{n}, a_{n}+\frac{1}{n!}\right)$. It follows that the sequence $a_{1}, a_{2}, \ldots$ is non-decreasing and bounded from above by $a_{1}+e$, so this sequence must converge to some limit $\alpha$.
|
| 455 |
-
|
| 456 |
-
If there exists a $k$ such that $a_{k}=\alpha$, then we have $a_{\ell}=\alpha$ for all $\ell>k$. For each positive integer $m$, there exists $\ell>k$ such that $m \mid \ell$ !. Plugging in $m n=\ell$ !, it then follows that
|
| 457 |
-
|
| 458 |
-
$$
|
| 459 |
-
f(m)=\left\lfloor\frac{f(\ell!)}{\ell!/ m}\right\rfloor=\lfloor\alpha m\rfloor
|
| 460 |
-
$$
|
| 461 |
-
|
| 462 |
-
for all $m$, so $f$ is of the desired form.
|
| 463 |
-
If there does not exist a $k$ such that $a_{k}=\alpha$, we must have $a_{k}<\alpha$ for all $k$. For each positive integer $m$, we can now pick an $\ell$ such that $m \mid \ell$ ! and $a_{\ell}=\alpha-x$ with $x$ arbitrarily small. It then follows from plugging in $m n=\ell$ ! that
|
| 464 |
-
|
| 465 |
-
$$
|
| 466 |
-
f(m)=\left\lfloor\frac{f(\ell!)}{\ell!/ m}\right\rfloor=\left\lfloor\frac{\ell!(\alpha-x)}{\ell!/ m}\right\rfloor=\lfloor\alpha m-m x\rfloor .
|
| 467 |
-
$$
|
| 468 |
-
|
| 469 |
-
If $\alpha m$ is an integer we can choose $\ell$ such that $m x<1$, and it follows that $f(m)=\lceil\alpha m\rceil-1$. If $\alpha m$ is not an integer we can choose $\ell$ such that $m x<\{\alpha m\}$, and it also follows that $f(m)=\lceil\alpha m\rceil-1$. We conclude that in this case $f$ is again of the desired form.
|
| 470 |
-
|
| 471 |
-
## §3.3 TSTST 2022/9, proposed by Vincent Huang
|
| 472 |
-
|
| 473 |
-
Available online at https://aops.com/community/p25517112.
|
| 474 |
-
|
| 475 |
-
## Problem statement
|
| 476 |
-
|
| 477 |
-
Let $k>1$ be a fixed positive integer. Prove that if $n$ is a sufficiently large positive integer, there exists a sequence of integers with the following properties:
|
| 478 |
-
|
| 479 |
-
- Each element of the sequence is between 1 and $n$, inclusive.
|
| 480 |
-
- For any two different contiguous subsequences of the sequence with length between 2 and $k$ inclusive, the multisets of values in those two subsequences is not the same.
|
| 481 |
-
- The sequence has length at least $0.499 n^{2}$.
|
| 482 |
-
|
| 483 |
-
For any positive integer $n$, define an $(n, k)$-good sequence to be a finite sequence of integers each between 1 and $n$ inclusive satisfying the second property in the problem statement. The problems asks to show that, for all sufficiently large integers $n$, there is an $(n, k)$-good sequence of length at least $0.499 n^{2}$.
|
| 484 |
-
Fix $k \geq 2$ and consider some prime power $n=p^{m}$ with $p>k+1$. Consider some $0<g<\frac{n}{k}-1$ with $\operatorname{gcd}(g, n)=1$ and let $a$ be the smallest positive integer with $g^{a} \equiv \pm 1$ $(\bmod n)$.
|
| 485 |
-
|
| 486 |
-
Claim (Main claim) — For $k, n, g, a$ defined as above, there is an $(n, k)$-good sequence of length $a(n+2)+2$.
|
| 487 |
-
To prove the main claim, we need some results about the structure of $\mathbb{Z} / n \mathbb{Z}$. Specifically, we'll first show that any nontrivial arithmetic sequence is uniquely recoverable.
|
| 488 |
-
|
| 489 |
-
## Lemma
|
| 490 |
-
|
| 491 |
-
Consider any arithmetic progression of length $i \leq k$ whose common difference is relatively prime to $n$, and let $S$ be the set of residues it takes modulo $n$. Then there exists a unique integer $0<d \leq \frac{n}{2}$ and a unique integer $0 \leq a<n$ such that
|
| 492 |
-
|
| 493 |
-
$$
|
| 494 |
-
S=\{a, a+d, \ldots, a+(i-1) d\}
|
| 495 |
-
$$
|
| 496 |
-
|
| 497 |
-
Proof of lemma. We'll split into cases, based on if $i$ is odd or not.
|
| 498 |
-
|
| 499 |
-
- Case $1: i$ is odd, so $i=2 j+1$ for some $j$. Then the middle term of the arithmetic progression is the average of all residues in $S$, which we can uniquely identify as some $u$ (and we know $n$ is coprime to $i$, so it is possible to average the residues). We need to show that there is only one choice of $d$, up to $\pm$, so that $S=\{u-$ $j d, u-(j-1) d, \ldots, u+j d\}$.
|
| 500 |
-
Let $X$ be the sum of squares of the residues in $S$, so we have
|
| 501 |
-
|
| 502 |
-
$$
|
| 503 |
-
X \equiv(u-j d)^{2}+(u-(j-1) d)^{2}+\cdots+(u+j d)^{2}=(2 j+1) u^{2}+d^{2} \frac{j(j+1)(2 j+1)}{3},
|
| 504 |
-
$$
|
| 505 |
-
|
| 506 |
-
which therefore implies
|
| 507 |
-
|
| 508 |
-
$$
|
| 509 |
-
3\left(X-(2 j+1) u^{2}\right)(j(j+1)(2 j+1))^{-1} \equiv d^{2}
|
| 510 |
-
$$
|
| 511 |
-
|
| 512 |
-
thus identifying $d$ uniquely up to sign as desired.
|
| 513 |
-
|
| 514 |
-
- Case 2: $i$ is even, so $i=2 j$ for some $j$. Once again we can compute the average $u$ of the residues in $S$, and we need to show that there is only one choice of $d$, up to $\pm$, so that $S=\{u-(2 j-1) d, u-(2 j-3) d, \ldots, u+(2 j-1) d\}$. Once again we compute the sum of squares $X$ of the residues in $S$, so that
|
| 515 |
-
$X \equiv(u-(2 j-1) d)^{2}+(u-(2 j-3) d)^{2}+\cdots+(u+(2 j-1) d)^{2}=2 j u^{2}+\frac{(2 j-1) 2 j(2 j+1)}{3}$
|
| 516 |
-
which therefore implies
|
| 517 |
-
|
| 518 |
-
$$
|
| 519 |
-
3\left(X-2 j u^{2}\right)((2 j-1) 2 j(2 j+1))^{-1} \equiv d^{2}
|
| 520 |
-
$$
|
| 521 |
-
|
| 522 |
-
again identifying $d$ uniquely up to sign as desired.
|
| 523 |
-
Thus we have shown that given the set of residues an arithmetic progression takes on modulo $n$, we can recover that progression up to sign. Here we have used the fact that given $d^{2}(\bmod n)$, it is possible to recover $d$ up to $\operatorname{sign}$ provided that $n$ is of the form $p^{m}$ with $p \neq 2$ and $\operatorname{gcd}(d, n)=1$.
|
| 524 |
-
|
| 525 |
-
Now, we will proceed by chaining many arithmetic sequences together.
|
| 526 |
-
Definition. For any integer $l$ between 0 and $a-1$, inclusive, define $C_{l}$ to be the sequence $0, g^{l}, g^{l}, 2 g^{l}, 3 g^{l}, \ldots,(n-1) g^{l},(n-1) g^{l}$ taken $(\bmod n)$. (This is just a sequence where the $i$ th term is $(i-1) g^{l}$, except the terms $g^{l},(n-1) g^{l}$ is repeated once.)
|
| 527 |
-
|
| 528 |
-
Definition. Consider the sequence $S_{n}$ of residues $\bmod n$ defined as follows:
|
| 529 |
-
|
| 530 |
-
- The first term of $S_{n}$ is 0 .
|
| 531 |
-
- For each $0 \leq l<a$, the next $n+2$ terms of $S_{n}$ are the terms of $C_{l}$ in order.
|
| 532 |
-
- The next and final term of $S_{n}$ is 0 .
|
| 533 |
-
|
| 534 |
-
We claim that $S_{n}$ constitutes a $k$-good string with respect to the alphabet of residues modulo $n$. We first make some initial observations about $S_{n}$.
|
| 535 |
-
|
| 536 |
-
## Lemma
|
| 537 |
-
|
| 538 |
-
$S_{n}$ has the following properties:
|
| 539 |
-
|
| 540 |
-
- $S_{n}$ has length $a(n+2)+2$.
|
| 541 |
-
- If a contiguous subsequence of $S_{n}$ of length $\leq k$ contains two of the same residue $(\bmod n)$, those two residues occur consecutively in the subsequence.
|
| 542 |
-
|
| 543 |
-
Proof of lemma. The first property is clear since each $C_{l}$ has length $n+2$, and there are $a$ of them, along with the 0s at beginning and end.
|
| 544 |
-
|
| 545 |
-
To prove the second property, consider any contiguous subsequence $S_{n}[i: i+k-1]$ of length $k$ which contains two of the same residue modulo $n$. If $S_{n}[i: i+k-1]$ is wholly contained within some $C_{l}$, it's clear that the only way $S_{n}[i: i+k-1]$ could repeat residues if it repeats one of the two consecutive values $g^{l}, g^{l}$ or $(n-1) g^{l},(n-1) g^{l}$, so assume that is not the case.
|
| 546 |
-
|
| 547 |
-
Now, it must be true that $S_{n}[i: i+k-1]$ consists of one contiguous subsequence of the form
|
| 548 |
-
|
| 549 |
-
$$
|
| 550 |
-
\left(n-k_{1}\right) g^{l-1},\left(n-\left(k_{1}-1\right)\right) g^{l-1}, \ldots,(n-1) g^{l-1},(n-1) g^{l-1}
|
| 551 |
-
$$
|
| 552 |
-
|
| 553 |
-
which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l-1}$, and then a second contiguous subsequence of the form
|
| 554 |
-
|
| 555 |
-
$$
|
| 556 |
-
0, g^{l}, g^{l}, 2 g^{l}, \ldots, k_{2} g^{l}
|
| 557 |
-
$$
|
| 558 |
-
|
| 559 |
-
which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l}$, and we obviously have $k_{2}+k_{1}=k-3$. For $S_{n}[i: i+k-1]$ to contain two of the same residue in non-consecutive positions, there would have to exist some $0<u \leq k_{1}, 0<v \leq k_{2}$ with $(n-u) g^{l-1} \equiv v g^{l}$ $(\bmod n)$, meaning that $u+g v \equiv 0(\bmod n)$. But we know since $k_{1}+k_{2}<k$ that $0<u+g v<k+k g<n$, so this is impossible, as desired.
|
| 560 |
-
|
| 561 |
-
Now we can prove the main claim.
|
| 562 |
-
Proof of main claim. Consider any multiset $M$ of $2 \leq i \leq k$ residues $(\bmod n)$ which corresponds to some unknown contiguous subsequence of $S_{n}$. We will show that it is possible to uniquely identify which contiguous subsequence $M$ corresponds to, thereby showing that $S_{n}$ has no twins of length $i$ for each $2 \leq i \leq k$, and then the result will follow.
|
| 563 |
-
|
| 564 |
-
First suppose $M$ contains some residue twice. By the last lemma there are only a few possible cases:
|
| 565 |
-
|
| 566 |
-
- $M$ contains multiple copies of the residue 0 . In this case we know $M$ contains the beginning of $S_{n}$, so the corresponding contiguous subsequence is just the first $i$ terms of $S_{n}$.
|
| 567 |
-
- $M$ contains multiple copies of multiple residues. By the last lemma and the structure of $S_{n}$, we can easily see that $M$ must contain two copies of $-g^{i-1}$ and two copies of $g^{i}$ for some $0 \leq i<a$ that can be identified uniquely, and $M$ must contain portions of both $C_{i-1}, C_{i}$. It follows $M$ 's terms can be partitioned into two portions, the first one being
|
| 568 |
-
|
| 569 |
-
$$
|
| 570 |
-
-i_{1} g^{i-1},-\left(i_{1}-1\right) g^{i-1}, \ldots,-g^{i-1},-g^{i-1}
|
| 571 |
-
$$
|
| 572 |
-
|
| 573 |
-
and the second one being
|
| 574 |
-
|
| 575 |
-
$$
|
| 576 |
-
0, g^{i}, g^{i}, 2 g^{i}, \ldots, i_{2} g^{i}
|
| 577 |
-
$$
|
| 578 |
-
|
| 579 |
-
for some $i_{1}$, $i_{2}$ with $i_{1}+i_{2}=i-3$, and we just need to uniquely identify $i_{1}, i_{2}$. Luckily, by dividing the residues in $M$ by $g^{i-1}$, we know we can partition $M$ 's terms into
|
| 580 |
-
|
| 581 |
-
$$
|
| 582 |
-
-i_{1},-\left(i_{1}-1\right), \ldots,-1,-1
|
| 583 |
-
$$
|
| 584 |
-
|
| 585 |
-
as well as
|
| 586 |
-
|
| 587 |
-
$$
|
| 588 |
-
0, g, g, 2 g, \ldots, i_{2} g
|
| 589 |
-
$$
|
| 590 |
-
|
| 591 |
-
Now since $i_{2} g \leq k g<n-k$ and $-i_{1} \equiv n-i_{1} \geq n-k$ it is easy to see that $i_{1}, i_{2}$ can be identified uniquely, as desired.
|
| 592 |
-
|
| 593 |
-
- $M$ contains multiple copies of only one residue $g^{i}$, for some $0 \leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the beginning of $C_{i}$ and possibly contain the last few terms of $C_{i-1}$, so $M$ must be of the form $g^{i}, g^{i}, 2 g^{i}, \ldots, i_{1} g^{i}$, along with possibly the term 0 or the terms $0,-g^{i-1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $g, g, 2 g, \ldots, i_{1} g$ along with possibly 0 or $0,-1$. Since $i_{1} g \leq k g<n-k$, we can easily disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$.
|
| 594 |
-
- $M$ contains multiple copies of only one residue $-g^{i}$, for some $0 \leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the end of $C_{i}$ and possibly the first terms of $C_{i+1}$, so $M$ must be of the form $-g^{i},-g^{i},-2 g^{i}, \ldots,-i_{1} g^{i}$, along with possibly the term 0 or the terms $0, g^{i+1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $-1,-1,-2, \ldots,-i_{1}$, along with possibly 0 or $0, g$. Since $-i_{1} \equiv n-i_{1} \geq \frac{n}{2}$ and $g<\frac{n}{2}$, we can disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$.
|
| 595 |
-
|
| 596 |
-
Thus in all cases where $M$ contains a repeated residue, we can identify the unique contiguous subsequence of $S_{n}$ corresponding to $M$.
|
| 597 |
-
|
| 598 |
-
When $M$ does not contain a repeated residue, it follows that $M$ cannot contain both of the $g^{i}$ terms or $(n-1) g^{i}$ terms at the beginning or end of each $C_{i}$. It follows that $M$ is either entirely contained in some $C_{i}$ or contained in the union of the end of some $C_{i}$ with the beginning of some $C_{i+1}$, meaning $M$ corresponds to a contiguous subsequence of $\left(-g^{i}, 0, g^{i+1}\right)$. In the first case, since each $C_{i}$ is an arithmetic progression when the repeated terms are ignored, Lemma 1 implies that we can uniquely determine the location of $M$, and in the second case, it is easy to tell which contiguous subsequence of $\left(-g^{i}, 0, g^{i+1}\right)$ corresponds to $M$.
|
| 599 |
-
|
| 600 |
-
Therefore, in all cases, for any multiset $M$ corresponding to some contiguous subsequence of $S_{n}$ of length $i \leq k$, we can uniquely identify the contiguous subsequence, meaning $S_{n}$ is $k$-good with respect to the alphabet of residues modulo $n$, as desired.
|
| 601 |
-
|
| 602 |
-
Now we will finish the problem. We observe the following.
|
| 603 |
-
Claim - Fix $k$ and let $p>k+1$ be a prime. Then for $n=p^{2}$ we can find a $(n, k)$-good sequence of length $\frac{p(p-1)\left(p^{2}+2\right)}{2}$.
|
| 604 |
-
|
| 605 |
-
Proof of last claim. Let $g$ be the smallest primitive root modulo $n=p^{2}$, so that $a=$ $\frac{p(p-1)}{2}$. As long as we can show that $g<\frac{n}{k}-1$, we can apply the previous claim to get the desired bound.
|
| 606 |
-
|
| 607 |
-
We will prove a stronger statement that $g<p$. Indeed, consider any primitive root $g_{0}$ $(\bmod p)$. Then $g_{0}+a p$ has order $p-1 \operatorname{modulo} p$, so its order modulo $p^{2}$ is divisible by $p-1$, hence $g_{0}+a p$ is a primitive root modulo $p^{2}$ as long as $\left(g_{0}+a p\right)^{p-1} \not \equiv 1\left(\bmod p^{2}\right)$. Now
|
| 608 |
-
|
| 609 |
-
$$
|
| 610 |
-
\left(g_{0}+a p\right)^{p-1}=\sum_{i} g_{0}^{p-1-i}(a p)^{i}\binom{p-1}{i} \equiv g_{0}^{p-1}+g_{0}^{p-2}(a p) \quad\left(\bmod p^{2}\right)
|
| 611 |
-
$$
|
| 612 |
-
|
| 613 |
-
In particular, of the values $g_{0}, g_{0}+p, \ldots, g_{0}+p(p-1)$, only one has order $p-1$ and the rest are primitive roots.
|
| 614 |
-
|
| 615 |
-
So for each $0<g_{0}<p$ which is a primitive root modulo $p$, either $g_{0}$ is a primitive root modulo $p^{2}$ or $g_{0}$ has order $p-1$ but $g_{0}+p, g_{0}+2 p, \ldots, g_{0}+p(p-1)$ are all primitive roots. By considering all choices of $g_{0}$, we either find a primitive root $\left(\bmod p^{2}\right)$ which is between 0 and $p$, or we find that all residues $\left(\bmod p^{2}\right)$ of order $p-1$ are between 0 and $p$. But if $\operatorname{ord}_{p^{2}}(a)=p-1$ then $\operatorname{ord}_{p^{2}}\left(a^{-1}\right)=p-1$, and two residues between $0, p$ cannot be inverses modulo $p^{2}$ (because with the exception of 1 , they cannot multiply to something $\geq p^{2}+1$ ), so there is always a primitive root between $0, p$ as desired.
|
| 616 |
-
|
| 617 |
-
Now for arbitrarily large $n$ we can choose $p<\sqrt{n}$ with $\frac{p}{\sqrt{n}}$ arbitrarily close to 1 ; by the previous claim, we can get an $(n, k)$-good sequence of length at least $\frac{p-1}{p} \cdot \frac{p^{4}}{2}$ for any constant, so for sufficiently large $n, p$ we get $(n, k)$-good sequences of length $0.499 n^{2}$.
|
| 618 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/md/en-sols-TSTST-2023.md
DELETED
|
@@ -1,1241 +0,0 @@
|
|
| 1 |
-
# USA TSTST 2023 Solutions <br> United States of America - TST Selection Test
|
| 2 |
-
|
| 3 |
-
Andrew Gu, Evan Chen, Gopal Goel<br>$65^{\text {th }}$ IMO 2024 United Kingdom and $13^{\text {th }}$ EGMO 2024 Georgia
|
| 4 |
-
|
| 5 |
-
## Contents
|
| 6 |
-
|
| 7 |
-
0 Problems ..... 2
|
| 8 |
-
1 Solutions to Day 1 ..... 4
|
| 9 |
-
1.1 TSTST 2023/1, proposed by Merlijn Staps ..... 4
|
| 10 |
-
1.2 TSTST 2023/2, proposed by Raymond Feng, Luke Robitaille ..... 9
|
| 11 |
-
1.3 TSTST 2023/3, proposed by Merlijn Staps ..... 13
|
| 12 |
-
2 Solutions to Day 2 ..... 16
|
| 13 |
-
2.1 TSTST 2023/4, proposed by Ankan Bhattacharya ..... 16
|
| 14 |
-
2.2 TSTST 2023/5, proposed by David Altizio ..... 17
|
| 15 |
-
2.3 TSTST 2023/6, proposed by Holden Mui ..... 20
|
| 16 |
-
3 Solutions to Day 3 ..... 24
|
| 17 |
-
3.1 TSTST 2023/7, proposed by Luke Robitaille ..... 24
|
| 18 |
-
3.2 TSTST 2023/8, proposed by Ankan Bhattacharya ..... 25
|
| 19 |
-
3.3 TSTST 2023/9, proposed by Holden Mui ..... 28
|
| 20 |
-
|
| 21 |
-
## §0 Problems
|
| 22 |
-
|
| 23 |
-
1. Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that
|
| 24 |
-
|
| 25 |
-
$$
|
| 26 |
-
\angle A B S=\angle A C R=180^{\circ}-\angle B G C .
|
| 27 |
-
$$
|
| 28 |
-
|
| 29 |
-
Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
| 30 |
-
2. Let $n \geq m \geq 1$ be integers. Prove that
|
| 31 |
-
|
| 32 |
-
$$
|
| 33 |
-
\sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}
|
| 34 |
-
$$
|
| 35 |
-
|
| 36 |
-
3. Find all positive integers $n$ for which it is possible to color some cells of an infinite grid of unit squares red, such that each rectangle consisting of exactly $n$ cells (and whose edges lie along the lines of the grid) contains an odd number of red cells.
|
| 37 |
-
4. Let $n \geq 3$ be an integer and let $K_{n}$ be the complete graph on $n$ vertices. Each edge of $K_{n}$ is colored either red, green, or blue. Let $A$ denote the number of triangles in $K_{n}$ with all edges of the same color, and let $B$ denote the number of triangles in $K_{n}$ with all edges of different colors. Prove that
|
| 38 |
-
|
| 39 |
-
$$
|
| 40 |
-
B \leq 2 A+\frac{n(n-1)}{3} .
|
| 41 |
-
$$
|
| 42 |
-
|
| 43 |
-
5. Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define
|
| 44 |
-
|
| 45 |
-
$$
|
| 46 |
-
p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} .
|
| 47 |
-
$$
|
| 48 |
-
|
| 49 |
-
Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
| 50 |
-
6. Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
| 51 |
-
7. The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up.
|
| 52 |
-
In a move, Vera may flip over one of the coins in the row, subject to the following rules:
|
| 53 |
-
|
| 54 |
-
- On the first move, Vera may flip over any of the 2023 coins.
|
| 55 |
-
- On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.)
|
| 56 |
-
|
| 57 |
-
Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.
|
| 58 |
-
8. Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$.
|
| 59 |
-
Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
| 60 |
-
9. Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by
|
| 61 |
-
|
| 62 |
-
$$
|
| 63 |
-
\begin{aligned}
|
| 64 |
-
& \Delta^{0} f(n)=f(n) \\
|
| 65 |
-
& \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots
|
| 66 |
-
\end{aligned}
|
| 67 |
-
$$
|
| 68 |
-
|
| 69 |
-
Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
| 70 |
-
|
| 71 |
-
## §1 Solutions to Day 1
|
| 72 |
-
|
| 73 |
-
## §1.1 TSTST 2023/1, proposed by Merlijn Staps
|
| 74 |
-
|
| 75 |
-
Available online at https://aops.com/community/p28015679.
|
| 76 |
-
|
| 77 |
-
## Problem statement
|
| 78 |
-
|
| 79 |
-
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that
|
| 80 |
-
|
| 81 |
-
$$
|
| 82 |
-
\angle A B S=\angle A C R=180^{\circ}-\angle B G C .
|
| 83 |
-
$$
|
| 84 |
-
|
| 85 |
-
Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
| 86 |
-
|
| 87 |
-
In all the following solutions, let $M$ and $N$ denote the midpoints of $\overline{A C}$ and $\overline{A B}$, respectively.
|
| 88 |
-
|
| 89 |
-
|
| 90 |
-
【 Solution 1 using power of a point. From the given condition that $\measuredangle A C R=\measuredangle C G M$, we get that
|
| 91 |
-
|
| 92 |
-
$$
|
| 93 |
-
M A^{2}=M C^{2}=M G \cdot M R \Longrightarrow \measuredangle R A C=\measuredangle M G A
|
| 94 |
-
$$
|
| 95 |
-
|
| 96 |
-
Analogously,
|
| 97 |
-
|
| 98 |
-
$$
|
| 99 |
-
\measuredangle B A S=\measuredangle A G N
|
| 100 |
-
$$
|
| 101 |
-
|
| 102 |
-
Hence,
|
| 103 |
-
|
| 104 |
-
$$
|
| 105 |
-
\measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle M G A+\measuredangle A G N=\measuredangle M G N=\measuredangle B G C .
|
| 106 |
-
$$
|
| 107 |
-
|
| 108 |
-
ब Solution 2 using similar triangles. As before, $\triangle M G C \sim \triangle M C R$ and $\triangle N G B \sim$ $\triangle N B S$. We obtain
|
| 109 |
-
|
| 110 |
-
$$
|
| 111 |
-
\frac{|A C|}{|C R|}=\frac{2|M C|}{|C R|}=\frac{2|M G|}{|G C|}=\frac{|G B|}{2|N G|}=\frac{|B S|}{2|B N|}=\frac{|B S|}{|A B|}
|
| 112 |
-
$$
|
| 113 |
-
|
| 114 |
-
which together with $\angle A C R=\angle A B S$ yields
|
| 115 |
-
|
| 116 |
-
$$
|
| 117 |
-
\triangle A C R \sim \triangle S B A \Longrightarrow \measuredangle B A S=\measuredangle C R A
|
| 118 |
-
$$
|
| 119 |
-
|
| 120 |
-
Hence
|
| 121 |
-
|
| 122 |
-
$$
|
| 123 |
-
\measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle R A C+\measuredangle C R A=-\measuredangle A C R=\measuredangle B G C,
|
| 124 |
-
$$
|
| 125 |
-
|
| 126 |
-
which proves the statement.
|
| 127 |
-
|
| 128 |
-
I Solution 3 using parallelograms. Let $M$ and $N$ be defined as above. Let $P$ be the reflection of $G$ in $M$ and let $Q$ the reflection of $G$ in $N$. Then $A G C P$ and $A G B Q$ are parallelograms.
|
| 129 |
-
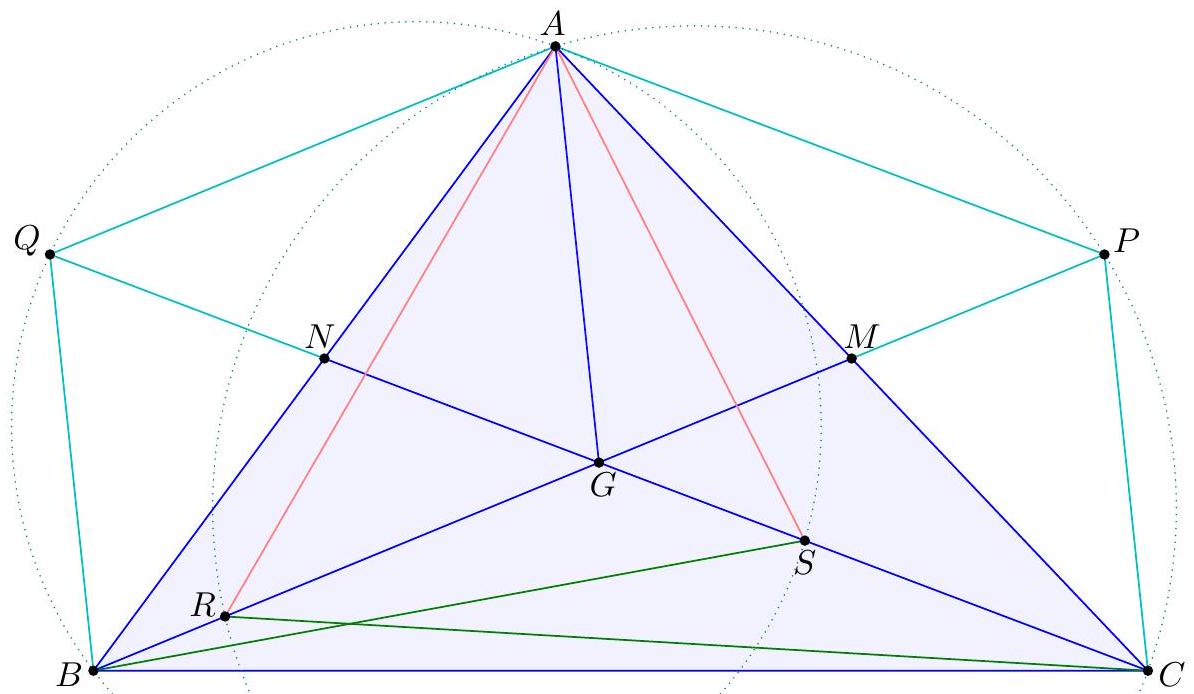
|
| 130 |
-
|
| 131 |
-
Claim - Quadrilaterals $A P C R$ and $A Q B S$ are concyclic.
|
| 132 |
-
|
| 133 |
-
Proof. Because $\measuredangle A P R=\measuredangle A P G=\measuredangle C G P=-\measuredangle B G C=\measuredangle A C R$.
|
| 134 |
-
Thus from $\overline{P C} \| \overline{G A}$ we get
|
| 135 |
-
|
| 136 |
-
$$
|
| 137 |
-
\measuredangle R A C=\measuredangle R P C=\measuredangle G P C=\measuredangle P G A
|
| 138 |
-
$$
|
| 139 |
-
|
| 140 |
-
and similarly
|
| 141 |
-
|
| 142 |
-
$$
|
| 143 |
-
\measuredangle B A S=\measuredangle B Q S=\measuredangle B Q G=\measuredangle A G Q
|
| 144 |
-
$$
|
| 145 |
-
|
| 146 |
-
We conclude that
|
| 147 |
-
|
| 148 |
-
$$
|
| 149 |
-
\measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle P G A+\measuredangle A G Q=\measuredangle P G Q=\measuredangle B G C
|
| 150 |
-
$$
|
| 151 |
-
|
| 152 |
-
ब Solution 4 also using parallelograms, by Ankan Bhattacharya. Construct parallelograms $A R C K$ and $A S B L$. Since
|
| 153 |
-
|
| 154 |
-
$$
|
| 155 |
-
\measuredangle C A K=\measuredangle A C R=\measuredangle C G B=\measuredangle C G K,
|
| 156 |
-
$$
|
| 157 |
-
|
| 158 |
-
it follows that $A G C K$ is cyclic. Similarly, $A G B L$ is also cyclic.
|
| 159 |
-
|
| 160 |
-
|
| 161 |
-
Finally, observe that
|
| 162 |
-
|
| 163 |
-
$$
|
| 164 |
-
\begin{aligned}
|
| 165 |
-
\angle R A S+\angle B A C & =\measuredangle B A S+\measuredangle R A C \\
|
| 166 |
-
& =\measuredangle A B L+\measuredangle K C A \\
|
| 167 |
-
& =\measuredangle A G L+\measuredangle K G A \\
|
| 168 |
-
& =\measuredangle K G L \\
|
| 169 |
-
& =\angle B G C
|
| 170 |
-
\end{aligned}
|
| 171 |
-
$$
|
| 172 |
-
|
| 173 |
-
as requested.
|
| 174 |
-
『 Solution 5 using complex numbers, by Milan Haiman. Note that $\angle R A S+\angle B A C=$ $\angle B A S+\angle R A C$. We compute $\angle B A S$ in complex numbers; then $\angle R A C$ will then be known by symmetry.
|
| 175 |
-
|
| 176 |
-
Let $a, b, c$ be points on the unit circle representing $A, B, C$ respectively. Let $g=\frac{1}{3}(a+b+c)$ represent the centroid $G$, and let $s$ represent $S$.
|
| 177 |
-
|
| 178 |
-
## Claim - We have
|
| 179 |
-
|
| 180 |
-
$$
|
| 181 |
-
\frac{s-a}{b-a}=\frac{a b-2 b c+c a}{2 a b-b c-c a} .
|
| 182 |
-
$$
|
| 183 |
-
|
| 184 |
-
Proof. Since $S$ is on line $C G$, which passes through the midpoint of segment $A B$, we have that
|
| 185 |
-
|
| 186 |
-
$$
|
| 187 |
-
s=\frac{a+b}{2}+t(c-g)
|
| 188 |
-
$$
|
| 189 |
-
|
| 190 |
-
for some $t \in \mathbb{R}$.
|
| 191 |
-
By the given angle condition, we have that
|
| 192 |
-
|
| 193 |
-
$$
|
| 194 |
-
\frac{(s-b) /(b-a)}{(c-g) /(g-b)} \in \mathbb{R}
|
| 195 |
-
$$
|
| 196 |
-
|
| 197 |
-
Note that
|
| 198 |
-
|
| 199 |
-
$$
|
| 200 |
-
\frac{s-b}{b-a}=t \frac{c-g}{b-a}-\frac{1}{2}
|
| 201 |
-
$$
|
| 202 |
-
|
| 203 |
-
So,
|
| 204 |
-
|
| 205 |
-
$$
|
| 206 |
-
t \frac{g-b}{b-a}-\frac{g-b}{2(c-g)} \in \mathbb{R}
|
| 207 |
-
$$
|
| 208 |
-
|
| 209 |
-
Thus
|
| 210 |
-
|
| 211 |
-
$$
|
| 212 |
-
t=\frac{\operatorname{Im}\left(\frac{g-b}{2(c-g)}\right)}{\operatorname{Im}\left(\frac{g-b}{b-a}\right)}=\frac{1}{2} \cdot \frac{\left(\frac{g-b}{c-g}\right)-\overline{\left(\frac{g-b}{c-g}\right)}}{\left(\frac{g-b}{b-a}\right)-\overline{\left(\frac{g-b}{b-a}\right)}}
|
| 213 |
-
$$
|
| 214 |
-
|
| 215 |
-
Let $N$ and $D$ be the numerator and denominator of the second factor above.
|
| 216 |
-
We want to compute
|
| 217 |
-
|
| 218 |
-
$$
|
| 219 |
-
\frac{s-a}{b-a}=\frac{1}{2}+t \frac{c-g}{b-a}=\frac{(b-a)+2 t(c-g)}{2(b-a)}=\frac{(b-a) D+(c-g) N}{2(b-a) D}
|
| 220 |
-
$$
|
| 221 |
-
|
| 222 |
-
We have
|
| 223 |
-
|
| 224 |
-
$$
|
| 225 |
-
\begin{aligned}
|
| 226 |
-
(c-g) N & =g-b-(c-g) \overline{\left(\frac{g-b}{c-g}\right)} \\
|
| 227 |
-
& =\frac{a+b+c}{3}-b-\left(c-\frac{a+b+c}{3}\right) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{c}-\frac{1}{a}-\frac{1}{b}-\frac{1}{c}} \\
|
| 228 |
-
& =\frac{(a+c-2 b)(2 a b-b c-c a)-(2 c-a-b)(a b+b c-2 c a)}{3(2 a b-b c-c a)} \\
|
| 229 |
-
& =\frac{3\left(a^{2} b+b^{2} c+c^{2} a-a b^{2}-b c^{2}-c a^{2}\right)}{3(2 a b-b c-c a)} \\
|
| 230 |
-
& =\frac{(a-b)(b-c)(a-c)}{2 a b-b c-c a}
|
| 231 |
-
\end{aligned}
|
| 232 |
-
$$
|
| 233 |
-
|
| 234 |
-
We also compute
|
| 235 |
-
|
| 236 |
-
$$
|
| 237 |
-
\begin{aligned}
|
| 238 |
-
(b-a) D & =g-b-(b-a) \overline{\left(\frac{g-b}{b-a}\right)} \\
|
| 239 |
-
& =\frac{a+b+c}{3}-b-(b-a) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{b}-\frac{3}{a}} \\
|
| 240 |
-
& =\frac{(a+c-2 b) c+(a b+b c-2 c a)}{3 c} \\
|
| 241 |
-
& =\frac{a b-b c-c a+c^{2}}{3 c} \\
|
| 242 |
-
& =\frac{(a-c)(b-c)}{3 c}
|
| 243 |
-
\end{aligned}
|
| 244 |
-
$$
|
| 245 |
-
|
| 246 |
-
So, we obtain
|
| 247 |
-
|
| 248 |
-
$$
|
| 249 |
-
\frac{s-a}{b-a}=\frac{\frac{1}{3 c}+\frac{a-b}{2 a b-b c-c a}}{\frac{2}{3 c}}=\frac{2 a b-b c-c a+3 c(a-b)}{2(2 a b-b c-c a)}=\frac{a b-2 b c+c a}{2 a b-b c-c a}
|
| 250 |
-
$$
|
| 251 |
-
|
| 252 |
-
By symmetry,
|
| 253 |
-
|
| 254 |
-
$$
|
| 255 |
-
\frac{r-a}{c-a}=\frac{a b-2 b c+c a}{2 c a-a b-b c}
|
| 256 |
-
$$
|
| 257 |
-
|
| 258 |
-
Hence their ratio
|
| 259 |
-
|
| 260 |
-
$$
|
| 261 |
-
\frac{s-a}{b-a} \div \frac{r-a}{c-a}=\frac{2 a b-b c-c a}{2 c a-a b-b c}
|
| 262 |
-
$$
|
| 263 |
-
|
| 264 |
-
has argument $\angle R A C+\angle B A S$.
|
| 265 |
-
|
| 266 |
-
We also have that $\angle B G C$ is the argument of
|
| 267 |
-
|
| 268 |
-
$$
|
| 269 |
-
\frac{b-g}{c-g}=\frac{2 b-a-c}{2 c-a-b}
|
| 270 |
-
$$
|
| 271 |
-
|
| 272 |
-
Note that these two complex numbers are inverse-conjugates, and thus have the same argument. So we're done.
|
| 273 |
-
|
| 274 |
-
## §1.2 TSTST 2023/2, proposed by Raymond Feng, Luke Robitaille
|
| 275 |
-
|
| 276 |
-
Available online at https://aops.com/community/p28015692.
|
| 277 |
-
|
| 278 |
-
## Problem statement
|
| 279 |
-
|
| 280 |
-
Let $n \geq m \geq 1$ be integers. Prove that
|
| 281 |
-
|
| 282 |
-
$$
|
| 283 |
-
\sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}
|
| 284 |
-
$$
|
| 285 |
-
|
| 286 |
-
We show several approaches.
|
| 287 |
-
【 First solution (authors). By Cauchy-Schwarz, we have
|
| 288 |
-
|
| 289 |
-
$$
|
| 290 |
-
\begin{aligned}
|
| 291 |
-
\sum_{k=m}^{n} \frac{k+1}{k^{3}} & =\sum_{k=m}^{n} \frac{\left(\frac{1}{k^{2}}\right)^{2}}{\frac{1}{k(k+1)}} \\
|
| 292 |
-
& \geq \frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m(m+1)}+\frac{1}{(m+1)(m+2)}+\cdots+\frac{1}{n(n+1)}} \\
|
| 293 |
-
& =\frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m}-\frac{1}{n+1}} \\
|
| 294 |
-
& >\frac{\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}}{\frac{1}{m}}
|
| 295 |
-
\end{aligned}
|
| 296 |
-
$$
|
| 297 |
-
|
| 298 |
-
as desired.
|
| 299 |
-
Remark (Bound on error). Let $A=\sum_{k=m}^{n} k^{-2}$ and $B=\sum_{k=m}^{n} k^{-3}$. The inequality above becomes tighter for large $m$ and $n \gg m$. If we use Lagrange's identity in place of Cauchy-Schwarz, we get
|
| 300 |
-
|
| 301 |
-
$$
|
| 302 |
-
A+B-m A^{2}=m \cdot \sum_{m \leq a<b} \frac{(a-b)^{2}}{a^{3} b^{3}(a+1)(b+1)}
|
| 303 |
-
$$
|
| 304 |
-
|
| 305 |
-
We can upper bound this error by
|
| 306 |
-
|
| 307 |
-
$$
|
| 308 |
-
\leq m \cdot \sum_{m \leq a<b} \frac{1}{a^{3}(a+1) b(b+1)}=m \cdot \sum_{m \leq a} \frac{1}{a^{3}(a+1)^{2}} \approx m \cdot \frac{1}{m^{4}}=\frac{1}{m^{3}},
|
| 309 |
-
$$
|
| 310 |
-
|
| 311 |
-
which is still generous as $(a-b)^{2} \ll b^{2}$ for $b$ not much larger than $a$, so the real error is probably around $\frac{1}{10 \mathrm{~m}^{3}}$. This exhibits the tightness of the inequality since it implies
|
| 312 |
-
|
| 313 |
-
$$
|
| 314 |
-
m A^{2}+O(B / m)>A+B
|
| 315 |
-
$$
|
| 316 |
-
|
| 317 |
-
Remark (Construction commentary, from author). My motivation was to write an inequality where Titu could be applied creatively to yield a telescoping sum. This can be difficult because most of the time, such a reverse-engineered inequality will be so loose it's trivial
|
| 318 |
-
anyways. My first attempt was the not-so-amazing inequality
|
| 319 |
-
|
| 320 |
-
$$
|
| 321 |
-
\frac{n^{2}+3 n}{2}=\sum_{1}^{n} i+1=\sum_{1}^{n} \frac{\frac{1}{i}}{\frac{1}{i(i+1)}}>\left(\sum_{1}^{n} \frac{1}{\sqrt{i}}\right)^{2}
|
| 322 |
-
$$
|
| 323 |
-
|
| 324 |
-
which is really not surprising given that $\sum \frac{1}{\sqrt{i}} \ll \frac{n}{\sqrt{2}}$. The key here is that we need "near-equality" as dictated by the Cauchy-Schwarz equality case, i.e. the square root of the numerators should be approximately proportional to the denominators.
|
| 325 |
-
|
| 326 |
-
This motivates using $\frac{1}{i^{4}}$ as the numerator, which works like a charm. After working out the resulting statement, the LHS and RHS even share a sum, which adds to the simplicity of the problem.
|
| 327 |
-
|
| 328 |
-
The final touch was to unrestrict the starting value of the sum, since this allows the strength of the estimate $\frac{1}{i^{2}} \approx \frac{1}{i(i+1)}$ to be fully exploited.
|
| 329 |
-
|
| 330 |
-
【 Second approach by inducting down, Luke Robitaille and Carl Schildkraut. Fix $n$; we'll induct downwards on $m$. For the base case of $n=m$ the result is easy, since the left side is $\frac{m+1}{m^{3}}$ and the right side is $\frac{m}{m^{4}}=\frac{1}{m^{3}}$.
|
| 331 |
-
|
| 332 |
-
For the inductive step, suppose we have shown the result for $m+1$. Let
|
| 333 |
-
|
| 334 |
-
$$
|
| 335 |
-
A=\sum_{k=m+1}^{n} \frac{1}{k^{2}} \quad \text { and } \quad B=\sum_{k=m+1}^{n} \frac{1}{k^{3}}
|
| 336 |
-
$$
|
| 337 |
-
|
| 338 |
-
We know $A+B \geq(m+1) A^{2}$, and we want to show
|
| 339 |
-
|
| 340 |
-
$$
|
| 341 |
-
\left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right) \geq m\left(A+\frac{1}{m^{2}}\right)^{2}
|
| 342 |
-
$$
|
| 343 |
-
|
| 344 |
-
Indeed,
|
| 345 |
-
|
| 346 |
-
$$
|
| 347 |
-
\begin{aligned}
|
| 348 |
-
\left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right)-m\left(A+\frac{1}{m^{2}}\right)^{2} & =A+B+\frac{m+1}{m^{3}}-m A^{2}-\frac{2 A}{m}-\frac{1}{m^{3}} \\
|
| 349 |
-
& =\left(A+B-(m+1) A^{2}\right)+\left(A-\frac{1}{m}\right)^{2} \geq 0
|
| 350 |
-
\end{aligned}
|
| 351 |
-
$$
|
| 352 |
-
|
| 353 |
-
and we are done.
|
| 354 |
-
|
| 355 |
-
I Third approach by reducing $n \rightarrow \infty$, Michael Ren and Carl Schildkraut. First, we give:
|
| 356 |
-
|
| 357 |
-
Claim (Reduction to $n \rightarrow \infty$ ) - If the problem is true when $n \rightarrow \infty$, it is true for all $n$.
|
| 358 |
-
|
| 359 |
-
Proof. Let $A=\sum_{k=m}^{n} k^{-2}$ and $B=\sum_{k=m}^{n} k^{-3}$. Consider the region of the $x y$-plane defined by $y>m x^{2}-x$. We are interested in whether $(A, B)$ lies in this region.
|
| 360 |
-
|
| 361 |
-
However, the region is bounded by a convex curve, and the sequence of points $(0,0)$, $\left(\frac{1}{m^{2}}, \frac{1}{m^{3}}\right),\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}, \frac{1}{m^{3}}+\frac{1}{(m+1)^{3}}\right), \ldots$ has successively decreasing slopes between consecutive points. Thus it suffices to check that the inequality is true when $n \rightarrow \infty$.
|
| 362 |
-
|
| 363 |
-
Set $n=\infty$ henceforth. Let
|
| 364 |
-
|
| 365 |
-
$$
|
| 366 |
-
A=\sum_{k=m}^{\infty} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{\infty} \frac{1}{k^{3}}
|
| 367 |
-
$$
|
| 368 |
-
|
| 369 |
-
we want to show $B \geq m A^{2}-A$, which rearranges to
|
| 370 |
-
|
| 371 |
-
$$
|
| 372 |
-
1+4 m B \geq(2 m A-1)^{2}
|
| 373 |
-
$$
|
| 374 |
-
|
| 375 |
-
Write
|
| 376 |
-
|
| 377 |
-
$$
|
| 378 |
-
C=\sum_{k=m}^{\infty} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{\infty} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}
|
| 379 |
-
$$
|
| 380 |
-
|
| 381 |
-
Then
|
| 382 |
-
|
| 383 |
-
$$
|
| 384 |
-
\frac{2}{2 k-1}-\frac{2}{2 k+1}=\frac{1}{k^{2}}+\frac{1}{k^{2}(2 k-1)(2 k+1)}
|
| 385 |
-
$$
|
| 386 |
-
|
| 387 |
-
and
|
| 388 |
-
|
| 389 |
-
$$
|
| 390 |
-
\frac{2}{(2 k-1)^{2}}-\frac{2}{(2 k+1)^{2}}=\frac{1}{k^{3}}+\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}},
|
| 391 |
-
$$
|
| 392 |
-
|
| 393 |
-
so that
|
| 394 |
-
|
| 395 |
-
$$
|
| 396 |
-
A=\frac{2}{2 m-1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-D
|
| 397 |
-
$$
|
| 398 |
-
|
| 399 |
-
Our inequality we wish to show becomes
|
| 400 |
-
|
| 401 |
-
$$
|
| 402 |
-
\frac{2 m+1}{2 m-1} C \geq D+m C^{2}
|
| 403 |
-
$$
|
| 404 |
-
|
| 405 |
-
We in fact show two claims:
|
| 406 |
-
Claim - We have
|
| 407 |
-
|
| 408 |
-
$$
|
| 409 |
-
\frac{2 m+1 / 2}{2 m-1} C \geq D
|
| 410 |
-
$$
|
| 411 |
-
|
| 412 |
-
Proof. We compare termwise; we need
|
| 413 |
-
|
| 414 |
-
$$
|
| 415 |
-
\frac{2 m+1 / 2}{2 m-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}
|
| 416 |
-
$$
|
| 417 |
-
|
| 418 |
-
for $k \geq m$. It suffices to show
|
| 419 |
-
|
| 420 |
-
$$
|
| 421 |
-
\frac{2 k+1 / 2}{2 k-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}
|
| 422 |
-
$$
|
| 423 |
-
|
| 424 |
-
which is equivalent to $k(2 k+1 / 2)(2 k+1) \geq 8 k^{2}-1$. This holds for all $k \geq 1$.
|
| 425 |
-
|
| 426 |
-
## Claim - We have
|
| 427 |
-
|
| 428 |
-
$$
|
| 429 |
-
\frac{1 / 2}{2 m-1} C \geq m C^{2}
|
| 430 |
-
$$
|
| 431 |
-
|
| 432 |
-
Proof. We need $C \leq 1 /(2 m(2 m-1))$; indeed,
|
| 433 |
-
|
| 434 |
-
$$
|
| 435 |
-
\frac{1}{2 m(2 m-1)}=\sum_{k=m}^{\infty}\left(\frac{1}{2 k(2 k-1)}-\frac{1}{2(k+1)(2 k+1)}\right)=\sum_{k=m}^{\infty} \frac{4 k+1}{2 k(2 k-1)(k+1)(2 k+1)}
|
| 436 |
-
$$
|
| 437 |
-
|
| 438 |
-
comparing term-wise with the definition of $C$ and using the inequality $k(4 k+1) \geq 2(k+1)$ for $k \geq 1$ gives the desired result.
|
| 439 |
-
|
| 440 |
-
Combining the two claims finishes the solution.
|
| 441 |
-
|
| 442 |
-
『 Fourth approach by bashing, Carl Schildkraut. With a bit more work, the third approach can be adapted to avoid the $n \rightarrow \infty$ reduction. Similarly to before, define
|
| 443 |
-
|
| 444 |
-
$$
|
| 445 |
-
A=\sum_{k=m}^{n} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{n} \frac{1}{k^{3}}
|
| 446 |
-
$$
|
| 447 |
-
|
| 448 |
-
we want to show $1+4 m B \geq(2 m A-1)^{2}$. Writing
|
| 449 |
-
|
| 450 |
-
$$
|
| 451 |
-
C=\sum_{k=m}^{n} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{n} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}
|
| 452 |
-
$$
|
| 453 |
-
|
| 454 |
-
We compute
|
| 455 |
-
|
| 456 |
-
$$
|
| 457 |
-
A=\frac{2}{2 m-1}-\frac{2}{2 n+1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-\frac{2}{(2 n+1)^{2}}-D .
|
| 458 |
-
$$
|
| 459 |
-
|
| 460 |
-
Then, the inequality we wish to show reduces (as in the previous solution) to
|
| 461 |
-
|
| 462 |
-
$$
|
| 463 |
-
\frac{2 m+1}{2 m-1} C+\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq D+m C^{2}+\frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C
|
| 464 |
-
$$
|
| 465 |
-
|
| 466 |
-
We deal first with the terms not containing the variable $n$, i.e. we show that
|
| 467 |
-
|
| 468 |
-
$$
|
| 469 |
-
\frac{2 m+1}{2 m-1} C \geq D+m C^{2}
|
| 470 |
-
$$
|
| 471 |
-
|
| 472 |
-
For this part, the two claims from the previous solution go through exactly as written above, and we have $C \leq 1 /(2 m(2 m-1))$. We now need to show
|
| 473 |
-
|
| 474 |
-
$$
|
| 475 |
-
\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq \frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C
|
| 476 |
-
$$
|
| 477 |
-
|
| 478 |
-
(this is just the inequality between the remaining terms); our bound on $C$ reduces this to proving
|
| 479 |
-
|
| 480 |
-
$$
|
| 481 |
-
\frac{4(2 m+1)(n-m+1)}{(2 m-1)(2 n+1)^{2}} \geq \frac{2}{(2 m-1)(2 n+1)}
|
| 482 |
-
$$
|
| 483 |
-
|
| 484 |
-
Expanding and writing in terms of $n$, this is equivalent to
|
| 485 |
-
|
| 486 |
-
$$
|
| 487 |
-
n \geq \frac{1+2(m-1)(2 m+1)}{4 m}=m-\frac{2 m+1}{4 m}
|
| 488 |
-
$$
|
| 489 |
-
|
| 490 |
-
which holds for all $n \geq m$.
|
| 491 |
-
|
| 492 |
-
## §1.3 TSTST 2023/3, proposed by Merlijn Staps
|
| 493 |
-
|
| 494 |
-
Available online at https://aops.com/community/p28015682.
|
| 495 |
-
|
| 496 |
-
## Problem statement
|
| 497 |
-
|
| 498 |
-
Find all positive integers $n$ for which it is possible to color some cells of an infinite grid of unit squares red, such that each rectangle consisting of exactly $n$ cells (and whose edges lie along the lines of the grid) contains an odd number of red cells.
|
| 499 |
-
|
| 500 |
-
We claim that this is possible for all positive integers $n$. Call a positive integer for which such a coloring is possible good. To show that all positive integers $n$ are good we prove the following:
|
| 501 |
-
(i) If $n$ is good and $p$ is an odd prime, then $p n$ is good;
|
| 502 |
-
(ii) For every $k \geq 0$, the number $n=2^{k}$ is good.
|
| 503 |
-
|
| 504 |
-
Together, (i) and (ii) imply that all positive integers are good.
|
| 505 |
-
【 Proof of (i). We simply observe that if every rectangle consisting of $n$ cells contains an odd number of red cells, then so must every rectangle consisting of $p n$ cells. Indeed, because $p$ is prime, a rectangle consisting of $p n$ cells must have a dimension (length or width) divisible by $p$ and can thus be subdivided into $p$ rectangles consisting of $n$ cells.
|
| 506 |
-
|
| 507 |
-
Thus every coloring that works for $n$ automatically also works for $p n$.
|
| 508 |
-
【 Proof of (ii). Observe that rectangles with $n=2^{k}$ cells have $k+1$ possible shapes: $2^{m} \times 2^{k-m}$ for $0 \leq m \leq k$.
|
| 509 |
-
|
| 510 |
-
Claim - For each of these $k+1$ shapes, there exists a coloring with two properties:
|
| 511 |
-
|
| 512 |
-
- Every rectangle with $n$ cells and shape $2^{m} \times 2^{k-m}$ contains an odd number of red cells.
|
| 513 |
-
- Every rectangle with $n$ cells and a different shape contains an even number of red cells.
|
| 514 |
-
|
| 515 |
-
Proof. This can be achieved as follows: assuming the cells are labeled with $(x, y) \in \mathbb{Z}^{2}$, color a cell red if $x \equiv 0\left(\bmod 2^{m}\right)$ and $y \equiv 0\left(\bmod 2^{k-m}\right)$. For example, a $4 \times 2$ rectangle gets the following coloring:
|
| 516 |
-
|
| 517 |
-
|
| 518 |
-
A $2^{m} \times 2^{k-m}$ rectangle contains every possible pair $\left(x \bmod 2^{m}, y \bmod 2^{k-m}\right)$ exactly once, so such a rectangle will contain one red cell (an odd number).
|
| 519 |
-
|
| 520 |
-
On the other hand, consider a $2^{\ell} \times 2^{k-\ell}$ rectangle with $\ell>m$. The set of cells this covers is $(x, y)$ where $x$ covers a range of size $2^{\ell}$ and $y$ covers a range of size $2^{k-\ell}$. The number of red cells is the count of $x$ with $x \equiv 0 \bmod 2^{m}$ multiplied by the count of $y$ with $y \equiv 0 \bmod 2^{k-m}$. The former number is exactly $2^{\ell-k}$ because $2^{k}$ divides $2^{\ell}$ (while the latter is 0 or 1) so the number of red cells is even. The $\ell<m$ case is similar.
|
| 521 |
-
|
| 522 |
-
Finally, given these $k+1$ colorings, we can add them up modulo 2, i.e. a cell will be colored red if it is red in an odd number of these $k+1$ coloring. We illustrate $n=4$ as an example; the coloring is 4 -periodic in both axes so we only show one $4 \times 4$ cell.
|
| 523 |
-

|
| 524 |
-
|
| 525 |
-
This solves the problem.
|
| 526 |
-
Remark. The final coloring can be described as follows: color $(x, y)$ red if
|
| 527 |
-
|
| 528 |
-
$$
|
| 529 |
-
\max \left(0, \min \left(\nu_{2}(x), k\right)+\min \left(\nu_{2}(y), k\right)-k+1\right)
|
| 530 |
-
$$
|
| 531 |
-
|
| 532 |
-
is odd.
|
| 533 |
-
|
| 534 |
-
Remark (Luke Robitaille). Alternatively for (i), if $n=2^{e} k$ for odd $k$ then one may dissect an $a \times b$ rectangle with area $n$ into $k$ rectangles of area $2^{e}$, each $2^{\nu_{2}(a)} \times 2^{\nu_{2}(b)}$. This gives a way to deduce the problem from (ii) without having to consider odd prime numbers.
|
| 535 |
-
|
| 536 |
-
【 Alternate proof of (ii) using generating functions. We will commit to constructing a coloring which is $n$-periodic in both directions. (This is actually forced, so it's natural to do so.) With that in mind, let
|
| 537 |
-
|
| 538 |
-
$$
|
| 539 |
-
f(x, y)=\sum_{i=0}^{2^{k}-1} \sum_{j=0}^{2^{k}-1} \lambda_{i, j} x^{i} y^{j}
|
| 540 |
-
$$
|
| 541 |
-
|
| 542 |
-
denote its generating function, where $f \in \mathbb{F}_{2}[x, y]$.
|
| 543 |
-
For this to be valid, we need that for any $2^{p} \times 2^{q}$ rectangle with area $n$, the sum of the coefficients of $f$ over it should be one, modulo $x^{2^{k}}=y^{2^{k}}=1$. In other words, whenever $p+q=k$, we must have
|
| 544 |
-
|
| 545 |
-
$$
|
| 546 |
-
f(x, y)\left(1+\cdots+x^{2^{p}-1}\right)\left(1+\cdots+y^{2^{q}-1}\right)=\left(1+\cdots+x^{2^{k}-1}\right)\left(1+\cdots+y^{2^{k}-1}\right)
|
| 547 |
-
$$
|
| 548 |
-
|
| 549 |
-
taken modulo $x^{2^{k}}=y^{2^{k}}=1$. The idea is to rewrite these expressions: because we're in characteristic 2, the given assertion is $(x+1)^{2^{k}}=(y+1)^{2^{k}}=0$, and the requested property is
|
| 550 |
-
|
| 551 |
-
$$
|
| 552 |
-
f(x, y)(x+1)^{2^{p}-1}(y+1)^{2^{q}-1}=(x+1)^{2^{k}-1}(y+1)^{2^{k}-1} .
|
| 553 |
-
$$
|
| 554 |
-
|
| 555 |
-
This suggests the substitution $g(x, y)=f(x+1, y+1)$ : then we can replace $(x+1, y+1) \mapsto$ $(x, y)$ to simplify the requested property significantly:
|
| 556 |
-
|
| 557 |
-
Whenever $p+q=k$, we must have
|
| 558 |
-
|
| 559 |
-
$$
|
| 560 |
-
g(x, y) x^{2^{p}-1} y^{2^{q}-1}=x^{2^{k}-1} y^{2^{k}-1}
|
| 561 |
-
$$
|
| 562 |
-
|
| 563 |
-
modulo $x^{2^{k}}$ and $y^{2^{k}}$.
|
| 564 |
-
|
| 565 |
-
However, now the construction of $g$ is very simple: for example, the choice
|
| 566 |
-
|
| 567 |
-
$$
|
| 568 |
-
g(x, y)=\sum_{p+q=k} x^{2^{k}-2^{p}} y^{2^{k}-2^{q}}
|
| 569 |
-
$$
|
| 570 |
-
|
| 571 |
-
works. The end.
|
| 572 |
-
Remark. Unraveling the substitutions seen here, it's possible to show that this is actually the same construction provided in the first solution.
|
| 573 |
-
|
| 574 |
-
## §2 Solutions to Day 2
|
| 575 |
-
|
| 576 |
-
## §2.1 TSTST 2023/4, proposed by Ankan Bhattacharya
|
| 577 |
-
|
| 578 |
-
Available online at https://aops.com/community/p28015691.
|
| 579 |
-
|
| 580 |
-
## Problem statement
|
| 581 |
-
|
| 582 |
-
Let $n \geq 3$ be an integer and let $K_{n}$ be the complete graph on $n$ vertices. Each edge of $K_{n}$ is colored either red, green, or blue. Let $A$ denote the number of triangles in $K_{n}$ with all edges of the same color, and let $B$ denote the number of triangles in $K_{n}$ with all edges of different colors. Prove that
|
| 583 |
-
|
| 584 |
-
$$
|
| 585 |
-
B \leq 2 A+\frac{n(n-1)}{3} \text {. }
|
| 586 |
-
$$
|
| 587 |
-
|
| 588 |
-
Consider all unordered pairs of different edges which share exactly one vertex (call these vees for convenience). Assign each vee a charge of +2 if its edge colors are the same, and a charge of -1 otherwise.
|
| 589 |
-
|
| 590 |
-
We compute the total charge in two ways.
|
| 591 |
-
|
| 592 |
-
## 【 Total charge by summing over triangles. Note that
|
| 593 |
-
|
| 594 |
-
- each monochromatic triangle has a charge of +6 ,
|
| 595 |
-
- each bichromatic triangle has a charge of 0 , and
|
| 596 |
-
- each trichromatic triangle has a charge of -3 .
|
| 597 |
-
|
| 598 |
-
Since each vee contributes to exactly one triangle, we obtain that the total charge is $6 A-3 B$.
|
| 599 |
-
|
| 600 |
-
【 Total charge by summing over vertices. We can also calculate the total charge by examining the centers of the vees. If a vertex has $a$ red edges, $b$ green edges, and $c$ blue edges, the vees centered at that vertex contribute a total charge of
|
| 601 |
-
|
| 602 |
-
$$
|
| 603 |
-
\begin{aligned}
|
| 604 |
-
& 2\left[\binom{a}{2}+\binom{b}{2}+\binom{c}{2}\right]-(a b+a c+b c) \\
|
| 605 |
-
= & \left(a^{2}-a+b^{2}-b+c^{2}-c\right)-(a b+a c+b c) \\
|
| 606 |
-
= & \left(a^{2}+b^{2}+c^{2}-a b-a c-b c\right)-(a+b+c) \\
|
| 607 |
-
= & \left(a^{2}+b^{2}+c^{2}-a b-a c-b c\right)-(n-1) \\
|
| 608 |
-
\geq & -(n-1) .
|
| 609 |
-
\end{aligned}
|
| 610 |
-
$$
|
| 611 |
-
|
| 612 |
-
In particular, the total charge is at least $-n(n-1)$.
|
| 613 |
-
đ Conclusion. Thus, we obtain
|
| 614 |
-
|
| 615 |
-
$$
|
| 616 |
-
6 A-3 B \geq-n(n-1) \Longleftrightarrow B \leq 2 A+\frac{n(n-1)}{3}
|
| 617 |
-
$$
|
| 618 |
-
|
| 619 |
-
as desired.
|
| 620 |
-
|
| 621 |
-
## §2.2 TSTST 2023/5, proposed by David Altizio
|
| 622 |
-
|
| 623 |
-
Available online at https://aops.com/community/p28015713.
|
| 624 |
-
|
| 625 |
-
## Problem statement
|
| 626 |
-
|
| 627 |
-
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define
|
| 628 |
-
|
| 629 |
-
$$
|
| 630 |
-
p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} .
|
| 631 |
-
$$
|
| 632 |
-
|
| 633 |
-
Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
| 634 |
-
|
| 635 |
-
We show $(p, q)=(-3,3)$ is the only possible ordered pair.
|
| 636 |
-
|
| 637 |
-
## 【T First solution.
|
| 638 |
-
|
| 639 |
-
Setup for proof Let us denote $a=y / x, b=z / y, c=x / z$, where $x, y, z$ are nonzero complex numbers. Then
|
| 640 |
-
|
| 641 |
-
$$
|
| 642 |
-
\begin{aligned}
|
| 643 |
-
p+3 & =3+\sum_{\text {cyc }}\left(\frac{x}{y}+\frac{y}{x}\right)=3+\frac{x^{2}(y+z)+y^{2}(z+x)+z^{2}(x+y)}{x y z} \\
|
| 644 |
-
& =\frac{(x+y+z)(x y+y z+z x)}{x y z} \\
|
| 645 |
-
q-3 & =-3+\sum_{\text {cyc }} \frac{y^{2}}{z x}=\frac{x^{3}+y^{3}+z^{3}-3 x y z}{x y z} \\
|
| 646 |
-
& =\frac{(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)}{x y z} .
|
| 647 |
-
\end{aligned}
|
| 648 |
-
$$
|
| 649 |
-
|
| 650 |
-
It follows that
|
| 651 |
-
|
| 652 |
-
$$
|
| 653 |
-
\begin{aligned}
|
| 654 |
-
\mathbb{R} & \ni 3(p+3)+(q-3) \\
|
| 655 |
-
& =\frac{(x+y+z)\left(x^{2}+y^{2}+z^{2}+2(x y+y z+z x)\right)}{x y z} \\
|
| 656 |
-
& =\frac{(x+y+z)^{3}}{x y z}
|
| 657 |
-
\end{aligned}
|
| 658 |
-
$$
|
| 659 |
-
|
| 660 |
-
Now, note that if $x+y+z=0$, then $p=-3, q=3$ so we are done.
|
| 661 |
-
Main proof We will prove that if $x+y+z \neq 0$ then we contradict either the hypothesis that $a, b, c \notin \mathbb{R}$ or that $a, b, c$ do not have absolute value 1 .
|
| 662 |
-
|
| 663 |
-
Scale $x, y, z$ in such a way that $x+y+z$ is nonzero and real; hence so is $x y z$. Thus, as $p+3 \in \mathbb{R}$, we conclude $x y+y z+z x \in \mathbb{R}$ as well. Hence, $x, y, z$ are the roots of a cubic with real coefficients. Thus,
|
| 664 |
-
|
| 665 |
-
- either all three of $\{x, y, z\}$ are real (which implies $a, b, c \in \mathbb{R}$ ),
|
| 666 |
-
- or two of $\{x, y, z\}$ are a complex conjugate pair (which implies one of $a, b, c$ has absolute value 1).
|
| 667 |
-
Both of these were forbidden by hypothesis.
|
| 668 |
-
|
| 669 |
-
Construction As we saw in the setup, $(p, q)=(-3,3)$ will occur as long as $x+y+z=0$, and no two of $x, y, z$ to share the same magnitude or are collinear with the origin. This is easy to do; for example, we could choose $(x, y, z)=(3,4 i,-(3+4 i))$. Hence $a=\frac{3}{4 i}$, $b=-\frac{4 i}{3+4 i}, c=-\frac{3+4 i}{3}$ satisfies the hypotheses of the problem statement.
|
| 670 |
-
|
| 671 |
-
I Second solution, found by contestants. The main idea is to make the substitution
|
| 672 |
-
|
| 673 |
-
$$
|
| 674 |
-
x=a+\frac{1}{c}, \quad y=b+\frac{1}{a}, \quad z=c+\frac{1}{b} .
|
| 675 |
-
$$
|
| 676 |
-
|
| 677 |
-
Then we can check that
|
| 678 |
-
|
| 679 |
-
$$
|
| 680 |
-
\begin{aligned}
|
| 681 |
-
x+y+z & =p \\
|
| 682 |
-
x y+y z+z x & =p+q+3 \\
|
| 683 |
-
x y z & =p+2 .
|
| 684 |
-
\end{aligned}
|
| 685 |
-
$$
|
| 686 |
-
|
| 687 |
-
Therefore $x, y, z$ are the roots of a cubic with real coefficients. As in the previous solution, we note that this cubic must either have all real roots, or a complex conjugate pair of roots. We also have the relation $a(y+1)=a b+a+1=x+1$, and likewise $b(z+1)=y+1, c(x+1)=z+1$. This means that if any of $x, y, z$ are equal to -1, then all are equal to -1 .
|
| 688 |
-
|
| 689 |
-
Assume for the sake of contradiction that none are equal to -1 . In the case where the cubic has three real roots, $a=\frac{x+1}{y+1}$ would be real. On the other hand, if there is a complex conjugate pair (without loss of generality, $x$ and $y$ ) then $a$ has magnitude 1. Therefore this cannot occur.
|
| 690 |
-
|
| 691 |
-
We conclude that $x=y=z=-1$, so $p=-3$ and $q=3$. The solutions $(a, b, c)$ can then be parameterized as $\left(a,-1-\frac{1}{a},-\frac{1}{1+a}\right)$. To construct a solution, we need to choose a specific value of $a$ such that none of the wrong conditions hold; when $a=2 i$, say, we obtain the solution $\left(2 i,-1+\frac{i}{2}, \frac{-1+2 i}{5}\right)$.
|
| 692 |
-
|
| 693 |
-
【 Third solution by Luke Robitaille and Daniel Zhu. The answer is $p=-3$ and $q=3$. Let's first prove that no other $(p, q)$ work.
|
| 694 |
-
|
| 695 |
-
Let $e_{1}=a+b+c$ and $e_{2}=a^{-1}+b^{-1}+c^{-1}=a b+a c+b c$. Also, let $f=e_{1} e_{2}$. Note that $p=e_{1}+e_{2}$.
|
| 696 |
-
|
| 697 |
-
Our main insight is to consider the quantity $q^{\prime}=\frac{b}{a}+\frac{c}{b}+\frac{a}{c}$. Note that $f=q+q^{\prime}+3$. Also,
|
| 698 |
-
|
| 699 |
-
$$
|
| 700 |
-
\begin{aligned}
|
| 701 |
-
q q^{\prime} & =3+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}+\frac{b c}{a^{2}}+\frac{a c}{b^{2}}+\frac{a b}{c^{2}} \\
|
| 702 |
-
& =3+a^{3}+b^{3}+c^{3}+a^{-3}+b^{-3}+c^{-3} \\
|
| 703 |
-
& =9+a^{3}+b^{3}+c^{3}-3 a b c+a^{-3}+b^{-3}+c^{-3}-3 a^{-1} b^{-1} c^{-1} \\
|
| 704 |
-
& =9+e_{1}\left(e_{1}^{2}-3 e_{2}\right)+e_{2}\left(e_{2}^{2}-3 e_{1}\right) \\
|
| 705 |
-
& =9+e_{1}^{3}+e_{2}^{3}-6 e_{1} e_{2} \\
|
| 706 |
-
& =9+p\left(p^{2}-3 f\right)-6 f \\
|
| 707 |
-
& =p^{3}-(3 p+6) f+9 .
|
| 708 |
-
\end{aligned}
|
| 709 |
-
$$
|
| 710 |
-
|
| 711 |
-
As a result, the quadratic with roots $q$ and $q^{\prime}$ is $x^{2}-(f-3) x+\left(p^{3}-(3 p+6) f+9\right)$, which implies that
|
| 712 |
-
|
| 713 |
-
$$
|
| 714 |
-
q^{2}-q f+3 q+p^{3}-(3 p+6) f+9=0 \Longleftrightarrow(3 p+q+6) f=p^{3}+q^{2}+3 q+9
|
| 715 |
-
$$
|
| 716 |
-
|
| 717 |
-
At this point, two miracles occur. The first is the following claim:
|
| 718 |
-
|
| 719 |
-
Claim - $f$ is not real.
|
| 720 |
-
Proof. Suppose $f$ is real. Since $\left(x-e_{1}\right)\left(x-e_{2}\right)=x^{2}-p x+f$, there are two cases:
|
| 721 |
-
|
| 722 |
-
- $e_{1}$ and $e_{2}$ are real. Then, $a, b$, and $c$ are the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$, and since every cubic with real coefficients has at least one real root, at least one of $a, b$, and $c$ is real, contradiction.
|
| 723 |
-
- $e_{1}$ and $e_{2}$ are conjugates. Then, the polynomial $x^{3}-\bar{e}_{2} x^{2}+\bar{e}_{1} x-1$, which has roots $\bar{a}^{-1}, \bar{b}^{-1}$, and $\bar{c}^{-1}$, is the same as the polynomial with $a, b, c$ as roots. We conclude that the multiset $\{a, b, c\}$ is invariant under inversion about the unit circle, so one of $a, b$, and $c$ must lie on the unit circle. This is yet another contradiction.
|
| 724 |
-
|
| 725 |
-
As a result, we know that $3 p+q+6=p^{3}+q^{2}+3 q+9=0$. The second miracle is that substituting $q=-3 p-6$ into $q^{2}+3 q+p^{3}+9=0$, we get
|
| 726 |
-
|
| 727 |
-
$$
|
| 728 |
-
0=p^{3}+9 p^{2}+27 p+27=(p+3)^{3}
|
| 729 |
-
$$
|
| 730 |
-
|
| 731 |
-
so $p=-3$. Thus $q=3$.
|
| 732 |
-
It remains to construct valid $a, b$, and $c$. To do this, let's pick some $e_{1}$, let $e_{2}=-3-e_{1}$, and let $a, b$, and $c$ be the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$. It is clear that this guarantees $p=-3$. By our above calculations, $q$ and $q^{\prime}$ are the roots of the quadratic $x^{2}-(f-3) x+(3 f-18)$, so one of $q$ and $q^{\prime}$ must be 3 ; by changing the order of $a, b$, and $c$ if needed, we can guarantee this to be $q$. It suffices to show that for some choice of $e_{1}$, none of $a, b$, or $c$ are real or lie on the unit circle.
|
| 733 |
-
|
| 734 |
-
To do this, note that we can rewrite $x^{3}-e_{1} x^{2}+\left(-3-e_{1}\right) x-1=0$ as
|
| 735 |
-
|
| 736 |
-
$$
|
| 737 |
-
e_{1}=\frac{x^{3}-3 x-1}{x^{2}+x}
|
| 738 |
-
$$
|
| 739 |
-
|
| 740 |
-
so all we need is a value of $e_{1}$ that is not $\frac{x^{3}-3 x-1}{x^{2}+x}$ for any real $x$ or $x$ on the unit circle. One way to do this is to choose any nonreal $e_{1}$ with $\left|e_{1}\right|<1 / 2$. This clearly rules out any real $x$. Also, if $|x|=1$, by the triangle inequality $\left|x^{3}-3 x-1\right| \geq|3 x|-\left|x^{3}\right|-|1|=1$ and $\left|x^{2}+x\right| \leq 2$, so $\left|\frac{x^{3}-3 x-1}{x^{2}+x}\right| \geq \frac{1}{2}$.
|
| 741 |
-
|
| 742 |
-
## §2.3 TSTST 2023/6, proposed by Holden Mui
|
| 743 |
-
|
| 744 |
-
Available online at https://aops.com/community/p28015708.
|
| 745 |
-
|
| 746 |
-
## Problem statement
|
| 747 |
-
|
| 748 |
-
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
| 749 |
-
|
| 750 |
-
We present three approaches.
|
| 751 |
-
『 Solution 1 (Ankit Bisain). Let $H$ be the orthocenter of $A B C$, and construct $P^{\prime}$ using the following claim.
|
| 752 |
-
|
| 753 |
-
Claim - There is a point $P^{\prime}$ for which
|
| 754 |
-
|
| 755 |
-
$$
|
| 756 |
-
\measuredangle A P H+\measuredangle A P^{\prime} H=\measuredangle B P H+\measuredangle B P^{\prime} H=\measuredangle C P H+\measuredangle C P^{\prime} H=0 .
|
| 757 |
-
$$
|
| 758 |
-
|
| 759 |
-
Proof. After inversion at $H$, this is equivalent to the fact that $P$ 's image has an isogonal conjugate in $A B C$ 's image.
|
| 760 |
-
|
| 761 |
-
Now, let $X, Y$, and $Z$ be the reflections of $P$ over $\overline{A H}, \overline{B H}$, and $\overline{C H}$ respectively. Additionally, let $Q^{\prime}$ be the image of $Q$ under inversion about ( $P X Y Z$ ).
|
| 762 |
-
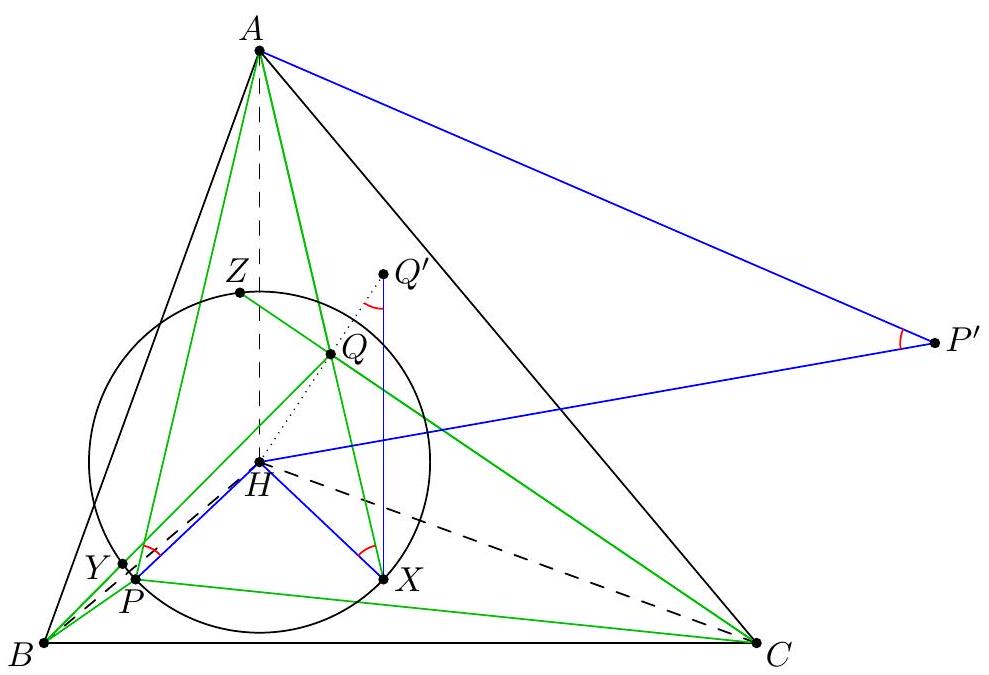
|
| 763 |
-
|
| 764 |
-
$$
|
| 765 |
-
\text { Claim }-A B C P^{\prime} \approx X Y Z Q^{\prime}
|
| 766 |
-
$$
|
| 767 |
-
|
| 768 |
-
Proof. Since
|
| 769 |
-
|
| 770 |
-
$$
|
| 771 |
-
\measuredangle Y X Z=\measuredangle Y P Z=\measuredangle(\overline{B H}, \overline{C H})=-\measuredangle B A C
|
| 772 |
-
$$
|
| 773 |
-
|
| 774 |
-
and cyclic variants, triangles $A B C$ and $X Y Z$ are similar. Additionally,
|
| 775 |
-
|
| 776 |
-
$$
|
| 777 |
-
\measuredangle H Q^{\prime} X=-\measuredangle H X Q=-\measuredangle H X A=\measuredangle H P A=-\measuredangle H P^{\prime} A
|
| 778 |
-
$$
|
| 779 |
-
|
| 780 |
-
and cyclic variants, so summing in pairs gives $\measuredangle Y Q^{\prime} Z=-\measuredangle B P^{\prime} C$ and cyclic variants; this implies the similarity.
|
| 781 |
-
|
| 782 |
-
Claim - $Q^{\prime}$ lies on the Euler line of triangle $X Y Z$.
|
| 783 |
-
|
| 784 |
-
Proof. Let $O$ be the circumcenter of $A B C$ so that $A B C O P^{\prime} \approx X Y Z H Q^{\prime}$. Then $\measuredangle H P^{\prime} A=-\measuredangle H Q^{\prime} X=\measuredangle O P^{\prime} A$, so $P^{\prime}$ lies on $\overline{O H}$. By the similarity, $Q^{\prime}$ must lie on the Euler line of $X Y Z$.
|
| 785 |
-
|
| 786 |
-
To finish the problem, let $G_{1}$ be the centroid of $A B C$ and $G_{2}$ be the centroid of $X Y Z$. Then with signed areas,
|
| 787 |
-
|
| 788 |
-
$$
|
| 789 |
-
\begin{aligned}
|
| 790 |
-
{\left[G_{1} H P\right]+\left[G_{1} H Q\right] } & =\frac{[A H P]+[B H P]+[C H P]}{3}+\frac{[A H Q]+[B H Q]+[C H Q]}{3} \\
|
| 791 |
-
& =\frac{[A H Q]-[A H X]+[B H Q]-[B H Y]+[C H Q]-[C H Z]}{3} \\
|
| 792 |
-
& =\frac{[H Q X]+[H Q Y]+[H Q Z]}{3} \\
|
| 793 |
-
& =\left[Q G_{2} H\right] \\
|
| 794 |
-
& =0
|
| 795 |
-
\end{aligned}
|
| 796 |
-
$$
|
| 797 |
-
|
| 798 |
-
where the last line follows from the last claim. Therefore $\overline{G_{1} H}$ bisects $\overline{P Q}$, as desired.
|
| 799 |
-
Remark. This solution characterizes the set of all points $P$ for which such a point $Q$ exists. It is the image of the Euler line under the mapping described in the first claim.
|
| 800 |
-
|
| 801 |
-
Solution 2 using complex numbers (Carl Schildkraut and Milan Haiman). Let $(A B C)$ be the unit circle in the complex plane, and let $A=a, B=b, C=c$ such that $|a|=|b|=|c|=1$. Let $P=p$ and $Q=q$, and $O=0$ and $H=h=a+b+c$ be the circumcenter and orthocenter of $A B C$ respectively.
|
| 802 |
-
|
| 803 |
-
The first step is to translate the given geometric conditions into a single usable equation:
|
| 804 |
-
|
| 805 |
-
Claim - We have the equation
|
| 806 |
-
|
| 807 |
-
$$
|
| 808 |
-
(p+q) \sum_{\mathrm{cyc}} a^{3}\left(b^{2}-c^{2}\right)=(\bar{p}+\bar{q}) a b c \sum_{\mathrm{cyc}}\left(b c\left(b^{2}-c^{2}\right)\right)
|
| 809 |
-
$$
|
| 810 |
-
|
| 811 |
-
Proof. The condition that the altitude $\overline{A H}$ bisects $\angle P A Q$ is equivalent to
|
| 812 |
-
|
| 813 |
-
$$
|
| 814 |
-
\begin{aligned}
|
| 815 |
-
& \frac{(p-a)(q-a)}{(h-a)^{2}}=\frac{(p-a)(q-a)}{(b+c)^{2}} \in \mathbb{R} \\
|
| 816 |
-
\Longrightarrow & \frac{(p-a)(q-a)}{(b+c)^{2}}=\frac{\left(\frac{(p-a)(q-a)}{(b+c)^{2}}\right)}{}=\frac{(a \bar{p}-1)(a \bar{q}-1) b^{2} c^{2}}{(b+c)^{2} a^{2}} \\
|
| 817 |
-
\Longrightarrow & a^{2}(p-a)(q-a)=b^{2} c^{2}(a \bar{p}-1)(a \bar{q}-1) \\
|
| 818 |
-
\Longrightarrow & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) .
|
| 819 |
-
\end{aligned}
|
| 820 |
-
$$
|
| 821 |
-
|
| 822 |
-
Writing the symmetric conditions that $\overline{B H}$ and $\overline{C H}$ bisect $\angle P B Q$ and $\angle P C Q$ gives three equations:
|
| 823 |
-
|
| 824 |
-
$$
|
| 825 |
-
\begin{aligned}
|
| 826 |
-
& a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) \\
|
| 827 |
-
& b^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(b^{4}-c^{2} a^{2}\right)=b^{3}(p+q)-b c^{2} a^{2}(\bar{p}+\bar{q})
|
| 828 |
-
\end{aligned}
|
| 829 |
-
$$
|
| 830 |
-
|
| 831 |
-
$$
|
| 832 |
-
c^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(c^{4}-a^{2} b^{2}\right)=c^{3}(p+q)-c a^{2} b^{2}(\bar{p}+\bar{q})
|
| 833 |
-
$$
|
| 834 |
-
|
| 835 |
-
Now, sum $\left(b^{2}-c^{2}\right)$ times the first equation, $\left(c^{2}-a^{2}\right)$ times the second equation, and $\left(a^{2}-b^{2}\right)$ times the third equation. On the left side, the coefficients of $p q$ and $\overline{p q}$ are 0 . Additionally, the coefficient of 1 (the parenthesized terms on the left sides of each equation) sum to 0 , since
|
| 836 |
-
|
| 837 |
-
$$
|
| 838 |
-
\sum_{\mathrm{cyc}}\left(a^{4}-b^{2} c^{2}\right)\left(b^{2}-c^{2}\right)=\sum_{\mathrm{cyc}}\left(a^{4} b^{2}-b^{4} c^{2}-a^{4} c^{2}+c^{4} b^{2}\right)
|
| 839 |
-
$$
|
| 840 |
-
|
| 841 |
-
This gives (1) as desired.
|
| 842 |
-
We can then factor (1):
|
| 843 |
-
Claim - The left-hand side of (1) factors as
|
| 844 |
-
|
| 845 |
-
$$
|
| 846 |
-
-(p+q)(a-b)(b-c)(c-a)(a b+b c+c a)
|
| 847 |
-
$$
|
| 848 |
-
|
| 849 |
-
while the right-hand side factors as
|
| 850 |
-
|
| 851 |
-
$$
|
| 852 |
-
-(\bar{p}+\bar{q})(a-b)(b-c)(c-a)(a+b+c)
|
| 853 |
-
$$
|
| 854 |
-
|
| 855 |
-
Proof. This can of course be verified by direct expansion, but here is a slightly more economic indirect proof.
|
| 856 |
-
|
| 857 |
-
Consider the cyclic sum on the left as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a^{3}\left(a^{2}-c^{2}\right)+a^{3}\left(c^{2}-a^{2}\right)+c^{3}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $f(a, b, c)(a-b)(b-c)(c-a)$ for some symmetric quadratic polynomial $f$, and thus it is some linear combination of $a^{2}+b^{2}+c^{2}$ and $a b+b c+c a$. When $a=0$, the whole expression is $b^{2} c^{2}(b-c)$, so $f(0, b, c)=-b c$, which implies that $f(a, b, c)=-(a b+b c+c a)$.
|
| 858 |
-
Similarly, consider the cyclic sum on the right as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a c\left(a^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)+a^{2}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $g(a, b, c)(a-b)(b-c)(c-a)$ where $g$ is a symmetric linear polynomial; hence, it is a scalar multiple of $a+b+c$. When $a=0$, the whole expression is $b c\left(b^{2}-c^{2}\right)$, so $g(0, b, c)=-b-c$, which implies that $g(a, b, c)=-(a+b+c)$.
|
| 859 |
-
|
| 860 |
-
Since $A, B$, and $C$ are distinct, we may divide by $(a-b)(b-c)(c-a)$ to obtain
|
| 861 |
-
|
| 862 |
-
$$
|
| 863 |
-
(p+q)(a b+b c+c a)=(\bar{p}+\bar{q}) a b c(a+b+c) \Longrightarrow(p+q) \bar{h}=(\bar{p}+\bar{q}) h
|
| 864 |
-
$$
|
| 865 |
-
|
| 866 |
-
This implies that $\frac{\frac{p+q}{h}-0}{h-0}$ is real, so the midpoint of $\overline{P Q}$ lies on line $\overline{O H}$.
|
| 867 |
-
【 Solution 3 also using complex numbers (Michael Ren). We use complex numbers as in the previous solution. The angle conditions imply that $\frac{(a-p)(a-q)}{(b-c)^{2}}, \frac{(b-p)(b-q)}{(c-a)^{2}}$, and $\frac{(c-p)(c-q)}{(a-b)^{2}}$ are real numbers. Take a linear combination of these with real coefficients $X$, $Y$, and $Z$ to be determined; after expansion, we obtain
|
| 868 |
-
|
| 869 |
-
$$
|
| 870 |
-
\begin{aligned}
|
| 871 |
-
& {\left[\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right] p q } \\
|
| 872 |
-
- & {\left[\frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}\right](p+q) }
|
| 873 |
-
\end{aligned}
|
| 874 |
-
$$
|
| 875 |
-
|
| 876 |
-
$$
|
| 877 |
-
+\left[\frac{a^{2} X}{(b-c)^{2}}+\frac{b^{2} Y}{(c-a)^{2}}+\frac{c^{2} Z}{(a-b)^{2}}\right]
|
| 878 |
-
$$
|
| 879 |
-
|
| 880 |
-
which is a real number. To get something about the midpoint of $P Q$, the $p q$ coefficient should be zero, which motivates the following lemma.
|
| 881 |
-
|
| 882 |
-
## Lemma
|
| 883 |
-
|
| 884 |
-
There exist real $X, Y, Z$ for which
|
| 885 |
-
|
| 886 |
-
$$
|
| 887 |
-
\begin{aligned}
|
| 888 |
-
& \frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}=0 \text { and } \\
|
| 889 |
-
& \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}} \neq 0 .
|
| 890 |
-
\end{aligned}
|
| 891 |
-
$$
|
| 892 |
-
|
| 893 |
-
Proof. Since $\mathbb{C}$ is a 2-dimensional vector space over $\mathbb{R}$, there exist real $X, Y, Z$ such that $(X, Y, Z) \neq(0,0,0)$ and the first condition holds. Suppose for the sake of contradiction that $\frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}=0$. Then
|
| 894 |
-
|
| 895 |
-
$$
|
| 896 |
-
\begin{aligned}
|
| 897 |
-
& \frac{(b-a) Y}{(c-a)^{2}}+\frac{(c-a) Z}{(a-b)^{2}} \\
|
| 898 |
-
= & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}-a\left(\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right) \\
|
| 899 |
-
= & 0
|
| 900 |
-
\end{aligned}
|
| 901 |
-
$$
|
| 902 |
-
|
| 903 |
-
We can easily check that $(Y, Z)=(0,0)$ is impossible, therefore $\frac{(b-a)^{3}}{(c-a)^{3}}=-\frac{Z}{Y}$ is real. This means $\angle B A C=60^{\circ}$ or $120^{\circ}$. By symmetry, the same is true of $\angle C B A$ and $\angle A C B$. This is impossible because $A B C$ is scalene.
|
| 904 |
-
|
| 905 |
-
With the choice of $X, Y, Z$ as in the lemma, there exist complex numbers $\alpha$ and $\beta$, depending only on $a, b$, and $c$, such that $\alpha \neq 0$ and $\alpha(p+q)+\beta$ is real. Therefore the midpoint of $P Q$, which corresponds to $\frac{p+q}{2}$, lies on a fixed line. It remains to show that this line is the Euler line. First, choose $P=Q$ to be the orthocenter to show that the orthocenter lies on the line. Secondly, choose $P$ and $Q$ to be the foci of the Steiner circumellipse to show that the centroid lies on the line. (By some ellipse properties, the external angle bisector of $\angle P A Q$ is the tangent to the circumellipse at $A$, which is the line through $A$ parallel to $B C$. Therefore these points are valid.) Therefore the fixed line of the midpoint is the Euler line.
|
| 906 |
-
|
| 907 |
-
Remark. This solution does not require fixing the origin of the complex plane or setting $(A B C)$ to be the unit circle.
|
| 908 |
-
|
| 909 |
-
## §3 Solutions to Day 3
|
| 910 |
-
|
| 911 |
-
## §3.1 TSTST 2023/7, proposed by Luke Robitaille
|
| 912 |
-
|
| 913 |
-
Available online at https://aops.com/community/p28015706.
|
| 914 |
-
|
| 915 |
-
## Problem statement
|
| 916 |
-
|
| 917 |
-
The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up.
|
| 918 |
-
|
| 919 |
-
In a move, Vera may flip over one of the coins in the row, subject to the following rules:
|
| 920 |
-
|
| 921 |
-
- On the first move, Vera may flip over any of the 2023 coins.
|
| 922 |
-
- On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.)
|
| 923 |
-
|
| 924 |
-
Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.
|
| 925 |
-
|
| 926 |
-
The answer is 4044 . In general, replacing 2023 with $4 n+3$, the answer is $8 n+4$.
|
| 927 |
-
|
| 928 |
-
Bound. Observe that the first and last coins must be flipped, and so every coin is flipped at least once. Then, the $2 n+1$ even-indexed coins must be flipped at least twice, so they are flipped at least $4 n+2$ times.
|
| 929 |
-
|
| 930 |
-
The $2 n+2$ odd-indexed coins must then be flipped at least $4 n+1$ times. Since there are an even number of these coins, the total flip count must be even, so they are actually flipped a total of at least $4 n+2$ times, for a total of at least $8 n+4$ flips in all.
|
| 931 |
-
|
| 932 |
-
【 Construction. For $k=0,1, \ldots, n-1$, flip $(4 k+1,4 k+2,4 k+3,4 k+2,4 k+3,4 k+$ $4,4 k+3,4 k+4)$ in that order; then at the end, flip $4 n+1,4 n+2,4 n+3,4 n+2$. This is illustrated below for $4 n+3=15$.
|
| 933 |
-
|
| 934 |
-
|
| 935 |
-
It is easy to check this works, and there are 4044 flips, as desired.
|
| 936 |
-
|
| 937 |
-
## §3.2 TSTST 2023/8, proposed by Ankan Bhattacharya
|
| 938 |
-
|
| 939 |
-
Available online at https://aops.com/community/p28015680.
|
| 940 |
-
|
| 941 |
-
## Problem statement
|
| 942 |
-
|
| 943 |
-
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$.
|
| 944 |
-
Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
| 945 |
-
|
| 946 |
-
The only possible value of the common perimeter, denoted $p$, is 1 .
|
| 947 |
-
|
| 948 |
-
【 Synthetic approach (from author). We prove the converse of the problem first:
|
| 949 |
-
Claim ( $p=1$ implies concurrence) - Suppose the six points are chosen so that triangles $A B_{2} C_{1}, B C_{2} A_{1}, C A_{2} B_{1}$ all have perimeter 1. Then lines $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}$, and $\overline{A_{1} B_{2}}$ are concurrent.
|
| 950 |
-
|
| 951 |
-
Proof. The perimeter conditions mean that $\overline{B_{2} C_{1}}, \overline{C_{2} A_{1}}$, and $\overline{A_{2} B_{1}}$ are tangent to the incircle of $\triangle A B C$.
|
| 952 |
-
|
| 953 |
-
|
| 954 |
-
Hence the result follows by Brianchon's theorem.
|
| 955 |
-
Now suppose $p \neq 1$. Let $\overline{B_{2}^{\prime} C_{1}^{\prime}}$ be the dilation of $\overline{B_{2} C_{1}}$ with ratio $\frac{1}{p}$ at center $A$, and define $C_{2}^{\prime}, A_{1}^{\prime}, A_{2}^{\prime}, B_{1}^{\prime}$ similarly. The following diagram showcases the situation $p<1$.
|
| 956 |
-
|
| 957 |
-
|
| 958 |
-
By the reasoning in the $p=1$ case, note that $\overline{B_{1}^{\prime} C_{2}^{\prime}}, \overline{C_{1}^{\prime} A_{2}^{\prime}}$, and $\overline{A_{1}^{\prime} B_{2}^{\prime}}$ are concurrent. However, $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}, \overline{A_{1} B_{2}}$ lie in the interior of quadrilaterals $B C B_{1}^{\prime} C_{2}^{\prime}, C A C_{1}^{\prime} A_{2}^{\prime}$, and $A B A_{1}^{\prime} B_{2}^{\prime}$, and these quadrilaterals do not share an interior point, a contradiction.
|
| 959 |
-
|
| 960 |
-
Thus $p \geq 1$. Similarly, we can show $p \leq 1$, and so $p=1$ is forced (and achieved if, for example, the three triangles are equilateral with side length $1 / 3$ ).
|
| 961 |
-
|
| 962 |
-
『 Barycentric solution (by Carl, Krit, Milan). We show that, if the common perimeter is 1 , then the lines concur. To do this, we use barycentric coordinates. Let $A=(1: 0: 0)$, $B=(0: 1: 0)$, and $C=(0: 0: 1)$. Let $A_{1}=\left(0: 1-a_{1}: a_{1}\right), A_{2}=\left(0: a_{2}: 1-a_{2}\right)$, $B_{1}=\left(b_{1}: 0: 1-b_{1}\right), B_{2}=\left(1-b_{2}: 0: b_{2}\right), C_{1}=\left(1-c_{1}: c_{1}: 0\right)$, and $C_{2}=\left(c_{2}: 1-c_{2}: 0\right)$. The line $B_{1} C_{2}$ is defined by the equation
|
| 963 |
-
|
| 964 |
-
$$
|
| 965 |
-
\operatorname{det}\left[\begin{array}{ccc}
|
| 966 |
-
x & y & z \\
|
| 967 |
-
b_{1} & 0 & 1-b_{1} \\
|
| 968 |
-
c_{2} & 1-c_{2} & 0
|
| 969 |
-
\end{array}\right]=0 \text {; }
|
| 970 |
-
$$
|
| 971 |
-
|
| 972 |
-
i.e.
|
| 973 |
-
|
| 974 |
-
$$
|
| 975 |
-
x\left(-\left(1-b_{1}\right)\left(1-c_{2}\right)\right)+y\left(\left(1-b_{1}\right) c_{2}\right)+z\left(b_{1}\left(1-c_{2}\right)\right)=0 .
|
| 976 |
-
$$
|
| 977 |
-
|
| 978 |
-
Computing the equations for the other lines cyclically, we get that the lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ concur if and only if
|
| 979 |
-
|
| 980 |
-
$$
|
| 981 |
-
\operatorname{det}\left[\begin{array}{ccc}
|
| 982 |
-
-\left(1-b_{1}\right)\left(1-c_{2}\right) & \left(1-b_{1}\right) c_{2} & b_{1}\left(1-c_{2}\right) \\
|
| 983 |
-
c_{1}\left(1-a_{2}\right) & -\left(1-c_{1}\right)\left(1-a_{2}\right) & \left(1-c_{1}\right) a_{2} \\
|
| 984 |
-
\left(1-a_{1}\right) b_{2} & a_{1}\left(1-b_{2}\right) & -\left(1-a_{1}\right)\left(1-b_{2}\right)
|
| 985 |
-
\end{array}\right]=0 .
|
| 986 |
-
$$
|
| 987 |
-
|
| 988 |
-
Let this matrix be $M$. We also define the similar matrix
|
| 989 |
-
|
| 990 |
-
$$
|
| 991 |
-
N=\left[\begin{array}{ccc}
|
| 992 |
-
-\left(1-b_{2}\right)\left(1-c_{1}\right) & \left(1-b_{2}\right) c_{1} & b_{2}\left(1-c_{1}\right) \\
|
| 993 |
-
c_{2}\left(1-a_{1}\right) & -\left(1-c_{2}\right)\left(1-a_{1}\right) & \left(1-c_{2}\right) a_{1} \\
|
| 994 |
-
\left(1-a_{2}\right) b_{1} & a_{2}\left(1-b_{1}\right) & -\left(1-a_{2}\right)\left(1-b_{1}\right)
|
| 995 |
-
\end{array}\right] .
|
| 996 |
-
$$
|
| 997 |
-
|
| 998 |
-
Geometrically, det $N=0$ if and only if $B_{2}^{\prime} C_{1}^{\prime}, C_{2}^{\prime} A_{1}^{\prime}$, and $A_{2}^{\prime} B_{1}^{\prime}$ concur, where for a point $P$ on a side of triangle $A B C, P^{\prime}$ denotes its reflection over that side's midpoint.
|
| 999 |
-
|
| 1000 |
-
Claim - We have $\operatorname{det} M=\operatorname{det} N$.
|
| 1001 |
-
|
| 1002 |
-
Proof. To show $\operatorname{det} M=\operatorname{det} N$, it suffices to demonstrate that the determinant above is invariant under swapping subscripts of " 1 " and " 2 ," an operation we call $\Psi$.
|
| 1003 |
-
|
| 1004 |
-
We use the definition of the determinant as a sum over permutations. The even permutations give us the following three terms:
|
| 1005 |
-
|
| 1006 |
-
$$
|
| 1007 |
-
\begin{aligned}
|
| 1008 |
-
-\left(1-b_{1}\right)\left(1-c_{2}\right)\left(1-c_{1}\right)\left(1-a_{2}\right)\left(1-a_{1}\right)\left(1-b_{2}\right) & =-\prod_{i=1}^{2}\left(\left(1-a_{i}\right)\left(1-b_{i}\right)\left(1-c_{i}\right)\right) \\
|
| 1009 |
-
\left(1-a_{1}\right) b_{2}\left(1-b_{1}\right) c_{2}\left(1-c_{1}\right) a_{2} & =\left(\left(1-a_{1}\right)\left(1-b_{1}\right)\left(1-c_{1}\right)\right)\left(a_{2} b_{2} c_{2}\right) \\
|
| 1010 |
-
c_{1}\left(1-a_{2}\right) a_{1}\left(1-b_{2}\right) b_{1}\left(1-c_{2}\right) & =\left(\left(1-a_{2}\right)\left(1-b_{2}\right)\left(1-c_{2}\right)\right)\left(a_{1} b_{1} c_{1}\right) .
|
| 1011 |
-
\end{aligned}
|
| 1012 |
-
$$
|
| 1013 |
-
|
| 1014 |
-
The first term is invariant under $\Psi$, while the second and third terms are swapped under $\Psi$. For the odd permutations, we have a contribution to the determinant of
|
| 1015 |
-
|
| 1016 |
-
$$
|
| 1017 |
-
\sum_{\mathrm{cyc}}\left(1-b_{1}\right)\left(1-c_{2}\right)\left(1-c_{1}\right) a_{2} a_{1}\left(1-b_{2}\right)
|
| 1018 |
-
$$
|
| 1019 |
-
|
| 1020 |
-
each summand is invariant under $\Psi$. This finishes the proof of our claim.
|
| 1021 |
-
Now, it suffices to show that, if $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ each have perimeter 1, then
|
| 1022 |
-
|
| 1023 |
-
$$
|
| 1024 |
-
\operatorname{det}\left[\begin{array}{ccc}
|
| 1025 |
-
-\left(1-b_{2}\right)\left(1-c_{1}\right) & \left(1-b_{2}\right) c_{1} & b_{2}\left(1-c_{1}\right) \\
|
| 1026 |
-
c_{2}\left(1-a_{1}\right) & -\left(1-c_{2}\right)\left(1-a_{1}\right) & \left(1-c_{2}\right) a_{1} \\
|
| 1027 |
-
\left(1-a_{2}\right) b_{1} & a_{2}\left(1-b_{1}\right) & -\left(1-a_{2}\right)\left(1-b_{1}\right) .
|
| 1028 |
-
\end{array}\right]=0
|
| 1029 |
-
$$
|
| 1030 |
-
|
| 1031 |
-
Indeed, we have $A B_{2}=b_{2}$ and $A C_{1}=c_{1}$, so by the law of cosines,
|
| 1032 |
-
|
| 1033 |
-
$$
|
| 1034 |
-
1-b_{2}-c_{1}=1-A B_{2}-A C_{1}=B_{2} C_{1}=\sqrt{b_{2}^{2}+c_{1}^{2}-b_{2} c_{1}}
|
| 1035 |
-
$$
|
| 1036 |
-
|
| 1037 |
-
This gives
|
| 1038 |
-
|
| 1039 |
-
$$
|
| 1040 |
-
\left(1-b_{2}-c_{1}\right)^{2}=b_{2}^{2}+c_{1}^{2}-b_{2} c_{1} \Longrightarrow 1-2 b_{2}-2 c_{1}+3 b_{2} c_{1}=0
|
| 1041 |
-
$$
|
| 1042 |
-
|
| 1043 |
-
Similarly, $1-2 c_{2}-2 a_{1}+3 c_{2} a_{1}=0$ and $1-2 a_{2}-2 b_{1}+3 a_{2} b_{1}=0$.
|
| 1044 |
-
Now,
|
| 1045 |
-
|
| 1046 |
-
$$
|
| 1047 |
-
\begin{aligned}
|
| 1048 |
-
N\left[\begin{array}{l}
|
| 1049 |
-
1 \\
|
| 1050 |
-
1 \\
|
| 1051 |
-
1
|
| 1052 |
-
\end{array}\right] & =\left[\begin{array}{l}
|
| 1053 |
-
-\left(1-b_{2}\right)\left(1-c_{1}\right)+\left(1-b_{2}\right) c_{1}+b_{2}\left(1-c_{1}\right) \\
|
| 1054 |
-
-\left(1-c_{2}\right)\left(1-a_{1}\right)+\left(1-c_{2}\right) a_{1}+c_{2}\left(1-a_{1}\right) \\
|
| 1055 |
-
-\left(1-a_{2}\right)\left(1-b_{1}\right)+\left(1-a_{2}\right) b_{1}+a_{2}\left(1-b_{1}\right)
|
| 1056 |
-
\end{array}\right] \\
|
| 1057 |
-
& =\left[\begin{array}{l}
|
| 1058 |
-
-1+2 b_{2}+2 c_{1}-3 b_{2} c_{1} \\
|
| 1059 |
-
-1+2 c_{2}+2 a_{1}-3 c_{2} a_{1} \\
|
| 1060 |
-
-1+2 a_{2}+2 b_{1}-2 a_{2} b_{1}
|
| 1061 |
-
\end{array}\right]=\left[\begin{array}{l}
|
| 1062 |
-
0 \\
|
| 1063 |
-
0 \\
|
| 1064 |
-
0
|
| 1065 |
-
\end{array}\right] .
|
| 1066 |
-
\end{aligned}
|
| 1067 |
-
$$
|
| 1068 |
-
|
| 1069 |
-
So it follows $\operatorname{det} N=0$, as desired.
|
| 1070 |
-
|
| 1071 |
-
## §3.3 TSTST 2023/9, proposed by Holden Mui
|
| 1072 |
-
|
| 1073 |
-
Available online at https://aops.com/community/p28015688.
|
| 1074 |
-
|
| 1075 |
-
## Problem statement
|
| 1076 |
-
|
| 1077 |
-
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by
|
| 1078 |
-
|
| 1079 |
-
$$
|
| 1080 |
-
\begin{aligned}
|
| 1081 |
-
& \Delta^{0} f(n)=f(n) \\
|
| 1082 |
-
& \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots
|
| 1083 |
-
\end{aligned}
|
| 1084 |
-
$$
|
| 1085 |
-
|
| 1086 |
-
Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$.
|
| 1087 |
-
|
| 1088 |
-
The answer is
|
| 1089 |
-
|
| 1090 |
-
$$
|
| 1091 |
-
\left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)}
|
| 1092 |
-
$$
|
| 1093 |
-
|
| 1094 |
-
【 First solution by author. For convenience in what follows, set $d=\nu_{p}(a)$, let $a=p^{d} \cdot b$, and let a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be essential if it equals one of its iterated finite differences.
|
| 1095 |
-
|
| 1096 |
-
The key claim is the following.
|
| 1097 |
-
Claim (Characterization of essential functions) - A function $f$ is essential if and only if
|
| 1098 |
-
|
| 1099 |
-
$$
|
| 1100 |
-
f(x)+f\left(x+p^{d}\right)+\cdots+f\left(x+(b-1) p^{d}\right)=0
|
| 1101 |
-
$$
|
| 1102 |
-
|
| 1103 |
-
for all $x$.
|
| 1104 |
-
As usual, we split the proof into two halves.
|
| 1105 |
-
Proof that essential implies the equation First, suppose that $f$ is essential, with $\Delta^{N} f=f$. Observe that $f$ is in the image of $\Delta^{k}$ for any $k$, because $\Delta^{m N} f=f$ for any $m$. The following lemma will be useful.
|
| 1106 |
-
|
| 1107 |
-
## Lemma
|
| 1108 |
-
|
| 1109 |
-
Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{p^{d}} g$. Then
|
| 1110 |
-
|
| 1111 |
-
$$
|
| 1112 |
-
h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \equiv 0 \quad(\bmod p)
|
| 1113 |
-
$$
|
| 1114 |
-
|
| 1115 |
-
for all $x$.
|
| 1116 |
-
|
| 1117 |
-
Proof. By definition,
|
| 1118 |
-
|
| 1119 |
-
$$
|
| 1120 |
-
h(x)=\Delta^{p^{d}} g(x)=\sum_{k=0}^{p^{d}}(-1)^{k}\binom{p^{d}}{k} g\left(x+p^{d}-k\right)
|
| 1121 |
-
$$
|
| 1122 |
-
|
| 1123 |
-
However, it is known that $\binom{p^{d}}{k}$ is a multiple of $p$ if $1 \leq k \leq p^{d}-1$, so
|
| 1124 |
-
|
| 1125 |
-
$$
|
| 1126 |
-
h(x) \equiv g\left(x+p^{d}\right)+(-1)^{p^{d}} g(x) \quad(\bmod p) .
|
| 1127 |
-
$$
|
| 1128 |
-
|
| 1129 |
-
Using this, we easily obtain
|
| 1130 |
-
|
| 1131 |
-
$$
|
| 1132 |
-
\begin{aligned}
|
| 1133 |
-
& h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \\
|
| 1134 |
-
\equiv & \begin{cases}0 & p>2 \\
|
| 1135 |
-
2\left(g(x)+g\left(x+p^{d}\right)+\cdots+g\left(x+(b-1) p^{d}\right)\right) & p=2\end{cases} \\
|
| 1136 |
-
\equiv & 0 \quad(\bmod p)
|
| 1137 |
-
\end{aligned}
|
| 1138 |
-
$$
|
| 1139 |
-
|
| 1140 |
-
as desired.
|
| 1141 |
-
|
| 1142 |
-
## Corollary
|
| 1143 |
-
|
| 1144 |
-
Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{e p^{d}} g$. Then
|
| 1145 |
-
|
| 1146 |
-
$$
|
| 1147 |
-
h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)=0
|
| 1148 |
-
$$
|
| 1149 |
-
|
| 1150 |
-
for all $x$.
|
| 1151 |
-
|
| 1152 |
-
Proof. Starting with the lemma, define
|
| 1153 |
-
|
| 1154 |
-
$$
|
| 1155 |
-
h_{1}(x)=\frac{h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)}{p} .
|
| 1156 |
-
$$
|
| 1157 |
-
|
| 1158 |
-
Applying the lemma to $h_{1}$ shows the corollary for $e=2$, since $h_{1}(x)$ is divisible by $p$, hence the numerator is divisible by $p^{2}$. Continue in this manner to get the result for general $e>2$.
|
| 1159 |
-
|
| 1160 |
-
This immediately settles this direction, since $f$ is in the image of $\Delta^{e p^{d}}$.
|
| 1161 |
-
|
| 1162 |
-
Proof the equation implies essential Let $\mathcal{S}$ be the set of all functions satisfying 2 ; then it's easy to see that $\Delta$ is a function on $\mathcal{S}$. To show that all functions in $\mathcal{S}$ are essential, it's equivalent to show that $\Delta$ is a permutation on $\mathcal{S}$.
|
| 1163 |
-
|
| 1164 |
-
We will show that $\Delta$ is injective on $\mathcal{S}$. Suppose otherwise, and consider two functions $f$, $g$ in $\mathcal{S}$ with $\Delta f=\Delta g$. Then, we obtain that $f$ and $g$ differ by a constant; say $g=f+\lambda$. However, then
|
| 1165 |
-
|
| 1166 |
-
$$
|
| 1167 |
-
\begin{aligned}
|
| 1168 |
-
& g(0)+g\left(p^{e}\right)+\cdots+g\left((b-1) p^{e}\right) \\
|
| 1169 |
-
= & (f(0)+\lambda)+\left(f\left(p^{e}\right)+\lambda\right)+\cdots+\left(f\left((b-1) p^{e}\right)+\lambda\right) \\
|
| 1170 |
-
= & b \lambda
|
| 1171 |
-
\end{aligned}
|
| 1172 |
-
$$
|
| 1173 |
-
|
| 1174 |
-
This should also be zero. Since $p \nmid b$, we obtain $\lambda=0$, as desired.
|
| 1175 |
-
|
| 1176 |
-
Counting Finally, we can count the essential functions: all but the last $p^{d}$ entries can be chosen arbitrarily, and then each remaining entry has exactly one possible choice. This leads to a count of
|
| 1177 |
-
|
| 1178 |
-
$$
|
| 1179 |
-
\left(p^{e}\right)^{a-p^{d}}=p^{e\left(a-p^{\nu_{p}(a)}\right)},
|
| 1180 |
-
$$
|
| 1181 |
-
|
| 1182 |
-
as promised.
|
| 1183 |
-
|
| 1184 |
-
II Second solution by Daniel Zhu. There are two parts to the proof: solving the $e=1$ case, and using the $e=1$ result to solve the general problem by induction on $e$. These parts are independent of each other.
|
| 1185 |
-
|
| 1186 |
-
The case $e=1 \quad$ Represent functions $f$ as elements
|
| 1187 |
-
|
| 1188 |
-
$$
|
| 1189 |
-
\alpha_{f}:=\sum_{k \in \mathbb{Z} / a \mathbb{Z}} f(-k) x^{k} \in \mathbb{F}_{p}[x] /\left(x^{a}-1\right)
|
| 1190 |
-
$$
|
| 1191 |
-
|
| 1192 |
-
Then, since $\alpha_{\Delta f}=(x-1) \alpha_{f}$, we wish to find the number of $\alpha \in \mathbb{F}_{p}[x] /\left(x^{a}-1\right)$ such that $(x-1)^{m} \alpha=\alpha$ for some $m$.
|
| 1193 |
-
|
| 1194 |
-
Now, make the substitution $y=x-1$ and let $P(y)=(y+1)^{a}-1$; we want to find $\alpha \in \mathbb{F}_{p}[y] /(P(y))$ such that $y^{m} \alpha=\alpha$ for some $m$.
|
| 1195 |
-
|
| 1196 |
-
If we write $P(y)=y^{d} Q(y)$ with $Q(0) \neq 0$, then by the Chinese Remainder Theorem we have the ring isomorphism
|
| 1197 |
-
|
| 1198 |
-
$$
|
| 1199 |
-
\mathbb{F}_{p}[y] /(P(y)) \cong \mathbb{F}_{p}[y] /\left(y^{d}\right) \times \mathbb{F}_{p}[y] /(Q(y))
|
| 1200 |
-
$$
|
| 1201 |
-
|
| 1202 |
-
Note that $y$ is nilpotent in the first factor, while it is a unit in the second factor. So the $\alpha$ that work are exactly those that are zero in the first factor; thus there are $p^{a-d}$ such $\alpha$. We can calculate $d=p^{v_{p}(a)}$ (via, say, Lucas's Theorem), so we are done.
|
| 1203 |
-
|
| 1204 |
-
The general problem The general idea is as follows: call a $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z} e$-good if $\Delta^{m} f=f$ for some $m$. Our result above allows us to count the 1-good functions. Then, if $e \geq 1$, every $(e+1)$-good function, when reduced $\bmod p^{e}$, yields an $e$-good function, so we count $(e+1)$-good functions by counting how many reduce to any given $e$-good function.
|
| 1205 |
-
|
| 1206 |
-
Formally, we use induction on $e$, with the $e=1$ case being treated above. Suppose now we have solved the problem for a given $e \geq 1$, and we now wish to solve it for $e+1$. For any function $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e+1} \mathbb{Z}$, let $\bar{g}: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be its reduction $\bmod p^{e}$. For a given $e$-good $f$, let $n(f)$ be the number of $(e+1)$-good $g$ with $\bar{g}=f$. The following two claims now finish the problem:
|
| 1207 |
-
|
| 1208 |
-
Claim - If $f$ is $e$-good, then $n(f)>0$.
|
| 1209 |
-
|
| 1210 |
-
Proof. Suppose $m$ is such that $\Delta^{m} f=f$. Pick any $g$ with $\bar{g}=f$, and consider the sequence of functions
|
| 1211 |
-
|
| 1212 |
-
$$
|
| 1213 |
-
g, \Delta^{m} g, \Delta^{2 m} g, \ldots
|
| 1214 |
-
$$
|
| 1215 |
-
|
| 1216 |
-
Since there are finitely many functions $\mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e+1} \mathbb{Z}$, there must exist $a<b$ such that $\Delta^{a m} g=\Delta^{b m} g$. We claim $\Delta^{a m} g$ is the desired $(e+1)$ good function. To see this, first note that since $\overline{\Delta^{k} g}=\Delta^{k} \bar{g}$, we must have $\overline{\Delta^{a m} g}=\Delta^{a m} f=f$. Moreover,
|
| 1217 |
-
|
| 1218 |
-
$$
|
| 1219 |
-
\Delta^{(b-a) m}\left(\Delta^{a m} g\right)=\Delta^{b m} g=\Delta^{a m} g
|
| 1220 |
-
$$
|
| 1221 |
-
|
| 1222 |
-
so $\Delta^{a m} g$ is $(e+1)$-good.
|
| 1223 |
-
|
| 1224 |
-
Claim - If $f$ is $e$-good, and $n(f)>0$, then $n(f)$ is exactly the number of 1-good functions, i.e. $p^{a-p^{v_{p}(a)}}$.
|
| 1225 |
-
|
| 1226 |
-
Proof. Let $g$ be any $(e+1)$-good function with $\bar{g}=f$. We claim that the $(e+1)$-good $g_{1}$ with $\bar{g}_{1}=f$ are exactly the functions of the form $g+p^{e} h$ for any 1-good $h$. Since these functions are clearly distinct, this characterization will prove the claim.
|
| 1227 |
-
|
| 1228 |
-
To show that this condition is sufficient, note that $\overline{g+p^{e} h}=\bar{g}=f$. Moreover, if $\Delta^{m} g=g$ and $\Delta^{m^{\prime}} h=h$, then
|
| 1229 |
-
|
| 1230 |
-
$$
|
| 1231 |
-
\Delta^{m m^{\prime}}\left(g+p^{e} h\right)=\Delta^{m m^{\prime}} g+p^{e} \Delta^{m m^{\prime}} h=g+p^{e} h .
|
| 1232 |
-
$$
|
| 1233 |
-
|
| 1234 |
-
To show that this condition is necessary, let $g_{1}$ be any $(e+1)$-good function such that $\bar{g}_{1}=f$. Then $g_{1}-g$ is also $(e+1)$-good, since if $\Delta^{m} g=g, \Delta^{m^{\prime}} g_{1}=g_{1}$, we have
|
| 1235 |
-
|
| 1236 |
-
$$
|
| 1237 |
-
\Delta^{m m^{\prime}}\left(g_{1}-g\right)=\Delta^{m m^{\prime}} g_{1}-\Delta^{m m^{\prime}} g=g_{1}-g .
|
| 1238 |
-
$$
|
| 1239 |
-
|
| 1240 |
-
On the other hand, we also know that $g_{1}-g$ is divisible by $p^{e}$. This means that it must be $p^{e} h$ for some function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p \mathbb{Z}$, and it is not hard to show that $g_{1}-g$ being $(e+1)$-good means that $h$ is 1 -good.
|
| 1241 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segment_script/segment_usamo.py
DELETED
|
@@ -1,320 +0,0 @@
|
|
| 1 |
-
# -----------------------------------------------------------------------------
|
| 2 |
-
# Author: Marina
|
| 3 |
-
# Date: 2024-11-15
|
| 4 |
-
# -----------------------------------------------------------------------------
|
| 5 |
-
"""Script to segment md files in en-usamo, en-tstst, en-tst, en-jmo folder using regex.
|
| 6 |
-
To run:
|
| 7 |
-
`python segment_script/segment_usamo.py`
|
| 8 |
-
"""
|
| 9 |
-
|
| 10 |
-
import json
|
| 11 |
-
from pathlib import Path
|
| 12 |
-
import warnings
|
| 13 |
-
|
| 14 |
-
warnings.filterwarnings("ignore", category=DeprecationWarning)
|
| 15 |
-
|
| 16 |
-
import os
|
| 17 |
-
import re
|
| 18 |
-
import pandas as pd
|
| 19 |
-
from rapidfuzz import fuzz
|
| 20 |
-
|
| 21 |
-
|
| 22 |
-
# "## §0 Problems" -> match
|
| 23 |
-
section_re = re.compile(r"^#{1,2}\s(?:Contents|Problem|§[\d.]+.*)")
|
| 24 |
-
# section_re = re.compile(r"^#{1,2}\s(?:§[\d.]+.*)")
|
| 25 |
-
|
| 26 |
-
# "## §1.3 USAMO 2024/3, proposed by Krit Boonsiriseth" ->3
|
| 27 |
-
# "## §2.3 TSTST 2011/6" ->6
|
| 28 |
-
# "## §1.1 TSTST 2021/1, proposed by Holden Mui" -> 1
|
| 29 |
-
# "## §1.2 USA TST 2020/2, proposed by Merlijn Staps" -> 2
|
| 30 |
-
# "# §1.3 USA TST 2019/3, proposed by Nikolai Beluhov" -> 3
|
| 31 |
-
solution_label_re = re.compile(
|
| 32 |
-
r"^#{1,2}\s§[\d.]+\s[A-Za-z0-9 ]+\s\d{4}/(\d+)(?:,\s.*)?$"
|
| 33 |
-
)
|
| 34 |
-
|
| 35 |
-
# "1. Prove that the average of the numbers $n" -> match
|
| 36 |
-
# "2 . For any nonempty set $S$ of real numbers,"" -> match
|
| 37 |
-
problem_re = re.compile(r"^(\d+)\s?\.\s(.*(?:\n\s+.*)*)")
|
| 38 |
-
|
| 39 |
-
# "## Problem statement extra text" -> match
|
| 40 |
-
# "Problem statement" -> match
|
| 41 |
-
# "##Problem statement (missing space)" -> match
|
| 42 |
-
solution_re = re.compile(r"^#{0,2}\s?Problem statement\b.*$")
|
| 43 |
-
|
| 44 |
-
# not actually used, only for debugging
|
| 45 |
-
pattern_debug = re.compile(
|
| 46 |
-
r"^[【『\\]*.*?\b(First|Second|Third|Fourth|Fifth|Sixth|Seventh|Eighth|Ninth|Tenth|Complex|Inversion|Synthetic|One|Another|Solution)\b.*\b(solution|approach|proof)\b.*",
|
| 47 |
-
re.IGNORECASE,
|
| 48 |
-
)
|
| 49 |
-
|
| 50 |
-
# "Solution 1" -> match
|
| 51 |
-
# "【 Solution 1" -> match
|
| 52 |
-
solution_split_re1 = re.compile(r"\bSolution\s[1-9]\b")
|
| 53 |
-
|
| 54 |
-
# "First solution" -> match
|
| 55 |
-
# "【 Third approach" -> match
|
| 56 |
-
# "【 Second approach" -> match
|
| 57 |
-
solution_split_re2 = re.compile(
|
| 58 |
-
r"\b(First|Second|Third|Fourth|Fifth|Sixth|Seventh|Eighth|Ninth|Synthetic)\b\s+(solution|approach|proof)\b"
|
| 59 |
-
)
|
| 60 |
-
|
| 61 |
-
# catch special cases (ugly but it works). To generate them run script with `DEBUG = True``
|
| 62 |
-
# and identify in console which special_cases should be catched as first line of a solution
|
| 63 |
-
DEBUG = False
|
| 64 |
-
special_cases = [
|
| 65 |
-
"【 First short solution, by Jeffrey Kwan. Let $p_{0",
|
| 66 |
-
"II Second longer solution using an invariant. Visu",
|
| 67 |
-
"【 Complex solution (Evan Chen). Toss on the comple",
|
| 68 |
-
"Second (longer) solution. If one does not notice t",
|
| 69 |
-
"『 Second calculation approach (along the lines of ",
|
| 70 |
-
"T Outline of second approach (by convexity, due t",
|
| 71 |
-
"I Inversion solution submitted by Ankan Bhattacha",
|
| 72 |
-
"【 Complex numbers approach with Apollonian circles",
|
| 73 |
-
" A second solution. Both lemmas above admit varia",
|
| 74 |
-
"【 A third remixed solution. We use Lemma I and Lem",
|
| 75 |
-
"【I A fourth remixed solution. We also can combine ",
|
| 76 |
-
"I First grid-based solution. The following solutio",
|
| 77 |
-
"Another short solution. Let $Z$ be on line $B D E$",
|
| 78 |
-
"【 Most common synthetic approach. The solution hin",
|
| 79 |
-
'\\ First "local" solution by swapping two points. L',
|
| 80 |
-
"Second general solution by angle chasing. By Rei",
|
| 81 |
-
"Third general solution by Pascal. Extend rays $A",
|
| 82 |
-
"【 Second length solution by tangent lengths. By $t",
|
| 83 |
-
"【 Angle chasing solution. Note that $(B D A)$ and",
|
| 84 |
-
"【 Harmonic solution (mine). Let $T$ be the point o",
|
| 85 |
-
"【 Pascal solution (Zuming Feng). Extend ray $F D$",
|
| 86 |
-
"『 A spiral similarity approach (Hans $\mathbf{Y u}",
|
| 87 |
-
"ब The author's original solution. Complete isoscel",
|
| 88 |
-
"l Evan's permutation-based solution. Retain the n",
|
| 89 |
-
"I Original proposer's solution. To this end, let's",
|
| 90 |
-
"【 Cartesian coordinates approach with power of a p",
|
| 91 |
-
"【 Cartesian coordinates approach without power of",
|
| 92 |
-
"I III-advised barycentric approach (outline). Use",
|
| 93 |
-
"【 Approach using difference of squares (from autho",
|
| 94 |
-
"【 Divisibility approach (Aharshi Roy). Since $p q-",
|
| 95 |
-
"Solution with Danielle Wang: the answer is that $|",
|
| 96 |
-
"【 Homothety solution (Alex Whatley). Let $G, N, O$",
|
| 97 |
-
"【 Power of a point solution (Zuming Feng, official",
|
| 98 |
-
"【 Solution by Luke Robitaille. Let $Q$ be the seco",
|
| 99 |
-
"ๆ Solution with coaxial circles (Pitchayut Saengru",
|
| 100 |
-
"【 Solution to generalization (Nikolai Beluhov). We",
|
| 101 |
-
"【 Approach by deleting teams (Gopal Goel). Initial",
|
| 102 |
-
"【 Approach by adding colors. For a constructive al",
|
| 103 |
-
"【 Solution using spiral similarity. We will ignore",
|
| 104 |
-
"『 Barycentric solution (by Carl, Krit, Milan). We",
|
| 105 |
-
"I A Menelaus-based approach (Kevin Ren). Let $P$ b",
|
| 106 |
-
"【 Barycentric solution. First, we find the coordin",
|
| 107 |
-
"【 Angle chasing solution (Mason Fang). Obviously $",
|
| 108 |
-
"【 Inversive solution (Kelin Zhu). Invert about $A$",
|
| 109 |
-
"l The one-liner. ",
|
| 110 |
-
" The external power solution. We distinguish betw",
|
| 111 |
-
"Cauchy-Schwarz approach. Apply Titu lemma to get",
|
| 112 |
-
"đ Cauchy-Schwarz approach. The main magical claim ",
|
| 113 |
-
"『 Alternate solution (by proposer). Let $L$ be dia",
|
| 114 |
-
]
|
| 115 |
-
|
| 116 |
-
|
| 117 |
-
def add_content(current_dict):
|
| 118 |
-
if not current_dict["lines"] or not current_dict["label"]:
|
| 119 |
-
return
|
| 120 |
-
text_str = " ".join(current_dict["lines"]).strip()
|
| 121 |
-
entry = {"label": current_dict["label"]}
|
| 122 |
-
if current_dict["class"] == "problem":
|
| 123 |
-
entry["problem"] = text_str
|
| 124 |
-
current_dict["problems"].append(entry)
|
| 125 |
-
elif current_dict["class"] == "solution":
|
| 126 |
-
entry["solution"] = text_str
|
| 127 |
-
entry["solution_lines"] = current_dict["lines"]
|
| 128 |
-
current_dict["solutions"].append(entry)
|
| 129 |
-
|
| 130 |
-
|
| 131 |
-
def parse(file: Path):
|
| 132 |
-
content = file.read_text(encoding="utf-8")
|
| 133 |
-
current = {
|
| 134 |
-
"label": None,
|
| 135 |
-
"class": None,
|
| 136 |
-
"lines": [],
|
| 137 |
-
"problems": [],
|
| 138 |
-
"solutions": [],
|
| 139 |
-
}
|
| 140 |
-
for line in content.splitlines():
|
| 141 |
-
if match := section_re.match(line): # match a section
|
| 142 |
-
add_content(current)
|
| 143 |
-
if "problems" in line.lower(): # match problem section
|
| 144 |
-
current["class"] = "problem"
|
| 145 |
-
elif sub_match := solution_label_re.match(
|
| 146 |
-
line
|
| 147 |
-
): # match solutions section, extract label for join
|
| 148 |
-
current["class"] = "other"
|
| 149 |
-
current["label"] = sub_match.group(1)
|
| 150 |
-
elif match := solution_re.match(line): # match solutions subsection
|
| 151 |
-
current["class"] = "solution"
|
| 152 |
-
else:
|
| 153 |
-
current["class"] = "other"
|
| 154 |
-
current["lines"] = []
|
| 155 |
-
elif match := problem_re.match(line): # match a problem
|
| 156 |
-
if current["class"] == "solution": # handle wrong problem match
|
| 157 |
-
current["lines"].append(line)
|
| 158 |
-
else:
|
| 159 |
-
add_content(current)
|
| 160 |
-
label, text = match.groups()
|
| 161 |
-
current["label"] = label
|
| 162 |
-
current["lines"] = [text]
|
| 163 |
-
else:
|
| 164 |
-
if current["class"] == "solution" or current["class"] == "problem":
|
| 165 |
-
current["lines"].append(line)
|
| 166 |
-
add_content(current)
|
| 167 |
-
problems_df = pd.DataFrame(current["problems"])
|
| 168 |
-
solutions_df = pd.DataFrame(current["solutions"])
|
| 169 |
-
return problems_df, solutions_df
|
| 170 |
-
|
| 171 |
-
|
| 172 |
-
def parse_solution(lines):
|
| 173 |
-
"""parses lines of a solution, finds multiple solutions and splits them"""
|
| 174 |
-
solutions = []
|
| 175 |
-
current = []
|
| 176 |
-
for line in lines:
|
| 177 |
-
if match := solution_split_re1.search(line): # match a solution (case1)
|
| 178 |
-
solutions.append(" ".join(current).strip())
|
| 179 |
-
current = [line]
|
| 180 |
-
elif match := solution_split_re2.search(line): # match a solution (case1)
|
| 181 |
-
solutions.append(" ".join(current).strip())
|
| 182 |
-
current = [line]
|
| 183 |
-
elif any(
|
| 184 |
-
case.lower() in line.lower() for case in special_cases
|
| 185 |
-
): # match a solution (handle special_case)
|
| 186 |
-
solutions.append(" ".join(current).strip())
|
| 187 |
-
current = [line]
|
| 188 |
-
elif any(
|
| 189 |
-
case.lower() in line[:50].lower()
|
| 190 |
-
for case in ["solution", "approach", "proof"]
|
| 191 |
-
):
|
| 192 |
-
if DEBUG:
|
| 193 |
-
if not any(
|
| 194 |
-
case.lower() in line[:50].lower()
|
| 195 |
-
for case in ["remark", "proof.", "proof", "approaches", "solutions"]
|
| 196 |
-
):
|
| 197 |
-
print(line[:50])
|
| 198 |
-
else:
|
| 199 |
-
current.append(line)
|
| 200 |
-
solutions.append(" ".join(current).strip())
|
| 201 |
-
return solutions
|
| 202 |
-
|
| 203 |
-
|
| 204 |
-
def find_mult_solutions(solutions_df):
|
| 205 |
-
"""apply parse_solution to all df"""
|
| 206 |
-
solutions_df["solution"] = solutions_df["solution_lines"].apply(
|
| 207 |
-
lambda v: parse_solution(v)
|
| 208 |
-
)
|
| 209 |
-
solutions_df = solutions_df.drop(columns=["solution_lines"])
|
| 210 |
-
solutions_df = solutions_df.explode("solution", ignore_index=True)
|
| 211 |
-
return solutions_df
|
| 212 |
-
|
| 213 |
-
|
| 214 |
-
def join(problems_df, solutions_df):
|
| 215 |
-
pairs_df = problems_df.merge(solutions_df, on=["label"], how="outer")
|
| 216 |
-
return pairs_df
|
| 217 |
-
|
| 218 |
-
|
| 219 |
-
def clean(pairs_df):
|
| 220 |
-
"""removes the problem statement from the solution in an approximate way"""
|
| 221 |
-
|
| 222 |
-
def find_closest_char(s, i, char):
|
| 223 |
-
left = s.rfind(char, 0, i) # Find the last '.' before index i
|
| 224 |
-
right = s.find(char, i) # Find the first '.' after or at index i
|
| 225 |
-
if left == -1 and right == -1:
|
| 226 |
-
return None # No '.' found
|
| 227 |
-
elif left == -1: # No '.' on the left
|
| 228 |
-
return right
|
| 229 |
-
elif right == -1: # No '.' on the right
|
| 230 |
-
return left
|
| 231 |
-
else: # Closest '.' on either side
|
| 232 |
-
return left if abs(i - left) <= abs(i - right) else right
|
| 233 |
-
|
| 234 |
-
def remove_approx_match(row, threshold=90):
|
| 235 |
-
problem = row["problem"]
|
| 236 |
-
solution = row["solution"]
|
| 237 |
-
similarity = fuzz.partial_ratio(problem, solution)
|
| 238 |
-
if similarity >= threshold:
|
| 239 |
-
i = find_closest_char(solution, len(problem), problem[-1])
|
| 240 |
-
if i is not None:
|
| 241 |
-
solution = solution[i + 1 :]
|
| 242 |
-
return solution
|
| 243 |
-
|
| 244 |
-
pairs_df["solution"] = pairs_df.apply(remove_approx_match, axis=1)
|
| 245 |
-
return pairs_df
|
| 246 |
-
|
| 247 |
-
|
| 248 |
-
def process_mult_solutions(pairs_df):
|
| 249 |
-
"""in case of multiple solutions, prepend common text to all solutions"""
|
| 250 |
-
|
| 251 |
-
def prepend_to_solution(group):
|
| 252 |
-
if len(group) == 1:
|
| 253 |
-
return group
|
| 254 |
-
first_row = group.iloc[0]
|
| 255 |
-
comment = f"{first_row['solution']}"
|
| 256 |
-
group = group.iloc[1:].copy()
|
| 257 |
-
group["solution"] = group["solution"].apply(lambda x: f"{comment} {x}")
|
| 258 |
-
return group
|
| 259 |
-
|
| 260 |
-
pairs_df = (
|
| 261 |
-
pairs_df.groupby("label", group_keys=False)
|
| 262 |
-
.apply(prepend_to_solution)
|
| 263 |
-
.reset_index(drop=True)
|
| 264 |
-
)
|
| 265 |
-
return pairs_df
|
| 266 |
-
|
| 267 |
-
|
| 268 |
-
def add_metadata(pairs_df, year, tier, resource_path):
|
| 269 |
-
pairs_df['year'] = year
|
| 270 |
-
pairs_df['tier'] = tier # according to omnimath
|
| 271 |
-
pairs_df['metadata'] = [{"resource_path": resource_path}] * len(pairs_df)
|
| 272 |
-
pairs_df['problem_type'] = None
|
| 273 |
-
pairs_df.rename(columns={'label': 'problem_label'}, inplace=True)
|
| 274 |
-
return pairs_df[['year', 'tier', 'problem_label', 'problem_type','problem', 'solution', 'metadata']]
|
| 275 |
-
|
| 276 |
-
|
| 277 |
-
def write_pairs(file_path, pairs_df):
|
| 278 |
-
pairs_df = pairs_df.replace({pd.NA: None, pd.NaT: None, float("nan"): None})
|
| 279 |
-
pairs_dict = pairs_df.to_dict(orient="records")
|
| 280 |
-
output_text = ""
|
| 281 |
-
for pair in pairs_dict:
|
| 282 |
-
output_text += json.dumps(pair, ensure_ascii=False) + "\n"
|
| 283 |
-
file_path.write_text(output_text, encoding="utf-8")
|
| 284 |
-
|
| 285 |
-
|
| 286 |
-
if __name__ == "__main__":
|
| 287 |
-
project_root = Path(__file__).parent.parent.parent
|
| 288 |
-
|
| 289 |
-
problem_count = 0
|
| 290 |
-
solution_count = 0
|
| 291 |
-
|
| 292 |
-
tier = "T0"
|
| 293 |
-
compet_base_path = Path(__file__).resolve().parent.parent
|
| 294 |
-
compet_md_path = compet_base_path / "md"
|
| 295 |
-
seg_output_path = compet_base_path / "segmented"
|
| 296 |
-
|
| 297 |
-
for md_file in compet_md_path.glob("**/*.md"):
|
| 298 |
-
year = re.search(r"\d{4}", md_file.name).group()
|
| 299 |
-
output_file = seg_output_path / md_file.relative_to(compet_md_path).with_suffix(".jsonl")
|
| 300 |
-
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 301 |
-
|
| 302 |
-
problems, solutions = parse(md_file)
|
| 303 |
-
solutions = find_mult_solutions(solutions)
|
| 304 |
-
pairs_df = join(problems, solutions)
|
| 305 |
-
pairs_df = clean(pairs_df)
|
| 306 |
-
pairs_df = process_mult_solutions(pairs_df)
|
| 307 |
-
pairs_df = add_metadata(
|
| 308 |
-
pairs_df, year, tier, output_file.relative_to(project_root).as_posix()
|
| 309 |
-
)
|
| 310 |
-
problem_count += len(problems)
|
| 311 |
-
solution_count += len(pairs_df)
|
| 312 |
-
write_pairs(output_file, pairs_df)
|
| 313 |
-
|
| 314 |
-
print(f"problem count: {problem_count}")
|
| 315 |
-
print(f"solution count: {solution_count}")
|
| 316 |
-
|
| 317 |
-
|
| 318 |
-
# en-tstst
|
| 319 |
-
# problem count: 105
|
| 320 |
-
# solution count: 168
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl
DELETED
|
@@ -1,9 +0,0 @@
|
|
| 1 |
-
{"year": "2011", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Find all real-valued functions $f$ defined on pairs of real numbers, having the following property: for all real numbers $a, b, c$, the median of $f(a, b), f(b, c), f(c, a)$ equals the median of $a, b, c$. (The median of three real numbers, not necessarily distinct, is the number that is in the middle when the three numbers are arranged in nondecreasing order.)", "solution": " We prove the following main claim, from which repeated applications can deduce the problem. Claim - Let $a<b<c$ be arbitrary. On $\\{a, b, c\\}^{2}, f$ takes one of the following two forms, where the column indicates the $x$-value and the row indicates the $y$-value. | $f$ | $a$ | $b$ | $c$ | | ---: | ---: | ---: | ---: | | $a$ | $a$ | $b$ | $\\geq c$ | | $b$ | $\\leq a$ | $b$ | $\\geq c$ | | $c$ | $\\leq a$ | $b$ | $c$ | or | $f$ | $a$ | $b$ | $c$ | | ---: | ---: | ---: | ---: | | $a$ | $a$ | $\\leq a$ | $\\leq a$ | | $b$ | $b$ | $b$ | $b$ | | $c$ | $\\geq c$ | $\\geq c$ | $c$ | - By considering the assertion for $(a, a, c)$ and $(a, c, c)$ we see that one of $f(a, c)$ and $f(c, a)$ is $\\geq c$ and the other is $\\leq a$. - Hence, by considering $(a, b, c)$ we find that one of $f(a, b)$ and $f(b, c)$ must be $b$, and similarly for $f(b, a)$ and $f(c, b)$. - Now, WLOG $f(b, a)=b$; we prove we get the first case. - By considering $(a, a, b)$ we deduce $f(a, b) \\leq a$, so $f(b, c)=b$ and then $f(c, b) \\geq c$. - Finally, considering $(c, b, a)$ once again in conjunction with the first bullet, we arrive at the conclusion that $f(a, c) \\leq a$; similarly $f(c, a) \\geq c$. From this it's easy to obtain that $f(x, y) \\equiv x$ or $f(x, y) \\equiv y$ are the only solutions.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 2 |
-
{"year": "2011", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Two circles $\\omega_{1}$ and $\\omega_{2}$ intersect at points $A$ and $B$. Line $\\ell$ is tangent to $\\omega_{1}$ at $P$ and to $\\omega_{2}$ at $Q$ so that $A$ is closer to $\\ell$ than $B$. Let $X$ and $Y$ be points on major $\\operatorname{arcs} \\widehat{P A}\\left(\\right.$ on $\\left.\\omega_{1}\\right)$ and $\\overparen{A Q}$ (on $\\left.\\omega_{2}\\right)$, respectively, such that $A X / P X=A Y / Q Y=c$. Extend segments $P A$ and $Q A$ through $A$ to $R$ and $S$, respectively, such that $A R=A S=c \\cdot P Q$. Given that the circumcenter of triangle $A R S$ lies on line $X Y$, prove that $\\angle X P A=\\angle A Q Y$.", "solution": " We begin as follows: Claim - There is a spiral similarity centered at $X$ mapping $A R$ to $P Q$. Similarly there is a spiral similarity centered at $Y$ mapping $S A$ to $P Q$. Now the composition of the two spiral similarities $$ A R \\stackrel{X}{\\mapsto} P Q \\stackrel{Y}{\\mapsto} S A $$ must be a rotation, since $A R=A S$. The center of this rotation must coincide with the circumcenter $O$ of $\\triangle A R S$, which is known to lie on line $X Y$.  As $O$ is a fixed-point of the composed map above, we may let $O^{\\prime}$ be the image of $O$ under the rotation at $X$, so that $$ \\triangle X P A \\AA \\triangle X O^{\\prime} O, \\quad \\triangle Y Q A \\AA \\triangle Y O^{\\prime} O . $$ Because $$ \\frac{X O}{X O^{\\prime}}=\\frac{X A}{X P}=c \\frac{Y Q}{Y A}=\\frac{Y O}{Y O^{\\prime}} $$ it follows $\\overline{O^{\\prime} O}$ bisects $\\angle X O^{\\prime} Y$. Finally, we have $$ \\measuredangle X P A=\\measuredangle X O^{\\prime} O=\\measuredangle O O^{\\prime} Y=\\measuredangle A Q Y $$ Remark. Indeed, this also shows $\\overline{X P} \\| \\overline{Y Q}$; so the positive homothety from $\\omega_{1}$ to $\\omega_{2}$ maps $P$ to $Q$ and $X$ to $Y$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 3 |
-
{"year": "2011", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Prove that there exists a real constant $c$ such that for any pair $(x, y)$ of real numbers, there exist relatively prime integers $m$ and $n$ satisfying the relation $$ \\sqrt{(x-m)^{2}+(y-n)^{2}}<c \\log \\left(x^{2}+y^{2}+2\\right) . $$", "solution": " This is actually the same problem as USAMO 2014/6. Surprise!", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 4 |
-
{"year": "2011", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Acute triangle $A B C$ is inscribed in circle $\\omega$. Let $H$ and $O$ denote its orthocenter and circumcenter, respectively. Let $M$ and $N$ be the midpoints of sides $A B$ and $A C$, respectively. Rays $M H$ and $N H$ meet $\\omega$ at $P$ and $Q$, respectively. Lines $M N$ and $P Q$ meet at $R$. Prove that $\\overline{O A} \\perp \\overline{R A}$.", "solution": " Let $M H$ and $N H$ meet the nine-point circle again at $P^{\\prime}$ and $Q^{\\prime}$, respectively. Recall that $H$ is the center of the homothety between the circumcircle and the nine-point circle. From this we can see that $P$ and $Q$ are the images of this homothety, meaning that $$ H Q=2 H Q^{\\prime} \\quad \\text { and } \\quad H P=2 H P^{\\prime} $$ Since $M, P^{\\prime}, Q^{\\prime}, N$ are cyclic, Power of a Point gives us $$ M H \\cdot H P^{\\prime}=H N \\cdot H Q^{\\prime} $$ Multiplying both sides by two, we thus derive $$ H M \\cdot H P=H N \\cdot H Q $$ It follows that the points $M, N, P, Q$ are concyclic.  Let $\\omega_{1}, \\omega_{2}, \\omega_{3}$ denote the circumcircles of $M N P Q, A M N$, and $A B C$, respectively. The radical axis of $\\omega_{1}$ and $\\omega_{2}$ is line $M N$, while the radical axis of $\\omega_{1}$ and $\\omega_{3}$ is line $P Q$. Hence the line $R$ lies on the radical axis of $\\omega_{2}$ and $\\omega_{3}$. But we claim that $\\omega_{2}$ and $\\omega_{3}$ are internally tangent at $A$. This follows by noting the homothety at $A$ with ratio 2 sends $M$ to $B$ and $N$ to $C$. Hence the radical axis of $\\omega_{2}$ and $\\omega_{3}$ is a line tangent to both circles at $A$. Hence $\\overline{R A}$ is tangent to $\\omega_{3}$. Therefore, $\\overline{R A} \\perp \\overline{O A}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 5 |
-
{"year": "2011", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "At a certain orphanage, every pair of orphans are either friends or enemies. For every three of an orphan's friends, an even number of pairs of them are enemies. Prove that it's possible to assign each orphan two parents such that every pair of friends shares exactly one parent, but no pair of enemies does, and no three parents are in a love triangle (where each pair of them has a child).", "solution": " Of course, we consider the graph with vertices as children and edges as friendships. Consider all the maximal cliques in the graph (i.e. repeatedly remove maximal cliques until no edges remain; thus all edges are in some clique). Claim - Every vertex is in at most two maximal cliques. Now, for every maximal clique we assign a particular parent to all vertices in that clique, adding in additional distinct parents if there are any deficient children. This satisfies the friendship/enemy condition. Moreover, one can readily check that there are no love triangles: given children $a, b, c$ such that $a$ and $b$ share a parent while $a$ and $c$ share another parent, according to the claim $b$ and $c$ can't share a third parent. This completes the problem. Ironically, the condition that there be no love triangle actually makes the problem easier, because it tells us exactly what to do!", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 6 |
-
{"year": "2011", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $a, b, c$ be real numbers in the interval $[0,1]$ with $a+b, b+c, c+a \\geq 1$. Prove that $$ 1 \\leq(1-a)^{2}+(1-b)^{2}+(1-c)^{2}+\\frac{2 \\sqrt{2} a b c}{\\sqrt{a^{2}+b^{2}+c^{2}}} $$", "solution": " We will prove the inequality for any $a, b, c$ the sides of a possibly degenerate triangle (which is implied by the condition), ignoring the particular constant 1. Homogenizing, we instead prove the problem in the following form: Claim - We have $$ k^{2} \\leq(k-a)^{2}+(k-b)^{2}+(k-c)^{2}+\\frac{2 \\sqrt{2} a b c}{\\sqrt{a^{2}+b^{2}+c^{2}}} $$ for any $a, b, c, k$ with $(a, b, c)$ the sides of a possibly degenerate triangle. Letting $x=\\frac{1}{2}(b+c-a)$ as is usual, the problem rearranges to In that case, the problem amounts to $$ (x+y+z)^{2} \\leq x^{2}+y^{2}+z^{2}+\\frac{2(x+y)(y+z)(z+x)}{\\sqrt{x^{2}+y^{2}+z^{2}+x y+y z+z x}} $$ or equivalently $$ x^{2}+y^{2}+z^{2}+x y+y z+z x \\leq\\left(\\frac{(x+y)(y+z)(z+x)}{x y+y z+z x}\\right)^{2} . $$ To show this, one may let $t=x y+y z+z x$, then using $(x+y)(x+z)=x^{2}+B$ this becomes $$ t^{2}\\left(x^{2}+y^{2}+z^{2}+t\\right) \\leq\\left(x^{2}+t\\right)\\left(y^{2}+t\\right)\\left(z^{2}+t\\right) $$ which is obvious upon expansion. Remark. The inequality holds actually for all real numbers $a, b$, $c$, with very disgusting proofs.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 7 |
-
{"year": "2011", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Let $A B C$ be a triangle. Its excircles touch sides $B C, C A, A B$ at $D, E, F$. Prove that the perimeter of triangle $A B C$ is at most twice that of triangle $D E F$.", "solution": " $$ \\begin{aligned} -s+\\sum_{\\mathrm{cyc}} E F & \\geq-s+\\sum_{\\mathrm{cyc}}[a-(s-a)(\\cos B+\\cos C)] \\\\ & =s-\\sum_{\\mathrm{cyc}} a \\cos A=\\sum_{\\mathrm{cyc}} a\\left(\\frac{1}{2}-\\cos A\\right) \\\\ & =R \\sum_{\\mathrm{cyc}} \\sin A(1-2 \\cos A) \\\\ & =R \\sum_{\\mathrm{cyc}}(\\sin A-\\sin 2 A) \\end{aligned} $$ Thus we're done upon noting that $$ \\frac{\\sin 2 B+\\sin 2 C}{2}=\\sin (B+C) \\cos (B-C)=\\sin A \\cos (B-C) \\leq \\sin A $$ (Alternatively, one can avoid trigonometry by substituting $\\cos A=\\frac{b^{2}+c^{2}-a^{2}}{2 b c}$ and doing some routine but long calculation.)", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 8 |
-
{"year": "2011", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $x_{0}, x_{1}, \\ldots, x_{n_{0}-1}$ be integers, and let $d_{1}, d_{2}, \\ldots, d_{k}$ be positive integers with $n_{0}=d_{1}>d_{2}>\\cdots>d_{k}$ and $\\operatorname{gcd}\\left(d_{1}, d_{2}, \\ldots, d_{k}\\right)=1$. For every integer $n \\geq n_{0}$, define $$ x_{n}=\\left\\lfloor\\frac{x_{n-d_{1}}+x_{n-d_{2}}+\\cdots+x_{n-d_{k}}}{k}\\right\\rfloor . $$ Show that the sequence $\\left(x_{n}\\right)$ is eventually constant.", "solution": " Note that if the initial terms are contained in some interval $[A, B]$ then they will remain in that interval. Thus the sequence is eventually periodic. Discard initial terms and let the period be $T$; we will consider all indices modulo $T$ from now on. Let $M$ be the maximal term in the sequence (which makes sense since the sequence is periodic). Note that if $x_{n}=M$, we must have $x_{n-d_{i}}=M$ for all $i$ as well. By taking a linear combination $\\sum c_{i} d_{i} \\equiv 1(\\bmod T)($ possibly be Bezout's theorem, since $\\operatorname{gcd}_{i}\\left(d_{i}\\right)=1$ ), we conclude $x_{n-1}=M$, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
| 9 |
-
{"year": "2011", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $n$ be a positive integer. Suppose we are given $2^{n}+1$ distinct sets, each containing finitely many objects. Place each set into one of two categories, the red sets and the blue sets, so that there is at least one set in each category. We define the symmetric difference of two sets as the set of objects belonging to exactly one of the two sets. Prove that there are at least $2^{n}$ different sets which can be obtained as the symmetric difference of a red set and a blue set.", "solution": " We can interpret the problem as working with binary strings of length $\\ell \\geq n+1$, with $\\ell$ the number of elements across all sets. Let $F$ be a field of cardinality $2^{\\ell}$, hence $F \\cong \\mathbb{F}_{2}^{\\oplus \\ell}$. Then, we can think of red/blue as elements of $F$, so we have some $B \\subseteq F$, and an $R \\subseteq F$. We wish to prove that $|B+R| \\geq 2^{n}$. Want $|B+R| \\geq 2^{n}$. Equivalently, any element of a set $X$ with $|X|=2^{n}-1$ should omit some element of $|B+R|$. To prove this: we know $|B|+|R|=2^{n}+1$, and define $$ P(b, r)=\\prod_{x \\in X}(b+r-x) $$ Consider $b^{|B|-1} r^{|R|-1}$. The coefficient of is $\\binom{2^{n}-1}{|B|-1}$, which is odd (say by Lucas theorem), so the nullstellensatz applies.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2011.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl
DELETED
|
@@ -1,13 +0,0 @@
|
|
| 1 |
-
{"year": "2012", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Determine all infinite strings of letters with the following properties: (a) Each letter is either $T$ or $S$, (b) If position $i$ and $j$ both have the letter $T$, then position $i+j$ has the letter $S$, (c) There are infinitely many integers $k$ such that position $2 k-1$ has the $k$ th $T$.", "solution": " We wish to find all infinite sequences $a_{1}, a_{2}, \\ldots$ of positive integers satisfying the following properties: (a) $a_{1}<a_{2}<a_{3}<\\cdots$, (b) there are no positive integers $i, j, k$, not necessarily distinct, such that $a_{i}+a_{j}=a_{k}$, (c) there are infinitely many $k$ such that $a_{k}=2 k-1$. If $a_{k}=2 k-1$ for some $k>1$, let $A_{k}=\\left\\{a_{1}, a_{2}, \\ldots, a_{k}\\right\\}$. By (b) and symmetry, we have $$ 2 k-1 \\geq \\frac{\\left|A_{k}-A_{k}\\right|-1}{2}+\\left|A_{k}\\right| \\geq \\frac{2\\left|A_{k}\\right|-2}{2}+\\left|A_{k}\\right|=2 k-1 . $$ But in order for $\\left|A_{k}-A_{k}\\right|=2\\left|A_{k}\\right|-1$, we must have $A_{k}$ an arithmetic progression, whence $a_{n}=2 n-1$ for all $n$ by taking $k$ arbitrarily large.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 2 |
-
{"year": "2012", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral with $A C=B D$. Diagonals $A C$ and $B D$ meet at $P$. Let $\\omega_{1}$ and $O_{1}$ denote the circumcircle and circumcenter of triangle $A B P$. Let $\\omega_{2}$ and $O_{2}$ denote the circumcircle and circumcenter of triangle $C D P$. Segment $B C$ meets $\\omega_{1}$ and $\\omega_{2}$ again at $S$ and $T$ (other than $B$ and $C$ ), respectively. Let $M$ and $N$ be the midpoints of minor arcs $\\widehat{S P}$ (not including $B$ ) and $\\overparen{T P}$ (not including $C$ ). Prove that $\\overline{M N} \\| \\overline{O_{1} O_{2}}$.", "solution": " Let $Q$ be the second intersection point of $\\omega_{1}, \\omega_{2}$. Suffice to show $\\overline{Q P} \\perp \\overline{M N}$. Now $Q$ is the center of a spiral congruence which sends $\\overline{A C} \\mapsto \\overline{B D}$. So $\\triangle Q A B$ and $\\triangle Q C D$ are similar isosceles. Now, $$ \\measuredangle Q P A=\\measuredangle Q B A=\\measuredangle D C Q=\\measuredangle D P Q $$ and so $\\overline{Q P}$ is bisects $\\angle B P C$.  Now, let $I=\\overline{B M} \\cap \\overline{C N} \\cap \\overline{P Q}$ be the incenter of $\\triangle P B C$. Then $I M \\cdot I B=I P \\cdot I Q=$ $I N \\cdot I C$, so $B M N C$ is cyclic, meaning $\\overline{M N}$ is antiparallel to $\\overline{B C}$ through $\\angle B I C$. Since $\\overline{Q P I}$ passes through the circumcenter of $\\triangle B I C$, it follows now $\\overline{Q P I} \\perp \\overline{M N}$ as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 3 |
-
{"year": "2012", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Let $\\mathbb{N}$ be the set of positive integers. Let $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ be a function satisfying the following two conditions: (a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime. (b) $n \\leq f(n) \\leq n+2012$ for all $n$. Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.", "solution": " 【 First short solution, by Jeffrey Kwan. Let $p_{0}, p_{1}, p_{2}, \\ldots$ denote the sequence of all prime numbers, in any order. Pick any primes $q_{i}$ such that $$ q_{0}\\left|f\\left(p_{0}\\right), \\quad q_{1}\\right| f\\left(p_{1}\\right), \\quad q_{2} \\mid f\\left(p_{2}\\right), \\text { etc. } $$ This is possible since each $f$ value above exceeds 1 . Also, since by hypothesis the $f\\left(p_{i}\\right)$ are pairwise coprime, the primes $q_{i}$ are all pairwise distinct. Claim - We must have $q_{i}=p_{i}$ for each $i$. (Therefore, $f\\left(p_{i}\\right)$ is a power of $p_{i}$ for each $i$.) $$ \\begin{array}{rr} m+i & \\equiv 0 \\\\ m & \\left(\\bmod q_{i}\\right) \\\\ m & \\equiv{ }^{\\prime} \\\\ \\left(\\bmod p_{i}\\right) \\end{array} $$ for $0 \\leq i \\leq 2012$. But now $f(m)$ should be coprime to all $f\\left(p_{i}\\right)$, ergo coprime to $q_{0} q_{1} \\ldots q_{2012}$, violating $m \\leq f(m) \\leq m+2012$. All that is left to do is note that whenever $p \\nmid n$, we have $\\operatorname{gcd}(f(p), f(n))=1$, hence $p \\nmid f(n)$. This is the contrapositive of the problem statement.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 4 |
-
{"year": "2012", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Let $\\mathbb{N}$ be the set of positive integers. Let $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ be a function satisfying the following two conditions: (a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime. (b) $n \\leq f(n) \\leq n+2012$ for all $n$. Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.", "solution": " 【 Second solution with a grid. Fix $n$ and $p$, and assume for contradiction $p \\nmid n$. Claim - There exists a large integer $N$ with $f(N)=N$, that also satisfies $N \\equiv 1$ $(\\bmod n)$ and $N \\equiv 0(\\bmod p)$. it to fill in the following table: | | $N+1$ | $N+2$ | $\\ldots$ | $N+2012$ | | :---: | :---: | :---: | :---: | :---: | | $M$ | $q_{0,1}$ | $q_{0,2}$ | $\\ldots$ | $q_{0,2012}$ | | $M+1$ | $q_{1,1}$ | $q_{1,2}$ | $\\ldots$ | $q_{1,2012}$ | | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ | | $M+2012$ | $q_{2012,1}$ | $q_{2012,2}$ | $\\ldots$ | $q_{2012,2012}$ |. By the Chinese Remainder Theorem, we can construct $N$ such that $N+1 \\equiv 0\\left(\\bmod q_{i, 1}\\right)$ for every $i$, and similarly for $N+2$, and so on. Moreover, we can also tack on the extra conditions $N \\equiv 0(\\bmod p)$ and $N \\equiv 1(\\bmod n)$ we wanted. Notice that $N$ cannot be divisible by any of the $q_{i, j}$ 's, since the $q_{i, j}$ 's are greater than 2012. After we've chosen $N$, we can pick $M$ such that $M \\equiv 0\\left(\\bmod q_{0, j}\\right)$ for every $j$, and similarly $M+1 \\equiv 0\\left(\\bmod q_{1, j}\\right)$, et cetera. Moreover, we can tack on the condition $M \\equiv 1$ $(\\bmod N)$, which ensures $\\operatorname{gcd}(M, N)=1$. What does this do? We claim that $f(N)=N$ now. Indeed $f(M)$ and $f(N)$ are relatively prime; but look at the table! The table tells us that $f(M)$ must have a common factor with each of $N+1, \\ldots, N+2012$. So the only possibility is that $f(N)=N$. Now we're basically done. Since $N \\equiv 1(\\bmod n)$, we have $\\operatorname{gcd}(N, n)=1$ and hence $1=\\operatorname{gcd}(f(N), f(n))=\\operatorname{gcd}(N, f(n))$. But $p \\mid N$ and $p \\mid f(n)$, contradiction.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 5 |
-
{"year": "2012", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "In scalene triangle $A B C$, let the feet of the perpendiculars from $A$ to $\\overline{B C}, B$ to $\\overline{C A}$, $C$ to $\\overline{A B}$ be $A_{1}, B_{1}, C_{1}$, respectively. Denote by $A_{2}$ the intersection of lines $B C$ and $B_{1} C_{1}$. Define $B_{2}$ and $C_{2}$ analogously. Let $D, E, F$ be the respective midpoints of sides $\\overline{B C}, \\overline{C A}, \\overline{A B}$. Show that the perpendiculars from $D$ to $\\overline{A A_{2}}, E$ to $\\overline{B B_{2}}$ and $F$ to $\\overline{C C_{2}}$ are concurrent.", "solution": " We claim that they pass through the orthocenter $H$. Indeed, consider the circle with diameter $\\overline{B C}$, which circumscribes quadrilateral $B C B_{1} C_{1}$ and has center $D$. Then by Brokard theorem, $\\overline{A A_{2}}$ is the polar of line $H$. Thus $\\overline{D H} \\perp \\overline{A A_{2}}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 6 |
-
{"year": "2012", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "A rational number $x$ is given. Prove that there exists a sequence $x_{0}, x_{1}, x_{2}, \\ldots$ of rational numbers with the following properties: (a) $x_{0}=x$; (b) for every $n \\geq 1$, either $x_{n}=2 x_{n-1}$ or $x_{n}=2 x_{n-1}+\\frac{1}{n}$; (c) $x_{n}$ is an integer for some $n$.", "solution": " Think of the sequence as a process over time. We'll show that: Claim - At any given time $t$, if the denominator of $x_{t}$ has some odd prime power $q=p^{e}$, then we can delete a factor of $p$ from the denominator, while only adding powers of two to the denominator. (Thus we can just delete off all the odd primes one by one and then double appropriately many times.) Indeed, let $n$ be large, and suppose $t<2^{r+1} q<2^{r+2} q<\\cdots<2^{r+m} q<n$. For some binary variables $\\varepsilon_{i} \\in\\{0,1\\}$ we can have $$ x_{n}=2^{n-t} x_{t}+c_{1} \\cdot \\frac{\\varepsilon_{1}}{q}+c_{2} \\cdot \\frac{\\varepsilon_{2}}{q} \\cdots+c_{s} \\cdot \\frac{\\varepsilon_{m}}{q} $$ where $c_{i}$ is some power of 2 (to be exact, $c_{i}=\\frac{2^{n-2^{r+i} q}}{2^{r+1}}$, but the exact value doesn't matter). If $m$ is large enough the set $\\left\\{0, c_{1}\\right\\}+\\left\\{0, c_{2}\\right\\}+\\cdots+\\left\\{0, c_{m}\\right\\}$ spans everything modulo p. (Actually, Cauchy-Davenport implies $m=p$ is enough, but one can also just use Pigeonhole to notice some residue appears more than $p$ times, for $m=O\\left(p^{2}\\right)$.) Thus we can eliminate one factor of $p$ from the denominator, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 7 |
-
{"year": "2012", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Positive real numbers $x, y, z$ satisfy $x y z+x y+y z+z x=x+y+z+1$. Prove that $$ \\frac{1}{3}\\left(\\sqrt{\\frac{1+x^{2}}{1+x}}+\\sqrt{\\frac{1+y^{2}}{1+y}}+\\sqrt{\\frac{1+z^{2}}{1+z}}\\right) \\leq\\left(\\frac{x+y+z}{3}\\right)^{5 / 8} . $$", "solution": " The key is the identity $$ \\begin{aligned} \\frac{x^{2}+1}{x+1} & =\\frac{\\left(x^{2}+1\\right)(y+1)(z+1)}{(x+1)(y+1)(z+1)} \\\\ & =\\frac{x(x y z+x y+x z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\\\ & =\\frac{x(x+y+z+1-y z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\\\ & =\\frac{(x+y)(x+z)+x^{2}+(x-x y z+y+z+1)}{2(1+x+y+z)} \\\\ & =\\frac{2(x+y)(x+z)}{2(1+x+y+z)} \\\\ & =\\frac{(x+y)(x+z)}{1+x+y+z} . \\end{aligned} $$ Remark. The \"trick\" can be rephrased as $\\left(x^{2}+1\\right)(y+1)(z+1)=2(x+y)(x+z)$. After this, straight Cauchy in the obvious way will do it (reducing everything to an inequality in $s=x+y+z$ ). One writes $$ \\begin{aligned} \\left(\\sum_{\\mathrm{cyc}} \\frac{\\sqrt{(x+y)(x+z)}}{\\sqrt{1+s}}\\right)^{2} & \\leq \\frac{\\left(\\sum_{\\mathrm{cyc}} x+y\\right)\\left(\\sum_{\\mathrm{cyc}} x+z\\right)}{1+s} \\\\ & =\\frac{4 s^{2}}{1+s} \\end{aligned} $$ and so it suffices to check that $\\frac{4 s^{2}}{1+s} \\leq 9(s / 3)^{5 / 4}$, which is true because $$ (s / 3)^{5} \\cdot 9^{4} \\cdot(1+s)^{4}-\\left(4 s^{2}\\right)^{4}=s^{5}(s-3)^{2}\\left(27 s^{2}+14 s+3\\right) \\geq 0 $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 8 |
-
{"year": "2012", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Triangle $A B C$ is inscribed in circle $\\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.", "solution": " By angle chasing, equivalent to show $\\overline{M N} \\| \\overline{A D}$, so discard the point $H$. We now present a three solutions. ब First solution using vectors. We first contend that: Claim - We have $Q B=P C$. Now notice that the vector $$ \\overrightarrow{M N}=\\frac{1}{2}(\\overrightarrow{B Q}+\\overrightarrow{C P}) $$ which must be parallel to the angle bisector since $\\overrightarrow{B Q}$ and $\\overrightarrow{C P}$ have the same magnitude.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 9 |
-
{"year": "2012", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Triangle $A B C$ is inscribed in circle $\\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.", "solution": " By angle chasing, equivalent to show $\\overline{M N} \\| \\overline{A D}$, so discard the point $H$. We now present a three solutions. 『 Second solution using spiral similarity. let $X$ be the arc midpoint of $B A C$. Then $A D M X$ is cyclic with diameter $\\overline{A M}$, and hence $X$ is the Miquel point $X$ of $Q B P C$ is the midpoint of arc $B A C$. Moreover $\\overline{X N D}$ collinear (as $X P=X Q, D P=D Q)$ on $(A P Q)$.  Then $\\triangle X N M \\sim \\triangle X P C$ spirally, and $$ \\measuredangle X M N=\\measuredangle X C P=\\measuredangle X C A=\\measuredangle X L A $$ thus done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 10 |
-
{"year": "2012", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Triangle $A B C$ is inscribed in circle $\\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.", "solution": " By angle chasing, equivalent to show $\\overline{M N} \\| \\overline{A D}$, so discard the point $H$. We now present a three solutions. 『 Third solution using barycentrics (mine). Once reduced to $\\overline{M N} \\| \\overline{A B}$, straight bary will also work. By power of a point one obtains $$ \\begin{aligned} P & =\\left(a^{2}: 0: 2 b(b+c)-a^{2}\\right) \\\\ Q & =\\left(a^{2}: 2 c(b+c)-a^{2}: 0\\right) \\\\ \\Longrightarrow N & =\\left(a^{2}(b+c): 2 b c(b+c)-b a^{2}: 2 b c(b+c)-c a^{2}\\right) . \\end{aligned} $$ Now the point at infinity along $\\overline{A D}$ is $(-(b+c): b: c)$ and so we need only verify $$ \\operatorname{det}\\left[\\begin{array}{ccc} a^{2}(b+c) & 2 b c(b+c)-b a^{2} & 2 b c(b+c)-c a^{2} \\\\ 0 & 1 & 1 \\\\ -(b+c) & b & c \\end{array}\\right]=0 $$ which follows since the first row is $-a^{2}$ times the third row plus $2 b c(b+c)$ times the second row.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 11 |
-
{"year": "2012", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $n$ be a positive integer. Consider a triangular array of nonnegative integers as follows:  Call such a triangular array stable if for every $0 \\leq i<j<k \\leq n$ we have $$ a_{i, j}+a_{j, k} \\leq a_{i, k} \\leq a_{i, j}+a_{j, k}+1 $$ For $s_{1}, \\ldots, s_{n}$ any nondecreasing sequence of nonnegative integers, prove that there exists a unique stable triangular array such that the sum of all of the entries in row $k$ is equal to $s_{k}$.", "solution": "Let $n$ be a positive integer. Consider a triangular array of nonnegative integers as follows: $$ \\begin{array}{clllll} \\text { Row 1: } & & & a_{0,1} \\\\ \\text { Row 2: } & & a_{0,2} & a_{1,2} & \\\\ & \\vdots & \\vdots & & \\ddots & \\\\ \\text { Row } n-1: & a_{0, n-1} & a_{1, n-1} & \\ldots & a_{n-2, n-1} \\\\ \\text { Row } n \\text { : } & a_{0, n} \\quad a_{1, n} \\quad a_{2, n} & & \\ldots & a_{n-1, n} \\end{array} $$ Call such a triangular array stable if for every $0 \\leq i<j<k \\leq n$ we have $$ a_{i, j}+a_{j, k} \\leq a_{i, k} \\leq a_{i, j}+a_{j, k}+1 $$ For $s_{1}, \\ldots, s_{n}$ any nondecreasing sequence of nonnegative integers, prove that there exists a unique stable triangular array such that the sum of all of the entries in row $k$ is equal to $s_{k}$. Firstly, here are illustrative examples showing the arrays for $\\left(s_{1}, s_{2}, s_{3}, s_{4}\\right)=(2,5,9, x)$ where $9 \\leq x \\leq 14$. (The array has been left justified.) $$ \\begin{aligned} & {\\left[\\begin{array}{cccc} 2 & \\swarrow & & \\\\ 4 & 1 & \\swarrow & \\\\ 5 & 3 & 1 & \\swarrow \\\\ 5 & 3 & 1 & 0 \\end{array}\\right]\\left[\\begin{array}{llll} 2 & \\swarrow & & \\\\ 4 & 1 & \\swarrow & \\\\ 5 & 3 & 1 & \\swarrow \\\\ 6 & 3 & 1 & 0 \\end{array}\\right]\\left[\\begin{array}{llll} 2 & \\swarrow & & \\\\ 4 & 1 & \\swarrow & \\\\ 5 & 3 & 1 & \\swarrow \\\\ 6 & 3 & 2 & 0 \\end{array}\\right]} \\\\ & {\\left[\\begin{array}{cccc} 2 & \\swarrow & & \\\\ 4 & 1 & \\swarrow & \\swarrow \\\\ 5 & 3 & 1 & \\swarrow \\\\ 6 & 4 & 2 & 0 \\end{array}\\right]\\left[\\begin{array}{llll} 2 & \\swarrow & \\\\ 4 & 1 & \\swarrow & \\\\ 5 & 3 & 1 & \\swarrow \\\\ 6 & 4 & 2 & 1 \\end{array}\\right]\\left[\\begin{array}{cccc} 2 & \\swarrow & \\\\ 4 & 1 & \\swarrow & \\\\ 5 & 3 & 1 & \\swarrow \\\\ 7 & 4 & 2 & 1 \\end{array}\\right]} \\end{aligned} $$ The base case $N=s_{n-1}$ is done by copying the $n-1$ st row and adding a zero at the end. This is also unique, since $a_{i, n} \\geq a_{i-1, n}+a_{n-1, n}$ for all $i=0, \\ldots, n-2$, whence $\\sum a_{i, n} \\geq s_{n-1}$ follows. Now the inductive step is based on the following lemma, which illustrates the idea of a \"unique increasable entry\". ## Lemma Fix a stable array Construct a tournament on the $n$ entries of the last row as follows: for $i<j$, - $a_{i, n} \\rightarrow a_{j, n}$ if $a_{i, n}=a_{i, j}+a_{j, n}$, and - $a_{j, n} \\rightarrow a_{i, n}$ if $a_{i, n}=a_{i, j}+a_{j, n}+1$. Then this tournament is transitive. Also, except for $N=s_{n-1}$, a 0 entry is never a source. Intuitively, $a_{i, n} \\rightarrow a_{j, n}$ if $a_{i, n}$ blocks $a_{j, n}$ from increasing. For instance, in the example $$ \\left[\\begin{array}{rrrr} 2 & \\swarrow & & \\\\ 4 & 1 & \\swarrow & \\\\ 5 & 3 & 1 & \\swarrow \\\\ \\mathbf{6} & 3 & 1 & 0 \\end{array}\\right] $$ the tournament is $1 \\rightarrow 3 \\rightarrow 0 \\rightarrow 6$. $$ \\left[\\begin{array}{ccc} p & \\swarrow & \\\\ s & q & \\swarrow \\\\ x & y & z \\end{array}\\right] $$ If $x \\rightarrow y \\rightarrow z \\rightarrow x$ happens, that means $x=y+p, y=q+z, x=s+z+1$, which gives $s=p+q-1$, contradiction. Similarly if $x \\leftarrow y \\leftarrow z \\leftarrow x$ then $x=y+p+1, y=q+z+1$, $x=s+z$, which gives $s=p+q+2$, also contradiction. Now this allows us to perform our induction. Indeed, to show existence from $N$ to $N+1$ we take a source of the tournament above and increase it. Conversely, to show uniqueness for $N$, note that we can take the (nonzero) sink of the tournament and decrement it, which gives $N-1$; our uniqueness inductive hypothesis now finishes. $$ s_{k}+\\sum_{i=1}^{k-1} a_{0, i} \\leq k a_{0, k} \\leq s_{k}+\\sum_{i=1}\\left(a_{0, i}+1\\right) $$ and similarly for other entries.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 12 |
-
{"year": "2012", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Given a set $S$ of $n$ variables, a binary operation $\\times$ on $S$ is called simple if it satisfies $(x \\times y) \\times z=x \\times(y \\times z)$ for all $x, y, z \\in S$ and $x \\times y \\in\\{x, y\\}$ for all $x, y \\in S$. Given a simple operation $\\times$ on $S$, any string of elements in $S$ can be reduced to a single element, such as $x y z \\rightarrow x \\times(y \\times z)$. A string of variables in $S$ is called full if it contains each variable in $S$ at least once, and two strings are equivalent if they evaluate to the same variable regardless of which simple $\\times$ is chosen. For example $x x x, x x$, and $x$ are equivalent, but these are only full if $n=1$. Suppose $T$ is a set of full strings such that any full string is equivalent to exactly one element of $T$. Determine the number of elements of $T$.", "solution": " The answer is $(n!)^{2}$. In fact it is possible to essentially find all $x$ : one assigns a real number to each variable in $S$. Then $x \\times y$ takes the larger of $\\{x, y\\}$, and in the event of a tie picks either \"left\" or \"right\", where the choice of side is fixed among elements of each size. 【 First solution (Steven Hao). The main trick is the two lemmas, which are not hard to show (and are motivated by our conjecture). $$ \\begin{aligned} x x & =x \\\\ x y x z x & =x y z x . \\end{aligned} $$ Consequently, define a double rainbow to be the concatenation of two full strings of length $n$, of which there are $(n!)^{2}$. We claim that these form equivalence classes for $T$. To see that any string $s$ is equivalent to a double rainbow, note that $s=s s$, and hence using the second identity above repeatedly lets us reduce ss to a double rainbow. To see two distinct double rainbows $R_{1}$ and $R_{2}$ aren't equivalent, one can use the construction mentioned in the beginning. Specifically, take two variables $a$ and $b$ which do not appear in the same order in $R_{1}$ and $R_{2}$. Then it's not hard to see that $a b a b, a b b a$, $b a a b, b a b a$ are pairwise non-equivalent by choosing \"left\" or \"right\" appropriately. Now construct $\\times$ on the whole set by having $a$ and $b$ be the largest variables, so the rest of the variables don't matter in the evaluation of the string.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
| 13 |
-
{"year": "2012", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Given a set $S$ of $n$ variables, a binary operation $\\times$ on $S$ is called simple if it satisfies $(x \\times y) \\times z=x \\times(y \\times z)$ for all $x, y, z \\in S$ and $x \\times y \\in\\{x, y\\}$ for all $x, y \\in S$. Given a simple operation $\\times$ on $S$, any string of elements in $S$ can be reduced to a single element, such as $x y z \\rightarrow x \\times(y \\times z)$. A string of variables in $S$ is called full if it contains each variable in $S$ at least once, and two strings are equivalent if they evaluate to the same variable regardless of which simple $\\times$ is chosen. For example $x x x, x x$, and $x$ are equivalent, but these are only full if $n=1$. Suppose $T$ is a set of full strings such that any full string is equivalent to exactly one element of $T$. Determine the number of elements of $T$.", "solution": " The answer is $(n!)^{2}$. In fact it is possible to essentially find all $x$ : one assigns a real number to each variable in $S$. Then $x \\times y$ takes the larger of $\\{x, y\\}$, and in the event of a tie picks either \"left\" or \"right\", where the choice of side is fixed among elements of each size. 【 Second solution outline (Ankan Bhattacharya). We outline a proof of the characterization claimed earlier, which will also give the answer $(n!)^{2}$. We say $a \\sim b$ if $a b \\neq b a$. Also, say $a>b$ if $a b=b a=a$. The following are proved by finite casework, using the fact that $\\{a b, b c, c a\\}$ always has exactly two distinct elements for any different $a, b, c$. - If $a>b$ and $b>c$ then $a>c$. - If $a \\sim b$ and $b \\sim c$ then $a b=a$ if and only if $b c=b$. - If $a \\sim b$ and $b \\sim c$ then $a \\sim c$. - If $a \\sim b$ and $a>c$ then $b>c$. - If $a \\sim b$ and $c>a$ then $c>b$. This gives us the total ordering on the elements and the equivalence classes by $\\sim$. In this we way can check the claimed operations are the only ones.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2012.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl
DELETED
|
@@ -1,9 +0,0 @@
|
|
| 1 |
-
{"year": "2013", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle and $D, E, F$ be the midpoints of $\\operatorname{arcs} B C, C A, A B$ on the circumcircle. Line $\\ell_{a}$ passes through the feet of the perpendiculars from $A$ to $\\overline{D B}$ and $\\overline{D C}$. Line $m_{a}$ passes through the feet of the perpendiculars from $D$ to $\\overline{A B}$ and $\\overline{A C}$. Let $A_{1}$ denote the intersection of lines $\\ell_{a}$ and $m_{a}$. Define points $B_{1}$ and $C_{1}$ similarly. Prove that triangles $D E F$ and $A_{1} B_{1} C_{1}$ are similar to each other.", "solution": " In fact, it is true for any points $D, E, F$ on the circumcircle. More strongly we contend: Claim - Point $A_{1}$ is the midpoint of $\\overline{H D}$.  Hence $A_{1} B_{1} C_{1}$ is similar to $D E F$ through a homothety at $H$ with ratio $\\frac{1}{2}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 2 |
-
{"year": "2013", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "A finite sequence of integers $a_{1}, a_{2}, \\ldots, a_{n}$ is called regular if there exists a real number $x$ satisfying $$ \\lfloor k x\\rfloor=a_{k} \\quad \\text { for } 1 \\leq k \\leq n $$ Given a regular sequence $a_{1}, a_{2}, \\ldots, a_{n}$, for $1 \\leq k \\leq n$ we say that the term $a_{k}$ is forced if the following condition is satisfied: the sequence $$ a_{1}, a_{2}, \\ldots, a_{k-1}, b $$ is regular if and only if $b=a_{k}$. Find the maximum possible number of forced terms in a regular sequence with 1000 terms.", "solution": " The answer is 985 . WLOG, by shifting $a_{1}=0$ (clearly $a_{1}$ isn't forced). Now, we construct regular sequences inductively using the following procedure. Start with the inequality $$ \\frac{0}{1} \\leq x<\\frac{1}{1} $$ Then for each $k=2,3, \\ldots, 1000$ we perform the following procedure. If there is no fraction of the form $F=\\frac{m}{k}$ in the interval $A \\leq x<B$, then $a_{k}$ is forced, and the interval of possible $x$ values does not change. Otherwise, $a_{k}$ is not forced, and we pick a value of $a_{k}$ and update the interval accordingly. The theory of Farey sequences tells us that when we have a stage $\\frac{a}{b} \\leq x<\\frac{c}{d}$ then the next time we will find a fraction in that interval is exactly $\\frac{a+c}{b+d}$ (at time $k=b+d$ ), and it will be the only such fraction. So essentially, starting with $\\frac{0}{1} \\leq x<\\frac{1}{1}$ we repeatedly replace one of the endpoints of the intervals with the mediant, until one of the denominators exceeds 1000; we are trying to minimize the number of non-forced terms, which is the number of denominators that appear in this process. It is not hard to see that this optimum occurs by always replacing the smaller of the denominators, so that the sequence is $\\frac{0}{1} \\leq x<\\frac{1}{1}$ $\\frac{0}{1} \\leq x<\\frac{1}{2}$ $\\frac{1}{3} \\leq x<\\frac{1}{2}$ $\\frac{1}{3} \\leq x<\\frac{2}{5}$ $\\frac{3}{8} \\leq x<\\frac{2}{5}$ $\\frac{3}{8} \\leq x<\\frac{5}{13}$ and so on; we see that the non-forced terms in this optimal configuration are exactly the Fibonacci numbers. There are 15 Fibonacci numbers less than 1000, hence the answer $1000-15=985$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 3 |
-
{"year": "2013", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Divide the plane into an infinite square grid by drawing all the lines $x=m$ and $y=n$ for $m, n \\in \\mathbb{Z}$. Next, if a square's upper-right corner has both coordinates even, color it black; otherwise, color it white (in this way, exactly $1 / 4$ of the squares are black and no two black squares are adjacent). Let $r$ and $s$ be odd integers, and let $(x, y)$ be a point in the interior of any white square such that $r x-s y$ is irrational. Shoot a laser out of this point with slope $r / s$; lasers pass through white squares and reflect off black squares. Prove that the path of this laser will from a closed loop.", "solution": " We re-color the white squares as red, blue, or green according as to whether they have a black square directly to the left/right, above/below, or neither, as shown below. Finally, we fix time zero to be a moment just before the laser passes a horizontal (WLOG) lattice line (not necessarily a wall). Shown below is an example for $(r, s)=(3,5)$.  The main idea is to keep track of every time the laser passes a lattice line (again, not necessarily a wall). There are four possible types of events: - A horizontal $h$ event where the laser switches from red to green (or vice-versa); - A horizontal $h$ event where the laser rebounds off a wall, remaining in a blue square, but flips the $x$-component of its velocity; - A vertical $v$ event where the laser switches from blue to green (or vice-versa) - A vertical $v$ event where the laser rebounds off a wall, remaining in a red square, but flips the $y$-component of its velocity. The first key observation is that: Claim - In the first second, the laser will encounter exactly $r$ horizontal events and $s$ vertical events. In every second after that, the same sequence of $r+s$ events occurs. We let the key-word be the sequence $w$ of $r+s$ letters corresponding to the sequence. For example, the picture above denotes an example with keyword $w=h v v h v v h v$; so no matter what, every second, the laser will encounter eight lattice lines, which are horizontal and vertical in that order. Claim - Color is periodic every 3 seconds. Now in a 3 -second period, consider the $3 r$ horizontal events and $3 s$ vertical events (both are odd). In order for the color to remain the same (as the only color changes are $R \\leftrightarrow G$ for $h$ and $B \\leftrightarrow G$ for $v$ ) there must have been an even number of color swaps for each orientation. Therefore there was an odd number of wall collisions of each orientation. So, the laser is pointing in the opposite direction at the end of 3 seconds. Finally, let $x_{t}$ be the fractional part of the $x$ coordinate after $t$ seconds (the $y$-coordinate is always zero by our setup at these moments). Note that $$ x_{t+1}= \\begin{cases}x_{t} & \\text { even number of vertical wall collisions } \\\\ 1-x_{t} & \\text { odd numbers of vertical wall collisions }\\end{cases} $$ Since over the there seconds there were an odd number of vertical collisions; it follows $x_{3}=1-x_{0}$. Thus at the end of three seconds, the laser is in a symmetric position from the start; and in 6 seconds it will form a closed loop.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 4 |
-
{"year": "2013", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Circle $\\omega$, centered at $X$, is internally tangent to circle $\\Omega$, centered at $Y$, at $T$. Let $P$ and $S$ be variable points on $\\Omega$ and $\\omega$, respectively, such that line $P S$ is tangent to $\\omega($ at $S)$. Determine the locus of $O$ - the circumcenter of triangle $P S T$.", "solution": " The answer is a circle centered at $Y$ with radius $\\sqrt{Y X \\cdot Y T}$, minus the two points on line $X Y$ itself. We let $P S$ meet $\\Omega$ again at $P^{\\prime}$, and let $O^{\\prime}$ be the circumcenter of $\\triangle T P S^{\\prime}$. Note that $O^{\\prime}, X, O$ are collinear on the perpendicular bisector of line $\\overline{T S}$ Finally, we let $M$ denote the arc midpoint of $P P^{\\prime}$ which lies on line $T S$ (by homothety).  By three applications of Salmon theorem, we have the following spiral similarities all centered at $T$ : $$ \\begin{aligned} \\triangle T S P & \\stackrel{+}{\\sim} \\triangle T O^{\\prime} Y \\\\ \\triangle T P^{\\prime} S & \\stackrel{ }{\\sim} \\triangle T Y O \\\\ \\triangle T P^{\\prime} P & \\stackrel{+}{\\sim} \\triangle T O^{\\prime} O \\end{aligned} $$ However, the shooting lemma also gives us two similarities: $$ \\begin{aligned} & \\triangle T P^{\\prime} M \\stackrel{ \\pm}{\\sim} \\triangle T S P \\\\ & \\triangle T M P \\stackrel{ \\pm}{\\sim} \\triangle T P^{\\prime} S \\end{aligned} $$ Putting everything together, we find that $$ T P^{\\prime} M P \\stackrel{ \\pm}{\\sim} T O^{\\prime} Y O $$ Then by shooting lemma, $Y O^{\\prime 2}=Y X \\cdot Y T$, so $O$ indeed lies on the claimed circle. As the line $\\overline{O^{\\prime} O}$ may be any line through $X$ other than line $X Y$ (one takes $S$ to be the reflection of $T$ across this line) one concludes the only two non-achievable points are the diametrically opposite ones on line $X Y$ of this circle (because this leads to the only degenerate situation where $S=T$ ).", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 5 |
-
{"year": "2013", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $p$ be a prime. Prove that in a complete graph with $1000 p$ vertices whose edges are labelled with integers, one can find a cycle whose sum of labels is divisible by $p$.", "solution": " Select $p-1$ disjoint triangles arbitrarily. If any of these triangles have 0 sum modulo $p$ we are done. Otherwise, we may label the vertices $u_{i}, x_{i}$, and $v_{i}$ (where $1 \\leq i \\leq p-1$ ) in such a way that $u_{i} x_{i}+x_{i} v_{i} \\neq u_{i} v_{i}$. Let $A_{i}=\\left\\{u_{i} x_{i}+x_{i} v_{i}, u_{i} v_{i}\\right\\}$. We can show that $\\left|A_{1}+A_{2}+\\cdots+A_{t}\\right| \\geq \\min \\{p, t+1\\}$ for each $1 \\leq t \\leq p-1$, by using induction on $t$ alongside Cauchy-Davenport. So, $A_{1}+A_{2}+\\cdots+A_{p-1}$ spans all of $\\mathbb{Z}_{p}$. All that's left to do is join the triangles together to form a cycle, and then delete either $u_{i} x_{i}, x_{i} v_{i}$ or $u_{i} v_{i}$ from each triangle in such a way that the final sum is $0 \\bmod p$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 6 |
-
{"year": "2013", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $\\mathbb{N}$ be the set of positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ that satisfy the equation $$ f^{a b c-a}(a b c)+f^{a b c-b}(a b c)+f^{a b c-c}(a b c)=a+b+c $$ for all $a, b, c \\geq 2$. (Here $f^{k}$ means $f$ applied $k$ times.)", "solution": " The answer is $f(n)=n-1$ for $n \\geq 3$ with $f(1)$ and $f(2)$ arbitrary; check these work. ## Lemma We have $f^{t^{2}-t}\\left(t^{2}\\right)=t$ for all $t$. $$ f^{t^{9}-t^{3}}\\left(t^{9}\\right)=t^{3} \\quad \\text { and } \\quad f^{t^{3}-t}\\left(t^{3}\\right)=t \\Longrightarrow f^{t^{9}-t}\\left(t^{9}\\right)=t $$ so $k=1$ and $k=3$ are good. Then taking $(a, b, c)=\\left(t, t^{4}, t^{4}\\right),(a, b, c)=\\left(t^{2}, t^{3}, t^{4}\\right)$ gives that $k=4$ and $k=2$ are good, respectively. The lemma follows from this $k=1$ and $k=2$ being good. Now, letting $t=a b c$ we combine $$ \\begin{aligned} f^{t-a}(a)+f^{t-b}(b)+f^{t-c}(c) & =a+b+c \\\\ f^{t^{2}-a b}\\left(t^{2}\\right)+f^{t^{2}-t}\\left(t^{2}\\right)+f^{t^{2}-c}\\left(t^{2}\\right) & =a b+t+c \\\\ \\Longrightarrow\\left[f^{t-a}(t)-a\\right]+\\left[f^{t-b}(t)-b\\right] & =\\left[f^{t-a b}(t)-a b\\right] \\end{aligned} $$ by subtracting and applying the lemma repeatedly. In other words, we have proven the second lemma: ## Lemma Let $t$ be fixed, and define $g_{t}(n)=f^{t-n}(t)-n$ for $n<t$. If $a, b \\geq 2$ and $a b \\mid t, a b<t$, then $g_{t}(a)+g_{t}(b)=g_{t}(a b)$. Now let $a, b \\geq 2$ be arbitrary, and let $p>q>\\max \\{a, b\\}$ be primes. Suppose $s=a^{p} b^{q}$ and $t=s^{2}$; then $$ p g_{t}(a)+q g_{t}(b)=g_{t}\\left(a^{p} b^{q}\\right)=g_{t}(s)=f^{s^{2}-s}(s)-s=0 $$ Now $$ q \\mid g_{t}(a)>-a \\quad \\text { and } \\quad p \\mid g_{t}(b)>-b \\Longrightarrow g_{t}(a)=g_{t}(b)=0 $$ and so we conclude $f^{t-a}(t)=a$ and $f^{t-b}(t)=b$ for $a, b \\geq 2$. In particular, if $a=n$ and $b=n+1$ then we deduce $f(n+1)=n$ for all $n \\geq 2$, as desired. Remark. If you let $c=(a b)^{2}$ after the first lemma, you recover the 2-variable version!", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 7 |
-
{"year": "2013", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "A country has $n$ cities, labelled $1,2,3, \\ldots, n$. It wants to build exactly $n-1$ roads between certain pairs of cities so that every city is reachable from every other city via some sequence of roads. However, it is not permitted to put roads between pairs of cities that have labels differing by exactly 1 , and it is also not permitted to put a road between cities 1 and $n$. Let $T_{n}$ be the total number of possible ways to build these roads. (a) For all odd $n$, prove that $T_{n}$ is divisible by $n$. (b) For all even $n$, prove that $T_{n}$ is divisible by $n / 2$.", "solution": " You can just spin the tree! Fixing $n$, the group $G=\\mathbb{Z} / n \\mathbb{Z}$ acts on the set of trees by rotation (where we imagine placing $1,2, \\ldots, n$ along a circle). Claim - For odd $n$, all trees have trivial stabilizer.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 8 |
-
{"year": "2013", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Define a function $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ by $f(1)=1, f(n+1)=f(n)+2^{f(n)}$ for every positive integer $n$. Prove that $f(1), f(2), \\ldots, f\\left(3^{2013}\\right)$ leave distinct remainders when divided by $3^{2013}$.", "solution": " I'll prove by induction on $k \\geq 1$ that any $3^{k}$ consecutive values of $f$ produce distinct residues modulo $3^{k}$. The base case $k=1$ is easily checked ( $f$ is always odd, hence $f$ cycles $1,0,2 \\bmod 3)$. For the inductive step, assume it's true up to $k$. Since $2^{\\bullet}\\left(\\bmod 3^{k+1}\\right)$ cycles every $2 \\cdot 3^{k}$, and $f$ is always odd, it follows that $$ \\begin{aligned} f\\left(n+3^{k}\\right)-f(n) & =2^{f(n)}+2^{f(n+1)}+\\cdots+2^{f\\left(n+3^{k}-1\\right)} \\quad\\left(\\bmod 3^{k+1}\\right) \\\\ & \\equiv 2^{1}+2^{3}+\\cdots+2^{2 \\cdot 3^{k}-1} \\quad\\left(\\bmod 3^{k+1}\\right) \\\\ & =2 \\cdot \\frac{4^{3^{k}}-1}{4-1} \\end{aligned} $$ Hence $$ f\\left(n+3^{k}\\right)-f(n) \\equiv C \\quad\\left(\\bmod 3^{k+1}\\right) \\quad \\text { where } \\quad C=2 \\cdot \\frac{4^{3^{k}}-1}{4-1} $$ noting that $C$ does not depend on $n$. Exponent lifting gives $\\nu_{3}(C)=k$ hence $f(n)$, $f\\left(n+3^{k}\\right), f\\left(n+2 \\cdot 3^{k}\\right)$ differ mod $3^{k+1}$ for all $n$, and the inductive hypothesis now solves the problem.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
| 9 |
-
{"year": "2013", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $r$ be a rational number in the interval $[-1,1]$ and let $\\theta=\\cos ^{-1} r$. Call a subset $S$ of the plane good if $S$ is unchanged upon rotation by $\\theta$ around any point of $S$ (in both clockwise and counterclockwise directions). Determine all values of $r$ satisfying the following property: The midpoint of any two points in a good set also lies in the set.", "solution": " The answer is that $r$ has this property if and only if $r=\\frac{4 n-1}{4 n}$ for some integer $n$. $$ \\omega=e^{i \\theta}=\\frac{a}{b} \\pm \\frac{\\sqrt{b^{2}-a^{2}}}{b} i $$ This means we may work with complex multiplication in the usual way; the rotation of $z$ through center $c$ is given by $z \\mapsto \\omega(z-c)+c$. - Start by letting $S_{0}=\\{0,1\\}$. - Let $S_{i}$ consist of $S_{i-1}$ plus all points that can be obtained by rotating a point of $S_{i-1}$ through a different point of $S_{i-1}$ (with scale factor $\\omega$ ). - Let $S_{\\infty}=\\bigcup_{i \\geq 0} S_{i}$. The set $S_{\\infty}$ is the (minimal, by inclusion) good set containing 0 and 1 . We are going to show that for most values of $r$, we have $\\frac{1}{2} \\notin S_{\\infty}$. Claim - If $b$ is odd, then $\\frac{1}{2} \\notin S_{\\infty}$. Consider the ring $$ A=\\mathbb{Z}_{\\{b\\}}=\\left\\{\\frac{s}{t}|s, t \\in \\mathbb{Z}, t| b^{\\infty}\\right\\} $$ which consists of all rational numbers whose denominators divide $b^{\\infty}$. Then, $0,1, \\omega \\in$ $A\\left[\\sqrt{b^{2}-a^{2}}\\right]$ and hence $S_{\\infty} \\subseteq A\\left[\\sqrt{b^{2}-a^{2}}\\right]$ too. (This works even if $\\sqrt{b^{2}-a^{2}} \\in \\mathbb{Z}$, in which case $S_{\\infty} \\subseteq A=A\\left[\\sqrt{b^{2}-a^{2}}\\right]$.) But $\\frac{1}{2} \\notin A\\left[\\sqrt{b^{2}-a^{2}}\\right]$. Claim - If $b$ is even and $|b-a| \\neq 1$, then $\\frac{1}{2} \\notin S_{\\infty}$. Let $D=b^{2}-a^{2} \\equiv 3(\\bmod 4)$. Let $p$ be a prime divisor of $b-a$. Because $\\operatorname{gcd}(a, b)=1$, we have $p \\neq 2$ and $p \\nmid b$. Consider the ring $$ A=\\mathbb{Z}_{(p)}=\\left\\{\\left.\\frac{s}{t} \\right\\rvert\\, s, t \\in \\mathbb{Z}, p \\perp t\\right\\} $$ which consists of all rational numbers whose denominators are coprime to $p$. Then, $0,1, \\omega \\in A[\\sqrt{-D}]$ and hence $S_{\\infty} \\subseteq A[\\sqrt{-D}]$ too. Now, there is a well-defined \"mod- $p$ \" ring homomorphism $$ \\Psi: A[\\sqrt{-D}] \\rightarrow \\mathbb{F}_{p} \\quad \\text { by } \\quad x+y \\sqrt{-D} \\mapsto x \\bmod p $$ which commutes with addition and multiplication (as $p \\mid D$ ). Under this map, $$ \\omega \\mapsto \\frac{a}{b} \\bmod p=1 $$ Consequently, the rotation $z \\mapsto \\omega(z-c)+c$ is just the identity map modulo $p$. In other words, the pre-image of any point in $S_{\\infty}$ under $\\Psi$ must be either $\\Psi(0)=0$ or $\\Psi(1)=1$. However, $\\Psi(1 / 2)=1 / 2$ is neither of these. So this point cannot be achieved. Claim - Suppose $a=2 n-1$ and $b=2 n$ for $n$ an odd integer. Then $\\frac{1}{2} \\notin S_{\\infty}$ This time, we define the ring $$ B=\\mathbb{Z}_{(2)}=\\left\\{\\left.\\frac{s}{t} \\right\\rvert\\, s, t \\in \\mathbb{Z}, t \\text { odd }\\right\\} $$ of rational numbers with odd denominator. We carefully consider the ring $B[\\omega]$ where $$ \\omega=\\frac{2 n-1 \\pm \\sqrt{1-4 n}}{2 n} $$ So $S_{\\infty} \\subseteq B[\\omega]$ as $0,1, \\omega \\in B[\\omega]$. I claim that $B[\\omega]$ is an integral extension of $B$; equivalently that $\\omega$ is integral over $B$. Indeed, $\\omega$ is the root of the monic polynomial $$ (T-1)^{2}+\\frac{1}{n}(T-1)-\\frac{1}{n}=0 $$ where $\\frac{1}{n} \\in B$ makes sense as $n$ is odd. On the other hand, $\\frac{1}{2}$ is not integral over $B$ so it is not an element of $B[\\omega]$. It remains to show that if $r=\\frac{4 n-1}{4 n}$, then goods sets satisfy the midpoint property. Again starting from the points $z_{0}=0, z_{1}=1$ construct the sequence $$ \\begin{aligned} z_{2} & =\\omega\\left(z_{1}-z_{0}\\right)+z_{0} \\\\ z_{3} & =\\omega^{-1}\\left(z_{0}-z_{2}\\right)+z_{2} \\\\ z_{4} & =\\omega^{-1}\\left(z_{2}-z_{3}\\right)+z_{3} \\\\ z_{5} & =\\omega\\left(z_{3}-z_{4}\\right)+z_{4} \\end{aligned} $$ as shown in the diagram below.  This construction shows that if we have the length-one segment $\\{0,1\\}$ then we can construct the length-one segment $\\{2 r-2,2 r-1\\}$. In other words, we can shift the segment to the left by $$ 1-(2 r-1)=2(1-r)=\\frac{1}{2 n} $$ Repeating this construction $n$ times gives the desired midpoint $\\frac{1}{2}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2013.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl
DELETED
|
@@ -1,6 +0,0 @@
|
|
| 1 |
-
{"year": "2014", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $\\leftarrow$ denote the left arrow key on a standard keyboard. If one opens a text editor and types the keys \"ab $\\leftarrow \\mathrm{cd} \\leftarrow \\leftarrow \\mathrm{e} \\leftarrow \\leftarrow \\mathrm{f}$ \", the result is \"faecdb\". We say that a string $B$ is reachable from a string $A$ if it is possible to insert some amount of $\\leftarrow$ 's in $A$, such that typing the resulting characters produces $B$. So, our example shows that \"faecdb\" is reachable from \"abcdef\". Prove that for any two strings $A$ and $B, A$ is reachable from $B$ if and only if $B$ is reachable from $A$.", "solution": " Obviously $A$ and $B$ should have the same multiset of characters, and we focus only on that situation. Claim - If $A=123 \\ldots n$ and $B=\\sigma(1) \\sigma(2) \\ldots \\sigma(n)$ is a permutation of $A$, then $B$ is reachable if and only if it is $\\mathbf{2 1 3}$-avoiding, i.e. there are no indices $i<j<k$ such that $\\sigma(j)<\\sigma(i)<\\sigma(k)$. Claim - A permutation $\\sigma$ on $\\{1, \\ldots, n\\}$ is 213 -avoiding if and only if the inverse $\\sigma^{-1}$ is. This essentially finishes the problem. Suppose $B$ is reachable from $A$. By using the typing pattern, we get some permutation $\\sigma:\\{1, \\ldots, n\\}$ such that the $i$ th character of $A$ is the $\\sigma(i)$ th character of $B$, and which is 213 -avoiding by the claim. (The permutation is unique if $A$ has all distinct characters, but there could be multiple if $A$ has repeated ones.) Then $\\sigma^{-1}$ is 213 -avoiding too and gives us a way to change $B$ into $A$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl"}}
|
| 2 |
-
{"year": "2014", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Consider a convex pentagon circumscribed about a circle. We name the lines that connect vertices of the pentagon with the opposite points of tangency with the circle gergonnians. (a) Prove that if four gergonnians are concurrent, then all five of them are concurrent. (b) Prove that if there is a triple of gergonnians that are concurrent, then there is another triple of gergonnians that are concurrent.", "solution": " This problem is insta-killed by taking a homography sending the concurrency point (in either part) to the center of the circle while fixing the incircle. Alternatively, one may send any four of the tangency points to a rectangle. Here are the details. Let $A B C D E$ be a pentagon with gergonnians $\\overline{A V}, \\overline{B W}, \\overline{C X}$, $\\overline{D Y}, \\overline{E Z}$. We prove the following lemma, which (up to a suitable permutation of point names) solves both parts (a) and (b). ## Lemma The gergonnians $\\overline{A V}, \\overline{C X}, \\overline{D Y}$ are concurrent if and only if the gergonnians $\\overline{A V}$, $\\overline{B W}, \\overline{E Z}$ are concurrent.  Then $X$ and $Y$ are symmetric around $\\overline{A P V}$ by hypothesis. Since $D=\\overline{V V} \\cap \\overline{P Y}$, $C=\\overline{V V} \\cap \\overline{P X}$, it follows that $C$ and $D$, and hence $Z$ and $W$, are also symmetric around $\\overline{A P V}$. Consequently $B$ and $E$ are symmetric too. So $\\overline{B W}$ and $\\overline{E Z}$ meet on $\\overline{A V}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl"}}
|
| 3 |
-
{"year": "2014", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Find all polynomials $P(x)$ with real coefficients that satisfy $$ P(x \\sqrt{2})=P\\left(x+\\sqrt{1-x^{2}}\\right) $$ for all real numbers $x$ with $|x| \\leq 1$.", "solution": " The answer is any polynomial of the form $P(x)=f(U(x / \\sqrt{2}))$, where $f \\in \\mathbb{R}[x]$ and $U$ is the unique polynomial satisfying $U(\\cos \\theta)=\\cos (8 \\theta)$. Let $Q(x)=P(x \\sqrt{2})$, then the condition reads $$ Q(\\cos \\theta)=Q\\left(\\frac{1}{\\sqrt{2}}(\\cos \\theta+\\sin \\theta)\\right)=Q\\left(\\cos \\left(\\theta-45^{\\circ}\\right)\\right) \\quad \\forall 0 \\leq \\theta \\leq 180^{\\circ} . $$ We call a polynomial good if it satisfies this functional equation. ## Lemma The minimal (by degree) good nonconstant polynomial is $U$. $$ \\begin{aligned} Q\\left(\\cos 136^{\\circ}\\right) & =Q\\left(\\cos 91^{\\circ}\\right)=Q\\left(\\cos 46^{\\circ}\\right)=Q\\left(\\cos 1^{\\circ}\\right)=Q\\left(\\cos -44^{\\circ}\\right) \\\\ & =Q\\left(\\cos 44^{\\circ}\\right)=Q\\left(\\cos 89^{\\circ}\\right)=Q\\left(\\cos 134^{\\circ}\\right)=Q\\left(\\cos 179^{\\circ}\\right) \\end{aligned} $$ Hence $Q$ is equal at eight distinct values (not nine since $\\cos -44^{\\circ}=\\cos 44^{\\circ}$ is repeated), so $\\operatorname{deg} Q \\geq 8$ (unless $Q$ is constant). Now, we claim $Q(x) \\equiv f(U(x))$ for some $f \\in \\mathbb{R}[x]$. Indeed, if $Q$ is good, then by minimality the quotient $Q \\bmod U$ must be constant, so $Q(x)=\\widetilde{Q}(x) \\cdot U(x)+c$ for some constant $c$, but then $\\widetilde{Q}(x)$ is good too and we finish iteratively.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl"}}
|
| 4 |
-
{"year": "2014", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Let $P(x)$ and $Q(x)$ be arbitrary polynomials with real coefficients, with $P \\neq 0$, and let $d=\\operatorname{deg} P$. Prove that there exist polynomials $A(x)$ and $B(x)$, not both zero, such that $\\max \\{\\operatorname{deg} A, \\operatorname{deg} B\\} \\leq d / 2$ and $P(x) \\mid A(x)+Q(x) \\cdot B(x)$.", "solution": " Let $V$ be the vector space of real polynomials with degree at most $d / 2$. Consider maps of linear spaces $$ \\begin{aligned} V^{\\oplus 2} & \\rightarrow \\mathbb{R}[x] /(P(x)) \\\\ \\text { by } \\quad(A, B) & \\mapsto A+Q B \\quad(\\bmod P) . \\end{aligned} $$ The domain has dimension $$ 2(\\lfloor d / 2\\rfloor+1) $$ while the codomain has dimension $d$. For dimension reasons it has nontrivial kernel.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl"}}
|
| 5 |
-
{"year": "2014", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Find the maximum number $E$ such that the following holds: there is an edge-colored graph with 60 vertices and $E$ edges, with each edge colored either red or blue, such that in that coloring, there is no monochromatic cycles of length 3 and no monochromatic cycles of length 5 .", "solution": " The answer is $E=30^{2}+2 \\cdot 15^{2}=6 \\cdot 15^{2}=1350$. First, we prove $E \\leq 1350$. Observe that: Claim - $G$ contains no $K_{5}$. Hence by Turán theorem we have $E \\leq\\binom{ 4}{2} \\cdot 15^{2}=1350$. To show this is achievable, take a red $K_{30,30}$, and on each side draw a blue $K_{15,15}$. This graph has no monochromatic odd cycles at all as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl"}}
|
| 6 |
-
{"year": "2014", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Suppose we have distinct positive integers $a, b, c, d$ and an odd prime $p$ not dividing any of them, and an integer $M$ such that if one considers the infinite sequence $$ \\begin{gathered} c a-d b \\\\ c a^{2}-d b^{2} \\\\ c a^{3}-d b^{3} \\\\ c a^{4}-d b^{4} \\end{gathered} $$ and looks at the highest power of $p$ that divides each of them, these powers are not all zero, and are all at most $M$. Prove that there exists some $T$ (which may depend on $a, b, c, d, p, M)$ such that whenever $p$ divides an element of this sequence, the maximum power of $p$ that divides that element is exactly $p^{T}$.", "solution": " By orders, the indices of terms divisible by $p$ is an arithmetic subsequence of $\\mathbb{N}$ : say they are $\\kappa, \\kappa+\\lambda, \\kappa+2 \\lambda, \\ldots$, where $\\lambda$ is the order of $a / b$. That means we want $$ \\nu_{p}\\left(c a^{\\kappa+n \\lambda}-d b^{\\kappa+n \\lambda}\\right)=\\nu_{p}\\left(\\left(\\frac{a^{\\lambda}}{b^{\\lambda}}\\right)^{n}-\\frac{d a^{\\kappa}}{c b^{\\kappa}}\\right) $$ to be constant. Thus, we have reduced the problem to the following proposition: ## Proposition Let $p$ be an odd prime. Let $x, y \\in \\mathbb{Q}_{>0}$ such that $x \\equiv y \\equiv 1(\\bmod p)$. If the sequence $\\nu_{p}\\left(x^{n}-y\\right)$ of positive integers is nonconstant, then it is unbounded. For this it would be sufficient to prove the following claim. Claim - Let $p$ be an odd prime. Let $x, y \\in \\mathbb{Q}>0$ such that $x \\equiv y \\equiv 1(\\bmod p)$. Suppose $m$ and $n$ are positive integers such that $$ d=\\nu_{p}\\left(x^{n}-y\\right)<\\nu_{p}\\left(x^{m}-y\\right)=e . $$ Then there exists $\\ell$ such that $\\nu_{p}\\left(x^{\\ell}-y\\right) \\geq e+1$. $$ \\nu_{p}\\left(x^{k}-1\\right)=e $$ namely $k=p^{e-d}|m-n|$. (In fact, one could also choose more carefully $k=p^{e-d} \\cdot \\operatorname{gcd}(m-$ $\\left.n, p^{\\infty}\\right)$, so that $k$ is a power of $p$.) Suppose we set $x^{k}=p^{e} u+1$ and $x^{m}=p^{e} v+y$ where $u, v \\in \\mathbb{Q}$ aren't divisible by $p$. Now for any integer $1 \\leq r \\leq p-1$ we consider $$ \\begin{aligned} x^{k r+m}-y & =\\left(p^{e} u+1\\right)^{r} \\cdot\\left(p^{e} v+y\\right)-y \\\\ & =p^{e}(v+y u \\cdot r)+p^{2 e}(\\ldots) \\end{aligned} $$ By selecting $r$ with $r \\equiv-v / u(\\bmod p)$, we ensure $p^{e+1} \\mid x^{k r+m}-y$, hence $\\ell=k r+m$ is as desired. $$ x^{\\ell-m} \\equiv 1 \\quad\\left(\\bmod p^{e}\\right) \\text { but } x^{\\ell-m} \\not \\equiv 1 \\quad\\left(\\bmod p^{e+1}\\right) $$ In particular, we need $\\nu_{p}\\left(x^{\\ell-m}-1\\right)=e$ exactly. So the $k$ in the claim must exist if we are going to succeed. On the other hand, if $k$ is some integer for which $\\nu_{p}\\left(x^{k}-1\\right)=e$, then by choosing $\\ell-m$ to be some multiple of $k$ with no extra factors of $p$, we hope that we can get $\\nu_{p}\\left(x^{\\ell}-y\\right)=e+1$. That's why we write $\\ell=k r+m$ and see what happens when we expand.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2014.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl
DELETED
|
@@ -1,9 +0,0 @@
|
|
| 1 |
-
{"year": "2015", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}$ be a sequence of real numbers, and let $m$ be a fixed positive integer less than $n$. We say an index $k$ with $1 \\leq k \\leq n$ is good if there exists some $\\ell$ with $1 \\leq \\ell \\leq m$ such that $$ a_{k}+a_{k+1}+\\cdots+a_{k+\\ell-1} \\geq 0 $$ where the indices are taken modulo $n$. Let $T$ be the set of all good indices. Prove that $$ \\sum_{k \\in T} a_{k} \\geq 0 $$", "solution": " First we prove the result if the indices are not taken modulo $n$. Call a number $\\ell$-good if $\\ell$ is the smallest number such that $a_{k}+a_{k+1}+\\cdots+a_{k+\\ell-1} \\geq 0$, and $\\ell \\leq m$. Then if $a_{k}$ is $\\ell$-good, the numbers $a_{k+1}, \\ldots, a_{k+\\ell-1}$ are good as well. Then by greedy from left to right, we can group all the good numbers into blocks with nonnegative sums. Repeatedly take the first good number, if $\\ell$-good, group it with the next $\\ell$ numbers. An example for $m=3$ : $$ \\langle 4\\rangle \\quad \\begin{array}{ccccccccc} -1 & -2 & 6\\rangle & -9 & -7 & \\langle 3\\rangle & \\langle-2 & 4\\rangle & \\langle-1 . \\end{array} $$ We can now return to the original problem. Let $N$ be a large integer; applying the algorithm to $N$ copies of the sequence, we deduce that $$ N \\sum_{k \\in T} a_{k}+c_{N} \\geq 0 $$ where $c_{N}$ represents some \"error\" from left-over terms. As $\\left|c_{N}\\right| \\leq \\sum\\left|a_{i}\\right|$, by taking $N$ large enough we deduce the problem.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 2 |
-
{"year": "2015", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.", "solution": " The main content of the problem: Claim - $\\angle H X_{a} G=90^{\\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. First proof by Brokard. To do this, it suffices to show that $M$ has the same power with respect to the circle with diameter $\\overline{A H}$ and the circle with diameter $\\overline{K L}$. In fact I claim both circles are orthogonal to the circle with diameter $\\overline{B C}$ ! The former follows from Brokard's theorem, noting that $A$ is on the polar of $H$, and the latter follows from the harmonic bundle.  Then $\\overline{A M}$ is the radical axis, so $X$ lies on both circles.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 3 |
-
{"year": "2015", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.", "solution": " The main content of the problem: Claim - $\\angle H X_{a} G=90^{\\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. Second proof by orthocenter reflection, Bendit Chan. As before, we know $M X \\cdot M A=$ $M K \\cdot M L=M B \\cdot M C$, but $X$ lies inside segment $A M$. Construct parallelogram $A B A^{\\prime} C$. Then $M X \\cdot M A^{\\prime}=M B \\cdot M C$, so $X B A^{\\prime} C$ is concyclic. However, it is well-known the circumcircle of $\\triangle B A^{\\prime} C$ (which is the reflection of $(A B C)$ across $\\overline{B C}$ ) passes through $H$ and in fact has diameter $\\overline{A^{\\prime} H}$. So this gives $\\angle H X A^{\\prime}=90^{\\circ}$ as needed.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 4 |
-
{"year": "2015", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.", "solution": " The main content of the problem: Claim - $\\angle H X_{a} G=90^{\\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. Third proof by barycentric coordinates. Alternatively we may just compute $X=\\left(a^{2}\\right.$ : $\\left.2 S_{A}: 2 S_{A}\\right)$. Let $F=\\left(0: S_{C}: S_{B}\\right)$ be the foot from $H$. Then we check that $X H F M$ is cyclic, which is power of a point from $A$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 5 |
-
{"year": "2015", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Let $P$ be the set of all primes, and let $M$ be a non-empty subset of $P$. Suppose that for any non-empty subset $\\left\\{p_{1}, p_{2}, \\ldots, p_{k}\\right\\}$ of $M$, all prime factors of $p_{1} p_{2} \\ldots p_{k}+1$ are also in $M$. Prove that $M=P$.", "solution": " Obviously $|M|=\\infty$. Assume for contradiction $p \\notin M$. We say a prime $q \\in M$ is sparse if there are only finitely many elements of $M$ which are $q(\\bmod p)$ (in particular there are finitely many sparse primes). Now let $C$ be the product of all sparse primes (note $p \\nmid C$ ). First, set $a_{0}=1$. For $k \\geq 0$, consider then the prime factorization of the number $$ C a_{k}+1 $$ No prime in its factorization is sparse, so consider the number $a_{k+1}$ obtained by replacing each prime in its factorization with some arbitrary representative of that prime's residue class. In this way we select a number $a_{k+1}$ such that - $a_{k+1} \\equiv C a_{k}+1(\\bmod p)$, and - $a_{k+1}$ is a product of distinct primes in $M$. In particular, $a_{k} \\equiv C^{k}+C^{k-1}+\\cdots+1(\\bmod p)$ But since $C \\not \\equiv 0(\\bmod p)$, we can find a $k$ such that $a_{k} \\equiv 0(\\bmod p)($ namely, $k=p-1$ if $C \\equiv 1$ and $k=p-2$ else) which is clearly impossible since $a_{k}$ is a product of primes in $M$ !", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 6 |
-
{"year": "2015", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Let $x, y, z$ be real numbers (not necessarily positive) such that $x^{4}+y^{4}+z^{4}+x y z=4$. Prove that $x \\leq 2$ and $$ \\sqrt{2-x} \\geq \\frac{y+z}{2} $$", "solution": " We prove that the condition $x^{4}+y^{4}+z^{4}+x y z=4$ implies $$ \\sqrt{2-x} \\geq \\frac{y+z}{2} $$ We first prove the easy part. Claim - We have $x \\leq 2$. $$ \\begin{aligned} 5=x^{4}+y^{4}+\\left(z^{4}+1\\right)+x y z & =\\frac{3 x^{4}}{4}+\\left(\\frac{x^{4}}{4}+y^{4}\\right)+\\left(z^{4}+1\\right)+x y z \\\\ & \\geq \\frac{3 x^{4}}{4}+x^{2} y^{2}+2 z^{2}+x y z . \\end{aligned} $$ We evidently have that $x^{2} y^{2}+2 z^{2}+x y z \\geq 0$ because the quadratic form $a^{2}+a b+2 b^{2}$ is positive definite, so $x^{4} \\leq \\frac{20}{3} \\Longrightarrow x \\leq 2$. Now, the desired statement is implied by its square, so it suffices to show that $$ 2-x \\geq\\left(\\frac{y+z}{2}\\right)^{2} $$ We are going to proceed by contradiction (it seems that many solutions do this) and assume that $$ 2-x<\\left(\\frac{y+z}{2}\\right)^{2} \\Longleftrightarrow 4 x+y^{2}+2 y z+z^{2}>8 $$ By AM-GM, $$ \\begin{aligned} x^{4}+3 & \\geq 4 x \\\\ \\frac{y^{4}+1}{2} & \\geq y^{2} \\\\ \\frac{z^{4}+1}{2} & \\geq z^{2} \\end{aligned} $$ which yields that $$ x^{4}+\\frac{y^{4}+z^{4}}{2}+2 y z+4>8 $$ If we replace $x^{4}=4-\\left(y^{4}+z^{4}+x y z\\right)$ now, this gives $$ -\\frac{y^{4}+z^{4}}{2}+(2-x) y z>0 \\Longrightarrow(2-x) y z>\\frac{y^{4}+z^{4}}{2} $$ Since $2-x$ and the right-hand side are positive, we have $y z \\geq 0$. Now $$ \\frac{y^{4}+z^{4}}{2 y z}<2-x<\\left(\\frac{y+z}{2}\\right)^{2} \\Longrightarrow 2 y^{4}+2 z^{4}<y z(y+z)^{2}=y^{3} z+2 y^{2} z^{2}+y z^{3} $$ This is clearly false by AM-GM, so we have a contradiction.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 7 |
-
{"year": "2015", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $\\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\\varphi(n)=m$ has at least 2015 solutions in $n$.", "solution": " 『 First solution with ad-hoc subsets, by Evan Chen. I consider the following eleven prime numbers: $$ S=\\{11,13,17,19,29,31,37,41,43,61,71\\} $$ This has the property that for any $p \\in S$, all prime factors of $p-1$ are one digit. Let $N=(210)^{\\text {billion }}$, and consider $M=\\varphi(N)$. For any subset $T \\subset S$, we have $$ M=\\varphi\\left(\\frac{N}{\\prod_{p \\in T}(p-1)} \\prod_{p \\in T} p\\right) $$ Since $2^{|S|}>2015$ we're done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 8 |
-
{"year": "2015", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $\\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\\varphi(n)=m$ has at least 2015 solutions in $n$.", "solution": " 【 Second solution with smallest primes, by Yang Liu. Let $2=p_{1}<p_{2}<\\cdots<p_{2015}$ be the smallest 2015 primes. Then the 2015 numbers $$ \\begin{aligned} n_{1} & =\\left(p_{1}-1\\right) p_{2} \\ldots p_{2015} \\\\ n_{2} & =p_{1}\\left(p_{2}-1\\right) \\ldots p_{2015} \\\\ & \\vdots \\\\ n_{2015} & =p_{1} p_{2} \\ldots\\left(p_{2015}-1\\right) \\end{aligned} $$ all have the same phi value, namely $$ \\varphi\\left(p_{1} p_{2} \\ldots p_{2015}\\right)=\\prod_{i=1}^{2015}\\left(p_{i}-1\\right) $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
| 9 |
-
{"year": "2015", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "A Nim-style game is defined as follows. Two positive integers $k$ and $n$ are specified, along with a finite set $S$ of $k$-tuples of integers (not necessarily positive). At the start of the game, the $k$-tuple $(~ n, 0,0, \\ldots, 0)$ is written on the blackboard. A legal move consists of erasing the tuple $\\left(a_{1}, a_{2}, \\ldots, a_{k}\\right)$ which is written on the blackboard and replacing it with $\\left(a_{1}+b_{1}, a_{2}+b_{2}, \\ldots, a_{k}+b_{k}\\right)$, where $\\left(b_{1}, b_{2}, \\ldots, b_{k}\\right)$ is an element of the set $S$. Two players take turns making legal moves, and the first to write a negative integer loses. In the event that neither player is ever forced to write a negative integer, the game is a draw. Prove that there is a choice of $k$ and $S$ with the following property: the first player has a winning strategy if $n$ is a power of 2 , and otherwise the second player has a winning strategy.", "solution": "  Now, the \"game\" is played as follows. The mechanics are controlled by the turn counters $A$ and $B$. Observe the game starts with Alice playing Init. Thereafter, we say that the game is - In the main part if $A+B=1$, and no one has played Init a second time. - In the death part otherwise. Observe that in the main state, on Alice's turn we always have $(A, B)=(1,0)$ and on Bob's turn we always have $(A, B)=(0,1)$. Claim - A player who plays Init a second time must lose. In particular, a player who makes a move when $A=B=0$ must lose. - Suppose the offending player is in a situation where $A=B=0$. Then he/she must play Init. At this point, the opposing player can respond by playing Kill. Then the offending player must play Init again. The opposing player now responds with Kill'. This iteration continues until $X$ reaches a negative number and the offending player loses. - Suppose Alice has $(A, B)=(1,0)$ but plays Init again anyways. Then Bob responds with PunB to punish her; he then wins as in the first case. - Suppose Bob has $(A, B)=(0,1)$ but plays Init again anyways. Alice responds with PunA in the same way. Thus we may assume that players avoid the death part at all costs. Hence the second moves consist of Bob playing Sleep, and then Alice playing Begin (thus restoring the value of $n$ in $X$ ), then Bob playing Sleep. Now we return to analysis of the main part. We say the game is in state $S$ for $S \\in$ $\\left\\{S_{X}^{0}, S_{X}, S_{X}^{\\prime}, S_{Y}^{0}, S_{Y}, S_{Y}^{\\prime}, \\mathrm{Cl}\\right\\}$ if $S=1$ and all other variables are zero. By construction, this is always the case. From then on the main part is divided into several phases: - An $X$-phase: this begins with Alice at $S_{X}^{0}$, and ends when the game is in a state other than $S_{X}$ and $S_{X}^{\\prime}$. (She can never return to $S_{X}^{0}$ during an $X$-phase.) - A $Y$-phase: this begins with Alice at $S_{Y}^{0}$, and ends when the game is in a state other than $S_{Y}$ and $S_{Y}^{\\prime}$. (She can never return to $S_{Y}^{0}$ during a $Y$-phase.) Claim - Consider an $X$-phase in which $(X, Y)=(x, 0), x>1$. Then Alice can complete the phase without losing if and only if $x$ is even; if so she begins a $Y$-phase with $(X, Y)=(0, x / 2)$. Now note that unless $X=0$, Bob now has a winning move WrongX. Conversely he may only play Sleep if $X=0$. We have an analogous claim for $Y$-phases. Thus if $n$ is not a power of 2 , we see that Alice eventually loses. Now suppose $n=2^{k}$; then Alice reaches $(X, Y)=\\left(0,2^{k-1}\\right),\\left(2^{k-2}, 0\\right), \\ldots$ until either reaching $(1,0)$ or $(0,1)$. At this point she can play ClaimX or ClaimY, respectively; the game is now in state Cl. Bob cannot play either FakeX or FakeY, so he must play Sleep, and then Alice wins by playing Win. Thus Alice has a winning strategy when $n=2^{k}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2015.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl
DELETED
|
@@ -1,8 +0,0 @@
|
|
| 1 |
-
{"year": "2016", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A=A(x, y)$ and $B=B(x, y)$ be two-variable polynomials with real coefficients. Suppose that $A(x, y) / B(x, y)$ is a polynomial in $x$ for infinitely many values of $y$, and a polynomial in $y$ for infinitely many values of $x$. Prove that $B$ divides $A$, meaning there exists a third polynomial $C$ with real coefficients such that $A=B \\cdot C$.", "solution": " This is essentially an application of the division algorithm, but the details require significant care. First, we claim that $A / B$ can be written as a polynomial in $x$ whose coefficients are rational functions in $y$. To see this, use the division algorithm to get $$ A=Q \\cdot B+R \\quad Q, R \\in(\\mathbb{R}(y))[x] $$ where $Q$ and $R$ are polynomials in $x$ whose coefficients are rational functions in $y$, and moreover $\\operatorname{deg}_{x} B>\\operatorname{deg}_{x} R$. Now, we claim that $R \\equiv 0$. Indeed, we have by hypothesis that for infinitely many values of $y_{0}$ that $B\\left(x, y_{0}\\right)$ divides $A\\left(x, y_{0}\\right)$, which means $B\\left(x, y_{0}\\right) \\mid R\\left(x, y_{0}\\right)$ as polynomials in $\\mathbb{R}[x]$. Now, we have $\\operatorname{deg}_{x} B\\left(x, y_{0}\\right)>\\operatorname{deg}_{x} R\\left(x, y_{0}\\right)$ outside of finitely many values of $y_{0}$ (but not all of them!); this means for infinitely many $y_{0}$ we have $R\\left(x, y_{0}\\right) \\equiv 0$. So each coefficient of $x^{i}$ (in $\\left.\\mathbb{R}(y)\\right)$ has infinitely many roots, hence is a zero polynomial. Consequently, we are able to write $A / B=F(x, y) / M(y)$ where $F \\in \\mathbb{R}[x, y]$ and $M \\in \\mathbb{R}[y]$ are each polynomials. Repeating the same argument now gives $$ \\frac{A}{B}=\\frac{F(x, y)}{M(y)}=\\frac{G(x, y)}{N(x)} $$ Now, by unique factorization of polynomials in $\\mathbb{R}[x, y]$, we can discuss GCD's. So, we tacitly assume $\\operatorname{gcd}(F, M)=\\operatorname{gcd}(G, N)=(1)$. Also, we obviously have $\\operatorname{gcd}(M, N)=(1)$. But $F \\cdot N=G \\cdot M$, so $M \\mid F \\cdot N$, thus we conclude $M$ is the constant polynomial. This implies the result. Remark. This fact does not generalize to arbitrary functions that are separately polynomial: see e.g. http://aops.com/community/c6h523650p2978180.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 2 |
-
{"year": "2016", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\\overline{A H}, \\overline{B C}$. Suppose the circle $\\gamma$ with diameter $\\overline{A H}$ meets the circumcircle of $A B C$ at $G \\neq A$, and meets line $\\overline{A N}$ at $Q \\neq A$. The tangent to $\\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\\triangle G N Q$ and $\\triangle M B C$ intersect on $\\overline{P N}$.", "solution": " 【 First solution (found by contestants). Denote by $\\triangle D E F$ the orthic triangle. Observe $\\overline{P A}$ and $\\overline{P G}$ are tangents to $\\gamma$, since $\\overline{O M}$ is the perpendicular bisector of $\\overline{A G}$. Also note that $\\overline{A G}, \\overline{E F}, \\overline{B C}$ are concurrent at some point $R$ by radical axis on $(A B C), \\gamma$, (BFEC). Now, consider circles (PAGM), (MFDNE), and (MBC). We already saw the point $R$ satisfies $$ R A \\cdot R G=R E \\cdot R F=R B \\cdot R C $$ and hence has equal powers to all three circles; but since the circles at $M$ already, they must actually be coaxial. Assume they meet again at $T \\in \\overline{R M}$, say. Then $\\angle P T M$ and $\\angle M T N$ are both right angles, hence $T$ lies on $\\overline{P N}$. Finally $H$ is the orthocenter of $\\triangle A R N$, and thus the circle with diameter $\\overline{R N}$ passes through $G, Q, N$. ", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 3 |
-
{"year": "2016", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\\overline{A H}, \\overline{B C}$. Suppose the circle $\\gamma$ with diameter $\\overline{A H}$ meets the circumcircle of $A B C$ at $G \\neq A$, and meets line $\\overline{A N}$ at $Q \\neq A$. The tangent to $\\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\\triangle G N Q$ and $\\triangle M B C$ intersect on $\\overline{P N}$.", "solution": " 『 Alternate solution (by proposer). Let $L$ be diametrically opposite $A$ on the circumcircle. Denote by $\\triangle D E F$ the orthic triangle. Let $X=\\overline{A H} \\cap \\overline{E F}$. Finally, let $T$ be the second intersection of (MFDNE) and (MBC).  We begin with a few easy observations. First, points $H, G, N, L$ are collinear and $\\angle A G L=90^{\\circ}$. Also, $Q$ is the foot from $H$ to $\\overline{A N}$. Consequently, lines $A G, E F, H Q$, $B C, T M$ concur at a point $R$ (radical axis). Moreover, we already know $\\angle M T N=90^{\\circ}$. This implies $T$ lies on the circle with diameter $\\overline{R N}$, which is exactly the circumcircle of $\\triangle G Q N$. Note by Brokard's Theorem on $A F H E$, the point $X$ is the orthocenter of $\\triangle M B C$. But $\\angle M T N=90^{\\circ}$ already, and $N$ is the midpoint of $\\overline{B C}$. Consequently, points $T, X$, $N$ are collinear. Finally, we claim $P, X, N$ are collinear, which solves the problem. Note $P=\\overline{G G} \\cap \\overline{A A}$. Set $K=\\overline{H N L} \\cap \\overline{A P}$. Then by noting $$ -1=(D, X ; A, H) \\stackrel{N}{=}(\\infty, \\overline{N X} \\cap \\overline{A K} ; A, K) $$ we see that $\\overline{N X}$ bisects segment $\\overline{A K}$, as desired. (A more projective finish is to show that $\\overline{P X N}$ is the polar of $R$ to $\\gamma$ ). Remark. The original problem proposal reads as follows: Let $A B C$ be a triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\\overline{A H}, \\overline{B C}$. Suppose ray $O M$ meets the line parallel to $\\overline{B C}$ through $A$ at $P$. Prove that the line through the circumcenter of $\\triangle M B C$ and the midpoint of $\\overline{O H}$ is parallel to $\\overline{N P}$. The points $G$ and $Q$ were added to the picture later to prevent the problem from being immediate by coordinates.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 4 |
-
{"year": "2016", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Decide whether or not there exists a nonconstant polynomial $Q(x)$ with integer coefficients with the following property: for every positive integer $n>2$, the numbers $$ Q(0), Q(1), Q(2), \\ldots, Q(n-1) $$ produce at most $0.499 n$ distinct residues when taken modulo $n$.", "solution": " We claim that $$ Q(x)=420\\left(x^{2}-1\\right)^{2} $$ works. Clearly, it suffices to prove the result when $n=4$ and when $n$ is an odd prime $p$. The case $n=4$ is trivial, so assume now $n=p$ is an odd prime. First, we prove the following easy claim. Claim - For any odd prime $p$, there are at least $\\frac{1}{2}(p-3)$ values of $a$ for which $\\left(\\frac{1-a^{2}}{p}\\right)=+1$. Remark. The above identity comes from starting with the equation $1-a^{2}=b^{2}$, and writing it as $\\left(\\frac{1}{b}\\right)^{2}-\\left(\\frac{a}{b}\\right)^{2}=1$. Then solve $\\frac{1}{b}-\\frac{a}{b}=k$ and $\\frac{1}{b}+\\frac{a}{b}=1 / k$ for $a$. Let $F(x)=\\left(x^{2}-1\\right)^{2}$. The range of $F$ modulo $p$ is contained within the $\\frac{1}{2}(p+1)$ quadratic residues modulo $p$. On the other hand, if for some $t$ neither of $1 \\pm t$ is a quadratic residue, then $t^{2}$ is omitted from the range of $F$ as well. Call such a value of $t$ useful, and let $N$ be the number of useful residues. We aim to show $N \\geq \\frac{1}{4} p-2$. We compute a lower bound on the number $N$ of useful $t$ by writing $$ \\begin{aligned} N & =\\frac{1}{4}\\left(\\sum_{t}\\left[\\left(1-\\left(\\frac{1-t}{p}\\right)\\right)\\left(1-\\left(\\frac{1+t}{p}\\right)\\right)\\right]-\\left(1-\\left(\\frac{2}{p}\\right)\\right)-\\left(1-\\left(\\frac{-2}{p}\\right)\\right)\\right) \\\\ & \\geq \\frac{1}{4} \\sum_{t}\\left[\\left(1-\\left(\\frac{1-t}{p}\\right)\\right)\\left(1-\\left(\\frac{1+t}{p}\\right)\\right)\\right]-1 \\\\ & =\\frac{1}{4}\\left(p+\\sum_{t}\\left(\\frac{1-t^{2}}{p}\\right)\\right)-1 \\\\ & \\geq \\frac{1}{4}\\left(p+(+1) \\cdot \\frac{1}{2}(p-3)+0 \\cdot 2+(-1) \\cdot\\left((p-2)-\\frac{1}{2}(p-3)\\right)\\right)-1 \\\\ & \\geq \\frac{1}{4}(p-5) . \\end{aligned} $$ Thus, the range of $F$ has size at most $$ \\frac{1}{2}(p+1)-\\frac{1}{2} N \\leq \\frac{3}{8}(p+3) . $$ This is less than $0.499 p$ for any $p \\geq 11$. Remark. In fact, the computation above is essentially an equality. There are only two points where terms are dropped: one, when $p \\equiv 3(\\bmod 4)$ there are no $k^{2}=-1$ in the lemma, and secondly, the terms $1-(2 / p)$ and $1-(-2 / p)$ are dropped in the initial estimate for $N$. With suitable modifications, one can show that in fact, the range of $F$ is exactly equal to $$ \\frac{1}{2}(p+1)-\\frac{1}{2} N=\\left\\{\\begin{array}{lll} \\frac{1}{8}(3 p+5) & p \\equiv 1 & (\\bmod 8) \\\\ \\frac{1}{8}(3 p+7) & p \\equiv 3 & (\\bmod 8) \\\\ \\frac{1}{8}(3 p+9) & p \\equiv 5 & (\\bmod 8) \\\\ \\frac{1}{8}(3 p+3) & p \\equiv 7 & (\\bmod 8) \\end{array}\\right. $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 5 |
-
{"year": "2016", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Prove that if $n$ and $k$ are positive integers satisfying $\\varphi^{k}(n)=1$, then $n \\leq 3^{k}$. (Here $\\varphi^{k}$ denotes $k$ applications of the Euler phi function.)", "solution": " The main observation is that the exponent of 2 decreases by at most 1 with each application of $\\varphi$. This will give us the desired estimate. Define the weight function $w$ on positive integers as follows: it satisfies $$ \\begin{aligned} w(a b) & =w(a)+w(b) \\\\ w(2) & =1 ; \\quad \\text { and } \\\\ w(p) & =w(p-1) \\quad \\text { for any prime } p>2 \\end{aligned} $$ By induction, we see that $w(n)$ counts the powers of 2 that are produced as $\\varphi$ is repeatedly applied to $n$. In particular, $k \\geq w(n)$. From $w(2)=1$, it suffices to prove that $w(p) \\geq \\log _{3} p$ for every $p>2$. We use strong induction and note that $$ w(p)=w(2)+w\\left(\\frac{p-1}{2}\\right) \\geq 1+\\log _{3}(p-1)-\\log _{3} 2 \\geq \\log _{3} p $$ for any $p>2$. This solves the problem. Moreover, the stronger bound $$ n \\leq 2 \\cdot 3^{k-1} $$ is true and best possible.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 6 |
-
{"year": "2016", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "In the coordinate plane are finitely many walls, which are disjoint line segments, none of which are parallel to either axis. A bulldozer starts at an arbitrary point and moves in the $+x$ direction. Every time it hits a wall, it turns at a right angle to its path, away from the wall, and continues moving. (Thus the bulldozer always moves parallel to the axes.) Prove that it is impossible for the bulldozer to hit both sides of every wall.", "solution": " We say a wall $v$ is above another wall $w$ if some point on $v$ is directly above a point on $w$. (This relation is anti-symmetric, as walls do not intersect). The critical claim is as follows: Claim - There exists a lowest wall, i.e. a wall not above any other walls. Now consider the leftmost vertical segment $\\overline{Q_{i} P_{i+1}}$ and the rightmost vertical segment $\\overline{Q_{j} P_{j+1}}$. The broken line gives a path from $P_{i+1}$ to $Q_{j}$, as well as a path from $P_{j+1}$ to $Q_{i}$. These clearly must intersect, contradiction. Remark. This claim is Iran TST 2010. Thus if the bulldozer eventually moves upwards indefinitely, it may never hit the bottom side of the lowest wall. Similarly, if the bulldozer eventually moves downwards indefinitely, it may never hit the upper side of the highest wall.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 7 |
-
{"year": "2016", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\\overline{B C}, \\overline{C A}$, $\\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\\overline{E F}$. Suppose that the circumcircle of $\\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\\triangle B B_{1} B_{2}$ and $\\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\\overline{D K}$.", "solution": " \\I First solution (Allen Liu). Let $X, Y, Z$ be midpoints of $E F, F D, D E$, and let $G$ be the Gergonne point. By radical axis on $(A E I F),(D E F),(A I C)$ we see that $B_{1}$, $X, B_{2}$ are collinear. Likewise, $B_{1}, Z, B_{2}$ are collinear, so lines $B_{1} B_{2}$ and $X Z$ coincide. Similarly, lines $C_{1} C_{2}$ and $X Y$ coincide. In particular lines $B_{1} B_{2}$ and $C_{1} C_{2}$ meet at $X$.  Note $G$ is the symmedian point of $D E F$, so it is well-known that $X G$ passes through the midpoint of $D K$. So we just have to prove $G$ lies on the radical axis. First, note that $\\triangle D E F$ is the cevian triangle of the Gergonne point $G$. Set $V=$ $\\overline{X Y} \\cap \\overline{A B}, W=\\overline{X Z} \\cap \\overline{A C}$, and $T=\\overline{B W} \\cap \\overline{C V}$. We begin with the following completely projective claim. Claim - The points $X, G, T$ are collinear. - By Cevian Nest on $\\triangle A B C$, it follows that $\\overline{A X}, \\overline{B Y}, \\overline{C Z}$ are concurrent. - Hence $\\triangle B Y V$ and $\\triangle C Z W$ are perspective. - Hence $\\triangle B Z W$ and $\\triangle C Y V$ are perspective too. - Hence we deduce by Desargues theorem that $T, X$, and $\\overline{B Z} \\cap \\overline{C Y}$ are collinear. - Finally, the Cevian Nest theorem applied on $\\triangle G B C$ (which has cevian triangles $\\triangle D F E, \\triangle X Z Y$ ) we deduce $G, X$, and $\\overline{B Z} \\cap \\overline{C Y}$, proving the claim. One could also proceed by using barycentric coordinates on $\\triangle D E F$. Remark (Eric Shen). The first four bullets can be replaced by non-projective means: one can check that $\\overline{B Z} \\cap \\overline{C Y}$ is the radical center of $(B I C),\\left(B B_{1} B_{2}\\right),\\left(C C_{1} C_{2}\\right)$ and therefore it lies on line $\\overline{X T}$. Now, we contend point $V$ is the radical center $\\left(C C_{1} C_{2}\\right),(A B C)$ and $(D E F)$. To see this, let $V^{\\prime}=\\overline{E D} \\cap \\overline{A B}$; then $\\left(F V^{\\prime} ; A B\\right)$ is harmonic, and $V$ is the midpoint of $\\overline{F V^{\\prime}}$, and thus $V A \\cdot V B=V F^{2}=V C_{1} \\cdot V C_{2}$. So in fact $\\overline{C V}$ is the radical axis of $(A B C)$ and $\\left(C C_{1} C_{2}\\right)$. Similarly, $\\overline{B W}$ is the radical axis of $(A B C)$ and $\\left(B B_{1} B_{2}\\right)$. Thus $T$ is the radical center of $(A B C),\\left(B B_{1} B_{2}\\right),\\left(C C_{1} C_{2}\\right)$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
| 8 |
-
{"year": "2016", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\\overline{B C}, \\overline{C A}$, $\\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\\overline{E F}$. Suppose that the circumcircle of $\\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\\triangle B B_{1} B_{2}$ and $\\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\\overline{D K}$.", "solution": " 『 Second solution (Evan Chen). As before, we just have to prove $G$ lies on the radical axis.  Construct parallelograms $G P F Q, G R D S, G T U E$ such that $P, R \\in D F, S, T \\in D E$, $Q, U \\in E F$. As $F G$ bisects $P Q$ and is isogonal to $F Z$, we find $P Q E D$, hence $P Q R U$, is cyclic. Repeating the same logic and noticing $P R, S T, Q U$ not concurrent, all six points $P Q R S T U$ are cyclic. Moreover, since $P Q$ bisects $G F$, we see that a dilation with factor 2 at $G$ sends $P Q$ to $P^{\\prime}, Q^{\\prime} \\in A B$, say, with $F$ the midpoint of $P^{\\prime} Q^{\\prime}$. Define $R^{\\prime}, S^{\\prime} \\in B C$ similarly now and $T^{\\prime}, U^{\\prime} \\in C A$. Note that $E Q P D S^{\\prime}$ is in cyclic too, as $\\measuredangle D S^{\\prime} Q=\\measuredangle D R S=\\measuredangle D E F$. By homothety through $B$, points $B, P, X$ are collinear; assume they meet ( $\\left.E Q P D S^{\\prime}\\right)$ again at $V$. Thus $E V Q P D S^{\\prime}$ is cyclic, and now $$ \\measuredangle B V S^{\\prime}=\\measuredangle P V S^{\\prime}=\\measuredangle P Q S=\\measuredangle P T S=\\measuredangle F E D=\\measuredangle X E Z=\\measuredangle X V Z $$ hence $V$ lies on $\\left(B Q^{\\prime} S^{\\prime}\\right)$. Since $F B \\| Q P$, we get $E V F B$ is cyclic too, so $X V \\cdot X B=X E \\cdot X F$ now; thus $X$ lies on the radical axis of $\\left(B S^{\\prime} Q^{\\prime}\\right)$ and $(D E F)$. By the same argument with $W \\in B Z$, we get $Z$ lies on the radical axis too. Thus the radical axis of $\\left(B S^{\\prime} Q^{\\prime}\\right)$ and ( $D E F$ ) must be line $X Z$, which coincides with $B_{1} B_{2}$; so $\\left(B B_{1} B_{2}\\right)=\\left(B S^{\\prime} Q^{\\prime}\\right)$. Analogously, $\\left(C C_{1} C_{2}\\right)=\\left(C R^{\\prime} U^{\\prime}\\right)$. Since $G=Q^{\\prime} S^{\\prime} \\cap R^{\\prime} U^{\\prime}$, we need only prove that $Q^{\\prime} R^{\\prime} S^{\\prime} U^{\\prime}$ is cyclic. But $Q R S U$ is cyclic, so we are done. The circle ( $P Q R S T U$ ) is called the Lemoine circle of $A B C$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2016.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl
DELETED
|
@@ -1,13 +0,0 @@
|
|
| 1 |
-
{"year": "2017", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with circumcircle $\\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \\neq A C$ and $\\angle A \\neq 90^{\\circ}$. Let $M$ and $N$ be the midpoints of $\\overline{A B}$ and $\\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\\Gamma$ with the circumcircle of $\\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\\overline{P R} \\perp \\overline{O H}$.", "solution": " 【 First solution (power of a point). Let $\\gamma$ denote the nine-point circle of $A B C$.  Note that - $P A^{2}=P M \\cdot P N$, so $P$ lies on the radical axis of $\\Gamma$ and $\\gamma$. - $R A \\cdot R Q=R E \\cdot R F$, so $R$ lies on the radical axis of $\\Gamma$ and $\\gamma$. Thus $\\overline{P R}$ is the radical axis of $\\Gamma$ and $\\gamma$, which is evidently perpendicular to $\\overline{O H}$. Remark. In fact, by power of a point one may also observe that $R$ lies on $\\overline{B C}$, since it is on the radical axis of $(A Q F H E),(B F E C),(A B C)$. Ironically, this fact is not used in the solution.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 2 |
-
{"year": "2017", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with circumcircle $\\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \\neq A C$ and $\\angle A \\neq 90^{\\circ}$. Let $M$ and $N$ be the midpoints of $\\overline{A B}$ and $\\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\\Gamma$ with the circumcircle of $\\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\\overline{P R} \\perp \\overline{O H}$.", "solution": " II Second solution (barycentric coordinates). Again note first $R \\in \\overline{B C}$ (although this can be avoided too). We compute the points in much the same way as before. Since $\\overline{A P} \\cap \\overline{B C}=\\left(0: b^{2}:-c^{2}\\right)$ we have $$ P=\\left(b^{2}-c^{2}: b^{2}:-c^{2}\\right) $$ (since $x=y+z$ is the equation of line $\\overline{M N}$ ). Now in Conway notation we have $$ R=\\overline{E F} \\cap \\overline{B C}=\\left(0: S_{C}:-S_{B}\\right)=\\left(0: a^{2}+b^{2}-c^{2}:-a^{2}+b^{2}-c^{2}\\right) . $$ Hence $$ \\overrightarrow{P R}=\\frac{1}{2\\left(b^{2}-c^{2}\\right)}\\left(b^{2}-c^{2}, c^{2}-a^{2}, a^{2}-b^{2}\\right) $$ On the other hand, we have $\\overrightarrow{O H}=\\vec{A}+\\vec{B}+\\vec{C}$. So it suffices to check that $$ \\sum_{\\mathrm{cyc}} a^{2}\\left(\\left(a^{2}-b^{2}\\right)+\\left(c^{2}-a^{2}\\right)\\right)=0 $$ which is immediate.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 3 |
-
{"year": "2017", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with circumcircle $\\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \\neq A C$ and $\\angle A \\neq 90^{\\circ}$. Let $M$ and $N$ be the midpoints of $\\overline{A B}$ and $\\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\\Gamma$ with the circumcircle of $\\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\\overline{P R} \\perp \\overline{O H}$.", "solution": " 『 Third solution (complex numbers). Let $A B C$ be the unit circle. We first compute $P$ as the midpoint of $A$ and $\\overline{A A} \\cap \\overline{B C}$ : $$ \\begin{aligned} p & =\\frac{1}{2}\\left(a+\\frac{a^{2}(b+c)-b c \\cdot 2 a}{a^{2}-b c}\\right) \\\\ & =\\frac{a\\left(a^{2}-b c\\right)+a^{2}(b+c)-2 a b c}{2\\left(a^{2}-b c\\right)} \\end{aligned} $$ Using the remark above, $R$ is the inverse of $D$ with respect to the circle with diameter $\\overline{B C}$, which has radius $\\left|\\frac{1}{2}(b-c)\\right|$. Thus $$ \\begin{aligned} r-\\frac{b+c}{2} & =\\frac{\\frac{1}{4}(b-c)\\left(\\frac{1}{b}-\\frac{1}{c}\\right)}{\\frac{1}{2}\\left(a-\\frac{b c}{a}\\right)} \\\\ r & =\\frac{b+c}{2}+\\frac{-\\frac{1}{2} \\frac{(b-c)^{2}}{b c}}{\\frac{1}{a}-\\frac{a}{b c}} \\\\ & =\\frac{b+c}{2}+\\frac{a(b-c)^{2}}{2\\left(a^{2}-b c\\right)} \\\\ & =\\frac{a(b-c)^{2}+(b+c)\\left(a^{2}-b c\\right)}{2\\left(a^{2}-b c\\right)} \\end{aligned} $$ Expanding and subtracting gives $$ p-r=\\frac{a^{3}-a b c-a b^{2}-a c^{2}+b^{2} c+b c^{2}}{2\\left(a^{2}-b c\\right)}=\\frac{(a+b+c)(a-b)(a-c)}{2\\left(a^{2}-b c\\right)} $$ which is visibly equal to the negation of its conjugate once the factor of $a+b+c$ is deleted. (Actually, one can guess this factorization ahead of time by noting that if $A=B$, then $P=B=R$, so $a-b$ must be a factor; analogously $a-c$ must be as well.)", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 4 |
-
{"year": "2017", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Ana and Banana are playing a game. First Ana picks a word, which is defined to be a nonempty sequence of capital English letters. Then Banana picks a nonnegative integer $k$ and challenges Ana to supply a word with exactly $k$ subsequences which are equal to Ana's word. Ana wins if she is able to supply such a word, otherwise she loses. For example, if Ana picks the word \"TST\", and Banana chooses $k=4$, then Ana can supply the word \"TSTST\" which has 4 subsequences which are equal to Ana's word. Which words can Ana pick so that she can win no matter what value of $k$ Banana chooses?", "solution": " First we introduce some notation. Define a block of letters to be a maximal contiguous subsequence of consecutive letters. For example, the word $A A B B B C A A A$ has four blocks, namely $A A, B B B, C, A A A$. Throughout the solution, we fix the word $A$ that Ana picks, and introduce the following notation for its $m$ blocks: $$ A=A_{1} A_{2} \\ldots A_{m}=\\underbrace{a_{1} \\ldots a_{1}}_{x_{1}} \\underbrace{a_{2} \\ldots a_{2}}_{x_{2}} \\cdots \\underbrace{a_{m} \\ldots a_{m}}_{x_{m}} $$ A rainbow will be a subsequence equal to Ana's initial word $A$ (meaning Ana seeks words with exactly $k$ rainbows). Finally, for brevity, let $A_{i}=\\underbrace{a_{i} \\ldots a_{i}}_{x_{i}}$, so $A=A_{1} \\ldots A_{m}$. We prove two claims that resolve the problem. Claim - If $x_{i}=1$ for some $i$, then for any $k \\geq 1$, the word $$ W=A_{1} \\ldots A_{i-1} \\underbrace{a_{i} \\ldots a_{i}}_{k} A_{i+1} \\ldots A_{m} $$ obtained by repeating the $i$ th letter $k$ times has exactly $k$ rainbows. Given a rainbow, consider the location of this singleton block in $W$. It cannot occur within the first $\\left|A_{1}\\right|+\\cdots+\\left|A_{i-1}\\right|$ letters, nor can it occur within the final $\\left|A_{i+1}\\right|+\\cdots+\\left|A_{m}\\right|$ letters. So it must appear in the $i$ th block of $W$. That implies that all the other $a_{i}$ 's in the $i$ th block of $W$ must be deleted, as desired. (This last argument is actually nontrivial, and has some substance; many students failed to realize that the upper bound requires care.) Claim - If $x_{i} \\geq 2$ for all $i$, then no word $W$ has exactly two rainbows. Let $W=w_{1} \\ldots w_{n}$ and consider the two rainbows of $W$. Since they are not the same, there must be a block $A_{p}$ of the rainbow, of length $\\ell \\geq 2$, which do not occupy the same locations in $W$. Assume the first rainbow uses $w_{i_{1}}, \\ldots, w_{i_{\\ell}}$ for this block and the second rainbow uses $w_{j_{1}}, \\ldots, w_{j_{\\ell}}$ for this block. Then among the letters $w_{q}$ for $\\min \\left(i_{1}, j_{1}\\right) \\leq q \\leq \\max \\left(i_{\\ell}, j_{\\ell}\\right)$, there must be at least $\\ell+1$ copies of the letter $a_{p}$. Moreover, given a choice of $\\ell$ copies of the letter $a_{p}$ in this range, one can complete the subsequence to a rainbow. So the number of rainbows is at least $\\binom{\\ell+1}{\\ell} \\geq \\ell+1$. Since $\\ell \\geq 2$, this proves $W$ has at least three rainbows. In summary, Ana wins if and only if $x_{i}=1$ for some $i$, since she can duplicate the isolated letter $k$ times; but if $x_{i} \\geq 2$ for all $i$ then Banana only needs to supply $k=2$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 5 |
-
{"year": "2017", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Consider solutions to the equation $$ x^{2}-c x+1=\\frac{f(x)}{g(x)} $$ where $f$ and $g$ are nonzero polynomials with nonnegative real coefficients. For each $c>0$, determine the minimum possible degree of $f$, or show that no such $f, g$ exist.", "solution": " Indeed, one simply takes $x=1$ to get $f(1) / g(1) \\leq 0$, impossible. For $c<2$, let $c=2 \\cos \\theta$, where $0<\\theta<\\pi$. We claim that $f$ exists and has minimum degree equal to $n$, where $n$ is defined as the smallest integer satisfying $\\sin n \\theta \\leq 0$. In other words $$ n=\\left\\lceil\\frac{\\pi}{\\arccos (c / 2)}\\right\\rceil $$ First we show that this is necessary. To see it, write explicitly $$ g(x)=a_{0}+a_{1} x+a_{2} x^{2}+\\cdots+a_{n-2} x^{n-2} $$ with each $a_{i} \\geq 0$, and $a_{n-2} \\neq 0$. Assume that $n$ is such that $\\sin (k \\theta) \\geq 0$ for $k=1, \\ldots, n-1$. Then, we have the following system of inequalities: $$ \\begin{aligned} & a_{1} \\geq 2 \\cos \\theta \\cdot a_{0} \\\\ & a_{0}+a_{2} \\geq 2 \\cos \\theta \\cdot a_{1} \\\\ & a_{1}+a_{3} \\geq 2 \\cos \\theta \\cdot a_{2} \\\\ & \\vdots \\\\ & a_{n-5}+a_{n-3} \\geq 2 \\cos \\theta \\cdot a_{n-4} \\\\ & a_{n-4}+a_{n-2} \\geq 2 \\cos \\theta \\cdot a_{n-3} \\\\ & a_{n-3} \\geq 2 \\cos \\theta \\cdot a_{n-2} . \\end{aligned} $$ Now, multiply the first equation by $\\sin \\theta$, the second equation by $\\sin 2 \\theta$, et cetera, up to $\\sin ((n-1) \\theta)$. This choice of weights is selected since we have $$ \\sin (k \\theta)+\\sin ((k+2) \\theta)=2 \\sin ((k+1) \\theta) \\cos \\theta $$ so that summing the entire expression cancels nearly all terms and leaves only $$ \\sin ((n-2) \\theta) a_{n-2} \\geq \\sin ((n-1) \\theta) \\cdot 2 \\cos \\theta \\cdot a_{n-2} $$ and so by dividing by $a_{n-2}$ and using the same identity gives us $\\sin (n \\theta) \\leq 0$, as claimed. This bound is best possible, because the example $$ a_{k}=\\sin ((k+1) \\theta) \\geq 0 $$ makes all inequalities above sharp, hence giving a working pair $(f, g)$. Remark. Calvin Deng points out that a cleaner proof of the lower bound is to take $\\alpha=\\cos \\theta+i \\sin \\theta$. Then $f(\\alpha)=0$, but by condition the imaginary part of $f(\\alpha)$ is apparently strictly positive, contradiction. Remark. Guessing that $c<2$ works at all (and realizing $c \\geq 2$ fails) is the first part of the problem. - Calvin Deng points out that it's possible to guess the answer from small cases: For $c \\leq 1$ we have $n=3$, tight at $\\frac{x^{3}+1}{x+1}=x^{2}-x+1$, and essentially the \"sharpest $n=3$ example\". A similar example exists at $n=4$ with $\\frac{x^{4}+1}{x^{2}+\\sqrt{2} x+1}=x^{2}-\\sqrt{2} x+1$ by the Sophie-Germain identity. In general, one can do long division to extract an optimal value of $c$ for any given $n$, although $c$ will be the root of some polynomial. The thresholds $c \\leq 1$ for $n=3, c \\leq \\sqrt{2}$ for $n=4, c \\leq \\frac{1+\\sqrt{5}}{2}$ for $n=5$, and $c \\leq 2$ for $n<\\infty$ suggest the unusual form of the answer via trigonometry. - One may imagine trying to construct a polynomial recursively / greedily by making all inequalities above hold (again the \"sharpest situation\" in which $f$ has few coefficients). If one sets $c=2 t$, then we have $$ a_{0}=1, \\quad a_{1}=2 t, \\quad a_{2}=4 t^{2}-1, \\quad a_{3}=8 t^{3}-4 t, \\quad \\ldots $$ which are the Chebyshev polynomials of the second type. This means that trigonometry is essentially mandatory. (One may also run into this when by using standard linear recursion techniques, and noting that the characteristic polynomial has two conjugate complex roots.) Remark. Mitchell Lee notes that an IMO longlist problem from 1997 shows that if $P(x)$ is any polynomial satisfying $P(x)>0$ for $x>0$, then $(x+1)^{n} P(x)$ has nonnegative coefficients for large enough $n$. This show that $f$ and $g$ at least exist for $c \\leq 2$, but provides no way of finding the best possible $\\operatorname{deg} f$. Meghal Gupta also points out that showing $f$ and $g$ exist is possible in the following way: $$ \\left(x^{2}-1.99 x+1\\right)\\left(x^{2}+1.99 x+1\\right)=\\left(x^{4}-1.9601 x^{2}+1\\right) $$ and so on, repeatedly multiplying by the \"conjugate\" until all coefficients become positive. To my best knowledge, this also does not give any way of actually minimizing $\\operatorname{deg} f$, although Ankan Bhattacharya points out that this construction is actually optimal in the case where $n$ is a power of 2 . Remark. It's pointed out that Matematicheskoe Prosveshchenie, issue 1, 1997, page 194 contains a nearly analogous result, available at https://mccme.ru/free-books/matpros/ pdf/mp-01.pdf with solutions presented in https://mccme.ru/free-books/matpros/pdf/ mp-05.pdf, pages 221-223; and https://mccme.ru/free-books/matpros/pdf/mp-10.pdf, page 274.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 6 |
-
{"year": "2017", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Find all nonnegative integer solutions to $$ 2^{a}+3^{b}+5^{c}=n! $$", "solution": "$$ 2^{a}+3^{b}+5^{c}=n! $$ $$ \\begin{aligned} & 2^{2}+3^{0}+5^{0}=3! \\\\ & 2^{1}+3^{1}+5^{0}=3! \\\\ & 2^{4}+3^{1}+5^{1}=4! \\end{aligned} $$ A tricky way to do this is to take modulo 120 , since $$ \\begin{aligned} 2^{a} \\quad(\\bmod 120) & \\in\\{1,2,4,8,16,32,64\\} \\\\ 3^{b} \\quad(\\bmod 120) & \\in\\{1,3,9,27,81\\} \\\\ 5^{c} \\quad(\\bmod 120) & \\in\\{1,5,25\\} \\end{aligned} $$ and by inspection one notes that no three elements have vanishing sum modulo 120 . - $a=1$ : since $3^{b}+5^{c} \\equiv 6(\\bmod 8)$, we find $b$ even and $c$ odd (hence $\\left.c \\neq 0\\right)$. Now looking modulo 5 gives that $3^{b}+5^{c} \\equiv 3(\\bmod 5)$, - $a=2$ : From $3^{b}+5^{c} \\equiv 4(\\bmod 8)$, we find $b$ is odd and $c$ is even. Now looking modulo 5 gives a contradiction, even if $c=0$, since $3^{b} \\in\\{2,3(\\bmod 5)\\}$ but $3^{b}+5^{c} \\equiv 1(\\bmod 5)$. Henceforth assume $a \\geq 3$. Next, by taking modulo 8 we have $3^{b}+5^{c} \\equiv 0(\\bmod 8)$, which forces both $b$ and $c$ to be odd (in particular, $b, c>0$ ). We now have $$ \\begin{aligned} & 2^{a}+5^{c} \\equiv 0 \\quad(\\bmod 3) \\\\ & 2^{a}+3^{b} \\equiv 0 \\quad(\\bmod 5) . \\end{aligned} $$ The first equation implies $a$ is even, but the second equation requires $a$ to be odd, contradiction. Hence no solutions with $n \\geq 5$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 7 |
-
{"year": "2017", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\\omega_{B}$ and $\\omega_{C}$ be the incircles of $\\triangle A B D$ and $\\triangle A C D$, respectively. Suppose that $\\omega_{B}$ and $\\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\\omega_{B}$ and $\\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\\triangle A B C$.", "solution": " 『 First solution (homothety). Let $Z$ be the diametrically opposite point on the incircle. We claim this is the desired intersection.  Note that: - $P$ is the insimilicenter of $\\omega_{B}$ and $\\omega_{C}$ - $C$ is the exsimilicenter of $\\omega$ and $\\omega_{C}$. Thus by Monge theorem, the insimilicenter of $\\omega_{B}$ and $\\omega$ lies on line $C P$. This insimilicenter should also lie on the line joining the centers of $\\omega$ and $\\omega_{B}$, which is $\\overline{B I}$, hence it coincides with the point $X$. So $X \\in \\overline{E Z}$ as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 8 |
-
{"year": "2017", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\\omega_{B}$ and $\\omega_{C}$ be the incircles of $\\triangle A B D$ and $\\triangle A C D$, respectively. Suppose that $\\omega_{B}$ and $\\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\\omega_{B}$ and $\\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\\triangle A B C$.", "solution": " 【 Second solution (harmonic). Let $T=\\overline{I_{B} I_{C}} \\cap \\overline{B C}$, and $W$ the foot from $I$ to $\\overline{B C}$. Define $Z=\\overline{F Y} \\cap \\overline{I W}$. Because $\\angle I_{B} D I_{C}=90^{\\circ}$, we have $$ -1=\\left(I_{B} I_{C} ; P T\\right) \\stackrel{B}{\\stackrel{B}{2}}\\left(I I_{C} ; Y C\\right) \\stackrel{F}{=}(I \\infty ; Z W) $$ So $I$ is the midpoint of $\\overline{Z W}$ as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 9 |
-
{"year": "2017", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\\omega_{B}$ and $\\omega_{C}$ be the incircles of $\\triangle A B D$ and $\\triangle A C D$, respectively. Suppose that $\\omega_{B}$ and $\\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\\omega_{B}$ and $\\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\\triangle A B C$.", "solution": " 【 Third solution (outline, barycentric, Andrew Gu). Let $A D=t, B D=x, C D=y$, so $a=x+y$ and by Stewart's theorem we have $$ (x+y)\\left(x y+t^{2}\\right)=b^{2} x+c^{2} y $$ We then have $D=(0: y: x)$ and so $$ \\overline{A I_{B}} \\cap \\overline{B C}=\\left(0: y+\\frac{t x}{c+t}: \\frac{c x}{c+t}\\right) $$ hence intersection with $B I$ gives $$ I_{B}=(a x: c y+a t: c x) $$ Similarly, $$ I_{C}=(a y: b y: b x+a t) $$ Then, we can compute $$ P=(2 a x y: y(a t+b x+c y): x(a t+b x+c y)) $$ since $P \\in \\overline{I_{B} I_{C}}$, and clearly $P \\in \\overline{A D}$. Intersection now gives $$ \\begin{aligned} & X=(2 a x: a t+b x+c y: 2 c x) \\\\ & Y=(2 a y: 2 b y: a t+b x+c y) \\end{aligned} $$ Finally, we have $B E=\\frac{1}{2}(c+x-t)$, and similarly for $C F$. Now if we reflect $D=$ $\\left(0, \\frac{s-c}{a}, \\frac{s-b}{a}\\right)$ over $I=\\left(\\frac{a}{2 s}, \\frac{b}{2 s}, \\frac{c}{2 s}\\right)$, we get the antipode $$ Q:=\\left(4 a^{2}:-a^{2}+2 a b-b^{2}+c^{2}:-a^{2}+2 a c-c^{2}+b^{2}\\right) . $$ We may then check $Q$ lies on each of lines $E X$ and $F Y$ (by checking $\\operatorname{det}(Q, E, X)=0$ using the equation (1)).", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 10 |
-
{"year": "2017", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "A sequence of positive integers $\\left(a_{n}\\right)_{n \\geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \\geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?", "solution": " 【 First solution (Kevin Sun). We are going to appeal to the so-called Zeckendorf theorem: Theorem (Zeckendorf) Every positive integer can be uniquely expressed as the sum of nonconsecutive Fibonacci numbers. This means every positive integer has a Zeckendorf (\"Fibonacci-binary\") representation where we put 1 in the $i$ th digit from the right if $F_{i+1}$ is used. The idea is then to take the following so-called Wythoff array: - Row 1: 1, 2, 3, 5, ... - Row 101: $1+3,2+5,3+8, \\ldots$ - Row 1001: $1+5,2+8,3+13, \\ldots$ - Row 10001: $1+8,2+13,3+21, \\ldots$ - Row 10101: $1+3+8,2+5+13,3+8+21, \\ldots$ - . . .et cetera. More concretely, the array has the following rows to start: | 1 | 2 | 3 | 5 | 8 | 13 | 21 | $\\ldots$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 4 | 7 | 11 | 18 | 29 | 47 | 76 | $\\ldots$ | | 6 | 10 | 16 | 26 | 42 | 68 | 110 | $\\ldots$ | | 9 | 15 | 24 | 39 | 63 | 102 | 165 | $\\ldots$ | | 12 | 20 | 32 | 52 | 84 | 136 | 220 | $\\ldots$ | | 14 | 23 | 37 | 60 | 97 | 157 | 254 | $\\ldots$ | | 17 | 28 | 45 | 73 | 118 | 191 | 309 | $\\ldots$ | | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\ddots$ | Here are the full details. $$ n-F_{k}<F_{k+1}-F_{k}=F_{k-1} . $$ In particular, repeatedly subtracting off the largest $F_{k}$ from $n$ will produce one such representation with no two consecutive Fibonacci numbers. On the other hand, this $F_{k}$ must be used, as $$ n \\geq F_{k}>F_{k-1}+F_{k-3}+F_{k-5}+\\cdots $$ This shows, by a simple inductive argument, that such a representation exists and unique. We write $n={\\bar{a} k \\ldots a_{1}}_{\\text {Fib }}$ for the Zeckendorf representation as we described (where $a_{i}=1$ if $F_{i+1}$ is used). Now for each ${\\bar{a} k \\ldots a_{1}}^{\\text {Fib }}$ with $a_{1}=1$, consider the sequence $$ {\\overline{a_{k} \\ldots a_{1}}}_{\\mathrm{Fib}},{\\overline{a_{k} \\ldots a_{1} 0}}_{\\mathrm{Fib}},{\\overline{a_{k} \\ldots a_{1} 00}}_{\\mathrm{Fib}}, \\ldots $$ These sequences are Fibonacci-type by definition, and partition the positive integers since each positive integer has exactly one Fibonacci base representation.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 11 |
-
{"year": "2017", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "A sequence of positive integers $\\left(a_{n}\\right)_{n \\geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \\geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?", "solution": " \\I Second solution. Call an infinite set of integers $S$ sandwiched if there exist increasing sequences $\\left\\{a_{i}\\right\\}_{i=0}^{\\infty},\\left\\{b_{i}\\right\\}_{i=0}^{\\infty}$ such that the following are true: - $a_{i}+a_{i+1}=a_{i+2}$ and $b_{i}+b_{i+1}=b_{i+2}$. - The intervals $\\left[a_{i}+1, b_{i}-1\\right]$ are disjoint and are nondecreasing in length. - $S=\\bigcup_{i=0}^{\\infty}\\left[a_{i}+1, b_{i}-1\\right]$. We claim that if $S$ is any nonempty sandwiched set, then $S$ can be partitioned into a Fibonacci-type sequence (involving the smallest element of $S$ ) and two smaller sandwiched sets. If this claim is proven, then we can start with $\\mathbb{N} \\backslash\\{1,2,3,5, \\ldots\\}$, which is a sandwiched set, and repeatedly perform this partition, which will eventually sort each natural number into a Fibonacci-type sequence. Let $S$ be a sandwiched set given by $\\left\\{a_{i}\\right\\}_{i=0}^{\\infty},\\left\\{b_{i}\\right\\}_{i=0}^{\\infty}$, so the smallest element in $S$ is $x=a_{0}+1$. Note that $y=a_{1}+1$ is also in $S$ and $x<y$. Then consider the Fibonaccitype sequence given by $f_{0}=x, f_{1}=y$, and $f_{k+2}=f_{k+1}+f_{k}$. We can then see that $f_{i} \\in\\left[a_{i}+1, b_{i}-1\\right]$, as the sum of numbers in the intervals $\\left[a_{k}+1, b_{k}-1\\right],\\left[a_{k+1}+1, b_{k+1}-1\\right]$ lies in the interval $$ \\left[a_{k}+a_{k+1}+2, b_{k}+b_{k+1}-2\\right]=\\left[a_{k+2}+2, b_{k+2}-2\\right] \\subset\\left[a_{k+2}+1, b_{k+2}-1\\right] $$ Therefore, this gives a natural partition of $S$ into this sequence and two sets: $$ \\begin{aligned} S_{1} & =\\bigcup_{i=0}^{\\infty}\\left[a_{i}+1, f_{i}-1\\right] \\\\ \\text { and } S_{2} & =\\bigcup_{i=0}^{\\infty}\\left[f_{i}+1, b_{i}-1\\right] . \\end{aligned} $$ (For convenience, $[x, x-1]$ will be treated as the empty set.) We now show that $S_{1}$ and $S_{2}$ are sandwiched. Since $\\left\\{a_{i}\\right\\},\\left\\{f_{i}\\right\\}$, and $\\left\\{b_{i}\\right\\}$ satisfy the Fibonacci recurrence, it is enough to check that the intervals have nondecreasing lengths. For $S_{1}$, that is equivalent to $f_{k+1}-a_{k+1} \\geq f_{k}-a_{k}$ for each $k$. Fortunately, for $k \\geq 1$, the difference is $f_{k-1}-a_{k-1} \\geq 0$, and for $k=0, f_{1}-a_{1}=1=f_{0}-a_{0}$. Similarly for $S_{2}$, checking $b_{k+1}-f_{k+1} \\geq b_{k}-f_{k}$ is easy for $k \\geq 1$ as $b_{k-1}-f_{k-1} \\geq 0$, and $$ \\left(b_{1}-f_{1}\\right)-\\left(b_{0}-f_{0}\\right)=\\left(b_{1}-a_{1}\\right)-\\left(b_{0}-a_{0}\\right) $$ which is nonnegative since the lengths of intervals in $S$ are nondecreasing. Therefore we have shown that $S_{1}$ and $S_{2}$ are sandwiched. (Note that some of the $\\left[a_{i}+1, f_{i}-1\\right]$ may be empty, which would shift some indices back.) Since this gives us a procedure to take a set $S$ and produce a Fibonacci-type sequence with its smallest element, along which two other sandwiched types, we can partition $\\mathbb{N}$ into an infinite number of Fibonacci-type sequences.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 12 |
-
{"year": "2017", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "A sequence of positive integers $\\left(a_{n}\\right)_{n \\geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \\geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?", "solution": " \\l Third solution. We add Fibonacci-type sequences one-by-one. At each step, let $x$ be the smallest number that has not been used in any previous sequence. We generate a new Fibonacci-type sequence as follows. Set $a_{0}=x$ and for $i \\geq 1$, set $$ a_{i}=\\left\\lfloor\\varphi a_{i-1}+\\frac{1}{2}\\right\\rfloor $$ Equivalently, $a_{i}$ is the closest integer to $\\varphi a_{i-1}$. It suffices to show that this sequence is Fibonacci-type and that no two sequences generated in this way overlap. We first show that for a positive integer $n$, $$ \\left\\lfloor\\varphi\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor+\\frac{1}{2}\\right\\rfloor=n+\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor . $$ Indeed, $$ \\begin{aligned} \\left\\lfloor\\varphi\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor+\\frac{1}{2}\\right\\rfloor & =\\left\\lfloor\\left(1+\\varphi^{-1}\\right)\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor+\\frac{1}{2}\\right\\rfloor \\\\ & =\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor+\\left\\lfloor\\varphi^{-1}\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor+\\frac{1}{2}\\right\\rfloor . \\end{aligned} $$ Note that $\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor=\\varphi n+c$ for some $|c| \\leq \\frac{1}{2}$; this implies that $\\varphi^{-1}\\left\\lfloor\\varphi n+\\frac{1}{2}\\right\\rfloor$ is within $\\varphi^{-1} \\cdot \\frac{1}{2}<\\frac{1}{2}$ of $n$, so its closest integer is $n$, proving the claim. Therefore these sequences are Fibonacci-type. Additionally, if $a \\neq b$, then $|\\varphi a-\\varphi b| \\geq$ $\\varphi>1$. Then $$ a \\neq b \\Longrightarrow\\left\\lfloor\\varphi a+\\frac{1}{2}\\right\\rfloor \\neq\\left\\lfloor\\varphi b+\\frac{1}{2}\\right\\rfloor, $$ and since the first term of each sequence is chosen to not overlap with any previous sequences, these sequences are disjoint. Remark. Ankan Bhattacharya points out that the same sequence essentially appears in IMO 1993, Problem 5 - in other words, a strictly increasing function $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ with $f(1)=2$, and $f(f(n))=f(n)+n$. Nikolai Beluhov sent us an older reference from March 1977, where Martin Gardner wrote in his column about Wythoff's Nim. The relevant excerpt goes: \"Imagine that we go through the infinite sequence of safe pairs (in the manner of Eratosthenes' sieve for sifting out primes) and cross out the infinite set of all safe pairs that are pairs in the Fibonacci sequence. The smallest pair that is not crossed out is $4 / 7$. We can now cross out a second infinite set of safe pairs, starting with $4 / 7$, that are pairs in the Lucas sequence. An infinite number of safe pairs, of which the lowest is now $6 / 10$, remain. This pair too begins another infinite Fibonacci sequence, all of whose pairs are safe. The process continues forever. Robert Silber, a mathematician at North Carolina State University, calls a safe pair \"primitive\" if it is the first safe pair that generates a Fibonacci sequence.\" The relevant article by Robert Silber is A Fibonacci Property of Wythoff Pairs, from The Fibonacci Quarterly 11/1976.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
| 13 |
-
{"year": "2017", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "A sequence of positive integers $\\left(a_{n}\\right)_{n \\geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \\geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?", "solution": " I Fourth solution (Mark Sellke). For later reference let $$ f_{1}=0, f_{2}=1, f_{3}=1, \\ldots $$ denote the ordinary Fibonacci numbers. We will denote the Fibonacci-like sequences by $F^{i}$ and the elements with subscripts; hence $F_{1}^{2}$ is the first element of the second sequence. Our construction amounts to just iteratively add new sequences; hence the following claim is the whole problem. ## Lemma For any disjoint collection of Fibonacci-like sequences $F^{1}, \\ldots, F^{k}$ and any integer $m$ contained in none of them, there is a new Fibonacci-like sequence $F^{k+1}$ beginning with $F_{1}^{k+1}=m$ which is disjoint from the previous sequences. Observe first that for each sequence $F^{j}$ there is $c^{j} \\in \\mathbb{R}^{n}$ such that $$ F_{n}^{j}=c^{j} \\phi^{n}+o(1) $$ where $$ \\phi=\\frac{1+\\sqrt{5}}{2} $$ Collapse the group $\\left(\\mathbb{R}^{+}, \\times\\right)$into the half-open interval $J=\\{x \\mid 1 \\leq x<\\phi\\}$ by defining $T(x)=y$ for the unique $y \\in J$ with $x=y \\phi^{n}$ for some integer $n$. Fix an interval $I=[a, b] \\subseteq[1.2,1.3]$ (the last condition is to avoid wrap-around issues) which contains none of the $c^{j}$, and take $\\varepsilon<0.001$ to be small enough that in fact each $c^{j}$ has distance at least $10 \\varepsilon$ from $I$; this means any $c_{j}$ and element of $I$ differ by at least a $(1+10 \\varepsilon)$ factor. The idea will be to take $F_{1}^{k+1}=m$ and $F_{2}^{k+1}$ to be a large such that the induced values of $F_{j}^{k+1}$ grow like $k \\phi^{j}$ for $j \\in T^{-1}(I)$, so that $F_{n}^{k+1}$ is separated from the $c^{j}$ after applying $T$. What's left to check is the convergence. Now let $$ c=\\lim _{n \\rightarrow \\infty} \\frac{f_{n}}{\\phi^{n}} $$ and take $M$ large enough that for $n>M$ we have $$ \\left|\\frac{f_{n}}{c \\phi^{n}}-1\\right|<\\varepsilon $$ Now $\\frac{T^{-1}(I)}{c}$ contains arbitrarily large integers, so there are infinitely many $N$ with $c N \\in T^{-1}(I)$ with $N>\\frac{10 m}{\\varepsilon}$. We claim that for any such $N$, the sequence $F^{(N)}$ defined by $$ F_{1}^{(N)}=m, F_{2}^{(N)}=N $$ will be very multiplicatively similar to the normal Fibonacci numbers up to rescaling; indeed for $j=2, j=3$ we have $\\frac{F_{2}^{(N)}}{f_{2}}=N, \\frac{F_{3}^{(N)}}{f_{3}}=N+m$ and so by induction we will have $$ \\frac{F_{j}^{(N)}}{f_{j}} \\in[N, N+m] \\subseteq[N, N(1+\\varepsilon)] $$ for $j \\geq 2$. Therefore, up to small multiplicative errors, we have $$ F_{j}^{(N)} \\approx N f_{j} \\approx c N \\phi^{j} $$ From this we see that for $j>M$ we have $$ T\\left(F_{j}^{(N)}\\right) \\in T(c N) \\cdot[1-2 \\varepsilon, 1+2 \\varepsilon] $$ In particular, since $T(c N) \\in I$ and $I$ is separated from each $c_{j}$ by a factor of $(1+10 \\varepsilon)$, we get that $F_{j}^{(N)}$ is not in any of $F^{1}, F^{2}, \\ldots, F^{k}$. Finishing is easy, since we now have a uniform estimate on how many terms we need to check for a new element before the exponential growth takes over. We will just use pigeonhole to argue that there are few possible collisions among those early terms, so we can easily pick a value of $N$ which avoids them all. We write it out below. For large $L$, the set $$ S_{L}=\\left(I \\cdot \\phi^{L}\\right) \\cap \\mathbb{Z} $$ contains at least $k_{I} \\phi^{L}$ elements. As $N$ ranges over $S_{L}$, for each fixed $j$, the value of $F_{j}^{(N)}$ varies by at most a factor of 1.1 because we imposed $I \\subseteq[1.2,1.3]$ and so this is true for the first two terms, hence for all subsequent terms by induction. Now suppose $L$ is very large, and consider a fixed pair $(i, j)$ with $i \\leq k$ and $j \\leq M$. We claim there is at most 1 possible value $k$ such that the term $F_{k}^{i}$ could equal $F_{j}^{(N)}$ for some $N \\in S_{L}$; indeed, the terms of $F^{i}$ are growing at exponential rate with factor $\\phi>1.1$, so at most one will be in a given interval of multiplicative width at most 1.1. Hence, of these $k_{I} \\phi^{L}$ values of $N$, at most $k M$ could cause problems, one for each pair $(i, j)$. However by monotonicity of $F_{j}^{(N)}$ in $N$, at most 1 value of $N$ causes a collision for each pair $(i, j)$. Hence for large $L$ so that $k_{I} \\phi^{L}>10 k M$ we can find a suitable $N \\in S_{L}$ by pigeonhole and the sequence $F^{(N)}$ defined by $(m, N, N+m, \\ldots)$ works.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2017.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl
DELETED
|
@@ -1,14 +0,0 @@
|
|
| 1 |
-
{"year": "2018", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "As usual, let $\\mathbb{Z}[x]$ denote the set of single-variable polynomials in $x$ with integer coefficients. Find all functions $\\theta: \\mathbb{Z}[x] \\rightarrow \\mathbb{Z}$ such that for any polynomials $p, q \\in$ $\\mathbb{Z}[x]$, - $\\theta(p+1)=\\theta(p)+1$, and - if $\\theta(p) \\neq 0$ then $\\theta(p)$ divides $\\theta(p \\cdot q)$.", "solution": " The answer is $\\theta: p \\mapsto p(c)$, for each choice of $c \\in \\mathbb{Z}$. Obviously these work, so we prove these are the only ones. In what follows, $x \\in \\mathbb{Z}[x]$ is the identity polynomial, and $c=\\theta(x)$. 【 First solution (Merlijn Staps). Consider an integer $n \\neq c$. Because $x-n \\mid p(x)-p(n)$, we have $$ \\theta(x-n)|\\theta(p(x)-p(n)) \\Longrightarrow c-n| \\theta(p(x))-p(n) . $$ On the other hand, $c-n \\mid p(c)-p(n)$. Combining the previous two gives $c-n \\mid$ $\\theta(p(x))-p(c)$, and by letting $n$ large we conclude $\\theta(p(x))-p(c)=0$, so $\\theta(p(x))=p(c)$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 2 |
-
{"year": "2018", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "As usual, let $\\mathbb{Z}[x]$ denote the set of single-variable polynomials in $x$ with integer coefficients. Find all functions $\\theta: \\mathbb{Z}[x] \\rightarrow \\mathbb{Z}$ such that for any polynomials $p, q \\in$ $\\mathbb{Z}[x]$, - $\\theta(p+1)=\\theta(p)+1$, and - if $\\theta(p) \\neq 0$ then $\\theta(p)$ divides $\\theta(p \\cdot q)$.", "solution": " The answer is $\\theta: p \\mapsto p(c)$, for each choice of $c \\in \\mathbb{Z}$. Obviously these work, so we prove these are the only ones. In what follows, $x \\in \\mathbb{Z}[x]$ is the identity polynomial, and $c=\\theta(x)$. II Second solution. First, we settle the case $\\operatorname{deg} p=0$. In that case, from the second property, $\\theta(m)=m+\\theta(0)$ for every integer $m \\in \\mathbb{Z}$ (viewed as a constant polynomial). Thus $m+\\theta(0) \\mid 2 m+\\theta(0)$, hence $m+\\theta(0) \\mid-\\theta(0)$, so $\\theta(0)=0$ by taking $m$ large. Thus $\\theta(m)=m$ for $m \\in \\mathbb{Z}$. Next, we address the case of $\\operatorname{deg} p=1$. We know $\\theta(x+b)=c+b$ for $b \\in \\mathbb{Z}$. Now for each particular $a \\in \\mathbb{Z}$, we have $$ c+k|\\theta(x+k)| \\theta(a x+a k)=\\theta(a x)+a k \\Longrightarrow c+k \\mid \\theta(a x)-a c . $$ for any $k \\neq-c$. Since this is true for large enough $k$, we conclude $\\theta(a x)=a c$. Thus $\\theta(a x+b)=a c+b$. We now proceed by induction on $\\operatorname{deg} p$. Fix a polynomial $p$ and assume it's true for all $p$ of smaller degree. Choose a large integer $n$ (to be determined later) for which $p(n) \\neq p(c)$. We then have $$ \\left.\\frac{p(c)-p(n)}{c-n}=\\theta\\left(\\frac{p-p(n)}{x-n}\\right) \\right\\rvert\\, \\theta(p-p(n))=\\theta(p)-p(n) $$ Subtracting off $c-n$ times the left-hand side gives $$ \\left.\\frac{p(c)-p(n)}{c-n} \\right\\rvert\\, \\theta(p)-p(c) $$ The left-hand side can be made arbitrarily large by letting $n \\rightarrow \\infty$, since $\\operatorname{deg} p \\geq 2$. Thus $\\theta(p)=p(c)$, concluding the proof. \\ Authorship comments. I will tell you a story about the creation of this problem. Yang Liu and I were looking over the drafts of December and January TST in October 2017, and both of us had the impression that the test was too difficult. This sparked a non-serious suggestion that we should try to come up with a problem now that would be easy enough to use. While we ended up just joking about changing the TST, we did get this problem out of it. Our idea was to come up with a functional equation that was different from the usual fare: at first we tried $\\mathbb{Z}[x] \\rightarrow \\mathbb{Z}[x]$, but then I suggested the idea of using $\\mathbb{Z}[x] \\rightarrow \\mathbb{Z}$, with the answer being the \"evaluation\" map. Well, what properties does that satisfy? One answer was $a-b \\mid p(a)-p(b)$; this didn't immediately lead to anything, but eventually we hit on the form of the problem above off this idea. At first we didn't require $\\theta(p) \\neq 0$ in the bullet, but without the condition the problem was too easy, since 0 divides only itself; and so the condition was added and we got the functional equation. I proposed the problem to USAMO 2018, but it was rejected (unsurprisingly; I think the problem may be too abstract for novice contestants). Instead it was used for TSTST, which I thought fit better.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 3 |
-
{"year": "2018", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "In the nation of Onewaynia, certain pairs of cities are connected by one-way roads. Every road connects exactly two cities (roads are allowed to cross each other, e.g., via bridges), and each pair of cities has at most one road between them. Moreover, every city has exactly two roads leaving it and exactly two roads entering it. We wish to close half the roads of Onewaynia in such a way that every city has exactly one road leaving it and exactly one road entering it. Show that the number of ways to do so is a power of 2 greater than 1 (i.e. of the form $2^{n}$ for some integer $n \\geq 1$ ).", "solution": " In the language of graph theory, we have a simple digraph $G$ which is 2 -regular and we seek the number of sub-digraphs which are 1-regular. We now present two solution paths. 『 First solution, combinatorial. We construct a simple undirected bipartite graph $\\Gamma$ as follows: - the vertex set consists of two copies of $V(G)$, say $V_{\\text {out }}$ and $V_{\\text {in }}$; and - for $v \\in V_{\\text {out }}$ and $w \\in V_{\\text {in }}$ we have an undirected edge $v w \\in E(\\Gamma)$ if and only if the directed edge $v \\rightarrow w$ is in $G$. Moreover, the desired sub-digraphs of $H$ correspond exactly to perfect matchings of $\\Gamma$. However the graph $\\Gamma$ is 2 -regular and hence consists of several disjoint (simple) cycles of even length. If there are $n$ such cycles, the number of perfect matchings is $2^{n}$, as desired. Remark. The construction of $\\Gamma$ is not as magical as it may first seem. Suppose we pick a road $v_{1} \\rightarrow v_{2}$ to use. Then, the other road $v_{3} \\rightarrow v_{2}$ is certainly not used; hence some other road $v_{3} \\rightarrow v_{4}$ must be used, etc. We thus get a cycle of forced decisions until we eventually return to the vertex $v_{1}$. These cycles in the original graph $G$ (where the arrows alternate directions) correspond to the cycles we found in $\\Gamma$. It's merely that phrasing the solution in terms of $\\Gamma$ makes it cleaner in a linguistic sense, but not really in a mathematical sense.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 4 |
-
{"year": "2018", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "In the nation of Onewaynia, certain pairs of cities are connected by one-way roads. Every road connects exactly two cities (roads are allowed to cross each other, e.g., via bridges), and each pair of cities has at most one road between them. Moreover, every city has exactly two roads leaving it and exactly two roads entering it. We wish to close half the roads of Onewaynia in such a way that every city has exactly one road leaving it and exactly one road entering it. Show that the number of ways to do so is a power of 2 greater than 1 (i.e. of the form $2^{n}$ for some integer $n \\geq 1$ ).", "solution": " In the language of graph theory, we have a simple digraph $G$ which is 2 -regular and we seek the number of sub-digraphs which are 1-regular. We now present two solution paths. 【 Second solution by linear algebra over $\\mathbb{F}_{2}$ (Brian Lawrence). This is actually not that different from the first solution. For each edge $e$, we create an indicator variable $x_{e}$. We then require for each vertex $v$ that: - If $e_{1}$ and $e_{2}$ are the two edges leaving $v$, then we require $x_{e_{1}}+x_{e_{2}} \\equiv 1(\\bmod 2)$. - If $e_{3}$ and $e_{4}$ are the two edges entering $v$, then we require $x_{e_{3}}+x_{e_{4}} \\equiv 1(\\bmod 2)$. We thus get a large system of equations. Moreover, the solutions come in natural pairs $\\vec{x}$ and $\\vec{x}+\\overrightarrow{1}$ and therefore the number of solutions is either zero, or a power of two. So we just have to prove there is at least one solution. For linear algebra reasons, there can only be zero solutions if some nontrivial linear combination of the equations gives the sum $0 \\equiv 1$. So suppose we added up some subset $S$ of the equations for which every variable appeared on the left-hand side an even number of times. Then every variable that did appear appeared exactly twice; and accordingly we see that the edges corresponding to these variables form one or more even cycles as in the previous solution. Of course, this means $|S|$ is even, so we really have $0 \\equiv 0(\\bmod 2)$ as needed. Remark. The author's original proposal contained a second part asking to show that it was not always possible for the resulting $H$ to be connected, even if $G$ was strongly connected. This problem is related to IMO Shortlist 2002 C6, which gives an example of a strongly connected graph which does have a full directed Hamiltonian cycle.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 5 |
-
{"year": "2018", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\\Gamma$. Let $M$ be the midpoint of $\\overline{A B}$. Ray $A I$ meets $\\overline{B C}$ at $D$. Denote by $\\omega$ and $\\gamma$ the circumcircles of $\\triangle B I C$ and $\\triangle B A D$, respectively. Line $M O$ meets $\\omega$ at $X$ and $Y$, while line $C O$ meets $\\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\\triangle A B C$ and $\\angle A Q M=\\angle A C B$. Consider the tangents to $\\omega$ at $X$ and $Y$ and the tangents to $\\gamma$ at $A$ and $D$. Given that $\\angle B A C \\neq 60^{\\circ}$, prove that these four lines are concurrent on $\\Gamma$.", "solution": " Henceforth assume $\\angle A \\neq 60^{\\circ}$; we prove the concurrence. Let $L$ denote the center of $\\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\\omega$ such that $\\overline{K L} \\| \\overline{A B}$ and $\\overline{K C} \\| \\overline{A L}$. Then $\\overline{K A}$ is tangent to $\\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\\overline{K A}$ is tangent to $\\gamma$ as well since $$ \\measuredangle K A D=\\measuredangle K A L=\\measuredangle K A C+\\measuredangle C A L=\\measuredangle K B C+\\measuredangle A B K=\\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \\neq O$, since $\\angle A \\neq 60^{\\circ} \\Longrightarrow O \\notin \\omega$. Moreover, we have $\\angle A O M=\\angle A C B$ too. Since $O$ and $Q$ both lie inside $\\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \\neq O$ we conclude $\\angle C Q A=90^{\\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\\overline{K X}$ and $\\overline{K Y}$ are tangent to $\\omega$. First proof of Claim, communicated by Milan Haiman. Observe that $\\triangle Q L C \\sim \\triangle L O C$ since both triangles are isosceles and share a base angle. Hence, $C L^{2}=C O \\cdot C Q$. Let $N$ be the midpoint of $\\overline{A C}$, which lies on $(A M O Q)$. Then, $$ x^{2}=C L^{2}=C O \\cdot C Q=C N \\cdot C A=\\frac{1}{2} C A^{2}=\\frac{1}{2} L K^{2} $$ where we have also used the fact $A Q O N$ is cyclic. Thus $L K=\\sqrt{2} x$ and so the rhombus $L X K Y$ is actually a square.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 6 |
-
{"year": "2018", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\\Gamma$. Let $M$ be the midpoint of $\\overline{A B}$. Ray $A I$ meets $\\overline{B C}$ at $D$. Denote by $\\omega$ and $\\gamma$ the circumcircles of $\\triangle B I C$ and $\\triangle B A D$, respectively. Line $M O$ meets $\\omega$ at $X$ and $Y$, while line $C O$ meets $\\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\\triangle A B C$ and $\\angle A Q M=\\angle A C B$. Consider the tangents to $\\omega$ at $X$ and $Y$ and the tangents to $\\gamma$ at $A$ and $D$. Given that $\\angle B A C \\neq 60^{\\circ}$, prove that these four lines are concurrent on $\\Gamma$.", "solution": " Henceforth assume $\\angle A \\neq 60^{\\circ}$; we prove the concurrence. Let $L$ denote the center of $\\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\\omega$ such that $\\overline{K L} \\| \\overline{A B}$ and $\\overline{K C} \\| \\overline{A L}$. Then $\\overline{K A}$ is tangent to $\\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\\overline{K A}$ is tangent to $\\gamma$ as well since $$ \\measuredangle K A D=\\measuredangle K A L=\\measuredangle K A C+\\measuredangle C A L=\\measuredangle K B C+\\measuredangle A B K=\\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \\neq O$, since $\\angle A \\neq 60^{\\circ} \\Longrightarrow O \\notin \\omega$. Moreover, we have $\\angle A O M=\\angle A C B$ too. Since $O$ and $Q$ both lie inside $\\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \\neq O$ we conclude $\\angle C Q A=90^{\\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\\overline{K X}$ and $\\overline{K Y}$ are tangent to $\\omega$. Second proof of Claim, Evan Chen. Observe that $Q$ lies on the circle with diameter $\\overline{A C}$, centered at $N$, say. This means that $O$ lies on the radical axis of $\\omega$ and $(N)$, hence $\\overline{N L} \\perp \\overline{C O}$ implying $$ \\begin{aligned} N O^{2}+C L^{2} & =N C^{2}+L O^{2}=N C^{2}+O C^{2}=N C^{2}+N O^{2}+N C^{2} \\\\ \\Longrightarrow x^{2} & =2 N C^{2} \\\\ \\Longrightarrow x & =\\sqrt{2} N C=\\frac{1}{\\sqrt{2}} A C=\\frac{1}{\\sqrt{2}} L K \\end{aligned} $$ So $L X K Y$ is a rhombus with $L K=\\sqrt{2} x$. Hence it is a square.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 7 |
-
{"year": "2018", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\\Gamma$. Let $M$ be the midpoint of $\\overline{A B}$. Ray $A I$ meets $\\overline{B C}$ at $D$. Denote by $\\omega$ and $\\gamma$ the circumcircles of $\\triangle B I C$ and $\\triangle B A D$, respectively. Line $M O$ meets $\\omega$ at $X$ and $Y$, while line $C O$ meets $\\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\\triangle A B C$ and $\\angle A Q M=\\angle A C B$. Consider the tangents to $\\omega$ at $X$ and $Y$ and the tangents to $\\gamma$ at $A$ and $D$. Given that $\\angle B A C \\neq 60^{\\circ}$, prove that these four lines are concurrent on $\\Gamma$.", "solution": " Henceforth assume $\\angle A \\neq 60^{\\circ}$; we prove the concurrence. Let $L$ denote the center of $\\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\\omega$ such that $\\overline{K L} \\| \\overline{A B}$ and $\\overline{K C} \\| \\overline{A L}$. Then $\\overline{K A}$ is tangent to $\\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\\overline{K A}$ is tangent to $\\gamma$ as well since $$ \\measuredangle K A D=\\measuredangle K A L=\\measuredangle K A C+\\measuredangle C A L=\\measuredangle K B C+\\measuredangle A B K=\\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \\neq O$, since $\\angle A \\neq 60^{\\circ} \\Longrightarrow O \\notin \\omega$. Moreover, we have $\\angle A O M=\\angle A C B$ too. Since $O$ and $Q$ both lie inside $\\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \\neq O$ we conclude $\\angle C Q A=90^{\\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\\overline{K X}$ and $\\overline{K Y}$ are tangent to $\\omega$. Third proof of Claim. A solution by trig is also possible. As in the previous claims, it suffices to show that $A C=\\sqrt{2} x$. First, we compute the length $C Q$ in two ways; by angle chasing one can show $\\angle C B Q=$ $180^{\\circ}-(\\angle B Q C+\\angle Q C B)=\\frac{1}{2} \\angle A$, and so $$ \\begin{aligned} A C \\sin B=C Q & =\\frac{B C}{\\sin \\left(90^{\\circ}+\\frac{1}{2} \\angle A\\right)} \\cdot \\sin \\frac{1}{2} \\angle A \\\\ \\Longleftrightarrow \\sin ^{2} B & =\\frac{\\sin A \\cdot \\sin \\frac{1}{2} \\angle A}{\\cos \\frac{1}{2} \\angle A} \\\\ \\Longleftrightarrow \\sin ^{2} B & =2 \\sin ^{2} \\frac{1}{2} \\angle A \\\\ \\Longleftrightarrow \\sin B & =\\sqrt{2} \\sin \\frac{1}{2} \\angle A \\\\ \\Longleftrightarrow 2 R \\sin B & =\\sqrt{2}\\left(2 R \\sin \\frac{1}{2} \\angle A\\right) \\\\ \\Longleftrightarrow A C & =\\sqrt{2} x \\end{aligned} $$ as desired (we have here used the fact $\\triangle A B C$ is acute to take square roots). It is interesting to note that $\\sin ^{2} B=2 \\sin ^{2} \\frac{1}{2} \\angle A$ can be rewritten as $$ \\cos A=\\cos ^{2} B $$ since $\\cos ^{2} B=1-\\sin ^{2} B=1-2 \\sin ^{2} \\frac{1}{2} \\angle A=\\cos A$; this is the condition for the existence of the point $Q$. We finish by proving that $$ K D=K A $$ and hence line $\\overline{K D}$ is tangent to $\\gamma$. Let $E=\\overline{B C} \\cap \\overline{K L}$. Then $$ L E \\cdot L K=L C^{2}=L X^{2}=\\frac{1}{2} L K^{2} $$ and so $E$ is the midpoint of $\\overline{L K}$. Thus $\\overline{M X O Y}, \\overline{B C}, \\overline{K L}$ are concurrent at $E$. As $\\overline{D L} \\| \\overline{K C}$, we find that $D L C K$ is a parallelogram, so $K D=C L=K A$ as well. Thus $\\overline{K D}$ and $\\overline{K A}$ are tangent to $\\gamma$. Remark. The condition $\\angle A \\neq 60^{\\circ}$ cannot be dropped, since if $Q=O$ the problem is not true. \\ Authorship comments. In the notation of the present points, the question originally sent to me by Yannick Yao read: Circles $(L)$ and $(O)$ are drawn, meeting at $B$ and $C$, with $L$ on $(O)$. Ray $C O$ meets $(L)$ at $Q$, and $A$ is on $(O)$ such that $\\angle C Q A=90^{\\circ}$. The angle bisector of $\\angle A O B$ meets $(L)$ at $X$ and $Y$. Show that $\\angle X L Y=90^{\\circ}$. Notice the points $M$ and $K$ are absent from the problem. I am told this was found as part of the computer game \"Euclidea\". Using this as the starting point, I constructed the TSTST problem by recognizing the significance of that special point $K$, which became the center of attention.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 8 |
-
{"year": "2018", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "For an integer $n>0$, denote by $\\mathcal{F}(n)$ the set of integers $m>0$ for which the polynomial $p(x)=x^{2}+m x+n$ has an integer root. (a) Let $S$ denote the set of integers $n>0$ for which $\\mathcal{F}(n)$ contains two consecutive integers. Show that $S$ is infinite but $$ \\sum_{n \\in S} \\frac{1}{n} \\leq 1 $$ (b) Prove that there are infinitely many positive integers $n$ such that $\\mathcal{F}(n)$ contains three consecutive integers.", "solution": " We prove the following. Claim - The set $S$ is given explicitly by $S=\\{x(x+1) y(y+1) \\mid x, y>0\\}$. $$ \\begin{aligned} m^{2}-4 n & =p^{2} \\\\ (m+1)^{2}-4 n & =q^{2} \\end{aligned} $$ Subtraction gives $2 m+1=q^{2}-p^{2}$, so $p$ and $q$ are different parities. We can thus let $q-p=2 x+1, q+p=2 y+1$, where $y \\geq x \\geq 0$ are integers. It follows that $$ \\begin{aligned} 4 n & =m^{2}-p^{2} \\\\ & =\\left(\\frac{q^{2}-p^{2}-1}{2}\\right)^{2}-p^{2}=\\left(\\frac{q^{2}-p^{2}-1}{2}-p\\right)\\left(\\frac{q^{2}-p^{2}-1}{2}+p\\right) \\\\ & =\\frac{q^{2}-\\left(p^{2}+2 p+1\\right)}{2} \\cdot \\frac{q^{2}-\\left(p^{2}-2 p+1\\right)}{2} \\\\ & =\\frac{1}{4}(q-p-1)(q-p+1)(q+p-1)(q+p+1)=\\frac{1}{4}(2 x)(2 x+2)(2 y)(2 y+2) \\\\ \\Longrightarrow n & =x(x+1) y(y+1) . \\end{aligned} $$ Since $n>0$ we require $x, y>0$. Conversely, if $n=x(x+1) y(y+1)$ for positive $x$ and $y$ then $m=\\sqrt{p^{2}+4 n}=\\sqrt{(y-x)^{2}+4 n}=2 x y+x+y=x(y+1)+(x+1) y$ and $m+1=2 x y+x+y+1=x y+(x+1)(y+1)$. Thus we conclude the main claim. From this, part (a) follows as $$ \\sum_{n \\in S} n^{-1} \\leq\\left(\\sum_{x \\geq 1} \\frac{1}{x(x+1)}\\right)\\left(\\sum_{y \\geq 1} \\frac{1}{y(y+1)}\\right)=1 \\cdot 1=1 $$ $$ \\begin{aligned} r^{2} & =(m+2)^{2}-4 n=m^{2}-4 n+4 m+4=p^{2}+2+2(2 m+1) \\\\ & =p^{2}+2\\left(q^{2}-p^{2}\\right)+2=2 q^{2}-p^{2}+2 \\\\ \\Longleftrightarrow 2 q^{2}+2 & =p^{2}+r^{2} \\quad(\\dagger) \\end{aligned} $$ with $q>p$ of different parity and $n=\\frac{1}{16}(q-p-1)(q-p+1)(q+p-1)(q+p+1)$. Note that (by taking modulo 8 ) we have $q \\not \\equiv p \\equiv r(\\bmod 2)$, and so there are no parity issues and we will always assume $p<q<r$ in ( $\\dagger$ ). Now, for every $q$, the equation ( $\\dagger$ ) has a canonical solution $(p, r)=(q-1, q+1)$, but this leaves $n=0$. Thus we want to show for infinitely many $q$ there is a third way to write $2 q^{2}+2$ as a sum of squares, which will give the desired $p$. To do this, choose large integers $q$ such that $q^{2}+1$ is divisible by at least three distinct $1 \\bmod 4$ primes. Since each such prime can be written as a sum of two squares, using Lagrange identity, we can deduce that $2 q^{2}+2$ can be written as a sum of two squares in at least three different ways, as desired. Remark. We can see that $n=144$ is the smallest integer such that $\\mathcal{F}(n)$ contains three consecutive integers and $n=15120$ is the smallest integer such that $\\mathcal{F}(n)$ contains four consecutive integers. It would be interesting to determine whether the number of consecutive elements in $\\mathcal{F}(n)$ can be arbitrarily large or is bounded.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 9 |
-
{"year": "2018", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with circumcircle $\\omega$, and let $H$ be the foot of the altitude from $A$ to $\\overline{B C}$. Let $P$ and $Q$ be the points on $\\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that the circumcircles of $\\triangle A E_{1} F_{1}$ and $\\triangle A E_{2} F_{2}$ are congruent, and the line through their centers is parallel to the tangent to $\\omega$ at $A$.", "solution": " Let $O$ be the center of $\\omega$, and let $M=\\overline{P Q} \\cap \\overline{A B}$ and $N=\\overline{P Q} \\cap \\overline{A C}$ be the midpoints of $\\overline{A B}$ and $\\overline{A C}$ respectively. Refer to the diagram below.  The main idea is to prove two key claims involving $O$, which imply the result: (i) quadrilaterals $A O E_{1} F_{1}$ and $A O E_{2} F_{2}$ are cyclic (giving the radical axis is $\\overline{A O}$ ), (ii) $\\triangle O E_{1} F_{1} \\cong \\triangle O E_{2} F_{2}$ (giving the congruence of the circles). We first note that (i) and (ii) are equivalent. Indeed, because $O P=O Q$, (ii) is equivalent to just the similarity $\\triangle O E_{1} F_{1} \\sim \\triangle O E_{2} F_{2}$, and then by the spiral similarity lemma (or even just angle chasing) we have (i) $\\Longleftrightarrow$ (ii). $$ \\measuredangle F_{2} E_{2} O=\\measuredangle Q E_{2} O=\\measuredangle Q N O=\\measuredangle M N O=\\measuredangle M A O=\\measuredangle F_{2} A O $$ and hence $E_{2} O A F_{2}$ is cyclic. Similarly, $E_{1} O A F_{1}$ is cyclic. $$ E_{1} P=\\sqrt{E_{1} A \\cdot E_{1} C}=\\sqrt{E_{2} A \\cdot E_{2} C}=E_{2} P $$ But also $O P=O Q$ and hence $\\triangle O P E_{1} \\cong \\triangle O Q E_{2}$. Similarly for the other pair. Now, $$ -1=(P Q ; N S) \\stackrel{T}{=}\\left(E_{1} E_{2} ; N \\infty\\right) $$ with $\\infty=\\overline{A C} \\cap \\overline{S T}$ the point at infinity. Hence $E_{1} N=N E_{2}$ and we can proceed as in the previous solution. Remark. The assumption that $\\triangle A B C$ is acute is not necessary; it is only present to ensure that $P$ lies on segment $E_{1} F_{1}$ and $Q$ lies on segment $E_{2} F_{2}$, which may be helpful for contestants. The argument presented above is valid in all configurations. When one of $\\angle B$ and $\\angle C$ is a right angle, some of the points $E_{1}, F_{1}, E_{2}, F_{2}$ lie at infinity; when one of them is obtuse, both $P$ and $Q$ lie outside segments $E_{1} F_{1}$ and $E_{2} F_{2}$ respectively. We place $A P B C Q$ on the unit circle. Since $\\overline{P Q} \\| \\overline{B C}$, we have $p q=b c$. Also, the midpoint of $\\overline{A B}$ lies on $\\overline{P Q}$, so $$ \\begin{aligned} p+q & =\\frac{a+b}{2}+\\overline{\\left(\\frac{a+b}{2}\\right)} \\cdot p q \\\\ & =\\frac{a+b}{2}+\\frac{a+b}{2 a b} \\cdot b c \\\\ & =\\frac{a(a+b)}{2 a}+\\frac{c(a+b)}{2 a} \\\\ & =\\frac{(a+b)(a+c)}{2 a} . \\end{aligned} $$ Now, $$ \\begin{aligned} p-e_{1} & =p-\\frac{p p(a+c)-a c(p+p)}{p p-a c} \\\\ & =\\frac{p\\left(p^{2}-p(a+c)+a c\\right)}{p p-a c}=\\frac{(p-a)(p-c)}{p^{2}-a c} \\\\ \\left|P E_{1}\\right|^{2} & =\\left(p-e_{1}\\right) \\cdot \\overline{p-e_{1}}=\\frac{(p-a)(p-c)}{p^{2}-a c} \\cdot \\frac{\\left(\\frac{1}{p}-\\frac{1}{a}\\right)\\left(\\frac{1}{p}-\\frac{1}{c}\\right)}{\\frac{1}{p^{2}}-\\frac{1}{a c}} \\\\ & =-\\frac{(p-a)^{2}(p-c)^{2}}{\\left(p^{2}-a c\\right)^{2}} \\end{aligned} $$ Similarly, $$ \\left|Q E_{2}\\right|^{2}=-\\frac{(q-a)^{2}(q-c)^{2}}{\\left(q^{2}-a c\\right)^{2}} $$ But actually, we claim that $$ \\frac{(p-a)(p-c)}{p^{2}-a c}=\\frac{(q-a)(q-c)}{q^{2}-a c} $$ One calculates $$ (p-a)(p-c)\\left(q^{2}-a c\\right)=p^{2} q^{2}-p q^{2} a-p q^{2} c+q^{2} a c-p^{2} a c+p a^{2} c+p a c^{2}-(a c)^{2} $$ Thus $(p-a)(p-c)\\left(q^{2}-a c\\right)-(q-a)(q-c)\\left(p^{2}-a c\\right)$ is equal to $$ \\begin{aligned} -(a+c)(p q) & (q-p)+\\left(q^{2}-p^{2}\\right) a c-\\left(p^{2}-q^{2}\\right) a c+a c(a+c)(p-q) \\\\ & =(p-q)[(a+c) p q-2(p+q) a c+a c(a+c)] \\\\ & =(p-q)\\left[(a+c) b c-2 \\cdot \\frac{(a+b)(a+c)}{2 a} \\cdot a c+a c(a+c)\\right] \\\\ & =(p-q)(a+c)[b c-c(a+b)+a c]=0 \\end{aligned} $$ This proves $\\left|E_{1} P\\right|=\\left|E_{2} Q\\right|$. Together with the similar $\\left|F_{1} P\\right|=\\left|F_{2} Q\\right|$, we have proved (ii). 【 Authorship comments. Ankan provides an extensive dialogue at https://aops.com/ community/c6h1664170p10571644 of how he came up with this problem, which at first was intended just to be an AMC-level question about an equilateral triangle. Here, we provide just the change-log of the versions of this problem. 0. (Original version) Let $A B C$ be an equilateral triangle with side 2 inscribed in circle $\\omega$, and let $P$ be a point on small arc $A B$ of its circumcircle. The tangent line to $\\omega$ at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$. If $P E=P F$, find $E F$. (Answer: 4.) 1. (Generalize to isosceles triangle) Let $A B C$ be an isosceles triangle with $A B=A C$, and let $M$ be the midpoint of $\\overline{B C}$. Let $P$ be a point on the circumcircle with $P A=P M$. The tangent to the circumcircle at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$, respectively. Show that $P E=P F$. 2. (Block coordinate bashes) Let $A B C$ be an isosceles triangle with $A B=A C$ and circumcircle $\\omega$, and let $M$ be the midpoint of $\\overline{B C}$. Let $P$ be a point on $\\omega$ with $P A=P M$. The tangent to $\\omega$ at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$, respectively. Show that the circumcircle of $\\triangle A E F$ passes through the center of $\\omega$. 3. (Delete isosceles condition) Let $A B C$ be a triangle with circumcircle $\\omega$, and let $H$ be the foot of the altitude from $A$ to $\\overline{B C}$. Let $P$ be a point on $\\omega$ with $P A=P H$. The tangent to $\\omega$ at $P$ intersects lines $A C$ and $A B$ at $E$ and $F$, respectively. Show that the circumcircle of $\\triangle A E F$ passes through the center of $\\omega$. 4. (Add in both tangents) Let $A B C$ be an acute triangle with circumcircle $\\omega$, and let $H$ be the foot of the altitude from $A$ to $\\overline{B C}$. Let $P$ and $Q$ be the points on $\\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that $E_{1} F_{1}=E_{2} F_{2}$. 5. (Merge v3 and v4) Let $A B C$ be an acute triangle with circumcircle $\\omega$, and let $H$ be the foot of the altitude from $A$ to $\\overline{B C}$. Let $P$ and $Q$ be the points on $\\omega$ with $P A=P H$ and $Q A=Q H$. The tangent to $\\omega$ at $P$ intersects lines $A C$ and $A B$ at $E_{1}$ and $F_{1}$ respectively; the tangent to $\\omega$ at $Q$ intersects lines $A C$ and $A B$ at $E_{2}$ and $F_{2}$ respectively. Show that the circumcircles of $\\triangle A E_{1} F_{1}$ and $\\triangle A E_{2} F_{2}$ are congruent, and the line through their centers is parallel to the tangent to $\\omega$ at $A$. The problem bears Evan's name only because he suggested the changes v2 and v5.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 10 |
-
{"year": "2018", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $S=\\{1, \\ldots, 100\\}$, and for every positive integer $n$ define $$ T_{n}=\\left\\{\\left(a_{1}, \\ldots, a_{n}\\right) \\in S^{n} \\mid a_{1}+\\cdots+a_{n} \\equiv 0 \\quad(\\bmod 100)\\right\\} $$ Determine which $n$ have the following property: if we color any 75 elements of $S$ red, then at least half of the $n$-tuples in $T_{n}$ have an even number of coordinates with red elements.", "solution": " We claim this holds exactly for $n$ even. \\I First solution by generating functions. Define $$ R(x)=\\sum_{s \\text { red }} x^{s}, \\quad B(x)=\\sum_{s \\text { blue }} x^{s} . $$ (Here \"blue\" means \"not-red\", as always.) Then, the number of tuples in $T_{n}$ with exactly $k$ red coordinates is exactly equal to $$ \\binom{n}{k} \\cdot \\frac{1}{100} \\sum_{\\omega} R(\\omega)^{k} B(\\omega)^{n-k} $$ where the sum is over all 100th roots of unity. So, we conclude the number of tuples in $T_{n}$ with an even (resp odd) number of red elements is exactly $$ \\begin{aligned} X & =\\frac{1}{100} \\sum_{\\omega} \\sum_{k \\text { even }}\\binom{n}{k} R(\\omega)^{k} B(\\omega)^{n-k} \\\\ Y & =\\frac{1}{100} \\sum_{\\omega} \\sum_{k \\text { odd }}\\binom{n}{k} R(\\omega)^{k} B(\\omega)^{n-k} \\\\ \\Longrightarrow X-Y & =\\frac{1}{100} \\sum_{\\omega}(B(\\omega)-R(\\omega))^{n} \\\\ & =\\frac{1}{100}\\left[(B(1)-R(1))^{n}+\\sum_{\\omega \\neq 1}(2 B(\\omega))^{n}\\right] \\\\ & =\\frac{1}{100}\\left[(B(1)-R(1))^{n}-(2 B(1))^{n}+2^{n} \\sum_{\\omega} B(\\omega)^{n}\\right] \\\\ & =\\frac{1}{100}\\left[(B(1)-R(1))^{n}-(2 B(1))^{n}\\right]+2^{n} Z \\\\ & =\\frac{1}{100}\\left[(-50)^{n}-50^{n}\\right]+2^{n} Z \\end{aligned} $$ where $$ Z:=\\frac{1}{100} \\sum_{\\omega} B(\\omega)^{n} \\geq 0 $$ counts the number of tuples in $T_{n}$ which are all blue. Here we have used the fact that $B(\\omega)+R(\\omega)=0$ for $\\omega \\neq 1$. We wish to show $X-Y \\geq 0$ holds for $n$ even, but may fail when $n$ is odd. This follows from two remarks: - If $n$ is even, then $X-Y=2^{n} Z \\geq 0$. - If $n$ is odd, then if we choose the coloring for which $s$ is red if and only if $s \\not \\equiv 2$ $(\\bmod 4)$; we thus get $Z=0$. Then $X-Y=-\\frac{2}{100} \\cdot 50^{n}<0$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 11 |
-
{"year": "2018", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $S=\\{1, \\ldots, 100\\}$, and for every positive integer $n$ define $$ T_{n}=\\left\\{\\left(a_{1}, \\ldots, a_{n}\\right) \\in S^{n} \\mid a_{1}+\\cdots+a_{n} \\equiv 0 \\quad(\\bmod 100)\\right\\} $$ Determine which $n$ have the following property: if we color any 75 elements of $S$ red, then at least half of the $n$-tuples in $T_{n}$ have an even number of coordinates with red elements.", "solution": " We claim this holds exactly for $n$ even. 『 Second solution by strengthened induction and random coloring. We again prove that $n$ even work. Let us define $$ T_{n}(a)=\\left\\{\\left(a_{1}, \\ldots, a_{n}\\right) \\in S^{n} \\mid a_{1}+\\cdots+a_{n} \\equiv a \\quad(\\bmod 100)\\right\\} $$ Also, call an $n$-tuple good if it has an even number of red elements. We claim that $T_{n}(a)$ also has at least $50 \\%$ good tuples, by induction. This follows by induction on $n \\geq 2$. Indeed, the base case $n=2$ can be checked by hand, since $T_{2}(a)=\\{(x, a-x) \\mid x \\in S\\}$. With the stronger claim, one can check the case $n=2$ manually and proceed by induction to go from $n-2$ to $n$, noting that $$ T_{n}(a)=\\bigsqcup_{b+c=a} T_{n-2}(b) \\oplus T_{2}(c) $$ where $\\oplus$ denotes concatenation of tuples, applied set-wise. The concatenation of an $(n-2)$-tuple and 2-tuple is good if and only if both or neither are good. Thus for each $b$ and $c$, if the proportion of $T_{n-2}(b)$ which is good is $p \\geq \\frac{1}{2}$ and the proportion of $T_{2}(c)$ which is good is $q \\geq \\frac{1}{2}$, then the proportion of $T_{n-2}(b) \\oplus T_{2}(c)$ which is good is $p q+(1-p)(1-q) \\geq \\frac{1}{2}$, as desired. Since each term in the union has at least half the tuples good, all of $T_{n}(a)$ has at least half the tuples good, as desired. It remains to fail all odd $n$. We proceed by a suggestion of Yang Liu and Ankan Bhattacharya by showing that if we pick the 75 elements randomly, then any particular tuple in $S^{n}$ has strictly less than $50 \\%$ chance of being good. This will imply (by linearity of expectation) that $T_{n}$ (or indeed any subset of $S^{n}$ ) will, for some coloring, have less than half good tuples. Let $\\left(a_{1}, \\ldots, a_{n}\\right)$ be such an $n$-tuple. If any element appears in the tuple more than once, keep discarding pairs of that element until there are zero or one; this has no effect on the good-ness of the tuple. If we do this, we obtain an $m$-tuple $\\left(b_{1}, \\ldots, b_{m}\\right)$ with no duplicated elements where $m \\equiv n \\equiv 1(\\bmod 2)$. Now, the probability that any element is red is $\\frac{3}{4}$, so the probability of being good is $$ \\begin{aligned} \\sum_{k \\text { even }}^{m}\\binom{m}{k}\\left(\\frac{3}{4}\\right)^{k}\\left(-\\frac{1}{4}\\right)^{m-k} & =\\frac{1}{2}\\left[\\left(\\frac{3}{4}+\\frac{1}{4}\\right)^{m}-\\left(\\frac{3}{4}-\\frac{1}{4}\\right)^{m}\\right] \\\\ & =\\frac{1}{2}\\left[1-\\left(\\frac{1}{2}\\right)^{m}\\right]<\\frac{1}{2} \\end{aligned} $$ Remark (Adam Hesterberg). Here is yet another proof that $n$ even works. Group elements of $T_{n}$ into equivalence classes according to the $n / 2$ sums of pairs of consecutive elements (first and second, third and fourth, ...). For each such pair sum, there are at least as many monochrome pairs with that sum as nonmonochrome ones, since every nonmonochrome pair uses one of the 25 non-reds. The monochromaticity of the pairs is independent. If $p_{i} \\leq \\frac{1}{2}$ is the probability that the $i$ th pair is nonmonochrome, then the probability that $k$ pairs are nonmonochrome is the coefficient of $x^{k}$ in $f(x)=\\prod_{i}\\left(x p_{i}+\\left(1-p_{i}\\right)\\right)$. Then the probability that evenly many pairs are nonmonochrome (and hence that evenly many coordinates are red) is the sum of the coefficients of even powers of $x$ in $f$, which is $$ (f(1)+f(-1)) / 2=\\left(1+\\prod_{i}\\left(1-2 p_{i}\\right)\\right) / 2 \\geq \\frac{1}{2}, \\text { as desired. } $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 12 |
-
{"year": "2018", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Let $n$ be a positive integer. A frog starts on the number line at 0 . Suppose it makes a finite sequence of hops, subject to two conditions: - The frog visits only points in $\\left\\{1,2, \\ldots, 2^{n}-1\\right\\}$, each at most once. - The length of each hop is in $\\left\\{2^{0}, 2^{1}, 2^{2}, \\ldots\\right\\}$. (The hops may be either direction, left or right.) Let $S$ be the sum of the (positive) lengths of all hops in the sequence. What is the maximum possible value of $S$ ?", "solution": " We claim the answer is $\\frac{4^{n}-1}{3}$. We first prove the bound. First notice that the hop sizes are in $\\left\\{2^{0}, 2^{1}, \\ldots, 2^{n-1}\\right\\}$, since the frog must stay within bounds the whole time. Let $a_{i}$ be the number of hops of size $2^{i}$ the frog makes, for $0 \\leq i \\leq n-1$. Claim - For any $k=1, \\ldots, n$ we have $$ a_{n-1}+\\cdots+a_{n-k} \\leq 2^{n}-2^{n-k} $$ Within each fixed residue modulo $2^{m}$, the frog can make at most $\\frac{2^{n}}{2^{m}}-1$ large jumps. So the total number of large jumps is at most $2^{m}\\left(\\frac{2^{n}}{2^{m}}-1\\right)=2^{n}-2^{m}$. (As an example, when $n=3$ this means there are at most four hops of length 4 , at most six hops of length 2 or 4 , and at most seven hops total. Of course, if we want to max the length of the hops, we see that we want $a_{2}=4, a_{1}=2, a_{0}=1$, and in general equality is achieved when $a_{m}=2^{m}$ for any $m$.) Now, the total distance the frog travels is $$ S=a_{0}+2 a_{1}+4 a_{2}+\\cdots+2^{n-1} a_{n-1} $$ We rewrite using the so-called \"summation by parts\": $$ \\begin{array}{rrrr} S & =a_{0}+a_{1}+a_{2}+ & a_{3}+\\ldots+ & a_{n-1} \\\\ & + & a_{1}+a_{2}+a_{3}+\\ldots+ & a_{n-1} \\\\ & + & 2 a_{2}+2 a_{3}+\\ldots+ & 2 a_{n-1} \\\\ & + & 4 a_{3}+\\ldots+ & 4 a_{n-1} \\\\ & \\vdots & \\ddots & \\vdots \\\\ & & & \\\\ + & & & 2^{n-2} a_{n-1} \\end{array} $$ Hence $$ \\begin{aligned} S & \\leq\\left(2^{n}-2^{0}\\right)+\\left(2^{n}-2^{1}\\right)+2\\left(2^{n}-2^{2}\\right)+\\cdots+2^{n-2}\\left(2^{n}-2^{n-1}\\right) \\\\ & =\\frac{4^{n}-1}{3} . \\end{aligned} $$ It remains to show that equality can hold. There are many such constructions but most are inductive. Here is one approach. We will construct two family of paths such that there are $2^{k}$ hops of size $2^{k}$, for every $0 \\leq k \\leq n-1$, and we visit each of $\\left\\{0, \\ldots, 2^{n}-1\\right\\}$ once, starting on 0 and ending on $x$, for the two values $x \\in\\left\\{1,2^{n}-1\\right\\}$. The base case $n=1$ is clear. To take a path from 0 to $2^{n+1}-1$. - Take a path on $\\left\\{0,2,4, \\ldots, 2^{n+1}-2\\right\\}$ starting from 0 and ending on 2 (by inductive hypothesis). - Take a path on $\\left\\{1,3,5, \\ldots, 2^{n+1}-1\\right\\}$ starting from 1 and ending on $2^{n+1}-1$ (by inductive hypothesis). - Link them together by adding a single jump $2 \\rightarrow 1$. The other case is similar, but we route $0 \\rightarrow\\left(2^{n+1}-2\\right) \\rightarrow\\left(2^{n+1}-1\\right) \\rightarrow 1$ instead. (This can also be visualized as hopping along a hypercube of binary strings; each inductive step takes two copies of the hypercube and links them together by a single edge.) Remark (Ashwin Sah). The problem can also be altered to ask for the minimum value of the sum of the reciprocals of the hop sizes, where further we stipulate that the frog must hit every point precisely once (to avoid triviality). With a nearly identical proof that also exploits the added condition $a_{0}+\\cdots+a_{n-1}=2^{n}-1$, the answer is $n$. This yields a nicer form for the generalization. The natural generalization changes the above problem by replacing $2^{k}$ with $a_{k}$ where $a_{k} \\mid a_{k+1}$, so that the interval covered by hops is of size $a_{n}$ and the hop sizes are restricted to the $a_{i}$, where $a_{0}=1$. In this case, similar bounding yields $$ \\sum_{i=1}^{2^{n}-1} \\frac{1}{b_{k}} \\geq \\sum_{i=0}^{n-1}\\left(\\frac{a_{k+1}}{a_{k}}-1\\right) $$ Bounds for the total distance traveled happen in the same way as the solution above, and equality for both can be constructed in an analogous fashion.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 13 |
-
{"year": "2018", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "For which positive integers $b>2$ do there exist infinitely many positive integers $n$ such that $n^{2}$ divides $b^{n}+1$ ?", "solution": " This problem is sort of the union of IMO 1990/3 and IMO 2000/5. The answer is any $b$ such that $b+1$ is not a power of 2 . In the forwards direction, we first prove more carefully the following claim. Claim - If $b+1$ is a power of 2 , then the only $n$ which is valid is $n=1$. $$ b^{2 n} \\equiv 1 \\quad(\\bmod p) $$ so the order of $b(\\bmod p)$ divides $\\operatorname{gcd}(2 n, p-1)=2$. Hence $p \\mid b^{2}-1=(b-1)(b+1)$. But since $b+1$ was a power of 2 , this forces $p \\mid b-1$. Then $0 \\equiv b^{n}+1 \\equiv 2(\\bmod p)$, contradiction. On the other hand, suppose that $b+1$ is not a power of 2 (and that $b>2$ ). We will inductively construct an infinite sequence of distinct primes $p_{0}, p_{1}, \\ldots$, such that the following two properties hold for each $k \\geq 0$ : - $p_{0}^{2} \\ldots p_{k-1}^{2} p_{k} \\mid b^{p_{0} \\ldots p_{k-1}}+1$, - and hence $p_{0}^{2} \\ldots p_{k-1}^{2} p_{k}^{2} \\mid b^{p_{0} \\ldots p_{k-1} p_{k}}+1$ by exponent lifting lemma. This will solve the problem. Initially, let $p_{0}$ be any odd prime dividing $b+1$. For the inductive step, we contend there exists an odd prime $q \\notin\\left\\{p_{0}, \\ldots, p_{k}\\right\\}$ such that $q \\mid b^{p_{0} \\ldots p_{k}}+1$. Indeed, this follows immediately by Zsigmondy theorem since $p_{0} \\ldots p_{k}$ divides $b^{p_{0} \\ldots p_{k-1}}+1$. Since $\\left(b^{p_{0} \\ldots p_{k}}\\right)^{q} \\equiv b^{p_{0} \\ldots p_{k}}(\\bmod q)$, it follows we can then take $p_{k+1}=q$. This finishes the induction. To avoid the use of Zsigmondy, one can instead argue as follows: let $p=p_{k}$ for brevity, and let $c=b^{p_{0} \\ldots p_{k-1}}$. Then $\\frac{\\frac{c}{}^{p}+1}{c+1}=c^{p-1}-c^{p-2}+\\cdots+1$ has GCD exactly $p$ with $c+1$. Moreover, this quotient is always odd. Thus as long as $c^{p}+1>p \\cdot(c+1)$, there will be some new prime dividing $c^{p}+1$ but not $c+1$. This is true unless $p=3$ and $c=2$, but we assumed $b>2$ so this case does not appear. Remark (On new primes). In going from $n^{2} \\mid b^{n}+1$ to $(n q)^{2} \\mid b^{n q}+1$, one does not necessarily need to pick a $q$ such that $q \\nmid n$, as long as $\\nu_{q}\\left(n^{2}\\right)<\\nu_{q}\\left(b^{n}+1\\right)$. In other words it suffices to just check that $\\frac{b^{n}+1}{n^{2}}$ is not a power of 2 in this process. However, this calculation is a little more involved with this approach. One proceeds by noting that $n$ is odd, hence $\\nu_{2}\\left(b^{n}+1\\right)=\\nu_{2}(b+1)$, and thus $\\frac{b^{n}+1}{n^{2}}=2^{\\nu_{2}(b+1)} \\leq b+1$, which is a little harder to bound than the analogous $c^{p}+1>p \\cdot(c+1)$ from the previous solution. \\ Authorship comments. I came up with this problem by simply mixing together the main ideas of IMO 1990/3 and IMO 2000/5, late one night after a class. On the other hand, I do not consider it very original; it is an extremely \"routine\" number theory problem for experienced contestants, using highly standard methods. Thus it may not be that interesting, but is a good discriminator of understanding of fundamentals. IMO 1990/3 shows that if $b=2$, then the only $n$ which work are $n=1$ and $n=3$. Thus $b=2$ is a special case and for this reason the problem explicitly requires $b>2$. An alternate formulation of the problem is worth mentioning. Originally, the problem statement asked whether there existed $n$ with at least 3 (or 2018, etc.) prime divisors, thus preventing the approach in which one takes a prime $q$ dividing $\\frac{b^{n}+1}{n^{2}}$. Ankan Bhattacharya suggested changing it to \"infinitely many $n$ \", which is more natural. These formulations are actually not so different though. Explicitly, suppose $k^{2} \\mid b^{k}+1$ and $p \\mid b^{k}+1$. Consider any $k \\mid n$ with $n^{2} \\mid b^{n}+1$, and let $p$ be an odd prime dividing $b^{k}+1$. Then $2 \\nu_{p}(n) \\leq \\nu_{p}\\left(b^{n}+1\\right)=\\nu_{p}(n / k)+\\nu_{p}\\left(b^{k}+1\\right)$ and thus $$ \\nu_{p}(n / k) \\leq \\nu_{p}\\left(\\frac{b^{k}+1}{k^{2}}\\right) . $$ Effectively, this means we can only add each prime a certain number of times.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
| 14 |
-
{"year": "2018", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Show that there is an absolute constant $c<1$ with the following property: whenever $\\mathcal{P}$ is a polygon with area 1 in the plane, one can translate it by a distance of $\\frac{1}{100}$ in some direction to obtain a polygon $\\mathcal{Q}$, for which the intersection of the interiors of $\\mathcal{P}$ and $\\mathcal{Q}$ has total area at most $c$.", "solution": " Suppose $\\mathcal{P}$ is a polygon of area 1 , and $\\varepsilon>0$ is a constant, such that for any translate $\\mathcal{Q}=\\mathcal{P}+v$, where $v$ has length exactly $\\frac{1}{100}$, the intersection of $\\mathcal{P}$ and $\\mathcal{Q}$ has area at least $1-\\varepsilon$. The problem asks us to prove a lower bound on $\\varepsilon$. ## Lemma Fix a sequence of $n$ vectors $v_{1}, v_{2}, \\ldots, v_{n}$, each of length $\\frac{1}{100}$. A grasshopper starts at a random point $x$ of $\\mathcal{P}$, and makes $n$ jumps to $x+v_{1}+\\cdots+v_{n}$. Then it remains in $\\mathcal{P}$ with probability at least $1-n \\varepsilon$. ## Corollary Fix a vector $w$ of length at most 8. A grasshopper starts at a random point $x$ of $\\mathcal{P}$, and jumps to $x+w$. Then it remains in $\\mathcal{P}$ with probability at least $1-800 \\varepsilon$. Now consider the process where we select a random starting point $x \\in \\mathcal{P}$ for our grasshopper, and a random vector $w$ of length at most 8 (sampled uniformly from the closed disk of radius 8 ). Let $q$ denote the probability of staying inside $\\mathcal{P}$ we will bound $q$ from above and below. - On the one hand, suppose we pick $w$ first. By the previous corollary, $q \\geq 1-800 \\varepsilon$ (irrespective of the chosen $w$ ). - On the other hand, suppose we pick $x$ first. Then the possible landing points $x+w$ are uniformly distributed over a closed disk of radius 8 , which has area $64 \\pi$. The probability of landing in $\\mathcal{P}$ is certainly at most $\\frac{[\\mathcal{P}]}{64 \\pi}$. Consequently, we deduce $$ 1-800 \\varepsilon \\leq q \\leq \\frac{[\\mathcal{P}]}{64 \\pi} \\Longrightarrow \\varepsilon>\\frac{1-\\frac{[\\mathcal{P}]}{64 \\pi}}{800}>0.001 $$ as desired. Remark. The choice of 800 jumps is only for concreteness; any constant $n$ for which $\\pi(n / 100)^{2}>1$ works. I think $n=98$ gives the best bound following this approach.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2018.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl
DELETED
|
@@ -1,15 +0,0 @@
|
|
| 1 |
-
{"year": "2019", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Find all binary operations $\\diamond: \\mathbb{R}_{>0} \\times \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{>0}$ (meaning $\\diamond$ takes pairs of positive real numbers to positive real numbers) such that for any real numbers $a, b, c>0$, - the equation $a \\diamond(b \\diamond c)=(a \\diamond b) \\cdot c$ holds; and - if $a \\geq 1$ then $a \\diamond a \\geq 1$.", "solution": " The answer is only multiplication and division, which both obviously work. 【 First solution using Cauchy FE. We prove: Claim - We have $a \\diamond b=a f(b)$ where $f$ is some involutive and totally multiplicative function. (In fact, this classifies all functions satisfying the first condition completely.) - Note that for any $x$, the function $y \\mapsto x \\diamond y$ is injective, because if $x \\diamond y_{1}=x \\diamond y_{2}$ then take $P\\left(1, x, y_{i}\\right)$ to get $y_{1}=y_{2}$. - Take $P(1, x, 1)$ and injectivity to get $x \\diamond 1=x$. - Take $P(1,1, y)$ to get $1 \\diamond(1 \\diamond y)=y$. - Take $P(x, 1,1 \\diamond y)$ to get $$ x \\diamond y=x \\cdot(1 \\diamond y) $$ Henceforth let us define $f(y)=1 \\diamond y$, so $f(1)=1, f$ is involutive and $$ x \\diamond y=x f(y) $$ Plugging this into the original condition now gives $f(b f(c))=f(b) c$, which (since $f$ is an involution) gives $f$ completely multiplicative. In particular, $f(1)=1$. We are now interested only in the second condition, which reads $f(x) \\geq 1 / x$ for $x \\geq 1$. Define the function $$ g(t)=\\log f\\left(e^{t}\\right) $$ so that $g$ is additive, and also $g(t) \\geq-t$ for all $t \\geq 0$. We appeal to the following theorem: ## Lemma If $h: \\mathbb{R} \\rightarrow \\mathbb{R}$ is an additive function which is not linear, then it is dense in the plane: for any point $\\left(x_{0}, y_{0}\\right)$ and $\\varepsilon>0$ there exists $(x, y)$ such that $h(x)=y$ and $\\sqrt{\\left(x-x_{0}\\right)^{2}+\\left(y-y_{0}\\right)^{2}}<\\varepsilon$. Applying this lemma with the fact that $g(t) \\geq-t$ implies readily that $g$ is linear. In other words, $f$ is of the form $f(x)=x^{r}$ for some fixed real number $r$. It is easy to check $r= \\pm 1$ which finishes.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 2 |
-
{"year": "2019", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Find all binary operations $\\diamond: \\mathbb{R}_{>0} \\times \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{>0}$ (meaning $\\diamond$ takes pairs of positive real numbers to positive real numbers) such that for any real numbers $a, b, c>0$, - the equation $a \\diamond(b \\diamond c)=(a \\diamond b) \\cdot c$ holds; and - if $a \\geq 1$ then $a \\diamond a \\geq 1$.", "solution": " The answer is only multiplication and division, which both obviously work. 【 Second solution manually. As before we arrive at $a \\diamond b=a f(b)$, with $f$ an involutive and totally multiplicative function. We prove that: Claim - For any $a>0$, we have $f(a) \\in\\{1 / a, a\\}$. Assume that $a b>1$; we show $a=b$. Note that for integers $m$ and $n$ with $a^{n} b^{m} \\geq 1$, we must have $$ a^{m} b^{n}=f(b)^{m} f(a)^{n}=f\\left(a^{n} b^{m}\\right) \\geq \\frac{1}{a^{n} b^{m}} \\Longrightarrow(a b)^{m+n} \\geq 1 $$ and thus we have arrived at the proposition $$ m+n<0 \\Longrightarrow n \\log _{b} a+m<0 $$ for all integers $m$ and $n$. Due to the density of $\\mathbb{Q}$ in the real numbers, this can only happen if $\\log _{b} a=1$ or $a=b$. Claim - The function $f$ is continuous. $$ |g(t)-g(s)|=\\left|\\log f\\left(e^{t-s}\\right)\\right|=|t-s| $$ since $f\\left(e^{t-s}\\right)=e^{ \\pm|t-s|}$. Therefore $g$ is Lipschitz. Hence $g$ continuous, and $f$ is too. Finally, we have from $f$ multiplicative that $$ f\\left(2^{q}\\right)=f(2)^{q} $$ for every rational number $q$, say. As $f$ is continuous this implies $f(x) \\equiv x$ or $f(x) \\equiv 1 / x$ identically (depending on whether $f(2)=2$ or $f(2)=1 / 2$, respectively). Therefore, $a \\diamond b=a b$ or $a \\diamond b=a \\div b$, as needed. Remark. The Lipschitz condition is one of several other ways to proceed. The point is that if $f(2)=2$ (say), and $x / 2^{q}$ is close to 1 , then $f(x) / 2^{q}=f\\left(x / 2^{q}\\right)$ is close to 1 , which is enough to force $f(x)=x$ rather than $f(x)=1 / x$. Remark. Compare to AMC 10A 2016 \\#23, where the second condition is $a \\diamond a=1$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 3 |
-
{"year": "2019", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with circumcircle $\\Omega$ and orthocenter $H$. Points $D$ and $E$ lie on segments $A B$ and $A C$ respectively, such that $A D=A E$. The lines through $B$ and $C$ parallel to $\\overline{D E}$ intersect $\\Omega$ again at $P$ and $Q$, respectively. Denote by $\\omega$ the circumcircle of $\\triangle A D E$. (a) Show that lines $P E$ and $Q D$ meet on $\\omega$. (b) Prove that if $\\omega$ passes through $H$, then lines $P D$ and $Q E$ meet on $\\omega$ as well.", "solution": " Claim - Points $L, D, P$ are collinear. $$ \\begin{aligned} \\measuredangle C L D & =\\measuredangle D H L=\\measuredangle D H A+\\measuredangle A H L=\\measuredangle D E A+\\measuredangle A H C \\\\ & =\\measuredangle A D E+\\measuredangle C B A=\\measuredangle A B P+\\measuredangle C B A=\\measuredangle C B P=\\measuredangle C L P . \\end{aligned} $$  Now let $K \\in \\omega$ such that $D H K E$ is an isosceles trapezoid, i.e. $\\measuredangle B A H=\\measuredangle K A E$. Claim - Points $D, K, P$ are collinear. $$ \\measuredangle K D E=\\measuredangle K A E=\\measuredangle B A H=\\measuredangle L A B=\\measuredangle L P B=\\measuredangle D P B=\\measuredangle P D E . $$ By symmetry, $\\overline{Q E}$ will then pass through the same $K$, as needed. Remark. These two claims imply each other, so guessing one of them allows one to realize the other. It is likely the latter is easiest to guess from the diagram, since it does not need any additional points. Claim - Point $K$ is the orthocenter of isosceles triangle $A P Q$. In light of the formula \" $A H^{2}=4 R^{2}-a^{2}$ \", this implies the conclusion. Let $M$ be the midpoint of $\\overline{P Q}$. Since $\\triangle A P Q$ is isosceles, $$ \\overline{A K M} \\perp \\overline{P Q} \\Longrightarrow M K \\cdot M A=M P^{2} $$ by orthocenter properties. So to summarize - The circle with diameter $\\overline{P Q}$ is orthogonal to $\\omega$. In other words, point $P$ lies on the polar of $Q$ with respect to $\\omega$. - The point $X=\\overline{Q D} \\cap \\overline{P E}$ is on $\\omega$. On the other hand, if we let $K^{\\prime}=\\overline{Q E} \\cap \\omega$, then by Brokard theorem on $X D K^{\\prime} E$, the polar of $Q=\\overline{X D} \\cap \\overline{K^{\\prime} E}$ pass through $\\overline{D K^{\\prime}} \\cap \\overline{X E}$; this point must therefore be $P$ and $K^{\\prime}=K$ as desired. $$ A=a^{2}, B=b^{2}, C=c^{2}, M=-b c, H=a^{2}+b^{2}+c^{2}, P=\\frac{a^{2} c}{b}, Q=\\frac{a^{2} b}{c} $$ where $M$ is the arc midpoint of $\\widehat{B C}$. By direct angle chasing we can verify that $\\overline{M B} \\| \\overline{D H}$. Also, $D \\in \\overline{A B}$. Therefore, we can compute $D$ as follows. $$ d+a^{2} b^{2} \\bar{d}=a^{2}+b^{2} \\text { and } \\frac{d-h}{\\bar{d}-\\bar{h}}=-m b^{2}=b^{3} c \\Longrightarrow d=\\frac{a^{2}\\left(a^{2} c+b^{2} c+c^{3}-b^{3}\\right)}{c\\left(b c+a^{2}\\right)} . $$ By symmetry, we have that $$ e=\\frac{a^{2}\\left(a^{2} b+b c^{2}+b^{3}-c^{3}\\right)}{b\\left(b c+a^{2}\\right)} . $$ To finish, we want to show that the angle between $\\overline{D P}$ and $\\overline{E Q}$ is angle $A$. To show this, we compute $\\frac{d-p}{e-q} / \\overline{\\frac{d-p}{e-q}}$. First, we compute $$ \\begin{aligned} d-p & =\\frac{a^{2}\\left(a^{2} c+b^{2} c+c^{3}-b^{3}\\right)}{c\\left(b c+a^{2}\\right)}-\\frac{a^{2} c}{b} \\\\ & =a^{2}\\left(\\frac{a^{2} c+b^{2} c+c^{3}-b^{3}}{c\\left(b c+a^{2}\\right)}-\\frac{c}{b}\\right)=\\frac{a^{2}\\left(a^{2} c-b^{3}\\right)(b-c)}{b c\\left(b c+a^{2}\\right)} \\end{aligned} $$ By symmetry, $$ \\frac{d-p}{e-q}=-\\frac{a^{2} c-b^{3}}{a^{2} b-c^{3}} \\Longrightarrow \\frac{d-p}{e-q} / \\overline{\\frac{d-p}{e-q}}=\\frac{a^{2} b^{3} c}{a^{2} b c^{3}}=\\frac{b^{2}}{c^{2}} $$ as desired. Recall: ## Lemma (Zack's lemma) Suppose points $A, B$ have degree $d_{1}, d_{2}$, and there are $k$ values of $t$ for which $A=B$. Then line $A B$ has degree at most $d_{1}+d_{2}-k$. Similarly, if lines $\\ell_{1}, \\ell_{2}$ have degrees $d_{1}, d_{2}$, and there are $k$ values of $t$ for which $\\ell_{1}=\\ell_{2}$, then the intersection $\\ell_{1} \\cap \\ell_{2}$ has degree at most $d_{1}+d_{2}-k$. Now, note that $H$ moves linearly in $C$ on line $B H$. Furthermore, angles $\\angle A H E$, $\\angle A H F$ are fixed, we get that $D$ and $E$ have degree 2 . One way to see this is using the lemma; $D$ lies on line $A B$, which is fixed, and line $H D$ passes through a point at infinity which is a constant rotation of the point at infinity on line $A H$, and therefore has degree 1. Then $D, E$ have degree at most $1+1-0=2$. Now, note that $P, Q$ move linearly in $C$. Both of these are because the circumcenter $O$ moves linearly in $C$, and $P, Q$ are reflections of $B, C$ in a line through $O$ with fixed direction, which also moves linearly. So by the lemma, the lines $P D, Q E$ have degree at most 3 . I claim they actually have degree 2; to show this it suffices to give an example of a choice of $C$ for which $P=D$ and one for which $Q=E$. But an easy angle chase shows that in the unique case when $P=B$, we get $D=B$ as well and thus $P=D$. Similarly when $Q=C, E=C$. It follows from the lemma that lines $P D, Q E$ have degree at most 2 . Let $\\ell_{\\infty}$ denote the line at infinity. I claim that the points $P_{1}=P D \\cap \\ell_{\\infty}, P_{2}=Q E \\cap \\ell_{\\infty}$ are projective in $C$. Since $\\ell_{\\infty}$ is fixed, it suffices to show by the lemma that there exists some value of $C$ for which $Q E=\\ell_{\\infty}$ and $P D=\\ell_{\\infty}$. But note that as $C \\rightarrow \\infty$, all four points $P, D, Q, E$ go to infinity. It follows that $P_{1}, P_{2}$ are projective in $C$. Then to finish, recall that we want to show that $\\angle(P D, Q E)$ is constant. It suffices then to show that there's a constant rotation sending $P_{1}$ to $P_{2}$. Since $P_{1}, P_{2}$ are projective, it suffices to verify this for 3 values of $C$. We can take $C$ such that $\\angle A B C=90, \\angle A C B=90$, or $A B=A C$, and all three cases are easy to check.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 4 |
-
{"year": "2019", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "On an infinite square grid we place finitely many cars, which each occupy a single cell and face in one of the four cardinal directions. Cars may never occupy the same cell. It is given that the cell immediately in front of each car is empty, and moreover no two cars face towards each other (no right-facing car is to the left of a left-facing car within a row, etc.). In a move, one chooses a car and shifts it one cell forward to a vacant cell. Prove that there exists an infinite sequence of valid moves using each car infinitely many times.", "solution": " Let $S$ be any rectangle containing all the cars. Partition $S$ into horizontal strips of height 1 , and color them red and green in an alternating fashion. It is enough to prove all the cars may exit $S$.  To do so, we outline a five-stage plan for the cars. 1. All vertical cars in a green cell may advance one cell into a red cell (or exit $S$ altogether), by the given condition. (This is the only place where the hypothesis about empty space is used!) 2. All horizontal cars on green cells may exit $S$, as no vertical cars occupy green cells. 3. All vertical cars in a red cell may advance one cell into a green cell (or exit $S$ altogether), as all green cells are empty. 4. All horizontal cars within red cells may exit $S$, as no vertical car occupy red cells. 5. The remaining cars exit $S$, as they are all vertical. The solution is complete. Remark (Higher-dimensional generalization by author). The natural higher-dimensional generalization is true, and can be proved in largely the same fashion. For example, in three dimensions, one may let $S$ be a rectangular prism and partition $S$ into horizontal slabs and color them red and green in an alternating fashion. Stages 1, 3, and 5 generalize immediately, and stages 2 and 4 reduce to an application of the two-dimensional problem. In the same way, the general problem is handled by induction on the dimension. Remark (Historical comments). For $k>1$, we could consider a variant of the problem where cars are $1 \\times k$ rectangles (moving parallel to the longer edge) instead of occupying single cells. In that case, if there are $2 k-1$ empty spaces in front of each car, the above proof works (with the red and green strips having height $k$ instead). On the other hand, at least $k$ empty spaces are necessary. We don't know the best constant in this case.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 5 |
-
{"year": "2019", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Consider coins with positive real denominations not exceeding 1. Find the smallest $C>0$ such that the following holds: if we are given any 100 such coins with total value 50 , then we can always split them into two stacks of 50 coins each such that the absolute difference between the total values of the two stacks is at most $C$.", "solution": " The answer is $C=\\frac{50}{51}$. The lower bound is obtained if we have 51 coins of value $\\frac{1}{51}$ and 49 coins of value 1. (Alternatively, 51 coins of value $1-\\frac{\\varepsilon}{51}$ and 49 coins of value $\\frac{\\varepsilon}{49}$ works fine for $\\varepsilon>0$.) We now present two (similar) proofs that this $C=\\frac{50}{51}$ suffices. 【 First proof (original). Let $a_{1} \\leq \\cdots \\leq a_{100}$ denote the values of the coins in ascending order. Since the 51 coins $a_{50}, \\ldots, a_{100}$ are worth at least $51 a_{50}$, it follows that $a_{50} \\leq \\frac{50}{51}$; likewise $a_{51} \\geq \\frac{1}{51}$. We claim that choosing the stacks with coin values $$ a_{1}, a_{3}, \\ldots, a_{49}, \\quad a_{52}, a_{54}, \\ldots, a_{100} $$ and $$ a_{2}, a_{4}, \\ldots, a_{50}, \\quad a_{51}, a_{53}, \\ldots, a_{99} $$ works. Let $D$ denote the (possibly negative) difference between the two total values. Then $$ \\begin{aligned} D & =\\left(a_{1}-a_{2}\\right)+\\cdots+\\left(a_{49}-a_{50}\\right)-a_{51}+\\left(a_{52}-a_{53}\\right)+\\cdots+\\left(a_{98}-a_{99}\\right)+a_{100} \\\\ & \\leq 25 \\cdot 0-\\frac{1}{51}+24 \\cdot 0+1=\\frac{50}{51} \\end{aligned} $$ Similarly, we have $$ \\begin{aligned} D & =a_{1}+\\left(a_{3}-a_{2}\\right)+\\cdots+\\left(a_{49}-a_{48}\\right)-a_{50}+\\left(a_{52}-a_{51}\\right)+\\cdots+\\left(a_{100}-a_{99}\\right) \\\\ & \\geq 0+24 \\cdot 0-\\frac{50}{51}+25 \\cdot 0=-\\frac{50}{51} \\end{aligned} $$ It follows that $|D| \\leq \\frac{50}{51}$, as required.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 6 |
-
{"year": "2019", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Consider coins with positive real denominations not exceeding 1. Find the smallest $C>0$ such that the following holds: if we are given any 100 such coins with total value 50 , then we can always split them into two stacks of 50 coins each such that the absolute difference between the total values of the two stacks is at most $C$.", "solution": " The answer is $C=\\frac{50}{51}$. The lower bound is obtained if we have 51 coins of value $\\frac{1}{51}$ and 49 coins of value 1. (Alternatively, 51 coins of value $1-\\frac{\\varepsilon}{51}$ and 49 coins of value $\\frac{\\varepsilon}{49}$ works fine for $\\varepsilon>0$.) We now present two (similar) proofs that this $C=\\frac{50}{51}$ suffices. 【 Second proof (Evan Chen). Again we sort the coins in increasing order $0<a_{1} \\leq$ $a_{2} \\leq \\cdots \\leq a_{100} \\leq 1$. A large gap is an index $i \\geq 2$ such that $a_{i}>a_{i-1}+\\frac{50}{51}$; obviously there is at most one such large gap. Claim - If there is a large gap, it must be $a_{51}>a_{50}+\\frac{50}{51}$. Now imagine starting with the coins $a_{1}, a_{3}, \\ldots, a_{99}$, which have total value $S \\leq 25$. We replace $a_{1}$ by $a_{2}$, then $a_{3}$ by $a_{4}$, and so on, until we replace $a_{99}$ by $a_{100}$. At the end of the process we have $S \\geq 25$. Moreover, since we did not cross a large gap at any point, the quantity $S$ changed by at most $C=\\frac{50}{51}$ at each step. So at some point in the process we need to have $25-C / 2 \\leq S \\leq 25+C / 2$, which proves $C$ works.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 7 |
-
{"year": "2019", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\\triangle A E F$, and suppose line $A K$ intersects $\\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\\overline{B C}$ meet on $\\Gamma$.", "solution": " 『 First solution (Andrew Gu). We begin with the following two observations. Claim - Point $K$ lies on the radical axis of $(B E H)$ and $(C F H)$. $$ \\measuredangle H E K=90^{\\circ}-\\measuredangle E A F=90^{\\circ}-\\measuredangle B A C=\\measuredangle H B E $$ implying the result. Since $K E=K F$, this implies the result. Claim - The second intersection $M$ of $(B E H)$ and $(C F H)$ lies on $\\Gamma$.  In particular, $M, H, K$ are collinear. Let $X$ be on $\\Gamma$ with $\\overline{D X} \\perp \\overline{B C}$; we then wish to show $X$ lies on the line $M H K$ we found. This is angle chasing: compute $$ \\measuredangle X M B=\\measuredangle X D B=90^{\\circ}-\\measuredangle D B C=90^{\\circ}-\\measuredangle D A C $$ $$ =90^{\\circ}-\\measuredangle K A F=\\measuredangle F E A=\\measuredangle H E B=\\measuredangle H M B $$ as needed.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 8 |
-
{"year": "2019", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\\triangle A E F$, and suppose line $A K$ intersects $\\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\\overline{B C}$ meet on $\\Gamma$.", "solution": " II Second solution (Ankan Bhattacharya). We let $D^{\\prime}$ be the second intersection of $\\overline{E F}$ with $(B H C)$ and redefine $D$ as the reflection of $D^{\\prime}$ across $\\overline{B C}$. We will first prove that this point $D$ coincides with the point $D$ given in the problem statement. The idea is that: Claim - $A$ is the $D$-excenter of $\\triangle D E F$. $$ \\begin{aligned} \\measuredangle D^{\\prime} D B & =\\measuredangle B D^{\\prime} D=\\measuredangle D^{\\prime} B C+90^{\\circ}=\\measuredangle D^{\\prime} H C+90^{\\circ} \\\\ & =\\measuredangle D^{\\prime} H C+\\measuredangle(H C, A B)=\\measuredangle\\left(D^{\\prime} H, A B\\right)=\\measuredangle D^{\\prime} E B \\end{aligned} $$ Now as $B D=B D^{\\prime}$, we obtain $\\overline{B E A}$ externally bisects $\\angle D E D^{\\prime} \\cong \\angle D E F$. Likewise $\\overline{F A}$ externally bisects $\\angle D F E$, so $A$ is the $D$-excenter of $\\triangle D E F$. Hence, by the so-called \"Fact 5 \", point $K$ lies on $\\overline{D A}$, so this point $D$ is the one given in the problem statement.  Now choose point $X$ on $(A B C)$ satisfying $\\overline{D X} \\perp \\overline{B C}$. Claim - Point $K$ lies on line $H X$. $$ \\frac{K D}{K A}=\\frac{K D}{K E}=\\frac{D E+D F}{E F} $$ On the other hand, if we let $r_{D}$ denote the $D$-exradius of $\\triangle D E F$ then $$ \\frac{X D}{X D^{\\prime}}=\\frac{[D E X]+[D F X]}{[X E F]}=\\frac{[D E X]+[D F X]}{[A E F]}=\\frac{D E \\cdot r_{D}+D F \\cdot r_{D}}{E F \\cdot r_{D}}=\\frac{D E+D F}{E F} $$ Thus $$ [A K X]=\\frac{K A}{K D} \\cdot[D K X]=\\frac{K A}{K D} \\cdot \\frac{X D}{X D^{\\prime}} \\cdot\\left[K D^{\\prime} X\\right]=\\left[D^{\\prime} K X\\right] $$ This is sufficient to prove $K$ lies on $\\overline{H X}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 9 |
-
{"year": "2019", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\\triangle A E F$, and suppose line $A K$ intersects $\\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\\overline{B C}$ meet on $\\Gamma$.", "solution": " I Fourth solution, complex numbers with spiral similarity (Evan Chen). First if $\\overline{A D} \\perp \\overline{B C}$ there is nothing to prove, so we assume this is not the case. Let $W$ be the antipode of $D$. Let $S$ denote the second intersection of $(A E F)$ and $(A B C)$. Consider the spiral similarity sending $\\triangle S E F$ to $\\triangle S B C$ : - It maps $H$ to a point $G$ on line $B C$, - It maps $K$ to $O$. - It maps the $A$-antipode of $\\triangle A E F$ to $D$. - Hence (by previous two observations) it maps $A$ to $W$. - Also, the image of line $A D$ is line $W O$, which does not coincide with line $B C$ (as $O$ does not lie on line $B C$ ). Therefore, $K$ is the unique point on line $\\overline{A D}$ for one can get a direct similarity $$ \\triangle A K H \\sim \\triangle W O G $$ for some point $G$ lying on line $\\overline{B C}$.  On the other hand, let us re-define $K$ as $\\overline{X H} \\cap \\overline{A D}$. We will show that the corresponding $G$ making $(\\triangle)$ true lies on line $B C$. We apply complex numbers with $\\Gamma$ the unit circle, with $a, b, c, d$ taking their usual meanings, $H=a+b+c, X=-b c / d$, and $W=-d$. Then point $K$ is supposed to satisfy $$ k+a d \\bar{k}=a+d $$ $$ \\begin{aligned} \\frac{k+\\frac{b c}{d}}{a+b+c+\\frac{b c}{d}} & =\\frac{\\bar{k}+\\frac{d}{b c}}{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}} \\\\ \\Longleftrightarrow \\frac{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}}{a+b+c+\\frac{b c}{d}}\\left(k+\\frac{b c}{d}\\right) & =\\bar{k}+\\frac{d}{b c} \\end{aligned} $$ Adding $a d$ times the last line to the first line and cancelling $a d \\bar{k}$ now gives $$ \\left(a d \\cdot \\frac{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}}{a+b+c+\\frac{b c}{d}}+1\\right) k=a+d+\\frac{a d^{2}}{b c}-a b c \\cdot \\frac{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}}{a+b+c+\\frac{b c}{d}} $$ or $$ \\begin{aligned} \\left(a d\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}\\right)+a+b+c+\\frac{b c}{d}\\right) k & =\\left(a+b+c+\\frac{b c}{d}\\right)\\left(a+d+\\frac{a d^{2}}{b c}\\right) \\\\ & -a b c \\cdot\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}\\right) . \\end{aligned} $$ We begin by simplifying the coefficient of $k$ : $$ \\begin{aligned} a d\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}\\right)+a+b+c+\\frac{b c}{d} & =a+b+c+d+\\frac{b c}{d}+\\frac{a d}{b}+\\frac{a d}{c}+\\frac{a d^{2}}{b c} \\\\ & =a+\\frac{b c}{d}+\\left(1+\\frac{a d}{b c}\\right)(b+c+d) \\\\ & =\\frac{a d+b c}{b c d}[b c+d(b+c+d)] \\\\ & =\\frac{(a d+b c)(d+b)(d+c)}{b c d} \\end{aligned} $$ Meanwhile, the right-hand side expands to $$ \\begin{aligned} \\mathrm{RHS}= & \\left(a+b+c+\\frac{b c}{d}\\right)\\left(a+d+\\frac{a d^{2}}{b c}\\right)-a b c \\cdot\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}+\\frac{d}{b c}\\right) \\\\ = & \\left(a^{2}+a b+a c+\\frac{a b c}{d}\\right)+(d a+d b+d c+b c) \\\\ & +\\left(\\frac{a^{2} d^{2}}{b c}+\\frac{a d^{2}}{c}+\\frac{a d^{2}}{b}+a d\\right)-(a b+b c+c a+a d) \\\\ = & a^{2}+d(a+b+c)+\\frac{a b c}{d}+\\frac{a^{2} d^{2}}{b c}+\\frac{a d^{2}}{b}+\\frac{a d^{2}}{c} \\\\ = & a^{2}+\\frac{a b c}{d}+d(a+b+c) \\cdot \\frac{a d+b c}{b c} \\\\ = & \\frac{a d+b c}{b c d}\\left[a b c+d^{2}(a+b+c)\\right] . \\end{aligned} $$ Therefore, we get $$ k=\\frac{a b c+d^{2}(a+b+c)}{(d+b)(d+c)} $$ In particular, $$ \\begin{aligned} k-a & =\\frac{a b c+d^{2}(a+b+c)-a(d+b)(d+c)}{(d+b)(d+c)} \\\\ & =\\frac{d^{2}(b+c)-d a(b+c)}{(d+b)(d+c)}=\\frac{d(b+c)(d-a)}{(d+b)(d+c)} \\end{aligned} $$ Now the corresponding point $G$ obeying $(\\Omega)$ satisfies $$ \\begin{aligned} \\frac{g-(-d)}{0-(-d)} & =\\frac{(a+b+c)-a}{k-a} \\\\ \\Longrightarrow g & =-d+\\frac{d(b+c)}{k-a} \\\\ & =-d+\\frac{(d+b)(d+c)}{d-a}=\\frac{d b+d c+b c+a d}{d-a} . \\\\ \\Longrightarrow b c \\bar{g} & =\\frac{b c \\cdot \\frac{a c+a b+a d+b c}{a b c d}}{\\frac{a-d}{a d}}=-\\frac{a b+a c+a d+b c}{d-a} . \\\\ \\Longrightarrow g+b c \\bar{g} & =\\frac{(d-a)(b+c)}{d-a}=b+c . \\end{aligned} $$ Hence $G$ lies on $B C$ and this completes the proof.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 10 |
-
{"year": "2019", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\\triangle A E F$, and suppose line $A K$ intersects $\\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\\overline{B C}$ meet on $\\Gamma$.", "solution": " 【 Seventh solution using moving points (Zack Chroman). We state the converse of the problem as follows: Take a point $D$ on $\\Gamma$, and let $G \\in \\Gamma$ such that $\\overline{D G} \\perp \\overline{B C}$. Then define $K$ to lie on $\\overline{G H}, \\overline{A D}$, and take $L \\in \\overline{A D}$ such that $K$ is the midpoint of $\\overline{A L}$. Then if we define $E$ and $F$ as the projections of $L$ onto $\\overline{A B}$ and $\\overline{A C}$ we want to show that $E, H, F$ are collinear. It's clear that solving this problem will solve the original. In fact we will show later that each line $E F$ through $H$ corresponds bijectively to the point $D$. We animate $D$ projectively on $\\Gamma$ (hence $\\operatorname{deg} D=2$ ). Since $D \\mapsto G$ is a projective map $\\Gamma \\rightarrow \\Gamma$, it follows $\\operatorname{deg} G=2$. By Zack's lemma, $\\operatorname{deg}(\\overline{A D}) \\leq 0+2-1=1$ (since $D$ can coincide with $A$ ), and $\\operatorname{deg}(\\overline{H G}) \\leq 0+2-0=2$. So again by Zack's lemma, $\\operatorname{deg} K \\leq 1+2-1=2$, since lines $A D$ and $G H$ can coincide once if $D$ is the reflection of $H$ over $\\overline{B C}$. It follows $\\operatorname{deg} L=2$, since it is obtained by dilating $K$ by a factor of 2 across the fixed point $A$. Let $\\infty_{C}$ be the point at infinity on the line perpendicular to $A C$, and similarly $\\infty_{B}$. Then $$ F=\\overline{A C} \\cap \\overline{\\infty_{C} L}, \\quad E=\\overline{A B} \\cap \\overline{\\infty_{B} L} . $$ We want to use Zack's lemma again on line $\\overline{\\infty_{B} L}$. Consider the case $G=B$; we get $\\overline{H G} \\| \\overline{A D}$, so $A D G H$ is a parallelogram, and then $K=L=\\infty_{B}$. Thus there is at least one $t$ where $L=\\infty_{B}$ and by Zack's lemma we get $\\operatorname{deg}\\left(\\overline{\\infty_{B} L}\\right) \\leq 0+2-1=1$. Again by Zack's lemma, we conclude $\\operatorname{deg} E \\leq 0+1-0=1$. Similarly, $\\operatorname{deg} F \\leq 1$. We were aiming to show $E, F, H$ collinear which is a condition of degree at most $1+1+0=2$. So it suffices to verify the problem for three distinct choices of $D$. - If $D=A$, then line $G H$ is line $A H$, and $L=\\overline{A D} \\cap \\overline{A H}=A$. So $E=F=A$ and the statement is true. - If $D=B, G$ is the antipode of $C$ on $\\Gamma$. Then $K=\\overline{H G} \\cap \\overline{A D}$ is the midpoint of $\\overline{A B}$, so $L=B$. Then $E=B$ and $F$ is the projection of $B$ onto $A C$, so $E, H, F$ collinear. - We finish similarly when $D=C$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 11 |
-
{"year": "2019", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Suppose $P$ is a polynomial with integer coefficients such that for every positive integer $n$, the sum of the decimal digits of $|P(n)|$ is not a Fibonacci number. Must $P$ be constant?", "solution": " The answer is yes, $P$ must be constant. By $S(n)$ we mean the sum of the decimal digits of $|n|$. We need two claims. Claim - If $P(x) \\in \\mathbb{Z}[x]$ is nonconstant with positive leading coefficient, then there exists an integer polynomial $F(x)$ such that all coefficients of $P \\circ F$ are positive except for the second one, which is negative. First, consider $T_{0}(x)=x^{3}+x+1$. Observe that in $T_{0}^{\\operatorname{deg} P}$, every coefficient is strictly positive, except for the second one, which is zero. Then, let $T_{1}(x)=x^{3}-\\frac{1}{D} x^{2}+x+1$. Using continuity as $D \\rightarrow \\infty$, it follows that if $D$ is large enough (in terms of $\\operatorname{deg} P$ ), then $T_{1}^{\\operatorname{deg} P}$ is good, with $-\\frac{3}{D} x^{3 \\operatorname{deg} P-1}$ being the only negative coefficient. Finally, we can let $F(x)=C T_{1}(x)$ where $C$ is a sufficiently large multiple of $D$ (in terms of the coefficients of $P$ ); thus the coefficients of $\\left(C T_{1}(x)\\right)^{\\operatorname{deg} P}$ dominate (and are integers), as needed. Claim - There are infinitely many Fibonacci numbers in each residue class modulo 9. $$ \\begin{aligned} F_{0}=0 & \\equiv 0 \\quad(\\bmod 9) \\\\ F_{1}=1 & \\equiv 1 \\quad(\\bmod 9) \\\\ F_{3}=2 & \\equiv 2 \\quad(\\bmod 9) \\\\ F_{4}=3 & \\equiv 3 \\quad(\\bmod 9) \\\\ F_{7}=13 & \\equiv 4 \\quad(\\bmod 9) \\\\ F_{5}=5 & \\equiv 5 \\quad(\\bmod 9) \\\\ F_{-4}=-3 & \\equiv 6 \\quad(\\bmod 9) \\\\ F_{9}=34 & \\equiv 7 \\quad(\\bmod 9) \\\\ F_{6}=8 & \\equiv 8 \\quad(\\bmod 9) . \\end{aligned} $$ We now show how to solve the problem with the two claims. WLOG $P$ satisfies the conditions of the first claim, and choose $F$ as above. Let $$ P(F(x))=c_{N} x^{N}-c_{N-1} x^{N-1}+c_{N-2} x^{N-2}+\\cdots+c_{0} $$ where $c_{i}>0$ (and $N=3 \\operatorname{deg} P$ ). Then if we select $x=10^{e}$ for $e$ large enough (say $\\left.x>10 \\max _{i} c_{i}\\right)$, the decimal representation $P\\left(F\\left(10^{e}\\right)\\right)$ consists of the concatenation of - the decimal representation of $c_{N}-1$, - the decimal representation of $10^{e}-c_{N-1}$ - the decimal representation of $c_{N-2}$, with several leading zeros, - the decimal representation of $c_{N-3}$, with several leading zeros, - ... - the decimal representation of $c_{0}$, with several leading zeros. (For example, if $P(F(x))=15 x^{3}-7 x^{2}+4 x+19$, then $P(F(1000))=14,993,004,019$.) Thus, the sum of the digits of this expression is equal to $$ S\\left(P\\left(F\\left(10^{e}\\right)\\right)\\right)=9 e+k $$ for some constant $k$ depending only on $P$ and $F$, independent of $e$. But this will eventually hit a Fibonacci number by the second claim, contradiction. Remark. It is important to control the number of negative coefficients in the created polynomial. If one tries to use this approach on a polynomial $P$ with $m>0$ negative coefficients, then one would require that the Fibonacci sequence is surjective modulo $9 m$ for any $m>1$, which is not true: for example the Fibonacci sequence avoids all numbers congruent to $4 \\bmod 11($ and thus $4 \\bmod 99)$. In bases $b$ for which surjectivity modulo $b-1$ fails, the problem is false. For example, $P(x)=11 x+4$ will avoid all Fibonacci numbers if we take sum of digits in base 12, since that base-12 sum is necessarily $4(\\bmod 11)$, hence not a Fibonacci number.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 12 |
-
{"year": "2019", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Let $f: \\mathbb{Z} \\rightarrow\\left\\{1,2, \\ldots, 10^{100}\\right\\}$ be a function satisfying $$ \\operatorname{gcd}(f(x), f(y))=\\operatorname{gcd}(f(x), x-y) $$ for all integers $x$ and $y$. Show that there exist positive integers $m$ and $n$ such that $f(x)=\\operatorname{gcd}(m+x, n)$ for all integers $x$.", "solution": " Let $\\mathcal{P}$ be the set of primes not exceeding $10^{100}$. For each $p \\in \\mathcal{P}$, let $e_{p}=\\max _{x} \\nu_{p}(f(x))$ and let $c_{p} \\in \\operatorname{argmax}_{x} \\nu_{p}(f(x))$. We show that this is good enough to compute all values of $x$, by looking at the exponent at each individual prime. Claim - For any $p \\in \\mathcal{P}$, we have $$ \\nu_{p}(f(x))=\\min \\left(\\nu_{p}\\left(x-c_{p}\\right), e_{p}\\right) $$ $$ \\operatorname{gcd}\\left(f\\left(c_{p}\\right), f(x)\\right)=\\operatorname{gcd}\\left(f\\left(c_{p}\\right), x-c_{p}\\right) $$ We then take $\\nu_{p}$ of both sides and recall $\\nu_{p}(f(x)) \\leq \\nu_{p}\\left(f\\left(c_{p}\\right)\\right)=e_{p}$; this implies the result. This essentially determines $f$, and so now we just follow through. Choose $n$ and $m$ such that $$ \\begin{aligned} n & =\\prod_{p \\in \\mathcal{P}} p^{e_{p}} \\\\ m & \\equiv-c_{p} \\quad\\left(\\bmod p^{e_{p}}\\right) \\quad \\forall p \\in \\mathcal{P} \\end{aligned} $$ the latter being possible by Chinese remainder theorem. Then, from the claim we have $$ \\begin{aligned} f(x) & =\\prod_{p \\in \\mathcal{P}} p^{\\nu_{p}(f(x))}=\\prod_{p \\mid n} p^{\\min \\left(\\nu_{p}\\left(x-c_{p}\\right), e_{p}\\right)} \\\\ & =\\prod_{p \\mid n} p^{\\min \\left(\\nu_{p}(x+m), \\nu_{p}(n)\\right)}=\\operatorname{gcd}(x+m, n) \\end{aligned} $$ for every $x \\in \\mathbb{Z}$, as desired. Remark. The functions $f(x)=x$ and $f(x)=|2 x-1|$ are examples satisfying the gcd equation (the latter always being strictly positive). Hence the hypothesis $f$ bounded cannot be dropped. Remark. The pair $(m, n)$ is essentially unique: every other pair is obtained by shifting $m$ by a multiple of $n$. Hence there is not really any choice in choosing $m$ and $n$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 13 |
-
{"year": "2019", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $\\mathcal{S}$ be a set of 16 points in the plane, no three collinear. Let $\\chi(\\mathcal{S})$ denote the number of ways to draw 8 line segments with endpoints in $\\mathcal{S}$, such that no two drawn segments intersect, even at endpoints. Find the smallest possible value of $\\chi(\\mathcal{S})$ across all such $\\mathcal{S}$.", "solution": " The answer is 1430 . In general, we prove that with $2 n$ points the answer is the $n^{\\text {th }}$ Catalan number $C_{n}=\\frac{1}{n+1}\\binom{2 n}{n}$. First of all, it is well-known that if $\\mathcal{S}$ is a convex $2 n$-gon, then $\\chi(\\mathcal{S})=C_{n}$. It remains to prove the lower bound. We proceed by (strong) induction on $n$, with the base case $n=0$ and $n=1$ clear. Suppose the statement is proven for $0,1, \\ldots, n$ and consider a set $\\mathcal{S}$ with $2(n+1)$ points. Let $P$ be a point on the convex hull of $\\mathcal{S}$, and label the other $2 n+1$ points $A_{1}, \\ldots, A_{2 n+1}$ in order of angle from $P$. Consider drawing a segment $\\overline{P A_{2 k+1}}$. This splits the $2 n$ remaining points into two halves $\\mathcal{U}$ and $\\mathcal{V}$, with $2 k$ and $2(n-k)$ points respectively.  Note that by choice of $P$, no segment in $\\mathcal{U}$ can intersect a segment in $\\mathcal{V}$. By the inductive hypothesis, $$ \\chi(\\mathcal{U}) \\geq C_{k} \\quad \\text { and } \\quad \\chi(\\mathcal{V}) \\geq C_{n-k} $$ Thus, drawing $\\overline{P A_{2 k+1}}$, we have at least $C_{k} C_{n-k}$ ways to complete the drawing. Over all choices of $k$, we obtain $$ \\chi(\\mathcal{S}) \\geq C_{0} C_{n}+\\cdots+C_{n} C_{0}=C_{n+1} $$ as desired. Remark. It is possible to show directly from the lower bound proof that convex $2 n$-gons achieve the minimum: indeed, every inequality is sharp, and no segment $\\overline{P A_{2 k}}$ can be drawn (since this splits the rest of the points into two halves with an odd number of points, and no crossing segment can be drawn). Bobby Shen points out that in the case of 6 points, a regular pentagon with its center also achieves equality, so this is not the only equality case. Remark. The result that $\\chi(S) \\geq 1$ for all $S$ is known (consider the choice of 8 segments with smallest sum), and appeared on Putnam 1979. However, it does not seem that knowing this gives an advantage for this problem, since the answer is much larger than 1.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 14 |
-
{"year": "2019", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\\triangle A B K$ and $\\triangle A B L$ are tangent at $P$, and the incircles of $\\triangle A C K$ and $\\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.", "solution": " 【 First solution, mostly elementary (original). Let $I_{B}, J_{B}, I_{C}, J_{C}$ be the incenters of $\\triangle A B K, \\triangle A B L, \\triangle A C K, \\triangle A C L$ respectively.  We begin with the following claim which does not depend on the existence of tangency points $P$ and $Q$. Claim - Lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at a point $R$ (possibly at infinity). $$ A\\left(B I ; I_{B} J_{B}\\right)=A\\left(I C ; I_{C} J_{C}\\right) . $$ It follows $\\left(B I ; I_{B} J_{B}\\right)=\\left(I C ; I_{C} J_{C}\\right)=\\left(C I ; J_{C} I_{C}\\right)$. (One could also check directly that both cross ratios equal $\\frac{\\sin \\angle B A K / 2}{\\sin \\angle C A K / 2} \\div \\frac{\\sin \\angle B A L / 2}{\\sin \\angle C A L / 2}$, rather than using rotation.) Therefore, the concurrence follows from the so-called prism lemma on $\\overline{I B I_{B} J_{B}}$ and $\\overline{I C J_{C} I_{C}}$. Remark (Nikolai Beluhov). This result is known; it appears as 4.5.32 in Akopyan's Geometry in Figures. The cross ratio is not necessary to prove this claim: it can be proven by length chasing with circumscribed quadrilaterals. (The generalization mentioned later also admits a trig-free proof for the analogous step.) We now bring $P$ and $Q$ into the problem. Claim - Line $P Q$ also passes through $R$. $$ \\frac{I_{B} P}{P I} \\cdot \\frac{I Q}{Q J_{C}} \\cdot \\frac{J_{C} R}{R I_{B}}=-1 \\Longrightarrow I P=I Q $$ Remark (Author's comments on drawing the diagram). Drawing the diagram directly is quite difficult. If one draws $\\triangle A B C$ first, they must locate both $K$ and $L$, which likely involves some trial and error due to the complex interplay between the two points. There are alternative simpler ways. For example, one may draw $\\triangle A K L$ first; then the remaining points $B$ and $C$ are not related and the task is much simpler (though some trial and error is still required). In fact, by breaking symmetry, we may only require one application of guesswork. Start by drawing $\\triangle A B K$ and its incircle; then the incircle of $\\triangle A B L$ may be constructed, and so point $L$ may be drawn. Thus only the location of point $C$ needs to be guessed. I would be interested in a method to create a general diagram without any trial and error.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
| 15 |
-
{"year": "2019", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\\triangle A B K$ and $\\triangle A B L$ are tangent at $P$, and the incircles of $\\triangle A C K$ and $\\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.", "solution": " 【 Second solution, inversion (Nikolai Beluhov). As above, the lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at some point $R$ (possibly at infinity). Let $\\omega_{1}, \\omega_{2}, \\omega_{3}, \\omega_{4}$ be the incircles of $\\triangle A B K$, $\\triangle A C L, \\triangle A B L$, and $\\triangle A C K$. Claim - There exists an inversion $\\iota$ at $R$ swapping $\\left\\{\\omega_{1}, \\omega_{2}\\right\\}$ and $\\left\\{\\omega_{3}, \\omega_{4}\\right\\}$. Claim - Circles $\\omega_{1}, \\omega_{2}, \\omega_{3}, \\omega_{4}$ share a common radical center. Then $k$ is actually orthogonal to $\\Omega, \\omega_{1}, \\omega_{3}$, so $k$ is fixed under $\\iota$ and $k$ is also orthogonal to $\\omega_{2}$ and $\\omega_{4}$. Thus the center of $k$ is the desired radical center. The desired statement immediately follows. Indeed, letting $S$ be the radical center, it follows that $\\overline{S P}$ and $\\overline{S Q}$ are the common internal tangents to $\\left\\{\\omega_{1}, \\omega_{3}\\right\\}$ and $\\left\\{\\omega_{2}, \\omega_{4}\\right\\}$. Since $S$ is the radical center, $S P=S Q$. In light of $\\angle S P I=\\angle S Q I=90^{\\circ}$, it follows that $I P=I Q$, as desired. Remark (Nikolai Beluhov). There exists a circle tangent to all four incircles, because circle $k$ is orthogonal to all four, and line $B C$ is tangent to all four; thus the inverse of line $B C$ in $k$ is a circle tangent to all four incircles. The amusing thing here is that Casey's theorem is completely unhelpful for proving this fact: all it can tell us is that there is a line or circle tangent to these incircles, and line $B C$ already satisfies this property. Remark (Generalization by Nikolai Beluhov). The following generalization holds: Let $A B C D$ be a quadrilateral circumscribed about a circle with center $I$. A line through $A$ meets $\\overrightarrow{B C}$ and $\\overrightarrow{D C}$ at $K$ and $L$; another line through $A$ meets $\\overrightarrow{B C}$ and $\\overrightarrow{D C}$ at $M$ and $N$. Suppose that the incircles of $\\triangle A B K$ and $\\triangle A B M$ are tangent at $P$, and the incircles of $\\triangle A C L$ and $\\triangle A C N$ are tangent at $Q$. Prove that $I P=I Q$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2019.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl
DELETED
|
@@ -1,10 +0,0 @@
|
|
| 1 |
-
{"year": "2020", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $a, b, c$ be fixed positive integers. There are $a+b+c$ ducks sitting in a circle, one behind the other. Each duck picks either rock, paper, or scissors, with $a$ ducks picking rock, $b$ ducks picking paper, and $c$ ducks picking scissors. A move consists of an operation of one of the following three forms: - If a duck picking rock sits behind a duck picking scissors, they switch places. - If a duck picking paper sits behind a duck picking rock, they switch places. - If a duck picking scissors sits behind a duck picking paper, they switch places. Determine, in terms of $a, b$, and $c$, the maximum number of moves which could take place, over all possible initial configurations.", "solution": " The maximum possible number of moves is $\\max (a b, a c, b c)$. First, we prove this is best possible. We define a feisty triplet to be an unordered triple of ducks, one of each of rock, paper, scissors, such that the paper duck is between the rock and scissors duck and facing the rock duck, as shown. (There may be other ducks not pictured, but the orders are irrelevant.)  Claim - The number of feisty triplets decreases by $c$ if a paper duck swaps places with a rock duck, and so on. Obviously the number of feisty triples is at most $a b c$ to start. Thus at most $\\max (a b, b c, c a)$ moves may occur, since the number of feisty triplets should always be nonnegative, at which point no moves are possible at all. To see that this many moves is possible, assume WLOG $a=\\min (a, b, c)$ and suppose we have $a$ rocks, $b$ papers, and $c$ scissors in that clockwise order.  Then, allow the scissors to filter through the papers while the rocks stay put. Each of the $b$ papers swaps with $c$ scissors, for a total of $b c=\\max (a b, a c, b c)$ swaps. Remark (Common errors). One small possible mistake: it is not quite kösher to say that \"WLOG $a \\leq b \\leq c$ \" because the condition is not symmetric, only cyclic. Therefore in this solution we only assume $a=\\min (a, b, c)$. It is true here that every pair of ducks swaps at most once, and some solutions make use of this fact. However, this fact implicitly uses the fact that $a, b, c>0$ and is false without this hypothesis.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 2 |
-
{"year": "2020", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle with incenter $I$. The incircle of $A B C$ touches $\\overline{B C}$, $\\overline{C A}, \\overline{A B}$ at points $D, E, F$, respectively. Let $P$ be the foot of the altitude from $D$ to $\\overline{E F}$, and let $M$ be the midpoint of $\\overline{B C}$. The rays $A P$ and $I P$ intersect the circumcircle of triangle $A B C$ again at points $G$ and $Q$, respectively. Show that the incenter of triangle $G Q M$ coincides with $D$.", "solution": " Refer to the figure below.  Claim - The point $Q$ is the Miquel point of $B F E C$. Also, $\\overline{Q D}$ bisects $\\angle B Q C$. The spiral similarity mentioned then gives $\\frac{Q B}{B F}=\\frac{Q C}{C E}$, so $\\overline{Q D}$ bisects $\\angle B Q C$. Remark. The point $Q$ and its properties mentioned in the first claim have appeared in other references. See for example Canada 2007/5, ELMO 2010/6, HMMT 2016 T-10, USA TST 2017/2, USA TST 2019/6 for a few examples. Claim - We have $(Q G ; B C)=-1$, so in particular $\\overline{G D}$ bisects $\\angle B G C$. $$ -1=(A I ; E F) \\stackrel{Q}{=}(\\overline{A Q} \\cap \\overline{E F}, P ; E, F) \\stackrel{A}{=}(Q G ; B C) $$ The last statement follows from Apollonian circle, or more bluntly $\\frac{G B}{G C}=\\frac{Q B}{Q C}=\\frac{B D}{D C}$. Hence $\\overline{Q D}$ and $\\overline{G D}$ are angle bisectors of $\\angle B Q C$ and $\\angle B G C$. However, $\\overline{Q M}$ and $\\overline{Q G}$ are isogonal in $\\angle B Q C$ (as median and symmedian), and similarly for $\\angle B G C$, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 3 |
-
{"year": "2020", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "We say a nondegenerate triangle whose angles have measures $\\theta_{1}, \\theta_{2}, \\theta_{3}$ is quirky if there exists integers $r_{1}, r_{2}, r_{3}$, not all zero, such that $$ r_{1} \\theta_{1}+r_{2} \\theta_{2}+r_{3} \\theta_{3}=0 $$ Find all integers $n \\geq 3$ for which a triangle with side lengths $n-1, n, n+1$ is quirky.", "solution": " The answer is $n=3,4,5,7$. We first introduce a variant of the $k$ th Chebyshev polynomials in the following lemma (which is standard, and easily shown by induction). ## Lemma For each $k \\geq 0$ there exists $P_{k}(X) \\in \\mathbb{Z}[X]$, monic for $k \\geq 1$ and with degree $k$, such that $$ P_{k}\\left(X+X^{-1}\\right) \\equiv X^{k}+X^{-k} . $$ The first few are $P_{0}(X) \\equiv 2, P_{1}(X) \\equiv X, P_{2}(X) \\equiv X^{2}-2, P_{3}(X) \\equiv X^{3}-3 X$. Suppose the angles of the triangle are $\\alpha<\\beta<\\gamma$, so the law of cosines implies that $$ 2 \\cos \\alpha=\\frac{n+4}{n+1} \\quad \\text { and } \\quad 2 \\cos \\gamma=\\frac{n-4}{n-1} $$ Claim - The triangle is quirky iff there exists $r, s \\in \\mathbb{Z}_{\\geq 0}$ not both zero such that $$ \\cos (r \\alpha)= \\pm \\cos (s \\gamma) \\quad \\text { or equivalently } \\quad P_{r}\\left(\\frac{n+4}{n+1}\\right)= \\pm P_{s}\\left(\\frac{n-4}{n-1}\\right) $$ If $r=0$, then by rational root theorem on $P_{s}(X) \\pm 2$ it follows $\\frac{n-4}{n-1}$ must be an integer which occurs only when $n=4$ (recall $n \\geq 3$ ). Similarly we may discard the case $s=0$. Thus in what follows assume $n \\neq 4$ and $r, s>0$. Then, from the fact that $P_{r}$ and $P_{s}$ are nonconstant monic polynomials, we find ## Corollary If $n \\neq 4$ works, then when $\\frac{n+4}{n+1}$ and $\\frac{n-4}{n-1}$ are written as fractions in lowest terms, the denominators have the same set of prime factors. But $\\operatorname{gcd}(n+1, n-1)$ divides 2 , and $\\operatorname{gcd}(n+4, n+1), \\operatorname{gcd}(n-4, n-1)$ divide 3 . So we only have three possibilities: - $n+1=2^{u}$ and $n-1=2^{v}$ for some $u, v \\geq 0$. This is only possible if $n=3$. Here $2 \\cos \\alpha=\\frac{7}{4}$ and $2 \\cos \\gamma=-\\frac{1}{2}$, and indeed $P_{2}(-1 / 2)=-7 / 4$. - $n+1=3 \\cdot 2^{u}$ and $n-1=2^{v}$ for some $u, v \\geq 0$, which implies $n=5$. Here $2 \\cos \\alpha=\\frac{3}{2}$ and $2 \\cos \\gamma=\\frac{1}{4}$, and indeed $P_{2}(3 / 2)=1 / 4$. - $n+1=2^{u}$ and $n-1=3 \\cdot 2^{v}$ for some $u, v \\geq 0$, which implies $n=7$. Here $2 \\cos \\alpha=\\frac{11}{8}$ and $2 \\cos \\gamma=\\frac{1}{2}$, and indeed $P_{3}(1 / 2)=-11 / 8$. Finally, $n=4$ works because the triangle is right, completing the solution. Remark (Major generalization due to Luke Robitaille). In fact one may find all quirky triangles whose sides are integers in arithmetic progression. Indeed, if the side lengths of the triangle are $x-y, x, x+y$ with $\\operatorname{gcd}(x, y)=1$ then the problem becomes $$ P_{r}\\left(\\frac{x+4 y}{x+y}\\right)= \\pm P_{s}\\left(\\frac{x-4 y}{x-y}\\right) $$ and so in the same way as before, we ought to have $x+y$ and $x-y$ are both of the form $3 \\cdot 2^{*}$ unless $r s=0$. This time, when $r s=0$, we get the extra solutions $(1,0)$ and $(5,2)$. For $r s \\neq 0$, by triangle inequality, we have $x-y \\leq x+y<3(x-y)$, and $\\min \\left(\\nu_{2}(x-\\right.$ $\\left.y), \\nu_{2}(x+y)\\right) \\leq 1$, so it follows one of $x-y$ or $x+y$ must be in $\\{1,2,3,6\\}$. An exhaustive check then leads to $$ (x, y) \\in\\{(3,1),(5,1),(7,1),(11,5)\\} \\cup\\{(1,0),(5,2),(4,1)\\} $$ In conclusion the equilateral triangle, $3-5-7$ triangle (which has a $120^{\\circ}$ angle) and $6-11-16$ triangle (which satisfies $B=3 A+4 C$ ) are exactly the new quirky triangles (up to similarity) whose sides are integers in arithmetic progression.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 4 |
-
{"year": "2020", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Find all pairs of positive integers $(a, b)$ satisfying the following conditions: (i) $a$ divides $b^{4}+1$, (ii) $b$ divides $a^{4}+1$, (iii) $\\lfloor\\sqrt{a}\\rfloor=\\lfloor\\sqrt{b}\\rfloor$.", "solution": " Obviously, $\\operatorname{gcd}(a, b)=1$, so the problem conditions imply $$ a b \\mid(a-b)^{4}+1 $$ since each of $a$ and $b$ divide the right-hand side. We define $$ k \\stackrel{\\text { def }}{=} \\frac{(b-a)^{4}+1}{a b} . $$ Claim (Size estimate) — We must have $k \\leq 16$. $$ \\begin{aligned} a b & \\geq n^{2}\\left(n^{2}+1\\right) \\geq n^{4}+1 \\\\ (b-a)^{4}+1 & \\leq(2 n)^{4}+1=16 n^{4}+1 \\end{aligned} $$ which shows $k \\leq 16$. Claim (Orders argument) - In fact, $k=1$. Thus $k$ is odd. However, every odd prime divisor of $(b-a)^{4}+1$ is congruent to 1 $(\\bmod 8)$ and is thus at least 17 , so $k=1$ or $k \\geq 17$. It follows that $k=1$. At this point, we have reduced to solving $$ a b=(b-a)^{4}+1 $$ $$ a^{2}-d a-\\left(d^{4}+1\\right)=0 $$ The discriminant $d^{2}+4\\left(d^{4}+1\\right)=4 d^{4}+d^{2}+4$ must be a perfect square. - The cases $d=0$ and $d=1$ lead to pairs $(1,1)$ and $(1,2)$. - If $d \\geq 2$, then we can sandwich $$ \\left(2 d^{2}\\right)^{2}<4 d^{4}+d^{2}+4<4 d^{4}+4 d^{2}+1=\\left(2 d^{2}+1\\right)^{2} $$ so the discriminant is not a square. Remark (Author remarks on origin). This comes from the problem of the existence of a pair of elliptic curves over $\\mathbb{F}_{a}, \\mathbb{F}_{b}$ respectively, such that the number of points on one is the field size of the other. The bound $n^{2} \\leq a, b<(n+1)^{2}$ is the Hasse bound. The divisibility conditions correspond to asserting that the embedding degree of each curve is 8 , so that they are pairing friendly. In this way, the problem is essentially the key result of https://arxiv.org/pdf/1803.02067.pdf, shown in Proposition 3.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 5 |
-
{"year": "2020", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $\\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\\left(x^{\\prime}, y^{\\prime}\\right)$ of $\\mathbb{N}^{2}$ with both $x^{\\prime} \\leq x$ and $y^{\\prime} \\leq y$. Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.", "solution": " Suppose $|S| \\geq 2$. For any $p \\in S$, let $R(p)$ denote the stable rectangle with upper-right corner $p$. We say such $p$ is pivotal if $p+(1,1) \\notin S$ and $|R(p)|$ is even.  Claim - If $|S| \\geq 2$, then a pivotal $p$ always exists. - If it has length at least 2 , one of the two rightmost points in it is pivotal. - Otherwise, the top row has length 1. Now either the top point or the point below it (which exists as $|S| \\geq 2$ ) is pivotal. We describe how to complete the induction, given some pivotal $p \\in S$. There is a partition $$ S=R(p) \\sqcup S_{1} \\sqcup S_{2} $$ where $S_{1}$ and $S_{2}$ are the sets of points in $S$ above and to the right of $p$ (possibly empty). Claim - The desired inequality holds for stable subsets containing $p$. Since $|R(p)|$ is even, exactly $E_{1} E_{2}+O_{1} O_{2}$ stable subsets containing $p$ are even, and exactly $E_{1} O_{2}+E_{2} O_{1}$ are odd. As $E_{1} \\geq O_{1}$ and $E_{2} \\geq O_{2}$ by inductive hypothesis, we obtain $E_{1} E_{2}+O_{1} O_{2} \\geq E_{1} O_{2}+E_{2} O_{1}$ as desired. By the inductive hypothesis, the desired inequality also holds for stable subsets not containing $p$, so we are done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 6 |
-
{"year": "2020", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\\triangle B C D, \\triangle C A D$, $\\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.", "solution": " Let $T$ be the concurrency point, and let $H$ be the orthocenter of $\\triangle A B C$.  Claim (Key claim) - $T$ is the midpoint of $\\overline{A P}, \\overline{B Q}, \\overline{C R}, \\overline{D H}$, and $D$ is the orthocenter of $\\triangle P Q R$. By symmetric reasoning, we get that $A Q C P B R$ is a hexagon with opposite sides parallel and concurrent diagonals as $\\overline{A P}, \\overline{B Q}, \\overline{C R}$ meet at $T$. This implies that the hexagon is centrally symmetric about $T$; indeed $$ \\frac{A T}{T P}=\\frac{T Q}{B T}=\\frac{C T}{T R}=\\frac{T P}{A T} $$ so all the ratios are equal to +1 . Next, $\\overline{P D} \\perp \\overline{B C} \\| \\overline{Q R}$, so by symmetry we get $D$ is the orthocenter of $\\triangle P Q R$. This means that $T$ is the midpoint of $\\overline{D H}$ as well. ## Corollary The configuration is now symmetric: we have four points $A, B, C, D$, and their reflections in $T$ are four orthocenters $P, Q, R, H$. Let $S$ be the centroid of $\\{A, B, C, D\\}$, and let $O$ be the reflection of $T$ in $S$. We are ready to conclude: Claim - $A, B, C, D$ are equidistant from $O$. Then $T^{\\prime}$ is the midpoint of $\\overline{A^{\\prime} D^{\\prime}}$, so $S^{\\prime}=\\frac{1}{4}\\left(A^{\\prime}+D^{\\prime}+B+C\\right)$ gives that $O^{\\prime}$ is the midpoint of $\\overline{B C}$. Thus $O B=O C$ and we're done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 7 |
-
{"year": "2020", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.", "solution": " The answer is $P(x)$ should be a polynomial of the form $P(x)=\\lambda x^{n}-\\mu$ where $|\\lambda|=|\\mu|$ and $\\operatorname{Re} \\mu=-\\frac{1}{2}$. One may check these all work; let's prove they are the only solutions. \\l First approach (Evan Chen). We introduce the following notations: $$ \\begin{aligned} P(x) & =c_{n} x^{n}+c_{n-1} x^{n-1}+\\cdots+c_{1} x+c_{0} \\\\ & =c_{n}\\left(x+\\alpha_{1}\\right) \\ldots\\left(x+\\alpha_{n}\\right) \\\\ P(x)-1 & =c_{n}\\left(x+\\beta_{1}\\right) \\ldots\\left(x+\\beta_{n}\\right) \\end{aligned} $$ By taking conjugates, $$ \\begin{aligned} \\left(x+\\alpha_{1}\\right) \\cdots\\left(x+\\alpha_{n}\\right) & =\\left(x+\\beta_{1}\\right) \\cdots\\left(x+\\beta_{n}\\right)+c_{n}^{-1} \\\\ \\Longrightarrow\\left(x+\\frac{1}{\\alpha_{1}}\\right) \\cdots\\left(x+\\frac{1}{\\alpha_{n}}\\right) & =\\left(x+\\frac{1}{\\beta_{1}}\\right) \\cdots\\left(x+\\frac{1}{\\beta_{n}}\\right)+\\left(\\overline{c_{n}}\\right)^{-1} \\end{aligned} $$ The equation $(\\boldsymbol{\\oplus})$ is the main player: Claim - We have $c_{k}=0$ for all $k=1, \\ldots, n-1$. $$ \\frac{c_{n-k}}{\\prod_{i} \\alpha_{i}}=\\frac{c_{n-k}}{\\prod_{i} \\beta_{i}} $$ but $\\prod_{i} \\alpha_{i}-\\prod_{i} \\beta_{i}=\\frac{1}{c_{n}} \\neq 0$. Hence $c_{k}=0$. It follows that $P(x)$ must be of the form $P(x)=\\lambda x^{n}-\\mu$, so that $P(x)=\\lambda x^{n}-(\\mu+1)$. This requires $|\\mu|=|\\mu+1|=|\\lambda|$ which is equivalent to the stated part.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 8 |
-
{"year": "2020", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.", "solution": " The answer is $P(x)$ should be a polynomial of the form $P(x)=\\lambda x^{n}-\\mu$ where $|\\lambda|=|\\mu|$ and $\\operatorname{Re} \\mu=-\\frac{1}{2}$. One may check these all work; let's prove they are the only solutions. II Second approach (from the author). We let $A=P$ and $B=P-1$ to make the notation more symmetric. We will as before show that $A$ and $B$ have all coefficients equal to zero other than the leading and constant coefficient; the finish is the same. First, we rule out double roots. Claim - Neither $A$ nor $B$ have double roots. Let $\\omega=e^{2 \\pi i / n}$, let $a_{1}, \\ldots, a_{n}$ be the roots of $A$, and let $b_{1}, \\ldots, b_{n}$ be the roots of $B$. For each $k$, let $A_{k}$ and $B_{k}$ be the points in the complex plane corresponding to $a_{k}$ and $b_{k}$ 。 Claim (Main claim) - For any $i$ and $j, \\frac{a_{i}}{a_{j}}$ is a power of $\\omega$. $$ \\frac{a_{i}-b_{1}}{a_{j}-b_{1}} \\cdots \\frac{a_{i}-b_{n}}{a_{j}-b_{n}}=\\frac{B\\left(a_{i}\\right)}{B\\left(a_{j}\\right)}=\\frac{A\\left(a_{i}\\right)-1}{A\\left(a_{j}\\right)-1}=\\frac{0-1}{0-1}=1 $$ Since the points $A_{i}, A_{j}, B_{k}$ all lie on the unit circle, interpreting the left-hand side geometrically gives $$ \\measuredangle A_{i} B_{1} A_{j}+\\cdots+\\measuredangle A_{i} B_{n} A_{j}=0 \\Longrightarrow n \\widehat{A_{i} A_{j}}=0 $$ where angles are directed modulo $180^{\\circ}$ and arcs are directed modulo $360^{\\circ}$. This implies that $\\frac{a_{i}}{a_{j}}$ is a power of $\\omega$. Now the finish is easy: since $a_{1}, \\ldots, a_{n}$ are all different, they must be $a_{1} \\omega^{0}, \\ldots, a_{1} \\omega^{n-1}$ in some order; this shows that $A$ is a multiple of $x^{n}-a_{1}^{n}$, as needed.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 9 |
-
{"year": "2020", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "For every positive integer $N$, let $\\sigma(N)$ denote the sum of the positive integer divisors of $N$. Find all integers $m \\geq n \\geq 2$ satisfying $$ \\frac{\\sigma(m)-1}{m-1}=\\frac{\\sigma(n)-1}{n-1}=\\frac{\\sigma(m n)-1}{m n-1} . $$", "solution": " The answer is that $m$ and $n$ should be powers of the same prime number. These all work because for a prime power we have $$ \\frac{\\sigma\\left(p^{e}\\right)-1}{p^{e}-1}=\\frac{\\left(1+p+\\cdots+p^{e}\\right)-1}{p^{e}-1}=\\frac{p\\left(1+\\cdots+p^{e-1}\\right)}{p^{e}-1}=\\frac{p}{p-1} $$ So we now prove these are the only ones. Let $\\lambda$ be the common value of the three fractions. $$ \\begin{aligned} \\sigma(m n) & \\geq \\sigma(m)+m \\sigma(n)-m \\\\ & =(\\lambda m-\\lambda+1)+m(\\lambda n-\\lambda+1)-m \\\\ & =\\lambda m n-\\lambda+1 \\end{aligned} $$ and so equality holds. Thus these are all the divisors of $m n$, for a count of $d(m)+d(n)-$ 1. Claim - If $d(m n)=d(m)+d(n)-1$ and $\\min (m, n) \\geq 2$, then $m$ and $n$ are powers of the same prime. Remark (Nikolai Beluhov). Here is a completion not relying on $|A \\cdot B|=|A|+|B|-1$. By the above arguments, we see that every divisor of $m n$ is either a divisor of $n$, or $n$ times a divisor of $m$. Now suppose that some prime $p \\mid m$ but $p \\nmid n$. Then $p \\mid m n$ but $p$ does not appear in the above classification, a contradiction. By symmetry, it follows that $m$ and $n$ have the same prime divisors. Now suppose we have different primes $p \\mid m$ and $q \\mid n$. Write $\\nu_{p}(m)=\\alpha$ and $\\nu_{p}(n)=\\beta$. Then $p^{\\alpha+\\beta} \\mid m n$, but it does not appear in the above characterization, a contradiction. Thus, $m$ and $n$ are powers of the same prime. Remark (Comments on the function in the problem). Let $f(n)=\\frac{\\sigma(n)-1}{n-1}$. Then $f$ is not really injective even outside the above solution; for example, we have $f\\left(6 \\cdot 11^{k}\\right)=\\frac{11}{5}$ for all $k$, plus sporadic equivalences like $f(14)=f(404)$, as pointed out by one reviewer during test-solving. This means that both relations should be used at once, not independently. Remark (Authorship remarks). Ankan gave the following story for how he came up with the problem while thinking about so-called almost perfect numbers. I was in some boring talk when I recalled a conjecture that if $\\sigma(n)=2 n-1$, then $n$ is a power of 2 . For some reason (divine intervention, maybe) I had the double idea of (1) seeing whether $m, n, m n$ all almost perfect implies $m, n$ powers of 2 , and (2) trying the naive divisor bound to resolve this. Through sheer dumb luck this happened to work out perfectly. I thought this was kinda cool but I felt that I hadn't really unlocked a lot of the potential this idea had: then I basically tried to find the \"general situation\" which allows for this manipulation, and was amazed that it led to such a striking statement.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
| 10 |
-
{"year": "2020", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Ten million fireflies are glowing in $\\mathbb{R}^{3}$ at midnight. Some of the fireflies are friends, and friendship is always mutual. Every second, one firefly moves to a new position so that its distance from each one of its friends is the same as it was before moving. This is the only way that the fireflies ever change their positions. No two fireflies may ever occupy the same point. Initially, no two fireflies, friends or not, are more than a meter away. Following some finite number of seconds, all fireflies find themselves at least ten million meters away from their original positions. Given this information, find the greatest possible number of friendships between the fireflies.", "solution": " In general, we show that when $n \\geq 70$, the answer is $f(n)=\\left\\lfloor\\frac{n^{2}}{3}\\right\\rfloor$. Construction: Choose three pairwise parallel lines $\\ell_{A}, \\ell_{B}, \\ell_{C}$ forming an infinite equilateral triangle prism (with side larger than 1). Split the $n$ fireflies among the lines as equally as possible, and say that two fireflies are friends iff they lie on different lines. To see this works: 1. Reflect $\\ell_{A}$ and all fireflies on $\\ell_{A}$ in the plane containing $\\ell_{B}$ and $\\ell_{C}$. 2. Reflect $\\ell_{B}$ and all fireflies on $\\ell_{B}$ in the plane containing $\\ell_{C}$ and $\\ell_{A}$. 3. Reflect $\\ell_{C}$ and all fireflies on $\\ell_{C}$ in the plane containing $\\ell_{A}$ and $\\ell_{B}$. Let $g(n)$ be the answer, given that there exist four pairwise friends (say $a, b, c, d$ ). Note that for a firefly to move, all its friends must be coplanar. Claim (No coplanar $K_{4}$ ) — We can't have four coplanar fireflies which are pairwise friends. Claim (Key claim — tetrahedrons don't share faces often) — There are at most 12 fireflies $e$ which are friends with at least three of $a, b, c, d$. WLOG, will assume that $e$ is friends with $a, b, c$. Then $e$ will always be located at one of two points $E_{1}$ and $E_{2}$ relative to $A B C$, such that $E_{1} A B C$ and $E_{2} A B C$ are two congruent tetrahedrons with fixed shape. We note that points $D, E_{1}$, and $E_{2}$ are all different: clearly $D \\neq E_{1}$ and $E_{1} \\neq E_{2}$. (If $D=E_{2}$, then some fireflies won't be able to move.) Consider the moment where firefly $a$ moves. Its friends must be coplanar at that time, so one of $E_{1}, E_{2}$ lies in plane $B C D$. Similar reasoning holds for planes $A C D$ and $A B D$. So, WLOG $E_{1}$ lies on both planes $B C D$ and $A C D$. Then $E_{1}$ lies on line $C D$, and $E_{2}$ lies in plane $A B D$. This uniquely determines $\\left(E_{1}, E_{2}\\right)$ relative to $A B C D$ : - $E_{1}$ is the intersection of line $C D$ with the reflection of plane $A B D$ in plane $A B C$. - $E_{2}$ is the intersection of plane $A B D$ with the reflection of line $C D$ in plane $A B C$. Accounting for WLOGs, there are at most 12 possibilities for the set $\\left\\{E_{1}, E_{2}\\right\\}$, and thus at most 12 possibilities for $E$. (It's not possible for both elements of one pair $\\left\\{E_{1}, E_{2}\\right\\}$ to be occupied, because then they couldn't move.) Thus, the number of friendships involving exactly one of $a, b, c, d$ is at most $(n-16)$. $2+12 \\cdot 3=2 n+4$, so removing these four fireflies gives $$ g(n) \\leq 6+(2 n+4)+\\max \\{f(n-4), g(n-4)\\} $$ $$ g(n) \\leq \\max \\{f(n),(2 n+10)+g(n-4)\\} \\quad \\forall n \\geq 24 $$ By iterating the above inequality, we get $$ \\begin{aligned} g(n) \\leq \\max \\{f(n),(2 n+10) & +(2(n-4)+10) \\\\ & +\\cdots+(2(n-4 r)+10)+g(n-4 r-4)\\} \\end{aligned} $$ where $r$ satisfies $n-4 r-4<24 \\leq n-4 r$. Now $$ \\begin{aligned} & (2 n+10)+(2(n-4)+10)+\\cdots+(2(n-4 r)+10)+g(n-4 r-4) \\\\ = & (r+1)(2 n-4 r+10)+g(n-4 r-4) \\\\ \\leq & \\left(\\frac{n}{4}-5\\right)(n+37)+\\binom{24}{2} . \\end{aligned} $$ This is less than $f(n)$ for $n \\geq 70$, which concludes the solution. Remark. There are positive integers $n$ such that it is possible to do better than $f(n)$ friendships. For instance, $f(5)=8$, whereas five fireflies $a, b, c, d$, and $e$ as in the proof of the Lemma ( $E_{1}$ being the intersection point of line $C D$ with the reflection of plane $(A B D)$ in plane $(A B C), E_{2}$ being the intersection point of plane $(A B D)$ with the reflection of line $C D$ in plane $(A B C)$, and tetrahedron $A B C D$ being sufficiently arbitrary that points $E_{1}$ and $E_{2}$ exist and points $D, E_{1}$, and $E_{2}$ are pairwise distinct) give a total of nine friendships. Remark (Author comments). It is natural to approach the problem by looking at the two-dimensional version first. In two dimensions, the following arrangement suggests itself almost immediately: We distribute all fireflies as equally as possible among two parallel lines, and two fireflies are friends if and only if they are on different lines. Similarly to the three-dimensional version, this attains the greatest possible number of friendships for all sufficiently large $n$, though not for all $n$. For instance, at least one friendlier arrangements exists for $n=4$, similarly to the above friendlier arrangement for $n=5$ in three dimensions. This observation strongly suggests that in three dimensions we should distribute the fireflies as equally as possible among two parallel planes, and that two fireflies should be friends if and only if they are on different planes. It was a great surprise for me to discover that this arrangement does not in fact give the correct answer! Remark. On the other hand, Ankan Bhattacharya gives the following reasoning as to why the answer should not be that surprising: I think the answer $\\left(10^{14}-1\\right) / 3$ is quite natural if you realize that $(n / 2)^{2}$ is probably optimal in 2D and $\\binom{n}{2}$ is optimal in super high dimensions (i.e. around $n$ ). So going from dimension 2 to 3 should increase the answer (and indeed it does).", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2020.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl
DELETED
|
@@ -1,28 +0,0 @@
|
|
| 1 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " 『 First solution, angle chasing only (Ankit Bisain). Let lines $B Q$ and $D P$ meet $(A B C D)$ again at $D^{\\prime}$ and $B^{\\prime}$, respectively.  Then $B B^{\\prime} \\| P X$ and $D D^{\\prime} \\| Q Y$ by Reim's theorem. Segments $B B^{\\prime}, D D^{\\prime}$, and $P Q$ share a perpendicular bisector which passes through $O$, so $O P=O Q$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 2 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " 【 Second solution via isosceles triangles (from contestants). Let $T=\\overline{B Q} \\cap \\overline{D P}$.  Note that $P Q T$ is isosceles because $$ \\measuredangle P Q T=\\measuredangle Y Q B=\\measuredangle B C D=\\measuredangle B A D=\\measuredangle X P D=\\measuredangle T P Q $$ Then $(B O D T)$ is cyclic because $$ \\measuredangle B O D=2 \\measuredangle B C D=\\measuredangle P Q T+\\measuredangle T P Q=\\measuredangle B T D . $$ Since $B O=O D, \\overline{T O}$ is an angle bisector of $\\measuredangle B T D$. Since $\\triangle P Q T$ is isosceles, $\\overline{T O} \\perp \\overline{P Q}$, so $O P=O Q$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 3 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " ब Third solution using a parallelogram (from contestants). Let $(B C Y)$ meet $\\overline{A B}$ again at $W$ and let $(A D X)$ meet $\\overline{C D}$ again at $Z$. Additionally, let $O_{1}$ be the center of $(A D X)$ and $O_{2}$ be the center of $(B C Y)$.  Note that $(W X Y Z)$ is cyclic since $$ \\measuredangle X W Y+\\measuredangle Y Z X=\\measuredangle Y W B+\\measuredangle X Z D=\\measuredangle Y C B+\\measuredangle X A D=0^{\\circ} $$ so let $O^{\\prime}$ be the center of ( $W X Y Z$ ). Since $\\overline{A D} \\| \\overline{W Y}$ and $\\overline{B C} \\| \\overline{X Z}$ by Reim's theorem, $O O_{1} O^{\\prime} O_{2}$ is a parallelogram. To finish the problem, note that projecting $O_{1}, O_{2}$, and $O^{\\prime}$ onto $\\overline{X Y}$ gives the midpoints of $\\overline{P X}, \\overline{Q Y}$, and $\\overline{X Y}$. Since $O O_{1} O^{\\prime} O_{2}$ is a parallelogram, projecting $O$ onto $\\overline{X Y}$ must give the midpoint of $\\overline{P Q}$, so $O P=O Q$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 4 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " ब Fourth solution using congruent circles (from contestants). Let the angle bisector of $\\measuredangle B O D$ meet $\\overline{X Y}$ at $K$.  Then $(B Q O K)$ is cyclic because $\\measuredangle K O D=\\measuredangle B A D=\\measuredangle K P D$, and $(D O P K)$ is cyclic similarly. By symmetry over $K O$, these circles have the same radius $r$, so $$ O P=2 r \\sin \\angle O K P=2 r \\sin \\angle O K Q=O Q $$ by the Law of Sines.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 5 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " 【 Fifth solution by ratio calculation (from contestants). Let $\\overline{X Y}$ meet $(A B C D)$ at $X^{\\prime}$ and $Y^{\\prime}$.  Since $\\measuredangle Y^{\\prime} B D=\\measuredangle P X^{\\prime} D$ and $\\measuredangle B Y^{\\prime} D=\\measuredangle B A D=\\measuredangle X^{\\prime} P D$, $$ \\triangle B Y^{\\prime} D \\sim \\triangle X P^{\\prime} D \\Longrightarrow P X^{\\prime}=B Y^{\\prime} \\cdot \\frac{D X^{\\prime}}{B D} $$ Similarly, $$ \\triangle B X^{\\prime} D \\sim \\triangle B Q Y^{\\prime} \\Longrightarrow Q Y^{\\prime}=D X^{\\prime} \\cdot \\frac{B Y^{\\prime}}{B D} $$ Thus $P X^{\\prime}=Q Y^{\\prime}$, which gives $O P=O Q$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 6 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " I Sixth solution using radical axis (from author). Without loss of generality, assume $\\overline{A D} \\nVdash \\overline{B C}$, as this case holds by continuity. Let $(B C Y)$ meet $\\overline{A B}$ again at $W$, let $(A D X)$ meet $\\overline{C D}$ again at $Z$, and let $\\overline{W Z}$ meet $(A D X)$ and $(B C Y)$ again at $R$ and $S$.  Note that $(W X Y Z)$ is cyclic since $$ \\measuredangle X W Y+\\measuredangle Y Z X=\\measuredangle Y W B+\\measuredangle X Z D=\\measuredangle Y C B+\\measuredangle X A D=0^{\\circ} $$ and $(P Q R S)$ is cyclic since $$ \\measuredangle P Q S=\\measuredangle Y Q S=\\measuredangle Y W S=\\measuredangle P X Z=\\measuredangle P R Z=\\measuredangle S R P $$ Additionally, $\\overline{A D} \\| \\overline{P R}$ since $$ \\measuredangle D A X+\\measuredangle A X P+\\measuredangle X P R=\\measuredangle Y W X+\\measuredangle W X Y+\\measuredangle X Y W=0^{\\circ}, $$ and $\\overline{B C} \\| \\overline{S Q}$ similarly. Lastly, $(A B C D)$ and $(P Q R S)$ are concentric; if not, using the radical axis theorem twice shows that their radical axis must be parallel to both $\\overline{A D}$ and $\\overline{B C}$, contradiction.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 7 |
-
{"year": "2021", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.", "solution": " 【 Seventh solution using Cayley-Bacharach (author). Define points $W, Z, R, S$ as in the previous solution.  The quartics $(A D X Z) \\cup(B C W Y)$ and $\\overline{X Y} \\cup \\overline{W Z} \\cup(A B C D)$ meet at the 16 points $$ A, B, C, D, W, X, Y, Z, P, Q, R, S, I, I, J, J $$ where $I$ and $J$ are the circular points at infinity. Since $\\overline{A B} \\cup \\overline{C D} \\cup(P Q R)$ contains the 13 points $$ A, B, C, D, P, Q, R, W, X, Y, Z, I, J $$ it must contain $S, I$, and $J$ as well, by quartic Cayley-Bacharach. Thus, $(P Q R S)$ is cyclic and intersects $(A B C D)$ at $I, I, J$, and $J$, implying that the two circles are concentric, as desired. Remark (Author comments). Holden says he came up with this problem via the CayleyBacharach solution, by trying to get two quartics to intersect.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 8 |
-
{"year": "2021", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}<a_{2}<a_{3}<a_{4}<\\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \\frac{a_{1}}{1}, \\frac{a_{2}}{2}, \\frac{a_{3}}{3}, \\frac{a_{4}}{4}, \\ldots $$", "solution": " 【 Solution 1 (Merlijn Staps). We argue by contradiction, so suppose that for each $\\lambda$ for which the set $S_{\\lambda}=\\left\\{k: a_{k} / k=\\lambda\\right\\}$ is non-empty, it contains at least two elements. Note that $S_{\\lambda}$ is always a finite set because $a_{k}=k \\lambda$ implies $k<1 / \\lambda$. Write $m_{\\lambda}$ and $M_{\\lambda}$ for the smallest and largest element of $S_{\\lambda}$, respectively, and define $T_{\\lambda}=\\left\\{m_{\\lambda}, m_{\\lambda}+1, \\ldots, M_{\\lambda}\\right\\}$ as the smallest set of consecutive positive integers that contains $S_{\\lambda}$. Then all $T_{\\lambda}$ are sets of at least two consecutive positive integers, and moreover the $T_{\\lambda}$ cover $\\mathbb{N}$. Additionally, each positive integer is covered finitely many times because there are only finitely many possible values of $m_{\\lambda}$ smaller than any fixed integer. Recall that if three intervals have a point in common then one of them is contained in the union of the other two. Thus, if any positive integer is covered more than twice by the sets $T_{\\lambda}$, we may throw out one set while maintaining the property that the $T_{\\lambda}$ cover $\\mathbb{N}$. By using the fact that each positive integer is covered finitely many times, we can apply this process so that each positive integer is eventually covered at most twice. Let $\\Lambda$ denote the set of the $\\lambda$-values for which $T_{\\lambda}$ remains in our collection of sets; then $\\bigcup_{\\lambda \\in \\Lambda} T_{\\lambda}=\\mathbb{N}$ and each positive integer is contained in at most two sets $T_{\\lambda}$. We now obtain $$ \\sum_{\\lambda \\in \\Lambda} \\sum_{k \\in T_{\\lambda}}\\left(a_{k+1}-a_{k}\\right) \\leq 2 \\sum_{k \\geq 1}\\left(a_{k+1}-a_{k}\\right) \\leq 2 $$ On the other hand, because $a_{m_{\\lambda}}=\\lambda m_{\\lambda}$ and $a_{M_{\\lambda}}=\\lambda M_{\\lambda}$, we have $$ \\begin{aligned} 2 \\sum_{k \\in T_{\\lambda}}\\left(a_{k+1}-a_{k}\\right) & \\geq 2 \\sum_{m_{\\lambda} \\leq k<M_{\\lambda}}\\left(a_{k+1}-a_{k}\\right)=2\\left(a_{M_{\\lambda}}-a_{m_{\\lambda}}\\right)=2\\left(M_{\\lambda}-m_{\\lambda}\\right) \\lambda \\\\ & =2\\left(M_{\\lambda}-m_{\\lambda}\\right) \\cdot \\frac{a_{m_{\\lambda}}}{m_{\\lambda}} \\geq\\left(M_{\\lambda}-m_{\\lambda}+1\\right) \\cdot \\frac{a_{1}}{m_{\\lambda}} \\geq a_{1} \\cdot \\sum_{k \\in T_{\\lambda}} \\frac{1}{k} . \\end{aligned} $$ Combining this with our first estimate, and using the fact that the $T_{\\lambda}$ cover $\\mathbb{N}$, we obtain $$ 4 \\geq 2 \\sum_{\\lambda \\in \\Lambda} \\sum_{k \\in T_{\\lambda}}\\left(a_{k+1}-a_{k}\\right) \\geq a_{1} \\sum_{\\lambda \\in \\Lambda} \\sum_{k \\in T_{\\lambda}} \\frac{1}{k} \\geq a_{1} \\sum_{k \\geq 1} \\frac{1}{k} $$ contradicting the fact that the harmonic series diverges.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 9 |
-
{"year": "2021", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}<a_{2}<a_{3}<a_{4}<\\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \\frac{a_{1}}{1}, \\frac{a_{2}}{2}, \\frac{a_{3}}{3}, \\frac{a_{4}}{4}, \\ldots $$", "solution": " 【 Solution 2 (Sanjana Das). Assume for the sake of contradiction that no number appears exactly once in the sequence. For every $i<j$ with $a_{i} / i=a_{j} / j$, draw an edge between $i$ and $j$, so every $i$ has an edge (and being connected by an edge is a transitive property). Call $i$ good if it has an edge with some $j>i$. First, each $i$ has finite degree - otherwise $$ \\frac{a_{x_{1}}}{x_{1}}=\\frac{a_{x_{2}}}{x_{2}}=\\cdots $$ for an infinite increasing sequence of positive integers $x_{i}$, but then the $a_{x_{i}}$ are unbounded. Now we use the following process to build a sequence of indices whose $a_{i}$ we can lower-bound: - Start at $x_{1}=1$, which is good. - If we're currently at good index $x_{i}$, then let $s_{i}$ be the largest positive integer such that $x_{i}$ has an edge to $x_{i}+s_{i}$. (This exists because the degrees are finite.) - Let $t_{i}$ be the smallest positive integer for which $x_{i}+s_{i}+t_{i}$ is good, and let this be $x_{i+1}$. This exists because if all numbers $k \\leq x \\leq 2 k$ are bad, they must each connect to some number less than $k$ (if two connect to each other, the smaller one is good), but then two connect to the same number, and therefore to each other this is the idea we will use later to bound the $t_{i}$ as well. Then $x_{i}=1+s_{1}+t_{1}+\\cdots+s_{i-1}+t_{i-1}$, and we have $$ a_{x_{i+1}}>a_{x_{i}+s_{i}}=\\frac{x_{i}+s_{i}}{x_{i}} a_{x_{i}}=\\frac{1+\\left(s_{1}+\\cdots+s_{i-1}+s_{i}\\right)+\\left(t_{1}+\\cdots+t_{i-1}\\right)}{1+\\left(s_{1}+\\cdots+s_{i-1}\\right)+\\left(t_{1}+\\cdots+t_{i-1}\\right)} a_{x_{i}} $$ This means $$ c_{n}:=\\frac{a_{x_{n}}}{a_{1}}>\\prod_{i=1}^{n-1} \\frac{1+\\left(s_{1}+\\cdots+s_{i-1}+s_{i}\\right)+\\left(t_{1}+\\cdots+t_{i-1}\\right)}{1+\\left(s_{1}+\\cdots+s_{i-1}\\right)+\\left(t_{1}+\\cdots+t_{i-1}\\right)} $$ ## Lemma $t_{1}+\\cdots+t_{n} \\leq s_{1}+\\cdots+s_{n}$ for each $n$. First we claim that if $x \\in\\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\\right)$, then $x$ cannot have an edge to $x_{j}$ for any $j \\leq i$. This is because $x>x_{i}+s_{i} \\geq x_{j}+s_{j}$, contradicting the fact that $x_{j}+s_{j}$ is the largest neighbor of $x_{j}$. This also means $x$ doesn't have an edge to $x_{j}+s_{j}$ for any $j \\leq i$, since if it did, it would have an edge to $x_{j}$. Second, no two bad values of $x$ can have an edge, since then the smaller one is good. This also means no two bad $x$ can have an edge to the same $y$. Then each of the $\\sum\\left(t_{i}-1\\right)$ values in the intervals $\\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\\right)$ for $1 \\leq i \\leq n$ must have an edge to an unique $y$ in one of the intervals $\\left(x_{i}, x_{i}+s_{i}\\right)$ (not necessarily with the same $i$ ). Therefore $$ \\sum\\left(t_{i}-1\\right) \\leq \\sum\\left(s_{i}-1\\right) \\Longrightarrow \\sum t_{i} \\leq \\sum s_{i} $$ Now note that if $a>b$, then $\\frac{a+x}{b+x}=1+\\frac{a-b}{b+x}$ is decreasing in $x$. This means $$ c_{n}>\\prod_{i=1}^{n-1} \\frac{1+2 s_{1}+\\cdots+2 s_{i-1}+s_{i}}{1+2 s_{1}+\\cdots+2 s_{i-1}}>\\prod_{i=1}^{n-1} \\frac{1+2 s_{1}+\\cdots+2 s_{i-1}+2 s_{i}}{1+2 s_{1}+\\cdots+2 s_{i-1}+s_{i}} $$ By multiplying both products, we have a telescoping product, which results in $$ c_{n}^{2} \\geq 1+2 s_{1}+\\cdots+2 s_{n}+2 s_{n+1} $$ The right hand side is unbounded since the $s_{i}$ are positive integers, while $c_{n}=a_{x_{n}} / a_{1}<$ $1 / a_{1}$ is bounded, contradiction.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 10 |
-
{"year": "2021", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}<a_{2}<a_{3}<a_{4}<\\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \\frac{a_{1}}{1}, \\frac{a_{2}}{2}, \\frac{a_{3}}{3}, \\frac{a_{4}}{4}, \\ldots $$", "solution": " 【 Solution 3 (Gopal Goel). Suppose for sake of contradiction that the problem is false. Call an index $i$ a pin if $$ \\frac{a_{j}}{j}=\\frac{a_{i}}{i} \\Longrightarrow j \\geq i $$ ## Lemma There exists $k$ such that if we have $\\frac{a_{i}}{i}=\\frac{a_{j}}{j}$ with $j>i \\geq k$, then $j \\leq 1.1 i$. Suppose no such $k$ exists. Then, take a pair $j_{1}>i_{1}$ such that $\\frac{a_{j_{1}}}{j_{1}}=\\frac{a_{i_{1}}}{i_{1}}$ and $j_{1}>1.1 i_{1}$, or $a_{j_{1}}>1.1 a_{i_{1}}$. Now, since $k=j_{1}$ can't work, there exists a pair $j_{2}>i_{2} \\geq i_{1}$ such that $\\frac{a_{j_{2}}}{j_{2}}=\\frac{a_{i_{2}}}{i_{2}}$ and $j_{2}>1.1 i_{2}$, or $a_{j_{2}}>1.1 a_{i_{2}}$. Continuing in this fashion, we see that $$ a_{j_{\\ell}}>1.1 a_{i_{\\ell}}>1.1 a_{j_{\\ell-1}} $$ so we have that $a_{j_{\\ell}}>1.1^{\\ell} a_{i_{1}}$. Taking $\\ell>\\log _{1.1}\\left(1 / a_{1}\\right)$ gives the desired contradiction. ## Lemma For $N>k^{2}$, there are at most $0.8 N$ pins in $[\\sqrt{N}, N)$. $$ p-N\\left(1-\\frac{1}{1.1}\\right) \\leq N-p $$ so $p \\leq 0.8 N$, as desired. We say that $i$ is the pin of $j$ if it is the smallest index such that $\\frac{a_{i}}{i}=\\frac{a_{j}}{j}$. The pin of $j$ is always a pin. Given an index $i$, let $f(i)$ denote the largest index less than $i$ that is not a pin (we leave the function undefined when no such index exists, as we are only interested in the behavior for large $i$ ). Then $f$ is weakly increasing and unbounded by the first lemma. Let $N_{0}$ be a positive integer such that $f\\left(\\sqrt{N_{0}}\\right)>k$. Take any $N>N_{0}$ such that $N$ is not a pin. Let $b_{0}=N$, and $b_{1}$ be the pin of $b_{0}$. Recursively define $b_{2 i}=f\\left(b_{2 i-1}\\right)$, and $b_{2 i+1}$ to be the pin of $b_{2 i}$. Let $\\ell$ be the largest odd index such that $b_{\\ell} \\geq \\sqrt{N}$. We first show that $b_{\\ell} \\leq 100 \\sqrt{N}$. Since $N>N_{0}$, we have $b_{\\ell+1}>k$. By the choice of $\\ell$ we have $b_{\\ell+2}<\\sqrt{N}$, so $$ b_{\\ell+1}<1.1 b_{\\ell+2}<1.1 \\sqrt{N} $$ by the first lemma. We see that all the indices from $b_{\\ell+1}+1$ to $b_{\\ell}$ must be pins, so we have at least $b_{\\ell}-1.1 \\sqrt{N}$ pins in $\\left[\\sqrt{N}, b_{\\ell}\\right)$. Combined with the second lemma, this shows that $b_{\\ell} \\leq 100 \\sqrt{N}$. Now, we have that $a_{b_{2 i}}=\\frac{b_{2 i}}{b_{2 i+1}} a_{b_{2 i+1}}$ and $a_{b_{2 i+1}}>a_{b_{2 i+2}}$, so combining gives us $$ \\frac{a_{b_{0}}}{a_{b_{\\ell}}}>\\frac{b_{0}}{b_{1}} \\frac{b_{2}}{b_{3}} \\cdots \\frac{b_{\\ell-1}}{b_{\\ell}} . $$ Note that there are at least $$ \\left(b_{1}-b_{2}\\right)+\\left(b_{3}-b_{4}\\right)+\\cdots+\\left(b_{\\ell-2}-b_{\\ell-1}\\right) $$ pins in $[\\sqrt{N}, N)$, so by the second lemma, that sum is at most $0.8 N$. Thus, $$ \\begin{aligned} \\left(b_{0}-b_{1}\\right)+\\left(b_{2}-b_{3}\\right)+\\cdots+\\left(b_{\\ell-1}-b_{\\ell}\\right) & =b_{0}-\\left[\\left(b_{1}-b_{2}\\right)+\\cdots+\\left(b_{\\ell-2}-b_{\\ell-1}\\right)\\right]-b_{\\ell} \\\\ & \\geq 0.2 N-100 \\sqrt{N} . \\end{aligned} $$ Then $$ \\begin{aligned} \\frac{b_{0}}{b_{1}} \\frac{b_{2}}{b_{3}} \\cdots \\frac{b_{\\ell-1}}{b_{\\ell}} & \\geq 1+\\frac{b_{0}-b_{1}}{b_{1}}+\\cdots+\\frac{b_{\\ell-1}-b_{\\ell}}{b_{\\ell}} \\\\ & >1+\\frac{b_{0}-b_{1}}{b_{0}}+\\cdots+\\frac{b_{\\ell-1}-b_{\\ell}}{b_{0}} \\\\ & \\geq 1+\\frac{0.2 N-100 \\sqrt{N}}{N} \\end{aligned} $$ which is at least 1.01 if $N_{0}$ is large enough. Thus, we see that $$ a_{N}>1.01 a_{b_{\\ell}} \\geq 1.01 a_{\\lfloor\\sqrt{N}\\rfloor} $$ if $N>N_{0}$ is not a pin. Since there are arbitrarily large non-pins, this implies that the sequence $\\left(a_{n}\\right)$ is unbounded, which is the desired contradiction.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 11 |
-
{"year": "2021", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Find all positive integers $k>1$ for which there exists a positive integer $n$ such that $\\binom{n}{k}$ is divisible by $n$, and $\\binom{n}{m}$ is not divisible by $n$ for $2 \\leq m<k$.", "solution": " Such an $n$ exists for any $k$. First, suppose $k$ is prime. We choose $n=(k-1)$ !. For $m<k$, it follows from $m!\\mid n$ that $$ \\begin{aligned} (n-1)(n-2) \\cdots(n-m+1) & \\equiv(-1)(-2) \\cdots(-m+1) \\\\ & \\equiv(-1)^{m-1}(m-1)! \\\\ & \\not \\equiv 0 \\bmod m! \\end{aligned} $$ We see that $\\binom{n}{m}$ is not a multiple of $m$. For $m=k$, note that $\\binom{n}{k}=\\frac{n}{k}\\binom{n-1}{k-1}$. Because $k \\nmid n$, we must have $k \\left\\lvert\\,\\binom{ n-1}{k-1}\\right.$, and it follows that $n \\left\\lvert\\,\\binom{ n}{k}\\right.$. Now suppose $k$ is composite. We will choose $n$ to satisfy a number of congruence relations. For each prime $p \\leq k$, let $$ t_{p}=\\nu_{p}(\\operatorname{lcm}(1,2, \\ldots, k-1))=\\max \\left(\\nu_{p}(1), \\nu_{p}(2), \\ldots, \\nu_{p}(k-1)\\right) $$ and choose $k_{p} \\in\\{1,2, \\ldots, k-1\\}$ as large as possible such that $\\nu_{p}\\left(k_{p}\\right)=t_{p}$. We now require $$ \\begin{aligned} n \\equiv 0 \\quad \\bmod p^{t_{p}+1} & \\text { if } p \\nmid k \\\\ \\nu_{p}\\left(n-k_{p}\\right)=t_{p}+\\nu_{p}(k) & \\text { if } p \\mid k \\end{aligned} $$ for all $p \\leq k$. From the Chinese Remainder Theorem, we know that an $n$ exists that satisfies (1) and (2) (indeed, a sufficient condition for (2) is the congruence $n \\equiv$ $\\left.k_{p}+p^{t_{p}+\\nu_{p}(k)} \\bmod p^{t_{p}+\\nu_{p}(k)+1}\\right)$. We show that this $n$ has the required property. We first will compute $\\nu_{p}(n-i)$ for primes $p<k$ and $1 \\leq i<k$. - If $p \\nmid k$, then we have $\\nu_{p}(i), \\nu_{p}(n-i) \\leq t_{p}$ and $\\nu_{p}(n)>t_{p}$, so $\\nu_{p}(n-i)=\\nu_{p}(i)$; - If $p \\mid k$ and $i \\neq k_{p}$, then we have $\\nu_{p}(i), \\nu_{p}(n-i) \\leq t_{p}$ and $\\nu_{p}(n) \\geq t_{p}$, so again $\\nu_{p}(n-i)=\\nu_{p}(i) ;$ - If $p \\mid k$ and $i=k_{p}$, then we have $\\nu_{p}(n-i)=\\nu_{p}(i)+\\nu_{p}(k)$ by (2). We conclude that $\\nu_{p}(n-i)=\\nu_{p}(i)$ always holds, except when $i=k_{p}$, when we have $\\nu_{p}(n-i)=\\nu_{p}(i)+\\nu_{p}(k)$ (this formula holds irrespective of whether $p \\mid k$ or $\\left.p \\nmid k\\right)$. We can now show that $\\binom{n}{k}$ is divisible by $n$, which amounts to showing that $k$ ! divides $(n-1)(n-2) \\cdots(n-k+1)$. Indeed, for each prime $p \\leq k$ we have $$ \\begin{aligned} \\nu_{p}((n-1)(n-2) \\ldots(n-k+1)) & =\\nu_{p}\\left(n-k_{p}\\right)+\\sum_{i<k, i \\neq k_{p}} \\nu_{p}(n-i) \\\\ & =\\nu_{p}\\left(k_{p}\\right)+\\nu_{p}(k)+\\sum_{i<k, i \\neq k_{p}} \\nu_{p}(i) \\end{aligned} $$ $$ =\\sum_{i=1}^{k} \\nu_{p}(i)=\\nu_{p}(k!) $$ so it follows that $(n-1)(n-2) \\cdots(n-k+1)$ is a multiple of $k$ !. Finally, let $1<m<k$. We will show that $n$ does not divide $\\binom{n}{m}$, which amounts to showing that $m$ ! does not divide $(n-1)(n-2) \\cdots(n-m+1)$. First, suppose that $m$ has a prime divisor $q$ that does not divide $k$. Then we have $$ \\begin{aligned} \\nu_{q}((n-1)(n-2) \\ldots(n-m+1)) & =\\sum_{i=1}^{m-1} \\nu_{q}(n-i) \\\\ & =\\sum_{i=1}^{m-1} \\nu_{q}(i) \\\\ & =\\nu_{q}((m-1)!)<\\nu_{q}(m!) \\end{aligned} $$ as desired. Therefore, suppose that $m$ is only divisible by primes that divide $k$. If there is such a prime $p$ with $\\nu_{p}(m)>\\nu_{p}(k)$, then it follows that $$ \\begin{aligned} \\nu_{p}((n-1)(n-2) \\ldots(n-m+1)) & =\\nu_{p}(k)+\\sum_{i=1}^{m-1} \\nu_{p}(i) \\\\ & <\\nu_{p}(m)+\\sum_{i=1}^{m-1} \\nu_{p}(i) \\\\ & =\\nu_{p}(m!) \\end{aligned} $$ so $m$ ! cannot divide $(n-1)(n-2) \\ldots(n-m+1)$. On the other hand, suppose that $\\nu_{p}(m) \\leq \\nu_{p}(k)$ for all $p \\mid k$, which would mean that $m \\mid k$ and hence $m \\leq \\frac{k}{2}$. Consider a prime $p$ dividing $m$. We have $k_{p} \\geq \\frac{k}{2}$, because otherwise $2 k_{p}$ could have been used instead of $k_{p}$. It follows that $m \\leq \\frac{k}{2} \\leq k_{p}$. Therefore, we obtain $$ \\begin{aligned} \\nu_{p}((n-1)(n-2) \\ldots(n-m+1)) & =\\sum_{i=1}^{m-1} \\nu_{p}(n-i) \\\\ & =\\sum_{i=1}^{m-1} \\nu_{p}(i) \\\\ & =\\nu_{p}((m-1)!)<\\nu_{p}(m!) \\end{aligned} $$ showing that $(n-1)(n-2) \\cdots(n-m+1)$ is not divisible by $m$ !. This shows that $\\binom{n}{m}$ is not divisible by $n$ for $m<k$, and hence $n$ does have the required property.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 12 |
-
{"year": "2021", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.", "solution": " Treating $a$ and $b$ as fixed, we are given that there are infinitely many quadrpules $(m, n, r, s)$ which satisfy the system $$ \\begin{aligned} m^{2}+a n+b & =(m+r)^{2} \\\\ n^{2}+a m+b & =(n+s)^{2} \\end{aligned} $$ We say that $(r, s)$ is exceptional if there exists infinitely many $(m, n)$ that satisfy. Claim - If $(r, s)$ is exceptional, then either - $0<r<a / 2$, and $0<s<\\frac{1}{4} a^{2}$; or - $0<s<a / 2$, and $0<r<\\frac{1}{4} a^{2}$; or - $r^{2}+s^{2} \\leq 2 b$. In particular, finitely many pairs $(r, s)$ can be exceptional. $$ r^{2}+s^{2}-2 b=(a-2 r) m+(a-2 s) n $$ If $0<r<a / 2$, then the idea is to use the bound $a n+b \\geq 2 m+1$ to get $m \\leq \\frac{a n+b-1}{2}$. Consequently, $$ (n+s)^{2}=n^{2}+a m+b \\leq n^{2}+a \\cdot \\frac{a n+b-1}{2}+b $$ For this to hold for infinitely many integers $n$, we need $2 s \\leq \\frac{a^{2}}{2}$, by comparing coefficients. A similar case occurs when $0<s<a / 2$. If $\\min (r, s)>a / 2$, then $(\\dagger)$ forces $r^{2}+s^{2} \\leq 2 b$, giving the last case. Hence, there exists some particular pair $(r, s)$ for which there are infinitely many solutions $(m, n)$. Simplifying the system gives $$ \\begin{aligned} & a n=2 r m+r^{2}-b \\\\ & 2 s n=a m+b-s^{2} \\end{aligned} $$ Since the system is linear, for there to be infinitely many solutions $(m, n)$ the system must be dependent. This gives $$ \\frac{a}{2 s}=\\frac{2 r}{a}=\\frac{r^{2}-b}{b-s^{2}} $$ so $a=2 \\sqrt{r s}$ and $b=\\frac{s^{2} \\sqrt{r}+r^{2} \\sqrt{s}}{\\sqrt{r}+\\sqrt{s}}$. Since $r s$ must be square, we can reparametrize as $r=k x^{2}, s=k y^{2}$, and $\\operatorname{gcd}(x, y)=1$. This gives $$ \\begin{aligned} a & =2 k x y \\\\ b & =k^{2} x y\\left(x^{2}-x y+y^{2}\\right) \\end{aligned} $$ Thus, $a \\mid 2 b$, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 13 |
-
{"year": "2021", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.", "solution": " The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 1 (Ankan Bhattacharya, Jeffery Li). ## Lemma If $S$ is an independent set of $T$, then $$ \\sum_{v \\in S} \\operatorname{deg}(v) \\leq n-1 $$ Equality holds if and only if $S$ is one of the two components of the unique 2-coloring of $T$. We are given that there exists an independent set of at least $\\frac{n+k-1}{2}$ vertices. By greedily choosing vertices of smallest degree, the sum of the degrees of these vertices is at least $$ k+2 \\cdot \\frac{n-k-1}{2}=n-1 $$ Thus equality holds everywhere, which implies that the independent set contains every leaf and is one of the components of the 2 -coloring.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 14 |
-
{"year": "2021", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.", "solution": " The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 2 (Andrew Gu). ## Lemma The vertices of $T$ can be partitioned into $k-1$ paths (i.e. the induced subgraph on each set of vertices is a path) such that all edges of $T$ which are not part of a path are incident to an endpoint of a path. Now given a path of $a$ vertices, at most $\\frac{a+1}{2}$ of those vertices can be in an independent set of $T$. By the lemma, $T$ can be partitioned into $k-1$ paths of $a_{1}, \\ldots, a_{k-1}$ vertices, so the maximum size of an independent set of $T$ is $$ \\sum \\frac{a_{i}+1}{2}=\\frac{n+k-1}{2} . $$ For equality to hold, each path in the partition must have an odd number of vertices, and has a unique 2 -coloring in red and blue where the endpoints are red. The unique independent set of $T$ of size $\\frac{n+k-1}{2}$ is then the set of red vertices. By the lemma, the edges of $T$ which are not part of a path connect an endpoint of a path (which is colored red) to another vertex (which must be blue, because the red vertices are independent). Thus the coloring of the paths extends to the unique 2 -coloring of $T$. The leaves of $T$ are endpoints of paths, so they are all red.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 15 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) Let the second tangent to $\\omega$ parallel to $E F$ meet lines $A B$ and $A C$ at $P$ and $Q$, respectively, and let the second tangent to $\\omega$ parallel to $B C$ meet lines $D E$ and $D F$ at $R$ and $S$, respectively. Furthermore, let $\\omega$ touch $P Q$ and $R S$ at $U$ and $V$, respectively. Let $h$ be inversion with respect to $\\omega$. Then $h$ maps $A, B$, and $C$ onto the midpoints of the sides of triangle $D_{1} E_{1} F_{1}$. So $h$ maps $k$ onto the Euler circle of triangle $D_{1} E_{1} F_{1}$. Similarly, $h$ maps $k$ onto the Euler circle of triangle $A_{1} B_{1} C_{1}$. Therefore, triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$ share a common nine-point circle $\\gamma$. Let $K$ be its center; its radius equals $\\frac{1}{2} r$. Let $H$ be the reflection of $I$ in $K$. Then $H$ is the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$. Let $\\gamma_{U}$ of center $K_{U}$ and radius $\\frac{1}{2} r$ be the Euler circle of triangle $U E_{1} F_{1}$, and let $\\gamma_{V}$ of center $K_{V}$ and radius $\\frac{1}{2} r$ be the Euler circle of triangle $V B_{1} C_{1}$. Let $H_{U}$ be the orthocenter of triangle $U E_{1} F_{1}$. Since quadrilateral $D_{1} E_{1} F_{1} U$ is cyclic, vectors $\\overrightarrow{H H_{U}}$ and $\\overrightarrow{D_{1} U}$ are equal. Consequently, $\\overrightarrow{K K_{U}}=\\frac{1}{2} \\overrightarrow{D_{1} U}$. Similarly, $\\overrightarrow{K K_{V}}=$ $\\frac{1}{2} \\overrightarrow{A_{1} V}$. Since both of $A_{1} U$ and $D_{1} V$ are diameters in $\\omega$, vectors $\\overrightarrow{D_{1} U}$ and $\\overrightarrow{A_{1} V}$ are equal. Therefore, $K_{U}$ and $K_{V}$ coincide, and so do $\\gamma_{U}$ and $\\gamma_{V}$. As above, $h$ maps $\\gamma_{U}$ onto the circumcircle of triangle $A P Q$ and $\\gamma_{V}$ onto the circumcircle of triangle $D R S$. Therefore, triangles $A P Q$ and $D R S$ are inscribed inside the same circle $\\Omega_{A D}$. Since $E F$ and $P Q$ are parallel, triangles $\\Delta_{A}$ and $A P Q$ are homothetic, and so are figures $\\Omega_{A} \\cup \\omega_{A}$ and $\\Omega_{A D} \\cup \\omega$. Consequently, we have $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{A D} \\cup \\omega\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right), $$ which solves part (a).", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 16 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (Michael Ren) As in the previous solution, let the second tangent to $\\omega$ parallel to $E F$ meet $A B$ and $A C$ at $P$ and $Q$, respectively. Let $(A P Q)$ meet $\\Omega$ again at $D^{\\prime}$, so that $D^{\\prime}$ is the Miquel point of $\\{A B, A C, B C, P Q\\}$. Since the quadrilateral formed by these lines has incircle $\\omega$, it is classical that $D^{\\prime} I$ bisects $\\angle P D^{\\prime} C$ and $B D^{\\prime} Q$ (e.g. by DDIT). Let $\\ell$ be the tangent to $\\Omega$ at $D^{\\prime}$ and $D^{\\prime} I$ meet $\\Omega$ again at $M$. We have $$ \\measuredangle\\left(\\ell, D^{\\prime} B\\right)=\\measuredangle D^{\\prime} C B=\\measuredangle D^{\\prime} Q P=\\measuredangle\\left(D^{\\prime} Q, E F\\right) . $$ Therefore $D^{\\prime} I$ also bisects the angle between $\\ell$ and the line parallel to $E F$ through $D^{\\prime}$. This means that $M$ is one of the arc midpoints of $E F$. Additionally, $D^{\\prime}$ lies on $\\operatorname{arc} B C$ not containing $A$, so $D^{\\prime}=D$. Similarly, letting the second tangent to $\\omega$ parallel to $B C$ meet $D E$ and $D F$ again at $R$ and $S$, we have $A D R S$ cyclic. ## Lemma There exists a circle $\\Omega_{A D}$ tangent to $\\Omega_{A}$ and $\\Omega_{D}$ at $A$ and $D$, respectively. $$ \\measuredangle O A O_{A}=\\measuredangle(\\perp E F, \\perp B C)=\\measuredangle(E F, B C) . $$ (Here, $\\perp E F$ means the direction perpendicular to $E F$.) By symmetry, this is equal to $\\measuredangle O_{D} D O$. The circle $(A D P Q)$ passes through $A$ and $D$, and is tangent to $\\Omega_{A}$ by homothety. Therefore it coincides with $\\Omega_{A D}$, as does ( $A D R S$ ). Like the previous solution, we finish with $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{A D} \\cup \\omega\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) . $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 17 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Andrew Gu) Construct triangles homothetic to $\\Delta_{A}$ and $\\Delta_{D}$ (with positive ratio) which have the same circumcircle; it suffices to show that these copies have the same incircle as well. Let $O$ be the center of this common circumcircle, which we take to be the origin, and $M_{X Y}$ denote the point on the circle such that the tangent at that point is parallel to line $X Y$ (from the two possible choices, we make the choice that corresponds to the arc midpoint on $\\Omega$, e.g. $M_{A B}$ should correspond to the arc midpoint on the internal angle bisector of $A C B$ ). The left diagram below shows the original triangles $A B C$ and $D E F$, while the right diagram shows the triangles homothetic to $\\Delta_{A}$ and $\\Delta_{D}$.  Using the fact that the incenter is the orthocenter of the arc midpoints, the incenter of $\\Delta_{A}$ in this reference frame is $M_{A B}+M_{A C}-M_{E F}$ and the incenter of $\\Delta_{D}$ in this reference frame is $M_{D E}+M_{D F}-M_{B C}$. Since $A B C$ and $D E F$ share a common incenter, we have $$ M_{A B}+M_{B C}+M_{C A}=M_{D E}+M_{E F}+M_{F D} $$ Thus the copies of $\\Delta_{A}$ and $\\Delta_{D}$ have the same incenter, and therefore the same incircle as well (Euler's theorem determines the inradius).", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 18 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) By Monge's theorem applied to $\\omega, \\omega_{A}$, and $\\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Therefore, $T_{A}=A D \\cap I_{A} I_{D}$. Let $p$ be pole-and-polar correspondence with respect to $\\omega$. Then $p$ maps $A$ onto line $E_{1} F_{1}$ and $D$ onto line $B_{1} C_{1}$. Consequently, $p$ maps line $A D$ onto $X_{A}=B_{1} C_{1} \\cap E_{1} F_{1}$. Furthermore, $p$ maps the line that bisects the angle formed by lines $A B$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} F_{1}$. Similarly, $p$ maps the line that bisects the angle formed by lines $A C$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} E_{1}$. So $p$ maps $I_{A}$ onto the midline of triangle $A_{1} E_{1} F_{1}$ opposite $A_{1}$. Similarly, $p$ maps $I_{D}$ onto the midline of triangle $D_{1} B_{1} C_{1}$ opposite $D_{1}$. Consequently, $p$ maps line $I_{A} I_{D}$ onto the intersection point $Y_{A}$ of this pair of midlines, and $p$ maps $T_{A}$ onto line $X_{A} Y_{A}$. Since the reflection of $H$ in line $B_{1} C_{1}$ lies on $\\omega, A_{1} H \\cdot H H_{A}$ equals half the power of $H$ with respect to $\\omega$. Similarly, $D_{1} H \\cdot H H_{D}$ equals half the power of $H$ with respect to $\\omega$. Then $A_{1} H \\cdot H H_{A}=D_{1} H \\cdot H H_{D}$ and $A_{1} H H_{D} \\sim D_{1} H H_{A}$. Since $\\angle H H_{D} L_{A}=90^{\\circ}=$ $\\angle H H_{A} L_{D}$, figures $A_{1} H H_{D} L_{A}$ and $D_{1} H H_{A} L_{D}$ are similar as well. Consequently, $$ \\frac{H L_{A}}{L_{A} A_{1}}=\\frac{H L_{D}}{L_{D} D_{1}}=s $$ as a signed ratio. Let the line through $A_{1}$ parallel to $E_{1} F_{1}$ and the line through $D_{1}$ parallel to $B_{1} C_{1}$ meet at $Z_{A}$. Then $H X_{A} / X_{A} Z_{A}=s$ and $Y_{A}$ is the midpoint of segment $X_{A} Z_{A}$. Therefore, $H$ lies on line $X_{A} Y_{A}$. This means that $T_{A}$ lies on the polar of $H$ with respect to $\\omega$, and by symmetry so do $T_{B}$ and $T_{C}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 19 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (author) As in the first solution to part (a), let $h$ be inversion with respect to $\\omega$, let $\\gamma$ of center $K$ be the common Euler circle of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$, and let $H$ be their common orthocenter. Let $K_{A}$ and $K_{D}$ be the centers of $\\gamma_{A}$ and $\\gamma_{D}$, respectively, and let $\\ell_{A}$ be the perpendicular bisector of segment $K_{A} K_{D}$. Since $\\gamma_{A}$ and $\\gamma_{D}$ are congruent (both of them are of radius $\\left.\\frac{1}{2} r\\right)$, they are reflections of each other across $\\ell_{A}$. Inversion $h$ maps the two common external tangents of $\\Omega_{A}$ and $\\Omega_{D}$ onto the two circles $\\alpha$ and $\\beta$ through $I$ that are tangent to both of $\\gamma_{A}$ and $\\gamma_{D}$ in the same way. (That is, either internally to both or externally to both.) Consequently, $\\alpha$ and $\\beta$ are reflections of each other in $\\ell_{A}$ and so their second point of intersection $S_{A}$, which $h$ maps $T_{A}$ onto, is the reflection of $I$ in $\\ell_{A}$. Define $\\ell_{B}, \\ell_{C}, S_{B}$, and $S_{C}$ similarly. Then $S_{B}$ is the reflection of $I$ in $\\ell_{B}$ and $S_{C}$ is the reflection of $I$ in $\\ell_{C}$. Therefore, all four points $I, S_{A}, S_{B}$, and $S_{C}$ lie on the circle of center $K$ that contains $I$. (This is also the circle on diameter $I H$.) Since points $S_{A}, S_{B}$, and $S_{C}$ are concyclic with $I$, their images $T_{A}, T_{B}$, and $T_{C}$ under $h$ are collinear, and the solution is complete.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 20 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Ankan Bhattacharya) From either of the first two solutions to part (a), we know that there is a circle $\\Omega_{A D}$ passing through $A$ and $D$ which is (internally) tangent to $\\Omega_{A}$ and $\\Omega_{D}$. By Monge's theorem applied to $\\Omega_{A}, \\Omega_{D}$, and $\\Omega_{A D}$, it follows that $A, D$, and $T_{A}$ are collinear. The inversion at $T_{A}$ swapping $\\Omega_{A}$ with $\\Omega_{D}$ also swaps $A$ with $D$ because $T_{A}$ lies on $A D$ and $A$ is not homologous to $D$. Let $\\Omega_{A}$ and $\\Omega_{D}$ meet $\\Omega$ again at $L_{A}$ and $L_{D}$. Since $A D L_{A} L_{D}$ is cyclic, the same inversion at $T_{A}$ also swaps $L_{A}$ and $L_{D}$, so $T_{A}=A D \\cap L_{A} L_{D}$. By Taiwan TST 2014, $L_{A}$ and $L_{D}$ are the tangency points of the $A$-mixtilinear and $D$-mixtilinear incircles, respectively, with $\\Omega$. Therefore $A L_{A} \\cap D L_{D}$ is the exsimilicenter $X$ of $\\Omega$ and $\\omega$. Then $T_{A}, T_{B}$, and $T_{C}$ all lie on the polar of $X$ with respect to $\\Omega$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 21 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 4 (Andrew Gu) We show that $T_{A}$ lies on the radical axis of the point circle at $I$ and $\\Omega$, which will solve the problem. Let $I_{A}$ and $I_{D}$ be the centers of $\\omega_{A}$ and $\\omega_{D}$ respectively. By the Monge's theorem applied to $\\omega, \\omega_{A}$, and $\\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Additionally, these other triples are collinear: $\\left(A, I_{A}, I\\right),\\left(D, I_{D}, I\\right),\\left(I_{A}, I_{D}, T\\right)$. By Menelaus's theorem, we have $$ \\frac{T_{A} D}{T_{A} A}=\\frac{I_{A} I}{I_{A} A} \\cdot \\frac{I_{D} D}{I_{D} I} . $$ If $s$ is the length of the side opposite $A$ in $\\Delta_{A}$, then we compute $$ \\begin{aligned} \\frac{I_{A} I}{I_{A} A} & =\\frac{s / \\cos (A / 2)}{r_{A} / \\sin (A / 2)} \\\\ & =\\frac{2 R_{A} \\sin (A) \\sin (A / 2)}{\\cos (A / 2)} \\\\ & =\\frac{4 R_{A} \\sin ^{2}(A / 2)}{r_{A}} \\\\ & =\\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} . \\end{aligned} $$ From part (a), we know that $\\frac{R_{A}}{r_{A}}=\\frac{R_{D}}{r_{D}}$. Therefore, doing a similar calculation for $\\frac{I_{D} D}{I_{D} I}$, we get $$ \\begin{aligned} \\frac{T_{A} D}{T_{A} A} & =\\frac{I_{A} I}{I_{A} A} \\cdot \\frac{I_{D} D}{I_{D} I} \\\\ & =\\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} \\cdot \\frac{r_{D} D I^{2}}{4 R_{D} r^{2}} \\\\ & =\\frac{D I^{2}}{A I^{2}} \\end{aligned} $$ Thus $T_{A}$ is the point where the tangent to $(A I D)$ at $I$ meets $A D$ and $T_{A} I^{2}=T_{A} A \\cdot T_{A} D$. This shows what we claimed at the start.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 22 |
-
{"year": "2021", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Triangles $A B C$ and $D E F$ share circumcircle $\\Omega$ and incircle $\\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\\Omega$. Let $\\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\\Delta_{B}, \\Delta_{C}, \\ldots, \\Delta_{F}$ similarly. Furthermore, let $\\Omega_{A}$ and $\\omega_{A}$ be the circumcircle and incircle of triangle $\\Delta_{A}$, respectively, and define circles $\\Omega_{B}, \\omega_{B}, \\ldots, \\Omega_{F}, \\omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$ and the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.", "solution": "  Let $I$ and $r$ be the center and radius of $\\omega$, and let $O$ and $R$ be the center and radius of $\\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\\Delta_{A}$, and define $O_{B}$, $I_{B}, \\ldots, I_{F}$ similarly. Let $\\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \\ldots, F_{1}$ similarly. $$ \\left(\\Omega_{A} \\cup \\omega_{A}\\right) \\sim\\left(\\Omega_{D} \\cup \\omega_{D}\\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 5 (Ankit Bisain) As in the previous solution, it suffices to show that $\\frac{I_{A} I}{A I_{A}} \\cdot \\frac{D I_{D}}{I_{D} I}=\\frac{D I^{2}}{A I^{2}}$. Let $A I$ and $D I$ meet $\\Omega$ again at $M$ and $N$, respectively. Let $\\ell$ be the line parallel to $B C$ and tangent to $\\omega$ but different from $B C$. Then $$ \\frac{D I_{D}}{I_{D} I}=\\frac{d(D, B C)}{d(B C, \\ell)}=\\frac{D B \\cdot D C / 2 R}{2 r}=\\frac{M I^{2}-M D^{2}}{4 R r} $$ Since $I D M \\sim I A N$, we have $$ \\frac{D I_{D}}{I_{D} I} \\cdot \\frac{I_{A} I}{A I_{A}}=\\frac{M I^{2}-M D^{2}}{N I^{2}-N A^{2}}=\\frac{D I^{2}}{A I^{2}} $$ as desired. Remark (Author comments on generalization of part (b) with a circumscribed hexagram). Let triangles $A B C$ and $D E F$ be circumscribed about the same circle $\\omega$ so that they form a hexagram. However, we do not require anymore that they are inscribed in the same circle. Define circles $\\Omega_{A}, \\omega_{A}, \\ldots, \\omega_{F}$ as in the problem. Let $T_{A}^{\\text {Circ }}$ be the intersection point of the two common external tangents to circles $\\Omega_{A}$ and $\\Omega_{D}$, and define points $T_{B}^{\\text {Circ }}$ and $T_{C}^{\\text {Circ }}$ similarly. Also let $T_{A}^{\\text {In }}$ be the intersection point of the two common external tangents to circles $\\omega_{A}$ and $\\omega_{D}$, and define points $T_{B}^{\\mathrm{In}}$ and $T_{C}^{\\mathrm{In}}$ similarly. Then points $T_{A}^{\\text {Circ }}, T_{B}^{\\text {Circ }}$, and $T_{C}^{\\mathrm{Circ}}$ are collinear and points $T_{A}^{\\mathrm{In}}, T_{B}^{\\mathrm{In}}$, and $T_{C}^{\\mathrm{In}}$ are also collinear. For the incircles part of the generalisation, we start out as in the first solution to part (b) of the problem, and eventually we reduce everything to the following: Let points $A_{1}, B_{1}, C_{1}, D_{1}, E_{1}$, and $F_{1}$ lie on circle $\\omega$. Let lines $B_{1} C_{1}$ and $E_{1} F_{1}$ meet at point $X_{A}$, let the line through $A_{1}$ parallel to $B_{1} C_{1}$ and the line through $D_{1}$ parallel to $E_{1} F_{1}$ meet at point $Z_{A}$, and define points $X_{B}, Z_{B}, X_{C}$, and $Z_{C}$ similarly. Then lines $X_{A} Z_{A}$, $X_{B} Z_{B}$, and $X_{C} Z_{C}$ are concurrent. Take $\\omega$ as the unit circle and assign complex numbers $u, v, w, x, y$, and $z$ to points $A_{1}$, $F_{1}, B_{1}, D_{1}, C_{1}$, and $E_{1}$, respectively, so that when we permute $u, v, w, x, y$, and $z$ cyclically the configuration remains unchanged. Then by standard complex bash formulas we obtain that each two out of our three lines meet at $\\varphi / \\psi$, where $$ \\varphi=\\sum_{\\mathrm{Cyc}} u^{2} v w(w x-w y+x y)(y-z) $$ and $$ \\psi=-u^{2} w^{2} y^{2}-v^{2} x^{2} z^{2}-4 u v w x y z+\\sum_{\\mathrm{Cyc}} u^{2}(v w x y-v w x z+v w y z-v x y z+w x y z) $$ (But the calculations were too difficult for me to do by hand, so I used SymPy.) Remark (Author comments on generalization of part (b) with an inscribed hexagram). Let triangles $A B C$ and $D E F$ be inscribed inside the same circle $\\Omega$ so that they form a hexagram. However, we do not require anymore that they are circumscribed about the same circle. Define points $T_{A}^{\\text {Circ }}, T_{B}^{\\text {Circ }}, \\ldots, T_{C}^{\\mathrm{In}}$ as in the previous remark. It looks like once again points $T_{A}^{\\text {Circ }}, T_{B}^{\\text {Circ }}$, and $T_{C}^{\\text {Circ }}$ are collinear and points $T_{A}^{\\mathrm{In}}, T_{B}^{\\mathrm{In}}$, and $T_{C}^{\\mathrm{In}}$ are also collinear. However, I do not have proofs of these claims. Remark (Further generalization from Andrew Gu). Let $A B C$ and $D E F$ be triangles which share an inconic, or equivalently share a circumconic. Define points $T_{A}^{\\text {Circ }}, T_{B}^{\\text {Circ }}, \\ldots, T_{C}^{\\mathrm{In}}$ as in the previous remarks. Then it is conjectured that points $T_{A}^{\\text {Circ }}, T_{B}^{\\text {Circ }}$, and $T_{C}^{\\text {Circ }}$ are collinear and points $T_{A}^{\\mathrm{In}}, T_{B}^{\\mathrm{In}}$, and $T_{C}^{\\mathrm{In}}$ are also collinear. (Note that extraversion may be required depending on the configuration of points, e.g. excircles instead of incircles.) Additionally, it appears that the insimilicenters of the circumcircles lie on a line perpendicular to the line through $T_{A}^{\\text {Circ }}, T_{B}^{\\text {Circ }}$, and $T_{C}^{\\text {Circ }}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 23 |
-
{"year": "2021", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.", "solution": " 【 Solution 1. We prove the statement by induction on $n$. We use $n=0$ as a base case, where the statement follows from $1 \\geq 2^{-|M|}$. For the inductive step, let $n>0$. There exists at least one mine-avoiding path, which must pass through either $(0,1)$ or $(1,0)$. We consider two cases: Case 1: there exist mine-avoiding paths starting at both $(1,0)$ and $(0,1)$. By the inductive hypothesis, there are at least $2^{n-1-|M|}$ mine-avoiding paths starting from each of $(1,0)$ and $(0,1)$. Then the total number of mine-avoiding paths is at least $2^{n-1-|M|}+2^{n-1-|M|}=2^{n-|M|}$. Case 2: only one of $(1,0)$ and $(0,1)$ is on a mine-avoiding path. Without loss of generality, suppose no mine-avoiding path starts at $(0,1)$. Then some element of $M$ must be of the form $(0, k)$ for $1 \\leq k \\leq n$ in order to block the path along the $y$-axis. This element can be ignored for any mine-avoiding path starting at (1,0). By the inductive hypothesis, there are at least $2^{n-1-(|M|-1)}=2^{n-|M|}$ mine-avoiding paths. This completes the induction step, which solves the problem.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 24 |
-
{"year": "2021", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.", "solution": " ## 【 Solution 2. ## Lemma If $|M|<n$, there is more than one mine-avoiding path. - Make the first $i+1$ points $P_{0}, P_{1}, \\ldots, P_{i}$. - If $P_{i} \\rightarrow P_{i+1}$ is one unit up, go right until $\\left(n-y_{i}, y_{i}\\right)$. - If $P_{i} \\rightarrow P_{i+1}$ is one unit right, go up until $\\left(x_{i}, n-x_{i}\\right)$.  The diagram above is an example for $n=5$ with the new segments formed by the $Q_{i}$ in red, and the line $x+y=n$ in blue. By definition, $M$ has less than $n$ points, none of which are in the original path. Since all $Q_{i}$ only intersect in the original path, each mine is in at most one of $Q_{0}, Q_{1}, \\ldots, Q_{n-1}$. By the Pigeonhole Principle, one of the $Q_{i}$ is mine-avoiding. Now, consider the following process: - Start at $(0,0)$. - If there is only one choice of next step that is part of a mine-avoiding path, make that choice. - Repeat the above until at a point with two possible steps that are part of mineavoiding paths. - Add a mine to the choice of next step with more mine-avoiding paths through it. If both have the same number of mine-avoiding paths through them, add a mine arbitrarily.  For instance, consider the above diagram for $n=4$. Lattice points are replaced with squares. Mines are black squares and each non-mine is labelled with the number of mine-avoiding paths passing through it. This process would start at $(0,0)$, go to $(1,0)$, then place a mine at $(1,1)$. This path increases the size of $M$ by one, and reduces the number of mine-avoiding paths to a nonzero number at most half of the original. Repeat this process until there is only one path left. By our lemma, the number of mines must be at least $n$ by the end of the process, so the process was iterated at least $n-|M|$ times. By the halving property, there must have been at least $2^{n-|M|}$ mine-avoiding paths before the process, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 25 |
-
{"year": "2021", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\\triangle A_{1} B_{1} C_{1}$ and $\\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\\triangle A_{2} B_{2} C_{2}$ and $\\triangle A B C$ are similar.", "solution": " ब Solution 1 (author). We'll use the following lemma. ## Lemma Suppose that $P Q R S$ is a convex quadrilateral with $\\angle P=\\angle R$. Then there is a point $T$ on $Q S$ such that $\\angle Q P T=\\angle S R P, \\angle T R Q=\\angle R P S$, and $P T=R T$. Before proving the lemma, we will show how it solves the problem. The lemma applied for the quadrilateral $A B_{1} A_{1} C_{1}$ with $\\angle A=\\angle A_{1}$ shows that $\\angle B_{1} A_{1} A_{2}=\\angle C_{1} A A_{1}$. This implies that the point $A_{2}$ in $\\triangle A_{1} B_{1} C_{1}$ corresponds to the point $A_{1}$ in $\\triangle A B C$. Then $\\triangle A_{2} B_{2} C_{2} \\sim \\triangle A_{1} B_{1} C_{1} \\sim \\triangle A B C$, as desired. Additionally, $P T=R T$ is a corollary of the angle conditions because $$ \\measuredangle P R T=\\measuredangle S R Q-\\measuredangle T R Q-\\measuredangle S R P=\\measuredangle Q P S-\\measuredangle R P S-\\measuredangle Q P T=\\measuredangle T P R $$ Therefore we only need to prove the angle conditions.  $$ \\begin{aligned} \\measuredangle P X T & =\\measuredangle R^{\\prime} P Q+\\measuredangle P Q S \\\\ & =\\measuredangle R^{\\prime} S Q+\\measuredangle P Q S \\\\ & =\\measuredangle Q S R+\\measuredangle P Q S \\\\ & =\\measuredangle(P Q, S R) \\\\ & =\\measuredangle Q P R+\\measuredangle P R S . \\end{aligned} $$ This means that $$ \\begin{aligned} \\measuredangle Q P T & =\\measuredangle Q P R-\\measuredangle T P R \\\\ & =\\measuredangle Q P R-\\measuredangle T X R \\\\ & =\\measuredangle Q P R-\\measuredangle P X T \\\\ & =\\measuredangle Q P R-\\measuredangle Q P R-\\measuredangle P R S \\\\ & =\\measuredangle S R P . \\end{aligned} $$ Similarly, $\\measuredangle Q R T=\\measuredangle S P R$, so we're done.  $$ \\frac{Q T}{T S}=\\frac{\\sin Q P T \\cdot P T / \\sin P Q T}{\\sin T P S \\cdot P T / \\sin T S P}=\\frac{P Q / \\sin P R Q}{P S / \\sin S R P}=\\frac{R(\\triangle P Q R)}{R(\\triangle P R S)} $$ which is symmetric in $P$ and $R$, so we're done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 26 |
-
{"year": "2021", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\\triangle A_{1} B_{1} C_{1}$ and $\\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\\triangle A_{2} B_{2} C_{2}$ and $\\triangle A B C$ are similar.", "solution": " Solution 2 (Ankan Bhattacharya). We prove the main claim $\\frac{B_{1} A_{2}}{A_{2} C_{1}}=\\frac{B A_{1}}{A_{1} C}$. Let $\\triangle A_{0} B_{0} C_{0}$ be the medial triangle of $\\triangle A B C$. In addition, let $A_{1}^{\\prime}$ be the reflection of $A_{1}$ over $\\overline{B_{1} C_{1}}$, and let $X$ be the point satisfying $\\triangle X B C \\approx \\triangle A B_{1} C_{1}$, so that we have a compound similarity $$ \\triangle A B C \\sqcup X \\approx \\triangle A_{1}^{\\prime} B_{1} C_{1} \\sqcup A . $$ Finally, let $O_{A}$ be the circumcenter of $\\triangle A_{1}^{\\prime} B_{1} C_{1}$, and let $A_{2}^{*}$ be the point on $\\overline{B_{1} C_{1}}$ satisfying $\\frac{B_{1} A_{2}^{*}}{A_{2}^{*} C_{1}}=\\frac{B A_{1}}{A_{1} C}$. Recall that $O$ is the Miquel point of $\\triangle A_{1} B_{1} C_{1}$, as well as its orthocenter. Claim $-\\overline{A A_{1}^{\\prime}} \\| \\overline{B C}$. $$ \\text { Claim }-\\overline{A X} \\| \\overline{B_{1} C_{1}} . $$ $$ \\measuredangle(\\overline{B C}, \\overline{A X})=\\measuredangle\\left(\\overline{A A_{1}^{\\prime}}, \\overline{B_{1} C_{1}}\\right) . $$ As $\\overline{A A_{1}^{\\prime}} \\| \\overline{B C}$, we obtain $\\overline{A X} \\| \\overline{B_{1} C_{1}}$. $$ \\text { Claim }-\\overline{A X} \\perp \\overline{A_{1} O} . $$ $$ \\text { Claim }-\\overline{A A_{1}^{\\prime}} \\perp \\overline{A_{2}^{*} O_{A}} $$ $$ \\triangle A B C \\sqcup X \\approx \\triangle A_{1}^{\\prime} B_{1} C_{1} \\sqcup A . $$ Claim $-A A_{2}^{*}=A_{1}^{\\prime} A_{2}$. Finally, $A_{1}^{\\prime} A_{2}^{*}=A_{1} A_{2}^{*}$ by reflections, so $A A_{2}^{*}=A_{1} A_{2}^{*}$, and $A_{2}^{*}=A_{2}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 27 |
-
{"year": "2021", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\\zeta=e^{\\frac{2 \\pi i}{q}}$. Find the least positive integer $n$ such that $$ \\sum_{\\substack{1 \\leq k \\leq q \\\\ \\operatorname{gcd}(k, p)=1}} \\frac{1}{\\left(1-\\zeta^{k}\\right)^{n}} $$ is not an integer. (The sum is over all $1 \\leq k \\leq q$ with $p$ not dividing $k$.)", "solution": " Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ). 【 Solution 1 (author). Let $\\zeta_{p}=e^{2 \\pi i / p}$ be a fixed primitive $p$ th root of unity. Observe that the given sum is an integer for all $n \\leq 0$ (e.g. because the sum is an integer symmetric polynomial in the primitive $q$ th roots of unity). By expanding polynomials in the basis $(1-x)^{k}$, it follows that if the sum in the problem statement is an integer for all $n<n_{0}$, then $$ \\sum_{\\omega \\in S_{q}} \\frac{f(\\omega)}{(1-\\omega)^{n}} \\in \\mathbb{Z} $$ for all $n<n_{0}$ and $f \\in \\mathbb{Z}[x]$, whereas for $n=n_{0}$ there is some $f \\in \\mathbb{Z}[x]$ for which the sum is not an integer (e.g. $f=1$ ). Let $z_{q}=r \\phi(q)-q / p=p^{r-1}[r(p-1)-1]$. We claim that the answer is $n=z_{q}+1$. We prove this by induction on $r$. First is the base case $r=1$. ## Lemma There exist polynomials $u, v \\in \\mathbb{Z}[x]$ such that $(1-\\omega)^{p-1} / p=u(\\omega)$ and $p /(1-\\omega)^{p-1}=$ $v(\\omega)$ for all $\\omega \\in S_{p}$. (What we are saying is that $p$ is $(1-\\omega)^{p-1}$ times a unit (invertible algebraic integer), namely $v(\\omega)$.) $$ \\frac{p}{(1-\\omega)^{p-1}}=\\frac{1-\\omega}{1-\\omega} \\cdot \\frac{1-\\omega^{2}}{1-\\omega} \\cdots \\frac{1-\\omega^{p-1}}{1-\\omega} $$ and take $$ v(x)=\\prod_{k=1}^{p-1} \\frac{1-x^{k}}{1-x} $$ Similarly, the polynomial $u$ is $$ u(x)=\\prod_{k=1}^{p-1} \\frac{1-x^{k \\ell_{k}}}{1-x^{k}} $$ where $\\ell_{k}$ is a multiplicative inverse of $k$ modulo $p$. Now, the main idea: given $g \\in \\mathbb{Z}[x]$, observe that $$ S=\\sum_{\\omega \\in S_{p}}(1-\\omega) g(\\omega) $$ is divisible by $1-\\zeta_{p}^{k}$ (i.e. it is $1-\\zeta_{p}^{k}$ times an algebraic integer) for every $k$ coprime to $p$. By symmetric sums, $S$ is an integer; since $S^{p-1}$ is divisible by $\\left(1-\\zeta_{p}\\right) \\cdots\\left(1-\\zeta_{p}^{p-1}\\right)=p$, the integer $S$ must itself be divisible by $p$. (Alternatively, since $h(x):=(1-x) g(x)$ vanishes at $x=1$, one can interpret $S$ using a roots of unity filter: $S=p \\cdot h\\left(\\left[x^{0}\\right]+\\left[x^{p}\\right]+\\cdots\\right) \\equiv 0$ $(\\bmod p)$.$) Now write$ $$ \\mathbb{Z} \\ni \\frac{S}{p}=\\sum_{\\omega \\in S_{p}} \\frac{(1-\\omega)^{p-1}}{p} \\frac{g(\\omega)}{(1-\\omega)^{p-2}}=\\sum_{\\omega \\in S_{p}} u(\\omega) \\frac{g(\\omega)}{(1-\\omega)^{p-2}} . $$ Taking $g=v \\cdot(1-x)^{k}$ for $k \\geq 0$, we see that the sum in the problem statement is an integer for any $n \\leq p-2$. Finally, we have $$ \\sum_{\\omega \\in S_{p}} \\frac{u(\\omega)}{(1-\\omega)^{p-1}}=\\sum_{\\omega \\in S_{p}} \\frac{1}{p}=\\frac{p-1}{p} \\notin \\mathbb{Z} $$ so the sum is not an integer for $n=p-1$. Now let $r \\geq 2$ and assume the induction hypothesis for $r-1$. ## Lemma There exist polynomials $U, V \\in \\mathbb{Z}[x]$ such that $(1-\\omega)^{p} /\\left(1-\\omega^{p}\\right)=U(\\omega)$ and $\\left(1-\\omega^{p}\\right) /(1-\\omega)^{p}=V(\\omega)$ for all $\\omega \\in S_{q}$. (Again, these are units.) $$ \\begin{aligned} U(x) & =\\prod_{k=1}^{p-1} \\frac{1-x^{(k q / p+1) \\ell_{k}}}{1-x^{k q / p+1}} \\\\ V(x) & =\\prod_{k=1}^{p-1} \\frac{1-x^{k q / p+1}}{1-x} \\end{aligned} $$ where $\\ell_{k}$ is a multiplicative inverse of $k q / p+1$ modulo $q$. ## Corollary If $\\omega \\in S_{q}$, then $(1-\\omega)^{\\phi(q)} / p$ is a unit. Thus we have polynomials $A, B \\in \\mathbb{Z}[x]$ such that $$ \\begin{aligned} & A(\\omega)=\\frac{p}{(1-\\omega)^{\\phi(q)}} V(\\omega)^{z_{q / p}} \\\\ & B(\\omega)=\\frac{(1-\\omega)^{\\phi(q)}}{p} U(\\omega)^{z_{q / p}} \\end{aligned} $$ for all $\\omega \\in S_{q}$. Given $g \\in \\mathbb{Z}[x]$, consider the $p$ th roots of unity filter $$ S(x):=\\sum_{k=0}^{p-1} g\\left(\\zeta_{p}^{k} x\\right)=p \\cdot h\\left(x^{p}\\right) $$ where $h \\in \\mathbb{Z}[x]$. Then $$ p h(\\eta)=S(\\omega)=\\sum_{\\omega^{p}=\\eta} g(\\omega) $$ for all $\\eta \\in S_{q / p}$, so $$ \\begin{aligned} \\frac{h(\\eta)}{(1-\\eta)^{z_{q / p}}}=\\frac{S(\\omega)}{p(1-\\eta)^{z_{q / p}}} & =\\sum_{\\omega^{p}=\\eta} \\frac{(1-\\omega)^{p z_{q / p}}}{\\left(1-\\omega^{p}\\right)^{z_{q / p}}} \\frac{g(\\omega)}{p(1-\\omega)^{p z_{q / p}}} \\\\ & =\\sum_{\\omega^{p}=\\eta} U(\\omega)^{z_{q / p}} \\frac{(1-\\omega)^{\\phi(q)}}{p} \\frac{g(\\omega)}{(1-\\omega)^{z_{q}}} \\end{aligned} $$ (Implicit in the last line is $z_{q}=\\phi(q)+p z_{q / p}$.) Since $U(\\omega)$ and $(1-\\omega)^{\\phi(q)} / p$ are units, we can let $g=A \\cdot f$ for arbitrary $f \\in \\mathbb{Z}[x]$, so that the expression in the summation simplifies to $f(\\omega) /(1-\\omega)^{z_{q}}$. From this we conclude that for any $f \\in \\mathbb{Z}[x]$, there exists $h \\in \\mathbb{Z}[x]$ such that $$ \\begin{aligned} \\sum_{\\omega \\in S_{q}} \\frac{f(\\omega)}{(1-\\omega)^{z_{q}}} & =\\sum_{\\eta \\in S_{q / p}} \\sum_{\\omega^{p}=\\eta} \\frac{f(\\omega)}{(1-\\omega)^{z_{q}}} \\\\ & =\\sum_{\\eta \\in S_{q / p}} \\frac{h(\\eta)}{(1-\\eta)^{z_{q / p}}} \\end{aligned} $$ By the inductive hypothesis, this is always an integer. In the other direction, for $\\eta \\in S_{q / p}$ we have $$ \\begin{aligned} \\sum_{\\omega^{p}=\\eta} \\frac{B(\\omega)}{(1-\\omega)^{1+z_{q}}} & =\\sum_{\\omega^{p}=\\eta} \\frac{1}{p\\left(1-\\omega^{p}\\right)^{z_{q / p}}(1-\\omega)} \\\\ & =\\frac{1}{p(1-\\eta)^{z_{q / p}}} \\sum_{\\omega^{p}=\\eta} \\frac{1}{1-\\omega} \\\\ & =\\frac{1}{p(1-\\eta)^{z_{q / p}}}\\left[\\frac{p x^{p-1}}{x^{p}-\\eta}\\right]_{x=1} \\\\ & =\\frac{1}{(1-\\eta)^{1+z_{q / p}}} \\end{aligned} $$ Summing over all $\\eta \\in S_{q / p}$, we conclude by the inductive hypothesis that $$ \\sum_{\\omega \\in S_{q}} \\frac{B(\\omega)}{(1-\\omega)^{1+z_{q}}}=\\sum_{\\eta \\in S_{q / p}} \\frac{1}{(1-\\eta)^{1+z_{q / p}}} $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
| 28 |
-
{"year": "2021", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\\zeta=e^{\\frac{2 \\pi i}{q}}$. Find the least positive integer $n$ such that $$ \\sum_{\\substack{1 \\leq k \\leq q \\\\ \\operatorname{gcd}(k, p)=1}} \\frac{1}{\\left(1-\\zeta^{k}\\right)^{n}} $$ is not an integer. (The sum is over all $1 \\leq k \\leq q$ with $p$ not dividing $k$.)", "solution": " Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ). Solution 2 (Nikolai Beluhov). Suppose that the complex numbers $\\frac{1}{1-\\omega}$ for $\\omega \\in S_{q}$ are the roots of $$ P(x)=x^{d}-c_{1} x^{d-1}+c_{2} x^{d-2}-\\cdots \\pm c_{d} $$ so that $c_{k}$ is their $k$-th elementary symmetric polynomial and $d=\\phi(q)=(p-1) p^{r-1}$. Additionally denote $$ S_{n}=\\sum_{\\omega \\in S_{q}} \\frac{1}{(1-\\omega)^{n}} $$ Then, by Newton's identities, $$ \\begin{aligned} S_{1} & =c_{1} \\\\ S_{2} & =c_{1} S_{1}-2 c_{2} \\\\ S_{3} & =c_{1} S_{2}-c_{2} S_{1}+3 c_{3} \\end{aligned} $$ and so on. The general pattern when $n \\leq d$ is $$ S_{n}=\\left[\\sum_{j=1}^{n-1}(-1)^{j+1} c_{j} S_{n-j}\\right]+(-1)^{n+1} n c_{n} $$ After that, when $n>d$, the pattern changes to $$ S_{n}=\\sum_{j=1}^{d}(-1)^{j+1} c_{j} S_{n-j} $$ ## Lemma All of the $c_{i}$ are integers except for $c_{d}$. Furthermore, $c_{d}$ is $1 / p$ times an integer. $$ \\Phi_{q}(x)=1+x^{p^{r-1}}+x^{2 p^{r-1}}+\\cdots+x^{(p-1) p^{r-1}} $$ The polynomial $$ Q(x)=1+(1+x)^{p^{r-1}}+(1+x)^{2 p^{r-1}}+\\cdots+(1+x)^{(p-1) p^{r-1}} $$ has roots $\\omega-1$ for $\\omega \\in S_{q}$, so it is equal to $p(-x)^{d} P(-1 / x)$ by comparing constant coefficients. Comparing the remaining coefficients, we find that $c_{n}$ is $1 / p$ times the $x^{n}$ coefficient of $Q$. Since $(x+y)^{p} \\equiv x^{p}+y^{p}(\\bmod p)$, we conclude that, modulo $p$, $$ \\begin{aligned} Q(x) & \\equiv 1+\\left(1+x^{p^{r-1}}\\right)+\\left(1+x^{p^{r-1}}\\right)^{2}+\\cdots+\\left(1+x^{p^{r-1}}\\right)^{p-1} \\\\ & \\equiv\\left[\\left(1+x^{p^{r-1}}\\right)^{p}-1\\right] / x^{p^{r-1}} \\end{aligned} $$ Since $\\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, it follows that all coefficients of $Q(x)$ are multiples of $p$ save for the leading one. Therefore, $c_{n}$ is an integer when $n<d$, while $c_{d}$ is $1 / p$ times an integer. By the recurrences above, $S_{n}$ is an integer for $n<d$. When $r=1$, we get that $d c_{d}$ is not an integer, so $S_{d}$ is not an integer, either. Thus the answer for $r=1$ is $n=p-1$. Suppose now that $r \\geq 2$. Then $d c_{d}$ does become an integer, so $S_{d}$ is an integer as well. ## Lemma For all $n$ with $1 \\leq n \\leq d$, we have $\\nu_{p}\\left(n c_{n}\\right) \\geq r-2$. Furthermore, the smallest $n$ such that $\\nu_{p}\\left(n c_{n}\\right)=r-2$ is $d-p^{r-1}+1$. $$ p^{r-1}(1+x)^{p^{r-1}-1}\\left[\\sum_{k=1}^{p-1} k(1+x)^{(k-1) p^{r-1}}\\right] . $$ What we want to prove reduces to showing that all coefficients of the polynomial in the square brackets are multiples of $p$ except for the leading one. Using the same trick $(x+y)^{p} \\equiv x^{p}+y^{p}(\\bmod p)$ as before and also writing $w$ for $x^{p^{r-1}}$, modulo $p$ the polynomial in the square brackets becomes $$ 1+2(1+w)+3(1+w)^{2}+\\cdots+(p-1)(1+w)^{p-2} $$ This is the derivative of $$ 1+(1+w)+(1+w)^{2}+\\cdots+(1+w)^{p-1}=\\left[(1+w)^{p}-1\\right] / w $$ and so, since $\\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, we are done. Finally, we finish the problem with the following claim. Claim - Let $m=d-p^{r-1}$. Then for all $k \\geq 0$ and $1 \\leq j \\leq d$, we have $$ \\begin{aligned} & \\nu_{p}\\left(S_{k d+m+1}\\right)=r-2-k \\\\ & \\nu_{p}\\left(S_{k d+m+j}\\right) \\geq r-2-k \\end{aligned} $$ $$ \\nu_{p}\\left((m+1) c_{m+1}\\right)=r-2 $$ and all other terms in the recurrence relation are divisible by $p^{r-1}$. We can similarly check that $\\nu_{p}\\left(S_{n}\\right) \\geq r-2$ for $m+1 \\leq n \\leq d$. Newton's identities combined with the first lemma now imply the following for $n>d$ : - If $\\nu_{p}\\left(S_{n-j}\\right) \\geq \\ell$ for all $1 \\leq j \\leq d$ and $\\nu_{p}\\left(S_{n-d}\\right) \\geq \\ell+1$, then $\\nu_{p}\\left(S_{n}\\right) \\geq \\ell$. - If $\\nu_{p}\\left(S_{n-j}\\right) \\geq \\ell$ for all $1 \\leq j \\leq d$ and $\\nu_{p}\\left(S_{n-d}\\right)=\\ell$, then $\\nu_{p}\\left(S_{n}\\right)=\\ell-1$. Together, these prove the claim by induction. By the claim, the smallest $n$ for which $\\nu_{p}\\left(S_{n}\\right)<0$ (equivalent to $S_{n}$ not being an integer, by the recurrences) is $$ n=(r-1) d+m+1=((p-1) r-1) p^{r-1}+1 $$ Remark. The original proposal was the following more general version: Let $n$ be an integer with prime power factorization $q_{1} \\cdots q_{m}$. Let $S_{n}$ denote the set of primitive $n$th roots of unity. Find all tuples of nonnegative integers $\\left(z_{1}, \\ldots, z_{m}\\right)$ such that $$ \\sum_{\\omega \\in S_{n}} \\frac{f(\\omega)}{\\left(1-\\omega^{n / q_{1}}\\right)^{z_{1}} \\cdots\\left(1-\\omega^{n / q_{m}}\\right)^{z_{m}}} \\in \\mathbb{Z} $$ for all polynomials $f \\in \\mathbb{Z}[x]$. The maximal $z_{i}$ are exponents in the prime ideal factorization of the different ideal of the cyclotomic extension $\\mathbb{Q}\\left(\\zeta_{n}\\right) / \\mathbb{Q}$. Remark. Let $F=\\left(x^{p}-1\\right) /(x-1)$ be the minimal polynomial of $\\zeta_{p}=e^{2 \\pi i / p}$ over $\\mathbb{Q}$. A calculation of Euler shows that $$ \\left(\\mathbb{Z}\\left[\\zeta_{p}\\right]\\right)^{*}:=\\left\\{\\alpha=g\\left(\\zeta_{p}\\right) \\in \\mathbb{Q}\\left[\\zeta_{p}\\right]: \\sum_{\\omega \\in S_{p}} f(\\omega) g(\\omega) \\in \\mathbb{Z} \\forall f \\in \\mathbb{Z}[x]\\right\\}=\\frac{1}{F^{\\prime}\\left(\\zeta_{p}\\right)} \\cdot \\mathbb{Z}\\left[\\zeta_{p}\\right], $$ where $$ F^{\\prime}\\left(\\zeta_{p}\\right)=\\frac{p \\zeta_{p}^{p-1}-\\left[1+\\zeta_{p}+\\cdots+\\zeta_{p}^{p-1}\\right]}{1-\\zeta_{p}}=p\\left(1-\\zeta_{p}\\right)^{-1} \\zeta_{p}^{p-1} $$ is $\\left(1-\\zeta_{p}\\right)^{[p-1]-1}=\\left(1-\\zeta_{p}\\right)^{p-2}$ times a unit of $\\mathbb{Z}\\left[\\zeta_{p}\\right]$. Here, $\\left(\\mathbb{Z}\\left[\\zeta_{p}\\right]\\right)^{*}$ is the dual lattice of $\\mathbb{Z}\\left[\\zeta_{p}\\right]$. Remark. Let $K=\\mathbb{Q}(\\omega)$, so $(p)$ factors as $(1-\\omega)^{p-1}$ in the ring of integers $\\mathcal{O}_{K}$ (which, for cyclotomic fields, can be shown to be $\\mathbb{Z}[\\omega])$. In particular, the ramification index $e$ of $(1-\\omega)$ over $p$ is the exponent, $p-1$. Since $e=p-1$ is not divisible by $p$, we have so-called tame ramification. Now by the ramification theory of Dedekind's different ideal, the exponent $z_{1}$ that works when $n=p$ is $e-1=p-2$. Higher prime powers are more interesting because of wild ramification: $p$ divides $\\phi\\left(p^{r}\\right)=$ $p^{r-1}(p-1)$ if and only if $r>1$. (This is a similar phenomena to how Hensel's lemma for $x^{2}-c$ is more interesting mod powers of 2 than mod odd prime powers.) Remark. Let $F=\\left(x^{q}-1\\right) /\\left(x^{q / p}-1\\right)$ be the minimal polynomial of $\\zeta_{q}=e^{2 \\pi i / q}$ over $\\mathbb{Q}$. The aforementioned calculation of Euler shows that $$ \\left(\\mathbb{Z}\\left[\\zeta_{q}\\right]\\right)^{*}:=\\left\\{\\alpha=g\\left(\\zeta_{q}\\right) \\in \\mathbb{Q}\\left[\\zeta_{q}\\right]: \\sum_{\\omega \\in S_{q}} f(\\omega) g(\\omega) \\in \\mathbb{Z} \\forall f \\in \\mathbb{Z}[x]\\right\\}=\\frac{1}{F^{\\prime}\\left(\\zeta_{q}\\right)} \\cdot \\mathbb{Z}\\left[\\zeta_{q}\\right] $$ where the chain rule implies (using the computation from the prime case) $$ F^{\\prime}\\left(\\zeta_{q}\\right)=\\left[p\\left(1-\\zeta_{p}\\right)^{-1} \\zeta_{p}^{p-1}\\right] \\cdot \\frac{q}{p} \\zeta_{q}^{(q / p)-1}=q\\left(1-\\zeta_{p}\\right)^{-1} \\zeta_{q}^{-1} $$ is $\\left(1-\\zeta_{q}\\right)^{r \\phi(q)-q / p}=\\left(1-\\zeta_{q}\\right)^{z_{q}}$ times a unit of $\\mathbb{Z}\\left[\\zeta_{q}\\right]$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2021.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl
DELETED
|
@@ -1,12 +0,0 @@
|
|
| 1 |
-
{"year": "2022", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold: - The sides of each rectangle are parallel to the sides of the unit square. - Each point in $S$ is not in the interior of any rectangle. - Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles. (The interior of a polygon does not contain its boundary.)", "solution": " We claim the answer is $k=2 n+2$. The lower bound is given by picking $$ S=\\left\\{\\left(s_{1}, s_{1}\\right),\\left(s_{2}, s_{2}\\right), \\ldots,\\left(s_{n}, s_{n}\\right)\\right\\} $$ for some real numbers $0<s_{1}<s_{2}<\\cdots<s_{n}<1$. Consider the $4 n$ points $$ S^{\\prime}=S+\\{(\\varepsilon, 0),(0, \\varepsilon),(-\\varepsilon, 0),(0,-\\varepsilon)\\} \\subset(0,1)^{2} $$ for some sufficiently small $\\varepsilon>0$. The four rectangles covering each of $$ \\left(s_{1}-\\varepsilon, s_{1}\\right),\\left(s_{1}, s_{1}-\\varepsilon\\right),\\left(s_{n}+\\varepsilon, s_{n}\\right),\\left(s_{n}, s_{n}+\\varepsilon\\right) $$ cannot cover any other points in $S^{\\prime}$; all other rectangles can only cover at most 2 points in $S^{\\prime}$, giving a bound of $$ k \\geq 4+\\frac{\\left|S^{\\prime}\\right|-4}{2}=2 n+2 $$  To prove that $2 n+2$ rectangles are sufficient, assume that the number of distinct $y$-coordinates is at least the number of distinct $x$-coordinates. Let $$ 0=x_{0}<x_{1}<\\cdots<x_{m}<x_{m+1}=1 $$ where $x_{1}, \\ldots, x_{m}$ are the distinct $x$-coordinates of points in $S$, and let $Y_{i}$ be the set of $y$-coordinates of points with $x$-coordinate $x_{i}$. For each $1 \\leq i \\leq m$, include the $\\left|Y_{i}\\right|+1$ rectangles $$ \\left(x_{i-1}, x_{i+1}\\right) \\times\\left((0,1) \\backslash Y_{i}\\right) $$ in the union, and also include $\\left(0, x_{1}\\right) \\times(0,1)$ and $\\left(x_{m}, 1\\right) \\times(0,1)$; this uses $m+n+2$ rectangles.  All remaining uncovered points are between pairs of points with the same $y$-coordinate and adjacent $x$-coordinates $\\left\\{x_{i}, x_{i+1}\\right\\}$. There are at most $n-m$ such pairs by the initial assumption, so covering the points between each pair with $$ \\left(x_{i}, x_{i+1}\\right) \\times(y-\\varepsilon, y+\\varepsilon) $$ for some sufficiently small $\\varepsilon>0$ gives a total of $$ (m+n+2)+(n-m)=2 n+2 $$ rectangles.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 2 |
-
{"year": "2022", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a triangle. Let $\\theta$ be a fixed angle for which $$ \\theta<\\frac{1}{2} \\min (\\angle A, \\angle B, \\angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\\angle B A S_{A}=\\angle T_{A} A C=\\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\\overline{A S_{A}}$ and $\\overline{A T_{A}}$ respectively. Then $\\ell_{A}$ is defined as the perpendicular bisector of $\\overline{P_{A} Q_{A}}$. Define $\\ell_{B}$ and $\\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\\theta$ ). Prove that $\\ell_{A}, \\ell_{B}$, and $\\ell_{C}$ are concurrent or all parallel.", "solution": " We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 First solution, by author. Let $X$ be the projection from $C$ to $A P_{A}, Y$ be the projection from $B$ to $A Q_{A}$.  Claim - Line $\\ell_{A}$ passes through $M_{A}$, the midpoint of $B C$. Also, quadrilateral $P_{A} Q_{A} Y X$ is cyclic with circumcenter $M_{A}$. $$ A P_{A} \\cdot A X=A B \\cdot A C \\cdot \\cos \\theta \\cos (\\angle A-\\theta)=A Q_{A} \\cdot A Y $$ it follows that $P_{A}, Q_{A}, Y, X$ are concyclic by power of a point. Moreover, by projection, the perpendicular bisector of $P_{A} X$ passes through $M_{A}$, similar for $Q_{A} Y$, implying that $M_{A}$ is the center of $P_{A} Q_{A} Y X$. Hence $\\ell_{A}$ passes through $M_{A}$. $$ \\text { Claim }-\\measuredangle\\left(M_{A} M_{C}, \\ell_{A}\\right)=\\measuredangle Y P_{A} Q_{A} $$ Therefore, $$ \\frac{\\sin \\angle\\left(M_{A} M_{C}, \\ell_{A}\\right)}{\\sin \\angle\\left(\\ell_{A}, M_{A} M_{B}\\right)}=\\frac{\\sin \\angle Y P_{A} Q_{A}}{\\sin \\angle P_{A} Q_{A} X}=\\frac{Y Q_{A}}{X P_{A}}=\\frac{B C \\sin (\\angle C+\\theta)}{B C \\sin (\\angle B+\\theta)}=\\frac{\\sin (\\angle C+\\theta)}{\\sin (\\angle B+\\theta)}, $$ and we conclude by trig Ceva theorem.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 3 |
-
{"year": "2022", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a triangle. Let $\\theta$ be a fixed angle for which $$ \\theta<\\frac{1}{2} \\min (\\angle A, \\angle B, \\angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\\angle B A S_{A}=\\angle T_{A} A C=\\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\\overline{A S_{A}}$ and $\\overline{A T_{A}}$ respectively. Then $\\ell_{A}$ is defined as the perpendicular bisector of $\\overline{P_{A} Q_{A}}$. Define $\\ell_{B}$ and $\\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\\theta$ ). Prove that $\\ell_{A}, \\ell_{B}$, and $\\ell_{C}$ are concurrent or all parallel.", "solution": " We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 Second solution via Jacobi, by Maxim Li. Let $D$ be the foot of the $A$-altitude. Note that line $B C$ is the external angle bisector of $\\angle P_{A} D Q_{A}$. Claim - $\\left(D P_{A} Q_{A}\\right)$ passes through the midpoint $M_{A}$ of $B C$. It follows that $M_{A}$ lies on $\\ell_{A}$; we need to identify a second point. We'll use the circumcenter $O_{A}$ of $\\left(D P_{A} Q_{A}\\right)$. The perpendicular bisector of $D P_{A}$ passes through $M_{C}$; indeed, we can easily show the angle it makes with $M_{C} M_{A}$ is $90^{\\circ}-\\theta-C$, so $\\angle O_{A} M_{C} M_{A}=90-\\theta-C$, and then by analogous angle-chasing we can finish with Jacobi's theorem on $\\triangle M_{A} M_{B} M_{C}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 4 |
-
{"year": "2022", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\\cdots$ satisfying the following properties: - the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \\ldots$ is periodic; and - $s_{s_{n}}-s_{s_{n-1}} \\leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.", "solution": " 【 Answer. All $N$ such that $t^{2} \\leq N<t^{2}+t$ for some positive integer $t$. Solution 1 (local). If $t^{2} \\leq N<t^{2}+t$ then the sequence $s_{n}=t n+1$ satisfies both conditions. It remains to show that no other values of $N$ work. Define $a_{n}:=s_{n}-s_{n-1}$, and let $p$ be the minimal period of $\\left\\{a_{n}\\right\\}$. For each $k \\in \\mathbb{Z}_{\\geq 0}$, let $f(k)$ be the integer such that $$ s_{f(k)}-s_{k} \\leq N<s_{f(k)+1}-s_{k} $$ Note that $f\\left(s_{n-1}\\right)=s_{n}$ for all $n$. Since $\\left\\{a_{n}\\right\\}$ is periodic with period $p, f(k+p)=f(k)+p$ for all $k$, so $k \\mapsto f(k)-k$ is periodic with period $p$. We also note that $f$ is nondecreasing: if $k<k^{\\prime}$ but $f\\left(k^{\\prime}\\right)<f(k)$ then $$ N<s_{f\\left(k^{\\prime}\\right)+1}-s_{k^{\\prime}}<s_{f(k)}-s_{k} \\leq N $$ which is absurd. We now claim that $$ \\max _{k}(f(k)-k)<p+\\min _{k}(f(k)-k) $$ Indeed, if $f\\left(k^{\\prime}\\right)-k^{\\prime} \\geq p+f(k)-k$ then we can shift $k$ and $k^{\\prime}$ so that $0 \\leq k-k^{\\prime}<p$, and it follows that $k \\leq k^{\\prime} \\leq f\\left(k^{\\prime}\\right)<f(k)$, violating the fact that $f$ is nondecreasing. Therefore $\\max _{k}(f(k)-k)<p+\\min _{k}(f(k)-k)$, so $f(k)-k$ is uniquely determined by its value modulo $p$. In particular, since $a_{n}=f\\left(s_{n-1}\\right)-s_{n-1}, a_{n}$ is also uniquely determined by its value modulo $p$, so $\\left\\{a_{n} \\bmod p\\right\\}$ also has minimal period $p$. Now work in $\\mathbb{Z} / p \\mathbb{Z}$ and consider the sequence $s_{0}, f\\left(s_{0}\\right), f\\left(f\\left(s_{0}\\right)\\right), \\ldots$. This sequence must be eventually periodic; suppose it has minimal period $p^{\\prime}$, which must be at most $p$. Then, since $$ f^{n}\\left(s_{0}\\right)-f^{n-1}\\left(s_{0}\\right)=s_{n}-s_{n-1}=a_{n} $$ and $\\left\\{a_{n} \\bmod p\\right\\}$ has minimal period $p$, we must have $p^{\\prime}=p$. Therefore the directed graph $G$ on $\\mathbb{Z} / p \\mathbb{Z}$ given by the edges $k \\rightarrow f(k)$ is simply a $p$-cycle, which implies that the map $k \\mapsto f(k)$ is a bijection on $\\mathbb{Z} / p \\mathbb{Z}$. Therefore, $f(k+1) \\neq f(k)$ for all $k$ (unless $p=1$, but in this case the following holds anyways), hence $$ f(k)<f(k+1)<\\cdots<f(k+p)=f(k)+p $$ This implies $f(k+1)=f(k)+1$ for all $k$, so $f(k)-k$ is constant, therefore $a_{n}=$ $f\\left(s_{n-1}\\right)-s_{n-1}$ is also constant. Let $a_{n} \\equiv t$. It follows that $t^{2} \\leq N<t^{2}+t$ as we wanted.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 5 |
-
{"year": "2022", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\\cdots$ satisfying the following properties: - the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \\ldots$ is periodic; and - $s_{s_{n}}-s_{s_{n-1}} \\leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.", "solution": " 【 Answer. All $N$ such that $t^{2} \\leq N<t^{2}+t$ for some positive integer $t$. 【 Solution 2 (global). Define $\\left\\{a_{n}\\right\\}$ and $f$ as in the previous solution. We first show that $s_{i} \\not \\equiv s_{j}(\\bmod p)$ for all $i<j<i+p$. Suppose the contrary, i.e. that $s_{i} \\equiv s_{j}$ $(\\bmod p)$ for some $i, j$ with $i<j<i+p$. Then $a_{s_{i}+k}=a_{s_{j}+k}$ for all $k \\geq 0$, therefore $s_{s_{i}+k}-s_{s_{i}}=s_{s_{j}+k}-s_{s_{j}}$ for all $k \\geq 0$, therefore $$ a_{i+1}=f\\left(s_{i}\\right)-s_{i}=f\\left(s_{j}\\right)-s_{j}=a_{j+1} \\quad \\text { and } \\quad s_{i+1}=f\\left(s_{i}\\right) \\equiv f\\left(s_{j}\\right)=s_{j+1} \\quad(\\bmod p) $$ Continuing this inductively, we obtain $a_{i+k}=a_{j+k}$ for all $k$, so $\\left\\{a_{n}\\right\\}$ has period $j-i<p$, which is a contradiction. Therefore $s_{i} \\not \\equiv s_{j}(\\bmod p)$ for all $i<j<i+p$, and this implies that $\\left\\{s_{i}, \\ldots, s_{i+p-1}\\right\\}$ forms a complete residue system modulo $p$ for all $i$. Consequently we must have $s_{i+p} \\equiv s_{i}(\\bmod p)$ for all $i$. Let $T=s_{p}-s_{0}=a_{1}+\\cdots+a_{p}$. Since $\\left\\{a_{n}\\right\\}$ is periodic with period $p$, and $\\{i+1, \\ldots, i+k p\\}$ contains exactly $k$ values of each residue class modulo $p$, $$ s_{i+k p}-s_{i}=a_{i+1}+\\cdots+a_{i+k p}=k T $$ for all $i, k$. Since $p \\mid T$, it follows that $s_{s_{p}}-s_{s_{0}}=\\frac{T}{p} \\cdot T=\\frac{T^{2}}{p}$. Summing up the inequalities $$ s_{s_{n}}-s_{s_{n-1}} \\leq N<s_{s_{n}+1}-s_{s_{n-1}}=s_{s_{n}}-s_{s_{n-1}}+a_{s_{n}+1} $$ for $n \\in\\{1, \\ldots, p\\}$ then implies $$ \\frac{T^{2}}{p}=s_{s_{p}}-s_{s_{0}} \\leq N p<\\frac{T^{2}}{p}+a_{s_{1}+1}+a_{s_{2}+1}+\\cdots+a_{s_{p}+1}=\\frac{T^{2}}{p}+T $$ where the last equality holds because $\\left\\{s_{1}+1, \\ldots, s_{p}+1\\right\\}$ is a complete residue system modulo $p$. Dividing this by $p$ yields $t^{2} \\leq N<t^{2}+t$ for $t:=\\frac{T}{p} \\in \\mathbb{Z}^{+}$. Remark (Author comments). There are some similarities between this problem and IMO 2009/3, mainly that they both involve terms of the form $s_{s_{n}}$ and $s_{s_{n}+1}$ and the sequence $s_{0}, s_{1}, \\ldots$ turns out to be an arithmetic progression. Other than this, I don't think knowing about IMO 2009/3 will be that useful on this problem, since in this problem the fact that $\\left\\{s_{n+1}-s_{n}\\right\\}$ is periodic is fundamentally important. The motivation for this problem comes from the following scenario: assume we have boxes that can hold some things of total size $\\leq N$, and a sequence of things of size $a_{1}, a_{2}, \\ldots$ (where $a_{i}:=s_{i+1}-s_{i}$ ). We then greedily pack the things in a sequence of boxes, 'closing' each box when it cannot fit the next thing. The number of things we put in each box gives a sequence $b_{1}, b_{2}, \\ldots$. This problem asks when we can have $\\left\\{a_{n}\\right\\}=\\left\\{b_{n}\\right\\}$, assuming that we start with a sequence $\\left\\{a_{n}\\right\\}$ that is periodic. (Extra motivation: I first thought about this scenario when I was pasting some text repeatedly into the Notes app and noticed that the word at the end of lines are also (eventually) periodic.)", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 6 |
-
{"year": "2022", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "A function $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers $$ f(m+1), f(m+2), \\ldots, f(m+f(n)) $$ is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.", "solution": " We start with the following claim: $$ \\text { Claim - If } a \\mid b \\text { then } f(a) \\mid f(b) $$ In what follows, let $a \\geq 2$ be any positive integer. Because $f(a)$ and $f(2 a)$ are both divisible by $f(a)$, there are $a+1$ consecutive values of $f$ of which at least two divisible by $f(a)$. It follows that $f(f(a)) \\leq a$. However, we also know that exactly one of $f(2), f(3), \\ldots, f(1+f(a))$ is divisible by $a$; let this be $f(t)$. Then we have $S_{a}=\\{t, t+f(a), t+2 f(a), \\ldots\\}$. Because $a|f(t)| f(2 t)$, we know that $2 t \\in S_{a}$, so $t$ is a multiple of $f(a)$. Because $2 \\leq t \\leq 1+f(a)$, and $f(a) \\geq 2$ for $a \\geq 2$, we conclude that we must have $t=f(a)$, so $f(f(a))$ is a multiple of $a$. Together with $f(f(a)) \\leq a$, this yields $f(f(a))=a$. Because $f(f(a))=a$ also holds for $a=1$ (from the given condition for $n=1$ it immediately follows that $f(1)=1$ ), we conclude that $f(f(a))=a$ for all $a$, and hence $f$ is a bijection. Moreover, we now have that $f(a) \\mid f(b)$ implies $f(f(a)) \\mid f(f(b))$, i.e. $a \\mid b$, so $a \\mid b$ if and only if $f(a) \\mid f(b)$. Together with the fact that $f$ is a bijection, this implies that $f(n)$ has the same number of divisors of $n$. Let $p$ be a prime. Then $f(p)=q$ must be a prime as well. If $q \\neq p$, then from $f(p) \\mid f(p q)$ and $f(q) \\mid f(p q)$ it follows that $p q \\mid f(p q)$, so $f(p q)=p q$ because $f(p q)$ and $p q$ must have the same number of divisors. Therefore, for every prime number $p$ we either have that $f(p)=p$ or $f(p f(p))=p f(p)$. From here, it is easy to see that $f(n)=n$ for infinitely many $n$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 7 |
-
{"year": "2022", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Let $A_{1}, \\ldots, A_{2022}$ be the vertices of a regular 2022 -gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.) In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \\ldots$, $\\left.A_{2022}\\right)$ and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \\ldots, A_{2022}$ in $Q$ rounds?", "solution": " The answer is 22 . To prove the lower bound, note that there are $2022 \\cdot 2021+2>2^{21}$ possible colorings. If Bob makes less than 22 queries, then he can only output $2^{21}$ possible colorings, which means he is wrong on some coloring. Now we show Bob can always win in 22 queries. A key observation is that the set of red points is convex, as is the set of blue points, so if a set of points is all the same color, then their convex hull is all the same color. ## Lemma Let $B_{0}, \\ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}$ and $B_{k+1}$ differ and are known. Then it is possible to determine the colors of $B_{1}$, $\\ldots, B_{k}$ in $\\left\\lceil\\log _{2} k\\right\\rceil$ queries. ## Lemma Let $B_{0}, \\ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}, B_{\\lceil k / 2\\rceil}, B_{k+1}$ are both red and are known. Then at least one of the following holds: all of $B_{1}, \\ldots, B_{\\lceil k / 2\\rceil}$ are red or all of $B_{\\lceil k / 2\\rceil}, \\ldots, B_{k}$ are red. Furthermore, in one query we can determine which one of the cases holds. Now the strategy is: Bob picks $A_{1}$. WLOG it is red. Now suppose Bob does not know the colors of $\\leq 2^{k}-1$ points $A_{i}, \\ldots, A_{j}$ with $j-i+1 \\leq 2^{k}-1$ and knows the rest are red. I claim Bob can win in $2 k-1$ queries. First, if $k=1$, there is one point and he wins by querying the point, so the base case holds, so assume $k>1$. Bob queries $A_{i+\\lceil(j-i+1) / 2\\rceil}$. If it is blue, he finishes in $2 \\log _{2}\\lceil(j-i+1) / 2\\rceil \\leq 2(k-1)$ queries by the first lemma, for a total of $2 k-1$ queries. If it is red, he can query one more point and learn some half of $A_{i}, \\ldots, A_{j}$ that are red by the second lemma, and then he has reduced it to the case with $\\leq 2^{k-1}-1$ points in two queries, at which point we induct.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 8 |
-
{"year": "2022", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\\overline{A H}$ intersects $\\overline{A B}$ and $\\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.", "solution": " \\ First solution, by author. Let $\\odot O X_{A} Y_{A}$ intersects $A B, A C$ again at $U, V$. Then by Reim's theorem $U V C B$ are concyclic. Hence the radical axis of $\\odot O X_{A} Y_{A}, \\odot O B C$ and $\\odot(U V C B)$ are concurrent, i.e. $O K_{A}, B C, U V$ are concurrent, Denote the intersection as $K_{A}^{*}$, which is indeed the inversion of $K_{A}$ with respect to $\\odot O$. (The inversion sends $\\odot O B C$ to the line $B C$ ). Let $P_{A}, P_{B}, P_{C}$ be the circumcenters of $\\triangle O B C, \\triangle O C A, \\triangle O A B$ respectively. Claim $-K_{A}^{*}$ coincides with the intersection of $P_{B} P_{C}$ and $B C$. Finally by Desargue's theorem, it suffices to show that $A P_{A}, B P_{B}, C P_{C}$ are concurrent. Note that $$ \\begin{aligned} & d\\left(P_{A}, A B\\right)=P_{A} B \\sin \\left(90^{\\circ}+\\angle C-\\angle A\\right) \\\\ & d\\left(P_{A}, A C\\right)=P_{A} C \\sin \\left(90^{\\circ}+\\angle B-\\angle A\\right) \\end{aligned} $$ Hence the symmetric product and trig Ceva finishes the proof. ", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 9 |
-
{"year": "2022", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\\overline{A H}$ intersects $\\overline{A B}$ and $\\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.", "solution": " I Second solution, from Jeffrey Kwan. Let $O_{A}$ be the circumcenter of $\\triangle A X_{A} Y_{A}$. The key claim is that: Claim $-O_{A} X_{A} Y_{A} O$ is cyclic. $$ \\frac{A X_{A}}{A B}=\\frac{A H / 2}{A D}=\\frac{R \\cos A}{A D} $$ and so $$ \\frac{A O}{A D}=R \\cdot \\frac{A X_{A}}{A B \\cdot R \\cos A}=\\frac{A X_{A}}{A E}=\\frac{A Y_{A}}{A F} $$ Hence $\\angle X_{A} O Y_{A}=180^{\\circ}-2 \\angle A=180^{\\circ}-\\angle X_{A} O_{A} Y_{A}$, which proves the claim. Let $P_{A}$ be the circumcenter of $\\triangle O B C$, and define $P_{B}, P_{C}$ similarly. By the claim, $A$ is the exsimilicenter of $\\left(O X_{A} Y_{A}\\right)$ and $(O B C)$, so $A P_{A}$ is the line between their two centers. In particular, $A P_{A}$ is the perpendicular bisector of $O K_{A}$.  Claim $-A P_{A}, B P_{B}, C P_{C}$ concur at $T$. Now $T$ lies on the perpendicular bisectors of $O K_{A}, O K_{B}$, and $O K_{C}$. Hence $O K_{A} K_{B} K_{C}$ is cyclic with center $T$, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 10 |
-
{"year": "2022", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that $$ 2 \\angle A E B=\\angle A D B+\\angle A C B, $$ and point $F$ lies on segment $B C$ such that $$ 2 \\angle D F A=\\angle D C A+\\angle D B A . $$ Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.", "solution": " Let the circle through $A, B$, and $E$ intersect $C D$ again at $E^{\\prime}$, and let the circle through $D$, $A$, and $F$ intersect $B C$ again at $F^{\\prime}$. Now $A B E E^{\\prime}$ and $D A F^{\\prime} F$ are cyclic quadrilaterals with two parallel sides, so they are isosceles trapezoids. From $K A=K B$, it now follows that $K E=K E^{\\prime}$, whereas from $K A=K D$ it follows that $K F=K F^{\\prime}$. Next, let the circle through $A, B$, and $E$ intersect $A C$ again at $S$. Then $$ \\angle A S B=\\angle A E B=\\frac{1}{2}(\\angle A D B+\\angle A C B)=\\frac{1}{2}(\\angle A D B+\\angle D A C)=\\frac{1}{2} \\angle A M B, $$ where $M$ is the intersection of $A C$ and $B D$. From $\\angle A S B=\\frac{1}{2} \\angle A M B$, it follows that $M S=M B$, so $S$ is the point on $M C$ such that $M S=M B=M D$. By symmetry, the circle through $A, D$, and $F$ also passes through $S$, and it follows that the line $A S$ is the radical axis of the circles $(A B E)$ and $(A D F)$. By power of a point, we now obtain $$ C E \\cdot C E^{\\prime}=C S \\cdot C A=C F \\cdot C F^{\\prime}, $$ from which it follows that $E, F, E^{\\prime}$, and $F^{\\prime}$ are concyclic. The segments $E E^{\\prime}$ and $F F^{\\prime}$ are not parallel, so their perpendicular bisectors only meet at one point, which is $K$. Hence $K E=K F$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 11 |
-
{"year": "2022", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{Z}$ such that $$ \\left\\lfloor\\frac{f(m n)}{n}\\right\\rfloor=f(m) $$ for all positive integers $m, n$.", "solution": " There are two families of functions that work: for each $\\alpha \\in \\mathbb{R}$ the function $f(n)=\\lfloor\\alpha n\\rfloor$, and for each $\\alpha \\in \\mathbb{R}$ the function $f(n)=\\lceil\\alpha n\\rceil-1$. (For irrational $\\alpha$ these two functions coincide.) It is straightforward to check that these functions indeed work; essentially, this follows from the identity $$ \\left\\lfloor\\frac{\\lfloor x n\\rfloor}{n}\\right\\rfloor=\\lfloor x\\rfloor $$ which holds for all positive integers $n$ and real numbers $x$. We now show that every function that works must be of one of the above forms. Let $f$ be a function that works, and define the sequence $a_{1}, a_{2}, \\ldots$ by $a_{n}=f(n!) / n!$. Applying the give condition with $(n!, n+1)$ yields $a_{n+1} \\in\\left[a_{n}, a_{n}+\\frac{1}{n!}\\right)$. It follows that the sequence $a_{1}, a_{2}, \\ldots$ is non-decreasing and bounded from above by $a_{1}+e$, so this sequence must converge to some limit $\\alpha$. If there exists a $k$ such that $a_{k}=\\alpha$, then we have $a_{\\ell}=\\alpha$ for all $\\ell>k$. For each positive integer $m$, there exists $\\ell>k$ such that $m \\mid \\ell$ !. Plugging in $m n=\\ell$ !, it then follows that $$ f(m)=\\left\\lfloor\\frac{f(\\ell!)}{\\ell!/ m}\\right\\rfloor=\\lfloor\\alpha m\\rfloor $$ for all $m$, so $f$ is of the desired form. If there does not exist a $k$ such that $a_{k}=\\alpha$, we must have $a_{k}<\\alpha$ for all $k$. For each positive integer $m$, we can now pick an $\\ell$ such that $m \\mid \\ell$ ! and $a_{\\ell}=\\alpha-x$ with $x$ arbitrarily small. It then follows from plugging in $m n=\\ell$ ! that $$ f(m)=\\left\\lfloor\\frac{f(\\ell!)}{\\ell!/ m}\\right\\rfloor=\\left\\lfloor\\frac{\\ell!(\\alpha-x)}{\\ell!/ m}\\right\\rfloor=\\lfloor\\alpha m-m x\\rfloor . $$ If $\\alpha m$ is an integer we can choose $\\ell$ such that $m x<1$, and it follows that $f(m)=\\lceil\\alpha m\\rceil-1$. If $\\alpha m$ is not an integer we can choose $\\ell$ such that $m x<\\{\\alpha m\\}$, and it also follows that $f(m)=\\lceil\\alpha m\\rceil-1$. We conclude that in this case $f$ is again of the desired form.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
| 12 |
-
{"year": "2022", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $k>1$ be a fixed positive integer. Prove that if $n$ is a sufficiently large positive integer, there exists a sequence of integers with the following properties: - Each element of the sequence is between 1 and $n$, inclusive. - For any two different contiguous subsequences of the sequence with length between 2 and $k$ inclusive, the multisets of values in those two subsequences is not the same. - The sequence has length at least $0.499 n^{2}$.", "solution": " For any positive integer $n$, define an $(n, k)$-good sequence to be a finite sequence of integers each between 1 and $n$ inclusive satisfying the second property in the problem statement. The problems asks to show that, for all sufficiently large integers $n$, there is an $(n, k)$-good sequence of length at least $0.499 n^{2}$. Fix $k \\geq 2$ and consider some prime power $n=p^{m}$ with $p>k+1$. Consider some $0<g<\\frac{n}{k}-1$ with $\\operatorname{gcd}(g, n)=1$ and let $a$ be the smallest positive integer with $g^{a} \\equiv \\pm 1$ $(\\bmod n)$. Claim (Main claim) — For $k, n, g, a$ defined as above, there is an $(n, k)$-good sequence of length $a(n+2)+2$. To prove the main claim, we need some results about the structure of $\\mathbb{Z} / n \\mathbb{Z}$. Specifically, we'll first show that any nontrivial arithmetic sequence is uniquely recoverable. ## Lemma Consider any arithmetic progression of length $i \\leq k$ whose common difference is relatively prime to $n$, and let $S$ be the set of residues it takes modulo $n$. Then there exists a unique integer $0<d \\leq \\frac{n}{2}$ and a unique integer $0 \\leq a<n$ such that $$ S=\\{a, a+d, \\ldots, a+(i-1) d\\} $$ - Case $1: i$ is odd, so $i=2 j+1$ for some $j$. Then the middle term of the arithmetic progression is the average of all residues in $S$, which we can uniquely identify as some $u$ (and we know $n$ is coprime to $i$, so it is possible to average the residues). We need to show that there is only one choice of $d$, up to $\\pm$, so that $S=\\{u-$ $j d, u-(j-1) d, \\ldots, u+j d\\}$. Let $X$ be the sum of squares of the residues in $S$, so we have $$ X \\equiv(u-j d)^{2}+(u-(j-1) d)^{2}+\\cdots+(u+j d)^{2}=(2 j+1) u^{2}+d^{2} \\frac{j(j+1)(2 j+1)}{3}, $$ which therefore implies $$ 3\\left(X-(2 j+1) u^{2}\\right)(j(j+1)(2 j+1))^{-1} \\equiv d^{2} $$ thus identifying $d$ uniquely up to sign as desired. - Case 2: $i$ is even, so $i=2 j$ for some $j$. Once again we can compute the average $u$ of the residues in $S$, and we need to show that there is only one choice of $d$, up to $\\pm$, so that $S=\\{u-(2 j-1) d, u-(2 j-3) d, \\ldots, u+(2 j-1) d\\}$. Once again we compute the sum of squares $X$ of the residues in $S$, so that $X \\equiv(u-(2 j-1) d)^{2}+(u-(2 j-3) d)^{2}+\\cdots+(u+(2 j-1) d)^{2}=2 j u^{2}+\\frac{(2 j-1) 2 j(2 j+1)}{3}$ which therefore implies $$ 3\\left(X-2 j u^{2}\\right)((2 j-1) 2 j(2 j+1))^{-1} \\equiv d^{2} $$ again identifying $d$ uniquely up to sign as desired. Thus we have shown that given the set of residues an arithmetic progression takes on modulo $n$, we can recover that progression up to sign. Here we have used the fact that given $d^{2}(\\bmod n)$, it is possible to recover $d$ up to $\\operatorname{sign}$ provided that $n$ is of the form $p^{m}$ with $p \\neq 2$ and $\\operatorname{gcd}(d, n)=1$. Now, we will proceed by chaining many arithmetic sequences together. Definition. For any integer $l$ between 0 and $a-1$, inclusive, define $C_{l}$ to be the sequence $0, g^{l}, g^{l}, 2 g^{l}, 3 g^{l}, \\ldots,(n-1) g^{l},(n-1) g^{l}$ taken $(\\bmod n)$. (This is just a sequence where the $i$ th term is $(i-1) g^{l}$, except the terms $g^{l},(n-1) g^{l}$ is repeated once.) Definition. Consider the sequence $S_{n}$ of residues $\\bmod n$ defined as follows: - The first term of $S_{n}$ is 0 . - For each $0 \\leq l<a$, the next $n+2$ terms of $S_{n}$ are the terms of $C_{l}$ in order. - The next and final term of $S_{n}$ is 0 . We claim that $S_{n}$ constitutes a $k$-good string with respect to the alphabet of residues modulo $n$. We first make some initial observations about $S_{n}$. ## Lemma $S_{n}$ has the following properties: - $S_{n}$ has length $a(n+2)+2$. - If a contiguous subsequence of $S_{n}$ of length $\\leq k$ contains two of the same residue $(\\bmod n)$, those two residues occur consecutively in the subsequence. To prove the second property, consider any contiguous subsequence $S_{n}[i: i+k-1]$ of length $k$ which contains two of the same residue modulo $n$. If $S_{n}[i: i+k-1]$ is wholly contained within some $C_{l}$, it's clear that the only way $S_{n}[i: i+k-1]$ could repeat residues if it repeats one of the two consecutive values $g^{l}, g^{l}$ or $(n-1) g^{l},(n-1) g^{l}$, so assume that is not the case. Now, it must be true that $S_{n}[i: i+k-1]$ consists of one contiguous subsequence of the form $$ \\left(n-k_{1}\\right) g^{l-1},\\left(n-\\left(k_{1}-1\\right)\\right) g^{l-1}, \\ldots,(n-1) g^{l-1},(n-1) g^{l-1} $$ which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l-1}$, and then a second contiguous subsequence of the form $$ 0, g^{l}, g^{l}, 2 g^{l}, \\ldots, k_{2} g^{l} $$ which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l}$, and we obviously have $k_{2}+k_{1}=k-3$. For $S_{n}[i: i+k-1]$ to contain two of the same residue in non-consecutive positions, there would have to exist some $0<u \\leq k_{1}, 0<v \\leq k_{2}$ with $(n-u) g^{l-1} \\equiv v g^{l}$ $(\\bmod n)$, meaning that $u+g v \\equiv 0(\\bmod n)$. But we know since $k_{1}+k_{2}<k$ that $0<u+g v<k+k g<n$, so this is impossible, as desired. Now we can prove the main claim. First suppose $M$ contains some residue twice. By the last lemma there are only a few possible cases: - $M$ contains multiple copies of the residue 0 . In this case we know $M$ contains the beginning of $S_{n}$, so the corresponding contiguous subsequence is just the first $i$ terms of $S_{n}$. - $M$ contains multiple copies of multiple residues. By the last lemma and the structure of $S_{n}$, we can easily see that $M$ must contain two copies of $-g^{i-1}$ and two copies of $g^{i}$ for some $0 \\leq i<a$ that can be identified uniquely, and $M$ must contain portions of both $C_{i-1}, C_{i}$. It follows $M$ 's terms can be partitioned into two portions, the first one being $$ -i_{1} g^{i-1},-\\left(i_{1}-1\\right) g^{i-1}, \\ldots,-g^{i-1},-g^{i-1} $$ and the second one being $$ 0, g^{i}, g^{i}, 2 g^{i}, \\ldots, i_{2} g^{i} $$ for some $i_{1}$, $i_{2}$ with $i_{1}+i_{2}=i-3$, and we just need to uniquely identify $i_{1}, i_{2}$. Luckily, by dividing the residues in $M$ by $g^{i-1}$, we know we can partition $M$ 's terms into $$ -i_{1},-\\left(i_{1}-1\\right), \\ldots,-1,-1 $$ as well as $$ 0, g, g, 2 g, \\ldots, i_{2} g $$ Now since $i_{2} g \\leq k g<n-k$ and $-i_{1} \\equiv n-i_{1} \\geq n-k$ it is easy to see that $i_{1}, i_{2}$ can be identified uniquely, as desired. - $M$ contains multiple copies of only one residue $g^{i}$, for some $0 \\leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the beginning of $C_{i}$ and possibly contain the last few terms of $C_{i-1}$, so $M$ must be of the form $g^{i}, g^{i}, 2 g^{i}, \\ldots, i_{1} g^{i}$, along with possibly the term 0 or the terms $0,-g^{i-1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $g, g, 2 g, \\ldots, i_{1} g$ along with possibly 0 or $0,-1$. Since $i_{1} g \\leq k g<n-k$, we can easily disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$. - $M$ contains multiple copies of only one residue $-g^{i}$, for some $0 \\leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the end of $C_{i}$ and possibly the first terms of $C_{i+1}$, so $M$ must be of the form $-g^{i},-g^{i},-2 g^{i}, \\ldots,-i_{1} g^{i}$, along with possibly the term 0 or the terms $0, g^{i+1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $-1,-1,-2, \\ldots,-i_{1}$, along with possibly 0 or $0, g$. Since $-i_{1} \\equiv n-i_{1} \\geq \\frac{n}{2}$ and $g<\\frac{n}{2}$, we can disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$. Thus in all cases where $M$ contains a repeated residue, we can identify the unique contiguous subsequence of $S_{n}$ corresponding to $M$. When $M$ does not contain a repeated residue, it follows that $M$ cannot contain both of the $g^{i}$ terms or $(n-1) g^{i}$ terms at the beginning or end of each $C_{i}$. It follows that $M$ is either entirely contained in some $C_{i}$ or contained in the union of the end of some $C_{i}$ with the beginning of some $C_{i+1}$, meaning $M$ corresponds to a contiguous subsequence of $\\left(-g^{i}, 0, g^{i+1}\\right)$. In the first case, since each $C_{i}$ is an arithmetic progression when the repeated terms are ignored, Lemma 1 implies that we can uniquely determine the location of $M$, and in the second case, it is easy to tell which contiguous subsequence of $\\left(-g^{i}, 0, g^{i+1}\\right)$ corresponds to $M$. Therefore, in all cases, for any multiset $M$ corresponding to some contiguous subsequence of $S_{n}$ of length $i \\leq k$, we can uniquely identify the contiguous subsequence, meaning $S_{n}$ is $k$-good with respect to the alphabet of residues modulo $n$, as desired. Now we will finish the problem. We observe the following. Claim - Fix $k$ and let $p>k+1$ be a prime. Then for $n=p^{2}$ we can find a $(n, k)$-good sequence of length $\\frac{p(p-1)\\left(p^{2}+2\\right)}{2}$. We will prove a stronger statement that $g<p$. Indeed, consider any primitive root $g_{0}$ $(\\bmod p)$. Then $g_{0}+a p$ has order $p-1 \\operatorname{modulo} p$, so its order modulo $p^{2}$ is divisible by $p-1$, hence $g_{0}+a p$ is a primitive root modulo $p^{2}$ as long as $\\left(g_{0}+a p\\right)^{p-1} \\not \\equiv 1\\left(\\bmod p^{2}\\right)$. Now $$ \\left(g_{0}+a p\\right)^{p-1}=\\sum_{i} g_{0}^{p-1-i}(a p)^{i}\\binom{p-1}{i} \\equiv g_{0}^{p-1}+g_{0}^{p-2}(a p) \\quad\\left(\\bmod p^{2}\\right) $$ In particular, of the values $g_{0}, g_{0}+p, \\ldots, g_{0}+p(p-1)$, only one has order $p-1$ and the rest are primitive roots. So for each $0<g_{0}<p$ which is a primitive root modulo $p$, either $g_{0}$ is a primitive root modulo $p^{2}$ or $g_{0}$ has order $p-1$ but $g_{0}+p, g_{0}+2 p, \\ldots, g_{0}+p(p-1)$ are all primitive roots. By considering all choices of $g_{0}$, we either find a primitive root $\\left(\\bmod p^{2}\\right)$ which is between 0 and $p$, or we find that all residues $\\left(\\bmod p^{2}\\right)$ of order $p-1$ are between 0 and $p$. But if $\\operatorname{ord}_{p^{2}}(a)=p-1$ then $\\operatorname{ord}_{p^{2}}\\left(a^{-1}\\right)=p-1$, and two residues between $0, p$ cannot be inverses modulo $p^{2}$ (because with the exception of 1 , they cannot multiply to something $\\geq p^{2}+1$ ), so there is always a primitive root between $0, p$ as desired. Now for arbitrarily large $n$ we can choose $p<\\sqrt{n}$ with $\\frac{p}{\\sqrt{n}}$ arbitrarily close to 1 ; by the previous claim, we can get an $(n, k)$-good sequence of length at least $\\frac{p-1}{p} \\cdot \\frac{p^{4}}{2}$ for any constant, so for sufficiently large $n, p$ we get $(n, k)$-good sequences of length $0.499 n^{2}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2022.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl
DELETED
|
@@ -1,22 +0,0 @@
|
|
| 1 |
-
{"year": "2023", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \\angle A B S=\\angle A C R=180^{\\circ}-\\angle B G C . $$ Prove that $\\angle R A S+\\angle B A C=\\angle B G C$.", "solution": "  【 Solution 1 using power of a point. From the given condition that $\\measuredangle A C R=\\measuredangle C G M$, we get that $$ M A^{2}=M C^{2}=M G \\cdot M R \\Longrightarrow \\measuredangle R A C=\\measuredangle M G A $$ Analogously, $$ \\measuredangle B A S=\\measuredangle A G N $$ Hence, $$ \\measuredangle R A S+\\measuredangle B A C=\\measuredangle R A C+\\measuredangle B A S=\\measuredangle M G A+\\measuredangle A G N=\\measuredangle M G N=\\measuredangle B G C . $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 2 |
-
{"year": "2023", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \\angle A B S=\\angle A C R=180^{\\circ}-\\angle B G C . $$ Prove that $\\angle R A S+\\angle B A C=\\angle B G C$.", "solution": "  ब Solution 2 using similar triangles. As before, $\\triangle M G C \\sim \\triangle M C R$ and $\\triangle N G B \\sim$ $\\triangle N B S$. We obtain $$ \\frac{|A C|}{|C R|}=\\frac{2|M C|}{|C R|}=\\frac{2|M G|}{|G C|}=\\frac{|G B|}{2|N G|}=\\frac{|B S|}{2|B N|}=\\frac{|B S|}{|A B|} $$ which together with $\\angle A C R=\\angle A B S$ yields $$ \\triangle A C R \\sim \\triangle S B A \\Longrightarrow \\measuredangle B A S=\\measuredangle C R A $$ Hence $$ \\measuredangle R A S+\\measuredangle B A C=\\measuredangle R A C+\\measuredangle B A S=\\measuredangle R A C+\\measuredangle C R A=-\\measuredangle A C R=\\measuredangle B G C, $$ which proves the statement.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 3 |
-
{"year": "2023", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \\angle A B S=\\angle A C R=180^{\\circ}-\\angle B G C . $$ Prove that $\\angle R A S+\\angle B A C=\\angle B G C$.", "solution": "  I Solution 3 using parallelograms. Let $M$ and $N$ be defined as above. Let $P$ be the reflection of $G$ in $M$ and let $Q$ the reflection of $G$ in $N$. Then $A G C P$ and $A G B Q$ are parallelograms.  Claim - Quadrilaterals $A P C R$ and $A Q B S$ are concyclic. Thus from $\\overline{P C} \\| \\overline{G A}$ we get $$ \\measuredangle R A C=\\measuredangle R P C=\\measuredangle G P C=\\measuredangle P G A $$ and similarly $$ \\measuredangle B A S=\\measuredangle B Q S=\\measuredangle B Q G=\\measuredangle A G Q $$ We conclude that $$ \\measuredangle R A S+\\measuredangle B A C=\\measuredangle R A C+\\measuredangle B A S=\\measuredangle P G A+\\measuredangle A G Q=\\measuredangle P G Q=\\measuredangle B G C $$", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 4 |
-
{"year": "2023", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \\angle A B S=\\angle A C R=180^{\\circ}-\\angle B G C . $$ Prove that $\\angle R A S+\\angle B A C=\\angle B G C$.", "solution": "  ब Solution 4 also using parallelograms, by Ankan Bhattacharya. Construct parallelograms $A R C K$ and $A S B L$. Since $$ \\measuredangle C A K=\\measuredangle A C R=\\measuredangle C G B=\\measuredangle C G K, $$ it follows that $A G C K$ is cyclic. Similarly, $A G B L$ is also cyclic.  Finally, observe that $$ \\begin{aligned} \\angle R A S+\\angle B A C & =\\measuredangle B A S+\\measuredangle R A C \\\\ & =\\measuredangle A B L+\\measuredangle K C A \\\\ & =\\measuredangle A G L+\\measuredangle K G A \\\\ & =\\measuredangle K G L \\\\ & =\\angle B G C \\end{aligned} $$ as requested.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 5 |
-
{"year": "2023", "tier": "T0", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \\angle A B S=\\angle A C R=180^{\\circ}-\\angle B G C . $$ Prove that $\\angle R A S+\\angle B A C=\\angle B G C$.", "solution": "  『 Solution 5 using complex numbers, by Milan Haiman. Note that $\\angle R A S+\\angle B A C=$ $\\angle B A S+\\angle R A C$. We compute $\\angle B A S$ in complex numbers; then $\\angle R A C$ will then be known by symmetry. Let $a, b, c$ be points on the unit circle representing $A, B, C$ respectively. Let $g=\\frac{1}{3}(a+b+c)$ represent the centroid $G$, and let $s$ represent $S$. ## Claim - We have $$ \\frac{s-a}{b-a}=\\frac{a b-2 b c+c a}{2 a b-b c-c a} . $$ $$ s=\\frac{a+b}{2}+t(c-g) $$ for some $t \\in \\mathbb{R}$. By the given angle condition, we have that $$ \\frac{(s-b) /(b-a)}{(c-g) /(g-b)} \\in \\mathbb{R} $$ Note that $$ \\frac{s-b}{b-a}=t \\frac{c-g}{b-a}-\\frac{1}{2} $$ So, $$ t \\frac{g-b}{b-a}-\\frac{g-b}{2(c-g)} \\in \\mathbb{R} $$ Thus $$ t=\\frac{\\operatorname{Im}\\left(\\frac{g-b}{2(c-g)}\\right)}{\\operatorname{Im}\\left(\\frac{g-b}{b-a}\\right)}=\\frac{1}{2} \\cdot \\frac{\\left(\\frac{g-b}{c-g}\\right)-\\overline{\\left(\\frac{g-b}{c-g}\\right)}}{\\left(\\frac{g-b}{b-a}\\right)-\\overline{\\left(\\frac{g-b}{b-a}\\right)}} $$ Let $N$ and $D$ be the numerator and denominator of the second factor above. We want to compute $$ \\frac{s-a}{b-a}=\\frac{1}{2}+t \\frac{c-g}{b-a}=\\frac{(b-a)+2 t(c-g)}{2(b-a)}=\\frac{(b-a) D+(c-g) N}{2(b-a) D} $$ We have $$ \\begin{aligned} (c-g) N & =g-b-(c-g) \\overline{\\left(\\frac{g-b}{c-g}\\right)} \\\\ & =\\frac{a+b+c}{3}-b-\\left(c-\\frac{a+b+c}{3}\\right) \\frac{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}-\\frac{3}{b}}{\\frac{3}{c}-\\frac{1}{a}-\\frac{1}{b}-\\frac{1}{c}} \\\\ & =\\frac{(a+c-2 b)(2 a b-b c-c a)-(2 c-a-b)(a b+b c-2 c a)}{3(2 a b-b c-c a)} \\\\ & =\\frac{3\\left(a^{2} b+b^{2} c+c^{2} a-a b^{2}-b c^{2}-c a^{2}\\right)}{3(2 a b-b c-c a)} \\\\ & =\\frac{(a-b)(b-c)(a-c)}{2 a b-b c-c a} \\end{aligned} $$ We also compute $$ \\begin{aligned} (b-a) D & =g-b-(b-a) \\overline{\\left(\\frac{g-b}{b-a}\\right)} \\\\ & =\\frac{a+b+c}{3}-b-(b-a) \\frac{\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}-\\frac{3}{b}}{\\frac{3}{b}-\\frac{3}{a}} \\\\ & =\\frac{(a+c-2 b) c+(a b+b c-2 c a)}{3 c} \\\\ & =\\frac{a b-b c-c a+c^{2}}{3 c} \\\\ & =\\frac{(a-c)(b-c)}{3 c} \\end{aligned} $$ So, we obtain $$ \\frac{s-a}{b-a}=\\frac{\\frac{1}{3 c}+\\frac{a-b}{2 a b-b c-c a}}{\\frac{2}{3 c}}=\\frac{2 a b-b c-c a+3 c(a-b)}{2(2 a b-b c-c a)}=\\frac{a b-2 b c+c a}{2 a b-b c-c a} $$ By symmetry, $$ \\frac{r-a}{c-a}=\\frac{a b-2 b c+c a}{2 c a-a b-b c} $$ Hence their ratio $$ \\frac{s-a}{b-a} \\div \\frac{r-a}{c-a}=\\frac{2 a b-b c-c a}{2 c a-a b-b c} $$ has argument $\\angle R A C+\\angle B A S$. We also have that $\\angle B G C$ is the argument of $$ \\frac{b-g}{c-g}=\\frac{2 b-a-c}{2 c-a-b} $$ Note that these two complex numbers are inverse-conjugates, and thus have the same argument. So we're done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 6 |
-
{"year": "2023", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $n \\geq m \\geq 1$ be integers. Prove that $$ \\sum_{k=m}^{n}\\left(\\frac{1}{k^{2}}+\\frac{1}{k^{3}}\\right) \\geq m \\cdot\\left(\\sum_{k=m}^{n} \\frac{1}{k^{2}}\\right)^{2} $$", "solution": " 【 First solution (authors). By Cauchy-Schwarz, we have $$ \\begin{aligned} \\sum_{k=m}^{n} \\frac{k+1}{k^{3}} & =\\sum_{k=m}^{n} \\frac{\\left(\\frac{1}{k^{2}}\\right)^{2}}{\\frac{1}{k(k+1)}} \\\\ & \\geq \\frac{\\left(\\frac{1}{m^{2}}+\\frac{1}{(m+1)^{2}}+\\cdots+\\frac{1}{n^{2}}\\right)^{2}}{\\frac{1}{m(m+1)}+\\frac{1}{(m+1)(m+2)}+\\cdots+\\frac{1}{n(n+1)}} \\\\ & =\\frac{\\left(\\frac{1}{m^{2}}+\\frac{1}{(m+1)^{2}}+\\cdots+\\frac{1}{n^{2}}\\right)^{2}}{\\frac{1}{m}-\\frac{1}{n+1}} \\\\ & >\\frac{\\left(\\sum_{k=m}^{n} \\frac{1}{k^{2}}\\right)^{2}}{\\frac{1}{m}} \\end{aligned} $$ as desired. Remark (Bound on error). Let $A=\\sum_{k=m}^{n} k^{-2}$ and $B=\\sum_{k=m}^{n} k^{-3}$. The inequality above becomes tighter for large $m$ and $n \\gg m$. If we use Lagrange's identity in place of Cauchy-Schwarz, we get $$ A+B-m A^{2}=m \\cdot \\sum_{m \\leq a<b} \\frac{(a-b)^{2}}{a^{3} b^{3}(a+1)(b+1)} $$ We can upper bound this error by $$ \\leq m \\cdot \\sum_{m \\leq a<b} \\frac{1}{a^{3}(a+1) b(b+1)}=m \\cdot \\sum_{m \\leq a} \\frac{1}{a^{3}(a+1)^{2}} \\approx m \\cdot \\frac{1}{m^{4}}=\\frac{1}{m^{3}}, $$ which is still generous as $(a-b)^{2} \\ll b^{2}$ for $b$ not much larger than $a$, so the real error is probably around $\\frac{1}{10 \\mathrm{~m}^{3}}$. This exhibits the tightness of the inequality since it implies $$ m A^{2}+O(B / m)>A+B $$ Remark (Construction commentary, from author). My motivation was to write an inequality where Titu could be applied creatively to yield a telescoping sum. This can be difficult because most of the time, such a reverse-engineered inequality will be so loose it's trivial anyways. My first attempt was the not-so-amazing inequality $$ \\frac{n^{2}+3 n}{2}=\\sum_{1}^{n} i+1=\\sum_{1}^{n} \\frac{\\frac{1}{i}}{\\frac{1}{i(i+1)}}>\\left(\\sum_{1}^{n} \\frac{1}{\\sqrt{i}}\\right)^{2} $$ which is really not surprising given that $\\sum \\frac{1}{\\sqrt{i}} \\ll \\frac{n}{\\sqrt{2}}$. The key here is that we need \"near-equality\" as dictated by the Cauchy-Schwarz equality case, i.e. the square root of the numerators should be approximately proportional to the denominators. This motivates using $\\frac{1}{i^{4}}$ as the numerator, which works like a charm. After working out the resulting statement, the LHS and RHS even share a sum, which adds to the simplicity of the problem. The final touch was to unrestrict the starting value of the sum, since this allows the strength of the estimate $\\frac{1}{i^{2}} \\approx \\frac{1}{i(i+1)}$ to be fully exploited.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 7 |
-
{"year": "2023", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $n \\geq m \\geq 1$ be integers. Prove that $$ \\sum_{k=m}^{n}\\left(\\frac{1}{k^{2}}+\\frac{1}{k^{3}}\\right) \\geq m \\cdot\\left(\\sum_{k=m}^{n} \\frac{1}{k^{2}}\\right)^{2} $$", "solution": " 【 Second approach by inducting down, Luke Robitaille and Carl Schildkraut. Fix $n$; we'll induct downwards on $m$. For the base case of $n=m$ the result is easy, since the left side is $\\frac{m+1}{m^{3}}$ and the right side is $\\frac{m}{m^{4}}=\\frac{1}{m^{3}}$. For the inductive step, suppose we have shown the result for $m+1$. Let $$ A=\\sum_{k=m+1}^{n} \\frac{1}{k^{2}} \\quad \\text { and } \\quad B=\\sum_{k=m+1}^{n} \\frac{1}{k^{3}} $$ We know $A+B \\geq(m+1) A^{2}$, and we want to show $$ \\left(A+\\frac{1}{m^{2}}\\right)+\\left(B+\\frac{1}{m^{3}}\\right) \\geq m\\left(A+\\frac{1}{m^{2}}\\right)^{2} $$ Indeed, $$ \\begin{aligned} \\left(A+\\frac{1}{m^{2}}\\right)+\\left(B+\\frac{1}{m^{3}}\\right)-m\\left(A+\\frac{1}{m^{2}}\\right)^{2} & =A+B+\\frac{m+1}{m^{3}}-m A^{2}-\\frac{2 A}{m}-\\frac{1}{m^{3}} \\\\ & =\\left(A+B-(m+1) A^{2}\\right)+\\left(A-\\frac{1}{m}\\right)^{2} \\geq 0 \\end{aligned} $$ and we are done.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 8 |
-
{"year": "2023", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $n \\geq m \\geq 1$ be integers. Prove that $$ \\sum_{k=m}^{n}\\left(\\frac{1}{k^{2}}+\\frac{1}{k^{3}}\\right) \\geq m \\cdot\\left(\\sum_{k=m}^{n} \\frac{1}{k^{2}}\\right)^{2} $$", "solution": " I Third approach by reducing $n \\rightarrow \\infty$, Michael Ren and Carl Schildkraut. First, we give: Claim (Reduction to $n \\rightarrow \\infty$ ) - If the problem is true when $n \\rightarrow \\infty$, it is true for all $n$. However, the region is bounded by a convex curve, and the sequence of points $(0,0)$, $\\left(\\frac{1}{m^{2}}, \\frac{1}{m^{3}}\\right),\\left(\\frac{1}{m^{2}}+\\frac{1}{(m+1)^{2}}, \\frac{1}{m^{3}}+\\frac{1}{(m+1)^{3}}\\right), \\ldots$ has successively decreasing slopes between consecutive points. Thus it suffices to check that the inequality is true when $n \\rightarrow \\infty$. Set $n=\\infty$ henceforth. Let $$ A=\\sum_{k=m}^{\\infty} \\frac{1}{k^{2}} \\text { and } B=\\sum_{k=m}^{\\infty} \\frac{1}{k^{3}} $$ we want to show $B \\geq m A^{2}-A$, which rearranges to $$ 1+4 m B \\geq(2 m A-1)^{2} $$ Write $$ C=\\sum_{k=m}^{\\infty} \\frac{1}{k^{2}(2 k-1)(2 k+1)} \\text { and } D=\\sum_{k=m}^{\\infty} \\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ Then $$ \\frac{2}{2 k-1}-\\frac{2}{2 k+1}=\\frac{1}{k^{2}}+\\frac{1}{k^{2}(2 k-1)(2 k+1)} $$ and $$ \\frac{2}{(2 k-1)^{2}}-\\frac{2}{(2 k+1)^{2}}=\\frac{1}{k^{3}}+\\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}, $$ so that $$ A=\\frac{2}{2 m-1}-C \\text { and } B=\\frac{2}{(2 m-1)^{2}}-D $$ Our inequality we wish to show becomes $$ \\frac{2 m+1}{2 m-1} C \\geq D+m C^{2} $$ We in fact show two claims: Claim - We have $$ \\frac{2 m+1 / 2}{2 m-1} C \\geq D $$ $$ \\frac{2 m+1 / 2}{2 m-1} \\cdot \\frac{1}{k^{2}(2 k-1)(2 k+1)} \\geq \\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ for $k \\geq m$. It suffices to show $$ \\frac{2 k+1 / 2}{2 k-1} \\cdot \\frac{1}{k^{2}(2 k-1)(2 k+1)} \\geq \\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ which is equivalent to $k(2 k+1 / 2)(2 k+1) \\geq 8 k^{2}-1$. This holds for all $k \\geq 1$. ## Claim - We have $$ \\frac{1 / 2}{2 m-1} C \\geq m C^{2} $$ $$ \\frac{1}{2 m(2 m-1)}=\\sum_{k=m}^{\\infty}\\left(\\frac{1}{2 k(2 k-1)}-\\frac{1}{2(k+1)(2 k+1)}\\right)=\\sum_{k=m}^{\\infty} \\frac{4 k+1}{2 k(2 k-1)(k+1)(2 k+1)} $$ comparing term-wise with the definition of $C$ and using the inequality $k(4 k+1) \\geq 2(k+1)$ for $k \\geq 1$ gives the desired result.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 9 |
-
{"year": "2023", "tier": "T0", "problem_label": "2", "problem_type": null, "problem": "Let $n \\geq m \\geq 1$ be integers. Prove that $$ \\sum_{k=m}^{n}\\left(\\frac{1}{k^{2}}+\\frac{1}{k^{3}}\\right) \\geq m \\cdot\\left(\\sum_{k=m}^{n} \\frac{1}{k^{2}}\\right)^{2} $$", "solution": " 『 Fourth approach by bashing, Carl Schildkraut. With a bit more work, the third approach can be adapted to avoid the $n \\rightarrow \\infty$ reduction. Similarly to before, define $$ A=\\sum_{k=m}^{n} \\frac{1}{k^{2}} \\text { and } B=\\sum_{k=m}^{n} \\frac{1}{k^{3}} $$ we want to show $1+4 m B \\geq(2 m A-1)^{2}$. Writing $$ C=\\sum_{k=m}^{n} \\frac{1}{k^{2}(2 k-1)(2 k+1)} \\text { and } D=\\sum_{k=m}^{n} \\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ We compute $$ A=\\frac{2}{2 m-1}-\\frac{2}{2 n+1}-C \\text { and } B=\\frac{2}{(2 m-1)^{2}}-\\frac{2}{(2 n+1)^{2}}-D . $$ Then, the inequality we wish to show reduces (as in the previous solution) to $$ \\frac{2 m+1}{2 m-1} C+\\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \\geq D+m C^{2}+\\frac{2(2 m+1)}{(2 n+1)^{2}}+\\frac{4 m}{2 n+1} C $$ We deal first with the terms not containing the variable $n$, i.e. we show that $$ \\frac{2 m+1}{2 m-1} C \\geq D+m C^{2} $$ For this part, the two claims from the previous solution go through exactly as written above, and we have $C \\leq 1 /(2 m(2 m-1))$. We now need to show $$ \\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \\geq \\frac{2(2 m+1)}{(2 n+1)^{2}}+\\frac{4 m}{2 n+1} C $$ (this is just the inequality between the remaining terms); our bound on $C$ reduces this to proving $$ \\frac{4(2 m+1)(n-m+1)}{(2 m-1)(2 n+1)^{2}} \\geq \\frac{2}{(2 m-1)(2 n+1)} $$ Expanding and writing in terms of $n$, this is equivalent to $$ n \\geq \\frac{1+2(m-1)(2 m+1)}{4 m}=m-\\frac{2 m+1}{4 m} $$ which holds for all $n \\geq m$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 10 |
-
{"year": "2023", "tier": "T0", "problem_label": "3", "problem_type": null, "problem": "Find all positive integers $n$ for which it is possible to color some cells of an infinite grid of unit squares red, such that each rectangle consisting of exactly $n$ cells (and whose edges lie along the lines of the grid) contains an odd number of red cells.", "solution": " We claim that this is possible for all positive integers $n$. Call a positive integer for which such a coloring is possible good. To show that all positive integers $n$ are good we prove the following: (i) If $n$ is good and $p$ is an odd prime, then $p n$ is good; (ii) For every $k \\geq 0$, the number $n=2^{k}$ is good. Together, (i) and (ii) imply that all positive integers are good. Thus every coloring that works for $n$ automatically also works for $p n$. Claim - For each of these $k+1$ shapes, there exists a coloring with two properties: - Every rectangle with $n$ cells and shape $2^{m} \\times 2^{k-m}$ contains an odd number of red cells. - Every rectangle with $n$ cells and a different shape contains an even number of red cells.  A $2^{m} \\times 2^{k-m}$ rectangle contains every possible pair $\\left(x \\bmod 2^{m}, y \\bmod 2^{k-m}\\right)$ exactly once, so such a rectangle will contain one red cell (an odd number). On the other hand, consider a $2^{\\ell} \\times 2^{k-\\ell}$ rectangle with $\\ell>m$. The set of cells this covers is $(x, y)$ where $x$ covers a range of size $2^{\\ell}$ and $y$ covers a range of size $2^{k-\\ell}$. The number of red cells is the count of $x$ with $x \\equiv 0 \\bmod 2^{m}$ multiplied by the count of $y$ with $y \\equiv 0 \\bmod 2^{k-m}$. The former number is exactly $2^{\\ell-k}$ because $2^{k}$ divides $2^{\\ell}$ (while the latter is 0 or 1) so the number of red cells is even. The $\\ell<m$ case is similar. Finally, given these $k+1$ colorings, we can add them up modulo 2, i.e. a cell will be colored red if it is red in an odd number of these $k+1$ coloring. We illustrate $n=4$ as an example; the coloring is 4 -periodic in both axes so we only show one $4 \\times 4$ cell.  This solves the problem. Remark. The final coloring can be described as follows: color $(x, y)$ red if $$ \\max \\left(0, \\min \\left(\\nu_{2}(x), k\\right)+\\min \\left(\\nu_{2}(y), k\\right)-k+1\\right) $$ is odd. Remark (Luke Robitaille). Alternatively for (i), if $n=2^{e} k$ for odd $k$ then one may dissect an $a \\times b$ rectangle with area $n$ into $k$ rectangles of area $2^{e}$, each $2^{\\nu_{2}(a)} \\times 2^{\\nu_{2}(b)}$. This gives a way to deduce the problem from (ii) without having to consider odd prime numbers. $$ f(x, y)=\\sum_{i=0}^{2^{k}-1} \\sum_{j=0}^{2^{k}-1} \\lambda_{i, j} x^{i} y^{j} $$ denote its generating function, where $f \\in \\mathbb{F}_{2}[x, y]$. For this to be valid, we need that for any $2^{p} \\times 2^{q}$ rectangle with area $n$, the sum of the coefficients of $f$ over it should be one, modulo $x^{2^{k}}=y^{2^{k}}=1$. In other words, whenever $p+q=k$, we must have $$ f(x, y)\\left(1+\\cdots+x^{2^{p}-1}\\right)\\left(1+\\cdots+y^{2^{q}-1}\\right)=\\left(1+\\cdots+x^{2^{k}-1}\\right)\\left(1+\\cdots+y^{2^{k}-1}\\right) $$ taken modulo $x^{2^{k}}=y^{2^{k}}=1$. The idea is to rewrite these expressions: because we're in characteristic 2, the given assertion is $(x+1)^{2^{k}}=(y+1)^{2^{k}}=0$, and the requested property is $$ f(x, y)(x+1)^{2^{p}-1}(y+1)^{2^{q}-1}=(x+1)^{2^{k}-1}(y+1)^{2^{k}-1} . $$ This suggests the substitution $g(x, y)=f(x+1, y+1)$ : then we can replace $(x+1, y+1) \\mapsto$ $(x, y)$ to simplify the requested property significantly: Whenever $p+q=k$, we must have $$ g(x, y) x^{2^{p}-1} y^{2^{q}-1}=x^{2^{k}-1} y^{2^{k}-1} $$ modulo $x^{2^{k}}$ and $y^{2^{k}}$. However, now the construction of $g$ is very simple: for example, the choice $$ g(x, y)=\\sum_{p+q=k} x^{2^{k}-2^{p}} y^{2^{k}-2^{q}} $$ works. The end. Remark. Unraveling the substitutions seen here, it's possible to show that this is actually the same construction provided in the first solution.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 11 |
-
{"year": "2023", "tier": "T0", "problem_label": "4", "problem_type": null, "problem": "Let $n \\geq 3$ be an integer and let $K_{n}$ be the complete graph on $n$ vertices. Each edge of $K_{n}$ is colored either red, green, or blue. Let $A$ denote the number of triangles in $K_{n}$ with all edges of the same color, and let $B$ denote the number of triangles in $K_{n}$ with all edges of different colors. Prove that $$ B \\leq 2 A+\\frac{n(n-1)}{3} . $$", "solution": "$ Consider all unordered pairs of different edges which share exactly one vertex (call these vees for convenience). Assign each vee a charge of +2 if its edge colors are the same, and a charge of -1 otherwise. We compute the total charge in two ways. ## 【 Total charge by summing over triangles. Note that - each monochromatic triangle has a charge of +6 , - each bichromatic triangle has a charge of 0 , and - each trichromatic triangle has a charge of -3 . Since each vee contributes to exactly one triangle, we obtain that the total charge is $6 A-3 B$. 【 Total charge by summing over vertices. We can also calculate the total charge by examining the centers of the vees. If a vertex has $a$ red edges, $b$ green edges, and $c$ blue edges, the vees centered at that vertex contribute a total charge of $$ \\begin{aligned} & 2\\left[\\binom{a}{2}+\\binom{b}{2}+\\binom{c}{2}\\right]-(a b+a c+b c) \\\\ = & \\left(a^{2}-a+b^{2}-b+c^{2}-c\\right)-(a b+a c+b c) \\\\ = & \\left(a^{2}+b^{2}+c^{2}-a b-a c-b c\\right)-(a+b+c) \\\\ = & \\left(a^{2}+b^{2}+c^{2}-a b-a c-b c\\right)-(n-1) \\\\ \\geq & -(n-1) . \\end{aligned} $$ In particular, the total charge is at least $-n(n-1)$. đ Conclusion. Thus, we obtain $$ 6 A-3 B \\geq-n(n-1) \\Longleftrightarrow B \\leq 2 A+\\frac{n(n-1)}{3} $$ as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 12 |
-
{"year": "2023", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}\\right) \\quad \\text { and } \\quad q=\\frac{a}{b}+\\frac{b}{c}+\\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.", "solution": " We show $(p, q)=(-3,3)$ is the only possible ordered pair. ## 【T First solution. $$ \\begin{aligned} p+3 & =3+\\sum_{\\text {cyc }}\\left(\\frac{x}{y}+\\frac{y}{x}\\right)=3+\\frac{x^{2}(y+z)+y^{2}(z+x)+z^{2}(x+y)}{x y z} \\\\ & =\\frac{(x+y+z)(x y+y z+z x)}{x y z} \\\\ q-3 & =-3+\\sum_{\\text {cyc }} \\frac{y^{2}}{z x}=\\frac{x^{3}+y^{3}+z^{3}-3 x y z}{x y z} \\\\ & =\\frac{(x+y+z)\\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\\right)}{x y z} . \\end{aligned} $$ It follows that $$ \\begin{aligned} \\mathbb{R} & \\ni 3(p+3)+(q-3) \\\\ & =\\frac{(x+y+z)\\left(x^{2}+y^{2}+z^{2}+2(x y+y z+z x)\\right)}{x y z} \\\\ & =\\frac{(x+y+z)^{3}}{x y z} \\end{aligned} $$ Now, note that if $x+y+z=0$, then $p=-3, q=3$ so we are done. Scale $x, y, z$ in such a way that $x+y+z$ is nonzero and real; hence so is $x y z$. Thus, as $p+3 \\in \\mathbb{R}$, we conclude $x y+y z+z x \\in \\mathbb{R}$ as well. Hence, $x, y, z$ are the roots of a cubic with real coefficients. Thus, - either all three of $\\{x, y, z\\}$ are real (which implies $a, b, c \\in \\mathbb{R}$ ), - or two of $\\{x, y, z\\}$ are a complex conjugate pair (which implies one of $a, b, c$ has absolute value 1). Both of these were forbidden by hypothesis. Construction As we saw in the setup, $(p, q)=(-3,3)$ will occur as long as $x+y+z=0$, and no two of $x, y, z$ to share the same magnitude or are collinear with the origin. This is easy to do; for example, we could choose $(x, y, z)=(3,4 i,-(3+4 i))$. Hence $a=\\frac{3}{4 i}$, $b=-\\frac{4 i}{3+4 i}, c=-\\frac{3+4 i}{3}$ satisfies the hypotheses of the problem statement.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 13 |
-
{"year": "2023", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}\\right) \\quad \\text { and } \\quad q=\\frac{a}{b}+\\frac{b}{c}+\\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.", "solution": " We show $(p, q)=(-3,3)$ is the only possible ordered pair. I Second solution, found by contestants. The main idea is to make the substitution $$ x=a+\\frac{1}{c}, \\quad y=b+\\frac{1}{a}, \\quad z=c+\\frac{1}{b} . $$ Then we can check that $$ \\begin{aligned} x+y+z & =p \\\\ x y+y z+z x & =p+q+3 \\\\ x y z & =p+2 . \\end{aligned} $$ Therefore $x, y, z$ are the roots of a cubic with real coefficients. As in the previous solution, we note that this cubic must either have all real roots, or a complex conjugate pair of roots. We also have the relation $a(y+1)=a b+a+1=x+1$, and likewise $b(z+1)=y+1, c(x+1)=z+1$. This means that if any of $x, y, z$ are equal to -1, then all are equal to -1 . Assume for the sake of contradiction that none are equal to -1 . In the case where the cubic has three real roots, $a=\\frac{x+1}{y+1}$ would be real. On the other hand, if there is a complex conjugate pair (without loss of generality, $x$ and $y$ ) then $a$ has magnitude 1. Therefore this cannot occur. We conclude that $x=y=z=-1$, so $p=-3$ and $q=3$. The solutions $(a, b, c)$ can then be parameterized as $\\left(a,-1-\\frac{1}{a},-\\frac{1}{1+a}\\right)$. To construct a solution, we need to choose a specific value of $a$ such that none of the wrong conditions hold; when $a=2 i$, say, we obtain the solution $\\left(2 i,-1+\\frac{i}{2}, \\frac{-1+2 i}{5}\\right)$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 14 |
-
{"year": "2023", "tier": "T0", "problem_label": "5", "problem_type": null, "problem": "Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\\left(\\frac{1}{a}+\\frac{1}{b}+\\frac{1}{c}\\right) \\quad \\text { and } \\quad q=\\frac{a}{b}+\\frac{b}{c}+\\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.", "solution": " We show $(p, q)=(-3,3)$ is the only possible ordered pair. 【 Third solution by Luke Robitaille and Daniel Zhu. The answer is $p=-3$ and $q=3$. Let's first prove that no other $(p, q)$ work. Let $e_{1}=a+b+c$ and $e_{2}=a^{-1}+b^{-1}+c^{-1}=a b+a c+b c$. Also, let $f=e_{1} e_{2}$. Note that $p=e_{1}+e_{2}$. Our main insight is to consider the quantity $q^{\\prime}=\\frac{b}{a}+\\frac{c}{b}+\\frac{a}{c}$. Note that $f=q+q^{\\prime}+3$. Also, $$ \\begin{aligned} q q^{\\prime} & =3+\\frac{a^{2}}{b c}+\\frac{b^{2}}{a c}+\\frac{c^{2}}{a b}+\\frac{b c}{a^{2}}+\\frac{a c}{b^{2}}+\\frac{a b}{c^{2}} \\\\ & =3+a^{3}+b^{3}+c^{3}+a^{-3}+b^{-3}+c^{-3} \\\\ & =9+a^{3}+b^{3}+c^{3}-3 a b c+a^{-3}+b^{-3}+c^{-3}-3 a^{-1} b^{-1} c^{-1} \\\\ & =9+e_{1}\\left(e_{1}^{2}-3 e_{2}\\right)+e_{2}\\left(e_{2}^{2}-3 e_{1}\\right) \\\\ & =9+e_{1}^{3}+e_{2}^{3}-6 e_{1} e_{2} \\\\ & =9+p\\left(p^{2}-3 f\\right)-6 f \\\\ & =p^{3}-(3 p+6) f+9 . \\end{aligned} $$ As a result, the quadratic with roots $q$ and $q^{\\prime}$ is $x^{2}-(f-3) x+\\left(p^{3}-(3 p+6) f+9\\right)$, which implies that $$ q^{2}-q f+3 q+p^{3}-(3 p+6) f+9=0 \\Longleftrightarrow(3 p+q+6) f=p^{3}+q^{2}+3 q+9 $$ At this point, two miracles occur. The first is the following claim: Claim - $f$ is not real. - $e_{1}$ and $e_{2}$ are real. Then, $a, b$, and $c$ are the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$, and since every cubic with real coefficients has at least one real root, at least one of $a, b$, and $c$ is real, contradiction. - $e_{1}$ and $e_{2}$ are conjugates. Then, the polynomial $x^{3}-\\bar{e}_{2} x^{2}+\\bar{e}_{1} x-1$, which has roots $\\bar{a}^{-1}, \\bar{b}^{-1}$, and $\\bar{c}^{-1}$, is the same as the polynomial with $a, b, c$ as roots. We conclude that the multiset $\\{a, b, c\\}$ is invariant under inversion about the unit circle, so one of $a, b$, and $c$ must lie on the unit circle. This is yet another contradiction. As a result, we know that $3 p+q+6=p^{3}+q^{2}+3 q+9=0$. The second miracle is that substituting $q=-3 p-6$ into $q^{2}+3 q+p^{3}+9=0$, we get $$ 0=p^{3}+9 p^{2}+27 p+27=(p+3)^{3} $$ so $p=-3$. Thus $q=3$. It remains to construct valid $a, b$, and $c$. To do this, let's pick some $e_{1}$, let $e_{2}=-3-e_{1}$, and let $a, b$, and $c$ be the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$. It is clear that this guarantees $p=-3$. By our above calculations, $q$ and $q^{\\prime}$ are the roots of the quadratic $x^{2}-(f-3) x+(3 f-18)$, so one of $q$ and $q^{\\prime}$ must be 3 ; by changing the order of $a, b$, and $c$ if needed, we can guarantee this to be $q$. It suffices to show that for some choice of $e_{1}$, none of $a, b$, or $c$ are real or lie on the unit circle. To do this, note that we can rewrite $x^{3}-e_{1} x^{2}+\\left(-3-e_{1}\\right) x-1=0$ as $$ e_{1}=\\frac{x^{3}-3 x-1}{x^{2}+x} $$ so all we need is a value of $e_{1}$ that is not $\\frac{x^{3}-3 x-1}{x^{2}+x}$ for any real $x$ or $x$ on the unit circle. One way to do this is to choose any nonreal $e_{1}$ with $\\left|e_{1}\\right|<1 / 2$. This clearly rules out any real $x$. Also, if $|x|=1$, by the triangle inequality $\\left|x^{3}-3 x-1\\right| \\geq|3 x|-\\left|x^{3}\\right|-|1|=1$ and $\\left|x^{2}+x\\right| \\leq 2$, so $\\left|\\frac{x^{3}-3 x-1}{x^{2}+x}\\right| \\geq \\frac{1}{2}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 15 |
-
{"year": "2023", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\\angle P A Q, \\angle P B Q$, and $\\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\\overline{P Q}$ lies on the Euler line of $A B C$.", "solution": " 『 Solution 1 (Ankit Bisain). Let $H$ be the orthocenter of $A B C$, and construct $P^{\\prime}$ using the following claim. Claim - There is a point $P^{\\prime}$ for which $$ \\measuredangle A P H+\\measuredangle A P^{\\prime} H=\\measuredangle B P H+\\measuredangle B P^{\\prime} H=\\measuredangle C P H+\\measuredangle C P^{\\prime} H=0 . $$ Now, let $X, Y$, and $Z$ be the reflections of $P$ over $\\overline{A H}, \\overline{B H}$, and $\\overline{C H}$ respectively. Additionally, let $Q^{\\prime}$ be the image of $Q$ under inversion about ( $P X Y Z$ ).  $$ \\text { Claim }-A B C P^{\\prime} \\approx X Y Z Q^{\\prime} $$ $$ \\measuredangle Y X Z=\\measuredangle Y P Z=\\measuredangle(\\overline{B H}, \\overline{C H})=-\\measuredangle B A C $$ and cyclic variants, triangles $A B C$ and $X Y Z$ are similar. Additionally, $$ \\measuredangle H Q^{\\prime} X=-\\measuredangle H X Q=-\\measuredangle H X A=\\measuredangle H P A=-\\measuredangle H P^{\\prime} A $$ and cyclic variants, so summing in pairs gives $\\measuredangle Y Q^{\\prime} Z=-\\measuredangle B P^{\\prime} C$ and cyclic variants; this implies the similarity. Claim - $Q^{\\prime}$ lies on the Euler line of triangle $X Y Z$. To finish the problem, let $G_{1}$ be the centroid of $A B C$ and $G_{2}$ be the centroid of $X Y Z$. Then with signed areas, $$ \\begin{aligned} {\\left[G_{1} H P\\right]+\\left[G_{1} H Q\\right] } & =\\frac{[A H P]+[B H P]+[C H P]}{3}+\\frac{[A H Q]+[B H Q]+[C H Q]}{3} \\\\ & =\\frac{[A H Q]-[A H X]+[B H Q]-[B H Y]+[C H Q]-[C H Z]}{3} \\\\ & =\\frac{[H Q X]+[H Q Y]+[H Q Z]}{3} \\\\ & =\\left[Q G_{2} H\\right] \\\\ & =0 \\end{aligned} $$ where the last line follows from the last claim. Therefore $\\overline{G_{1} H}$ bisects $\\overline{P Q}$, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 16 |
-
{"year": "2023", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\\angle P A Q, \\angle P B Q$, and $\\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\\overline{P Q}$ lies on the Euler line of $A B C$.", "solution": " Solution 2 using complex numbers (Carl Schildkraut and Milan Haiman). Let $(A B C)$ be the unit circle in the complex plane, and let $A=a, B=b, C=c$ such that $|a|=|b|=|c|=1$. Let $P=p$ and $Q=q$, and $O=0$ and $H=h=a+b+c$ be the circumcenter and orthocenter of $A B C$ respectively. The first step is to translate the given geometric conditions into a single usable equation: Claim - We have the equation $$ (p+q) \\sum_{\\mathrm{cyc}} a^{3}\\left(b^{2}-c^{2}\\right)=(\\bar{p}+\\bar{q}) a b c \\sum_{\\mathrm{cyc}}\\left(b c\\left(b^{2}-c^{2}\\right)\\right) $$ $$ \\begin{aligned} & \\frac{(p-a)(q-a)}{(h-a)^{2}}=\\frac{(p-a)(q-a)}{(b+c)^{2}} \\in \\mathbb{R} \\\\ \\Longrightarrow & \\frac{(p-a)(q-a)}{(b+c)^{2}}=\\frac{\\left(\\frac{(p-a)(q-a)}{(b+c)^{2}}\\right)}{}=\\frac{(a \\bar{p}-1)(a \\bar{q}-1) b^{2} c^{2}}{(b+c)^{2} a^{2}} \\\\ \\Longrightarrow & a^{2}(p-a)(q-a)=b^{2} c^{2}(a \\bar{p}-1)(a \\bar{q}-1) \\\\ \\Longrightarrow & a^{2} p q-a^{2} b^{2} c^{2} \\overline{p q}+\\left(a^{4}-b^{2} c^{2}\\right)=a^{3}(p+q)-a b^{2} c^{2}(\\bar{p}+\\bar{q}) . \\end{aligned} $$ Writing the symmetric conditions that $\\overline{B H}$ and $\\overline{C H}$ bisect $\\angle P B Q$ and $\\angle P C Q$ gives three equations: $$ \\begin{aligned} & a^{2} p q-a^{2} b^{2} c^{2} \\overline{p q}+\\left(a^{4}-b^{2} c^{2}\\right)=a^{3}(p+q)-a b^{2} c^{2}(\\bar{p}+\\bar{q}) \\\\ & b^{2} p q-a^{2} b^{2} c^{2} \\overline{p q}+\\left(b^{4}-c^{2} a^{2}\\right)=b^{3}(p+q)-b c^{2} a^{2}(\\bar{p}+\\bar{q}) \\end{aligned} $$ $$ c^{2} p q-a^{2} b^{2} c^{2} \\overline{p q}+\\left(c^{4}-a^{2} b^{2}\\right)=c^{3}(p+q)-c a^{2} b^{2}(\\bar{p}+\\bar{q}) $$ Now, sum $\\left(b^{2}-c^{2}\\right)$ times the first equation, $\\left(c^{2}-a^{2}\\right)$ times the second equation, and $\\left(a^{2}-b^{2}\\right)$ times the third equation. On the left side, the coefficients of $p q$ and $\\overline{p q}$ are 0 . Additionally, the coefficient of 1 (the parenthesized terms on the left sides of each equation) sum to 0 , since $$ \\sum_{\\mathrm{cyc}}\\left(a^{4}-b^{2} c^{2}\\right)\\left(b^{2}-c^{2}\\right)=\\sum_{\\mathrm{cyc}}\\left(a^{4} b^{2}-b^{4} c^{2}-a^{4} c^{2}+c^{4} b^{2}\\right) $$ This gives (1) as desired. We can then factor (1): Claim - The left-hand side of (1) factors as $$ -(p+q)(a-b)(b-c)(c-a)(a b+b c+c a) $$ while the right-hand side factors as $$ -(\\bar{p}+\\bar{q})(a-b)(b-c)(c-a)(a+b+c) $$ Consider the cyclic sum on the left as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a^{3}\\left(a^{2}-c^{2}\\right)+a^{3}\\left(c^{2}-a^{2}\\right)+c^{3}\\left(a^{2}-a^{2}\\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $f(a, b, c)(a-b)(b-c)(c-a)$ for some symmetric quadratic polynomial $f$, and thus it is some linear combination of $a^{2}+b^{2}+c^{2}$ and $a b+b c+c a$. When $a=0$, the whole expression is $b^{2} c^{2}(b-c)$, so $f(0, b, c)=-b c$, which implies that $f(a, b, c)=-(a b+b c+c a)$. Similarly, consider the cyclic sum on the right as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a c\\left(a^{2}-c^{2}\\right)+c a\\left(c^{2}-a^{2}\\right)+a^{2}\\left(a^{2}-a^{2}\\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $g(a, b, c)(a-b)(b-c)(c-a)$ where $g$ is a symmetric linear polynomial; hence, it is a scalar multiple of $a+b+c$. When $a=0$, the whole expression is $b c\\left(b^{2}-c^{2}\\right)$, so $g(0, b, c)=-b-c$, which implies that $g(a, b, c)=-(a+b+c)$. Since $A, B$, and $C$ are distinct, we may divide by $(a-b)(b-c)(c-a)$ to obtain $$ (p+q)(a b+b c+c a)=(\\bar{p}+\\bar{q}) a b c(a+b+c) \\Longrightarrow(p+q) \\bar{h}=(\\bar{p}+\\bar{q}) h $$ This implies that $\\frac{\\frac{p+q}{h}-0}{h-0}$ is real, so the midpoint of $\\overline{P Q}$ lies on line $\\overline{O H}$.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 17 |
-
{"year": "2023", "tier": "T0", "problem_label": "6", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\\angle P A Q, \\angle P B Q$, and $\\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\\overline{P Q}$ lies on the Euler line of $A B C$.", "solution": " 【 Solution 3 also using complex numbers (Michael Ren). We use complex numbers as in the previous solution. The angle conditions imply that $\\frac{(a-p)(a-q)}{(b-c)^{2}}, \\frac{(b-p)(b-q)}{(c-a)^{2}}$, and $\\frac{(c-p)(c-q)}{(a-b)^{2}}$ are real numbers. Take a linear combination of these with real coefficients $X$, $Y$, and $Z$ to be determined; after expansion, we obtain $$ \\begin{aligned} & {\\left[\\frac{X}{(b-c)^{2}}+\\frac{Y}{(c-a)^{2}}+\\frac{Z}{(a-b)^{2}}\\right] p q } \\\\ - & {\\left[\\frac{a X}{(b-c)^{2}}+\\frac{b Y}{(c-a)^{2}}+\\frac{c Z}{(a-b)^{2}}\\right](p+q) } \\end{aligned} $$ $$ +\\left[\\frac{a^{2} X}{(b-c)^{2}}+\\frac{b^{2} Y}{(c-a)^{2}}+\\frac{c^{2} Z}{(a-b)^{2}}\\right] $$ which is a real number. To get something about the midpoint of $P Q$, the $p q$ coefficient should be zero, which motivates the following lemma. ## Lemma There exist real $X, Y, Z$ for which $$ \\begin{aligned} & \\frac{X}{(b-c)^{2}}+\\frac{Y}{(c-a)^{2}}+\\frac{Z}{(a-b)^{2}}=0 \\text { and } \\\\ & \\frac{a X}{(b-c)^{2}}+\\frac{b Y}{(c-a)^{2}}+\\frac{c Z}{(a-b)^{2}} \\neq 0 . \\end{aligned} $$ $$ \\begin{aligned} & \\frac{(b-a) Y}{(c-a)^{2}}+\\frac{(c-a) Z}{(a-b)^{2}} \\\\ = & \\frac{a X}{(b-c)^{2}}+\\frac{b Y}{(c-a)^{2}}+\\frac{c Z}{(a-b)^{2}}-a\\left(\\frac{X}{(b-c)^{2}}+\\frac{Y}{(c-a)^{2}}+\\frac{Z}{(a-b)^{2}}\\right) \\\\ = & 0 \\end{aligned} $$ We can easily check that $(Y, Z)=(0,0)$ is impossible, therefore $\\frac{(b-a)^{3}}{(c-a)^{3}}=-\\frac{Z}{Y}$ is real. This means $\\angle B A C=60^{\\circ}$ or $120^{\\circ}$. By symmetry, the same is true of $\\angle C B A$ and $\\angle A C B$. This is impossible because $A B C$ is scalene. With the choice of $X, Y, Z$ as in the lemma, there exist complex numbers $\\alpha$ and $\\beta$, depending only on $a, b$, and $c$, such that $\\alpha \\neq 0$ and $\\alpha(p+q)+\\beta$ is real. Therefore the midpoint of $P Q$, which corresponds to $\\frac{p+q}{2}$, lies on a fixed line. It remains to show that this line is the Euler line. First, choose $P=Q$ to be the orthocenter to show that the orthocenter lies on the line. Secondly, choose $P$ and $Q$ to be the foci of the Steiner circumellipse to show that the centroid lies on the line. (By some ellipse properties, the external angle bisector of $\\angle P A Q$ is the tangent to the circumellipse at $A$, which is the line through $A$ parallel to $B C$. Therefore these points are valid.) Therefore the fixed line of the midpoint is the Euler line.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 18 |
-
{"year": "2023", "tier": "T0", "problem_label": "7", "problem_type": null, "problem": "The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up. In a move, Vera may flip over one of the coins in the row, subject to the following rules: - On the first move, Vera may flip over any of the 2023 coins. - On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.) Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.", "solution": " The answer is 4044 . In general, replacing 2023 with $4 n+3$, the answer is $8 n+4$. Bound. Observe that the first and last coins must be flipped, and so every coin is flipped at least once. Then, the $2 n+1$ even-indexed coins must be flipped at least twice, so they are flipped at least $4 n+2$ times. The $2 n+2$ odd-indexed coins must then be flipped at least $4 n+1$ times. Since there are an even number of these coins, the total flip count must be even, so they are actually flipped a total of at least $4 n+2$ times, for a total of at least $8 n+4$ flips in all. 【 Construction. For $k=0,1, \\ldots, n-1$, flip $(4 k+1,4 k+2,4 k+3,4 k+2,4 k+3,4 k+$ $4,4 k+3,4 k+4)$ in that order; then at the end, flip $4 n+1,4 n+2,4 n+3,4 n+2$. This is illustrated below for $4 n+3=15$.  It is easy to check this works, and there are 4044 flips, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 19 |
-
{"year": "2023", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.", "solution": " The only possible value of the common perimeter, denoted $p$, is 1 . 【 Synthetic approach (from author). We prove the converse of the problem first: Claim ( $p=1$ implies concurrence) - Suppose the six points are chosen so that triangles $A B_{2} C_{1}, B C_{2} A_{1}, C A_{2} B_{1}$ all have perimeter 1. Then lines $\\overline{B_{1} C_{2}}, \\overline{C_{1} A_{2}}$, and $\\overline{A_{1} B_{2}}$ are concurrent.  Hence the result follows by Brianchon's theorem. Now suppose $p \\neq 1$. Let $\\overline{B_{2}^{\\prime} C_{1}^{\\prime}}$ be the dilation of $\\overline{B_{2} C_{1}}$ with ratio $\\frac{1}{p}$ at center $A$, and define $C_{2}^{\\prime}, A_{1}^{\\prime}, A_{2}^{\\prime}, B_{1}^{\\prime}$ similarly. The following diagram showcases the situation $p<1$.  By the reasoning in the $p=1$ case, note that $\\overline{B_{1}^{\\prime} C_{2}^{\\prime}}, \\overline{C_{1}^{\\prime} A_{2}^{\\prime}}$, and $\\overline{A_{1}^{\\prime} B_{2}^{\\prime}}$ are concurrent. However, $\\overline{B_{1} C_{2}}, \\overline{C_{1} A_{2}}, \\overline{A_{1} B_{2}}$ lie in the interior of quadrilaterals $B C B_{1}^{\\prime} C_{2}^{\\prime}, C A C_{1}^{\\prime} A_{2}^{\\prime}$, and $A B A_{1}^{\\prime} B_{2}^{\\prime}$, and these quadrilaterals do not share an interior point, a contradiction. Thus $p \\geq 1$. Similarly, we can show $p \\leq 1$, and so $p=1$ is forced (and achieved if, for example, the three triangles are equilateral with side length $1 / 3$ ).", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 20 |
-
{"year": "2023", "tier": "T0", "problem_label": "8", "problem_type": null, "problem": "Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.", "solution": " The only possible value of the common perimeter, denoted $p$, is 1 . 『 Barycentric solution (by Carl, Krit, Milan). We show that, if the common perimeter is 1 , then the lines concur. To do this, we use barycentric coordinates. Let $A=(1: 0: 0)$, $B=(0: 1: 0)$, and $C=(0: 0: 1)$. Let $A_{1}=\\left(0: 1-a_{1}: a_{1}\\right), A_{2}=\\left(0: a_{2}: 1-a_{2}\\right)$, $B_{1}=\\left(b_{1}: 0: 1-b_{1}\\right), B_{2}=\\left(1-b_{2}: 0: b_{2}\\right), C_{1}=\\left(1-c_{1}: c_{1}: 0\\right)$, and $C_{2}=\\left(c_{2}: 1-c_{2}: 0\\right)$. The line $B_{1} C_{2}$ is defined by the equation $$ \\operatorname{det}\\left[\\begin{array}{ccc} x & y & z \\\\ b_{1} & 0 & 1-b_{1} \\\\ c_{2} & 1-c_{2} & 0 \\end{array}\\right]=0 \\text {; } $$ i.e. $$ x\\left(-\\left(1-b_{1}\\right)\\left(1-c_{2}\\right)\\right)+y\\left(\\left(1-b_{1}\\right) c_{2}\\right)+z\\left(b_{1}\\left(1-c_{2}\\right)\\right)=0 . $$ Computing the equations for the other lines cyclically, we get that the lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ concur if and only if $$ \\operatorname{det}\\left[\\begin{array}{ccc} -\\left(1-b_{1}\\right)\\left(1-c_{2}\\right) & \\left(1-b_{1}\\right) c_{2} & b_{1}\\left(1-c_{2}\\right) \\\\ c_{1}\\left(1-a_{2}\\right) & -\\left(1-c_{1}\\right)\\left(1-a_{2}\\right) & \\left(1-c_{1}\\right) a_{2} \\\\ \\left(1-a_{1}\\right) b_{2} & a_{1}\\left(1-b_{2}\\right) & -\\left(1-a_{1}\\right)\\left(1-b_{2}\\right) \\end{array}\\right]=0 . $$ Let this matrix be $M$. We also define the similar matrix $$ N=\\left[\\begin{array}{ccc} -\\left(1-b_{2}\\right)\\left(1-c_{1}\\right) & \\left(1-b_{2}\\right) c_{1} & b_{2}\\left(1-c_{1}\\right) \\\\ c_{2}\\left(1-a_{1}\\right) & -\\left(1-c_{2}\\right)\\left(1-a_{1}\\right) & \\left(1-c_{2}\\right) a_{1} \\\\ \\left(1-a_{2}\\right) b_{1} & a_{2}\\left(1-b_{1}\\right) & -\\left(1-a_{2}\\right)\\left(1-b_{1}\\right) \\end{array}\\right] . $$ Geometrically, det $N=0$ if and only if $B_{2}^{\\prime} C_{1}^{\\prime}, C_{2}^{\\prime} A_{1}^{\\prime}$, and $A_{2}^{\\prime} B_{1}^{\\prime}$ concur, where for a point $P$ on a side of triangle $A B C, P^{\\prime}$ denotes its reflection over that side's midpoint. Claim - We have $\\operatorname{det} M=\\operatorname{det} N$. We use the definition of the determinant as a sum over permutations. The even permutations give us the following three terms: $$ \\begin{aligned} -\\left(1-b_{1}\\right)\\left(1-c_{2}\\right)\\left(1-c_{1}\\right)\\left(1-a_{2}\\right)\\left(1-a_{1}\\right)\\left(1-b_{2}\\right) & =-\\prod_{i=1}^{2}\\left(\\left(1-a_{i}\\right)\\left(1-b_{i}\\right)\\left(1-c_{i}\\right)\\right) \\\\ \\left(1-a_{1}\\right) b_{2}\\left(1-b_{1}\\right) c_{2}\\left(1-c_{1}\\right) a_{2} & =\\left(\\left(1-a_{1}\\right)\\left(1-b_{1}\\right)\\left(1-c_{1}\\right)\\right)\\left(a_{2} b_{2} c_{2}\\right) \\\\ c_{1}\\left(1-a_{2}\\right) a_{1}\\left(1-b_{2}\\right) b_{1}\\left(1-c_{2}\\right) & =\\left(\\left(1-a_{2}\\right)\\left(1-b_{2}\\right)\\left(1-c_{2}\\right)\\right)\\left(a_{1} b_{1} c_{1}\\right) . \\end{aligned} $$ The first term is invariant under $\\Psi$, while the second and third terms are swapped under $\\Psi$. For the odd permutations, we have a contribution to the determinant of $$ \\sum_{\\mathrm{cyc}}\\left(1-b_{1}\\right)\\left(1-c_{2}\\right)\\left(1-c_{1}\\right) a_{2} a_{1}\\left(1-b_{2}\\right) $$ each summand is invariant under $\\Psi$. This finishes the proof of our claim. Now, it suffices to show that, if $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ each have perimeter 1, then $$ \\operatorname{det}\\left[\\begin{array}{ccc} -\\left(1-b_{2}\\right)\\left(1-c_{1}\\right) & \\left(1-b_{2}\\right) c_{1} & b_{2}\\left(1-c_{1}\\right) \\\\ c_{2}\\left(1-a_{1}\\right) & -\\left(1-c_{2}\\right)\\left(1-a_{1}\\right) & \\left(1-c_{2}\\right) a_{1} \\\\ \\left(1-a_{2}\\right) b_{1} & a_{2}\\left(1-b_{1}\\right) & -\\left(1-a_{2}\\right)\\left(1-b_{1}\\right) . \\end{array}\\right]=0 $$ Indeed, we have $A B_{2}=b_{2}$ and $A C_{1}=c_{1}$, so by the law of cosines, $$ 1-b_{2}-c_{1}=1-A B_{2}-A C_{1}=B_{2} C_{1}=\\sqrt{b_{2}^{2}+c_{1}^{2}-b_{2} c_{1}} $$ This gives $$ \\left(1-b_{2}-c_{1}\\right)^{2}=b_{2}^{2}+c_{1}^{2}-b_{2} c_{1} \\Longrightarrow 1-2 b_{2}-2 c_{1}+3 b_{2} c_{1}=0 $$ Similarly, $1-2 c_{2}-2 a_{1}+3 c_{2} a_{1}=0$ and $1-2 a_{2}-2 b_{1}+3 a_{2} b_{1}=0$. Now, $$ \\begin{aligned} N\\left[\\begin{array}{l} 1 \\\\ 1 \\\\ 1 \\end{array}\\right] & =\\left[\\begin{array}{l} -\\left(1-b_{2}\\right)\\left(1-c_{1}\\right)+\\left(1-b_{2}\\right) c_{1}+b_{2}\\left(1-c_{1}\\right) \\\\ -\\left(1-c_{2}\\right)\\left(1-a_{1}\\right)+\\left(1-c_{2}\\right) a_{1}+c_{2}\\left(1-a_{1}\\right) \\\\ -\\left(1-a_{2}\\right)\\left(1-b_{1}\\right)+\\left(1-a_{2}\\right) b_{1}+a_{2}\\left(1-b_{1}\\right) \\end{array}\\right] \\\\ & =\\left[\\begin{array}{l} -1+2 b_{2}+2 c_{1}-3 b_{2} c_{1} \\\\ -1+2 c_{2}+2 a_{1}-3 c_{2} a_{1} \\\\ -1+2 a_{2}+2 b_{1}-2 a_{2} b_{1} \\end{array}\\right]=\\left[\\begin{array}{l} 0 \\\\ 0 \\\\ 0 \\end{array}\\right] . \\end{aligned} $$ So it follows $\\operatorname{det} N=0$, as desired.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 21 |
-
{"year": "2023", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $p$ be a fixed prime and let $a \\geq 2$ and $e \\geq 1$ be fixed integers. Given a function $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ and an integer $k \\geq 0$, the $k$ th finite difference, denoted $\\Delta^{k} f$, is the function from $\\mathbb{Z} / a \\mathbb{Z}$ to $\\mathbb{Z} / p^{e} \\mathbb{Z}$ defined recursively by $$ \\begin{aligned} & \\Delta^{0} f(n)=f(n) \\\\ & \\Delta^{k} f(n)=\\Delta^{k-1} f(n+1)-\\Delta^{k-1} f(n) \\quad \\text { for } k=1,2, \\ldots \\end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \\geq 1$ for which $\\Delta^{k} f=f$ 。", "solution": "Let $p$ be a fixed prime and let $a \\geq 2$ and $e \\geq 1$ be fixed integers. Given a function $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ and an integer $k \\geq 0$, the $k$ th finite difference, denoted $\\Delta^{k} f$, is the function from $\\mathbb{Z} / a \\mathbb{Z}$ to $\\mathbb{Z} / p^{e} \\mathbb{Z}$ defined recursively by $$ \\begin{aligned} & \\Delta^{0} f(n)=f(n) \\\\ & \\Delta^{k} f(n)=\\Delta^{k-1} f(n+1)-\\Delta^{k-1} f(n) \\quad \\text { for } k=1,2, \\ldots \\end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \\geq 1$ for which $\\Delta^{k} f=f$. The answer is $$ \\left(p^{e}\\right)^{a} \\cdot p^{-e p^{\\nu} p(a)}=p^{e\\left(a-p^{\\nu_{p}(a)}\\right)} $$ 【 First solution by author. For convenience in what follows, set $d=\\nu_{p}(a)$, let $a=p^{d} \\cdot b$, and let a function $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ be essential if it equals one of its iterated finite differences. The key claim is the following. Claim (Characterization of essential functions) - A function $f$ is essential if and only if $$ f(x)+f\\left(x+p^{d}\\right)+\\cdots+f\\left(x+(b-1) p^{d}\\right)=0 $$ for all $x$. ## Lemma Let $g: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ be any function, and let $h=\\Delta^{p^{d}} g$. Then $$ h(x)+h\\left(x+p^{d}\\right)+\\cdots+h\\left(x+(b-1) p^{d}\\right) \\equiv 0 \\quad(\\bmod p) $$ for all $x$. $$ h(x)=\\Delta^{p^{d}} g(x)=\\sum_{k=0}^{p^{d}}(-1)^{k}\\binom{p^{d}}{k} g\\left(x+p^{d}-k\\right) $$ However, it is known that $\\binom{p^{d}}{k}$ is a multiple of $p$ if $1 \\leq k \\leq p^{d}-1$, so $$ h(x) \\equiv g\\left(x+p^{d}\\right)+(-1)^{p^{d}} g(x) \\quad(\\bmod p) . $$ Using this, we easily obtain $$ \\begin{aligned} & h(x)+h\\left(x+p^{d}\\right)+\\cdots+h\\left(x+(b-1) p^{d}\\right) \\\\ \\equiv & \\begin{cases}0 & p>2 \\\\ 2\\left(g(x)+g\\left(x+p^{d}\\right)+\\cdots+g\\left(x+(b-1) p^{d}\\right)\\right) & p=2\\end{cases} \\\\ \\equiv & 0 \\quad(\\bmod p) \\end{aligned} $$ as desired. ## Corollary Let $g: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ be any function, and let $h=\\Delta^{e p^{d}} g$. Then $$ h(x)+h\\left(x+p^{d}\\right)+\\cdots+h\\left(x+(b-1) p^{d}\\right)=0 $$ for all $x$. $$ h_{1}(x)=\\frac{h(x)+h\\left(x+p^{d}\\right)+\\cdots+h\\left(x+(b-1) p^{d}\\right)}{p} . $$ Applying the lemma to $h_{1}$ shows the corollary for $e=2$, since $h_{1}(x)$ is divisible by $p$, hence the numerator is divisible by $p^{2}$. Continue in this manner to get the result for general $e>2$. This immediately settles this direction, since $f$ is in the image of $\\Delta^{e p^{d}}$. We will show that $\\Delta$ is injective on $\\mathcal{S}$. Suppose otherwise, and consider two functions $f$, $g$ in $\\mathcal{S}$ with $\\Delta f=\\Delta g$. Then, we obtain that $f$ and $g$ differ by a constant; say $g=f+\\lambda$. However, then $$ \\begin{aligned} & g(0)+g\\left(p^{e}\\right)+\\cdots+g\\left((b-1) p^{e}\\right) \\\\ = & (f(0)+\\lambda)+\\left(f\\left(p^{e}\\right)+\\lambda\\right)+\\cdots+\\left(f\\left((b-1) p^{e}\\right)+\\lambda\\right) \\\\ = & b \\lambda \\end{aligned} $$ This should also be zero. Since $p \\nmid b$, we obtain $\\lambda=0$, as desired. Counting Finally, we can count the essential functions: all but the last $p^{d}$ entries can be chosen arbitrarily, and then each remaining entry has exactly one possible choice. This leads to a count of $$ \\left(p^{e}\\right)^{a-p^{d}}=p^{e\\left(a-p^{\\nu_{p}(a)}\\right)}, $$ as promised.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
| 22 |
-
{"year": "2023", "tier": "T0", "problem_label": "9", "problem_type": null, "problem": "Let $p$ be a fixed prime and let $a \\geq 2$ and $e \\geq 1$ be fixed integers. Given a function $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ and an integer $k \\geq 0$, the $k$ th finite difference, denoted $\\Delta^{k} f$, is the function from $\\mathbb{Z} / a \\mathbb{Z}$ to $\\mathbb{Z} / p^{e} \\mathbb{Z}$ defined recursively by $$ \\begin{aligned} & \\Delta^{0} f(n)=f(n) \\\\ & \\Delta^{k} f(n)=\\Delta^{k-1} f(n+1)-\\Delta^{k-1} f(n) \\quad \\text { for } k=1,2, \\ldots \\end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \\geq 1$ for which $\\Delta^{k} f=f$ 。", "solution": "Let $p$ be a fixed prime and let $a \\geq 2$ and $e \\geq 1$ be fixed integers. Given a function $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ and an integer $k \\geq 0$, the $k$ th finite difference, denoted $\\Delta^{k} f$, is the function from $\\mathbb{Z} / a \\mathbb{Z}$ to $\\mathbb{Z} / p^{e} \\mathbb{Z}$ defined recursively by $$ \\begin{aligned} & \\Delta^{0} f(n)=f(n) \\\\ & \\Delta^{k} f(n)=\\Delta^{k-1} f(n+1)-\\Delta^{k-1} f(n) \\quad \\text { for } k=1,2, \\ldots \\end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \\geq 1$ for which $\\Delta^{k} f=f$. The answer is $$ \\left(p^{e}\\right)^{a} \\cdot p^{-e p^{\\nu} p(a)}=p^{e\\left(a-p^{\\nu_{p}(a)}\\right)} $$ II Second solution by Daniel Zhu. There are two parts to the proof: solving the $e=1$ case, and using the $e=1$ result to solve the general problem by induction on $e$. These parts are independent of each other. The case $e=1 \\quad$ Represent functions $f$ as elements $$ \\alpha_{f}:=\\sum_{k \\in \\mathbb{Z} / a \\mathbb{Z}} f(-k) x^{k} \\in \\mathbb{F}_{p}[x] /\\left(x^{a}-1\\right) $$ Then, since $\\alpha_{\\Delta f}=(x-1) \\alpha_{f}$, we wish to find the number of $\\alpha \\in \\mathbb{F}_{p}[x] /\\left(x^{a}-1\\right)$ such that $(x-1)^{m} \\alpha=\\alpha$ for some $m$. Now, make the substitution $y=x-1$ and let $P(y)=(y+1)^{a}-1$; we want to find $\\alpha \\in \\mathbb{F}_{p}[y] /(P(y))$ such that $y^{m} \\alpha=\\alpha$ for some $m$. If we write $P(y)=y^{d} Q(y)$ with $Q(0) \\neq 0$, then by the Chinese Remainder Theorem we have the ring isomorphism $$ \\mathbb{F}_{p}[y] /(P(y)) \\cong \\mathbb{F}_{p}[y] /\\left(y^{d}\\right) \\times \\mathbb{F}_{p}[y] /(Q(y)) $$ Note that $y$ is nilpotent in the first factor, while it is a unit in the second factor. So the $\\alpha$ that work are exactly those that are zero in the first factor; thus there are $p^{a-d}$ such $\\alpha$. We can calculate $d=p^{v_{p}(a)}$ (via, say, Lucas's Theorem), so we are done. The general problem The general idea is as follows: call a $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z} e$-good if $\\Delta^{m} f=f$ for some $m$. Our result above allows us to count the 1-good functions. Then, if $e \\geq 1$, every $(e+1)$-good function, when reduced $\\bmod p^{e}$, yields an $e$-good function, so we count $(e+1)$-good functions by counting how many reduce to any given $e$-good function. Formally, we use induction on $e$, with the $e=1$ case being treated above. Suppose now we have solved the problem for a given $e \\geq 1$, and we now wish to solve it for $e+1$. For any function $g: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e+1} \\mathbb{Z}$, let $\\bar{g}: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e} \\mathbb{Z}$ be its reduction $\\bmod p^{e}$. For a given $e$-good $f$, let $n(f)$ be the number of $(e+1)$-good $g$ with $\\bar{g}=f$. The following two claims now finish the problem: Claim - If $f$ is $e$-good, then $n(f)>0$. $$ g, \\Delta^{m} g, \\Delta^{2 m} g, \\ldots $$ Since there are finitely many functions $\\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p^{e+1} \\mathbb{Z}$, there must exist $a<b$ such that $\\Delta^{a m} g=\\Delta^{b m} g$. We claim $\\Delta^{a m} g$ is the desired $(e+1)$ good function. To see this, first note that since $\\overline{\\Delta^{k} g}=\\Delta^{k} \\bar{g}$, we must have $\\overline{\\Delta^{a m} g}=\\Delta^{a m} f=f$. Moreover, $$ \\Delta^{(b-a) m}\\left(\\Delta^{a m} g\\right)=\\Delta^{b m} g=\\Delta^{a m} g $$ so $\\Delta^{a m} g$ is $(e+1)$-good. Claim - If $f$ is $e$-good, and $n(f)>0$, then $n(f)$ is exactly the number of 1-good functions, i.e. $p^{a-p^{v_{p}(a)}}$. To show that this condition is sufficient, note that $\\overline{g+p^{e} h}=\\bar{g}=f$. Moreover, if $\\Delta^{m} g=g$ and $\\Delta^{m^{\\prime}} h=h$, then $$ \\Delta^{m m^{\\prime}}\\left(g+p^{e} h\\right)=\\Delta^{m m^{\\prime}} g+p^{e} \\Delta^{m m^{\\prime}} h=g+p^{e} h . $$ To show that this condition is necessary, let $g_{1}$ be any $(e+1)$-good function such that $\\bar{g}_{1}=f$. Then $g_{1}-g$ is also $(e+1)$-good, since if $\\Delta^{m} g=g, \\Delta^{m^{\\prime}} g_{1}=g_{1}$, we have $$ \\Delta^{m m^{\\prime}}\\left(g_{1}-g\\right)=\\Delta^{m m^{\\prime}} g_{1}-\\Delta^{m m^{\\prime}} g=g_{1}-g . $$ On the other hand, we also know that $g_{1}-g$ is divisible by $p^{e}$. This means that it must be $p^{e} h$ for some function $f: \\mathbb{Z} / a \\mathbb{Z} \\rightarrow \\mathbb{Z} / p \\mathbb{Z}$, and it is not hard to show that $g_{1}-g$ being $(e+1)$-good means that $h$ is 1 -good.", "metadata": {"resource_path": "USA_TST_TST/segmented/en-sols-TSTST-2023.jsonl"}}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|