Fix EGMO data errors
Browse files
EGMO/segment_script/segment.py
CHANGED
|
@@ -34,7 +34,7 @@ def find_problem_with_solution(
|
|
| 34 |
return match.start()
|
| 35 |
|
| 36 |
|
| 37 |
-
def
|
| 38 |
text = text.replace('The proof can be divided in two steps:\n\n1. Proving', 'The proof can be divided in two steps:\n\n1). Proving')
|
| 39 |
text = text.replace('M P \cdot M Q=M U \cdot M V=M B^{2}\n$$\n\n2. Conclude the', 'M P \cdot M Q=M U \cdot M V=M B^{2}\n$$\n\n2). Conclude the')
|
| 40 |
text = text.replace(
|
|
@@ -56,7 +56,6 @@ def analyze(text: str) -> Tuple[List, int]:
|
|
| 56 |
Returns:
|
| 57 |
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 58 |
"""
|
| 59 |
-
text = enhance_text(text)
|
| 60 |
problem_pattern = re.compile(r'(?:(?:\n|# )(?:Problem|Problems)\s+(\d+)\.?|\n(\d+)\.)(?:\s*\(.+?\)\n)?', re.IGNORECASE)
|
| 61 |
solution_pattern = re.compile(r'(?:\n|# |\n\#*\s*\d+\.\s*)Solution(?:\s*\d*\s*\(.+?\)|\s+\d+[\.\:])?.?', re.IGNORECASE)
|
| 62 |
|
|
@@ -140,7 +139,7 @@ def main():
|
|
| 140 |
output_file = seg_output_path / egmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 141 |
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 142 |
|
| 143 |
-
text = '\n' + egmo_md.read_text(encoding="utf-8")
|
| 144 |
|
| 145 |
tags, problem_num = analyze(text)
|
| 146 |
|
|
|
|
| 34 |
return match.start()
|
| 35 |
|
| 36 |
|
| 37 |
+
def clean_text(text: str) -> str:
|
| 38 |
text = text.replace('The proof can be divided in two steps:\n\n1. Proving', 'The proof can be divided in two steps:\n\n1). Proving')
|
| 39 |
text = text.replace('M P \cdot M Q=M U \cdot M V=M B^{2}\n$$\n\n2. Conclude the', 'M P \cdot M Q=M U \cdot M V=M B^{2}\n$$\n\n2). Conclude the')
|
| 40 |
text = text.replace(
|
|
|
|
| 56 |
Returns:
|
| 57 |
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 58 |
"""
|
|
|
|
| 59 |
problem_pattern = re.compile(r'(?:(?:\n|# )(?:Problem|Problems)\s+(\d+)\.?|\n(\d+)\.)(?:\s*\(.+?\)\n)?', re.IGNORECASE)
|
| 60 |
solution_pattern = re.compile(r'(?:\n|# |\n\#*\s*\d+\.\s*)Solution(?:\s*\d*\s*\(.+?\)|\s+\d+[\.\:])?.?', re.IGNORECASE)
|
| 61 |
|
|
|
|
| 139 |
output_file = seg_output_path / egmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 140 |
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 141 |
|
| 142 |
+
text = '\n' + clean_text(egmo_md.read_text(encoding="utf-8"))
|
| 143 |
|
| 144 |
tags, problem_num = analyze(text)
|
| 145 |
|
EGMO/segmented/en-2018-solutions.jsonl
CHANGED
|
@@ -2,8 +2,8 @@
|
|
| 2 |
{"year": "2018", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Consider the set\n\n$$\nA=\\left\\{1+\\frac{1}{k}: k=1,2,3, \\ldots\\right\\}\n$$\n\n(a) Prove that every integer $x \\geq 2$ can be written as the product of one or more elements of $A$, which are not necessarily different.\n(b) For every integer $x \\geq 2$, let $f(x)$ denote the minimum integer such that $x$ can be written as the product of $f(x)$ elements of $A$, which are not necessarily different.\nProve that there exist infinitely many pairs $(x, y)$ of integers with $x \\geq 2, y \\geq 2$, and\n\n$$\nf(x y)<f(x)+f(y) .\n$$\n\n(Pairs $\\left(x_{1}, y_{1}\\right)$ and $\\left(x_{2}, y_{2}\\right)$ are different if $x_{1} \\neq x_{2}$ or $\\left.y_{1} \\neq y_{2}\\right)$.\n(Mihail Baluna, Romania)", "solution": "Every integer $x \\geq 2$ can be written as the telescopic product of $x-1$ elements of $A$ as\n\n$$\nx=\\left(1+\\frac{1}{x-1}\\right) \\cdot\\left(1+\\frac{1}{x-2}\\right) \\cdot \\ldots \\cdot\\left(1+\\frac{1}{2}\\right) \\cdot\\left(1+\\frac{1}{1}\\right)\n$$\n\nwhich is enough to establish part (a). We now consider part (b). Notice that for any positive integer $k$ we have\n\n$$\nf\\left(2^{k}+1\\right) \\leq k+1\n$$\n\nbecause $2^{k}+1=\\left(1+\\frac{1}{2^{k}}\\right) \\cdot 2^{k}$ is a representation of $2^{k}+1$ as a product of $k+1$ elements of $A$. We claim that all the pairs $(x, y)$ of the form\n\n$$\nx=5, \\quad y=\\frac{2^{4 k+2}+1}{5}\n$$\n\nsatisfy the required inequality. Notice that $y$ is an integer for any positive value of $k$, because $2^{4 k+2}+1 \\equiv 16^{k} \\cdot 4+1 \\equiv 5 \\equiv 0(\\bmod 5)$. Furthermore, $f(x y)=f\\left(2^{4 k+2}+1\\right) \\leq 4 k+3$ (and $f(x)=f\\left(2^{2}+1\\right) \\leq 3$ ) by the above. We now need some lower bounds on the values of $f$. Notice that no element of $A$ exceeds 2, and therefore the product of at most $k$ elements of $A$ does not exceed $2^{k}$ : it follows that\n\n$$\nf(n) \\geq\\left\\lceil\\log _{2}(n)\\right\\rceil\n$$\n\nand in particular that\n\n$$\nf(5)=f\\left(2^{2}+1\\right) \\geq\\left\\lceil\\log _{2}(5)\\right\\rceil=3\n$$\n\nWe have thus proven $f(x)=f(5)=3$. We want to show $f(x y)<f(x)+f(y)$, and since we know $f(x y) \\leq 4 k+3$ and $f(x)=3$ we are reduced to showing $f(y)>4 k$. Since $y>2^{4 k-1}$, from (Q2.1) we already know that $f(y) \\geq 4 k$, and hence we just need to exclude that $f(y)=4 k$. Let us assume that we can represent $y$ in the form $a_{1} \\cdot \\ldots a_{4 k}$ with every $a_{i}$ in $A$. At least one of the $a_{i}$ is not 2 (otherwise the product would be a power of 2 , while $y$ is odd), and hence it is less than or equal to $3 / 2$. It follows that\n\n$$\na_{1} \\cdot \\ldots \\cdot a_{4 k} \\leq 2^{4 k-1} \\cdot \\frac{3}{2}=15 \\cdot \\frac{2^{4 k-2}}{5}<\\frac{2^{4 k+2}}{5}<y\n$$\n\nwhich contradicts the fact that $a_{1} \\cdot \\ldots \\cdot a_{4 k}$ is a representation of $y$.\nNote. Using a similar approach one can also prove that all pairs of the form\n\n$$\n\\left(3, \\frac{2^{2 k+1}+1}{3}\\right) \\quad \\text { and } \\quad\\left(11, \\frac{2^{10 k+5}+1}{11}\\right)\n$$\n\nsatisfy the required inequality.\nSecond solution As in the previous solution we obtain the lower bound (Q2.1).\nNow we claim that all the pairs of the form\n\n$$\nx=2^{k}+1, \\quad y=4^{k}-2^{k}+1\n$$\n\nsatisfy the required inequality when $k$ is large enough. To begin with, it is easy to see that\n\n$$\n2^{k}+1=\\frac{2^{k}+1}{2^{k}} \\cdot \\underbrace{2 \\cdot \\ldots \\cdot 2}_{k \\text { terms }} \\quad \\text { and } \\quad 2^{3 k}+1=\\frac{2^{3 k}+1}{2^{3 k}} \\cdot \\underbrace{2 \\cdot \\ldots \\cdot 2}_{3 k \\text { terms }}\n$$\n\nwhich shows that $f\\left(2^{k}+1\\right) \\leq k+1$ and $f\\left(2^{3 k}+1\\right) \\leq 3 k+1$. On the other hand, from (Q2.1) we deduce that the previous inequalities are actually equalities, and therefore\n\n$$\nf(x)=k+1 \\quad \\text { and } \\quad f(x y)=3 k+1\n$$\n\nTherefore, it remain to show that $f(y)>2 k$. Since $y>2^{2 k-1}$ (for $k \\geq 1$ ), from (Q2.1) we already know that $f(y) \\geq 2 k$, and hence we just need to exclude that $f(y)=2 k$. Let us assume that we can represent $y$ in the form $a_{1} \\cdot \\ldots \\cdot a_{2 k}$. At least one of the factors is not 2 , and hence it is less than or equal to $3 / 2$. Thus when $k$ is large enough it follows that\n\n$$\na_{1} \\cdot \\ldots \\cdot a_{2 k} \\leq 2^{2 k-1} \\cdot \\frac{3}{2}=\\frac{3}{4} \\cdot 2^{2 k}<2^{2 k}-2^{k}<y\n$$\n\nwhich contradicts the fact that $a_{1} \\cdot \\ldots \\cdot a_{2 k}$ is a representation of $y$.\nThird solution Let's start by showing that $(x, y)=(7,7)$ satisfies $f(x y)<f(x)+f(y)$. We have $f(7) \\geq 4$ since 7 cannot be written as the product of 3 or fewer elements of $A$ : indeed $2^{3}>7$, and any other product of at most three elements of $A$ does not exceed $2^{2} \\cdot \\frac{3}{2}=6<7$. On the other hand, $f(49) \\leq 7$ since $49=2 \\cdot 2 \\cdot 2 \\cdot 2 \\cdot 2 \\cdot \\frac{3}{2} \\cdot \\frac{49}{48}$.\n\nSuppose by contradiction that there exist only finitely many pairs $(x, y)$ that satisfy $f(x y)<$ $f(x)+f(y)$. This implies that there exists $M$ large enough so that whenever $a>M$ or $b>M$ holds we have $f(a b)=f(a)+f(b)$ (indeed, it is clear that the reverse inequality $f(a b) \\leq f(a)+f(b)$ is always satisfied).\n\nNow take any pair $(x, y)$ that satisfies $f(x y)<f(x)+f(y)$ and let $n>M$ be any integer. We obtain\n\n$$\nf(n)+f(x y)=f(n x y)=f(n x)+f(y)=f(n)+f(x)+f(y),\n$$\n\nwhich contradicts $f(x y)<f(x)+f(y)$.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 2", "solution_match": "\nSolution "}}
|
| 3 |
{"year": "2018", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "The $n$ contestants of an EGMO are named $C_{1}, \\ldots, C_{n}$. After the competition they queue in front of the restaurant according to the following rules.\n\n- The Jury chooses the initial order of the contestants in the queue.\n- Every minute, the Jury chooses an integer $i$ with $1 \\leq i \\leq n$.\n- If contestant $C_{i}$ has at least $i$ other contestants in front of her, she pays one euro to the Jury and moves forward in the queue by exactly $i$ positions.\n- If contestant $C_{i}$ has fewer than $i$ other contestants in front of her, the restaurant opens and the process ends.\n(a) Prove that the process cannot continue indefinitely, regardless of the Jury's choices.\n(b) Determine for every $n$ the maximum number of euros that the Jury can collect by cunningly choosing the initial order and the sequence of moves.\n(Hungary)", "solution": "The maximal number of euros is $2^{n}-n-1$.\nTo begin with, we show that it is possible for the Jury to collect this number of euros. We argue by induction. Let us assume that the Jury can collect $M_{n}$ euros in a configuration with $n$ contestants. Then we show that the Jury can collect at least $2 M_{n}+n$ moves in a configuration with $n+1$ contestants. Indeed, let us begin with all the contestants lined up in reverse order. In the first $M_{n}$ moves the Jury keeps $C_{n+1}$ in first position and reverses the order of the remaining contestants, then in the next $n$ moves all contestants $C_{1}, \\ldots, C_{n}$ (in this order) jump over $C_{n+1}$ and end up in the first $n$ positions of the line in reverse order, and finally in the last $M_{n}$ moves the Jury rearranges the first $n$ positions.\n\nSince $M_{1}=0$ and $M_{n+1} \\geq 2 M_{n}+n$, an easy induction shows that $M_{n} \\geq 2^{n}-n-1$.\n\nLet us show now that at most $2^{n}-n-1$ moves are possible. To this end, let us identify a line of contestants with a permutation $\\sigma$ of $\\{1, \\ldots, n\\}$. To each permutation we associate the set of reverse pairs\n\n$$\nR(\\sigma):=\\{(i, j): 1 \\leq i<j \\leq n \\text { and } \\sigma(i)>\\sigma(j)\\}\n$$\n\nand the nonnegative integer\n\n$$\nW(\\sigma):=\\sum_{(i, j) \\in R(\\sigma)} 2^{i}\n$$\n\nwhich we call the total weight of the permutation. We claim that the total weight decreases after any move of the contestants. Indeed, let us assume that $C_{i}$ moves forward in the queue, let $\\sigma$ be the permutation before the move, and let $\\sigma^{\\prime}$ denote the permutation after the move. Since $C_{i}$ jumps over exactly $i$ contestants, necessarily she jumps over at least one contestant $C_{j}$ with index\n$j>i$. This means that the pair $(i, j)$ is reverse with respect to $\\sigma$ but not with respect to $\\sigma^{\\prime}$, and this yields a reduction of $2^{i}$ in the total weight. On the other hand, the move by $C_{i}$ can create new reverse pairs of the form $(k, i)$ with $k<i$, but their total contribution is at most\n\n$$\n2^{0}+2^{1}+\\ldots+2^{i-1}=2^{i}-1\n$$\n\nIn conclusion, when passing from $\\sigma$ to $\\sigma^{\\prime}$, at least one term $2^{i}$ disappears from the computation of the total weight, and the sum of all the new terms that might have been created is at most $2^{i}-1$. This shows that $W\\left(\\sigma^{\\prime}\\right) \\leq W(\\sigma)-1$.\n\nWe conclude by observing that the maximum possible value of $W(\\sigma)$ is realized when all pairs are reverse, in which case\n\n$$\nW(\\sigma)=\\sum_{i=1}^{n}(i-1) 2^{i}=2^{n}-n-1 .\n$$\n\nThis proves that the number of moves is less than or equal to $2^{n}-n-1$, and in particular it is finite.\n\nAlternative solution As in the previous solution, the fundamental observation is again that, when a contestant $C_{i}$ moves forward, necessarily she has to jump over at least one contestant $C_{j}$ with $j>i$.\n\nLet us show now that the process ends after a finite number of moves. Let us assume that this is not the case. Then at least one contestant moves infinitely many times. Let $i_{0}$ be the largest index such that $C_{i_{0}}$ moves infinitely many times. Then necessarily $C_{i_{0}}$ jumps infinitely many times over some fixed $C_{j_{0}}$ with $j_{0}>i_{0}$. On the other hand, we know that $C_{j_{0}}$ makes only a finite number of moves, and therefore she can precede $C_{i_{0}}$ in the line only a finite number of times, which is absurd.\n\nIn order to estimate from above the maximal number of moves, we show that the contestant $C_{i}$ can make at most $2^{n-i}-1$ moves. Indeed, let us argue by \"backward extended induction\". To begin with, we observe that the estimate is trivially true for $C_{n}$ because she has no legal move.\n\nLet us assume now that the estimate has been proved for $C_{i}, C_{i+1}, \\ldots, C_{n}$, and let us prove it for $C_{i-1}$. When $C_{i-1}$ moves, at least one contestant $C_{j}$ with $j>i-1$ must precede her in the line. The initial configuration can provide at most $n-i$ contestants with larger index in front of $C_{i-1}$, which means at most $n-i$ moves for $C_{i-1}$. All other moves are possible only if some contestant in the range $C_{i}, C_{i+1}, \\ldots, C_{n}$ jumps over $C_{i-1}$ during her moves. As a consequence, the total number of moves of $C_{i-1}$ is at most\n\n$$\nn-i+\\sum_{k=i}^{n}\\left(2^{n-k}-1\\right)=2^{n-i+1}-1\n$$\n\nSumming over all indices we obtain that\n\n$$\n\\sum_{i=1}^{n}\\left(2^{n-i}-1\\right)=2^{n}-n-1\n$$\n\nwhich gives an estimate for the total number of moves.\nThe same example of the first solution shows that this upper bound can actually be achieved.\nComment In every move of the example, the moving contestant jumps over exactly one contestant with larger index (and as a consequence over all contestants with smaller index).", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 3", "solution_match": "\nSolution "}}
|
| 4 |
{"year": "2018", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "A domino is a $1 \\times 2$ or $2 \\times 1$ tile.\nLet $n \\geq 3$ be an integer. Dominoes are placed on an $n \\times n$ board in such a way that each domino covers exactly two cells of the board, and dominoes do not overlap.\n\nThe value of a row or column is the number of dominoes that cover at least one cell of this row or column. The configuration is called balanced if there exists some $k \\geq 1$ such that each row and each column has a value of $k$.\n\nProve that a balanced configuration exists for every $n \\geq 3$, and find the minimum number of dominoes needed in such a configuration.\n(Merlijn Staps, The Netherlands)", "solution": "The minimal number of dominoes required in a balanced configuration is $2 n / 3$ if $n$ is a multiple of 3 , and $2 n$ otherwise.\n\nIn order to show that this number is necessary, we count in two different ways the number of elements of the set $S$ of all pairs $(\\ell, d)$, where $\\ell$ is a row or a column of the board, and $d$ is a domino that covers at least one cell of that row or column. On the one hand, since each row or column intersects the same number $k$ of dominoes, the set $S$ has $2 n k$ elements. On the other hand, since each domino intersects 3 rows/columns, the set $S$ has $3 D$ elements, where $D$ is the total number of dominoes on the board. This leads to the equality\n\n$$\n2 n k=3 D\n$$\n\nIf $n$ is a multiple of 3 , from the trivial inequality $k \\geq 1$ we obtain that $D \\geq 2 n / 3$. If $n$ is not a multiple of 3 , then $k$ is a multiple of 3 , which means that $k \\geq 3$ and hence $D \\geq 2 n$.\n\nNow we need to exhibit a balanced configuration with this number of dominoes. The following diagram shows a balanced configuration with $n=3$ and $k=1$.\n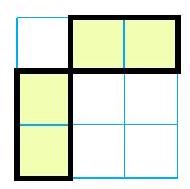\n\nIf $n$ is any multiple of 3 , we can obtain a balanced configuration with $k=1$ by using $n / 3$ of these $3 \\times 3$ blocks along the principal diagonal of the board.\n\nThe following diagrams show balanced configurations with $k=3$ and $n \\in\\{4,5,6,7\\}$.\n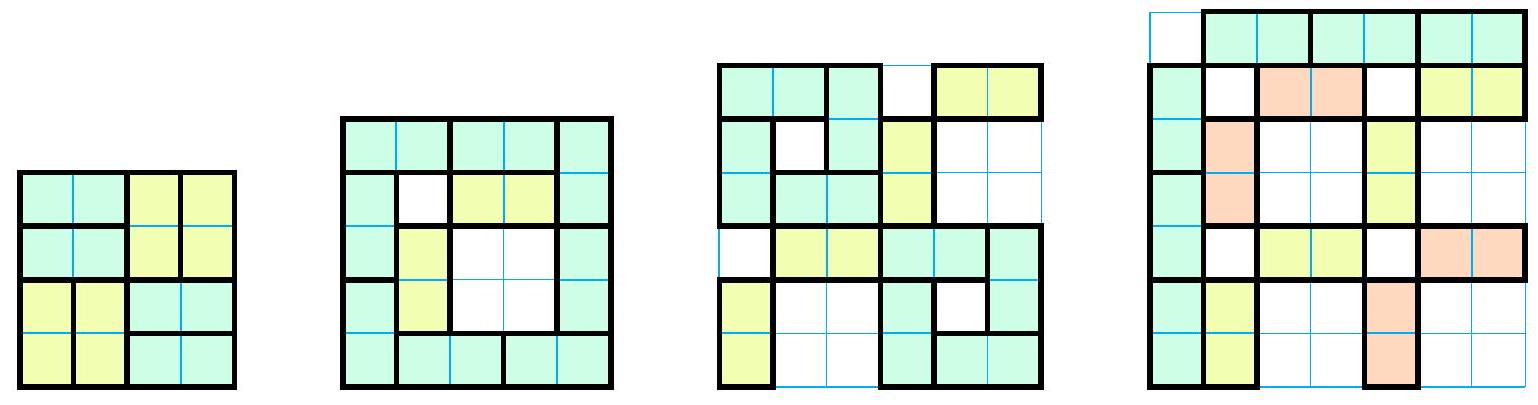\n\nAny $n \\geq 8$ can be written in the form $4 A+r$ where $A$ is a positive integer and $r \\in\\{4,5,6,7\\}$. Therefore, we can obtain a balanced configuration with $n \\geq 8$ and $k=3$ by using one block with size $r \\times r$, and $A$ blocks with size $4 \\times 4$ along the principal diagonal of the board. In particular, this construction covers all the cases where $n$ is not a multiple of 3 .", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution "}}
|
| 5 |
-
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "1 Let $M$ be the midpoint of the arc $A B$ that does not contain $C$, let $V$ be the intersection of $\\Omega$ and $\\Gamma$, and let $U$ be the intersection of $\\Omega$ and $A B$.\n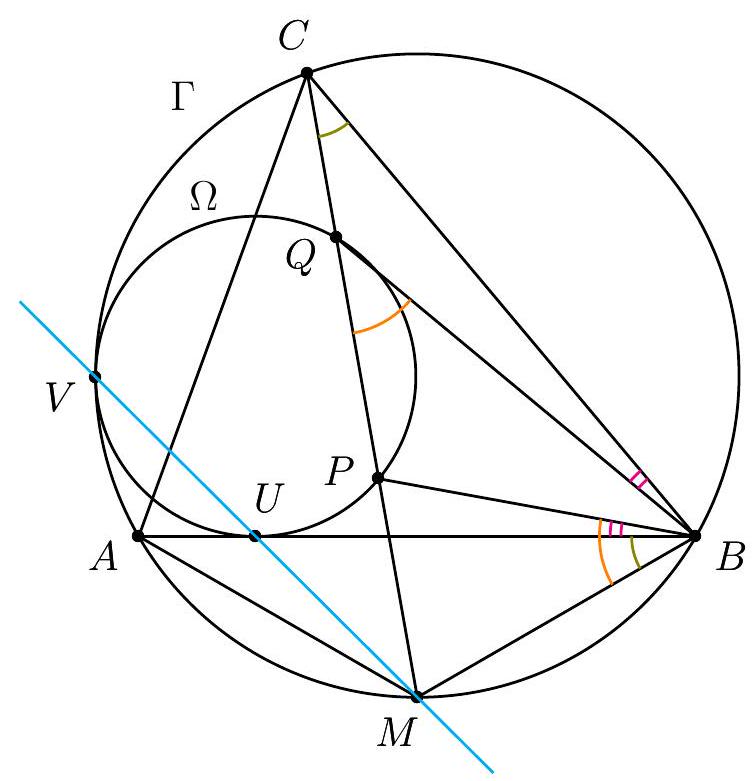\n\nThe proof can be divided in two steps:\n\n1. Proving that $M P \\cdot M Q=M B^{2}$.\n\nIt is well-known that $V, U$ and $M$ are collinear (indeed the homothety with center in $V$ that sends $\\Omega$ to $\\Gamma$ sends $U$ to the point of $\\Gamma$ where the tangent to $\\Gamma$ is parallel to $A B$, and this point is $M$ ), and\n\n$$\nM V \\cdot M U=M A^{2}=M B^{2}\n$$\n\nThis follows from the similitude between the triangles $\\triangle M A V$ and $\\triangle M U A$. Alternatively, it is a consequence of the following well-known lemma: Given a circle $\\Gamma$ with a chord $A B$, let $M$ be the middle point of one of the two arcs $A B$. Take a line through $M$ which intersects $\\Gamma$ again at $X$ and $A B$ at $Y$. Then $M X \\cdot M Y$ is independent of the choice of the line.\nComputing the power of $M$ with respect to $\\Omega$ we obtain that\n\n$$\nM P \\cdot M Q=M U \\cdot M V=M B^{2}\n$$\n\n2. Conclude the proof given that $M P \\cdot M Q=M B^{2}$.\n\nThe relation $M P \\cdot M Q=M B^{2}$ in turn implies that triangle $\\triangle M B P$ is similar to triangle $\\triangle M Q B$, and in particular $\\angle M B P=\\angle M Q B$. Keeping into account that $\\angle M C B=$ $\\angle M B A$, we finally conclude that\n\n$$\n\\angle Q B C=\\angle M Q B-\\angle M C B=\\angle M B P-\\angle M B A=\\angle P B A\n$$\n\nas required
|
| 6 |
-
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "The second solution is in fact a different proof of the first part of Solution 1.\nLet us consider the inversion with respect to circle with center $M$ and radius $M A=M B$. This inversion switches $A B$ and $\\Gamma$, and fixes the line passing through $M, U, V$. As a consequence, it keeps $\\Omega$ fixed, and therefore it switches $P$ and $Q$. This is because they are the intersections between the fixed line $M C$ and $\\Omega$, and the only fixed point on the segment $M C$ is its intersection with the inversion circle (thus $P$ and $Q$ are switched). This implies that $M P \\cdot M Q=M B^{2}
|
| 7 |
-
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "This solution is instead a different proof of the second step of Solution 1.\nLet $I$ and $J$ be the incenter and the $C$-excenter of $\\triangle A B C$ respectively. It is well-known that $M A=M I=M J$, therefore the relation $M P \\cdot M Q=M A^{2}$ implies that $(P, Q, I, J)=-1$.\n\nNow observe that $\\angle I B J=90^{\\circ}$, thus $B I$ is the angle bisector of $\\angle P B Q$ as it is well-known from the theory of harmonic pencils, and this leads easily to the conclusion
|
| 8 |
-
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "Let $D$ denote the intersection of $A B$ and $C M$. Let us consider an inversion with respect to $B$, and let us use primes to denote corresponding points in the transformed diagram, with the gentlemen agreement that $B^{\\prime}=B$.\n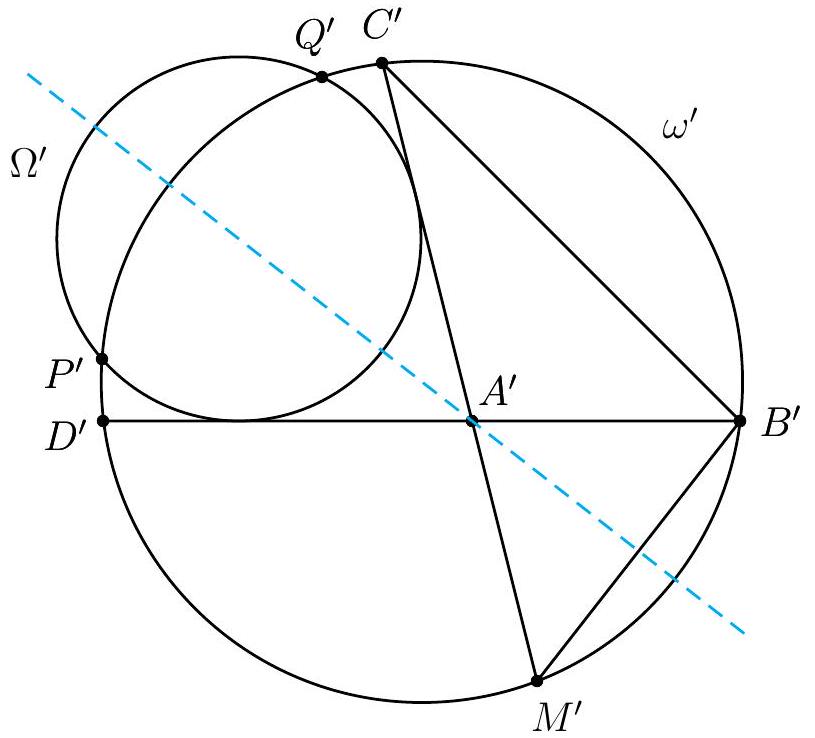\n\nSince inversion preserves angles, it turns out that\n\n$$\n\\angle A^{\\prime} B^{\\prime} M^{\\prime}=\\angle A^{\\prime} M^{\\prime} B^{\\prime}=\\angle A C B,\n$$\n\nand in particular triangle $A^{\\prime} B^{\\prime} M^{\\prime}$ is isosceles with basis $B^{\\prime} M^{\\prime}$.\nThe image of $C M$ is the circumcircle of $B^{\\prime} C^{\\prime} M^{\\prime}$, which we denote by $\\omega^{\\prime}$. It follows that the centers of both $\\omega^{\\prime}$ and the image $\\Omega^{\\prime}$ of $\\Omega$ lie on the perpendicular bisector of $B^{\\prime} M^{\\prime}$. Therefore, the whole transformed diagram is symmetric with respect to the perpendicular bisector of $B^{\\prime} M^{\\prime}$, and in particular the $\\operatorname{arcs} D^{\\prime} P^{\\prime}$ and $Q^{\\prime} C^{\\prime}$ of $\\omega^{\\prime}$ are equal.\n\nThis is enough to conclude that $\\angle D^{\\prime} B^{\\prime} P^{\\prime}=\\angle Q^{\\prime} B^{\\prime} C^{\\prime}$, which implies the conclusion.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 5", "solution_match": "\nSolution "}}
|
| 9 |
{"year": "2018", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "(a) Prove that for every real number $t$ such that $0<t<\\frac{1}{2}$ there exists a positive integer $n$ with the following property: for every set $S$ of $n$ positive integers there exist two different elements $x$ and $y$ of $S$, and a non-negative integer $m$ (i.e. $m \\geq 0$ ), such that\n\n$$\n|x-m y| \\leq t y\n$$\n\n(b) Determine whether for every real number $t$ such that $0<t<\\frac{1}{2}$ there exists an infinite set $S$ of positive integers such that\n\n$$\n|x-m y|>t y\n$$\n\nfor every pair of different elements $x$ and $y$ of $S$ and every positive integer $m$ (i.e. $m>0$ ).\n(Merlijn Staps, The Netherlands)", "solution": "Part (a) Let $n$ be any positive integer such that\n\n$$\n(1+t)^{n-1} \\geq \\frac{1}{t}\n$$\n\n(this inequality is actually true for every large enough $n$ due to Bernoulli's inequality).\nLet $S$ be any set of $n$ distinct positive integers, which we denote by\n\n$$\ns_{1}<s_{2}<\\ldots<s_{n}\n$$\n\nWe distinguish two cases.\n\n- If $s_{i+1} \\leq(1+t) s_{i}$ for some $i \\in\\{1, \\ldots, n-1\\}$, then\n\n$$\n\\left|s_{i+1}-s_{i}\\right|=s_{i+1}-s_{i} \\leq t s_{i}\n$$\n\nand therefore the required inequality is satisfied with $x=s_{i+1}, y=s_{i}$, and $m=1$.\n\n- If $s_{i+1}>(1+t) s_{i}$ for every $i \\in\\{1, \\ldots, n-1\\}$, then by induction we obtain that\n\n$$\ns_{n}>(1+t)^{n-1} s_{1} .\n$$\n\nAs a consequence, from (Q6.1) it follows that\n\n$$\n\\left|s_{1}\\right|=s_{1}<\\frac{1}{(1+t)^{n-1}} \\cdot s_{n} \\leq t s_{n}\n$$\n\nand therefore the required inequality is satisfied with $x=s_{1}, y=s_{n}$, and $m=0$.\n\nPart (b) (Explicit formula) We claim that an infinite set with the required property exists. To this end, we rewrite the required condition in the form\n\n$$\n\\left|\\frac{x}{y}-m\\right|>t\n$$\n\nThis is equivalent to saying that the distance between the ratio $x / y$ and the set of positive integers is greater than $t$.\n\nNow we construct an increasing sequence $s_{n}$ of odd coprime positive integers satisfying\n\n$$\n\\frac{1}{2}-\\frac{1}{2 s_{n}}>t \\quad \\forall n \\geq 1\n$$\n\nand such that for every $j>i$ it turns out that\n\n$$\n\\frac{s_{i}}{s_{j}}<\\frac{1}{2} \\quad \\text { and } \\quad t<\\left\\{\\frac{s_{j}}{s_{i}}\\right\\}<\\frac{1}{2}\n$$\n\nwhere $\\{\\alpha\\}$ denotes the fractional part of $\\alpha$. This is enough to show that the set $S:=\\left\\{s_{n}: n \\geq 1\\right\\}$ has the required property.\n\nTo this end, we consider the sequence defined recursively by\n\n$$\ns_{n+1}=\\frac{\\left(s_{1} \\cdot \\ldots \\cdot s_{n}\\right)^{2}+1}{2}\n$$\n\nwith $s_{1}$ large enough. An easy induction shows that this is an increasing sequence of odd positive integers. For every $i \\in\\{1, \\ldots, n\\}$ it turns out that\n\n$$\n\\frac{s_{i}}{s_{n+1}} \\leq \\frac{2}{s_{i}} \\leq \\frac{2}{s_{1}}<\\frac{1}{2}\n$$\n\nbecause $s_{1}$ is large enough, which proves the first relation in (Q6.3). Moreover, it turns out that\n\n$$\n\\frac{s_{n+1}}{s_{i}}=\\frac{\\left(s_{1} \\cdot \\ldots \\cdot s_{n}\\right)^{2}}{2 s_{i}}+\\frac{1}{2 s_{i}}\n$$\n\nThe first term is a positive integer plus $1 / 2$, from which it follows that the distance of $s_{n+1} / s_{i}$ from the positive integers is greater than or equal to\n\n$$\n\\frac{1}{2}-\\frac{1}{2 s_{i}} \\geq \\frac{1}{2}-\\frac{1}{2 s_{1}}\n$$\n\nwhich is greater than $t$ if $s_{1}$ is large enough. This proves the second relation in (Q6.3).\nPart (b) (Arithmetic approach) We produce an increasing sequence $s_{n}$ of odd and coprime positive integers that satisfies (Q6.3) every $j>i$. As in the previous solution, this is enough to conclude.\n\nWe argue by induction. To begin with, we choose $s_{1}$ to be any odd integer satisfying the inequality in (Q6.2). Let us assume now that $s_{1}, \\ldots, s_{n}$ have already been chosen, and let us choose $s_{n+1}$ in such a way that\n\n$$\ns_{n+1} \\equiv \\frac{s_{i}-1}{2} \\quad\\left(\\bmod s_{i}\\right) \\quad \\forall i \\in\\{1, \\ldots, n\\}\n$$\n\nWe can solve this system because the previously chosen integers are odd and coprime. Moreover, any solution of this system is coprime with $s_{1}, \\ldots, s_{n}$. Indeed, for every $1 \\leq i \\leq n$ it turns out that\n\n$$\ns_{n+1}=\\frac{s_{i}-1}{2}+k_{i} s_{i}\n$$\n\nfor some positive integer $k_{i}$. Therefore, any prime $p$ that divides both $s_{n+1}$ and $s_{i}$ divides also $\\left(2 k_{i}+1\\right) s_{i}-2 s_{n+1}=1$, which is absurd. Finally, we observe that we can assume that $s_{n+1}$ is odd and large enough. In this way we can guarantee that\n\n$$\n\\frac{s_{i}}{s_{n+1}}<\\frac{1}{2} \\quad \\forall i \\in\\{1, \\ldots, n\\}\n$$\n\nwhich is the first requirement in (Q6.3), and\n\n$$\nk_{i}+t<k_{i}+\\frac{1}{2}-\\frac{1}{2 s_{i}}=\\frac{s_{n+1}}{s_{i}}<k_{i}+\\frac{1}{2} \\quad \\forall i \\in\\{1, \\ldots, n\\}\n$$\n\nwhich implies the second requirement in (Q6.3).\nPart (b) (Algebraic approach) Again we produce an increasing sequence $s_{n}$ of positive integers that satisfies (Q6.3) every $j>i$.\n\nTo this end, for every positive integer $x$, we define its security region\n\n$$\nS(x):=\\bigcup_{n \\geq 1}\\left((n+t) x,\\left(n+\\frac{1}{2}\\right) x\\right) .\n$$\n\nThe security region $S(x)$ is a periodic countable union of intervals of length $\\left(\\frac{1}{2}-t\\right) x$, whose left-hand or right-hand endpoints form an arithmetic sequence. It has the property that\n\n$$\nt<\\left\\{\\frac{y}{x}\\right\\}<\\frac{1}{2} \\quad \\forall y \\in S(x)\n$$\n\nNow we prove by induction that we can choose a sequence $s_{n}$ of positive integers satisfying (Q6.3) and in addition the fact that every interval of the security region $S\\left(s_{n}\\right)$ contains at least one interval of $S\\left(s_{n-1}\\right)$.\n\nTo begin with, we choose $s_{1}$ large enough so that the length of the intervals of $S\\left(s_{1}\\right)$ is larger than 1. This guarantees that any interval of $S\\left(s_{1}\\right)$ contains at least a positive integer. Now let us choose a positive integer $s_{2} \\in S\\left(s_{1}\\right)$ that is large enough. This guarantees that $s_{1} / s_{2}$ is small enough, that the fractional part of $s_{2} / s_{1}$ is in $(t, 1 / 2)$, and that every interval of the security region $S\\left(s_{2}\\right)$ contains at least one interval of $S\\left(s_{1}\\right)$, and hence at least one positive integer.\n\nLet us now assume that $s_{1}, \\ldots, s_{n}$ have been already chosen with the required properties. We know that every interval of $S\\left(s_{n}\\right)$ contains at least one interval of $S\\left(s_{n-1}\\right)$, which in turn contains an interval in $S\\left(s_{n-2}\\right)$, and so on up to $S\\left(s_{1}\\right)$. As a consequence, we can choose a large enough positive integer $s_{n+1}$ that lies in $S\\left(s_{k}\\right)$ for every $k \\in\\{1, \\ldots, n\\}$. Since $s_{n+1}$ is large enough, we are sure that\n\n$$\n\\frac{s_{k}}{s_{n+1}}<t \\quad \\forall k \\in\\{1, \\ldots, n\\}\n$$\n\nMoreover, we are sure also that all the intervals of $S\\left(s_{n+1}\\right)$ are large enough, and therefore they contain at least one interval of $S\\left(s_{n}\\right)$, which in turn contains at least one interval of $S\\left(s_{n-1}\\right)$, and so on. Finally, the condition\n\n$$\nt<\\left\\{\\frac{s_{n-1}}{s_{n}}\\right\\}<\\frac{1}{2}\n$$\n\nis guaranteed by the fact that $s_{n+1}$ was chosen in an interval that is contained in $S\\left(s_{k}\\right)$ for every $k \\in\\{1, \\ldots, n\\}$. This completes the induction.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "# Problem 6", "solution_match": "# Solution"}}
|
|
|
|
| 2 |
{"year": "2018", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Consider the set\n\n$$\nA=\\left\\{1+\\frac{1}{k}: k=1,2,3, \\ldots\\right\\}\n$$\n\n(a) Prove that every integer $x \\geq 2$ can be written as the product of one or more elements of $A$, which are not necessarily different.\n(b) For every integer $x \\geq 2$, let $f(x)$ denote the minimum integer such that $x$ can be written as the product of $f(x)$ elements of $A$, which are not necessarily different.\nProve that there exist infinitely many pairs $(x, y)$ of integers with $x \\geq 2, y \\geq 2$, and\n\n$$\nf(x y)<f(x)+f(y) .\n$$\n\n(Pairs $\\left(x_{1}, y_{1}\\right)$ and $\\left(x_{2}, y_{2}\\right)$ are different if $x_{1} \\neq x_{2}$ or $\\left.y_{1} \\neq y_{2}\\right)$.\n(Mihail Baluna, Romania)", "solution": "Every integer $x \\geq 2$ can be written as the telescopic product of $x-1$ elements of $A$ as\n\n$$\nx=\\left(1+\\frac{1}{x-1}\\right) \\cdot\\left(1+\\frac{1}{x-2}\\right) \\cdot \\ldots \\cdot\\left(1+\\frac{1}{2}\\right) \\cdot\\left(1+\\frac{1}{1}\\right)\n$$\n\nwhich is enough to establish part (a). We now consider part (b). Notice that for any positive integer $k$ we have\n\n$$\nf\\left(2^{k}+1\\right) \\leq k+1\n$$\n\nbecause $2^{k}+1=\\left(1+\\frac{1}{2^{k}}\\right) \\cdot 2^{k}$ is a representation of $2^{k}+1$ as a product of $k+1$ elements of $A$. We claim that all the pairs $(x, y)$ of the form\n\n$$\nx=5, \\quad y=\\frac{2^{4 k+2}+1}{5}\n$$\n\nsatisfy the required inequality. Notice that $y$ is an integer for any positive value of $k$, because $2^{4 k+2}+1 \\equiv 16^{k} \\cdot 4+1 \\equiv 5 \\equiv 0(\\bmod 5)$. Furthermore, $f(x y)=f\\left(2^{4 k+2}+1\\right) \\leq 4 k+3$ (and $f(x)=f\\left(2^{2}+1\\right) \\leq 3$ ) by the above. We now need some lower bounds on the values of $f$. Notice that no element of $A$ exceeds 2, and therefore the product of at most $k$ elements of $A$ does not exceed $2^{k}$ : it follows that\n\n$$\nf(n) \\geq\\left\\lceil\\log _{2}(n)\\right\\rceil\n$$\n\nand in particular that\n\n$$\nf(5)=f\\left(2^{2}+1\\right) \\geq\\left\\lceil\\log _{2}(5)\\right\\rceil=3\n$$\n\nWe have thus proven $f(x)=f(5)=3$. We want to show $f(x y)<f(x)+f(y)$, and since we know $f(x y) \\leq 4 k+3$ and $f(x)=3$ we are reduced to showing $f(y)>4 k$. Since $y>2^{4 k-1}$, from (Q2.1) we already know that $f(y) \\geq 4 k$, and hence we just need to exclude that $f(y)=4 k$. Let us assume that we can represent $y$ in the form $a_{1} \\cdot \\ldots a_{4 k}$ with every $a_{i}$ in $A$. At least one of the $a_{i}$ is not 2 (otherwise the product would be a power of 2 , while $y$ is odd), and hence it is less than or equal to $3 / 2$. It follows that\n\n$$\na_{1} \\cdot \\ldots \\cdot a_{4 k} \\leq 2^{4 k-1} \\cdot \\frac{3}{2}=15 \\cdot \\frac{2^{4 k-2}}{5}<\\frac{2^{4 k+2}}{5}<y\n$$\n\nwhich contradicts the fact that $a_{1} \\cdot \\ldots \\cdot a_{4 k}$ is a representation of $y$.\nNote. Using a similar approach one can also prove that all pairs of the form\n\n$$\n\\left(3, \\frac{2^{2 k+1}+1}{3}\\right) \\quad \\text { and } \\quad\\left(11, \\frac{2^{10 k+5}+1}{11}\\right)\n$$\n\nsatisfy the required inequality.\nSecond solution As in the previous solution we obtain the lower bound (Q2.1).\nNow we claim that all the pairs of the form\n\n$$\nx=2^{k}+1, \\quad y=4^{k}-2^{k}+1\n$$\n\nsatisfy the required inequality when $k$ is large enough. To begin with, it is easy to see that\n\n$$\n2^{k}+1=\\frac{2^{k}+1}{2^{k}} \\cdot \\underbrace{2 \\cdot \\ldots \\cdot 2}_{k \\text { terms }} \\quad \\text { and } \\quad 2^{3 k}+1=\\frac{2^{3 k}+1}{2^{3 k}} \\cdot \\underbrace{2 \\cdot \\ldots \\cdot 2}_{3 k \\text { terms }}\n$$\n\nwhich shows that $f\\left(2^{k}+1\\right) \\leq k+1$ and $f\\left(2^{3 k}+1\\right) \\leq 3 k+1$. On the other hand, from (Q2.1) we deduce that the previous inequalities are actually equalities, and therefore\n\n$$\nf(x)=k+1 \\quad \\text { and } \\quad f(x y)=3 k+1\n$$\n\nTherefore, it remain to show that $f(y)>2 k$. Since $y>2^{2 k-1}$ (for $k \\geq 1$ ), from (Q2.1) we already know that $f(y) \\geq 2 k$, and hence we just need to exclude that $f(y)=2 k$. Let us assume that we can represent $y$ in the form $a_{1} \\cdot \\ldots \\cdot a_{2 k}$. At least one of the factors is not 2 , and hence it is less than or equal to $3 / 2$. Thus when $k$ is large enough it follows that\n\n$$\na_{1} \\cdot \\ldots \\cdot a_{2 k} \\leq 2^{2 k-1} \\cdot \\frac{3}{2}=\\frac{3}{4} \\cdot 2^{2 k}<2^{2 k}-2^{k}<y\n$$\n\nwhich contradicts the fact that $a_{1} \\cdot \\ldots \\cdot a_{2 k}$ is a representation of $y$.\nThird solution Let's start by showing that $(x, y)=(7,7)$ satisfies $f(x y)<f(x)+f(y)$. We have $f(7) \\geq 4$ since 7 cannot be written as the product of 3 or fewer elements of $A$ : indeed $2^{3}>7$, and any other product of at most three elements of $A$ does not exceed $2^{2} \\cdot \\frac{3}{2}=6<7$. On the other hand, $f(49) \\leq 7$ since $49=2 \\cdot 2 \\cdot 2 \\cdot 2 \\cdot 2 \\cdot \\frac{3}{2} \\cdot \\frac{49}{48}$.\n\nSuppose by contradiction that there exist only finitely many pairs $(x, y)$ that satisfy $f(x y)<$ $f(x)+f(y)$. This implies that there exists $M$ large enough so that whenever $a>M$ or $b>M$ holds we have $f(a b)=f(a)+f(b)$ (indeed, it is clear that the reverse inequality $f(a b) \\leq f(a)+f(b)$ is always satisfied).\n\nNow take any pair $(x, y)$ that satisfies $f(x y)<f(x)+f(y)$ and let $n>M$ be any integer. We obtain\n\n$$\nf(n)+f(x y)=f(n x y)=f(n x)+f(y)=f(n)+f(x)+f(y),\n$$\n\nwhich contradicts $f(x y)<f(x)+f(y)$.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 2", "solution_match": "\nSolution "}}
|
| 3 |
{"year": "2018", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "The $n$ contestants of an EGMO are named $C_{1}, \\ldots, C_{n}$. After the competition they queue in front of the restaurant according to the following rules.\n\n- The Jury chooses the initial order of the contestants in the queue.\n- Every minute, the Jury chooses an integer $i$ with $1 \\leq i \\leq n$.\n- If contestant $C_{i}$ has at least $i$ other contestants in front of her, she pays one euro to the Jury and moves forward in the queue by exactly $i$ positions.\n- If contestant $C_{i}$ has fewer than $i$ other contestants in front of her, the restaurant opens and the process ends.\n(a) Prove that the process cannot continue indefinitely, regardless of the Jury's choices.\n(b) Determine for every $n$ the maximum number of euros that the Jury can collect by cunningly choosing the initial order and the sequence of moves.\n(Hungary)", "solution": "The maximal number of euros is $2^{n}-n-1$.\nTo begin with, we show that it is possible for the Jury to collect this number of euros. We argue by induction. Let us assume that the Jury can collect $M_{n}$ euros in a configuration with $n$ contestants. Then we show that the Jury can collect at least $2 M_{n}+n$ moves in a configuration with $n+1$ contestants. Indeed, let us begin with all the contestants lined up in reverse order. In the first $M_{n}$ moves the Jury keeps $C_{n+1}$ in first position and reverses the order of the remaining contestants, then in the next $n$ moves all contestants $C_{1}, \\ldots, C_{n}$ (in this order) jump over $C_{n+1}$ and end up in the first $n$ positions of the line in reverse order, and finally in the last $M_{n}$ moves the Jury rearranges the first $n$ positions.\n\nSince $M_{1}=0$ and $M_{n+1} \\geq 2 M_{n}+n$, an easy induction shows that $M_{n} \\geq 2^{n}-n-1$.\n\nLet us show now that at most $2^{n}-n-1$ moves are possible. To this end, let us identify a line of contestants with a permutation $\\sigma$ of $\\{1, \\ldots, n\\}$. To each permutation we associate the set of reverse pairs\n\n$$\nR(\\sigma):=\\{(i, j): 1 \\leq i<j \\leq n \\text { and } \\sigma(i)>\\sigma(j)\\}\n$$\n\nand the nonnegative integer\n\n$$\nW(\\sigma):=\\sum_{(i, j) \\in R(\\sigma)} 2^{i}\n$$\n\nwhich we call the total weight of the permutation. We claim that the total weight decreases after any move of the contestants. Indeed, let us assume that $C_{i}$ moves forward in the queue, let $\\sigma$ be the permutation before the move, and let $\\sigma^{\\prime}$ denote the permutation after the move. Since $C_{i}$ jumps over exactly $i$ contestants, necessarily she jumps over at least one contestant $C_{j}$ with index\n$j>i$. This means that the pair $(i, j)$ is reverse with respect to $\\sigma$ but not with respect to $\\sigma^{\\prime}$, and this yields a reduction of $2^{i}$ in the total weight. On the other hand, the move by $C_{i}$ can create new reverse pairs of the form $(k, i)$ with $k<i$, but their total contribution is at most\n\n$$\n2^{0}+2^{1}+\\ldots+2^{i-1}=2^{i}-1\n$$\n\nIn conclusion, when passing from $\\sigma$ to $\\sigma^{\\prime}$, at least one term $2^{i}$ disappears from the computation of the total weight, and the sum of all the new terms that might have been created is at most $2^{i}-1$. This shows that $W\\left(\\sigma^{\\prime}\\right) \\leq W(\\sigma)-1$.\n\nWe conclude by observing that the maximum possible value of $W(\\sigma)$ is realized when all pairs are reverse, in which case\n\n$$\nW(\\sigma)=\\sum_{i=1}^{n}(i-1) 2^{i}=2^{n}-n-1 .\n$$\n\nThis proves that the number of moves is less than or equal to $2^{n}-n-1$, and in particular it is finite.\n\nAlternative solution As in the previous solution, the fundamental observation is again that, when a contestant $C_{i}$ moves forward, necessarily she has to jump over at least one contestant $C_{j}$ with $j>i$.\n\nLet us show now that the process ends after a finite number of moves. Let us assume that this is not the case. Then at least one contestant moves infinitely many times. Let $i_{0}$ be the largest index such that $C_{i_{0}}$ moves infinitely many times. Then necessarily $C_{i_{0}}$ jumps infinitely many times over some fixed $C_{j_{0}}$ with $j_{0}>i_{0}$. On the other hand, we know that $C_{j_{0}}$ makes only a finite number of moves, and therefore she can precede $C_{i_{0}}$ in the line only a finite number of times, which is absurd.\n\nIn order to estimate from above the maximal number of moves, we show that the contestant $C_{i}$ can make at most $2^{n-i}-1$ moves. Indeed, let us argue by \"backward extended induction\". To begin with, we observe that the estimate is trivially true for $C_{n}$ because she has no legal move.\n\nLet us assume now that the estimate has been proved for $C_{i}, C_{i+1}, \\ldots, C_{n}$, and let us prove it for $C_{i-1}$. When $C_{i-1}$ moves, at least one contestant $C_{j}$ with $j>i-1$ must precede her in the line. The initial configuration can provide at most $n-i$ contestants with larger index in front of $C_{i-1}$, which means at most $n-i$ moves for $C_{i-1}$. All other moves are possible only if some contestant in the range $C_{i}, C_{i+1}, \\ldots, C_{n}$ jumps over $C_{i-1}$ during her moves. As a consequence, the total number of moves of $C_{i-1}$ is at most\n\n$$\nn-i+\\sum_{k=i}^{n}\\left(2^{n-k}-1\\right)=2^{n-i+1}-1\n$$\n\nSumming over all indices we obtain that\n\n$$\n\\sum_{i=1}^{n}\\left(2^{n-i}-1\\right)=2^{n}-n-1\n$$\n\nwhich gives an estimate for the total number of moves.\nThe same example of the first solution shows that this upper bound can actually be achieved.\nComment In every move of the example, the moving contestant jumps over exactly one contestant with larger index (and as a consequence over all contestants with smaller index).", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 3", "solution_match": "\nSolution "}}
|
| 4 |
{"year": "2018", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "A domino is a $1 \\times 2$ or $2 \\times 1$ tile.\nLet $n \\geq 3$ be an integer. Dominoes are placed on an $n \\times n$ board in such a way that each domino covers exactly two cells of the board, and dominoes do not overlap.\n\nThe value of a row or column is the number of dominoes that cover at least one cell of this row or column. The configuration is called balanced if there exists some $k \\geq 1$ such that each row and each column has a value of $k$.\n\nProve that a balanced configuration exists for every $n \\geq 3$, and find the minimum number of dominoes needed in such a configuration.\n(Merlijn Staps, The Netherlands)", "solution": "The minimal number of dominoes required in a balanced configuration is $2 n / 3$ if $n$ is a multiple of 3 , and $2 n$ otherwise.\n\nIn order to show that this number is necessary, we count in two different ways the number of elements of the set $S$ of all pairs $(\\ell, d)$, where $\\ell$ is a row or a column of the board, and $d$ is a domino that covers at least one cell of that row or column. On the one hand, since each row or column intersects the same number $k$ of dominoes, the set $S$ has $2 n k$ elements. On the other hand, since each domino intersects 3 rows/columns, the set $S$ has $3 D$ elements, where $D$ is the total number of dominoes on the board. This leads to the equality\n\n$$\n2 n k=3 D\n$$\n\nIf $n$ is a multiple of 3 , from the trivial inequality $k \\geq 1$ we obtain that $D \\geq 2 n / 3$. If $n$ is not a multiple of 3 , then $k$ is a multiple of 3 , which means that $k \\geq 3$ and hence $D \\geq 2 n$.\n\nNow we need to exhibit a balanced configuration with this number of dominoes. The following diagram shows a balanced configuration with $n=3$ and $k=1$.\n\n\nIf $n$ is any multiple of 3 , we can obtain a balanced configuration with $k=1$ by using $n / 3$ of these $3 \\times 3$ blocks along the principal diagonal of the board.\n\nThe following diagrams show balanced configurations with $k=3$ and $n \\in\\{4,5,6,7\\}$.\n\n\nAny $n \\geq 8$ can be written in the form $4 A+r$ where $A$ is a positive integer and $r \\in\\{4,5,6,7\\}$. Therefore, we can obtain a balanced configuration with $n \\geq 8$ and $k=3$ by using one block with size $r \\times r$, and $A$ blocks with size $4 \\times 4$ along the principal diagonal of the board. In particular, this construction covers all the cases where $n$ is not a multiple of 3 .", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution "}}
|
| 5 |
+
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "1 Let $M$ be the midpoint of the arc $A B$ that does not contain $C$, let $V$ be the intersection of $\\Omega$ and $\\Gamma$, and let $U$ be the intersection of $\\Omega$ and $A B$.\n\n\nThe proof can be divided in two steps:\n\n1). Proving that $M P \\cdot M Q=M B^{2}$.\n\nIt is well-known that $V, U$ and $M$ are collinear (indeed the homothety with center in $V$ that sends $\\Omega$ to $\\Gamma$ sends $U$ to the point of $\\Gamma$ where the tangent to $\\Gamma$ is parallel to $A B$, and this point is $M$ ), and\n\n$$\nM V \\cdot M U=M A^{2}=M B^{2}\n$$\n\nThis follows from the similitude between the triangles $\\triangle M A V$ and $\\triangle M U A$. Alternatively, it is a consequence of the following well-known lemma: Given a circle $\\Gamma$ with a chord $A B$, let $M$ be the middle point of one of the two arcs $A B$. Take a line through $M$ which intersects $\\Gamma$ again at $X$ and $A B$ at $Y$. Then $M X \\cdot M Y$ is independent of the choice of the line.\nComputing the power of $M$ with respect to $\\Omega$ we obtain that\n\n$$\nM P \\cdot M Q=M U \\cdot M V=M B^{2}\n$$\n\n2). Conclude the proof given that $M P \\cdot M Q=M B^{2}$.\n\nThe relation $M P \\cdot M Q=M B^{2}$ in turn implies that triangle $\\triangle M B P$ is similar to triangle $\\triangle M Q B$, and in particular $\\angle M B P=\\angle M Q B$. Keeping into account that $\\angle M C B=$ $\\angle M B A$, we finally conclude that\n\n$$\n\\angle Q B C=\\angle M Q B-\\angle M C B=\\angle M B P-\\angle M B A=\\angle P B A\n$$\n\nas required.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 5", "solution_match": "\nSolution "}}
|
| 6 |
+
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "2 The second solution is in fact a different proof of the first part of Solution 1.\nLet us consider the inversion with respect to circle with center $M$ and radius $M A=M B$. This inversion switches $A B$ and $\\Gamma$, and fixes the line passing through $M, U, V$. As a consequence, it keeps $\\Omega$ fixed, and therefore it switches $P$ and $Q$. This is because they are the intersections between the fixed line $M C$ and $\\Omega$, and the only fixed point on the segment $M C$ is its intersection with the inversion circle (thus $P$ and $Q$ are switched). This implies that $M P \\cdot M Q=M B^{2}$.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 5", "solution_match": "\nSolution "}}
|
| 7 |
+
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "3 This solution is instead a different proof of the second step of Solution 1.\nLet $I$ and $J$ be the incenter and the $C$-excenter of $\\triangle A B C$ respectively. It is well-known that $M A=M I=M J$, therefore the relation $M P \\cdot M Q=M A^{2}$ implies that $(P, Q, I, J)=-1$.\n\nNow observe that $\\angle I B J=90^{\\circ}$, thus $B I$ is the angle bisector of $\\angle P B Q$ as it is well-known from the theory of harmonic pencils, and this leads easily to the conclusion.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 5", "solution_match": "\nSolution "}}
|
| 8 |
+
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of triangle $A B C$. A circle $\\Omega$ is tangent to the line segment $A B$ and is tangent to $\\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\\angle B C A$ intersects $\\Omega$ at two different points $P$ and $Q$.\n\nProve that $\\angle A B P=\\angle Q B C$.\n(Dominika Regiec, Poland)", "solution": "4 Let $D$ denote the intersection of $A B$ and $C M$. Let us consider an inversion with respect to $B$, and let us use primes to denote corresponding points in the transformed diagram, with the gentlemen agreement that $B^{\\prime}=B$.\n\n\nSince inversion preserves angles, it turns out that\n\n$$\n\\angle A^{\\prime} B^{\\prime} M^{\\prime}=\\angle A^{\\prime} M^{\\prime} B^{\\prime}=\\angle A C B,\n$$\n\nand in particular triangle $A^{\\prime} B^{\\prime} M^{\\prime}$ is isosceles with basis $B^{\\prime} M^{\\prime}$.\nThe image of $C M$ is the circumcircle of $B^{\\prime} C^{\\prime} M^{\\prime}$, which we denote by $\\omega^{\\prime}$. It follows that the centers of both $\\omega^{\\prime}$ and the image $\\Omega^{\\prime}$ of $\\Omega$ lie on the perpendicular bisector of $B^{\\prime} M^{\\prime}$. Therefore, the whole transformed diagram is symmetric with respect to the perpendicular bisector of $B^{\\prime} M^{\\prime}$, and in particular the $\\operatorname{arcs} D^{\\prime} P^{\\prime}$ and $Q^{\\prime} C^{\\prime}$ of $\\omega^{\\prime}$ are equal.\n\nThis is enough to conclude that $\\angle D^{\\prime} B^{\\prime} P^{\\prime}=\\angle Q^{\\prime} B^{\\prime} C^{\\prime}$, which implies the conclusion.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "\nProblem 5", "solution_match": "\nSolution "}}
|
| 9 |
{"year": "2018", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "(a) Prove that for every real number $t$ such that $0<t<\\frac{1}{2}$ there exists a positive integer $n$ with the following property: for every set $S$ of $n$ positive integers there exist two different elements $x$ and $y$ of $S$, and a non-negative integer $m$ (i.e. $m \\geq 0$ ), such that\n\n$$\n|x-m y| \\leq t y\n$$\n\n(b) Determine whether for every real number $t$ such that $0<t<\\frac{1}{2}$ there exists an infinite set $S$ of positive integers such that\n\n$$\n|x-m y|>t y\n$$\n\nfor every pair of different elements $x$ and $y$ of $S$ and every positive integer $m$ (i.e. $m>0$ ).\n(Merlijn Staps, The Netherlands)", "solution": "Part (a) Let $n$ be any positive integer such that\n\n$$\n(1+t)^{n-1} \\geq \\frac{1}{t}\n$$\n\n(this inequality is actually true for every large enough $n$ due to Bernoulli's inequality).\nLet $S$ be any set of $n$ distinct positive integers, which we denote by\n\n$$\ns_{1}<s_{2}<\\ldots<s_{n}\n$$\n\nWe distinguish two cases.\n\n- If $s_{i+1} \\leq(1+t) s_{i}$ for some $i \\in\\{1, \\ldots, n-1\\}$, then\n\n$$\n\\left|s_{i+1}-s_{i}\\right|=s_{i+1}-s_{i} \\leq t s_{i}\n$$\n\nand therefore the required inequality is satisfied with $x=s_{i+1}, y=s_{i}$, and $m=1$.\n\n- If $s_{i+1}>(1+t) s_{i}$ for every $i \\in\\{1, \\ldots, n-1\\}$, then by induction we obtain that\n\n$$\ns_{n}>(1+t)^{n-1} s_{1} .\n$$\n\nAs a consequence, from (Q6.1) it follows that\n\n$$\n\\left|s_{1}\\right|=s_{1}<\\frac{1}{(1+t)^{n-1}} \\cdot s_{n} \\leq t s_{n}\n$$\n\nand therefore the required inequality is satisfied with $x=s_{1}, y=s_{n}$, and $m=0$.\n\nPart (b) (Explicit formula) We claim that an infinite set with the required property exists. To this end, we rewrite the required condition in the form\n\n$$\n\\left|\\frac{x}{y}-m\\right|>t\n$$\n\nThis is equivalent to saying that the distance between the ratio $x / y$ and the set of positive integers is greater than $t$.\n\nNow we construct an increasing sequence $s_{n}$ of odd coprime positive integers satisfying\n\n$$\n\\frac{1}{2}-\\frac{1}{2 s_{n}}>t \\quad \\forall n \\geq 1\n$$\n\nand such that for every $j>i$ it turns out that\n\n$$\n\\frac{s_{i}}{s_{j}}<\\frac{1}{2} \\quad \\text { and } \\quad t<\\left\\{\\frac{s_{j}}{s_{i}}\\right\\}<\\frac{1}{2}\n$$\n\nwhere $\\{\\alpha\\}$ denotes the fractional part of $\\alpha$. This is enough to show that the set $S:=\\left\\{s_{n}: n \\geq 1\\right\\}$ has the required property.\n\nTo this end, we consider the sequence defined recursively by\n\n$$\ns_{n+1}=\\frac{\\left(s_{1} \\cdot \\ldots \\cdot s_{n}\\right)^{2}+1}{2}\n$$\n\nwith $s_{1}$ large enough. An easy induction shows that this is an increasing sequence of odd positive integers. For every $i \\in\\{1, \\ldots, n\\}$ it turns out that\n\n$$\n\\frac{s_{i}}{s_{n+1}} \\leq \\frac{2}{s_{i}} \\leq \\frac{2}{s_{1}}<\\frac{1}{2}\n$$\n\nbecause $s_{1}$ is large enough, which proves the first relation in (Q6.3). Moreover, it turns out that\n\n$$\n\\frac{s_{n+1}}{s_{i}}=\\frac{\\left(s_{1} \\cdot \\ldots \\cdot s_{n}\\right)^{2}}{2 s_{i}}+\\frac{1}{2 s_{i}}\n$$\n\nThe first term is a positive integer plus $1 / 2$, from which it follows that the distance of $s_{n+1} / s_{i}$ from the positive integers is greater than or equal to\n\n$$\n\\frac{1}{2}-\\frac{1}{2 s_{i}} \\geq \\frac{1}{2}-\\frac{1}{2 s_{1}}\n$$\n\nwhich is greater than $t$ if $s_{1}$ is large enough. This proves the second relation in (Q6.3).\nPart (b) (Arithmetic approach) We produce an increasing sequence $s_{n}$ of odd and coprime positive integers that satisfies (Q6.3) every $j>i$. As in the previous solution, this is enough to conclude.\n\nWe argue by induction. To begin with, we choose $s_{1}$ to be any odd integer satisfying the inequality in (Q6.2). Let us assume now that $s_{1}, \\ldots, s_{n}$ have already been chosen, and let us choose $s_{n+1}$ in such a way that\n\n$$\ns_{n+1} \\equiv \\frac{s_{i}-1}{2} \\quad\\left(\\bmod s_{i}\\right) \\quad \\forall i \\in\\{1, \\ldots, n\\}\n$$\n\nWe can solve this system because the previously chosen integers are odd and coprime. Moreover, any solution of this system is coprime with $s_{1}, \\ldots, s_{n}$. Indeed, for every $1 \\leq i \\leq n$ it turns out that\n\n$$\ns_{n+1}=\\frac{s_{i}-1}{2}+k_{i} s_{i}\n$$\n\nfor some positive integer $k_{i}$. Therefore, any prime $p$ that divides both $s_{n+1}$ and $s_{i}$ divides also $\\left(2 k_{i}+1\\right) s_{i}-2 s_{n+1}=1$, which is absurd. Finally, we observe that we can assume that $s_{n+1}$ is odd and large enough. In this way we can guarantee that\n\n$$\n\\frac{s_{i}}{s_{n+1}}<\\frac{1}{2} \\quad \\forall i \\in\\{1, \\ldots, n\\}\n$$\n\nwhich is the first requirement in (Q6.3), and\n\n$$\nk_{i}+t<k_{i}+\\frac{1}{2}-\\frac{1}{2 s_{i}}=\\frac{s_{n+1}}{s_{i}}<k_{i}+\\frac{1}{2} \\quad \\forall i \\in\\{1, \\ldots, n\\}\n$$\n\nwhich implies the second requirement in (Q6.3).\nPart (b) (Algebraic approach) Again we produce an increasing sequence $s_{n}$ of positive integers that satisfies (Q6.3) every $j>i$.\n\nTo this end, for every positive integer $x$, we define its security region\n\n$$\nS(x):=\\bigcup_{n \\geq 1}\\left((n+t) x,\\left(n+\\frac{1}{2}\\right) x\\right) .\n$$\n\nThe security region $S(x)$ is a periodic countable union of intervals of length $\\left(\\frac{1}{2}-t\\right) x$, whose left-hand or right-hand endpoints form an arithmetic sequence. It has the property that\n\n$$\nt<\\left\\{\\frac{y}{x}\\right\\}<\\frac{1}{2} \\quad \\forall y \\in S(x)\n$$\n\nNow we prove by induction that we can choose a sequence $s_{n}$ of positive integers satisfying (Q6.3) and in addition the fact that every interval of the security region $S\\left(s_{n}\\right)$ contains at least one interval of $S\\left(s_{n-1}\\right)$.\n\nTo begin with, we choose $s_{1}$ large enough so that the length of the intervals of $S\\left(s_{1}\\right)$ is larger than 1. This guarantees that any interval of $S\\left(s_{1}\\right)$ contains at least a positive integer. Now let us choose a positive integer $s_{2} \\in S\\left(s_{1}\\right)$ that is large enough. This guarantees that $s_{1} / s_{2}$ is small enough, that the fractional part of $s_{2} / s_{1}$ is in $(t, 1 / 2)$, and that every interval of the security region $S\\left(s_{2}\\right)$ contains at least one interval of $S\\left(s_{1}\\right)$, and hence at least one positive integer.\n\nLet us now assume that $s_{1}, \\ldots, s_{n}$ have been already chosen with the required properties. We know that every interval of $S\\left(s_{n}\\right)$ contains at least one interval of $S\\left(s_{n-1}\\right)$, which in turn contains an interval in $S\\left(s_{n-2}\\right)$, and so on up to $S\\left(s_{1}\\right)$. As a consequence, we can choose a large enough positive integer $s_{n+1}$ that lies in $S\\left(s_{k}\\right)$ for every $k \\in\\{1, \\ldots, n\\}$. Since $s_{n+1}$ is large enough, we are sure that\n\n$$\n\\frac{s_{k}}{s_{n+1}}<t \\quad \\forall k \\in\\{1, \\ldots, n\\}\n$$\n\nMoreover, we are sure also that all the intervals of $S\\left(s_{n+1}\\right)$ are large enough, and therefore they contain at least one interval of $S\\left(s_{n}\\right)$, which in turn contains at least one interval of $S\\left(s_{n-1}\\right)$, and so on. Finally, the condition\n\n$$\nt<\\left\\{\\frac{s_{n-1}}{s_{n}}\\right\\}<\\frac{1}{2}\n$$\n\nis guaranteed by the fact that $s_{n+1}$ was chosen in an interval that is contained in $S\\left(s_{k}\\right)$ for every $k \\in\\{1, \\ldots, n\\}$. This completes the induction.", "metadata": {"resource_path": "EGMO/segmented/en-2018-solutions.jsonl", "problem_match": "# Problem 6", "solution_match": "# Solution"}}
|
EGMO/segmented/en-2019-solutions-day2.jsonl
CHANGED
|
@@ -3,10 +3,10 @@
|
|
| 3 |
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "(Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.", "solution": "Like before, notice that $A Q \\cdot A C=A P \\cdot A B=A I^{2}$. Consider the positive inversion $\\Psi$ with center $A$ and power $A I^{2}$. This maps $P$ to $B$ (and vice-versa), $Q$ to $C$\n(and vice-versa), and keeps the incenter $I$ fixed. The problem statement will follow from the fact that the image of the incircle of triangle $A B C$ under $\\Psi$ is the so-called mixtilinear incircle of $A B C$, which is defined to be the circle tangent to the lines $A B, A C$, and the circumcircle of $A B C$. Indeed, since the image of the line $Q P$ is the circumcircle of $A B C$, and inversion preserves tangencies, this implies that $Q P$ is tangent to the incircle of $A B C$.\n\nWe justify the claim as follows: let $\\gamma$ be the incircle of $A B C$ and let $\\Gamma_{A}$ be the $A$-mixtilinear incircle of $A B C$. Let $K$ and $L$ be the tangency points of $\\gamma$ with the sides $A B$ and $A C$, and let $U$ and $V$ be the tangency points of $\\Gamma_{A}$ with the sides $A B$ and $A C$, respectively. It is well-known that the incenter $I$ is the midpoint of segment $U V$. In particular, since also $A I \\perp U V$, this implies that $A U=A V=\\frac{A I}{\\cos \\frac{A}{2}}$. Note that $A K=A L=A I \\cdot \\cos \\frac{A}{2}$. Therefore, $A U \\cdot A K=A V \\cdot A L=A I^{2}$, which means that $U$ and $V$ are the images of $K$ and $L$ under $\\Psi$. Since $\\Gamma_{A}$ is the unique circle simultaneously tangent to $A B$ at $U$ and to $A C$ at $V$, it follows that the image of $\\gamma$ under $\\Psi$ must be precisely $\\Gamma_{A}$, as claimed.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution 3. "}}
|
| 4 |
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "(Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.", "solution": "by Achilleas Sinefakopoulos, Greece. From the power of a point theorem, we have\n\n$$\nA P \\cdot A B=A I^{2}=A Q \\cdot A C\n$$\n\nHence $P B C Q$ is cyclic, and so, $\\angle A P Q=\\angle B C A$. Let $K$ be the circumcenter of $\\triangle B I P$ and let $L$ be the circumcenter of $\\triangle Q I C$. Then $\\overline{K L}$ is perpendicular to $\\overline{A I}$ at $I$.\n\nLet $N$ be the point of intersection of line $\\overline{K L}$ with $\\overline{A B}$.Then in the right triangle $\\triangle N I A$, we have $\\angle A N I=90^{\\circ}-\\frac{\\angle B A C}{2}$ and from the external angle theorem for triangle $\\triangle B N I$, we have $\\angle A N I=\\frac{\\angle A B C}{2}+\\angle N I B$. Hence\n\n$$\n\\angle N I B=\\angle A N I-\\frac{\\angle A B C}{2}=\\left(90^{\\circ}-\\frac{\\angle B A C}{2}\\right)-\\frac{\\angle A B C}{2}=\\frac{\\angle B C A}{2} .\n$$\n\nSince $M I$ is tangent to the circumcircle of $\\triangle B I P$ at $I$, we have\n\n$$\n\\angle B P I=\\angle B I M=\\angle N I M-\\angle N I B=90^{\\circ}-\\frac{\\angle B C A}{2} .\n$$\n\nAlso, since $\\angle A P Q=\\angle B C A$, we have\n\n$$\n\\angle Q P I=180^{\\circ}-\\angle A P Q-\\angle B P I=180^{\\circ}-\\angle B C A-\\left(90^{\\circ}-\\frac{\\angle B C A}{2}\\right)=90^{\\circ}-\\frac{\\angle B C A}{2}\n$$\n\nas well. Hence $I$ lies on the angle bisector of $\\angle B P Q$, and so it is equidistant from its sides $\\overline{P Q}$ and $\\overline{P B}$. Therefore, the distance of $I$ from $\\overline{P Q}$ equals the inradius of $\\triangle A B C$, as desired.\n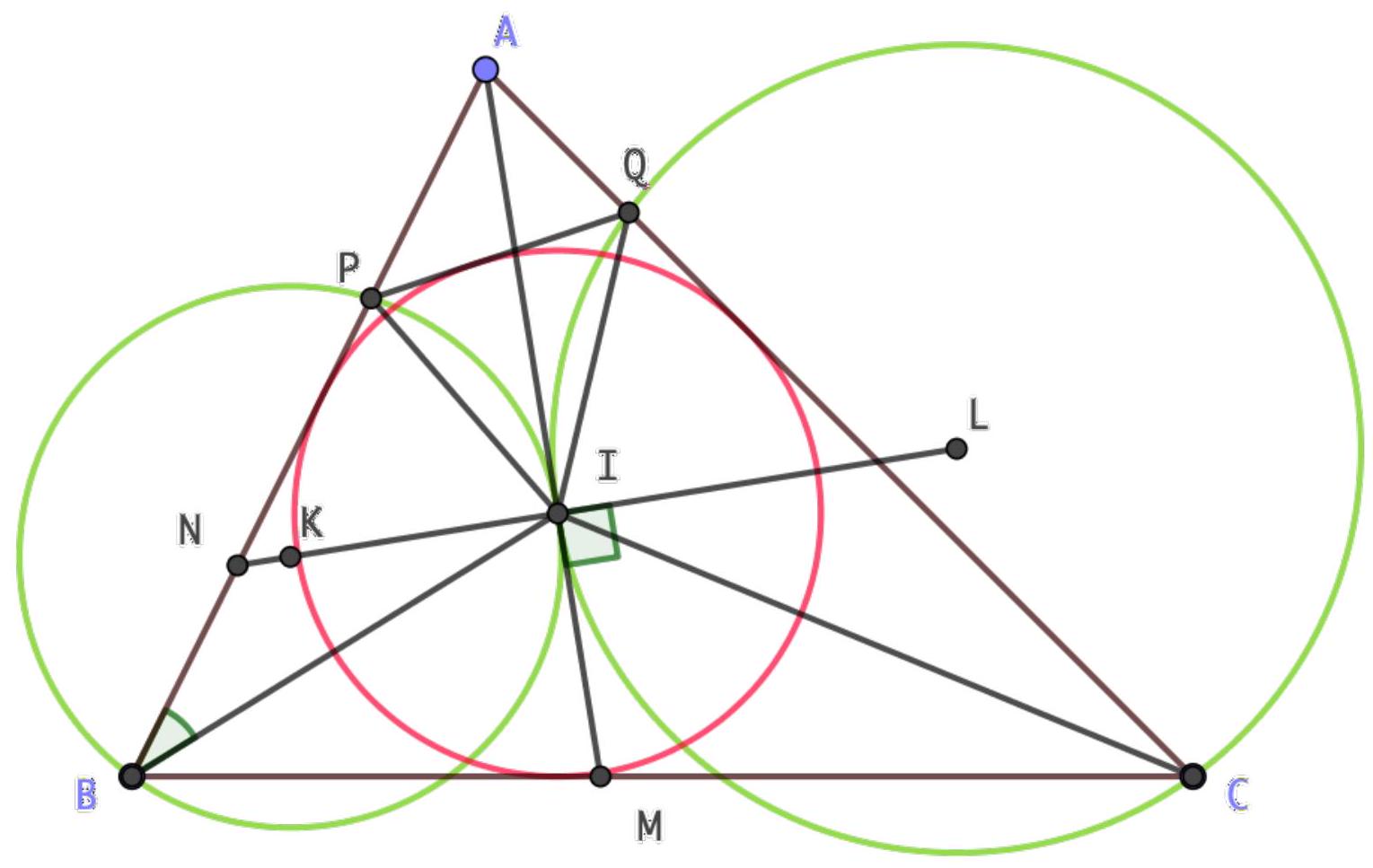", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution "}}
|
| 5 |
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "(Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.", "solution": "by Eirini Miliori (HEL2). Let $D$ be the point of intersection of $\\overline{A I}$ and $\\overline{B C}$ and let $R$ be the point of intersection of $\\overline{A I}$ and $\\overline{P Q}$. We have $\\angle R I P=\\angle P B I=\\frac{\\angle B}{2}$, $\\angle R I Q=\\angle I C Q=\\frac{\\angle C}{2}, \\angle I Q C=\\angle D I C=x$ and $\\angle B P I=\\angle B I D=\\varphi$, since $\\overline{A I}^{2}$ is tangent to both circles.\n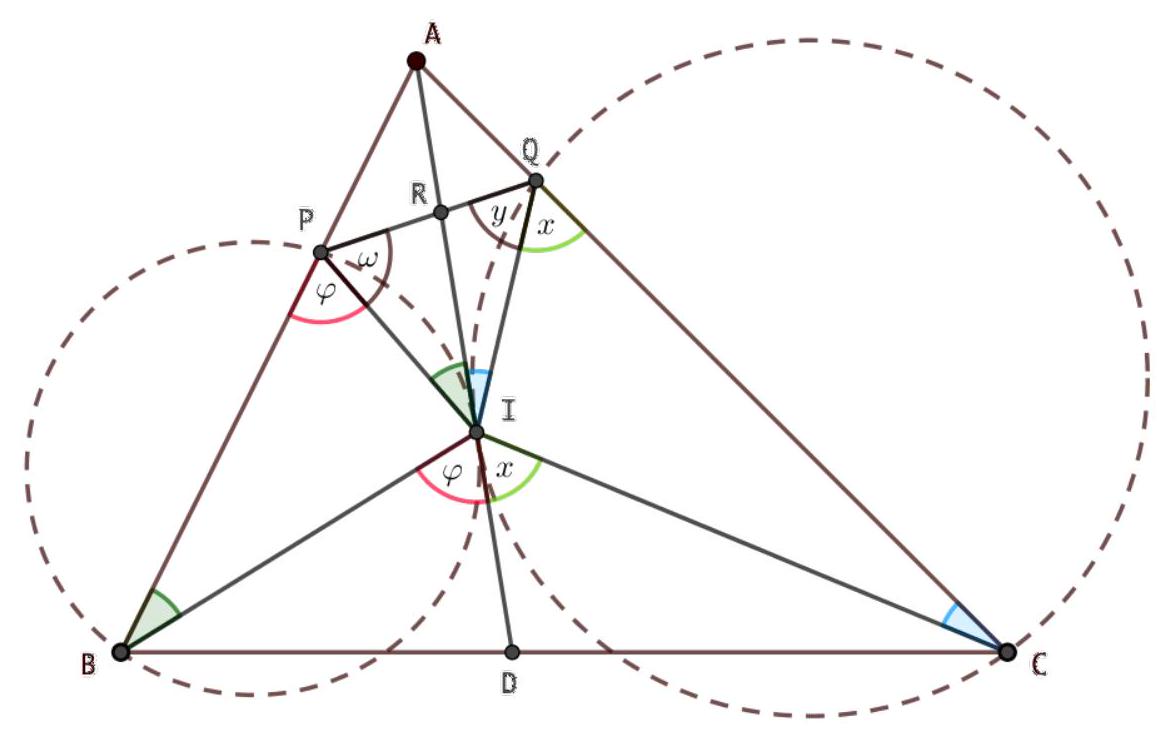\n\nFrom the angle bisector theorem, we have\n\n$$\n\\frac{R Q}{R P}=\\frac{A Q}{A P} \\quad \\text { and } \\quad \\frac{A C}{A B}=\\frac{D C}{B D}\n$$\n\nSince $\\overline{A I}$ is tangent to both circles at $I$, we have $A I^{2}=A Q \\cdot A C$ and $A I^{2}=A P \\cdot A B$. Therefore,\n\n$$\n\\frac{R Q}{R P} \\cdot \\frac{D C}{B D}=\\frac{A Q \\cdot A C}{A B \\cdot A P}=1\n$$\n\nFrom the sine law in triangles $\\triangle Q R I$ and $\\triangle P R I$, it follows that $\\frac{R Q}{\\sin \\frac{\\angle C}{2}}=\\frac{R I}{\\sin y}$ and $\\frac{R P}{\\sin \\frac{\\angle B}{2}}=\\frac{R I}{\\sin \\omega}$, respectively. Hence\n\n$$\n\\frac{R Q}{R P} \\cdot \\frac{\\sin \\frac{\\angle B}{2}}{\\sin \\frac{\\angle C}{2}}=\\frac{\\sin \\omega}{\\sin y}\n$$\n\nSimilarly, from the sine law in triangles $\\triangle I D C$ and $\\triangle I D B$, it is $\\frac{D C}{\\sin x}=\\frac{I D}{\\sin \\frac{\\angle C}{2}}$ and $\\frac{B D}{\\sin \\varphi}=\\frac{I D}{\\sin \\frac{\\angle B}{2}}$, and so\n\n$$\n\\frac{D C}{B D} \\cdot \\frac{\\sin \\varphi}{\\sin x}=\\frac{\\sin \\frac{\\angle B}{2}}{\\sin \\frac{\\angle C}{2}}\n$$\n\nBy multiplying equations (2) with (3), we obtain $\\frac{R Q}{R P} \\cdot \\frac{D C}{B D} \\cdot \\frac{\\sin \\varphi}{\\sin x}=\\frac{\\sin \\omega}{\\sin y}$, which combined with (1) and cross-multiplying yields\n\n$$\n\\sin \\varphi \\cdot \\sin y=\\sin \\omega \\cdot \\sin x\n$$\n\nLet $\\theta=90^{\\circ}+\\frac{\\angle A}{2}$. Since $I$ is the incenter of $\\triangle A B C$, we have $x=90^{\\circ}+\\frac{\\angle A}{2}-\\varphi=\\theta-\\phi$. Also, in triangle $\\triangle P I Q$, we see that $\\omega+y+\\frac{\\angle B}{2}+\\frac{\\angle C}{2}=180^{\\circ}$, and so $y=\\theta-\\omega$.\nTherefore, equation (4) yields\n\n$$\n\\sin \\varphi \\cdot \\sin (\\theta-\\omega)=\\sin \\omega \\cdot \\sin (\\theta-\\varphi)\n$$\n\nor\n\n$$\n\\frac{1}{2}(\\cos (\\varphi-\\theta+\\omega)-\\cos (\\varphi+\\theta-\\omega))=\\frac{1}{2}(\\cos (\\omega-\\theta+\\varphi)-\\cos (\\omega+\\theta-\\varphi))\n$$\n\nwhich is equivalent to\n\n$$\n\\cos (\\varphi+\\theta-\\omega)=\\cos (\\omega+\\theta-\\varphi)\n$$\n\nSo\n\n$$\n\\varphi+\\theta-\\omega=2 k \\cdot 180^{\\circ} \\pm(\\omega+\\theta-\\varphi), \\quad(k \\in \\mathbb{Z} .)\n$$\n\nIf $\\varphi+\\theta-\\omega=2 k \\cdot 180^{\\circ}+(\\omega+\\theta-\\varphi)$, then $2(\\varphi-\\omega)=2 k \\cdot 180^{\\circ}$, with $|\\varphi-\\omega|<180^{\\circ}$ forcing $k=0$ and $\\varphi=\\omega$. If $\\varphi+\\theta-\\omega=2 k \\cdot 180^{\\circ}-(\\omega+\\theta-\\varphi)$, then $2 \\theta=2 k \\cdot 180^{\\circ}$, which contradicts the fact that $0^{\\circ}<\\theta<180^{\\circ}$. Hence $\\varphi=\\omega$, and so $P I$ is the angle bisector of $\\angle Q P B$.\n\nTherefore the distance of $I$ from $\\overline{P Q}$ is the same with the distance of $I$ from $A B$, which is equal to the inradius of $\\triangle A B C$. Consequently, $\\overline{P Q}$ is tangent to the incircle of $\\triangle A B C$.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution "}}
|
| 6 |
-
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1. $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2. the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3. $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)
|
| 7 |
-
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1. $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2. the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3. $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)
|
| 8 |
-
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1. $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2. the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3. $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)
|
| 9 |
-
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1. $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2. the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3. $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)
|
| 10 |
-
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1. $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2. the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3. $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)\n\nSo", "solution": "can assume that all $a_{i} \\in\\{0,1, \\ldots, n-1\\}$, as we can deduct $n$ from both $a_{i}$ and $b_{i}$ for arbitrary $i$ without violating any of the three conditions from the problem statement. We shall also assume that $a_{1} \\leq \\ldots \\leq a_{n}$.\nNow let us provide an algorithm for constructing $b_{1}, \\ldots, b_{n}$.\n\nWe start at step 1 by choosing $f(1)$ to be the maximum $i$ in $\\{1, \\ldots, n\\}$ such that $a_{i} \\leq n-1$, that is $f(1)=n$. We set $b_{f(1)}=n-1$.\nHaving performed steps 1 through $j$, at step $j+1$ we set $f(j+1)$ to be the maximum $i$ in $\\{1, \\ldots, n\\} \\backslash\\{f(1), \\ldots, f(j)\\}$ such that $a_{i} \\leq n-j-1$, if such an index exists. If it does, we set $b_{f(j+1)}=n-j-1$. If there is no such index, then we define $T=j$ and assign to the terms $b_{i}$, where $i \\notin f(\\{1, \\ldots, j\\})$, the values $n, n+1 \\ldots, 2 n-j-1$, in any order, thus concluding the run of our algorithm.\n\nNotice that the sequence $\\left(b_{i}\\right)_{i=1}^{n}$ satisfies the first and second required conditions by construction. We wish to show that it also satisfies the third.\n\nNotice that, since the values chosen for the $b_{i}$ 's are those from $n-T$ to $2 n-T-1$, we have\n\n$$\n\\sum_{i=1}^{n} b_{i}=\\frac{n(n-1)}{2}+(n-T) n\n$$\n\nIt therefore suffices to show that\n\n$$\n\\left[\\frac{a_{1}+\\ldots+a_{n}}{n}\\right] \\geq n-T\n$$\n\nor (since the RHS is obviously an integer) $a_{1}+\\ldots+a_{n} \\geq(n-T) n$.\nFirst, we show that there exists $1 \\leq i \\leq T$ such that $n-i=b_{f(i)}=a_{f(i)}$.\nIndeed, this is true if $a_{n}=n-1$, so we may suppose $a_{n}<n-1$ and therefore $a_{n-1} \\leq n-2$, so that $T \\geq 2$. If $a_{n-1}=n-2$, we are done. If not, then $a_{n-1}<n-2$ and therefore $a_{n-2} \\leq n-3$ and $T \\geq 3$. Inductively, we actually obtain $T=n$ and necessarily $f(n)=1$ and $a_{1}=b_{1}=0$, which gives the desired result.\n\nNow let $t$ be the largest such index $i$. We know that $n-t=b_{f(t)}=a_{f(t)}$ and therefore $a_{1} \\leq \\ldots \\leq a_{f(t)} \\leq n-t$. If we have $a_{1}=\\ldots=a_{f(t)}=n-t$, then $T=t$ and we have $a_{i} \\geq n-T$ for all $i$, hence $\\sum_{i} a_{i} \\geq n(n-T)$. Otherwise, $T>t$ and in fact one can show $T=t+f(t+1)$ by proceeding inductively and using the fact that $t$ is the last time for which $a_{f(t)}=b_{f(t)}$.\n\nNow we get that, since $a_{f(t+1)+1} \\geq n-t$, then $\\sum_{i} a_{i} \\geq(n-t)(n-f(t+1))=(n-T+f(t+$ 1) $)(n-f(t+1))=n(n-T)+n f(t+1)-f(t+1)(n-T+f(t+1))=n(n-T)+t f(t+1) \\geq$ $n(n-T)$.\n\nGreedy algorithm variant $\\mathbf{1}$ (ISR). Consider the residues $0, \\ldots, n-1$ modulo $n$ arranged in a circle clockwise, and place each $a_{i}$ on its corresponding residue; so that on each residue there is a stack of all $a_{i}$ s congruent to it modulo $n$, and the sum of the sizes of all stacks is exactly $n$. We iteratively flatten and spread the stacks forward, in such a way that the $a_{i}$ s are placed in the nearest available space on the circle clockwise (skipping over any already flattened residue or still standing stack). We may choose the order in which the stacks are flattened. Since the total amount of numbers equals the total number of spaces, there is always an available space and at the end all spaces are covered. The $b_{i} \\mathrm{~s}$ are then defined by adding to each $a_{i}$ the number of places it was moved forward, which clearly satifies (i) and (ii), and we must prove that they satisfy (iii) as well.\n\nSuppose that we flatten a stack of $k$ numbers at a residue $i$, causing it to overtake a stack of $l$ numbers at residue $j \\in(i, i+k)$ (we can allow $j$ to be larger than $n$ and identify it\nwith its residue modulo $n$ ). Then in fact in fact in whichever order we would flatten the two stacks, the total number of forward steps would be the same, and the total sum of the corresponding $b_{t}$ (such that $a_{t} \\bmod n \\in\\{i, j\\}$ ) would be the same. Moreover, we can merge the stacks to a single stack of $k+l$ numbers at residue $i$, by replacing each $a_{t} \\equiv j$ $(\\bmod n)$ by $a_{t}^{\\prime}=a_{t}-(j-i)$, and this stack would be flattened forward into the same positions as the separate stacks would have been, so applying our algorithm to the new stacks will yield the same total sum of $\\sum b_{i}-$ but the $a_{i}$ s are strictly decreased, so $\\sum a_{i}$ is decreased, so $\\left\\lfloor\\frac{\\sum a_{i}}{n}\\right\\rfloor$ is not increased - so by merging the stacks, we can only make the inequality we wish to prove tighter.\n\nThus, as long as there is some stack that when flattened will overtake another stack, we may merge stacks and only make the inequality tighter. Since the amount of numbers equals the amount of places, the merging process terminates with stacks of sizes $k_{1}, \\ldots, k_{m}$, such that the stack $j$, when flattened, will exactly cover the interval to the next stack. Clearly the numbers in each such stack were advanced by a total of $\\sum_{t=1}^{k_{j}-1}=\\frac{k_{j}\\left(k_{j}-1\\right)}{2}$, thus $\\sum b_{i}=\\sum a_{i}+\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2}$. Writing $\\sum a_{i}=n \\cdot r+s$ with $0 \\leq s<n$, we must therefore show\n\n$$\ns+\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2} \\leq \\frac{n(n-1)}{2}\n$$\n\nEnding 1. Observing that both sides of the last inequality are congruent modulo $n$ (both are congruent to the sum of all different residues), and that $0 \\leq s<n$, the inequality is eqivalent to the simpler $\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2} \\leq \\frac{n(n-1)}{2}$. Since $x(x-1)$ is convex, and $k_{j}$ are nonnegative integers with $\\sum_{j} k_{j}=n$, the left hand side is maximal when $k_{j^{\\prime}}=n$ and the rest are 0 , and then eqaulity is achieved. (Alternatively it follows easily for any non-negative reals from AM-GM.)\n\nEnding 2. If $m=1$ (and $k_{1}=n$ ), then all numbers are in a single stack and have the same residue, so $s=0$ and equality is attained. If $m \\geq 2$, then by convexity $\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2}$ is maximal for $m=2$ and $\\left(k_{1}, k_{2}\\right)=(n-1,1)$, where it equals $\\frac{(n-1)(n-2)}{2}$. Since we always have $s \\leq n-1$, we find\n\n$$\ns+\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2} \\leq(n-1)+\\frac{(n-1)(n-2)}{2}=\\frac{n(n-1)}{2}\n$$\n\nas required.\nGreedy algorithm variant 1' (ISR). We apply the same algorithm as in the previous solution. However, this time we note that we may merge stacks not only when they overlap after flattening, but also when they merely touch front-to-back: That is, we relax the condition $j \\in(i, i+k)$ to $j \\in(i, i+k]$; the argument for why such merges are allowed is exactly the same (But note that this is now sharp, as merging non-touching stacks can cause the sum of $b_{i}$ s to decrease).\n\nWe now observe that as long as there at least two stacks left, at least one will spread to touch (or overtake) the next stack, so we can perform merges until there is only one stack left. We are left with verifying that the inequality indeed holds for the case of only one stack which is spread forward, and this is indeed immediate (and in fact equality is achieved).\n\nGreedy algorithm variant 2 (ISR). Let $c_{i}=a_{i} \\bmod n$. Iteratively define $b_{i}=a_{i}+l_{i}$ greedily, write $d_{i}=c_{i}+l_{i}$, and observe that $l_{i} \\leq n-1$ (since all residues are present in $\\left.a_{i}, \\ldots, a_{i}+n-1\\right)$, hence $0 \\leq d_{i} \\leq 2 n-2$. Let $I=\\left\\{i \\in I: d_{i} \\geq n\\right\\}$, and note that $d_{i}=b_{i}$ $\\bmod n$ if $i \\notin I$ and $d_{i}=\\left(b_{i} \\bmod n\\right)+n$ if $i \\in I$. Then we must show\n\n$$\n\\begin{aligned}\n& \\sum\\left(a_{i}+l_{i}\\right)=\\sum b_{i} \\leq \\frac{n(n-1)}{2}+n\\left\\lfloor\\frac{\\sum a_{i}}{n}\\right\\rfloor \\\\\n\\Longleftrightarrow & \\sum\\left(c_{i}+l_{i}\\right) \\leq \\sum\\left(b_{i} \\bmod n\\right)+n\\left\\lfloor\\frac{\\sum c_{i}}{n}\\right\\rfloor \\\\\n\\Longleftrightarrow & \\left.n|I| \\leq n\\left\\lfloor\\frac{\\sum c_{i}}{n}\\right\\rfloor \\Longleftrightarrow|I| \\leq \\left\\lvert\\, \\frac{\\sum c_{i}}{n}\\right.\\right\\rfloor \\Longleftrightarrow|I| \\leq \\frac{\\sum c_{i}}{n}\n\\end{aligned}\n$$\n\nLet $k=|I|$, and for each $0 \\leq m<n$ let $J_{m}=\\left\\{i: c_{i} \\geq n-m\\right\\}$. We claim that there must be some $m$ for which $\\left|J_{m}\\right| \\geq m+k$ (clearly for such $m$, at least $k$ of the sums $d_{j}$ with $j \\in J_{m}$ must exceed $n$, i.e. at least $k$ of the elements of $J_{m}$ must also be in $I$, so this $m$ is a \"witness\" to the fact $|I| \\geq k$ ). Once we find such an $m$, then we clearly have\n\n$$\n\\sum c_{i} \\geq(n-m)\\left|J_{m}\\right| \\geq(n-m)(k+m)=n k+m(n-(k+m)) \\geq n k=n|I|\n$$\n\nas required. We now construct such an $m$ explicitly.\nIf $k=0$, then clearly $m=n$ works (and also the original inequality is trivial). Otherwise, there are some $d_{i}$ s greater than $n$, and let $r+n=\\max d_{i}$, and suppose $d_{t}=r+n$ and let $s=c_{t}$. Note that $r<s<r+n$ since $l_{t}<n$. Let $m \\geq 0$ be the smallest number such that $n-m-1$ is not in $\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$, or equivalently $m$ is the largest such that $[n-m, n) \\subset\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$. We claim that this $m$ satisfies the required property. More specifically, we claim that $J_{m}^{\\prime}=\\left\\{i \\leq t: d_{i} \\geq n-m\\right\\}$ contains exactly $m+k$ elements and is a subset of $J_{m}$.\n\nNote that by the greediness of the algorithm, it is impossible that for $\\left[c_{i}, d_{i}\\right)$ to contain numbers congruent to $d_{j} \\bmod n$ with $j>i$ (otherwise, the greedy choice would prefer $d_{j}$ to $d_{i}$ at stage $i$ ). We call this the greedy property. In particular, it follows that all $i$ such that $d_{i} \\in\\left[s, d_{t}\\right)=\\left[c_{t}, d_{t}\\right)$ must satisfy $i<t$. Additionally, $\\left\\{d_{i}\\right\\}$ is disjoint from $[n+r+1,2 n)$ (by maximality of $d_{t}$ ), but does intersect every residue class, so it contains $[r+1, n)$ and in particular also $[s, n)$. By the greedy property the latter can only be attained by $d_{i}$ with $i<t$, thus $[s, n) \\subset\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$, and in particular $n-m \\leq s$ (and in particular $m \\geq 1$ ).\nOn the other hand $n-m>r$ (since $r \\notin\\left\\{d_{i}\\right\\}$ at all), so $n-m-1 \\geq r$. It follows that there is a time $t^{\\prime} \\geq t$ for which $d_{t^{\\prime}} \\equiv n-m-1(\\bmod n)$ : If $n-m-1=r$ then this is true for $t^{\\prime}=t$ with $d_{t}=n+r=2 n-m-1$; whereas if $n-m-1 \\in[r+1, n)$ then there is some $t^{\\prime}$ for which $d_{t^{\\prime}}=n-m-1$, and by the definition of $m$ it satisfies $t^{\\prime}>t$.\n\nTherefore for all $i<t \\leq t^{\\prime}$ for which $d_{i} \\geq n-m$, necessarily also $c_{i} \\geq n-m$, since otherwise $d_{t^{\\prime}} \\in\\left[c_{i}, d_{i}\\right)$, in contradiction to the greedy property. This is also true for $i=t$, since $c_{t}=s \\geq n-m$ as previously shown. Thus, $J_{m}^{\\prime} \\subset J_{m}$ as claimed.\nFinally, since by definition of $m$ and greediness we have $[n-m, n) \\cup\\left\\{d_{i}: i \\in I\\right\\} \\subset$ $\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$, we find that $\\left\\{d_{j}: j \\in J_{m}^{\\prime}\\right\\}=[n-m, n) \\cup\\left\\{d_{i}: i \\in I\\right\\}$ and thus $\\left|J_{m}^{\\prime}\\right|=$ $|[n-m, n)|+|I|=m+k$ as claimed.\n\n## P", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 5", "solution_match": "\nSolution 5. "}}
|
| 11 |
-
{"year": "2019", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "
|
| 12 |
-
{"year": "2019", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "
|
|
|
|
| 3 |
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "(Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.", "solution": "Like before, notice that $A Q \\cdot A C=A P \\cdot A B=A I^{2}$. Consider the positive inversion $\\Psi$ with center $A$ and power $A I^{2}$. This maps $P$ to $B$ (and vice-versa), $Q$ to $C$\n(and vice-versa), and keeps the incenter $I$ fixed. The problem statement will follow from the fact that the image of the incircle of triangle $A B C$ under $\\Psi$ is the so-called mixtilinear incircle of $A B C$, which is defined to be the circle tangent to the lines $A B, A C$, and the circumcircle of $A B C$. Indeed, since the image of the line $Q P$ is the circumcircle of $A B C$, and inversion preserves tangencies, this implies that $Q P$ is tangent to the incircle of $A B C$.\n\nWe justify the claim as follows: let $\\gamma$ be the incircle of $A B C$ and let $\\Gamma_{A}$ be the $A$-mixtilinear incircle of $A B C$. Let $K$ and $L$ be the tangency points of $\\gamma$ with the sides $A B$ and $A C$, and let $U$ and $V$ be the tangency points of $\\Gamma_{A}$ with the sides $A B$ and $A C$, respectively. It is well-known that the incenter $I$ is the midpoint of segment $U V$. In particular, since also $A I \\perp U V$, this implies that $A U=A V=\\frac{A I}{\\cos \\frac{A}{2}}$. Note that $A K=A L=A I \\cdot \\cos \\frac{A}{2}$. Therefore, $A U \\cdot A K=A V \\cdot A L=A I^{2}$, which means that $U$ and $V$ are the images of $K$ and $L$ under $\\Psi$. Since $\\Gamma_{A}$ is the unique circle simultaneously tangent to $A B$ at $U$ and to $A C$ at $V$, it follows that the image of $\\gamma$ under $\\Psi$ must be precisely $\\Gamma_{A}$, as claimed.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution 3. "}}
|
| 4 |
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "(Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.", "solution": "by Achilleas Sinefakopoulos, Greece. From the power of a point theorem, we have\n\n$$\nA P \\cdot A B=A I^{2}=A Q \\cdot A C\n$$\n\nHence $P B C Q$ is cyclic, and so, $\\angle A P Q=\\angle B C A$. Let $K$ be the circumcenter of $\\triangle B I P$ and let $L$ be the circumcenter of $\\triangle Q I C$. Then $\\overline{K L}$ is perpendicular to $\\overline{A I}$ at $I$.\n\nLet $N$ be the point of intersection of line $\\overline{K L}$ with $\\overline{A B}$.Then in the right triangle $\\triangle N I A$, we have $\\angle A N I=90^{\\circ}-\\frac{\\angle B A C}{2}$ and from the external angle theorem for triangle $\\triangle B N I$, we have $\\angle A N I=\\frac{\\angle A B C}{2}+\\angle N I B$. Hence\n\n$$\n\\angle N I B=\\angle A N I-\\frac{\\angle A B C}{2}=\\left(90^{\\circ}-\\frac{\\angle B A C}{2}\\right)-\\frac{\\angle A B C}{2}=\\frac{\\angle B C A}{2} .\n$$\n\nSince $M I$ is tangent to the circumcircle of $\\triangle B I P$ at $I$, we have\n\n$$\n\\angle B P I=\\angle B I M=\\angle N I M-\\angle N I B=90^{\\circ}-\\frac{\\angle B C A}{2} .\n$$\n\nAlso, since $\\angle A P Q=\\angle B C A$, we have\n\n$$\n\\angle Q P I=180^{\\circ}-\\angle A P Q-\\angle B P I=180^{\\circ}-\\angle B C A-\\left(90^{\\circ}-\\frac{\\angle B C A}{2}\\right)=90^{\\circ}-\\frac{\\angle B C A}{2}\n$$\n\nas well. Hence $I$ lies on the angle bisector of $\\angle B P Q$, and so it is equidistant from its sides $\\overline{P Q}$ and $\\overline{P B}$. Therefore, the distance of $I$ from $\\overline{P Q}$ equals the inradius of $\\triangle A B C$, as desired.\n", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution "}}
|
| 5 |
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "(Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.", "solution": "by Eirini Miliori (HEL2). Let $D$ be the point of intersection of $\\overline{A I}$ and $\\overline{B C}$ and let $R$ be the point of intersection of $\\overline{A I}$ and $\\overline{P Q}$. We have $\\angle R I P=\\angle P B I=\\frac{\\angle B}{2}$, $\\angle R I Q=\\angle I C Q=\\frac{\\angle C}{2}, \\angle I Q C=\\angle D I C=x$ and $\\angle B P I=\\angle B I D=\\varphi$, since $\\overline{A I}^{2}$ is tangent to both circles.\n\n\nFrom the angle bisector theorem, we have\n\n$$\n\\frac{R Q}{R P}=\\frac{A Q}{A P} \\quad \\text { and } \\quad \\frac{A C}{A B}=\\frac{D C}{B D}\n$$\n\nSince $\\overline{A I}$ is tangent to both circles at $I$, we have $A I^{2}=A Q \\cdot A C$ and $A I^{2}=A P \\cdot A B$. Therefore,\n\n$$\n\\frac{R Q}{R P} \\cdot \\frac{D C}{B D}=\\frac{A Q \\cdot A C}{A B \\cdot A P}=1\n$$\n\nFrom the sine law in triangles $\\triangle Q R I$ and $\\triangle P R I$, it follows that $\\frac{R Q}{\\sin \\frac{\\angle C}{2}}=\\frac{R I}{\\sin y}$ and $\\frac{R P}{\\sin \\frac{\\angle B}{2}}=\\frac{R I}{\\sin \\omega}$, respectively. Hence\n\n$$\n\\frac{R Q}{R P} \\cdot \\frac{\\sin \\frac{\\angle B}{2}}{\\sin \\frac{\\angle C}{2}}=\\frac{\\sin \\omega}{\\sin y}\n$$\n\nSimilarly, from the sine law in triangles $\\triangle I D C$ and $\\triangle I D B$, it is $\\frac{D C}{\\sin x}=\\frac{I D}{\\sin \\frac{\\angle C}{2}}$ and $\\frac{B D}{\\sin \\varphi}=\\frac{I D}{\\sin \\frac{\\angle B}{2}}$, and so\n\n$$\n\\frac{D C}{B D} \\cdot \\frac{\\sin \\varphi}{\\sin x}=\\frac{\\sin \\frac{\\angle B}{2}}{\\sin \\frac{\\angle C}{2}}\n$$\n\nBy multiplying equations (2) with (3), we obtain $\\frac{R Q}{R P} \\cdot \\frac{D C}{B D} \\cdot \\frac{\\sin \\varphi}{\\sin x}=\\frac{\\sin \\omega}{\\sin y}$, which combined with (1) and cross-multiplying yields\n\n$$\n\\sin \\varphi \\cdot \\sin y=\\sin \\omega \\cdot \\sin x\n$$\n\nLet $\\theta=90^{\\circ}+\\frac{\\angle A}{2}$. Since $I$ is the incenter of $\\triangle A B C$, we have $x=90^{\\circ}+\\frac{\\angle A}{2}-\\varphi=\\theta-\\phi$. Also, in triangle $\\triangle P I Q$, we see that $\\omega+y+\\frac{\\angle B}{2}+\\frac{\\angle C}{2}=180^{\\circ}$, and so $y=\\theta-\\omega$.\nTherefore, equation (4) yields\n\n$$\n\\sin \\varphi \\cdot \\sin (\\theta-\\omega)=\\sin \\omega \\cdot \\sin (\\theta-\\varphi)\n$$\n\nor\n\n$$\n\\frac{1}{2}(\\cos (\\varphi-\\theta+\\omega)-\\cos (\\varphi+\\theta-\\omega))=\\frac{1}{2}(\\cos (\\omega-\\theta+\\varphi)-\\cos (\\omega+\\theta-\\varphi))\n$$\n\nwhich is equivalent to\n\n$$\n\\cos (\\varphi+\\theta-\\omega)=\\cos (\\omega+\\theta-\\varphi)\n$$\n\nSo\n\n$$\n\\varphi+\\theta-\\omega=2 k \\cdot 180^{\\circ} \\pm(\\omega+\\theta-\\varphi), \\quad(k \\in \\mathbb{Z} .)\n$$\n\nIf $\\varphi+\\theta-\\omega=2 k \\cdot 180^{\\circ}+(\\omega+\\theta-\\varphi)$, then $2(\\varphi-\\omega)=2 k \\cdot 180^{\\circ}$, with $|\\varphi-\\omega|<180^{\\circ}$ forcing $k=0$ and $\\varphi=\\omega$. If $\\varphi+\\theta-\\omega=2 k \\cdot 180^{\\circ}-(\\omega+\\theta-\\varphi)$, then $2 \\theta=2 k \\cdot 180^{\\circ}$, which contradicts the fact that $0^{\\circ}<\\theta<180^{\\circ}$. Hence $\\varphi=\\omega$, and so $P I$ is the angle bisector of $\\angle Q P B$.\n\nTherefore the distance of $I$ from $\\overline{P Q}$ is the same with the distance of $I$ from $A B$, which is equal to the inradius of $\\triangle A B C$. Consequently, $\\overline{P Q}$ is tangent to the incircle of $\\triangle A B C$.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "\nProblem 4", "solution_match": "\nSolution "}}
|
| 6 |
+
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1). $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2). the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3). $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)", "solution": "We define the $b_{i}$ recursively by letting $b_{i}$ be the smallest integer such that $b_{i} \\geq a_{i}$ and such that $b_{i}$ is not congruent to any of $b_{1}, \\ldots, b_{i-1}$ modulo $n$. Then $b_{i}-a_{i} \\leq i-1$, since of the $i$ consecutive integers $a_{i}, a_{i}+1, \\ldots, a_{i}+i-1$, at most $i-1$ are congruent to one of $b_{1}, \\ldots, b_{i-1}$ modulo $n$. Since all $b_{i}$ are distinct modulo $n$, we have $\\sum_{i=1}^{n} b_{i} \\equiv \\sum_{i=1}^{n}(i-1)=\\frac{1}{2} n(n-1)$ modulo $n$, so $n$ divides $\\sum_{i=1}^{n} b_{i}-\\frac{1}{2} n(n-1)$. Moreover, we have $\\sum_{i=1}^{n} b_{i}-\\sum_{i=1}^{n} a_{i} \\leq \\sum_{i=1}^{n}(i-1)=\\frac{1}{2} n(n-1)$, hence $\\sum_{i=1}^{n} b_{i}-\\frac{1}{2} n(n-1) \\leq \\sum_{i=1}^{n}$. As the left hand side is divisible by $n$, we have\n\n$$\n\\frac{1}{n}\\left(\\sum_{i=1}^{n} b_{i}-\\frac{1}{2} n(n-1)\\right) \\leq\\left[\\frac{1}{n} \\sum_{i=1}^{n} a_{i}\\right]\n$$\n\nwhich we can rewrite as\n\n$$\n\\sum_{i=1}^{n} b_{i} \\leq n\\left(\\frac{n-1}{2}+\\left[\\frac{1}{n} \\sum_{i=1}^{n} a_{i}\\right]\\right)\n$$\n\nas required.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 5", "solution_match": "\nSolution 1. "}}
|
| 7 |
+
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1). $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2). the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3). $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)", "solution": "Note that the problem is invariant under each of the following operations:\n\n- adding a multiple of $n$ to some $a_{i}$ (and the corresponding $b_{i}$ );\n- adding the same integer to all $a_{i}$ (and all $b_{i}$ );\n- permuting the index set $1,2, \\ldots, n$.\n\nWe may therefore remove the restriction that our $a_{i}$ and $b_{i}$ be positive.\nFor each congruence class $\\bar{k}$ modulo $n(\\bar{k}=\\overline{0}, \\ldots, \\overline{n-1})$, let $h(k)$ be the number of $i$ such that $a_{i}$ belongs to $\\bar{k}$. We will now show that the problem is solved if we can find a $t \\in \\mathbb{Z}$ such that\n\n$$\n\\begin{array}{cl}\nh(t) & \\geq 1, \\\\\nh(t)+h(t+1) & \\geq 2 \\\\\nh(t)+h(t+1)+h(t+2) & \\geq 3\n\\end{array}\n$$\n\nIndeed, these inequalities guarantee the existence of elements $a_{i_{1}} \\in \\bar{t}, a_{i_{2}} \\in \\bar{t} \\cup \\overline{t+1}$, $a_{i_{3}} \\in \\bar{t} \\cup \\overline{t+1} \\cup \\overline{t+2}$, et cetera, where all $i_{k}$ are different. Subtracting appropriate\nmultiples of $n$ and reordering our elements, we may assume $a_{1}=t, a_{2} \\in\\{t, t+1\\}$, $a_{3} \\in\\{t, t+1, t+2\\}$, et cetera. Finally subtracting $t$ from the complete sequence, we may assume $a_{1}=0, a_{2} \\in\\{0,1\\}, a_{3} \\in\\{0,1,2\\}$ et cetera. Now simply setting $b_{i}=i-1$ for all $i$ suffices, since $a_{i} \\leq b_{i}$ for all $i$, the $b_{i}$ are all different modulo $n$, and\n\n$$\n\\sum_{i=1}^{n} b_{i}=\\frac{n(n-1)}{2} \\leq \\frac{n(n-1)}{2}+n\\left[\\frac{\\sum_{i=1}^{n} a_{i}}{n}\\right] .\n$$\n\nPut $x_{i}=h(i)-1$ for all $i=0, \\ldots, n-1$. Note that $x_{i} \\geq-1$, because $h(i) \\geq 0$. If we have $x_{i} \\geq 0$ for all $i=0, \\ldots, n-1$, then taking $t=0$ completes the proof. Otherwise, we can pick some index $j$ such that $x_{j}=-1$. Let $y_{i}=x_{i}$ where $i=0, \\ldots, j-1, j+1, \\ldots, n-1$ and $y_{j}=0$. For sequence $\\left\\{y_{i}\\right\\}$ we have\n\n$$\n\\sum_{i=0}^{n-1} y_{i}=\\sum_{i=0}^{n-1} x_{i}+1=\\sum_{i=0}^{n-1} h(i)-n+1=1\n$$\n\nso from Raney's lemma there exists index $k$ such that $\\sum_{i=k}^{k+j} y_{i}>0$ for all $j=0, \\ldots, n-1$ where $y_{n+j}=y_{j}$ for $j=0, \\ldots, k-1$. Taking $t=k$ we will have\n\n$$\n\\sum_{t=k}^{k+i} h(t)-(i+1)=\\sum_{t=k}^{k+i} x(t) \\geq \\sum_{t=k}^{k+i} y(t)-1 \\geq 0\n$$\n\nfor all $i=0, \\ldots, n-1$ and we are done.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 5", "solution_match": "\nSolution 2. "}}
|
| 8 |
+
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1). $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2). the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3). $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)", "solution": "Choose a random permutation $c_{1}, \\ldots, c_{n}$ of the integers $1,2, \\ldots, n$. Let $b_{i}=a_{i}+f\\left(c_{i}-a_{i}\\right)$, where $f(x) \\in\\{0, \\ldots, n-1\\}$ denotes a remainder of $x$ modulo $n$. Observe, that for such defined sequence the first two conditions hold. The expected value of $B:=b_{1}+\\ldots+b_{n}$ is easily seen to be equal to $a_{1}+\\ldots+a_{n}+n(n-1) / 2$. Indeed, for each $i$ the random number $c_{i}-a_{i}$ has uniform distribution modulo $n$, thus the expected value of $f\\left(c_{i}-a_{i}\\right)$ is $(0+\\ldots+(n-1)) / n=(n-1) / 2$. Therefore we may find such $c$ that $B \\leq a_{1}+\\ldots+a_{n}+n(n-1) / 2$. But $B-n(n-1) / 2$ is divisible by $n$ and therefore $B \\leq n\\left[\\left(a_{1}+\\ldots+a_{n}\\right) / n\\right]+n(n-1) / 2$ as needed.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 5", "solution_match": "\nSolution 3. "}}
|
| 9 |
+
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1). $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2). the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3). $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)", "solution": "We will prove the required statement for all sequences of non-negative integers $a_{i}$ by induction on $n$.\nCase $n=1$ is obvious, just set $b_{1}=a_{1}$.\nNow suppose that the statement is true for some $n \\geq 1$; we shall prove it for $n+1$.\nFirst note that, by subtracting a multiple of $n+1$ to each $a_{i}$ and possibly rearranging indices we can reduce the problem to the case where $0 \\leq a_{1} \\leq a_{2} \\leq \\cdots \\leq a_{n} \\leq a_{n+1}<$ $n+1$.\n\nNow, by the induction hypothesis there exists a sequence $d_{1}, d_{2}, \\ldots, d_{n}$ which satisfies the properties required by the statement in relation to the numbers $a_{1}, \\ldots, a_{n}$. Set $I=\\{i \\mid 1 \\leq$ $i \\leq n$ and $\\left.d_{i} \\bmod n \\geq a_{i}\\right\\}$ and construct $b_{i}$, for $i=1, \\ldots, n+1$, as follows:\n\n$$\nb_{i}=\\left\\{\\begin{array}{l}\nd_{i} \\bmod n, \\text { when } i \\in I, \\\\\nn+1+\\left(d_{i} \\bmod n\\right), \\text { when } i \\in\\{1, \\ldots, n\\} \\backslash I, \\\\\nn, \\text { for } i=n+1\n\\end{array}\\right.\n$$\n\nNow, $a_{i} \\leq d_{i} \\bmod n \\leq b_{i}$ for $i \\in I$, while for $i \\notin I$ we have $a_{i} \\leq n \\leq b_{i}$. Thus the sequence $\\left(b_{i}\\right)_{i=1}^{n+1}$ satisfies the first condition from the problem statement.\nBy the induction hypothesis, the numbers $d_{i} \\bmod n$ are distinct for $i \\in\\{1, \\ldots, n\\}$, so the values $b_{i} \\bmod (n+1)$ are distinct elements of $\\{0, \\ldots, n-1\\}$ for $i \\in\\{1, \\ldots, n\\}$. Since $b_{n+1}=n$, the second condition is also satisfied.\n\nDenote $k=|I|$. We have\n\n$$\n\\begin{gathered}\n\\sum_{i=1}^{n+1} b_{i}=\\sum_{i=1}^{n} b_{i}+n=\\sum_{i=1}^{n} d_{i} \\bmod n+(n-k)(n+1)+n= \\\\\n\\frac{n(n+1)}{2}+(n-k)(n+1)\n\\end{gathered}\n$$\n\nhence we need to show that\n\n$$\n\\frac{n(n+1)}{2}+(n-k)(n+1) \\leq \\frac{n(n+1)}{2}+(n+1)\\left[\\frac{\\sum_{i=1}^{n+1} a_{i}}{n+1}\\right]\n$$\n\nequivalently, that\n\n$$\nn-k \\leq\\left[\\frac{\\sum_{i=1}^{n+1} a_{i}}{n+1}\\right]\n$$\n\nNext, from the induction hypothesis we have\n\n$$\n\\begin{gathered}\n\\frac{n(n-1)}{2}+n\\left[\\frac{\\sum_{i=1}^{n} a_{i}}{n}\\right] \\geq \\sum_{i=1}^{n} d_{i}=\\sum_{i \\in I} d_{i}+\\sum_{i \\notin I} d_{i} \\geq \\\\\n\\sum_{i \\in I} d_{i} \\bmod n+\\sum_{i \\notin I}\\left(n+d_{i} \\bmod n\\right)=\\frac{n(n-1)}{2}+(n-k) n\n\\end{gathered}\n$$\n\nor\n\n$$\nn-k \\leq\\left[\\frac{\\sum_{i=1}^{n} a_{i}}{n}\\right]\n$$\n\nThus, it's enough to show that\n\n$$\n\\frac{\\sum_{i=1}^{n} a_{i}}{n} \\leq \\frac{\\sum_{i=1}^{n+1} a_{i}}{n+1}\n$$\n\nbecause then\n\n$$\nn-k \\leq\\left[\\frac{\\sum_{i=1}^{n} a_{i}}{n}\\right] \\leq\\left[\\frac{\\sum_{i=1}^{n+1} a_{i}}{n+1}\\right]\n$$\n\nBut the required inequality is equivalent to $\\sum_{i=1}^{n} a_{i} \\leq n a_{n+1}$, which is obvious.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 5", "solution_match": "\nSolution 4. "}}
|
| 10 |
+
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Netherlands).\n\nLet $n \\geq 2$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \\ldots, b_{n}$ satisfying the following three conditions:\n\n1). $a_{i} \\leq b_{i}$ for $i=1,2, \\ldots, n$;\n2). the remainders of $b_{1}, b_{2}, \\ldots, b_{n}$ on division by $n$ are pairwise different; and\n3). $b_{1}+\\cdots+b_{n} \\leq n\\left(\\frac{n-1}{2}+\\left\\lfloor\\frac{a_{1}+\\cdots+a_{n}}{n}\\right\\rfloor\\right)$.\n(Here, $\\lfloor x\\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)", "solution": "We can assume that all $a_{i} \\in\\{0,1, \\ldots, n-1\\}$, as we can deduct $n$ from both $a_{i}$ and $b_{i}$ for arbitrary $i$ without violating any of the three conditions from the problem statement. We shall also assume that $a_{1} \\leq \\ldots \\leq a_{n}$.\nNow let us provide an algorithm for constructing $b_{1}, \\ldots, b_{n}$.\n\nWe start at step 1 by choosing $f(1)$ to be the maximum $i$ in $\\{1, \\ldots, n\\}$ such that $a_{i} \\leq n-1$, that is $f(1)=n$. We set $b_{f(1)}=n-1$.\nHaving performed steps 1 through $j$, at step $j+1$ we set $f(j+1)$ to be the maximum $i$ in $\\{1, \\ldots, n\\} \\backslash\\{f(1), \\ldots, f(j)\\}$ such that $a_{i} \\leq n-j-1$, if such an index exists. If it does, we set $b_{f(j+1)}=n-j-1$. If there is no such index, then we define $T=j$ and assign to the terms $b_{i}$, where $i \\notin f(\\{1, \\ldots, j\\})$, the values $n, n+1 \\ldots, 2 n-j-1$, in any order, thus concluding the run of our algorithm.\n\nNotice that the sequence $\\left(b_{i}\\right)_{i=1}^{n}$ satisfies the first and second required conditions by construction. We wish to show that it also satisfies the third.\n\nNotice that, since the values chosen for the $b_{i}$ 's are those from $n-T$ to $2 n-T-1$, we have\n\n$$\n\\sum_{i=1}^{n} b_{i}=\\frac{n(n-1)}{2}+(n-T) n\n$$\n\nIt therefore suffices to show that\n\n$$\n\\left[\\frac{a_{1}+\\ldots+a_{n}}{n}\\right] \\geq n-T\n$$\n\nor (since the RHS is obviously an integer) $a_{1}+\\ldots+a_{n} \\geq(n-T) n$.\nFirst, we show that there exists $1 \\leq i \\leq T$ such that $n-i=b_{f(i)}=a_{f(i)}$.\nIndeed, this is true if $a_{n}=n-1$, so we may suppose $a_{n}<n-1$ and therefore $a_{n-1} \\leq n-2$, so that $T \\geq 2$. If $a_{n-1}=n-2$, we are done. If not, then $a_{n-1}<n-2$ and therefore $a_{n-2} \\leq n-3$ and $T \\geq 3$. Inductively, we actually obtain $T=n$ and necessarily $f(n)=1$ and $a_{1}=b_{1}=0$, which gives the desired result.\n\nNow let $t$ be the largest such index $i$. We know that $n-t=b_{f(t)}=a_{f(t)}$ and therefore $a_{1} \\leq \\ldots \\leq a_{f(t)} \\leq n-t$. If we have $a_{1}=\\ldots=a_{f(t)}=n-t$, then $T=t$ and we have $a_{i} \\geq n-T$ for all $i$, hence $\\sum_{i} a_{i} \\geq n(n-T)$. Otherwise, $T>t$ and in fact one can show $T=t+f(t+1)$ by proceeding inductively and using the fact that $t$ is the last time for which $a_{f(t)}=b_{f(t)}$.\n\nNow we get that, since $a_{f(t+1)+1} \\geq n-t$, then $\\sum_{i} a_{i} \\geq(n-t)(n-f(t+1))=(n-T+f(t+$ 1) $)(n-f(t+1))=n(n-T)+n f(t+1)-f(t+1)(n-T+f(t+1))=n(n-T)+t f(t+1) \\geq$ $n(n-T)$.\n\nGreedy algorithm variant $\\mathbf{1}$ (ISR). Consider the residues $0, \\ldots, n-1$ modulo $n$ arranged in a circle clockwise, and place each $a_{i}$ on its corresponding residue; so that on each residue there is a stack of all $a_{i}$ s congruent to it modulo $n$, and the sum of the sizes of all stacks is exactly $n$. We iteratively flatten and spread the stacks forward, in such a way that the $a_{i}$ s are placed in the nearest available space on the circle clockwise (skipping over any already flattened residue or still standing stack). We may choose the order in which the stacks are flattened. Since the total amount of numbers equals the total number of spaces, there is always an available space and at the end all spaces are covered. The $b_{i} \\mathrm{~s}$ are then defined by adding to each $a_{i}$ the number of places it was moved forward, which clearly satifies (i) and (ii), and we must prove that they satisfy (iii) as well.\n\nSuppose that we flatten a stack of $k$ numbers at a residue $i$, causing it to overtake a stack of $l$ numbers at residue $j \\in(i, i+k)$ (we can allow $j$ to be larger than $n$ and identify it\nwith its residue modulo $n$ ). Then in fact in fact in whichever order we would flatten the two stacks, the total number of forward steps would be the same, and the total sum of the corresponding $b_{t}$ (such that $a_{t} \\bmod n \\in\\{i, j\\}$ ) would be the same. Moreover, we can merge the stacks to a single stack of $k+l$ numbers at residue $i$, by replacing each $a_{t} \\equiv j$ $(\\bmod n)$ by $a_{t}^{\\prime}=a_{t}-(j-i)$, and this stack would be flattened forward into the same positions as the separate stacks would have been, so applying our algorithm to the new stacks will yield the same total sum of $\\sum b_{i}-$ but the $a_{i}$ s are strictly decreased, so $\\sum a_{i}$ is decreased, so $\\left\\lfloor\\frac{\\sum a_{i}}{n}\\right\\rfloor$ is not increased - so by merging the stacks, we can only make the inequality we wish to prove tighter.\n\nThus, as long as there is some stack that when flattened will overtake another stack, we may merge stacks and only make the inequality tighter. Since the amount of numbers equals the amount of places, the merging process terminates with stacks of sizes $k_{1}, \\ldots, k_{m}$, such that the stack $j$, when flattened, will exactly cover the interval to the next stack. Clearly the numbers in each such stack were advanced by a total of $\\sum_{t=1}^{k_{j}-1}=\\frac{k_{j}\\left(k_{j}-1\\right)}{2}$, thus $\\sum b_{i}=\\sum a_{i}+\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2}$. Writing $\\sum a_{i}=n \\cdot r+s$ with $0 \\leq s<n$, we must therefore show\n\n$$\ns+\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2} \\leq \\frac{n(n-1)}{2}\n$$\n\nEnding 1. Observing that both sides of the last inequality are congruent modulo $n$ (both are congruent to the sum of all different residues), and that $0 \\leq s<n$, the inequality is eqivalent to the simpler $\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2} \\leq \\frac{n(n-1)}{2}$. Since $x(x-1)$ is convex, and $k_{j}$ are nonnegative integers with $\\sum_{j} k_{j}=n$, the left hand side is maximal when $k_{j^{\\prime}}=n$ and the rest are 0 , and then eqaulity is achieved. (Alternatively it follows easily for any non-negative reals from AM-GM.)\n\nEnding 2. If $m=1$ (and $k_{1}=n$ ), then all numbers are in a single stack and have the same residue, so $s=0$ and equality is attained. If $m \\geq 2$, then by convexity $\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2}$ is maximal for $m=2$ and $\\left(k_{1}, k_{2}\\right)=(n-1,1)$, where it equals $\\frac{(n-1)(n-2)}{2}$. Since we always have $s \\leq n-1$, we find\n\n$$\ns+\\sum_{j} \\frac{k_{j}\\left(k_{j}-1\\right)}{2} \\leq(n-1)+\\frac{(n-1)(n-2)}{2}=\\frac{n(n-1)}{2}\n$$\n\nas required.\nGreedy algorithm variant 1' (ISR). We apply the same algorithm as in the previous solution. However, this time we note that we may merge stacks not only when they overlap after flattening, but also when they merely touch front-to-back: That is, we relax the condition $j \\in(i, i+k)$ to $j \\in(i, i+k]$; the argument for why such merges are allowed is exactly the same (But note that this is now sharp, as merging non-touching stacks can cause the sum of $b_{i}$ s to decrease).\n\nWe now observe that as long as there at least two stacks left, at least one will spread to touch (or overtake) the next stack, so we can perform merges until there is only one stack left. We are left with verifying that the inequality indeed holds for the case of only one stack which is spread forward, and this is indeed immediate (and in fact equality is achieved).\n\nGreedy algorithm variant 2 (ISR). Let $c_{i}=a_{i} \\bmod n$. Iteratively define $b_{i}=a_{i}+l_{i}$ greedily, write $d_{i}=c_{i}+l_{i}$, and observe that $l_{i} \\leq n-1$ (since all residues are present in $\\left.a_{i}, \\ldots, a_{i}+n-1\\right)$, hence $0 \\leq d_{i} \\leq 2 n-2$. Let $I=\\left\\{i \\in I: d_{i} \\geq n\\right\\}$, and note that $d_{i}=b_{i}$ $\\bmod n$ if $i \\notin I$ and $d_{i}=\\left(b_{i} \\bmod n\\right)+n$ if $i \\in I$. Then we must show\n\n$$\n\\begin{aligned}\n& \\sum\\left(a_{i}+l_{i}\\right)=\\sum b_{i} \\leq \\frac{n(n-1)}{2}+n\\left\\lfloor\\frac{\\sum a_{i}}{n}\\right\\rfloor \\\\\n\\Longleftrightarrow & \\sum\\left(c_{i}+l_{i}\\right) \\leq \\sum\\left(b_{i} \\bmod n\\right)+n\\left\\lfloor\\frac{\\sum c_{i}}{n}\\right\\rfloor \\\\\n\\Longleftrightarrow & \\left.n|I| \\leq n\\left\\lfloor\\frac{\\sum c_{i}}{n}\\right\\rfloor \\Longleftrightarrow|I| \\leq \\left\\lvert\\, \\frac{\\sum c_{i}}{n}\\right.\\right\\rfloor \\Longleftrightarrow|I| \\leq \\frac{\\sum c_{i}}{n}\n\\end{aligned}\n$$\n\nLet $k=|I|$, and for each $0 \\leq m<n$ let $J_{m}=\\left\\{i: c_{i} \\geq n-m\\right\\}$. We claim that there must be some $m$ for which $\\left|J_{m}\\right| \\geq m+k$ (clearly for such $m$, at least $k$ of the sums $d_{j}$ with $j \\in J_{m}$ must exceed $n$, i.e. at least $k$ of the elements of $J_{m}$ must also be in $I$, so this $m$ is a \"witness\" to the fact $|I| \\geq k$ ). Once we find such an $m$, then we clearly have\n\n$$\n\\sum c_{i} \\geq(n-m)\\left|J_{m}\\right| \\geq(n-m)(k+m)=n k+m(n-(k+m)) \\geq n k=n|I|\n$$\n\nas required. We now construct such an $m$ explicitly.\nIf $k=0$, then clearly $m=n$ works (and also the original inequality is trivial). Otherwise, there are some $d_{i}$ s greater than $n$, and let $r+n=\\max d_{i}$, and suppose $d_{t}=r+n$ and let $s=c_{t}$. Note that $r<s<r+n$ since $l_{t}<n$. Let $m \\geq 0$ be the smallest number such that $n-m-1$ is not in $\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$, or equivalently $m$ is the largest such that $[n-m, n) \\subset\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$. We claim that this $m$ satisfies the required property. More specifically, we claim that $J_{m}^{\\prime}=\\left\\{i \\leq t: d_{i} \\geq n-m\\right\\}$ contains exactly $m+k$ elements and is a subset of $J_{m}$.\n\nNote that by the greediness of the algorithm, it is impossible that for $\\left[c_{i}, d_{i}\\right)$ to contain numbers congruent to $d_{j} \\bmod n$ with $j>i$ (otherwise, the greedy choice would prefer $d_{j}$ to $d_{i}$ at stage $i$ ). We call this the greedy property. In particular, it follows that all $i$ such that $d_{i} \\in\\left[s, d_{t}\\right)=\\left[c_{t}, d_{t}\\right)$ must satisfy $i<t$. Additionally, $\\left\\{d_{i}\\right\\}$ is disjoint from $[n+r+1,2 n)$ (by maximality of $d_{t}$ ), but does intersect every residue class, so it contains $[r+1, n)$ and in particular also $[s, n)$. By the greedy property the latter can only be attained by $d_{i}$ with $i<t$, thus $[s, n) \\subset\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$, and in particular $n-m \\leq s$ (and in particular $m \\geq 1$ ).\nOn the other hand $n-m>r$ (since $r \\notin\\left\\{d_{i}\\right\\}$ at all), so $n-m-1 \\geq r$. It follows that there is a time $t^{\\prime} \\geq t$ for which $d_{t^{\\prime}} \\equiv n-m-1(\\bmod n)$ : If $n-m-1=r$ then this is true for $t^{\\prime}=t$ with $d_{t}=n+r=2 n-m-1$; whereas if $n-m-1 \\in[r+1, n)$ then there is some $t^{\\prime}$ for which $d_{t^{\\prime}}=n-m-1$, and by the definition of $m$ it satisfies $t^{\\prime}>t$.\n\nTherefore for all $i<t \\leq t^{\\prime}$ for which $d_{i} \\geq n-m$, necessarily also $c_{i} \\geq n-m$, since otherwise $d_{t^{\\prime}} \\in\\left[c_{i}, d_{i}\\right)$, in contradiction to the greedy property. This is also true for $i=t$, since $c_{t}=s \\geq n-m$ as previously shown. Thus, $J_{m}^{\\prime} \\subset J_{m}$ as claimed.\nFinally, since by definition of $m$ and greediness we have $[n-m, n) \\cup\\left\\{d_{i}: i \\in I\\right\\} \\subset$ $\\left\\{d_{1}, \\ldots, d_{t}\\right\\}$, we find that $\\left\\{d_{j}: j \\in J_{m}^{\\prime}\\right\\}=[n-m, n) \\cup\\left\\{d_{i}: i \\in I\\right\\}$ and thus $\\left|J_{m}^{\\prime}\\right|=$ $|[n-m, n)|+|I|=m+k$ as claimed.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 5", "solution_match": "\nSolution 5. "}}
|
| 11 |
+
{"year": "2019", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "(United Kingdom).\n\nOn a circle, Alina draws 2019 chords, the endpoints of which are all different. A point is considered marked if it is either\n(i) one of the 4038 endpoints of a chord; or\n(ii) an intersection point of at least two chords.\n\nAlina labels each marked point. Of the 4038 points meeting criterion (i), Alina labels 2019 points with a 0 and the other 2019 points with a 1 . She labels each point meeting criterion (ii) with an arbitrary integer (not necessarily positive).\nAlong each chord, Alina considers the segments connecting two consecutive marked points. (A chord with $k$ marked points has $k-1$ such segments.) She labels each such segment in yellow with the sum of the labels of its two endpoints and in blue with the absolute value of their difference.\n\nAlina finds that the $N+1$ yellow labels take each value $0,1, \\ldots, N$ exactly once. Show that at least one blue label is a multiple of 3 .\n(A chord is a line segment joining two different points on a circle.)", "solution": "First we prove the following:\nLemma: if we color all of the points white or black, then the number of white-black edges, which we denote $E_{W B}$, is equal modulo 2 to the number of white (or black) points on the circumference, which we denote $C_{W}$, resp. $C_{B}$.\n\nObserve that changing the colour of any interior point does not change the parity of $E_{W B}$, as each interior point has even degree, so it suffices to show the statement holds when all interior points are black. But then $E_{W B}=C_{W}$ so certainly the parities are equal.\n\nNow returning to the original problem, assume that no two adjacent vertex labels differ by a multiple of three, and three-colour the vertices according to the residue class of the labels modulo 3. Let $E_{01}$ denote the number of edges between 0 -vertices and 1 -vertices, and $C_{0}$ denote the number of 0 -vertices on the boundary, and so on.\n\nThen, consider the two-coloring obtained by combining the 1-vertices and 2-vertices. By applying the lemma, we see that $E_{01}+E_{02} \\equiv C_{0} \\bmod 2$.\n\n$$\n\\text { Similarly } E_{01}+E_{12} \\equiv C_{1}, \\quad \\text { and } E_{02}+E_{12} \\equiv C_{2}, \\quad \\bmod 2\n$$\n\nUsing the fact that $C_{0}=C_{1}=2019$ and $C_{2}=0$, we deduce that either $E_{02}$ and $E_{12}$ are even and $E_{01}$ is odd; or $E_{02}$ and $E_{12}$ are odd and $E_{01}$ is even.\n\nBut if the edge labels are the first $N$ non-negative integers, then $E_{01}=E_{12}$ unless $N \\equiv 0$ modulo 3 , in which case $E_{01}=E_{02}$. So however Alina chooses the vertex labels, it is not possible that the multiset of edge labels is $\\{0, \\ldots, N\\}$.\nHence in fact two vertex labels must differ by a multiple of 3 .", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 6", "solution_match": "\nSolution 1. "}}
|
| 12 |
+
{"year": "2019", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "(United Kingdom).\n\nOn a circle, Alina draws 2019 chords, the endpoints of which are all different. A point is considered marked if it is either\n(i) one of the 4038 endpoints of a chord; or\n(ii) an intersection point of at least two chords.\n\nAlina labels each marked point. Of the 4038 points meeting criterion (i), Alina labels 2019 points with a 0 and the other 2019 points with a 1 . She labels each point meeting criterion (ii) with an arbitrary integer (not necessarily positive).\nAlong each chord, Alina considers the segments connecting two consecutive marked points. (A chord with $k$ marked points has $k-1$ such segments.) She labels each such segment in yellow with the sum of the labels of its two endpoints and in blue with the absolute value of their difference.\n\nAlina finds that the $N+1$ yellow labels take each value $0,1, \\ldots, N$ exactly once. Show that at least one blue label is a multiple of 3 .\n(A chord is a line segment joining two different points on a circle.)", "solution": "As before, colour vertices based on their label modulo 3.\nSuppose this gives a valid 3-colouring of the graph with 2019 0s and 2019 1s on the\ncircumference. Identify pairs of 0-labelled vertices and pairs of 1-labelled vertices on the circumference, with one 0 and one 1 left over. The resulting graph has even degrees except these two leaves. So the connected component $\\mathcal{C}$ containing these leaves has an Eulerian path, and any other component has an Eulerian cycle.\n\nLet $E_{01}^{*}$ denote the number of edges between 0 -vertices and 1 -vertices in $\\mathcal{C}$, and let $E_{01}^{\\prime}$ denote the number of such edges in the other components, and so on. By studying whether a given vertex has label congruent to 0 modulo 3 or not as we go along the Eulerian path in $\\mathcal{C}$, we find $E_{01}^{*}+E_{02}^{*}$ is odd, and similarly $E_{01}^{*}+E_{12}^{*}$ is odd. Since neither start nor end vertex is a 2 -vertex, $E_{02}^{*}+E_{12}^{*}$ must be even.\n\nApplying the same argument for the Eulerian cycle in each other component and adding up, we find that $E_{01}^{\\prime}+E_{02}^{\\prime}, E_{01}^{\\prime}+E_{12}^{\\prime}, E_{02}^{\\prime}+E_{12}^{\\prime}$ are all even. So, again we find $E_{01}+E_{02}$, $E_{01}+E_{12}$ are odd, and $E_{02}+E_{12}$ is even, and we finish as in the original solution.", "metadata": {"resource_path": "EGMO/segmented/en-2019-solutions-day2.jsonl", "problem_match": "# Problem 6", "solution_match": "\nSolution 2. "}}
|
EGMO/segmented/en-2023-solutions.jsonl
CHANGED
|
The diff for this file is too large to render.
See raw diff
|
|
|
EGMO/segmented/en-2024-solutions.jsonl
CHANGED
|
@@ -1,11 +1,11 @@
|
|
| 1 |
-
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "
|
| 2 |
-
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "
|
| 3 |
-
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "
|
| 4 |
-
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "
|
| 5 |
-
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "
|
| 6 |
-
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "
|
| 7 |
-
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "
|
| 8 |
-
{"year": "2024", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "
|
| 9 |
-
{"year": "2024", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "
|
| 10 |
-
{"year": "2024", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "
|
| 11 |
-
{"year": "2024", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "6 (LUX+BEL)\n\nProblem. Find all positive integers $d$ for which there exists a degree $d$ polynomial $P$ with real coefficients such that there are at most $d$ different values among $P(0), P(1), \\ldots, P\\left(d^{2}-\\right.$ d).\n\nRemark 1 You can add a constant to a polynomial satisfying the conditions and obtain another polynomial satisfying the conditions.\n\nRemark 2 This problem is equivalent to: Find all positive integers $d$ for which there exists a polynomial $P$ of degree $d$ that takes at most $d$ different values at members of a an arithmetic progression with $d^{2}-d+1$ (different) terms.\nThe answer to this EGMO problem implies a solution to this more general problem by scaling and translating, and the general result solves the EGMO problem as a special case. This means that instead of working with $0,1, \\ldots, d^{2}-d$ we have the option of working with a region that is symmetric about the origin. Irrespective of the parity of $d$ we can use the $d^{2}-d+1$ integers which run from $-\\left(d^{2}-d\\right) / 2$ to $\\left(d^{2}-d\\right) / 2$ inclusive.\n\nThe advantage of using an arithmetic progression which is symmetric about the 0 is that $P(X)$ is a polynomial which works for the problem if, and only if, $P(-X)$ is a polynomial which works for the problem. This means that working at one end of the run of integers is the reflection of the activity at the other end. T Remarks dismissing the cases at the other end of the run as similar now become obviously correct rather than having to be studied", "solution": ".\n\nSolution. We claim that such polynomials exist if and only if $d \\leq 3$. The following examples show that such polynomials do exist for $d \\leq 3$ :\n\n$$\n\\left.\\begin{array}{lll}\nd=1: & d^{2}-d=0, & P_{1}(x)=x,\n\\end{array} \\begin{array}{ll} \n& P(0)=0 ;\n\\end{array}\\right\\}\n$$\n\nWe can make more examples by adding constants.\nNow we will show that there are no examples of degree greater than 3.\nFrom now on we assume (without loss of generality) that the leading coefficient of our polynomial $P$ is positive and that all values $P(i)$ are positive (by adding a constant if necessary) for integers $i$ in the range $0 \\leq i \\leq d^{2}-d+1$.\n\nAssume (for contradiction) that $P$ is a polynomial of degree $d \\geq 4$ that satisfies the conditions of the problem and let $P(0), \\ldots, P\\left(d^{2}-d\\right)$ take values among $p_{1}<\\cdots<p_{d}$. For $i=1, \\ldots, d$, let $n_{i} \\geq 0$ be the number of appearances of $p_{i}$ among $P(0), \\ldots, P\\left(d^{2}-d\\right)$.\n\nBy definition $n_{1}+\\cdots+n_{d}=d^{2}-d+1$. Since $P$ has degree $d, n_{i} \\leq d$. The key observation is now the following.\n\nClaim 1 Make the convention that $n_{0}=n_{d+1}=0$. If $n_{i}=d$ for some $i$ in the range $1 \\leq i \\leq d$, then $n_{i \\pm 1} \\leq d-2$.\n\nProof. Up to scaling and hence without loss of generality, $P$ has leading coefficient +1 . $\\overline{\\text { Since }} n_{i}=d$, there exist non-negative integers $a_{1, i}<\\cdots<a_{d, i} \\leq d^{2}-d$ such that\n\n$$\nP(X)=\\left(X-a_{1, i}\\right) \\cdots\\left(X-a_{d, i}\\right)+p_{i} .\n$$\n\nBy construction, each of the $d-1$ intervals $I_{j}=\\left[a_{j, i}, a_{j+1, i}\\right]$ contains at least one local extremum of $P$, so contains exactly one such extremum because $P$, having degree $d$, has at most $d-1$ such extrema. Suppose that $i \\leq d-1$ and that $P(m)=p_{i+1}>p_{i}$ for some $m \\in\\left\\{0, \\ldots, d^{2}-d\\right\\}$. Since $P$ has positive leading coefficient,\n\n$$\nm \\in\\left(a_{d, i}, \\infty\\right) \\cup\\left(a_{d-2, i}, a_{d-1, i}\\right) \\cup \\cdots \\cup\\left(a_{i, 1}, a_{2, i}\\right)\n$$\n\nif $d$ is odd or\n\n$$\nm \\in\\left(a_{d, i}, \\infty\\right) \\cup\\left(a_{d-2, i}, a_{d-1, i}\\right) \\cup \\cdots \\cup\\left(-\\infty, a_{1, i}\\right)\n$$\n\nif $d$ is even.\nSuppose that $a_{j, i}<m<a_{j+1, i}$, for some $j \\in\\{1, \\ldots, d-1\\}$. If $a_{j, i}+1<m<a_{j+1, i}-1$, then, because $I_{j}$ contains exactly one local extremum (which is a maximum),\n\nEither $p_{i+1}=P(m)>P\\left(a_{j, i}+1\\right)$ or $p_{i+1}=P(m)>P\\left(a_{j+1, i}-1\\right)$. Since $P\\left(a_{j, i}+1\\right)>$ $P\\left(a_{j, i}\\right)=p_{i}$ and $P\\left(a_{j, i}-1\\right)>P\\left(a_{j+1, i}\\right)=p_{i}$, this contradicts the requirement that $P\\left(a_{j, i}+1\\right), P\\left(a_{j+1, i}-1\\right) \\in\\left\\{p_{1}, \\ldots, p_{d}\\right\\}$. Hence $m=a_{j, i}+1$ or $m=a_{j, i}-1$. Similarly, if $m>a_{d, i}$, then $m=a_{d, i}+1$, but if $m<a_{i, 1}$ (which may arise when $d$ is even), then $m=a_{i, 1}-1$. This shows that $m$ belongs to this list:\n\n$$\na_{d, i}+1, a_{d-1, i}-1, \\ldots, a_{2, i}+(-1)^{d}, a_{1, i}-(-1)^{d}\n$$\n\nThis list contains at most $d$ different integers. It follows in particular that, if $n_{i+1}>d-2$, then either\n\n$$\nP\\left(a_{d, i}+1\\right)=p_{i+1}=P\\left(a_{d-1, i}-1\\right)\n$$\n\nor\n\n$$\nP\\left(a_{2, i}+(-1)^{d}\\right)=p_{i+1}=P\\left(a_{1, i}-(-1)^{d}\\right)\n$$\n\nwith, additionally, $a_{2, i}+(-1)^{d} \\neq a_{1, i}-(-1)^{d}$.\nWe have\n\n$$\n\\left|P\\left(a_{1, i} \\pm 1\\right)-p_{i}\\right|=1 \\cdot\\left|a_{1, i} \\pm 1-a_{2, i}\\right| \\cdot \\prod_{j=3}^{d}\\left|a_{1, i} \\pm 1-a_{j, i}\\right|\n$$\n\nand\n\n$$\n\\left|P\\left(a_{2, i} \\mp 1\\right)-p_{i}\\right|=\\left|a_{2, i} \\mp 1-a_{1, i}\\right| \\cdot 1 \\cdot \\prod_{j=3}^{d}\\left|a_{2, i} \\mp 1-a_{j, i}\\right| .\n$$\n\nAs $a_{1, i}<a_{2, i}<a_{3, i}<\\ldots<a_{d, i}$ we have $\\left|a_{1, i} \\pm 1-a_{j, i}\\right| \\geq\\left|a_{2, i} \\mp 1-a_{j, i}\\right|$ with equality possible only if $a_{1, i}+1=a_{2, i}-1$. We also have $\\left|a_{1, i} \\pm 1-a_{2, i}\\right|=\\left|a_{2, i} \\mp 1-a_{1, i}\\right|$, which can be zero only if $a_{1, i}+1=a_{2, i}-1$. We conclude that $\\left|P\\left(a_{1, i} \\pm 1\\right)-p_{i}\\right|>\\left|P\\left(a_{2, i} \\mp 1\\right)-p_{i}\\right|$ or $a_{1, i}+1=a_{2, i}-1$.\n\nLooking at the other end of the list of $\\left(a_{j, i}\\right)$ as $j$ varies, we have\n\n$$\n\\left|P\\left(a_{d-1, i}-1\\right)-p_{i}\\right|=1 \\cdot\\left|a_{d-1, i}-1-a_{d, i}\\right| \\cdot \\prod_{j=1}^{d-2}\\left|a_{d-1, i}-1-a_{j, i}\\right|\n$$\n\nand\n\n$$\n\\left|P\\left(a_{d, i}+1\\right)-p_{i}\\right|=\\left|a_{d, i}+1-a_{d-1, i}\\right| \\cdot 1 \\cdot \\prod_{j=1}^{d-2}\\left|a_{d, i}+1-a_{j, i}\\right|\n$$\n\nIn these two formulas the shared factor outside the product is at least 2 and so is not 0 . Now look at the factors behind the product symbols. As $a_{1, i}<a_{2, i}<a_{3, i}<\\ldots<a_{d, i}$, for $j \\leq d-2$ we have $\\left|a_{d, i}+1-a_{j, i}\\right|>\\left|a_{d-1, i}-1-a_{j, i}\\right|$. We conclude that $\\left|P\\left(a_{d, i}+1\\right)-p_{i}\\right|>$ $\\left|P\\left(a_{d-1, i}-1\\right)-p_{i}\\right|$. Claim 1 is proved.\n\nFor each $i \\in\\{1, \\ldots, d-1\\}$, there are three possibilities:\n\n- $n_{i}, n_{i+1} \\leq d-1$\n- $n_{i}=d$ and $n_{i+1} \\leq d-2$\n- $n_{i+1}=d$ and $n_{i} \\leq d-2$.\n\nIn all three cases, $n_{i}+n_{i+1} \\leq 2(d-1)$. If $n$ is even, this leads to the contradiction\n\n$$\nd^{2}-d+1=\\left(n_{1}+n_{2}\\right)+\\cdots+\\left(n_{d-1}+n_{d}\\right) \\leq(d / 2)[2(d-1)]=d^{2}-d\n$$\n\nThis is an important staging point in the argument because we have eliminated the possibility of a polynomial of even degree $d$ satisfying the conditions of the problem if $d \\geq 4$.\n\nFrom now on we assume that $d \\geq 5$ is odd, and\n$d^{2}-d+1=\\left(n_{1}+n_{2}\\right)+\\cdots+\\left(n_{d-2}+n_{d-1}\\right)+n_{d} \\leq[(d-1) / 2][2(d-1)]+d=d^{2}-d+1$.\nEquality must therefore hold throughout. Since the sum can also be grouped as\n\n$$\nn_{1}+\\left(n_{2}+n_{3}\\right)+\\cdots+\\left(n_{d-1}+n_{d}\\right)\n$$\n\nthis requires $n_{1}=n_{d}=d, n_{i}+n_{i+1}=2(d-1)$ for $i=1,2, \\ldots, d-1$ i.e. $n_{i}=d$ for odd $i$ and $n_{i}=d-2$ for even $i$.\n\nWe are interested in the degree of $P$ being $d \\geq 5$ and odd, and showing that no polynomial $P$ satisfying the conditions of the problem can exist. There are $d-1 \\geq 4$ extremal points points which alternate between local maxima and minima (in that order) as you read from left to right (we normalize so that $P$ is monic). For any $p_{i}$ with $i$ odd, the line $y=p_{i}$ (with\n$i$ odd) crosses the graph of $P$ in $d$ places with $x$-coordinates in the real closed interval $\\left[0, d^{2}-d\\right]$ at points $\\left(z, p_{i}\\right)$ so each $z$ must be an integer. Suppose that $J$ is a real interval on the $x$-axis ending at adjacent local extrema. The function defined by $P$ is monotonic on each $J$. The line $y=p_{i}$ ( $i$ odd) meets the graph at most once on $J$. Therefore it meets the graph of $P$ exactly once in the interior of each $J$ (there are $d-2$ such intervals) and at the only two possible places outside the union of these intervals.\n\nNow consider $p_{j}$ when $j$ is even (so $n_{j}=d-2$ ). These $d-2$ intervals $J$ afford $d-2$ real values at which $P$ will take $p_{j}$ as a value where $j$ is fixed and even. The question is, are the corresponding arguments integers? The proof of Claim 1 tells us that in the middle of the run $\\left\\{0,1, \\ldots, d^{2}-d+1\\right\\}$ all is well: the polynomial is assuming the value $p_{j}$ at an integer where the polynomial assumes the values $p_{j-1}$ and $p_{j+1}$ at adjacent integers in some order. The problem is at the ends of the run where $\\left|P\\left(a_{1, i}+1\\right)-p_{i}\\right|>\\left|P\\left(a_{2, i}-1\\right)-p_{i}\\right|$ and $\\left|P\\left(a_{d, i}+1\\right)-p_{i}\\right|>\\left|P\\left(a_{d-1, i}-1\\right)-p_{i}\\right|$. When $j$ is even, two of the roots of $P(x)-p_{j}$ are not integers, and we now know approximately where this trouble is happening (at the ends).\n\nAt this point we could finish if $d \\geq 7$, because the run of regular behaviour in the middle is sufficiently long that we could obtain a contradiction. However we have to work a little harder to include the case $d=5$. We now show that the run of regular behaviour is slightly longer than we have currently established. We do this using Claim 2.\n\nClaim 2. If $d$ is odd, and $n_{i}=d, n_{i \\pm 1}=d-2$ for some $i$, then $P$ attains $p_{i \\pm 1}$ precisely at the $d-2$ integers\n\n$$\na_{2, i}-1, a_{3, i}+1, \\cdots, a_{d-2, i}-1, a_{d-1, i}+1\n$$\n\nProof Suppose (for contradiction) $a_{1, i}+1 \\neq a_{2, i}-1$ and $P\\left(a_{1, i}+1\\right)=p_{i+1}$. Now $a_{1, i}<a_{2, i}$ so either $a_{1, i}+1<a_{2, i}-1$ or $a_{1, i}=a_{2, i}-1$. In the latter case, $P\\left(a_{1, i}+1\\right)=P\\left(a_{2, i}\\right)=p_{i}$, a contradiction. In the former case, the proof of Claim 1 shows that\n\n$$\n\\left|P\\left(a_{2, i}-1\\right)-p_{i}\\right|<\\left|P\\left(a_{1, i}+1\\right)-p_{i}\\right|=\\left|p_{i+1}-p_{i}\\right|=p_{i+1}-p_{i}\n$$\n\nso $P\\left(a_{2, i}-1\\right)<p_{i+1}$. The polynomial is decreasing on the interval $\\left(a_{2, d}, a_{2,1}\\right)$ so $p_{i}<P\\left(a_{2, i}-1\\right)<p_{i+1}$ which is absurd because $P\\left(a_{2, i}-1\\right)=p_{j}$ for some $j$. Therefore $P\\left(a_{2, i}-1\\right)=p_{i+1}$ for all odd $i$. A similar argument shows that $P\\left(a_{d-1, i}+1\\right)=p_{i+1}$ so Claim 2 is established.\n\nNow we have n sequence of alternating falling then rising then falling etc. full runs starting at $\\left(a_{2, d}, p_{d}\\right)$ and ending at $\\left(a_{d-1,1}, p_{1}\\right)$ so the initial run of $3 d+1$ terms of this run of values is\n\n$$\np_{d}, p_{d-1}, \\cdots p_{1}, p_{1}, p_{2}, \\ldots, p_{d}, p_{d}, p_{d-1}, \\cdots p_{1}, p_{1}\n$$\n\nwhich starts at $\\left(a_{2, d}, p_{d}\\right)$ and ends at $\\left(a_{4,1}+1, p_{1}\\right)$ which is fine because $4 \\leq d-1$.\nThere are now various ways we can finish.\n(a) Consider the run of length $2 d$ consecutive values\n\n$$\np_{d}, p_{d-1}, \\cdots p_{1}, p_{1}, p_{2}, \\ldots, p_{d}\n$$\n\nThe first $d+1$ points determine $P(x)$. The last $d+1$ values also determine $P$ but the values are in the reverse order, so $P(X)=P(c-X)$ for some constant $c$. However, the coefficients of $X^{d}$ are have opposite signs ( $d$ is odd) so this is absurd.\n(b) The idea in (a) can be expressed in terms of Lagrange interpolation to obtain essentially the same contradiction. Construct $P$ in two ways using Lagrange interpolation on both the first $d+1$ and the last $d+1$ points. The symmetry in the data forces the graph of $P$ to have a vertical axis of symmetry. This is absurd because the degree of $P$ is odd.\n(c) The initial fragment length $3 d+1$ mentioned above at $(*)$ includes two identical runs of values of $P$ (in the same order) of length $d+1$. The polynomial $P$ is determined by each of them and so $P(X)=P(X+c)$ for some constant $c$ and so the polynomial defines a bounded function which is absurd.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 6 (LUX+BEL)\n", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:\n(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.\n(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.\n\nDetermine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.", "solution": "We will show that the answer are the integer pairs $(u, v)$ such that $u \\neq 0$, $v \\neq 0,\\{u, v\\} \\neq\\{-1,1\\}$ and $u>0$ or $v>0$.\n\nIf $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers. Hence, if $u=0$ or $v=0$, we cannot reach every possible $y$. From now on, assume $u \\neq 0$ and $v \\neq 0$.\n\nIf both numbers $u, v$ were negative, we will show that there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$. From now on, assume that at least one of $u, v$ is positive. Without loss of generality take $u<v$, and so $v>0$.\n\nAfter one step, we can have the numbers $u, v, u+v$, which are mutually distinct due to $u, v$ being nonzero. Notice that the equation $u x^{2}+(u+v) x+v=0$ has a root -1 , and so we can have -1 on the board.\n\nWe now check two cases: case $v=1$, and case $v>1$.\nIf $v=1$, then $u<0$. Further split the case of $v=1$ based on whether $u=-1$ or $u<-1$.\n\nIf $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\\{a, b, c\\}$ to $\\{-1,0,1\\}$ in any order only has solutions for $x$ in $\\{-1,0,1\\}$. Hence, if $\\{u, v\\}=\\{-1,1\\}$, then we cannot reach every possible $y$.\n\nIf $v=1$ and $u<-1$, we can use operation (i) on numbers $u,-1$ (and then repeat choosing the obtained result and -1 ) to get any negative number smaller than $u$, and operation (i) on numbers $(u, 1)$ (and then repeat choosing the obtained result and 1 ) to get any negative number larger than $u$, as well as 0 . Then, we set $(a, b, c)=(0,1,-2)$ and apply operation (ii) to additionally get number 2. Applying (i) on $(2,1)$ (and then repeat choosing the obtained result and 1), we can get all the remaining integers too.\n\nFrom now on, assume $v>1$. Recall that we can make $u+v$ and -1 .\nWe will now apply operation (i). First, $(v,-1)$ gives $v-1$. Next, $(v, v-1)$ gives $2 v-1$. Since $v>1$, we know $v \\neq 2 v-1$, so we can apply operation (i) on $(v, 2 v-1)$ to get $3 v-1$, and then continue adding $(v, k v-1)$ to get $(k+1) v-1$ for any positive $k$. Since $v>1$, we can get an arbitrarily large integer by repeating this.\n\nIf $a$ is any positive number on the board, applying (i) to $(a,-1)$ gives $a-1$. By repeating this, we have that we can get all numbers smaller than $a$ and larger than or equal to -1 . Together with previously having found a way to get an arbitrarily large integer, we have that we can get any integer $l \\geq-1$ on the board.\n\nNow, we set $(a, b, c)=(0,1,2)$ and apply operation (ii) to additionally get number -2 . Then we can repeat operation (i) on ( $-1,-2$ ) (and afterwards on -1 and the obtained result) to get any negative number.\n\nTherefore, if $u \\neq 0, v \\neq 0,\\{u, v\\} \\neq\\{-1,1\\}$ and $u>0$ or $v>0$, we can write every integer on the board.\n\nRemark. There are of course many other ways to create all integers in case of $(u, v)$ that satisfies all the requirements. Basically you will always use (i) to create arbitrarily large numbers and then (ii) to create a number in a range that you didn't have before.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 1 (SVK)\n", "solution_match": "\nSolution 1. "}}
|
| 2 |
+
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:\n(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.\n(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.\n\nDetermine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.", "solution": "If $u=0$ or $v=0$ then we can only get $\\{u, v\\}$.\n\nProof. If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers.\n\nIf $\\max (u, v)<0$, we cannot get non-negative numbers.\n\nProof. For $a, b, c<0$ :\n(i) cannot generate a non-negative number as $a+b<0$.\n(ii) cannot generate a non-negative number as for $x \\geq 0$ : $a x^{2}+b x+c \\leq c<0$.\n\nIf $u+v \\neq 0, u, v \\neq 0$ and $\\max (u, v)>0$, we can get every number.\n\nProof. $u \\neq v \\rightarrow u+v$ can be written. $u \\neq 0$, so $u+v \\neq v \\rightarrow u+2 v$ can be written. $v \\neq 0$, so $u+2 v \\neq u$, meaning that $2 u+2 v$ can be written. If for $n>1, n(u+v)$ can be written then $(n+1)(u+v)=n(u+v)+(u+v)$ can also be written, because $u+v \\neq 0$, so $n(u+v) \\neq(u+v)$. Therefore, by induction for all $n>0$ the number $n(u+v)$ can be written.\n\nTaking $n=2,3, \\ldots$ and $(u+v)(x+1)(x+n)=(u+v) x^{2}+(u+v)(n+1) x+(u+v) n=0$ gives $x=-1$ and $x=-n \\rightarrow$ for all $n>0$ we can get $-n$ (we can get all the negative numbers). Additionally, we can get $u+(-u)=0$.\n\nFor $n \\geq 1$ we can take $0 \\cdot x^{2}+u x+(-u n)=0$ as $u \\neq 0 \\rightarrow u,-n u, 0$ are all distinct, therefore we can get $n$. Thus, we can get all the numbers.\n\nIf $u+v=0$ and $\\max (u, v)>1$ we can get all the numbers.\n\nProof. We can get $0=u+v$ as $u \\neq v$. Take $0 \\cdot x^{2}+u x-u=0$ so we can get 1 written on the board. Take $\\left(u^{\\prime}, v^{\\prime}\\right)=(1, \\max (u, v))$ and then use the result from claim 3. As $0<u^{\\prime}=1<\\max (u, v)=v^{\\prime}$ and $u^{\\prime}+v^{\\prime}>0$ we can get all the numbers.\n\nRemaining case: If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\\{a, b, c\\}$ to $\\{-1,0,1\\}$ in any order only has solutions for $x$ in $\\{-1,0,1\\}$. Hence, if $\\{u, v\\}=\\{-1,1\\}$, then we cannot reach every possible $y$.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 1 (SVK)\n", "solution_match": "\nSolution 2. "}}
|
| 3 |
+
{"year": "2024", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:\n(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.\n(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.\n\nDetermine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.", "solution": "We show none of the initial number can be 0 , as in Solution 1. Then, we split into three cases: initial numbers having different signs, both being positive, and both being negative.\n\nCase 1. Suppose we have two numbers $u, v$ with different signs such that $\\operatorname{gcd}(u, v)=k$ for some $k \\in \\mathbb{Z}^{+}$. Without loss of generality assume that $u>0$ and $v<0$.\n\nCase 1.1. $v<-k$ :\nWe can generate all numbers $y$ such that $k \\mid y$ and $y \\leq u$.\n\nProof. Define $u^{\\prime}=\\frac{u}{k}, v^{\\prime}=\\frac{v}{k}$. Note that by definition, $\\operatorname{gcd}\\left(u^{\\prime}, v^{\\prime}\\right)=1$. If starting with numbers $u^{\\prime}, v^{\\prime}$, we can make a sequence of applications of only the (i) rule to write a number $y=p \\cdot u^{\\prime}+q \\cdot v^{\\prime}$ on the board, then we can apply the same sequence of moves to $u, v$ to write $k \\cdot y=p \\cdot u+q \\cdot v$ on the board.\n\nTherefore, we will prove instead that if $v^{\\prime}<-1$, we can write all numbers $y<u^{\\prime}$ on the board, which is equivalent to the lemma.\n\nWe attempt to write numbers $u^{\\prime}+q \\cdot v^{\\prime}$ for $q \\in \\mathbb{Z}^{+}$on the board by repeatedly adding $v^{\\prime}$ to $u^{\\prime}$. This process can only ever halt if we reach a point where $u^{\\prime}+q \\cdot v^{\\prime}=v^{\\prime}$. That cannot occur, as it would imply $u^{\\prime}=(1-q) \\cdot v^{\\prime}$. Taking into account that $u^{\\prime}, v^{\\prime} \\neq 0$, that implies $\\operatorname{gcd}\\left(u^{\\prime}, v^{\\prime}\\right)=\\left|v^{\\prime}\\right|$. That is a contradiction, as $\\left|v^{\\prime}\\right|>1$.\n\nTherefore, we can write all numbers of the form $u^{\\prime}+q \\cdot v^{\\prime}$ on the board for $q \\in \\mathbb{Z}^{+}$. We will use these numbers to construct an arbitrary integer $y$.\n\nIf we want to write a number $y<u^{\\prime}$ on the board, and we already have a number $n<y$ on the board such that $y \\equiv n\\left(\\bmod u^{\\prime}\\right)$, then we can construct $y$ by repeatedly adding $u^{\\prime}$ to $n$ until we reach $y$, skipping all numbers that are already on the board. As $y<u^{\\prime}$, none of the numbers we attempt to add $u^{\\prime}$ to will be equal to $u^{\\prime}$.\n\nSuppose we fix any number $y<u^{\\prime}$. As $\\operatorname{gcd}\\left(u^{\\prime}, v^{\\prime}\\right)=1, q \\cdot v^{\\prime}$ takes all residues modulo $u^{\\prime}$ as $q$ runs through the positive integers. Therefore, we will always be able to find a number $n$ of the form $u^{\\prime}+q \\cdot v^{\\prime}$ such that $y \\equiv n \\bmod u^{\\prime}$. We can generate an arbitrarily small $n^{\\prime}$ by taking $n^{\\prime}=n+l \\cdot u^{\\prime} \\cdot v^{\\prime}=u^{\\prime}+\\left(q+l \\cdot u^{\\prime}\\right) \\cdot v^{\\prime}$ for large enough $l$, making both $n^{\\prime}<y$ and $n^{\\prime} \\equiv y \\bmod u^{\\prime}$ true.\n\nTherefore, we can write all numbers $y<u^{\\prime}$ on the board. Thus, starting from $u$ and $v$, we can get all numbers $y \\leq u$ s.t. $k \\mid y$.\n\nThe numbers $k, 0$ and all negative multiples of $k$ are a subset of the integers $y \\leq u$ s.t. $k \\mid y$. Therefore, we have all of those numbers on the board.\n\nWe can now get an arbitrary nonzero number by applying (ii) to the polynomial $k \\cdot(x-$ $n)(x+n)=k \\cdot x^{2}+0 \\cdot x-n^{2} \\cdot k$. The coefficients of this polynomial are distinct for all integers $n \\neq 0$, and they are from the set $\\{k, 0\\} \\cup\\{q \\cdot k \\mid q<0\\}$, which we have on the board. Therefore the rule application is valid.\n\nAs this works for all integers $n \\in \\mathbb{Z} \\backslash\\{0\\}$, and 0 is already on the board, we have proven that we can write all integers on the board.\n\nCase 1.2.: $v=-k$ :\nCase 1.2.1.: $k \\neq 1$.\nIf $k \\neq 1$, we can generate -1 from the polynomial $u \\cdot x^{2}+(u+v) x+v$. We can now repeatedly add -1 to $v=-k$ until we reach $-2 k$ on the board. Now, we can appeal to Case 1.1.\n\nCase 1.2.2. $k=1$.\nTo restate the conditions of this sub-case, $v=-k=-1$, and $u$ is an arbitrary positive number.\n\nCase 1.2.2.1. $u=1$.\nIf $u=1$, we are only ever able to construct the numbers $-1,0,1$, no matter how we apply the rules.\n\nCase 1.2.2.2. $u \\neq 1$.\nWe can subtract 1 from $u$ until we reach 0 . This procedure also generates 1 . We now add 1 to $u$ until we get all positive numbers.\n\nNow, we find an arbitrary polynomial with different positive coefficients that have a negative root smaller than -1 . An example is $(x+3)^{2}$.\n\nWe will now keep adding -1 to -3 to get all the negative numbers $y \\leq-3$. To get -2 , we can add -3 to 1 , generating all integers.\n\nCase 2 Suppose that both of $u, v$ are positive.\nWe can now use any method from the previous solutions to generate a negative number, and then appeal to Case 1.\n\nCase 3 Suppose $u<0, v<0$.\nThen there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 1 (SVK)\n", "solution_match": "\nSolution 3. "}}
|
| 4 |
+
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\\overparen{D F}$ and $\\overparen{D E}$ of the incircle, respectively, such that $\\angle B X D=\\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\\Omega$ such that $K T$ is tangent to $\\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\\Omega$.", "solution": "By the alternate segment theorem we have that:\n\n$$\n180^{\\circ}=\\angle D C Y+\\angle C Y D+\\angle Y D C=\\angle D C Y+\\angle D X B+\\angle Y X D=\\angle D C Y+\\angle Y X B\n$$\n\nTherefore opposite angle of $B X Y C$ are supplementary and so $C Y X B$ cyclic.\nOne can apply power of a point at $K$ :\n\n$$\nK T^{2}=K B \\cdot K C=K X \\cdot K Y=K D^{2} \\Longrightarrow K T=K D .\n$$\n\n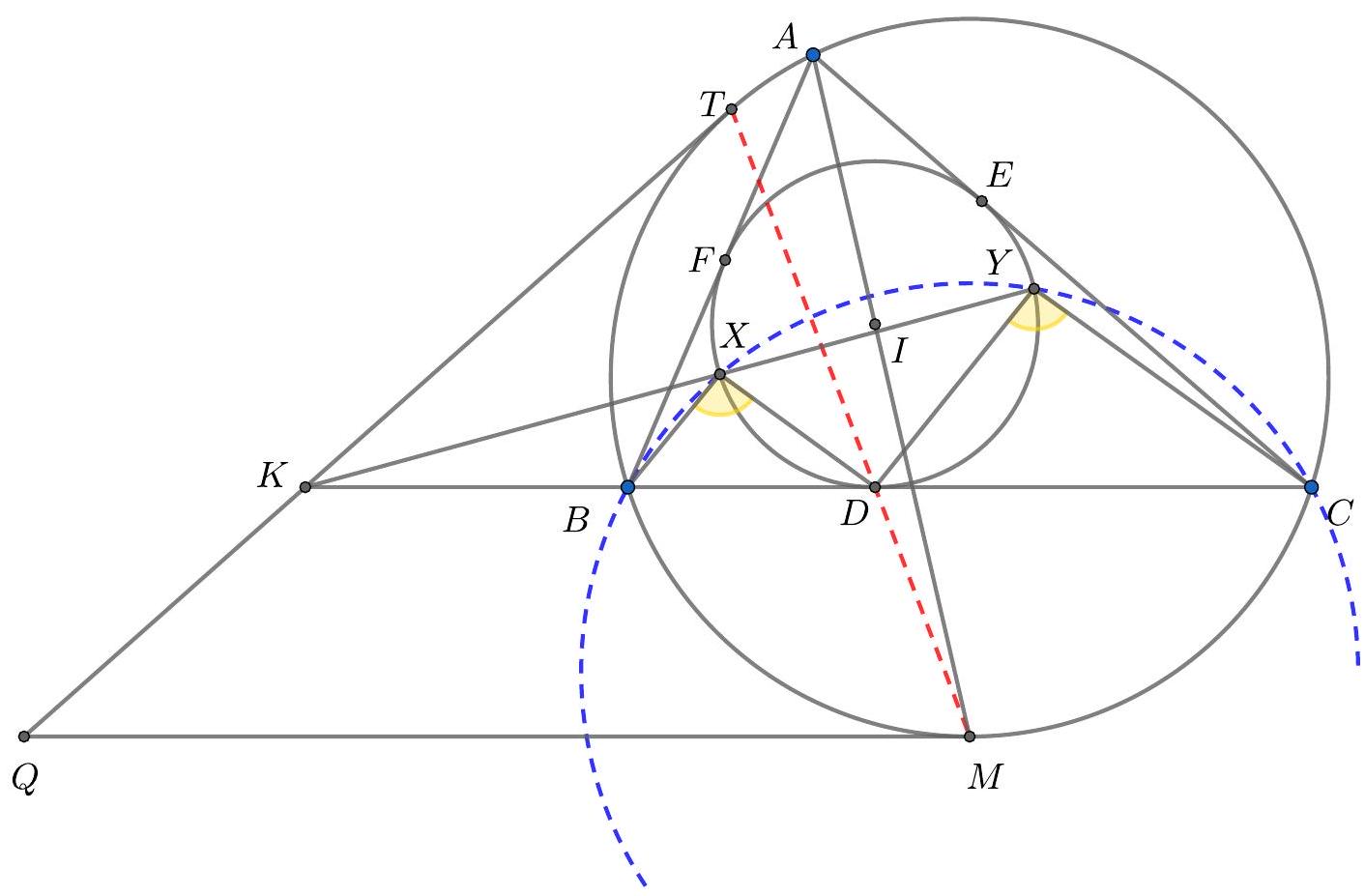\n\nFigure 1: The proposer's solution using a new point $Q$\n(Alternatively you can sidestep power of a point by observing that $K$ is the radical centre of the incircle $D E F$, the circumcircle $\\Gamma$ and the circle $C Y X B$ and so $K T^{2}=K D^{2}$.)\n\nNow let $A I$ meet $\\Omega$ at $M$, the midpoint of $\\widehat{B C}$ not containing $A$. Let the tangent at $M$ meet $K T$ at $Q$. Observe that $Q M \\| K D$ so $\\angle T K D=\\angle T Q M$ and also $K T=K D$, $Q T=Q M$ hence $\\triangle T K D \\sim \\triangle T Q M$. As $T, K, Q$ are collinear, this means that $T, D, M$ are collinear so $T D$ and $A I$ meet at $M$ which lies on $\\Omega$.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 2 (UNK)\n", "solution_match": "\nSolution 1. "}}
|
| 5 |
+
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\\overparen{D F}$ and $\\overparen{D E}$ of the incircle, respectively, such that $\\angle B X D=\\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\\Omega$ such that $K T$ is tangent to $\\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\\Omega$.", "solution": "The role of $X$ and $Y$ in this problem is secondary. Draw any circle through $B$ and $C$ which meets the incircle at $X$ and $Y$ and you determine the same point $K$. This is because $K$ is the radical centre of the three circles in play. Therefore $K$ is the intersection of $B C$ with the radical axis of the circumcircle $\\Omega$ and the incircle $D E F$, and so is independent of the choice of circle through $B$ and $C$ which gives rise to $X$ and $Y$. In the problem as posed, this is disguised, with angle properties of $X$ and $Y$ giving rise the the circle $B X Y C$.\n\nYou can now work with the simplified diagram shown in Figure 2.\n\nSomehow we must use a characterization of $M$ in order to finish. In the proposer's solution, we used the tangent to the circumcircle $\\Omega$ at $M$ being parallel to $B C$. In this alternative, we use the fact that the internal angle bisector of angle $\\angle C T B$ meets $\\Omega$ again at $M$.\n\nTriangle $T K D$ is isosceles with apex $K$ so\n\n$$\n\\angle K D T=\\angle D T K=\\angle D T B+\\angle B T K .\n$$\n\n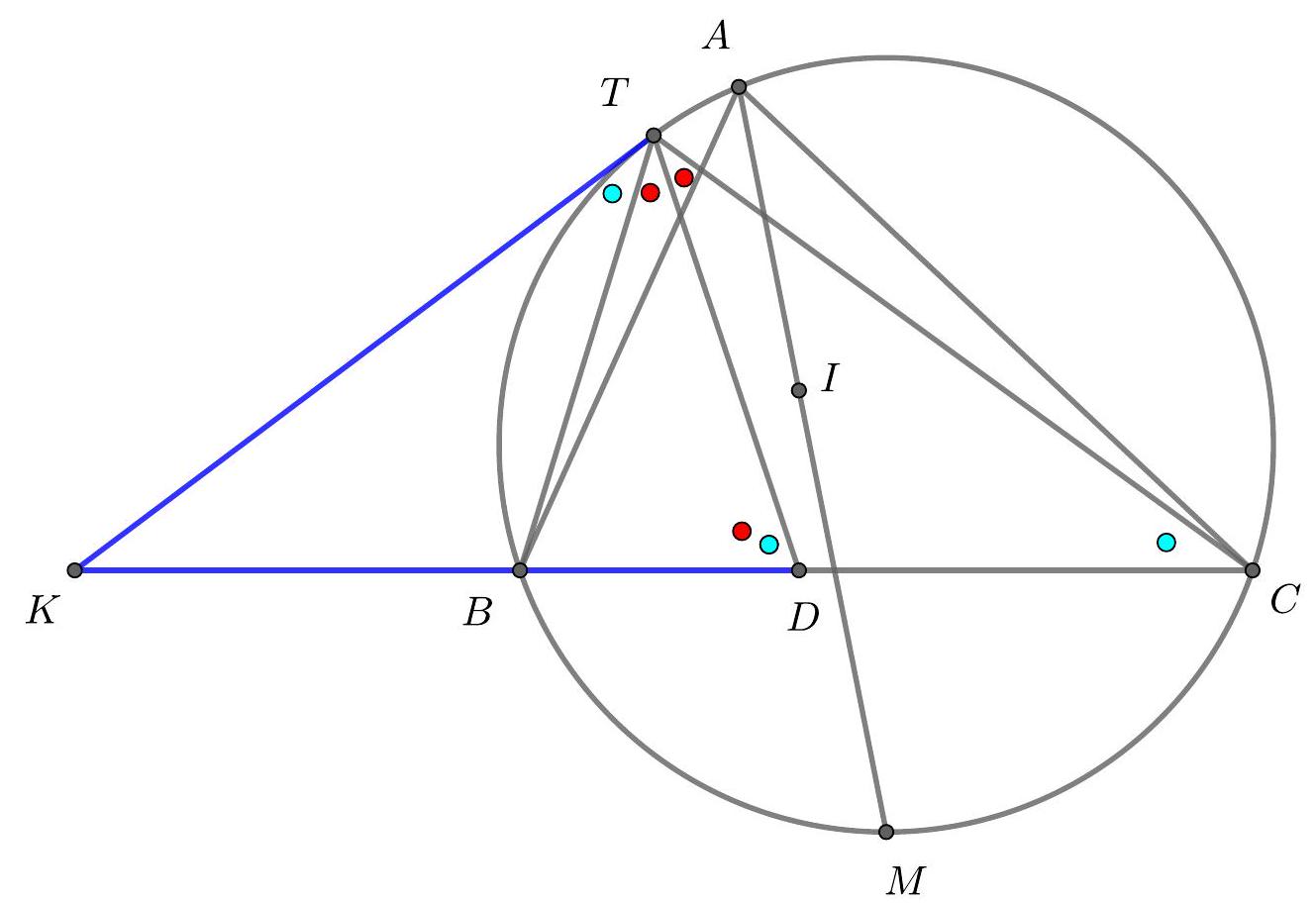\n\nFigure 2: Illustration of an angle chase\n\nBy the alternate segment theorem, $\\angle B T K=\\angle B C T=\\angle D C T$. Now angle $\\angle K D T$ is an exterior angle of triangle $D C T$ so $\\angle C T D=\\angle D T B$.\n\nTherefore the line $T D$ is the internal angle bisector of angle $\\angle C T B$ and so must pass through $M$, the midpoint of the arc $\\widehat{B C}$ of $\\Omega$ which does not contain $T$.\n\nObservation This affords a construction of the radical axis of the incircle and circumcircle of triangle $A B C: M$ and $D$ determine $T$ and the tangent at $T$ meets $B C$ at a point on the required radical axis. See Figure 3. Now do a cyclic change of letters of $A B C$ and find a point on $C A$ which is also on the radical axis (the dashed magenta line).", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 2 (UNK)\n", "solution_match": "\nSolution 2. "}}
|
| 6 |
+
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\\overparen{D F}$ and $\\overparen{D E}$ of the incircle, respectively, such that $\\angle B X D=\\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\\Omega$ such that $K T$ is tangent to $\\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\\Omega$.", "solution": "The centre of direct enlargement from the incircle to the circumcircle gives another way to finish the proof. This enlargement carries $D$ to $M$ since the tangent lines to their associated circles are parallel. The centre of enlargement therefore lies on the line $M D$. Let $M D$ meet the incircle again at $U$ and the circumcircle again at $V$. Draw the tangent to the incircle at $U$ to meet $B C$ at $W$ so triangle $W D U$ is isosceles with apex $W$ and has equal base angles $\\angle W D U$ and $\\angle D U W$. The enlargement carries the line $W U$ to the tangent line to the circumcircle at $V$ which meets $B C$ at $S$. Enlargements carry lines to parallel lines, so $\\angle D V K^{\\prime}=\\angle D U W=\\angle W D U=\\angle K^{\\prime} D V$. Therefore triangle $K^{\\prime} D V$ is isosceles with apex $K^{\\prime}$.\n\n\nFigure 3: The three points $K$ on the radical axis.\n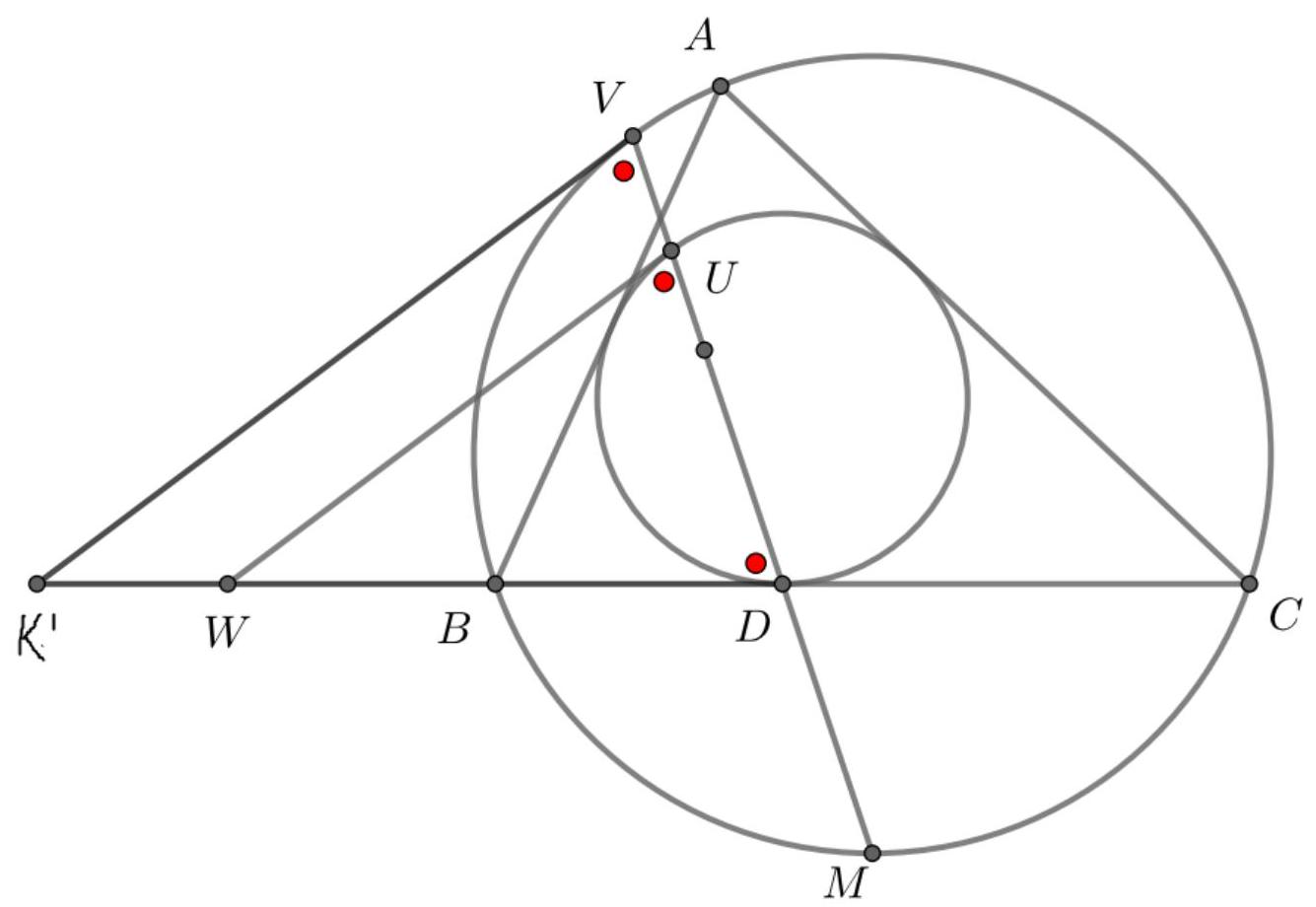\n\nFigure 4: The enlargement of $W$ gives $K^{\\prime}$.\n\nThis identifies $S$ as the intersection of the radical axis of the two circles with $B C$, so $K^{\\prime}=K$ and $V=T$ and the proof is complete.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 2 (UNK)\n", "solution_match": "\nSolution 3. "}}
|
| 7 |
+
{"year": "2024", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\\overparen{D F}$ and $\\overparen{D E}$ of the incircle, respectively, such that $\\angle B X D=\\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\\Omega$ such that $K T$ is tangent to $\\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\\Omega$.", "solution": "Let $\\phi$ be the inversion with center $K$ and radius $K D$. Note that this inversion maps incirlce of $A B C$ to itself and $K, X, Y$ are collinear, hence $\\phi(X)=Y$. Also $\\phi(D)=D$, so $\\phi$ maps circle $X B D$ to cicle $Y D B^{\\prime}$, where $B^{\\prime}:=\\phi(B)$ is the point on $B C$ different from $B$ such that $\\angle B X D=\\angle D Y B^{\\prime}$, hence $\\phi(B)=C$. From $\\phi(B)=C$ we get that $K D=K T$ as $K D^{2}=K B \\cdot K C=K T^{2}$ since $K D$ is the radius of inversion.\n\nThe rest of the solutions is the same as in the other solutions.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 2 (UNK)\n", "solution_match": "\nSolution 4. "}}
|
| 8 |
+
{"year": "2024", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Problem. For a sequence $a_{1}<a_{2}<\\cdots<a_{n}$ of integers, a pair $\\left(a_{i}, a_{j}\\right)$ with $1 \\leq i<j \\leq n$ is called interesting if there exists a pair $\\left(a_{k}, a_{l}\\right)$ of integers with $1 \\leq k<l \\leq n$ such that\n\n$$\n\\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2\n$$\n\nFor each $n \\geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.\n\nAnswer. $\\frac{1}{2}(n-1)(n-2)+1$.", "solution": "Consider the numbers $a_{i}=2^{i}$ for $2 \\leq i \\leq n$ and $a_{1}=0$, and choose any pair $(i, j)$ with $1 \\leq i<j \\leq n$.\n\nIf $i=1$, the pair $(1, j)$ is interesting for all $2 \\leq j \\leq n-1$, as $\\frac{a_{j+1}-a_{1}}{a_{j}-a_{1}}=\\frac{2^{j+1}}{2^{j}}=2$.\nIf $i \\geq 2$, the pair $(i, j)$ is also interesting for all $j$ such that $i+1 \\leq j \\leq n-1$, since $\\frac{a_{j+1}-a_{i+1}}{a_{j}-a_{i}}=\\frac{2^{j+1}-2^{i+1}}{2^{j}-2^{i}}=2$.\n\nIn addition, the pair $(n-1, n)$ is interesting, as $\\frac{a_{n}-a_{0}}{a_{n}-a_{n-1}}=2$.\nHence, all pairs in which $j \\leq n-1$, and additionally the pair $(n-1, n)$, are interesting, giving $\\frac{1}{2}(n-1)(n-2)+1$ pairs in total.\n\nNow, let's show that there can't be more interesting pairs. To this end we show that at least $\\frac{1}{2} n(n-1)-\\left(\\frac{1}{2}(n-1)(n-2)+1\\right)=n-2$ pairs are not interesting. Clearly, the pair $(1, n)$ is not interesting.\n\nLet's make the following observation: if a pair $(i, j)$ is interesting and it's not $(1, n)$, then $a_{j}-a_{i}$ can't exceed $\\frac{1}{2}\\left(a_{n}-a_{1}\\right)$. (Since, if $(i, j)$ is interesting then $a_{l}-a_{k}=2\\left(a_{j}-a_{i}\\right)$ for some pair $(k, l)$. If then $2\\left(a_{j}-a_{i}\\right)>a_{n}-a_{1}$ we would have $a_{l}-a_{k}>a_{n}-a_{1}$, which is not possible.)\n\nFinally, for any $2 \\leq i \\leq n-1$ consider pairs $(1, i)$ and $(i, n)$. If both of them are interesting, then, following the observation above, the only possibility is $a_{i}-a_{1}=a_{n}-a_{i}=\\frac{a_{n}-a_{1}}{2}$. Clearly, this is possible for at most one $i$, so for all other $n-3$ values of $i$, at least one of pairs $(1, i)$ and $(i, n)$ is not interesting. Combining with the pair $(1, n)$, we get at least $n-2$ not interesting pairs in total, as desired.\n\nComment: The originally proposed formulation considered a sequence $a_{1}<a_{2}<\\cdots<$ $a_{n}$ of $n$ real numbers, rather than integers. The conclusion is however the same and the solution is identical.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 4 (UKR)\n", "solution_match": "\nSolution."}}
|
| 9 |
+
{"year": "2024", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Problem. Let $\\mathbb{N}$ denote the set of positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :\n\n- $x$ and $f(x)$ have the same number of positive divisors.\n- If $x$ does not divide $y$ and $y$ does not divide $x$, then\n\n$$\n\\operatorname{gcd}(f(x), f(y))>f(\\operatorname{gcd}(x, y))\n$$\n\nHere $\\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.", "solution": "Throughout this proof, when we write divisors we mean positive divisors.\nLet $f$ be a function satisfying these properties. From the first one, it follows that $f(1)=1$ and for each prime number $p, f(p)=q_{p}$ for some prime number $q_{p}$. Assume $p \\neq 2$, the pair $(2, p)$ in property 2 gives\n\n$$\n\\operatorname{gcd}\\left(q_{2}, q_{p}\\right)=\\operatorname{gcd}(f(2), f(p))>f(\\operatorname{gcd}(2, p))=f(1)=1\n$$\n\nso $q_{p}=q_{2}$ for all $p$. Set $q=q_{2}$.\nDenote by $d(n)$ the number of divisors of a positive integer $n$.\nWe will prove the following claim by induction on $k \\geq 0$, the number of distinct prime divisors of $n$ : For a positive integer $n, f(n)$ is a power of $q$.\n\nThe claim, together with the first property, imply that $f(n)=q^{d(n)-1}$.\nFor $k=0$ the claim is already proved.\nFor $k=1$, we need to prove that $f\\left(p^{m}\\right)$ is a power of $q$ for all positive $m$. The case $m=1$ was already proved. Assume now the result being proved for all positive integers $\\leq m$. As $d\\left(p^{t}\\right)=t+1$, we then know $f\\left(p^{t}\\right)=q^{t}$ for all $t \\leq m$. Now we consider $t=m+1$.\n\nLet $r \\neq p$ be a prime. Plug the pair $\\left(p^{m-1} r, p^{m}\\right)$ into the second property:\n\n$$\n\\operatorname{gcd}\\left(f\\left(p^{m-1} r\\right), q^{m}\\right)=\\operatorname{gcd}\\left(f\\left(p^{m-1} r\\right), f\\left(p^{m}\\right)\\right)>f\\left(p^{m-1}\\right)=q^{m-1}\n$$\n\nThis implies $q^{m}$ divides $f\\left(p^{m-1} r\\right)$. Since $f\\left(p^{m-1} r\\right)$ has $2 m$ divisors, and $v_{q}\\left(f\\left(p^{m-1} r\\right)\\right) \\geq m$, it follows that $f\\left(p^{m-1} r\\right)$ does not have prime divisors other than $q$, since it would then have at least $2 \\cdot\\left(v_{q}\\left(f\\left(p^{m-1} r\\right)\\right)+1\\right)>2 m$ divisors. Thus, $f\\left(p^{m-1} r\\right)$ is a power of $q$. And since it has $2 m$ divisors, we must have $f\\left(p^{m-1} r\\right)=q^{2 m-1}$.\n\nNow, plug the pair $\\left(p^{m+1}, p^{m-1} r\\right)$ into the second property. We have\n\n$$\n\\operatorname{gcd}\\left(f\\left(p^{m+1}\\right), q^{2 m-1}\\right)=\\operatorname{gcd}\\left(f\\left(p^{m+1}\\right), f\\left(p^{m-1} r\\right)\\right)>f\\left(p^{m-1}\\right)=q^{m-1} .\n$$\n\nThen $f\\left(p^{m+1}\\right)$ is divisible by $q^{m}$. If $f\\left(p^{m+1}\\right)$ had a prime factor other than $q$, it would have at least $2(m+1)$ divisors, but it has $m+2$ divisors and $2(m+1)>m+2$ since $m \\geq 1$. Hence, $f\\left(p^{m+1}\\right)$ must also be a power of $q$. By induction, the proof is finished for $k=1$.\n\nSuppose the claim is true for all integers $n$ with at most $k$ distinct prime factors, for some $k \\geq 1$. In order to prove the claim for integers with $k+1$ distinct prime factors, it suffices\nto show that for every positive integer $N$ with $k$ distinct prime factors, every positive integer $m$ and every prime $p$ which does not divide $N$, the number $f\\left(N p^{m}\\right)$ is a power of $q$. We will prove this by induction on $m$. The case $m=0$ follows from the previous induction hypothesis. Now suppose it has already been proved for a certain $m \\geq 0$.\n\nLet $s$ be a prime divisor of $N$. Consider the numbers $\\left(N p^{m+1}, N s p^{m}\\right)$. By the second property,\n\n$$\n\\operatorname{gcd}\\left(f\\left(N p^{m+1}\\right), q^{d\\left(N s p^{m}\\right)-1}\\right)=\\operatorname{gcd}\\left(f\\left(N p^{m+1}\\right), f\\left(N s p^{m}\\right)\\right)>f\\left(N p^{m}\\right)=q^{d\\left(N p^{m}\\right)-1}\n$$\n\nThen $q^{d\\left(N p^{m}\\right)}$ divides $f\\left(N p^{m+1}\\right)$. If $f\\left(N p^{m+1}\\right)$ has a prime factor other than $q$, it would have at least $2\\left(d\\left(N p^{m}\\right)+1\\right)=2((m+1) d(N)+1)=(2 m+2) d(N)+2$ divisors, but it has only $(m+2) d(N)$ divisors. Hence, $f\\left(N p^{m+1}\\right)$ must also be a power of $q$.\n\nFinally, let us check that the function $f(n)=q^{d(n)-1}$ does satisfy the properties of the problem for any prime number $q$. The first property obviously holds. To check the second one, note that\n\n$$\n\\operatorname{gcd}(f(x), f(y))=q^{\\min (d(x), d(y))}>q^{d(\\operatorname{gcd}(x, y))}=f(\\operatorname{gcd}(x, y))\n$$\n\nwhenever $x \\nmid y$ and $y \\nmid x$.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 5 (HRV)\n", "solution_match": "\nSolution 1. "}}
|
| 10 |
+
{"year": "2024", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Problem. Let $\\mathbb{N}$ denote the set of positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :\n\n- $x$ and $f(x)$ have the same number of positive divisors.\n- If $x$ does not divide $y$ and $y$ does not divide $x$, then\n\n$$\n\\operatorname{gcd}(f(x), f(y))>f(\\operatorname{gcd}(x, y))\n$$\n\nHere $\\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.", "solution": "Firstly, one can prove that for any prime $p$ and any $m \\geq 0, f\\left(p^{m}\\right)=q^{m}$, in the same way as in the first solution.\n\nWe will prove the claim this time by induction on $k=d(n)$. We notice again that the claim implies that $f(n)=q^{d(n)-1}$.\n\nThe cases $k=1,2,3$ are then already proved. Now suppose that for some $k \\geq 3$ we have proved the claim for all positive integers $n$ with at most $k$ divisors.\n\nConsider a positive integer $n$ with $k+1$ divisors. If $n$ is a power of a prime, then it is already proved that $f(n)$ is a power of $q$. Suppose $n$ is not a power of a prime. Consider distinct prime numbers $p_{1}$ and $p_{2}$ which divide $n$, such that $v_{p_{1}}(n) \\leq v_{p_{2}}(n)$. Consider the number $\\frac{n p_{2}}{p_{1}}$ : its number of divisors is $\\frac{v_{p_{1}}(n)\\left(v_{p_{2}}(n)+2\\right)}{\\left(v_{p_{1}}(n)+1\\right)\\left(v_{p_{2}}(n)+1\\right)} d(n)$, which is strictly less than the number of divisors of $n$. Thus, by induction hypothesis, $f\\left(\\frac{n p_{2}}{p_{1}}\\right)$ is a power of $q$.\n\nBy applying the second property to the pair $\\left(n, \\frac{n p_{2}}{p_{1}}\\right)$, we have\n\n$$\n\\operatorname{gcd}\\left(f(n), q^{d\\left(\\frac{n p_{2}}{p_{1}}\\right)-1}\\right)=\\operatorname{gcd}\\left(f(n), f\\left(\\frac{n p_{2}}{p_{1}}\\right)\\right)>f\\left(\\frac{n}{p_{1}}\\right)=q^{d\\left(\\frac{n}{p_{1}}\\right)-1}\n$$\n\nThis implies that $q^{d\\left(\\frac{n}{p_{1}}\\right)}$ divides $f(n)$. Again, if other primes than $q$ divided $f(n)$, it would have at least $2\\left(d\\left(\\frac{n}{p_{1}}\\right)+1\\right)$ divisors. But $2\\left(d\\left(\\frac{n}{p_{1}}\\right)+1\\right)=2\\left(\\frac{v_{p_{1}}(n)}{v_{p_{1}}(n)+1} d(n)+1\\right)>d(n)$. So $f(n)$ is a power of $q$ and the Claim is proved.\n\nWe finally check as in the first solution that $f(n)=q^{d(n)-1}$ satisfies the 2 properties for all prime $q$.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 5 (HRV)\n", "solution_match": "\nSolution 2. "}}
|
| 11 |
+
{"year": "2024", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Problem. Find all positive integers $d$ for which there exists a degree $d$ polynomial $P$ with real coefficients such that there are at most $d$ different values among $P(0), P(1), \\ldots, P\\left(d^{2}-\\right.$ d).\n\nRemark 1 You can add a constant to a polynomial satisfying the conditions and obtain another polynomial satisfying the conditions.\n\nRemark 2 This problem is equivalent to: Find all positive integers $d$ for which there exists a polynomial $P$ of degree $d$ that takes at most $d$ different values at members of a an arithmetic progression with $d^{2}-d+1$ (different) terms.\nThe answer to this EGMO problem implies a solution to this more general problem by scaling and translating, and the general result solves the EGMO problem as a special case. This means that instead of working with $0,1, \\ldots, d^{2}-d$ we have the option of working with a region that is symmetric about the origin. Irrespective of the parity of $d$ we can use the $d^{2}-d+1$ integers which run from $-\\left(d^{2}-d\\right) / 2$ to $\\left(d^{2}-d\\right) / 2$ inclusive.\n\nThe advantage of using an arithmetic progression which is symmetric about the 0 is that $P(X)$ is a polynomial which works for the problem if, and only if, $P(-X)$ is a polynomial which works for the problem. This means that working at one end of the run of integers is the reflection of the activity at the other end. T Remarks dismissing the cases at the other end of the run as similar now become obviously correct rather than having to be studied separately.", "solution": "We claim that such polynomials exist if and only if $d \\leq 3$. The following examples show that such polynomials do exist for $d \\leq 3$ :\n\n$$\n\\left.\\begin{array}{lll}\nd=1: & d^{2}-d=0, & P_{1}(x)=x,\n\\end{array} \\begin{array}{ll} \n& P(0)=0 ;\n\\end{array}\\right\\}\n$$\n\nWe can make more examples by adding constants.\nNow we will show that there are no examples of degree greater than 3.\nFrom now on we assume (without loss of generality) that the leading coefficient of our polynomial $P$ is positive and that all values $P(i)$ are positive (by adding a constant if necessary) for integers $i$ in the range $0 \\leq i \\leq d^{2}-d+1$.\n\nAssume (for contradiction) that $P$ is a polynomial of degree $d \\geq 4$ that satisfies the conditions of the problem and let $P(0), \\ldots, P\\left(d^{2}-d\\right)$ take values among $p_{1}<\\cdots<p_{d}$. For $i=1, \\ldots, d$, let $n_{i} \\geq 0$ be the number of appearances of $p_{i}$ among $P(0), \\ldots, P\\left(d^{2}-d\\right)$.\n\nBy definition $n_{1}+\\cdots+n_{d}=d^{2}-d+1$. Since $P$ has degree $d, n_{i} \\leq d$. The key observation is now the following.\n\nClaim 1 Make the convention that $n_{0}=n_{d+1}=0$. If $n_{i}=d$ for some $i$ in the range $1 \\leq i \\leq d$, then $n_{i \\pm 1} \\leq d-2$.\n\nProof. Up to scaling and hence without loss of generality, $P$ has leading coefficient +1 . $\\overline{\\text { Since }} n_{i}=d$, there exist non-negative integers $a_{1, i}<\\cdots<a_{d, i} \\leq d^{2}-d$ such that\n\n$$\nP(X)=\\left(X-a_{1, i}\\right) \\cdots\\left(X-a_{d, i}\\right)+p_{i} .\n$$\n\nBy construction, each of the $d-1$ intervals $I_{j}=\\left[a_{j, i}, a_{j+1, i}\\right]$ contains at least one local extremum of $P$, so contains exactly one such extremum because $P$, having degree $d$, has at most $d-1$ such extrema. Suppose that $i \\leq d-1$ and that $P(m)=p_{i+1}>p_{i}$ for some $m \\in\\left\\{0, \\ldots, d^{2}-d\\right\\}$. Since $P$ has positive leading coefficient,\n\n$$\nm \\in\\left(a_{d, i}, \\infty\\right) \\cup\\left(a_{d-2, i}, a_{d-1, i}\\right) \\cup \\cdots \\cup\\left(a_{i, 1}, a_{2, i}\\right)\n$$\n\nif $d$ is odd or\n\n$$\nm \\in\\left(a_{d, i}, \\infty\\right) \\cup\\left(a_{d-2, i}, a_{d-1, i}\\right) \\cup \\cdots \\cup\\left(-\\infty, a_{1, i}\\right)\n$$\n\nif $d$ is even.\nSuppose that $a_{j, i}<m<a_{j+1, i}$, for some $j \\in\\{1, \\ldots, d-1\\}$. If $a_{j, i}+1<m<a_{j+1, i}-1$, then, because $I_{j}$ contains exactly one local extremum (which is a maximum),\n\nEither $p_{i+1}=P(m)>P\\left(a_{j, i}+1\\right)$ or $p_{i+1}=P(m)>P\\left(a_{j+1, i}-1\\right)$. Since $P\\left(a_{j, i}+1\\right)>$ $P\\left(a_{j, i}\\right)=p_{i}$ and $P\\left(a_{j, i}-1\\right)>P\\left(a_{j+1, i}\\right)=p_{i}$, this contradicts the requirement that $P\\left(a_{j, i}+1\\right), P\\left(a_{j+1, i}-1\\right) \\in\\left\\{p_{1}, \\ldots, p_{d}\\right\\}$. Hence $m=a_{j, i}+1$ or $m=a_{j, i}-1$. Similarly, if $m>a_{d, i}$, then $m=a_{d, i}+1$, but if $m<a_{i, 1}$ (which may arise when $d$ is even), then $m=a_{i, 1}-1$. This shows that $m$ belongs to this list:\n\n$$\na_{d, i}+1, a_{d-1, i}-1, \\ldots, a_{2, i}+(-1)^{d}, a_{1, i}-(-1)^{d}\n$$\n\nThis list contains at most $d$ different integers. It follows in particular that, if $n_{i+1}>d-2$, then either\n\n$$\nP\\left(a_{d, i}+1\\right)=p_{i+1}=P\\left(a_{d-1, i}-1\\right)\n$$\n\nor\n\n$$\nP\\left(a_{2, i}+(-1)^{d}\\right)=p_{i+1}=P\\left(a_{1, i}-(-1)^{d}\\right)\n$$\n\nwith, additionally, $a_{2, i}+(-1)^{d} \\neq a_{1, i}-(-1)^{d}$.\nWe have\n\n$$\n\\left|P\\left(a_{1, i} \\pm 1\\right)-p_{i}\\right|=1 \\cdot\\left|a_{1, i} \\pm 1-a_{2, i}\\right| \\cdot \\prod_{j=3}^{d}\\left|a_{1, i} \\pm 1-a_{j, i}\\right|\n$$\n\nand\n\n$$\n\\left|P\\left(a_{2, i} \\mp 1\\right)-p_{i}\\right|=\\left|a_{2, i} \\mp 1-a_{1, i}\\right| \\cdot 1 \\cdot \\prod_{j=3}^{d}\\left|a_{2, i} \\mp 1-a_{j, i}\\right| .\n$$\n\nAs $a_{1, i}<a_{2, i}<a_{3, i}<\\ldots<a_{d, i}$ we have $\\left|a_{1, i} \\pm 1-a_{j, i}\\right| \\geq\\left|a_{2, i} \\mp 1-a_{j, i}\\right|$ with equality possible only if $a_{1, i}+1=a_{2, i}-1$. We also have $\\left|a_{1, i} \\pm 1-a_{2, i}\\right|=\\left|a_{2, i} \\mp 1-a_{1, i}\\right|$, which can be zero only if $a_{1, i}+1=a_{2, i}-1$. We conclude that $\\left|P\\left(a_{1, i} \\pm 1\\right)-p_{i}\\right|>\\left|P\\left(a_{2, i} \\mp 1\\right)-p_{i}\\right|$ or $a_{1, i}+1=a_{2, i}-1$.\n\nLooking at the other end of the list of $\\left(a_{j, i}\\right)$ as $j$ varies, we have\n\n$$\n\\left|P\\left(a_{d-1, i}-1\\right)-p_{i}\\right|=1 \\cdot\\left|a_{d-1, i}-1-a_{d, i}\\right| \\cdot \\prod_{j=1}^{d-2}\\left|a_{d-1, i}-1-a_{j, i}\\right|\n$$\n\nand\n\n$$\n\\left|P\\left(a_{d, i}+1\\right)-p_{i}\\right|=\\left|a_{d, i}+1-a_{d-1, i}\\right| \\cdot 1 \\cdot \\prod_{j=1}^{d-2}\\left|a_{d, i}+1-a_{j, i}\\right|\n$$\n\nIn these two formulas the shared factor outside the product is at least 2 and so is not 0 . Now look at the factors behind the product symbols. As $a_{1, i}<a_{2, i}<a_{3, i}<\\ldots<a_{d, i}$, for $j \\leq d-2$ we have $\\left|a_{d, i}+1-a_{j, i}\\right|>\\left|a_{d-1, i}-1-a_{j, i}\\right|$. We conclude that $\\left|P\\left(a_{d, i}+1\\right)-p_{i}\\right|>$ $\\left|P\\left(a_{d-1, i}-1\\right)-p_{i}\\right|$. Claim 1 is proved.\n\nFor each $i \\in\\{1, \\ldots, d-1\\}$, there are three possibilities:\n\n- $n_{i}, n_{i+1} \\leq d-1$\n- $n_{i}=d$ and $n_{i+1} \\leq d-2$\n- $n_{i+1}=d$ and $n_{i} \\leq d-2$.\n\nIn all three cases, $n_{i}+n_{i+1} \\leq 2(d-1)$. If $n$ is even, this leads to the contradiction\n\n$$\nd^{2}-d+1=\\left(n_{1}+n_{2}\\right)+\\cdots+\\left(n_{d-1}+n_{d}\\right) \\leq(d / 2)[2(d-1)]=d^{2}-d\n$$\n\nThis is an important staging point in the argument because we have eliminated the possibility of a polynomial of even degree $d$ satisfying the conditions of the problem if $d \\geq 4$.\n\nFrom now on we assume that $d \\geq 5$ is odd, and\n$d^{2}-d+1=\\left(n_{1}+n_{2}\\right)+\\cdots+\\left(n_{d-2}+n_{d-1}\\right)+n_{d} \\leq[(d-1) / 2][2(d-1)]+d=d^{2}-d+1$.\nEquality must therefore hold throughout. Since the sum can also be grouped as\n\n$$\nn_{1}+\\left(n_{2}+n_{3}\\right)+\\cdots+\\left(n_{d-1}+n_{d}\\right)\n$$\n\nthis requires $n_{1}=n_{d}=d, n_{i}+n_{i+1}=2(d-1)$ for $i=1,2, \\ldots, d-1$ i.e. $n_{i}=d$ for odd $i$ and $n_{i}=d-2$ for even $i$.\n\nWe are interested in the degree of $P$ being $d \\geq 5$ and odd, and showing that no polynomial $P$ satisfying the conditions of the problem can exist. There are $d-1 \\geq 4$ extremal points points which alternate between local maxima and minima (in that order) as you read from left to right (we normalize so that $P$ is monic). For any $p_{i}$ with $i$ odd, the line $y=p_{i}$ (with\n$i$ odd) crosses the graph of $P$ in $d$ places with $x$-coordinates in the real closed interval $\\left[0, d^{2}-d\\right]$ at points $\\left(z, p_{i}\\right)$ so each $z$ must be an integer. Suppose that $J$ is a real interval on the $x$-axis ending at adjacent local extrema. The function defined by $P$ is monotonic on each $J$. The line $y=p_{i}$ ( $i$ odd) meets the graph at most once on $J$. Therefore it meets the graph of $P$ exactly once in the interior of each $J$ (there are $d-2$ such intervals) and at the only two possible places outside the union of these intervals.\n\nNow consider $p_{j}$ when $j$ is even (so $n_{j}=d-2$ ). These $d-2$ intervals $J$ afford $d-2$ real values at which $P$ will take $p_{j}$ as a value where $j$ is fixed and even. The question is, are the corresponding arguments integers? The proof of Claim 1 tells us that in the middle of the run $\\left\\{0,1, \\ldots, d^{2}-d+1\\right\\}$ all is well: the polynomial is assuming the value $p_{j}$ at an integer where the polynomial assumes the values $p_{j-1}$ and $p_{j+1}$ at adjacent integers in some order. The problem is at the ends of the run where $\\left|P\\left(a_{1, i}+1\\right)-p_{i}\\right|>\\left|P\\left(a_{2, i}-1\\right)-p_{i}\\right|$ and $\\left|P\\left(a_{d, i}+1\\right)-p_{i}\\right|>\\left|P\\left(a_{d-1, i}-1\\right)-p_{i}\\right|$. When $j$ is even, two of the roots of $P(x)-p_{j}$ are not integers, and we now know approximately where this trouble is happening (at the ends).\n\nAt this point we could finish if $d \\geq 7$, because the run of regular behaviour in the middle is sufficiently long that we could obtain a contradiction. However we have to work a little harder to include the case $d=5$. We now show that the run of regular behaviour is slightly longer than we have currently established. We do this using Claim 2.\n\nClaim 2. If $d$ is odd, and $n_{i}=d, n_{i \\pm 1}=d-2$ for some $i$, then $P$ attains $p_{i \\pm 1}$ precisely at the $d-2$ integers\n\n$$\na_{2, i}-1, a_{3, i}+1, \\cdots, a_{d-2, i}-1, a_{d-1, i}+1\n$$\n\nProof Suppose (for contradiction) $a_{1, i}+1 \\neq a_{2, i}-1$ and $P\\left(a_{1, i}+1\\right)=p_{i+1}$. Now $a_{1, i}<a_{2, i}$ so either $a_{1, i}+1<a_{2, i}-1$ or $a_{1, i}=a_{2, i}-1$. In the latter case, $P\\left(a_{1, i}+1\\right)=P\\left(a_{2, i}\\right)=p_{i}$, a contradiction. In the former case, the proof of Claim 1 shows that\n\n$$\n\\left|P\\left(a_{2, i}-1\\right)-p_{i}\\right|<\\left|P\\left(a_{1, i}+1\\right)-p_{i}\\right|=\\left|p_{i+1}-p_{i}\\right|=p_{i+1}-p_{i}\n$$\n\nso $P\\left(a_{2, i}-1\\right)<p_{i+1}$. The polynomial is decreasing on the interval $\\left(a_{2, d}, a_{2,1}\\right)$ so $p_{i}<P\\left(a_{2, i}-1\\right)<p_{i+1}$ which is absurd because $P\\left(a_{2, i}-1\\right)=p_{j}$ for some $j$. Therefore $P\\left(a_{2, i}-1\\right)=p_{i+1}$ for all odd $i$. A similar argument shows that $P\\left(a_{d-1, i}+1\\right)=p_{i+1}$ so Claim 2 is established.\n\nNow we have n sequence of alternating falling then rising then falling etc. full runs starting at $\\left(a_{2, d}, p_{d}\\right)$ and ending at $\\left(a_{d-1,1}, p_{1}\\right)$ so the initial run of $3 d+1$ terms of this run of values is\n\n$$\np_{d}, p_{d-1}, \\cdots p_{1}, p_{1}, p_{2}, \\ldots, p_{d}, p_{d}, p_{d-1}, \\cdots p_{1}, p_{1}\n$$\n\nwhich starts at $\\left(a_{2, d}, p_{d}\\right)$ and ends at $\\left(a_{4,1}+1, p_{1}\\right)$ which is fine because $4 \\leq d-1$.\nThere are now various ways we can finish.\n(a) Consider the run of length $2 d$ consecutive values\n\n$$\np_{d}, p_{d-1}, \\cdots p_{1}, p_{1}, p_{2}, \\ldots, p_{d}\n$$\n\nThe first $d+1$ points determine $P(x)$. The last $d+1$ values also determine $P$ but the values are in the reverse order, so $P(X)=P(c-X)$ for some constant $c$. However, the coefficients of $X^{d}$ are have opposite signs ( $d$ is odd) so this is absurd.\n(b) The idea in (a) can be expressed in terms of Lagrange interpolation to obtain essentially the same contradiction. Construct $P$ in two ways using Lagrange interpolation on both the first $d+1$ and the last $d+1$ points. The symmetry in the data forces the graph of $P$ to have a vertical axis of symmetry. This is absurd because the degree of $P$ is odd.\n(c) The initial fragment length $3 d+1$ mentioned above at $(*)$ includes two identical runs of values of $P$ (in the same order) of length $d+1$. The polynomial $P$ is determined by each of them and so $P(X)=P(X+c)$ for some constant $c$ and so the polynomial defines a bounded function which is absurd.", "metadata": {"resource_path": "EGMO/segmented/en-2024-solutions.jsonl", "problem_match": "# Problem 6 (LUX+BEL)\n", "solution_match": "\nSolution."}}
|