Add data for romanian master of mathematics (RMM) (#1)
Browse files- Add download script and data for RMM (cec0b1055f13426fedb09d323e52466cc9f26d54)
- add segmented RMM problems and solutions (28fe836e74c83efb579b7e8c381d635802a17372)
This view is limited to 50 files because it contains too many changes.
See raw diff
- RMM/download_script/download.py +120 -0
- RMM/md/en-2011-Sols2011D1.md +168 -0
- RMM/md/en-2011-Sols2011D2.md +171 -0
- RMM/md/en-2012-Solutions2012-1.md +123 -0
- RMM/md/en-2012-Solutions2012-2.md +90 -0
- RMM/md/en-2013-Solutions2013-1.md +95 -0
- RMM/md/en-2013-Solutions2013-2.md +142 -0
- RMM/md/en-2015-Solutions_RMM2015-1.md +114 -0
- RMM/md/en-2015-Solutions_RMM2015-2.md +104 -0
- RMM/md/en-2016-Solutions_RMM2016-1.md +92 -0
- RMM/md/en-2016-Solutions_RMM2016-2.md +76 -0
- RMM/md/en-2017-Solutions_RMM2017-1.md +149 -0
- RMM/md/en-2017-Solutions_RMM2017-2.md +190 -0
- RMM/md/en-2018-RMM2018-Day1-English.md +73 -0
- RMM/md/en-2018-RMM2018-Day2-English.md +157 -0
- RMM/md/en-2019-RMM2019-Day1-English.md +123 -0
- RMM/md/en-2019-RMM2019-Day2-English.md +29 -0
- RMM/md/en-2021-RMM2021-Day1-English_Solutions.md +55 -0
- RMM/md/en-2021-RMM2021-Day2-English_Solutions.md +117 -0
- RMM/md/en-2023-RMM2023-Day1-English_Solutions.md +205 -0
- RMM/md/en-2023-RMM2023-Day2-English_Solutions.md +163 -0
- RMM/md/en-2024-RMM2024-Day1-English.md +30 -0
- RMM/md/en-2024-RMM2024-Day2-English.md +21 -0
- RMM/raw/en-2011-Sols2011D1.pdf +3 -0
- RMM/raw/en-2011-Sols2011D2.pdf +3 -0
- RMM/raw/en-2012-Solutions2012-1.pdf +3 -0
- RMM/raw/en-2012-Solutions2012-2.pdf +3 -0
- RMM/raw/en-2013-Solutions2013-1.pdf +3 -0
- RMM/raw/en-2013-Solutions2013-2.pdf +3 -0
- RMM/raw/en-2015-Solutions_RMM2015-1.pdf +3 -0
- RMM/raw/en-2015-Solutions_RMM2015-2.pdf +3 -0
- RMM/raw/en-2016-Solutions_RMM2016-1.pdf +3 -0
- RMM/raw/en-2016-Solutions_RMM2016-2.pdf +3 -0
- RMM/raw/en-2017-Solutions_RMM2017-1.pdf +3 -0
- RMM/raw/en-2017-Solutions_RMM2017-2.pdf +3 -0
- RMM/raw/en-2018-RMM2018-Day1-English.pdf +3 -0
- RMM/raw/en-2018-RMM2018-Day2-English.pdf +3 -0
- RMM/raw/en-2019-RMM2019-Day1-English.pdf +3 -0
- RMM/raw/en-2019-RMM2019-Day2-English.pdf +3 -0
- RMM/raw/en-2021-RMM2021-Day1-English_Solutions.pdf +3 -0
- RMM/raw/en-2021-RMM2021-Day2-English_Solutions.pdf +3 -0
- RMM/raw/en-2023-RMM2023-Day1-English_Solutions.pdf +3 -0
- RMM/raw/en-2023-RMM2023-Day2-English_Solutions.pdf +3 -0
- RMM/raw/en-2024-RMM2024-Day1-English.pdf +3 -0
- RMM/raw/en-2024-RMM2024-Day2-English.pdf +3 -0
- RMM/segment_script/segment.py +128 -0
- RMM/segmented/en-2011-Sols2011D1.jsonl +3 -0
- RMM/segmented/en-2011-Sols2011D2.jsonl +3 -0
- RMM/segmented/en-2012-Solutions2012-1.jsonl +7 -0
- RMM/segmented/en-2012-Solutions2012-2.jsonl +5 -0
RMM/download_script/download.py
ADDED
|
@@ -0,0 +1,120 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
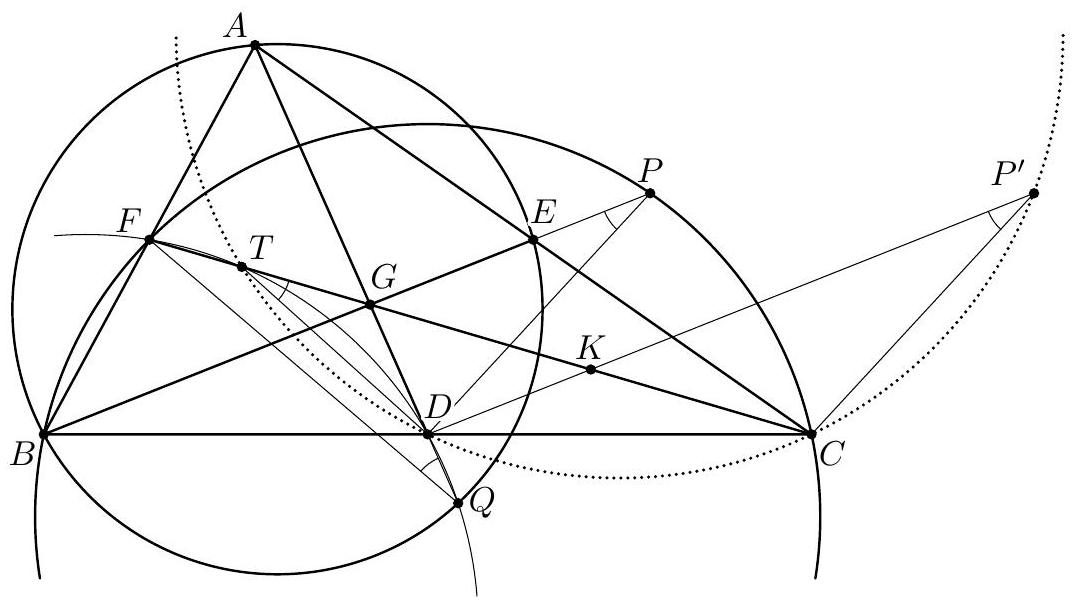
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-11-20
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download script for RMM
|
| 7 |
+
Manual review is required to remove some duplicate files.
|
| 8 |
+
To run:
|
| 9 |
+
`python RMM\download_script\download.py`
|
| 10 |
+
'''
|
| 11 |
+
|
| 12 |
+
import requests
|
| 13 |
+
from requests.adapters import HTTPAdapter
|
| 14 |
+
from tqdm import tqdm
|
| 15 |
+
from bs4 import BeautifulSoup
|
| 16 |
+
from urllib.parse import urljoin
|
| 17 |
+
from urllib3.util.retry import Retry
|
| 18 |
+
from pathlib import Path
|
| 19 |
+
|
| 20 |
+
|
| 21 |
+
def build_session(
|
| 22 |
+
max_retries: int = 3,
|
| 23 |
+
backoff_factor: int = 2,
|
| 24 |
+
session: requests.Session = None
|
| 25 |
+
) -> requests.Session:
|
| 26 |
+
"""
|
| 27 |
+
Build a requests session with retries
|
| 28 |
+
|
| 29 |
+
Args:
|
| 30 |
+
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 31 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 32 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 33 |
+
"""
|
| 34 |
+
session = session or requests.Session()
|
| 35 |
+
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 36 |
+
session.mount("http://", adapter)
|
| 37 |
+
session.mount("https://", adapter)
|
| 38 |
+
session.headers.update({
|
| 39 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 40 |
+
})
|
| 41 |
+
|
| 42 |
+
return session
|
| 43 |
+
|
| 44 |
+
|
| 45 |
+
def main():
|
| 46 |
+
req_session = build_session()
|
| 47 |
+
|
| 48 |
+
# Output directory
|
| 49 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 50 |
+
output_dir.mkdir(exist_ok=True)
|
| 51 |
+
|
| 52 |
+
# Get a list of competition years
|
| 53 |
+
resp = req_session.get("https://rmms.lbi.ro/")
|
| 54 |
+
soup = BeautifulSoup(resp.text, "html.parser")
|
| 55 |
+
a_eles = soup.select_one("#header").find_all("a")[2:]
|
| 56 |
+
urls = [f"{_['href']}/" for _ in a_eles] + [resp.url]
|
| 57 |
+
|
| 58 |
+
for url in tqdm(urls):
|
| 59 |
+
year = url.split("/")[-2].replace("rmm", "")
|
| 60 |
+
donwload_urls = []
|
| 61 |
+
|
| 62 |
+
# Make request url
|
| 63 |
+
sol_page_url = urljoin(url, "index.php?id=solutions_math")
|
| 64 |
+
prob_page_url = urljoin(url, "index.php?id=problems_math")
|
| 65 |
+
|
| 66 |
+
# Make requests
|
| 67 |
+
sol_page_resp = req_session.get(sol_page_url)
|
| 68 |
+
prob_page_resp = req_session.get(prob_page_url)
|
| 69 |
+
|
| 70 |
+
sol_page_soup = BeautifulSoup(sol_page_resp.text, "html.parser")
|
| 71 |
+
prob_page_soup = BeautifulSoup(prob_page_resp.text, "html.parser")
|
| 72 |
+
|
| 73 |
+
# Check if the page has pdf container
|
| 74 |
+
sol_content_container = sol_page_soup.select_one("#inside_content")
|
| 75 |
+
prob_content_container = prob_page_soup.select_one("#inside_content")
|
| 76 |
+
if sol_content_container is None and prob_content_container is None:
|
| 77 |
+
continue
|
| 78 |
+
|
| 79 |
+
sol_a_eles = sol_page_soup.select_one("#inside_content").find_all("a")
|
| 80 |
+
sol_iframe_eles = sol_page_soup.select_one("#inside_content").find_all("iframe")
|
| 81 |
+
|
| 82 |
+
# Check if the page has solutions pdf
|
| 83 |
+
if len(sol_iframe_eles) != 0 or len(sol_a_eles) != 0:
|
| 84 |
+
if len(sol_a_eles) != 0:
|
| 85 |
+
donwload_urls = [_["href"] for _ in sol_a_eles]
|
| 86 |
+
elif len(sol_iframe_eles) != 0:
|
| 87 |
+
donwload_urls = [_["src"] for _ in sol_iframe_eles]
|
| 88 |
+
else:
|
| 89 |
+
# Check if the page has problems pdf
|
| 90 |
+
prob_a_eles = prob_page_soup.select_one("#inside_content").find_all("a")
|
| 91 |
+
prob_iframe_eles = prob_page_soup.select_one("#inside_content").find_all("iframe")
|
| 92 |
+
|
| 93 |
+
if len(prob_iframe_eles) != 0 or len(prob_a_eles) != 0:
|
| 94 |
+
if len(prob_a_eles) != 0:
|
| 95 |
+
donwload_urls = [_["href"] for _ in prob_a_eles]
|
| 96 |
+
elif len(prob_iframe_eles) != 0:
|
| 97 |
+
donwload_urls = [_["src"] for _ in prob_iframe_eles]
|
| 98 |
+
|
| 99 |
+
# Download pdf
|
| 100 |
+
for du in donwload_urls:
|
| 101 |
+
if "grading" in du.lower():
|
| 102 |
+
continue
|
| 103 |
+
|
| 104 |
+
download_url = urljoin(url, du)
|
| 105 |
+
|
| 106 |
+
output_file = output_dir / f"en-{year}-{Path(download_url).name}"
|
| 107 |
+
if output_file.exists():
|
| 108 |
+
continue
|
| 109 |
+
|
| 110 |
+
pdf_resp = requests.get(download_url)
|
| 111 |
+
|
| 112 |
+
if pdf_resp.status_code != 200:
|
| 113 |
+
print(f"pdf download failed: {download_url}")
|
| 114 |
+
continue
|
| 115 |
+
|
| 116 |
+
output_file.write_bytes(pdf_resp.content)
|
| 117 |
+
|
| 118 |
+
|
| 119 |
+
if __name__ == "__main__":
|
| 120 |
+
main()
|
RMM/md/en-2011-Sols2011D1.md
ADDED
|
@@ -0,0 +1,168 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $4^{\text {th }}$ Romanian Master of Mathematics Competition - Solutions Day 1: Friday, February 25, 2011, Bucharest
|
| 2 |
+
|
| 3 |
+
Problem 1. Prove that there exist two functions
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
f, g: \mathbb{R} \rightarrow \mathbb{R}
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
such that $f \circ g$ is strictly decreasing, while $g \circ f$ is strictly increasing.
|
| 10 |
+
(Poland) Andrzej KomisArsKi \& Marcin Kuczma
|
| 11 |
+
|
| 12 |
+
## Solution. Let
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\begin{aligned}
|
| 16 |
+
& \cdot A=\bigcup_{k \in \mathbb{Z}}\left(\left[-2^{2 k+1},-2^{2 k}\right) \bigcup\left(2^{2 k}, 2^{2 k+1}\right]\right) \\
|
| 17 |
+
& \cdot B=\bigcup_{k \in \mathbb{Z}}\left(\left[-2^{2 k},-2^{2 k-1}\right) \bigcup\left(2^{2 k-1}, 2^{2 k}\right]\right)
|
| 18 |
+
\end{aligned}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Thus $A=2 B, B=2 A, A=-A, B=-B, A \cap B=\varnothing$, and finally $A \cup B \cup\{0\}=\mathbb{R}$. Let us take
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
f(x)=\left\{\begin{array}{lll}
|
| 25 |
+
x & \text { for } & x \in A \\
|
| 26 |
+
-x & \text { for } & x \in B \\
|
| 27 |
+
0 & \text { for } & x=0
|
| 28 |
+
\end{array}\right.
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Take $g(x)=2 f(x)$. Thus $f(g(x))=f(2 f(x))=-2 x$ and $g(f(x))=2 f(f(x))=2 x$.
|
| 32 |
+
|
| 33 |
+
Problem 2. Determine all positive integers $n$ for which there exists a polynomial $f(x)$ with real coefficients, with the following properties:
|
| 34 |
+
(1) for each integer $k$, the number $f(k)$ is an integer if and only if $k$ is not divisible by $n$;
|
| 35 |
+
(2) the degree of $f$ is less than $n$.
|
| 36 |
+
(Hungary) GÉza Kós
|
| 37 |
+
Solution. We will show that such polynomial exists if and only if $n=1$ or $n$ is a power of a prime.
|
| 38 |
+
|
| 39 |
+
We will use two known facts stated in Lemmata 1 and 2.
|
| 40 |
+
Lemma 1. If $p^{a}$ is a power of a prime and $k$ is an integer, then $\frac{(k-1)(k-2) \ldots\left(k-p^{a}+1\right)}{\left(p^{a}-1\right)!}$ is divisible by $p$ if and only if $k$ is not divisible by $p^{a}$.
|
| 41 |
+
|
| 42 |
+
Proof. First suppose that $p^{a} \mid k$ and consider
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
\frac{(k-1)(k-2) \cdots\left(k-p^{a}+1\right)}{\left(p^{a}-1\right)!}=\frac{k-1}{p^{a}-1} \cdot \frac{k-2}{p^{a}-2} \cdots \frac{k-p^{a}+1}{1}
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
In every fraction on the right-hand side, $p$ has the same maximal exponent in the numerator as in the denominator.
|
| 49 |
+
|
| 50 |
+
Therefore, the product (which is an integer) is not divisible by $p$.
|
| 51 |
+
|
| 52 |
+
Now suppose that $p^{a} \nmid k$. We have
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\frac{(k-1)(k-2) \cdots\left(k-p^{a}+1\right)}{\left(p^{a}-1\right)!}=\frac{p^{a}}{k} \cdot \frac{k(k-1) \cdots\left(k-p^{a}+1\right)}{\left(p^{a}\right)!} .
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
The last fraction is an integer. In the fraction $\frac{p^{a}}{k}$, the denominator $k$ is not divisible by $p^{a}$.
|
| 59 |
+
Lemma 2. If $g(x)$ is a polynomial with degree less than $n$ then
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\sum_{\ell=0}^{n}(-1)^{\ell}\binom{n}{\ell} g(x+n-\ell)=0
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
Proof. Apply induction on $n$. For $n=1$ then $g(x)$ is a constant and
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
\binom{1}{0} g(x+1)-\binom{1}{1} g(x)=g(x+1)-g(x)=0
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Now assume that $n>1$ and the Lemma holds for $n-1$. Let $h(x)=g(x+1)-g(x)$; the degree of $h$ is less than the degree of $g$, so the induction hypothesis applies for $g$ and $n-1$ :
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
\begin{gathered}
|
| 75 |
+
\sum_{\ell=0}^{n-1}(-1)^{\ell}\binom{n-1}{\ell} h(x+n-1-\ell)=0 \\
|
| 76 |
+
\sum_{\ell=0}^{n-1}(-1)^{\ell}\binom{n-1}{\ell}(g(x+n-\ell)-g(x+n-1-\ell))=0 \\
|
| 77 |
+
\binom{n-1}{0} g(x+n)+\sum_{\ell=1}^{n-1}(-1)^{\ell}\left(\binom{n-1}{\ell-1}+\right. \\
|
| 78 |
+
\left.\binom{n-1}{\ell}\right) g(x+n-\ell)-(-1)^{n-1}\binom{n-1}{n-1} g(x)=0 \\
|
| 79 |
+
\sum_{\ell=0}^{n}(-1)^{\ell}\binom{n}{\ell} g(x+n-\ell)=0
|
| 80 |
+
\end{gathered}
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
Lemma 3. If $n$ has at least two distinct prime divisors then the greatest common divisor of $\binom{n}{1},\binom{n}{2}, \ldots,\binom{n}{n-1}$ is 1 .
|
| 84 |
+
|
| 85 |
+
Proof. Suppose to the contrary that $p$ is a common prime divisor of $\binom{n}{1}, \ldots,\binom{n}{n-1}$. In particular, $p \left\lvert\,\binom{ n}{1}=n\right.$. Let $a$ be the exponent of $p$ in the prime factorization of $n$. Since $n$ has at least two prime divisors, we have $1<p^{a}<n$. Hence, $\binom{n}{p^{a}-1}$ and $\binom{n}{p^{a}}$ are listed among $\binom{n}{1}, \ldots,\binom{n}{n-1}$ and thus $p \left\lvert\,\binom{ n}{p^{a}}\right.$ and $p \left\lvert\,\binom{ n}{p^{a}-1}\right.$. But then $p$ divides $\binom{n}{p^{a}}-\binom{n}{p^{a}-1}=\binom{n-1}{p^{a}-1}$, which contradicts Lemma 1.
|
| 86 |
+
|
| 87 |
+
Next we construct the polynomial $f(x)$ when $n=1$ or $n$ is a power of a prime.
|
| 88 |
+
|
| 89 |
+
For $n=1, f(x)=\frac{1}{2}$ is such a polynomial.
|
| 90 |
+
If $n=p^{a}$ where $p$ is a prime and $a$ is a positive integer then let
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
f(x)=\frac{1}{p}\binom{x-1}{p^{a}-1}=\frac{1}{p} \cdot \frac{(x-1)(x-2) \cdots\left(x-p^{a}+1\right)}{\left(p^{a}-1\right)!} .
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
The degree of this polynomial is $p^{a}-1=n-1$.
|
| 97 |
+
The number $\frac{(k-1)(k-2) \cdots\left(k-p^{a}+1\right)}{\left(p^{a}-1\right)!}$ is an integer for any integer $k$, and, by Lemma 1 , it is divisible by $p$ if and only if $k$ is not divisible by $p^{a}=n$.
|
| 98 |
+
|
| 99 |
+
Finally we prove that if $n$ has at least two prime divisors then no polynomial $f(x)$ satisfies $(1,2)$. Suppose that some polynomial $f(x)$ satisfies (1,2), and apply Lemma 2 for $g=f$ and $x=-k$ where $1 \leq k \leq n-1$. We get that
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
\binom{n}{k} f(0)=\sum_{0 \leq \ell \leq n, \ell \neq k}(-1)^{k-\ell}\binom{n}{\ell} f(-k+\ell)
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
Since $f(-k), \ldots, f(-1)$ and $f(1), \ldots, f(n-k)$ are all integers, we conclude that $\binom{n}{k} f(0)$ is an integer for every $1 \leq k \leq n-1$.
|
| 106 |
+
By dint of Lemma 3, the greatest common divisor of $\binom{n}{1},\binom{n}{2}, \ldots,\binom{n}{n-1}$ is 1 . Hence, there will exist some integers $u_{1}, u_{2}, \ldots, u_{n-1}$ for which $u_{1}\binom{n}{1}+\cdots+u_{n-1}\binom{n}{n-1}=1$. Then
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
f(0)=\left(\sum_{k=1}^{n-1} u_{k}\binom{n}{k}\right) f(0)=\sum_{k=1}^{n-1} u_{k}\binom{n}{k} f(0)
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
is a sum of integers. This contradicts the fact that $f(0)$ is not an integer. So such polynomial $f(x)$ does not exist.
|
| 113 |
+
|
| 114 |
+
Alternative Solution. (I. Bogdanov) We claim the answer is $n=p^{\alpha}$ for some prime $p$ and nonnegative $\alpha$.
|
| 115 |
+
|
| 116 |
+
Lemma. For every integers $a_{1}, \ldots, a_{n}$ there exists an integervalued polynomial $P(x)$ of degree $<n$ such that $P(k)=a_{k}$ for all $1 \leq k \leq n$.
|
| 117 |
+
|
| 118 |
+
Proof. Induction on $n$. For the base case $n=1$ one may set $P(x)=a_{1}$. For the induction step, suppose that the polynomial $P_{1}(x)$ satisfies the desired property for all $1 \leq k \leq n-1$. Then set $P(x)=P_{1}(x)+\left(a_{n}-P_{1}(n)\right)\binom{x-1}{n-1}$; since $\binom{k-1}{n-1}=0$ for $1 \leq k \leq n-1$ and $\binom{n-1}{n-1}=1$, the polynomial $P(x)$ is a sought one.
|
| 119 |
+
|
| 120 |
+
Now, if for some $n$ there exists some polynomial $f(x)$ satisfying the problem conditions, one may choose some integer-valued polynomial $P(x)$ (of degree $<n-1$ ) coinciding with $f(x)$ at points $1, \ldots, n-1$. The difference $f_{1}(x)=$ $f(x)-P(x)$ also satisfies the problem conditions, therefore we may restrict ourselves to the polynomials vanishing at points $1, \ldots, n-1-$ that are, the polynomials of the form $f(x)=c \prod_{i=1}^{n-1}(x-i)$ for some (surely rational) constant $c$.
|
| 121 |
+
|
| 122 |
+
Let $c=p / q$ be its irreducible form, and $q=\prod_{j=1}^{d} p_{j}^{\alpha_{j}}$ be the prime decomposition of the denominator.
|
| 123 |
+
|
| 124 |
+
1. Assume that a desired polynomial $f(x)$ exists. Since $f(0)$ is not an integer, we have $9 \nmid(-1)^{n-1}(n-1)$ ! and hence $p_{j}^{\alpha_{j}} \nmid(-1)^{n-1}(n-1)$ ! for some $j$. Hence
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\prod_{i=1}^{n-1}\left(p_{j}^{\alpha_{j}}-i\right) \equiv(-1)^{n-1}(n-1)!\not \equiv 0 \quad\left(\bmod p_{j}^{\alpha_{j}}\right)
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
therefore $f\left(p_{i}^{\alpha_{i}}\right)$ is not integer, too. By the condition (i), this means that $n \mid p_{i}^{\alpha_{i}}$, and hence $n$ should be a power of a prime.
|
| 131 |
+
2. Now let us construct a desired polynomial $f(x)$ for any power of a prime $n=p^{\alpha}$. We claim that the polynomial
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
f(x)=\frac{1}{p}\binom{x-1}{n-1}=\frac{n}{p x}\binom{x}{n}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
fits. Actually, consider some integer $x$. From the first representation, the denominator of the irreducible form of $f(x)$ may be 1 or $p$ only. If $p^{\alpha} \nmid x$, then the prime decomposition of the fraction $n /(p x)$ contains $p$ with a nonnegative exponent; hence $f(x)$ is integer. On the other hand, if $n=p^{\alpha} \mid x$, then the numbers $x-1, x-2, \ldots, x-(n-1)$ contain the same exponents of primes as the numbers $n-1, n-2, \ldots, 1$ respectively; hence the number
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
\binom{x-1}{n-1}=\frac{\prod_{i=1}^{n-1}(x-i)}{\prod_{i=1}^{n-1}(n-i)}
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
is not divisible by $p$. Thus $f(x)$ is not an integer.
|
| 144 |
+
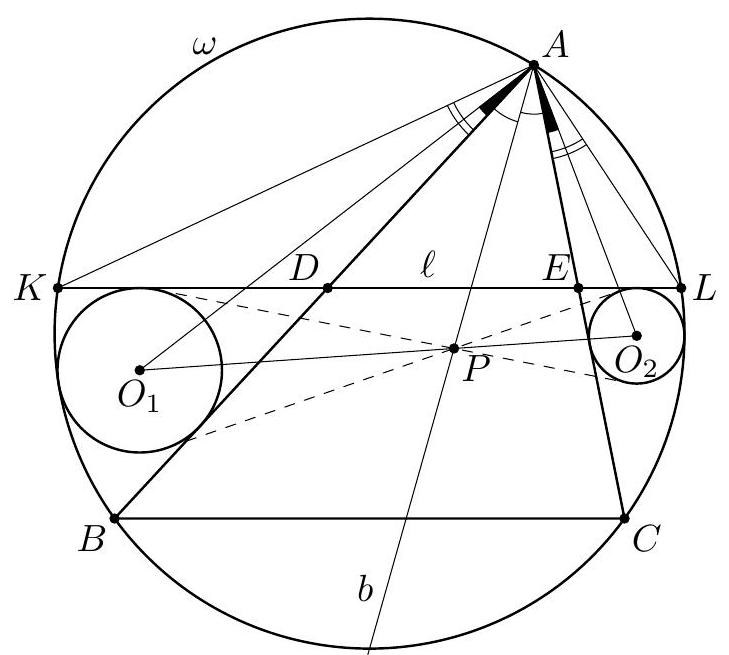
Problem 3. A triangle $A B C$ is inscribed in a circle $\omega$. A variable line $\ell$ chosen parallel to $B C$ meets segments $A B$, $A C$ at points $D, E$ respectively, and meets $\omega$ at points $K, L$ (where $D$ lies between $K$ and $E$ ). Circle $\gamma_{1}$ is tangent to the segments $K D$ and $B D$ and also tangent to $\omega$, while circle $\gamma_{2}$ is tangent to the segments $L E$ and $C E$ and also tangent to $\omega$. Determine the locus, as $\ell$ varies, of the meeting point of the common inner tangents to $\gamma_{1}$ and $\gamma_{2}$.
|
| 145 |
+
(Russia) VASily Mokin \& Fedor IvLev
|
| 146 |
+
Solution. Let $P$ be the meeting point of the common inner tangents to $\gamma_{1}$ and $\gamma_{2}$. Also, let $b$ be the angle bisector of $\angle B A C$. Since $K L \| B C, b$ is also the angle bisector of $\angle K A L$.
|
| 147 |
+
|
| 148 |
+
Let $\mathfrak{H}$ be the composition of the symmetry $\mathfrak{S}$ with respect to $b$ and the inversion $\mathfrak{I}$ of centre $A$ and ratio $\sqrt{A K \cdot A L}$ (it is readily seen that $\mathfrak{S}$ and $\mathfrak{I}$ commute, so since $\mathfrak{S}^{2}=\mathfrak{I}^{2}=$ id, then also $\mathfrak{H}^{2}=\mathrm{id}$, the identical transformation). The elements of the configuration interchanged by $\mathfrak{H}$ are summarized in Table I.
|
| 149 |
+
|
| 150 |
+
Let $O_{1}$ and $O_{2}$ be the centres of circles $\gamma_{1}$ and $\gamma_{2}$. Since the circles $\gamma_{1}$ and $\gamma_{2}$ are determined by their construction (in a unique way), they are interchanged by $\mathfrak{H}$, therefore the rays $A O_{1}$ and $A O_{2}$ are symmetrical with respect
|
| 151 |
+
to $b$. Denote by $\rho_{1}$ and $\rho_{2}$ the radii of $\gamma_{1}$ and $\gamma_{2}$. Since $\angle O_{1} A B=\angle O_{2} A C$, we have $\rho_{1} / \rho_{2}=A O_{1} / A O_{2}$. On the other hand, from the definition of $P$ we have $O_{1} P / O_{2} P=$ $\rho_{1} / \rho_{2}=A O_{1} / A O_{2}$; this means that $A P$ is the angle bisector of $\angle O_{1} A O_{2}$ and therefore of $\angle B A C$.
|
| 152 |
+
|
| 153 |
+
The limiting, degenerated, cases are when the parallel line passes through $A$ - when $P$ coincides with $A$; respectively when the parallel line is $B C$ - when $P$ coincides with the foot $A^{\prime} \in B C$ of the angle bisector of $\angle B A C$ (or any other point on $B C$ ). By continuity, any point $P$ on the open segment $A A^{\prime}$ is obtained for some position of the parallel, therefore the locus is the open segment $A A^{\prime}$ of the angle bisector $b$ of $\angle B A C$.
|
| 154 |
+
|
| 155 |
+
| point $K$ | $\longleftrightarrow$ | point $L$ |
|
| 156 |
+
| :---: | :---: | :---: |
|
| 157 |
+
| line $K L$ | $\longleftrightarrow$ | circle $\omega$ |
|
| 158 |
+
| ray $A B$ | $\longleftrightarrow$ | ray $A C$ |
|
| 159 |
+
| point $B$ | $\longleftrightarrow$ | point $E$ |
|
| 160 |
+
| point $C$ | $\longleftrightarrow$ | point $D$ |
|
| 161 |
+
| segment $B D$ | $\longleftrightarrow$ | segment $E C$ |
|
| 162 |
+
| $\operatorname{arc} B K$ | $\longleftrightarrow$ | segment $E L$ |
|
| 163 |
+
| $\operatorname{arc} C L$ | $\longleftrightarrow$ | segment $D K$ |
|
| 164 |
+
|
| 165 |
+
|
| 166 |
+
|
| 167 |
+
TABLE I: Elements interchanged by $\mathfrak{H}$.
|
| 168 |
+
|
RMM/md/en-2011-Sols2011D2.md
ADDED
|
@@ -0,0 +1,171 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $4^{\text {th }}$ Romanian Master of Mathematics Competition - Solutions Day 2: Saturday, February 26, 2011, Bucharest
|
| 2 |
+
|
| 3 |
+
Problem 4. Given a positive integer $n=\prod_{i=1}^{s} p_{i}^{\alpha_{i}}$, we write $\Omega(n)$ for the total number $\sum_{i=1}^{s} \alpha_{i}$ of prime factors of $n$, counted with multiplicity. Let $\lambda(n)=(-1)^{\Omega(n)}$ (so, for example, $\left.\lambda(12)=\lambda\left(2^{2} \cdot 3^{1}\right)=(-1)^{2+1}=-1\right)$.
|
| 4 |
+
|
| 5 |
+
Prove the following two claims:
|
| 6 |
+
i) There are infinitely many positive integers $n$ such that $\lambda(n)=\lambda(n+1)=+1 ;$
|
| 7 |
+
ii) There are infinitely many positive integers $n$ such that $\lambda(n)=\lambda(n+1)=-1$.
|
| 8 |
+
(ROMANIA) DAN SchwARZ
|
| 9 |
+
|
| 10 |
+
Solution. Notice that we have $\Omega(m n)=\Omega(m)+\Omega(n)$ for all positive integers $m, n$ ( $\Omega$ is a completely additive arithmetic function), translating into $\lambda(m n)=\lambda(m) \cdot \lambda(n)$ (so $\lambda$ is a completely multiplicative arithmetic function), hence $\lambda(p)=-1$ for any prime $p$, and $\lambda\left(k^{2}\right)=\lambda(k)^{2}=+1$ for all positive integers $k$.[1]
|
| 11 |
+
The start (first 100 terms) of the sequence $\mathfrak{S}=(\lambda(n))_{n \geq 1}$ is
|
| 12 |
+
$+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,-1,-1,-1,+1,+1,+1,-1,-1,-1,-1$,
|
| 13 |
+
$+1,+1,-1,+1,+1,+1,-1,-1,-1,-1,-1,-1,+1,+1,+1,+1,-1,+1,+1,+1$,
|
| 14 |
+
$-1,-1,-1,-1,-1,+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,+1,+1,+1,-1,+1$,
|
| 15 |
+
$-1,+1,-1,+1,+1,-1,-1,-1,+1,-1,-1,-1,-1,+1,-1,-1,+1,-1,-1,-1$,
|
| 16 |
+
$+1,+1,-1,+1,+1,+1,+1,+1,-1,+1,+1,-1,+1,+1,+1,+1,-1,-1,-1,+1$.
|
| 17 |
+
i) The Pell equation $x^{2}-6 y^{2}=1$ has infinitely many solutions in positive integers; all solutions are given by $\left(x_{n}, y_{n}\right)$, where $x_{n}+y_{n} \sqrt{6}=(5+2 \sqrt{6})^{n}$. Since $\lambda\left(6 y^{2}\right)=1$ and also $\lambda\left(6 y^{2}+1\right)=\lambda\left(x^{2}\right)=1$, the thesis is proven.
|
| 18 |
+
|
| 19 |
+
Alternative Solution. Take any existing pair with $\lambda(n)=$ $\lambda(n+1)=1$. Then $\lambda\left((2 n+1)^{2}-1\right)=\lambda\left(4 n^{2}+4 n\right)=\lambda(4) \cdot \lambda(n)$. $\lambda(n+1)=1$, and also $\lambda\left((2 n+1)^{2}\right)=\lambda(2 n+1)^{2}=1$, so we have built a larger $(1,1)$ pair.
|
| 20 |
+
ii) The equation $3 x^{2}-2 y^{2}=1$ (again Pell theory) has also infinitely many solutions in positive integers, given by $\left(x_{n}, y_{n}\right)$, where $x_{n} \sqrt{3}+y_{n} \sqrt{2}=(\sqrt{3}+\sqrt{2})^{2 n+1}$. Since $\lambda\left(2 y^{2}\right)=$ -1 and $\lambda\left(2 y^{2}+1\right)=\lambda\left(3 x^{2}\right)=-1$, the thesis is proven.
|
| 21 |
+
|
| 22 |
+
Alternative Solution. Assume $(\lambda(n-1), \lambda(n))$ is the largest $(-1,-1)$ pair, therefore $\lambda(n+1)=1$ and $\lambda\left(n^{2}+n\right)=\lambda(n)$. $\lambda(n+1)=-1$, therefore again $\lambda\left(n^{2}+n+1\right)=1$. But then $\lambda\left(n^{3}-1\right)=\lambda(n-1) \cdot \lambda\left(n^{2}+n+1\right)=-1$, and also $\lambda\left(n^{3}\right)=$ $\lambda(n)^{3}=-1$, so we found yet a larger such pair than the one we started with, contradiction.
|
| 23 |
+
|
| 24 |
+
Alternative Solution. Assume the pairs of consecutive terms $(-1,-1)$ in $\mathfrak{S}$ are finitely many. Then from some rank on we only have subsequences ( $1,-1,1,1, \ldots, 1,-1,1$ ). By
|
| 25 |
+
"doubling" such a subsequence (like at point ii)), we will produce
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
(-1, ?, 1, ?,-1, ?,-1, ?, \ldots, ?,-1, ?, 1, ?,-1)
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
According with our assumption, all ?-terms ought to be 1 , hence the produced subsequence is
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
(-1,1,1,1,-1,1,-1,1, \ldots, 1,-1,1,1,1,-1)
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
and so the "separating packets" of l's contain either one or three terms. Now assume some far enough ( $1,1,1,1)$ or $(-1,1,1,-1)$ subsequence of $\mathfrak{S}$ were to exist. Since it lies within some "doubled" subsequence, it contradicts the structure described above, which thus is the only prevalent from some rank on. But then all the positions of the ( -1 )terms will have the same parity. However though, we have $\lambda(p)=\lambda\left(2 p^{2}\right)=-1$ for all odd primes $p$, and these terms have different parity of their positions. A contradiction has been reached.[2]
|
| 38 |
+
|
| 39 |
+
Alternative Solution for both i) and ii). (I. Bogdanov) Take $\varepsilon \in\{-1,1\}$. There obviously exist infinitely many $n$ such that $\lambda(2 n+1)=\varepsilon$ (just take $2 n+1$ to be the product of an appropriate number of odd primes). Now, if either $\lambda(2 n)=\varepsilon$ or $\lambda(2 n+2)=\varepsilon$, we are done; otherwise $\lambda(n)=-\lambda(2 n)=$ $-\lambda(2 n+2)=\lambda(n+1)=\varepsilon$. Therefore, for such an $n$, one of the three pairs $(n, n+1),(2 n, 2 n+1)$ or $(2 n+1,2 n+2)$ fits the bill.
|
| 40 |
+
|
| 41 |
+
We have thus proved the existence in $\mathfrak{S}$ of infinitely many occurrences of all possible subsequences of length 1 , viz. $(+1)$ and $(-1)$, and of length 2 , viz. $(+1,-1),(-1,+1)$, $(+1,+1)$ and $(-1,-1) .[3]$
|
| 42 |
+
|
| 43 |
+
Problem 5. For every $n \geq 3$, determine all the configurations of $n$ distinct points $X_{1}, X_{2}, \ldots, X_{n}$ in the plane, with the property that for any pair of distinct points $X_{i}, X_{j}$ there exists a permutation $\sigma$ of the integers $\{1, \ldots, n\}$, such that $\mathrm{d}\left(X_{i}, X_{k}\right)=\mathrm{d}\left(X_{j}, X_{\sigma(k)}\right)$ for all $1 \leq k \leq n$.
|
| 44 |
+
(We write $\mathrm{d}(X, Y)$ to denote the distance between points $X$ and $Y$.)
|
| 45 |
+
(United Kingdom) LuKe BetTs
|
| 46 |
+
Solution. Let us first prove that the points must be concyclic. Assign to each point $X_{k}$ the vector $x_{k}$ in a system of orthogonal coordinates whose origin is the point of mass of the configuration, thus $\frac{1}{n} \sum_{k=1}^{n} x_{k}=0$.
|
| 47 |
+
|
| 48 |
+
Then $\mathrm{d}^{2}\left(X_{i}, X_{k}\right)=\left\|x_{i}-x_{k}\right\|^{2}=\left\langle x_{i}-x_{k}, x_{i}-x_{k}\right\rangle=$ $\left\|x_{i}\right\|^{2}-2\left\langle x_{i}, x_{k}\right\rangle+\left\|x_{k}\right\|^{2}$, hence $\sum_{k=1}^{n} \mathrm{~d}^{2}\left(X_{i}, X_{k}\right)=n\left\|x_{i}\right\|^{2}-$
|
| 49 |
+
$2\left\langle x_{i}, \sum_{k=1}^{n} x_{k}\right\rangle+\sum_{k=1}^{n}\left\|x_{k}\right\|^{2}=n\left\|x_{i}\right\|^{2}+\sum_{k=1}^{n}\left\|x_{k}\right\|^{2}=n\left\|x_{j}\right\|^{2}+$ $\sum_{k=1}^{n}\left\|x_{\sigma(k)}\right\|^{2}=\sum_{k=1}^{n} \mathrm{~d}^{2}\left(X_{j}, X_{\sigma(k)}\right)$, therefore $\left\|x_{i}\right\|=\left\|x_{j}\right\|$ for all pairs $(i, j)$. The points are thus concyclic (lying on a circle centred at $O(0,0)$ ).
|
| 50 |
+
Let now $m$ be the least angular distance between any two points. Two points situated at angular distance $m$ must be adjacent on the circle. Let us connect each pair of such two points with an edge. The graph $G$ obtained must be regular, of degree $\operatorname{deg}(G)=1$ or 2 . If $n$ is odd, since $\sum_{k=1}^{n} \operatorname{deg}\left(X_{k}\right)=$ $n \operatorname{deg}(G)=2|E|$, we must have $\operatorname{deg}(G)=2$, hence the configuration is a regular $n$-gon.
|
| 51 |
+
|
| 52 |
+
If $n$ is even, we may have the configuration of a regular $n$-gon, but we also may have $\operatorname{deg}(G)=1$. In that case, let $M$ be the next least angular distance between any two points; such points must also be adjacent on the circle. Let us connect each pair of such two points with an edge, in order to get a graph $G^{\prime}$. A similar reasoning yields $\operatorname{deg}\left(G^{\prime}\right)=1$, thus the configuration is that of an equiangular $n$-gon (with alternating equal side-lengths).
|
| 53 |
+
|
| 54 |
+
Problem 6. The cells of a square $2011 \times 2011$ array are labelled with the integers $1,2, \ldots, 2011^{2}$, in such a way that every label is used exactly once. We then identify the lefthand and right-hand edges, and then the top and bottom, in the normal way to form a torus (the surface of a doughnut).
|
| 55 |
+
|
| 56 |
+
Determine the largest positive integer $M$ such that, no matter which labelling we choose, there exist two neighbouring cells with the difference of their labels at least M.[4]
|
| 57 |
+
(ROMANIA) DAN SchwarZ
|
| 58 |
+
Preamble. For a planar $N \times N$ array, it is folklore that this value is $M=N$, with some easy models shown below. As such, the problem is mentioned in [Béla Bollobás - The Art of Mathematics], 21. Neighbours in a Matrix.
|
| 59 |
+
|
| 60 |
+
This is not necessarily a flaw on the actual problem, which is presented in a brand novel setting; on the contrary, some general previous knowledge on such type of problems (which we think must be encouraged) is beneficial in searching for the right ideas of a proof.
|
| 61 |
+
|
| 62 |
+
The idea for a proof goes along the lines of finding a moment in the consecutive filling with numbers of the array, when there are at least $N$ pairs of adjacent filled/yet-unfilled cells (with either distinct filled cells or distinct yet-unfilled cells). Then, when the cell next to that bearing the least label is filled, the difference between its label and the one being filled will be at least $N$.
|
| 63 |
+
|
| 64 |
+
| 1 | 2 | $\ldots$ | N |
|
| 65 |
+
| :---: | :---: | :---: | :---: |
|
| 66 |
+
| $\mathrm{~N}+1$ | $\mathrm{~N}+2$ | $\ldots$ | 2 N |
|
| 67 |
+
| $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
|
| 68 |
+
| $(\mathrm{~N}-1) \mathrm{N}+1$ | $(\mathrm{~N}-1) \mathrm{N}+2$ | $\ldots$ | $\mathrm{~N}^{2}$ |
|
| 69 |
+
|
| 70 |
+
A planar parallel $N \times N$ model array.
|
| 71 |
+
|
| 72 |
+
| 1 | 2 | 4 | $\ldots$ | | $\mathrm{~N}(\mathrm{~N}-1) / 2+1$ |
|
| 73 |
+
| :---: | :---: | :---: | :---: | :---: | :---: |
|
| 74 |
+
| 3 | 5 | $\ldots$ | $\mathrm{~N}(\mathrm{~N}-1) / 2+2$ | | |
|
| 75 |
+
| 6 | | $\ldots$ | | | |
|
| 76 |
+
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | $\vdots$ |
|
| 77 |
+
| | $\mathrm{~N}(\mathrm{~N}+1) / 2-1$ | $\ldots$ | | $\mathrm{~N}^{2}-2$ | |
|
| 78 |
+
| $\mathrm{~N}(\mathrm{~N}+1) / 2$ | | $\ldots$ | $\mathrm{~N}^{2}-1$ | $\mathrm{~N}^{2}$ | |
|
| 79 |
+
|
| 80 |
+
A planar diagonal $N \times N$ model array.
|
| 81 |
+
|
| 82 |
+
Solution. For the toroidal case, it is clear the statement of the problem is referring to the cells of a $\mathbb{Z}_{N} \times \mathbb{Z}_{N}$ lattice on the surface of the torus, labeled with the numbers $1,2, \ldots, N^{2}$, where one has to determine the least possible maximal absolute value $M$ of the difference of labels assigned to orthogonally adjacent cells.
|
| 83 |
+
|
| 84 |
+
The toroidal $N=2$ case is trivially seen to be $M=2$ (thus coinciding with the planar case).
|
| 85 |
+
|
| 86 |
+
|
| 87 |
+
The unique $2 \times 2$ toroidal array.
|
| 88 |
+
|
| 89 |
+
For $N \geq 3$ we will prove that value to be at least $M \geq$ $2 N-1$. Consider such a configuration, and color all cells of the square in white. Go along the cells labeled 1, 2, etc. coloring them in black, stopping just on the cell bearing the least label $k$ which, after assigned and colored in black, makes that all lines of a same orientation (rows, or columns, or both) contain at least two black cells (that is, before coloring in black the cell labeled $k$, at least one row and at least one column contained at most one black cell). Wlog assume this happens for rows. Then at most one row is all black, since if two were then the stopping condition would have been fulfilled before cell labeled $k$ (if the cell labeled $k$ were to be on one of these rows, then all rows would have contained at least two black cells before, while if not, then all columns would have contained at least two black cells before).
|
| 90 |
+
|
| 91 |
+
Now color in red all those black cells adjacent to a white cell. Since each row, except the potential all black one, contained at least two black and one white cell, it will now contain at least two red cells. For the potential all black row, any of the neighbouring rows contains at least one white cell, and so the cell adjacent to it has been colored red. In total we have therefore colored red at least $2(N-1)+1=2 N-1$ cells.
|
| 92 |
+
|
| 93 |
+
The least label of the red cells has therefore at most the value $k+1-(2 N-1)$. When the white cell adjacent to it will eventually be labeled, its label will be at least $k+1$, therefore their difference is at least $(k+1)-(k+1-(2 N-1))=2 N-1$.
|
| 94 |
+

|
| 95 |
+
|
| 96 |
+
Example of coloring the array.
|
| 97 |
+
The models are kind of hard to find, due to the fact that the direct proof offers little as to their structure (it is difficult to determine the equality case during the argument involving the inequality with the bound, and then, even this is not sure to be prone to being prolonged to a full labeling of the array).
|
| 98 |
+
|
| 99 |
+
The weaker fact the value $M$ is not larger than $2 N$ is proved by the general model exhibited below (presented so that partial credits may be awarded).
|
| 100 |
+
|
| 101 |
+
| $\mathrm{N}+1$ | $\mathrm{~N}+2$ | $\ldots$ | 2 N |
|
| 102 |
+
| :---: | :---: | :---: | :---: |
|
| 103 |
+
| $3 \mathrm{~N}+1$ | $3 \mathrm{~N}+2$ | $\cdots$ | 4 N |
|
| 104 |
+
| $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
|
| 105 |
+
| $(2 \ell-1) \mathrm{N}+1$ | $(2 \ell-1) \mathrm{N}+2$ | $\ldots$ | $2 \ell \mathrm{~N}$ |
|
| 106 |
+
| $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
|
| 107 |
+
| $2 k \mathrm{~N}+1$ | $2 k \mathrm{~N}+2$ | $\ldots$ | $(2 k+1) \mathrm{N}$ |
|
| 108 |
+
| $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
|
| 109 |
+
| $2 \mathrm{~N}+1$ | $2 \mathrm{~N}+2$ | $\ldots$ | 3 N |
|
| 110 |
+
| 1 | 2 | $\ldots$ | N |
|
| 111 |
+
|
| 112 |
+
A general model for $M=2 N$ in a $N \times N$ array.
|
| 113 |
+
By examining some small $N>2$ cases, one comes up with the idea of spiral models for the true value $M=2 N-1$. The models presented are for odd $N$ (since 2011 is odd); similar models exist for even $N$ (but are less symmetric). The color red (preceded by green) marks the moment where the largest difference $M=2 N-1$ first appears.
|
| 114 |
+
[1] Also see Sloane's Online Encyclopædia of Integer Sequences (OEIS), sequence A001222 for $\Omega$ and sequence A008836 for $\lambda$, which is called Liouville's function. Its summatory function $\sum_{d \mid n} \lambda(d)$ is equal to 1 for a perfect square $n$, and 0 otherwise.
|
| 115 |
+
Pólya conjectured that $L(n):=\sum_{k=1}^{n} \lambda(k) \leq 0$ for all $n$, but this has been proven false by Minoru Tanaka, who in 1980 computed that for $n=906,151,257$ its value was positive. Turán showed that if $T(n):=\sum_{k=1}^{n} \frac{\lambda(k)}{k} \geq 0$ for all large enough $n$, that
|
| 116 |
+
|
| 117 |
+
| 7 | 2 | 6 |
|
| 118 |
+
| :--- | :--- | :--- |
|
| 119 |
+
| 3 | 1 | 5 |
|
| 120 |
+
| 8 | 4 | 9 |
|
| 121 |
+
|
| 122 |
+
TABLE I: The spiral $3 \times 3$ array.
|
| 123 |
+
|
| 124 |
+
| 16 | 14 | 7 | 13 | 16 |
|
| 125 |
+
| :---: | :---: | :---: | :---: | :---: |
|
| 126 |
+
| 12 | 8 | 2 | 6 | 12 |
|
| 127 |
+
| 9 | 3 | 1 | 5 | 9 |
|
| 128 |
+
| 15 | 10 | 4 | 11 | 15 |
|
| 129 |
+
| 16 | 14 | 7 | 13 | |
|
| 130 |
+
| | | | | |
|
| 131 |
+
|
| 132 |
+
TABLE II: The spiral $4 \times 4$ array.
|
| 133 |
+
|
| 134 |
+
| 23 | 16 | 7 | 15 | 22 |
|
| 135 |
+
| :---: | :---: | :---: | :---: | :---: |
|
| 136 |
+
| 17 | 8 | 2 | 6 | 14 |
|
| 137 |
+
| 9 | 3 | 1 | 5 | 13 |
|
| 138 |
+
| 18 | 10 | 4 | 12 | 21 |
|
| 139 |
+
| 24 | 19 | 11 | 20 | 25 |
|
| 140 |
+
|
| 141 |
+
TABLE III: The spiral $5 \times 5$ array.
|
| 142 |
+
|
| 143 |
+
| 47 | 40 | 29 | 16 | 28 | 39 | 46 |
|
| 144 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 145 |
+
| 41 | 30 | 17 | 7 | 15 | 27 | 38 |
|
| 146 |
+
| 31 | 18 | 8 | 2 | 6 | 14 | 26 |
|
| 147 |
+
| 19 | 9 | 3 | 1 | 5 | 13 | 25 |
|
| 148 |
+
| 32 | 20 | 10 | 4 | 12 | 24 | 37 |
|
| 149 |
+
| 42 | 33 | 21 | 11 | 23 | 36 | 45 |
|
| 150 |
+
| 48 | 43 | 34 | 22 | 35 | 44 | 49 |
|
| 151 |
+
|
| 152 |
+
TABLE IV: The spiral $7 \times 7$ array.
|
| 153 |
+
|
| 154 |
+
| $(2 \mathrm{n}+1)^{2}-2$ | $(2 \mathrm{n}+1)^{2}-9$ | $\ldots$ | | $\mathrm{n}(2 \mathrm{n}-1)+1$ | | $\ldots$ | $(2 \mathrm{n}+1)^{2}-10$ | $(2 \mathrm{n}+1)^{2}-3$ |
|
| 155 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 156 |
+
| $(2 \mathrm{n}+1)^{2}-8$ | | $\ldots$ | $\mathrm{n}(2 \mathrm{n}-1)+2$ | | $\mathrm{n}(2 \mathrm{n}-1)$ | $\ldots$ | | $(2 \mathrm{n}+1)^{2}-11$ |
|
| 157 |
+
| $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $2 \mathrm{n}(\mathrm{n}+1)+3$ | $\vdots$ |
|
| 158 |
+
| | $2 \mathrm{n}^{2}$ | $\ldots$ | 8 | 2 | 6 | $\ldots$ | $2 \mathrm{n}(\mathrm{n}-1)+2$ | $2 \mathrm{n}(\mathrm{n}+1)+2$ |
|
| 159 |
+
| $2 \mathrm{n}^{2}+1$ | | $\ldots$ | 3 | 1 | 5 | $\ldots$ | | $2 \mathrm{n}(\mathrm{n}+1)+1$ |
|
| 160 |
+
| | $2 \mathrm{n}^{2}+2$ | $\ldots$ | 10 | 4 | 12 | $\ldots$ | $2 \mathrm{n}(\mathrm{n}+1)$ | |
|
| 161 |
+
| | $\vdots$ | $\ddots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | $\vdots$ |
|
| 162 |
+
| $\vdots$ | $\vdots$ | $\ldots$ | $\mathrm{n}(2 \mathrm{n}+1)$ | | $\mathrm{n}(2+1)+2$ | $\ldots$ | | $(2 \mathrm{n}+1)^{2}-4$ |
|
| 163 |
+
| $(2 \mathrm{n}+1)^{2}-7$ | | $\ldots$ | $\mathrm{n}(2 \mathrm{n}+1)+1$ | | $\ldots$ | $(2 \mathrm{n}+1)^{2}-5$ | $(2 \mathrm{n}+1)^{2}$ | |
|
| 164 |
+
| $(2 \mathrm{n}+1)^{2}-1$ | $(2 \mathrm{n}+1)^{2}-6$ | $\ldots$ | | | | | | |
|
| 165 |
+
|
| 166 |
+
TABLE V: The general spiral $N \times N$ array for $N=2 n+1 \geq 5$.
|
| 167 |
+
will imply Riemann's Hypothesis; however, Haselgrove proved it is negative infinitely often.
|
| 168 |
+
[2] Using the same procedure for point i), we only need notice that $\lambda\left((2 k+1)^{2}\right)=\lambda\left((2 k)^{2}\right)=1$, and these terms again are of different parity of their position.
|
| 169 |
+
[3] Is this true for subsequences of all lengths $\ell=3,4$, etc.? If no, up to which length $\ell \geq 2$ ?
|
| 170 |
+
[4] Cells with coordinates $(x, y)$ and $\left(x^{\prime}, y^{\prime}\right)$ are considered to be neighbours if $x=x^{\prime}$ and $y-y^{\prime} \equiv \pm 1(\bmod 2011)$, or if $y=y^{\prime}$ and $x-x^{\prime} \equiv \pm 1(\bmod 2011)$.
|
| 171 |
+
|
RMM/md/en-2012-Solutions2012-1.md
ADDED
|
@@ -0,0 +1,123 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $5^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Solutions for the Day 1
|
| 4 |
+
|
| 5 |
+
Problem 1. Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
| 6 |
+
|
| 7 |
+
Solution 1. A set $X$ of boys is separated from a set $Y$ of girls if no boy in $X$ is an acquaintance of a girl in $Y$. Similarly, a set $Y$ of girls is separated from a set $X$ of boys if no girl in $Y$ is an acquaintance of a boy in $X$. Since acquaintance is assumed mutual, separation is symmetric: $X$ is separated from $Y$ if and only if $Y$ is separated from $X$.
|
| 8 |
+
|
| 9 |
+
This enables doubly counting the number $n$ of ordered pairs $(X, Y)$ of separated sets $X$, of boys, and $Y$, of girls, and thereby showing that it is congruent modulo 2 to both numbers in question.
|
| 10 |
+
|
| 11 |
+
Given a set $X$ of boys, let $Y_{X}$ be the largest set of girls separated from $X$, to deduce that $X$ is separated from exactly $2^{\left|Y_{X}\right|}$ sets of girls. Consequently, $n=\sum_{X} 2^{\left|Y_{X}\right|}$ which is clearly congruent modulo 2 to the number of covering sets of boys.
|
| 12 |
+
|
| 13 |
+
Mutatis mutandis, the argument applies to show $n$ congruent modulo 2 to the number of covering sets of girls.
|
| 14 |
+
|
| 15 |
+
Remark. The argument in this solution translates verbatim in terms of the adjancency matrix of the associated acquaintance graph.
|
| 16 |
+
|
| 17 |
+
Solution 2. (Ilya Bogdanov) Let $B$ denote the set of boys, let $G$ denote the set of girls and induct on $|B|+|G|$. The assertion is vacuously true if either set is empty.
|
| 18 |
+
|
| 19 |
+
Next, fix a boy $b$, let $B^{\prime}=B \backslash\{b\}$, and let $G^{\prime}$ be the set of all girls who do not know $b$. Notice that:
|
| 20 |
+
(1) a covering set of boys in $B^{\prime} \cup G$ is still one in $B \cup G$; and
|
| 21 |
+
(2) a covering set of boys in $B \cup G$ which is no longer one in $B^{\prime} \cup G$ is precisely the union of a covering set of boys in $B^{\prime} \cup G^{\prime}$ and $\{b\}$,
|
| 22 |
+
so the number of covering sets of boys in $B \cup G$ is the sum of those in $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$. On the other hand,
|
| 23 |
+
$\left(1^{\prime}\right)$ a covering set of girls in $B \cup G$ is still one in $B^{\prime} \cup G$; and
|
| 24 |
+
$\left(2^{\prime}\right)$ a covering set of girls in $B^{\prime} \cup G$ which is no longer one in $B \cup G$ is precisely a covering set of girls in $B^{\prime} \cup G^{\prime}$,
|
| 25 |
+
so the number of covering sets of girls in $B \cup G$ is the difference of those in $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$. Since the assertion is true for both $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$ by the induction hypothesis, the conclusion follows.
|
| 26 |
+
|
| 27 |
+
Solution 3. (Géza Kós) Let $B$ and $G$ denote the sets of boys and girls, respectively. For every pair $(b, g) \in B \times G$, write $f(b, g)=0$ if they know each other, and $f(b, g)=1$ otherwise. A set $X$ of boys is covering if and only if
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\prod_{g \in G}\left(1-\prod_{b \in X} f(b, g)\right)=1
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Hence the number of covering sets of boys is
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\begin{aligned}
|
| 37 |
+
\sum_{X \subseteq B} \prod_{g \in G}\left(1-\prod_{b \in X} f(b, g)\right) & \equiv \sum_{X \subseteq B} \prod_{g \in G}\left(1+\prod_{b \in X} f(b, g)\right) \\
|
| 38 |
+
& =\sum_{X \subseteq B} \sum_{Y \subseteq G} \prod_{b \in X} \prod_{g \in Y} f(b, g) \quad(\bmod 2)
|
| 39 |
+
\end{aligned}
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
By symmetry, the same is valid for the number of covering sets of girls.
|
| 43 |
+
|
| 44 |
+
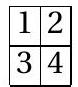
Problem 2. Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
| 45 |
+
|
| 46 |
+
Solution 1. We will use the following lemma.
|
| 47 |
+
Lemma. Let $A D$ be a median in triangle $A B C$. Then $\cot \angle B A D=2 \cot A+\cot B$ and $\cot \angle A D C=\frac{1}{2}(\cot B-\cot C)$.
|
| 48 |
+
|
| 49 |
+
Proof. Let $C C_{1}$ and $D D_{1}$ be the perpendiculars from $C$ and $D$ to $A B$. Using the signed lengths we write
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\cot B A D=\frac{A D_{1}}{D D_{1}}=\frac{\left(A C_{1}+A B\right) / 2}{C C_{1} / 2}=\frac{C C_{1} \cot A+C C_{1}(\cot A+\cot B)}{C C_{1}}=2 \cot A+\cot B
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Similarly, denoting by $A_{1}$ the projection of $A$ onto $B C$, we get
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\cot A D C=\frac{D A_{1}}{A A_{1}}=\frac{B C / 2-A_{1} C}{A A_{1}}=\frac{\left(A A_{1} \cot B+A A_{1} \cot C\right) / 2-A A_{1} \cot C}{A A_{1}}=\frac{\cot B-\cot C}{2} .
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
The Lemma is proved.
|
| 62 |
+
Turning to the solution, by the Lemma we get
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\begin{aligned}
|
| 66 |
+
\cot \angle B P D & =2 \cot \angle B P C+\cot \angle P B C=2 \cot \angle B F C+\cot \angle P B C \quad(\text { from circle } B F P C) \\
|
| 67 |
+
& =2 \cdot \frac{1}{2}(\cot A-\cot B)+2 \cot B+\cot C=\cot A+\cot B+\cot C
|
| 68 |
+
\end{aligned}
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Similarly, $\cot \angle G Q F=\cot A+\cot B+\cot C$, so $\angle G P R=\angle G Q F$ and $G P R Q$ is cyclic.
|
| 72 |
+
Remark. The angle $\angle G P R=\angle G Q F$ is the Brocard angle.
|
| 73 |
+
Solution 2. (Ilya Bogdanov and Marian Andronache) We also prove that $\angle(R P, P G)=\angle(R Q, Q G)$, or $\angle(D P, P G)=\angle(F Q, Q G)$.
|
| 74 |
+
|
| 75 |
+
Let $S$ be the point on ray $G D$ such that $A G \cdot G S=C G \cdot G F$ (so the points $A, S, C, F$ are concyclic). Then $G P \cdot G E=G P \cdot \frac{1}{2} G B=\frac{1}{2} C G \cdot G F=\frac{1}{2} A G \cdot G S=G D \cdot G S$, hence the points $E, P, D, S$ are also concyclic, and $\angle(D P, P G)=\angle(G S, S E)$. The problem may therefore be rephrased as follows:
|
| 76 |
+
Given a triangle $A B C$, let $D, E$ and $F$ respectively denote the midpoints of the sides $B C, C A$ and $A B$. The circle $A B E$, respectively, $A C F$, and the line $A D$ meet again at $Q$, respectively, $S$. Prove that $\angle A Q F=\angle A S E($ and $E S=F Q)$.
|
| 77 |
+
|
| 78 |
+
|
| 79 |
+
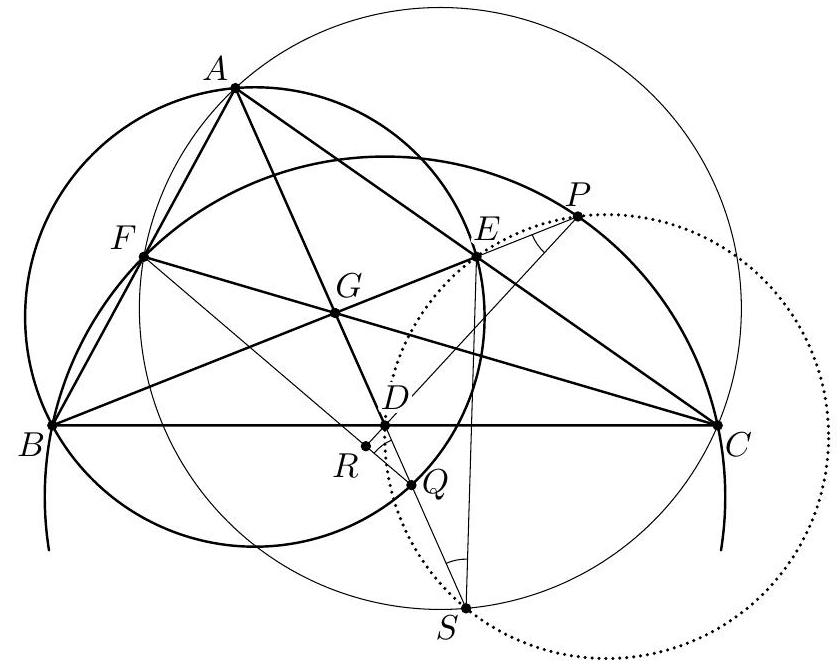
Upon inversion of pole $A$, the problem reads:
|
| 80 |
+
Given a triangle $A E^{\prime} F^{\prime}$, let the symmedian from $A$ meet the medians from $E^{\prime}$ and $F^{\prime}$ at $K=Q^{\prime}$ and $L=S^{\prime}$, respectively. Prove that the angles $A E^{\prime} L$ and $A F^{\prime} K$ are congruent.
|
| 81 |
+
|
| 82 |
+
|
| 83 |
+
To prove this, denote $E^{\prime}=X, F^{\prime}=Y$. Let the symmedian from $A$ meet the side $X Y$ at $V$ and let the lines $X L$ and $Y K$ meet the sides $A Y$ and $A X$ at $M$ and $N$, respectively. Since the points $K$ and $L$ lie on the medians, we have $V M\|A X, V N\| A Y$. Hence $A M V N$ is a parallelogram, the symmedian $A V$ of triangle $A X Y$ supports the median of triangle $A M N$, which implies that the triangles $A M N$ and $A X Y$ are similar. Hence the points $M, N, X, Y$ are concyclic, and $\angle A X M=\angle A Y N$, QED.
|
| 84 |
+
|
| 85 |
+
Remark 1. We know that the points $X, Y, M, N$ are concyclic. Invert back from $A$ and consider the circles $A F Q$ and $A E S$ : the former meets $A C$ again at $M^{\prime}$ and the latter meets $A B$ again at $N^{\prime}$. Then the points $E, F, M^{\prime}, N^{\prime}$ are concyclic.
|
| 86 |
+
|
| 87 |
+
Remark 2. The inversion at pole $A$ also allows one to show that $\angle A Q F$ is the Brocard angle, thus providing one more solution. In our notation, it is equivalent to the fact that the points $Y$, $K$, and $Z$ are collinear, where $Z$ is the Brocard point (so $\angle Z A X=\angle Z Y A=\angle Z X Y$ ). This is valid because the lines $A V, X K$, and $Y Z$ are the radical axes of the following circles: (i) passing through $X$ and tangent to $A Y$ at $A$; (ii) passing through $Y$ and tangent to $A X$ at $A$; and (iii) passing through $X$ and tangent to $A Y$ at $Y$. The point $K$ is the radical center of these three circles.
|
| 88 |
+
|
| 89 |
+
Solution 3. (Ilya Bogdanov) Again, we will prove that $\angle(D P, P G)=\angle(F Q, Q G)$. Mark a point $T$ on the ray $G F$ such that $G F \cdot G T=G Q \cdot G D$; then the points $F, Q, D, T$ are concyclic, and $\angle(F Q, Q G)=\angle(T G, T D)=\angle(T C, T D)$.
|
| 90 |
+
|
| 91 |
+
|
| 92 |
+
Shift the point $P$ by the vector $\overrightarrow{B D}$ to obtain point $P^{\prime}$. Then $\angle(D P, P G)=\angle\left(C P^{\prime}, P^{\prime} D\right)$, and we need to prove that $\angle\left(C P^{\prime}, P^{\prime} D\right)=\angle(C T, T D)$. This is precisely the condition that the points $T, D, C, P^{\prime}$ be concyclic.
|
| 93 |
+
|
| 94 |
+
Denote $G E=x, G F=y$. Then $G P \cdot G B=G C \cdot G F$, so $G P=y^{2} / x$. On the other hand, $G B \cdot G E=G Q \cdot G A=2 G Q \cdot G D=2 G T \cdot G F$, so $G T=x^{2} / y$. Denote by $K$ the point of intersection of $D P^{\prime}$ and $C T$; we need to prove that $T K \cdot K C=D K \cdot K P^{\prime}$.
|
| 95 |
+
|
| 96 |
+
Now, $D P^{\prime}=B P=B G+G P=2 x+y^{2} / x, C T=C G+G T=2 y+x^{2} / y, D K=B G / 2=x$, $C K=C G / 2=y$. Hence the desired equality reads $x\left(x+y^{2} / x\right)=y\left(y+x^{2} / y\right)$ which is obvious.
|
| 97 |
+
|
| 98 |
+
Remark. The points $B, T, E$, and $C$ are concyclic, hence the point $T$ is also of the same kind as $P$ and $Q$.
|
| 99 |
+
|
| 100 |
+
Problem 3. Each positive integer number is coloured red or blue. A function $f$ from the set of positive integer numbers into itself has the following two properties:
|
| 101 |
+
(a) if $x \leq y$, then $f(x) \leq f(y)$; and
|
| 102 |
+
(b) if $x, y$ and $z$ are all (not necessarily distinct) positive integer numbers of the same colour and $x+y=z$, then $f(x)+f(y)=f(z)$.
|
| 103 |
+
|
| 104 |
+
Prove that there exists a positive number $a$ such that $f(x) \leq a x$ for all positive integer numbers $x$.
|
| 105 |
+
|
| 106 |
+
Solution. For integer $x, y$, by a segment $[x, y]$ we always mean the set of all integers $t$ such that $x \leq t \leq y$; the length of this segment is $y-x$.
|
| 107 |
+
|
| 108 |
+
If for every two positive integers $x, y$ sharing the same colour we have $f(x) / x=f(y) / y$, then one can choose $a=\max \{f(r) / r, f(b) / b\}$, where $r$ and $b$ are arbitrary red and blue numbers, respectively. So we can assume that there are two red numbers $x, y$ such that $f(x) / x \neq f(y) / y$.
|
| 109 |
+
|
| 110 |
+
Set $m=x y$. Then each segment of length $m$ contains a blue number. Indeed, assume that all the numbers on the segment $[k, k+m]$ are red. Then
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
\begin{aligned}
|
| 114 |
+
& f(k+m)=f(k+x y)=f(k+x(y-1))+f(x)=\cdots=f(k)+y f(x), \\
|
| 115 |
+
& f(k+m)=f(k+x y)=f(k+(x-1) y)+f(y)=\cdots=f(k)+x f(y),
|
| 116 |
+
\end{aligned}
|
| 117 |
+
$$
|
| 118 |
+
|
| 119 |
+
so $y f(x)=x f(y)$ - a contradiction. Now we consider two cases.
|
| 120 |
+
Case 1. Assume that there exists a segment $[k, k+m]$ of length $m$ consisting of blue numbers. Define $D=\max \{f(k), \ldots, f(k+m)\}$. We claim that $f(z)-f(z-1) \leq D$, whatever $z>k$, and the conclusion follows. Consider the largest blue number $b_{1}$ not exceeding $z$, so $z-b_{1} \leq m$, and some blue number $b_{2}$ on the segment $\left[b_{1}+k, b_{1}+k+m\right]$, so $b_{2}>z$. Write $f\left(b_{2}\right)=f\left(b_{1}\right)+f\left(b_{2}-b_{1}\right) \leq f\left(b_{1}\right)+D$ to deduce that $f(z+1)-f(z) \leq f\left(b_{2}\right)-f\left(b_{1}\right) \leq D$, as claimed.
|
| 121 |
+
|
| 122 |
+
Case 2. Each segment of length $m$ contains numbers of both colours. Fix any red number $R \geq 2 m$ such that $R+1$ is blue and set $D=\max \{f(R), f(R+1)\}$. Now we claim that $f(z+1)-f(z) \leq D$, whatever $z>2 m$. Consider the largest red number $r$ not exceeding $z$ and the largest blue number $b$ smaller than $r$; then $0<z-b=(z-r)+(r-b) \leq 2 m$, and $b+1$ is red. Let $t=b+R+1$; then $t>z$. If $t$ is blue, then $f(t)=f(b)+f(R+1) \leq f(b)+D$, and $f(z+1)-f(z) \leq f(t)-f(b) \leq D$. Otherwise, $f(t)=f(b+1)+f(R) \leq f(b+1)+D$, hence $f(z+1)-f(z) \leq f(t)-f(b+1) \leq D$, as claimed.
|
| 123 |
+
|
RMM/md/en-2012-Solutions2012-2.md
ADDED
|
@@ -0,0 +1,90 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $5^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Solutions for the Day 2
|
| 4 |
+
|
| 5 |
+
Problem 4. Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
| 6 |
+
|
| 7 |
+
Solution 1. Throughout the solution $n$ stands for a positive integer. By Euler's theorem, $\left(2^{3^{n}}+1\right)\left(2^{3^{n}}-1\right)=2^{2 \cdot 3^{n}}-1 \equiv 0\left(\bmod 3^{n+1}\right)$. Since $2^{3^{n}}-1 \equiv 1(\bmod 3)$, it follows that $2^{3^{n}}+1$ is divisible by $3^{n+1}$.
|
| 8 |
+
|
| 9 |
+
The number $\left(2^{3^{n+1}}+1\right) /\left(2^{3^{n}}+1\right)=2^{2 \cdot 3^{n}}-2^{3^{n}}+1$ is greater than 3 and congruent to 3 modulo 9 , so it has a prime factor $p_{n}>3$ that does not divide $2^{3^{n}}+1$ (otherwise, $2^{3^{n}} \equiv-1$ (mod $\left.p_{n}\right)$, so $2^{2 \cdot 3^{n}}-2^{3^{n}}+1 \equiv 3\left(\bmod p_{n}\right)$, contradicting the fact that $p_{n}$ is a factor greater than 3 of $2^{2 \cdot 3^{n}}-2^{3^{n}}+1$ ).
|
| 10 |
+
|
| 11 |
+
We now show that $a_{n}=3^{n} p_{n}$ satisfies the conditions in the statement. Since $2^{a_{n}}+1 \equiv$ $2^{3^{n}}+1 \not \equiv 0\left(\bmod p_{n}\right)$, it follows that $a_{n}$ does not divide $2^{a_{n}}+1$.
|
| 12 |
+
|
| 13 |
+
On the other hand, $3^{n+1}$ divides $2^{3^{n}}+1$ which in turn divides $2^{a_{n}}+1$, so $2^{3^{n+1}}+1$ divides $2^{2^{a_{n}}+1}+1$. Finally, both $3^{n}$ and $p_{n}$ divide $2^{3^{n+1}}+1$, so $a_{n}$ divides $2^{2^{a_{n}}+1}+1$.
|
| 14 |
+
|
| 15 |
+
As $n$ runs through the positive integers, the $a_{n}$ are clearly pairwise distinct and the conclusion follows.
|
| 16 |
+
|
| 17 |
+
Solution 2. (Géza Kós) We show that the numbers $a_{n}=\left(2^{3^{n}}+1\right) / 9, n \geq 2$, satisfy the conditions in the statement. To this end, recall the following well-known facts:
|
| 18 |
+
(1) If $N$ is an odd positive integer, then $\nu_{3}\left(2^{N}+1\right)=\nu_{3}(N)+1$, where $\nu_{3}(a)$ is the exponent of 3 in the decomposition of the integer $a$ into prime factors; and
|
| 19 |
+
(2) If $M$ and $N$ are odd positive integers, then $\left(2^{M}+1,2^{N}+1\right)=2^{(M, N)}+1$, where $(a, b)$ is the greatest common divisor of the integers $a$ and $b$.
|
| 20 |
+
By (1), $a_{n}=3^{n-1} m$, where $m$ is an odd positive integer not divisible by 3 , and by (2),
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\left(m, 2^{a_{n}}+1\right) \left\lvert\,\left(2^{3^{n}}+1,2^{a_{n}}+1\right)=2^{\left(3^{n}, a_{n}\right)}+1=2^{3^{n-1}}+1<\frac{2^{3^{n}}+1}{3^{n+1}}=m\right.
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
so $m$ cannot divide $2^{a_{n}}+1$.
|
| 27 |
+
On the other hand, $3^{n-1} \mid 2^{2^{a_{n}}+1}+1$, for $\nu_{3}\left(2^{2^{a_{n}}+1}+1\right)>\nu_{3}\left(2^{a_{n}}+1\right)>\nu_{3}\left(a_{n}\right)=n-1$, and $m \mid 2^{2^{a_{n}}+1}+1$, for $3^{n-1} \mid a_{n}$, so $3^{n} \mid 2^{a_{n}}+1$ whence $m\left|2^{3^{n}}+1\right| 2^{2^{a_{n}}+1}+1$. Since $3^{n-1}$ and $m$ are coprime, the conclusion follows.
|
| 28 |
+
|
| 29 |
+
Remarks. There are several variations of these solutions. For instance, let $b_{1}=3$ and $b_{n+1}=$ $2^{b_{n}}+1, n \geq 1$, and notice that $b_{n}$ divides $b_{n+1}$. It can be shown that there are infinitely many indices $n$ such that some prime factor $p_{n}$ of $b_{n+1}$ does not divide $b_{n}$. One checks that for these $n$ 's the $a_{n}=p_{n} b_{n-1}$ satisfy the required conditions.
|
| 30 |
+
|
| 31 |
+
Finally, the numbers $3^{n} \cdot 571, n \geq 2$, form yet another infinite set of positive integers fulfilling the conditions in the statement - the details are omitted.
|
| 32 |
+
|
| 33 |
+
Solution 3. (Dušan Djukić) Assume that $n$ satisfies the conditions of the problem. We claim that the number $N=2^{n}+1>n$ also satisfies these conditions.
|
| 34 |
+
|
| 35 |
+
Firstly, since $n \nmid N$, the fact (2) from Solution 2 allows to conclude that $2^{n}+1 \nmid 2^{N}+1$, or $N \nmid 2^{N}+1$. Next, since $n \mid 2^{2^{n}+1}+1=2^{N}+1$, we obtain from the same fact that $N=2^{n}+1 \mid 2^{2^{N}+1}+1$, thus confirming our claim.
|
| 36 |
+
|
| 37 |
+
Hence, it suffices to provide only one example, hence obtaining an infinite series by the claim. For instance, one may easily check that the number $n=57$ fits.
|
| 38 |
+
|
| 39 |
+
Problem 5. Given a positive integer number $n \geq 3$, colour each cell of an $n \times n$ square array one of $\left[(n+2)^{2} / 3\right]$ colours, each colour being used at least once. Prove that the cells of some $1 \times 3$ or $3 \times 1$ rectangular subarray have pairwise distinct colours.
|
| 40 |
+
|
| 41 |
+
Solution. For more convenience, say that a subarray of the $n \times n$ square array bears a colour if at least two of its cells share that colour.
|
| 42 |
+
|
| 43 |
+
We shall prove that the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays, which is $2 n(n-2)$, exceeds the number of such subarrays, each of which bears some colour. The key ingredient is the estimate in the lemma below.
|
| 44 |
+
|
| 45 |
+
Lemma. If a colour is used exactly $p$ times, then the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays bearing that colour does not exceed $3(p-1)$.
|
| 46 |
+
|
| 47 |
+
Assume the lemma for the moment, let $N=\left[(n+2)^{2} / 3\right]$ and let $n_{i}$ be the number of cells coloured the $i$ th colour, $i=1, \ldots, N$, to deduce that the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays, each of which bears some colour, is at most
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\sum_{i=1}^{N} 3\left(n_{i}-1\right)=3 \sum_{i=1}^{N} n_{i}-3 N=3 n^{2}-3 N<3 n^{2}-\left(n^{2}+4 n\right)=2 n(n-2)
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
and thereby conclude the proof.
|
| 54 |
+
Back to the lemma, the assertion is clear if $p=1$, so let $p>1$.
|
| 55 |
+
We begin by showing that if a row contains exactly $q$ cells coloured $C$, then the number $r$ of $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $3 q / 2-1$; of course, a similar estimate holds for a column. To this end, notice first that the case $q=1$ is trivial, so we assume that $q>1$. Consider the incidence of a cell $c$ coloured $C$ and a $3 \times 1$ rectangular subarray $R$ bearing $C$ :
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\langle c, R\rangle= \begin{cases}1 & \text { if } c \subset R \\ 0 & \text { otherwise. }\end{cases}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Notice that, given $R, \sum_{c}\langle c, R\rangle \geq 2$, and, given $c, \sum_{R}\langle c, R\rangle \leq 3$; moreover, if $c$ is the leftmost or rightmost cell, then $\sum_{R}\langle c, R\rangle \leq 2$. Consequently,
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
2 r \leq \sum_{R} \sum_{c}\langle c, R\rangle=\sum_{c} \sum_{R}\langle c, R\rangle \leq 2+3(q-2)+2=3 q-2
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
whence the conclusion.
|
| 68 |
+
Finally, let the $p$ cells coloured $C$ lie on $k$ rows and $\ell$ columns and notice that $k+\ell \geq 3$, for $p>1$. By the preceding, the total number of $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-k$, and the total number of $1 \times 3$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-\ell$, so the total number of $1 \times 3$ and $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $(3 p / 2-k)+(3 p / 2-\ell)=3 p-(k+\ell) \leq 3 p-3=3(p-1)$. This completes the proof.
|
| 69 |
+
|
| 70 |
+
Remarks. In terms of the total number of cells, the number $N=\left[(n+2)^{2} / 3\right]$ of colours is asymptotically close to the minimum number of colours required for some $1 \times 3$ or $3 \times 1$ rectangular subarray to have all cells of pairwise distinct colours, whatever the colouring. To see this, colour the cells with the coordinates $(i, j)$, where $i+j \equiv 0(\bmod 3)$ and $i, j \in\{0,1, \ldots, n-1\}$, one colour each, and use one additional colour $C$ to colour the remaining cells. Then each $1 \times 3$ and each $3 \times 1$ rectangular subarray has exactly two cells coloured $C$, and the number of colours is $\left\lceil n^{2} / 3\right\rceil+1$ if $n \equiv 1$ or $2(\bmod 3)$, and $\left\lceil n^{2} / 3\right\rceil$ if $n \equiv 0(\bmod 3)$. Consequently, the minimum number of colours is $n^{2} / 3+O(n)$.
|
| 71 |
+
|
| 72 |
+
Problem 6. Let $A B C$ be a triangle and let $I$ and $O$ respectively denote its incentre and circumcentre. Let $\omega_{A}$ be the circle through $B$ and $C$ and tangent to the incircle of the triangle $A B C$; the circles $\omega_{B}$ and $\omega_{C}$ are defined similarly. The circles $\omega_{B}$ and $\omega_{C}$ through $A$ meet again at $A^{\prime}$; the points $B^{\prime}$ and $C^{\prime}$ are defined similarly. Prove that the lines $A A^{\prime}, B B^{\prime}$ and $C C^{\prime}$ are concurrent at a point on the line $I O$.
|
| 73 |
+
|
| 74 |
+
Solution. Let $\gamma$ be the incircle of the triangle $A B C$ and let $A_{1}, B_{1}, C_{1}$ be its contact points with the sides $B C, C A, A B$, respectively. Let further $X_{A}$ be the point of contact of the circles $\gamma$ and $\omega_{A}$. The latter circle is the image of the former under a homothety centred at $X_{A}$. This homothety sends $A_{1}$ to a point $M_{A}$ on $\omega_{A}$ such that the tangent to $\omega_{A}$ at $M_{A}$ is parallel to $B C$. Consequently, $M_{A}$ is the midpoint of the arc $B C$ of $\omega_{A}$ not containing $X_{A}$. It follows that the angles $M_{A} X_{A} B$ and $M_{A} B C$ are congruent, so the triangles $M_{A} B A_{1}$ and $M_{A} X_{A} B$ are similar: $M_{A} B / M_{A} X_{A}=M_{A} A_{1} / M_{A} B$. Rewrite the latter $M_{A} B^{2}=M_{A} A_{1} \cdot M_{A} X_{A}$ to deduce that $M_{A}$ lies on the radical axis $\ell_{B}$ of $B$ and $\gamma$. Similarly, $M_{A}$ lies on the radical axis $\ell_{C}$ of $C$ and $\gamma$.
|
| 75 |
+
|
| 76 |
+
Define the points $X_{B}, X_{C}, M_{B}, M_{C}$ and the line $\ell_{A}$ in a similar way and notice that the lines $\ell_{A}, \ell_{B}, \ell_{C}$ support the sides of the triangle $M_{A} M_{B} M_{C}$. The lines $\ell_{A}$ and $B_{1} C_{1}$ are both perpendicular to $A I$, so they are parallel. Similarly, the lines $\ell_{B}$ and $\ell_{C}$ are parallel to $C_{1} A_{1}$ and $A_{1} B_{1}$, respectively. Consequently, the triangle $M_{A} M_{B} M_{C}$ is the image of the triangle $A_{1} B_{1} C_{1}$ under a homothety $\Theta$. Let $K$ be the centre of $\Theta$ and let $k=M_{A} K / A_{1} K=M_{B} K / B_{1} K=$ $M_{C} K / C_{1} K$ be the similitude ratio. Notice that the lines $M_{A} A_{1}, M_{B} B_{1}$ and $M_{C} C_{1}$ are concurrent at $K$.
|
| 77 |
+
|
| 78 |
+
Since the points $A_{1}, B_{1}, X_{A}, X_{B}$ are concyclic, $A_{1} K \cdot K X_{A}=B_{1} K \cdot K X_{B}$. Multiply both sides by $k$ to get $M_{A} K \cdot K X_{A}=M_{B} K \cdot K X_{B}$ and deduce thereby that $K$ lies on the radical axis $C C^{\prime}$ of $\omega_{A}$ and $\omega_{B}$. Similarly, both lines $A A^{\prime}$ and $B B^{\prime}$ pass through $K$.
|
| 79 |
+
|
| 80 |
+
|
| 81 |
+
Finally, consider the image $O^{\prime}$ of $I$ under $\Theta$. It lies on the line through $M_{A}$ parallel to $A_{1} I$ (and hence perpendicular to $B C$ ); since $M_{A}$ is the midpoint of the $\operatorname{arc} B C$, this line must be $M_{A} O$. Similarly, $O^{\prime}$ lies on the line $M_{B} O$, so $O^{\prime}=O$. Consequently, the points $I, K$ and $O$ are collinear.
|
| 82 |
+
|
| 83 |
+
Remark 1. Many steps in this solution allow different reasonings. For instance, one may
|
| 84 |
+
see that the lines $A_{1} X_{A}$ and $B_{1} X_{B}$ are concurrent at point $K$ on the radical axis $C C^{\prime}$ of the circles $\omega_{A}$ and $\omega_{B}$ by applying Newton's theorem to the quadrilateral $X_{A} X_{B} A_{1} B_{1}$ (since the common tangents at $X_{A}$ and $X_{B}$ intersect on $C C^{\prime}$ ). Then one can conclude that $K A_{1} / K B_{1}=$ $K M_{A} / K M_{B}$, thus obtaining that the triangles $M_{A} M_{B} M_{C}$ and $A_{1} B_{1} C_{1}$ are homothetical at $K$ (and therefore $K$ is the radical center of $\omega_{A}, \omega_{B}$, and $\omega_{C}$ ). Finally, considering the inversion with the pole $K$ and the power equal to $K X_{1} \cdot K M_{A}$ followed by the reflection at $P$ we see that the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$ are invariant under this transform; next, the image of $\gamma$ is the circumcircle of $M_{A} M_{B} M_{C}$ and it is tangent to all the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$, hence its center is $O$, and thus $O, I$, and $K$ are collinear.
|
| 85 |
+
|
| 86 |
+
Remark 2. Here is an outline of an alternative approach to the first part of the solution. Let $J_{A}$ be the excentre of the triangle $A B C$ opposite $A$. The line $J_{A} A_{1}$ meets $\gamma$ again at $Y_{A}$; let $Z_{A}$ and $N_{A}$ be the midpoints of the segments $A_{1} Y_{A}$ and $J_{A} A_{1}$, respectively. Since the segment $I J_{A}$ is a diameter in the circle $B C Z_{A}$, it follows that $B A_{1} \cdot C A_{1}=Z_{A} A_{1} \cdot J_{A} A_{1}$, so $B A_{1} \cdot C A_{1}=N_{A} A_{1} \cdot Y_{A} A_{1}$. Consequently, the points $B, C, N_{A}$ and $Y_{A}$ lie on some circle $\omega_{A}^{\prime}$.
|
| 87 |
+
|
| 88 |
+
It is well known that $N_{A}$ lies on the perpendicular bisector of the segment $B C$, so the tangents to $\omega_{A}^{\prime}$ and $\gamma$ at $N_{A}$ and $A_{1}$ are parallel. It follows that the tangents to these circles at $Y_{A}$ coincide, so $\omega_{A}^{\prime}$ is in fact $\omega_{A}$, whence $X_{A}=Y_{A}$ and $M_{A}=N_{A}$. It is also well known that the midpoint $S_{A}$ of the segment $I J_{A}$ lies both on the circumcircle $A B C$ and on the perpendicular bisector of $B C$. Since $S_{A} M_{A}$ is a midline in the triangle $A_{1} I J_{A}$, it follows that $S_{A} M_{A}=r / 2$, where $r$ is the radius of $\gamma$ (the inradius of the triangle $A B C$ ). Consequently, each of the points $M_{A}, M_{B}$ and $M_{C}$ is at distance $R+r / 2$ from $O$ (here $R$ is the circumradius). Now proceed as above.
|
| 89 |
+
|
| 90 |
+
|
RMM/md/en-2013-Solutions2013-1.md
ADDED
|
@@ -0,0 +1,95 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $6^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
## Solutions for the Day 1
|
| 4 |
+
|
| 5 |
+
Problem 1. For a positive integer $a$, define a sequence of integers $x_{1}, x_{2}, \ldots$ by letting $x_{1}=a$ and $x_{n+1}=2 x_{n}+1$ for $n \geq 1$. Let $y_{n}=2^{x_{n}}-1$. Determine the largest possible $k$ such that, for some positive integer $a$, the numbers $y_{1}, \ldots, y_{k}$ are all prime.
|
| 6 |
+
(Russia) Valery Senderov
|
| 7 |
+
Solution. The largest such is $k=2$. Notice first that if $y_{i}$ is prime, then $x_{i}$ is prime as well. Actually, if $x_{i}=1$ then $y_{i}=1$ which is not prime, and if $x_{i}=m n$ for integer $m, n>1$ then $2^{m}-1 \mid 2^{x_{i}}-1=y_{i}$, so $y_{i}$ is composite. In particular, if $y_{1}, y_{2}, \ldots, y_{k}$ are primes for some $k \geq 1$ then $a=x_{1}$ is also prime.
|
| 8 |
+
|
| 9 |
+
Now we claim that for every odd prime $a$ at least one of the numbers $y_{1}, y_{2}, y_{3}$ is composite (and thus $k<3$ ). Assume, to the contrary, that $y_{1}, y_{2}$, and $y_{3}$ are primes; then $x_{1}, x_{2}, x_{3}$ are primes as well. Since $x_{1} \geq 3$ is odd, we have $x_{2}>3$ and $x_{2} \equiv 3(\bmod 4)$; consequently, $x_{3} \equiv 7$ $(\bmod 8)$. This implies that 2 is a quadratic residue modulo $p=x_{3}$, so $2 \equiv s^{2}(\bmod p)$ for some integer $s$, and hence $2^{x_{2}}=2^{(p-1) / 2} \equiv s^{p-1} \equiv 1(\bmod p)$. This means that $p \mid y_{2}$, thus $2^{x_{2}}-1=x_{3}=2 x_{2}+1$. But it is easy to show that $2^{t}-1>2 t+1$ for all integer $t>3$. A contradiction.
|
| 10 |
+
|
| 11 |
+
Finally, if $a=2$, then the numbers $y_{1}=3$ and $y_{2}=31$ are primes, while $y_{3}=2^{11}-1$ is divisible by 23 ; in this case we may choose $k=2$ but not $k=3$.
|
| 12 |
+
|
| 13 |
+
Remark. The fact that $23 \mid 2^{11}-1$ can be shown along the lines in the solution, since 2 is a quadratic residue modulo $x_{4}=23$.
|
| 14 |
+
|
| 15 |
+
Problem 2. Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
|
| 16 |
+
(United Kingdom) Alexander Betts
|
| 17 |
+
Solution 1. Such a tester pair exists. We may biject $\mathbb{R}$ with the closed unit interval, so it suffices to find a tester pair for that instead. We give an explicit example: take some positive real numbers $\alpha, \beta$ (which we will specify further later). Take
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
g(x)=\max (x-\alpha, 0) \quad \text { and } \quad h(x)=\min (x+\beta, 1) .
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Say a set $S \subseteq[0,1]$ is invariant if $f(S) \subseteq S$ for all functions $f$ commuting with both $g$ and $h$. Note that intersections and unions of invariant sets are invariant. Preimages of invariant sets under $g$ and $h$ are also invariant; indeed, if $S$ is invariant and, say, $T=g^{-1}(S)$, then $g(f(T))=$ $f(g(T)) \subseteq f(S) \subseteq S$, thus $f(T) \subseteq T$.
|
| 24 |
+
|
| 25 |
+
We claim that (if we choose $\alpha+\beta<1$ ) the intervals $[0, n \alpha-m \beta]$ are invariant where $n$ and $m$ are nonnegative integers with $0 \leq n \alpha-m \beta \leq 1$. We prove this by induction on $m+n$.
|
| 26 |
+
|
| 27 |
+
The set $\{0\}$ is invariant, as for any $f$ commuting with $g$ we have $g(f(0))=f(g(0))=f(0)$, so $f(0)$ is a fixed point of $g$. This gives that $f(0)=0$, thus the induction base is established.
|
| 28 |
+
|
| 29 |
+
Suppose now we have some $m, n$ such that $\left[0, n^{\prime} \alpha-m^{\prime} \beta\right]$ is invariant whenever $m^{\prime}+n^{\prime}<$ $m+n$. At least one of the numbers $(n-1) \alpha-m \beta$ and $n \alpha-(m-1) \beta$ lies in $(0,1)$. Note however that in the first case $[0, n \alpha-m \beta]=g^{-1}([0,(n-1) \alpha-m \beta])$, so $[0, n \alpha-m \beta]$ is invariant. In the second case $[0, n \alpha-m \beta]=h^{-1}([0, n \alpha-(m-1) \beta])$, so again $[0, n \alpha-m \beta]$ is invariant. This completes the induction.
|
| 30 |
+
|
| 31 |
+
We claim that if we choose $\alpha+\beta<1$, where $0<\alpha \notin \mathbb{Q}$ and $\beta=1 / k$ for some integer $k>1$, then all intervals $[0, \delta]$ are invariant for $0 \leq \delta<1$. This occurs, as by the previous claim, for all nonnegative integers $n$ we have $[0,(n \alpha \bmod 1)]$ is invariant. The set of $n \alpha \bmod 1$ is dense in $[0,1]$, so in particular
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
[0, \delta]=\bigcap_{(n \alpha \bmod 1)>\delta}[0,(n \alpha \bmod 1)]
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
is invariant.
|
| 38 |
+
A similar argument establishes that $[\delta, 1]$ is invariant, so by intersecting these $\{\delta\}$ is invariant for $0<\delta<1$. Yet we also have $\{0\},\{1\}$ both invariant, which proves $f$ to be the identity.
|
| 39 |
+
|
| 40 |
+
Solution 2. Let us agree that a sequence $\mathbf{x}=\left(x_{n}\right)_{n=1,2, \ldots}$ is cofinally non-constant if for every index $m$ there exists an index $n>m$ such that $x_{m} \neq x_{n}$.
|
| 41 |
+
|
| 42 |
+
Biject $\mathbb{R}$ with the set of cofinally non-constant sequences of 0 's and 1 's, and define $g$ and $h$ by
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
g(\epsilon, \mathbf{x})=\left\{\begin{array}{ll}
|
| 46 |
+
\epsilon, \mathbf{x} & \text { if } \epsilon=0 \\
|
| 47 |
+
\mathbf{x} & \text { else }
|
| 48 |
+
\end{array} \quad \text { and } \quad h(\epsilon, \mathbf{x})= \begin{cases}\epsilon, \mathbf{x} & \text { if } \epsilon=1 \\
|
| 49 |
+
\mathbf{x} & \text { else }\end{cases}\right.
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
where $\epsilon, \mathbf{x}$ denotes the sequence formed by appending $\mathbf{x}$ to the single-element sequence $\epsilon$. Note that $g$ fixes precisely those sequences beginning with 0 , and $h$ fixes precisely those beginning with 1.
|
| 53 |
+
|
| 54 |
+
Now assume that $f$ commutes with both $f$ and $g$. To prove that $f(\mathbf{x})=\mathbf{x}$ for all $\mathbf{x}$ we show that $\mathbf{x}$ and $f(\mathbf{x})$ share the same first $n$ terms, by induction on $n$.
|
| 55 |
+
|
| 56 |
+
The base case $n=1$ is simple, as we have noticed above that the set of sequences beginning with a 0 is precisely the set of $g$-fixed points, so is preserved by $f$, and similarly for the set of sequences starting with 1.
|
| 57 |
+
|
| 58 |
+
Suppose that $f(\mathbf{x})$ and $\mathbf{x}$ agree for the first $n$ terms, whatever $\mathbf{x}$. Consider any sequence, and write it as $\mathbf{x}=\epsilon, \mathbf{y}$. Without loss of generality, we may (and will) assume that $\epsilon=0$, so $f(\mathbf{x})=0, \mathbf{y}^{\prime}$ by the base case. Yet then $f(\mathbf{y})=f(h(\mathbf{x}))=h(f(\mathbf{x}))=h\left(0, \mathbf{y}^{\prime}\right)=\mathbf{y}^{\prime}$. Consequently, $f(\mathbf{x})=0, f(\mathbf{y})$, so $f(\mathbf{x})$ and $\mathbf{x}$ agree for the first $n+1$ terms by the inductive hypothesis.
|
| 59 |
+
|
| 60 |
+
Thus $f$ fixes all of cofinally non-constant sequences, and the conclusion follows.
|
| 61 |
+
Solution 3. (Ilya Bogdanov) We will show that there exists a tester pair of bijective functions $g$ and $h$.
|
| 62 |
+
|
| 63 |
+
First of all, let us find out when a pair of functions is a tester pair. Let $g, h: \mathbb{R} \rightarrow \mathbb{R}$ be arbitrary functions. We construct a directed graph $G_{g, h}$ with $\mathbb{R}$ as the set of vertices, its edges being painted with two colors: for every vertex $x \in \mathbb{R}$, we introduce a red edge $x \rightarrow g(x)$ and a blue edge $x \rightarrow h(x)$.
|
| 64 |
+
|
| 65 |
+
Now, assume that the function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$. This means exactly that if there exists an edge $x \rightarrow y$, then there also exists an edge $f(x) \rightarrow f(y)$ of the same color; that is $-f$ is an endomorphism of $G_{g, h}$.
|
| 66 |
+
|
| 67 |
+
Thus, a pair $(g, h)$ is a tester pair if and only if the graph $G_{g, h}$ admits no nontrivial endomorphisms. Notice that each endomorphism maps a component into a component. Thus, to construct a tester pair, it suffices to construct a continuum of components with no nontrivial endomorphisms and no homomorphisms from one to another. It can be done in many ways; below we present one of them.
|
| 68 |
+
|
| 69 |
+
Let $g(x)=x+1$; the construction of $h$ is more involved. For every $x \in[0,1)$ we define the set $S_{x}=x+\mathbb{Z}$; the sets $S_{x}$ will be exactly the components of $G_{g, h}$. Now we will construct these components.
|
| 70 |
+
|
| 71 |
+
Let us fix any $x \in[0,1)$; let $x=0 . x_{1} x_{2} \ldots$ be the binary representation of $x$. Define $h(x-n)=x-n+1$ for every $n>3$. Next, let $h(x-3)=x, h(x)=x-2, h(x-2)=x-1$, and $h(x-1)=x+1$ (that would be a "marker" which fixes a point in our component).
|
| 72 |
+
|
| 73 |
+
Next, for every $i=1,2, \ldots$, we define
|
| 74 |
+
(1) $h(x+3 i-2)=x+3 i-1, h(x+3 i-1)=x+3 i$, and $h(x+3 i)=x+3 i+1$, if $x_{i}=0$;
|
| 75 |
+
(2) $h(x+3 i-2)=x+3 i, h(x+3 i)=3 i-1$, and $h(x+3 i-1)=x+3 i+1$, if $x_{i}=1$.
|
| 76 |
+
|
| 77 |
+
Clearly, $h$ is a bijection mapping each $S_{x}$ to itself. Now we claim that the graph $G_{g, h}$ satisfies the desired conditions.
|
| 78 |
+
|
| 79 |
+
Consider any homomorphism $f_{x}: S_{x} \rightarrow S_{y}$ ( $x$ and $y$ may coincide). Since $g$ is a bijection, consideration of the red edges shows that $f_{x}(x+n)=x+n+k$ for a fixed real $k$. Next, there exists a blue edge $(x-3) \rightarrow x$, and the only blue edge of the form $(y+m-3) \rightarrow(y+m)$ is $(y-3) \rightarrow y$; thus $f_{x}(x)=y$, and $k=0$.
|
| 80 |
+
|
| 81 |
+
Next, if $x_{i}=0$ then there exists a blue edge $(x+3 i-2) \rightarrow(x+3 i-1)$; then the edge $(y+3 i-2) \rightarrow(y+3 i-1)$ also should exist, so $y_{i}=0$. Analogously, if $x_{i}=1$ then there exists a blue edge $(x+3 i-2) \rightarrow(x+3 i)$; then the edge $(y+3 i-2) \rightarrow(y+3 i)$ also should exist, so $y_{i}=1$. We conclude that $x=y$, and $f_{x}$ is the identity mapping, as required.
|
| 82 |
+
|
| 83 |
+
Remark. If $g$ and $h$ are injections, then the components of $G_{g, h}$ are at most countable. So the set of possible pairwise non-isomorphic such components is continual; hence there is no bijective tester pair for a hyper-continual set instead of $\mathbb{R}$.
|
| 84 |
+
|
| 85 |
+
Problem 3. Let $A B C D$ be a quadrilateral inscribed in a circle $\omega$. The lines $A B$ and $C D$ meet at $P$, the lines $A D$ and $B C$ meet at $Q$, and the diagonals $A C$ and $B D$ meet at $R$. Let $M$ be the midpoint of the segment $P Q$, and let $K$ be the common point of the segment $M R$ and the circle $\omega$. Prove that the circumcircle of the triangle $K P Q$ and $\omega$ are tangent to one another.
|
| 86 |
+
(Russia) MedeubeK Kungozhin
|
| 87 |
+
Solution. Let $O$ be the centre of $\omega$. Notice that the points $P, Q$, and $R$ are the poles (with respect to $\omega$ ) of the lines $Q R, R P$, and $P Q$, respectively. Hence we have $O P \perp Q R, O Q \perp R P$, and $O R \perp P Q$, thus $R$ is the orthocentre of the triangle $O P Q$. Now, if $M R \perp P Q$, then the points $P$ and $Q$ are the reflections of one another in the line $M R=M O$, and the triangle $P Q K$ is symmetrical with respect to this line. In this case the statement of the problem is trivial.
|
| 88 |
+
|
| 89 |
+
Otherwise, let $V$ be the foot of the perpendicular from $O$ to $M R$, and let $U$ be the common point of the lines $O V$ and $P Q$. Since $U$ lies on the polar line of $R$ and $O U \perp M R$, we obtain that $U$ is the pole of $M R$. Therefore, the line $U K$ is tangent to $\omega$. Hence it is enough to prove that $U K^{2}=U P \cdot U Q$, since this relation implies that $U K$ is also tangent to the circle $K P Q$.
|
| 90 |
+
|
| 91 |
+
From the rectangular triangle $O K U$, we get $U K^{2}=U V \cdot U O$. Let $\Omega$ be the circumcircle of triangle $O P Q$, and let $R^{\prime}$ be the reflection of its orthocentre $R$ in the midpoint $M$ of the side $P Q$. It is well known that $R^{\prime}$ is the point of $\Omega$ opposite to $O$, hence $O R^{\prime}$ is the diameter of $\Omega$. Finally, since $\angle O V R^{\prime}=90^{\circ}$, the point $V$ also lies on $\Omega$, hence $U P \cdot U Q=U V \cdot U O=U K^{2}$, as required.
|
| 92 |
+
|
| 93 |
+
|
| 94 |
+
Remark. The statement of the problem is still true if $K$ is the other common point of the line $M R$ and $\omega$.
|
| 95 |
+
|
RMM/md/en-2013-Solutions2013-2.md
ADDED
|
@@ -0,0 +1,142 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $6^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
## Solutions for the Day 2
|
| 4 |
+
|
| 5 |
+
Problem 4. Let $P$ and $P^{\prime}$ be two convex quadrilateral regions in the plane (regions contain their boundary). Let them intersect, with $O$ a point in the intersection. Suppose that for every line $\ell$ through $O$ the segment $\ell \cap P$ is strictly longer than the segment $\ell \cap P^{\prime}$. Is it possible that the ratio of the area of $P^{\prime}$ to the area of $P$ is greater than 1.9?
|
| 6 |
+
(Bulgaria) Nikolai Beluhov
|
| 7 |
+
Solution. The answer is in the affirmative: Given a positive $\epsilon<2$, the ratio in question may indeed be greater than $2-\epsilon$.
|
| 8 |
+
|
| 9 |
+
To show this, consider a square $A B C D$ centred at $O$, and let $A^{\prime}, B^{\prime}$, and $C^{\prime}$ be the reflections of $O$ in $A, B$, and $C$, respectively. Notice that, if $\ell$ is a line through $O$, then the segments $\ell \cap A B C D$ and $\ell \cap A^{\prime} B^{\prime} C^{\prime}$ have equal lengths, unless $\ell$ is the line $A C$.
|
| 10 |
+
|
| 11 |
+
Next, consider the points $M$ and $N$ on the segments $B^{\prime} A^{\prime}$ and $B^{\prime} C^{\prime}$, respectively, such that $B^{\prime} M / B^{\prime} A^{\prime}=B^{\prime} N / B^{\prime} C^{\prime}=(1-\epsilon / 4)^{1 / 2}$. Finally, let $P^{\prime}$ be the image of the convex quadrangle $B^{\prime} M O N$ under the homothety of ratio $(1-\epsilon / 4)^{1 / 4}$ centred at $O$. Clearly, the quadrangles $P \equiv A B C D$ and $P^{\prime}$ satisfy the conditions in the statement, and the ratio of the area of $P^{\prime}$ to the area of $P$ is exactly $2-\epsilon / 2$.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
Remarks. (1) With some care, one may also construct such example with a point $O$ being interior for both $P$ and $P^{\prime}$. In our example, it is enough to replace vertex $O$ of $P^{\prime}$ by a point on the segment $O D$ close enough to $O$. The details are left to the reader.
|
| 15 |
+
(2) On the other hand, one may show that the ratio of areas of $P^{\prime}$ and $P$ cannot exceed 2 (even if $P$ and $P^{\prime}$ are arbitrary convex polygons rather than quadrilaterals). Further on, we denote by $[S]$ the area of $S$.
|
| 16 |
+
|
| 17 |
+
In order to see that $\left[P^{\prime}\right]<2[P]$, let us fix some ray $r$ from $O$, and let $r_{\alpha}$ be the ray from $O$ making an (oriented) angle $\alpha$ with $r$. Denote by $X_{\alpha}$ and $Y_{\alpha}$ the points of $P$ and $P^{\prime}$, respectively, lying on $r_{\alpha}$ farthest from $O$, and denote by $f(\alpha)$ and $g(\alpha)$ the lengths of the segments $O X_{\alpha}$ and $O Y_{\alpha}$, respectively. Then
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
[P]=\frac{1}{2} \int_{0}^{2 \pi} f^{2}(\alpha) d \alpha=\frac{1}{2} \int_{0}^{\pi}\left(f^{2}(\alpha)+f^{2}(\pi+\alpha)\right) d \alpha
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
and similarly
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\left[P^{\prime}\right]=\frac{1}{2} \int_{0}^{\pi}\left(g^{2}(\alpha)+g^{2}(\pi+\alpha)\right) d \alpha
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
But $X_{\alpha} X_{\pi+\alpha}>Y_{\alpha} Y_{\pi+\alpha}$ yields $2 \cdot \frac{1}{2}\left(f^{2}(\alpha)+f^{2}(\pi+\alpha)\right)=O X_{\alpha}^{2}+O X_{\pi+\alpha}^{2} \geq \frac{1}{2} X_{\alpha} X_{\pi+\alpha}^{2}>$ $\frac{1}{2} Y_{\alpha} Y_{\pi+\alpha}^{2} \geq \frac{1}{2}\left(O Y_{\alpha}^{2}+O Y_{\pi+\alpha}^{2}\right)=\frac{1}{2}\left(g^{2}(\alpha)+g^{2}(\pi+\alpha)\right)$. Integration then gives us $2[P]>\left[P^{\prime}\right]$, as needed.
|
| 30 |
+
|
| 31 |
+
This can also be proved via elementary methods. Actually, we will establish the following more general fact.
|
| 32 |
+
|
| 33 |
+
Fact. Let $P=A_{1} A_{2} A_{3} A_{4}$ and $P^{\prime}=B_{1} B_{2} B_{3} B_{4}$ be two convex quadrangles in the plane, and let $O$ be one of their common points different from the vertices of $P^{\prime}$. Denote by $\ell_{i}$ the line $O B_{i}$, and assume that for every $i=1,2,3,4$ the length of segment $\ell_{i} \cap P$ is greater than the length of segment $\ell_{i} \cap P^{\prime}$. Then $\left[P^{\prime}\right]<2[P]$.
|
| 34 |
+
Proof. One of (possibly degenerate) quadrilaterals $O B_{1} B_{2} B_{3}$ and $O B_{1} B_{4} B_{3}$ is convex; the same holds for $O B_{2} B_{3} B_{4}$ and $O B_{2} B_{1} B_{4}$. Without loss of generality, we may (and will) assume that the quadrilaterals $O B_{1} B_{2} B_{3}$ and $O B_{2} B_{3} B_{4}$ are convex.
|
| 35 |
+
|
| 36 |
+
Denote by $C_{i}$ such a point that $\ell_{i} \cap P^{\prime}$ is the segment $B_{i} C_{i}$; let $a_{i}$ be the length of $\ell_{i} \cap P$, and let $\alpha_{i}$ be the angle between $\ell_{i}$ and $\ell_{i+1}$ (hereafter, we use the cyclic notation, thus $\ell_{5}=\ell_{1}$ and so on). Thus $C_{2}$ and $C_{3}$ belong to the segment $B_{1} B_{4}, C_{1}$ lies on $B_{3} B_{4}$, and $C_{4}$ lies on $B_{1} B_{2}$. Assume that there exists an index $i$ such that the area of $B_{i} B_{i+1} C_{i} C_{i+1}$ is at least $\left[P^{\prime}\right] / 2$; then we have
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
\frac{\left[P^{\prime}\right]}{2} \leq\left[B_{i} B_{i+1} C_{i} C_{i+1}\right]=\frac{B_{i} C_{i} \cdot B_{i+1} C_{i+1} \cdot \sin \alpha_{i}}{2}<\frac{a_{i} a_{i+1} \sin \alpha_{i}}{2} \leq[P]
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
as desired. Assume, to the contrary, that such index does not exist. Two cases are possible.
|
| 43 |
+
|
| 44 |
+
|
| 45 |
+
Case 1. Assume that the rays $B_{1} B_{2}$ and $B_{4} B_{3}$ do not intersect (see the left figure above). This means, in particular, that $d\left(B_{1}, B_{3} B_{4}\right) \leq d\left(B_{2}, B_{3} B_{4}\right)$.
|
| 46 |
+
|
| 47 |
+
Since the ray $B_{3} O$ lies in the angle $B_{1} B_{3} B_{4}$, we obtain $d\left(B_{1}, B_{3} C_{3}\right) \leq d\left(C_{4}, B_{3} C_{3}\right)$; hence $\left[B_{3} B_{4} B_{1}\right] \leq\left[B_{3} B_{4} C_{3} C_{4}\right]<\left[P^{\prime}\right] / 2$. Similarly, $\left[B_{1} B_{2} B_{4}\right] \leq\left[B_{1} B_{2} C_{1} C_{2}\right]<\left[P^{\prime}\right] / 2$. Thus,
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\begin{aligned}
|
| 51 |
+
{\left[B_{2} B_{3} C_{2} C_{3}\right] } & =\left[P^{\prime}\right]-\left[B_{1} B_{2} C_{3}\right]-\left[B_{3} B_{4} C_{2}\right]=\left[P^{\prime}\right]-\frac{B_{1} C_{3}}{B_{1} B_{4}} \cdot\left[B_{1} B_{2} B_{4}\right]-\frac{B_{4} C_{2}}{B_{1} B_{4}} \cdot\left[B_{3} B_{4} B_{1}\right] \\
|
| 52 |
+
& >\left[P^{\prime}\right]\left(1-\frac{B_{1} C_{3}+B_{4} C_{2}}{2 B_{1} B_{4}}\right) \geq \frac{\left[P^{\prime}\right]}{2} .
|
| 53 |
+
\end{aligned}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
A contradiction.
|
| 57 |
+
Case 2. Assume now that the rays $B_{1} B_{2}$ and $B_{4} B_{3}$ intersect at some point (see the right figure above). Denote by $L$ the common point of $B_{2} C_{1}$ and $B_{3} C_{4}$. We have $\left[B_{2} C_{4} C_{1}\right] \geq\left[B_{2} C_{4} B_{3}\right]$, hence $\left[C_{1} C_{4} L\right] \geq\left[B_{2} B_{3} L\right]$. Thus we have
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\begin{aligned}
|
| 61 |
+
{\left[P^{\prime}\right]>\left[B_{1} B_{2} C_{1} C_{2}\right]+\left[B_{3} B_{4} C_{3} C_{4}\right] } & =\left[P^{\prime}\right]+\left[L C_{1} C_{2} C_{3} C_{4}\right]-\left[B_{2} B_{3} L\right] \\
|
| 62 |
+
& \geq\left[P^{\prime}\right]+\left[C_{1} C_{4} L\right]-\left[B_{2} B_{3} L\right] \geq\left[P^{\prime}\right] .
|
| 63 |
+
\end{aligned}
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
A final contradiction.
|
| 67 |
+
|
| 68 |
+
Problem 5. Given an integer $k \geq 2$, set $a_{1}=1$ and, for every integer $n \geq 2$, let $a_{n}$ be the smallest $x>a_{n-1}$ such that:
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
x=1+\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor .
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
Prove that every prime occurs in the sequence $a_{1}, a_{2}, \ldots$.
|
| 75 |
+
(Bulgaria) Alexander Ivanov
|
| 76 |
+
Solution 1. We prove that the $a_{n}$ are precisely the $k$ th-power-free positive integers, that is, those divisible by the $k$ th power of no prime. The conclusion then follows.
|
| 77 |
+
|
| 78 |
+
Let $B$ denote the set of all $k$ th-power-free positive integers. We first show that, given a positive integer $c$,
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\sum_{b \in B, b \leq c}\left\lfloor\sqrt[k]{\frac{c}{b}}\right\rfloor=c
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
To this end, notice that every positive integer has a unique representation as a product of an element in $B$ and a $k$ th power. Consequently, the set of all positive integers less than or equal to $c$ splits into
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
C_{b}=\left\{x: x \in \mathbb{Z}_{>0}, x \leq c, \text { and } x / b \text { is a } k \text { th power }\right\}, \quad b \in B, b \leq c .
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Clearly, $\left|C_{b}\right|=\lfloor\sqrt[k]{c / b}\rfloor$, whence the desired equality.
|
| 91 |
+
Finally, enumerate $B$ according to the natural order: $1=b_{1}<b_{2}<\cdots<b_{n}<\cdots$. We prove by induction on $n$ that $a_{n}=b_{n}$. Clearly, $a_{1}=b_{1}=1$, so let $n \geq 2$ and assume $a_{m}=b_{m}$ for all indices $m<n$. Since $b_{n}>b_{n-1}=a_{n-1}$ and
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
b_{n}=\sum_{i=1}^{n}\left\lfloor\sqrt[k]{\frac{b_{n}}{b_{i}}}\right\rfloor=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{b_{n}}{b_{i}}}\right\rfloor+1=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{b_{n}}{a_{i}}}\right\rfloor+1
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
the definition of $a_{n}$ forces $a_{n} \leq b_{n}$. Were $a_{n}<b_{n}$, a contradiction would follow:
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
a_{n}=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{a_{n}}{b_{i}}}\right\rfloor=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{a_{n}}{a_{i}}}\right\rfloor=a_{n}-1
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Consequently, $a_{n}=b_{n}$. This completes the proof.
|
| 104 |
+
Solution 2. (Ilya Bogdanov) For every $n=1,2,3, \ldots$, introduce the function
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
f_{n}(x)=x-1-\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Denote also by $g_{n}(x)$ the number of the indices $i \leq n$ such that $x / a_{i}$ is the $k$ th power of an integer. Then $f_{n}(x+1)-f_{n}(x)=1-g_{n}(x)$ for every integer $x \geq a_{n}$; hence $f_{n}(x)+1 \geq f_{n}(x+1)$. Moreover, $f_{n}\left(a_{n-1}\right)=-1$ (since $f_{n-1}\left(a_{n-1}\right)=0$ ). Now a straightforward induction shows that $f_{n}(x)<0$ for all integers $x \in\left[a_{n-1}, a_{n}\right)$.
|
| 111 |
+
|
| 112 |
+
Next, if $g_{n}(x)>0$ then $f_{n}(x) \leq f_{n}(x-1)$; this means that such an $x$ cannot equal $a_{n}$. Thus $a_{j} / a_{i}$ is never the $k$ th power of an integer if $j>i$.
|
| 113 |
+
|
| 114 |
+
Now we are prepared to prove by induction on $n$ that $a_{1}, a_{2}, \ldots, a_{n}$ are exactly all $k$ th-power-free integers in $\left[1, a_{n}\right]$. The base case $n=1$ is trivial.
|
| 115 |
+
|
| 116 |
+
Assume that all the $k$ th-power-free integers on $\left[1, a_{n}\right]$ are exactly $a_{1}, \ldots, a_{n}$. Let $b$ be the least integer larger than $a_{n}$ such that $g_{n}(b)=0$. We claim that: (1) $b=a_{n+1}$; and (2) $b$ is the least $k$ th-power-free number greater than $a_{n}$.
|
| 117 |
+
|
| 118 |
+
To prove (1), notice first that all the numbers of the form $a_{j} / a_{i}$ with $1 \leq i<j \leq n$ are not $k$ th powers of rational numbers since $a_{i}$ and $a_{j}$ are $k$ th-power-free. This means that for every integer $x \in\left(a_{n}, b\right)$ there exists exactly one index $i \leq n$ such that $x / a_{i}$ is the $k$ th power of an integer (certainly, $x$ is not $k$ th-power-free). Hence $f_{n+1}(x)=f_{n+1}(x-1)$ for each such $x$, so $f_{n+1}(b-1)=f_{n+1}\left(a_{n}\right)=-1$. Next, since $b / a_{i}$ is not the $k$ th power of an integer, we have $f_{n+1}(b)=f_{n+1}(b-1)+1=0$, thus $b=a_{n+1}$. This establishes (1).
|
| 119 |
+
|
| 120 |
+
Finally, since all integers in $\left(a_{n}, b\right)$ are not $k$ th-power-free, we are left to prove that $b$ is $k$ th-power-free to establish (2). Otherwise, let $y>1$ be the greatest integer such that $y^{k} \mid b$; then $b / y^{k}$ is $k$ th-power-free and hence $b / y^{k}=a_{i}$ for some $i \leq n$. So $b / a_{i}$ is the $k$ th power of an integer, which contradicts the definition of $b$.
|
| 121 |
+
|
| 122 |
+
Thus $a_{1}, a_{2}, \ldots$ are exactly all $k$ th-power-free positive integers; consequently all primes are contained in this sequence.
|
| 123 |
+
|
| 124 |
+
Problem 6. $2 n$ distinct tokens are placed at the vertices of a regular $2 n$-gon, with one token placed at each vertex. A move consists of choosing an edge of the $2 n$-gon and interchanging the two tokens at the endpoints of that edge. Suppose that after a finite number of moves, every pair of tokens have been interchanged exactly once. Prove that some edge has never been chosen.
|
| 125 |
+
(Russia) Alexander Gribalko
|
| 126 |
+
Solution. Step 1. Enumerate all the tokens in the initial arrangement in clockwise circular order; also enumerate the vertices of the $2 n$-gon accordingly. Consider any three tokens $i<j<k$. At each moment, their cyclic order may be either $i, j, k$ or $i, k, j$, counted clockwise. This order changes exactly when two of these three tokens have been switched. Hence the order has been reversed thrice, and in the final arrangement token $k$ stands on the arc passing clockwise from token $i$ to token $j$. Thus, at the end, token $i+1$ is a counter-clockwise neighbor of token $i$ for all $i=1,2, \ldots, 2 n-1$, so the tokens in the final arrangement are numbered successively in counter-clockwise circular order.
|
| 127 |
+
|
| 128 |
+
This means that the final arrangement of tokens can be obtained from the initial one by reflection in some line $\ell$.
|
| 129 |
+
|
| 130 |
+
Step 2. Notice that each token was involved into $2 n-1$ switchings, so its initial and final vertices have different parity. Hence $\ell$ passes through the midpoints of two opposite sides of a $2 n$-gon; we may assume that these are the sides $a$ and $b$ connecting $2 n$ with 1 and $n$ with $n+1$, respectively.
|
| 131 |
+
|
| 132 |
+
During the process, each token $x$ has crossed $\ell$ at least once; thus one of its switchings has been made at edge $a$ or at edge $b$. Assume that some two its switchings were performed at $a$ and at $b$; we may (and will) assume that the one at $a$ was earlier, and $x \leq n$. Then the total movement of token $x$ consisted at least of: (i) moving from vertex $x$ to $a$ and crossing $\ell$ along $a$; (ii) moving from $a$ to $b$ and crossing $\ell$ along $b$; (iii) coming to vertex $2 n+1-x$. This tales at least $x+n+(n-x)=2 n$ switchings, which is impossible.
|
| 133 |
+
|
| 134 |
+
Thus, each token had a switching at exactly one of the edges $a$ and $b$.
|
| 135 |
+
Step 3. Finally, let us show that either each token has been switched at $a$, or each token has been switched at $b$ (then the other edge has never been used, as desired). To the contrary, assume that there were switchings at both $a$ and at $b$. Consider the first such switchings, and let $x$ and $y$ be the tokens which were moved clockwise during these switchings and crossed $\ell$ at $a$ and $b$, respectively. By Step $2, x \neq y$. Then tokens $x$ and $y$ initially were on opposite sides of $\ell$.
|
| 136 |
+
|
| 137 |
+
Now consider the switching of tokens $x$ and $y$; there was exactly one such switching, and we assume that it has been made on the same side of $\ell$ as vertex $y$. Then this switching has been made after token $x$ had traced $a$. From this point on, token $x$ is on the clockwise arc from token $y$ to $b$, and it has no way to leave out from this arc. But this is impossible, since token $y$ should trace $b$ after that moment. A contradiction.
|
| 138 |
+
|
| 139 |
+
Remark. The same statement for $(2 n-1)$-gon is also valid. The problem is stated for a polygon with an even number of sides only to avoid case consideration.
|
| 140 |
+
|
| 141 |
+
Let us outline the solution in the case of a $(2 n-1)$-gon. We prove the existence of line $\ell$ as in Step 1. This line passes through some vertex $x$, and through the midpoint of the opposite edge $a$. Then each token either passes through $x$, or crosses $\ell$ along $a$ (but not both; this can be shown as in Step 2). Finally, since a token is involved into an even number of moves, it passes through $x$ but not through $a$, and $a$ is never used.
|
| 142 |
+
|
RMM/md/en-2015-Solutions_RMM2015-1.md
ADDED
|
@@ -0,0 +1,114 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $7^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
## Solutions for the Day 1
|
| 4 |
+
|
| 5 |
+
Problem 1. Does there exist an infinite sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ such that $a_{m}$ and $a_{n}$ are coprime if and only if $|m-n|=1$ ?
|
| 6 |
+
(Peru) Jorge Tipe
|
| 7 |
+
Solution. The answer is in the affirmative.
|
| 8 |
+
The idea is to consider a sequence of pairwise distinct primes $p_{1}, p_{2}, p_{3}, \ldots$, cover the positive integers by a sequence of finite non-empty sets $I_{n}$ such that $I_{m}$ and $I_{n}$ are disjoint if and only if $m$ and $n$ are one unit apart, and set $a_{n}=\prod_{i \in I_{n}} p_{i}, n=1,2,3, \ldots$.
|
| 9 |
+
|
| 10 |
+
One possible way of finding such sets is the following. For all positive integers $n$, let
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
\begin{array}{rlr}
|
| 14 |
+
2 n \in I_{k} & \text { for all } k=n, n+3, n+5, n+7, \ldots ; & \text { and } \\
|
| 15 |
+
2 n-1 \in I_{k} & & \text { for all } k=n, n+2, n+4, n+6, \ldots
|
| 16 |
+
\end{array}
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Clearly, each $I_{k}$ is finite, since it contains none of the numbers greater than $2 k$. Next, the number $p_{2 n}$ ensures that $I_{n}$ has a common element with each $I_{n+2 i}$, while the number $p_{2 n-1}$ ensures that $I_{n}$ has a common element with each $I_{n+2 i+1}$ for $i=1,2, \ldots$. Finally, none of the indices appears in two consecutive sets.
|
| 20 |
+
|
| 21 |
+
Remark. The sets $I_{n}$ from the solution above can explicitly be written as
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
I_{n}=\{2 n-4 k-1: k=0,1, \ldots,\lfloor(n-1) / 2\rfloor\} \cup\{2 n-4 k-2: k=1,2, \ldots,\lfloor n / 2\rfloor-1\} \cup\{2 n\},
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
The above construction can alternatively be described as follows: Let $p_{1}, p_{1}^{\prime}, p_{2}, p_{2}^{\prime}, \ldots$, $p_{n}, p_{n}^{\prime}, \ldots$ be a sequence of pairwise distinct primes. With the standard convention that empty products are 1, let
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
P_{n}= \begin{cases}p_{1} p_{2}^{\prime} p_{3} p_{4}^{\prime} \cdots p_{n-4} p_{n-3}^{\prime} p_{n-2}, & \text { if } n \text { is odd } \\ p_{1}^{\prime} p_{2} p_{3}^{\prime} p_{4} \cdots p_{n-3}^{\prime} p_{n-2}, & \text { if } n \text { is even }\end{cases}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
and define $a_{n}=P_{n} p_{n} p_{n}^{\prime}$.
|
| 34 |
+
|
| 35 |
+
Problem 2. For an integer $n \geq 5$, two players play the following game on a regular $n$-gon. Initially, three consecutive vertices are chosen, and one counter is placed on each. A move consists of one player sliding one counter along any number of edges to another vertex of the $n$-gon without jumping over another counter. A move is legal if the area of the triangle formed by the counters is strictly greater after the move than before. The players take turns to make legal moves, and if a player cannot make a legal move, that player loses. For which values of $n$ does the player making the first move have a winning strategy?
|
| 36 |
+
(United Kingdom) Jeremy King
|
| 37 |
+
Solution. We shall prove that the first player wins if and only the exponent of 2 in the prime decomposition of $n-3$ is odd.
|
| 38 |
+
|
| 39 |
+
Since the game is identical for both players, has finitely many possible states and always terminates, we can label the possible states Wins od Losses according as whether a player faced with that position has a winning strategy or not. A state is a Win if and only if there is some legal move taking the state to a Loss, and a state is a Loss if and only if all moves take that state to a Win (including the case where there are no legal moves).
|
| 40 |
+
Lemma. Any configuration in which the triangle formed by the three counters is not isosceles is necessarily a Win.
|
| 41 |
+
|
| 42 |
+
Proof. Label the positions of the counters $X, Y, Z$ so that the arc $Y Z$ of the circumcircle is shortest and the $\operatorname{arc} Z X$ is longest. Begin by moving the counter at $Z$ around the polygon on the arc $Y Z X$ until it forms an isosceles triangle $X Y Z^{\prime}$ with apex at $Y$ (note that the $\operatorname{arc} X Y$ is less than half the circle, so that $Z$ does not jump over the counter at $X$ ). If this configuration is a Loss, we are done.
|
| 43 |
+
|
| 44 |
+
If instead this configuration is a Win, then the counters can be moved legally from triangle $X Y Z^{\prime}$ to reach a losing state. This cannot involve the counter at $Y$, so by symmetry a Loss state can be reached by moving the counter at $Z^{\prime}$ to a new location $Z^{\prime \prime}$. But then the counter at $Z$ could have been moved to $Z^{\prime \prime}$ in the first place, so the original configuration was a Win as well.
|
| 45 |
+
|
| 46 |
+
For every nonzero integer $x$, denote by $v_{2}(x)$ the exponent of 2 in the prime decomposition of $x$. Now, given a configuration in which the triangle formed by the three counters is isosceles, the arcs between the vertices having lengths $a, a, b$ respectively (in appropriate units so that $2 a+b=n$ ), we show that the configuration is a Win if and only if $a \neq b$ and $v_{2}(a-b)$ is odd.
|
| 47 |
+
|
| 48 |
+
Write $b=a \pm|a-b|$ and notice that the only other isosceles triangle that can be reached from the original configuration is one with arc lengths $a, a \pm|a-b| / 2, a \pm|a-b| / 2$. If $|a-b|$ is odd, this is of course impossible, so the configuration is a Loss, since all non-isosceles configurations are Wins, by the lemma.
|
| 49 |
+
|
| 50 |
+
If instead $|a-b|$ is even, then all states that can be reached from the original configuration are Wins, except possibly the state with arc lengths $a, a \pm|a-b| / 2, a \pm|a-b| / 2$. Consequently, $(a, a, b)$ is a Win if and only if ( $a, a \pm|a-b| / 2, a \pm|a-b| / 2$ ) is a Loss. Since the side lengths of this new triangle differ by $|a-b| / 2$, the conclusion follows inductively once the exceptional and trivial case $a=b$ is dealt with.
|
| 51 |
+
|
| 52 |
+
As an immediate corollary, the configuration with arc lengths $1,1, n-2$ (the starting configuration of the question) is a Win if and only if $v_{2}(n-3)$ is odd.
|
| 53 |
+
|
| 54 |
+
Remark. Relying on the solution presented above, one may also derive an explicit winning strategy. Denote the position in the game by the multiset $\{a, b, c\}$ of thr lengths of the three arcs between the tokens (again in appropriate units so that $a+b+c=n$ ). A move now consists in choosing two of the three numbers $a, b$, $c$, and replacing them by two numbers with the same sum so as to strictly increase the minimum of the pair.
|
| 55 |
+
|
| 56 |
+
The winning strategy for a player is to obtain at the end of each of his moves the positions of the form $\{a, a, b\}$, where $a=b$ or $v_{2}(a-b)$ is even; we say that such position is good. At the beginning of the game, the position is good exactly if $v_{2}(n-3)$ is even.
|
| 57 |
+
|
| 58 |
+
Now, there is at most one position of the form $\left\{a^{\prime}, a^{\prime}, b^{\prime}\right\}$ which may be obtained by a move from a good position $\{a, a, b\}$ - that is, with $b^{\prime}=a$. This position is not good, thus it suffices to show that it is possible to obtain a good position from any non-good one by a move.
|
| 59 |
+
|
| 60 |
+
Let now $\{a, b, c\}$ be a non-good position, with $a \leq b \leq c$. If $a+c=2 b$ then one may get the good position $(b, b, b)$. Assume now that $a+c \neq 2 b$. If $v_{2}(c+a-2 b)$ is even, then it is possible to achieve the good position $\{b, b, c+a-b\}$; otherwise, $c+a$ is necessarily even, and one may get the good position $\{(c+a) / 2,(c+a) / 2, b\}$.
|
| 61 |
+
|
| 62 |
+
Problem 3. A finite list of rational numbers is written on a blackboard. In an operation, we choose any two numbers $a, b$, erase them, and write down one of the numbers
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
a+b, a-b, b-a, a \times b, a / b(\text { if } b \neq 0), b / a(\text { if } a \neq 0) .
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
Prove that, for every integer $n>100$, there are only finitely many integers $k \geq 0$, such that, starting from the list
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
k+1, k+2, \ldots, k+n
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
it is possible to obtain, after $n-1$ operations, the value $n$ !.
|
| 75 |
+
(United Kingdom) Alexander Betts
|
| 76 |
+
Solution. We prove the problem statement even for all positive integer $n$.
|
| 77 |
+
There are only finitely many ways of constructing a number from $n$ pairwise distinct numbers $x_{1}, \ldots, x_{n}$ only using the four elementary arithmetic operations, and each $x_{k}$ exactly once. Each such formula for $k>1$ is obtained by an elementary operation from two such formulas on two disjoint sets of the $x_{i}$.
|
| 78 |
+
|
| 79 |
+
A straightforward induction on $n$ shows that the outcome of each such construction is a number of the form
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\frac{\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} a_{\alpha_{1}, \ldots, \alpha_{n}} x_{1}^{\alpha_{1}} \cdots x_{n}^{\alpha_{n}}}{\sum_{\alpha_{1}, \alpha_{n} \in\{0,1\}} b_{\alpha_{1}, \ldots, \alpha_{n}} x_{1}^{\alpha_{1}} \cdots x_{n}^{\alpha_{n}}},
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
where the $a_{\alpha_{1}, \ldots, \alpha_{n}}$ and $b_{\alpha_{1}, \ldots, \alpha_{n}}$ are all in the set $\{0, \pm 1\}$, not all zero of course, $a_{0, \ldots, 0}=b_{1, \ldots, 1}=0$, and also $a_{\alpha_{1}, \ldots, \alpha_{n}} \cdot b_{\alpha_{1}, \ldots, \alpha_{n}}=0$ for every set of indices.
|
| 86 |
+
|
| 87 |
+
Since $\left|a_{\alpha_{1}, \ldots, \alpha_{n}}\right| \leq 1$, and $a_{0,0, \ldots, 0}=0$, the absolute value of the numerator does not exceed $\left(1+\left|x_{1}\right|\right) \cdots\left(1+\left|x_{n}\right|\right)-1$; in particular, if $c$ is an integer in the range $-n, \ldots,-1$, and $x_{k}=c+k$, $k=1, \ldots, n$, then the absolute value of the numerator is at most $(-c)!(n+c+1)!-1 \leq n!-1<n!$.
|
| 88 |
+
|
| 89 |
+
Consider now the integral polynomials,
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
P=\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} a_{\alpha_{1}, \ldots, \alpha_{n}}(X+1)^{\alpha_{1}} \cdots(X+n)^{\alpha_{n}}
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
and
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
Q=\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} b_{\alpha_{1}, \ldots, \alpha_{n}}(X+1)^{\alpha_{1}} \cdots(X+n)^{\alpha_{n}}
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
where the $a_{\alpha_{1}, \ldots, \alpha_{n}}$ and $b_{\alpha_{1}, \ldots, \alpha_{n}}$ are all in the set $\{0, \pm 1\}$, not all zero, $a_{\alpha_{1}, \ldots, \alpha_{n}} b_{\alpha_{1}, \ldots, \alpha_{n}}=0$ for every set of indices, and $a_{0, \ldots, 0}=b_{1, \ldots, 1}=0$. By the preceding, $|P(c)|<n$ ! for every integer $c$ in the range $-n, \ldots,-1$; and since $b_{1, \ldots, 1}=0$, the degree of $Q$ is less than $n$.
|
| 102 |
+
|
| 103 |
+
Since every non-zero polynomial has only finitely many roots, and the number of roots does not exceed the degree, to complete the proof it is sufficient to show that the polynomial $P-n!Q$ does not vanish identically, provided that $Q$ does not (which is the case in the problem).
|
| 104 |
+
|
| 105 |
+
Suppose, if possible, that $P=n!Q$, where $Q \neq 0$. Since $\operatorname{deg} Q<n$, it follows that $\operatorname{deg} P<n$ as well, and since $P \neq 0$, the number of roots of $P$ does not exceed $\operatorname{deg} P<n$, so $P(c) \neq 0$ for some integer $c$ in the range $-n, \ldots,-1$. By the preceding, $|P(c)|$ is consequently a positive integer less than $n!$. On the other hand, $|P(c)|=n!|Q(c)|$ is an integral multiple of $n!$. A contradiction.
|
| 106 |
+
|
| 107 |
+
Remark. Alternatively, it can be shown by induction on $n$ that
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\max (|P(c)|, 2|Q(c)|) \leq \prod_{k=1}^{n} \max (|c+k|, 2)
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
for all integers $c$. In case $n>8$, this provides a solution along the same lines.
|
| 114 |
+
|
RMM/md/en-2015-Solutions_RMM2015-2.md
ADDED
|
@@ -0,0 +1,104 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $7^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
## Solutions for the Day 2
|
| 4 |
+
|
| 5 |
+
Problem 4. Let $A B C$ be a triangle, let $D$ be the touchpoint of the side $B C$ and the incircle of the triangle $A B C$, and let $J_{b}$ and $J_{c}$ be the incentres of the triangles $A B D$ and $A C D$, respectively. Prove that the circumcentre of the triangle $A J_{b} J_{c}$ lies on the bisectrix of the angle $B A C$.
|
| 6 |
+
(Russia) Fedor Ivlev
|
| 7 |
+
Solution. Let the incircle of the triangle $A B C$ meet $C A$ and $A B$ at points $E$ and $F$, respectively. Let the incircles of the triangles $A B D$ and $A C D$ meet $A D$ at points $X$ and $Y$, respectively. Then $2 D X=D A+D B-A B=D A+D B-B F-A F=D A-A F$; similarly, $2 D Y=D A-A E=2 D X$. Hence the points $X$ and $Y$ coincide, so $J_{b} J_{c} \perp A D$.
|
| 8 |
+
|
| 9 |
+
Now let $O$ be the circumcentre of the triangle $A J_{b} J_{c}$. Then $\angle J_{b} A O=\pi / 2-\angle A O J_{b} / 2=$ $\pi / 2-\angle A J_{c} J_{b}=\angle X A J_{c}=\frac{1}{2} \angle D A C$. Therefore, $\angle B A O=\angle B A J_{b}+\angle J_{b} A O=\frac{1}{2} \angle B A D+$ $\frac{1}{2} \angle D A C=\frac{1}{2} \angle B A C$, and the conclusion follows.
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
Fig. 1
|
| 13 |
+
|
| 14 |
+
Problem 5. Let $p \geq 5$ be a prime number. For a positive integer $k$ we denote by $R(k)$ the remainder of $k$ when divided by $p$. Determine all positive integers $a<p$ such that
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
m+R(m a)>a
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
for every $m=1,2, \ldots, p-1$.
|
| 21 |
+
(Bulgaria) Alexander Ivanov
|
| 22 |
+
Solution. The required integers are $p-1$ along with all the numbers of the form $\lfloor p / q\rfloor, q=$ $2, \ldots, p-1$. In other words, these are $p-1$, along with the numbers $1,2, \ldots,\lfloor\sqrt{p}\rfloor$, and also the (distinct) numbers $\lfloor p / q\rfloor, q=2, \ldots,\left\lfloor\sqrt{p}-\frac{1}{2}\right\rfloor$.
|
| 23 |
+
|
| 24 |
+
We begin by showing that these numbers satisfy the conditions in the statement. It is readily checked that $p-1$ satisfies the required inequalities, since $m+R(m(p-1))=m+(p-m)=$ $p>p-1$ for all $m=1, \ldots, p-1$.
|
| 25 |
+
|
| 26 |
+
Now, consider any number $a$ of the form $a=\lfloor p / q\rfloor$, where $q$ is an integer greater than 1 but less than $p$; then $p=a q+r$ with $0<r<q$. Choose any integer $m \in(0, p)$ and write $m=x q+y$ with $x, y \in \mathbb{Z}, 0<y \leq q$ (notice that $x$ is nonnegative). Then
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
R(m a)=R(a y+x a q)=R(a y+x p-x r)=R(a y-x r) .
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
Since $a y-x r \leq a y \leq a q<p$, we obtain $R(a y-x r) \geq a y-x r$ and hence
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
m+R(m a) \geq(x q+y)+(a y-x r)=x(q-r)+y(a+1) \geq a+1
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
by $q>r$ and $y \geq 1$. Thus $a$ satisfies the required condition.
|
| 39 |
+
Finally, we show that if an integer $a \in(0, p-1)$ satisfies the required condition then $a$ is indeed of the form $a=\lfloor p / q\rfloor$ for some integer $q \in(0, p)$. This is clear for $a=1$, so we may (and will) assume that $a \geq 2$.
|
| 40 |
+
|
| 41 |
+
Write $p=a q+r$ with $q, r \in \mathbb{Z}$ and $0<r<a$; since $a \geq 2$ we have $q<p / 2$. Choose $m=q+1<p$; we have $R(m a)=R(a q+a)=R(p+(a-r))=a-r$, so
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
a<m+R(m a)=q+1+a-r,
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
which yields $r<q+1$. Moreover, if $r=q$, then $p=q(a+1)$ which is impossible by $1<a+1<p$. Thus $r<q$, and we have
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
0 \leq \frac{p}{q}-a=\frac{r}{q}<1,
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
which proves $a=\lfloor p / q\rfloor$.
|
| 54 |
+
|
| 55 |
+
Problem 6. Given a positive integer $n$, determine the largest real number $\mu$ satisfying the following condition: for every $4 n$-point configuration $C$ in an open unit square $U$, there exists an open rectangle in $U$, whose sides are parallel to those of $U$, which contains exactly one point of $C$, and has an area greater than or equal to $\mu$.
|
| 56 |
+
(Bulgaria) Nikolai Beluhov
|
| 57 |
+
Solution. The required maximum is $\frac{1}{2 n+2}$. To show that the condition in the statement is not met if $\mu>\frac{1}{2 n+2}$, let $U=(0,1) \times(0,1)$, choose a small enough positive $\epsilon$, and consider the configuration $C$ consisting of the $n$ four-element clusters of points $\left(\frac{i}{n+1} \pm \epsilon\right) \times\left(\frac{1}{2} \pm \epsilon\right), i=1, \ldots, n$, the four possible sign combinations being considered for each $i$. Clearly, every open rectangle in $U$, whose sides are parallel to those of $U$, which contains exactly one point of $C$, has area at $\operatorname{most}\left(\frac{1}{n+1}+\epsilon\right) \cdot\left(\frac{1}{2}+\epsilon\right)<\mu$ if $\epsilon$ is small enough.
|
| 58 |
+
|
| 59 |
+
We now show that, given a finite configuration $C$ of points in an open unit square $U$, there always exists an open rectangle in $U$, whose sides are parallel to those of $U$, which contains exactly one point of $C$, and has an area greater than or equal to $\mu_{0}=\frac{2}{|C|+4}$.
|
| 60 |
+
|
| 61 |
+
To prove this, usage will be made of the following two lemmas whose proofs are left at the end of the solution.
|
| 62 |
+
Lemma 1. Let $k$ be a positive integer, and let $\lambda<\frac{1}{\lfloor k / 2\rfloor+1}$ be a positive real number. If $t_{1}, \ldots, t_{k}$ are pairwise distinct points in the open unit interval $(0,1)$, then some $t_{i}$ is isolated from the other $t_{j}$ by an open subinterval of $(0,1)$ whose length is greater than or equal to $\lambda$.
|
| 63 |
+
Lemma 2. Given an integer $k \geq 2$ and positive integers $m_{1}, \ldots, m_{k}$,
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\left\lfloor\frac{m_{1}}{2}\right\rfloor+\sum_{i=1}^{k}\left\lfloor\frac{m_{i}}{2}\right\rfloor+\left\lfloor\frac{m_{k}}{2}\right\rfloor \leq \sum_{i=1}^{k} m_{i}-k+2
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Back to the problem, let $U=(0,1) \times(0,1)$, project $C$ orthogonally on the $x$-axis to obtain the points $x_{1}<\cdots<x_{k}$ in the open unit interval $(0,1)$, let $\ell_{i}$ be the vertical through $x_{i}$, and let $m_{i}=\left|C \cap \ell_{i}\right|, i=1, \ldots, k$.
|
| 70 |
+
|
| 71 |
+
Setting $x_{0}=0$ and $x_{k+1}=1$, assume that $x_{i+1}-x_{i-1}>\left(\left\lfloor m_{i} / 2\right\rfloor+1\right) \mu_{0}$ for some index $i$, and apply Lemma 1 to isolate one of the points in $C \cap \ell_{i}$ from the other ones by an open subinterval $x_{i} \times J$ of $x_{i} \times(0,1)$ whose length is greater than or equal to $\mu_{0} /\left(x_{i+1}-x_{i-1}\right)$. Consequently, $\left(x_{i-1}, x_{i+1}\right) \times J$ is an open rectangle in $U$, whose sides are parallel to those of $U$, which contains exactly one point of $C$ and has an area greater than or equal to $\mu_{0}$.
|
| 72 |
+
|
| 73 |
+
Next, we rule out the case $x_{i+1}-x_{i-1} \leq\left(\left\lfloor m_{i} / 2\right\rfloor+1\right) \mu_{0}$ for all indices $i$. If this were the case, notice that necessarily $k>1$; also, $x_{1}-x_{0}<x_{2}-x_{0} \leq\left(\left\lfloor m_{1} / 2\right\rfloor+1\right) \mu_{0}$ and $x_{k+1}-x_{k}<$ $x_{k+1}-x_{k-1} \leq\left(\left\lfloor m_{k} / 2\right\rfloor+1\right) \mu_{0}$. With reference to Lemma 2, write
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\begin{aligned}
|
| 77 |
+
2=2\left(x_{k+1}-x_{0}\right) & =\left(x_{1}-x_{0}\right)+\sum_{i=1}^{k}\left(x_{i+1}-x_{i-1}\right)+\left(x_{k+1}-x_{k}\right) \\
|
| 78 |
+
& <\left(\left(\left\lfloor\frac{m_{1}}{2}\right\rfloor+1\right)+\sum_{i=1}^{k}\left(\left\lfloor\frac{m_{i}}{2}\right\rfloor+1\right)+\left(\left\lfloor\frac{m_{k}}{2}\right\rfloor+1\right)\right) \cdot \mu_{0} \\
|
| 79 |
+
& \leq\left(\sum_{i=1}^{k} m_{i}+4\right) \mu_{0}=(|C|+4) \mu_{0}=2
|
| 80 |
+
\end{aligned}
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
and thereby reach a contradiction.
|
| 84 |
+
|
| 85 |
+
Finally, we prove the two lemmas.
|
| 86 |
+
Proof of Lemma 1. Suppose, if possible, that no $t_{i}$ is isolated from the other $t_{j}$ by an open subinterval of $(0,1)$ whose length is greater than or equal to $\lambda$. Without loss of generality, we may (and will) assume that $0=t_{0}<t_{1}<\cdots<t_{k}<t_{k+1}=1$. Since the open interval $\left(t_{i-1}, t_{i+1}\right)$ isolates $t_{i}$ from the other $t_{j}$, its length, $t_{i+1}-t_{i-1}$, is less than $\lambda$. Consequently, if $k$ is odd we have $1=\sum_{i=0}^{(k-1) / 2}\left(t_{2 i+2}-t_{2 i}\right)<\lambda\left(1+\frac{k-1}{2}\right)<1$; if $k$ is even, we have $1<1+t_{k}-t_{k-1}=$ $\sum_{i=0}^{k / 2-1}\left(t_{2 i+2}-t_{2 i}\right)+\left(t_{k+1}-t_{k-1}\right)<\lambda\left(1+\frac{k}{2}\right)<1$. A contradiction in either case.
|
| 87 |
+
Proof of Lemma 2. Let $I_{0}$, respectively $I_{1}$, be the set of all indices $i$ in the range $2, \ldots, k-1$ such that $m_{i}$ is even, respectively odd. Clearly, $I_{0}$ and $I_{1}$ form a partition of that range. Since $m_{i} \geq 2$ if $i$ is in $I_{0}$, and $m_{i} \geq 1$ if $i$ is in $I_{1}$ (recall that the $m_{i}$ are positive integers),
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\sum_{i=2}^{k-1} m_{i}=\sum_{i \in I_{0}} m_{i}+\sum_{i \in I_{1}} m_{i} \geq 2\left|I_{0}\right|+\left|I_{1}\right|=2(k-2)-\left|I_{1}\right|, \quad \text { or } \quad\left|I_{1}\right| \geq 2(k-2)-\sum_{i=2}^{k-1} m_{i}
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
Therefore,
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
\begin{aligned}
|
| 97 |
+
\left\lfloor\frac{m_{1}}{2}\right\rfloor+\sum_{i=1}^{k}\left\lfloor\frac{m_{i}}{2}\right\rfloor+\left\lfloor\frac{m_{k}}{2}\right\rfloor & \leq m_{1}+\left(\sum_{i=2}^{k-1} \frac{m_{i}}{2}-\frac{\left|I_{1}\right|}{2}\right)+m_{k} \\
|
| 98 |
+
& \leq m_{1}+\left(\frac{1}{2} \sum_{i=2}^{k-1} m_{i}-(k-2)+\frac{1}{2} \sum_{i=2}^{k-1} m_{i}\right)+m_{k} \\
|
| 99 |
+
& =\sum_{i=1}^{k} m_{i}-k+2
|
| 100 |
+
\end{aligned}
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Remark. In case $4 n$ is replaced by a positive integer $k$ not divisible by 4 , we do not yet know the maximal $\mu$ satisfying the corresponding condition.
|
| 104 |
+
|
RMM/md/en-2016-Solutions_RMM2016-1.md
ADDED
|
@@ -0,0 +1,92 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $8^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 1 — Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
| 6 |
+
|
| 7 |
+
Solution 1. (Ilya Bogdanov) Let $\sigma$ denote reflection in the line $B C$. Since $\angle B D F=\angle B A C=$ $\angle C D E$, by concyclicity, the lines $D E$ and $D F$ are images of one another under $\sigma$, so the lines $A C$ and $D F$ meet at $P^{\prime}=\sigma(P)$, and the lines $A B$ and $D E$ meet at $Q^{\prime}=\sigma(Q)$. Consequently, the lines $P Q$ and $P^{\prime} Q^{\prime}=\sigma(P Q)$ meet at some (possibly ideal) point $R$ on the line $B C$.
|
| 8 |
+
|
| 9 |
+
Since the pairs of lines $(C A, Q D),(A B, D P),(B C, P Q)$ meet at three collinear points, namely $P^{\prime}, Q^{\prime}, R$ respectively, the triangles $A B C$ and $D P Q$ are perspective, i.e., the lines $A D, B P, C Q$ are concurrent, by the Desargues theorem.
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
Fig. 1
|
| 13 |
+
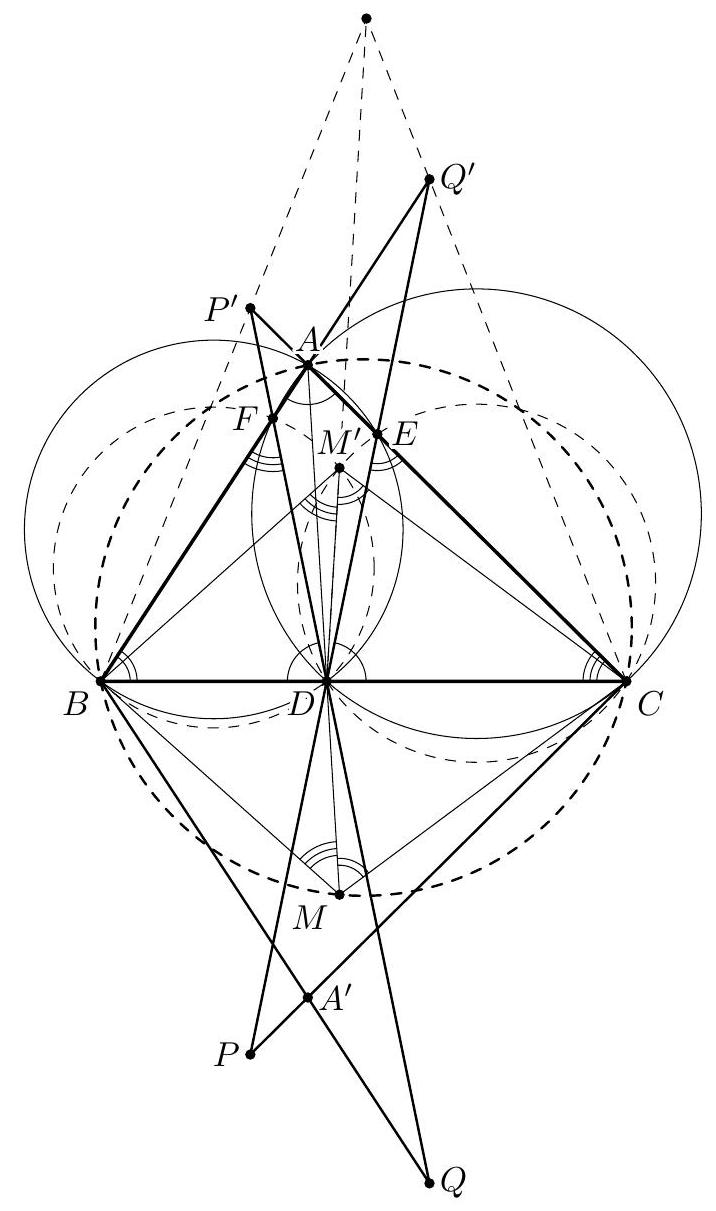
|
| 14 |
+
|
| 15 |
+
Fig. 2
|
| 16 |
+
|
| 17 |
+
Solution 2. As in the first solution, $\sigma$ denotes reflection in the line $B C$, the lines $D E$ and $D F$ are images of one another under $\sigma$, the lines $A C$ and $D F$ meet at $P^{\prime}=\sigma(P)$, and the lines $A B$ and $D E$ meet at $Q^{\prime}=\sigma(Q)$.
|
| 18 |
+
|
| 19 |
+
Let the line $A D$ meet the circle $A B C$ again at $M$. Letting $M^{\prime}=\sigma(M)$, it is sufficient to prove that the lines $D M^{\prime}=\sigma(A D), B P^{\prime}=\sigma(B P)$ and $C Q^{\prime}=\sigma(C Q)$ are concurrent.
|
| 20 |
+
|
| 21 |
+
Begin by noticing that $\angle\left(B M^{\prime}, M^{\prime} D\right)=-\angle(B M, M A)=-\angle(B C, C A)=\angle(B F, F D)$, to infer that $M^{\prime}$ lies on the circle $B D F$. Similarly, $M^{\prime}$ lies on the circle $C D E$, so the line $D M^{\prime}$ is the radical axis of the circles $B D F$ and $C D E$.
|
| 22 |
+
|
| 23 |
+
Since $P^{\prime}$ lies on the lines $A C$ and $D F$, it is the radical centre of the circles $A B C, A D C$, and $B D F$; hence the line $B P^{\prime}$ is the radical axis of the circles $B D F$ and $A B C$. Similarly, the line $C Q^{\prime}$ is the radical axis of the circles $C D E$ and $A B C$. So the conclusion follows: the lines $D M^{\prime}$, $B P^{\prime}$ and $C Q^{\prime}$ are concurrent at the radical centre of the circles $A B C, B D F$ and $C D E$; thus the lines $D M, B P^{\prime}$ and $C Q^{\prime}$ are also concurrent.
|
| 24 |
+
|
| 25 |
+
Solution 3. (Ilya Bogdanov) As in the previous solutions, $\sigma$ denotes reflection in the line $B C$. Let the lines $B E$ and $C F$ meet at $X$. Due to the circles $B D E A$ and $C D F A$, we have $\angle X B D=$ $\angle E A D=\angle X F D$, so the quadrilateral $B F X D$ is cyclic; similarly, the quadrilateral $C E X D$ is cyclic. Hence $\angle X D B=\angle C F A=\angle C D A$, the lines $D X$ and $D A$ are therefore images of one another under $\sigma$, and $X^{\prime}=\sigma(X)$ lies on the line $A D$. Let $E^{\prime}=\sigma(E)$ and $F^{\prime}=\sigma(F)$, and apply the Pappus theorem to the hexagon $B P F^{\prime} C Q E^{\prime}$ to infer that $X^{\prime}, D$, and $B P \cap C Q$ are collinear. The conclusion follows.
|
| 26 |
+
|
| 27 |
+
|
| 28 |
+
Fig. 3
|
| 29 |
+
|
| 30 |
+
Remark. In fact, the point $X$ in Solution 3 and the point $M$ in Solution 2 coincide.
|
| 31 |
+
Problem 2. Given positive integers $m$ and $n \geq m$, determine the largest number of dominoes ( $1 \times 2$ or $2 \times 1$ rectangles) that can be placed on a rectangular board with $m$ rows and $2 n$ columns consisting of cells ( $1 \times 1$ squares) so that:
|
| 32 |
+
(i) each domino covers exactly two adjacent cells of the board;
|
| 33 |
+
(ii) no two dominoes overlap;
|
| 34 |
+
(iii) no two form a $2 \times 2$ square; and
|
| 35 |
+
(iv) the bottom row of the board is completely covered by $n$ dominoes.
|
| 36 |
+
|
| 37 |
+
Solution 1. The required maximum is $m n-\lfloor m / 2\rfloor$ and is achieved by the brick-like vertically symmetric arrangement of blocks of $n$ and $n-1$ horizontal dominoes placed on alternate rows, so that the bottom row of the board is completely covered by $n$ dominoes.
|
| 38 |
+
|
| 39 |
+
To show that the number of dominoes in an arrangement satisfying the conditions in the statement does not exceed $m n-\lfloor m / 2\rfloor$, label the rows upwards $0,1, \ldots, m-1$, and, for each
|
| 40 |
+
$i$ in this range, draw a vertically symmetric block of $n-i$ fictitious horizontal dominoes in the $i$-th row (so the block on the $i$-th row leaves out $i$ cells on either side) - Figure 4 illustrates the case $m=n=6$. A fictitious domino is good if it is completely covered by a domino in the arrangement; otherwise, it is bad.
|
| 41 |
+
|
| 42 |
+
If the fictitious dominoes are all good, then the dominoes in the arrangement that cover no fictitious domino, if any, all lie in two triangular regions of side-length $m-1$ at the upper-left and upper-right corners of the board. Colour the cells of the board chess-like and notice that in each of the two triangular regions the number of black cells and the number of white cells differ by $\lfloor m / 2\rfloor$. Since each domino covers two cells of different colours, at least $\lfloor m / 2\rfloor$ cells are not covered in each of these regions, and the conclusion follows.
|
| 43 |
+
|
| 44 |
+
|
| 45 |
+
Fig. 4
|
| 46 |
+
|
| 47 |
+
|
| 48 |
+
Fig. 5
|
| 49 |
+
|
| 50 |
+
To deal with the remaining case where bad fictitious dominoes are present, we show that an arrangement satisfying the conditions in the statement can be transformed into another such with at least as many dominoes, but fewer bad fictitious dominoes. A finite number of such transformations eventually leads to an arrangement of at least as many dominoes all of whose fictitious dominoes are good, and the conclusion follows by the preceding.
|
| 51 |
+
|
| 52 |
+
Consider the row of minimal rank containing bad fictitious dominoes - this is certainly not the bottom row - and let $D$ be one such. Let $\ell$, respectively $r$, be the left, respectively right, cell of $D$ and notice that the cell below $\ell$, respectively $r$, is the right, respectively left, cell of a domino $D_{1}$, respectively $D_{2}$, in the arrangement.
|
| 53 |
+
|
| 54 |
+
If $\ell$ is covered by a domino $D_{\ell}$ in the arrangement, since $D$ is bad and no two dominoes in the arrangement form a square, it follows that $D_{\ell}$ is vertical. If $r$ were also covered by a domino $D_{r}$ in the arrangement, then $D_{r}$ would also be vertical, and would therefore form a square with $D_{\ell}$ - a contradiction. Hence $r$ is not covered, and there is room for $D_{\ell}$ to be placed so as to cover $D$, to obtain a new arrangement satisfying the conditions in the statement; the latter has as many dominoes as the former, but fewer bad fictitious dominoes. The case where $r$ is covered is dealt with similarly.
|
| 55 |
+
|
| 56 |
+
Finally, if neither cell of $D$ is covered, addition of an extra domino to cover $D$ and, if necessary, removal of the domino above $D$ to avoid formation of a square, yields a new arrangement satisfying the conditions in the statement; the latter has at least as many dominoes as the former, but fewer bad fictitious dominoes. (Figure 5 illustrates the two cases.)
|
| 57 |
+
|
| 58 |
+
Solution 2. (sketch by Ilya Bogdanov) We present an alternative proof of the bound.
|
| 59 |
+
Label the rows upwards $0,1, \ldots, m-1$, and the columns from the left to the right by $0,1, \ldots, 2 n-1$; label each cell by the pair of its column's and row's numbers, so that $(1,0)$ is the second left cell in the bottom row. Colour the cells chess-like so that $(0,0)$ is white. For $0 \leq i \leq n-1$, we say that the $i$ th white diagonal is the set of cells of the form $(2 i+k, k)$, where $k$ ranges over all appropriate indices. Similarly, the ith black diagonal is the set of cells of the form $(2 i+1-k, k)$. (Notice that the white cells in the upper-left corner and the black cells in the upper-right corner are not covered by these diagonals.)
|
| 60 |
+
Claim. Assume that $K$ lowest cells of some white diagonal are all covered by dominoes. Then all these $K$ dominoes face right or up from the diagonal. (In other words, the black cell of any such
|
| 61 |
+
domino is to the right or to the top of its white cell.) Similarly, if $K$ lowest cells of some black diagonal are covered by dominoes, then all these dominoes face left or up from the diagonal.
|
| 62 |
+
|
| 63 |
+
Proof. By symmetry, it suffices to prove the first statement. Assume that $K$ lowest cells of the $i$ th white diagonal is completely covered. We prove by induction on $k<K$ that the required claim holds for the domino covering $(2 i+k, k)$. The base case $k=0$ holds due to the problem condition. To establish the step, one observes that if $(2 i+k, k)$ is covered by a domino facing up of right, while $(2 i+k+1, k+1)$ is covered by a domino facing down or left, then these two dominoes form a square.
|
| 64 |
+
|
| 65 |
+
We turn to the solution. We will prove that there are at least $d=\lfloor m / 2\rfloor$ empty white cells. Since each domino covers exactly one white cell, the required bound follows.
|
| 66 |
+
|
| 67 |
+
If each of the first $d$ white diagonals contains an empty cell, the result is clear. Otherwise, let $i<d$ be the least index of a completely covered white diagonal. We say that the dominoes covering our diagonal are distinguished. After removing the distinguished dominoes, the board splits into two parts; the left part $L$ contains $i$ empty white cells on the previous diagonals. So, it suffices to prove that the right part $R$ contains at least $d-i$ empty white cells.
|
| 68 |
+
|
| 69 |
+
Let $j$ be the number of distinguished dominoes facing up. Then at least $j-i$ of these dominoes cover some cells of (distinct) black diagonals (the relation $m \leq n$ is used). Each such domino faces down from the corresponding black diagonal - so, by the Claim, each such black diagonal contains an empty cell in $R$. Thus, $R$ contains at least $j-i$ empty black cells.
|
| 70 |
+
|
| 71 |
+
Now, let $w$ be the number of white cells in $R$. Then the number of black cells in $R$ is $w-d+j$, and at least $i-j$ of those are empty. Thus, the number of dominoes in $R$ is at most $(w-d+j)-(j-i)=w-(d-i)$, so $R$ contains at least $d-i$ empty white cells, as we wanted to show.
|
| 72 |
+
|
| 73 |
+
Remark. The conclusion still holds if some row, not necessarily the bottom row, is completely covered by $n$ dominoes - apply the result in the problem to the upper and lower parts of the board overlapping along a row completely covered by $n$ dominoes.
|
| 74 |
+
|
| 75 |
+
However, omission of the condition that the bottom row be covered by $n$ dominoes reduces the minimal number of uncovered cells dramatically. For instance, all but two cells of a $(2 k+1) \times(4 k+2)$ board can be covered by dominoes no two of which form a $2 \times 2$ square.
|
| 76 |
+
|
| 77 |
+
Problem 3. A cubic sequence is a sequence of integers given by $a_{n}=n^{3}+b n^{2}+c n+d$, where $b, c$ and $d$ are integer constants and $n$ ranges over all integers, including negative integers.
|
| 78 |
+
(a) Show that there exists a cubic sequence such that the only terms of the sequence which are squares of integers are $a_{2015}$ and $a_{2016}$.
|
| 79 |
+
(b) Determine the possible values of $a_{2015} \cdot a_{2016}$ for a cubic sequence satisfying the condition in part (a).
|
| 80 |
+
|
| 81 |
+
Solution. The only possible value of $a_{2015} \cdot a_{2016}$ is 0 . For simplicity, by performing a translation of the sequence (which may change the defining constants $b, c$ and $d$ ), we may instead concern ourselves with the values $a_{0}$ and $a_{1}$, rather than $a_{2015}$ and $a_{2016}$.
|
| 82 |
+
|
| 83 |
+
Suppose now that we have a cubic sequence $a_{n}$ with $a_{0}=p^{2}$ and $a_{1}=q^{2}$ square numbers. We will show that $p=0$ or $q=0$. Consider the line $y=(q-p) x+p$ passing through $(0, p)$ and $(1, q)$; the latter are two points the line under consideration and the cubic $y^{2}=x^{3}+b x^{2}+c x+d$ share. Hence the two must share a third point whose $x$-coordinate is the third root of the polynomial $t^{3}+\left(b-(q-p)^{2}\right) t^{2}+(c-2(q-p) p) t+\left(d-p^{2}\right)$ (it may well happen that this third point coincide with one of the other two points the line and the cubic share).
|
| 84 |
+
|
| 85 |
+
Notice that the sum of the three roots is $(q-p)^{2}-b$, so the third intersection has integral $x$-coordinate $X=(q-p)^{2}-b-1$. Its $y$-coordinate $Y=(q-p) X+p$ is also an integer, and hence $a_{X}=X^{3}+b X^{2}+c X+d=Y^{2}$ is a square. This contradicts our assumption on the sequence unless $X=0$ or $X=1$, i.e. unless $(q-p)^{2}=b+1$ or $(q-p)^{2}=b+2$.
|
| 86 |
+
|
| 87 |
+
Applying the same argument to the line through $(0,-p)$ and $(1, q)$, we find that $(q+p)^{2}=b+1$ or $b+2$ also. Since $(q-p)^{2}$ and $(q+p)^{2}$ have the same parity, they must be equal, and hence $p q=0$, as desired.
|
| 88 |
+
|
| 89 |
+
It remains to show that such sequences exist, say when $p=0$. Consider the sequence $a_{n}=$ $n^{3}+\left(q^{2}-2\right) n^{2}+n$, chosen to satisfy $a_{0}=0$ and $a_{1}=q^{2}$. We will show that when $q=1$, the only square terms of the sequence are $a_{0}=0$ and $a_{1}=1$. Indeed, suppose that $a_{n}=n\left(n^{2}-n+1\right)$ is square. Since the second factor is positive, and the two factors are coprime, both must be squares; in particular, $n \geq 0$. The case $n=0$ is clear, so let $n \geq 1$. Finally, if $n>1$, then $(n-1)^{2}<n^{2}-n+1<n^{2}$, so $n^{2}-n+1$ is not a square. Consequently, $n=0$ or $n=1$, and the conclusion follows.
|
| 90 |
+
|
| 91 |
+
Remark. The values $q=3$ and $q=4$ work as well. In the former case, the only square terms of the sequence $a_{n}=n\left(n^{2}+7 n+1\right)$ are $a_{0}=0$ and $a_{1}=9$. In the other case, the only square terms of the sequence $a_{n}=n\left(n^{2}+14 n+1\right)$ are $a_{0}=0$ and $a_{1}=16$.
|
| 92 |
+
|
RMM/md/en-2016-Solutions_RMM2016-2.md
ADDED
|
@@ -0,0 +1,76 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $8^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 2 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 4. Let $x$ and $y$ be positive real numbers such that $x+y^{2016} \geq 1$. Prove that $x^{2016}+y>$ 1 - 1/100.
|
| 6 |
+
|
| 7 |
+
Solution. If $x \geq 1-1 /(100 \cdot 2016)$, then
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
x^{2016} \geq\left(1-\frac{1}{100 \cdot 2016}\right)^{2016}>1-2016 \cdot \frac{1}{100 \cdot 2016}=1-\frac{1}{100}
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
by Bernoulli's inequality, whence the conclusion.
|
| 14 |
+
If $x<1-1 /(100 \cdot 2016)$, then $y \geq(1-x)^{1 / 2016}>(100 \cdot 2016)^{-1 / 2016}$, and it is sufficient to show that the latter is greater than $1-1 / 100=99 / 100$; alternatively, but equivalently, that
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
\left(1+\frac{1}{99}\right)^{2016}>100 \cdot 2016
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
To establish the latter, refer again to Bernoulli's inequality to write
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\left(1+\frac{1}{99}\right)^{2016}>\left(1+\frac{1}{99}\right)^{99 \cdot 20}>\left(1+99 \cdot \frac{1}{99}\right)^{20}=2^{20}>100 \cdot 2016
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
Remarks. (1) Although the constant $1 / 100$ is not sharp, it cannot be replaced by the smaller constant $1 / 400$, as the values $x=1-1 / 210$ and $y=1-1 / 380$ show.
|
| 27 |
+
(2) It is natural to ask whether $x^{n}+y \geq 1-1 / k$, whenever $x$ and $y$ are positive real numbers such that $x+y^{n} \geq 1$, and $k$ and $n$ are large. Using the inequality $\left(1+\frac{1}{k-1}\right)^{k}>\mathrm{e}$, it can be shown along the lines in the solution that this is indeed the case if $k \leq \frac{n}{2 \log n}(1+o(1))$. It seems that this estimate differs from the best one by a constant factor.
|
| 28 |
+
|
| 29 |
+
Problem 5. A convex hexagon $A_{1} B_{1} A_{2} B_{2} A_{3} B_{3}$ is inscribed in a circle $\Omega$ of radius $R$. The diagonals $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ concur at $X$. For $i=1,2,3$, let $\omega_{i}$ be the circle tangent to the segments $X A_{i}$ and $X B_{i}$, and to the arc $A_{i} B_{i}$ of $\Omega$ not containing other vertices of the hexagon; let $r_{i}$ be the radius of $\omega_{i}$.
|
| 30 |
+
(a) Prove that $R \geq r_{1}+r_{2}+r_{3}$.
|
| 31 |
+
(b) If $R=r_{1}+r_{2}+r_{3}$, prove that the six points where the circles $\omega_{i}$ touch the diagonals $A_{1} B_{2}, A_{2} B_{3}, A_{3} B_{1}$ are concyclic.
|
| 32 |
+
|
| 33 |
+
Solution. (a) Let $\ell_{1}$ be the tangent to $\Omega$ parallel to $A_{2} B_{3}$, lying on the same side of $A_{2} B_{3}$ as $\omega_{1}$. The tangents $\ell_{2}$ and $\ell_{3}$ are defined similarly. The lines $\ell_{1}$ and $\ell_{2}, \ell_{2}$ and $\ell_{3}, \ell_{3}$ and $\ell_{1}$ meet at $C_{3}, C_{1}, C_{2}$, respectively (see Fig. 1). Finally, the line $C_{2} C_{3}$ meets the rays $X A_{1}$ and $X B_{1}$ emanating from $X$ at $S_{1}$ and $T_{1}$, respectively; the points $S_{2}, T_{2}$, and $S_{3}, T_{3}$ are defined similarly.
|
| 34 |
+
|
| 35 |
+
Each of the triangles $\Delta_{1}=\triangle X S_{1} T_{1}, \Delta_{2}=\triangle T_{2} X S_{2}$, and $\Delta_{3}=\triangle S_{3} T_{3} X$ is similar to $\Delta=\triangle C_{1} C_{2} C_{3}$, since their corresponding sides are parallel. Let $k_{i}$ be the ratio of similitude of $\Delta_{i}$ and $\Delta$ (e.g., $k_{1}=X S_{1} / C_{1} C_{2}$ and the like). Since $S_{1} X=C_{2} T_{3}$ and $X T_{2}=S_{3} C_{1}$, it follows that $k_{1}+k_{2}+k_{3}=1$, so, if $\rho_{i}$ is the inradius of $\Delta_{i}$, then $\rho_{1}+\rho_{2}+\rho_{3}=R$.
|
| 36 |
+
|
| 37 |
+
Finally, notice that $\omega_{i}$ is interior to $\Delta_{i}$, so $r_{i} \leq \rho_{i}$, and the conclusion follows by the preceding.
|
| 38 |
+
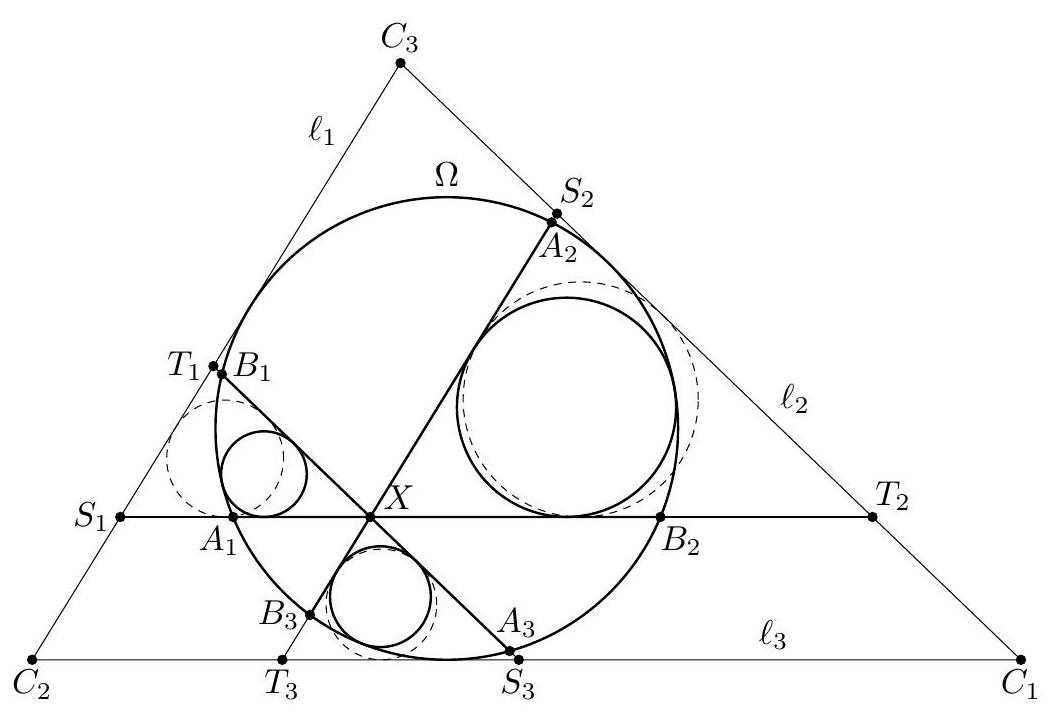
|
| 39 |
+
|
| 40 |
+
Fig. 1
|
| 41 |
+
|
| 42 |
+
|
| 43 |
+
Fig. 2
|
| 44 |
+
(b) By part (a), the equality $R=r_{1}+r_{2}+r_{3}$ holds if and only if $r_{i}=\rho_{i}$ for all $i$, which implies in turn that $\omega_{i}$ is the incircle of $\Delta_{i}$. Let $K_{i}, L_{i}, M_{i}$ be the points where $\omega_{i}$ touches the sides $X S_{i}, X T_{i}, S_{i} T_{i}$, respectively. We claim that the six points $K_{i}$ and $L_{i}(i=1,2,3)$ are equidistant from $X$.
|
| 45 |
+
|
| 46 |
+
Clearly, $X K_{i}=X L_{i}$, and we are to prove that $X K_{2}=X L_{1}$ and $X K_{3}=X L_{2}$. By similarity, $\angle T_{1} M_{1} L_{1}=\angle C_{3} M_{1} M_{2}$ and $\angle S_{2} M_{2} K_{2}=\angle C_{3} M_{2} M_{1}$, so the points $M_{1}, M_{2}, L_{1}, K_{2}$ are collinear. Consequently, $\angle X K_{2} L_{1}=\angle C_{3} M_{1} M_{2}=\angle C_{3} M_{2} M_{1}=\angle X L_{1} K_{2}$, so $X K_{2}=X L_{1}$. Similarly, $X K_{3}=X L_{2}$.
|
| 47 |
+
|
| 48 |
+
Remark. Under the assumption in part (b), the point $M_{i}$ is the centre of a homothety mapping $\omega_{i}$ to $\Omega$. Since this homothety maps $X$ to $C_{i}$, the points $M_{i}, C_{i}, X$ are collinear, so $X$ is the Gergonne point of the triangle $C_{1} C_{2} C_{3}$. This condition is in fact equivalent to $R=r_{1}+r_{2}+r_{3}$.
|
| 49 |
+
|
| 50 |
+
Problem 6. A set of $n$ points in Euclidean 3-dimensional space, no four of which are coplanar, is partitioned into two subsets $\mathcal{A}$ and $\mathcal{B}$. An $\mathcal{A B}$-tree is a configuration of $n-1$ segments, each of which has an endpoint in $\mathcal{A}$ and the other in $\mathcal{B}$, and such that no segments form a closed polyline. An $\mathcal{A B}$-tree is transformed into another as follows: choose three distinct segments $A_{1} B_{1}, B_{1} A_{2}$ and $A_{2} B_{2}$ in the $\mathcal{A B}$-tree such that $A_{1}$ is in $\mathcal{A}$ and $A_{1} B_{1}+A_{2} B_{2}>A_{1} B_{2}+A_{2} B_{1}$, and remove the segment $A_{1} B_{1}$ to replace it by the segment $A_{1} B_{2}$. Given any $\mathcal{A B}$-tree, prove that every sequence of successive transformations comes to an end (no further transformation is possible) after finitely many steps.
|
| 51 |
+
|
| 52 |
+
Solution. The configurations of segments under consideration are all bipartite geometric trees on the points $n$ whose vertex-parts are $\mathcal{A}$ and $\mathcal{B}$, and transforming one into another preserves the degree of any vertex in $\mathcal{A}$, but not necessarily that of a vertex in $\mathcal{B}$.
|
| 53 |
+
|
| 54 |
+
The idea is to devise a strict semi-invariant of the process, i.e., assign each $\mathcal{A B}$-tree a real number strictly decreasing under a transformation. Since the number of trees on the $n$ points is finite, the conclusion follows.
|
| 55 |
+
|
| 56 |
+
To describe the assignment, consider an $\mathcal{A B}$-tree $\mathcal{T}=(\mathcal{A} \sqcup \mathcal{B}, \mathcal{E})$. Removal of an edge $e$ of $\mathcal{T}$ splits the graph into exactly two components. Let $p_{\mathcal{T}}(e)$ be the number of vertices in $\mathcal{A}$ lying in the component of $\mathcal{T}-e$ containing the $\mathcal{A}$-endpoint of $e$; since $\mathcal{T}$ is a tree, $p_{\mathcal{T}}(e)$ counts the number of paths in $\mathcal{T}-e$ from the $\mathcal{A}$-endpoint of $e$ to vertices in $\mathcal{A}$ (including the one-vertex path). Define $f(\mathcal{T})=\sum_{e \in \mathcal{E}} p_{\mathcal{T}}(e)|e|$, where $|e|$ is the Euclidean length of $e$.
|
| 57 |
+
|
| 58 |
+
We claim that $f$ strictly decreases under a transformation. To prove this, let $\mathcal{T}^{\prime}$ be obtained from $\mathcal{T}$ by a transformation involving the polyline $A_{1} B_{1} A_{2} B_{2}$; that is, $A_{1}$ and $A_{2}$ are in $\mathcal{A}, B_{1}$
|
| 59 |
+
and $B_{2}$ are in $\mathcal{B}, A_{1} B_{1}+A_{2} B_{2}>A_{1} B_{2}+A_{2} B_{1}$, and $\mathcal{T}^{\prime}=\mathcal{T}-A_{1} B_{1}+A_{1} B_{2}$. It is readily checked that $p_{\mathcal{T}^{\prime}}(e)=p_{\mathcal{T}}(e)$ for every edge $e$ of $\mathcal{T}$ different from $A_{1} B_{1}, A_{2} B_{1}$ and $A_{2} B_{2}, p_{\mathcal{T}^{\prime}}\left(A_{1} B_{2}\right)=$ $p_{\mathcal{T}}\left(A_{1} B_{1}\right), p_{\mathcal{T}^{\prime}}\left(A_{2} B_{1}\right)=p_{\mathcal{T}}\left(A_{2} B_{1}\right)+p_{\mathcal{T}}\left(A_{1} B_{1}\right)$, and $p_{\mathcal{T}^{\prime}}\left(A_{2} B b_{2}\right)=p_{\mathcal{T}}\left(A_{2} B_{2}\right)-p_{\mathcal{T}}\left(A_{1} B_{1}\right)$. Consequently,
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\begin{aligned}
|
| 63 |
+
f\left(\mathcal{T}^{\prime}\right)-f(\mathcal{T})= & p_{\mathcal{T}^{\prime}}\left(A_{1} B_{2}\right) \cdot A_{1} B_{2}+\left(p_{\mathcal{T}^{\prime}}\left(A_{2} B_{1}\right)-p_{\mathcal{T}}\left(A_{2} B_{1}\right)\right) \cdot A_{2} B_{1}+ \\
|
| 64 |
+
& \left(p_{\mathcal{T}^{\prime}}\left(A_{2} B_{2}\right)-p_{\mathcal{T}}\left(A_{2} B_{2}\right)\right) \cdot A_{2} B_{2}-p_{\mathcal{T}}\left(A_{1} B_{1}\right) \cdot A_{1} B_{1} \\
|
| 65 |
+
= & p_{\mathcal{T}}\left(A_{1} B_{1}\right)\left(A_{1} B_{2}+A_{2} B_{1}-A_{2} B_{2}-A_{1} B_{1}\right)<0
|
| 66 |
+
\end{aligned}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Remarks. (1) The solution above does not involve the geometric structure of the configurations, so the conclusion still holds if the Euclidean length (distance) is replaced by any real-valued function on $\mathcal{A} \times \mathcal{B}$.
|
| 70 |
+
(2) There are infinitely many strict semi-invariants that can be used to establish the conclusion, as we are presently going to show. The idea is to devise a non-strict real-valued semiinvariant $f_{A}$ for each $A$ in $\mathcal{A}$ (i.e., $f_{A}$ does not increase under a transformation) such that $\sum_{A \in \mathcal{A}} f_{A}=f$. It then follows that any linear combination of the $f_{A}$ with positive coefficients is a strict semi-invariant.
|
| 71 |
+
|
| 72 |
+
To describe $f_{A}$, where $A$ is a fixed vertex in $\mathcal{A}$, let $\mathcal{T}$ be an $\mathcal{A B}$-tree. Since $\mathcal{T}$ is a tree, by orienting all paths in $\mathcal{T}$ with an endpoint at $A$ away from $A$, every edge of $\mathcal{T}$ comes out with a unique orientation so that the in-degree of every vertex of $\mathcal{T}$ other than $A$ is 1 . Define $f_{A}(\mathcal{T})$ to be the sum of the Euclidean lengths of all out-going edges from $\mathcal{A}$. It can be shown that $f_{A}$ does not increase under a transformation, and it strictly decreases if the paths from $A$ to each of $A_{1}$, $A_{2}, B_{1}, B_{2}$ all pass through $A_{1}$ - i.e., of these four vertices, $A_{1}$ is combinatorially nearest to $A$. In particular, this is the case if $A_{1}=A$, i.e., the edge-switch in the transformation occurs at $A$. It is not hard to prove that $\sum_{A \in \mathcal{A}} f_{A}(\mathcal{T})=f(\mathcal{T})$.
|
| 73 |
+
|
| 74 |
+
The conclusion of the problem can also be established by resorting to a single carefully chosen $f_{A}$. Suppose, if possible, that the process is infinite, so some tree $\mathcal{T}$ occurs (at least) twice. Let $A$ be the vertex in $\mathcal{A}$ at which the edge-switch occurs in the transformation of the first occurrence of $\mathcal{T}$. By the preceding paragraph, consideration of $f_{A}$ shows that $\mathcal{T}$ can never occur again.
|
| 75 |
+
(3) Recall that the degree of any vertex in $\mathcal{A}$ is invariant under a transformation, so the linear combination $\sum_{A \in \mathcal{A}}(\operatorname{deg} A-1) f_{A}$ is a strict semi-invariant for $\mathcal{A B}$-trees $\mathcal{T}$ whose vertices in $\mathcal{A}$ all have degrees exceeding 1. Up to a factor, this semi-invariant can alternatively, but equivalently be described as follows. Fix a vertex $*$ and assign each vertex $X$ a number $g(X)$ so that $g(*)=0$, and $g(A)-g(B)=A B$ for every $A$ in $\mathcal{A}$ and every $B$ in $\mathcal{B}$ joined by an edge. Next, let $\beta(\mathcal{T})=\frac{1}{|\mathcal{B}|} \sum_{B \in \mathcal{B}} g(B)$, let $\alpha(\mathcal{T})=\frac{1}{|\mathcal{E}|-|\mathcal{A}|} \sum_{A \in \mathcal{A}}(\operatorname{deg} A-1) g(A)$, where $\mathcal{E}$ is the edge-set of $\mathcal{T}$, and set $\mu(\mathcal{T})=\beta(\mathcal{T})-\alpha(\mathcal{T})$. It can be shown that $\mu$ strictly decreases under a transformation; in fact, $\mu$ and $\sum_{A \in \mathcal{A}}(\operatorname{deg} A-1) f_{A}$ are proportional to one another.
|
| 76 |
+
|
RMM/md/en-2017-Solutions_RMM2017-1.md
ADDED
|
@@ -0,0 +1,149 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $9^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 1 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. (a) Prove that every positive integer $n$ can be written uniquely in the form
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
n=\sum_{j=1}^{2 k+1}(-1)^{j-1} 2^{m_{j}}
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
where $k \geq 0$ and $0 \leq m_{1}<m_{2}<\cdots<m_{2 k+1}$ are integers.
|
| 12 |
+
This number $k$ is called the weight of $n$.
|
| 13 |
+
(b) Find (in closed form) the difference between the number of positive integers at most $2^{2017}$ with even weight and the number of positive integers at most $2^{2017}$ with odd weight.
|
| 14 |
+
|
| 15 |
+
## Vjekoslav Kovač, Croatia
|
| 16 |
+
|
| 17 |
+
Solution. (a) We show by induction on the integer $M \geq 0$ that every integer $n$ in the range $-2^{M}+1$ through $2^{M}$ can uniquely be written in the form $n=\sum_{j=1}^{\ell}(-1)^{j-1} 2^{m_{j}}$ for some integers $\ell \geq 0$ and $0 \leq m_{1}<m_{2}<\cdots<m_{\ell} \leq M$ (empty sums are 0 ); moreover, in this unique representation $\ell$ is odd if $n>0$, and even if $n \leq 0$. The integer $w(n)=\lfloor\ell / 2\rfloor$ is called the weight of $n$.
|
| 18 |
+
|
| 19 |
+
Existence once proved, uniqueness follows from the fact that there are as many such representations as integers in the range $-2^{M}+1$ through $2^{M}$, namely, $2^{M+1}$.
|
| 20 |
+
|
| 21 |
+
To prove existence, notice that the base case $M=0$ is clear, so let $M \geq 1$ and let $n$ be an integer in the range $-2^{M}+1$ through $2^{M}$.
|
| 22 |
+
|
| 23 |
+
If $-2^{M}+1 \leq n \leq-2^{M-1}$, then $1 \leq n+2^{M} \leq 2^{M-1}$, so $n+2^{M}=\sum_{j=1}^{2 k+1}(-1)^{j-1} 2^{m_{j}}$ for some integers $k \geq 0$ and $0 \leq m_{1}<\cdots<m_{2 k+1} \leq M-1$ by the induction hypothesis, and $n=\sum_{j=1}^{2 k+2}(-1)^{j-1} 2^{m_{j}}$, where $m_{2 k+2}=M$.
|
| 24 |
+
|
| 25 |
+
The case $-2^{M-1}+1 \leq n \leq 2^{M-1}$ is covered by the induction hypothesis.
|
| 26 |
+
Finally, if $2^{M-1}+1 \leq n \leq 2^{M}$, then $-2^{M-1}+1 \leq n-2^{M} \leq 0$, so $n-2^{M}=\sum_{j=1}^{2 k}(-1)^{j-1} 2^{m_{j}}$ for some integers $k \geq 0$ and $0 \leq m_{1}<\cdots<m_{2 k} \leq M-1$ by the induction hypothesis, and $n=\sum_{j=1}^{2 k+1}(-1)^{j-1} 2^{m_{j}}$, where $m_{2 k+1}=M$.
|
| 27 |
+
(b) First Approach. Let $M \geq 0$ be an integer. The solution for part (a) shows that the number of even (respectively, odd) weight integers in the range 1 through $2^{M}$ coincides with the number of subsets in $\{0,1,2, \ldots, M\}$ whose cardinality has remainder 1 (respectively, 3) modulo 4. Therefore, the difference of these numbers is
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\sum_{k=0}^{\lfloor M / 2\rfloor}(-1)^{k}\binom{M+1}{2 k+1}=\frac{(1+\mathrm{i})^{M+1}-(1-\mathrm{i})^{M+1}}{2 \mathrm{i}}=2^{(M+1) / 2} \sin \frac{(M+1) \pi}{4}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
where $\mathrm{i}=\sqrt{-1}$ is the imaginary unit. Thus, the required difference is $2^{1009}$.
|
| 34 |
+
Second Approach. For every integer $M \geq 0$, let $A_{M}=\sum_{n=-2^{M}+1}^{0}(-1)^{w(n)}$ and let $B_{M}=$ $\sum_{n=1}^{2^{M}}(-1)^{w(n)}$; thus, $B_{M}$ evaluates the difference of the number of even weight integers in the range 1 through $2^{M}$ and the number of odd weight integers in that range.
|
| 35 |
+
|
| 36 |
+
Notice that
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
w(n)= \begin{cases}w\left(n+2^{M}\right)+1 & \text { if }-2^{M}+1 \leq n \leq-2^{M-1} \\ w\left(n-2^{M}\right) & \text { if } 2^{M-1}+1 \leq n \leq 2^{M}\end{cases}
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
to get
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
\begin{aligned}
|
| 46 |
+
& A_{M}=-\sum_{n=-2^{M}+1}^{-2^{M-1}}(-1)^{w\left(n+2^{M}\right)}+\sum_{n=-2^{M-1}+1}^{0}(-1)^{w(n)}=-B_{M-1}+A_{M-1}, \\
|
| 47 |
+
& B_{M}=\sum_{n=1}^{2^{M-1}}(-1)^{w(n)}+\sum_{n=2^{M-1}+1}^{2^{M}}(-1)^{w\left(n-2^{M}\right)}=B_{M-1}+A_{M-1} .
|
| 48 |
+
\end{aligned}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Iteration yields
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\begin{aligned}
|
| 55 |
+
B_{M} & =A_{M-1}+B_{M-1}=\left(A_{M-2}-B_{M-2}\right)+\left(A_{M-2}+B_{M-2}\right)=2 A_{M-2} \\
|
| 56 |
+
& =2 A_{M-3}-2 B_{M-3}=2\left(A_{M-4}-B_{M-4}\right)-2\left(A_{M-4}+B_{M-4}\right)=-4 B_{M-4}
|
| 57 |
+
\end{aligned}
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Thus, $B_{2017}=(-4)^{504} B_{1}=2^{1008} B_{1}$; since $B_{1}=(-1)^{w(1)}+(-1)^{w(2)}=2$, it follows that $B_{2017}=$ $2^{1009}$ 。
|
| 61 |
+
|
| 62 |
+
Problem 2. Determine all positive integers $n$ satisfying the following condition: for every monic polynomial $P$ of degree at most $n$ with integer coefficients, there exists a positive integer $k \leq n$, and $k+1$ distinct integers $x_{1}, x_{2}, \ldots, x_{k+1}$ such that
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
P\left(x_{1}\right)+P\left(x_{2}\right)+\cdots+P\left(x_{k}\right)=P\left(x_{k+1}\right)
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
Semen Petrov, Russia
|
| 69 |
+
Note. A polynomial is monic if the coefficient of the highest power is one.
|
| 70 |
+
Solution. There is only one such integer, namely, $n=2$. In this case, if $P$ is a constant polynomial, the required condition is clearly satisfied; if $P=X+c$, then $P(c-1)+P(c+1)=$ $P(3 c)$; and if $P=X^{2}+q X+r$, then $P(X)=P(-X-q)$.
|
| 71 |
+
|
| 72 |
+
To rule out all other values of $n$, it is sufficient to exhibit a monic polynomial $P$ of degree at most $n$ with integer coefficients, whose restriction to the integers is injective, and $P(x) \equiv 1$ $(\bmod n)$ for all integers $x$. This is easily seen by reading the relation in the statement modulo $n$, to deduce that $k \equiv 1(\bmod n)$, so $k=1$, since $1 \leq k \leq n$; hence $P\left(x_{1}\right)=P\left(x_{2}\right)$ for some distinct integers $x_{1}$ and $x_{2}$, which contradicts injectivity.
|
| 73 |
+
|
| 74 |
+
If $n=1$, let $P=X$, and if $n=4$, let $P=X^{4}+7 X^{2}+4 X+1$. In the latter case, clearly, $P(x) \equiv 1(\bmod 4)$ for all integers $x$; and $P$ is injective on the integers, since $P(x)-P(y)=$ $(x-y)\left((x+y)\left(x^{2}+y^{2}+7\right)+4\right)$, and the absolute value of $(x+y)\left(x^{2}+y^{2}+7\right)$ is either 0 or at least 7 for integral $x$ and $y$.
|
| 75 |
+
|
| 76 |
+
Assume henceforth $n \geq 3, n \neq 4$, and let $f_{n}=(X-1)(X-2) \cdots(X-n)$. Clearly, $f_{n}(x) \equiv$ $0(\bmod n)$ for all integers $x$. If $n$ is odd, then $f_{n}$ is non-decreasing on the integers; and if, in addition, $n>3$, then $f_{n}(x) \equiv 0(\bmod n+1)$ for all integers $x$, since $f_{n}(0)=-n!=-1 \cdot 2 \cdot \ldots$. $\frac{n+1}{2} \cdots \cdot n \equiv 0(\bmod n+1)$.
|
| 77 |
+
|
| 78 |
+
Finally, let $P=f_{n}+n X+1$ if $n$ is odd, and let $P=f_{n-1}+n X+1$ if $n$ is even. In either case, $P$ is strictly increasing, hence injective, on the integers, and $P(x) \equiv 1(\bmod n)$ for all integers $x$.
|
| 79 |
+
|
| 80 |
+
Remark. The polynomial $P=f_{n}+n X+1$ works equally well for even $n>2$. To prove injectivity, notice that $P$ is strictly monotone, hence injective, on non-positive (respectively, positive) integers. Suppose, if possible, that $P(a)=P(b)$ for some integers $a \leq 0$ and $b>0$. Notice that $P(a) \geq P(0)=n!+1>n^{2}+1=P(n)$, since $n \geq 4$, to infer that $b \geq n+1$. It is therefore sufficient to show that $P(x)>P(n+1-x)>P(x-1)$ for all integers $x \geq n+1$. The former inequality is trivial, since $f_{n}(x)=f_{n}(n+1-x)$ for even $n$. For the latter, write
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\begin{aligned}
|
| 84 |
+
P(n+1-x)-P(x-1) & =(x-1) \cdots(x-n)-(x-2) \cdots(x-n-1)+n(n+2-2 x) \\
|
| 85 |
+
& =n((x-2) \cdots(x-n)+(n-2)-2(x-2)) \geq n(n-2)>0,
|
| 86 |
+
\end{aligned}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
since $(x-3) \cdots(x-n) \geq 2$.
|
| 90 |
+
|
| 91 |
+
Problem 3. Let $n$ be an integer greater than 1 and let $X$ be an $n$-element set. A non-empty collection of subsets $A_{1}, \ldots, A_{k}$ of $X$ is tight if the union $A_{1} \cup \cdots \cup A_{k}$ is a proper subset of $X$ and no element of $X$ lies in exactly one of the $A_{i}$ s. Find the largest cardinality of a collection of proper non-empty subsets of $X$, no non-empty subcollection of which is tight.
|
| 92 |
+
|
| 93 |
+
Note. A subset $A$ of $X$ is proper if $A \neq X$. The sets in a collection are assumed to be distinct. The whole collection is assumed to be a subcollection.
|
| 94 |
+
|
| 95 |
+
## Alexander Polyansky, Russia
|
| 96 |
+
|
| 97 |
+
Solution 1. (Ilya Bogdanov) The required maximum is $2 n-2$. To describe a ( $2 n-2$ )-element collection satisfying the required conditions, write $X=\{1,2, \ldots, n\}$ and set $B_{k}=\{1,2, \ldots, k\}$, $k=1,2, \ldots, n-1$, and $B_{k}=\{k-n+2, k-n+3, \ldots, n\}, k=n, n+1, \ldots, 2 n-2$. To show that no subcollection of the $B_{k}$ is tight, consider a subcollection $\mathcal{C}$ whose union $U$ is a proper subset of $X$, let $m$ be an element in $X \backslash U$, and notice that $\mathcal{C}$ is a subcollection of $\left\{B_{1}, \ldots, B_{m-1}, B_{m+n-1}, \ldots, B_{2 n-2}\right\}$, since the other $B$ 's are precisely those containing $m$. If $U$ contains elements less than $m$, let $k$ be the greatest such and notice that $B_{k}$ is the only member of $\mathcal{C}$ containing $k$; and if $U$ contains elements greater than $m$, let $k$ be the least such and notice that $B_{k+n-2}$ is the only member of $\mathcal{C}$ containing $k$. Consequently, $\mathcal{C}$ is not tight.
|
| 98 |
+
|
| 99 |
+
We now proceed to show by induction on $n \geq 2$ that the cardinality of a collection of proper non-empty subsets of $X$, no subcollection of which is tight, does not exceed $2 n-2$. The base case $n=2$ is clear, so let $n>2$ and suppose, if possible, that $\mathcal{B}$ is a collection of $2 n-1$ proper non-empty subsets of $X$ containing no tight subcollection.
|
| 100 |
+
|
| 101 |
+
To begin, notice that $\mathcal{B}$ has an empty intersection: if the members of $\mathcal{B}$ shared an element $x$, then $\mathcal{B}^{\prime}=\{B \backslash\{x\}: B \in \mathcal{B}, B \neq\{x\}\}$ would be a collection of at least $2 n-2$ proper non-empty subsets of $X \backslash\{x\}$ containing no tight subcollection, and the induction hypothesis would be contradicted.
|
| 102 |
+
|
| 103 |
+
Now, for every $x$ in $X$, let $\mathcal{B}_{x}$ be the (non-empty) collection of all members of $\mathcal{B}$ not containing $x$. Since no subcollection of $\mathcal{B}$ is tight, $\mathcal{B}_{x}$ is not tight, and since the union of $\mathcal{B}_{x}$ does not contain $x$, some $x^{\prime}$ in $X$ is covered by a single member of $\mathcal{B}_{x}$. In other words, there is a single set in $\mathcal{B}$ covering $x^{\prime}$ but not $x$. In this case, draw an arrow from $x$ to $x^{\prime}$. Since there is at least one arrow from each $x$ in $X$, some of these arrows form a (minimal) cycle $x_{1} \rightarrow x_{2} \rightarrow \cdots \rightarrow x_{k} \rightarrow x_{k+1}=x_{1}$ for some suitable integer $k \geq 2$. Let $A_{i}$ be the unique member of $\mathcal{B}$ containing $x_{i+1}$ but not $x_{i}$, and let $X^{\prime}=\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}$.
|
| 104 |
+
|
| 105 |
+
Remove $A_{1}, A_{2}, \ldots, A_{k}$ from $\mathcal{B}$ to obtain a collection $\mathcal{B}^{\prime}$ each member of which either contains or is disjoint from $X^{\prime}$ : for if a member $B$ of $\mathcal{B}^{\prime}$ contained some but not all elements of $X^{\prime}$, then $B$ should contain $x_{i+1}$ but not $x_{i}$ for some $i$, and $B=A_{i}$, a contradiction. This rules out the case $k=n$, for otherwise $\mathcal{B}=\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}$, so $|\mathcal{B}|<2 n-1$.
|
| 106 |
+
|
| 107 |
+
To rule out the case $k<n$, consider an extra element $x^{*}$ outside $X$ and let
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\mathcal{B}^{*}=\left\{B: B \in \mathcal{B}^{\prime}, B \cap X^{\prime}=\varnothing\right\} \cup\left\{\left(B \backslash X^{\prime}\right) \cup\left\{x^{*}\right\}: B \in \mathcal{B}^{\prime}, X^{\prime} \subseteq B\right\} ;
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
thus, in each member of $\mathcal{B}^{\prime}$ containing $X^{\prime}$, the latter is collapsed to singleton $x^{*}$. Notice that $\mathcal{B}^{*}$ is a collection of proper non-empty subsets of $X^{*}=\left(X \backslash X^{\prime}\right) \cup\left\{x^{*}\right\}$, no subcollection of which is tight. By the induction hypothesis, $\left|\mathcal{B}^{\prime}\right|=\left|\mathcal{B}^{*}\right| \leq 2\left|X^{*}\right|-2=2(n-k)$, so $|\mathcal{B}| \leq 2(n-k)+k=$ $2 n-k<2 n-1$, a final contradiction.
|
| 114 |
+
|
| 115 |
+
Solution 2. Proceed again by induction on $n$ to show that the cardinality of a collection of proper non-empty subsets of $X$, no subcollection of which is tight, does not exceed $2 n-2$.
|
| 116 |
+
|
| 117 |
+
Consider any collection $\mathcal{B}$ of proper non-empty subsets of $X$ with no tight subcollection (we call such collection good). Assume that there exist $M, N \in \mathcal{B}$ such that $M \cup N$ is distinct from $M, N$, and $X$. In this case, we will show how to modify $\mathcal{B}$ so that it remains good, contains the same number of sets, but the total number of elements in the sets of $\mathcal{B}$ increases.
|
| 118 |
+
|
| 119 |
+
Consider a maximal (relative to set-theoretic inclusion) subcollection $\mathcal{C} \subseteq \mathcal{B}$ such that the set $C=\bigcup_{A \in \mathcal{C}} A$ is distinct from $X$ and from all members of $\mathcal{C}$. Notice here that the union of any subcollection $\mathcal{D} \subset \mathcal{B}$ cannot coincide with any $K \in \mathcal{B} \backslash \mathcal{D}$, otherwise $\{K\} \cup \mathcal{D}$ would be tight. Surely, $\mathcal{C}$ exists (since $\{M, N\}$ is an example of a collection satisfying the requirements on $\mathcal{C}$, except for maximality); moreover, $C \notin \mathcal{B}$ by the above remark.
|
| 120 |
+
|
| 121 |
+
Since $C \neq X$, there exists an $L \in \mathcal{C}$ and $x \in L$ such that $L$ is the unique set in $\mathcal{C}$ containing $x$. Now replace in $\mathcal{B}$ the set $L$ by $C$ in order to obtain a new collection $\mathcal{B}^{\prime}$ (then $\left.\left|\mathcal{B}^{\prime}\right|=|\mathcal{B}|\right)$. We claim that $\mathcal{B}^{\prime}$ is good.
|
| 122 |
+
|
| 123 |
+
Assume, to the contrary, that $\mathcal{B}^{\prime}$ contained a tight subcollection $\mathcal{T}$; clearly, $C \in \mathcal{T}$, otherwise $\mathcal{B}$ is not good. If $\mathcal{T} \subseteq \mathcal{C} \cup\{C\}$, then $C$ is the unique set in $\mathcal{T}$ containing $x$ which is impossible. Therefore, there exists $P \in \mathcal{T} \backslash(\mathcal{C} \cup\{C\})$. By maximality of $\mathcal{C}$, the collection $\mathcal{C} \cup\{P\}$ does not satisfy the requirements imposed on $\mathcal{C}$; since $P \cup C \neq X$, this may happen only if $C \cup P=P$, i.e., if $C \subset P$. But then $\mathcal{G}=(\mathcal{T} \backslash\{C\}) \cup \mathcal{C}$ is a tight subcollection in $\mathcal{B}$ : all elements of $C$ are covered by $\mathcal{G}$ at least twice (by $P$ and an element of $\mathcal{C}$ ), and all the rest elements are covered by $\mathcal{G}$ the same number of times as by $\mathcal{T}$. A contradiction. Thus $\mathcal{B}^{\prime}$ is good.
|
| 124 |
+
|
| 125 |
+
Such modifications may be performed finitely many times, since the total number of elements of sets in $\mathcal{B}$ increases. Thus, at some moment we arrive at a good collection $\mathcal{B}$ for which the procedure no longer applies. This means that for every $M, N \in \mathcal{B}$, either $M \cup N=X$ or one of them is contained in the other.
|
| 126 |
+
|
| 127 |
+
Now let $M$ be a minimal (with respect to inclusion) set in $\mathcal{B}$. Then each set in $\mathcal{B}$ either contains $M$ or forms $X$ in union with $M$ (i.e., contains $X \backslash M$ ). Now one may easily see that the two collections
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\mathcal{B}_{+}=\{A \backslash M: A \in \mathcal{B}, M \subset A, A \neq M\}, \quad \mathcal{B}_{-}=\{A \cap M: A \in \mathcal{B}, X \backslash M \subset A, A \neq X \backslash M\}
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
are good as collections of subsets of $X \backslash M$ and $M$, respectively; thus, by the induction hypothesis, we have $\left|\mathcal{B}_{+}\right|+\left|\mathcal{B}_{-}\right| \leq 2 n-4$.
|
| 134 |
+
|
| 135 |
+
Finally, each set $A \in \mathcal{B}$ either produces a set in one of the two new collections, or coincides with $M$ or $X \backslash M$. Thus $|\mathcal{B}| \leq\left|\mathcal{B}_{+}\right|+\left|\mathcal{B}_{-}\right|+2 \leq 2 n-2$, as required.
|
| 136 |
+
|
| 137 |
+
Solution 3. We provide yet another proof of the estimate $|\mathcal{B}| \leq 2 n-2$, using the notion of a good collection from Solution 2. Arguing indirectly, we assume that there exists a good collection $\mathcal{B}$ with $|\mathcal{B}| \geq 2 n-1$, and choose one such for the minimal possible value of $n$. Clearly, $n>2$.
|
| 138 |
+
|
| 139 |
+
Firstly, we perform a different modification of $\mathcal{B}$. Choose any $x \in X$, and consider the subcollection $\mathcal{B}_{x}=\{B: B \in \mathcal{B}, x \notin B\}$. By our assumption, $\mathcal{B}_{x}$ is not tight. As the union of sets in $\mathcal{B}_{x}$ is distinct from $X$, either this collection is empty, or there exists an element $y \in X$ contained in a unique member $A_{x}$ of $\mathcal{B}_{x}$. In the former case, we add the set $B_{x}=X \backslash\{x\}$ to $\mathcal{B}$, and in the latter we replace $A_{x}$ by $B_{x}$, to form a new collection $\mathcal{B}^{\prime}$. (Notice that if $B_{x} \in \mathcal{B}$, then $B_{x} \in \mathcal{B}_{x}$ and $y \in B_{x}$, so $B_{x}=A_{x}$.)
|
| 140 |
+
|
| 141 |
+
We claim that the collection $\mathcal{B}^{\prime}$ is also good. Indeed, if $\mathcal{B}^{\prime}$ has a tight subcollection $\mathcal{T}$, then $B_{x}$ should lie in $\mathcal{T}$. Then, as the union of the sets in $\mathcal{T}$ is distinct from $X$, we should have $\mathcal{T} \subseteq \mathcal{B}_{x} \cup\left\{B_{x}\right\}$. But in this case an element $y$ is contained in a unique member of $\mathcal{T}$, namely $B_{x}$, so $\mathcal{T}$ is not tight - a contradiction.
|
| 142 |
+
|
| 143 |
+
Perform this procedure for every $x \in X$, to get a good collection $\mathcal{B}$ containing the sets $B_{x}=X \backslash\{x\}$ for all $x \in X$. Consider now an element $x \in X$ such that $\left|\mathcal{B}_{x}\right|$ is maximal. As we have mentioned before, there exists an element $y \in X$ belonging to a unique member (namely, $B_{x}$ ) of $\mathcal{B}_{x}$. Thus, $\mathcal{B}_{x} \backslash\left\{B_{x}\right\} \subset \mathcal{B}_{y}$; also, $B_{y} \in \mathcal{B}_{y} \backslash \mathcal{B}_{x}$. Thus we get $\left|\mathcal{B}_{y}\right| \geq\left|\mathcal{B}_{x}\right|$, which by the maximality assumption yields the equality, which in turn means that $\mathcal{B}_{y}=\left(\mathcal{B}_{x} \backslash\left\{B_{x}\right\}\right) \cup\left\{B_{y}\right\}$.
|
| 144 |
+
|
| 145 |
+
Therefore, each set in $\mathcal{B} \backslash\left\{B_{x}, B_{y}\right\}$ contains either both $x$ and $y$, or none of them. Collapsing $\{x, y\}$ to singleton $x^{*}$, we get a new collection of $|\mathcal{B}|-2$ subsets of $(X \backslash\{x, y\}) \cup\left\{x^{*}\right\}$ containing no tight subcollection. This contradicts minimality of $n$.
|
| 146 |
+
|
| 147 |
+
Remarks. 1. Removal of the condition that subsets be proper would only increase the maximum by 1. The 'non-emptiness' condition could also be omitted, since the empty set forms a tight collection by itself, but the argument is a bit too formal to be considered.
|
| 148 |
+
2. There are many different examples of good collections of $2 n-2$ sets. E.g., applying the algorithm from the first part of Solution 2 to the example shown in Solution 1, one may get the following example: $B_{k}=\{1,2, \ldots, k\}, k=1,2, \ldots, n-1$, and $B_{k}=X \backslash\{k-n+1\}$, $k=n, n+1, \ldots, 2 n-2$.
|
| 149 |
+
|
RMM/md/en-2017-Solutions_RMM2017-2.md
ADDED
|
@@ -0,0 +1,190 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $9^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 2 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 4. In the Cartesian plane, let $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ be the graphs of the quadratic functions $f_{1}(x)=p_{1} x^{2}+q_{1} x+r_{1}$ and $f_{2}(x)=p_{2} x^{2}+q_{2} x+r_{2}$, where $p_{1}>0>p_{2}$. The graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ cross at distinct points $A$ and $B$. The four tangents to $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ at $A$ and $B$ form a convex quadrilateral which has an inscribed circle. Prove that the graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ have the same axis of symmetry.
|
| 6 |
+
|
| 7 |
+
## Alexey Zaslavsky, Russia
|
| 8 |
+
|
| 9 |
+
Solution 1. Let $\mathcal{A}_{i}$ and $\mathcal{B}_{i}$ be the tangents to $\mathcal{G}_{i}$ at $A$ and $B$, respectively, and let $C_{i}=\mathcal{A}_{i} \cap \mathcal{B}_{i}$. Since $f_{1}(x)$ is convex and $f_{2}(x)$ is concave, the convex quadrangle formed by the four tangents is exactly $A C_{1} B C_{2}$.
|
| 10 |
+
Lemma. If $C A$ and $C B$ are the tangents drawn from a point $C$ to the graph $\mathcal{G}$ of a quadratic trinomial $f(x)=p x^{2}+q x+r, A, B \in \mathcal{G}, A \neq B$, then the abscissa of $C$ is the arithmetic mean of the abscissae of $A$ and $B$.
|
| 11 |
+
Proof. Assume, without loss of generality, that $C$ is at the origin, so the equations of the two tangents have the form $y=k_{a} x$ and $y=k_{b} x$. Next, the abscissae $x_{A}$ and $x_{B}$ of the tangency points $A$ and $B$, respectively, are multiple roots of the polynomials $f(x)-k_{a} x$ and $f(x)-k_{b} x$, respectively. By the Vieta theorem, $x_{A}^{2}=r / p=x_{B}^{2}$, so $x_{A}=-x_{B}$, since the case $x_{A}=x_{B}$ is ruled out by $A \neq B$.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
The Lemma shows that the line $C_{1} C_{2}$ is parallel to the $y$-axis and the points $A$ and $B$ are equidistant from this line.
|
| 15 |
+
|
| 16 |
+
Suppose, if possible, that the incentre $O$ of the quadrangle $A C_{1} B C_{2}$ does not lie on the line $C_{1} C_{2}$. Assume, without loss of generality, that $O$ lies inside the triangle $A C_{1} C_{2}$ and let $A^{\prime}$ be the reflection of $A$ in the line $C_{1} C_{2}$. Then the ray $C_{i} B$ emanating from $C_{i}$ lies inside the angle $A C_{i} A^{\prime}$, so $B$ lies inside the quadrangle $A C_{1} A^{\prime} C_{2}$, whence $A$ and $B$ are not equidistant from $C_{1} C_{2}-$ a contradiction.
|
| 17 |
+
|
| 18 |
+
Thus $O$ lies on $C_{1} C_{2}$, so the lines $A C_{i}$ and $B C_{i}$ are reflections of one another in the line $C_{1} C_{2}$, and $B=A^{\prime}$. Hence $y_{A}=y_{B}$, and since $f_{i}(x)=y_{A}+p_{i}\left(x-x_{A}\right)\left(x-x_{B}\right)$, the line $C_{1} C_{2}$ is the axis of symmetry of both parabolas, as required.
|
| 19 |
+
|
| 20 |
+
Solution 2. Use the standard equation of a tangent to a smooth curve in the plane, to deduce that the tangents at two distinct points $A$ and $B$ on the parabola of equation $y=p x^{2}+q x+r$,
|
| 21 |
+
$p \neq 0$, meet at some point $C$ whose coordinates are
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
x_{C}=\frac{1}{2}\left(x_{A}+x_{B}\right) \quad \text { and } \quad y_{C}=p x_{A} x_{B}+q \cdot \frac{1}{2}\left(x_{A}+x_{B}\right)+r .
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
Usage of the standard formula for Euclidean distance yields
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
C A=\frac{1}{2}\left|x_{B}-x_{A}\right| \sqrt{1+\left(2 p x_{A}+q\right)^{2}} \quad \text { and } \quad C B=\frac{1}{2}\left|x_{B}-x_{A}\right| \sqrt{1+\left(2 p x_{B}+q\right)^{2}},
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
so, after obvious manipulations,
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
C B-C A=\frac{2 p\left(x_{B}-x_{A}\right)\left|x_{B}-x_{A}\right|\left(p\left(x_{A}+x_{B}\right)+q\right)}{\sqrt{1+\left(2 p x_{A}+q\right)^{2}}+\sqrt{1+\left(2 p x_{B}+q\right)^{2}}}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
Now, write the condition in the statement in the form $C_{1} B-C_{1} A=C_{2} B-C_{2} A$, apply the above formula and clear common factors to get
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\frac{p_{1}\left(p_{1}\left(x_{A}+x_{B}\right)+q_{1}\right)}{\sqrt{1+\left(2 p_{1} x_{A}+q_{1}\right)^{2}}+\sqrt{1+\left(2 p_{1} x_{B}+q_{1}\right)^{2}}}=\frac{p_{2}\left(p_{2}\left(x_{A}+x_{B}\right)+q_{2}\right)}{\sqrt{1+\left(2 p_{2} x_{A}+q_{2}\right)^{2}}+\sqrt{1+\left(2 p_{2} x_{B}+q_{2}\right)^{2}}}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Next, use the fact that $x_{A}$ and $x_{B}$ are the solutions of the quadratic equation $\left(p_{1}-p_{2}\right) x^{2}+$ $\left(q_{1}-q_{2}\right) x+r_{1}-r_{2}=0$, so $x_{A}+x_{B}=-\left(q_{1}-q_{2}\right) /\left(p_{1}-p_{2}\right)$, to obtain
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\frac{p_{1}\left(p_{1} q_{2}-p_{2} q_{1}\right)}{\sqrt{1+\left(2 p_{1} x_{A}+q_{1}\right)^{2}}+\sqrt{1+\left(2 p_{1} x_{B}+q_{1}\right)^{2}}}=\frac{p_{2}\left(p_{1} q_{2}-p_{2} q_{1}\right)}{\sqrt{1+\left(2 p_{2} x_{A}+q_{2}\right)^{2}}+\sqrt{1+\left(2 p_{2} x_{B}+q_{2}\right)^{2}}} .
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Finally, since $p_{1} p_{2}<0$ and the denominators above are both positive, the last equality forces $p_{1} q_{2}-p_{2} q_{1}=0$; that is, $q_{1} / p_{1}=q_{2} / p_{2}$, so the two parabolas have the same axis.
|
| 52 |
+
|
| 53 |
+
Remarks. The are, of course, several different proofs of the Lemma in Solution 1 - in particular, computational. Another argument relies on the following consequence of focal properties: The tangents to a parabola at two points meet at the circumcentre of the triangle formed by the focus and the orthogonal projections of those points on the directrix. Since the directrix of the parabola in the lemma is parallel to the axis of abscissae, the conclusion follows.
|
| 54 |
+
|
| 55 |
+
Problem 5. Fix an integer $n \geq 2$. An $n \times n$ sieve is an $n \times n$ array with $n$ cells removed so that exactly one cell is removed from every row and every column. A stick is a $1 \times k$ or $k \times 1$ array for any positive integer $k$. For any sieve $A$, let $m(A)$ be the minimal number of sticks required to partition $A$. Find all possible values of $m(A)$, as $A$ varies over all possible $n \times n$ sieves.
|
| 56 |
+
|
| 57 |
+
Palmer Mebane and Nikolai Beluhov
|
| 58 |
+
Solution 1. Given $A, m(A)=2 n-2$, and it is achieved, for instance, by dissecting $A$ along all horizontal (or vertical) grid lines. It remains to prove that $m(A) \geq 2 n-2$ for every $A$.
|
| 59 |
+
|
| 60 |
+
By holes we mean the cells which are cut out from the board. The cross of a hole in $A$ is the union of the row and the column through that hole.
|
| 61 |
+
|
| 62 |
+
Arguing indirectly, consider a dissection of $A$ into $2 n-3$ or fewer sticks. Horizontal sticks are all labelled $h$, and vertical sticks are labelled $v ; 1 \times 1$ sticks are both horizontal and vertical, and labelled arbitrarily. Each cell of $A$ inherits the label of the unique containing stick.
|
| 63 |
+
|
| 64 |
+
Assign each stick in the dissection to the cross of the unique hole on its row, if the stick is horizontal; on its column, if the stick is vertical.
|
| 65 |
+
|
| 66 |
+
Since there are at most $2 n-3$ sticks and exactly $n$ crosses, there are two crosses each of which is assigned to at most one stick in the dissection. Let the crosses be $c$ and $d$, centred at $a=\left(x_{a}, y_{a}\right)$ and $b=\left(x_{b}, y_{b}\right)$, respectively, and assume, without loss of generality, $x_{a}<x_{b}$ and $y_{a}<y_{b}$. The sticks covering the cells $\left(x_{a}, y_{b}\right)$ and $\left(x_{b}, y_{a}\right)$ have like labels, for otherwise one of the two crosses would be assigned to at least two sticks. Say the common label is $v$, so each of $c$ and $d$ contains a stick covering one of those two cells. It follows that the lower (respectively, upper) arm of $c$ (respectively, $d$ ) is all- $h$, and the horizontal arms of both crosses are all- $v$, as illustrated below.
|
| 67 |
+
|
| 68 |
+
|
| 69 |
+
Each of the rows between the rows of $a$ and $b$, that is, rows $y_{a}+1, y_{a}+2, \ldots, y_{b}-1$, contains a hole. The column of each such hole contains at least two $v$-sticks. All other columns contain at least one $v$-stick each. In addition, all rows below $a$ and all rows above $b$ contain at least one $h$-stick each. This amounts to a total of at least $2\left(y_{b}-y_{a}-1\right)+\left(n-y_{b}+y_{a}+1\right)+\left(n-y_{b}\right)+\left(y_{a}-1\right)=2 n-2$ sticks. A contradiction.
|
| 70 |
+
|
| 71 |
+
Remark. One may find a different argument finishing the solution. Since $c$ and $d$ are proven to contain one stick each, there is a third cross $e$ centred at $\left(x_{*}, y_{*}\right)$ also containing at most one stick. It meets the horizontal arms of $c$ and $d$ at two $v$-cells, so all the cells where two of the three crosses meet are labelled with $v$. Now, assuming (without loss of generality) that $y_{a}<y_{*}<y_{b}$, we obtain that both vertical arms of $e$ contain $v$-cells, so $e$ is assigned to two different $v$-sticks. A contradiction.
|
| 72 |
+
|
| 73 |
+
Solution 2. (Ilya Bogdanov) We provide a different proof that $m(A) \geq 2 n-2$.
|
| 74 |
+
|
| 75 |
+
Call a stick vertical if it is contained in some column, and horizontal if it is contained in some row; $1 \times 1$ sticks may be called arbitrarily, but any of them is supposed to have only one direction. Assign to each vertical/horizontal stick the column/row it is contained in. If each row and each column is assigned to some stick, then there are at least $2 n$ sticks, which is even more than we want. Thus we assume, without loss of generality, that some exceptional row $R$ is not assigned to any stick. This means that all $n-1$ existing cells in $R$ belong to $n-1$ distinct vertical sticks; call these sticks central.
|
| 76 |
+
|
| 77 |
+
Now we mark $n-1$ cells on the board in the following manner. ( $\downarrow$ ) For each hole $c$ below $R$, we mark the cell just under $c$; $(\uparrow)$ for each hole $c$ above $R$, we mark the cell just above $c$; and $(\bullet)$ for the hole $r$ in $R$, we mark both the cell just above it and just below it. We have described $n+1$ cells, but exactly two of them are out of the board; so $n-1$ cells are marked within the board. A sample marking is shown in the figure below, where the marked cells are crossed.
|
| 78 |
+

|
| 79 |
+
|
| 80 |
+
Notice that all the marked cells lie in different rows, and all of them are marked in different columns, except for those two marked for $(\bullet)$; but the latter two have a hole $r$ between them. So no two marked cells may belong to the same stick. Moreover, none of them lies in a central stick, since the marked cells are separated from $R$ by the holes. Thus the marked cells should be covered by $n-1$ different sticks (call them border) which are distinct from the central sticks. This shows that there are at least $(n-1)+(n-1)=2 n-2$ distinct sticks, as desired.
|
| 81 |
+
|
| 82 |
+
Solution 3. In order to prove $m(A) \geq 2 n-2$, it suffices to show that there are $2 n-2$ cells in $A$, no two of which may be contained in the same stick.
|
| 83 |
+
|
| 84 |
+
To this end, consider the bipartite graph $G$ with parts $G_{h}$ and $G_{v}$, where the vertices in $G_{h}$ (respectively, $G_{v}$ ) are the $2 n-2$ maximal sticks $A$ is dissected into by all horizontal (respectively, vertical) grid lines, two sticks being joined by an edge in $G$ if and only if they share a cell.
|
| 85 |
+
|
| 86 |
+
We show that $G$ admits a perfect matching by proving that it fulfils the condition in Hall's theorem; the $2 n-2$ cells corresponding to the edges of this matching form the desired set. It is sufficient to show that every subset $S$ of $G_{h}$ has at least $|S|$ neighbours (in $G_{v}$, of course).
|
| 87 |
+
|
| 88 |
+
Let $L$ be the set of all sticks in $S$ that contain a cell in the leftmost column of $A$, and let $R$ be the set of all sticks in $S$ that contain a cell in the rightmost column of $A$; let $\ell$ be the length of the longest stick in $L$ (zero if $L$ is empty), and let $r$ be the length of the longest stick in $R$ (zero if $R$ is empty).
|
| 89 |
+
|
| 90 |
+
Since every row of $A$ contains exactly one hole, $L$ and $R$ partition $S$; and since every column of $A$ contains exactly one hole, neither $L$ nor $R$ contains two sticks of the same size, so $\ell \geq|L|$ and $r \geq|R|$, whence $\ell+r \geq|L|+|R|=|S|$.
|
| 91 |
+
|
| 92 |
+
If $\ell+r \leq n$, we are done, since there are at least $\ell+r \geq|S|$ vertical sticks covering the cells of the longest sticks in $L$ and $R$. So let $\ell+r>n$, in which case the sticks in $S$ span all $n$ columns, and notice that we are again done if $|S| \leq n$, to assume further $|S|>n$.
|
| 93 |
+
|
| 94 |
+
Let $S^{\prime}=G_{h} \backslash S$, let $T$ be set of all neighbours of $S$, and let $T^{\prime}=G_{v} \backslash T$. Since the sticks in $S$ span all $n$ columns, $|T| \geq n$, so $\left|T^{\prime}\right| \leq n-2$. Transposition of the above argument (replace $S$ by $T^{\prime}$, shows that $\left|T^{\prime}\right| \leq\left|S^{\prime}\right|$, so $|S| \leq|T|$.
|
| 95 |
+
Remark. Here is an alternative argument for $s=|S|>n$. Add to $S$ two empty sticks formally present to the left of the leftmost hole and to the right of the rightmost one. Then there are at
|
| 96 |
+
least $s-n+2$ rows containing two sticks from $S$, so two of them are separated by at least $s-n$ other rows. Each hole in those $s-n$ rows separates two vertical sticks from $G_{v}$ both of which are neighbours of $S$. Thus the vertices of $S$ have at least $n+(s-n)$ neighbours.
|
| 97 |
+
|
| 98 |
+
Solution 4. Yet another proof of the estimate $m(A) \geq 2 n-2$. We use the induction on $n$. Now we need the base cases $n=2,3$ which can be completed by hands.
|
| 99 |
+
|
| 100 |
+
Assume now that $n>3$ and consider any dissection of $A$ into sticks. Define the cross of a hole as in Solution 1, and notice that each stick is contained in some cross. Thus, if the dissection contains more than $n$ sticks, then there exists a cross containing at least two sticks. In this case, remove this cross from the sieve to obtain an $(n-1) \times(n-1)$ sieve. The dissection of the original sieve induces a dissection of the new array: even if a stick is partitioned into two by the removed cross, then the remaining two parts form a stick in the new array. After this operation has been performed, the number of sticks decreases by at least 2, and by the induction hypothesis the number of sticks in the new dissection is at least $2 n-4$. Hence, the initial dissection contains at least $(2 n-4)+2=2 n-2$ sticks, as required.
|
| 101 |
+
|
| 102 |
+
It remains to rule out the case when the dissection contains at most $n$ sticks. This can be done in many ways, one of which is removal a cross containing some stick. The resulting dissection of an $(n-1) \times(n-1)$ array contains at most $n-1$ sticks, which is impossible by the induction hypothesis since $n-1<2(n-1)-2$.
|
| 103 |
+
|
| 104 |
+
Remark. The idea of removing a cross containing at least two sticks arises naturally when one follows an inductive approach. But it is much trickier to finish the solution using this approach, unless one starts to consider removing each cross instead of removing a specific one.
|
| 105 |
+
|
| 106 |
+
Problem 6. Let $A B C D$ be any convex quadrilateral and let $P, Q, R, S$ be points on the segments $A B, B C, C D$, and $D A$, respectively. It is given that the segments $P R$ and $Q S$ dissect $A B C D$ into four quadrilaterals, each of which has perpendicular diagonals. Show that the points $P, Q, R, S$ are concyclic.
|
| 107 |
+
|
| 108 |
+
NikOlai Beluhov
|
| 109 |
+
Solution 1. We start with a lemma which holds even in a more general setup.
|
| 110 |
+
Lemma 1. Let $P Q R S$ be a convex quadrangle whose diagonals meet at $O$. Let $\omega_{1}$ and $\omega_{2}$ be the circles on diameters $P Q$ and $R S$, respectively, and let $\ell$ be their radical axis. Finally, choose the points $A, B$, and $C$ outside this quadrangle so that: the point $P$ (respectively, $Q$ ) lies on the segment $A B$ (respectively, $B C$ ); and $A O \perp P S, B O \perp P Q$, and $C O \perp Q R$. Then the three lines $A C, P Q$, and $\ell$ are concurrent or parallel.
|
| 111 |
+
|
| 112 |
+
Proof. Assume first that the lines $P R$ and $Q S$ are not perpendicular. Let $H_{1}$ and $H_{2}$ be the orthocentres of the triangles $O S P$ and $O Q R$, respectively; notice that $H_{1}$ and $H_{2}$ do not coincide.
|
| 113 |
+
|
| 114 |
+
Since $H_{1}$ is the radical centre of the circles on diameters $R S, S P$, and $P Q$, it lies on $\ell$. Similarly, $H_{2}$ lies on $\ell$, so the lines $H_{1} H_{2}$ and $\ell$ coincide.
|
| 115 |
+
|
| 116 |
+
The corresponding sides of the triangles $A P H_{1}$ and $C Q H_{2}$ meet at $O, B$, and the orthocentre of the triangle $O P Q$ (which lies on $O B$ ). By Desargues' theorem, the lines $A C, P Q$ and $\ell$ are concurrent or parallel.
|
| 117 |
+
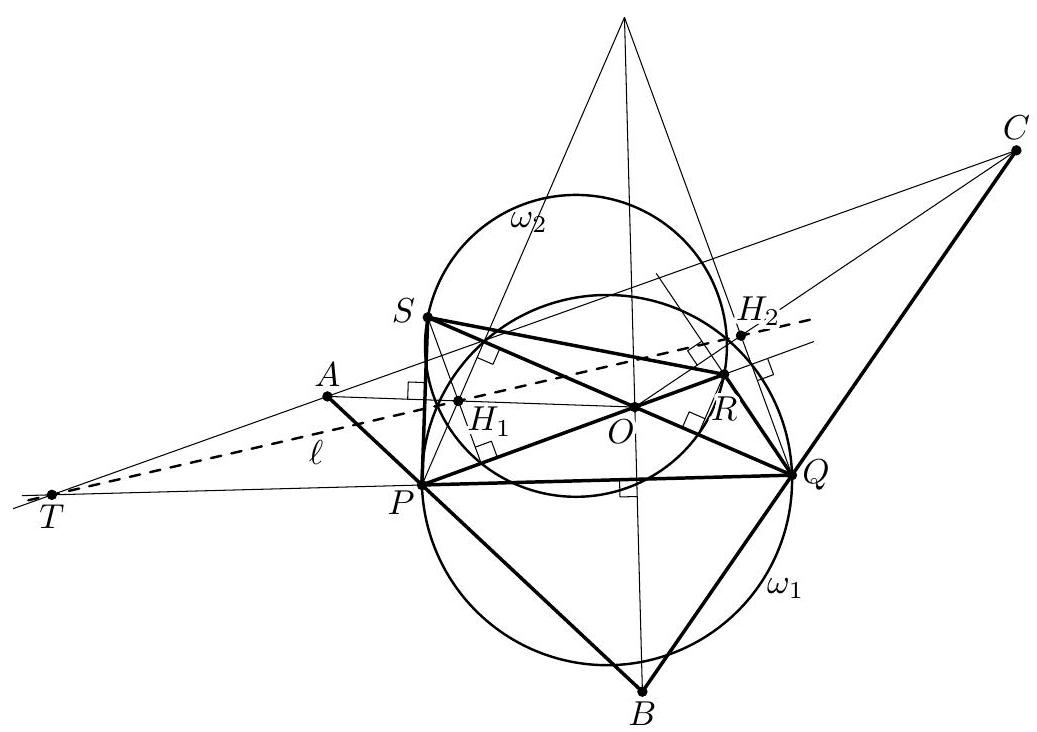
|
| 118 |
+
|
| 119 |
+
The case when $P R \perp Q S$ may be considered as a limit case, since the configuration in the statement of the lemma allows arbitrarily small perturbations. The lemma is proved.
|
| 120 |
+
|
| 121 |
+
Back to the problem, let the segments $P R$ and $Q S$ cross at $O$, let $\omega_{1}$ and $\omega_{2}$ be the circles on diameters $P Q$ and $R S$, respectively, and let $\ell$ be their radical axis. By the Lemma, the three lines $A C$, $\ell$, and $P Q$ are concurrent or parallel, and similarly so are the three lines $A C, \ell$, and $R S$. Thus, if the lines $A C$ and $\ell$ are distinct, all four lines are concurrent or pairwise parallel.
|
| 122 |
+
|
| 123 |
+
This is clearly the case when the lines $P S$ and $Q R$ are not parallel (since $\ell$ crosses $O A$ and $O C$ at the orthocentres of $O S P$ and $O Q R$, these orthocentres being distinct from $A$ and $C$ ). In this case, denote the concurrency point by $T$. If $T$ is not ideal, then we have $T P \cdot T Q=T R \cdot T S$ (as $T \in \ell$ ), so $P Q R S$ is cyclic. If $T$ is ideal (i.e., all four lines are parallel), then the segments $P Q$ and $R S$ have the same perpendicular bisector (namely, the line of centers of $\omega_{1}$ and $\omega_{2}$ ), and $P Q R S$ is cyclic again.
|
| 124 |
+
|
| 125 |
+
Assume now $P S$ and $Q R$ parallel. By symmetry, $P Q$ and $R S$ may also be assumed parallel: otherwise, the preceding argument goes through after relabelling. In this case, we need to prove that the parallelogram $P Q R S$ is a rectangle.
|
| 126 |
+
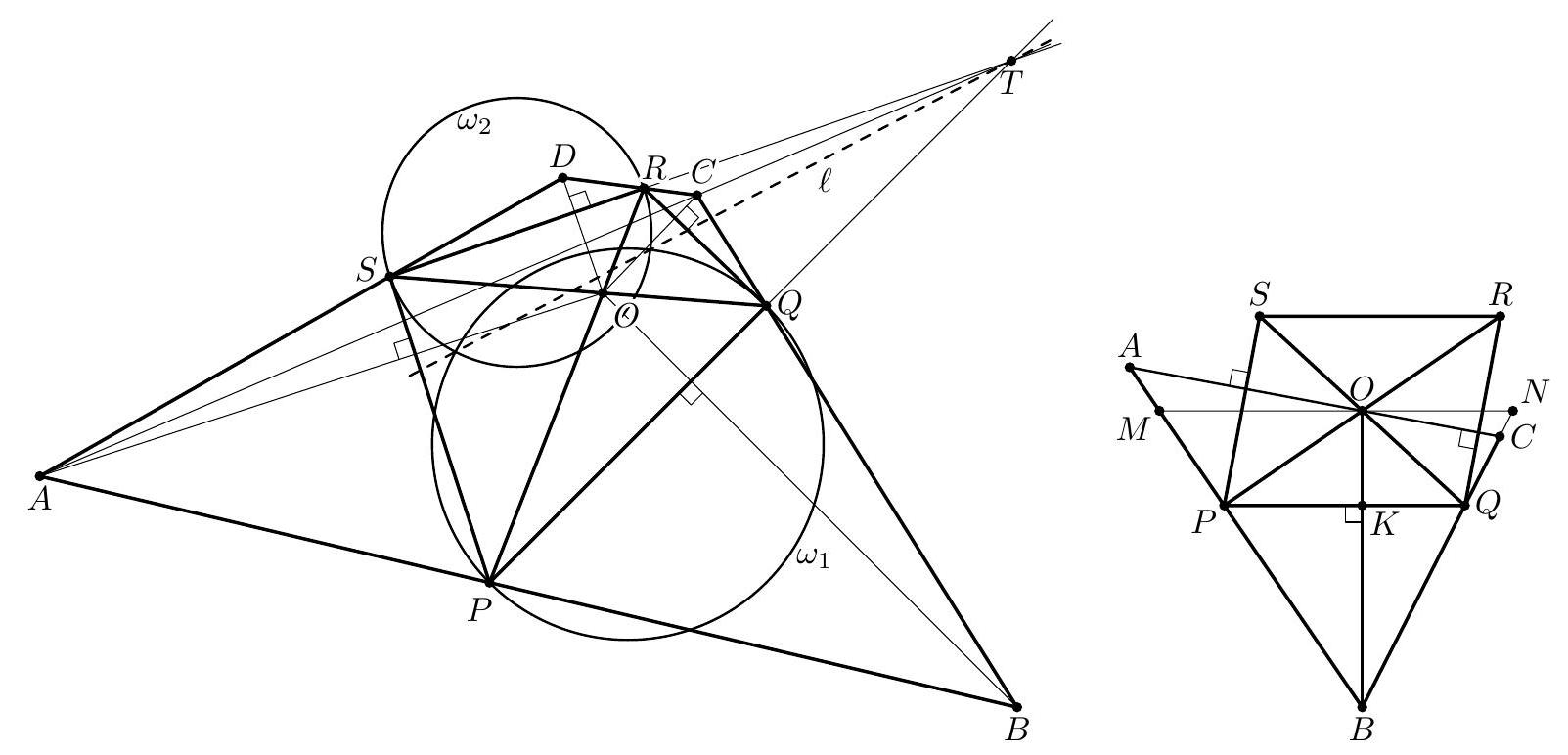
|
| 127 |
+
|
| 128 |
+
Suppose, by way of contradiction, that $O P>O Q$. Let the line through $O$ and parallel to $P Q$ meet $A B$ at $M$, and $C B$ at $N$. Since $O P>O Q$, the angle $S P Q$ is acute and the angle $P Q R$ is obtuse, so the angle $A O B$ is obtuse, the angle $B O C$ is acute, $M$ lies on the segment $A B$, and $N$ lies on the extension of the segment $B C$ beyond $C$. Therefore: $O A>O M$, since the angle $O M A$ is obtuse; $O M>O N$, since $O M: O N=K P: K Q$, where $K$ is the projection of $O$ onto $P Q$; and $O N>O C$, since the angle $O C N$ is obtuse. Consequently, $O A>O C$.
|
| 129 |
+
|
| 130 |
+
Similarly, $O R>O S$ yields $O C>O A$ : a contradiction. Consequently, $O P=O Q$ and $P Q R S$ is a rectangle. This ends the proof.
|
| 131 |
+
|
| 132 |
+
Solution 2. (Ilya Bogdanov) To begin, we establish a useful lemma.
|
| 133 |
+
Lemma 2. If $P$ is a point on the side $A B$ of a triangle $O A B$, then
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\frac{\sin A O P}{O B}+\frac{\sin P O B}{O A}=\frac{\sin A O B}{O P}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Proof. Let $[X Y Z]$ denote the area of a triangle $X Y Z$, to write
|
| 140 |
+
$0=2([A O B]-[P O B]-[P O C])=O A \cdot O B \cdot \sin A O B-O B \cdot O P \cdot \sin P O B-O P \cdot O A \cdot \sin A O P$,
|
| 141 |
+
and divide by $O A \cdot O B \cdot O P$ to get the required identity.
|
| 142 |
+
A similar statement remains valid if the point $C$ lies on the line $A B$; the proof is obtained by using signed areas and directed lengths.
|
| 143 |
+
|
| 144 |
+
We now turn to the solution. We first prove some sort of a converse statement, namely:
|
| 145 |
+
Claim. Let $P Q R S$ be a cyclic quadrangle with $O=P R \cap Q S$; assume that no its diagonal is perpendicular to a side. Let $\ell_{A}, \ell_{B}, \ell_{C}$, and $\ell_{D}$ be the lines through $O$ perpendicular to $S P$, $P Q, Q R$, and $R S$, respectively. Choose any point $A \in \ell_{A}$ and successively define $B=A P \cap \ell_{B}$, $C=B Q \cap \ell_{C}, D=C R \cap \ell_{D}$, and $A^{\prime}=D S \cap \ell_{A}$. Then $A^{\prime}=A$.
|
| 146 |
+
|
| 147 |
+
Proof. We restrict ourselves to the case when the points $A, B, C, D$, and $A^{\prime}$ lie on $\ell_{A}, \ell_{B}$, $\ell_{C}, \ell_{D}$, and $\ell_{A}$ on the same side of $O$ as their points of intersection with the respective sides of the quadrilateral $P Q R S$. Again, a general case is obtained by suitable consideration of directed lengths.
|
| 148 |
+
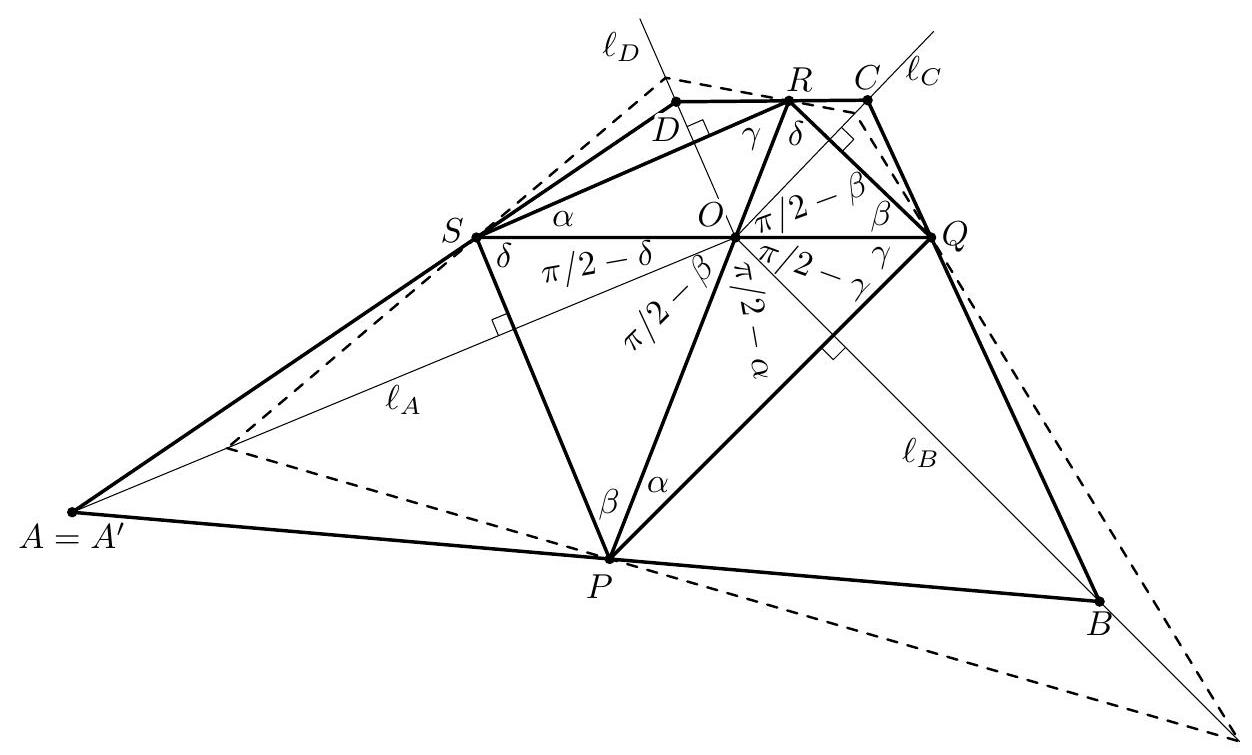
|
| 149 |
+
|
| 150 |
+
Denote
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
\begin{gathered}
|
| 154 |
+
\alpha=\angle Q P R=\angle Q S R=\pi / 2-\angle P O B=\pi / 2-\angle D O S \\
|
| 155 |
+
\beta=\angle R P S=\angle R Q S=\pi / 2-\angle A O P=\pi / 2-\angle Q O C \\
|
| 156 |
+
\gamma=\angle S Q P=\angle S R P=\pi / 2-\angle B O Q=\pi / 2-\angle R O D \\
|
| 157 |
+
\delta=\angle P R Q=\angle P S Q=\pi / 2-\angle C O R=\pi / 2-\angle S O A
|
| 158 |
+
\end{gathered}
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
By Lemma 2 applied to the lines $A P B, P Q C, C R D$, and $D S A^{\prime}$, we get
|
| 162 |
+
|
| 163 |
+
$$
|
| 164 |
+
\begin{array}{ll}
|
| 165 |
+
\frac{\sin (\alpha+\beta)}{O P}=\frac{\cos \alpha}{O A}+\frac{\cos \beta}{O B}, & \frac{\sin (\beta+\gamma)}{O Q}=\frac{\cos \beta}{O B}+\frac{\cos \gamma}{O C} \\
|
| 166 |
+
\frac{\sin (\gamma+\delta)}{O R}=\frac{\cos \gamma}{O C}+\frac{\cos \delta}{O D}, & \frac{\sin (\delta+\alpha)}{O S}=\frac{\cos \delta}{O D}+\frac{\cos \alpha}{O A^{\prime}}
|
| 167 |
+
\end{array}
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
Adding the two equalities on the left and subtracting the two on the right, we see that the required equality $A=A^{\prime}$ (i.e., $\cos \alpha / O A=\cos \alpha / O A^{\prime}$, in view of $\cos \alpha \neq 0$ ) is equivalent to the relation
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
\frac{\sin Q P S}{O P}+\frac{\sin S R Q}{O R}=\frac{\sin P Q R}{O Q}+\frac{\sin R S P}{O S}
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
Let $d$ denote the circumdiameter of $P Q R S$, so $\sin Q P S=\sin S R Q=Q S / d$ and $\sin R S P=$ $\sin P Q R=P R / d$. Thus the required relation reads
|
| 177 |
+
|
| 178 |
+
$$
|
| 179 |
+
\frac{Q S}{O P}+\frac{Q S}{O R}=\frac{P R}{O S}+\frac{P R}{O Q}, \quad \text { or } \quad \frac{Q S \cdot P R}{O P \cdot O R}=\frac{P R \cdot Q S}{O S \cdot O Q}
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
The last relation is trivial, due again to cyclicity.
|
| 183 |
+
Finally, it remains to derive the problem statement from our Claim. Assume that $P Q R S$ is not cyclic, e.g., that $O P \cdot O R>O Q \cdot O S$, where $O=P R \cap Q S$. Mark the point $S^{\prime}$ on the ray $O S$ so that $O P \cdot O R=O Q \cdot O S^{\prime}$. Notice that no diagonal of $P Q R S$ is perpendicular to a side, so the quadrangle $P Q R S^{\prime}$ satisfies the conditions of the claim.
|
| 184 |
+
|
| 185 |
+
Let $\ell_{A}^{\prime}$ and $\ell_{D}^{\prime}$ be the lines through $O$ perpendicular to $P S^{\prime}$ and $R S^{\prime}$, respectively. Then $\ell_{A}^{\prime}$ and $\ell_{D}^{\prime}$ cross the segments $A P$ and $R D$, respectively, at some points $A^{\prime}$ and $D^{\prime}$. By the Claim, the line $A^{\prime} D^{\prime}$ passes through $S^{\prime}$. This is impossible, because the segment $A^{\prime} D^{\prime}$ crosses the segment $O S$ at some interior point, while $S^{\prime}$ lies on the extension of this segment. This contradiction completes the proof.
|
| 186 |
+
|
| 187 |
+
Remark. According to the author, there is a remarkable corollary that is worth mentioning: Four lines dissect a convex quadrangle into nine smaller quadrangles to make it into a $3 \times 3$ array
|
| 188 |
+
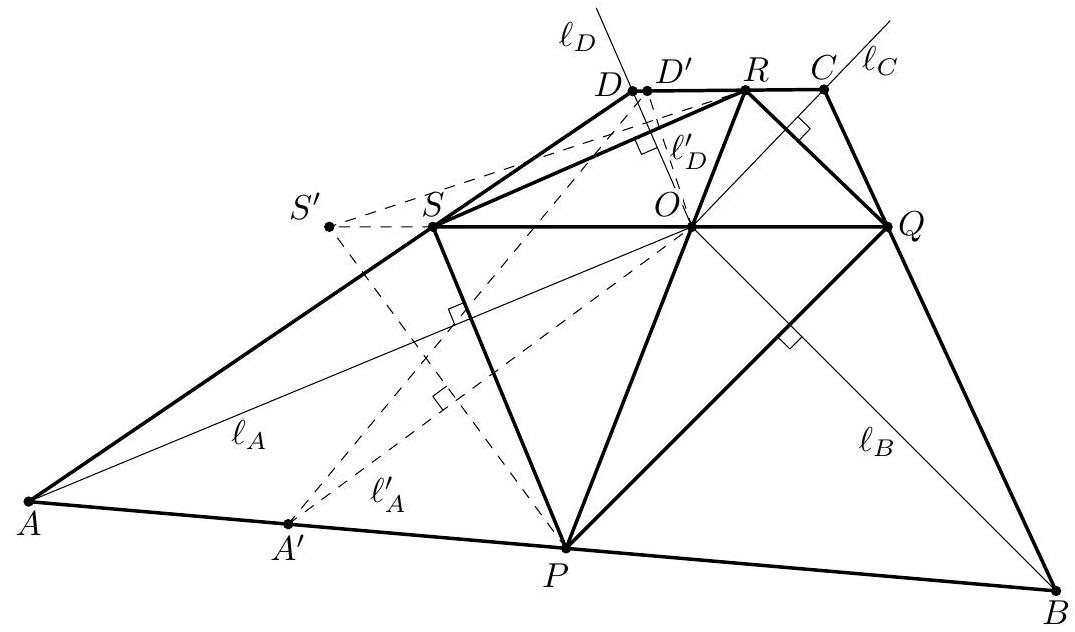
|
| 189 |
+
of quadrangular cells. Label these cells 1 through 9 from left to right and from top to bottom. If the first eight cells are orthodiagonal, then so is the ninth.
|
| 190 |
+
|
RMM/md/en-2018-RMM2018-Day1-English.md
ADDED
|
@@ -0,0 +1,73 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $10^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 1 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. Let $A B C D$ be a cyclic quadrangle and let $P$ be a point on the side $A B$. The diagonal $A C$ crosses the segment $D P$ at $Q$. The parallel through $P$ to $C D$ crosses the extension of the side $B C$ beyond $B$ at $K$, and the parallel through $Q$ to $B D$ crosses the extension of the side $B C$ beyond $B$ at $L$. Prove that the circumcircles of the triangles $B K P$ and $C L Q$ are tangent.
|
| 6 |
+
|
| 7 |
+
## AleksandR Kuznetsov, Russia
|
| 8 |
+
|
| 9 |
+
Solution. We show that the circles $B K P$ and $C L Q$ are tangent at the point $T$ where the line $D P$ crosses the circle $A B C D$ again.
|
| 10 |
+
|
| 11 |
+
Since $B C D T$ is cyclic, we have $\angle K B T=\angle C D T$. Since $K P \| C D$, we get $\angle C D T=\angle K P T$. Thus, $\angle K B T=\angle C D T=\angle K P T$, which shows that $T$ lies on the circle $B K P$. Similarly, the equalities $\angle L C T=\angle B D T=\angle L Q T$ show that $T$ also lies on the circle $C L Q$.
|
| 12 |
+
|
| 13 |
+
It remains to prove that these circles are indeed tangent at $T$. This follows from the fact that the chords $T P$ and $T Q$ in the circles $B K T P$ and $C L T Q$, respectively, both lie along the same line and subtend equal angles $\angle T B P=\angle T B A=\angle T C A=\angle T C Q$.
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
Remarks. The point $T$ may alternatively be defined as the Miquel point of (any four of) the five lines $A B, B C, A C, K P$, and $L Q$.
|
| 17 |
+
|
| 18 |
+
Of course, the result still holds if $P$ is chosen on the line $A B$, and the other points lie on the corresponding lines rather than segments/rays. The current formulation was chosen in order to avoid case distinction based on the possible configurations of points.
|
| 19 |
+
|
| 20 |
+
Problem 2. Determine whether there exist non-constant polynomials $P(x)$ and $Q(x)$ with real coefficients satisfying
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
P(x)^{10}+P(x)^{9}=Q(x)^{21}+Q(x)^{20} .
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
## Ilya Bogdanov, Russia
|
| 27 |
+
|
| 28 |
+
Solution 1. The answer is in the negative. Comparing the degrees of both sides in (*) we get $\operatorname{deg} P=21 n$ and $\operatorname{deg} Q=10 n$ for some positive integer $n$. Take the derivative of $(*)$ to obtain
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
P^{\prime} P^{8}(10 P+9)=Q^{\prime} Q^{19}(21 Q+20)
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
Since $\operatorname{gcd}(10 P+9, P)=\operatorname{gcd}(10 P+9, P+1)=1$, it follows that $\operatorname{gcd}\left(10 P+9, P^{9}(P+1)\right)=1$, so $\operatorname{gcd}(10 P+9, Q)=1$, by $(*)$. Thus $(* *)$ yields $10 P+9 \mid Q^{\prime}(21 Q+20)$, which is impossible since $0<\operatorname{deg}\left(Q^{\prime}(21 Q+20)\right)=20 n-1<21 n=\operatorname{deg}(10 P+9)$. A contradiction.
|
| 35 |
+
|
| 36 |
+
Remark. A similar argument shows that there are no non-constant solutions of $P^{m}+P^{m-1}=$ $Q^{k}+Q^{k-1}$, where $k$ and $m$ are positive integers with $k \geq 2 m$. A critical case is $k=2 m$; but in this case there exist more routine ways of solving the problem. Thus, we decided to choose $k=2 m+1$.
|
| 37 |
+
|
| 38 |
+
Solution 2. Letting $r$ and $s$ be integers such that $r \geq 2$ and $s \geq 2 r$, we show that if $P^{r}+P^{r-1}=$ $Q^{s}+Q^{s-1}$, then $Q$ is constant.
|
| 39 |
+
|
| 40 |
+
Let $m=\operatorname{deg} P$ and $n=\operatorname{deg} Q$. A degree inspection in the given relation shows that $m \geq 2 n$.
|
| 41 |
+
We will prove that $P(P+1)$ has at least $m+1$ distinct complex roots. Assuming this for the moment, notice that $Q$ takes on one of the values 0 or -1 at each of those roots. Since $m+1 \geq 2 n+1$, it follows that $Q$ takes on one of the values 0 and -1 at more than $n$ distinct points, so $Q$ must be constant.
|
| 42 |
+
|
| 43 |
+
Finally, we prove that $P(P+1)$ has at least $m+1$ distinct complex roots. This can be done either by referring to the Mason-Stothers theorem or directly, in terms of multiplicities of the roots in question.
|
| 44 |
+
|
| 45 |
+
Since $P$ and $P+1$ are relatively prime, the Mason-Stothers theorem implies that the number of distinct roots of $P(P+1)$ is greater than $m$, hence at least $m+1$.
|
| 46 |
+
|
| 47 |
+
For a direct proof, let $z_{1}, \ldots, z_{t}$ be the distinct complex roots of $P(P+1)$, and let $z_{k}$ have multiplicity $\alpha_{k}, k=1, \ldots, t$. Since $P$ and $P+1$ have no roots in common, and $P^{\prime}=(P+1)^{\prime}$, it follows that $P^{\prime}$ has a root of multiplicity $\alpha_{k}-1$ at $z_{k}$. Consequently, $m-1=\operatorname{deg} P^{\prime} \geq$ $\sum_{k=1}^{t}\left(\alpha_{k}-1\right)=\sum_{k=1}^{t} \alpha_{k}-t=2 m-t$; that is, $t \geq m+1$. This completes the prof.
|
| 48 |
+
|
| 49 |
+
Remark. The Mason-Stothers theorem (in a particular case over the complex field) claims that, given coprime complex polynomials $P(x), Q(x)$, and $R(x)$, not all constant, such that $P(x)+Q(x)=R(x)$, the total number of their complex roots (not regarding multiplicities) is at least $\max \{\operatorname{deg} P, \operatorname{deg} Q, \operatorname{deg} R\}+1$. This theorem was a part of motivation for the famous $a b c$-conjecture.
|
| 50 |
+
|
| 51 |
+
Problem 3. Ann and Bob play a game on an infinite checkered plane making moves in turn; Ann makes the first move. A move consists in orienting any unit grid-segment that has not been oriented before. If at some stage some oriented segments form an oriented cycle, Bob wins. Does Bob have a strategy that guarantees him to win?
|
| 52 |
+
|
| 53 |
+
Maxim Didin, Russia
|
| 54 |
+
|
| 55 |
+
Solution. The answer is in the negative: Ann has a strategy allowing her to prevent Bob's victory.
|
| 56 |
+
|
| 57 |
+
We say that two unit grid-segments form a low-left corner (or LL-corner) if they share an endpoint which is the lowest point of one and the leftmost point of the other. An up-right corner (or $U R$-corner) is defined similarly. The common endpoint of two unit grid-segments at a corner is the joint of that corner.
|
| 58 |
+
|
| 59 |
+
Fix a vertical line on the grid and call it the midline; the unit grid-segments along the midline are called middle segments. The unit grid-segments lying to the left/right of the midline are called left/right segments. Partition all left segments into LL-corners, and all right segments into UR-corners.
|
| 60 |
+
|
| 61 |
+
We now describe Ann's strategy. Her first move consists in orienting some middle segment arbitrarily. Assume that at some stage, Bob orients some segment $s$. If $s$ is a middle segment, Ann orients any free middle segment arbitrarily. Otherwise, $s$ forms a corner in the partition with some other segment $t$. Then Ann orients $t$ so that the joint of the corner is either the source of both arrows, or the target of both. Notice that after any move of Ann's, each corner in the partition is either completely oriented or completely not oriented. This means that Ann can always make a required move.
|
| 62 |
+
|
| 63 |
+
Assume that Bob wins at some stage, i.e., an oriented cycle $C$ occurs. Let $X$ be the lowest of the leftmost points of $C$, and let $Y$ be the topmost of the rightmost points of $C$. If $X$ lies (strictly) to the left of the midline, then $X$ is the joint of some corner whose segments are both oriented. But, according to Ann's strategy, they are oriented so that they cannot occur in a cycle - a contradiction. Otherwise, $Y$ lies to the right of the midline, and a similar argument applies. Thus, Bob will never win, as desired.
|
| 64 |
+
|
| 65 |
+
Remarks. (1) There are several variations of the argument in the solution above. For instance, instead of the midline, Ann may choose any infinite in both directions down going polyline along the grid (i.e., consisting of steps to the right and steps-down alone). Alternatively, she may split the plane into four quadrants, use their borders as "trash bin" (as the midline was used in the solution above), partition all segments in the upper-right quadrant into UR-corners, all segments in the lower-right quadrant into LR-corners, and so on.
|
| 66 |
+
(2) The problem becomes easier if Bob makes the first move. In this case, his opponent just partitions the whole grid into LL-corners. In particular, one may change the problem to say that the first player to achieve an oriented cycle wins (in this case, the result is a draw).
|
| 67 |
+
|
| 68 |
+
On the other hand, this version is closer to known problems. In particular, the following problem is known:
|
| 69 |
+
|
| 70 |
+
Ann and Bob play the game on an infinite checkered plane making moves in turn (Ann makes the first move). A move consists in painting any unit grid segment that has not been painted before (Ann paints in blue, Bob paints in red). If a player creates a cycle of her/his color, (s)he wins. Does any of the players have a winning strategy?
|
| 71 |
+
|
| 72 |
+
Again, the solution is pairing strategy with corners of a fixed orientation (with a little twist for Ann's strategy - in this problem, it is clear that Ann has better chances).
|
| 73 |
+
|
RMM/md/en-2018-RMM2018-Day2-English.md
ADDED
|
@@ -0,0 +1,157 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $10^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 2 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 4. Let $a, b, c, d$ be positive integers such that $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$. Prove that, as $n$ runs through the positive integers, the values $\operatorname{gcd}(a n+b, c n+d)$ may achieve form the set of all positive divisors of some integer.
|
| 6 |
+
|
| 7 |
+
Raul Alcantara, Peru
|
| 8 |
+
|
| 9 |
+
Solution 1. We extend the problem statement by allowing $a$ and $c$ take non-negative integer values, and allowing $b$ and $d$ to take arbitrary integer values. (As usual, the greatest common divisor of two integers is non-negative.) Without loss of generality, we assume $0 \leq a \leq c$. Let $S(a, b, c, d)=\left\{\operatorname{gcd}(a n+b, c n+d): n \in \mathbb{Z}_{>0}\right\}$.
|
| 10 |
+
|
| 11 |
+
Now we induct on $a$. We first deal with the inductive step, leaving the base case $a=0$ to the end of the solution. So, assume that $a>0$; we intend to find a 4 -tuple $\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)$ satisfying the requirements of the extended problem, such that $S\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=S(a, b, c, d)$ and $0 \leq a^{\prime}<a$, which will allow us to apply the induction hypothesis.
|
| 12 |
+
|
| 13 |
+
The construction of this 4 -tuple is provided by the step of the Euclidean algorithm. Write $c=a q+r$, where $q$ and $r$ are both integers and $0 \leq r<a$. Then for every $n$ we have
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\operatorname{gcd}(a n+b, c n+d)=\operatorname{gcd}(a n+b, q(a n+b)+r n+d-q b)=\operatorname{gcd}(a n+b, r n+(d-q b))
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
so a natural intention is to define $a^{\prime}=r, b^{\prime}=d-q b, c^{\prime}=a$, and $d^{\prime}=b$ (which are already shown to satisfy $S\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=S(a, b, c, d)$ ). The check of the problem requirements is straightforward: indeed,
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
a^{\prime} d^{\prime}-b^{\prime} c^{\prime}=(c-q a) b-(d-q b) a=-(a d-b c) \neq 0
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
and
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
\operatorname{gcd}\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=\operatorname{gcd}(c-q a, b-q d, a, b)=\operatorname{gcd}(c, d, a, b)=1
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Thus the step is verified.
|
| 32 |
+
It remains to deal with the base case $a=0$, i.e., to examine the set $S(0, b, c, d)$ with $b c \neq 0$ and $\operatorname{gcd}(b, c, d)=1$. Let $b^{\prime}$ be the integer obtained from $b$ by ignoring all primes $b$ and $c$ share (none of them divides $c n+d$ for any integer $n$, otherwise $\operatorname{gcd}(b, c, d)>1)$. We thus get $\operatorname{gcd}\left(b^{\prime}, c\right)=1$ and $S\left(0, b^{\prime}, c, d\right)=S(0, b, c, d)$.
|
| 33 |
+
|
| 34 |
+
Finally, it is easily seen that $S\left(0, b^{\prime}, c, d\right)$ is the set of all positive divisors of $b^{\prime}$. Each member of $S\left(0, b^{\prime}, c, d\right)$ is clearly a divisor of $b^{\prime}$. Conversely, if $\delta$ is a positive divisor of $b^{\prime}$, then $c n+d \equiv \delta$ $\left(\bmod b^{\prime}\right)$ for some $n$, since $b^{\prime}$ and $c$ are coprime, so $\delta$ is indeed a member of $S\left(0, b^{\prime}, c, d\right)$.
|
| 35 |
+
|
| 36 |
+
Solution 2. (Alexander Betts) For positive integers $s$ and $t$ and prime $p$, we will denote by $\operatorname{gcd}_{p}(s, t)$ the greatest common $p$-power divisor of $s$ and $t$.
|
| 37 |
+
Claim 1. For any positive integer $n, \operatorname{gcd}(a n+b, c n+d) \mid a d-b c$.
|
| 38 |
+
Proof. This is clear from the identity
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
a(c n+d)-c(a n+b)=a d-b c
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Claim 2. The set of values taken by $\operatorname{gcd}(a n+b, c n+d)$ is exactly the set of values taken by the product
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
\prod_{p \mid a d-b c} \operatorname{gcd}_{p}\left(a n_{p}+b, c n_{p}+d\right)
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
as the $\left(n_{p}\right)_{p \mid a d-b c}$ each range over positive integers.
|
| 51 |
+
|
| 52 |
+
Proof. From the identity
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\operatorname{gcd}(a n+b, c n+d)=\prod_{p \mid a d-b c} \operatorname{gcd}_{p}(a n+b, c n+d)
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
it is clear that every value taken by $\operatorname{gcd}(a n+b, c n+d)$ is also a value taken by the product (with all $n_{p}=n$ ). Conversely, it suffices to show that, given any positive integers $\left(n_{p}\right)_{p \mid a d-b c}$, there is a positive integer $n$ such that $\operatorname{gcd}_{p}(a n+b, c n+d)=\operatorname{gcd}_{p}\left(a n_{p}+b, c n_{p}+d\right)$ for each $p \mid a d-b c$. This can be achieved by requiring that $n$ be congruent to $n_{p}$ modulo a sufficiently large ${ }^{1}$ power of $p$ (using the Chinese Remainder Theorem).
|
| 59 |
+
|
| 60 |
+
Using Claim 2, it suffices to determine the sets of values taken by $\operatorname{gcd}_{p}(a n+b, c n+d)$ as $n$ ranges over all positive integers. There are two cases.
|
| 61 |
+
|
| 62 |
+
Claim 3. If $p \mid a, c$, then $\operatorname{gcd}_{p}(a n+b, c n+d)=1$ for all $n$.
|
| 63 |
+
Proof. If $p \mid a n+b, c n+d$, then we would have $p \mid a, b, c, d$, which is not the case.
|
| 64 |
+
Claim 4. If $p \nmid a$ or $p \nmid c$, then the values taken by $\operatorname{gcd}_{p}(a n+b, c n+d)$ are exactly the $p$-power divisors of $a d-b c$.
|
| 65 |
+
Proof. Assume without loss of generality that $p \nmid a$. Then from identity $(\dagger)$ we have $\operatorname{grd}_{p}(a n+$ $b, c n+d)=\operatorname{gcd}_{p}(a n+b, a d-b c)$. But since $p \nmid a$, the arithmetic progression $a n+b$ takes all possible values modulo the highest $p$-power divisor of $a d-b c$, and in particular the values taken by $\operatorname{gcd}_{p}(a n+b, a d-b c)$ are exactly the $p$-power divisors of $a d-b c$.
|
| 66 |
+
Conclusion. Using claims 2,3 and 4 , we see that the set of values taken by $\operatorname{gcd}(a n+b, c n+d)$ is equal to the set of products of $p$-power divisors of $a d-b c$, where we only consider those primes $p$ not dividing $\operatorname{gcd}(a, c)$. Thus the set of values of $\operatorname{gcd}(a n+b, c n+d)$ is equal to the set of divisors of the largest factor of $a d-b c$ coprime to $\operatorname{gcd}(a, c)$.
|
| 67 |
+
|
| 68 |
+
Remarks. (1) If $S(a, b, c, d)$ is the set of all positive divisors of some integer, then necessarily $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$ : finiteness of $S(a, b, c, d)$ forces the former, and membership of 1 forces the latter.
|
| 69 |
+
(2) One may modify the problem statement according to the first paragraph of the solution. However, it seems that in this case one needs to include a clarification of the agreement on gcd being necessarily non-negative.
|
| 70 |
+
|
| 71 |
+
Problem 5. Let $n$ be a positive integer and fix $2 n$ distinct points on a circumference. Split these points into $n$ pairs and join the points in each pair by an arrow (i.e., an oriented line segment). The resulting configuration is good if no two arrows cross, and there are no arrows $\overrightarrow{A B}$ and $\overrightarrow{C D}$ such that $A B C D$ is a convex quadrangle oriented clockwise. Determine the number of good configurations.
|
| 72 |
+
|
| 73 |
+
Fedor Petrov, Russia
|
| 74 |
+
Solution 1. The required number is $\binom{2 n}{n}$. To prove this, trace the circumference counterclockwise to label the points $a_{1}, a_{2}, \ldots, a_{2 n}$.
|
| 75 |
+
|
| 76 |
+
Let $\mathcal{C}$ be any good configuration and let $O(\mathcal{C})$ be the set of all points from which arrows emerge. We claim that every $n$-element subset $S$ of $\left\{a_{1}, \ldots, a_{2 n}\right\}$ is an $O$-image of a unique good configuration; clearly, this provides the answer.
|
| 77 |
+
|
| 78 |
+
To prove the claim induct on $n$. The base case $n=1$ is clear. For the induction step, consider any $n$-element subset $S$ of $\left\{a_{1}, \ldots, a_{2 n}\right\}$, and assume that $S=O(\mathcal{C})$ for some good configuration $\mathcal{C}$. Take any index $k$ such that $a_{k} \in S$ and $a_{k+1} \notin S$ (assume throughout that indices are cyclic modulo $2 n$, i.e., $a_{2 n+1}=a_{1}$ etc.).
|
| 79 |
+
|
| 80 |
+
If the arrow from $a_{k}$ points to some $a_{\ell}, k+1<\ell(<2 n+k)$, then the arrow pointing to $a_{k+1}$ emerges from some $a_{m}, m$ in the range $k+2$ through $\ell-1$, since these two arrows do not cross. Then the arrows $a_{k} \rightarrow a_{\ell}$ and $a_{m} \rightarrow a_{k+1}$ form a prohibited quadrangle. Hence, $\mathcal{C}$ contains an arrow $a_{k} \rightarrow a_{k+1}$.
|
| 81 |
+
|
| 82 |
+
On the other hand, if any configuration $\mathcal{C}$ contains the arrow $a_{k} \rightarrow a_{k+1}$, then this arrow cannot cross other arrows, neither can it occur in prohibited quadrangles.
|
| 83 |
+
|
| 84 |
+
Thus, removing the points $a_{k}, a_{k+1}$ from $\left\{a_{1}, \ldots, a_{2 n}\right\}$ and the point $a_{k}$ from $S$, we may apply the induction hypothesis to find a unique good configuration $\mathcal{C}^{\prime}$ on $2 n-2$ points compatible with the new set of sources (i.e., points from which arrows emerge). Adjunction of the arrow $a_{k} \rightarrow a_{k+1}$ to $\mathcal{C}^{\prime}$ yields a unique good configuration on $2 n$ points, as required.
|
| 85 |
+
|
| 86 |
+
Solution 2. Use the counterclockwise labelling $a_{1}, a_{2}, \ldots, a_{2 n}$ in the solution above.
|
| 87 |
+
Letting $D_{n}$ be the number of good configurations on $2 n$ points, we establish a recurrence relation for the $D_{n}$. To this end, let $C_{n}=\frac{(2 n)!}{n!(n+1)!}$ the $n$th Catalan number; it is well-known that $C_{n}$ is the number of ways to connect $2 n$ given points on the circumference by $n$ pairwise disjoint chords.
|
| 88 |
+
|
| 89 |
+
Since no two arrows cross, in any good configuration the vertex $a_{1}$ is connected to some $a_{2 k}$. Fix $k$ in the range 1 through $n$ and count the number of good configurations containing the arrow $a_{1} \rightarrow a_{2 k}$. Let $\mathcal{C}$ be any such configuration.
|
| 90 |
+
|
| 91 |
+
In $\mathcal{C}$, the vertices $a_{2}, \ldots, a_{2 k-1}$ are paired off with one other, each arrow pointing from the smaller to the larger index, for otherwise it would form a prohibited quadrangle with $a_{1} \rightarrow a_{2 k}$. Consequently, there are $C_{k-1}$ ways of drawing such arrows between $a_{2}, \ldots, a_{2 k-1}$.
|
| 92 |
+
|
| 93 |
+
On the other hand, the arrows between $a_{2 k+1}, \ldots, a_{2 n}$ also form a good configuration, which can be chosen in $D_{n-k}$ ways. Finally, it is easily seen that any configuration of the first kind and any configuration of the second kind combine together to yield an overall good configuration.
|
| 94 |
+
|
| 95 |
+
Thus the number of good configurations containing the arrow $a_{1} \rightarrow a_{2 k}$ is $C_{k-1} D_{n-k}$. Clearly, this is also the number of good configurations containing the arrow $a_{2(n-k+1)} \rightarrow a_{1}$, so
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
D_{n}=2 \sum_{k=1}^{n} C_{k-1} D_{n-k} .
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
To find an explicit formula for $D_{n}$, let $d(x)=\sum_{n=0}^{\infty} D_{n} x^{n}$ and let $c(x)=\sum_{n=0}^{\infty} C_{n} x^{n}=$ $\frac{1-\sqrt{1-4 x}}{2 x}$ be the generating functions of the $D_{n}$ and the $C_{n}$, respectively. Since $D_{0}=1$, relation ( $*$ )
|
| 102 |
+
yields $d(x)=2 x c(x) d(x)+1$, so
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\begin{aligned}
|
| 106 |
+
d(x)=\frac{1}{1-2 x c(x)}=(1-4 x)^{-1 / 2} & =\sum_{n \geq 0}\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right) \ldots\left(-\frac{2 n-1}{2}\right) \frac{(-4 x)^{n}}{n!} \\
|
| 107 |
+
& =\sum_{n \geq 0} \frac{2^{n}(2 n-1)!!}{n!} x^{n}=\sum_{n \geq 0}\binom{2 n}{n} x^{n} .
|
| 108 |
+
\end{aligned}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
Consequently, $D_{n}=\binom{2 n}{n}$.
|
| 112 |
+
Solution 3. Let $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$ denote the $n$th Catalan number and recall that there are exactly $C_{n}$ ways to join $2 n$ distinct points on a circumference by $n$ pairwise disjoint chords. Such a configuration of chords will be referred to as a Catalan n-configuration. An orientation of the chords in a Catalan configuration $\mathcal{C}$ making it into a good configuration (in the sense defined in the statement of the problem) will be referred to as a good orientation for $\mathcal{C}$.
|
| 113 |
+
|
| 114 |
+
We show by induction on $n$ that there are exactly $n+1$ good orientations for any Catalan $n$-configuration, so there are exactly $(n+1) C_{n}=\binom{2 n}{n}$ good configurations on $2 n$ points. The base case $n=1$ is clear.
|
| 115 |
+
|
| 116 |
+
For the induction step, let $n>1$, let $\mathcal{C}$ be a Catalan $n$-configuration, and let $a b$ be a chord of minimal length in $\mathcal{C}$. By minimality, the endpoints of the other chords in $\mathcal{C}$ all lie on the major $\operatorname{arc} a b$ of the circumference.
|
| 117 |
+
|
| 118 |
+
Label the $2 n$ endpoints $1,2, \ldots, 2 n$ counterclockwise so that $\{a, b\}=\{1,2\}$, and notice that the good orientations for $\mathcal{C}$ fall into two disjoint classes: Those containing the arrow $1 \rightarrow 2$, and those containing the opposite arrow.
|
| 119 |
+
|
| 120 |
+
Since the arrow $1 \rightarrow 2$ cannot be involved in a prohibited quadrangle, the induction hypothesis applies to the Catalan $(n-1)$-configuration formed by the other chords to show that the first class contains exactly $n$ good orientations.
|
| 121 |
+
|
| 122 |
+
Finally, the second class consists of a single orientation, namely, $2 \rightarrow 1$, every other arrow emerging from the smaller endpoint of the respective chord; a routine verification shows that this is indeed a good orientation. This completes the induction step and ends the proof.
|
| 123 |
+
|
| 124 |
+
Remark. Combining the arguments from Solutions 1 and 3 one gets a way (though not the easiest) to compute the Catalan number $C_{n}$.
|
| 125 |
+
|
| 126 |
+
Solution 4, sketch. (Sang-il Oum) As in the previous solution, we intend to count the number of good orientations of a Catalan $n$-configuration.
|
| 127 |
+
|
| 128 |
+
For each such configuration, we consider its dual graph $T$ whose vertices are finite regions bounded by chords and the circle, and an edge connects two regions sharing a boundary segment. This graph $T$ is a plane tree with $n$ edges and $n+1$ vertices.
|
| 129 |
+
|
| 130 |
+
There is a canonical bijection between orientations of chords and orientations of edges of $T$ in such a way that each chord crosses an edge of $T$ from the right to the left of the arrow on that edge. A good orientation of chords corresponds to an orientation of the tree containing no two edges oriented towards each other. Such an orientation is defined uniquely by its source vertex, i.e., the unique vertex having no in-arrows.
|
| 131 |
+
|
| 132 |
+
Therefore, for each tree $T$ on $n+1$ vertices, there are exactly $n+1$ ways to orient it so that the source vertex is unique - one for each choice of the source. Thus, the answer is obtained in the same way as above.
|
| 133 |
+
|
| 134 |
+
Problem 6. Fix a circle $\Gamma$, a line $\ell$ tangent to $\Gamma$, and another circle $\Omega$ disjoint from $\ell$ such that $\Gamma$ and $\Omega$ lie on opposite sides of $\ell$. The tangents to $\Gamma$ from a variable point $X$ on $\Omega$ cross $\ell$ at $Y$ and $Z$. Prove that, as $X$ traces $\Omega$, the circle $X Y Z$ is tangent to two fixed circles.
|
| 135 |
+
|
| 136 |
+
Russia, Ivan Frolov
|
| 137 |
+
Solution. Assume $\Gamma$ of unit radius and invert with respect to $\Gamma$. No reference will be made to the original configuration, so images will be denoted by the same letters. Letting $\Gamma$ be centred at $G$, notice that inversion in $\Gamma$ maps tangents to $\Gamma$ to circles of unit diameter through $G$ (hence internally tangent to $\Gamma$ ). Under inversion, the statement reads as follows:
|
| 138 |
+
|
| 139 |
+
Fix a circle $\Gamma$ of unit radius centred at $G$, a circle $\ell$ of unit diameter through $G$, and a circle $\Omega$ inside $\ell$ disjoint from $\ell$. The circles $\eta$ and $\zeta$ of unit diameter, through $G$ and a variable point $X$ on $\Omega$, cross $\ell$ again at $Y$ and $Z$, respectively. Prove that, as $X$ traces $\Omega$, the circle $X Y Z$ is tangent to two fixed circles.
|
| 140 |
+
|
| 141 |
+
|
| 142 |
+
Since $\eta$ and $\zeta$ are the reflections of the circumcircle $\ell$ of the triangle $G Y Z$ in its sidelines $G Y$ and $G Z$, respectively, they pass through the orthocentre of this triangle. And since $\eta$ and $\zeta$ cross again at $X$, the latter is the orthocentre of the triangle $G Y Z$. Hence the circle $\xi$ through $X, Y, Z$ is the reflection of $\ell$ in the line $Y Z$; in particular, $\xi$ is also of unit diameter.
|
| 143 |
+
|
| 144 |
+
Let $O$ and $L$ be the centres of $\Omega$ and $\ell$, respectively, and let $R$ be the (variable) centre of $\xi$. Let $G X \operatorname{cross} \xi$ again at $X^{\prime}$; then $G$ and $X^{\prime}$ are reflections of one another in the line $Y Z$, so $G L R X^{\prime}$ is an isosceles trapezoid. Then $L R \| G X$ and $\angle(L G, G X)=\angle\left(G X^{\prime}, X^{\prime} R\right)=\angle(R X, X G)$, i.e., $L G \| R X$; this means that $G L R X$ is a parallelogram, so $\overrightarrow{X R}=\overrightarrow{G L}$ is constant.
|
| 145 |
+
|
| 146 |
+
Finally, consider the fixed point $N$ defined by $\overrightarrow{O N}=\overrightarrow{G L}$. Then $X R N O$ is a parallelogram, so the distance $R N=O X$ is constant. Consequently, $\xi$ is tangent to the fixed circles centred at $N$ of radii $|1 / 2-O X|$ and $1 / 2+O X$.
|
| 147 |
+
|
| 148 |
+
One last check is needed to show that the inverse images of the two obtained circles are indeed circles and not lines. This might happen if one of them contained $G$; we show that this is
|
| 149 |
+
impossible. Indeed, since $\Omega$ lies inside $\ell$, we have $O L<1 / 2-O X$, so
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
N G=|\overrightarrow{G L}+\overrightarrow{L O}+\overrightarrow{O N}|=|2 \overrightarrow{G L}+\overrightarrow{L O}| \geq 2|\overrightarrow{G L}|-|\overrightarrow{L O}|>1-(1 / 2-O X)=1 / 2+O X
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
this shows that $G$ is necessarily outside the obtained circles.
|
| 156 |
+
Remarks. (1) The last check could be omitted, if we allowed in the problem statement to regard a line as a particular case of a circle. On the other hand, the Problem Selection Committee suggests not to punish students who have not performed this check.
|
| 157 |
+
(2) Notice that the required fixed circles are also tangent to $\Omega$.
|
RMM/md/en-2019-RMM2019-Day1-English.md
ADDED
|
@@ -0,0 +1,123 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $11^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 1 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. Amy and Bob play the game. At the beginning, Amy writes down a positive integer on the board. Then the players take moves in turn, Bob moves first. On any move of his, Bob replaces the number $n$ on the blackboard with a number of the form $n-a^{2}$, where $a$ is a positive integer. On any move of hers, Amy replaces the number $n$ on the blackboard with a number of the form $n^{k}$, where $k$ is a positive integer. Bob wins if the number on the board becomes zero. Can Amy prevent Bob's win?
|
| 6 |
+
|
| 7 |
+
Russia, Maxim Didin
|
| 8 |
+
|
| 9 |
+
Solution. The answer is in the negative. For a positive integer $n$, we define its square-free part $S(n)$ to be the smallest positive integer $a$ such that $n / a$ is a square of an integer. In other words, $S(n)$ is the product of all primes having odd exponents in the prime expansion of $n$. We also agree that $S(0)=0$.
|
| 10 |
+
|
| 11 |
+
Now we show that (i) on any move of hers, Amy does not increase the square-free part of the positive integer on the board; and (ii) on any move of his, Bob always can replace a positive integer $n$ with a non-negative integer $k$ with $S(k)<S(n)$. Thus, if the game starts by a positive integer $N$, Bob can win in at most $S(N)$ moves.
|
| 12 |
+
|
| 13 |
+
Part (i) is trivial, as the definition of the square-part yields $S\left(n^{k}\right)=S(n)$ whenever $k$ is odd, and $S\left(n^{k}\right)=1 \leq S(n)$ whenever $k$ is even, for any positive integer $n$.
|
| 14 |
+
|
| 15 |
+
Part (ii) is also easy: if, before Bob's move, the board contains a number $n=S(n) \cdot b^{2}$, then Bob may replace it with $n^{\prime}=n-b^{2}=(S(n)-1) b^{2}$, whence $S\left(n^{\prime}\right) \leq S(n)-1$.
|
| 16 |
+
|
| 17 |
+
Remarks. (1) To make the argument more transparent, Bob may restrict himself to subtract only those numbers which are divisible by the maximal square dividing the current number. This restriction having been put, one may replace any number $n$ appearing on the board by $S(n)$, omitting the square factors.
|
| 18 |
+
|
| 19 |
+
After this change, Amy's moves do not increase the number, while Bob's moves decrease it. Thus, Bob wins.
|
| 20 |
+
(2) In fact, Bob may win even in at most 4 moves of his. For that purpose, use Lagrange's four squares theorem in order to expand $S(n)$ as the sum of at most four squares of positive integers: $S(n)=a_{1}^{2}+\cdots+a_{s}^{2}$. Then, on every move of his, Bob can replace the number $\left(a_{1}^{2}+\cdots+a_{k}^{2}\right) b^{2}$ on the board by $\left(a_{1}^{2}+\cdots+a_{k-1}^{2}\right) b^{2}$. The only chance for Amy to interrupt this process is to replace a current number by its even power; but in this case Bob wins immediately.
|
| 21 |
+
|
| 22 |
+
On the other hand, four is indeed the minimum number of moves in which Bob can guarantee himself to win. To show that, let Amy choose the number 7, and take just the first power on each of her subsequent moves.
|
| 23 |
+
|
| 24 |
+
Problem 2. Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
|
| 25 |
+
|
| 26 |
+
Slovenia, Jakob Jurij Snou
|
| 27 |
+
Solution 1. If $A B C D$ is a rectangle, the statement is trivial due to symmetry. Hence, in what follows we assume $A D \nVdash B C$.
|
| 28 |
+
|
| 29 |
+
Let $F$ be the midpoint of $B D$; by symmetry, both $\omega$ and $\Omega$ pass through $F$. Let $P^{\prime}$ be the meeting point of tangents to $\omega$ at $F$ and to $\Omega$ at $E$. We aim to show that $P^{\prime}=P$, which yields the required result. For that purpose, we show that $P^{\prime} A$ and $P^{\prime} D$ are tangent to $\omega$ and $\Omega$, respectively.
|
| 30 |
+
|
| 31 |
+
Let $K$ be the midpoint of $A F$. Then $E K$ is a midline in the triangle $A C F$, so $\angle(A E, E K)=$ $\angle(E C, C F)$. Since $P^{\prime} E$ is tangent to $\Omega$, we get $\angle(E C, C F)=\angle\left(P^{\prime} E, E F\right)$. Thus, $\angle(A E, E K)=$ $\angle\left(P^{\prime} E, E F\right)$, so $E P^{\prime}$ is a symmedian in the triangle $A E F$. Therefore, $E P^{\prime}$ and the tangents to $\omega$ at $A$ and $F$ are concurrent, and the concurrency point is $P^{\prime}$ itself. Hence $P^{\prime} A$ is tangent to $\omega$.
|
| 32 |
+
|
| 33 |
+
The second claim is similar. Taking $L$ to be the midpoint of $D E$, we have $\angle(D F, F L)=$ $\angle(F B, B E)=\angle\left(P^{\prime} F, F E\right)$, so $P^{\prime} F$ is a symmedian in the triangle $D E F$, and hence $P^{\prime}$ is the meeting point of the tangents to $\Omega$ at $D$ and $E$.
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
Remark. The above arguments may come in different orders. E.g., one may define $P^{\prime}$ to be the point of intersection of the tangents to $\Omega$ at $D$ and $E$ - hence obtaining that $P^{\prime} F$ is a symmedian in $\triangle D E F$, then deduce that $P^{\prime} F$ is tangent to $\omega$, and then apply a similar argument to show that $P^{\prime} E$ is a symmedian in $\triangle A E F$, whence $P^{\prime} A$ is tangent to $\omega$.
|
| 37 |
+
|
| 38 |
+
Solution 2. Let $Q$ be the isogonal conjugate of $P$ with respect to $\triangle A E D$, so $\angle(Q A, A D)=$ $\angle(E A, A P)=\angle(E B, B A)$ and $\angle(Q D, D A)=\angle(E D, D P)=\angle(E C, C D)$. Now our aim is to prove that $Q E \| C D$; this will yield that $\angle(E C, C D)=\angle(A E, E Q)=\angle(P E, E D)$, whence $P E$ is tangent to $\Omega$.
|
| 39 |
+
|
| 40 |
+
Let $D Q$ meet $A B$ at $X$. Then we have $\angle(X D, D A)=\angle(E C, C D)=\angle(E A, A B)$ and $\angle(D A, A X)=\angle(A B, B C)$, hence the triangles $D A X$ and $A B C$ are similar. Since $\angle(A B, B E)=$ $\angle(D A, A Q)$, the points $Q$ and $E$ correspond to each other in these triangles, hence $Q$ is the midpoint of $D X$. This yields that the points $Q$ and $E$ lie on the midline of the trapezoid parallel to $C D$, as desired.
|
| 41 |
+
|
| 42 |
+
|
| 43 |
+
Remark. The last step could be replaced with another application of isogonal conjugacy in the following manner. Reflect $Q$ in the common perpendicular bisector of $A B$ and $C D$ to obtain a point $R$ such that $\angle(C B, B R)=\angle(Q A, A D)=\angle(E B, B A)$ and $\angle(B C, C R)=\angle(Q D, D A)=$ $\angle(E C, C D)$. These relations yield that the points $E$ and $R$ are isogonally conjugate in a triangle $B C I$, where $I$ is the (ideal) point of intersection of $B A$ with $C D$. Since $E$ is equidistant from $A B$ and $C D, R$ is also equidistant from them, which yields what we need. (The last step deserves some explanation, since one vertex of the triangle is ideal. Such explanation may be obtained in many different ways - e.g., by a short computation in sines, or by noticing that, as in the usual case, $R$ is the circumcenter of the triangle formed by the reflections of $E$ in the sidelines $A B$, $B C$, and $C D$.)
|
| 44 |
+
|
| 45 |
+
Solution 3. (Dan Carmon) Let $O$ be the intersection of the diagonals $A C$ and $B D$. Let $F$ be the midpoint of $B D$. Let $S$ be the second intersection point of the circumcircles of triangles $A O F$ and $D O E$. We will prove that $S D$ and $S E$ are tangent to $\Omega$; the symmetric argument would then imply also that $S A$ and $S F$ are tangent to $\Gamma$. Thus $S=P$ and the claimed tangency holds.
|
| 46 |
+
|
| 47 |
+
We first prove that $O S$ is parallel to $A B$ and $D C$. Compute the powers of the points $A, B$ with respect to the circumcircles of $A O F$ and $D O E$ :
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\begin{gathered}
|
| 51 |
+
d(A, A O F)=0, \quad d(A, D O E)=A O \cdot A E \\
|
| 52 |
+
d(B, A O F)=B O \cdot B F, \quad d(B, D O E)=B O \cdot B D=2 B O \cdot B F
|
| 53 |
+
\end{gathered}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
And therefore
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
d(B, D O E)-d(B, A O F)=B O \cdot B F=A O \cdot A E=d(A, D O E)-d(A, A O F)
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
Thus both $A$ and $B$ belong to a locus of the form
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
d(X, D O E)-d(X, A O F)=\mathrm{const}
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
which is always a lines parallel to the radical axis of the respective circles. Since this radical axis is $O S$ by definition, it follows that $A B$ is parallel to $O S$, as claimed.
|
| 69 |
+
|
| 70 |
+
Now by angle chasing in the cyclic quadrilateral $D S O E$, we find
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
\begin{gathered}
|
| 74 |
+
\angle(S D, D E)=\angle(S O, O E)=\angle(D C, C E), \\
|
| 75 |
+
\angle(S E, E D)=\angle(S O, O D)=\angle(D C, D B)=\angle(A C, C D)=\angle(E C, C D),
|
| 76 |
+
\end{gathered}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
and these angle equalities are exactly the conditions of $S D, S E$ being tanget to $\Omega$, as claimed.
|
| 80 |
+
Remarks. (1) The solution was motivated by the following observation: Suppose $P$ is the intersection of the tangents to $\Omega$ at $D$ and $E$ as claimed. Then by single angle chasing we observe that the isogonal conjugate of $P$ in the triangle $D O E$ is the common ideal point at infinity of $D C$ and $E F$. This implies that $P$ is on the circumcircle of $D O E$ and that $O P$ is parallel to $D C$ (to be precise, it implies that the reflection of $O P$ in the angle bisector of $D O E$ is parallel to $D C$ and $E F$ - but the angle bisector is also parallel to these lines, so in fact $O P$ is the angle bisector). By symmetry it follows that $P$ is also on the circumcircle of $A O F$, thus the construction.
|
| 81 |
+
(2) The key parts of the proof can be described as (1) Constructing $S$, (2) Proving that $O S$ is parallel to $A B$ and $C D$, and (3) Concluding that $S=P$ and finishing the problem. Parts (2) and (3) can be performed in various other ways. For example, part (2) can be proved by showing that the circumcentres of $A O F$ and $D O E$ lie on a line perpendicular to the trapezium's bases; part (3) can be proved considering the spiral map taking the circumcircle of $D O C$ to the circumcircle of $D S E$. Since $O$ is the second intersction point of these circles, and since $O C E$ are collinear and $S O$ is tangent to the circumcircle of $D O C$ at $O$ (by symmetry), it follows that the spiral map sends $C$ to $E$ and $O$ to $S$, i.e. the triangle $D S E$ is similar to the isoceles triangle $D O C$, from which the remainder of the angle chase is trivial.
|
| 82 |
+
|
| 83 |
+
Problem 3. Given any positive real number $\varepsilon$, prove that, for all but finitely many positive integers $v$, any graph on $v$ vertices with at least $(1+\varepsilon) v$ edges has two distinct simple cycles of equal lengths.
|
| 84 |
+
(Recall that the notion of a simple cycle does not allow repetition of vertices in a cycle.)
|
| 85 |
+
|
| 86 |
+
Russia, Fedor Petrov
|
| 87 |
+
|
| 88 |
+
Solution. Fix a positive real number $\varepsilon$, and let $G$ be a graph on $v$ vertices with at least $(1+\varepsilon) v$ edges, all of whose simple cycles have pairwise distinct lengths.
|
| 89 |
+
|
| 90 |
+
Assuming $\varepsilon^{2} v \geq 1$, we exhibit an upper bound linear in $v$ and a lower bound quadratic in $v$ for the total number of simple cycles in $G$, showing thereby that $v$ cannot be arbitrarily large, whence the conclusion.
|
| 91 |
+
|
| 92 |
+
Since a simple cycle in $G$ has at most $v$ vertices, and each length class contains at most one such, $G$ has at most $v$ pairwise distinct simple cycles. This establishes the desired upper bound.
|
| 93 |
+
|
| 94 |
+
For the lower bound, consider a spanning tree for each component of $G$, and collect them all together to form a spanning forest $F$. Let $A$ be the set of edges of $F$, and let $B$ be the set of all other edges of $G$. Clearly, $|A| \leq v-1$, so $|B| \geq(1+\varepsilon) v-|A| \geq(1+\varepsilon) v-(v-1)=\varepsilon v+1>\varepsilon v$.
|
| 95 |
+
|
| 96 |
+
For each edge $b$ in $B$, adjoining $b$ to $F$ produces a unique simple cycle $C_{b}$ through $b$. Let $S_{b}$ be the set of edges in $A$ along $C_{b}$. Since the $C_{b}$ have pairwise distinct lengths, $\sum_{b \in B}\left|S_{b}\right| \geq$ $2+\cdots+(|B|+1)=|B|(|B|+3) / 2>|B|^{2} / 2>\varepsilon^{2} v^{2} / 2$.
|
| 97 |
+
|
| 98 |
+
Consequently, some edge in $A$ lies in more than $\varepsilon^{2} v^{2} /(2 v)=\varepsilon^{2} v / 2$ of the $S_{b}$. Fix such an edge $a$ in $A$, and let $B^{\prime}$ be the set of all edges $b$ in $B$ whose corresponding $S_{b}$ contain $a$, so $\left|B^{\prime}\right|>\varepsilon^{2} v / 2$.
|
| 99 |
+
|
| 100 |
+
For each 2-edge subset $\left\{b_{1}, b_{2}\right\}$ of $B^{\prime}$, the union $C_{b_{1}} \cup C_{b_{2}}$ of the cycles $C_{b_{1}}$ and $C_{b_{2}}$ forms a $\theta$-graph, since their common part is a path in $F$ through $a$; and since neither of the $b_{i}$ lies along this path, $C_{b_{1}} \cup C_{b_{2}}$ contains a third simple cycle $C_{b_{1}, b_{2}}$ through both $b_{1}$ and $b_{2}$. Finally, since $B^{\prime} \cap C_{b_{1}, b_{2}}=\left\{b_{1}, b_{2}\right\}$, the assignment $\left\{b_{1}, b_{2}\right\} \mapsto C_{b_{1}, b_{2}}$ is injective, so the total number of simple cycles in $G$ is at least $\binom{\left|B^{\prime}\right|}{2}>\binom{\varepsilon^{2} v / 2}{2}$. This establishes the desired lower bound and concludes the proof.
|
| 101 |
+
|
| 102 |
+
Remarks. (1) The problem of finding two cycles of equal lengths in a graph on $v$ vertices with $2 v$ edges is known and much easier - simply consider all cycles of the form $C_{b}$.
|
| 103 |
+
|
| 104 |
+
The solution above shows that a graph on $v$ vertices with at least $v+\Theta\left(v^{3 / 4}\right)$ edges has two cycles of equal lengths. The constant $3 / 4$ is not sharp; a harder proof seems to show that $v+\Theta(\sqrt{v \log v})$ edges would suffice. On the other hand, there exist graphs on $v$ vertices with $v+\Theta(\sqrt{v})$ edges having no such cycles.
|
| 105 |
+
(2) To avoid graph terminology, the statement of the problem may be rephrased as follows:
|
| 106 |
+
|
| 107 |
+
Given any positive real number $\varepsilon$, prove that, for all but finitely many positive integers $v$, any $v$-member company, within which there are at least $(1+\varepsilon) v$ friendship relations, satisfies the following condition: For some integer $u \geq 3$, there exist two distinct $u$ member cyclic arrangements in each of which any two neighbours are friends. (Two arrangements are distinct if they are not obtained from one another through rotation and/or symmetry; a member of the company may be included in neither arrangement, in one of them or in both.)
|
| 108 |
+
|
| 109 |
+
Sketch of solution 2. (Po-Shen Loh) Recall that the girth of a graph $G$ is the minimal length of a (simple) cycle in this graph.
|
| 110 |
+
|
| 111 |
+
Lemma. For any fixed positive $\delta$, a graph on $v$ vertices whose girth is at least $\delta v$ has at most $v+o(v)$ edges.
|
| 112 |
+
Proof. Define $f(v)$ to be the maximal number $f$ such that a graph on $v$ vertices whose girth is at least $\delta v$ may have $v+f$ edges. We are interested in the recursive estimates for $f$.
|
| 113 |
+
|
| 114 |
+
Let $G$ be a graph on $v$ vertices whose gifth is at least $\delta v$ containing $v+f(v)$ edges. If $G$ contains a leaf (i.e., a vertex of degree 1 ), then one may remove this vertex along with its edge, obtaining a graph with at most $v-1+f(v-1)$ edges. Thus, in this case $f(v) \leq f(v-1)$.
|
| 115 |
+
|
| 116 |
+
Define an isolated path of length $k$ to be a sequence of vertices $v_{0}, v_{1}, \ldots, v_{k}$, such that $v_{i}$ is connected to $v_{i+1}$, and each of the vertices $v_{1}, \ldots, v_{k-1}$ has degree 2 (so, these vertices are connected only to their neighbors in the path). If $G$ contains an isolated path $v_{0}, \ldots, v_{k}$ of length, say, $k>\sqrt{v}$, then one may remove all its middle vertices $v_{1}, \ldots, v_{k-1}$, along with all their $k$ edges. We obtain a graph on $v-k+1$ vertices with at most $(v-k+1)+f(v-k+1)$ edges. Thus, in this case $f(v) \leq f(v-k+1)+1$.
|
| 117 |
+
|
| 118 |
+
Assume now that the lengths of all isolated paths do not exceed $\sqrt{v}$; we show that in this case $v$ is bounded from above. For that purpose, we replace each maximal isolated path by an edge between its endpoints, removing all middle vertices. We obtain a graph $H$ whose girth is at least $\delta v / \sqrt{v}=\delta \sqrt{v}$. Each vertex of $H$ has degree at least 3. By the girth condition, the neighborhood of any vertex $x$ of radius $r=\lfloor(\delta \sqrt{v}-1) / 2\rfloor$ is a tree rooted at $x$. Any vertex at level $i<r$ has at least two sons; so the tree contains at least $2^{\lfloor(\delta \sqrt{v}-1) / 2\rfloor}$ vertices (even at the last level). So, $v \geq 2^{\lfloor(\delta \sqrt{v}-1) / 2\rfloor}$ which may happen only for a finite number of values of $v$.
|
| 119 |
+
|
| 120 |
+
Thus, for all large enough values of $v$, we have either $f(v) \leq f(v-1)$ or $f(v) \leq f(v-k+1)$ for some $k>\sqrt{v}$. This easily yields $f(v)=o(v)$, as desired.
|
| 121 |
+
|
| 122 |
+
Now we proceed to the problem. Consider a graph on $v$ vertices containing no two simple cycles of the same length. Take its $\lfloor\varepsilon v / 2\rfloor$ shortest cycles (or all its cycles, if their total number is smaller) and remove an edge from each. We get a graph of girth at least $\varepsilon v / 2$. By the lemma, the number of edges in the obtained graph is at most $v+o(v)$, so the number of edges in the initial graph is at most $v+\varepsilon v / 2+o(v)$, which is smaller than $(1+\varepsilon) v$ if $v$ is large enough.
|
| 123 |
+
|
RMM/md/en-2019-RMM2019-Day2-English.md
ADDED
|
@@ -0,0 +1,29 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $11^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 2: Saturday, February 23, 2019, Bucharest
|
| 4 |
+
|
| 5 |
+
Language: English
|
| 6 |
+
|
| 7 |
+
Problem 4. Prove that for every positive integer $n$ there exists a (not necessarily convex) polygon with no three collinear vertices, which admits exactly $n$ different triangulations.
|
| 8 |
+
(A triangulation is a dissection of the polygon into triangles by interior diagonals which have no common interior points with each other nor with the sides of the polygon.)
|
| 9 |
+
|
| 10 |
+
Problem 5. Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
f(x+y f(x))+f(x y)=f(x)+f(2019 y)
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
for all real numbers $x$ and $y$.
|
| 17 |
+
Problem 6. Find all pairs of integers $(c, d)$, both greater than 1 , such that the following holds:
|
| 18 |
+
|
| 19 |
+
For any monic polynomial $Q$ of degree $d$ with integer coefficients and for any prime $p>c(2 c+1)$, there exists a set $S$ of at most $\left(\frac{2 c-1}{2 c+1}\right) p$ integers, such that
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
\bigcup_{s \in S}\{s, Q(s), Q(Q(s)), Q(Q(Q(s))), \ldots\}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
is a complete residue system modulo $p$ (i.e., intersects with every residue class modulo $p$ ).
|
| 26 |
+
|
| 27 |
+
Each of the three problems is worth 7 points.
|
| 28 |
+
Time allowed $4 \frac{1}{2}$ hours.
|
| 29 |
+
|
RMM/md/en-2021-RMM2021-Day1-English_Solutions.md
ADDED
|
@@ -0,0 +1,55 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $13^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 1 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. Let $T_{1}, T_{2}, T_{3}, T_{4}$ be pairwise distinct collinear points such that $T_{2}$ lies between $T_{1}$ and $T_{3}$, and $T_{3}$ lies between $T_{2}$ and $T_{4}$. Let $\omega_{1}$ be a circle through $T_{1}$ and $T_{4}$; let $\omega_{2}$ be the circle through $T_{2}$ and internally tangent to $\omega_{1}$ at $T_{1}$; let $\omega_{3}$ be the circle through $T_{3}$ and externally tangent to $\omega_{2}$ at $T_{2}$; and let $\omega_{4}$ be the circle through $T_{4}$ and externally tangent to $\omega_{3}$ at $T_{3}$. A line crosses $\omega_{1}$ at $P$ and $W, \omega_{2}$ at $Q$ and $R, \omega_{3}$ at $S$ and $T$, and $\omega_{4}$ at $U$ and $V$, the order of these points along the line being $P, Q, R, S, T, U, V, W$. Prove that $P Q+T U=R S+V W$.
|
| 6 |
+
|
| 7 |
+
Hungary, Geza Kos
|
| 8 |
+
|
| 9 |
+
Solution. Let $O_{i}$ be the centre of $\omega_{i}, i=1,2,3,4$. Notice that the isosceles triangles $O_{i} T_{i} T_{i-1}$ are similar (indices are reduced modulo 4 ), to infer that $\omega_{4}$ is internally tangent to $\omega_{1}$ at $T_{4}$, and $O_{1} O_{2} O_{3} O_{4}$ is a (possibly degenerate) parallelogram.
|
| 10 |
+
|
| 11 |
+
Let $F_{i}$ be the foot of the perpendicular from $O_{i}$ to $P W$. The $F_{i}$ clearly bisect the segments $P W, Q R, S T$ and $U V$, respectively.
|
| 12 |
+
|
| 13 |
+
The proof can now be concluded in two similar ways.
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
First Approach. Since $O_{1} O_{2} O_{3} O_{4}$ is a parallelogram, $\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{3} F_{4}}=\mathbf{0}$ and $\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{4} F_{1}}=\mathbf{0}$; this still holds in the degenerate case, for if the $O_{i}$ are collinear, then they all lie on the line $T_{1} T_{4}$, and each $O_{i}$ is the midpoint of the segment $T_{i} T_{i+1}$. Consequently,
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\begin{aligned}
|
| 20 |
+
\overrightarrow{P Q}-\overrightarrow{R S}+\overrightarrow{T U}-\overrightarrow{V W}= & \left(\overrightarrow{P F_{1}}+\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{2} Q}\right)-\left(\overrightarrow{R F_{2}}+\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{3} S}\right) \\
|
| 21 |
+
& +\left(\overrightarrow{T F_{3}}+\overrightarrow{F_{3} F_{4}}+\overrightarrow{F_{4} U}\right)-\left(\overrightarrow{V F_{4}}+\overrightarrow{F_{4} F_{1}}+\overrightarrow{F_{1} W}\right) \\
|
| 22 |
+
= & \left(\overrightarrow{P F_{1}}-\overrightarrow{F_{1} W}\right)-\left(\overrightarrow{R F_{2}}-\overrightarrow{F_{2} Q}\right)+\left(\overrightarrow{T F_{3}}-\overrightarrow{F_{3} S}\right)-\left(\overrightarrow{V F_{4}}-\overrightarrow{F_{4} U}\right) \\
|
| 23 |
+
& +\left(\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{3} F_{4}}\right)-\left(\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{4} F_{1}}\right)=\mathbf{0}
|
| 24 |
+
\end{aligned}
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
Alternatively, but equivalently, $\overrightarrow{P Q}+\overrightarrow{T U}=\overrightarrow{R S}+\overrightarrow{V W}$, as required.
|
| 28 |
+
Second Approach. This is merely another way of reading the previous argument. Fix an orientation of the line $P W$, say, from $P$ towards $W$, and use a lower case letter to denote the coordinate of a point labelled by the corresponding upper case letter.
|
| 29 |
+
|
| 30 |
+
Since the diagonals of a parallelogram bisect one another, $f_{1}+f_{3}=f_{2}+f_{4}$, the common value being twice the coordinate of the projection to $P W$ of the point where $O_{1} O_{3}$ and $O_{2} O_{4}$ cross; the relation clearly holds in the degenerate case as well.
|
| 31 |
+
|
| 32 |
+
Plug $f_{1}=\frac{1}{2}(p+w), f_{2}=\frac{1}{2}(q+r), f_{3}=\frac{1}{2}(s+t)$ and $f_{4}=\frac{1}{2}(u+v)$ into the above equality to get $p+w+s+t=q+r+u+v$. Alternatively, but equivalently, $(q-p)+(u-t)=(s-r)+(w-v)$, that is, $P Q+T U=R Q+V W$, as required.
|
| 33 |
+
|
| 34 |
+
Problem 2. Xenia and Sergey play the following game. Xenia thinks of a positive integer $N$ not exceeding 5000. Then she fixes 20 distinct positive integers $a_{1}, a_{2}, \ldots, a_{20}$ such that, for each $k=1,2, \ldots, 20$, the numbers $N$ and $a_{k}$ are congruent modulo $k$. By a move, Sergey tells Xenia a set $S$ of positive integers not exceeding 20, and she tells him back the set $\left\{a_{k}: k \in S\right\}$ without spelling out which number corresponds to which index. How many moves does Sergey need to determine for sure the number Xenia thought of?
|
| 35 |
+
|
| 36 |
+
Russia, Sergey Kudrya
|
| 37 |
+
Solution. Sergey can determine Xenia's number in 2 but not fewer moves.
|
| 38 |
+
We first show that 2 moves are sufficient. Let Sergey provide the set $\{17,18\}$ on his first move, and the set $\{18,19\}$ on the second move. In Xenia's two responses, exactly one number occurs twice, namely, $a_{18}$. Thus, Sergey is able to identify $a_{17}, a_{18}$, and $a_{19}$, and thence the residue of $N$ modulo $17 \cdot 18 \cdot 19=5814>5000$, by the Chinese Remainder Theorem. This means that the given range contains a single number satisfying all congruences, and Sergey achieves his goal.
|
| 39 |
+
|
| 40 |
+
To show that 1 move is not sufficient, let $M=\operatorname{lcm}(1,2, \ldots, 10)=2^{3} \cdot 3^{2} \cdot 5 \cdot 7=2520$. Notice that $M$ is divisible by the greatest common divisor of every pair of distinct positive integers not exceeding 20. Let Sergey provide the set $S=\left\{s_{1}, s_{2}, \ldots, s_{k}\right\}$. We show that there exist pairwise distinct positive integers $b_{1}, b_{2}, \ldots, b_{k}$ such that $1 \equiv b_{i}\left(\bmod s_{i}\right)$ and $M+1 \equiv b_{i-1}\left(\bmod s_{i}\right)$ (indices are reduced modulo $k$ ). Thus, if in response Xenia provides the set $\left\{b_{1}, b_{2}, \ldots, b_{k}\right\}$, then Sergey will be unable to distinguish 1 from $M+1$, as desired.
|
| 41 |
+
|
| 42 |
+
To this end, notice that, for each $i$, the numbers of the form $1+m s_{i}, m \in \mathbb{Z}$, cover all residues modulo $s_{i+1}$ which are congruent to $1(\equiv M+1)$ modulo $\operatorname{gcd}\left(s_{i}, s_{i+1}\right) \mid M$. Xenia can therefore choose a positive integer $b_{i}$ such that $b_{i} \equiv 1\left(\bmod s_{i}\right)$ and $b_{i} \equiv M+1\left(\bmod s_{i+1}\right)$. Clearly, such choices can be performed so as to make the $b_{i}$ pairwise distinct, as required.
|
| 43 |
+
|
| 44 |
+
Problem 3. A number of 17 workers stand in a row. Every contiguous group of at least 2 workers is a brigade. The chief wants to assign each brigade a leader (which is a member of the brigade) so that each worker's number of assignments is divisible by 4. Prove that the number of such ways to assign the leaders is divisible by 17 .
|
| 45 |
+
|
| 46 |
+
Russia, Mikhail Antipov
|
| 47 |
+
|
| 48 |
+
Solution. Assume that every single worker also forms a brigade (with a unique possible leader). In this modified setting, we are interested in the number $N$ of ways to assign leadership so that each worker's number of assignments is congruent to 1 modulo 4.
|
| 49 |
+
|
| 50 |
+
Consider the variables $x_{1}, x_{2}, \ldots, x_{17}$ corresponding to the workers. Assign each brigade (from the $i$-th through the $j$-th worker) the polynomial $f_{i j}=x_{i}+x_{i+1}+\cdots+x_{j}$, and form the product $f=\prod_{1 \leq i \leq j \leq 17} f_{i j}$. The number $N$ is the sum $\Sigma(f)$ of the coefficients of all monomials $x_{1}^{\alpha_{1}} x_{2}^{\alpha_{2}} \ldots x_{17}^{\alpha_{17}}$ in the expansion of $f$, where the $\alpha_{i}$ are all congruent to 1 modulo 4 . For any polynomial $P$, let $\Sigma(P)$ denote the corresponding sum. From now on, all polynomials are considered with coefficients in the finite field $\mathbb{F}_{17}$.
|
| 51 |
+
|
| 52 |
+
Recall that for any positive integer $n$, and any integers $a_{1}, a_{2}, \ldots, a_{n}$, there exist indices $i \leq j$ such that $a_{i}+a_{i+1}+\cdots+a_{j}$ is divisible by $n$. Consequently, $f\left(a_{1}, a_{2}, \ldots, a_{17}\right)=0$ for all $a_{1}, a_{2}, \ldots, a_{17}$ in $\mathbb{F}_{17}$.
|
| 53 |
+
|
| 54 |
+
Now, if some monomial in the expansion of $f$ is divisible by $x_{i}^{17}$, replace that $x_{i}^{17}$ by $x_{i}$; this does not alter the above overall vanishing property (by Fermat's Little Theorem), and preserves $\Sigma(f)$. After several such changes, $f$ transforms into a polynomial $g$ whose degree in each variable does not exceed 16 , and $g\left(a_{1}, a_{2}, \ldots, a_{17}\right)=0$ for all $a_{1}, a_{2}, \ldots, a_{17}$ in $\mathbb{F}_{17}$. For such a polynomial, an easy induction on the number of variables shows that it is identically zero. Consequently, $\Sigma(g)=0$, so $\Sigma(f)=0$ as well, as desired.
|
| 55 |
+
|
RMM/md/en-2021-RMM2021-Day2-English_Solutions.md
ADDED
|
@@ -0,0 +1,117 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $13^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 2 - Solutions
|
| 4 |
+
|
| 5 |
+
Problem 4. Consider an integer $n \geq 2$ and write the numbers $1,2, \ldots, n$ down on a board. A move consists in erasing any two numbers $a$ and $b$, and, for each $c$ in $\{a+b,|a-b|\}$, writing $c$ down on the board, unless $c$ is already there; if $c$ is already on the board, do nothing. For all integers $n \geq 2$, determine whether it is possible to be left with exactly two numbers on the board after a finite number of moves.
|
| 6 |
+
|
| 7 |
+
## China
|
| 8 |
+
|
| 9 |
+
Solution. The answer is in the affirmative for all $n \geq 2$. Induct on $n$. Leaving aside the trivial case $n=2$, deal first with particular cases $n=5$ and $n=6$.
|
| 10 |
+
|
| 11 |
+
If $n=5$, remove first the pair $(2,5)$, notice that $3=|2-5|$ is already on the board, so $7=2+5$ alone is written down. Removal of the pair $(3,4)$ then leaves exactly two numbers on the board, 1 and 7 , since $|3 \pm 4|$ are both already there.
|
| 12 |
+
|
| 13 |
+
If $n=6$, remove first the pair $(1,6)$, notice that $5=|1-6|$ is already on the board, so $7=1+6$ alone is written down. Next, remove the pair $(2,5)$ and notice that $|2 \pm 5|$ are both already on the board, so no new number is written down. Finally, removal of the pair $(3,4)$ provides a single number to be written down, $1=|3-4|$, since $7=3+4$ is already on the board. At this stage, the process comes to an end: 1 and 7 are the two numbers left.
|
| 14 |
+
|
| 15 |
+
In the remaining cases, the problem for $n$ is brought down to the corresponding problem for $\lceil n / 2\rceil<n$ by a finite number of moves. The conclusion then follows by induction.
|
| 16 |
+
|
| 17 |
+
Let $n=4 k$ or $4 k-1$, where $k$ is a positive integer. Remove the pairs $(1,4 k-1),(3,4 k-3), \ldots$, $(2 k-1,2 k+1)$ in turn. Each time, two odd numbers are removed, and the corresponding $c=|a \pm b|$ are even numbers in the range 2 through $4 k$, of which one is always $4 k$. These even numbers are already on the board at each stage, so no $c$ is to be written down, unless $n=4 k-1$ in which case $4 k$ is written down during the first move. The outcome of this $k$-move round is the string of even numbers 2 through $4 k$ written down on the board. At this stage, the problem is clearly brought down to the case where the numbers on the board are $1,2, \ldots, 2 k=\lceil n / 2\rceil$, as desired.
|
| 18 |
+
|
| 19 |
+
Finally, let $n=4 k+1$ or $4 k+2$, where $k \geq 2$. Remove first the pair $(4,2 k+1)$ and notice that no new number is to be written down on the board, since $4+(2 k+1)=2 k+5 \leq 4 k+1 \leq n$. Next, remove the pairs $(1,4 k+1),(3,4 k-1), \ldots,(2 k-1,2 k+3)$ in turn. As before, at each of these stages, two odd numbers are removed; the corresponding $c=|a \pm b|$ are even numbers, this time in the range 4 through $4 k+2$, of which one is always $4 k+2$; and no new numbers are to be written down on the board, except $4=|(2 k-1)-(2 k+3)|$ during the last move, and, possibly, $4 k+2=1+(4 k+1)$ during the first move if $n=4 k+1$. Notice that 2 has not yet been involved in the process, to conclude that the outcome of this $(k+1)$-move round is the string of even numbers 2 through $4 k+2$ written down on the board. At this stage, the problem is clearly brought down to the case where the numbers on the board are $1,2, \ldots, 2 k+1=\lceil n / 2\rceil$, as desired.
|
| 20 |
+
|
| 21 |
+
Solution 2. We will prove the following, more general statement:
|
| 22 |
+
Claim. Write down a finite number (at least two) of pairwise distinct positive integers on a board. A move consists in erasing any two numbers $a$ and $b$, and, for each $c$ in $\{a+b,|a-b|\}$, writing $c$ down on the board, unless $c$ is already there; if $c$ is already on the board, do nothing. Then it is possible to be left with exactly two numbers on the board after a finite number of moves.
|
| 23 |
+
|
| 24 |
+
Notice that, if we divide all numbers on the board by some common factor, the resulting process goes on equally well. Such a reduction can therefore be performed after any move.
|
| 25 |
+
|
| 26 |
+
Notice that we cannot be left with less than two numbers. So it suffices to show that, given $k$ positive integers on the board, $k \geq 3$, we can always decrease their number by at least 1 . Arguing indirectly, choose a set of $k \geq 3$ positive integers $S=\left\{a_{1}, \ldots, a_{k}\right\}$ which cannot be reduced in size by a sequence of moves, having a minimal possible sum $\sigma$. So, in any sequence of moves applied to $S$, two numbers are erased and exactly two numbers appear on each move. Moreover, the sum of any resulting set of $k$ numbers is at least $\sigma$.
|
| 27 |
+
|
| 28 |
+
Notice that, given two numbers $a>b$ on the board, we can replace them by $a+b$ and $a-b$, and then, performing a move on the two new numbers, by $(a+b)+(a-b)=2 a$ and $(a+b)-(a-b)=2 b$. So we can double any two numbers on the board.
|
| 29 |
+
|
| 30 |
+
We now show that, if the board contains two even numbers $a$ and $b$, we can divide them both by 2 , while keeping the other numbers unchanged. If $k$ is even, split the other numbers into pairs to multiply each pair by 2 ; then clear out the common factor 2 . If $k$ is odd, split all numbers but $a$ into pairs to multiply each by 2 ; then do the same for all numbers but $b$; finally, clear out the common factor 4.
|
| 31 |
+
|
| 32 |
+
Back to the problem, if two of the numbers $a_{1}, \ldots, a_{k}$ are even, reduce them both by 2 to get a set with a smaller sum, which is impossible. Otherwise, two numbers, say, $a_{1}<a_{2}$, are odd, and we may replace them by the two even numbers $a_{1}+a_{2}$ and $a_{2}-a_{1}$, and then by $\frac{1}{2}\left(a_{1}+a_{2}\right)$ and $\frac{1}{2}\left(a_{2}-a_{1}\right)$, to get a set with a smaller sum, which is again impossible.
|
| 33 |
+
|
| 34 |
+
Problem 5. Let $n$ be a positive integer. The kingdom of Zoomtopia is a convex polygon with integer sides, perimeter $6 n$, and $60^{\circ}$ rotational symmetry (that is, there is a point $O$ such that a $60^{\circ}$ rotation about $O$ maps the polygon to itself). In light of the pandemic, the government of Zoomtopia would like to relocate its $3 n^{2}+3 n+1$ citizens at $3 n^{2}+3 n+1$ points in the kingdom so that every two citizens have a distance of at least 1 for proper social distancing. Prove that this is possible. (The kingdom is assumed to contain its boundary.)
|
| 35 |
+
|
| 36 |
+
USA, Ankan Bhattacharya
|
| 37 |
+
Solution. Let $P$ denote the given polygon, i.e., the kingdom of Zoomtopia. Throughout the solution, we interpret polygons with integer sides and perimeter $6 k$ as $6 k$-gons with unit sides (some of their angles may equal $180^{\circ}$ ). The argument hinges on the claim below:
|
| 38 |
+
Claim. Let $P$ be a convex polygon satisfying the problem conditions - i.e., it has integer sides, perimeter $6 n$, and $60^{\circ}$ rotational symmetry. Then $P$ can be tiled with unit equilateral triangles and unit lozenges with angles at least $60^{\circ}$, with tiles meeting completely along edges, so that the tile configuration has a total of exactly $3 n^{2}+3 n+1$ distinct vertices.
|
| 39 |
+
Proof. Induct on $n$. The base case, $n=1$, is clear.
|
| 40 |
+
Now take a polygon $P$ of perimeter $6 n \geq 12$. Place six equilateral triangles inwards on six edges corresponding to each other upon rotation at $60^{\circ}$. It is possible to stick a lozenge to each other edge, as shown in the Figure below.
|
| 41 |
+
|
| 42 |
+
We show that all angles of the lozenges are at least $60^{\circ}$. Let an edge $X Y$ of the polygon bearing some lozenge lie along a boundary segment between edges $A B$ and $C D$ bearing equilateral triangles $A B P$ and $C D Q$. Then the angle formed by $\overrightarrow{X Y}$ and $\overrightarrow{B P}$ is between those formed by $\overrightarrow{A B}, \overrightarrow{B P}$ and $\overrightarrow{C D}, \overrightarrow{C Q}$, i.e., between $60^{\circ}$ and $120^{\circ}$, as desired.
|
| 43 |
+
|
| 44 |
+
Removing all obtained tiles, we get a $60^{\circ}$-symmetric convex $6(n-1)$-gon with unit sides which can be tiled by the inductive hypothesis. Finally, the number of vertices in the tiling of $P$ is $6 n+3(n-1)^{2}+3(n-1)+1=3 n^{2}+3 n+1$, as desired.
|
| 45 |
+
|
| 46 |
+
|
| 47 |
+
Using the Claim above, we now show that the citizens may be placed at the $3 n^{2}+3 n+1$ tile vertices.
|
| 48 |
+
|
| 49 |
+
Consider any tile $T_{1}$; its vertices are at least 1 apart from each other. Moreover, let $B A C$ be a part of the boundary of some tile $T$, and let $X$ be any point of the boundary of $T$, lying outside the half-open intervals $[A, B)$ and $[A, C)$ (in this case, we say that $X$ is not adjacent to $A$ ). Then $A X \geq \sqrt{3} / 2$.
|
| 50 |
+
|
| 51 |
+
Now consider any two tile vertices $A$ and $B$. If they are vertices of the same tile we already know $A B \geq 1$; otherwise, the segment $A B$ crosses the boundaries of some tiles containing $A$ and $B$ at some points $X$ and $Y$ not adjacent to $A$ and $B$, respectively. Hence $A B \geq A X+Y B \geq \sqrt{3}>1$.
|
| 52 |
+
|
| 53 |
+
Problem 6. Initially, a non-constant polynomial $S(x)$ with real coefficients is written down on a board. Whenever the board contains a polynomial $P(x)$, not necessarily alone, one can write down on the board any polynomial of the form $P(C+x)$ or $C+P(x)$, where $C$ is a real constant. Moreover, if the board contains two (not necessarily distinct) polynomials $P(x)$ and $Q(x)$, one can write $P(Q(x))$ and $P(x)+Q(x)$ down on the board. No polynomial is ever erased from the board.
|
| 54 |
+
|
| 55 |
+
Given two sets of real numbers, $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$, a polynomial $f(x)$ with real coefficients is $(A, B)$-nice if $f(A)=B$, where $f(A)=\left\{f\left(a_{i}\right): i=1,2, \ldots, n\right\}$.
|
| 56 |
+
|
| 57 |
+
Determine all polynomials $S(x)$ that can initially be written down on the board such that, for any two finite sets $A$ and $B$ of real numbers, with $|A|=|B|$, one can produce an $(A, B)$-nice polynomial in a finite number of steps.
|
| 58 |
+
|
| 59 |
+
Iran, Navid SafaEi
|
| 60 |
+
Solution. The required polynomials are all polynomials of an even degree $d \geq 2$, and all polynomials of odd degree $d \geq 3$ with negative leading coefficient.
|
| 61 |
+
|
| 62 |
+
Part I. We begin by showing that any (non-constant) polynomial $S(x)$ not listed above is not $(A, B)$-nice for some pair $(A, B)$ with either $|A|=|B|=2$, or $|A|=|B|=3$.
|
| 63 |
+
|
| 64 |
+
If $S(x)$ is linear, then so are all the polynomials appearing on the board. Therefore, none of them will be $(A, B)$-nice, say, for $A=\{1,2,3\}$ and $B=\{1,2,4\}$, as desired.
|
| 65 |
+
|
| 66 |
+
Otherwise, $\operatorname{deg} S=d \geq 3$ is odd, and the leading coefficient is positive. In this case, we make use of the following technical fact, whose proof is presented at the end of the solution.
|
| 67 |
+
|
| 68 |
+
Claim. There exists a positive constant $T$ such that $S(x)$ satisfies the following condition:
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
S(b)-S(a) \geq b-a \quad \text { whenever } \quad b-a \geq T
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
Fix a constant $T$ provided by the Claim. Then, an immediate check shows that all newly appearing polynomials on the board also satisfy $(*)$ (with the same value of $T$ ). Therefore, none of them will be $(A, B)$-nice, say, for $A=\{0, T\}$ and $B=\{0, T / 2\}$, as desired.
|
| 75 |
+
|
| 76 |
+
Part II. We show that the polynomials listed in the Answer satisfy the requirements. We will show that for any $a_{1}<a_{2}<\cdots<a_{n}$ and any $b_{1} \leq b_{2} \leq \cdots \leq b_{n}$ there exists a polynomial $f(x)$ satisfying $f\left(a_{i}\right)=b_{\sigma(i)}$ for all $i=1,2, \ldots, n$, where $\sigma$ is some permutation.
|
| 77 |
+
|
| 78 |
+
The proof goes by induction on $n \geq 2$. It is based on the following two lemmas, first of which is merely the base case $n=2$; the proofs of the lemmas are also at the end of the solution.
|
| 79 |
+
|
| 80 |
+
Lemma 1. For any $a_{1}<a_{2}$ and any $b_{1}, b_{2}$ one can write down on the board a polynomial $F(x)$ satisfying $F\left(a_{i}\right)=b_{i}, i=1,2$.
|
| 81 |
+
|
| 82 |
+
Lemma 2. For any distinct numbers $a_{1}<a_{2}<\cdots<a_{n}$ one can produce a polynomial $F(x)$ on the board such that the list $F\left(a_{1}\right), F\left(a_{2}\right), \ldots, F\left(a_{n}\right)$ contains exactly $n-1$ distinct numbers, and $F\left(a_{1}\right)=F\left(a_{2}\right)$.
|
| 83 |
+
|
| 84 |
+
Now, in order to perform the inductive step, we may replace the polynomial $S(x)$ with its shifted copy $S(C+x)$ so that the values $S\left(a_{i}\right)$ are pairwise distinct. Applying Lemma 2 , we get a polynomial $f(x)$ such that only two among the numbers $c_{i}=f\left(a_{i}\right)$ coincide, namely $c_{1}$ and $c_{2}$. Now apply Lemma 1 to get a polynomial $g(x)$ such that $g\left(a_{1}\right)=b_{1}$ and $g\left(a_{2}\right)=b_{2}$. Apply the inductive hypothesis in order to obtain a polynomial $h(x)$ satisfying $h\left(c_{i}\right)=b_{i}-g\left(a_{i}\right)$ for all $i=2,3, \ldots, n$. Then the polynomial $h(f(x))+g(x)$ is a desired one; indeed, we have $h\left(f\left(a_{i}\right)\right)+g\left(a_{i}\right)=h\left(c_{i}\right)+g\left(a_{i}\right)=b_{i}$ for all $i=2,3, \ldots, n$, and finally $h\left(f\left(a_{1}\right)\right)+g\left(a_{1}\right)=$ $h\left(c_{1}\right)+g\left(a_{1}\right)=b_{2}-g\left(a_{2}\right)+g\left(a_{1}\right)=b_{1}$.
|
| 85 |
+
|
| 86 |
+
It remains to prove the Claim and the two Lemmas.
|
| 87 |
+
Proof of the Claim. There exists some segment $\Delta=\left[\alpha^{\prime}, \beta^{\prime}\right]$ such that $S(x)$ is monotone increasing outside that segment. Now one can choose $\alpha \leq \alpha^{\prime}$ and $\beta \geq \beta^{\prime}$ such that $S(\alpha)<\min _{x \in \Delta} S(x)$ and
|
| 88 |
+
$S(\beta)>\max _{x \in \Delta} S(x)$. Therefore, for any $x, y, z$ with $x \leq \alpha \leq y \leq \beta \leq z$ we get $S(x) \leq S(\alpha) \leq$ $S(y) \leq S(\beta) \leq S(z)$.
|
| 89 |
+
|
| 90 |
+
We may decrease $\alpha$ and increase $\beta$ (preserving the condition above) so that, in addition, $S^{\prime}(x)>3$ for all $x \notin[\alpha, \beta]$. Now we claim that the number $T=3(\beta-\alpha)$ fits the bill.
|
| 91 |
+
|
| 92 |
+
Indeed, take any $a$ and $b$ with $b-a \geq T$. Even if the segment $[a, b]$ crosses $[\alpha, \beta]$, there still is a segment $\left[a^{\prime}, b^{\prime}\right] \subseteq[a, b] \backslash(\alpha, \beta)$ of length $b^{\prime}-a^{\prime} \geq(b-a) / 3$. Then
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
S(b)-S(a) \geq S\left(b^{\prime}\right)-S\left(a^{\prime}\right)=\left(b^{\prime}-a^{\prime}\right) \cdot S^{\prime}(\xi) \geq 3\left(b^{\prime}-a^{\prime}\right) \geq b-a
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
for some $\xi \in\left(a^{\prime}, b^{\prime}\right)$.
|
| 99 |
+
Proof of Lemma 1. If $S(x)$ has an even degree, then the polynomial $T(x)=S\left(x+a_{2}\right)-S\left(x+a_{1}\right)$ has an odd degree, hence there exists $x_{0}$ with $T\left(x_{0}\right)=S\left(x_{0}+a_{2}\right)-S\left(x_{0}+a_{1}\right)=b_{2}-b_{1}$. Setting $G(x)=S\left(x+x_{0}\right)$, we see that $G\left(a_{2}\right)-G\left(a_{1}\right)=b_{2}-b_{1}$, so a suitable shift $F(x)=G(x)+\left(b_{1}-G\left(a_{1}\right)\right)$ fits the bill.
|
| 100 |
+
|
| 101 |
+
Assume now that $S(x)$ has odd degree and a negative leading coefficient. Notice that the polynomial $S^{2}(x):=S(S(x))$ has an odd degree and a positive leading coefficient. So, the polynomial $S^{2}\left(x+a_{2}\right)-S^{2}\left(x+a_{1}\right)$ attains all sufficiently large positive values, while $S\left(x+a_{2}\right)-$ $S\left(x+a_{1}\right)$ attains all sufficiently large negative values. Therefore, the two-variable polynomial $S^{2}\left(x+a_{2}\right)-S^{2}\left(x+a_{1}\right)+S\left(y+a_{2}\right)-S\left(y+a_{1}\right)$ attains all real values; in particular, there exist $x_{0}$ and $y_{0}$ with $S^{2}\left(x_{0}+a_{2}\right)+S\left(y_{0}+a_{2}\right)-S^{2}\left(x_{0}+a_{1}\right)-S\left(y_{0}+a_{1}\right)=b_{2}-b_{1}$. Setting $G(x)=S^{2}\left(x+x_{0}\right)+S\left(x+y_{0}\right)$, we see that $G\left(a_{2}\right)-G\left(a_{1}\right)=b_{2}-b_{1}$, so a suitable shift of $G$ fits the bill.
|
| 102 |
+
|
| 103 |
+
Proof of Lemma 2. Let $\Delta$ denote the segment $\left[a_{1} ; a_{n}\right]$. We modify the proof of Lemma 1 in order to obtain a polynomial $F$ convex (or concave) on $\Delta$ such that $F\left(a_{1}\right)=F\left(a_{2}\right)$; then $F$ is a desired polynomial. Say that a polynomial $H(x)$ is good if $H$ is convex on $\Delta$.
|
| 104 |
+
|
| 105 |
+
If $\operatorname{deg} S$ is even, and its leading coefficient is positive, then $S(x+c)$ is good for all sufficiently large negative $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large negative values for such $c$. Similarly, $S(x+c)$ is good for all sufficiently large positive $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large positive values for such $c$. Therefore, there exist large $c_{1}<0<c_{2}$ such that $S\left(x+c_{1}\right)+S\left(x+c_{2}\right)$ is a desired polynomial. If the leading coefficient of $H$ is negative, we similarly find a desired polynomial which is concave on $\Delta$.
|
| 106 |
+
|
| 107 |
+
If $\operatorname{deg} S \geq 3$ is odd (and the leading coefficient is negative), then $S(x+c)$ is good for all sufficiently large negative $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large negative values for such $c$. Similarly, $S^{2}(x+c)$ is good for all sufficiently large positive $c$, and $S^{2}\left(a_{2}+c\right)-S^{2}\left(a_{1}+c\right)$ attains all sufficiently large positive values for such $c$. Therefore, there exist large $c_{1}<0<c_{2}$ such that $S\left(x+c_{1}\right)+S^{2}\left(x+c_{2}\right)$ is a desired polynomial.
|
| 108 |
+
|
| 109 |
+
Comment. Both parts above allow some variations.
|
| 110 |
+
In Part I, the same scheme of the proof works for many conditions similar to (*), e.g.,
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
S(b)-S(a)>T \quad \text { whenever } \quad b-a>T
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
Let us sketch an alternative approach for Part II. It suffices to construct, for each $i$, a polynomial $f_{i}(x)$ such that $f_{i}\left(a_{i}\right)=b_{i}$ and $f_{i}\left(a_{j}\right)=0, j \neq i$. The construction of such polynomials may be reduced to the construction of those for $n=3$ similarly to what happens in the proof of Lemma 2. However, this approach (as well as any in this part) needs some care in order to work properly.
|
| 117 |
+
|
RMM/md/en-2023-RMM2023-Day1-English_Solutions.md
ADDED
|
@@ -0,0 +1,205 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Problem 1. Determine all prime numbers $p$ and all positive integers $x$ and $y$ satisfying $x^{3}+y^{3}=$ $p(x y+p)$.
|
| 2 |
+
|
| 3 |
+
Solution 1. Up to a swap of the first two entries, the only solutions are $(x, y, p)=(1,8,19)$, $(x, y, p)=(2,7,13)$ and $(x, y, p)=(4,5,7)$. The verification is routine.
|
| 4 |
+
|
| 5 |
+
Set $s=x+y$. Rewrite the equation in the form $s\left(s^{2}-3 x y\right)=p(p+x y)$, and express $x y$ :
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
x y=\frac{s^{3}-p^{2}}{3 s+p}
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
In particular,
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
s^{2} \geq 4 x y=\frac{4\left(s^{3}-p^{2}\right)}{3 s+p}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
or
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
(s-2 p)\left(s^{2}+s p+2 p^{2}\right) \leq p^{2}-p^{3}<0
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
so $s<2 p$.
|
| 24 |
+
If $p \mid s$, then $s=p$ and $x y=p(p-1) / 4$ which is impossible for $x+y=p$ (the equation $t^{2}-p t+p(p-1) / 4=0$ has no integer solutions).
|
| 25 |
+
|
| 26 |
+
If $p \nmid s$, rewrite $(*)$ in the form
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
27 x y=\left(9 s^{2}-3 s p+p^{2}\right)-\frac{p^{2}(p+27)}{3 s+p}
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
Since $p \nmid s$, this could be integer only if $3 s+p \mid$ $p+27$, and hence $3 s+p \mid 27-s$.
|
| 33 |
+
|
| 34 |
+
If $s \neq 9$, then $|3 s-27| \geq 3 s+p$, so $27-3 s \geq$ $3 s+p$, or $27-p \geq 6 s$, whence $s \leq 4$. These cases are ruled out by hand.
|
| 35 |
+
|
| 36 |
+
If $s=x+y=9$, then $(*)$ yields $x y=27-p$. Up to a swap of $x$ and $y$, all such triples $(x, y, p)$ are $(1,8,19),(2,7,13)$, and $(4,5,7)$.
|
| 37 |
+
|
| 38 |
+
Solution 2. Set again $s=x+y$. It is readily checked that $s \leq 8$ provides no solutions, so assume $s \geq 9$. Notice that $x^{3}+y^{3}=s\left(x^{2}-x y+y^{2}\right) \geq$ $\frac{1}{4} s^{3}$ and $x y \leq \frac{1}{4} s^{2}$. The condition in the statement then implies $s^{2}(s-p) \leq 4 p^{2}$, so $s<p+4$.
|
| 39 |
+
|
| 40 |
+
Notice that $p$ divides one of $s$ and $x^{2}-x y+y^{2}$. The case $p \mid s$ is easily ruled out by the condition $s<p+4$ : The latter forces $s=p$,
|
| 41 |
+
|
| 42 |
+
## Serbia, Dushan DuUkitch
|
| 43 |
+
|
| 44 |
+
so $x^{2}-x y+y^{2}=x y+p$, i. e., $(x-y)^{2}=p$, which is impossible.
|
| 45 |
+
|
| 46 |
+
Hence $p \mid x^{2}-x y+y^{2}$, so $x^{2}-x y+y^{2}=k p$ and $x y+p=k s$ for some positive integer $k$, implying
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
s^{2}+3 p=k(3 s+p)
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Recall that $p \nmid s$ to infer that $3 k \equiv s(\bmod p)$. We now present two approaches.
|
| 53 |
+
1st Approach. Write $3 k=s+m p$ for some integer $m$ and plug $k=\frac{1}{3}(s+m p)$ into ( $\left.* *\right)$ to get $s=(9-m p) /(3 m+1)$. The condition $s \geq 9$ then forces $m=0$, so $s=9$, in which case, up to a swap of the first two entries, the solutions turn out to be $(x, y, p)=(1,8,19),(x, y, p)=(2,7,13)$ and $(x, y, p)=(4,5,7)$.
|
| 54 |
+
2nd Approach. Notice that $k=\frac{s^{2}+3 p}{3 s+p}=3+$ $\frac{s(s-9)}{3 s+p} \leq 3+\frac{1}{3}(s-9)=\frac{1}{3} s \leq \frac{1}{3}(p+3)$, since $s<p+4$. Hence $3 k \leq p+3$, and the congruence $3 k \equiv s$ $(\bmod p)$ then forces either $3 k=s-p$ or $3 k=s$.
|
| 55 |
+
|
| 56 |
+
The case $3 k=s-p$ is easily ruled out: Otherwise, $(* *)$ boils down to $2 s+p+9=0$, which is clearly impossible.
|
| 57 |
+
|
| 58 |
+
Finally, if $3 k=s$, then $(* *)$ reduces to $s=9$. In this case, up to a swap of the first two entries, the only solutions are $(x, y, p)=(1,8,19)$, $(x, y, p)=(2,7,13)$ and $(x, y, p)=(4,5,7)$.
|
| 59 |
+
|
| 60 |
+
Remark. The upper bound for $k$ can equally well be established by considering the variation of $\left(s^{2}+3 p\right) /(3 s+p)$ for $1 \leq s \leq p+3$. The maximum is achieved at $s=p+3$ :
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
\begin{array}{r}
|
| 64 |
+
\max _{1 \leq s \leq p+3} \frac{s^{2}+3 p}{3 s+p}=\frac{(p+3)^{2}+3 p}{3(p+3)+p}=\frac{p^{2}+9 p+9}{4 p+9} \\
|
| 65 |
+
<\frac{p+4}{3}
|
| 66 |
+
\end{array}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
so the integer $3 k \leq p+3<p+9 \leq p+s$ and the remainder of the proof now goes along the few final lines above.
|
| 70 |
+
|
| 71 |
+
|
| 72 |
+
#### Abstract
|
| 73 |
+
|
| 74 |
+
Problem 2. Fix an integer $n \geqslant 3$. Let $\mathcal{S}$ be a set of $n$ points in the plane, no three of which are collinear. Given different points $A, B, C$ in $\mathcal{S}$, the triangle $A B C$ is nice for $A B$ if Area $(A B C) \leqslant \operatorname{Area}(A B X)$ for all $X$ in $\mathcal{S}$ different from $A$ and $B$. (Note that for a segment $A B$ there could be several nice triangles.) A triangle is beautiful if its vertices are all in $\mathcal{S}$ and it is nice for at least two of its sides.
|
| 75 |
+
|
| 76 |
+
|
| 77 |
+
Prove that there are at least $\frac{1}{2}(n-1)$ beautiful triangles.
|
| 78 |
+
|
| 79 |
+
# Bulgaria, Alexander Ivanov
|
| 80 |
+
|
| 81 |
+
Solution. For convenience, a triangle whose vertices all lie in $\mathcal{S}$ will be referred to as a triangle in $\mathcal{S}$. The argument hinges on the following observation:
|
| 82 |
+
|
| 83 |
+
Given any partition of $\mathcal{S}$, amongst all triangles in $\mathcal{S}$ with at least one vertex in each part, those of minimal area are all adequate.
|
| 84 |
+
|
| 85 |
+
Indeed, amongst the triangles under consideration, one of minimal area is suitable for both sides with endpoints in different parts.
|
| 86 |
+
|
| 87 |
+
We now present two approaches for the lower bound.
|
| 88 |
+
1st Approach. By the above observation, the 3uniform hypergraph of adequate triangles is connected. It is a well-known fact that such a hypergraph has at least $\frac{1}{2}(n-1)$ hyperedges, whence the required lower bound
|
| 89 |
+
2nd Approach. For a partition $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$, an area minimising triangle as above will be called $(\mathcal{A}, \mathcal{B})$ minimal. Thus, $(\mathcal{A}, \mathcal{B})$-minimal triangles are all adequate.
|
| 90 |
+
|
| 91 |
+
Consider now a partition of $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$, where $|\mathcal{A}|=1$. Choose an $(\mathcal{A}, \mathcal{B})$-minimal triangle and add to $\mathcal{A}$ its vertices from $\mathcal{B}$ to obtain a new partition also written $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$. Continuing, choose an $(\mathcal{A}, \mathcal{B})$-minimal triangle and add to $\mathcal{A}$ its vertices/vertex from $\mathcal{B}$ and so on and so forth all the way down for at least another $\frac{1}{2}(n-5)$ steps - this works at least as many times, since at each step, $\mathcal{B}$ loses at most two points. Clearly, each step provides a new adequate triangle, so the overall number of adequate triangles is at least $\frac{1}{2}(n-1)$, as required.
|
| 92 |
+
|
| 93 |
+
Remark. In fact, $\lfloor n / 2\rfloor$ is the smallest possible number of adequate triangles, as shown by the the configurations described below.
|
| 94 |
+
|
| 95 |
+
Let first $n=2 k-1$. Consider a regular $n$-gon
|
| 96 |
+
$\mathcal{P}=A_{1} A_{2} \ldots A_{n}$. Choose a point $B_{i}$ on the perpendicular bisector of $A_{i} A_{i+1}$ outside $\mathcal{P}$ and sufficiently close to the segment $A_{i} A_{i+1}$. We claim that there are exactly $k-1=\lfloor n / 2\rfloor$ adequate triangles in the set
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\mathcal{S}=\left\{A_{1}, A_{2}, \ldots, A_{k}, B_{1}, B_{2}, \ldots, B_{k-1}\right\}
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
Notice here that the arc $A_{1} A_{2} \ldots A_{k}$ is less than half of the circumcircle of $\mathcal{P}$, so the angles $\angle A_{u} A_{v} A_{w}$, $1 \leq u<v<w \leq k$, are all obtuse.
|
| 103 |
+
|
| 104 |
+
|
| 105 |
+
To prove the claim, list the suitable triangles for each segment.
|
| 106 |
+
|
| 107 |
+
For segments $A_{i} A_{i+1}, A_{i} B_{i}$, and $B_{i} A_{i+1}$, it is $A_{i} B_{i} A_{i+1}$.
|
| 108 |
+
|
| 109 |
+
For segment $A_{i} A_{j+1}, j \geq i+1$, those are $A_{i} B_{i} A_{j+1}$ and $A_{i} B_{j} A_{j+1}$.
|
| 110 |
+
|
| 111 |
+
For segment $A_{i} B_{j}, j \geq i+1$, it is $A_{i} B_{i} B_{j}$.
|
| 112 |
+
For segment $B_{i} A_{j+1}, j \geq i+1$, it is $B_{i} B_{j} A_{j+1}$.
|
| 113 |
+
For segment $B_{i} B_{j}, i<j$, those are $B_{i} A_{i+1} B_{j}$ and $B_{i} A_{j} B_{j}$.
|
| 114 |
+
|
| 115 |
+
It is easily seen that the only triangles occurring twice are $A_{i} B_{i} A_{i+1}$, hence they are the only adequate triangles.
|
| 116 |
+
|
| 117 |
+
For $n=2 k-2$, just remove $A_{k}$ from the above example. This removes the adequate triangle $A_{k-1} B_{k-1} A_{k}$ and provides only one new such instead, namely, $B_{k-2} A_{k-1} B_{k-1}$. Consequently, there are exactly $k-1=\lfloor n / 2\rfloor$ adequate triangles in the set
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\mathcal{S}=\left\{A_{1}, A_{2}, \ldots, A_{k-1}, B_{1}, B_{2}, \ldots, B_{k-1}\right\}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
Problem 3. Let $n \geqslant 2$ be an integer, and let $f$ be a $4 n$-variable polynomial with real coefficients. Assume that, for any $2 n$ points $\left(x_{1}, y_{1}\right), \ldots,\left(x_{2 n}, y_{2 n}\right)$ in the plane, $f\left(x_{1}, y_{1}, \ldots, x_{2 n}, y_{2 n}\right)=0$ if and only if the points form the vertices of a regular $2 n$-gon in some order, or are all equal.
|
| 124 |
+
|
| 125 |
+
Determine the smallest possible degree of $f$.
|
| 126 |
+
|
| 127 |
+
Solution. The smallest possible degree is $2 n$. In what follows, we will frequently write $A_{i}=$ $\left(x_{i}, y_{i}\right)$, and abbreviate $P\left(x_{1}, y_{1}, \ldots, x_{2 n}, y_{2 n}\right)$ to $P\left(A_{1}, \ldots, A_{2 n}\right)$ or as a function of any $2 n$ points.
|
| 128 |
+
|
| 129 |
+
Suppose that $f$ is valid. First, we note a key property:
|
| 130 |
+
|
| 131 |
+
Claim (Sign of $f$ ). $f$ attains wither only nonnegative values, or only nonpositive values.
|
| 132 |
+
|
| 133 |
+
Proof. This follows from the fact that the zero-set of $f$ is very sparse: if $f$ takes on a positive and a negative value, we can move $A_{1}, \ldots, A_{2 n}$ from the negative value to the positive value without ever having them form a regular $2 n$-gon - a contradiction.
|
| 134 |
+
|
| 135 |
+
The strategy for showing $\operatorname{deg} f \geq 2 n$ is the following. We will animate the points $A_{1}, \ldots, A_{2 n}$ linearly in a variable $t$; then $g(t)=f\left(A_{1}, \ldots, A_{2 n}\right)$ will have degree at most $\operatorname{deg} f$ (assuming it is not zero). The claim above then establishes that any root of $g$ must be a multiple root, so if we can show that there are at least $n$ roots, we will have shown $\operatorname{deg} g \geq 2 n$, and so $\operatorname{deg} f \geq 2 n$.
|
| 136 |
+
|
| 137 |
+
Geometrically, our goal is to exhibit $2 n$ linearly moving points so that they form a regular $2 n$-gon a total of $n$ times, but not always form one.
|
| 138 |
+
|
| 139 |
+
We will do this as follows. Draw $n$ mirrors through the origin, as lines making angles of $\frac{\pi}{n}$ with each other. Then, any point $P$ has a total of $2 n$ reflections in the mirrors, as shown below for $n=5$. (Some of these reflections may overlap.)
|
| 140 |
+
|
| 141 |
+
Draw the $n$ angle bisectors of adjacent mirrors. Observe that the reflections of $P$ form a regular $2 n$ gon if and only if $P$ lies on one of the bisectors.
|
| 142 |
+
|
| 143 |
+
We will animate $P$ on any line $\ell$ which intersects all $n$ bisectors (but does not pass through the origin), and let $P_{1}, \ldots, P_{2 n}$ be its reflections. Clearly, these are also all linearly animated, and because of the reasons above, they will form a regular $2 n$-gon exactly $n$ times, when $\ell$ meets each bisector. So this establishes $\operatorname{deg} f \geq 2 n$ for the reasons described previously.
|
| 144 |
+
|
| 145 |
+
Now we pass to constructing a polynomial $f$ of degree $2 n$ having the desired property. First of all, we will instead find a polynomial $g$ which has this property, but only when points with sum zero are input. This still solves the problem, because then
|
| 146 |
+
we can choose
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
f\left(A_{1}, A_{2}, \ldots, A_{2 n}\right)=g\left(A_{1}-\bar{A}, \ldots, A_{2 n}-\bar{A}\right)
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
where $\bar{A}$ is the centroid of $A_{1}, \ldots, A_{2 n}$. This has the upshot that we can now always assume $A_{1}+\cdots+A_{2 n}=0$, which will simplify the ensuing discussion.
|
| 153 |
+
|
| 154 |
+
|
| 155 |
+
We will now construct a suitable $g$ as a sum of squares. This means that, if we write $g=g_{1}^{2}+g_{2}^{2}+$ $\cdots+g_{m}^{2}$, then $g=0$ if and only if $g_{1}=\cdots=g_{m}=0$, and that if their degrees are $d_{1}, \ldots, d_{m}$, then $g$ has degree at most $2 \max \left(d_{1}, \ldots, d_{m}\right)$.
|
| 156 |
+
|
| 157 |
+
Thus, it is sufficient to exhibit several polynomials, all of degree at most $n$, such that $2 n$ points with zero sum are the vertices of a regular $2 n$-gon if and only if the polynomials are all zero at those points.
|
| 158 |
+
|
| 159 |
+
First, we will impose the constraints that all $\left|A_{i}\right|^{2}=x_{i}^{2}+y_{i}^{2}$ are equal. This uses multiple degree 2 constraints.
|
| 160 |
+
|
| 161 |
+
Now, we may assume that the points $A_{1}, \ldots, A_{2 n}$ all lie on a circle with centre 0 , and $A_{1}+\cdots+A_{2 n}=0$. If this circle has radius 0 , then all $A_{i}$ coincide, and we may ignore this case.
|
| 162 |
+
|
| 163 |
+
Otherwise, the circle has positive radius. We will use the following lemma.
|
| 164 |
+
Lemma. Suppose that $a_{1}, \ldots, a_{2 n}$ are complex numbers of the same non-zero magnitude, and suppose that $a_{1}^{k}+\cdots+a_{2 n}^{k}=0, k=1, \ldots, n$. Then $a_{1}, \ldots, a_{2 n}$ form a regular $2 n$-gon centred at the origin. (Conversely, this is easily seen to be sufficient.)
|
| 165 |
+
Proof. Since all the hypotheses are homogenous, we may assume (mostly for convenience) that $a_{1}, \ldots, a_{2 n}$ lie on the unit circle. By Newton's sums, the $k$-th symmetric sums of $a_{1}, \ldots, a_{2 n}$ are all zero for $k$ in the range $1, \ldots, n$.
|
| 166 |
+
|
| 167 |
+
Taking conjugates yields $a_{1}^{-k}+\cdots+a_{2 n}^{-k}=0$, $k=1, \ldots, n$. Thus, we can repeat the above logic to obtain that the $k$-th symmetric sums of $a_{1}^{-1}, \ldots, a_{2 n}^{-1}$ are also all zero for $k=1, \ldots, n$. However, these are simply the $(2 n-k)$-th symmetric sums of $a_{1}, \ldots, a_{2 n}$ (divided by $a_{1} \cdots a_{2 n}$ ), so the first $2 n-1$ symmetric sums of $a_{1}, \ldots, a_{2 n}$ are all zero. This implies that $a_{1}, \ldots, a_{2 n}$ form a regular $2 n$-gon centred at the origin.
|
| 168 |
+
|
| 169 |
+
We will encode all of these constraints into our polynomial. More explicitly, write $a_{r}=x_{r}+y_{r} i$; then the constraint $a_{1}^{k}+\cdots+a_{2 n}^{k}=0$ can be expressed as $p_{k}+q_{k} i=0$, where $p_{k}$ and $q_{k}$ are real polynomials in the coordinates. To incorporate this, simply impose the constraints $p_{k}=0$ and $q_{k}=0$; these are conditions of degree $k \leq n$, so their squares are all of degree at most $2 n$.
|
| 170 |
+
|
| 171 |
+
To recap, taking the sum of squares of all of these constraints gives a polynomial $f$ of degree at most $2 n$ which works whenever $A_{1}+\cdots+A_{2 n}=0$. Finally, the centroid-shifting trick gives a polynomial which works in general, as wanted.
|
| 172 |
+
|
| 173 |
+
Remark 1. Here is a more detailed approach of the mirror-reflection argument. Let $r e^{i \theta}$ be the polar representation of the point $P$. The polar representations of its mirrored images are then
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
\begin{array}{ll}
|
| 177 |
+
r e^{i \theta}, & r e^{-i \theta}, \quad r e^{i\left(\frac{2 \pi}{n}+\theta\right)}, \quad r e^{i\left(\frac{2 \pi}{n}-\theta\right)} \\
|
| 178 |
+
\ldots, & r e^{i\left(\frac{2(n-1) \pi}{n}+\theta\right)}, \quad r e^{i\left(\frac{2(n-1) \pi}{n}-\theta\right)}
|
| 179 |
+
\end{array}
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
Clearly, they are all linear with respect to $P$ and lie on the circle of radius $r$ centred at the origin. As listed above, the $2 n$ images are not necessarily in
|
| 183 |
+
circular order around the circle. For convenience, assume $0 \leq \theta \leq \frac{\pi}{n}$, so the list now displays them in circular order. These images form the vertices of a regular $2 n$-gon if and only if the angle between every two consecutive terms in the list (read circularly) is $\frac{\pi}{n}$. This is clearly the case if and only if $\theta=\frac{\pi}{2 n}$. Consequently, the images are the vertices of a regular $2 n$-gon if and only if $P$ lies on the internal bisector of the angle formed by some pair of consecutive mirrors.
|
| 184 |
+
|
| 185 |
+
Remark 2. We sketch here some versions of the arguments in the solution above.
|
| 186 |
+
|
| 187 |
+
To show that $\operatorname{deg} f \geq 2 n$, we use the same constancy of sign claim and the convention that the polynomial is a function of points ( $=$ pairs of coordinates) $A_{1}, A_{2}, \ldots, A_{2 n}$. Assume that the values of $f$ are all non-negative.
|
| 188 |
+
|
| 189 |
+
Write $B(\phi)=(\cos \phi, \sin \phi)$. Choose a substitution $A_{2 i-1}=B\left((2 i-1) \frac{\pi}{n}+\phi\right)$ and $A_{2 i}=$ $B\left(2 i \frac{\pi}{n}-\phi\right), i=1,2, \ldots, n$. Notice that the coordinates of the points $A_{1}, A_{2}, \ldots, A_{2 n}$ are all linear functions in $c=\cos \phi$ and $s=\sin \phi$, so, substituting these expressions into $f$, we get a polynomial $g(c, s)$ with $\operatorname{deg} g \leq \operatorname{deg} f$.
|
| 190 |
+
|
| 191 |
+
Now, the values of $g$ are all non-negative (each being one of $f$ ), and, on the circle $c^{2}+s^{2}=1$, it vanishes at exactly $2 n$ points, namely, $(c, s)=$ $\left(\cos \frac{\pi}{n} k, \sin \frac{\pi}{n} k\right), k=1, \ldots, 2 n$. We show that these properties already yield $\operatorname{deg} g \geq 2 n$.
|
| 192 |
+
|
| 193 |
+
Obviously, if $g(c, s)$ possesses the properties listed above, then so does $g(c,-s)$, and hence so does $\bar{g}(c, s)=g(c, s)+g(c,-s)$.
|
| 194 |
+
|
| 195 |
+
The polynomial $\bar{g}$ is even in $s$, so it in fact depends only on $s^{2}$, and we may plug $s^{2}=1-c^{2}$ into it, to obtain a polynomial $h(c)$ with $\operatorname{deg} h \leq \operatorname{deg} g$ which is non-negative on $[-1,1]$ and vanishes on this segment exactly at $c=\cos \frac{\pi}{n} k$. These are $n+1$ such points, and, except $c= \pm 1$, they should all be roots of $h$ of even multiplicity, due to sign conservation. All in all, this provides $2 n$ roots of $h$, counted with multiplicity, hence $\operatorname{deg} f \geq \operatorname{deg} g \geq \operatorname{deg} h \geq 2 n$, as desired.
|
| 196 |
+
|
| 197 |
+
For a bit alternative construction of a suitable $f$, one may notice that the Lemma in the above solution can be changed to impose vanishing of the elementary symmetric polynomials $\sigma_{i}\left(a_{1}, a_{2}, \ldots, a_{2 n}\right)$, $i=1,2, \ldots, n$, instead of Newton sums. Indeed, if the $\sigma_{i}$ all vanish, then so do the polynomials
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
\sigma_{i}\left(\bar{a}_{1}, a_{2}, \ldots, \bar{a}_{2 n}\right)=\frac{\left|a_{1}\right|^{2 i} \sigma_{2 n-i}\left(a_{1}, a_{2}, \ldots, a_{2 n}\right)}{\bar{a}_{1} \bar{a}_{2} \ldots \bar{a}_{2 n}}
|
| 201 |
+
$$
|
| 202 |
+
|
| 203 |
+
so $\sigma_{i}\left(a_{1}, \ldots, a_{2 n}\right)$ also vanishes for $i=n+1, \ldots, 2 n-$
|
| 204 |
+
|
| 205 |
+
1. Hence $a_{1}, a_{2}, \ldots, a_{2 n}$ are the roots of $z^{2 n}-\left|a_{1}\right|^{n}$, as desired.
|
RMM/md/en-2023-RMM2023-Day2-English_Solutions.md
ADDED
|
@@ -0,0 +1,163 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Problem 4. Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
|
| 2 |
+
|
| 3 |
+
# Russia, Vasily Mokin
|
| 4 |
+
|
| 5 |
+
Solution 1. Fix the origin at $O$ and the real axis along $\ell$. A lower case letter denotes the complex coordinate of the corresponding point in the configuration. For convenience, let $|a|=|b|=|c|=1$.
|
| 6 |
+
|
| 7 |
+
Clearly, $k=a+\frac{1}{2}(b+c), p=a+\frac{1}{2}\left(b+\frac{1}{b}\right)$ and $q=a+\frac{1}{2}\left(c+\frac{1}{c}\right)$.
|
| 8 |
+
|
| 9 |
+
Then $|k-p|=\left|a+\frac{1}{2}\left(c-\frac{1}{b}\right)\right|=\frac{1}{2}|2 a b+b c-1|$, since $|b|=1$.
|
| 10 |
+
|
| 11 |
+
Similarly, $|k-q|=\frac{1}{2}|2 a c+b c-1|$, so, since $|a|=1$,
|
| 12 |
+
$|k-p|+|k-q|=\frac{1}{2}|2 a b+b c-1|+\frac{1}{2}|2 a c+b c-1|$
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\geq \frac{1}{2}|2 a(b-c)|=|b-c|,
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
as required.
|
| 19 |
+
Solution 2. Let $M$ be the midpoint of $B C$, and let $R$ be the projection of $M$ onto $\ell$. In other words, $R$ is the midpoint of $P Q$. Since $\angle B P O=\angle B M O=$ $90^{\circ}$, the points $B, P, O$, and $M$ are concyclic, so $\angle(O M, O B)=\angle(P M, P B)=\angle(P M, M R)$, so the right triangles $M R P$ and $O M B$ are similar and have different orientation. Similarly, the triangles $M R Q$ and $O M C$ are similar and have different orientation, hence so are the triangles $O B C$ and $M P Q$.
|
| 20 |
+
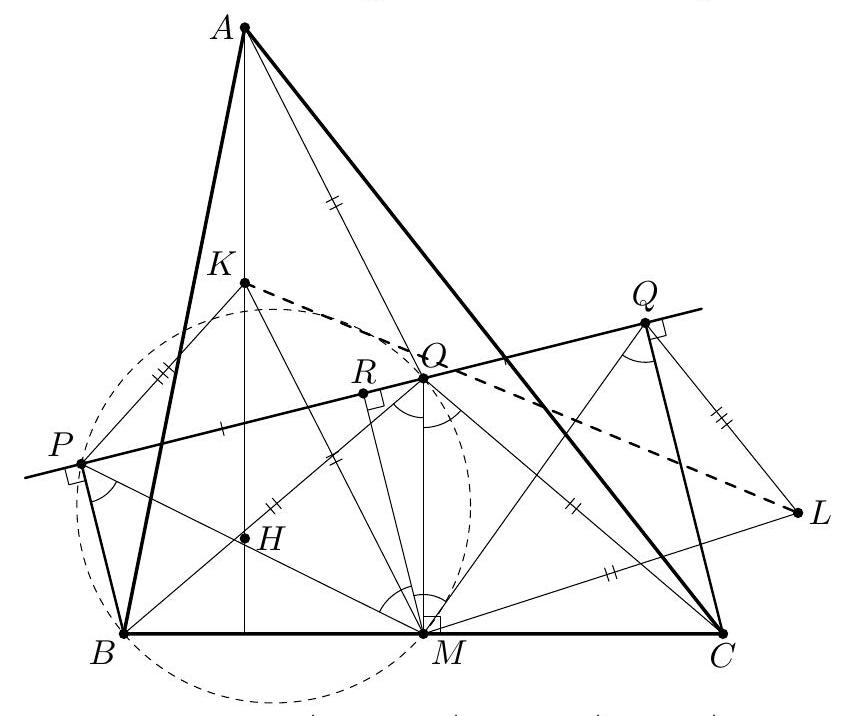
|
| 21 |
+
|
| 22 |
+
Recall that $\overrightarrow{A H}=2 \overrightarrow{O M}$, so $\overrightarrow{O M}=\overrightarrow{A K}$. Hence $A O M K$ is a parallelogram, so $M K=O A=O B=$ $O C$.
|
| 23 |
+
|
| 24 |
+
Consider the rotation through $\angle(\overrightarrow{O C}, \overrightarrow{O B})$ about $M$. It maps $P$ to $Q$; let it map $K$ to some point $L$. Then $M K=M L=O B=O C$ and $\angle L M K=\angle B O C$, so the triangles $O B C$ and $M K L$ are congruent. Hence $B C=K L \leq K Q+L Q=$ $K Q+K P$, as required.
|
| 25 |
+
Solution 3. Let $\alpha=\angle(P B, B C)=\angle(Q C, B C)$. Since $P$ lies on the circle of diameter $O B$, $\angle(O P, O M)=\alpha$. Since also $Q$ lies on the circle of diameter $O C$, it immediately follows that
|
| 26 |
+
$M P=M Q=R \sin \alpha$ by sine theorem in triangles $\triangle O P M$ and $\triangle O Q M$.
|
| 27 |
+
|
| 28 |
+
Because $P Q$ is the projection of $B C$ on line $\ell$, it follows that $P Q=B C \sin \alpha$. Just like in the first solution, $K M=A O=R$ (the circumradius of triangle $\triangle A B C)$.
|
| 29 |
+
|
| 30 |
+
Now apply Ptolemy's inequality for the quadrilateral $K P M Q$ : $K P \cdot M Q+K Q \cdot M P \geq P Q \cdot K M$, and now substitute the relations from above, leading to
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
R \sin \alpha(K P+K Q) \geq R \sin \alpha \cdot B C
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
which is precisely the conclusion whenever $\sin \alpha \neq 0$. The case when $\sin \alpha=0$ can be treated either directly, or via a limit argument.
|
| 37 |
+
Solution 4. Denote by $R$ and $O$ the circumradius and the circumcentre of triangle $A B C$, respectively. As in Solution 1, we see that $M K=R$.
|
| 38 |
+
|
| 39 |
+
Assume now that $\ell$ is fixed, while $A$ moves along the fixed circle $(A B C)$. Then $K$ will move along a cricle centred at $M$ with radius $R$. We must show that for each point $K$ on this circle we have $B C \leq K P+K Q$. In doing so, we prove that the afore-mentioned circle contains an ellipse with foci at $Q$ and $P$ with distance $B C$.
|
| 40 |
+
|
| 41 |
+
Let $S$ be the foot of the perpendicular from $M$ to $P Q$, it is easy to verify that $S$ is the center of the ellipse. We shall then consider it as the origin. Let $u=\frac{B C}{2}$ and $t=\frac{P Q}{2}$; notice that $u$ is the major semi-axis of the ellipse and $\sqrt{u^{2}-t^{2}}$ is the minor one. Assume $X(x, y)$ is a point on this ellipse. We now need to prove $M X \leq R$.
|
| 42 |
+
|
| 43 |
+
Since $X$ is on the ellipse, we can write $(x, y)=$ $\left(u \cos \theta, \sqrt{u^{2}-t^{2}} \sin \theta\right)$, for some $\theta \in(0,2 \pi)$. Since $M X^{2}=x^{2}+(y+M S)^{2}$, we can expand and obtain $M X^{2}=u^{2}+M S^{2}-t^{2} \cdot \sin ^{2} \theta+2 M S \cdot \sqrt{u^{2}-t^{2}} \cdot \sin \theta$.
|
| 44 |
+
|
| 45 |
+
Add and subtract $M S^{2}\left(u^{2}-t^{2}\right) / t^{2}$ in order to obtain a square on the right hand side: $M X^{2}=u^{2}+$ $M S^{2}+\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}}-\left(t \sin \theta-\frac{M S \sqrt{u^{2}-t^{2}}}{t}\right)^{2}$. It now suffices to show that $u^{2}+M S^{2}+\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}}=$ $R^{2}$, since then it would immediately follow that $M X^{2} \leq R^{2}$.
|
| 46 |
+
|
| 47 |
+
Applying Pythagorean theorem in triangles $O B M$ and $O S M$, we obtain $R^{2}=u^{2}+O M^{2}$ and $O M^{2}=M S^{2}+O S^{2}$, so it remains to prove that $O S^{2}=\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}} . \quad$ Let $\alpha=\angle(O P, B M)$, then $O S / M S=\tan ^{t^{2}} \alpha$ and $t / u=\cos \alpha$, so $O S^{2}=$ $M S^{2} \tan ^{2} \alpha=M S^{2}\left(\frac{1-\cos ^{2} \alpha}{\cos ^{2} \alpha}\right)=M S^{2} \cdot \frac{u^{2}-t^{2}}{t^{2}}$, which is the desired result.
|
| 48 |
+
|
| 49 |
+
Problem 5. Let $P(x), Q(x), R(x)$ and $S(x)$ be non-constant polynomials with real coefficients such that $P(Q(x))=R(S(x))$. Suppose that the degree of $P(x)$ is divisible by the degree of $R(x)$.
|
| 50 |
+
Prove that there is a polynomial $T(x)$ with real coefficients such that $P(x)=R(T(x))$.
|
| 51 |
+
|
| 52 |
+
## Iran, NaVid Safaei
|
| 53 |
+
|
| 54 |
+
Solution 1. Degree comparison of $P(Q(x))$ and $R(S(x))$ implies that $q=\operatorname{deg} Q \mid \operatorname{deg} S=s$. We will show that $S(x)=T(Q(x))$ for some polynomial $T$. Then $P(Q(x))=R(S(x))=R(T(Q(x)))$, so the polynomial $P(t)-R(T(t))$ vanishes upon substitution $t=S(x)$; it therefore vanishes identically, as desired.
|
| 55 |
+
|
| 56 |
+
Choose the polynomials $T(x)$ and $M(x)$ such that
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
S(x)=T(Q(x))+M(x)
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
where $\operatorname{deg} M$ is minimised; if $M=0$, then we get the desired result. For the sake of contradiction, suppose $M \neq 0$. Then $q \nmid m=\operatorname{deg} M$; otherwise, $M(x)=\beta Q(x)^{m / q}+M_{1}(x)$, where $\beta$ is some number and $\operatorname{deg} M_{1}<\operatorname{deg} M$, contradicting the choice of $M$. In particular, $0<m<s$ and hence $\operatorname{deg} T(Q(x))=s$.
|
| 63 |
+
|
| 64 |
+
Substitute now (*) into $R(S(x))-P(Q(x))=$ 0 ; let $\alpha$ be the leading coefficient of $R(x)$ and let $r=\operatorname{deg} R(x)$. Expand the brackets to get a sum of powers of $Q(x)$ and other terms including powers of $M(x)$ as well. Amongst the latter, the unique term of highest degree is $\operatorname{arM}(x) T(Q(x))^{r-1}$. So, for some polyno$\operatorname{mial} N(x), \quad N(Q(x))=\alpha r M(x) T(Q(x))^{r-1}+$ a polynomial of lower degree.
|
| 65 |
+
|
| 66 |
+
This is impossible, since $q$ divides the degree of the left-hand member, but not that of the righthand member.
|
| 67 |
+
|
| 68 |
+
Solution 2. All polynomials in the solution have real coefficients. As usual, the degree of a polynomial $f(x)$ is denoted $\operatorname{deg} f(x)$.
|
| 69 |
+
|
| 70 |
+
Of all pairs of polynomials $P(x), R(x)$, satisfying the conditions in the statement, choose one, say, $P_{0}(x), R_{0}(x)$, so that $P_{0}(Q(x))=R_{0}(S(x))$ has a minimal (positive) degree. We will show that $\operatorname{deg} R_{0}(x)=1$, say, $R_{0}(x)=\alpha x+\beta$ for some real numbers $\alpha \neq 0$ and $\beta$, so $P_{0}(Q(x))=\alpha S(x)+\beta$. Hence $S(x)=T(Q(x))$ for some polynomial $T(x)$.
|
| 71 |
+
|
| 72 |
+
Now, if $P(x)$ and $R(x)$ are polynomials satisfying $P(Q(x))=R(S(x))$, then $P(Q(x))=$ $R(T(Q(x)))$. Since $Q(x)$ is not constant, it takes infinitely many values, so $P(x)$ and $R(T(x))$ agree at infinitely many points, implying that $P(x)=$ $R(T(x))$, as required.
|
| 73 |
+
|
| 74 |
+
It is therefore sufficient to solve the problem in the particular case where $F(x)=P(Q(x))=$ $R(S(x))$ has a minimal degree. Let $d=$ $\operatorname{gcd}(\operatorname{deg} Q(x), \operatorname{deg} S(x))$ to write $\operatorname{deg} Q(x)=a d$ and $\operatorname{deg} S(x)=b d$, where $\operatorname{gcd}(a, b)=1$. Then
|
| 75 |
+
$\operatorname{deg} P(x)=b c, \operatorname{deg} R(x)=a c$ and $\operatorname{deg} F(x)=a b c d$ for some positive integer $c$. We will show that minimality of $\operatorname{deg} F(x)$ forces $c=1$, so $\operatorname{deg} P(x)=b$, $\operatorname{deg} R(x)=a$ and $\operatorname{deg} F(x)=a b d$. The conditions $a=\operatorname{deg} R(x) \mid \operatorname{deg} P(x)=b$ and $\operatorname{gcd}(a, b)=1$ then force $a=1$, as stated above.
|
| 76 |
+
|
| 77 |
+
Consequently, the only thing we are left with is the proof of the fact that $c=1$. For convenience, we may and will assume that $P(x), Q(x), R(x), S(x)$ are all monic; hence so is $F(x)$. The argument hinges on the lemma below.
|
| 78 |
+
Lemma. If $f(x)$ is a monic polynomial of degree $m n$, then there exists a degree $n$ monic polynomial $g(x)$ such that $\operatorname{deg}\left(f(x)-g(x)^{m}\right)<(m-1) n$. (If $m=0$ or 1 , or $n=0$, the conclusion is still consistent with the usual convention that the identically zero polynomial has degree $-\infty$.)
|
| 79 |
+
Proof. Write $f(x)=\sum_{k=0}^{m n} \alpha_{k} x^{k}, \alpha_{m n}=1$, and seek $g(x)=\sum_{k=0}^{n} \beta_{k} x^{k}, \beta_{n}=1$, so as to fit the bill. To this end, notice that, for each positive integer $k \leq n$, the coefficient of $x^{m n-k}$ in the expansion of $g(x)^{m}$ is of the form $m \beta_{n-k}+\varphi_{k}\left(\beta_{n}, \ldots, \beta_{n-k+1}\right)$, where $\varphi_{k}\left(\beta_{n}, \ldots, \beta_{n-k+1}\right)$ is an algebraic expression in $\beta_{n}, \ldots, \beta_{n-k+1}$. Recall that $\beta_{n}=1$ to determine the $\beta_{n-k}$ recursively by requiring $\beta_{n-k}=$ $\frac{1}{m}\left(a_{m n-k}-\varphi_{k}\left(\beta_{n}, \ldots, \beta_{n-k+1}\right)\right), k=1, \ldots, n$.
|
| 80 |
+
|
| 81 |
+
The outcome is then the desired polynomial $g(x)$.
|
| 82 |
+
|
| 83 |
+
We are now in a position to prove that $c=$ 1. Suppose, if possible, that $c>1$. By the lemma, there exist monic polynomials $U(x)$ and $V(x)$ of degree $b$ and $a$, respectively, such that $\operatorname{deg}\left(P(x)-U(x)^{c}\right)<(c-1) b$ and $\operatorname{deg}(R(x)-$ $\left.V(x)^{c}\right)<(c-1) a$. Then $\operatorname{deg}\left(F(x)-U(Q(x))^{c}\right)=$ $\operatorname{deg}\left(P(Q(x))-U(Q(x))^{c}\right)<(c-1) a b d, \operatorname{deg}(F(x)-$ $\left.V(S(x))^{c}\right)=\operatorname{deg}\left(R(S(x))-V(S(x))^{c}\right)<(c-1) a b d$, so $\operatorname{deg}\left(U(Q(x))^{c}-V(S(x))^{c}\right)=\operatorname{deg}((F(x)-$ $\left.\left.V(S(x))^{c}\right)-\left(F(x)-U(Q(x))^{c}\right)\right)<(c-1) a b d$.
|
| 84 |
+
|
| 85 |
+
On the other hand, $U(Q(x))^{c}-V(S(x))^{c}=$ $(U(Q(x))-V(S(x)))\left(U(Q(x))^{c-1}+\cdots+\right.$ $\left.V(S(x))^{c-1}\right)$.
|
| 86 |
+
|
| 87 |
+
By the preceding, the degree of the left-hand member is (strictly) less than $(c-1) a b d$ which is precisely the degree of the second factor in the righthand member. This forces $U(Q(x))=V(S(x))$, so $U(Q(x))=V(S(x))$ has degree $a b d<a b c d=$ $\operatorname{deg} F(x)$ - a contradiction. Consequently, $c=1$. This completes the argument and concludes the proof.
|
| 88 |
+
|
| 89 |
+
Problem 6. Let $r, g, b$ be non-negative integers. Let $\Gamma$ be a connected graph on $r+g+b+1$ vertices. The edges of $\Gamma$ are each coloured red, green or blue. It turns out that $\Gamma$ has
|
| 90 |
+
|
| 91 |
+
- a spanning tree in which exactly $r$ of the edges are red,
|
| 92 |
+
- a spanning tree in which exactly $g$ of the edges are green and
|
| 93 |
+
- a spanning tree in which exactly $b$ of the edges are blue.
|
| 94 |
+
|
| 95 |
+
Prove that $\Gamma$ has a spanning tree in which exactly $r$ of the edges are red, exactly $g$ of the edges are green and exactly $b$ of the edges are blue.
|
| 96 |
+
|
| 97 |
+
Russia, Vasily Mokin
|
| 98 |
+
|
| 99 |
+
Solution 1. Induct on $n=r+g+b$. The base case, $n=1$, is clear.
|
| 100 |
+
|
| 101 |
+
Let now $n>1$. Let $V$ denote the vertex set of $\Gamma$, and let $T_{r}, T_{g}$, and $T_{b}$ be the trees with exactly $r$ red edges, $g$ green edges, and $b$ blue edges, respectively. Consider two cases.
|
| 102 |
+
Case 1: There exists a partition $V=A \sqcup B$ of the vertex set into two non-empty parts such that the edges joining the parts all bear the same colour, say, blue.
|
| 103 |
+
|
| 104 |
+
Since $\Gamma$ is connected, it has a (necessarily blue) edge connecting $A$ and $B$. Let $e$ be one such.
|
| 105 |
+
|
| 106 |
+
Assume that $T$, one of the three trees, does not contain $e$. Then the graph $T \cup\{e\}$ has a cycle $C$ through $e$. The cycle $C$ should contain another edge $e^{\prime}$ connecting $A$ and $B$; the edge $e^{\prime}$ is also blue. Replace $e^{\prime}$ by $e$ in $T$ to get another tree $T^{\prime}$ with the same number of edges of each colour as in $T$, but containing $e$.
|
| 107 |
+
|
| 108 |
+
Performing such an operation to all three trees, we arrive at the situation where the three trees $T_{r}^{\prime}$, $T_{g}^{\prime}$, and $T_{b}^{\prime}$ all contain $e$. Now shrink $e$ by identifying its endpoints to obtain a graph $\Gamma^{*}$, and set $r^{*}=r, g^{*}=g$, and $b^{*}=b-1$. The new graph satisfies the conditions in the statement for those new values - indeed, under the shrinking, each of the trees $T_{r}^{\prime}, T_{g}^{\prime}$, and $T_{b}^{\prime}$ loses a blue edge. So $\Gamma^{*}$ has a spanning tree with exactly $r$ red, exactly $g$
|
| 109 |
+
green, and exactly $b-1$ blue edges. Finally, pass back to $\Gamma$ by restoring $e$, to obtain the a desired spanning tree in $\Gamma$.
|
| 110 |
+
|
| 111 |
+
Case 2: There is no such a partition.
|
| 112 |
+
Consider all possible collections $(R, G, B)$, where $R, G$ and $B$ are acyclic sets consisting of $r$ red edges, $g$ green edges, and $b$ blue edges, respectively. By the problem assumptions, there is at least one such collection. Amongst all such collections, consider one such that the graph on $V$ with edge set $R \cup G \cup B$ has the smallest number $k$ of components. If $k=1$, then the collection provides the edges of a desired tree (the number of edges is one less than the number of vertices).
|
| 113 |
+
|
| 114 |
+
Assume now that $k \geq 2$; then in the resulting graph some component $K$ contains a cycle $C$. Since $R, G$, and $B$ are acyclic, $C$ contains edges of at least two colours, say, red and green. By assumption, the edges joining $V(K)$ to $V \backslash V(K)$ bear at least two colours; so one of these edges is either red or green. Without loss of generality, consider a red such edge $e$.
|
| 115 |
+
|
| 116 |
+
Let $e^{\prime}$ be a red edge in $C$ and set $R^{\prime}=R \backslash\left\{e^{\prime}\right\} \cup$ $\{e\}$. Then $\left(R^{\prime}, G, B\right)$ is a valid collection providing a smaller number of components. This contradicts minimality of the choice above and concludes the proof.
|
| 117 |
+
|
| 118 |
+
Problem 6. Let $r, g, b$ be non-negative integers. Let $\Gamma$ be a connected graph on $r+g+b+1$ vertices. The edges of $\Gamma$ are each coloured red, green or blue. It turns out that $\Gamma$ has
|
| 119 |
+
|
| 120 |
+
- a spanning tree in which exactly $r$ of the edges are red,
|
| 121 |
+
- a spanning tree in which exactly $g$ of the edges are green and
|
| 122 |
+
- a spanning tree in which exactly $b$ of the edges are blue.
|
| 123 |
+
|
| 124 |
+
Prove that $\Gamma$ has a spanning tree in which exactly $r$ of the edges are red, exactly $g$ of the edges are green and exactly $b$ of the edges are blue.
|
| 125 |
+
|
| 126 |
+
Solution 2. For a spanning tree $T$ in $\Gamma$, denote by $r(T), g(T)$, and $b(T)$ the number of red, green, and blue edges in $T$, respectively.
|
| 127 |
+
|
| 128 |
+
Assume that $\mathcal{C}$ is some collection of spanning trees in $\Gamma$. Write
|
| 129 |
+
|
| 130 |
+
$$
|
| 131 |
+
\begin{array}{rlrl}
|
| 132 |
+
r(\mathcal{C}) & =\min _{T \in \mathcal{C}} r(T), & & g(\mathcal{C})=\min _{T \in \mathcal{C}} g(T) \\
|
| 133 |
+
b(\mathcal{C}) & =\min _{T \in \mathcal{C}} b(T), & & R(\mathcal{C})=\max _{T \in \mathcal{C}}(T) \\
|
| 134 |
+
G(\mathcal{C}) & =\max _{T \in \mathcal{C}} g(T), & B(\mathcal{C})=\max _{T \in \mathcal{C}} b(T)
|
| 135 |
+
\end{array}
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
Say that a collection $\mathcal{C}$ is good if $r \in[r(\mathcal{C}, R(\mathcal{C})]$, $g \in[g(\mathcal{C}, G(\mathcal{C})]$, and $b \in[b(\mathcal{C}, B(\mathcal{C})]$. By the problem conditions, the collection of all spanning trees in $\Gamma$ is good.
|
| 139 |
+
|
| 140 |
+
For a good collection $\mathcal{C}$, say that an edge $e$ of $\Gamma$ is suspicious if $e$ belongs to some tree in $\mathcal{C}$ but not to all trees in $\mathcal{C}$. Choose now a good collection $\mathcal{C}$ minimizing the number of suspicious edges. If $\mathcal{C}$ contains a desired tree, we are done. Otherwise, without loss of generality, $r(\mathcal{C})<r$ and $G(\mathcal{C})>g$.
|
| 141 |
+
|
| 142 |
+
We now distinguish two cases.
|
| 143 |
+
Case 1: $B(\mathcal{C})=b$ 。
|
| 144 |
+
Let $T^{0}$ be a tree in $\mathcal{C}$ with $g\left(T^{0}\right)=g(\mathcal{C}) \leq g$. Since $G(\mathcal{C})>g$, there exists a green edge $e$ contained in some tree in $\mathcal{C}$ but not in $T^{0}$; clearly, $e$ is suspicious. Fix one such green edge $e$.
|
| 145 |
+
|
| 146 |
+
Now, for every $T$ in $\mathcal{C}$, define a spanning tree $T_{1}$ of $\Gamma$ as follows. If $T$ does not contain $e$, then $T_{1}=T$; in particular, $\left(T^{0}\right)_{1}=T^{0}$. Otherwise, the graph $T \backslash\{e\}$ falls into two components. The tree $T_{0}$ contains some edge $e^{\prime}$ joining those components; this edge is necessarily suspicious. Choose one such edge and define $T_{1}=T \backslash\{e\} \cup\left\{e^{\prime}\right\}$.
|
| 147 |
+
|
| 148 |
+
Let $\mathcal{C}_{1}=\left\{T_{1}: T \in \mathcal{C}\right\}$. All edges suspicious for $\mathcal{C}_{1}$ are also suspicious for $\mathcal{C}$, but no tree in $\mathcal{C}_{1}$ con-
|
| 149 |
+
|
| 150 |
+
## Russia, Vasily Mokin
|
| 151 |
+
|
| 152 |
+
tains $e$. So the number of suspicious edges for $\mathcal{C}_{1}$ is strictly smaller than that for $\mathcal{C}$.
|
| 153 |
+
|
| 154 |
+
We now show that $\mathcal{C}_{1}$ is good, reaching thereby a contradiction with the choice of $\mathcal{C}$. For every $T$ in $\mathcal{C}$, the tree $T_{1}$ either coincides with $T$ or is obtained from it by removing a green edge and adding an edge of some colour. This already shows that $g\left(\mathcal{C}_{1}\right) \leq g(\mathcal{C}) \leq g, G\left(\mathcal{C}_{1}\right) \geq G(\mathcal{C})-1 \geq g$, $R\left(\mathcal{C}_{1}\right) \geq R(\mathcal{C}) \geq r, r\left(\mathcal{C}_{1}\right) \leq r(\mathcal{C})+1 \leq r$, and $B\left(\mathcal{C}_{1}\right) \geq B(\mathcal{C}) \geq b$. Finally, we get $b\left(T^{0}\right) \leq$ $B(\mathcal{C})=b$; since $\mathcal{C}_{1}$ contains $T^{0}$, it follows that $b\left(\mathcal{C}_{1}\right) \leq b\left(T^{0}\right) \leq b$, which concludes the proof.
|
| 155 |
+
Case 2: $B(\mathcal{C})>b$.
|
| 156 |
+
Consider a tree $T^{0}$ in $\mathcal{C}$ satisfying $r\left(T^{0}\right)=$ $R(\mathcal{C}) \geq r$. Since $r(\mathcal{C})<r$, the tree $T^{0}$ contains a suspicious red edge. Fix one such edge $e$.
|
| 157 |
+
|
| 158 |
+
Now, for every $T$ in $\mathcal{C}$, define a spanning tree $T_{2}$ of $\Gamma$ as follows. If $T$ contains $e$, then $T_{2}=T$; in particular, $\left(T^{0}\right)_{2}=T^{0}$. Otherwise, the graph $T \cup\{e\}$ contains a cycle $C$ through $e$. This cycle contains an edge $e^{\prime}$ absent from $T^{0}$ (otherwise $T^{0}$ would contain the cycle $C$ ), so $e^{\prime}$ is suspicious. Choose one such edge and define $T_{2}=T \backslash\left\{e^{\prime}\right\} \cup\{e\}$.
|
| 159 |
+
|
| 160 |
+
Let $\mathcal{C}_{2}=\left\{T_{2}: T \in \mathcal{C}\right\}$. All edges suspicious for $\mathcal{C}_{2}$ are also suspicious for $\mathcal{C}$, but all trees in $\mathcal{C}_{2}$ contain $e$. So the number of suspicious edges for $\mathcal{C}_{2}$ is strictly smaller than that for $\mathcal{C}$.
|
| 161 |
+
|
| 162 |
+
We now show that $\mathcal{C}_{2}$ is good, reaching again a contradiction. For every $T$ in $\mathcal{C}$, the tree $T_{2}$ either coincides with $T$ or is obtained from it by removing some edge and adding a red edge. This shows that $r\left(\mathcal{C}_{2}\right) \leq r(\mathcal{C})+1 \leq r, R\left(\mathcal{C}_{2}\right) \geq R(\mathcal{C}) \geq r$, $G\left(\mathcal{C}_{2}\right) \geq G(\mathcal{C})-1 \geq g, g\left(\mathcal{C}_{2}\right) \leq g(\mathcal{C}) \leq g$, $b\left(\mathcal{C}_{1}\right) \leq b(\mathcal{C}) \leq b$ and $B\left(\mathcal{C}_{2}\right) \geq B(\mathcal{C})-1 \geq b$. This concludes the proof.
|
| 163 |
+
|
RMM/md/en-2024-RMM2024-Day1-English.md
ADDED
|
@@ -0,0 +1,30 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $15^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 1: Wednesday, February $28^{\text {th }}$, 2024, Bucharest
|
| 4 |
+
|
| 5 |
+
Language: English
|
| 6 |
+
|
| 7 |
+
Problem 1. Let $n$ be a positive integer. Initially, a bishop is placed in each square of the top row of a $2^{n} \times 2^{n}$ chessboard; those bishops are numbered from 1 to $2^{n}$, from left to right. A jump is a simultaneous move made by all bishops such that the following conditions are satisfied:
|
| 8 |
+
|
| 9 |
+
- each bishop moves diagonally, in a straight line, some number of squares, and
|
| 10 |
+
- at the end of the jump, the bishops all stand in different squares of the same row.
|
| 11 |
+
|
| 12 |
+
Find the total number of permutations $\sigma$ of the numbers $1,2, \ldots, 2^{n}$ with the following property: There exists a sequence of jumps such that all bishops end up on the bottom row arranged in the order $\sigma(1), \sigma(2), \ldots, \sigma\left(2^{n}\right)$, from left to right.
|
| 13 |
+
|
| 14 |
+
Problem 2. Consider an odd prime $p$ and a positive integer $N<50 p$. Let $a_{1}, a_{2}, \ldots, a_{N}$ be a list of positive integers less than $p$ such that any specific value occurs at most $\frac{51}{100} N$ times and $a_{1}+a_{2}+\cdots+a_{N}$ is not divisible by $p$. Prove that there exists a permutation $b_{1}, b_{2}, \ldots, b_{N}$ of the $a_{i}$ such that, for all $k=1,2, \ldots, N$, the sum $b_{1}+b_{2}+\cdots+b_{k}$ is not divisible by $p$.
|
| 15 |
+
|
| 16 |
+
Problem 3. Given a positive integer $n$, a set $\mathcal{S}$ is $n$-admissible if
|
| 17 |
+
|
| 18 |
+
- each element of $\mathcal{S}$ is an unordered triple of integers in $\{1,2, \ldots, n\}$,
|
| 19 |
+
- $|\mathcal{S}|=n-2$, and
|
| 20 |
+
- for each $1 \leq k \leq n-2$ and each choice of $k$ distinct $A_{1}, A_{2}, \ldots, A_{k} \in \mathcal{S}$,
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\left|A_{1} \cup A_{2} \cup \cdots \cup A_{k}\right| \geq k+2
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
Is it true that, for all $n>3$ and for each $n$-admissible set $\mathcal{S}$, there exist pairwise distinct points $P_{1}, \ldots, P_{n}$ in the plane such that the angles of the triangle $P_{i} P_{j} P_{k}$ are all less than $61^{\circ}$ for any triple $\{i, j, k\}$ in $\mathcal{S}$ ?
|
| 27 |
+
|
| 28 |
+
Each problem is worth 7 marks.
|
| 29 |
+
Time allowed: $4 \frac{1}{2}$ hours.
|
| 30 |
+
|
RMM/md/en-2024-RMM2024-Day2-English.md
ADDED
|
@@ -0,0 +1,21 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# The $15^{\text {th }}$ Romanian Master of Mathematics Competition
|
| 2 |
+
|
| 3 |
+
Day 2: Thursday, February $29^{\text {th }}$, 2024, Bucharest
|
| 4 |
+
|
| 5 |
+
Language: English
|
| 6 |
+
|
| 7 |
+
Problem 4. Fix integers $a$ and $b$ greater than 1 . For any positive integer $n$, let $r_{n}$ be the (non-negative) remainder that $b^{n}$ leaves upon division by $a^{n}$. Assume there exists a positive integer $N$ such that $r_{n}<2^{n} / n$ for all integers $n \geq N$. Prove that $a$ divides $b$.
|
| 8 |
+
|
| 9 |
+
Problem 5. Let $B C$ be a fixed segment in the plane, and let $A$ be a variable point in the plane not on the line $B C$. Distinct points $X$ and $Y$ are chosen on the rays $\overrightarrow{C A}$ and $\overrightarrow{B A}$, respectively, such that $\angle C B X=\angle Y C B=\angle B A C$. Assume that the tangents to the circumcircle of $A B C$ at $B$ and $C$ meet line $X Y$ at $P$ and $Q$, respectively, such that the points $X, P, Y$, and $Q$ are pairwise distinct and lie on the same side of $B C$. Let $\Omega_{1}$ be the circle through $X$ and $P$ centred on $B C$. Similarly, let $\Omega_{2}$ be the circle through $Y$ and $Q$ centred on $B C$. Prove that $\Omega_{1}$ and $\Omega_{2}$ intersect at two fixed points as $A$ varies.
|
| 10 |
+
|
| 11 |
+
Problem 6. A polynomial $P$ with integer coefficients is square-free if it is not expressible in the form $P=Q^{2} R$, where $Q$ and $R$ are polynomials with integer coefficients and $Q$ is not constant. For a positive integer $n$, let $\mathcal{P}_{n}$ be the set of polynomials of the form
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
1+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
with $a_{1}, a_{2}, \ldots, a_{n} \in\{0,1\}$. Prove that there exists an integer $N$ so that, for all integers $n \geq N$, more than $99 \%$ of the polynomials in $\mathcal{P}_{n}$ are square-free.
|
| 18 |
+
|
| 19 |
+
Each problem is worth 7 marks.
|
| 20 |
+
Time allowed: $4 \frac{1}{2}$ hours.
|
| 21 |
+
|
RMM/raw/en-2011-Sols2011D1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:ce8d78396bd2283dbfd8bb25140d51427b9e0546ac19b649998e25a8db67fea2
|
| 3 |
+
size 64262
|
RMM/raw/en-2011-Sols2011D2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:68571a0d147cc74578a89185b655890ffcb2b9c9b4a76e21af4765b5a31f0188
|
| 3 |
+
size 101945
|
RMM/raw/en-2012-Solutions2012-1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:9b3dbd271d9c0a8e84a0e4c30a96a78eaa2a5e1605aeeadeb84766b232672d99
|
| 3 |
+
size 62148
|
RMM/raw/en-2012-Solutions2012-2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:8159e649bdb58319b60b1ac011dfc5663be5defdc1fe6289160162489a8718f1
|
| 3 |
+
size 69503
|
RMM/raw/en-2013-Solutions2013-1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:bd28ceb151a6ed96706f0fb6fff948976dca87642f4e061081de119bcfebc957
|
| 3 |
+
size 192918
|
RMM/raw/en-2013-Solutions2013-2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:861f545e68a397fc8d65d3970bd0a87a6efae0fe1f8c91ad162e596f25212d76
|
| 3 |
+
size 188229
|
RMM/raw/en-2015-Solutions_RMM2015-1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:b44077fb72520e64dcadaebf5e427ffe5ced194e0d809993df30d54784ef316a
|
| 3 |
+
size 170097
|
RMM/raw/en-2015-Solutions_RMM2015-2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:a02b84b874cdfd5244f7b7063f598304aa8f8dfae50549140b338b358e246533
|
| 3 |
+
size 177510
|
RMM/raw/en-2016-Solutions_RMM2016-1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:04a6e1d44f501fd3747976c7caddf6479bb54ba5f774065580cfc70de3ab743e
|
| 3 |
+
size 174522
|
RMM/raw/en-2016-Solutions_RMM2016-2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:218f8098fa64e27bf96cd8327aea2debb4e1dfd4b5b51ab7ce1df890e56b3edc
|
| 3 |
+
size 164651
|
RMM/raw/en-2017-Solutions_RMM2017-1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:d3477e9ff25c655154a73706ed8637de4ce6b4a747313e241f49e0fd207a5cab
|
| 3 |
+
size 192072
|
RMM/raw/en-2017-Solutions_RMM2017-2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:ce47e2e521aca8dd7570aedfe8b75d80f650b6b4a50a18a26fc878c2549304b0
|
| 3 |
+
size 234135
|
RMM/raw/en-2018-RMM2018-Day1-English.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:70cfc8fdfea49982ab6757fc92387e3957531d2311d95f03ed473e4d83b2c83d
|
| 3 |
+
size 153298
|
RMM/raw/en-2018-RMM2018-Day2-English.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:6aec41927452927cb805f83fd66995019862f4c74057c9872a1db155b9966c15
|
| 3 |
+
size 232116
|
RMM/raw/en-2019-RMM2019-Day1-English.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:0ff926f8db74c4d7b9c47b1202711d40f74181fb506a496b52b3482cfc4366f6
|
| 3 |
+
size 194832
|
RMM/raw/en-2019-RMM2019-Day2-English.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:9b25b347b805a365e23ff1967fd29440addd9fc6e2f83cf4449e3267cbbb65d9
|
| 3 |
+
size 108870
|
RMM/raw/en-2021-RMM2021-Day1-English_Solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:ec35b4e5afd0b62972dbb8d7e96cadd4eaf6fbf07933de706160a5e8bd53b8f3
|
| 3 |
+
size 166910
|
RMM/raw/en-2021-RMM2021-Day2-English_Solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:8d99c660cc7373a41dcff12fde03dc4f72fff2a2f4717e34353eea40bda77f91
|
| 3 |
+
size 160341
|
RMM/raw/en-2023-RMM2023-Day1-English_Solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:546e9271262297d281454cbbd51f83750f967bf9e63e28ed9ea3fd5e65ef6509
|
| 3 |
+
size 407570
|
RMM/raw/en-2023-RMM2023-Day2-English_Solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3a0348a4083e0390993a4fe041b81f981a44dba530a1ab41dbfd3bffb7009f6e
|
| 3 |
+
size 364971
|
RMM/raw/en-2024-RMM2024-Day1-English.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:82826fe7a40e3ec7dba03c71ece91f4a877084984be7f485ac03225bd66bd8ee
|
| 3 |
+
size 122264
|
RMM/raw/en-2024-RMM2024-Day2-English.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:1514ed91a3f25faa9fb2c95e21834581484076889818b0f1f2e64ba45a9d2247
|
| 3 |
+
size 117542
|
RMM/segment_script/segment.py
ADDED
|
@@ -0,0 +1,128 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
problem_tag = 'Problem'
|
| 12 |
+
solution_tag = 'Solution'
|
| 13 |
+
problem_pattern = re.compile(r'(?:\n|# )Problem\s+(\d+)(.)?')
|
| 14 |
+
solution_pattern = re.compile(r'(?:\n|# )Solution(?:\s+(\d+)|\.|\n)')
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 18 |
+
"""
|
| 19 |
+
Analyze the text and return the tags and problem number.
|
| 20 |
+
|
| 21 |
+
Args:
|
| 22 |
+
text (str): The markdown text to analyze.
|
| 23 |
+
|
| 24 |
+
Returns:
|
| 25 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 26 |
+
"""
|
| 27 |
+
tags = []
|
| 28 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text)])
|
| 29 |
+
problem_num = len(tags)
|
| 30 |
+
|
| 31 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text)])
|
| 32 |
+
tags.sort(key=lambda x: x[0].start())
|
| 33 |
+
return tags, problem_num
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
def segment(text: str, tags):
|
| 37 |
+
starts = []
|
| 38 |
+
ends = []
|
| 39 |
+
|
| 40 |
+
for i in range(len(tags)):
|
| 41 |
+
starts.append(tags[i][0].end())
|
| 42 |
+
if i + 1 < len(tags):
|
| 43 |
+
ends.append(tags[i + 1][0].start())
|
| 44 |
+
else:
|
| 45 |
+
ends.append(len(text))
|
| 46 |
+
|
| 47 |
+
return [text[start:end].strip() for start, end in zip(starts, ends)]
|
| 48 |
+
|
| 49 |
+
|
| 50 |
+
def join(tags, segments):
|
| 51 |
+
problem, solution = '', ''
|
| 52 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 53 |
+
pairs = []
|
| 54 |
+
|
| 55 |
+
has_solution = any([tag[1] == solution_tag for tag in tags])
|
| 56 |
+
|
| 57 |
+
for tag, segment in zip(tags, segments):
|
| 58 |
+
if tag[1] == problem_tag:
|
| 59 |
+
problem = segment
|
| 60 |
+
problem_match = tag[0].group(0)
|
| 61 |
+
problem_label = tag[0].group(1)
|
| 62 |
+
|
| 63 |
+
# If there is no solution, add an empty solution
|
| 64 |
+
if not has_solution:
|
| 65 |
+
pairs.append((problem, '', problem_label, problem_match, ''))
|
| 66 |
+
else:
|
| 67 |
+
solution = segment
|
| 68 |
+
solution_match = tag[0].group(0)
|
| 69 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 70 |
+
|
| 71 |
+
return pairs
|
| 72 |
+
|
| 73 |
+
|
| 74 |
+
def write_pairs(output_file: Path, pairs):
|
| 75 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 76 |
+
|
| 77 |
+
output_jsonl_text = ""
|
| 78 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 79 |
+
output_jsonl_text += json.dumps(
|
| 80 |
+
{
|
| 81 |
+
'year': year,
|
| 82 |
+
'problem_label': problem_label,
|
| 83 |
+
'tier': 1,
|
| 84 |
+
'problem': problem,
|
| 85 |
+
'solution': solution,
|
| 86 |
+
'problem_match': problem_match,
|
| 87 |
+
'solution_match': solution_match
|
| 88 |
+
},
|
| 89 |
+
ensure_ascii=False
|
| 90 |
+
) + '\n'
|
| 91 |
+
|
| 92 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 93 |
+
|
| 94 |
+
|
| 95 |
+
def main():
|
| 96 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 97 |
+
compet_md_path = compet_base_path / "md"
|
| 98 |
+
seg_output_path = compet_base_path / "segmented"
|
| 99 |
+
|
| 100 |
+
total_problem_count = 0
|
| 101 |
+
total_solution_count = 0
|
| 102 |
+
|
| 103 |
+
for apmo_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 104 |
+
output_file = seg_output_path / apmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 105 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 106 |
+
|
| 107 |
+
text = '\n' + apmo_md.read_text(encoding="utf-8")
|
| 108 |
+
|
| 109 |
+
tags, problem_num = analyze(text)
|
| 110 |
+
|
| 111 |
+
if problem_num != 6 and problem_num != 3:
|
| 112 |
+
logger.warning(f"{apmo_md} problem number is {problem_num}")
|
| 113 |
+
|
| 114 |
+
if problem_num > 0:
|
| 115 |
+
segments = segment(text, tags)
|
| 116 |
+
pairs = join(tags, segments)
|
| 117 |
+
write_pairs(output_file, pairs)
|
| 118 |
+
|
| 119 |
+
total_problem_count += problem_num
|
| 120 |
+
total_solution_count += len(pairs)
|
| 121 |
+
else:
|
| 122 |
+
logger.warning(f"No problem found in {apmo_md}")
|
| 123 |
+
|
| 124 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 125 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 126 |
+
|
| 127 |
+
if __name__ == '__main__':
|
| 128 |
+
main()
|
RMM/segmented/en-2011-Sols2011D1.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "1", "tier": 1, "problem": "Prove that there exist two functions\n\n$$\nf, g: \\mathbb{R} \\rightarrow \\mathbb{R}\n$$\n\nsuch that $f \\circ g$ is strictly decreasing, while $g \\circ f$ is strictly increasing.\n(Poland) Andrzej KomisArsKi \\& Marcin Kuczma\n\n#", "solution": "Let\n\n$$\n\\begin{aligned}\n& \\cdot A=\\bigcup_{k \\in \\mathbb{Z}}\\left(\\left[-2^{2 k+1},-2^{2 k}\\right) \\bigcup\\left(2^{2 k}, 2^{2 k+1}\\right]\\right) \\\\\n& \\cdot B=\\bigcup_{k \\in \\mathbb{Z}}\\left(\\left[-2^{2 k},-2^{2 k-1}\\right) \\bigcup\\left(2^{2 k-1}, 2^{2 k}\\right]\\right)\n\\end{aligned}\n$$\n\nThus $A=2 B, B=2 A, A=-A, B=-B, A \\cap B=\\varnothing$, and finally $A \\cup B \\cup\\{0\\}=\\mathbb{R}$. Let us take\n\n$$\nf(x)=\\left\\{\\begin{array}{lll}\nx & \\text { for } & x \\in A \\\\\n-x & \\text { for } & x \\in B \\\\\n0 & \\text { for } & x=0\n\\end{array}\\right.\n$$\n\nTake $g(x)=2 f(x)$. Thus $f(g(x))=f(2 f(x))=-2 x$ and $g(f(x))=2 f(f(x))=2 x$.", "problem_match": "\nProblem 1.", "solution_match": "# Solution."}
|
| 2 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "Determine all positive integers $n$ for which there exists a polynomial $f(x)$ with real coefficients, with the following properties:\n(1) for each integer $k$, the number $f(k)$ is an integer if and only if $k$ is not divisible by $n$;\n(2) the degree of $f$ is less than $n$.\n(Hungary) GÉza Kós", "solution": "We will show that such polynomial exists if and only if $n=1$ or $n$ is a power of a prime.\n\nWe will use two known facts stated in Lemmata 1 and 2.\nLemma 1. If $p^{a}$ is a power of a prime and $k$ is an integer, then $\\frac{(k-1)(k-2) \\ldots\\left(k-p^{a}+1\\right)}{\\left(p^{a}-1\\right)!}$ is divisible by $p$ if and only if $k$ is not divisible by $p^{a}$.\n\nProof. First suppose that $p^{a} \\mid k$ and consider\n\n$$\n\\frac{(k-1)(k-2) \\cdots\\left(k-p^{a}+1\\right)}{\\left(p^{a}-1\\right)!}=\\frac{k-1}{p^{a}-1} \\cdot \\frac{k-2}{p^{a}-2} \\cdots \\frac{k-p^{a}+1}{1}\n$$\n\nIn every fraction on the right-hand side, $p$ has the same maximal exponent in the numerator as in the denominator.\n\nTherefore, the product (which is an integer) is not divisible by $p$.\n\nNow suppose that $p^{a} \\nmid k$. We have\n\n$$\n\\frac{(k-1)(k-2) \\cdots\\left(k-p^{a}+1\\right)}{\\left(p^{a}-1\\right)!}=\\frac{p^{a}}{k} \\cdot \\frac{k(k-1) \\cdots\\left(k-p^{a}+1\\right)}{\\left(p^{a}\\right)!} .\n$$\n\nThe last fraction is an integer. In the fraction $\\frac{p^{a}}{k}$, the denominator $k$ is not divisible by $p^{a}$.\nLemma 2. If $g(x)$ is a polynomial with degree less than $n$ then\n\n$$\n\\sum_{\\ell=0}^{n}(-1)^{\\ell}\\binom{n}{\\ell} g(x+n-\\ell)=0\n$$\n\nProof. Apply induction on $n$. For $n=1$ then $g(x)$ is a constant and\n\n$$\n\\binom{1}{0} g(x+1)-\\binom{1}{1} g(x)=g(x+1)-g(x)=0\n$$\n\nNow assume that $n>1$ and the Lemma holds for $n-1$. Let $h(x)=g(x+1)-g(x)$; the degree of $h$ is less than the degree of $g$, so the induction hypothesis applies for $g$ and $n-1$ :\n\n$$\n\\begin{gathered}\n\\sum_{\\ell=0}^{n-1}(-1)^{\\ell}\\binom{n-1}{\\ell} h(x+n-1-\\ell)=0 \\\\\n\\sum_{\\ell=0}^{n-1}(-1)^{\\ell}\\binom{n-1}{\\ell}(g(x+n-\\ell)-g(x+n-1-\\ell))=0 \\\\\n\\binom{n-1}{0} g(x+n)+\\sum_{\\ell=1}^{n-1}(-1)^{\\ell}\\left(\\binom{n-1}{\\ell-1}+\\right. \\\\\n\\left.\\binom{n-1}{\\ell}\\right) g(x+n-\\ell)-(-1)^{n-1}\\binom{n-1}{n-1} g(x)=0 \\\\\n\\sum_{\\ell=0}^{n}(-1)^{\\ell}\\binom{n}{\\ell} g(x+n-\\ell)=0\n\\end{gathered}\n$$\n\nLemma 3. If $n$ has at least two distinct prime divisors then the greatest common divisor of $\\binom{n}{1},\\binom{n}{2}, \\ldots,\\binom{n}{n-1}$ is 1 .\n\nProof. Suppose to the contrary that $p$ is a common prime divisor of $\\binom{n}{1}, \\ldots,\\binom{n}{n-1}$. In particular, $p \\left\\lvert\\,\\binom{ n}{1}=n\\right.$. Let $a$ be the exponent of $p$ in the prime factorization of $n$. Since $n$ has at least two prime divisors, we have $1<p^{a}<n$. Hence, $\\binom{n}{p^{a}-1}$ and $\\binom{n}{p^{a}}$ are listed among $\\binom{n}{1}, \\ldots,\\binom{n}{n-1}$ and thus $p \\left\\lvert\\,\\binom{ n}{p^{a}}\\right.$ and $p \\left\\lvert\\,\\binom{ n}{p^{a}-1}\\right.$. But then $p$ divides $\\binom{n}{p^{a}}-\\binom{n}{p^{a}-1}=\\binom{n-1}{p^{a}-1}$, which contradicts Lemma 1.\n\nNext we construct the polynomial $f(x)$ when $n=1$ or $n$ is a power of a prime.\n\nFor $n=1, f(x)=\\frac{1}{2}$ is such a polynomial.\nIf $n=p^{a}$ where $p$ is a prime and $a$ is a positive integer then let\n\n$$\nf(x)=\\frac{1}{p}\\binom{x-1}{p^{a}-1}=\\frac{1}{p} \\cdot \\frac{(x-1)(x-2) \\cdots\\left(x-p^{a}+1\\right)}{\\left(p^{a}-1\\right)!} .\n$$\n\nThe degree of this polynomial is $p^{a}-1=n-1$.\nThe number $\\frac{(k-1)(k-2) \\cdots\\left(k-p^{a}+1\\right)}{\\left(p^{a}-1\\right)!}$ is an integer for any integer $k$, and, by Lemma 1 , it is divisible by $p$ if and only if $k$ is not divisible by $p^{a}=n$.\n\nFinally we prove that if $n$ has at least two prime divisors then no polynomial $f(x)$ satisfies $(1,2)$. Suppose that some polynomial $f(x)$ satisfies (1,2), and apply Lemma 2 for $g=f$ and $x=-k$ where $1 \\leq k \\leq n-1$. We get that\n\n$$\n\\binom{n}{k} f(0)=\\sum_{0 \\leq \\ell \\leq n, \\ell \\neq k}(-1)^{k-\\ell}\\binom{n}{\\ell} f(-k+\\ell)\n$$\n\nSince $f(-k), \\ldots, f(-1)$ and $f(1), \\ldots, f(n-k)$ are all integers, we conclude that $\\binom{n}{k} f(0)$ is an integer for every $1 \\leq k \\leq n-1$.\nBy dint of Lemma 3, the greatest common divisor of $\\binom{n}{1},\\binom{n}{2}, \\ldots,\\binom{n}{n-1}$ is 1 . Hence, there will exist some integers $u_{1}, u_{2}, \\ldots, u_{n-1}$ for which $u_{1}\\binom{n}{1}+\\cdots+u_{n-1}\\binom{n}{n-1}=1$. Then\n\n$$\nf(0)=\\left(\\sum_{k=1}^{n-1} u_{k}\\binom{n}{k}\\right) f(0)=\\sum_{k=1}^{n-1} u_{k}\\binom{n}{k} f(0)\n$$\n\nis a sum of integers. This contradicts the fact that $f(0)$ is not an integer. So such polynomial $f(x)$ does not exist.\n\nAlternative Solution. (I. Bogdanov) We claim the answer is $n=p^{\\alpha}$ for some prime $p$ and nonnegative $\\alpha$.\n\nLemma. For every integers $a_{1}, \\ldots, a_{n}$ there exists an integervalued polynomial $P(x)$ of degree $<n$ such that $P(k)=a_{k}$ for all $1 \\leq k \\leq n$.\n\nProof. Induction on $n$. For the base case $n=1$ one may set $P(x)=a_{1}$. For the induction step, suppose that the polynomial $P_{1}(x)$ satisfies the desired property for all $1 \\leq k \\leq n-1$. Then set $P(x)=P_{1}(x)+\\left(a_{n}-P_{1}(n)\\right)\\binom{x-1}{n-1}$; since $\\binom{k-1}{n-1}=0$ for $1 \\leq k \\leq n-1$ and $\\binom{n-1}{n-1}=1$, the polynomial $P(x)$ is a sought one.\n\nNow, if for some $n$ there exists some polynomial $f(x)$ satisfying the problem conditions, one may choose some integer-valued polynomial $P(x)$ (of degree $<n-1$ ) coinciding with $f(x)$ at points $1, \\ldots, n-1$. The difference $f_{1}(x)=$ $f(x)-P(x)$ also satisfies the problem conditions, therefore we may restrict ourselves to the polynomials vanishing at points $1, \\ldots, n-1-$ that are, the polynomials of the form $f(x)=c \\prod_{i=1}^{n-1}(x-i)$ for some (surely rational) constant $c$.\n\nLet $c=p / q$ be its irreducible form, and $q=\\prod_{j=1}^{d} p_{j}^{\\alpha_{j}}$ be the prime decomposition of the denominator.\n\n1. Assume that a desired polynomial $f(x)$ exists. Since $f(0)$ is not an integer, we have $9 \\nmid(-1)^{n-1}(n-1)$ ! and hence $p_{j}^{\\alpha_{j}} \\nmid(-1)^{n-1}(n-1)$ ! for some $j$. Hence\n\n$$\n\\prod_{i=1}^{n-1}\\left(p_{j}^{\\alpha_{j}}-i\\right) \\equiv(-1)^{n-1}(n-1)!\\not \\equiv 0 \\quad\\left(\\bmod p_{j}^{\\alpha_{j}}\\right)\n$$\n\ntherefore $f\\left(p_{i}^{\\alpha_{i}}\\right)$ is not integer, too. By the condition (i), this means that $n \\mid p_{i}^{\\alpha_{i}}$, and hence $n$ should be a power of a prime.\n2. Now let us construct a desired polynomial $f(x)$ for any power of a prime $n=p^{\\alpha}$. We claim that the polynomial\n\n$$\nf(x)=\\frac{1}{p}\\binom{x-1}{n-1}=\\frac{n}{p x}\\binom{x}{n}\n$$\n\nfits. Actually, consider some integer $x$. From the first representation, the denominator of the irreducible form of $f(x)$ may be 1 or $p$ only. If $p^{\\alpha} \\nmid x$, then the prime decomposition of the fraction $n /(p x)$ contains $p$ with a nonnegative exponent; hence $f(x)$ is integer. On the other hand, if $n=p^{\\alpha} \\mid x$, then the numbers $x-1, x-2, \\ldots, x-(n-1)$ contain the same exponents of primes as the numbers $n-1, n-2, \\ldots, 1$ respectively; hence the number\n\n$$\n\\binom{x-1}{n-1}=\\frac{\\prod_{i=1}^{n-1}(x-i)}{\\prod_{i=1}^{n-1}(n-i)}\n$$\n\nis not divisible by $p$. Thus $f(x)$ is not an integer.", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}
|
| 3 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "A triangle $A B C$ is inscribed in a circle $\\omega$. A variable line $\\ell$ chosen parallel to $B C$ meets segments $A B$, $A C$ at points $D, E$ respectively, and meets $\\omega$ at points $K, L$ (where $D$ lies between $K$ and $E$ ). Circle $\\gamma_{1}$ is tangent to the segments $K D$ and $B D$ and also tangent to $\\omega$, while circle $\\gamma_{2}$ is tangent to the segments $L E$ and $C E$ and also tangent to $\\omega$. Determine the locus, as $\\ell$ varies, of the meeting point of the common inner tangents to $\\gamma_{1}$ and $\\gamma_{2}$.\n(Russia) VASily Mokin \\& Fedor IvLev", "solution": "Let $P$ be the meeting point of the common inner tangents to $\\gamma_{1}$ and $\\gamma_{2}$. Also, let $b$ be the angle bisector of $\\angle B A C$. Since $K L \\| B C, b$ is also the angle bisector of $\\angle K A L$.\n\nLet $\\mathfrak{H}$ be the composition of the symmetry $\\mathfrak{S}$ with respect to $b$ and the inversion $\\mathfrak{I}$ of centre $A$ and ratio $\\sqrt{A K \\cdot A L}$ (it is readily seen that $\\mathfrak{S}$ and $\\mathfrak{I}$ commute, so since $\\mathfrak{S}^{2}=\\mathfrak{I}^{2}=$ id, then also $\\mathfrak{H}^{2}=\\mathrm{id}$, the identical transformation). The elements of the configuration interchanged by $\\mathfrak{H}$ are summarized in Table I.\n\nLet $O_{1}$ and $O_{2}$ be the centres of circles $\\gamma_{1}$ and $\\gamma_{2}$. Since the circles $\\gamma_{1}$ and $\\gamma_{2}$ are determined by their construction (in a unique way), they are interchanged by $\\mathfrak{H}$, therefore the rays $A O_{1}$ and $A O_{2}$ are symmetrical with respect\nto $b$. Denote by $\\rho_{1}$ and $\\rho_{2}$ the radii of $\\gamma_{1}$ and $\\gamma_{2}$. Since $\\angle O_{1} A B=\\angle O_{2} A C$, we have $\\rho_{1} / \\rho_{2}=A O_{1} / A O_{2}$. On the other hand, from the definition of $P$ we have $O_{1} P / O_{2} P=$ $\\rho_{1} / \\rho_{2}=A O_{1} / A O_{2}$; this means that $A P$ is the angle bisector of $\\angle O_{1} A O_{2}$ and therefore of $\\angle B A C$.\n\nThe limiting, degenerated, cases are when the parallel line passes through $A$ - when $P$ coincides with $A$; respectively when the parallel line is $B C$ - when $P$ coincides with the foot $A^{\\prime} \\in B C$ of the angle bisector of $\\angle B A C$ (or any other point on $B C$ ). By continuity, any point $P$ on the open segment $A A^{\\prime}$ is obtained for some position of the parallel, therefore the locus is the open segment $A A^{\\prime}$ of the angle bisector $b$ of $\\angle B A C$.\n\n| point $K$ | $\\longleftrightarrow$ | point $L$ |\n| :---: | :---: | :---: |\n| line $K L$ | $\\longleftrightarrow$ | circle $\\omega$ |\n| ray $A B$ | $\\longleftrightarrow$ | ray $A C$ |\n| point $B$ | $\\longleftrightarrow$ | point $E$ |\n| point $C$ | $\\longleftrightarrow$ | point $D$ |\n| segment $B D$ | $\\longleftrightarrow$ | segment $E C$ |\n| $\\operatorname{arc} B K$ | $\\longleftrightarrow$ | segment $E L$ |\n| $\\operatorname{arc} C L$ | $\\longleftrightarrow$ | segment $D K$ |\n\n\n\nTABLE I: Elements interchanged by $\\mathfrak{H}$.", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}
|
RMM/segmented/en-2011-Sols2011D2.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Given a positive integer $n=\\prod_{i=1}^{s} p_{i}^{\\alpha_{i}}$, we write $\\Omega(n)$ for the total number $\\sum_{i=1}^{s} \\alpha_{i}$ of prime factors of $n$, counted with multiplicity. Let $\\lambda(n)=(-1)^{\\Omega(n)}$ (so, for example, $\\left.\\lambda(12)=\\lambda\\left(2^{2} \\cdot 3^{1}\\right)=(-1)^{2+1}=-1\\right)$.\n\nProve the following two claims:\ni) There are infinitely many positive integers $n$ such that $\\lambda(n)=\\lambda(n+1)=+1 ;$\nii) There are infinitely many positive integers $n$ such that $\\lambda(n)=\\lambda(n+1)=-1$.\n(ROMANIA) DAN SchwARZ", "solution": "Notice that we have $\\Omega(m n)=\\Omega(m)+\\Omega(n)$ for all positive integers $m, n$ ( $\\Omega$ is a completely additive arithmetic function), translating into $\\lambda(m n)=\\lambda(m) \\cdot \\lambda(n)$ (so $\\lambda$ is a completely multiplicative arithmetic function), hence $\\lambda(p)=-1$ for any prime $p$, and $\\lambda\\left(k^{2}\\right)=\\lambda(k)^{2}=+1$ for all positive integers $k$.[1]\nThe start (first 100 terms) of the sequence $\\mathfrak{S}=(\\lambda(n))_{n \\geq 1}$ is\n$+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,-1,-1,-1,+1,+1,+1,-1,-1,-1,-1$,\n$+1,+1,-1,+1,+1,+1,-1,-1,-1,-1,-1,-1,+1,+1,+1,+1,-1,+1,+1,+1$,\n$-1,-1,-1,-1,-1,+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,+1,+1,+1,-1,+1$,\n$-1,+1,-1,+1,+1,-1,-1,-1,+1,-1,-1,-1,-1,+1,-1,-1,+1,-1,-1,-1$,\n$+1,+1,-1,+1,+1,+1,+1,+1,-1,+1,+1,-1,+1,+1,+1,+1,-1,-1,-1,+1$.\ni) The Pell equation $x^{2}-6 y^{2}=1$ has infinitely many solutions in positive integers; all solutions are given by $\\left(x_{n}, y_{n}\\right)$, where $x_{n}+y_{n} \\sqrt{6}=(5+2 \\sqrt{6})^{n}$. Since $\\lambda\\left(6 y^{2}\\right)=1$ and also $\\lambda\\left(6 y^{2}+1\\right)=\\lambda\\left(x^{2}\\right)=1$, the thesis is proven.\n\nAlternative Solution. Take any existing pair with $\\lambda(n)=$ $\\lambda(n+1)=1$. Then $\\lambda\\left((2 n+1)^{2}-1\\right)=\\lambda\\left(4 n^{2}+4 n\\right)=\\lambda(4) \\cdot \\lambda(n)$. $\\lambda(n+1)=1$, and also $\\lambda\\left((2 n+1)^{2}\\right)=\\lambda(2 n+1)^{2}=1$, so we have built a larger $(1,1)$ pair.\nii) The equation $3 x^{2}-2 y^{2}=1$ (again Pell theory) has also infinitely many solutions in positive integers, given by $\\left(x_{n}, y_{n}\\right)$, where $x_{n} \\sqrt{3}+y_{n} \\sqrt{2}=(\\sqrt{3}+\\sqrt{2})^{2 n+1}$. Since $\\lambda\\left(2 y^{2}\\right)=$ -1 and $\\lambda\\left(2 y^{2}+1\\right)=\\lambda\\left(3 x^{2}\\right)=-1$, the thesis is proven.\n\nAlternative Solution. Assume $(\\lambda(n-1), \\lambda(n))$ is the largest $(-1,-1)$ pair, therefore $\\lambda(n+1)=1$ and $\\lambda\\left(n^{2}+n\\right)=\\lambda(n)$. $\\lambda(n+1)=-1$, therefore again $\\lambda\\left(n^{2}+n+1\\right)=1$. But then $\\lambda\\left(n^{3}-1\\right)=\\lambda(n-1) \\cdot \\lambda\\left(n^{2}+n+1\\right)=-1$, and also $\\lambda\\left(n^{3}\\right)=$ $\\lambda(n)^{3}=-1$, so we found yet a larger such pair than the one we started with, contradiction.\n\nAlternative Solution. Assume the pairs of consecutive terms $(-1,-1)$ in $\\mathfrak{S}$ are finitely many. Then from some rank on we only have subsequences ( $1,-1,1,1, \\ldots, 1,-1,1$ ). By\n\"doubling\" such a subsequence (like at point ii)), we will produce\n\n$$\n(-1, ?, 1, ?,-1, ?,-1, ?, \\ldots, ?,-1, ?, 1, ?,-1)\n$$\n\nAccording with our assumption, all ?-terms ought to be 1 , hence the produced subsequence is\n\n$$\n(-1,1,1,1,-1,1,-1,1, \\ldots, 1,-1,1,1,1,-1)\n$$\n\nand so the \"separating packets\" of l's contain either one or three terms. Now assume some far enough ( $1,1,1,1)$ or $(-1,1,1,-1)$ subsequence of $\\mathfrak{S}$ were to exist. Since it lies within some \"doubled\" subsequence, it contradicts the structure described above, which thus is the only prevalent from some rank on. But then all the positions of the ( -1 )terms will have the same parity. However though, we have $\\lambda(p)=\\lambda\\left(2 p^{2}\\right)=-1$ for all odd primes $p$, and these terms have different parity of their positions. A contradiction has been reached.[2]\n\nAlternative Solution for both i) and ii). (I. Bogdanov) Take $\\varepsilon \\in\\{-1,1\\}$. There obviously exist infinitely many $n$ such that $\\lambda(2 n+1)=\\varepsilon$ (just take $2 n+1$ to be the product of an appropriate number of odd primes). Now, if either $\\lambda(2 n)=\\varepsilon$ or $\\lambda(2 n+2)=\\varepsilon$, we are done; otherwise $\\lambda(n)=-\\lambda(2 n)=$ $-\\lambda(2 n+2)=\\lambda(n+1)=\\varepsilon$. Therefore, for such an $n$, one of the three pairs $(n, n+1),(2 n, 2 n+1)$ or $(2 n+1,2 n+2)$ fits the bill.\n\nWe have thus proved the existence in $\\mathfrak{S}$ of infinitely many occurrences of all possible subsequences of length 1 , viz. $(+1)$ and $(-1)$, and of length 2 , viz. $(+1,-1),(-1,+1)$, $(+1,+1)$ and $(-1,-1) .[3]$", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}
|
| 2 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "For every $n \\geq 3$, determine all the configurations of $n$ distinct points $X_{1}, X_{2}, \\ldots, X_{n}$ in the plane, with the property that for any pair of distinct points $X_{i}, X_{j}$ there exists a permutation $\\sigma$ of the integers $\\{1, \\ldots, n\\}$, such that $\\mathrm{d}\\left(X_{i}, X_{k}\\right)=\\mathrm{d}\\left(X_{j}, X_{\\sigma(k)}\\right)$ for all $1 \\leq k \\leq n$.\n(We write $\\mathrm{d}(X, Y)$ to denote the distance between points $X$ and $Y$.)\n(United Kingdom) LuKe BetTs", "solution": "Let us first prove that the points must be concyclic. Assign to each point $X_{k}$ the vector $x_{k}$ in a system of orthogonal coordinates whose origin is the point of mass of the configuration, thus $\\frac{1}{n} \\sum_{k=1}^{n} x_{k}=0$.\n\nThen $\\mathrm{d}^{2}\\left(X_{i}, X_{k}\\right)=\\left\\|x_{i}-x_{k}\\right\\|^{2}=\\left\\langle x_{i}-x_{k}, x_{i}-x_{k}\\right\\rangle=$ $\\left\\|x_{i}\\right\\|^{2}-2\\left\\langle x_{i}, x_{k}\\right\\rangle+\\left\\|x_{k}\\right\\|^{2}$, hence $\\sum_{k=1}^{n} \\mathrm{~d}^{2}\\left(X_{i}, X_{k}\\right)=n\\left\\|x_{i}\\right\\|^{2}-$\n$2\\left\\langle x_{i}, \\sum_{k=1}^{n} x_{k}\\right\\rangle+\\sum_{k=1}^{n}\\left\\|x_{k}\\right\\|^{2}=n\\left\\|x_{i}\\right\\|^{2}+\\sum_{k=1}^{n}\\left\\|x_{k}\\right\\|^{2}=n\\left\\|x_{j}\\right\\|^{2}+$ $\\sum_{k=1}^{n}\\left\\|x_{\\sigma(k)}\\right\\|^{2}=\\sum_{k=1}^{n} \\mathrm{~d}^{2}\\left(X_{j}, X_{\\sigma(k)}\\right)$, therefore $\\left\\|x_{i}\\right\\|=\\left\\|x_{j}\\right\\|$ for all pairs $(i, j)$. The points are thus concyclic (lying on a circle centred at $O(0,0)$ ).\nLet now $m$ be the least angular distance between any two points. Two points situated at angular distance $m$ must be adjacent on the circle. Let us connect each pair of such two points with an edge. The graph $G$ obtained must be regular, of degree $\\operatorname{deg}(G)=1$ or 2 . If $n$ is odd, since $\\sum_{k=1}^{n} \\operatorname{deg}\\left(X_{k}\\right)=$ $n \\operatorname{deg}(G)=2|E|$, we must have $\\operatorname{deg}(G)=2$, hence the configuration is a regular $n$-gon.\n\nIf $n$ is even, we may have the configuration of a regular $n$-gon, but we also may have $\\operatorname{deg}(G)=1$. In that case, let $M$ be the next least angular distance between any two points; such points must also be adjacent on the circle. Let us connect each pair of such two points with an edge, in order to get a graph $G^{\\prime}$. A similar reasoning yields $\\operatorname{deg}\\left(G^{\\prime}\\right)=1$, thus the configuration is that of an equiangular $n$-gon (with alternating equal side-lengths).", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}
|
| 3 |
+
{"year": "2011", "problem_label": "6", "tier": 1, "problem": "The cells of a square $2011 \\times 2011$ array are labelled with the integers $1,2, \\ldots, 2011^{2}$, in such a way that every label is used exactly once. We then identify the lefthand and right-hand edges, and then the top and bottom, in the normal way to form a torus (the surface of a doughnut).\n\nDetermine the largest positive integer $M$ such that, no matter which labelling we choose, there exist two neighbouring cells with the difference of their labels at least M.[4]\n(ROMANIA) DAN SchwarZ\nPreamble. For a planar $N \\times N$ array, it is folklore that this value is $M=N$, with some easy models shown below. As such, the problem is mentioned in [Béla Bollobás - The Art of Mathematics], 21. Neighbours in a Matrix.\n\nThis is not necessarily a flaw on the actual problem, which is presented in a brand novel setting; on the contrary, some general previous knowledge on such type of problems (which we think must be encouraged) is beneficial in searching for the right ideas of a proof.\n\nThe idea for a proof goes along the lines of finding a moment in the consecutive filling with numbers of the array, when there are at least $N$ pairs of adjacent filled/yet-unfilled cells (with either distinct filled cells or distinct yet-unfilled cells). Then, when the cell next to that bearing the least label is filled, the difference between its label and the one being filled will be at least $N$.\n\n| 1 | 2 | $\\ldots$ | N |\n| :---: | :---: | :---: | :---: |\n| $\\mathrm{~N}+1$ | $\\mathrm{~N}+2$ | $\\ldots$ | 2 N |\n| $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ |\n| $(\\mathrm{~N}-1) \\mathrm{N}+1$ | $(\\mathrm{~N}-1) \\mathrm{N}+2$ | $\\ldots$ | $\\mathrm{~N}^{2}$ |\n\nA planar parallel $N \\times N$ model array.\n\n| 1 | 2 | 4 | $\\ldots$ | | $\\mathrm{~N}(\\mathrm{~N}-1) / 2+1$ |\n| :---: | :---: | :---: | :---: | :---: | :---: |\n| 3 | 5 | $\\ldots$ | $\\mathrm{~N}(\\mathrm{~N}-1) / 2+2$ | | |\n| 6 | | $\\ldots$ | | | |\n| $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ | $\\vdots$ |\n| | $\\mathrm{~N}(\\mathrm{~N}+1) / 2-1$ | $\\ldots$ | | $\\mathrm{~N}^{2}-2$ | |\n| $\\mathrm{~N}(\\mathrm{~N}+1) / 2$ | | $\\ldots$ | $\\mathrm{~N}^{2}-1$ | $\\mathrm{~N}^{2}$ | |\n\nA planar diagonal $N \\times N$ model array.", "solution": "For the toroidal case, it is clear the statement of the problem is referring to the cells of a $\\mathbb{Z}_{N} \\times \\mathbb{Z}_{N}$ lattice on the surface of the torus, labeled with the numbers $1,2, \\ldots, N^{2}$, where one has to determine the least possible maximal absolute value $M$ of the difference of labels assigned to orthogonally adjacent cells.\n\nThe toroidal $N=2$ case is trivially seen to be $M=2$ (thus coinciding with the planar case).\n\n\nThe unique $2 \\times 2$ toroidal array.\n\nFor $N \\geq 3$ we will prove that value to be at least $M \\geq$ $2 N-1$. Consider such a configuration, and color all cells of the square in white. Go along the cells labeled 1, 2, etc. coloring them in black, stopping just on the cell bearing the least label $k$ which, after assigned and colored in black, makes that all lines of a same orientation (rows, or columns, or both) contain at least two black cells (that is, before coloring in black the cell labeled $k$, at least one row and at least one column contained at most one black cell). Wlog assume this happens for rows. Then at most one row is all black, since if two were then the stopping condition would have been fulfilled before cell labeled $k$ (if the cell labeled $k$ were to be on one of these rows, then all rows would have contained at least two black cells before, while if not, then all columns would have contained at least two black cells before).\n\nNow color in red all those black cells adjacent to a white cell. Since each row, except the potential all black one, contained at least two black and one white cell, it will now contain at least two red cells. For the potential all black row, any of the neighbouring rows contains at least one white cell, and so the cell adjacent to it has been colored red. In total we have therefore colored red at least $2(N-1)+1=2 N-1$ cells.\n\nThe least label of the red cells has therefore at most the value $k+1-(2 N-1)$. When the white cell adjacent to it will eventually be labeled, its label will be at least $k+1$, therefore their difference is at least $(k+1)-(k+1-(2 N-1))=2 N-1$.\n\n\nExample of coloring the array.\nThe models are kind of hard to find, due to the fact that the direct proof offers little as to their structure (it is difficult to determine the equality case during the argument involving the inequality with the bound, and then, even this is not sure to be prone to being prolonged to a full labeling of the array).\n\nThe weaker fact the value $M$ is not larger than $2 N$ is proved by the general model exhibited below (presented so that partial credits may be awarded).\n\n| $\\mathrm{N}+1$ | $\\mathrm{~N}+2$ | $\\ldots$ | 2 N |\n| :---: | :---: | :---: | :---: |\n| $3 \\mathrm{~N}+1$ | $3 \\mathrm{~N}+2$ | $\\cdots$ | 4 N |\n| $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ |\n| $(2 \\ell-1) \\mathrm{N}+1$ | $(2 \\ell-1) \\mathrm{N}+2$ | $\\ldots$ | $2 \\ell \\mathrm{~N}$ |\n| $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ |\n| $2 k \\mathrm{~N}+1$ | $2 k \\mathrm{~N}+2$ | $\\ldots$ | $(2 k+1) \\mathrm{N}$ |\n| $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ |\n| $2 \\mathrm{~N}+1$ | $2 \\mathrm{~N}+2$ | $\\ldots$ | 3 N |\n| 1 | 2 | $\\ldots$ | N |\n\nA general model for $M=2 N$ in a $N \\times N$ array.\nBy examining some small $N>2$ cases, one comes up with the idea of spiral models for the true value $M=2 N-1$. The models presented are for odd $N$ (since 2011 is odd); similar models exist for even $N$ (but are less symmetric). The color red (preceded by green) marks the moment where the largest difference $M=2 N-1$ first appears.\n[1] Also see Sloane's Online Encyclopædia of Integer Sequences (OEIS), sequence A001222 for $\\Omega$ and sequence A008836 for $\\lambda$, which is called Liouville's function. Its summatory function $\\sum_{d \\mid n} \\lambda(d)$ is equal to 1 for a perfect square $n$, and 0 otherwise.\nPólya conjectured that $L(n):=\\sum_{k=1}^{n} \\lambda(k) \\leq 0$ for all $n$, but this has been proven false by Minoru Tanaka, who in 1980 computed that for $n=906,151,257$ its value was positive. Turán showed that if $T(n):=\\sum_{k=1}^{n} \\frac{\\lambda(k)}{k} \\geq 0$ for all large enough $n$, that\n\n| 7 | 2 | 6 |\n| :--- | :--- | :--- |\n| 3 | 1 | 5 |\n| 8 | 4 | 9 |\n\nTABLE I: The spiral $3 \\times 3$ array.\n\n| 16 | 14 | 7 | 13 | 16 |\n| :---: | :---: | :---: | :---: | :---: |\n| 12 | 8 | 2 | 6 | 12 |\n| 9 | 3 | 1 | 5 | 9 |\n| 15 | 10 | 4 | 11 | 15 |\n| 16 | 14 | 7 | 13 | |\n| | | | | |\n\nTABLE II: The spiral $4 \\times 4$ array.\n\n| 23 | 16 | 7 | 15 | 22 |\n| :---: | :---: | :---: | :---: | :---: |\n| 17 | 8 | 2 | 6 | 14 |\n| 9 | 3 | 1 | 5 | 13 |\n| 18 | 10 | 4 | 12 | 21 |\n| 24 | 19 | 11 | 20 | 25 |\n\nTABLE III: The spiral $5 \\times 5$ array.\n\n| 47 | 40 | 29 | 16 | 28 | 39 | 46 |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| 41 | 30 | 17 | 7 | 15 | 27 | 38 |\n| 31 | 18 | 8 | 2 | 6 | 14 | 26 |\n| 19 | 9 | 3 | 1 | 5 | 13 | 25 |\n| 32 | 20 | 10 | 4 | 12 | 24 | 37 |\n| 42 | 33 | 21 | 11 | 23 | 36 | 45 |\n| 48 | 43 | 34 | 22 | 35 | 44 | 49 |\n\nTABLE IV: The spiral $7 \\times 7$ array.\n\n| $(2 \\mathrm{n}+1)^{2}-2$ | $(2 \\mathrm{n}+1)^{2}-9$ | $\\ldots$ | | $\\mathrm{n}(2 \\mathrm{n}-1)+1$ | | $\\ldots$ | $(2 \\mathrm{n}+1)^{2}-10$ | $(2 \\mathrm{n}+1)^{2}-3$ |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $(2 \\mathrm{n}+1)^{2}-8$ | | $\\ldots$ | $\\mathrm{n}(2 \\mathrm{n}-1)+2$ | | $\\mathrm{n}(2 \\mathrm{n}-1)$ | $\\ldots$ | | $(2 \\mathrm{n}+1)^{2}-11$ |\n| $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\ddots$ | $2 \\mathrm{n}(\\mathrm{n}+1)+3$ | $\\vdots$ |\n| | $2 \\mathrm{n}^{2}$ | $\\ldots$ | 8 | 2 | 6 | $\\ldots$ | $2 \\mathrm{n}(\\mathrm{n}-1)+2$ | $2 \\mathrm{n}(\\mathrm{n}+1)+2$ |\n| $2 \\mathrm{n}^{2}+1$ | | $\\ldots$ | 3 | 1 | 5 | $\\ldots$ | | $2 \\mathrm{n}(\\mathrm{n}+1)+1$ |\n| | $2 \\mathrm{n}^{2}+2$ | $\\ldots$ | 10 | 4 | 12 | $\\ldots$ | $2 \\mathrm{n}(\\mathrm{n}+1)$ | |\n| | $\\vdots$ | $\\ddots$ | $\\vdots$ | $\\vdots$ | $\\vdots$ | $\\ddots$ | $\\vdots$ | $\\vdots$ |\n| $\\vdots$ | $\\vdots$ | $\\ldots$ | $\\mathrm{n}(2 \\mathrm{n}+1)$ | | $\\mathrm{n}(2+1)+2$ | $\\ldots$ | | $(2 \\mathrm{n}+1)^{2}-4$ |\n| $(2 \\mathrm{n}+1)^{2}-7$ | | $\\ldots$ | $\\mathrm{n}(2 \\mathrm{n}+1)+1$ | | $\\ldots$ | $(2 \\mathrm{n}+1)^{2}-5$ | $(2 \\mathrm{n}+1)^{2}$ | |\n| $(2 \\mathrm{n}+1)^{2}-1$ | $(2 \\mathrm{n}+1)^{2}-6$ | $\\ldots$ | | | | | | |\n\nTABLE V: The general spiral $N \\times N$ array for $N=2 n+1 \\geq 5$.\nwill imply Riemann's Hypothesis; however, Haselgrove proved it is negative infinitely often.\n[2] Using the same procedure for point i), we only need notice that $\\lambda\\left((2 k+1)^{2}\\right)=\\lambda\\left((2 k)^{2}\\right)=1$, and these terms again are of different parity of their position.\n[3] Is this true for subsequences of all lengths $\\ell=3,4$, etc.? If no, up to which length $\\ell \\geq 2$ ?\n[4] Cells with coordinates $(x, y)$ and $\\left(x^{\\prime}, y^{\\prime}\\right)$ are considered to be neighbours if $x=x^{\\prime}$ and $y-y^{\\prime} \\equiv \\pm 1(\\bmod 2011)$, or if $y=y^{\\prime}$ and $x-x^{\\prime} \\equiv \\pm 1(\\bmod 2011)$.", "problem_match": "\nProblem 6.", "solution_match": "\nSolution."}
|
RMM/segmented/en-2012-Solutions2012-1.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)", "solution": ". A set $X$ of boys is separated from a set $Y$ of girls if no boy in $X$ is an acquaintance of a girl in $Y$. Similarly, a set $Y$ of girls is separated from a set $X$ of boys if no girl in $Y$ is an acquaintance of a boy in $X$. Since acquaintance is assumed mutual, separation is symmetric: $X$ is separated from $Y$ if and only if $Y$ is separated from $X$.\n\nThis enables doubly counting the number $n$ of ordered pairs $(X, Y)$ of separated sets $X$, of boys, and $Y$, of girls, and thereby showing that it is congruent modulo 2 to both numbers in question.\n\nGiven a set $X$ of boys, let $Y_{X}$ be the largest set of girls separated from $X$, to deduce that $X$ is separated from exactly $2^{\\left|Y_{X}\\right|}$ sets of girls. Consequently, $n=\\sum_{X} 2^{\\left|Y_{X}\\right|}$ which is clearly congruent modulo 2 to the number of covering sets of boys.\n\nMutatis mutandis, the argument applies to show $n$ congruent modulo 2 to the number of covering sets of girls.\n\nRemark. The argument in this solution translates verbatim in terms of the adjancency matrix of the associated acquaintance graph.", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 1"}
|
| 2 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)", "solution": ". (Ilya Bogdanov) Let $B$ denote the set of boys, let $G$ denote the set of girls and induct on $|B|+|G|$. The assertion is vacuously true if either set is empty.\n\nNext, fix a boy $b$, let $B^{\\prime}=B \\backslash\\{b\\}$, and let $G^{\\prime}$ be the set of all girls who do not know $b$. Notice that:\n(1) a covering set of boys in $B^{\\prime} \\cup G$ is still one in $B \\cup G$; and\n(2) a covering set of boys in $B \\cup G$ which is no longer one in $B^{\\prime} \\cup G$ is precisely the union of a covering set of boys in $B^{\\prime} \\cup G^{\\prime}$ and $\\{b\\}$,\nso the number of covering sets of boys in $B \\cup G$ is the sum of those in $B^{\\prime} \\cup G$ and $B^{\\prime} \\cup G^{\\prime}$. On the other hand,\n$\\left(1^{\\prime}\\right)$ a covering set of girls in $B \\cup G$ is still one in $B^{\\prime} \\cup G$; and\n$\\left(2^{\\prime}\\right)$ a covering set of girls in $B^{\\prime} \\cup G$ which is no longer one in $B \\cup G$ is precisely a covering set of girls in $B^{\\prime} \\cup G^{\\prime}$,\nso the number of covering sets of girls in $B \\cup G$ is the difference of those in $B^{\\prime} \\cup G$ and $B^{\\prime} \\cup G^{\\prime}$. Since the assertion is true for both $B^{\\prime} \\cup G$ and $B^{\\prime} \\cup G^{\\prime}$ by the induction hypothesis, the conclusion follows.", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}
|
| 3 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)", "solution": ". (Géza Kós) Let $B$ and $G$ denote the sets of boys and girls, respectively. For every pair $(b, g) \\in B \\times G$, write $f(b, g)=0$ if they know each other, and $f(b, g)=1$ otherwise. A set $X$ of boys is covering if and only if\n\n$$\n\\prod_{g \\in G}\\left(1-\\prod_{b \\in X} f(b, g)\\right)=1\n$$\n\nHence the number of covering sets of boys is\n\n$$\n\\begin{aligned}\n\\sum_{X \\subseteq B} \\prod_{g \\in G}\\left(1-\\prod_{b \\in X} f(b, g)\\right) & \\equiv \\sum_{X \\subseteq B} \\prod_{g \\in G}\\left(1+\\prod_{b \\in X} f(b, g)\\right) \\\\\n& =\\sum_{X \\subseteq B} \\sum_{Y \\subseteq G} \\prod_{b \\in X} \\prod_{g \\in Y} f(b, g) \\quad(\\bmod 2)\n\\end{aligned}\n$$\n\nBy symmetry, the same is valid for the number of covering sets of girls.", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 3"}
|
| 4 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.", "solution": ". We will use the following lemma.\nLemma. Let $A D$ be a median in triangle $A B C$. Then $\\cot \\angle B A D=2 \\cot A+\\cot B$ and $\\cot \\angle A D C=\\frac{1}{2}(\\cot B-\\cot C)$.\n\nProof. Let $C C_{1}$ and $D D_{1}$ be the perpendiculars from $C$ and $D$ to $A B$. Using the signed lengths we write\n\n$$\n\\cot B A D=\\frac{A D_{1}}{D D_{1}}=\\frac{\\left(A C_{1}+A B\\right) / 2}{C C_{1} / 2}=\\frac{C C_{1} \\cot A+C C_{1}(\\cot A+\\cot B)}{C C_{1}}=2 \\cot A+\\cot B\n$$\n\nSimilarly, denoting by $A_{1}$ the projection of $A$ onto $B C$, we get\n\n$$\n\\cot A D C=\\frac{D A_{1}}{A A_{1}}=\\frac{B C / 2-A_{1} C}{A A_{1}}=\\frac{\\left(A A_{1} \\cot B+A A_{1} \\cot C\\right) / 2-A A_{1} \\cot C}{A A_{1}}=\\frac{\\cot B-\\cot C}{2} .\n$$\n\nThe Lemma is proved.\nTurning to the solution, by the Lemma we get\n\n$$\n\\begin{aligned}\n\\cot \\angle B P D & =2 \\cot \\angle B P C+\\cot \\angle P B C=2 \\cot \\angle B F C+\\cot \\angle P B C \\quad(\\text { from circle } B F P C) \\\\\n& =2 \\cdot \\frac{1}{2}(\\cot A-\\cot B)+2 \\cot B+\\cot C=\\cot A+\\cot B+\\cot C\n\\end{aligned}\n$$\n\nSimilarly, $\\cot \\angle G Q F=\\cot A+\\cot B+\\cot C$, so $\\angle G P R=\\angle G Q F$ and $G P R Q$ is cyclic.\nRemark. The angle $\\angle G P R=\\angle G Q F$ is the Brocard angle.", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}
|
| 5 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.", "solution": ". (Ilya Bogdanov and Marian Andronache) We also prove that $\\angle(R P, P G)=\\angle(R Q, Q G)$, or $\\angle(D P, P G)=\\angle(F Q, Q G)$.\n\nLet $S$ be the point on ray $G D$ such that $A G \\cdot G S=C G \\cdot G F$ (so the points $A, S, C, F$ are concyclic). Then $G P \\cdot G E=G P \\cdot \\frac{1}{2} G B=\\frac{1}{2} C G \\cdot G F=\\frac{1}{2} A G \\cdot G S=G D \\cdot G S$, hence the points $E, P, D, S$ are also concyclic, and $\\angle(D P, P G)=\\angle(G S, S E)$. The problem may therefore be rephrased as follows:\nGiven a triangle $A B C$, let $D, E$ and $F$ respectively denote the midpoints of the sides $B C, C A$ and $A B$. The circle $A B E$, respectively, $A C F$, and the line $A D$ meet again at $Q$, respectively, $S$. Prove that $\\angle A Q F=\\angle A S E($ and $E S=F Q)$.\n\n\nUpon inversion of pole $A$, the problem reads:\nGiven a triangle $A E^{\\prime} F^{\\prime}$, let the symmedian from $A$ meet the medians from $E^{\\prime}$ and $F^{\\prime}$ at $K=Q^{\\prime}$ and $L=S^{\\prime}$, respectively. Prove that the angles $A E^{\\prime} L$ and $A F^{\\prime} K$ are congruent.\n\n\nTo prove this, denote $E^{\\prime}=X, F^{\\prime}=Y$. Let the symmedian from $A$ meet the side $X Y$ at $V$ and let the lines $X L$ and $Y K$ meet the sides $A Y$ and $A X$ at $M$ and $N$, respectively. Since the points $K$ and $L$ lie on the medians, we have $V M\\|A X, V N\\| A Y$. Hence $A M V N$ is a parallelogram, the symmedian $A V$ of triangle $A X Y$ supports the median of triangle $A M N$, which implies that the triangles $A M N$ and $A X Y$ are similar. Hence the points $M, N, X, Y$ are concyclic, and $\\angle A X M=\\angle A Y N$, QED.\n\nRemark 1. We know that the points $X, Y, M, N$ are concyclic. Invert back from $A$ and consider the circles $A F Q$ and $A E S$ : the former meets $A C$ again at $M^{\\prime}$ and the latter meets $A B$ again at $N^{\\prime}$. Then the points $E, F, M^{\\prime}, N^{\\prime}$ are concyclic.\n\nRemark 2. The inversion at pole $A$ also allows one to show that $\\angle A Q F$ is the Brocard angle, thus providing one more solution. In our notation, it is equivalent to the fact that the points $Y$, $K$, and $Z$ are collinear, where $Z$ is the Brocard point (so $\\angle Z A X=\\angle Z Y A=\\angle Z X Y$ ). This is valid because the lines $A V, X K$, and $Y Z$ are the radical axes of the following circles: (i) passing through $X$ and tangent to $A Y$ at $A$; (ii) passing through $Y$ and tangent to $A X$ at $A$; and (iii) passing through $X$ and tangent to $A Y$ at $Y$. The point $K$ is the radical center of these three circles.", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}
|
| 6 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.", "solution": ". (Ilya Bogdanov) Again, we will prove that $\\angle(D P, P G)=\\angle(F Q, Q G)$. Mark a point $T$ on the ray $G F$ such that $G F \\cdot G T=G Q \\cdot G D$; then the points $F, Q, D, T$ are concyclic, and $\\angle(F Q, Q G)=\\angle(T G, T D)=\\angle(T C, T D)$.\n\n\nShift the point $P$ by the vector $\\overrightarrow{B D}$ to obtain point $P^{\\prime}$. Then $\\angle(D P, P G)=\\angle\\left(C P^{\\prime}, P^{\\prime} D\\right)$, and we need to prove that $\\angle\\left(C P^{\\prime}, P^{\\prime} D\\right)=\\angle(C T, T D)$. This is precisely the condition that the points $T, D, C, P^{\\prime}$ be concyclic.\n\nDenote $G E=x, G F=y$. Then $G P \\cdot G B=G C \\cdot G F$, so $G P=y^{2} / x$. On the other hand, $G B \\cdot G E=G Q \\cdot G A=2 G Q \\cdot G D=2 G T \\cdot G F$, so $G T=x^{2} / y$. Denote by $K$ the point of intersection of $D P^{\\prime}$ and $C T$; we need to prove that $T K \\cdot K C=D K \\cdot K P^{\\prime}$.\n\nNow, $D P^{\\prime}=B P=B G+G P=2 x+y^{2} / x, C T=C G+G T=2 y+x^{2} / y, D K=B G / 2=x$, $C K=C G / 2=y$. Hence the desired equality reads $x\\left(x+y^{2} / x\\right)=y\\left(y+x^{2} / y\\right)$ which is obvious.\n\nRemark. The points $B, T, E$, and $C$ are concyclic, hence the point $T$ is also of the same kind as $P$ and $Q$.", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 3"}
|
| 7 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Each positive integer number is coloured red or blue. A function $f$ from the set of positive integer numbers into itself has the following two properties:\n(a) if $x \\leq y$, then $f(x) \\leq f(y)$; and\n(b) if $x, y$ and $z$ are all (not necessarily distinct) positive integer numbers of the same colour and $x+y=z$, then $f(x)+f(y)=f(z)$.\n\nProve that there exists a positive number $a$ such that $f(x) \\leq a x$ for all positive integer numbers $x$.", "solution": "For integer $x, y$, by a segment $[x, y]$ we always mean the set of all integers $t$ such that $x \\leq t \\leq y$; the length of this segment is $y-x$.\n\nIf for every two positive integers $x, y$ sharing the same colour we have $f(x) / x=f(y) / y$, then one can choose $a=\\max \\{f(r) / r, f(b) / b\\}$, where $r$ and $b$ are arbitrary red and blue numbers, respectively. So we can assume that there are two red numbers $x, y$ such that $f(x) / x \\neq f(y) / y$.\n\nSet $m=x y$. Then each segment of length $m$ contains a blue number. Indeed, assume that all the numbers on the segment $[k, k+m]$ are red. Then\n\n$$\n\\begin{aligned}\n& f(k+m)=f(k+x y)=f(k+x(y-1))+f(x)=\\cdots=f(k)+y f(x), \\\\\n& f(k+m)=f(k+x y)=f(k+(x-1) y)+f(y)=\\cdots=f(k)+x f(y),\n\\end{aligned}\n$$\n\nso $y f(x)=x f(y)$ - a contradiction. Now we consider two cases.\nCase 1. Assume that there exists a segment $[k, k+m]$ of length $m$ consisting of blue numbers. Define $D=\\max \\{f(k), \\ldots, f(k+m)\\}$. We claim that $f(z)-f(z-1) \\leq D$, whatever $z>k$, and the conclusion follows. Consider the largest blue number $b_{1}$ not exceeding $z$, so $z-b_{1} \\leq m$, and some blue number $b_{2}$ on the segment $\\left[b_{1}+k, b_{1}+k+m\\right]$, so $b_{2}>z$. Write $f\\left(b_{2}\\right)=f\\left(b_{1}\\right)+f\\left(b_{2}-b_{1}\\right) \\leq f\\left(b_{1}\\right)+D$ to deduce that $f(z+1)-f(z) \\leq f\\left(b_{2}\\right)-f\\left(b_{1}\\right) \\leq D$, as claimed.\n\nCase 2. Each segment of length $m$ contains numbers of both colours. Fix any red number $R \\geq 2 m$ such that $R+1$ is blue and set $D=\\max \\{f(R), f(R+1)\\}$. Now we claim that $f(z+1)-f(z) \\leq D$, whatever $z>2 m$. Consider the largest red number $r$ not exceeding $z$ and the largest blue number $b$ smaller than $r$; then $0<z-b=(z-r)+(r-b) \\leq 2 m$, and $b+1$ is red. Let $t=b+R+1$; then $t>z$. If $t$ is blue, then $f(t)=f(b)+f(R+1) \\leq f(b)+D$, and $f(z+1)-f(z) \\leq f(t)-f(b) \\leq D$. Otherwise, $f(t)=f(b+1)+f(R) \\leq f(b+1)+D$, hence $f(z+1)-f(z) \\leq f(t)-f(b+1) \\leq D$, as claimed.", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}
|
RMM/segmented/en-2012-Solutions2012-2.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.", "solution": ". Throughout the solution $n$ stands for a positive integer. By Euler's theorem, $\\left(2^{3^{n}}+1\\right)\\left(2^{3^{n}}-1\\right)=2^{2 \\cdot 3^{n}}-1 \\equiv 0\\left(\\bmod 3^{n+1}\\right)$. Since $2^{3^{n}}-1 \\equiv 1(\\bmod 3)$, it follows that $2^{3^{n}}+1$ is divisible by $3^{n+1}$.\n\nThe number $\\left(2^{3^{n+1}}+1\\right) /\\left(2^{3^{n}}+1\\right)=2^{2 \\cdot 3^{n}}-2^{3^{n}}+1$ is greater than 3 and congruent to 3 modulo 9 , so it has a prime factor $p_{n}>3$ that does not divide $2^{3^{n}}+1$ (otherwise, $2^{3^{n}} \\equiv-1$ (mod $\\left.p_{n}\\right)$, so $2^{2 \\cdot 3^{n}}-2^{3^{n}}+1 \\equiv 3\\left(\\bmod p_{n}\\right)$, contradicting the fact that $p_{n}$ is a factor greater than 3 of $2^{2 \\cdot 3^{n}}-2^{3^{n}}+1$ ).\n\nWe now show that $a_{n}=3^{n} p_{n}$ satisfies the conditions in the statement. Since $2^{a_{n}}+1 \\equiv$ $2^{3^{n}}+1 \\not \\equiv 0\\left(\\bmod p_{n}\\right)$, it follows that $a_{n}$ does not divide $2^{a_{n}}+1$.\n\nOn the other hand, $3^{n+1}$ divides $2^{3^{n}}+1$ which in turn divides $2^{a_{n}}+1$, so $2^{3^{n+1}}+1$ divides $2^{2^{a_{n}}+1}+1$. Finally, both $3^{n}$ and $p_{n}$ divide $2^{3^{n+1}}+1$, so $a_{n}$ divides $2^{2^{a_{n}}+1}+1$.\n\nAs $n$ runs through the positive integers, the $a_{n}$ are clearly pairwise distinct and the conclusion follows.", "problem_match": "\nProblem 4.", "solution_match": "\nSolution 1"}
|
| 2 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.", "solution": ". (Géza Kós) We show that the numbers $a_{n}=\\left(2^{3^{n}}+1\\right) / 9, n \\geq 2$, satisfy the conditions in the statement. To this end, recall the following well-known facts:\n(1) If $N$ is an odd positive integer, then $\\nu_{3}\\left(2^{N}+1\\right)=\\nu_{3}(N)+1$, where $\\nu_{3}(a)$ is the exponent of 3 in the decomposition of the integer $a$ into prime factors; and\n(2) If $M$ and $N$ are odd positive integers, then $\\left(2^{M}+1,2^{N}+1\\right)=2^{(M, N)}+1$, where $(a, b)$ is the greatest common divisor of the integers $a$ and $b$.\nBy (1), $a_{n}=3^{n-1} m$, where $m$ is an odd positive integer not divisible by 3 , and by (2),\n\n$$\n\\left(m, 2^{a_{n}}+1\\right) \\left\\lvert\\,\\left(2^{3^{n}}+1,2^{a_{n}}+1\\right)=2^{\\left(3^{n}, a_{n}\\right)}+1=2^{3^{n-1}}+1<\\frac{2^{3^{n}}+1}{3^{n+1}}=m\\right.\n$$\n\nso $m$ cannot divide $2^{a_{n}}+1$.\nOn the other hand, $3^{n-1} \\mid 2^{2^{a_{n}}+1}+1$, for $\\nu_{3}\\left(2^{2^{a_{n}}+1}+1\\right)>\\nu_{3}\\left(2^{a_{n}}+1\\right)>\\nu_{3}\\left(a_{n}\\right)=n-1$, and $m \\mid 2^{2^{a_{n}}+1}+1$, for $3^{n-1} \\mid a_{n}$, so $3^{n} \\mid 2^{a_{n}}+1$ whence $m\\left|2^{3^{n}}+1\\right| 2^{2^{a_{n}}+1}+1$. Since $3^{n-1}$ and $m$ are coprime, the conclusion follows.\n\nRemarks. There are several variations of these solutions. For instance, let $b_{1}=3$ and $b_{n+1}=$ $2^{b_{n}}+1, n \\geq 1$, and notice that $b_{n}$ divides $b_{n+1}$. It can be shown that there are infinitely many indices $n$ such that some prime factor $p_{n}$ of $b_{n+1}$ does not divide $b_{n}$. One checks that for these $n$ 's the $a_{n}=p_{n} b_{n-1}$ satisfy the required conditions.\n\nFinally, the numbers $3^{n} \\cdot 571, n \\geq 2$, form yet another infinite set of positive integers fulfilling the conditions in the statement - the details are omitted.", "problem_match": "\nProblem 4.", "solution_match": "\nSolution 2"}
|
| 3 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.", "solution": ". (Dušan Djukić) Assume that $n$ satisfies the conditions of the problem. We claim that the number $N=2^{n}+1>n$ also satisfies these conditions.\n\nFirstly, since $n \\nmid N$, the fact (2) from Solution 2 allows to conclude that $2^{n}+1 \\nmid 2^{N}+1$, or $N \\nmid 2^{N}+1$. Next, since $n \\mid 2^{2^{n}+1}+1=2^{N}+1$, we obtain from the same fact that $N=2^{n}+1 \\mid 2^{2^{N}+1}+1$, thus confirming our claim.\n\nHence, it suffices to provide only one example, hence obtaining an infinite series by the claim. For instance, one may easily check that the number $n=57$ fits.", "problem_match": "\nProblem 4.", "solution_match": "\nSolution 3"}
|
| 4 |
+
{"year": "2012", "problem_label": "5", "tier": 1, "problem": "Given a positive integer number $n \\geq 3$, colour each cell of an $n \\times n$ square array one of $\\left[(n+2)^{2} / 3\\right]$ colours, each colour being used at least once. Prove that the cells of some $1 \\times 3$ or $3 \\times 1$ rectangular subarray have pairwise distinct colours.", "solution": "For more convenience, say that a subarray of the $n \\times n$ square array bears a colour if at least two of its cells share that colour.\n\nWe shall prove that the number of $1 \\times 3$ and $3 \\times 1$ rectangular subarrays, which is $2 n(n-2)$, exceeds the number of such subarrays, each of which bears some colour. The key ingredient is the estimate in the lemma below.\n\nLemma. If a colour is used exactly $p$ times, then the number of $1 \\times 3$ and $3 \\times 1$ rectangular subarrays bearing that colour does not exceed $3(p-1)$.\n\nAssume the lemma for the moment, let $N=\\left[(n+2)^{2} / 3\\right]$ and let $n_{i}$ be the number of cells coloured the $i$ th colour, $i=1, \\ldots, N$, to deduce that the number of $1 \\times 3$ and $3 \\times 1$ rectangular subarrays, each of which bears some colour, is at most\n\n$$\n\\sum_{i=1}^{N} 3\\left(n_{i}-1\\right)=3 \\sum_{i=1}^{N} n_{i}-3 N=3 n^{2}-3 N<3 n^{2}-\\left(n^{2}+4 n\\right)=2 n(n-2)\n$$\n\nand thereby conclude the proof.\nBack to the lemma, the assertion is clear if $p=1$, so let $p>1$.\nWe begin by showing that if a row contains exactly $q$ cells coloured $C$, then the number $r$ of $3 \\times 1$ rectangular subarrays bearing $C$ does not exceed $3 q / 2-1$; of course, a similar estimate holds for a column. To this end, notice first that the case $q=1$ is trivial, so we assume that $q>1$. Consider the incidence of a cell $c$ coloured $C$ and a $3 \\times 1$ rectangular subarray $R$ bearing $C$ :\n\n$$\n\\langle c, R\\rangle= \\begin{cases}1 & \\text { if } c \\subset R \\\\ 0 & \\text { otherwise. }\\end{cases}\n$$\n\nNotice that, given $R, \\sum_{c}\\langle c, R\\rangle \\geq 2$, and, given $c, \\sum_{R}\\langle c, R\\rangle \\leq 3$; moreover, if $c$ is the leftmost or rightmost cell, then $\\sum_{R}\\langle c, R\\rangle \\leq 2$. Consequently,\n\n$$\n2 r \\leq \\sum_{R} \\sum_{c}\\langle c, R\\rangle=\\sum_{c} \\sum_{R}\\langle c, R\\rangle \\leq 2+3(q-2)+2=3 q-2\n$$\n\nwhence the conclusion.\nFinally, let the $p$ cells coloured $C$ lie on $k$ rows and $\\ell$ columns and notice that $k+\\ell \\geq 3$, for $p>1$. By the preceding, the total number of $3 \\times 1$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-k$, and the total number of $1 \\times 3$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-\\ell$, so the total number of $1 \\times 3$ and $3 \\times 1$ rectangular subarrays bearing $C$ does not exceed $(3 p / 2-k)+(3 p / 2-\\ell)=3 p-(k+\\ell) \\leq 3 p-3=3(p-1)$. This completes the proof.\n\nRemarks. In terms of the total number of cells, the number $N=\\left[(n+2)^{2} / 3\\right]$ of colours is asymptotically close to the minimum number of colours required for some $1 \\times 3$ or $3 \\times 1$ rectangular subarray to have all cells of pairwise distinct colours, whatever the colouring. To see this, colour the cells with the coordinates $(i, j)$, where $i+j \\equiv 0(\\bmod 3)$ and $i, j \\in\\{0,1, \\ldots, n-1\\}$, one colour each, and use one additional colour $C$ to colour the remaining cells. Then each $1 \\times 3$ and each $3 \\times 1$ rectangular subarray has exactly two cells coloured $C$, and the number of colours is $\\left\\lceil n^{2} / 3\\right\\rceil+1$ if $n \\equiv 1$ or $2(\\bmod 3)$, and $\\left\\lceil n^{2} / 3\\right\\rceil$ if $n \\equiv 0(\\bmod 3)$. Consequently, the minimum number of colours is $n^{2} / 3+O(n)$.", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}
|
| 5 |
+
{"year": "2012", "problem_label": "6", "tier": 1, "problem": "Let $A B C$ be a triangle and let $I$ and $O$ respectively denote its incentre and circumcentre. Let $\\omega_{A}$ be the circle through $B$ and $C$ and tangent to the incircle of the triangle $A B C$; the circles $\\omega_{B}$ and $\\omega_{C}$ are defined similarly. The circles $\\omega_{B}$ and $\\omega_{C}$ through $A$ meet again at $A^{\\prime}$; the points $B^{\\prime}$ and $C^{\\prime}$ are defined similarly. Prove that the lines $A A^{\\prime}, B B^{\\prime}$ and $C C^{\\prime}$ are concurrent at a point on the line $I O$.", "solution": "Let $\\gamma$ be the incircle of the triangle $A B C$ and let $A_{1}, B_{1}, C_{1}$ be its contact points with the sides $B C, C A, A B$, respectively. Let further $X_{A}$ be the point of contact of the circles $\\gamma$ and $\\omega_{A}$. The latter circle is the image of the former under a homothety centred at $X_{A}$. This homothety sends $A_{1}$ to a point $M_{A}$ on $\\omega_{A}$ such that the tangent to $\\omega_{A}$ at $M_{A}$ is parallel to $B C$. Consequently, $M_{A}$ is the midpoint of the arc $B C$ of $\\omega_{A}$ not containing $X_{A}$. It follows that the angles $M_{A} X_{A} B$ and $M_{A} B C$ are congruent, so the triangles $M_{A} B A_{1}$ and $M_{A} X_{A} B$ are similar: $M_{A} B / M_{A} X_{A}=M_{A} A_{1} / M_{A} B$. Rewrite the latter $M_{A} B^{2}=M_{A} A_{1} \\cdot M_{A} X_{A}$ to deduce that $M_{A}$ lies on the radical axis $\\ell_{B}$ of $B$ and $\\gamma$. Similarly, $M_{A}$ lies on the radical axis $\\ell_{C}$ of $C$ and $\\gamma$.\n\nDefine the points $X_{B}, X_{C}, M_{B}, M_{C}$ and the line $\\ell_{A}$ in a similar way and notice that the lines $\\ell_{A}, \\ell_{B}, \\ell_{C}$ support the sides of the triangle $M_{A} M_{B} M_{C}$. The lines $\\ell_{A}$ and $B_{1} C_{1}$ are both perpendicular to $A I$, so they are parallel. Similarly, the lines $\\ell_{B}$ and $\\ell_{C}$ are parallel to $C_{1} A_{1}$ and $A_{1} B_{1}$, respectively. Consequently, the triangle $M_{A} M_{B} M_{C}$ is the image of the triangle $A_{1} B_{1} C_{1}$ under a homothety $\\Theta$. Let $K$ be the centre of $\\Theta$ and let $k=M_{A} K / A_{1} K=M_{B} K / B_{1} K=$ $M_{C} K / C_{1} K$ be the similitude ratio. Notice that the lines $M_{A} A_{1}, M_{B} B_{1}$ and $M_{C} C_{1}$ are concurrent at $K$.\n\nSince the points $A_{1}, B_{1}, X_{A}, X_{B}$ are concyclic, $A_{1} K \\cdot K X_{A}=B_{1} K \\cdot K X_{B}$. Multiply both sides by $k$ to get $M_{A} K \\cdot K X_{A}=M_{B} K \\cdot K X_{B}$ and deduce thereby that $K$ lies on the radical axis $C C^{\\prime}$ of $\\omega_{A}$ and $\\omega_{B}$. Similarly, both lines $A A^{\\prime}$ and $B B^{\\prime}$ pass through $K$.\n\n\nFinally, consider the image $O^{\\prime}$ of $I$ under $\\Theta$. It lies on the line through $M_{A}$ parallel to $A_{1} I$ (and hence perpendicular to $B C$ ); since $M_{A}$ is the midpoint of the $\\operatorname{arc} B C$, this line must be $M_{A} O$. Similarly, $O^{\\prime}$ lies on the line $M_{B} O$, so $O^{\\prime}=O$. Consequently, the points $I, K$ and $O$ are collinear.\n\nRemark 1. Many steps in this solution allow different reasonings. For instance, one may\nsee that the lines $A_{1} X_{A}$ and $B_{1} X_{B}$ are concurrent at point $K$ on the radical axis $C C^{\\prime}$ of the circles $\\omega_{A}$ and $\\omega_{B}$ by applying Newton's theorem to the quadrilateral $X_{A} X_{B} A_{1} B_{1}$ (since the common tangents at $X_{A}$ and $X_{B}$ intersect on $C C^{\\prime}$ ). Then one can conclude that $K A_{1} / K B_{1}=$ $K M_{A} / K M_{B}$, thus obtaining that the triangles $M_{A} M_{B} M_{C}$ and $A_{1} B_{1} C_{1}$ are homothetical at $K$ (and therefore $K$ is the radical center of $\\omega_{A}, \\omega_{B}$, and $\\omega_{C}$ ). Finally, considering the inversion with the pole $K$ and the power equal to $K X_{1} \\cdot K M_{A}$ followed by the reflection at $P$ we see that the circles $\\omega_{A}, \\omega_{B}$, and $\\omega_{C}$ are invariant under this transform; next, the image of $\\gamma$ is the circumcircle of $M_{A} M_{B} M_{C}$ and it is tangent to all the circles $\\omega_{A}, \\omega_{B}$, and $\\omega_{C}$, hence its center is $O$, and thus $O, I$, and $K$ are collinear.\n\nRemark 2. Here is an outline of an alternative approach to the first part of the solution. Let $J_{A}$ be the excentre of the triangle $A B C$ opposite $A$. The line $J_{A} A_{1}$ meets $\\gamma$ again at $Y_{A}$; let $Z_{A}$ and $N_{A}$ be the midpoints of the segments $A_{1} Y_{A}$ and $J_{A} A_{1}$, respectively. Since the segment $I J_{A}$ is a diameter in the circle $B C Z_{A}$, it follows that $B A_{1} \\cdot C A_{1}=Z_{A} A_{1} \\cdot J_{A} A_{1}$, so $B A_{1} \\cdot C A_{1}=N_{A} A_{1} \\cdot Y_{A} A_{1}$. Consequently, the points $B, C, N_{A}$ and $Y_{A}$ lie on some circle $\\omega_{A}^{\\prime}$.\n\nIt is well known that $N_{A}$ lies on the perpendicular bisector of the segment $B C$, so the tangents to $\\omega_{A}^{\\prime}$ and $\\gamma$ at $N_{A}$ and $A_{1}$ are parallel. It follows that the tangents to these circles at $Y_{A}$ coincide, so $\\omega_{A}^{\\prime}$ is in fact $\\omega_{A}$, whence $X_{A}=Y_{A}$ and $M_{A}=N_{A}$. It is also well known that the midpoint $S_{A}$ of the segment $I J_{A}$ lies both on the circumcircle $A B C$ and on the perpendicular bisector of $B C$. Since $S_{A} M_{A}$ is a midline in the triangle $A_{1} I J_{A}$, it follows that $S_{A} M_{A}=r / 2$, where $r$ is the radius of $\\gamma$ (the inradius of the triangle $A B C$ ). Consequently, each of the points $M_{A}, M_{B}$ and $M_{C}$ is at distance $R+r / 2$ from $O$ (here $R$ is the circumradius). Now proceed as above.\n", "problem_match": "\nProblem 6.", "solution_match": "\nSolution."}
|