add segmented Dutch-TST 2006-2024 problems and solutions
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- Dutch_TST/md/nl-2008-uitwerkingen.md +2 -1
- Dutch_TST/segment_script/segment.py +130 -0
- Dutch_TST/segment_script/segment2.py +133 -0
- Dutch_TST/segmented/nl-2006-uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2007-uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2008-uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2009-uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2010-B_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2010-C_uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2010-D_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2011-B_uitwerkingen.jsonl +9 -0
- Dutch_TST/segmented/nl-2011-C_uitwerkingen.jsonl +9 -0
- Dutch_TST/segmented/nl-2011-D_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2012-B_uitwerkingen.jsonl +9 -0
- Dutch_TST/segmented/nl-2012-C_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2012-D_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2013-B_uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl +11 -0
- Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl +11 -0
- Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl +4 -0
- Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl +7 -0
- Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl +6 -0
- Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl +5 -0
- Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl +8 -0
- Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl +7 -0
Dutch_TST/md/nl-2008-uitwerkingen.md
CHANGED
|
@@ -108,7 +108,8 @@ $$
|
|
| 108 |
|
| 109 |
en dat is wat we moesten bewijzen.
|
| 110 |
|
| 111 |
-
Opgave 5.
|
|
|
|
| 112 |
De lijn $B C$ is een raaklijn aan $\Gamma$, dus geldt $\angle C B P=\angle B A P=\angle Q A P$. Omdat de driehoeken $C B P$ en $Q A P$ beide gelijkbenig zijn, zijn ze gelijkvormig. Zij $\alpha=\angle B C P$, dan geldt
|
| 113 |
|
| 114 |
$$
|
|
|
|
| 108 |
|
| 109 |
en dat is wat we moesten bewijzen.
|
| 110 |
|
| 111 |
+
Opgave 5.
|
| 112 |
+
Oplossing 1. Zij $S$ het snijpunt van $\Gamma$ en $C Q$. We moeten bewijzen dat $|Q S|=|S C|$.
|
| 113 |
De lijn $B C$ is een raaklijn aan $\Gamma$, dus geldt $\angle C B P=\angle B A P=\angle Q A P$. Omdat de driehoeken $C B P$ en $Q A P$ beide gelijkbenig zijn, zijn ze gelijkvormig. Zij $\alpha=\angle B C P$, dan geldt
|
| 114 |
|
| 115 |
$$
|
Dutch_TST/segment_script/segment.py
ADDED
|
@@ -0,0 +1,130 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
problem_tag = 'Problem'
|
| 12 |
+
solution_tag = 'Solution'
|
| 13 |
+
problem_pattern = re.compile(r'(?:\n|# )Opgave\s+(\d+)\.', re.IGNORECASE)
|
| 14 |
+
solution_pattern = re.compile(r'(?:\n|# )Oplossing(?:\s+(\d+)\.|\s+(I{1,3}|IV|V|VI{1,3}|IX)\.|\.|\n|:)', re.IGNORECASE)
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 18 |
+
"""
|
| 19 |
+
Analyze the text and return the tags and problem number.
|
| 20 |
+
|
| 21 |
+
Args:
|
| 22 |
+
text (str): The markdown text to analyze.
|
| 23 |
+
|
| 24 |
+
Returns:
|
| 25 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 26 |
+
"""
|
| 27 |
+
tags = []
|
| 28 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text)])
|
| 29 |
+
problem_num = len(tags)
|
| 30 |
+
|
| 31 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text)])
|
| 32 |
+
tags.sort(key=lambda x: x[0].start())
|
| 33 |
+
return tags, problem_num
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
def segment(text: str, tags):
|
| 37 |
+
starts = []
|
| 38 |
+
ends = []
|
| 39 |
+
|
| 40 |
+
for i in range(len(tags)):
|
| 41 |
+
starts.append(tags[i][0].end())
|
| 42 |
+
if i + 1 < len(tags):
|
| 43 |
+
ends.append(tags[i + 1][0].start())
|
| 44 |
+
else:
|
| 45 |
+
ends.append(len(text))
|
| 46 |
+
|
| 47 |
+
return [text[start:end].strip().rstrip("#").strip() for start, end in zip(starts, ends)]
|
| 48 |
+
|
| 49 |
+
|
| 50 |
+
def join(tags, segments):
|
| 51 |
+
problem, solution = '', ''
|
| 52 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 53 |
+
pairs = []
|
| 54 |
+
|
| 55 |
+
has_solution = any([tag[1] == solution_tag for tag in tags])
|
| 56 |
+
|
| 57 |
+
for tag, segment in zip(tags, segments):
|
| 58 |
+
if tag[1] == problem_tag:
|
| 59 |
+
problem = segment
|
| 60 |
+
problem_match = tag[0].group(0)
|
| 61 |
+
problem_label = tag[0].group(1) if tag[0].group(1) else tag[0].group(2)
|
| 62 |
+
|
| 63 |
+
# If there is no solution, add an empty solution
|
| 64 |
+
if not has_solution:
|
| 65 |
+
pairs.append((problem, '', problem_label, problem_match, ''))
|
| 66 |
+
else:
|
| 67 |
+
solution = segment
|
| 68 |
+
solution_match = tag[0].group(0)
|
| 69 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 70 |
+
|
| 71 |
+
return pairs
|
| 72 |
+
|
| 73 |
+
|
| 74 |
+
def write_pairs(output_file: Path, pairs):
|
| 75 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 76 |
+
|
| 77 |
+
output_jsonl_text = ""
|
| 78 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 79 |
+
output_jsonl_text += json.dumps(
|
| 80 |
+
{
|
| 81 |
+
'year': year,
|
| 82 |
+
'problem_label': problem_label,
|
| 83 |
+
'tier': 1,
|
| 84 |
+
'problem': problem,
|
| 85 |
+
'solution': solution,
|
| 86 |
+
'problem_match': problem_match,
|
| 87 |
+
'solution_match': solution_match
|
| 88 |
+
},
|
| 89 |
+
ensure_ascii=False
|
| 90 |
+
) + '\n'
|
| 91 |
+
|
| 92 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 93 |
+
|
| 94 |
+
|
| 95 |
+
def main():
|
| 96 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 97 |
+
compet_md_path = compet_base_path / "md"
|
| 98 |
+
seg_output_path = compet_base_path / "segmented"
|
| 99 |
+
|
| 100 |
+
total_problem_count = 0
|
| 101 |
+
total_solution_count = 0
|
| 102 |
+
|
| 103 |
+
for dutch_tst_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 104 |
+
output_file = seg_output_path / dutch_tst_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 105 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 106 |
+
|
| 107 |
+
text = '\n' + dutch_tst_md.read_text(encoding="utf-8")
|
| 108 |
+
|
| 109 |
+
if all([y not in dutch_tst_md.name for y in ["2007", "2008"]]):
|
| 110 |
+
tags, problem_num = analyze(text)
|
| 111 |
+
|
| 112 |
+
if problem_num != 4 and problem_num != 5:
|
| 113 |
+
logger.warning(f"{dutch_tst_md} problem number is {problem_num}")
|
| 114 |
+
|
| 115 |
+
segments = segment(text, tags)
|
| 116 |
+
pairs = join(tags, segments)
|
| 117 |
+
|
| 118 |
+
if pairs and problem_num > 0:
|
| 119 |
+
write_pairs(output_file, pairs)
|
| 120 |
+
total_problem_count += problem_num
|
| 121 |
+
total_solution_count += len(pairs)
|
| 122 |
+
else:
|
| 123 |
+
logger.warning(f"No problem found in {dutch_tst_md}")
|
| 124 |
+
|
| 125 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 126 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 127 |
+
|
| 128 |
+
|
| 129 |
+
if __name__ == '__main__':
|
| 130 |
+
main()
|
Dutch_TST/segment_script/segment2.py
ADDED
|
@@ -0,0 +1,133 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
problem_pattern = re.compile(r'\n(\d+)\.\s+', re.IGNORECASE)
|
| 12 |
+
solution_pattern = re.compile(r'(?:\n|# )Opgave\s+(\d+)\.', re.IGNORECASE)
|
| 13 |
+
|
| 14 |
+
|
| 15 |
+
def analyze_problem(text: str) -> Tuple[List, int]:
|
| 16 |
+
tags = list(problem_pattern.finditer(text))
|
| 17 |
+
problem_num = len(tags)
|
| 18 |
+
tags.sort(key=lambda x: x.start())
|
| 19 |
+
return tags, problem_num
|
| 20 |
+
|
| 21 |
+
|
| 22 |
+
def analyze_solution(text: str) -> Tuple[List, int]:
|
| 23 |
+
tags = list(solution_pattern.finditer(text))
|
| 24 |
+
solution_num = len(tags)
|
| 25 |
+
tags.sort(key=lambda x: x.start())
|
| 26 |
+
return tags, solution_num
|
| 27 |
+
|
| 28 |
+
|
| 29 |
+
def segment(text: str, tags: list):
|
| 30 |
+
starts = []
|
| 31 |
+
ends = []
|
| 32 |
+
|
| 33 |
+
for i, t in enumerate(tags):
|
| 34 |
+
starts.append(t.end())
|
| 35 |
+
if i + 1 < len(tags):
|
| 36 |
+
ends.append(tags[i + 1].start())
|
| 37 |
+
else:
|
| 38 |
+
ends.append(len(text))
|
| 39 |
+
|
| 40 |
+
return [text[start:end].strip() for start, end in zip(starts, ends)]
|
| 41 |
+
|
| 42 |
+
|
| 43 |
+
def join(problems, solutions):
|
| 44 |
+
pairs = []
|
| 45 |
+
|
| 46 |
+
for problem in problems:
|
| 47 |
+
key = problem[0].group(1)
|
| 48 |
+
|
| 49 |
+
problem_content = problem[1]
|
| 50 |
+
problem_label = key
|
| 51 |
+
problem_match = problem[0].group(0)
|
| 52 |
+
solution_content, solution_match = [], ''
|
| 53 |
+
# (a) Oplossing 1.
|
| 54 |
+
for s in solutions:
|
| 55 |
+
if s[0].group(1) == key:
|
| 56 |
+
solution_content = s[1]
|
| 57 |
+
solution_match = s[0].group(0)
|
| 58 |
+
break
|
| 59 |
+
|
| 60 |
+
pairs.append((problem_content, solution_content, problem_label, problem_match, solution_match))
|
| 61 |
+
|
| 62 |
+
return pairs
|
| 63 |
+
|
| 64 |
+
|
| 65 |
+
def write_pairs(output_file: Path, pairs):
|
| 66 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 67 |
+
|
| 68 |
+
output_jsonl_text = ""
|
| 69 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 70 |
+
output_jsonl_text += json.dumps(
|
| 71 |
+
{
|
| 72 |
+
'year': year,
|
| 73 |
+
'problem_label': problem_label,
|
| 74 |
+
'tier': 1,
|
| 75 |
+
'problem': problem,
|
| 76 |
+
'solution': solution,
|
| 77 |
+
'problem_match': problem_match,
|
| 78 |
+
'solution_match': solution_match
|
| 79 |
+
},
|
| 80 |
+
ensure_ascii=False
|
| 81 |
+
) + '\n'
|
| 82 |
+
|
| 83 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 84 |
+
|
| 85 |
+
|
| 86 |
+
def main():
|
| 87 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 88 |
+
compet_md_path = compet_base_path / "md"
|
| 89 |
+
seg_output_path = compet_base_path / "segmented"
|
| 90 |
+
|
| 91 |
+
special_years_md = {
|
| 92 |
+
"2007": {
|
| 93 |
+
"problem": "nl-2007-opgaven.md",
|
| 94 |
+
"solution": "nl-2007-uitwerkingen.md"
|
| 95 |
+
},
|
| 96 |
+
"2008": {
|
| 97 |
+
"problem": "nl-2008-opgaven.md",
|
| 98 |
+
"solution": "nl-2008-uitwerkingen.md"
|
| 99 |
+
}
|
| 100 |
+
}
|
| 101 |
+
|
| 102 |
+
total_problem_count = 0
|
| 103 |
+
total_solution_count = 0
|
| 104 |
+
|
| 105 |
+
for year, md in tqdm(special_years_md.items()):
|
| 106 |
+
problem_path = compet_md_path / md["problem"]
|
| 107 |
+
solution_path = compet_md_path / md["solution"]
|
| 108 |
+
|
| 109 |
+
output_file = seg_output_path / solution_path.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 110 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 111 |
+
|
| 112 |
+
problem_content = problem_path.read_text(encoding="utf-8")
|
| 113 |
+
problem_tags, problem_num = analyze_problem(problem_content)
|
| 114 |
+
segmented_problems = segment(problem_content, problem_tags)
|
| 115 |
+
problems = zip(problem_tags, segmented_problems)
|
| 116 |
+
|
| 117 |
+
solution_content = solution_path.read_text(encoding="utf-8")
|
| 118 |
+
solution_tags, solution_num = analyze_solution(solution_content)
|
| 119 |
+
segmented_solutions = segment(solution_content, solution_tags)
|
| 120 |
+
solutions = zip(solution_tags, segmented_solutions)
|
| 121 |
+
|
| 122 |
+
pairs = join(problems, solutions)
|
| 123 |
+
write_pairs(output_file, pairs)
|
| 124 |
+
|
| 125 |
+
total_problem_count += problem_num
|
| 126 |
+
total_solution_count += len(pairs)
|
| 127 |
+
|
| 128 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 129 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 130 |
+
|
| 131 |
+
|
| 132 |
+
if __name__ == "__main__":
|
| 133 |
+
main()
|
Dutch_TST/segmented/nl-2006-uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2006", "problem_label": "1", "tier": 1, "problem": "Als we een verzameling punten in de ruimte hebben, mogen we een punt van de verzameling spiegelen in een ander punt van de verzameling en het beeld hiervan toevoegen aan de verzameling.\nAls we beginnen met een verzameling bestaande uit zeven van de acht hoekpunten van een kubus, kunnen we dan het achtste hoekpunt in de verzameling krijgen na een eindig aantal stappen?", "solution": "Als we op de getallenlijn een punt $x$ spiegelen in een punt $y$, dan krijgen we als spiegelbeeld het punt $S_{y}(x)=y-(x-y)=2 y-x$. Hetzelfde geldt voor punten in de ruimte: spiegelen we een willekeurig punt $\\left(x_{1}, x_{2}, x_{3}\\right)$ in een punt $\\left(y_{1}, y_{2}, y_{3}\\right)$, dan krijgen we $S_{\\left(y_{1}, y_{2}, y_{3}\\right)}\\left(x_{1}, x_{2}, x_{3}\\right)=\\left(2 y_{1}-x_{1}, 2 y_{2}-x_{2}, 2 y_{3}-x_{3}\\right)$.\nWe bekijken nu alleen punten met gehele coördinaten. Hoe we het roosterpunt ( $y_{1}, y_{2}, y_{3}$ ) ook kiezen, de coördinaten van het beeld $S_{\\left(y_{1}, y_{2}, y_{3}\\right)}\\left(x_{1}, x_{2}, x_{3}\\right)$ van $\\left(x_{1}, x_{2}, x_{3}\\right)$ hebben alle drie dezelfde pariteit als de coördinaten van $\\left(x_{1}, x_{2}, x_{3}\\right)$. Er zijn $2^{3}=8$ verschillende mogelijkheden voor de pariteitscombinaties van de roosterpunten. We kunnen de punten van ons rooster dus kleuren met 8 kleuren, zodanig dat de kleur van een punt invariant is onder spiegeling in een willekeurig roosterpunt.\nBeschouw nu de kubus met hoekpunten $(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1)$, $(1,1,0),(1,1,1)$. Deze hoekpunten hebben in bovengenoemde kleuring elk een andere kleur. Als er dus één hoekpunt ontbreekt, kunnen we deze niet verkijgen door het herhaald spiegelen van één van de andere hoekpunten, want je krijgt dan alleen maar punten van een kleur die je al had.", "problem_match": "# Opgave 1.", "solution_match": "# Oplossing:"}
|
| 2 |
+
{"year": "2006", "problem_label": "2", "tier": 1, "problem": "In een groep van scholieren spreken 50 scholieren Duits, 50 scholieren Frans en 50 scholieren Spaans. Sommige scholieren spreken meer dan één taal.\nBewijs dat de scholieren in 5 groepen verdeeld kunnen worden zodat in elke groep precies 10 scholieren Duits spreken, 10 Frans en 10 Spaans.", "solution": "Scholieren die geen enkele taal spreken kunnen we buiten beschouwing laten, want we kunnen ze willekeurig over de groepen verdelen.\nWe onderscheiden zeven typen scholieren, al naar gelang de talen die ze spreken: DFS, FS, SD, DF, D, F en S, waarbij bijvoorbeeld een S-scholier alleen Spaans spreekt.\nMaak een Venn-diagram met de aantallen scholieren (zie figuur 1 op bladzijde 6): $d$ DFSscholieren, $a$ FS-scholieren, $b$ SD-scholieren en $c$ DF-scholieren. Dus zijn er $50-d-b-c$ D-scholieren, $50-d-c-a$ F-scholieren en $50-d-a-b$ S-scholieren. Definiëren we $t=a+b+c+d$, dan geldt dat er $50-t+a$ D-scholieren zijn, $50-t+b$ F-scholieren en $50-t+c$ S-scholieren.\nGa er z.b.d.a. van uit dat $a \\leq b \\leq c$. We gaan eerst groepjes maken van 1 FS-scholier, 1 SD-scholier en 1 DF-scholier. Deze spreken samen alle drie de talen twee maal. Nadat we $a$ van zulke groepjes hebben gemaakt, maken we $d$ groepjes bestaande uit 1 DFS-scholier. Nu houden we de volgende aantallen over:\n0 FS-scholieren; $b-a \\geq 0$ SD-scholieren en $c-a \\geq 0$ DF-scholieren; $50-d-b-c$ Dscholieren, $50-d-c-a$ F-scholieren en $50-d-a-b$ S-scholieren. Maken we $b-a$ groepjes van 1 SD-scholier en 1 F-scholier en ook $c-a$ groepjes van 1 DF-scholier en 1 S-scholier, dan houden we $50-d-b-c$ D-scholieren, $50-d-c-a-(b-a)=50-d-c-b$ F-scholieren en $50-d-a-b-(c-a)=50-d-b-c$ S-scholieren over, die samen $50-d-b-c$ groepjes van 1 D-scholier, 1 F-scholier en 1 S-scholier vormen.\nIn alle tot nu toe gevormde groepjes worden de drie talen alle drie 1 keer, ofwel alle drie 2 keer gesproken. Voeg eerst de groepjes samen waarin alle drie de talen 2 keer worden gesproken, steeds totdat de talen 10 keer worden gesproken. Ga daarna verder met het toevoegen van groepjes waarin de talen 1 keer worden gesproken.\nDan krijgen we groepen waarin alle drie de talen 10 keer worden gesproken. Aangezien elke taal 50 keer wordt gesproken, leidt dit tot 5 van dergelijke groepen.", "problem_match": "# Opgave 2.", "solution_match": "# Oplossing:"}
|
| 3 |
+
{"year": "2006", "problem_label": "3", "tier": 1, "problem": "Cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$ snijden elkaar in $P$ en $Q$. Zij $A$ een punt op $\\Gamma_{1}$ niet gelijk aan $P$ of $Q$. De lijnen $A P$ en $A Q$ snijden $\\Gamma_{2}$ nogmaals in respectievelijk $B$ en $C$.\nBewijs dat de hoogtelijn uit $A$ in driehoek $A B C$ door een punt gaat dat onafhankelijk is van de keuze van $A$.", "solution": "Door het tekenen van verscheidene nette plaatjes hebben we het vermoeden gekregen dat de genoemde hoogtelijn altijd door het middelpunt van $\\Gamma_{1}$ gaat. Dat dat ook daadwerkelijk zo is, gaan we nu bewijzen.\nHet voetpunt van de hoogtelijn uit $A$ op (het verlengde van) $B C$ noemen we $K$, en het andere snijpunt van deze hoogtelijn met $\\Gamma_{1}$ noemen we $D$. Te bewijzen: $A D$ is een middellijn van $\\Gamma_{1}$.\nEr zijn verschillende configuraties mogelijk. We noemen boog $P Q$ het deel van $\\Gamma_{1}$ dat binnen $\\Gamma_{2}$ ligt, en boog $Q P$ het andere deel van $\\Gamma_{1}$. We bekijken eerst het geval dat $D$ op boog $P Q$ ligt (zie figuur 2 op bladzijde 6). In dit geval geldt:\n\n$$\n\\begin{aligned}\n\\angle D Q C+\\angle P Q D=\\angle P Q C & =\\pi-\\angle C B P(\\text { wegens koordenvierhoek } P Q C B) \\\\\n& =\\pi-\\angle K B P(\\text { zelfde hoek }) \\\\\n& =\\pi-\\angle K B A(\\text { zelfde hoek }) \\\\\n& =\\angle B A K+\\angle A K B \\text { (hoekensom driehoek) } \\\\\n& =\\angle B A K+\\frac{1}{2} \\pi(A K \\text { was hoogtelijn) } \\\\\n& =\\angle P A D+\\frac{1}{2} \\pi \\text { (zelfde hoek) } \\\\\n& =\\angle P Q D+\\frac{1}{2} \\pi(\\text { omtrekshoek })\n\\end{aligned}\n$$\n\nzodat $\\angle D Q C=\\frac{1}{2} \\pi$. Uit $\\angle A Q D+\\angle D Q C=\\angle A Q C=\\pi$ (gestrekte hoek) volgt nu dat $\\angle A Q D=\\frac{1}{2} \\pi$, zodat we wegens Thales kunnen concluderen dat $A D$ een middellijn is van $\\Gamma_{1}$.\nBekijk nu het geval dat $\\angle B$ stomp is en dat $B$ en $C$ nog wel aan dezelfde kant van $P Q$ liggen (zie figuur 3 op bladzijde 6). In dit geval geldt:\n\n$$\n\\begin{aligned}\n\\angle D Q C-\\angle D Q P=\\angle P Q C & =\\pi-\\angle C B P(\\text { wegens koordenvierhoek } P Q C B) \\\\\n& =\\angle P B K(\\text { gestrekte hoek }) \\\\\n& =\\angle A B K(\\text { zelfde hoek }) \\\\\n& =\\pi-\\angle K A B-\\angle B K A \\text { (hoekensom driehoek) } \\\\\n& =\\frac{1}{2} \\pi-\\angle K A B(A K \\text { was hoogtelijn) } \\\\\n& =\\frac{1}{2} \\pi-\\angle D A P \\text { (zelfde hoek) } \\\\\n& =\\frac{1}{2} \\pi-\\angle D Q P(\\text { omtrekshoek })\n\\end{aligned}\n$$\n\nzodat $\\angle D Q C=\\frac{1}{2} \\pi$. Uit $\\angle A Q D+\\angle D Q C=\\angle A Q C=\\pi$ volgt wederom dat $\\angle A Q D=\\frac{1}{2} \\pi$, zodat we wegens Thales kunnen concluderen dat $A D$ een middellijn is van $\\Gamma_{1}$.\nAlle andere configuraties gaan analoog. Door met georiënteerde hoeken te werken zouden we geen gevalsonderscheiding hoeven te gebruiken.", "problem_match": "# Opgave 3.", "solution_match": "# Oplossing:"}
|
| 4 |
+
{"year": "2006", "problem_label": "4", "tier": 1, "problem": "Zij $\\mathbb{R}_{>0}$ de verzameling van positieve reële getallen. Laat $a \\in \\mathbb{R}_{>0}$ gegeven zijn. Vind alle functies $f: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}$ zodanig dat $f(a)=1$ en\n\n$$\n\\forall x, y \\in \\mathbb{R}_{>0}: f(x) f(y)+f\\left(\\frac{a}{x}\\right) f\\left(\\frac{a}{y}\\right)=2 f(x y)\n$$", "solution": "Invullen van $x=a$ en $y=1$ in (1) geeft $f(a) f(1)+f\\left(\\frac{a}{a}\\right) f\\left(\\frac{a}{1}\\right)=2 f(a \\cdot 1)$, wat wegens $f(a)=1$ leidt tot $f(1)+f(1)=2$, dus\n\n$$\nf(1)=1\n$$\n\nInvullen van $y=1$ in (1) geeft $f(x) f(1)+f\\left(\\frac{a}{x}\\right) f\\left(\\frac{a}{1}\\right)=2 f(x \\cdot 1)$, wat wegens $f(a)=f(1)=1$ leidt tot $f(x)+f\\left(\\frac{a}{x}\\right)=2 f(x)$, dus\n\n$$\nf(x)=f\\left(\\frac{a}{x}\\right) .\n$$\n\nMaar dan gaat (1) over in $f(x) f(y)+f(x) f(y)=2 f(x y)$, dus\n\n$$\nf(x) f(y)=f(x y)\n$$\n\nUit (3) en (4) volgt dat $f(x) f(x)=f(x) f\\left(\\frac{a}{x}\\right)=f\\left(x \\cdot \\frac{a}{x}\\right)=f(a)=1$, dus voor elke $x \\in \\mathbb{R}_{>0}$ geldt $f(x)=1$ of $f(x)=-1$.\nAangezien we positieve $x$ kunnen schrijven als $\\sqrt{x} \\sqrt{x}$, vinden we m.b.v. (4) dat $f(x)=$ $f(\\sqrt{x} \\sqrt{x})=f(\\sqrt{x}) f(\\sqrt{x})=( \\pm 1)^{2}=1$, dus $f(x)=1$ voor elke $x \\in \\mathbb{R}_{>0}$. We concluderen dat de enige mogelijkheid voor $f$ blijkbaar de constante functie $f: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}: x \\mapsto 1$ is.\nTen slotte controleren we of de constante functie $\\forall x: f(x)=1$ daadwerkelijk voldoet. Aan $f(a)=1$ wordt voldaan, terwijl (1) neerkomt op $1 \\cdot 1+1 \\cdot 1=2 \\cdot 1$, wat geldt.\nEr is dus precies één functie $f$ die aan de gevraagde voorwaarden voldoet, namelijk $f$ : $\\mathbb{R}_{>0} \\rightarrow \\mathbb{R}: x \\mapsto 1$.", "problem_match": "# Opgave 4.", "solution_match": "# Oplossing:"}
|
| 5 |
+
{"year": "2006", "problem_label": "5", "tier": 1, "problem": "Zij $\\lfloor x\\rfloor$ het grootste gehele getal kleiner dan of gelijk aan $x$. Laat $n \\in \\mathbb{N}, n \\geq 7$ gegeven zijn.\nBewijs dat $\\binom{n}{7}-\\left\\lfloor\\frac{n}{7}\\right\\rfloor$ deelbaar is door 7 .", "solution": "Schrijf $n=7 k+\\ell$ voor gehele $k$ en $\\ell$ met $0 \\leq \\ell \\leq 6$, dan geldt $\\left\\lfloor\\frac{n}{7}\\right\\rfloor=\\left\\lfloor k+\\frac{\\ell}{7}\\right\\rfloor=k$.\nTe bewijzen: $\\binom{n}{7} \\equiv k(\\bmod 7)$.\nBewijs: Het uitschrijven van de binomiaalcoëfficiënt geeft\n\n$$\n\\binom{n}{7}=\\frac{n!}{7!(n-7)!}=\\frac{n(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)}{7 \\cdot 6 \\cdot 5 \\cdot 4 \\cdot 3 \\cdot 2 \\cdot 1}\n$$\n\nDe factor $(n-\\ell)$ in de teller is gelijk aan $7 k$, zodat\n$\\binom{n}{7}=\\frac{7 k \\cdot n(n-1) \\cdots(\\widehat{n-\\ell}) \\cdots(n-5)(n-6)}{7 \\cdot 6 \\cdot 5 \\cdot 4 \\cdot 3 \\cdot 2 \\cdot 1}=k \\cdot \\frac{n(n-1) \\cdots(\\widehat{n-\\ell}) \\cdots(n-5)(n-6)}{6 \\cdot 5 \\cdot 4 \\cdot 3 \\cdot 2 \\cdot 1}$,\nwaar $(\\widehat{n-\\ell})$ betekent dat we de factor $(n-\\ell)$ hebben weggelaten. Modulo 7 stonden in de teller de 7 restklassen modulo 7 , maar nu we $(n-\\ell) \\equiv 0(\\bmod 7)$ hebben weggelaten staan in de teller precies de restklassen $1,2,3,4,5$ en 6 , net als in de noemer, die dus tegen elkaar wegvallen modulo het priemgetal 7 . We houden over dat\n\n$$\n\\binom{n}{7}=k \\cdot \\frac{n(n-1) \\cdots(\\widehat{n-\\ell}) \\cdots(n-5)(n-6)}{6 \\cdot 5 \\cdot 4 \\cdot 3 \\cdot 2 \\cdot 1} \\equiv k \\cdot 1=k \\quad(\\bmod 7)\n$$\n\nhetgeen te bewijzen was.", "problem_match": "# Opgave 5.", "solution_match": "# Oplossing:"}
|
Dutch_TST/segmented/nl-2007-uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2007", "problem_label": "1", "tier": 1, "problem": "Zij $m$ een positief geheel getal. Bewijs dat voor alle positieve reële getallen $a$ en $b$ geldt:\n\n$$\n\\left(1+\\frac{a}{b}\\right)^{m}+\\left(1+\\frac{b}{a}\\right)^{m} \\geq 2^{m+1}\n$$", "solution": "We gebruiken dat $x+\\frac{1}{x} \\geq 2$ voor alle $x \\in \\mathbb{R}_{>0}$. Er geldt\n\n$$\n\\begin{aligned}\n\\left(1+\\frac{a}{b}\\right)^{m}+\\left(1+\\frac{b}{a}\\right)^{m} & =\\sum_{i=0}^{m}\\binom{m}{i}\\left(\\frac{a}{b}\\right)^{i}+\\sum_{i=0}^{m}\\binom{m}{i}\\left(\\frac{b}{a}\\right)^{i} \\\\\n& =\\sum_{i=0}^{m}\\binom{m}{i}\\left(\\left(\\frac{a}{b}\\right)^{i}+\\left(\\frac{b}{a}\\right)^{i}\\right) \\\\\n& =\\sum_{i=0}^{m}\\binom{m}{i}\\left(\\frac{a^{i}}{b^{i}}+\\frac{b^{i}}{a^{i}}\\right) \\\\\n& \\geq \\sum_{i=0}^{m}\\binom{m}{i} \\cdot 2 \\\\\n& =2^{m+1} .\n\\end{aligned}\n$$\n\n## Alternatieve oplossing.\n\nPas de ongelijkheid van het rekenkundig en meetkundig gemiddelde toe op 1 en $\\frac{a}{b}$ :\n\n$$\n1+\\frac{a}{b} \\geq 2 \\sqrt{\\frac{a}{b}}\n$$\n\ndus\n\n$$\n\\left(1+\\frac{a}{b}\\right)^{m} \\geq\\left(2 \\sqrt{\\frac{a}{b}}\\right)^{m}\n$$\n\nAnaloog geldt natuurlijk\n\n$$\n\\left(1+\\frac{b}{a}\\right)^{m} \\geq\\left(2 \\sqrt{\\frac{b}{a}}\\right)^{m}\n$$\n\nNu passen we opnieuw de ongelijkheid van het rekenkundig en meetkundig gemiddelde toe:\n\n$$\n\\left(2 \\sqrt{\\frac{a}{b}}\\right)^{m}+\\left(2 \\sqrt{\\frac{b}{a}}\\right)^{m} \\geq 2 \\sqrt{\\left(2 \\sqrt{\\frac{a}{b}}\\right)^{m} \\cdot\\left(2 \\sqrt{\\frac{b}{a}}\\right)^{m}}=2^{m+1}\n$$\n\nDit bewijst het gevraagde.", "problem_match": "\n1. ", "solution_match": "\nOpgave 1."}
|
| 2 |
+
{"year": "2007", "problem_label": "2", "tier": 1, "problem": "Vier punten $P, Q, R$ en $S$ liggen in deze volgorde op een cirkel, zodat $\\angle P S R=90^{\\circ}$. Zij $H$ en $K$ de voetpunten van de loodlijnen uit $Q$ op respectievelijk $P R$ en $P S$. Zij $T$ het snijpunt van $H K$ en $Q S$. Bewijs dat $|S T|=|T Q|$.", "solution": "Omdat $\\angle P S R$ recht is, is $P R$ een middellijn en is dus ook $\\angle P Q R$ recht. Verder is $P Q H K$ een koordenvierhoek (en $P Q R S$ natuurlijk ook), dus\n\n$$\n\\angle Q S R=\\angle Q P R=\\angle Q P H=\\angle Q K H\n$$\n\nDus\n\n$$\n\\angle T K S=90^{\\circ}-\\angle Q K H=90^{\\circ}-\\angle Q S R=\\angle Q S K\n$$\n\nDus $\\triangle T S K$ is gelijkbenig met $|K T|=|T S|$. Verder is $\\angle Q S R=\\angle K Q S$, omdat $S R$ en $Q K$ beide loodrecht op $P S$ staan, dus\n\n$$\n\\angle K Q S=\\angle Q S R=\\angle Q K H,\n$$\n\nzodat ook driehoek $K Q T$ gelijkbenig is met $|T Q|=|T K|$. Dus $|T Q|=|T K|=|T S|$.", "problem_match": "\n2. ", "solution_match": "\nOpgave 2."}
|
| 3 |
+
{"year": "2007", "problem_label": "3", "tier": 1, "problem": "Je hebt 2007 kaarten. Op elke kaart is een positief geheel getal kleiner dan 2008 geschreven. Als je een aantal (minstens 1) van deze kaarten neemt, is de som van de getallen op de kaarten niet deelbaar door 2008. Bewijs dat op elke kaart hetzelfde getal staat.", "solution": "Stel niet. Noem de getallen op de kaarten $n_{1}, \\ldots, n_{2007}$ waarbij $n_{1} \\neq n_{2}$. Zij\n\n$$\ns_{i}=n_{1}+n_{2}+\\ldots+n_{i},\n$$\n\nvoor $i=1,2, \\ldots, 2007$. We weten nu dat $s_{i} \\equiv \\equiv(\\bmod 2008)$ voor alle $i$. Stel dat $s_{i} \\equiv s_{j}$ $(\\bmod 2008)$ met $i<j$, dan geldt\n\n$$\nn_{i+1}+\\ldots+n_{j} \\equiv 0 \\quad(\\bmod 2008)\n$$\n\ntegenspraak. Dus $s_{1}, \\ldots, s_{2007}$ nemen modulo 2008 precies de waarden 1, 2, .., 2007 aan. Bekijk nu $n_{2}$. We weten dat $n_{2} \\not \\equiv 0(\\bmod 2008)$, dus $n_{2} \\equiv s_{i}(\\bmod 2008)$ voor een of andere $i$. Voor $i=1$ staat hier $n_{2} \\equiv n_{1}(\\bmod 2008)$, wat wegens $n_{1}, n_{2} \\in\\{1, \\ldots, 2007\\}$ impliceert dat $n_{1}=n_{2}$; tegenspraak. En voor $i>1$ betekent het dat de niet-lege som $s_{i}-n_{2}=n_{1}+n_{3}+n_{4}+\\ldots+n_{i}$ gelijk is aan 0 modulo 2008; wederom tegenspraak.", "problem_match": "\n3. ", "solution_match": "\nOpgave 3."}
|
| 4 |
+
{"year": "2007", "problem_label": "4", "tier": 1, "problem": "$\\mathrm{Zij} n \\geq 1$. Vind alle permutaties $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ van $(1,2, \\ldots, n)$ waarvoor geldt\n\n$$\n\\frac{a_{k}^{2}}{a_{k+1}} \\leq k+2 \\quad \\text { voor } k=1,2, \\ldots, n-1\n$$", "solution": "Stel dat voor zekere $i \\leq n-1$ geldt dat $a_{i}>i$. Er geldt $\\frac{a_{i}^{2}}{a_{i+1}} \\leq i+2$, dus\n\n$$\na_{i+1} \\geq \\frac{a_{i}^{2}}{i+2} \\geq \\frac{(i+1)^{2}}{i+2}=\\frac{i^{2}+2 i+1}{i+2}>i .\n$$\n\nAls $a_{i} \\geq i+2$, dan geldt op dezelfde manier $a_{i+1}>i+1$. Als $a_{i}=i+1$, dan is $i+1$ niet meer beschikbaar als waarde voor $a_{i+1}$, dus geldt ook $a_{i+1}>i+1$.\nDus als $a_{i}>i$, dan ook $a_{i+1}>i+1$. Aangezien $a_{n} \\leq n$, kan er dus geen enkele $i$ zijn met $a_{i}>i$. Hieruit volgt dat $a_{i}=i$ voor alle $i$.", "problem_match": "\n4. ", "solution_match": "\nOpgave 4."}
|
| 5 |
+
{"year": "2007", "problem_label": "5", "tier": 1, "problem": "Bewijs dat er oneindig veel paren positieve gehele getallen $(x, y)$ zijn met\n\n$$\n\\frac{x+1}{y}+\\frac{y+1}{x}=4 .\n$$", "solution": "We kunnen de vergelijking herschrijven tot $(x+1) x+(y+1) y=4 x y$, dus\n\n$$\nx^{2}-(4 y-1) x+\\left(y^{2}+y\\right)=0 .\n$$\n\nAls we dit zien als een vergelijking in $x$ met parameter $y$, dan geldt er voor de twee oplossingen $x_{0}$ en $x_{1}$ wegens Vieta dat (i): $x_{0}+x_{1}=4 y-1$ en (ii): $x_{0} \\cdot x_{1}=y^{2}+y$.\nStel nou dat $x_{0} \\in \\mathbb{N}$ en $y_{0} \\in \\mathbb{N}$ een willekeurige oplossing vormen. Dan is er bij deze waarde van $y_{0}$ dus nog een oplossing $x_{1}$, die wegens (i) weer geheel is, en wegens (ii) weer positief. Voor deze andere oplossing geldt wegens (i): $x_{1}=4 y_{0}-1-x_{0}$. Kortom, elk oplossingspaar $(x, y)$ leidt tot een oplossingspaar $(4 y-1-x, y)$. De truc is nou om te bedenken dat dan ook $(y, 4 y-1-x)$ een oplossingspaar is.\nHet paar $(1,1)$ is duidelijk een oplossing. Beschouw nu de rij $z_{1}=1, z_{2}=1$, en $z_{n+2}=$ $4 z_{n+1}-1-z_{n}(n \\geq 1)$, dan is elk paar $\\left(z_{n}, z_{n+1}\\right)$ dus blijkbaar een oplossing van de gegeven vergelijking.\n\nTot slot moeten we nog bewijzen dat dit tot echt allemaal verschillende oplossingen $\\left(z_{n}, z_{n+1}\\right)$ leidt. Hiertoe bewijzen we met inductie dat $\\forall n \\geq 2: z_{n+1} \\geq 2 z_{n} \\wedge z_{n+1} \\geq 1$.\nVoor $n=2$ is dit duidelijk, want $z_{3}=2$ en $z_{2}=1$. Stel het geldt voor zekere $n \\geq 2$, dus $z_{n+1} \\geq 2 z_{n} \\wedge z_{n+1} \\geq 1$. Dan $z_{n+2}=4 z_{n+1}-1-z_{n} \\geq 4 z_{n+1}-z_{n+1}-z_{n+1}=2 z_{n+1} \\geq 2>1$, dus zien we dat het ook geldt voor $n+1$.", "problem_match": "\n5. ", "solution_match": "\nOpgave 5."}
|
Dutch_TST/segmented/nl-2008-uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2008", "problem_label": "1", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ die voldoen aan\n\n$$\nf(f(f(n)))+f(f(n))+f(n)=3 n\n$$\n\nvoor alle $n \\in \\mathbb{Z}_{>0}$.", "solution": "Uit $f(m)=f(n)$ volgt $3 m=3 n$ dus $m=n$. Dus $f$ is injectief. Nu bewijzen we met volledige inductie naar $n$ dat $f(n)=n$ voor alle $n$.\nOmdat $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ geldt $f(1) \\geq 1, f(f(1)) \\geq 1$ en $f(f(f(1))) \\geq 1$. Vullen we nu $n=1$ in de functievergelijking in, dan zien we dat\n\n$$\nf(f(f(1)))+f(f(1))+f(1)=3,\n$$\n\ndus moet overal gelijkheid gelden: $f(1)=f(f(1))=f(f(f(1)))=1$.\nZij nu $k \\geq 2$ en stel dat we voor alle $n<k$ bewezen hebben dat $f(n)=n$. Dan volgt uit de injectiviteit van $f$ dat voor alle $m \\geq k$ geldt dat $f(m) \\geq k$; de lagere functiewaardes worden immers al aangenomen. Dus in het bijzonder geldt $f(k) \\geq k$ en dan ook $f(f(k)) \\geq k$ en daarom ook $f(f(f(k))) \\geq k$. Vullen we nu $n=k$ in de functievergelijking in, dan zien we dat\n\n$$\nf(f(f(k)))+f(f(k))+f(k)=3 k\n$$\n\nWe zien dat ook nu weer overal gelijkheid moet gelden, dus $f(k)=k$. Dit voltooit de inductie.\nDe enige functie die kan voldoen is dus $f(n)=n$ voor alle $n$. Deze functie voldoet ook daadwerkelijk, want\n\n$$\nf(f(f(n)))+f(f(n))+f(n)=n+n+n=3 n\n$$", "problem_match": "\n1. ", "solution_match": "\nOpgave 1."}
|
| 2 |
+
{"year": "2008", "problem_label": "2", "tier": 1, "problem": "Julian en Johan spelen een spel met een even aantal, zeg $2 n$, kaarten ( $n \\in \\mathbb{Z}_{>0}$ ). Op elke kaart staat een positief geheel getal. De kaarten worden geschud en in een rij op tafel gelegd met de getallen zichtbaar. Een speler die aan de beurt is, mag ofwel de meest linker kaart ofwel de meest rechter kaart pakken. De spelers zijn om en om aan de beurt.\nJohan begint, dus Julian pakt uiteindelijk de laatste kaart. De score van Johan is de som van de getallen op de $n$ kaarten die hij heeft gepakt en voor Julian net zo. Bewijs dat Johan altijd een minstens even hoge score als Julian kan behalen.", "solution": "Zij $2 n$ het aantal kaarten en ga ervan uit dat de kaarten in de rij achtereenvolgens $a_{1}, a_{2}, \\ldots, a_{2 n}$ zijn. We bewijzen met inductie naar $n$ dat Johan dan altijd kan zorgen dat hij naar keuze alle oneven kaarten $a_{1}, a_{3}, a_{5}, \\ldots$ pakt of juist alle even kaarten $a_{2}, a_{4}, a_{6}, \\ldots$ Voor $n=1$ pakt Johan kaart $a_{1}$ als hij de oneven kaarten wil en kaart $a_{2}$ als hij de even kaarten wil. Stel we hebben het bewezen voor zekere $n$. Bekijk de kaarten $a_{1}$, $a_{2}, \\ldots, a_{2 n+2}$. Als Johan de oneven kaarten wil, pakt hij eerst $a_{1}$. Julian pakt vervolgens $a_{2}$ of $a_{2 n+2}$. Daarna blijft over de rij $b_{1}, b_{2}, \\ldots, b_{2 n}$. In het eerste geval geldt $b_{i}=a_{i+2}$ voor alle $i$ en kan Johan volgens de inductiehypothese alle oneven $b_{i}$ krijgen, wat hem samen met de kaart $a_{1}$ alle oneven kaarten oplevert. In het tweede geval geldt $b_{i}=a_{i+1}$ voor alle $i$ en kan Johan volgens de inductiehypothese alle even $b_{i}$ krijgen, wat hem samen met de kaart $a_{1}$ alle oneven kaarten oplevert. Johan kan dus zorgen dat hij alle oneven kaarten krijgt. Analoog kan hij ook zorgen dat hij alle even kaarten krijgt. Dit voltooit de inductie. Johan kan nu zorgen dat hij minstens evenveel punten scoort als Julian op de volgende manier: als de som van de getallen op de oneven kaarten minstens even groot is als de som van de getallen op de even kaarten, dan kiest hij alle oneven kaarten. Zo niet, dan kiest hij alle even kaarten.\n\n#", "problem_match": "\n2. ", "solution_match": "\nOpgave 2."}
|
| 3 |
+
{"year": "2008", "problem_label": "3", "tier": 1, "problem": "Laat $m, n$ positieve gehele getallen zijn. Bekijk een rijtje positieve gehele getallen $a_{1}$, $a_{2}, \\ldots, a_{n}$ dat voldoet aan $m=a_{1} \\geq a_{2} \\geq \\cdots \\geq a_{n} \\geq 1$. Voor $1 \\leq i \\leq m$ definiëren we\n\n$$\nb_{i}=\\#\\left\\{j \\in\\{1,2, \\ldots, n\\}: a_{j} \\geq i\\right\\}\n$$\n\ndus $b_{i}$ is het aantal getallen $a_{j}$ uit het rijtje waarvoor geldt $a_{j} \\geq i$. Voor $1 \\leq j \\leq n$ definiëren we\n\n$$\nc_{j}=\\#\\left\\{i \\in\\{1,2, \\ldots, m\\}: b_{i} \\geq j\\right\\}\n$$\n\ndus $c_{j}$ is het aantal getallen $b_{i}$ waarvoor geldt $b_{i} \\geq j$.\nVoorbeeld: bij het a-rijtje 5, 3, 3, 2, 1, 1 hoort het b-rijtje 6, 4, 3, 1, 1 .\n(a) Bewijs dat $a_{j}=c_{j}$ voor $1 \\leq j \\leq n$.\n(b) Bewijs dat voor $1 \\leq k \\leq m$ geldt: $\\sum_{i=1}^{k} b_{i}=k \\cdot b_{k}+\\sum_{j=b_{k}+1}^{n} a_{j}$.", "solution": "(a) Oplossing 1. Merk op dat voor $1 \\leq i \\leq m$ en $1 \\leq j \\leq n$ geldt:\n\n| $a_{j} \\geq i$ | $\\Longleftrightarrow$ |\n| ---: | :--- |\n| $a_{1}, a_{2}, \\ldots, a_{j} \\geq i$ | $\\Longleftrightarrow$ |\n| minstens $j$ van de $a^{\\prime}$ 'tjes zijn groter of gelijk aan $i$ | $\\Longleftrightarrow$ |\n| $b_{i} \\geq j$ | $\\Longleftrightarrow$ |\n| $b_{1}, b_{2}, \\ldots, b_{i} \\geq j$ | $\\Longleftrightarrow$ |\n| minstens $i$ van de $b^{\\prime}$ tjes zijn groter of gelijk aan $j$ | $\\Longleftrightarrow$ |\n| $c_{j} \\geq i$. | |\n\nZij nu $j$ gegeven. Neem dan eerst $i=a_{j}$, dan is de eerste regel waar, dus de laatste ook: $c_{j} \\geq a_{j}$. Neem andersom $i=c_{j}$, dan is de laatste regel waar, dus de eerste ook: $a_{j} \\geq c_{j}$. Nu volgt $a_{j}=c_{j}$.\n\nOplossing 2. Wegens de niet-stijgendheid geldt $b_{i}=\\max \\left\\{l: a_{l} \\geq i\\right\\}$ en $c_{j}=\\max \\{i$ : $\\left.b_{i} \\geq j\\right\\}$. Dus voor $1 \\leq j \\leq n$ geldt\n\n$$\nc_{j}=\\max \\left\\{i: b_{i} \\geq j\\right\\}=\\max \\left\\{i: \\max \\left\\{l: a_{l} \\geq i\\right\\} \\geq j\\right\\}\n$$\n\nVoor een vaste $i$ geldt:\n\n$$\n\\max \\left\\{l: a_{l} \\geq i\\right\\} \\geq j \\quad \\Longleftrightarrow \\quad a_{j} \\geq i\n$$\n\ndus $c_{j}=\\max \\left\\{i: a_{j} \\geq i\\right\\}=a_{j}$.\n(b) Oplossing 1. Voor $1 \\leq k \\leq m$ geldt\n\n$$\n\\sum_{i=1}^{k}\\left(b_{i}-b_{k}\\right)=\\sum_{i=1}^{k}\\left(\\#\\left\\{l: a_{l} \\geq i\\right\\}-\\#\\left\\{l: a_{l} \\geq k\\right\\}\\right)=\\sum_{i=1}^{k} \\#\\left\\{l: k>a_{l} \\geq i\\right\\}\n$$\n\nElk element $a_{l}$ uit de rij (met $k>a_{l}$ ) wordt hierin precies $a_{l}$ maal geteld (namelijk voor elke $i \\leq a_{l}$ ) dus dit is niets anders dan de som van al dergelijke $a_{l}$. Nu is (zie oplossing 1 van onderdeel a) $k \\leq a_{l}$ dan en slechts dan als $l \\leq b_{k}$, dus $k>a_{l}$ dan en slechts dan als $l>b_{k}$, dus\n\n$$\n\\sum_{i=1}^{k}\\left(b_{i}-b_{k}\\right)=\\sum_{l: k>a_{l}} a_{l}=\\sum_{l=b_{k}+1}^{n} a_{l}\n$$\n\nen hier volgt het te bewijzen direct uit.\nOplossing 2. We bewijzen dit met inductie naar $k$. Voor $k=1$ staat er\n\n$$\nb_{1} \\stackrel{?}{=} b_{1}+\\sum_{j=b_{1}+1}^{n} a_{j}\n$$\n\nen dit is waar omdat $b_{1}=\\#\\left\\{j: a_{j} \\geq 1\\right\\}=n$, dus de som aan de rechterkant is leeg. Stel nu dat we het bewezen hebben voor zekere $k$ met $1 \\leq k \\leq m-1$. Dan geldt\n\n$$\n\\begin{aligned}\n\\sum_{i=1}^{k+1} b_{i} & =\\sum_{i=1}^{k} b_{i}+b_{k+1} \\\\\n& \\stackrel{\\mathrm{IH}}{=} k \\cdot b_{k}+\\sum_{j=b_{k}+1}^{n} a_{j}+b_{k+1} \\\\\n& =(k+1) \\cdot b_{k+1}+\\sum_{j=b_{k+1}+1}^{n} a_{j}+k\\left(b_{k}-b_{k+1}\\right)-\\sum_{j=b_{k+1}+1}^{b_{k}} a_{j} \\\\\n& =(k+1) \\cdot b_{k+1}+\\sum_{j=b_{k+1}+1}^{n} a_{j}+k\\left(b_{k}-b_{k+1}\\right)-\\sum_{j=b_{k+1}+1}^{b_{k}} k \\\\\n& =(k+1) \\cdot b_{k+1}+\\sum_{j=b_{k+1}+1}^{n} a_{j} .\n\\end{aligned}\n$$", "problem_match": "\n3. ", "solution_match": "# Opgave 3."}
|
| 4 |
+
{"year": "2008", "problem_label": "4", "tier": 1, "problem": "Zij $n$ een geheel getal zo dat $\\sqrt{1+12 n^{2}}$ een geheel getal is.\n\nBewijs dat $2+2 \\sqrt{1+12 n^{2}}$ het kwadraat van een geheel getal is.", "solution": "Zij a zo dat $1+12 n^{2}=a^{2}$. We kunnen dit herschrijven als\n\n$$\n12 n^{2}=a^{2}-1=(a+1)(a-1)\n$$\n\nDe linkerkant is deelbaar door 2, dus de rechterkant ook, dus $a$ is oneven. Omdat links een even aantal factoren 2 staat, moeten zowel $a+1$ en $a-1$ deelbaar zijn door een oneven aantal factoren 2 (de een is namelijk deelbaar door precies één factor 2). Verder geldt $\\operatorname{ggd}(a+1, a-1)=2$, dus alle oneven priemfactoren die voorkomen in $n$, komen voor in precies één van $a+1$ en $a-1$. Voor de priemfactoren groter dan 3 geldt dat ze rechts een even aantal keer voorkomen; de priemfactor 3 komt een oneven aantal keer voor. Concluderend zijn er twee mogelijkheden:\n\n$$\na+1=6 b^{2} \\quad \\text { en } \\quad a-1=2 c^{2}\n$$\n\nvoor zekere gehele $b$ en $c$ met $b c=n$ of\n\n$$\na+1=2 b^{2} \\quad \\text { en } \\quad a-1=6 c^{2}\n$$\n\nvoor zekere gehele $b$ en $c$ met $b c=n$. Bekijk eerst het eerste geval. Dan is $a+1$ deelbaar door 3 en dus $a-1 \\equiv 1 \\bmod 3$. Maar daaruit volgt $c^{2} \\equiv 2 \\bmod 3$ en dat is onmogelijk. Dus het tweede geval moet gelden. Maar dan is\n\n$$\n2+2 \\sqrt{1+12 n^{2}}=2+2 a=2(a+1)=4 b^{2}=(2 b)^{2},\n$$\n\nen dat is wat we moesten bewijzen.", "problem_match": "\n4. ", "solution_match": "\nOpgave 4."}
|
| 5 |
+
{"year": "2008", "problem_label": "5", "tier": 1, "problem": "Laat $\\triangle A B C$ een rechthoekige driehoek zijn met $\\angle B=90^{\\circ}$ en $|A B|>|B C|$; en zij $\\Gamma$ de halve cirkel met middellijn $A B$ aan de kant van $A B$ waar ook $C$ ligt. Zij punt $P$ op $\\Gamma$ zo dat $|B P|=|B C|$ en zij $Q$ op lijnstuk $A B$ zo dat $|A P|=|A Q|$. Bewijs dat het midden van $C Q$ op $\\Gamma$ ligt.", "solution": "Oplossing 1. Zij $S$ het snijpunt van $\\Gamma$ en $C Q$. We moeten bewijzen dat $|Q S|=|S C|$.\nDe lijn $B C$ is een raaklijn aan $\\Gamma$, dus geldt $\\angle C B P=\\angle B A P=\\angle Q A P$. Omdat de driehoeken $C B P$ en $Q A P$ beide gelijkbenig zijn, zijn ze gelijkvormig. Zij $\\alpha=\\angle B C P$, dan geldt\n\n$$\n\\alpha=\\angle B C P=\\angle C P B=\\angle Q P A=\\angle A Q P\n$$\n\nWe zien nu dat\n\n$$\n\\angle C P Q=\\angle C P B+\\angle B P Q=\\angle Q P A+\\angle B P Q=\\angle B P A=90^{\\circ} .\n$$\n\nDus $P$ ligt, net als $B$, op de cirkel met middellijn $C Q$. Punt $S$ ligt op deze middellijn en we willen laten zien dat $S$ het middelpunt van de cirkel is, dus het is voldoende om te laten zien dat\n\n$$\n\\angle B S P=2 \\alpha=2 \\angle B C P .\n$$\n\nIn koordenvierhoek $Q B C P$ geldt $\\angle C P B=\\angle C Q B$, dus\n$2 \\alpha=\\angle C Q B+\\angle A Q P=180^{\\circ}-\\angle P Q C=180^{\\circ}-\\angle P B C=90^{\\circ}+\\angle Q B C-\\angle P B C=90^{\\circ}+\\angle Q B P$.\nIn koordenvierhoek $A B S P$, waarin $A B$ de middellijn is, zien we\n\n$$\n90^{\\circ}+\\angle Q B P=90^{\\circ}+\\angle A B P=\\angle B S A+\\angle A S P=\\angle B S P,\n$$\n\nzodat we kunnen concluderen\n\n$$\n2 \\alpha=\\angle B S P\n$$\n\nen dat is wat we wilden bewijzen.\n\nOplossing 2. Merk eerst op (net als in de vorige oplossing) dat de twee gelijkbenige driehoeken gelijkvormig zijn. Omdat $B C$ loodrecht op $A B$ staat, is de ene driehoek $90^{\\circ}$ gedraaid ten opzichte van de andere. Zij $l_{1}$ de bissectrice van $\\angle P B C$ en $l_{2}$ de bissectrice $\\operatorname{van} \\angle P A Q$. Deze bissectrices staan nu loodrecht op elkaar. Zij $T$ het snijpunt van $l_{1}$ en $l_{2}$. Dan geldt dus $\\angle A T B=90^{\\circ}$, dus $T$ ligt op $\\Gamma$.\nNu is $P$ het beeld van $C$ onder spiegeling in $l_{1}$ en $Q$ is het beeld van $P$ onder spiegeling in $l_{2}$. De samenstelling van deze twee spiegelingen is de rotatie in $T$ om $2 \\cdot 90=180$ graden. Onder deze rotatie gaat $C$ over in $Q$, dus $C T Q$ is een rechte lijn. Dus $T=S$. Wegens de rotatie geldt ook $|T C|=|T Q|$, dus $S$ is het midden van $C Q$.", "problem_match": "\n5. ", "solution_match": "\nOpgave 5."}
|
Dutch_TST/segmented/nl-2009-uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2009", "problem_label": "1", "tier": 1, "problem": "Zij $n \\geq 10$ een geheel getal. We schrijven $n$ in het tientallig stelsel. Zij $S(n)$ de som van de cijfers van $n$. Een stomp van $n$ is een positief geheel getal dat verkregen is door een aantal (minstens één, maar niet alle) cijfers van $n$ aan het rechteruiteinde weg te halen. Bijvoorbeeld: 23 is een stomp van 2351. $\\mathrm{Zij} T(n)$ de som van alle stompen van $n$. Bewijs dat $n=S(n)+9 \\cdot T(n)$.", "solution": "Van rechts naar links geven we de cijfers van $n$ aan met $a_{0}, a_{1}, \\ldots, a_{k}$. Er geldt dus\n\n$$\nn=a_{0}+10 a_{1}+\\cdots+10^{k} a_{k} .\n$$\n\nEen stomp van $n$ bestaat van rechts naar links uit de cijfers $a_{i}, a_{i+1}, \\ldots, a_{k}$ waarbij $1 \\leq i \\leq k$. Zo'n stomp is dan gelijk aan $a_{i}+10 a_{i+1}+\\cdots+10^{k-i} a_{k}$. Als we dit sommeren over alle $i$, krijgen we $T(n)$. We kunnen vervolgens $T(n)$ makkelijker schrijven door alle termen met $a_{1}$ samen te nemen, alle termen met $a_{2}$, enzovoorts (dit komt hieronder neer op het verwisselen van de sommatietekens: eerst sommeren over $i$ van 1 tot en met $k$ en daarna per $i$ nog over $j$ van $i$ tot en met $k$, is hetzelfde als eerst sommeren over $j$ van 1 tot en met $k$ en daarna per $j$ nog over $i$ van 1 tot en met $j$ ):\n\n$$\n\\begin{gathered}\nT(n)=\\sum_{i=1}^{k}\\left(a_{i}+10 a_{i+1}+\\cdots+10^{k-i} a_{k}\\right)=\\sum_{i=1}^{k} \\sum_{j=i}^{k} 10^{j-i} a_{j} \\\\\n=\\sum_{j=1}^{k} \\sum_{i=1}^{j} 10^{j-i} a_{j}=\\sum_{j=1}^{k}\\left(1+10+\\cdots+10^{j-1}\\right) a_{j}=\\sum_{j=1}^{k} \\frac{10^{j}-1}{10-1} a_{j} .\n\\end{gathered}\n$$\n\nIn de laatste stap hebben we de somformule voor de meetkundige reeks gebruikt. We krijgen nu\n\n$$\n9 \\cdot T(n)=\\sum_{j=1}^{k}\\left(10^{j}-1\\right) a_{j}=\\sum_{j=0}^{k}\\left(10^{j}-1\\right) a_{j}\n$$\n\nBedenk nu dat $S(n)=\\sum_{j=0}^{k} a_{j}$. Er geldt dus\n\n$$\nS(n)+9 \\cdot T(n)=\\sum_{j=0}^{k}\\left(10^{j}-1+1\\right) a_{j}=\\sum_{j=0}^{k} 10^{j} a_{j}=n\n$$", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2009", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek, punt $P$ het midden van $B C$ en punt $Q$ op lijnstuk $C A$ zodat $|C Q|=2|Q A|$. Zij $S$ het snijpunt van $B Q$ en $A P$. Bewijs dat $|A S|=|S P|$.", "solution": "Trek een lijn door $P$ evenwijdig aan $A C$ en zij $T$ het snijpunt van deze lijn met $B Q$. Dan is $P T$ een middenparallel in driehoek $B C Q$, dus geldt $|P T|=\\frac{1}{2}|C Q|=|Q A|$. Nu is $A T P Q$ een vierhoek met een paar even lange, evenwijdige zijden, dus $A T P Q$ is een parallellogram. Van een parallellogram weten we dat de diagonalen elkaar middendoor snijden, dus $|A S|=|S P|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2009", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek, punt $P$ het midden van $B C$ en punt $Q$ op lijnstuk $C A$ zodat $|C Q|=2|Q A|$. Zij $S$ het snijpunt van $B Q$ en $A P$. Bewijs dat $|A S|=|S P|$.", "solution": "We passen de stelling van Menelaos toe in driehoek $P C A$. We weten dat de punten $B, S$ en $Q$ op één lijn liggen, dus\n\n$$\n-1=\\frac{P B}{B C} \\cdot \\frac{C Q}{Q A} \\cdot \\frac{A S}{S P}=\\frac{-1}{2} \\cdot \\frac{2}{1} \\cdot \\frac{A S}{S P}=-\\frac{A S}{S P}\n$$\n\nDus $\\frac{A S}{S P}=1$, waaruit volgt dat $S$ midden tussen $A$ en $P$ ligt.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2009", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek, punt $P$ het midden van $B C$ en punt $Q$ op lijnstuk $C A$ zodat $|C Q|=2|Q A|$. Zij $S$ het snijpunt van $B Q$ en $A P$. Bewijs dat $|A S|=|S P|$.", "solution": "Zij $M$ het midden van $Q C$ en noem $x=[A Q S]=[Q M S]=[M C S]$ en $y=[C P S]=[P B S]$. Omdat $[C P A]=[P B A]$ geldt dat $[A S B]=3 x$. Maar dan is $[A Q B]=x+3 x$ terwijl anderzijds $2[A Q B]=[Q C B]$, dus $2 x+2 y=[Q C B]=2[A Q B]=8 x$. Dus $y=3 x$. Maar dan $[A S B]=3 x=y=[S P B]$, dus $|A S|=|S P|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 5 |
+
{"year": "2009", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek, punt $P$ het midden van $B C$ en punt $Q$ op lijnstuk $C A$ zodat $|C Q|=2|Q A|$. Zij $S$ het snijpunt van $B Q$ en $A P$. Bewijs dat $|A S|=|S P|$.", "solution": "Zij $R$ het snijpunt van $C S$ en $A B$. Volgens de stelling van Ceva geldt\n\n$$\n\\frac{A R}{R B} \\cdot \\frac{B P}{P C} \\cdot \\frac{C Q}{Q A}=1\n$$\n\nwaaruit volgt $2|A R|=|R B|$. Zij $a=[P S C], b=[Q S C], c=[Q S A], d=[R S A]$, $e=[R S B]$ en $f=[P S B]$. Nu geldt\n\n$$\nb+a+f=2(c+d+e) \\quad \\text { en } \\quad a+e+f=2(b+c+d)\n$$\n\nwaaruit volgt\n\n$$\nb-e=2 e-2 b\n$$\n\ndus $b=e$. Verder geldt $2 d=e$ en $2 c=b$, dus ook $c=d$ en $c+d=e$. Uit $a+e+f=$ $2(b+c+d)$ volgt nu\n\n$$\na+f=b+2 c+2 d=b+c+d+e,\n$$\n\ndus\n\n$$\n2(a+f)=a+b+c+d+e+f=[A B C] .\n$$\n\nDus $2|P S|=|P A|$, dus $|P S|=|A S|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing IV."}
|
| 6 |
+
{"year": "2009", "problem_label": "3", "tier": 1, "problem": "Laat $a, b$ en $c$ positieve reële getallen zijn die voldoen aan $a+b+c \\geq a b c$. Bewijs dat\n\n$$\na^{2}+b^{2}+c^{2} \\geq \\sqrt{3} a b c\n$$", "solution": "We weten dat $a^{2}+b^{2}+c^{2} \\geq a b+b c+c a$ en dus $3\\left(a^{2}+b^{2}+c^{2}\\right) \\geq(a+b+c)^{2}$. Wegens de ongelijkheid van het meetkundig en rekenkundig gemiddelde geldt $a+b+c \\geq$ $3(a b c)^{\\frac{1}{3}}$ en anderzijds is gegeven dat $a+b+c \\geq a b c$. Dus we hebben twee ongelijkheden:\n\n$$\n\\begin{aligned}\n& a^{2}+b^{2}+c^{2} \\geq \\frac{1}{3}(a+b+c)^{2} \\geq 3(a b c)^{\\frac{2}{3}} \\\\\n& a^{2}+b^{2}+c^{2} \\geq \\frac{1}{3}(a+b+c)^{2} \\geq \\frac{1}{3}(a b c)^{2}\n\\end{aligned}\n$$\n\nWe doen de eerste ongelijkheid tot de macht $\\frac{3}{4}$ en de tweede tot de macht $\\frac{1}{4}$ (en dit mogen we doen omdat alles positief is):\n\n$$\n\\begin{aligned}\n& \\left(a^{2}+b^{2}+c^{2}\\right)^{\\frac{3}{4}} \\geq 3^{\\frac{3}{4}}(a b c)^{\\frac{1}{2}} \\\\\n& \\left(a^{2}+b^{2}+c^{2}\\right)^{\\frac{1}{4}} \\geq 3^{-\\frac{1}{4}}(a b c)^{\\frac{1}{2}}\n\\end{aligned}\n$$\n\nNu vermenigvuldigen we deze beide en dan krijgen we\n\n$$\na^{2}+b^{2}+c^{2} \\geq 3^{\\frac{1}{2}}(a b c)\n$$\n\nwat het gevraagde is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2009", "problem_label": "4", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ die voldoen aan\n\n$$\nf(m+n)+f(m n-1)=f(m) f(n)+2\n$$\n\nvoor alle $m, n \\in \\mathbb{Z}$.", "solution": "Stel eerst dat er een $c \\in \\mathbb{Z}$ is met $f(n)=c$ voor alle $n$. Dan hebben we $2 c=c^{2}+2$, dus $c^{2}-2 c+2=0$ en dat heeft geen oplossing voor $c$. Dus is $f$ niet constant. Vul nu in $m=0$. Dat geeft $f(n)+f(-1)=f(n) f(0)+2$, waaruit we concluderen dat $f(n)(1-f(0))$ een constante is. Omdat $f(n)$ niet constant is, volgt hieruit $f(0)=1$. Uit dezelfde vergelijking krijgen we nu $f(-1)=2$. Vul nu in $m=n=-1$, dat geeft $f(-2)+f(0)=f(-1)^{2}+2$, waaruit volgt $f(-2)=5$. Vul vervolgens in $m=1$ en $n=-1$, dan krijgen we $f(0)+f(-2)=f(1) f(-1)+2$, waaruit volgt $f(1)=2$.\nVul nu in $m=1$, dan krijgen we $f(n+1)+f(n-1)=f(1) f(n)+2$, ofwel\n\n$$\nf(n+1)=2 f(n)+2-f(n-1) .\n$$\n\nMet inductie bewijzen we nu gemakkelijk dat $f(n)=n^{2}+1$ voor alle $n \\geq 0$ en vervolgens met de vergelijking\n\n$$\nf(n-1)=2 f(n)+2-f(n+1)\n$$\n\nook voor $n \\leq 0$. Dus $f(n)=n^{2}+1$ voor alle $n$ en deze functie voldoet.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 8 |
+
{"year": "2009", "problem_label": "5", "tier": 1, "problem": "Van een gegeven $n$-hoek met alle zijden even lang hebben alle hoekpunten rationale coördinaten. Bewijs dat $n$ even is.", "solution": "Laat $\\left(x_{1}, y_{1}\\right), \\ldots,\\left(x_{n}, y_{n}\\right)$ de coördinaten van de hoekpunten van de $n$-hoek zijn. Definieer $a_{i}=x_{i+1}-x_{i}, b_{i}=y_{i+1}-y_{i}$ voor $i=1,2, \\ldots, n$, waarbij $x_{n+1}=x_{1}$ en $y_{n+1}=y_{1}$. Gegeven is nu dat $a_{i}, b_{i} \\in \\mathbb{Q}$ en $\\sum_{i=1}^{n} a_{i}=\\sum_{i=1}^{n} b_{i}=0$; en de som $a_{i}^{2}+b_{i}^{2}$ is voor alle $i$ gelijk. Door alle noemers weg te vermenigvuldigen en eventuele gemeenschappelijke delers van de tellers weg te delen, mogen we aannemen dat $a_{i}, b_{i} \\in \\mathbb{Z}$ en $\\operatorname{ggd}\\left(a_{1}, \\ldots, a_{n}, b_{1}, \\ldots, b_{n}\\right)=1$. Zij $c$ het gehele getal zodat $a_{i}^{2}+b_{i}^{2}=c$ voor alle $i$.\nStel eerst dat $c \\equiv 1 \\bmod 2$. Dan is voor elke $i$ precies één van $a_{i}, b_{i}$ oneven. Dus van alle $2 n$ getallen $a_{i}, b_{i}$ zijn er precies $n$ even en $n$ oneven. Dus $0=\\sum_{i=1}^{n}\\left(a_{i}+b_{i}\\right) \\equiv n \\bmod 2$. Dus $n$ is even.\nStel nu dat $c \\equiv 0 \\bmod 2$. Dan geldt voor alle $i$ dat $a_{i} \\equiv b_{i} \\bmod 2$. Als er een $i$ is met $a_{i}$ en $b_{i}$ allebei oneven, dan is $c=a_{i}^{2}+b_{i}^{2} \\equiv 1+1 \\equiv 2 \\bmod 4$. Als er een $i$ is met $a_{i}$ en $b_{i}$ allebei even, dan is $c=a_{i}^{2}+b_{i}^{2} \\equiv 0+0 \\equiv 0 \\bmod 4$. Dit kan niet allebei tegelijk. Dus óf alle $a_{i}$ en $b_{i}$ zijn oneven, óf alle $a_{i}$ en $b_{i}$ zijn even. Het laatste is een tegenspraak met onze aanname over de ggd van alle $a_{i}$ en $b_{i}$. Het eerste geeft $0=\\sum_{i=1}^{n} a_{i} \\equiv n \\bmod 2$, dus $n$ is even.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2010-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2010", "problem_label": "1", "tier": 1, "problem": "Zij $A B C D$ een trapezium met $A B \\| C D, 2|A B|=|C D|$ en $B D \\perp B C$. Zij $M$ het midden van $C D$ en zij $E$ het snijpunt van $B C$ en $A D$. Zij $O$ het snijpunt van $A M$ en $B D$. $\\operatorname{Zij} N$ het snijpunt van $O E$ en $A B$.\n(a) Bewijs dat $A B M D$ een ruit is.\n(b) Bewijs dat de lijn $D N$ door het midden van lijnstuk $B E$ gaat.", "solution": "Uit 2 $|A B|=|C D|$ en $A B \\| C D$ volgt dat $A B$ een middenparallel in driehoek $C D E$ is. Dus $A$ is het midden van $D E$. Omdat $\\angle D B E=90^{\\circ}$, geldt volgens Thales dat $A$ het middelpunt is van de cirkel door $D, B$ en $E$. Dus $|A D|=|A E|=|A B|$ en we wisten al dat $|A B|=|D M|=|M C|$. Op dezelfde manier met Thales laten we zien dat $|B M|=|C M|=|D M|$, dus van vierhoek $A B M D$ zijn alle zijden even lang. Het is dus een ruit (a). De diagonalen van een ruit delen elkaar middendoor, dus $O$ is het midden van $B D$. Omdat $A$ ook het midden van $D E$ is, is $N$ het zwaartepunt van driehoek $B D E$. Dus $D N$ gaat door het midden van $B E$ (b).", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2010", "problem_label": "1", "tier": 1, "problem": "Zij $A B C D$ een trapezium met $A B \\| C D, 2|A B|=|C D|$ en $B D \\perp B C$. Zij $M$ het midden van $C D$ en zij $E$ het snijpunt van $B C$ en $A D$. Zij $O$ het snijpunt van $A M$ en $B D$. $\\operatorname{Zij} N$ het snijpunt van $O E$ en $A B$.\n(a) Bewijs dat $A B M D$ een ruit is.\n(b) Bewijs dat de lijn $D N$ door het midden van lijnstuk $B E$ gaat.", "solution": "Omdat $A B$ en $D M$ evenwijdig zijn en $|A B|=\\frac{1}{2}|C D|=|D M|$, is $A B M D$ een parallellogram. Wegens $A B \\| C D$ en $|C D|=2|A B|$ geldt verder $\\triangle E A B \\sim \\triangle E D C$ met vergrotingsfactor 2. Dus $A$ is het midden van $D E$. Daarom is $A M$ de middenparallel in $\\triangle E C D$ evenwijdig aan $E C$. Omdat $E C$ en $B D$ loodrecht op elkaar staan (wegens $B D \\perp B C$ ) staan ook $A M$ en $B D$ loodrecht op elkaar. Dus $A B M D$ is een parallellogram waarvan de diagonalen loodrecht op elkaar staan. Dus $A B M D$ is een ruit (a). Onderdeel (b) gaat hetzelfde als in de eerste oplossing.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2010", "problem_label": "2", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ die voldoen aan\n\n$$\nf(x) f(y)=f(x+y)+x y\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Merk eerst op dat de functie $f(x)=0$ voor alle $x \\in \\mathbb{R}$ niet voldoet. Er is dus zeker een $x_{0} \\in \\mathbb{R}$ waarvoor $f\\left(x_{0}\\right) \\neq 0$. Vul nu $x=x_{0}$ en $y=0$ in: $f\\left(x_{0}\\right) f(0)=f\\left(x_{0}\\right)$. We mogen delen door $f\\left(x_{0}\\right)$, waardoor we krijgen: $f(0)=1$. Vul nu $x=1$ en $y=-1$ in: $f(1) f(-1)=f(0)-1=1-1=0$. Dus $f(1)=0$ of $f(-1)=0$.\nWe onderscheiden gevallen. Stel eerst dat $f(1)=0$ en vul $x=1 \\mathrm{in}: 0=f(1) f(y)=$ $f(1+y)+y$ voor alle $y \\in \\mathbb{R}$, dus $f(1+y)=-y$ voor alle $y \\in \\mathbb{R}$. Substitueren we nu $y=t-1$, dan zien we $f(t)=-t+1$ voor alle $t \\in \\mathbb{R}$. Dit is onze eerste kandidaatoplossing. Stel nu dat $f(-1)=0$ en vul $x=-1$ in: $0=f(-1) f(y)=f(-1+y)-y$ voor alle $y \\in \\mathbb{R}$, dus $f(-1+y)=y$ voor alle $y \\in \\mathbb{R}$. Substitueren we nu $y=t+1$, dan zien we $f(t)=t+1$ voor alle $t \\in \\mathbb{R}$. Dit is onze tweede kandidaatoplossing.\nWe hebben alle gevallen gehad, dus er zijn twee mogelijke oplossingen. We controleren ze allebei. Stel eerst dat $f(t)=-t+1$ voor alle $t \\in \\mathbb{R}$, dan geldt voor alle $x, y \\in \\mathbb{R}$ :\n\n$$\nf(x) f(y)=(-x+1)(-y+1)=x y-x-y+1=(-x-y+1)+x y=f(x+y)+x y\n$$\n\nStel nu dat $f(t)=t+1$ voor alle $t \\in \\mathbb{R}$, dan geldt voor alle $x, y \\in \\mathbb{R}$ :\n\n$$\nf(x) f(y)=(x+1)(y+1)=x y+x+y+1=(x+y+1)+x y=f(x+y)+x y\n$$\n\nBeide oplossingen voldoen dus.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2010", "problem_label": "3", "tier": 1, "problem": "Zij $N$ het aantal geordende vijftallen $\\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\\right)$ van positieve gehele getallen waarvoor geldt\n\n$$\n\\frac{1}{a_{1}}+\\frac{1}{a_{2}}+\\frac{1}{a_{3}}+\\frac{1}{a_{4}}+\\frac{1}{a_{5}}=1 .\n$$\n\n(Bij geordende vijftallen doet de volgorde er toe, dus $(2,3,15,15,30)$ en $(15,2,15,3,30)$ zijn verschillende geordende vijftallen.)\nIs $N$ een even of een oneven getal?", "solution": "Bekijk een ongeordend vijftal dat voldoet en stel dat het uit de verschillende getallen $b_{1}, \\ldots, b_{k}$ bestaat (met $k \\leq 5$ ), waarbij $b_{i}$ precies $t_{i}$ keer voorkomt. Er geldt dus $t_{1}+\\cdots+t_{k}=5$. Nu geldt dat dit vijftal op $\\frac{5!}{t_{1}!\\cdots t_{k}!}$ manieren geordend kan worden. Dit is oneven dan en slechts dan als in de noemer drie factoren 2 zitten. Dat geldt dan en slechts dan als er 4! of 5! in de noemer voorkomt. Kortom, de enige ongeordende vijftallen die op een oneven aantal manieren geordend kunnen worden, zijn die bestaande uit minstens vier dezelfde getallen.\nZo'n vijftal ziet er dus uit als ( $a, a, a, a, b$ ), waarbij $b$ eventueel gelijk zou kunnen zijn aan $a$ en waarbij $a$ en $b$ positieve gehele getallen zijn. We krijgen de vergelijking $\\frac{4}{a}+\\frac{1}{b}=1$, oftewel $4 b+a=a b$. We zien dat $b$ een deler moet zijn van $a$ en dat $a$ een deler moet zijn van $4 b$. Er zijn dus drie opties: $a=b, a=2 b$ en $a=4 b$. In het eerste geval krijgen we $5 b=b^{2}$, dus $b=5$. Dit geeft de oplossing $(5,5,5,5,5)$. In het tweede geval krijgen we $6 b=2 b^{2}$, dus $b=3$. Dit geeft de oplossing $(6,6,6,6,3)$. In het derde geval krijgen we $8 b=4 b^{2}$, dus $b=2$. Dit geeft de oplossing $(8,8,8,8,2)$. Er zijn dus drie ongeordende vijftallen die op een oneven aantal manieren geordend kunnen worden. Dus $N$ is oneven.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 5 |
+
{"year": "2010", "problem_label": "3", "tier": 1, "problem": "Zij $N$ het aantal geordende vijftallen $\\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\\right)$ van positieve gehele getallen waarvoor geldt\n\n$$\n\\frac{1}{a_{1}}+\\frac{1}{a_{2}}+\\frac{1}{a_{3}}+\\frac{1}{a_{4}}+\\frac{1}{a_{5}}=1 .\n$$\n\n(Bij geordende vijftallen doet de volgorde er toe, dus $(2,3,15,15,30)$ en $(15,2,15,3,30)$ zijn verschillende geordende vijftallen.)\nIs $N$ een even of een oneven getal?", "solution": "$\\mathrm{Zij}\\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\\right)$ een geordend vijftal dat voldoet. Dan voldoet ook het vijftal $\\left(a_{2}, a_{1}, a_{3}, a_{4}, a_{5}\\right)$. Als $a_{1} \\neq a_{2}$, is dit echt een ander vijftal. Zo zien we dat er een even aantal oplossingen $\\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\\right)$ met $a_{1} \\neq a_{2}$ is. We bekijken nu verder alleen de oplossingen met $a_{1}=a_{2}$. Op dezelfde manier zien we dat er een even aantal oplossingen $\\left(a_{1}, a_{1}, a_{3}, a_{4}, a_{5}\\right)$ met $a_{3} \\neq a_{4}$ is. We bekijken nu verder alleen de oplossingen met $a_{1}=a_{2}$ en $a_{3}=a_{4}$. Voor elke oplossing $\\left(a_{1}, a_{1}, a_{3}, a_{3}, a_{5}\\right)$ met $a_{1} \\neq a_{3}$ is er nog een andere oplossing $\\left(a_{3}, a_{3}, a_{1}, a_{1}, a_{5}\\right)$, dus ook van de oplossingen $\\left(a_{1}, a_{1}, a_{3}, a_{3}, a_{5}\\right)$ met $a_{1} \\neq a_{3}$ is er een even aantal. We bekijken nu verder alleen de oplossingen van de vorm ( $a, a, a, a, b$ ), waarbij $b$ eventueel nog gelijk aan $a$ zou kunnen zijn.\nWe krijgen de vergelijking $\\frac{4}{a}+\\frac{1}{b}=1$, oftewel $4 b+a=a b$. Dit kunnen we herschrijven als $(a-4)(b-1)=4$. Omdat $b$ een positief geheel getal moet zijn, geldt $b-1 \\geq 0$. Dus $b-1$ is een positieve deler van 4 , te weten 1,2 of 4 . Dit leidt tot respectievelijk $(a, b)=(8,2)$, $(a, b)=(6,3)$ en $(a, b)=(5,5)$. Dit zijn drie oplossingen. Het aantal eerder beschouwde oplossingen is even, dus $N$ is oneven.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 6 |
+
{"year": "2010", "problem_label": "4", "tier": 1, "problem": "De twee cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$ snijden elkaar in $P$ en $Q$. De gemeenschappelijke raaklijn aan de kant van $P$ raakt de cirkels in $A$ resp. $B$. De raaklijn aan $\\Gamma_{1}$ in $P$ snijdt $\\Gamma_{2}$ voor de tweede keer in $C$ en de raaklijn aan $\\Gamma_{2}$ in $P$ snijdt $\\Gamma_{1}$ voor de tweede keer in $D$. Het snijpunt van de lijnen $A P$ en $B C$ noemen we $E$ en het snijpunt van de lijnen $B P$ en $A D$ noemen we $F$. Zij $M$ de puntspiegeling van $P$ in het midden van $A B$. Bewijs dat $A M B E Q F$ een koordenzeshoek is.", "solution": "We gaan alle relevante hoeken uitdrukken in $\\alpha=\\angle B A P$ en $\\beta=\\angle P B A$. Het midden van $A B$ is per definitie ook het midden van $P M$, dus de diagonalen van vierhoek $A P B M$ snijden elkaar middendoor. Daarom is $A P B M$ een parallellogram en geldt $\\angle A M B=\\angle A P B$. Wegens hoekensom van $\\triangle A B P$ geldt $\\angle A P B+\\alpha+\\beta=180^{\\circ}$. Dus $180^{\\circ}-\\angle A M B=\\alpha+\\beta$.\nWegens de raaklijnomtrekshoekstelling met raaklijn $A B$ aan $\\Gamma_{1}$ geldt $\\alpha=\\angle A D P$. Vervolgens volgt uit de omtrekshoekstelling op koorde $A P$ van $\\Gamma_{1}$ dat $\\angle A D P=\\angle A Q P$. Dus $\\alpha=\\angle A Q P$. Zo ook $\\beta=\\angle P C B=\\angle P Q B$. Dus $\\angle A Q B=\\angle A Q P+\\angle P Q B=\\alpha+\\beta=$ $180^{\\circ}-\\angle A M B$. Hieruit concluderen we dat $A Q B M$ een koordenvierhoek is.\nZij $S$ het snijpunt van $D P$ en $A B$. Met de raaklijnomtrekshoekstelling zien we dat $\\angle S P B=\\angle P C B=\\angle P B S=\\angle P B A=\\beta$. Dus $\\angle D P F=\\angle S P B=\\beta$ wegens overstaande hoeken. Nu passen we de buitenhoekstelling toe op $\\triangle D F P$, zodat geldt: $\\angle A F B=$ $\\angle A F P=\\angle F D P+\\angle D P F=\\alpha+\\beta=\\angle A Q B$. Dus $A F Q B$ is een koordenvierhoek. Daaruit volgt dat $F$ op de omgeschreven cirkel van koordenvierhoek $A Q B M$ ligt. Analoog zien we dat $E$ daar ook op ligt. Dus $A M B E Q F$ is een koordenzeshoek.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2010", "problem_label": "5", "tier": 1, "problem": "Voor een niet-negatief geheel getal $n$ noemen we een permutatie $\\left(a_{0}, a_{1}, \\ldots, a_{n}\\right)$ van $\\{0,1, \\ldots, n\\}$ kwadratisch als $k+a_{k}$ een kwadraat is voor $k=0,1, \\ldots, n$. Bewijs dat er voor elke niet-negatieve gehele $n$ een kwadratische permutatie van $\\{0,1, \\ldots, n\\}$ bestaat.", "solution": "We bewijzen dit met inductie naar $n$. Voor $n=0$ werkt de permutatie ( 0 ), want $0+0$ is een kwadraat. Zij nu $l \\geq 0$ en neem aan dat er voor elke $n \\leq l$ een kwadratische permutatie bestaat (de inductiehypothese). We bekijken $n=l+1$. Zij $m$ zodat $m^{2}$ het kleinste kwadraat groter dan of gelijk aan $l+1$ is. Nu geldt $l \\geq(m-1)^{2}=m^{2}-2 m+1$, dus $2(l+1) \\geq 2 m^{2}-4 m+4=m^{2}+(m-2)^{2} \\geq m^{2}$. Dit betekent dat we een gehele $p$ met $0 \\leq p \\leq l+1$ kunnen vinden zodat $(l+1)+p=m^{2}$. Nu definiëren we onze permutatie als volgt. Als $p \\geq 1$, nemen we voor $\\left(a_{0}, a_{1}, \\ldots, a_{p-1}\\right)$ een kwadratische permutatie van $\\{0,1, \\ldots, p-1\\}$; deze bestaat volgens de inductiehypothese omdat $p-1 \\leq l$. Voor $p \\leq i \\leq l+1$ definiëren we $a_{i}=m^{2}-i$. (Merk op dat we voor $p=0 \\mathrm{nu}$ ook een volledige permutatie hebben gedefinieerd.) Het rijtje $\\left(a_{p}, a_{p+1}, \\ldots, a_{l+1}\\right)$ is nu precies $(l+1, l, \\ldots, p)$, zodat we samen met het beginstuk nu alle waarden van 0 tot en met $l+1$ gebruikt hebben. Verder is $a_{i}+i$ een kwadraat voor alle $i$. Dus $\\left(a_{0}, a_{1}, \\ldots, a_{l+1}\\right)$ is een kwadratische permutatie van $\\{0,1, \\ldots, l+1\\}$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2010-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2010", "problem_label": "1", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek met de eigenschap $\\angle B A C=45^{\\circ}$. Zij $D$ het voetpunt van de loodlijn vanuit $C$ op $A B$. Zij $P$ een inwendig punt van het lijnstuk $C D$. Bewijs dat de lijnen $A P$ en $B C$ loodrecht op elkaar staan dan en slechts dan als $|A P|=|B C|$.", "solution": "Zij $E$ het snijpunt van $A P$ en $B C$. Merk op dat $\\angle D C A=90^{\\circ}-\\angle C A D=$ $90^{\\circ}-\\angle C A B=45^{\\circ}$, dus $\\triangle A C D$ is gelijkbenig: $|A D|=|C D|$.\nStel nu dat $|A P|=|B C|$. Omdat $\\angle A D P=90^{\\circ}=\\angle C D B$, geldt $\\triangle A D P \\cong \\triangle C D B$ wegens (ZZR). Dus $\\angle A P D=\\angle C B D$, waaruit volgt\n\n$$\n\\begin{gathered}\n\\angle C E A=\\angle C E P=180^{\\circ}-\\angle E P C-\\angle P C E=180^{\\circ}-\\angle A P D-\\angle D C B \\\\\n=180^{\\circ}-\\angle C B D-\\angle D C B=\\angle B D C=90^{\\circ},\n\\end{gathered}\n$$\n\ndus $A P$ staat loodrecht op $B C$.\nStel andersom dat $A P$ loodrecht op $B C$ staat, oftewel $\\angle C E P=90^{\\circ}$. Dan geldt\n\n$$\n\\angle A P D=\\angle E P C=90^{\\circ}-\\angle P C E=90^{\\circ}-\\angle D C B=\\angle C B D .\n$$\n\nOmdat ook $\\angle A D P=90^{\\circ}=\\angle C D B$, volgt nu met $(\\mathrm{ZHH})$ dat $\\triangle A D P \\cong \\triangle C D B$. Dus $|A P|=|B C|$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2010", "problem_label": "2", "tier": 1, "problem": "Laat $A$ en $B$ positieve gehele getallen zijn. Definieer de rekenkundige rij $a_{0}, a_{1}, a_{2}, \\ldots$ door $a_{n}=A n+B$. Neem aan dat er minstens één $n \\geq 0$ is zodat $a_{n}$ een kwadraat is. $\\mathrm{Zij} M$ een positief geheel getal zodat $M^{2}$ het kleinste kwadraat in de rij is. Bewijs dat $M<A+\\sqrt{B}$.", "solution": "Als $M \\leq A$, dan zeker $M<A+\\sqrt{B}$, dus zijn we klaar.\nAls $M>A$, zij dan $k$ zodat $a_{k}=M^{2}$. Dan geldt dus $A k+B=M^{2}$. Omdat $0<M-A<$ $M$, is $(M-A)^{2}$ kleiner dan $M^{2}$. Er geldt $(M-A)^{2}=M^{2}-2 M A+A^{2}=M^{2}-A(2 M-A)$. Als $k-(2 M-A) \\geq 0$, dan is\n$a_{k-(2 M-A)}=A(k-(2 M-A))+B=(A k+B)-2 M A+A^{2}=M^{2}-2 M A+A^{2}=(M-A)^{2}$.\nMaar dan is $M^{2}$ niet het kleinste kwadraat in de rij, tegenspraak. Dus geldt $k-(2 M-A)<$ 0 . Hieruit volgt $A(k-(2 M-A))+B<B$, oftewel $(M-A)^{2}<B$. Omdat $M-A$ positief is, mogen we concluderen dat $M-A<\\sqrt{B}$, oftewel $M<A+\\sqrt{B}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2010", "problem_label": "3", "tier": 1, "problem": "Zij $n \\geq 2$ een positief geheel getal en $p$ een priemgetal zodat $n \\mid p-1$ en $p \\mid n^{3}-1$. Bewijs dat $4 p-3$ een kwadraat is.", "solution": "Uit $n \\mid p-1$ volgt $n<p$. Omdat $p$ priem is, is $p$ een deler van één van de twee factoren van $n^{3}-1=(n-1)\\left(n^{2}+n+1\\right)$, maar $p$ is te groot om een deler van $n-1>0$ te zijn. Dus $p \\mid n^{2}+n+1$. Wegens $n \\mid p-1$ kunnen we $p$ schrijven als $k n+1$, met $k$ een positief geheel getal. Uit $k n+1 \\mid n^{2}+n+1$ volgt\n\n$$\nk n+1 \\mid k\\left(n^{2}+n+1\\right)-(n+1)(k n+1)=k-n-1 .\n$$\n\nWe onderscheiden nu drie gevallen.\nGeval 1: $k>n+1$. Dan is $k-n-1$ positief en moet gelden $k n+1 \\leq k-n-1$. Daaruit volgt $(k+1) n \\leq k-2$, maar links staat nu iets dat duidelijk groter is dan wat er rechts staat. Dit geval kan dus niet.\nGeval 2: $k<n+1$. Dan is $k-n-1$ negatief en moet gelden $k n+1 \\leq n+1-k$. Daaruit volgt $(k-1) n \\leq-k$, maar links staat nu iets niet-negatiefs en rechts iets negatiefs. Dit geval kan dus ook niet.\nGeval 3: $k=n+1$. Nu geldt $p=(n+1) n+1=n^{2}+n+1$. Dus $4 p-3=4 n^{2}+4 n+1=$ $(2 n+1)^{2}$ en dit is een kwadraat.\nWe concluderen dat in het enige mogelijke geval $4 p-3$ een kwadraat is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2010", "problem_label": "3", "tier": 1, "problem": "Zij $n \\geq 2$ een positief geheel getal en $p$ een priemgetal zodat $n \\mid p-1$ en $p \\mid n^{3}-1$. Bewijs dat $4 p-3$ een kwadraat is.", "solution": "Zoals in de eerste oplossing laten we zien dat $p \\mid n^{2}+n+1$. Als $p=n^{2}+n+1$, dan geldt $4 p-3=4 n^{2}+4 n+1=(2 n+1)^{2}$ en dit is een kwadraat. Stel nu dat $p \\neq n^{2}+n+1$. Dan is er een geheel getal $m>1$ zodat $p m=n^{2}+n+1$. Modulo $n$ staat hier $p m \\equiv 1$ $\\bmod n$. Uit $n \\mid p-1$ volgt dat $p \\equiv 1 \\bmod n$, dus we krijgen $m \\equiv 1 \\bmod n$. Dus $p$ en $m$ zijn beide minstens $n+1$. Echter, $(n+1)^{2}=n^{2}+2 n+1>n^{2}+n+1=p m$, tegenspraak.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2010", "problem_label": "4", "tier": 1, "problem": "Zij $A B C D$ een koordenvierhoek met de eigenschap dat $\\angle A B D=\\angle D B C$. Zij $E$ het snijpunt van de diagonalen $A C$ en $B D$. Zij $M$ het midden van $A E$ en $N$ het midden van $D C$. Bewijs dat $M B C N$ een koordenvierhoek is.", "solution": "Omdat $A B C D$ een koordenvierhoek is, weten we dat $\\angle B D C=\\angle B A C=$ $\\angle B A E$. Daarnaast volgt uit het gegeven dat $\\angle C B D=\\angle E B A$. Samen geeft dit $\\triangle D C B \\sim$ $\\triangle A E B$ (hh). We gaan nu bewijzen dat hieruit volgt $\\triangle N C B \\sim \\triangle M E B$. Allereerst vinden we dat $\\angle N C B=\\angle D C B=\\angle A E B=\\angle M E B$. Verder zien we dat $\\frac{|N C|}{|M E|}=$ $\\frac{2|N C|}{2|M E|}=\\frac{|D C|}{|A E|}=\\frac{|C B|}{|E B|}$. Met (zhz) concluderen we dat inderdaad $\\triangle N C B \\sim \\triangle M E B$. Dus $\\angle B M C=\\angle B M E=\\angle B N C$, waaruit volgt dat $M B C N$ een koordenvierhoek is.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2010", "problem_label": "4", "tier": 1, "problem": "Zij $A B C D$ een koordenvierhoek met de eigenschap dat $\\angle A B D=\\angle D B C$. Zij $E$ het snijpunt van de diagonalen $A C$ en $B D$. Zij $M$ het midden van $A E$ en $N$ het midden van $D C$. Bewijs dat $M B C N$ een koordenvierhoek is.", "solution": "Net als in de eerste oplossing leiden we af dat $\\triangle D C B \\sim \\triangle A E B$. Merk nu op dat de lijnen $B M$ en $B N$ zwaartelijnen in deze twee gelijkvormige driehoeken zijn. Daaruit volgt dat de corresponderende hoeken $\\angle B M E$ en $\\angle B N C$ even groot zijn. Dus $\\angle B M C=\\angle B M E=\\angle B N C$, waaruit volgt dat $M B C N$ een koordenvierhoek is.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2010", "problem_label": "4", "tier": 1, "problem": "Zij $A B C D$ een koordenvierhoek met de eigenschap dat $\\angle A B D=\\angle D B C$. Zij $E$ het snijpunt van de diagonalen $A C$ en $B D$. Zij $M$ het midden van $A E$ en $N$ het midden van $D C$. Bewijs dat $M B C N$ een koordenvierhoek is.", "solution": "Zij $K$ het midden van $D E$. Nu is $M K$ een middenparallel in driehoek $E A D$ evenwijdig aan $A D$, dus $\\angle M K B=\\angle M K E=\\angle A D E=\\angle A D B$. In koordenvierhoek $A B C D$ zien we $\\angle A D B=\\angle A C B=\\angle M C B$, dus $\\angle M K B=\\angle M C B$, waaruit volgt dat $M K C B$ een koordenvierhoek is.\nVerder is $K N$ een middenparallel in driehoek $C E D$ evenwijdig aan $C E$, dus $180^{\\circ}-$ $\\angle K N C=\\angle K N D=\\angle E C D=\\angle A C D$. Vanwege koordenvierhoek $A B C D$ geldt $\\angle A C D=$ $\\angle A B D$ en volgens het gegeven is dit gelijk aan $\\angle D B C$. Dus $180^{\\circ}-\\angle K N C=\\angle D B C=$ $\\angle K B C$. Hieruit volgt dat $K N C B$ een koordenvierhoek is.\nWe concluderen dat zowel $M$ als $N$ op de omgeschreven cirkel van driehoek $B C K$ liggen. Dus $M B C N$ is een koordenvierhoek.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing III."}
|
| 8 |
+
{"year": "2010", "problem_label": "5", "tier": 1, "problem": "Vind alle drietallen $(x, y, z)$ van reële (maar niet noodzakelijk positieve) getallen die voldoen aan\n\n$$\n\\begin{aligned}\n3\\left(x^{2}+y^{2}+z^{2}\\right) & =1 \\\\\nx^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} & =x y z(x+y+z)^{3} .\n\\end{aligned}\n$$", "solution": "We gaan laten zien dat voor reële getallen $x, y$ en $z$ die aan de eerste voorwaarde voldoen, geldt\n\n$$\nx^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \\geq x y z(x+y+z)^{3} .\n$$\n\nDe oplossingen die we zoeken, zijn dus de gelijkheidsgevallen van deze ongelijkheid.\nLaat $a, b$ en $c$ reële getallen zijn. Er geldt $(a-b)^{2} \\geq 0$, dus $\\frac{a^{2}+b^{2}}{2} \\geq a b$ met gelijkheid d.e.s.d.a. $a=b$. Dit doen we analoog voor $b$ en $c$ en voor $c$ en $a$, zodat opgeteld volgt dat\n\n$$\na^{2}+b^{2}+c^{2} \\geq a b+b c+c a\n$$\n\nmet gelijkheid d.e.s.d.a. $a=b=c$.\nPassen we dit toe op $(x y, y z, z x)$, dan vinden we dat\n\n$$\nx^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \\geq x y^{2} z+y z^{2} x+z x^{2} y=x y z(x+y+z)\n$$\n\nmet gelijkheid d.e.s.d.a. $x y=y z=z x$. Door het ook toe te passen op $(x, y, z)$ vinden we $x^{2}+y^{2}+z^{2} \\geq x y+y z+z x$, dus volgens de eerste eis geldt\n$1=3\\left(x^{2}+y^{2}+z^{2}\\right)=\\left(x^{2}+y^{2}+z^{2}\\right)+2\\left(x^{2}+y^{2}+z^{2}\\right) \\geq x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x=(x+y+z)^{2}$, met gelijkheid d.e.s.d.a. $x=y=z$. We willen nu deze twee ongelijkheden,\n\n$$\nx^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \\geq x y z(x+y+z)\n$$\n\nen\n\n$$\n1 \\geq(x+y+z)^{2}\n$$\n\nmet elkaar combineren. Hiervoor vermenigvuldigen we eerst (3) met de niet-negatieve factor $x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}$; dan krijgen we\n\n$$\n\\left(x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}\\right) \\cdot 1 \\geq\\left(x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}\\right) \\cdot(x+y+z)^{2}\n$$\n\nmet gelijkheid d.e.s.d.a. $x=y=z$ of $x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}=0$. Verder vermenigvuldigen (2) met de niet-negatieve factor $(x+y+z)^{2}$, waaruit volgt\n\n$$\n\\left(x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}\\right) \\cdot(x+y+z)^{2} \\geq x y z(x+y+z) \\cdot(x+y+z)^{2}\n$$\n\nmet gelijkheid d.e.s.d.a. $x y=y z=z x$ of $x+y+z=0$. Al met al vinden we $\\left(x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}\\right) \\cdot 1 \\geq\\left(x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}\\right) \\cdot(x+y+z)^{2} \\geq x y z(x+y+z) \\cdot(x+y+z)^{2}$,\noftewel (1), met gelijkheid d.e.s.d.a.\n\n$$\n\\left(x=y=z \\text { of } x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}=0\\right) \\text { en }(x y=y z=z x \\text { of } x+y+z=0) .\n$$\n\nNu zegt de tweede vergelijking dat hier inderdaad gelijkheid moet gelden, dus we zitten in het zojuist beschreven gelijkheidsgeval. Daarnaast zegt de eerste eis nog steeds dat $3\\left(x^{2}+y^{2}+z^{2}\\right)=1:$\n\n$$\n\\begin{aligned}\n& 3\\left(x^{2}+y^{2}+z^{2}\\right)=1 \\\\\n& x=y=z \\text { of } \\\\\n& x y=y z=z x \\text { of } \\\\\n& x+y+y^{2} z^{2}+z^{2} x^{2}=0 \\\\\n& x y=0\n\\end{aligned}\n$$\n\nWe onderscheiden twee gevallen. Stel eerst $x=y=z$. Dan wordt automatisch voldaan aan $x y=y z=z x$. We vinden met behulp van de eerste eis dat $1=3\\left(x^{2}+y^{2}+z^{2}\\right)=$ $9 x^{2}=(3 x)^{2}$, dus $x=y=z= \\pm \\frac{1}{3}$.\nStel nu dat $x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}=0$; dan moet wel elk van de termen nul zijn, dus $x y=y z=z x=0$, dus ook nu wordt voldaan aan $x y=y z=z x$. Uit $x y=0$ volgt dat (z.b.d.a.) $x=0$. Uit $y z=0$ ook z.b.d.a. dat $y=0$. Zo vinden we de oplossingen $\\left(0,0, \\pm \\frac{1}{3} \\sqrt{3}\\right)$ en daarnaast ook $\\left(0, \\pm \\frac{1}{3} \\sqrt{3}, 0\\right)$ en $\\left( \\pm \\frac{1}{3} \\sqrt{3}, 0,0\\right)$.\n\nOpmerking. Als je (2) en (3) hebt bewezen, kun je (1) ook vinden door (3) te vermenigvuldigen met $x y z(x+y+z)$. Hiervoor moet je dan wel aantonen dat $x y z(x+y+z)$ niet-negatief is. We weten vanwege de tweede eis in de opgave dat $x y z(x+y+z)^{3}$ gelijk is aan een som van kwadraten en dus niet-negatief. Als $x+y+z \\neq 0$, volgt hieruit $x y z(x+y+z) \\geq 0$. Als $x+y+z=0$, dan geldt $x y z(x+y+z)=0$. Dus in beide gevallen geldt $x y z(x+y+z) \\geq 0$.\nHet gelijkheidsgeval wordt bij deze methode:\n\n$$\n\\begin{aligned}\n& 3\\left(x^{2}+y^{2}+z^{2}\\right)=1 \\\\\n& \\quad x y=y z=z x \\\\\n& x=y=z \\quad \\text { of } \\quad x y z(x+y+z)=0 .\n\\end{aligned}\n$$", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2010-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2010", "problem_label": "1", "tier": 1, "problem": "Bekijk rijen $a_{1}, a_{2}, a_{3}, \\ldots$ van positieve gehele getallen. Bepaal de kleinst mogelijke waarde van $a_{2010}$ als gegeven is:\n(i) $a_{n}<a_{n+1}$ voor alle $n \\geq 1$,\n(ii) $a_{i}+a_{l}>a_{j}+a_{k}$ voor alle viertallen $(i, j, k, l)$ met $1 \\leq i<j \\leq k<l$.", "solution": "We bewijzen met inductie dat $a_{n}-a_{1} \\geq 2^{n-1}-1$ voor alle $n \\geq 2$. Voor $n=2$ staat hier $a_{2}-a_{1} \\geq 1$ en dat volgt uit voorwaarde (i). $\\mathrm{Zij} \\mathrm{nu} m \\geq 2$ en stel dat $a_{m}-a_{1} \\geq 2^{m-1}-1$. We passen voorwaarde (ii) toe met $i=1, j=k=m$ en $l=m+1$. We vinden dat $a_{1}+a_{m+1}>2 a_{m}$. Dus\n\n$$\na_{m+1}-a_{1}>2 a_{m}-2 a_{1} \\stackrel{\\mathrm{IH}}{\\geq} 2\\left(2^{m-1}-1\\right)=2^{m}-2,\n$$\n\nen aangezien $a_{m+1}$ positief en geheel is, volgt hieruit $a_{m+1}-a_{1} \\geq 2^{m}-1$. Dit voltooit de inductie.\nNu zien we dat voor $n \\geq 1$ geldt:\n\n$$\na_{n} \\geq 2^{n-1}-1+a_{1} \\geq 2^{n-1}\n$$\n\nen in het bijzonder $a_{2010} \\geq 2^{2009}$.\nAnderzijds bewijzen we dat $a_{2010}=2^{2009}$ mogelijk is door te laten zien dat de rij gegeven door $a_{n}=2^{n-1}$ aan de voorwaarden voldoet. Deze rij bestaat uit positieve gehele getallen en is strikt stijgend (voorwaarde (i)). Zij nu ( $i, j, k, l)$ een viertal dat voldoet aan $1 \\leq i<$ $j \\leq k<l$. Er geldt\n\n$$\na_{j}+a_{k}=2^{j-1}+2^{k-1} \\leq 2^{k-1}+2^{k-1}=2^{k} \\leq 2^{l-1}<2^{i-1}+2^{l-1},\n$$\n\ndus ook aan voorwaarde (ii) is voldaan.\nWe concluderen dat de kleinst mogelijke waarde van $a_{2010}$ gelijk is aan $2^{2009}$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2010", "problem_label": "2", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ waarvoor geldt dat\n\n$$\nf(x)=\\max _{y \\in \\mathbb{R}}(2 x y-f(y))\n$$\n\nvoor alle $x \\in \\mathbb{R}$.\n(In het algemeen betekent de uitdrukking $a=\\max _{s \\in S} g(s)$ : er geldt $a \\geq g(s)$ voor alle $s \\in S$ en bovendien is er een $s \\in S$ waarvoor $a=g(s)$.)", "solution": "Voor alle $x \\in \\mathbb{R}$ geldt\n\n$$\nf(x)=\\max _{y \\in \\mathbb{R}}(2 x y-f(y)) \\geq 2 x^{2}-f(x)\n$$\n\ndus $2 f(x) \\geq 2 x^{2}$, oftewel $f(x) \\geq x^{2}$.\nOmdat $(x-y)^{2} \\geq 0$, geldt $x^{2} \\geq 2 x y-y^{2}$ voor alle $x, y \\in \\mathbb{R}$. Omdat we al hebben laten zien dat $f(y) \\geq y^{2}$, geldt $2 x y-f(y) \\leq 2 x y-y^{2} \\leq x^{2}$ en dus\n\n$$\nf(x)=\\max _{y \\in \\mathbb{R}}(2 x y-f(y)) \\leq x^{2}\n$$\n\nWe concluderen $f(x)=x^{2}$.\nWe controleren nog dat deze functie voldoet. Kies een willekeurige $x \\in \\mathbb{R}$. Omdat $(x-y)^{2} \\geq$ 0 , geldt $x^{2} \\geq 2 x y-y^{2}$ voor alle $y \\in \\mathbb{R}$ met gelijkheid als $x=y$, dus\n\n$$\nx^{2}=\\max _{y \\in \\mathbb{R}}\\left(2 x y-y^{2}\\right)\n$$", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2010", "problem_label": "3", "tier": 1, "problem": "(a) Laat $a$ en $b$ positieve gehele getallen zijn zodat $M(a, b)=a-\\frac{1}{b}+b\\left(b+\\frac{3}{a}\\right)$ een geheel getal is. Bewijs dat $M(a, b)$ een kwadraat is.\n(b) Vind gehele getallen $a$ en $b$, beide ongelijk aan nul, zodat $M(a, b)$ een positief geheel getal is, maar geen kwadraat.", "solution": "(a) Omdat $a+b^{2}$ een geheel getal is, is ook $-\\frac{1}{b}+\\frac{3 b}{a}$ een geheel getal. Dit kunnen we schrijven als $\\frac{-a+3 b^{2}}{a b}$. We zien dat $a b$ een deler is van $3 b^{2}-a$. In het bijzonder is $b$ een deler van $3 b^{2}-a$ en dus geldt $b \\mid a$. Maar dat betekent dat $b^{2}$ een deler is van $a b$ en dus ook van $3 b^{2}-a$, waaruit volgt $b^{2} \\mid a$. We schrijven nu $a=m b^{2}$ met $m$ een positief geheel getal. Dan geldt dat $m b^{3}$ een deler is van $3 b^{2}-m b^{2}$, dus is $m b$ een deler van $3-m$. Hieruit volgt dat $m$ een deler is van 3 (oftewel $m=1$ of $m=3$ ) en dat $b$ een deler is van $3-m$.\nStel eerst dat $m=3$. Dan geldt $a=3 b^{2}$. Dit invullen geeft $M\\left(3 b^{2}, b\\right)=3 b^{2}-\\frac{1}{b}+$ $b^{2}+\\frac{1}{b}=4 b^{2}$ en dat is het kwadraat van $2 b$.\nStel nu dat $m=1$. Uit $b \\mid 3-m$ volgt nu $b=1$ of $b=2$. In het eerste geval geldt $a=1$ en in het tweede geval geldt $a=4$. De eerste mogelijkheid invullen geeft $M(1,1)=1-1+1+3=4$ en dat is een kwadraat. De tweede mogelijkheid invullen geeft $M(4,2)=4-\\frac{1}{2}+4+\\frac{3}{2}=9$ en dat is ook een kwadraat.\nWe concluderen dat $M(a, b)$ in alle gevallen een kwadraat is.\n(b) Neem $a=4$ en $b=-2$. Dan geldt $M(4,-2)=7$. Dat is een positief geheel getal, maar geen kwadraat. Na al het werk van onderdeel (a) is dit antwoord niet moeilijk te vinden. Je weet dat a van de vorm $m b^{2}$ moet zijn, nu met $m \\in \\mathbb{Z}$, en dat $m$ een deler moet zijn van 3. Bovendien werkt $m=3$ niet, want dan kriggen we altijd een kwadraat. De rest van de mogelijkheden voor $m$ kun je simpel uitproberen.", "problem_match": "# Opgave 3.", "solution_match": "# Oplossing."}
|
| 4 |
+
{"year": "2010", "problem_label": "4", "tier": 1, "problem": "Gegeven is een vierkant $A B C D$ met omgeschreven cirkel $\\Gamma_{1}$. Zij $P$ een punt op boog $A C$ waar ook $B$ op ligt. Een cirkel $\\Gamma_{2}$ raakt inwendig aan $\\Gamma_{1}$ in $P$ en raakt daarnaast diagonal $A C$ in $Q$. Zij $R$ een punt op $\\Gamma_{2}$ zodat de lijn $D R$ raakt aan $\\Gamma_{2}$. Bewijs dat $|D R|=|D A|$.", "solution": "Zij $M$ het snijpunt van $A C$ en $B D$ (oftewel het middelpunt van $\\Gamma_{1}$ ) en zij $N$ het middelpunt van $\\Gamma_{2}$. We gaan allereerst bewijzen dat $P, Q$ en $D$ op een lijn liggen. Als $P=B$, dan is $Q=M$ en is het triviaal. Zo niet, definieer dan $S$ als het snijpunt van $P Q$ en $B D$. We willen bewijzen dat $S=D$. Merk op dat $M, N$ en $P$ op een lijn liggen en dat $Q N$ evenwijdig is aan $D B$. Hieruit volgt wegens $F$-hoeken $\\angle P S B=\\angle P Q N=\\angle N P Q$, dat laatste vanwege $|N P|=|N Q|$. Met $Z$-hoeken zien we dat $\\angle P M B=\\angle M N Q$ en vanwege de buitenhoekstelling in driehoek $P Q N$ is dat gelijk aan $\\angle P Q N+\\angle N P Q=2 \\angle P S B$. Dus $\\angle P M B=2 \\angle P S B$, waaruit met de middelpuntsomtrekshoekstelling volgt dat $S$ op $\\Gamma_{1}$ ligt. Dus $S=D$, waaruit volgt dat $P, Q$ en $D$ op een lijn liggen.\nOmdat $\\angle D P B=\\angle D M Q=90^{\\circ}$ en $\\angle P D B=\\angle Q D M$, geldt $\\triangle D P B \\sim \\triangle D M Q$. Hieruit volgt $\\frac{|D P|}{|D B|}=\\frac{|D M|}{|D Q|}$. Aangezien $|D B|=2|D M|$, staat hier $|D P||D Q|=2|D M|^{2}$. Uit de machtstelling op $\\Gamma_{2}$ volgt $|D P||D Q|=|D R|^{2}$, dus $|D R|=\\sqrt{2}|D M|=|D A|$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 5 |
+
{"year": "2010", "problem_label": "4", "tier": 1, "problem": "Gegeven is een vierkant $A B C D$ met omgeschreven cirkel $\\Gamma_{1}$. Zij $P$ een punt op boog $A C$ waar ook $B$ op ligt. Een cirkel $\\Gamma_{2}$ raakt inwendig aan $\\Gamma_{1}$ in $P$ en raakt daarnaast diagonal $A C$ in $Q$. Zij $R$ een punt op $\\Gamma_{2}$ zodat de lijn $D R$ raakt aan $\\Gamma_{2}$. Bewijs dat $|D R|=|D A|$.", "solution": "Zij $M$ het snijpunt van $A C$ en $B D$ (oftewel het middelpunt van $\\Gamma_{1}$ ) en zij $N$ het middelpunt van $\\Gamma_{2}$. We gaan allereerst bewijzen dat $P, Q$ en $D$ op een lijn liggen. Bekijk een puntvermenigvuldiging vanuit $P$ die $N$ overvoert in $M$. Dan gaat $\\Gamma_{2}$ over in $\\Gamma_{1}$. De raaklijn $A C$ aan $\\Gamma_{2}$ gaat over in een lijn evenwijdig aan $A C$ die raakt aan $\\Gamma_{1}$. Dit moet de raaklijn in $D$ zijn. Dus $Q$ gaat over in $D$, waaruit volgt dat $P, Q$ en $D$ op een lijn liggen.\nVerder gaat het bewijs zoals in de eerste oplossing.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 6 |
+
{"year": "2010", "problem_label": "5", "tier": 1, "problem": "Het polynoom $A(x)=x^{2}+a x+b$ met gehele coëfficiënten heeft de eigenschap dat voor elk priemgetal $p$ er een geheel getal $k$ bestaat zodat $A(k)$ en $A(k+1)$ beide deelbaar zijn door $p$. Bewijs dat er een geheel getal $m$ bestaat zodat $A(m)=A(m+1)=0$.", "solution": "Zij $p$ een priemgetal en zij $k$ zodat $A(k)$ en $A(k+1)$ beide deelbaar zijn door $p$. Het verschil van $A(k)$ en $A(k+1)$ is dan ook deelbaar door $p$ en dit is gelijk aan\n\n$$\nA(k+1)-A(k)=(k+1)^{2}+a(k+1)+b-\\left(k^{2}+a k+b\\right)=2 k+1+a,\n$$\n\ndus $2 k \\equiv-1-a \\bmod p$. Omdat $A(k)$ deelbaar is door $p$, is $4 A(k)$ dat ook, dus modulo $p$ geldt\n\n$$\n4 A(k)=4 k^{2}+4 a k+4 b \\equiv(-1-a)^{2}+2(-1-a) a+4 b=-a^{2}+4 b+1 \\quad \\bmod p\n$$\n\nDe rechterkant is niet meer afhankelijk van $k$. We zien dus dat voor elk priemgetal $p$ het getal $-a^{2}+4 b+1$ deelbaar moet zijn door $p$. Dit kan alleen als $-a^{2}+4 b+1=0$. Dus geldt $a^{2}=4 b+1$. We zien dat $a$ oneven moet zijn en we schrijven $a=2 c+1$ met $c \\in \\mathbb{Z}$. Dan geldt $4 b+1=a^{2}=4 c^{2}+4 c+1$, dus $b=c^{2}+c$. Het polynoom is daarom van de vorm $A(x)=x^{2}+(2 c+1) x+\\left(c^{2}+c\\right)$ met $c$ geheel. We kunnen dit ontbinden als $A(x)=(x+c)(x+c+1)$, waaruit volgt dat $x=-c$ en $x=-c-1$ de nulpunten zijn van het polynoom. Deze zijn beide geheel. We concluderen dat $m=-c-1$ voldoet aan $A(m)=A(m+1)=0$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 7 |
+
{"year": "2010", "problem_label": "5", "tier": 1, "problem": "Het polynoom $A(x)=x^{2}+a x+b$ met gehele coëfficiënten heeft de eigenschap dat voor elk priemgetal $p$ er een geheel getal $k$ bestaat zodat $A(k)$ en $A(k+1)$ beide deelbaar zijn door $p$. Bewijs dat er een geheel getal $m$ bestaat zodat $A(m)=A(m+1)=0$.", "solution": "Zoals in de eerste oplossing vinden we voor alle $p$ en bijbehorende $k$ dat $2 k \\equiv-1-a \\bmod p$. Als we dit toepassen voor $p=2$, zien we dat $a$ oneven is. Dus $-1-a$ is even. Voor oneven $p$ mogen we delen door 2 en geldt dus $k \\equiv \\frac{-1-a}{2} \\bmod p$. Zij nu $k_{0}=\\frac{-1-a}{2}$. Dan geldt $k_{0} \\equiv k \\bmod p$ en daarom ook $A\\left(k_{0}\\right) \\equiv A(k) \\equiv 0 \\bmod p$. Net zo geldt $A\\left(k_{0}+1\\right) \\equiv A(k+1) \\equiv 0 \\bmod p$. Merk op dat $k_{0}$ onafhankelijk is van $p$. Het getal $A\\left(k_{0}\\right)$ is deelbaar door $p$ voor oneindig veel priemgetallen $p$ (namelijk alle oneven $p$ ) en moet dus wel gelijk zijn aan 0 . Zo ook is $A\\left(k_{0}+1\\right)$ gelijk aan 0 . Dus $m=k_{0}$ voldoet.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2011-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "1", "tier": 1, "problem": "Alle positieve gehele getallen worden rood of groen gekleurd, zodat aan de volgende voorwaarden wordt voldaan:\n\n- Er zijn zowel rode als groene getallen.\n- De som van drie (niet noodzakelijk verschillende) rode getallen is rood.\n- De som van drie (niet noodzakelijk verschillende) groene getallen is groen.\n\nVind alle mogelijke kleuringen die hieraan voldoen.", "solution": "Stel dat we het getal $k$ rood kleuren. We bewijzen met inductie naar $n$ dat dan ook $(2 n+1) k$ rood is voor alle $n \\geq 0$. Voor $n=0$ is dit natuurlijk waar. Stel dat $(2 n-1) k$ rood is voor zekere $n$, dan is ook $k+k+(2 n-1) k=(2 n+1) k$ rood. Dit voltooit de inductie. Analoog geldt dat als $k$ groen gekleurd is, dat dan ook $(2 n+1) k$ groen gekleurd is voor alle $n \\geq 0$.\nZonder verlies van algemeenheid kunnen we aannemen dat 1 rood is. Dan zijn dus alle oneven getallen rood. Stel nu dat er ook een even getal $2 m$ is dat rood is. Omdat nu 1 en $2 m$ beide rood zijn, kunnen we weer makkelijk met inductie laten zien dat $2 m+2 n$ rood is voor alle $n \\geq 0$. Er zijn nu nog maar eindig veel getallen over die groen kunnen zijn, namelijk de even getallen kleiner dan $2 m$. Echter, als één van die getallen groen is, dan moeten ook alle oneven veelvouden van dat getal groen zijn en dat zijn er oneindig veel, tegenspraak. Als anderzijds geen van die getallen groen is, dan hebben we een tegenspraak met de eerste voorwaarde. We concluderen dat er geen even getal is dat rood is. Dus alle even getallen zijn groen.\nDeze kleuring voldoet ook aan alle voorwaarden: de som van drie oneven getallen is altijd oneven en de som van drie even getallen is altijd even, waaruit blijkt dat aan de tweede en derde voorwaarde voldaan is. Aan de eerste voorwaarde is duidelijk ook voldaan.\nDe enige mogelijke kleuringen zijn dus: alle even getallen groen en alle oneven getallen rood, of alle oneven getallen groen en alle even getallen rood.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "In de scherphoekige driehoek $A B C$ is $\\angle C$ groter dan $\\angle A$. Zij $E$ zodat $A E$ een middellijn is van de omgeschreven cirkel $\\Gamma$ van $\\triangle A B C$. Zij $K$ het snijpunt van $A C$ en de raaklijn in $B$ aan $\\Gamma$. Zij $L$ het voetpunt van de loodlijn vanuit $K$ op $A E$ en zij $D$ het snijpunt van $K L$ en $A B$.\nBewijs dat $C E$ de bissectrice van $\\angle B C D$ is.", "solution": "Door de voorwaarden in de opgave ligt de configuratie vast. Omdat $\\angle L A D=$ $\\angle E A B=\\angle E C B$ vanwege de omtrekshoekstelling op koorde $E B$ van $\\Gamma$, geldt\n\n$$\n\\begin{gathered}\n\\angle B D K=\\angle A D L=180^{\\circ}-\\angle D L A-\\angle L A D=90^{\\circ}-\\angle L A D=90^{\\circ}-\\angle E C B \\\\\n=\\angle E C A-\\angle E C B=\\angle B C A=180^{\\circ}-\\angle B C K .\n\\end{gathered}\n$$\n\nHieruit volgt dat $B D K C$ een koordenvierhoek is. Dus $\\angle B C D=\\angle B K D$. We gaan nu bewijzen dat $\\angle B K D=2 \\angle B C E$, waaruit het gevraagde volgt.\nVanwege de raaklijnomtrekshoekstelling geldt $\\angle E B K=\\angle B C E$, dus $\\angle A B K=\\angle A B E+$ $\\angle E B K=90^{\\circ}+\\angle B C E$. Met de hoekensom in driehoek $A B K$ zien we vervolgens dat\n\n$$\n\\angle A K B=180^{\\circ}-\\left(90^{\\circ}+\\angle B C E\\right)-\\angle B A K=90^{\\circ}-\\angle B C E-\\angle B A K\n$$\n\nDe omtrekhoekstelling vertelt ons dat $\\angle B A K=\\angle E A K+\\angle B A E=\\angle E A K+\\angle B C E$, dus we vinden dat\n\n$$\n\\angle A K B=90^{\\circ}-2 \\angle B C E-\\angle E A K=90^{\\circ}-2 \\angle B C E-\\angle L A K .\n$$\n\nUit de hoekensom in driehoek $A K L$ volgt dat $\\angle A K L=90^{\\circ}-\\angle L A K$, dus\n\n$$\n\\angle A K B=\\angle A K L-2 \\angle B C E .\n$$\n\nDit geeft\n\n$$\n\\angle B K D=\\angle A K L-\\angle A K B=2 \\angle B C E,\n$$\n\nwat is wat we wilden bewijzen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "In de scherphoekige driehoek $A B C$ is $\\angle C$ groter dan $\\angle A$. Zij $E$ zodat $A E$ een middellijn is van de omgeschreven cirkel $\\Gamma$ van $\\triangle A B C$. Zij $K$ het snijpunt van $A C$ en de raaklijn in $B$ aan $\\Gamma$. Zij $L$ het voetpunt van de loodlijn vanuit $K$ op $A E$ en zij $D$ het snijpunt van $K L$ en $A B$.\nBewijs dat $C E$ de bissectrice van $\\angle B C D$ is.", "solution": "Omdat $A E$ een middellijn is, geldt wegens de stelling van Thales dat $\\angle E B A=90^{\\circ}$ en ook $\\angle E C A=90^{\\circ}$. Verder geldt natuurlijk $\\angle K L A=90^{\\circ}$. Dus volgens de stelling van Thales liggen $B$ en $L$ op de cirkel met middellijn $D E$, dus is $B D L E$ een koordenvierhoek. Wegens de rechte hoeken bij $C$ en $L$ is zo ook $C K L E$ een koordenvierhoek.\nWe passen de machtstelling toe op het punt $A$ en de koordenvierhoek $B D L E$ : er geldt $A B \\cdot A D=A E \\cdot A L$. De machtstelling op punt $A$ en koordenvierhoek $C K L E$ geeft juist $A E \\cdot A L=A C \\cdot A K$. Combineren van beide geeft dat $A B \\cdot A D=A C \\cdot A K$. Daaruit volgt met alweer de machtstelling vanuit punt $A$ dat $B D K C$ een koordenvierhoek is. Vanaf hier kunnen we het bewijs vervolgen als in oplossing 1.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Vind alle drietallen reële getallen $(x, y, z)$ die voldoen aan\n\n$$\nx^{2}+y^{2}+z^{2}+1=x y+y z+z x+|x-2 y+z|\n$$", "solution": "We herschrijven de gegeven vergelijking als\n\n$$\n\\frac{1}{2} x^{2}-x y+\\frac{1}{2} y^{2}+\\frac{1}{2} y^{2}-y z+\\frac{1}{2} z^{2}+\\frac{1}{2} z^{2}-z x+\\frac{1}{2} x^{2}+1=|x-2 y+z|,\n$$\n\noftewel als\n\n$$\n\\frac{1}{2}(x-y)^{2}+\\frac{1}{2}(y-z)^{2}+\\frac{1}{2}(z-x)^{2}+1=|(x-y)+(z-y)| .\n$$\n\nSubstitueer nu $a=x-y$ en $b=z-y$. Dan geldt $x-z=a-b$, dus krijgen we\n\n$$\n\\frac{1}{2} a^{2}+\\frac{1}{2} b^{2}+\\frac{1}{2}(a-b)^{2}+1=|a+b| .\n$$\n\nUit $(a-b)^{2} \\geq 0$ volgt $a^{2}-2 a b+b^{2} \\geq 0$, dus $2 a^{2}+2 b^{2} \\geq a^{2}+b^{2}+2 a b$, wat betekent dat $a^{2}+b^{2} \\geq \\frac{(a+b)^{2}}{2}$ met gelijkheid dan en slechts dan als $a=b$. Verder geldt natuurlijk ook $(a-b)^{2} \\geq 0$. Dus\n\n$$\n|a+b|=\\frac{1}{2} a^{2}+\\frac{1}{2} b^{2}+\\frac{1}{2}(a-b)^{2}+1 \\geq \\frac{(a+b)^{2}}{4}+1\n$$\n\nSchrijf nu $c=|a+b|$, dan staat hier\n\n$$\nc \\geq \\frac{c^{2}}{4}+1\n$$\n\nDit kunnen we herschrijven naar $c^{2}-4 c+4 \\leq 0$, oftewel $(c-2)^{2} \\leq 0$. Omdat links een kwadraat staat, moet hier wel gelijkheid gelden, dus $c=2$. Verder moet nu ook in onze eerdere afschatting gelijkheid gelden, dus $a=b$. Dit invullen in (2) geeft $a^{2}+1=2$, dus $a= \\pm 1$. Zo vinden we de drietallen $(y+1, y, y+1)$ en $(y-1, y, y-1)$ voor willekeurige $y \\in \\mathbb{R}$. Invullen in de vergelijking (1) (die equivalent is aan de oorspronkelijke vergelijking) laat zien dat deze drietallen inderdaad oplossingen zijn voor alle $y \\in \\mathbb{R}$. Alle oplossingen worden dus gegeven door $(y+1, y, y+1)$ en $(y-1, y, y-1)$ met $y \\in \\mathbb{R}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 5 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Vind alle drietallen reële getallen $(x, y, z)$ die voldoen aan\n\n$$\nx^{2}+y^{2}+z^{2}+1=x y+y z+z x+|x-2 y+z|\n$$", "solution": "Leid net als hierboven vergelijking (2) af. Merk nu op dat $|a+b| \\leq|a|+|b|$ volgens de driehoeksongelijkheid, dus\n\n$$\n\\frac{1}{2} a^{2}+\\frac{1}{2} b^{2}+\\frac{1}{2}(a-b)^{2}+1=|a+b| \\leq|a|+|b| .\n$$\n\nDit kunnen we herschrijven als\n\n$$\n\\frac{1}{2}(|a|-1)^{2}+\\frac{1}{2}(|b|-1)^{2}+\\frac{1}{2}(a-b)^{2} \\leq 0 .\n$$\n\nLinks staat de som van drie kwadraten, dus deze moeten allemaal gelijk aan 0 zijn. Dus $|a|=1,|b|=1$ en $a=b$. Zo vinden we weer de drietallen $(y+1, y, y+1)$ en $(y-1, y, y-1)$ voor willekeurige $y \\in \\mathbb{R}$. Zie verder eerste oplossing.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 6 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Vind alle drietallen reële getallen $(x, y, z)$ die voldoen aan\n\n$$\nx^{2}+y^{2}+z^{2}+1=x y+y z+z x+|x-2 y+z|\n$$", "solution": "We onderscheiden twee gevallen: $x-2 y+z \\geq 0$ of $x-2 y+z<0$. In het eerste geval wordt de vergelijking\n\n$$\nx^{2}+y^{2}+z^{2}+1=x y+y z+z x+x-2 y+z .\n$$\n\nWe kunnen dit beschouwen als kwadratische vergelijking in $x$ :\n\n$$\nx^{2}+(-y-z-1) x+\\left(y^{2}+z^{2}+1-y z+2 y-z\\right)=0 .\n$$\n\nWe berekenen hiervan de discriminant:\n\n$$\n\\begin{gathered}\nD=(-y-z-1)^{2}-4\\left(y^{2}+z^{2}+1-y z+2 y-z\\right)=-3 y^{2}-3 z^{2}-3+6 y z-6 y+6 z \\\\\n=-3\\left(y^{2}+z^{2}+1-2 y z+2 y-2 z\\right)=-3(y-z+1)^{2} .\n\\end{gathered}\n$$\n\nWe zien dat $D \\leq 0$, terwijl de kwadratische vergelijking alleen een oplossing heeft als $D \\geq 0$. Er moet dus gelden $D=0$. Hieruit volgt $y-z+1=0$, dus $z=y+1$. We krijgen dan met abc-formule $x=\\frac{-(-y-z-1) \\pm \\sqrt{0}}{2}=y+1$. Zo vinden we het drietal $(y+1, y, y+1)$ voor willekeurige $y \\in \\mathbb{R}$. We moeten hiervoor nog controleren dat $x-2 y+z \\geq 0$. Dit geldt inderdaad, want $x-2 y+z=2$. Dus dit drietal is een oplossing.\nNu bekijken we het geval $x-2 y+z<0$. We krijgen weer een kwadratische vergelijking in $x$ :\n\n$$\nx^{2}+(-y-z+1) x+\\left(y^{2}+z^{2}+1-y z-2 y+z\\right)=0 .\n$$\n\nDeze heeft als discriminant\n\n$$\n\\begin{gathered}\nD=(-y-z+1)^{2}-4\\left(y^{2}+z^{2}+1-y z-2 y+z\\right)=-3 y^{2}-3 z^{2}-3+6 y z+6 y-6 z \\\\\n=-3\\left(y^{2}+z^{2}+1-2 y z-2 y+2 z\\right)=-3(y-z-1)^{2} .\n\\end{gathered}\n$$\n\nWe zien weer $D \\leq 0$, waaruit weer volgt dat $D=0$, dus $z=y-1$. We vinden vervolgens $x=\\frac{-(-y-z+1) \\pm \\sqrt{0}}{2}=y-1$. Zo vinden we het drietal $(y-1, y, y-1)$ voor willekeurige $y \\in \\mathbb{R}$. Er geldt nu $x-2 y+z=-2<0$, dus dit drietal is een oplossing.\nAl met al zijn de enige oplossingen $(y+1, y, y+1)$ en $(y-1, y, y-1)$ voor willekeurige $y \\in \\mathbb{R}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing III."}
|
| 7 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Zij $n \\geq 2$ een geheel getal. Zij $a$ het grootste positieve gehele getal waarvoor geldt $2^{a} \\mid 5^{n}-3^{n}$. Zij $b$ het grootste positieve gehele getal waarvoor geldt $2^{b} \\leq n$. Bewijs dat $a \\leq b+3$.", "solution": "We bewijzen dit allereerst voor oneven getallen $n$. Hiervoor geldt modulo 4 dat $5^{n} \\equiv 1^{n}=1$ en $3^{n} \\equiv(-1)^{n} \\equiv-1$, dus $5^{n}-3^{n} \\equiv 2 \\bmod 4$. Dus als $n$ oneven is, geldt $a=1$. Omdat $b \\geq 1$, is nu voldaan aan $a \\leq b+3$.\nStel nu dat $n \\equiv 2 \\bmod 4$. Schrijf $n=2 k$ met $k$ een oneven positief geheel getal. Merk op dat $5^{2 k}-3^{2 k}=\\left(5^{k}-3^{k}\\right)\\left(5^{k}+3^{k}\\right)$. We hebben net laten zien dat $5^{k}-3^{k}$ precies één factor 2 bevat, aangezien $k$ oneven is. We bekijken nu $5^{k}+3^{k}$ modulo 16 . Voor $m=1,2,3,4$ geldt dat $5^{m}$ modulo 16 congruent is aan respectievelijk $5,9,13,1$. Omdat $5^{4} \\equiv 1 \\bmod 16$, geldt dat $5^{k} \\equiv 5$ voor alle $k \\equiv 1 \\bmod 4$ en $5^{k} \\equiv 13$ voor alle $k \\equiv 3 \\bmod 4$. Voor $m=1,2,3,4$ geldt dat $3^{m}$ modulo 16 congruent is aan respectievelijk $3,9,11,1$. Omdat $3^{4} \\equiv 1 \\bmod 16$, geldt dat $3^{k} \\equiv 3$ voor alle $k \\equiv 1 \\bmod 4$ en $3^{k} \\equiv 11$ voor alle $k \\equiv 3 \\bmod 4$. Al met al zien we dat $5^{k}+3^{k} \\equiv 5+3 \\equiv 8 \\bmod 16$ als $k \\equiv 1 \\bmod 4$ en $5^{k}+3^{k} \\equiv 13+11=24 \\equiv 8$ $\\bmod 16$ als $k \\equiv 3 \\bmod 4$. In beide gevallen bevat $5^{k}+3^{k}$ precies 3 factoren 2 .\nWe concluderen dat voor $n \\equiv 2 \\bmod 4$ geldt: $a=4$. Omdat $b \\geq 1$, is nu voldaan aan $a \\leq b+3$.\nWe bewijzen nu met inductie naar $m$ dat $a \\leq b+3$ voor alle positieve gehele getallen $n$ met precies $m \\geq 1$ factoren 2 . De inductiebasis is $m=1$, oftewel het geval $n \\equiv 2 \\bmod 4$. Hiervoor hebben we dit al bewezen.\nZij nu $m \\geq 1$ en neem als inductiehypothese aan dat we al $a \\leq b+3$ hebben laten zien voor alle getallen $n$ met precies $m$ factoren 2 . Bekijk nu een getal $n$ met $m+1$ factoren 2. We schrijven $n=2 k$, waarbij $k$ precies $m$ factoren 2 heeft. Laat voor de duidelijkheid $a(k)$ en $b(k)$ de $a$ en $b$ zijn die horen bij $k$, en $a(n)$ en $b(n)$ de $a$ en $b$ die horen bij $n$. De inductiehypothese zegt dat $a(k) \\leq b(k)+3$. We willen bewijzen dat $a(n) \\leq b(n)+3$.\nEr geldt $5^{n}-3^{n}=5^{2 k}-3^{2 k}=\\left(5^{k}-3^{k}\\right)\\left(5^{k}+3^{k}\\right)$. Omdat $k$ even is (hij bevat $m \\geq 1$ factoren 2) geldt modulo 4 dat $5^{k}+3^{k} \\equiv 1^{k}+(-1)^{k} \\equiv 2 \\bmod 4$. Dus $5^{k}+3^{k}$ bevat precies één factor 2. Verder bevat $5^{k}-3^{k}$ precies $a(k)$ factoren 2 . Dus $a(n)=a(k)+1$. We weten daarnaast dat $2^{b(k)} \\leq k$ en $2^{b(k)+1}>k$, waaruit volgt dat $2^{b(k)+1} \\leq 2 k$ en $2^{b(k)+2}>2 k$. Dus $b(n)=b(k)+1$. Nu kunnen we concluderen: $a(n)=a(k)+1 \\leq b(k)+3+1=b(n)+3$, waarmee de inductie voltooid is.\nDit bewijst dat $a \\leq b+3$ voor alle gehele getallen $n \\geq 2$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 8 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Gegeven is een trapezium $A B C D$ met $B C \\| A D$. Neem aan dat de bissectrices van de hoeken $B A D$ en $C D A$ elkaar snijden op de middelloodlijn van lijnstuk $B C$. Bewijs dat $|A B|=|C D|$ of $|A B|+|C D|=|A D|$.", "solution": "Zij $M$ het midden van $B C$ en zij $P$ het snijpunt van de middelloodlijn van $B C$ met $A D$. Noem $K$ het snijpunt van $M P$ en de twee bissectrices. Laat $L$ en $N$ de voetpunten zijn van $K$ op respectievelijk zijden $A B$ en $D C$. Omdat $A K$ en $D K$ bissectrices zijn, geldt $|K L|=|K P|=|K N|$. Verder ligt $K$ ook op de middelloodlijn van $B C$, dus $|K B|=|K C|$. Omdat driehoeken $B L K$ en $C N K$ ook beide een rechte hoek hebben, zijn ze met (ZZR) congruent.\nWe onderscheiden nu vier gevallen. Bekijk eerst het geval dat $L$ en $N$ op het inwendige van respectievelijk zijden $A B$ en $D C$ liggen. Merk op dat driehoek $K B C$ gelijkbenig is, zodat $\\angle K B C=\\angle B C K$. Dus geldt vanwege $\\triangle B L K \\cong \\triangle C N K$ :\n\n$$\n\\angle A B C=\\angle L B K+\\angle K B C=\\angle N C K+\\angle B C K=\\angle B C D .\n$$\n\nHieruit volgt dat $A B C D$ een gelijkbenig trapezium is en dat dus geldt $|A B|=|C D|$.\nIn het geval dat $L$ en $N$ beide op het verlengde van de zijden $A B$ en $D C$ liggen, kunnen we op analoge wijze laten zien dat $|A B|=|C D|$.\nNu bekijken we het geval dat $L$ op het inwendige van zijde $A B$ ligt, maar $N$ op het verlengde van zijde $D C$. Omdat $A K$ en $D K$ bissectrices zijn, geldt $|A L|=|A P|$ en $|D N|=|D P|$. Dus geldt vanwege $\\triangle B L K \\cong \\triangle C N K$ :\n\n$$\n|A B|+|C D|=(|A L|+|L B|)+(|D N|-|N C|)=|A P|+|L B|+|D P|-|L B|=|A D|\n$$\n\nIn het geval dat $L$ juist op het verlengde van $A B$ ligt en $N$ op het inwendige van $D C$, laten we op analoge wijze zien dat $|A B|+|C D|=|A D|$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 9 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Gegeven is een trapezium $A B C D$ met $B C \\| A D$. Neem aan dat de bissectrices van de hoeken $B A D$ en $C D A$ elkaar snijden op de middelloodlijn van lijnstuk $B C$. Bewijs dat $|A B|=|C D|$ of $|A B|+|C D|=|A D|$.", "solution": "Zij $K$ het snijpunt van de middelloodlijn van $B C$ en de twee bissectrices. Spiegel $B$ in de lijn $A K$ en noem het beeld $E$. Omdat $A K$ een bissectrice is, ligt $E$ op $A D$, geldt $|A B|=|A E|$ en is $A K$ de middelloodlijn van $B E$, zodat $|K B|=|K E|$. Spiegel nu ook $C$ in $D K$ en noem het beeld $F$. Ook $F$ ligt op $A D$ en verder geldt $|D C|=|D F|$ en $|K C|=|K F|$. Als $E$ en $F$ hetzelfde punt zijn, zien we dat $|A B|+|C D|=|A E|+|F D|=$ $|A D|$.\nStel nu dat $E$ en $F$ niet hetzelfde punt zijn. Omdat $K$ op de middelloodlijn van $B C$ ligt, geldt $|K B|=|K C|$. We wisten al $|K B|=|K E|$ en $|K C|=|K F|$, dus $K$ ligt op gelijke afstand van de vier punten $B, C, E$ en $F$. Dat betekent dat deze vier punten op een cirkel liggen. We nemen aan dat de volgorde van de punten op deze cirkel $B C F E$ is; het geval dat de volgorde $B C E F$ is, gaat analoog. Er geldt nu\n\n$$\n\\angle F C B=180^{\\circ}-\\angle F E B=\\angle A E B=\\angle E B A .\n$$\n\nAnaloog geldt $\\angle E B C=\\angle F C D$. Dus\n\n$$\n\\angle B C D=\\angle F C B+\\angle F C D=\\angle E B A+\\angle E B C=\\angle A B C .\n$$\n\nHieruit volgt dat $A B C D$ een gelijkbenig trapezium is en dat dus geldt $|A B|=|C D|$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2011-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "1", "tier": 1, "problem": "Vind alle paren $(x, y)$ van gehele getallen die voldoen aan\n\n$$\nx^{2}+y^{2}+3^{3}=456 \\sqrt{x-y} .\n$$", "solution": "Omdat links een geheel getal staat, moet rechts ook een geheel getal staan. De wortel uit een geheel getal is ofwel geheel ofwel irrationaal (maar nooit een niet-gehele breuk), dus moet $\\sqrt{x-y}$ wel geheel zijn. De rechterkant van de vergelijking is deelbaar door 3 , dus de linkerkant moet dat ook zijn. Dus $3 \\mid x^{2}+y^{2}$. Maar kwadraten zijn modulo 3 altijd congruent aan 0 of 1 , dus dit kan alleen als $x^{2} \\equiv y^{2} \\equiv 0 \\bmod 3$. Dus $x$ en $y$ zijn beide deelbaar door 3 . Schrijf nu $x=3 a$ en $y=3 b$ en vul dit in:\n\n$$\n9 a^{2}+9 b^{2}+3^{3}=456 \\sqrt{3 a-3 b}\n$$\n\nWortels uit gehele getallen zijn in het algemeen geheel of irrationaal. Maar $\\sqrt{3 a-3 b}$ kan niet irrationaal zijn, want het is gelijk aan $\\frac{9 a^{2}+9 b^{2}+3^{3}}{456}$, dus het is geheel. Daarom is $3 a-3 b$ een kwadraat, dat ook nog deelbaar is door 3 , dus moet het deelbaar door 9 zijn. We kunnen nu beide kanten van de vergelijking door 9 delen:\n\n$$\na^{2}+b^{2}+3=152 \\sqrt{\\frac{a-b}{3}}\n$$\n\nSchrijf $a-b=3 c^{2}$ en substitueer $a=b+3 c^{2}$ :\n\n$$\n9 c^{4}+6 c^{2} b+2 b^{2}+3=152 c\n$$\n\nOmdat aan de linkerkant allemaal positieve termen staan, moet gelden $9 c^{4}<152 c$, dus $c^{3}<\\frac{152}{9}=16+\\frac{8}{9}$. Aangezien voor $c \\geq 3$ geldt: $c^{3} \\geq 3^{3}=27>16+\\frac{8}{9}$, volgt hieruit $c \\leq 2$. Verder is $152 c$ even, net als $6 c^{2} b+2 b^{2}$, dus moet $9 c^{4}+3$ ook even zijn, waardoor we zien dat $c$ oneven moet zijn. Dus de enige mogelijkheid is $c=1$. Als we dit invullen, krijgen we\n\n$$\n9+6 b+2 b^{2}+3=152\n$$\n\noftewel\n\n$$\nb^{2}+3 b-70=0\n$$\n\nDit kunnen we ook schrijven als $(b-7)(b+10)=0$. Dus $b=7$ of $b=-10$. In het eerste geval krijgen we nu $a=b+3 c^{2}=10$ en dus $x=30$ en $y=21$. In het tweede geval krijgen we $a=b+3 c^{2}=-7$ en dus $x=-21$ en $y=-30$. Controleren laat zien dat beide paren voldoen. Dus de oplossingen zijn $(x, y)=(30,21)$ en $(x, y)=(-21,-30)$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "We bekijken betegelingen van een rechthoekig $m \\times n$-bord met $1 \\times 2$-tegels. De tegels mogen zowel horizontaal als verticaal liggen, maar ze mogen elkaar niet overlappen en niet buiten het bord uitsteken. Alle velden van het bord moeten bedekt worden door een tegel.\na) Bewijs dat bij elke betegeling van een $4 \\times 2010$-bord met $1 \\times 2$-tegels er een rechte lijn is die het bord in twee stukken verdeelt zodat elke tegel in zijn geheel binnen één van de stukken ligt.\nb) Bewijs dat er een betegeling van een $5 \\times 2010$-bord met $1 \\times 2$-tegels bestaat zodat er geen rechte lijn is die het bord in twee stukken verdeelt zodat elke tegel in zijn geheel binnen één van de stukken ligt.", "solution": "a) Noem een rechte lijn die het bord in twee stukken verdeelt zodat elke tegel in zijn geheel binnen één van de stukken ligt, een scheidingslijn. Stel dat er een betegeling bestaat waar geen scheidingslijn te vinden is. Bekijk de kolommen $k$ en $k+1$, met $1 \\leq k \\leq 2009$. Er moet dan een horizontale tegel zijn die in deze twee kolommen ligt; anders is de verticale lijn tussen de kolommen een scheidingslijn. In de kolommen 1 tot en met $k$ zitten totaal $4 k$ velden, dus een even aantal. Omdat elke tegel die helemaal binnen de kolommen 1 tot en met $k$ ligt, een even aantal velden bedekt, moet er een even aantal tegels horizontaal in kolommen $k$ en $k+1$ liggen. We hebben gezien dat het er minstens één is en dus zijn het er minstens twee.\nVoor elke $k$ met $1 \\leq k \\leq 2009$ zijn er dus twee tegels die horizontaal in kolommen $k$ en $k+1$ liggen. Deze tegels bedekken samen $2 \\cdot 2009 \\cdot 2$ velden. Verder moet er nog voor elke $i$ met $1 \\leq i \\leq 3$ een verticale tegel zijn die in de rijen $i$ en $i+1$ ligt. Deze tegels bedekken samen $3 \\cdot 2$ velden. Het totaal aantal velden dat bedekt wordt door al deze tegels, is dus $(2 \\cdot 2009+3) \\cdot 2>2 \\cdot 2010 \\cdot 2$. Maar het bord bevat slechts $4 \\cdot 2010$ velden, tegenspraak.\nb) We bewijzen met inductie naar $n$ dat we voor alle $n \\geq 3$ een $5 \\times 2 n$-bord kunnen betegelen zonder scheidingslijn. Voor $n=3$ kan dit als volgt:\n\n\nStel nu dat we een betegeling van een $5 \\times 2 n$-bord hebben zonder scheidingslijn. Dan liggen minstens vier tegels verticaal. Dus is er een $k$ met $1 \\leq k \\leq 2 n-1$ uit zodat er in kolom $k$ een tegel verticaal ligt. Voeg nu twee kolommen in tussen kolom $k$ en kolom $k+1$; noem deze kolommen $k_{1}$ en $k_{2}$. Elke tegel die horizontaal in kolommen $k$\nen $k+1$ lag, vervangen we door twee horizontale tegels, één in kolommen $k$ en $k_{1}$ en één in kolommen $k_{2}$ en $k+1$. Omdat kolom $k$ een verticale tegel bevat, zijn nu nog niet alle velden van de kolommen $k_{1}$ en $k_{2}$ bezet. Als in een rij het veld van kolom $k_{1}$ nog niet bezet is, is in dezelfde rij het veld van kolom $k_{2}$ ook nog niet bezet. We kunnen hier dus een horizontale tegel neerleggen. Zo vullen we alle velden van de nieuwe kolommen.\n\nHet is nu duidelijk dat er tussen geen enkel tweetal rijen een scheidingslijn ontstaan kan zijn en ook in geen enkele kolom waar niets veranderd is. Verder ligt er nu minstens één horizontale tegel in kolommen $k_{1}$ en $k_{2}$, dus er is geen scheidingslijn tussen deze twee kolommen. In het oude bord was er geen scheidingslijn tussen de kolommen $k$ en $k+1$, dus lag er een horizontale tegel in deze kolommen. Dat betekent dat er nu een horizontale tegel in kolommen $k$ en $k_{1}$ ligt en een horizontale tegel in kolommen $k_{2}$ en $k+1$, zodat ook tussen die twee paren kolommen geen scheidingslijn is. Het hele nieuwe bord bevat dus geen enkele scheidingslijn.\n\nDit voltooit de inductie. Nu volgt dat er een $5 \\times 2010$-bord bestaat zonder scheidingslijn.", "problem_match": "\nOpgave 2.", "solution_match": "# Oplossing."}
|
| 3 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "De cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$ snijden elkaar in $D$ en $P$. De gemeenschappelijke raaklijn van de twee cirkels het dichtste bij punt $D$ raakt $\\Gamma_{1}$ in $A$ en $\\Gamma_{2}$ in $B$. De lijn $A D$ snijdt $\\Gamma_{2}$ voor de tweede keer in $C$. Zij $M$ het midden van lijnstuk $B C$.\nBewijs dat $\\angle D P M=\\angle B D C$.", "solution": "Zij $S$ het snijpunt van $P D$ en $A B$. Dan ligt $S$ op de machtlijn van de twee cirkels en geldt dus $|S A|=|S B|$. Dus $P S$ is een zwaartelijn in driehoek $P A B$.\nVanwege de raaklijnomtrekshoekstelling op $\\Gamma_{1}$ met koorde $A P$ geldt $\\angle B A P=180^{\\circ}-$ $\\angle A D P=\\angle C D P=\\angle C B P$. Vanwege de raaklijnomtrekshoekstelling op $\\Gamma_{2}$ met koorde $B P$ geldt $\\angle A B P=\\angle B C P$. Dus $\\triangle P A B \\sim \\triangle P B C$ (hh). Omdat $P M$ een zwaartelijn in driehoek $P B C$ is, geldt $\\angle S P B=\\angle M P C$. Dus\n$\\angle D P M=\\angle D P B+\\angle B P M=\\angle S P B+\\angle B P M=\\angle M P C+\\angle B P M=\\angle B P C=\\angle B D C$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "De cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$ snijden elkaar in $D$ en $P$. De gemeenschappelijke raaklijn van de twee cirkels het dichtste bij punt $D$ raakt $\\Gamma_{1}$ in $A$ en $\\Gamma_{2}$ in $B$. De lijn $A D$ snijdt $\\Gamma_{2}$ voor de tweede keer in $C$. Zij $M$ het midden van lijnstuk $B C$.\nBewijs dat $\\angle D P M=\\angle B D C$.", "solution": "Zij $S$ het snijpunt van $P D$ en $A B$. Dan ligt $S$ op de machtlijn van de twee cirkels en geldt dus $|S A|=|S B|$. Dus $S M$ is een middenparallel in $\\triangle A B C$. Hieruit volgt\n\n$$\n\\angle S M B=\\angle A C B=\\angle D C B=\\angle D P B=\\angle S P B\n$$\n\nDus $S B M P$ is een koordenvierhoek. Dat betekent\n\n$$\n\\angle B P M=\\angle B S M=\\angle B A C\n$$\n\nVerder geldt wegens de raaklijnomtrekshoekstelling op koorde $D B$ dat\n\n$$\n\\angle A B D=\\angle B P D .\n$$\n\nDe buitenhoekstelling in $\\triangle A B D$ geeft dat $\\angle B D C=\\angle B A C+\\angle A B D$. Als we dit combineren met (1) en (2), zien we dat $\\angle B D C=\\angle B P M+\\angle B P D=\\angle D P M$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Bepaal alle gehele getallen $n$ waarvoor het polynoom $P(x)=3 x^{3}-n x-n-2$ te schrijven is als het product van twee niet-constante polynomen met gehele coëfficiënten.", "solution": "Stel dat $P(x)$ te schrijven is als $P(x)=A(x) B(x)$ met $A$ en $B$ niet-constante polynomen met gehele coëfficiënten. Omdat $A$ en $B$ niet constant zijn, hebben ze elk graad minstens 1. De som van de twee graden is gelijk aan de graad van $P$, dus gelijk aan 3. Dit betekent dat de twee graden 1 en 2 moeten zijn. We kunnen dus zonder verlies van algemeenheid schrijven $A(x)=a x^{2}+b x+c$ en $B(x)=d x+e$ met $a, b, c, d$ en $e$ gehele getallen. Het product van de kopcoëfficiënten $a$ en $d$ is gelijk aan de kopcoëfficiënt van $P$, dus gelijk aan 3. Omdat we $A$ en $B$ ook beide met -1 zouden kunnen vermenigvuldigen, mogen we aannemen dat $a$ en $d$ beide positief zijn en dus in een of andere volgorde gelijk aan 1 en 3.\nStel eerst dat $d=1$ Vul nu $x=-1$ in. Er geldt\n\n$$\nP(-1)=3 \\cdot(-1)^{3}+n-n-2=-5,\n$$\n\ndus\n\n$$\n-5=P(-1)=A(-1) B(-1)=A(-1) \\cdot(-1+e) .\n$$\n\nWe zien dat $-1+e$ een deler is van -5 , dus gelijk is aan $-5,-1,1$ of 5 . Dat geeft vier mogelijke waarden voor $e$, namelijk $-4,0,2$ of 6 . Verder is $x=-e$ een nulpunt van $B$ en dus ook van $P$.\nAls $e=-4$, dan geldt\n\n$$\n0=P(4)=3 \\cdot 4^{3}-4 n-n-2=190-5 n\n$$\n\ndus $n=38$. We kunnen dan $P(x)$ inderdaad ontbinden:\n\n$$\n3 x^{3}-38 x-40=\\left(3 x^{2}+12 x+10\\right)(x-4)\n$$\n\nAls $e=0$, dan geldt\n\n$$\n0=P(0)=-n-2\n$$\n\ndus $n=-2$. We kunnen dan $P(x)$ inderdaad ontbinden:\n\n$$\n3 x^{3}+2 x=\\left(3 x^{2}+2\\right) x\n$$\n\nAls $e=2$, dan geldt\n\n$$\n0=P(-2)=3 \\cdot(-2)^{3}+2 n-n-2=-26+n\n$$\n\ndus $n=26$. We kunnen dan $P(x)$ inderdaad ontbinden:\n\n$$\n3 x^{3}-26 x-28=\\left(3 x^{2}-6 x-14\\right)(x+2)\n$$\n\nAls $e=6$, dan geldt\n\n$$\n0=P(-6)=3 \\cdot(-6)^{3}+6 n-n-2=-650+5 n\n$$\n\ndus $n=130$. We kunnen dan $P(x)$ inderdaad ontbinden:\n\n$$\n3 x^{3}-130 x-132=\\left(3 x^{2}-18 x-22\\right)(x+6)\n$$\n\nStel nu dat $d=3$. Er geldt nu\n\n$$\n-5=P(-1)=A(-1) B(-1)=A(-1) \\cdot(-3+e)\n$$\n\nWe zien dat $-3+e$ een deler is van -5 , dus gelijk is aan $-5,-1,1$ of 5 . Dat geeft vier mogelijke waarden voor $e$, namelijk $-2,2,4$ of 8 . Verder is $x=\\frac{-e}{3}$ een nulpunt van $B$ en dus ook van $P$. We zien dat $e$ nooit deelbaar is door 3. Er geldt nu\n\n$$\n0=P\\left(\\frac{-e}{3}\\right)=3 \\cdot\\left(\\frac{-e}{3}\\right)^{3}+\\frac{e}{3} n-n-2=-\\frac{e^{3}}{9}+\\frac{e-3}{3} n-2,\n$$\n\ndus $\\frac{e-3}{3} n=\\frac{e^{3}}{9}+2$, dus $(e-3) n=\\frac{e^{3}}{3}+6$. Maar dit geeft een tegenspraak, want links staat een geheel getal en rechts niet, aangezien 3 geen deler is van $e$.\nWe concluderen dat de oplossingen zijn: $n=38, n=-2, n=26$ en $n=130$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Bepaal alle gehele getallen $n$ waarvoor het polynoom $P(x)=3 x^{3}-n x-n-2$ te schrijven is als het product van twee niet-constante polynomen met gehele coëfficiënten.", "solution": "Net als in oplossing I schrijven we schrijven $P(x)=\\left(a x^{2}+b x+c\\right)(d x+e)$ en leiden we af dat $a=1$ en $d=3$, of $a=3$ en $d=1$. Door het vergelijken van de coëfficiënten krijgen we nog drie voorwaarden:\n\n$$\n\\begin{aligned}\na e+b d & =0, \\\\\nb e+d c & =-n, \\\\\nc e & =-n-2 .\n\\end{aligned}\n$$\n\nStel eerst dat $a=3$ en $d=1$. Uit (3) volgt nu $b=-3 e$. Uit (4) en (5) krijgen we nu\n\n$$\n\\begin{aligned}\n& -n=-3 e^{2}+c \\\\\n& -n=c e+2\n\\end{aligned}\n$$\n\ndus $-3 e^{2}+c=c e+2$, dus\n\n$$\nc=\\frac{-3 e^{2}-2}{e-1}=\\frac{-3 e(e-1)-3 e-2}{e-1}=-3 e+\\frac{-3(e-1)-5}{e-1}=-3 e-3-\\frac{5}{e-1} .\n$$\n\nOmdat $c$ geheel moet zijn, moet $e-1$ een deler zijn van 5 en dus gelijk zijn aan $-5,-1$, 1 of 5 . Dat geeft vier mogelijke waarden voor $e$, namelijk $-4,0,2$ of 6 . Als $e=-4$, krijgen we $c=(-3)(-4)-3-\\frac{5}{-5}=10$ en dus $n=-10 \\cdot(-4)-2=38$. Als $e=0$, krijgen we $c=(-3) \\cdot 0-3-\\frac{5}{-1}=2$ en dus $n=-2 \\cdot 0-2=-2$. Als $e=2$, krijgen we $c=(-3) \\cdot 2-3-\\frac{5}{1}=-14$ en dus $n=14 \\cdot 2-2=26$. Als $e=6$, krijgen we $c=(-3) \\cdot 6-3-\\frac{5}{5}=-22$ en dus $n=22 \\cdot 6-2=130$. Al deze waarden van $n$ voldoen, zoals we in oplossing I hebben gezien.\n\nStel nu dat $a=1$ en $d=3$. Uit (3) volgt nu $e=-3 b$. Uit (4) en (5) krijgen we nu\n\n$$\n\\begin{aligned}\n& -n=-3 b^{2}+3 c \\\\\n& -n=-3 b c+2\n\\end{aligned}\n$$\n\ndus $-3 b^{2}+3 c=-3 b c+2$. Echter, elke term van deze gelijkheid is deelbaar door 3 behalve de term 2, wat een tegenspraak is. Dit geval geeft dus geen oplossingen.\nWe concluderen dat de oplossingen zijn: $n=38, n=-2, n=26$ en $n=130$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Zij $A B C$ een driehoek met $|A B|>|B C|$. Zij $D$ het midden van $A C$. Zij $E$ het snijpunt van de bissectrice van $\\angle A B C$ met de lijn $A C$. Zij $F$ op $B E$ zo dat $C F$ loodrecht op $B E$ staat. Zij verder $G$ het snijpunt van $C F$ en $B D$.\nBewijs dat $D F$ het lijnstuk $E G$ doormidden snijdt.", "solution": "Merk op dat vanwege de voorwaarde $|A B|>|B C|$ de punten $D$ en $E$ verschillend zijn en de volgorde van punten op de lijn $A C$ is: $A, D, E, C$. Verder is $\\angle B C A>\\angle C A B$, dus $\\angle B C A+\\frac{1}{2} \\angle A B C>90^{\\circ}$, waaruit volgt dat $F$ op het inwendige van $B E$ ligt. Daarmee ligt ook $G$ op het inwendige van $B D$.\nZij nu $K$ het snijpunt van $C F$ en $A B$. Omdat $B E$ de bissectrice van $\\angle A B C$ is, is $\\angle K B F=$ $\\angle F B C$. Verder geldt $\\angle B F K=90^{\\circ}=\\angle C F B$ en $|B F|=|B F|$, dus wegens (HZH) geldt $\\triangle K B F \\sim \\triangle C B F$. Hieruit volgt $|B K|=|B C|$ en $|K F|=|C F|$. In het bijzonder is $F$ het midden van $C K$. Omdat $D$ het midden van $A C$ is, betekent dit dat $D F$ een middenparallel is in $\\triangle A K C$, dus $D F \\| A K$ en $|D F|=\\frac{1}{2}|A K|$.\nUit $D F \\| A B$ volgt $\\triangle K G B \\sim \\triangle F G D$ (hh), dus\n\n$$\n\\frac{|D G|}{|B G|}=\\frac{|F D|}{|K B|}=\\frac{\\frac{1}{2}|A K|}{|K B|}=\\frac{\\frac{1}{2}(|A B|-|K B|)}{|K B|}=\\frac{\\frac{1}{2}(|A B|-|B C|)}{|B C|} .\n$$\n\nDe bissectricestelling zegt dat $\\frac{|A E|}{|C E|}=\\frac{|A B|}{|C B|}$, oftewel $\\frac{|A C|-|C E|}{|C E|}=\\frac{|A B|}{|B C|}$. Dit geeft $|B C| \\cdot(|A C|-$ $|C E|)=|A B| \\cdot|C E|$, dus $|B C| \\cdot|A C|=|C E| \\cdot(|A B|+|B C|)$, dus\n\n$$\n|C E|=\\frac{|B C| \\cdot|A C|}{|A B|+|B C|}\n$$\n\nWe berekenen nu verder\n\n$$\n\\begin{gathered}\n|D E|=|D C|-|C E|=\\frac{1}{2}|A C|-|C E|=\\frac{\\frac{1}{2}|A C| \\cdot(|A B|+|B C|)-|A C| \\cdot|B C|}{|A B|+|B C|} \\\\\n=\\frac{\\frac{1}{2}|A C| \\cdot(|A B|-|B C|)}{|A B|+|B C|} .\n\\end{gathered}\n$$\n\nDus\n\n$$\n\\frac{|D E|}{|C E|}=\\frac{\\frac{\\frac{1}{2}|A C| \\cdot(|A B|-|B C|)}{|A B|+|B C|}}{\\frac{|B C| \\cdot|A C|}{|A B|+|B C|}}=\\frac{\\frac{1}{2}(|A B|-|B C|)}{|B C|}\n$$\n\nGecombineerd met (6) zien we nu dat\n\n$$\n\\frac{|D E|}{|C E|}=\\frac{|D G|}{|B G|}\n$$\n\nIn driehoek $D B C$ betekent dit dat $E G \\| B C$. Noem $S$ nu het snijpunt van $D F$ en $E G$. Dan weten we\n\n$$\n\\angle S G F=\\angle E G F=\\angle F C B=\\angle F K B=\\angle G F D=\\angle G F S,\n$$\n\ndus $\\triangle S F G$ is gelijkbenig met $|S F|=|S G|$. Verder is\n\n$$\n\\angle S E F=\\angle G E F=90^{\\circ}-\\angle E G F=90^{\\circ}-\\angle G F S=\\angle S F E,\n$$\n\ndus ook $\\triangle S F E$ is gelijkbenig met $|S F|=|S E|$. We concluderen dat $|S G|=|S E|$, dus dat $S$ het midden van $E G$ is.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 8 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Zij $A B C$ een driehoek met $|A B|>|B C|$. Zij $D$ het midden van $A C$. Zij $E$ het snijpunt van de bissectrice van $\\angle A B C$ met de lijn $A C$. Zij $F$ op $B E$ zo dat $C F$ loodrecht op $B E$ staat. Zij verder $G$ het snijpunt van $C F$ en $B D$.\nBewijs dat $D F$ het lijnstuk $E G$ doormidden snijdt.", "solution": "Net als in bovenstaande oplossing leiden we af dat $D F \\| A K$. Daarmee wordt $D F$ ook de middenparallel van $\\triangle A B C$, dus het snijpunt $H$ van $D F$ en $B C$ is het midden van $B C$. Zij nu $G^{\\prime}$ het snijpunt van $C F$ en de lijn door $E$ evenwijdig aan $C B$. Zij $T$ het snijpunt van $D H$ en $E G^{\\prime}$. Omdat $E G^{\\prime} \\| C B$, geldt $\\triangle E G^{\\prime} F \\sim \\triangle B C F$ en ook $\\triangle E T F \\sim \\triangle B H F$. Dus\n\n$$\n\\frac{|E T|}{\\left|E G^{\\prime}\\right|}=\\frac{|E T|}{|E F|} \\cdot \\frac{|E F|}{\\left|E G^{\\prime}\\right|}=\\frac{|B H|}{|B F|} \\cdot \\frac{|B F|}{|B C|}=\\frac{|B H|}{|B C|}=\\frac{1}{2} .\n$$\n\nWe zien dat $T$ het midden is van $E G^{\\prime}$. Als we nu bewijzen dat $G^{\\prime}=G$, dan weten we direct dat $D F$ het lijnstuk $E G$ doormidden snijdt en zijn we dus klaar. Vanwege $E G^{\\prime} \\| C B$ geldt $\\triangle D T E \\sim \\triangle D H C$, dus\n\n$$\n\\frac{\\left|E G^{\\prime}\\right|}{|C B|}=\\frac{2|E T|}{2|C H|}=\\frac{|E T|}{|C H|}=\\frac{|E D|}{|C D|}\n$$\n\nMet (zhz) zien we nu dat $\\triangle E D G^{\\prime} \\sim \\triangle C D B$. Hieruit volgt $\\angle E D G^{\\prime}=\\angle C D B$, dus $G^{\\prime}$ ligt op de lijn $D B$. Dus $G^{\\prime}$ is het snijpunt van $D B$ en $C F$ en daarmee gelijk aan $G$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
| 9 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Zij $A B C$ een driehoek met $|A B|>|B C|$. Zij $D$ het midden van $A C$. Zij $E$ het snijpunt van de bissectrice van $\\angle A B C$ met de lijn $A C$. Zij $F$ op $B E$ zo dat $C F$ loodrecht op $B E$ staat. Zij verder $G$ het snijpunt van $C F$ en $B D$.\nBewijs dat $D F$ het lijnstuk $E G$ doormidden snijdt.", "solution": "De middelloodlijn van $A C$ (de lijn door $D$ loodrecht op $A C$ ) snijdt de bissectrice van hoek $\\angle A B C$ op de omgeschreven cirkel van $\\triangle A B C$, want ze snijden allebei de boog $A C$ in twee gelijke stukken. Noem dit snijpunt $S$. Omdat $\\angle C F S$ en $\\angle C D S$ allebei $90^{\\circ}$ zijn, is $C F D S$ een koordenvierhoek volgens Thales. Hiermee vinden we $\\angle F D C=$ $\\angle F S C=\\angle B S C=\\angle B A C$, dus $D F \\| A B$ wegens F-hoeken.\nNoem het midden van zijde $B C$ nu $H$. Omdat $D H$ een middenparallel is in driehoek $A B C$ is $D H$ ook evenwijdig aan $A B$. Dus $D F$ en $D H$ zijn dezelfde lijn, oftewel: $D, F$ en $H$ liggen op één lijn. Nu geeft de stelling van Ceva op $\\triangle B C D$ met de punten $E, G$ en $H$, dat\n\n$$\n1=\\frac{|C E|}{|E D|} \\frac{|D G|}{|G B|} \\frac{|B H|}{|H C|}=\\frac{|C E|}{|E D|} \\frac{|D G|}{|G B|}\n$$\n\nDaaruit volgt $\\frac{|D G|}{|G B|}=\\frac{|D E|}{|E C|}$. Wegens evenredigheid leiden we hieruit af dat $G E$ evenwijdig is aan $B C$. Omdat $D F$ het lijnstuk $B C$ midden doorsnijdt, snijdt zij dus ook $G E$ middendoor.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing III."}
|
Dutch_TST/segmented/nl-2011-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "1", "tier": 1, "problem": "Laat $n \\geq 2$ en $k \\geq 1$ gehele getallen zijn. In een land zijn $n$ steden en tussen elk paar steden is een busverbinding in twee richtingen. Laat $A$ en $B$ twee verschillende steden zijn. Bewijs dat het aantal manieren waarop je van $A$ naar $B$ kunt reizen met precies $k$ bussen gelijk is aan\n\n$$\n\\frac{(n-1)^{k}-(-1)^{k}}{n}\n$$", "solution": "Zij $\\alpha(k)$ het aantal manieren om van stad $A$ naar stad $B \\neq A$ te reizen met $k$ bussen. Zij $\\beta(k)$ het aantal manieren om van stad $A$ naar stad $A$ te reizen met $k$ bussen. Als we beginnen in stad $A$ en daarna $k$ keer een bus nemen, dan kan dat op $(n-1)^{k}$ manieren. In $\\beta(k)$ van de gevallen komen we uit bij stad $A$ en in $(n-1) \\alpha(k)$ van de gevallen bij een andere stad dan $A$. Dus\n\n$$\n(n-1) \\alpha(k)+\\beta(k)=(n-1)^{k} .\n$$\n\nNeem nu even $k \\geq 2$. Om van stad $A$ naar stad $A$ te reizen met precies $k$ bussen, nemen we een bus van $A$ naar een willekeurige stad (dit kan op $(n-1)$ manieren); vervolgens moeten we van een stad ongelijk aan $A$ naar stad $A$ reizen met $k-1$ bussen, wat kan op $\\alpha(k-1)$ manieren. Dus\n\n$$\n\\beta(k)=(n-1) \\alpha(k-1) \\quad \\text { voor } k \\geq 2\n$$\n\nWe vullen nu deze uitdrukking voor $\\beta(k)$ in in (1). Hiermee vinden we voor $k \\geq 2$ dat\n\n$$\n(n-1) \\alpha(k)+(n-1) \\alpha(k-1)=(n-1)^{k}\n$$\n\nen dus\n\n$$\n\\alpha(k)=(n-1)^{k-1}-\\alpha(k-1) .\n$$\n\nWe gaan nu met inductie naar $k$ bewijzen dat voor $n \\geq 2$ en $k \\geq 1$ geldt\n\n$$\n\\alpha(k)=\\frac{(n-1)^{k}-(-1)^{k}}{n} .\n$$\n\nVoor $k=1$ staat hier $\\alpha(1)=\\frac{(n-1)+1}{n}=1$ en dat klopt, omdat er precies één manier is om van stad $A$ naar stad $B \\neq A$ te reizen met één bus. Zij nu $m \\geq 1$ geheel en stel nu dat we de uitdrukking voor $\\alpha(k)$ bewezen hebben voor $k=m$. Dan geldt, gebruikmakend van (3), voor $k=m+1 \\geq 2$ dat\n\n$$\n\\begin{aligned}\n& \\alpha(m+1)=(n-1)^{m}-\\alpha(m)=(n-1)^{m}-\\frac{(n-1)^{m}-(-1)^{m}}{n} \\\\\n& =\\frac{n(n-1)^{m}-(n-1)^{m}+(-1)^{m}}{n}=\\frac{(n-1)^{m+1}-(-1)^{m+1}}{n}\n\\end{aligned}\n$$\n\nen dat is precies de uitdrukking die we wilden bewijzen voor $k=m+1$. Dit voltooit de inductie.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ waarvoor geldt dat\n\n$$\nx f(x+x y)=x f(x)+f\\left(x^{2}\\right) f(y)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Invullen van $x=0$ en $y=0$ geeft $0=f(0)^{2}$, dus $f(0)=0$. Invullen van $x=1$ en $y=-1$ geeft $f(0)=f(1)+f(1) f(-1)$, dus $0=f(1)(1+f(-1))$, dus $f(1)=0$ of $f(-1)=-1$. Invullen van $x=-1$ geeft\n\n$$\n-f(-1-y)=-f(-1)+f(1) f(y) \\quad \\text { voor alle } y \\in \\mathbb{R}\n$$\n\nStel dat $f(1)=0$, dan staat hier $-f(-1-y)=-f(-1)$ en omdat $-1-y$ alle waarden in $\\mathbb{R}$ kan aannemen, betekent dit dat $f$ constant is. Omdat $f(0)=0$, moet dan wel gelden $f(x)=0$ voor alle $x$. Het is duidelijk dat deze functie voldoet aan de oorspronkelijke vergelijking. We hebben dus de eerste oplossing gevonden: $f(x)=0$ voor alle $x \\in \\mathbb{R}$.\nNeem nu verder aan dat $f(1) \\neq 0$, zodat $f(-1)=-1$. Vul nu $y=-1$ in in (4), dan krijgen we $-f(0)=-f(-1)+f(1) f(-1)$, dus $0=1-f(1)$, dus $f(1)=1$. Invullen van $x=1$ in de oorspronkelijke vergelijking geeft\n\n$$\nf(1+y)=1+f(y) \\quad \\text { voor alle } y \\in \\mathbb{R}\n$$\n\nVerder geeft $y=-1$ in de oorspronkelijke vergelijking dat $x f(0)=x f(x)-f\\left(x^{2}\\right)$, dus\n\n$$\nx f(x)=f\\left(x^{2}\\right) \\quad \\text { voor alle } x \\in \\mathbb{R}\n$$\n\nDe oorspronkelijke vergelijking kunnen we nu schrijven als\n\n$$\nx f(x+x y)=x f(x)+x f(x) f(y)=x f(x)(1+f(y))\n$$\n\nAls $x \\neq 0$, kunnen we links en rechts delen door $x$ en geeft het toepassen van (5)\n\n$$\nf(x+x y)=f(x) f(1+y) \\quad \\text { voor } x \\neq 0\n$$\n\nMerk op dat dit ook waar is voor $x=0$. Noem nu $z=1+y$. Omdat dit alle waarden in $\\mathbb{R}$ kan aannemen, krijgen we\n\n$$\nf(x z)=f(x) f(z) \\quad \\text { voor alle } x, z \\in \\mathbb{R}\n$$\n\nAls we dit toepassen op (6), vinden we\n\n$$\nx f(x)=f\\left(x^{2}\\right)=f(x) f(x),\n$$\n\ndus voor alle $x$ geldt $f(x)=0$ of $f(x)=x$. Stel nu dat er een $x \\neq 0$ is met $f(x)=0$, dan geldt\n\n$$\n1=f(1)=f\\left(x \\cdot \\frac{1}{x}\\right)=f(x) f\\left(\\frac{1}{x}\\right)=0,\n$$\n\ntegenspraak. Dus voor alle $x \\neq 0$ geldt $f(x)=x$. Ook voor $x=0$ is dit waar. Invullen in de oorspronkelijke vergelijking laat zien dat dit een oplossing is. De twee functies die voldoen zijn dus $f(x)=0$ voor alle $x \\in \\mathbb{R}$ en $f(x)=x$ voor alle $x \\in \\mathbb{R}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Laat $\\Gamma_{1}$ en $\\Gamma_{2}$ twee snijdende cirkels met middelpunten respectievelijk $O_{1}$ en $O_{2}$ zijn, zodat $\\Gamma_{2}$ het lijnstuk $O_{1} O_{2}$ snijdt in een punt $A$. De snijpunten van $\\Gamma_{1}$ en $\\Gamma_{2}$ zijn $C$ en $D$. De lijn $A D$ snijdt $\\Gamma_{1}$ een tweede keer in $S$. De lijn $C S$ snijdt $O_{1} O_{2}$ in $F$. Laat $\\Gamma_{3}$ de omgeschreven cirkel van driehoek $A D F$ zijn. Noem $E$ het tweede snijpunt van $\\Gamma_{1}$ en $\\Gamma_{3}$.\nBewijs dat $O_{1} E$ raakt aan $\\Gamma_{3}$.", "solution": "We gaan $\\angle O_{1} E A$ berekenen. Omdat driehoek $O_{1} E D$ gelijkbenig is met top $O_{1}$ en omdat $A E F D$ een koordenvierhoek is, geldt\n\n$$\n\\angle O_{1} E A=\\angle O_{1} E D-\\angle A E D=90^{\\circ}-\\frac{1}{2} \\angle E O_{1} D-\\angle A F D .\n$$\n\nVerder is\n\n$$\n\\begin{aligned}\n\\frac{1}{2} \\angle E O_{1} D & =\\angle E S D \\quad \\text { middelpunts-omtrekshoekstelling op } \\Gamma_{1} \\\\\n& =\\angle C S D-\\angle C S E \\\\\n& =\\angle C S D-\\angle C D E \\quad \\text { omtrekshoekstelling in koordenvierhoek } C S D E \\\\\n& =\\angle F C D-\\angle S D C-\\angle C D E \\quad \\text { buitenhoekstelling in } \\triangle C S D \\\\\n& =\\angle F C D-\\angle S D E \\\\\n& =\\angle F C D-\\angle A D E \\quad \\\\\n& =\\angle F C D-\\angle A F E . \\quad \\text { omtrekshoekstelling in koordenvierhoek } A E F D\n\\end{aligned}\n$$\n\nHieruit volgt nu samen met (7) dat\n\n$$\n\\angle O_{1} E A=90^{\\circ}-\\angle F C D+\\angle A F E-\\angle A F D\n$$\n\nDe lijn $O_{1} O_{2}$ staat loodrecht $C D$ en deelt het lijnstuk $C D$ middendoor, dus het is de middelloodlijn van $C D$. Dus $F$ ligt op de middelloodlijn van $C D$, waaruit volgt dat driehoek $C D F$ gelijkbenig is met top $F$. Dus\n\n$$\n\\angle F C D=90^{\\circ}-\\frac{1}{2} \\angle C F D=90^{\\circ}-\\angle A F D .\n$$\n\nGecombineerd met (8) geeft dit\n\n$$\n\\angle O_{1} E A=\\angle A F D+\\angle A F E-\\angle A F D=\\angle A F E\n$$\n\nNu volgt met de raaklijnomtrekshoekstelling op $\\Gamma_{3}$ dat $O_{1} E$ raakt aan $\\Gamma_{3}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Laat $\\Gamma_{1}$ en $\\Gamma_{2}$ twee snijdende cirkels met middelpunten respectievelijk $O_{1}$ en $O_{2}$ zijn, zodat $\\Gamma_{2}$ het lijnstuk $O_{1} O_{2}$ snijdt in een punt $A$. De snijpunten van $\\Gamma_{1}$ en $\\Gamma_{2}$ zijn $C$ en $D$. De lijn $A D$ snijdt $\\Gamma_{1}$ een tweede keer in $S$. De lijn $C S$ snijdt $O_{1} O_{2}$ in $F$. Laat $\\Gamma_{3}$ de omgeschreven cirkel van driehoek $A D F$ zijn. Noem $E$ het tweede snijpunt van $\\Gamma_{1}$ en $\\Gamma_{3}$.\nBewijs dat $O_{1} E$ raakt aan $\\Gamma_{3}$.", "solution": "Het snijpunt van $O_{1} O_{2}$ met de boog $S D$ van $\\Gamma_{1}$ waar $C$ op ligt, noemen we $T$. Omdat $A$ in het inwendige van $\\Gamma_{1}$ ligt, weten we nu\n\n$$\n\\begin{array}{rlr}\n\\angle O_{1} A S & =\\angle A T S+\\angle T S A & \\quad \\text { buitenhoekstelling in } \\triangle A T S \\\\\n& =\\angle O_{1} T S+\\angle T S D & \\\\\n& =\\angle T S O_{1}+\\angle T S D \\quad \\triangle O_{1} S T \\text { is gelijkbenig met tophoek } O_{1}\n\\end{array}\n$$\n\nDe lijn $O_{1} O_{2}$ staat loodrecht $C D$ en deelt het lijnstuk $C D$ middendoor, dus het is de middelloodlijn van $C D$. Dus $T$ ligt op de middelloodlijn van $C D$, waaruit volgt dat de bogen $T C$ en $T D$ even groot zijn. Dus volgens de omtrekshoekstelling is $\\angle T S D=\\angle C S T$. Dus\n\n$$\n\\angle O_{1} A S=\\angle T S O_{1}+\\angle T S D=\\angle T S O_{1}+\\angle C S T=\\angle C S O_{1}=\\angle F S O_{1}\n$$\n\nDit betekent dat $\\triangle O_{1} A S \\sim \\triangle O_{1} S F$ (hh). Hieruit volgt\n\n$$\n\\frac{\\left|O_{1} A\\right|}{\\left|O_{1} S\\right|}=\\frac{\\left|O_{1} S\\right|}{\\left|O_{1} F\\right|},\n$$\n\ndus $\\left|O_{1} A\\right| \\cdot\\left|O_{1} F\\right|=\\left|O_{1} S\\right|^{2}=\\left|O_{1} E\\right|^{2}$. Omdat $A$ en $F$ aan dezelfde kant van $O_{1}$ liggen, geldt zelfs $O_{1} A \\cdot O_{1} F=O_{1} E^{2}$. Met de machtstelling zien we nu dat $O_{1} E$ raakt aan de omgeschreven cirkel van $\\triangle A F E$ en dat is $\\Gamma_{3}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Bewijs dat er geen oneindige rij priemgetallen $p_{0}, p_{1}, p_{2}, \\ldots$ bestaat met de eigenschap dat voor alle positieve gehele $k$ geldt:\n\n$$\np_{k}=2 p_{k-1}+1 \\quad \\text { of } \\quad p_{k}=2 p_{k-1}-1\n$$", "solution": "Stel dat er zo'n oneindige rij bestaat. Door eventueel de eerste twee elementen weg te laten, kunnen we zorgen dat het eerste priemgetal in de rij minstens 5 is. We nemen dus zonder verlies van algemeenheid aan dat $p_{0} \\geq 5$. Dan weten we dat $p_{0} \\not \\equiv 0 \\bmod 3$.\nStel dat $p_{0} \\equiv 1 \\bmod 3$. We bewijzen dan met inductie naar $k$ dat voor alle positieve gehele $k$ geldt: $p_{k} \\equiv 1 \\bmod 3$ en $p_{k}=2 p_{k-1}-1$. Stel namelijk dat $k \\geq 1$ en $p_{k-1} \\equiv 1 \\bmod 3$. Dan is $2 p_{k-1} \\equiv 2 \\bmod 3$, dus $2 p_{k-1}+1$ is deelbaar door 3 . Omdat $p_{k}$ een priemgetal groter dan 3 moet zijn, geldt dus $p_{k}=2 p_{k-1}-1$ en $p_{k} \\equiv 2-1 \\equiv 1 \\bmod 3$. Dit voltooit de inductie.\nAls juist $p_{0} \\equiv 2 \\bmod 3$, dan kunnen we geheel analoog bewijzen dat $p_{k} \\equiv 2 \\bmod 3$ en $p_{k}=2 p_{k-1}+1$ voor alle positieve gehele $k$.\nWe kunnen nu een directe formule van de rij opstellen. Als $p_{0} \\equiv 1 \\bmod 3$, dan krijgen we $p_{k}=\\left(p_{0}-1\\right) 2^{k}+1$ voor alle $k \\geq 0$. Als $p_{0} \\equiv 2 \\bmod 3$, dan krijgen we $p_{k}=\\left(p_{0}+1\\right) 2^{k}-1$. We kunnen deze formules weer simpel met inductie bewijzen.\nVolgens de kleine stelling van Fermat geldt $2^{p_{0}-1} \\equiv 1 \\bmod p_{0}$, dus ook $\\left(-p_{0}+1\\right) 2^{p_{0}-1} \\equiv 1$ $\\bmod p_{0}$ en $\\left(p_{0}+1\\right) 2^{p_{0}-1} \\equiv 1 \\bmod p_{0}$. Hieruit volgt $p_{0} \\mid\\left(p_{0}-1\\right) 2^{p_{0}-1}+1$ en $p_{0} \\mid$ $\\left(p_{0}+1\\right) 2^{p_{0}-1}-1$. We zien dat $p_{0}$ altijd een deler is van $p_{p_{0}-1}$. Omdat ook duidelijk is dat $p_{p_{0}-1}$ groter is dan $p_{0}$, volgt hieruit dat $p_{p_{0}-1}$ geen priemgetal is. Tegenspraak.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Vind alle drietallen $(a, b, c)$ van positieve gehele getallen met $a+b+c=10$ zodat er $a$ rode, $b$ blauwe en $c$ groene punten (allemaal verschillend) in het vlak bestaan met de volgende eigenschappen:\n\n- voor elk rood punt en elk blauw punt bekijken we de afstand tussen deze twee punten; de som van al deze afstanden is 37 ;\n- voor elk groen punt en elk rood punt bekijken we de afstand tussen deze twee punten; de som van al deze afstanden is 30 ;\n- voor elk blauw punt en elk groen punt bekijken we de afstand tussen deze twee punten; de som van al deze afstanden is 1 ;", "solution": "We maken driehoeken bestaande uit een blauw, een rood en een groen punt. Deze driehoeken mogen ook gedegenereerd zijn. In elk van de driehoeken geldt de (nietstrikte) driehoeksongelijkheid: de afstand tussen het blauwe en het rode punt is hoogstens gelijk aan de som van de afstanden tussen het blauwe en het groene en tussen het rode en het groene punt. We tellen al deze driehoeksongelijkheden bij elkaar op (één voor elke driehoek die we kunnen vormen met een blauw, een rood en een groen punt). We tellen nu elke afstand tussen een rood en een blauw punt $c$ keer (want met een vast gekozen blauw en rood punt kun je nog $c$ punten kiezen als derde, groene hoekpunt), elke afstand tussen een groen en een rood punt $b$ keer en elke afstand tussen een blaww en een groen punt $a$ keer. We krijgen dus\n\n$$\n37 c \\leq 30 b+a\n$$\n\nOmdat $a+b+c=10$, volgt hieruit $37 c \\leq 30 b+(10-b-c)=10+29 b-c$, dus $38 c \\leq 10+29 b$. Oftewel\n\n$$\n\\frac{38 c-10}{29} \\leq b\n$$\n\nWe kunnen de driehoeksongelijkheid ook anders toepassen: de afstand tussen het groene en het rode punt is hoogstens gelijk aan de som van de afstanden tussen het rode en het blauwe en tussen het blauwe en het groene punt. Als we al deze ongelijkheden bij elkaar optellen, krijgen we\n\n$$\n30 b \\leq 37 c+a\n$$\n\nDit geeft nu $30 b \\leq 37 c+(10-b-c)=10+36 c-b$, dus $31 b \\leq 10+36 c$, oftewel\n\n$$\nb \\leq \\frac{10+36 c}{31}\n$$\n\nCombineren van (9) en (10) geeft\n\n$$\n\\frac{38 c-10}{29} \\leq \\frac{10+36 c}{31}\n$$\n\ndus $31(38 c-10) \\leq 29(10+36 c)$. Uitwerken geeft $134 c \\leq 600$, dus $c \\leq 4$. We lopen nu één voor één de mogelijkheden voor $c$ af.\n\nStel $c=1$. Dan geeft (10) dat $b \\leq \\frac{46}{31}<2$, waaruit volgt $b=1$. We krijgen nu $(a, b, c)=$ $(8,1,1)$.\nStel $c=2$. Dan volgt uit (9) en (10) dat $2<\\frac{66}{29} \\leq b \\leq \\frac{82}{31}<3$, dus er is geen gehele $b$ die voldoet.\nStel $c=3$. Dan volgt uit (9) en (10) dat $3<\\frac{104}{29} \\leq b \\leq \\frac{118}{31}<4$, dus er is geen gehele $b$ die voldoet.\nStel $c=4$. Dan volgt uit (9) en (10) dat $4<\\frac{142}{29} \\leq b \\leq \\frac{154}{31}<5$, dus er is geen gehele $b$ die voldoet.\nHet enige drietal dat mogelijk zou kunnen voldoen is dus $(8,1,1)$. We laten nu zien dat we daadwerkelijk 8 rode punten, 1 blauw punt en 1 groen punt in het vlak kunnen kiezen zodat aan alle voorwaarden voldaan wordt. We gebruik een standaard assenstelsel. Kies voor het blauwe punt $(0,0)$ en voor het groene punt $(1,0)$. Kies rode punten $(i, 0)$ met $2 \\leq i \\leq 8$. Kies bovendien nog een rood punt zo dat dat punt samen met het groene en het blauwe punt een gelijkbenige driehoek vormt met twee zijden van lengte 2. De som van de afstanden tussen rode punten en het blauwe punt is nu $2+2+3+\\cdots+8=37$. De som van de afstanden tussen rode punten en het groene punt is $2+1+2+\\cdots+7=30$. De afstand tussen het blauwe punt en het groene punt is 1 .\nWe concluderen dat de enige oplossing $(8,1,1)$ is.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2012-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Bestaan er kwadratische polynomen $P(x)$ en $Q(x)$ met reële coëfficiënten zodat het polynoom $P(Q(x))$ als nulpunten precies $x=2, x=3, x=5$ en $x=7$ heeft?", "solution": "Stel dat zulke polynomen bestaan en schrijf $Q(x)=a x^{2}+b x+c$. Als we 2, 3, 5 en 7 in $Q$ stoppen, moeten er precies de (hoogstens) twee nulpunten van $P$ uitkomen. Omdat er niet meer dan twee keer dezelfde waarde uit $Q(x)$ kan komen (want $Q$ is kwadratisch) krijgen we dus twee verschillende waarden elk precies twee keer.\nStel nu $Q(n)=Q(m)$ voor verschillende getallen $m$ en $n$. Dan geldt $a n^{2}+b n+c=$ $a m^{2}+b m+c$, dus $a\\left(n^{2}-m^{2}\\right)=b(m-n)$, dus $a(n+m)(n-m)=-b(n-m)$. Omdat $m-n \\neq 0$, volgt hieruit $a(n+m)=-b$, oftewel $n+m=\\frac{-b}{a}$.\nWe weten dat we in $2,3,5$ en 7 twee verschillende paren $(m, n)$ en $(k, l)$ kunnen vinden zodat $Q(m)=Q(n)$ en $Q(k)=Q(l)$. Er geldt dan dus $m+n=\\frac{-b}{a}=k+l$. We moeten dus de vier getallen $2,3,5$ en 7 op kunnen delen in twee paren die dezelfde som hebben. Dit is echter onmogelijk, aangezien $2+3+5+7=17$ oneven is. We concluderen dat er geen polynomen $P$ en $Q$ met de gevraagde eigenschappen bestaan.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek en zij $X$ een punt binnen de driehoek. De lijnen $X A$, $X B$ en $X C$ snijden de omgeschreven cirkel van $\\triangle A B C$ nogmaals in respectievelijk $P, Q$ en $R$. Zij $U$ een punt op de halfrechte $X P$ (d.w.z. op de lijn $X P$ zodat $P$ en $U$ aan dezelfde kant van $X$ liggen). De lijn door $U$ evenwijdig aan $A B$ snijdt $B Q$ in $V$. De lijn door $U$ evenwijdig aan $A C$ snijdt $C R$ in $W$.\nBewijs dat $Q, R, V$ en $W$ op één cirkel liggen.", "solution": "Omdat $A B$ en $U V$ evenwijdig zijn, geldt $\\triangle A B X \\sim \\triangle U V X$ (hh). Zo ook is $\\triangle A C X \\sim \\triangle U W X$. Uit deze gelijkvormigheden verkrijgen we de verhoudingen\n\n$$\n\\frac{|X A|}{|X B|}=\\frac{|X U|}{|X V|} \\quad \\text { en } \\quad \\frac{|X A|}{|X C|}=\\frac{|X U|}{|X W|}\n$$\n\nHieruit volgt\n\n$$\n\\frac{|X B|}{|X C|}=\\frac{|X B|}{|X A|} \\frac{|X A|}{|X C|}=\\frac{|X V|}{|X U|} \\frac{|X U|}{|X W|}=\\frac{|X V|}{|X W|}\n$$\n\nMet behulp van de machtstelling vanuit het punt $X$ op de koordenvierhoek $B C Q R$ volgt nu\n\n$$\n|X C| \\cdot|X R|=|X B| \\cdot|X Q|=\\frac{|X B|}{|X C|} \\cdot|X C| \\cdot|X Q|=\\frac{|X V|}{|X W|} \\cdot|X C| \\cdot|X Q|\n$$\n\ndus\n\n$$\n|X W| \\cdot|X R|=|X V| \\cdot|X Q| .\n$$\n\nUit de gegeven configuratie ( $X$ binnen de driehoek, $U$ en $P$ op de lijn $X P$ aan dezelfde kant van $X$ ) volgt dat $R$ en $W$ op de lijn $X C$ aan dezelfde kant van $X$ liggen, en ook $V$ en $Q$ op de lijn $X B$ liggen aan dezelfde kant van $X$. Dus geldt ook zonder absoluutstrepen: $X W \\cdot X R=X V \\cdot X Q$. De machtstelling zegt vervolgens dat dan $W, R, V$ en $Q$ op een cirkel liggen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek en zij $X$ een punt binnen de driehoek. De lijnen $X A$, $X B$ en $X C$ snijden de omgeschreven cirkel van $\\triangle A B C$ nogmaals in respectievelijk $P, Q$ en $R$. Zij $U$ een punt op de halfrechte $X P$ (d.w.z. op de lijn $X P$ zodat $P$ en $U$ aan dezelfde kant van $X$ liggen). De lijn door $U$ evenwijdig aan $A B$ snijdt $B Q$ in $V$. De lijn door $U$ evenwijdig aan $A C$ snijdt $C R$ in $W$.\nBewijs dat $Q, R, V$ en $W$ op één cirkel liggen.", "solution": "Omdat $A B$ en $U V$ evenwijdig zijn, geldt $\\triangle A B X \\sim \\triangle U V X$ (hh). Zo ook is $\\triangle A C X \\sim \\triangle U W X$. Met deze gelijkvormigheden kunnen we $\\frac{|X U|}{|X A|}$ op twee manieren uitdrukken:\n\n$$\n\\frac{|U V|}{|A B|}=\\frac{|X U|}{|X A|}=\\frac{|U W|}{|A C|}\n$$\n\nVerder volgt uit de evenwijdigheden ook\n\n$$\n\\angle V U W=\\angle V U A+\\angle A U W=\\angle B A U+\\angle U A C=\\angle B A C .\n$$\n\nNu zien we dat $\\triangle V U W \\sim \\triangle B A C$ (zhz). Hieruit volgt, samen met Z-hoeken (beide bij het tweede $=$-teken):\n\n$$\n\\angle W V B=\\angle W V U-\\angle B V U=\\angle C B A-\\angle V B A=\\angle C B V .\n$$\n\nBekijk nu de configuratie dat $V$ tussen $Q$ en $X$ ligt en $W$ tussen $X$ en $R$. Dan geldt\n\n$$\n\\angle C B V=\\angle C B Q=\\angle C R Q=\\angle W R Q,\n$$\n\ndus\n\n$$\n180^{\\circ}-\\angle W V Q=\\angle W V B=\\angle C B V=\\angle W R Q\n$$\n\nDit betekent dat $W V Q R$ een koordenvierhoek is.\nBij andere configuraties waarbij $V \\neq Q$ en $W \\neq R$ verloopt het bewijs analoog. Als $V=Q$ of $W=R$, dan zijn de vier punten $W, R, V$ en $Q$ er in feite maar drie (of nog minder), die dus zeker samen op een cirkel liggen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek en zij $X$ een punt binnen de driehoek. De lijnen $X A$, $X B$ en $X C$ snijden de omgeschreven cirkel van $\\triangle A B C$ nogmaals in respectievelijk $P, Q$ en $R$. Zij $U$ een punt op de halfrechte $X P$ (d.w.z. op de lijn $X P$ zodat $P$ en $U$ aan dezelfde kant van $X$ liggen). De lijn door $U$ evenwijdig aan $A B$ snijdt $B Q$ in $V$. De lijn door $U$ evenwijdig aan $A C$ snijdt $C R$ in $W$.\nBewijs dat $Q, R, V$ en $W$ op één cirkel liggen.", "solution": "Als $V=Q$ of $W=R$, dan zijn de vier punten $W, R$, $V$ en $Q$ er in feite maar drie (of nog minder), die dus zeker samen op een cirkel liggen. Bekijk nu de configuratie dat $U$ tussen $X$ en $P$ ligt, $V$ tussen $Q$ en $X$, en $W$ tussen $X$ en $R$. Het bewijs in andere configuraties gaat analoog, tenzij $U=P$. Dat geval behandelen we aan het eind nog even.\nWegens Z-hoeken geldt\n\n$$\n\\angle W U A=\\angle P A C=\\angle P R C=\\angle P R W .\n$$\n\nDus $\\angle P U W=180^{\\circ}-\\angle W U A=180^{\\circ}-\\angle P R W$, waaruit we concluderen dat $P U W R$ een koordenvierhoek is. Op een vergelijkbare manier kunnen we laten zien dat $P U V Q$ een koordenvierhoek is. Nu passen we de machtstelling toe vanuit het punt $X$ op beide koordenvierhoeken:\n\n$$\nX W \\cdot X R=X U \\cdot X P=X V \\cdot X Q\n$$\n\nNu zegt de machtstelling weer dat $W, R, V$ en $Q$ op een cirkel liggen.\nBekijk nu het geval dat $U=P$. Wegens Z-hoeken geldt\n\n$$\n\\angle W U A=\\angle U A C=\\angle U R C=\\angle U R W .\n$$\n\nBekijk de cirkel door $U, W$ en $R$. Daar is $\\angle U R W$ de omtrekshoek op koorde $U W$. Omdat $\\angle W U A$ even groot is, is dat blijkbaar de raaklijnhoek op die koorde, dus raakt $A U$ aan de cirkel. Daaruit volgt dat de macht van $X$ ten opzichte van deze cirkel gelijk is aan $X U^{2}$. Analoog is de macht van $X$ ten opzichte van de cirkel door $U, V$ en $Q$ ook gelijk aan $X U^{2}$. Dus\n\n$$\nX W \\cdot X R=X U^{2}=X V \\cdot X Q\n$$\n\nNu zegt de machtstelling weer dat $W, R, V$ en $Q$ op een cirkel liggen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 5 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Bepaal alle paren positieve gehele getallen $(x, y)$ waarvoor\n\n$$\nx^{3}+y^{3}=4\\left(x^{2} y+x y^{2}-5\\right) .\n$$", "solution": "We kunnen de vergelijking als volgt herschrijven:\n\n$$\n(x+y)\\left(x^{2}-x y+y^{2}\\right)=4 x y(x+y)-20\n$$\n\nNu is $x+y$ een deler van de linkerkant en van de eerste term rechts, dus ook van de tweede term rechts: $x+y \\mid 20$. Omdat $x+y \\geq 2$, geeft dit voor $x+y$ de mogelijkheden $2,4,5,10,20$. Als van $x$ en $y$ er precies één even en één oneven is, is de linkerkant van de vergelijking oneven en de rechterkant even, tegenspraak. Dus $x+y$ is even, waarmee $x+y=5$ afvalt. Als $x+y=2$, geldt $x=y=1$ en dan staat links iets positiefs en rechts iets negatiefs, dus deze mogelijkheid valt ook af.\nOm de andere mogelijkheden te proberen, schrijven we de vergelijking nog iets anders:\n\n$$\n(x+y)\\left((x+y)^{2}-3 x y\\right)=4 x y(x+y)-20\n$$\n\nAls $x+y=4$, staat er $4 \\cdot(16-3 x y)=16 x y-20$, dus $16-3 x y=4 x y-5$, dus $21=7 x y$, oftewel $x y=3$. Dus geldt $(x, y)=(3,1)$ of $(x, y)=(1,3)$. Allebei de paren voldoen.\nAls $x+y=10$, krijgen we $100-3 x y=4 x y-2$, dus $7 x y=102$. Maar 102 is niet deelbaar door 7 , dus dit kan niet.\nAls $x+y=20$, krijgen we $400-3 x y=4 x y-1$, dus $7 x y=401$. Maar 401 is niet deelbaar door 7 , dus dit kan niet.\nHiermee hebben we alle mogelijkheden gehad, dus we concluderen dat $(1,3)$ en $(3,1)$ de enige oplossingen zijn.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Bepaal alle paren positieve gehele getallen $(x, y)$ waarvoor\n\n$$\nx^{3}+y^{3}=4\\left(x^{2} y+x y^{2}-5\\right) .\n$$", "solution": "Er geldt $(x+y)^{3}=x^{3}+3 x^{2} y+3 x y^{2}+y^{3}$, dus uit de gegeven vergelijking volgt\n\n$$\n\\begin{aligned}\n(x+y)^{3} & =x^{3}+y^{3}+3 x^{2} y+3 x y^{2} \\\\\n& =4\\left(x^{2} y+x y^{2}-5\\right)+3 x^{2} y+3 x y^{2} \\\\\n& =7 x^{2} y+7 x y^{2}-20 \\\\\n& =7 x y(x+y)-20 .\n\\end{aligned}\n$$\n\nOmdat $x+y$ een deler is van $(x+y)^{3}$ en van $7 x y(x+y)$, is $x+y$ ook een deler van 20. Omdat $x+y \\geq 2$, geeft dit voor $x+y$ de mogelijkheden $2,4,5,10,20$.\nNu lezen we $(x+y)^{3}=7 x y(x+y)-20$ modulo 7 , dan krijgen we\n\n$$\n(x+y)^{3} \\equiv-20 \\equiv 1 \\quad \\bmod 7\n$$\n\nWe proberen voor alle mogelijkheden van $x+y$ of de derde macht congruent aan 1 modulo 7 is. Er geldt $5^{3} \\equiv(-2)^{3}=-8 \\equiv-1 \\bmod 7$, dus $x+y=5$ kan niet. Er geldt\n$10^{3} \\equiv 3^{3}=27 \\equiv-1 \\bmod 7$, dus $x+y=10$ kan ook niet. Er geldt $20^{3} \\equiv(-1)^{3}=-1$ $\\bmod 7$, dus ook $x+y=20$ kan niet. We houden alleen over $x+y=2$ en $x+y=4$.\nAls $x+y=2$, geldt $x=y=1$ en dan staat links iets positiefs en rechts iets negatiefs, dus deze mogelijkheid valt ook af. Als $x+y=4$, is $(x, y)$ gelijk aan $(1,3),(2,2)$ of $(3,1)$. Invullen laat zien dat alleen $(1,3)$ en $(3,1)$ voldoen.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Zij $A B C D$ een convexe vierhoek (d.w.z. alle binnenhoeken zijn kleiner dan $180^{\\circ}$ ), zodat er een punt $M$ op lijnstuk $A B$ en een punt $N$ op lijnstuk $B C$ bestaan met de eigenschap dat $A N$ de vierhoek in twee stukken van gelijke oppervlakte deelt, en $C M$ dat ook doet.\nBewijs dat $M N$ de diagonaal $B D$ middendoor deelt.", "solution": "Noteer de oppervlakte van veelhoek $\\mathcal{P}$ met $O(\\mathcal{P})$. Laat $S$ het snijpunt van $A N$ en $C M$ zijn. Er geldt\n$O(A S M)+O(S M B N)=O(A B N)=\\frac{1}{2} O(A B C D)=O(C B M)=O(C N S)+O(S M B N)$,\ndus $O(A S M)=O(C N S)$. Als we hier links en rechts $O(S M N)$ bij optellen, vinden we dat $O(M N A)=O(M N C)$. Deze driehoeken hebben dezelfde basis $M N$ en dus kennelijk ook dezelfde hoogte. Dat betekent dat de lijn $A C$ evenwijdig is aan de basis $M N$.\nLaat nu $X$ en $Y$ de snijpunten zijn van respectievelijk $A B$ en $B C$ met de lijn door $D$ die evenwijdig aan $A C$ (en dus ook evenwijdig aan $M N$ ) loopt. De driehoeken $A C Y$ en $A C D$ hebben dezelfde basis $A C$ en dezelfde hoogte, dus $O(A C Y)=O(A C D)$. Hieruit volgt\n\n$$\nO(A N Y)=O(A N C)+O(A C Y)=O(A N C)+O(A C D)=O(A N C D)=O(A N B)\n$$\n\nwaarbij de laatste gelijkheid geldt omdat $A N$ de vierhoek in twee stukken van gelijke oppervlakte deelt. De driehoeken $A N Y$ en $A N B$ hebben dezelfde hoogte, dus moeten ze ook dezelfde basis hebben. Dus $N$ is het midden van $B Y$.\nZo ook laten we zien dat $M$ het midden is van $B X$. We vinden dat $M N$ een middenparallel van $\\triangle B X Y$ is. Omdat $D$ op $X Y$ ligt, snijdt $M N$ het lijnstuk $B D$ middendoor.\n\nAlternatief bewijs voor $A C \\| M N$. Er geldt $O(A B N)=\\frac{1}{2} \\cdot|A B| \\cdot|B N| \\cdot \\sin \\angle B$ en $O(M B C)=\\frac{1}{2} \\cdot|M B| \\cdot|B C| \\cdot \\sin \\angle B$. Omdat ook geldt $O(A B N)=\\frac{1}{2} O(A B C D)=$ $O(M B C)$, zien we dat\n\n$$\n\\frac{1}{2} \\cdot|A B| \\cdot|B N| \\cdot \\sin \\angle B=\\frac{1}{2} \\cdot|M B| \\cdot|B C| \\cdot \\sin \\angle B\n$$\n\noftewel\n\n$$\n|A B| \\cdot|B N|=|M B| \\cdot|B C| .\n$$\n\nDat betekent\n\n$$\n\\frac{|M B|}{|B N|}=\\frac{|A B|}{|B C|}\n$$\n\nwaaruit met (zhz) volgt dat $\\triangle M B N \\sim \\triangle A B C$. Hieruit volgt dat $\\angle N M B=\\angle C A B$, dus zien we met F-hoeken dat $M N \\| A C$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 8 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Zij $A B C D$ een convexe vierhoek (d.w.z. alle binnenhoeken zijn kleiner dan $180^{\\circ}$ ), zodat er een punt $M$ op lijnstuk $A B$ en een punt $N$ op lijnstuk $B C$ bestaan met de eigenschap dat $A N$ de vierhoek in twee stukken van gelijke oppervlakte deelt, en $C M$ dat ook doet.\nBewijs dat $M N$ de diagonaal $B D$ middendoor deelt.", "solution": "Noteer de oppervlakte van veelhoek $\\mathcal{P}$ met $O(\\mathcal{P})$. Noem $T$ het midden van $B D$. Nu hebben driehoeken $C D T$ en $C B T$ een even lange basis, namelijk $|D T|=$ $|B T|$, en dezelfde hoogte, dus zijn hun oppervlaktes gelijk. Op dezelfde manier geldt $O(A D T)=O(A B T)$. Dus $O(A T C D)=\\frac{1}{2} O(A B C D)=O(A N C D)$. Merk nu op dat $T$ niet binnen driehoek $A C D$ kan liggen, want dan zou $O(A T C D)<O(A C D)$, terwijl juist $O(A N C D)>O(A C D)$. Dus\n\n$$\nO(A T C)=O(A T C D)-O(A C D)=O(A N C D)-O(A C D)=O(A N C)\n$$\n\nDriehoeken $A T C$ en $A N C$ hebben dezelfde basis $A C$, dus ze hebben gelijke hoogte. Dat betekent dat de lijn $N T$ evenwijdig is aan de basis $A C$.\nOp analoge manier laten we zien dat $M T$ evenwijdig is aan $A C$. Dus $N T \\| M T$ en daaruit volgt dat $M, N$ en $T$ op één lijn liggen. Dus $M N$ gaat door het midden van $B D$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 9 |
+
{"year": "2012", "problem_label": "5", "tier": 1, "problem": "Laat $A$ een verzameling van positieve gehele getallen zijn met de volgende eigenschap: voor elk positief geheel getal $n$ zit precies één van de drie getallen $n, 2 n$ en $3 n$ in $A$. Verder is gegeven dat $2 \\in A$. Bewijs dat $13824 \\notin A$.", "solution": "We bewijzen de volgende twee beweringen:\n(i) Als $m \\in A$ met $2 \\mid m$, dan $6 m \\in A$.\n(ii) Als $m \\in A$ met $3 \\mid m$, dan $\\frac{4}{3} m \\in A$.\n\nEerst bewering (i). Neem aan dat $m \\in A$ met $2 \\mid m$. Door $n=\\frac{m}{2}$ te kiezen, zien we dat $\\frac{m}{2}$ en $\\frac{3}{2} m$ niet in $A$ zitten. Door $n=m$ te kiezen, zien we dat $2 m$ en $3 m$ niet in $A$ zitten. Als we nu $n=\\frac{3}{2} m$ bekijken, dan blijkt $2 n=3 m$ niet in $A$ te zitten en $n=\\frac{3}{2} m$ zelf ook niet, dus $3 n=\\frac{9}{2} m$ wel. Met $n=\\frac{9}{2} m$ krijgen we nu dat $9 m \\notin A$. Ten slotte bekijken we $n=3 m$ : we weten dat $3 m \\notin A$ en $9 m \\notin A$, dus $6 m \\in A$.\nNu bewering (ii). Neem aan dat $m \\in A$ met $3 \\mid m$. Door $n=\\frac{m}{3}$ te kiezen, zien we dat $\\frac{m}{3}$ en $\\frac{2}{3} m$ niet in $A$ zitten. Door $n=m$ te kiezen, zien we dat $2 m$ niet in $A$ zit. Als we nu $n=\\frac{2}{3} m$ kiezen, hebben we dus dat $n$ en $3 n$ niet in $A$ zitten, dus zit $2 n=\\frac{4}{3} m$ dat wel. Dit bewijst bewering (ii).\nWe weten dat $2 \\in A$. Door herhaaldelijk beweringen (i) en (ii) toe te passen, kunnen we laten zien dat de volgende getallen ook allemaal in $A$ zitten:\n\n$$\n2 \\xrightarrow{\\text { (i) }} 2^{2} \\cdot 3 \\xrightarrow{\\text { (i) }} 2^{3} \\cdot 3^{2} \\xrightarrow{\\text { (i) }} 2^{4} \\cdot 3^{3} \\xrightarrow{\\text { (i) }} 2^{5} \\cdot 3^{4} \\xrightarrow{\\text { (ii) }} 2^{7} \\cdot 3^{3} \\xrightarrow{\\text { (ii) }} 2^{9} \\cdot 3^{2} .\n$$\n\nOmdat $2^{9} \\cdot 3^{2} \\in A$, geldt $2^{9} \\cdot 3^{3} \\notin A$. Aangezien $13824=2^{9} \\cdot 3^{3}$, is dit wat we moesten bewijzen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2012-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Zij $I$ het middelpunt van de ingeschreven cirkel van driehoek $A B C$. Een lijn door $I$ snijdt het inwendige van lijnstuk $A B$ in $M$ en het inwendige van lijnstuk $B C$ in $N$. We nemen aan dat $B M N$ een scherphoekige driehoek is. Laat nu $K$ en $L$ punten op lijnstuk $A C$ zijn zodat $\\angle B M I=\\angle I L A$ en $\\angle B N I=\\angle I K C$.\nBewijs dat $|A M|+|K L|+|C N|=|A C|$.", "solution": "Noem $D, E$ en $F$ de voetpunten van $I$ op respectievelijk $B C, C A$ en $A B$. Er geldt dat $N$ tussen $C$ en $D$ ligt: als namelijk $N$ tussen $D$ en $B$ ligt, dan is $\\angle B N I$ groter dan $\\angle B D I=90^{\\circ}$, maar gegeven is dat $\\triangle B M N$ scherphoekig is. Dus $N$ ligt tussen $C$ en $D$. Zo ook ligt $M$ tussen $A$ en $F$. Verder kan $L$ niet tussen $A$ en $E$ liggen, want dan zou $\\angle I L A>90^{\\circ}$, terwijl juist $\\angle I L A=\\angle B M I<90^{\\circ}$. Dus $L$ ligt tussen $E$ en $C$. Zo ook ligt $K$ tussen $A$ en $E$. Al met al ligt $E$ tussen $K$ en $L$.\nEr geldt\n\n$$\n|A C|=|A E|+|C E|=|A F|+|C D|=|A M|+|M F|+|C N|+|N D|,\n$$\n\nwaarbij het tweede =-teken geldt omdat de raaklijnstukjes aan de ingeschreven cirkel even lang zijn.\nVerder is $\\angle I K E=\\angle I K C=\\angle B N I=\\angle D N I$ en $\\angle K E I=90^{\\circ}=\\angle I D N$, dus $\\triangle I K E \\sim$ $\\triangle I N D$ (hh). Omdat lijnstukken $E I$ en $D I$ beide de straal van de ingeschreven cirkel zijn, zijn deze even lang, dus geldt zelfs $\\triangle I K E \\cong \\triangle I N D$. Hieruit volgt $|E K|=|N D|$.\nZo ook kunnen we afleiden dat $|E L|=|M F|$. We krijgen dus\n\n$$\n|A C|=|A M|+|M F|+|N D|+|C N|=|A M|+|E L|+|E K|+|C N|=|A M|+|K L|+|C N|\n$$", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Laat $a, b, c$ en $d$ positieve reële getallen zijn. Bewijs dat\n\n$$\n\\frac{a-b}{b+c}+\\frac{b-c}{c+d}+\\frac{c-d}{d+a}+\\frac{d-a}{a+b} \\geq 0\n$$", "solution": "Er geldt\n\n$$\n\\frac{a-b}{b+c}=\\frac{a-b+b+c}{b+c}-1=\\frac{a+c}{b+c}-1\n$$\n\nDoor hetzelfde met de andere drie breuken te doen en daarna de vier keer -1 naar de andere kant te halen, krijgen we dat we moeten bewijzen:\n\n$$\n\\frac{a+c}{b+c}+\\frac{b+d}{c+d}+\\frac{c+a}{d+a}+\\frac{d+b}{a+b} \\geq 4\n$$\n\nNu passen we de ongelijkheid van het harmonisch en rekenkundig gemiddelde toe op de twee positieve getallen $b+c$ en $d+a$ :\n\n$$\n\\frac{2}{\\frac{1}{b+c}+\\frac{1}{d+a}} \\leq \\frac{(b+c)+(d+a)}{2}\n$$\n\ndus\n\n$$\n\\frac{1}{b+c}+\\frac{1}{d+a} \\geq \\frac{4}{a+b+c+d}\n$$\n\nZo ook geldt\n\n$$\n\\frac{1}{c+d}+\\frac{1}{a+b} \\geq \\frac{4}{a+b+c+d}\n$$\n\nHiermee kunnen we de linkerkant van (1) afschatten:\n\n$$\n\\begin{aligned}\n\\frac{a+c}{b+c}+\\frac{b+d}{c+d}+\\frac{c+a}{d+a}+\\frac{d+b}{a+b} & =(a+c)\\left(\\frac{1}{b+c}+\\frac{1}{d+a}\\right)+(b+d)\\left(\\frac{1}{c+d}+\\frac{1}{a+b}\\right) \\\\\n& \\geq(a+c) \\cdot \\frac{4}{a+b+c+d}+(b+d) \\cdot \\frac{4}{a+b+c+d} \\\\\n& =4 \\cdot \\frac{(a+c)+(b+d)}{a+b+c+d} \\\\\n& =4 .\n\\end{aligned}\n$$\n\nDaarmee hebben we (1) bewezen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Bepaal alle positieve gehele getallen die niet geschreven kunnen worden als $\\frac{a}{b}+\\frac{a+1}{b+1}$ met $a, b$ positief en geheel.", "solution": "Er geldt\n\n$$\n\\frac{a}{b}+\\frac{a+1}{b+1}=\\frac{2 a b+a+b}{b(b+1)}\n$$\n\nNeem aan dat dit gelijk is aan een geheel getal $n$. Dan geldt $b \\mid 2 a b+a+b$ en $b+1 \\mid$ $2 a b+a+b$. Uit het eerste volgt $b \\mid a$ en dus ook $b \\mid a-b$. Uit het tweede volgt $b+1 \\mid(2 a b+a+b)-(b+1) \\cdot 2 a=-a+b$, dus ook $b+1 \\mid a-b$. Omdat de ggd van $b$ en $b+1$ gelijk aan 1 is, mogen we hieruit concluderen dat $b(b+1) \\mid a-b$. We kunnen $a$ dus schrijven als $a=b(b+1) \\cdot k+b$. Omdat $a$ positief moet zijn, moet $k$ hier een niet-negatief geheel getal zijn. Dit vullen we in:\n\n$$\n\\begin{aligned}\nn & =\\frac{2 a b+a+b}{b(b+1)} \\\\\n& =\\frac{2 \\cdot(b(b+1) \\cdot k+b) \\cdot b+(b(b+1) \\cdot k+b)+b}{b(b+1)} \\\\\n& =\\frac{b(b+1) \\cdot(2 k b+k)+2 b^{2}+2 b}{b(b+1)} \\\\\n& =(2 b+1) k+2 .\n\\end{aligned}\n$$\n\nDus $n$ is van de vorm $n=(2 b+1) k+2$. Hieruit zien we dat $n \\geq 2$ (want $k \\geq 0)$ en dat $n-2$ deelbaar moet zijn door een oneven getal groter dan 1 (namelijk $2 b+1 \\geq 3$ ).\nStel omgekeerd dat voor een getal $n$ geldt dat $n \\geq 2$ en $n-2$ is deelbaar door een oneven getal groter dan 1 , zeg door $2 b+1$ met $b \\geq 1$ en geheel. Dan is er dus een $k \\geq 0$ met $n=(2 b+1) k+2$. Kies nu $a=b(b+1) \\cdot k+b$, dan is $a$ positief geheel en geldt\n\n$$\n\\frac{a}{b}+\\frac{a+1}{b+1}=((b+1) k+1)+(b k+1)=(2 b+1) k+2=n\n$$\n\nWe kunnen nu concluderen dat de getallen die geschreven kunnen worden als $\\frac{a}{b}+\\frac{a+1}{b+1}$ met $a$ en $b$ positief geheel, precies de getallen $n \\geq 2$ zijn waarvoor geldt dat $n-2$ deelbaar is door een oneven getal groter dan 1. De getallen die niet zo geschreven kunnen worden, zijn dus precies 1 en de getallen $n \\geq 2$ waarvoor geldt dat $n-2$ geen oneven deler groter dan 1 heeft, oftewel waarvoor geldt dat $n-2$ een tweemacht $2^{m}$ met $m \\geq 0$ is.\nWe concluderen dat de getallen die niet geschreven kunnen worden als $\\frac{a}{b}+\\frac{a+1}{b+1}$, precies 1 en de getallen van de vorm $2^{m}+2$ met $m \\geq 0$ zijn.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Zij $n$ een positief geheel getal deelbaar door 4. We bekijken permutaties $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ van $(1,2, \\ldots, n)$ met de volgende eigenschap: voor elke $j$ geldt dat als we $i=a_{j}$ nemen, dan $a_{i}+j=n+1$. Bewijs dat er precies $\\frac{\\left(\\frac{1}{2} n\\right)!}{\\left(\\frac{1}{4} n\\right)!}$ zulke permutaties zijn.", "solution": "Zij $t \\in\\{1,2, \\ldots, n\\}$. Stel dat $a_{t}=t$, dan kunnen we $i=j=t$ kiezen en geldt dus $a_{t}+t=n+1$, dus $2 t=n+1$. Maar $n$ is deelbaar door 4 , dus $n+1$ is oneven. Tegenspraak. Stel nu dat $a_{t}=n+1-t$. Dan kunnen we $i=n+1-t$ en $j=t$ kiezen en geldt dus $a_{n+1-t}+t=n+1$, dus $a_{n+1-t}=n+1-t$. We hebben echter net gezien dat dit niet kan voorkomen.\nStel nu dat $a_{t}=u$ met $u \\neq t, u \\neq n+1-t$. Dan kunnen we $i=u$ en $j=t$ kiezen en geldt dus $a_{u}+t=n+1$, dus $a_{u}=n+1-t$. Vervolgens kunnen we $i=n+1-t$ en $j=u$ kiezen en geldt dus $a_{n+1-t}=n+1-u$. Nu kiezen we $i=n+1-u$ en $j=n+1-t$ en zien we dat $a_{n+1-u}=n+1-(n+1-t)=t$. Al met al hebben we dus:\n\n$$\n\\begin{aligned}\na_{t} & =u, \\\\\na_{u} & =n+1-t, \\\\\na_{n+1-t} & =n+1-u, \\\\\na_{n+1-u} & =t .\n\\end{aligned}\n$$\n\nOmdat $u \\neq t$ en $u \\neq n+1-t$, zijn de vier getallen aan de rechterkant allemaal verschillend. Verder zijn de vier getallen op te delen in twee paren van de vorm $(v, n+1-v)$. We hebben nu dus vier getallen waarvoor geldt dat op dezelfde posities in de permutatie dezelfde vier getallen staan, maar in een andere volgorde. We kunnen nu een $t^{\\prime}$ ongelijk aan één van deze vier getallen kiezen en een $u^{\\prime}$ met $a_{t^{\\prime}}=u^{\\prime}$ en op dezelfde manier een viertal vinden waar $t^{\\prime}$ in zit. Merk op dat nu $n+1-t^{\\prime}$ en $n+1-u^{\\prime}$ niet al in het eerste viertal kunnen zitten, want dan zouden $u^{\\prime}$ en $t^{\\prime}$ er ook al in zitten. Zo kunnen we doorgaan totdat alle $n$ getallen opgedeeld zijn in viertallen.\nWe zien dat we precies alle permutaties kunnen maken door het volgende recept toe te passen:\n\n- Kies het kleinste getal $k$ waarvoor $a_{k}$ nog niet bepaald is. Neem $a_{k}=u$ voor een zekere $u$ waarvan $a_{u}$ nog niet bepaald was en waarvoor geldt $u \\neq k, u \\neq n+1-k$. Dit bepaalt ook de waarden van $a_{u}, a_{n+1-u}$ en $a_{n+1-k}$.\n- Herhaal de vorige stap net zo vaak totdat alle waarden $a_{k}$ bepaald zijn.\n\nBij de eerste $k$ hebben we voor $u$ nog $n-2$ mogelijkheden. Bij de volgende stap hebben we nog $n-6$ mogelijkheden. Bij de stap daarna nog $n-10$, enzovoorts. Dus het aantal permutaties dat aan deze eigenschap voldoet, is\n\n$$\n2 \\cdot 6 \\cdot 10 \\cdot \\ldots \\cdot(n-10) \\cdot(n-6) \\cdot(n-2)\n$$\n\nSchrijf $n=4 m$, dan kunnen we dit schrijven als\n\n$$\n\\begin{gathered}\n2^{m} \\cdot 1 \\cdot 3 \\cdot 5 \\cdot \\ldots \\cdot(2 m-5) \\cdot(2 m-3) \\cdot(2 m-1)=2^{m} \\cdot \\frac{(2 m)!}{2 \\cdot 4 \\cdot \\ldots \\cdot(2 m)} \\\\\n=\\frac{(2 m)!}{1 \\cdot 2 \\cdot 3 \\cdot \\ldots \\cdot m}=\\frac{(2 m)!}{m!}=\\frac{\\left(\\frac{1}{2} n\\right)!}{\\left(\\frac{1}{4} n\\right)!}\n\\end{gathered}\n$$", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2012", "problem_label": "5", "tier": 1, "problem": "Zij $\\Gamma$ de omgeschreven cirkel van de scherphoekige driehoek $A B C$. De bissectrice van hoek $A B C$ snijdt $A C$ in het punt $B_{1}$ en de korte boog $A C$ van $\\Gamma$ in het punt $P$. De lijn door $B_{1}$ loodrecht op $B C$ snijdt de korte boog $B C$ van $\\Gamma$ in $K$. De lijn door $B$ loodrecht op $A K$ snijdt $A C$ in $L$. Bewijs dat $K, L$ en $P$ op een lijn liggen.", "solution": "Dat de bissectrice van hoek $A B C$ de korte boog $A C$ snijdt in $P$, betekent dat $P$ precies midden in deze boog $A C$ ligt. We moeten bewijzen dat $K L$ ook door $P$ gaat, dus dat $K L$ de boog $A C$ doormidden snijdt. Omdat $K$ op $\\Gamma$ ligt, betekent dat dat we moeten bewijzen dat $K L$ de bissectrice van $\\angle A K C$ is.\nNoem $S$ het snijpunt van $B_{1} K$ en $B C$ en noem $T$ het snijpunt van $B L$ en $A K$. Dan is $\\angle B S K=90^{\\circ}$ en $\\angle B T K=90^{\\circ}$, dus $B T S K$ is een koordenvierhoek. Hieruit volgt\n\n$$\n\\angle C B L=\\angle S B T=\\angle S K T=\\angle B_{1} K A .\n$$\n\nOmdat $A B K C$ een koordenvierhoek is, geldt $\\angle B_{1} A K=\\angle C A K=\\angle C B K$. Volgens de buitenhoekstelling is $\\angle L B_{1} K=\\angle B_{1} A K+\\angle B_{1} K A$, dus geldt met behulp van (2) dat\n\n$$\n\\angle L B_{1} K=\\angle B_{1} A K+\\angle B_{1} K A=\\angle C B K+\\angle C B L=\\angle L B K .\n$$\n\nHieruit volgt dat $L K B B_{1}$ een koordenvierhoek is, wat weer betekent dat $\\angle L B B_{1}=$ $\\angle L K B_{1}$. Als we hier gelijkheid (2) bij optellen, krijgen we\n\n$$\n\\angle C B B_{1}=\\angle C B L+\\angle L B B_{1}=\\angle B_{1} K A+\\angle L K B_{1}=\\angle L K A .\n$$\n\nDus\n\n$$\n\\angle L K A=\\angle C B B_{1}=\\frac{1}{2} \\angle C B A=\\frac{1}{2} \\angle C K A,\n$$\n\nwaarbij we nog gebruikt hebben dat $A B K C$ een koordenvierhoek is. Hieruit volgt dat $K L$ de bissectrice $\\operatorname{van} \\angle A K C$ is, wat we wilden bewijzen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2012-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Voor positieve gehele getallen $a$ en $b$ definiëren we $a \\ominus b=\\frac{a-b}{\\operatorname{ggd}(a, b)}$. Bewijs dat voor elk geheel getal $n>1$ geldt: $n$ is een priemmacht (d.w.z. dat $n$ te schrijven is als $n=p^{k}$ met $p$ een priemgetal en $k$ een positief geheel getal) dan en slechts dan als voor alle positieve gehele $m<n$ geldt dat $\\operatorname{ggd}(n, n \\ominus m)=1$.", "solution": "Stel eerst dat $n=p^{k}$ met $p$ priem en $k>0$. We moeten bewijzen dat $\\operatorname{ggd}(n, n \\ominus m)=1$ voor alle $m<n$. Dus bekijk een willekeurig positief geheel getal $m<n$. We schrijven $m=p^{l} s$ met $p \\nmid s$ en $0 \\leq l<k$. Nu is $\\operatorname{ggd}(n, m)=\\operatorname{ggd}\\left(p^{k}, p^{l} s\\right)=p^{l}$, dus\n\n$$\nn \\ominus m=\\frac{p^{k}-p^{l} s}{p^{l}}=p^{k-l}-s\n$$\n\nOmdat $k-l \\geq 1$, geldt $\\operatorname{ggd}\\left(p^{k-l}-s, p\\right)=\\operatorname{ggd}(-s, p)=1$ en dus $\\operatorname{ggd}(n, n \\ominus m)=$ $\\operatorname{ggd}\\left(p^{k}, p^{k-l}-s\\right)=1$.\nStel nu dat $n$ geen priemmacht is. We moeten bewijzen dat er een $m<n$ is waarvoor $\\operatorname{ggd}(n, n \\ominus m) \\neq 1$. Zij $q$ het kleinste priemgetal dat een deler is van $n$ en zij $t$ het positieve gehele getal zodat $q^{t} \\mid n$ en $q^{t+1} \\nmid n$. Omdat $n$ geen $q$-macht is, bevat $n$ nog een priemdeler $p>q$. Dus $\\frac{n}{q^{t}} \\geq p>q$, waaruit volgt $n>q^{t+1}$. Kies nu $m=n-q^{t+1}$. Dan geldt $\\operatorname{ggd}(n, m)=\\operatorname{ggd}\\left(n, q^{t+1}\\right)=q^{t}$, dus\n\n$$\nn \\ominus m=\\frac{n-\\left(n-q^{t+1}\\right)}{q^{t}}=\\frac{q^{t+1}}{q^{t}}=q .\n$$\n\nOmdat $q \\mid n$, geldt nu $\\operatorname{ggd}(n, n \\ominus m)=q>1$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "We hebben twee dozen met ballen. In de ene doos zitten $m$ ballen, in de andere doos $n$ ballen, waarbij $m, n>0$. Twee verschillende handelingen zijn toegestaan:\n(i) Verwijder uit beide dozen een gelijk aantal ballen.\n(ii) Vergroot het aantal ballen in één van de dozen met een factor $k$.\n\nIs het altijd mogelijk om alle ballen uit beide dozen te verwijderen met deze twee handelingen,\na) als $k=2$ ?\nb) als $k=3$ ?", "solution": "Bekijk eerst het geval $k=2$. We kunnen alle ballen uit beide dozen verwijderen op de volgende manier.\nAls $m=n$, dan halen we $m$ ballen uit beide dozen en zijn we klaar. Als $m \\neq n$, kunnen we zonder verlies van algemeenheid aannemen dat $m<n$. Als bovendien geldt $2 m<n$, dan verdubbelen we het aantal ballen in de eerste doos totdat we $m^{\\prime}$ ballen in de eerste doos hebben met de eigenschap dat $m^{\\prime}<n$ en $2 m^{\\prime} \\geq n$. We kunnen dus ook zonder verlies van algemeenheid aannemen dat $2 m \\geq n$. Verwijder nu uit beide dozen $2 m-n \\geq 0$ ballen. In de eerste doos blijven er $m-(2 m-n)=n-m>0$ ballen over; in de tweede doos blijven er $n-(2 m-n)=2 n-2 m=2(n-m)>0$ ballen over. Verdubbel nu het aantal ballen in de eerste doos en verwijder vervolgens uit beide dozen $2(n-m)$ ballen; dan zijn beide dozen leeg.\nBekijk nu het geval $k=3$. Noem $S$ het aantal ballen in de eerste doos min het aantal ballen in de tweede doos. Als we de eerste handeling toepassen, verandert $S$ niet. Als we de tweede handeling toepassen, zeg op een doos met $t$ ballen, dan verandert de pariteit van het aantal ballen in die doos niet (want $3 t \\equiv t \\bmod 2)$. De pariteit van $S$ verandert dus ook niet. We concluderen dat de pariteit van $S$ nooit verandert. Als we nu beginnen met $m=1$ en $n=2$, dan is $S=-1 \\equiv 1 \\bmod 2$. We kunnen nu nooit de situatie bereiken dat beide dozen leeg zijn, want dan zou $S \\equiv 0 \\bmod 2$. Als $k=3$ kunnen we dus niet altijd beide dozen leeghalen.\n\nAlternatieve oplossing voor $k=2$ : Als $m=n$, dan halen we $m$ ballen uit beide dozen en zijn we klaar. Als $m \\neq n$, kunnen we zonder verlies van algemeenheid aannemen dat $m<n$. Haal nu uit beide dozen $m-1$ ballen weg. Dan blijft er in de eerste doos 1 over. We kunnen nu steeds het aantal ballen in de eerste doos verdubbelen (van 1 naar 2) en vervolgens uit beide dozen 1 weghalen. Hiermee kunnen we doorgaan totdat de tweede doos nog maar 1 bal bevat. Dan halen we uit beide dozen 1 bal weg en zijn beide dozen leeg.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Bepaal alle paren $(x, y)$ van positieve gehele getallen die voldoen aan\n\n$$\nx+y+1 \\mid 2 x y \\quad \\text { en } \\quad x+y-1 \\mid x^{2}+y^{2}-1\n$$", "solution": "Er geldt\n\n$$\n\\left(x^{2}+y^{2}-1\\right)-(x+y+1)(x+y-1)=\\left(x^{2}+y^{2}-1\\right)-\\left(x^{2}+y^{2}+2 x y-1\\right)=-2 x y .\n$$\n\nOmdat $x+y-1$ een deler is van $x^{2}+y^{2}-1$ en natuurlijk ook van $(x+y+1)(x+y-1)$, zien we dat $x+y-1$ een deler is van $2 x y$. We weten dat $x+y+1$ ook een deler is van $2 x y$. Maar de ggd van $x+y-1$ en $x+y+1$ is 1 of 2 , aangezien het verschil van de twee getallen 2 is. Dus geldt dat $2 x y$ deelbaar is door $(x+y-1)(x+y+1)$ (als de ggd 1 is) of door $\\frac{(x+y-1)(x+y+1)}{2}$ (als de ggd 2 is). In beide gevallen geldt dat $4 x y$ deelbaar is door $(x+y-1)(x+y+1)$ en dus dat voor een zekere $k \\geq 1$ geldt:\n\n$$\n4 x y=k(x+y-1)(x+y+1)=k\\left(x^{2}+y^{2}+2 x y-1\\right) \\geq k(4 x y-1)\n$$\n\nwaarbij de laatste ongelijkheid geldt omdat voor alle reële getallen (en dus zeker voor positieve gehele) $x$ en $y$ geldt $x^{2}+y^{2} \\geq 2 x y$.\nAls $k \\geq 2$, dan geldt dus $4 x y \\geq 2 \\cdot(4 x y-1)$, dus $4 x y \\leq 2$. Tegenspraak, want $x$ en $y$ zijn positief en geheel, dus $4 x y \\geq 4$. We concluderen dat moet gelden $k=1$ en dus $4 x y=x^{2}+y^{2}+2 x y-1$. Hieruit volgt $x^{2}+y^{2}-1-2 x y=0$, wat we kunnen herschrijven tot $(x-y)^{2}=1$. Er moet dus gelden $x=y-1$ of $x=y+1$.\nDe mogelijke paren die voldoen zijn dus $(x, x+1)$ met $x \\geq 1$ en $(x, x-1)$ met $x \\geq 2$. We vullen het eerste paar in om te controleren: $2 x+2$ moet een deler zijn van $2 x(x+1)$ en dat klopt; en $2 x$ moet een deler zijn van $x^{2}+(x+1)^{2}-1=2 x^{2}+2 x$ en dat klopt ook. Analoog voldoet het tweede paar ook. Dus de oplossingen zijn: alle paren $(x, x+1)$ met $x \\geq 1$ en alle paren $(x, x-1)$ met $x \\geq 2$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Gegeven is een driehoek $A B C$. De bissectrice van $\\angle C A B$ snijdt $B C$ in $L$. Op het inwendige van zijden $A C$ en $A B$ liggen respectievelijk de punten $M$ en $N$, zodat $A L$, $B M$ en $C N$ door één punt gaan en zodat $\\angle A M N=\\angle A L B$. Bewijs dat $\\angle N M L=90^{\\circ}$.", "solution": "Noem $T$ het snijpunt van $M N$ en $B C$. Merk op dat omdat $\\angle A C B=\\angle A L B-$ $\\angle L A C=\\angle A M N-\\angle L A C<\\angle A M N$, geldt dat $T$ aan dezelfde kant van $C$ ligt als $B$ (en aan dezelfde kant van $M$ als $N$. Omdat $\\angle A M T=\\angle A M N=\\angle A L B=\\angle A L T$, is $A M L T$ een koordenvierhoek. Dus $\\angle N M L=\\angle T M L=\\angle T A L$. Het is dus voldoende om te laten zien dat $\\angle T A L=90^{\\circ}$. Dat is precies het geval als $A T$ de buitenbissectrice van $\\angle C A B$ is, want de binnen- en buitenbissectrice staan loodrecht op elkaar. Dit gaan we dus bewijzen. Omdat $A L, B M$ en $C N$ elkaar snijden in één punt, geldt volgens de stelling van Ceva dat\n\n$$\n\\frac{B L}{L C} \\cdot \\frac{C M}{M A} \\cdot \\frac{A N}{N B}=1\n$$\n\nOmdat $M, N$ en $T$ op een lijn liggen, geldt volgens de stelling van Menelaos dat\n\n$$\n\\frac{B T}{T C} \\cdot \\frac{C M}{M A} \\cdot \\frac{A N}{N B}=-1\n$$\n\nUit deze twee gelijkheden volgt dat\n\n$$\n\\frac{B L}{L C}=-\\frac{B T}{T C}\n$$\n\nVolgens de bissectricestelling is $\\frac{|B L|}{|L C|}=\\frac{|B A|}{|C A|}$, dus geldt ook $\\frac{|B T|}{|T C|}=\\frac{|B A|}{|C A|}$. Dat betekent weer met de bissectricestelling dat $A T$ de buitenbissectrice van $\\angle C A B$ is. Dat is wat we wilden bewijzen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2012", "problem_label": "5", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ die voldoen aan\n\n$$\nf(x+x y+f(y))=\\left(f(x)+\\frac{1}{2}\\right)\\left(f(y)+\\frac{1}{2}\\right)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Vul in $y=-1$, dan staat er:\n\n$$\nf(f(-1))=\\left(f(x)+\\frac{1}{2}\\right)\\left(f(-1)+\\frac{1}{2}\\right) .\n$$\n\nAls $f(-1) \\neq-\\frac{1}{2}$, dan kunnen we delen door $f(-1)+\\frac{1}{2}$ en krijgen we\n\n$$\nf(x)+\\frac{1}{2}=\\frac{f(f(-1))}{f(-1)+\\frac{1}{2}},\n$$\n\nwat betekent dat $f$ constant is. Dan is er dus een $c \\in \\mathbb{R}$ zodat $f(x)=c$ voor alle $x \\in \\mathbb{R}$. Nu staat er in de functievergelijking:\n\n$$\nc=\\left(c+\\frac{1}{2}\\right)\\left(c+\\frac{1}{2}\\right),\n$$\n\nwat we kunnen herschrijven als $0=c^{2}+\\frac{1}{4}$, maar dat heeft geen reële oplossing in $c$. Dus $f$ kan niet constant zijn.\nDe enige mogelijkheid is dus dat $f(-1)=-\\frac{1}{2}$. Dit betekent bovendien dat $f(f(-1))=0$, dus dat $f\\left(-\\frac{1}{2}\\right)=0$. Vul nu $x=0$ en $y=-\\frac{1}{2}$ in, dat geeft:\n\n$$\nf\\left(f\\left(-\\frac{1}{2}\\right)\\right)=\\left(f(0)+\\frac{1}{2}\\right)\\left(f\\left(-\\frac{1}{2}\\right)+\\frac{1}{2}\\right),\n$$\n\nen dus\n\n$$\nf(0)=\\left(f(0)+\\frac{1}{2}\\right) \\cdot \\frac{1}{2}\n$$\n\nwaaruit volgt dat $f(0)=\\frac{1}{2}$.\nStel dat er een $a \\neq-1$ is met $f(a)=-\\frac{1}{2}$. Vul $y=a$ in:\n\n$$\nf\\left(x(1+a)-\\frac{1}{2}\\right)=0 .\n$$\n\nOmdat $1+a \\neq 0$, kan $x(1+a)-\\frac{1}{2}$ alle waarden in $\\mathbb{R}$ aannemen als $x$ varieert over $\\mathbb{R}$. Dus nu volgt dat $f$ constant 0 is, maar we hadden al gezien dat $f$ niet constant kon zijn. We concluderen dat er geen $a \\neq-1$ is met $f(a)=-\\frac{1}{2}$. Er is dus maar één $x$ waarvoor $f(x)=-\\frac{1}{2}$ en dat is $x=-1$.\nBekijk een willekeurige $b$ met $f(b)=0$. We vullen $x=b-\\frac{1}{2}$ en $y=0$ in:\n\n$$\nf\\left(b-\\frac{1}{2}+\\frac{1}{2}\\right)=\\left(f\\left(b-\\frac{1}{2}\\right)+\\frac{1}{2}\\right)\\left(\\frac{1}{2}+\\frac{1}{2}\\right),\n$$\n\noftewel\n\n$$\nf(b)=\\left(f\\left(b-\\frac{1}{2}\\right)+\\frac{1}{2}\\right) .\n$$\n\nOmdat $f(b)=0$, is $f\\left(b-\\frac{1}{2}\\right)=-\\frac{1}{2}$. We hebben gezien dat dan moet gelden $b-\\frac{1}{2}=-1$, dus $b=-\\frac{1}{2}$.\nEr is dus maar één $x$ waarvoor $f(x)=0$ en dat is $x=-\\frac{1}{2}$. Vul nu $x=-1$ in:\n\n$$\nf(-1-y+f(y))=0\n$$\n\nHieruit volgt $-1-y+f(y)=-\\frac{1}{2}$, dus $f(y)=y+\\frac{1}{2}$. De enige kandidaatfunctie is dus de functie gegeven door $f(x)=x+\\frac{1}{2}$ voor alle $x \\in \\mathbb{R}$.\nWe controleren deze functie. Links in de functievergelijking komt te staan: $x+x y+y+1$. Rechts komt te staan $(x+1)(y+1)$ en dat is gelijk aan $x y+x+y+1$. De functie voldoet dus. We concluderen dat er precies één oplossing is: $f(x)=x+\\frac{1}{2}$ voor alle $x \\in \\mathbb{R}$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2013-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "problem_label": "1", "tier": 1, "problem": "In trapezium $A B C D$ is $A B \\| C D$. Zij $M$ het midden van diagonaal $A C$. Neem aan dat driehoeken $A B M$ en $A C D$ dezelfde oppervlakte hebben. Bewijs dat $D M \\| B C$.", "solution": "Omdat $M$ het midden van $A C$ is, is de oppervlakte van driehoek $A B M$ gelijk aan de oppervlakte van driehoek $B C M$. Dus de oppervlakte van driehoek $A B C$ is twee keer zo groot als de oppervlakte van driehoek $A B M$ en daarmee ook twee keer zo groot als de oppervlakte van driehoek $A C D$. De hoogte van driehoek $A C D$ ten opzichte van basis $C D$ is de afstand tussen de evenwijdige lijnen $A B$ en $C D$. Dat is ook de hoogte van driehoek $A B C$ ten opzichte van basis $A B$. Omdat die hoogtes dus even groot zijn, moet $|A B|=2 \\cdot|C D|$.\nZij nu $K$ het midden van $A B$. Dan is $K M$ een middenparallel van $\\triangle A B C$ en dus is $K M \\| B C$. Verder is $|K B|=\\frac{1}{2}|A B|=|C D|$, dus vierhoek $K B C D$ heeft een paar evenwijdige en even lange zijden, waarmee het een parallellogram is. Dus $D K \\| B C$. Maar dat betekent dat $D K$ en $K M$ dezelfde lijn zijn (want beide door $K$ en beide evenwijdig aan $B C)$, zodat $D M$ ook wel deze lijn moet zijn. Dus $D M$ is ook evenwijdig met $B C$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Gegeven is een drietal verschillende positieve gehele getallen $(a, b, c)$ met $a+b+c=2013$. Een stap bestaat uit het vervangen van het drietal $(x, y, z)$ door het drietal $(y+z-x, z+x-y, x+y-z)$. Bewijs dat we uitgaande van het drietal $(a, b, c)$ na 10 stappen een drietal krijgen dat minstens één negatief getal bevat.", "solution": "Het verschil tussen de eerste twee getallen in het nieuwe drietal $(y+z-$ $x, z+x-y, x+y-z)$ is $(y+z-x)-(z+x-y)=2 y-2 x$, terwijl het verschil tussen de eerste twee getallen in het oude drietal $(x, y, z) \\operatorname{nog} x-y$ was. Het verschil is dus in één stap vermenigvuldigd met -2 en het absolute verschil dus met 2. Dit geldt ook voor het verschil tussen het tweede en derde getal en voor het verschil tussen het eerste en derde getal. Omdat de drie getallen $a, b$ en $c$ verschillend zijn, zijn er twee bij met absoluut verschil minstens 2 . Na het uitvoeren van tien stappen op het drietal $(a, b, c)$, zijn er dus twee getallen met absoluut verschil minstens $2 \\cdot 2^{10}=2048$.\nMerk nu op dat de som van de getallen in een drietal gelijk blijft bij het uitvoeren van een stap, want\n\n$$\n(y+z-x)+(z+x-y)+(x+y-z)=x+y+z .\n$$\n\nDus het drietal dat ontstaan is door tien stappen uit te voeren op $(a, b, c)$, heeft nog steeds som 2013. We hadden gezien dat er twee getallen met absoluut verschil minstens 2048 zijn. Als alle drie de getallen niet-negatief zijn, is de som dus minstens 2048 en dat is weer groter dan 2013; tegenspraak. Dus bevat het drietal een negatief getal.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Gegeven is een drietal verschillende positieve gehele getallen $(a, b, c)$ met $a+b+c=2013$. Een stap bestaat uit het vervangen van het drietal $(x, y, z)$ door het drietal $(y+z-x, z+x-y, x+y-z)$. Bewijs dat we uitgaande van het drietal $(a, b, c)$ na 10 stappen een drietal krijgen dat minstens één negatief getal bevat.", "solution": "Omdat de som van $a, b$ en $c$ gelijk aan 2013 is, kunnen we schrijven\n\n$$\n(a, b, c)=(671+u, 671+v, 671+w)\n$$\n\nmet $u+v+w=0$. $\\mathrm{Zij}\\left(a_{i}, b_{i}, c_{i}\\right)$ het drietal dat je krijgt na $i$ stappen. Na één stap is het eerste getal vervangen door\n$a_{1}=b+c-a=(671+v)+(671+w)-(671+u)=671+v+w-u=671+(v+w+u)-2 u=671-2 u$.\nHet verschil met 671 is dus na één stap vermenigvuldigd met -2 . Hetzelfde geldt voor het tweede en derde getal in het drietal. Met inductie zien we nu direct dat\n\n$$\n\\left(a_{i}, b_{i}, c_{i}\\right)=\\left(671+(-2)^{i} \\cdot u, 671+(-2)^{i} \\cdot v, 671+(-2)^{i} \\cdot w\\right)\n$$\n\nOmdat $u+v+w=0$ en ze allemaal verschillend moeten zijn, is er minstens één getal van die drie dat negatief is, zeg $u$. Dan is\n\n$$\na_{10}=671+(-2)^{10} \\cdot u=671+1024 u \\leq 671-1024<0 .\n$$", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Gegeven is een drietal verschillende positieve gehele getallen $(a, b, c)$ met $a+b+c=2013$. Een stap bestaat uit het vervangen van het drietal $(x, y, z)$ door het drietal $(y+z-x, z+x-y, x+y-z)$. Bewijs dat we uitgaande van het drietal $(a, b, c)$ na 10 stappen een drietal krijgen dat minstens één negatief getal bevat.", "solution": "Noem $S=x+y+z$. Dan wordt het drietal $(x, y, z)$ in een stap vervangen door het drietal $(S-2 x, S-2 y, S-2 z)$. De som van deze drie getallen is $3 S-2 S=S$. De som van de getallen van een drietal verandert dus niet als je een stap uitvoert.\n$\\mathrm{Zij}\\left(a_{i}, b_{i}, c_{i}\\right)$ het drietal dat je krijgt na $i$ stappen op het drietal $(a, b, c)$. We hebben nu $S=a+b+c=2013$. Er geldt $a_{1}=S-2 a$, dus $a_{1}$ is van de vorm $m \\cdot S+n \\cdot a$ met $n=-2$. We bewijzen met inductie dat elke $a_{i}$ in deze vorm te schrijven is waarbij $n$ gelijk is aan $(-2)^{i}$. De inductiebasis hebben we zojuist gedaan. Zij nu $i \\geq 2$ en stel dat $a_{i-1}$ van de vorm $m \\cdot S+n \\cdot a$ is met $n=(-2)^{i-1}$. We weten dat $a_{i}=S-2 a_{i-1}$. Dus $a_{i}$ is van de vorm $m^{\\prime} \\cdot S+n^{\\prime} \\cdot a$ met $n^{\\prime}=-2 n=(-2)^{i}$. Dit voltooit de inductiestap. In het bijzonder weten we nu voor $i=10$ dat er een $M$ is met $a_{10}=M \\cdot S+1024 \\cdot a$. Als we dezelfde redenering toepassen op $b$ en $c$ komt daar dezelfde $M$ uit, dus $b_{10}=M \\cdot S+1024 \\cdot b$ en $c_{10}=M \\cdot S+1024 \\cdot c$.\nVerder weten we nog steeds dat de som van de getallen $S$ is. Dus\n\n$$\nS=a_{10}+b_{10}+c_{10}=3 M \\cdot S+1024 \\cdot(a+b+c)=(3 M+1024) \\cdot S\n$$\n\nWe concluderen dat $3 M+1024=1$, dus $3 M=-1023$, dus $M=-341$.\nStel nu dat $a_{10}, b_{10}$ en $c_{10}$ alle drie niet-negatief zijn. Dan is $-341 \\cdot S+1024 \\cdot a \\geq 0$, waarbij we ook nog weten dat $S=2013$. Dus\n\n$$\na \\geq \\frac{341 \\cdot 2013}{1024}=\\frac{1023 \\cdot 2013}{3 \\cdot 1024}=\\frac{1023}{1024} \\cdot 671>\\frac{670}{671} \\cdot 671=670 .\n$$\n\nDus $a \\geq 671$. Maar op dezelfde manier zien we dat $b \\geq 671$ en $c \\geq 671$. Bovendien zijn $a$, $b$ en $c$ verschillend, dus $2013=a+b+c \\geq 671+672+673=2016$. Tegenspraak. Dus $a_{10}$, $b_{10}$ en $c_{10}$ zijn niet alle drie niet-negatief.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 5 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Vind alle drietallen $(x, n, p)$ van positieve gehele getallen $x$ en $n$ en priemgetallen $p$ waarvoor geldt\n\n$$\nx^{3}+3 x+14=2 \\cdot p^{n} \\text {. }\n$$", "solution": "Omdat de rechterkant een product is van priemfactoren, zou het handig zijn als de linkerkant ook een product is. Het zou dan te factoriseren moeten zijn in een eerstegraads en een tweedegraads polynoom in $x$. Proberen geeft dan de volgende ontbinding. We kunnen de linkerkant ontbinden als $(x+2)\\left(x^{2}-2 x+7\\right)$. Er moet dus gelden\n\n$$\n(x+2)\\left(x^{2}-2 x+7\\right)=2 p^{n} .\n$$\n\nStel nu eerst dat $x$ even is. Dan moet $x+2=2 p^{a}$ voor zekere gehele $a \\geq 0$ en $x^{2}-2 x+7=$ $p^{n-a}$. (Merk op dat dit ook goed gaat als $p=2$.) Omdat $x$ een positief geheel getal is, is $x+2 \\geq 3$ en kunnen we $a=0$ dus uitsluiten. Verder geldt $x^{2}-3 x+5>\\left(x-\\frac{3}{2}\\right)^{2} \\geq 0$ voor alle $x$, dus $x^{2}-2 x+7>x+2$. Dat betekent dat $n-a>a$. We vullen nu $x=2 p^{a}-2$ in in $x^{2}-2 x+7=p^{n-a}$ :\n\n$$\n\\left(2 p^{a}-2\\right)^{2}-2\\left(2 p^{a}-2\\right)+7=p^{n-a},\n$$\n\noftewel\n\n$$\n4 p^{2 a}-12 p^{a}+15=p^{n-a} .\n$$\n\nOmdat $n-a>a$, geldt $p^{a} \\mid p^{n-a}$. Verder geldt naturrlijk ook $p^{a} \\mid p^{a}$ en $p^{a} \\mid p^{2 a}$. Dus $p^{a}$ moet ook een deler zijn van 15. Daaruit volgt $p=3$ of $p=5$ en verder $a=1$. Als $p=3$, staat er links 15 en rechts $3^{n-1}$; dat geeft geen oplossing. Als $p=5$, staat er links 55 en rechts $5^{n-1}$; dat geeft ook geen oplossing.\nStel nu dat $x$ oneven is. Dan moet $x+2=p^{a}$ voor zekere gehele $a \\geq 0$ en $x^{2}-2 x+7=2 p^{n-a}$. Omdat $x$ een positief geheel getal is, is $x+2 \\geq 3$ en valt $a=0$ dus weer af. Verder geldt dat $x \\neq 2$, dus dat $x^{2}-4 x+3=(x-2)^{2}-1 \\geq 0$, dus $x^{2}-2 x+7 \\geq 2(x+2)$. Dus $n-a \\geq a$. We vullen nu $x=p^{a}-2$ in in $x^{2}-2 x+7=2 p^{n-a}$ :\n\n$$\n\\left(p^{a}-2\\right)^{2}-2\\left(p^{a}-2\\right)+7=2 p^{n-a}\n$$\n\noftewel\n\n$$\np^{2 a}-6 p^{a}+15=2 p^{n-a} .\n$$\n\nOmdat $n-a \\geq a$, geldt $p^{a} \\mid p^{n-a}$. Dus vinden we ook hier dat $p^{a} \\mid 15$, waaruit volgt $p=3$ of $p=5$ en verder $a=1$. Als $p=3$, staat er links 6 en rechts $2 \\cdot 3^{n-1}$, dus $n=2$. We vinden $x=3-2=1$. Inderdaad is $(1,2,3)$ een oplossing. Als $p=5$, staat er links 10 en rechts $2 \\cdot 5^{n-1}$, dus $n=2$. We vinden $x=5-2=3$. Inderdaad is $(3,2,5)$ een oplossing. Er zijn dus twee oplossingen, namelijk $(1,2,3)$ en $(3,2,5)$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2013", "problem_label": "4", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ die voldoen aan\n\n$$\nf(x+y f(x))=f(x f(y))-x+f(y+f(x))\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Vul in $x=y=0$ : dat geeft\n\n$$\nf(0)=f(0)-0+f(f(0))\n$$\n\ndus $f(f(0))=0$. Vul in $x=y=1$ : dat geeft\n\n$$\nf(1+f(1))=f(f(1))-1+f(1+f(1))\n$$\n\ndus $f(f(1))=1$. Vul nu in $x=1, y=0$ :\n\n$$\nf(1)=f(f(0))-1+f(f(1))\n$$\n\nWe weten dat $f(f(0))=0$ en $f(f(1))=1$, dus we vinden nu $f(1)=0$. Omdat $f(f(1))=1$, geeft dit ook $f(0)=1$. Vul nu in $y=0$ :\n\n$$\nf(x)=f(x)-x+f(f(x)) \\quad \\text { voor alle } x \\in \\mathbb{R}\n$$\n\ndus $f(f(x))=x$ voor alle $x \\in \\mathbb{R}$. Vul in $x=1$ : dat geeft\n\n$$\nf(1)=f(f(y))-1+f(y) \\quad \\text { voor alle } x \\in \\mathbb{R}\n$$\n\nSamen met $f(1)=0$ en $f(f(y))=y$ krijgen we nu $0=y-1+f(y)$, dus $f(y)=1-y$ voor alle $y \\in \\mathbb{R}$. We hebben nu gevonden dat de enige mogelijke oplossing kan zijn: $f(x)=1-x$ voor alle $x \\in \\mathbb{R}$. Als we dit invullen in de oorspronkelijke funtievergelijking, krijgen we links\n\n$$\n1-(x+y(1-x))=1-x-y+x y\n$$\n\nen rechts\n\n$$\n1-x(1-y)-x+1-(y+1-x)=1-x+x y-x+1-y-1+x=1-x-y+x y\n$$\n\nDus deze functie voldoet en is daarmee de enige oplossing.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "Zij $A B C D$ een koordenvierhoek met $|A D|=|B D|$. Zij $M$ het snijpunt van $A C$ en $B D$. Zij $I$ het middelpunt van de ingeschreven cirkel van $\\triangle B C M$. Zij $N$ het tweede snijpunt van $A C$ met de omgeschreven cirkel van $\\triangle B M I$. Bewijs dat $|A N| \\cdot|N C|=$ $|C D| \\cdot|B N|$.", "solution": "Zij $\\alpha=\\angle D A B$. Omdat $|A D|=|B D|$, is dan ook $\\angle A B D=\\alpha$. Vanwege de omtrekshoekstelling vinden we ook $\\angle A C D=\\alpha$, terwijl de koordenvierhoekstelling geeft dat $\\angle B C D=180^{\\circ}-\\alpha$. Dus $\\angle B C A=180^{\\circ}-2 \\alpha$. De hoekensom in driehoek $B I M$ geeft, samen met het feit dat $I$ het snijpunt van de bissectrices van $\\triangle B C M$ is, dat\n\n$$\n\\begin{gathered}\n\\angle B I M=180^{\\circ}-\\angle I M B-\\angle M B I=90^{\\circ}+90^{\\circ}-\\frac{1}{2} \\angle C M B-\\frac{1}{2} \\angle M B C \\\\\n=90^{\\circ}+\\frac{1}{2} \\angle B C M=90^{\\circ}+\\frac{1}{2} \\angle B C A=90^{\\circ}+90^{\\circ}-\\alpha=180^{\\circ}-\\alpha .\n\\end{gathered}\n$$\n\nOmdat BIMN een koordenvierhoek is, volgt hieruit $\\angle B N M=\\alpha$. De hoekensom in $\\triangle B N C$ geeft nu\n$\\angle N B C=180^{\\circ}-\\angle B C N-\\angle C N B=180^{\\circ}-\\angle B C A-\\angle M N B=180^{\\circ}-\\left(180^{\\circ}-2 \\alpha\\right)-\\alpha=\\alpha$.\nDit betekent dat\n\n$$\n\\angle A B N=\\angle A B C-\\angle N B C=\\angle A B C-\\alpha=\\angle A B C-\\angle A B D=\\angle C B D .\n$$\n\nDit gecombineerd met $\\angle N A B=\\angle C A B=\\angle C D B$, wat geldt vanwege de omtrekshoekstelling, geeft $\\triangle A B N \\sim \\triangle D B C$ (hh). Dus\n\n$$\n\\frac{|A N|}{|C D|}=\\frac{|B N|}{|C B|}\n$$\n\noftewel $|C D| \\cdot|B N|=|A N| \\cdot|C B|$. We weten dat $\\angle N B C=\\alpha=\\angle B N M=\\angle B N C$, dus $\\triangle B N C$ is gelijkbenig met tophoek $C$, dus $|C B|=|C N|$. Er geldt dus $|C D| \\cdot|B N|=$ $|A N| \\cdot|C N|$ en dat is wat we wilden bewijzen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 8 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "Zij $A B C D$ een koordenvierhoek met $|A D|=|B D|$. Zij $M$ het snijpunt van $A C$ en $B D$. Zij $I$ het middelpunt van de ingeschreven cirkel van $\\triangle B C M$. Zij $N$ het tweede snijpunt van $A C$ met de omgeschreven cirkel van $\\triangle B M I$. Bewijs dat $|A N| \\cdot|N C|=$ $|C D| \\cdot|B N|$.", "solution": "Zij $E$ het tweede snijpunt van $B N$ met de omgeschreven cirkel van $A B C D$. Dan volgt uit de machtstelling dat $|N B| \\cdot|N E|=|N A| \\cdot|N C|$. Het is dus voldoende om te bewijzen dat $|N E|=|C D|$. Net als in oplossing I noemen we $\\alpha=\\angle D A B$, die ook gelijk is aan $\\angle A B D$ en $\\angle A C D$. Verder volgt net als in oplossing I dat $\\angle B N M=\\alpha$. Dus geldt $\\angle B N C=\\angle B N M=\\alpha$. Dus $\\angle B N C=\\angle A C D=\\angle N C D$, wat betekent dat met Z-hoeken $B N$ en $C D$ evenwijdig zijn. Verder is $\\angle B E D=\\angle B A D=\\alpha=\\angle B N C$, dus volgt met F-hoeken dat $E D$ en $C N$ evenwijdig zijn. Van de vierhoek $N E D C$ zijn dus de twee paren overstaande zijden evenwijdig aan elkaar, wat betekent dat het een parallellogram is. Dus $|N E|=|C D|$, wat we nog moesten bewijzen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "problem_label": "1", "tier": 1, "problem": "Vind alle viertallen $(a, b, c, d)$ van reële getallen waarvoor geldt\n\n$$\n\\begin{aligned}\n& a b+c+d=3, \\\\\n& b c+d+a=5, \\\\\n& c d+a+b=2, \\\\\n& d a+b+c=6 .\n\\end{aligned}\n$$", "solution": "De eerste twee vergelijkingen van elkaar aftrekken geeft\n\n$$\n2=5-3=(b c+d+a)-(a b+c+d)=b(c-a)+a-c=(b-1)(c-a) .\n$$\n\nDe laatste twee vergelijkingen van elkaar aftrekken geeft\n\n$$\n4=6-2=(d a+b+c)-(c d+a+b)=d(a-c)+c-a=(1-d)(c-a)\n$$\n\nWe zien dat $c-a$ niet gelijk aan 0 is (want dan zou het product van $c-a$ met iets anders 0 moeten zijn) en we kunnen dus concluderen dat $1-d=2(b-1)$, oftewel $3=2 b+d$.\nOp dezelfde manier combineren we de tweede en derde vergelijking; dat levert $3=(c-$ $1)(b-d)$ op. En combineren van de eerste en vierde vergelijking geeft $3=(1-a)(b-d)$. Dus $c-1=1-a$, oftewel $a+c=2$.\nNu tellen we de eerste twee vergelijkingen bij elkaar op. Dat geeft\n$8=3+5=a b+c+d+b c+d+a=b(a+c)+(a+c)+2 d=2 b+2+2 d=2+3+d=5+d$,\ndus $d=3$. Vanwege $2 b+d=3$ volgt hieruit dat $b=0$. De eerste vergelijking wordt nu $0+c+3=3$, dus $c=0$. In de tweede vergelijking vinden we ten slotte $0+3+a=5$, dus $a=2$. We hebben nu gevonden dat de enige mogelijke oplossing is: $(a, b, c, d)=(2,0,0,3)$. Controleren laat zien dat dit viertal inderdaad aan alle vier de vergelijkingen voldoet.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Vind alle gehele getallen $n$ waarvoor $\\frac{4 n-2}{n+5}$ het kwadraat van een rationaal getal is. (Een rationaal getal is een getal in $\\mathbb{Q}$.)", "solution": "Stel dat $\\frac{4 n-2}{n+5}$ het kwadraat van een rationaal getal is. Dan kunnen we het dus schrijven als $\\frac{p^{2}}{q^{2}}$ met $p, q$ niet-negatieve gehele getallen, $q \\neq 0$ en $\\operatorname{ggd}(p, q)=1$. Vanwege de voorwaarde $\\operatorname{ggd}(p, q)=1$, is $\\frac{p^{2}}{q^{2}}$ de meest vereenvoudigde versie van deze breuk, dus er is een gehele $c \\neq 0$ zodat $4 n-2=c p^{2}$ en $n+5=c q^{2}$. Nu is\n\n$$\n22=4(n+5)-(4 n-2)=4 c q^{2}-c p^{2}=c\\left((2 q)^{2}-p^{2}\\right)=c(2 q-p)(2 q+p)\n$$\n\nDus $c$ is een deler van 22. Verder is 22 deelbaar door 2, dus de rechterkant is ook deelbaar door 2 . Als er een factor 2 in $2 q-p$ zit, zit er ook een factor 2 in $2 q+p$, want die twee factoren schelen $2 p$ en dat is even. En andersom, als $2 q+p$ deelbaar is door 2 , dan is $2 q-p$ dat ook. Maar 22 bevat maar één factor 2 , dus het kan niet dat $2 q-p$ en $2 q+p$ beide deelbaar zijn door 2 . We concluderen dat $2 q-p$ en $2 q+p$ juist oneven zijn en $c$ dus even is. Ten slotte geldt dat $p \\geq 0$ en $q \\geq 1$, dus $2 q+p \\geq 2$, dus de factor 11 uit 22 moet juist in $2 q+p$ zitten. We concluderen dat er slechts twee mogelijkheden zijn:\n\n- $c=2,2 q+p=11,2 q-p=1$;\n- $c=-2,2 q+p=11,2 q-p=-1$.\n\nIn het eerste geval vinden we $2 p=11-1=10$, dus $p=5$ en $q=3$. Dit geeft $4 n-2=50$, dus $n=13$. Controleren: $\\frac{4 n-2}{n+5}=\\frac{50}{18}=\\frac{25}{9}=\\frac{5^{2}}{3^{2}}$, dus $n=13$ voldoet inderdaad. In het tweede geval vinden we $2 p=11--1=12$, dus $p=6$, maar dan kan $q$ niet meer geheel zijn, dus dit geval valt af. We concluderen dat er precies één oplossing is en dat is $n=13$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Gegeven is een driehoek $A B C . \\mathrm{Zij} \\Gamma_{1}$ de cirkel door $B$ die raakt aan zijde $A C$ in $A$. Zij $\\Gamma_{2}$ de cirkel door $C$ die raakt aan zijde $A B$ in $A$. Het tweede snijpunt van $\\Gamma_{1}$ en $\\Gamma_{2}$ noemen we $D$. De lijn $A D$ snijdt de omgeschreven cirkel van $\\triangle A B C$ nog een keer in $E$. Bewijs dat $D$ het midden is van $A E$.", "solution": "We bekijken de configuratie waar $D$ binnen $\\triangle A B C$ ligt. De andere configuratie gaat analoog. Vanwege de raaklijnomtrekshoekstelling in $\\Gamma_{1}$ geldt $\\angle D A C=\\angle D B A$. Vanwege de raaklijnomtrekshoekstelling in $\\Gamma_{2}$ geldt $\\angle D A B=\\angle D C A$. Er geldt dus $\\triangle A B D \\sim \\triangle C A D$ (hh), waaruit volgt\n\n$$\n\\frac{|B D|}{|A D|}=\\frac{|A D|}{|C D|}, \\quad \\text { oftewel } \\quad|A D|^{2}=|B D| \\cdot|C D|\n$$\n\nVolgens de omtrekshoekstelling geldt $\\angle E C B=\\angle E A B=\\angle D A B=\\angle D C A$. Dus $\\angle E C D=$ $\\angle E C B+\\angle B C D=\\angle D C A+\\angle B C D=\\angle B C A$. Verder is $\\angle D E C=\\angle A E C=\\angle A B C$ vanwege de omtrekshoekstelling. Dus $\\triangle C D E \\sim \\triangle C A B$ (hh). Analoog zien we dat $\\triangle B D E \\sim \\triangle B A C$. We concluderen dat $\\triangle C D E \\sim \\triangle E D B$, waaruit volgt\n\n$$\n\\frac{|C D|}{|D E|}=\\frac{|E D|}{|D B|}, \\quad \\text { oftewel } \\quad|D E|^{2}=|B D| \\cdot|C D|\n$$\n\nSamen met (1) geeft dit $|D E|^{2}=|A D|^{2}$, dus $|D E|=|A D|$, wat betekent dat $D$ het midden $\\operatorname{van} A E$ is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Gegeven is een driehoek $A B C . \\mathrm{Zij} \\Gamma_{1}$ de cirkel door $B$ die raakt aan zijde $A C$ in $A$. Zij $\\Gamma_{2}$ de cirkel door $C$ die raakt aan zijde $A B$ in $A$. Het tweede snijpunt van $\\Gamma_{1}$ en $\\Gamma_{2}$ noemen we $D$. De lijn $A D$ snijdt de omgeschreven cirkel van $\\triangle A B C$ nog een keer in $E$. Bewijs dat $D$ het midden is van $A E$.", "solution": "We bekijken de configuratie waar $D$ binnen $\\triangle A B C$ ligt. De andere configuratie gaat analoog. Vanwege de raaklijnomtrekshoekstelling in $\\Gamma_{2}$ geldt $\\angle D A B=\\angle D C A$. De buitenhoekstelling geeft nu dat\n\n$$\n\\angle C D E=\\angle D C A+\\angle C A D=\\angle D A B+\\angle C A D=\\angle C A B .\n$$\n\nNoem $B^{\\prime}$ het tweede snijpunt van $B D$ met de omgeschreven cirkel van $\\triangle A B C$. Vanwege de raaklijnomtrekshoekstelling in $\\Gamma_{1}$ geldt $\\angle C A D=\\angle A B D=\\angle A B B^{\\prime}=\\angle A C B^{\\prime}$, waarbij de laatste $=$ een toepassing van de omtrekshoekstelling is. Dus\n\n$$\n\\angle D C B^{\\prime}=\\angle D C A+\\angle A C B^{\\prime}=\\angle D A B+\\angle C A D=\\angle C A B .\n$$\n\nVerder is $\\angle C B^{\\prime} D=\\angle C B^{\\prime} B=\\angle C A B$ vanwege de omtrekshoekstelling. We zien dat $\\triangle D B^{\\prime} C$ gelijkbenig is met tophoek $D$. Ook geeft (2) samen met (3) dat $\\angle C D E=\\angle D C B^{\\prime}$, waaruit volgt $C B^{\\prime} \\| D E$, oftewel $C B^{\\prime} \\| A E$. Volgens de stelling van Julian geeft dit $\\left|A B^{\\prime}\\right|=|C E|$. We hebben nu een gelijkbenig trapezium $A E C B^{\\prime}$. De middelloodlijnen van de evenwijdige zijden $A E$ en $C B^{\\prime}$ hiervan vallen samen. De middelloodlijn van $C B^{\\prime}$ gaat door $D$ omdat $\\triangle D B^{\\prime} C$ gelijkbenig is. Dus de middelloodlijn van $A E$ gaat ook door $D$, wat betekent dat $D$ het midden van $A E$ is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Gegeven is een driehoek $A B C . \\mathrm{Zij} \\Gamma_{1}$ de cirkel door $B$ die raakt aan zijde $A C$ in $A$. Zij $\\Gamma_{2}$ de cirkel door $C$ die raakt aan zijde $A B$ in $A$. Het tweede snijpunt van $\\Gamma_{1}$ en $\\Gamma_{2}$ noemen we $D$. De lijn $A D$ snijdt de omgeschreven cirkel van $\\triangle A B C$ nog een keer in $E$. Bewijs dat $D$ het midden is van $A E$.", "solution": "Vanwege de raaklijnomtrekshoekstelling in $\\Gamma_{1}$ geldt $\\angle D A C=\\angle D B A$. Vanwege de raaklijnomtrekshoekstelling in $\\Gamma_{2}$ geldt $\\angle D A B=\\angle D C A$. Er geldt dus $\\triangle A B D \\sim \\triangle C A D(\\mathrm{hh})$. Noem nu $M$ het midden van $A B$ en $N$ het midden van $A C$. Dan is $D M$ een zwaartelijn in $\\triangle D B A$ en is $D N$ de corresponderende zwaartelijn in $\\triangle D A C$. Daardoor weten we dat $\\angle B D M=\\angle A D N$. Dus\n\n$$\n\\begin{array}{rlr}\n\\angle M D N & =\\angle M D A+\\angle A D N & \\text { (opsplitsen hoek) } \\\\\n& =\\angle M D A+\\angle B D M & \\text { (gelijkheid van hiervoor) } \\\\\n& =\\angle B D A & \\text { (optellen hoeken) } \\\\\n& =180^{\\circ}-\\angle A B D-\\angle B A D & \\text { (hoekensom } \\triangle A B D) \\\\\n& =180^{\\circ}-\\angle C A D-\\angle B A D & \\text { (gelijkvormigheid } \\triangle A B D \\sim \\triangle C A D) \\\\\n& =180^{\\circ}-\\angle C A B & \\text { (optellen hoeken) } \\\\\n& =180^{\\circ}-\\angle N A M & \\text { (zelfde hoek.) }\n\\end{array}\n$$\n\nWe concluderen dat $M D N A$ een koordenvierhoek is. Dus $\\angle M D A=\\angle M N A$. Omdat $M N$ een middenparallel in $\\triangle A B C$ is, is $\\angle M N A=\\angle B C A$ en dat is wegens de omtrekshoekstelling weer gelijk aan $\\angle B E A$. Al met al hebben we $\\angle M D A=\\angle B E A$, wat betekent dat $M D$ evenwijdig is met $B E$. Aangezien $M$ het midden van $A B$ is, moet nu $D$ ook het midden van $A E$ zijn.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing III."}
|
| 6 |
+
{"year": "2013", "problem_label": "4", "tier": 1, "problem": "Zij $n \\geq 3$ een geheel getal en bekijk een $n \\times n$-bord, opgedeeld in $n^{2}$ eenheidsvierkantjes. We hebben voor elke $m \\geq 1$ willekeurig veel $1 \\times m$-rechthoeken (type I) en willekeurig veel $m \\times 1$-rechthoeken (type II) beschikbaar. We bedekken het bord met $N$ van deze rechthoeken, die elkaar niet overlappen en niet uitsteken buiten het bord. Het totaal aantal rechthoeken van type I op het bord moet hierbij gelijk zijn aan het totaal aantal rechthoeken van type II op het bord. (Merk op dat een $1 \\times 1$-rechthoek zowel van type I als van type II is.) Wat is de kleinste waarde van $N$ waarvoor dit mogelijk is?", "solution": "We bewijzen dat de minimale waarde $N=2 n-1$ is. We construeren eerst een voorbeeld door middel van inductie.\nInductiebasis. Voor $n=3$ is $N=5$ mogelijk, door in het middelste veld een $1 \\times 1$-rechthoek te leggen en de overige velden te bedekken met vier $2 \\times 1$ - en $1 \\times 2$-rechthoeken. Er zijn dan drie rechthoeken met hoogte 1 (type I) en drie rechthoeken met breedte 1 (type II), waarbij de $1 \\times 1$-rechthoek twee keer geteld wordt.\nInductiestap. Zij $k \\geq 3$ en neem aan dat we een $k \\times k$-bord kunnen bedekken met $2 k-1$ rechthoeken zodat aan alle voorwaarden is voldaan. Bekijk een $(k+1) \\times(k+1)$-bord en bedek het $k \\times k$-deelvierkant rechtsonder volgens de inductiehypothese. Bedek vervolgens de linkerkolom met een rechthoek met breedte 1 en hoogte $k+1$ en vervolgens de overgebleven ruimte met een rechthoek met hoogte 1 en breedte $k$. We hebben nu één rechthoek met breedte 1 en één rechthoek met hoogte 1 meer gebruikt, dus aan de voorwaarde is voldaan en we hebben $2 k-1+2=2(k+1)-1$ rechthoeken gebruikt. Hiermee hebben we een voorbeeld voor $n=k+1$ geconstrueerd.\nHiermee is bewezen dat het mogelijk is om het bord te bedekken met $N=2 n-1$ rechthoeken. We willen nu nog bewijzen dat het niet met minder rechthoeken kan. Zij $k$ het aantal rechthoeken met breedte 1 en hoogte groter dan 1 . Dan is ook het aantal rechthoeken met hoogte 1 en breedte groter dan 1 , gelijk aan $k$. Zij verder $l$ het aantal rechthoeken van $1 \\times 1$. Er geldt dus $N=2 k+l$. Als $k \\geq n$, geldt $N \\geq 2 n$, dus in dit geval is er niets te bewijzen. We nemen dus aan dat $k<n$ en we gaan bewijzen dat dan $l \\geq 2 n-2 k-1$, zodat $N \\geq 2 n-1$.\nElke rechthoek met breedte 1 kan alleen velden in één kolom bedekken. Er zijn dus $n-k$ kolommen waarin geen enkel veld wordt bedekt door een rechthoek met breedte 1 en hoogte groter dan 1. Zo ook zijn er $n-k$ rijen waarin geen enkel veld wordt bedekt door een rechthoek met hoogte 1 en breedte groter dan 1. Bekijk de $(n-k)^{2}$ velden die in zowel zo'n rij als zo'n kolom liggen. Deze velden moeten bedekt worden door $1 \\times 1$-rechthoeken. Dus $l \\geq(n-k)^{2}$.\nEr geldt $(k-n+1)^{2} \\geq 0$, dus $k^{2}+n^{2}+1-2 k n+2 k-2 n \\geq 0$, dus $n^{2}-2 k n+k^{2} \\geq 2 n-2 k-1$. We concluderen dat $l \\geq(n-k)^{2} \\geq 2 n-2 k-1$ en dat is precies wat we wilden bewijzen. Dus in alle gevallen is $N \\geq 2 n-1$ en dat bewijst dat de minimale waarde van $N$ gelijk is aan $2 n-1$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "Laat $a, b$ en $c$ positieve reële getallen zijn met $a b c=1$. Bewijs dat\n\n$$\na+b+c \\geq \\sqrt{\\frac{(a+2)(b+2)(c+2)}{3}}\n$$", "solution": "Laat $x, y$ en $z$ positieve reële getallen zijn zodat $x^{3}=a, y^{3}=b$ en $z^{3}=c$. Dan geldt $x^{3} y^{3} z^{3}=1$, dus ook $x y z=1$. We kunnen nu $a+2$ schrijven als $x^{3}+2 x y z=x\\left(x^{2}+2 y z\\right)$, en analoog kunnen we $b+2$ en $c+2$ herschrijven, waarmee we krijgen\n$(a+2)(b+2)(c+2)=x y z\\left(x^{2}+2 y z\\right)\\left(y^{2}+2 z x\\right)\\left(z^{2}+2 x y\\right)=\\left(x^{2}+2 y z\\right)\\left(y^{2}+2 z x\\right)\\left(z^{2}+2 x y\\right)$.\nNu passen we rekenkundig-meetkundig toe op de positieve termen $x^{2}+2 y z, y^{2}+2 z x$ en $z^{2}+2 x y:$\n$\\left(x^{2}+2 y z\\right)\\left(y^{2}+2 z x\\right)\\left(z^{2}+2 x y\\right) \\leq\\left(\\frac{x^{2}+2 y z+y^{2}+2 z x+z^{2}+2 x y}{3}\\right)^{3}=\\left(\\frac{(x+y+z)^{2}}{3}\\right)^{3}$.\nWe hebben tot nu toe dus gevonden:\n\n$$\n(a+2)(b+2)(c+2) \\leq \\frac{1}{27}\\left((x+y+z)^{3}\\right)^{2}\n$$\n\nWe gaan nu bewijzen dat $(x+y+z)^{3} \\leq 9\\left(x^{3}+y^{3}+z^{3}\\right)$. Voor wie het machtsgemiddelde kent: dit volgt direct uit de ongelijkheid van het rekenkundig gemiddelde en het derdemachtsgemiddelde. Er geldt\n\n$$\n(x+y+z)^{3}=x^{3}+y^{3}+z^{3}+3\\left(x^{2} y+y^{2} z+z^{2} x+x y^{2}+y z^{2}+z x^{2}\\right)+6 x y z .\n$$\n\nMet rekenkundig-meetkundig op alleen maar positieve termen weten we dat\n\n$$\n2 x^{3}+y^{3}=x^{3}+x^{3}+y^{3} \\geq 3 \\sqrt[3]{x^{6} y^{3}}=3 x^{2} y\n$$\n\nen analoog $x^{3}+2 y^{3} \\geq 3 x y^{2}$. Als we deze beide ongelijkheden cyclisch doordraaien, vinden we\n\n$$\n3\\left(x^{2} y+y^{2} z+z^{2} x+x y^{2}+y z^{2}+z x^{2}\\right) \\leq 6\\left(x^{3}+y^{3}+z^{3}\\right) .\n$$\n\nWe weten natuurlijk ook $x^{3}+y^{3}+z^{3} \\geq 3 \\sqrt[3]{x^{3} y^{3} z^{3}}=3 x y z$, dus al met al krijgen we\n\n$$\n(x+y+z)^{3} \\leq\\left(x^{3}+y^{3}+z^{3}\\right)+6\\left(x^{3}+y^{3}+z^{3}\\right)+2\\left(x^{3}+y^{3}+z^{3}\\right)=9\\left(x^{3}+y^{3}+z^{3}\\right) .\n$$\n\nGecombineerd met (4) krijgen we nu\n\n$$\n(a+2)(b+2)(c+2) \\leq \\frac{1}{27}\\left(9\\left(x^{3}+y^{3}+z^{3}\\right)\\right)^{2}=3(a+b+c)^{2}\n$$\n\nLinks en rechts delen door 3 en daarna de worteltrekken (beide kanten zijn positief) geeft nu precies het gevraagde.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 8 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "Laat $a, b$ en $c$ positieve reële getallen zijn met $a b c=1$. Bewijs dat\n\n$$\na+b+c \\geq \\sqrt{\\frac{(a+2)(b+2)(c+2)}{3}}\n$$", "solution": "Merk op dat $a, b$ en $c$ positief zijn, zodat we hieronder steeds rekenkundigmeetkundig mogen toepassen. Allereerst passen we rekenkundig-meetkundig toe op $a^{2}$ en 1 :\n\n$$\na^{2}+1 \\geq 2 \\sqrt{a^{2}}=2 a\n$$\n\nDit kunnen we cyclisch doordraaien en optellen, zodat we vinden:\n\n$$\na^{2}+b^{2}+c^{2}+3 \\geq 2 a+2 b+2 c\n$$\n\nVerder passen we rekenkundig-meetkundig toe op $b c, c a$ en $a b$ :\n\n$$\nb c+c a+a b \\geq 3 \\sqrt[3]{a^{2} b^{2} c^{2}}=3\n$$\n\nwaarbij we gebruikt hebben dat $a b c=1$. Ook passen we rekenkundig-meetkundig toe op $a^{2}, b^{2}$ en $c^{2}$ :\n\n$$\na^{2}+b^{2}+c^{2} \\geq 3 \\sqrt[3]{a^{2} b^{2} c^{2}}=3\n$$\n\nNu nemen we 2 keer (5), 4 keer (6) en 1 keer (7) en tellen dat op. Dan krijgen we:\n\n$$\n2 a^{2}+2 b^{2}+2 c^{2}+6+4 b c+4 c a+4 a b+a^{2}+b^{2}+c^{2} \\geq 4 a+4 b+4 c+12+3\n$$\n\nGelijke termen bij elkaar nemen, links en rechts 6 aftrekken en links en rechts $2 a b+2 b c+2 c a$ optellen geeft:\n\n$$\n3 a^{2}+3 b^{2}+3 c^{2}+6 a b+6 b c+6 c a \\geq 2 a b+2 b c+2 c a+4 a+4 b+4 c+9\n$$\n\nNu staat links $3\\left(a^{2}+b^{2}+c^{2}+2 a b+2 b c+2 c a\\right)=3(a+b+c)^{2}$. Rechts kunnen we 9 schrijven als $8+a b c$ en dan staat daar precies $(a+2)(b+2)(c+2)$. Als we dan ten slotte links en rechts delen door 3 en de wortel trekken (alles is nog steeds positief) dan krijgen we\n\n$$\na+b+c \\geq \\sqrt{\\frac{(a+2)(b+2)(c+2)}{3}}\n$$", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "problem_label": "1", "tier": 1, "problem": "Bewijs dat\n\n$$\n\\sum_{n=0}^{2013} \\frac{4026!}{(n!(2013-n)!)^{2}}\n$$\n\nhet kwadraat van een geheel getal is.", "solution": "Door 2013 te vervangen door 1, 2, 3 en 4 en de som dan uit te rekenen, krijg je een vermoeden voor welk getal in het kwadraat deze som oplevert. De faculteiten suggereren dat je het in de binomiaalcoëfficiënten moet zoeken. We bewijzen iets algemeners:\n\n$$\n\\sum_{n=0}^{m} \\frac{(2 m)!}{(n!(m-n)!)^{2}}=\\binom{2 m}{m}^{2}\n$$\n\nHieruit volgt het gevraagde.\nEr geldt\n\n$$\n\\frac{(2 m)!}{(n!(m-n)!)^{2}}=\\frac{(m!)^{2}}{(n!(m-n)!)^{2}} \\cdot \\frac{(2 m)!}{(m!)^{2}}=\\binom{m}{n}^{2} \\cdot\\binom{2 m}{m}\n$$\n\nHet is dus voldoende te bewijzen dat\n\n$$\n\\sum_{n=0}^{m}\\binom{m}{n}^{2}=\\binom{2 m}{m}\n$$\n\nWe doen dit combinatorisch. Bekijk $2 m$ ballen genummerd van 1 tot en met $2 m$, waarbij de ballen van 1 tot en met $m$ blauw gekleurd zijn en de ballen van $m+1$ tot en met $2 m$ rood gekleurd zijn. Je wilt hier totaal $m$ ballen van uitkiezen. Dat kan op $\\binom{2 m}{m}$ manieren. Anderzijds kunnen we ook eerst $n$ blauwe ballen uitkiezen, met $0 \\leq n \\leq m$, en vervolgens $m-n$ rode ballen. Dat komt op hetzelfde neer als eerst $n$ blauwe ballen uitkiezen en daarna $n$ rode ballen niet uitkiezen. Dus het aantal manieren om $m$ ballen uit te kiezen is ook gelijk aan\n\n$$\n\\sum_{n=0}^{m}\\binom{m}{n}^{2}\n$$\n\nDus deze som is gelijk aan $\\binom{2 m}{m}$. En daarmee hebben we (1) bewezen.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Zij $P$ het snijpunt van de diagonalen van een convexe vierhoek $A B C D$. Laat $X, Y$ en $Z$ punten op het inwendige van respectievelijk $A B, B C$ en $C D$ zijn zodat\n\n$$\n\\frac{|A X|}{|X B|}=\\frac{|B Y|}{|Y C|}=\\frac{|C Z|}{|Z D|}=2\n$$\n\nVeronderstel bovendien dat $X Y$ raakt aan de omgeschreven cirkel van $\\triangle C Y Z$ en dat $Y Z$ raakt aan de omgeschreven cirkel van $\\triangle B X Y$. Bewijs dat $\\angle A P D=\\angle X Y Z$.", "solution": "Vanwege de raaklijnomtrekshoekstelling is $\\angle C Z Y=\\angle B Y X$ en $\\angle B X Y=$ $\\angle C Y Z$. Hieruit volgt ten eerste dat\n\n$$\n\\angle X Y Z=180^{\\circ}-\\angle B Y X-\\angle C Y Z=180^{\\circ}-\\angle B Y X-\\angle B X Y=\\angle X B Y=\\angle A B C .\n$$\n\nTen tweede zien we dat $\\triangle X B Y \\sim \\triangle Y C Z$ (hh). Dit betekent\n\n$$\n\\frac{|X B|}{|B Y|}=\\frac{|Y C|}{|C Z|}\n$$\n\nGegeven is dat $|X B|=\\frac{1}{3}|A B|,|B Y|=\\frac{2}{3}|B C|,|Y C|=\\frac{1}{3}|B C|$ en $|C Z|=\\frac{2}{3}|C D|$. Dit invullen geeft\n\n$$\n\\frac{\\frac{1}{3}|A B|}{\\frac{2}{3}|B C|}=\\frac{\\frac{1}{3}|B C|}{\\frac{2}{3}|C D|}\n$$\n\nen dus\n\n$$\n\\frac{|A B|}{|B C|}=\\frac{|B C|}{|C D|}\n$$\n\nUit de gelijkvormigheid volgt ook $\\angle A B C=\\angle X B Y=\\angle Y C Z=\\angle B C D$. Als we dit combineren met de gevonden verhouding, krijgen we een nieuwe gelijkvormigheid: $\\triangle A B C \\sim \\triangle B C D$ (zhz). Dus $\\angle C A B=\\angle D B C$. Dit geeft\n\n$$\n\\angle P A B+\\angle A B P=\\angle C A B+\\angle A B D=\\angle D B C+\\angle A B D=\\angle A B C .\n$$\n\nWe wisten al dat $\\angle A B C=\\angle X Y Z$. Met de buitenhoekstelling in driehoek $A B P$ krijgen we nu\n\n$$\n\\angle B P C=\\angle P A B+\\angle A B P=\\angle A B C=\\angle X Y Z .\n$$\n\nAangezien $\\angle B P C=\\angle A P D$, geldt $\\angle A P D=\\angle X Y Z$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \\ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt\n\n$$\na_{p k+1}=p a_{k}-3 a_{p}+13\n$$\n\nBepaal alle mogelijke waarden van $a_{2013}$.", "solution": "Laat $q$ en $t$ priemgetallen zijn. Vul in $k=q, p=t$ :\n\n$$\na_{q t+1}=t a_{q}-3 a_{t}+13\n$$\n\nVul ook in $k=t, p=q$ :\n\n$$\na_{q t+1}=q a_{t}-3 a_{q}+13\n$$\n\nBeide uitdrukkingen rechts zijn dus gelijk aan elkaar, waaruit volgt\n\n$$\nt a_{q}-3 a_{t}=q a_{t}-3 a_{q}\n$$\n\noftewel\n\n$$\n(t+3) a_{q}=(q+3) a_{t}\n$$\n\nIn het bijzonder geldt $5 a_{3}=6 a_{2}$ en $5 a_{7}=10 a_{2}$. Vul nu $k=3, p=2$ in:\n\n$$\na_{7}=2 a_{3}-3 a_{2}+13=2 \\cdot \\frac{6}{5} a_{2}-3 a_{2}+13\n$$\n\nOmdat $a_{7}=\\frac{10}{5} a_{2}$, vinden we nu\n\n$$\n\\frac{13}{5} a_{2}=13\n$$\n\ndus $a_{2}=5$. Nu geldt voor elk priemgetal $p$ dat $a_{p}=\\frac{(p+3) a_{2}}{5}=p+3$.\nVul in $k=4, p=3$ :\n\n$$\na_{13}=3 a_{4}-3 a_{3}+13\n$$\n\nWe weten dat $a_{13}=16$ en $a_{3}=6$, dus dit geeft $3 a_{4}=21$, oftewel $a_{4}=7$.\nVul ten slotte $k=4$ en $p=503$ in:\n$a_{2013}=a_{4 \\cdot 503+1}=503 \\cdot a_{4}-3 a_{503}+13=503 \\cdot 7-3 \\cdot(503+3)+13=503 \\cdot 4-9+13=2016$.\nDus $a_{2013}=2016$ en dit is de enige mogelijke waarde.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \\ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt\n\n$$\na_{p k+1}=p a_{k}-3 a_{p}+13\n$$\n\nBepaal alle mogelijke waarden van $a_{2013}$.", "solution": "Leid net als in oplossing I af dat $a_{2}=5$ en $a_{p}=p+3$ voor alle priemgetallen $p$. Dan geldt dus $a_{3}=6$. Invullen van $k=1$ en $p=2$ geeft\n\n$$\na_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,\n$$\n\ndus $2 a_{1}=a_{3}+2=8$, dus $a_{1}=4$. Nu hebben we $a_{1}$ en $a_{2}$ berekend. Voor $n \\geq 3$ geldt dat er altijd een priemgetal $p$ is met $p \\mid n-1$, dus dat we altijd $p$ en $k$ kunnen vinden zodat\n$n=k p+1$. Dus ligt de waarde van $a_{n}$ vast als we alle waarden $a_{m}$ met $1 \\leq m<n$ al kennen. Er kan dus maar één rij zijn die voldoet. We proberen nu of $a_{n}=n+3$ voldoet. Dan geldt\n\n$$\np a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}\n$$\n\nDus dit voldoet inderdaad. De enige rij die voldoet is dus degene met $a_{n}=n+3$ voor alle $n \\geq 1$, waaruit volgt dat de enige mogelijke waarde voor $a_{2013}$ gelijk is aan 2016.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2013", "problem_label": "4", "tier": 1, "problem": "Bepaal alle gehele getallen $n \\geq 2$ waarvoor geldt dat\n\n$$\ni+j \\equiv\\binom{n}{i}+\\binom{n}{j} \\quad \\bmod 2\n$$\n\nvoor alle $i$ en $j$ met $0 \\leq i \\leq j \\leq n$.", "solution": "We laten eerst zien dat $n$ voldoet dan en slechts dan als $\\binom{n}{i} \\equiv i+1 \\bmod 2$ voor alle $i$ met $0 \\leq i \\leq n$. Stel dat $\\binom{n}{i} \\equiv i+1 \\bmod 2$ voor alle $i$, dan geldt $\\binom{n}{i}+\\binom{n}{j} \\equiv$ $i+1+j+1 \\equiv i+j \\bmod 2$ voor alle $i$ en $j$. Dus $n$ voldoet dan aan de voorwaarde in de opgave. Stel andersom dat $n$ voldoet. Omdat $\\binom{n}{0}=1$, geldt dan $i \\equiv 1+\\binom{n}{i} \\bmod 2$ voor alle $i$, dus $\\binom{n}{i} \\equiv i-1 \\equiv i+1 \\bmod 2$ voor alle $i$.\nSchrijf nu $n$ als $n=2^{k}+m$ met $0 \\leq m<2^{k}$. Omdat $n \\geq 2$, mogen we aannemen $k \\geq 1$. Bekijk\n\n$$\n\\binom{n}{2^{k}-2}=\\binom{2^{k}+m}{2^{k}-2}=\\frac{\\left(2^{k}+m\\right)\\left(2^{k}+m-1\\right) \\cdots(m+4)(m+3)}{\\left(2^{k}-2\\right)\\left(2^{k}-3\\right) \\cdots 2 \\cdot 1} .\n$$\n\nHet product in de noemer bevat $\\left\\lfloor\\frac{2^{k}-2}{2}\\right\\rfloor$ factoren deelbaar door $2,\\left\\lfloor\\frac{2^{k}-2}{4}\\right\\rfloor$ factoren deelbaar door $4, \\ldots,\\left\\lfloor\\frac{2^{k}-2}{2^{k-1}}\\right\\rfloor$ factoren deelbaar door $2^{k-1}$ en geen factoren deelbaar door $2^{k}$. Het product in de teller bestaat uit $2^{k}-2$ opeenvolgende factoren en bevat daarom minstens $\\left\\lfloor\\frac{2^{k}-2}{2}\\right\\rfloor$ factoren deelbaar door 2 , minstens $\\left\\lfloor\\frac{2^{k}-2}{4}\\right\\rfloor$ factoren deelbaar door $4, \\ldots$, minstens $\\left\\lfloor\\frac{2^{k}-2}{2^{k-1}}\\right\\rfloor$ factoren deelbaar door $2^{k-1}$. Het product in de teller bevat dus minstens evenveel factoren 2 als het product in de noemer. Het product in de teller bevat zeker meer factoren 2 dan het product in de noemer als $2^{k}$ voorkomt als factor in de teller. Dat is zo als $m+3 \\leq 2^{k}$, oftewel als $m \\leq 2^{k}-3$. Dus als $m \\leq 2^{k}-3$, dan is $\\binom{n}{2^{k}-2}$ even, terwijl $2^{k}-2$ ook even is. Dan voldoet $n=2^{k}+m$ dus niet.\nDus $n$ kan alleen voldoen als er een $k \\geq 2$ is met $2^{k}-2 \\leq n \\leq 2^{k}-1$. Als $n$ oneven is, geldt $\\binom{n}{0}+\\binom{n}{1}=1+n \\equiv 0 \\bmod 2$, dus dan voldoet $n$ niet. Dus $n$ kan alleen voldoen als hij van de vorm $n=2^{k}-2$ met $k \\geq 2$ is. Stel nu dat $n$ inderdaad van die vorm is. We gaan laten zien dat $n$ voldoet. Er geldt\n\n$$\n\\binom{2^{k}-2}{c}=\\frac{\\left(2^{k}-2\\right)\\left(2^{k}-3\\right) \\cdots\\left(2^{k}-c\\right)\\left(2^{k}-c-1\\right)}{c \\cdot(c-1) \\cdots 2 \\cdot 1} .\n$$\n\nHet aantal factoren 2 in $2^{k}-i$ is gelijk aan het aantal factoren 2 in $i$ voor $1 \\leq i \\leq 2^{k}-1$. Dus het aantal factoren 2 in de teller is gelijk aan het aantal factoren 2 in het product $(c+1) \\cdot c \\cdot(c-1) \\cdots 2$, oftewel het aantal factoren 2 in de noemer plus het aantal factoren 2 in $c+1$. Dus $\\binom{2^{k}-2}{c}$ is even dan en slechts dan als $c$ oneven is. Dit betekent dat $n=2^{k}-2$ voldoet.\nWe concluderen dat $n$ voldoet dan en slechts dan als $n=2^{k}-2$ met $k \\geq 2$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "In een koordenzeshoek $A B C D E F$ geldt $A B \\perp B D$ en $|B C|=|E F|$. Noem $P$ het snijpunt van $B C$ en $A D$ en noem $Q$ het snijpunt van $E F$ en $A D$. Neem aan dat $P$ en $Q$ allebei aan de kant van $D$ liggen waar $A$ niet ligt. Zij $S$ het midden van $A D$. Laat $K$ en $L$ de middelpunten zijn van de ingeschreven cirkels van respectievelijk $\\triangle B P S$ en $E Q S$. Bewijs dat $\\angle K D L=90^{\\circ}$.", "solution": "Het is bij deze opgave nuttig om te analyseren wat er gebeurt als je met punten schuift. Je kunt namelijk lijnstuk EF verschuiven zonder dat dat invloed op $K$ heeft. Dus L kan onafhankelijk van $K$ bewegen. Kennelijk beweegt $L$ dan wel altijd over een lijn door D die loodrecht op KD staat. De hoek $\\angle L D S$ is blijkbaar onafhankelijk van de positie van lijnstuk EF. Omdat we met een cirkel te maken hebben, suggereert dit dat $\\angle L D S$ misschien gelijk is aan een bepaalde omtrekshoek. Dan zou $\\angle K D S$ ook gelijk aan een omtrekshoek worden, en wel zo dat die twee omtrekshoeken samen $90^{\\circ}$ zijn. Op deze manier kun je ideeën krijgen om uiteindelijk tot het volgende bewijs te komen.\nDe configuratie ligt vast door de gegeven volgorde van de punten $A$ tot en met $F$ op de cirkel en door het gegeven over de punten $P$ en $Q$ op de lijn $A D$. We hoeven dus geen verschillende configuraties te onderscheiden. (De punten $P$ en $Q$ kunnen wel verwisseld worden op de lijn $A D$, maar dat is niet relevant.)\nMerk eerst op dat $S$ het middelpunt van de cirkel is, aangezien vanwege $\\angle A B D=90^{\\circ}$ de lijn $A D$ middellijn is, en $S$ het midden van $A D$ is. We gaan nu bewijzen dat $\\angle K D S=\\angle K B S$. We weten dat $K S$ een bissectrice is, dus $\\angle B S K=\\angle K S D$. Verder is $|S D|=|S B|$, omdat beide lengtes gelijk zijn aan de straal van de cirkel. Omdat ook $|S K|=|S K|$, vinden we $\\triangle D S K \\cong \\triangle B S K$ (ZHZ). Dus $\\angle K D S=\\angle K B S$.\nOmdat ook $B K$ een bissectrice is, geldt $\\angle K B S=\\angle C B K=\\frac{1}{2} \\angle C B S$. Dus $\\angle K D S=$ $\\frac{1}{2} \\angle C B S$.\nHelemaal analoog leiden we af dat $\\angle L D S=\\frac{1}{2} \\angle Q E S$, waaruit volgt dat $\\angle L D S=\\frac{1}{2}$. $\\left(180^{\\circ}-\\angle F E S\\right)=90^{\\circ}-\\frac{1}{2} \\angle F E S$. Dus $\\angle L D S+\\angle K D S=90^{\\circ}-\\frac{1}{2} \\angle F E S+\\frac{1}{2} \\angle C B S$. Merk nu verder op dat $\\triangle S B C \\cong \\triangle S E F$ (ZZZ), zodat $\\angle F E S=\\angle C B S$. Nu kunnen we concluderen dat $\\angle K D L=\\angle L D S+\\angle K D S=90^{\\circ}$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "Vind alle niet-negatieve gehele getallen $n$ waarvoor er gehele getallen $a$ en $b$ bestaan met $n^{2}=a+b$ en $n^{3}=a^{2}+b^{2}$.", "solution": "Vanwege de ongelijkheid van het rekenkundig en meetkundig gemiddelde, toegepast op $a^{2}$ en $b^{2}$, geldt $a^{2}+b^{2} \\geq 2 a b$. Aangezien $2 a b=(a+b)^{2}-\\left(a^{2}+b^{2}\\right)$, volgt hieruit $n^{3} \\geq\\left(n^{2}\\right)^{2}-n^{3}$, oftewel $2 n^{3} \\geq n^{4}$. Dit betekent $n=0$ of $2 \\geq n$. Dus $n=0, n=1$ en $n=2$ zijn de enige mogelijkheden. Voor $n=0$ vinden we $a=b=0$ als oplossing, voor $n=1$ vinden we $a=0, b=1$ als oplossing en voor $n=2$ vinden we $a=b=2$ als oplossing. De getallen $n$ die voldoen zijn dus precies $n=0, n=1$ en $n=2$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "Vind alle niet-negatieve gehele getallen $n$ waarvoor er gehele getallen $a$ en $b$ bestaan met $n^{2}=a+b$ en $n^{3}=a^{2}+b^{2}$.", "solution": "Schrijf $b=n^{2}-a$ en vul dat in:\n\n$$\nn^{3}=a^{2}+b^{2}=a^{2}+\\left(n^{2}-a\\right)^{2}=a^{2}+n^{4}-2 a n^{2}+a^{2} .\n$$\n\nDus\n\n$$\n2 a^{2}-2 n^{2} a+n^{4}-n^{3}=0 .\n$$\n\nDit is een kwadratische vergelijking in $a$, waarvan de discriminant gelijk is aan\n\n$$\nD=\\left(-2 n^{2}\\right)^{2}-4 \\cdot 2 \\cdot\\left(n^{4}-n^{3}\\right)=-4 n^{4}+8 n^{3}=4 n^{2}\\left(-n^{2}+2 n\\right) .\n$$\n\nVoor $n \\geq 3$ geldt $-n^{2}+2 n \\leq-3 n+2 n=-n<0$, dus dan is er geen oplossing voor $a$. Er moet dus gelden $n \\leq 2$. Voor $n=0$ vinden we $a=b=0$ als oplossing, voor $n=1$ vinden we $a=0, b=1$ als oplossing en voor $n=2$ vinden we $a=b=2$ als oplossing. De getallen $n$ die voldoen zijn dus precies $n=0, n=1$ en $n=2$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\backslash\\{0\\} \\rightarrow \\mathbb{R}$ waarvoor geldt:\n\n$$\nx f(x y)+f(-y)=x f(x)\n$$\n\nvoor alle reële $x, y$ ongelijk aan 0 .", "solution": "Vul in $x=1$, dat geeft $f(y)+f(-y)=f(1)$, oftewel $f(-y)=f(1)-f(y)$ voor alle $y$. Vul nu in $y=-1$, dat geeft $x f(-x)+f(1)=x f(x)$. Als we hierin $f(-x)=$ $f(1)-f(x)$ invullen, krijgen we $x(f(1)-f(x))+f(1)=x f(x)$, dus $x f(1)+f(1)=2 x f(x)$. We zien dat $f$ van de vorm $f(x)=c+\\frac{c}{x}$ is voor zekere $c \\in \\mathbb{R}$. Deze familie van functies controleren we. Links staat dan $x f(x y)+f(-y)=x\\left(c+\\frac{c}{x y}\\right)+c+\\frac{c}{-y}=x c+c$ en rechts staat $x f(x)=x\\left(c+\\frac{c}{x}\\right)=x c+c$. Deze twee zijn aan elkaar gelijk, dus deze functie voldoet voor alle $c \\in \\mathbb{R}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "In driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel. Een cirkel raakt aan $A I$ in $I$ en gaat verder door $B$. Deze cirkel snijdt $A B$ nogmaals in $P$ en $B C$ nogmaals in $Q$. De lijn $Q I$ snijdt $A C$ in $R$. Bewijs dat $|A R| \\cdot|B Q|=|P I|^{2}$.", "solution": "Er is maar één configuratie. Er geldt\n\n$$\n\\begin{array}{rlr}\n\\angle A I P & =\\angle I B P & \\text { (raaklijn-omtrekshoekstelling) } \\\\\n& =\\angle I B Q & (I B \\text { is bissectrice) } \\\\\n& =\\angle I P Q & \\text { (koordenvierhoek } P B Q I \\text { ) }\n\\end{array}\n$$\n\ndus vanwege Z-hoeken geldt nu $A I \\| P Q$. Dit betekent $\\angle I A B=\\angle Q P B=\\angle Q I B$, waarbij de laatste gelijkheid geldt vanwege de koordenvierhoek. We hadden al gezien dat $\\angle A I P=\\angle I B Q$, dus $\\triangle I A P \\sim \\triangle B I Q$ (hh). Dus\n\n$$\n\\frac{|A P|}{|P I|}=\\frac{|Q I|}{|B Q|}\n$$\n\nDaarnaast is $\\angle R I A$ de overstaande hoek van een raaklijnhoek en daarom gelijk aan $\\angle I P Q$, waarvan we al wisten dat die gelijk is aan $\\angle A I P$. Dus $\\angle R I A=\\angle A I P$. Vanwege de bissectrice $A I$ geldt ook $\\angle R A I=\\angle P A I$, dus $\\triangle R A I \\cong \\triangle P A I$ (HZH). Hieruit volgt $|A R|=|A P|$. Verder is $I$ het midden van boog $P Q$, aangezien $B I$ een bissectrice is, dus $|P I|=|Q I|$. Deze twee dingen vullen we in in (1):\n\n$$\n\\frac{|A R|}{|P I|}=\\frac{|P I|}{|B Q|}\n$$\n\nwaaruit volgt $|A R| \\cdot|B Q|=|P I|^{2}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "Laat $m \\geq 3$ en $n$ positieve gehele getallen zijn met $n>m(m-2)$. Vind het grootste positieve gehele getal $d$ zodat $d \\mid n$ ! en $k \\nmid d$ voor alle $k \\in\\{m, m+1, \\ldots, n\\}$.", "solution": "We gaan bewijzen dat $d=m-1$ de grootste is die voldoet. Merk eerst op dat $m-1 \\mid n$ ! en dat voor $k \\geq m$ geldt $k \\nmid m-1$, dus $d=m-1$ voldoet inderdaad.\nStel nu dat voor zekere $d$ geldt: $d \\mid n$ ! en $k \\nmid d$ voor alle $k \\in\\{m, m+1, \\ldots, n\\}$. We gaan bewijzen dat $d \\leq m-1$. Schrijf $d=p_{1} p_{2} \\cdots p_{t}$ met $p_{i}$ priem voor alle $i$ (niet noodzakelijk allemaal verschillend). Als $t=0$, is $d=1 \\leq m-1$, dus we mogen aannemen $t \\geq 1$. Uit de eerste voorwaarde op $d$ volgt $p_{i} \\leq n$ voor alle $i$. Uit de tweede voorwaarde op $d$ volgt dat $p_{i} \\notin\\{m, m+1, \\ldots, n\\}$ voor alle $i$. Dus $p_{i} \\leq m-1$ voor alle $i$. Bekijk nu de getallen $p_{1}, p_{1} p_{2}, \\ldots, p_{1} p_{2} \\cdots p_{t}$. Dit zijn allemaal delers van $d$ en daarom allemaal ongelijk aan getallen uit $\\{m, m+1, \\ldots, n\\}$. Verder weten we dat $p_{1} \\leq m-1$. Bekijk nu de grootste $j \\leq t$ waarvoor geldt dat $p_{1} p_{2} \\cdots p_{j} \\leq m-1$. Als $j<t$ geldt\n\n$$\np_{1} p_{2} \\cdots p_{j} p_{j+1} \\leq(m-1) p_{j+1} \\leq(m-1)(m-1)=m(m-2)+1 \\leq n\n$$\n\nMaar dat betekent dat ook $p_{1} p_{2} \\cdots p_{j} p_{j+1} \\leq m-1$. Tegenspraak met de maximaliteit van $j$. Dus moet gelden $j=t$, oftewel $d=p_{1} p_{2} \\cdots p_{t} \\leq m-1$.\nWe concluderen dat $d=m-1$ inderdaad de grootste $d$ is die aan de eisen voldoet.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2014", "problem_label": "5", "tier": 1, "problem": "Zij $n$ een positief geheel getal. Daniël en Merlijn spelen een spel. Daniël heeft $k$ vellen papier die naast elkaar op tafel liggen, waarbij $k$ een positief geheel getal is. Hij schrijft op elk vel papier een aantal van de getallen 1 tot en met $n$ (geen enkel getal mag ook, alle getallen mag ook). Op de achterkant van elk vel papier schrijft hij juiste de overige getallen van 1 tot en met $n$. Als Daniël klaar is, mag Merlijn een aantal vellen papier met de achterkant boven leggen (hij mag dit ook bij geen enkel vel of juist alle vellen doen). Als het hem lukt om de getallen 1 tot en met $n$ allemaal tegelijk zichtbaar te maken (waarbij dubbele mogen voorkomen), dan wint hij.\nBepaal de kleinste $k$ waarvoor Merlijn altijd kan winnen, wat Daniël ook doet.", "solution": "We geven de vellen papier van Daniël allemaal een andere kleur. Verder hebben we $n$ doosjes met daarop de getallen 1 tot en met $n$. We zorgen ook voor voldoende beschikbare fiches in precies de kleuren van de vellen papier van Daniël. Per vel bekijkt hij de getallen op de voorkant van het vel en stopt een fiche met de kleur van dit vel in elk van die doosjes. Elk doosje bevat daarna dus de fiches in de kleuren van de vellen papier waar dat getal op de voorkant staat, en juist niet de fiches in de kleuren van de vellen papier waar dat getal op de achterkant staat.\nAls Merlijn de door hem gewenste vellen papier met de achterkant boven heeft gelegd, pakt hij uit de voorraad precies de fiches in de kleuren van die vellen. Een getal is niet zichtbaar op tafel precies als de vellen waar dit getal op de voorkant staat, de vellen zijn die Merlijn omgedraaid heeft, oftewel precies als de verzameling fiches in zijn hand gelijk is aan de verzameling fiches in het doosje van dit getal. Merlijn wint dus dan en slechts dan als de verzameling fiches in zijn hand niet voorkomt in één van de doosjes, want dan zijn alle getallen zichtbaar. We beweren nu dat Merlijn kan winnen dan en slechts dan als $2^{k}>n$. De kleinste $k$ waarvoor Merlijn wint, is dan dus de kleinste $k$ met $2^{k}>n$.\nStel dat $2^{k}>n$. Het aantal mogelijke verzamelingen van kleuren is $2^{k}$ en daarom groter dan $n$. Er zijn $n$ doosjes, dus niet alle verzamelingen van kleuren kunnen precies de kleuren van fiches in een doosje zijn. Merlijn kan dus een verzameling kleuren kiezen die niet in een doosje voorkomt en de vellen daarvan met de achterkant boven leggen. Dan wint hij. Stel nu dat $2^{k} \\leq n$. Daniël vult nu eerst de doosjes met verzamelingen fiches, zodat elke mogelijke verzameling voorkomt in een doosje. Dat kan, want het aantal mogelijke verzamelingen is $2^{k}$ en we hebben minstens $2^{k}$ doosjes. Nu schrijft Daniël op elk vel gekleurd papier op de voorkant precies de getallen van de doosjes waar een fiche van de juiste kleur in zit, en op de achterkant de rest. Op deze manier corresponderen de fiches in de doosjes weer precies met de getallen op de voorkant van de vellen. Welke verzameling kleuren Merlijn nu ook uitkiest, er is altijd een doosje met precies die verzameling kleuren. Merlijn kan dus niet winnen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 7 |
+
{"year": "2014", "problem_label": "5", "tier": 1, "problem": "Zij $n$ een positief geheel getal. Daniël en Merlijn spelen een spel. Daniël heeft $k$ vellen papier die naast elkaar op tafel liggen, waarbij $k$ een positief geheel getal is. Hij schrijft op elk vel papier een aantal van de getallen 1 tot en met $n$ (geen enkel getal mag ook, alle getallen mag ook). Op de achterkant van elk vel papier schrijft hij juiste de overige getallen van 1 tot en met $n$. Als Daniël klaar is, mag Merlijn een aantal vellen papier met de achterkant boven leggen (hij mag dit ook bij geen enkel vel of juist alle vellen doen). Als het hem lukt om de getallen 1 tot en met $n$ allemaal tegelijk zichtbaar te maken (waarbij dubbele mogen voorkomen), dan wint hij.\nBepaal de kleinste $k$ waarvoor Merlijn altijd kan winnen, wat Daniël ook doet.", "solution": "We gaan laten zien dat Merlijn kan winnen dan en slechts dan als $2^{k}>n$. De kleinste $k$ waarvoor Merlijn wint, is dan dus de kleinste $k$ met $2^{k}>n$.\nStel dat $2^{k}>n$. Merlijn kiest één voor één bij elk vel of hij het wel of niet omdraait. Bij het eerste vel legt hij de kant boven waar de meeste getallen op staan (dus minstens de\nhelft van de getallen 1 tot en met $n$ ). Bij elk volgende vel legt hij de kant naar boven waar zoveel mogelijk getallen op staan die hij nog niet op eerdere vellen zichtbaar had liggen. Laat $b_{j}$ het aantal getallen zijn dat nog niet zichtbaar is op de vellen 1 tot en met $j$ nadat Merlijn voor deze vellen een keuze heeft gemaakt. Dan is $b_{1} \\leq \\frac{1}{2} n$ en $b_{j} \\leq \\frac{1}{2} b_{j-1}$ voor $j \\geq 2$. Dus $b_{j} \\leq\\left(\\frac{1}{2}\\right)^{j} n$ en in het bijzonder $b_{k} \\leq\\left(\\frac{1}{2}\\right)^{k} n$. Omdat $2^{k}>n$, is $\\left(\\frac{1}{2}\\right)^{k} n<1$, dus $b_{k}<1$. Omdat $b_{k}$ geheel moet zijn, geldt $b_{k}=0$. Dus na Merlijns keuze voor alle $k$ vellen zijn er geen getallen meer onzichtbaar.\nNu bewijzen we dat voor $2^{k} \\leq n$ Daniël kan zorgen dat Merlijn niet kan winnen. Dit doen we met inductie naar $k$. Voor $k=1$ geldt $n \\geq 2$. Daniël schrijft nu het getal 1 op de ene kant van het vel en alle andere getallen (dat is er minstens één) op de andere kant. Merlijn kan dit vel nu niet zo draaien dat hij kan winnen. Dat is de inductiebasis. Zij nu $k \\geq 1$ en neem aan dat Daniël $k$ vellen zo kan beschrijven met $n \\geq 2^{k}$ getallen dat Merlijn niet kan winnen. We bekijken nu $k+1$ vellen. Beschrijf de eerste $k$ vellen op zo'n manier met de getallen 1 tot en met $2^{k}$ dat Merlijn met alleen die getallen niet kan winnen; dit kan volgens de inductiehypothese. Schrijf vervolgens op elk vel weer dezelfde getallen voor en achter, maar dan verhoogd met $2^{k}$, zodat deze getallen van $2^{k}+1$ tot en met $2^{k+1}$ lopen. Schrijf ten slotte alle getallen $m$ met $2^{k+1}<m \\leq n$ op de achterkant van elk vel. Nu bevat elk van deze $k$ vellen de getallen 1 tot en met $n$. Op vel nummer $k+1$ schrijven we aan de voorkant de getallen 1 tot en met $2^{k}$ en aan de achterkant de getallen $2^{k}+1$ tot en met $n$. Stel dat Merlijn het laatste vel met de voorkant boven laat liggen. Dan moet hij in ieder geval de getallen $2^{k}+1$ tot en met $2^{k+1}$ nog zichtbaar maken op de eerste $k$ vellen, maar dat kan niet volgens de inductiehypothese. Stel dat Merlijn het laatste vel juist met de achterkant boven legt. Dan moet hij de getallen 1 tot en met $2^{k}$ nog zichtbaar maken op de eerste $k$ vellen, maar dat kan ook weer niet volgens de inductiehypothese. Merlijn kan dus met deze vellen niet winnen. Dit voltooit het bewijs.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,11 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "Bepaal alle paren $(a, b)$ van positieve gehele getallen waarvoor\n\n$$\na^{2}+b \\mid a^{2} b+a \\quad \\text { en } \\quad b^{2}-a \\mid a b^{2}+b .\n$$", "solution": "Uit $a^{2}+b \\mid a^{2} b+a$ volgt\n\n$$\na^{2}+b \\mid\\left(a^{2} b+a\\right)-b\\left(a^{2}+b\\right)=a-b^{2}\n$$\n\nUit $b^{2}-a \\mid a b^{2}+b$ volgt\n\n$$\nb^{2}-a \\mid\\left(a b^{2}+b\\right)-a\\left(b^{2}-a\\right)=b+a^{2} .\n$$\n\nWe zien dus dat $a^{2}+b\\left|a-b^{2}\\right| a^{2}+b$. Dat betekent dat $a^{2}+b$ op eventueel het teken na gelijk is aan $a-b^{2}$. We krijgen dus twee gevallen: $a^{2}+b=b^{2}-a$ en $a^{2}+b=a-b^{2}$. In het tweede geval geldt $a^{2}+b^{2}=a-b$. Maar $a^{2} \\geq a$ en $b^{2} \\geq b>-b$, dus dit is onmogelijk. We moeten dus wel het eerste geval hebben: $a^{2}+b=b^{2}-a$. Hieruit volgt $a^{2}-b^{2}=-a-b$, dus $(a+b)(a-b)=-(a+b)$. Aangezien $a+b$ positief is, mogen we erdoor delen en krijgen we $a-b=-1$, dus $b=a+1$. Alle paren die kunnen voldoen zijn dus van de vorm $(a, a+1)$ voor een positieve gehele $a$.\nWe controleren deze paren. Er geldt $a^{2}+b=a^{2}+a+1$ en $a^{2} b+a=a^{2}(a+1)+a=$ $a^{3}+a^{2}+a=a\\left(a^{2}+a+1\\right)$, dus aan de eerste deelbaarheidsrelatie wordt voldaan. Verder is $b^{2}-a=(a+1)^{2}-a=a^{2}+a+1$ en $a b^{2}+b=a(a+1)^{2}+(a+1)=a^{3}+2 a^{2}+2 a+1=$ $a\\left(a^{2}+a+1\\right)+a^{2}+a+1=(a+1)\\left(a^{2}+a+1\\right)$, dus aan de tweede deelbaarheidsrelatie wordt ook voldoen. De paren $(a, a+1)$ voldoen dus en zijn daarmee precies de oplossingen.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.", "solution": "Er is maar één configuratie. Zij $N$ het midden van $A C$. Dan is $M N$ een middenparallel. Wegens Z-hoeken is $\\angle E A D=\\angle M A B=\\angle A M N$, maar ook geldt $\\angle E A D=\\angle D E A=\\angle M E C$. Dus $\\angle A M N=\\angle C E M$. Als nu $S$ het snijpunt van $M N$ en $C E$ is, dan is $\\triangle S E M$ dus gelijkbenig met $|S E|=|S M|$. Verder is $S M$ een middenparallel in driehoek $C D B$, dus $2|S M|=|D B|$ en is $S$ dan het midden van $C D$, zodat $|C S|=|S D|$. Als we dit alles combineren, vinden we\n\n$$\n|C E|=|C S|+|S E|=|S D|+|S E|=2|S E|+|D E|=2|S M|+|A D|=|D B|+|A D|=|A B| .\n$$", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.", "solution": "Er is maar één configuratie. Zij $K$ een punt op $A M$ zodat $M$ het midden van lijnstuk $A K$ is. Dan snijden $A K$ en $B C$ elkaar middendoor, dus $A B K C$ is een parallellogram. Dat betekent\n\n$$\n\\angle C K A=\\angle K A B=\\angle E A D=\\angle D E A=\\angle C E K\n$$\n\ndus driehoek $C K E$ is gelijkbenig met tophoek $C$. Daaruit volgt $|C E|=|C K|$. Vanwege het parallellogram is $|C K|=|A B|$, dus $|C E|=|A B|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.", "solution": "We passen Menelaos toe op de lijn door $A, E$ en $M$ in driehoek $B C D$. Er geldt dus\n\n$$\n\\frac{|B M|}{|M C|} \\cdot \\frac{|C E|}{|E D|} \\cdot \\frac{|D A|}{|A B|}=1 .\n$$\n\nOmdat $M$ het midden van $B C$ is, is $\\frac{|B M|}{|M C|}=1$. En gegeven is dat $|A D|=|D E|$. Dit geeft samen dat $|C E|=|A B|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 5 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.", "solution": "We bewijzen eerst dat $A$ en $B$ aan dezelfde kant van de middelloodlijn van $B C$ liggen. Stel namelijk dat $A$ en $C$ juist aan dezelfde kant liggen of $A$ op de middelloodlijn ligt. Dan geldt $|A B| \\geq|A C|$ en zegt de bissectricestelling dus dat de bissectrice vanuit hoek $A$ de zijde $B C$ snijdt tussen $M$ en $C$. Dus $\\angle B A M \\leq \\angle C A M$. Maar\n\n$$\n\\begin{aligned}\n\\angle A E C & =180^{\\circ}-\\angle A E D=180^{\\circ}-\\angle D A E=180^{\\circ}-\\angle B A M \\\\\n& \\geq 180^{\\circ}-\\angle C A M=\\angle A E C+\\angle A C E>\\angle A E C .\n\\end{aligned}\n$$\n\nTegenspraak. Dit bewijst onze claim.\n\nSpiegel nu $A$ in de middelloodlijn van $B C$ en noem het beeld $A^{\\prime}$. Dan is $\\angle M A^{\\prime} C=$ $\\angle M A B=\\angle E A D$. Vanwege de gelijkbenigheid is $\\angle E A D=\\angle D E A=\\angle M E C$, dus $\\angle M A^{\\prime} C=\\angle M E C$. Omdat $A^{\\prime}$ en $C$ aan dezelfde kant van de middelloodlijn van $B C$ liggen en $E$ juist aan de andere kant (want $E$ ligt op $A M$ ), betekent dat dat $M C A^{\\prime} E$ een koordenvierhoek is. Daarom is\n\n$$\n\\angle E A^{\\prime} C=180^{\\circ}-\\angle E M C=\\angle E M B=\\angle A M B=\\angle A^{\\prime} M C=\\angle A^{\\prime} E C,\n$$\n\nwaarbij we ook de spiegeling nogmaals gebruikt hebben. Dus is driehoek $A^{\\prime} E C$ gelijkbenig met top $C$. Dus $|C E|=\\left|C A^{\\prime}\\right|=|B A|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing IV."}
|
| 6 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.", "solution": "De sinusregel in driehoek $M A B$ geeft\n\n$$\n\\frac{|M B|}{\\sin \\angle M A B}=\\frac{|A B|}{\\sin \\angle A M B}=\\frac{|A B|}{\\sin \\angle A M C},\n$$\n\nwaarbij het laatste $=$-teken geldt omdat $\\angle A M B+\\angle A M C=180^{\\circ}$. De sinusregel in driehoek EMC geeft\n\n$$\n\\frac{|M C|}{\\sin \\angle M E C}=\\frac{|E C|}{\\sin \\angle E M C} .\n$$\n\nEr geldt $|M B|=|M C|$ en $\\angle A M C=\\angle E M C$. Ook is $\\angle M A B=\\angle E A D=\\angle D E A=$ $\\angle M E C$. Dit alles combineren geeft\n\n$$\n\\frac{|A B|}{\\sin \\angle A M C}=\\frac{|M B|}{\\sin \\angle M A B}=\\frac{|M C|}{\\sin \\angle M E C}=\\frac{|E C|}{\\sin \\angle E M C}=\\frac{|E C|}{\\sin \\angle A M C},\n$$\n\ndus $|A B|=|E C|$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing V."}
|
| 7 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "Laat $a, b$ en $c$ rationale getallen zijn waarvoor $a+b c, b+a c$ en $a+b$ allemaal ongelijk aan 0 zijn en waarvoor geldt dat\n\n$$\n\\frac{1}{a+b c}+\\frac{1}{b+a c}=\\frac{1}{a+b}\n$$\n\nBewijs dat $\\sqrt{(c-3)(c+1)}$ rationaal is.", "solution": "Er geldt\n\n$$\n\\frac{1}{a+b c}+\\frac{1}{b+a c}=\\frac{(b+a c)+(a+b c)}{(a+b c)(b+a c)}=\\frac{(a+b)+(a+b) c}{a b+a^{2} c+b^{2} c+a b c^{2}}\n$$\n\nUit de gegeven gelijkheid volgt dus\n\n$$\n(a+b)((a+b)+(a+b) c)=a b+a^{2} c+b^{2} c+a b c^{2}\n$$\n\noftewel\n\n$$\n\\begin{aligned}\n(a+b)^{2} & =a b+a^{2} c+b^{2} c+a b c^{2}-(a+b)^{2} c \\\\\n& =a b+a b c^{2}-2 a b c \\\\\n& =a b(c-1)^{2}\n\\end{aligned}\n$$\n\nDus $(c-1)^{2}=0$ of $a b$ is het kwadraat van een rationaal getal. Als $(c-1)^{2}=0$, dan is $c=1$ en staat er in de oorspronkelijke vergelijking\n\n$$\n\\frac{1}{a+b}+\\frac{1}{a+b}=\\frac{1}{a+b}\n$$\n\nwat niet waar kan zijn. Dus $(c-1)^{2} \\neq 0$, waaruit volgt dat $a b$ het kwadraat van een rationaal getal is.\nVerder zien we dat\n\n$$\n\\begin{aligned}\n(a-b)^{2} & =(a+b)^{2}-4 a b \\\\\n& =a b+a b c^{2}-2 a b c-4 a b \\\\\n& =a b c^{2}-2 a b c-3 a b \\\\\n& =a b(c-3)(c+1) .\n\\end{aligned}\n$$\n\nDus $a=0$ of $b=0$ of $(c-3)(c+1)$ is het kwadraat van een rationaal getal. Als $a=0$ staat er in de oorspronkelijke vergelijking\n\n$$\n\\frac{1}{b c}+\\frac{1}{b}=\\frac{1}{b}\n$$\n\nwat niet waar kan zijn. Dus $a \\neq 0$ en op vergelijkbare manier zien we dat $b \\neq 0$. Dus $(c-3)(c+1)$ is het kwadraat van een rationaal getal.", "problem_match": "\nOpgave 3.", "solution_match": "# Oplossing I."}
|
| 8 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "Laat $a, b$ en $c$ rationale getallen zijn waarvoor $a+b c, b+a c$ en $a+b$ allemaal ongelijk aan 0 zijn en waarvoor geldt dat\n\n$$\n\\frac{1}{a+b c}+\\frac{1}{b+a c}=\\frac{1}{a+b}\n$$\n\nBewijs dat $\\sqrt{(c-3)(c+1)}$ rationaal is.", "solution": "Er geldt\n\n$$\n\\frac{1}{a+b c}+\\frac{1}{b+a c}=\\frac{(b+a c)+(a+b c)}{(a+b c)(b+a c)}=\\frac{a+b+a c+b c}{a b+a^{2} c+b^{2} c+a b c^{2}} .\n$$\n\nUit de gegeven gelijkheid volgt dus\n\n$$\n(a+b)(a+b+a c+b c)=a b+a^{2} c+b^{2} c+a b c^{2}\n$$\n\noftewel\n\n$$\na^{2}+a b+a^{2} c+a b c+a b+b^{2}+a b c+b^{2} c=a b+a^{2} c+b^{2} c+a b c^{2}\n$$\n\noftewel\n\n$$\na^{2}+2 a b c+a b-a b c^{2}+b^{2}=0\n$$\n\nWe kunnen dit zien als kwadratische vergelijking in $a$, waarvan we weten dat het een rationale oplossing heeft. De discriminant van deze vergelijking moet dus het kwadraat van een rationaal getal zijn. Deze discriminant is gelijk aan\n\n$$\n\\begin{aligned}\nD & =\\left(2 b c+b-b c^{2}\\right)^{2}-4 b^{2} \\\\\n& =\\left(2 b c+b-b c^{2}-2 b\\right)\\left(2 b c+b-b c^{2}+2 b\\right) \\\\\n& =b^{2}\\left(2 c-1-c^{2}\\right)\\left(2 c+3-c^{2}\\right) \\\\\n& =b^{2}\\left(c^{2}-2 c+1\\right)\\left(c^{2}-2 c-3\\right) \\\\\n& =b^{2}(c-1)^{2}(c+1)(c-3) .\n\\end{aligned}\n$$\n\nNet als in de vorige oplossing zien we dat $b=0$ en $c=1$ geen oplossingen geven, dus volgt hieruit dat\n\n$$\n(c-3)(c+1)=\\frac{D}{b^{2}(c-1)^{2}}\n$$\n\nhet kwadraat van een rationaal getal is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 9 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek met $|A C|=2|A B|$ en zij $O$ het middelpunt van de omgeschreven cirkel. Zij $D$ het snijpunt van de bissectrice van $\\angle A$ met $B C$. Zij $E$ de loodrechte projectie van $O$ op $A D$ en zij $F \\neq D$ het punt op $A D$ waarvoor $|C D|=|C F|$. Bewijs dat $\\angle E B F=\\angle E C F$.", "solution": "Als $E=F$ zijn hoeken $E B F$ en $E C F$ beide 0 , dus aan elkaar gelijk. We nemen dus verder aan dat $E \\neq F$. Zij $G$ het tweede snijpunt van $A D$ en de omgeschreven cirkel van $\\triangle A B C$. Er zijn meerdere configuraties mogelijk. We bekijken de configuratie waarbij de punten op de lijn $A D$ in de volgorde $A, E, D, G, F$ liggen, waarbij eventueel mag gelden $D=E$ en $F=G$. Andere configuraties gaan analoog.\nZij $M$ het midden van $A C$. Omdat $|A B|=\\frac{|A C|}{2}=|A M|$ en omdat $A D$ de bissectrice van $\\angle B A M$ is, is $M$ het beeld van $B$ onder spiegeling in $A D$. Er geldt dus $\\angle E B F=\\angle E M F$, dus om te bewijzen dat $\\angle E B F=\\angle E C F$ is het voldoende om te bewijzen dat $\\angle E M F=$ $\\angle E C F$. Dat is equivalent met dat de punten $E, M, C$ en $F$ op een cirkel liggen, aangezien $M$ en $C$ aan dezelfde kant van $E F$ liggen.\nOm dit te bewijzen laten we zien dat $\\angle E F C+\\angle E M C=180^{\\circ}$, oftewel dat $\\angle E F C=$ $\\angle A M E$. Omdat $\\triangle C D F$ gelijkbenig is, vinden we\n\n$$\n\\angle E F C=\\angle D F C=\\angle F D C=180^{\\circ}-\\angle A D C=\\angle D A C+\\angle A C D=\\frac{\\angle A}{2}+\\angle C .\n$$\n\nVerder geldt dat de middelloodlijn van een koorde door het middelpunt van de bijbehorende cirkel gaat, dus $M O$ staat loodrecht op $A C$. Dit betekent met Thales dat $E$ en $M$ beide op de cirkel met middellijn $A O$ liggen. Hieruit volgt dat $\\angle A M E=\\angle A O E$. Dan is $\\triangle A O G$ gelijkbenig, dus hoogtelijn $O E$ is in deze driehoek ook bissectrice. We vinden dus met de middelpunt-omtrekhoeksstelling dat\n\n$$\n\\angle A O E=\\frac{\\angle A O G}{2}=\\angle A C G=\\angle A C B+\\angle B C G=\\angle A C B+\\angle B A G=\\angle C+\\frac{\\angle A}{2} .\n$$\n\nEr geldt dus\n\n$$\n\\angle A M E=\\angle A O E=\\angle C+\\frac{\\angle A}{2}=\\angle E F C,\n$$\n\nprecies wat we moesten bewijzen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 10 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek met $|A C|=2|A B|$ en zij $O$ het middelpunt van de omgeschreven cirkel. Zij $D$ het snijpunt van de bissectrice van $\\angle A$ met $B C$. Zij $E$ de loodrechte projectie van $O$ op $A D$ en zij $F \\neq D$ het punt op $A D$ waarvoor $|C D|=|C F|$. Bewijs dat $\\angle E B F=\\angle E C F$.", "solution": "Zij $G \\neq A$ het snijpunt van $A D$ met de omgeschreven cirkel van $\\triangle A B C$. Dan geldt $|A G|=2|A E|$ omdat de projectie van het middelpunt van een cirkel op een koorde van die cirkel het midden van die koorde is. Zij $M$ het midden van $A C$. Omdat $|A B|=\\frac{|A C|}{2}=|A M|$ en omdat $A D$ de bissectrice van $\\angle B A M$ is, is $M$ het beeld van $B$ onder spiegeling in $A D$. Nu geldt er $\\angle D G C=\\angle A G C=\\angle A B C=\\angle A B D=$ $\\angle D M A=180^{\\circ}-\\angle D M C$, dus $D M C G$ is een koordenvierhoek. Nu is $A M^{2}=\\frac{A M \\cdot A C}{2}=$ $\\frac{A D \\cdot A G}{2}=A D \\cdot A E$, dus $\\triangle A M E \\sim \\triangle A D M$ (zhz). Nu geldt $180^{\\circ}-\\angle E M C=\\angle E M A=$ $\\angle M D A=\\angle B D A=\\angle C D F=\\angle D F C=\\angle E F C$, dus $E M C F$ is een koordenvierhoek. Nu is $\\angle E B F=\\angle E M F=\\angle E C F$, precies wat we moesten bewijzen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 11 |
+
{"year": "2014", "problem_label": "5", "tier": 1, "problem": "Op een $2014 \\times 2014$-bord staat op elk van de $2014^{2}$ vakjes een lamp. Lampen kunnen aan of uit staan. In de beginsituatie is een aantal van de lampen aan. In een zet kies je een rij of kolom waarin minstens 1007 lampen aan staan en verander je van alle 2014 lampen in die rij of kolom de status (van aan naar uit en van uit naar aan). Vind de kleinste niet-negatieve gehele $k$ zodat geldt: vanuit elke beginsituatie kun je in een eindig aantal stappen naar een situatie waarin hoogstens $k$ lampen aan staan.", "solution": "Nummer de rijen van 1 tot en met 2014 en de kolommen ook. Bekijk de volgende beginsituatie: in rij $i$ zijn de lampen in de kolommen $i, i+1, \\ldots, i+1005$ aan en de rest uit, waarbij we de kolomnummers modulo 2014 rekenen. Nu zijn in elke rij en in elke kolom precies 1006 lampen aan. Er is dus geen zet mogelijk. Het is dus niet altijd mogelijk om naar een situatie met minder dan 2014 • 1006 lampen aan toe te gaan.\nNu laten we zien dat we wel altijd naar een situatie met hoogstens 2014 • 1006 lampen aan toe kunnen. Stel uit het ongerijmde dat er in een bepaalde situatie minstens 2014•1006+1 lampen aan staan en het toch niet mogelijk is om naar minder lampen aan toe te gaan. Als er een rij of kolom is met 1008 of meer lampen aan, dan kunnen we de status van de lampen in deze rij of kolom veranderen en zijn er daarna minder lampen aan, tegenspraak. Dus in elke rij en kolom staan hoogstens 1007 lampen aan.\nZij $I$ de verzameling rijen met precies 1007 lampen aan en zij $J_{1}$ de verzameling kolommen met precies 1007 lampen aan. We zijn van plan om de status van de lampen in alle rijen in $I$ om te zetten. Dit noemen we het grote plan. Als na het uitvoeren van het grote plan een kolom ontstaat met 1008 of meer lampen aan, krijgen we weer een tegenspraak, dus we nemen aan dat dat niet zo is. $\\mathrm{Zij} J_{2}$ de verzameling kolommen die na het uitvoeren van het grote plan precies 1007 lampen aan zullen hebben. Als er een vakje $(i, j)$ bestaat met $i \\in I$ en $j \\in J_{1}$ waarvan de lamp uit staat, kan ik rij $i$ omzetten en krijg ik in kolom $j$ meer dan 1007 lampen aan, tegenspraak. Dus elke lamp op $(i, j)$ met $i \\in I$ en $j \\in J_{1}$ is aan. Als er een vakje $(i, j)$ bestaat met $i \\in I$ en $j \\in J_{2}$ waarvan de lamp na het uitvoeren van het grote plan uit staat, krijg ik op dezelfde manier een tegenspraak. Dus elke lamp op $(i, j)$ met $i \\in I$ en $j \\in J_{2}$ staat na het uitvoeren van het grote plan aan. Omdat de kolommen in $J_{2}$ na het uitvoeren van het grote plan elk precies 1007 lampen aan hebben, hebben ze vóór het uitvoeren van het grote plan dus $1007-|I|$ lampen aan. (De notatie $|X|$ geeft het aantal elementen in de verzameling $X$ aan.) De kolommen in $J_{1}$ hebben precies 1007 lampen aan en dit betekent ook dat $J_{1}$ en $J_{2}$ disjunct zijn (geen overlappende kolommen hebben). De overige kolommen hebben hoogstens 1006 lampen aan. Het totaal aantal lampen aan vóór het grote plan is dus hoogstens\n$(1007-|I|)\\left|J_{2}\\right|+1007\\left|J_{1}\\right|+1006\\left(2014-\\left|J_{1}\\right|-\\left|J_{2}\\right|\\right)=1006 \\cdot 2014+\\left|J_{1}\\right|+\\left|J_{2}\\right|-|I| \\cdot\\left|J_{2}\\right|$.\nDit moet minstens $1006 \\cdot 2014+1$ zijn, dus $\\left|J_{1}\\right|+\\left|J_{2}\\right|-|I| \\cdot\\left|J_{2}\\right| \\geq 1$. Hieruit volgt $\\left|J_{1}\\right|>(|I|-1)\\left|J_{2}\\right|$. Als $|I| \\geq 2$, dan $\\left|J_{1}\\right|>\\left|J_{2}\\right|$. Door het uitvoeren van het grote plan wordt dan dus het aantal kolommen met 1007 lampen aan verkleind. Maar daarna hebben we weer een situatie met $|I|$ rijen met 1007 lampen aan, waarbij $J_{1}$ en $J_{2}$ precies verwisseld zijn. Dus kunnen we hier een nieuw groot plan uitvoeren waardoor het aantal kolommen\nmet 1007 lampen aan weer kleiner wordt. Tegenspraak, want we zijn nu weer terug in de uitgangssituatie. We concluderen dat moet gelden $|I|=1$.\nWe hebben dus de situatie dat er precies één rij is met precies 1007 lampen aan. Analoog kunnen we laten zien dat er ook één kolom moet zijn met precies 1007 lampen aan. Omdat er $1006 \\cdot 2014+1$ lampen aan staan, moeten er in elke andere rij en kolom precies 1006 lampen aan staan. Verander nu de status van lampen in de rij met 1007 lampen aan. In 1007 kolommen staan vervolgens $1006+1=1007$ lampen aan. We hebben al gezien dat we in deze situatie het aantal lampen dat aan staat, kunnen verminderen.\nWe zien dat als er meer dan 1006 • 2014 lampen aan staan, het altijd mogelijk is om dit aantal te verminderen. Dus de kleinste $k$ is $1006 \\cdot 2014$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "Zij $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{R}$ een functie waarvoor geldt: voor alle $n>1$ is er een priemdeler $p$ van $n$ zodat\n\n$$\nf(n)=f\\left(\\frac{n}{p}\\right)-f(p)\n$$\n\nBovendien is gegeven dat $f\\left(2^{2014}\\right)+f\\left(3^{2015}\\right)+f\\left(5^{2016}\\right)=2013$.\nBereken $f\\left(2014^{2}\\right)+f\\left(2015^{3}\\right)+f\\left(2016^{5}\\right)$.", "solution": "Als $n=q$ met $q$ priem, dan is er maar één priemdeler van $n$, namelijk $q$, dus moet gelden dat $f(q)=f(1)-f(q)$, dus $f(q)=\\frac{1}{2} f(1)$. Als $n=q^{2}$ met $q$ priem, dan heeft $n$ ook maar één priemdeler, dus geldt $f\\left(q^{2}\\right)=f(q)-f(q)=0$. We bewijzen nu met inductie naar $k$ dat $f\\left(q^{k}\\right)=\\frac{2-k}{2} f(1)$ als $q$ een priemgetal is en $k$ een positief geheel getal. Voor $k=1$ en $k=2$ hebben we dit al laten zien. Stel nu dat $f\\left(q^{k}\\right)=\\frac{2-k}{2} f(1)$ voor zekere $k \\geq 2$ en vul in $n=q^{k+1}$. Er geldt\n\n$$\nf\\left(q^{k+1}\\right)=f\\left(q^{k}\\right)-f(q)=\\frac{2-k}{2} f(1)-\\frac{1}{2} f(1)=\\frac{2-(k+1)}{2} f(1)\n$$\n\nDit voltooit de inductie.\nNu gebruiken we ons tweede gegeven. Er geldt\n\n$$\n\\begin{aligned}\n2013 & =f\\left(2^{2014}\\right)+f\\left(3^{2015}\\right)+f\\left(5^{2016}\\right) \\\\\n& =\\frac{2-2014}{2} f(1)+\\frac{2-2015}{2} f(1)+\\frac{2-2016}{2} f(1) \\\\\n& =-\\frac{6039}{2} f(1)\n\\end{aligned}\n$$\n\ndus $f(1)=\\frac{2013 \\cdot 2}{-6039}=-\\frac{2}{3}$. En dan geldt voor elk priemgetal $q$ dat $f(q)=\\frac{1}{2} f(1)=-\\frac{1}{3}$.\nWe bewijzen vervolgens dat als $n=p_{1} p_{2} \\cdots p_{m}$ met $p_{1}, p_{2}, \\ldots, p_{m}$ niet noodzakelijk verschillende priemgetallen en $m \\geq 0$, dat dan geldt $f(n)=\\frac{m-2}{3}$. Dit doen we met inductie naar $m$. Voor $m=0$ is $n=1$ en $f(1)=-\\frac{2}{3}=\\frac{0-2}{3}$, dus hiervoor klopt het. Stel nu dat we het bewezen hebben voor zekere $m \\geq 0$. Bekijk een willekeurige $n$ van de vorm $n=p_{1} p_{2} \\cdots p_{m+1}$. Dan is $n>1$, dus is er een priemfactor $p \\mid n$ waarvoor geldt $f(n)=f\\left(\\frac{n}{p}\\right)-f(p)$; zonder verlies van algemeenheid is dit $p=p_{m+1}$. Nu volgt\n\n$$\nf(n)=f\\left(p_{1} p_{2} \\cdots p_{m}\\right)-f\\left(p_{m+1}\\right)=\\frac{m-2}{3}--\\frac{1}{3}=\\frac{(m+1)-2}{3} .\n$$\n\nDit voltooit de inductie.\nWe kunnen nu het gevraagde berekenen. De priemfactorisaties van 2014, 2015 en 2016 zijn $2014=2 \\cdot 19 \\cdot 53,2015=5 \\cdot 13 \\cdot 31$ en $2016=2^{5} \\cdot 3^{2} \\cdot 7$, dus\n\n$$\nf\\left(2014^{2}\\right)+f\\left(2015^{3}\\right)+f\\left(2016^{5}\\right)=\\frac{6-2}{3}+\\frac{9-2}{3}+\\frac{40-2}{3}=\\frac{49}{3} .\n$$", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "De verzamelingen $A$ en $B$ zijn deelverzamelingen van de positieve gehele getallen. De som van elke twee verschillende elementen uit $A$ is een element van $B$. Het quotiënt van elke twee verschillende elementen van $B$ (waarbij we de grootste door de kleinste delen) is een element van $A$. Bepaal het maximale aantal elementen in $A \\cup B$.", "solution": "Stel dat $A$ minstens drie elementen bevat, zeg $a<b<c$. Dan bevat $B$ de drie verschillende elementen $a+b<a+c<b+c$. Dus $A$ bevat in elk geval het element $\\frac{b+c}{a+c}$. Deze breuk is kennelijk geheel, dus $a+c \\mid b+c$. Maar dan volgt $a+c \\mid(b+c)-(a+c)=b-a$. We weten $b>a$, dus $b-a$ is positief, dus moet gelden $a+c \\leq b-a$. Dit geeft $c \\leq b-2 a<b$, een tegenspraak met $c>b$. Dus $A$ bevat hoogstens twee elementen.\nStel dat $B$ minstens vier elementen bevat, zeg $a<b<c<d$. Dan bevat $A$ de drie verschillende elementen $\\frac{d}{a}, \\frac{d}{b}$ en $\\frac{d}{c}$. Maar $A$ kan geen drie verschillende elementen bevatten, tegenspraak. Dus $B$ bevat hoogstens drie elementen.\nIn totaal bevat $A \\cup B$ dus hoogstens 5 elementen. Dit is mogelijk, bijvoorbeeld met $A=\\{2,4\\}$ en $B=\\{3,6,12\\}$. Nu is $2+4=6 \\in B$ en $\\frac{12}{6}=\\frac{6}{3}=2 \\in A$ en $\\frac{12}{3}=4 \\in A$, dus dit paar verzamelingen voldoet. We concluderen dat $A \\cup B$ maximaal 5 elementen bevat.\nHet vinden van een paar verzamelingen dat voldoet, kan bijvoorbeeld als volgt. Stel B bevat de elementen $a<b<c$. Dan bevat $A$ de elementen $\\frac{c}{b}, \\frac{b}{a}$ en $\\frac{c}{a}$, waarvan $\\frac{c}{a}$ in elk geval de grootste is. Omdat A maar twee elementen bevat, moet wel gelden $\\frac{c}{b}=\\frac{b}{a}$. Verder moet de som van de twee elementen in $A$ weer in $B$ zitten, dus $\\frac{b}{a}+\\frac{c}{a} \\in B$. Schrijf $b=t a$, dan $c=t b=t^{2} a$ en $\\frac{b}{a}+\\frac{c}{a}=t+t^{2}$. Nu zie je dat $b$ gelijk kan zijn aan $t+t^{2}$ door $a=t+1$ te kiezen. Met $t=1$ krijg je $b=a$, dus die voldoet niet; met $t=2$ krijg je bovenstaande oplossing.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "Zij $H$ het hoogtepunt van een scherphoekige driehoek $A B C$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $B C$ snijden elkaar in $D$. De cirkel met middelpunt $C$ door $H$ snijdt de omgeschreven cirkel van driehoek $A B C$ in de punten $E$ en $F$. Bewijs dat $|D E|=|D F|=|A B|$.", "solution": "De driehoek is scherphoekig, dus $H$ ligt binnen de driehoek. Dat betekent dat $E$ en $F$ op de korte bogen $A C$ en $B C$ liggen. Neem aan dat $E$ op de korte boog $A C$ ligt en $F$ op de korte boog $B C$.\nAls we $H$ spiegelen in $A C$, komt het spiegelbeeld $H^{\\prime}$ op de omgeschreven cirkel van $\\triangle A B C$ terecht. (Dit is een bekend feit, te bewijzen door met wat hoekenjagen te laten zien dat $\\angle A H C=180^{\\circ}-\\angle A B C$.) Anderzijds ligt dit spiegelbeeld ook op de cirkel met middelpunt $C$ door $H$, aangezien $\\left|C H^{\\prime}\\right|=|C H|$. Dus $H^{\\prime}$ is het snijpunt van de twee cirkels en dat is $E$. We concluderen dat $E$ het spiegelbeeld van $H$ is onder spiegeling in $A C$.\nDit betekent dat $E H$ loodrecht op $A C$ staat en dus dezelfde lijn is als $B H$. Omdat $A D$ ook loodrecht op $A C$ staat, zijn $B E$ en $A D$ evenwijdig. Verder ligt $D$ op de omgeschreven cirkel van $\\triangle A B C$ omdat $\\angle C A D+\\angle C B D=90^{\\circ}+90^{\\circ}=180^{\\circ}$. We hadden al gezien dat $E$ op de korte boog $A C$ ligt, dus is $E A D B$ een koordenvierhoek in die volgorde. Nu is $\\angle B E A+\\angle E A D=180^{\\circ}$ wegens U-hoeken, maar ook $\\angle E B D+\\angle E A D=180^{\\circ}$ vanwege de koordenvierhoek. Dus $\\angle B E A=\\angle E B D$, dus de bijbehorende koorden $B A$ en $E D$ zijn even lang.\nAnaloog kunnen we bewijzen dat $|A B|=|D F|$, waarmee het gevraagde bewezen is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "Zij $H$ het hoogtepunt van een scherphoekige driehoek $A B C$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $B C$ snijden elkaar in $D$. De cirkel met middelpunt $C$ door $H$ snijdt de omgeschreven cirkel van driehoek $A B C$ in de punten $E$ en $F$. Bewijs dat $|D E|=|D F|=|A B|$.", "solution": "Op dezelfde manier als in de eerste oplossing laten we zien dat $E$ het spiegelbeeld van $H$ is onder spiegeling in $A C$ en dat $E A D B$ een koordenvierhoek is in die volgorde. Vanwege de spiegeling is $|A E|=|A H|$. Omdat zowel $B D$ als $A H$ loodrecht op $B C$ staan, zijn ze evenwijdig. Analoog zijn ook $A D$ en $B H$ evenwijdig, dus is $A D B H$ een parallellogram. Dus is $|A H|=|B D|$, waarmee we zien dat $|A E|=|B D|$. We hebben nu een koorde $E A$ naast een koorde $A D$, en verder een koorde $B D$ (even lang als $E A$ ) naast weer dezelfde koorde $A D$. We laten nu zien dat de overspannende koorden $E D$ en $A B$ daarom gelijk zijn. Er geldt $\\angle A E D=\\angle A B D$. En omdat $|A E|=|B D|$ geldt $\\angle A D E=\\angle B A D$. Dus $\\triangle E A D \\cong \\triangle B D A(\\mathrm{ZHH})$, waaruit volgt $|D E|=|A B|$.\nAnaloog kunnen we bewijzen dat $|A B|=|D F|$, waarmee het gevraagde bewezen is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "Bepaal alle paren $(p, q)$ van priemgetallen waarvoor $p^{q+1}+q^{p+1}$ een kwadraat is.", "solution": "Stel eerst dat $p$ en $q$ beide oneven zijn. Dan zijn in $p^{q+1}+q^{p+1}$ beide exponenten even, waaruit volgt dat beide termen congruent $1 \\bmod 4$ zijn. De som is dus congruent 2 $\\bmod 4$, maar dat is nooit een kwadraat.\nStel nu dat $p$ en $q$ beide even zijn. Dan zijn ze beide gelijk aan 2 . Dat geeft $p^{q+1}+q^{p+1}=$ $2^{3}+2^{3}=16=4^{2}$, dus dit tweetal voldoet.\nStel ten slotte dat één beide, zeg $p$, even is en de ander oneven. We hebben dan dus $p=2$ en $2^{q+1}+q^{3}=a^{2}$ voor een zeker positief geheel getal $a$. Schrijf $q+1=2 b$ met $b$ positief geheel, dan staat er $2^{2 b}+q^{3}=a^{2}$, oftewel\n\n$$\nq^{3}=a^{2}-2^{2 b}=\\left(a-2^{b}\\right)\\left(a+2^{b}\\right)\n$$\n\nBeide factoren rechts moeten nu een $q$-macht zijn, zeg $a-2^{b}=q^{k}$ en $a+2^{b}=q^{l}$ met $l>k \\geq 0$. Beide factoren zijn deelbaar door $q^{k}$, dus ook het verschil is daardoor deelbaar. Dus $q^{k} \\mid 2 \\cdot 2^{b}=2^{b+1}$. Maar $q$ is een oneven priemgetal, dus de enige $q$-macht die een deler van een tweemacht is, is 1 . Dus $k=0$. We krijgen nu $q^{3}=a+2^{b}$ en $a-2^{b}=1$, dus $q^{3}=\\left(2^{b}+1\\right)+2^{b}=2^{b+1}+1$. Daaruit volgt\n\n$$\n2^{b+1}=q^{3}-1=(q-1)\\left(q^{2}+q+1\\right)\n$$\n\nEchter, $q^{2}+q+1 \\equiv 1 \\bmod 2$ en verder is $q^{2}+q+1>1$, dus dit kan nooit een tweemacht zijn. Tegenspraak.\nWe concluderen dat de enige oplossing $(p, q)=(2,2)$ is.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2014", "problem_label": "5", "tier": 1, "problem": "Zij $P(x)$ een polynoom met gehele coëfficiënten en graad $n \\leq 10$ waarvoor geldt dat er voor elke $k \\in\\{1,2, \\ldots, 10\\}$ een gehele $m$ is met $P(m)=k$. Verder is gegeven dat $|P(10)-P(0)|<1000$. Bewijs dat er voor elke gehele $k$ een gehele $m$ is met $P(m)=k$.", "solution": "Laat voor $i=1,2, \\ldots, 10$ het gehele getal $c_{i}$ zo zijn dat $P\\left(c_{i}\\right)=i$. Er geldt voor $i \\in\\{1,2, \\ldots, 9\\}$ dat\n\n$$\nc_{i+1}-c_{i} \\mid P\\left(c_{i+1}\\right)-P\\left(c_{i}\\right)=(i+1)-i=1\n$$\n\ndus $c_{i+1}-c_{i}= \\pm 1$ voor alle $i \\in\\{1,2, \\ldots, 9\\}$. Verder geldt dat $c_{i} \\neq c_{j}$ voor $i \\neq j$, want $P\\left(c_{i}\\right)=i \\neq j=P\\left(c_{j}\\right)$. We concluderen dat $c_{1}, c_{2}, \\ldots, c_{10}$ tien opeenvolgende getallen zijn, ofwel stijgend ofwel dalend. We onderscheiden dus twee gevallen:\n(A) $c_{i}=c_{1}-1+i$ voor $i=1,2, \\ldots, 10$ (dus $c_{1}, c_{2}, \\ldots, c_{10}$ is een stijgend rijtje opeenvolgende getallen),\n(B) $c_{i}=c_{1}+1-i$ voor $i=1,2, \\ldots, 10$ (dus $c_{1}, c_{2}, \\ldots, c_{10}$ is een dalend rijtje opeenvolgende getallen).\n\nBekijk eerst geval (A). Definieer $Q(x)=1+x-c_{1}$. Dan geldt voor $1 \\leq i \\leq 10$ dat\n\n$$\nQ\\left(c_{i}\\right)=Q\\left(c_{1}-1+i\\right)=1+\\left(c_{1}-1+i\\right)-c_{1}=i=P\\left(c_{i}\\right)\n$$\n\ndus $P\\left(c_{i}\\right)-Q\\left(c_{i}\\right)=0$. Dus kunnen we schrijven\n\n$$\nP(x)-Q(x)=R(x) \\cdot \\prod_{i=1}^{10}\\left(x-c_{i}\\right)\n$$\n\noftewel\n\n$$\nP(x)=1+x-c_{1}+R(x) \\cdot \\prod_{i=1}^{10}\\left(x-c_{i}\\right)\n$$\n\nOmdat de graad van $P$ hoogstens 10 is, mag de graad van $R$ niet groter dan 0 zijn. Dus $R(x)$ is een constante, zeg $R(x)=a$ met $a \\in \\mathbb{Z}$. We krijgen dan\n\n$$\nP(x)=1+x-c_{1}+a \\cdot \\prod_{i=1}^{10}\\left(x-c_{i}\\right)\n$$\n\nWe vullen nu $x=10$ en $x=0$ in:\n\n$$\n\\begin{gathered}\nP(10)-P(0)=1+10-c_{1}+a \\cdot \\prod_{i=1}^{10}\\left(10-c_{i}\\right)-\\left(1+0-c_{1}\\right)-a \\cdot \\prod_{i=1}^{10}\\left(0-c_{i}\\right) \\\\\n=10+a \\cdot\\left(\\prod_{i=1}^{10}\\left(10-c_{i}\\right)-\\prod_{i=1}^{10}\\left(0-c_{i}\\right)\\right)\n\\end{gathered}\n$$\n\nDe getallen $10-c_{1}, 10-c_{2}, \\ldots, 10-c_{10}$ zijn tien opeenvolgende getallen en de getallen $0-c_{1}, 0-c_{2}, \\ldots, 0-c_{10}$ volgen daar weer precies op. Dus er is een $N$ zodat\n\n$$\n\\prod_{i=1}^{10}\\left(10-c_{i}\\right)-\\prod_{i=1}^{10}\\left(0-c_{i}\\right)=(N+20)(N+19) \\cdots(N+11)-(N+10)(N+9) \\cdots(N+1)\n$$\n\nWe gaan dit afschatten. We nemen eerst aan dat $N+1>0$. Dan geldt\n\n$$\n\\begin{aligned}\n(N+20)( & N+19) \\cdots(N+11)-(N+10)(N+9) \\cdots(N+1) \\\\\n& >(N+20)(N+9) \\cdots(N+1)-(N+10)(N+9) \\cdots(N+1) \\\\\n& =10 \\cdot(N+9)(N+8) \\cdots(N+1) \\\\\n& \\geq 10!.\n\\end{aligned}\n$$\n\nAls juist $N+20<0$, zijn alle factoren negatief. Helemaal analoog is het absolute verschil ook weer groter dan 10 !. Als $N+20 \\geq 0$ en $N+1 \\leq 0$, zit er dus ergens een 0 tussen de factoren. Dus precies één van de twee termen is gelijk aan 0 en de ander is in absolute waarde minstens 10 !. We concluderen dat het absolute verschil altijd minstens 10 ! is. Dus als $a \\neq 0$ is $|P(10)-P(0)| \\geq 10!-10>1000$. Gegeven is echter dat $|P(10)-P(0)|<1000$, dus blijkbaar moet gelden dat $a=0$. Nu vinden we dat\n\n$$\nP(x)=1+x-c_{1} .\n$$\n\nZij $k \\in \\mathbb{Z}$ willekeurig en kies $m=k-1+c_{1}$. Dan geldt $P(m)=1+\\left(k-1+c_{1}\\right)-c_{1}=k$. Dus voor elke gehele $k$ is er een gehele $m$ met $P(m)=k$.\nBekijk nu geval (B). We kunnen precies dezelfde redenering volgen, waarbij we nu $Q(x)=$ $1-x+c_{1}$ definiëren en uiteindelijk krijgen dat\n\n$$\nP(x)=1-x+c_{1}+a \\cdot \\prod_{i=1}^{10}\\left(x-c_{i}\\right)\n$$\n\nWe leiden op dezelfde manier af dat $a=0$, zodat\n\n$$\nP(x)=1-x+c_{1} .\n$$\n\nEn nu volgt weer dat er voor elke gehele $k$ een gehele $m$ is met $P(m)=k$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Laat $m$ en $n$ positieve gehele getallen zijn zodat $5 m+n$ een deler is van $5 n+m$. Bewijs dat $m$ een deler is van $n$.", "solution": "Er is een positieve gehele $k$ met $(5 m+n) k=5 n+m$. Dus $5 k m-m=5 n-k n$, oftewel $(5 k-1) m=(5-k) n$. De linkerkant is positief, dus de rechterkant ook, waaruit volgt dat $k<5$. Als $k=1$, dan is $4 m=4 n$, dus $m=n$, dus $m \\mid n$. Als $k=2$, dan is $9 m=3 n$, dus $3 m=n$, dus $m \\mid n$. Als $k=3$, dan is $14 m=2 n$, dus $7 m=n$, dus $m \\mid n$. Als $k=4$, dan is $19 m=n$, dus $m \\mid n$. We zien dat in alle gevallen geldt dat $m \\mid n$. $\\square$", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Laat $m$ en $n$ positieve gehele getallen zijn zodat $5 m+n$ een deler is van $5 n+m$. Bewijs dat $m$ een deler is van $n$.", "solution": "Zij $d=\\operatorname{ggd}(m, n)$ en schrijf $m=a d, n=b d$. Dan zijn $a$ en $b$ positieve gehele getallen met $\\operatorname{ggd}(a, b)=1$. Uit $5 m+n \\mid 5 n+m$ volgt $5 a d+b d \\mid 5 b d+a d$, dus $5 a+b \\mid 5 b+a$. Nu geldt ook\n\n$$\n5 a+b \\mid(5 b+a)-5(5 a+b)=-24 a\n$$\n\nen\n\n$$\n5 a+b \\mid 5(5 b+a)-(5 a+b)=24 b\n$$\n\nDus $5 a+b \\mid \\operatorname{ggd}(24 a, 24 b)=24$. Als $a=1$ geldt altijd $a \\mid b$. Als $a \\geq 2$ is $5 a+b \\geq 11$, dus kan $5 a+b$ alleen gelijk zijn aan 12 of 24 . Als $5 a+b=12$, dan moet gelden $a=2$ en $b=2$, maar die zijn niet copriem, tegenspraak. Als $5 a+b=24$, dan moet $a=2$ en $b=14$ of $a=3$ en $b=9$ of $a=4$ en $b=4$. In alle drie zijn $a$ en $b$ niet copriem, tegenspraak. Dus alleen $a=1$ kan gelden en dan is $a \\mid b$, waaruit volgt $a d \\mid b d$, dus $m \\mid n$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Gegeven zijn positieve gehele getallen $r$ en $k$ en een oneindige rij positieve gehele getallen $a_{1} \\leq a_{2} \\leq \\ldots$ zodat $\\frac{r}{a_{r}}=k+1$. Bewijs dat er een $t$ is met $\\frac{t}{a_{t}}=k$.", "solution": "We bewijzen dit uit het ongerijmde. Stel dat zo'n $t$ niet bestaat. Als $a_{k}=1$, dan zou $\\frac{k}{a_{k}}=k$, tegenspraak met onze aanname. Dus $a_{k} \\geq 2$. We bewijzen nu met inductie naar $i$ dat $a_{i k} \\geq i+1$. De inductiebasis hebben we zojuist gedaan. Stel nu dat voor zekere $i \\geq 1$ geldt dat $a_{i k} \\geq i+1$. Dan is ook $a_{(i+1) k} \\geq i+1$. Als $a_{(i+1) k}=i+1$, dan is $\\frac{(i+1) k}{a_{(i+1) k}}=k$, tegenspraak. Dus $a_{(i+1) k} \\geq i+2$. Dit voltooit de inductiestap. Neem nu $i=a_{r}$, dan is dus $a_{a_{r} k} \\geq a_{r}+1$. En omdat $r=a_{r}(k+1)$ geldt $a_{r}=a_{a_{r}(k+1)} \\geq a_{a_{r} k} \\geq a_{r}+1$, tegenspraak.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Zij $n \\geq 2$ een positief geheel getal. Ieder vakje van een $n \\times n$-bord wordt rood of blauw gekleurd. We leggen dominostenen op het bord, die elk twee vakjes bedekken. We noemen een dominosteen effen als hij op twee rode of twee blauwe vakjes ligt en kleurrijk als hij op een rood en een blauw vakje ligt. Vind het grootste positieve gehele getal $k$ met de volgende eigenschap: hoe de rood/blauw-kleuring van het bord ook gebeurt, het is altijd mogelijk om $k$ niet-overlappende dominostenen op het bord te leggen die ofwel allemaal effen zijn ofwel allemaal kleurrijk.", "solution": "We bewijzen dat $k=\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ de grootst mogelijke waarde is.\nStel dat $n$ even is. Dan is het mogelijk om het bord te bedekken met $\\frac{n^{2}}{2}$ dominostenen (zonder op kleuren te letten). Omdat er $\\frac{n^{2}}{2}$ dominostenen zijn die allemaal kleurrijk of effen zijn, zijn er of minstens $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor=\\frac{n^{2}}{4}$ kleurrijke of minstens $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor=\\frac{n^{2}}{4}$ effen dominostenen. Als $n$ oneven is, kunnen we het bord bedekken met $\\frac{n^{2}-1}{2}$ dominostenen. (Merk op dat dit getal geheel en even is.) Van deze dominostenen zijn er of minstens $\\frac{n^{2}-1}{4}=\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ kleurrijk, of minstens $\\frac{n^{2}-1}{4}=\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ effen. Dit bewijst dat het altijd mogelijk is om op het bord minstens $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ kleurrijke dominostenen of minstens $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ effen dominostenen neer te leggen. We bewijzen nu dat het mogelijk is om de kleuring in rode en blauwe vakjes zo te kiezen, dat er niet meer dan $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ effen en ook niet meer dan $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ kleurrijke dominostenen neer te leggen zijn.\nKleur de vakjes van het bord zwart-wit als op een schaakbord, zodat het vakje linksonder wit is. Als $n$ even is, zijn er evenveel witte als zwarte vakjes, namelijk $\\frac{n^{2}}{2}$. Als $n$ oneven is, is er een zwart vakje minder en is het aantal zwarte vakjes gelijk aan $\\frac{n^{2}-1}{2}=\\left\\lfloor\\frac{n^{2}}{2}\\right\\rfloor$. In beide gevallen is dit een even aantal vakjes, aangezien voor oneven $n$ geldt dat $n^{2} \\equiv 1$ mod 4. Kleur de helft van de zwarte vakjes rood en alle andere vakjes blauw. Dan zijn er $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ rode vakjes, dus we kunnen maximaal $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ niet-overlappende kleurrijke dominostenen op het bord leggen: elk van deze dominostenen bedekt immers een rood vakje. Een effen dominosteen kan geen twee rode vakjes bedekken, want er zijn geen twee vakjes naast elkaar rood gekleurd. Hij moet dus wel twee blauwe vakjes bedekken. Daar zit in elk geval een zwart vakje bij, dus het aantal effen dominostenen is hoogstens het aantal zwart-blauwe vakjes en dat is $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$. Dus zowel van de kleurrijke als van de effen dominostenen kunnen er hooguit $\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ tegelijk op het bord worden gelegd.\nWe concluderen dat de maximale $k$ inderdaad $k=\\left\\lfloor\\frac{n^{2}}{4}\\right\\rfloor$ is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "In een driehoek $A B C$ is $D$ het snijpunt van de binnenbissectrice van $\\angle B A C$ met zijde $B C$. Zij $P$ het tweede snijpunt van de buitenbissectrice van $\\angle B A C$ met de omgeschreven cirkel van $\\triangle A B C$. Een cirkel door $A$ en $P$ snijdt lijnstuk $B P$ inwendig in $E$ en lijnstuk $C P$ inwendig in $F$. Bewijs dat $\\angle D E P=\\angle D F P$.", "solution": "We bekijken de configuratie waarbij de punten $A, C, B$ en $P$ in die volgorde op de omgeschreven cirkel liggen. Het andere geval gaat analoog.\nVanwege de omtrekshoekstelling in de omgeschreven cirkel van $\\triangle A B C$ geldt\n\n$$\n\\angle A B E=\\angle A B P=\\angle A C P=\\angle A C F .\n$$\n\nVerder is wegens de omtrekshoekstelling in de cirkel door $A, P, E$ en $F$ :\n\n$$\n\\angle A E B=180^{\\circ}-\\angle A E P=180^{\\circ}-\\angle A F P=\\angle A F C .\n$$\n\nMet (hh) concluderen we dat $\\triangle A B E \\sim \\triangle A C F$. Hieruit volgt\n\n$$\n\\frac{|A B|}{|A C|}=\\frac{|B E|}{|C F|}\n$$\n\nVolgens de bissectricestelling geldt\n\n$$\n\\frac{|A B|}{|A C|}=\\frac{|D B|}{|D C|}\n$$\n\ndus samen geeft dit\n\n$$\n\\frac{|B E|}{|C F|}=\\frac{|D B|}{|D C|}\n$$\n\nKies $Z$ op $P A$ zodat $A$ tussen $P$ en $Z$ ligt. Omdat $A P$ de buitenbissectrice van $\\angle B A C$ is, geldt $\\angle P A B=\\angle Z A C=180^{\\circ}-\\angle P A C$. Dus met behulp van de omtrekshoekstelling en koordenvierhoekstelling krijgen we nu\n\n$$\n\\angle D C F=\\angle P C B=\\angle P A B=180^{\\circ}-\\angle P A C=\\angle P B C=\\angle E B D .\n$$\n\n(Alternatief voor het bewijs $\\angle D C F=\\angle E B D$ : noem $Q$ het tweede snijpunt van de binnenbissectrice van $\\angle B A C$ met de omgeschreven cirkel van $\\triangle A B C$. Omdat $\\angle C A Q=\\angle B A Q$, zijn de bogen $B Q$ en $C Q$ even lang. De buitenbissectrice en de binnenbissectrice staan loodrecht op elkaar, dus met Thales zien we dat $P Q$ een middellijn van de omgeschreven cirkel is. Daaruit volgt dat ook de bogen $B P$ en $C P$ even lang zijn. Dus $|B P|=|C P|$ en daarmee ook\n\n$$\n\\angle E B D=\\angle P B C=\\angle B C P=\\angle D C F\n$$\n\nwat we wilden bewijzen.)\nGecombineerd met (1) krijgen we nu $\\triangle B E D \\sim \\triangle C F D$ (zhz). Hieruit volgt dat $\\angle B E D=$ $\\angle C F D$ en dus ook $\\angle D E P=180^{\\circ}-\\angle B E D=180^{\\circ}-\\angle C F D=\\angle D F P$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2015", "problem_label": "5", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ met\n\n$$\n\\left(x^{2}+y^{2}\\right) f(x y)=f(x) f(y) f\\left(x^{2}+y^{2}\\right)\n$$\n\nvoor alle reële $x$ en $y$.", "solution": "Vul in $x=y=0$, dan staat er $0=f(0)^{3}$, dus $f(0)=0$. We bekijken nu twee gevallen: $f$ is nog ergens anders ook 0 of juist niet. Voor het eerste geval nemen we dus aan dat er nog een $a \\neq 0$ is zodat $f(a)=0$. Dan geeft $x=a$ invullen dat $\\left(a^{2}+y^{2}\\right) f(a y)=0$ voor alle $y$. Omdat $a^{2}+y^{2}>0$ aangezien $a \\neq 0$, is $f(a y)=0$ voor alle $y$. Maar $a y$ kan alle waarden in $\\mathbb{R}$ aannemen, dus $f(x)=0$ voor alle $x$. Dit is meteen een kandidaatfunctie en deze voldoet.\nWe bekijken nu verder het tweede geval: $f(x) \\neq 0$ voor alle $x \\neq 0$. Neem nu $x \\neq 0$ en $y=1$. Dan geldt $\\left(x^{2}+1\\right) f(x)=f(x) f(1) f\\left(x^{2}+1\\right)$ en $f(x) \\neq 0$, dus we kunnen hier delen door $f(x)$. We krijgen $\\left(x^{2}+1\\right)=f(1) f\\left(x^{2}+1\\right)$. Noem $f(1)=c$. We weten $c \\neq 0$, dus $f\\left(x^{2}+1\\right)=\\frac{x^{2}+1}{c}$. Omdat $x^{2}+1$ alle reële waarden groter dan 1 kan aannemen, geldt nu $f(x)=\\frac{x}{c}$ voor alle $x>1$.\nNeem $x=y=2$ en vul dit in: $(4+4) f(4)=f(2) f(2) f(4+4)$. Voor $x>1$ weten we de functiewaarde, dus in het bijzonder weten we ook $f(2), f(4)$ en $f(8)$. Dus $8 \\cdot \\frac{4}{c}=\\frac{2}{c} \\cdot \\frac{2}{c} \\cdot \\frac{8}{c}$, oftewel $\\frac{1}{c}=\\frac{1}{c^{3}}$. We zien dat $c^{2}=1$, dus $c=1$ of $c=-1$. Omdat $c^{2}=1$, kunnen we nu ook schrijven $f(x)=c x$ voor alle $x \\geq 1$.\nNeem $x>1$ en vul $y=\\frac{1}{x}$ in. Dat geeft $\\left(x^{2}+\\frac{1}{x^{2}}\\right) f(1)=f(x) f\\left(\\frac{1}{x}\\right) f\\left(x^{2}+\\frac{1}{x^{2}}\\right)$. Omdat $x>1$, is ook $x^{2}+\\frac{1}{x^{2}}>1$, dus hier staat $\\left(x^{2}+\\frac{1}{x^{2}}\\right) c=x c \\cdot f\\left(\\frac{1}{x}\\right) \\cdot c\\left(x^{2}+\\frac{1}{x^{2}}\\right)$, oftewel $1=x c \\cdot f\\left(\\frac{1}{x}\\right)$. Dus $f\\left(\\frac{1}{x}\\right)=\\frac{1}{x c}=c \\cdot \\frac{1}{x}$. We concluderen dat $f(x)=c x$ voor alle $x>0$ met $x \\neq 1$. Maar ook voor $x=1$ geldt $f(x)=c x$, want $f(1)=c$. Dus $f(x)=c x$ voor alle $x>0$.\nVul nu $x=y=-1 \\mathrm{in}$. Dat geeft $2 f(1)=f(-1)^{2} f(2)$. We weten $f(1)=c$ en $f(2)=2 c$, dus $2 c=f(-1)^{2} \\cdot 2 c$, oftewel $f(-1)^{2}=1$ aangezien $c \\neq 0$. Dus $f(-1)=1$ of $f(-1)=-1$. Neem $x>0$ en $y=-1$. Dat geeft $\\left(x^{2}+1\\right) f(-x)=f(x) f(-1) f\\left(x^{2}+1\\right)$, dus $\\left(x^{2}+1\\right) f(-x)=$ $c x \\cdot f(-1) \\cdot c\\left(x^{2}+1\\right)$, oftewel $f(-x)=c^{2} x f(-1)=x f(-1)$. Als we $d=f(-1)$ noemen, geldt dus $f(x)=-d x$ voor alle $x<0$, met $d^{2}=1$.\nWe concluderen dat er vier mogelijke kandidaatfuncties zijn (naast $f(x)=0$, die we al gecontroleerd hadden): $f(x)=x, f(x)=-x, f(x)=|x|$ en $f(x)=-|x|$. We controleren eerst $f(x)=t x$ met $t= \\pm 1$. Dan staat er links $\\left(x^{2}+y^{2}\\right) \\cdot t x y$ en rechts $t x \\cdot t y \\cdot t\\left(x^{2}+y^{2}\\right)$. Omdat $t^{2}=1$, staat links en rechts hetzelfde. Dus deze twee functies voldoen. Nu controleren we $f(x)=t|x|$, waarbij weer $t= \\pm 1$. Nu staat links $\\left(x^{2}+y^{2}\\right) \\cdot t|x y|$ en rechts $t|x| \\cdot t|y| \\cdot t\\left|x^{2}+y^{2}\\right|$. Omdat $x^{2}+y^{2}=\\left|x^{2}+y^{2}\\right|$ en $|x y|=|x||y|$, staat links en rechts hetzelfde. Dus ook deze twee functies voldoen.\nEr zijn dus vijf oplossingen: $f(x)=0, f(x)=x, f(x)=-x, f(x)=|x|$ en $f(x)=-|x|$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,11 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Voor vierhoek $A B C D$ geldt $\\angle A=\\angle C=90^{\\circ}$. Zij $E$ een punt binnen de vierhoek. Zij $M$ het midden van $B E$. Bewijs dat $\\angle A D B=\\angle E D C$ dan en slechts dan als $|M A|=|M C|$.", "solution": "Zij $N$ het midden van $B D$. Wegens Thales gaat de cirkel met middellijn $B D$ ook door $A$ en $C$ en punt $N$ is hiervan het middelpunt. Verder geldt dat $M N \\| D E$ : als $E$ niet op $B D$ ligt, is $M N$ een middenparallel in driehoek $B D E$, en als $E$ wel op $B D$ ligt, dan zijn $M N$ en $D E$ dezelfde lijn.\nDe bewering $|A M|=|C M|$ is equivalent met dat $M$ op de middelloodlijn van $A C$ ligt. Omdat die middelloodlijn door het middelpunt $N$ van de cirkel gaat, is dit dus equivalent met de bewering $M N \\perp A C$. En dat is het geval dan en slechts dan als $D E \\perp A C$. Noem $T$ het snijpunt van $D E$ en $A C$, dan geldt dus: $|A M|=|C M|$ dan en slechts dan als $\\angle D T C=90^{\\circ}$.\nMet de hoekensom vinden we $\\angle D T C=180^{\\circ}-\\angle T D C-\\angle D C T=180^{\\circ}-\\angle E D C-\\angle D C A$. Er geldt $\\angle D C A=90^{\\circ}-\\angle A C B=90^{\\circ}-\\angle A D B$, waarbij we voor de laatste gelijkheid de koordenvierhoek $A B C D$ hebben gebruikt. Dus $\\angle D T C=180^{\\circ}-\\angle E D C-\\left(90^{\\circ}-\\angle A D B\\right)=$ $90^{\\circ}-\\angle E D C+\\angle A D B$. Nu volgt onmiddelijk dat $\\angle A D B=\\angle E D C$ dan en slechts dan als $\\angle D T C=90^{\\circ}$ en we hadden al gezien dat dat laatste equivalent was met $|A M|=|C M|$. Merk op dat dit bewijs geldt in iedere configuratie.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom\n\n$$\nQ(x)=(x+1) P(x-1)-(x-1) P(x)\n$$\n\nconstant is.", "solution": "Stel dat $P(x)$ een constant polynoom is, zeg $P(x)=a$ met $a \\in \\mathbb{R}$. Dan is\n\n$$\nQ(x)=(x+1) a-(x-1) a=a x+a-a x+a=2 a,\n$$\n\nen dat is constant. Dus elk constant polynoom $P(x)$ voldoet.\nWe nemen nu verder aan dat $P$ niet constant is. We kunnen dan schrijven $P(x)=a_{n} x^{n}+$ $a_{n-1} x^{n-1}+\\ldots+a_{1} x+a_{0}$ met $n \\geq 1$ en $a_{n} \\neq 0$. Bekijk de coëfficiënt van $x^{n}$ in $Q(x)$. Deze is de som van de coëfficiënten van $x^{n}$ in $x P(x-1), P(x-1),-x P(x)$ en $P(x)$. In de eerste is deze coëfficiënt gelijk aan $a_{n-1}-n a_{n}$, in de tweede aan $a_{n}$, in de derde aan $-a_{n-1}$ en in de vierde aan $a_{n}$. Samen is dat\n\n$$\na_{n-1}-n a_{n}+a_{n}-a_{n-1}+a_{n}=(2-n) a_{n} .\n$$\n\nMaar in $Q(x)$ moet deze coëfficiënt gelijk zijn aan 0 . Omdat $a_{n} \\neq 0$, volgt hieruit $n=2$. Dus $P(x)=a_{2} x^{2}+a_{1} x+a_{0}$ met $a_{2} \\neq 0$.\nBekijk nu de constante coëfficiënt van $Q(x)$. Deze is de som van de constante coëfficiënten van $x P(x-1), P(x-1),-x P(x)$ en $P(x)$. Dit zijn achtereenvolgens $0, a_{2}-a_{1}+a_{0}, 0$ en $a_{0}$. Samen is dat $a_{2}-a_{1}+2 a_{0}$. Anderzijds kunnen we $Q(1)$ uitrekenen:\n\n$$\nQ(1)=2 P(0)-0=2 a_{0}\n$$\n\nOmdat $Q$ constant is, is $Q(1)$ gelijk aan de constante coëfficiënt van $Q$, dus $2 a_{0}=a_{2}-a_{1}+$ $2 a_{0}$. We zien dat $a_{2}=a_{1}$. Dus $P(x)$ is van de vorm $P(x)=b x^{2}+b x+a=b x(x+1)+a$ met $a, b \\in \\mathbb{R}$ en $b \\neq 0$. Om te kijken of alle polynomen van deze vorm voldoen, vullen we dit in:\n\n$$\n\\begin{aligned}\nQ(x) & =(x+1)(b(x-1) x+a)-(x-1)(b x(x+1)+a) \\\\\n& =(x-1) x(x+1) b+(x+1) a-(x-1) x(x+1) b-(x-1) a \\\\\n& =2 a\n\\end{aligned}\n$$\n\nDat is inderdaad constant, dus alle polynomen van deze vorm voldoen. In feite is elk constant polynoom ook van deze vorm, maar dan met $b=0$. We concluderen dat de oplossingen zijn: alle polynomen van de vorm $P(x)=b x^{2}+b x+a$ met $a, b \\in \\mathbb{R}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom\n\n$$\nQ(x)=(x+1) P(x-1)-(x-1) P(x)\n$$\n\nconstant is.", "solution": "Er geldt\n\n$$\nQ(1)=2 P(0)-0=2 P(0)\n$$\n\nen\n\n$$\nQ(-1)=0--2 P(-1)=2 P(-1)\n$$\n\nOmdat $Q$ constant is, volgt hieruit $P(0)=P(-1)$. Schrijf $P(0)=c$ en bekijk het polynoom $P(x)-c$. Dit polynoom heeft nulpunten bij $x=0$ en $x=-1$, dus\n\n$$\nP(x)-c=x(x+1) R(x)\n$$\n\nvoor een zeker polynoom $R(x)$ met reële coëfficiënten. Dus $P(x)=x(x+1) R(x)+c$ en dit vullen we in:\n\n$$\n\\begin{aligned}\nQ(x) & =(x+1)((x-1) x R(x-1)+c)-(x-1)(x(x+1) R(x)+c) \\\\\n& =(x-1) x(x+1) R(x-1)+(x+1) c-(x-1) x(x+1) R(x)-(x-1) c \\\\\n& =(x-1) x(x+1)(R(x-1)-R(x))+2 c\n\\end{aligned}\n$$\n\nDit moet constant zijn, dus $R(x-1)-R(x)$ moet het nulpolynoom zijn. Dus $R(x-1)=$ $R(x)$ voor alle $x$. In het bijzonder geldt $R(0)=R(1)=R(2)=\\ldots$, dus $R$ neemt dezelfde waarde aan op oneindig veel punten. Dat betekent dat $R$ gelijk moet zijn aan een constant polynoom, zeg $R(x)=d$. Dan geldt\n\n$$\nP(x)=x(x+1) d+c=d x^{2}+d x+c .\n$$\n\nNet als in de eerste oplossing controleren we dat alle polynomen van deze vorm, met $c, d \\in \\mathbb{R}$, voldoen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom\n\n$$\nQ(x)=(x+1) P(x-1)-(x-1) P(x)\n$$\n\nconstant is.", "solution": "We noemen $p=P(1)$ en $q$ de constante waarde die $Q(x)$ aanneemt. We bewijzen met inductie naar $m$ dat $P(m)=\\frac{1}{2} m(m+1) p-\\left(\\frac{1}{2} m(m+1)-1\\right) \\cdot \\frac{q}{2}$ voor alle gehele $m \\geq 1$.\nVoor $m=1$ staat er $P(1)=\\frac{1}{2} \\cdot 1 \\cdot 2 \\cdot p-\\left(\\frac{1}{2} \\cdot 1 \\cdot 2-1\\right) \\cdot \\frac{q}{2}=p-0=P(1)$, dus dat klopt. Zij nu $k \\geq 1$ en neem aan dat we de claim bewezen hebben voor $m=k$. Uit de gegeven vergelijking volgt voor $x \\neq 1$ :\n\n$$\nP(x)=\\frac{(x+1) P(x-1)-q}{x-1} .\n$$\n\nVul nu $x=k+1$ in (merk op dat $x \\neq 1$, want $k \\geq 1$ ):\n\n$$\n\\begin{aligned}\nP(k+1) & =\\frac{(k+2) P(k)-q}{k} \\\\\n& =\\frac{(k+2) \\cdot\\left(\\frac{1}{2} k(k+1) p-\\left(\\frac{1}{2} k(k+1)-1\\right) \\cdot \\frac{q}{2}\\right)-q}{k} \\\\\n& =(k+2) \\cdot\\left(\\frac{1}{2}(k+1) p-\\left(\\frac{1}{2}(k+1)-\\frac{1}{k}\\right) \\cdot \\frac{q}{2}\\right)-\\frac{q}{k} \\\\\n& =\\frac{1}{2}(k+1)(k+2) p-\\frac{1}{2}(k+1)(k+2) \\cdot \\frac{q}{2}+\\frac{k+2}{k} \\cdot \\frac{q}{2}-\\frac{q}{k} \\\\\n& =\\frac{1}{2}(k+1)(k+2) p-\\frac{1}{2}(k+1)(k+2) \\cdot \\frac{q}{2}+\\frac{q}{2}+\\frac{2}{k} \\cdot \\frac{q}{2}-\\frac{q}{k} \\\\\n& =\\frac{1}{2}(k+1)(k+2) p-\\left(\\frac{1}{2}(k+1)(k+2)-1\\right) \\cdot \\frac{q}{2} .\n\\end{aligned}\n$$\n\nDit voltooit de inductiestap.\nDus $P(x)$ valt op oneindig veel punten (namelijk alle positieve gehele getallen) samen met het polynoom $\\frac{1}{2} x(x+1) p-\\left(\\frac{1}{2} x(x+1)-1\\right) \\cdot \\frac{q}{2}$. Daarom moet hij gelijk zijn aan dit polynoom. Als we dit herschrijven tot de standaardnotatie, krijgen we\n\n$$\nP(x)=\\left(\\frac{1}{2} p-\\frac{1}{4} q\\right) \\cdot x^{2}+\\left(\\frac{1}{2} p-\\frac{1}{4} q\\right) \\cdot x+\\frac{q}{2} .\n$$\n\nDit is van de vorm $P(x)=b x^{2}+b x+a$ met $a$ en $b$ constanten in $\\mathbb{R}$. Net als in de eerste oplossing controleren we dat alle polynomen van deze vorm voldoen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 5 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Zij $n$ een positief geheel getal. We bekijken rijtjes getallen $a_{0}, a_{1}, \\ldots, a_{k}$ en $b_{0}, b_{1}, \\ldots, b_{k}$ die voldoen aan $a_{0}=b_{0}=1$ en $a_{k}=b_{k}=n$ en waarbij voor elke $i$ met $1 \\leq i \\leq k$ geldt dat $\\left(a_{i}, b_{i}\\right)$ gelijk is aan ofwel $\\left(1+a_{i-1}, b_{i-1}\\right)$ ofwel $\\left(a_{i-1}, 1+b_{i-1}\\right)$. Definieer voor $1 \\leq i \\leq k$ het getal\n\n$$\nc_{i}= \\begin{cases}a_{i} & \\text { als } a_{i}=a_{i-1} \\\\ b_{i} & \\text { als } b_{i}=b_{i-1}\\end{cases}\n$$\n\nBewijs dat $c_{1}+c_{2}+\\cdots+c_{k}=n^{2}-1$.", "solution": "We bewijzen met inductie naar $j$ dat $c_{1}+\\ldots+c_{j}=a_{j} b_{j}-1$. Voor $j=1$ staat hier $c_{1}=a_{1} b_{1}-1$ en dat is waar aangezien $\\left(a_{1}, b_{1}\\right) \\in\\{(1,2),(2,1)\\}$. Stel nu dat $c_{1}+\\ldots+c_{i-1}=a_{i-1} b_{i-1}-1$. Neem zonder verlies van algemeenheid aan dat $\\left(a_{i}, b_{i}\\right)=$ $\\left(a_{i-1}, 1+b_{i-1}\\right)$, zodat $a_{i}=a_{i-1}$ en dus $c_{i}=a_{i-1}$. Er geldt nu\n\n$$\n\\left(c_{1}+\\ldots+c_{i-1}\\right)+c_{i}=\\left(a_{i-1} b_{i-1}-1\\right)+a_{i-1}=a_{i-1}\\left(b_{i-1}+1\\right)-1=a_{i} b_{i}-1\n$$\n\nwat de inductie voltooit. Voor $j=k$ zien we nu dat $c_{1}+\\ldots+c_{k}=a_{k} b_{k}-1=n^{2}-1$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Zij $n$ een positief geheel getal. We bekijken rijtjes getallen $a_{0}, a_{1}, \\ldots, a_{k}$ en $b_{0}, b_{1}, \\ldots, b_{k}$ die voldoen aan $a_{0}=b_{0}=1$ en $a_{k}=b_{k}=n$ en waarbij voor elke $i$ met $1 \\leq i \\leq k$ geldt dat $\\left(a_{i}, b_{i}\\right)$ gelijk is aan ofwel $\\left(1+a_{i-1}, b_{i-1}\\right)$ ofwel $\\left(a_{i-1}, 1+b_{i-1}\\right)$. Definieer voor $1 \\leq i \\leq k$ het getal\n\n$$\nc_{i}= \\begin{cases}a_{i} & \\text { als } a_{i}=a_{i-1} \\\\ b_{i} & \\text { als } b_{i}=b_{i-1}\\end{cases}\n$$\n\nBewijs dat $c_{1}+c_{2}+\\cdots+c_{k}=n^{2}-1$.", "solution": "We definiëren een rijtje van $k$ letters: de $i$-de letter in het rijtje is gelijk aan $A$ als $a_{i}=1+a_{i-1}$ en gelijk aan $B$ als $b_{i}=1+b_{i-1}$. Omdat de rijtjes $a_{i}$ en $b_{i}$ beide van 1 naar $n$ gaan, moet er $n-1$ keer een $A$ staan en $n-1$ keer een $B$. Als voor zekere $i$ de $i$-de letter gelijk is aan $A$, dan is $c_{i}=b_{i}$ en dat is gelijk aan 1 plus het aantal letters $B$ dat eerder in het rijtje staat (want $b_{0}=1$ en voor elke $B$ is $b_{j}$ met 1 omhoog gegaan en bij elke $A$ is $b_{j}$ niet veranderd). En andersom geldt dat als de $i$-de letter een $B$ is, dan $c_{i}$ gelijk is aan 1 plus het aantal letters $A$ dat eerder in het rijtje staat.\nBekijk nu een oude situatie met de $i$-de letter gelijk aan $A$ en de $i+1$-ste letter gelijk aan $B$ en een nieuwe situatie waarin dit precies andersom is. De $c_{j}$ die hoort bij de letter $A$ is in de nieuwe situatie 1 groter dan in de oude, omdat er een keer $B$ extra voorafgaat aan de $A$. De $c_{j}$ die hoort bij de letter $B$ is juist 1 kleiner geworden. De rest van de $c_{j}$ 's is ongewijzigd, dus de som van de $c_{j}$ 's is ook ongewijzigd. Een verwisseling van $A B$ naar $B A$ heeft dus geen invloed op de som van de $c_{j}$ 's. We kunnen nu net zo lang $A B$ vervangen door $B A$ tot het letterrijtje bestaat uit eerst $n-1$ keer $B$ en daarna $n-1$ keer $A$. De bijbehorende $c_{j}$ 's zijn dan achtereenvolgens $1,1, \\ldots, 1, n, n, \\ldots, n$, waarbij de 1 precies $n-1$ keer voorkomt en de $n$ ook. De som hiervan is $(n-1)(n+1)=n^{2}-1$ en dat geldt dus ook voor de som van $c_{j}$ 's in het oorspronkelijke rijtje.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Zij $n$ een positief geheel getal. We bekijken rijtjes getallen $a_{0}, a_{1}, \\ldots, a_{k}$ en $b_{0}, b_{1}, \\ldots, b_{k}$ die voldoen aan $a_{0}=b_{0}=1$ en $a_{k}=b_{k}=n$ en waarbij voor elke $i$ met $1 \\leq i \\leq k$ geldt dat $\\left(a_{i}, b_{i}\\right)$ gelijk is aan ofwel $\\left(1+a_{i-1}, b_{i-1}\\right)$ ofwel $\\left(a_{i-1}, 1+b_{i-1}\\right)$. Definieer voor $1 \\leq i \\leq k$ het getal\n\n$$\nc_{i}= \\begin{cases}a_{i} & \\text { als } a_{i}=a_{i-1} \\\\ b_{i} & \\text { als } b_{i}=b_{i-1}\\end{cases}\n$$\n\nBewijs dat $c_{1}+c_{2}+\\cdots+c_{k}=n^{2}-1$.", "solution": "We definiëren een rijtje van $k$ letters: de $i$-de letter in het rijtje is gelijk aan $A$ als $a_{i}=1+a_{i-1}$ en gelijk aan $B$ als $b_{i}=1+b_{i-1}$. Verder definiëren we voor $1 \\leq i \\leq k$\n\n$$\nd_{i}= \\begin{cases}b_{i} & \\text { als } a_{i}=a_{i-1} \\\\ a_{i} & \\text { als } b_{i}=b_{i-1}\\end{cases}\n$$\n\nAls voor zekere $i$ de $i$-de letter gelijk is aan $A$, dan is $d_{i}=a_{i}$ en dat is gelijk aan 1 plus het aantal letters $A$ dat tot en met deze plek in het rijtje staat (want $a_{0}=1$ en voor elke $A$ is $a_{j}$ met 1 omhoog gegaan en bij elke $B$ is $a_{j}$ niet veranderd). De $d_{i}$ die corresponderen met de plekken waar een $A$ staat, zijn dus precies de getallen 2 tot en met $n$. De $d_{i}$ die corresponderen met de plekken waar een $B$ staat, zijn ook precies de getallen 2 tot en met $n$. Dus de som van alle $d_{i}$ is gelijk aan $(n-1)(n+2)=n^{2}+n-2$.\nVoor elke $i$ geldt $c_{i}+d_{i}=a_{i}+b_{i}=1+\\left(a_{i-1}+b_{i-1}\\right)$ en $c_{1}+d_{1}=1+2=3$, dus met een simpele inductie $c_{i}+d_{i}=i+2$. De totale som van alle $c_{i}$ en $d_{i}$ bij elkaar is dus $3+4+\\ldots+2 n=\\frac{1}{2}(2 n+3)(2 n-2)=(2 n+3)(n-1)=2 n^{2}+n-3$. We concluderen dat de som van de $c_{i}$ gelijk is aan $\\left(2 n^{2}+n-3\\right)-\\left(n^{2}+n-2\\right)=n^{2}-1$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing III."}
|
| 8 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "Laat cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$, met middelpunten respectievelijk $O_{1}$ en $O_{2}$, elkaar snijden in twee verschillende punten $A$ en $B$. De lijn $O_{1} A$ snijdt $\\Gamma_{2}$ nogmaals in $C$ en de lijn $O_{2} A$ snijdt $\\Gamma_{1}$ nogmaals in $D$. De lijn door $B$ evenwijdig met $A D$ snijdt $\\Gamma_{1}$ nogmaals in $E$. Veronderstel dat $O_{1} A$ evenwijdig is met $D E$. Bewijs dat $C D$ loodrecht op $O_{2} C$ staat.", "solution": "In alle oplossingen bekijken we de configuratie waarin $A, B, E$ en $D$ in die volgorde op een cirkel liggen, $O_{1}, A$ en $C$ in die volgorde op een lijn en $O_{2}, A$ en $D$ in die volgorde op een lijn. De andere configuraties gaan analoog.\nVanwege koordenvierhoek $A B E D$ geldt $\\angle B E D=180^{\\circ}-\\angle D A B$. Verder geldt wegens de twee evenwijdigheden dat $\\angle B E D=\\angle D A O_{1}$ en omdat $\\left|O_{1} A\\right|=\\left|O_{1} D\\right|$ geldt $\\angle D A O_{1}=$ $\\angle A D O_{1}$. We concluderen dat $180^{\\circ}-\\angle D A B=\\angle A D O_{1}$. Met U-hoeken volgt nu dat $D O_{1}$ en $A B$ evenwijdig zijn.\nWe hadden al gezien dat $\\angle A D O_{1}=\\angle D A O_{1}$. Vanwege overstaande hoeken en het feit dat $\\left|O_{2} A\\right|=\\left|O_{2} C\\right|$ geldt $\\angle D A O_{1}=\\angle O_{2} A C=\\angle O_{2} C A$. Dus $\\angle O_{2} D O_{1}=\\angle A D O_{1}=$ $\\angle O_{2} C A=\\angle O_{2} C O_{1}$, wat betekent dat $O_{1} D C O_{2}$ een koordenvierhoek is.\nDe lijn $O_{1} O_{2}$ is de middelloodlijn van $A B$ en staat dus ook loodrecht op $D O_{1}$, omdat die evenwijdig aan $A B$ is. Dus $\\angle O_{2} O_{1} D=90^{\\circ}$. Omdat $O_{1} D C O_{2}$ een koordenvierhoek is, is nu ook $\\angle O_{2} C D=90^{\\circ}$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 9 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "Laat cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$, met middelpunten respectievelijk $O_{1}$ en $O_{2}$, elkaar snijden in twee verschillende punten $A$ en $B$. De lijn $O_{1} A$ snijdt $\\Gamma_{2}$ nogmaals in $C$ en de lijn $O_{2} A$ snijdt $\\Gamma_{1}$ nogmaals in $D$. De lijn door $B$ evenwijdig met $A D$ snijdt $\\Gamma_{1}$ nogmaals in $E$. Veronderstel dat $O_{1} A$ evenwijdig is met $D E$. Bewijs dat $C D$ loodrecht op $O_{2} C$ staat.", "solution": "Noem $\\alpha=\\angle D E B$. Zij $S$ het snijpunt van $B E$ en $A C$, zodat $E S A D$ een parallellogram is. Dus is $\\angle D A O_{1}=\\angle D A S=\\angle D E S=\\angle D E B=\\alpha$. Omdat driehoek $A O_{1} D$ gelijkbenig is met top $O_{1}$, geldt $\\angle O_{1} A D=\\angle D A O_{1}=\\alpha$. Wegens overstaande hoeken en de gelijkbenigheid van $\\triangle C O_{2} A$ geldt nu ook $\\angle O_{2} C A=\\angle C A O_{2}=\\angle O_{1} A D=\\alpha$. Wegens koordenvierhoek $B A D E$ geldt verder $\\angle O_{2} A B=180^{\\circ}-\\angle D A B=\\angle D E B=\\alpha$, en vanwege de gelijkbenigheid van $\\triangle A O_{2} B$ geldt ook $\\angle O_{2} B A=\\angle O_{2} A B=\\alpha$. Nu zijn $\\triangle A O_{2} B$ en $\\triangle A O_{2} C$ twee driehoeken met twee hoeken gelijk aan $\\alpha$ en een gemeenschappelijke zijde $A O_{2}$, dus ze zijn congruent (ZHH), waaruit volgt $|A B|=|A C|$.\nEen koordenvierhoek met twee evenwijdige zijden is een gelijkbenig trapezium (stelling van Julian) dus $|D E|=|A B|$. Samen met de vorige gelijkheid krijgen we nu $|D E|=$ $|A C|$. Omdat $D E$ en $A C$ ook evenwijdig zijn, vinden we een parallellogram $A C D E$. Dit betekent dat $\\angle D C A=\\angle A E D$. Wegens de middelpunt-omtrekhoekstelling geldt $\\angle A E D=\\frac{1}{2} \\angle A O_{1} D=90^{\\circ}-\\angle O_{1} A D=90^{\\circ}-\\alpha$. Dus $\\angle D C A=90^{\\circ}-\\alpha . \\mathrm{Nu}$ is $\\angle D C O_{2}=\\angle D C A+\\angle O_{2} C A=90^{\\circ}-\\alpha+\\alpha=90^{\\circ}$, wat we moesten bewijzen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 10 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "Laat cirkels $\\Gamma_{1}$ en $\\Gamma_{2}$, met middelpunten respectievelijk $O_{1}$ en $O_{2}$, elkaar snijden in twee verschillende punten $A$ en $B$. De lijn $O_{1} A$ snijdt $\\Gamma_{2}$ nogmaals in $C$ en de lijn $O_{2} A$ snijdt $\\Gamma_{1}$ nogmaals in $D$. De lijn door $B$ evenwijdig met $A D$ snijdt $\\Gamma_{1}$ nogmaals in $E$. Veronderstel dat $O_{1} A$ evenwijdig is met $D E$. Bewijs dat $C D$ loodrecht op $O_{2} C$ staat.", "solution": "Zij $S$ het snijpunt van $B E$ en $A C$, zodat $E S A D$ een parallellogram is. Zij $T$ het snijpunt van $B E$ en $C O_{2}$. Er geldt $\\angle C S T=\\angle A S B=\\angle D A S$ vanwege $B E \\| A D$ en $\\angle D A S=\\angle O_{2} A C=\\angle O_{2} C A=\\angle T C S$ omdat $\\left|O_{2} A\\right|=\\left|O_{2} C\\right|$. Dus $\\angle C S T=\\angle T C S$, wat betekent dat $|T S|=|T C|$. Verder is nu $\\angle B T C=\\angle S T C=180^{\\circ}-2 \\angle O_{2} C A$. Daarnaast hadden we al gezien dat $\\angle O_{2} C A=\\angle O_{2} A C=\\angle D A S$. Vanwege het parallellogram geldt $\\angle D A S=\\angle D E S=\\angle D E B=180^{\\circ}-\\angle D A B=\\angle O_{2} A B$. Dus $\\angle O_{2} C A=\\angle O_{2} A B$. Hiermee zien we dat $\\angle B T C=180^{\\circ}-2 \\angle O_{2} C A=180^{\\circ}-\\angle O_{2} A C-\\angle O_{2} A B=180^{\\circ}-\\angle B A C$.\n\nDus $B A C T$ is een koordenvierhoek, oftewel $T$ ligt op $\\Gamma_{2}$. Wegens Thales vinden we nu $\\angle T A C=90^{\\circ}$. Maar $T S C$ is gelijkbenig en de lijn $T A$ is een hoogtelijn vanuit de top, dus ook een zwaartelijn. Dus $A$ is het midden van $S C$.\nEen koordenvierhoek met twee evenwijdige zijden is een gelijkbenig trapezium (stelling van Julian) dus $|D E|=|A B|$. Vanwege het parallellogram is ook $|D E|=|S A|$, dus $|A B|=|S A|=|A C|$. Dus $A$ ligt op de middelloodlijn van $B C$. Die middelloodlijn gaat ook door het middelpunt van de cirkel waar $B C$ een koorde van is en is dus de lijn $O_{2} A$. Dus $D$ ligt ook op deze middelloodlijn, zodat $|D C|=|D B|$. In het bijzonder is nu zwaartelijn $D A$ in driehoek $B C D$ ook een bissectrice, dus $\\angle C D B=2 \\angle A D B$. Met de middelpuntsomtrekshoekstelling is ook $\\angle A O_{1} B=2 \\angle A D B$. Dus driehoeken $C D B$ en $A O_{1} B$ zijn gelijkbenig met dezelfde tophoek, waardoor ze gelijkvormig zijn. Dus $\\angle O_{1} A B=$ $\\angle D C B$. Omdat met de omtrekshoekstelling geldt $\\angle B A T=\\angle B C T$, geldt nu\n\n$$\n\\angle D C O_{2}=\\angle D C T=\\angle D C B+\\angle B C T=\\angle O_{1} A B+\\angle B A T=\\angle O_{1} A T=90^{\\circ} .\n$$", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing III."}
|
| 11 |
+
{"year": "2015", "problem_label": "5", "tier": 1, "problem": "Voor een positief geheel getal $n$ definiëren we $D_{n}$ als het grootste getal dat een deler is van $a^{n}+(a+1)^{n}+(a+2)^{n}$ voor alle positieve gehele $a$.\na) Bewijs dat voor elke positieve gehele $n$ het getal $D_{n}$ van de vorm $3^{k}$ is met $k \\geq 0$.\nb) Bewijs dat er voor elke $k \\geq 0$ een positieve gehele $n$ bestaat zodat $D_{n}=3^{k}$.", "solution": "a) $\\mathrm{Zij} p$ een priemgetal en stel dat $p$ een deler is van $D_{n}$. Dan is $p$ een deler van\n\n$$\n\\left((a+1)^{n}+(a+2)^{n}+(a+3)^{n}\\right)-\\left(a^{n}+(a+1)^{n}+(a+2)^{n}\\right)=(a+3)^{n}-a^{n}\n$$\n\nvoor alle positieve gehele $a$. Kies nu $a=p$, dan $p \\mid(p+3)^{n}-p^{n}$, oftewel $(p+3)^{n}-p^{n} \\equiv$ $0 \\bmod p$. Hier staat gewoon $3 \\equiv 0 \\bmod p$, dus $p=3$. We concluderen dat $D_{n}$ alleen priemfactoren 3 bevat en dus van de vorm $3^{k}$ is met $k \\geq 0$.\nb) Voor $k=0$ nemen we $n=2$. Er geldt $1^{2}+2^{2}+3^{2}=14$ en $2^{2}+3^{2}+4^{2}=29$ en die twee hebben geen enkele priemfactor gemeenschappelijk, dus $D_{2}=1$. Neem nu verder aan dat $k \\geq 1$. We gaan bewijzen dat $D_{n}=3^{k}$ voor $n=3^{k-1}$.\nEerst laten we zien dat $1^{n}+2^{n}+3^{n}$ voor $n=3^{k-1}$ deelbaar is door $3^{k}$, maar niet door $3^{k+1}$. Voor $k=1$ is $n=1$ en geldt inderdaad dat $1+2+3=6$ deelbaar is door 3 , maar niet door $3^{2}$. Voor $k \\geq 2$ geldt dat $n>k$ en dus dat $3^{n}$ deelbaar is door $3^{k+1}$. Het te bewijzen is dus equivalent aan: $1+2^{n}$ voor $n=3^{k-1}$ is deelbaar door $3^{k}$ maar niet door $3^{k+1}$. We bewijzen dit met inductie naar $k$. Voor $k=2$ is $n=3$ en geldt inderdaad dat $1+8=9$ deelbaar is door 9 , maar niet door 27 . Zij $m \\geq 2$ en stel dat we dit hebben bewezen voor $k=m$. Neem $n=3^{m-1}$. We weten dat $1+2^{n}$ deelbaar is door $3^{m}$, maar niet door $3^{m+1}$. We willen laten zien dat $1+2^{3 n}$ deelbaar is door $3^{m+1}$, maar niet door $3^{m+2}$. Schrijf $1+2^{n}=3^{m} c$ met $3 \\nmid c$. Dan is $2^{n}=3^{m} c-1$, dus\n\n$$\n1+2^{3 n}=1+\\left(3^{m} c-1\\right)^{3}=3^{3 m} c^{3}-3 \\cdot 3^{2 m} c^{2}+3 \\cdot 3^{m} c\n$$\n\nModulo $3^{m+2}$ is dit congruent aan $3^{m+1} c$ en omdat $3 \\nmid c$ volgt hieruit dat dit deelbaar is door $3^{m+1}$, maar niet door $3^{m+2}$, zoals we wilden bewijzen. Dit voltooit de inductie. Nu laten we zien dat voor $n=3^{k-1}$ geldt dat $(a+3)^{n}-a^{n}$ deelbaar is door $3^{k}$ voor alle positieve gehele $a$. We bewijzen dit weer met inductie naar $k$. Voor $k=1$ is $n=1$ en geldt inderdaad dat $(a+3)-a=3$ deelbaar is door 3 . Zij nu $m \\geq 1$ en neem aan dat we dit bewezen hebben voor $k=m$. Neem $n=3^{m-1}$. Dan weten we dat $(a+3)^{n}-a^{n}$ deelbaar is door $3^{m}$, dus we kunnen schrijven $(a+3)^{n}=a^{n}+3^{m} c$ voor een zekere gehele $c$. Links en rechts de derde macht nemen geeft dan\n\n$$\n(a+3)^{3 n}=a^{3 n}+3 a^{2 n} \\cdot 3^{m} c+3 a^{n} \\cdot 3^{2 m} c^{2}+3^{3 m} c^{3},\n$$\n\ndus\n\n$$\n(a+3)^{3 n}-a^{3 n}=a^{2 n} \\cdot 3^{m+1} c+a^{n} \\cdot 3^{2 m+1} c^{2}+3^{3 m} c^{3} .\n$$\n\nDit is deelbaar door $3^{m+1}$, wat de inductie voltooit.\nWe hebben nu voor $n=3^{k-1}$ bewezen dat $3^{k} \\mid 1^{n}+2^{n}+3^{n}$ en $3^{k} \\mid(a+3)^{n}-a^{n}$ voor alle positieve gehele $a$, waaruit met inductie naar $a$ direct volgt dat $3^{k} \\mid a^{n}+$ $(a+1)^{n}+(a+2)^{n}$ voor alle $a$. Dus $3^{k} \\mid D_{n}$. Omdat $3^{k+1} \\nmid 1^{n}+2^{n}+3^{n}$ geldt ook $3^{k+1} \\nmid D_{n}$. Dus $D_{n}=3^{k}$.", "problem_match": "\nOpgave 5.", "solution_match": "# Oplossing."}
|
Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Laat $a$ en $b$ twee positieve gehele getallen zijn die voldoen aan $\\operatorname{ggd}(a, b)=1$. Beschouw een pion die op roosterpunt $(x, y)$ staat. Een stap van type A bestaat uit het verplaatsen van de pion naar één van de volgende velden: $(x+a, y+a),(x+a, y-a),(x-$ $a, y+a)$ of $(x-a, y-a)$. Een stap van type B bestaat uit het verplaatsen van de pion naar $(x+b, y+b),(x+b, y-b),(x-b, y+b)$ of $(x-b, y-b)$.\nZet nu een pion op $(0,0)$. Je mag een (eindig) aantal stappen uitvoeren, en wel om en om stappen van type A en type B, beginnend met een stap van type A. Je mag een even aantal of een oneven aantal stappen uitvoeren, dus de laatste stap mag zowel van type A als van type B zijn. Bepaal de verzameling van alle roosterpunten $(x, y)$ die je met zo'n serie van stappen kunt bereiken.", "solution": "We gaan bewijzen dat een roosterpunt $(x, y)$ bereikbaar is dan en slechts dan als $x+y \\equiv 0 \\bmod 2$.\nAls we de pion verplaatsen van $(x, y)$ naar $(x \\pm a, y \\pm a)$, dan wordt de som van de nieuwe coördinaten gelijk aan $x+y+2 a, x+y$ of $x+y-2 a$, dus modulo 2 congruent aan de som van de oude coördinaten. Hetzelfde geldt bij het doen van een stap van type B. Omdat de pion begint op $(0,0)$, geldt op elk moment (na het uitvoeren van een aantal stappen) dat de som van de coördinaten van het punt waar hij op staat, even is. De punten $(x, y)$ met $x+y \\equiv 1 \\bmod 2$ zijn dus niet te bereiken.\nNu laten we zien dat alle andere punten wel te bereiken zijn. Omdat $\\operatorname{ggd}(a, b)=1$, bestaan er gehele getallen $m, n$ met $m a+n b=1$. Dan geldt $2 m a+2 n b=2$. Van de getallen $m$ en $n$ moet er eentje positief en eentje negatief zijn. We nemen aan dat $m$ positief is. Het andere geval gaat analoog. We gaan nu eerst $2 m$ stappen van type A en $2 m$ stappen van type B doen. Voor de stappen van type A kiezen we $m$ keer $(x, y) \\mapsto(x+a, y+a)$ en $m$ keer $(x, y) \\mapsto(x+a, y-a)$. Voor de stappen van type B kiezen we $m$ keer $(x, y) \\mapsto(x+b, y+b)$ en $m$ keer $(x, y) \\mapsto(x-b, y-b)$. Het effect van al deze stappen samen is dat de $x$ coördinaat $2 m a$ groter wordt en de $y$-coördinaat gelijk blijft (in feite doen de B-stappen helemaal niets). Hierna doen we nog $2|n|$ stappen van type A en $2|n|$ stappen van type B. Voor de stappen van type A kiezen we $|n|$ keer $(x, y) \\mapsto(x+a, y+a)$ en $|n|$ keer $(x, y) \\mapsto(x-a, y-a)$. Voor de stappen van type B kiezen we $|n|$ keer $(x, y) \\mapsto(x-b, y+b)$ en $|n|$ keer $(x, y) \\mapsto(x-b, y-b)$. Het effect van al deze stappen samen is dat de $x$-coördinaat $2|n| b$ kleiner wordt en de $y$-coördinaat gelijk blijft (in feite doen nu de A-stappen helemaal niets). Al met al hebben we na deze $4 m+4|n|$ stappen de pion verplaatst van een beginpunt $(x, y)$ naar het punt $(x+2 m a-2|n| b, y)=(x+2, y)$. We kunnen een analoge serie stappen construeren die de pion van $(x, y)$ naar $(x, y+2)$ verplaatst, en ook analoge series stappen\ndie de pion van $(x, y)$ verplaatsen naar $(x-2, y)$ en $(x, y-2)$. Elk van deze series begint met een stap van type A en eindigt met een stap van type B.\nDoor dit soort series achter elkaar te plakken, kunnen we de pion van $(0,0)$ verplaatsen naar elk punt $(x, y)$ met $x \\equiv y \\equiv 0 \\bmod 2$. Bekijk nu een punt $(x, y)$ met $x \\equiv y \\equiv 1$ $\\bmod 2$. Omdat $\\operatorname{ggd}(a, b)=1$, is minstens één van $a$ en $b$ oneven. Stel dat $a$ oneven is. Dan is het punt $(x-a, y-a)$ een punt met twee even coördinaten, waarnaartoe we dus een serie stappen kunnen construeren, die eindigt op een stap van type B. We voegen hierachter nu een stap van type A toe waarmee we van $(x-a, y-a)$ op $(x, y)$ komen. Stel vervolgens dat $a$ even is. Dan is $b$ oneven. Het punt $(x-b, y-b)$ heeft nu twee even coördinaten, dus dit punt kunnen we bereiken met een serie stappen die eindigt op een stap van type B. We voeren nog drie stappen hierna uit:\n\n$$\n(x-b, y-b) \\stackrel{\\mathrm{A}}{\\longmapsto}(x-b-a, y-b-a) \\stackrel{\\mathrm{B}}{\\longmapsto}(x-a, y-a) \\stackrel{\\mathrm{A}}{\\longmapsto}(x, y) .\n$$\n\nZo kunnen we het punt $(x, y)$ dus ook bereiken.\nWe concluderen dat we alle punten $(x, y)$ met $x+y \\equiv 0 \\bmod 2$ kunnen bereiken en alle overige punten niet.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Bepaal alle positieve gehele getallen $n$ waarvoor er positieve gehele getallen $a_{1}, a_{2}, \\ldots, a_{n}$ bestaan met\n\n$$\na_{1}+2 a_{2}+3 a_{3}+\\ldots+n a_{n}=6 n\n$$\n\nen\n\n$$\n\\frac{1}{a_{1}}+\\frac{2}{a_{2}}+\\frac{3}{a_{3}}+\\ldots+\\frac{n}{a_{n}}=2+\\frac{1}{n}\n$$", "solution": "Als we de ongelijkheid van het rekenkundig en harmonisch gemiddelde toepassen op $a_{1}$, twee keer $a_{2}$, drie keer $a_{3}, \\ldots, n$ keer $a_{n}$, dan vinden we\n\n$$\n\\frac{6 n}{\\frac{1}{2} n(n+1)}=\\frac{a_{1}+2 a_{2}+3 a_{3}+\\ldots+n a_{n}}{\\frac{1}{2} n(n+1)} \\geq \\frac{\\frac{1}{2} n(n+1)}{\\frac{1}{a_{1}}+\\frac{2}{a_{2}}+\\frac{3}{a_{3}}+\\ldots+\\frac{n}{a_{n}}}=\\frac{\\frac{1}{2} n(n+1)}{2+\\frac{1}{n}}\n$$\n\nEr geldt\n\n$$\n\\frac{6 n}{\\frac{1}{2} n(n+1)}=\\frac{12}{n+1}<\\frac{12}{n}\n$$\n\nen\n\n$$\n\\frac{\\frac{1}{2} n(n+1)}{2+\\frac{1}{n}}=\\frac{\\frac{1}{2} n^{2}(n+1)}{2 n+1}>\\frac{\\frac{1}{2} n^{2}(n+1)}{2 n+2}=\\frac{1}{4} n^{2}\n$$\n\nAlles bij elkaar vinden we $\\frac{12}{n}>\\frac{1}{4} n^{2}$, oftewel $48>n^{3}$, waaruit volgt $n \\leq 3$.\nMet $n=1$ krijgen we $a_{1}=6$ en $\\frac{1}{a_{1}}=3$, wat in tegenspraak met elkaar is. Dus $n=1$ kan niet.\nMet $n=2$ krijgen we $a_{1}+2 a_{2}=12$ en $\\frac{1}{a_{1}}+\\frac{2}{a_{2}}=2+\\frac{1}{2}$. Als $a_{2} \\geq 2$ geldt $\\frac{1}{a_{1}}+\\frac{2}{a_{2}} \\leq 1+1$ en dat is te klein. Dus moet $a_{2}=1$, maar dan vinden we $a_{1}=12-2=10$ en dus $\\frac{1}{a_{1}}+\\frac{2}{a_{2}}=\\frac{1}{10}+2$, tegenspraak. Dus $n=2$ kan niet.\nBij $n=3$ is er een oplossing, namelijk $a_{1}=6, a_{2}=3$ en $a_{3}=2$ (invullen laat zien dat deze voldoet). Dus $n=3$ kan wel en we concluderen dat $n=3$ de enige oplossing is.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Gegeven is een gelijkzijdige driehoek $A B C$. Op de lijn door $B$ evenwijdig aan $A C$ ligt een punt $D$, zodat $D$ en $C$ aan dezelfde kant van lijn $A B$ liggen. De middelloodlijn van $C D$ snijdt de lijn $A B$ in $E$. Bewijs dat driehoek $C D E$ gelijkzijdig is.", "solution": "We bekijken in alle oplossingen de configuratie waarin $E$ tussen $A$ en $B$ ligt. Het geval dat $B$ tussen $A$ en $E$ ligt gaat analoog. (En vanwege de voorwaarde dat $D$ en $C$ aan dezelfde kant van $A B$ liggen, kan $A$ niet tussen $B$ en $E$ liggen, dus hebben we zo alle gevallen gehad.)\nOmdat $E$ op de middelloodlijn van $C D$ ligt, geldt $|E C|=|E D|$. Het is dus voldoende om te bewijzen dat tophoek $\\angle C E D=60^{\\circ}$. Stel eerst dat $E=B$. Dan is $\\angle C E D=\\angle C B D=$ $\\angle A C B=60^{\\circ}$ wegens Z-hoeken, dus zijn we klaar. Stel nu dat $E \\neq B$.\nOmdat $B D$ evenwijdig aan $A C$ is, geldt $\\angle C B D=\\angle A C B=60^{\\circ}=\\angle C B A$. Het punt $E$ is dus het snijpunt van de middelloodlijn van $C D$ en de buitenbissectrice van $\\angle C B D$. Dat betekent dat $E$ op de omgeschreven cirkel van driehoek $C D B$ ligt. (Dit is een bekend feit, maar het is ook als volgt te bewijzen. Zij $E^{\\prime}$ het snijpunt van de buitenbissectrice van $\\angle C B D$ en de omgeschreven cirkel van $\\triangle C B D$. Omdat $B E^{\\prime}$ de buitenbissectrice is, geldt $\\angle C B E^{\\prime}=180^{\\circ}-\\angle D B E^{\\prime}$. Dus koorden $C E^{\\prime}$ en $D E^{\\prime}$ zijn even lang, wat betekent dat $E^{\\prime}$ op de middelloodlijn van $C D$ ligt.) We concluderen dat $C E B D$ een koordenvierhoek is. Dus $\\angle C E D=\\angle C B D=60^{\\circ}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Gegeven is een gelijkzijdige driehoek $A B C$. Op de lijn door $B$ evenwijdig aan $A C$ ligt een punt $D$, zodat $D$ en $C$ aan dezelfde kant van lijn $A B$ liggen. De middelloodlijn van $C D$ snijdt de lijn $A B$ in $E$. Bewijs dat driehoek $C D E$ gelijkzijdig is.", "solution": "Zij $E^{\\prime}$ het tweede snijpunt van $A B$ met de omgeschreven cirkel van $\\triangle B C D$. Wegens koordenvierhoek $B E^{\\prime} C D$ geldt dan $\\angle E^{\\prime} D C=\\angle E^{\\prime} B C=\\angle A B C=60^{\\circ}$ en $\\angle E^{\\prime} C D=180^{\\circ}-\\angle E^{\\prime} B D=60^{\\circ}$ wegens de evenwijdigheid. Dus driehoek $C D E^{\\prime}$ heeft twee hoeken van $60^{\\circ}$ en is daarom gelijkzijdig. Vanwege deze gelijkzijdigheid ligt verder $E^{\\prime}$ op de middelloodlijn van $C D$, dus $E^{\\prime}=E$. Dus $\\triangle C D E$ is gelijkzijdig.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Gegeven is een gelijkzijdige driehoek $A B C$. Op de lijn door $B$ evenwijdig aan $A C$ ligt een punt $D$, zodat $D$ en $C$ aan dezelfde kant van lijn $A B$ liggen. De middelloodlijn van $C D$ snijdt de lijn $A B$ in $E$. Bewijs dat driehoek $C D E$ gelijkzijdig is.", "solution": "Zij $E^{\\prime}$ een punt op $A B$ met $\\left|A E^{\\prime}\\right|=|B D|$, zodat $E^{\\prime}$ en $B$ aan dezelfde kant van $A$ liggen. Er geldt $|A C|=|B C|$ en $\\angle C A E=60^{\\circ}=\\angle C B D$ wegens Z-hoeken en de gelijkzijdigheid. Dus $\\triangle C A E^{\\prime} \\cong \\triangle C B D$ (ZHZ). Hieruit volgt $\\left|C E^{\\prime}\\right|=|C D|$ en $\\angle E^{\\prime} C A=\\angle D C B$. Uit het laatste volgt $\\angle E^{\\prime} C D=\\angle E^{\\prime} C B+\\angle B C D=\\angle E^{\\prime} C B+$ $\\angle E^{\\prime} C A=\\angle A C B=60^{\\circ}$. Dus driehoek $C D E^{\\prime}$ is gelijkbenig met tophoek $60^{\\circ}$, dus gelijkzijdig. Vanwege deze gelijkzijdigheid ligt verder $E^{\\prime}$ op de middelloodlijn van $C D$, dus $E^{\\prime}=E$. Dus $\\triangle C D E$ is gelijkzijdig.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing III."}
|
| 6 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "Je mag elk van de getallen 1 tot en met 2014 een kleur geven, waarbij precies de helft rood moet worden en de andere helft blauw. Vervolgens bekijk je het aantal $k$ van positieve gehele getallen die te schrijven zijn als de som van een rood en een blauw getal. Bepaal de maximale waarde van $k$ die je kunt bereiken.", "solution": "Noem $n=2014$. We gaan bewijzen dat de maximale $k$ gelijk is aan $2 n-5$. Het kleinste getal dat je zou kunnen schrijven als de som van een rood en een blauw getal is $1+2=3$ en het grootste getal is $(n-1)+n=2 n-1$. Er zijn dus hoogstens $2 n-3$ getallen te schrijven als de som van een rood en een blauw getal.\nStel dat de getallen zo gekleurd kunnen worden dat er $2 n-3$ of $2 n-4$ getallen te schrijven zijn als som van een rood en een blauw getal. Er is nu hooguit één getal van 3 tot en met $2 n-1$ dat niet zo te schrijven is. We laten nu eerst zien dat we zonder verlies van algemeenheid mogen aannemen dat dit getal minstens $n+1$ is. We kunnen namelijk een tweede kleuring maken waarbij een getal $i$ blauw is dan en slechts dan als in de eerste kleuring $n+1-i$ blauw was. Dan is een getal $m$ bij de tweede kleuring te schrijven als som van rood en blauw dan en slechts dan als $2 n+2-m$ in de eerste kleuring te schrijven was als som van rood en blauw. Dus als in de eerste kleuring een getal kleiner dan $n+1$ niet te schrijven was als som van rood en blauw, dan is in de tweede kleuring juist een getal groter dan $2 n+2-(n+1)=n+1$ niet te schrijven als som van rood en blauw.\nWe mogen dus aannemen dat de getallen 3 tot en met $n$ allemaal te schrijven zijn als som van rood en blauw. Omdat rood en blauw verwisselbaar zijn, mogen we ook nog zonder verlies van algemeenheid aannemen dat 1 blauw gekleurd is. Omdat 3 te schrijven is als som van rood en blauw en dat alleen $3=1+2$ kan zijn, moet 2 rood zijn. Stel nu dat we weten dat 2 tot en met $l$ rood zijn, voor zekere $l$ met $2 \\leq l \\leq n-2$. Dan zijn in alle mogelijke sommen $a+b=l+2$ met $a, b \\geq 2$ beide getallen rood gekleurd, maar we weten dat we $l+2$ kunnen schrijven als som van rood en blauw (want $l+2 \\leq n$ ), dus moet dat wel $1+(l+1)$ zijn. Dus $l+1$ is ook rood gekleurd. Met inductie zien we nu dus dat de getallen 2 tot en met $n-1$ allemaal rood zijn. Dat zijn $n-2=2012$ getallen. Maar er zijn slechts $\\frac{1}{2} n=1007$ getallen rood, tegenspraak.\nWe concluderen dat er minstens twee getallen van 3 tot en met $2 n-1$ niet te schrijven zijn als som van een rood en een blauw getal. We laten nu zien dat we de getallen zo kunnen kleuren dat alle getallen van 4 tot en met $2 n-2$ te schrijven zijn als som van een rood en een blauw getal, zodat de maximale $k$ gelijk is aan $2 n-5$.\nKleur hiervoor alle even getallen behalve $n$ blauw en verder ook nog het getal 1. Alle oneven getallen behalve 1 kleuren we rood en verder ook nog het getal $n$. Door 1 op te tellen bij een oneven getal (ongelijk aan 1) kunnen we alle even getallen van 4 tot en met $n$ schrijven als som van een rood en een blauw getal. Door 2 op te tellen bij een oneven getal (ongelijk aan 1) kunnen we alle oneven getallen van 5 tot en met $n+1$ schrijven als som van een rood en een blauw getal. Door $n-1$ op te tellen bij een even getal (ongelijk aan $n$ ) kunnen we alle oneven getallen van $n+1$ tot en met $2 n-3$ schrijven als som van een rood en een blauw getal. Door $n$ op te tellen bij een even getal (ongelijk aan $n$ ) kunnen we alle even getallen van $n+2$ tot en met $2 n-2$ schrijven als som van een rood en een\nblauw getal. Al met al kunnen we dus alle getallen van 4 tot en met $2 n-2$ schrijven als som van een rood en een blauw getal.\nWe concluderen dat de maximale $k$ gelijk is aan $2 n-5=4023$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2015", "problem_label": "5", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ zodat $f(1)=2$ en zodat voor alle $m, n \\in \\mathbb{Z}_{>0}$ geldt dat $\\min (2 m+2 n, f(m+n)+1)$ deelbaar is door $\\max (f(m)+f(n), m+n)$.", "solution": "Invullen van $m=n$ geeft dat $\\min (4 n, f(2 n)+1)$ deelbaar is door $\\max (2 f(n), 2 n)$. Een getal hoogstens gelijk aan $4 n$ is dus deelbaar door een getal minstens gelijk aan $2 f(n)$. Daaruit volgt $4 n \\geq 2 f(n)$, dus $f(n) \\leq 2 n$ voor alle $n$.\nInvullen van $m=n=1$ geeft dat $\\min (4, f(2)+1)$ deelbaar is door $\\max (2 f(1), 2)=$ $\\max (4,2)=4$. Dus $\\min (4, f(2)+1)$ kan niet kleiner dan 4 zijn, dus $f(2)+1 \\geq 4$. Maar we hebben net ook al gezien dat $f(2) \\leq 2 \\cdot 2=4$, dus $f(2)=3$ of $f(2)=4$.\nStel eerst dat $f(2)=3$. We bewijzen met inductie naar $n$ dat $f(n)=n+1$ voor alle $n$. Stel namelijk dat dit waar is voor $n=r-1$ voor zekere $r \\geq 3$ en vul in $m=1$ en $n=r-1$. Dan krijgen we dat $\\min (2 r, f(r)+1)$ deelbaar is door $\\max (f(1)+f(r-1), r)=$ $\\max (r+2, r)=r+2$. Aangezien $\\min (2 r, f(r)+1) \\leq 2 r<2(r+2)$ moet er gelden dat $\\min (2 r, f(r)+1)=r+2$. Omdat $r \\geq 3$ is $2 r>r+2$, dus er geldt $f(r)+1=r+2$ oftewel $f(r)=r+1$. Dit voltooit de inductie. We krijgen dus de kandidaatfunctie $f(n)=n+1$. We controleren meteen of deze functie voldoet. Er geldt dan voor alle $m, n \\in \\mathbb{N}$ dat $\\min (2 m+2 n, f(m+n)+1)=\\min (2 m+2 n, m+n+2)=m+n+2$ omdat $m, n \\geq 1$, en $\\max (f(m)+f(n), m+n)=\\max (m+n+2, m+n)=m+n+2$. Het eerste is deelbaar door het tweede (want gelijk aan het tweede), dus deze functie voldoet.\nStel nu dat $f(2)=4$. We bewijzen met inductie naar $n$ dat $f(n)=2 n$ voor alle $n$. Stel namelijk dat dit waar is voor $n=r-1$ voor zekere $r \\geq 3$. We bewijzen dat ook $f(r)=2 r$. Vul eerst $m=1$ en $n=r-1$ in. Dan vinden we dat $\\min (2 r, f(r)+1)$ deelbaar is door $\\max (f(1)+f(r-1), 1+r-1)=\\max (2 r, r)=2 r$. Dus $\\min (2 r, f(r)+1)$ kan niet kleiner dan $2 r$ zijn, dus $f(r) \\geq 2 r-1$. Maar we wisten ook al dat $f(r) \\leq 2 r$, dus $f(r) \\in\\{2 r-1,2 r\\}$. Veronderstel dat $f(r)=2 r-1$. Vul dan $m=1$ en $n=r$ in. Dan vinden we dat $\\min (2(r+$ 1), $f(r+1)+1)$ deelbaar is door $\\max (f(1)+f(r), 1+r)=\\max (2+2 r-1, r+1)=2 r+1$. Omdat $2 r+1 \\nmid 2(r+1)$, kan $2(r+1)$ niet het minimum zijn, dus moet $f(r+1)+1<2 r+2$ en het moet ook deelbaar zijn door $2 r+1$, dus $f(r+1)=2 r$. Vul ook $m=2$ en $n=r-1$ in. Dan vinden we dat $\\min (2(r+1), f(r+1)+1)=\\min (2 r+2,2 r+1)=2 r+1$ deelbaar is door $\\max (f(2)+f(r-1), 1+r)=\\max (4+2 r-2, r+1)=2 r+2$, tegenspraak. We concluderen dat $f(r)=2 r$, waarmee de inductie voltooid is. We krijgen hiermee de kandidaatfunctie $f(n)=2 n$ voor alle $n$. We controleren of deze functie voldoet. Voor alle $m, n$ geldt dan dat $\\min (2 m+2 n, f(m+n)+1)=\\min (2 m+2 n, 2 m+2 n+1)=2 m+2 n$ en $\\max (f(m)+f(n), m+n)=\\max (2 m+2 n, m+n)=2 m+2 n$. Het eerste is deelbaar door het tweede (want gelijk aan het tweede), dus deze functie voldoet.\nWe concluderen dat er precies twee oplossingen zijn: de functie $f(n)=n+1$ voor alle $n$ en de functie $f(n)=2 n$ voor alle $n$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Voor een positief geheel getal $n$ dat geen tweemacht is, definiëren we $t(n)$ als de grootste oneven deler van $n$ en $r(n)$ als de kleinste positieve oneven deler van $n$ die ongelijk aan 1 is. Bepaal alle positieve gehele getallen $n$ die geen tweemacht zijn en waarvoor geldt\n\n$$\nn=3 t(n)+5 r(n)\n$$", "solution": "Als $n$ oneven is, geldt $t(n)=n$ dus is $3 t(n)$ groter dan $n$, tegenspraak. Als $n$ deelbaar door 2 is maar niet deelbaar door 4 , dan geldt $t(n)=\\frac{1}{2} n$ en is $3 t(n)$ weer groter dan $n$, opnieuw tegenspraak. We kunnen concluderen dat $n$ in elk geval deelbaar door 4 moet zijn. Als $n$ deelbaar door 16 is, dan is $t(n) \\leq \\frac{1}{16} n$. Verder is $r(n) \\leq t(n)$, dus $3 t(n)+5 r(n) \\leq 8 t(n) \\leq \\frac{1}{2} n<n$, tegenspraak. Dus $n$ is niet deelbaar door 16 . We kunnen dus schrijven $n=4 m$ of $n=8 m$ met $m \\geq 3$ oneven.\nStel $n=4 m$ met $m \\geq 3$ oneven. Dan geldt $t(n)=m$, dus $4 m=3 m+5 r(n)$, dus $5 r(n)=m$. Omdat $r(n)$ gelijk is aan de kleinste oneven priemdeler van $n$, wat ook de kleinste priemdeler van $m$ is, moet nu $m$ van de vorm $m=5 p$ zijn met $p \\leq 5$ een oneven priemgetal. Dus $m=15$ of $m=25$, wat $n=60$ of $n=100$ geeft. Beide oplossingen voldoen.\nStel dat $n=8 m$ met $m \\geq 3$ oneven. Opnieuw geldt $t(n)=m$, dus $8 m=3 m+5 r(n)$, dus $5 r(n)=5 m$, oftewel $r(n)=m$. We zien dat $m$ priem is. Dus $n=8 p$ met $p$ een oneven priemgetal. Deze familie van oplossingen voldoet ook.\nWe vinden als oplossingen dus $n=60, n=100$ en $n=8 p$ met $p$ een oneven priemgetal.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Voor een positief geheel getal $n$ dat geen tweemacht is, definiëren we $t(n)$ als de grootste oneven deler van $n$ en $r(n)$ als de kleinste positieve oneven deler van $n$ die ongelijk aan 1 is. Bepaal alle positieve gehele getallen $n$ die geen tweemacht zijn en waarvoor geldt\n\n$$\nn=3 t(n)+5 r(n)\n$$", "solution": "Noem $p$ de kleinste oneven priemdeler van $n$. Dan is $r(n)=p$. We kunnen nu schrijven $n=2^{t} m p$ met $m$ oneven en $t \\geq 0$. Er geldt dan $t(n)=p m$, dus de gegeven gelijkheid gaat over in $2^{t} m p=3 p m+5 p$, oftewel $\\left(2^{t}-3\\right) m p=5 p$, dus $\\left(2^{t}-3\\right) m=5$. We zien dat $m$ een deler van 5 moet zijn, dus $m=1$ of $m=5$. Als $m=1$ geldt $2^{t}=8$, dus $t=3$. We krijgen dan $n=8 p$ met $p$ een oneven priem. Deze oplossing voldoet voor alle oneven priemgetallen $p$. Als $m=5$ geldt $2^{t}=4$, dus $t=2$. We krijgen dan $n=4 \\cdot 5 \\cdot p$ met $p$ een oneven priem. Deze oplossing voldoet alleen als $p$ de kleinste oneven priemdeler is, dus als $p=3$ of $p=5$. Zo vinden we nog twee oplossingen: $n=60$ en $n=100$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Bepaal alle drietallen $(x, y, z)$ van niet-negatieve reële getallen die voldoen aan het stelsel vergelijkingen\n\n$$\n\\begin{aligned}\n& x^{2}-y=(z-1)^{2} \\\\\n& y^{2}-z=(x-1)^{2} \\\\\n& z^{2}-x=(y-1)^{2}\n\\end{aligned}\n$$", "solution": "Haakjes uitwerken en alles bij elkaar optellen geeft\n\n$$\nx^{2}+y^{2}+z^{2}-(x+y+z)=x^{2}+y^{2}+z^{2}-2(x+y+z)+3,\n$$\n\ndus $x+y+z=3$. Zonder verlies van algemeenheid nemen we aan dat $x \\leq y, z$. Dan geldt $0 \\leq x \\leq 1$. Dus $x^{2} \\leq x$, dus $x^{2}-y \\leq x-y \\leq 0$. Anderzijds is $x^{2}-y=(z-1)^{2} \\geq 0$. Dus moet gelijkheid gelden in o.a. $x^{2} \\leq x$ en $x-y \\leq 0$. Uit de eerste gelijkheid volgt $x=0$ of $x=1$ en uit de tweede $x=y$. Stel $x=y=0$, dan volgt uit $x+y+z=3$ dat $z=3$. Maar dan geldt niet $x^{2}-y=(z-1)^{2}$, tegenspraak. We houden alleen het geval over dat $x=y=1$. Dan geldt $z=3-1-1=1$. Dit drietal voldoet inderdaad en is daarmee de enige oplossing.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $\\triangle A B C$ een rechthoekige driehoek met $\\angle A=90^{\\circ}$ en omgeschreven cirkel $\\Gamma$. De ingeschreven cirkel raakt aan $B C$ in een punt $D$. Zij $E$ het midden van de boog $A B$ van $\\Gamma$ waar $C$ niet op ligt en zij $F$ het midden van de boog $A C$ van $\\Gamma$ waar $B$ niet op ligt.\na) Bewijs dat $\\triangle A B C \\sim \\triangle D E F$.\nb) Bewijs dat $E F$ door de raakpunten van de ingeschreven cirkel aan $A B$ en $A C$ gaat.", "solution": "a) Het midden $E$ van boog $A B$ waar $C$ niet op ligt, ligt op de bissectrice $C I$. Net zo ligt $F$ op $B I$. Er geldt $\\angle I F C=\\angle B F C=\\angle B A C=90^{\\circ}$ omdat $A B C F$ een koordenvierhoek is en $\\angle I D C=90^{\\circ}$ omdat $D$ het raakpunt van de ingeschreven cirkel aan $B C$ is. Dus $\\angle I F C+\\angle I D C=180^{\\circ}$, waaruit volgt dat $F I D C$ een koordenvierhoek is. Nu geldt $\\angle D F I=\\angle D C I=\\frac{1}{2} \\angle A C B$, terwijl ook $\\angle I F E=\\angle B F E=\\angle B C E=$ $\\frac{1}{2} \\angle A C B$. Dus $\\angle D F E=\\frac{1}{2} \\angle A C B+\\frac{1}{2} \\angle A C B=\\angle A C B$. Analoog is $\\angle D E F=\\angle A B C$. Samen geeft dit $\\triangle D E F \\sim \\triangle A B C$.\nb) $\\mathrm{Zij} S$ het snijpunt van $E F$ met $A B$. In het vorige onderdeel hebben we gezien dat $B F$ de bissectrice is van $\\angle D F E=\\angle D F S$. Ook is $B F$ de bissectrice van $\\angle A B C=$ $\\angle S B D$. Dus $\\triangle B D F \\cong \\triangle B S F$ vanwege (HZH). Dit betekent dat $|B D|=|B S|$. Anderzijds zijn de afstanden van $B$ tot de raakpunten van de ingeschreven cirkel aan $B C$ en $B A$ gelijk en het ene raakpunt is $D$, dus het andere raakpunt moet $S$ zijn. Dus $E F$ gaat door het raakpunt van de ingeschreven cirkel aan $A B$. Analoog gaat hij ook door het raakpunt van de ingeschreven cirkel aan $A C$.", "problem_match": "\nOpgave 3.", "solution_match": "# Oplossing I."}
|
| 5 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $\\triangle A B C$ een rechthoekige driehoek met $\\angle A=90^{\\circ}$ en omgeschreven cirkel $\\Gamma$. De ingeschreven cirkel raakt aan $B C$ in een punt $D$. Zij $E$ het midden van de boog $A B$ van $\\Gamma$ waar $C$ niet op ligt en zij $F$ het midden van de boog $A C$ van $\\Gamma$ waar $B$ niet op ligt.\na) Bewijs dat $\\triangle A B C \\sim \\triangle D E F$.\nb) Bewijs dat $E F$ door de raakpunten van de ingeschreven cirkel aan $A B$ en $A C$ gaat.", "solution": "a) Zoals in de eerste oplossing bewijzen we dat FIDC een koordenvierhoek is. Vanwege de buitenhoekstelling is $\\angle C I F=\\angle I C B+\\angle I B C=\\frac{1}{2} \\angle A C B+\\frac{1}{2} \\angle A B C=90^{\\circ}-$ $\\frac{1}{2} \\angle B A C=45^{\\circ}$. Dus $\\angle C D F=\\angle C I F=45^{\\circ}$. Analoog is $\\angle B D E=45^{\\circ}$, zodat $\\angle E D F=180^{\\circ}-45^{\\circ}-45^{\\circ}=90^{\\circ}$. Zij nu $M$ het midden van $B C$. Dan is $M$ ook het midden van de omgeschreven cirkel van $\\triangle A B C$ dus staat $M F$ loodrecht op $A C$. Dat betekent dat $M F \\| A B$. Zo ook is $M E \\| A C$. Dus $\\angle E M F=90^{\\circ}$. We zien dat $\\angle E M F=\\angle E D F$, dus $D, E, F$ en $M$ liggen op één cirkel. We onderscheiden nu twee gevallen.\nAls $D=M$, dan geldt $45^{\\circ}=\\angle C D F=\\angle C M F=\\angle C B A$ wegens $F$-hoeken, dus $\\triangle A B C$ is een gelijkbenige rechthoekige driehoek. Omdat $M$ het middelpunt van de omgeschreven cirkel is, waar ook $E$ en $F$ op liggen, is $|M E|=|M F|$, dus ook $\\triangle M E F$ is een gelijkbenige rechthoekige driehoek. Dus $\\triangle A B C \\sim \\triangle M E F=\\triangle D E F$.\n\nIn het andere geval geldt $D \\neq M$. Zonder verlies van algemeenheid nemen we aan dat $D$ dichter bij $C$ ligt dan $M$. Dan geldt $\\angle D E F=\\angle D M F=\\angle C B A$ wegens F-hoeken en $\\angle D F E=180^{\\circ}-\\angle D M E=\\angle B M E=\\angle B C A$ wegens F-hoeken. Dus met (hh) is nu ook $\\triangle D E F \\sim \\triangle A B C$.\nb) $\\mathrm{Zij} L$ het raakpunt van de ingeschreven cirkel aan $A C$. We hebben al gezien dat $F I D C$ een koordenvierhoek is wegens $\\angle I D C=90^{\\circ}=\\angle I F C$. Omdat ook $\\angle I L C=$ $90^{\\circ}$, ligt $L$ op dezelfde cirkel. Dus\n\n$$\n\\angle L F B=\\angle L F I=\\angle L C I=\\angle A C E=\\angle E C B=\\angle E F B,\n$$\n\nwaaruit volgt dat $E, F$ en $L$ op een lijn liggen. Dus $E F$ gaat door het raakpunt $L$. Analoog gaat $E F$ ook door het raakpunt van de ingeschreven cirkel aan $A B$.", "problem_match": "\nOpgave 3.", "solution_match": "# Oplossing II."}
|
| 6 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $\\triangle A B C$ een rechthoekige driehoek met $\\angle A=90^{\\circ}$ en omgeschreven cirkel $\\Gamma$. De ingeschreven cirkel raakt aan $B C$ in een punt $D$. Zij $E$ het midden van de boog $A B$ van $\\Gamma$ waar $C$ niet op ligt en zij $F$ het midden van de boog $A C$ van $\\Gamma$ waar $B$ niet op ligt.\na) Bewijs dat $\\triangle A B C \\sim \\triangle D E F$.\nb) Bewijs dat $E F$ door de raakpunten van de ingeschreven cirkel aan $A B$ en $A C$ gaat.", "solution": "a) Zoals in de vorige oplossing bewijzen we dat $\\angle C D F=45^{\\circ}=\\angle B D E$. Zij nu $F^{\\prime}$ de spiegeling van $F$ in $B C$. Omdat $B C$ de middellijn van $\\Gamma$ is, ligt $F^{\\prime}$ weer op $\\Gamma$. Verder is $\\angle C D F^{\\prime}=\\angle C D F=45^{\\circ}$ en $\\angle C D E=180^{\\circ}-\\angle B D E=135^{\\circ}$, dus $\\angle C D F^{\\prime}+\\angle C D E=180^{\\circ}$, waaruit volgt dat $F^{\\prime}, D$ en $E$ op een lijn liggen. We zien dat\n\n$$\n\\angle F E D=\\angle F E F^{\\prime}=\\angle F B F^{\\prime}=2 \\angle F B C=2 \\cdot \\frac{1}{2} \\angle A B C=\\angle A B C .\n$$\n\nAnaloog geldt $\\angle E F D=\\angle A C B$, dus met (hh) geldt $\\triangle D E F \\sim \\triangle A B C$.\nb) Laat $K$ en $L$ de raakpunten zijn van de inschreven cirkel aan respectievelijk $A B$ en $A C$. Omdat $\\angle A K I=\\angle A L I=90^{\\circ}$ en ook $\\angle K A L=90^{\\circ}$, is $A K I L$ een rechthoek. Het is zelfs een vierkant, aangezien $|I K|=|I L|$. Dus diagonaal $K L$ is de middelloodlijn van $A I$. We gaan nu bewijzen dat $E F$ ook de middelloodlijn van $A I$ is, zodat $E F$ samenvalt met $K L$ en het gevraagde bewezen is.\nEr geldt\n\n$$\n\\angle F A I=\\angle F A C+\\angle C A I=\\angle F B C+\\angle C A I=\\frac{1}{2} \\angle A B C+\\frac{1}{2} \\angle B A C\n$$\n\nen verder, wegens de buitenhoekstelling in $\\triangle A B I$,\n\n$$\n\\angle A I F=\\angle I A B+\\angle I B A=\\frac{1}{2} \\angle A B C+\\frac{1}{2} \\angle B A C .\n$$\n\nDus $\\angle F A I=\\angle A I F$, waaruit volgt $|A F|=|I F|$. Dat betekent dat $F$ op de middelloodlijn van $A I$ ligt. Analoog kunnen we laten zien dat ook $E$ op de middelloodlijn van $A I$ ligt. Dus $E F$ is inderdaad de middelloodlijn van $A I$.", "problem_match": "\nOpgave 3.", "solution_match": "# Oplossing III."}
|
| 7 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "De Facebookgroep Olympiadetraining heeft minstens vijf leden. Er is een zeker getal $k$ met de eigenschap: voor elk $k$-tal leden geldt dat er minstens één lid van dat $k$-tal bevriend is met de andere $k-1$. (Vriendschap is wederzijds: als $A$ bevriend is met $B$, dan is $B$ ook bevriend met $A$.)\na) Stel $k=4$. Kun je met zekerheid zeggen dat de Facebookgroep een lid heeft dat vrienden is met alle andere leden?\nb) Stel $k=5$. Kun je met zekerheid zeggen dat de Facebookgroep een lid heeft dat vrienden is met alle andere leden?", "solution": "a) Ja, dat kan. Als iedereen bevriend is met iedereen, dan zijn we klaar. Stel dus dat er twee leden zijn, zeg $A$ en $B$, die geen vrienden met elkaar zijn. Als we een groep van vier bekijken met $A, B$ en twee andere leden, dan moet één van die andere twee bevriend zijn met de ander en met $A$ en $B$. In het bijzonder zijn die twee anderen bevriend met elkaar. Dit geldt voor elke twee leden (ongelijk aan $A$ en $B$ ) die we kiezen, dus elk tweetal zonder $A$ en $B$ is bevriend met elkaar. Neem nu $A, B, C$ en $D$ en zeg dat $C$ bevriend is met $A, B$ en $D$. Hij is verder ook bevriend met alle andere leden van de groep, dus $C$ is iemand die bevriend is met iedereen.\nb) Nee, dat kan niet. We geven een tegenvoorbeeld. Stel dat de Facebookgroep zes leden heeft, namelijk $A, B, C, D, E$ en $F$. Zij zijn allemaal vrienden van elkaar, behalve het paar $(A, B)$, het paar $(C, D)$ en het paar $(E, F)$. Dat betekent dat er geen enkel lid vrienden is van alle andere leden. Als we een groep van vijf nemen, dan is dat zonder verlies van algemeenheid $A, B, C, D$ en $E$. Hierbij is iemand die vrienden is met de andere vier, namelijk $E$. Dus aan de voorwaarde is voldaan.", "problem_match": "\nOpgave 4.", "solution_match": "# Oplossing."}
|
| 8 |
+
{"year": "2016", "problem_label": "5", "tier": 1, "problem": "Bepaal alle paren $(m, n)$ van positieve gehele getallen waarvoor\n\n$$\n(m+n)^{3} \\mid 2 n\\left(3 m^{2}+n^{2}\\right)+8\n$$", "solution": "Stel dat het quotiënt van $2 n\\left(3 m^{2}+n^{2}\\right)+8$ en $(m+n)^{3}$ niet gelijk aan 1 is. Dan is het minstens 2, dus geldt\n\n$$\n(m+n)^{3} \\leq n\\left(3 m^{2}+n^{2}\\right)+4\n$$\n\noftewel\n\n$$\nm^{3}+3 m^{2} n+3 m n^{2}+n^{3} \\leq 3 m^{2} n+n^{3}+4\n$$\n\noftewel\n\n$$\nm^{3}+3 m n^{2} \\leq 4\n$$\n\nHieruit volgt meteen $m<2$, dus $m=1$. Dan staat er $1+3 n^{2} \\leq 4$, dus ook $n=1$. Het paar $(m, n)=(1,1)$ is inderdaad een oplossing, want er geldt $2^{3} \\mid 2 \\cdot 4+8$.\nDe andere mogelijkheid is dat het quotiënt juist wel gelijk aan 1 is. Dan geldt\n\n$$\n(m+n)^{3}=2 n\\left(3 m^{2}+n^{2}\\right)+8\n$$\n\noftewel\n\n$$\nm^{3}+3 m^{2} n+3 m n^{2}+n^{3}=6 m^{2} n+2 n^{3}+8\n$$\n\noftewel\n\n$$\nm^{3}-3 m^{2} n+3 m n^{2}-n^{3}=8\n$$\n\nDe linkerkant kunnen we ontbinden als $(m-n)^{3}$. Dus er geldt $m-n=2$, oftewel $m=n+2$. Uit de voorgaande berekeningen volgt direct ook dat $(m, n)=(n+2, n)$ inderdaad een oplossing is voor alle positieve gehele $n$.\nWe concluderen dat de oplossingen zijn: $(m, n)=(1,1)$ en $(m, n)=(n+2, n)$ voor $n \\geq 1$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "$\\mathrm{Zij} A B C$ een scherphoekige driehoek. $\\mathrm{Zij} H$ het voetpunt van de hoogtelijn vanuit $C$ op $A B$. Veronderstel dat $|A H|=3|B H|$. Laat $M$ en $N$ de middens van respectievelijk $A B$ en $A C$ zijn. Zij $P$ een punt zodat $|N P|=|N C|$ en $|C P|=|C B|$ en zodat $B$ en $P$ aan verschillende kanten van de lijn $A C$ liggen.\nBewijs dat $\\angle A P M=\\angle P B A$.", "solution": "Er is maar één configuratie. Omdat $N$ het midden van $A C$ is, is $|N C|=|N A|$. Gegeven was ook dat $|N P|=|N C|$, dus $N$ is het middelpunt van een cirkel door $A, C$ en $P$. Met de stelling van Thales volgt hieruit dat $\\angle A P C=90^{\\circ}$. Omdat $|A H|=3|B H|$ en $M$ het midden van $A B$ is, geldt $|M H|=|B H|$. Omdat ook nog $\\angle C H B=90^{\\circ}=\\angle C H M$ zijn driehoeken $C H B$ en $C H M$ congruent, waaruit volgt dat $|C M|=|C B|$. Gegeven was verder dat $|C P|=|C B|$, dus $C$ is het middelpunt van een cirkel door $P, M$ en $B$. Omdat $\\angle A P C=90^{\\circ}$, is $A P$ een raaklijn aan deze cirkel. Met de raaklijnomtrekshoekstelling krijgen we nu $\\angle A P M=\\angle P B M=\\angle P B A$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Zij $n$ een positief geheel getal en bekijk een vierkant met afmetingen $2^{n} \\times 2^{n}$. We bedekken dit vierkant met een aantal (minstens 2) niet-overlappende rechthoeken, zodat elke rechthoek gehele afmetingen heeft en een tweemacht als oppervlakte. Bewijs dat twee van de rechthoeken in de bedekking dezelfde afmetingen hebben. (Twee rechthoeken hebben dezelfde afmetingen als ze dezelfde breedte en dezelfde hoogte hebben, waarbij ze niet gedraaid mogen worden.)", "solution": "Merk eerst op dat een rechthoek met gehele afmetingen een tweemacht als oppervlakte heeft precies dan als de afmetingen beide tweemachten zijn.\nBekijk een bedekking waarin geen twee rechthoeken met dezelfde afmetingen voorkomen. We bewijzen eerst dat er dan geen rechthoeken met breedte 1 voorkomen. Stel namelijk dat er wel zo'n rechthoek voorkomt. Kleur alle vakjes blauw die bedekt worden door een rechthoek met breedte 1. Noem $M$ het totaal aantal blauwe vakjes. Dit is de som van de hoogtes van alle rechthoeken met breedte 1, dus de som van verschillende tweemachten (minstens één). Noem $2^{k}$ de grootste tweemacht die daarbij zit. Omdat $2^{k}-1=2^{k-1}+$ $2^{k-2}+\\ldots+2+1$, zijn er minder dan $2^{k}$ blauwe vakjes buiten die ene rechthoek met hoogte $2^{k}$, dus is er minstens één rij waar alleen een blauw vakje van die rechthoek met hoogte $2^{k}$ zit en geen ander blauw vakje. Maar in deze rij is er dan nog een oneven aantal vakjes over, die bedekt moeten worden met allemaal rechthoeken met een even breedte (de breedte moet dan immers een tweemacht groter dan 1 zijn). Tegenspraak. Dus er zijn geen rechthoeken met breedte 1. Analoog komen er in de bedekking geen rechthoeken met hoogte 1 voor. Dus alle rechthoeken hebben een even breedte en hoogte.\nBekijk nu de kleinste $n$ waarvoor zo'n bedekking bestaat waarin geen twee rechthoeken met dezelfde afmetingen voorkomen. Omdat alle rechthoeken een even breedte en hoogte hebben, kunnen we alle afmetingen (van zowel het vierkant als de rechthoeken) door 2 delen en krijgen we een twee keer zo klein vierkant dat bedekt is door rechthoeken met gehele afmetingen die elk een tweemacht als oppervlakte hebben. Tegenspraak met de minimaliteit van $n$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Zij $n$ een positief geheel getal en bekijk een vierkant met afmetingen $2^{n} \\times 2^{n}$. We bedekken dit vierkant met een aantal (minstens 2) niet-overlappende rechthoeken, zodat elke rechthoek gehele afmetingen heeft en een tweemacht als oppervlakte. Bewijs dat twee van de rechthoeken in de bedekking dezelfde afmetingen hebben. (Twee rechthoeken hebben dezelfde afmetingen als ze dezelfde breedte en dezelfde hoogte hebben, waarbij ze niet gedraaid mogen worden.)", "solution": "We geven een alternatieve manier om te bewijzen dat er geen rechthoeken met breedte 1 voorkomen in een bedekking waarin geen twee rechthoeken met dezelfde afmetingen voorkomen. De rest van het bewijs gaat hetzelfde als in oplossing I. Stel dus er wel een rechthoek met breedte 1 voorkomt. Kleur nu alle oneven kolommen blauw en alle even kolommen rood. Dan zijn er $2^{2 n-1}$ blauwe en $2^{2 n-1}$ rode vakjes. Iedere rechthoek met breedte minstens 2 bedekt evenveel blauwe als rode vakjes. De rechthoeken met breedte 1 bedekken samen dus ook evenveel rode als blauwe vakjes; noem dit aantal rode vakjes $V$. Bekijk de rechthoek met breedte 1 met de kleinste hoogte $2^{\\ell}$. Stel zonder verlies van algemeenheid dat deze rode vakjes bedekt. Iedere andere rechthoek met breedte 1 in een rode kolom heeft hoogte minstens $2^{\\ell+1}$ en bedekt dus een aantal rode vakjes dat 0 is modulo $2^{\\ell+1}$. Dus $V \\equiv 2^{\\ell} \\bmod 2^{\\ell+1}$. Maar alle rechthoeken met breedte 1 in een blauwe kolom hebben ook hoogte minstens $2^{\\ell+1}$, dus het aantal blauwe vakjes dat door rechthoeken met breedte 1 wordt bedekt, is 0 modulo $2^{\\ell+1}$. Dus $0 \\equiv V \\equiv 2^{\\ell} \\bmod 2^{\\ell+1}$, tegenspraak.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Vind alle positieve gehele $k$ waarvoor de vergelijking\n\n$$\n\\operatorname{kgv}(m, n)-\\operatorname{ggd}(m, n)=k(m-n)\n$$\n\ngeen positieve gehele oplossingen $(m, n)$ met $m \\neq n$ heeft.", "solution": "Noem $d=\\operatorname{ggd}(m, n)$ en schrijf $m=d a$ en $n=d b$. Er geldt $\\operatorname{kgv}(m, n)$. $\\operatorname{ggd}(m, n)=m n$, dus we kunnen de gegeven vergelijking schrijven als\n\n$$\n\\frac{d a \\cdot d b}{d}-d=k(d a-d b)\n$$\n\noftewel\n\n$$\na b-1=k(a-b) .\n$$\n\nWe kijken vanaf nu naar het equivalente vraagstuk: vind alle positieve gehele $k$ waarvoor deze nieuwe vergelijking geen positieve gehele oplossingen $(a, b)$ met $a \\neq b$ en $\\operatorname{ggd}(a, b)=1$ heeft. Merk op dat als een paar $(a, b)$ aan deze vergelijking voldoet, automatisch geldt dat $\\operatorname{ggd}(a, b)=1$. Stel namelijk dat $t \\mid a$ en $t \\mid b$, dan geldt $t \\mid a b$ en $t \\mid a-b$, dus $t \\mid 1$, dus $a$ en $b$ hebben geen gemeenschappelijke deler groter dan 1.\nStel eerst dat $k \\geq 3$. We beweren dat $(a, b)=\\left(k^{2}-k-1, k-1\\right)$ een oplossing is. Er geldt dan namelijk\n$a b-1=a(k-1)-1=k a-a-1=k a-k^{2}+k+1-1=k a-k^{2}+k=k(a-k+1)=k(a-b)$.\nWe hebben al gezien dat nu direct volgt dat $\\operatorname{ggd}(a, b)=1$. We moeten nog checken dat $a$ en $b$ positief zijn en dat ze ongelijk aan elkaar zijn. Omdat $k \\geq 3$, is $b=k-1 \\geq 2$ en is $a=k^{2}-k-1 \\geq 2 k-k-1=k-1 \\geq 2$, dus ze zijn allebei positief. Stel dat $a=b$, dan geldt $k^{2}-k-1=k-1$, oftewel $k^{2}=2 k$, oftewel $k=2$, tegenspraak. Dus ons paar $(a, b)$ voldoet aan alle eisen. Voor elke $k \\geq 3$ heeft de vergelijking dus minstens één oplossing $(a, b)$ met $a \\neq b$ en $\\operatorname{ggd}(a, b)=1$.\nStel nu dat $k=1$. We beweren dat $(a, b)=(2,1)$ een oplossing is. Overduidelijk zijn $a$ en $b$ positief en ongelijk aan elkaar. Verder geldt\n\n$$\na b-1=2-1=1=1 \\cdot(2-1)=k(a-b)\n$$\n\nDus voor $k=1$ heeft de vergelijking ook minstens één oplossing $(a, b)$ met $a \\neq b$ en $\\operatorname{ggd}(a, b)=1$.\nStel ten slotte dat $k=2$. De vergelijking wordt dan\n\n$$\na b-1=2(a-b) .\n$$\n\nDe rechterkant is hooguit $2 a-2$ omdat $b$ positief en geheel is, dus $a b-1 \\leq 2 a-2$, dus $a b<2 a$, dus $b<2$. Er moet dus gelden $b=1$. De vergelijking wordt dan $a-1=2(a-1)$, waaruit volgt $a-1=0$. We hebben dan $a=1$ en $b=1$, dus $a=b$. We concluderen dat er geen oplossingen $(a, b)$ met $a \\neq b$ zijn.\nDus de enige $k$ waarvoor de oorspronkelijke vergelijking geen positieve gehele oplossingen $(m, n)$ met $m \\neq n$ heeft, is $k=2$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ die voldoen aan\n\n$$\nf(x y-1)+f(x) f(y)=2 x y-1\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Als $f$ constant is, staat links altijd hetzelfde, terwijl rechts kan variëren, tegenspraak. Dus $f$ is niet constant. Vul nu $x=0$ in: $f(-1)+f(0) f(y)=-1$, dus $f(0) f(y)$ neemt voor alle $y \\in \\mathbb{R}$ dezelfde waarde aan. Omdat $f$ niet constant is, geeft dit $f(0)=0$. We kunnen dan ook onmiddellijk concluderen dat $f(-1)=-1$. Vul nu $x=y=1$ in: $f(0)+f(1)^{2}=1$, dus $f(1)=1$ of $f(1)=-1$.\nInvullen van $y=1+\\frac{1}{x}$ met $x \\neq 0$ geeft $f(x+1-1)+f(x) f\\left(1+\\frac{1}{x}\\right)=2 x+2-1$, dus\n\n$$\nf(x) f\\left(1+\\frac{1}{x}\\right)=2 x+1-f(x) \\quad \\text { voor alle } x \\neq 0\n$$\n\nInvullen van $y=\\frac{1}{x}$ met $x \\neq 0$ geeft $f(1-1)+f(x) f\\left(\\frac{1}{x}\\right)=2-1$, dus\n\n$$\nf(x) f\\left(\\frac{1}{x}\\right)=1 \\quad \\text { voor alle } x \\neq 0\n$$\n\nInvullen van $y=1, x=z+1$ geeft $f(z+1-1)+f(z+1) f(1)=2 z+2-1$, dus\n\n$$\nf(z)+f(z+1) f(1)=2 z+1 \\quad \\text { voor alle } z\n$$\n\nWe kiezen in deze vergelijking nu $z=\\frac{1}{x}$ met $x \\neq 0$ en vermenigvuldigen het geheel met $f(x)$ :\n\n$$\nf(x) f\\left(\\frac{1}{x}\\right)+f\\left(\\frac{1}{x}+1\\right) f(1) f(x)=\\frac{2}{x} f(x)+f(x) \\quad \\text { voor alle } x \\neq 0\n$$\n\nWe herschrijven de eerste en tweede term met behulp van respectievelijk (2) en (1), zodat we krijgen:\n\n$$\n1+2 x f(1)+f(1)-f(x) f(1)=\\frac{2}{x} f(x)+f(x) \\quad \\text { voor alle } x \\neq 0\n$$\n\nDit kunnen we herschrijven tot\n\n$$\nf(x) \\cdot\\left(\\frac{2}{x}+1+f(1)\\right)=1+2 x f(1)+f(1) \\quad \\text { voor alle } x \\neq 0\n$$\n\nAls de tweede factor links niet 0 is, kunnen we erdoor delen, dus:\n\n$$\nf(x)=\\frac{1+2 x f(1)+f(1)}{\\frac{2}{x}+1+f(1)} \\quad \\text { als } x \\neq 0 \\text { en } \\frac{2}{x}+1+f(1) \\neq 0 \\text {. }\n$$\n\nWe hadden twee mogelijke waarden voor $f(1)$. Stel eerst $f(1)=1$. Dan staat hier\n\n$$\nf(x)=\\frac{2+2 x}{\\frac{2}{x}+2}=x \\quad \\text { als } x \\neq 0 \\text { en } \\frac{2}{x}+2 \\neq 0\n$$\n\nEr geldt alleen $\\frac{2}{x}+2=0$ als $x=-1$, maar we wisten al dat $f(-1)=-1$. Ook hadden we al $f(0)=0$. We zien dus dat $f(x)=x$ voor alle $x$. We controleren deze functie: in\nde oorspronkelijke functievergelijking krijgen we dan links $x y-1+x y=2 x y-1$, dus het klopt.\nStel anderzijds juist $f(1)=-1$. Dan staat hier\n\n$$\nf(x)=\\frac{-2 x}{\\frac{2}{x}}=-x^{2} \\quad \\text { als } x \\neq 0 \\text { en } \\frac{2}{x} \\neq 0\n$$\n\nOmdat $\\frac{2}{x}=0$ niet kan voorkomen, concluderen we dat $f(x)=-x^{2}$ voor alle $x \\neq 0$. Ook $f(0)=0$ voldoet aan deze formule. We controleren de functie $f(x)=-x^{2}$ voor alle $x$ : in de oorspronkelijke functievergelijking krijgen we dan links $-x^{2} y^{2}-1+2 x y+x^{2} y^{2}=2 x y-1$, dus het klopt.\nWe concluderen dat er twee oplossingen zijn, namelijk $f(x)=x$ voor alle $x$ en $f(x)=-x^{2}$ voor alle $x$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Bewijs dat voor alle positieve reële getallen $a, b, c$ geldt:\n\n$$\na+\\sqrt{a b}+\\sqrt[3]{a b c} \\leq \\frac{4}{3}(a+b+c)\n$$", "solution": "We kunnen $\\sqrt[3]{a b c}$ schrijven als $\\sqrt[3]{\\frac{a}{4} \\cdot b \\cdot 4 c}$. Toepassen van de ongelijkheid van het rekenkundig en meetkundig gemiddelde op de (positieve) termen $\\frac{a}{4}, b$ en $4 c$ geeft dan\n\n$$\n\\sqrt[3]{a b c}=\\sqrt[3]{\\frac{a}{4} \\cdot b \\cdot 4 c} \\leq \\frac{\\frac{a}{4}+b+4 c}{3}=\\frac{a}{12}+\\frac{b}{3}+\\frac{4 c}{3} .\n$$\n\nDaarnaast passen we rekenkundig-meetkundig toe op $\\frac{a}{2}$ en $2 b$ :\n\n$$\n\\sqrt{a b}=\\sqrt{\\frac{a}{2} \\cdot 2 b} \\leq \\frac{\\frac{a}{2}+2 b}{2}=\\frac{a}{4}+b .\n$$\n\nDeze twee ongelijkheden tellen we bij elkaar op en we tellen er ook nog $a$ bij op:\n\n$$\na+\\sqrt{a b}+\\sqrt[3]{a b c} \\leq a+\\frac{a}{4}+b+\\frac{a}{12}+\\frac{b}{3}+\\frac{4 c}{3}=\\frac{4}{3}(a+b+c) .\n$$", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Bepaal alle paren $(a, b)$ van gehele getallen met de volgende eigenschap: er is een gehele $d \\geq 2$ zodat $a^{n}+b^{n}+1$ deelbaar is door $d$ voor alle positieve gehele getallen $n$.", "solution": "Bekijk een paar $(a, b)$ dat voldoet, met bijbehorende $d$. Zij $p$ een priemdeler van $d$ (die bestaat omdat $d \\geq 2$ ). Omdat $d \\mid a^{n}+b^{n}+1$ voor alle $n$, geldt ook $p \\mid a^{n}+b^{n}+1$ voor alle $n$. Bekijk nu $n=p-1$. Dan geldt $a^{n} \\equiv 0 \\bmod p$ als $p \\mid a$ en $a^{n} \\equiv 1 \\bmod p$ als $p \\nmid a$, wegens de kleine stelling van Fermat. Hetzelfde geldt voor $b$. Dus $a^{n}+b^{n}+1$ kan modulo $p$ de waarden 1 , 2 en 3 aannemen. Omdat het anderzijds 0 modulo $p$ moet zijn, zien we dat $p=2$ of $p=3$. We onderscheiden dus twee gevallen.\nStel dat $p=3$. Dan moet dus $3 \\nmid a, 3 \\nmid b$. Het geval $n=1$ geeft verder dat $3 \\mid a+b+1$, dus $a+b \\equiv 2 \\bmod 3$. Die twee eisen samen betekenen dat $a \\equiv b \\equiv 1 \\bmod 3$. In dit geval geldt voor alle positieve gehele $n$ dat $a^{n}+b^{n}+1 \\equiv 1+1+1 \\equiv 0 \\bmod 3$, dus elk zo'n tweetal voldoet, met $d=3$.\nStel nu dat $p=2$. Dan moet 2 een deler zijn van precies één van $a$ en $b$. In dat geval geldt voor alle positieve gehele $n$ dat $a^{n}+b^{n}+1 \\equiv 0+1+1 \\equiv 0 \\bmod 2$, dus elk zo'n tweetal voldoet, met $d=2$.\nWe concluderen dat dit de paren zijn die voldoen: $(a, b)$ met $a \\equiv b \\equiv 1 \\bmod 3,(a, b)$ met $a \\equiv 1, b \\equiv 0 \\bmod 2$, en $(a, b)$ met $a \\equiv 0, b \\equiv 1 \\bmod 2$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $\\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Laat $D, E$ en $F$ punten zijn op de respectievelijke lijnstukken $B C, C A$ en $A B$ zodat $|B F|=|B E|$ en zodat $E D$ de binnenbissectrice van $\\angle B E C$ is.\nBewijs dat $|B D|=|E F|$ dan en slechts dan als $|A F|=|E C|$.", "solution": "Uit het gegeven en de bissectricestelling volgt dat\n\n$$\n\\frac{|B F|}{|B D|}=\\frac{|B E|}{|B D|}=\\frac{|C E|}{|C D|}\n$$\n\nVanwege de gelijkbenigheid van $\\triangle A B C$ geldt verder $\\angle F B D=\\angle E C D$, wat samen geeft dat $\\triangle B F D \\sim \\triangle C E D$. Hieruit volgt dat $\\angle B F D=\\angle C E D=\\angle B E D$, dus $B D E F$ is een koordenvierhoek. Met de stelling van Julian geldt dus $|B D|=|E F|$ dan en slechts dan als $D E \\| B F$. Er geldt $|A F|=|E C|$ dan en slechts dan als $|B F|=|A E|$ (aangezien $|A B|=|A C|$ ), oftewel dan en slechts dan als $|E A|=|E B|$, en dat geldt dan en slechts dan als $\\angle B A E=\\angle A B E$. Aangezien $2 \\angle B E D=\\angle B E C=\\angle B A E+\\angle A B E$ vanwege de buitenhoekstelling, is $\\angle B A E=\\angle A B E$ equivalent met $\\angle B E D=\\angle A B E$ en dat is weer equivalent met $D E \\| B F$. Kortom, $|B D|=|E F|$ dan en slechts dan als $D E \\| B F$ en dat geldt dan en slechts dan als $|A F|=|E C|$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $\\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Laat $D, E$ en $F$ punten zijn op de respectievelijke lijnstukken $B C, C A$ en $A B$ zodat $|B F|=|B E|$ en zodat $E D$ de binnenbissectrice van $\\angle B E C$ is.\nBewijs dat $|B D|=|E F|$ dan en slechts dan als $|A F|=|E C|$.", "solution": "Stel eerst $|B D|=|E F|$. Vanwege de buitenhoekstelling en het gegeven dat $|B F|=|B E|$ geldt $\\angle A E F=\\angle B F E-\\angle F A E=\\angle B E F-\\angle F A E$. Dus\n$180^{\\circ}-2 \\angle B E D=\\angle A E F+\\angle B E F=2 \\angle B E F-\\angle F A E=2 \\angle B E F-\\left(180^{\\circ}-2 \\angle A B C\\right)$.\nHieruit volgt\n\n$$\n180^{\\circ}=\\angle B E D+\\angle B E F+\\angle A B C=\\angle D E F+\\angle F B D,\n$$\n\ndus $B D E F$ is een koordenvierhoek. Vanwege $|B D|=|E F|$ krijgen we met de stelling van Julian dat $B F \\| D E$. Dus\n\n$$\n\\angle B F D=\\angle B E D=\\angle D E C=\\angle B A C,\n$$\n\nwat betekent dat $F D \\| A C$. Dus $F A E D$ is een parallellogram. Verder zijn driehoeken $B F D$ en $B A C$ nu gelijkvormig wegens gelijke hoeken bij $A$ en $F$, dus $B F D$ is ook gelijkbenig. Dus geldt $|A E|=|F D|=|F B|$. Vanwege $|A B|=|A C|$ volgt daaruit $|E C|=|A F|$. Stel nu andersom dat $|E C|=|A F|$. Dat betekent $|A E|=|B F|=|B E|$, dus $\\triangle A E B$ is gelijkbenig. Hieruit volgt $\\angle B A C=\\angle A B E$, dus hebben de gelijkbenige driehoeken $\\triangle A B C$ en $\\triangle B E F$ dezelfde tophoek. Dat maakt dat ze gelijkvormig zijn. Noem de tophoek van deze driehoeken even $\\alpha$ en de basishoek $\\beta$. Dan is $\\angle D B E=\\angle D B A-\\angle E B F=\\beta-\\alpha=\\angle A E F$ vanwege de buitenhoekstelling in $\\triangle A F E$. Verder is $\\angle B E D=\\frac{1}{2} \\angle B E C=\\frac{1}{2} \\cdot 2 \\alpha=\\alpha$ vanwege de buitenhoekstelling in $\\triangle A E B$. Driehoeken $\\triangle A F E$ en $\\triangle E D B$ hebben dus twee paren gelijke hoeken. Daarnaast is $|A E|=|E B|$, dus deze driehoeken zijn congruent. Daaruit volgt $|D B|=|E F|$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "Bepaal het aantal verzamelingen $A=\\left\\{a_{1}, a_{2}, \\ldots, a_{1000}\\right\\}$ van positieve gehele getallen met $a_{1}<a_{2}<\\ldots<a_{1000} \\leq 2014$, waarvoor geldt dat de verzameling\n\n$$\nS=\\left\\{a_{i}+a_{j} \\mid 1 \\leq i, j \\leq 1000 \\text { en } i+j \\in A\\right\\}\n$$\n\neen deelverzameling is van $A$.", "solution": "We bewijzen dat er $2^{14}$ zulke verzamelingen zijn. We bewijzen in het bijzonder dat de verzamelingen $A$ die voldoen van de vorm $B \\cup C$ zijn, met $C$ een deelverzameling van $\\{2001, \\ldots, 2014\\}$ en $B=\\{1,2, \\ldots, 1000-|C|\\}$. Noem verzamelingen van die vorm \"leuk\". Omdat er $2^{14}$ deelverzamelingen van $\\{2001, \\ldots, 2014\\}$ zijn, zijn er $2^{14}$ leuke verzamelingen. We laten eerst zien dat iedere leuke verzameling $A$ voldoet. Stel dat $i, j \\leq 1000$ met $i+j \\in A$. Dan is $i+j \\leq 2000$, dus $i+j \\in B$. Er bestaat dan dus een $k$ met $k \\leq 1000-|C|$ zodat $i+j=a_{k}(=k)$. Omdat $a_{k} \\leq 1000-|C|$ geldt ook $i, j \\leq 1000-|C|$, dus $a_{i}=i$ en $a_{j}=j$. Dat betekent $a_{i}+a_{j}=i+j=a_{k}$ en dat is een element van $A$. Dus elk element van $S$ is een element van $A$, waaruit volgt dat $A$ voldoet.\nWe laten nu zien dat iedere verzameling $A$ die voldoet, leuk is. Stel allereerst dat er een $k$ met $1 \\leq k \\leq 1000$ bestaat zodat $a_{k} \\in\\{1001, \\ldots, 2000\\}$. Dan is $a_{k}=1000+i$ voor zekere $i$ met $i \\leq 1000$, dus $a_{1000}+a_{i}$ is een element van $S$ en moet daarom ook een element van $A$ zijn. Er geldt echter $a_{1000}+a_{i}>a_{1000}$, tegenspraak. Dus zo'n $a_{k}$ kan niet voorkomen. Dit betekent dat $A$ te schrijven is als de disjuncte vereniging $B \\cup C$, met $C \\subseteq\\{2001, \\ldots, 2014\\}$ en $B \\subseteq\\{1,2, \\ldots, 1000\\}$. Zij $b$ het aantal elementen van $B$. Dan is $b \\geq 986$, want $C$ heeft hoogstens 14 elementen. Om te bewijzen dat $A$ leuk is, moeten we bewijzen dat $B=\\{1,2, \\ldots, b\\}$. Hiertoe is het voldoende om te bewijzen dat $a_{b}$, het grootste element van $B$, gelijk is aan $b$. Stel daarom uit het ongerijmde dat $a_{b}>b$. Voor $i$ met $i=a_{b}-b$ geldt dan $b+i=a_{b} \\leq 1000$, dus $i \\leq 1000-b \\leq 14<b$. Daarom is $a_{i} \\leq 1000$ en dus $a_{b}+a_{i} \\leq$ 2000. Omdat $i+b=a_{b} \\in A$, geldt $a_{b}+a_{i} \\in S \\subset A$, maar dan is $a_{b}+a_{i}$ een groter element van $B$ dan $a_{b}$, het maximale element. Tegenspraak. Dus $a_{b}=b$, waaruit volgt dat $B=\\{1,2, \\ldots, b\\}$. Dus $A$ is leuk.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Zij $n$ een natuurlijk getal. In een dorp wonen $n$ jongens en $n$ meisjes. Voor het jaarlijkse bal moeten $n$ danskoppels worden gevormd, die elk uit één jongen en één meisje bestaan. Elk meisje geeft een lijstje door, bestaande uit de naam van de jongen met wie ze het liefst zou willen dansen, plus nul of meer namen van andere jongens met wie ze ook wel zou willen dansen. Het blijkt dat er $n$ danskoppels kunnen worden gevormd zodat elk meisje danst met een jongen die op haar lijstje staat.\nBewijs dat het mogelijk is om $n$ danskoppels te vormen zodat elk meisje danst met een jongen die op haar lijstje staat en waarbij ten minste één meisje danst met de jongen met wie ze het liefst wil dansen.", "solution": "Noem bij elk meisje de jongen met wie ze het liefst zou willen dansen, haar lievelingsjongen. We bewijzen de opgave met inductie naar $n$. Als $n=1$, dan danst het meisje met de enige jongen, dus danst ze met haar lievelingsjongen. Zij nu $k \\geq 1$ en neem aan dat we de opgave bewezen hebben voor $n=k$. Bekijk vervolgens het geval $n=k+1$. We onderscheiden twee gevallen. Stel eerst dat elke jongen precies één keer voorkomt als lievelingsjongen. Dan koppelen we elk meisjes aan haar lievelingsjongens en vormen zo $n$ danskoppels. Dit geval is hiermee afgehandeld. Bekijk nu het andere geval: niet elke jongen komt precies één keer voor als lievelingsjongen. Er worden $n$ lievelingsjongens genoemd en er zijn $n$ jongens, dus dan is er een jongen, zeg jongen $X$, die helemaal niet genoemd wordt als lievelingsjongen (en een ander die vaker genoemd wordt). We nemen nu de danskoppels die volgens de opgave bestaan, waarin elk meisje danst met een jongen van haar lijstje. In deze koppeling danst jongen $X$ met meisje $Y$. We verwijderen nu jongen $X$ en meisje $Y$ uit het dorp. Er blijven $k$ jongens en $k$ meisjes over. Dezelfde koppeling heeft nog steeds de eigenschap dat elk meisje danst met een jongen die op haar lijstje staat. Verder is het nog steeds zo dat elk meisje één van de $k$ jongens heeft uitverkoren als lievelingsjongen (want niemand had jongen $X$ gekozen). We kunnen dus de inductiehypothese toepassen om een koppeling te maken van $k$ danskoppels waarbij minstens één meisje danst met haar lievelingsjongen. Vervolgens voegen we het koppel $X-Y$ weer toe en dan wordt aan het gevraagde voldaan. Dit voltooit de inductie.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Voor reële getallen $a_{1}, a_{2}, \\ldots, a_{n}$, allemaal verschillend, berekenen we de $\\frac{n(n-1)}{2}$ sommen $a_{i}+a_{j}$ met $1 \\leq i<j \\leq n$ en sorteren deze vervolgens van klein naar groot. Bepaal alle gehele $n \\geq 3$ waarvoor er $a_{1}, a_{2}, \\ldots, a_{n}$ bestaan zodat dit rijtje van $\\frac{n(n-1)}{2}$ sommen een rekenkundige rij vormt (d.w.z. dat het verschil tussen twee opeenvolgende termen steeds hetzelfde is).", "solution": "Voor $n=3$ bekijken we $\\left(a_{1}, a_{2}, a_{3}\\right)=(1,2,3)$. De sommen van steeds twee elementen zijn gelijk aan 3,4 en 5 , dus die vormen een rekenkundige rij. Voor $n=4$ bekijken we $\\left(a_{1}, a_{2}, a_{3}, a_{4}\\right)=(1,3,4,5)$. De sommen van steeds twee elementen zijn gelijk aan $4,5,6,7,8$ en 9 , dus die vormen een rekenkundige rij.\nNeem nu $n \\geq 5$ en stel dat $a_{1}, a_{2}, \\ldots, a_{n}$ voldoet. Zonder verlies van algemeenheid nemen we aan dat $a_{1}<a_{2}<\\ldots<a_{n}$. $\\mathrm{Zij} d$ het verschil van twee opeenvolgende termen van de bijbehorende rekenkundige rij. De kleinste som is $a_{1}+a_{2}$ en de op een na kleinste is $a_{1}+a_{3}$. Hier zit een verschil $d$ tussen, dus $a_{3}-a_{2}=d$. De grootste som is $a_{n}+a_{n-1}$ en de op een na grootste is $a_{n}+a_{n-2}$, dus ook $a_{n-1}-a_{n-2}=d$. Dit betekent dat\n\n$$\na_{2}+a_{n-1}=\\left(a_{3}-d\\right)+\\left(a_{n-2}+d\\right)=a_{3}+a_{n-2} .\n$$\n\nAls $n \\geq 6$ staan hier links en rechts twee verschillende sommen $a_{i}+a_{j}$ met $i \\neq j$, maar het verschil tussen twee verschillende zulke sommen zou minstens $d$ moeten zijn. Tegenspraak. Dus voor $n \\geq 6$ is er geen oplossing.\nVoor $n=5$ hebben we dat $a_{3}-a_{2}=d$ en $a_{4}-a_{3}=d$. Dat betekent dat de op twee na kleinste som gelijk moet zijn aan $a_{1}+a_{4}$ (want die is $d$ groter dan $a_{1}+a_{3}$ ) en de op twee na grootste som gelijk aan $a_{5}+a_{2}$. Hiertussen zitten de sommen $a_{2}+a_{3}<a_{2}+a_{4}<a_{3}+a_{4}$, steeds met verschil $d$, en verder nog $a_{1}+a_{5}$. Dus $a_{1}+a_{5}$ is de vierde som in het rijtje, ofwel vanaf de kleinste kant geteld ofwel vanaf de grootste kant. Neem zonder verlies van algemeenheid aan dat het vanaf de kleinste kant is. We hebben dan\n$a_{1}+a_{2}<a_{1}+a_{3}<a_{1}+a_{4}<a_{1}+a_{5}<a_{2}+a_{3}<a_{2}+a_{4}<a_{3}+a_{4}<a_{2}+a_{5}<a_{3}+a_{5}<a_{4}+a_{5}$.\nDan geldt dus $\\left(a_{5}+a_{2}\\right)-\\left(a_{3}+a_{4}\\right)=d$, waaruit volgt $a_{5}-a_{4}=d+a_{3}-a_{2}=d+d$. Anderzijds weten we ook dat $\\left(a_{1}+a_{5}\\right)-\\left(a_{1}+a_{4}\\right)=d$, dus $a_{5}-a_{4}=d$. Tegenspraak. Dus ook $n=5$ voldoet niet.\nWe concluderen dat er $a_{1}, a_{2}, \\ldots, a_{n}$ bestaan die aan de voorwaarde voldoen voor $n=3$ en $n=4$, maar niet voor $n \\geq 5$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $k$ een positief geheel getal en geef de som van de cijfers van een positief geheel getal $n$ aan met $s(n)$. Bewijs dat er onder de positieve gehele getallen met $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen $n$ die voldoen aan $s(n)>s(2 n)$.", "solution": "We bewijzen dat er onder de positieve gehele getallen met hoogstens $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen die voldoen aan $s(n)>s(2 n)$. Het gevraagde volgt hieruit door dit resultaat voor $k$ en voor $k-1$ te combineren.\nWe gaan nu elk getal $n$ met hoogstens $k$ cijfers koppelen aan een ander getal $m$ met hoogstens $k$ cijfers. Definieer $m$ als $999 \\cdots 999-n$, waarbij het eerste getal uit $k$ negens bestaat. Nu heeft $m$ hoogstens $k$ cijfers. We gaan bewijzen dat $s(m)-s(2 m)=s(2 n)-s(n)$. Om $m$ uit te rekenen, trekken we $n$ af van $999 \\cdots 999$, waarbij elk cijfer van $n$ natuurlijk hooguit 9 is. Dus elk cijfer van $m$ is gelijk aan 9 min het bijbehorende cijfer van $n$ (zonder dat er ergens iets overgedragen wordt). Hierbij beschouwen we $m$ en $n$ beide als getallen van precies $k$ cijfers, door eventueel vooraan nullen aan te vullen. We zien dus dat $s(m)+s(n)=s(999 \\cdots 999)=9 k$. Nu bekijken we $2 m$ en $2 n$. Er geldt $2 m=$ 1999...998-2n (met $k-1$ negens). We beschouwen $2 m$ en $2 n$ nu als getallen met precies $k+1$ cijfers, waarbij het eerste cijfer van $2 n$ een 0 of 1 is. Als we dat afhalen van $1999 \\cdots 998$ wordt het eerste cijfer van $2 m$ dus $1-1=0$ of $1-0=1$. Het laatste cijfer van $2 m$ wordt 8 min het laatste cijfer van $2 n$, dat geen 9 kan zijn omdat $2 n$ even is. Alle overige cijfers van $2 m$ zijn gelijk aan 9 min het bijbehorende cijfer van $2 n$. Al met al zien we dat $s(2 m)+s(2 n)=s(1999 \\cdots 998)=1+9(k-1)+9=9 k$. We concluderen dat $s(m)+s(n)=s(2 m)+s(2 n)$, zodat $s(m)-s(2 m)=s(2 n)-s(n)$.\nNu zien we dat $s(m)>s(2 m)$ dan en slechts dan als $s(n)<s(2 n)$. Merk verder op dat geen enkel getal aan zichzelf wordt gekoppeld omdat $999 \\cdots 99$ oneven is. Er zijn dus precies evenveel getallen met $s(n)<s(2 n)$ als getallen met $s(n)>s(2 n)$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Zij $k$ een positief geheel getal en geef de som van de cijfers van een positief geheel getal $n$ aan met $s(n)$. Bewijs dat er onder de positieve gehele getallen met $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen $n$ die voldoen aan $s(n)>s(2 n)$.", "solution": "We bewijzen hier op een alternatieve manier dat $s(m)-s(2 m)=s(2 n)-$ $s(n)$. Zij $t(n)$ het aantal cijfers groter of gelijk aan 5 in het getal $n$. Als we $n$ bij zichzelf optellen, dan wordt er in deze optelling bij sommige cijfers wel een 1 overgedragen aan het volgende cijfer en bij sommige cijfers niet. Dit overgedragen gebeurt dan en slechts dan als het betreffende cijfer in $n$ een 5 of hoger is. Of er bij het vorige cijfer iets overgedragen is, is hierop niet van invloed. Als er iets overgedragen wordt, dan komt in de som niet het dubbele van het cijfer te staan, maar een cijfer 10 kleiner dan dat, terwijl anderzijds het volgende cijfer juist 1 groter wordt. Dus voor elke keer 1 overdragen wordt de som van de cijfers van $2 n$ precies 9 kleiner dan wanneer gewoon elk cijfer verdubbeld zou worden. Dat geeft dus $s(2 n)=2 s(n)-9 t(n)$.\nZoals in de vorige oplossing zien we dat elk cijfer van $m$ gelijk is aan 9 min het bijbehorende\ncijfer van $n$. Dus $s(m)=9 k-s(n)$ en $t(m)=k-t(n)$. Er geldt\n\n$$\n\\begin{aligned}\ns(m)-s(2 m) & =s(m)-(2 s(m)-9 t(m)) \\\\\n& =s(m)-(2 s(m)-9 k+9 t(n)) \\\\\n& =-s(m)+9 k-9 t(n) \\\\\n& =-9 k+s(n)+9 k-9 t(n) \\\\\n& =s(n)-9 t(n) \\\\\n& =s(2 n)-s(n)\n\\end{aligned}\n$$", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "Gegeven zijn cirkels $\\Gamma_{1}$ met middelpunt $A$ en $\\Gamma_{2}$ met middelpunt $B$, waarbij $A$ op $\\Gamma_{2}$ ligt. Op $\\Gamma_{2}$ ligt verder een variabel punt $P$, niet op $A B$. Een lijn door $P$ die $\\Gamma_{1}$ raakt in $S$, snijdt $\\Gamma_{2}$ nogmaals in $Q$, waarbij $P$ en $Q$ aan dezelfde kant van $A B$ liggen. Een andere lijn door $Q$ raakt $\\Gamma_{1}$ in $T$. Zij verder $M$ het voetpunt van de loodlijn vanuit $P$ op $A B$. Zij $N$ het snijpunt van $A Q$ en $M T$. Bewijs dat $N$ op een lijn ligt die onafhankelijk is van de plaats van $P$ op $\\Gamma_{2}$.", "solution": "Punt $P$ ligt buiten $\\Gamma_{1}$, omdat er anders geen raaklijn $P S$ aan $\\Gamma_{1}$ bestaat. Aangezien $P$ en $Q$ aan dezelfde kant van $A B$ liggen, ligt $S$ op het deel van $\\Gamma_{1}$ aan diezelfde kant van $A B$ dat buiten $\\Gamma_{2}$ ligt. (In het extreme geval dat $P$ op $A B$ zou liggen, zou $S$ namelijk in het snijpunt van $\\Gamma_{1}$ en $\\Gamma_{2}$ terecht komen wegens Thales.) We bekijken de configuratie waarin $Q$ tussen $P$ en $S$ ligt; daarmee ligt $Q$ ook op de korte boog $A P$. De andere configuratie gaat analoog. (Merk op dat $P \\neq Q$ volgens de opgave.)\nWe bewijzen dat $N$ op de machtlijn van $\\Gamma_{1}$ en $\\Gamma_{2}$ ligt. Er geldt $\\angle A S P=90^{\\circ}=\\angle A M P$, dus $A S P M$ is een koordenvierhoek vanwege Thales. Hieruit volgt\n\n$$\n\\angle P S M=\\angle P A M=\\angle P A B=90^{\\circ}-\\frac{1}{2} \\angle A B P=90^{\\circ}-\\left(180^{\\circ}-\\angle A Q P\\right)=90^{\\circ}-\\angle A Q S,\n$$\n\nwaarbij we in de eennalaatste stap de middelpunts-omtrekshoekstelling toegepast hebben. Verder geldt wegens de hoekensom in $\\triangle A Q S$ dat $90^{\\circ}-\\angle A Q S=\\angle Q A S$. Omdat $A S Q T$ een koordenvierhoek is met $|Q T|=|Q S|$ (gelijke raaklijnstukjes) is $\\angle Q A S=\\angle Q T S=\\angle Q S T$. Al met al vinden we $\\angle P S M=90^{\\circ}-\\angle A Q S=\\angle Q A S=\\angle Q S T=\\angle P S T$. Dus $S, T$ en $M$ liggen op een lijn.\nDaaruit volgt dat $N$ het snijpunt is van $S T$ en $A Q$. In koordenvierhoek $A S Q T$ vinden we met de machtstelling nu $N T \\cdot N S=N A \\cdot N Q$. Maar links staat ook de macht van $N$ ten opzichte van $\\Gamma_{1}$ en rechts de macht van $N$ ten opzichte van $\\Gamma_{2}$. Dus $N$ ligt op de machtlijn $\\operatorname{van} \\Gamma_{1}$ en $\\Gamma_{2}$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "Gegeven zijn cirkels $\\Gamma_{1}$ met middelpunt $A$ en $\\Gamma_{2}$ met middelpunt $B$, waarbij $A$ op $\\Gamma_{2}$ ligt. Op $\\Gamma_{2}$ ligt verder een variabel punt $P$, niet op $A B$. Een lijn door $P$ die $\\Gamma_{1}$ raakt in $S$, snijdt $\\Gamma_{2}$ nogmaals in $Q$, waarbij $P$ en $Q$ aan dezelfde kant van $A B$ liggen. Een andere lijn door $Q$ raakt $\\Gamma_{1}$ in $T$. Zij verder $M$ het voetpunt van de loodlijn vanuit $P$ op $A B$. Zij $N$ het snijpunt van $A Q$ en $M T$. Bewijs dat $N$ op een lijn ligt die onafhankelijk is van de plaats van $P$ op $\\Gamma_{2}$.", "solution": "We bekijken dezelfde configuratie als in de eerste oplossing. We geven een alternatief bewijs voor het feit dat $S, T$ en $M$ op een lijn liggen; daarna kun je het afmaken zoals in oplossing I.\nNoem $R$ het spiegelbeeld van $P$ in de lijn $A B$. Dan ligt $R$ ook op $\\Gamma_{2}$ en geldt $\\angle P B A=$ $\\angle R B A$. Vanwege de middelpuntsomtrekshoekstelling is $\\angle R Q A=\\frac{1}{2} \\angle R B A$ en $180^{\\circ}-$ $\\angle P Q A=\\frac{1}{2} \\angle P B A$. Dus $\\angle R Q A=180^{\\circ}-\\angle P Q A=\\angle S Q A$. Vanwege gelijke raaklijnstukjes is $\\angle S Q A=\\angle T Q A$, waaruit we concluderen $\\angle R Q A=\\angle T Q A$. Dat betekent dat $R, Q$ en $T$ op een lijn liggen.\nNu bekijken we driehoek $P Q R$ en het punt $A$ op zijn omgeschreven cirkel. De loodlijnen vanuit $A$ op de zijden van de driehoek hebben voetpunten $S, T$ en $M$. Dit is een Simsonlijn, dus $S, T$ en $M$ liggen op een lijn.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Zij $n$ een even positief geheel getal. Een rijtje van $n$ reële getallen noemen we volledig als voor elke gehele $m$ met $1 \\leq m \\leq n$ geldt dat de som van de eerste $m$ termen of de som van de laatste $m$ termen van het rijtje geheel is. Bepaal het minimale aantal gehele getallen in een volledig rijtje van $n$ getallen.", "solution": "We bewijzen dat het minimale aantal gehele getallen in een volledig rijtje gelijk aan 2 is. Bekijk eerst het geval $n=2$. Noem $a_{1}$ en $a_{2}$ de getallen in het rijtje. Dan is $a_{1}$ of $a_{2}$ geheel, zeg zonder verlies van algemeenheid $a_{1}$. Verder is $a_{1}+a_{2}$ geheel, maar dan is ook $a_{2}$ geheel. Dus het rijtje bevat minstens twee gehele getallen.\nBekijk nu het geval $n>2$. Schrijf $n=2 k$ (want $n$ is even) met $k \\geq 2$. Dan is $a_{1}+a_{2}+\\ldots+a_{k}$ of $a_{k+1}+a_{k+2}+\\ldots+a_{2 k}$ geheel. Maar omdat de som van beide uitdrukkingen ook geheel is, zijn ze allebei geheel. Verder is $a_{1}+a_{2}+\\ldots+a_{k-1}$ of $a_{k+2}+a_{k+3}+\\ldots+a_{2 k}$ geheel. Hieruit volgt dat $a_{k}$ of $a_{k+1}$ geheel is. Daarnaast weten we dat $a_{1}$ of $a_{2 k}$ geheel is en die vallen niet samen met $a_{k}$ of $a_{k+1}$ omdat $k \\geq 2$. Dus minstens twee verschillende getallen zijn geheel.\nTen slotte laten we zien dat het voor elke even $n$ mogelijk is om een volledig rijtje met precies twee gehele getallen te maken. Schrijf weer $n=2 k$. Als $k$ oneven is, nemen we $a_{1}=a_{k+1}=1$ en alle overige termen gelijk aan $\\frac{1}{2}$. De som van alle getallen in het rijtje is geheel, dus het is voldoende om nog te laten zien dat de som van de eerste of laatste $m$ termen geheel is met $1 \\leq m \\leq k$; de gevallen met $m>k$ volgen dan direct. Voor oneven $m \\leq k$ zijn de eerste $m$ termen samen geheel, voor even $m<k$ juist de laatste $m$ termen. Als $k$ even is, nemen we juist $a_{1}=a_{k}=1$ en alle overige termen gelijk aan $\\frac{1}{2}$. Nu is voor oneven $m<k$ de som van de eerste $m$ termen geheel en voor even $m \\leq k$ de som van de laatste $m$ termen. Verder is de som van alle termen bij elkaar geheel, dus het gevraagde volgt ook voor $m>k$.\nWe concluderen dat het minimale aantal gehele getallen in een volledig rijtje van $n$ getallen 2 is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Gegeven is de functie $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}$ die voldoet aan de eigenschappen:\n(i) $f(p)=1$ voor alle priemgetallen $p$,\n(ii) $f(x y)=y f(x)+x f(y)$ voor alle $x, y \\in \\mathbb{Z}_{>0}$.\n\nBepaal de kleinste $n \\geq 2016$ met $f(n)=n$.", "solution": "We bewijzen allereerst dat voor priemgetallen $p$ en positieve gehele getallen $k$ geldt dat $f\\left(p^{k}\\right)=k p^{k-1}$. Dit doen we met inductie naar $k$. Voor $k=1$ staat er $f(p)=1$ en dat is gegeven. Zij nu $l \\geq 1$ en stel dat we het bewezen hebben voor $k=l$. Bekijk $k=l+1$. Dan passen we de tweede eigenschap toe met $x=p$ en $y=p^{l}$ :\n\n$$\nf\\left(p^{l+1}\\right)=f\\left(p \\cdot p^{l}\\right)=p^{l} \\cdot f(p)+p \\cdot f\\left(p^{l}\\right)=p^{l}+p \\cdot l p^{l-1}=(l+1) p^{l} .\n$$\n\nDit voltooit de inductie. Nu bewijzen we dat voor verschillende priemgetallen $p_{1}, p_{2}, \\ldots$, $p_{t}$ en positieve gehele getallen $a_{1}, a_{2}, \\ldots, a_{t}$ geldt dat\n\n$$\nf\\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{t}^{a_{t}}\\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{t}^{a_{t}} \\cdot\\left(\\frac{a_{1}}{p_{1}}+\\frac{a_{2}}{p_{2}}+\\cdots+\\frac{a_{t}}{p_{t}}\\right) .\n$$\n\nWe bewijzen dit met inductie naar $t$. Voor $t=1$ is het precies de formule die we hiervoor bewezen hebben. Zij nu $r \\geq 1$ en stel dat we het bewezen hebben voor $t=r$. Dan passen we weer de tweede eigenschap toe:\n\n$$\n\\begin{aligned}\nf\\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} \\cdot p_{r+1}^{a_{r+1}}\\right) & =p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} \\cdot f\\left(p_{r+1}^{a_{r+1}}\\right)+p_{r+1}^{a_{r+1}} \\cdot f\\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}}\\right) \\\\\n& =p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} \\cdot a_{r+1} p_{r+1}^{a_{r+1}-1}+p_{r+1}^{a_{r+1}} \\cdot p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} \\cdot\\left(\\frac{a_{1}}{p_{1}}+\\frac{a_{2}}{p_{2}}+\\cdots+\\frac{a_{r}}{p_{r}}\\right) \\\\\n& =p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \\cdot \\frac{a_{r+1}}{p_{r+1}}+p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \\cdot\\left(\\frac{a_{1}}{p_{1}}+\\frac{a_{2}}{p_{2}}+\\cdots+\\frac{a_{r}}{p_{r}}\\right) \\\\\n& =p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \\cdot\\left(\\frac{a_{1}}{p_{1}}+\\frac{a_{2}}{p_{2}}+\\cdots+\\frac{a_{r}}{p_{r}}+\\frac{a_{r+1}}{p_{r+1}}\\right) .\n\\end{aligned}\n$$\n\nDit voltooit de inductie.\nVoor een geheel getal $n>1$ van de vorm $n=p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{t}^{a_{t}}$ met de $p_{i}$ verschillende priemgetallen, is de eigenschap $f(n)=n$ dus equivalent met\n\n$$\np_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{t}^{a_{t}} \\cdot\\left(\\frac{a_{1}}{p_{1}}+\\frac{a_{2}}{p_{2}}+\\cdots+\\frac{a_{t}}{p_{t}}\\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{t}^{a_{t}}\n$$\n\noftewel\n\n$$\n\\frac{a_{1}}{p_{1}}+\\frac{a_{2}}{p_{2}}+\\cdots+\\frac{a_{t}}{p_{t}}=1 .\n$$\n\nVermenigvuldigen met $p_{1} p_{2} \\cdots p_{t}$ geeft\n\n$$\na_{1} p_{2} p_{3} \\cdots p_{t}+a_{2} p_{1} p_{3} \\cdots p_{t}+\\ldots+a_{t} p_{1} p_{2} \\cdots p_{t-1}=p_{1} p_{2} \\cdots p_{t}\n$$\n\nNeem zonder verlies van algemeenheid aan dat $p_{1}$ het kleinste priemgetal is dat voorkomt in de priemfactorisatie van $n$. In de uitdrukking hierboven is $p_{1}$ een deler van de rechterkant en van elke term aan de linkerkant behalve eventueel de eerste. Maar dan moet $p_{1}$ ook een deler van de eerste term zijn. Aangezien $p_{2}, \\ldots, p_{t}$ allemaal priemgetallen ongelijk aan $p_{1}$ zijn, kan dat alleen als $p_{1} \\mid a_{1}$. In het bijzonder geldt dan $a_{1} \\geq p_{1}$, zodat $\\frac{a_{1}}{p_{1}} \\geq 1$. We zien nu dat hier gelijkheid moet gelden en dat $t=1$, omdat de som van alle $\\frac{a_{i}}{p_{i}}$ anders groter dan 1 wordt. Dus $n=p^{p}$ voor een zeker priemgetal $p$.\nWe zoeken dus de kleinste $n \\geq 2016$ van de vorm $n=p^{p}$. Er geldt $3^{3}=27$ en $5^{5}=3125$, dus de gevraagde $n$ is gelijk aan 3125 .", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Zij $A B C$ een driehoek met $\\angle A=90^{\\circ}$ en zij $D$ het voetpunt van de hoogtelijn vanuit $A$. De middens van $A D$ en $A C$ noemen we respectievelijk $E$ en $F$. Zij $M$ het middelpunt van de omschreven cirkel van $\\triangle B E F$. Bewijs dat $A C \\| B M$.", "solution": "Vanwege de rechte hoeken bij $A$ en $D$ geldt $\\triangle A D B \\sim \\triangle C A B$ (hh). Hieruit volgt $\\frac{|A D|}{|A B|}=\\frac{|C A|}{|C B|}$. Omdat $|A E|=\\frac{1}{2}|A D|$ en $|C F|=\\frac{1}{2}|C A|$ geldt ook $\\frac{|A E|}{|A B|}=\\frac{|C F|}{|C B|}$. Uit de vorige gelijkvormigheid volgt ook dat $\\angle B A E=\\angle B A D=\\angle B C A=\\angle B C F$, dus met (zhz) krijgen we nu $\\triangle A E B \\sim \\triangle C F B$. Hieruit volgt $\\angle A B E=\\angle C B F$.\nVerder is $E F$ een middenparallel in driehoek $A D C$, dus $E F \\| B C$. Met Z-hoeken geeft dit $\\angle C B F=\\angle B F E$. Vanwege de middelpunts-omtrekshoekstelling en vervolgens de hoekensom in gelijkbenige driehoek $E B M$ geldt $\\angle B F E=\\frac{1}{2} \\angle B M E=90^{\\circ}-\\angle E B M$. Dus $\\angle A B E=\\angle C B F=90^{\\circ}-\\angle E B M$. We concluderen dat $\\angle A B M=\\angle A B E+\\angle E B M=90^{\\circ}$. Dus $A C \\| B M$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Een viertal $(a, b, c, d)$ van positieve gehele getallen met $a \\leq b \\leq c \\leq d$ noemen we goed indien we ieder geheel getal rood, blauw, groen of paars kunnen kleuren zodat\n\n- van iedere $a$ opeenvolgende getallen er tenminste één rood is;\n- van iedere $b$ opeenvolgende getallen er tenminste één blauw is;\n- van iedere $c$ opeenvolgende getallen er tenminste één groen is;\n- van iedere $d$ opeenvolgende getallen er tenminste één paars is.\n\nBepaal alle goede viertallen met $a=2$.", "solution": "We bekijken steeds alleen viertallen $(a, b, c, d)$ van positieve gehele getallen met $a \\leq b \\leq c \\leq d$. Ieder viertal met $b \\geq 6$ voldoet: we kleuren dan de even getallen rood en de oneven getallen achtereenvolgens blauw, groen, paars, blauw, groen, paars, etc. Verder voldoet ieder viertal met $b \\geq 4$ en $c \\geq 8$ : we kleuren dan de even getallen rood, de getallen $1 \\bmod 4$ blauw, de getallen $3 \\bmod 8$ groen en de getallen $7 \\bmod 8$ paars. We gaan bewijzen dat dit de enige mogelijkheden zijn.\nStel $(2, b, c, d)$ is goed. We bekijken een paars getal. De buren van dit getal moeten rood zijn, dus dan hebben we 3 opeenvolgende getallen waarvan er geen blauw is. Dus $b \\geq 4$. Als $b \\geq 6$, dan voldoet het viertal, zoals we hebben gezien. Stel nu dus dat $b=4$ of $b=5$. We bekijken een paars getal. Deze heeft twee rode buren. Aan minstens één van beide kanten staat een blauw getal, zeg links. Daar weer links van komt een rood getal. Dus we hebben $R B R P R$. Bij de volgende twee getallen in het rijtje zit in elk geval een rode en in elk geval een blauwe, dus zeker geen groene. We hebben daarmee 7 opeenvolgende getallen zonder groene, dus $c \\geq 8$. We hebben al gezien dat dit geval voldoet.\nWe concluderen dat de volgende viertallen $(2, b, c, d)$ de goede viertallen zijn: die met $b \\geq 6$ en die met $b \\geq 4$ en $c \\geq 8$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2017", "problem_label": "5", "tier": 1, "problem": "Bepaal alle paren priemgetallen $(p, q)$ zodat $p^{2}+5 p q+4 q^{2}$ het kwadraat van een geheel getal is.", "solution": "Schrijf $p^{2}+5 p q+4 q^{2}=a^{2}$, met $a \\geq 0$ een geheel getal. De linkerkant is gelijk aan $(p+2 q)^{2}+p q$, dus we kunnen dit herschrijven tot $p q=a^{2}-(p+2 q)^{2}$, oftewel $p q=(a-p-2 q)(a+p+2 q)$. De tweede factor rechts is groter dan $p$ en groter dan $q$, maar het is wel een deler van $p q$. Omdat $p$ en $q$ priem zijn, moet het wel gelijk zijn aan $p q$, dus $a+p+2 q=p q$. En dan is $a-p-2 q=1$. Trek deze twee van elkaar af: $p q-1=(a+p+2 q)-(a-p-2 q)=2(p+2 q)$, oftewel $p q-2 p-4 q-1=0$. Dit kunnen we herschrijven tot $(p-4)(q-2)=9$. De factor $q-2$ kan niet negatief zijn, dus is $p-4$ dat ook niet. De factoren moeten dus gelijk zijn aan 1 en 9 of aan 9 en 1 of aan 3 en 3. Dit geeft respectievelijk voor $(p, q)$ de mogelijkheden $(5,11),(13,3)$ en $(7,5)$. Controleren laat zien dat $p^{2}+5 p q+4 q^{2}$ in elk van die gevallen een kwadraat is, namelijk respectievelijk $28^{2}, 20^{2}$ en $18^{2}$. Dus deze drie tweetallen zijn de oplossingen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Zij $n$ een positief geheel getal. Gegeven zijn cirkelvormige schijven met stralen $1,2, \\ldots, n$. Van elke grootte hebben we twee schijven: een doorzichtige en een ondoorzichtige. In elke schijf zit een gaatje, precies in het midden, waarmee we de schijven op een rechtopstaand staafje kunnen stapelen. We willen nu stapels maken die aan de volgende voorwaarden voldoen:\n\n- Van elke grootte ligt er precies één schijf op de stapel.\n- Als we recht van boven kijken, kunnen we de buitenranden van alle $n$ schijven op de stapel zien. (Dat wil zeggen, als er een ondoorzichtige schijf op de stapel ligt, dan mogen daaronder geen kleinere schijven liggen.)\n\nBepaal het aantal verschillende stapels dat we kunnen maken onder deze voorwaarden. (Twee stapels zijn verschillend als ze niet precies dezelfde verzameling schijven gebruiken, maar ook als ze wel precies dezelfde verzameling schijven gebruiken maar niet in dezelfde volgorde.)", "solution": "Noem een stapel geldig als hij aan de voorwaarden voldoet. Zij $a_{n}$ het aantal geldige stapels met $n$ schijven (met straal $1,2, \\ldots, n$ ). We bewijzen met inductie dat $a_{n}=(n+1)!$. Voor $n=1$ kunnen we twee stapels maken: met de doorzichtige schijf met straal 1 en met de ondoorzichtige schijf met straal 1 , dus $a_{1}=2=2$. Stel nu dat we voor zekere $n \\geq 1$ bewezen hebben dat $a_{n}=(n+1)$ !. Bekijk een geldige stapel met $n+1$ schijven. Als we de schijf met straal $n+1$ weghalen, zijn nog steeds alle schijven van bovenaf zichtbaar, dus we houden een geldige stapel met $n$ schijven over. Elke geldige stapel met $n+1$ schijven is dus te maken door in een geldige stapel met $n$ schijven de schijf met straal $n+1$ op een geschikte plek in te voegen. In principe zijn er $n+1$ posities waarop we de schijf met straal $n+1$ kunnen invoegen: boven de bovenste schijf, boven de tweede schijf, ..., boven de onderste schijf en ook nog onder de onderste schijf. De schijf met straal $n+1$ zelf is altijd zichtbaar, waar we hem ook invoegen. Als we de schijf met straal $n+1$ invoegen onder de onderste schijf, dan mag hij zowel doorzichtig als ondoorzichtig zijn; in beide gevallen wordt het zicht op de andere schijven niet geblokkeerd. Er zijn dus $2 a_{n}$ geldige stapels waarbij de schijf met straal $n+1$ onderop liggen. Als we echter op een andere positie een ondoorzichtige schijf met straal $n+1$ invoegen, dan blokkeert hij het zicht op de schijven eronder. We kunnen dus op de andere $n$ posities alleen de doorzichtige schijf met straal $n+1$ invoegen. Er zijn dus $n a_{n}$ geldige stapels waarbij de schijf met straal\n$n+1$ niet onderop ligt. Zo vinden we\n\n$$\na_{n+1}=2 a_{n}+n a_{n}=(n+2) a_{n}=(n+2)(n+1)!=(n+2)!\n$$\n\nDit voltooit de inductie.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Zij $n \\geq 4$ een geheel getal. Bekijk een regelmatige $2 n$-hoek waarbij aan elk hoekpunt een geheel getal is toegekend, wat we de waarde van dat hoekpunt noemen. Als vier verschillende hoekpunten van deze $2 n$-hoek een rechthoek vormen, dan noemen we de som van de waarden van deze hoekpunten een rechthoekssom.\nBepaal voor welke gehele (niet-noodzakelijk positieve) $m$ we de getallen $m+1, m+2$, $\\ldots, m+2 n$ als waarden kunnen toekennen aan de hoekpunten (in een of andere volgorde) zodat elke rechthoekssom een priemgetal is. (Priemgetallen zijn per definitie positief.)", "solution": "Nummer de hoekpunten van de $2 n$-hoek met de klok mee 1 tot en met $2 n$ en zij $a_{i}$ de waarde van hoekpunt $i$. Omdat het aantal hoekpunten van de veelhoek even is, kunnen we elk hoekpunt koppelen aan het punt er precies tegenover. We tellen de waarden van elk tweetal tegenoverliggende hoekpunten bij elkaar op en verkrijgen zo de getallen $s_{i}=a_{i}+a_{i+n}$ met $1 \\leq i \\leq n$.\nAls vier hoekpunten $A, B, C$ en $D$ in die volgorde een rechthoek vormen, dan is $\\angle A B C=$ $90^{\\circ}$ en $\\angle A D C=90^{\\circ}$, dus $B$ en $D$ liggen volgens Thales op de cirkel met middellijn $A C$. Omdat alle hoekpunten van de veelhoek op zijn omgeschreven cirkel liggen, is $A C$ blijkbaar een middellijn van de omgeschreven cirkel. Dus $A$ en $C$ zijn tegenoverliggende hoekpunten en hetzelfde geldt voor $B$ en $D$. Andersom geldt dat als $A$ en $C$ tegenoverliggende hoekpunten zijn en $B$ en $D$ ook, dat dan $A B C D$ een rechthoek is, ook wegens Thales. Kortom, vier punten vormen een rechthoek dan en slechts dan als ze tot twee paren tegenoverliggende hoekpunten behoren.\nEr moet dus gelden dat $s_{i}+s_{j}$ priem is voor alle $1 \\leq i<j \\leq n$. Stel dat minstens drie van de getallen $s_{i}$ dezelfde pariteit hebben, zeg $s_{j}, s_{k}$ en $s_{l}$. Dan is de som van elke twee van die drie even, maar tegelijkertijd priem, dus die som moet in alle gevallen gelijk aan 2 zijn. Dus $s_{j}+s_{k}=s_{k}+s_{l}=s_{j}+s_{l}$, waaruit volgt dat $s_{j}=s_{k}=s_{l}$. Maar omdat $s_{j}+s_{k}=2$, geeft dit $s_{j}=s_{k}=s_{l}=1$. We concluderen dat hoogstens twee van de getallen $s_{i}$ even zijn, en dat als er drie of meer oneven zijn, deze allemaal gelijk moeten zijn aan 1.\nDe totale som van alle $s_{i}$ is gelijk aan de som van alle getallen bij de hoekpunten, dus gelijk aan\n\n$$\n(m+1)+(m+2)+\\ldots+(m+2 n)=2 m n+\\frac{1}{2} \\cdot 2 n \\cdot(2 n+1)=2 m n+n(2 n+1)\n$$\n\nModulo 2 is deze som congruent aan $n$. Anderzijds moet deze som modulo 2 congruent zijn aan het aantal oneven $s_{i}$. Dus het aantal oneven $s_{i}$ heeft dezelfde pariteit als $n$. Omdat er totaal $n$ getallen $s_{i}$ zijn, is het aantal even $s_{i}$ dus even. We hebben al gezien dat dat er hoogstens twee zijn, dus het zijn er nul of twee.\nStel dat $n=4$ en stel dat er twee $s_{i}$ even zijn en dus ook twee $s_{i}$ oneven. Dan is de som van de twee even $s_{i}$ gelijk aan 2 en de som van de twee oneven $s_{i}$ ook gelijk aan 2, dus de totale som van de $s_{i}$ is $4=n$. Stel nu dat $n \\geq 5$ en stel dat er twee $s_{i}$ even zijn. Dan zijn er $n-2 \\geq 3$ van de $s_{i}$ oneven, dus alle oneven $s_{i}$ zijn gelijk aan 1 . De twee even $s_{i}$ samen zijn gelijk aan 2. Dus de totale som van de $s_{i}$ is $(n-2)+2=n$. (Je kunt ook bewijzen dat het geval met precies twee even $s_{i}$ onmogelijk is.) Stel nu dat er geen even $s_{i}$ zijn. Dan\nzijn alle $s_{i}$ oneven en dus ook allemaal gelijk aan 1, dus is de totale som van de $s_{i}$ gelijk aan $n$.\nIn alle gevallen is de totale som van de $s_{i}$ dus $n$. We hebben ook gezien dat deze som gelijk is aan $2 m n+n(2 n+1)$. Dus $2 m n+n(2 n+1)=n$, waaruit na deling door $n \\neq 0$ volgt $2 m+2 n+1=1$, dus $m=-n$.\nWe laten nu zien dat als $m=-n$, er inderdaad een oplossing bestaat. Neem $a_{i}=i$ en $a_{n+i}=1-i$ voor $1 \\leq i \\leq n$. Dan worden de getallen $1,2, \\ldots, n$ en de getallen $0,-1, \\ldots,-n+1$ gebruikt en dat zijn samen precies de getallen $m+1, m+2, \\ldots, m+2 n$. Verder geldt $s_{i}=i+(1-i)=1$ voor alle $i$. Dus elke rechthoekssom is gelijk aan 2 en dat is een priemgetal.\nWe concluderen dat $m=-n$ de enige waarde van $m$ is die voldoet.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Bepaal alle mogelijke waarden van $\\frac{1}{x}+\\frac{1}{y}$ als $x$ en $y$ reële getallen (ongelijk aan $0)$ zijn die voldoen aan $x^{3}+y^{3}+3 x^{2} y^{2}=x^{3} y^{3}$.", "solution": "We herschrijven het gegeven naar $x^{3}+y^{3}-x^{3} y^{3}=-3 x^{2} y^{2}$, waarmee we vinden\n\n$$\n\\begin{aligned}\n(x+y)^{3}-x^{3} y^{3} & =x^{3}+3 x^{2} y+3 x y^{2}+y^{3}-x^{3} y^{3} \\\\\n& =-3 x^{2} y^{2}+3 x^{2} y+3 x y^{2}=3 x y(-x y+x+y)\n\\end{aligned}\n$$\n\nDoor te gebruiken dat $a^{3}-b^{3}=(a-b)\\left(a^{2}+a b+b^{2}\\right)$ kunnen we anderzijds ook schrijven\n\n$$\n\\begin{aligned}\n(x+y)^{3}-x^{3} y^{3} & =(x+y-x y)\\left((x+y)^{2}+x y(x+y)+(x y)^{2}\\right) \\\\\n& =(x+y-x y)\\left(x^{2}+y^{2}+2 x y+x^{2} y+x y^{2}+x^{2} y^{2}\\right)\n\\end{aligned}\n$$\n\nAls we nu de twee rechterkanten aan elkaar gelijk stellen, dan zien we dat ofwel $x+y-x y=0$ ofwel $x^{2}+y^{2}+2 x y+x^{2} y+x y^{2}+x^{2} y^{2}=3 x y$. Het laatste geval laat zich herschrijven tot\n\n$$\n\\begin{aligned}\n0 & =x^{2}+y^{2}-x y+x^{2} y+x y^{2}+x^{2} y^{2} \\\\\n& =\\frac{1}{2}(x-y)^{2}+\\frac{1}{2} x^{2}\\left(y^{2}+2 y+1\\right)+\\frac{1}{2} y^{2}\\left(x^{2}+2 x+1\\right) \\\\\n& =\\frac{1}{2}(x-y)^{2}+\\frac{1}{2} x^{2}(y+1)^{2}+\\frac{1}{2} y^{2}(x+1)^{2} .\n\\end{aligned}\n$$\n\nDe som van drie kwadraten moet dus 0 zijn, waaruit volgt dat elk van de kwadraten 0 moet zijn. Dus $x=y=-1$. In dit geval wordt inderdaad aan de gegeven vergelijking voldaan en geldt $\\frac{1}{x}+\\frac{1}{y}=-2$.\nIn het andere geval is $x+y-x y=0$, dus $\\frac{1}{y}+\\frac{1}{x}-1=0$, waaruit volgt dat $\\frac{1}{x}+\\frac{1}{y}=1$. Dit wordt bijvoorbeeld aangenomen voor $x=y=2$.\nWe concluderen dat de gevraagde waarden -2 en 1 zijn.\n\nAlternatieve aanpak. Ook met minder algebraïsch gegoochel is het mogelijk de gewenste vorm van de gegeven relatie te vinden. We beschrijven hier een mogelijke aanpak.\nDelen door $x^{3} y^{3}$ geeft\n\n$$\n\\frac{1}{x^{3}}+\\frac{1}{y^{3}}+\\frac{3}{x y}=1\n$$\n\nHier zien we alvast iets met $\\frac{1}{x}$ en $\\frac{1}{y}$ in terug. We substitueren $a=\\frac{1}{x}$ en $b=\\frac{1}{y}$ om de notatie makkelijker te maken. Dan staat er\n\n$$\na^{3}+b^{3}+3 a b=1\n$$\n\nen zijn we op zoek naar de waarde van $a+b$. Waarschijnlijk zijn er wel oplossingen met $a=b$. We krijgen dan $2 a^{3}+3 a^{2}=1$. Getalletjes proberen of dit ontbinden geeft dat $a=-1$ en $a=\\frac{1}{2}$ voldoen. Nu wordt $a+b$ gelijk aan -2 of 1 . We kunnen nu gokken dat misschien wel alle paren $(a, b)$ met $a+b=-2$ of alle paren $(a, b)$ met $a+b=1$ werken;\ndan zou de uitdrukking deelbaar zijn door $a+b+2$ respectievelijk $a+b-1$. Proberen laat zien dat het laatste inderdaad het geval is. We kunnen herschrijven tot\n\n$$\n(a+b-1)\\left(a^{2}+b^{2}-a b+a+b+1\\right)=0\n$$\n\nWe weten inmiddels ook dat $a+b=-2$ niet voor alle $a$ en $b$ een oplossing geeft, maar wel voor $a=b=-1$. Dus zouden we voor de rechterfactor iets met $a+1$ en $b+1$ willen. Het is nu makkelijk te zien dat de rechterfactor de som is van drie kwadraten. We kunnen het nu verder afmaken (vergelijkbaar met hierboven).", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "In driehoek $A B C$ is $M$ het midden van $A B$ en $N$ het midden van $C M$. Zij $X$ een punt dat voldoet aan $\\angle X M C=\\angle M B C$ en $\\angle X C M=\\angle M C B$, zo dat $X$ en $B$ aan verschillende kanten van $C M$ liggen. $\\mathrm{Zij} \\Omega$ de omgeschreven cirkel van driehoek $A M X$.\na) Bewijs dat $C M$ raakt aan $\\Omega$.\nb) Bewijs dat de lijnen $N X$ en $A C$ snijden op $\\Omega$.\n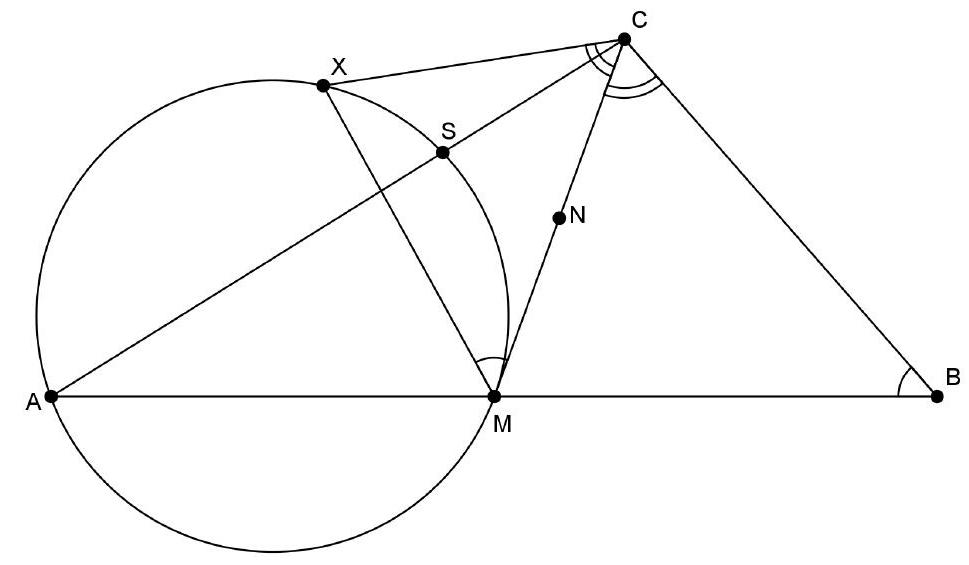", "solution": "We bekijken de configuratie in de figuur; andere configuraties gaan analoog.\na) Uit de gegevens volgt dat $\\triangle X M C \\sim \\triangle M B C$. Er geldt nu $\\angle A M X=180^{\\circ}-$ $\\angle X M C-\\angle B M C=180^{\\circ}-\\angle X M C-\\angle M X C=\\angle M C X$ en\n\n$$\n\\frac{|A M|}{|M X|}=\\frac{|B M|}{|M X|}=\\frac{|M C|}{|C X|}\n$$\n\ndus met zhz zien we dat $\\triangle A M X \\sim \\triangle M C X$. Hieruit volgt dat $\\angle X A M=\\angle X M C$, dus met de omgekeerde raaklijnomtrekhoekstelling zien we dat $C M$ raakt aan $\\Omega$.\nb) Zij $S$ het tweede snijpunt van $A C$ en $\\Omega$ (of het raakpunt van $A C$ en $\\Omega$; dat is dan A). We moeten bewijzen dat $S$ op $N X$ ligt. Vanwege de raaklijnomtrekshoekstelling geldt $\\angle S M C=\\angle S A M=\\angle C A M$. (Als $S=A$, dan volgt $\\angle S M C=\\angle C A M$ uit het feit dat $C A$ en $C M$ beide raaklijnstukjes zijn en dus $\\triangle C A M$ gelijkbenig is.) Hieruit volgt $\\triangle C S M \\sim \\triangle C M A$ (hh), dus $\\frac{|C M|}{|C A|}=\\frac{|S M|}{|M A|}$. Aangezien $|C M|=2|M N|$ en $|M A|=\\frac{1}{2}|A B|$, geldt ook $\\frac{|M N|}{|C A|}=\\frac{|S M|}{|A B|}$. Samen met $\\angle S M N=\\angle S M C=\\angle C A M=$ $\\angle C A B$ betekent dit $\\triangle S N M \\sim \\triangle B C A$. Dus $\\angle M S N=\\angle A B C$. Verder is $\\angle X S M=$ $180^{\\circ}-\\angle X A M$. In het vorige onderdeel hebben we gezien dat $\\angle X A M=\\angle X M C=$ $\\angle M B C=\\angle A B C$, dus $\\angle X S M=180^{\\circ}-\\angle A B C=180^{\\circ}-\\angle M S N$. Hieruit volgt dat $S$ op $X N$ ligt.\n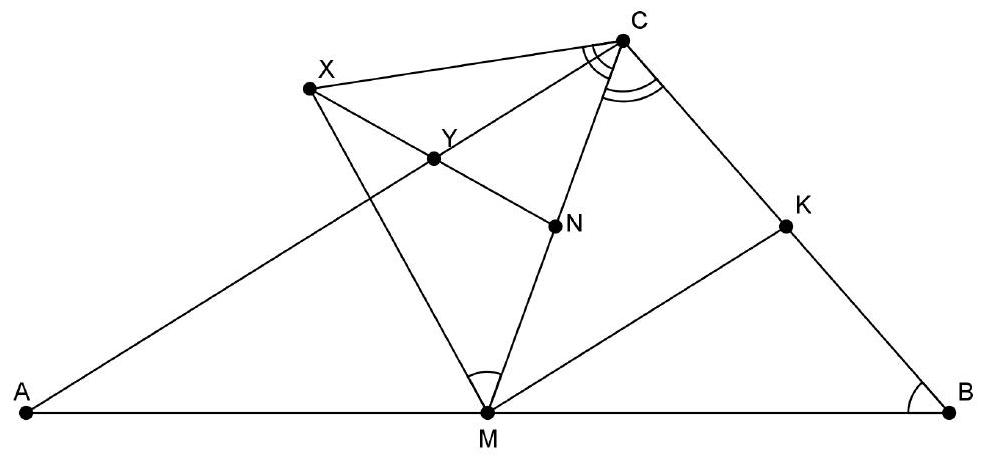\n\nOplossing II voor deel b Zij $K$ het midden van $B C$. Uit de gelijkvormigheid $\\triangle X M C \\sim$ $\\triangle M B C$ volgt ook dat $\\triangle X M N \\sim \\triangle M B K$. Omdat lijn $X M$ en lijn $B M$ een hoek van $\\angle A M X$ maken, zijn de andere zijden $N X$ en $K M$ niet evenwijdig. Aangezien $K M$ een middenparallel is in driehoek $A B C$, is $K M$ evenwijdig aan $A C$. Dus hebben $N X$ en $A C$ een snijpunt $Y$. We zien nu dat $\\angle B M K=\\angle M X N=\\angle M X Y$. Vanwege de middenparallel geldt verder $\\angle M A Y=\\angle M A C=\\angle B M K$. Dus $\\angle M X Y=\\angle M A Y$, waaruit volgt dat $Y$ op $\\Omega$ ligt.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Laat $a, b$ en $c$ positieve gehele getallen zijn, allemaal verschillend, en veronderstel dat $p=a b+b c+c a$ een priemgetal is.\na) Bewijs dat $a^{2}, b^{2}$ en $c^{2}$ verschillende resten geven bij deling door $p$.\nb) Bewijs dat $a^{3}, b^{3}$ en $c^{3}$ verschillende resten geven bij deling door $p$.", "solution": "a) We bewijzen dit uit het ongerijmde. Stel dat twee van $a^{2}, b^{2}$ en $c^{2}$ dezelfde rest geven bij deling door $p$, zeg dat $a^{2} \\equiv b^{2} \\bmod p$. Dan geldt $p \\mid a^{2}-b^{2}=(a-b)(a+b)$, dus $p \\mid a-b$ of $p \\mid a+b$. In het laatste geval geldt $p \\leq a+b \\leq c(a+b)<a b+b c+c a=p$, tegenspraak. In het eerste geval geldt vanwege $a \\neq b$ dat $p \\leq|a-b| \\leq a+b<p$, tegenspraak.\nb) We bewijzen dit uit het ongerijmde. Stel dat twee van $a^{3}, b^{3}$ en $c^{3}$ dezelfde rest geven bij deling door $p$, zeg dat $a^{3} \\equiv b^{3} \\bmod p$. Dan geldt $p \\mid a^{3}-b^{3}=(a-b)\\left(a^{2}+a b+b^{2}\\right)$, dus $p \\mid a-b$ of $p \\mid a^{2}+a b+b^{2}$. Het eerste geval geeft net als bij (a) een tegenspraak. We bekijken het andere geval: $p \\mid a^{2}+a b+b^{2}$. Daaruit volgt dat $p \\mid a^{2}+a b+b^{2}+$ $(a b+b c+c a)=(a+b)(a+b+c)$ en dus $p \\mid a+b$ of $p \\mid a+b+c$. Er geldt echter $a+b<a+b+c<a b+b c+c a$ omdat $a, b$ en $c$ niet allemaal gelijk kunnen zijn aan 1. Dus $p$ is geen deler van $a+b$ of $a+b+c$, tegenspraak.", "problem_match": "\nOpgave 1.", "solution_match": "# Oplossing."}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "De ingeschreven cirkel van een niet-gelijkbenige driehoek $\\triangle A B C$ heeft middelpunt $I$ en raakt aan $B C$ en $C A$ in respectievelijk $D$ en $E$. Zij $H$ het hoogtepunt van $\\triangle A B I$, zij $K$ het snijpunt van $A I$ en $B H$ en zij $L$ het snijpunt van $B I$ en $A H$. Bewijs dat de omgeschreven cirkels van $\\triangle D K H$ en $\\triangle E L H$ snijden op de ingeschreven cirkel van $\\triangle A B C$.\n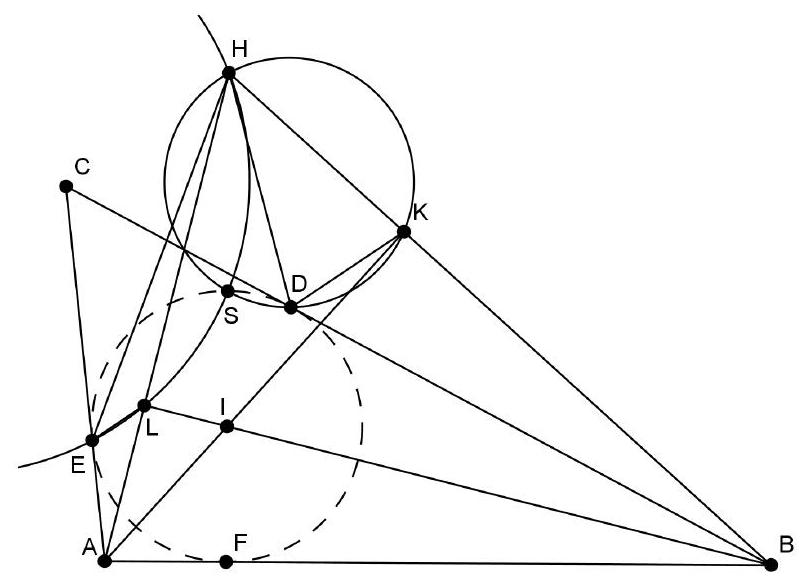", "solution": "We bekijken de configuratie in de figuur; andere configuraties gaan analoog. Er geldt $\\angle I D B=90^{\\circ}=\\angle I K B$, dus $B K D I$ is een koordenvierhoek. Verder is $\\angle A L B=$ $90^{\\circ}=\\angle A K B$, dus ook $B K L A$ is een koordenvierhoek. Dus\n\n$$\n\\angle B K D=180^{\\circ}-\\angle B I D=180^{\\circ}-\\left(90^{\\circ}-\\frac{1}{2} \\angle A B C\\right)=180^{\\circ}-\\angle B A L=\\angle B K L .\n$$\n\nHieruit volgt dat $K, D$ en $L$ op een lijn liggen. Analoog liggen ook $K, E$ en $L$ op een lijn en dat is dezelfde lijn, dus $D$ ligt hier ook op.\nZij $S$ het tweede snijpunt van de omgeschreven cirkels van $\\triangle D K H$ en $\\triangle E L H$. Dan geldt\n\n$$\n\\begin{gathered}\n\\angle D S E=360^{\\circ}-\\angle D S H-\\angle H S E=\\angle D K H+180^{\\circ}-\\angle H L E=\\angle L K H+\\angle H L K \\\\\n=180^{\\circ}-\\angle K H L .\n\\end{gathered}\n$$\n\nOmdat ook HLIK een koordenvierhoek is (wegens twee rechte hoeken) geldt\n$180^{\\circ}-\\angle K H L=\\angle K I L=\\angle A I B=180^{\\circ}-\\angle I B A-\\angle I A B=180^{\\circ}-\\frac{1}{2} \\angle C B A-\\frac{1}{2} \\angle C A B$.\nDus $\\angle D S E=180^{\\circ}-\\frac{1}{2} \\angle C B A-\\frac{1}{2} \\angle C A B$. Noem nu $F$ het raakpunt van de ingeschreven cirkel aan zijde $A B$, dan zijn $A F I E$ en $B F I D$ ook koordenvierhoeken (allebei wegens twee rechte hoeken). Dus geldt\n\n$$\n\\angle D F E=\\angle D F I+\\angle I F E=\\angle D B I+\\angle I A E=\\frac{1}{2} \\angle C B A+\\frac{1}{2} \\angle C A B .\n$$\n\nWe concluderen dat $\\angle D F E+\\angle D S E=180^{\\circ}$, waaruit volgt dat $S$ op de omgeschreven cirkel van $\\triangle D E F$ ligt en dat is precies de ingeschreven cirkel van $\\triangle A B C$.\n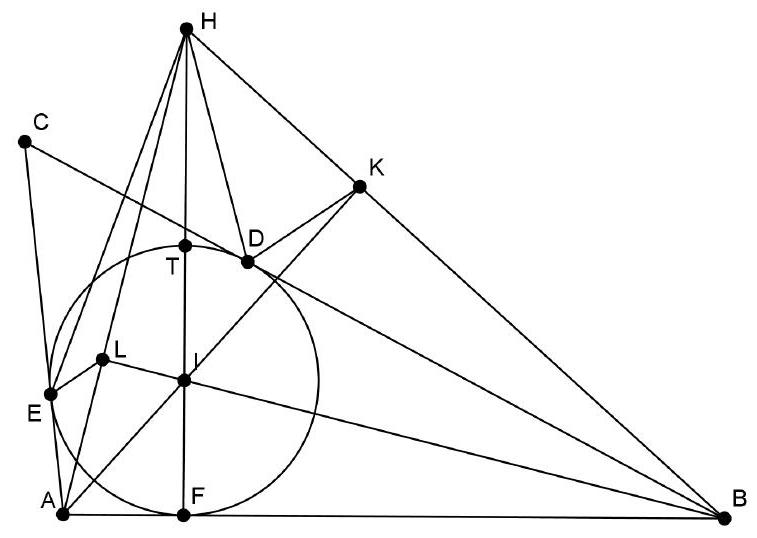", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "De ingeschreven cirkel van een niet-gelijkbenige driehoek $\\triangle A B C$ heeft middelpunt $I$ en raakt aan $B C$ en $C A$ in respectievelijk $D$ en $E$. Zij $H$ het hoogtepunt van $\\triangle A B I$, zij $K$ het snijpunt van $A I$ en $B H$ en zij $L$ het snijpunt van $B I$ en $A H$. Bewijs dat de omgeschreven cirkels van $\\triangle D K H$ en $\\triangle E L H$ snijden op de ingeschreven cirkel van $\\triangle A B C$.\n", "solution": "We bewijzen net als in oplossing I dat $K, D, E$ en $L$ op een lijn liggen. Noem nu $T \\neq F$ het snijpunt van $H I$ en de ingeschreven cirkel. Als $T=H$, dan is er niets te bewijzen. Neem nu aan $T \\neq H$. Dan is het voldoende te laten zien dat KDTH en ELTH koordenvierhoeken zijn. Wegens koordenvierhoeken ETDF (ingeschreven cirkel) en $E I F A$ (twee rechte hoeken) geldt: $\\angle E D T=\\angle E F T=\\angle E F I=\\angle E A I=\\frac{1}{2} \\angle C A B$. En vanwege koordenvierhoek $H K F A$ (twee rechte hoeken) geldt verder $\\angle K H T=\\angle K H F=$ $\\angle K A F=\\frac{1}{2} \\angle C A B$. Dus $\\angle K H T=\\angle E D T=180^{\\circ}-\\angle K D T$ aangezien $K, D$ en $E$ op een lijn liggen. We concluderen dat $K D T H$ een koordenvierhoek is. De andere koordenvierhoek gaat analoog.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Zij $k>2$ een geheel getal. Een positief geheel getal $\\ell$ noemen we $k$-pabel als we de getallen $1,3,5, \\ldots, 2 k-1$ kunnen opdelen in twee verzamelingen $A$ en $B$ zodat de som van de elementen van $A$ precies $\\ell$ keer zo groot is als de som van de elementen van $B$. Bewijs dat het kleinste $k$-pabele getal relatief priem is met $k$.", "solution": "We gaan bewijzen dat als $p$ de kleinste priemdeler van $k$ is, dat dan $p-1$ het kleinste $k$-pabele getal is. Hieruit volgt het gevraagde, want er geldt dan $\\operatorname{ggd}(p-1, k)=1$. Er geldt $1+3+5+\\ldots+(2 k-1)=k^{2}$. Als $\\ell$ een $k$-pabel getal is en $s$ is de bijbehorende som van de elementen uit $B$, dan is de som van de elementen uit $A$ gelijk aan $\\ell s$, dus is de totale som $(\\ell+1) s$ en dat moet gelijk zijn aan $k^{2}$. Dus $\\ell+1 \\mid k^{2}$. Omdat $\\ell+1 \\geq 2$ geldt nu $\\ell+1 \\geq p$, waarbij $p$ de kleinste priemdeler van $k$ is. Dus $\\ell \\geq p-1$. We gaan nu bewijzen dat $\\ell=p-1$ een $k$-pabel getal is, waaruit dan onmiddellijk volgt dat het het kleinste $k$-pabele getal is. En daarmee zijn we klaar, want $\\operatorname{ggd}(k, p-1)=1$ omdat er geen priemdelers kleiner dan $p$ in $k$ zitten.\nStel eerst dat $k$ even is, zodat $p=2$. Dan moeten we dus bewijzen dat we de verzameling $\\{1,3, \\ldots, 2 k-1\\}$ kunnen opdelen in twee verzamelingen met gelijke som van de elementen. Dit bewijzen we met inductie naar $k$. Voor $k=4$ en $k=6$ hebben we respectievelijk $\\{1,7\\},\\{3,5\\}$ en $\\{1,3,5,9\\},\\{7,11\\}$. Als we de verzameling $\\{1,3, \\ldots, 2 k-1\\}$ zo kunnen opdelen, kan dat ook voor de verzameling $\\{1,3, \\ldots, 2(k+4)-1\\}$ door van de nieuwe elementen $\\{2 k+1,2 k+3,2 k+5,2 k+7\\}$ de elementen $2 k+1$ en $2 k+7$ in de ene verzameling te stoppen en de elementen $2 k+3$ en $2 k+5$ in de andere. Dat voltooit de inductie. Stel nu dat $k$ oneven is. Schrijf $k=p m$. Dan is het voldoende dat we een deelverzameling $B$ van $\\{1,3, \\ldots, 2 k-1\\}$ kunnen vinden waarvan de som van de elementen gelijk is aan $p m^{2}$, want dan is de som van de elementen in de verzameling $A=\\{1,3, \\ldots, 2 k-1\\} \\backslash B$ gelijk aan $k^{2}-p m^{2}=p^{2} m^{2}-p m^{2}=(p-1) p m^{2}$ en dus precies $p-1$ keer zo groot als de som van de elementen in $B$. Bekijk de verzameling $B=\\{p, 3 p, \\ldots,(2 m-1) p\\} \\subset\\{1,3, \\ldots, 2 k-1\\}$. Dan is de som van de elementen in $B$ gelijk aan\n\n$$\np+3 p+\\cdots+(2 m-1) p=p(1+3+\\cdots+(2 m-1))=p m^{2}\n$$\n\nprecies wat de bedoeling was.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Bepaal alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ zodat\n\n$$\n(y+1) f(x)+f(x f(y)+f(x+y))=y\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Invullen van $x=0$ geeft $(y+1) f(0)+f(f(y))=y$, dus $f(f(y))=y \\cdot(1-$ $f(0))-f(0)$. Als $f(0) \\neq 1$, is de rechterkant een bijectieve functie in $y$ en de linkerkant dus ook. Daarmee is in dit geval $f$ bijectief.\nWe gaan nu laten zien dat in het geval $f(0)=1$ ook geldt dat $f$ bijectief is. Dus stel $f(0)=1$. Dan krijgen we $f(f(y))=-1$ voor alle $y \\in \\mathbb{R}$. Invullen van $y=0$ geeft $f(x)+f(x+f(x))=0$, dus $f(x+f(x))=-f(x)$. Vul vervolgens $x=f(z)$ en $y=z$ in en vervang $f(f(z))$ door -1 :\n\n$$\n(z+1) \\cdot-1+f(f(z) f(z)+f(z+f(z)))=z\n$$\n\ndus, als we ook nog gebruiken dat $f(z+f(z))=-f(z)$,\n\n$$\nf\\left(f(z)^{2}-f(z)\\right)=2 z+1\n$$\n\nHieruit volgt direct dat $f$ surjectief is. Als er $a$ en $b$ zijn met $f(a)=f(b)$, dan geeft $z=a$ en daarna $z=b$ invullen in deze laatste vergelijking links twee keer hetzelfde, terwijl er rechts eerst $2 a+1$ en daarna $2 b+1$ staat. Dus $a=b$, waaruit volgt dat $f$ injectief is. We zien dat $f$ ook in dit geval bijectief is.\nWe kunnen dus vanaf nu aannemen dat $f$ bijectief is, waarbij we de aanname $f(0)=1$ weer laten vallen. We weten $f(f(y))=y \\cdot(1-f(0))-f(0)$ en dus vinden we met $y=-1$ dat $f(f(-1))=-1$. Invullen van $y=-1$ in de oorspronkelijke vergelijking geeft\n\n$$\nf(x f(-1)+f(x-1))=-1=f(f(-1))\n$$\n\nOmdat $f$ injectief is, volgt hieruit dat $x f(-1)+f(x-1)=f(-1)$, dus $f(x-1)=$ $f(-1) \\cdot(1-x)$. Als we nu $x=z+1$ nemen, zien we dat $f(z)=-f(-1) z$ voor alle $z \\in \\mathbb{R}$. Dus de functie is van de vorm $f(x)=c x$ voor $x \\in \\mathbb{R}$, waarbij $c \\in \\mathbb{R}$ een constante is. We controleren deze functie. Er geldt\n$(y+1) f(x)+f(x f(y)+f(x+y))=(y+1) c x+c(x c y+c x+c y)=c x y+c x+c^{2} x y+c^{2} x+c^{2} y$.\nDit moet gelijk zijn aan $y$ voor alle $x, y \\in \\mathbb{R}$. Met $y=0$ en $x=1$ staat er $c+c^{2}=0$, dus $c=0$ of $c=-1$. Met $x=0$ en $y=1$ staat er $c^{2}=1$, dus $c=1$ of $c=-1$. We concluderen dat $c=-1$ en dan zien we dat deze functie inderdaad voldoet. Dus de enige oplossing is $f(x)=-x$ voor $x \\in \\mathbb{R}$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Bepaal alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ zodat\n\n$$\n(y+1) f(x)+f(x f(y)+f(x+y))=y\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "We geven een alternatief bewijs voor het geval $f(0)=1$. Net als in de eerste oplossing vinden we $f(f(y))=-1$ voor alle $y \\in \\mathbb{R}$. Vul nu $x=f(0)=1$ in:\n\n$$\n(y+1) f(f(0))+f(f(y)+f(1+y))=y\n$$\n\nEr geldt $f(f(0))=-1$, dus\n\n$$\nf(f(y)+f(1+y))=2 y+1\n$$\n\nAls we nu links en rechts $f$ toepassen, vinden we\n\n$$\nf(f(f(y)+f(1+y)))=f(2 y+1)\n$$\n\nLinks staat hier gewoon -1 , dus $f$ is overal gelijk aan -1 , maar dat is een tegenspraak met $f(0)=1$. In dit geval zijn er dus geen oplossingen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Gegeven is cirkel $\\omega$ met middellijn $A K$. Punt $M$ ligt binnen de cirkel, niet op lijn $A K$. De lijn $A M$ snijdt $\\omega$ nogmaals in $Q$. De raaklijn aan $\\omega$ in $Q$ snijdt de lijn door $M$ loodrecht op $A K$ in $P$. Punt $L$ ligt op $\\omega$ zodat $P L$ een raaklijn is, met $L \\neq Q$. Bewijs dat $K, L$ en $M$ op een lijn liggen.\n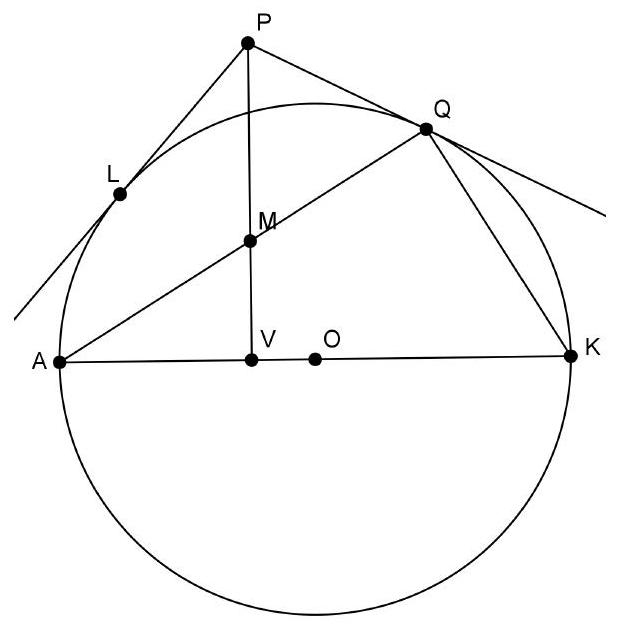", "solution": "Noem $O$ het middelpunt van $\\omega$ en zij $V$ het snijpunt van $M P$ met $A K$. We bewijzen nu eerst dat $\\angle P V L=\\angle P O L$. Als $V$ en $O$ samenvallen, dan is er niets te bewijzen. Als $V$ en $O$ niet samenvallen, dan geldt $\\angle O V P=90^{\\circ}=\\angle O L P$, dus $O V P L$ of $V O P L$ is een koordenvierhoek. (In feite ligt $Q$ ook nog op de bijbehorende omgeschreven cirkel.) Hieruit volgt dat $\\angle P V L=\\angle P O L$. We hebben nu in alle gevallen $\\angle M V L=\\angle P V L=\\angle P O L$. Omdat $P L$ en $P Q$ raken aan $\\omega$, geldt $\\triangle O Q P \\cong \\triangle O L P$, dus $\\angle P O L=\\frac{1}{2} \\angle Q O L$. Vanwege de middelpuntsomtrekshoekstelling toegepast op $\\omega$ is die hoek bovendien gelijk aan $\\angle Q A L$. Al met al vinden we\n\n$$\n\\angle M V L=\\angle P O L=\\angle Q A L=\\angle M A L\n$$\n\nwaaruit volgt dat $M V A L$ een koordenvierhoek is. Dus $\\angle A L M=180^{\\circ}-\\angle A V M=90^{\\circ}$. Verder geldt wegens Thales dat $\\angle A L K=90^{\\circ}$, dus $\\angle A L M=\\angle A L K$, wat betekent dat $L$, $M$ en $K$ op een lijn liggen.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Gegeven is cirkel $\\omega$ met middellijn $A K$. Punt $M$ ligt binnen de cirkel, niet op lijn $A K$. De lijn $A M$ snijdt $\\omega$ nogmaals in $Q$. De raaklijn aan $\\omega$ in $Q$ snijdt de lijn door $M$ loodrecht op $A K$ in $P$. Punt $L$ ligt op $\\omega$ zodat $P L$ een raaklijn is, met $L \\neq Q$. Bewijs dat $K, L$ en $M$ op een lijn liggen.\n", "solution": "We definiëren $V$ als in de eerste oplossing. Er geldt wegens Thales dat $\\angle M Q K=90^{\\circ}=\\angle M V K$, dus $M Q K V$ is een koordenvierhoek. Dus $\\angle P M Q=180^{\\circ}-$\n$\\angle V M Q=\\angle V K Q=\\angle A K Q$. Omdat $P Q$ raakt aan $\\omega$ geldt $\\angle A K Q=\\angle A Q P=\\angle M Q P$. Al met al geldt dus $\\angle P M Q=\\angle M Q P$, wat betekent dat $\\triangle M Q P$ gelijkbenig is met $|P M|=|P Q|$. Vanwege gelijke raaklijnstukjes is ook $|P Q|=|P L|$, dus $P$ is het middelpunt van de cirkel door $M, Q$ en $L$. Daaruit volgt\n\n$$\n\\angle Q L M=\\frac{1}{2} \\angle Q P M=90^{\\circ}-\\angle M Q P=90^{\\circ}-\\angle A K Q=\\angle Q A K=\\angle Q L K\n$$\n\nWe concluderen dat $L, M$ en $K$ op een lijn liggen.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "$\\mathrm{Zij} a_{1}, a_{2}, \\ldots, a_{n}$ een rijtje reële getallen zodat $a_{1}+\\cdots+a_{n}=0$ en definieer $b_{i}=a_{1}+\\cdots+a_{i}$ voor $1 \\leq i \\leq n$. Veronderstel dat $b_{i}\\left(a_{j+1}-a_{i+1}\\right) \\geq 0$ voor alle $1 \\leq i \\leq$ $j \\leq n-1$. Bewijs dat\n\n$$\n\\max _{1 \\leq \\ell \\leq n}\\left|a_{\\ell}\\right| \\geq \\max _{1 \\leq m \\leq n}\\left|b_{m}\\right|\n$$", "solution": "Er geldt $b_{n}=0$. Stel dat er een $i \\leq n-1$ is met $b_{i}>0$ en $a_{i+1} \\geq 0$. Dan volgt uit $b_{i}\\left(a_{j+1}-a_{i+1}\\right) \\geq 0$ dat $a_{j+1} \\geq a_{i+1} \\geq 0$ voor alle $i \\leq j \\leq n-1$. Dus $b_{n}=b_{i}+a_{i+1}+a_{i+2}+\\ldots+a_{n} \\geq b_{i}>0$, tegenspraak. We concluderen dat uit $b_{i}>0$ volgt dat $a_{i+1}<0$. En analoog: als $b_{i}<0$, dan geldt $a_{i+1}>0$.\nZij nu $k$ zo dat $\\left|b_{k}\\right|=\\max _{1 \\leq m \\leq n}\\left|b_{m}\\right|$. We kunnen zonder verlies van algemeenheid aannemen dat $b_{k}>0$ (anders vermenigvuldigen we alle $a_{i}$ met -1 ). Als $k=1$, dan geldt $b_{k}=a_{1}$, dus $\\left|b_{k}\\right|=\\left|a_{1}\\right| \\leq \\max _{1 \\leq \\ell \\leq n}\\left|a_{\\ell}\\right|$ en dan zijn we klaar. Stel nu $k>1$. Als $b_{k-1}>0$, dan geldt volgens bovenstaande dat $a_{k}<0$. Anderzijds is $a_{k}=b_{k}-b_{k-1} \\geq 0$ omdat $b_{k}$ maximaal was, tegenspraak. Dus $b_{k-1} \\leq 0$. Nu is $a_{k}=b_{k}-b_{k-1}=b_{k}+\\left|b_{k-1}\\right| \\geq b_{k}$, dus $\\left|b_{k}\\right| \\leq\\left|a_{k}\\right| \\leq \\max _{1 \\leq \\ell \\leq n}\\left|a_{\\ell}\\right|$, wat we moesten bewijzen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "$\\mathrm{Zij} a_{1}, a_{2}, \\ldots, a_{n}$ een rijtje reële getallen zodat $a_{1}+\\cdots+a_{n}=0$ en definieer $b_{i}=a_{1}+\\cdots+a_{i}$ voor $1 \\leq i \\leq n$. Veronderstel dat $b_{i}\\left(a_{j+1}-a_{i+1}\\right) \\geq 0$ voor alle $1 \\leq i \\leq$ $j \\leq n-1$. Bewijs dat\n\n$$\n\\max _{1 \\leq \\ell \\leq n}\\left|a_{\\ell}\\right| \\geq \\max _{1 \\leq m \\leq n}\\left|b_{m}\\right|\n$$", "solution": "Net als in oplossing I vinden we dat uit $b_{i}>0$ volgt dat $a_{i+1}<0$ en uit $b_{i}<0$ volgt $a_{i+1}>0$. Zij nu $M=\\max _{1 \\leq \\ell \\leq n}\\left|a_{\\ell}\\right|$. We bewijzen met inductie naar $t$ dat $\\left|b_{t}\\right| \\leq M$ voor $1 \\leq t \\leq n$. Voor $t=1$ geldt $\\left|b_{1}\\right|=\\left|a_{1}\\right| \\leq M$. Zij nu $r \\geq 1$ en neem aan dat $\\left|b_{r}\\right| \\leq M$. Nu bewijzen we dat $\\left|b_{r+1}\\right| \\leq M$. We onderscheiden drie gevallen. Als $b_{r}=0$, dan geldt $\\left|b_{r+1}\\right|=\\left|b_{r}+a_{r+1}\\right|=\\left|a_{r+1}\\right| \\leq M$. Stel nu $b_{r}>0$. Dan weten we $a_{r+1}<0$, dan geldt $b_{r+1}=b_{r}+a_{r+1}$, dus $a_{r+1}<b_{r+1}<b_{r}$. Vanwege de inductiehypothese is $b_{r} \\leq M$ en verder weten we $a_{r+1} \\geq-M$, dus $-M<b_{r+1}<M$, wat betekent dat $\\left|b_{r+1}\\right| \\leq M$. Stel ten slotte dat $b_{r}<0$. Dan weten we $a_{r+1}>0$, dus zien we op dezelfde manier als hierboven $-M \\leq b_{r}<b_{r+1}<a_{r+1} \\leq M$, dus $\\left|b_{r+1}\\right| \\leq M$. Dit voltooit de inductie. We concluderen dat $\\left|b_{t}\\right| \\leq M$ voor alle $t$ en daaruit volgt direct het gevraagde.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Bepaal het product van alle positieve gehele getallen $n$ waarvoor $3(n!+1)$ deelbaar is door $2 n-5$.", "solution": "De getallen $n=1$ tot en met $n=4$ voldoen, want $2 n-5$ is dan gelijk aan respectievelijk $-3,-1,1$ en 3 , dus altijd een deler dan $3(n!+1)$. Vanaf nu bekijken we alleen $n>4$ en dan is $2 n-5>3$.\nWe bewijzen eerst dat als $n$ voldoet, dan $2 n-5$ priem moet zijn. We onderscheiden twee gevallen. Stel eerst dat $2 n-5$ niet priem is en een priemdeler $p>3$ heeft. Omdat $p \\neq 2 n-5$ en omdat $2 n-5$ oneven is, geldt $p \\leq \\frac{2 n-5}{3}<n$. Dus $p \\mid n!$, maar dan $p \\nmid n!+1$ en dus ook $p \\nmid 3(n!+1)$ aangezien $p \\neq 3$. Dus $2 n-5 \\nmid 3(n!+1)$, wat betekent dat $n$ niet voldoet. Stel nu dat $2 n-5$ niet priem is, maar alleen priemdelers 3 heeft; dan is het dus een driemacht groter dan 3. Echter, voor $n>4$ is $3 \\nmid n!+1$, dus $3(n!+1)$ is deelbaar door precies één factor 3 en niet meer. We zien dat $n$ ook in dit geval niet kan voldoen.\nVoor een $n>4$ die voldoet, weten we nu dat $2 n-5$ een priemgetal groter dan 3 is. Schrijf $q=2 n-5$. Dan $q \\mid n!+1$, oftewel $n!\\equiv-1 \\bmod q$. Verder zegt de stelling van Wilson dat $(q-1)!\\equiv-1 \\bmod q$. Dus\n\n$$\n\\begin{aligned}\n-1 & \\equiv(2 n-6)! \\\\\n& \\equiv(2 n-6)(2 n-7) \\cdots(n+1) \\cdot n! \\\\\n& \\equiv(-1) \\cdot(-2) \\cdots \\cdots(-n+6) \\cdot n! \\\\\n& \\equiv(-1)^{n-6} \\cdot(n-6)!\\cdot n! \\\\\n& \\equiv(-1)^{n} \\cdot(n-6)!\\cdot-1 \\quad \\bmod q .\n\\end{aligned}\n$$\n\nDus $(n-6)!\\equiv(-1)^{n} \\bmod q$. Omdat $n!\\equiv-1 \\bmod q$, volgt daaruit $n \\cdot(n-1) \\cdots \\cdot \\cdot(n-5) \\equiv$ $(-1)^{n-1} \\bmod q$. We vermenigvuldigen dit met $2^{6}$ :\n\n$$\n2 n \\cdot(2 n-2) \\cdot(2 n-4) \\cdot(2 n-6) \\cdot(2 n-8) \\cdot(2 n-10) \\equiv(-1)^{n-1} \\cdot 64 \\bmod q .\n$$\n\nModulo $q=2 n-5$ staat links $5 \\cdot 3 \\cdot 1 \\cdot-1 \\cdot-3 \\cdot-5=-225$.\nStel $n$ is oneven. Dan hebben we dus $-225 \\equiv 64 \\bmod q$, dus $q \\mid-225-64=-289=-17^{2}$. Dus $q=17$ en dan $n=\\frac{17+5}{2}=11$. Stel nu $n$ is even. Dan hebben we $-225 \\equiv-64 \\bmod q$, dus $q \\mid-225+64=-161=-7 \\cdot 23$. Dus $q=7$ of $q=23$ en dat geeft respectievelijk $n=6$ en $n=14$.\nWe controleren deze drie mogelijkheden. Voor $n=11$ en $2 n-5=17$ :\n\n$$\n\\begin{aligned}\n11! & =1 \\cdot(2 \\cdot 9) \\cdot(3 \\cdot 6) \\cdot(5 \\cdot 7) \\cdot 4 \\cdot 8 \\cdot 10 \\cdot 11 \\\\\n& \\equiv 4 \\cdot 8 \\cdot 10 \\cdot 11=88 \\cdot 40 \\equiv 3 \\cdot 6 \\equiv 1 \\quad \\bmod 17\n\\end{aligned}\n$$\n\ndus $n=11$ voldoet niet. Voor $n=14$ en $2 n-5=23$ :\n\n$$\n\\begin{aligned}\n14! & =1 \\cdot(2 \\cdot 12) \\cdot(3 \\cdot 8) \\cdot(4 \\cdot 6) \\cdot(5 \\cdot 14) \\cdot(7 \\cdot 10) \\cdot 9 \\cdot 11 \\cdot 13 \\\\\n& \\equiv 9 \\cdot 11 \\cdot 13=117 \\cdot 11 \\equiv 2 \\cdot 11 \\equiv-1 \\quad \\bmod 23\n\\end{aligned}\n$$\n\ndus $n=14$ voldoet. Voor $n=6$ en $2 n-5=7$ ten slotte volgt $6!\\equiv-1 \\bmod 7$ uit de stelling van Wilson, dus $n=6$ voldoet ook.\nWe concluderen dat de getallen $n$ die voldoen, zijn: $1,2,3,4,6$ en 14. Het product daarvan is 2016.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Zij $n \\geq 2$ een geheel getal. Bepaal de kleinste positieve gehele $m$ zodat geldt: gegeven $n$ punten in het vlak, geen drie op een lijn, zijn er $m$ lijnen te vinden, zodat geen enkele lijn door één van de gegeven punten gaat en zodat voor elk tweetal gegeven punten $X \\neq Y$ geldt dat er een lijn is waarvan $X$ en $Y$ aan weerszijden liggen.", "solution": "We bewijzen dat de kleinste $m$ gelijk is aan $\\frac{n}{2}$ als $n$ even is en $\\frac{n+1}{2}$ als $n$ oneven. Kies de $n$ punten allemaal op dezelfde cirkel en noem ze $P_{1}, P_{2}, \\ldots, P_{n}$ in de volgorde waarin ze op de cirkel liggen. De $n$ lijnstukken $P_{1} P_{2}, P_{2} P_{3}, \\ldots, P_{n} P_{1}$ moeten allemaal gesneden worden door minstens één lijn. Elke lijn snijdt hoogstens twee van zulke lijnstukken, aangezien elke lijn de cirkel hoogstens twee keer snijdt. Dus het aantal lijnen is minstens $\\frac{n}{2}$ en dus voor oneven $n$ minstens $\\frac{n+1}{2}$.\nNu bewijzen we dat dit voldoende is. Eerst laten we zien dat gegeven vier verschillende punten $P_{1}, P_{2}$ en $Q_{1}, Q_{2}$ er altijd een lijn bestaat zodat $P_{1}$ en $P_{2}$ aan weerszijden van de lijn liggen en $Q_{1}$ en $Q_{2}$ ook. Neem hiervoor de lijn door het midden van $P_{1} P_{2}$ en door het midden van $Q_{1} Q_{2}$. Stel dat deze lijn door $P_{1}$ heen gaat. Dan gaat hij ook door $P_{2}$ heen, maar niet door $Q_{1}$ of $Q_{2}$, omdat er nooit drie punten op een lijn liggen. Schuif hem dan een klein stukje op zodat hij net niet door het midden van $Q_{1} Q_{2}$ heen gaat, maar nog wel door het midden van $P_{1} P_{2}$, dan gaat hij niet meer door één van deze vier punten heen. Analoog als de lijn door één van de andere drie punten heen zou gaan. Als de nu gekozen lijn door één van de overige gegeven punten in het vlak gaat, schuif je hem (nog) een heel klein beetje op zodat dat niet meer zo is. Omdat er maar eindig veel punten zijn, lukt dit altijd. Deze lijn heeft nu $P_{1}$ en $P_{2}$ aan weerszijden en $Q_{1}$ en $Q_{2}$ ook.\nNeem nu aan dat $n$ even is; als $n$ oneven is, voegen we een willekeurig punt (niet op een lijn met twee van de andere punten) toe. De lijnen die we dan construeren, werken ook als je het extra punt weer weglaat. We moeten dus nu $\\frac{n}{2}$ lijnen construeren. Kies een willekeurige lijn in een richting zodat geen enkele lijn door twee van de gegeven punten evenwijdig aan deze lijn loopt (dat kan omdat er maar eindig veel punten zijn en dus ook maar eindig veel tweetallen, terwijl er oneindig veel richtingen te kiezen zijn). Schuif nu de gekozen lijn op. Hierbij komt hij één voor één de gegeven punten tegen. Er is dus een moment dat er geen punten op de lijn liggen en er aan weerszijden van de lijn precies $\\frac{n}{2}$ punten liggen. Daar leggen we deze eerste lijn vast.\nHet vlak wordt nu in twee gebieden verdeeld, laten we zeggen het linker- en rechtergebied. We gaan nu lijnen toevoegen zodat elke lijn een nieuw deelgebied creëert in zowel het linker- als het rechtergebied. (We tellen alleen deelgebieden waarin minstens één punt ligt.) Hiervoor nemen we steeds twee punten in het linkergebied die nog niet gescheiden worden door een lijn en twee punten in het rechtergebied die nog niet gescheiden worden door een lijn. We kiezen nu een lijn zodat de twee punten links aan weerszijden van deze lijn liggen en de twee punten rechts ook; we hebben eerder laten zien dat dit kan. Er is nu zowel links als rechts minstens één extra deelgebied ontstaan, want het deelgebied met de twee punten erin is in tweeën gesplitst. Mochten er op een gegeven moment aan één van beide kanten geen twee punten meer zijn waar nog geen lijn tussendoor loopt, dan gebruiken we alleen nog punten aan de andere kant. Uiteindelijk hebben we na het toevoegen van $\\frac{n}{2}-1$ lijnen\nzowel links als rechts minstens $\\frac{n}{2}$ deelgebieden met elk minstens één punt erin; er moet dus wel precies één punt in elk deelgebied zitten. Elk punt ligt dus in zijn eigen deelgebied, waardoor aan de voorwaarde voldaan wordt. In totaal hebben we $\\frac{n}{2}$ lijnen gebruikt. Dus met $\\frac{n}{2}$ lijnen lukt het altijd om aan de voorwaarde te voldoen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal de kleinste waarde van $n$ met de volgende eigenschap: als je de 1000 ballen willekeurig in een cirkel legt, zijn er altijd $n$ ballen naast elkaar te vinden waarbij minstens 20 verschillende kleuren voorkomen.", "solution": "Bekijk de cirkel van ballen waarbij de 25 ballen van één kleur steeds allemaal naast elkaar liggen. Om nu 20 verschillende kleuren te hebben, moet je minstens 18 van deze groepen nemen plus nog een bal aan de ene kant daarvan en een bal aan de andere kant. Totaal heb je dus minimaal $18 \\cdot 25+2=452$ ballen naast elkaar nodig. Dus $n \\geq 452$. Nu bewijzen we dat je in elke cirkel van ballen genoeg hebt aan 452 ballen naast elkaar om 20 verschillende kleuren te krijgen. Bekijk daarvoor een willekeurige cirkel van ballen en alle mogelijke series van ballen naast elkaar die samen precies 20 kleuren hebben. (Er bestaat minstens één zo'n serie: pak een willekeurige bal en voeg de ballen ernaast één voor één toe, totdat je precies 20 kleuren hebt.) Neem een serie daarvan met zo min mogelijk ballen erin. Zeg dat de eerste bal daarvan wit is. Als er nog een bal in de serie wit is, dan hadden we de eerste bal kunnen weglaten om een serie te krijgen met evenveel kleuren, maar minder ballen. Dat is een tegenspraak met de minimaliteit van de serie. Dus er is geen enkele andere bal wit. In het bijzonder is ook de laatste bal van de serie niet wit; zeg dat deze zwart is. We zien op dezelfde manier dat geen enkele andere bal in de serie zwart is. Dus er is één witte bal, één zwarte bal en daarnaast nog ballen in 18 andere kleuren, hooguit 25 per kleur. Samen zijn dat hooguit $18 \\cdot 25+2=452$ ballen. Dus inderdaad kun je altijd een serie van 452 ballen naast elkaar vinden met daarin minstens 20 verschillende kleuren. We concluderen dat de gevraagde minimale $n$ gelijk is aan 452 .", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal de kleinste waarde van $n$ met de volgende eigenschap: als je de 1000 ballen willekeurig in een cirkel legt, zijn er altijd $n$ ballen naast elkaar te vinden waarbij minstens 20 verschillende kleuren voorkomen.", "solution": "We geven een alternatief bewijs voor het tweede deel van de oplossing. We doen dit uit het ongerijmde. Stel dat we een cirkel van ballen hebben waar elke serie van 452 ballen hooguit 19 kleuren bevat. Omdat $452=18 \\cdot 25+2$ bevat elk zo'n serie dan precies 19 kleuren en zitten er van elke kleur minstens twee ballen in. Bekijk nu zo'n serie en schuif hem steeds één bal op. Bij zo'n verschuiving verdwijnt één bal uit de serie, zeg bal $A$, en komt er ook eentje bij, zeg bal $B$. De kleur van bal $A$ komt minstens nog een keer voor in de serie, dus de kleur van bal $A$ verdwijnt niet. Maar er mag ook geen extra kleur bijkomen, dus bal $B$ moet van een kleur zijn die al in de serie zat. Elke keer dat we één opschuiven, blijft de verzameling van kleuren die voorkomen in de serie, dus dezelfde verzameling van 19 kleuren. Als we zo de hele cirkel rondgaan, komen we dus maar 19\nverschillende kleuren tegen, terwijl er 40 verschillende kleuren zijn. Tegenspraak. Dus er is een serie van 452 ballen met minstens 20 verschillende kleuren.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Zij $\\triangle A B C$ een driehoek waarvan de zijdelengtes positieve gehele getallen zijn die paarsgewijs relatief priem zijn. De raaklijn in $A$ aan de omgeschreven cirkel snijdt de lijn $B C$ in $D$. Bewijs dat $|B D|$ geen geheel getal is.\n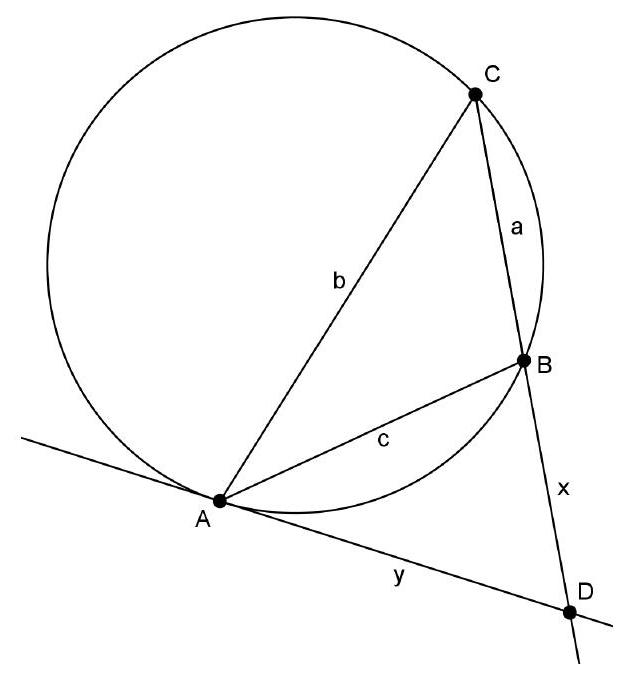", "solution": "Er zijn twee configuraties mogelijk. Neem zonder verlies van algemeenheid aan dat $B$ tussen $D$ en $C$ ligt. Schrijf $a=|B C|, b=|C A|, c=|A B|, x=|B D|$ en $y=|A D|$. Vanwege de raaklijnomtrekshoekstelling geldt $\\angle B A D=\\angle A C B=\\angle A C D$, dus $\\triangle A B D \\sim \\triangle C A D(\\mathrm{hh})$, dus $\\frac{|B D|}{|A D|}=\\frac{|A B|}{|C A|}=\\frac{|A D|}{|C D|}$, oftewel $\\frac{x}{y}=\\frac{c}{b}=\\frac{y}{a+x}$. We vinden hieruit $y c=b x$ en $a c+x c=b y$, dus ook byc $=b^{2} x$ en $a c^{2}+x c^{2}=b y c$. Dit combineren geeft $b^{2} x=a c^{2}+x c^{2}$, oftewel $x\\left(b^{2}-c^{2}\\right)=a c^{2}$.\nStel nu uit het ongerijmde dat $x$ geheel is. Dan is $b^{2}-c^{2}$ een deler van $a c^{2}$. Maar we weten $\\operatorname{ggd}(b, c)=1$, dus ook $\\operatorname{ggd}\\left(b^{2}-c^{2}, c\\right)=\\operatorname{ggd}\\left(b^{2}, c\\right)=1$. Dus $b^{2}-c^{2}$ moet een deler zijn van $a$. Daaruit volgt $b^{2}-c^{2} \\leq a$. Merk op dat $b^{2}-c^{2}>0$ aangezien $x\\left(b^{2}-c^{2}\\right)=a c^{2}$; er geldt dus ook $b-c>0$. Dus $b^{2}-c^{2}=(b-c)(b+c) \\geq 1 \\cdot(b+c)$ omdat $b$ en $c$ positieve gehele getallen zijn. Dus $a \\geq b+c$, wat in tegenspraak is met de driehoeksongelijkheid. Dus $x=|B D|$ kan niet geheel zijn.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Zij $p$ een priemgetal. Bewijs dat het mogelijk is om een permutatie $a_{1}, a_{2}, \\ldots, a_{p}$ van $1,2, \\ldots, p$ te kiezen zodat de getallen $a_{1}, a_{1} a_{2}, a_{1} a_{2} a_{3}, \\ldots, a_{1} a_{2} a_{3} \\cdots a_{p}$ allemaal verschillende resten geven na deling door $p$.", "solution": "Noem $b_{i}=a_{1} a_{2} \\cdots a_{i}$, voor $1 \\leq i \\leq p$. We bewijzen dat het mogelijk is de permutatie zo te kiezen dat $b_{i} \\equiv i \\bmod p$ voor alle $i$. Voor $i \\geq 2$ is $a_{i} \\equiv b_{i} \\cdot b_{i-1}^{-1} \\bmod p$ als $b_{i-1} \\not \\equiv 0 \\bmod p$. We kiezen nu dus $a_{1}=1$ en $a_{i} \\equiv i \\cdot(i-1)^{-1} \\bmod p$ voor $2 \\leq i \\leq p$. Het is nu voldoende te bewijzen dat $a_{i} \\not \\equiv 1 \\bmod p$ voor alle $2 \\leq i \\leq p$ en $a_{i} \\not \\equiv a_{j} \\bmod p$ voor alle $2 \\leq j<i \\leq p$.\nStel uit het ongerijmde dat $a_{i} \\equiv 1 \\bmod p$ voor zekere $2 \\leq i \\leq p$. Dan is $i \\cdot(i-1)^{-1} \\equiv 1$ $\\bmod p$, dus $i \\equiv i-1 \\bmod p$, dus $0 \\equiv-1 \\bmod p$. Omdat $p \\geq 2$ is dit een tegenspraak. Stel nu dat $a_{i} \\equiv a_{j} \\bmod p$ voor zekere $2 \\leq j<i \\leq p$. Dan geldt $i \\cdot(i-1)^{-1} \\equiv j \\cdot(j-1)^{-1}$ $\\bmod p$ dus $i(j-1) \\equiv j(i-1) \\bmod p$ dus $i j-i \\equiv i j-j \\bmod p$ dus $-i \\equiv-j \\bmod p$. Maar we hadden $2 \\leq j<i \\leq p$, dus dit kan niet.\nWe concluderen dat als we de $a_{i}$ kiezen zoals hierboven aangegeven, alle $a_{i}$ verschillend worden, zodat het inderdaad een permutatie van $1,2, \\ldots, p$ is. Verder geldt nu per definitie dat $a_{1} a_{2} \\cdots a_{i} \\equiv i \\bmod p$, zodat ook aan de tweede eis is voldaan.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "In een niet-gelijkbenige driehoek $\\triangle A B C$ geldt $\\angle B A C=60^{\\circ}$. Zij $D$ het snijpunt van de bissectrice van $\\angle B A C$ met de zijde $B C, O$ het middelpunt van de omgeschreven cirkel van $\\triangle A B C$ en $E$ het snijpunt van $A O$ met $B C$. Bewijs dat $\\angle A E D+\\angle A D O=90^{\\circ}$.\n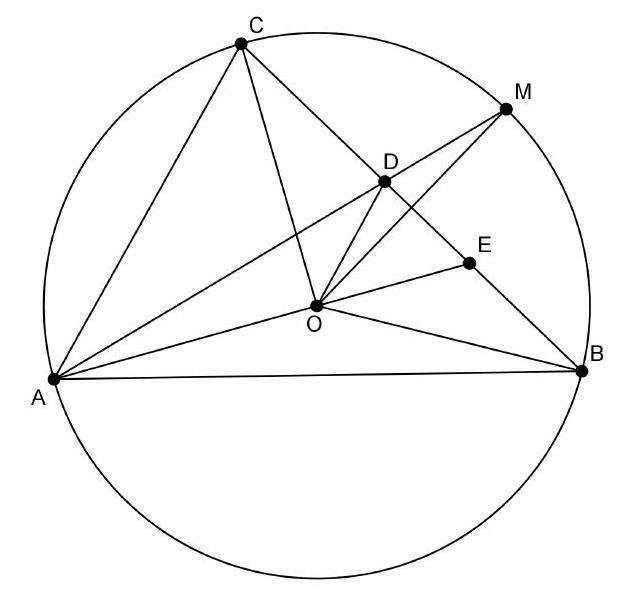", "solution": "Zij $M$ het tweede snijpunt van $A D$ met de omgeschreven cirkel van $\\triangle A B C$. Dan is $M$ het midden van de boog $B C$ waar $A$ niet op ligt. Er geldt nu $\\angle C O M=$ $\\frac{1}{2} \\angle C O B=\\angle C A B=60^{\\circ}$. Verder is natuurlijk $|O C|=|O M|$, dus $\\triangle O C M$ is gelijkbenig met een tophoek van $60^{\\circ}$. Dat betekent dat hij gelijkzijdig is, dus $|C M|=|C O|$. Omdat $O M$ loodrecht op $B C$ staat, volgt hieruit dat $M$ de spiegeling is van $O$ in zijde $B C$, en dus $\\angle D O M=\\angle D M O$.\nVerder geldt $\\angle D M O=\\angle A M O=\\angle M A O$ vanwege $|O A|=|O M|$. We vinden nu $\\angle O D E=90^{\\circ}-\\angle D O M=90^{\\circ}-\\angle D M O=90^{\\circ}-\\angle M A O=90^{\\circ}-\\angle D A E$. Dus $\\angle O D E+\\angle D A E=90^{\\circ}$. In driehoek $A D E$ geldt $180^{\\circ}=\\angle D A E+\\angle A E D+\\angle O D E+\\angle A D O$, dus we concluderen dat $\\angle A E D+\\angle A D O=90^{\\circ}$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2018", "problem_label": "5", "tier": 1, "problem": "Gegeven is een positief geheel getal $n$. Bepaal alle positieve reële getallen $x$ met\n\n$$\nn x^{2}+\\frac{2^{2}}{x+1}+\\frac{3^{2}}{x+2}+\\ldots+\\frac{(n+1)^{2}}{x+n}=n x+\\frac{n(n+3)}{2} .\n$$", "solution": "Voor $1 \\leq i \\leq n$ geldt\n$\\frac{(i+1)^{2}}{x+i}=i+1+\\frac{(i+1)^{2}-(i+1)(x+i)}{x+i}=i+1+\\frac{i+1-(i+1) x}{x+i}=i+1+\\frac{(i+1)(1-x)}{x+i}$,\ndus kunnen we de linkerkant van de gegeven vergelijking herschrijven tot\n\n$$\nn x^{2}+2+3+\\ldots+(n+1)+\\frac{2(1-x)}{x+1}+\\frac{3(1-x)}{x+2}+\\ldots+\\frac{(n+1)(1-x)}{x+n}\n$$\n\nEr geldt $2+3+\\ldots+(n+1)=\\frac{1}{2} n(n+3)$ dus deze som valt weg tegen $\\frac{n(n+3)}{2}$ aan de rechterkant van de gegeven vergelijking. Verder kunnen we $n x^{2}$ naar de andere kant halen en in alle breuken $1-x$ buiten haakjes halen. De vergelijking laat zich dus herschrijven tot\n\n$$\n(1-x) \\cdot\\left(\\frac{2}{x+1}+\\frac{3}{x+2}+\\ldots+\\frac{n+1}{x+n}\\right)=n x-n x^{2} .\n$$\n\nDe rechterkant kunnen we ontbinden als $n x(1-x)$. We zien nu dat $x=1$ een oplossing is van deze vergelijking. Als er nog een oplossing $x \\neq 1$ zou zijn, dan moet die voldoen aan\n\n$$\n\\frac{2}{x+1}+\\frac{3}{x+2}+\\ldots+\\frac{n+1}{x+n}=n x .\n$$\n\nVoor $0<x<1$ geldt echter\n\n$$\n\\frac{2}{x+1}+\\frac{3}{x+2}+\\ldots+\\frac{n+1}{x+n}>\\frac{2}{2}+\\frac{3}{3}+\\ldots+\\frac{n+1}{n+1}=n>n x\n$$\n\nterwijl voor $x>1$ juist geldt\n\n$$\n\\frac{2}{x+1}+\\frac{3}{x+2}+\\ldots+\\frac{n+1}{x+n}<\\frac{2}{2}+\\frac{3}{3}+\\ldots+\\frac{n+1}{n+1}=n<n x .\n$$\n\nEr zijn dus geen oplossingen met $x \\neq 1$. We concluderen dat voor alle $n$ de enige oplossing $x=1$ is.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Gegeven is een bord met $2 m$ rijen en $2 n$ kolommen, waarbij $m$ en $n$ positieve gehele getallen zijn. Je mag één pion plaatsen op een vakje van dit bord, maar niet het vakje linksonder of het vakje rechtsboven. Vervolgens begint een slak een wandeling te maken over het bord. De slak begint in het vakje linksonder en mag horizontaal en verticaal bewegen. De slak komt niet op het vakje met de pion, maar wil verder elk vakje precies één keer aandoen, waarbij het vakje rechtsboven zijn eindpunt is. Op welke vakjes kun je de pion neerzetten zodat de slak in zijn opzet kan slagen?", "solution": "Nummer de rijen van beneden naar boven met 1 tot en met $2 m$ en nummer de kolommen van links naar rechts met 1 tot en met $2 n$. De slak begint dus in vakje $(1,1)$ en eindigt in vakje $(2 m, 2 n)$. Kleur nu de vakjes als een schaakbord, waarbij vakje $(i, j)$ zwart wordt als $i+j$ even is en wit als $i+j$ oneven is. Omdat $2 m$ en $2 n$ even zijn, zijn er evenveel zwarte als witte vakjes. De slak begint en eindigt op een zwart vakje en bezoekt tijdens zijn wandeling om en om zwarte en witte vakjes. Het aantal zwarte vakjes waar hij komt, is dus 1 groter dan het aantal witte vakjes waar hij komt. Daarom moet de pion wel op een wit vakje staan, dus een vakje $(i, j)$ met $i+j$ oneven.\nWe laten nu zien dat als de pion op zo'n vakje staat, de slak altijd zijn wandeling kan maken. Zij $1 \\leq k \\leq m$ en $1 \\leq l \\leq n$ zo dat de pion in één van de rijen $2 k-1$ en $2 k$ staat en in één van de kolommen $2 l-1$ en $2 l$. Laat de slak alle rijen met rijnummer kleiner dan $2 k-1$ in zijn geheel aflopen: de oneven rijen van links naar rechts, dan één vakje omhoog en de even rijen van rechts naar links terug. Vervolgens weer één vakje omhoog en dan is hij weer op een oneven rij. Op een gegeven moment komt de slak aan in rij $2 k-1$ en staat dan op het vakje helemaal links. Zolang de slak nog in de kolommen met nummer kleiner dan $2 l-1$ zit, bezoekt hij elk $2 \\times 2$-vierkantje (in rijen $2 k-1,2 k$ ) in de volgorde linksonder-linksboven-rechtsboven-rechtsonder. En dan komt hij linksonder weer aan in het volgende $2 \\times 2$-vierkantje. Op een gegeven moment arriveert hij in kolom $2 l-1$. Hij staat dan op vakje $(2 k-1,2 l-1)$ en daar kan de pion niet staan, want $2 k-1+2 l-1$ is even. In dit $2 \\times 2$-vierkantje staat de pion ofwel linksboven ofwel rechtsonder. In het eerste geval loopt de slak linksonder-rechtsonder-rechtsboven en in het tweede geval loopt hij linksonder-linksboven-rechtsboven. In beide gevallen eindigt hij in dit $2 \\times 2$-vierkantje in het vakje rechtsboven. De rest van de $2 \\times 2$-vierkantjes in deze rijen kan hij dus in de volgorde linksboven-linksonder-rechtsonder-rechtsboven bezoeken. Steeds eindigt hij rechtsboven. Als hij uiteindelijk in de laatste kolom is aangekomen, gaat hij een rij omhoog, naar rij $2 k+1$. Daar komt hij dus rechtsonderin aan. De overige rijen loopt hij weer in z'n geheel af: de oneven rijen van rechts naar links, dan een vakje omhoog en de even rijen van links\nnaar rechts terug. In rij $2 m$ eindigt hij dus rechtsboven, precies zoals gevraagd. We concluderen dat de pion op de vakjes $(i, j)$ met $i+j$ oneven neergezet kan worden.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Gegeven is een driehoek $\\triangle A B C$ met $\\angle C=90^{\\circ}$. Het midden van $A C$ noemen we $D$ en de loodrechte projectie van $C$ op $B D$ noemen we $E$. Bewijs dat de raaklijn in $C$ aan de omgeschreven cirkel van $\\triangle A E C$ loodrecht op $A B$ staat.\n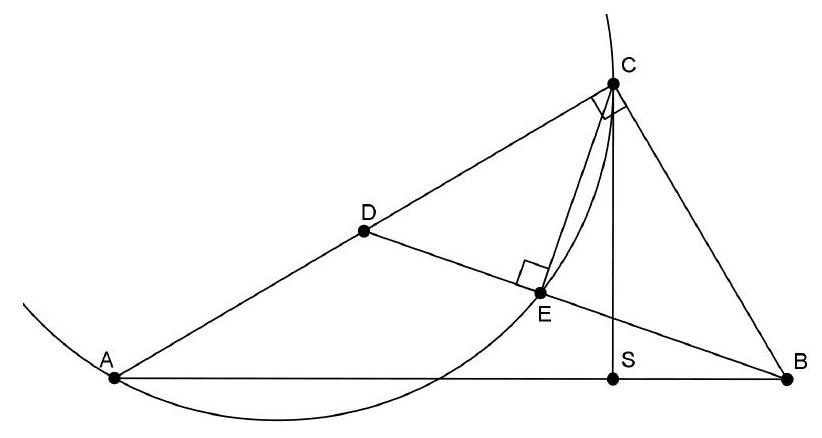", "solution": "Noem $S$ het snijpunt van de raaklijn en $A B$. We moeten dus bewijzen dat $\\angle B S C=90^{\\circ}$.\nVanwege $\\angle B C D=90^{\\circ}=\\angle C E D$ geldt $\\triangle B C D \\sim \\triangle C E D$, dus $\\frac{|D C|}{|D B|}=\\frac{|D E|}{|D C|}$. Omdat $|D A|=|D C|$ volgt hieruit $\\frac{|D A|}{|D B|}=\\frac{|D E|}{|D A|}$. Samen met $\\angle B D A=\\angle E D A$ geeft dit $\\triangle A D E \\sim \\triangle B D A$ (zhz). Dus $\\angle A B D=\\angle E A D$. Omdat $S C$ een raaklijn is aan de omgeschreven cirkel van $\\triangle A E C$ geldt vanwege de raaklijnomtrekshoekstelling ook dat $\\angle E A D=\\angle E A C=\\angle S C E$. Dus $\\angle S C E=\\angle A B D=\\angle S B E$. Hieruit volgt dat $S B C E$ een koordenvierhoek is. Dus $\\angle B S C=\\angle B E C=90^{\\circ}$.\n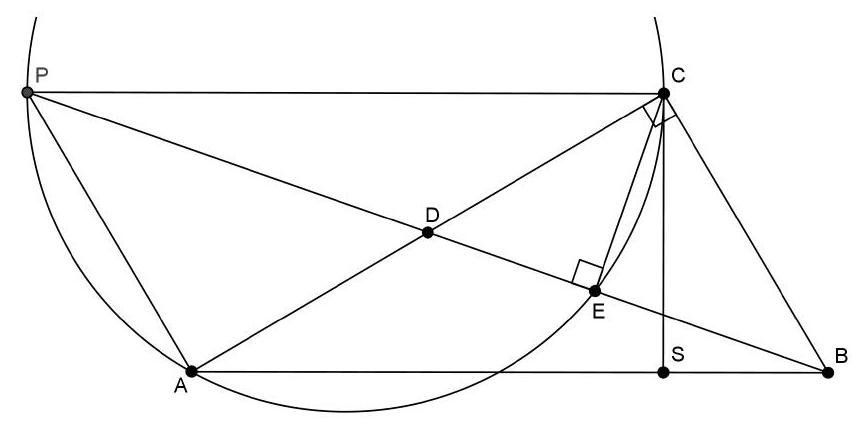", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Gegeven is een driehoek $\\triangle A B C$ met $\\angle C=90^{\\circ}$. Het midden van $A C$ noemen we $D$ en de loodrechte projectie van $C$ op $B D$ noemen we $E$. Bewijs dat de raaklijn in $C$ aan de omgeschreven cirkel van $\\triangle A E C$ loodrecht op $A B$ staat.\n", "solution": "Zij $P$ de spiegeling van $B$ in $D$. Dan snijden $A C$ en $P B$ elkaar middendoor, dus is $C B A P$ een parallellogram. Dus $\\angle C A P=\\angle A C B=90^{\\circ}=\\angle C E P$. Dit betekent dat $C E A P$ een koordenvierhoek is en dat $C P$ een middellijn van zijn omgeschreven cirkel is. De raaklijn in $C$ aan deze omgeschreven cirkel staat loodrecht op de middellijn $C P$. Aangezien in het parallellogram $A B \\| C P$, staat de raaklijn dus ook loodrecht op $A B$.\n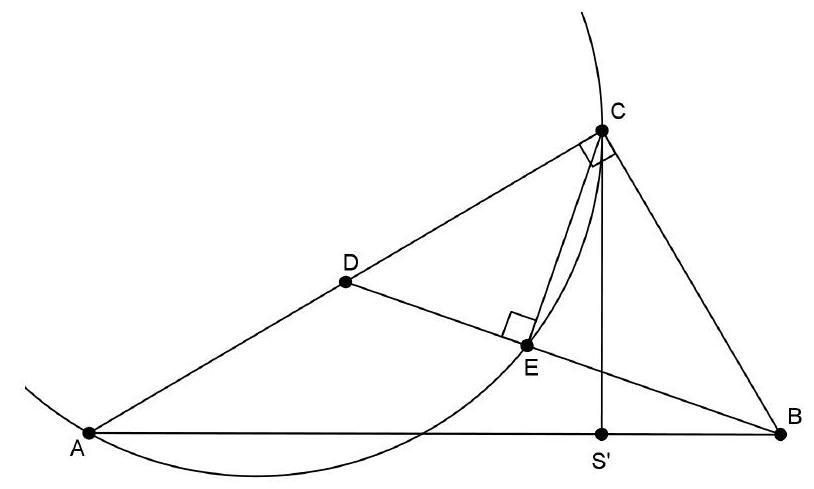", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Gegeven is een driehoek $\\triangle A B C$ met $\\angle C=90^{\\circ}$. Het midden van $A C$ noemen we $D$ en de loodrechte projectie van $C$ op $B D$ noemen we $E$. Bewijs dat de raaklijn in $C$ aan de omgeschreven cirkel van $\\triangle A E C$ loodrecht op $A B$ staat.\n", "solution": "Zij $S^{\\prime}$ de loodrechte projectie van $C$ op $A B$. Er geldt dan $\\angle B S^{\\prime} C=$ $90^{\\circ}=\\angle B E C$, dus $B C S^{\\prime} E$ is een koordenvierhoek. Er volgt dat $\\angle E D C=90^{\\circ}-\\angle E C D=$ $\\angle E C B=180^{\\circ}-\\angle E S^{\\prime} C=\\angle E S^{\\prime} A$, dus $\\angle E D A=180^{\\circ}-\\angle E D C=180^{\\circ}-\\angle E S^{\\prime} A$, waaruit volgt dat $A D E S^{\\prime}$ een koordenvierhoek is. Nu is $\\angle S^{\\prime} A E=\\angle S^{\\prime} D E$. Verder is vanwege Thales $D$ het middelpunt van de cirkel door $A, C$ en $S^{\\prime}$, dus is $\\angle D S^{\\prime} A=\\angle S^{\\prime} A D$. Deze twee resultaten samen geven $\\angle E A C=\\angle S^{\\prime} A C-\\angle S^{\\prime} A E=\\angle S^{\\prime} A D-\\angle S^{\\prime} A E=\\angle D S^{\\prime} A-$ $\\angle S^{\\prime} D E$. Met de buitenhoekstelling in driehoek $D S^{\\prime} B$ is dit gelijk aan $\\angle S^{\\prime} B D=\\angle S^{\\prime} B E$ en vanwege koordenvierhoek $B C S^{\\prime} E$ is dat weer gelijk aan $\\angle S^{\\prime} C E$. Dus $\\angle E A C=\\angle S^{\\prime} C E$. Met de raaklijnomtrekshoekstelling volgt hieruit dat $S^{\\prime} C$ raakt aan de omgeschreven cirkel van $\\triangle E A C$. Deze raaklijn $S^{\\prime} C$ staat dus inderdaad loodrecht op $A B$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 5 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Zij $n \\geq 0$ een geheel getal. Een rij $a_{0}, a_{1}, a_{2}, \\ldots$ van gehele getallen wordt als volgt gedefinieerd: er geldt $a_{0}=n$ en voor $k \\geq 1$ is $a_{k}$ het kleinste gehele getal groter dan $a_{k-1}$ waarvoor $a_{k}+a_{k-1}$ het kwadraat van een geheel getal is. Bewijs dat er precies $\\lfloor\\sqrt{2 n}\\rfloor$ positieve gehele getallen zijn die niet te schrijven zijn in de vorm $a_{k}-a_{\\ell}$ met $k>\\ell \\geq 0$.", "solution": "Zij $m=\\lfloor\\sqrt{2 n}\\rfloor$. We bewijzen eerst dat de rij kwadraten $a_{0}+a_{1}, a_{1}+a_{2}$, ... precies de rij $(m+1)^{2},(m+2)^{2}, \\ldots$ is. Vervolgens laten we zien dat de verschillen $a_{i}-a_{i-1}$ een rij opeenvolgende even getallen en een rij opeenvolgende oneven getallen vormen. Hiermee kunnen we daarna het gevraagde bewijzen.\nMerk op dat $a_{0}+a_{1}$ het kleinste kwadraat is dat groter is dan $2 n$. Er geldt dus $a_{0}+a_{1}=$ $(m+1)^{2}$. We bewijzen nu met inductie naar $i$ dat $a_{i-1}+a_{i}=(m+i)^{2}$. Voor $i=1$ hebben we dit zojuist bewezen. Stel dat $a_{j-1}+a_{j}=(m+j)^{2}$. Dat betekent dat $a_{j-1} \\geq \\frac{(m+j-1)^{2}}{2}$ (anders had $a_{j}$ zo gekozen kunnen worden dat $\\left.a_{j-1}+a_{j}=(m+j-1)^{2}\\right)$ en dus\n\n$$\n\\begin{aligned}\na_{j} & =(m+j)^{2}-a_{j-1} \\\\\n& \\leq(m+j)^{2}-\\frac{(m+j-1)^{2}}{2} \\\\\n& =\\frac{2 m^{2}+4 m j+2 j^{2}-\\left(m^{2}+2 m j+j^{2}+1-2 m-2 j\\right)}{2} \\\\\n& =\\frac{m^{2}+2 m j+j^{2}-1+2 m+2 j}{2} \\\\\n& <\\frac{m^{2}+2 m j+j^{2}+1+2 m+2 j}{2} \\\\\n& =\\frac{(m+j+1)^{2}}{2} .\n\\end{aligned}\n$$\n\nHieruit volgt dat $a_{j}+a_{j+1} \\leq(m+j+1)^{2}$. Er geldt bovendien $a_{j}+a_{j+1}>a_{j-1}+a_{j}=(m+j)^{2}$, dus $a_{j}+a_{j+1}=(m+j+1)^{2}$. Dit voltooit de inductie.\nDefinieer nu $b_{i}=a_{i}-a_{i-1}$ voor alle $i \\geq 1$. Dan geldt\n\n$$\n\\begin{aligned}\nb_{i+2}-b_{i} & =a_{i+2}-a_{i+1}-a_{i}+a_{i-1} \\\\\n& =\\left(a_{i+2}+a_{i+1}\\right)+\\left(a_{i}+a_{i-1}\\right)-2\\left(a_{i+1}+a_{i}\\right) \\\\\n& =(m+i+2)^{2}+(m+i)^{2}-2(m+i+1)^{2} \\\\\n& =(m+i)^{2}+4(m+i)+4+(m+i)^{2}-2(m+i)^{2}-4(m+i)-2 \\\\\n& =2\n\\end{aligned}\n$$\n\nvoor alle $i \\geq 1$. We zien nu dat\n\n$$\n\\left(b_{1}, b_{3}, b_{5}, \\ldots\\right)=\\left(b_{1}, b_{1}+2, b_{1}+4, \\ldots\\right), \\quad\\left(b_{2}, b_{4}, b_{6}, \\ldots\\right)=\\left(b_{2}, b_{2}+2, b_{2}+4, \\ldots\\right)\n$$\n\nEr geldt $b_{1}+b_{2}=\\left(a_{2}-a_{1}\\right)+\\left(a_{1}-a_{0}\\right)=\\left(a_{2}+a_{1}\\right)-\\left(a_{1}+a_{0}\\right)=(m+2)^{2}-(m+1)^{2}=2 m+3$. In het bijzonder hebben $b_{1}$ en $b_{2}$ verschillende pariteit. Nu kunnen in elk geval alle getallen\nmet dezelfde pariteit als $b_{1}$ en minstens gelijk aan $b_{1}$ geschreven worden als $a_{k}-a_{k-1}$ voor zekere $k$. Hetzelfde geldt voor de getallen met dezelfde pariteit als $b_{2}$ en minstens gelijk aan $b_{2}$. Alle getallen van de vorm $a_{k}-a_{\\ell}$ met $k \\geq \\ell+2$ zijn minstens gelijk aan $b_{k}+b_{k-1} \\geq b_{1}+b_{2}$ en dus groter dan $b_{1}$ en groter dan $b_{2}$. We kunnen op deze manier dus geen nieuwe getallen meer maken. De getallen die niet te schrijven zijn als $a_{k}-a_{\\ell}$ met $k>\\ell \\geq 0$ zijn dus precies de getallen met dezelfde pariteit als $b_{1}$ en kleiner dan $b_{1}$ en de getallen met dezelfde pariteit als $b_{2}$ en kleiner dan $b_{2}$. Dit zijn in totaal\n\n$$\n\\left\\lfloor\\frac{b_{1}-1}{2}\\right\\rfloor+\\left\\lfloor\\frac{b_{2}-1}{2}\\right\\rfloor\n$$\n\ngetallen, waarbij binnen de haken van de entierfunctie precies één van beide keren een geheel getal staat. We kunnen dit dus schrijven als\n\n$$\n\\frac{b_{1}-1}{2}+\\frac{b_{2}-1}{2}-\\frac{1}{2}=\\frac{b_{1}+b_{2}-3}{2}=\\frac{2 m}{2}=m \\text {. }\n$$\n\nEr zijn dus precies $m=\\lfloor\\sqrt{2 n}\\rfloor$ positieve gehele getallen die niet op de gevraagde manier te schrijven zijn.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "Gegeven is een verzameling $A$ van functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$. Voor alle $f_{1}, f_{2} \\in A$ bestaat er een $f_{3} \\in A$ zodat\n\n$$\nf_{1}\\left(f_{2}(y)-x\\right)+2 x=f_{3}(x+y)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$. Bewijs dat voor alle $f \\in A$ geldt:\n\n$$\nf(x-f(x))=0\n$$\n\nvoor alle $x \\in \\mathbb{R}$.", "solution": "Invullen van $x=0$ geeft\n\n$$\nf_{1}\\left(f_{2}(y)\\right)=f_{3}(y)\n$$\n\ndus de $f_{3}$ die bij $f_{1}$ en $f_{2}$ hoort, is blijkbaar de samenstelling $f_{3}(x)=f_{1}\\left(f_{2}(x)\\right)$. Invullen van $x=-y$ geeft nu dat voor alle $f_{1}, f_{2} \\in A$\n\n$$\nf_{1}\\left(f_{2}(y)+y\\right)-2 y=f_{3}(0)=f_{1}\\left(f_{2}(0)\\right)\n$$\n\nvoor alle $y \\in \\mathbb{R}$.\nInvullen van $x=f_{2}(y)$ geeft dat er voor alle $f_{1}, f_{2} \\in A$ een $f_{3} \\in A$ bestaat met\n\n$$\nf_{1}(0)+2 f_{2}(y)=f_{3}\\left(f_{2}(y)+y\\right)\n$$\n\nvoor alle $y \\in \\mathbb{R}$. We hebben hiervoor gezien dat we $f_{3}\\left(f_{2}(y)+y\\right)$ kunnen schrijven als $2 y+f_{3}\\left(f_{2}(0)\\right)$. Dus\n\n$$\n2 f_{2}(y)=2 y+f_{3}\\left(f_{2}(0)\\right)-f_{1}(0)\n$$\n\nvoor alle $y \\in \\mathbb{R}$. We concluderen dat er een $d \\in \\mathbb{R}$ is, onafhankelijk van $y$, zodat $f_{2}(y)=y+d$ voor alle $y \\in \\mathbb{R}$.\nDus elke $f \\in A$ is van de vorm $f(x)=x+d$ met $d$ een constante. Er geldt dan\n\n$$\nf(x-f(x))=f(x-(x+d))=f(-d)=-d+d=0\n$$", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "a) Als $c\\left(a^{3}+b^{3}\\right)=a\\left(b^{3}+c^{3}\\right)=b\\left(c^{3}+a^{3}\\right)$ voor positieve reële getallen $a, b, c$, geldt dan noodzakelijk $a=b=c$ ?\nb) Als $a\\left(a^{3}+b^{3}\\right)=b\\left(b^{3}+c^{3}\\right)=c\\left(c^{3}+a^{3}\\right)$ voor positieve reële getallen $a, b, c$, geldt dan noodzakelijk $a=b=c$ ?", "solution": "a) We beweren dat $(a, b, c)=(2,2,-1+\\sqrt{5})$ aan de gegeven gelijkheden voldoet. In dit drietal zijn alle getallen positief reëel en ze zijn niet allemaal gelijk, dus het antwoord op de vraag is dan nee.\nWe berekenen $c^{3}=(-1+\\sqrt{5})^{3}=-1+3 \\cdot \\sqrt{5}-3 \\cdot 5+5 \\sqrt{5}=-16+8 \\sqrt{5}$. Nu geldt $c\\left(a^{3}+b^{3}\\right)=(-1+\\sqrt{5}) \\cdot 2 \\cdot 8=-16+16 \\sqrt{5}$ en $a\\left(b^{3}+c^{3}\\right)=b\\left(c^{3}+a^{3}\\right)=$ $2 \\cdot(-16+8 \\sqrt{5}+8)=-16+16 \\sqrt{5}$. De gegeven gelijkheden gelden dus inderdaad.\nHier een mogelijke aanpak om dit drietal te vinden. Neem zonder verlies van algemeenheid aan dat $c \\leq a, b$. Herschrijf $a\\left(b^{3}+c^{3}\\right)=b\\left(c^{3}+a^{3}\\right)$ tot $a b\\left(b^{2}-a^{2}\\right)=c^{3}(b-a)$. Als $a \\neq b$ kunnen we delen door $b-a$ en volgt $a b(a+b)=c^{3}$. Maar $c \\leq a, b$ en alles is positief, dus $c^{3}<2 c^{3} \\leq a^{2} b+a b^{2}=a b(a+b)$, tegenspraak. Er moet dus wel gelden $a=b$. Nu kunnen we $c\\left(a^{3}+b^{3}\\right)=a\\left(b^{3}+c^{3}\\right)$ herschrijven tot $a^{3} c-a c^{3}=a^{4}-a^{3} c$ en dan verder tot ac $\\left(a^{2}-c^{2}\\right)=a^{3}(a-c)$. Nu geldt $a=c$ (en dus $a=b=c$ ) of $a c(a+c)=a^{3}$. Dit tweede is een kwadratische vergelijking in $c$. Dit oplossen geeft dat $c=\\left(-\\frac{1}{2}+\\frac{1}{2} \\sqrt{5}\\right) a$. Zo vinden we oneindig veel drietallen die voldoen.\nb) We gaan bewijzen dat altijd moet gelden dat $a=b=c$. Neem zonder verlies van algemeenheid aan dat $c \\leq a, b$. Nu zijn er twee gevallen (want de gegeven gelijkheden zijn slechts cyclisch en niet symmetrisch).\nStel eerst dat $a \\geq b \\geq c$. Dan geldt\n\n$$\na\\left(a^{3}+b^{3}\\right) \\geq c\\left(a^{3}+b^{3}\\right) \\geq c\\left(a^{3}+c^{3}\\right)=a\\left(a^{3}+b^{3}\\right)\n$$\n\ndus er moet steeds gelijkheid gelden. Omdat alles positief is, volgt daaruit $a=c$ bij de eerste ongelijkheid en $b=c$ bij de tweede. Dus $a=b=c$.\n\nStel nu dat $b \\geq a \\geq c$. Dan geldt\n\n$$\nb\\left(b^{3}+c^{3}\\right) \\geq c\\left(b^{3}+c^{3}\\right) \\geq c\\left(a^{3}+c^{3}\\right)=b\\left(b^{3}+c^{3}\\right)\n$$\n\ndus ook hier moet steeds gelijkheid gelden. We vinden nu $b=c$ bij de eerste ongelijkheid en $b=a$ bij de tweede, dus $a=b=c$.\n\nOplossing II voor b). Neem zonder verlies van algemeenheid aan dat $a \\geq b, c$. Dan geldt\n\n$$\na\\left(a^{3}+b^{3}\\right) \\geq b\\left(a^{3}+b^{3}\\right) \\geq b\\left(c^{3}+b^{3}\\right)=a\\left(a^{3}+b^{3}\\right)\n$$\n\ndus er moet steeds gelijkheid gelden. Omdat alles positief is, volgt daaruit $a=b$ bij de eerste ongelijkheid en $a=c$ bij de tweede. Dus $a=b=c$.", "problem_match": "# Opgave 1.", "solution_match": "# Oplossing I."}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Vind alle positieve gehele getallen $n$ waarvoor er een positief geheel getal $k$ bestaat zodat voor iedere positieve deler $d$ van $n$ geldt dat ook $d-k$ een (niet noodzakelijk positieve) deler van $n$ is.", "solution": "Als $n=1$ of $n$ is een priemgetal, dan zijn de enige positieve delers van $n$ gelijk aan 1 en $n$ (die samenvallen in het geval $n=1$ ). Neem nu $k=n+1$, dan moeten $1-(n+1)=-n$ en $n-(n+1)=-1$ ook delers zijn van $n$. Dat klopt precies. Dus $n=1$ en $n$ is priem voldoen met $k=n+1$. Als $n=4$, zijn de positieve delers 1,2 en 4 . We kiezen $k=3$, waardoor $-2,-1$ en 1 delers van 4 moeten zijn en dat klopt. Dus $n=4$ voldoet met $k=3$. Als $n=6$, dan zijn de positieve delers $1,2,3$ en 6 . We kiezen $k=4$, waardoor $-3,-2,-1$ en 2 ook delers van 6 moeten zijn en dat klopt. Dus $n=6$ voldoet met $k=4$. Al met al weten we nu dat $n \\leq 6$ en alle priemgetallen $n$ voldoen.\nStel nu dat $n>6$ en $n$ is niet priem. Neem aan dat $n$ voldoet. Omdat $n$ een positieve deler is van $n$, is $n-k$ ook een deler van $n$. De grootste deler kleiner dan $n$ is hoogstens $\\frac{1}{2} n$, dus $n-k \\leq \\frac{1}{2} n$, dus $k \\geq \\frac{1}{2} n$. Verder is 1 een positieve deler van $n$, dus is $1-k$ een deler van $n$. We weten nu $1-k \\leq 1-\\frac{1}{2} n$. Aangezien $n>6$, is $\\frac{1}{6} n>1$, dus $\\frac{1}{2} n-\\frac{1}{3} n>1$, dus $-\\frac{1}{3} n>1-\\frac{1}{2} n$. De enige delers die hoogstens $1-\\frac{1}{2} n$ zijn, zijn dus $-n$ en (als $n$ even is) $-\\frac{1}{2} n$. We concluderen dat $1-k=-n$ of $1-k=-\\frac{1}{2} n$.\nIn het laatste geval geldt $k=\\frac{1}{2} n+1$, dus $n-k=\\frac{1}{2} n-1$. Echter, analoog aan het voorgaande is er voor $n>6$ geen deler gelijk aan $\\frac{1}{2} n-1$ (want na $\\frac{1}{2} n$ is de volgende mogelijke deler $\\frac{1}{3} n$ en die is al kleiner dan $\\frac{1}{2} n-1$ ). Tegenspraak, want $n-k$ moet een deler van $n$ zijn.\nWe houden het geval $1-k=-n$ over. Dus $k=n+1$. Omdat $n$ niet priem is, is er een deler $d$ met $1<d<n$. Daarom is $d-k=d-n-1$ ook een deler. Maar $d \\leq \\frac{1}{2} n$, dus $d-n-1 \\leq-\\frac{1}{2} n-1$, maar de enige deler kleiner dan of gelijk aan $-\\frac{1}{2} n-1$ is $-n$. We zien dat $d-n-1=-n$, dus $d=1$, tegenspraak.\nWe concluderen dat alle $n$ met $n>6$ en $n$ niet priem niet voldoen, dus de enige oplossingen zijn alle $n$ met $n \\leq 6$ en alle $n$ die priem zijn.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Vind alle positieve gehele getallen $n$ waarvoor er een positief geheel getal $k$ bestaat zodat voor iedere positieve deler $d$ van $n$ geldt dat ook $d-k$ een (niet noodzakelijk positieve) deler van $n$ is.", "solution": "Bekijk een $n \\geq 2$ die voldoet. Omdat 1 een positieve deler van $n$ is, is $1-k$ een deler van $n$. Dit moet een negatieve deler zijn, aangezien $k$ positief geheel is. Als we deze deler als $-d$ schrijven met $d$ een positieve deler van $n$, geldt $1-k=-d$, dus $d+1=k$. Omdat $n$ een positieve deler van $n$ is, is ook $n-k=n-d-1$ een deler van $n$. Merk op dat $\\operatorname{ggd}(d, n-d-1)=\\operatorname{ggd}(d,-1)=1$ omdat $d \\mid n$. Dit betekent dat $d(n-d-1)$ ook een deler van $n$ is. Er geldt dan $d(n-d-1) \\leq n$.\nStel $d=n$. Bekijk de kleinste priemdeler $p$ van $n$ en schrijf $n=p m$ met $m$ positief geheel. Er geldt nu dat $m$ de grootste deler van $n$ is die kleiner is dan $n$, en verder is $p-k=p-d-1=p-n-1$ een deler van $n$. Maar $p-n-1>-n$ en $p-n-1=$ $p-p m-1=p(1-m)-1 \\leq 2(1-m)-1=-2 m+1 \\leq-m$. Er zijn echter geen delers tussen $-n$ en $-m$, dus moet in de laatste ongelijkheid wel gelijkheid gelden. Dat kan alleen als $m=1$ en dat betekent dat $n$ priem is.\n\nStel nu $d<n$. Dan geldt $2 d \\leq n$. Uit $d(n-d-1) \\leq n$ volgt $-d^{2}-d \\leq n-d n$, dus $d^{2}+d \\geq n(d-1) \\geq 2 d(d-1)=2 d^{2}-2 d$. Hieruit volgt dat $d^{2} \\leq 3 d$ oftewel $d \\leq 3$. Nu is $n-d-1 \\geq n-4$. Omdat $n-d-1$ een deler van $n$ kleiner dan $n$ is, geldt $2(n-4) \\leq 2(n-d-1) \\leq n$, dus $n \\leq 8$.\nWe weten nu dat als $n$ voldoet, dat dan $n$ priem is of $n \\leq 8$ (hier valt ook het geval $n=1$ onder, dat we in eerste instantie hadden overgeslagen). We bekijken $n=8$. De delers 1 en 2 van 8 zijn opeenvolgend, dus moeten $1-k$ en $2-k$ ook opeenvolgend zijn. Dat moeten dan wel -2 en -1 zijn, dus $k=3$. Maar $8-3=5$ is geen deler van $n$, tegenspraak. Dus als $n$ voldoet, dan moet $n$ priem zijn of $n \\leq 6$. Net als in oplossing I kunnen we laten zien dat al deze waarden van $n$ voldoen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek en zij $D$ het voetpunt van de hoogtelijn uit $A$. Op $A D$ liggen verschillende punten $E$ en $F$ zodat $|A E|=|B E|$ en $|A F|=|C F|$. Een punt $T \\neq D$ voldoet aan $\\angle B T E=\\angle C T F=90^{\\circ}$. Toon aan dat $|T A|^{2}=|T B| \\cdot|T C|$.\n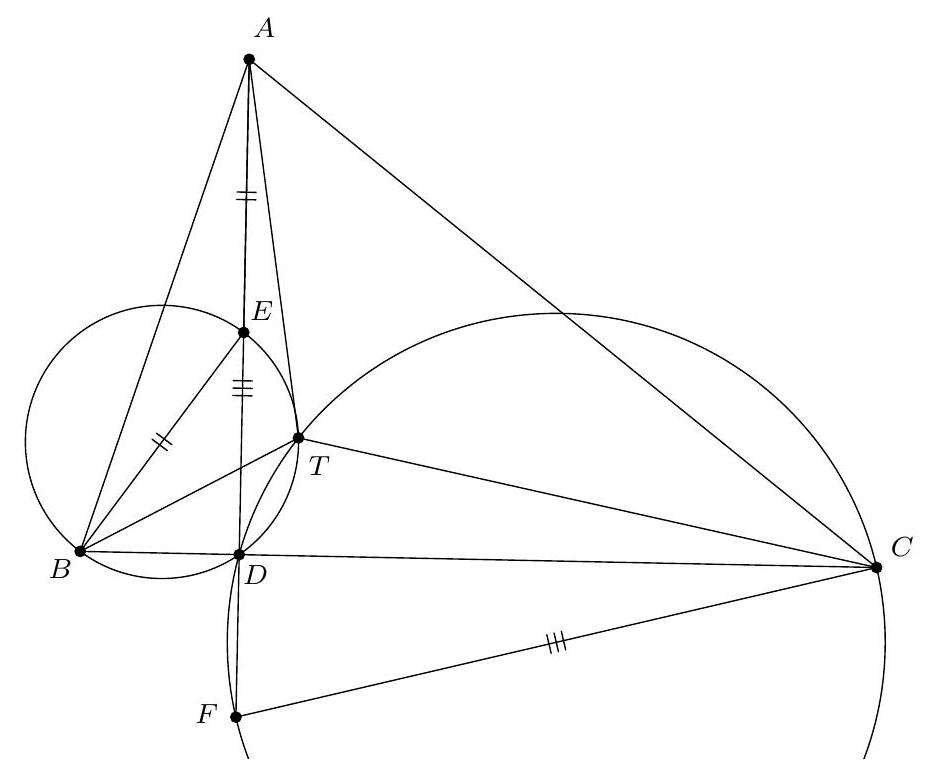\n\nWe bekijken de configuratie met de volgorde van de punten zoals in het plaatje.", "solution": "Zij $M$ het midden van $A B$ en zij $N$ het midden van $A C$. Uit de gegevens volgt dat $E$ op de middelloodlijn van $A B$ ligt, dus $\\angle B M E=90^{\\circ}$. Omdat ook $\\angle B T E=90^{\\circ}$ en $\\angle B D E=90^{\\circ}$, is $B D T E M$ een koordenvijfhoek wegens Thales. Zo ook is $C F D T N$ een koordenvijfhoek. Er geldt nu $\\angle N T M=360^{\\circ}-\\angle D T N-\\angle M T D=\\left(180^{\\circ}-\\angle D T N\\right)+$ $\\left(180^{\\circ}-\\angle M T D\\right)=\\angle D C N+\\angle M B D=\\angle B C A+\\angle A B C=180^{\\circ}-\\angle C A B=180^{\\circ}-\\angle N A M$. Dus $A M T N$ is een koordenvierhoek. (Dit laatste volgt ook direct uit de stelling van Miquel.) Met alleen hoekenjagen gaan we nu bewijzen dat $\\triangle T B A \\sim \\triangle T A C$. Er geldt $\\angle N T C=$ $\\angle N F C=90^{\\circ}-\\angle F C N$ omdat $\\angle F N C=90^{\\circ}$. Verder is $\\angle F C N=\\angle F C A=\\angle C A F$ vanwege $|A F|=|C F|$, dus $\\angle N T C=90^{\\circ}-\\angle C A F=90^{\\circ}-\\angle C A D=\\angle D C A=\\angle B C A$. Nu krijgen we $\\angle A C T=\\angle N C T=180^{\\circ}-\\angle N T C-\\angle C N T=180^{\\circ}-\\angle B C A-\\angle C N T$. Omdat $M N$ een middenparallel in driehoek $A B C$ is, geldt $M N \\| B C$ en met U-hoeken volgt daaruit $180^{\\circ}-\\angle B C A=\\angle C N M$. Dus $\\angle A C T=\\angle C N M-\\angle C N T=\\angle T N M=$ $\\angle T A M=\\angle T A B$, waarbij we ook koordenvierhoek $A M T N$ nog gebruikt hebben. Analoog geldt $\\angle A B T=\\angle T A C$, dus $\\triangle T B A \\sim \\triangle T A C$. Hieruit volgt dat $\\frac{|T B|}{|T A|}=\\frac{|T A|}{|T C|}$, dus $|T A|^{2}=$ $|T B| \\cdot|T C|$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 5 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek en zij $D$ het voetpunt van de hoogtelijn uit $A$. Op $A D$ liggen verschillende punten $E$ en $F$ zodat $|A E|=|B E|$ en $|A F|=|C F|$. Een punt $T \\neq D$ voldoet aan $\\angle B T E=\\angle C T F=90^{\\circ}$. Toon aan dat $|T A|^{2}=|T B| \\cdot|T C|$.\n\n\nWe bekijken de configuratie met de volgorde van de punten zoals in het plaatje.", "solution": "We volgen oplossing I tot en met de bewering dat $A M T N$ een koordenvierhoek is.\nOmdat $M N$ een middenparallel in driehoek $A B C$ is, staat $A D$ loodrecht op $M N$ en wordt hij door $M N$ doormidden gedeeld. Daarom is $D$ de spiegeling van $A$ in $M N$. Hieruit volgt\ndat $\\angle D M N=\\angle A M N=\\angle A B C=\\angle M B D$, dus vanwege de raaklijnomtrekshoekstelling kunnen we nu concluderen dat $M N$ raakt aan de cirkel door $B, D, T, E$ en $M$. We vinden nu dat $\\angle T A C=\\angle T A N=\\angle T M N=\\angle T B M=\\angle T B A$. Analoog geldt $\\angle T C A=\\angle T A B$, dus $\\triangle T B A \\sim \\triangle T A C$. Hieruit volgt dat $\\frac{|T B|}{|T A|}=\\frac{|T A|}{|T C|}$, dus $|T A|^{2}=|T B| \\cdot|T C|$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 6 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "In een klas van minstens vier mensen geldt het volgende: als er vier van hen aan een ronde tafel gaan zitten, is er altijd iemand die allebei zijn buren kent of allebei zijn buren niet kent. Bewijs dat het mogelijk is om de mensen over twee groepen (waarvan er eentje leeg mag zijn) te verdelen, zodat in de ene groep iedereen elkaar kent en in de andere groep juist niemand elkaar kent.\n(Als persoon $A$ persoon $B$ kent, dan kent $B$ ook $A$.)", "solution": "Van alle mogelijke groepen mensen die we in deze klas kunnen maken, bekijken we de groepen waarin iedereen elkaar kent en daarvan nemen we er eentje met zoveel mogelijk mensen erin. (Deze grootste groep bestaat: er zijn eindig veel mensen en er is in elk geval een groep van mensen die elkaar allemaal kennen, namelijk een groep bestaande uit één persoon.) Noem deze groep $X$. We bewijzen dat de groep $X$ en de groep bestaande uit de rest van de mensen aan de voorwaarde voldoet.\nOmdat in $X$ alle mensen elkaar kennen, hoeven we alleen te bewijzen dat alle mensen buiten $X$ elkaar niet kennen. Stel dat er wel $A$ en $B$ buiten $X$ bestaan die elkaar kennen. Omdat $X$ zo groot mogelijk is, bevat $X$ een persoon $A^{\\prime}$ die geen kennis van $A$ is. Net zo bevat $X$ een persoon $B^{\\prime}$ die geen kennis van $B$ is. We bewijzen nu eerst dat we $A^{\\prime}$ en $B^{\\prime}$ verschillend van elkaar kunnen kiezen. Zo niet, is er in $X$ een unieke persoon $C=A^{\\prime}=B^{\\prime}$ die $A$ en $B$ niet kent. Voor alle andere mensen in $X$ geldt dan dat ze $A$ en $B$ wel kennen. Bekijk nu de verzameling $(X \\backslash C) \\cup\\{A, B\\}$. In deze groep mensen kent iedereen elkaar: de mensen uit $X$ kennen elkaar, $A$ en $B$ kennen elkaar en iedereen in $X$ kent zowel $A$ als $B$. Deze groep is echter groter dan $X$, tegenspraak.\nDus we mogen aannemen dat $A^{\\prime}$ en $B^{\\prime}$ verschillende personen zijn. Merk op dat $A^{\\prime}$ en $B^{\\prime}$ elkaar kennen, want ze zitten allebei in $X$. Als nu $A, B, B^{\\prime}$ en $A^{\\prime}$ in die volgorde aan een ronde tafel gaan zitten, kent iedereen precies één van zijn buren: $A$ en $B$ kennen elkaar en $A^{\\prime}$ en $B^{\\prime}$ kennen elkaar, maar $A$ en $A^{\\prime}$ kennen elkaar juist niet en hetzelfde geldt voor $B$ en $B^{\\prime}$. Dit is een tegenspraak met het gegeven. We concluderen dat de opdeling in $X$ en de rest van de mensen voldoet.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 7 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "In een klas van minstens vier mensen geldt het volgende: als er vier van hen aan een ronde tafel gaan zitten, is er altijd iemand die allebei zijn buren kent of allebei zijn buren niet kent. Bewijs dat het mogelijk is om de mensen over twee groepen (waarvan er eentje leeg mag zijn) te verdelen, zodat in de ene groep iedereen elkaar kent en in de andere groep juist niemand elkaar kent.\n(Als persoon $A$ persoon $B$ kent, dan kent $B$ ook $A$.)", "solution": "We bewijzen dit met inductie naar het aantal mensen $n$ in de klas. We nemen $n=3$ als inductiebasis; het gegeven over vier mensen aan een tafel is dan een lege eis. We delen de drie mensen willekeurig in in een groep van één en een groep van twee. Die twee mensen kennen elkaar wel of niet; in beide gevallen klopt het. Stel nu dat we het voor alle klassen van $n$ mensen bewezen hebben. Bekijk een klas van $n+1$ mensen. Noem er eentje $N$. De overige $n$ mensen delen we in twee groepen op volgens de inductiehypothese. Noem groep $\\mathcal{K}$ de groep mensen die elkaar allemaal kennen en groep $\\mathcal{L}$ de groep mensen die elkaar allemaal niet kennen. Als $N$ iedereen in $\\mathcal{K}$ kent, kunnen we $N$ aan $\\mathcal{K}$ toevoegen. Als $N$ niemand in $\\mathcal{L}$ kent, kunnen we $N$ aan $\\mathcal{L}$ toevoegen. In de andere gevallen kent $N$ minstens één iemand in $\\mathcal{K}$ niet en kent hij minstens één iemand in $\\mathcal{L}$ wel.\nStel dat hij in $\\mathcal{K}$ minstens twee mensen $K_{1}$ en $K_{2}$ niet kent, terwijl hij in $\\mathcal{L}$ minstens twee mensen $L_{1}$ en $L_{2}$ wel kent. Als nu $K_{1}$ en $L_{1}$ elkaar kennen, dan zetten we $K_{1}, L_{1}, L_{2}, N$ in die volgorde om een ronde tafel; tegenspraak. Als juiste $K_{1}$ en $L_{1}$ elkaar niet kennen,\ndan zetten we $K_{1}, L_{1}, N, K_{2}$ in die volgorde om een ronde tafel; tegenspraak. Dit geval is dus onmogelijk.\nStel dat $N$ in $\\mathcal{K}$ minstens twee mensen $K_{1}$ en $K_{2}$ niet kent, terwijl hij in $\\mathcal{L}$ precies één persoon $L$ wel kent. Neem een willekeurige $K$ in $\\mathcal{K}$. Dan zetten we $K, L, N$ en $K_{i}$ in die volgorde aan een ronde tafel, waarbij $i$ gelijk is aan 1 of 2 , zodat $K \\neq K_{i}$. Nu zien we dat als $K$ en $L$ elkaar niet kennen, dit een tegenspraak geeft, dus $K$ en $L$ kennen elkaar wel. Dus $L$ kent iedereen in $\\mathcal{K}$. Nu voegen $L$ aan $\\mathcal{K}$ toe. Omdat $N$ verder niemand in $\\mathcal{L}$ kent, kunnen we dan $N$ bij $\\mathcal{L}$ zetten.\nStel dat $N$ in $\\mathcal{K}$ precies één persoon niet kent, terwijl hij in $\\mathcal{L}$ minstens twee personen wel kent. Dan kunnen we analoog aan het vorige geval de groepsindeling maken.\nStel ten slotte dat $N$ in $\\mathcal{K}$ precies één persoon $K_{1}$ niet kent, terwijl hij in $\\mathcal{L}$ precies één persoon $L$ wel kent. Zonder verlies van algemeenheid nemen we aan dat $K_{1}$ en $L$ elkaar kennen. Neem een willekeurige $K \\neq K_{1}$ in $\\mathcal{K}$. Dan zetten we $K, L, N$ en $K_{1}$ in die volgorde aan een ronde tafel. Nu zien we dat als $K$ en $L$ elkaar niet kennen, dit een tegenspraak geeft, dus $K$ en $L$ kennen elkaar wel. Dus $L$ kent iedereen in $\\mathcal{K}$. Nu voegen $L$ aan $\\mathcal{K}$ toe. Omdat $N$ verder niemand in $\\mathcal{L}$ kent, kunnen we dan $N$ bij $\\mathcal{L}$ zetten.\nIn alle gevallen lukt het dus om een groepsindeling te maken met $n+1$ personen. Dit voltooit de inductie.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Een verzameling lijnen in het vlak noemen we mooi indien elke lijn in de verzameling een oneven aantal van de andere lijnen in de verzameling snijdt.\nBepaal het kleinste gehele getal $k \\geq 0$ met de volgende eigenschap: voor iedere 2018 verschillende lijnen $\\ell_{1}, \\ell_{2}, \\ldots, \\ell_{2018}$ in het vlak bestaan er lijnen $\\ell_{2018+1}, \\ell_{2018+2}, \\ldots$, $\\ell_{2018+k}$ zodat de lijnen $\\ell_{1}, \\ell_{2}, \\ldots, \\ell_{2018+k}$ allemaal verschillend zijn en een mooie verzameling vormen.", "solution": "We bewijzen eerst dat in een mooie verzameling het aantal lijnen even moet zijn. Stel namelijk dat het aantal lijnen oneven zou zijn. Dan ligt op elk van het oneven aantal lijnen een oneven aantal snijpunten, dus het totale aantal snijpunten is dan ook oneven. Elk snijpunt wordt hier echter twee keer geteld (één keer voor elke lijn waar hij op ligt), dus het totaal zou even moeten zijn. Tegenspraak. Dus het aantal lijnen in een mooie verzameling moet even zijn. In het bijzonder moet $2018+k$ ook even zijn, dus $k$ moet even zijn.\nStel nu dat er 1009 richtingen zijn zodat er in elke richting twee van de oorspronkelijke lijnen liggen. Dan is elke lijn evenwijdig met precies één andere lijn. Als $k<1010$ is $k \\leq 1008$, dus moet er een richting zijn waarin we geen lijn toevoegen. Bekijk een oorspronkelijke lijn $\\ell$ in deze richting. Die snijdt in de uiteindelijke verzameling alle lijnen behalve zichzelf en de lijn waar hij evenwijdig mee was. Dit is een even aantal. Dus dan is de resulterende verzameling niet mooi. Er is dus een voorbeeld waarbij minstens 1010 lijnen nodig zijn.\nWe laten nu zien dat het mogelijk is om precies 1010 lijnen toe te voegen zodat de totale verzameling uiteindelijk mooi is. We bekijken alle richtingen waarin een even aantal (groter dan 0) van de oorspronkelijke lijnen liggen. Er zijn hoogstens 1009 van zulke richtingen. Voor elk van deze richtingen voegen we een lijn toe. Elke lijn loopt dan evenwijdig aan een even aantal (mogelijk 0) andere lijnen. Stel eerst dat het totaal aantal lijnen nu even is. Dan snijdt elke lijn een oneven aantal lijnen (het totaal minus zichzelf en een even aantal andere lijnen). Stel nu dat het totaal aantal lijnen nu oneven is. Dan snijdt elke lijn een even aantal lijnen. We voegen een lijn toe in een nieuwe richting die dus alle lijnen snijdt (een oneven aantal), zodat daarna elke lijn een oneven aantal andere lijnen snijdt.\nNu is de verzameling mooi en we hebben hooguit $1009+1=1010$ lijnen toegevoegd. Mogelijk zijn het er echt nog minder dan 1010. In dat geval is het aantal toegevoegde lijnen wel even, want het totaal aantal lijnen van een mooie verzameling is altijd even. We kiezen een richting waarin al minstens één lijn loopt. We voegen nu steeds een tweetal lijnen in diezelfde richting toe. Deze lijnen snijden alle lijnen in andere richtingen; dat is totaal een oneven aantal. Die andere lijnen hebben er elk twee snijpunten bijgekregen,\ndus zij houden een oneven aantal snijpunten. Dat laatste geldt ook voor de lijnen die er al waren in de gekozen richting, want zij krijgen nul nieuwe snijpunten. De verzameling blijft dus mooi. We voegen net zo lang zulke tweetallen toe totdat we in totaal 1010 lijnen hebben toegevoegd.\nWe concluderen dat de minimale $k$ die voldoet $k=1010$ is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ waarvoor\n\n$$\nf\\left(x^{2}\\right)-f\\left(y^{2}\\right) \\leq(f(x)+y)(x-f(y))\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Invullen van $x=y=0$ geeft $0 \\leq f(0) \\cdot-f(0)$. Maar kwadraten zijn nietnegatief, dus hieruit volgt $f(0)^{2}=0$ en daarmee $f(0)=0$. Nu geeft $x=0$ en $y=t$ dat $-f\\left(t^{2}\\right) \\leq t \\cdot-f(t)$, terwijl $x=t$ en $y=0$ geeft dat $f\\left(t^{2}\\right) \\leq f(t) \\cdot t$. We vinden $t f(t) \\leq f\\left(t^{2}\\right) \\leq t f(t)$, dus $f\\left(t^{2}\\right)=t f(t)$ voor alle $t \\in \\mathbb{R}$. We kunnen nu links in de functieongelijkheid $f\\left(x^{2}\\right)-f\\left(y^{2}\\right)$ vervangen door $x f(x)-y f(y)$. Door rechts haakjes uit te werken krijgen we daar $x f(x)-y f(y)+x y-f(x) f(y)$, dus krijgen we\n\n$$\nf(x) f(y) \\leq x y\n$$\n\nUit $f\\left(t^{2}\\right)=t f(t)$ volgt $f(1)=-f(-1)$. Door nu eerst $y=1$ te nemen en daarna $y=-1$, krijgen we voor alle $x \\in \\mathbb{R}$ :\n\n$$\nx \\geq f(x) f(1)=-f(x) f(-1) \\geq-x \\cdot-1=x\n$$\n\nDus er moet steeds gelijkheid gelden, wat betekent dat $f(x) f(1)=x$. Hieruit volgt in het bijzonder $f(1)^{2}=1$, dus $f(1)=1$ of $f(1)=-1$. In het eerste geval krijgen we $f(x)=x$ voor alle $x$ en in het tweede geval $f(x)=-x$ voor alle $x$.\nAls we $f(x)=x$ controleren in de oorspronkelijke functieongelijkheid, komt er links $x^{2}-y^{2}$ en rechts $(x+y)(x-y)=x^{2}-y^{2}$, dus deze functie voldoet. Als we $f(x)=-x$ controleren, komt er links $-x^{2}+y^{2}$ en rechts $(-x+y)(x+y)=-x^{2}+y^{2}$, dus deze functie voldoet ook. We concluderen dat de oplossingen zijn: $f(x)=x$ voor alle $x \\in \\mathbb{R}$ en $f(x)=-x$ voor alle $x \\in \\mathbb{R}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ waarvoor\n\n$$\nf\\left(x^{2}\\right)-f\\left(y^{2}\\right) \\leq(f(x)+y)(x-f(y))\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Net als in oplossing I leiden we af dat $f(0)=0$ en $f\\left(t^{2}\\right)=t f(t)$ voor alle $t \\in \\mathbb{R}$. Daaruit volgt\n\n$$\nt f(t)=f\\left(t^{2}\\right)=f\\left((-t)^{2}\\right)=-t f(-t)\n$$\n\ndus voor $t \\neq 0$ geldt $f(-t)=-f(t)$. We wisten al $f(0)=0$, dus dit geldt ook voor $t=0$. Vul nu $y=-x$ in in de functieongelijkheid:\n\n$$\n0 \\leq(f(x)-x)(x-f(-x))=(f(x)-x)(x+f(x))=f(x)^{2}-x^{2}\n$$\n\ndus $f(x)^{2} \\geq x^{2}$. Anderzijds volgt uit het invullen van $y=x$ dat\n\n$$\n0 \\leq(f(x)+x)(x-f(x))=x^{2}-f(x)^{2}\n$$\n\ndus ook $f(x)^{2} \\leq x^{2}$. We concluderen dat $f(x)^{2}=x^{2}$ en dus dat $f(x)= \\pm x$ voor alle $x \\in \\mathbb{R}$. We hebben nu in elk geval de kandidaatoplossingen $f(x)=x$ voor alle $x$ en $f(x)=-x$ voor alle $x$ en deze voldoen (zoals in oplossing I). Nu willen we nog de mixfuncties uitsluiten.\n\nStel dat er $x \\neq y$, allebei ongelijk aan 0 , bestaan met $f(x)=x$ en $f(y)=-y$. Dan geldt $f\\left(x^{2}\\right)=x f(x)=x^{2}$ en $f\\left(y^{2}\\right)=y f(y)=-y^{2}$, zodat de functieongelijkheid geeft:\n\n$$\nx^{2}+y^{2} \\leq(x+y)(x--y)=x^{2}+2 x y+y^{2} .\n$$\n\nDus $2 x y \\geq 0$. Maar $x$ en $y$ waren ongelijk aan 0 , dus $x$ en $y$ zijn beide positief of beide negatief. Zeg zonder verlies van algemeenheid dat ze beide positief zijn. Neem vervolgens een $z<0$. Dan geldt $f(z)=z$ of $f(z)=-z$, dus bovenstaande redenering kunnen we ook toepassen op het tweetal $(z, x)$ (als $f(z)=-z$ ) of juist op $(z, y)$ (als $f(z)=z$ ). Daaruit volgt dat $z$ en $x$ (of juist $z$ en $y$ ) hetzelfde teken hebben, maar dat is een tegenspraak.\nWe concluderen dat voor alle $x, y \\neq 0$ geldt dat $f(x)=x$ en $f(y)=y$ of juist $f(x)=-x$ en $f(y)=-y$. Omdat $f(0)=0=-0$ geldt dus voor alle $x \\in \\mathbb{R}$ dat $f(x)=x$ of voor alle $x \\in \\mathbb{R}$ dat $f(x)=-x$. Dus dit zijn de twee oplossingen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Bepaal alle paren $(a, b)$ van positieve gehele getallen zodat $(a+b)^{3}-2 a^{3}-2 b^{3}$ een tweemacht is.", "solution": "We bepalen eerst de paren $(a, b)$ met $\\operatorname{ggd}(a, b)=1$. Er geldt\n\n$$\n\\begin{aligned}\n(a+b)^{3}-2 a^{3}-2 b^{3} & =a^{3}+3 a^{2} b+3 a b^{2}+b^{3}-2 a^{3}-2 b^{3} \\\\\n& =-a^{3}-b^{3}+3 a b(a+b) \\\\\n& =-(a+b)\\left(a^{2}-a b+b^{2}\\right)+3 a b(a+b) \\\\\n& =(a+b)\\left(-a^{2}+a b-b^{2}+3 a b\\right) \\\\\n& =(a+b)\\left(-a^{2}-b^{2}+4 a b\\right) .\n\\end{aligned}\n$$\n\nDit moet een tweemacht zijn. Omdat $a+b$ positief is, moet de andere factor ook positief zijn en zijn het dus beide tweemachten. Vanwege $\\operatorname{ggd}(a, b)=1$ is minstens één van $a$ en $b$ oneven. Dan is $a^{2}+b^{2}$ congruent aan 1 of 2 modulo 4 , dus $-a^{2}-b^{2}+4 a b$ is congruent aan 3 of 2 modulo 4 . Het moet echter een tweemacht zijn, dus het getal 3 modulo 4 is onmogelijk en in het geval 2 modulo 4 kan het alleen gelijk aan 2 zijn. We concluderen dat $-a^{2}-b^{2}+4 a b=2$.\nStel dat $a+b$ minstens 8 is. Omdat het een tweemacht is, is het dan deelbaar door 8 , dus kunnen we $b=8 m-a$ schrijven voor zekere positieve gehele $m$. Er geldt dan\n\n$$\n\\begin{aligned}\n2 & =-a^{2}-b^{2}+4 a b \\\\\n& =-a^{2}-(8 m-a)^{2}+4 a(8 m-a) \\\\\n& =-a^{2}-64 m^{2}+16 m a-a^{2}+32 m a-4 a^{2} \\\\\n& =-6 a^{2}+48 m a-64 m^{2},\n\\end{aligned}\n$$\n\ndus\n\n$$\n1=-3 a^{2}+24 m a-32 m^{2}\n$$\n\nModulo 8 staat hier nu $1 \\equiv-3 a^{2}$. Als $a$ even is, dan staat er rechts iets wat even is, en als $a$ oneven is, dan staat er rechts -3 modulo 8 . In beide gevallen klopt deze vergelijking niet modulo 8 . We concluderen dat $a+b$ niet minstens 8 is. Omdat $a$ en $b$ beide minstens 1 zijn, moet $a+b$ dan gelijk zijn aan 2 of aan 4 .\n\n- Als $a+b=2$, dan geldt $a=b=1 . \\mathrm{Nu}$ is $-a^{2}-b^{2}+4 a b=2$, dus het product van de twee factoren is inderdaad een tweemacht (namelijk 4). Dus $(1,1)$ is een oplossing.\n- Als $a+b=4$, dan moet wegens $\\operatorname{ggd}(a, b)=1$ gelden dat $a=1$ en $b=3$ of andersom. Nu is $-a^{2}-b^{2}+4 a b=2$, dus ook nu is het product van de twee factoren een tweemacht (namelijk 8). Dus $(1,3)$ en $(3,1)$ zijn oplossingen.\n\nBekijk nu een oplossing $(a, b)$ met $\\operatorname{ggd}(a, b)=d>1$. Dan is $d$ een deler van $(a+b)^{3}-2 a^{3}-$ $2 b^{3}$, dus $d$ moet zelf een tweemacht zijn. We zien nu dat $\\left(\\frac{a}{d}, \\frac{b}{d}\\right)$ ook een oplossing is, want\nuit de tweemacht $(a+b)^{3}-2 a^{3}-2 b^{3}$ wordt $d^{3}$ weggedeeld, waardoor er weer een tweemacht overblijft. Dus $\\left(\\frac{a}{d}, \\frac{b}{d}\\right)$ moet één van de drie eerder gevonden paren zijn. Andersom geeft elk van die drie paren vermenigvuldigd met een willekeurige tweemacht weer een oplossing. We concluderen dat alle oplossingen gegeven worden door\n\n$$\n(a, b)=\\left(2^{k}, 2^{k}\\right), \\quad(a, b)=\\left(2^{k}, 3 \\cdot 2^{k}\\right), \\quad \\text { en } \\quad(a, b)=\\left(3 \\cdot 2^{k}, 2^{k}\\right),\n$$\n\nwaarbij $k$ varieert over de niet-negatieve gehele getallen.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "In een niet-gelijkbenige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel. De bissectrice van $\\angle B A C$ snijdt de omgeschreven cirkel van $\\triangle A B C$ nogmaals in $D$. De lijn door $I$ loodrecht op $A D$ snijdt $B C$ in $F$. Het midden van boog $B C$ waar $A$ op ligt, noemen we $M$. De lijn $M I$ snijdt de cirkel door $B, I$ en $C$ nogmaals in $N$. Bewijs dat $F N$ raakt aan de cirkel door $B, I$ en $C$.\n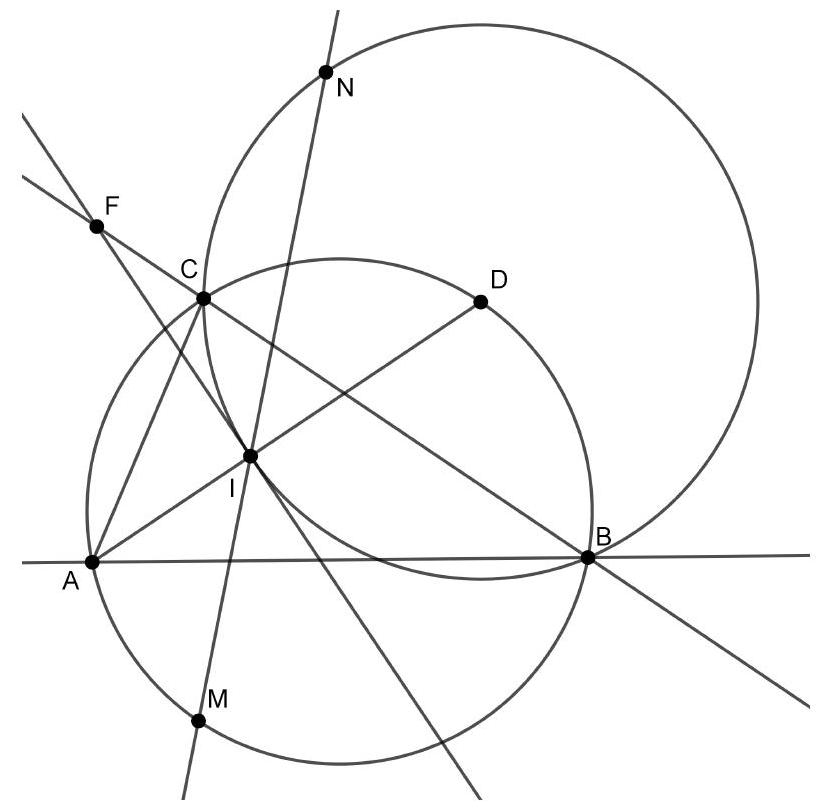\n\nWe bekijken de configuratie waar $|A B|>|A C|$ zodat $C$ tussen $B$ en $F$ ligt. Andere configuraties gaan analoog.", "solution": "Omdat $\\angle D A C=\\angle B A D$ is $D$ het midden van de boog $B C$ waar $A$ niet op ligt. De lijn $D M$ is dus een middellijn van de cirkel. Met Thales zien we dan dat $\\angle D B M=90^{\\circ}$. Zij nu $K$ het snijpunt van $B C$ en $D M$. Omdat $D M$ de middelloodlijn van $B C$ is, geldt nu $\\angle B K M=90^{\\circ}=\\angle D B M$. Dus $\\triangle M K B \\sim \\triangle M B D$ (hh). Hieruit volgt $\\frac{|M B|}{|M K|}=\\frac{|M D|}{|M B|}$, dus $|M D| \\cdot|M K|=|M B|^{2}$. Omdat $K$ inwendig op $M D$ ligt, geldt deze gelijkheid ook gericht: $M D \\cdot M K=M B^{2}$.\nOmdat $D$ het midden van boog $B C$ is, geldt $|D B|=|D C|$. Verder is $\\angle C D I=\\angle C D A=$ $\\angle C B A$ en $\\angle D C I=\\angle D C B+\\angle B C I=\\angle D A B+\\angle B C I=\\frac{1}{2} \\angle C A B+\\frac{1}{2} \\angle B C A$. Met de hoekensom in driehoek $D C I$ zien we nu dat $\\angle D I C=180^{\\circ}-\\angle C B A-\\frac{1}{2} \\angle C A B-\\frac{1}{2} \\angle B C A=$ $\\frac{1}{2} \\angle C A B+\\frac{1}{2} \\angle B C A=\\angle D C I$. Dus driehoek $D C I$ is gelijkbenig met $|D C|=|D I|$. We conluderen dat $D$ het middelpunt is van de cirkel door $B, C$ en $I$. (Dit noemen we ook wel de tussengeschreven cirkel.) Nu is $D B$ een straal van deze cirkel en $D B$ staat loodrecht op $M B$, waaruit volgt dat $M B$ een raaklijn is. Met de machtstelling weten we nu $M B^{2}=M I \\cdot M N$. Samen met het voorgaande concluderen we dat $M D \\cdot M K=M I \\cdot M N$. Dus vanwege de machtstelling is $N D K I$ een koordenvierhoek.\nWe weten ook dat $\\angle F I D=90^{\\circ}=\\angle F K D$, dus $D K I F$ is een koordenvierhoek. We concluderen dat $N D K I F$ een koordenvijfhoek is. Hieruit volgt $\\angle D N F=180^{\\circ}-\\angle D I F=90^{\\circ}$.\n\nDus $N F$ staat loodrecht op de straal $D N$ van de cirkel door $B, I$ en $C$; dat betekent dat $F N$ raakt aan deze cirkel.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "In een niet-gelijkbenige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel. De bissectrice van $\\angle B A C$ snijdt de omgeschreven cirkel van $\\triangle A B C$ nogmaals in $D$. De lijn door $I$ loodrecht op $A D$ snijdt $B C$ in $F$. Het midden van boog $B C$ waar $A$ op ligt, noemen we $M$. De lijn $M I$ snijdt de cirkel door $B, I$ en $C$ nogmaals in $N$. Bewijs dat $F N$ raakt aan de cirkel door $B, I$ en $C$.\n\n\nWe bekijken de configuratie waar $|A B|>|A C|$ zodat $C$ tussen $B$ en $F$ ligt. Andere configuraties gaan analoog.", "solution": "We definiëren net als in oplossing I punt $K$ als het snijpunt van $B C$ en $D M$ en leiden af dat $\\angle B K M=90^{\\circ}$. Verder geldt wegens Thales dat $\\angle D C M=90^{\\circ}=\\angle C K D$, dus $\\triangle D C M \\sim \\triangle D K C$ (hh). Dus $\\frac{|D C|}{|D M|}=\\frac{|D K|}{|D C|}$, dus $|D C|^{2}=|D M| \\cdot|D K|$. Ook net als in oplossing I zien we dat $D$ het middelpunt is van de cirkel door $B, C$ en $I$. In het bijzonder geldt $|D I|=|D C|$, dus $|D I|^{2}=|D M| \\cdot|D K|$. Omdat $K$ inwendig op $M D$ ligt, geldt deze gelijkheid ook gericht: $D I^{2}=D M \\cdot D K$. Met de machtstelling volgt hieruit dat $D I$ raakt aan de cirkel door $I, K$ en $M$. De raaklijnomtrekshoekstelling zegt dan dat $\\angle I M K=\\angle D I K$.\nVerder geldt $\\angle D I F=90^{\\circ}=\\angle D K F$, dus $D K I F$ is een koordenvierhoek. Dus $\\angle D I K=$ $\\angle D F K$ en samen met het voorgaande geeft dat $\\angle I M K=\\angle D F K$. Definieer nu $X$ als het snijpunt van $D F$ en $N M$. Dan zien we $\\angle X M K=\\angle I M K=\\angle D F K=\\angle X F K$, wat betekent dat $X K M F$ een koordenvierhoek is. Nu zien we $\\angle F X M=\\angle F K M=90^{\\circ}$.\nDus $F D$ staat loodrecht op $I N$. Omdat $D$ het middelpunt is van de cirkel met koorde $I N$, is $F D$ de middelloodlijn van $I N$. Dus $I$ en $N$ zijn elkaars gespiegelde in $F D$. Bij deze spiegeling gaat de cirkel door $B, I$ en $C$ in zichzelf over, dus raaklijn $F I$ gaat over in raaklijn $F N$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Bewijs dat er voor elke positieve gehele $n$ hoogstens twee paren $(a, b)$ van positieve gehele getallen bestaan met de volgende twee eigenschappen:\n(i) $a^{2}+b=n$,\n(ii) $a+b$ is een tweemacht, d.w.z. er is een gehele $k \\geq 0$ met $a+b=2^{k}$.", "solution": "Stel dat er drie of meer zulke paren bestaan bij dezelfde $n$. Dan zijn er wegens het ladenprincipe minstens twee, zeg $(a, b)$ en $(c, d)$, zodat $a \\equiv c \\bmod 2$. Schrijf $a+b=2^{k}$ en $c+d=2^{\\ell}$ met $k$ en $\\ell$ positieve gehele getallen. Neem zonder verlies van algemeenheid aan dat $\\ell \\geq k$. We zien dat\n\n$$\n\\begin{aligned}\n2^{\\ell}-2^{k} & =(c+d)-(a+b) \\\\\n& =\\left(c+n-c^{2}\\right)-\\left(a+n-a^{2}\\right)=c-a-c^{2}+a^{2}=(a+c-1)(a-c) .\n\\end{aligned}\n$$\n\nOmdat $\\ell \\geq k$ is $2^{k}$ een deler van $2^{\\ell}-2^{k}$. Omdat $a \\equiv c \\bmod 2$, is $a+c-1$ oneven, dus moet $2^{k}$ een deler zijn van $a-c$. Omdat $2^{\\ell}-2^{k} \\geq 0$ en $a+c-1>0$ is $a-c \\geq 0$. Anderzijds geldt $a-c<a+b=2^{k}$, dus $0 \\leq a-c<2^{k}$, terwijl $2^{k} \\mid a-c$. We concluderen dat $a-c=0$, dus $a=c$. Nu geldt $b=n-a^{2}=n-c^{2}=d$, dus de paren $(a, b)$ en $(c, d)$ zijn identiek. Tegenspraak. Er zijn dus hoogstens twee paren $(a, b)$ die voldoen.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek en zij $I$ het middelpunt van de ingeschreven cirkel van deze driehoek. De lijn door $I$ loodrecht op $A I$ snijdt de omgeschreven cirkel van $\\triangle A B C$ in de punten $P$ en $Q$, waarbij $P$ aan dezelfde kant van $A I$ ligt als $B$. Zij $S$ het tweede snijpunt van de omgeschreven cirkels van $\\triangle B I P$ en $\\triangle C I Q$. Bewijs dat $S I$ de bissectrice $\\operatorname{van} \\angle P S Q$ is.\n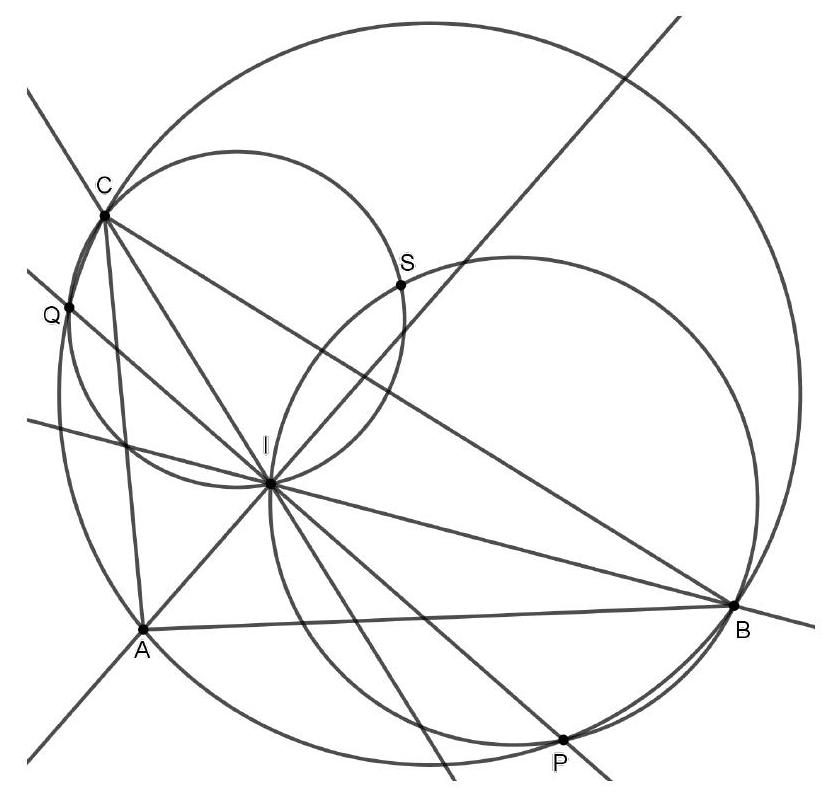\n\nWe bekijken de configuratie waarin $S$ en $A$ aan verschillende kanten van $P Q$ liggen. De configuratie waarin $S$ en $A$ aan dezelfde kant van $P Q$ liggen, gaat analoog.", "solution": "Laat $M$ en $N$ de snijpunten zijn van respectievelijk $B I$ en $C I$ met de omgeschreven cirkel van $\\triangle A B C$. Schrijf verder $\\angle C A B=2 \\alpha, \\angle A B C=2 \\beta$ en $\\angle B C A=$ $2 \\gamma$. Dan geldt vanwege de omtrekshoekstelling\n\n$$\n\\angle A M N=\\angle A C N=\\angle A C I=\\gamma\n$$\n\nen\n\n$$\n\\angle M A C=\\angle M B C=\\angle I B C=\\beta,\n$$\n\nzodat\n\n$$\n\\angle A M N+\\angle M A I=\\gamma+\\angle M A C+\\angle C A I=\\gamma+\\beta+\\alpha=90^{\\circ} .\n$$\n\nHieruit volgt dat $M N \\perp A I$. Aangezien gegeven is dat ook $P Q \\perp A I$, geldt $M N \\| P Q$. Koordenvierhoek $M N P Q$ is dus een gelijkbenig trapezium en daarin zijn de diagonalen even lang, dus $|M P|=|N Q|$. Hieruit volgt $\\angle P B M=\\angle N C Q$. Met nog twee keer omtrekshoekstelling vinden we nu\n\n$$\n\\angle P S I=\\angle P B I=\\angle P B M=\\angle N C Q=\\angle I C Q=\\angle I S Q\n$$\n\nWe concluderen dat $S I$ de bissectrice van $\\angle P S Q$ is.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een driehoek en zij $I$ het middelpunt van de ingeschreven cirkel van deze driehoek. De lijn door $I$ loodrecht op $A I$ snijdt de omgeschreven cirkel van $\\triangle A B C$ in de punten $P$ en $Q$, waarbij $P$ aan dezelfde kant van $A I$ ligt als $B$. Zij $S$ het tweede snijpunt van de omgeschreven cirkels van $\\triangle B I P$ en $\\triangle C I Q$. Bewijs dat $S I$ de bissectrice $\\operatorname{van} \\angle P S Q$ is.\n\n\nWe bekijken de configuratie waarin $S$ en $A$ aan verschillende kanten van $P Q$ liggen. De configuratie waarin $S$ en $A$ aan dezelfde kant van $P Q$ liggen, gaat analoog.", "solution": "Schrijf $\\angle C A B=2 \\alpha, \\angle A B C=2 \\beta$ en $\\angle B C A=2 \\gamma$. Er geldt vanwege de hoekensom in $\\triangle A I B$ dat\n\n$$\n\\angle B I A=180^{\\circ}-\\angle I A B-\\angle A B I=180^{\\circ}-\\alpha-\\beta=90^{\\circ}+\\gamma,\n$$\n\ndus\n\n$$\n\\angle B I P=\\angle B I A-\\angle A I P=90^{\\circ}+\\gamma-90^{\\circ}=\\gamma=\\angle B C I .\n$$\n\nVerder geldt met behulp van de koordenvierhoekstelling\n\n$$\n180^{\\circ}-\\angle B P I=180^{\\circ}-\\angle B P Q=\\angle B C Q=\\angle B C I+\\angle I C Q \\text {. }\n$$\n\nAls we nu de hoekensom in driehoek $B P I$ bekijken en beide resultaten hierboven gebruiken, vinden we\n\n$$\n\\angle P B I=180^{\\circ}-\\angle B P I-\\angle B I P=\\angle B C I+\\angle I C Q-\\angle B C I=\\angle I C Q\n$$\n\nMet nog twee keer omtrekshoekstelling volgt nu\n\n$$\n\\angle P S I=\\angle P B I=\\angle I C Q=\\angle I S Q\n$$\n\ndus $S I$ is de bissectrice van hoek $P S Q$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Laat $x$ en $y$ positieve reële getallen zijn.\na) Bewijs: als $x^{3}-y^{3} \\geq 4 x$, dan geldt $x^{2}>2 y$.\nb) Bewijs: als $x^{5}-y^{3} \\geq 2 x$, dan geldt $x^{3} \\geq 2 y$.", "solution": "a) Er geldt $x^{3}-4 x \\geq y^{3}>0$, dus $x\\left(x^{2}-4\\right)>0$. Omdat $x$ positief is, volgt hieruit dat $x^{2}-4>0$, dus $x^{2}>4$. Dat betekent $x>2$. Verder geldt $x^{3}-y^{3} \\geq 4 x>0$, dus $x>y$. Combineren van deze twee resultaten (wat mag omdat $x$ en $y$ beide positief zijn) geeft $x^{2}=x \\cdot x>2 \\cdot y=2 y$.\nb) Er geldt $\\left(x^{4}-4\\right)^{2} \\geq 0$. Uitwerken geeft $x^{8}-8 x^{4}+16 \\geq 0$. Omdat $x$ positief is, kunnen we dit met $x$ vermenigvuldigen zonder dat het teken omklapt, dus geldt ook $x^{9} \\geq 8 x^{5}-16 x$. Uit de gegeven ongelijkheid volgt $x^{5}-2 x \\geq y^{3}$. Als we dat combineren met het voorgaande, krijgen we $x^{9} \\geq 8\\left(x^{5}-2 x\\right) \\geq 8 y^{3}$. Hieruit volgt $x^{3} \\geq 2 y$.", "problem_match": "\nOpgave 3.", "solution_match": "# Oplossing."}
|
| 5 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Bestaan er een positief geheel getal $k$ en een niet-constante rij $a_{1}, a_{2}, a_{3}, \\ldots$ van positieve gehele getallen zodat $a_{n}=\\operatorname{ggd}\\left(a_{n+k}, a_{n+k+1}\\right)$ voor alle positieve gehele getallen $n$ ?", "solution": "Zo'n $k$ en bijbehorende rij bestaan niet. We bewijzen dit uit het ongerijmde, dus stel dat ze wel bestaan. Merk op dat $a_{n} \\mid a_{n+k}$ en $a_{n} \\mid a_{n+k+1}$ voor alle $n \\geq 1$. Met een eenvoudige inductie volgt ook dat $a_{n} \\mid a_{n+\\ell k}$ en $a_{n} \\mid a_{n+\\ell k+\\ell}$ voor alle $l \\geq 0$. We bewijzen nu met inductie naar $m$ dat $a_{n} \\mid a_{n+m k+(m+1)}$ voor alle $0 \\leq m \\leq k-1$. Voor $m=k-1$ volgt dit uit $a_{n} \\mid a_{n+k \\cdot k}=a_{n+(k-1) k+k}$. Stel nu dat voor zekere $m$ met $1 \\leq m \\leq k-1$ geldt dat $a_{n} \\mid a_{n+m k+(m+1)}$. We weten ook dat $a_{n} \\mid a_{n+m k+m}$, dus vanwege $a_{n+(m-1) k+m}=\\operatorname{ggd}\\left(a_{n+m k+m}, a_{n+m k+m+1}\\right)$ geldt ook $a_{n} \\mid a_{n+(m-1) k+m}$. Dit voltooit de inductiestap. Invulen van $m=0$ geeft nu $a_{n} \\mid a_{n+1}$.\nOmdat $a_{n} \\mid a_{n+1}$, geldt ook $\\operatorname{ggd}\\left(a_{n}, a_{n+1}\\right)=a_{n}$ voor alle $n$. Dus $a_{n}=a_{n-k}$ voor alle $n \\geq k+1$. We hebben nu $a_{n-k}\\left|a_{n-k+1}\\right| a_{n-k+2}|\\ldots| a_{n}=a_{n-k}$. Omdat het om allemaal positieve gehele getallen gaat, moeten $a_{n-k}, a_{n-k+1}, \\ldots, a_{n}$ allemaal gelijk zijn. Dit geldt voor alle $n \\geq k+1$, dus de rij is constant. Tegenspraak.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Bestaan er een positief geheel getal $k$ en een niet-constante rij $a_{1}, a_{2}, a_{3}, \\ldots$ van positieve gehele getallen zodat $a_{n}=\\operatorname{ggd}\\left(a_{n+k}, a_{n+k+1}\\right)$ voor alle positieve gehele getallen $n$ ?", "solution": "Zo'n $k$ en bijbehorende rij bestaan niet. We bewijzen dit uit het ongerijmde, dus stel dat ze wel bestaan. Merk op dat $a_{n} \\mid a_{n+k}$ en $a_{n} \\mid a_{n+k+1}$ voor alle $n \\geq 1$. Zij nu $0 \\leq \\ell \\leq k$ een geheel getal. Dan geldt $k^{2}+\\ell=(k-\\ell) \\cdot k+\\ell \\cdot(k+1)$. Door de eerste deelbaarheid $k-\\ell$ keer toe te passen en vervolgens de tweede $\\ell$ keer, vinden we hiermee dat $a_{n} \\mid a_{n+k^{2}+\\ell}$. Er geldt dus $a_{n} \\mid a_{n+k^{2}+\\ell}$ voor alle $0 \\leq \\ell \\leq k$.\nWe bewijzen nu dat als $a_{n} \\mid a_{i}, a_{i+1}, \\ldots, a_{i+k}$, dat dan ook $a_{n} \\mid a_{i-1}$. Er geldt $a_{i-1}=$ $\\operatorname{ggd}\\left(a_{i+k-1}, a_{i+k}\\right)$. Omdat $a_{n}$ ook een gemeenschappelijke deler van $a_{i+k-1}$ en $a_{i+k}$ is, moet er gelden dat $a_{n} \\mid a_{i-1}$.\nWe weten $a_{n} \\mid a_{n+k^{2}}, a_{n+k^{2}+1}, \\ldots, a_{n+k^{2}+k}$, dus door het bovenstaande toe te passen, vinden we $a_{n} \\mid a_{n+k^{2}-1}$. Met inductie krijgen we nu $a_{n} \\mid a_{n+k^{2}-m}$ voor alle $m<n+k^{2}$. In het bijzonder vinden we $a_{n} \\mid a_{n+1}$ voor alle $n$, maar ook $a_{n} \\mid a_{n-1}$ voor alle $n \\geq 2$. Dus geldt voor alle positieve gehele $j$ zowel $a_{j} \\mid a_{j+1}$ als $a_{j+1} \\mid a_{j}$. Er geldt dus $a_{j}=a_{j+1}$ voor alle $j$, dus de rij is constant. Tegenspraak.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2019", "problem_label": "5", "tier": 1, "problem": "In een land zijn 2018 steden, waarvan sommige met elkaar verbonden zijn door wegen. Elke stad is verbonden met ten minste drie andere steden. Het is mogelijk om van elke willekeurige stad naar elke andere willekeurige stad te reizen via één of meer wegen. Bekijk voor elk tweetal steden de kortste route tussen deze twee steden. Wat is het grootste aantal wegen dat in zo'n kortste route zou kunnen voorkomen?", "solution": "Het grootste aantal wegen dat in een kortste route kan voorkomen, is 1511. We geven eerst een land waarvoor dit aantal aangenomen wordt. Deel de steden op in 504 groepen: twee groepen van vijf steden $\\left(A_{0}, B_{0}, C_{0}, D_{0}, E_{0}\\right)$ en $\\left(A_{503}, B_{503}, C_{503}, D_{503}, E_{503}\\right)$ en verder groepen van vier steden $\\left(A_{i}, B_{i}, C_{i}, D_{i}\\right)$ voor $1 \\leq i \\leq 502$. Voor alle $i$ met $0 \\leq i \\leq 503$ : verbind $A_{i}$ met $B_{i}$, verbind $A_{i}$ met $C_{i}$, verbind $B_{i}$ met $D_{i}$ en verbind $C_{i}$ met $D_{i}$. Verbind verder $E_{0}$ met $A_{0}, B_{0}$ en $C_{0}$. Verbind $E_{503}$ met $B_{503}, C_{503}$ en $D_{503}$. Voor $1 \\leq i \\leq 502$ : verbind $B_{i}$ met $C_{i}$. Ten slotte voor $0 \\leq i \\leq 502$ : verbind $D_{i}$ met $A_{i+1}$. Nu is elke stad met precies drie andere steden verbonden.\nAls we nu van $A_{0}$ naar $D_{503}$ willen, dan moet dat via alle $A_{i}$ en $D_{i}$, omdat daar de enige verbindingen tussen de verschillende groepen lopen en elke groep alleen verbonden is met de vorige en volgende groep. Verder is voor $0 \\leq i \\leq 503$ de stad $A_{i}$ niet verbonden met $D_{i}$, dus de route binnen groep $i$ moet via $B_{i}$ of $C_{i}$ lopen. Minstens drie van de vier of vijf steden in zo'n groep worden dus aangedaan op de route. In totaal bevat de route dus minstens $3 \\cdot 504=1512$ steden en daarmee minstens 1511 wegen.\nWe laten vervolgens zien dat een kortste route tussen twee steden nooit meer dan 1511 wegen kan doorlopen. Bekijk zo'n korste route waarbij achtereenvolgens de steden $A_{0}, A_{1}$, $\\ldots, A_{k}$ worden aangedaan. Elk van de steden $A_{i}$ is behalve met zijn buren $A_{i-1}$ en $A_{i+1}$ nog met minstens één andere stad verbonden, zeg met $B_{i}$ (hierbij hoeven $B_{0}, B_{1}, \\ldots, B_{k}$ niet allemaal verschillende steden te zijn). Verder zijn $A_{0}$ en $A_{k}$ nog met een derde stad verbonden, zeg $C_{0} \\neq B_{0}$ en $C_{k} \\neq B_{k}$. Als één van de steden $B_{i}$ of $C_{i}$ gelijk is aan één van de steden $A_{j}$, dan hadden we een kortere route kunnen vinden door direct van $A_{i}$ naar $A_{j}$ te lopen (of andersom), tegenspraak. Dus de steden $B_{i}$ en $C_{i}$ zijn allemaal ongelijk aan alle steden $A_{j}$.\nAls één van de steden $B_{i}$ in totaal met vier steden $A_{j}$ verbonden is, zeg $B_{i}$ is verbonden met $A_{i}, A_{m}, A_{n}$ en $A_{p}$ met $i<m<n<p$, dan zouden we de route kunnen inkorten door van $A_{i}$ naar $B_{i}$ en dan naar $A_{p}$ te lopen. We slaan dan minimaal twee steden uit de oorspronkelijke route over (namelijk $A_{m}$ en $A_{n}$ ) en bezoeken in plaats daarvan alleen $B_{i}$ extra, dus deze nieuwe route is korter. Tegenspraak. De steden $B_{i}$ met $3 \\leq i \\leq k-3$ zijn dus minstens $\\frac{k-5}{3}$ verschillende steden. Voor $B_{0}$ en $C_{0}$ geldt dat we de route kunnen inkorten als één van deze steden gelijk is aan $B_{i}$ met $i \\geq 3$. Dat zou een tegenspraak zijn, dus $B_{0}$ en $C_{0}$ zijn twee verschillende steden ongelijk aan $B_{i}$ met $i \\geq 3$. Zo ook zijn $B_{k}$ en $C_{k}$ twee verschillende steden ongelijk aan $B_{i}$ met $i \\leq k-3$. Al met al hebben we op de route zelf $k+1$ steden en daarnaast nog minstens $\\frac{k-5}{3}+2+2$ andere steden. Dus $\\frac{k-5}{3}+k+5 \\leq 2018$, dus $4 k-5+15 \\leq 3 \\cdot 2018=6054$, dus $4 k \\leq 6044$, dus $k \\leq 1511$.\nWe concluderen dat het grootst mogelijke aantal wegen in een kortste route gelijk aan 1511.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Gegeven is een kwadratisch polynoom $P(x)$ met twee verschillende reële nulpunten. Voor alle reële getallen $a$ en $b$ met $|a|,|b| \\geq 2017$ geldt dat $P\\left(a^{2}+b^{2}\\right) \\geq P(2 a b)$. Bewijs dat minstens één van de nulpunten van $P$ negatief is.", "solution": "Schrijf $P(x)=c(x-d)(x-e)$, waarbij $d$ en $e$ de nulpunten zijn, dus $d \\neq e$. Verder geldt $c \\neq 0$, anders is $P$ niet kwadratisch. Voor $|a|,|b| \\geq 2017$ volgt nu uit $P\\left(a^{2}+b^{2}\\right) \\geq P(2 a b)$ dat\n\n$$\nc\\left(a^{2}+b^{2}-d\\right)\\left(a^{2}+b^{2}-e\\right) \\geq c(2 a b-d)(2 a b-e)\n$$\n\nWe werken haakjes uit en strepen links en rechts de term cde weg:\n\n$$\nc\\left(\\left(a^{2}+b^{2}\\right)^{2}-(d+e)\\left(a^{2}+b^{2}\\right)\\right) \\geq c\\left((2 a b)^{2}-(d+e) \\cdot 2 a b\\right) .\n$$\n\nWe halen $c(2 a b)^{2}$ naar links, zodat daar een merkwaardig product ontstaat; en we zetten de termen met een factor $(d+e)$ samen rechts. Nu vinden we\n\n$$\nc\\left(a^{2}+b^{2}-2 a b\\right)\\left(a^{2}+b^{2}+2 a b\\right) \\geq c(d+e)\\left(a^{2}+b^{2}-2 a b\\right)\n$$\n\nWe factoriseren beide kanten:\n\n$$\nc(a-b)^{2}(a+b)^{2} \\geq c(d+e)(a-b)^{2}\n$$\n\nVoor $a \\neq b$ is $(a-b)^{2}>0$, dus kunnen we daardoor delen, zonder dat het teken omklapt. We krijgen\n\n$$\nc(a+b)^{2} \\geq c(d+e)\n$$\n\nWe onderscheiden nu twee gevallen. Stel eerst dat $c>0$. Dan kunnen we links en rechts door $c$ delen en klapt het teken niet om. Als we vervolgens kiezen voor $a=2017, b=-2017$ krijgen we $0 \\geq d+e$. Omdat $d \\neq e$ volgt hieruit dat minstens één van $d$ en $e$ negatief moet zijn.\nNu het tweede geval: $c<0$. Dan klapt het teken om bij deling door $c$ en krijgen we $(a+b)^{2} \\leq d+e$ voor alle $a \\neq b$ met $|a|,|b| \\geq 2017$. Door het variëren van $a$ en $b$ kan de linkerkant willekeurig groot worden, terwijl de rechterkant constant is. Tegenspraak.\n\nWe concluderen dat het eerste geval moet gelden en dus minstens één van de nulpunten van $P$ negatief is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Gegeven is een kwadratisch polynoom $P(x)$ met twee verschillende reële nulpunten. Voor alle reële getallen $a$ en $b$ met $|a|,|b| \\geq 2017$ geldt dat $P\\left(a^{2}+b^{2}\\right) \\geq P(2 a b)$. Bewijs dat minstens één van de nulpunten van $P$ negatief is.", "solution": "Schrijf $P(x)=c(x-d)(x-e)$, waarbij $d$ en $e$ de nulpunten zijn, dus $d \\neq e$. Verder geldt $c \\neq 0$, anders is $P$ niet kwadratisch. We onderscheiden twee gevallen. Stel eerst dat $c>0$. We nemen $b=-a=2017$ in $P\\left(a^{2}+b^{2}\\right) \\geq P(2 a b)$, waardoor we krijgen $P\\left(2 a^{2}\\right) \\geq P\\left(-2 a^{2}\\right)$, dus\n\n$$\nc\\left(2 a^{2}-d\\right)\\left(2 a^{2}-e\\right) \\geq c\\left(-2 a^{2}-d\\right)\\left(-2 a^{2}-2\\right)\n$$\n\nWe delen door $c>0$, werken haakjes uit en strepen links en rechts de termen $4 a^{4}$ en de weg:\n\n$$\n-(d+e) \\cdot 2 a^{2} \\geq(d+e) \\cdot 2 a^{2}\n$$\n\noftewel\n\n$$\n4 a^{2}(d+e) \\leq 0\n$$\n\nWe kunnen delen door $4 a^{2}=4 \\cdot 2017^{2}$, zodat we vinden dat $d+e \\leq 0$. Omdat de twee nulpunten verschillend zijn, moet nu minstens één van beide negatief zijn.\nStel nu dat $c<0$. Dan hebben we te maken met een bergparabool, die rechts voorbij de top dalend is. Kies nu $a \\neq b$ met $a, b \\geq 2017$ en $a$ en $b$ rechts van de top, dan geldt volgens de ongelijkheid van het rekenkundig-meetkundig $a^{2}+b^{2}>2 a b$ (geen gelijkheid want $a \\neq b$ ). Omdat $a$ en $b$ positief en groter dan 1 zijn en rechts van de top liggen, geldt $2 a b>a$, dus ligt ook $2 a b$ rechts van de top (en daarmee $a^{2}+b^{2}$ ook). Dus omdat $P$ dalend is, geldt $P\\left(a^{2}+b^{2}\\right)<P(2 a b)$, in tegenspraak met het gegeven.\nWe concluderen dat het eerste geval moet gelden en dus minstens één van de nulpunten van $P$ negatief is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Schrijf $S_{n}$ voor de verzameling $\\{1,2, \\ldots, n\\}$. Bepaal alle positieve gehele $n$ waarvoor er functies $f: S_{n} \\rightarrow S_{n}$ en $g: S_{n} \\rightarrow S_{n}$ bestaan zodat voor elke $x$ precies één van de gelijkheden $f(g(x))=x$ en $g(f(x))=x$ waar is.", "solution": "We laten eerst zien dat als $n=2 m$ voor zekere positieve gehele $m$, er dan zulke functies bestaan. Definieer\n\n$$\nf(x)=\\left\\{\\begin{array}{ll}\nx & \\text { als } 1 \\leq x \\leq m, \\\\\nx-m & \\text { als } m+1 \\leq x \\leq 2 m,\n\\end{array} \\quad g(x)= \\begin{cases}x+m & \\text { als } 1 \\leq x \\leq m \\\\\nx & \\text { als } m+1 \\leq x \\leq 2 m\\end{cases}\\right.\n$$\n\nMerk op dat alle voorgeschreven functiewaarden in $S_{n}$ vallen, dus dit zijn inderdaad functies van $S_{n}$ naar $S_{n}$. Verder is het bereik van $f$ gelijk aan $\\{1,2, \\ldots, m\\}$ en dat van $g$ aan $\\{m+1, m+2, \\ldots, 2 m\\}$. Dus $f(g(x)) \\neq x$ als $x \\geq m+1$ en $g(f(x)) \\neq x$ als $x \\leq m$. Voor $x \\leq m$ geldt daarnaast $f(g(x))=f(x+m)=x+m-m=x$ en vor $x \\geq m+1$ geldt juist $g(f(x))=g(x-m)=x-m+m=x$. We zien dat voor elke $x$ inderdaad aan precies één van $g(f(x))=x$ en $f(g(x))=x$ voldaan wordt. Dus $n=2 m$ voldoet.\nStel nu dat $n$ oneven is, zeg $n=2 m+1$, en stel dat $f$ en $g$ functies zijn die aan de voorwaarden voldoen. Dan geldt zonder verlies van algemeenheid minstens $m+1$ keer $f(g(x))=x$, zeg voor $x_{1}, \\ldots, x_{m+1}$. Stel nu dat voor een zekere $i, j$ met $1 \\leq i, j \\leq m+1$ geldt dat $g\\left(x_{i}\\right)=x_{j}$. Dan is $f\\left(x_{j}\\right)=f\\left(g\\left(x_{i}\\right)\\right)=x_{i}$, dus $g\\left(f\\left(x_{j}\\right)\\right)=g\\left(x_{i}\\right)=x_{j}$. Maar nu geldt zowel $f(g(x))=x$ als $g(f(x))=x$ voor $x=x_{j}$ en dat mag niet. Dus voor alle $i$ met $1 \\leq i \\leq m+1$ geldt dat $g\\left(x_{i}\\right)$ niet één van de getallen $x_{j}$ met $1 \\leq j \\leq m+1$ is. Er zijn echter nog slechts $m$ andere getallen in $S_{n}$, terwijl er $m+1$ waarden van $i$ mogelijk zijn, dus twee van de functiewaarden moeten gelijk zijn. Zeg $g\\left(x_{k}\\right)=g\\left(x_{l}\\right)$ voor $1 \\leq k<l \\leq m+1$. Maar nu is $x_{k}=f\\left(g\\left(x_{k}\\right)\\right)=f\\left(g\\left(x_{l}\\right)\\right)=x_{l}$, tegenspraak. Voor oneven $n$ kunnen dus geen functies bestaan die aan de voorwaarde voldoen.\nWe concluderen dat alle even $n$ voldoen en alle oneven $n$ niet.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Schrijf $S_{n}$ voor de verzameling $\\{1,2, \\ldots, n\\}$. Bepaal alle positieve gehele $n$ waarvoor er functies $f: S_{n} \\rightarrow S_{n}$ en $g: S_{n} \\rightarrow S_{n}$ bestaan zodat voor elke $x$ precies één van de gelijkheden $f(g(x))=x$ en $g(f(x))=x$ waar is.", "solution": "Elke $x \\in S_{n}$ is een dekpunt van precies één van de functies $f \\circ g$ en $g \\circ f$. We laten nu eerst zien dat als $x$ een dekpunt van $f \\circ g$ is, dat dan $x$ geen dekpunt van $g$ is. Immers, als wel zou gelden $f(g(x))=x$ en $g(x)=x$, dan is ook $f(x)=f(g(x))=x$, dus $g(f(x))=g(x)=x$, tegenspraak. Dus als $x$ een dekpunt van $f \\circ g$ is, dan geldt $g(x) \\neq x$. Noem nu $y=g(x)$. Dan is $f(y)=f(g(x))=x$, dus $g(f(y))=g(x)=y$, dus $y$ is een dekpunt van $g \\circ f$. Bij elk dekpunt $x$ van $f \\circ g$ hoort dus een dekpunt $y=g(x)$ van $g \\circ f$. Analoog hoort bij dat dekpunt $y$ van $g \\circ f$ ook weer een dekpunt $x^{\\prime}=f(y)$ van $f \\circ g$; bovendien geldt $x^{\\prime}=x$ want we hadden al gezien dat $f(y)=x$. We kunnen dus de getallen in $S_{n}$ opdelen in paren $(x, y)$ waarbij $x$ een dekpunt van $f \\circ g$ is en $y$ een dekpunt van $g \\circ f$ en waarvoor geldt $x \\neq y$. Het aantal elementen van $S_{n}$ moet dus even zijn, dus $n$ is even. Voor even $n$ kunnen we vervolgens net als in oplossing I laten zien dat zulke functies bestaan.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Gegeven is een positief geheel getal $n$. Bepaal de maximale waarde van $\\operatorname{ggd}(a, b)+\\operatorname{ggd}(b, c)+\\operatorname{ggd}(c, a)$, onder de voorwaarde dat $a, b$ en $c$ positieve gehele getallen zijn met $a+b+c=5 n$.", "solution": "Schrijf $G=\\operatorname{ggd}(a, b)+\\operatorname{ggd}(b, c)+\\operatorname{ggd}(c, a)$. Zonder verlies van algemeenheid nemen we aan dat $a \\leq b \\leq c$. Nu geldt $\\operatorname{ggd}(a, b) \\leq a, \\operatorname{ggd}(b, c) \\leq b$ en $\\operatorname{ggd}(c, a) \\leq a$. Dus\n\n$$\nG \\leq a+b+a \\leq a+b+c=5 n\n$$\n\nAls $3 \\mid n$, dan is $G=5 n$ haalbaar, namelijk met $a=b=c=\\frac{5}{3} n$. Alle drie de ggd's zijn dan gelijk aan $\\frac{5}{3} n$, dus $G=3 \\cdot \\frac{5}{3} n=5 n$.\nStel nu verder dat $3 \\nmid n$. Dan weten we dat $a, b$ en $c$ niet allemaal gelijk kunnen zijn. We onderscheiden een aantal gevallen:\n\nGeval 1a: $b=c$ en $b \\leq 2 n$. Omdat nu $a \\neq b$, geldt $\\operatorname{ggd}(a, b)=\\operatorname{ggd}(a, b-a) \\leq b-a$. Dus $G \\leq(b-a)+b+a=2 b \\leq 4 n$.\n\nGeval 1b: $b=c$ en $b>2 n$. Er geldt $a+2 b=5 n$, dus $a=5 n-2 b$, waaruit volgt dat $G \\leq a+b+a=10 n-4 b+b=10 n-3 b<10 n-6 n=4 n$.\n\nGeval 2a: $b \\neq c$ en $c-a \\geq n$. Nu geldt $G \\leq a+b+a=(a+b+c)-(c-a)=5 n-(c-a) \\leq$ $5 n-n=4 n$.\n\nGeval 2b: $b \\neq c$ en $c-a<n$. Omdat $a \\leq b \\leq c$ geldt nu ook $c-b<n$. Verder is $b \\neq c$ en dus ook $a \\neq c$. Dus $\\operatorname{ggd}(c, a)=\\operatorname{ggd}(c-a, a) \\leq c-a<n$ en $\\operatorname{ggd}(b, c)=\\operatorname{ggd}(b, c-b) \\leq c-b<n$. Daarnaast is $a \\leq \\frac{5 n}{3}$. We conluderen dat $G<\\frac{5 n}{3}+n+n<4 n$.\n\nWe zien dat in alle gevallen $G \\leq 4 n$. De waarde $G=4 n$ is haalbaar met $a=n, b=2 n$ en $c=2 n$, want dan geldt $\\operatorname{ggd}(a, b)=\\operatorname{ggd}(c, a)=n$ en $\\operatorname{ggd}(b, c)=2 n$.\nDus de maximale waarde van $G$ is $5 n$ als $3 \\mid n$ en $4 n$ als $3 \\nmid n$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Gegeven is een positief geheel getal $n$. Bepaal de maximale waarde van $\\operatorname{ggd}(a, b)+\\operatorname{ggd}(b, c)+\\operatorname{ggd}(c, a)$, onder de voorwaarde dat $a, b$ en $c$ positieve gehele getallen zijn met $a+b+c=5 n$.", "solution": "We bewijzen op een alternatieve manier dat $G \\leq 4 n$ voor het geval $3 \\nmid n$. We nemen hier in eerste instantie niet aan dat $a \\leq b \\leq c$. We onderscheiden twee gevallen.\n\nGeval 1: twee van $a, b$ en $c$ zijn gelijk, zeg $a=b$. Schrijf $d=\\operatorname{ggd}(a, c)$. Dan geldt $G=a+d+d$. Verder is $5 n=a+b+c=2 a+c$. Omdat $d \\mid a$ en $d \\mid c$ geldt ook $d \\mid 5 n$ en bovendien $3 d \\leq 2 a+c=5 n$. Er is dus een $k \\geq 3$ met $k d=5 n$. Maar $3 \\nmid n$, dus $k=3$ kan niet. We onderscheiden nu weer twee gevallen:\n\nGeval 1a: $k=4$. Dan is $4 d=5 n=2 a+c$, terwijl $a$ en $c$ beide veelvouden van $d$ zijn. Dan geldt $a<2 d$, dus $a=d$. We vinden nu $G=a+2 d=3 d=\\frac{3}{4} \\cdot 5 n=\\frac{15}{4} n<4 n$.\nGeval 1b: $k \\geq 5$. Dan geldt $5 n=k d \\geq 5 d$, dus $n \\geq d$. Verder is $c \\geq d$, dus $G=a+2 d=$ $\\frac{5 n-c}{2}+2 d \\leq \\frac{5 n-d}{2}+2 d=\\frac{5}{2} n+\\frac{3}{2} d \\leq \\frac{5}{2} n+\\frac{3}{2} n=4 n$.\n\nGeval 2: $a, b$ en $c$ zijn allemaal verschillend. Neem zonder verlies van algemeenheid aan dat $a<b<c$. Er geldt nu $\\operatorname{ggd}(a, b) \\leq \\frac{b}{2}, \\operatorname{ggd}(b, c) \\leq \\frac{c}{2}$ en $\\operatorname{ggd}(c, a) \\leq a$, dus $6 G \\leq 3 b+3 c+6 a<3 b+3 c+4 a+b+c=4 a+4 b+4 c=20 n$, dus $G<\\frac{20 n}{6}<4 n$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Gegeven is een driehoek $A B C$. Op zijde $A C$ liggen punten $D$ en $E$ zodat de volgorde van punten op deze lijn $A, E, D, C$ is. De lijn door $E$ evenwijdig aan $B C$ snijdt de omgeschreven cirkel van $\\triangle A B D$ in een punt $F$, waarbij $E$ en $F$ aan weerszijden van $A B$ liggen. De lijn door $E$ evenwijdig aan $A B$ snijdt de omgeschreven cirkel van $\\triangle B C D$ in een punt $G$, waarbij $E$ en $G$ aan weerszijden van $B C$ liggen. Bewijs dat $D E F G$ een koordenvierhoek is.\n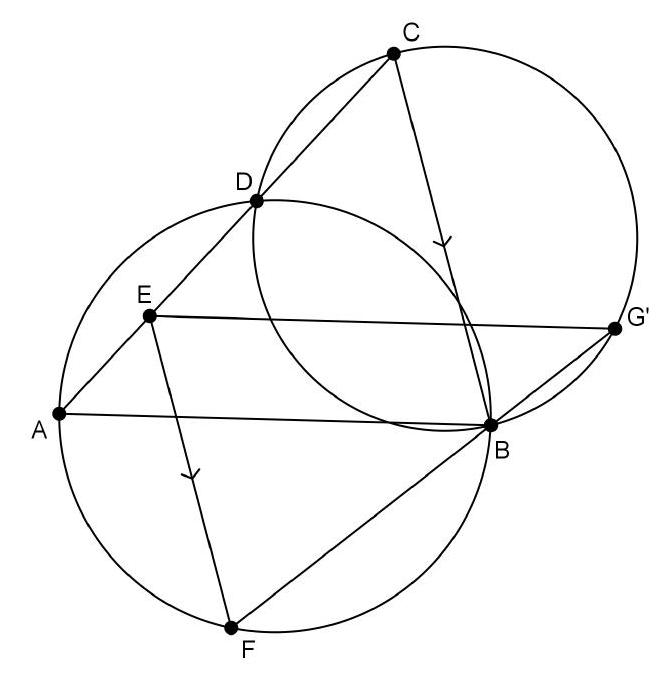", "solution": "Zij $G^{\\prime}$ het snijpunt van de lijn $B F$ en de omgeschreven cirkel van $\\triangle B C D$. We bewijzen dat $D E F G^{\\prime}$ een koordenvierhoek is en vervolgens dat $G=G^{\\prime}$, waarmee het bewijs compleet is.\nWegens $E F \\| B C$ geldt $180^{\\circ}-\\angle D E F=\\angle A E F=\\angle A C B$ en vanwege koordenvierhoek $B D C G^{\\prime}$ is $\\angle A C B=\\angle D C B=\\angle D G^{\\prime} B=\\angle D G^{\\prime} F$, dus $180^{\\circ}-\\angle D E F=\\angle D G^{\\prime} F$. Hieruit volgt dat $D E F G^{\\prime}$ een koordenvierhoek is. Dit betekent dat $\\angle D E G^{\\prime}=\\angle D F G^{\\prime}=\\angle D F B$. Vanwege koordenvierhoek $A D B F$ geldt $\\angle D F B=\\angle D A B$, dus $\\angle D E G^{\\prime}=\\angle D A B$, wat betekent dat $E G^{\\prime} \\| A B$. Omdat $G^{\\prime}$ ook op de omgeschreven cirkel van $\\triangle B C D$ ligt, moet nu $G=G^{\\prime}$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Op een middelbare school zit in elke klas een oneven aantal leerlingen. Verder heeft elke leerling een beste vriend (mogelijk uit een andere klas). Iedereen is de beste vriend van zijn of haar beste vriend. Bij de stedenreis gaat elke leerling naar Rome of Parijs. Bewijs dat de leerlingen over de twee bestemmingen kunnen worden verdeeld zodat\n(i) iedere leerling samen met zijn beste vriend op stedenreis gaat;\n(ii) voor iedere klas het absolute verschil tussen het aantal leerlingen dat naar Rome gaat en het aantal leerlingen dat naar Parijs gaat gelijk is aan 1.", "solution": "Noem een losse leerling een leerling van wie de beste vriend in een andere klas zit. We gaan nu eerst alle losse leerlingen een bestemming geven. Begin met een willekeurige losse leerling $A_{1}$ en stuur deze naar Parijs samen met zijn beste vriend $A_{2}$. Kies in de klas van $A_{2}$ een andere losse leerling $A_{3}$ (als dat mogelijk is) en stuur deze naar Rome samen met zijn beste vriend $A_{4}$. Ga nu verder in de klas van leerling $A_{4}$, enzovoorts. Preciezer: als we leerlingen $A_{1}$ tot en met $A_{2 k}$ gekozen hebben met $k \\geq 1$, dan kiezen we in de klas van $A_{2 k}$ nog een nieuwe losse leerling $A_{2 k+1}$ (als dat kan) en sturen deze naar de andere bestemming dan $A_{2 k}$, samen met zijn beste vriend $A_{2 k+2}$. Zo gaan we door totdat we bij een $k \\geq 1$ komen waarvoor er in de klas van $A_{2 k}$ geen losse leerlingen meer zijn die nog niet gekozen zijn. We gaan dan verder in de klas van $A_{1}$ en kiezen daar nog een nieuwe losse leerling $A_{0}$ (als dat kan), die samen met zijn beste vriend $A_{-1}$ naar Rome gaat (want $A_{1}$ ging naar Parijs). Zo breiden we de keten ook in deze richting uit, totdat we bij een $m \\leq 0$ komen waarvoor in de klas van $A_{2 m+1}$ geen losse leerlingen meer zijn die nog niet gekozen zijn. Merk op dat dit niet opnieuw klas $A_{2 k}$ kan zijn, want daar waren geen losse leerlingen meer. We hebben nu leerlingen $A_{2 m+1}, A_{2 m+2}, \\ldots, A_{2 k-1}, A_{2 k}$ zodat steeds $A_{2 i-1}$ en $A_{2 i}$ beste vrienden zijn en zodat steeds $A_{2 i}$ en $A_{2 i+1}$ in dezelfde klas zitten maar niet naar dezelfde bestemming gaan. In elke klas behalve de klas van $A_{2 m+1}$ en die van $A_{2 k}$ hebben nu evenveel leerlingen bestemming Parijs als bestemming Rome gekregen. In de klas van $A_{2 m+1}$ en van $A_{2 k}$ gaat één leerling meer naar de ene bestemming dan naar de andere, maar in deze klassen hebben we alle losse leerlingen al een bestemming gegeven. We herhalen dit proces totdat alle losse leerlingen een bestemming hebben. Alle leerlingen zonder bestemming hebben nu een beste vriend in hun eigen klas, dus in elke klas is nog een even aantal leerlingen zonder bestemming en heeft een oneven aantal leerlingen een bestemming gekregen. Dan moet elke klas een keer als einde van een keten voorgekomen zijn (en dat was meteen de laatste keer dat deze klas in een keten zat). In elke klas is er\ndaarom precies één losse leerling meer voor de ene bestemming dan voor de andere. Bekijk nu een willekeurige klas en zeg dat er één losse leerling meer naar Parijs gaat dan naar Rome. We geven nu bestemmingen aan de leerlingen in de klas die met hun beste vriend in dezelfde klas zitten. Als er een even aantal van dit soort paren is, sturen we de helft van de paren naar Parijs en de andere helft naar Rome. Als er een oneven aantal van dit soort paren is, sturen we één paar meer naar Rome dan naar Parijs. Omdat van de losse leerlingen juist één leerling meer naar Parijs ging, gaat nu in totaal in deze klas één leerling meer naar Rome. We zien dat in alle gevallen het verschil tussen het aantal Parijsgangers en het aantal Romegangers in een klas in absolute waarde gelijk aan 1 is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Bepaal alle viertallen $(a, b, c, d)$ van positieve reële getallen die voldoen aan $a+b+c+d=1$ en\n\n$$\n\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right) \\cdot \\max \\left(\\frac{c^{2}}{d}, \\frac{d^{2}}{c}\\right)=(\\min (a+b, c+d))^{4}\n$$", "solution": "Als $a \\geq b$ dan $\\frac{a}{b} \\geq \\frac{b}{a}$ en als juist $a \\leq b$ dan $\\frac{a}{b} \\leq \\frac{b}{a}$, dus het rijtje $(a, b)$ en het rijtje $\\left(\\frac{a}{b}, \\frac{b}{a}\\right)$ zijn gelijk geordend. De herschikkingsongelijkheid zegt nu dat\n\n$$\na \\cdot \\frac{a}{b}+b \\cdot \\frac{b}{a} \\geq a \\cdot \\frac{b}{a}+b \\cdot \\frac{a}{b}\n$$\n\nWe kunnen dit herschrijven tot $\\frac{a^{2}}{b}+\\frac{b^{2}}{a} \\geq a+b$. Als we dit combineren met $\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right) \\geq$ $\\frac{\\frac{a^{2}}{b}+\\frac{b^{2}}{a}}{2}$, dan zien we\n\n$$\n\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right) \\geq \\frac{a+b}{2} .\n$$\n\nAnaloog geldt ook\n\n$$\n\\max \\left(\\frac{c^{2}}{d}, \\frac{d^{2}}{d}\\right) \\geq \\frac{c+d}{2}\n$$\n\ndus\n\n$$\n\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right) \\cdot \\max \\left(\\frac{c^{2}}{d}, \\frac{d^{2}}{c}\\right) \\geq \\frac{(a+b)(c+d)}{4}\n$$\n\nZonder verlies van algemeenheid nemen we aan dat $\\min (a+b, c+d)=a+b$. Vanwege $a+b+c+d=1$ geldt dan $a+b \\leq \\frac{1}{2}$. Dus\n\n$$\n\\frac{(a+b)(c+d)}{4} \\geq \\frac{1}{4} \\cdot(a+b)^{2} \\geq(a+b)^{2} \\cdot(a+b)^{2}=(a+b)^{4}\n$$\n\nWe concluderen dat\n\n$$\n\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right) \\cdot \\max \\left(\\frac{c^{2}}{d}, \\frac{d^{2}}{c}\\right) \\geq(a+b)^{4}\n$$\n\nGegeven is dat hier juist gelijkheid geldt. Omdat alles positief is, moet dan hiervoor overal ook gelijkheid gelden. In het bijzonder moet $a+b=\\frac{1}{2}$ en verder moet $\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right)=\\frac{\\frac{a^{2}}{b}+\\frac{b^{2}}{a}}{a}$, dus $\\frac{a^{2}}{b}=\\frac{b^{2}}{a}$, waaruit volgt dat $a^{3}=b^{3}$, dus $a=b$. Dat betekent dat $a=b=\\frac{1}{4}$. Omdat $c+d=1-(a+b)=\\frac{1}{2}$ kunnen we op een vergelijkbare manier afleiden dat $c=d=\\frac{1}{4}$.\nHet enige viertal dat kan voldoen, is dus $(a, b, c, d)=\\left(\\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}\\right)$. Dit invullen laat zien dat in de gegeven gelijkheid dan zowel links als rechts $\\frac{1}{16}$ staat, dus dit viertal voldoet.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Bepaal alle viertallen $(a, b, c, d)$ van positieve reële getallen die voldoen aan $a+b+c+d=1$ en\n\n$$\n\\max \\left(\\frac{a^{2}}{b}, \\frac{b^{2}}{a}\\right) \\cdot \\max \\left(\\frac{c^{2}}{d}, \\frac{d^{2}}{c}\\right)=(\\min (a+b, c+d))^{4}\n$$", "solution": "Zonder verlies van algemeenheid nemen we aan dat $a+b \\leq c+d$, aangezien $a$ en $b$ samen te verwisselen zijn met $c$ en $d$ zonder dat de opgave verandert. Ook kunnen\nwe aannemen dat $a \\leq b$ en $c \\leq d$, omdat $a$ en $b$ onderling te verwisselen en zijn en $c$ en $d$ onderling ook. Nu geldt $a^{3} \\leq b^{3}$ dus $\\frac{a^{2}}{b} \\leq \\frac{b^{2}}{a}$, en analoog $\\frac{c^{2}}{d} \\leq \\frac{d^{2}}{c}$. De gegeven gelijkheid wordt nu\n\n$$\n\\frac{b^{2}}{a} \\cdot \\frac{d^{2}}{c}=(a+b)^{4}\n$$\n\nEr geldt $\\frac{b^{2}}{a} \\geq b$ en $\\frac{d^{2}}{c} \\geq d$, dus de linkerkant is minstens $b d$. We gaan nu bewijzen dat $b d \\geq(a+b)^{4}$ is, waaruit dan volgt dat overal gelijkheid moet gelden.\nVanwege $a \\leq b$ geldt $b \\geq \\frac{1}{2}(a+b)$ en analoog is $d \\geq \\frac{1}{2}(c+d)$ en omdat $c+d \\geq a+b$ volgt daaruit $d \\geq \\frac{1}{2}(a+b)$. Verder volgt uit $a+b+c+d=1$ en $a+b \\leq c+d$ dat $a+b \\leq \\frac{1}{2}$, dus\n\n$$\nb d \\geq \\frac{1}{4}(a+b)^{2} \\geq(a+b)^{2}(a+b)^{2}=(a+b)^{4} .\n$$\n\nNu moet dus in alle gebruikte ongelijkheden gelijkheid gelden. In $\\frac{b^{2}}{a} \\geq b$ betekent dat dat $a=b$ en analoog geldt ook $c=d$. En in $a+b \\leq \\frac{1}{2}$ betekent dat $a+b=\\frac{1}{2}$. Dus volgt nu $a=b=\\frac{1}{4}$ en ook $c=d=\\frac{1}{4}$.\nHet enige viertal dat kan voldoen, is dus $(a, b, c, d)=\\left(\\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}\\right)$. Dit invullen laat zien dat in de gegeven gelijkheid dan zowel links als rechts $\\frac{1}{16}$ staat, dus dit viertal voldoet.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek met $O$ het middelpunt van de omgeschreven cirkel. Punt $Q$ ligt op de omgeschreven cirkel van $\\triangle B O C$ zodat $O Q$ een middellijn is. Punt $M$ ligt op $C Q$ en punt $N$ ligt inwendig op lijnstuk $B C$ zodat $A N C M$ een parallellogram is. Bewijs dat de omgeschreven cirkel van $\\triangle B O C$ en de lijnen $A Q$ en $N M$ door één punt gaan.\n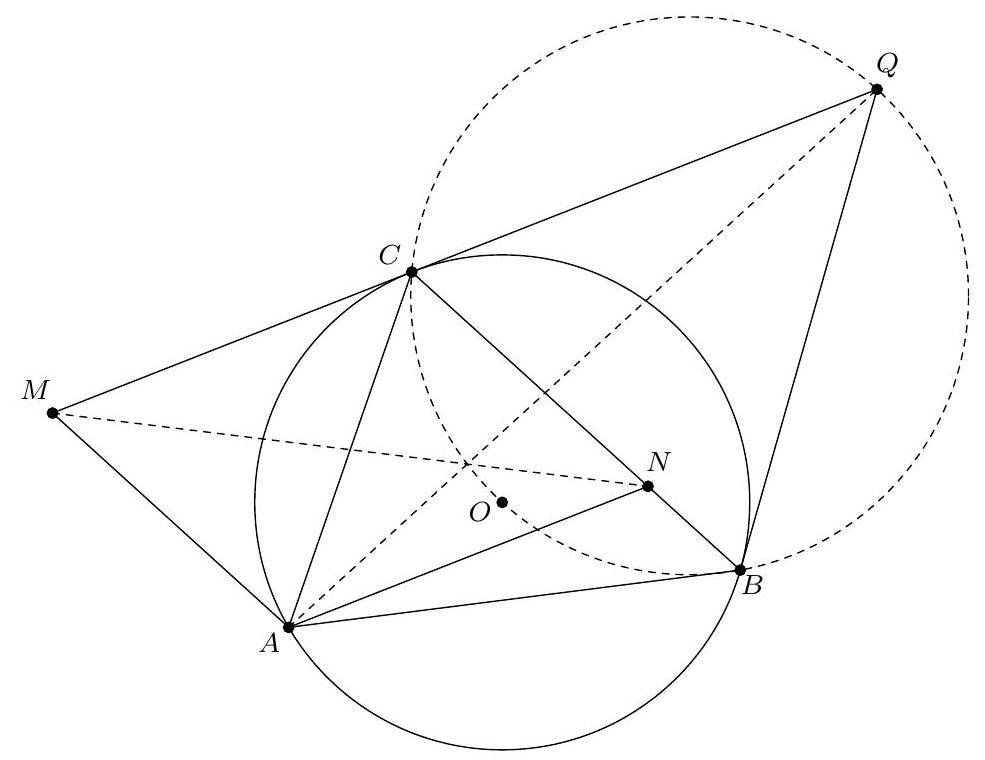", "solution": "Definieer $T$ als het snijpunt van de omgeschreven cirkel van $\\triangle B O C$ en de lijn $A Q$. We gaan bewijzen dat $T$ op $N M$ ligt. Schrijf $\\alpha=\\angle B A C$. Dan geldt $\\angle B O C=2 \\alpha$ vanwege de middelpuntsomtrekshoekstelling. Aangezien $|O B|=|O C|$ en $\\angle O C Q=90^{\\circ}=$ $\\angle O B Q$ wegens Thales, geldt $\\triangle O B Q \\cong \\triangle O C Q$ (ZZR). Dus geldt $\\angle C O Q=\\angle B O Q=\\alpha$. Vanwege parallellogram $A N C M$ geldt $\\angle A M C=180^{\\circ}-\\angle M C N=\\angle Q C N=\\angle Q C B=$ $\\angle Q O B=\\alpha$, dus ook $\\angle C N A=\\angle A M C=\\alpha$. Nu zien we dat $\\angle Q T B=\\angle Q O B=\\alpha=$ $\\angle C N A$, waaruit volgt dat $\\angle A T B=180^{\\circ}-\\angle Q T B=180^{\\circ}-\\angle C N A=\\angle A N B$. Dit betekent dat $A T N B$ een koordenvierhoek is. Ook is $A T C M$ een koordenvierhoek omdat $\\angle A M C=\\alpha=\\angle C O Q=\\angle C T Q=180^{\\circ}-\\angle A T C$.\nKoordenvierhoek $A T C M$ geeft $\\angle A T M=\\angle A C M=180^{\\circ}-\\angle Q C B-\\angle B C A$ vanwege de gestrekte hoek bij $C$. We weten $\\angle Q C B=\\angle Q O B=\\alpha=\\angle C A B$, dus met een hoekensom in driehoek $A B C$ krijgen we $\\angle A T M=180^{\\circ}-\\angle C A B-\\angle B C A=\\angle A B C$. Nu gebruiken we koordenvierhoek $A T N B$ om te vinden dat $\\angle A B C=\\angle A B N=180^{\\circ}-\\angle A T N$, zodat al met al geldt $\\angle A T M=180^{\\circ}-\\angle A T N$. Dit betekent dat $M, T$ en $N$ op een lijn liggen, zoals we wilden bewijzen.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ die voldoen aan\n\n- $f(p)>0$ voor alle priemgetallen $p$,\n- $p \\mid(f(x)+f(p))^{f(p)}-x$ voor alle $x \\in \\mathbb{Z}$ en alle priemgetallen $p$.", "solution": "Vul $x=p$ in: $p \\mid(2 f(p))^{f(p)}-p$ en $p$ is priem, dus $p \\mid 2 f(p)$. We zien dat $p=2$ of $p \\mid f(p)$. Vul nu $x=0$ in: $p \\mid(f(0)+f(p))^{f(p)}-0$ en $p$ is priem, dus $p \\mid f(0)+f(p)$. Aangezien $p \\mid f(p)$ voor $p \\neq 2$, zien we nu ook $p \\mid f(0)$ voor $p \\neq 2$. Dus $f(0)$ is deelbaar door oneindig veel priemgetallen en moet daarom wel 0 zijn. Nu volgt uit $2 \\mid f(0)+f(2)$ ook dat $2 \\mid f(2)$, dus $p \\mid f(p)$ voor alle priemgetallen $p$.\nDe gegeven deelrelatie laat zich nu vertalen tot $f(x)^{f(p)} \\equiv x \\bmod p$ voor alle gehele getallen $x$ en priemgetallen $p$. We zien dat $p \\mid f(x)$ dan en slechts dan als $p \\mid x$. Als we dit nu toepassen voor $x=q$ met $q$ een priemgetal ongelijk aan $p$, dan zien we dat $f(q)$ door geen enkele $p \\neq q$ deelbaar is en dus wel een macht van $q$ moet zijn. De kleine stelling van Fermat zegt voor alle priemgetallen $p$ en gehele getallen $n$ dat $n^{p} \\equiv n \\bmod p$, dus ook $n^{p^{t}} \\equiv n \\bmod p$ voor alle positieve gehele $t$. Nu is $f(p)$ voor alle priemgetallen $p$ van de vorm $p^{t}$ met $t$ positief geheel, dus uit de gegeven deelrelatie kunnen we nu concluderen dat $f(x) \\equiv x \\bmod p$ voor alle gehele getallen $x$ en priemgetallen $p$. Dus $p \\mid f(x)-x$ voor alle $x$ en $p$. Dus voor een vaste $x \\in \\mathbb{Z}$ geldt dat $f(x)-x$ deelbaar is door oneindig veel priemgetallen $p$, waaruit volgt dat $f(x)-x=0$. Dus $f(x)=x$ voor alle $x$.\nWe controleren deze functie. Er geldt inderdaad $f(p)>0$ voor priemgetallen $p$. En verder is\n\n$$\n(f(x)+f(p))^{f(p)}-x=(x+p)^{p}-x \\equiv x^{p}-x \\equiv 0 \\quad \\bmod p\n$$\n\nvoor alle $x \\in \\mathbb{Z}$ en alle priemgetallen $p$. Dus de functie $f(x)=x$ voldoet.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "In koordenvierhoek $A B C D$ is $E$ het snijpunt van de diagonalen. Een lijn door $E$, ongelijk aan $A C$ of $B D$, snijdt $A B$ in $P$ en $B C$ in $Q$. De cirkel die raakt aan $P Q$ in $E$ en verder door $D$ gaat, snijdt de omgeschreven cirkel van $A B C D$ nogmaals in punt $R$. Bewijs dat $B, P, R$ en $Q$ op een cirkel liggen.\n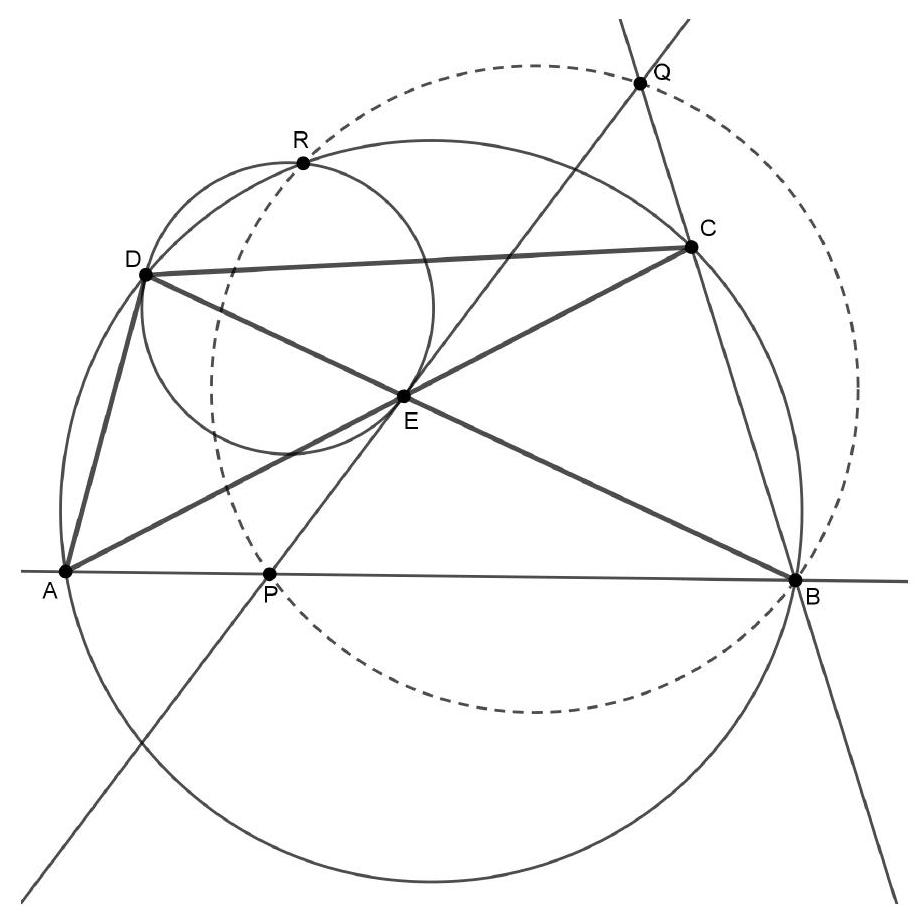\n\nWe bekijken de configuratie waar $P$ inwendig op $A B$ ligt en $Q$ uitwendig op $B C$; andere configuraties gaan analoog.", "solution": "Vanwege koordenvierhoek $D B C R$ geldt $\\angle Q C R=180^{\\circ}-\\angle B C R=\\angle B D R$. Omdat $E Q$ raakt aan de cirkel door $E, D$ en $R$ geldt $\\angle B D R=\\angle E D R=\\angle Q E R$, dus $\\angle Q C R=\\angle Q E R$. Dit betekent dat $E R Q C$ een koordenvierhoek is. Analoog is ook $E P A R$ een koordenvierhoek.\nWe vinden nu $\\angle P R Q=\\angle P R E+\\angle E R Q=\\angle P A E+180^{\\circ}-\\angle E C Q=\\angle B A E+\\angle E C B$. Vanwege de hoekensom in $\\triangle A B C$ is dit gelijk aan $180^{\\circ}-\\angle A B C=180^{\\circ}-\\angle P B Q$. Dus $\\angle P R Q=180^{\\circ}-\\angle P B Q$ en daaruit volgt dat $B P R Q$ een koordenvierhoek is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "In koordenvierhoek $A B C D$ is $E$ het snijpunt van de diagonalen. Een lijn door $E$, ongelijk aan $A C$ of $B D$, snijdt $A B$ in $P$ en $B C$ in $Q$. De cirkel die raakt aan $P Q$ in $E$ en verder door $D$ gaat, snijdt de omgeschreven cirkel van $A B C D$ nogmaals in punt $R$. Bewijs dat $B, P, R$ en $Q$ op een cirkel liggen.\n\n\nWe bekijken de configuratie waar $P$ inwendig op $A B$ ligt en $Q$ uitwendig op $B C$; andere configuraties gaan analoog.", "solution": "Analoog aan oplossing I bewijzen we dat $E P A R$ een koordenvierhoek is. (In deze oplossing hebben we koordenvierhoek $E R Q C$ niet nodig.) We vinden nu $\\angle B R P=$ $\\angle B R A-\\angle P R A=\\angle B C A-\\angle P E A=\\left(180^{\\circ}-\\angle Q C E\\right)-\\left(180^{\\circ}-\\angle Q E A\\right)=\\angle Q E A-\\angle Q C E$. Vanwege de buitenhoekstelling in driehoek $Q C E$ is dit gelijk aan $\\angle E Q C=\\angle P Q B$. Dus $\\angle B R P=\\angle P Q B$, waaruit volgt dat $B P R Q$ een koordenvierhoek is.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Zij $n$ een positief geheel getal. Bewijs dat $n^{2}+n+1$ niet te schrijven is als het product van twee positieve gehele getallen die minder dan $2 \\sqrt{n}$ van elkaar verschillen.", "solution": "Stel dat $a$ en $b$ positieve gehele getallen zijn met $a b=n^{2}+n+1$. We gaan bewijzen dat $|a-b| \\geq 2 \\sqrt{n}$. Merk op dat $(a-b)^{2} \\geq 0$. Aan beide kanten $4 a b$ optellen geeft\n\n$$\n(a+b)^{2}=(a-b)^{2}+4 a b \\geq 4 a b=4 n^{2}+4 n+4>4 n^{2}+4 n+1=(2 n+1)^{2} .\n$$\n\nOmdat $(a+b)^{2}$ een kwadraat is, geldt $(a+b)^{2} \\geq(2 n+2)^{2}$. Dan volgt\n\n$$\n(a-b)^{2}=(a+b)^{2}-4 a b \\geq(2 n+2)^{2}-4\\left(n^{2}+n+1\\right)=4 n\n$$\n\ndus $|a-b| \\geq 2 \\sqrt{n}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Zij $n$ een positief geheel getal. Bewijs dat $n^{2}+n+1$ niet te schrijven is als het product van twee positieve gehele getallen die minder dan $2 \\sqrt{n}$ van elkaar verschillen.", "solution": "Stel dat $n^{2}+n+1$ het product van twee positieve gehele getallen is en noem de kleinste $n-a$ met $a$ geheel. Omdat $(n+1)^{2}=n^{2}+2 n+1>n^{2}+n+1$, is $n-a \\leq n$, dus $a \\geq 0$. Nu geldt $(n-a)(n+a+1)=n^{2}+n-a(a+1)<n^{2}+n+1$, dus dit product is te klein; de tweede factor is daarom minstens $n+a+2$. Als $n>(a+1)^{2}$ geldt\n\n$$\n\\begin{gathered}\n(n-a)(n+a+2)=n^{2}+2 n-a(a+2)>n^{2}+n+(a+1)^{2}-a(a+2) \\\\\n=n^{2}+n+a^{2}+2 a+1-a^{2}-2 a=n^{2}+n+1,\n\\end{gathered}\n$$\n\ndus dit product is al te groot, tegenspraak. Er geldt dus $n \\leq(a+1)^{2}$, wat te schrijven is als $a+1 \\geq \\sqrt{n}$. Het verschil tussen de twee factoren is dan minstens\n\n$$\n(n+a+2)-(n-a)=2 a+2 \\geq 2 \\sqrt{n}\n$$", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Zij $n$ een positief geheel getal. Bewijs dat $n^{2}+n+1$ niet te schrijven is als het product van twee positieve gehele getallen die minder dan $2 \\sqrt{n}$ van elkaar verschillen.", "solution": "Stel dat $a$ en $b$ positieve gehele getallen zijn met $a b=n^{2}+n+1$. We gaan bewijzen dat $|a-b| \\geq 2 \\sqrt{n}$. Neem zonder verlies van algemeenheid aan dat $b$ de kleinste is. Omdat $(n+1)^{2}=n^{2}+2 n+1>n^{2}+n+1$, is $b \\leq n$. Schrijf $b=n+1-c$ met $c \\geq 1$ geheel. Modulo $b$ geldt nu $n \\equiv c-1$. Dus\n\n$$\nn^{2}+n+1 \\equiv(c-1)^{2}+(c-1)+1=c^{2}-2 c+1+c-1+1=c^{2}-c+1 \\bmod b .\n$$\n\nAnderzijds is $b$ een deler van $n^{2}+n+1$, dus geldt $n^{2}+n+1 \\equiv 0 \\bmod b$. Dus $c^{2}-c \\equiv-1$ $\\bmod b$. Maar de linkerkant is niet-negatief want $c \\geq 1$, dus het is minstens gelijk aan $-1+b=-1+(n+1-c)=n-c$. Dus $c^{2}-c \\geq n-c$, waaruit volgt dat $c^{2} \\geq n$, dus $c \\geq \\sqrt{n}$.\nMerk nu op dat $n^{2}+n+1=(n-\\sqrt{n}+1)(n+\\sqrt{n}+1)$. We weten nu $b=n+1-c \\leq n-\\sqrt{n}+1$, dus $a \\geq n+\\sqrt{n}+1$. Het verschil tussen de twee factoren is daarom minstens $2 \\sqrt{n}$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing III."}
|
| 6 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ die voldoen aan de volgende twee voorwaarden:\n(i) voor alle gehele getallen $x$ geldt $f(f(x))=x$;\n(ii) voor alle gehele getallen $x$ en $y$ zodat $x+y$ oneven is geldt er dat $f(x)+f(y) \\geq x+y$.", "solution": "De functie $f(x)=x$ voor alle $x$ voldoet. Neem nu verder aan dat niet voor alle $x$ geldt $f(x)=x$. Vanwege (i) is er dan zowel een waarde van $x$ met $f(x)>x$ als een waarde van $x$ met $f(x)<x$. We nemen nu een $a \\in \\mathbb{Z}$ met $f(a)<a$ en bekijken een willekeurige $x$ met $x \\not \\equiv a \\bmod 2$. Er geldt dat $f(x)+f(a) \\geq x+a$, dus $f(x) \\geq x+a-f(a)>x$. Schrijf $w=f(x)$, dan geldt $f(w)=f(f(x))=x<f(x)=w$. Als $w \\not \\equiv a \\bmod 2$, zou juist $f(w)>w$, tegenspraak. Dus $f(x)=w \\equiv a \\bmod 2$ en dus ook $f(x) \\not \\equiv x$.\nNeem nu een $x_{1}$ en een $x_{2}$ die beide niet dezelfde pariteit als $a$ hebben. Dan hebben ze beide ook niet dezelfde pariteit als hun functiewaarden, dus $x_{1}+f\\left(x_{2}\\right)$ en $x_{2}+f\\left(x_{1}\\right)$ zijn oneven. Door $x=x_{1}, y=f\\left(x_{2}\\right)$ en ook $x=x_{2}, y=f\\left(x_{1}\\right)$ in te vullen, zien we dat\n\n$$\nf\\left(x_{1}\\right)+x_{2}=f\\left(x_{1}\\right)+f\\left(f\\left(x_{2}\\right)\\right) \\geq x_{1}+f\\left(x_{2}\\right)=f\\left(f\\left(x_{1}\\right)\\right)+f\\left(x_{2}\\right) \\geq f\\left(x_{1}\\right)+x_{1}\n$$\n\nEr moet nu overal gelijkheid gelden, dus $f\\left(x_{1}\\right)+x_{2}=x_{1}+f\\left(x_{2}\\right)$. Fixeer $x_{1}$ en schrijf $c=f\\left(x_{1}\\right)-x_{1}$, dan geldt $f\\left(x_{2}\\right)=x_{2}+c$ voor alle $x_{2}$ die niet dezelfde pariteit hebben als $a$. We weten verder dat $c$ oneven is. Schrijf $z=x_{2}+c$, dan kan $z$ alle mogelijke waarden aannemen die niet dezelfde pariteit hebben als $x_{2}$ en dus wel dezelfde als $a$. Er geldt\n\n$$\nf(z)=f\\left(x_{2}+c\\right)=f\\left(f\\left(x_{2}\\right)\\right)=x_{2}=z-c\n$$\n\nSchrijf nu $d=c$ als $a$ oneven en $d=-c$ als $a$ even, dan voldoet de functie aan\n\n$$\nf(x)= \\begin{cases}x+d & \\text { als } x \\text { even } \\\\ x-d & \\text { als } x \\text { oneven }\\end{cases}\n$$\n\nWe controleren nu functies van deze vorm voor een willekeurige oneven $d$. We zien dat $f(x)$ en $x$ nooit dezelfde pariteit hebben, dus $f(f(x))=x+d-d=x$, waarmee aan (i) voldaan wordt. Verder geldt als $x+y$ oneven is dat $x$ en $y$ verschillende pariteiten hebben, dus $f(x)+f(y)=x+y+d-d=x+y \\geq x+y$, waarmee ook aan (ii) voldaan wordt. We concluderen dat de functies van deze vorm samen met de functie $f(x)=x$ voor alle $x$ de oplossingen zijn.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Aan een wiskundewedstrijd doen 300 deelnemers mee. Na de wedstrijd spelen sommige deelnemers wat potjes schaak. Elke twee deelnemers spelen hooguit één keer tegen elkaar. Er zijn geen drie deelnemers bij deze wedstrijd die onderling allemaal tegen elkaar schaken. Bepaal de maximale $n$ waarvoor het mogelijk is dat aan de volgende voorwaarden tegelijk voldaan wordt: elke deelnemer speelt hooguit $n$ potjes schaak, en voor elke $m$ met $1 \\leq m \\leq n$ is er een deelnemer die precies $m$ potjes schaak speelt.", "solution": "We laten zien dat $n$ maximaal 200 is. We geven eerst een voorbeeld waarin $n=200$ geldt. Bekijk spelers $A_{1}, A_{2}, \\ldots, A_{200}$ en $B_{1}, B_{2}, \\ldots, B_{100}$. Dit zijn 300 spelers in totaal. Laat $B_{i}$ schaak spelen tegen de spelers $A_{j}$ met $1 \\leq j \\leq i+100$, terwijl verder geen andere deelnemers tegen elkaar schaken. Dan schaakt $B_{i}$ tegen precies $100+i$ andere deelnemers, dus voor $101 \\leq m \\leq 200$ is er een deelnemer die precies $m$ potjes schaak speelt. Verder schaakt $A_{j}$ voor $j>100$ tegen de deelnemers $B_{i}$ met $i \\geq j-100$; dat zijn er $100-(j-101)=201-j$. Omdat $j$ hier kan variëren van 101 tot en met 200, varieert dit getal van 100 tot en met 1 . Voor $1 \\leq m \\leq 100$ is er dus ook een deelnemer die precies $m$ potjes schaak speelt. Ten slotte schaakt $A_{j}$ voor $j \\leq 100$ tegen alle $B_{i}$; dat zijn er 100. Er zijn dus geen deelnemers die meer dan 200 potjes schaak spelen. We zien dat dit voorbeeld aan de eisen voldoet voor $n=200$.\nNu bewijzen we dat $n>200$ niet kan. Dit doen we uit het ongerijmde, dus stel dat $n>200$. Dan is er in elk geval een deelnemer $A$ die precies 201 potjes schaak speelt, tegen spelers $B_{1}, B_{2}, \\ldots, B_{201}$. Er zijn in totaal 300 deelnemers, dus naast hen en $A$ zijn er nog $300-1-201=98$ andere deelnemers, die we $C_{1}, \\ldots, C_{98}$ noemen. Als een deelnemer $B_{i}$ schaakt tegen een andere deelnemer $B_{j}$, vormen zij samen met $A$ een drietal dat onderling drie potjes schaakt; dat mag niet. Dus $B_{i}$ schaakt niet tegen een andere deelnemer $B_{j}$. Hij speelt dus hooguit $1+98=99$ potjes schaak. Dat betekent dat de deelnemers die tegen precies $m$ andere deelnemers schaken met $100 \\leq m \\leq 200$ allemaal onder de deelnemers $C_{i}$ te vinden moeten zijn. Echter, dat zijn maar 98 verschillende mensen, tegenspraak. We concluderen dat $n>200$ niet kan en dat dus $n=200$ maximaal is.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Voor een geheel getal $n \\geq 3$ bekijken we een cirkel met $n$ punten erop. We plaatsen een positief geheel getal bij elk punt, waarbij de getallen niet noodzakelijk verschillend hoeven te zijn. Zo'n plaatsing van getallen heet stabiel als drie getallen naast elkaar altijd product $n$ hebben. Voor hoeveel waarden van $n$ met $3 \\leq n \\leq 2020$ is het mogelijk om getallen op een stabiele manier te plaatsen?", "solution": "Stel dat $n$ geen veelvoud van 3 is en dat we een stabiele plaatsing hebben van de getallen $a_{1}, a_{2}, \\ldots, a_{n}$, die in die volgorde op de cirkel liggen. Er geldt dan $a_{i} a_{i+1} a_{i+2}=3$ voor alle $i$, waarbij we de indices modulo $n$ rekenen. Dus\n\n$$\na_{i+1} a_{i+2} a_{i+3}=n=a_{i} a_{i+1} a_{i+2}\n$$\n\nwaaruit volgt dat $a_{i+3}=a_{i}$ (aangezien alle getallen positief zijn). Met inductie vinden we dat voor alle $k \\geq 0$ geheel geldt $a_{3 k+1}=a_{1}$. Omdat $n$ geen drievoud is, nemen de getallen $3 k+1$ voor $k \\geq 0$ alle waarden modulo $n$ aan: immers, 3 heeft een multiplicatieve inverse modulo $n$, dus $k \\equiv 3^{-1} \\cdot(b-1)$ geeft $3 k+1 \\equiv b \\bmod n$ voor alle $b$. We concluderen dat alle getallen op de cirkel gelijk zijn aan $a_{1}$. Er moet dus gelden dat $a_{1}^{3}=n$, waarbij $a_{1}$ positief geheel is. Dus als $n$ geen drievoud is, dan moet $n$ een derdemacht zijn.\n\nAls $n$ een drievoud is, dan zetten we achteraanvolgens de getallen $1,1, n, 1,1, n, \\ldots$ neer op de cirkel. Het product van drie getallen naast elkaar is nu altijd $1 \\cdot 1 \\cdot n=n$. Als $n$ een derdemacht is, zeg $n=m^{3}$, dan zetten we de getallen $m, m, m, \\ldots$ neer op de cirkel. Het product van drie getallen naast elkaar is nu altijd $m^{3}=n$.\n\nWe conluderen dat er een stabiele plaatsing mogelijk is dan en slechts dan als $n$ een drievoud of een derdemacht is. We moeten nu nog dit aantal tellen. De drievouden $n$ met $3 \\leq n \\leq 2020$ zijn $3,6,9, \\ldots, 2019$ en dat zijn er $\\frac{2019}{3}=673$. De derdemachten $n$ met $3 \\leq n \\leq 2020$ zijn $2^{3}, 3^{3}, \\ldots, 12^{3}$, want $12^{3}=1728 \\leq 2020$ en $13^{3}=2197>2020$. Dit zijn 11 derdemachten, waarvan er 4 deelbaar zijn door 3 , dus er zijn 7 derdemachten die geen drievoud zijn. Alles bij elkaar zijn er $673+7=680$ waarden van $n$ die voldoen.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "In een scherphoekige driehoek $A B C$ is $D$ het voetpunt van de hoogtelijn vanuit $A$. Laat $D_{1}$ en $D_{2}$ de spiegelbeelden zijn van $D$ in respectievelijk $A B$ en $A C$. Het snijpunt van $B C$ en de lijn door $D_{1}$ evenwijdig aan $A B$, noemen we $E_{1}$. Het snijpunt van $B C$ en de lijn door $D_{2}$ evenwijdig aan $A C$, noemen we $E_{2}$. Bewijs dat $D_{1}, D_{2}, E_{1}$ en $E_{2}$ op een cirkel liggen waarvan het middelpunt op de omgeschreven cirkel van $\\triangle A B C$ ligt.\n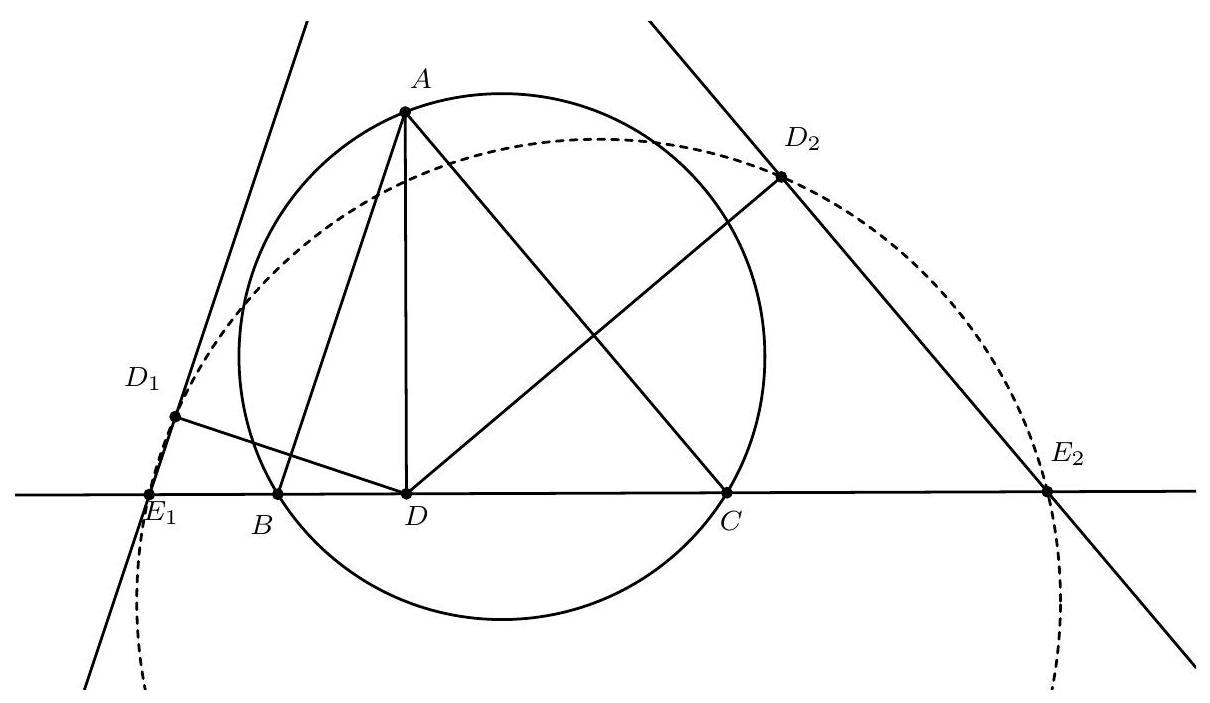", "solution": "Het midden van $D D_{1}$ noemen we $K$ en het midden van $D D_{2}$ noemen we $L$. Dan ligt $K$ op $A B$ en $L$ op $A C$. Wegens $\\angle A K D=90^{\\circ}=\\angle A L D$ is $A K D L$ een koordenvierhoek. Dus $\\angle D L K=\\angle D A K=\\angle D A B=90^{\\circ}-\\angle A B C$. Verder is $K L$ een middenparallel in driehoek $D D_{1} D_{2}$, dus $\\angle D L K=\\angle D D_{2} D_{1}$. We concluderen dat $\\angle D D_{2} D_{1}=90^{\\circ}-\\angle A B C$.\n\nOmdat $A C \\perp D D_{2}$ en $D_{2} E_{2} \\| A C$, geldt $\\angle D D_{2} E_{2}=90^{\\circ}$. Dus $\\angle D_{1} D_{2} E_{2}=\\angle D_{1} D_{2} D+$ $\\angle D D_{2} E_{2}=90^{\\circ}-\\angle A B C+90^{\\circ}=180^{\\circ}-\\angle A B C$. Anderzijds geldt vanwege $D_{1} E_{1} \\| A B$ dat $\\angle D_{1} E_{1} E_{2}=\\angle A B C$, dus we zien $\\angle D_{1} D_{2} E_{2}=180^{\\circ}-\\angle D_{1} E_{1} E_{2}$. We concluderen dat $D_{1} E_{1} E_{2} D_{2}$ een koordenvierhoek is.\n\nNoem nu $M$ het punt zodat $A M$ een middellijn is van de omgeschreven cirkel van $\\triangle A B C$. Wegens Thales geldt dan $\\angle A C M=90^{\\circ}$. Dus $C M \\perp A C$, waaruit volgt dat $C M \\perp D_{2} E_{2}$ en $C M \\| D D_{2}$. Verder is $L$ het midden van $D D_{2}$ en geldt $L C \\| D_{2} E_{2}$, dus $L C$ is een middenparallel in driehoek $D D_{2} E_{2}$. Dit betekent dat $C$ het midden van $D E_{2}$ is. Aangezien $C M \\| D D_{2}$ volgt nu dat $C M$ ook een middenparallel is, dus $C M$ snijdt $D_{2} E_{2}$ middendoor. Omdat ook $C M \\perp D_{2} E_{2}$, is $C M$ de middelloodlijn van $D_{2} E_{2}$. Analoog geldt dat $B M$ de middelloodlijn van $D_{1} E_{1}$ is. Dus $M$ is het snijpunt van de middelloodlijnen van twee van de koorden van de cirkel door $D_{1}, D_{2}, E_{1}$ en $E_{2}$ en is daarmee het middelpunt van deze cirkel.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ die voldoen aan\n\n$$\nf\\left(x^{2} y\\right)+2 f\\left(y^{2}\\right)=\\left(x^{2}+f(y)\\right) \\cdot f(y)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Invullen van $x=1$ geeft $f(y)+2 f\\left(y^{2}\\right)=(1+f(y)) f(y)$, dus\n\n$$\n2 f\\left(y^{2}\\right)=f(y)^{2}\n$$\n\nWe kunnen hiermee in de oorspronkelijke functievergelijking de term $2 f\\left(y^{2}\\right)$ links wegstrepen tegen $f(y)^{2}$ rechts:\n\n$$\nf\\left(x^{2} y\\right)=x^{2} f(y) .\n$$\n\nInvullen van $y=1$ hierin geeft $f\\left(x^{2}\\right)=x^{2} f(1)$ en invullen van $y=-1$ geeft $f\\left(-x^{2}\\right)=$ $x^{2} f(-1)$. Omdat $x^{2}$ alle niet-negatieve getallen aanneemt als $x \\in \\mathbb{R}$, geldt nu\n\n$$\nf(x)= \\begin{cases}c x & \\text { als } x \\geq 0 \\\\ d x & \\text { als } x<0\\end{cases}\n$$\n\nmet $c=f(1)$ en $d=-f(-1)$. Vul nu $y=1$ in bij (1), dat geeft $2 f(1)=f(1)^{2}$, dus $2 c=c^{2}$. Hieruit volgt $c=0$ of $c=2$. Vullen we juist $y=-1$ in bij (1), dan vinden we $2 f(1)=f(-1)^{2}$, dus $2 c=(-d)^{2}$. Voor $c=0$ geeft dit $d=0$ en voor $c=2$ geeft dit $d=2$ of $d=-2$. We hebben dus drie gevallen:\n\n- $c=0, d=0$ : dan is $f(x)=0$ voor alle $x$;\n- $c=2, d=2$ : dan is $f(x)=2 x$ voor alle $x$;\n- $c=2, d=-2$ : dan is $f(x)=2 x$ voor $x \\geq 0$ en $f(x)=-2 x$ voor $x<0$, oftewel $f(x)=2|x|$ voor alle $x$.\n\nMet de eerste functie komt er in de functievergelijking links en rechts 0 , dus deze voldoet. Met de tweede functie komt er in de functievergelijking links $2 x^{2} y+4 y^{2}$ en rechts $\\left(x^{2}+2 y\\right)$. $2 y=2 x^{2} y+4 y^{2}$, dus die functie voldoet. Met de derde functie komt er links $2\\left|x^{2} y\\right|+4\\left|y^{2}\\right|=$ $2 x^{2}|y|+4 y^{2}$ en rechts $\\left(x^{2}+2|y|\\right) \\cdot 2|y|=2 x^{2}|y|+4|y|^{2}=2 x^{2}|y|+4 y^{2}$, dus die functie voldoet ook.\n\nAl met al hebben we drie oplossingen gevonden: $f(x)=0, f(x)=2 x$ en $f(x)=2|x|$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ die voldoen aan\n\n$$\nf\\left(x^{2} y\\right)+2 f\\left(y^{2}\\right)=\\left(x^{2}+f(y)\\right) \\cdot f(y)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Invullen van $y=0$ geeft $f(0)+2 f(0)=\\left(x^{2}+f(0)\\right) f(0)$. Dus $f(0)=0$ of $3=x^{2}+f(0)$ voor alle $x \\in \\mathbb{R}$. Dat laatste kan niet waar zijn, dus $f(0)=0$.\n\nVul nu in $x=0, y=1$. Dan krijgen we $f(0)+2 f(1)=f(1)^{2}$, dus $2 f(1)=f(1)^{2}$, dus $f(1)=0$ of $f(1)=2$. Vervolgens geeft $y=1$ dat $f\\left(x^{2}\\right)+2 f(1)=\\left(x^{2}+f(1)\\right) \\cdot f(1)$, wat met de twee mogelijke waarden van $f(1)$ oplevert:\n\n$$\nf\\left(x^{2}\\right)= \\begin{cases}0 & \\text { als } f(1)=0 \\\\ 2 x^{2} & \\text { als } f(1)=2\\end{cases}\n$$\n\nOmdat $x^{2}$ alle niet-negatieve getallen aanneemt als $x \\in \\mathbb{R}$, zijn nu de functiewaarden van alle niet-negatieve getallen bepaald. Merk op dat de term $2 f\\left(y^{2}\\right)$ in de functievergelijking nu ook voor alle $y$ uitgerekend kan worden.\n\nBekijk nu eerst het geval dat $f(1)=0$. Er geldt dus $f(x)=0$ voor alle $x \\geq 0$. Vul $x=1$ in, dat geeft $f(y)+0=(1+f(y)) f(y)$, dus $0=f(y)^{2}$, dus $f(y)=0$ voor alle $y \\in \\mathbb{R}$. De functie $f(x)=0$ voor alle $x$ voldoet inderdaad aan de functievergelijking en is dus een oplossing.\n\nBekijk nu het geval dat $f(1)=2$. Er geldt dus $f(x)=2 x$ voor alle $x \\geq 0$. Vul $x=1$ in, dat geeft $f(y)+4 y^{2}=(1+f(y)) f(y)$, dus $4 y^{2}=f(y)^{2}$. We vinden nu voor alle $y$ dat $f(y)=2 y$ of $f(y)=-2 y$. Voor $y \\geq 0$ weten we al dat altijd het eerste geldt. We willen nu uitsluiten dat voor $y<0$ allebei de mogelijkheden voorkomen. Neem dus een $a, b<0$ met $a \\neq b$ zodat $f(a)=2 a$ en $f(b)=-2 b$. Kies $y=b$ en $x^{2}=\\frac{a}{b}$, wat kan omdat $\\frac{a}{b}>0$. Dan geldt $x^{2} y=a$, dus invullen in de functievergelijking geeft\n\n$$\n2 a+2 f\\left(b^{2}\\right)=\\left(\\frac{a}{b}-2 b\\right) \\cdot-2 b,\n$$\n\noftewel $2 f\\left(b^{2}\\right)=-4 a+4 b^{2}$. We weten dat $f\\left(b^{2}\\right)$ gelijk is aan $2 b^{2}$, want $f(x)=2 x$ voor $x \\geq 0$. Dus $4 b^{2}=-4 a+4 b^{2}$, oftewel $-4 a=0$, tegenspraak met $a<0$. We concluderen dat ofwel voor alle $y<0$ geldt dat $f(y)=2 y$, ofwel voor alle $y<0$ geldt dat $f(y)=-2 y$.\n\nDat geeft nog twee mogelijke functies: $f(x)=2 x$ voor alle $x$ en $f(x)=2|x|$ voor alle $x$. Met de eerste functie komt er in de functievergelijking links $2 x^{2} y+4 y^{2}$ en rechts $\\left(x^{2}+2 y\\right) \\cdot 2 y=2 x^{2} y+4 y^{2}$, dus die functie voldoet. Met de tweede functie komt er links $2\\left|x^{2} y\\right|+4\\left|y^{2}\\right|=2 x^{2}|y|+4 y^{2}$ en rechts $\\left(x^{2}+2|y|\\right) \\cdot 2|y|=2 x^{2}|y|+4|y|^{2}=2 x^{2}|y|+4 y^{2}$, dus die functie voldoet ook.\n\nAl met al hebben we drie oplossingen gevonden: $f(x)=0, f(x)=2 x$ en $f(x)=2|x|$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Op een cirkel met middelpunt $M$ liggen drie verschillende punten $A, B$ en $C$ zodat $|A B|=|B C|$. Punt $D$ ligt binnen de cirkel op zo'n manier dat $\\triangle B C D$ gelijkzijdig is. Het tweede snijpunt van $A D$ met de cirkel noemen we $F$. Bewijs dat $|F D|=|F M|$.\n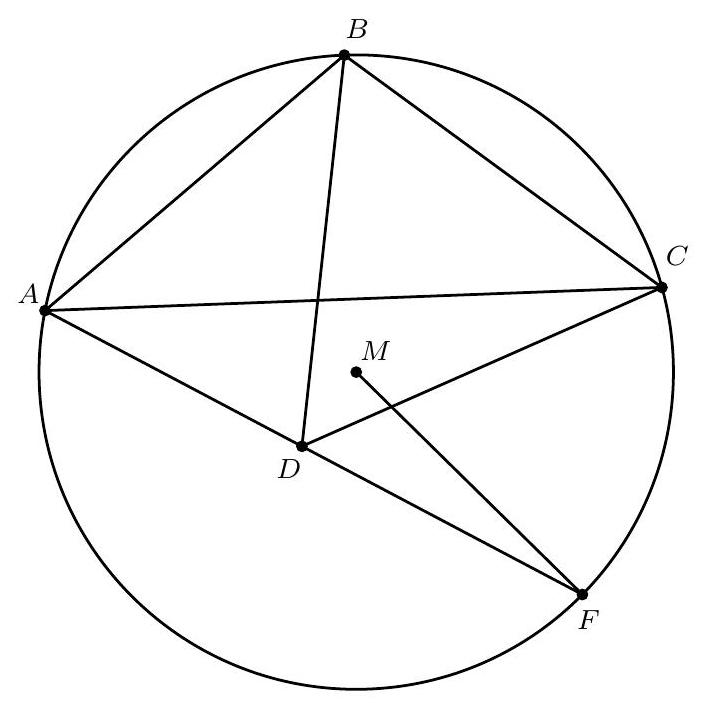", "solution": "We gaan bewijzen dat $|F D|=|F C|$ en dat $|F C|=|F M|$, waaruit het gevraagde volgt.\n\nIn koordenvierhoek $A B C F$ is $\\angle B C F=180^{\\circ}-\\angle B A F$. Wegens $|A B|=|B C|=|B D|$ geldt verder $\\angle B A F=\\angle B A D=\\angle A D B$, dus $\\angle B D F=180^{\\circ}-\\angle A D B=180^{\\circ}-\\angle B A F$. We zien dat $\\angle B C F=\\angle B D F$. Verder zijn $\\angle D F B=\\angle A F B$ en $\\angle C F B$ omtrekshoeken op de gelijke koorden $A B$ en $B C$, dus $\\angle D F B=\\angle C F B$. Driehoeken $B C F$ en $B D F$ hebben dus twee paren hoeken gelijk; omdat ze ook nog zijde $B F$ gemeenschappelijk hebben, zijn ze congruent wegens ZHH. We concluderen dat $|F C|=|F D|$ en dat $\\angle D B F=\\angle C B F$.\n\nVanwege de middelpunt-omtrekhoekstelling geldt $\\angle C M F=2 \\angle C B F$. Uit de zojuist gevonden gelijkheid $\\angle D B F=\\angle C B F$ volgt dat $2 \\angle C B F=\\angle C B D=60^{\\circ}$, dus $\\angle C M F=$ $60^{\\circ}$. Verder is $|M C|=|M F|$ (straal van de cirkel) dus $\\triangle C M F$ is gelijkbenig met een tophoek van $60^{\\circ}$, waaruit volgt dat hij gelijkzijdig is. Dit betekent dat $|F C|=|F M|$.\n\nHiermee hebben we bewezen dat $|F D|=|F C|=|F M|$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Een verzameling $S$ die bestaat uit 2019 (verschillende) positieve gehele getallen heeft de volgende eigenschap: het product van elke 100 elementen van $S$ is een deler van het product van de overige 1919 elementen. Wat is het maximale aantal priemgetallen dat $S$ kan bevatten?", "solution": "Het maximale aantal priemgetallen is 1819.\n\nWe beginnen met de constructie. Kies verschillende priemgetallen $p_{1}, p_{2}, \\ldots, p_{1819}$ en zij $P=p_{1} p_{2} \\cdots p_{1819}$. Neem\n\n$$\nS=\\left\\{p_{1}, p_{2}, \\ldots, p_{1819}, P, P \\cdot p_{1}, \\ldots, P \\cdot p_{199}\\right\\}\n$$\n\nVoor elke $p_{i}$ geldt dat er 201 getallen in $S$ zijn die deelbaar zijn door $p_{i}$ (namelijk $p_{i}$ en alle getallen deelbaar door $P$ ). Hiervan is er hoogstens één getal met twee factoren $p_{i}$; de rest heeft één factor $p_{i}$. Nemen we nu 100 getallen uit $S$, dan zitten in hun product hoogstens 101 factoren $p_{i}$. Bij de overige getallen zitten nog minstens 101 getallen deelbaar door $p_{i}$, dus hun product heeft minstens 101 factoren $p_{i}$. Omdat dit voor elke $p_{i}$ geldt en de getallen uit $S$ geen andere priemfactoren hebben, betekent dit dat $S$ de gewenste eigenschap heeft.\n\nWe bewijzen nu dat $S$ niet meer dan 1819 priemgetallen kan bevatten. Bekijk een priemdeler $q$ van een getal in $S$. Stel dat hooguit 199 getallen in $S$ deelbaar zijn door $q$. Dan nemen we de 100 elementen van $S$ met de meeste factoren $q$ erin; die hebben samen altijd meer factoren $q$ dan de overige elemenenten, tegenspraak met de voorwaarde in de opgave. Dus er zijn minstens 200 getallen in $S$ deelbaar door $q$. Als het er precies 200 zijn, volgt bovendien dat het aantal priemfactoren $q$ in al deze getallen gelijk moet zijn, anders krijgen we weer een tegenspraak als we de 100 elementen met de meeste factoren $p$ kiezen.\n\nWe zien nu dat $S$ minstens 199 niet-priemgetallen moet bevatten, want een priemgetal $p$ in $S$ deelt nog minstens 199 andere elementen van $S$. Stel nu dat $S$ precies 199 nietpriemgetallen bevat. Dan komt de priemfactor $p$ in elk van deze 199 niet-priemgetallen precies één keer voor (namelijk net zo vaak als in het priemgetal $p$ ). Verder kunnen getallen in $S$ nu niet deelbaar zijn door een priemgetal $r$ dat zelf niet in $S$ zit, want dan moeten er wel in totaal minstens 200 veelvouden van $r$ in $S$ zitten en dat zijn dan 200 niet-priemgetallen, tegenspraak. Hieruit volgt dat elk van de 199 niet-priemgetallen in $S$ het product moet zijn van de priemgetallen in $S$ en in het bijzonder zijn deze 199 getallen dus niet verschillend van elkaar. Dit is een tegenspraak, dus $S$ moet minstens 200 niet-priemgetallen bevatten en daarmee hoogstens 1819 priemgetallen.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "In scherphoekige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel en geldt $|A C|+|A I|=|B C|$. Bewijs dat $\\angle B A C=2 \\angle A B C$.\n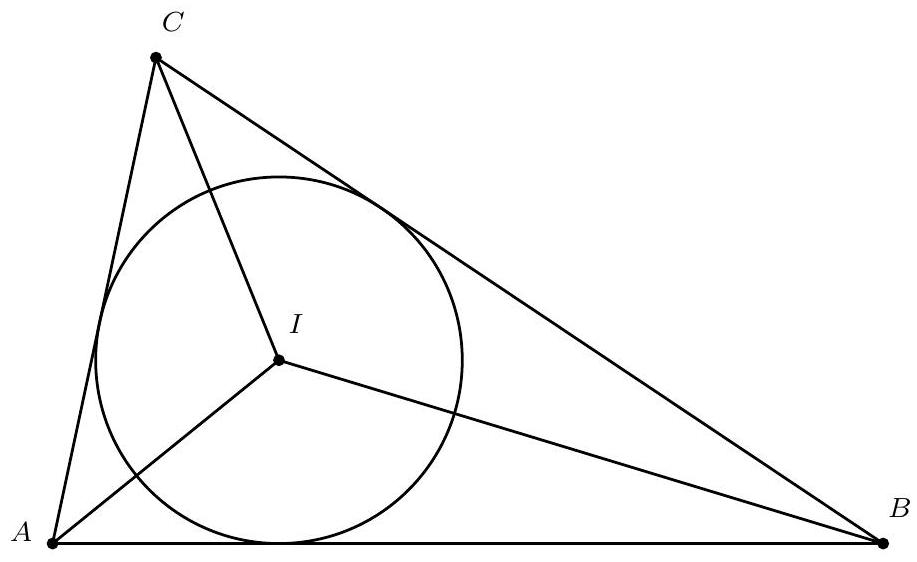", "solution": "Definieer een punt $D$ op zijde $B C$ zodat $|C D|=|A C|$. Vanwege het gegeven dat $|B C|=|A C|+|A I|$ ligt $D$ dan inwendig op zijde $B C$ en geldt $|B D|=|A I|$. Omdat driehoek $A C D$ nu gelijkbenig is, is bissectrice $C I$ ook middelloodlijn van $A D$, dus zijn $A$ en $D$ elkaars gespiegelde in $C I$. Hieruit volgt $\\angle C D I=\\angle C A I=\\angle I A B$, dus $180^{\\circ}-\\angle B D I=\\angle I A B$, wat betekent dat $A B D I$ een koordenvierhoek is. In deze koordenvierhoek zijn $B D$ en $A I$ even lang. Volgens de stelling van Julian zijn dan $A B$ en $I D$ evenwijdig. Dus $A B D I$ is een gelijkbenig trapezium en daarvan zijn de basishoeken gelijk. Dus $\\angle C B A=\\angle D B A=\\angle B A I=\\frac{1}{2} \\angle B A C$, waaruit het gevraagde direct volgt.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "In scherphoekige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel en geldt $|A C|+|A I|=|B C|$. Bewijs dat $\\angle B A C=2 \\angle A B C$.\n", "solution": "Definieer een punt $E$ op lijn $A C$ zodat $A$ tussen $E$ en $C$ ligt en $|A E|=|A I|$. Vanwege het gegeven dat $|B C|=|A C|+|A I|$ geldt dan $|B C|=|C E|$. Dus driehoeken $E C I$ en $B C I$ hebben zijden $|B C|=|C E|$ en $|C I|$ even lang en er geldt $\\angle E C I=\\angle B C I$ vanwege de bissectrice $C I$. Dus $\\triangle E C I \\cong \\triangle B C I$ (ZHZ). In gelijkbenige driehoek $E A I$\ngeldt $\\angle I E A=\\frac{1}{2}\\left(180^{\\circ}-\\angle E A I\\right)=\\frac{1}{2} \\angle C A I$. Dus $\\angle A B C=2 \\angle I B C=2 \\angle I E C=2 \\angle I E A=$ $\\angle C A I=\\frac{1}{2} \\angle B A C$, waaruit het gevraagde direct volgt.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor geldt\n\n$$\nP\\left(x^{2}\\right)+2 P(x)=P(x)^{2}+2 .\n$$", "solution": "Herschrijf de gegeven vergelijking naar\n\n$$\nP\\left(x^{2}\\right)-1=(P(x)-1)^{2} \\text {. }\n$$\n\nSchrijf $Q(x)=P(x)-1$, dan is $Q$ een polynoom met reële coëfficiënten waarvoor geldt dat\n\n$$\nQ\\left(x^{2}\\right)=Q(x)^{2}\n$$\n\nStel dat $Q$ constant is, zeg $Q(x)=c$ met $c \\in \\mathbb{R}$. Dan geldt $c=c^{2}$, dus $c=0$ of $c=1$. Beide mogelijkheden voldoen. We kunnen nu verder aannemen dat $Q$ niet constant is, dus kunnen we schrijven $Q(x)=b x^{n}+R(x)$ met $n \\geq 1, b \\neq 0$ en $R(x)$ een polynoom met reële coëfficiënten van graad hoogstens $n-1$. De polynoomvergelijking wordt nu\n\n$$\nb x^{2 n}+R\\left(x^{2}\\right)=b^{2} x^{2 n}+2 b x^{n} \\cdot R(x)+R(x)^{2} .\n$$\n\nDoor de coëfficiënten van $x^{2 n}$ links en rechts te vergelijken, krijgen we $b=b^{2}$. Aangezien $b \\neq 0$ volgt daaruit dat $b=1$. Als we nu links en rechts $x^{2 n}$ aftrekken, vinden we\n\n$$\nR\\left(x^{2}\\right)=2 x^{n} \\cdot R(x)+R(x)^{2} .\n$$\n\nAls $R$ niet het nulpolynoom is, dan heeft hij een graad $m \\geq 0$. Er geldt $m<n$. De linkerkant van deze vergelijking heeft dan graad $2 m$ en de rechterkant graad $m+n$, want $m+n>2 m$. Tegenspraak. Dus $R$ moet het nulpolynoom zijn, waaruit volgt dat $Q(x)=x^{n}$. Dit voldoet inderdaad aan de polynoomvergelijking voor $Q$.\n\nDit geeft voor $P$ de oplossingen $P(x)=1, P(x)=2$ en $P(x)=x^{n}+1$ met $n \\geq 1$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor geldt\n\n$$\nP\\left(x^{2}\\right)+2 P(x)=P(x)^{2}+2 .\n$$", "solution": "Stel dat $P$ constant is, zeg $P(x)=c$ met $c \\in \\mathbb{R}$. Dan geldt $c+2 c=c^{2}+2$, dus $c^{2}-3 c+2=0$, dus $(c-2)(c-1)=0$, dus $c=2$ of $c=1$. Beide mogelijkheden voldoen. We kunnen nu verder aannemen dat $P$ niet constant is, dus kunnen we schrijven $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\\ldots+a_{1} x+a_{0}$ met $n \\geq 1$ en $a_{n} \\neq 0$. Door nu links en rechts de coëfficiënten van $x^{2 n}$ te vergelijken, zien we dat $a_{n}=a_{n}^{2}$. Omdat $a_{n} \\neq 0$, volgt hieruit dat $a_{n}=1$.\n\nWe bewijzen nu met inductie naar $k$ dat $a_{k}=0$ voor alle $1 \\leq k \\leq n-1$. Als inductiehypothese nemen we aan dat voor zekere $k$ met $1 \\leq k \\leq n-1$ geldt dat $a_{i}=0$ voor alle\n$k<i \\leq n-1$. (We hebben nu geen inductiebasis nodig; als $k=n-1$ is de inductiehypothese een lege bewering.) In $P\\left(x^{2}\\right)$ is de eerste term na $x^{2 n}$ die mogelijk niet 0 is, die met $x^{2 k}$. Omdat $k \\leq n-1$, is de coëfficiënt van $x^{n+k}$ dus zeker gelijk aan 0 . De term $2 P(x)$ kan niet aan deze coëfficiënt bijdragen, want $k \\geq 1$. Dus links is de coëfficiënt van $x^{n+k}$ gelijk aan 0 . Rechts is de 2 niet relevant omdat $n+k>0$. In $P(x)^{2}$ is de coëfficiënt van $x^{n+k}$ gelijk aan $\\sum_{j=k}^{n} a_{j} a_{n+k-j}$. Omdat $a_{i}=0$ voor $k<i \\leq n-1$ is deze som gelijk aan $a_{k} a_{n}+a_{n} a_{k}$. We concluderen dat $2 a_{n} a_{k}=0$, wat betekent dat $a_{k}=0$. Dit voltooit de inductie.\n\nWe weten nu dat $P$ van de vorm $P(x)=x^{n}+c$ is. Door $x=0$ in te vullen in de gegeven polynoomvergelijking zien we bovendien dat $c+2 c=c^{2}+2$. We hebben eerder al gezien dat deze vergelijking $c=1$ of $c=2$ geeft. We controleren nu dus de twee mogelijke oplossingen $P(x)=x^{n}+1$ en $P(x)=x^{n}+2$. In het eerste geval staat er links $\\left(x^{2 n}+1\\right)+2\\left(x^{n}+1\\right)$ en rechts $\\left(x^{n}+1\\right)^{2}+2$, wat allebei gelijk is aan $x^{2 n}+2 x^{n}+3$, dus dit polynoom voldoet. In het tweede geval staat er links $\\left(x^{2 n}+2\\right)+2\\left(x^{n}+2\\right)=x^{2 n}+2 x^{n}+6$ en rechts $\\left(x^{n}+2\\right)^{2}+2=x^{2 n}+4 x^{n}+6$, wat niet gelijk is aan elkaar, dus dit polynoom voldoet niet.\n\nWe concluderen dat de oplossingen zijn: $P(x)=1, P(x)=2$ en $P(x)=x^{n}+1$ met $n \\geq 1$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Voor een positief geheel getal $n$ bekijken we een $n \\times n$-bord en tegels met afmetingen $1 \\times 1,1 \\times 2, \\ldots, 1 \\times n$. Op hoeveel manieren kunnen er precies $\\frac{1}{2} n(n+1)$ vakjes van het bord rood worden gekleurd, zodat de rode vakjes allemaal bedekt kunnen worden door de $n$ tegels allemaal horizontaal te plaatsen, maar ook door de $n$ tegels allemaal verticaal te plaatsen? Twee kleuringen die niet identiek zijn, maar door draaiing of spiegeling van het bord in elkaar overgaan, tellen als verschillend.", "solution": "Het aantal rode vakjes is het precies gelijk aan het totaal aantal vakjes dat door de $n$ tegels bedekt kan worden, dus de tegels worden alleen op rode vakjes gelegd. Bekijk een kleuring van het bord en de bijbehorende horizontale bedekking van de tegels (waarin alle tegels horizontaal liggen) en verticale bedekking. We leiden een aantal eigenschappen van de kleuring af en tellen daarna hoeveel mogelijkheden er zijn. Noem de tegel met afmetingen $1 \\times k$ de $k$-tegel.\n\nOmdat de horizontale bedekking een $n$-tegel bevat, bevat elke kolom minstens één rood vakje. In de verticale bedekking moet daarom in elke kolom minstens één tegel liggen; omdat er precies $n$ tegels zijn, betekent dat dat er in elke kolom precies één tegel moet liggen. Net zo moet er in de horizontale bedekking in elke rij precies één tegel liggen. Nummer nu de rijen en kolommen afhankelijk van het nummer van de tegel die daarin ligt: dus rij $i$ is de rij waarin de $i$-tegel ligt in de horizontale bedekking, en analoog voor de kolommen.\n\nWe bewijzen nu eerst dat het vakje in rij $i$ en kolom $j$ (noem dit vakje $(i, j)$ ) rood is dan en slechts dan als $i+j \\geq n+1$. We bewijzen dit met inductie naar $i$. In rij 1 is er slechts één rood vakje en dat moet wel in de kolom zijn waar de $n$-tegel ligt in de verticale bedekking, dus in kolom $n$. Dus het vakje $(1, j)$ is rood dan en slechts als $j=n$, oftewel dan en slechts dan als $1+j \\geq n+1$. Zij nu $k \\geq 1$ en neem aan dat we dit bewezen hebben voor alle $i \\leq k$. We willen het nu bewijzen voor $i=k+1$, dus dat een vakje $(k+1, j)$ rood is dan en slechts dan als $k+1+j \\geq n+1$, oftewel als $j \\geq n-k$. Bekijk dus een kolom $j \\geq n-k$. We weten wegens de inductiehypothese precies hoeveel rode vakjes deze kolom heeft in de rijen $1,2, \\ldots, k$ : het vakje $(i, j)$ is namelijk rood dan en slechts dan als $i+j \\geq n+1$, oftewel $i \\geq n+1-j$, dus dat zijn er $k-(n-j)=j+k-n$. In de overige $n-k$ rijen heeft deze kolom dus nog $j-(j+k-n)=n-k$ rode vakjes nodig. Dus deze kolom heeft een rood vakje in elk van die rijen en in het bijzonder ook in rij $i=k+1$. In rij $i=k+1$ zijn dus de vakjes $(i, j)$ met $j \\geq n-k$ allemaal rood en dat zijn er $k+1$. Dus dit zijn precies alle rode vakjes in rij $i=k+1$, dus het vakje $(i, j)$ is rood dan en slechts dan als $j \\geq n-k$, oftewel dan en slechts dan als $i+j \\geq n-k+k+1=n+1$. Dit voltooit de inductie.\n\nBekijk nu twee rijen direct boven elkaar met rijnummers $a$ en $b$, met $a>b$. In kolom $n-b$ zit een rood vakje in rij $a$ (want $a+n-b>n$ ) maar niet in rij $b$. In de rij direct aan de andere kant van rij $b$ (als deze bestaat) mag daarom geen rood vakje in kolom $n-b$ zitten, want anders zouden de rode vakjes in kolom $n-b$ niet aaneengesloten zijn en kan de\ntegel met nummer $n-b$ hier niet liggen. Het rijnummer van deze rij moet daarom kleiner dan $b$ zijn. We concluderen dat de rijnummers niet eerst kunnen dalen en daarna weer stijgen. Boven en onder rij $n$ moet wel een rij met een kleiner nummer zitten (of helemaal geen rij meer) dus dalen vanaf daar de rijnummers allebei de kanten op. We zien dat de rijnummers van boven naar beneden eerst oplopend moeten zijn tot aan rij $n$ en daarna aflopend. Hetzelfde kunnen we bewijzen voor de kolomnummers.\n\nAndersom moeten we bewijzen dat als de rijnummers en kolomnummers eerst oplopend en dan aflopend zijn, dat we dan de horizontale en verticale tegels allebei neer kunnen leggen. Hiervoor kleuren we de vakje $(i, j)$ rood dan en slechts dan als $i+j \\geq n+1$. Voor vaste $i$ zijn de rode vakjes dus de vakjes $(i, j)$ met $j \\geq n+1-i$; vanwege de vorm van de kolomnummers zijn die kolommen aaneengesloten. Dus in elke rij zijn de rode vakjes aaneengesloten. We kunnen dus de horizontale tegels precies op de rode vakjes leggen. Net zo goed lukt dit met de verticale tegels. We hadden bij dezelfde rij- en kolomnummers niet een andere kleuring kunnen kiezen waarvoor de betegeling werkt, want we weten al dat bij elke goede betegeling geldt dat $(i, j)$ rood is dan en slechts dan als $i+j \\geq n+1$.\n\nAl met al zijn we dus op zoek naar het aantal manieren om zowel de rij- als de kolomnummers te kiezen in een volgorde die eerst oplopend en daarna aflopend is; bij elk van die keuzes hoort precies één manier om de rode vakjes te kleuren die aan de voorwaarde voldoet. Het aantal manieren om de getallen 1 tot en met $n$ in een volgorde te zetten die eerst oplopend en dan aflopend is, is gelijk aan het aantal deelverzamelingen van $\\{1,2, \\ldots, n-1\\}$, namelijk de deelverzameling van getallen die vóór het getal $n$ komen; deze kunnen maar op één manier gesorteerd worden (oplopend) en de rest van de getallen moet juist aflopend gesorteerd worden en na $n$ neergezet worden. Het aantal deelverzamelingen is $2^{n-1}$. Dus het totaal aantal kleuringen dat aan de opgave voldoet is $\\left(2^{n-1}\\right)^{2}=2^{2 n-2}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Voor een positief geheel getal $n$ bekijken we een $n \\times n$-bord en tegels met afmetingen $1 \\times 1,1 \\times 2, \\ldots, 1 \\times n$. Op hoeveel manieren kunnen er precies $\\frac{1}{2} n(n+1)$ vakjes van het bord rood worden gekleurd, zodat de rode vakjes allemaal bedekt kunnen worden door de $n$ tegels allemaal horizontaal te plaatsen, maar ook door de $n$ tegels allemaal verticaal te plaatsen? Twee kleuringen die niet identiek zijn, maar door draaiing of spiegeling van het bord in elkaar overgaan, tellen als verschillend.", "solution": "Net als in oplossing I leiden we af dat er in de horizontale bedekking in elke rij precies één tegel moet liggen en in de verticale bedekking in elke kolom precies één tegel. Bekijk nu eerst een volgorde voor de tegels in de verticale bedekking. We gaan afleiden aan welke eisen deze volgorde moet voldoen en hoeveel mogelijkheden er per volgorde zijn om de tegels neer te leggen (en daarmee de kleuring te kiezen).\n\nBekijk de kolom met de $n$-tegel. Deze tegel kan maar op één manier in deze kolom liggen. Bekijk vervolgens een willekeurige andere tegel met lengte $i$. Deze bedekt $i$ vakjes in zijn kolom. In elke rij moeten de rode vakjes aaneengesloten zijn, dus in de $i$ rijen waarin de $i$-tegel ligt, zijn er rode vakjes vanaf de kolom met de $i$-tegel tot en met de kolom met de $n$-tegel. In de kolommen daartussen liggen dus tegels met lengte minstens $i$. We zien dus dat de tegelnummers van links naar rechts oplopend moeten zijn tot aan de $n$-tegel en daarna juist aflopend. Het aantal manieren om de verticale tegels in zo'n volgorde te kiezen, is $2^{n-1}$ (zie het einde van oplossing I).\n\nWe bekijken nu één van deze volgordes. We gaan de verticale tegels in de kolommen leggen en tegelijkertijd de vakjes die ze bedekken, rood kleuren. De $(n-1)$-tegel kan op twee manieren in zijn kolom liggen. De enige rij waarin hij niet ligt, moet nu wel de rij zijn waarin maar één rood vakje komt, want alle andere rijen hebben al minstens twee rode vakjes. In deze rij (de bovenste of onderste) mag dus geen tegel meer gelegd worden; we noemen deze rij klaar. Vervolgens zijn er daardoor twee manieren om de $(n-2)$-tegel in zijn kolom te leggen, want die moet binnen de $n-1$ rijen van de $(n-1)$-tegel vallen. Na het neerleggen van de ( $n-2$ )-tegel is er een tweede rij klaar, namelijk de tweede rij waar deze tegel niet in ligt en waar dus precies twee rode vakjes zijn. Deze twee rode vakjes zijn nu automatisch aaneengesloten. De rest van de rijen (die nog niet klaar zijn) hebben nu minstens drie rode vakjes. Hierna moet de $(n-3)$-tegel binnen de $n-2$ rijen van de $(n-2)$-tegel liggen, waardoor er een derde rij klaar is, namelijk die met precies drie rode vakjes. Deze rode vakjes zijn ook weer aaneengesloten. Enzovoorts. Voor elke volgende tegel zijn er dus precies twee opties om hem neer te leggen. In totaal geeft dit $2^{n-1}$ mogelijkheden. Nadat we voor elke tegel een keuze hebben gemaakt, zijn de aantallen rode vakjes per rij precies de getallen $1,2,3, \\ldots, n$ en liggen in alle rijen de rode vakjes aaneengesloten. Dit betekent dat het lukt om de horizontale tegels precies op de rode vakjes te leggen. We hebben in totaal $2^{n-1} \\cdot 2^{n-1}=2^{2 n-2}$ mogelijke manieren waarop we nu het bord gekleurd hebben. Elk van deze manieren voldoet aan alle voorwaarden. Dus het totaal aantal kleuringen dat aan de opgave voldoet is $2^{2 n-2}$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Laat $\\mathrm{a}, \\mathrm{b} \\geq 2$ positieve gehele getallen met $\\operatorname{ggd}(\\mathrm{a}, \\mathrm{b})=1$ zijn. Zij r de kleinste positieve waarde die aangenomen wordt bij een uitdrukking van de vorm $\\frac{a}{b}-\\frac{c}{d}$, met C en d positieve gehele getallen die voldoen aan $\\mathbf{c} \\leq \\mathrm{a}$ en $\\mathrm{d} \\leq \\mathrm{b}$ Bewijs dat $\\frac{1}{r}$ geheel is.", "solution": "We laten eerst zien dat het mogelijk is om $\\mathbf{C}$ en $\\mathbf{d}$ zo te kiezen dat $\\frac{a}{b}-\\frac{c}{d}=\\frac{1}{b d}$.\nOmdat $\\operatorname{ggd}(\\mathrm{a}, \\mathrm{b})=1$, bestaat er een multiplicatieve inverse $\\mathrm{b}^{-1}$ van b modulo a . Kies nu c met $1 \\leq \\mathrm{c} \\leq \\mathrm{a}$ zo dat $\\mathrm{c} \\equiv-\\mathrm{b}^{-1} \\bmod \\mathrm{a}$. Er geldt dan $\\mathrm{b} \\equiv-1 \\bmod \\mathrm{a}$, dus $\\mathrm{a} \\mid \\mathrm{bc}+1$. Definieer vervolgens $\\mathrm{d}=\\frac{b c+1}{a}$, dan is d een positief geheel getal. Er geldt $\\mathrm{d}=\\frac{b c+1}{a} \\leq \\frac{b a+1}{a}=\\mathrm{b}+\\frac{1}{a}$. Omdat $\\mathrm{a} \\geq 2$ en d een geheel getal is, volgt hieruit $\\mathrm{d} \\leq \\mathrm{b}$ Aan alle voorwaarden is daarom voldaan. Er geldt nu $\\frac{a}{b}-\\frac{c}{d}=\\frac{a d-b c}{b d}=\\frac{b c+1-b c}{b d}=\\frac{1}{b d}$.\n\nAls dit de kleinst mogelijke uitkomst positieve is, dan zijn we klaar, want dan geldt $\\frac{1}{r}=\\mathrm{bd}$ en dat is geheel. We willen dus laten zien dat er geen kleinere positieve uitkomst mogelijk is. Neem C en d zoals hierboven en stel dat er positieve gehele getallen $\\mathrm{c}^{\\prime} \\leq \\mathrm{a}$ en $\\mathrm{d}^{\\prime} \\leq \\mathrm{b}$ bestaan zodat $0<\\frac{a}{b}-\\frac{c^{\\prime}}{d^{\\prime}}<\\frac{1}{b d}$. We gaan een tegenspraak afleiden.\n\nSchrijf $\\mathbf{x}=\\mathrm{ad}-\\mathrm{bc}^{\\prime}$, dan geldt $\\frac{a}{b}-\\frac{c^{\\prime}}{d^{\\prime}}=\\frac{x}{b d^{\\prime}}$, dus $\\mathbf{x b d}<\\mathrm{bd}$, waaruit volgt dat $\\mathbf{x d}<\\mathrm{d}^{\\prime}$. We weten verder dat $x>0$. Dus $0<x d<d^{\\prime} \\leq \\mathrm{b}$ wat betekent dat $x d$ en $d^{\\prime}$ twee verschillende getallen zijn met verschil kleiner dan b . Verder volgt uit $\\mathrm{x}=\\mathrm{ad}$ - $\\mathrm{bc}^{\\prime}$ dat $\\mathbf{x} \\equiv \\mathbf{a d} \\bmod \\mathbf{b}$. Anderzijds weten we dat $\\mathbf{a d}-\\mathbf{b}=1$, dus $\\mathbf{a d} \\equiv 1 \\bmod \\mathbf{b}$ dus $\\mathbf{x a d} \\equiv \\mathbf{x}$ $\\bmod \\mathbf{b} . \\quad$ Dit combineren geeft $\\mathrm{ad} \\equiv \\mathrm{xad} \\bmod \\mathbf{b}$ Omdat $\\operatorname{ggd}(\\mathrm{a}, \\mathrm{b})=1$ mogen we delen door $a$, dus $\\mathrm{d}^{\\prime} \\equiv x d \\bmod \\mathbf{b}$ Echter, we hadden gezien dat $d^{\\prime}$ en $x d$ verschillende getallen zijn met verschil kleiner dan b dus dit is onmogelijk.\n\nWe concluderen dat de gevonden $\\mathbf{C}$ en $\\mathbf{d}$ inderdaad de kleinste uitkomst geven en dat dus $\\frac{1}{r}$ geheel is.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Gegeven zijn reële getallen $a_{1}, a_{2}, \\ldots, a_{2020}$, niet noodzakelijk verschillend. Voor elke $n \\geq 2020$ wordt nu $a_{n+1}$ gedefinieerd als het kleinste reële nulpunt van het polynoom\n\n$$\nP_{n}(x)=x^{2 n}+a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+\\ldots+a_{n-1} x^{2}+a_{n}\n$$\n\nals dat bestaat. Veronderstel dat $a_{n+1}$ bestaat voor alle $n \\geq 2020$. Bewijs dat $a_{n+1} \\leq a_{n}$ voor alle $n \\geq 2021$.", "solution": "Als $x=\\alpha$ een nulpunt van $P_{n}$ is, dan is $x=-\\alpha$ ook een nulpunt, aangezien alle termen in $P_{n}(x)$ een even graad hebben. Het kleinste nulpunt van $P_{n}$ kan dus nooit positief zijn. Er geldt daarom $a_{n} \\leq 0$ voor alle $n>2020$. Er geldt $P_{n+1}(x)=x^{2} \\cdot P_{n}(x)+a_{n+1}$. Vul nu $x=a_{n+1}$ in: we weten dat dat een nulpunt van $P_{n}$ is, dus $P_{n+1}\\left(a_{n+1}\\right)=0+a_{n+1} \\leq 0$.\n\nOmdat de term in $P_{n}(x)$ met de hoogste graad $x^{2 n}$ is, is er een $N<0$ zodat $P_{n}(x)>0$ voor alle $x<N$. Neem bijvoorbeeld $-N=\\max \\left(2,\\left|a_{1}\\right|+\\left|a_{2}\\right|+\\ldots+\\left|a_{n}\\right|\\right)$, dan geldt voor $x<N$ dat $x^{2 i-2} \\leq x^{2 n-2}$ voor $1 \\leq i \\leq n$ en dus\n\n$$\n\\begin{aligned}\n\\mid a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+ & \\ldots+a_{n-1} x^{2}+a_{n} \\mid \\\\\n& \\leq\\left|a_{1} x^{2 n-2}\\right|+\\left|a_{2} x^{2 n-4}\\right|+\\ldots+\\left|a_{n-1} x^{2}\\right|+\\left|a_{n}\\right| \\\\\n& \\leq\\left|a_{1}\\right| x^{2 n-2}+\\left|a_{2}\\right| x^{2 n-2}+\\ldots+\\left|a_{n-1}\\right| x^{2 n-2}+\\left|a_{n}\\right| x^{2 n-2} \\\\\n& \\leq\\left(\\left|a_{1}\\right|+\\left|a_{2}\\right|+\\ldots+\\left|a_{n}\\right|\\right) x^{2 n-2} \\\\\n& \\leq-N \\cdot x^{2 n-2} \\\\\n& <x^{2 n},\n\\end{aligned}\n$$\n\ndus $x^{2 n}+a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+\\ldots+a_{n-1} x^{2}+a_{n}>0$. Dus voor $n \\geq 2021$ is er een zekere $N<0$ met $P_{n}(x)>0$ voor $x<N$, terwijl $P_{n}\\left(a_{n}\\right) \\leq 0$. Dat betekent dat $P_{n}(x)$ een nulpunt heeft kleiner dan of gelijk aan $a_{n}$. Aangezien $a_{n+1}$ het kleinste nulpunt is, geldt $a_{n+1} \\leq a_{n}$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Ward en Gabriëlle spelen een spel op een groot vel papier. In het begin staan er 999 enen op het papier geschreven. Ward en Gabriëlle zijn om en om aan de beurt, waarbij Ward begint. Een speler die aan de beurt is, mag twee getallen $a$ en $b$ van het papier uitkiezen waarvoor geldt $\\operatorname{ggd}(a, b)=1$, deze getallen weggummen en het getal $a+b$ erbij schrijven. De eerste die geen zet meer kan doen, verliest. Bepaal wie van Ward en Gabriëlle dit spel met zekerheid kan winnen.", "solution": "Gabriëlle kan winnen met de volgende strategie: ze kiest steeds de grootste twee getallen op het papier als $a$ en $b$. We bewijzen met inductie naar $k$ dat ze dit altijd mag doen en dat na haar $k$-de zet het getal $2 k+1$ en verder $998-2 k$ enen op het papier staan.\n\nIn de eerste beurt van Ward kan hij alleen maar $a=b=1$ kiezen. Daarna staat er op het papier het getal 2 en verder 997 enen. Gabriëlle kiest nu de twee grootste getallen, dus $a=2$ en $b=1$ en komt uit op het getal 3 en verder 996 enen. Dit bewijst de inductiebasis $k=1$. Stel nu dat voor zekere $m \\geq 1$ geldt dat na de $m$-de beurt van Gabriëlle op het papier het getal $2 m+1$ en verder $998-2 m$ enen staan. Als $998-2 m=0$, dan kan Ward geen zet doen. Zo niet, dan kan Ward twee dingen doen: $a=b=1$ kiezen of $a=2 m+1$ en $b=1$. We bekijken deze twee gevallen apart:\n\n- Als Ward $a=b=1$ kiest, dan wordt de situatie daarna: het getal $2 m+1$, het getal 2 en verder $996-2 m$ enen. Gabriëlle kiest nu weer de grootste twee getallen, dus $a=2 m+1$ en $b=2$ (dit mag want de ggd is 1 ). Na haar zet staat er dan het getal $2 m+3=2(m+1)+1$ en verder $996-2 m=998-2(m+1)$ enen.\n- Als Ward $a=2 m+1$ en $b=1$ kiest, dan wordt de situatie daarna: het getal $2 m+2$ en verder $997-2 m$ enen. Gabriëlle kiest nu weer de grootste twee getallen, dus $a=2 m+2$ en $b=1$ (dit mag want de ggd is 1 ). Merk op dat er nog een 1 beschikbaar is, want $997-2 m$ kan niet gelijk aan 0 zijn aangezien het oneven is. Na haar zet staat er dan het getal $2 m+3=2(m+1)+1$ en verder $996-2 m=998-2(m+1)$ enen.\n\nDit voltooit de inductie.\nWe zien dat Gabriëlle altijd een zet kan doen. Na zet nummer 499 van Gabriëlle bevat het papier alleen nog het getal 999, dus kan Ward geen zet meer doen en wint Gabriëlle.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Bepaal alle paren $(a, b)$ van positieve gehele getallen waarvoor\n\n$$\na+b=\\varphi(a)+\\varphi(b)+\\operatorname{ggd}(a, b) .\n$$\n\nHier is $\\varphi(n)$ het aantal getallen $k$ uit $\\{1,2, \\ldots, n\\}$ met $\\operatorname{ggd}(n, k)=1$.", "solution": "Stel eerst dat $a=1$. Er geldt $\\varphi(1)=1$. Voor alle positieve gehele $b$ is nu $\\operatorname{ggd}(a, b)=1$, dus de vergelijking wordt $1+b=1+\\varphi(b)+1$, dus $\\varphi(b)=b-1$. Er is dus precies één getal uit $\\{1,2, \\ldots, b\\}$ dat niet copriem met $b$ is; dat moet $b$ zelf zijn (want $\\operatorname{ggd}(b, b)>1$ tenzij $b=1$, maar in dat geval geldt $\\varphi(b)=b$ ). Hieruit volgt dat $b$ een priemgetal is. Voor alle priemgetallen klopt de vergelijking. We concluderen dat $(1, p)$ een oplossing is voor alle priemgetallen $p$. Net zo goed geeft $b=1$ de oplossingen $(p, 1)$.\n\nWe nemen nu verder aan dat $a, b \\geq 2$. Omdat $\\operatorname{ggd}(b, b)>1$ geldt $\\varphi(b) \\leq b-1$. Dus\n\n$$\n\\operatorname{ggd}(a, b)=a+b-\\varphi(a)-\\varphi(b) \\geq a-\\varphi(a)+1\n$$\n\nZij nu $p$ de kleinste priemdeler van $a$ (die bestaat, want $a \\geq 2$ ). Omdat voor alle $p$-vouden $t p \\leq a$ geldt dat $\\operatorname{ggd}(t p, a)>1$, is $a-\\varphi(a) \\geq \\frac{1}{p} \\cdot a$. Er geldt dus\n\n$$\n\\operatorname{ggd}(a, b) \\geq a-\\varphi(a)+1 \\geq \\frac{a}{p}+1\n$$\n\nDe grootste twee delers van $a$ zijn $a$ en $\\frac{a}{p}$. Omdat $\\operatorname{ggd}(a, b)$ een deler van $a$ is die minstens $\\frac{a}{p}+1$ is, moet hij gelijk zijn aan $a$. Dus $\\operatorname{ggd}(a, b)=a$. Volkomen analoog kunnen we bewijzen dat $\\operatorname{ggd}(a, b)=b$. Dus $a=b$.\n\nNu gaat de vergelijking over in $2 a=2 \\varphi(a)+a$, oftewel $a=2 \\varphi(a)$. We zien dat $2 \\mid a$. Schrijf daarom $a=2^{k} \\cdot m$ met $k \\geq 1$ en $m$ oneven. Dan geldt wegens een bekende eigenschap van de $\\varphi$-functie dat $\\varphi(a)=\\varphi\\left(2^{k}\\right) \\varphi(m)=2^{k-1} \\cdot \\varphi(m)$, dus de vergelijking gaat over in $2^{k} \\cdot m=2 \\cdot 2^{k-1} \\cdot \\varphi(m)$, oftewel $m=\\varphi(m)$. Hieruit volgt $m=1$. Dus $a=b=2^{k}$ en dan klopt de vergelijking inderdaad.\n\nWe concluderen dat de oplossingen zijn: $(1, p)$ en $(p, 1)$ voor alle priemgetallen $p$, en $\\left(2^{k}, 2^{k}\\right)$ voor alle positieve gehele $k$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Bepaal alle paren $(a, b)$ van positieve gehele getallen waarvoor\n\n$$\na+b=\\varphi(a)+\\varphi(b)+\\operatorname{ggd}(a, b) .\n$$\n\nHier is $\\varphi(n)$ het aantal getallen $k$ uit $\\{1,2, \\ldots, n\\}$ met $\\operatorname{ggd}(n, k)=1$.", "solution": "Schrijf $a=x d, b=y d$ met $d=\\operatorname{ggd}(a, b)$. Dan gaat de vergelijking over in\n\n$$\nx d+y d=\\varphi(x d)+\\varphi(y d)+d\n$$\n\nVan de getallen $\\{1,2, \\ldots, x\\}$ zijn er $\\varphi(x)$ die copriem zijn met $x$, dus hooguit $\\varphi(x)$ die copriem zijn met $x d$. Hetzelfde geldt voor de getallen $\\{x+1, x+2, \\ldots, 2 x\\}$ en meer\nalgemeen voor de getallen $\\{t x+1, t x+2, \\ldots,(t+1) x\\}$. Door de getallen $\\{1,2, \\ldots, x d\\}$ in $d$ van dit soort groepjes op te delen, zien we dat hooguit $d \\cdot \\varphi(x)$ van deze getallen copriem zijn met $x d$. Dus $\\varphi(x d) \\leq d \\cdot \\varphi(x)$. Analoog geldt $\\varphi(y d) \\leq d \\cdot \\varphi(y)$. Dus krijgen we\n\n$$\nx d+y d \\leq d \\cdot \\varphi(x)+d \\cdot \\varphi(y)+d\n$$\n\nDelen door $d$ geeft\n\n$$\nx+y \\leq \\varphi(x)+\\varphi(y)+1\n$$\n\nAls $x, y \\geq 2$ geldt $\\varphi(x) \\leq x-1, \\varphi(y) \\leq y-1$ en kan dit niet waar zijn. Dus minstens één van $x$ en $y$ is gelijk aan 1.\n\nStel dat $x=y=1$. Dan geldt $a=b$. Net als in de eerste oplossing leiden we af dat dan $a=b=2^{k}$ met $k \\geq 1$.\n\nStel nu dat $x=1$ en $y \\neq 1$. Dan moet gelden $\\varphi(y) \\geq y-1$, dus $y$ moet dan een priemgetal zijn. Verder moet er gelijkheid gelden in $\\varphi(x d) \\leq d \\cdot \\varphi(x)$. Invullen van $x=1$ geeft dus $\\varphi(d)=d \\cdot \\varphi(1)=d$. Dat kan alleen als $d=1$. We vinden $(a, b)=(1, p)$ voor een priemgetal $p$. Analoog volgt uit $x \\neq 1$ en $y=1$ de oplossing $(p, 1)$.\n\nWe concluderen dat de oplossingen zijn: $(1, p)$ en $(p, 1)$ voor alle priemgetallen $p$, en $\\left(2^{k}, 2^{k}\\right)$ voor alle positieve gehele $k$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek en zij $P$ het snijpunt van de raaklijnen in $B$ en $C$ aan de omgeschreven cirkel van $\\triangle A B C$. De lijn door $A$ loodrecht op $A B$ en de lijn door $C$ loodrecht op $A C$ snijden in $X$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $A B$ snijden in $Y$. Toon aan dat $A P \\perp X Y$.\n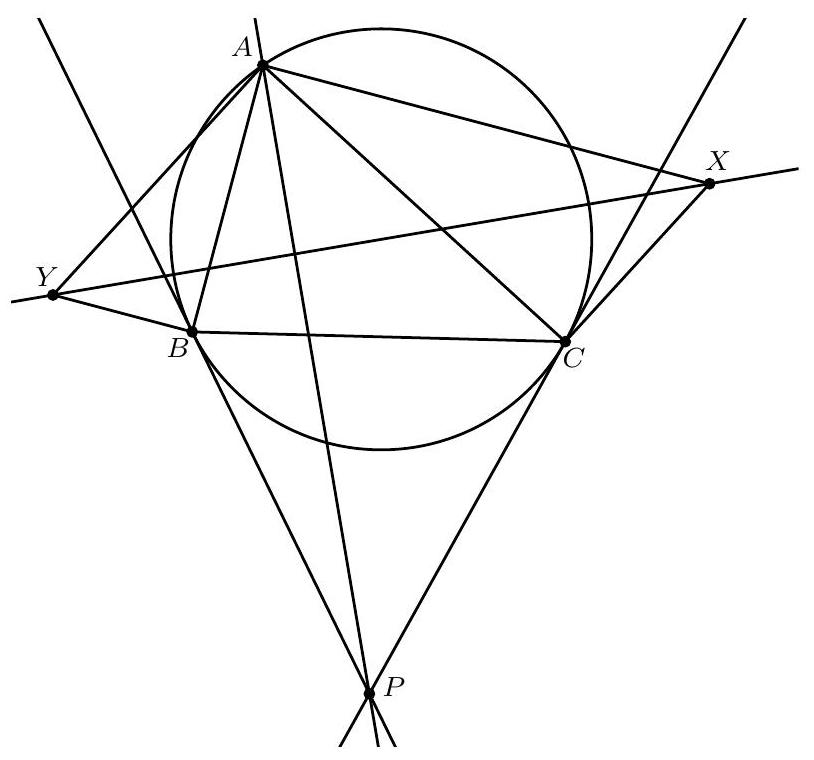", "solution": "Zij $M$ het midden van de omgeschreven cirkel van $\\triangle A B C$ en schrijf $\\alpha=$ $\\angle B A C$. We bewijzen eerst dat $\\triangle B Y A \\sim \\triangle B M P$ en vervolgens dat $\\triangle Y B M \\sim \\triangle A B P$. Wegens de middelpunt-omtrekshoekstelling geldt $\\angle B M C=2 \\angle B A C=2 \\alpha$. Vierhoek $P B M C$ is een vlieger met symmetrie-as $P M$ (wegens gelijke stralen $|M B|=|M C|$ en gelijke raaklijnstukjes $|P B|=|P C|$ ), dus $M P$ deelt hoek $\\angle B M C$ in tweeën. We concluderen dat $\\angle B M P=\\frac{1}{2} \\angle B M C=\\alpha$. Verder geldt $\\angle P B M=90^{\\circ}$ (raaklijn staat loodrecht op de straal) en dus wegens hoekensom dat $\\angle M P B=90^{\\circ}-\\alpha$. Anderzijds geldt dat $\\angle A B Y=90^{\\circ}$ (gegeven) en dat $\\angle Y A B=\\angle Y A C-\\angle B A C=90^{\\circ}-\\alpha$. Dus $\\angle A B Y=\\angle P B M$ en $\\angle Y A B=\\angle M P B$, waaruit volgt dat $\\triangle B Y A \\sim \\triangle B M P$. Uit deze gelijkvormigheid volgt dat $\\frac{|Y B|}{|A B|}=\\frac{|M B|}{|P B|}$. Combineren we dit met de hoekengelijkheid\n\n$$\n\\angle Y B M=\\angle Y B A+\\angle A B M=90^{\\circ}+\\angle A B M=\\angle A B M+\\angle M B P=\\angle A B P\n$$\n\ndan zien we dat bovendien $\\triangle Y B M \\sim \\triangle A B P$. Noemen we nu $T$ het snijpunt van $A P$ en $Y M$, dan zien we dus dat\n\n$$\n\\angle B Y T=\\angle B Y M=\\angle B A P=\\angle B A T\n$$\n\nwaaruit volgt dat $B Y A T$ een koordenvierhoek is. We concluderen dat $\\angle A T Y=\\angle A B Y=$ $90^{\\circ}$, dus dat $A P \\perp Y M$. Analoog vinden we dat $A P \\perp X M$. Maar dat betekent dat de\nlijnen $Y M$ en $X M$ samenvallen en dat $A P \\perp X Y$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek en zij $P$ het snijpunt van de raaklijnen in $B$ en $C$ aan de omgeschreven cirkel van $\\triangle A B C$. De lijn door $A$ loodrecht op $A B$ en de lijn door $C$ loodrecht op $A C$ snijden in $X$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $A B$ snijden in $Y$. Toon aan dat $A P \\perp X Y$.\n", "solution": "Zij $S$ het snijpunt van $C X$ en $B Y$. De lijnen $A X$ en $B Y$ staan allebei loodrecht op $A B$, dus geldt $A X \\| B Y$, en analoog $A Y \\| C X$. Dus $A X S Y$ is een parallellogram. Daarnaast geldt $\\angle A B S=90^{\\circ}=\\angle A C S$, dus wegens Thales is $A S$ een middellijn van de omgeschreven cirkel van $\\triangle A B C$. Het middelpunt $M$ van deze cirkel is daarom het midden van $A S$. De diagonalen van een parallellogram snijden elkaar middendoor, dus $X Y$ gaat door het midden van $A S$, dus door $M$.\n\nZij nu $T$ op $X Y$ zodat $\\angle A T X=90^{\\circ}$. Er geldt dan $\\angle A T X=\\angle A C X$, dus $A T C X$ is een koordenvierhoek. Net zo is $A T B Y$ een koordenvierhoek. Nu geldt $\\angle A T C=180^{\\circ}-\\angle A X C$, en wegens $A C \\perp C X$ en $A B \\perp A X$ geldt $\\angle A X C=90^{\\circ}-\\angle C A X=\\angle C A B$. Dus $\\angle A T C=180^{\\circ}-\\angle C A B$. Analoog geldt ook $\\angle A T B=180^{\\circ}-\\angle C A B$. Dus $\\angle B T C=360^{\\circ}-$ $\\left(180^{\\circ}-\\angle C A B\\right)-\\left(180^{\\circ}-\\angle C A B\\right)=2 \\angle C A B$. Wegens de middelpuntsomtrekshoekstelling geldt bovendien $\\angle B M C=2 \\angle B A C$, dus $\\angle B T C=\\angle B M C$. Hieruit volgt dat $B M T C$ een koordenvierhoek is.\n\nOmdat $B P$ en $C P$ raaklijnen aan de omgeschreven cirkel van $\\triangle A B C$ zijn, geldt $\\angle M B P=$ $90^{\\circ}=\\angle M C P$, dus $M B P C$ is een koordenvierhoek met middellijn $M P$. Maar we hebben net gezien dat $T$ ook op deze cirkel ligt. Er geldt dus $\\angle M T P=\\angle M B P=90^{\\circ}$. Aangezien nu $\\angle A T M+\\angle M T P=180^{\\circ}$, ligt $T$ dus op $A P$. We concluderen dat $A P \\perp X Y$.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Voor een positief getal $n$ schrijven we $d(n)$ voor het aantal positieve delers van $n$. Bepaal alle positieve gehele getallen $k$ waarvoor er positieve gehele getallen $a$ en $b$ bestaan met de eigenschap\n\n$$\nk=d(a)=d(b)=d(2 a+3 b)\n$$", "solution": "Voor $i \\geq 0$ kiezen we $a=2 \\cdot 5^{i}$ en $b=3 \\cdot 5^{i}$. Dan hebben $a$ en $b$ elk $2(i+1)$ delers. Verder is $2 a+3 b=4 \\cdot 5^{i}+9 \\cdot 5^{i}=13 \\cdot 5^{i}$ en dat heeft ook $2(i+1)$ delers. Dus dit voldoet met $k=2(i+1)$. We zien dat alle even waarden van $k$ voldoen.\n\nStel nu dat $k$ oneven is. Dan heeft $a$ een oneven aantal delers en is dus een kwadraat, zeg $a=x^{2}$. Net zo is $b$ een kwadraat, zeg $b=y^{2}$, en is $2 a+3 b$ een kwadraat, zeg $2 a+3 b=z^{2}$. Er geldt dus\n\n$$\n2 x^{2}+3 y^{2}=z^{2}\n$$\n\nWe bewijzen dat deze vergelijking geen oplossingen in de positieve gehele getallen heeft. Stel er bestaan wel zulke oplossing, kies dan de oplossing $(x, y, z)=(u, v, w)$ met de minimale waarde van $x+y+z$. Er geldt dus $2 u^{2}+3 v^{2}=w^{2}$. Als we deze vergelijking modulo 3 bekijken, staat er $2 u^{2}=w^{2}$. Als $u$ niet deelbaar door 3 is, dan is $u^{2} \\equiv 1 \\bmod 3$, dus $w^{2}=2 u^{2} \\equiv 2 \\bmod 3$, maar dat kan niet. Dus $u$ is deelbaar door 3 en dan volgt dat $w$ ook deelbaar door 3 is. Nu is $2 u^{2}$ deelbaar door 9 en $w^{2}$ ook, dus $3 v^{2}$ is deelbaar door 9 . Daaruit volgt dat $v$ ook deelbaar door 3 is. Nu voldoet echter $(x, y, z)=\\left(\\frac{u}{3}, \\frac{v}{3}, \\frac{w}{3}\\right)$ ook aan de vergelijking, terwijl deze oplossing een kleinere waarde van $x+y+z$ heeft. Tegenspraak. Er bestaan dus geen oplossingen in de positieve gehele getallen.\n\nDaaruit volgt dat een oneven waarde van $k$ nooit kan voldoen. De enige oplossingen zijn dus alle even getallen.\n\nAlternatief voor het tweede deel. Net als in de oplossing hierboven bekijken we de vergelijking $2 x^{2}+3 y^{2}=z^{2}$. We gaan laten zien dat deze vergelijking geen oplossing in de positieve gehele getallen heeft. Bekijk de vergelijking eerst modulo 2. Dan staat er\n$3 y^{2} \\equiv z^{2}$, dus $y$ en $z$ zijn beide even of beide oneven. Stel dat ze beide oneven zijn. Bekijk dan de vergelijking modulo 8 . We weten dan $y^{2} \\equiv z^{2} \\equiv 1 \\bmod 8$, dus $2 x^{2} \\equiv 1-3 \\equiv 6$ $\\bmod 8$. Hieruit volgt $x^{2} \\equiv 3 \\bmod 4$, maar dat kan niet. We concluderen dat $y$ en $z$ niet allebei oneven kunnen zijn, dus moeten ze allebei even zijn. Nu is de rechterkant van de vergelijking deelbaar door 4 , dus de linkerkant ook. Ook $3 y^{2}$ is deelbaar door 4 , dus $2 x^{2}$ moet deelbaar door 4 zijn. Hieruit volgt dat $x$ even is. We zien dat voor elke oplossing $(x, y, z)$ geldt dat $x, y$ en $z$ alle drie even zijn. Nu kunnen we net als in de oplossing hierboven beginnen met een oplossing $(x, y, z)=(u, v, w)$ met minimale waarde van $x+y+z$. Dan is $(x, y, z)=\\left(\\frac{u}{2}, \\frac{v}{2}, \\frac{w}{2}\\right)$ ook een oplossing van de vergelijking met een kleinere waarde van $x+y+z$, tegenspraak.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Gegeven is een driehoek $A B C$ met zijn omgeschreven cirkel en met $|A C|<$ $|A B|$. Op de korte boog $A C$ ligt een variabel punt $D$ ongelijk aan $A$. Zij $E$ de spiegeling van $A$ in de binnenbissectrice van $\\angle B D C$. Bewijs dat de lijn $D E$ door een vast punt gaat, onafhankelijk van de plek van $D$.\n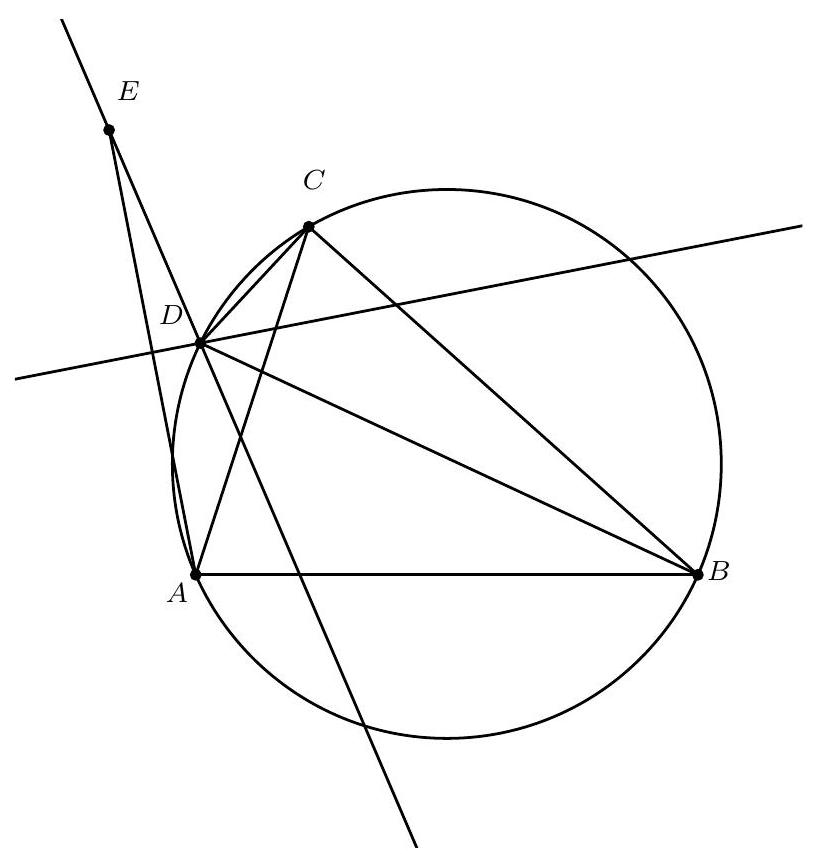", "solution": "Zij $M$ het snijpunt van de binnenbissectrice van $\\angle B D C$ met de omgeschreven cirkel van $\\triangle A B C$. Omdat $D$ op de korte boog $A C$ ligt, ligt $M$ op de boog $B C$ waar $A$ niet op ligt. Er geldt $\\angle B D M=\\angle M D C$ omdat $D M$ de binnenbissectrice van $\\angle B D C$ is, dus bogen $B M$ en $C M$ zijn even lang. Hieruit volgt dat de plek van $M$ niet afhangt van de plek van $D$.\n\nZij $S$ het snijpunt van $D E$ en de omgeschreven cirkel van $\\triangle A B C$. We gaan bewijzen dat $S$ niet afhangt van de plek van $D$. Omdat $S$ en $M$ op de omgeschreven cirkel van $\\triangle A B C$ liggen, geldt $\\angle A M D=\\angle A S D=\\angle A S E$. Omdat $E$ de spiegeling van $A$ in $D M$ is, zien we nu $\\angle A M E=2 \\angle A M D=2 \\angle A S E$. Bekijk de cirkel met middelpunt $M$ die door $A$ heen gaat. Vanwege opnieuw de spiegeling is $|M A|=|M E|$, dus deze cirkel gaat ook door $E$. De middelpunt-omtrekshoekstelling zegt nu dat uit $\\angle A M E=2 \\angle A S E$ volgt dat $S$ ook op deze cirkel ligt. We zien dat $S$ het tweede snijpunt is van de omgeschreven cirkel van $\\triangle A B C$ en de cirkel met middelpunt $M$ die door $A$ gaat. Dat legt $S$ vast, onafhankelijk van de plek van $D$. Omdat $D E$ door $S$ heen gaat, is $S$ het gevraagde punt.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Gegeven is een driehoek $A B C$ met zijn omgeschreven cirkel en met $|A C|<$ $|A B|$. Op de korte boog $A C$ ligt een variabel punt $D$ ongelijk aan $A$. Zij $E$ de spiegeling van $A$ in de binnenbissectrice van $\\angle B D C$. Bewijs dat de lijn $D E$ door een vast punt gaat, onafhankelijk van de plek van $D$.\n", "solution": "Zij $T$ het spiegelbeeld van $A$ in de middelloodlijn van $B C$. Dit punt hangt\nniet af van $D$. We gaan bewijzen dat $D E$ altijd door $T$ heen gaat. We doen dit door te laten zien dat $\\angle E D C+\\angle C D B+\\angle B D T=180^{\\circ}$.\n\nPunt $T$ ligt op de omgeschreven cirkel van $\\triangle A B C$, want deze cirkel gat in zichzelf over bij spiegeling in de middelloodlijn van $B C$. Dus $\\angle B D T=\\angle B C T$. Wegens de spiegeling in de middelloodlijn van $B C$ is $A C B T$ een gelijkbenig trapezium met basis $B C$ en dus is $\\angle B C T=\\angle C B A$. Dus $\\angle B D T=\\angle C B A$.\n\nVerder gaat bij spiegeling in de bissectrice van $\\angle B D C$ punt $A$ over in punt $E$ en lijn $B D$ in lijn $C D$, dus $\\angle E D C=\\angle A D B$. Vanwege de omtrekshoekstelling is $\\angle A D B=\\angle A C B$, dus $\\angle E D C=\\angle A C B$.\n\nTen slotte is $\\angle C D B=\\angle C A B$. We vinden dus\n\n$$\n\\angle E D C+\\angle C D B+\\angle B D T=\\angle A C B+\\angle C A B+\\angle C B A=180^{\\circ} .\n$$", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ die voldoen aan\n\n$$\nf(-f(x)-f(y))=1-x-y\n$$\n\nvoor alle $x, y \\in \\mathbb{Z}$.", "solution": "Invullen van $x=y=1$ geeft $f(-2 f(1))=-1$. Invullen van $x=n, y=1$ geeft $f(-f(n)-f(1))=-n$. Nu kiezen we $x=-f(n)-f(1)$ en $y=-2 f(1)$, dat geeft\n\n$$\nf(-f(-f(n)-f(1))-f(-2 f(1)))=1-(-f(n)-f(1))-(-2 f(1))\n$$\n\nwaarbij we de linkerkant verder kunnen uitrekenen als $f(--n--1)=f(n+1)$ en de rechterkant verder als $1+f(n)+f(1)+2 f(1)=f(n)+3 f(1)+1$. Schrijf nu $3 f(1)+1=c$, dan staat er\n\n$$\nf(n+1)=f(n)+c\n$$\n\nMet inductie twee kanten op volgt dat $f(n+k)=f(n)+c k$ voor alle $k \\in \\mathbb{Z}$, waarna $n=0$ geeft dat $f(k)=f(0)+c k$ voor alle $k \\in \\mathbb{Z}$, dus $f$ is een lineaire functie.\n\nOm te controleren vullen we $f(x)=a x+b$ in met $a, b \\in \\mathbb{Z}$. Dan wordt de linkerkant van de functievergelijking\n\n$$\nf(-f(x)-f(y))=a(-a x-b-a y-b)+b=-a^{2} x-a^{2} y-2 a b+b\n$$\n\nDit moet voor alle $x$ en $y$ gelijk zijn aan $1-x-y$. De coëfficiënt voor de $x$ moet daarom gelijk zijn (want met $y$ vast moet aan beide kanten dezelfde functie van $x$ staan) dus $-a^{2}=-1$, dus $a=1$ of $a=-1$. Met $a=-1$ en $x=y=0$ krijgen we $2 b+b=1$, wat geen gehele $b$ oplevert. Met $a=1$ en $x=y=0$ krijgen we $-2 b+b=1$ dus $b=-1$. Inderdaad komt er voor $a=1$ en $b=-1$ links ook $1-x-y$ te staan, dus de enige functie die voldoet is $f(x)=x-1$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 5 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ die voldoen aan\n\n$$\nf(-f(x)-f(y))=1-x-y\n$$\n\nvoor alle $x, y \\in \\mathbb{Z}$.", "solution": "Stel dat er $a, b \\in \\mathbb{Z}$ zijn met $f(a)=f(b)$. Dan geeft $y=0$ invullen en vervolgens eerst $x=a$ en dan $x=b$ dat\n\n$$\n1-a=f(-f(a)-f(0))=f(-f(b)-f(0))=1-b\n$$\n\ndus $a=b$. We conluderen dat $f$ injectief is.\nVul nu eerst $x=n, y=1$ in en daarna $x=n+1, y=0$, dat geeft\n\n$$\nf(-f(n)-f(1))=1-n-1=1-(n+1)-0=f(-f(n+1)-f(0))\n$$\n\nwaaruit wegens de injectiviteit volgt dat $-f(n)-f(1)=-f(n+1)-f(0)$, oftewel $f(n+1)=f(n)+f(1)-f(0)$. Nu volgt net als in de vorige oplossing dat $f$ een lineaire functie is, waarna controleren laat zien dat de enige oplossing $f(x)=x-1$ is.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 6 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Gegeven zijn twee positieve gehele getallen $k$ en $n$ met $k \\leq n \\leq 2 k-1$. Julian heeft een grote stapel rechthoekige $k \\times 1$-tegels. Merlijn noemt een positief geheel getal $m$ en ontvangt van Julian $m$ tegels om op een $n \\times n$-bord te plaatsen. Op elke tegel schrijft Julian eerst of het een horizontale of een verticale tegel moet worden. Tegels mogen op het bord niet overlappen en ze mogen ook niet uitsteken. Wat is het grootste getal $m$ dat Merlijn kan noemen als hij zeker wil weten dat hij alle tegels volgens het voorschrift van Julian kwijt kan op het bord?", "solution": "We bewijzen dat de grootste $m$ die Merlijn kan noemen, gelijk is aan $\\min (n, 3(n-$ $k)+1$. Eerst bewijzen we dat $m \\leq \\min (n, 3(n-k)+1)$. Als Merlijn $n+1$ tegels bestelt, kan Julian ze allemaal als horizontaal bestempelen. Aangezien $n \\leq 2 k-1$ is het niet mogelijk om meer dan één horizontale tegel in dezelfde rij te plaatsen, dus heeft Merlijn $n+1$ rijen nodig, tegenspraak. Er moet dus gelden $m \\leq n$.\n\nStel nu dat Merlijn 3( $n-k)+2$ tegels bestelt. Julian kan nu $n-k+1$ tegels verticaal maken en $2 n-2 k+1$ tegels horizontaal. Verticale tegels kunnen vakjes uit de bovenste $k$ rijen bedekken of uit de onderste $k$ rijen of uit $k$ rijen ergens daartussenin, maar in alle gevallen bedekken ze vakjes uit de $k-(n-k)=2 k-n \\geq 1$ rijen in het midden van het bord. In elk van deze middelste rijen bedekken de verticale tegels dus minimaal $n-k+1$ vakjes, waardoor er nog $k-1$ vakjes over zijn voor de horizontale tegels. Daar past geen horizontale tegel meer in, dus de $2 k-n$ middelste rijen bevatten geen horizontale tegels. Alle horizontale tegels liggen daarom in de overige $n-(2 k-n)=2 n-2 k$ rijen, maar er zijn $2 n-2 k+1$ horizontale tegels, tegenspraak. Er moet dus gelden $m \\leq 3(n-k)+1$. Al met al geldt $m \\leq \\min (n, 3(n-k)+1)$.\n\nNu bewijzen we dat het altijd mogelijk is om een collectie van $\\min (n, 3(n-k)+1)$ tegels op het bord te plaatsen. We bekijken eerst twee speciale configuraties. Leg $n-k$ horizontale tegels linksonder, die een rechthoek van $n-k$ hoog en $k$ breed bedekken. Rechts daarnaast passen dan nog precies $n-k$ verticale tegels (zo ver mogelijk naar beneden geschoven), die een rechthoek van $n-k$ breed en $k$ hoog bedekken. Vervolgens kunnen daarboven nog precies $n-k$ horizontale tegels (zo ver mogelijk naar rechts geschoven) en blijft er linksboven ruimte over voor $n-k$ verticale tegels. We kunnen dus $2(n-k)$ horizontale en $2(n-k)$ verticale tegels kwijt. Een andere manier om het bord te bedekken is als volgt. Leg $n$ verticale tegels bovenin, die een rechthoek van $n$ breed en $k$ hoog bedekken. Er is daaronder dan nog ruimte voor $n-k$ horizontale tegels (elk op hun eigen rij; de precieze plaatsing maakt verder niet uit). Het is dus ook mogelijk om $n$ verticale en $n-k$ horizontale tegels te plaatsen.\n\nStel nu dat Merlijn $A$ horizontale tegels van Julian krijgt en $B$ verticale. Dan geldt $A+B \\leq n$ en $A+B \\leq 3(n-k)+1$. Zonder verlies van algemeenheid nemen we aan dat $A \\leq B$. Als nu $A \\leq n-k$, dan gebruikt Merlijn de tweede speciale configuratie en laat daar indien nodig nog tegels weg. Omdat $B \\leq n$, lukt dit. Stel anderzijds dat $A \\geq n-k+1$.\n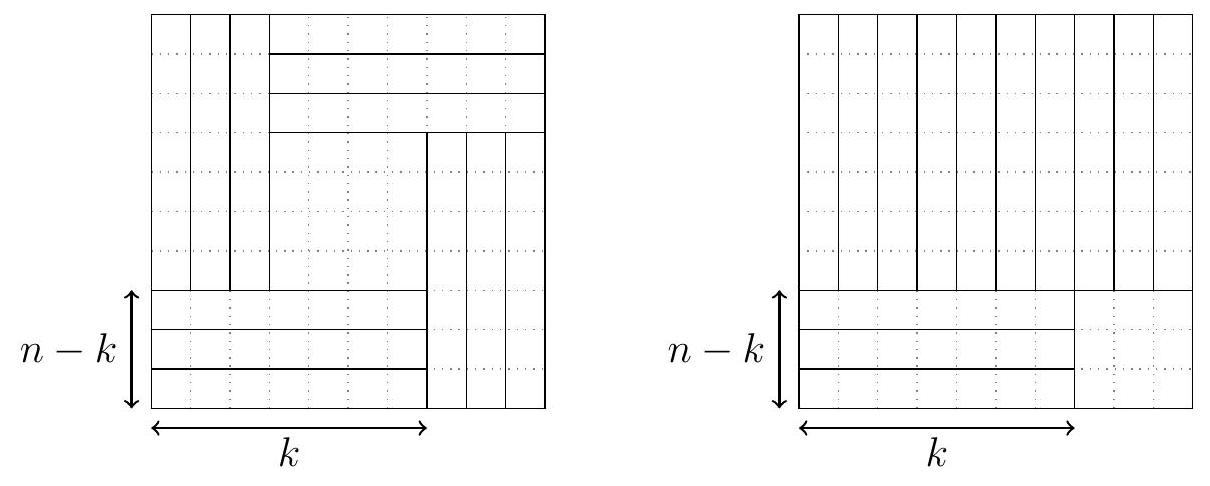\n\nDan is $B \\leq 3(n-k)+1-A \\leq 3(n-k)+1-(n-k+1)=2(n-k)$. Omdat $A \\leq B$ geldt ook $A \\leq B \\leq 2(n-k)$. Dus Merlijn kan de eerste speciale configuratie gebruiken, waarin hij indien nodig nog wat tegels weglaat. Het lukt Merlijn dus altijd om $\\min (n, 3(n-k)+1)$ tegels op het bord te leggen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Gegeven is een koordenvierhoek $A B C D$ met $|A B|=|B C|$. Punt $E$ ligt op de boog $C D$ waar $A$ en $B$ niet op liggen. Het snijpunt van $B E$ en $C D$ noemen we $P$, het snijpunt van $A E$ en $B D$ noemen we $Q$. Bewijs dat $P Q \\| A C$.\n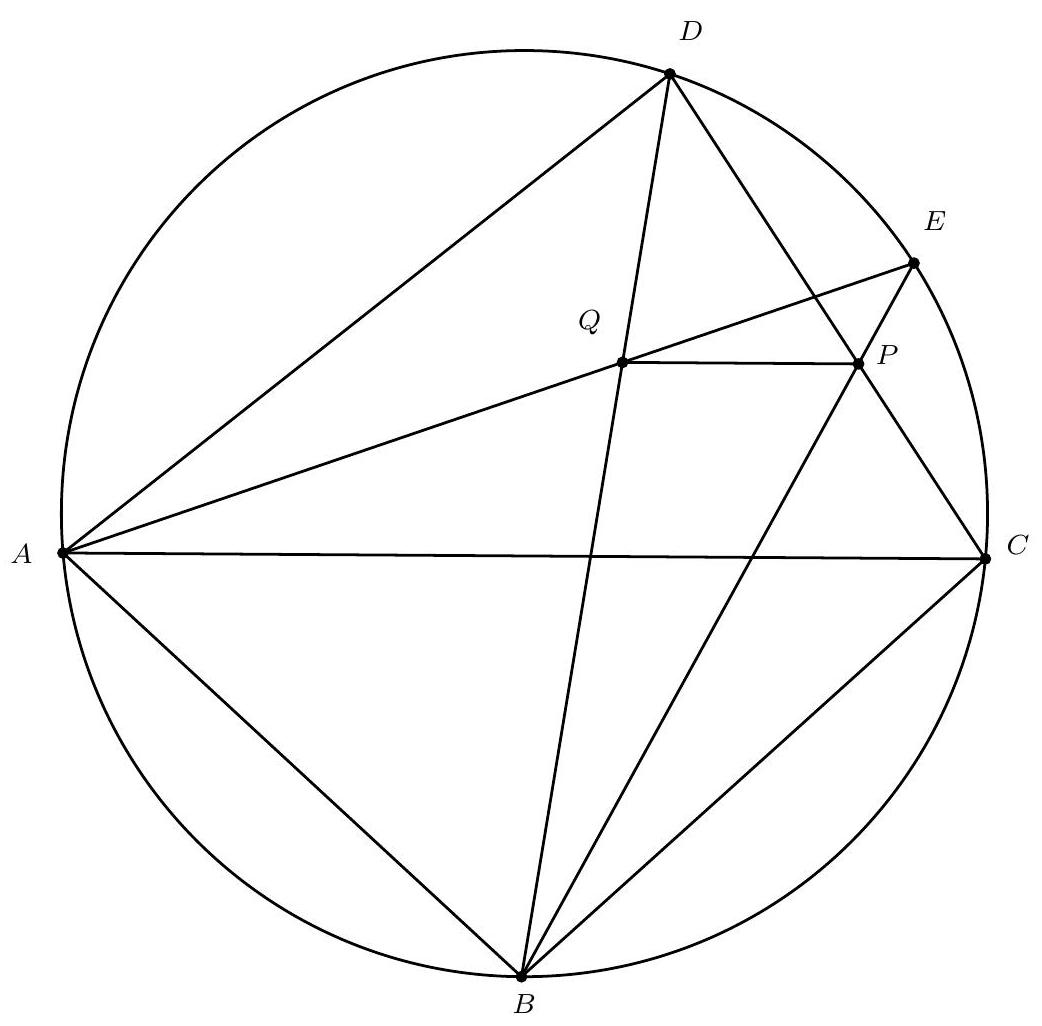", "solution": "Omdat $|A B|=|B C|$ geldt $\\angle A E B=\\angle B D C$, dus $\\angle Q E P=\\angle A E B=$ $\\angle B D C=\\angle Q D P$, waaruit volgt dat $Q P E D$ een koordenvierhoek is. Dus $\\angle Q P D=$ $\\angle Q E D=\\angle A E D=\\angle A C D$. Dit betekent wegens F-hoeken dat $Q P$ en $A C$ evenwijdig zijn.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Bepaal alle drietallen $(x, y, z)$ van reële getallen waarvoor geldt\n\n$$\n\\begin{aligned}\n& x^{2}-y z=|y-z|+1, \\\\\n& y^{2}-z x=|z-x|+1, \\\\\n& z^{2}-x y=|x-y|+1\n\\end{aligned}\n$$", "solution": "Het stelsel vergelijkingen is symmetrisch: verwissel je bijvoorbeeld $x$ en $y$, dan blijft de derde vergelijking hetzelfde en wisselen de eerste twee vergelijkingen om. We kunnen dus zonder verlies van algemeenheid aannemen dat $x \\geq y \\geq z$. Dan wordt het stelsel:\n\n$$\n\\begin{aligned}\n& x^{2}-y z=y-z+1, \\\\\n& y^{2}-z x=x-z+1 \\\\\n& z^{2}-x y=x-y+1\n\\end{aligned}\n$$\n\nDe eerste twee vergelijkingen van elkaar afhalen geeft $x^{2}-y^{2}+z(x-y)=y-x$, oftewel $(x-y)(x+y+z+1)=0$. Hieruit volgt $x=y$ of $x+y+z=-1$. De tweede en derde vergelijking van elkaar afhalen geeft $y^{2}-z^{2}+x(y-z)=y-z$, oftewel $(y-z)(y+z+x-1)=0$. Hieruit volgt $y=z$ of $x+y+z=1$.\n\nWe onderscheiden nu twee gevallen: $x=y$ en $x \\neq y$. In het eerste geval geldt $y \\neq z$, want anders zou $x=y=z$ en dat geeft in de eerste vergelijking $0=1$, tegenspraak. Er volgt dus nu $x+y+z=1$, oftewel $2 x+z=1$. Invullen van $y=x$ en $z=1-2 x$ in de eerste vergelijking geeft $x^{2}-x(1-2 x)=x-(1-2 x)+1$, wat we herleiden tot $3 x^{2}-x=3 x$, oftewel $3 x^{2}=4 x$. Dit geeft $x=0$ of $x=\\frac{4}{3}$. Met $x=0$ vinden we $y=0, z=1$, maar dit voldoet niet aan onze aanname $x \\geq y \\geq z$. We houden dus alleen de optie $x=\\frac{4}{3}$ over en dat geeft het drietal $\\left(\\frac{4}{3}, \\frac{4}{3},-\\frac{5}{3}\\right)$. Controleren laat zien dat dit een oplossing is.\n\nNu het geval $x \\neq y$. Dan geldt $x+y+z=-1$, dus kan niet ook gelden $x+y+z=1$, dus we zien dat $y=z$. Nu geeft $x+y+z=-1$ dat $x+2 z=-1$, dus $x=-1-2 z$. De eerste vergelijking wordt nu $(-1-2 z)^{2}-z^{2}=1$, wat we herleiden tot $3 z^{2}+4 z=0$. Hieruit vinden we $z=0$ of $z=-\\frac{4}{3}$. Met $z=0$ vinden we $y=0, x=-1$, maar dit voldoet niet aan onze aanname $x \\geq y \\geq z$. We houden dus alleen de optie $z=-\\frac{4}{3}$ over en dat geeft het drietal $\\left(\\frac{5}{3},-\\frac{4}{3},-\\frac{4}{3}\\right)$. Controleren laat zien dat dit een oplossing is.\n\nDoor de permutaties van deze twee oplossingen ook mee te nemen, vinden we al met al zes oplossingen: $\\left(\\frac{4}{3}, \\frac{4}{3},-\\frac{5}{3}\\right),\\left(\\frac{4}{3},-\\frac{5}{3}, \\frac{4}{3}\\right),\\left(-\\frac{5}{3}, \\frac{4}{3}, \\frac{4}{3}\\right),\\left(\\frac{5}{3},-\\frac{4}{3},-\\frac{4}{3}\\right),\\left(-\\frac{4}{3}, \\frac{5}{3},-\\frac{4}{3}\\right)$ en $\\left(-\\frac{4}{3},-\\frac{4}{3}, \\frac{5}{3}\\right)$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 3 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Zij $p$ een priemgetal groter dan 2. Patricia wil 7 niet-noodzakelijk verschillende getallen uit $\\{1,2, \\ldots, p\\}$ aan de zwarte stippen in onderstaande figuur toekennen, op zo'n manier dat het product van drie getallen op een lijn of cirkel altijd dezelfde rest bij deling door $p$ heeft.\n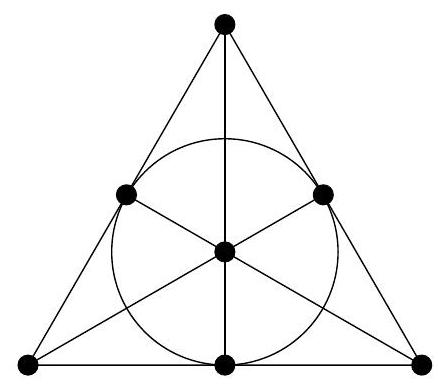\n(a) Stel dat Patricia het getal $p$ minstens één keer gebruikt. Hoe vaak heeft ze het getal $p$ dan in totaal minimaal nodig?\n(b) Stel dat Patricia het getal $p$ niet gebruikt. Op hoeveel manieren kan zij dan de getallen toekennen? (Twee manieren zijn verschillend als er aan minstens één zwarte stip verschillende getallen zijn toegekend. De figuur wordt niet gedraaid of gespiegeld.)", "solution": "(a) Met 'lijnen' bedoelen we in het vervolg van dit onderdeel de zes lijnen en de cirkel. Zodra het getal $p$ ergens gebruikt wordt, is er een 'lijn' met product deelbaar door $p$, dus met rest 0 na deling door $p$. Alle 'lijnen' moeten dan rest 0 geven, dus alle 'lijnen' bevatten minstens één keer $p$. Dit kunnen we bereiken door het getal $p$ aan de onderste drie stippen toe te kennen. Stel dat het ook al kan met hooguit twee keer $p$. Elke stip ligt op precies drie 'lijnen', dus dan zijn er hooguit zes 'lijnen' waar een getal $p$ op ligt. Er zijn echter zeven 'lijnen', dus dit kan niet. We concluderen dat ze $p$ in totaal minimaal drie keer nodig heeft.\n(b) Noem de onderste drie getallen van links naar rechts $a, b$ en $c$. Noem het getal midden op de linkerzijkant van de driehoek $d$. We kunnen nu alle getallen modulo $p$ uitrekenen; merk op dat alle getallen inverteerbaar zijn modulo $p$ omdat $p$ zelf niet meedoet en $p$ priem is. De onderste lijn heeft product $a b c$. De linkerzijde van de driehoek dus ook, dus het getal helemaal bovenin is modulo $p$ congruent aan $a b c(a d)^{-1}=b c d^{-1}$. Als we de lijn van rechtsonder naar het midden van de linkerzijde bekijken, zien we dat het middelste getal congruent moet zijn aan $a b c(c d)^{-1}=a b d^{-1}$. Door de cirkel te bekijken, vinden we dat het getal rechts in het midden $a b c(b d)^{-1}=$ $a c d^{-1}$ is.\n\nOp de rechterzijde krijgen we nu de vergelijking $b c d^{-1} \\cdot a c d^{-1} \\cdot c \\equiv a b c \\bmod p$, dus $c^{2} \\equiv d^{2} \\bmod p$. Analoog vinden we op de verticale lijn $b^{2} \\equiv d^{2}$ en op de lijn van linksonder naar rechts midden $a^{2} \\equiv d^{2} \\bmod p$. We concluderen dat de getallen $a, b, c$ en $d$ allemaal hetzelfde kwadraat moeten hebben. Uit $x^{2} \\equiv y^{2} \\operatorname{volgt}(x-y)(x+y) \\equiv 0$ $\\bmod p$, dus $p \\mid x-y$ of $p \\mid x+y$, want $p$ is priem. Dus geldt $x \\equiv y$ of $x \\equiv-y$. Dat zijn twee opties, want zou $y \\equiv-y$, dan $2 y \\equiv 0$, dus $p \\mid 2 y$, dus $p \\mid y$ wegens $p>2$; tegenspraak. Er geldt dus dat de getallen $b, c$ en $d$ allemaal congruent aan $a$ of $-a$ moeten zijn. Als aan deze voorwaarde voldaan is, dan geldt $a^{2} \\equiv b^{2} \\equiv c^{2} \\equiv d^{2}$ en dan volgt uit het voorgaande dat op alle zes de lijnen en op de cirkel het product congruent aan $a b c$ is.\nEr zijn $p-1$ mogelijkheden voor het getal $a$ en daarna 2 mogelijkheden voor elk van de getallen $b, c$ en $d$. Dus totaal zijn er $8(p-1)$ manieren om de getallen toe te kennen.", "problem_match": "\nOpgave 3.", "solution_match": "# Oplossing I."}
|
| 4 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Zij $p$ een priemgetal groter dan 2. Patricia wil 7 niet-noodzakelijk verschillende getallen uit $\\{1,2, \\ldots, p\\}$ aan de zwarte stippen in onderstaande figuur toekennen, op zo'n manier dat het product van drie getallen op een lijn of cirkel altijd dezelfde rest bij deling door $p$ heeft.\n\n(a) Stel dat Patricia het getal $p$ minstens één keer gebruikt. Hoe vaak heeft ze het getal $p$ dan in totaal minimaal nodig?\n(b) Stel dat Patricia het getal $p$ niet gebruikt. Op hoeveel manieren kan zij dan de getallen toekennen? (Twee manieren zijn verschillend als er aan minstens één zwarte stip verschillende getallen zijn toegekend. De figuur wordt niet gedraaid of gespiegeld.)", "solution": "Als alternatieve oplossing voor onderdeel (b) laten we zien dat ofwel alle zeven getallen hetzelfde zijn, dan wel dat er een 'lijn' $k$ is waarvan de drie punten waarde $x$ hebben terwijl de overige vier punten waarde $-x$ hebben. Merk op dat $-x \\not \\equiv x$ wegens $p>2$.\n\nMerk op dat deze toekenningen in ieder geval voldoen: in het eerste geval is het product van de drie punten op elke 'lijn' uiteraard hetzelfde; in het tweede geval is het $x^{3}$ voor 'lijn' $k$, en $x(-x)^{2}=x^{3}$ voor elk van de zes andere lijnen, waarbij we gebruiken dat elk van deze andere lijnen precies één punt met $k$ gemeen heeft. Het aantal manieren waarop ze dit kan doen is $p-1$ in het eerste geval, en $7(p-1)$ in het tweede geval (namelijk 7 keuzes voor de 'lijn' $k$ en per keuze vervolgens $p-1$ keuzes voor $x)$, dus in totaal $(p-1)+7(p-1)=8(p-1)$.\n\nGegeven twee verschillende stippen met waarden $x$ en $y$. Noem de waarde bij de derde stip op de lijn door $x$ en $y$ nu $z$ en de andere vier waarden $a, b, c, d$, dan geldt (z.b.d.a.) dat $x a b \\equiv x c d \\equiv y c b \\equiv y a d \\equiv z a c \\equiv z b d \\equiv x y z$. Dus $x^{2} a b c d=(x a b)(x c d) \\equiv(y c d)(y a d)=$ $y^{2}(a b c d)$, dus $x^{2} \\equiv y^{2}$, omdat we mogen delen door $a b c d \\not \\equiv 0$. Uit $p \\mid x^{2}-y^{2}=(x-y)(x+y)$ volgt dat $p \\mid x-y$ of $p \\mid x+y$, dus $y \\equiv x$ of $y \\equiv-x$. Houden we een punt met waarde $x$ vast, dan zien we dat elk ander punt dus waarde $x$ of $-x$ heeft.\n\nStel dat niet alle punten dezelfde waarde hebben. Dan komen $x$ en $y \\equiv-x$ dus beide voor, dus is er een lijn met daarop de punten $x, y$ en (z.b.d.a.) $z=y$. Deze heeft product $x y^{2}=-y^{3}$. Omdat $y^{3} \\not \\equiv-y^{3}$ (anders zou $p \\mid 2 y^{3}$ dus $p \\mid y$ ), bevat nu elke lijn precies 1 of 3 keer een punt met waarde $x$. De producten die we voor de overige zes 'lijnen' vinden zijn $x a b \\equiv x c d \\equiv y c b \\equiv y a d \\equiv y a c \\equiv y b d$. De laatste vier producten kunnen niet uit drie maal factor $x$ bestaan, dus bevatten precies één $x$, dus geldt z.b.d.a. $(a, b, c, d)=(x, x, y, y)$. Dat betekent dat $(x, a, b)=(x, x, x)$, terwijl de punten die niet op deze lijn liggen allemaal waarde $y \\equiv-x$ hebben, zoals we wilden bewijzen.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Jesse en Tjeerd spelen een spelletje. Jesse heeft de beschikking over $n \\geq 2$ stenen. Er zijn twee dozen: in de zwarte doos is ruimte voor de helft van de stenen (naar beneden afgerond) en in de witte doos is ruimte voor de helft van de stenen (naar boven afgerond). Jesse en Tjeerd zijn om en om aan de beurt, waarbij Jesse begint. Jesse pakt in zijn beurt steeds één nieuwe steen, schrijft een positief reëel getal op de steen en legt hem in één van de dozen die nog niet vol is. Tjeerd ziet al deze getallen op de stenen in de dozen en mag in zijn beurt één steen naar keuze uit een doos verplaatsen naar de andere doos als die nog niet vol is, maar hij mag er ook voor kiezen om niets te doen. Het spel stopt zodra beide dozen vol zijn. Als dan de totale waarde van de stenen in de zwarte doos groter is dan de totale waarde van de stenen in de witte doos, wint Jesse; anders wint Tjeerd. Bepaal voor elke $n \\geq 2$ wie er met zekerheid kan winnen (en geef een bijbehorende winnende strategie).", "solution": "Als $n$ even is, komen er in allebei de dozen precies evenveel stenen. Jesse kan nu winnen door de eerste $n-1$ stenen allemaal waarde 2 te geven en ze in een willekeurige doos te stoppen. Tjeerd verplaatst na elke zet van Jesse eventueel een steen. Als Jesse's laatste steen in de zwarte doos moet, geeft hij deze steen waarde 3. Dan wint hij, want de totale waarde in de zwarte doos is dan 1 groter dan in de witte doos. Als zijn laatste steen in de witte doos moet, geeft hij deze steen waarde 1 . Ook nu is de totale waarde in de zwarte doos 1 groter dan in de witte doos, dus Jesse wint.\n\nBekijk nu het geval dat $n$ oneven is, zeg $n=2 m+1$ met $m \\geq 1$. In de zwarte doos kunnen $m$ stenen en in de witte kunnen $m+1$ stenen. Jesse kan nu weer winnen. De eerste $n-2$ stenen geeft hij allemaal waarde 1 en legt hij in een willekeurige doos. Tjeerd verplaatst na elke zet van Jesse weer eventueel een steen. We onderscheiden nu twee gevallen voor het moment dat Jesse aan de beurt is en er nog twee lege plekken in de dozen zijn.\n\n- Geval 1: de zwarte doos is vol. De waarde van de zwarte doos is nu $m$, die van de witte doos $m-1$. Jesse legt nu een steen met waarde $\\frac{1}{4}$ in de witte doos. Als Tjeerd vervolgens niet een steen verplaatst, geeft Jesse de laatste steen ook waarde $\\frac{1}{4}$. De totale waarde van de witte doos is dan $(m-1)+\\frac{1}{4}+\\frac{1}{4}=m-\\frac{1}{2}$ en dat is kleiner dan de totale waarde in de zwarte doos. Als Tjeerd wel iets verplaatst, dan moet dat een steen uit de zwarte doos zijn die naar de witte doos gaat (immers, de zwarte doos is vol). Daarmee is de waarde in de witte doos $(m-1)+\\frac{1}{4}+1=m+\\frac{1}{4}$ geworden en die in de zwarte doos $m-1$. Jesse legt nu de laatste steen met waarde 2 in de zwarte doos, zodat de totale waarde in de zwarte doos $(m-1) \\cdot 1+1 \\cdot 2=m+1$ wordt.\n- Geval 2: de zwarte doos is nog niet vol. Jesse legt nu een steen met waarde 3 in de zwarte doos. Als Tjeerd deze steen niet verplaatst, geeft Jesse de laatste steen waarde 1. Dan is de totale waarde in de witte doos $m+1$ en in de zwarte doos $(m-1) \\cdot 1+1 \\cdot 3=m+2$. Als Tjeerd de steen met waarde 3 wel verplaatst, dan komt er een plek vrij in de zwarte doos, dus daar legt Jesse zijn laatste steen en deze\ngeeft hij waarde 5 . De totale waarde van de witte doos is nu $m \\cdot 1+1 \\cdot 3=m+3$ en de totale waarde van de zwarte doos $(m-1) \\cdot 1+1 \\cdot 5=m+4$.\n\nWe zien dat Jesse in alle gevallen ervoor kan zorgen dat de totale waarde in de zwarte doos groter is dan die in de witte doos, dus Jesse wint altijd.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Jesse en Tjeerd spelen een spelletje. Jesse heeft de beschikking over $n \\geq 2$ stenen. Er zijn twee dozen: in de zwarte doos is ruimte voor de helft van de stenen (naar beneden afgerond) en in de witte doos is ruimte voor de helft van de stenen (naar boven afgerond). Jesse en Tjeerd zijn om en om aan de beurt, waarbij Jesse begint. Jesse pakt in zijn beurt steeds één nieuwe steen, schrijft een positief reëel getal op de steen en legt hem in één van de dozen die nog niet vol is. Tjeerd ziet al deze getallen op de stenen in de dozen en mag in zijn beurt één steen naar keuze uit een doos verplaatsen naar de andere doos als die nog niet vol is, maar hij mag er ook voor kiezen om niets te doen. Het spel stopt zodra beide dozen vol zijn. Als dan de totale waarde van de stenen in de zwarte doos groter is dan de totale waarde van de stenen in de witte doos, wint Jesse; anders wint Tjeerd. Bepaal voor elke $n \\geq 2$ wie er met zekerheid kan winnen (en geef een bijbehorende winnende strategie).", "solution": "De volgende oplossing laat zien dat het niet uitmaakt hoe groot de capaciteit van de twee dozen is, als de capaciteit in totaal maar $n$ is (en minstens 1 per stuk). Jesse kan altijd winnen en doet dat door eerst de tweemacht $2^{0}=1$ te spelen, en vervolgens telkens de eerstvolgende kleinere of grotere tweemacht. Dus als hij op zeker moment al\n\n$$\n2^{-i}, 2^{-(i-1)}, \\ldots, 2^{-1}, 2^{0}, 2^{1}, \\ldots, 2^{j-1}, 2^{j}\n$$\n\nheeft gespeeld, speelt hij in de volgende beurt ofwel $2^{-(i+1)}$, dan wel $2^{j+1}$.\nJesse kan er door handig te spelen voor zorgen dat de grootste tweemacht onder de gespeelde stenen na zijn beurt altijd in de zwarte doos zit. We bewijzen deze claim met inductie. Bij zijn eerste zet plaatst hij de steen met waarde $2^{0}$ in de zwarte doos en klopt de claim; dit bewijst de inductiebasis. Als hij later weer aan de beurt is en Tjeerd heeft in de vorige zet de tot dan toe grootste tweemacht, die volgens de inductiehypothese in de zwarte doos zat, verplaatst naar de witte doos, dan is er in de zwarte doos een plek vrijgekomen en kan Jesse daar de volgende grotere tweemacht neerzetten en klopt de claim weer. Als Tjeerd iets anders heeft verplaatst of niets heeft gedaan, dan staat de tot dan toe grootste tweemacht nog altijd in de zwarte doos en speelt Jesse juist de volgende kleinere tweemacht; het maakt niet uit waar hij die neerzet. Ook nu klopt de claim weer. Dit bewijst de inductiestap, waarmee we de claim hebben bewezen.\n\nNa het spelen van de laatste steen staat de grootste gespeelde tweemacht dus in de zwarte doos. Die is groter dan de som van alle gespeelde kleinere tweemachten $\\left(2^{j}>2^{j}-2^{-i}=\\right.$ $\\left.2^{j-1}+2^{j-2}+\\cdots+2^{-(i-1)}+2^{-i}\\right)$, dus zeker groter dan de som van alle tweemachten in de witte doos. Dus de totale waarde van de zwarte doos is groter dan de totale waarde van de witte doos.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Gegeven is een driehoek $A B C$ met de eigenschap dat $|A B|+|A C|=3|B C|$. Zij $T$ het punt op lijnstuk $A C$ zodat $|A C|=4|A T|$. Laat $K$ en $L$ punten zijn op het inwendige van respectievelijk lijnstukken $A B$ en $A C$ zodat ten eerste $K L \\| B C$ en ten tweede $K L$ raakt aan de ingeschreven cirkel van $\\triangle A B C$. $\\mathrm{Zij} S$ het snijpunt van $B T$ en $K L$. Bepaal de verhouding $\\frac{|S L|}{|K L|}$.\n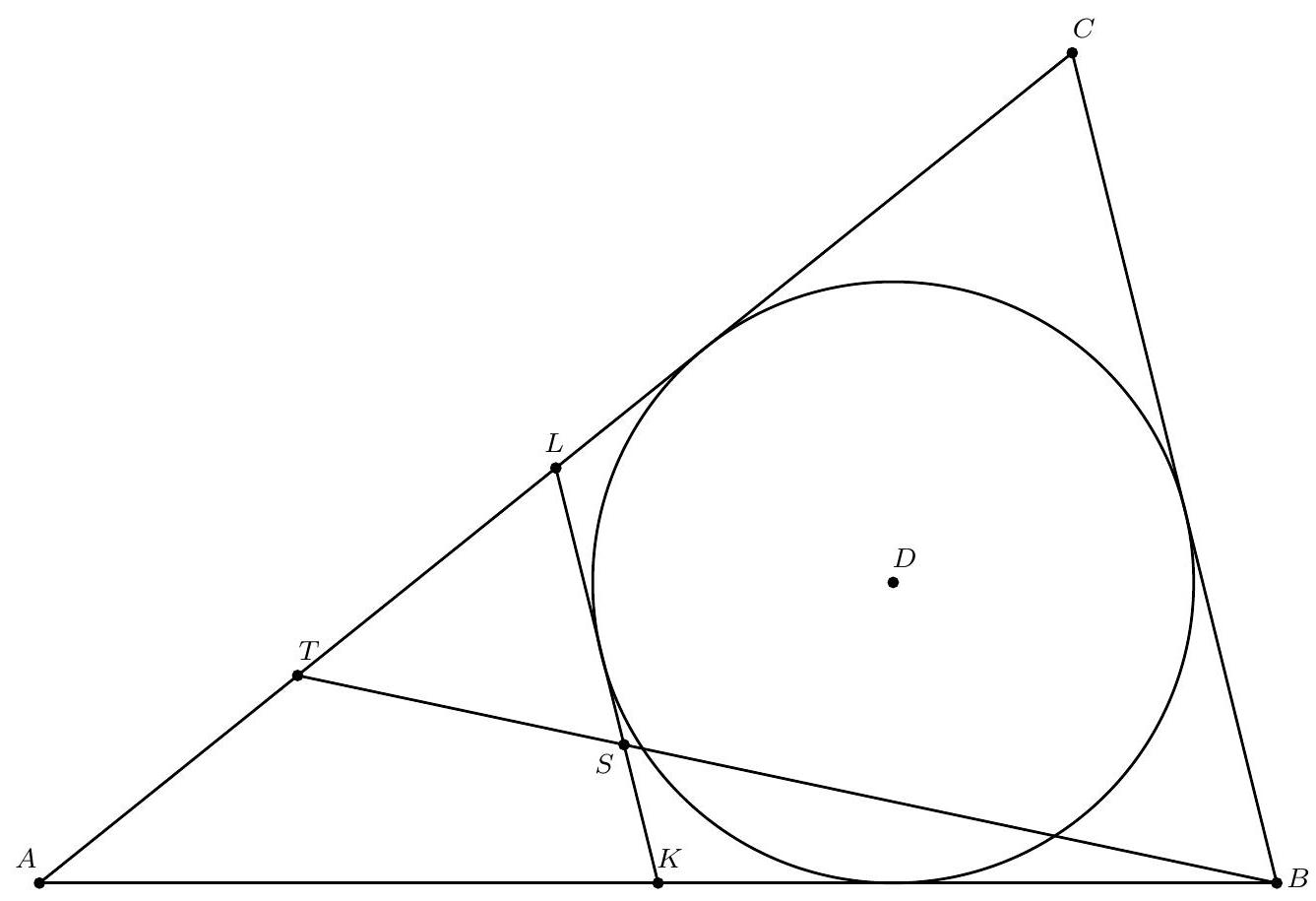", "solution": "De vierhoek $K B C L$ raakt met alle zijden aan de ingeschreven cirkel van $\\triangle A B C$. Bij elk hoekpunt zitten twee gelijke raaklijnstukjes. Twee overstaande zijden van de vierhoek bestaan samen precies uit de vier verschillende raaklijnstukjes, dus geldt $|K B|+|L C|=|K L|+|B C|$.\n\nVanwege $K L \\| B C$ geldt $\\triangle A K L \\sim \\triangle A B C$. Noem $t$ de vermenigvuldigingsfactor van deze gelijkvormigheid, dus $|A K|=t|A B|,|A L|=t|A C|$ en $|K L|=t|B C|$. Dan is $|B K|=$ $|A B|-|A K|=|A B|-t|A B|=(1-t)|A B|$. Analoog geldt $|C L|=(1-t)|A C|$. Er geldt nu\n$t|B C|+|B C|=|K L|+|B C|=|K B|+|L C|=(1-t)|A B|+(1-t)|A C|=3(1-t)|B C|$,\nwaarbij de laatste gelijkheid geldt vanwege het gegeven in de opgave. Delen door $|B C|$ geeft nu $1+t=3-3 t$, oftewel $4 t=2$ dus $t=\\frac{1}{2}$. We concluderen dat $K$ het midden van $A B$ is en $L$ het midden van $A C$.\n\nWe wisten al $\\triangle A K L \\sim \\triangle A B C$, waaruit volgt $\\frac{|K L|}{|B C|}=\\frac{|A L|}{|A C|}$. Er geldt wegens $K L \\| B C$ ook $\\triangle T S L \\sim \\triangle T B C$, dus $\\frac{|S L|}{|B C|}=\\frac{|T L|}{|T C|}$. Combineren we deze verhoudingen, dan krijgen we\n\n$$\n\\frac{|S L|}{|K L|}=\\frac{|S L|}{|B C|} \\cdot \\frac{|B C|}{|K L|}=\\frac{|T L|}{|T C|} \\cdot \\frac{|A C|}{|A L|} .\n$$\n\nWe weten dat $\\frac{|A C|}{|A L|}=2$, omdat $L$ het midden van $A C$ is. Dit betekent ook dat $T$ het midden van $A L$ is, aangezien $4|A T|=|A C|=2|A L|$. Dus $\\frac{|T L|}{|T C|}=\\frac{\\frac{1}{4}|A C|}{\\frac{3}{4}|A C|}=\\frac{1}{3}$. We concluderen dat $\\frac{|S L|}{|K L|}=\\frac{1}{3} \\cdot 2=\\frac{2}{3}$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing I."}
|
| 8 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Gegeven is een driehoek $A B C$ met de eigenschap dat $|A B|+|A C|=3|B C|$. Zij $T$ het punt op lijnstuk $A C$ zodat $|A C|=4|A T|$. Laat $K$ en $L$ punten zijn op het inwendige van respectievelijk lijnstukken $A B$ en $A C$ zodat ten eerste $K L \\| B C$ en ten tweede $K L$ raakt aan de ingeschreven cirkel van $\\triangle A B C$. $\\mathrm{Zij} S$ het snijpunt van $B T$ en $K L$. Bepaal de verhouding $\\frac{|S L|}{|K L|}$.\n", "solution": "Noem $r$ de straal van de ingeschreven cirkel van $\\triangle A B C$. De oppervlakte van driehoek $A B C$ is te schrijven als\n\n$$\n\\frac{1}{2}|A B| \\cdot r+\\frac{1}{2}|B C| \\cdot r+\\frac{1}{2}|A C|=\\frac{1}{2} r \\cdot(3|B C|+|B C|)=2 r|B C| .\n$$\n\nAnderzijds is de oppervlakte van driehoek $A B C$ gelijk aan $\\frac{1}{2} h|B C|$ met $h$ de hoogte vanuit $A$. Dus $h=4 r$. Omdat de afstand van $K L$ tot $B C$ precies $2 r$ is, is de afstand van $A$ tot $K L$ ook $2 r$. Driehoek $A K L$ en $A B C$ zijn gelijkvormig wegens $K L \\| B C$, met de hoogtes vanuit $A$ gelijk aan respectievelijk $2 r$ en $4 r$, dus de vermenigvuldigingsfactor is precies 2. Dus $K$ is het midden van $A B$ en $L$ is het midden van $A C$.\n\nVoor punt $T$ geldt $|A C|=4|A T|$, dus $|A T|=\\frac{1}{4}|A C|=\\frac{1}{2}|A L|$, dus $T$ is het midden van $A L$. Bekijk nu driehoek $A B L$. Hierin is $B T$ een zwaartelijn, want $T$ is het midden van $A L$. Ook is $L K$ een zwaartelijn, want $K$ is het midden van $A B$. Dus hun snijpunt $S$ is het zwaartepunt, waaruit volgt dat $\\frac{|S L|}{|K L|}=\\frac{2}{3}$.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "De rij positieve gehele getallen $a_{0}, a_{1}, a_{2}, \\ldots$ is gedefinieerd door $a_{0}=3$ en\n\n$$\na_{n+1}-a_{n}=n\\left(a_{n}-1\\right)\n$$\n\nvoor alle $n \\geq 0$. Bepaal alle gehele getallen $m \\geq 2$ waarvoor geldt dat $\\operatorname{ggd}\\left(m, a_{n}\\right)=1$ voor alle $n \\geq 0$.", "solution": "Een directe formule voor de rij wordt gegeven door $a_{n}=2 \\cdot n!+1$ voor $n \\geq 0$. (We gebruiken de gangbare definitie $0!=1$, die voldoet aan $1!=1 \\cdot 0$ !, zoals ook voor grotere $n$ geldt $n!=n \\cdot(n-1)!$.) We bewijzen de directe formule met inductie. Er geldt $a_{0}=3$ en dat is gelijk aan $2 \\cdot 0!+1$. Stel nu dat voor zekere $k \\geq 0$ geldt $a_{k}=2 \\cdot k!+1$, dan is\n\n$$\na_{k+1}=a_{k}+k\\left(a_{k}-1\\right)=2 \\cdot k!+1+k \\cdot 2 \\cdot k!=2 \\cdot k!\\cdot(1+k)+1=2 \\cdot(k+1)!+1\n$$\n\nDit voltooit de inductie.\n\nWe zien dat $a_{n}$ altijd oneven is, dus $\\operatorname{ggd}\\left(2, a_{n}\\right)=1$ voor alle $n$. Daaruit volgt ook dat $\\operatorname{ggd}\\left(2^{i}, a_{n}\\right)=1$ voor alle $i \\geq 1$. Dus $m=2^{i}$ met $i \\geq 1$ voldoet. Neem nu een $m \\geq 2$ die geen tweemacht is. Dan heeft $m$ een oneven priemdeler, zeg $p$. We laten zien dat $p$ een deler is van $a_{p-3}$. Wegens de stelling van Wilson geldt $(p-1)!\\equiv-1 \\bmod p$. Dus\n$2 \\cdot(p-3)!\\equiv 2 \\cdot(p-1)!\\cdot((p-2)(p-1))^{-1} \\equiv 2 \\cdot-1 \\cdot(-2 \\cdot-1)^{-1} \\equiv 2 \\cdot-1 \\cdot 2^{-1} \\equiv-1 \\quad \\bmod p$.\nDus inderdaad geldt $a_{p-3}=2 \\cdot(p-3)!+1 \\equiv 0 \\bmod p$. We concluderen dat $m$ niet voldoet. Dus de enige waarden van $m$ die voldoen zijn de tweemachten.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing."}
|
| 2 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Vind alle viertallen $\\left(x_{1}, x_{2}, x_{3}, x_{4}\\right)$ van reële getallen zodat de volgende zes gelijkheden gelden:\n\n$$\n\\begin{aligned}\n& x_{1}+x_{2}=x_{3}^{2}+x_{4}^{2}+6 x_{3} x_{4}, \\\\\n& x_{1}+x_{3}=x_{2}^{2}+x_{4}^{2}+6 x_{2} x_{4}, \\\\\n& x_{1}+x_{4}=x_{2}^{2}+x_{3}^{2}+6 x_{2} x_{3}, \\\\\n& x_{2}+x_{3}=x_{1}^{2}+x_{4}^{2}+6 x_{1} x_{4}, \\\\\n& x_{2}+x_{4}=x_{1}^{2}+x_{3}^{2}+6 x_{1} x_{3}, \\\\\n& x_{3}+x_{4}=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2} .\n\\end{aligned}\n$$", "solution": "De eerste twee vergelijkingen van elkaar afhalen geeft $x_{2}-x_{3}=x_{3}^{2}-x_{2}^{2}+$ $6 x_{4}\\left(x_{3}-x_{2}\\right)$, wat we kunnen ontbinden als $0=\\left(x_{3}-x_{2}\\right)\\left(x_{3}+x_{2}+1+6 x_{4}\\right)$. We zien dat $x_{2}=x_{3}$ of $x_{2}+x_{3}+1+6 x_{4}=0$. Analoog geldt ook dat $x_{2}=x_{3}$ of $x_{2}+x_{3}+1+6 x_{1}=0$. Dus als $x_{2} \\neq x_{3}$, dan geldt in beide gevallen de tweede gelijkheid; die van elkaar afhalen geeft $x_{1}=x_{4}$. We conluderen dat $x_{2}=x_{3}$ of $x_{1}=x_{4}$. Analoog geldt voor elke permutatie $(i, j, k, l) \\operatorname{van}(1,2,3,4)$ dat $x_{i}=x_{j}$ of $x_{k}=x_{l}$.\n\nWe bewijzen nu dat minstens drie van de $x_{i}$ gelijk aan elkaar zijn. Als ze alle vier gelijk zijn, is dat natuurlijk waar. Anders zijn er twee die ongelijk zijn, zeg zonder verlies van algemeenheid $x_{1} \\neq x_{2}$. Dan geldt $x_{3}=x_{4}$. Als nu $x_{1}=x_{3}$, dan zijn er drie elementen aan elkaar gelijk. Anders is $x_{1} \\neq x_{3}$, dus $x_{2}=x_{4}$ en ook dan zijn er drie elementen aan elkaar gelijk. Het viertal $\\left(x_{1}, x_{2}, x_{3}, x_{4}\\right)$ is dus op volgorde na van de vorm $(x, x, x, y)$, waarbij eventueel mag gelden dat $x=y$.\n\nDit invullen in de gegeven vergelijkingen geeft $x+y=8 x^{2}$ en $2 x=x^{2}+y^{2}+6 x y$. Tel deze twee vergelijkingen bij elkaar op: $3 x+y=9 x^{2}+y^{2}+6 x y$. De rechterkant is te ontbinden als $(3 x+y)^{2}$. Met $s=3 x+y$ staat er dus $s=s^{2}$, waaruit volgt $s=0$ of $s=1$. Er geldt $s=3 x+y=2 x+(x+y)=2 x+8 x^{2}$. Dus $8 x^{2}+2 x=0$ of $8 x^{2}+2 x=1$.\n\nIn het eerste geval geldt $x=0$ of $x=-\\frac{1}{4}$. We vinden $y=0-3 x=0$ respectievelijk $y=$ $0-3 x=\\frac{3}{4}$. In het tweede geval kunnen we de vergelijking ontbinden als $(4 x-1)(2 x+1)=0$, dus $x=\\frac{1}{4}$ of $x=-\\frac{1}{2}$. We vinden $y=1-3 x=\\frac{1}{4}$ respectievelijk $y=1-3 x=\\frac{5}{2}$.\n\nAlles bij elkaar hebben we de volgende viertallen gevonden: $(0,0,0,0),\\left(-\\frac{1}{4},-\\frac{1}{4},-\\frac{1}{4}, \\frac{3}{4}\\right)$ en de permutaties hiervan, $\\left(\\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}\\right)$ en $\\left(-\\frac{1}{2},-\\frac{1}{2},-\\frac{1}{2}, \\frac{5}{2}\\right)$ en de permutaties hiervan. Controleren laat zien dat al deze viertallen voldoen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 3 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Vind alle viertallen $\\left(x_{1}, x_{2}, x_{3}, x_{4}\\right)$ van reële getallen zodat de volgende zes gelijkheden gelden:\n\n$$\n\\begin{aligned}\n& x_{1}+x_{2}=x_{3}^{2}+x_{4}^{2}+6 x_{3} x_{4}, \\\\\n& x_{1}+x_{3}=x_{2}^{2}+x_{4}^{2}+6 x_{2} x_{4}, \\\\\n& x_{1}+x_{4}=x_{2}^{2}+x_{3}^{2}+6 x_{2} x_{3}, \\\\\n& x_{2}+x_{3}=x_{1}^{2}+x_{4}^{2}+6 x_{1} x_{4}, \\\\\n& x_{2}+x_{4}=x_{1}^{2}+x_{3}^{2}+6 x_{1} x_{3}, \\\\\n& x_{3}+x_{4}=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2} .\n\\end{aligned}\n$$", "solution": "Alle gelijkheden optellen geeft\n\n$$\n3\\left(x_{1}+x_{2}+x_{3}+x_{4}\\right)=3\\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}\\right)+6\\left(x_{1} x_{2}+x_{1} x_{3}+x_{1} x_{4}+x_{2} x_{3}+x_{2} x_{4}+x_{3} x_{4}\\right) .\n$$\n\nDe rechterkant laat zich ontbinden als $3\\left(x_{1}+x_{2}+x_{3}+x_{4}\\right)^{2}$. Schrijf $s=x_{1}+x_{2}+x_{3}+x_{4}$, dan vinden we dus nu de vergelijking $3 s=3 s^{2}$ met oplossingen $s=0$ en $s=1$.\n\nZij $(i, j, k, l)$ een permutatie van $(1,2,3,4)$. Dan geldt\n\n$$\ns-\\left(x_{i}+x_{j}\\right)=x_{k}+x_{l}=x_{i}^{2}+x_{j}^{2}+6 x_{i} x_{j}\n$$\n\ndus\n\n$$\nx_{i}^{2}+x_{j}^{2}+6 x_{i} x_{j}+x_{i}+x_{j}-s=0 .\n$$\n\nVoor een vaste $j$ is dit een kwadratische vergelijking in $x_{i}$, met maximaal twee oplossingen. Bij een vaste $j$ kunnen we voor $i$ drie verschillende waarden kiezen, dus volgens het ladenprincipe zijn twee van die mogelijke $x_{i}$ gelijk aan elkaar. Voor elke $x_{j}$ geldt dus dat van $x_{i}, x_{k}$ en $x_{l}$ er twee gelijk aan elkaar zijn.\n\nIn het bijzonder zijn twee van $x_{2}, x_{3}$ en $x_{4}$ gelijk aan elkaar, zeg $x_{3}=x_{4}$. Nu nemen we $j=3$ en zien we dat van $x_{1}, x_{2}$ en $x_{4}$ er twee gelijk aan elkaar zijn. Als $x_{4}$ daarbij zit, hebben we drie gelijke elementen. Als $x_{4}$ er niet bij zit, geldt $x_{1}=x_{2}$ en $x_{3}=x_{4}$. Op volgorde na moeten de viertallen dus van de vorm $(x, x, x, y)$ of $(x, x, y, y)$ zijn. Vul nu in (1) $x_{i}=x$ en $x_{j}=x$ in. Dan staat er $8 x^{2}+2 x-s=0$. We gaan nu gevallen naar $s$ onderscheiden.\n\nStel dat $s=0$. Dan geldt er $8 x^{2}+2 x=0$, dus $x=0$ of $x=-\\frac{1}{4}$. Als $x=0$, dan zijn dus twee of drie van de elementen gelijk aan 0 . Verder weten we dat de som van de vier elementen nul moet zijn en dat als er nog twee elementen over zijn, die gelijke waarde moeten hebben. We zien dat alleen $(0,0,0,0)$ mogelijk is. Als $x=-\\frac{1}{4}$, dan vullen we $x$ en $y$ in in (1). Dat geeft $y^{2}+\\frac{1}{16}-\\frac{6}{4} y+y-\\frac{1}{4}=0$, oftewel $y^{2}-\\frac{1}{2} y-\\frac{3}{16}=0$. Dit kunnen we herschrijven als $\\left(y+\\frac{1}{4}\\right)\\left(y-\\frac{3}{4}\\right)=0$, dus $y=-\\frac{1}{4}$ of $y=\\frac{3}{4}$. Omdat de som van de vier elementen 0 moet zijn, kan (op volgorde na) alleen ( $-\\frac{1}{4},-\\frac{1}{4},-\\frac{1}{4}, \\frac{3}{4}$ ).\n\nStel dat $s=1$. Dan geldt er $8 x^{2}+2 x-1=0$, wat te schrijven is als $(4 x-1)(2 x+1)=0$, dus $x=\\frac{1}{4}$ of $x=-\\frac{1}{2}$. Als $x=\\frac{1}{4}$, dan vullen we $x$ en $y$ in in (1). Dat geeft $y^{2}+\\frac{1}{16}+\\frac{6}{4} y+y+\\frac{1}{4}-1=$ 0 , oftewel $y^{2}+\\frac{5}{2} y-\\frac{11}{16}=0$. Dit kunnen we herschrijven als $\\left(y-\\frac{1}{4}\\right)\\left(y+\\frac{11}{4}\\right)=0$, dus $y=\\frac{1}{4}$ of $y=-\\frac{11}{4}$. Omdat de som van de vier elementen 1 moet zijn, kan alleen $\\left(\\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}\\right)$. Als $x=-\\frac{1}{2}$, dan vullen we $x$ en $y$ in in (1). Dat geeft $y^{2}+\\frac{1}{4}-3 y+y-\\frac{1}{2}-1=0$, oftewel $y^{2}-2 y-\\frac{5}{4}=0$. Dit kunnen we herschrijven als $\\left(y+\\frac{1}{2}\\right)\\left(y-\\frac{5}{2}\\right)=0$, dus $y=-\\frac{1}{2}$ of $y=\\frac{5}{2}$. Omdat de som van de vier elementen 1 moet zijn, kan (op volgorde na) alleen $\\left(-\\frac{1}{2},-\\frac{1}{2},-\\frac{1}{2}, \\frac{5}{2}\\right)$.\n\nAlles bij elkaar hebben we de volgende viertallen gevonden: $(0,0,0,0),\\left(-\\frac{1}{4},-\\frac{1}{4},-\\frac{1}{4}, \\frac{3}{4}\\right)$ en de permutaties hiervan, $\\left(\\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}, \\frac{1}{4}\\right)$ en $\\left(-\\frac{1}{2},-\\frac{1}{2},-\\frac{1}{2}, \\frac{5}{2}\\right)$ en de permutaties hiervan. Controleren laat zien dat al deze viertallen voldoen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 4 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Zij $A B C$ een scherphoekige en niet-gelijkbenige driehoek met hoogtepunt $H$. Zij $O$ het middelpunt van de omgeschreven cirkel van driehoek $A B C$ en zij $K$ het middelpunt van de omgeschreven cirkel van driehoek $A H O$. Bewijs dat de spiegeling van $K$ in $O H$ op $B C$ ligt.\n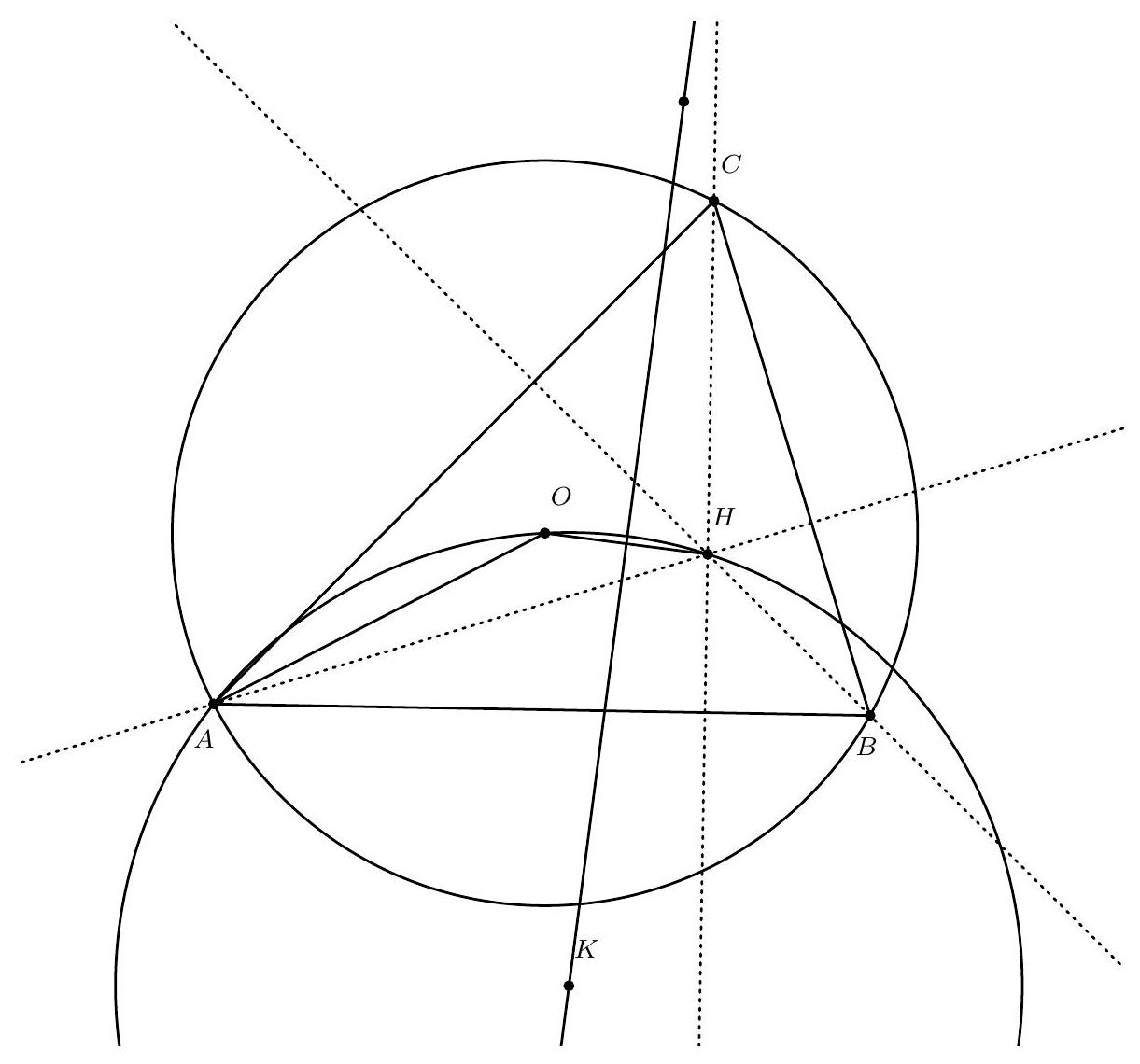", "solution": "We bekijken de configuratie zoals in de figuur. Andere configuraties gaan analoog. Noem $D$ het tweede snijpunt van $A H$ met de omgeschreven cirkel van $\\triangle A B C$. Noem $S$ het tweede snijpunt van de omgeschreven cirkel van $A B C$ en de omgeschreven cirkel van $A H O$. (Omdat $\\triangle A B C$ scherphoekig is, liggen $O$ en $H$ inwendig in driehoek $A B C$ en dus ook in zijn omgeschreven cirkel, dus $D$ en $S$ bestaan allebei.)\n\nEr geldt\n\n$$\n\\angle O S H=\\angle O A H=\\angle O A D=\\angle O D A=\\angle O D H,\n$$\n\nwaarbij we gebruiken dat $|O A|=|O D|$. Verder geldt\n\n$$\n\\angle O H D=180^{\\circ}-\\angle O H A=180^{\\circ}-\\angle O S A=180^{\\circ}-\\angle O A S=\\angle O H S,\n$$\n\nwaarbij we gebruiken dat $|O A|=|O S|$. We concluderen nu dat $\\triangle O H S \\cong \\triangle O H D$ (ZHH). Hieruit volgt dat $D$ en $S$ elkaars gespiegelde in $O H$ zijn.\n\nAls we het middelpunt $K$ van de omgeschreven cirkel van $\\triangle O H S$ spiegelen in $O H$, krijgen we dus het middelpunt $L$ van de omgeschreven cirkel van $\\triangle O H D$. We moeten nu bewijzen dat $L$ op $B C$ ligt.\n\nPunt $D$ is de spiegeling van $H$ in $B C$. Dit is een bekend feit, dat we als volgt kunnen bewijzen: $\\angle D B C=\\angle D A C=\\angle H A C=90^{\\circ}-\\angle A C B=\\angle H B C$ en analoog is $\\angle D C B=\\angle H C B$, dus $\\triangle D B C \\cong \\triangle H B C(\\mathrm{HZH})$. Dus inderdaad is $D$ de spiegeling van $H$ in $B C$, waaruit volgt dat $B C$ de middelloodlijn van $H D$ is. Omdat $L$ op de middelloodlijn van $H D$ ligt, ligt $L$ op $B C$ en dat is wat we wilden bewijzen.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Op een rechthoekig bord met $m \\times n$ vakjes ( $m, n \\geq 3$ ) liggen domino's ( $2 \\times 1$ of $1 \\times 2$-tegels), die elkaar niet overlappen en niet uitsteken buiten het bord. Elke domino bedekt precies twee vakjes van het bord. Neem aan dat de bedekking met domino's de eigenschap heeft dat er geen enkele domino meer bijgeplaatst kan worden op het bord en dat de vier hoekvakjes van het bord niet allemaal leeg zijn. Bewijs dat minstens $\\frac{2}{3}$ van de vakjes van het bord bedekt zijn met domino's.", "solution": "Koppel elk leeg vakje aan de domino die direct rechts van dit vakje ligt (tenzij het vakje aan de rechterrand van het bord ligt). Stel dat er nu twee lege vakjes aan dezelfde domino gekoppeld worden, dan moet deze domino verticaal liggen en zijn beide vakjes links van hem leeg. Echter, dan zou er daar nog een extra domino passen, tegenspraak. Dus er worden geen twee lege vakjes aan dezelfde domino gekoppeld.\n\nDe lege vakjes aan de rechterrand van het bord zijn nog niet gekoppeld. We proberen deze vakjes elk te koppelen aan een domino die direct links van zich geen leeg vakje heeft (en dus nog niet gekoppeld was). Neem eerst even aan dat het lukt om alle lege vakjes van de rechterrand op deze manier te koppelen aan verschillende domino's. We hebben dan alle lege vakjes van het bord gekoppeld aan een domino, waarbij geen domino twee keer gebruikt wordt. Omdat elke domino twee vakjes van het bord bedekt, zijn er voor elk leeg vakje twee bedekte vakjes en is dus hooguit $\\frac{1}{3}$ van de vakjes van het bord leeg. Dan zijn we klaar.\n\nWe gaan nu laten zien dat deze koppeling altijd lukt. Noem $k$ het aantal lege vakjes aan de rechterrand en $\\ell$ het aantal lege vakjes aan de linkerrand. De lege vakjes aan de linkerrand mogen niet naast elkaar liggen, dus liggen er minstens $\\ell-1$ domino's aan de linkerrand en deze hebben allemaal geen leeg vakje links van zich. Als $\\ell>k$, dan liggen er dus genoeg domino's aan de linkerrand liggen om alle lege vakjes van de rechterrand te koppelen. Als $\\ell<k$, dan zouden we de hele situatie kunnen omdraaien en juist alle lege vakjes koppelen aan de domino links daarvan en zouden we daarmee ook kunnen bewijzen dat hooguit $\\frac{1}{3}$ van de vakjes van het bord leeg is. De enige situatie die nog over is, is als $\\ell=k$ en er zowel links als rechts precies $k-1$ domino's aan de rand liggen. Aan beide randen geldt dan dat er tussen elke twee domino's een leeg vakje zit en er ook een leeg vakje in de hoeken zit. Maar dit is in tegenspraak met de voorwaarde in de opgave dat niet alle hoekvakjes leeg zijn. Deze situatie kan dus niet voorkomen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Zij $\\Gamma$ de omgeschreven cirkel van een driehoek $A B C$ en zij $D$ een punt op lijnstuk $B C$. De cirkel door $B$ en $D$ die raakt aan $\\Gamma$ en de cirkel door $C$ en $D$ die raakt aan $\\Gamma$ snijden in een punt $E \\neq D$. De lijn $D E$ snijdt $\\Gamma$ in twee punten $X$ en $Y$. Bewijs dat $|E X|=|E Y|$.", "solution": "We bekijken de configuratie zoals in de figuur, waarbij $E$ minstens zo dicht bij $B$ ligt als bij $C$. De configuratie waarbij dit andersom is, gaat analoog. Zij $O$ het middelpunt van $\\Gamma$. De hoek tussen de lijn $B C$ en de gemeenschappelijke raaklijn in $B$ is volgens de raaklijnomtrekshoekstelling enerzijds gelijk aan $\\angle B E D$ en anderzijds aan $\\angle B A C$. Dus $\\angle B E D=\\angle B A C$. Analoog geldt $\\angle C E D=\\angle B A C$, dus $\\angle B E C=\\angle B E D+\\angle C E D=2 \\angle B A C=\\angle B O C$, waarbij we in de laatste stap de middelpuntomtrekshoekstelling gebruiken. Nu volgt dat $E$ op de cirkel door $B, O$ en $C$ ligt. Als $E=O$, dan zijn we direct klaar, want dan zijn $|E X|$ en $|E Y|$ beide de straal van de cirkel. Zo niet, dan is (in onze configuratie) $B E O C$ een koordenvierhoek.\n\nDus $\\angle B E O=180^{\\circ}-\\angle B C O$. Verder geldt in gelijkbenige driehoek $B O C$ dat $\\angle B C O=$ $90^{\\circ}-\\frac{1}{2} \\angle B O C=90^{\\circ}-\\angle B A C$, dus $\\angle B E O=180^{\\circ}-\\left(90^{\\circ}-\\angle B A C\\right)=90^{\\circ}+\\angle B A C$. Hiermee vinden we $\\angle D E O=\\angle B E O-\\angle B E D=90^{\\circ}+\\angle B A C-\\angle B A C=90^{\\circ}$. Dus $E O$ staat loodrecht op $D E$ en daarmee ook loodrecht op koorde $X Y$, waaruit volgt dat $E$ het midden van $X Y$ is. Dus $|E X|=|E Y|$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Zij $\\Gamma$ de omgeschreven cirkel van een driehoek $A B C$ en zij $D$ een punt op lijnstuk $B C$. De cirkel door $B$ en $D$ die raakt aan $\\Gamma$ en de cirkel door $C$ en $D$ die raakt aan $\\Gamma$ snijden in een punt $E \\neq D$. De lijn $D E$ snijdt $\\Gamma$ in twee punten $X$ en $Y$. Bewijs dat $|E X|=|E Y|$.", "solution": "Zij $O$ het middelpunt van $\\Gamma$, zij $\\Gamma_{B}$ de cirkel door $B, D$ en $E$ en zij $\\Gamma_{C}$ de cirkel door $C$, $D$ en $E$. De gemeenschappelijke raaklijn van $\\Gamma$ en $\\Gamma_{B}$ is de machtlijn van deze twee cirkels; zo ook is de raaklijn in $C$ de machtlijn van $\\Gamma$ en $\\Gamma_{C}$. Noem $P$ het snijpunt van de twee raaklijnen; dan is $P$ het machtpunt van de drie cirkels. Aangezien $D E$ de machtlijn van $\\Gamma_{B}$ en $\\Gamma_{C}$ is, ligt $P$ op $D E$. Zij nu $M$ het midden van $B C$. Dan is $O M$ de middelloodlijn van $B C$ en die gaat door het snijpunt van de raaklijnen in $B$ en $C$, dus $P$ ligt ook op $O M$. Er geldt $\\angle P B O=90^{\\circ}$ omdat $P B$ de raaklijn aan $\\Gamma$ is. Maar dan raakt $P B$ ook aan de cirkel met middellijn $O B$, die wegens Thales door $M$ gaat aangezien $\\angle O M B=90^{\\circ}$. Met de machtstelling vinden we nu $P B^{2}=P M \\cdot P O$, terwijl de machtstelling op $\\Gamma_{B}$ geeft dat $P B^{2}=P D \\cdot P E$. Dus $P M \\cdot P O=P D \\cdot P E$, waaruit volgt dat $D, M, O$ en $E$ op een cirkel liggen. Omdat $\\angle D M O=90^{\\circ}$ is $O M$ een middellijn van deze cirkel. Als $E=O$, dan zijn we direct klaar, want dan zijn $|E X|$ en $|E Y|$ beide de straal van de cirkel. Zo niet, dan geldt $\\angle D E O=90^{\\circ}$. Dus $E O$ staat loodrecht op $D E$ en daarmee ook loodrecht op koorde $X Y$, waaruit volgt dat $E$ het midden van $X Y$ is. Dus $|E X|=|E Y|$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Stekel en Prik spelen een spel op een $m \\times n$-bord, waarbij $m$ en $n$ positieve gehele getallen zijn. Ze zijn afwisselend aan de beurt, waarbij Stekel begint. Stekel zet in zijn beurt steeds een pion op een vakje waar nog geen pion staat. Prik doet in zijn beurt hetzelde, maar zijn pion moet altijd komen in een vakje dat met een zijde grenst aan het vakje waar Stekel net in zijn vorige beurt een pion in gezet heeft. Prik wint als het hele bord vol met pionnen staat. Stekel wint als Prik geen pion meer kan zetten in zijn beurt, terwijl er nog wel minstens een leeg vakje op het bord is. Bepaal voor alle paren $(m, n)$ wie er een winnende strategie heeft.", "solution": "Als $m$ (het aantal rijen) even is, dan koppelen we de vakjes van het bord in tweetallen aan elkaar: in elke kolom vormen de bovenste twee vakjes een tweetal, en het derde en vierde vakje, enzovoorts. Omdat er een even aantal rijen is, lukt dit. Prik kan nu de volgende strategie hanteren: als Stekel een vakje van zo'n tweetal bezet, zet hij een pion in het andere vakje van dit tweetal. Na elke zet van Prik zijn op deze manier alle tweetallen met nul of met twee pionnen bezet, dus hij kan deze strategie steeds blijven uitvoeren. Hij voldoet automatisch aan de voorwaarde dat zijn pion grenst aan de pion die Stekel net heeft neergezet. Prik kan dus zorgen dat het hele bord vol met pionnen komt en wint. Als $n$ even is, heeft Prik analoog ook een winnende strategie.\n\nAls $m=n=1$ hoeft Prik geen enkele pion te zetten om te winnen. Als $m=1$ en $n=3$ of andersom, zet Prik zijn eerste pion op een vakje dat grenst aan het vakje waar Stekel net een pion heeft neergezet; dat lukt altijd. Het bord is dan na de volgende zet van Stekel vol, dus Prik wint.\n\nBekijk nu het geval dat $m=n=3$. Stekel kan de volgende strategie volgen. Hij zet zijn eerste pion in het middelste vakje. Prik moet in dezelfde rij of in dezelfde kolom een pion zetten; zonder verlies van algemeenheid nemen we aan dat de pion van Prik in dezelfde kolom komt. Stekel zet nu in het derde vakje van deze kolom een pion. Op dat moment zijn de linker- en rechterkolom nog helemaal leeg. Prik moet in één van beide een pion zetten. Stekel kiest vervolgens de andere kolom: daar zijn nog drie vakjes leeg. Hij plaatst daar een pion en dwingt Prik daarmee om ook in die kolom een pion te zetten; de vakjes in de middelste kolom zijn immmers allemaal al vol. Stekel plaatst vervolgens een pion in het laatste vakje van die kolom, waarna Prik niet meer kan. Dus Stekel wint.\n\nBlijft over het geval dat $m$ en $n$ allebei oneven zijn en dat $m \\geq 5$ of $n \\geq 5$ (of allebei). We bekijken het geval dat $n$ (het aantal kolommen) minstens 5 is. Het andere geval gaat analoog. Stekel kan nu de volgende strategie volgen. Hij zet zijn pionnen steeds in de middelste kolom, totdat die kolom vol is. Als Stekel vervolgens weer aan de beurt is, staat er een even aantal pionnen op het bord, allemaal in de middelste drie kolommen, waarbij de middelste kolom in elk geval helemaal vol is. De linker- en rechterkolom zijn nog helemaal leeg. Er is nog een oneven aantal vakjes open, dus ofwel het gebied links van de middelste kolom ofwel het gebied rechts van de middelste kolom bevat een oneven aantal lege vakjes.\n\nStekel kiest dat gebied en plaatst vervolgens al zijn pionnen daar, op willekeurige plekken. Omdat de middelste kolom helemaal vol is, moet Prik nu ook al zijn pionnen in dat gebied zetten. Er was een oneven aantal vakjes leeg in dit gebied, dus Stekel bezet in principe het laatste vakje. Prik kan daarna niet meer zetten, dus Stekel wint. Mocht Prik al in een eerdere beurt niet meer kunnen zetten, dan wint Stekel ook.\n\nWe concluderen dat Stekel wint als $m$ en $n$ oneven zijn en $m \\geq 5$, als $m$ en $n$ oneven zijn en $n \\geq 5$, en als $m=n=3$. Prik wint in alle overige gevallen: als $m$ even is, als $n$ even is, als $m=n=1$, als $m=1$ en $n=3$ en als $m=3$ en $n=1$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing."}
|
| 4 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Bewijs dat voor elk positief geheel getal $n$ er positieve gehele getallen $a$ en $b$ bestaan met\n\n$$\nn \\mid 4 a^{2}+9 b^{2}-1\n$$", "solution": "Voor $n=1$ voldoet elke keuze van $a$ en $b$. Stel nu dat $n>1$ en zij $p$ een priemdeler van $n$. Zij $k$ het aantal factoren $p$ in $n$. We geven een voorwaarde voor $a$ en $b$ modulo $p^{k}$ die garandeert dat $p^{k} \\mid 4 a^{2}+9 b^{2}-1$. Door dit voor elke priemdeler van $n$ te doen, krijgen we een stelsel van eisen voor $a$ en $b$ modulo de verschillende priemmachten. De Chinese reststelling vertelt ons vervolgens dat er nu een $n$ te vinden is die aan alle eisen tegelijk voldoet.\n\nAls $p \\neq 2$ nemen we als voorwaarde dat $2 a \\equiv 1 \\bmod p^{k}$ en $b \\equiv 0 \\bmod p^{k}$. Omdat 2 een multiplicatieve inverse heeft modulo $p^{k}$, is dit mogelijk. We zien nu dat\n\n$$\n4 a^{2}+9 b^{2}-1=(2 a)^{2}+9 b^{2}-1 \\equiv 1^{2}+9 \\cdot 0-1=0 \\quad \\bmod p^{k} .\n$$\n\nDus deze keuze voor $a$ en $b$ voldoet.\nAls $p=2$ nemen we als voorwaarde $a \\equiv 0 \\bmod 2^{k}$ en $3 b \\equiv 1 \\bmod 2^{k}$. Omdat 3 een multiplicatieve inverse heeft modulo $2^{k}$, is dit mogelijk. We zien nu dat\n\n$$\n4 a^{2}+9 b^{2}-1=4 a^{2}+(3 b)^{2}-1 \\equiv 4 \\cdot 0+1^{2}-1=0 \\quad \\bmod 2^{k}\n$$\n\nDus deze keuze voor $a$ en $b$ voldoet.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 5 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Bepaal alle positieve gehele getallen $n$ met de volgende eigenschap: voor ieder drietal $(a, b, c)$ van positieve reële getallen is er een drietal $(k, \\ell, m)$ van niet-negatieve gehele getallen zodat dat $a n^{k}, b n^{\\ell}$ en $c n^{m}$ de lengtes van de zijden van een (niet-gedegenereerde) driehoek vormen.", "solution": "Het is duidelijk dat $n=1$ niet voldoet, want niet elke drie positieve reële getallen $a, b$ en $c$ zijn de lengtes van een driehoek. We bewijzen nu eerst dat $n \\geq 5$ niet voldoet door het drietal $(1,2,3)$ te bekijken. Stel dat er $k, \\ell, m$ bestaan zodat $n^{k}, 2 n^{\\ell}$ en $3 n^{m}$ de lengtes van de zijden van een driehoek vormen. Merk allereerst op dat geen twee van deze drie getallen gelijk aan elkaar kunnen zijn, aangezien $n \\neq 2,3$. Door de driehoek eventueel een aantal keer met een factor $n$ te verkleinen, kunnen we verder aannemen dat één van de getallen $k$, $\\ell$ en $m$ gelijk aan 0 is. Stel dat de andere twee allebei positief zijn, dan zijn de bijbehorende zijdelengtes allebei een veelvoud van $n$. Hun verschil is dus ook tenminste $n$, terwijl de derde zijde hooguit 3 is. Dit is in tegenspraak met de driehoeksongelijkheid. Dus van $k, \\ell$ en $m$ moeten er minstens twee gelijk aan 0 zijn. De bijbehorende twee zijdelengtes hebben som hoogstens 5 , dus de derde zijde moet kleiner dan 5 zijn. Uit $n \\geq 5$ volgt dan dat die derde zijde ook geen factor $n$ in zijn lengte heeft. Dus $k$, $\\ell$ en $m$ zijn alle drie gelijk aan 0 , maar dan zouden 1,2 en 3 de lengtes van de zijden van een driehoek moeten zijn, terwijl $3=2+1$. Tegenspraak. We concluderen dat $n \\geq 5$ niet voldoet.\n\nBekijk nu $n=2,3,4$. We construeren $(k, \\ell, m)$ als volgt. Neem een drietal $(a, b, c)$. Als dit al de zijden van een driehoek zijn, nemen we $k=\\ell=m=0$. Anders is er een driehoeksongelijkheid die niet geldt, zeg zonder verlies van algemeenheid dat er geldt $a \\geq$ $b+c$. Vermenigvuldig nu de kleinste van $b$ en $c$ met $n$. Als daarmee de rechterkant nog niet groter dan $a$ is, vermenigvuldigen we nog een keer de kleinste (van de nieuwe twee termen) met $n$. Algemeen geldt dus: als $a \\geq n^{i} b+n^{j} c$, dan vermenigvuldigen we de kleinste van $n^{i} b$ en $n^{j} c$ met $n$ en kijken dan opnieuw of de ongelijkheid nog geldt. Dit proces stopt gegarandeerd, want er is een $i$ zodat $n^{i}>a$. Bekijk nu de $i$ en $j$ zodat $a \\geq n^{i} b+n^{j} c$ en dit de laatste stap is waarin deze ongelijkheid geldt. Neem zonder verlies van algemeenheid aan dat $n^{i} b \\leq n^{j} c$, dan geldt dus $a<n^{i+1} b+n^{j} c$. We beweren nu dat we ( $k, \\ell, m$ ) gelijk kunnen nemen aan een van $(0, i+1, j)$ en $(0, i+1, j+1)$.\n\nPer definitie geldt $a<n^{i+1} b+n^{j} c$ en verder is $n^{j} c<n^{i} b+n^{j} c \\leq a<a+n^{i+1} b$, dus als $(0, i+1, j)$ niet voldoet, dan moet dat komen omdat $n^{i+1} b \\geq a+n^{j} c$. Verder is $n^{i} b \\leq n^{j} c$, dus $n^{i+1} b \\leq n^{j+1} c<a+n^{j+1} c$. Ook is natuurlijk $a<n^{i+1} b+n^{j+1} c$, dus als $(0, i+1, j+1)$ niet voldoet, dan moet dat komen omdat $n^{j+1} c \\geq a+n^{i+1} b$. We gaan een tegenspraak afleiden in het geval dat beide drietallen niet voldoen. We weten dan dus dat zowel $n^{i+1} b \\geq a+n^{j} c$ als $n^{j+1} c \\geq a+n^{i+1} b$.\n\nDeze ongelijkheden bij elkaar optellen en links en rechts $n^{i+1} b$ wegstrepen geeft $n^{j+1} c \\geq$\n$2 a+n^{j} c$, oftewel $(n-1) n^{j} c \\geq 2 a$. Dus\n\n$$\nn^{i+1} b \\geq a+n^{j} c \\geq a+\\frac{2 a}{n-1}=\\left(1+\\frac{2}{n-1}\\right) a\n$$\n\nwaaruit volgt dat\n\n$$\na \\geq n^{i} b+n^{j} c \\geq \\frac{1}{n}\\left(1+\\frac{2}{n-1}\\right) a+\\frac{2}{n-1} a=\\frac{(n-1)+2+2 n}{n(n-1)} a=\\frac{3 n+1}{n(n-1)} a .\n$$\n\nDus $3 n+1 \\leq n(n-1)$. Voor $n=2,3,4$ staat hier respectievelijk $7 \\leq 2,10 \\leq 6$ en $13 \\leq 12$, wat in alle gevallen een tegenspraak is.\n\nWe concluderen dat de waarden van $n$ die voldoen, precies $n=2,3,4$ zijn.\n\nAlternatieve oplossing voor het eerste deel. We bewijzen op een andere manier dat $n \\geq 5$ niet voldoet. We bekijken weer het drietal $(1,2,3)$. Stel dat er $k, \\ell, m$ bestaan zodat $n^{k}, 2 n^{\\ell}$ en $3 n^{m}$ de lengtes van de zijden van een driehoek vormen. Uit de driehoeksongelijkheid volgt\n\n$$\n\\begin{aligned}\nn^{k} & <2 n^{\\ell}+3 n^{m} \\\\\n2 n^{\\ell} & <n^{k}+3 n^{m} \\\\\n3 n^{m} & <n^{k}+2 n^{\\ell}\n\\end{aligned}\n$$\n\nAls $m \\leq \\ell-1$ en $k \\leq \\ell$, dan volgt\n\n$$\nn^{k}+3 n^{m} \\leq n^{\\ell}+\\frac{3}{n} n^{\\ell}=\\left(1+\\frac{3}{n}\\right) \\cdot n^{\\ell} \\leq 2 n^{\\ell}\n$$\n\nwat in tegenspraak is met de tweede driehoeksongelijkheid. Dus $m \\geq \\ell$ of $k \\geq \\ell+1$. Analoog kunnen we uit de eerste driehoeksongelijkheid afleiden dat $\\ell \\geq k$ of $m \\geq k$ en uit de derde dat $k \\geq m+1$ of $\\ell \\geq m+1$.\n\nWe onderscheiden nu twee gevallen: $m \\geq \\ell$ of $k \\geq \\ell+1$. Stel eerst dat $m \\geq \\ell$. Dan geldt niet $\\ell \\geq m+1$, dus moet wel $k \\geq m+1$. Maar dan geldt niet $m \\geq k$, dus moet wel $\\ell \\geq k$. We vinden nu $m \\geq \\ell \\geq k \\geq m+1$, tegenspraak. Stel vervolgens dat juist $k \\geq \\ell+1$. Dan geldt niet $\\ell \\geq k$, dus wel $m \\geq k$. Maar dan geldt niet $k \\geq m+1$, dus wel $\\ell \\geq m+1$. We vinden nu $k \\geq \\ell+1 \\geq m+2 \\geq k+2$, tegenspraak. We concluderen dat $n \\geq 5$ niet voldoet.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Laat $m$ en $n$ natuurlijke getallen zijn met $m n$ even. Jetze gaat een $m \\times n$ bord (dus bestaande uit $m$ rijen en $n$ kolommen) bedekken met dominostenen, zodat elke dominosteen precies twee vakjes bedekt, dominostenen niet uitsteken of overlappen, en alle vakjes bedekt worden door een dominosteen. Merlijn gaat vervolgens alle dominostenen op het bord rood of blauw kleuren. Bepaal het kleinste niet-negatieve gehele getal $V$ (afhankelijk van $m$ en $n$ ) zodat Merlijn er altijd voor kan zorgen dat in elke rij het aantal vakjes bedekt door een rode dominosteen en het aantal vakjes bedekt door een blauwe dominosteen ten hoogste $V$ van elkaar verschillen, hoe Jetze het bord ook bedekt.", "solution": "Stel eerst dat $n$ oneven is. Dan is het duidelijk dat $V \\geq 1$; het verschil is immers altijd oneven. We laten zien dat $V=1$ altijd mogelijk is. Kleur hiertoe de verticale dominostenen in oneven kolommen rood en de verticale dominostenen in even kolommen blauw. Omdat in elke rij elke horizontale dominosteen een vakje in een even en een vakje in een oneven kolom bedekt, is er nu in elke rij één vakje meer door een rode dominosteen dan door een blauwe dominosteen bedekt. Kleur de horizontale dominostenen in elke rij nu afwisselend blauw, rood, blauw, rood, .... Als het aantal horizontale domino's even is, is er uiteindelijk één rood vakje meer; is het aantal horizontale domino's oneven, dan is er uiteindelijk één blauw vakje meer. Het verschil is dus altijd 1.\n\nAls $n \\equiv 2 \\bmod 4$ geldt er dat $V \\geq 2$ als Jetze elke dominosteen horizontaal legt; dan liggen er in elke rij immers een oneven aantal dominostenen. We laten nu zien dat $V=2$ altijd mogelijk is. Gebruik daartoe dezelfde strategie als in het oneven geval. Na het kleuren van de verticale dominostenen zijn er in elke rij evenveel vakjes rood als blauw. Als we daarna weer de horizontale dominostenen per rij afwisselend rood en blauw kleuren, is in elke rij het verschil tussen het aantal rode en blauwe vakjes gelijk aan 0 of 2 .\n\nWe bekijken ten slotte het geval waarin $n \\equiv 0 \\bmod 4$. We laten daarin zien dat $V=0$ altijd mogelijk is. Nummer de rijen van boven naar beneden van 1 tot en met $m$ en zij $b_{i}$ het aantal verticale dominostenen waarvan het bovenste vakje in rij $i$ ligt. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ even is, waarbij we gebruiken dat een horizontale dominosteen altijd een even aantal vakjes in een rij bedekt. We kleuren de verticale dominostenen in rij $i$ en rij $i+1 \\mathrm{nu}$ als volgt: als $b_{i} \\equiv 0 \\bmod 4$ kleuren we de helft rood en\nde helft blauw, en als $b_{i} \\equiv 2$ mod 4 kleuren we er twee meer rood dan blauw als $i$ even is, en twee meer blauw dan rood als $i$ oneven is. We laten nu zien dat we in elke rij $k$ de horizontale dominostenen zo kunnen kleuren dat deze rij evenveel rode als blauwe vakjes heeft. Als $b_{k-1} \\equiv b_{k} \\equiv 0 \\bmod 4$ dan bedekken verticale dominostenen in rij $k$ evenveel rode als blauwe vakjes. Bovendien is het aantal horizontale dominostenen in rij $k$ nu even, dus we kleuren simpelweg de helft rood en de helft blauw. Als $b_{k-1} \\equiv b_{k} \\equiv 2 \\bmod 4$ geldt wederom dat de verticale dominostenen in rij $k$ evenveel rode als blauwe vakjes bedekken, omdat er van $k-1$ en $k$ één even en één oneven is. Verder is het aantal horizontale dominostenen in rij $k$ weer even, dus kunnen we weer de helft rood en de helft blauw kleuren. Als $b_{k-1} \\not \\equiv b_{k} \\bmod 4$ is het verschil tussen rode en blauwe vakjes bedekt door verticale dominostenen gelijk aan 2. Het aantal horizontale dominostenen in rij $k$ is nu oneven. We kunnen dus de horizontale dominostenen zo kleuren dat uiteindelijk evenveel vakjes rood als blauw zijn.\n\nWe concluderen dat de minimale waarden zijn: $V=1$ als $n$ oneven is, $V=2$ als $n \\equiv 2$ $\\bmod 4$ en $V=0$ als $n \\equiv 0 \\bmod 4$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Laat $m$ en $n$ natuurlijke getallen zijn met $m n$ even. Jetze gaat een $m \\times n$ bord (dus bestaande uit $m$ rijen en $n$ kolommen) bedekken met dominostenen, zodat elke dominosteen precies twee vakjes bedekt, dominostenen niet uitsteken of overlappen, en alle vakjes bedekt worden door een dominosteen. Merlijn gaat vervolgens alle dominostenen op het bord rood of blauw kleuren. Bepaal het kleinste niet-negatieve gehele getal $V$ (afhankelijk van $m$ en $n$ ) zodat Merlijn er altijd voor kan zorgen dat in elke rij het aantal vakjes bedekt door een rode dominosteen en het aantal vakjes bedekt door een blauwe dominosteen ten hoogste $V$ van elkaar verschillen, hoe Jetze het bord ook bedekt.", "solution": "Nummer de rijen van boven naar beneden van 1 tot en met $m$ en zij $b_{i}$ $(1 \\leq i \\leq m-1)$ het aantal verticale dominostenen waarvan het bovenste vakje in rij $i$ ligt en het onderste vakje in rij $i+1$. Definieer $b_{0}=0$ en $b_{m}=0$.\n\nStel eerst dat $n$ oneven is. Schrijf $n=\\frac{1}{2}(n-1)+\\frac{1}{2}(n+1)$; precies een van deze twee termen is even en de ander is oneven; schrijf $n_{\\mathrm{e}}$ voor de even term en $n_{\\mathrm{o}}$ voor de oneven term. We hebben nu dus $n=n_{\\mathrm{e}}+n_{\\mathrm{o}}$ terwijl $n_{\\mathrm{e}}$ en $n_{\\mathrm{o}}$ precies 1 verschillen. Het is allereerst duidelijk dat $V \\geq 1$; het verschil is immers altijd oneven. We laten zien dat $V=1$ altijd mogelijk is. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ oneven is voor oneven $i$ en even voor even $i$, waarbij we gebruiken dat een horizontale dominosteen altijd een even aantal vakjes in een rij bedekt. Voor oneven $i$ hebben we in rij $i$ te maken met een oneven aantal $b_{i}$ verticale stenen die naar beneden uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i-1}$ die naar boven uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $n_{\\mathrm{o}}$ vakjes rood en juist de laatste $n_{\\mathrm{e}}$ vakjes blauw. Voor even $i$ hebben we in rij $i$ te maken met een oneven aantal $b_{i-1}$ verticale stenen die naar boven uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i}$ die naar beneden uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $n_{\\mathrm{o}}$ vakjes rood en juist de laatste $n_{\\mathrm{e}}$ vakjes blauw. Op deze manier is in elke rij in ieder geval elke horizontale dobbelsteen monochroom (de twee vakjes hebben dezelfde kleur), terwijl we voor twee opeenvolgende rijen de vakjes op de verticale dominostenen in beide rijen ook dezelfde kleur hebben gegeven. De kleuring is dus correct en voldoet aan $V=1$.\n\nAls $n \\equiv 2 \\bmod 4$ is $\\frac{1}{2} n$ oneven en schrijven we $\\frac{1}{2} n=n_{\\mathrm{e}}+n_{\\mathrm{o}}$ met $n_{\\mathrm{e}}$ en $n_{\\mathrm{o}}$ even en oneven\ngetallen die precies 1 verschillen. Er geldt dat $V \\geq 2$ als Jetze elke dominosteen horizontaal legt; dan liggen er in elke rij immers een oneven aantal dominostenen. We laten nu zien dat $V=2$ altijd mogelijk is. Gebruik daartoe dezelfde strategie als in het oneven geval. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ even is voor alle $i$. Voor oneven $i$ hebben we in rij $i$ te maken met een even aantal $b_{i}$ verticale stenen die naar beneden uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i-1}$ die naar boven uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{\\mathrm{o}}$ vakjes rood en juist de laatste $2 n_{\\mathrm{e}}$ vakjes blauw. Voor even $i$ hebben we in rij $i$ te maken met een even aantal $b_{i-1}$ verticale stenen die naar boven uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i}$ die naar beneden uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{\\mathrm{o}}$ vakjes rood en juist de laatste $2 n_{\\mathrm{e}}$ vakjes blauw. Op deze manier is in elke rij in ieder geval elke horizontale dobbelsteen monochroom (de twee vakjes hebben dezelfde kleur), terwijl we voor twee opeenvolgende rijen de vakjes op de verticale dominostenen in beide rijen ook dezelfde kleur hebben gegeven. De kleuring is dus correct en voldoet aan $V=2$.\n\nAls $n \\equiv 0 \\bmod 4$ is $\\frac{1}{2} n$ even en schrijven we $\\frac{1}{2} n=2 n_{0}$. We laten nu zien dat $V=0$ altijd mogelijk is. Gebruik daartoe dezelfde strategie als in het vorige geval. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ even is voor alle $i$. Voor oneven $i$ hebben we in rij $i$ te maken met een even aantal $b_{i}$ verticale stenen die naar beneden uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i-1}$ die naar boven uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{0}$ vakjes rood en juist de laatste $2 n_{0}$ vakjes blauw. Voor even $i$ hebben we in rij $i$ te maken met een even aantal $b_{i-1}$ verticale stenen die naar boven uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i}$ die naar beneden uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{0}$ vakjes rood en juist de laatste $2 n_{0}$ vakjes blauw. Op deze manier is in elke rij in ieder geval elke horizontale dobbelsteen monochroom (de twee vakjes hebben dezelfde kleur), terwijl we voor twee opeenvolgende rijen de vakjes op de verticale dominostenen in beide rijen ook dezelfde kleur hebben gegeven. De kleuring is dus correct en voldoet aan $V=0$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een rechthoekige driehoek met $\\angle C=90^{\\circ}$ en zij $D$ het voetpunt van de hoogtelijn uit $C$. Zij $E$ het zwaartepunt van driehoek $A C D$ en zij $F$ het zwaartepunt van driehoek $B C D$. Het punt $P$ voldoet aan $\\angle C E P=90^{\\circ}$ en $|C P|=|A P|$, terwijl het punt $Q$ voldoet aan $\\angle C F Q=90^{\\circ}$ en $|C Q|=|B Q|$.\nToon aan dat $P Q$ door het zwaartepunt van driehoek $A B C$ gaat.\n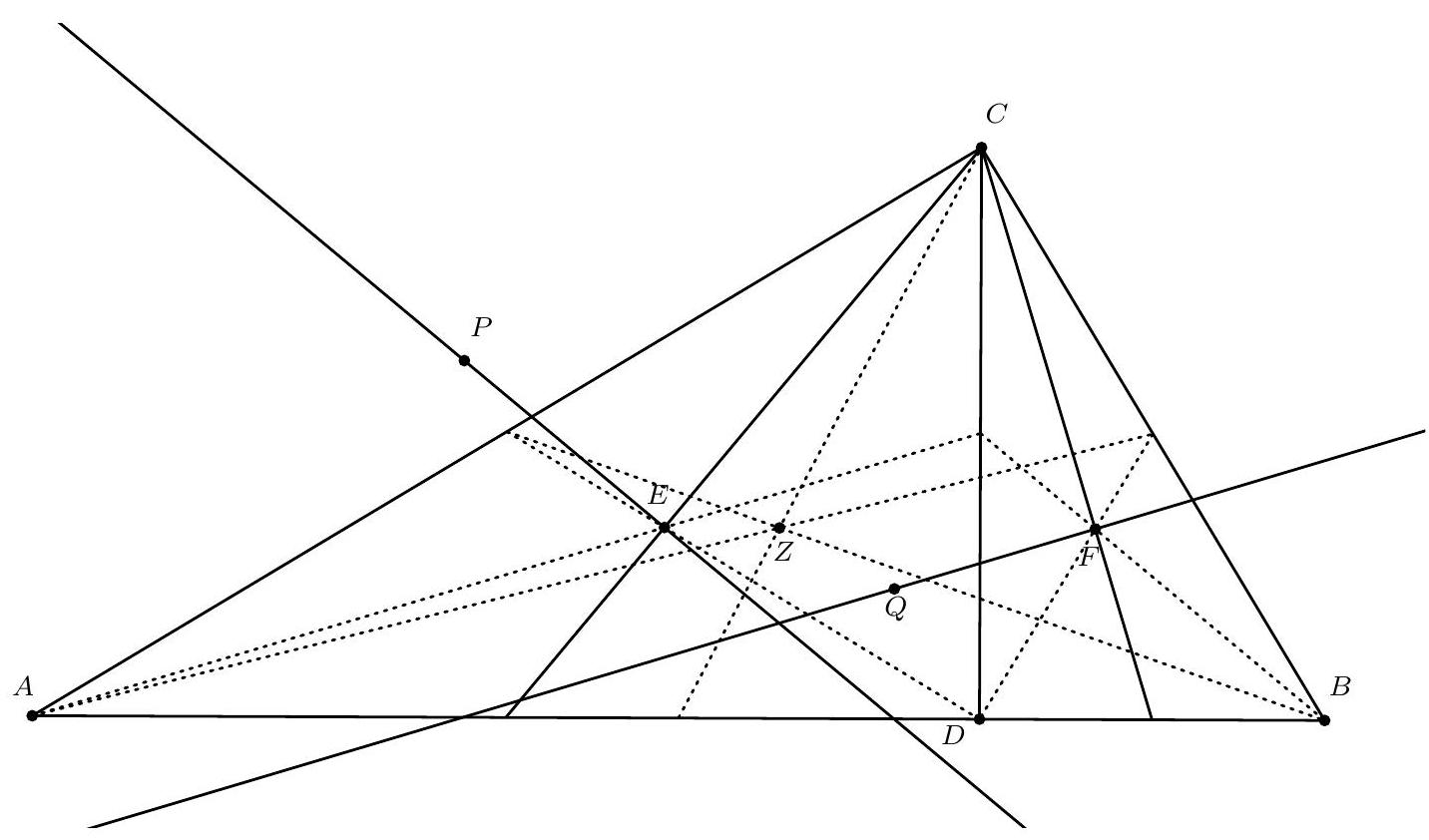", "solution": "Noem $M, N, R$ en $S$ de middens van respectievelijk zijden $B C, C A, B D$ en $A D$. Zij $Z$ het zwaartepunt van $\\triangle A B C$. Vierhoek $Q F M C$ is een koordenveriehoek wegens rechte hoeken $\\angle Q F C=90^{\\circ}=\\angle Q M C$. Merk op dat $C Q$ dus de middellijn van de omgeschreven cirkel is. Analoog zien we dat $P N E C$ een koordenvierhoek is, met $C P$ de middellijn van de omgeschreven cirkel.\n\nWe bewijzen nu dat $Z$ ook op deze koordenvierhoeken ligt. Driehoek $C Z M$ gaat onder de gelijkvormigheid $\\triangle B C A \\sim \\triangle B D C$ over in driehoek $D F R$, want $C$ gaat naar $D$, het zwaartepunt $Z$ gaat naar het zwaartepunt $F$, en het midden $M$ van $B C$ gaat naar het midden van $B D$ en dat is $R$. Dus $\\triangle C Z M \\sim \\triangle D F R$, waaruit in het bijzonder volgt dat $\\angle C Z M=\\angle D F R=\\angle C F M$ wegens overstaande hoeken. Dus $Z$ ligt op koordenvierhoek $Q F M C$. Analoog volgt dat $\\angle C Z N=\\angle D E S=\\angle C E N$, waaruit volgt dat $Z$ op koordenvierhoek $P N E C$ ligt.\n\nWe kunnen nu bewijzen dat $Z$ op $P Q$ ligt. Omdat $C Q$ de middellijn is van de cirkel door $Q, F, M, C, Z$, geldt $\\angle Q Z C=90^{\\circ}$. Omdat $C P$ de middellijn is van de cirkel door $P, N, E, Z, C$, geldt ook $\\angle C Z P=90^{\\circ}$. Samen kunnen we hieruit concluderen dat $P, Z$ en $Q$ op een lijn liggen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing I."}
|
| 4 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een rechthoekige driehoek met $\\angle C=90^{\\circ}$ en zij $D$ het voetpunt van de hoogtelijn uit $C$. Zij $E$ het zwaartepunt van driehoek $A C D$ en zij $F$ het zwaartepunt van driehoek $B C D$. Het punt $P$ voldoet aan $\\angle C E P=90^{\\circ}$ en $|C P|=|A P|$, terwijl het punt $Q$ voldoet aan $\\angle C F Q=90^{\\circ}$ en $|C Q|=|B Q|$.\nToon aan dat $P Q$ door het zwaartepunt van driehoek $A B C$ gaat.\n", "solution": "Noem $M, N, K$ en $L$ de middens van respectievelijk zijden $B C, C A, A B$ en $C D$. Zij $Z$ het zwaartepunt van $\\triangle A B C$. Omdat $M L$ een middenparallel in driehoek $B C D$ is, geldt $M L \\| B D$ en dus $M L \\| A B$. Zo is ook $N L \\| A B$, dus $M, N$ en $L$ liggen op een lijn $\\ell$ evenwijdig aan $A B$. Verder geldt vanwege $M L \\| B D$ dat $\\triangle B D F \\sim \\triangle L M F$, waarbij de vermenigvuldigingsfactor tussen deze twee driehoeken gelijk aan 2 is. Dus de afstand van $F$ tot $\\ell$ (wat de lijn $M L$ is) is twee keer zo klein als de afstand van $F$ tot $A B$ (wat de lijn $B D$ is). Net zo is de afstand van $E$ tot $\\ell$ twee keer zo klein als de afstand van $E$ tot $A B$, en hetzelfde geldt voor $Z$. Dus $E, F$ en $Z$ liggen allemaal op een lijn evenwijdig aan $A B$ die twee keer zo ver van $A B$ af ligt als van $\\ell$.\n(Een andere manier om dit in te zien, is door gebruik te maken van het feit dat zwaartepunten altijd op $\\frac{1}{3}$ hoogte van een zwaartelijn liggen. De punten $E, F$ en $Z$ liggen allemaal op $\\frac{1}{3}$ hoogte van de corresponderende zwaartelijnen uit $C$, waaruit het gestelde volgt.)\n\nHieruit volgt in het bijzonder dat $\\angle C Z E=\\angle C K A$ (F-hoeken). We gaan dit gebruiken om aan te tonen dat de punten $Z, E, N$ en $C$ samen op een cirkel liggen. Bekijk hiervoor eerst de gelijkvormige driehoeken $\\triangle A B C$ en $\\triangle A C D$. Er geldt nu $\\frac{|A K|}{|A N|}=\\frac{|A B|}{|A C|}=\\frac{|A C|}{|A D|}$, dus $\\triangle A K C \\sim \\triangle A N D$ (zhz). Hieruit volgt $\\angle C K A=\\angle D N A$. Al met al vinden we nu\n\n$$\n\\angle C Z E=\\angle C K A=\\angle D N A=180^{\\circ}-\\angle D N C=180^{\\circ}-\\angle E N C,\n$$\n\ndus $C Z E N$ is een koordenvierhoek.\nOmdat $|C P|=|A P|$ ligt $P$ op de middelloodlijn van $A C$. Er geldt dus $\\angle C N P=90^{\\circ}=$ $\\angle C E P$, wat betekent dat $C, E, N$ en $P$ op een cirkel liggen. We hebben zojuist gezien dat $Z$ ook op deze cirkel ligt. Dus geldt $\\angle C Z P=\\angle C E P=90^{\\circ}$. Analoog volgt $\\angle C Z Q=90^{\\circ}$. Samen kunnen we hieruit concluderen dat $P, Z$ en $Q$ op een lijn liggen.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ met\n\n$$\nf(x+y f(x+y))=y^{2}+f(x) f(y)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Merk op dat de functie $f(x)=0$ voor alle $x$ niet voldoet. Er is dus een $a$ met $f(a) \\neq 0$. Vul $x=a$ en $y=0$ in, dat geeft $f(a)=f(a) f(0)$, dus $f(0)=1$. Vul nu $x=1$ en $y=-1$ in, dat geeft $f(1-f(0))=1+f(1) f(-1)$. Omdat $f(0)=1$, staat hier $1=1+f(1) f(-1)$, dus $f(1)=0$ of $f(-1)=0$. We onderscheiden deze twee gevallen.\n\nStel eerst dat $f(1)=0$. Vul $x=t$ en $y=1-t$ in, en vervolgens $x=1-t$ en $y=t$, dan krijgen we de twee vergelijkingen\n\n$$\n\\begin{aligned}\nf(t) & =(1-t)^{2}+f(t) f(1-t) \\\\\nf(1-t) & =t^{2}+f(t) f(1-t)\n\\end{aligned}\n$$\n\nDeze van elkaar afhalen geeft $f(t)-f(1-t)=(1-t)^{2}-t^{2}=1-2 t$, dus $f(1-t)=f(t)+2 t-1$. Dit invullen in de eerste van bovenstaande twee vergelijkingen geeft\n\n$$\nf(t)=(1-t)^{2}+f(t)^{2}+(2 t-1) f(t)\n$$\n\nwat we kunnen herschrijven tot\n\n$$\nf(t)^{2}+(2 t-2) f(t)+(1-t)^{2}=0\n$$\n\noftewel $(f(t)-(1-t))^{2}=0$. We concluderen dat $f(t)=1-t$. Controleren van deze functie in de oorspronkelijke functievergelijking geeft links $1-(x+y(1-x-y))=1-$ $\\left(x+y-x y-y^{2}\\right)=1-x-y+x y+y^{2}$ en rechts $y^{2}+(1-x)(1-y)=y^{2}+1-x-y+x y$ en dat is hetzelfde, dus de functie voldoet.\n\nStel nu $f(-1)=0$. Vul $x=t$ en $y=-1-t$ in, en vervolgens $x=-1-t$ en $y=t$, dan krijgen we de twee vergelijkingen\n\n$$\n\\begin{aligned}\nf(t) & =(-1-t)^{2}+f(t) f(-1-t), \\\\\nf(-1-t) & =t^{2}+f(t) f(-1-t)\n\\end{aligned}\n$$\n\nDeze van elkaar afhalen geeft $f(t)-f(-1-t)=(-1-t)^{2}-t^{2}=1+2 t$, dus $f(-1-t)=$ $f(t)-2 t-1$. Dit invullen in de eerste van bovenstaande twee vergelijkingen geeft\n\n$$\nf(t)=(-1-t)^{2}+f(t)^{2}+(-2 t-1) f(t)\n$$\n\nwat we kunnen herschrijven tot\n\n$$\nf(t)^{2}-(2 t+2) f(t)+(t+1)^{2}=0\n$$\n\noftewel $(f(t)-(t+1))^{2}=0$. We concluderen dat $f(t)=t+1$. Controleren van deze functie in de oorspronkelijke functievergelijking geeft links $x+y(x+y+1)+1=x+x y+y^{2}+y+1$ en rechts $y^{2}+(x+1)(y+1)=y^{2}+x y+x+y+1$ en dat is hetzelfde, dus de functie voldoet.\n\nWe concluderen dat er precies twee oplossingen zijn: $f(x)=1-x$ voor alle $x$ en $f(x)=x+1$ voor alle $x$.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing I."}
|
| 6 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ met\n\n$$\nf(x+y f(x+y))=y^{2}+f(x) f(y)\n$$\n\nvoor alle $x, y \\in \\mathbb{R}$.", "solution": "Net als in de eerste oplossing leiden we af dat $f(0)=1$ en dat $f(1)=0$ of $f(-1)=0$.\n\nStel eerst dat $f(1)=0$. Invullen van $x=t-1$ en $y=1$ geeft $f(t-1+f(t))=1$. Anderzijds geldt ook $f(0)=1$. We laten nu zien dat $f(z)=1$ impliceert dat $z=0$. Stel $f(z)=1$. Invullen van $x=1$ en $y=z-1$ geeft $f(1+(z-1) f(z))=(z-1)^{2}$, dus $f(z)=(z-1)^{2}$, oftewel $1=(z-1)^{2}$. Dus $z=0$ of $z=2$. Stel $z=2$, dan geeft invullen van $x=0$ en $y=2$ dat $f(2 f(2))=4+f(0) f(2)$, wat met $f(2)=f(z)=1$ leidt tot $f(2)=5$, in tegenspraak met $f(2)=1$. Dus $z=0$. In het bijzonder volgt uit $f(t-1+f(t))=1$ dus dat $t-1+f(t)=0$, dus $f(t)=1-t$. Deze functie voldoet (zie eerste oplossing).\n\nStel nu dat $f(-1)=0$. Invullen van $x=t+1$ en $y=-1$ geeft $f(t+1-f(t))=1$. Anderzijds geldt ook $f(0)=1$. We laten nu wederom zien dat $f(z)=1$ impliceert dat $z=0$. Stel $f(z)=1$. Invullen van $x=-1$ en $y=z+1$ geeft $f(-1+(z+1) f(z))=(z+1)^{2}$, dus $f(z)=(z+1)^{2}$, oftewel $1=(z+1)^{2}$. Dus $z=0$ of $z=-2$. Stel $z=-2$, dan geeft invullen van $x=0$ en $y=-2$ dat $f(-2 f(-2))=4+f(0) f(-2)$, wat met $f(-2)=f(z)=1$ leidt tot $f(-2)=5$, in tegenspraak met $f(-2)=1$. Dus $z=0$. In het bijzonder volgt uit $f(t+1-f(t))=1$ dus dat $t+1-f(t)=0$, dus $f(t)=t+1$. Deze functie voldoet ook (zie eerste oplossing).", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing II."}
|
| 7 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Zij $p>10$ een priemgetal. Bewijs dat er positieve gehele getallen $m$ en $n$ met $m+n<p$ bestaan waarvoor $p$ een deler is van $5^{m} 7^{n}-1$.", "solution": "Wegens de kleine stelling van Fermat geldt $a^{p-1} \\equiv 1 \\bmod p$ voor alle $a$ met $p \\nmid a$. Omdat $p>10$ is $p$ oneven, dus $p-1$ is even. Er geldt\n\n$$\n\\left(a^{\\frac{p-1}{2}}-1\\right)\\left(a^{\\frac{p-1}{2}}+1\\right)=a^{p-1}-1 \\equiv 0 \\quad \\bmod p\n$$\n\nDus $p \\left\\lvert\\,\\left(a^{\\frac{p-1}{2}}-1\\right)\\left(a^{\\frac{p-1}{2}}+1\\right)\\right.$, dus $p$ is een deler van minstens één van beide factoren. Dus $a^{\\frac{p-1}{2}}$ is modulo $p$ congruent aan 1 of -1 .\n\nWe passen dit toe op $a=5$ en $a=7$. Merk op dat $p>10$ dus $p \\neq 5,7$. Als $5^{\\frac{p-1}{2}} \\equiv 1$ $\\bmod p$ en $7^{\\frac{p-1}{2}} \\equiv 1 \\bmod p$, dan nemen we $m=n=\\frac{p-1}{2}$ en dat voldoet. Hetzelfde geldt als ze beide $-1 \\bmod p$ zijn. Blijft over het geval dat één van beide 1 en de ander -1 is. Neem aan dat $5^{\\frac{p-1}{2}} \\equiv 1 \\bmod p$ en $7^{\\frac{p-1}{2}} \\equiv-1 \\bmod p$. Het geval waarin het andersom is, gaat precies analoog.\n\nAls er een $n$ is met $0<n<\\frac{p-1}{2}$ en $7^{n} \\equiv 1 \\bmod p$, dan kiezen we deze $n$ en verder $m=\\frac{p-1}{2}$. Dat voldoet. Zo niet, dan kan er ook geen $n$ zijn met $\\frac{p-1}{2}<n<p-1$ en $7^{n} \\equiv 1 \\bmod p$, want dan zou $7^{p-1-n} \\equiv 7^{p-1} \\cdot\\left(7^{n}\\right)^{-1} \\equiv 1 \\bmod p$, terwijl $0<p-1-n<\\frac{p-1}{2}$, tegenspraak. Verder kunnen er nu geen $i$ en $j$ zijn met $1 \\leq i<j \\leq p-1$ zodat $7^{i} \\equiv 7^{j} \\bmod p$, want als die wel zouden bestaan, dan is $7^{j-i} \\equiv 1 \\bmod p$ met $1 \\leq j-i<p-1$. We concluderen dat $7^{i}$ met $1 \\leq i \\leq p-1$ allemaal verschillende waarden aanneemt modulo $p$, en daar zit waarde 0 niet bij, dus het zijn precies alle waarden van 1 tot en met $p-1$.\n\nIn het bijzonder is er een $n$ zodat $7^{n} \\equiv 5^{-1} \\bmod p$. Er geldt $n \\leq p-2$, want $7^{p-1} \\equiv 1 \\not \\equiv 5^{-1}$ $\\bmod p$. We kiezen nu deze $n$ en verder $m=1$ en dan geldt $7^{n} \\cdot 5^{m} \\equiv 5^{-1} \\cdot 5 \\equiv 1 \\bmod p$.\n\nWe zien dat het in alle gevallen mogelijk is om $m$ en $n$ te vinden die aan de voorwaarden voldoen.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing I."}
|
| 8 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Zij $p>10$ een priemgetal. Bewijs dat er positieve gehele getallen $m$ en $n$ met $m+n<p$ bestaan waarvoor $p$ een deler is van $5^{m} 7^{n}-1$.", "solution": "We bekijken alle getallen van de vorm $5^{i} 7^{j}$ voor $1 \\leq i, j \\leq p-1$. Dit zijn $(p-1)^{2}$ getallen. Modulo $p$ nemen deze getallen nooit de waarde 0 aan, want vanwege $p>10$ geldt $p \\neq 5,7$. Dus modulo $p$ worden er hooguit $p-1$ verschillende waarden aangenomen. Vanwege het ladenprincipe is er nu een waarde $k$ zodat minstens $\\frac{(p-1)^{2}}{p-1}=p-1$ van deze paren $(i, j)$ voldoen aan $5^{i} 7^{j} \\equiv k \\bmod p$. Noem deze paren $k$-waardig.\n\nNeem zo'n $k$-waardig paar $(i, j)=(a, b)$. We gaan eerst laten zien dat niet alle $k$-waardige paren van de vorm $(x, b)$ zijn. Bijvoorbeeld $(a+1, b)$ (en net zo goed $(a-1, b)$ als net toevallig $a=p-1$ ) is niet $k$-waardig, want uit $5^{a+1} 7^{b} \\equiv 5^{a} 7^{b} \\bmod p$ zou volgen dat $5 \\equiv 1$\n$\\bmod p$ dus $p \\mid 4$, tegenspraak. Omdat er minstens $p-1$ paren $k$-waardig zijn, volgt nu dat niet alle $k$-waardige paren van de vorm $(x, b)$ kunnen zijn. Dus er is een $k$-waardig paar $(c, d)$ met $d \\neq b$. Net zo bestaat er een $k$-waardig paar $(e, f)$ met $e \\neq a$. Als nu $a \\neq c$, dan zijn $(a, b)$ en $(c, d)$ twee paren met twee verschillende getallen in de eerste component en twee verschillende getallen in de tweede component. Als $b \\neq f$, zijn $(a, b)$ en $(e, f)$ zulke paren. Als $a=c$ en $b=f$, dan zijn juist $(c, d)=(a, d)$ en $(e, f)=(e, b)$ zulke paren.\n\nWe kunnen dus altijd twee $k$-waardige paren $\\left(i_{1}, j_{1}\\right)$ en $\\left(i_{2}, j_{2}\\right)$ vinden met $i_{1} \\neq i_{2}$ en $j_{1} \\neq j_{2}$. Er geldt nu\n\n$$\n5^{i_{1}-i_{2}} 7^{j_{1}-j_{2}} \\equiv 5^{i_{1}}\\left(5^{i_{2}}\\right)^{-1} \\cdot 7^{j_{1}}\\left(7^{j_{2}}\\right)^{-1} \\equiv k \\cdot k^{-1} \\equiv 1 \\quad \\bmod p .\n$$\n\nUit de kleine stelling van Fermat volgt $u^{p-1} \\equiv 1 \\bmod p$ als $u \\in\\{5,7\\}$. Voor $t \\in \\mathbb{Z}$ geldt nu $u^{p-1+t} \\equiv u^{p-1} u^{t} \\equiv u^{t} \\bmod p$. Schrijf $m^{\\prime}=i_{1}-i_{2}$ als $i_{1}>i_{2}$ en $m^{\\prime}=p-1+i_{1}-i_{2}$ als $i_{1}<i_{2}$, dan geldt dus $5^{m^{\\prime}} \\equiv 5^{i_{1}-i_{2}} \\bmod p$. Verder is $1 \\leq m^{\\prime} \\leq p-2$. Analoog definiëren we $n^{\\prime}$ zodat $7^{n^{\\prime}} \\equiv 7^{j_{1}-j_{2}} \\bmod p$ en $1 \\leq n^{\\prime} \\leq p-2$. We hebben nu $5^{m^{\\prime}} 7^{n^{\\prime}} \\equiv 1 \\bmod p$.\n\nAls $n^{\\prime}+m^{\\prime}<p$, dan kiezen we $m=m^{\\prime}$ en $n=n^{\\prime}$ en zijn we klaar. Zo niet, dan kiezen we $m=p-1-m^{\\prime}$ en $n=p-1-n^{\\prime}$ en geldt $5^{m} 7^{n} \\equiv 5^{p-1}\\left(5^{m^{\\prime}}\\right)^{-1} \\cdot 7^{p-1}\\left(7^{n^{\\prime}}\\right)^{-1} \\equiv 1 \\cdot 1^{-1} \\equiv 1$ $\\bmod p$. Nu geldt $n+m=2(p-2)-\\left(n^{\\prime}+m^{\\prime}\\right) \\leq 2 p-4-p=p-4$, dus zijn we ook klaar.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing II."}
|
Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2022", "problem_label": "1", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ waarvoor geldt dat $f(n) \\mid f(m)-n$ dan en slechts dan als $n \\mid m$ voor alle natuurlijke getallen $m$ en $n$.", "solution": "Als we $m=n$ invullen, dan vinden we dat $f(n) \\mid f(n)-n$, dus voor alle natuurlijke getallen geldt $f(n) \\mid n$. Als we dat weer gebruiken op de originele functievoorwaarde vinden we dat $f(n) \\mid f(m)$ dan en slechts dan als $n \\mid m$.\n\nNu bewijzen we dat $f(n)=n$ via inductie naar het aantal priemdelers van $n$ geteld met multipliciteit. Als inductiebasis hebben we dat $f(1) \\mid 1$, dus inderdaad $f(1)=1$. Stel dat $f(k)=k$ voor alle getallen $k$ met minder delers dan $n$ en dat $f(n) \\mid n$ een strikte deler is van $n$. Dan bestaat er dus een priemgetal $p$ zo dat $f(n) \\mid n / p=f(n / p)$ door de inductiehypothese. Maar $n$ is geen deler van $n / p$, dus onze aanname dat $f(n) \\neq n$ leidt tot een tegenspraak.\n\nWe controleren dat $f(n)=n$ inderdaad een oplossing is: $n \\mid m$ dan en slechts dan als $n \\mid m-n$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing I."}
|
| 2 |
+
{"year": "2022", "problem_label": "1", "tier": 1, "problem": "Vind alle functies $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ waarvoor geldt dat $f(n) \\mid f(m)-n$ dan en slechts dan als $n \\mid m$ voor alle natuurlijke getallen $m$ en $n$.", "solution": "We kunnen ook sterke inductie doen naar $n$. De basis is hetzelfde als hierboven. Stel dat $f(k)=k$ voor alle $k<n$ (dat is de inductiehypothese). Om een tegenspraak af te leiden stellen we ook dat $f(n)<n$. Dan geldt door $k=f(n)$ te nemen dat $f(f(n))=f(n)$. En in het bijzonder dus dat $f(n) \\mid f(f(n))$. Doordat $f(n) \\mid f(m)$ dan en slechts dan als $n \\mid m$ volgt hieruit dat $n \\mid f(n)$. Maar dat is in tegenspraak met $f(n)<n$, dus $f(n)=n$.", "problem_match": "\nOpgave 1.", "solution_match": "\nOplossing II."}
|
| 3 |
+
{"year": "2022", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek met $D$ het voetpunt van de hoogtelijn vanuit $A$. De cirkel met middelpunt $A$ die door $D$ gaat, snijdt de omgeschreven cirkel van driehoek $A B C$ in $X$ en $Y$, waarbij de volgorde van de punten op deze omgeschreven cirkel is: $A, X, B, C, Y$. Bewijs dat $\\angle B X D=\\angle C Y D$.", "solution": "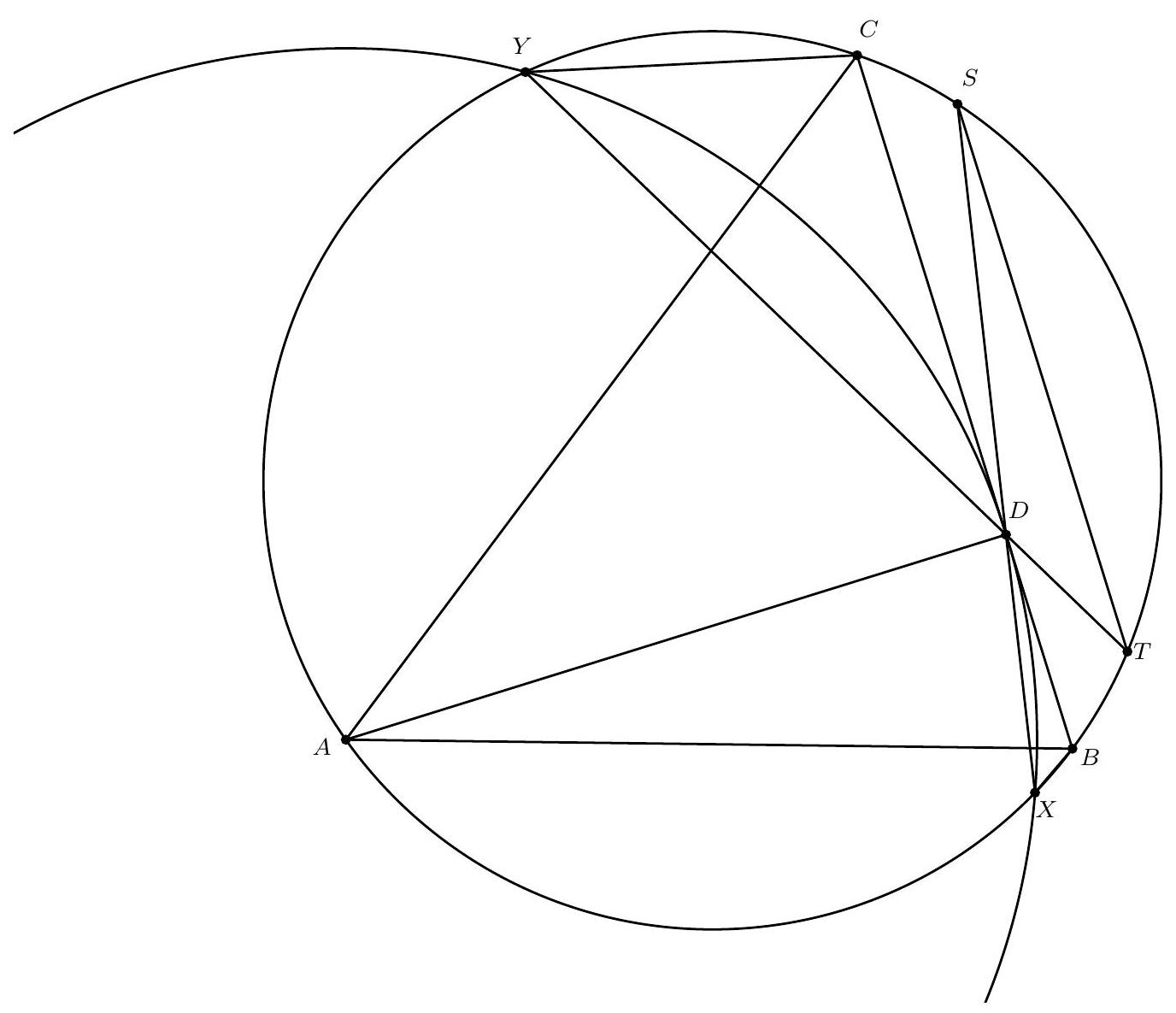\n\nOmdat de straal $A D$ loodrecht staat op $B C$, raakt $B C$ aan de omgeschreven cirkel van $\\triangle D X Y$. Wegens de raaklijn-omtrekshoekstelling geldt daardoor dat de hoek tussen de raaklijn en de koorde $D X$ gelijk is aan de omtrekshoek op deze koorde, oftewel $\\angle X D B=$ $\\angle X Y D$. Verder weten we dat $B C Y X$ een koordenvierkhoek is. Dat betekent dat de overstaande hoeken optellen tot $180^{\\circ}$, dus $\\angle C B X+\\angle X Y C=180^{\\circ}$. Vanwege de hoekensom in $\\triangle B D X$ vinden we dan dat $\\angle B X D=180^{\\circ}-\\angle D B X-\\angle X D B=\\left(180^{\\circ}-\\angle C B X\\right)-$ $\\angle X D B=\\angle X Y C-\\angle X Y D$ waar we de twee gevonden vergelijkingen hebben gebruikt. Deze laatste twee hoeken kunnen we gewoon van elkaar aftrekken: $\\angle X Y C-\\angle X Y D=$ $\\angle D Y C$, waaruit volgt dat $\\angle B X D=\\angle D Y C$.", "problem_match": "\nOpgave 2.", "solution_match": "# Oplossing I."}
|
| 4 |
+
{"year": "2022", "problem_label": "2", "tier": 1, "problem": "Zij $A B C$ een scherphoekige driehoek met $D$ het voetpunt van de hoogtelijn vanuit $A$. De cirkel met middelpunt $A$ die door $D$ gaat, snijdt de omgeschreven cirkel van driehoek $A B C$ in $X$ en $Y$, waarbij de volgorde van de punten op deze omgeschreven cirkel is: $A, X, B, C, Y$. Bewijs dat $\\angle B X D=\\angle C Y D$.", "solution": "Zij $S$ het tweede snijpunt van $X D$ en de omgeschreven cirkel van $\\triangle A B C$. Zij $T$ het tweede snijpunt van $Y D$ en de omgeschreven cirkel van $\\triangle A B C$. Dan geldt $\\angle D S T=\\angle X S T=\\angle X Y T=\\angle X Y D$. Verder geldt $A D \\perp B C$ en $A$ is het middelpunt van de cirkel door $D, X$ en $Y$, dus $B C$ raakt aan deze cirkel. Met de raaklijnomtrekshoekstelling vinden we dan $\\angle X Y D=\\angle X D B$. Dus $\\angle D S T=\\angle X D B$, waaruit met F-hoeken volgt dat $B D$ evenwijdig aan $S T$ is.\n\nDus $B C$ en $S T$ zijn evenwijdig, waaruit met de stelling van Julian volgt dat $|B S|=|C T|$. De omtrekshoeken op deze koorden zijn gelijk, oftewel $\\angle B X S=\\angle C Y T$. Dit betekent dat $\\angle B X D=\\angle C Y D$.", "problem_match": "\nOpgave 2.", "solution_match": "\nOplossing II."}
|
| 5 |
+
{"year": "2022", "problem_label": "3", "tier": 1, "problem": "Vind alle paren priemgetallen $(p, q)$ waarvoor geldt dat\n\n$$\np\\left(p^{2}-p-1\\right)=q(2 q+3)\n$$", "solution": "Antwoord: de enige oplossing is $(p, q)=(13,31)$.\nAls $p=q$, dan moet ook gelden dat $p^{2}-p-1=2 q+3=2 p+3$. Dit kunnen we ontbinden als $(p-4)(p+1)=0$. Omdat 4 en -1 geen priemgetallen zijn, levert dit dus geen oplossingen op.\n\nIn het andere geval hebben we $p \\mid 2 q+3$ en $q \\mid p^{2}-p-1$. Omdat $2 q+3$ en $p^{2}-p-1$ positief zijn, volgt hieruit dat $p \\leq 2 q+3$ en $q \\leq p^{2}-p-1$. Om een scherpere ondergrens voor $p$ te vinden vermenigvuldigen we de twee relaties\n\n$$\n\\begin{aligned}\np q & \\mid(2 q+3)\\left(p^{2}-p-1\\right) \\\\\n& \\mid 2 q p^{2}-2 q p-2 q+3\\left(p^{2}-p-1\\right) \\\\\n& \\mid 3\\left(p^{2}-p-1\\right)-2 q,\n\\end{aligned}\n$$\n\nwaarbij we termen met een factor $p q$ hebben weggegooid. Merk nu op dat $3\\left(p^{2}-p-1\\right)-2 q \\geq$ $3 q-2 q=q>0$. Dat betekent dat de bovenstaande deelrelatie leidt tot\n\n$$\n\\begin{aligned}\np q & \\leq 3\\left(p^{2}-p-1\\right)-2 q \\\\\n& =3 p^{2}-3 p-(2 q+3) \\\\\n& \\leq 3 p^{2}-3 p-p \\\\\n& =3 p^{2}-4 p .\n\\end{aligned}\n$$\n\nAls we $4 p$ naar de andere kant halen en delen door $p$ vinden we dus dat $q+4 \\leq 3 p$, oftewel\n\n$$\n\\frac{2 q+3}{6}<\\frac{q+4}{3} \\leq p\n$$\n\nAangezien $p$ een deler is van $2 q+3$ leiden we hieruit af dat $2 q+3=k p$ met $k \\in\\{1,2,3,4,5\\}$. Als $k=1$, dan hebben we $2 q+3=p$ en dus ook $q=p^{2}-p-1$. Maar dan zou gelden dat $p=2 q+3=2\\left(p^{2}-p-1\\right)+3=2 p^{2}-2 p+1$. Dat kunnen we ontbinden als $(2 p-1)(p-1)=0$, wat geen oplossingen heeft met $p$ priem. Als $k=2$ of $k=4$, dan is $k p$ even. Maar $2 q+3$ is oneven, dus die vallen af. Als $k=3$, dan volgt uit $2 q+3=3 p$ dat $q$ een drievoud moet zijn. Omdat $q$ priem is, hebben we dan $q=3$, en dus ook $p=(2 q+3) / 3=3$. Controleren geeft dat dit geen oplossing is van de oorspronkelijke vergelijking.\n\nHet laatste geval is $k=5$. Dan hebben we $5 p=2 q+3$ en wegens de oorspronkelijke vergelijking dus dat $5 q=p^{2}-p-1$. Als we dat invullen, vinden we $25 p=5(2 q+3)=$ $2\\left(p^{2}-p-1\\right)+15=2 p^{2}-2 p+13$. Dit kunnen we ontbinden als $(p-13)(2 p-1)=0$. Dit geeft als mogelijke oplossing $p=13$ met daarbij $q=(5 p-3) / 2=31$. We controleren dat $(p, q)=(13,31)$ inderdaad een oplossing is van de opgave.", "problem_match": "\nOpgave 3.", "solution_match": "\nOplossing."}
|
| 6 |
+
{"year": "2022", "problem_label": "4", "tier": 1, "problem": "Gegeven zijn positieve, reële getallen $a_{1}, a_{2}, \\ldots, a_{n}$ met $n \\geq 2$ waarvoor geldt dat $a_{1} a_{2} \\cdots a_{n}=1$. Bewijs dat\n\n$$\n\\left(\\frac{a_{1}}{a_{2}}\\right)^{n-1}+\\left(\\frac{a_{2}}{a_{3}}\\right)^{n-1}+\\ldots+\\left(\\frac{a_{n-1}}{a_{n}}\\right)^{n-1}+\\left(\\frac{a_{n}}{a_{1}}\\right)^{n-1} \\geq a_{1}^{2}+a_{2}^{2}+\\ldots+a_{n}^{2}\n$$\n\nen bepaal wanneer gelijkheid geldt.", "solution": "We nemen het rekenkundig-meetkundig gemiddelde op $\\frac{1}{2} n(n-1)$ termen:\n\n$$\n\\begin{aligned}\n\\frac{(n-1)\\left(\\frac{a_{1}}{a_{2}}\\right)^{n-1}+(n-2)\\left(\\frac{a_{2}}{a_{3}}\\right)^{n-1}+\\ldots+\\left(\\frac{a_{n-1}}{a_{n}}\\right)^{n-1}}{\\frac{1}{2} n(n-1)} & \\geq\\left(\\left(\\frac{a_{1}}{a_{2}}\\right)^{(n-1)^{2}}\\left(\\frac{a_{2}}{a_{3}}\\right)^{(n-1)(n-2)} \\cdots\\left(\\frac{a_{n-1}}{a_{n}}\\right)^{n-1}\\right)^{\\frac{2}{n(n-1)}} \\\\\n& =\\left(\\left(\\frac{a_{1}}{a_{2}}\\right)^{n-1}\\left(\\frac{a_{2}}{a_{3}}\\right)^{n-2} \\cdots\\left(\\frac{a_{n-1}}{a_{n}}\\right)\\right)^{\\frac{2}{n}} \\\\\n& =\\left(a_{1}^{n-1} a_{2}^{-1} a_{3}^{-1} \\cdots a_{n}^{-1}\\right)^{\\frac{2}{n}} \\\\\n& =a_{1}^{2}\\left(a_{1}^{-1} a_{2}^{-1} a_{2}^{-1} \\cdots a_{n}^{-1}\\right)^{\\frac{2}{n}}\n\\end{aligned}\n$$\n\nAangezien gegeven is dat $a_{1} a_{2} \\cdots a_{n}=1$ is dit gelijk aan $a_{1}^{2}$. Als we deze ongelijkheid cyclisch roteren krijgen we één ongelijkheid voor elke $a_{i}^{2}$. Het optellen van deze $n$ ongelijkheden geeft precies het gevraagde: de rechterkant is duidelijk $a_{1}^{2}+a_{2}^{2}+\\ldots+a_{n}^{2}$ en aan de linkerkant krijgen hebben we alleen termen van de vorm $\\left(\\frac{a_{i}}{a_{i+1}}\\right)^{n-1}$ elk met een factor $\\frac{1}{\\frac{1}{2} n(n-1)}((n-1)+(n-2)+\\ldots+1)=1$.\n\nEr geldt gelijkheid dan en slechts dan als er gelijkheid geldt voor elk van de $n$ ongelijkheden. Voor elk van deze $n$ ongelijkheden geldt gelijkheid wanneer de $n-1$ verschillende termen gelijk zijn. Voor $n=2$ is dit triviaal waar, dus geldt er gelijkheid voor alle $a_{1}, a_{2}$ met $a_{1} a_{2}=1$. Voor $n>2$ zijn de gelijkheidsgevallen de cyclische permutaties van $\\frac{a_{1}}{a_{2}}=\\frac{a_{2}}{a_{3}}=\\ldots=\\frac{a_{n-1}}{a_{n}}$. Als we twee permutaties combineren krijgen we $\\frac{a_{1}}{a_{2}}=\\frac{a_{2}}{a_{3}}=\\ldots=\\frac{a_{n}}{a_{1}}=a$ voor een zekere positieve reële $a$, en dan geldt de gelijkheid ook voor alle permutaties. Het product van al deze breuken kunnen we dan uitrekenen als $a^{n}=\\frac{a_{1}}{a_{2}} \\frac{a_{2}}{a_{3}} \\cdots \\frac{a_{n}}{a_{1}}=1$, dus $a=1$. We concluderen dat alle $a_{i}$ hetzelfde moeten zijn. Wegens de voorwaarde zijn ze dan allemaal gelijk aan 1.", "problem_match": "\nOpgave 4.", "solution_match": "\nOplossing."}
|
| 7 |
+
{"year": "2022", "problem_label": "5", "tier": 1, "problem": "Op een vismarkt staan 10 kraampjes die allemaal dezelfde 10 vissoorten verkopen. Alle vissen zijn gevangen in de Noordzee of de Middellandse Zee, en elk kraampje heeft per vissoort maar één zee van afkomst. Een aantal, $k$, klanten koopt van elk kraampje één vis zo dat ze één vis van elke soort hebben. Verder weten we dat elk tweetal klanten een vissoort hebben met verschillende afkomst. We beschouwen alle mogelijke manieren om de kraampjes te vullen volgens de bovenstaande spelregels.\n\nWat is de maximaal mogelijke waarde van $k$ ?", "solution": "Het antwoord is $2^{10}-10$. Ten eerste merken we op dat er $2^{10}$ mogelijke combinaties zijn voor de afkomsten per vissoort. We gaan laten zien dat er altijd minstens 10 uitzonderingen zijn (mogelijkheden die afvallen) en dat er een marktopzet is waarbij er precies 10 uitzonderingen zijn.\n\nWe ordenen zowel de kraampjes als de vissen van 1 tot 10. Voor een kraampje $i$ definiëren we het rijtje $a_{i} \\in\\{M, N\\}^{10}$ als de afkomsten van de 10 vissoorten in dit kraampje (bijvoorbeeld $a_{1}=(M, M, M, N, M, N, N, M, M, M)$ ). Zij $c_{i}$ het complement van dit rijtje: we vervangen alle $M$ door $N$ en vice versa. Aangezien elke klant een vis heeft gekocht van kraampje $i$ kan geen enkele klant het rijtje $c_{i}$ hebben. Als de rijtjes $c_{i}$ met $1 \\leq i \\leq 10$ allemaal verschillend zijn, dan hebben we dus 10 uitzonderingen.\n\nStel aan de andere kant dat kraampjes $i$ en $j$ vissen van precies dezelfde zeeën verkopen, oftewel $a_{i}=a_{j}$. Dan ook $c_{i}=c_{j}$. Dan definiëren we de rijtjes $d_{k}$ met $1 \\leq k \\leq 10$ door in het rijtje $c_{i}$ de afkomst van vis $k$ te wisselen. Dit zijn precies de rijtjes die één zee overeenkomstig hebben met het rijtje $a_{i}=a_{j}$. Als een klant een rijtje $d_{k}$ heeft ingekocht, dan kan daar dus maximaal één vis tussen zitten van kraampje $i$ of $j$. Dit is in tegenspraak met het feit dat de klant bij beide kraampjes een vis heeft gekocht. We concluderen dat we in dat geval ook minstens 10 uitzonderingen $d_{k}$ hebben (en in feite ook nog $c_{i}$ ).\n\nWe construeren als volgt een markt waar je $2^{10}-10$ verschillende combinaties van afkomsten van vissen kan kopen zoals in de opgave: kraampje $i$ verkoopt alleen vis uit de Noordzee met uitzondering van vis $i$ uit de Middellandse Zee. Zij $b \\in\\{M, N\\}^{10}$ een rijtje afkomsten zo dat er niet precies één $N$ in voorkomt. We gaan laten zien dat we 10 verschillende vissen van 10 verschillende kraampjes kunnen kopen zo dat $b$ het rijtje afkomsten is. We splitsen de vissen in $b$ op in een verzameling $A$ uit de Middellandse Zee en een verzameling $B$ uit de Noordzee, dat wil zeggen $A$ is de verzameling indices waar in $b$ een $M$ staat en $B$ is de verzameling indices waar een $N$ staat. Voor $i \\in A$ kopen we vissoort $i$ bij kraampje $i$, zodat we inderdaad een vis uit de Middellandse Zee krijgen. Als $B$ leeg is, dan zijn we klaar. Anders heeft $B$ minstens twee elementen en schrijven we $B=\\left\\{i_{1}, \\ldots, i_{n}\\right\\} \\subset\\{1, \\ldots, 10\\}$. Voor $i_{k} \\in B$ kopen we vissoort $i_{k}$ bij kraampje $i_{k+1}$, waarbij we de indices modulo $n$ rekenen. Omdat $n \\neq 1$ geldt dat $i_{k+1} \\neq i_{k}$, dus deze vis komt inderdaad uit de Noordzee.", "problem_match": "\nOpgave 5.", "solution_match": "\nOplossing."}
|