add segmented French-TSTs 2011-2023 problems and solutions
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- French_TST_Senior/md/fr-2011-2012-ofm-2011-2012-test-mars-corrige.md +8 -4
- French_TST_Senior/md/fr-2013-2014-ofm-2013-2014-test-mai-corrige.md +3 -2
- French_TST_Senior/md/fr-2017-2018-Corrig%c3%a9-03-2018.md +2 -1
- French_TST_Senior/segment_script/segment.py +126 -0
- French_TST_Senior/segmented/fr-2011-2012-ofm-2011-2012-test-janvier-corrige.jsonl +4 -0
- French_TST_Senior/segmented/fr-2011-2012-ofm-2011-2012-test-mars-corrige.jsonl +9 -0
- French_TST_Senior/segmented/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl +8 -0
- French_TST_Senior/segmented/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl +8 -0
- French_TST_Senior/segmented/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl +8 -0
- French_TST_Senior/segmented/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl +7 -0
- French_TST_Senior/segmented/fr-2013-2014-ofm-2013-2014-test-mai-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2014-2015-ofm-2014-2015-test-fevrier-corrige.jsonl +4 -0
- French_TST_Senior/segmented/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl +4 -0
- French_TST_Senior/segmented/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl +7 -0
- French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl +4 -0
- French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2017-2018-Corrig%c3%a9-03-2018.jsonl +7 -0
- French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl +4 -0
- French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl +6 -0
- French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2018-2019-Test-09-01-Corrigé.jsonl +6 -0
- French_TST_Senior/segmented/fr-2018-2019-Test-15-05-Corrigé.jsonl +7 -0
- French_TST_Senior/segmented/fr-2018-2019-Test-20-03-Corrigé-web.jsonl +6 -0
- French_TST_Senior/segmented/fr-2018-2019-Test-26-02-Corrige.jsonl +4 -0
- French_TST_Senior/segmented/fr-2018-2019-Test-27-02-Corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl +3 -0
- French_TST_Senior/segmented/fr-2019-2020-Corrigé-Web-05-2020.jsonl +12 -0
- French_TST_Senior/segmented/fr-2019-2020-Corrigé-Web.jsonl +10 -0
- French_TST_Senior/segmented/fr-2019-2020-corrigé-test-janvier.jsonl +9 -0
- French_TST_Senior/segmented/fr-2019-2020-corrigé-test-novembre.jsonl +4 -0
- French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-1.jsonl +4 -0
- French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-2.jsonl +16 -0
- French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-3-Web.jsonl +21 -0
- French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-4-Web.jsonl +13 -0
- French_TST_Senior/segmented/fr-2020-2021-Corrigé-Web-Test-5.jsonl +9 -0
- French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-1.jsonl +13 -0
- French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-2.jsonl +7 -0
- French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-3.jsonl +14 -0
- French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-4.jsonl +7 -0
- French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-5.jsonl +10 -0
- French_TST_Senior/segmented/fr-2022-2023-Corrige-Test-3.jsonl +11 -0
- French_TST_Senior/segmented/fr-2022-2023-Corrige-Test-4.jsonl +8 -0
French_TST_Senior/md/fr-2011-2012-ofm-2011-2012-test-mars-corrige.md
CHANGED
|
@@ -26,7 +26,7 @@ Prouver que les droites $(A P),(B C),(O H)$ sont concourantes si, et seulement s
|
|
| 26 |
|
| 27 |
## Solution.
|
| 28 |
|
| 29 |
-
 \perp(A C)$ et donc $(B H) / /(V C)$. De même on voit que $(C H) / /(V B)$. Il s'ensuit que $B H C V$ est un parallélogramme de centre $M$. Les points $H, M, V$ sont donc alignés. Si on note $U$ la deuxième intersection de $(H V)$ avec $\Gamma$, par cocyclicité on obtient $\widehat{A U V}=\widehat{A B V}=90^{\circ}$. Comme $\widehat{A P V}=\widehat{A P M}=90^{\circ}$, on conclut que $U=P$ et donc que $P, H, M$ sont alignés.
|
| 32 |
|
|
@@ -137,7 +137,8 @@ f_{k}(n)=\underbrace{f \circ f \circ \cdots \circ f}_{k \text { fois }}(n)
|
|
| 137 |
$$
|
| 138 |
|
| 139 |
Pour quels $k$ existe-t-il une fonction $k$-tastrophique?
|
| 140 |
-
|
|
|
|
| 141 |
|
| 142 |
On procède maintenant de la façon suivante. On pose $f(1)=1$, et si $n$ est le plus petit entier pour lequel $f(n)$ n'est pas encore défini, alors:
|
| 143 |
|
|
@@ -192,7 +193,10 @@ Ainsi, dans tous les cas, on a $f_{k}(n)=n^{k}$. Ce qui achève la récurrence,
|
|
| 192 |
## Exercice 5
|
| 193 |
|
| 194 |
Déterminer tous les polynômes $X^{n}+a_{1} X^{n-1}+\cdots+a_{n-1} X+a_{n}$, non constants et à coefficients entiers, dont les racines sont exactement les nombres $a_{1}, \ldots, a_{n-1}, a_{n}$ (avec multiplicité).
|
| 195 |
-
|
|
|
|
|
|
|
|
|
|
| 196 |
|
| 197 |
$$
|
| 198 |
P(X)=\prod_{i=1}^{n}\left(X-a_{i}\right)
|
|
@@ -251,7 +255,7 @@ Soit $A B C D$ un quadrilatère convexe tel que les droites $(A D)$ et $(B C)$ n
|
|
| 251 |
Prouver que le milieu de $[E F]$ appartient à la droite passant par les deux points d'intersection de $\Gamma_{E}$ et $\Gamma_{F}$.
|
| 252 |
|
| 253 |
Solution.
|
| 254 |
-
,(A B),(B C),(C D)$. Les points $P$ et $Q$ appartiennent au cercle de diamètre $[A E]$ de sorte que $\widehat{Q P E}=\widehat{Q A E}$. De même, $\widehat{Q R E}=\widehat{Q B E}$. Ainsi :
|
| 257 |
|
|
|
|
| 26 |
|
| 27 |
## Solution.
|
| 28 |
|
| 29 |
+
|
| 30 |
|
| 31 |
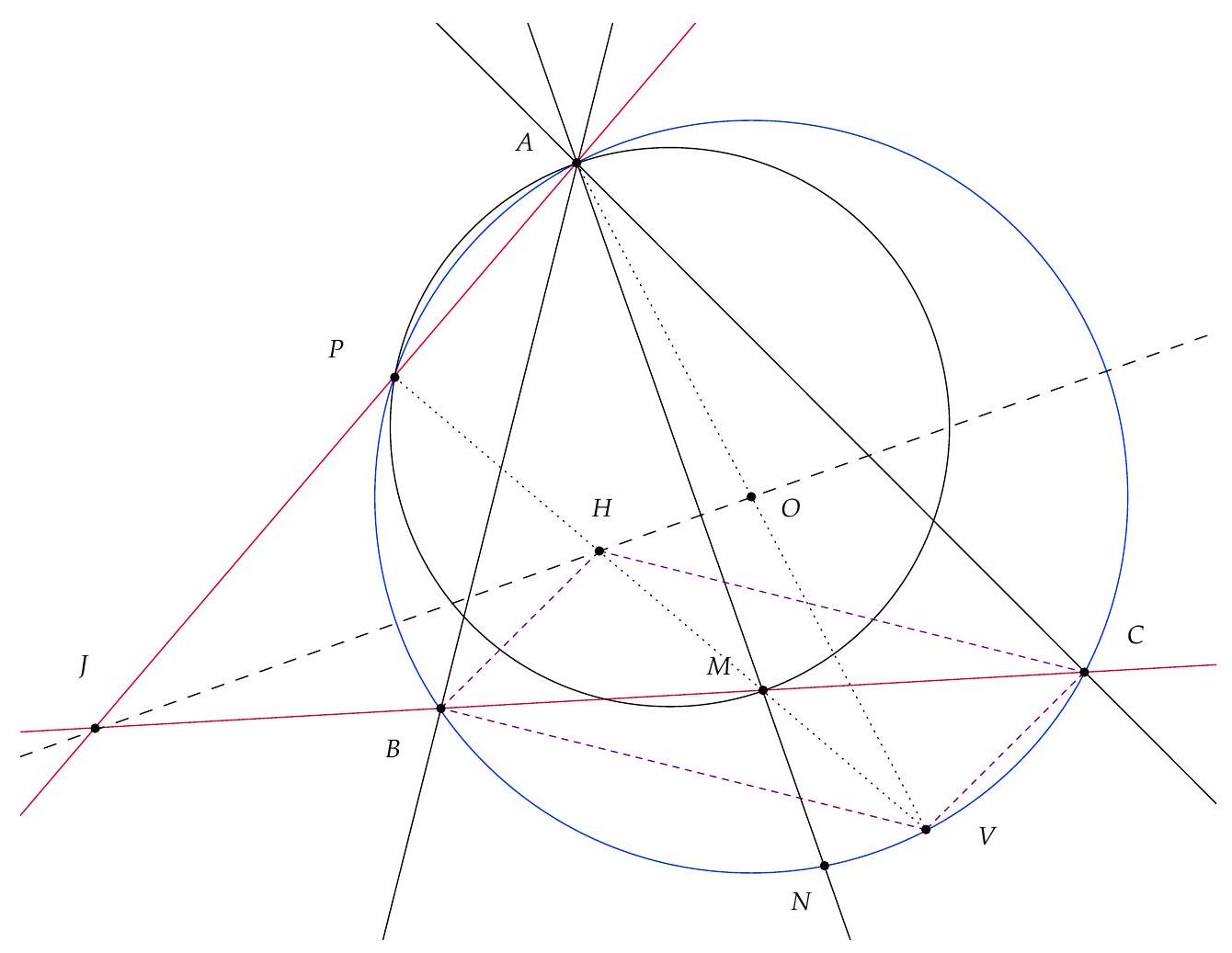
Montrons d'abord que $P, H, M$ sont alignés. À cet effet, introduisons $V$, le point diamétralement opposé à $A$ sur $\Gamma$. Alors $(V C) \perp(A C)$ et donc $(B H) / /(V C)$. De même on voit que $(C H) / /(V B)$. Il s'ensuit que $B H C V$ est un parallélogramme de centre $M$. Les points $H, M, V$ sont donc alignés. Si on note $U$ la deuxième intersection de $(H V)$ avec $\Gamma$, par cocyclicité on obtient $\widehat{A U V}=\widehat{A B V}=90^{\circ}$. Comme $\widehat{A P V}=\widehat{A P M}=90^{\circ}$, on conclut que $U=P$ et donc que $P, H, M$ sont alignés.
|
| 32 |
|
|
|
|
| 137 |
$$
|
| 138 |
|
| 139 |
Pour quels $k$ existe-t-il une fonction $k$-tastrophique?
|
| 140 |
+
## Solution. On va prouver que, pour tout entier $k \geq 1$, il existe une fonction $k$-tastrophique.
|
| 141 |
+
Clairement, la fonction $f: n \longmapsto n$ est 1-tastrophique. On suppose donc que $k \geq 2$.
|
| 142 |
|
| 143 |
On procède maintenant de la façon suivante. On pose $f(1)=1$, et si $n$ est le plus petit entier pour lequel $f(n)$ n'est pas encore défini, alors:
|
| 144 |
|
|
|
|
| 193 |
## Exercice 5
|
| 194 |
|
| 195 |
Déterminer tous les polynômes $X^{n}+a_{1} X^{n-1}+\cdots+a_{n-1} X+a_{n}$, non constants et à coefficients entiers, dont les racines sont exactement les nombres $a_{1}, \ldots, a_{n-1}, a_{n}$ (avec multiplicité).
|
| 196 |
+
|
| 197 |
+
## Solution. \text{Soit } P(X) = X^n + a_1 X^{n-1} + \cdots + a_{n-1} X + a_n \; \text{un polynôme à coefficients entiers.}
|
| 198 |
+
|
| 199 |
+
Alors $P(X)$ est une solution du problème ssi
|
| 200 |
|
| 201 |
$$
|
| 202 |
P(X)=\prod_{i=1}^{n}\left(X-a_{i}\right)
|
|
|
|
| 255 |
Prouver que le milieu de $[E F]$ appartient à la droite passant par les deux points d'intersection de $\Gamma_{E}$ et $\Gamma_{F}$.
|
| 256 |
|
| 257 |
Solution.
|
| 258 |
+
|
| 259 |
|
| 260 |
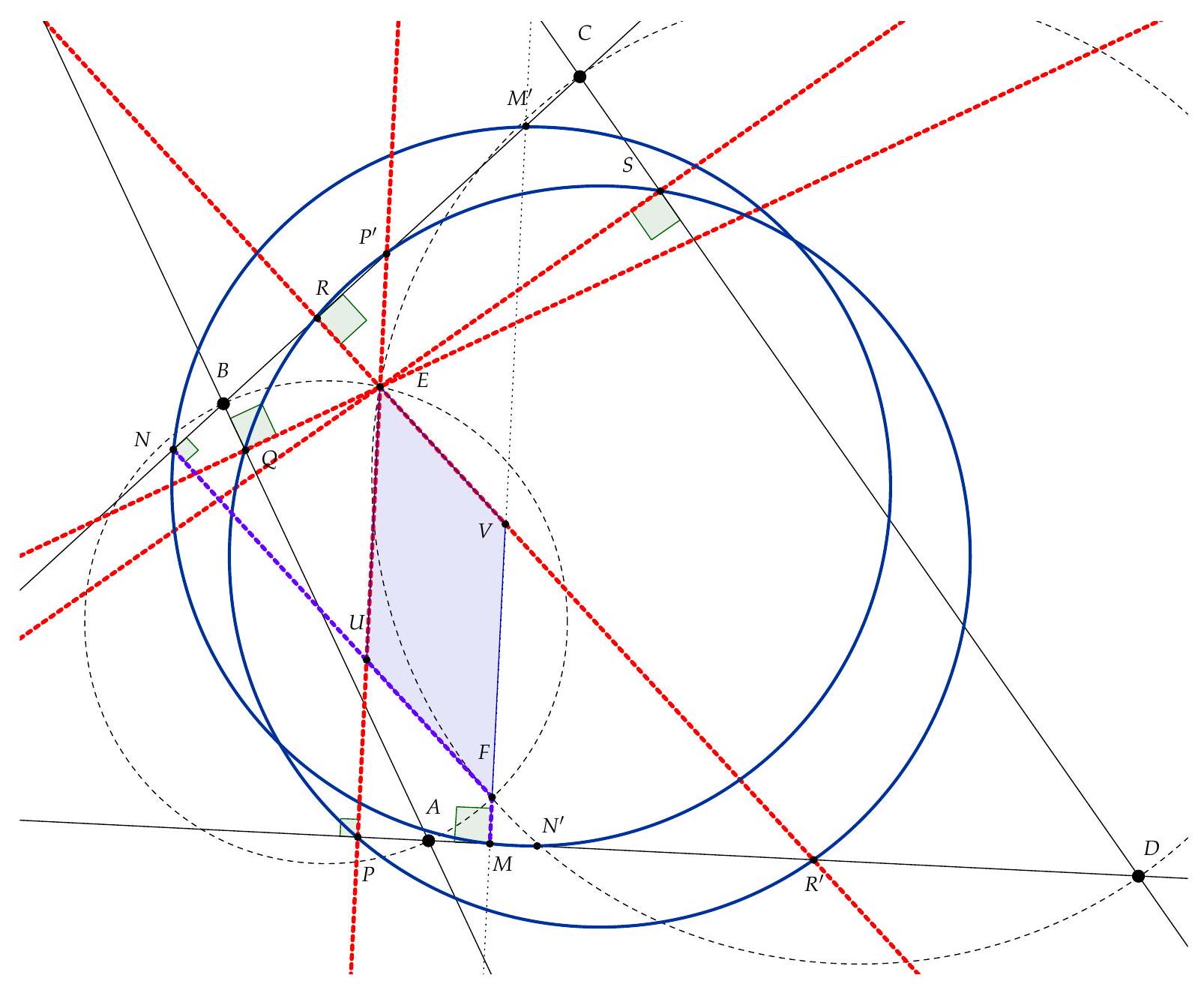
Soient $P, Q, R, S$ les projections de $E$ sur les droites $(D A),(A B),(B C),(C D)$. Les points $P$ et $Q$ appartiennent au cercle de diamètre $[A E]$ de sorte que $\widehat{Q P E}=\widehat{Q A E}$. De même, $\widehat{Q R E}=\widehat{Q B E}$. Ainsi :
|
| 261 |
|
French_TST_Senior/md/fr-2013-2014-ofm-2013-2014-test-mai-corrige.md
CHANGED
|
@@ -6,7 +6,7 @@ TEST DES 13 ET 14 MAI 2014
|
|
| 6 |
|
| 7 |
CORRIGÉ
|
| 8 |
|
| 9 |
-
Exercice
|
| 10 |
|
| 11 |
Solution de l'exercice J1. Cet exercice découle en fait d'une utilisation astucieuse du principe des tiroirs. Soit $E$ une partie de $\{1,2, \ldots, 2014\}$ ne contenant que des entiers dont la différence n'est jamais égale à 17 .
|
| 12 |
Tout d'abord, pour tout entier $a$, on note $S_{a}$ l'ensemble $\{a, a+17\}$, et $T_{a}$ l'ensemble $\{a, a+$ $1, \ldots, a+33\}$ : alors on sait que $E \cap S_{a}$ contient au plus un élément, quelque soit l'entier $a$ considéré : autrement dit, $\left|E \cap S_{a}\right| \leq 1$. Puisque $2014=34 \times 59+8$, on sait que
|
|
@@ -23,7 +23,8 @@ $$
|
|
| 23 |
|
| 24 |
D'autre part, en choisissant exactement $E=\bigcup_{i=0}^{58}\left(\bigcup_{a=34 i+1}^{34 i+17}\{a\}\right) \cup \bigcup_{a=2009}^{2014}\{a\}$, on obtient bien une partie de $\{1,2, \ldots, 2014\}$ ne contenant que des entiers dont la différence n'est jamais égale à 17 , et dont le cardinal est précisément $|E|=1011$.
|
| 25 |
Ainsi, le nombre recherché était bien 1011.
|
| 26 |
-
|
|
|
|
| 27 |
Solution de l'exercice J2. La puissance du point $P$ par rapport au cercle $\mathcal{C}$ est égale à $P B^{2}=P Q$. $\overline{P R}$. Ainsi, on a égalité des rapports de longueurs $\frac{P R}{P B}=\frac{P B}{P Q}$, ce qui montre que les triangles $P R B$ et $P B Q$ sont indirectement semblables. En particulier, on en déduit que $\frac{P B}{P R}=\frac{B Q}{B R}$. Puis, $A$ et $B$ jouant des rôles symétriques, on a également $\frac{P A}{P R}=\frac{A Q}{A R}$.
|
| 28 |
Soit alors $O$ le centre du cercle $\mathcal{C}$ ainsi que $N_{1}$ le milieu de $[Q R]$ et $N_{2}$ le milieu de $[B S]$. Les cordes $Q R$ et $B S$ étant parallèles, on sait que $\left(N_{1} O\right)=\left(N_{2} O\right)$ est la médiatrice commune à $[Q R]$ et à $[B S]$, c'est-à-dire un axe de symétrie du trapèze $Q S B R$. Il s'ensuit que $\frac{B Q}{B R}=\frac{S R}{S Q}$. On en déduit donc que
|
| 29 |
|
|
|
|
| 6 |
|
| 7 |
CORRIGÉ
|
| 8 |
|
| 9 |
+
Exercice J1. Déterminer le plus grand nombre d'entiers que l'on peut extraire de l'ensemble $\{1,2, \ldots, 2014\}$ de sorte que la différence de deux quelconques de ces entiers soit différente de 17.
|
| 10 |
|
| 11 |
Solution de l'exercice J1. Cet exercice découle en fait d'une utilisation astucieuse du principe des tiroirs. Soit $E$ une partie de $\{1,2, \ldots, 2014\}$ ne contenant que des entiers dont la différence n'est jamais égale à 17 .
|
| 12 |
Tout d'abord, pour tout entier $a$, on note $S_{a}$ l'ensemble $\{a, a+17\}$, et $T_{a}$ l'ensemble $\{a, a+$ $1, \ldots, a+33\}$ : alors on sait que $E \cap S_{a}$ contient au plus un élément, quelque soit l'entier $a$ considéré : autrement dit, $\left|E \cap S_{a}\right| \leq 1$. Puisque $2014=34 \times 59+8$, on sait que
|
|
|
|
| 23 |
|
| 24 |
D'autre part, en choisissant exactement $E=\bigcup_{i=0}^{58}\left(\bigcup_{a=34 i+1}^{34 i+17}\{a\}\right) \cup \bigcup_{a=2009}^{2014}\{a\}$, on obtient bien une partie de $\{1,2, \ldots, 2014\}$ ne contenant que des entiers dont la différence n'est jamais égale à 17 , et dont le cardinal est précisément $|E|=1011$.
|
| 25 |
Ainsi, le nombre recherché était bien 1011.
|
| 26 |
+
|
| 27 |
+
Exercice J2. Soit $P$ un point à l'extérieur d'un cercle $\mathcal{C}$. Les tangentes à $\mathcal{C}$ passant par $P$ touchent $\mathcal{C}$ en $A$ et $B$. Une droite passant par $P$ intersecte $\mathcal{C}$ aux points $Q$ et $R$. Soit $S$ un point de $\mathcal{C}$ tel que $(B S) / /(Q R)$. Montrer que $(S A)$ passe par le milieu de $[Q R]$.
|
| 28 |
Solution de l'exercice J2. La puissance du point $P$ par rapport au cercle $\mathcal{C}$ est égale à $P B^{2}=P Q$. $\overline{P R}$. Ainsi, on a égalité des rapports de longueurs $\frac{P R}{P B}=\frac{P B}{P Q}$, ce qui montre que les triangles $P R B$ et $P B Q$ sont indirectement semblables. En particulier, on en déduit que $\frac{P B}{P R}=\frac{B Q}{B R}$. Puis, $A$ et $B$ jouant des rôles symétriques, on a également $\frac{P A}{P R}=\frac{A Q}{A R}$.
|
| 29 |
Soit alors $O$ le centre du cercle $\mathcal{C}$ ainsi que $N_{1}$ le milieu de $[Q R]$ et $N_{2}$ le milieu de $[B S]$. Les cordes $Q R$ et $B S$ étant parallèles, on sait que $\left(N_{1} O\right)=\left(N_{2} O\right)$ est la médiatrice commune à $[Q R]$ et à $[B S]$, c'est-à-dire un axe de symétrie du trapèze $Q S B R$. Il s'ensuit que $\frac{B Q}{B R}=\frac{S R}{S Q}$. On en déduit donc que
|
| 30 |
|
French_TST_Senior/md/fr-2017-2018-Corrig%c3%a9-03-2018.md
CHANGED
|
@@ -36,7 +36,8 @@ $$
|
|
| 36 |
$$
|
| 37 |
|
| 38 |
On en déduit que $B C=C E+B E=A D+B D$.
|
| 39 |
-
Exercice 3. Trouver tous les entiers naturels non nuls $k, \ell$ tels que $2^{k}+3^{\ell}$ soit un carré parfait.
|
|
|
|
| 40 |
Puisque $k \geqslant 1$ et $\ell \geqslant 1$, on a donc $2^{k} \equiv 1(\bmod 3)$ et $3^{\ell} \equiv 1(\bmod 8)$, ce qui signifie que $k$ et $\ell$ sont pairs. En posant $\mathrm{a}=\mathrm{k} / 2, \mathrm{~b}=\ell / 2$ et $\mathrm{c}=\sqrt{2^{k}+3^{\ell}}$, on remarque alors que $\left(\mathrm{c}-2^{\mathrm{a}}\right)\left(\mathrm{c}+2^{\mathrm{a}}\right)=$ $c^{2}-2^{k}=3^{\ell}$ est une puissance de 3 .
|
| 41 |
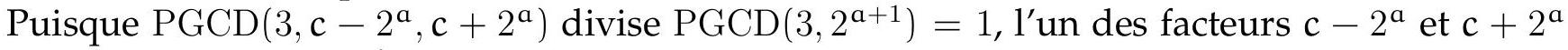 vaut nécessairement $3^{\ell}$, tandis que l'autre vaut 1 . Le facteur $c+2^{a}$ est le plus grand des deux, ce qui montre que $c-2^{a}=1$ et $\mathrm{c}+2^{a}=3^{\ell}$, donc que $2^{a+1}=3^{\ell}-1=9^{b}-1=\left(3^{b}-1\right)\left(3^{b}+1\right)$. De même, puisque $3^{\mathrm{b}}-1$ et $3^{\mathrm{b}}+1$ sont pairs et que $\operatorname{PGCD}\left(2,3^{\mathrm{b}}-1,3^{\mathrm{b}}+1\right)$ divise 2 , l'un des facteurs $3^{b}-1$ et $3^{b}+1$ vaut nécessairement $2^{a}$, tandis que l'autre vaut 2 . Par conséquent, $3^{\mathrm{b}}-1=2$ et $3^{\mathrm{b}}+1=2^{\mathrm{a}}$, ce qui montre que $\mathrm{a}=2$ et $\mathrm{b}=1$, ou encore $\mathrm{k}=4$ et $\ell=2$.
|
| 42 |
Réciproquement, si $(k, \ell)=(4,2)$, on a bien $2^{k}+3^{\ell}=2^{4}+3^{2}=16+9=25=5^{2}$. Ceci montre que la paire $(k, \ell)=(4,2)$ est la seule solution du problème.
|
|
|
|
| 36 |
$$
|
| 37 |
|
| 38 |
On en déduit que $B C=C E+B E=A D+B D$.
|
| 39 |
+
Exercice 3. Trouver tous les entiers naturels non nuls $k, \ell$ tels que $2^{k}+3^{\ell}$ soit un carré parfait.
|
| 40 |
+
Solution de l'exercice 3 Une première idée est de consiérer l'équation de l'énoncé modulo $n$, où n est un nombre pas trop grand tel que $\mathbb{Z} / \mathrm{n} \mathbb{Z}$ ne contienne pas trop de résidus quadratiques. Dans ces conditions, $n=3$ et $n=8$ semblent de bons candidats, car les carrés modulo 3 sont 0 et 1 , alors que les carrés modulo 8 sont 0,1 et 4 .
|
| 41 |
Puisque $k \geqslant 1$ et $\ell \geqslant 1$, on a donc $2^{k} \equiv 1(\bmod 3)$ et $3^{\ell} \equiv 1(\bmod 8)$, ce qui signifie que $k$ et $\ell$ sont pairs. En posant $\mathrm{a}=\mathrm{k} / 2, \mathrm{~b}=\ell / 2$ et $\mathrm{c}=\sqrt{2^{k}+3^{\ell}}$, on remarque alors que $\left(\mathrm{c}-2^{\mathrm{a}}\right)\left(\mathrm{c}+2^{\mathrm{a}}\right)=$ $c^{2}-2^{k}=3^{\ell}$ est une puissance de 3 .
|
| 42 |
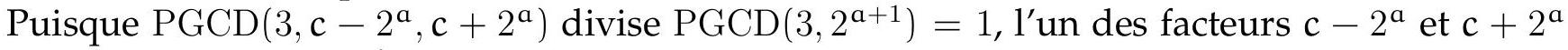 vaut nécessairement $3^{\ell}$, tandis que l'autre vaut 1 . Le facteur $c+2^{a}$ est le plus grand des deux, ce qui montre que $c-2^{a}=1$ et $\mathrm{c}+2^{a}=3^{\ell}$, donc que $2^{a+1}=3^{\ell}-1=9^{b}-1=\left(3^{b}-1\right)\left(3^{b}+1\right)$. De même, puisque $3^{\mathrm{b}}-1$ et $3^{\mathrm{b}}+1$ sont pairs et que $\operatorname{PGCD}\left(2,3^{\mathrm{b}}-1,3^{\mathrm{b}}+1\right)$ divise 2 , l'un des facteurs $3^{b}-1$ et $3^{b}+1$ vaut nécessairement $2^{a}$, tandis que l'autre vaut 2 . Par conséquent, $3^{\mathrm{b}}-1=2$ et $3^{\mathrm{b}}+1=2^{\mathrm{a}}$, ce qui montre que $\mathrm{a}=2$ et $\mathrm{b}=1$, ou encore $\mathrm{k}=4$ et $\ell=2$.
|
| 43 |
Réciproquement, si $(k, \ell)=(4,2)$, on a bien $2^{k}+3^{\ell}=2^{4}+3^{2}=16+9=25=5^{2}$. Ceci montre que la paire $(k, \ell)=(4,2)$ est la seule solution du problème.
|
French_TST_Senior/segment_script/segment.py
ADDED
|
@@ -0,0 +1,126 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import os
|
| 2 |
+
import re
|
| 3 |
+
import json
|
| 4 |
+
|
| 5 |
+
from tqdm import tqdm
|
| 6 |
+
from loguru import logger
|
| 7 |
+
|
| 8 |
+
from pathlib import Path
|
| 9 |
+
from typing import Tuple, List
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
problem_tag = 'Problem'
|
| 13 |
+
solution_tag = 'Solution'
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
def clean(text: str) -> str:
|
| 17 |
+
return re.sub(r'\$\\underline\{\\text \{ (Solution de l\'exercice) \} (\d*)\}\$', r'\n\1 \2\n', text)
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 21 |
+
"""
|
| 22 |
+
Analyze the text and return the tags and problem number.
|
| 23 |
+
|
| 24 |
+
Args:
|
| 25 |
+
text (str): The markdown text to analyze.
|
| 26 |
+
|
| 27 |
+
Returns:
|
| 28 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 29 |
+
"""
|
| 30 |
+
problem_pattern = re.compile(r"(?i)(?:\n|##* )Exercice (\d+)[\.\n]")
|
| 31 |
+
solution_pattern = re.compile(r"(?i)(?:\n|##* )(?:Solution de l'exercice\s*\d*|Solution\s*(\d+\s*)?[:\.\n]|(?:Première|Deuxième|Troisième|Quatrième) démonstration|Démonstration[:\.\n]|Corrigé[:\.\n]|Solution alternative)")
|
| 32 |
+
|
| 33 |
+
tags = []
|
| 34 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text)])
|
| 35 |
+
problem_num = len(tags)
|
| 36 |
+
|
| 37 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text)])
|
| 38 |
+
tags.sort(key=lambda x: x[0].start())
|
| 39 |
+
return tags, problem_num
|
| 40 |
+
|
| 41 |
+
|
| 42 |
+
def segment(text: str, tags):
|
| 43 |
+
starts = []
|
| 44 |
+
ends = []
|
| 45 |
+
|
| 46 |
+
for i in range(len(tags)):
|
| 47 |
+
starts.append(tags[i][0].end())
|
| 48 |
+
if i + 1 < len(tags):
|
| 49 |
+
ends.append(tags[i + 1][0].start())
|
| 50 |
+
else:
|
| 51 |
+
ends.append(len(text))
|
| 52 |
+
|
| 53 |
+
return [text[start:end].strip().strip('#').strip() for start, end in zip(starts, ends)]
|
| 54 |
+
|
| 55 |
+
|
| 56 |
+
def join(tags, segments):
|
| 57 |
+
problem, solution = '', ''
|
| 58 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 59 |
+
pairs = []
|
| 60 |
+
|
| 61 |
+
for tag, segment in zip(tags, segments):
|
| 62 |
+
if tag[1] == problem_tag:
|
| 63 |
+
problem = segment
|
| 64 |
+
problem_match = tag[0].group(0)
|
| 65 |
+
problem_label = tag[0].group(1)
|
| 66 |
+
elif problem != '':
|
| 67 |
+
solution = segment
|
| 68 |
+
solution_match = tag[0].group(0)
|
| 69 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 70 |
+
|
| 71 |
+
return pairs
|
| 72 |
+
|
| 73 |
+
|
| 74 |
+
def write_pairs(output_file: Path, pairs):
|
| 75 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 76 |
+
|
| 77 |
+
output_jsonl_text = ""
|
| 78 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 79 |
+
output_jsonl_text += json.dumps(
|
| 80 |
+
{
|
| 81 |
+
'year': year,
|
| 82 |
+
'problem_label': problem_label,
|
| 83 |
+
'tier': 1,
|
| 84 |
+
'problem': problem,
|
| 85 |
+
'solution': solution,
|
| 86 |
+
'problem_match': problem_match,
|
| 87 |
+
'solution_match': solution_match
|
| 88 |
+
},
|
| 89 |
+
ensure_ascii=False
|
| 90 |
+
) + '\n'
|
| 91 |
+
|
| 92 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 93 |
+
|
| 94 |
+
|
| 95 |
+
def main():
|
| 96 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 97 |
+
compet_md_path = compet_base_path / "md"
|
| 98 |
+
seg_output_path = compet_base_path / "segmented"
|
| 99 |
+
|
| 100 |
+
total_problem_count = 0
|
| 101 |
+
total_solution_count = 0
|
| 102 |
+
|
| 103 |
+
for fr_tsts_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 104 |
+
output_file = seg_output_path / fr_tsts_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 105 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 106 |
+
|
| 107 |
+
text = '\n' + clean(fr_tsts_md.read_text(encoding="utf-8"))
|
| 108 |
+
|
| 109 |
+
tags, problem_num = analyze(text)
|
| 110 |
+
|
| 111 |
+
segments = segment(text, tags)
|
| 112 |
+
pairs = join(tags, segments)
|
| 113 |
+
if pairs and problem_num > 0:
|
| 114 |
+
write_pairs(output_file, pairs)
|
| 115 |
+
|
| 116 |
+
total_problem_count += problem_num
|
| 117 |
+
total_solution_count += len(pairs)
|
| 118 |
+
else:
|
| 119 |
+
logger.warning(f"No problem found in {fr_tsts_md}")
|
| 120 |
+
|
| 121 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 122 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 123 |
+
|
| 124 |
+
|
| 125 |
+
if __name__ == '__main__':
|
| 126 |
+
main()
|
French_TST_Senior/segmented/fr-2011-2012-ofm-2011-2012-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "1", "tier": 1, "problem": "Dans le plan on se donne 2011 points deux à deux distincts colorés soit en bleu, soit en rouge.\n(i) On suppose que pour tout point bleu le disque de centre ce point et de rayon 1 contienne exactement deux points rouges. Quel est le plus grand nombre possible de points bleus?\n(ii) On suppose que pour tout point bleu le cercle de centre ce point et de rayon 1 contienne exactement deux points rouges. Quel est le plus grand nombre possible de points bleus?", "solution": "(i) S'il existe un point bleu, il doit exister au moins deux points rouges donc il ne peut y avoir plus de 2009 points bleus.\n\nRéciproquement, si l'on considère 2009 disques de rayon 1 ayant un intérieur commun à tous qui soit non vide, il suffit de marquer deux points rouges dans cette partie commune et de marquer en bleu les centres de ces 2009 disques pour obtenir une configuration à 2009 points bleus qui vérifie les conditions de l'énoncé.\n\nLe maximum cherché est donc 2009.\n(ii) Considérons une configuration de $r$ points rouges et $b$ points bleus vérifiant les conditions de l'énoncé, avec $r+b=2011$. Comme ci-dessus, on a $r \\geq 2$.\n\nSi $R_{1}$ et $R_{2}$ sont deux points rouges distincts, on note $n\\left(R_{1}, R_{2}\\right)$ le nombre de points bleus qui sont centres de cercles de rayon 1 passant par $R_{1}$ et $R_{2}$.\n\nPuisque tout cercle de rayon 1 et centré en un point bleu passe par exactement deux points rouges, cela assure que:\n\n- tout point bleu est compté au moins une fois dans un certain $n\\left(R_{1}, R_{2}\\right)$,\n- si $\\left\\{R_{1}, R_{2}\\right\\}$ et $\\left\\{R_{1}^{\\prime}, R_{2}^{\\prime}\\right\\}$ sont deux paires distinctes de points rouges, alors les points bleus comptés dans $n\\left(R_{1}, R_{2}\\right)$ sont deux à deux distincts des points bleus comptés dans $n\\left(R_{1}^{\\prime}, R_{2}^{\\prime}\\right)$.\nAinsi, chaque point bleu est compté une et une seule fois dans un certain $n\\left(R_{1}, R_{2}\\right)$. En sommant sur les paires de points rouges, il vient\n\n$$\n\\sum_{\\left\\{R_{1}, R_{2}\\right\\}} n\\left(R_{1}, R_{2}\\right)=b\n$$\n\nD'autre part, pour toute paire de points du plan, il n'existe qu'au plus deux cercles de rayon 1 qui passent par ces deux points, on a donc $n\\left(R_{1}, R_{2}\\right) \\leq 2$ pour toute paire $R_{1}, R_{2}$ de points rouges. Comme il y a $r(r-1) / 2$ paires de points rouges, on a alors :\n\n$$\nb=\\sum_{\\left\\{R_{1}, R_{2}\\right\\}} n\\left(R_{1}, R_{2}\\right) \\leq \\sum_{\\left\\{R_{1}, R_{2}\\right\\}} 2=r(r-1),\n$$\n\net donc $r(r-1) \\geq 2011-r$, ou encore $r^{2} \\geq 2011$. On en déduit facilement que $r \\geq 45$, et donc que $b \\leq 1966$.\n\nRéciproquement, considérons 45 points rouges, tous situés sur un même segment de longueur 1. Deux quelconques de ces points rouges appartiennent alors toujours à deux cercles de rayon 1. On trace seulement 1966 de ces cercles (on pourrait en tracer $1980=$ $45 \\times 44$ ), et on marque en bleu les centres de ces cercles. Il est facile de vérifier que l'on obtient ainsi une configuration à 2011 points colorés qui vérifie les conditions de l'énoncé.\n\nLe maximum cherché est donc 1966.", "problem_match": "## Exercice 1\n", "solution_match": "## Solution."}
|
| 2 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "Trouver toutes les fonctions $f$ de $\\mathbb{R}$ dans $\\mathbb{R}$ telles que $f(a b)=f(a+b)$ pour tous nombres irrationnels $a$ et $b$.", "solution": "Il est clair que les fonctions constantes conviennent. Montrons que ce sont les seules. Soit $u$ un nombre irrationnel positif. Alors $\\sqrt{u}$ est irrationnel. En prenant $(a, b)=$ $(\\sqrt{u},-\\sqrt{u})$, il vient $f(-u)=f(0)$. En prenant $(a, b)=(-\\sqrt{u},-\\sqrt{u})$, il vient $f(u)=$ $f(-2 \\sqrt{u})=f(0)$ car $-2 \\sqrt{u}$ est un nombre irrationnel négatif. Ainsi, on a $f(u)=f(0)$ pour $u \\notin \\mathbb{Q}$.\n\nMaintenant soit $r \\in \\mathbb{Q}$ non nul, et écrivons $r=\\sqrt{2}+(r-\\sqrt{2})$. Comme $\\sqrt{2}$ est irrationnel, il est clair que $\\sqrt{2}, r-\\sqrt{2}, \\sqrt{2}(r-\\sqrt{2})$ sont tous irrationnels. Alors :\n\n$$\nf(r)=f(\\sqrt{2}(r-\\sqrt{2}))=f(0)\n$$\n\nd'après ce qui précède. Donc $f$ est constante.", "problem_match": "## Exercice 2\n", "solution_match": "\nSolution."}
|
| 3 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Soit $A B C D$ un quadrilatère inscrit dans un cercle de centre $O$. On note $\\Delta_{1}$ et $\\Delta_{2}$ les images de la droite $(A B)$ par les symétries dont les axes sont respectivement les bissectrices intérieures de $\\widehat{C A D}$ et $\\widehat{C B D}$. Soit $P$ l'intersection de $\\Delta_{1}$ et $\\Delta_{2}$.\n\nProuver que $(O P)$ et $(C D)$ sont perpendiculaires.", "solution": "On traite uniquement le cas où $O$ est à l'intérieur de $A B C D$ (les autres cas étant similaires). D'après les propriétés de l'angle inscrit, les deux bissectrices considérées s'intersectent en un point du cercle noté $S$, qui est le milieu de l'arc $C D$. En particulier, (OS) et $(C D)$ sont perpendiculaires. Il suffit donc de montrer que $P, O, S$ sont alignés.\n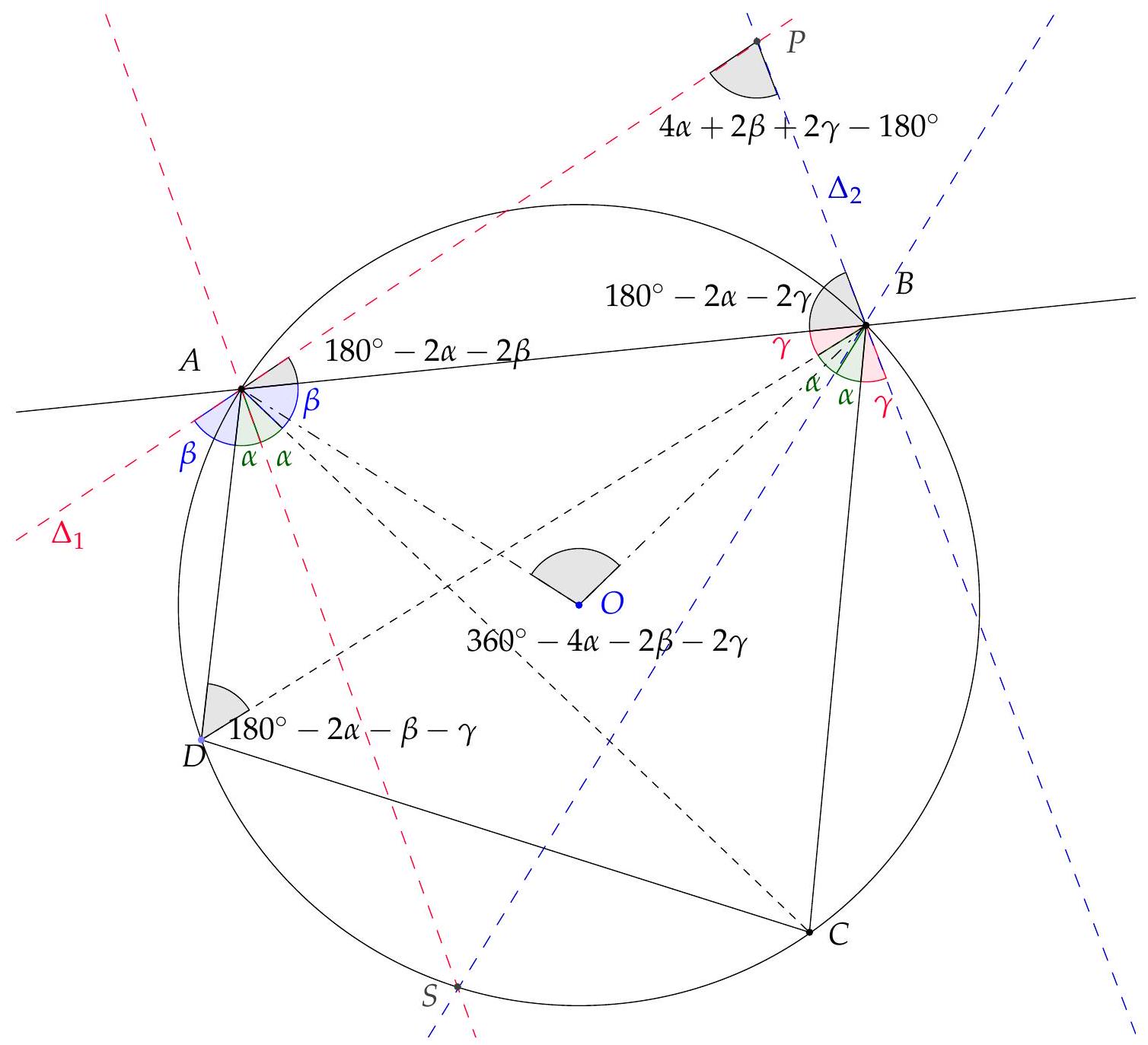\n\nUne chasse aux angles (voir figure) fournit $\\widehat{A P B}+\\widehat{A O B}=180^{\\circ}$. Ainsi, $A, P, B, O$ sont cocycliques. Alors $\\widehat{P O B}=\\widehat{P A B}=180^{\\circ}-2 \\alpha-2 \\beta$. Comme $A, B, C, D$ sont cocyliques, on a $\\widehat{B O C}=2 \\widehat{B A C}=2 \\beta$ et $\\widehat{C O S}=2 \\widehat{S B C}=2 \\alpha$. Ainsi, $\\widehat{P O B}+\\widehat{B O C}+\\widehat{C O S}=180^{\\circ}$. Les points $P, O, S$ sont donc alignés, ce qui conclut.", "problem_match": "## Exercice 3\n", "solution_match": "\nSolution."}
|
| 4 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Soit $a, b, c, d$ des entiers naturels tels que $0<|a d-b c|<\\min (c, d)$.\nProuver que pour tous entiers $x, y>1$ premiers entre eux, le nombre $x^{a}+y^{b}$ n'est pas divisible par $x^{c}+y^{d}$.", "solution": "Par l'absurde : on suppose que les entiers $x, y>1$ sont premiers entre eux et que $s=x^{c}+y^{d}$ divise $x^{a}+y^{b}$. On a alors:\n\n$$\nx^{c}=-y^{d} \\quad \\bmod s \\quad \\text { et } \\quad x^{a}=-y^{b} \\quad \\bmod s .\n$$\n\nD'où\n\n$$\nx^{a d}=(-1)^{d} y^{b d} \\bmod s \\quad \\text { et } \\quad x^{b c}=(-1)^{c} y^{b d} \\bmod s .\n$$\n\nAinsi $x^{a d}=(-1)^{b-d} x^{b c} \\bmod s$.\nOr, puisque $c>0$ et que $x$ et $y$ sont premiers entre eux, on a clairement $x$ et $s$ premiers entre eux. On peut donc diviser par $x^{\\min (a d, b c)}$ dans la congruence ci-dessus, et il vient $x^{|a d-b c|}=(-1)^{b-d} \\bmod s$. De même, on a $y^{|a d-b c|}=(-1)^{a-c} \\bmod s$.\n\nOn en déduit que :\n\n$$\nx^{|a d-b c|}+y^{|a d-b c|} \\text { ou } x^{|a d-b c|}-y^{|a d-b c|} \\text { est divisible par } s .\n$$\n\nMais on a $x^{|a d-b c|}-y^{|a d-b c|} \\neq 0$ car $x$ et $y$ sont premiers entre eux, supérieurs à 1 , et $|a d-b c|>0$. De plus $|a d-b c|<\\min (c, d)$ donc on a les inégalités\n\n$$\n0<\\left|x^{|a d-b c|}-y^{|a d-b c|}\\right|<x^{|a d-b c|}+y^{|a d-b c|}<x^{c}+y^{d}=s,\n$$\n\nce qui contredit (1).", "problem_match": "## Exercice 4\n", "solution_match": "\nSolution."}
|
French_TST_Senior/segmented/fr-2011-2012-ofm-2011-2012-test-mars-corrige.jsonl
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "problem_label": "1", "tier": 1, "problem": "Soient $n$ et $k$ deux entiers strictement positifs. On considère une assemblée de $k$ personnes telle que, pour tout groupe de $n$ personnes, il y en ait une $(n+1)$-ième qui les connaisse toutes (si $A$ connaît $B$ alors $B$ connaît $A$ ).\n\n1) Si $k=2 n+1$, prouver qu'il existe une personne qui connaît toutes les autres.\n2) Si $k=2 n+2$, donner un exemple d'une telle assemblée dans laquelle personne ne connaît tous les autres.", "solution": "1) On commence par construire, par récurrence, un groupe de $n+1$ personnes qui se connaissent deux à deux : il est clair que l'on peut trouver deux personnes qui se connaissent. Supposons que pour $p \\in\\{2, \\ldots, n\\}$ fixé, on ait réussi à trouver un groupe de $p$ personnes qui se connaîssent deux à deux. En complétant ce groupe par $n-p$ personnes quelconques, on forme un groupe de $n$ personnes dont on sait qu'il en existe une $(n+1)^{i e ̀ m e}$ qui les connaît toutes. En ajoutant cette personne à notre groupe de $p$ personnes, on forme ainsi un groupe de $p+1$ personnes qui se connaissent deux à deux.\nOn considère donc un groupe $G$ de $n+1$ personnes qui se connaissent deux à deux. Puisque $k=2 n+1$, il reste donc $n$ personnes qui forment un groupe $G^{\\prime}$ disjoint du précédent. Pour ce groupe $G^{\\prime}$, on sait qu'il existe une personne appartenant nécessairement à $G$ qui en connaît tous les membres. Cette personne connaît alors tout le monde.\n2) On divise les personnes en $n+1$ paires disjointes, et on suppose que chaque personne connaît toutes les autres sauf celle qui est dans la même paire qu'elle. Ainsi, personne ne connaît tout le monde.\nSoit $G$ un groupe de $n$ personnes de cette assemblée. Puisqu'il y a $n+1$ paires, c'est donc qu'il existe une paire, disons $\\{A, B\\}$, dont aucun des deux membres n'est dans $G$. Par suite, $A$ connaît tous les membres de $G$, et les conditions de l'énoncé sont satisfaites.", "problem_match": "## Exercice 1\n", "solution_match": "## Solution."}
|
| 2 |
+
{"year": "2011", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle acutangle avec $A B \\neq A C$. On note $\\Gamma$ son cercle circonscrit, $H$ son orthocentre et $O$ le centre de $\\Gamma$. Soit $M$ le milieu de $[B C]$. La droite $(A M)$ recoupe $\\Gamma$ en $N$ et le cercle de diamètre $[A M]$ recoupe $\\Gamma$ en $P$.\n\nProuver que les droites $(A P),(B C),(O H)$ sont concourantes si, et seulement si, $A H=H N$.", "solution": "\n\nMontrons d'abord que $P, H, M$ sont alignés. À cet effet, introduisons $V$, le point diamétralement opposé à $A$ sur $\\Gamma$. Alors $(V C) \\perp(A C)$ et donc $(B H) / /(V C)$. De même on voit que $(C H) / /(V B)$. Il s'ensuit que $B H C V$ est un parallélogramme de centre $M$. Les points $H, M, V$ sont donc alignés. Si on note $U$ la deuxième intersection de $(H V)$ avec $\\Gamma$, par cocyclicité on obtient $\\widehat{A U V}=\\widehat{A B V}=90^{\\circ}$. Comme $\\widehat{A P V}=\\widehat{A P M}=90^{\\circ}$, on conclut que $U=P$ et donc que $P, H, M$ sont alignés.\n\nSoit J l'intersection de $(A P)$ et de (BC). Comme $(A H)$ et $(M P)$ sont des hauteurs du triangle $A J M, H$ est aussi l'orthocentre de $A J M$. Ainsi, $(O H)$ passe par $J$ si, et seulement si, $(O H) \\perp(A N)$. Or $O A=O N$, ce qui implique que $(O H) \\perp(A N)$ si, et seulement si $(O H)$ est la médiatrice de de $[A N]$, c'est-à-dire si, et seulement si, $H A=H N$.", "problem_match": "## Exercice 2\n", "solution_match": "## Solution."}
|
| 3 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Soit $p$ un nombre premier. Trouver tous les entiers $a, b, c \\geq 1$ tels que:\n\n$$\na^{p}+b^{p}=p^{c}\n$$", "solution": "La réponse est:\n\n(i) $p=2$ et $(a, b, c)=\\left(2^{u}, 2^{u}, 2 u+1\\right)$ pour un entier $u \\geq 0$\n(ii) $p=3$ et $(a, b, c)=\\left(2 \\cdot 3^{u}, 3^{u}, 2+3 u\\right)$ ou $(a, b, c)=\\left(3^{u}, 2 \\cdot 3^{u}, 2+3 u\\right)$ pour un entier $u \\geq 0$.\n\nPour un entier $n \\geq 1$ et un nombre premier $p$ on note $v_{p}(n)$ le plus grand entier $k \\geq 0$ tel que $p^{k}$ divise $n$. On montre d'abord trois lemmes.\n\n## Lemme 1\n\nSoit $p$ un nombre premier. Alors, pour $1 \\leq j \\leq p-1,\\binom{p}{j}$ est divisible par $p$.", "problem_match": "## Exercice 3\n", "solution_match": "## Solution."}
|
| 4 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Soit $p$ un nombre premier. Trouver tous les entiers $a, b, c \\geq 1$ tels que:\n\n$$\na^{p}+b^{p}=p^{c}\n$$", "solution": "On a $j!(p-j)!\\binom{p}{j}=p$ !. Comme $1 \\leq j<p$ et $1 \\leq p-j<p, j$ et $p-j$ sont premiert avec $p$ de sorte que $p$ divise $\\binom{p}{j}$.\n\n## Lemme 2\n\nSoit $p$ un nombre premier impair et soient $a, j$ des entiers strictement positifs avec $2 \\leq j \\leq p$. On pose $u=v_{p}(a)$ et on considère un entier $k>u$. Alors:\n\n$$\nv_{p}\\left(\\binom{p}{j} p^{j k} a^{p-j}\\right) \\geq k+u(p-1)+2\n$$", "problem_match": "## Exercice 3\n", "solution_match": "\nDémonstration:"}
|
| 5 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Soit $p$ un nombre premier. Trouver tous les entiers $a, b, c \\geq 1$ tels que:\n\n$$\na^{p}+b^{p}=p^{c}\n$$", "solution": "D'après le lemme 1, pour $2 \\leq j \\leq p-1$, on a $v_{p}\\left(\\left({ }_{j}^{p}\\right) p^{j k} a^{p-j}\\right) \\geq 1+j k+$ $u(p-j)$. Il suffit donc de prouver que $1+j k+u(p-j) \\geq k+u(p-1)+2$, ce qui est équivalent au fait que $(j-1)(k-u) \\geq 1$, ce qui est clairement vérifié. Pour $j=p$, on a $v_{p}\\left(\\binom{p}{j} p^{j k} a^{p-j}\\right)=p k$, qui est supérieur ou égal à $k+u(p-1)+2$ car l'inégalité $p k \\geq$ $k+u(p-1)+2$ est équivalente à $(p-1)(k-u) \\geq 2$, qui est clairement vraie.\n\n## Lemme 3\n\nOn a $(2 n)^{\\frac{1}{n-1}}<2$ pour tout entier $n \\geq 5$.", "problem_match": "## Exercice 3\n", "solution_match": "\nDémonstration:"}
|
| 6 |
+
{"year": "2011", "problem_label": "3", "tier": 1, "problem": "Soit $p$ un nombre premier. Trouver tous les entiers $a, b, c \\geq 1$ tels que:\n\n$$\na^{p}+b^{p}=p^{c}\n$$", "solution": "On raisonne par récurrence sur $n$. Pour $n=5$, on a clairement $10<2^{4}$. On suppose que $2 n<2^{n-1}$. Alors $2(n+1)=2 n+2 \\leq 2^{n-1}+1<2^{n}$ car $2^{n}-2^{n-1}=2^{n-1}>1$. Ceci clôt la preuve.\n\nRésolvons maintenant l'exercice. On considère en un premier temps le cas $p=2$. Si $c<2$, la seule solution est $a=b=c=1$. Si $c \\geq 2$ et $a^{2}+b^{2}=2^{c}$, en raisonnant modulo 4, on voit que $a$ et $b$ doivent être pairs. Soit $u=\\min \\left(v_{2}(a), v_{2}(b)\\right)$. Alors $\\left(a / 2^{u}\\right)^{2}+\\left(b / 2^{u}\\right)^{2}=$ $2^{c-2 u}$. Si $c-2 u \\geq 2$, alors $a / 2^{u}$ et $b / 2^{u}$ sont des entiers pairs, ce qui contredit la définition de $u$. Donc $c-2 u=1$ et $a=b=2^{u}$. Pour conclure, on vérifie aisément que pour tout entier $u \\geq 0$ :\n\n$$\n\\left(2^{u}\\right)^{2}+\\left(2^{u}\\right)^{2}=2^{2 u+1} .\n$$\n\nOn suppose maintenant que $p>2$. Soient $a, b, c \\geq 1$ des entiers tels que $a^{p}+b^{p}=p^{c}$. Sans perte de généralité, supposons $a \\geq b$. Comme $a+b$ divise $a^{p}+b^{p}$, il existe un entier $k \\geq 1$ tel que :\n\n$$\na+b=p^{k}\n$$\n\nSoit $u=v_{p}(a)$. En particulier, (5) implique que $a<p^{k}$ de sorte que $u<k$. Alors, en utilisant le fait que $p$ est impair\n\n$$\na^{p}+b^{p}=a^{p}+\\left(p^{k}-a\\right)^{p}=\\sum_{j=2}^{p}(-1)^{j+1} u_{j}+u_{1}, \\quad \\text { où } \\quad u_{j}=\\binom{p}{j} p^{j k} a^{p-j}\n$$\n\nD'après le Lemme 2 , on a $v_{p}\\left(u_{j}\\right) \\geq k+u(p-1)+2$ pour $2 \\leq j \\leq p$. De plus, comme $v_{p}\\left(u_{1}\\right)=i+k+u(p-1)$, il en découle que $v_{p}\\left(a^{n}+b^{n}\\right)=1+k+u(p-1)$. Comme $a^{p}+b^{p}$ est une puissance de $p$, on conclut que:\n\n$$\na^{p}+b^{p}=p^{1+k+u(p-1)}=p(a+b) p^{u(p-1)},\n$$\n\noù l'on a utilisé le fait que $a+b=p^{k}$ pour la dernière égalité. Puisque $a \\geq b$, ceci impose $a^{p} \\leq 2 p a p^{u(p-1)}$. Ainsi :\n\n$$\na \\leq(2 p)^{\\frac{1}{p-1}} p^{u}\n$$\n\nMais par définition $u=v_{p}(a)$, de sorte que $a \\geq p^{u}$. De plus, $a>p^{u}$ implique $a \\geq 2 p^{u}$ D'après le Lemme 3 , comme $(2 p)^{\\frac{1}{p-1}}<2$ pour $p \\geq 5$, on en déduit que $p \\geq 5$ implique $a=p^{u}$, et que $p=3$ implique $a=3^{u}$ ou $a=2 \\cdot 3^{u}$ (le cas $p=2$ est exclu car $p$ est impair).\n\nOn étudie d'abord le cas $a=p^{u}$. On a alors:\n\n$$\nb^{p}=p^{u p}\\left(p^{c-u p}-1\\right),\n$$\n\nde sorte que $v_{p}(b)=p^{u}$. Comme $a \\geq b$ et $a=p^{u}$, ceci implique $a=b$, et donc 2 divise $p$, ce qui est exclu car $p$ est impair.\n\nOn a donc prouvé que ( $p$ est impair) :\n\n$$\na^{p}+b^{p}=p^{c} \\text { et } a \\geq b \\quad \\Longrightarrow \\quad p=3, \\quad a=2 \\cdot 3^{u} .\n$$\n\nDans la suite on suppose donc que $p=3$ et $a=2 \\cdot 3^{u}$. Alors $b^{3}=3^{3 u}\\left(3^{c-3 u}-8\\right)$. Donc $3^{u}$ divise $b$. Par suite $3^{u} \\leq b \\leq a=2 \\cdot 3^{u}$. Si $b=a$, alors 2 divise $p^{c}$, ce qui contredit le fait\nque $p$ est impair. Donc $b=3^{u}$, ce qui implique $\\left(3^{u}\\right)^{3}+\\left(2 \\cdot 3^{u}\\right)^{3}=3^{3 u+2}=3^{c}$. Finalement, $c=3 u+2$ et on vérifie aisément que pour tout entier $u \\geq 0$ :\n\n$$\n\\left(2 \\cdot 3^{u}\\right)^{3}+\\left(3^{u}\\right)^{3}=3^{2+3 u} .\n$$\n\nAinsi $p=3, a=2 \\cdot 3^{u}, b=3^{u}, c=2+3 u$ pour un certain entier $u \\geq 0$.\n\nRemarque. Il est possible d'utiliser le lemme dit LTE (voir poly sur le site d'Animath) pour aborder l'exercice : si $p$ est un nombre premier impair tel que $p$ ne divise pas $a$ et ne divise pas $b$, alors:\n\n$$\nv_{p}\\left(a^{p}+b^{p}\\right)=1+v_{p}(a+b) .\n$$", "problem_match": "## Exercice 3\n", "solution_match": "\nDémonstration:"}
|
| 7 |
+
{"year": "2011", "problem_label": "4", "tier": 1, "problem": "Soit $k>1$ un entier. Une fonction $f: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ est dite $k$-tastrophique lorsque pour tout entier $n>0$, on a $f_{k}(n)=n^{k}$ où $f_{k}$ est la $k$-ième itérée de f :\n\n$$\nf_{k}(n)=\\underbrace{f \\circ f \\circ \\cdots \\circ f}_{k \\text { fois }}(n)\n$$\n\nPour quels $k$ existe-t-il une fonction $k$-tastrophique?", "solution": "On va prouver que, pour tout entier $k \\geq 1$, il existe une fonction $k$-tastrophique.\n Clairement, la fonction $f: n \\longmapsto n$ est 1-tastrophique. On suppose donc que $k \\geq 2$.\n\nOn procède maintenant de la façon suivante. On pose $f(1)=1$, et si $n$ est le plus petit entier pour lequel $f(n)$ n'est pas encore défini, alors:\n\n- si $n=a^{k}$ pour un certain entier $a \\geq 2$, on pose :\n\n$$\nf(n)=f(a)^{k}\n$$\n\n- si $n$ n'est pas la puissance $k^{i e ̀ m e}$ d'un entier, on note $n_{1}=n, n_{2}, \\ldots, n_{k}$ les $k$ plus petits entiers (dans l'ordre) qui ne sont pas des puissances $k^{i e ̀ m e s}$ d'entiers et pour lesquels $f$ n'est pas définie, et on pose:\n\n$$\nf\\left(n_{1}\\right)=n_{2}, f\\left(n_{2}\\right)=n_{3}, \\ldots, f\\left(n_{k-1}\\right)=n_{k}, \\text { et } f\\left(n_{k}\\right)=n_{1}^{k}=n^{k}\n$$\n\nIl est clair que l'on définit ainsi une fonction $f: \\mathbb{N} \\longrightarrow \\mathbb{N}$. Il reste à vérifier qu'elle est $k$-tastrophique. Soit $a \\geq 2$ un entier. On commence par noter que, d'après (1), on a :\n\n$$\nf_{2}\\left(a^{k}\\right)=f\\left(f\\left(a^{k}\\right)\\right)=f\\left(f(a)^{k}\\right)=[f(f(a))]^{k}=\\left[f_{2}(a)\\right]^{k}\n$$\n\net, par une récurrence immédiate, on a\n\n$$\nf_{p}\\left(a^{k}\\right)=\\left[f_{p}(a)\\right]^{k} \\text { pour tout entier } p \\geq 1\n$$\n\nOn prouve alors que $f$ est $k$-tastrophique par récurrence (forte) : On a évidemment $f_{k}(1)=1=1^{k}$. Supposons que $n \\geq 2$ soit un entier et que $f_{k}(m)=m^{k}$ pour tout entier naturel $m \\leq n-1$.\n\n- Si $n=a^{k}$ pour un certain entier $a \\geq 2$. Alors $a \\leq n-1$ et on a\n\n$$\n\\begin{aligned}\nf_{k}(n) & =f_{k}\\left(a^{k}\\right)=\\left[f_{k}(a)\\right]^{k} \\quad \\text { d'après }(4) \\\\\n& =\\left(a^{k}\\right)^{k} \\quad \\text { d'après l'hypothèse de récurrence } \\\\\n& =n^{k}\n\\end{aligned}\n$$\n\n- Si $n$ n'est pas la puissance $k^{i e ̀ m e} d^{\\prime}$ un entier, on sait qu'il existe des entiers $n_{1}, n_{2}, \\ldots, n_{k}$ pour lesquels on a (3) et avec $n=n_{i}$ pour un certain $i \\in\\{1, \\ldots, k\\}$. Alors, d'après (3) et (4),\nil vient\n\n$$\n\\begin{aligned}\nf_{k}(n) & =f_{k}\\left(n_{i}\\right)=f_{k+i-1}\\left(n_{1}\\right)=f_{i-1}\\left(f_{k}\\left(n_{1}\\right)\\right) \\\\\n& =f_{i-1}\\left(f\\left(n_{k}\\right)\\right)=f_{i-1}\\left(n_{1}^{k}\\right)=\\left[f_{i-1}\\left(n_{1}\\right)\\right]^{k}=n_{i}^{k}=n^{k}\n\\end{aligned}\n$$\n\nAinsi, dans tous les cas, on a $f_{k}(n)=n^{k}$. Ce qui achève la récurrence, et la démonstration.", "problem_match": "## Exercice 4\n", "solution_match": "## Solution."}
|
| 8 |
+
{"year": "2011", "problem_label": "5", "tier": 1, "problem": "Déterminer tous les polynômes $X^{n}+a_{1} X^{n-1}+\\cdots+a_{n-1} X+a_{n}$, non constants et à coefficients entiers, dont les racines sont exactement les nombres $a_{1}, \\ldots, a_{n-1}, a_{n}$ (avec multiplicité).", "solution": "\\text{Soit } P(X) = X^n + a_1 X^{n-1} + \\cdots + a_{n-1} X + a_n \\; \\text{un polynôme à coefficients entiers.}\n\nAlors $P(X)$ est une solution du problème ssi\n\n$$\nP(X)=\\prod_{i=1}^{n}\\left(X-a_{i}\\right)\n$$\n\nSupposons tout d'abord que $a_{n}=0$. Soit alors $i$ minimal tel que $a_{n-i} \\neq 0$. On a donc $P(X)=X^{i}\\left(X^{n-i}+a_{1} X^{n-i-1}+\\cdots+a_{n-i-1}\\right)$ et ainsi (5) est vérifiée si et seulement si $Q(X)=X^{n-i}+a_{1} X^{n-i-1}+\\cdots+a_{n-i-1}$ est constant ou est lui-même une solution du problème. Le premier cas correspond à $P(X)=X^{n}$, qui convient bien.\n\nOn supposera donc dans ce qui suit que $P(X)$ est une solution avec $a_{n} \\neq 0$. Dans ces conditions, on en déduit tout de suite que l'on ne peut avoir $X+a_{1}=X-a_{1}$ et donc qu'il n'y a pas de polynôme de degré 1 qui soit solution. On suppose donc que $n \\geq 2$. De $P(0)=a_{n}=(-1)^{n} \\prod_{i=1}^{n} a_{i}$, on déduit alors que\n\n$$\n(-1)^{n} \\prod_{i=1}^{n-1} a_{i}=1\n$$\n\nEt, puisque les $a_{i}$ sont des entiers, on a $a_{i}=1$ ou $a_{i}=-1$ pour tout $i \\leq n-1$. On note $k$ le nombre d'entre eux qui valent -1 (et donc $0 \\leq k \\leq n-1$ ). On peut noter que (6) montre alors que $k$ et $n$ ont la même parité. Les relations entre coefficients et racines conduisent à\n\n$$\n-a_{1}=\\sum_{i=1}^{n} a_{i}=a_{n}+(n-1-k)-k\n$$\n\nd'où\n\n$$\na_{n}=2 k-n \\quad \\text { ou } \\quad a_{n}=2 k-n+2\n$$\n\nPour $n=2$, puisque $a_{2} \\neq 0$ et que $k$ doit être pair et ne pas dépasser 1 , la seule possibilité est $k=0, a_{1}=1, a_{2}=-2$, et donc $P(X)=X^{2}+X-2=(X-1)(X+2)$, qui est bien solution.\n\nOn suppose maintenant que $n \\geq 3$. Alors\n\n$$\na_{2}=\\sum_{1 \\leq i<j \\leq n} a_{i} a_{j}=a_{n} \\sum_{i=1}^{n-1} a_{i}+\\frac{k(k-1)}{2}+\\frac{(n-1-k)(n-2-k)}{2}-k(n-1-k)\n$$\n\net donc\n\n$$\n2 a_{2}=2 a_{n}(n-1-2 k)+n^{2}+4 k^{2}-4 k n-3 n+4 k+2\n$$\n\nCompte-tenu de (7), deux cas se présentent:\n\n- Si $a_{n}=2 k-n$ : De (8), on tire $(n-2 k)^{2}+n=2-2 a_{2}$, avec $a_{2}=1$ ou $a_{2}=-1$. Donc $a_{2}=-1$ et, puisque $n-2 k=-a_{n} \\neq 0$, la seule possibilité est $n=3$ et $(n-2 k)^{2}=1$. De $k \\leq n-1$ et de même parité que $n$, on déduit que $k=1$, puis que $a_{1}=1$ et $a_{3}=-1$, d'où $P(X)=X^{3}+X^{2}-X-X=(X+1)^{2}(X-1)$, qui est bien solution.\n- Si $a_{n}=2 k-n+2$ : Comme ci-dessus, on obtient cette fois\n\n$$\n(n-2 k-2)^{2}+n=2-2 a_{2}\n$$\n\net donc $a_{2}=-1, n=3, k=1, a_{1}=1, a_{3}=1$, d'où $P(X)=X^{3}+X^{2}-X+1 \\neq$ $(X-1)^{2}(X+1)$, qui n'est pas solution.\nEn définitive, les solutions du problème sont les polynômes $P(X)=X^{n}$ pour $n \\geq 1$, $P(X)=X^{n}\\left(X^{2}+X-2\\right)$ ou $P(X)=X^{n}\\left(X^{3}+X^{2}-X-X\\right)$ pour $n \\geq 0$.", "problem_match": "## Exercice 5\n", "solution_match": "## Solution."}
|
| 9 |
+
{"year": "2011", "problem_label": "6", "tier": 1, "problem": "Soit $A B C D$ un quadrilatère convexe tel que les droites $(A D)$ et $(B C)$ ne sont pas parallèles. On suppose que les cercles de diamètre $[A B]$ et $[C D]$ se coupent en deux points $E$ et $F$ situés à l'intérieur de $A B C D$. Soit $\\Gamma_{E}$ le cercle qui passe par les projetés orthogonaux de $E$ sur $(A B),(B C)$ et $(C D)$, et $\\Gamma_{F}$ le cercle qui passe par les projetés orthogonaux de $F$ sur $(C D),(D A)$ et $(A B)$.\n\nProuver que le milieu de $[E F]$ appartient à la droite passant par les deux points d'intersection de $\\Gamma_{E}$ et $\\Gamma_{F}$.", "solution": "\n\nSoient $P, Q, R, S$ les projections de $E$ sur les droites $(D A),(A B),(B C),(C D)$. Les points $P$ et $Q$ appartiennent au cercle de diamètre $[A E]$ de sorte que $\\widehat{Q P E}=\\widehat{Q A E}$. De même, $\\widehat{Q R E}=\\widehat{Q B E}$. Ainsi :\n\n$$\n\\widehat{Q P E}+\\widehat{Q R E}=\\widehat{Q A E}+\\widehat{Q B E}=90^{\\circ}\n$$\n\nDe même, on montre que $\\widehat{Q P S}+\\widehat{Q R S}=90^{\\circ}+90^{\\circ}=180^{\\circ}$. Ainsi, les points $P, Q, R, S$ appartiennent à $\\Gamma_{E}$. De même, les projetés orthogonaux de $F$ sur les côtés de $A B C D$ sont sur $\\Gamma_{F}$.\n\nSoit $K$ le point d'intersection de $(A D)$ et $(B C)$. Sans perte de généralité, on suppose que $A \\in[D K]$. On voit facilement que $\\widehat{C K D}<90^{\\circ}$ (sinon le cercle de diamètre $[C D]$ couvre entièrement $A B C D$ ). Les droites $(E P)$ et $(B C)$ s'intersectent donc en un point $P^{\\prime}$ et les droites $(E R)$ et $(A D)$ en un point $R^{\\prime}$. Montrons que $P^{\\prime}$ et $R^{\\prime}$ sont sur $\\Gamma_{E}$. Par cocyclicité des points $R, E, Q, B$ :\n\n$$\n\\widehat{Q R K}=\\widehat{Q E B}=90^{\\circ}-\\widehat{Q B E}=\\widehat{Q A E}=\\widehat{Q P E} .\n$$\n\nDonc $\\widehat{Q R K}=\\widehat{Q P P^{\\prime}}$, ce qui implique que $P^{\\prime} \\in \\Gamma_{E}$. De même, $R^{\\prime} \\in \\Gamma_{E}$.\nDe même, soient $M$ et $N$ les projections respectives de $F$ sur $(A D)$ et (BC), et soient $M^{\\prime}$ le point d'intersection de $(F M)$ et $(B C)$ et $N^{\\prime}$ le point d'intersection de $(F N)$ et $(A D)$. En utilisant les mêmes arguments que précédemment on voit que $M^{\\prime}$ et $N^{\\prime}$ sont sur $\\Gamma_{F}$.\n\nSoient finalement $U$ l'intersection de $\\left(N N^{\\prime}\\right)$ avec $\\left(P P^{\\prime}\\right)$ et $V$ l'intersection de ( $\\left.M M^{\\prime}\\right)$ avec $\\left(R R^{\\prime}\\right)$. Comme les angles en $N$ et $P$ sont droits, $N, N^{\\prime}, P, P^{\\prime}$ sont cocycliques. La puissance de $U$ par rapport au cercle passant par ces points vaut donc:\n\n$$\nU N \\cdot U N^{\\prime}=U P \\cdot U P^{\\prime}\n$$\n\nAinsi, $U$ appartient à l'axe radical de $\\Gamma_{E}$ et $\\Gamma_{F}$. De même $V$ appartient à cet axe radical. Or $E U F V$ est un parallelogramme, ce qui implique que $(U V)$ coupe $[E F]$ en son milieu.", "problem_match": "## Exercice 6\n", "solution_match": "\nSolution."}
|
French_TST_Senior/segmented/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Si $k$ est un entier strictement positif, on désigne par $S(k)$ la somme des chiffres de son écriture décimale.\n\n1) Existe-t-il deux entiers $a$ et $b$ strictement positifs tels que $S(a)=S(b)=S(a+b)=2013$ ?\n2) Existe-t-il deux entiers $a$ et $b$ strictement positifs tels que $S(a)=S(b)=S(a+b)=2016$ ?", "solution": "1) Rappelons que pour tout $a$, les entiers a et $S(a)$ sont congrus modulo 9. En effet, si $\\overline{a_{k} \\cdots a_{1} a_{0}}$ est l'écriture décimale de $a$, alors comme $10 \\equiv 1[9]$, on a pour tout $j \\geqslant 0: 10^{j} \\equiv 1^{j}=1[9]$, donc $a=\\sum_{j=0}^{k} a_{j} 10^{j} \\equiv \\sum_{j=0}^{k} a_{j}=S(a)$ [9].\n\nSupposons par l'absurde qu'il existe a et b comme dans l'énoncé. Modulo 9 , on a\n\n$$\n\\begin{aligned}\na & \\equiv S(a) \\equiv 2013 \\equiv 6 \\\\\nb & \\equiv S(b) \\equiv 2013 \\equiv 6 \\\\\na+b & \\equiv S(a+b) \\equiv 2013 \\equiv 6\n\\end{aligned}\n$$\n\nOn ajoute les deux premières congruences et on retranche la troisième, ce qui donne $0 \\equiv 6+6-6=$ 6 [9]. Impossible.\n2) On remarque que $2016=9 \\times 224$, donc on peut prendre $\\mathrm{a}=\\mathrm{b}=9090 \\cdots 09$ où le chiffre 9 apparaît 224 fois, et $a+b=1818 \\cdots 18$ où le motif 18 apparaît 224 fois.\n", "problem_match": "\nExercice 1.", "solution_match": "## Solution."}
|
| 2 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Les réels $a, b, c$ sont distincts et non nuls, et on suppose qu'il existe deux réels $x$ et $y$ tels que $a^{3}+a x+y=0, b^{3}+b x+y=0$ et $c^{3}+c x+y=0$.\n\nProuver que $a+b+c=0$.", "solution": "On a\n\n$$\n\\left\\{\\begin{array}{l}\na^{3}+a x+y=0 \\\\\nb^{3}+b x+y=0 \\\\\nc^{3}+c x+y=0\n\\end{array}\\right.\n$$\n\nOn retranche la première et la troisième équation : $\\left(a^{3}-c^{3}\\right)+(a-c) x=0$. Or, $a^{3}-c^{3}=(a-c)\\left(a^{2}+\\right.$ $\\left.a c+c^{2}\\right)$, donc $(a-c)\\left(a^{2}+a c+c^{2}+x\\right)=0$. Comme $a-c \\neq 0$ il vient\n\n$$\n\\mathrm{a}^{2}+\\mathrm{ac}+\\mathrm{c}^{2}+\\mathrm{x}=0\n$$\n\nDe même, on montre que $b^{2}+b c+c^{2}+x=0$. En retranchant les deux dernières équations, on obtient $0=a^{2}-b^{2}+a c-b c=(a-b)(a+b+c)$. Comme $a-b \\neq 0$, on en déduit que $a+b+c=0$.\n", "problem_match": "\nExercice 2.", "solution_match": "## Solution."}
|
| 3 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Sur le cercle $\\Gamma$, on choisit les points $A, B, C$ de sorte que $A C=B C$. Soit $P$ un point de l'arc $A B$ de $\\Gamma$ qui ne contient pas $C$. La droite passant par $C$ et perpendiculaire à la droite ( PB ) rencontre (PB) en D.\n\nProuver que $\\mathrm{PA}+\\mathrm{PB}=2 \\mathrm{PD}$.", "solution": "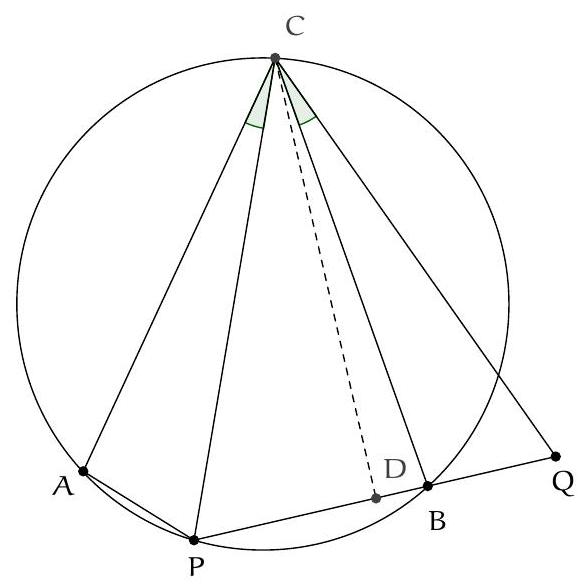\n\nProlongeons la demi-droite $[\\mathrm{PB})$ et introduisons le point Q tel que $B Q=P A$.\nOn a donc $A P=B Q$ et $A C=B C$ ainsi que $\\widehat{\\mathrm{QBC}}=\\pi-\\widehat{\\mathrm{CBP}}=\\widehat{\\mathrm{PAC}}$. Cela assure que les triangles $C B Q$ et $C A P$ sont égaux, et donc que $C P=C Q$. Par suite, le triangle $C P Q$ est isocèle et le point $D$, pied de la hauteur issue de $C$, est alors le milieu de $[\\mathrm{PQ}]$.\n\nOn a donc $P A+P B=B Q+P B=P Q=2 P D$.\n", "problem_match": "\nExercice 3.", "solution_match": "## Solution."}
|
| 4 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Sur un terrain, $2013 \\times 2013$ chaises sont placées sur les sommets d'un quadrillage. Chaque chaise est occupée par une personne. Certaines personnes décident alors de changer de place : certaines se décalent d'un cran vers la droite, d'autres de 2 crans vers l'avant, d'autres de 3 crans vers la gauche, et d'autres de 6 crans vers l'arrière. A la fin, chaque chaise est toujours occupée par une seule personne.\n\nProuver qu'au moins une personne n'a pas changé de place.", "solution": "Soit a (resp. b, c, d) le nombre de personnes qui se décalent vers la droite (resp. la gauche, l'avant, l'arrière). On peut supposer qu'il existe un repère tel que les personnes ont toutes des coordonnées entières $\\left(x_{i}, y_{i}\\right)$. Comme $\\sum_{i} x_{i}$ ne change pas, mais que le déplacement d'un cran vers la droite (resp. 3 crans vers la gauche) a pour effet de faire augmenter (resp. diminuer) $\\sum_{i} x_{i}$ de la quantité $a$ (resp. 3c), on en déduit que $a=3 c$, et donc $a$ et $c$ ont la même parité. De même, $2 \\mathrm{~b}=6 \\mathrm{~d}$ donc b et $d$ ont la même parité. Finalement, $a+b+c+d=(a+b)+(c+d)$ est pair, donc ne peut pas être égal à 2013, ce qui implique qu'au moins une personne ne s'est pas déplacée.\n\n\n## Sujet Olympique", "problem_match": "\nExercice 4.", "solution_match": "## Solution."}
|
| 5 |
+
{"year": "2012", "problem_label": "5", "tier": 1, "problem": "Soit $0 \\leqslant x_{1} \\leqslant x_{2} \\leqslant \\cdots \\leqslant x_{n} \\leqslant 1$ et $0 \\leqslant y_{1} \\leqslant y_{2} \\leqslant \\cdots \\leqslant y_{n} \\leqslant 1$ des réels. On pose $x_{n+1}=1$.\n\nProuver que\n\n$$\n\\sum_{i=1}^{n}\\left(x_{i}-y_{i}\\right)+n \\sum_{i=1}^{n}\\left(x_{i+1}-x_{i}\\right) y_{i} \\geqslant 0\n$$", "solution": "On va raisonner par récurrence sur $\\mathrm{n} \\geqslant 1$.\n\n- Pour $n=1$, on considère deux réels $x_{1}, y_{1} \\in[0,1]$ et on pose $x_{2}=1$. Il s'agit de prouver que $\\left(x_{1}-y_{1}\\right)+\\left(x_{2}-x_{1}\\right) y_{1} \\geqslant 0$.\n\nOr, on a $\\left(x_{1}-y_{1}\\right)+\\left(x_{2}-x_{1}\\right) y_{1}=\\left(x_{1}-y_{1}\\right)+\\left(1-x_{1}\\right) y_{1}=x_{1}\\left(1-y_{1}\\right) \\geqslant 0$, ce qui conclut.\n\n- Supposons que pour un certain $n \\geqslant 1$ et pour tous réels $0 \\leqslant a_{1} \\leqslant a_{2} \\leqslant \\cdots \\leqslant a_{n} \\leqslant 1$ et $0 \\leqslant b_{1} \\leqslant b_{2} \\leqslant \\cdots \\leqslant b_{n} \\leqslant 1$ et avec $a_{n+1}=1$, on ait\n\n$$\n\\sum_{i=1}^{n}\\left(a_{i}-b_{i}\\right)+n \\sum_{i=1}^{n}\\left(a_{i+1}-a_{i}\\right) b_{i} \\geqslant 0\n$$\n\nOn considère alors des réels $0 \\leqslant x_{1} \\leqslant x_{2} \\leqslant \\cdots \\leqslant x_{n+1} \\leqslant 1$ et $0 \\leqslant y_{1} \\leqslant y_{2} \\leqslant \\cdots \\leqslant y_{n+1} \\leqslant 1$ et on pose $x_{n+2}=1$.\n\nEn isolant les contributions de $x_{1}$ et $y_{1}$, on a\n\n$$\n\\begin{aligned}\n& \\sum_{i=1}^{n+1}\\left(x_{i}-y_{i}\\right)+(n+1) \\sum_{i=1}^{n+1}\\left(x_{i+1}-x_{i}\\right) y_{i} \\\\\n&= \\sum_{i=2}^{n+1}\\left(x_{i}-y_{i}\\right)+n \\sum_{i=2}^{n+1}\\left(x_{i+1}-x_{i}\\right) y_{i}+x_{1}-y_{1}+\\sum_{i=2}^{n+1}\\left(x_{i+1}-x_{i}\\right) y_{i} \\\\\n& \\quad+(n+1)\\left(x_{2}-x_{1}\\right) y_{1}\n\\end{aligned}\n$$\n\nappliquée aux réels $a_{i}=x_{i+1}$ et $b_{i}=y_{i+1}$\n\n$$\n\\geqslant x_{1}-y_{1}+\\sum_{i=2}^{n+1}\\left(x_{i+1}-x_{i}\\right) y_{1}+(n+1)\\left(x_{2}-x_{1}\\right) y_{1} \\text { puisque } y_{1} \\leqslant y_{i} \\text { et } x_{i+1} \\geqslant x_{i} \\text { pour }\n$$\n\ntout $i$\n\n$$\n\\begin{aligned}\n& =x_{1}+y_{1}\\left[-1+(n+1)\\left(x_{2}-x_{1}\\right)+\\sum_{i=2}^{n+1}\\left(x_{i+1}-x_{i}\\right)\\right] \\\\\n& =x_{1}+y_{1}\\left[n x_{2}-(n+1) x_{1}\\right] \\\\\n& =x_{1}\\left(1-y_{1}\\right)+n y_{1}\\left(x_{2}-x_{1}\\right) \\\\\n& \\geqslant 0\n\\end{aligned}\n$$\n\nce qui prouve le résultat cherché pour la valeur $n+1$ et achève la démonstration.\n", "problem_match": "\nExercice 5.", "solution_match": "## Solution."}
|
| 6 |
+
{"year": "2012", "problem_label": "6", "tier": 1, "problem": "Trouver le plus grand entier $\\mathrm{n} \\geqslant 3$, vérifiant:\n\"pour tout entier $k \\in\\{2,3, \\cdots, \\mathfrak{n}\\}$ si $k$ et $\\boldsymbol{n}$ sont premiers entre eux alors $k$ est un nombre premier.\"", "solution": "On remarque d'abord que $\\mathrm{n}=30$ vérifie la propriété. En effet, si $\\mathrm{k}>1$ est premier avec n , alors il est premier avec $2,3,5$. Si de plus k n'est pas premier, alors il admet une factorisation non triviale $\\mathrm{k}=\\mathrm{lm}$ avec $\\ell, \\mathrm{m}>1$. Comme $\\ell$, m sont premiers avec n , ils sont premiers avec $2,3,5$, donc $\\ell$, $\\mathrm{m} \\geqslant 7$, ce qui entraîne que $k \\geqslant 7 \\times 7=49>n$.\n\nRéciproquement, montrons que si $n$ vérifie la propriété alors $n \\leqslant 30$. Supposons par l'absurde que $n>30$. Soit $p$ le plus petit entier premier ne divisant pas $n$. Comme $p^{2} n$ 'est pas premier mais est premier avec $n$, on a $p^{2}>n>30>5^{2}$ donc $p \\geqslant 7$. En particulier, 2,3 et 5 divisent $n$ donc 30 divise $n$. Comme $\\mathrm{n}>30$, on en déduit que $\\mathrm{p}^{2}>\\mathrm{n} \\geqslant 60>7^{2}$ donc $\\mathrm{p}>7$, par conséquent $\\mathrm{p} \\geqslant 11$.\n\nNotons $p_{1}<p_{2}<p_{3}<\\cdots$ la liste des nombres premiers ( $p_{1}=2$, $p_{2}=3$, etc.). Ce qui précède montre que $p=p_{k+1}$ où $k \\geqslant 4$. De plus, $p_{1}, \\ldots, p_{k}$ divisent $n$ donc $p_{k+1}^{2}>n \\geqslant p_{1} \\cdots p_{k}$, ce qui contredit l'inégalité de Bonse.\n\nRemarque: si on ne connaît pas l'inégalité de Bonse, on la retrouve facilement à partir du postulat de Bertrand qui dit que $\\boldsymbol{p}_{j+1}<2 p_{j}$ pour tout $\\boldsymbol{j}$. En effet,\n\n$$\n\\mathrm{p}_{\\mathrm{k}+1}^{2}<4 \\mathrm{p}_{\\mathrm{k}}^{2}<8 \\mathrm{p}_{\\mathrm{k}-1} \\mathrm{p}_{\\mathrm{k}}<2 \\times 3 \\times 5 \\times \\mathrm{p}_{\\mathrm{k}-1} \\mathrm{p}_{\\mathrm{k}} \\leqslant \\mathrm{p}_{1} \\mathrm{p}_{2} \\cdots \\mathrm{p}_{\\mathrm{k}}\n$$\n\nsi $k \\geqslant 5$. De plus, si $k=4$ on vérifie directement que $p_{k+1}^{2}=121<210=2 \\times 3 \\times 5 \\times 7=p_{1} \\cdots p_{k}$.\nRemarque : il existe une démonstration élémentaire de l'inégalité de Bonse n'utilisant pas le postulat de Bertrand. On vérifie d'abord à la main que si $4 \\leqslant n \\leqslant 7$ alors $p_{1} p_{2} \\cdots p_{n}>p_{n+1}^{2}$.\n\nSupposons par l'absurde qu'il existe $n \\geqslant 8$ tel que $p_{1} p_{2} \\cdots p_{n} \\leqslant p_{n+1}^{2}$. Soit $m=\\left[\\frac{n}{2}\\right]$. On a\n\n$$\n\\left(p_{1} p_{2} \\cdots p_{m}\\right)^{2}<p_{1} p_{2} \\cdots p_{n} \\leqslant p_{n+1}^{2}\n$$\n\ndonc $\\mathrm{p}_{1} \\mathrm{p}_{2} \\cdots \\mathrm{p}_{\\mathrm{m}}<\\mathrm{p}_{\\mathrm{n}+1}$.\nConsidérons les entiers $N_{j}=j p_{1} p_{2} \\cdots p_{m-1}-1\\left(1 \\leqslant j \\leqslant p_{m}\\right)$. Pour tout $j$, on a $N_{j}<p_{1} p_{2} \\cdots p_{m}<$ $p_{n+1}$ et $N_{j}$ est premier avec $p_{1}, p_{2}, \\ldots, p_{m-1}$. Donc si $q_{j}$ est le plus petit entier premier divisant $N_{j}$, on a $p_{m} \\leqslant q_{j} \\leqslant p_{n}$.\n\nLes $q_{j}$ sont distincts car si $j<\\ell$ et $q_{j}=q_{\\ell}$, alors $q_{j}$ divise $N_{\\ell}-N_{j}=(\\ell-j) p_{1} p_{2} \\cdots p_{m}$, donc $q_{j}$ divise $\\ell-\\mathfrak{j}$, ce qui est impossible puisque $1 \\leqslant \\ell-\\mathfrak{j}<p_{m} \\leqslant q_{j}$.\n\nPar conséquent, il y a au moins $p_{m}$ nombres premiers distincts compris entre $p_{m}$ et $p_{n}$ : autrement dit, $p_{m} \\leqslant n-m+1$. Or, $n \\leqslant 2 m+1$ donc $p_{m} \\leqslant m+2$.\n\nComme $p_{m} \\geqslant 2 m-1$ pour tout $m \\geqslant 1$, cela entraîne $2 m-1 \\leqslant m+2$, donc $m \\leqslant 3$, et donc $n \\leqslant 7$.\n", "problem_match": "\nExercice 6.", "solution_match": "## Solution."}
|
| 7 |
+
{"year": "2012", "problem_label": "7", "tier": 1, "problem": "A, B, C, D, E sont cinq points d'un même cercle, de sorte que $A B C D E$ soit convexe et que l'on ait $A B=B C$ et $C D=D E$. On suppose que les droites $(A D)$ et $(B E)$ se coupent en $P$, et que la droite (BD) rencontre la droite (CA) en $Q$ et la droite (CE) en $T$.\n\nProuver que le triangle PQT est isocèle.", "solution": "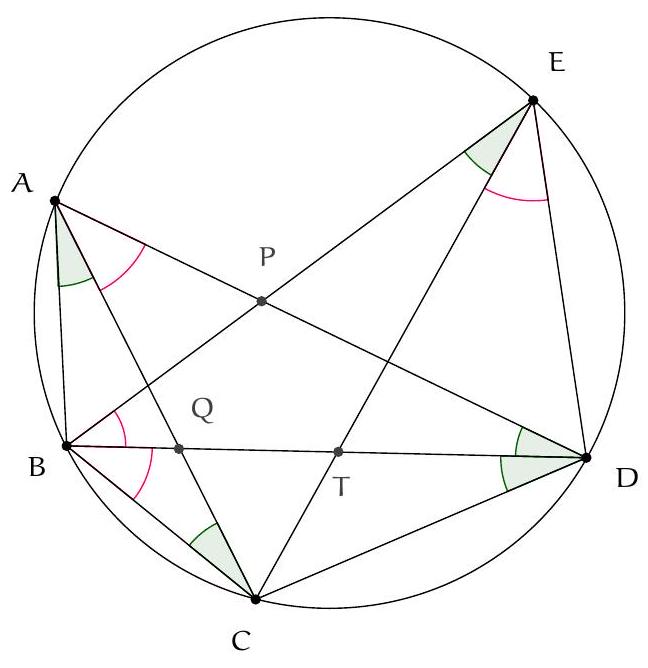\n\nNotons $\\alpha$ et $\\beta$ les angles $(\\overrightarrow{A B}, \\overrightarrow{A C})$ et $(\\overrightarrow{A C}, \\overrightarrow{A D})$ respectivement. D'après le théorème de l'angle inscrit et les hypothèses de l'énoncé, on a\n\n$$\n\\begin{aligned}\n& \\alpha=(\\overrightarrow{\\mathrm{DB}}, \\overrightarrow{\\mathrm{DC}})=(\\overrightarrow{\\mathrm{EB}}, \\overrightarrow{\\mathrm{EC}})=(\\overrightarrow{\\mathrm{CA}}, \\overrightarrow{\\mathrm{CB}})=(\\overrightarrow{\\mathrm{DA}}, \\overrightarrow{\\mathrm{DB}}) \\\\\n& \\beta=(\\overrightarrow{\\mathrm{BC}}, \\overrightarrow{\\mathrm{BD}})=(\\overrightarrow{\\mathrm{EC}}, \\overrightarrow{\\mathrm{ED}})=(\\overrightarrow{\\mathrm{BD}}, \\overrightarrow{\\mathrm{BE}})=(\\overrightarrow{\\mathrm{CD}}, \\overrightarrow{\\mathrm{CE}})\n\\end{aligned}\n$$\n\nOn en déduit que\n\n$$\n\\begin{aligned}\n(\\overrightarrow{\\mathrm{BD}}, \\overrightarrow{\\mathrm{BP}}) & =\\beta=(\\overrightarrow{\\mathrm{BC}}, \\overrightarrow{\\mathrm{BQ}}) \\\\\n(\\overrightarrow{\\mathrm{DP}}, \\overrightarrow{\\mathrm{DB}}) & =\\alpha=(\\overrightarrow{\\mathrm{CA}}, \\overrightarrow{\\mathrm{CB}})\n\\end{aligned}\n$$\n\ndonc BPD et $B Q C$ sont semblables. Il s'ensuit $\\frac{B Q}{B P}=\\frac{B C}{B D}$.\nOr, $(\\overrightarrow{B Q}, \\overrightarrow{B P})=\\beta=(\\overrightarrow{B C}, \\overrightarrow{B D})$, donc $B Q P$ et $B C D$ sont semblables, ce qui entrainne que $\\frac{B P}{P Q}=\\frac{B D}{C D}$.\nEn échangeant les rôles de $(A, B)$ et de $(E, D)$, on obtient que $\\frac{D P}{P T}=\\frac{B D}{B C}$. En divisant les deux égalités précédentes, on en déduit que\n\n$$\n\\frac{B P}{D P} \\times \\frac{P T}{P Q}=\\frac{B C}{C D}\n$$\n\nOr, $B D P$ et $B D C$ sont (indirectement) semblables, puisque $(\\overrightarrow{B D}, \\overrightarrow{B P})=\\beta=(\\overrightarrow{B C}, \\overrightarrow{B D})$ et $(\\overrightarrow{D P}, \\overrightarrow{D B})=$ $\\alpha=(\\overrightarrow{D B}, \\overrightarrow{D C})$, donc $\\frac{B P}{D P}=\\frac{B C}{C D}$, et finalement $P T=P Q$.\n$\\underline{\\text { Solution analytique. }}$\n\nOn peut supposer que les affixes $a, b, c, d, e$ des points $A, B, C, D, E$ sont des nombres complexes de module 1. Le fait que $A B C$ est isocèle en $B$ se traduit par l'égalité $b^{2}=a c$ puisque $\\frac{b}{a}=e^{i \\theta}=\\frac{c}{b}$ où $\\theta$ est l'angle $(\\overrightarrow{O A}, \\overrightarrow{O B})=(\\overrightarrow{O B}, \\overrightarrow{O C})$. De même, on a $d^{2}=c e$.\n\nPour calculer l'affixe $p$ du point $P$, on exprime que $B, P, E$ sont alignés, ce qui se traduit par le fait que $\\frac{p-b}{p-e}$ est réel, ou encore\n\n$$\n\\frac{p-b}{p-e}=\\frac{\\bar{p}-\\bar{b}}{\\bar{p}-\\bar{e}}\n$$\n\nOn chasse les dénominateurs et on simplifie :\n\n$$\n(\\bar{b}-\\bar{e}) p-(b-e) \\bar{p}+b \\bar{e}-\\bar{b} e=0\n$$\n\nComme $\\overline{\\mathrm{b}}-\\overline{\\mathrm{e}}=\\frac{1}{\\mathrm{~b}}-\\frac{1}{\\mathrm{e}}=-\\frac{\\mathrm{b}-\\mathrm{e}}{\\mathrm{be}}$ et $\\mathrm{b} \\overline{\\mathrm{e}}-\\overline{\\mathrm{b}} e=\\frac{\\mathrm{b}}{\\mathrm{e}}-\\frac{\\mathrm{e}}{\\mathrm{b}}=\\frac{\\mathrm{b}^{2}-\\mathrm{e}^{2}}{\\mathrm{be}}=\\frac{(\\mathrm{b}-\\mathrm{e})(\\mathrm{b}+\\mathrm{e})}{\\mathrm{be}}$, on en déduit\n\n$$\n-\\frac{(b-e)}{b e} p-(b-e) \\bar{p}+(b-e) \\frac{b+e}{b e}=0\n$$\n\nce qui se simplifie en\n\n$$\np+b e \\bar{p}=b+e\n$$\n\nDe même, le fait que $A, P, D$ sont alignés se traduit par $p+a d \\bar{p}=a+d$. En soustrayant les deux égalités précédentes et en divisant par be - ad, on obtient\n\n$$\n\\bar{p}=\\frac{b+e-a-d}{b e-a d} .\n$$\n\nDe même, $\\bar{q}=\\frac{b+d-a-c}{b d-a c}$. On soustrait les deux égalités précédentes :\n\n$$\n\\overline{\\mathrm{p}}-\\overline{\\mathrm{q}}=\\frac{(\\mathrm{bd}-\\mathrm{ac})(\\mathrm{b}+\\mathrm{e}-\\mathrm{a}-\\mathrm{d})-(\\mathrm{be}-\\mathrm{ad})(\\mathrm{b}+\\mathrm{d}-\\mathrm{a}-\\mathrm{c})}{(\\mathrm{be}-\\mathrm{ac})(\\mathrm{bd}-\\mathrm{ac})}\n$$\n\nOn développe le numérateur et on remplace tous les $b^{2}$ par $a c$ et tous les $\\mathrm{d}^{2}$ par ce , ce qui donne\n\n$$\n\\begin{aligned}\n\\bar{p}-\\bar{q} & =\\frac{a(-b c+a c+c d-a d+b e-c e)}{(b e-a d)(b d-a c)} \\\\\n& =\\frac{a(-b c+a c+c d-a d+b e-c e)}{b(b e-a d)(d-b)}\n\\end{aligned}\n$$\n\ncompte tenu de $\\mathrm{ac}=\\mathrm{b}^{2}$. En échangeant les rôles de $(\\boldsymbol{a}, \\mathrm{b})$ et $(e, d)$, on obtient\n\n$$\n\\bar{p}-\\bar{t}=\\frac{e(-c d+c e+b c-b e+a d-a c)}{d(a d-b e)(b-d)}\n$$\n\nOn voit que $\\bar{p}-\\overline{\\mathrm{t}}=-\\frac{\\mathrm{be}}{\\mathrm{ad}}(\\overline{\\mathrm{p}}-\\overline{\\mathrm{q}})$. En prenant le module des deux membres, on en conclut que $\\mathrm{PQ}=\\mathrm{PT}$.\n", "problem_match": "\nExercice 7.", "solution_match": "## Solution."}
|
| 8 |
+
{"year": "2012", "problem_label": "8", "tier": 1, "problem": "Soit $\\mathrm{n}>0$ un entier. Anne écrit au tableau n entiers strictement positifs distincts. Bernard efface alors certains de ces nombres (éventuellement aucun, mais pas tous). Devant chacun des nombres restants, il écrit un + ou un -, et effectue l'addition correspondante. Si le résultat est divisible par 2013, c'est Bernard qui gagne, sinon c'est Anne.\n\nDéterminer, selon la valeur de n , lequel des deux possède une stratégie gagnante.", "solution": "Montrons que si $n \\geqslant 11$ alors Bernard a une stratégie gagnante. En effet, si $x_{1}, \\ldots, x_{n}$ sont des nombres entiers, d'après le principe des tiroirs les restes modulo 2013 des entiers de la forme $a_{1} \\chi_{1}+$ $\\cdots+a_{n} x_{n}\\left(a_{i} \\in\\{0,1\\}\\right)$ ne peuvent pas être tous distincts puisque le nombre de telles écritures est $2^{n} \\geqslant 2^{11}=2048>2013$. Il existe donc $\\left(a_{1}, \\ldots, a_{n}\\right)$ et $\\left(b_{1}, \\ldots, b_{n}\\right) \\in\\{0,1\\}^{n}$ distincts tels que $a_{1} x_{1}+\\cdots+a_{n} x_{n} \\equiv b_{1} x_{1}+\\cdots+b_{n} x_{n}$ [2013]. Si on pose $c_{i}=a_{i}-b_{i}$, alors les $c_{i}$ valent 0,1 ou -1 , ne sont pas tous nuls, et $c_{1} x_{1}+\\cdots+c_{n} x_{n}$ est divisible par 2013.\n\nMontrons que si $n \\leqslant 10$ alors Anne possède une stratégie gagnante. En effet, elle choisit les nombres $1,2, \\ldots, 2^{n-1}$. Si Bernard gagnait, cela signifierait qu'il pourrait trouver $c_{1}, \\ldots, c_{k}, d_{1}, \\ldots, d_{\\ell}$ deux à deux distincts dans $\\{0,1, \\ldots, \\mathfrak{n}-1\\}$ tels que $(k, \\ell) \\neq(0,0)$ et $2^{\\mathrm{c}_{1}}+\\cdots+2^{\\mathrm{c}_{\\mathrm{k}}} \\equiv 2^{\\mathrm{d}_{1}}+\\cdots+2^{\\mathrm{d}_{\\ell}}[2013]$. Or, les deux nombres $2^{\\mathrm{c}_{1}}+\\cdots+2^{\\mathrm{c}_{\\mathrm{k}}}$ et $2^{\\mathrm{d}_{1}}+\\cdots+2^{\\mathrm{d}_{\\ell}}$ sont compris entre 0 et $1+2+\\cdots+2^{\\text {n-1 }}=$ $2^{n}-1 \\leqslant 2^{10}-1=1023$, donc s'ils sont congrus modulo 2013 c'est qu'ils sont égaux :\n\n$$\n2^{c_{1}}+\\cdots+2^{c_{k}}=2^{d_{1}}+\\cdots+2^{d_{\\ell}}\n$$\n\nce qui contredit l'unicité de l'écriture en base 2 d'un entier.\n\n\nFin", "problem_match": "\nExercice 8.", "solution_match": "## Solution."}
|
French_TST_Senior/segmented/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Soit $A B C$ un triangle isocèle en $A$. On note $O$ le centre de son cercle circonscrit. Soit $D$ un point de $[B C]$. La droite parallèle à $(A B)$ passant par $D$ coupe $(A C)$ en $E$. La droite parallèle à $(A C)$ passant par $D$ coupe $(A B)$ en $F$. Montrer que $A, E, O, F$ sont cocycliques.", "solution": "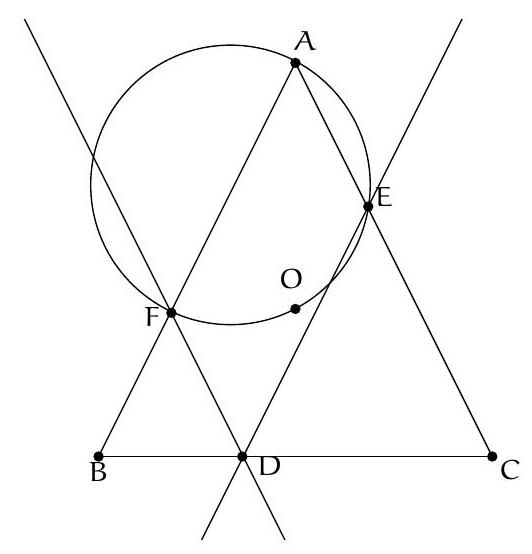\n\nSoit $R$ la rotation de centre $O$ et d'angle $(\\overrightarrow{O B}, \\overrightarrow{O A})$. On a $R(B)=A$ et $R(A)=C$.\nComme ( DF$) / /(\\mathrm{AC})$, on a $\\widehat{\\mathrm{FDB}}=\\widehat{\\mathrm{ACB}}=\\widehat{\\mathrm{CBA}}=\\widehat{\\mathrm{DBF}}$, donc FBD est isocèle en F. Par conséquent, $\\mathrm{BF}=\\mathrm{FD}$. Or, $A E D F$ est un parallélogramme, donc $\\mathrm{FD}=A E$, d'où $B F=A E$. On en déduit que $R(F)$ et $E$ sont deux points de $[A, C]$ qui sont à même distance de $A$, donc $R(F)=E$.\n\nOn en déduit l'égalité entre les angles de vecteurs $(\\overrightarrow{O F}, \\overrightarrow{O E})=(\\overrightarrow{O B}, \\overrightarrow{O A})$. Par conséquent, $2(\\overrightarrow{O F}, \\overrightarrow{O E})=$ $(\\overrightarrow{O B}, \\overrightarrow{O A})+(\\overrightarrow{O A}, \\overrightarrow{O C})=(\\overrightarrow{O B}, \\overrightarrow{O C})=2(\\overrightarrow{A B}, \\overrightarrow{A C})=2(\\overrightarrow{A F}, \\overrightarrow{A E})$, donc les angles de droites $(A F, A E)$ et $(\\mathrm{OF}, \\mathrm{OE})$ sont égaux, ce qui conclut.\n", "problem_match": "\nExercice 1.", "solution_match": "## Solution."}
|
| 2 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Soit $\\left(a_{n}\\right)_{n \\in \\mathbb{N}}$ une suite croissante et non constante d'entiers strictement positifs tels que $a_{n}$ divise $n^{2}$ pour tout $n \\geqslant 1$. Prouver que l'une des affirmations suivantes est vraie:\na) Il existe un entier $n_{1}>0$ tel que $a_{n}=n$ pour tout $n \\geqslant n_{1}$.\nb) Il existe un entier $n_{2}>0$ tel que $a_{n}=n^{2}$ pour tout $n \\geqslant n_{2}$.", "solution": "Tout d'abord, puisque pour tout entier $n$, on a $a_{n} \\in \\mathbb{N}^{*}$, et que la suite ( $a_{n}$ ) est croissante et non constante, il existe un entier $n_{0}$ tel que $a_{n} \\geqslant 2$ pour tout $n \\geqslant n_{0}$. Par conséquent, pour tout nombre premier $p>n_{0}$, on a $a_{p}=p$ ou $a_{p}=p^{2}$.\n\n- Supposons que, pour tout entier $n \\geqslant 1$, on ait $a_{n} \\leqslant n$. Soit $p>n_{0}$ un nombre premier. Prouvons par récurrence que $a_{n}=n$ pour tout $n \\geqslant p$. En effet, d'après ci-dessus, on a $a_{p}=p$. De plus, si $a_{n}=n$ pour un certain $n \\geqslant p \\geqslant 2$, alors $n=a_{n} \\leqslant a_{n+1} \\leqslant n+1$, d'où $a_{n+1}=n$ ou $a_{n+1}=n+1$. Mais, $a_{n+1}$ divise $(n+1)^{2}$, tandis que $n$ ne divise pas $(n+1)^{2}$. Ainsi, on a $a_{n+1}=n+1$, ce qui achève la récurrence.\n\nIl suffit alors de choisir $\\mathrm{n}_{1}=\\mathrm{p}$ pour conclure dans ce cas.\n\n- Supposons qu'il existe un entier $m \\geqslant 1$ tel que $a_{m}>m$. S'agissant d'entiers, c'est donc que $a_{m} \\geqslant m+1$. Mais, $m+1 \\geqslant 2$ et $m+1$ est premier avec $m^{2}$, donc $m+1$ ne peut diviser $m^{2}$, et on a alors $a_{m} \\geqslant m+2$. On en déduit que $a_{m+1} \\geqslant a_{m}>m+1$. Une récurrence immédiate assure donc que $a_{n}>n$ pour tout $n \\geqslant m$.\n\nEn particulier, compte-tenu de notre remarque initiale, si $p \\geqslant m$ est un nombre premier, on a $a_{p}=p^{2}$. Soit donc $p>m$ un nombre premier impair. Nous allons prouver par récurrence que $a_{n}=n^{2}$ pour tout $n \\geqslant p$. Nous venons de voir que c'est vrai pour $n=p$. Supposons que $a_{n}=n^{2}$ pour un certain entier $n \\geqslant p$. Alors $n \\geqslant 3$, d'où $a_{n+1} \\geqslant a_{n}=n^{2}>\\frac{1}{2}(n+1)^{2}$. Or, $a_{n+1}$ divise $(n+1)^{2}$, donc $\\mathrm{a}_{\\mathrm{n}+1}=(\\mathrm{n}+1)^{2}$. Cela achève la récurrence.\n\nIl suffit donc de choisir $\\mathrm{n}_{2}=\\mathrm{p}$ pour conclure dans ce cas.\n", "problem_match": "\nExercice 2.", "solution_match": "## Solution."}
|
| 3 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Prouver que pour tous réels strictement positifs $a, b, c$ tels que $a b c=1$, on a\n\n$$\n\\frac{1}{1+a^{2}+(b+1)^{2}}+\\frac{1}{1+b^{2}+(c+1)^{2}}+\\frac{1}{1+c^{2}+(a+1)^{2}} \\leqslant \\frac{1}{2}\n$$", "solution": "Soit $a, b, c$ des réels strictement positifs.\nCompte tenu de l'inégalité bien connue $x^{2}+y^{2} \\geqslant 2 x y$ valable pour tous réels $x, y$, on a\n\n$$\n\\frac{1}{1+a^{2}+(b+1)^{2}}=\\frac{1}{2+a^{2}+b^{2}+2 b} \\leqslant \\frac{1}{2(1+a b+b)}\n$$\n\nDe même, et puisque $a b c=1$, on a\n\n$$\n\\frac{1}{1+b^{2}+(c+1)^{2}} \\leqslant \\frac{1}{2(1+b c+c)}=\\frac{a b}{2\\left(a b+a b^{2} c+a b c\\right)}=\\frac{a b}{2(1+a b+b)}\n$$\n\net\n\n$$\n\\frac{1}{1+c^{2}+(a+1)^{2}} \\leqslant \\frac{1}{2(1+a c+a)}=\\frac{b}{2(b+a b c+a b)}=\\frac{b}{2(1+a b+b)}\n$$\n\nen sommant membre à membre, il vient\n\n$$\n\\begin{aligned}\n& \\frac{1}{1+\\mathrm{a}^{2}+(\\mathrm{b}+1)^{2}}+\\frac{1}{1+\\mathrm{b}^{2}+(\\mathrm{c}+1)^{2}}+\\frac{1}{1+\\mathrm{c}^{2}+(\\mathrm{a}+1)^{2}} \\\\\n& \\leqslant \\frac{1}{2}\\left(\\frac{1}{1+\\mathrm{ab}+\\mathrm{b}}+\\frac{\\mathrm{ab}}{1+\\mathrm{ab}+\\mathrm{b}}+\\frac{\\mathrm{b}}{1+\\mathrm{ab}+\\mathrm{b}}\\right)=\\frac{1}{2}\n\\end{aligned}\n$$\n\n", "problem_match": "\nExercice 3.", "solution_match": "## Solution."}
|
| 4 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Dans le plan, on considère l'ensemble $S$ des points de coordonnées $(x, y)$, où $x, y \\in$ $\\{1,2, \\ldots, 2013\\}$. Deux points de $S$ sont dits voisins s'ils sont à une distance 1 l'un de l'autre. A chaque seconde, une mouche et des araignées se déplacent sur les points de $S$ de la façon suivante : tout d'abord, la mouche soit ne bouge pas, soit va sur un point voisin de celui sur lequel elle se trouve. Puis, chaque araignée soit ne bouge pas, soit va sur un point voisin de celui sur lequel elle se trouve. Plusieurs araignées peuvent se trouver simultanément sur un même point, et la mouche ainsi que les araignées connaissent les positions respectives des unes et des autres.\na) Déterminer le plus petit entier $k$ pour lequel $k$ araignées pourront toujours finir par attraper la mouche en un temps fini, et ce quelles que soient les positions initiales de la mouche et des araignées sur les points de $S$.\nb) Répondre à la même question si l'on suppose cette fois que l'on est dans l'espace usuel et que $S$ est l'ensemble des points de coordonnéees $(x, y, z)$ où $x, y, z \\in\\{1,2, \\ldots, 2013\\}$.", "solution": "Une seule araignée ne peut attraper la mouche : en effet, la mouche peut attendre jusqu'à ce que l'araignée soit sur un point voisin de celui sur lequel elle se trouve. A partir de ce moment, elle se déplace à chaque fois sur un point diagonalement opposé à celui sur lequel est l'araignée si celle-ci est sur un point voisin, et sinon attend où elle est.\n\nOn va prouver maintenant que, dans le plan comme dans l'espace, deux araignées suffisent pour attraper la mouche.\n\nPour cela, on note $M$ la mouche, et on désigne par $P$ et $Q$ les deux araignées. Pour chaque animal $A$, on note respectivement $A_{x}, A_{y}$ et $A_{z}$ son abscisse, son ordonnée et sa cote.\na) Les araignées $P$ et $Q$ se placent tout d'abord sur le point de coordonnées $(1,1)$. Puisque $M$ ne peut s'enfuir indéfiniment vers la droite, $P$ peut alors en un temps fini, et en ne se déplaçant qu'horizontalement, se trouver en un point tel que $P_{x}=M_{x}$ et $P_{y}=1$. De même, $Q$ se place en un point tel que $Q_{x}=1$ et $Q_{y}=M_{y}$ (il est clair que si $P$, par exemple, atteint ce premier objectif avant $Q$, elle peut suivre les déplacements de $M$ en conservant $P_{x}=M_{x}$ et $P_{y}=1$ et attendre le positionnement adéquat de Q).\n\nA partir de ces positions, atteintes au temps $t_{0}$ :\n\n- si $M$ se déplace horizontalement (c'est-à-dire de sorte que $M_{x}$ change) alors $P$ fait de même afin de conserver $\\mathrm{P}_{\\mathrm{x}}=\\mathrm{M}_{\\mathrm{x}}$.\n- sinon, $P$ se déplace verticalement, en allant vers $M$.\n\nL'araignée $Q$ procède de la même façon, mais en échangeant les rôles des abscisses et ordonnées.\nEn utilisant cette stratégie et à partir de $t_{0}$, la quantité $\\left|P_{y}-M_{y}\\right|+\\left|Q_{x}-M_{x}\\right|$ n'augmente jamais. Mais, cette quantité ne reste constante que lors d'un déplacement de $M$ vers la droite ou vers le haut, ce qui ne peut arriver qu'un nombre fini de fois. Par suite, après un temps fini, au moins l'un des deux termes de la somme va être égal à 0 , signifiant ainsi la perte de la mouche.\nb) Les deux araignées se placent tout d'abord sur le point $(1,1,1)$. Puis, en restant dans le plan $\\pi$ d'équation $z=1$ et par utilisation de la stratégie du a), l'une d'elles va attraper l'ombre de $M$ dans $\\pi$ (i.e. la projection orthogonale de $M$ sur $\\pi$ ). Sans perte de généralité, on peut supposer qu'il s'agit de $P$, et on a donc $P_{x}=M_{x}$ et $P_{y}=M_{y}$. Une fois ceci réalisé, $P$ calque ses déplacements sur ceux de $M$ de façon à conserver ces deux égalités. Toutefois, si $M$ se déplace parallèlement à l'axe des cotes ou reste immobile, alors $P$ se déplace parallèlement à l'axe des cotes, mais en allant vers $M$ (et on note qu'on a toujours $P_{z} \\leqslant M_{z}$ ). Puisque $M_{z}$ ne peut augmenter indéfiniment, $M$ ne peut échapper à $P$ qu'en ne faisant qu'un nombre fini de déplacements parallèlement à l'axe des cotes et en ne restant immobile\nqu'un nombre fini de fois. Par conséquent, à partir d'un instant $t_{1}$, la mouche $M$ ne se déplacera plus que dans un même plan $\\pi^{\\prime}$ d'équation $z=$ constante, et sans rester immobile.\n\nL'araignée Q vient alors se placer dans le plan $\\pi^{\\prime}$. Quitte à rester immobile, elle peut rendre la quantité $f=\\left|Q_{x}-M_{x}\\right|+\\left|Q_{y}-M_{y}\\right|$ paire. A partir de cet instant, noté $t_{2}, Q$ suit la procédure suivante :\n\n- Si $\\left|Q_{x}-M_{x}\\right|>\\left|Q_{y}-M_{y}\\right|$ alors $Q$ se déplace parallèlement à l'axe des abscisses, de sorte que $\\left|Q_{x}-M_{x}\\right|$ n'augmente pas ( $Q$ se déplace horizontalement, le long d'une droite $d$, en allant vers la projection de $M$ sur la droite $d$ ).\n- Sinon, $Q$ se déplace parallèlement à l'axe des ordonnées, dans des conditions analogues.\n\nPour se fixer les idées, on peut supposer que pour tout $t \\in \\mathbb{N}$, la mouche se déplace à l'instant $t+\\frac{1}{3}$ et l'araignée à l'instant $t+\\frac{2}{3}$. Puisque ni $M$ ni $Q$ ne reste immobile, le mouvement de $M$ fait augmenter ou diminuer $f$ d'une unité et le mouvement de $Q$ fait diminuer $f$ d'une unité, donc pour tout $t \\in \\mathbb{N}, f(t)$ est pair (en particulier, $Q$ ne se placera jamais sur un point voisin de $M$ ) et de plus $f(t+1) \\leqslant f(t)$.\n\nSoit $g=\\max \\left(\\left|Q_{x}-M_{x}\\right|,\\left|Q_{y}-M_{y}\\right|\\right)$. On observe que le mouvement de $Q$ ne peut que faire décroître g. De plus,\n\n- Si le mouvement de $M$ à l'instant $t+\\frac{1}{3}$ fait décroître $g$, alors $g(t+1) \\leqslant g(t)$.\n- Supposons que le mouvement de $M$ à l'instant $t+\\frac{1}{3}$ fait croître $g$. Si par exemple $M$ s'est déplacée dans la direction des $x$, nécessairement $\\left|Q_{x}(t)-M_{x}(t)\\right| \\geqslant\\left|Q_{y}(t)-M_{y}(t)\\right|$ et $M$ s'est éloignée de $Q$, donc après le mouvement de $M$ on a $\\left|Q_{x}-M_{x}\\right|>\\left|Q_{y}-M_{y}\\right|$. Par conséquent l'araignée se déplace dans le même sens que la mouche et on a $g(t+1)=g(t)$.\nDans tous les cas, on voit que $g(t+1) \\leqslant g(t)$ pour tout $t \\in \\mathbb{N}$, donc il existe $t_{2} \\in \\mathbb{N}$ tel que $g(t)=g\\left(t_{2}\\right)$ et $f(t)=f\\left(t_{2}\\right)$ pour tout $t \\geqslant t_{2}$. Supposons par l'absurde que $g\\left(t_{2}\\right)>0$.\n\nQuitte changer l'orientation des axes, on peut supposer que $Q_{x}\\left(t_{2}\\right) \\leqslant M_{x}\\left(t_{2}\\right)$ et $Q_{y}\\left(t_{2}\\right) \\leqslant M_{y}\\left(t_{2}\\right)$. - Premier cas: $Q_{y}\\left(t_{2}\\right)=M_{y}\\left(t_{2}\\right)$. Comme $f\\left(t_{2}\\right)$ est pair, on a $M_{x}\\left(t_{2}\\right) \\geqslant Q_{x}\\left(t_{2}\\right)+2$. Si entre les instants $t_{2}$ et $t_{2}+1$ la mouche se déplace dans la direction des $y$, alors l'araignée se déplace vers la droite, et $g\\left(t_{2}+1\\right)=g\\left(t_{2}\\right)-1$. Impossible. Si la mouche se déplace vers la gauche, alors son déplacement fait diminuer f d'une unité, donc $\\mathrm{f}\\left(\\mathrm{t}_{2}+1\\right)=\\mathrm{f}\\left(\\mathrm{t}_{2}\\right)-2$. Impossible. On en déduit que la mouche se déplace vers la droite, et du coup l'araignée également. Par une récurrence immédiate, on obtient que $M_{x}\\left(t_{2}+k\\right)=M_{x}\\left(t_{2}\\right)+k$ pour tout $k \\in \\mathbb{N}$, ce qui est impossible.\n\n- Deuxième cas: $Q_{x}\\left(t_{2}\\right)=M_{x}\\left(t_{2}\\right)$. Analogue.\n- Troisième cas: $\\mathrm{Q}_{\\mathrm{x}}\\left(\\mathrm{t}_{2}\\right)<\\mathrm{M}_{\\mathrm{x}}\\left(\\mathrm{t}_{2}\\right)$ et $\\mathrm{Q}_{\\mathrm{y}}\\left(\\mathrm{t}_{2}\\right)<\\mathrm{M}_{\\mathrm{y}}\\left(\\mathrm{t}_{2}\\right)$. Comme le déplacement de Q fait diminuer strictement la quantité f , le déplacement de $M$ doit faire augmenter f d'une unité. Par conséquent, entre les instants $t_{2}$ et $t_{2}+1$, la mouche doit se déplacer vers la droite ou vers le haut. On en déduit facilement que $Q_{x}\\left(t_{2}+1\\right)<M_{x}\\left(t_{2}+1\\right)$ et $Q_{y}\\left(t_{2}+1\\right)<M_{y}\\left(t_{2}+1\\right)$. Par une récurrence immédiate, la suite $\\left(M_{x}\\left(t_{2}+k\\right)+M_{y}\\left(t_{2}+k\\right)\\right)_{k \\in \\mathbb{N}}$ est strictement croissante, ce qui est impossible puisqu'elle est bornée et à valeurs entières.\nDans tous les cas on a abouti à une contradiction, ce qui prouve que $\\mathrm{g}\\left(\\mathrm{t}_{2}\\right)=0$ et que l'araignée a rattrapé la mouche à l'instant $t_{2}$.", "problem_match": "\nExercice 4.", "solution_match": "## Solution."}
|
| 5 |
+
{"year": "2012", "problem_label": "5", "tier": 1, "problem": "$\\mathbb{N}^{*}$ désigne l'ensemble des entiers supérieurs ou égaux à un. Trouver toutes les applications $\\mathrm{f}: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ vérifiant :\ni) quel que soit $n$ appartenant à $\\mathbb{N}^{*}, f(n+f(n))=f(n)$\nii) $f(2013)=1$.", "solution": "Soit f une solution éventuelle.\nSoit $a \\in \\mathbb{N}^{*}$ tel que $f(a)=1$.\nAlors $f(a+1)=f(a+f(a))=f(a)=1$.\nPuisque $f(2013)=1$, on en déduit par r��currence que $f(n)=1$ pour tout entier $\\mathfrak{n} \\geqslant 2013$.\nD'autre part, supposons que $a \\geqslant 2$ soit un entier tel que $f(n)=1$ pour tout $n \\geqslant a$.\nAlors, $a-1 \\geqslant 1$ et $f(a-1) \\geqslant 1$, d'où $a-1+f(a-1) \\geqslant a$ et donc d'après le premier paragraphe $f(a-1)=f(a-1+f(a-1))=1$.\n\nCela assure que $f(n)=1$ pour tout $n \\geqslant a-1$.\nPuisque l'on a vu que $f(n)=1$ pour tout $n \\geqslant 2013$, on en déduit par récurrence descendante que $f(n)=1$ pour tout $n \\geqslant 1$.\n\nRéciproquement, il est clair que la fonction constante $\\mathrm{f}: \\mathrm{n} \\longmapsto 1$ est une solution du problème.\nFinalement, la seule solution est la fonction constante $\\mathrm{f}: \\mathfrak{n} \\longmapsto 1$.\n", "problem_match": "\nExercice 5.", "solution_match": "## Solution."}
|
| 6 |
+
{"year": "2012", "problem_label": "6", "tier": 1, "problem": "1) Soient $a$ et $b$ deux nombres réels tels que $a^{n}+b^{n}$ est un entier pour $n=1,2,3,4$. Montrer que $a^{n}+b^{n}$ est un entier pour tout $n \\in \\mathbb{N}^{*}$.\n2) Est-il vrai que si $a$ et $b$ sont deux nombres réels tels que $a^{n}+b^{n}$ est un entier pour $\\boldsymbol{n}=1,2,3$ alors $a^{n}+b^{n}$ est un entier pour tout $n \\in \\mathbb{N}^{*}$ ?", "solution": "1) Notons $s=a+b$ et $p=a b$. Soit $S_{n}=a^{n}+b^{n}$. Par hypothèse, $S_{n}$ est un entier pour $1 \\leqslant n \\leqslant 4$. Comme pour tout $\\mathrm{n} \\geqslant 1$ on a\n\n$$\nS_{n+1}=a^{n+1}+b^{n+1}=(a+b)\\left(a^{n}+b^{n}\\right)-a b\\left(a^{n-1}+b^{n-1}\\right)=S_{1} S_{n}-p S_{n-1},\n$$\n\nsi on montre que $p$ est un entier alors par récurrence immédiate il s'ensuivra que $S_{n}$ est un entier pour tout $n$.\n\nOn a\n\n$$\nS_{2}=(a+b)^{2}-2 a b=s^{2}-2 p\n$$\n\ndonc $2 p=S_{1}^{2}-S_{2}$ est un entier. On a\n\n$$\nS_{4}=\\left(a^{2}+b^{2}\\right)^{2}-2(a b)^{2}=S_{2}^{2}-2 p^{2}\n$$\n\ndonc $2 p^{2}=S_{2}^{2}-S_{4}$ est un entier. On en déduit que $(2 p)^{2}=2\\left(2 p^{2}\\right)$ est un entier pair. Comme $2 p$ est entier, il est pair donc $p$ est bien entier.\n2) On a\n\n$$\nS_{3}=(a+b)\\left(a^{2}+b^{2}\\right)-a b^{2}-a^{2} b=S_{1} S_{2}-p s\n$$\n\ndonc si $p$ est un demi-entier (c'est-à-dire que $p-\\frac{1}{2}$ est un entier) et si $s$ est un entier pair, alors $S_{1}, S_{2}, S_{3}$ sont des entiers alors que $S_{4}$ est un demi-entier. Par exemple, si $a=1+\\frac{1}{\\sqrt{2}}$ et $b=1-\\frac{1}{\\sqrt{2}}$ alors $s=2$, $p=\\frac{1}{2}, S_{1}=2, S_{2}=3, S_{3}=5, S_{4}=17 / 2$.\n", "problem_match": "\nExercice 6.", "solution_match": "\nSolution."}
|
| 7 |
+
{"year": "2012", "problem_label": "7", "tier": 1, "problem": "Partant d'un triplet d'entiers relatifs $(x, y, z)$, une opération consiste à ajouter à l'un de ces trois entiers un multiple de l'un des deux autres (ce multiple peut être positif ou négatif). Prouver que si $a, b, c$ sont des entiers premiers entre eux dans leur ensemble, on peut passer du triplet ( $a, b, c$ ) au triplet $(1,0,0)$ en au plus cinq opérations.", "solution": "Si $b$ et $c$ sont nuls alors, puisque $\\operatorname{pgcd}(a, b, c)=1$, on doit avoir $a=1$ ou $a=-1$. Dans le premier cas, il n'y a rien à faire. Dans le second, par trois opérations successives, on peut passer de $(-1,0,0)$ à $(-1,1,0)$, puis à $(1,1,0)$ et enfin à $(1,0,0)$.\n\nOn peut donc supposer que b ou c est non nul.\nL'objectif est d'atteindre un triplet de la forme $(1, \\mathrm{~s}, \\mathrm{t})$ en au plus trois étapes, puisqu'avec deux étapes supplémentaires, il est alors immédiat d'obtenir $(1,0,0)$.\n\nOn suppose que $\\mathrm{c} \\neq 0$, le cas $\\mathrm{b} \\neq 0$ se traitant de façon analogue.\nAfin d'atteindre l'objectif ci-dessus, il suffit de trouver un entier n tel que c et $\\mathrm{b}+\\mathrm{na}$ soient premiers entre eux : en effet, supposons pour le moment qu'un tel entier n ait été déterminé et voyons comment la conclusion va en découler.\n\nOn pose $b^{\\prime}=b+n a$ et, avec une première opération, on peut passer de $(a, b, c) a ̀\\left(a, b^{\\prime}, c\\right)$. Ensuite, d'après le théorème de Bézout, on sait qu'il existe deux entiers $u$ et $v$ tels que $u b^{\\prime}+v c=1$. Après multiplication par $a-1$, il existe donc deux entiers $x$ et $y$ tels que $x b^{\\prime}+y c=a-1$. On utilise alors une seconde opération pour passer de $\\left(a, b^{\\prime}, c\\right)$ à $\\left(a-x b^{\\prime}, b^{\\prime}, c\\right)$, puis une troisième pour passer de $\\left(a-x b^{\\prime}, b^{\\prime}, c\\right) a ̀\\left(a-x b^{\\prime}-y c, b^{\\prime} c\\right)=\\left(1, b^{\\prime}, c\\right)$.\n\nPour conclure, il ne reste donc plus qu'à prouver qu'un tel entier n existe.\nSoit E l'ensemble des diviseurs premiers de c qui divisent également au moins un nombre de la forme $b+k a$, où $k \\in \\mathbb{Z}$.\n$\\operatorname{Si} E=\\emptyset$ alors tout entier n est tel que $\\operatorname{pgcd}(\\mathrm{c}, \\mathrm{b}+\\mathrm{na})=1$.\nSinon, on note tout d'abord que E est fini car il ne contient que des diviseurs premiers de c , avec $c \\neq 0$. Ensuite, pour chaque $p \\in E$, il existe un entier $k_{p}$ tel que $b+k_{p} a=0 \\bmod [p]$. On remarque qu'un tel nombre $p$ ne divise pas a car sinon $p$ diviserait aussi $b$, en contradiction avec $\\operatorname{pgcd}(a, b, c)=1$.\n\nD'après le théorème chinois, il existe un entier $n$ tel que $n=k_{p}+1 \\bmod [p]$ pour tout $p \\in E$. Prouvons que cet entier n convient :\n\n- Si $p$ divise $c$ et $p \\notin E$ alors $p$ ne divise aucun nombre de la forme $b+k a$ et donc, en particulier, ne divise pas b + na.\n- Si $p \\in E$ alors $b+n a=b+k_{p} a+a=a \\neq 0 \\bmod [p]$.\n\nAinsi, aucun diviseur premier de c ne divise $\\mathrm{b}+\\mathrm{na}$, ce qui assure que c et $\\mathrm{b}+\\mathrm{na}$ sont bien premiers entre eux.\n", "problem_match": "\nExercice 7.", "solution_match": "## Solution."}
|
| 8 |
+
{"year": "2012", "problem_label": "8", "tier": 1, "problem": "Soit $A B C$ un triangle. Soient $D \\in[A C]$ et $E \\in[A B]$ tels que $B E=C D$. Soit $P$ le point d'intersection de (BD) et ( $C E$ ). Les cercles circonscrits à BEP et CDP se recoupent en Q. Soient $K$ et $L$ les milieux respectifs de [BE] et [CD]. Soit R l'intersection entre la perpendiculaire à (QK) passant par K et la perpendiculaire à ( QL ) passant par L . Montrer que\n\n1) $R$ se trouve sur le cercle circonscrit à $A B C$;\n2) $Q$ se trouve sur la bissectrice de l'angle $\\widehat{B A C}$.", "solution": "Rappelons d'abord la méthode de construction du centre d'une similitude directe qui envoie deux points distincts $A$ et $B$ sur deux points distincts $A^{\\prime}$ et $B^{\\prime}$ respectivement.\n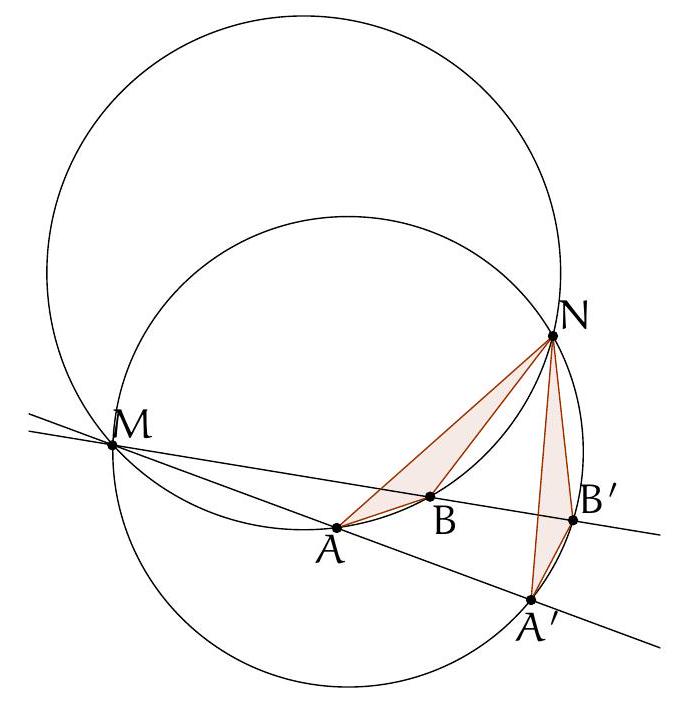\n\nSupposons que $A \\neq A^{\\prime}, B \\neq B^{\\prime}$, et que les droites $\\left(A A^{\\prime}\\right)$ et $\\left(B B^{\\prime}\\right)$ ne sont pas parallèles. Soit $M$ le point d'intersection de $\\left(A A^{\\prime}\\right)$ et de ( $\\left.B B^{\\prime}\\right)$. Alors les cercles $M A B$ et $M A^{\\prime} B^{\\prime}$ se recoupent en un point $N$. Comme $(N A, N B)=(M A, M B)=\\left(M A^{\\prime}, M B^{\\prime}\\right)=\\left(N A^{\\prime}, N B^{\\prime}\\right)$ et $(A B, A N)=(M B, M N)=$ $\\left(M B^{\\prime}, M N\\right)=\\left(A^{\\prime} B^{\\prime}, A^{\\prime} N\\right)$, les triangles $N A B$ et $N A^{\\prime} B^{\\prime}$ sont directement semblables, donc la similitude de centre $N$ et de rapport $N A^{\\prime} / N A$ envoie $A$ sur $A^{\\prime}$ et $B$ sur $B^{\\prime}$. On vérifie que le résultat reste vrai si $A=A^{\\prime}$ ou $B=B^{\\prime}$.\n$\\mathrm{Si}\\left(A A^{\\prime}\\right)$ et $\\left(B B^{\\prime}\\right)$ sont parallèles, alors $N$ est le point d'intersection de $(A B)$ et de $\\left(A^{\\prime} B^{\\prime}\\right)$.\nRevenons à l'exercice. Montrons d'abord la deuxième assertion.\n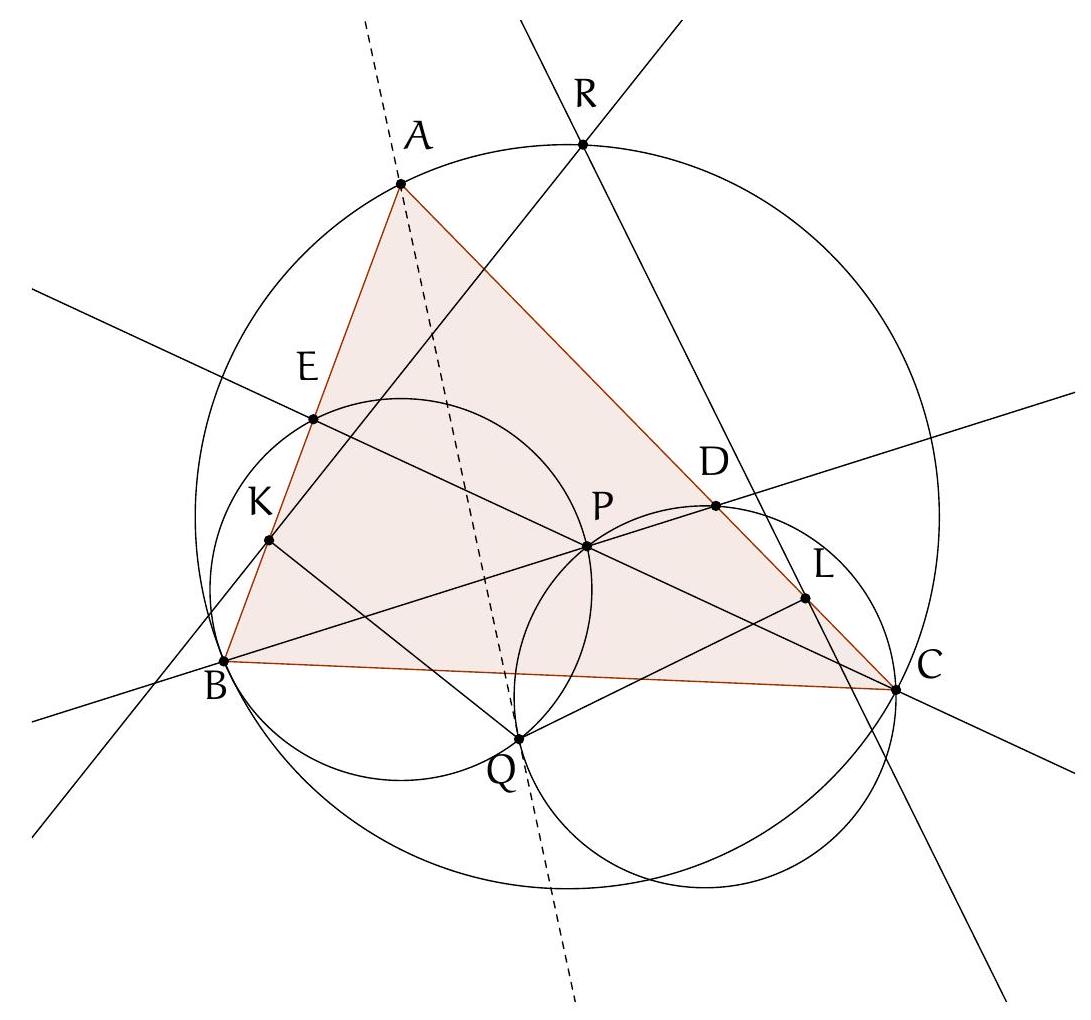\n\nD'après le préliminaire, $Q$ est le centre de la similitude directe qui envoie $B$ sur $D$ et $E$ sur $C$. Comme $B E=C D$, cette similitude est une rotation sur l'on notera $r$. Comme $r$ envoie ( $A B$ ) sur ( $A C$ ), $Q$ est équidistant de $(A B)$ et de $(A C)$ donc $Q$ est sur une bissectrice de l'angle $\\widehat{B A C}$. Vérifions que c'est la bissectrice intérieure.\n\nPar un argument de continuité, il suffit de se restreindre au cas où $E$ et $D$ sont strictement à l'intérieur des segments $[A B]$ et $[A C]$. Dans ce cas, $A, B$ et $E$ étant alignés donc non-cocycliques, $Q \\neq A$.\n\nDe plus, lorsque $A B C$ est isocèle en $A$ et que $D$ et $E$ tendent vers $A$, les cercles circonscrits à $B P E$ et CPD tendent vers les cercles $\\Gamma_{1}$ passant par B et tangent à (AC) en $A$ et $\\Gamma_{2}$ passant par $C$ et tangent à $(A B)$ en $A$. Or, le cercle $\\Gamma_{1}$ et le triangle sont du même côté de la droite $(A C)$, le cercle $\\Gamma_{2}$ et le triangle sont du même côté de $(A B)$, donc $Q$ tend vers un point à l'intérieur de l'angle $\\widehat{B A C}$ ou de celui opposé par le sommet. Ce sera donc un point de la bissectrice intérieure (différent de $A$ puisque $(A B) \\neq(A C)$ ).\n\nEn faisant varier les points $A, D$ et $E$, le point $Q$ reste sur la réunion des deux bissectrices et ne passe pas par $A$, donc il doit par continuité rester sur la bissectrice intérieure.\n\nMontrons maintenant la première assertion. Comme $r$ envoie ( $Q K$ ) sur ( $Q L$ ) et ( $A K$ ) sur ( $A L$ ), les angles de droites $(Q K, Q L$ ) et ( $A K, A L$ ) sont égaux donc $A, K, Q, L$ sont cocycliques.\n\nComme les triangles $K Q R$ et $L Q R$ sont rectangles en $K$ et $L$, le cercle de diamètre $[Q R]$ passe par $K$ et $L$, donc le cercle circonscrit à $Q K L$ rencontre $R$, ce qui montre que $A, K, Q, L, R$ sont cocycliques.\n\nSoit $r^{\\prime}$ la similitude directe qui envoie $K$ sur $B$ et $L$ sur $C$. D'après le préliminaire, le centre de $r^{\\prime}$ est le second point d'intersection du cercle ABC avec le cercle AKL, c'est-à-dire R. Comme $r^{\\prime}$ envoie les droites $(R K)$ et $(R L)$ sur $(R B)$ et $(R C)$ respectivement, on en déduit que $(R B, R C)=(R K, R L)=$ $(A K, A L)=(A B, A C)$ où la deuxème égalité provient de la cocyclicité de $A, K, L, R$. Ceci prouve que $A, B, C, R$ sont cocycliques.\n", "problem_match": "\nExercice 8.", "solution_match": "## Solution."}
|
French_TST_Senior/segmented/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "problem_label": "1", "tier": 1, "problem": "Soit $k \\geqslant 2$ un entier.\n\n1) Soit $n>k$ un entier.\n\nExiste-t-il $n$ entiers strictement positifs tels que $k$ quelconques ne sont jamais premiers entre eux dans leur ensemble, mais $k+1$ quelconques sont toujours premiers entre eux dans leur ensemble?\n2) Existe-t-il une suite infinie d'entiers strictement positifs vérifiant les deux conditions ci-dessus?", "solution": "1) Soit $A$ l'ensemble des parties de $\\{1, \\ldots, n\\}$ de cardinal $k$. Comme l'ensemble des nombres premiers est infini, il existe une famille $\\left(p_{I}\\right)_{I \\in A}$ de nombres premiers deux à deux distincts indexée par $A$. Pour tout $i$, notons $A(i)$ l'ensemble des parties $I$ de $\\{1, \\ldots, n\\}$ de cardinal $k$ telles que $i \\in I$. On définit\n\n$$\na_{i}=\\prod_{I \\in A(i)} p_{I}\n$$\n\nSi $J$ est une partie de $\\{1, \\ldots, n\\}$, alors les $a_{j}(j \\in J)$ ne sont pas premiers entre eux dans leur ensemble\n$\\Longleftrightarrow$ ils ont un facteur premier commun\n$\\Longleftrightarrow$ il existe $I \\in A$ tel que $p_{I} \\mid a_{j}$ pour tout $j \\in J$\n$\\Longleftrightarrow$ il existe $I \\in A$ tel que $j \\in I$ pour tout $j \\in J$\n$\\Longleftrightarrow$ il existe $I \\in A$ tel que $J \\subset I$\n$\\Longleftrightarrow \\operatorname{Card}(J) \\leqslant k$.\nCeci montre que la famille $\\left(a_{i}\\right)_{1 \\leqslant i \\leqslant n}$ convient.\n2) Supposons par l'absurde qu'il y a une famille $\\left(a_{n}\\right)_{n \\in \\mathbb{N}}$ d'entiers strictement positifs telle que $k$ quelconques ne sont jamais premiers entre eux dans leur ensemble.\nNotons $p_{1}, \\ldots, p_{m}$ les diviseurs premiers de $a_{0}$. Comme $k \\geqslant 2$, pour tout $n \\in \\mathbb{N}$, $a_{n}$ possède un diviseur parmi $p_{1}, \\ldots, p_{m}$. Notons $p_{i(n)}$ l'un d'eux. Comme la suite $\\left(p_{i(n)}\\right)_{n \\in \\mathbb{N}}$ ne prend qu'un nombre fini de valeurs, au moins une de ses valeurs (que nous noterons $p_{\\ell}$ ) est atteinte une infinité de fois. Il existe donc $i_{1}<\\cdots<i_{k+1}$ tels que $p_{\\ell}$ divise $a_{i_{1}}, \\ldots, a_{i_{k+1}}$, ce qui montre que $a_{i_{1}}, \\ldots, a_{i_{k+1}}$ ne sont pas premiers entre eux dans leur ensemble.", "problem_match": "## Exercice 1.", "solution_match": "\nSolution."}
|
| 2 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\omega$ un cercle qui passe par $A$ et $B$ et recoupe les côtés $[B C]$ et $[A C]$ respectivement en $D$ et $E$. Les points $K$ et $L$ sont respectivement les centres du cercle inscrit dans $D A C$ et du cercle inscrit dans $B E C$. Soit $N$ l'intersection des droites $(E L)$ et $(D K)$.\n\nProuver que le triangle $K N L$ est isocèle.", "solution": "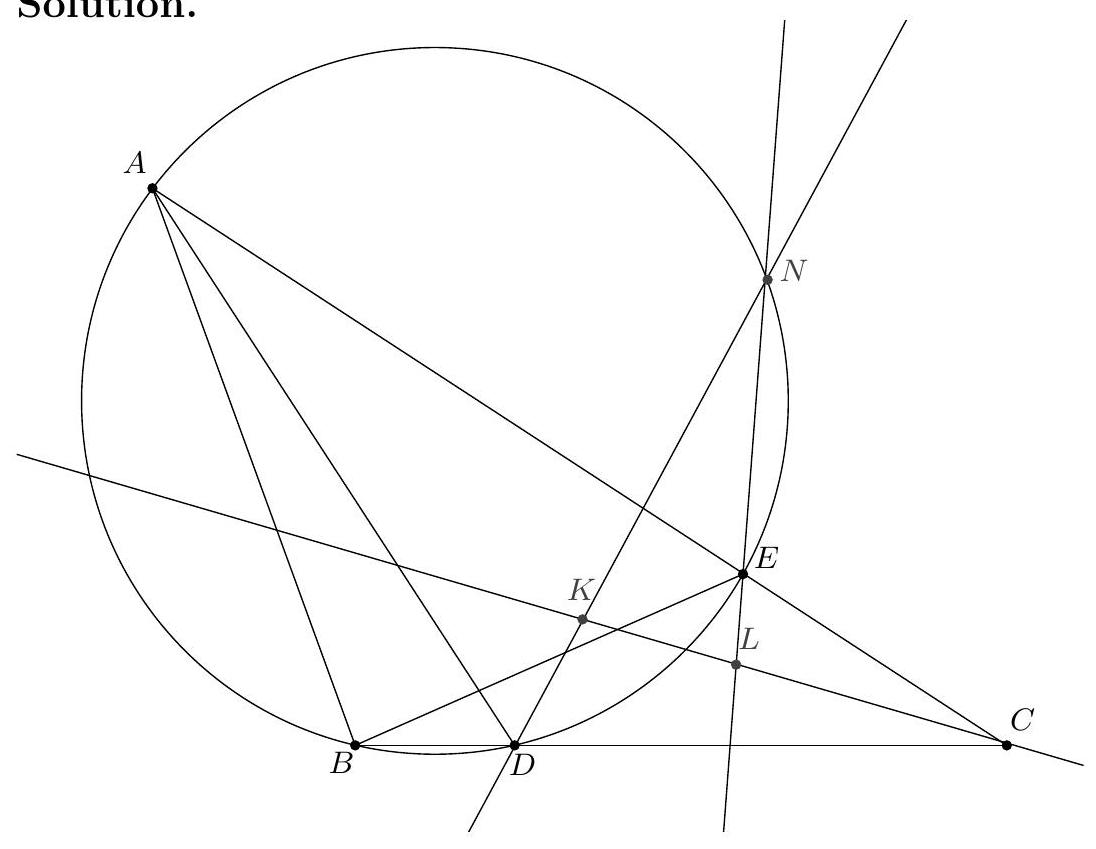", "problem_match": "## Exercice 2.", "solution_match": "\nSolution."}
|
| 3 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\omega$ un cercle qui passe par $A$ et $B$ et recoupe les côtés $[B C]$ et $[A C]$ respectivement en $D$ et $E$. Les points $K$ et $L$ sont respectivement les centres du cercle inscrit dans $D A C$ et du cercle inscrit dans $B E C$. Soit $N$ l'intersection des droites $(E L)$ et $(D K)$.\n\nProuver que le triangle $K N L$ est isocèle.", "solution": "On va montrer l'égalité entre les angles de droites ( $K L, K N$ ) et $(L N, K L)$. Notons d'abord que $C, K, L$ sont alignés (sur la bissectrice intérieure en $C$ du triangle $A B C$ ).\n\n$$\n\\begin{aligned}\n(K L, K N) & =(C K, C D)+(D C, D N)=\\frac{1}{2}((\\overrightarrow{C A}, \\overrightarrow{C B})+(\\overrightarrow{D C}, \\overrightarrow{D A})) \\\\\n& =\\frac{1}{2}[(\\overrightarrow{C A}, \\overrightarrow{C B})+\\Pi+(\\overrightarrow{D B}, \\overrightarrow{D A})]\n\\end{aligned}\n$$\n\noù $\\Pi$ est l'angle plat, et\n\n$$\n\\begin{aligned}\n(L N, K L) & =(E L, E C)+(E C, C K)=\\frac{1}{2}((\\overrightarrow{E B}, \\overrightarrow{E C})+(\\overrightarrow{C E}, \\overrightarrow{C B})) \\\\\n& =\\frac{1}{2}[(\\overrightarrow{E B}, \\overrightarrow{E A})+\\Pi+(\\overrightarrow{C A}, \\overrightarrow{C B})]\n\\end{aligned}\n$$\n\nOr, les angles de vecteurs $(\\overrightarrow{D B}, \\overrightarrow{D A})$ et $(\\overrightarrow{E B}, \\overrightarrow{E A})$ sont égaux puisque $E$ et $D$ sont sur le même arc délimité par $A$ et $B$, ce qui conclut.", "problem_match": "## Exercice 2.", "solution_match": "\nSolution 1."}
|
| 4 |
+
{"year": "2012", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\omega$ un cercle qui passe par $A$ et $B$ et recoupe les côtés $[B C]$ et $[A C]$ respectivement en $D$ et $E$. Les points $K$ et $L$ sont respectivement les centres du cercle inscrit dans $D A C$ et du cercle inscrit dans $B E C$. Soit $N$ l'intersection des droites $(E L)$ et $(D K)$.\n\nProuver que le triangle $K N L$ est isocèle.", "solution": "Comme $A, B, D, E$ sont cocycliques, on a les égalités d'angles orientés de droites\n\n$$\n\\begin{aligned}\n& (D A, D C)=(D A, D B)=(E A, E B)=(E C, E B) \\\\\n& (A D, A C)=(A D, A E)=(B D, B E)=(B C, B E)\n\\end{aligned}\n$$\n\ndonc les angles orientés de $C A D$ et $C B E$ sont deux à deux opposés, par conséquent les triangles $C A D$ et $C B E$ sont indirectement semblables. Soit $f$ la similitude indirecte qui envoie $C, A, D$ sur $C, B, E$ respectivement. Alors $f$ envoie le centre du cercle inscrit de $C A D$ sur celui de $C B E$ : autrement dit, $f(K)=L$.\nOn a $(L K, L N)=(L K, E L)=(C L, E L)$ car $C, K, L$ sont alignés (sur la bissectrice intérieure en $C$ du triangle $A B C$ ). De plus, $f$ envoie $C, D, K$ sur $C, E, L$ respectivement, donc $(C L, E L)=-(C K, D K)=(K D, K C)=$ $(K N, K L)$. Finalement, $(L K, L N)=(K N, K L)$ donc $L K N$ est isocèle en $N$.", "problem_match": "## Exercice 2.", "solution_match": "\nSolution 2."}
|
| 5 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Prouver que, pour tous réels $a, b, c>0$ et tout réel $t \\geqslant 0$, on a\n\n$$\n\\frac{a}{b+t c}+\\frac{b}{c+t a}+\\frac{c}{a+t b} \\geqslant \\frac{3}{1+t} .\n$$", "solution": "Posons $x=b+t c, y=c+t a, z=a+t b$. On vérifie que\n\n$$\n\\begin{aligned}\n\\left(1+t^{3}\\right) a & =z-t x+t^{2} y \\\\\n\\left(1+t^{3}\\right) b & =x-t y+t^{2} z \\\\\n\\left(1+t^{3}\\right) c & =y-t z+t^{2} x\n\\end{aligned}\n$$\n\ndonc, d'après l'inégalité arithmético-géométrique,\n\n$$\n\\begin{aligned}\n\\left(1+t^{3}\\right)\\left(\\frac{a}{b+t c}+\\frac{b}{c+t a}+\\frac{c}{a+t b}\\right) & =\\frac{z-t x+t^{2} y}{x}+\\frac{x-t y+t^{2} z}{y}+\\frac{y-t z+t^{2} x}{z} \\\\\n& =\\left(\\frac{z}{x}+\\frac{x}{y}+\\frac{y}{z}\\right)+t^{2}\\left(\\frac{y}{x}+\\frac{z}{y}+\\frac{x}{z}\\right)-3 t \\\\\n& \\geqslant 3 \\sqrt[3]{\\frac{z}{x} \\frac{x}{y} \\frac{y}{z}}+3 t^{2} \\sqrt[3]{\\frac{y}{x} \\frac{z}{y} \\frac{x}{z}}-3 t \\\\\n& =3\\left(1-t+t^{2}\\right)=3 \\frac{1+t^{3}}{1+t}\n\\end{aligned}\n$$\n\nd'où la conclusion.", "problem_match": "## Exercice 3.", "solution_match": "\nSolution 1."}
|
| 6 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Prouver que, pour tous réels $a, b, c>0$ et tout réel $t \\geqslant 0$, on a\n\n$$\n\\frac{a}{b+t c}+\\frac{b}{c+t a}+\\frac{c}{a+t b} \\geqslant \\frac{3}{1+t} .\n$$", "solution": "Puisque l'inégalité est homogène en $a, b, c$, on peut supposer que $a+b+c=1$. Comme le membre de gauche est égal à $a f(x)+b f(y)+c f(z)$ où $x=b+t c, y=c+t a, z=a+t b$ et $f(x)$ est la fonction convexe $x \\mapsto \\frac{1}{x}$, d'après l'inégalité de Jensen le membre de gauche est supérieur ou égal à\n\n$$\nf(a x+b y+t z)=\\frac{1}{a b+t a c+b c+t b a+c a+t a b}=\\frac{1}{(1+t)(a b+b c+c a)},\n$$\n\ndonc il suffit de prouver que $a b+b c+c a \\leqslant \\frac{1}{3}$.\nOr, $1=(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(a b+b c+c a)$ donc il suffit de montrer que $a^{2}+b^{2}+c^{2} \\geqslant \\frac{1}{3}$, ce qui découle de l'inégalité entre la moyenne arithmétique et la moyenne quadratique de $a, b, c$.", "problem_match": "## Exercice 3.", "solution_match": "\nSolution 2."}
|
| 7 |
+
{"year": "2012", "problem_label": "3", "tier": 1, "problem": "Prouver que, pour tous réels $a, b, c>0$ et tout réel $t \\geqslant 0$, on a\n\n$$\n\\frac{a}{b+t c}+\\frac{b}{c+t a}+\\frac{c}{a+t b} \\geqslant \\frac{3}{1+t} .\n$$", "solution": "D'après l'inégalité de Cauchy-Schwarz,\n$\\left(\\frac{a^{2}}{a b+t c a}+\\frac{b^{2}}{b c+t a b}+\\frac{c^{2}}{c a+t b c}\\right) \\cdot((a b+t c a)+(b c+t a b)+(c a+t b c)) \\geqslant(a+b+c)^{2}$ ce qui s'écrit\n\n$$\n\\left(\\frac{a}{b+t c}+\\frac{b}{c+t a}+\\frac{c}{a+t b}\\right) \\cdot(1+t)(a b+b c+c a) \\geqslant a^{2}+b^{2}+c^{2}+2(a b+b c+c a) .\n$$\n\nOr, on a $a^{2}+b^{2}+c^{2} \\geqslant a b+b c+c a$ d'après l'inégalité de réordonnement (ou d'après celle de Cauchy-Schwarz), donc\n\n$$\n\\left(\\frac{a}{b+t c}+\\frac{b}{c+t a}+\\frac{c}{a+t b}\\right) \\cdot(1+t)(a b+b c+c a) \\geqslant 3(a b+b c+c a)\n$$\n\nL'inégalité demandée en découle après division par $(1+t)(a b+b c+c a)$.", "problem_match": "## Exercice 3.", "solution_match": "\nSolution 3."}
|
| 8 |
+
{"year": "2012", "problem_label": "4", "tier": 1, "problem": "Déterminer tous les entiers naturels $m, n$ et tous les nombres premiers $p$ tels que\n\n$$\nm\\left(4 m^{2}+m+12\\right)=3\\left(p^{n}-1\\right)\n$$", "solution": "On récrit l'équation sous la forme\n\n$$\n3 p^{n}=4 m^{3}+m^{2}+12 m+3=(4 m+1)\\left(m^{2}+3\\right)\n$$\n\nOn en déduit qu'il existe $u, v, a, b$ entiers naturels tels que $4 m+1=3^{u} p^{a}$ et $m^{2}+3=3^{v} p^{b}$ avec $u+v=1$ et $a+b=n$.\nSi $m=0$, l'équation devient $3 p^{n}=3$, donc $n=0$ et tout nombre premier convient.\nSupposons désormais $m \\geqslant 1$. Alors $4 m+1>3$ et $m^{2}+3>3$, donc $a \\geqslant 1$ et $b \\geqslant 1$.\nOn a\n\n$$\n\\begin{aligned}\n16 \\times 3^{v} p^{b} & =16\\left(m^{2}+3\\right)=(4 m)^{2}+48=((4 m+1)-1)^{2}+48 \\\\\n& =3^{2 u} p^{2 a}-2 \\times 3^{u} p^{a}+49\n\\end{aligned}\n$$\n\nComme $p$ divise le membre de gauche, il divise le membre de droite, donc $p \\mid 49$, ce qui donne $p=7$. On remplace alors 49 par $p^{2}$ :\n\n$$\n16 \\times 3^{v} p^{b}=3^{2 u} p^{2 a}-2 \\times 3^{u} p^{a}+p^{2}\n$$\n\nSi $a=1$ alors $4 m+1$ vaut 7 ou 21 . Comme $m$ est un entier, on a $4 m+1=21$, ou encore $m=5$, ce qui entraîne $3^{v} p^{b}=m^{2}+3=28$. Impossible. Donc $a \\geqslant 2$. On en déduit que $3^{2 u} p^{2 a}-2 \\times 3^{u} p^{a}+p^{2}$ est divisible par $p^{2}$, donc $16 \\times 3^{v} p^{b}$ est divisible par $p^{2}$, d'où $b \\geqslant 2$.\nSi $a \\geqslant 3$, alors $16 \\times 3^{v} p^{b}=3^{2 u} p^{2 a}-2 \\times 3^{u} p^{a}+p^{2}$ est congru à $p^{2}$ modulo $p^{3}$, donc n'est pas divisible par $p^{3}$, par conséquent $b=2$. En divisant par $p^{2}$, on obtient que $16 \\times 3^{v} \\equiv 1[p]$. Pour $v=0$ cela donne $16 \\equiv 1[7]$ et pour $v=1$ cela donne $48 \\equiv 1[7]$. Impossible.\nDonc on a nécessairement $a=2$ et $4 m+1=3^{u} \\times 49$. Si $u=0$ alors $m=12$ et $n=4$. Si $u=1$ alors $4 m+1=147$, ce qui est impossible.\nConclusion: les seules solutions sont\n\n- $m=0, n=0, p$ premier quelconque, et\n- $m=12, n=4, p=7$.", "problem_match": "## Exercice 4.", "solution_match": "\nSolution."}
|
French_TST_Senior/segmented/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "problem_label": "1", "tier": 1, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers tels que\n\n$$\nx^{2}+y^{2}+z^{2}=16(x+y+z)\n$$", "solution": "Tout d'abord, remarquons que l'équation peut se réécrire\n\n$$\nx(x-16)+y(y-16)+z(z-16)=0\n$$\n\nCela invite donc à effectuer un changement de variables, en posant $X=x-8, Y=y-8$ et $Z=z-8$. L'équation devient alors\n\n$$\nX^{2}+Y^{2}+Z^{2}=3 \\times 8^{2}\n$$\n\nOn introduit alors le lemme suivant, sur les sommes de trois carrés : si $a, b$ et c sont trois entiers tels que $a^{2}+b^{2}+c^{2} \\equiv 0(\\bmod 4)$, alors $a, b$ et $c$ sont tous les trois pairs. En effet, le carré d'un entier pair vaut $0(\\bmod 4)$, et que le carré d'un entier impair vaut $1(\\bmod 4)$.\nEn appliquant 3 fois de suite le lemme, on montre donc que $X, Y$ et $Z$ sont multiples de 8 . Encore une fois, on change de variables, en posant $u=\\frac{X}{8}=\\frac{x}{8}-1, v=\\frac{Y}{8}=\\frac{y}{8}-1$ et $w=\\frac{Z}{8}=\\frac{z}{8}-1$. L'équation devient\n\n$$\nu^{2}+v^{2}+w^{2}=3\n$$\n\nIl est alors clair que $(u, v, w)$ convient si et seulement si $u^{2}=v^{2}=w^{2}=1$, c'est-à-dire si et seulement si $u, v$ et $w$ appartiennent tous trois à l'ensemble $\\{-1,1\\}$. L'équation initiale avait donc pour solutions les triplets $(x, y, z)$ tels que $x, y$ et $z$ appartiennent tous trois à l'ensemble \\{0, 16\\}.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Sur une droite se trouvent 400 points bleus et 200 points verts. Montrer que l'on peut trouver un segment qui contient exactement 200 points bleus et 100 points verts.", "solution": "Notons $A_{1}, \\ldots, A_{600}$ les points de la droite, alignés dans cet ordre. Il s'agit de montrer qu'il existe un entier $k \\in\\{0, \\ldots, 300\\}$ tel que, parmi les points $A_{k+1}, \\ldots, A_{k+300}$, il y en a exactement 100 verts (il y en aura alors forcément 200 bleus).\nIntroduisons la fonction $\\mathrm{f}:\\{0, \\ldots, 300\\} \\longrightarrow \\mathbb{N}$ qui à un entier $k$ associe le nombre de points verts parmi $A_{k+1}, \\ldots, A_{k+300}$. On veut montrer que f prend la valeur 100 . Pour cela, remarquons deux choses:\n\n1. Tout d'abord, la somme $f(0)+f(300)$ compte le nombre total de points verts, et elle vaut donc 200. Ainsi, l'un des deux termes de la somme est supérieur ou égal à 100 tandis que l'autre ne dépasse pas 100. Quitte à changer le sens de parcours des points sur la droite, on peut supposer que $f(0) \\leqslant 100 \\leqslant f(300)$.\n2. Intéressons-nous maintenant à la différence $f(k)-f(k-1)$, où $k \\geqslant 1$ :\n\n- si $A_{k+300}$ et $A_{k}$ sont de même couleur, elle vaut 0 ;\n- si $A_{k+300}$ est vert et $A_{k}$ est bleu, elle vaut 1;\n- si $A_{k+300}$ est bleu et $A_{k}$ est vert, elle vaut -1 .\n\nEn particulier, on a $f(k)-f(k-1) \\leqslant 1$ pour tout $k \\in\\{1, \\ldots, 300\\}$.\nConsidérons maintenant le plus petit entier $p$ tel que $f(p) \\geqslant 100$ : cet entier existe bien, puisque $f(300) \\geqslant 100$. Si $p=0$, il n'y a plus rien à faire : en effet, dans ce cas, on a $f(0) \\geqslant 100$ et $f(0) \\leqslant 100$,\nd'où $f(0)=100$. Si $p>0$, la minimalité de $p$ assure que $f(p-1) \\leqslant 99$ et donc, d'après ci-dessus, on a alors $100 \\leqslant f(p) \\leqslant f(p-1)+1 \\leqslant 100$, et ainsi $f(p)=100$.\nFinalement, dans tous les cas, la valeur 100 est bien atteinte par la fonction $f$, ce qui conclut.\n\n## Exercices communs", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Soit $a, b, c, d>0$ des réels tels que $a b c d=1$.\nProuver que\n\n$$\n\\frac{1}{a+b+2}+\\frac{1}{b+c+2}+\\frac{1}{c+d+2}+\\frac{1}{d+a+2} \\leqslant 1 .\n$$", "solution": "Il est bien connu que, si $x, y>0$ sont des réels, on a $x+y \\geqslant 2 \\sqrt{x y}$.\nPar suite, $\\frac{1}{a+b+2} \\leqslant \\frac{1}{2(\\sqrt{a b}+1)}$ et $\\frac{1}{c+d+2} \\leqslant \\frac{1}{2(\\sqrt{c d}+1)}$, d'où\n\n$$\n\\begin{aligned}\n\\frac{1}{a+b+2}+\\frac{1}{c+d+2} & \\leqslant \\frac{1}{2(\\sqrt{a b}+1)}+\\frac{1}{2(\\sqrt{c d}+1)}=\\frac{1}{2(\\sqrt{a b}+1)}+\\frac{1}{2\\left(\\frac{1}{\\sqrt{a b}}+1\\right)} \\\\\n& =\\frac{1}{2(\\sqrt{a b}+1)}+\\frac{\\sqrt{a b}}{2(\\sqrt{a b}+1)}=\\frac{1}{2}\n\\end{aligned}\n$$\n\nOn prouve de même que $\\frac{1}{\\mathrm{~b}+\\mathrm{c}+2}+\\frac{1}{\\mathrm{~d}+\\mathrm{a}+2} \\leqslant \\frac{1}{2}$.\nEn sommant les deux inégalités précédentes, on déduit immédiatement la conclusion désirée.", "problem_match": "## Exercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2013", "problem_label": "4", "tier": 1, "problem": "Soient deux cercles extérieurs $\\mathcal{C}$ et $\\mathcal{C}^{\\prime}$ de centres $O$ et $\\mathrm{O}^{\\prime}$. On mène deux rayons parallèles de même sens $[O M]$ et $\\left[O^{\\prime} M^{\\prime}\\right]$, et deux autres rayons parallèles de même sens [OP] et $\\left[\\mathrm{O}^{\\prime} \\mathrm{P}^{\\prime}\\right]$. La droite $\\left(M M^{\\prime}\\right.$ ) recoupe $\\mathcal{C}^{\\prime}$ en $N$ et la droite ( $\\mathrm{PP}^{\\prime}$ ) recoupe $\\mathcal{C}^{\\prime}$ en Q . Montrer que $M, N, P, Q$ sont cocycliques.", "solution": "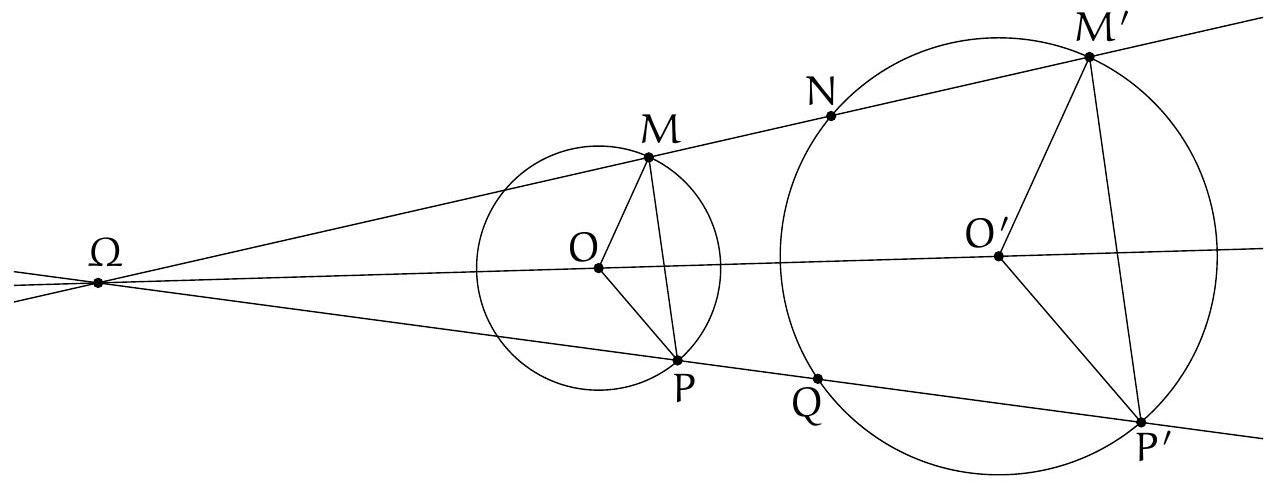\n\nLes triangles OMP et $\\mathrm{O}^{\\prime} \\mathrm{M}^{\\prime} \\mathrm{P}^{\\prime}$ sont isocèles en O et $\\mathrm{O}^{\\prime}$ respectivement. De plus, les angles $(\\overrightarrow{\\mathrm{OM}}, \\overrightarrow{\\mathrm{OP}})$ et $\\left(\\overrightarrow{\\mathrm{O}^{\\prime} \\mathrm{M}^{\\prime}}, \\overrightarrow{\\mathrm{O}^{\\prime} \\mathrm{P}^{\\prime}}\\right)$ sont égaux, donc ces deux triangles sont directement semblables. Comme de plus (OM) et $\\left(O^{\\prime} M^{\\prime}\\right)$ sont parallèles, (MP) et $\\left(M^{\\prime} \\mathrm{P}^{\\prime}\\right)$ le sont.\n\nOn en déduit $(M P, M N)=\\left(M^{\\prime} P^{\\prime}, M^{\\prime} N\\right)=\\left(Q^{\\prime}, Q N\\right)=(Q P, Q N)$, donc MNPQ est inscriptible.\nAutre solution. Supposons que les cercles sont de rayons différents. Soit $\\Omega$ le centre de l'homothétie $h$ de rapport $\\lambda>0$ qui transforme le premier cercle en le deuxième. Le point $h(M)$ vérifie la même condition de l'énoncé que le point $M^{\\prime}$, donc $h(M)=M^{\\prime}$. De même, $h(P)=P^{\\prime}$. On a $\\Omega N \\cdot \\Omega M^{\\prime}=\\Omega Q \\cdot \\Omega P^{\\prime}$ (puissance d'un point par rapport à un cercle), donc $\\lambda \\Omega N \\cdot \\Omega M=$ $\\lambda Q \\cdot \\Omega P$. En simplifiant par $\\lambda$ et en utilisant encore la puissance d'un point par rapport à un cercle, on en déduit que $M, N, P, Q$ sont cocycliques.\nSi les cercles sont de même rayon, alors il existe une translation qui envoie $M$ et $P$ sur $M^{\\prime}$ et $P^{\\prime}$ respectivement, donc comme ci-dessus on a $(M P, M N)=\\left(M^{\\prime} P^{\\prime}, M^{\\prime} N\\right)=\\left(Q^{\\prime}, Q N\\right)=$ (QP, QN).\n\n## Exercices du groupe A", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "Soit $n>0$ un entier, et $a, b, c$ des entiers strictement positifs tels que\n\n$$\n(a+b c)(b+a c)=19^{n}\n$$\n\nProuver que n est pair.", "solution": "Procédons par l'absurde, et supposons qu'il existe un triplet ( $a, b, c$ ) tel que $(\\mathrm{a}+\\mathrm{bc})(\\mathrm{b}+\\mathrm{ac})=19^{\\mathrm{n}}$, où $n$ est un entier impair. Sans perte de généralité, on peut supposer que $a \\geqslant b$ et que la somme $a+b+c$ est minimale.\nPuisque 19 est premier, on sait que $b+a c \\geqslant 2$ est une puissance de 19 , donc que $b+a c \\equiv 0$ $(\\bmod 19)$. Si 19 divise $a$, alors 19 divise bégalement : alors le triplet $(\\alpha, \\beta, c)=\\left(\\frac{a}{19}, \\frac{b}{19}, c\\right)$ est tel que $(\\alpha+\\beta c)(\\beta+\\alpha c)=19^{n-2}$, de sorte que la somme $a+b+c$ n'est pas minimale. On sait donc que $\\operatorname{PGCD}(\\mathbf{a}, 19)=1$.\nEn outre, si $\\mathrm{c}=1$, alors $(a+b c)(b+a c)=(a+b)^{2}$ est un carré, donc $n$ est nécessairement pair. De même, si $a=b$, alors $(a+b c)(b+a c)=(a+a c)^{2}$ est un carré, et $n$ est pair. On sait donc que $c>1$ et que $a>b$.\nAlors $b+a c=(a+b c)+(a-b)(c-1)>a+b c$, de sorte qu'il existe deux entiers naturels $u$ et $v$ tels que $a+b c=19^{u}$ et $b+a c=19^{u+v}$. En particulier, $a(c-1)(c+1)=a c^{2}-a=$ $(b+a c) c-(a+b c)=19^{u}\\left(19^{v} c-1\\right)$. On sait donc que $19^{u}$ divise $(c-1)(c+1)$ et, puisque $\\operatorname{PGCD}\\left(19^{\\mathbf{u}}, \\mathfrak{c}-1, \\mathrm{c}+1\\right)=\\operatorname{PGCD}\\left(19^{\\mathbf{u}}, \\boldsymbol{c}-1,2\\right)=1$, on en déduit que $19^{\\mathbf{u}}$ divise soit $\\mathbf{c}-1$ soit $\\mathrm{c}+1$.\nOr, on sait que $19^{\\mathrm{u}}=\\mathrm{a}+\\mathrm{bc}>\\mathrm{b}+\\mathrm{bc} \\geqslant \\mathrm{c}+1>\\mathrm{c}-1>0$. Il est donc impossible que $19^{\\mathrm{u}}$ divise $\\mathrm{c}-1$ ou $\\mathrm{c}+1$, de sorte que notre supposition initiale était fausse, et donc que $n$ est nécessairement pair.\nRemarque. Le raisonnement utilisé ci-dessus permet en fait de montrer que, si $p$ est un nombre premier impair, les triplets ( $a, b, c$ ) d'entiers strictement positifs tels que $(a+b c)(b+a c)$ soit une puissance de $p$ sont les triplets de la forme ( $\\mathfrak{a}, \\mathfrak{p}^{\\mathrm{k}}-\\mathfrak{a}, 1$ ) ou bien ( $\\mathfrak{p}^{k}, \\mathfrak{p}^{\\mathrm{k}}, \\mathfrak{p}^{\\ell}-1$ ).\nLe fait que $p$ soit impair est très important, car l'exercice est faux si on prend $p=2$, comme en témoigne l'égalité $(3+1 \\times 5)(1+3 \\times 5)=2^{7}$.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2013", "problem_label": "6", "tier": 1, "problem": "Soient $n$ et $p$ des entiers $\\geqslant 1$. Dans une assemblée de $n$ personnes, deux personnes quelconques ont au plus $p$ connaissances communes ; bien sûr, si A connaît B, alors B connaît $A$. Montrer que le nombre de paires non ordonnées $\\{A, B\\}$ de personnes qui se connaissent est inférieur ou égal à $\\sqrt{\\mathrm{pn}^{3}}$.", "solution": "Notons $A_{1}, \\cdots, A_{n}$ les personnes et, considérons le graphe simple et non orienté dont les sommets sont les $A_{i}$, et où deux personnes $A_{i}$ et $A_{j}$ sont reliées par une arête si et seulement si elles se connaissent.\nPour tout $i$, notons $d_{i}$ le degré de $A_{i}$ (c'est-à-dire le nombre de personnes que connaît $A_{i}$ ). Il s'agit de prouver que le nombre d'arêtes a de ce graphe vérifie $a \\leqslant \\sqrt{\\mathrm{pn}^{3}}$.\nIl est bien connu que $2 a=\\sum_{i=1}^{n} d_{i}$.\nSoit $M$ le nombre de paires d'arêtes $\\{X Y, Y Z\\}$ ayant un sommet commun.\nPour tout $i$, le sommet $A_{i}$ joue le rôle de $Y$ autant de fois que l'on peut choisir deux sommets adjacents à $A_{i}$. Ainsi,\n\n$$\nM=\\sum_{i=1}^{n}\\binom{d_{i}}{2}\n$$\n\nD'autre part, d'après l'énoncé, deux sommets quelconques ont toujours au plus p sommets adjacents communs. Ainsi,\n\n$$\nM \\leqslant p\\binom{n}{2} .\n$$\n\nDe (1) et (2), on déduit que\n\n$$\n\\sum_{i=1}^{n}\\binom{d_{i}}{2} \\leqslant p\\binom{n}{2}\n$$\n\nOr, la fonction $x \\longmapsto \\frac{1}{2} \\chi(x-1)$ est convexe sur $\\mathbb{R}$ donc, d'après l'inégalité de Jensen, on a\n\n$$\n\\sum_{i=1}^{n}\\binom{d_{i}}{2} \\geqslant \\frac{n}{2}\\left(\\frac{2 a}{n}\\right)\\left(\\frac{2 a}{n}-1\\right)\n$$\n\nDe (3) et (4), on obtient que $2 a(2 a-n) \\leqslant p^{2}(n-1) \\leqslant n^{3}$, ou encore $4 a^{2}-2 n a-p n^{3} \\leqslant 0$. Si $a>\\sqrt{p n^{3}}$, alors $0>4 a^{2}-2 n a-a^{2}=(3 a-2 n) a \\geqslant(3 \\sqrt{p n}-2) n a \\geqslant n a \\geqslant 0$, ce qui conclut.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "problem_label": "1", "tier": 1, "problem": "Soient $C$ et $\\mathrm{C}^{\\prime}$ deux cercles de centres $O$ et $\\mathrm{O}^{\\prime}$, extérieurs l'un à l'autre. Une tangente commune extérieure coupe les deux tangentes communes intérieures aux points M et N .\n\nMontrer que (OM) est perpendiculaire à ( $O^{\\prime} M$ ) et que ( $O N$ ) est perpendiculaire à ( $O^{\\prime} N$ ).", "solution": "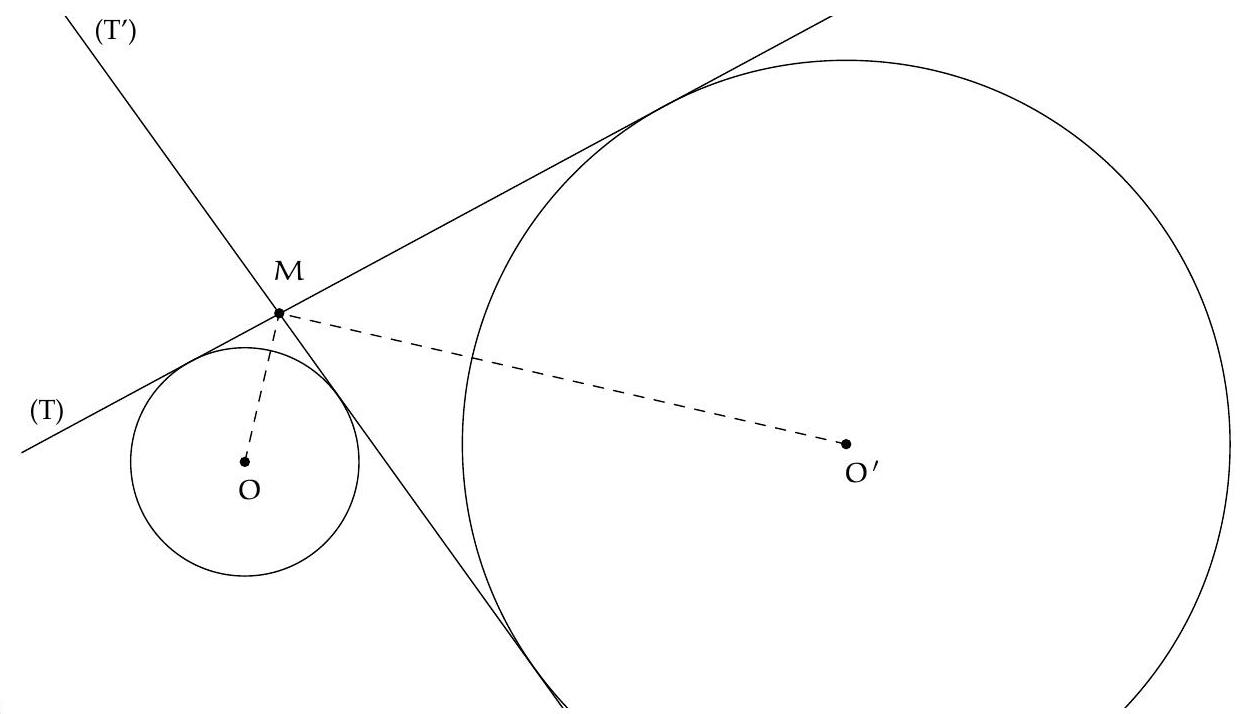\n\nSoit (T) la tangente commune extérieure de l'énoncé. Soit ( $\\mathrm{T}^{\\prime}$ ) la tangente commune intérieure passant par $M$. Les droites $(T)$ et $\\left(T^{\\prime}\\right)$ sont donc les deux tangentes à $C$ issues de $M$.\n\nComme ces deux tangentes sont symétriques par rapport à (OM), la droite (OM) est une bissectrice de ( $T$ ) et $\\left(T^{\\prime}\\right)$. De même, $\\left(O^{\\prime} M\\right.$ ) est une bissectrice de $(T)$ et $\\left(T^{\\prime}\\right)$.\n\nComme les bissectrices de deux droites sont perpendiculaires, $(O M)$ et $\\left(O^{\\prime} M\\right.$ ) sont perpendiculaires ou confondues.\n\nSi elles étaient confondues, $\\mathrm{O}, \\mathrm{O}^{\\prime}, \\mathrm{M}$ seraient alignés, et les deux tangentes à ( C ) passant par $M$ seraient extérieures, ce qui n'est pas le cas.\n\nPar conséquent, $(O M) \\perp\\left(O^{\\prime} M\\right)$. On montre de même que $(O N) \\perp\\left(O^{\\prime} N\\right)$.", "problem_match": "\nExercice 1.", "solution_match": "## Solution de l'exercice 1"}
|
| 2 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Soit $k \\geqslant 1$ un entier. À chaque client, un opérateur téléphonique propose $k$ numéros pour lesquels la communication est gratuite (si une personne $A$ choisit le numéro de $B$, alors les appels de $A$ vers $B$ et de $B$ vers $A$ sont gratuits). On considère un groupe de $n$ personnes.\n\n1) Si $n \\geqslant 2 k+2$, montrer qu'il existe deux personnes qui ne pourront pas communiquer gratuitement.\n2) $\\operatorname{Si} n=2 k+1$, montrer que les $n$ personnes peuvent faire en sorte que toute personne peut communiquer gratuitement avec n'importe quelle autre.", "solution": "On dira pour simplifier qu'une personne $A$ choisit une personne B si le numéro de $B$ fait parti des numéros choisis par $A$ vers lesquels la communication est gratuite.\n3) Comme chaque personne peut choisir au plus k autre personnes, il y a au plus kn paires de personnes qui peuvent communiquer gratuitement. Or le nombre total de paires de personnes est $n(n-1) / 2$, et on a\n\n$$\n\\frac{n(n-1)}{2} \\geqslant \\frac{n(2 k+1)}{2}>k n\n$$\n\nAinsi, le nombre total de paires de personnes est strictement supérieur au nombre de paires de personnes qui peuvent communiquer gratuitement. Il existe donc forcément deux personnes qui ne pourront pas communiquer gratuitement.\n2) Plaçons les $2 k+1$ personnes sur un cercle. Chaque personne choisit alors de communiquer gratuitement avec les $k$ personnes qui sont situées juste après elle. On vérifie aisément que cette configuration permet à toute personne de communiquer gratuitement avec n'importe quelle autre : par construction, chaque personne peut communiquer avec les $k$ personnes situées juste après elle ainsi qu'avec les $k$ personnes situées juste avant elles, autrement dit tout le monde.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Soit $n \\geqslant 1$ un entier. Déterminer tous les entiers $p \\geqslant 1$ pour lesquels il existe des entiers strictement positifs $x_{1}<x_{2}<\\cdots<x_{n}$ tels que\n\n$$\n\\frac{1}{x_{1}}+\\frac{2}{x_{2}}+\\cdots+\\frac{n}{x_{n}}=p\n$$", "solution": "Nous allons montrer que l'ensemble des solutions est l'ensemble $\\{1,2, \\ldots, n\\}$. Soient $p \\geqslant 1$ un entier et des entiers strictement positifs $x_{1}<x_{2}<\\cdots<x_{n}$ tels que\n\n$$\n\\frac{1}{x_{1}}+\\frac{2}{x_{2}}+\\cdots+\\frac{n}{x_{n}}=p\n$$\n\nOn remarque tout d'abord que $p \\leqslant n$. En effet, si $i$ et $j$ sont deux entiers tels que $i>j$, alors $i \\geqslant j+1$. On en déduit que $x_{i} \\geqslant i$ pour tout entier $1 \\leqslant i \\leqslant n$. Ainsi\n\n$$\n\\frac{1}{x_{1}}+\\frac{2}{x_{2}}+\\cdots+\\frac{n}{x_{n}} \\leqslant \\frac{1}{1}+\\frac{2}{2}+\\cdots+\\frac{n}{n} \\leqslant n .\n$$\n\nDonc $p \\leqslant n$.\nRéciproquement, soit $1 \\leqslant p \\leqslant \\mathrm{n}$ et montrons qu'il existe des entiers strictement positifs $x_{1}<x_{2}<\\cdots<x_{n}$ tels que\n\n$$\n\\frac{1}{x_{1}}+\\frac{2}{x_{2}}+\\cdots+\\frac{n}{x_{n}}=p .\n$$\n\nPour cela, on choisit les $x_{i}$ de sorte que parmi les différents quotients $i / x_{i}(1 \\leqslant i \\leqslant n)$ on ait $p-1$ quotients égaux à 1 et les $n-p+1$ autres égaux à $1 /(n-p+1)$. Plus précisément, on choisit:\n$x_{1}=1, x_{2}=2, \\ldots, x_{p-1}=p-1, x_{p}=p(n-p+1), x_{p+1}=(p+1)(n-p+1), \\ldots, x_{n}=n(n-p+1)$.\n\nOn vérifie aisément que $x_{1}<x_{2}<\\cdots<x_{n}$ et que\n\n$$\n\\frac{1}{x_{1}}+\\frac{2}{x_{2}}+\\cdots+\\frac{n}{x_{n}}=p-1+(n-p+1) \\cdot \\frac{1}{n-p+1}=p .\n$$\n\n## Exercice commun", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2013", "problem_label": "4", "tier": 1, "problem": "Soit $A B C$ un triangle dont les angles sont aigus, et tel que $A B \\neq A C$. On note $D$ le pied de la bissectrice de $\\widehat{B A C}$. Le point $E$ (resp. $F$ ) désigne le pied de la hauteur issue de $B$ (resp. de C). Le cercle circonscrit au triangle DBF rencontre le cercle circonscrit au triangle DCE en un point $M$ autre que $D$.\n\nProuver que ME $=M F$.", "solution": "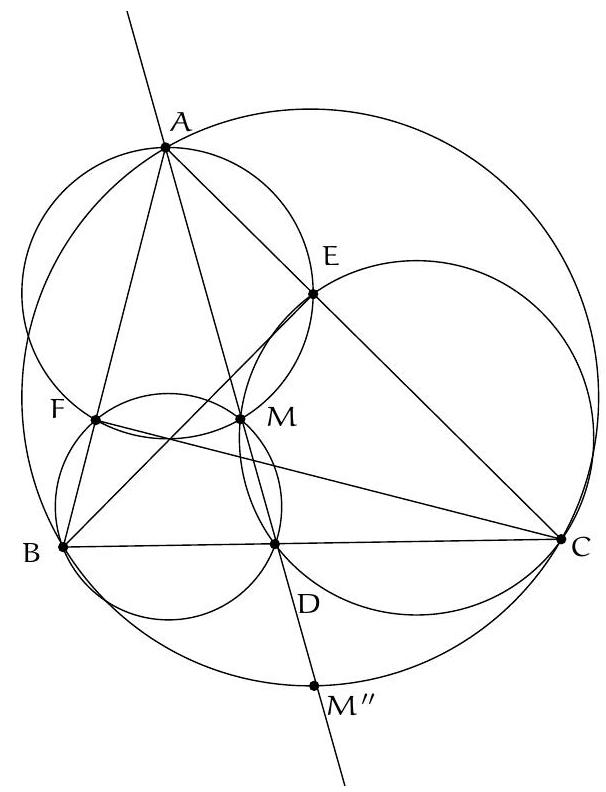\n\nLemme 1. Les cercles AEF, BDF et CDE sont concourants en $M$.\nCela découle immédiatement du théorème de Miquel mais rappelons tout de même la démonstration:\n$(M F, M E)=(M F, M D)+(M D, M E)=(B F, B D)+(C D, C E)=(A B, C D)+(C D, A C)=$ ( $A B, A C$ ) donc $A, E, F, M$ sont cocycliques.\n\nLemme 2. Les triangles $A E F$ et $A B C$ sont (indirectement) semblables.\nLes triangles $A F C$ et $A E B$ sont rectangles en $F$ et en $E$, et leurs angles en $A$ sont égaux, donc ils sont semblables. On en déduit que $\\frac{A E}{A F}=\\frac{A B}{A C}$. Ceci s'écrit encore $\\frac{A E}{A B}=\\frac{A F}{A C}$. Comme $\\widehat{E A F}=\\widehat{B A C}$, les triangles EAF et $B A C$ sont semblables. Il est clair que la similitude est indirecte puisque les angles orientés $(\\overrightarrow{A B}, \\overrightarrow{A C})$ et $(\\overrightarrow{A E}, \\overrightarrow{A F})$ sont opposés.\n\nRevenons à l'exercice. Soit $M^{\\prime}$ le point d'intersection autre que $A$ entre la bissectrice de $\\widehat{B A C}$ et le cercle $A E F$. De même, on définit $M^{\\prime \\prime}$ comme le point d'intersection autre que $A$ entre la bissectrice de $\\widehat{B A C}$ et le cercle $A B C$. Montrons que $M^{\\prime}=M$.\n\n$$\n\\begin{aligned}\n\\left(M^{\\prime} F, M^{\\prime} D\\right) & =\\left(M^{\\prime} F, M^{\\prime} A\\right) \\quad \\text { car } A, M, D \\text { alignés } \\\\\n& =(E F, E A) \\quad \\text { car } A, E, F, M \\text { cocycliques } \\\\\n& =(B A, B C) \\quad \\text { car } A E F \\text { et } A B C \\text { indirectement semblables } \\\\\n& =(B F, B F) .\n\\end{aligned}\n$$\n\nOn en déduit que $M^{\\prime}$ appartient au cercle BDF. De même, il appartient au cercle CDE. Par conséquent, il est l'intersection des trois cercles BDF, CDE et $A E F$ : ceci prouve que $M^{\\prime}=M$.\n\nEnfin, comme les arcs MF et ME sont égaux (puisque (AM) est la bissectrice de $\\widehat{F A E}$ ), on a $M F=M E$.\n\n## Autre solution.\n\nLemme 1. Deux cordes $\\left[\\mathrm{BB}^{\\prime}\\right]$ et $\\left[\\mathrm{CC}^{\\prime}\\right]$ d'un cercle se coupent en un point extérieur $A$. Alors les triangles $A B C$ et $A C^{\\prime} B^{\\prime}$ sont indirectement semblables.\n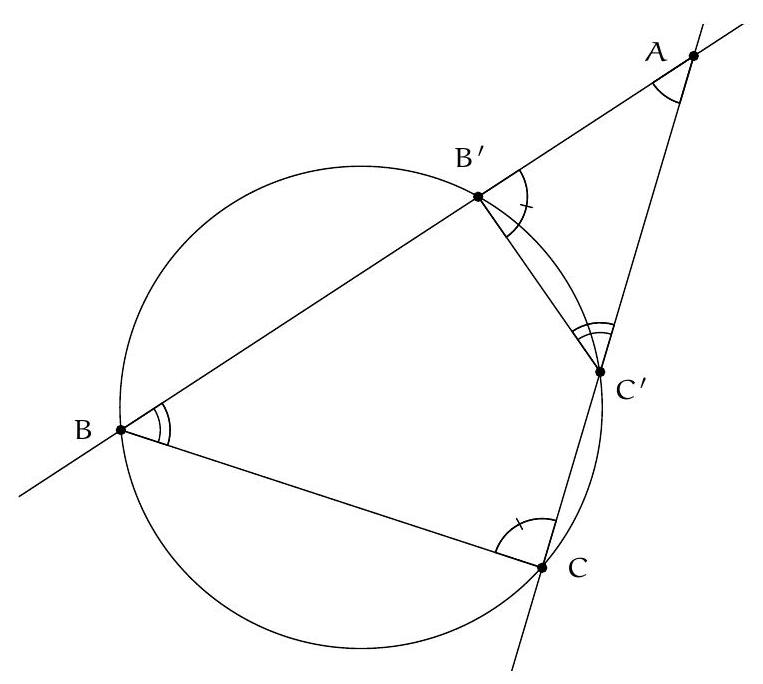\n\nOn a $\\left(B^{\\prime} C^{\\prime}, B^{\\prime} A\\right)=\\left(B^{\\prime} C^{\\prime}, B^{\\prime} B\\right)=\\left(C C^{\\prime}, C B\\right)=(C A, C B)$ et de même $\\left(C^{\\prime} A, C^{\\prime} B^{\\prime}\\right)=(B C, B A)$.\nLemme 2. $\\frac{D B}{D C}=\\frac{A B}{A C}$.\nD'après la loi des sinus, on a $\\frac{A B}{D B}=\\frac{\\sin \\widehat{A D B}}{\\sin \\frac{\\widehat{B A C}}{2}}=\\frac{\\sin \\widehat{C D A}}{\\sin \\frac{\\widehat{B A C}}{2}}=\\frac{A C}{D C}$.\nRevenons à l'exercice. Comme AFC et AEB sont rectangles en $F$ et $E$ et ont le même angle en $A$, ils sont semblables. On en déduit $\\frac{A F}{A E}=\\frac{A C}{A B}$, ce qui s'écrit encore $A F \\cdot A B=A E \\cdot A C$. Autrement dit, $A$ a la même puissance par rapport aux deux cercles BFD et CED. Par conséquent, $A$ se trouve sur l'axe radical (MD).\n$D^{\\prime}$ 'autre part, le lemme 1 entraîne que $A F M$ et $A D B$ sont semblables, donc $\\frac{B D}{B A}=\\frac{M F}{M A}$. De même, $\\frac{C D}{C A}=\\frac{M E}{M A}$. D'après le lemme 2 , on a $\\frac{B D}{B A}=\\frac{C D}{C A}$ donc $M F=M E$.\n\n## Exercices du groupe A", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "On dit qu'une suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ est Sicilienne si $u_{1}$ est un entier strictement positif, et si pour tout $n$,\n\n$$\nu_{n+1}= \\begin{cases}u_{n} / 2 & \\text { si } u_{n} \\text { est pair, et } \\\\ u_{n}+\\left[\\sqrt{u_{n}}\\right] & \\text { si } u_{n} \\text { est impair. }\\end{cases}\n$$\n\nExiste-t-il une suite Sicilienne $\\left(u_{n}\\right)_{n \\geqslant 1}$ telle que $u_{n}>1$ pour tout $n$ ?\n(N.B. $[x]$ désigne la partie entière de $x$. Par exemple, $[2,71828]=2$.)", "solution": "Commençons par une simple remarque. Soit $\\mathrm{f}: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ la fonction qui, à tout entier naturel non nul $n$, associe l'entier $n / 2$ si $n$ est pair, et $n+[\\sqrt{n}]$ si $n$ est impair. Il est clair que l'image $f(n)$ est bien un entier naturel non nul.\n\nNous allons maintenant montrer que la réponse à la question de l'énoncé est négative : toute suite Sicilienne $\\left(u_{n}\\right)_{n \\geqslant 1}$ contient un terme $u_{n}=1$.\n\nSoit $\\left(u_{n}\\right)_{n \\geqslant 1}$ une suite Sicilienne : on note que $u_{n+1}=f\\left(u_{n}\\right)$ pour tout entier $n \\geqslant 1$. Soit alors $E=\\left\\{u_{n} \\mid n \\geqslant 1\\right\\}$ l'ensemble des valeurs prises par les termes de cette suite. $E$ est un ensemble d'entiers non vide, de sorte qu'il admet un minimum $M$, tel que $M \\geqslant 1$ : il existe alors un entier $n \\geqslant 1$ tel que $M=u_{n}$. Notre but est de montrer que $M=1$. Nous allons donc procéder par l'absurde, et supposer que $M \\geqslant 2$.\n\nSi $M$ est pair, alors $u_{n+1}=f\\left(u_{n}\\right)=f(M)=M / 2<M$ et, puisque $u_{n+1} \\in E$, cela contredit la minimalité de $M$.\n\nSi $M$ est impair, soit $k$ l'entier naturel non nul tel que $k^{2} \\leqslant M<(k+1)^{2}$. Si $k$ est impair, alors $u_{n+1}=f(M)=M+k$, donc $M+k$ est pair, et $u_{n+2}=f\\left(u_{n+1}\\right)=f(M+k)=\\frac{M+k}{2}$. Or, $M>1$, donc $M-k \\geqslant M-\\sqrt{M}=\\sqrt{M}(\\sqrt{M}-1)>0$, de sorte que $u_{n+2}<M$ : puisque $u_{n+2} \\in E$, cela contredit la minimalité de $M$.\n\nAinsi, on sait que $M$ est impair et que $k$ est pair, donc que $k^{2}+1 \\leqslant M<(k+1)^{2}$.\n\n- Si $k^{2}+1 \\leqslant M \\leqslant k^{2}+k$, alors $k^{2} \\leqslant f(M)=M+k<(k+1)^{2}$, puis $(k+1)^{2} \\leqslant f^{2}(M)=$ $M+2 k<(k+2)^{2}$, donc $f^{3}(M)=M+3 k+1$ est pair, et enfin $f^{4}(M)=\\frac{M+3 k+1}{2}$.\n- Si $k^{2}+k+1 \\leqslant M<(k+1)^{2}$, alors $(k+1)^{2} \\leqslant f(M)=M+k<(k+2)^{2}$, donc $f^{2}(M)=$ $M+2 k+1$ est pair, et enfin $f^{3}(M)=\\frac{M+2 k+1}{2}$.\nIl s'ensuit que $M=\\min E \\leqslant \\min \\left\\{f^{3}(M), f^{4}(M)\\right\\} \\leqslant \\frac{M+3 k+1}{2}$, donc que $M \\leqslant 3 k+1$.\nEn particulier, $k^{2} \\leqslant 3 k+1$, ce qui signifie que $k^{2}-3 k-1=\\left(k-\\frac{3}{2}\\right)^{2}-\\frac{13}{4} \\leqslant 0$, donc que $k \\leqslant \\frac{3}{2}+\\sqrt{\\frac{13}{4}}<2+\\sqrt{4}=4$. Puisque $k$ est pair et $M$ impair, en déduit que $k=2$ et que $M \\in\\{5,7\\}$. On conclut donc l'exercice en montrant que $\\mathbf{f}^{5}(5)=3<5$ et que $\\mathrm{f}^{4}(7)=3<7$, ce qui permet bien d'établir que nulle valeur $M \\geqslant 2$ n'est possible.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2013", "problem_label": "6", "tier": 1, "problem": "Déterminer tous les couples d'entiers positifs ou nuls $(x, y)$ pour lesquels $x^{2}+y^{2}$ divise à la fois $x^{3}+y$ et $x+y^{3}$.", "solution": "Tout d'abord, remarquons que les couples $(x, y) \\in\\{(0,0),(1,0),(0,1),(1,1)\\}$ sont solutions.\n\nOn se place maintenant dans le cas où $(x, y)$ est une solution éventuelle autre que celles-ci. De plus, $x$ et $y$ jouant des rôles symétriques, on suppose ici que $x \\leqslant y$, donc que $y \\geqslant 2$. Si $x=0$, le problème revient à trouver $y$ tel que $y^{2}$ divise à la fois $y$ et $y^{3}$, ce qui est incompatible avec la contrainte $y \\geqslant 2$. Ainsi, $y \\geqslant 2$ et $x \\geqslant 1$, donc $x y-1 \\geqslant 1$.\n\nSoit alors $d$ le PGCD de $x$ et $y$ : on note $x=d X$ et $y=d Y$, avec $X$ et $Y$ premiers entre eux : notons que $d>0$ et que $X^{2}+Y^{2}>0$. Il s'ensuit que $d\\left(X^{2}+Y^{2}\\right)$ divise à la fois $d^{2} X^{3}+Y$ et $X+d^{2} Y^{3}$. En particulier, $d$ divise à la fois $X$ et $Y$, donc $d=1$. Par conséquent, $\\operatorname{PGCD}\\left(x^{2}+y^{2}, x\\right)=$ $\\operatorname{PGCD}\\left(\\mathrm{y}^{2}, \\mathrm{x}\\right)=1$.\n\nEn outre, $x^{2}+y^{2}$ divise $y\\left(x^{3}+y\\right)-\\left(x^{2}+y^{2}\\right)=x^{2}(x y-1)$, de sorte que, d'après le théorème de Gauss, $x^{2}+y^{2}$ divise $x y-1$. Puisque $x y-1 \\neq 0$, on en déduit que $x^{2}+y^{2} \\leqslant x y-1$. Or, $x^{2}+y^{2}=(x y-1)+\\left(x y+1+(x-y)^{2}\\right)>x y-1$. On a ainsi montré que les quatre solutions sus-mentionnées sont les seules solutions au problème.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2013", "problem_label": "7", "tier": 1, "problem": "On répartit des poids de respectivement $1 \\mathrm{~g}, 2 \\mathrm{~g}, \\ldots, 200 \\mathrm{~g}$ sur les deux plateaux d'une balance de sorte que chaque plateau contienne 100 poids.\n\nProuver que l'on peut échanger 50 poids d'un plateau avec 50 poids de l'autre plateau pour que la balance devienne équilibrée.", "solution": "Dans cette solution, on dira que deux poids sont complémentaires s'ils pèsent 201 grammes à eux deux.\n\nConsidérons alors les 100 poids situés sur le plateau de gauche. On peut les classer en trois catégories:\n\n1. les poids $a_{1}, \\ldots, a_{n}$ de 100 grammes ou moins, dont le complémentaire est également sur le plateau de gauche;\n2. leurs complémentaires, qui sont les poids $A_{1}, \\ldots, A_{n}$ de 101 grammes ou plus, dont le complémentaire est également sur le plateau de gauche (avec $A_{k}=201-a_{k}$ );\n3. enfin, les poids $b_{1}, \\ldots, b_{\\ell}$ dont le complémentaire est sur le plateau de droite.\n\nDe même, on peut classer les 100 poids du plateau de droite en trois catégories :\n\n1. les poids $c_{1}, \\ldots, c_{m}$ de 100 grammes ou moins, dont le complémentaire est également sur le plateau de droite;\n2. leurs complémentaires, qui sont les poids $C_{1}, \\ldots, C_{m}$ de 101 grammes ou plus, dont le complémentaire est également sur le plateau de gauche ; (avec $\\mathrm{C}_{\\mathrm{k}}=201-\\mathrm{c}_{\\mathrm{k}}$ );\n3. enfin, les poids $B_{1}, \\ldots, B_{\\ell}$ qui sont les complémentaires des poids $b_{1}, \\ldots, b_{\\ell}$ (avec $B_{k}=$ $201-b_{k}$ ) ; ce sont les poids du plateau de droite dont le complémentaire est sur le plateau de gauche.\nNotons que $100=2 \\mathrm{n}+\\ell=2 \\mathrm{~m}+\\ell$, de sorte que $\\mathrm{m}=\\mathrm{n}$. Deux possibilités s'offrent alors à nous:\n4. si $m=n \\geqslant 25$, on conserve sur le plateau de gauche les 50 poids $a_{1}, \\ldots, a_{25}$ et $A_{1}, \\ldots, A_{25}$, et on $y$ transfère les 50 poids $c_{1}, \\ldots, c_{25}$ et $C_{1}, \\ldots, C_{25}$; tous les autres poids sont mis sur le plateau de droite;\n5. si $\\mathrm{m}=\\mathrm{n}<25$, cela signifie que $\\ell>50$; dans ce cas, on conserve sur le plateau de gauche les 50 poids $b_{1}, \\ldots, b_{50}$ et on y transfère les 50 poids $B_{1}, \\ldots, B_{50}$; tous les autres poids sont mis sur le plateau de droite.\nDans les deux cas, on a transféré 50 poids du plateau de gauche vers le plateau de droite, et réciproquement. En outre, chacun des deux plateaux est maintenant formé de 50 paires de poids complémentaires, de sorte que chacune pèse $50 \\times 201$ grammes, et donc qu'elles ont bien le même poids.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2013-2014-ofm-2013-2014-test-mai-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "problem_label": "1", "tier": 1, "problem": "Soit $n$ un entier strictement positif. Trouver le plus petit entier $k$ ayant la propriété suivante : pour tous réels $a_{1}, \\ldots, a_{d}$ vérifiant $a_{1}+a_{2}+\\cdots+a_{d}=n$ et $0 \\leqslant a_{i} \\leqslant 1$ pour $i=1,2, \\ldots, d$, il est possible de regrouper les nombres en $k$ paquets (éventuellement vides) de sorte que la somme des nombres de chaque paquet soit $\\leqslant 1$.", "solution": "$\\triangleright$ Les réels $a_{1}=\\ldots=a_{2 n-1}=\\frac{n}{2 n-1}$ appartiennent à l'intervalle $\\left.] \\frac{1}{2}, 1\\right]$ et leur somme vaut $n$. Comme chaque réel est strictement plus grand que $\\frac{1}{2}$, chaque paquet contient au plus un de ces $2 n-1$ réels (car la somme de deux d'entre eux est strictement supérieure à 1 ) : il faut donc au moins $2 n-1$ paquets.\n$\\triangleright$ Supposons que l'on ait partitionné notre ensemble de réels $a_{1}, \\ldots, a_{d}$ en $k \\geq 2 n$ paquets et notons $\\alpha_{1} \\leq \\ldots \\leq \\alpha_{k}$ les sommes associées à ces paquets classées par ordre croissant. Alors, en regroupant ces nombres deux par deux, on obtient\n\n$$\n\\begin{aligned}\nn & =\\alpha_{1}+\\alpha_{2}+\\ldots+\\alpha_{k} \\\\\n& =\\left(\\alpha_{1}+\\alpha_{2}\\right)+\\left(\\alpha_{3}+\\alpha_{4}\\right)+\\ldots \\\\\n& \\geq\\left\\lfloor\\frac{k}{2}\\right\\rfloor\\left(\\alpha_{1}+\\alpha_{2}\\right) \\geq n\\left(\\alpha_{1}+\\alpha_{2}\\right)\n\\end{aligned}\n$$\n\nAinsi, $\\alpha_{1}+\\alpha_{2} \\leq 1$ et on peut regrouper les deux paquets correspondants en un nouveau paquet de somme totale inférieure ou égale à 1 et on est ramené à $k-1$ paquets.\n$\\triangleright$ En conclusion, il est nécessaire d'avoir $2 n-1$ paquets et, si l'on a partitionné en plus de $2 n$ paquets, on peut procéder à un regroupement et faire diminuer le nombre de paquets nécessaires. La valeur recherchée est donc $2 n-1$.", "problem_match": "\nExercice 1.", "solution_match": "## Solution de l'exercice 1"}
|
| 2 |
+
{"year": "2013", "problem_label": "2", "tier": 1, "problem": "Deux cercles $O_{1}$ et $O_{2}$ se coupent en $M$ et $N$. La tangente commune aux deux cercles la plus proche de $M$ touche $O_{1}$ et $O_{2}$ en $A$ et $B$ respectivement. Soient $C$ et $D$ les symétriques de $A$ et $B$ par rapport à $M$ respectivement. Le cercle circonscrit au triangle $D C M$ intersecte les cercles $O_{1}$ et $O_{2}$ respectivement en des points $E$ et $F$ distincts de $M$. Montrer que les cercles circonscrits aux triangles $M E F$ et $N E F$ sont de même rayon.", "solution": "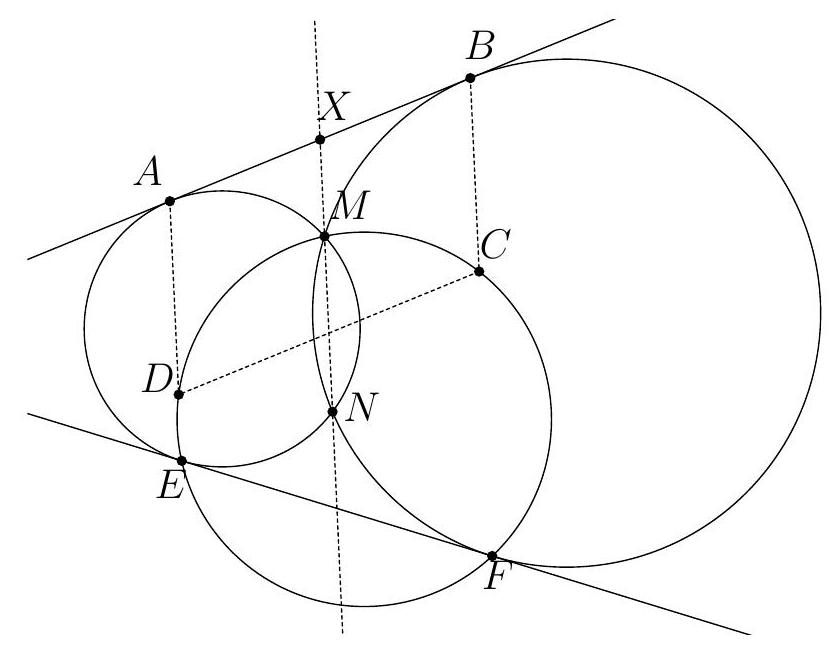\n\nMontrons d'abord que $(E F)$ l'autre tangente commune aux deux cercles.\nSoient $E^{\\prime}$ et $F^{\\prime}$ les points de contact de l'autre tangente commune. Soit $X$ le point d'intersection de $(A B)$ et de $(M N)$. On a $A X=B X$ car $X$ se situe sur l'axe radical des deux cercles. Comme $A B C D$ est un parallélogramme de centre $M$, on a $(M X) / /(A D)$, ce qui entraîne $(A D) \\perp\\left(O_{1} O_{2}\\right)$.\n\nDe plus, $A$ et $E$ étant symétriques par rapport à $\\left(O_{1} O_{2}\\right)$ on obtient que $A, D, E$ sont alignés, et de même $B, C, F$ sont alignés.\nD'après le cas limite du théorème de l'angle inscrit dans le cercle $O_{1}$, on a $(E M, E A)=(A M, A B)$, donc $(C M, C D)=(C A, C D)=(A M, A B)=(E M, E A)=(E M, E D)$, par conséquent $E^{\\prime}$ appartient au cercle $M C D$. On en conclut que $E=E^{\\prime}$, et de même $F=F^{\\prime}$.\nEn appliquant la symétrie d'axe $\\left(O_{1} O_{2}\\right)$ puis la symétrie de centre $M$ au cercle $(N E F)$, on obtient successivement le cercle $M A B$, puis le cercle $M C D$, c'est-à-dire le cercle $M E F$. Comme une symétrie conserve les longueurs, les cercles $M E F$ et $N E F$ ont même rayon.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2013", "problem_label": "3", "tier": 1, "problem": "Montrer qu'il existe une infinité d'entiers positifs $n$ tels que le plus grand facteur premier de $n^{4}+n^{2}+1$ soit égal au plus grand facteur premier de $(n+1)^{4}+(n+1)^{2}+1$.", "solution": "Pour tout $n \\geq 1$, on note $p_{n}$ le plus grand diviseur premier de $n^{4}+n^{2}+1$, et $q_{n}$ le plus grand diviseur premier de $n^{2}+n+1$.\nOn donc $p_{n}=q_{n^{2}}$.\nDe plus, de l'identité\n\n$$\nn^{4}+n^{2}+1=\\left(n^{2}+n+1\\right)\\left(n^{2}-n+1\\right)=\\left(n^{2}+n+1\\right)\\left((n-1)^{2}+(n-1)+1\\right)\n$$\n\nil découle que $p_{n}=\\max \\left(q_{n}, q_{n-1}\\right)$ pour tout $n \\geq 2$.\nD'autre part, le nombre $n^{2}-n+1=n(n-1)+1$ est impair, donc\n\n$$\n\\operatorname{pgcd}\\left(n^{2}+n+1, n^{2}-n+1\\right)=\\operatorname{pgcd}\\left(2 n, n^{2}-n+1\\right)=\\operatorname{pgcd}\\left(n, n^{2}-n+1\\right)=1\n$$\n\nAinsi, on a $q_{n} \\neq q_{n-1}$.\nPour conclure, il suffit alors de prouver que l'ensemble\n\n$$\nS=\\left\\{n \\geq 2 \\mid q_{n}>q_{n-1} \\text { et } q_{n}>q_{n+1}\\right\\}\n$$\n\nest infini, puisque pour tout $n \\in S$, on a\n\n$$\np_{n}=\\max \\left(q_{n}, q_{n-1}\\right)=q_{n}=\\max \\left(q_{n}, q_{n+1}\\right)=p_{n+1} .\n$$\n\nPar l'absurde: supposons que $S$ soit fini.\nPuisque $q_{2}=q_{4}=7<13=q_{3}$, on peut affirmer que $S$ n'est pas vide. Puisqu'il est fini, il possède alors un plus grand élément, disons $m$.\nLa suite $\\left(q_{n}\\right)_{n \\geq m}$ ne peut être strictement décroissante puisqu'elle est formée d'entiers positifs. Il existe donc $k \\geq m$ tel que $q_{k}<q_{k+1}$ (on rappelle que $q_{k} \\neq q_{k+1}$ ). Mais, il est également impossible d'avoir $\\left(q_{n}\\right)_{n \\geq k}$ strictement croissante car $q_{(k+1)^{2}}=p_{k+1}=\\max \\left(q_{k}, q_{k+1}\\right)=q_{k+1}$. Notons alors $t$ le plus petit entier supérieur ou égal à $k+1$ tel que $q_{t}>q_{t+1}$. La minimalité de $t$ assure que l'on a $q_{t-1}<q_{t}$, et donc que $t \\in S$.\nPourtant, on a $t \\geq k+1>k \\geq m$, ce qui contredit la maximalité de $m$.\nPar suite, on a $S$ infini, ce qui conclut.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2013", "problem_label": "4", "tier": 1, "problem": "On note $\\mathbb{N}^{*}$ l'ensemble des entiers naturels strictement positifs. Trouver toutes les $^{2}$ fonctions $f: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ telles que\n\n$$\nm^{2}+f(n) \\mid m f(m)+n\n$$\n\npour tous entiers strictement positifs $m$ et $n$.", "solution": "Soit $f$ une solution éventuelle du problème.\nOn note ( $\\left.{ }^{*}\\right)$ la condition \" $m^{2}+f(n)$ divise $m f(m)+n$ \".\nEn choisissant $m=n=2$ dans $\\left(^{*}\\right.$ ), il vient que $4+f(2)$ divise $2 f(2)+2$. Or, on a $2 f(2)+2<$ $2(f(2)+4)$, et il faut donc que $f(2)+4=2 f(2)+2$, d'où $f(2)=2$.\n\nEn choisissant maintenant $m=2$, la condition ( ${ }^{*}$ ) assure que, pour tout $n \\geq 1$, le nombre $4+f(n)$ divise $4+n$, ce qui conduit à $f(n) \\leq n$, pour tout $n \\geq 1$. (i)\n\nD'autre part, en choisissant $m=n$ dans $\\left({ }^{*}\\right)$, on déduit cette fois que, pour tout $n \\geq 1$, le nombre $n^{2}+f(n)$ divise $n f(n)+n$, d'où $n^{2}+f(n) \\leq n f(n)+n$. Ainsi, on a $(n-1)(f(n)-n) \\geq 0$, ce qui conduit à $f(n) \\geq n$, pour tout $n \\geq 2$. Puisqu'on a clairement $f(1) \\geq 1$, c'est donc que $f(n) \\geq n$ pour tout $n \\geq 1$. (ii)\n\nDe (i) et (ii), on déduit que $f(n)=n$ pour tout $n \\geq 1$.\nRéciproquement, il est évident que $f: n \\longmapsto n$ est bien une solution du problème.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2013", "problem_label": "5", "tier": 1, "problem": "Soit $n$ un entier strictement positif et $x_{1}, \\ldots, x_{n}$ des réels strictement positifs. Montrer qu'il existe des nombres $a_{1}, \\ldots, a_{n} \\in\\{-1,1\\}$ tels que :\n\n$$\na_{1} x_{1}^{2}+a_{2} x_{2}^{2}+\\cdots+a_{n} x_{n}^{2} \\geqslant\\left(a_{1} x_{1}+a_{2} x_{2}+\\cdots+a_{n} x_{n}\\right)^{2} .\n$$", "solution": "Commençons par ordonner les réels $x_{k}$ de sorte à ce que $x_{1} \\geq x_{2} \\geq \\ldots \\geq x_{n}>0$.\nMontrons par récurrence forte qu'une solution est fournie par la suite de coefficients définie par $a_{k}=1$ si $k$ est impair et $a_{k}=-1$ si $k$ est pair.\n$\\triangleright \\operatorname{Si} n=1, a_{1} x_{1}^{2}=\\left(a_{1} x_{1}\\right)^{2}$ donc l'inégalité est vérifiée.\n$\\triangleright$ Si $n=2, a_{1} x_{1}^{2}+a_{2} x_{2}^{2}=x_{1}^{2}-x_{2}^{2} \\geq x_{1}^{2}-2 x_{1} x_{2}+x_{2}^{2}=\\left(x_{1}-x_{2}\\right)^{2}$ car $x_{1} \\geq x_{2}$; l'inégalité est encore vérifiée.\n$\\triangleright$ Soit $n \\geq 3$. Supposons que le résultat est établi jusqu'au rang $n-1$ et montrons l'inégalité au rang $n$.\nLa différence des deux membres est alors\n\n$$\na_{1} x_{1}^{2}+\\ldots+a_{n} x_{n}^{2}-\\left(a_{1} x_{1}+\\ldots+a_{n} x_{n}\\right)^{2}=\\alpha x_{1}+\\beta\n$$\n\navec\n\n$$\n\\alpha=-2\\left(a_{2} x_{2}+\\ldots+a_{n} x_{n}\\right)=2\\left(\\left(x_{2}-x_{3}\\right)+\\left(x_{4}-x_{5}\\right)+\\ldots\\right) \\leq 0\n$$\n\ncar $x_{2} \\geq x_{3}, x_{4} \\geq x_{5}, \\ldots$ Par conséquent, en utilisant la croissance de la fonction $x \\mapsto \\alpha x+\\beta$ et $x_{1} \\geq x_{2}$,\n\n$$\n\\begin{aligned}\na_{1} x_{1}^{2}+\\ldots+a_{n} x_{n}^{2}-\\left(a_{1} x_{1}+\\ldots+a_{n} x_{n}\\right)^{2} & \\geq \\alpha x_{2}+\\beta \\\\\n& \\geq a_{1} x_{2}^{2}+a_{2} x_{2}^{2} \\ldots+a_{n} x_{n}^{2}-\\left(a_{1} x_{2}+a_{2} x_{2}+\\ldots+a_{n} x_{n}\\right)^{2} \\\\\n& \\geq a_{3} x_{1}^{3}+\\ldots+a_{n} x_{n}^{2}-\\left(a_{3} x_{3}+\\ldots+a_{n} x_{n}\\right)^{2}\n\\end{aligned}\n$$\n\ncar $a_{1}=-a_{2}$ et donc $a_{1} x_{1}^{2}+a_{2} x_{2}^{2}=a_{1} x_{1}+a_{2} x_{2}=0$. Le dernier terme est positif d'après l'hypothèse de récurrence avec les réels $x_{3}, \\ldots, x_{n}$ ce qui termine la preuve de l'inégalité au rang $n$.", "problem_match": "\nExercice 5.", "solution_match": "## Solution de l'exercice 5"}
|
| 6 |
+
{"year": "2013", "problem_label": "6", "tier": 1, "problem": "Soit $\\omega$ le cercle circonscrit à un triangle $A B C$. On désigne par $M$ et $N$ les milieux des côtés $[A B]$ et $[A C]$ respectivement, et par $T$ le milieu de l'arc $B C$ de $\\omega$ ne contenant pas $A$. Les cercles circonscrits aux triangles $A M T$ et $A N T$ rencontrent les médiatrices de $[A C]$ et $[A B]$ aux points $X$ et $Y$ respectivement; on suppose que $X$ et $Y$ sont à l'intérieur du triangle $A B C$. Les droites $(M N)$ et $(X Y)$ se coupent en $K$. Montrer que $K A=K T$.", "solution": "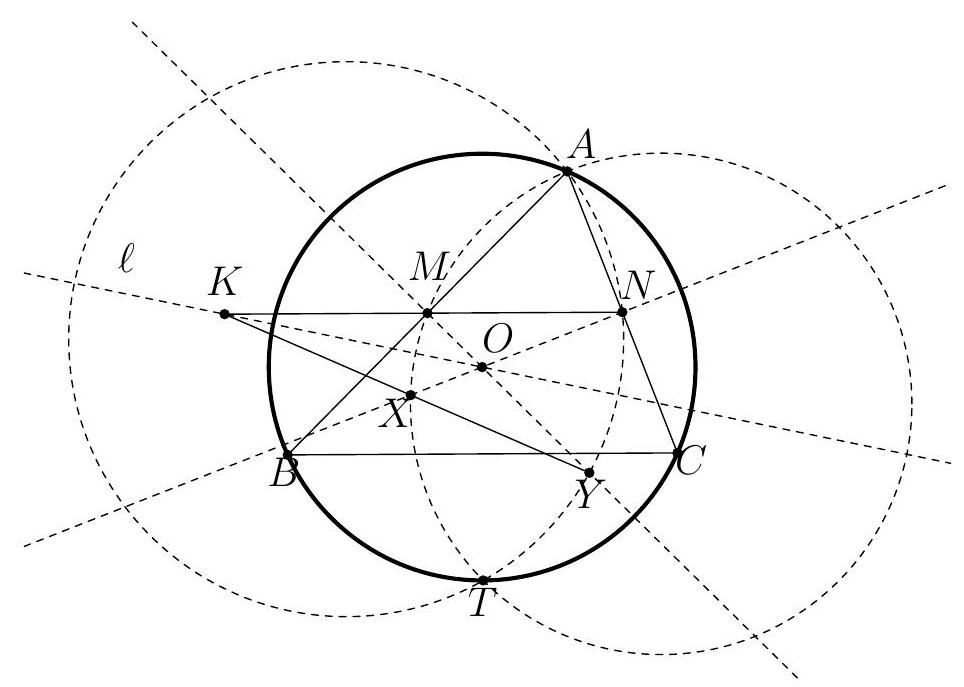\n\nNotons $O$ le centre du cercle $\\omega$. On a $O=(M Y) \\cap(N X)$. Soit $\\ell$ la médiatrice de $[A T]$. Elle passe par $O$.\nNotons $s$ la symétrie par rapport à $\\ell$. Comme $(A T)$ est la bissectrice de $\\widehat{B A C}$, la droite $s(A B)$ est parallèle à $(A C)$. Comme $(O M) \\perp(A B)$ et $(O N) \\perp(A C)$, la droite $s(O M)$ est parallèle à $(O N)$. Or, elle passe par $O$, donc $s(O M)=(O N)$.\nDe plus, le cercle circonscrit $\\gamma$ à $A M T$ est symétrique par rapport à $\\ell$, c'est-à-dire $s(\\gamma)=\\gamma$, donc $s(M)$ appartient à la fois à $\\gamma$ et à $s(O M)=(O N)$. Nécessairement, $s(M)=X$. De même, $s(N)=Y$. On en déduit que $s(M N)=(X Y)$. Le point commun $K \\operatorname{de}(M N)$ et $(X Y)$ appartient ainsi à la droite $\\ell$, ce qui implique que $K A=K T$.", "problem_match": "\nExercice 6.", "solution_match": "## Solution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2014-2015-ofm-2014-2015-test-fevrier-corrige.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "Dans un pays, se trouvent 100 villes. Chacune de ces villes est reliée à exactement trois autres villes par des routes directes dans les deux sens. Prouver qu'il existe une ville $A$ à partir de laquelle on peut aller de ville en ville et revenir en $A$, sans jamais passer deux fois par une même route, et en utilisant un nombre total de routes qui n'est pas divisible par 3 (il n'est pas demandé que toutes les villes du pays soient visitées au cours de ce voyage).", "solution": "Puisqu'il n'y a qu'un nombre fini de villes, on peut considérer un chemin C de longueur maximale. Soit $v_{0}$ une des villes extrémités de C et parcourons C en partant de $v_{0}$ en numérotant les villes au fur et à mesure. La maximalité de C assure que les trois villes reliées à $v_{0}$ par une route sont dans C. Il s'agit de $v_{1}, \\nu_{i}$ et $v_{j}$ avec $1<i<j$. On a ainsi identifié trois cycles :\n\n$$\n\\begin{gathered}\nv_{0}, v_{1}, \\cdots, v_{i}, v_{0} \\text {, de longueur } \\mathfrak{i}+1, \\\\\nv_{0}, v 1, \\cdots, v_{j}, v_{0} \\text {, de longueur } \\mathfrak{j}+1 \\\\\nv_{0}, v_{i}, v_{i+1}, \\cdots, v_{j}, v_{0}, \\text { de longueur } \\mathfrak{j}-\\mathfrak{i}+2\n\\end{gathered}\n$$\n\nSi $i+1$ ou $j+1$ n'est pas divisible par 3, l'un des deux premiers cycles convient. Sinon, c'est que $\\boldsymbol{i}=\\mathbf{j}=-1 \\bmod 3, d^{\\prime}$ où $\\boldsymbol{j}-\\mathfrak{i}+2=2 \\bmod 3$ et le troisième cycle permet de conclure.", "problem_match": "\nExercice 1.", "solution_match": "## Solution de l'exercice 1"}
|
| 2 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Déterminer tous les polynômes P à coefficients dans $\\mathbb{Z}$ tels que, pour tous $p$ premier et $u$ et $v$ dans $\\mathbb{Z}$ tels que $p \\mid u v-1$ on ait : $p \\mid P(u) P(v)-1$.", "solution": "Soit f un tel polynôme, et $\\mathrm{n} \\geqslant 0$ son degré. Clairement $\\mathrm{f} \\mathrm{n}^{\\prime}$ est pas le polynôme nul.\nPosons $g(X)=X^{n} f\\left(\\frac{1}{X}\\right)$. Alors $g$ est un polynôme à coefficients entiers.\nSoit $x$ un entier non nul, et $p$ un nombre premier avec $p>\\max \\left(|x|,\\left|f(x) g(x)-x^{n}\\right|\\right)$. Alors $x$ est inversible modulo $p$, et il existe $y>0$ tel que $x y=1 \\bmod p$. On vérifie facilement que $x^{n} f(y)=g(x) \\bmod [p]$.\n\nD'autre part, on sait que $f(x) f(y)=1 \\bmod p$, $d^{\\prime}$ où $x^{n}=x^{n} f(x) f(y)=f(x) g(x) \\bmod [p]$. Ainsi $p$ divise $f(x) g(x)-x^{n}$ avec $p>\\left|f(x) g(x)-x^{n}\\right|$, d'où $f(x) g(x)=x^{n}$, pour tout $x \\neq 0$ (et donc aussi pour $x=0$ comme égalité entre deux polynômes).\n\nPuisque $f$ est de degré $n$, on en déduit que $g$ est constant et que $f(X)=a X^{n}$, où $a$ est un entier. En reportant dans $f(x) g(x)=x^{n}$, il vient immédiatement $a= \\pm 1$, et donc $f(X)= \\pm X^{n}$.\n\nRéciproquement, tout polynôme de la forme $f(X)= \\pm X^{n}$ est bien une solution du problème puisque, pour tous entiers $u$ et $v$ et tout nombre premier $p$, si $u v=1 \\bmod [p]$ alors $u^{n} v^{n}=$ $1 \\bmod [p]$.\n\nFinalement, les polynômes cherchés sont ceux de la forme $f(X)= \\pm X^{n}$, avec $n \\in \\mathbb{N}$.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle non isocèle en $A$ et $\\Gamma$ son cercle circonscrit. Soit $N$ le milieu de l'arc de $\\Gamma$ entre $B$ et $C$ qui contient $A$. Soient $I$ le centre du cercle inscrit à $A B C, J$ le centre du cercle $A$-exinscrit à $A B C$ et $K$ le point d'intersection de ( $B C)$ avec la bissectrice extérieure de $\\angle B A C$.\n\nMontrer que $(\\mathrm{JN}) \\perp(\\mathrm{IK})$.", "solution": "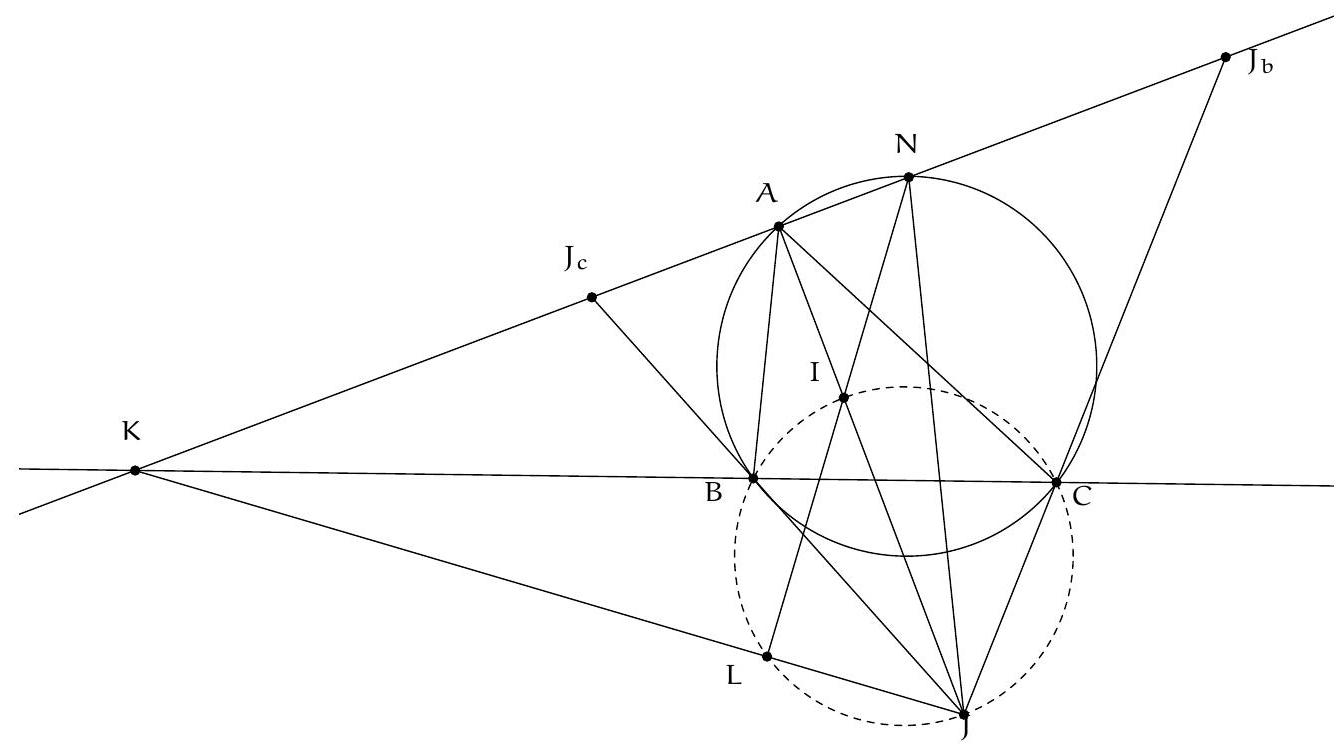\n\nNotons $\\mathrm{J}_{\\mathrm{b}}$ et $\\mathrm{J}_{\\mathrm{c}}$ les centres des cercles exinscrits dans les angles $\\widehat{\\mathrm{B}}$ et $\\widehat{\\mathrm{C}}$. Alors I est l'orthocentre de $J_{b} J_{c}$. En utilisant le fait que $B$ et $C$ sont sur le cercle de diamètre $J_{b} J_{c}$, et que $A, B, C, N$ sont cocycliques, on a $\\overline{\\mathrm{KJ}_{\\mathrm{b}}} \\cdot \\overline{\\mathrm{KJ}} \\mathrm{c}=\\overline{\\mathrm{KB}} \\cdot \\overline{\\mathrm{KC}}=\\overline{\\mathrm{KA}} \\cdot \\overline{\\mathrm{KN}}$, donc\n\n$$\n\\begin{aligned}\n\\left(\\overline{\\mathrm{KA}}+\\overline{A J_{b}}\\right)\\left(\\overline{\\mathrm{KA}}+\\overline{A J_{c}}\\right) & =\\overline{\\mathrm{KA}} \\cdot(\\overline{\\mathrm{KA}}+\\overline{\\mathrm{AN}}) \\\\\n\\overline{\\mathrm{KA}}\\left(\\overline{A J_{b}}+\\overline{A J_{c}}+\\overline{N A}\\right) & =-\\overline{A J_{b}} \\cdot \\overline{A J_{c}}\n\\end{aligned}\n$$\n\nOr, $\\overline{A J_{b}}+\\overline{A J_{c}}+\\overline{N A}=\\overline{N J_{b}}+\\overline{A J_{c}}=\\overline{J_{c} N}+\\overline{A J_{c}}=\\overline{A N}$, donc $\\overline{K A}=-\\frac{\\overline{A J_{b}} \\cdot \\overline{A J_{c}}}{\\overline{A N}}$.\nOr, I étant l'orthocentre de $J_{b} J_{c}$, on a $\\frac{I A}{A J_{b}}=\\frac{A J_{c}}{A J}$. Il vient $\\frac{I A}{K A}=\\frac{A N}{A J}$, donc les triangles rectangles KAI et JAN sont semblables. Comme $(\\mathrm{KA}) \\perp(\\mathrm{JA})$, il vient $(\\mathrm{KI}) \\perp(\\mathrm{JN})$.\n\nAutre solution. Il suffit de montrer que I est l'orthocentre de KJN . Comme $(\\mathrm{AJ}) \\perp(\\mathrm{KN})$, il suffit de voir que (NI) $\\perp(\\mathrm{KJ})$.\n\nSoit $\\omega$ le cercle de diamètre $[\\mathrm{IJ}]$. Il contient les points B et C . Soit L le second point d'intersection de (KJ) avec $\\omega$. On a $\\overline{\\mathrm{KL}} \\cdot \\overline{\\mathrm{KJ}}=\\overline{\\mathrm{KB}} \\cdot \\overline{\\mathrm{KC}}=\\overline{\\mathrm{KA}} \\cdot \\overline{\\mathrm{KN}}$ donc $A, N, L$, J sont cocycliques.\n\nOr, $(J A) \\perp($ AN $)$, donc $(J L) \\perp(L N)$.\nDe plus, comme $\\omega$ a pour diamètre [IJ], on a (JL) $\\perp$ (IL), donc N, I, L sont alignés. Il vient $(\\mathrm{NI}) \\perp(\\mathrm{JL})$.", "problem_match": "\nExercice 3.", "solution_match": "## Solution de l'exercice 3"}
|
| 4 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "Déterminer tous les polynômes P et Q à coefficients entiers tels que, si l'on définit la suite $\\left(x_{n}\\right)$ par $x_{0}=2015, x_{2 n+1}=P\\left(x_{2 n}\\right)$ et $x_{2 n+2}=\\mathrm{Q}\\left(x_{2 n+1}\\right)$ pour tout $n \\geqslant 0$, alors tout entier $\\mathrm{m}>0$ divise au moins un terme non nul de la suite.", "solution": "Soit P et Q deux tels polynômes.\nOn dira qu'une suite $\\left(\\mathrm{y}_{\\mathrm{n}}\\right)$ d'entiers possède la propriété D si tout entier $\\mathrm{m}>0$ divise au moins un terme non nul de cette suite. On dira qu'un polynôme T à coefficients entiers possède la propriété D s'il existe un entier a tel que la suite $\\left(x_{n}\\right)$ définie par $x_{0}=a$ et $x_{n+1}=T\\left(x_{n}\\right)$ possède la propriété D.\n\nNous débutons maintenant par trois lemmes.\nLemme 1. Soit ( $x_{n}$ ) une suite d'entiers et soit $k$ un entier naturel non nul. Alors ( $x_{n}$ ) possède la propriété D si et seulement si l'une des $k$ suites $\\left(x_{k n}\\right),\\left(x_{k n+1}\\right), \\ldots,\\left(x_{k n+k-1}\\right)$ possède la propriété D.\n\nPreuve du lemme 1. Supposons d'abord qu'aucune des $k$ suites $\\left(x_{k n}\\right),\\left(x_{k n+1}\\right), \\ldots,\\left(x_{k n+k-1}\\right)$ ne possède la propriété $D$. Alors, pour chaque entier $\\ell \\in\\{0,1, \\ldots, k-1\\}$, il existe un entier $M_{\\ell}$ qui ne divise aucun terme non nul de la suite ( $x_{k n+\\ell}$ ). En particulier, l'entier $\\prod_{\\ell=0}^{k-1} M_{\\ell}$ ne peut donc diviser aucun terme non nul de la suite $\\left(x_{n}\\right)$, qui ne peut posséder la propriété D non plus.\n\nRéciproquement, si une suite $\\left(x_{k n+\\ell}\\right)$ a la propriété $D$, alors clairement $\\left(x_{n}\\right)$ a la propriété $D$ aussi.\n\nLemme 2. Soit T un polynôme à coefficients entiers, de degré d et de coefficient dominant $\\rho$. Si R possède la propriété D , alors $\\mathrm{d}=1$ et $|\\rho|<4$.\n\nPreuve du lemme 2. Si T est constant, la suite ( $x_{n}$ ) ne prend qu'un nombre fini de valeurs distinctes, ce qui lui interdit d'avoir la propriété D. Procédons maintenant par l'absurde, et supposons que $d \\geqslant 2$ ou que $d=1$ et $|\\rho| \\geqslant 4$. Il existe alors un réel $c>0$ tel que\n\n$$\n|\\mathrm{T}(\\mathrm{x})|>3|x| \\text { pour tout } x \\text { tel que }|x|>c \\text {. (1) }\n$$\n\nOn note qu'il n'existe qu'un nombre fini d'entiers dans [-c; c] et que chacun d'eux ne peut être atteint qu'un nombre fini de fois par $T$. Ainsi, il existe un entier $N \\geqslant 0$ tel que $\\left|x_{N}\\right|>c$. Une récurrence immédiate à l'aide de (1) montre qu'alors $\\left|x_{i}\\right|>c$ pour tout $i \\geqslant N$.\n\nDe plus, sans perte de généralité, on peut choisir $N$ minimal ayant cette propriété. On a donc\n\n$$\n\\left|x_{i}\\right| \\leqslant c \\text { pour tout } i<N, \\text { et }\\left|x_{i}\\right|>c \\text { pour tout } i \\geqslant N \\text {. (2) }\n$$\n\nEn particulier, de (1) et (2), on déduit que $\\left|x_{N+1}\\right|>\\max \\left(c,\\left|x_{0}\\right|, \\cdots,\\left|x_{N}\\right|\\right)$.\nPosons $m=\\left|x_{N+1}-x_{N}\\right|$, qui est bien un entier strictement positif. Alors:\n$m \\geqslant\\left|x_{N+1}\\right|-\\left|x_{N}\\right|>2\\left|x_{N}\\right|>\\max \\left(\\left|x_{0}\\right|, \\cdots,\\left|x_{N}\\right|\\right)$, ce qui assure $m$ ne divise aucun $x_{i}$ non nul lorsque $i \\leqslant N$. Mais alors $m$ ne divise pas $x_{N+1}$ non plus.\n\nD'autre part, puisque $T$ est à coefficients entiers, $x_{n+1}-x_{n}=T\\left(x_{n}\\right)-T\\left(x_{n-1}\\right)$ est divisible par $x_{n}-x_{n-1}$ pour tout $n \\geqslant 1$. En particulier, pour tout $n \\geqslant N$, on a $x_{n+1}-x_{n}$ divisible par $m$, et donc\n\n$$\nx_{n+1}-x_{N+1}=\\left(x_{n+1}-x_{n}\\right)+\\left(x_{n}-x_{n-1}\\right)+\\cdots+\\left(x_{N+2}-x_{N+1}\\right)\n$$\n\nest lui aussi divisible par $m$. Mais, $m$ ne divisant pas $x_{N+1}$, il ne divise donc pas non plus $x_{n}$ pour tout $n \\geqslant N+1$. Finalement, $m$ ne divise aucun terme non nul de la suite, en contradiction avec l'hypothèse que $\\left(x_{n}\\right)$ possède la propriété $D$.\n\nLemme 3. Soit $T(X)=\\rho X+\\theta$ un polynôme à coefficients entiers. Si $T$ possède la propriété $D$, alors $\\rho=1$.\n\nPreuve du lemme 3. Si T possède la propriété D , soit $x_{0}$ un entier tel que la suite ( $x_{n}$ ) définie par $x_{n+1}=T\\left(x_{n}\\right)$ ait la propriété $D$. D'après le lemme 1, l'une des suites $\\left(x_{2 n}\\right)$ et $\\left(x_{2 n+1}\\right)$ a la propriété $D$, et satisfait bien $x_{n+2}=T\\left(T\\left(x_{n}\\right)\\right)$. Le polynôme $T(T(X))$ a donc également la propriété D .\n\nOr, $T(T(X))$ est de coefficient dominant $\\rho^{2}$. Le lemme 2 montre donc que $\\rho^{2}<4$, donc que $\\rho \\in\\{-1,0,1\\}$. Puisque $\\rho$ est un coefficient dominant de $T$, on a nécessairement $\\rho \\neq 0$. De plus, si $\\rho=-1$, alors $T(T(X))=X$ n'a pas la propriété $D$. Il s'ensuit que $\\rho=1$.\n\nRevenons maintenant à l'exercice.\nOn pose $H(X)=P(Q(X))$ et $K(X)=Q(P(X))$.\nD'après le lemme 1, l'une des deux suites ( $\\mathrm{x}_{2 \\mathrm{k}}$ ) et $\\left(\\mathrm{x}_{2 \\mathrm{k}+1}\\right)$ possède la propriété D , donc l'un des polynômes H et K possède la propriété D , car $\\mathrm{x}_{2 \\mathrm{k}+2}=\\mathrm{H}\\left(\\mathrm{x}_{2 \\mathrm{k}}\\right)$ et $\\mathrm{x}_{2 \\mathrm{k}+3}=\\mathrm{K}\\left(\\mathrm{x}_{2 \\mathrm{k}+1}\\right)$.\n\nPuisque $\\operatorname{deg} H=(\\operatorname{deg} P) \\cdot(\\operatorname{deg} Q)=\\operatorname{deg} K$, le lemme 2 indique que $\\operatorname{deg} H=\\operatorname{deg} P=\\operatorname{deg} \\mathbf{Q}=$ $\\operatorname{deg} K=1$. Notons alors $P(X)=a X+b$ et $Q(X)=c X+d$. On a alors $H(X)=a c X+a d+b$ et $K(X)=a c X+b c+d$, donc le lemme 3 indique que $a=c= \\pm 1$.\n\nFinalement, notons que $x_{2 n}=2015+(a d+b) n$ et que $x_{2 n+1}=(a 2015+d)+(b c+d) n$. Or, une suite arithmétique $\\left(y_{n}\\right)$ de raison $r$ a la propriété $D$ si et seulement si $r$ divise $y_{0}$ :\n\n- si $y_{0}=q r$, et si $m \\in \\mathbb{N}^{*}$, alors $q^{2} m-q \\geqslant 0$ et $m$ divise $y_{q^{2} m-q}=q^{2} m r$;\n- si $r$ ne divise pas $y_{0}$, alors $r$ ne divise aucun entier $y_{n}$.\n\nOr, le lemme 1 inidique que $\\left(x_{n}\\right)$ a la propriété $D$ si et seulement si $\\left(x_{2 n}\\right)$ ou $\\left(x_{2 n+1}\\right)$ a la propriété $D$. Dans le premier cas, cela signifie que $a d+b$ divise $x_{0}=2005$. Dans le second cas, cela signifie que $b c+d$ divise $x_{1}=2005 c+d$. Or, notons que $|a d+b|=|b c+d|$.\n\nLes paires des polynômes $(P(X), Q(X))$ recherchées sont donc les paires $(P(X), Q(X))=$ $(\\varepsilon X+b, \\varepsilon X+d)$ telles que $\\varepsilon= \\pm 1$ et $b+\\varepsilon$ d divise 2005 ou $2005+\\varepsilon d$.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
French_TST_Senior/segmented/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "Déterminer tous les nombres réels $x, y, z$ satisfaisant le système d'équations suivant : $x=\\sqrt{2 y+3}, y=\\sqrt{2 z+3}, z=\\sqrt{2 x+3}$.", "solution": "Il est évident que les nombres $x, y, z$ doivent être strictement positifs. Les deux premières équations donnent $x^{2}=2 y+3$ et $y^{2}=2 z+3$. En les soustrayant, on obtient $x^{2}-y^{2}=2(y-z)$. On en déduit que si $x \\leqslant y$ alors $y \\leqslant z$, et de même si $y \\leqslant z$ alors $z \\leqslant x$. Donc si $x \\leqslant y$, on a $x \\leqslant y \\leqslant z \\leqslant x$, ce qui impose que $x=y=z$.\n\nOn montre de même que si $x \\geqslant y$ alors $x=y=z$. Donc dans tous les cas, $x, y, z$ sont égaux, et leur valeur commune satisfait l'équation $x^{2}=2 x+3$, qui s'écrit encore $(x-3)(x+1)=0$. Or, $x$ est strictement positif, donc nécessairement $x=y=z=3$. Réciproquement, on vérifie immédiatement que $x=y=z=3$ est bien solution du système.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Soient $n$ et $k$ des entiers strictement positifs. Il y a $n k$ objets (de même taille) et $k$ boîtes qui peuvent contenir chacune $n$ objets. Chaque objet est colorié en une couleur parmi $k$ couleurs possibles. Montrer qu'il est possible de ranger les objets dans les boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.", "solution": "On le montre par récurrence sur $k$. Si $k=1 c^{\\prime}$ est évident. Supposons la propriété vraie pour tous les entiers $<k$.\n\nSi l'une des couleurs $c$ est prise exactement $n$ fois, on range tous les objets dont la couleur est $c$ dans la dernière boîte. L'hypothèse de récurrence permet de ranger les $n(k-1)$ objets restants dans les $k-1$ premières boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.\n\nSupposons donc qu'aucune couleur ne soit prise exactement $n$ fois. Si toutes les couleurs sont prises $\\leqslant n-1$ fois, alors il y a au plus $(n-1) k$ objets au total, ce qui contredit l'hypothèse. Donc l'une des couleurs $c_{1}$ est prise $\\geqslant n+1$ fois. De même, l'une des couleurs $c_{2}$ est prise $\\leqslant n-1$ fois.\n\nOn place alors tous les objets de couleur $c_{2}$ dans la dernière boîte. On complète cette boîte avec des objets de couleur $c_{1}$. L'hypothèse de récurrence permet de ranger les $n(k-1)$ objets restants dans les $k-1$ premières boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "On dit qu'un entier strictement positif $n$ est amusant si pour tout diviseur strictement positif $d$ de $n$, l'entier $d+2$ est premier. Déterminer tous les entiers amusants dont le nombre de diviseurs est maximum.", "solution": "Soit $n$ un entier amusant et $p$ un diviseur premier de $n$. Alors $p$ est impair, puisque $p+2$ est premier.\n\nSupposons que $p \\geqslant 5$. Alors $p+2$ est premier, et $p+2>3$, donc $p+2$ n'est pas divisible par 3. On en déduit que $p$ n'est pas congru à 1 modulo 3 . Il est clair que $p \\mathrm{n}^{\\prime}$ est pas congru à 0 modulo 3 , donc $p \\equiv 2(\\bmod 3)$. Supposons que $p^{2} \\mid n$. Alors $p^{2} \\equiv 1(\\bmod 3)$, donc $p^{2}+2 \\equiv 0$ $(\\bmod 3)$. De plus, $p^{2}+2$ est premier, donc $p^{2}+2=3$, ce qui est impossible.\n\nOn déduit de ce qui précède que si $p \\geqslant 5$ est un diviseur premier de $n$, alors $p^{2}$ ne divise pas $n$.\n\nDe même, si $p_{1}$ et $p_{2}$ sont des diviseurs premiers distincts $\\geqslant 5$ de $n$, alors $p_{1} p_{2}$ divise $n$, donc $p_{1} p_{2}+2$ est divisible par 3 , ce qui est impossible.\n\nPar conséquent, tout entier amusant $n$ est de la forme $n=3^{k}$ ou bien $3^{k} p$ où $p$ est premier.\nOn vérifie que $3+2,3^{2}+2,3^{3}+2$ et $3^{4}+2$ sont premiers mais $3^{5}+2$ ne l'est pas, donc $k \\leqslant 4$. Les entiers amusants de la forme $3^{k}$ ont donc au plus 5 diviseurs.\n\nSi $n=3^{4} \\times 5=405$, alors $n+2$ n'est pas premier donc $n$ n'est pas amusant.\nSi $n=3^{k} p$ avec $p \\geqslant 7$ premier, et $k \\geqslant 3$, alors les nombres $p, 3 p, 9 p, 27 p$ sont des diviseurs de $n$ congrus à $p, 3 p, 4 p, 2 p$ modulo 5 . Aucun n'est congru à 0 modulo 5 , et les congruences de ces quatre nombres modulo 5 sont deux à deux distinctes, donc à l'ordre près valent $1,2,3,4$. On en déduit qu'il existe un diviseur $d \\geqslant 7$ de $n$ tel que $d \\equiv 3(\\bmod 5)$. On a donc $d+2>5$ et $5 \\mid d$, ce qui entraîne que $d$ n'est pas premier.\n\nOn déduit de ce qui précède que les entiers amusants de la forme $3^{k} p$ vérifient $k \\leqslant 2$ ou bien $(k \\leqslant 3$ et $p=5$ ), donc ont au plus 8 diviseurs, avec égalité seulement lorsque $k=3$ et $p=5$. Réciproquement, on vérifie que $3^{3} \\times 5$ est amusant, donc l'unique entier ammusant ayant un nombre maximal de diviseurs est $3^{3} \\times 5=135$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "Soit $A B C$ un triangle non isocèle. Soit $\\omega$ le cercle inscrit et $I$ son centre. On note $M, N, P$ les points de contact de $\\omega$ avec les côtés $[B C],[C A],[A B]$. Soit $J$ le point d'intersection entre $(M N)$ et $(I C)$. La droite $(P J)$ recoupe $\\omega$ en $K$. Montrer que\na) $C K I P$ est cyclique;\nb) $(C I)$ est la bissectrice de $\\widehat{P C K}$.", "solution": "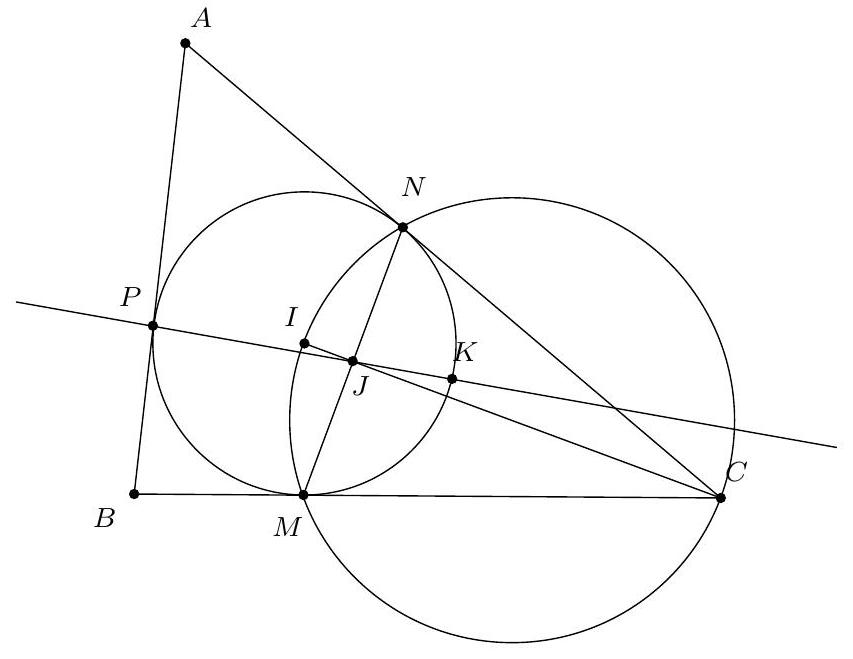\na) Comme $(I N) \\perp(N C)$ et $(I M) \\perp(M C)$, les points $M$ et $N$ sont situés sur le cercle de diamètre [IC], donc $I, M, C, N$ sont cocycliques.\n\nD'après la puissance d'un point par rapport à ce cercle, on a $J I \\cdot J C=J M \\cdot J N$. D'autre part, en utilisant la puissance par rapport au cercle inscrit, on a $J M \\cdot J N=J K \\cdot J P$, donc finalement $J I \\cdot J C=J K \\cdot J P$, ce qui entraîne que $P, I, K, C$ sont cocycliques.\nb) D'après la question a), on a $\\widehat{I C P}=\\widehat{I K P}$ et $\\widehat{K C I}=\\widehat{K P I}$. Or, $I P K$ est isocèle en $I$, donc $\\widehat{I K P}=\\widehat{K P I}$, ce qui entraîne que $\\widehat{I C P}=\\widehat{K C I}$.", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
French_TST_Senior/segmented/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "problem_label": "1", "tier": 1, "problem": "a) Prouver que, pour tous réels strictement positifs $a, b, k$ tels que $a<b$, on a\n\n$$\n\\frac{a}{b}<\\frac{a+k}{b+k}\n$$\n\nb) Prouver que\n\n$$\n\\frac{1}{100}+\\frac{4}{101}+\\frac{7}{102}+\\frac{10}{103}+\\cdots+\\frac{148}{149}>25\n$$", "solution": "a) On a $a k<b k$, donc $a b+a k<a b+b k$. Ceci s'écrit $a(b+k)<b(a+k)$, ou encore $\\frac{a}{b}<\\frac{a+k}{b+k}$.\nb) Soit $A=\\frac{1}{100}+\\frac{4}{101}+\\frac{7}{102}+\\frac{10}{103}+\\cdots+\\frac{148}{149}$. En appliquant ce qui précède, on en déduit\n\n$$\nA>\\frac{1}{100}+\\frac{3}{100}+\\frac{5}{100}+\\frac{7}{100}+\\cdots+\\frac{99}{100}=\\frac{50+2(0+1+2+3+\\cdots+49)}{100}\n$$\n\nIl suffit donc de vérifier que ce dernier terme vaut 25 , soit en calculant à la main le numérateur, soit en utilisant la formule\n\n$$\n1+2+3+\\cdots+n=\\frac{n(n+1)}{2}\n$$\n\nqui donne\n\n$$\n\\frac{50+2(0+1+2+3+\\cdots+49)}{100}=\\frac{50+49 \\times 50}{100}=25\n$$", "problem_match": "\nExercice 1.", "solution_match": "## Solution de l'exercice 1"}
|
| 2 |
+
{"year": "2014", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle acutangle tel que $A C>A B, D \\operatorname{sur}(B C)$ tel que $A D=A B$ et $D$ différent de $B$. Soit $\\Gamma$ le cercle circonscrit à $A B C, \\Delta$ la tangente à $\\Gamma$ en $C, E$ l'intersection de $(A D)$ et $\\Delta$.\nMontrer que $C D^{2}=A D \\cdot D E-B D \\cdot D C$.", "solution": "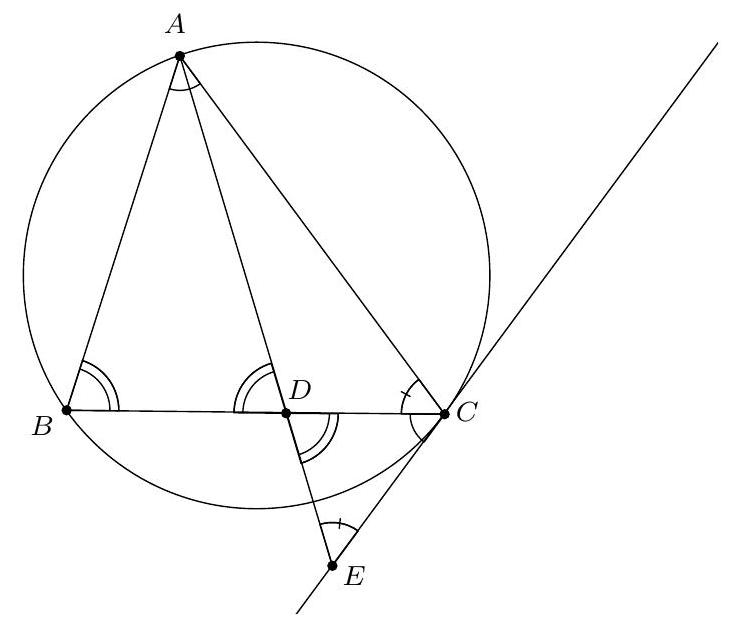\n\nOn a $\\widehat{E D C}=\\widehat{A D B}=\\widehat{C B A}$ et $\\widehat{D C E}=\\widehat{B A C}$ donc $A B C$ et $C D E$ sont semblables. On en déduit que $\\frac{A B}{C D}=\\frac{B C}{D E}$, donc\n\n$$\nA D \\cdot D E-B D \\cdot D C=A B \\cdot D E-B D \\cdot D C=B C \\cdot C D-B D \\cdot C D=(B C-B D) C D=C D^{2} .\n$$", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2014", "problem_label": "3", "tier": 1, "problem": "Soit $n$ un entier strictement positif tel que $n(n+2015)$ est le carré d'un entier.\na) Prouver que $n$ n'est pas un nombre premier.\nb) Donner un exemple d'un tel entier $n$.", "solution": "a) Supposons que $n$ est premier et qu'il existe un entier $m$ vérifiant $n(n+2015)=m^{2}$. Alors $n$ divise $m^{2}$, donc $n$ divise $m$. On peut donc écrire $m=n r$. Il vient $n(n+2015)=n^{2} r^{2}$, puis $n+2015=n r^{2}$. Par conséquent, $2015=n r^{2}-n=n\\left(r^{2}-1\\right)$ est divisible par $n$.\nOr, $2015=5 \\times 13 \\times 31$, donc $n$ est l'un des entiers 5, 13, 31 .\nSi $n=5$ alors $r^{2}-1=13 \\times 31=403$, ce qui est impossible car 404 n'est pas un carré parfait. De même, $5 \\times 31+1=156$ et $5 \\times 13+1=66$ ne sont pas des carrés parfaits, ce qui exclut les cas $n=13$ et $n=31$.\nb) On cherche $n$ et $m$ entiers tels que\n\n$$\n(2 m)^{2}=4 n(n+2015)=(2 n)^{2}+2 \\times(2 n) \\times 2015=(2 n+2015)^{2}-2015^{2}\n$$\n\nCeci équivaut à $2015^{2}=(2 n+2015)^{2}-(2 m)^{2}=(2 n+2015+2 m)(2 n+2015-2 m)$.\nSoient $a=2015 \\times 5$ et $b=\\frac{2015}{5}$. Il suffit donc que\n\n$$\n2 n+2015+2 m=a \\text { et } 2 n+2015-2 m=b\n$$\n\nEn additionnant ces égalités, on trouve que $4 n+4030=a+b=403 \\times 25+403$, donc $\\underline{n=1612}$, et en soustrayant on obtient $4 m=a-b=403 \\times 24$ donc $m=403 \\times 6$.", "problem_match": "\nExercice 3.", "solution_match": "## Solution de l'exercice 3"}
|
| 4 |
+
{"year": "2014", "problem_label": "4", "tier": 1, "problem": "On veut colorier les parties à trois éléments de $\\{1,2,3,4,5,6,7\\}$, de sorte que si deux de ces parties n'ont pas d'élément en commun alors elles soient de couleurs différentes. Quel est le nombre minimum de couleurs pour réaliser cet objectif?", "solution": "Considérons la suite de parties $\\{1,2,3\\},\\{4,5,6\\},\\{1,2,7\\},\\{3,4,6\\},\\{1,5,7\\},\\{2,3,6\\},\\{4,5,7\\}$, $\\{1,2,3\\}$.\nChaque partie doit avoir une couleur différente de la suivante, donc déjà il y a au moins deux couleurs. S'il n'y avait qu'exactement deux couleurs, alors les couleurs devraient alterner, ce qui est impossible car la dernière partie est la même que la première et devrait être de couleur opposée.\nRéciproquement, montrons que trois couleurs suffisent:\n\n- On colorie en bleu les parties qui contiennent au moins deux éléments parmi 1, 2, 3.\n- On colorie en vert les parties non coloriées en bleu et qui contiennent au moins deux éléments parmi 4, 5, 6 .\n- On colorie en rouge les parties non coloriées en bleu ou en vert.\n\nIl est évident que deux parties bleues ont un élément en commun parmi 1, 2, 3 ; de même, deux parties vertes ont un élément en commun parmi $4,5,6$. Enfin, toute partie rouge contient trois éléments, dont contient nécessairement l'élément 7 : deux parties rouges ont donc également un élément en commun.", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2014", "problem_label": "5", "tier": 1, "problem": "Soit $A B C D$ un trapèze tel que $(A B) / /(C D)$. Deux cercles $\\omega_{1}$ et $\\omega_{2}$ sont situés à l'intérieur du trapèze de sorte que $\\omega_{1}$ est tangent à $(D A),(A B),(B C)$ et $\\omega_{2}$ est tangent à $(B C),(C D),(D A)$. Soit $d_{1}$ une droite passant par $A$, autre que $(A D)$, tangente à $\\omega_{2}$. Soit $d_{2}$ une droite passant par $C$, autre que $(C B)$, tangente à $\\omega_{1}$. Montrer que $d_{1} / / d_{2}$.", "solution": "Par continuité, on peut supposer que $A B \\neq C D$. De plus, quitte à échanger $A$ et $B$ avec $C$ et $D$, ainsi que $\\omega_{1}$ et $\\omega_{2}$, on peut supposer $A B>C D$.\n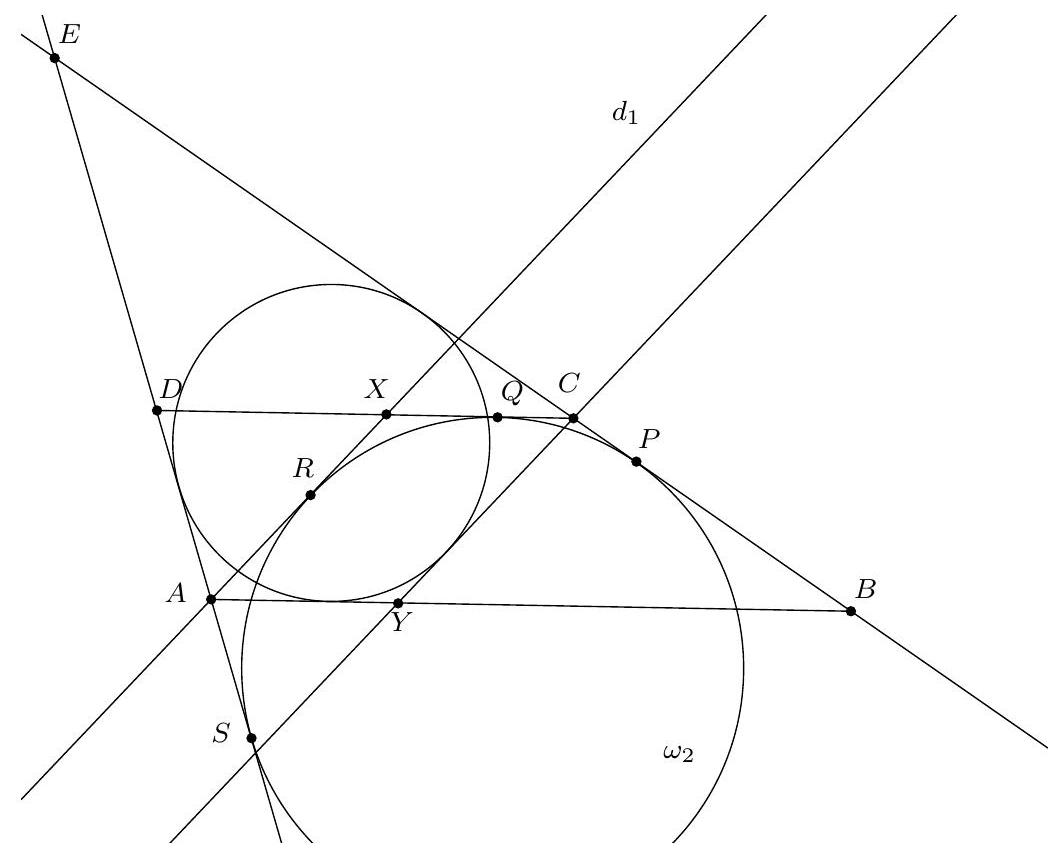\n\nSoit $E$ l'intersection de $(A D)$ et $(B C)$. Supposons que $(C D)$ coupe $\\omega_{1}$.\nOn note $P, Q, R, S$ les points de contact de $\\omega_{2}$ avec $(B C),(C D), d_{1},(D A)$. Soit $X$ l'intersection de $(C D)$ avec $d_{1}$. Soit $d_{2}^{\\prime}$ la parallèle à $d_{1}$ passant par $C$ et $Y=(A B) \\cap d_{2}^{\\prime}$. On oriente les droites de sorte que les mesures algébriques $\\overline{E A}, \\overrightarrow{A B}, \\overline{B C}, \\overline{D C}, \\overline{A X}, \\overline{Y C}$ soient positives.\n\n$$\n\\begin{aligned}\n(E A+Y C)-(C E+A Y) & =(\\overline{E A}+\\overline{Y C})-(\\overline{C E}+\\overline{A Y}) \\\\\n& =\\overline{E S}+\\overline{S A}+\\overline{A X}-\\overline{C P}-\\overline{P E}-\\overline{X C} \\\\\n& =\\overline{S A}+\\overline{A X}-\\overline{C P}-\\overline{X C} \\operatorname{car} \\overline{E S}=\\overline{P E} \\\\\n& =\\overline{R A}+\\overline{A X}-\\overline{X Q}=\\overline{R X}-\\overline{X Q}=0\n\\end{aligned}\n$$\n\ndonc $E A Y C$ est circonscriptible. Il vient $d_{2}^{\\prime}=(C Y)=d_{2}$, donc $d_{1} / / d_{2}$.\nSi maintenant $(C D)$ ne coupe pas $\\omega_{1}$, on définit cette fois $d_{1}^{\\prime}$ la parallèle à $d_{2}$ passant par $A$, $X=(C D) \\cap d_{1}^{\\prime}$ et $Y=(A B) \\cap d_{2}$. On montre comme ci-dessus que EAXC est circonscriptible (la preuve est laissée au lecteur).\n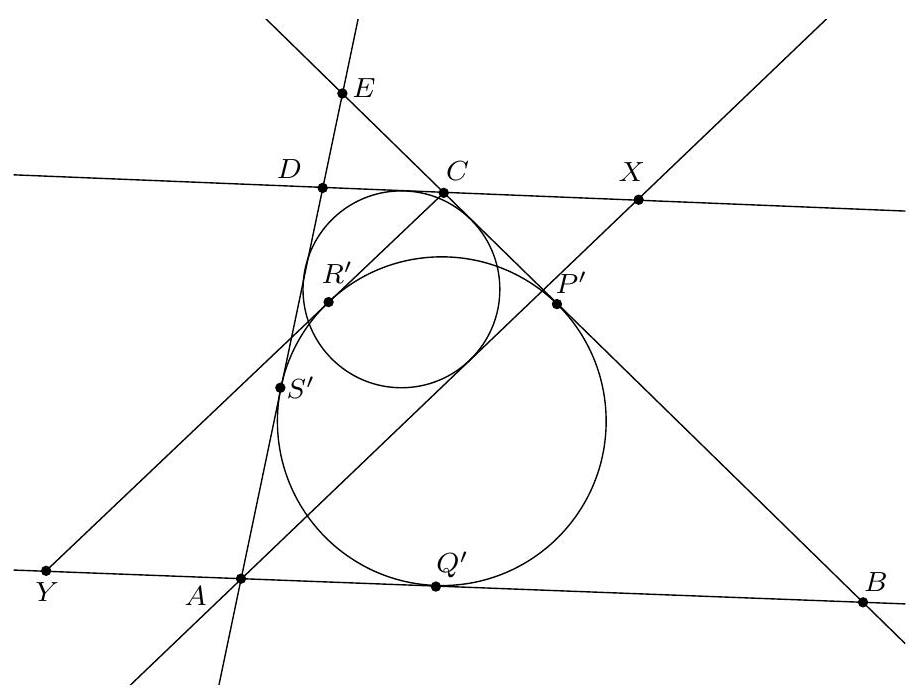", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2014", "problem_label": "6", "tier": 1, "problem": "Soit $a_{1}, a_{2}, \\ldots, a_{n}$ des entiers strictement positifs. Pour tout $k=1,2, \\ldots, n$, on note\n\n$$\nm_{k}=\\max _{1 \\leq \\ell \\leq k} \\frac{a_{k-\\ell+1}+a_{k-\\ell+2}+\\cdots+a_{k}}{\\ell} .\n$$\n\nMontrer que pour tout $\\alpha>0$, le nombre d'entiers $k$ tel que $m_{k}>\\alpha$ est strictement plus petit que $\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{\\alpha}$.", "solution": "Soit $k_{1}$ le plus grand entier $k$ tel que $m_{k}>\\alpha$. Il existe $\\ell_{1}$ tel que $a_{k_{1}-\\ell_{1}+1}+\\cdots+a_{k_{1}}>\\ell_{1} \\alpha$.\nSoit $k_{2}$ le plus grand entier $\\leqslant k_{1}-\\ell_{1}$ tel que $m_{k}>\\alpha$. Il existe $\\ell_{2}$ tel que $a_{k_{2}-\\ell_{2}+1}+\\cdots+a_{k_{2}}>\\ell_{2} \\alpha$. ...\nOn construit ainsi une suite finie $k_{1}>k_{2}>\\cdots>k_{r}$ telle que tout entier $k$ vérifiant $m_{k}>\\alpha$ se trouve dans l'un des intervalles $I_{j}=\\llbracket k_{j}-\\ell_{j}+1, k_{j} \\rrbracket$. De plus, ces intervalles sont deux à deux disjoints.\nPar conséquent, le nombre d'entiers $k$ tels que $m_{k}>\\alpha$ est inférieur ou égal à la somme des longueurs des intervalles, à savoir $\\ell_{1}+\\cdots+\\ell_{r}$.\nOr, $\\sum_{j=1}^{r} \\ell_{j}<\\frac{1}{\\alpha} \\sum_{j}\\left(a_{k_{j}-\\ell_{j}+1}+\\cdots+a_{k_{j}}\\right) \\leqslant \\frac{1}{\\alpha}\\left(a_{1}+\\cdots+a_{n}\\right)$. CQFD.", "problem_match": "\nExercice 6.", "solution_match": "## Solution de l'exercice 6"}
|
| 7 |
+
{"year": "2014", "problem_label": "7", "tier": 1, "problem": "Soit $a, b, c, n$ des entiers, avec $n \\geq 2$. Soit $p$ un nombre premier qui divise $a^{2}+a b+b^{2}$ et $a^{n}+b^{n}+c^{n}$, mais qui ne divise pas $a+b+c$.\nProuver que $n$ et $p-1$ ne sont pas premiers entre eux.", "solution": "Si $p$ divise $a$ et $b$, alors $p$ divise $c^{n}$ donc $p$ divise $c$, ce qui contredit la dernière assertion. Donc, quitte à échanger $a$ et $b$, on suppose que $p$ ne divise pas $b$. Quitte à multiplier $a, b, c$ par un inverse de $b$ modulo $p$, on peut supposer que $b=1$ et donc\n\n$$\np\\left|a^{2}+a+1, \\quad p\\right| a^{n}+1+c^{n}, \\quad p \\nmid a+1+c .\n$$\n\nComme $a^{2}+a+1$ est impair, $p$ l'est aussi.\nComme $p$ divise $\\left(a^{2}+a+1\\right)(a-1)=a^{3}-1$, l'ordre de $a$ modulo $p$ est 1 ou 3 .\nPremier cas: $a \\equiv 1(\\bmod p)$. Alors $p=3$, donc $c^{n} \\equiv-1-a^{n} \\equiv 1(\\bmod 3)$.\nEn particulier, $c$ est inversible modulo 3 , donc $c \\equiv \\pm 1(\\bmod 3)$. Comme $p \\nmid a+1+c$, on a nécessairement $c \\equiv-1(\\bmod 3)$. Enfin, comme $c^{n} \\equiv 1(\\bmod 3)$, l'entier $n$ est pair donc n'est pas premier avec $p-1$.\nDeuxième cas: l'ordre de $a$ modulo $p$ est 3 . Comme par ailleurs l'ordre de $a$ modulo $p$ divise $p-1$ en vertu du petit théorème de Fermat, on a $3 \\mid p-1$.\nSupposons que $n$ est premier avec $p-1$. Alors $x \\mapsto x^{n}$ est une bijection de $\\mathbb{Z} / p \\mathbb{Z}$ sur lui-même :\n\n- si $n \\equiv 1(\\bmod 3)$ alors $c^{n} \\equiv-a^{n}-1 \\equiv-a-1 \\equiv a^{2} \\equiv\\left(a^{2}\\right)^{n}(\\bmod p)$ donc par bijectivité de $x \\mapsto x^{n}$ dans $\\mathbb{Z} / p \\mathbb{Z}$ on a $c \\equiv a^{2} \\equiv-a-1(\\bmod p):$ contradiction!\n- si $n \\equiv 2(\\bmod 3)$ alors $c^{n} \\equiv-a^{n}-1 \\equiv-a^{2}-1 \\equiv a \\equiv\\left(a^{2}\\right)^{n}(\\bmod p)$ donc par bijectivité de $x \\mapsto x^{n}$ dans $\\mathbb{Z} / p \\mathbb{Z}$ on a $c \\equiv a^{2} \\equiv-a-1(\\bmod p):$ contradiction!\nOn en déduit que $n \\equiv 0(\\bmod 3)$, donc 3 est un diviseur commun de $n$ et de $p-1$.", "problem_match": "\nExercice 7.", "solution_match": "## Solution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Soit $a_{1}, a_{2}, \\ldots, a_{2 n}$ des réels tels que $a_{1}+a_{2}+\\cdots+a_{2 n}=0$.\nProuver qu'il existe au moins $2 n-1$ couples $\\left(a_{i}, a_{j}\\right)$ avec $i<j$ tels que $a_{i}+a_{j} \\geqslant 0$.", "solution": "Sans perte de généralité, on peut supposer que $a_{1} \\leq a_{2} \\leq \\cdots \\leq a_{2 n}$. On distingue deux cas :\n\n- Si $a_{n}+a_{2 n-1} \\geq 0$ alors on a $a_{i}+a_{2 n-1} \\geq 0$ pour $i=n, \\cdots, 2 n-2$, et $a_{i}+a_{2 n} \\geq 0$ pour $i=n \\cdots, 2 n-1$. Cela fournit bien $2 n-1$ sommes positives ou nulles.\n- Si $a_{n}+a_{2 n-1}<0$ alors\n\n$$\na_{1}+\\cdots+a_{n-1}+a_{n+1}+\\cdots a_{2 n-2}+a_{2 n}>0\n$$\n\nD'autre part, on a $0>a_{n}+a_{2 n-1} \\geq a_{n-1}+a_{2 n-2} \\geq \\cdots \\geq a_{2}+a_{n+1}$, donc\n\n$$\na_{2}+a_{3}+\\cdots+a_{n-1}+a_{n+1}+\\cdots+a_{2 n-2}<0\n$$\n\nDe (1) et (2), on déduit que $a_{1}+a_{2 n} \\geq 0$, ce qui assure que $a_{i}+a_{2 n} \\geq 0$ pour $i=1, \\cdots 2 n-1$.\nAutre solution. Notons $b_{1} \\leqslant b_{2} \\leqslant \\cdots \\leqslant b_{\\ell}$ les entiers positifs ou nuls parmi $a_{1}, \\ldots, a_{2 n}$. Premier cas: $\\ell>n$. Alors il y a au moins $\\frac{\\ell(\\ell-1)}{2} \\geq \\frac{n(n+1)}{2}$ couples $\\left(a_{i}, a_{j}\\right)$ avec $i<j, a_{i} \\geqslant 0$ et $a_{j} \\geqslant 0$. Or, $\\frac{n(n+1)}{2}-(2 n-1)=\\frac{n^{2}-3 n+2}{2}=\\frac{(n-1)(n-2)}{2} \\geqslant 0$, donc il y a au moins $2 n-1$ couples $\\left(a_{i}, a_{j}\\right)$ avec $i<j$ tels que $a_{i}+a_{j} \\geqslant 0$.\nDeuxième cas : $\\ell \\leqslant n$. Notons $c_{1} \\leqslant \\cdots \\leqslant c_{\\ell}$ les plus petits entiers parmi $a_{1}, \\ldots, a_{2 n}$. Comme $\\ell \\leqslant n$, on a $c_{\\ell}<0$. De plus, $\\sum_{i=1}^{2 n} a_{i}$ est égal à la somme de $\\sum_{i=1}^{\\ell}\\left(b_{i}+c_{i}\\right)$ et de termes négatifs, donc $\\sum_{i=1}^{\\ell}\\left(b_{i}+c_{i}\\right) \\geqslant 0$. Or, $b_{\\ell}+c_{\\ell} \\geqslant b_{i}+c_{i}$ pour tout $i$, donc $b_{\\ell}+c_{\\ell} \\geqslant 0$.\nOn forme ainsi déjà $2 n-\\ell$ couples $\\left(a_{i}, a_{j}\\right)$ en prenant $a_{j}=b_{\\ell}$ et $a_{i}$ autre que $c_{1}, \\ldots, c_{\\ell-1}, b_{\\ell}$.\nDe plus, pour tout $k=1, \\ldots, \\ell-1$, on a $\\sum_{i=1}^{\\ell}\\left(b_{i}+c_{i+k}\\right) \\geqslant 0$ (où par convention $c_{\\ell+1}=c_{1}$, $c_{\\ell+2}=c_{2}$, etc.), donc pour tout $k$ il existe $i$ tel que $b_{i}+c_{i+k} \\geqslant 0$. Ceci fournit encore $\\ell-1$ couples supplémentaires.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle dont tous les angles sont aigus, et $H$ son orthocentre. Les bissectrices de $\\widehat{A B H}$ et $\\widehat{A C H}$ se coupent en un point $I$. Montrer que $I$ est aligné avec les milieux de $[B C]$ et de $[A H]$.", "solution": "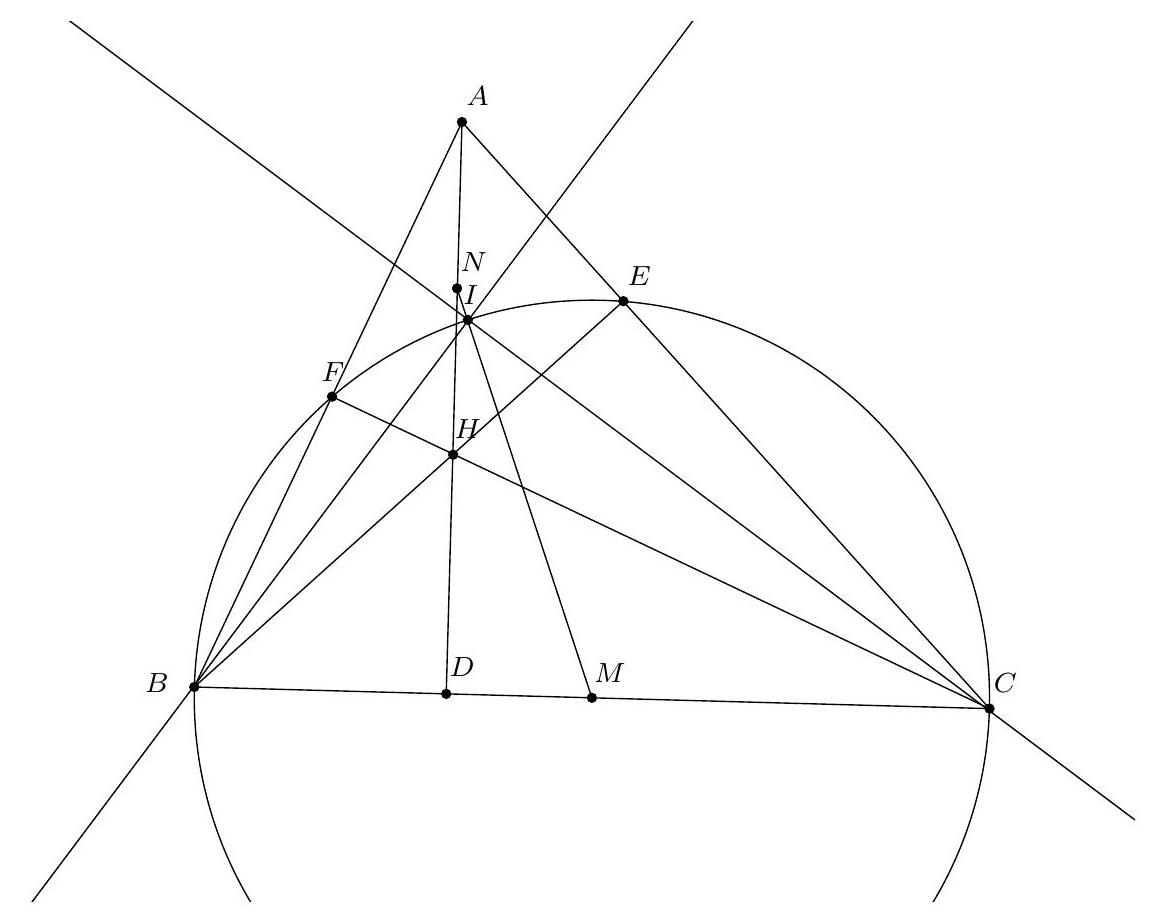\n\nNotons $D, E, F$ les pieds des hauteurs, $O$ le centre du cercle circonscrit, $M$ le milieu de $[B C]$ et $N$ le milieu de $[A H]$. On a $2 \\overrightarrow{M N}=2 \\overrightarrow{O N}-2 \\overrightarrow{O M}=\\overrightarrow{O A}+\\overrightarrow{O H}-\\overrightarrow{O B}-\\overrightarrow{O C}$.\nOr, $\\overrightarrow{O H}=\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}$ donc $\\overrightarrow{M N}=\\overrightarrow{O A}$. Par conséquent, il suffit de montrer que ( $M I$ ) est parallèle à $(O A)$.\nComme $B C F$ est un triangle rectangle en $F$, le point $F$ est situé sur le cercle de centre $M$ passant par $B$ et $C$. Il en va de même pour le point $E$. La bissectrice de $\\widehat{A B H}$ passe par le milieu de l'arc $E F$, et de même pour la bissectrice de $\\widehat{A C H}$, donc $I$ est le milieu de l'arc $E F$. En notant $C^{\\prime}$ le milieu de $[A B]$, on en déduit les égalités d'angles de droites $(M I, M B)=2(C I, C B)=$ $(C E, C B)+(C F, C B)=(C A, C B)+(C F, A B)+(A B, C B)$.\nD'autre part, $(O A, M B)=\\left(O A, O C^{\\prime}\\right)+\\left(O C^{\\prime}, A B\\right)+(A B, M B)=(C A, C B)+(C F, A B)+$ $(A B, C B)$ car $\\left(O C^{\\prime}\\right)$ et $(C F)$ sont parallèles.\nPar conséquent, $(O A, M B)=(M I, M B)$, ce qui prouve que $(O A)$ et $(M I)$ sont parallèles.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Pour tout entier $n \\in \\mathbb{N}^{*}$, on note $v_{3}(n)$ la valuation 3 -adique de $n$, c'est-à-dire le plus grand entier $k$ tel que $n$ est divisible par $3^{k}$. On pose $u_{1}=2$ et $u_{n}=4 v_{3}(n)+2-\\frac{2}{u_{n-1}}$ pour tout $n \\geqslant 2$ (si tant est que $u_{n-1}$ soit défini et non nul).\nMontrer que, pour tout nombre rationnel strictement positif $q$, il existe un et un seul entier $n \\geqslant 1$ tel que $u_{n}=q$.", "solution": "Tout d'abord, notons que $u_{1}=2, u_{2}=1, u_{3}=3, u_{4}=\\frac{3}{2}, u_{5}=\\frac{2}{3}$ et $u_{6}=3$. On prouve par récurrence que, pour tout entier $n \\geq 2$, on a $0<u_{n}$ et\n\n$$\n0<u_{3 n-1}<1<u_{3 n-2}<2<u_{3 n}=2+u_{n}:\n$$\n\nc'est déjà vrai pour $n=2$.\nPuisque $u_{3 n}=u_{n}+2$, on montre successivement que $u_{3 n+1}, u_{3 n+2}$ et $u_{3 n+3}$ sont bien définis, avec\n\n$$\n\\begin{aligned}\n& u_{3 n+1}=2-\\frac{2}{u_{3 n}}=1+\\frac{u_{n}}{2+u_{n}}, \\text { donc } 1<u_{3 n+1}<2 ; \\\\\n& u_{3 n+2}=2-\\frac{2}{u_{3 n+1}}=1+\\frac{u_{n}}{1+u_{n}}, \\text { donc } 0<u_{3 n+2}<1 ; \\\\\n& u_{3 n+3}=4 v_{3}(3(n+1))+2-\\frac{2}{u_{3 n+2}}=4 v_{3}(n)+4-\\frac{2}{u_{n}}=2+u_{n+1} .\n\\end{aligned}\n$$\n\nCeci conclut la récurrence.\nMaintenant, considérons la fonction $\\varphi:\\{x \\in \\mathbb{Q}: 0<x$ et $x \\notin\\{1,2\\}\\} \\mapsto\\{x \\in \\mathbb{Q}: 0<x\\}$ telle que\n\n$$\n\\begin{aligned}\n\\varphi: & x \\mapsto \\frac{x}{1-x} \\text { si } 0<x<1 ; \\\\\n& x \\mapsto 2 \\frac{x-1}{2-x} \\text { si } 1<x<2 ; \\\\\n& x \\mapsto x-2 \\text { si } 2<x\n\\end{aligned}\n$$\n\nEn outre, pour toute fraction irréductible $\\frac{p}{q}$, avec $p \\geq 0$ et $q>0$, on pose $\\left\\|\\frac{p}{q}\\right\\|=p+q$. Alors :\n\n- $\\left\\|\\varphi\\left(\\frac{p}{q}\\right)\\right\\|=\\left\\|\\frac{p}{q-p}\\right\\|=p<p+q=\\left\\|\\frac{p}{q}\\right\\|$ si $0<p<q$ ;\n- $\\left\\|\\varphi\\left(1+\\frac{p}{q}\\right)\\right\\|=\\left\\|2 \\frac{p}{q-p}\\right\\| \\leq 2 q<(p+q)+q=\\left\\|1+\\frac{p}{q}\\right\\|$ si $0<p<q$ ;\n- $\\left\\|\\varphi\\left(2+\\frac{p}{q}\\right)\\right\\|=\\left\\|\\frac{p}{q}\\right\\|=p+q<(p+2 q)+q=\\left\\|2+\\frac{p}{q}\\right\\|$ si $0<p$ et $0<q$.\n\nDans tous les cas, si $x$ est un rationnel strictement positif tel que $x \\notin\\{1,2\\}$, on a $\\|\\varphi(x)\\|<\\|x\\|$. Or, pour tout rationnel strictement positif $x$ et pour tout entier $n \\geq 1$ :\n\n- si $0<x<1$, alors $u_{n}=\\varphi(x) \\Leftrightarrow u_{3 n+2}=x ;$\n- si $1<x<2$, alors $u_{n}=\\varphi(x) \\Leftrightarrow u_{3 n+1}=x$;\n- si $2<x$, alors $u_{n}=\\varphi(x) \\Leftrightarrow u_{3 n}=x$.\n\nUne récurrence sur $\\|x\\|$ montre donc immédiatement que, pour tout rationnel strictement positif $x$, il existe un entier unique entier $n \\geq 1$ tel que $u_{n}=x$, ce qui conclut l'exercice.", "problem_match": "\nExercice 3.", "solution_match": "## Solution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Prouver que, pour tout entier $n \\geq 2$, on a : $\\sum_{k=2}^{n} \\frac{1}{\\sqrt[k]{(2 k)!}} \\geq \\frac{n-1}{2 n+2}$.\nN.B. Si $a>0$, on note $\\sqrt[k]{a}$ l'unique nombre réel $b>0$ tel que $b^{k}=a$.", "solution": "On raisonne par récurrence sur $n \\geq 2$.\nPour $n=2$, on a bien $\\frac{1}{\\sqrt{24}}>\\frac{1}{6}$.\nSupposons que l'inégalité désirée soit vraie pour la valeur $n-1 \\geq 2$. Pour la valeur $n$, le membre de droite augmente de $\\frac{n-1}{2 n+2}-\\frac{n-2}{2 n}=\\frac{1}{n(n+1)}$.\nD'après l'hypothèse de récurrence, il suffit donc de prouver que $\\frac{1}{\\sqrt[n]{(2 n)!}} \\geq \\frac{1}{n(n+1)}$.\nOr, pour $k=1,2, \\cdots, n$, on a $(n-k)(n-k+1) \\geq 0$, donc $0 \\leq k(2 n-k+1) \\leq n(n+1)$.\nEn multipliant ces inégalités membre à membre, il vient $(2 n)!\\leq(n(n+1))^{n}$, $\\mathrm{d}^{\\prime}$ où la conclusion.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle non rectangle tel que $A B<A C$. On note $H$ le projeté de $A$ sur $(B C)$, et $E, F$ les projetés respectifs de $H$ sur $(A B)$ et $(A C)$. La droite $(E F)$ coupe $(B C)$ au point $D$. On considère le demi-cercle de diamètre $[C D]$ situé dans le même demi-plan délimité par $(C D)$ que $A$. Soit $K$ le point de ce demi-cercle qui se projette sur $B$. Montrer que $(D K)$ est tangente au cercle $K E F$.", "solution": "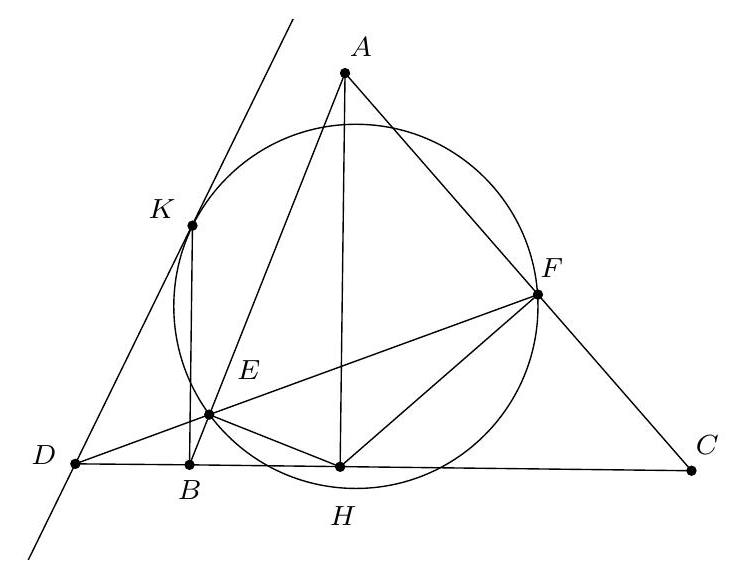\n\nComme $A E H F$ sont cocycliques (sur le cercle de diamètre $[A H]$ ), on a $(E F, E A)=(H F, H A)=$ $(H F, C A)+(C A, C B)+(C B, H A)=(C A, C B)=(C F, C B)$, donc $(E F, E B)=(C F, C B)$. Par conséquent, $B, E, F, C$ sont cocycliques. D'après la puissance d'un point par rapport à un cercle, on a $D E \\cdot D F=D B \\cdot D C$. D'autre part, comme $D K C$ est rectangle en $K$, les triangles $D K B$ et $D C K$ sont semblables, ce qui implique $\\frac{D K}{D B}=\\frac{D C}{D K}$, ou encore $D K^{2}=D B \\cdot D C$.\nIl vient $D K^{2}=D E \\cdot D F$, et donc d'après la puissance de $D$ par rapport au cercle $K E F$, on en déduit que $(D K)$ est tangente en $K$ au cercle $K E F$.\nRemarque : le choix du demi-cercle n'a pas d'importance.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Soit $n \\geq 1$ un entier. Un groupe de $2 n$ personnes se réunit. Chacune de ces personnes possède au moins $n$ amies dans ce groupe (en particulier, si $A$ est amie avec $B$ alors $B$ est amie avec $A$, et on n'est pas ami avec soi-même). Prouver que l'on peut disposer ces $2 n$ personnes autour d'une table ronde de sorte que chacune soit entre deux de ses amies.", "solution": "Considérons une disposition arbitraire des invités :\nAB.... $A$.\noù $A, B$ désignent des personnes différentes, mais les deux $A$ représentent la même personne (on est autour d'une table ronde).\nDans ce qui suit, on considérera la disposition comme une suite de personnes, ordonnée de gauche à droite.\nSi deux voisins ne sont pas amis, on dira que c'est une tension.\nS'il n'y a aucune tension, c'est fini.\nS'il existe une tension, par symétrie circulaire, on peut toujours supposer que $A$ et $B$ ne sont pas amis.\nComme $B$ a au moins $n$ amis, plus lui-même, on en déduit que $B$ a au plus $n-1$ \"ennemis\".\nSupposons que dans la disposition ci-dessus et après $B$, on ne trouve jamais deux voisins $A^{\\prime}$ et $B^{\\prime}$ (dans cet ordre) qui sont amies respectivement de $A$ et de $B$.\nAlors, comme une telle disposition n'arrive pas non plus avant $B$, on en déduit qu'elle n'apparaît jamais, et donc qu'à droite de chaque ami de $A$ doit se trouver un ennemi de $B$. Donc, le nombre d'ennemis de $B$ est au moins égal au nombre d'amis de $A$, ce qui implique $n-1 \\geq n$. Contradiction.\n\nPar suite, on peut trouver deux voisins $A^{\\prime}$ et $B^{\\prime}$ (dans cet ordre) qui sont amies respectivement de $A$ et de $B$.\nLa disposition est alors de la forme :\n\n$$\nA B \\ldots A^{\\prime} B^{\\prime} \\ldots A\n$$\n\nDans ces conditions, on peut éliminer la tension entre $A$ et $B$ en renversant l'ordre des personnes entre $B$ et $A^{\\prime}$ :\n\n$$\nA\\left(B \\ldots A^{\\prime}\\right) B^{\\prime} \\ldots A \\rightarrow A\\left(A^{\\prime} \\ldots B\\right) B^{\\prime} \\ldots A\n$$\n\nCela fournit une nouvelle disposition mais avec au moins une tension de moins que dans la précédente, puisque clairement la modification ne crée pas de nouvelle tension (par contre, elle peut éliminer une tension éventuelle entre $A^{\\prime}$ et $B^{\\prime}$ ).\nEn répétant cette procédure autant que nécessaire (un nombre fini de fois en tout cas, puisque le nombre initial de tensions est fini), on fait disparaître toutes les tensions, et l'objectif est atteint.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Les cases d'une grille à 10 lignes et 10 colonnes sont coloriées en blanc et en noir. Un coloriage de ces cases est dit homogène s'il contient un carré $3 \\times 3$ monochrome, et inhomogène sinon. Montrer qu'il existe plus de coloriages inhomogènes que de coloriages homogènes.", "solution": "Il y a $2^{100}$ coloriages possibles. Si $c$ est un carré $3 \\times 3$, le nombre de coloriages tels que $c$ soit monochrome est égal à $2 \\times 2^{91}=2^{92}$. Or, il y a 64 carrés $3 \\times 3$, donc il y a au plus $64 \\times 2^{92}=2^{98}$ coloriages homogènes.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Montrer que si $a, b, c$ sont des nombres réels positifs vérifiant $a+b+c=1$ alors\n\n$$\n\\frac{7+2 b}{1+a}+\\frac{7+2 c}{1+b}+\\frac{7+2 a}{1+c} \\geqslant \\frac{69}{4}\n$$", "solution": "Comme $7+2 b=5+2(1+b)$, on écrit le membre de gauche sous la forme\n\n$$\n5\\left(\\frac{1}{1+a}+\\frac{1}{1+b}+\\frac{1}{1+c}\\right)+2\\left(\\frac{1+b}{1+a}+\\frac{1+c}{1+b}+\\frac{1+a}{1+c}\\right)\n$$\n\nEn utilisant l'inégalité $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z} \\geqslant \\frac{9}{x+y+z}$, on minore le premier terme par $\\frac{45}{4}$.\nEn utilisant l'inégalité $x+y+z \\geqslant 3 \\sqrt[3]{x y z}$, on minore le second terme par 6 . L'assertion à démontrer en découle.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle, et $M$ le milieu de $[B C]$. On note $I_{b}$ et $I_{c}$ les centres des cercles inscrits à $A M B$ et $A M C$. Montrer que le second point d'intersection des cercles circonscrits aux triangles $A B I_{b}$ et $A C I_{c}$ se situe sur la droite $(A M)$.", "solution": "Soit $T$ l'intersection entre le cercle de diamètre $[B C]$ et la demi-droite $\\left[M A\\right.$ ). Il suffit de montrer que $T$ appartient au cercle $A B I_{b}$ (par symétrie des rôles de $B$ et $C$, ceci montrera qu'il appartient également au cercle $A C I_{c}$ ).\nComme $\\widehat{B T C}$ est droit, on a $\\widehat{A T B}=90^{\\circ}+\\frac{1}{2} \\widehat{A M B}=\\widehat{A I_{b} B}$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "Soit $n \\geqslant 1$ un entier. On suppose qu'il existe exactement 2005 couples $(x, y)$ d'entiers naturels tels que $\\frac{1}{x}+\\frac{1}{y}=\\frac{1}{n}$. Montrer que $n$ est le carré d'un entier.\nN.B. Si $x \\neq y$ alors $(x, y) \\neq(y, x)$.", "solution": "On remarque que $x>n$ et $y>n$.\nL'équation s'écrit $x y=n(x+y)$, ou encore $n^{2}=(x-n)(y-n)$. On en déduit qu'il y a exactement 2005 couples d'entiers naturels $(u, v)$ tels que $n^{2}=u v$.\nSi $n^{2}=u v$ alors $u$ est un diviseur de $n^{2}$. Réciproquement, si $u$ est un diviseur de $n^{2}$ alors l'équation $n^{2}=u v$ détermine uniquement $v$. On en déduit que $n^{2}$ admet exactement 2005 diviseurs.\nEcrivons $n=p_{1}^{\\alpha_{1}} \\cdots p_{r}^{\\alpha_{r}}$ avec $p_{i}$ premiers distincts et $\\alpha_{i}$ entiers. On a donc $n^{2}=p_{1}^{2 \\alpha_{1}} \\cdots p_{r}^{2 \\alpha_{r}}$. On sait que le nombre de diviseurs de $n^{2}$ est égal à $\\left(2 \\alpha_{1}+1\\right) \\cdots\\left(2 \\alpha_{r}+1\\right)$. Or, la décomposition en facteurs premiers de 2005 est $5 \\times 401$, donc soit $r=1$ et $2 \\alpha_{1}+1=2005$, soit $r=2$ et $2 \\alpha_{1}+1=5$, $2 \\alpha_{2}+1=401$. Dans tous les cas, les $\\alpha_{i}$ sont pairs donc $n$ est un carré parfait.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
French_TST_Senior/segmented/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "problem_label": "1", "tier": 1, "problem": "Soit $A B C$ un triangle isocèle en $A$, dont l'angle en $A$ n'est pas droit. Soit $D$ le point de $(B C)$ tel que $(A D) \\perp(A B)$. Soit $E$ le projeté orthogonal de $D$ sur $(A C)$. Soit enfin $H$ le milieu de $[B C]$. Montrer que $A H=H E$.", "solution": "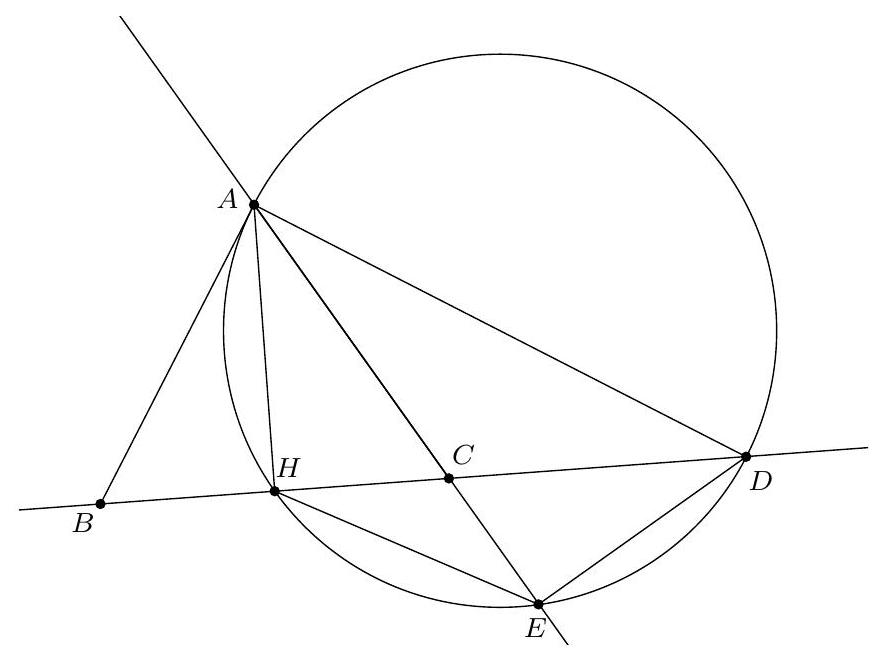\n\nTout d'abord, comme les angles $\\widehat{A H D}$ et $\\widehat{A E D}$ sont droits, les points $A, H, E, D$ sont sur le cercle de diamètre $[A D]$.\nNotons $\\theta=\\widehat{C B A}=\\widehat{A C B}$. Comme $A H C$ est rectangle en $H, \\widehat{H A C}=90^{\\circ}-\\theta$. Comme $B A D$ est rectangle en $A, \\widehat{A D B}=90^{\\circ}-\\theta$, et donc $\\widehat{A D H}=\\widehat{H A E}$.\nPar cocyclicité de $A, H, E, D$, les angles $\\widehat{A D H}$ et $\\widehat{A E H}$ sont égaux ou supplémentaires, donc $\\widehat{H A E}=\\widehat{A E H}$ ou $\\widehat{H A E}+\\widehat{A E H}=180^{\\circ}$.\nLe deuxième cas ne peut pas se produire car la somme des angles du triangle $A E H$ vaut $180^{\\circ}$, donc on a $\\widehat{H A E}=\\widehat{A E H}$. On en déduit que $H A E$ est isocèle en $H$, d'où $H A=H E$.\nAutre approche avec les angles de droites. On sait que si $T$ est une tangente en un point $A$ à un cercle $(C)$ et si $B$ et $M$ sont deux autres points de $(C)$, alors $(T, A B)=(M A, M B)$.\nDans l'exercice, comme $(A B)$ est perpendiculaire au diamètre $(A D)$, elle est tangente au cercle donc d'après ce qui précède on a $(A B, A H)=(E A, E H)$. Or, comme $A B C$ est isocèle on a $(A B, A H)=(A H, A C)$ donc $(A H, A E)=(A H, A C)=(A B, A H)=(E A, E H)$. On en conclut que $H A E$ est isocèle en $H$, d'où $H A=H E$.", "problem_match": "\nExercice 1.", "solution_match": "## Solution de l'exercice 1"}
|
| 2 |
+
{"year": "2015", "problem_label": "2", "tier": 1, "problem": "Trouver tous les entiers $m \\geqslant 1$ et $n \\geqslant 1$ tels que $\\frac{5^{m}+2^{n+1}}{5^{m}-2^{n+1}}$ soit le carré d'un entier.", "solution": "La démonstration qui suit est valable pour $m, n \\in \\mathbb{N}$.\nDéjà, $5^{m}-2^{n+1}$ doit diviser $5^{m}+2^{n+1}$, donc divise $5^{m}+2^{n+1}-\\left(5^{m}-2^{n+1}\\right)=2^{n+2}$, par conséquent c'est une puissance de 2 . Or, $5^{m}-2^{n+1}$ est impair, donc $5^{m}-2^{n+1}=1$.\nEcrivons $5^{m}+2^{n+1}=a^{2}$. On a donc $(a-1)(a+1)=a^{2}-1=5^{m}+2^{n+1}-5^{m}+2^{n+1}=2^{n+2}$, donc $a-1$ et $a+1$ sont des puissances de 2 .\nEcrivons $a-1=2^{c}$ et $a+1=2^{d}$ avec $c+d=n+2$. Alors $c<d$ donc $a-1=2^{c}$ divise $2^{d}-2^{c}=(a+1)-(a-1)=2$, donc $a-1=1$ ou $a-1=2$.\nSi $a=2$ alors $2^{d}=a+1=3$, ce qui est impossible.\nOn en déduit que $a=3, c=1, d=2$ et $n+2=3$, ce qui donne $n=1$ et $5^{m}=1+2^{n+1}=5$, puis $m=1$.\nFinalement, $m=n=1$.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2015", "problem_label": "3", "tier": 1, "problem": "On considère 7 îles $A_{1}, \\ldots, A_{7}$. On est autorisé à construire des ponts, soit entre une île $A_{i}$ et l'île suivante $A_{i+1}$ (pour $i \\in\\{1,2, \\ldots, 6\\}$ ), soit entre une île $A_{i}$ et la dernière $A_{7}$ (pour $i \\in\\{1,2, \\ldots, 6\\}$ ). De combien de manières peut-on réaliser ces constructions avec le moins de ponts possibles de sorte que l'on puisse se rendre d'une île vers n'importe quelle autre ?\n\nExemple pour 3 îles au lieu de 7 : les trois constructions possibles utilisant deux ponts sont 1) un pont entre $A_{1}$ et $A_{2}$, et un pont entre $A_{1}$ et $A_{3}$\n2) un pont entre $A_{1}$ et $A_{2}$, et un pont entre $A_{2}$ et $A_{3}$\n3) un pont entre $A_{1}$ et $A_{3}$, et un pont entre $A_{2}$ et $A_{3}$.", "solution": "On dira qu'une configuration est bonne si elle satisfait les conditions de l'énoncé.\nNotons $a_{n}$ le nombre de bonnes configurations avec $n$ îles. On a $a_{1}=a_{2}=1$ et $a_{3}=3$.\nPartant d'une bonne configuration avec $n$ îles telle que $A_{n-1}$ et $A_{n}$ ne soient pas reliées, alors $A_{n-1}$ et $A_{n-2}$ sont nécessairement reliées, donc si on supprime l'île $A_{n-1}$ on obtient une bonne configuration avec $n-1$ îles. Réciproquement, toute bonne configuration avec $n-1$ îles provient d'une et une seule bonne configuration avec $n$ îles dont les deux dernières ne sont pas reliées : il suffit en effet d'intercaler une île entre les deux dernières et de mettre un pont entre celle-ci et la $n$ - 2-ième.\nOn en déduit qu'il y a $a_{n-1}$ bonnes configurations avec $n$ îles telles que $A_{n-1}$ et $A_{n}$ ne soient pas reliées.\nD'autre part, partant d'une bonne configuration avec des ponts entre $A_{n}$ et $A_{n-1}, A_{n-1}$ et $A_{n-2}, \\ldots$, $A_{n-k+1}$ et $A_{n-k}(k \\geqslant 1)$ mais pas entre $A_{n-k}$ et $A_{n_{k}-1}$, si on supprime les îles $A_{n-1}, \\ldots, A_{n-k}$ alors on obtient une bonne configuration avec $n-k$ îles. On en déduit comme ci-dessus qu'il y a $a_{n-1}+a_{n-2}+\\cdots+a_{1}$ bonnes configurations comportant un pont entre $A_{n}$ et $A_{n-1}$.\nOn voit donc que $a_{n}=2 a_{n-1}+a_{n-2}+\\cdots+a_{1}$.\nOn en déduit de proche en proche que $a_{4}=8, a_{5}=21, a_{6}=55$ et $a_{7}=144$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2015", "problem_label": "4", "tier": 1, "problem": "Déterminer toutes les fonctions $f$ de $\\mathbb{R}$ dans $\\mathbb{R}$ telles que, pour tous $x$ et $y$ réels, on ait l'égalité\n\n$$\nf(x+y)=f(x-y)+f(f(1-x y))\n$$", "solution": "Pour $y=0$ on trouve que $f(x)=f(x)+f(f(1))$ donc $f(f(1))=0$. Pour $x=0$ on trouve $f(y)=f(-y)+f(f(1))$ donc $f(y)=f(-y)$ pour tout $y$.\nPour $y=1$ on obtient $f(x+1)=f(x-1)+f(f(1-x))$. En remplaçant $x$ par $-x+2$, il vient $f(-x+3)=f(-x+1)+f(f(x-1))$.\n\nOr, $f(x-1)=f(1-x)$ donc $f(f(1-x))=f(f(x-1))$. Par conséquent, $f(x+1)=f(x-1)+$ $f(-x+3)-f(-x+1)=f(x-3)$ puisque $f(-t)=f(t)$ pour tout $t$.\nOn en déduit, en remplaçant $x$ par $x+1$, que $f(x+2)=f(x-2)$ pour tout $x$.\nPrenons $y=2$ dans l'équation fonctionnelle. On a $f(x+2)=f(x-2)+f(f(1-2 x))$, donc $f(f(1-2 x))=0$ pour tout $x$. En remplaçant $x$ par $(1-t) / 2$, on trouve que $f(f(t))=0$ pour tout $r$.\nOn revient à l'équation fonctionnelle : $f(x+y)=f(x-y)+f(f(1-x y))$, donc $f(x+y)=f(x-y)$ pour tous $x$ et $y$. On prend $x=y=t / 2$ : il vient $f(t)=f(0)$, donc $f$ est constante. Comme $f(f(1))=0$, cette constante est nulle, et finalement $f(x)=0$ pour tout $x$.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2015", "problem_label": "5", "tier": 1, "problem": "a) Trouver tous les entiers $m \\geqslant 1$ et $n \\geqslant 1$ tels que $\\frac{5^{m}+2^{n+1}}{5^{m}-2^{n+1}}$ soit le carré d'un entier.\nb) Plus généralement, trouver tous les entiers $m \\geqslant 1$ et $n \\geqslant 1$, ainsi que les nombres premiers $p$, tels que $\\frac{5^{m}+2^{n} p}{5^{m}-2^{n} p}$ soit le carré d'un entier.", "solution": "a) Voir exercice 2 ci-dessus.\nb) Supposons que $p=5$. Alors $\\frac{5^{m-1}+2^{n}}{5^{m-1}-2^{n}}$ est le carré d'un entier. D'après la partie a) (qui marchait aussi dans le cas d'entiers $\\geqslant 0$, on a $m=n=2$.\nSupposons enfin $p \\neq 2$ et $p \\neq 5$. Soit $d$ le PGCD de $5^{m}+2^{n} p$ et de $5^{m}-2^{n} p$. Alors $d$ divise $5^{m}+2^{n} p+5^{m}-2^{n} p=2 \\times 5^{m}$. Comme $d$ est le PGCD de deux nombres impairs, il est impair, doncil divise $5^{m}$.\nDe plus, $d$ divise $5^{m}+2^{n} p-\\left(5^{m}-2^{n} p\\right)=2^{n+1} p$ et il est impair, donc il divise $p$. Comme $p$ et 5 sont premiers entre eux, en en déduit que $d=1$ et que $5^{m}-2^{n} p=1$; de plus, $5^{m}+2^{n} p=a^{2}$ pour un certain entier $a$.\nOn a donc $(a-1)(a+1)=a^{2}-1=2^{n+1} p$.\nLe PGCD de $a-1$ et de $a+1$ divise $(a+1)-(a-1)=2$, donc il vaut 1 ou 2 . De plus, $a-1$ et $a+1$ sont de même parité, et leur produit est pair, donc leur PGCD vaut 2 . On en déduit que $\\left(a-1=2, a+1=2^{n} p\\right)$ ou $\\left(a-1=2 p, a+1=2^{n}\\right)$ ou $\\left(a-1=2^{n}, a+1=2 p\\right)$.\nDans le premier cas on aurait $a=3$, donc $4=a+1=2^{n} p$, ce qui est impossible.\nDans le deuxième cas, on a $p=2^{n-1}-1$. Comme $p$ est premier, $n=1$ et $n=2$ ne conviennent pas donc $n \\geqslant 3$. Par conséquent, $5^{m}=2^{n} p+1 \\equiv 1[8]$. Comme $5^{2 \\ell+1}=5 \\times 25^{\\ell} \\equiv 5 \\times 1^{\\ell}=5$ [8], l'entier $m$ est nécessairement pair. Posons $m=2 \\ell$, alors $\\left(5^{\\ell}-1\\right)\\left(5^{\\ell}+1\\right)=2^{n} p$. L'un des facteurs est égal à $2 p$ et l'autre à $2^{n-1}$. Comme leur différence est égale 2 , on a $\\pm 2=2 p-2^{n-1}=2 p-(p+1)=p-1$, donc $p=3, n=3$ et $m=2$.\nDans le troisième cas, on a $p=2^{n-1}+1$. On ne peut pas avoir $n=1$, $\\operatorname{sinon} p=2$. Si $n=2$ alors $p=3$ et $5^{m}=1+2^{n} p=13$. Impossible. Donc $n \\geqslant 3$. Le même raisonnement que plus haut conduit à $m=2 \\ell$ avec $\\pm 2=2 p-2^{n-1}=2 p-(p-1)=p+1$, ce qui contredit $p \\geqslant 3$.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2015", "problem_label": "6", "tier": 1, "problem": "Soit $I$ le centre du cercle inscrit à un triangle $A B C$. Soit $D$ le point diamétralement opposé à $A$ sur le cercle circonscrit. On suppose que le point $E$ de la demi-droite $[B A)$ et le point $F$ de la demi-droite $[C A)$ satisfont la condition\n\n$$\nB E=C F=\\frac{A B+B C+C A}{2} .\n$$\n\nMontrer que $(E F) \\perp(D I)$.", "solution": "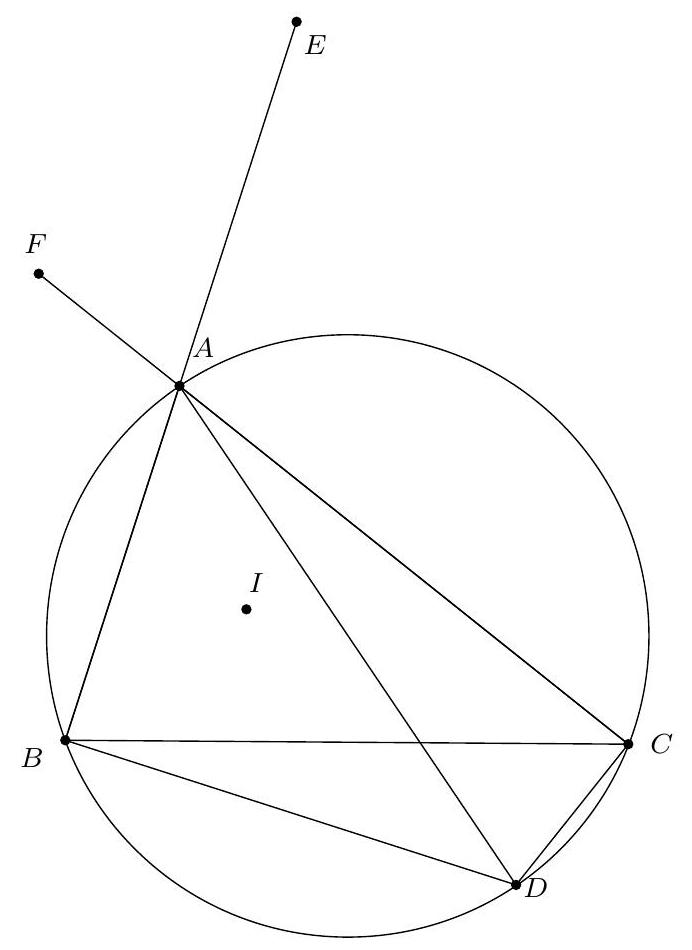\n\nNotons $a, b, c$ les longueurs des côtés, $r$ le rayon du cercle inscrit et $p=(a+b+c) / 2$. Comme $[A D]$ est un diamètre, les angles $\\widehat{A B D}$ et $\\widehat{A C D}$ sont droits donc\n\n$$\n\\begin{aligned}\nD E^{2}-D F^{2} & =\\left(D B^{2}+B E^{2}\\right)-\\left(D C^{2}+C F^{2}\\right)=D B^{2}-D C^{2} \\\\\n& =\\left(A D^{2}-D C^{2}\\right)-\\left(A D^{2}-D B^{2}\\right)=A C^{2}-A B^{2} \\\\\n& =b^{2}-c^{2} .\n\\end{aligned}\n$$\n\nD'autre part, si $C^{\\prime}$ est le point de contact du cercle inscrit avec $[A B]$, on sait que $B C^{\\prime}=p-b$, donc $C^{\\prime} E=B E-B C^{\\prime}=b$. Il vient $I E^{2}=\\left(I C^{\\prime}\\right)^{2}+\\left(C^{\\prime} E\\right)^{2}=r^{2}+b^{2}$, et de même $I F^{2}=r^{2}-c^{2}$, donc\n\n$$\nD E^{2}-D F^{2}=I E^{2}-I F^{2}\n$$\n\nCeci signifie que les points $D$ et $I$ ont la même différence de puissances par rapport à $E$ et $F$ (considérés comme des cercles de rayon nul), donc $(D I) \\perp(E F)$.\n\nPrécision : expliquons pourquoi si $C$ et $C^{\\prime}$ sont deux cercles de centres $O$ et $O^{\\prime}$, et si $P_{C}(A)$ -$P_{C^{\\prime}}(A)=P_{C}(B)-P_{C^{\\prime}}(B)$ alors $(A B) \\perp\\left(O O^{\\prime}\\right)$. Notons $R$ et $R^{\\prime}$ les rayons des cercles et $C, D$ les projetés respectifs de $A$ et $B$ sur $\\left(O O^{\\prime}\\right)$.\nOn a $P_{C}(A)-P_{C^{\\prime}}(A)=O A^{2}-O^{\\prime} A^{2}-\\left(R^{2}-\\left(R^{\\prime}\\right)^{2}\\right)=O C^{2}-O^{\\prime} C^{2}-\\left(R^{2}-\\left(R^{\\prime}\\right)^{2}\\right)$, donc $O C^{2}-$ $O^{\\prime} C^{2}=O D^{2}-O^{\\prime} D^{2}$. Ceci s'écrit encore $\\left(\\overline{O C}-\\overline{O^{\\prime} C}\\right)\\left(\\overline{O C}+\\overline{O^{\\prime} C}\\right)=\\left(\\overline{O D}-\\overline{O^{\\prime} D}\\right)\\left(\\overline{O D}+\\overline{O^{\\prime} D}\\right)$, ou encore $2 \\overline{O^{\\prime} O} \\cdot \\overline{M C}=2 \\overline{O^{\\prime} O} \\cdot \\overline{M D}$ où $M$ est le milieu de $\\left[O^{\\prime} O\\right]$. Par conséquent, $C=D$, et donc $(A B)=(A C) \\perp\\left(O O^{\\prime}\\right)$.", "problem_match": "\nExercice 6.", "solution_match": "## Solution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Résoudre en nombres réels le système d'équations\n\n$$\n\\begin{gathered}\nx_{1}\\left(x_{1}-1\\right)=x_{2}-1 \\\\\nx_{2}\\left(x_{2}-1\\right)=x_{3}-1 \\\\\n\\cdots \\\\\nx_{2016}\\left(x_{2016}-1\\right)=x_{2017}-1 \\\\\nx_{2017}\\left(x_{2017}-1\\right)=x_{1}-1 .\n\\end{gathered}\n$$", "solution": "Posons par convention $x_{2018}=x_{1}$. Pour tout $i=1, \\ldots, 2017$, on a $x_{i+1}-$ $x_{i}=x_{i}\\left(x_{i}-1\\right)+1-x_{i}=\\left(x_{i}-1\\right)^{2} \\geqslant 0$, donc $x_{1}=x_{2018} \\geqslant x_{2017} \\geqslant \\cdots \\geqslant x_{1}$. On en déduit que les $x_{i}$ sont tous égaux, donc $0=x_{i+1}-x_{i}=\\left(x_{i}-1\\right)^{2}=0$. Par conséquent, $x_{i}=1$ pour tout $i$. Réciproquement, il est clair que $x_{i}=1$ est solution.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Soit $a$ et $b$ des entiers strictement positifs. Prouver que si\n\n$$\na+\\frac{b}{a}-\\frac{1}{b}\n$$\n\nest un entier alors c'est un carré.", "solution": "En multipliant par $a$, on obtient que $a^{2}+b-\\frac{a}{b}$ est un entier, donc $k=\\frac{a}{b}$ est un entier.\nDe même, en multipliant par $b$ on voit que $\\frac{b^{2}}{a}$ est un entier. Comme $\\frac{b^{2}}{a}=\\frac{b}{k}$, on a $b=k c$ où $c$ est un entier.\nComme $\\frac{b}{a}-\\frac{1}{b}=\\frac{1}{k}-\\frac{1}{k c}$ est un entier, en multipliant par $k$ on voit que $\\frac{1}{c}$ est un entier, donc $c=1$, $b=k$ et $a=k^{2}$. Finalement, $a+\\frac{b}{a}-\\frac{1}{b}=k^{2}$ est un carré.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "On considère 2017 droites du plan, qui se rencontrent deux à deux en des points distincts. On appelle $E$ l'ensemble de ces points d'intersection.\nOn veut attribuer une couleur à chacun des points de $E$ de sorte que deux quelconques de ces points qui appartiennent à une même droite et dont le segment qui les relient ne contient aucun autre point de $E$, soient de couleurs différentes.\nCombien faut-il au minimum de couleurs pour pouvoir réaliser une telle coloration?", "solution": "Le minimum $m$ cherché est $m=3$ et, avec ce qui suit, il sera assez évident que le résultat reste vrai pour $n \\geq 3$ droites.\nTout d'abord, on note que, dans la configuration obtenue, il y a au moins une région non subdivisée qui est un triangle. En effet, trois droites non concourantes et deux jamais parallèles forment un triangle. Or, toute droite qui traverse un triangle, le partage en deux polygones dont\nau moins un est un triangle et donc, en partant de trois des droites données et en \"ajoutant\" une par une les 2014 autres, on est assuré de l'existence d'une telle région triangulaire dans la configuration finale. Les trois sommets d'un tel triangle doivent être de couleurs distinctes, ce qui implique que $m \\geq 3$.\nPour conclure, nous allons construire une coloration adéquate à trois couleurs. On commence par remarquer que, puisqu'il n'y a qu'un nombre fini de points d'intersection, on peut choisir un repère orthogonal dans lequel ces points ont des abscisses deux à deux distinctes. On numérote alors les points $M_{1}, M_{2} \\ldots, M_{k}$ selon les abscisses croissantes (et où $k=\\frac{2017 \\times 2016}{2}$ ). Pour tout $i$, le point $M_{i}$ possède au plus quatre voisins et, s'il appartient à un segment qui joint deux de ses voisins, un seul de ces deux voisins a une abscisse inférieure à celle de $M_{i}$. Cela assure que, pour tout $i \\leq k$, parmi les voisins de $M_{i}$, il y en a au plus deux qui ont des indices inférieurs à $i$. On peut alors colorier les $M_{i}$ dans l'ordre de la numérotation selon la procédure suivante : on colorie $M_{1}$ en vert et $M_{2}$ en rouge. Et, pour tout $i$ tel que $2 \\leq i \\leq k-1$, si l'on suppose que les points $M_{1}, M_{2} \\ldots, M_{i}$ ont été colorés chacun soit en vert, soit en rouge, soit en bleu de sorte que deux points voisins ne soient pas (encore) de la même couleur alors, d'après la remarque précédente, au plus deux voisins de $M_{i+1}$ ont déjà été colorés, ce qui laisse une couleur libre pour $M_{i+1}$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "Soit $A B C$ un triangle dont tous les angles sont aigus.\nLes hauteurs $\\left[A A_{1}\\right],\\left[B B_{1}\\right]$ et $\\left[C C_{1}\\right]$ se coupent au point $H$. Soit $A_{2}$ le symétrique de $A$ par rapport à $\\left(B_{1} C_{1}\\right)$, et soit $O$ le centre du cercle circonscrit à $A B C$.\na) Prouver que les points $O, A_{2}, B_{1}, C$ sont cocycliques.\nb) Prouver que $O, H, A_{1}, A_{2}$ sont cocycliques.", "solution": "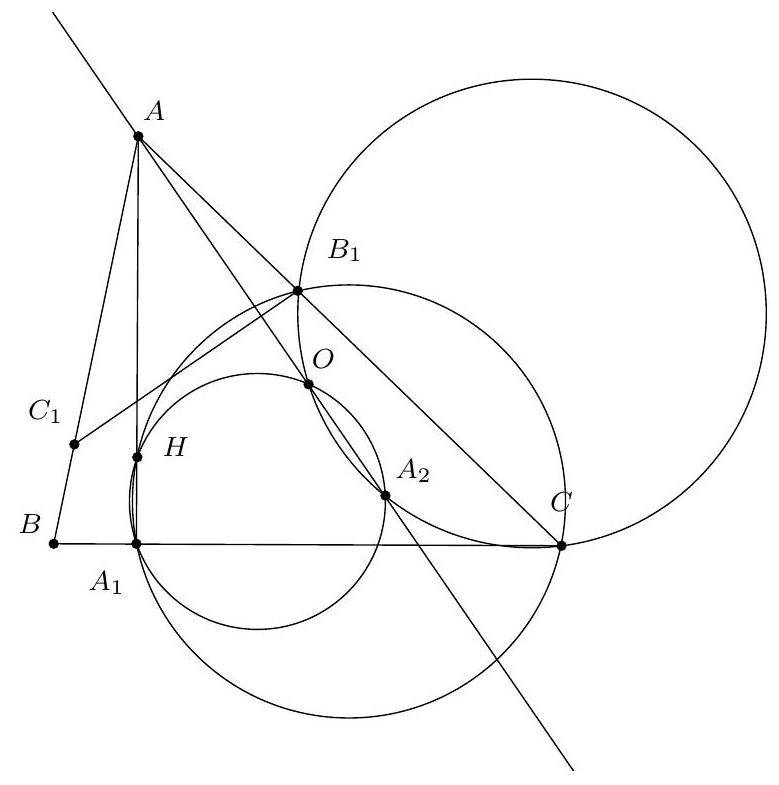\na) $A, H, B_{1}, C_{1}$ sont cocycliques sur le cercle de diamètre $[A H]$, donc $\\widehat{A B_{1} C_{1}}=\\widehat{A H C_{1}}=90^{\\circ}-$ $\\widehat{C_{1} A H}$. Or, $\\left(A A_{2}\\right) \\perp\\left(B_{1} C_{1}\\right)$ donc $\\widehat{A_{2} A B_{1}}=\\widehat{C_{1} A H}$, i.e. les demi-droites $[A H)$ et $\\left[A A_{2}\\right)$ sont symétriques par rapport à la bissectrice de $\\widehat{B A C}$. On en déduit que $A_{2} \\in[A O)$. Comme $A O=$ $C O$, on a $\\widehat{A C O}=\\widehat{O A C}=\\widehat{A A_{2} B_{1}}$, donc $O, A_{2}, B_{1}, C$ sont cocycliques.\nb) En utilisant la puissance de $A$ par rapport aux cercles $O, A_{2}, B_{1}, C$ et $H, A_{1}, C, B_{1}$, on a $A B_{1}$. $A C=A O \\cdot A A_{2}$ et $A B_{1} \\cdot A C=A H \\cdot A A_{1}$. Par conséquent, $A O \\cdot A A_{2}=A H \\cdot A A_{1}$. D'après la puissance d'un point par rapport à un cercle, on en déduit que $O A_{2}, H, A_{1}$ sont cocycliques.\n\nRemarque. L'hypothèse que $A B C$ est acutangle est superflue.", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2016", "problem_label": "5", "tier": 1, "problem": "Soit $a_{0}, a_{1}, . ., a_{99}, b_{0}, b_{1}, \\ldots, b_{99}$ des réels strictement positifs.\nPour $k=0,1, \\ldots, 198$, on pose $S_{k}=\\sum_{i=0}^{198} a_{i} b_{k-i}$, avec $a_{j}=0$ et $b_{j}=0$ si $j<0$ ou $j>99$.\nEst-il possible que les nombres $S_{0}, S_{1}, \\ldots, S_{198}$ soient tous égaux?", "solution": "Non. Raisonnons par l'absurde. En effet, comme $a_{0} b_{0}=a_{0} b_{99}+\\cdots+a_{99} b_{0}$ où les $\\cdots$ représentent des termes strictement positifs, on a $a_{0} b_{0}>a_{0} b_{99}$ donc $b_{0}>b_{99}$, et de même $a_{0}>a_{99}$. Par conséquent, $S_{0}=a_{0} b_{0}>a_{99} b_{99}=S_{198}$, ce qui est contradictoire.\n\nAutre démonstration qui ne nécessite pas l'hypothèse de positivité (mais seulement le fait que $a_{99} \\neq 0$ et $b_{99} \\neq 0$ :\nsupposons que $S_{0}=S_{1}=\\ldots=S_{198}=\\alpha$.\nNotons que $\\alpha \\neq 0$.\nOn pose $P(x)=a_{0}+a_{1} x+\\ldots+a_{99} x^{99}$ et $Q(x)=b_{0}+b_{1} x+\\ldots+b_{99} x^{99}$. Comme $P(x) Q(x)=S_{0}+S_{1} x+\\ldots+S_{198} x^{198}=\\alpha\\left(1+x+\\ldots+x^{198}\\right)$\n$=\\alpha \\frac{1-x^{199}}{1-x}$ pour $x \\neq 1$, on constate que $P(x) Q(x) \\neq 0$ pour tout $x \\neq 1$. D'autre\npart, on a $\\alpha \\neq 0$ puisque $P$ et $Q$ sont des polynômes non nuls, donc $P(1) Q(1)=199 \\alpha \\neq 0$.\nPar conséquent, $P(x) Q(x) \\neq 0$ pour tout réel $x$, et donc $P$ n'admet pas de racine réelle. Ceci contredit le fait que $P$ est de degré impair.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2016", "problem_label": "6", "tier": 1, "problem": "1) Pierre répartit les entiers $1,2, \\ldots, 2012$ en deux groupes disjoints dont les sommes respectives des éléments sont égales.\nSans même regarder la répartion choisie par Pierre, Clara affirme alors que l'on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.\nProuver que Clara a raison.\n2) Pierre répartit les entiers $1,2, \\ldots, 20$ en deux groupes disjoints dont les sommes respectives des éléments sont égales.\nSans même regarder la répartion choisie par Pierre, Clara affirme alors que l'on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.\nProuver que, cette fois, Clara aurait peut-être mieux fait de regarder avant de parler.", "solution": "On colorie les éléments du groupe $G_{1}$ en rouge, et ceux de $G_{2}$ en bleu. Sans perte de généralité, on peut supposer que 1 est rouge. Lorsque deux entiers consécutifs ne sont pas dans le même groupe, on dit que l'on a une alternance.\n\n- Si l'on a au moins quatre alternances, on peut trouver la configuration ...rb...br...rb...br..., où les pointillés indiquent toujours que l'on reste sur la même couleur, sauf peut-être pour le dernier paquet. Dans la situation décrite, la conclusion est assurée en éliminant les entiers responsables des première et quatrième alternances (on ne peut utiliser les deux premières alternances car $c^{\\prime}$ est peut-être le même nombre bleu qui est concerné).\n- Si l'on a exactement trois alternances ...rb...br...rb... avec au moins deux bleus successifs dans le premier paquet de bleus, on peut effacer les nombres impliqués dans les deux premières alternances. De même, s'il y a au moins deux rouges successifs dans le second paquet de rouges, on peut effacer les nombres impliqués dans les seconde et troisième alternances.\n\nSi l'on n'est pas dans un de ces deux cas, c'est que l'on a ...rbrb...., où le premier groupe de pointillés ne désigne que des rouges, et le second groupe de pointillés ne désigne que des bleus. On appelle $k$ le nombre de rouges dans ce premier paquet. La somme des nombres rouges est alors $\\frac{k(k+1)}{2}+(k+2)$, alors que la somme de tous les entiers de 1 à 2012 vaut $2012 \\times 2013 / 2$. Puisque la somme des nombres dans chaque groupe est la même, on doit avoir $\\frac{k(k+1)}{2}+(k+2)=$ $2012 \\times 2012 / 4$, autrement dit, $k(k+3)+4=2012 \\times 2013 / 2$. Or, cette équation n'a pas de solution modulo 3, ce qui assure que cette configuration n'est finalement pas possible.\n\n- Si l'on a exactement deux alternances, on est forcément dans la configuration ....rb...br...., où les pointillés indiquent qu'il n'y a pas de changements de couleurs. S'il y a au moins deux bleus, on peut effacer les nombres impliqués dans les deux alternances. Sinon, c'est qu'il n'y a qu'un bleu, mais alors il doit être égal à 1012539, ce qui est impossible.\n- S'il n'y a qu'une alternance, c'est que l'on est dans la configuration ....rb... Si, comme ci-dessus, on note $k$ le nombre de rouges, on doit avoir $\\frac{k(k+1)}{2}=1012539$, soit $k(k+1)=2025078$ qui n'a pas non plus de solution entière (on peut le voir modulo 10).\nFinalement, dans tous les cas, on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.\n\n2) Par exemple, pour $n=20$, on colorie en rouge les entiers de 1 à 14 , et les autres en bleu. Les sommes des deux groupes sont égales, mais si l'on élimine deux rouges, la somme des rouges diminuera d'au plus $14+13=27$, alors que si on élimine deux bleus, la somme des bleus diminuera d'au moins $15+16=31$. Il est alors impossible qu'après élimination, les deux groupes aient encore des sommes égales.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que\n\n$$\nf\\left(a^{2}\\right)-f\\left(b^{2}\\right) \\leqslant(f(a)+b)(a-f(b)), \\quad \\text { pour tous } a, b \\in \\mathbb{R}\n$$", "solution": "En prenant $(a, b)=(0,0)$, on obtient $f(0)^{2} \\leqslant 0$ donc $f(0)=0$. En prenant $(a, b)=(x, 0)$ puis $(a, b)=(0, x)$, on trouve que $f\\left(x^{2}\\right)=x f(x)$. En remplaçant dans l'équation initiale, on en déduit que $a f(a)-b f(b) \\leqslant(f(a)+b)(a-f(b)$, donc $f(a) f(b) \\leqslant a b$ pour tous $a, b$. D'autre part, $f\\left(x^{2}\\right)=x f(x)$ entraîne que $x f(x)=-x f(-x)$, donc $f$ est impaire. En remplaçant $b$ par $-b$ dans $f(a) f(b) \\leqslant a b$, on en déduit que $f(a) f(b)=a b$ pour tous $a$ et $b$. En particulier, $f(1)^{2}=1$ donc $f(1)=1$ ou $f(1)=-1$. Comme $f(a) f(1)=a$ pour tout $a$, on en déduit que $f(x)=x$ ou $f(x)=-x$ pour tout $x$.\nRéciproquement, on vérifie facilement que les fonctions $f(x)=x$ et $f(x)=-x$ sont solutions de l'équation fonctionnelle.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Soit $S$ l'ensemble des nombres à deux chiffres qui ne contiennent pas le chiffre 0. Deux nombres de $S$ sont dits amis si leurs plus grands chiffres sont égaux, et si la différence entre leurs plus petits chiffres est égale à 1 . Par exemple, 68 et 85 sont amis, 78 et 88 sont amis, mais 58 et 75 ne sont pas amis.\nDéterminer le plus grand entier $m$ tel qu'il existe une partie $T$ de $S$ possédant $m$ éléments, telle que deux éléments quelconques de $T$ ne soient pas amis.", "solution": "Réponse : 45 . On peut prendre pour $T$ l'ensemble des nombres dont le plus petit chiffre est impair.\nRéciproquement, si $x=\\overline{a b}$ avec $1 \\leqslant b<a \\leqslant 9$ alors $x$ et $x+1$ sont amis. Si $x=\\overline{a b}$ avec $2 \\leqslant a<b \\leqslant 9$ et $a$ pair, alors $x$ et $x+10$ sont amis. On a ainsi trouvé 36 paires d'amis disjointes. Par conséquent, parmi les 72 nombres $\\geqslant 21, T$ ne peut contenir qu'au plus 36 nombres, donc $|T| \\leqslant 9+36=45$.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Soit $P(x)=x^{4}-x^{3}-3 x^{2}-x+1$. Montrer qu'il existe une infinité d'entiers $n$ tels que $P\\left(3^{n}\\right)$ ne soit pas premier.", "solution": "On observe que $3^{2} \\equiv-1(\\bmod 5)$ et $3^{4} \\equiv 1(\\bmod 5)$. Soit $n \\geqslant 1$. Soit $x=3^{4 n+1}$, alors $x=\\left(3^{4}\\right)^{n} \\times 3 \\equiv 3(\\bmod 5)$, donc $P(x) \\equiv 3^{4}-3^{3}-3^{3}-3+1 \\equiv 1+3+3-3+1 \\equiv 0$ $(\\bmod 5)$.\nD'autre part, $P(x)>x^{4}-x^{3}-3 x^{3}-x^{3}=x^{3}(x-5)>x-5>3^{4 n}-5>5$, donc $P\\left(3^{4 n+1}\\right)$ n'est $^{\\prime}$ pas premier.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2016", "problem_label": "4", "tier": 1, "problem": "Soit $A B C$ un triangle rectangle en $C$. Soient $D$ le pied de la hauteur issue de $C$, et $Z$ le point de $[A B]$ tel que $A C=A Z$. La bissectrice de $\\widehat{B A C}$ coupe $(C B)$ et $(C Z)$ en $X$ et $Y$ respectivement. Montrer que les quatre points $B, X, Y, D$ sont sur un même cercle.", "solution": "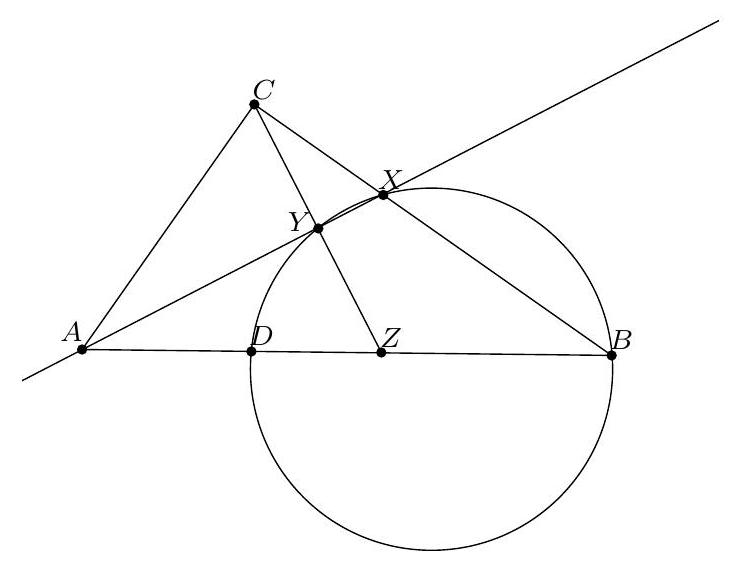\n$C A Z$ est isocèle en $A$ donc $(A Y)$, qui est la bissectrice de $\\widehat{C A Z}$, est perpendiculaire à $(C Z)$. Donc $A D Y C$ est cyclique.\nOn a alors $\\widehat{D Y X}=180^{\\circ}-\\widehat{A Y D}=180^{\\circ}-\\widehat{A C D}=180^{\\circ}-\\widehat{X B D}$.", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2016", "problem_label": "5", "tier": 1, "problem": "Soit $a \\in[0 ; 1]$. On définit la suite $\\left(x_{n}\\right)$ par\n$x_{0}=a$ et $x_{n+1}=1-\\left|1-2 x_{n}\\right|$, pour tout $n \\geq 0$.\nProuver que la suite $\\left(x_{n}\\right)$ est périodique à partir d'un certain rang si et seulement si $a$ est un nombre rationnel.\n(Note: on dit que $\\left(x_{n}\\right)$ est périodique à partir d'un certain rang s'il existe des entiers $T>0$ et $n \\geqslant 0$ tels que $x_{k+T}=x_{k}$ pour tout $k \\geqslant n$.)", "solution": "On note tout d'abord que si $x_{n} \\in[0 ; 1]$ alors $-1 \\leq 1-2 x_{n} \\leq 1$, d'où $0 \\leq x_{n+1} \\leq 1$. Puisque $x_{0} \\in[0 ; 1]$, on déduit ainsi par récurrence que $x_{n} \\in[0 ; 1]$ pour tout $n \\geq 0$.\n\n- Supposons que $a$ soit un nombre rationnel. Une récurrence immédiate assure alors que, pour tout $\\mathrm{n} \\geq 0, x_{n}$ est un nombre rationnel.\nPour tout $n \\geq 0$, on pose $x_{n}=\\frac{p_{n}}{q_{n}}$, avec $p_{n}$ et $q_{n}$ entiers positifs et premiers entre eux. Alors $x_{n+1}=\\frac{q_{n}-\\left|q_{n}-2 p_{n}\\right|}{q_{n}}$, d'où $q_{n+1} \\leq q_{n}$.\nLa suite $\\left(q_{n}\\right)$, suite décroissante d'entiers naturels, est alors stationnaire à partir d'un certain rang. Il existe donc des entiers $q>0$ et $N \\geq 0$ tels que $q_{n}=q$ pour tout $n \\geq N$.\nPour tout $n \\geq N$, le nombre $x_{n}$ est donc un nombre rationnel de $[0 ; 1]$ dont le dénominateur vaut $q$. Or, il n'y a qu'un nombre fini de tels rationnels et il existe donc $n_{0} \\geq N$ et $k>0$ tels que $x_{n_{0}+k}=x_{n_{0}}$. La définition par récurrence de $\\left(x_{n}\\right)$ assure alors que $\\left(x_{n}\\right)_{n \\geq n_{0}}$ est périodique de période $k$.\n- Supposons maintenant qu'il existe des entiers $k>0$ et $N \\geq 0$ tels que $x_{n+k}=x_{n}$ pour tout $n \\geq N$.\nPour $n \\geq 0$, on a $x_{n+1}=2 x_{n}$ ou $x_{n+1}=2-2 x_{n}$ selon que $1-2 x_{n}$ est positif ou négatif. On peut donc poser $x_{n+1}=a+2 b x_{n}$, où $a$ est un entier et $b= \\pm 1$. On prouve alors facilement par récurrence que, pour tout $i \\geq 0$, il existe un entier $a_{i}$ tel que $x_{N+i}=a_{i}+2^{i} b_{i} x_{N}$ avec $b_{i}= \\pm 1$.\n\nEn particulier, on a $x_{N}=x_{N+k}=a_{k}+2^{k} b_{k} x_{N}$. Puisque $2^{k} b_{k}= \\pm 2^{k} \\neq 1$, cette équation du premier degré en $x_{N}$ admet une unique solution $x_{N}=\\frac{a_{k}}{1-2^{k} b_{k}}$. Ainsi, $x_{N}$ est un nombre rationnel. Or, il est facile de vérifier que, pour $m \\geq 0$, si $x_{m+1}$ et rationnel alors $x_{m}$ est rationnel donc, par récurrence descendante, on déduit que $a=x_{0}$ est rationnel.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2016", "problem_label": "6", "tier": 1, "problem": "Prouver qu'il existe un entier $n>0$ tel que parmi les 2016 chiffres de droite dans $l^{\\prime}$ écriture décimale de $2^{n}$, il y a au moins 1008 chiffres 9.", "solution": "On peut légitimement se demander quand trouver des 9 à la droite de l'écriture décimale de $2^{n}$. On peut penser que c'est quand la puissance de 2 est légèrement inférieure à une puissance de 10 . On va donc chercher des nombres de la forme $2^{n}+1$ qui sont divisibles par 5 selon une puissance élevée. Pour un tel nombre, en multipliant par la puissance de 2 adéquate, on obtiendra un nombre de la forme $2^{k}\\left(2^{n}+1\\right)=2^{n+k}+2^{k}$ divisible par une grande puissance de 10 , et il suffira de retrancher le $2^{k}$ en question pour obtenir le type de puissance de 2 cherché.\nLemme. Pour tout entier $k \\geq 1$, le nombre $a_{k}=2^{2 \\cdot 5^{k-1}}+1$ est divisible par $5^{k}$.\nPreuve du lemme. On raisonne par récurrence sur $k$ :\n\n- Pour $k=1$, on a $a_{1}=5$ qui est bien divisible par 5.\n- Supposons le résultat établi pour un certain $k \\geq 1$.\n\nPosons $a=4^{5^{k-1}}=a_{k}-1$. On note qu'alors $a=-1 \\bmod 5$.\nOn a alors $a_{k+1}=4^{5^{k}}+1=a^{5}+1=(a+1)\\left(a^{4}-a^{3}+a^{2}-a+1\\right)$.\nD'après l'hypothèse de récurrence, on a $a+1=0 \\bmod 5^{k-1}$.\nD'autre part, puisque $a=-1 \\bmod 5$, on a $a^{4}-a^{3}+a^{2}-a+1=0 \\bmod 5$.\nAinsi, $a_{k+1}$ est divisible par $5^{k}$, ce qui achève la récurrence.\nComme prévu, on en déduit que, pour tout $k \\geq 1$, le nombre $2^{2 k}\\left(2^{2 \\cdot 5^{2 k-1}}+1\\right)=2^{2 k+2 \\cdot 5^{2 k-1}}+2^{2 k}$ est divisible par $10^{2 k}$. Son écriture décimale se termine donc par au moins $2 k$ chiffres 0 .\nOr, pour $k \\geq 1$, on a $2^{2 k}<10^{k}$. Ainsi, l'écriture décimale de $2^{2 k} n^{\\prime}$ utilise pas plus de $k$ chiffres. Par suite, parmi les $2 k$ chiffres de droite de l'écriture décimale de $2^{2 k+2 \\cdot 5^{2 k-1}}$, il y a au moins $k$ chiffres 9.\nLe résultat demandé correspond à $k=1008$.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "problem_label": "1", "tier": 1, "problem": "Soit $n \\geq 5$ un entier, et $E_{1}, E_{2}, \\ldots, E_{2 n-1}$ des parties distinctes à deux éléments de $\\{1,2, \\ldots, n\\}$.\nProuver que, parmi les $2 n-1$ parties $E_{i}$, on peut en choisir $n$ de sorte que la réunion de ces $n$ parties ne contienne pas plus de $\\frac{2}{3} n+1$ éléments.", "solution": "On va prouver par récurrence sur $k \\leq \\frac{2 n-1}{3}$ que l'on peut toujours éliminer $3 k$ des $2 n-1$ parties de sorte que la réunion des $2 n-1-3 k$ restantes ne contienne pas plus de $n-k$ éléments.\nLe cas $k=0$ est immédiat.\nSoit maintenant $1 \\leq k \\leq \\frac{2 n-1}{3}$. On suppose que l'on a éliminé $3(k-1)$ des $E_{i}$ de sorte que la réunion $U_{k-1}$ des $2 n-1-3(k-1)$ autres ne contienne pas plus de $n-k+1$ éléments.\nChacun des $E_{i}$ contient deux éléments. De $2(2 n-1-3(k-1))<4(n-k+1)$, on déduit alors qu'il existe un élément $x$ de $U_{k-1}$ qui n'appartient qu'à au plus trois de $E_{i}$ qui forment $U_{k-1}$. Ainsi, en éliminant encore trois des $E_{i}$ non déà éliminés, dont tous ceux qui contiennent $x$, cela assure que la réunion des $n-3 k$ restants ne contient pas plus de $n-k$ éléments.\nCela achève la récurrence.\nPour $k=\\left\\lfloor\\frac{n-1}{3}\\right\\rfloor$, on a $n-\\left\\lfloor\\frac{n-1}{3}\\right\\rfloor \\leq n-\\frac{n-1}{3}=\\frac{2}{3} n+1$, ce qui conclut.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2016", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle. On note $P$ le symétrique de $B$ par rapport à $(A C)$ et $Q$ le symétrique de $C$ par rapport à $(A B)$.\nSoit $T$ l'intersection entre $(P Q)$ et la tangente en $A$ au cercle circonscrit à $(A P Q)$.\nMontrer que le symétrique de $T$ par rapport à $A$ appartient à $(B C)$.", "solution": "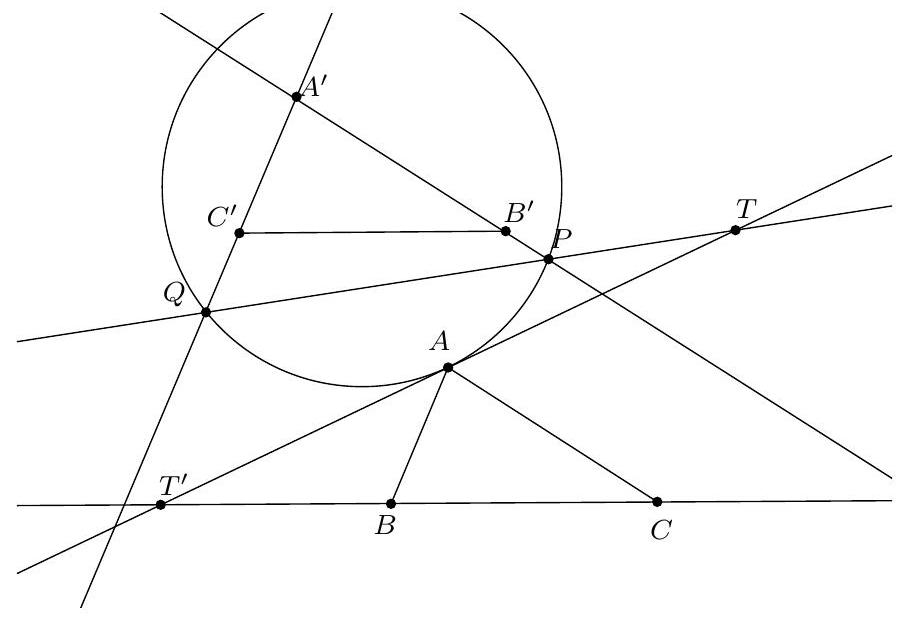\n\nSoient $B^{\\prime}$ et $C^{\\prime}$ les symétriques de $B$ et $C$ par rapport à $A$. Comme le triangle $A B^{\\prime} P$ est isocèle en $A$, on a $\\widehat{A B^{\\prime} P}=\\frac{1}{2}\\left(180^{\\circ}-\\widehat{B^{\\prime} A P}\\right)=\\frac{1}{2} \\widehat{P A B}=\\widehat{B A C}$, donc $\\left(B^{\\prime} P\\right) \\|(A C)$.\nDe même, $\\left(C^{\\prime} Q\\right) \\|(A B)$, donc les droites $\\left(B^{\\prime} P\\right)$ et $\\left(C^{\\prime} Q\\right)$ sont sécantes. Notons $A^{\\prime}$ leur point d'intersection.\nLes triangles $A^{\\prime} B^{\\prime} C^{\\prime}$ et $A C B$ sont semblables car leurs côtés sont deux à deux parallèles.\nDe plus, $A B^{\\prime} P$ et $A C^{\\prime} Q$ sont semblables car $\\widehat{A B^{\\prime} P}=\\widehat{A C^{\\prime} Q}$ et car ces deux triangles sont isocèles en $A$.\nMontrons maintenant l'assertion demandée. Par symétrie par rapport à $A$, il revient au même de montrer que $T, B^{\\prime}, C^{\\prime}$ sont alignés. En appliquant le théorème de Ménélaüs dans $A^{\\prime} P Q$, cela équivaut à\n\n$$\n\\frac{B^{\\prime} P}{B^{\\prime} A^{\\prime}} \\times \\frac{C^{\\prime} A^{\\prime}}{C^{\\prime} Q} \\times \\frac{T Q}{T P}=1 \\quad(E)\n$$\n\nComme $T A Q$ et $T P A$ sont semblables, on a $\\frac{T A}{T P}=\\frac{T Q}{T A}=\\frac{A Q}{A P}$, donc $\\frac{T Q}{T P}=\\frac{A Q^{2}}{A P^{2}}=\\frac{A C^{2}}{A B^{2}}$.\nComme $A^{\\prime} B^{\\prime} C^{\\prime}$ et $A C B$ sont semblables, on a $\\frac{C^{\\prime} A^{\\prime}}{B^{\\prime} A^{\\prime}}=\\frac{A B}{A C}$.\nComme $A B^{\\prime} P$ et $A C^{\\prime} Q$ sont semblables, on a $\\frac{B^{\\prime} P}{C^{\\prime} Q}=\\frac{A P}{A Q}=\\frac{A B}{A C}$.\nOn en déduit que $(E)$ est vraie.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2016", "problem_label": "3", "tier": 1, "problem": "Déterminer tous les entiers $a>0$ pour lesquels il existe des entiers strictement positifs $n, s, m_{1}, \\cdots, m_{n}, k_{1}, \\cdots, k_{s}$ tels que\n\n$$\n\\left(a^{m_{1}}-1\\right) \\cdots\\left(a^{m_{n}}-1\\right)=\\left(a^{k_{1}}+1\\right) \\cdots\\left(a^{k_{s}}+1\\right)\n$$", "solution": "On va prouver que les entiers $a$ cherchés sont $a=2$ et $a=3$.\nTout d'abord, on constate que $2^{2}-1=2+1$ et que $(3-1)(3-1)=3+1$, ce qui assure que $a=2$ et $a=3$ sont effectivement des solutions du problème.\nRéciproquement, soit $a, n, s, m_{1}, \\cdots, m_{n}, k_{1}, \\cdots, k_{s}$ des entiers strictement positifs tels que\n\n$$\n\\left(a^{m_{1}}-1\\right) \\cdots\\left(a^{m_{n}}-1\\right)=\\left(a^{k_{1}}+1\\right) \\cdots\\left(a^{k_{s}}+1\\right)\n$$\n\nClairement, on a $a \\neq 1$, puisque si $a=1$ le membre de droite vaut 0 mais pas celui de gauche.\nPar l'absurde: supposons que $a>3$.\nOn pose $A=\\left(a^{m_{1}}-1\\right) \\cdots\\left(a^{m_{n}}-1\\right)=\\left(a^{k_{1}}+1\\right) \\cdots\\left(a^{k_{s}}+1\\right)$.\nLemme 1. Chacun des nombres $m_{1}, \\cdots, m_{n}$ et $a-1$ est une puissance de 2.\nPreuve du lemme 1. Soit $i \\in\\{1, \\cdots, n\\}$ et $\\gamma$ un diviseur impair de $m_{i}$ (éventuellement $\\gamma=1$ ), disons $m_{i}=\\gamma \\times b$. Soit $p$ un diviseur premier de $a^{\\gamma}-1$.\nPuisque $a^{\\gamma} \\equiv 1(\\bmod p)$, on a $a^{m_{i}} \\equiv\\left(a^{\\gamma}\\right)^{b} \\equiv 1(\\bmod p)$.\nAinsi $A$ est divisible par $p$, ce qui assure qu'il existe $j$ tel que $a^{k_{j}}+1$ soit divisible par $p$. Comme ci-dessus, on a alors $\\left(a^{\\gamma}\\right)^{k_{j}}-1 \\equiv 0(\\bmod p)$ et, puisque $\\gamma$ est impair, on a aussi $\\left(a^{k_{j}}\\right)^{\\gamma} \\equiv-1$ $(\\bmod p)$.\nPar suite $p$ divise $\\left(\\left(a^{k_{j}}\\right)^{\\gamma}+1\\right)-\\left(\\left(a^{\\gamma}\\right)^{k_{j}}-1\\right)=2$, d'où $p=2$.\nAinsi, le seul diviseur premier de $a^{\\gamma}-1$ est $p=2$, ce qui prouve que $a^{\\gamma}-1$ est une puissance de 2. Il existe donc un entier $c$ tel que\n\n$$\n2^{c}=a^{\\gamma}-1=(a-1)\\left(a^{\\gamma-1}+\\cdots+a+1\\right) .\n$$\n\nEn particulier, $a-1$ est donc une puissance de 2 et $a$ est impair. Mais, puisque $\\gamma$ est impair, $a^{\\gamma-1}+\\cdots+a+1$ est impair et doit aussi être une puissance de 2 . Cela implique que $\\gamma=1$ et donc que le seul diviseur impair de $m_{i}$ est 1 , ce qui conclut la preuve du lemme 1.\nD'après le lemme, on a $a-1=2^{c}$ et $a-1>2$, donc $a-1$ est divisible par 4. Pour tout entier $k \\geq 0$, on a alors $a^{k}+1 \\equiv 2(\\bmod 4)$.\nPour tout $i$, on pose $a_{i}=\\frac{1}{2}\\left(a^{2^{i}}+1\\right)$. On sait donc que $a_{i}$ est un entier impair.\nOn vérifie facilement par récurrence que, pour tout entier $d \\geq 0$ :\n\n$$\na^{2^{d}}-1=(a-1)(a+1)\\left(a^{2}+1\\right) \\cdots\\left(a^{2^{d-1}}+1\\right)=2^{c} \\cdot 2^{d} \\cdot a_{0} a_{1} \\cdots a_{d-1}\n$$\n\nLemme 2. Les nombres $a_{0}, a_{1}, a_{2}, \\cdots$ sont deux à deux premiers entre eux.\nPreuve du lemme 2. Soit $0 \\leq i<j$. On note que $a_{i}$ et $a_{j}$ sont impairs donc leur pgcd $d$ est impair. D'après (1), le nombre $a^{2^{j}}-1$ est divisible par $a_{i}$. Puisque $a^{2^{j}}+1=2 a_{j}$, on en déduit que tout diviseur commun à $a_{i}$ et $a_{j}$ divise aussi $\\left(a^{2^{j}}+1\\right)-\\left(a^{2^{j}}-1\\right)=2$. Ainsi $d$ est impair et divise 2, donc $d=1$. On a donc $a_{i}$ et $a_{j}$ premiers entre eux, et cela achève la preuve du lemme 2.\nD'après le lemme 1, on sait que chaque $m_{i}$ est une puissance de 2 . En utilisant (1) pour chaque $m_{i}$, on déduit que $A$ peut s'écrire sous la forme\n\n$$\nA=2^{N}\\left(a_{0}\\right)^{N_{0}} \\cdots\\left(a_{q}\\right)^{N_{q}}(2),\n$$\n\navec $N>N_{0}+\\cdots N_{q}$. Puisque chaque $a^{k_{j}}+1$ est congru à 2 modulo 4 , on doit donc avoir $s=N$. Or, pour tout $j$, si l'on pose $k_{j}=2^{r} t$ avec $t$ impair, alors $a^{k_{j}}+1=\\left(a^{2^{r}}\\right)^{t}+1 \\equiv(-1)^{t}+1 \\equiv 0$ $(\\bmod 2)^{r}+1$. Ainsi $a^{k_{j}}+1$ est divisible par $a_{r}$.\nAinsi, chacun des nombres $a^{k_{j}}+1$ est divisible par un des $a_{i}$. Puisque $s>N_{0}+\\cdots N_{q}$, il existe $i$ pour lequel $a_{i}$ divise plus de $N_{i}$ des $a^{k_{j}}+1$. Par suite, $A$ est divisible par $\\left(a_{i}\\right)^{N_{i}+1}$, ce qui est impossible d'après (2), puisque $a_{i}$ est impair et premier avec chacun des autres $a_{j}$ d'après le lemme 2.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2017-2018-Corrig%c3%a9-03-2018.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Les entiers $1,2, \\ldots, 2018$ sont écrits au tableau. On effectue alors 2017 opérations comme suit : choisir deux nombres $a$ et $b$, les effacer, et écrire $a+b+2 a b$ à la place. À la fin, il ne reste qu'un seul entier sur le tableau.\nQuelles sont les valeurs que son chiffre des unités peut prendre?", "solution": "Puisqu'il y a 1009 nombres impairs entre 1 et 2018, on sait que la somme des entiers initialement inscrits au tableau est impaire. En outre, l'un de ces entiers est congru à $2(\\bmod 5)$. Une récurrence immédiate permet alors de montrer que, après chaque opération, la somme des entiers écrits sur le tableau reste impaire, et l'un de ces entiers est congru à 2 $(\\bmod 5)$. Par conséquent, le dernier entier écrit sur le tableau est congru à $1(\\bmod 2)$ et à 2 $(\\bmod 5)$, c'est-à-dire à $7(\\bmod 10)$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle isocèle en $A$, tel que $\\widehat{B A C}=100^{\\circ}$. Soit $D$ le point d'intersection de (AC) et de la bissectrice de $\\widehat{A B C}$.\nMontrer que BC $=A D+B D$.", "solution": "D'après la loi des sinus, notons que $\\mathrm{BD} \\leqslant \\mathrm{BC}$ si et seulement $\\operatorname{si} \\sin (\\widehat{\\mathrm{BCD}}) \\leqslant$ $\\sin (\\widehat{\\mathrm{BDC}})$. Puisque $\\widehat{\\mathrm{BDC}}=130^{\\circ}$ et $\\widehat{\\mathrm{BCD}}=40^{\\circ}$, on a bien $\\mathrm{BD} \\geqslant \\mathrm{BC}$. Soit E le point de $[\\mathrm{BC}]$ tel que $B D=B E$, et soit $A^{\\prime}$ le symétrique de $A$ par rapport à ( $A D$ ).\nLa loi des sinus indique alors que\n\n$$\n\\mathrm{CE}=\\frac{\\sin (\\widehat{\\mathrm{CDE}})}{\\sin (\\widehat{\\mathrm{ECD}})} \\mathrm{DE}=\\frac{\\sin (\\widehat{\\mathrm{CDE}})}{\\sin (\\widehat{\\mathrm{ECD}})} \\times \\frac{\\sin (\\widehat{\\mathrm{EA}} \\widehat{\\mathrm{D}})}{\\sin \\left(\\widehat{\\mathrm{A}^{\\prime} \\mathrm{ED}}\\right)} A^{\\prime} \\mathrm{D}=\\frac{\\sin \\left(40^{\\circ}\\right) \\sin \\left(80^{\\circ}\\right)}{\\sin \\left(40^{\\circ}\\right) \\sin \\left(80^{\\circ}\\right)} A D=A D .\n$$\n\nOn en déduit que $B C=C E+B E=A D+B D$.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Trouver tous les entiers naturels non nuls $k, \\ell$ tels que $2^{k}+3^{\\ell}$ soit un carré parfait.", "solution": "Une première idée est de consiérer l'équation de l'énoncé modulo $n$, où n est un nombre pas trop grand tel que $\\mathbb{Z} / \\mathrm{n} \\mathbb{Z}$ ne contienne pas trop de résidus quadratiques. Dans ces conditions, $n=3$ et $n=8$ semblent de bons candidats, car les carrés modulo 3 sont 0 et 1 , alors que les carrés modulo 8 sont 0,1 et 4 .\nPuisque $k \\geqslant 1$ et $\\ell \\geqslant 1$, on a donc $2^{k} \\equiv 1(\\bmod 3)$ et $3^{\\ell} \\equiv 1(\\bmod 8)$, ce qui signifie que $k$ et $\\ell$ sont pairs. En posant $\\mathrm{a}=\\mathrm{k} / 2, \\mathrm{~b}=\\ell / 2$ et $\\mathrm{c}=\\sqrt{2^{k}+3^{\\ell}}$, on remarque alors que $\\left(\\mathrm{c}-2^{\\mathrm{a}}\\right)\\left(\\mathrm{c}+2^{\\mathrm{a}}\\right)=$ $c^{2}-2^{k}=3^{\\ell}$ est une puissance de 3 .\n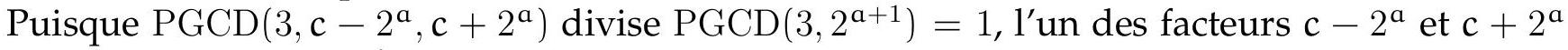 vaut nécessairement $3^{\\ell}$, tandis que l'autre vaut 1 . Le facteur $c+2^{a}$ est le plus grand des deux, ce qui montre que $c-2^{a}=1$ et $\\mathrm{c}+2^{a}=3^{\\ell}$, donc que $2^{a+1}=3^{\\ell}-1=9^{b}-1=\\left(3^{b}-1\\right)\\left(3^{b}+1\\right)$. De même, puisque $3^{\\mathrm{b}}-1$ et $3^{\\mathrm{b}}+1$ sont pairs et que $\\operatorname{PGCD}\\left(2,3^{\\mathrm{b}}-1,3^{\\mathrm{b}}+1\\right)$ divise 2 , l'un des facteurs $3^{b}-1$ et $3^{b}+1$ vaut nécessairement $2^{a}$, tandis que l'autre vaut 2 . Par conséquent, $3^{\\mathrm{b}}-1=2$ et $3^{\\mathrm{b}}+1=2^{\\mathrm{a}}$, ce qui montre que $\\mathrm{a}=2$ et $\\mathrm{b}=1$, ou encore $\\mathrm{k}=4$ et $\\ell=2$.\nRéciproquement, si $(k, \\ell)=(4,2)$, on a bien $2^{k}+3^{\\ell}=2^{4}+3^{2}=16+9=25=5^{2}$. Ceci montre que la paire $(k, \\ell)=(4,2)$ est la seule solution du problème.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Soit $a, b, c, d$ des réels tels que $0 \\leqslant a \\leqslant b \\leqslant c \\leqslant d$. Montrer que\n\n$$\na b^{3}+b c^{3}+c d^{3}+d a^{3} \\geqslant a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\n$$", "solution": "Une première idée est de considérer les sommes «symétriques $\\gg$ l'une de l'autre $S_{1}=a b^{3}+b^{3}+c d^{3}+d a^{3}$ et $S_{2}=a^{3} b+b^{3} c+c^{3} d+d^{3} a$. On constate alors que\n$S_{1}-S_{2}=\\left(d^{3}-b^{3}\\right)(c-a)+\\left(c^{3}-a^{3}\\right)(b-d)=(d-b)(c-a)\\left(d^{2}+b d+d^{2}-c^{2}-a c-a^{2}\\right) \\geqslant 0$.\nL'inégalit�� de Cauchy-Schwarz indique alors que $S_{1}^{2} \\geqslant S_{1} S_{2} \\geqslant\\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\\right)^{2}$, ce qui conclut.\n\n## Exercices du groupe A - Énoncés et solutions", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2017", "problem_label": "5", "tier": 1, "problem": "Soit $n$ un entier naturel impair, et soit $a_{1}, \\ldots, a_{n}$ des entiers naturels non nuls. On note $A$ le produit des entiers $a_{i}$, et $d$ leur plus grand diviseur commun.\nMontrer que\n\n$$\n\\operatorname{PGCD}\\left(a_{1}^{n}+A, a_{2}^{n}+A, \\ldots, a_{n}^{n}+A\\right) \\leqslant 2 d^{n}\n$$", "solution": "Pour tout $i$, on pose $b_{i}=a_{i} / d$, de sorte que $\\operatorname{PGCD}\\left(b_{1}, \\ldots, b_{n}\\right)=1$, et on pose également $B=b_{1} \\times \\ldots \\times b_{n}$ et $\\Delta=\\operatorname{PGCD}\\left(b_{1}^{n}+B, b_{2}^{n}+B, \\ldots, b_{n}^{n}+B\\right)$. Alors $\\operatorname{PGCD}\\left(a_{1}^{n}+A, a_{2}^{n}+A, \\ldots, a_{n}^{n}+A\\right)=d^{n} \\times \\Delta$, et il reste à démontrer que $\\Delta \\leqslant 2$.\nOn considère alors un éventuel facteur premier $p$ de $\\Delta$. Si $p$ divise un des entiers $b_{i}$, alors il divise $B$ également, donc il divise chaque entier $b_{j}$, ce qui est absurde. Par conséquent, $p$ ne divise aucun des entiers $b_{i}$, et ne divise pas $B$ non plus. Cela montre que $\\Delta$ est premier avec $B$. Or, puisque $b_{1}^{n} \\equiv b_{2}^{n} \\equiv \\ldots \\equiv b_{n}^{n}=-B(\\bmod \\Delta)$, alors $B^{n} \\equiv b_{1}^{n} \\times \\ldots \\times b_{n}^{n} \\equiv(-1)^{n} B^{n} \\equiv-B^{n}$ $(\\bmod \\Delta)$. Par conséquent, $\\Delta$ divise $2 \\mathrm{~B}^{n}$. On en déduit que $\\Delta$ divise 2 , ce qui conclut.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2017", "problem_label": "6", "tier": 1, "problem": "Soit q un nombre réel. Margaret a écrit 10 nombres réels, deux à deux distincts, sur une ligne. Puis elle ajoute trois lignes comme suit :\n$\\triangleright$ sur la $2^{\\text {nde }}$ ligne, elle écrit tous les nombres de la forme $a-b$, où $a$ et $b$ sont deux réels (non nécessairement distincts) de la $1{ }^{\\text {ère }}$ ligne;\n$\\triangleright$ sur la $3^{\\text {ème }}$ ligne, elle écrit tous les nombres de la forme $q a b$, où $a$ et $b$ sont deux réels (non nécessairement distincts) de la $2^{\\text {nde }}$ ligne;\n$\\triangleright$ sur la $4^{\\text {ème }}$ ligne, elle écrit tous les nombres de la forme $a^{2}+b^{2}-c^{2}-d^{2}$, où $a, b, c$ et $d$ sont des réels (non nécessairement distincts) de la $2^{\\text {nde }}$ ligne.\nTrouver tous les réels q tels que, quels que soient les 10 nombres écrits sur la $1{ }^{\\text {ère }}$ ligne, chaque nombre de la $3^{\\text {ème }}$ ligne soit également sur la $4^{\\text {ème }}$ ligne.", "solution": "On va dire qu'un réel q est bon s'il a la propriété demandée dans l'énoncé. Tout d'abord, il est clair que, si q est bon, alors - q l'est aussi, et réciproquement. D'autre part, $q=0$ est manifestement bon. On cherche donc les bons réels $q>0$, s'il y en a.\nSoit $\\lambda$ un grand nombre réel et soit $\\varepsilon=1 / \\lambda$. On suppose que Margaret a écrit dix nombres $x_{1}, \\ldots, x_{10}$ tels que $0 \\leqslant x_{1}<\\ldots<x_{8} \\leqslant \\varepsilon, x_{9}=1$ et $x_{10}=\\lambda$. Alors la $2^{\\text {nde }}$ ligne contient les nombres $\\pm \\lambda, \\pm(\\lambda-1)$ et $\\pm 1$, ainsi que des éléments de l'ensemble $\\Omega_{2}=[0,1] \\cup[\\lambda-\\varepsilon, \\lambda]$ et leurs opposés. En particulier, Margaret écrit donc les réels $q \\lambda^{2}$ et $q \\lambda$ sur la $3^{\\text {ème }}$ ligne.\n\nOn considère alors un nombre de la $4^{\\text {ème }}$ ligne, de la forme $z=a^{2}+b^{2}-c^{2}-d^{2}$, et tel que $z \\geqslant 0$. Chacun des réels $\\mathrm{a}^{2}, \\mathrm{~b}^{2}, \\mathrm{c}^{2}, \\mathrm{~d}^{2}$ appartient à l'ensemble $\\left\\{0, \\lambda^{2}\\right\\}+\\{-2 \\lambda, 0\\}+[0,2]$, donc $z$ appartient à l'ensemble $\\Omega_{4}=\\left\\{0, \\lambda^{2}, 2 \\lambda^{2}\\right\\}+\\{-4 \\lambda,-2 \\lambda, 0,2 \\lambda, 4 \\lambda\\}+[-4,4]$.\nSi q est bon, alors $q \\lambda^{2}$ et $\\mathrm{q} \\lambda$ appartiennent à $\\Omega_{4}$, donc en faisant tendre $\\lambda$ vers $+\\infty$ on en déduit respectivement que $q \\in\\{1,2\\}$ et que $q \\in\\{2,4\\}$. Cela montre que seul $q=2$ est susceptible d'être bon.\nRéciproquement, si $q=2$, tout nombre de la $3^{\\text {ème }}$ est de la forme $2(a-b)(c-d)$ avec $a, b, c, d$ des réels de la $1^{\\text {ère }}$ ligne. Puisque $2(a-b)(c-d)=(a-d)^{2}+(b-c)^{2}-(a-c)^{2}-(b-d)^{2}$, ce nombre est figure également sur la $4^{\\text {ème }}$ ligne. Par conséquent, les bons réels sont $-2,0$ et 2 .", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2017", "problem_label": "7", "tier": 1, "problem": "Soit $A B C$ un triangle acutangle non isocèle. Soit O le centre du cercle circonscrit à $A B C$ et $H$ l'orthocentre de $A B C$. Soit $P$ et $Q$ les points d'intersection respectifs de ( $A O)$ avec (BH) et (CH).\nMontrer que le centre du cercle circonscrit à $P Q H$ se situe sur une médiane du triangle $A B C$.", "solution": "Soit $\\Omega$ le cercle circonscrit à $A B C, \\omega$ le cercle circonscrit à PQH , et $X$ le centre de $\\omega$. Puisque $B$ et $C$ jouent des rôles symétriques, on va montrer que $X$ se trouve sur la médiane issue de $A$. Soit alors $M$ le point d'intersection des droites $(A X)$ et (BC) : montrons que $M$ est le milieu de $[B C]$, c'est-à-dire que $\\widehat{C M O}=90^{\\circ}$.\nTout d'abord, une simple chasse aux angles montre que $\\widehat{\\mathrm{QHP}}=\\widehat{\\mathrm{CAB}}, \\widehat{\\mathrm{HPQ}}=\\widehat{\\mathrm{ABC}}$ et $\\widehat{\\mathrm{PQH}}=$ $\\widehat{P H A}=\\widehat{B C A}$. Les triangles $A B C$ et $H P Q$ sont donc semblables, et il existe une similitude $s$ telle que $s(A)=H, s(B)=P, s(C)=Q$ et $s(O)=X$.\n$D^{\\prime}$ autre part, puisque $\\widehat{P Q H}=\\widehat{P H A}$ on sait que $(A H)$ est tangente à $\\omega$ en $H$. Par conséquent, si on pose $S=s^{-1}(\\mathcal{A})$, alors on sait que $S$ est le point d'intersection de (BC) et de la tangente à $\\Omega$ en $A$. Puisque s envoie $B S O$ sur $P A X$, on en déduit que $\\widehat{M S O}=\\widehat{B S O}=\\widehat{\\mathrm{XAP}}=\\widehat{\\mathrm{MAO}}$, donc que les points $M, S, O$ et $A$ sont cocycliques. Or, $\\widehat{S A O}=90^{\\circ}$. Il s'ensuit que $\\widehat{S M O}=90^{\\circ}$ également, ce qui conclut.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Soit $n \\geq 3$ un entier et considérons $n$ droites en position générale (c'est-à-dire que trois droites ne sont jamais concourantes et deux droites jamais parallèles). Combien de triangles sont formés par ces droites?\nN.B. Par exemple, dans la figure ci-dessous, il y a 4 triangles.\n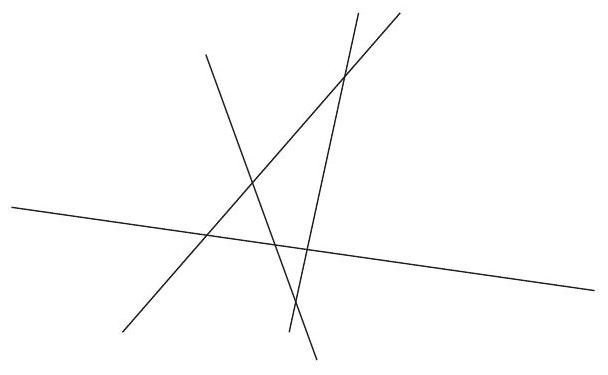", "solution": "Si on numérote de 1 à $n$ les $n$ droites, on remarque que chaque triangle est codé par la donnée d'un sous-ensemble de $\\{1,2, \\ldots, n\\}$ à trois éléments. Il y a donc $\\binom{n}{3}=$ $\\frac{n(n-1)(n-2)}{6}$ triangles.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle. On note $L, M, N$ les milieux de $[B C],[C A]$ et $[A B]$. Notons $(d)$ la tangente en $A$ au cercle circonscrit à $A B C$. La droite $(L M)$ coupe $(d)$ en $P$, et la droite $(L N)$ coupe $(d)$ en $Q$. Montrer que $(C P)$ et $(B Q)$ sont parallèles.", "solution": "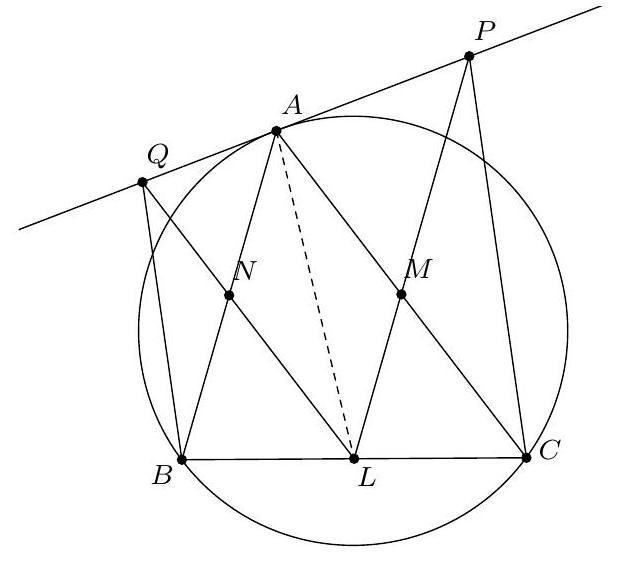\n\nOn a $(A Q, A B)=(C A, C B)=(L Q, L B)$ donc $A, Q, B, L$ sont cocycliques, et de même $A, P, C, M$ sont cocycliques. On a donc $(C P, B C)=(C P, C L)=(A P, A L)=(A Q, A L)=(B Q, B L)=$ $(B Q, B C)$, donc $(C P)$ et $(B Q)$ sont parallèles.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Soient $p$ et $n$ des entiers strictement positifs, avec $p$ premier, et $n \\geqslant p$. On suppose que $1+n p$ est un carré parfait. Montrer que $n+1$ est une somme de $p$ carrés parfaits non nuls (non nécessairement distincts).", "solution": "Soit $k$ tel que $1+n p=k^{2}$, alors $n p=(k-1)(k+1)$.\nPremier cas : $p$ divise $k-1$. Alors on peut écrire $k-1=p \\ell$, donc $k=p \\ell+1$. En reportant dans l'égalité, on obtient que $n+1=p \\ell^{2}+2 \\ell+1=(p-1) \\ell^{2}+(\\ell+1)^{2}$.\nDeuxième cas : $p$ divise $k+1$. On obtient avec la même méthode $n+1=p \\ell^{2}-2 \\ell+1=$ $(p-1) \\ell^{2}+(\\ell-1)^{2}$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Soit $n \\geqslant 1$ un entier. Pour tout sous-ensemble non vide $A$ de $\\{1,2, \\ldots, n\\}$, on note $P(A)$ le produit de tous les éléments de $A$. Par exemple, pour $A=\\{2,4,7\\}$, on a $P(A)=$ 56. Déterminer la somme des $\\frac{1}{P(A)}$ lorsque $A$ parcourt tous les sous-ensembles non vides de $\\{1,2, \\ldots, n\\}$.", "solution": "On a l'identité $\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right)=1+\\sum x_{i}+\\sum_{i<j} x_{i} x_{j}+\\cdots$. En prenant $x_{i}=\\frac{1}{a_{i}}$, on obtient\n\n$$\n\\sum_{k \\geqslant 0} \\sum_{a_{1}<\\cdots<a_{k}} \\frac{1}{a_{1} a_{2} \\cdots a_{k}}=\\left(1+\\frac{1}{1}\\right) \\cdots\\left(1+\\frac{1}{n}\\right)=\\frac{2}{1} \\times \\frac{3}{2} \\times \\frac{4}{3} \\cdots \\times \\frac{n+1}{n}=n+1\n$$\n\nOn a donc $1+\\sum_{A} \\frac{1}{P(A)}=n+1$ donc $\\sum_{A} \\frac{1}{P(A)}=n$.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Déterminer la valeur maximale de $\\sqrt{x}+\\sqrt{2 y+2}+\\sqrt{3 z+6}$ lorsque $x, y, z$ sont des nombres réels strictement positifs vérifiant $x+y+z=3$.", "solution": "D'après l'inégalité de Cauchy-Schwarz, on a\n\n$$\n\\sqrt{x} \\sqrt{1}+\\sqrt{y+1} \\sqrt{2}+\\sqrt{z+2} \\sqrt{3} \\leqslant \\sqrt{x+y+1+z+2} \\sqrt{1+2+3}=6\n$$\n\nL'égalité est atteinte lorsque $x=y=z=1$. Donc la valeur maximale est 6 .", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle acutangle, et soit $P$ un point situé à l'intérieur du triangle $A B C$. Soit $D$ le milieu du segment $[P C], E$ le point d'intersection des droites $(A P)$ et $(B C)$, et $Q$ le point d'intersection des droites $(B P)$ et $(D E)$. Montrer que, si les angles $\\widehat{P A C}$ et $\\widehat{P C B}$ sont égaux, alors $\\sin (\\widehat{B C Q})=\\sin (\\widehat{B A P})$.", "solution": "Soit $R$ le point d'intersection des droites $(C Q)$ et $(A P)$. Il suffit de prouver l'égalité des angles de droites $(C B, C Q)=(A B, A R)$. Pour ce faire, il suffit de prouver que les points $B, C, A, R$ sont cocycliques, c'est-à-dire que $(B R, B C)=(A R, R C)$. Comme $(A R, A C)=$ $(C P, C B)$, il suffit de prouver que $(B R, B C)=(C P, C B)$, donc que les droites $(B R)$ et $(P C)$ sont parallèles.\nPour ce dernier point, on peut utiliser que si $X=(C P) \\cap(B R)$ alors $(X, D, P, C)$ est une division harmonique. On peut également se passer de géométrie projective comme suit :\nOn utilise le théorème de Ceva dans le triangle $P C E$, puisque les droites $(P B),(D E)$ et $(R C)$ sont concourantes en $Q$, avec $R \\in(P E)$ et $B \\in(C E)$. On en déduit que\n\n$$\n1=\\frac{C B}{E B} \\cdot \\frac{P D}{C D} \\cdot \\frac{R E}{R P}=\\frac{C B}{E B} \\cdot \\frac{R E}{R P}\n$$\n\nc'est-à-dire\n\n$$\n\\frac{R E}{E B}=\\frac{R P}{C B}\n$$\n\nEn appliquant la réciproque du théorème de Thalès aux triangles $B R E$ et $C P E$, on déduit de cette dernière égalité que les droites $(B R)$ et $(P C)$ sont bien parallèles, ce qui conclut.\n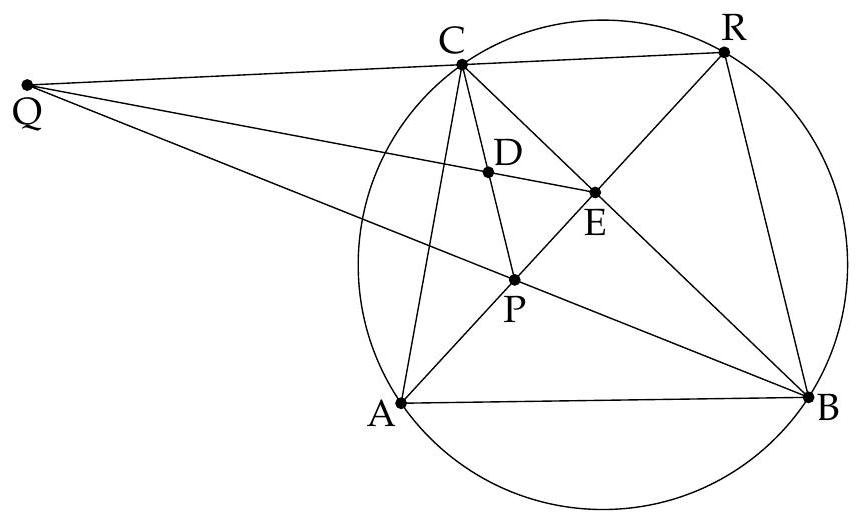", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Trouver toutes les valeurs possibles pour $f(2018)$ où $f$ est une fonction de $\\mathbb{Q}$ dans $\\mathbb{R}_{+}$vérifiant les trois conditions suivantes:\n\n- $f(2)=1 / 2$ ;\n- pour tout rationnel $x$, si $f(x) \\leqslant 1$, alors $f(x+1) \\leqslant 1$;\n- $f(x y)=f(x) f(y)$ pour tous rationnels $x$ et $y$.", "solution": "Tout d'abord, l'égalité $1 / 2=f(2)=f(1 \\times 2)=f(1) f(2)=f(1) / 2$ montre que $f(1)=1$, et donc que $f(n) \\leqslant 1$ pour tout entier naturel non nul $n$.\nNotons de plus que pour tous $x, y$ avec $y \\neq 0$ on a $f(y) \\neq 0$, et $f(x / y)=f(x) / f(y)$ puisque $f(x / y) f(y)=f((x / y) y)=f(x)$. En particulier, $f(1 / 2)=2$. Enfin, pour tout rationnel $x$, on a $f(x)^{2}=f\\left(x^{2}\\right)=f(-x)^{2}$, donc $f$ est paire.\nSoit alors $k$ un entier naturel impair, de la forme $k=2 n+1$ : on a nécessairement $f(k) \\leqslant 1$. On sait également que $f(-k / 2)>1$, puisque $1 / 2=-k / 2+(n+1)$, donc $f(-2 / k)=1 / f(-k / 2) \\leqslant 1$, ce qui implique que $f\\left(\\frac{k-2}{k}\\right)=f\\left(-\\frac{2}{k}+1\\right) \\leqslant 1$, par conséquent $f(k-2) \\leqslant f(k)$.\nCeci permet de montrer par récurrence que pour tout $k \\geqslant 1$ impair on a $f(k) \\geqslant 1$, et donc $f(k)=1$.\nOn déduit de tout ceci que $f(2018)=f(2) f(1009)=1 / 2$.\nRéciproquement, il reste à vérifier qu'une fonction $f$ telle que décrite dans l'énoncé existe bien. Il suffit pour ce faire de constater que la fonction $f$ définie par\n\n$$\nf: p / q \\mapsto \\begin{cases}0 & \\text { si } p=0 \\\\ 2^{v_{2}(q)-v_{2}(p)} & \\text { si } p \\neq 0\\end{cases}\n$$\n\noù $v_{2}(n)$ désigne la valuation 2-adique de l'entier $n$, satisfait bien les conditions de l'énoncé.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Pour tout entier naturel $n$, on note $S(n)$ la somme des chiffres de l'écriture décimale de $n$. On dit qu'un entier naturel $n$ est joli si $S(n)=S\\left(n^{2}\\right)$. Déterminer toutes les valeurs possibles de $S(n)$ pour les entiers jolis $n$.", "solution": "Modulo 9, $S(n)$ vérifie l'équation $x^{2}=x$. On vérifie en testant $x=$ $0,1, \\ldots, 8$ que les seules solutions (modulo 9) sont 0 et 1 , donc $S(n)$ est nécessairement congru à 0 ou 1 modulo 9 . Réciproquement, on vérifie que si $n=10^{k}-1=99 \\cdots 9$ ( $k$ fois) alors $n^{2}=99 \\cdots 9800 \\cdots 01$ (avec $k-1$ chiffres 9 et $k-1$ chiffres 0 ), donc $S(n)=S\\left(n^{2}\\right)=9 k$. De même, si $n=2 \\times 10^{k}-1=199 \\cdots 9$ alors $n^{2}=399 \\cdots 9600 \\cdots 01$ donc $S(n)=S\\left(n^{2}\\right)=9 k+1$.\nOn en conclut que les valeurs possibles de $S(n)$ sont les entiers naturels congrus à 0 ou à 1 modulo 9.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "On fixe un entier naturel $n \\geqslant 2$. Déterminer tous les nombres réels $x \\geqslant-1$ tels que pour tous nombres réels $a_{1}, \\ldots, a_{n} \\geqslant 1$ on ait\n\n$$\n\\frac{a_{1}+x}{2} \\times \\cdots \\times \\frac{a_{n}+x}{2} \\leqslant \\frac{a_{1} a_{2} \\cdots a_{n}+x}{2} .\n$$", "solution": "En prenant $a_{i}=1$ pour tout $i$, on obtient la condition $\\left(\\frac{1+x}{2}\\right)^{n} \\leqslant \\frac{1+x}{2}$. Notons $y=\\frac{1+x}{2}$. Par hypothèse, $y \\geqslant 0$. Comme $y^{n} \\leqslant y$, on a $y^{n-1} \\leqslant 1$ donc $y \\leqslant 1$, ce qui implique $x \\leqslant 1$.\nRéciproquement, montrons que tout $x \\in[-1,1]$ convient. On raisonne par récurrence sur $n$. Pour $n=1$ l'inégalité est évidente. Supposons qu'elle soit vraie au rang $n-1$. Le membre de gauche de l'inégalité est alors inférieur ou égal à $\\frac{a+x}{2} \\times \\frac{b+x}{2}$, où $a=a_{1} a_{2} \\cdots a_{n-1}$ et $b=a_{n}$. Il suffit alors de montrer que $\\left(\\frac{a+x}{2}\\right)\\left(\\frac{b+x}{2}\\right) \\leqslant\\left(\\frac{a b+x}{2}\\right)$. En développant, l'inégalité devient $(a+b-2) x+x^{2} \\leqslant a b$. Comme $a+b-2 \\geqslant 0$, et comme $x \\leqslant 1$ et $x^{2} \\leqslant 1$, le membre de gauche de l'inégalité est majoré par $(a+b-2)+1$, donc suffit de montrer que $(a+b-2)+1 \\leqslant a b$, ou encore que $0 \\leqslant a b-a-b+1$. Or, on a $a b-a-b+1=(a-1)(b-1)$. Comme $a \\geqslant 1$ et $b \\geqslant 1$, l'inégalité $(a-1)(b-1) \\geqslant 0$ est bien vérifiée.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Soit $n \\geqslant 2$ un entier naturel. On se donne $2 n$ boules. Sur chacune de ces boules est écrit un nombre. On suppose que, à chaque fois que l'on regroupe les boules en $n$ paires, deux de ces paires ont la même somme.\n(a) Montrer que quatre de ces boules comportent le même nombre.\n(b) Montrer que le nombre de valeurs distinctes inscrites sur les boules est $\\leqslant n-1$.", "solution": "(a) On note $a_{1} \\geqslant a_{2} \\geqslant \\cdots \\geqslant a_{2 n}$ les valeurs prises par les $2 n$ boules dans l'ordre décroissant. On les apparie ainsi : $\\left(a_{1}, a_{2}\\right),\\left(a_{3}, a_{4}\\right), \\ldots$ Comme il existe $i<j$ impairs tels que $a_{i}+a_{i+1}=a_{j}+a_{j+1}$, et comme $a_{i} \\geqslant a_{i+1} \\geqslant a_{j} \\geqslant a_{j+1}$, on a $a_{i}=a_{i+1}=a_{j}=a_{j+1}$.\n(b) Supposons qu'il y ait au moins $n$ valeurs distinctes, que l'on ordonne par ordre décroissant $b_{1}>b_{2}>\\cdots>b_{n}$. On ordonne les autres boules dans l'ordre décroissant $c_{1} \\geqslant \\cdots \\geqslant c_{n}$. On forme les $n$ paires $\\left(b_{i}, c_{i}\\right)$, et on constate que si $i<j$ alors $b_{i}+c_{i}>b_{j}+c_{j}$, ce qui contredit le fait que deux de ces sommes doivent être égales.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Soit $A B C D$ un quadrilatère convexe d'aire $S$. On note $a=A B, b=B C, c=C D$ et $d=D A$. Pour toute permutation $x, y, z, t$ de $a, b, c, d$, montrer que\n\n$$\nS \\leqslant \\frac{1}{2}(x y+z t)\n$$", "solution": "Si $x$ et $y$ sont adjacents, sans perte de généralité on se ramène à montrer que $S \\leqslant \\frac{1}{2}(a b+c d)$. Cela découle de $S_{A B C}=\\frac{1}{2} A B \\cdot B C \\cdot \\sin \\widehat{A B C} \\leqslant \\frac{1}{2} a b$, et de même $S_{C D A} \\leqslant \\frac{1}{2} c d$. Si $x$ et $y$ sont des côtés opposés, on doit montrer que $S \\leqslant \\frac{1}{2}(a c+b d)$. Soit $A^{\\prime}$ le symétrique de $A$ par rapport à la médiatrice de $[B D]$. Alors $B A^{\\prime} D$ est isométrique à $D A B$. On applique ce qui précède à $A^{\\prime} B C D$, ce qui donne $S=S_{B A D}+S_{B C D}=S_{B A^{\\prime} D}+S_{B C D}=S_{A^{\\prime} B C D} \\leqslant \\frac{1}{2}\\left(A^{\\prime} B \\cdot B C+\\right.$ $\\left.C D \\cdot D A^{\\prime}\\right)=\\frac{1}{2}(a c+b d)$.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2017", "problem_label": "5", "tier": 1, "problem": "Déterminer tous les nombres réels $a$ tels qu'il existe une suite infinie de nombres réels strictement positifs $x_{0}, x_{1}, x_{2}, x_{3}, \\ldots$ vérifiant pour tout $n$ l'égalité\n\n$$\nx_{n+2}=\\sqrt{a x_{n+1}-x_{n}} .\n$$", "solution": "Si $a>1$, on peut prendre la suite constante égale à $a-1$. Supposons $a \\leqslant 1$. Comme la racine carré est bien définie, on a nécessairement $a x_{n+1}-x_{n}>0$, donc déjà $a \\geqslant 0$, et de plus $x_{n+1} \\geqslant a x_{n+1}>x_{n}$. Par conséquent, la suite est strictement croissante.\nComme $x_{n+1} \\leqslant x_{n+2} \\leqslant \\sqrt{x_{n+1}-x_{n}}<\\sqrt{x_{n+1}}$, on en déduit que $x_{n}<1$ pour tout $n$. De plus, $x_{n+1}^{2} \\leqslant x_{n+1}-x_{n}$ donc $x_{n+1} \\geqslant x_{n+1}^{2}+x_{n} \\geqslant x_{n} x_{0}+x_{n}=\\left(1+x_{0}\\right) x_{n}$, ce qui montre que $x_{n} \\geqslant$ $\\left(1+x_{0}\\right)^{n} x_{0}$ pour tout $n$. Ceci contredit que $x_{n} \\leqslant 1$.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2017", "problem_label": "6", "tier": 1, "problem": "Dans un pays se trouvent 64 villes. Il existe des routes qui relient certaines paires de villes, mais Bob ne sait pas lesquelles (les routes ne se croisent pas mais peuvent éventuellement passer les unes au-dessus des autres ; de plus, les routes peuvent être parcourues dans les deux sens). Alice, elle, connaît parfaitement le réseau. Bob peut choisir n'importe quelle paire de villes et demander à Alice si elles sont reliées directement par une route. Le but de Bob est de déterminer s'il est possible de voyager de n'importe quelle ville à n'importe quelle autre (en empruntant éventuellement plusieurs routes successives). Montrer qu'il n'existe aucun algorithme (c'est-à-dire aucune stratégie en fonction des réponses successives d'Alice) lui permettant de le savoir à coup sûr en moins de 2016 questions.", "solution": "On remarque que $2016=64 \\times 63 / 2=\\binom{64}{2}$, donc il y a exactement 2016 paires de villes. Le réseau routier est un graphe non orienté ayant 64 sommets. Chaque paire de villes correspond à une\nquestion, et on veut savoir si en moins de 2016 questions Bob peut déterminer si le graphe est connexe. Supposons par l'absurde que Bob possède un algorithme en moins de 2016 questions : par conséquent, pour tout graphe ayant 64 sommets, si Bob suit son algorithme en posant une suite de questions $Q_{1}, Q_{2}, \\ldots$ et s'arrête à une question $Q_{n}$ dès qu'il peut conclure à coup sûr si le graphe est connexe ou non, alors $n \\leqslant 2015$ (l'entier $n$ dépend du graphe). Remarquons que la réponse à $Q_{n}$ est nécessairement \"oui\" si le graphe est connexe et \"non\" si le graphe est non connexe, sinon Bob aurait déjà pu conclure à la question $Q_{n-1}$.\nOn part du graphe $G_{0}$ ne possédant aucune arête. Bob, en utilisant son algorithme, pose une suite de questions $Q_{1}, Q_{2}, \\ldots, Q_{n_{0}}$ à Alice.\nLa question $Q_{n_{0}}$ correspond à une paire de villes. Soit $G_{1}$ le graphe consistant à rajouter une arête entre ces deux villes. En suivant son algorithme, Bob pose à nouveau les questions $Q_{1}, \\ldots, Q_{n_{0}}$, et d'autres questions $Q_{n_{0}+1}, \\ldots, Q_{n_{1}}$. On a bien $n_{1}>n_{0}$ car, pour le graphe $G_{1}$, la réponse à $Q_{n_{0}}$ est \"oui\", et la réponse à $Q_{n_{1}}$ est \"non\" puisque le graphe $G_{1}$ n'est pas connexe.\nOn continue la procédure, et on construit ainsi une suite de graphes $G_{0}, G_{1}, G_{2}, \\ldots$, chaque graphe étant construit à partir du précédent en rajoutant une arête, jusqu'à obtenir un graphe connexe $G_{k}$. Comme $n_{k-1}>n_{k-1}>\\cdots>n_{0} \\geqslant 1$, on a $n_{k-1} \\geqslant k$ donc $k \\leqslant 2015$.\nOr, $G_{k}$ possède $k$ arêtes, donc il existe une paire de villes $X$ et $Y$ qui ne sont pas reliées directement. En revanche, comme $G_{k}$ est connexe on peut aller de $X$ vers $Y$ en suivant un chemin consistant en des arêtes de $G_{k}$. Soit $j$ le plus grand indice tel que l'une des arêtes $A$ de ce chemin appartient à $G_{j}$ mais pas à $G_{j-1}$. Soit $G^{\\prime}$ le graphe obtenu en enlevant l'arête $A$ au graphe $G_{k}$ et en ajoutant l'arête $X Y$, alors la réponse aux questions $Q_{1}, \\ldots, Q_{n_{j-1}}$ est la même pour $G^{\\prime}$ que pour $G_{j-1}$. Or, Bob a pu conclure à coup sûr que $G_{j-1}{\\text { n'est pas connexe, donc } G^{\\prime}}^{\\prime}$ ne l'est pas non plus.\nMais ceci est contradictoire car, $G_{k}$ étant connexe, $G^{\\prime}$ l'est aussi.", "problem_match": "\nExercice 6.", "solution_match": "## Solution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Trouver tous les triplets ( $a, b, c$ ) de réels strictement positifs tels que\n\n$$\n\\left\\{\\begin{array}{l}\na \\sqrt{b}-c=a \\\\\nb \\sqrt{c}-a=b \\\\\nc \\sqrt{a}-b=c\n\\end{array}\\right.\n$$", "solution": "On remarque que $\\mathrm{a}=\\mathrm{b}=\\mathrm{c}=4$ est solution. On va montrer que c'est en fait la seule.\nSi deux des trois nombres sont égaux à 4 (disons a et b), on vérifie facilement que le troisième aussi, car $4 \\sqrt{4}-\\mathrm{c}=4$, donc $\\mathrm{c}=4$. Si un des trois nombres vaut 4 (disons a), alors $c \\sqrt{a}-b=c$ devient $2 \\mathrm{c}-\\mathrm{b}=\\mathrm{c}$, donc $\\mathrm{b}=\\mathrm{c}$. De plus, on $\\mathrm{a} \\sqrt{\\mathrm{b}}-\\mathrm{b}=4$, qui se réécrit $(\\sqrt{\\mathrm{b}}-2)^{2}=0$, donc $\\mathrm{b}=4$ et $\\mathrm{c}=4$. Il reste à montrer qu'il est impossible que les trois nombres soient différents de 4.\n\nSi c'est le cas, alors soit au moins deux des nombres sont strictement supérieurs à 4 , soit au moins deux sont strictement inférieurs à 4 . On traite les deux cas séparément.\nSi au moins deux des nombres sont $>4$, mettons que c soit le plus petit des trois nombres. Alors $a, b>4$, donc $a=a \\sqrt{b}-c>2 a-c$, donc $c>a>4$, ce qui contredit la minimalité de $c$. De même, si au moins deux des nombres sont $<4$, supposons que $c$ est le plus grand. Alors $a, b<4$, donc $a=a \\sqrt{b}-c<2 a-c$, donc $c<a$, ce qui contredit la maximalité de $c$. La seule solution est donc bien $(4,4,4)$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Trouver toutes les paires (m,n) d'entiers strictement positifs telles que\n\n$$\n\\mathrm{m}!+\\mathrm{n}!=\\mathrm{m}^{\\mathrm{n}}\n$$\n\nRemarque. Pour tout entier $n$, on rappelle que $n$ ! désigne l'entier $1 \\times 2 \\times 3 \\times \\cdots \\times n$.", "solution": "On vérifie facilement que les paires $(2,2)$ et $(2,3)$ sont solutions. On va montrer que ce sont les seules.\nOn commence par traiter le cas où $m$ ou $n$ vaut 1 ou 2 . Si $m=1$, alors $m^{n}=1$ mais $m!+n!\\geqslant 2$, donc il n'y a pas de solution. Si $m=2$, l'équation devient $2+n!=2^{n-1}$. Si $n \\geqslant 4$, alors le membre de gauche est congru à 2 modulo 4 , et le membre de droite à 0 , donc $n$ vaut 1,2 ou 3 , et $n=1$ ne marche pas. Si $n=1$, l'équation devient $m!+1=m$, mais $m$ divise $m$ ! et $m$, donc $m$ divise 1 et $m=1$, mais $(1,1) n^{\\prime}$ est pas solution. Enfin, si $n=2$, on obtient $m!+2=m^{2}$. Mais $m$ divise $m$ ! et $m^{2}$ donc $m$ divise 2 , donc $m$ vaut 1 ou 2 et on retombe sur des cas déjà traités.\nOn traite maintenant le cas $2<\\mathrm{m} \\leqslant \\mathrm{n}$. Dans ce cas m ! divise $n$ ! donc m ! divise $\\mathrm{m}^{\\mathrm{n}}$. En particulier, $m-1$ divise $m$ ! donc aussi $m^{n}$, mais $m-1$ est premier avec $m$, donc aussi avec $m^{n}$. Par conséquent, $\\mathrm{m}-1$ ne peut valoir que 1 donc $\\mathrm{m}=2$, contradiction.\nEnfin, on traite le cas $2<n<m$. Dans ce cas $n$ ! divise $m$ !, donc on peut écrire $n!\\left(1+\\frac{m!}{n!}\\right)=m^{n}$. En particulier, $1+\\frac{m!}{n!}$ divise $m^{n}$. Mais $\\frac{m!}{n!}=(n+1)(n+2) \\ldots$ m est divisible par $m$, donc $1+\\frac{m!}{n!}$ est premier avec $m$, donc avec $m^{n}$. On a donc $1+\\frac{n!}{m!}=1$, ce qui est impossible.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Soit $A B C D$ un trapèze tel que $(A B)$ et $(C D)$ sont parallèles. On suppose que $A D<$ $C D$ et que $A B C D$ est inscrit dans un cercle $\\Gamma$. Soit $P$ sur $\\Gamma$ tel que (DP) est parallèle à ( $A C$ ). La tangente à $\\Gamma$ en $D$ recoupe $(A B)$ en $E$, et les cordes $[B P]$ et $[C D]$ s'intersectent en $Q$. Montrer que $E Q=A C$.", "solution": "On sait que (CQ) est parallèle à $(\\mathrm{AE})$, donc l'énoncé revient à montrer que $A C Q E$ est un parallélogramme, donc il suffit de montrer que (EQ) et (AC) sont parallèles. Le quadrilatère BQDE est un trapèze, avec $(B E)$ et (DQ) parallèles. On va d'abord montrer que c'est un trapèze isocèle. En effet, on a\n\n$$\n\\widehat{\\mathrm{EDQ}}=\\widehat{\\mathrm{EDC}}=180^{\\circ}-\\widehat{\\mathrm{DAC}}\n$$\n\nd'après le cas limite du théorème de l'angle inscrit. D'autre part, on a\n\n$$\n\\widehat{\\mathrm{DQB}}=180^{\\circ}-\\widehat{\\mathrm{BDC}}-\\widehat{\\mathrm{DBP}}=180^{\\circ}-\\widehat{\\mathrm{BAC}}-\\widehat{\\mathrm{DAP}}\n$$\n\nOr, les quadrilatères $A B C D$ et $A C P D$ sont des trapèzes inscriptibles, donc isocèles, donc $P C=$ $A D=B C$, donc $C$ est le milieu de l'arc entre $B$ et $P$. On a donc $\\widehat{B A C}=\\widehat{C A P}$, donc\n\n$$\n\\widehat{\\mathrm{DQB}}=180^{\\circ}-\\widehat{\\mathrm{CAP}}-\\widehat{\\mathrm{DAP}}=180^{\\circ}-\\widehat{\\mathrm{DAC}}=\\widehat{\\mathrm{EDQ}}\n$$\n\ndonc le trapèze EBQD est bien isocèle, et a un axe de symétrie. On en déduit\n\n$$\n\\widehat{\\mathrm{DQE}}=\\widehat{\\mathrm{QDB}}=\\widehat{\\mathrm{CDB}}=\\widehat{\\mathrm{DCA}},\n$$\n\nen utilisant à la fin le fait que $A B C D$ a un axe de symétrie. Cela montre que ( QE ) et ( $A C$ ) sont parallèles, ce qui conclut.\n\n## Exercice commun aux groupes A et B - Énoncé et solution", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2017", "problem_label": "4", "tier": 1, "problem": "Un grand carré de côté $n$ est découpé en $n^{2}$ petits carrés de côté 1 . On veut colorier en rouge ou bleu chacun des $(n+1)^{2}$ sommets des petits carrés de telle manière que chacun des petits carrés a exactement 2 sommets rouges. Combien y a-t-il de coloriages possibles?", "solution": "La réponse est $2^{\\mathrm{n}+2}-2$. Pour le montrer, on commence par colorier les $n+1$ sommets les plus hauts. Il y a $2^{n+1}$ manières de le faire.\nSi il existe deux sommets consécutifs de même couleur sur la rangée supérieure ( $2^{n+1}-2$ coloriages de la rangée supérieure), alors ils fixent les couleurs sur la rangée juste en-dessous, et ainsi de suite, ce qui donne $2^{n+1}-2$ coloriages.\nSi les couleurs sur la rangée supérieure sont alternées ( 2 coloriages de la rangée supérieure), alors on est obligé d'alterner les couleurs sur la rangée d'en-dessous, et sur les suivantes... On peut cependant, à chaque ligne, choisir la couleur par laquelle on commence, ce qui donne $2 \\times 2^{n}$ coloriages, donc $2^{n+2}-2$ au total.\n\n## Exercices du groupe A - Énoncés et solutions", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2017", "problem_label": "5", "tier": 1, "problem": "Déterminer tous les entiers $n \\geqslant 2$ vérifiant la propriété suivante : pour tous entiers $a_{1}, a_{2}, \\ldots, a_{n}$ dont la somme n'est pas divisible par $n$, $i l$ existe un indice $i$ tel qu'aucun des nombres\n\n$$\na_{i}, a_{i}+a_{i+1}, \\ldots, a_{i}+\\cdots+a_{i+n-1}\n$$\n\nn'est divisible par $n$ (pour $i>n$, on pose $a_{i}=a_{i-n}$ ).", "solution": "Ce sont exactement les nombres premiers!\n\nEn effet, si $n=a b$, on peut prendre $a_{1}=0$ et $a_{2}=\\cdots=a_{n}=a$. La somme des $a_{i}$ vaut $a(n-1)$ donc n'est pas divisible par $n$. Cependant, soit $1 \\leqslant i \\leqslant n$. Si $i+b-1 \\leqslant n$, alors le nombre $a_{i}+\\cdots+a_{i+b-1}=a b=n$ est divisible par $n$. Si $i+b-1>n$, alors le nombre $a_{i}+\\cdots+a_{i+b}=a b=n$ est divisible par $n$.\nRéciproquement, supposons $n$ premier, et soient $a_{1}, \\ldots, a_{n}$ des entiers dont la somme n'est pas divisible par $n$. Si $n$ ne vérifie pas la propriété, alors pour tout indice $i$, il existe $j(i)$ avec $\\mathfrak{i}+1 \\leqslant \\mathfrak{j}(\\mathfrak{i}) \\leqslant \\mathfrak{i}+\\boldsymbol{n}$ tel que\n\n$$\na_{i}+a_{i+1}+\\cdots+a_{j(i)-1}\n$$\n\nest divisible par $n$. De plus, comme la somme des $a_{i} n^{\\prime}$ est pas divisible par $n$, on ne peut pas avoir $\\mathfrak{j}(\\mathfrak{i})=\\mathfrak{i}+\\mathfrak{n}$, donc $\\mathfrak{i}+1 \\leqslant \\mathfrak{j}(\\mathfrak{i}) \\leqslant \\mathfrak{i}+\\mathfrak{n}-1$. On définit alors par récurrence une suite $d^{\\prime}$ 'indices $\\left(i_{n}\\right)$ par $i_{1}=1$ et $i_{n+1}=j\\left(i_{n}\\right)$. On sait que pour tout $k$, l'entier\n\n$$\na_{i_{k}}+\\cdots+a_{i_{k+1}-1}\n$$\n\nest divisible par n donc, en sommant, pour tous indices $k<\\ell$, l'entier\n\n$$\na_{i_{k}}+\\cdots+a_{i_{\\ell}-1}\n$$\n\nest divisible par $n$. Par le principe des tiroirs, il existe $1 \\leqslant k<\\ell \\leqslant n+1$ tels que $\\mathfrak{i}_{k} \\equiv \\mathfrak{i}_{\\ell}(\\bmod n)$. Le nombre de termes de la somme (1) vaut alors $\\mathfrak{i}_{\\ell}-\\mathfrak{i}_{k}$ donc est divisible par $n$, donc chacun des $a_{i} y$ apparaît exactement $\\frac{\\boldsymbol{i}_{\\ell}-\\mathfrak{i}_{k}}{n}$ fois. De plus, on sait que $\\mathfrak{i}_{j+1}-\\mathfrak{i}_{j} \\leqslant n-1$ pour tout $j$ et que $\\ell-k \\leqslant n$, donc $\\mathfrak{i}_{\\ell}-\\mathfrak{i}_{k} \\leqslant n(n-1)$. La somme (1) vaut donc\n\n$$\n\\frac{\\mathfrak{i}_{\\ell}-\\mathfrak{i}_{k}}{n} \\times \\sum_{i=1}^{n} a_{i} .\n$$\n\nMais $\\frac{i_{\\ell}-i_{k}}{n} \\leqslant n-1$ donc ne peut pas être divisible par $n$, et la somme des $a_{i}$ ne l'est pas non plus. Comme n est premier, la somme (1) n'est pas divisible par n , d'où la contradiction.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2017", "problem_label": "6", "tier": 1, "problem": "Soit $A B C$ un triangle avec $A B \\neq A C$, et soit $\\omega$ le cercle $A$-exinscrit à $A B C$. On note $D, E$ et $F$ les points de tangence de $\\omega$ avec $[B C],[A C)$ et $[A B)$. Le cercle circonscrit à $A E F$ recoupe ( $B C$ ) en $P$ et $Q$. On note $M$ le milieu de $[A D]$. Montrer que le cercle circonscrit à MPQ est tangent à $\\omega$.\nRemarque. On rappelle que le cercle $A$-exinscrit à $A B C$ est l'unique cercle tangent au segment $[B C]$, à la demi-droite $[A B)$ au-delà de $B$ et à la demi-droite $[A C)$ au-delà de $C$.", "solution": "On note $\\Gamma$ le cercle passant par $A, E, F, P$ et $Q$. Soit $T$ le second point d'intersection de (AD) avec $\\omega$. On va montrer que $\\omega$ et le cercle circonscrit à MPQ sont tangents en $T$. On commence pour cela par montrer que $M, P, Q$ et $T$ sont cocycliques.\nSoient $J$ le centre de $\\omega$, et $N$ le milieu de [DT]. Alors les angles $\\widehat{A E J}$ et $\\widehat{A F J}$ sont droits, donc $E$ et $F$ sont sur le cercle de diamètre $[A J]$, donc $\\Gamma$ est le cercle de diamètre $[A J]$. De plus, la droite (JN) est la médiatrice de [DT], donc l'angle $\\widehat{A N J}$ est aussi droit et $N \\in \\Gamma$. La puissance de $D$ par rapport à $\\Gamma$ donne alors\n\n$$\n\\mathrm{DP} \\times \\mathrm{DQ}=\\mathrm{DA} \\times \\mathrm{DN}=\\mathrm{DA} \\times \\frac{1}{2} \\mathrm{DT}=\\frac{1}{2} \\mathrm{DA} \\times \\mathrm{DT}=\\mathrm{DM} \\times \\mathrm{DT}\n$$\n\ndonc $M, T, P$ et Q sont bien cocycliques.\nOn trace maintenant la tangente en $T$ à $\\omega$, qui recoupe ( $B C$ ) en $X$. On a $X D=X T$, donc les points $X$, J et $N$ sont alignés sur la médiatrice de [DT]. Les triangles XND et XDJ sont alors\nrectangles en $N$ et $D$ et partagent l'angle $\\widehat{D R J}$, donc ils sont semblables, donc $\\frac{X N}{X D}=\\frac{X D}{X J}$, donc $\\mathrm{XD}^{2}=\\mathrm{XN} \\times \\mathrm{XJ}$. On sait aussi que $\\mathrm{XT}=\\mathrm{XD}$, et la puissance de $X$ par rapport à $\\Gamma$ donne $\\mathrm{XN} \\times X \\mathrm{~J}=\\mathrm{XP} \\times \\mathrm{XQ}$. On obtient donc\n\n$$\nX T^{2}=X P \\times X Q\n$$\n\ndonc $(X T)$ est tangente au cercle circonscrit à PQT, ce qui conclut.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "problem_label": "1", "tier": 1, "problem": "Trouver tous les quadruplets ( $\\mathfrak{p}, \\mathrm{q}, \\mathrm{r}, \\mathfrak{n}$ ) d'entiers strictement positifs vérifiant les trois conditions suivantes:\n\n- $p$ et $q$ sont premiers,\n- $p+q$ n'est $^{\\text {pas divisible par 3, }}$\n$-p+q=r(p-q)^{n}$.", "solution": "On suppose d'abord que $\\mathrm{p} \\neq 3$ et $\\mathrm{q} \\neq 3$, et on considère p et q modulo 3. Puisque $p+q \\not \\equiv 0[3]$, on n'a pas $p \\equiv 1[3]$ et $q \\equiv 2[3]$, ni $p \\equiv 2[3]$ et $q \\equiv 1[3]$. On est donc assuré que $p \\equiv q \\equiv 1[3]$ ou bien que $p \\equiv q \\equiv 2$ [3]. Dans ces deux cas, 3 divise $p-q$ et donc divise $\\mathrm{p}+\\mathrm{q}=\\mathrm{r}(\\mathrm{p}-\\mathrm{q})^{\\mathrm{n}}$ puisque $\\mathrm{n} \\geqslant 1$. Ceci est absurde et invalide donc notre supposition, ce qui montre que $p=3$ ou $q=3$.\nD'autre part, puisque $n \\geqslant 0$, on sait que $p-q$ divise $p+q$, donc $p \\neq q$, de sorte que $p$ et $q$ sont premiers entre eux. Puisque $p-q$ divise $(p+q)+(p-q)=2 p$ et $(p+q)-(p-q)=2 q$, on sait donc que $p-q$ divise $\\operatorname{PGCD}(2 \\mathfrak{p}, 2 \\mathrm{q})=2 \\operatorname{PGCD}(p, q)=2$. Il s'ensuit que $p-q \\in\\{-2,-1,1,2\\}$. On en déduit donc que $(p, q) \\in\\{(2,3),(3,2),(3,5),(5,3)\\}$; on traite ces quatre cas un à un :\n- si $(p, q)=(2,3)$, l'équation devient $5=(-1)^{\\mathrm{n}} r$; ses solutions sont $\\mathrm{r}=5$ et $n \\in 2 \\mathbb{N}^{*}$;\n- si $(p, q)=(3,2), l^{\\prime}$ 'equation devient $5=1^{n} r$; ses solutions sont $r=5$ et $n \\in \\mathbb{N}^{*}$;\n- si $(p, q)=(3,5)$, l'équation devient $8=(-2)^{\\mathrm{n}} \\mathrm{r}$; ses solutions sont $(\\mathrm{r}, \\mathfrak{n})=(2,2)$;\n- si $(p, q)=(5,3)$, l'équation devient $8=2^{\\mathfrak{n}} r$; ses solutions sont $(r, n)=(1,3),(2,2)$ et $(4,1)$.\n\nEn conclusion, les solutions sont : $(2,3,5,2 \\mathfrak{n})_{\\mathfrak{n} \\in \\mathbb{N}^{*}},(3,2,5, \\mathfrak{n})_{\\mathfrak{n} \\in \\mathbb{N}^{*}},(3,5,2,2),(5,3,1,3),(5,3,2,2)$ et $(5,3,4,1)$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2017", "problem_label": "2", "tier": 1, "problem": "Soient deux cercles $\\omega_{1}, \\omega_{2}$ tangents l'un à l'autre en un point $T$, tels que $\\omega_{1}$ soit à l'intérieur de $\\omega_{2}$. Soient $M$ et $N$ deux points distincts sur $\\omega_{1}$, différents de $T$. Soient [AB] et [CD] deux cordes du cercle $\\omega_{2}$ passant respectivement par $M$ et $N$. On suppose que les segments [BD], $[A C]$, et $[M N]$ s'intersectent en un point $K$.\nMontrer que (TK) est la bissectrice de l'angle $\\widehat{M T N}$.", "solution": "Soit $E$ et $F$ les points d'intersection respectifs de (TM) et (TN) avec $\\omega_{2}$, autres que $T$. Puisque $\\omega_{1}$ et $\\omega_{2}$ sont tangents en $T$, l'homothétie de centre T et qui envoie $\\omega_{1}$ sur $\\omega_{2}$ envoie également $M$ sur $E$ et $N$ sur $F$. On en déduit que\n\n$$\n\\frac{\\mathrm{TM}}{\\mathrm{TN}}=\\frac{\\mathrm{ME}}{\\mathrm{NF}}\n$$\n\nEn outre, la puissance des points $M$ et $N$ par rapport à $\\omega_{2}$ vaut respectivement $A M \\cdot M B=T M \\cdot M E$ et $C N \\cdot N D=T N \\cdot N F$. Cela montre que\n\n$$\n\\frac{\\mathrm{TM}^{2}}{\\mathrm{TN}^{2}}=\\frac{\\mathrm{TM} \\cdot \\mathrm{ME}}{\\mathrm{TN} \\cdot \\mathrm{NF}}=\\frac{\\mathrm{AM} \\cdot \\mathrm{MB}}{\\mathrm{CN} \\cdot \\mathrm{ND}}\n$$\n\nD'autre part, dans les triangles $A M K$ et $D N K$, la loi des sinus indique que\n\n$$\nA M \\cdot \\sin (\\widehat{M A K})=M K \\cdot \\sin (\\widehat{A K M}) \\text { et que DN } \\cdot \\sin (\\widehat{N D K})=N K \\cdot \\sin (\\widehat{D K N}) .\n$$\n\nPuisque $A, B, C$ et $D$ sont cocycliques, on a également $\\sin (\\widehat{B A C})=\\sin (\\widehat{B D C})$, de sorte que\n\n$$\n\\sin (\\widehat{M A K})=\\sin (\\widehat{B A C})=\\sin (\\widehat{B D C})=\\sin (\\widehat{K D N})\n$$\n\nIl s'ensuit que $\\frac{A M}{D N}=\\frac{M K \\cdot \\sin (\\widehat{A K M})}{N K \\cdot \\sin (\\widehat{D K N})}$ et, de même, que $\\frac{B M}{C N}=\\frac{M K \\cdot \\sin (\\widehat{B K M})}{N K \\cdot \\sin (\\widehat{C K N})}$. Puisque les angles $\\widehat{B K M}$ et $\\widehat{D K N}$ d'une part, et $\\widehat{A K M}$ et $\\widehat{C K M}$ d'autre part, sont opposés par le sommet, donc sont égaux deux à deux, on en déduit que\n\n$$\n\\frac{A M \\cdot M B}{D N \\cdot N C}=\\frac{M K^{2}}{N K^{2}}\n$$\n\nOn en conclut que TM $\\cdot N K=T N \\cdot M K$.\nLa loi des sinus dans les triangles TKM et TKN indique en outre que\n\n$$\n\\mathrm{TM} \\cdot \\sin (\\widehat{\\mathrm{KTM}})=\\mathrm{KM} \\cdot \\sin (\\widehat{\\mathrm{MKT}}) \\text { et que } \\mathrm{TN} \\cdot \\sin (\\widehat{\\mathrm{KTN}})=\\mathrm{KN} \\cdot \\sin (\\widehat{\\mathrm{NKT}})\n$$\n\nPuisque $\\widehat{M K T}$ et $\\widehat{N K T}$ sont supplémentaires, ils ont même sinus, de sorte que\n\n$$\n\\frac{\\sin (\\widehat{K T M})}{\\sin (\\widehat{\\mathrm{KTN}})}=\\frac{\\mathrm{KM} \\cdot \\sin (\\widehat{\\mathrm{MKT}}) \\cdot \\mathrm{TN}}{\\mathrm{TM} \\cdot \\mathrm{KN} \\cdot \\sin (\\widehat{\\mathrm{NKT}})}=1\n$$\n\nce qui prouve que (TK) est la bissectrice de $\\widehat{M T N}$.\n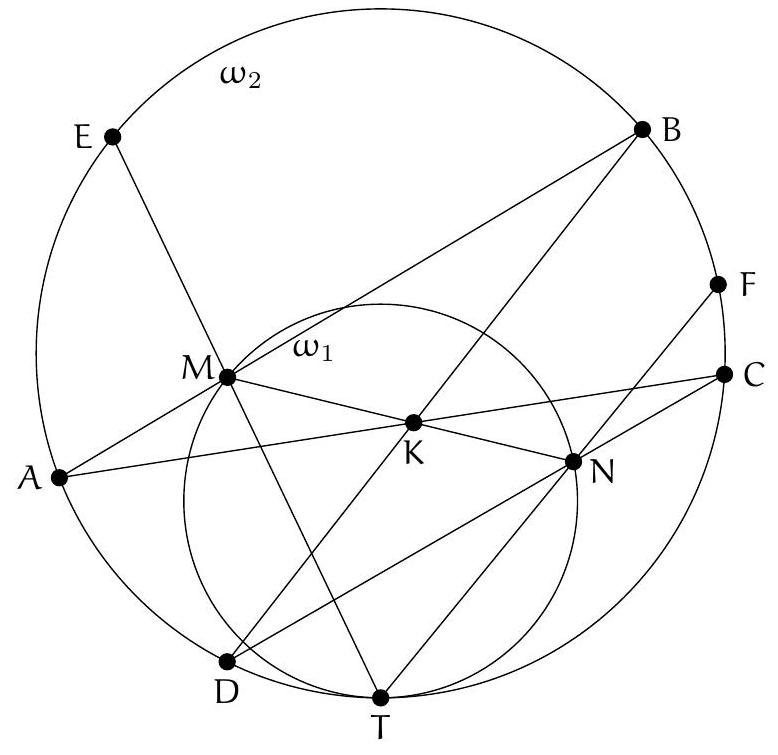", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2017", "problem_label": "3", "tier": 1, "problem": "Dans les cases d'un tableau rectangulaire à $n$ lignes et $m$ colonnes sont écrits des nombres réels. On suppose que pour toute ligne ou colonne, la somme des nombres écrits sur cette ligne ou colonne est un entier. Montrer qu'il est possible de remplacer chaque réel $x$ par l'entier $\\lfloor x\\rfloor$ ou $\\lceil x\\rceil$ de sorte que les sommes de chaque colonne et de chaque ligne demeurent inchangées.\nRemarque : On rappelle que si $x$ est un nombre réel, $\\lfloor x\\rfloor$ est l'unique entier tel que $\\lfloor x\\rfloor \\leqslant x<\\lfloor x\\rfloor+1$, et $\\lceil x\\rceil$ est l'unique entier tel que $\\lceil x\\rceil-1<x \\leqslant\\lceil x\\rceil$.", "solution": "Quitte à soustraire sa partie entière à chaque entrée du tableau, on peut supposer que chaque nombre est compris entre 0 et 1 . On dit qu'une case est « fractionnaire $\\gg$ si son nombre n'est pas entier. Remarquons que, si C est une case fractionnaire, alors il existe nécessairement une autre case fractionnaire sur la même ligne que C , et il existe aussi une autre case fractionnaire sur la même colonne que C .\nChoisissons donc une case $C_{0}$ fractionnaire, puis, pour tout $n \\in \\mathbb{N}$ :\n\n- si $n$ est pair, on choisit une case $C_{n+1}$ fractionnaire sur la même ligne que $C_{n}$;\n- si $n$ est impair, on choisit une case $C_{n+1}$ fractionnaire sur la même colonne que $C_{n}$.\n\nPar principe des tiroirs, il existe deux entiers $k<\\ell$ tels que $C_{k}=C_{\\ell}$. Sans perte de généralité, on suppose que $\\ell$ est aussi petit que possible, parmi tous les choix de cases $C_{0}, C_{1}, \\ldots$ et d'entiers $k<\\ell$ que l'on aura pu faire.\nOn a donc $k=0$, et l'on dispose ainsi d'un $«$ cycle $\\gg C_{0}, \\ldots, C_{\\ell-1}, C_{\\ell}$ de cases fractionnaires deux à deux distinctes (sauf $C_{0}$ et $C_{\\ell}$ ) et telles que les segments $\\left[C_{i}, C_{i+1}\\right]$ sont alternativement horizontaux et verticaux. Ce cycle étant de longueur $\\ell$ minimale, on sait que chaque ligne et chaque colonne contient soit 0 , soit 2 cases du cycle, et que ces cases sont consécutives dans le cycle.\nPour tout $i<\\ell-1$, on note $x_{i}$ le nombre écrit sur la case $C_{i}$, et l'on pose $y_{i}=x_{i}$ si $i$ est pair, et $y_{i}=1-x_{i}$ si $i$ est impair. Puis l'on remplace $x_{i}$ par le réel\n\n$$\nx_{i}^{\\prime}=x_{i}+(-1)^{i} \\varepsilon\n$$\n\noù $\\varepsilon=\\min \\left\\{y_{i} \\mid i<\\ell\\right\\}$. Par construction de $\\varepsilon$, on a donc $0 \\leqslant x_{i}^{\\prime} \\leqslant 1$ pour tout $i<\\ell$, avec $x_{i}^{\\prime}=0$ ou $x_{i}^{\\prime}=1$ pour au moins un entier $i$.\nCe procédé n'a modifié la somme d'aucune ligne ni colonne, et a permis de réduire le nombre de cases fractionnaires, tout en affectant à chaque case modifiée une valeur $x_{i}^{\\prime}$ telle que\n\n$$\n\\left\\{\\left\\lfloor x_{i}^{\\prime}\\right\\rfloor,\\left\\lceil x_{i}^{\\prime}\\right\\rceil\\right\\} \\subseteq\\{0,1\\}=\\left\\{\\left\\lfloor x_{i}\\right\\rfloor,\\left\\lceil x_{i}\\right\\rceil\\right\\} .\n$$\n\nOn peut donc réitérer ce procédé jusqu'à éliminer toutes les cases fractionnaires, ce qui conclut le problème.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2018-2019-Test-09-01-Corrigé.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Soit $x$ et $y$ deux entiers tels que $5 x+6 y$ et $6 x+5 y$ soient des carrés parfaits. Montrer que $x$ et $y$ sont tous deux divisibles par 11.\nNote : on dit qu'un entier $n$ est un carré parfait si c'est le carré d'un entier.", "solution": "Soit $a$ et $b$ deux entiers tels que $5 x+6 y=a^{2}$ et $6 x+5 y=b^{2}$. On note que $a^{2}+b^{2}=11(x+y)$ est divisible par 11 . Or, modulo 11 , les carrés sont $0,1,3,4,5$ et 9 : ainsi, la somme de deux carrés est nulle (mod. 11) si et seulement si les deux carrés en question sont nuls (mod. 11) eux aussi.\nDans notre cas, cela signifie que $a$ et $b$ sont divisibles par 11. Il existe donc des entiers $A$ et $B$ tels que $a=11 A$ et $b=11 \\mathrm{~B}$. Mais alors\n\n$$\n11 x=(6 \\times 6-5 \\times 5) x=6\\left(b^{2}-5 y^{2}\\right)-5\\left(a^{2}-6 y\\right)=6 b^{2}-5 a^{2}=11^{2}\\left(6 B^{2}-5 A^{2}\\right)\n$$\n\nde sorte que $x=11\\left(6 B^{2}-5 A^{2}\\right)$ est bien divisible par 11. De même, on montre que $y=$ $11\\left(6 A^{2}-5 B^{2}\\right)$ est lui aussi divisible par 11.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Soit $\\Gamma$ un cercle de centre $O$ et de rayon $r$ et $\\ell$ une droite qui ne coupe pas $\\Gamma$. On note $E$ le point d'intersection entre $\\ell$ et la droite perpendiculaire à $\\ell$ passant par $O$.\nSoit $M$ un point de $\\ell$ différent de $E$. Les tangentes au cercle $\\Gamma$ et passant par $M$ touchent $\\Gamma$ en $A$ et $B$. Enfin, soit $H$ le point d'intersection des droites ( $A B$ ) et ( $O E$ ).\nMontrer que $\\mathrm{OH}=\\mathrm{r}^{2} / \\mathrm{OE}$.", "solution": "Tout d'abord, les triangles OAM, OBM et OEM sont respectivement rectangles en $A, B$ et $E$, de sorte que les points $A, O, B, E, M$ appartiennent tous à un même cercle de diamètre [OM].\nOr, d'après la loi des sinus dans les triangles OBH et OEA, on sait que\n\n$$\n\\frac{\\mathrm{OH} \\times \\mathrm{OE}}{\\mathrm{r}^{2}}=\\frac{\\mathrm{OH}}{\\mathrm{OB}} \\times \\frac{\\mathrm{OE}}{\\mathrm{OA}}=\\frac{\\sin (\\widehat{\\mathrm{OBA}})}{\\sin (\\widehat{\\mathrm{OHB}})} \\times \\frac{\\sin (\\widehat{\\mathrm{OAE}})}{\\sin (\\widehat{\\mathrm{OEA}})}\n$$\n\nLes points $O, B, E$ et $A$ étant cocycliques, on sait que $\\widehat{O B A}=\\widehat{O E A}$. D'autre part, puisque les droites $(\\mathrm{AH})$ et $(\\mathrm{HO})$ sont respectivement perpendiculaires à $(\\mathrm{OM})$ et $(\\mathrm{ME})$, on sait également que\n\n$$\n\\widehat{\\mathrm{OHB}}=180^{\\circ}-\\widehat{\\mathrm{AHO}}=180^{\\circ}-\\widehat{\\mathrm{OME}}=180^{\\circ}-\\widehat{\\mathrm{OAE}}\n$$\n\nCela montre que $\\sin (\\widehat{O B A})=\\sin (\\widehat{O E A})$ et que $\\sin (\\widehat{O H B})=\\sin (\\widehat{O A E})$, ce qui conclut.\n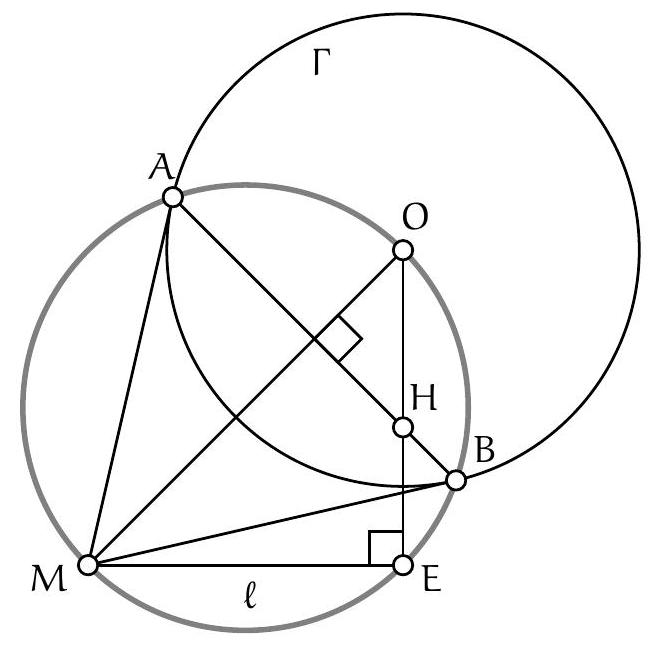", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Soit $n$ un entier naturel. Un escalier de taille $n$ est constitué de petits carrés $1 \\times 1$, avec 1 carré pour la première marche, 2 carrés pour la deuxième marche, et ainsi de suite, jusqu'à $n$ carrés pour la $n^{\\text {ème }}$ marche.\nOn dispose de pierres carrées (de coté entier) de toutes les tailles pour construire cet escalier et on note $f(n)$ le nombre minimum de pierres que l'on doit utiliser pour un escalier de taille $n$. Par exemple, $f(2)=3$ et $f(4)=7$, comme illustré ci-dessous.\n\n\n1. Trouver tous les entiers $n \\geqslant 0$ tels que $f(n)=n$.\n2. Trouver tous les entiers $n \\geqslant 0$ tels que $f(n)=n+1$", "solution": "Commençons par quelques définitions et observations générales. Dans la suite, on note $(i, j)$ le petit carré $1 \\times 1$ situé au jème étage de la $i^{\\text {ème }}$ marche. On appellera carré supérieur chaque petit carré ( $k, k$ ), c'est-à-dire chaque carré situé tout en haut d'une marche.\nOn considère une construction de l'escalier de taille $n$ à partir de $f(n)$ pierres carrées. Deux carrés supérieurs distincts ne peuvent appartenir à la même pierre. Puisqu'il y a exactement $n$ carrés supérieurs dans un escalier de taille $n$, on en déduit que $f(n) \\geqslant n$ pour tout $n \\geqslant 0$. On traite maintenant les questions 1 et 2.\n\n1. Tout d'abord, il est clair que $f(0)=0$. Soit maintenant $n \\geqslant 1$ un entier tel que $f(n)=n$.\n\nAu vu de l'observation ci-dessus, chaque pierre contient un unique carré supérieur. C'est en particulier le cas de la pierre contenant le carré ( $n, 1$ ). Mais alors cette pierre sépare l'escalier en 2 parties symétriques. Ainsi, chaque partie forme un escalier de taille $(n-1) / 2$, tel que $f((n-1) / 2)=(n-1) / 2$. Par conséquent, une récurrence immédiate montre qu'il existe un entier $k \\geqslant 0$ tel que $n=2^{k}-1$.\nRéciproquement, et en suivant cette construction dans l'autre sens, une récurrence immédiate montre que $f\\left(2^{k}-1\\right)=2^{k}-1$ pour tout entier $k \\geqslant 0$.\nLes entiers $n$ recherchés sont donc bien les entiers de la forme $n=2^{k}-1$ avec $k \\geqslant 0$.\n2. Cette fois-ci, on sait que $n \\geqslant 2$. D'autre part, la pierre contenant le carré ( $n, 1$ ) ne saurait contenir de carré supérieur; en effet, si c'était le cas, elle couperait l'escalier en 2 parties symétriques, formant chacune un escalier de taille ( $n-1$ )/2, de sorte que $f(n)-n$ devrait être pair.\nIl s'agit donc de la seule la seule pierre qui ne contient pas de carré supérieur. Soit $\\ell \\times \\ell$ les dimensions de cette pierre. Une fois $\\ell$ et $n$ fixés, chaque autre pierre doit contenir un carré supérieur, et les dimensions des pierres sont donc prescrites. En particulier, une récurrence immédiate sur $n+i-j$ montre que les pierres contenant les carrés ( $i, j$ ) et $(\\mathfrak{n}+1-\\mathfrak{j}, \\mathfrak{n}+1-\\mathfrak{i})$ occupent en fait des positions symétriques.\nAfin de se ramener à ne traiter que des escaliers où chaque pierre contient un carré supérieur, on s'intéresse donc spécifiquement aux pierres contenant les carrés ( $\\mathrm{n}, 1$ ), $(n-\\ell, 1),(n, \\ell+1)$ et $(n-\\ell, \\ell+1)$; cette dernière pierre n'existe que si $n \\neq 2 \\ell$.\nOn suppose tout d'abord que $n \\neq 2 \\ell$. Dans ce cas, nos quatre pierres sont deux à deux disjointes, de tailles respectives $\\ell \\times \\ell,(n+1-\\ell) / 2,(n+1-\\ell) / 2$ et $(n+1-2 \\ell) / 2$, et elles coupent l'escalier en quatre petits escaliers : deux escaliers de taille ( $n-1-\\ell$ ) /2 et deux escaliers de taille $(n-1-2 \\ell) / 2$. Au vu des résultats de la première question, il existe donc deux entiers naturels non nuls $k$ et $k^{\\prime}$ tels que $n=2^{\\mathrm{k}}+\\ell-1=2^{\\mathrm{k}^{\\prime}}+2 \\ell-1$.\n\nCela signifie que $\\ell=2^{k}-2^{k^{\\prime}}$, donc que $k \\geqslant k^{\\prime}$ et que $n=2^{k+1}-2^{k^{\\prime}}-1$. Réciproquement, s'il existe des entiers $k \\geqslant k^{\\prime} \\geqslant 1$ tels que $n=2^{k+1}-2^{k^{\\prime}}-1$, il suffit en effet de choisir $\\ell=2^{k}-2^{k^{\\prime}}$ pour que notre construction fonctionne.\nDe même, si $n=2 \\ell$, on a en fait trois pierres, qui coupent l'escalier en quatre petits escaliers de taille $(n-1-\\ell) / 2=(\\ell-1) / 2$, donc il existe un entier naturel non nul $k$ tel que $\\ell=2^{k}-1$ et $n=2^{k+1}-2$. Réciproquement, s'il existe un entier $k \\geqslant 1$ tel que $\\mathrm{n}=2^{\\mathrm{k}+1}-2$, il suffit en effet de choisir $\\ell=\\mathrm{n} / 2$ pour que notre construction fonctionne. Les entiers $n$ recherchés sont donc bien les entiers de la forme $n=2^{k+1}-2^{k^{\\prime}}-1$ avec $k \\geqslant k^{\\prime} \\geqslant 0$.\n\n## Exercice commun aux groupes Junior et Senior", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{N} \\rightarrow \\mathbb{N}$ telles que\n\n$$\nx f(y)+y f(x)=(x+y) f\\left(x^{2}+y^{2}\\right)\n$$\n\npour tous les entiers naturels $x$ et $y$.\nNote : on rappelle que $\\mathbb{N}$ désigne l'ensemble des entiers naturels, c'est-à-dire $\\mathbb{N}=\\{0,1,2, \\ldots\\}$.", "solution": "Dans la suite, on notera $\\mathbf{E}_{x, y}$ l'équation de l'énoncé.\nTout d'abord, l'équation $E_{x, 0}$ indique que $x f(0)=x f\\left(x^{2}\\right)$, ce qui montre que $f\\left(x^{2}\\right)=f(0)$ pour tout entier $x \\geqslant 1$. Par conséquent, pour tout entier $y \\geqslant 1$, l'équation $\\mathbf{E}_{x, y^{2}}$ indique que $x+y^{2}$ divise $x(f(0)-f(x))$. Cette relation de divisibilité étant valide même quand $y$ est arbitrairement grand, on en déduit que $f(x)=f(0)$ quel que soit $x$.\nRéciproquement, on vérifie aisément que les fonctions constantes sont bien des solutions de l'équation.\n\n## Exercices du groupe Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2018", "problem_label": "5", "tier": 1, "problem": "Soit $n$ un entier impair, et soit $S$ un ensemble de $n$ points du plan à coordonnées entières. On considère une permutation $\\mathrm{f}: \\mathrm{S} \\rightarrow \\mathrm{S}$ qui satisfait la propriété suivante :\nPour toute paire de points $A$ et $B$ appartenant à $S$, la distance entre $f(A)$ et $f(B)$ est supérieure ou égale à la distance entre $A$ et $B$.\nMontrer qu'il existe un point $X$, appartenant à $S$, tel que $f(X)=X$.", "solution": "Puisque $S$ est de cardinal impair, f admet une orbite de cardinal impair. Sans perte de généralité, on peut donc supposer que $S$ est égal à cette orbite, et même que $S=\\left\\{P_{1}, \\ldots, P_{n}\\right\\}$ avec $f\\left(P_{i}\\right)=P_{i+1}$ pour tout $i \\leqslant n$, en posant $P_{1}=n+1$.\nSi f n'a aucun point fixe, $\\mathrm{c}^{\\prime}$ est donc que $n \\geqslant 3$. Montrons que ce cas est en fait impossible.\nEn effet, dans ces conditions, l'énoncé montre que $P_{1} P_{2} \\leqslant P_{2} P_{3} \\leqslant \\ldots \\leqslant P_{n} P_{1}$, de sorte que toutes ces inégalités sont en fait des égalités. En outre, toujours sans perte de généralité, quitte à considérer un point $P_{i}$ plutôt que $P_{1}$ et quitte à effectuer des translations à coordonnées entières et à diviser toutes nos coordonnées par 2, on peut supposer que les coordonnées du vecteur $\\overrightarrow{\\mathrm{P}_{1} \\mathrm{P}_{2}}$ ne sont pas toutes les deux paires. Maintenant, on va noter $x_{i}$ et $y_{i}$ les coordonnées du point $P_{i}$.\n\nPuisque les carrés modulo 4 sont 0 et 1 , on en déduit que $P_{i} P_{i+1}^{2}=P_{1} P_{2}^{2}=\\left(x_{i}-x_{i+1}\\right)^{2}+$ $\\left(y_{i}-y_{i+1}\\right)^{2}$ est congru à 1 ou 2 modulo 4 .\nDans le premier cas, $c^{\\prime}$ est donc que la somme $\\Delta_{i}=x_{i}+y_{i}+x_{i+1}+y_{i+1} \\equiv 1(\\bmod 2)$. On en déduit que\n\n$$\nn \\equiv \\sum_{i=1}^{n} \\Delta_{i} \\equiv 2 \\sum_{i=1}^{n}\\left(x_{i}+y_{i}\\right) \\equiv 0 \\quad(\\bmod 2)\n$$\n\nDans le deuxième cas, on a directement $\\Delta_{i}^{x}=x_{i}+x_{i+1} \\equiv 1(\\bmod 2)$ et $\\Delta_{i}^{y}=y_{i}+y_{i+1} \\equiv 1$ $(\\bmod 2)$, de sorte que\n\n$$\nn \\equiv \\sum_{i=1}^{n} \\Delta_{i}^{x} \\equiv 2 \\sum_{i=1}^{n} x_{i} \\equiv 0 \\quad(\\bmod 2)\n$$\n\nPuisque n est impair, aucun de ces deux cas n'est possible, ce qui conclut.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2018", "problem_label": "6", "tier": 1, "problem": "Soit $A B C$ un triangle, et soit $E$ et $F$ deux points appartenant respectivement aux droites $(A B)$ et $(A C)$, distincts de $A, B$ et $C$. Soit également $\\Omega$ le cercle circoncscrit à $A B C$, soit $O$ le centre de $\\Omega$, et soit $\\Gamma$ le cercle circonscrit à $A E F$. Enfin, soit $P$ le point d'intersection $\\operatorname{de} \\Gamma$ et $\\Omega$ autre que $A$, et soit $Q$ le symétrique de $P$ par rapport à la droite (EF).\nMontrer que Q appartient à la droite ( BC ) si et seulement si O appartient au cercle $\\Gamma$.", "solution": "Puisque (BC) et (EF) sont deux droites d'intérêt notoire, on note 7 leur point d'intersection, éventuellement rejeté à l'infini. Alors Q appartient à la droite ( BC ) si et seulement si, en angles de droites, on a (BT, ET) $=(\\mathrm{ET}, \\mathrm{PT})$.\nOr, toujours en angles de droites, on sait déjà que\n\n$$\n\\begin{aligned}\n(\\mathrm{PB}, \\mathrm{PE}) & =(\\mathrm{PB}, \\mathrm{PA})+(\\mathrm{PA}, \\mathrm{PE})=(\\mathrm{CB}, \\mathrm{CA})+(\\mathrm{FA}, \\mathrm{FE}) \\\\\n& =(\\mathrm{CT}, \\mathrm{CF})+(\\mathrm{CF}, \\mathrm{FT})=(\\mathrm{CT}, \\mathrm{FT})=(\\mathrm{TB}, \\mathrm{TE}),\n\\end{aligned}\n$$\n\nce qui signifie que les points $\\mathrm{P}, \\mathrm{E}, \\mathrm{B}$ et T sont cocycliques. Par conséquent, on sait que $(B T, E T)=(B P, E P)$ et $(E T, P T)=(E B, P B)=(A B, P B)$.\nOn sait aussi que $2(B A, B P)=(O A, O P)$ et que $(E A, E P)=(B A, B P)+(B P, E P)$. Ainsi,\n\n$$\n\\begin{aligned}\n\\text { Q appartient à la droite }(\\mathrm{BC}) & \\Leftrightarrow(\\mathrm{BP}, \\mathrm{EP})=(\\mathrm{AB}, \\mathrm{~PB}) \\\\\n& \\Leftrightarrow(\\mathrm{EA}, \\mathrm{EP})=2(\\mathrm{BA}, \\mathrm{BP})=(\\mathrm{OA}, \\mathrm{OP}) \\\\\n& \\Leftrightarrow \\mathrm{O} \\text { appartient au cercle } \\Gamma .\n\\end{aligned}\n$$\n\n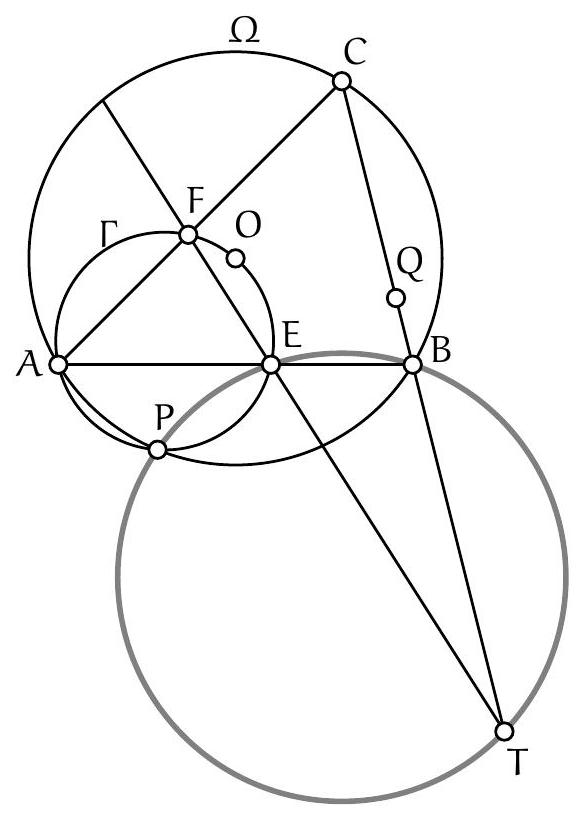", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2018-2019-Test-15-05-Corrigé.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Soit $S$ un ensemble d'entiers. On dit que $S$ est insommable si, pour tous les entiers $x$ et $y$ appartenant à $S$, la somme $x+y$ n'appartient pas à $S$. Pour tout entier $n \\geqslant 1$, on note $s_{n}$ le nombre de sous-ensembles de $\\{1,2, \\ldots, 2 n\\}$ qui sont insommables.\nDémontrer que $s_{n} \\geqslant 2^{n}$.", "solution": "Soit $S$ une partie de $\\{n+1, \\ldots, 2 n\\}$. Une telle partie est insommable, puisque, pour tous les entiers $x, y$ et $z$ appartenant à $S$, on a $x+y \\geqslant 2(n+1)>2 n \\geqslant z$. Or, il existe $2^{n}$ parties de $\\{n+1, \\ldots, 2 n\\}$. On en déduit bien que $s_{n} \\geqslant 2^{n}$.\n\nNote : On peut en fait démontrer que $2^{\\mathfrak{n}+4} \\geqslant s_{n} \\geqslant 2^{\\mathfrak{n}+1}$ pour tout $n \\geqslant 3$. L'inégalité $s_{n} \\geqslant$ $2^{\\mathrm{n}+1}$ s'obtient, par exemple, comme suit.\nPour tout entier $k \\in\\{1, \\ldots, 2 \\mathfrak{n}\\}$, on note $E_{k}$ l'ensemble des parties de $\\{\\lfloor k / 2\\rfloor+1, \\ldots, k\\}$ auxquelles appartient $k$. $S i$ un ensemble $S$ appartient à $E_{k}$, alors pour tous $x$ et $y$ appartenant à $S$, on a bien $x+y \\geqslant 2\\lfloor k / 2\\rfloor+2>k=\\max S$, donc $S$ est insommable.\nOr, $E_{k}$ contient exactement $2^{k-\\lfloor k / 2\\rfloor-1}$ ensembles, et $k$ est l'élément maximum de tout ensemble $S$ appartenant à $E_{k}$, donc les ensembles $E_{k}$ sont deux à deux disjoints. Si on pose $k=2 \\ell-\\varepsilon$, avec $\\varepsilon=0$ ou $\\varepsilon=1$, on a alors $k-\\lfloor k / 2\\rfloor-1=2 \\ell-\\varepsilon-(\\ell-\\varepsilon)-1=\\ell-1$, donc $\\left|E_{k}\\right|=2^{\\ell-1}$.\nEnfin, puisque $\\boldsymbol{n} \\geqslant 3$, les ensembles $\\{1,2 \\mathfrak{n}\\}$ et $\\{2,2 \\mathfrak{n}\\}$ sont tous deux insommables, et n'appartiennent pas à $E_{2 n}$. On en déduit que\n\n$$\ns_{2 n} \\geqslant 2+\\sum_{k=1}^{2 n}\\left|E_{k}\\right|=2+\\sum_{\\ell=1}^{n}\\left|E_{2 \\ell-1}\\right|+\\left|E_{2 \\ell}\\right|=2+2 \\sum_{\\ell=1}^{n} 2^{\\ell-1}=2+2^{n+1}-2=2^{n+1} .\n$$", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Soit $m$ et $n$ deux entiers naturels. Démontrer que $n!\\neq m^{2}+2019$.", "solution": "Procédons par l'absurde, et supposons que l'on dispose de deux entiers naturels $m$ et $n$ tels que $n!=m^{2}+2019$. Tout d'abord, on sait que $n!\\geqslant 2019>6!=720$, donc que $n \\geqslant 7$. Par conséquent, $n!$ est divisible par $7!=2^{4} \\times 3^{2} \\times 5 \\times 7$, et l'on a $0 \\equiv m^{2}+2019$ $(\\bmod 7!)$.\nEn vertu de la décomposition en produit de facteurs premiers énoncée ci-dessus et du théorème Chinois, cela signifie que -2019 est un carré modulo $k$ pour tout entier $k$, parmi $2^{4}, 3^{2}$, 5 et 7 .\nOn pourrait démontrer que cela ne constitue pas une contradiction pour $k=5$ et $k=7$. En revanche, -2019 n'est pas un carré modulo 9 (ni modulo 16). En effet, si m² $\\equiv-2019 \\equiv-3$ $(\\bmod 9)$, alors 3 divise $m$, donc 9 divise $m^{2}$, qui devrait donc être congru à la fois à 0 et à -3 modulo 9.\nAinsi, dès lors que $n \\geqslant 7$, on a en fait $n!\\equiv 0 \\not \\equiv m^{2}-3 \\equiv m^{2}+2019(\\bmod 9)$, ce qui montre bien que nulle paire d'entiers naturels ( $m, n$ ) ne peut satisfaire l'équation $n!=m^{2}+2019$.\nNote : On a également $-2019 \\equiv 5(\\bmod 8)$, alors que $n^{2} \\equiv 1(\\bmod 8)$ pour tout entier $n$ impair. Ainsi, comme prévu, -2019 n'est pas un carré modulo 8 , donc modulo $2^{4}$ non plus.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle, et soit $M$ le pied de la médiane issue de $A$. Soit également $\\ell_{\\mathrm{b}}$ la bissectrice de $\\widehat{A M B}$ et $\\ell_{c}$ la bissectrice de $\\widehat{A M C}$. Enfin, soit $B^{\\prime}$ le projeté orthogonal de $B$ sur $\\ell_{b}$, soit $C^{\\prime}$ le projeté orthogonal de $C$ sur $\\ell_{c}$, et soit $A^{\\prime}$ le point $d^{\\prime}$ intersection des droites $(A M)$ et ( $B^{\\prime} C^{\\prime}$ ).\nDémontrer que $A^{\\prime} B^{\\prime}=A^{\\prime} C^{\\prime}$.", "solution": "Soit $\\beta$ l'angle $\\widehat{A M B^{\\prime}}$ et $\\gamma$ l'angle $\\widehat{A M C^{\\prime}}$. Par construction, on sait que $2(\\beta+\\gamma)=180^{\\circ}$, donc que $\\widehat{\\mathrm{B}^{\\prime} \\mathrm{MC}^{\\prime}}=\\beta+\\gamma=90^{\\circ}$. Ainsi, la droite $\\ell_{\\mathrm{b}}=\\left(\\mathrm{MB}^{\\prime}\\right)$ est perpendiculaire aux droites $\\left(\\mathrm{BB}^{\\prime}\\right)$ et $\\ell_{c}=\\left(M C^{\\prime}\\right)$, et la droite $\\ell_{c}=\\left(M C^{\\prime}\\right)$ est perpendiculaire aux droites $\\left(C C^{\\prime}\\right)$ et $\\ell_{b}=\\left(M B^{\\prime}\\right)$.\n$D^{\\prime}$ autre part, on remarque que $\\widehat{\\mathrm{B}^{\\prime} \\mathrm{BM}}=180^{\\circ}-\\widehat{\\mathrm{BB}^{\\prime} M}-\\widehat{\\mathrm{BMB}^{\\prime}}=180^{\\circ}-90^{\\circ}-\\beta=\\gamma$ et que, de même, $\\widehat{C^{\\prime} C M}=\\beta$. Ainsi, les deux triangles $B B^{\\prime} M$ et $M C^{\\prime} C$ sont semblables. En outre, puisque $M$ est le pied de la médiane de $A B C$ issue de $A$, $c^{\\prime}$ est en fait le milieu de [BC], donc $B M=M C$. Les deux triangles $B B^{\\prime} M$ et $M C C^{\\prime}$ sont donc isométriques.\nEn particulier, on en déduit que $B B^{\\prime}=M C^{\\prime}$ et que $C C^{\\prime}=M B^{\\prime}$. Mais alors, puisque le triangle $M B^{\\prime} C^{\\prime}$ est rectangle en $M$, il a un angle et deux côtés de mêmes mesures que le triangle $B^{\\prime} M B$, et il est donc isométrique avec $B^{\\prime} M B$ et avec $C^{\\prime} C M$.\nOn en déduit notamment que\n\n$$\n\\widehat{A^{\\prime} C^{\\prime} M}=\\widehat{B^{\\prime} C^{\\prime} M}=\\widehat{M B B^{\\prime}}=\\gamma=\\widehat{A M C^{\\prime}}=\\widehat{A^{\\prime} M C^{\\prime}}\n$$\n\ndonc que le triangle $A^{\\prime} C^{\\prime} M$ est isocèle en $A^{\\prime}$. De même, le triangle $A^{\\prime} B^{\\prime} M$ est isocèle en $A^{\\prime}$, et on en conclut comme prévu que $A^{\\prime} B^{\\prime}=A^{\\prime} M=A^{\\prime} C^{\\prime}$.\n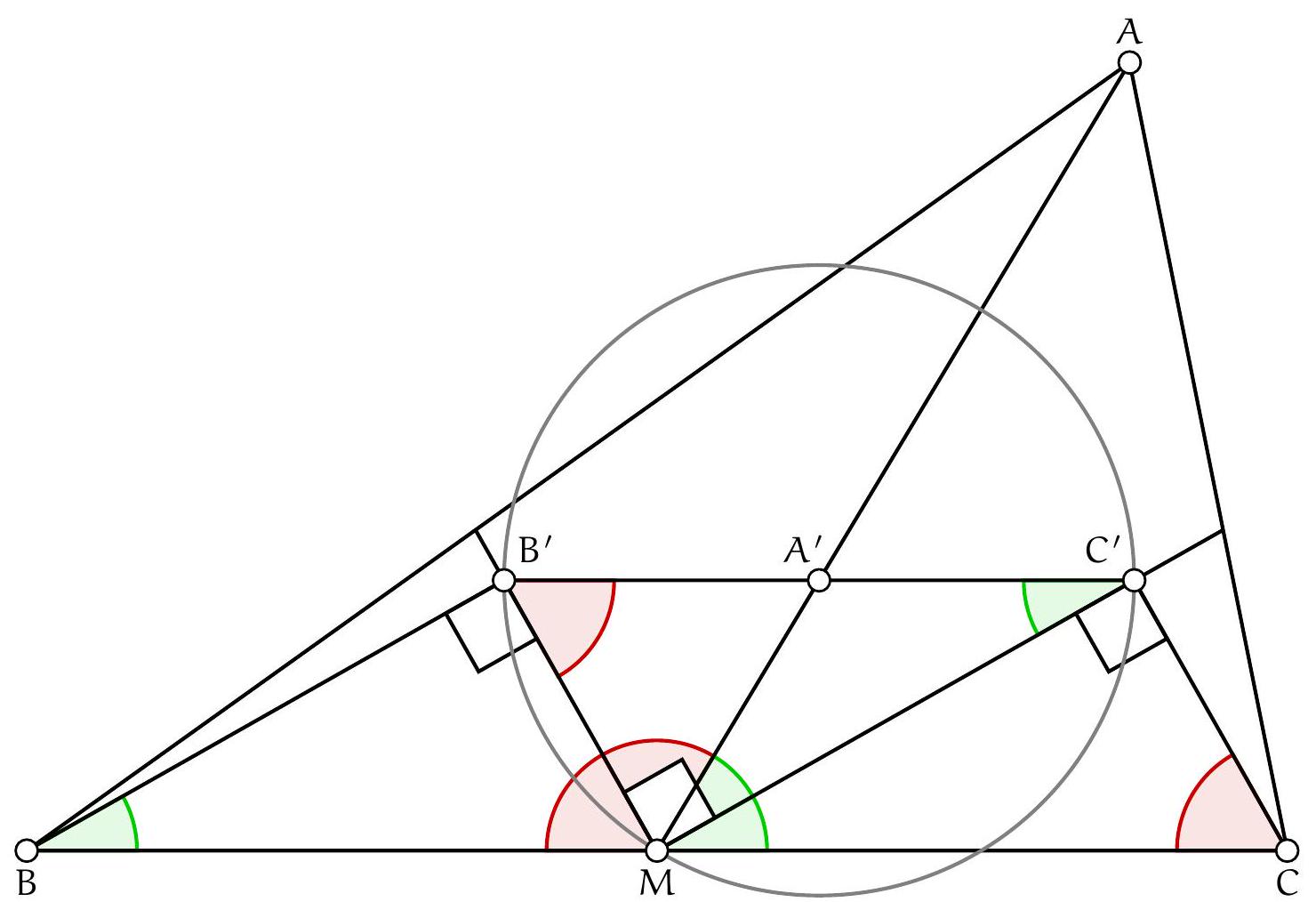", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "Soit $\\mathrm{f}: \\mathbb{Z} \\mapsto \\mathbb{R}$ une fonction telle que\n\n$$\n\\mathbf{f}(\\mathrm{n}+2)=(f(n+1)+\\mathbf{f}(\\mathrm{n})) / 2\n$$\n\npour tout entier $n$. On suppose que f est bornée, c'est-à-dire qu'il existe un réel $\\mathbf{F}$ tel que $-F \\leqslant f(n) \\leqslant F$ pour tout $n$.\nDémontrer que $f$ est une fonction constante.", "solution": "Supposons que f n'est pas constante. Il existe donc un entier n et un réel $\\varepsilon \\neq 0$ tels que $f(n+1)-f(n)=\\varepsilon$.\nPour tout entier $k$, posons $\\Delta_{k}=f(k+1)-f(k)$. Alors\n\n$$\n\\Delta_{k+1}=f(k+2)-f(k+1)=(f(k+1)+f(k)) / 2-f(k+1)=-\\Delta_{k} / 2\n$$\n\net, réciproquement, $\\Delta_{\\mathrm{k}-1}=-2 \\Delta_{\\mathrm{k}}$. Une récurrence immédiate indique alors que $\\Delta_{\\mathrm{n}-\\mathrm{k}}=$ $(-2)^{k} \\varepsilon$ pour tout $k \\geqslant 0$.\nOr, pour tout entier $k$, on sait que $\\left|\\Delta_{k}\\right| \\leqslant|\\mathbf{f}(k+1)|+|f(k)| \\leqslant 2 \\mathbf{F}$. Mais ceci est incompatible avec le fait que $\\left|\\Delta_{n-k}\\right|=2^{k}|\\varepsilon|$ pout tout $k \\geqslant 0$. Notre supposition initiale était donc absurde, et $f$ est bien constante.\n\n## Exercices du groupe Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2018", "problem_label": "5", "tier": 1, "problem": "Soit $A, B, C$ et $P$ quatre points du plan tels que $A B C$ soit un triangle équilatéral et que $A P<B P<C P$. On suppose que la seule donnée des longueurs $A P, B P$ et $C P$ nous permet de déterminer, de manière unique, la longueur $A B$.\nDémontrer que P appartient au cercle circonscrit à $A B C$.", "solution": "Soit $\\Gamma_{\\mathrm{a}}, \\Gamma_{\\mathrm{b}}$ et $\\Gamma_{\\mathrm{c}}$ les cercles de centre P et passant respectivement par $A$, $B$ et $C$. Soit également $C^{\\bullet}$ le symétrique de $C$ par rapport à ( $A P$ ). Notons que $C^{\\bullet}$ est le seul point de $\\Gamma_{\\mathrm{c}}$, autre que C lui-même, tel que $A C=A C^{\\bullet}$.\nOn note maintenant r la rotation de centre $\\mathcal{A}$ et d'angle $60^{\\circ}$ dans le sens horaire. Quitte à faire subir une symétrie à la figure de répart, on suppose que $C=r(B)$.\nPuis, à tout point $B^{\\prime}$ de $\\Gamma_{b}$, on associe le point $C^{\\prime}=r\\left(B^{\\prime}\\right)$. Le triangle $A B^{\\prime} C^{\\prime}$ est équilatéral, et l'hypothèse de l'énoncé stipule donc que, pour tout $B^{\\prime}$, le point $C^{\\prime}$ ne peut appartenir à $\\Gamma_{c}$ que s'il est égal à $C$ ou à $C^{\\bullet}$.\nOr, quand $B^{\\prime}$ décrit $\\Gamma_{b}$, le point $C^{\\prime}$ décrit le cercle $r\\left(\\Gamma_{b}\\right)$, de centre $r(P)$ et de rayon $P B$. Ce cercle ne peut contenir à la fois les points $C$ et $C^{\\bullet}$, puisque alors son centre se trouverait sur la médiatrice (AP) de $\\left[C^{\\bullet}\\right]$, ce qui n'est pas le cas de $r(P)$.\nComme $\\mathrm{r}\\left(\\Gamma_{\\mathrm{b}}\\right)$ contient déjà C , il ne peut donc pas contenir d'autre point de $\\Gamma_{\\mathrm{c}}$, et puisque $\\mathrm{r}(\\mathrm{P}) A=\\mathrm{PA}<\\mathrm{PB}$, on sait que $A$ est situé à l'intérieur $\\operatorname{de} \\mathrm{r}\\left(\\Gamma_{\\mathrm{b}}\\right)$, qui est donc tangent intérieurement, en le point $C$, à $\\Gamma_{\\mathrm{c}}$.\nComme $P B=r(P) C<P C, c^{\\prime}$ est en fait que les points $C, r(P)$ et $P$ sont alignés dans cet ordre. On en déduit que $P C=r(P) C+r(P) P=P B+P A$, ou encore que $C P \\cdot A B=B P \\cdot A C+A P$. $B C$. L'égalité de Ptolémée indique donc que les points $A, B, C$ et $P$ sont cocycliques, ce qui conclut.\n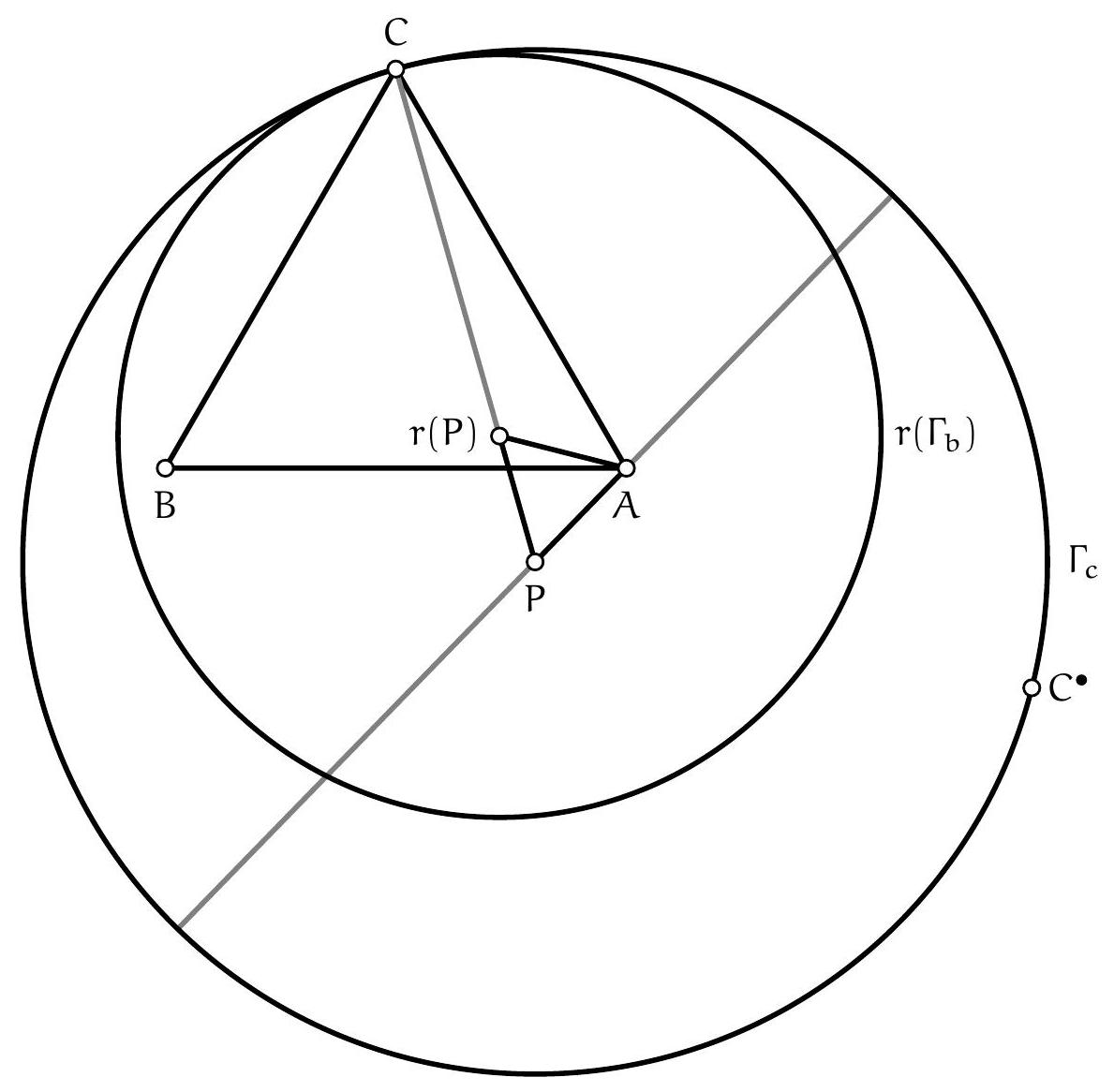", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2018", "problem_label": "6", "tier": 1, "problem": "Soit $a_{0}, a_{1}, \\ldots, a_{d}$ des entiers tels que $\\operatorname{PGCD}\\left(a_{0}, a_{1}\\right)=1$. Pour tout entier $n \\geqslant 1$, on pose\n\n$$\nu_{n}=\\sum_{k=0}^{d} a_{k} \\varphi(n+k)\n$$\n\nDémontrer que 1 est le seul entier naturel divisant tous les entiers $u_{n}$.\nOn rappelle que $\\varphi(n+k)$ est le nombre d'entiers naturels $\\ell<n+k$ tels que $\\operatorname{PGCD}(\\ell, n+k)=1$.", "solution": "Procédons par l'absurde, et supposons qu'il existe un nombre premier $p$ qui divise tous les entiers $u_{n}$.\nTout d'abord, puisque $\\varphi(1)=\\varphi(2)=1$ et que $\\varphi(\\mathfrak{n})$ est pair pour tout $\\mathfrak{n} \\geqslant 2$, on remarque que $u_{1} \\equiv a_{0}+a_{1}(\\bmod 2)$ et que $u_{2} \\equiv a_{0}(\\bmod 2)$. Comme $a_{0}$ et $a_{1}$ sont premiers entre eux, les entiers $\\mathfrak{u}_{1}$ et $\\mathfrak{u}_{2}$ ne peuvent donc pas être pairs tous les deux, de sorte que $p \\geqslant 3$.\nSoit alors $\\delta$ le plus grand entier tel que $p$ ne divise pas $a_{\\delta}$. Pour tout entier $n \\geqslant 1$, on note $T_{n}$ le $\\delta$-uplet $(\\varphi(n), \\varphi(n+1), \\ldots, \\varphi(n+\\delta-1))$, considéré modulo $p$. Puisque $u_{n} \\equiv 0(\\bmod p)$, $c^{\\prime}$ est que\n\n$$\n\\varphi(n+\\delta) \\equiv-a_{\\delta}^{-1} \\sum_{k=0}^{\\delta-1} a_{k} \\varphi(n+k) \\quad(\\bmod p)\n$$\n\nAinsi, si l'on note $\\lambda:(\\mathbb{Z} / \\mathrm{p} \\mathbb{Z})^{\\delta} \\mapsto(\\mathbb{Z} / \\mathrm{p} \\mathbb{Z})^{\\delta}$ la fonction définie par\n\n$$\n\\lambda:\\left(x_{0}, x_{1}, \\ldots, x_{\\delta-1}\\right) \\mapsto\\left(x_{1}, x_{2}, \\ldots, x_{\\delta-1},-a_{\\delta}^{-1} \\sum_{k=0}^{\\delta-1} a_{k} x_{k}\\right)\n$$\n\non a $\\mathbf{T}_{\\mathfrak{n}+1}=\\lambda\\left(\\mathbf{T}_{\\mathfrak{n}}\\right)$. Or, d'après le principe des tiroirs, il existe deux entiers $k, \\ell \\geqslant 1$ tels que $\\mathbf{T}_{\\mathrm{k}}=\\mathbf{T}_{\\mathrm{k}+\\ell}$. On a alors $\\mathbf{T}_{\\mathbf{n}}=\\mathbf{T}_{\\mathrm{n}+\\ell}$ et $\\varphi(\\mathrm{n}) \\equiv \\varphi(\\mathrm{n}+\\ell)(\\bmod p)$ pour tout $n \\geqslant k$.\nOn montre alors le lemme suivant : pour tous les entiers $a \\geqslant 1$ et $b \\geqslant 3$, il existe un nombre premier $q>a$ tel que $q \\not \\equiv 1(\\bmod b)$. En effet, l'entier $m=\\max \\{a, b\\}!-1$ est congru à -1 $(\\bmod b)$, donc il admet nécessairement un facteur premier $q \\not \\equiv 1(\\bmod b)$, et $q$ ne peut pas diviser $\\mathrm{m}+1=\\max \\{\\mathrm{a}, \\mathrm{b}\\}!$, donc $\\mathrm{q}>\\mathrm{a}$.\nEn appliquant ce lemme deux fois de suite, on en déduit qu'il existe deux nombres premiers $q$ et $r$ tels que $q, r \\not \\equiv 1(\\bmod p)$ et $q>r>k+\\ell$. Mais alors $q$ est premier avec $\\ell$, donc $q^{\\varphi(\\ell)} \\equiv 1(\\bmod \\ell)$, et $\\varphi\\left(q^{\\varphi(\\ell)} n\\right) \\equiv \\varphi(n)(\\bmod p)$ pour tout $n \\geqslant k$.\nPuisque $q>r \\geqslant k$, on en déduit que\n\n$$\n\\begin{array}{rlr}\n(q-1) q^{\\varphi(\\ell)} & \\equiv \\varphi\\left(q^{\\varphi(\\ell)+1}\\right) \\equiv \\varphi(q) & \\equiv q-1 \\quad(\\bmod p) \\\\\n(r-1)(q-1) q^{\\varphi(\\ell)-1} & \\equiv \\varphi\\left(r q^{\\varphi(\\ell)}\\right) & \\equiv \\varphi(r)\n\\end{array}\n$$\n\nComme $q, r \\not \\equiv 1(\\bmod p), c^{\\prime}$ est que $q^{\\varphi(\\ell)} \\equiv(q-1) q^{\\varphi(\\ell)-1} \\equiv 1(\\bmod p)$, donc que $q^{\\varphi(\\ell)-1} \\equiv 0$ $(\\bmod p)$, ce qui est impossible. On a ainsi obtenu la contradiction souhaitée, ce qui conclut.\n\nNote : On peut aussi faire appel au théorème de Dirichlet, qui affirme que, pour tous les entiers $a$ et $b$ premiers entre eux, il existe une infinité de nombres premiers $q \\equiv a(\\bmod b)$. Il existe alors des nombres premiers $q_{0}>q_{1}>\\ldots>q_{d}>p+d$ congrus à $1(\\bmod p)$. Puis, si on choisit $k \\in\\{0,1\\}$ tel que $p$ ne divise pas $a_{k}$, il existe aussi un nombre premier $r$ tel que $r \\equiv 2(\\bmod p)$ et $r \\equiv k-i\\left(\\bmod q_{i}\\right)$ pour tout $i \\neq k$. Alors $p$ ne divise pas $u_{r-k}$.\n\nExercice 7 . Soit $n \\geqslant 2$ un entier. Clara dispose d'un plateau de taille $3 n \\times 3 n$, semblable à un échiquier. Elle vient d'inventer une nouvelle pièce, le léopard, qu'elle peut mouvoir comme suit : en le déplaçant d'une case vers le haut, d'une case vers la droite, ou bien d'une case en diagonale, vers le bas et la gauche. Clara a posé son léopard sur une des cases du plateau, puis elle l'a déplacé, de sorte qu'il ne passe jamais deux fois par la même case, jusqu'à ce qu'il revienne à sa case de départ.\nQuelle est le plus grand nombre possible de déplacements que Clara a pu effectuer en procédant de la sorte?", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2018", "problem_label": "6", "tier": 1, "problem": "Soit $a_{0}, a_{1}, \\ldots, a_{d}$ des entiers tels que $\\operatorname{PGCD}\\left(a_{0}, a_{1}\\right)=1$. Pour tout entier $n \\geqslant 1$, on pose\n\n$$\nu_{n}=\\sum_{k=0}^{d} a_{k} \\varphi(n+k)\n$$\n\nDémontrer que 1 est le seul entier naturel divisant tous les entiers $u_{n}$.\nOn rappelle que $\\varphi(n+k)$ est le nombre d'entiers naturels $\\ell<n+k$ tels que $\\operatorname{PGCD}(\\ell, n+k)=1$.", "solution": "Tout d'abord, Clara peut effectuer $9 \\mathfrak{n}^{2}-3$ en procédant comme illustré ci-dessous dans le cas où $\\mathrm{n}=3$.\n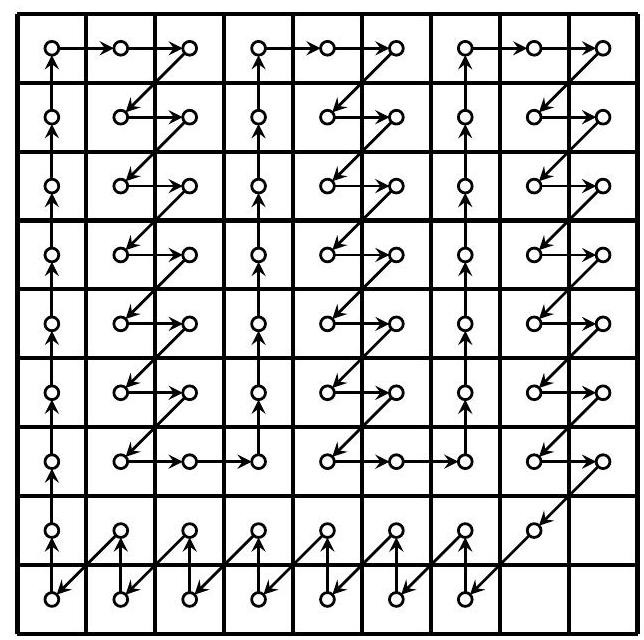\n\nMontrons maintenant qu'elle ne peut pas mieux faire. Tout d'abord, on identifie chaque case en ligne $i$ (en partant du bas) et en colonne $j$ (en partant de la gauche) à la paire ( $i, j$ ), où $1 \\leqslant i, j \\leqslant 3 n$. Puis on colorie les cases du plateau de trois couleurs $C_{0}, C_{1}$ et $C_{2}$, en affectant à la case $(\\mathfrak{i}, \\mathfrak{j})$ la couleur $\\mathrm{C}_{\\boldsymbol{i}+\\boldsymbol{j}}(\\bmod 3)$. Chaque mouvement du léopard consiste à se mouvoir d'un vecteur $(0,1),(1,0)$ ou $(-1,-1)$. Par conséquent, il passe systématiquement d'une case de couleur $C_{k}$ à une case de couleur $C_{k+1}(\\bmod 3)$. Il a donc effectué un nombre de déplacements divisible par 3, et il suffit de démontrer qu'il n'a pas pu passer par toutes les cases.\nÀ cette fin, remarquons que son parcours décrit un graphe planaire formé d'un seul cycle, qui contient donc une face interne (finie) et une face externe. Or, si le léopard est passé par la case $(1,3 \\mathfrak{n})$, il a dû utiliser l'arête $(1,3 \\mathfrak{n}) \\rightarrow(2,3 \\mathfrak{n})$, donc contourner sa face interne dans le sens horaire. Mais, de même, s'il est passé par la case ( $3 n, 1$ ), il a dû utiliser l'arête $(3 n, 1) \\rightarrow(3 n, 2)$, donc contourner sa face interne dans le sens anti-horaire. Il n'a donc pas pu passer par ces deux cases lors du même trajet, ce qui conclut.\n\n\n[^0]: Animath,\n Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2018-2019-Test-20-03-Corrigé-web.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Soit $A B C D$ un trapèze tel que $(A B)$ soit parallèle à $(C D)$. Soit $P$ un point de $[A C]$ et $Q$ un point de $[B D]$ tels que $\\widehat{A P D}=\\widehat{\\mathrm{BQC}}$.\nDémontrer que $\\widehat{A Q D}=\\widehat{\\mathrm{BPC}}$.", "solution": "L'énoncé nous donne plein d'égalités d'angles : exploitons-les! Tout d'abord, on remarque que\n\n$$\n\\widehat{\\mathrm{DPC}}=180^{\\circ}-\\widehat{\\mathrm{APD}}=180^{\\circ}-\\widehat{\\mathrm{CQB}}=\\widehat{\\mathrm{DQC}},\n$$\n\nce qui signifie que les points $C, D, P$ et $Q$ sont cocycliques.\nOn en déduit que\n\n$$\n\\widehat{\\mathrm{BQP}}=180^{\\circ}-\\widehat{\\mathrm{PQD}}=180^{\\circ}-\\widehat{\\mathrm{PCD}}=180^{\\circ}-\\widehat{\\mathrm{PAB}}\n$$\n\nce qui signifie là encore que les points $A, B, P$ et $Q$ sont cocycliques.\nOn en conclut que\n\n$$\n\\begin{aligned}\n\\widehat{\\mathrm{AQD}} & =\\widehat{\\mathrm{AQP}}+\\widehat{\\mathrm{PQD}}=\\widehat{\\mathrm{ABP}}+\\widehat{\\mathrm{PCD}}=(\\widehat{\\mathrm{ABC}}-\\widehat{\\mathrm{PBC}})+(\\widehat{\\mathrm{BCD}}-\\widehat{\\mathrm{BCP}}) \\\\\n& =(\\widehat{\\mathrm{ABC}}+\\widehat{\\mathrm{BCD}})-(\\widehat{\\mathrm{PBC}}+\\widehat{\\mathrm{BCP}})=180^{\\circ}-\\left(180^{\\circ}-\\widehat{\\mathrm{CPB}}\\right)=\\widehat{\\mathrm{CPB}}\n\\end{aligned}\n$$\n\n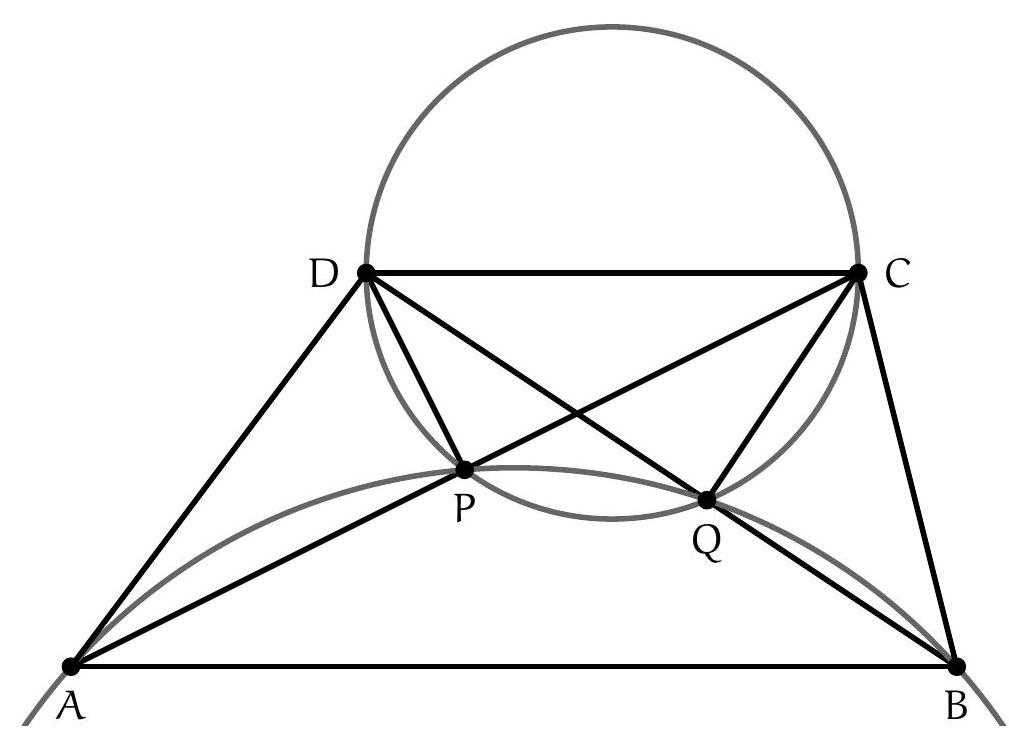", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Soit $a, b, c$ des nombres réels positifs ou nuls tels que $a+b+c=1$.\nDémontrer que\n\n$$\n\\frac{5+2 b+c^{2}}{1+a}+\\frac{5+2 c+a^{2}}{1+b}+\\frac{5+2 a+b^{2}}{1+c} \\geqslant 13\n$$", "solution": "Soit $S$ la somme\n\n$$\n\\frac{5+2 b+c^{2}}{1+a}+\\frac{5+2 c+a^{2}}{1+b}+\\frac{5+2 a+b^{2}}{1+c}\n$$\n\nNotons également $x_{i}$ le $i^{\\text {ème }}$ plus petit élément de l'ensemble $\\{a, b, c\\}$. L'inégalité du réordonnement indique que\n\n$$\n\\begin{aligned}\n& \\frac{b}{1+a}+\\frac{c}{1+b}+\\frac{a}{1+c} \\geqslant \\frac{x_{1}}{1+x_{1}}+\\frac{x_{2}}{1+x_{2}}+\\frac{x_{3}}{1+x_{3}} \\text { et } \\\\\n& \\frac{c^{2}}{1+a}+\\frac{a^{2}}{1+b}+\\frac{b^{2}}{1+c} \\geqslant \\frac{x_{1}^{2}}{1+x_{1}}+\\frac{x_{2}^{2}}{1+x_{2}}+\\frac{x_{3}^{2}}{1+x_{3}},\n\\end{aligned}\n$$\n\nde sorte que\n\n$$\n\\begin{aligned}\nS & \\geqslant \\frac{5+2 x_{1}+x_{1}^{2}}{1+x_{1}}+\\frac{5+2 x_{2}+x_{2}^{2}}{1+x_{2}}+\\frac{5+2 x_{3}+x_{3}^{2}}{1+x_{3}} \\\\\n& \\geqslant 4\\left(\\frac{1}{1+x_{1}}+\\frac{1}{1+x_{2}}+\\frac{1}{1+x_{3}}\\right)+\\left(1+x_{1}\\right)+\\left(1+x_{2}\\right)+\\left(1+x_{3}\\right) \\\\\n& \\geqslant 4+4\\left(\\frac{1}{1+x_{1}}+\\frac{1}{1+x_{2}}+\\frac{1}{1+x_{3}}\\right)\n\\end{aligned}\n$$\n\nLa fonction $\\mathrm{f}: \\mathrm{x} \\mapsto 1 /(1+x)$ étant convexe, on sait en outre que\n\n$$\n\\frac{1}{1+x_{1}}+\\frac{1}{1+x_{2}}+\\frac{1}{1+x_{3}}=f\\left(x_{1}\\right)+\\mathbf{f}\\left(x_{2}\\right)+\\mathbf{f}\\left(x_{3}\\right) \\geqslant 3 \\mathbf{f}\\left(\\frac{x_{1}+x_{2}+x_{3}}{3}\\right)=3 \\mathbf{f}(1 / 3)=9 / 4\n$$\n\nOn en déduit que $S \\geqslant 4+9=13$.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "On dit qu'une paire d'entiers ( $\\mathbf{a}, \\mathrm{b}$ ) est chypriote si $\\mathrm{a} \\geqslant \\mathrm{b} \\geqslant 2$, si a et b sont premiers entre eux, et si $a+b$ divise $a^{b}+b^{a}$.\nDémontrer qu'il existe une infinité de paires chypriotes distinctes.", "solution": "Posons $k=a-b$. Puisque $a$ et $b$ sont premiers entre eux, on sait que $a \\neq b$, donc que $k \\geqslant 1$. Ainsi,\n\n$$\na^{b}+b^{a} \\equiv a^{b}+(-a)^{a} \\equiv a^{b}\\left(1+(-1)^{a} a^{k}\\right) \\quad(\\bmod a+b)\n$$\n\nOr, $a$ est premier avec $b$ donc avec $a+b$ aussi.\nD'après le théorème de Gauss, on souhaite donc que $a+b=2 a-k$ divise $1+(-1)^{a} a^{k}$, ou encore $a^{\\mathrm{k}}+(-1)^{\\mathrm{a}}$.\nFaute de mieux, étudions maintenant les petites valeurs de k. Choisir $k=1$ reviendrait à souhaiter que $a+b$ divise $a \\pm 1$, ce qui est impossible puisque $a+b>a+1>a-1$. On regarde donc $k=2$.\nDans ce cas, on souhaite que $2 a-2=2(a-1)$ divise $a^{2}+(-1)^{a}$. Or, notons que $a^{2}+(-1)^{a} \\equiv$ $1+(-1)^{\\mathrm{a}}(\\bmod a-1)$. Par conséquent, et puisque $a \\geqslant 2$, il nous faut nécessairement choisir $a$ impair. Dans ce cas, il reste à faire en sorte que $2(a-1)$ divise $a^{2}-1=(a-1)(a+1)$, c'est-à-dire que 2 divise $a-1$. Mais c'est justement le cas, puisque a est impair.\nEn conclusion, on a bien montré que toutes les paires $(2 k+1,2 k-1)$, où $k \\geqslant 2$, étaient chypriotes.\n\nNote : Il existe d'autres paires chypriotes. On laisse ainsi au lecteur le plaisir de vérifier que les entiers $\\mathrm{a}=(2 \\ell)^{4 \\ell}+2 \\ell-1$ et $\\mathrm{b}=(2 \\ell)^{4 \\ell}-2 \\ell-1$ forment également une paire chypriote pour tout entier $\\ell \\geqslant 1$.\n\n## Exercice commun aux groupes Junior et Senior", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "Soit $\\mathcal{C}$ un cercle de rayon 1 , et soit $T$ un nombre réel. On dit qu'un ensemble de triangles est T-méraire s'il satisfait les trois conditions suivantes:\n$\\triangleright$ les sommets de chaque triangle appartiennent à $\\mathcal{C}$;\n$\\triangleright$ les triangles sont d'intérieurs deux à deux disjoints (mais deux triangles peuvent partager un côté ou un sommet);\n$\\triangleright$ chaque triangle est de périmètre strictement plus grand que $\\mathbf{T}$.\nTrouver tous les réels $\\mathbf{T}$ tels que, pour tout entier $\\mathrm{n} \\geqslant 1$, il existe un ensemble T-méraire contenant exactement n triangles.", "solution": "Nous allons démontrer que les réels recherchés sont exactement les réels $\\mathbf{T} \\leqslant 4$. Pour ce faire, fixons on réel $\\mathbf{T} \\leqslant 4$. On commence par montrer qu'il existe des ensembles T-méraires de n'importe quelle taille, grâce à la construction suivante. Soit $[A B]$ un diamètre de $\\mathcal{C}$, et soit $P$ un point quelconque de $\\mathcal{C}$, autre que $A$ et $B$. L'inégalité triangulaire indique que $A B P$ est de périmètre $A B+B P+P A>2 A B=4 \\geqslant T$.\nForts de cette remarque, on montre par récurrence sur $n$ qu'il existe $n$ points $P_{1}, \\ldots, P_{n}$, placés dans cet ordre sur l'un des deux demi-cercles $\\overline{A B}$ (avec $P_{1}$ proche de $A$ et $P_{n}$ proche de B), et tel que l'ensemble formé des triangles $A P_{i} P_{i+1}$ (pour $i \\leqslant n-1$ ) et $A B P_{n}$ soit $T$ méraire. Pour $n=1$, on vient de voir qu'il suffit de placer $P_{1} n$ 'importe où sur $\\overline{A B}$.\nPuis, une fois acquise l'existence des points $P_{1}, \\ldots, P_{n}$, construisons le point $P_{n+1}$. Pour ce faire, on considère le réel $\\varepsilon=A B+B P_{n}+P_{n} A-T$, qui est strictement positif par hypothèse. On place alors $\\mathrm{P}_{n+1}$ n'importe où sur l'arc $\\overline{B P_{n}}$, de sorte que $B P_{n+1}<\\varepsilon / 2$. En effet, dans ces conditions, nos $n+1$ triangles sont bien d'intérieurs deux à deux disjoints, et il suffit de vérifier que $A B P_{n+1}$ et $A P_{n} P_{n+1}$ sont de périmètre strictement plus grand que $T$.\nLe premier cas est un cas particulier de notre remarque initiale, et le deuxième cas découle encore une fois de l'inégalité triangulaire, puisque $A P_{n} P_{n+1}$ est de périmètre\n\n$$\nA P_{n}+P_{n} P_{n+1}+P_{n+1} A \\geqslant A P_{n}+\\left(P_{n} B-B P_{n+1}\\right)+\\left(A B-B P_{n+1}\\right)=T+\\varepsilon-2 B P_{n+1}>T\n$$\n\nCeci conclut notre récurrence, et donc le fait que l'on a bien des ensembles T-méraires de n'importe quelle taille.\nRéciproquement, considérons un réel $\\mathbf{T}>4$, et posons $\\varepsilon=(\\mathbf{T}-4) / 2>0$. Soit également $A B C$ un triangle dont les sommets appartiennent à $\\mathcal{C}$ et dont le périmètre est strictement plus grand que T. En notant $a, b$ et $c$ les longueurs $B C, C A$ et $A B$, et $p=(a+b+c) / 2>T / 2$ le demi-périmètre de $A B C$, la formule de Héron indique que $A B C$ est d'aire\n\n$$\n\\mathcal{S}=\\sqrt{p(p-a)(p-b)(p-c)}\n$$\n\nPuisque $p-a \\geqslant p-2 \\geqslant T / 2-2=\\varepsilon$ et que, de même, $p-b \\geqslant \\varepsilon$ et $p-c \\geqslant \\varepsilon$ on en déduit que $\\mathcal{S} \\geqslant \\sqrt{\\mathrm{p} \\mathrm{\\varepsilon}^{3}} \\geqslant \\sqrt{2 \\varepsilon^{3}}$.\nPar conséquent, si un ensemble T-méraire contient $n$ triangles, ceux-ci étant d'intérieurs deux à deux disjoints, ils couvrent, dans leur ensemble, une surface égale à $n \\sqrt{2 \\varepsilon^{3}}$ au moins. Cette surface ne pouvant pas dépasser $\\pi$, qui est la surface du disque contenu à l'intérieur $\\mathcal{C}$, on en déduit que $n \\leqslant \\pi / \\sqrt{2 \\mathcal{\\varepsilon}^{3}}$, ce qui conclut le problème.\nNote : En invoquant d'autres arguments, et sans faire appel à la formule de Héron, on pourrait également montrer que $n \\leqslant \\pi / \\varepsilon$, ce qui nous fournit une meilleure approximation dès lors que T est proche de 4.\n\n## Exercices du groupe Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2018", "problem_label": "5", "tier": 1, "problem": "Soit u un entier naturel non nul.\nDémontrer qu'il n'existe qu'un nombre fini de triplets d'entiers naturels ( $a, b, n$ ) tels que $\\mathrm{n}!=\\mathrm{u}^{\\mathrm{a}}-\\mathrm{u}^{\\mathrm{b}}$.\nNote : on rappelle que $0!=1!=1$.", "solution": "Soit $p$ un nombre premier impair qui ne divise pas $u$, et soit $k$ un entier tel que $p^{k}>u^{p-1}-1$. Posons $q=p^{k-1}$. On montre tout d'abord que $u$ n'est $^{\\text {pres }}$ une puissance $q^{\\text {ème }}\\left(\\bmod p^{k}\\right)$. En effet, si $u$ était une puissance $q^{\\text {ème }}\\left(\\bmod p^{k}\\right)$, alors il existerait un entier $v$ tel que $u \\equiv v^{q}\\left(\\bmod p^{k}\\right)$, et alors on aurait $1 \\equiv v^{\\varphi\\left(p^{k}\\right)} \\equiv v^{q(p-1)} \\equiv \\mathfrak{u}^{p-1}$ $\\left(\\bmod p^{k}\\right)$, ce qui $n^{\\prime}$ est pas le cas.\nPar conséquent, on sait également, pour tout entier $\\ell \\geqslant k$, que $u$ n'est pas non plus une puissance $q^{\\text {ème }}\\left(\\bmod p^{\\ell}\\right)$. On en déduit que $p^{\\ell-k}$ divise $\\omega_{p^{\\ell}}(u)$, où $\\omega_{p^{\\ell}}(u)$ désigne l'ordre de $u\\left(\\bmod p^{\\ell}\\right)$. En effet, soit $g$ une racine primitive $\\left(\\bmod p^{\\ell}\\right)$, et soit $x$ un entier tel que $u \\equiv g^{x}$ $\\left(\\bmod \\mathfrak{p}^{\\ell}\\right)$. Alors $1 \\equiv u^{\\omega_{p^{\\ell}}(\\mathfrak{u})} \\equiv \\mathrm{g}^{x \\omega_{p^{\\ell}}(\\mathfrak{u})}\\left(\\bmod \\mathrm{p}^{\\ell}\\right)$, ce qui signifie que $\\varphi\\left(\\mathrm{p}^{\\ell}\\right)=(p-1) \\mathrm{p}^{\\ell-1}$ divise $x \\omega_{p^{\\ell}}(u)$. Puisque $q=p^{k-1}$ ne divise pas $x$, $c^{\\prime}$ est donc que $p^{\\ell-k}$ divise $\\omega_{p^{\\ell}}(u)$.\nSupposons enfin qu'il existe un triplet ( $a, b, n$ ) d'entiers tels que $u^{a}-u^{b}=n$ ! et $n \\geqslant k p$. Posons également $d=a-b$ et $\\ell=\\lfloor n / p\\rfloor$. Alors $p^{\\ell}$ divise $n!=u^{b}\\left(u^{d}-1\\right)$ et, puisque $p$ ne divise pas $u$, $c^{\\prime}$ est donc que $a^{d} \\equiv 1\\left(\\bmod p^{\\ell}\\right)$. On en déduit que $\\omega_{p^{\\ell}}(u)$ divise $d$, donc que $p^{\\ell-k}$ divise $d$ également. Cela signifie en particulier que $d \\geqslant p^{\\ell-k}$, donc que\n\n$$\n2^{\\mathfrak{n}(\\mathfrak{n}+1)} \\geqslant \\mathfrak{n}^{n+1} \\geqslant n!+1 \\geqslant \\mathfrak{u}^{d} \\geqslant \\mathfrak{u}^{p^{\\ell-k}} \\geqslant \\mathfrak{u}^{p^{p / p-k}},\n$$\n\nou encore que $p^{k} n(n+1) \\geqslant p^{n / p} \\log _{2}(u)$.\nUne fois les entiers $u, p$ et $k$ fixés, le membre de droite croît beaucoup plus vite que le membre de gauche. Il existe donc un entier $\\mathbf{N}$, qui ne dépend que de $u$, $p$ et $k$, et tel que $n \\leqslant N$.\nAinsi, seul un nombre fini d'entiers $n$ appartient à un triplet ( $a, b, n$ ) tel que $n!=u^{a}-u^{b}$. Or, une fois un tel entier $n$ fixé, on sait que $u^{a}>u^{b}$, donc que $a \\geqslant b+1$, et donc que $n!\\geqslant \\mathfrak{u}^{\\mathrm{a}}-\\mathfrak{u}^{\\mathrm{a}-1}=(\\mathfrak{u}-1) \\mathfrak{u}^{\\mathrm{a}-1}$, ce qui montre que $a$ et $b$ sont eux-mêmes bornés. Ceci conlut notre solution.\n\nNote : Il n'était pas nécessaire de recourir directement à l'existence d'une racine primitive $\\left(\\bmod p^{\\ell}\\right)$, par exemple en procédant comme suit. Soit $s$ l'ordre de $_{u}(\\bmod p)$, et soit $k$ la valuation $p$-adique de $u^{s}-1$. Alors, pour tout $\\ell \\geqslant k$, on peut en fait montrer que $u$ est $d^{\\prime}$ ordre $\\omega=p^{\\ell-\\mathrm{k}} s\\left(\\bmod p^{\\ell}\\right)$.\nPour ce faire, on va d'abord montrer par récurrence, pour tout $m \\geqslant 1$, les racines $p^{\\text {èmes }}$ de l'unité $^{\\left(\\bmod p^{\\mathrm{m}}\\right)}$ sont les entiers congrus à $1\\left(\\bmod p^{\\mathrm{m}-1}\\right)$. En effet, le résultat est immédiat pour $m=1$. Puis, si $m \\geqslant 2$ et si $x^{p} \\equiv 1\\left(\\bmod p^{\\mathfrak{m}}\\right)$, alors $x^{p} \\equiv 1\\left(\\bmod p^{m-1}\\right)$, donc on peut écrire $x=1+y^{\\mathrm{m}-2}$, et en développant un binôme de Newton on en déduit que $1 \\equiv x^{\\mathfrak{p}} \\equiv 1+y^{\\mathfrak{m}-1}\\left(\\bmod \\mathfrak{p}^{\\mathfrak{m}}\\right)$, ce qui conclut la récurrence.\nÀ l'aide de la récurrence ci-dessus, on remarque donc que $u^{s}$ est d'ordre $\\varpi=p^{\\ell-k}$ $\\left(\\bmod p^{\\ell}\\right)$. Puisque $s$ divise $\\omega$, on sait en outre que $\\omega=s \\varpi$, ce qui conclut.\nDe manière générale, ce raisonnement joue en fait un rôle crucial dans la preuve de l'existence $d^{\\prime}$ une racine primitive $\\left(\\bmod p^{\\ell}\\right)$.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2018", "problem_label": "6", "tier": 1, "problem": "Soit $A B C$ un triangle, soit I le centre du cercle inscrit dans $A B C$. Soit $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ trois points respectivement situés sur (AI), (BI) et (CI). On suppose que $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ sont distincts de $A, B, C$ et $I$, et qu'ils sont alignés. Enfin, soit $P_{A}$ le point d'intersection des médiatrices de $\\left[\\mathrm{BB}^{\\prime}\\right]$ et $\\left[\\mathrm{CC}^{\\prime}\\right]$. De même, soit $\\mathrm{P}_{\\mathrm{B}}$ le point d'intersection des médiatrices de $\\left[C C^{\\prime}\\right]$ et $\\left[A A^{\\prime}\\right]$, et soit $P_{C}$ le point d'intersection des médiatrices de $\\left[A A^{\\prime}\\right]$ et $\\left[B B^{\\prime}\\right]$.\nDémontrer que les cercles circonscrits aux triangles $A B C$ et $P_{A} P_{B} P_{C}$ sont tangents l'un à l'autre.", "solution": "On commence par tracer une figure comme ci-dessous, sans oublier la droite $\\ell$ qui passe par $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ ni les cercles $\\Omega$ et $\\Gamma$, respectivement circonscrits à $A B C$ et à $\\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{B}} \\mathrm{P}_{\\mathrm{C}}$.\n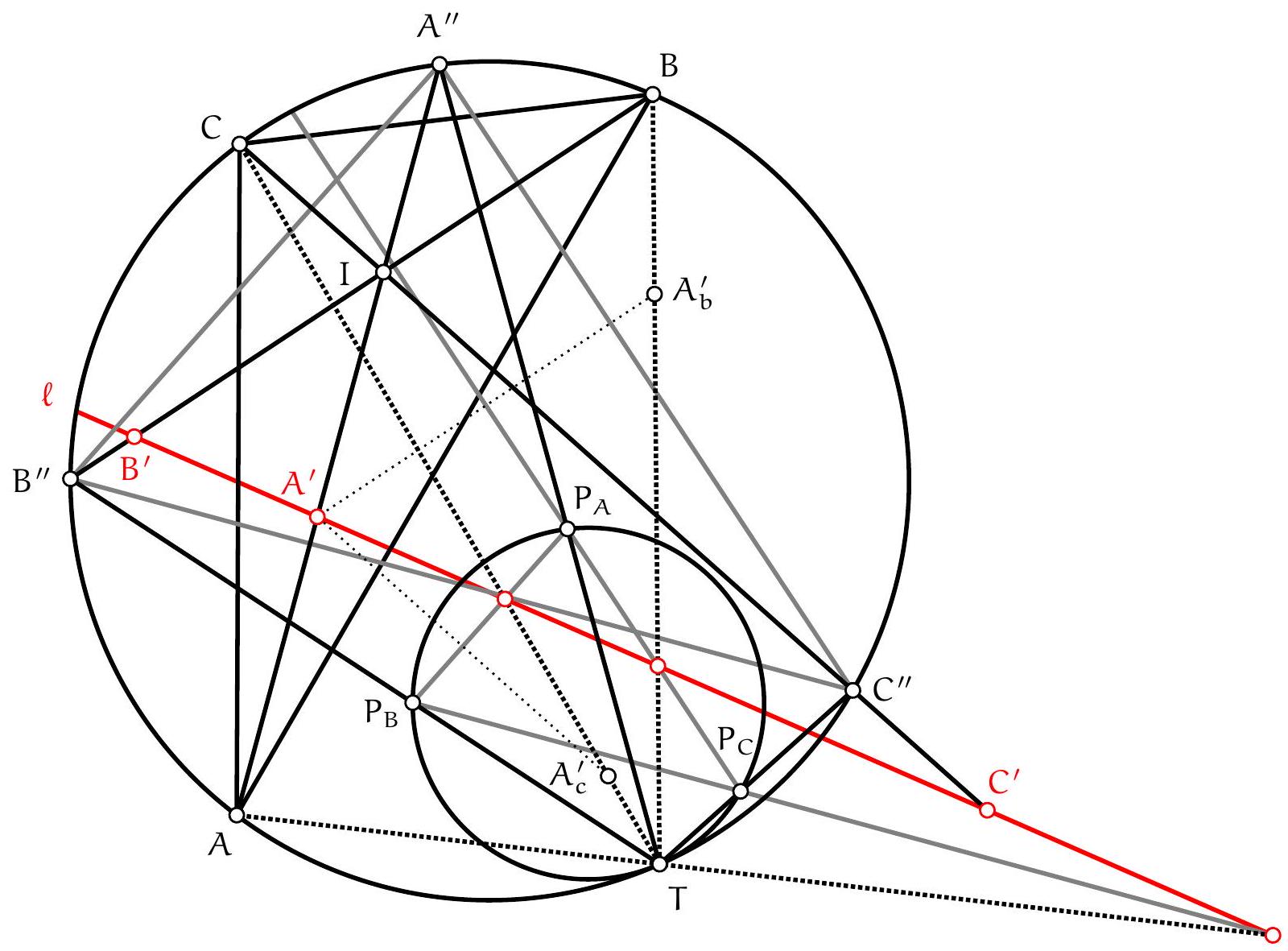\n\nAu vu de l'énoncé, une approche raisonnable est de trouver une caractérisation adaptée du point de tangence éventuel, que l'on notera $T$, entre $\\Omega$ et $\\Gamma$. Une telle caractérisation est la suivante : T est le centre d'une des deux homothéties envoyant $\\Gamma$ sur $\\Omega$. Soit h cette homothétie : il s'agit de l'homothétie de rapport positif si l'un des deux cercles est inclus à l'intérieur de l'autre, et de l'homothétie de rapport négatif sinon.\nAu vu de la définition de $\\Gamma$ et $\\Omega$, il est tentant d'étudier l'image de $\\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{B}} \\mathrm{P}_{\\mathrm{C}}$ par $h$, ou bien celle de $A B C$ par $\\mathrm{h}^{-1}$. Or, sur la figure, on constate deux choses:\n$\\triangleright$ les points $h\\left(P_{A}\\right), h\\left(P_{B}\\right)$ et $h\\left(P_{C}\\right)$ semblent être les points d'intersection respectifs de (AI), (BI) et (CI) avec $\\Omega$;\n$\\triangleright$ les droites $(A T),(B T)$ et $(C T)$ semblent recouper la droite $\\ell$ en des points de $\\left(P_{B} P_{C}\\right)$, $\\left(\\mathrm{P}_{C} \\mathrm{P}_{\\mathrm{A}}\\right)$ et $\\left(\\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{B}}\\right)$ respectivement.\nExploitons ces idées!\n\nTout d'abord, on note donc $A^{\\prime \\prime}, B^{\\prime \\prime}$ et $C^{\\prime \\prime}$ ces points d'intersection. Le point $A^{\\prime \\prime} n^{\\prime}$ est autre que le pôle sud de $A B C$ par rapport au sommet $A$. On sait donc que $A^{\\prime \\prime} B=A^{\\prime \\prime} C=A^{\\prime \\prime} \\mathrm{I}$. De même, on a $B^{\\prime \\prime} C=B^{\\prime \\prime} A=B^{\\prime \\prime} I$ et $C^{\\prime \\prime} A=C^{\\prime \\prime} B=C^{\\prime \\prime}$. Ainsi, les droites $\\left(A^{\\prime \\prime} B^{\\prime \\prime}\\right)$ et $\\left(P_{A} P_{B}\\right)$ sont les médiatrices respectives de [CI] et de $\\left[C^{\\prime}\\right]$, ce qui montre en particulier qu'elles sont parallèles. De même, $\\left(B^{\\prime \\prime} C^{\\prime \\prime}\\right)$ est parallèle à $\\left(P_{B} P_{C}\\right)$ et $\\left(C^{\\prime \\prime} A^{\\prime \\prime}\\right)$ est parallèle à $\\left(P_{A}, P_{B}\\right)$. Cela montre que les triangles $P_{A} P_{B} P_{C}$ et $A^{\\prime \\prime} B^{\\prime \\prime} C^{\\prime \\prime}$ sont homothétiques l'un de l'autre.\nEn particulier, il existe une unique homothétie qui envoie $P_{A} P_{B} P_{C}$ sur $A^{\\prime \\prime} B^{\\prime \\prime} C^{\\prime \\prime}$. On peut effectivement la noter $h$, et noter $T$ son centre, de sorte que $h$ envoie $\\Omega$ sur $\\Gamma$. Ici, le point T n'est autre que le point de concours des droites $\\left(A^{\\prime \\prime} P_{A}\\right),\\left(B^{\\prime \\prime} P_{B}\\right)$ et $\\left(C^{\\prime \\prime} P_{C}\\right)$, et il reste à montrer que $T$ appartient à $\\Omega$.\nD'autre part, puisque ( $\\mathrm{P}_{A} \\mathrm{P}_{B}$ ) est a médiatrice de $\\left[C C^{\\prime}\\right]$, et si (TC) recoupe ( $\\mathrm{P}_{A} \\mathrm{P}_{B}$ ) en un point $X$ qui appartient aussi à $\\ell$, alors les droites $\\ell$ et $(T C)=(C X)$ sont symétriques l'une de l'autre par rapport à ( $\\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{B}}$ ). Réciproquement, on note $\\ell_{\\mathrm{a}}, \\ell_{b}$ et $\\ell_{c}$ les symétriques respectifs de $\\ell$ par rapport à $\\left(P_{B} P_{C}\\right),\\left(P_{C} P_{A}\\right)$ et $\\left(P_{A} P_{B}\\right)$.\nOn peut alors chercher à montrer que les droites $\\ell_{a}, \\ell_{b}$ et $\\ell_{c}$ sont concourantes en un point $\\hat{T}$ qui appartiendra à $\\Omega$, puis que les points $\\hat{T}, \\mathrm{P}_{A}$ et $A^{\\prime \\prime}$ sont alignés: on en déduira que $T=\\hat{T}$, ce qui conclura le problème. Soit alors $T_{c}$ le point d'intersection de $\\ell_{a}$ et $\\ell_{b}$. On remarque que\n\n$$\n\\begin{aligned}\n\\left(\\mathrm{T}_{\\mathrm{c}} A, \\mathrm{~T}_{\\mathrm{c}} \\mathrm{~B}\\right) & =\\left(\\ell_{\\mathrm{a}}, \\ell_{\\mathrm{b}}\\right)=\\left(\\ell_{\\mathrm{a}}, \\ell\\right)+\\left(\\ell, \\ell_{\\mathrm{b}}\\right)=2\\left(\\mathrm{P}_{\\mathrm{B}} \\mathrm{P}_{\\mathrm{C}}, \\ell\\right)+2\\left(\\ell, \\mathrm{P}_{\\mathrm{C}} \\mathrm{P}_{\\mathrm{A}}\\right)=2\\left(\\mathrm{P}_{\\mathrm{B}} \\mathrm{P}_{\\mathrm{C}}, \\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{C}}\\right) \\\\\n& =2\\left(\\mathrm{~B}^{\\prime \\prime} \\mathrm{C}^{\\prime \\prime}, \\mathrm{A}^{\\prime \\prime} \\mathrm{C}^{\\prime \\prime}\\right)=2\\left(\\mathrm{~B}^{\\prime \\prime} \\mathrm{C}^{\\prime \\prime}, C C^{\\prime \\prime}\\right)+2\\left(C C^{\\prime \\prime}, A^{\\prime \\prime} \\mathrm{C}^{\\prime \\prime}\\right) \\\\\n& =\\left(A C^{\\prime \\prime}, C C^{\\prime \\prime}\\right)+\\left(C C^{\\prime \\prime}, B C^{\\prime \\prime}\\right)=\\left(A C^{\\prime \\prime}, B C^{\\prime \\prime}\\right)=(A C, B C) .\n\\end{aligned}\n$$\n\nCeci montre que les points $T_{c}, A, B$ et $C^{\\prime \\prime}$ sont cocycliques, donc que $T_{c}$ appartient bien à $\\Omega$. Or, si $T_{c}=A$, alors $\\ell_{b}=(A B)$, donc $(A C, B C)=\\left(\\ell_{a}, \\ell_{b}\\right)=\\left(\\ell_{a}, B A\\right)$, donc $\\ell_{a}$ est la tangente à $\\Omega$ en $A$, et $T_{c}$ est nécessairement le point d'intersection de $\\ell_{a}, \\ell_{b}$ et $\\ell_{c}$. De même, on introduit les points $T_{a}$ et $T_{b}$. Si l'un de ces trois points est $A, B$ ou $C$, alors il constitue bien le point $\\hat{T}$ désiré. Sinon, $T_{c}$ est le point d'intersection de $\\ell_{a}$ avec $\\Omega$ autre que $A$, mais également le point d'intersection de $\\ell_{b}$ avec $\\Omega$ autre que $B$, et en raisonnant de manière analogue sur $T_{a}$ et $T_{b}$ on constate bien que $T_{a}=T_{b}=T_{c}$ appartient à $\\Omega$.\nPar ailleurs, et puisque l'on a obtenu les droites $\\ell_{a}, \\ell_{b}$ et $\\ell_{c}$ en appliquant à $\\ell$ des symétries axiales, il est important d'appliquer ces symétries à d'autres points en particulier, notamment les points $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ présents sur $\\ell$. Ainsi, on note $A_{b}^{\\prime}$ et $A_{c}^{\\prime}$ les symétriques de $A^{\\prime}$ par rapport à $\\left(\\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{C}}\\right)$ et à $\\left(\\mathrm{P}_{\\mathrm{A}} \\mathrm{P}_{\\mathrm{B}}\\right)$ : ils se trouvent sur $\\ell_{\\mathrm{b}}$ et $\\ell_{\\mathrm{c}}$.\nDans ces conditions,\n\n$$\n\\begin{aligned}\n\\left(P_{A} A_{b}^{\\prime}, P_{A} A_{c}^{\\prime}\\right) & =\\left(P_{A} A_{b}^{\\prime}, P_{A} A^{\\prime}\\right)+\\left(P_{A} A^{\\prime}, P_{A} A_{c}^{\\prime}\\right)=2\\left(P_{A} P_{C}, P_{A} A^{\\prime}\\right)+2\\left(P_{A} A^{\\prime}, P_{A} P_{B}\\right) \\\\\n& =2\\left(P_{A} P_{C}, P_{A} P_{B}\\right)=\\left(\\ell_{b}, \\ell_{c}\\right)=\\left(\\hat{T} A_{b}^{\\prime}, \\hat{T} A_{c}^{\\prime}\\right) .\n\\end{aligned}\n$$\n\nCela signifie que les points $\\mathrm{P}_{\\mathrm{A}}, \\mathrm{A}_{\\mathrm{b}}^{\\prime}, \\hat{T}$ et $A_{c}^{\\prime}$ sont cocycliques.\nD'autre part, puisque $P_{A} A_{b}^{\\prime}=P_{A} A^{\\prime}=P_{A} A_{c}^{\\prime}$, on sait que le triangle $P_{A} A_{b}^{\\prime} A_{c}^{\\prime}$ est isocèle en $P_{A}$. On en déduit que\n\n$$\n\\begin{aligned}\n& \\left(\\ell_{b}, P_{A} \\hat{T}\\right)=\\left(A_{b}^{\\prime} \\hat{T}, P_{A} \\hat{T}\\right)=\\left(A_{b}^{\\prime} A_{c}^{\\prime}, P_{A} A_{c}^{\\prime}\\right) \\\\\n& =90^{\\circ}-\\left(A_{b}^{\\prime} \\mathrm{P}_{\\mathrm{A}}, \\mathcal{A}_{\\mathrm{c}}^{\\prime} \\mathrm{P}_{\\mathrm{A}}\\right) / 2=90^{\\circ}-\\left(\\mathrm{P}_{\\mathrm{C}} \\mathrm{P}_{\\mathrm{A}}, \\mathrm{P}_{\\mathrm{B}} \\mathrm{P}_{\\mathrm{A}}\\right) \\\\\n& =90^{\\circ}+(\\mathrm{BI}, \\mathrm{IC})=(\\mathrm{BA}, \\mathrm{AI})=\\left(\\mathrm{BA}, \\mathrm{AA}^{\\prime \\prime}\\right)=\\left(\\mathrm{B} \\hat{\\mathrm{~T}}, \\hat{\\mathrm{~T}} \\mathrm{~A}^{\\prime \\prime}\\right)=\\left(\\ell_{\\mathrm{b}}, \\hat{\\mathrm{~T}} \\mathrm{~A}^{\\prime \\prime}\\right) .\n\\end{aligned}\n$$\n\nCela signifie que $\\hat{\\top}$ est bien aligné avec $P_{A}$ et $A^{\\prime \\prime}$. On montre de même que $\\hat{T}$ est aligné avec $P_{B}$ et $B^{\\prime \\prime}$, ainsi qu'avec $P_{C}$ et $C^{\\prime \\prime}$. Par conséquent, on a bien $T=\\hat{T}$, ce qui conclut.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
French_TST_Senior/segmented/fr-2018-2019-Test-26-02-Corrige.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Soit $a$ et $b$ deux réels tels que $a b \\geqslant a^{3}+b^{3}$.\nDémontrer que $a+b \\leqslant 1$.", "solution": "Puisque $(a+b)^{2}=(a-b)^{2}+4 a b \\geqslant 4 a b$, on en déduit que\n\n$$\n(a+b)^{3}=a^{3}+b^{3}+3(a+b) a b \\leqslant(3 a+3 b+1) a b \\leqslant(3 a+3 b+1)(a+b)^{2} / 4\n$$\n\nSi $a+b>1$, on peut diviser notre inégalité par $(a+b)^{2} / 4$, ce qui signifie que $4(a+b) \\leqslant$ $3 a+3 b+1$, donc que $a+b \\leqslant 1$ tout de même.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Un coloriage de $\\mathbb{Q}$ consiste à colorier tout nombre rationnel soit en rouge, soit en bleu. On dit qu'un coloriage de $\\mathbb{Q}$ est harmonieux si, pour tous les rationnels $x$ et $y$ d'une même couleur, le rationnel $x+y$ est encore de la même couleur.\nTrouver tous les coloriages de $\\mathbb{Q}$ qui sont harmonieux.", "solution": "On va montrer que les coloriages recherchés sont les suivants :\n$\\triangleright$ on colorie tous les rationnels avec la même couleur;\n$\\triangleright$ on colorie tous les rationnels positifs ou nuls avec une même couleur, et tous les rationnels strictement négatifs avec l'autre couleur;\n$\\triangleright$ on colorie tous les rationnels strictement positifs avec une même couleur, et tous les rationnels négatifs ou nuls avec l'autre couleur.\nTout d'abord, il est clair que chacun de ces coloriages est harmonieux. Montrons que ce sont les seuls.\nDans la suite, on supposera que l'on dispose d'un coloriage harmonieux fixé. On note B l'ensemble des rationnels coloriés en bleu et R l'ensemble des rationnels coloriés en rouge.\nAvec ces notations, si $x$ est un rationnel quelconque appartenant à un ensemble $E \\in\\{B, R\\}$, on va d'abord montrer que pour tout nombre rationnel $p / q$ strictement positif, $p x / q$ appartient aussi à $E$. En effet, si $x / q \\notin E$, alors une récurrence immédiate montre que $x=q x / q \\notin E$, ce qui $n^{\\prime}$ est pas possible. On en déduit que $x / q \\in E$, puis que $p x / q \\in E$, toujours par récurrence immédiate.\nAinsi, tous les rationnels strictement positifs sont de la même couleur que 1, et tous les rationnels strictement négatifs sont de la même couleur que -1 . Vu notre objectif, il reste à montrer que, si 1 et -1 sont de la même couleur, alors 0 est de cette couleur là également : ceci découle précisément du fait que $0=1+(-1)$ est du caractère harmonieux de notre coloriage.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle isocèle en $A$, et soit $D$ un point sur ( $A C$ ) tel que $A$ soit situé entre C et D , mais ne soit pas le milieu de [CD].\nOn note $d_{1}$ et $d_{2}$ les bissectrices intérieure et extérieure de l'angle $\\widehat{B A C}$, et $\\Delta$ la médiatrice de [BD]. Enfin, soit $E$ et $F$ les points d'intersection respectifs de $\\Delta$ avec les droites $d_{1}$ et $d_{2}$.\nDémontrer que les points $A, D, E$ et $F$ sont cocycliques.", "solution": "Une jolie figure suggère même que les points $A, B, D, E$ et $F$ sont cocycliques : c'est ce que nous allons montrer.\nSoit $\\Gamma$ le cercle circonscrit à $A B D$, et soit $G_{1}$ et $G_{2}$ les points d'intersection respectifs des droites $d_{1}$ et $d_{2}$ avec $\\Gamma$, et autres que $D$ lui-même. Il nous suffit de montrer que $E=G_{1}$ et que $\\mathrm{F}=\\mathrm{G}_{2}$.\nPuisque $\\mathrm{d}_{2}$ est la bissectrice extérieure de $\\widehat{B A C}$, donc la bissectrice intérieure de $\\widehat{B A D}$, le théorème du pôle Sud indique que $\\mathrm{G}_{2}$ est équidistant de B et D . De même, $\\mathrm{d}_{1}$ est la bissectrice intérieure de $\\widehat{B A C}$, donc la bissectrice extérieure de $\\widehat{B A D}$, et le théorème du pôle Nord indique que $\\mathrm{G}_{1}$ est équidistant de B et D .\nMais alors $\\left(G_{1} G_{2}\\right)$ est bien la médiatrice de $[B D]$, donc $G_{1}=E$ et $G_{2}=F$, ce qui conclut.\n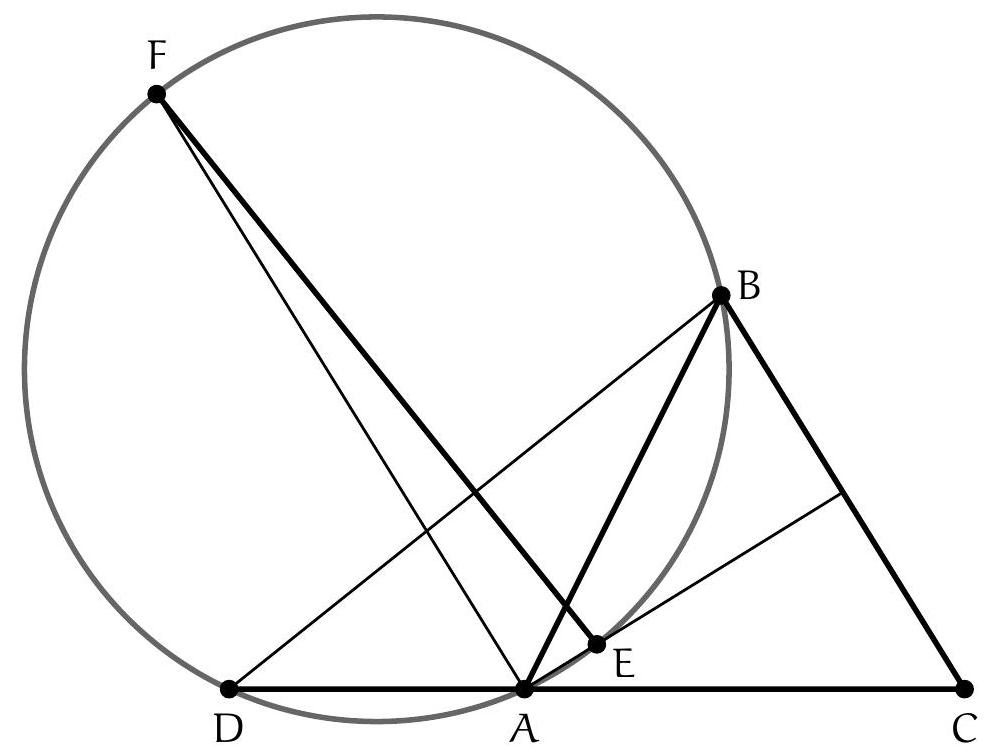", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2018", "problem_label": "4", "tier": 1, "problem": "Dans un tournoi auxquels participent $n$ joueurs, numérotés de 1 à $n$, chaque paire de joueurs se rencontre exactement une fois. Cette rencontre se termine par la victoire d'un des deux joueurs et la défaite de l'autre joueur. On note $v_{\\mathrm{k}}$ le nombre de victoires du joueur $k$ au cours du tournoi, et $d_{k}$ son nombre de défaites.\nDémontrer que $\\sum_{k=1}^{n} v_{k}^{2}=\\sum_{k=1}^{n} d_{k}^{2}$.", "solution": "Puisque chaque joueur a disputé $n-1$ parties et que l'ensemble des joueurs a totalisé $n(n-1) / 2$ victoires, on sait que\n\n$$\n\\sum_{k=1}^{n} v_{k}=n(n-1) / 2\n$$\n\net que $v_{k}+d_{k}=n-1$ pour tout $k \\leqslant n$. On en déduit que\n\n$$\n\\sum_{k=1}^{n} d_{k}^{2}=\\sum_{k=1}^{n}\\left(n-1-v_{k}\\right)^{2}=n(n-1)^{2}-2(n-1) \\sum_{k=1}^{n} v_{k}+\\sum_{k=1}^{n} v_{k}^{2}=\\sum_{k=1}^{n} v_{k}^{2}\n$$", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
French_TST_Senior/segmented/fr-2018-2019-Test-27-02-Corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Carine et Cyril jouent au jeu suivant. Tout d'abord, Cyril choisit un entier $\\mathrm{n} \\geqslant 1$. Puis, dans chacune des cases d'une grille $3 \\times 3$ (apparentée à un jeu de morpion), il écrit un entier.\nVient ensuite le tour de Carine. Elle peut, autant de fois qu'elle le souhaite, effectuer l'opération suivante : elle choisit une case $\\mathbf{c}$, puis augmente de 1 la valeur de $\\mathbf{c}$ et de ses voisines (c'est-à-dire des cases qui partagent un côté avec c). Carine gagne la partie si elle réussit à faire en sorte que les 9 entiers soient tous égaux modulo $n$.\nQuel est le joueur qui dispose d'une stratégie gagnante?", "solution": "On va montrer que Carine a une stratégie gagnante. Tout d'abord, adoptons quelques notations. On note ( $\\mathfrak{i}, \\mathfrak{j}$ ) la case située en ligne $\\boldsymbol{i}$ et en colonne $\\mathfrak{j}$, et on note $k_{i, j}$ l'entier écrit sur cette case. Sans perte de généralité, on suppose que nos entiers sont écrits modulo $n$.\nOn va également noter $a_{i, j}$ une action de Carine consistant à choisir la case $(i, j)$, donc à augmenter de 1 les entiers $k_{\\hat{i}, \\hat{j}}$ tels que $|\\mathfrak{i}-\\hat{\\mathfrak{i}}|+|\\mathfrak{j}-\\hat{j}| \\leqslant 1$. Au vu de la condition de victoire de Carine, on suppose aussi qu'elle dispose d'une opération $a_{\\infty}$ qui consiste à ôter 1 à toutes les cases.\nAlors, en effectuant les actions $a_{1,1}, a_{3,1}, a_{2,3}$ et $a_{\\infty}$, Carine se débrouille pour augmenter $l^{\\prime}$ entier $k_{2,1}$ de 1 sans changer les autres. De même, elle peut augmenter isolément chacun des entiers $k_{2,3}, k_{1,2}$ et $k_{3,2}$. On appelle $b_{2,1,2,3}, b_{1,2}$ et $b_{3,2}$ les \"actions\" correspondantes.\nPuis, en réalisant l'action $a_{1,1}$ et en réalisant $n-1$ fois les actions $b_{2,1}$ et $b_{1,2}$, Carine a augmenté l'entier $k_{1,1}$ sans changer les autres. De même, elle peut augmenter isolément les entiers $k_{1,3}, k_{3,1}$ et $k_{3,3}$.\nIl lui suffit donc de modifier les valeurs de chacune des cases autres que $(2,2)$ pour que tous les entiers deviennent égaux, et alors elle aura gagné.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "Trouver les fonctions $f: \\mathbb{R} \\mapsto \\mathbb{R}$ telles que, pour tous les réels $x$ et $y$, on ait:\n\n$$\nf\\left(x^{2}+x+f(y)\\right)=y+f(x)+f(x)^{2}\n$$", "solution": "Tout d'abord, il est clair que la fonction $\\mathrm{f}: x \\mapsto x$ est une solution. On va montrer que c'est la seule.\nDans la suite, on notera $E_{x, y}$ l'équation $f\\left(x^{2}+x+f(y)\\right)=y+f(x)+f(x)^{2}$. En premier lieu, $E_{0, y}$ indique que $f(f(y))=y+f(0)+f(0)^{2}$, ce qui montre que $f$ est à la fois injective et surjective, donc bijective.\nD'autre part, pour tous les réels $x$ et $t$, notons que $x^{2}+x=t^{2}+t$ si et seulement si $0=$ $x^{2}-t^{2}+x-t=(x-t)(x+t+1)$, c'est-à-dire si $x=t$ ou $t=-1-x$. En particulier, en posant $t=-1-x$, alors $E_{x, y}$ et $E_{t, y}$ indiquent que $f(x)+(x)^{2}=f(t)+(t)^{2}$. Par conséquent, si $x \\neq-1 / 2$, et puisque l'on a alors $t \\neq x$ et que $f$ est injective, on a également $f(t)=-1-f(x)$ et $f(x) \\neq-1 / 2$. On en déduit notamment que $f(-1 / 2)=-1 / 2$.\nOn vient de montrer que $-1 / 2$ est un point fixe de $f$. Or, si $y$ et $x$ sont des points fixes de $f$, l'équation $\\mathbf{E}_{x, y}$ montre que $x^{2}+x+y$ en est un également. De même, si $x$ et $x^{2}+x+y$ sont des points fixes de $f$, et puisque $f$ est bijective, alors $y$ en est un également. Ici, en choisissant $x=-1 / 2$, on constate donc que, dès lors que $y$ est un point fixe de $f, y-1 / 4$ et $y+1 / 4$ en sont aussi. En particulier, 0 et $1 / 4$ sont des points fixes.\nDans ces conditions, $E_{x, 0}$ et $E_{0, y}$ montrent respectivement que $f\\left(x^{2}+x\\right)=f(x)+f(x)^{2}$ et que $f(f(y))=y$. Puis, si $t$ est un réel positif, soit $x$ un réel tel que $x^{2}+x=t-1 / 4$. Alors $\\mathbf{E}_{x, 1 / 4}$ indique que\n\n$$\n\\mathbf{f}(\\mathbf{t})=\\mathbf{f}\\left(\\left(\\mathrm{x}^{2}+x+\\mathbf{f}(1 / 4)\\right)=1 / 4+\\boldsymbol{f}(\\mathrm{x})+\\mathrm{f}(\\mathrm{x})^{2} \\geqslant 0\\right.\n$$\n\nPar ailleurs, si $z$ est un réel tel que $z^{2}+z=\\mathrm{t}$, alors $\\mathbf{E}_{z, \\mathrm{f}(\\mathrm{y})}$ indique que\n\n$$\nf(t+y)=f(y)+f(z)+f(z)^{2}=f(y)+f\\left(z^{2}+z\\right)=f(y)+f(t)\n$$\n\nOn en déduit à la fois que $f$ est croissante et que $f$ est en fait additive.\nLa fonction $f$ est donc linéaire, c'est-à-dire de la forme $f: x \\mapsto \\lambda x$. On conclut en observant que, puisque $-1 / 2$ est un point fixe de f , $\\mathrm{c}^{\\prime}$ est que $\\lambda=1$, donc que f est bien la fonction identité.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "Soit p un nombre premier.\nDémontrer qu'il existe un nombre premier $q$ tel que $\\mathfrak{n}^{p} \\not \\equiv p$ pour tout $n \\in \\mathbb{Z}$.", "solution": "Tout d'abord, si $p$ ne divise pas $q-1$, alors $x \\mapsto x^{p}$ est une bijection de $\\mathbb{Z} / q \\mathbb{Z}$ dans lui-même, donc $q$ ne peut pas convenir. On en vient à chercher $q \\equiv 1(\\bmod p)$ tel que, pour tout $n \\not \\equiv 0(\\bmod q), n$ soit d'ordre $\\omega_{q}(n) \\neq p \\omega_{q}(p)$ modulo $q$, où $\\omega_{q}(p)$ est l'ordre de $p$ modulo $q$.\nPuisque les ordres possibles sont exactement les diviseurs de $q-1$, cela signifie que $q-1$ doit être divisible par $p$ et par $\\omega_{q}(p)$ mais pas $p \\omega_{q}(p)$. Par conséquent, $p$ doit nécessairement diviser $\\omega_{q}(p)$, et une première idée serait de vérifier si on ne peut pas justement avoir $\\omega_{q}(p)=p$.\nDans cette optique, $q$ doit diviser $p^{p}-1$ mais pas $p-1$. Ainsi, $q$ doit diviser l'entier\n\n$$\n\\mathbf{N}=\\frac{p^{p}-1}{p-1}=1+p+p^{2}+\\ldots+p^{p-1}\n$$\n\nDans ces conditions, si $q$ divise quand même $p-1$, alors $\\mathbf{N} \\equiv p(\\bmod q)$, ce qui est impossible. Ainsi, on est ici assuré que $q$ ne divise pas $p-1$, donc que $\\omega_{q}(p)=p$.\nIl reste donc à s'assurer que l'on peut choisir $q$ de sorte que $q \\not \\equiv 1\\left(\\bmod p^{2}\\right)$. Si un tel $q$ $n^{\\prime}$ existait pas, alors $N$ lui même serait congru à $1\\left(\\bmod p^{2}\\right)$. On conclut donc le problème en remarquant que $\\mathbf{N} \\equiv 1+p \\not \\equiv 1\\left(\\bmod p^{2}\\right)$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "problem_label": "1", "tier": 1, "problem": "Un pays comprend $2018 n+1$ villes, où $n$ est un entier naturel non nul. Certaines paires de villes sont reliées par des lignes directes de chemin de fer, de sorte qu'il y ait au plus une ligne entre deux villes ; chaque ligne va dans les deux sens. La distance entre deux villes $A$ et $B$ est alors le nombre minimal de lignes à prendre pour aller de $A$ à $B$.\nTrouver l'ensemble des entiers $n$ pour lesquels il possible de construire un réseau ferré respectant le critère suivant:\nPour toute ville C et pour tout $i \\in\\{1,2, \\ldots, 2018\\}$, il y a exactement $n$ villes à distance $i$ de $C$.", "solution": "Dans toute la suite, on va bien sûr réinterpréter l'énoncé en termes de graphes, et on va montrer que les entiers n recherchés sont les entiers pairs.\nSupposons d'abord que l'on dispose d'un entier $n$ et d'un graphe respectant le critère de l'énoncé. Alors tout sommet est de degré $n$. La somme des degrés des sommets du graphe vaut donc $(2018 n+1) n$. Or, cette somme est toujours paire. On en déduit que\n\n$$\nn \\equiv(2018 n+1) n \\equiv 0 \\quad(\\bmod 2)\n$$\n\nc'est-à-dire que $n$ est pair.\nRéciproquement, si $n$ est pair, on forme d'abord un cycle de $2018 n+1$ sommets. Puis on rajoute des arêtes auxiliaires entre deux sommets $u$ et $v$ dès lors que la distance entre $u$ et $v$ (dans notre cycle sans arêtes auxiliaires) est comprise entre 2 et $n / 2$. Il est alors aisé de vérifier que ce graphe (avec arêtes auxiliaires) respecte le critère de l'énoncé.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2018", "problem_label": "2", "tier": 1, "problem": "On dispose, dans le plan, 16 points deux à deux distincts, que l'on note $A_{i, j}$ pour $i, j \\in\\{1,2,3,4\\}$. Ces points vérifient les relations d'alignement et de cocyclicité suivantes :\n$\\triangleright$ pour tout $i \\in\\{1,2,3,4\\}$, les points $A_{i, 1}, A_{i, 2}, A_{i, 3}$ et $A_{i, 4}$ sont alignés;\n$\\triangleright$ pour tout $j \\in\\{1,2,3,4\\}$, les points $A_{1, j}, A_{2, j}, A_{3, j}$ et $A_{4, j}$ sont alignés;\n$\\triangleright$ les quadrilatères $A_{1,1} A_{1,2} A_{2,2} A_{2,1}, A_{2,1} A_{2,2} A_{3,2} A_{3,1}, A_{3,1} A_{3,2} A_{4,2} A_{4,1}, A_{1,2} A_{1,3} A_{2,3} A_{2,2}$, $A_{1,3} A_{1,4} A_{2,4} A_{2,3}, A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ sont cycliques.\nMontrer que le quadrilatère $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ est lui aussi cyclique.\nNote: on dit qu'un quadrilatère est cyclique si ses quatre sommets sont sur un même cercle.", "solution": "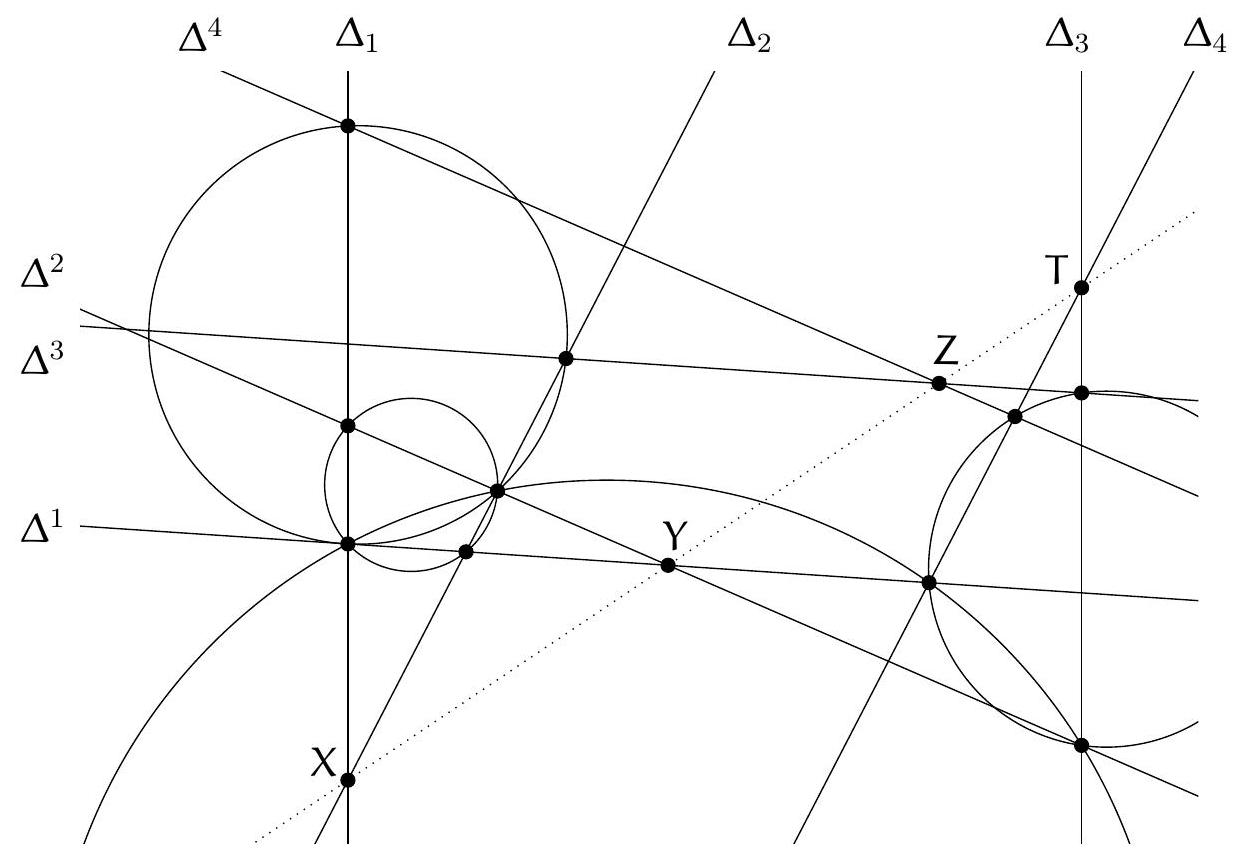\n\nCi-dessous, on notera $\\Delta_{i}$ la droite $\\left(A_{i, 1} A_{i, 2}\\right)$ et $\\Delta^{j}$ la droite $\\left(A_{1, j} A_{2, j}\\right)$. Une figure et une chasse aux angles nous montrent que les droites $\\Delta_{1}$ et $\\Delta_{3}$ sont parallèles, puisque ( $\\Delta_{1}, \\Delta^{1}$ ) $\\equiv$ $\\left(\\Delta^{2}, \\Delta_{2}\\right) \\equiv\\left(\\Delta_{3}, \\Delta^{1}\\right)\\left(\\bmod 180^{\\circ}\\right)$. De même, on sait que $\\Delta_{2} / / \\Delta_{4}$, que $\\Delta^{1} / / \\Delta^{3}$ et que $\\Delta^{2} / / \\Delta^{4}$.\nCe faisant, et sous réserve que le quadrilatère $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ formé par les droites $\\Delta_{1}, \\Delta^{1}$, $\\Delta_{2}$ et $\\Delta^{2}$ soit cyclique, il suffit de définir le point $A_{i, j}$ comme le point d'intersection de $\\Delta_{i}$ et $\\Delta^{j}$ pour être assuré de nos relations d'alginement, et pour être certain que nos cinq premiers quadrilatères sont cycliques. En particulier, toujours par chasse aux angles, chaque quadrilatère $A_{i, j} A_{i+1, j} A_{i+1, j+1} A_{i, j+1}$ est alors cyclique.\nDans toute la suite, on supposera ces relations d'alignement et de cocyclicité acquises, et on s'intéresse maintenant au quadrilatère $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$. Vu le rôle symétrique qu'il semble jouer avec les quadrilatères $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ d'une part et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ d'autre part, il serait bon de trouver un critère simple qui soit équivalent avec son caractère cyclique.\nOr, il ne met en jeu que les droites $\\Delta_{1}$ et $\\Delta_{2}$ d'une part, et les quatre droites $\\Delta^{j}$ d'autre part, les paires $\\left(\\Delta^{1}, \\Delta^{2}\\right)$ et $\\left(\\Delta^{3}, \\Delta^{4}\\right)$ jouant des rôles symétriques. On en vient alors à considérer les points d'intersection $X=\\Delta_{1} \\cap \\Delta_{2}, Y=\\Delta^{1} \\cap \\Delta^{2}$ et $Z=\\Delta^{3} \\cap \\Delta^{4}$, dont la figure semble montrer qu'ils sont alignés. Cela suggère le lemme suivant.\nLemme: Le quadrilatère $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ est cyclique si et seulement si $X$, $Y$ et $Z$ sont alignés. Démonstration : Supposons d'abord $\\mathrm{X}, \\mathrm{Y}$ et Z alignés. Le théorème de Thalès indique alors que les quadrilatères $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ et $A_{1,3} A_{2,3} A_{2,4} A_{3,4}$ sont homothétiques l'un de l'autre, doncque $\\left(A_{2,1} A_{1,2}\\right) / /\\left(A_{2,3} A_{1,4}\\right)$. On en déduit que ( $\\left.A_{1,1} A_{1,4}, A_{1,1} A_{2,2}\\right) \\equiv\\left(A_{1,1} A_{1,2}, A_{1,1} A_{2,2}\\right) \\equiv$ $\\left(A_{2,1} A_{1,2}, A_{2,1} A_{2,2}\\right) \\equiv\\left(A_{2,3} A_{1,4}, A_{2,3} A_{2,2}\\right)\\left(\\bmod 180^{\\circ}\\right)$, ce qui signifie que $A_{1,1} A_{1,4} A_{2,3} A_{2,2}$ est bien cyclique.\nRéciproquement, une fois fixées les droites $\\Delta_{1}, \\Delta_{2}, \\Delta^{1}, \\Delta^{2}$ et $\\Delta^{3}$, le point $A_{4,1}$ puis la droite $\\Delta^{4}$ sont définis de manière unique, donc $Z$ se retrouve nécessairement aligné avec $X$ et $Y$.\nOn en profite aussi pour poser $T=\\Delta_{3} \\cap \\Delta_{4}$. Ici, puisque $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ sont cycliques, le lemme montre l'alignement des points $X, Y$ et $Z$, et $X, Y$ et $T$ d'autre part. Ainsi, les points $T, Y$ et $Z$ sont alignés, et le lemme montre cette fois-ci que le quadrilatère $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ est cyclique.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2018", "problem_label": "3", "tier": 1, "problem": "On dit qu'un entier $k$ est olympique s'il existe quatre entiers $a, b, c$ et $d$, tous premiers avec $k$, tels que $k$ divise $a^{4}+b^{4}+c^{4}+d^{4}$. Soit $n$ un entier quelconque.\nMontrer que $n^{2}-2$ est olympique.", "solution": "Soit $p_{1}^{\\alpha_{1}} \\cdots p_{\\ell}^{\\alpha_{\\ell}}$ la décomposition de $n^{2}-2$ en produits de facteurs premiers. Grâce au théorème Chinois, il nous suffit en fait de montrer que chacun des entiers $p_{i}^{\\alpha_{i}}$ est olympique.\nSupposons tout d'abord que $p_{i}=2$. Puisque $n^{2}-2 \\equiv\\{2,3\\}(\\bmod 4)$, on sait que $\\alpha_{i} \\leqslant 1$. Or, il est clair que 2 est olympique, puisque $1+1+1+1 \\equiv 0(\\bmod 2)$.\nOn considère maintenant un diviseur premier $p$ impair de $n^{2}-2$. Puisque 2 n'est pas carré modulo 3 ou 5 , on sait en fait que $p \\geqslant 7$. Par ailleurs, si $p^{\\alpha}$ est olympique, alors $p$ l'est clairement lui aussi. Réciproquement, si $p$ est olympique (et impair), le lemme de Hensel montre que les puissances $4{ }^{\\text {èmes }}$ modulo $p^{k}$ sont exactement les entiers dont les résidus (modulo $p$ ) sont des puissances $4^{\\text {èmes }}$ modulo $p$, et il s'ensuit que $p^{\\alpha}$ est également olympique.\nOn se ramène donc à montrer que tout nombre premier $p \\geqslant 7$ tel que 2 soit un carré modulo $p$ est olympique. On va procéder par disjonction de cas, selon la valeur de $p$ modulo 4 ou 8 . Cependant, on rappelle d'abord le petit théorème de Fermat, qui stipule que l'ordre $\\omega_{p}(x)$ d'un élément inversible modulo $p$ doit diviser $p-1$. On rappelle également que $\\mathbb{Z} / p \\mathbb{Z}$\ncontient un élément d'ordre $p-1$, comme l'indique le Théorème 17 du cours d'Arithmétique de la POFM sur les propriétés de $\\mathbb{Z} / \\mathrm{n} \\mathbb{Z}$. On en déduit le lemme suivant.\nLemme : Les puissances $k^{\\text {èmes }}$ sont les éléments $x$ dont l'ordre $\\omega_{p}(x)$ divise $(p-1) / \\delta$, où $\\delta=\\operatorname{PGCD}(k, p-1)$.\nDémonstration : Soit $z$ un élément d'ordre $p-1$. Les puissances $k^{\\text {èmes }}$ sont les éléments de la forme $z^{a k+b(p-1)}$, avec a et b entiers, c'est-à-dire les éléments de la forme $z^{\\mathrm{c} \\mathrm{\\delta}}$ avec c entier. L'ordre de ces éléments modulo $p$ divise clairement $(p-1) / \\delta$.\nRéciproquement, $\\omega_{p}(x)$ divise $(p-1) / \\delta$ si et seulement si $x$ est une des racines du polynôme $P(X)=1-X^{(\\mathfrak{p}-1) / \\delta}$. Or, les éléments de la forme $z^{\\mathfrak{c} \\delta}$ constituent déjà $(p-1) / \\delta$ racines de $P(X)$. Par conséquent, les puissances ${ }^{k e \\text { èmes }}$ sont exactement les racines de $P(X)$, ce qui conclut la preuve du lemme.\nOn procède enfin à la disjonction de cas annoncée ci-dessus.\n\n1. Si $p \\equiv 1(\\bmod 8)$, et puisque -1 est d'ordre 2 , c'est une puissance $4^{\\text {ème }}$. Comme $0 \\equiv$ $1+1+(-1)+(-1)(\\bmod p)$, l'entier $p$ est olympique.\n2. Si $p \\equiv 5(\\bmod 8)$, alors -1 est un carré. Soit $i$ et $-i$ ses racines carrées. Elles sont d'ordre 4 , donc ce ne sont pas des carrés. Or, $(1+i)^{2} \\equiv 2 i(\\bmod p)$. Puisque l'ensemble des carrés est clos par produit et par inverse (donc par division), 2 n'est donc pas un carré, ce qui signifiait en fait que $p$ ne divisait pas $n^{2}-2$. Ce cas s'avère donc impossible.\n3. Si $p \\equiv 3(\\bmod 4)$, alors être une puissance $4{ }^{\\text {ème }}$ revient en fait à être un carré. Il suffit donc de montrer que 0 est somme de quatre carrés non nuls modulo $p$.\nOn va d'abord montrer que c'est une somme de $\\ell$ carrés non nuls, avec $2 \\leqslant \\ell \\leqslant 4$. En effet, soit Q l'ensemble des carrés. Notons que $|Q|=(p+1) / 2$, puisque tout carré non nul a exactement deux racines carrés modulo $p$. Ainsi, pour tout $k \\in \\mathbb{Z} / p \\mathbb{Z}$, et par principe des tiroirs, $l^{\\prime}$ ensemble $(k-Q) \\cap Q$ est non vide, ce qui signifie que $k$ est somme de deux carrés. Si $k \\neq 0$, l'un de ces carrés est même non nul. Mais alors, en écrivant $0 \\equiv k+(-k)(\\bmod p)$, on peut bien écrire 0 comme une somme de quatre carrés dont au moins deux sont non nuls.\nPuis, en vertu de l'identité $k^{2} \\equiv(3 k / 5)^{2}+(4 k / 5)^{2}(\\bmod p)$, tout carré non nul est en fait somme de deux carrés non nuls. Par conséquent, 0 est bien somme de quatre carrés non nuls, ce qui signifie que $p$ est olympique.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2019-2020-Corrigé-Web-05-2020.jsonl
ADDED
|
@@ -0,0 +1,12 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Soit $x$ et $y$ deux nombres réels. On pose\n\n$$\nM=\\max \\{x y+1, x y-x-y+3,-2 x y+x+y+2\\} .\n$$\n\nDémontrer que $M \\geqslant 2$, et déterminer les cas d'égalité.", "solution": "Parmi les trois nombres $x y+1, x y-x-y+3$ et $-2 x y+x+y+2$, on note $K$ le plus petit, $L$ le deuxième plus petit et $M$ le plus grand. Alors $K \\leqslant L \\leqslant M$ donc\n\n$$\n3 M \\geqslant K+L+M=(x y+1)+(x y-x-y+3)+(-2 x y+x+y+2)=6,\n$$\n\nce qui signifie que $M \\geqslant 2$.\nEn outre, si $M=2$, les inégalités $K \\leqslant L \\leqslant M$ sont en fait des égalités, ce qui signifie que\n\n$$\nx y+1=x y-x-y+3=-2 x y+x+y+2=2\n$$\n\nEn notant $p$ le produit $x y$ et $s$ la somme $x+y$, les égalités de l'équation (1) sont vérifiées si et seulement si $p=1$ et $s=2$.\nOr, l'inégalité arithmético-géométrique indique, de manière générale, que\n\n$$\n\\frac{s^{2}}{4}=\\left(\\frac{x+y}{2}\\right)^{2} \\geqslant x y=p\n$$\n\navec égalité si et seulement si $x=y$. Ce résultat se retrouve bien si l'on remarque que\n\n$$\n\\left(\\frac{x+y}{2}\\right)^{2}=\\left(\\frac{x-y}{2}\\right)^{2}+x y\n$$\n\nIci, puisque l'on souhaite avoir $s^{2} / 4=1=p$, il nous faut donc également avoir $x=y$, de sorte que $x=y=1$.\nEnfin, réciproquement, on vérifie aisément, si $x=y=1$, que\n\n$$\nx y+1=x y-x-y+3=-2 x y+x+y+2=2\n$$\n\nde sorte que $M=2$ également.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Soit $x$ et $y$ deux nombres réels. On pose\n\n$$\nM=\\max \\{x y+1, x y-x-y+3,-2 x y+x+y+2\\} .\n$$\n\nDémontrer que $M \\geqslant 2$, et déterminer les cas d'égalité.", "solution": "$n^{\\circ} 1$ Voici une autre manière de démontrer que les égalités de l'équation (1) sont vérifiées si et seulement si $x=y=1$. Tout d'abord, si $x=y=1$, ces égalités sont clairement vérifiées.\nRéciproquement, si elles sont vérifiées, alors on peut réécrire l'égalité $x y-x-y+3=2$ comme $0=x y-x-y+1=(x-1)(y-1)$. Puisque $x$ et $y$ jouent des rôles symétriques, on peut supposer, sans perte de généralité, que $x=1$. Pour que l'égalité $x y+1=2$ soit vérifiée, il est alors nécessaire que $y=1$, ce qui conclut ici.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 3 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Soit $x$ et $y$ deux nombres réels. On pose\n\n$$\nM=\\max \\{x y+1, x y-x-y+3,-2 x y+x+y+2\\} .\n$$\n\nDémontrer que $M \\geqslant 2$, et déterminer les cas d'égalité.", "solution": "$n^{\\circ} 2$ Avoir pensé à introduire les variables $p$ et $s$, comme dans la première solution, ou bien à utiliser directement l'égalité $x y-x-y+3=2$ pour obtenir une factorisation, comme dans la deuxième solution, pourrait passer pour miraculeux. Il n'en est bien sûr rien, et ces approchent découlent en fait de ce que l'on appelle les relations de Viète.\nCes relations consistent à dire que $x$ et $y$ sont les deux racines, éventuellement confondues, du polynôme\n\n$$\nP(X)=(X-x)(X-y)=X^{2}-(x+y) X+x y=X^{2}-s X+p .\n$$\n\nPuisque les égalités de l'équation (1) sont symétriques en $x$ et en $y$, un résultat général (valable même si on avait eu trois inconnues $x, y$ et $z$, ou même un nombre quelconque d'inconnues) permet en fait de démontrer qu'elles peuvent s'exprimer directement à partir des valeurs que prend le polynôme $P$.\nPar exemple, les égalités $p+1=2, p-s+3=2$ et $-2 p+s+2=2$ peuvent se réécrire comme $P(0)=1, P(1)=0$ et $P(1 / 2)=1 / 4$. Ici, l'égalité $P(1)=0$ signifie précisément que $(x-1)(y-1)=0$, ce qui est la factorisation utilisée dans notre deuxième solution.\nOn pourrait également procéder de manière plus systématique. En effet, puisque $P(1)=0$, on sait que le polynôme $P(X)$ est divisible par $X-1$. On peut donc l'écrire sous la forme $P(X)=(X-1)(X-a)$, puis vérifier que $P(0)=a$, et donc que $P(X)=(X-1)^{2}$.\nSi l'on avait été moins chanceux, et que l'on n'avait pas identifié de racine de notre polynôme $P$, il aurait toujours été possible d'écrire $P$ comme un polynôme d'interpolation de Lagrange. Ici, cette méthode nous permet d'écrire que\n\n$$\n\\begin{aligned}\nP(X) & =\\frac{X-1}{0-1} \\frac{X-1 / 2}{0-1 / 2} P(0)+\\frac{X-1}{1 / 2-1} \\frac{X-0}{1 / 2-0} P(1 / 2)+\\frac{X-1 / 2}{1-1 / 2} \\frac{X-0}{1-0} P(1) \\\\\n& =2(X-1)(X-1 / 2)-X(X-1)=X^{2}-2 X+1=(X-1)^{2}\n\\end{aligned}\n$$\n\nd'où le fait que les deux racines de $P$ soient $x=y=1$.\nCommentaire des correcteurs L'exercice a été plutôt bien résolu. Peu d'élèves ont vu que la première inégalité était une conséquence simple du fait que le maximum est plus grand que la moyenne arithmétique.\nAttention au maniement des inégalités : certains élèves ont écrit que $x y<1$ et $x+y \\geqslant x y$ pour en conclure que $x+y \\geqslant 1$, ce qui n'est pas vrai. D'autres élèves ont démontré l'inégalité demandée mais oublié de regarder les cas d'égalité alors que c'était une partie importante de l'exercice : contrairement à des cas d'égalité dans des inégalités classiques, celui-là était plus dur à trouver, et affirmer sans preuve que $x=y=1$ ne suffisait pas.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Dans le train, alors qu'elles rentrent de EGMOnd an Zee, Clara et Edwige jouent au jeu suivant. Initialement, l'entier $n=1 \\times 2 \\times \\cdots \\times 20$ est écrit sur une feuille de papier. Puis, chacune à son tour, et en commençant par Clara, les joueuses remplacent l'entier $n$ par un des nombres $k n / 10$, où $k$ est un entier compris entre 1 et 9 inclus. La première joueuse à écrire un nombre qui n'est pas entier perd, et son adversaire gagne.\nClara et Edwige sont deux joueuses redoutables, et jouent donc de manière optimale. Laquelle des deux va-t-elle gagner?", "solution": "Intéressons-nous au nombre $n$ écrit sur la feuille de papier au moment où la joueuse X s'apprête à jouer, et avant que la partie ne se termine. On factorise partiellement $n$ comme produit de nombres premiers : $n=2^{x} \\times 5^{y} \\times m$, où $x$ et $y$ sont des entiers naturels et $m$ est un entier naturel non nul premier avec 2 et 5 .\nOn va alors démontrer la propriété $\\mathcal{P}_{n}$ par récurrence sur $n$ : la joueuse X perdra si $x$ et $y$ sont tous deux pairs, et gagnera dans le cas contraire. Tout d'abord, $\\mathcal{P}_{1}$ est évidente, puisque X devra remplacer le nombre $n=1$ par un nombre compris entre $1 / 10$ et $9 / 10$.\nSoit alors $n \\geqslant 1$ un entier quelconque. On suppose $\\mathcal{P}_{1}, \\ldots, \\mathcal{P}_{n}$, et on va démontrer $\\mathcal{P}_{n+1}$.\n$\\triangleright$ Si $x$ et/ou $y$ est impair, on note $r$ et $s$ les restes de $x$ et $y$ modulo 2. Alors la joueuse X remplace l'entier $n$ par l'entier $n^{\\prime}=n /\\left(2^{r} \\times 5^{s}\\right)$. Puisque $n^{\\prime}=2^{x-r} \\times 5^{y-s} \\times m$, la propriété $\\mathcal{P}_{n^{\\prime}}$ assure alors que l'adversaire de X perdra.\n$\\triangleright$ Si $x$ et $y$ sont pairs, on suppose tout de même que X remplace $n$ par un entier $n^{\\prime}$ (ce qui n'est possible que si $x \\geqslant 1$ ou $y \\geqslant 1$ ). Si X remplace $n$ par le nombre $n^{\\prime}=n / 2=$ $2^{x-1} \\times 5^{y} \\times m$, alors $\\mathcal{P}_{n^{\\prime}}$ assure que l'aversaire de $X$ gagnera. Sinon, on peut écrire $n^{\\prime}$ sous la forme $n^{\\prime}=2^{x^{\\prime}} \\times 5^{y-1} \\times m^{\\prime}$ (avec $m^{\\prime}$ premier avec et 2 et 5 ): quelles que soient les valeurs de $x^{\\prime}$ et de $m^{\\prime}$, la propriété $\\mathcal{P}_{n^{\\prime}}$ assure quand même que l'adversaire de X perdra.\nOn dispose donc de la propriété $\\mathcal{P}_{20!}$, où l'on a posé $20!=1 \\times 2 \\times \\cdots \\times 20$. En particulier, on constate aisément que $20!=2^{18} \\times 5^{4} \\times m$, où l'on a posé $m=3^{8} \\times 7^{2} \\times 11 \\times 13 \\times 17 \\times 19$. Puisque Clara qui joue la première, $c^{\\prime}$ est donc Edwige qui gagnera.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 5 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Dans le train, alors qu'elles rentrent de EGMOnd an Zee, Clara et Edwige jouent au jeu suivant. Initialement, l'entier $n=1 \\times 2 \\times \\cdots \\times 20$ est écrit sur une feuille de papier. Puis, chacune à son tour, et en commençant par Clara, les joueuses remplacent l'entier $n$ par un des nombres $k n / 10$, où $k$ est un entier compris entre 1 et 9 inclus. La première joueuse à écrire un nombre qui n'est pas entier perd, et son adversaire gagne.\nClara et Edwige sont deux joueuses redoutables, et jouent donc de manière optimale. Laquelle des deux va-t-elle gagner?", "solution": "$n^{\\circ} 1$ Nous allons de nouveau fournir une stratégie gagnante pour Edwige, qui diffère légèrement de la stratégie précédente. Cette stratégie est toute simple (même si montrer qu'elle convient l'est moins) : si Clara vient de transformer son nombre $n$ en un nouveau nombre $n^{\\prime}=k n / 10$, alors Edwige transforme de nouveau $n^{\\prime}$ en $n^{\\prime \\prime}=k n^{\\prime} / 10$.\nPour montrer que cette stratégie permettra à Edwige de gagner, et puisque la partie durera au plus $20!=1 \\times 2 \\times \\cdots \\times 20$ coups, il suffit de démontrer que $n^{\\prime \\prime}$ sera nécessairement un entier. Ainsi, Edwige ne pourra pas perdre, et elle gagnera donc.\nTout d'abord, on constate que l'entier 20! est égal à $u^{2} \\times v$, où l'on a posé $u=2^{9} \\times 2^{4} \\times 5^{2} \\times 7$ et $v=11 \\times 13 \\times 17 \\times 19$. On va maintenant démontrer que, si Edwige applique la stratégie ci-dessus, alors chacun des entiers $n$ qu'elle laissera à Clara sera de la forme $n=\\hat{u}^{2} v$, avec $\\hat{u}$ entier et $v=11 \\times 13 \\times 17 \\times 19$.\nC'est déjà le cas au début du jeu. Puis, si Clara transforme un entier $n=\\hat{u}^{2} v$ en un autre entier $n^{\\prime}=k n / 10$, Edwige transformera $n^{\\prime}$ en le nombre $n^{\\prime \\prime}=k n^{\\prime} / 10=(k \\hat{u} / 10)^{2} v$. Il s'agit donc de démontrer que $k \\hat{u} / 10$ est un entier, c'est-à-dire que 2 et 5 divisent tous deux $k \\hat{u}$.\nPuisque $n^{\\prime}$ est un entier, et comme $10 n^{\\prime}=k n=k \\hat{u}^{2} v$, on sait que 2 et 5 divisent tous deux $k \\hat{u}^{2} v$. Or, 2 ne divise pas $v$, et divise donc $k$ ou $\\hat{u}$ : il divise donc aussi $k \\hat{u}$. De même, 5 ne divise pas $v$, et divise donc $k$ ou $\\hat{u}$ : il divise donc aussi $k \\hat{u}$. Cela conclut notre démonstration.\n\nCommentaire des correcteurs Beaucoup d'élèves ont eu des bonnes idées sur le problème, mais peu ont réussi à obtenir une vraie preuve du fait qu'Edwige a une stratégie gagnante. En effet, un certain nombre d'élèves donne dès le départ une «stratégie optimale »à Clara : pour démontrer qu'Edwige gagne, il faut donner une stratégie à Edwige et vérifier quen peu importe ce que Clara faitn Edwige gagnera. En particulier, Clara n'a aucune raison de suivre une stratégie qui semble être la meilleure à vue d'œil (et qui, assez souvent, ne l'est pas).\nCertains élèves ont rapidement considéré que seuls les seules valeurs de $k$ importantes étaient $k=1, k=2$ et $k=5$, en tant que diviseurs de 10 . Cependant, $k=4$ et $k=8$ étaient tout aussi importants, permettant d'obtenir des valuations 2-adiques inaccessibles autrement.\nPar ailleurs, plusieurs élèves ont bien compris que Edwige avait intérêt à laisser Clara à chaque étape avec un entier de la forme $2^{x} 5^{y} m$, avec $m$ entier premier avec 10 et $x$ et $y$ pairs, mais n'ont pas prouvé que Edwige pouvait bien laisser Clara à chaque fois dans un tel état; et surtout qu'Edwige pouvait jouer le coup en question!\nEnfin, il aurait été bien de prouver que la partie termine dans tous les cas, ce sans quoi Edwige ne gagne bien sûr pas.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 6 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Déterminer tous les entiers naturels $x, y$ et $z$ tels que\n\n$$\n45^{x}-6^{y}=2019^{z}\n$$", "solution": "On commence par décomposer chaque terme en produit de facteurs premiers. L'équation devient alors\n\n$$\n3^{2 x} \\cdot 5^{x}-3^{y} \\cdot 2^{y}=3^{z} \\cdot 673^{z}\n$$\n\nNous allons maintenant traiter différents cas :\n$\\triangleright$ Si $y>2 x$, alors $3^{z} \\cdot 673^{z}=3^{2 x}\\left(5^{x}-3^{y-2 x} \\times 2^{y}\\right)$. Le théorème de Gauss indique alors que $3^{z}$ divise $3^{2 x}$ (car $5^{x}-3^{y-2 x} \\times 2^{y}$ n'est pas divisible par 3, doncest premier avec $3^{z}$ ) et que $3^{2 x}$ divise $3^{z}$ (car $673^{z}$ n'est pas divisible par 3 , donc est premier avec $3^{2 x}$. On en déduit que $z=2 x$, et l'équation devient\n\n$$\n673^{2 x}=5^{x}-3^{y-2 x} \\cdot 2^{y}\n$$\n\nMais, puisque $673^{2 x} \\geqslant 5^{x}$, cette équation n'a en fait pas de solution, et ce cas est donc impossible.\n$\\triangleright$ Si $y=2 x$, alors $3^{z} \\cdot 673^{z}=3^{2 x}\\left(5^{x}-2^{y}\\right)$. Comme précédemment, le théorème de Gauss indique que $3^{2 x}$ divise $3^{z}$. On en déduit que $2 x \\leqslant z$, et l'équation devient\n\n$$\n3^{z-2 x} \\cdot 673^{z}=5^{x}-2^{y}\n$$\n\nMais, puisque $673^{z} \\geqslant 5^{z} \\geqslant 5^{x}$, cette équation n'a pas de solution elle non plus, et ce cas est donc impossible.\n$\\triangleright$ Si $y<2 x$, alors $3^{z} \\cdot 673^{z}=3^{y}\\left(3^{2 x-y} \\cdot 5^{x}-2^{y}\\right)$. Une fois encore, puisque ni $673^{z} \\mathrm{ni}$ $3^{2 x-y} \\cdot 5^{x}-2^{y}$ ne sont divisibles par 3 , le théorème de Gauss indique que $3^{z}$ et $3^{y}$ se divisent mutuellement. On en déduit que $z=y$, et l'équation devient\n\n$$\n673^{y}=3^{2 x-y} \\cdot 5^{x}-2^{y}\n$$\n\nOn distingue alors plusieurs sous-cas :\n$\\triangleright$ Si $y=0$, l'équation devient $2=3^{2 x} \\cdot 5^{x}$, et n'a bien sûr aucune solution.\n$\\triangleright$ Si $y=1$, l'équation devient $675=3^{2 x-1} \\cdot 5^{x}$. Puisque $675=3^{3} \\times 5^{2}$, on en déduit l'existence de la solution $(x, y, z)=(2,1,1)$.\n$\\triangleright$ Si $y \\geqslant 2$, considérons notre équation modulo 4 : elle devient $1 \\equiv 3^{y}(\\bmod 4)$, ce qui signifie que $y$ est pair.\nPuis, comme on a nécessairement $x \\geqslant 1$, et si on considère l'équation modulo 5 , celle-ci devient $(-2)^{y} \\equiv-2^{y}(\\bmod 5)$, ce qui signifie que $y$ est impair. L'équation n'admet donc aucune solution dans ce sous-cas.\nL'unique solution de l'équation est donc le triplet $(2,1,1)$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 7 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Déterminer tous les entiers naturels $x, y$ et $z$ tels que\n\n$$\n45^{x}-6^{y}=2019^{z}\n$$", "solution": "$n^{\\circ} 1$ On peut traiter directement les cas $y>2 x$ et $y=2 x$ en une seule fois, en reprentant les arguments mentionn��s ci-dessus dans un ordre légèrement différent. Tout d'abord, puisque $2019^{z}<45^{x} \\leqslant 2019^{x}$, on en déduit que $z<x$. En outre, si l'un des trois entiers $2 x, y$ et $z$ (on l'appellera $t$ ) est strictement plus petit que les deux autres, alors l'entier $3^{2 x} \\cdot 5^{x}-3^{y} \\cdot 2^{y}-3^{z} \\cdot 673^{z}$ n'est pas divisible par $3^{t+1}$, ce qui est impossible puisqu'il est censé être nul. Puisque l'on sait déjà que $z<x \\leqslant 2 x$, on en déduit que $y=z$, et donc que $y=z<x$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution alternative"}
|
| 8 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Déterminer tous les entiers naturels $x, y$ et $z$ tels que\n\n$$\n45^{x}-6^{y}=2019^{z}\n$$", "solution": "$n^{\\circ} 2$ On travaille directement à partir de l'équation\n\n$$\n45^{x}-6^{y}=2019^{z}\n$$\n\nTout d'abord, puisque $45^{x}>2019^{z}$, on sait que $x \\geqslant 1$. Considérée modulo 5 , l'équation se réécrit\n\n$$\n-1 \\equiv-1^{y} \\equiv(-1)^{z} \\quad(\\bmod 5)\n$$\n\nCela signifie que $z$ est un entier impair.\nPuis, en considérant l'équation modulo 4, et puisque $z$ est impair, celle-ci se réécrit\n\n$$\n1-2^{y} \\equiv 45^{x}-6^{y} \\equiv 2019^{z} \\equiv(-1)^{z} \\equiv-1 \\quad(\\bmod 4)\n$$\n\nCela signifie que $y=1$.\nEnfin, puisque $x \\geqslant 1$, en considérant l'équation modulo 9 , celle-ci se réécrit\n\n$$\n3 \\equiv 45^{x}-6^{y} \\equiv 3^{z} \\quad(\\bmod 9)\n$$\n\nCela signifie que $z=1$.\nL'équation devient alors $45^{x}=6^{y}+2019^{z}=2025=45^{2}$, et le triplet $(x, y, z)=(2,1,1)$ apparaît alors manifestement comme une solution de l'équation de l'énoncé.\nEn conclusion, l'unique solution recherchée est le triplet $(2,1,1)$.\nCommentaire des correcteurs L'exercice a été bien résolu. En particulier, de nombreux élèves ont commencé par écrire les petites puissances de 45, 6 et 2019, ce qui leur a permis de voir des relations remarquables modulo 10 , puis de prendre conscience que regarder l'équation modulo de petits nombres pouvait être utile. D'autres ont reconnu, à juste titre, que 45, 6 et 2019 étaient des multiples de 3, ce qui les a poussés à utiliser la notion de valuation 3-adique. Dans les deux cas, il s'agit d'excellents réflexes, qui n'ont pas manqué de porter leurs fruits. On peut néanmoins regretter que plusieurs élèves aient implicitement supposé $x, y$ et $z$ non nuls, alors que rien ne venait le garantir a priori : il faut faire attention de bien lire l'énoncé pour éviter de perdre ainsi, par naïveté, des points pas faciles à obtenir par ailleurs!", "problem_match": "\nExercice 3.", "solution_match": "\nSolution alternative"}
|
| 9 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\Gamma$ un cercle passant par $A$. On suppose que $\\Gamma$ recoupe les segments $[A B]$ et $[A C]$ en deux points, que l'on appelle respectivement $D$ et $E$, et qu'il coupe le segment $[B C]$ en deux points, que l'on appelle $F$ et $G$, de sorte que $F$ se trouve entre $B$ et $G$. Soit $T$ le point d'intersection entre la tangente en $F$ au cercle circonscrit à $B D F$ et la tangente en $G$ au cercle circonscrit à $C E G$.\nDémontrer que, si les points $A$ et $T$ sont distincts, alors $(A T)$ et $(B C)$ sont parallèles.", "solution": "Commençons par tracer une figure.\n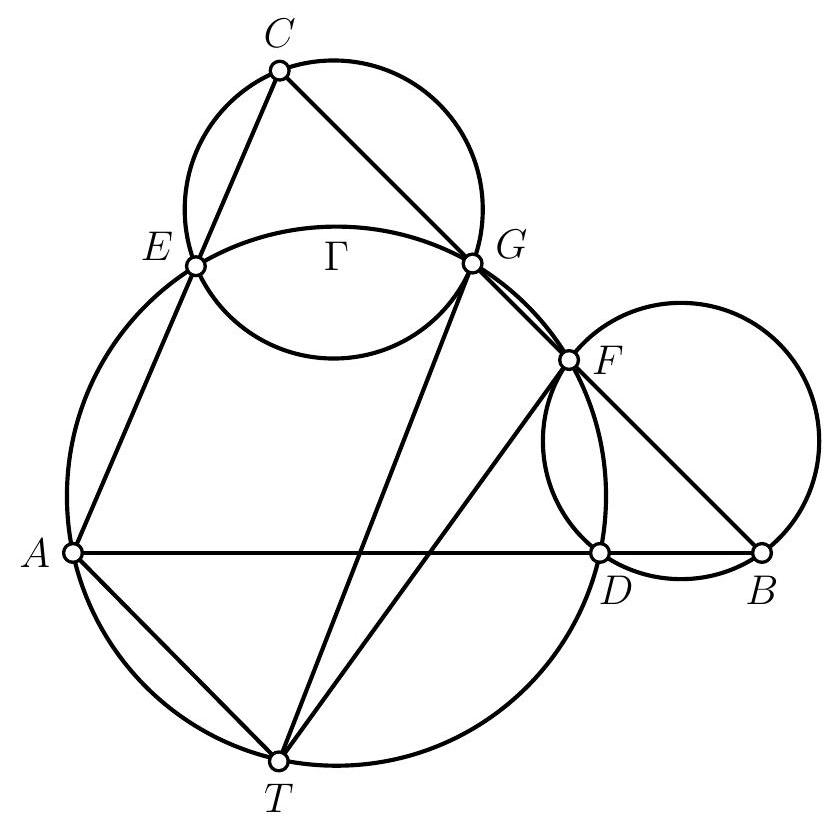\n\nUne première remarque frappante est que $T$ semble être situé sur le cercle $\\Gamma$. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites, en utilisant les relations de cocyclicité et le cas limite du théorème de l'angle au centre :\n\n$$\n\\begin{aligned}\n(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\\\\n& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F)\n\\end{aligned}\n$$\n\nLes points $A, F, G$ et $T$ sont donc cocycliques, et $T$ appartient à bien $\\Gamma$. Mais alors\n\n$$\n\\begin{aligned}\n(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\\\\n& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\\circ},\n\\end{aligned}\n$$\n\nce qui signifie précisément que les droites $(A T)$ et $(B C)$ sont parallèles.\nCommentaire des correcteurs L'exercice a été correctement résolu par 7 élèves. Quelques élèves, même s'ils n'ont pas complètement résolu le problème, ont utilisé leur figure pour conjecturer que le point $T$ appartenait au cercle $\\Gamma$ et ont conclu en admettant ce résultat. Ce procédé a été grandement apprécié car c'est la bonne attitude face à un problème de géometrie.\n\n## Exercices Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 10 |
+
{"year": "2019", "problem_label": "5", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\Gamma$ un cercle passant par $A$. On suppose que $\\Gamma$ recoupe les segments $[A B]$ et $[A C]$ en deux points, que l'on appelle respectivement $D$ et $E$, et qu'il coupe le segment $[B C]$ en deux points, que l'on appelle $F$ et $G$, de sorte que $F$ se trouve entre $B$ et $G$. Soit $T$ le point d'intersection entre la tangente en $F$ au cercle circonscrit à $B D F$ et la tangente en $G$ au cercle circonscrit à $C E G$.\nDémontrer que, si les points $A$ et $T$ sont distincts, alors $(A T)$ et $(B C)$ sont parallèles.", "solution": "Commençons par tracer une figure.\n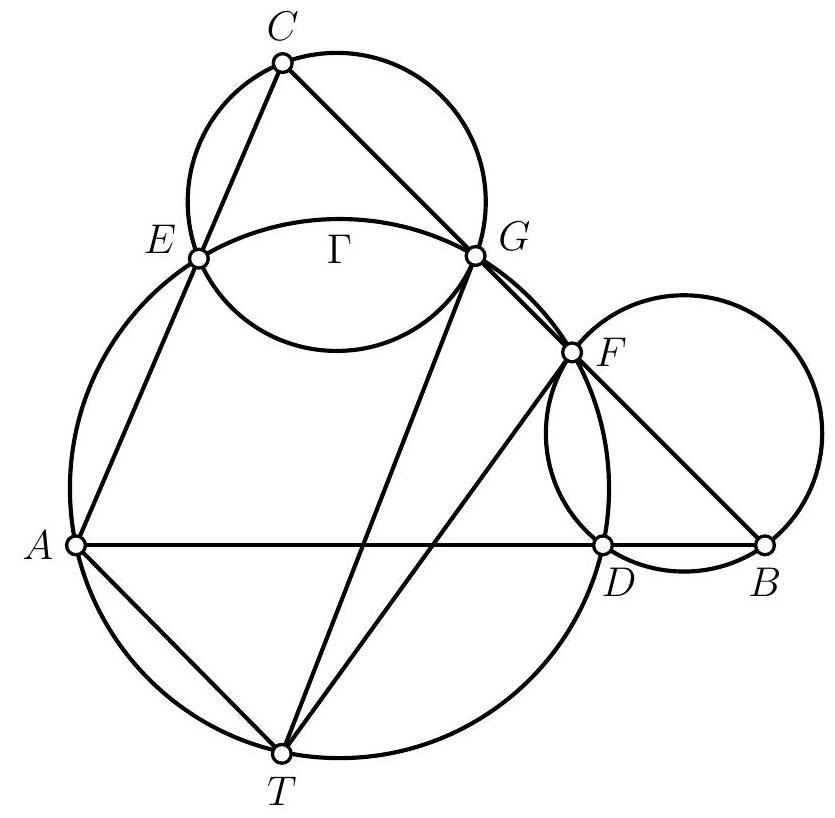\n\nUne première remarque frappante est que $T$ semble être situé sur le cercle $\\Gamma$. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites, en utilisant les relations de cocyclicité et le cas limite du théorème de l'angle au centre :\n\n$$\n\\begin{aligned}\n(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\\\\n& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F) .\n\\end{aligned}\n$$\n\nLes points $A, F, G$ et $T$ sont donc cocycliques, et $T$ appartient à bien $\\Gamma$. Mais alors\n\n$$\n\\begin{aligned}\n(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\\\\n& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\\circ},\n\\end{aligned}\n$$\n\nce qui signifie précisément que les droites $(A T)$ et $(B C)$ sont parallèles.\nCommentaire des correcteurs L'exercice a été très bien réussi! Les élèves les plus efficaces ont noté qu'il suffisait de montrer que le point $T^{\\prime} \\mathrm{d}^{\\prime}$ intersection de la droite parallèle à la droite $(B C)$ passant par le point $A$ avec le cercle $\\Gamma$ appartenait aux deux tangentes. Il est dommage de constater que plusieurs élèves ont rendu une figure très propre mais n'ont pas cherché à effectuer de conjectures à partir de cette figure, alors même que le point $T$ appartient visiblement au cercle $\\Gamma$.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 11 |
+
{"year": "2019", "problem_label": "6", "tier": 1, "problem": "Soit $S$ un ensemble d'entiers relatifs. On dit que $S$ est beau s'il contient tous les entiers de la forme $2^{a}-2^{b}$, où $a$ et $b$ sont des entiers naturels non nuls. On dit également que $S$ est fort si, pour tout polynôme $P(X)$ non constant et à coefficients dans $S$, les racines entières de $P(X)$ appartiennent également à $S$.\nTrouver tous les ensembles qui sont à la fois beaux et forts.", "solution": "L'ensemble $\\mathbb{Z}$ est clairement beau et fort. Nous allons démontrer que c'est le seul. Pour ce faire, considérons un ensemble $S$ beau et fort : nous allons en fait prouver, par récurrence forte sur $n$, que les entiers $n$ et $-n$ appartiennent nécessairement à $S$.\nTout d'abord, puisque $S$ est beau, il contient les entiers $2^{1}-2^{1}=0,2^{2}-2^{1}=2$ et $2^{1}-2^{2}=-2$. Il contient donc aussi les entiers 1 et -1 , qui sont des racines respectives des polynômes $2-2 X$ et $2+2 X$.\nOn considère désormais un entier $n \\geqslant 3$ tel que $-n-1, \\ldots, n-1$ appartiennent tous à $S$. Soit $\\alpha$ la valuation 2 -adique de $n$, et $m$ l'entier impair tel que $n=2^{\\alpha} m$. En notant $\\varphi(m)$ l'indicatrice d'Euler de $m$, on constate alors que l'entier $k=2^{\\alpha+\\varphi(m)+1}-2^{\\alpha+1}$, qui appartient manifestement à $S$, est également un multiple de $2^{\\alpha}$ et de $m$, donc de $n$.\nSoit $\\overline{a_{\\ell} a_{\\ell-1} \\ldots a_{0}}$ l'écriture de $k / n$ en base $n$. Tous les entiers $\\pm a_{0}, \\ldots, \\pm a_{\\ell}$ sont compris entre $1-n$ et $n-1$, donc appartiennent à $S$. Par construction, $n$ est une racine entière du polynôme $P(X)=k-\\sum_{i=0}^{\\ell} a_{i} X^{i+1}$, dont tous les coefficients sont dans $S$, donc $n$ est dans $S$ lui aussi. De même, $-n$ est une racine entière du polynôme $Q(X)=k-\\sum_{i=0}^{\\ell} a_{i}(-X)^{i+1}$, donc $-n \\in S$, ce qui conclut la récurrence et la démonstration.\n\nRemarque: Au vu de l'énoncé, on pouvait se douter qu'utiliser des polynomes de degré $d \\geqslant 2$ pourrait être utile, ce sans quoi les créateurs de l'énoncé auraient directement choisi de définir, tout simplement, les ensembles forts comme les ensembles stables par division. La remarque ci-dessous a pour but principal d'illustrer le fait que, si l'on cherche à simplifier drastiquement une hypothèse d'un énoncé mathématique, ici avec pour objectif de montrer que $\\mathbb{Z}$ serait le seul ensemble beau stable par division, il est très important de chercher des constructions simples qui permettraient d'invalider cette simplification.\nOn va en fait démontrer qu'il existe un ensemble $S$ beau et stable par division, mais différent de $\\mathbb{Z}$ : cela démontre qu'utiliser des polynomes de degré $d \\geqslant 2$ était en fait nécessaire pour résoudre cet exercice. Pour construire cet ensemble, on a besoin du théorème de Zsygmondy ainsi que de la propriété connue suivante : il existe des nombres de Fermat (c'est-à-dire les entiers de la forme $2^{p}-1$ ) qui ne sont pas premiers, même si $p$ est assez grand (ci-dessous, on aura besoin de l'inégalité $p \\geqslant 7$ ). C'est le cas, par exemple, quand $p=11$, car $2^{11}-1=23 \\times 89$. En effet, écrivons $2^{p}-1$ comme le produit $2^{p}-1=q \\times r \\times m$, où $q$ et $r$ sont deux nombres premiers, et $m$ est un entier quelconque. On considère alors l'ensemble $S$ formé de 0 ainsi que des entiers de la forme\n\n$$\n\\pm 2^{a} \\prod_{k \\geqslant 2}\\left(2^{k}-1\\right)^{\\alpha_{k}}\n$$\n\noù les $\\alpha_{k}$ sont des entiers relatifs dont seul un nombre fini est non nul. L'ensemble $S$ est manifestement beau et stable par division.\nSupposons maintenant que $q \\in S$ : on écrit alors $q$ sous la forme\n\n$$\nq=\\prod_{k \\geqslant 2}\\left(2^{k}-1\\right)^{\\alpha_{k}}\n$$\n\net on note $\\ell$ l'indice maximal tel que $\\alpha_{\\ell} \\neq 0$. Puisque l'ordre de 2 modulo $q$ et $r$ divise $p$, il est égal à $p$, de sorte que $\\ell \\geqslant p \\geqslant 7$.\n\nLe théorème de Zsygmondy indique alors qu'il existe un nombre premier $s$ qui divise $2^{\\ell}-1$ et aucun entier $2^{k}-1$ pour $1 \\leqslant k \\leqslant \\ell-1$. On remarque alors que\n\n$$\nv_{s}(q)=\\sum_{k \\geqslant 2} \\alpha_{k} v_{s}\\left(2^{k}-1\\right)=\\alpha_{\\ell} v_{s}\\left(2^{\\ell}-1\\right) \\neq 0 .\n$$\n\nOn en déduit que $s=q$, donc que $\\ell=p$, et que $v_{q}\\left(2^{\\ell}-1\\right)=1$. Cela signifie en particulier que $r \\neq q$. Mais alors, même pour $\\ell=p$, et au lieu de choisir $s=q$, on aurait pu satisfaire le théorème de Zsygmondy en choisissant $s=r$, obtenant ainsi une contradiction. On en conclut donc bien que $q \\notin S$, et donc que $S \\neq \\mathbb{Z}$.\n\nCommentaire des correcteurs Ce problème de théorie des nombres était assez difficile car nécessitait une astuce : la solution la plus simple faisait appel à la décomposition d'un entier en base $b$. Seuls cinq élèves y ont pensé et ils ont tous obtenu la note maximale. Le barème valorisait cette astuce, si bien qu'il était impossible d'avoir une note strictement supérieure à 3 si cet élément de décomposition en base n'était pas évoqué.\nQuasiment tous les élèves se sont rendus compte que le seul ensemble beau et fort serait $\\mathbb{Z}$, sans forcément savoir le prouver.\nBeaucoup d'élèves ont pensé à montrer que tout entier (parfois en ne se restreignant qu'aux entiers impairs ou premiers) possédait un multiple dans $S$, ce qui était essentiel dans la suite. Beaucoup ont également montré que $S$ était symétrique par rapport à 0 (c'est-à-dire que, $n \\in S$, alors $-n \\in S$ ), ce qui permet d'éviter de se préoccuper des entiers négatifs dans la suite.\nRevenons enfin sur quelques erreurs régulièrement rencontrées:\n$\\triangleright$ La gestion des entiers négatifs a parfois été source d'une erreur importante, notamment quand les élèves ont entrepris de démontrer par récurrence que $\\llbracket 1, n \\rrbracket \\subseteq S$ pour tout $n \\geqslant 1$. Certains élèves ont en effet introduit un entier $k \\geqslant 1$ tel que $n k \\in S$, et ils ont affirmé que $n-k$ appartenait par hypothèse de récurrence à $S$ en tant qu'entier strictement inférieur à $n$. Cependant, ces élèves n'ont pas écarté le cas où $k \\geqslant 2 n$, de sorte que l'on pouvait avoir $n-k \\leqslant-n$, remettant ainsi en cause tout leur raisonnement.\n$\\triangleright$ Quelques élèves ont remarqué qu'il suffisait que tous les nombres premiers soient dans $S$ pour conclure. C'est vrai, mais aucune solution connue ne prouve immédiatement ce résultat. En l'occurence, plusieurs élèves pensaient avoir résolu l'exercice en montrant ce résultat. Ils se fondaient sur la croyance (erronnée, comme indiqué dans la remarque ci-dessus) que, si $n$ et $m$ sont deux entiers naturels impairs distincts, alors l'ordre de 2 modulo $n$ est différent de celui de 2 modulo $m$. Cette erreur est équivalente à la méconnaissance du théorème de Zsigmondy consistant à croire que pour $n \\notin\\{1,6\\}$, $2^{n}-1$ a exactement un diviseur premier primitif.\n$\\triangleright$ Enfin, les raisonnements vagues du style « on construit de plus en plus d'entiers en prenant les racines entières de polynômes à coefficients dans un ensemble de plus en plus grand » peuvent aider à se faire une idée, mais ne rapportent évidemment aucun point\nSoulignons le fait que, dans un exercice comme celui-ci, vérifier explicitement que les petites valeurs de $n$ (par exemple $n=0, n=1$ et $n=2$ ) sont dans $S$ rapporte forcément un point, et pourtant quelques élèves n'ont pas eu ce réflexe.\nEnfin, beaucoup d'élèves prouvent que si $a b \\in S$ et $a \\in S$ non nul, alors $b \\in S$. Ce résultat certes correct est en fait trompeur, car il invite à n'utiliser que les polynômes de degré 1 de l'énoncé, qui ne suffisent manifestement pas à conclure, comme indiqué dans la remarque ci-dessus.\n si l'égalité\n\n$$\nf(f(x+y)+y)=f(f(x)+y)\n$$\n\nest vérifiée pour tous les entiers $x$ et $y$. On dit également qu'un entier $v$ est $f$-rare si l'ensemble des entiers $x$ tels que $f(x)=v$ est un ensemble fini et non vide.\na) Démontrer qu'il existe une fonction $f$ russe pour laquelle il existe un entier $f$-rare.\nb) Démontrer que, pour toute fonction $f$ russe, il existe au plus un entier $f$-rare.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 12 |
+
{"year": "2019", "problem_label": "6", "tier": 1, "problem": "Soit $S$ un ensemble d'entiers relatifs. On dit que $S$ est beau s'il contient tous les entiers de la forme $2^{a}-2^{b}$, où $a$ et $b$ sont des entiers naturels non nuls. On dit également que $S$ est fort si, pour tout polynôme $P(X)$ non constant et à coefficients dans $S$, les racines entières de $P(X)$ appartiennent également à $S$.\nTrouver tous les ensembles qui sont à la fois beaux et forts.", "solution": "a) Soit $f$ la fonction définie par $f(0)=0$ et $f(n)=2^{v_{2}(n)+1}$, où $v_{2}(n)$ est la valuation 2 adique de $n$. Tout d'abord, il est clair que 0 est $f$-rare, puisque son seul antécédent par $f$ est 0 lui-même.\nD'autre part, soit $x$ et $y$ deux entiers relatifs : en posant $v_{2}(0)=\\infty$ et $\\infty+1=\\infty$, il apparaît que $v_{2}(f(x))=v_{2}(x)+1$, que $v_{2}(x+y)=\\min \\left\\{v_{2}(x), v_{2}(y)\\right\\}$ si $v_{2}(x) \\neq v_{2}(y)$, et que $v_{2}(x+y) \\geqslant \\min \\left\\{v_{2}(x), v_{2}(y)\\right\\}+1$ sinon.\nEnfin, on a $f(x)=f(y)$ si et seulement si $v_{2}(x)=v_{2}(y)$. Par conséquent, $\\triangleright \\operatorname{si} v_{2}(x) \\geqslant v_{2}(y)$, alors\n\n$$\nv_{2}(f(x+y))=v_{2}(x+y)+1 \\geqslant v_{2}(y)+1\n$$\n\ndonc $v_{2}(f(x+y)+y)=v_{2}(y)=v_{2}(f(x)+y)$ et $f(f(x+y)+y)=f(f(x)+y)$;\n$\\triangleright \\operatorname{si} v_{2}(x)<v_{2}(y)$, alors\n\n$$\nv_{2}(f(x+y))=v_{2}(x+y)+1=v_{2}(x)+1=v_{2}(f(x))\n$$\n\ndonc $f(x+y)=f(x)$ et $f(f(x+y)+y)=f(f(x)+y)$.\nAinsi, $f$ est une fonction russe, ce qui répond à la question.\nb) Soit $v$ un éventuel entier $f$-rare. On pose $X_{v}=\\{x \\in \\mathbb{Z}: f(x)=v\\}$, puis $a=\\min \\left(X_{v}\\right)$ et $b=\\max \\left(X_{v}\\right)$.\nTout d'abord, une récurrence immédiate sur $k$ montre que $f(f(x)+y)=f(f(x+k y)+y)$ pour tous les entiers relatifs $x, y$ et $k$. Par conséquent, si on pose $y=a-f(x)$, alors\n\n$$\nf(f(x+k y)+y)=f(f(x)+y)=f(a)=v\n$$\n\ndonc $f(x+k y)+y \\in X_{v}$, de sorte que $f(x+k y) \\geqslant a-y=f(x)$ pour tout $k \\in \\mathbb{Z}$. De même, si on pose $z=b-f(x)$, alors $f(x+\\ell z)+z \\in X_{v}$, de sorte que $f(x+\\ell z) \\leqslant b-z=f(x)$ pour tout $\\ell \\in \\mathbb{Z}$.\nL'ensemble $X_{f(x)}$ contient donc l'entier $x+m y z$ pour tout $m \\in \\mathbb{Z}$. Par conséquent, si l'entier $r=f(x)$ est $f$-rare, c'est que $y z=0$, et donc que $r=f(x) \\in\\{a, b\\} \\subseteq X_{v}$. Ainsi, seuls les éléments de $X_{v}$ sont susceptibles d'être $f$-rares.\nMais alors, pour tout entier $w$ qui serait $f$-rare, on sait que $v$ appartient à la fois à $X_{v}$ et à $X_{w}$, ce qui démontre que $v=w$, comme attendu.\n\nCommentaire des correcteurs Ce problème très difficile a été substantiellement résolu par trois élèves. Ceux-ci ont, ce faisant, dépassé les attentes que les correcteurs avaient formulées au vu de la difficulté du problème.\nPar ailleurs, plusieurs élèves ont proposé des fonctions russes qui n'en étaient en fait pas : il est important d'être méticuleux quand on vérifie qu'une fonction satisfait les conditions d'un énoncé, d'autant plus si cette vérification n'a rien d'évident, comme c'était le cas ici, et qu'elle est censée fournir une réponse toute faite à une question de l'énoncé.", "problem_match": "\nExercice 6.", "solution_match": "## Solution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2019-2020-Corrigé-Web.jsonl
ADDED
|
@@ -0,0 +1,10 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Soit $a_{1}, a_{2}, \\ldots$ la suite d'entiers telle que $a_{1}=1$ et, pour tout entier $n \\geqslant 1$,\n\n$$\na_{n+1}=a_{n}^{2}+a_{n}+1\n$$\n\nDémontrer, pour tout entier $n \\geqslant 1$, que $a_{n}^{2}+1$ divise $a_{n+1}^{2}+1$.", "solution": "Pour tout entier $n \\geqslant 1$, posons $b_{n}=a_{n}^{2}+1$. On conclut en constatant directement que\n\n$$\nb_{n+1} \\equiv\\left(a_{n}^{2}+a_{n}+1\\right)^{2}+1 \\equiv\\left(b_{n}+a_{n}\\right)^{2}+1 \\equiv a_{n}^{2}+1 \\equiv b_{n} \\equiv 0 \\quad\\left(\\bmod b_{n}\\right)\n$$\n\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ Il suffit de constater, pour tout entier $n \\geqslant 1$, que\n\n$$\n\\begin{aligned}\na_{n+1}^{2}+1 & =\\left(a_{n}^{2}+a_{n}+1\\right)^{2}+1 \\\\\n& =a_{n}^{4}+2 a_{n}^{3}+3 a_{n}^{2}+2 a_{n}+2 \\\\\n& =a_{n}^{2}\\left(a_{n}^{2}+1\\right)+2 a_{n}^{3}+2 a_{n}^{2}+2 a_{n}+2 \\\\\n& =a_{n}^{2}\\left(a_{n}^{2}+1\\right)+2 a_{n}\\left(a_{n}^{2}+1\\right)+2 a_{n}^{2}+2 \\\\\n& =a_{n}^{2}\\left(a_{n}^{2}+1\\right)+2 a_{n}\\left(a_{n}^{2}+1\\right)+2\\left(a_{n}^{2}+1\\right) \\\\\n& =\\left(a_{n}^{2}+2 a_{n}+2\\right)\\left(a_{n}^{2}+1\\right)\n\\end{aligned}\n$$\n\nest effectivement un multiple de $a_{n}^{2}+1$.\nCommentaire des correcteurs L'exercice a été bien résolu. Certains ont tenté une récurrence, sans grand succès, car il était difficile d'obtenir le résultat par récurrence. Peu de copies ont travaillé modulo $a_{n}^{2}+1$, ce qui simplifiait pourtant grandement les calculs.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "On répartit les entiers de $1,2, \\ldots, 8$ en deux ensembles $A$ et $B$, puis on note $P_{A}$ le produit de tous les éléments de $A$ et $P_{B}$ le produit de tous les éléments de $B$.\nQuelles sont les valeurs minimale et maximale que peut prendre la somme $P_{A}+P_{B}$ ?\nNote : si un ensemble $E$ est vide, on considérera que le produit de ses éléments est égal à 1.", "solution": "Soit $A$ et $B$ deux ensembles disjoints dont la réunion est égale à l'ensemble $E=\\{1, \\ldots, 8\\}$.\nTâchons tout d'abord de maximiser la somme $P_{A}+P_{B}$. Sans perte de généralité, on peut supposer que $P_{A} \\leqslant P_{B}$. Puis, si $A$ contient un entier $k \\geqslant 2$, on pose $A^{\\prime}=A \\backslash\\{k\\}$ et $B^{\\prime}=$ $B \\cup\\{k\\}$. Alors\n\n$$\nP_{A^{\\prime}}+P_{B^{\\prime}} \\geqslant P_{B^{\\prime}}=k P_{B} \\geqslant 2 P_{B} \\geqslant P_{A}+P_{B} .\n$$\n\nAinsi, lorsque la somme $P_{A}+P_{B}$ atteint sa valeur maximale, on sait que $A \\subseteq\\{1\\}$, donc que $P_{A}=1$ et que $P_{B}=8!$, de sorte que $P_{A}+P_{B}=8!+1=40321$.\nTâchons maintenant de minimiser la somme $P_{A}+P_{B}$. L'inégalité arithmético-géométrique indique que $P_{A}+P_{B} \\geqslant 2 c$, où l'on a posé $c=\\sqrt{P_{A} P_{B}}=\\sqrt{8!}$. Comme $401^{2}=160801<$ $161280=4 c^{2}$, on sait que $2 c>401$, et donc que $P_{A}+P_{B} \\geqslant\\lceil 2 c\\rceil \\geqslant 402$.\nUn premier réflexe est donc de rechercher deux ensembles $A$ et $B$ tels que $P_{A}+P_{B}=402$. On formule alors quelques remarques préliminaires à cette recherche. Tout d'abord, savoir quel ensemble contient l'entier 1 ne change rien. Puis on démontre que l'un des deux ensembles contient l'entier 6 et que l'autre contient les entiers 2 et 3 . En effet, soit $X$ l'ensemble qui contient 6 et $Y$ celui qui ne contient pas 6 :\n$\\triangleright$ puisque $P_{Y} \\equiv 402-P_{X} \\equiv 0(\\bmod 6)$, c'est que $Y$ contient l'entier 3 ainsi qu'un entier pair;\n$\\triangleright$ si c'est $X$ qui contient l'entier 2, alors $P_{Y} \\equiv 402-P_{X} \\equiv 2(\\bmod 4)$, donc $X$ contient un entier pair mais pas divisible par 4 , ce qui est impossible.\nQuitte à supprimer les entiers $1,2,3$ et 6 des ensembles $A$ et $B$, on se ramène donc à trouver une partition de l'ensemble $\\hat{E}=\\{4,5,7,8\\}$ en deux sous-ensembles $\\hat{A}$ et $\\hat{B}$ tels que $P_{\\hat{A}}+$ $P_{\\hat{B}}=402 / 6=67$. Supposons, sans perte de généralité, que $\\hat{A}$ contient l'entier 4. Alors $P_{\\hat{B}} \\equiv 67-P_{\\hat{A}} \\equiv 1(\\bmod 2)$, donc $\\hat{A}$ contient aussi l'entier 8 . En outre, si $\\hat{A}$ contient également l'un des deux entiers 5 ou 7 , alors $P_{\\hat{A}}+P_{\\hat{B}} \\geqslant P_{\\hat{A}} \\geqslant 4 \\times 5 \\times 8 \\geqslant 160>67$. On a donc nécessairement $\\hat{A}=\\{4,8\\}$ et $\\hat{B}=\\{5,7\\}$, et on est tout heureux de vérifier que, dans ce cas, on a effectivement $P_{\\hat{A}}+P_{\\hat{B}}=32+35=67$.\nEn conclusion, la valeur maximale de $P_{A}+P_{B}$ est égale à $P_{\\emptyset}+P_{E}=8!+1=40321$, et la valeur minimale de $P_{A}+P_{B}$ est égale à $P_{\\{2,3,5,7\\}}+P_{\\{1,4,6,8\\}}=402$.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "On répartit les entiers de $1,2, \\ldots, 8$ en deux ensembles $A$ et $B$, puis on note $P_{A}$ le produit de tous les éléments de $A$ et $P_{B}$ le produit de tous les éléments de $B$.\nQuelles sont les valeurs minimale et maximale que peut prendre la somme $P_{A}+P_{B}$ ?\nNote : si un ensemble $E$ est vide, on considérera que le produit de ses éléments est égal à 1.", "solution": "$n^{\\circ} 1$ Soit $A$ et $B$ deux ensembles disjoints dont la réunion est égale à l'ensemble $E=\\{1, \\ldots, 8\\}$, et soit $c=\\sqrt{8}$ !. Sans perte de généralité, on peut supposer que $P_{A} \\leqslant P_{B} ;$ puisque $P_{A} \\times P_{B}=P_{E}=c^{2}$, cela signifie que $P_{A} \\leqslant c$.\nMais alors $P_{A}+P_{B}=f\\left(P_{A}\\right)$, où l'on a posé $f(x)=x+c^{2} / x$, et il nous reste donc à trouver les valeurs minimale et maximale que peut prendre $f\\left(P_{A}\\right)$. On étudie donc le sens de variation de $f$ : si $x \\leqslant y \\leqslant c$, alors\n\n$$\nf(y)-f(x)=\\frac{y^{2}+c^{2}}{y}-\\frac{x^{2}+c^{2}}{x}=\\frac{\\left(c^{2}-x y\\right)(x-y)}{x y} \\leqslant 0 .\n$$\n\nLa fonction $f$ est donc décroissante sur l'intervalle $(0, c]$ et, par conséquent :\n$\\triangleright$ afin de maximiser $f\\left(P_{A}\\right)$, il suffit de minimiser $P_{A}$, c'est-à-dire de choisir $A$ vide, ou encore $P_{A}=1$;\n$\\triangleright$ afin de minimiser $f\\left(P_{A}\\right)$, il suffit de maximiser $P_{A}$, sachant que $P_{A}$ est un produit d'éléments de $E$ et que $P_{A} \\leqslant c$.\nIl nous faut donc calculer la valeur de l'entier $\\lfloor c\\rfloor$. Puisque $c^{2}=8!=40320$ et que\n\n$$\n200^{2}=40000<40320<40401=201^{2}\n$$\n\n$c^{\\prime}$ est donc que $\\lfloor c\\rfloor=200$. On étudie donc les entiers $200,199,198, \\ldots$ jusqu'à tomber sur un entier $n$ que l'on pourra écrire comme un produit d'éléments de $E$. Au lieu de procéder brutalement, on peut formuler deux remarques préalables:\n$\\triangleright$ de manière générale, $n$ doit diviser $8!=2^{7} \\times 3^{2} \\times 5 \\times 7$;\n$\\triangleright$ en outre, si $n$ est impair, alors $n$ divise même $3 \\times 5 \\times 7=105$, donc $n \\leqslant 105$.\nOn déduit de la première remarque que $n$ ne peut prendre aucune des valeurs\n\n$$\n200=2^{3} \\times 5^{2}, 198=11 \\times 18,196=4 \\times 7^{2}, 194=2 \\times 97\n$$\n\nde sorte que $n=192=4 \\times 6 \\times 8$ est en fait l'entier recherché.\nPar conséquent, la valeur maximale de $P_{A}+P_{B}$ est égale à $f(1)=8!+1=40321$, et la valeur minimale de $P_{A}+P_{B}$ est égale à $f(192)=192+210=402$.\n\nCommentaire des correcteurs L'exercice a été résolu de façon très hétérogène. Beaucoup d'élèves ont trouvé la valeur du maximum, mais peu ont fourni une bonne justification de sa maximalité : on pouvait par exemple utiliser l'inégalité du réordonnement, ou bien affirmer que si $P_{A}<8$ !, on a forcément $P_{a} \\leqslant 8!/ 2$.\nPour le minimum, il était déjà plus difficile de trouver comment obtenir la valeur minimale de 402, et peu d'élèves ont vu comment utiliser une inégalité arithmético-géométrique permettait de montrer que celle-ci était optimale. Néanmoins, certains ont utilisé des approches plus atypiques et trouvé des résultats, notamment via l'étude de fonctions ou via des comparaisons astucieuses. Nombreux ont dit qu'il fallait obtenir les termes les plus proches possible pour avoir égalité : l'idée est intéressante, mais il fallait formaliser pour obtenir des résultats rigoureux.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle et soit $\\omega$ son cercle circonscrit. Soit $\\ell_{B}$ et $\\ell_{C}$ deux droites parallèles l'une à l'autre, passant respectivement par les points $B$ et $C$. On note $D$ le point d'intersection, autre que $B$, entre $\\omega$ et la droite $\\ell_{B}$. De même, on note $E$ le point d'intersection, autre que $C$, entre $\\omega$ et la droite $\\ell_{C}$.\nOn suppose que les droites $\\ell_{C}$ et $(A D)$ se coupent en un point $F$, et que les droites $\\ell_{B}$ et $(A E)$ se coupent en un point $G$. On note alors $O, O_{1}$ et $O_{2}$ le centres respectifs des cercles circonscrits aux triangles $A B C, A D G$ et $A E F$. Enfin, on note $P$ le centre du cercle circonscrit au triangle $O O_{1} O_{2}$.\nDémontrer que la droite $(O P)$ est parallèle aux deux droites $\\ell_{B}$ et $\\ell_{C}$.", "solution": "Commençons par tracer une figure, en prenant soin de faire apparaître le triangle $O O_{1} O_{2}$, puisque $P$ en est le centre du cercle circonscrit. On en profite pour noter $\\omega_{1}, \\omega_{2}$ et $\\omega^{\\prime}$ les cercles circonscrits à $A D G$, à $A E F$ et à $O O_{1} O_{2}$.\n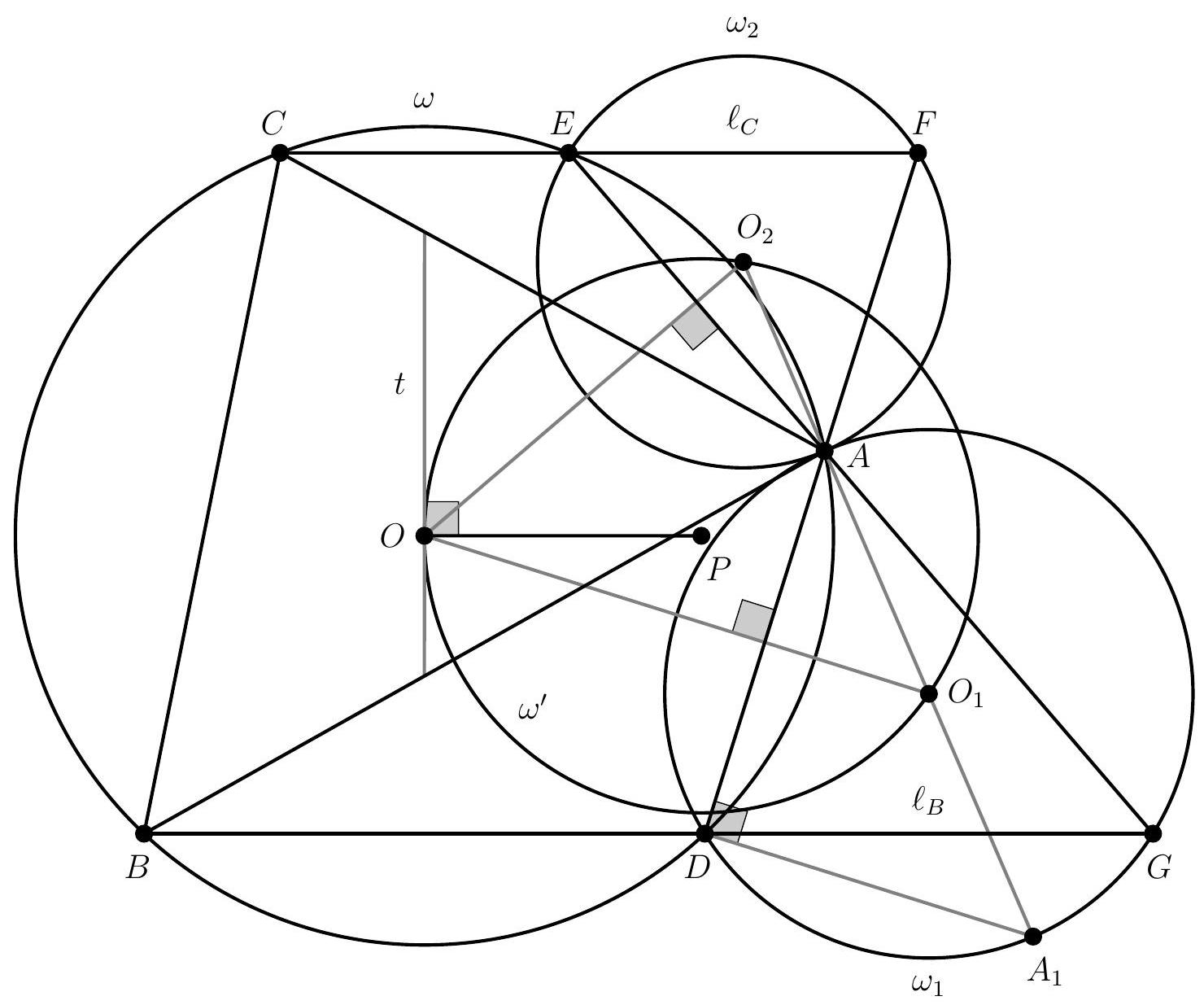\n\nOn remarque tout de suite que les points $A, O_{1}$ et $O_{2}$ semblent alignés, et on s'empresse donc de le démontrer. En effet, les droites $(D G)$ et $(E F)$ sont parallèles l'une à l'autre. Le théorème de Thalès indique alors qu'il existe une homothétie $h$, de centre $A$, qui envoie le triangle $A D G$ sur le triangle $A F E$. On en déduit que $O_{2}=h\\left(O_{1}\\right)$, et donc que les points $A$, $O_{1}$ et $O_{2}$ sont bien alignés.\nAfin de démontrer que $(O P)$ est parallèle à $\\ell_{B}$ et à $\\ell_{C}$, on va maintenant calculer l'angle de droites $\\left(O P, \\ell_{B}\\right)$. Pour ce faire, on commence par se débarrasser du point $P$, en invoquant la\ntangente en $O$ à $\\omega^{\\prime}$ : si l'on note $t$ cette tangente, alors\n\n$$\n\\begin{aligned}\n\\left(O P, \\ell_{B}\\right) & =(O P, t)+\\left(t, O O_{2}\\right)+\\left(O O_{2}, \\ell_{B}\\right) \\\\\n& =90^{\\circ}+\\left(O_{1} O, O_{1} O_{2}\\right)+\\left(O O_{2}, \\ell_{B}\\right) \\\\\n& =90^{\\circ}+\\left(O_{1} O, O_{1} A\\right)+\\left(O O_{2}, \\ell_{B}\\right) .\n\\end{aligned}\n$$\n\nPuis, comme $(A D)$ est l'axe radical des cercles $\\omega_{1}$ et $\\omega^{\\prime}$, les droites $(A D)$ et $\\left(O O_{1}\\right)$ sont perpendiculaires l'une à l'autre. De même, $(\\mathrm{AE})$ et $\\left(\\mathrm{OO}_{2}\\right)$ sont perpendiculaires. On en déduit que\n\n$$\n\\begin{aligned}\n\\left(O P, \\ell_{B}\\right) & =90^{\\circ}+\\left(O_{1} O, O_{1} A\\right)+\\left(O O_{2}, \\ell_{B}\\right) \\\\\n& =90^{\\circ}+\\left(O_{1} O, A D\\right)+\\left(A D, O_{1} A\\right)+\\left(O O_{2}, A E\\right)+\\left(A E, \\ell_{B}\\right) \\\\\n& =90^{\\circ}+90^{\\circ}+\\left(A D, O_{1} A\\right)+90^{\\circ}+\\left(A E, \\ell_{B}\\right) \\\\\n& =90^{\\circ}+\\left(A D, O_{1} A\\right)+\\left(A E, \\ell_{B}\\right)\n\\end{aligned}\n$$\n\nCe faisant, on s'est déjà débarrassés des points $P, O$ et $O_{2}$, ce qui suggère que l'on est sur la bonne voie. Notre prochaine victime sera donc le point $O_{1}$. En effet, si l'on note $A_{1}$ le symétrique de $A$ par rapport à $O_{1}$, alors $\\left[A A_{1}\\right]$ est un diamètre de $\\omega_{1}$, de sorte que\n\n$$\n\\left(A D, O_{1} A\\right)=\\left(A D, A A_{1}\\right)=\\left(A D, D A_{1}\\right)+\\left(D A_{1}, A A_{1}\\right)=90^{\\circ}+(D G, A G)=90^{\\circ}+(B D, A E)\n$$\n\nMais alors on a déjà gagné, puisque\n\n$$\n\\left(O P, \\ell_{B}\\right)=90^{\\circ}+\\left(A D, O_{1} A\\right)+\\left(A E, \\ell_{B}\\right)=90^{\\circ}+90^{\\circ}+(B D, A E)+\\left(A E, \\ell_{B}\\right)=\\left(B D, \\ell_{B}\\right),\n$$\n\nce qui conclut.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ On réutilise, ci-dessous, les noms des points et cercles introduits dans la solution précédente.\nPuisque les droites $\\ell_{B}$ et $\\ell_{C}$ sont parallèles, et comme $A, B, C, D$ et $E$ sont cocycliques, on sait tout d'abord que $(G A, G D)=(E A, E F)$ et que, de même, $(F E, F A)=(D G, D A)$. Les triangles $A E F$ et $A G D$ sont donc semblables. Par conséquent, les triangles $F O_{2} A$ et $D O_{1} A$ sont également semblables, de sorte que $\\left(A F, A O_{2}\\right)=\\left(A D, A O_{1}\\right)$, et donc que les points $O_{1}$, $A$ et $O_{2}$ sont alignés.\nEnsuite, puisque la droite $(A D)$ est l'axe radical des cercles $\\omega$ et $\\omega_{1}$, elle est perpendiculaire à $\\left(O O_{1}\\right)$. On en déduit, d'après le théorème de l'angle au centre, et en notant $A_{1}$ le symétrique de $A$ par rapport à $O_{1}$, que\n\n$$\n\\begin{aligned}\n\\left(O_{1} O_{2}, O_{1} O\\right) & =\\left(A A_{1}, A D\\right)+\\left(A D, O O_{1}\\right)=\\left(A A_{1}, D A_{1}\\right)+\\left(D A_{1}, A D\\right)+90^{\\circ} \\\\\n& =(A G, D G)+90^{\\circ}+90^{\\circ}=(G A, G D) .\n\\end{aligned}\n$$\n\nOn montre de même que $\\left(O_{2} O, O_{2} O_{1}\\right)=(F E, F A)=(D G, D A)$. Les triangles $O O_{1} O_{2}$ et $A G D$ sont donc indirectement semblables.\nMais alors les triangles $O O_{1} P$ et $A G O_{1}$ sont, aux aussi, indirectement semblables. On en conclut que\n\n$$\n\\left(O P, O_{1} O_{2}\\right)=\\left(G D, A O_{1}\\right)=\\left(G D, O_{1} O_{2}\\right),\n$$\n\nce qui signifie bien que $(O P)$ est parallèle à la droite $(G D)=\\ell_{B}$, donc à $\\ell_{C}$ également.\n\nRemarque: Si l'on entreprend d'utiliser des angles de droites, il est important de ne jamais diviser brutalement les angles par deux, par exemple pour utiliser le théorème de l'angle au centre ou bien quand on rencontre un triangle isocèle ou une bissectrice. En effet, voici un exemple d'horreur à laquelle on pourrait aboutir si on ne prend pas cette peine :\n«Puisque la droite $\\left(O O_{1}\\right)$ est la bissectrice de l'angle $\\widehat{A O_{1} D}$, on sait que $\\left(O_{1} O, O_{1} A\\right)=\\left(O_{1} D, O_{1} A\\right) / 2$. Puisque $A O_{1} D$ est isocèle en $O_{1}$, on en déduit que\n\n$$\n\\left(A D, A O_{1}\\right)=\\left(\\left(D O_{1}, D A\\right)+\\left(A D, A O_{1}\\right)\\right) / 2=\\left(D O_{1}, A O_{1}\\right) / 2=\\left(O_{1} O, O_{1} A\\right)\n$$\n\nMais cette égalité est bien sûr complètement fausse, puisque l'on a en fait $\\left(A D, A O_{1}\\right)=\\left(O_{1} O, O_{1} A\\right)+90^{\\circ}$. Oups!»\nLa raison pour laquelle le raisonnement ci-dessus est faux est que les angles de droites sont des angles modulo $180^{\\circ}$. Par conséquent, si on divise un angle de droite par deux, on récupère une relation qui n'est valide que modulo $90^{\\circ}$. On s'abstiendra donc à tout prix, si on décide d'utiliser des angles de droites, de diviser des angles par deux.\n\nCommentaire des correcteurs L'exercice a été résolu par un faible nombre de personnes. Cependant, de nombreux élèves ont réussi à avancer significativement dans le problème, en essayant de démontrer ce qu'ils pouvaient conjecturer à partir de leur figure, ce qui est une excellente démarche. Des remarques simples, comme le fait que les droites $\\left(O O_{1}\\right)$ et $(A D)$ sont perpendiculaires, étaient en fait précieuses pour la résolution du problème et étaient alors récompensées. N'hésitez pas à écrire toutes vos idées, même les remarques qui pourraient sembler anodines.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 5 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Au pays des merveilles se trouvent $n$ villes. Chaque paire de villes est reliée par une route à sens unique, qui part d'une des deux villes et arrive à l'autre. Afin de s'y retrouver, Alice interroge le roi de cœur : à chaque question, Alice choisit une paire de villes, et le roi de cœur lui dit quelle est la ville de départ de la route qui relie ces deux villes.\nDémontrer que, en $5 n$ questions ou moins, Alice peut arriver à savoir s'il existe une ville d'où part au plus une route.", "solution": "Nous allons décrire une stratégie qu'Alice peut mettre en place pour aboutir à ses fins en $5 n$ questions ou moins. À tout moment, on dira qu'une ville $v$ est mauvaise si Alice a déjà trouvé deux routes qui partent de $v$, et que $v$ est bonne sinon. De même, on dira qu'une paire de villes $\\{v, w\\}$ est explorée si Alice a déjà interrogé le roi de cœur sur cette paire-là, et inexplorée sinon.\nEnfin, en parallèle de ces questions, Alice a dessiné une carte sur laquelle les $n$ villes sont représentées par $n$ sommets, et elle ajoute une arête sur cette carte, entre les villes $v$ et $w$ à chaque question qu'elle pose sur la paire $\\{v, w\\}$. Dans la suite, nous allons identifier le pays des merveilles au graphe qu'Alice est en train de construire.\nTout d'abord, Alice n'a manifestement jamais intérêt à interroger le roi de cœur sur une paire de villes qui seraient toutes deux mauvaises, ou sur une paire de villes déjà explorée. La stratégie d'Alice débute donc comme suit. Tant qu'il existe une paire inexplorée $\\{v, w\\}$ formée de deux bonnes villes, Alice choisit une telle paire et interroge le roi de cœur sur cette paire. À la fin de cette première étape, nul sommet de notre graphe n'a strictement plus de deux arêtes sortantes. Alice a donc posé au plus $2 n$ questions.\nEn outre, soit $X$ l'ensemble des villes toujours bonnes à l'issue de cette étape, et soit $x$ le cardinal de $X$, de sorte qu'il y a $x(x-1) / 2$ routes entre villes de $X$. Toute paire $\\{v, w\\}$ formée de deux villes de $X$ est manifestement explorée; et toute ville de $X$, puisqu'elle est bonne, est donc à l'origine d'au plus une route allant vers une autre ville de $X$. Il y a donc au plus $x$ routes entre villes de $X$, ce qui signifie que $x \\leqslant 3$.\nAlice n'a donc plus qu'à interroger le roi de cœur sur toutes les paires $\\{v, x\\}$ où $x \\in X$ : cela fera $n x \\leqslant 3 n$ questions supplémentaires, à l'issue desquelles Alice saura exactement combien de routes partent de chacune des villes de $X$. Si, à cette étape de l'algorithme, il reste une bonne ville $v$, c'est qu'il n'y avait effectivement pas plus d'une route qui partait de $v$.\n\nCommentaire des correcteurs Du fait de sa difficulté, cet exercice a été résolu par un faible nombre d'élèves. Nombreux sont ceux qui ont remarqué que, pour $n \\leqslant 11$, Alice pouvait se contenter de demander le sens de toutes les routes; malheureusement, cela ne faisait pas avancer le problème. La clé consistait à s'apercevoir que, en général, il fallait éviter de poser une question sur une ville dont deux routes sortaient.\nQuelques élèves ont proposé des stratégies qui ne marchaient pas en $5 n$ questions, mais en $6 n$ questions ou plus (par exemple 10n questions) et cela a été valorisé. Quelques élèves ont également obtenu des points en montrant qu'au plus 3 villes pouvaient avoir moins de 2 routes sortantes.\n\n## Exercices Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 6 |
+
{"year": "2019", "problem_label": "5", "tier": 1, "problem": "Au pays des merveilles se trouvent $n$ villes. Chaque paire de villes est reliée par une route à sens unique, qui part d'une des deux villes et arrive à l'autre. Afin de s'y retrouver, Alice interroge le roi de cœur : à chaque question, Alice choisit une paire de villes, et le roi de cœur lui dit quelle est la ville de départ de la route qui relie ces deux villes.\nDémontrer que, en $5 n$ questions ou moins, Alice peut arriver à savoir s'il existe une ville d'où part au plus une route.", "solution": "Nous allons décrire une stratégie qu'Alice peut mettre en place pour aboutir à ses fins en $5 n$ questions ou moins. À tout moment, on dira qu'une ville $v$ est mauvaise si Alice a déjà trouvé deux routes qui partent de $v$, et que $v$ est bonne sinon. De même, on dira qu'une paire de villes $\\{v, w\\}$ est explorée si Alice a déjà interrogé le roi de cœur sur cette paire-là, et inexplorée sinon.\nEnfin, en parallèle de ces questions, Alice a dessiné une carte sur laquelle les $n$ villes sont représentées par $n$ sommets, et elle ajoute une arête sur cette carte, entre les villes $v$ et $w$ à chaque question qu'elle pose sur la paire $\\{v, w\\}$. Dans la suite, nous allons identifier le pays des merveilles au graphe qu'Alice est en train de construire.\nTout d'abord, Alice n'a manifestement jamais intérêt à interroger le roi de cœur sur une paire de villes qui seraient toutes deux mauvaises, ou sur une paire de villes déjà explorée. La stratégie d'Alice débute donc comme suit. Tant qu'il existe une paire inexplorée $\\{v, w\\}$ formée de deux bonnes villes, Alice choisit une telle paire et interroge le roi de cœur sur cette paire. À la fin de cette première étape, nul sommet de notre graphe n'a strictement plus de deux arêtes sortantes. Alice a donc posé au plus $2 n$ questions.\nEn outre, soit $X$ l'ensemble des villes toujours bonnes à l'issue de cette étape, et soit $x$ le cardinal de $X$, de sorte qu'il y a $x(x-1) / 2$ routes entre villes de $X$. Toute paire $\\{v, w\\}$ formée de deux villes de $X$ est manifestement explorée; et toute ville de $X$, puisqu'elle est bonne, est donc à l'origine d'au plus une route allant vers une autre ville de $X$. Il y a donc au plus $x$ routes entre villes de $X$, ce qui signifie que $x \\leqslant 3$.\nAlice n'a donc plus qu'à interroger le roi de cœur sur toutes les paires $\\{v, x\\}$ où $x \\in X$ : cela fera $n x \\leqslant 3 n$ questions supplémentaires, à l'issue desquelles Alice saura exactement combien de routes partent de chacune des villes de $X$. Si, à cette étape de l'algorithme, il reste une bonne ville $v$, c'est qu'il n'y avait effectivement pas plus d'une route qui partait de $v$.\n\nCommentaire des correcteurs Du fait de sa difficulté, cet exercice a été résolu par un faible nombre d'élèves. Nombreux sont ceux qui ont remarqué que, pour $n \\leqslant 11$, Alice pouvait se contenter de demander le sens de toutes les routes; malheureusement, cela ne faisait pas avancer le problème. La clé consistait à s'apercevoir que, en général, il fallait éviter de poser une question sur une ville dont deux routes sortaient.\nQuelques élèves ont proposé des stratégies qui ne marchaient pas en $5 n$ questions, mais en $6 n$ questions ou plus (par exemple 10n questions) et cela a été valorisé. Quelques élèves ont également obtenu des points en montrant qu'au plus 3 villes pouvaient avoir moins de 2 routes sortantes.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 7 |
+
{"year": "2019", "problem_label": "6", "tier": 1, "problem": "Soit $A B C$ un triangle acutangle tel que $\\widehat{C A B}>\\widehat{B C A}$ et soit $P$ le point du segment $[B C]$ tel que $\\widehat{P A B}=\\widehat{B C A}$. Soit $Q$ le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B P$ et la droite $(A C)$. Soit ensuite $D$ le point du segment $[A P]$ tel que $\\widehat{Q D C}=\\widehat{C A P}$, puis $E$ le point de $(B D)$, autre que $D$, tel que $C E=C D$. Enfin, soit $F$ le point d'intersection, autre que $C$, entre le cercle circonscrit à $C Q E$ et la droite ( $C D$ ), et soit $G$ le point d'intersection des droites $(Q F)$ et $(B C)$.\nDémontrer que les points $B, D, F$ et $G$ sont cocycliques.", "solution": "Commençons par tracer une figure. Une première difficulté est de construire le point $P$ : une manière simple de procéder est alors de construire le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B C$ et le cercle de centre $B$ et de rayon $A$. En effet, si l'on note $P^{\\prime}$ ce point, les arcs $\\overline{A B}$ et $\\overline{B P^{\\prime}}$ ont même mesure, donc $\\widehat{B C A}=\\widehat{P^{\\prime} A B}=\\widehat{P A B}$, et il suffit de construire $P$ comme le point d'intersection des droites $(B C)$ et $\\left(A P^{\\prime}\\right)$.\nDe même, puisque l'on souhaite que $\\widehat{Q D C}=\\widehat{C A P}=\\widehat{Q A P}=\\widehat{Q B P}=\\widehat{Q B C}$, on peut construire le point $D$ comme le point d'intersection entre la droite $(A P)$ et le cercle circonscrit à $B C Q$.\nOn obtient alors la figure suivante, où l'on a tracé en pointillés tous les cercle utiles à notre construction, en gris le cercle dont on souhaite montrer qu'il existe, et où l'on a bien sûr marqué les angles $\\widehat{P A B}=\\widehat{B C A}$ et $\\widehat{Q D C}=\\widehat{C A P}$, qui ont de fortes chances d'avoir un rôle à jouer dans la suite.\n\n\nUne première remarque qui apparaît nettement sur la figure est que les points $A, B, P^{\\prime}, C$ et $E$ semblent cocycliques. On commence donc par le démontrer, au moyen de la chasse aux angles de droites suivante:\n\n$$\n\\begin{aligned}\n(E C, E B) & =(D B, D C)=(Q B, Q C)=(Q B, Q A)=(P B, P A) \\\\\n& =(C B, P A)=(C B, A B)+(A B, P A) \\\\\n& =(C B, A B)+(A C, C B)=(A C, A B) .\n\\end{aligned}\n$$\n\nPuisque aucune autre remarque ne saute manifestement aux yeux, on se concentre alors sur la propriété à démontrer, dans le but de la transformer en une propriété équivalente qui aura des chances d'être plus facile à observer. Ainsi, il s'agit de démontrer que\n\n$$\n(D F, D B)=(G F, G B)=(Q F, B C)=(Q F, C F)+(C F, B C)=(Q E, C E)+(D F, B C)\n$$\n\nc'est-à-dire que $(Q E, C E)=(B C, D B)=(B C, B E)=(A C, A E)$, ou encore que les triangles $A C E$ et $E C Q$ sont (indirectement) semblables, puisqu'ils ont déjà même angle en $\\widehat{C}$.\nAu vu de la relation $C D^{2}=C E^{2}$, notre objectif devient donc de démontrer que $C A \\cdot C Q=$ $C E^{2}=C D^{2}$. Mais l'égalité $C A \\cdot C Q=C D^{2}$ découle justement du fait que les triangles $C A D$ et $C D Q$ sont semblables, puisqu'ils ont même angle en $\\widehat{C}$ et que $\\widehat{C A D}=\\widehat{Q D C}$. Ceci conclut donc notre solution.\n\nCommentaire des correcteurs L'exercice a été très réussi! Plusieurs approches étaient possibles. Quelques élèves étaient, sans le savoir, très proches de la conclusion. D'autres ont effectué une chasse aux angles intéressante sans pour autant voir que cela impliquait que des points étaient cocycliques ou que des droites étaient parallèles, ce qui est toujours dommage.\nPlusieurs élèves ont tenté de réduire le problème ou de le ramener à la démonstration d'une autre propriété de la figure. C'est une bonne idée mais, la plupart du temps, démontrer cette autre propriété n'est pas spécialement plus simple que le problème de départ.\nOn notera qu'il n'était pas nécessaire de déployer des outils techniques pour cet exercice et qu'une simple chasse aux angles ou l'usage de la puissance d'un point par rapport à un cercle était largement suffisants.\nUne fois de plus, on déplore le cas d'élèves n'ayant pas respecté la consigne concernant les figures. On insiste sur l'intérêt de figures propres et exactes qui sont la base de la réflexion en géométrie, surtout lorsque l'exercice devient rééllement corsé. L'habitude de tracer des figures exactes est donc essentiel. À l'inverse, de nombreux élèves ont su utiliser leur figure pour conjecturer diverses propriétés et en fournir un début de démonstration.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 8 |
+
{"year": "2019", "problem_label": "7", "tier": 1, "problem": "Soit $C$ un entier naturel non nul. Trouver toutes les fonctions $f: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ telles que, pour tous les entiers $a$ et $b$ de somme $a+b \\geqslant C$, l'entier $a+f(b)$ divise $a^{2}+b f(a)$.", "solution": "Tout d'abord, toute fonction linéaire strictement croissante est solution. En effet, pour tout entier $k \\geqslant 1$, l'entier $a+k b$ divise bien $a^{2}+b \\times(k a)=a(a+k b)$. Réciproquement, montrons que toute solution est une fonction linéaire (qui sera strictement croissante, puisque à valeurs dans $\\mathbb{N}^{*}$ ).\nConsidérons un entier $n \\geqslant C$, et posons $\\varphi=f(1)$. Alors\n\n$$\n\\varphi^{2}+f(n) \\equiv n^{2}+f(n) \\equiv 0 \\quad(\\bmod n+\\varphi)\n$$\n\ndonc $f(n)+\\varphi^{2}$ est un multiple non nul de $n+\\varphi$, de sorte que $f(n) \\geqslant n+\\varphi-\\varphi^{2}$.\nD'autre part, puisque $1+f(n)$ divise $1+\\varphi n$, soit $g(n)=(1+\\varphi n) /(1+f(n))$. Alors\n\n$$\n\\varphi(1+f(n)) \\geqslant \\varphi\\left(n+1+\\varphi-\\varphi^{2}\\right)=(1+f(n)) g(n)-1+\\left(1+\\varphi-\\varphi^{2}\\right) \\varphi\n$$\n\nCela signifie que $\\Phi \\geqslant(1+f(n))(g(n)-\\varphi)$, où l'on a posé $\\Phi=\\varphi^{3}-\\varphi^{2}-\\varphi+1$. Par conséquent, si $n \\geqslant \\Phi+\\varphi^{2}-\\varphi$, on sait que $1+f(n)>\\Phi$, et donc que $g(n) \\leqslant \\varphi$.\nChoisissons maintenant un entier $a \\geqslant 1$, et démontrons que $f(a)=\\varphi a$. Pour ce faire, on construit un entier $n \\geqslant \\max \\left\\{\\Phi+\\varphi^{2}-\\varphi, C\\right\\}$ comme suit :\n$\\triangleright$ on prend $n \\equiv 2(\\bmod 4)$ si $\\varphi$ est impair, et $n$ impair si $\\varphi$ est pair : dans tous les cas, $n \\varphi+1$ est impair;\n$\\triangleright$ pour tout nombre premier $p \\leqslant \\max \\{a, \\varphi\\}$ impair, on choisit $n \\equiv 1(\\bmod p)$ ou $n \\equiv 2$ $(\\bmod p)$ de sorte que $n \\varphi \\not \\equiv-1(\\bmod p)$.\nD'après le théorème chinois, un tel choix est bien faisable, et ce pour une infinité d'entiers $n$. Sans perte de généralité, on suppose donc même que $n \\geqslant 2 \\max \\{\\varphi a, f(a)\\}$.\nAlors $g(n)$ est un diviseur de $1+\\varphi n$, et l'on sait que $g(n) \\leqslant \\varphi$. Par construction, l'entier $1+\\varphi n$ n'a aucun facteur premier $p \\leqslant \\varphi$, de sorte que $g(n)=1$, et donc que $f(n)=\\varphi n$. Mais alors $a+\\varphi n=a+f(n)$ divise\n\n$$\n\\left(a^{2}+n f(a)\\right)+(a+\\varphi n)(\\varphi n-a)=(\\varphi n)^{2}+n f(a)=\\left(\\varphi^{2} n+f(a)\\right) n\n$$\n\nOr, on a construit $n$ de sorte qu'il n'ait aucun facteur premier impair commun avec $a$, et ne soit pas divisible par 4. Par conséquent, si l'on pose $d=\\operatorname{PGCD}(a+\\varphi n, n)$, alors $d=\\operatorname{PGCD}(a, n)$ divise 2. Puis, si l'on pose $\\alpha=(a+\\varphi n) / d$ et $n^{\\prime}=n / d$, on constate que $\\operatorname{PGCD}\\left(\\alpha, n^{\\prime}\\right)=1$ et que $\\alpha$ divise $\\left(\\varphi^{2} n+f(a)\\right) n^{\\prime}$, de sorte que $\\alpha$ divise $\\varphi^{2} n+f(a)$. L'entier $\\alpha$ divise donc également\n\n$$\n\\left(\\varphi^{2} n+f(a)\\right)-d \\varphi \\alpha=f(a)-\\varphi a\n$$\n\nOr, comme $n \\geqslant 2 \\max \\{\\varphi a, f(a)\\}$, on sait que\n\n$$\n\\alpha>\\varphi n / d \\geqslant \\varphi n / 2 \\geqslant \\max \\{\\varphi a, f(a)\\} \\geqslant|f(a)-\\varphi a| .\n$$\n\nC'est donc que $f(a)=\\varphi a$, ce qui conclut.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 9 |
+
{"year": "2019", "problem_label": "7", "tier": 1, "problem": "Soit $C$ un entier naturel non nul. Trouver toutes les fonctions $f: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ telles que, pour tous les entiers $a$ et $b$ de somme $a+b \\geqslant C$, l'entier $a+f(b)$ divise $a^{2}+b f(a)$.", "solution": "$n^{\\circ} 1$ Comme précédemment, on pose $\\varphi=f(1)$, et on démontre que, si $f$ est une fonction solution, alors $f(n)=\\varphi n$ pour tout entier $n \\geqslant 1$.\nTout d'abord, pour tout entier $n \\geqslant C$, l'énoncé indique que $1+f(n)$ divise $1+n \\varphi$. On en déduit que $1+f(n) \\leqslant 1+n \\varphi$, donc que $f(n) \\leqslant n \\varphi$.\nOn considère maintenant un entier $m \\geqslant 2$ quelconque, puis un entier $k \\geqslant 1$ tel que $k m-$ $f(m) \\geqslant C$. Si l'on pose $a=k m-f(m)$, et puique $a+m \\geqslant a \\geqslant C$, l'énoncé indique que\n\n$$\nf(m)^{2}+n f(a) \\equiv f(m)^{2}+b f(a) \\equiv(-a)^{2}+m f(a) \\equiv 0 \\quad(\\bmod a+f(m)) .\n$$\n\nL'entier $f(m)^{2}+m f(a)$ est donc divisible par $a+f(m)=k m$, et par $m$ également. On en conclut que $f(m)^{2}$ est lui aussi divisible par $m$; bien sûr, cette relation de divisibilité également valable pour $m=1$, mais on n'en aura pas besoin.\nEn particulier, si $p$ est un nombre premier, et comme $p$ divise $f(p)^{2}$, l'entier $p$ divise aussi $f(p)$ : dans la suite, on pose $g(p)=f(p) / p$, et l'on sait que $1 \\leqslant g(p) \\leqslant \\varphi$. Si, en outre, $p \\geqslant$ $\\max \\{C, \\varphi+1\\}$, alors $p+1 \\geqslant C$, et l'énoncé indique donc que $p+\\varphi$ divise $p^{2}+f(p)=p(p+g(p))$. Puisque $p>\\varphi$, c'est que $p$ et $p+\\varphi$ sont premiers entre eux, donc que $p+\\varphi$ divise $p+g(p)$. Comme $1 \\leqslant g(p) \\leqslant \\varphi$, on en déduit que $g(p)=\\varphi$, c'est-à-dire que $f(p)=\\varphi p$.\nEnfin, soit $\\ell \\geqslant 1$ un entier quelconque, et soit $p$ un nombre premier tel que $p \\geqslant \\max \\{C, \\varphi+$ $1, \\ell+1\\}$. On vient de voir que $f(p)=\\varphi p$. En outre, puisque $\\ell+p \\geqslant p \\geqslant C$, l'énoncé indique que\n\n$$\np(f(\\ell)-\\varphi \\ell) \\equiv p f(\\ell)-\\ell f(p) \\equiv p f(\\ell)+\\ell^{2} \\equiv 0 \\quad(\\bmod \\ell+f(p))\n$$\n\nOr, comme $1 \\leqslant \\ell \\leqslant p-1$, on sait que $p$ est premier avec $\\ell$, donc avec $\\ell+\\varphi p=\\ell+f(p)$ également. On en déduit que $\\ell+\\varphi p=\\ell+f(p)$ divise $f(\\ell)-\\varphi \\ell$. Ceci étant valable pour des nombres premiers $p$ arbitrairement grands, on en déduit que $f(\\ell)=\\ell \\varphi$, ce qui conclut.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|
| 10 |
+
{"year": "2019", "problem_label": "7", "tier": 1, "problem": "Soit $C$ un entier naturel non nul. Trouver toutes les fonctions $f: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ telles que, pour tous les entiers $a$ et $b$ de somme $a+b \\geqslant C$, l'entier $a+f(b)$ divise $a^{2}+b f(a)$.", "solution": "$n^{\\circ} 2$ On présente une autre façon, légèrement différente, de conclure une fois que l'on a montré que $p$ divise $f(p)$ pour tout nombre premier $p$.\nSoit $p$ un nombre premier, et soit $g(p)$ l'entier $f(p) / p$. Puisque $g(p) \\leqslant \\varphi$ dès lors que $p \\geqslant C$, la fonction $g$ est bornée. Il existe donc un entier $\\gamma$ et une infinité de nombres premiers $p$ pour lesquels $g(p)=\\gamma$.\nSoit alors $\\ell$ un entier, puis $p \\geqslant \\max \\{C, \\ell+1\\}$ un nombre premier pour lequel $g(p)=\\gamma$. Alors $p$ est premier avec $\\ell$, donc avec $\\ell+\\gamma p=\\ell+f(p)$. Or, puisque $\\ell+p \\geqslant p \\geqslant C$, l'énoncé indique que\n\n$$\np(f(\\ell)-\\gamma \\ell) \\equiv p f(\\ell)-\\ell f(p) \\equiv p f(\\ell)+\\ell^{2} \\equiv 0 \\quad(\\bmod \\ell+f(p))\n$$\n\nOn en déduit que $\\ell+\\gamma p=\\ell+f(p)$ divise $f(\\ell)-\\gamma \\ell$. Ceci étant valable pour des nombres premiers $p$ arbitrairement grands, on en déduit que $f(\\ell)=\\gamma \\ell$, ce qui conclut.\n\nCommentaire des correcteurs Cet exercice difficile a été résolu entièrement par cinq élèves, ce qui est très satisfaisant, d'autant que deux autres élèves avaient presque une solution complète!\nIl y avait de très nombreuses preuves différentes, certaines ne contenant même presque aucune manipulation arithmétique. Beaucoup d'élèves mentionnent le théorème de Dirichlet, de manière très judicieuse, soit pour démontrer que tout nombre $p$ premier divise $f(p)$, soit pour démontrer directement qu'il existe une infinité d'entiers $b$ tels que $f(b)=b f(1)$. D'autres élèves ne connaissaient manifestement pas ce théorème : ce n'est pas grave, et c'est le moment de le découvrir!\nDe très loin, l'erreur la plus fréquente est de ne pas faire dépendre les variables que vous introduisez des paramètres $a$ et $b$. Par exemple, mieux vaut écrire $a^{2}+b f(a)=k_{a, b}(a+f(b))$ plutôt que simplement $a^{2}+b f(a)=k(a+f(b))$. En effet, dans la suite, et à cause de cette notation, de nombreux élèves ont oublié que $k$ dépendait à la fois de $a$ et de $b$, et ont alors utilisé le raisonnement faux suivant:\n«En choisissant $a=b$, on obtient $(a-k)(a+f(a))$, donc $k=a$. Par conséquent, dans le cas général, puisque $k=a$, cela signifie que $a^{2}+b f(a)=a^{2}+a f(b)$, c'est-à-dire que $f$ est linéaire! »\nÉvidemment, on avait bien $k_{a, a}=a$, mais rien $\\mathrm{n}^{\\prime}$ indiquait que $k_{a, b}=a$ quand $a \\neq b$.\n\nAutre conseil : même si conjecturer que les fonctions affines étaient solutions n'était pas valorisé directement ici, rechercher des solutions simples, telles que l'identité, est toujours une bonne idée. En effet, plusieurs élèves ont perdu du temps à essayer de voir ce qu'impliquerait un défaut d'injectivité de $f$ et ont fondé leur copie là-dessus; s'ils avaient remarqué que l'identité était solution, ils en auraient vite conclu que se focaliser sur les cas des fonctions non injectives était en fait loin de suffire, et qu'il fallait donc se concentrer sur d'autres approches.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2019-2020-corrigé-test-janvier.jsonl
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Clara et Isabelle jouent au jeu suivant. Au début du jeu, elles choisissent un entier $n \\geqslant 1$, puis mettent $n$ bonbons dans un saladier. Puis elles jouent à tour de rôle, en commençant par Clara. À chaque tour, si le saladier contient $k$ bonbons, la joueuse dont c'est le tour choisit un entier $\\ell$ premier avec $k$, tel que $\\ell \\leqslant k$, puis elle mange $\\ell$ bonbons; c'est alors à l'autre joueuse de jouer. La joueuse qui mange le dernier bonbon gagne la partie.\nPour quelles valeurs de $n$ Clara dispose-t-elle d'une stratégie gagnante?", "solution": "Tout d'abord, si $n$ est impair, Clara peut commencer par choisir $\\ell=$ $n-2$. En effet, puisque $n$ est impair, on sait que $\\operatorname{PGCD}(n, n-2)=\\operatorname{PGCD}(n, 2)=1$. Mais alors Isabelle se retrouve avec deux bonbons, elle est obligée d'en manger un seul, et laisse le dernier bonbon à Clara, qui gagne donc.\nAu contraire, si $n$ est pair, Clara est obligée de choisir un entier $\\ell$ impair, et elle laisse donc $k=n-\\ell$ bonbons à Isabelle, l'entier $k$ étant donc impair. Si $k=1$, Isabelle a déjà gagné, et si $k \\geqslant 3$, Isabelle peut copier la stratégie présentée ci-dessus, et manger $k-2$ bonbons, s'assurant ainsi la victoire.\n\nLes entiers $n$ recherchés sont donc les entiers impairs.\nCommentaire des correcteurs Ce problème a été globalement bien réussi. Cependant, les correcteurs y ont repéré quelques erreurs récurrentes :\n$\\triangleright$ Plusieurs élèves ont mal compris l'énoncé : il ne fallait pas retirer un nombre premier de billes, mais un nombre premier avec le nombre total de billes.\n$\\triangleright$ Après avoir constaté que Clara gagnait lorsque $n$ était impair, il ne fallait pas oublié de démontrer qu'Isabelle gagnait lorsque $n$ étiat pair.\n$\\triangleright$ Certains élèves n'ont pas vu que Clara pouvait se contenter d'enlever une seule bille : même si 1 divise le nombre $n$ de billes, 1 et $n$ sont quand même premiers entre eux!\n$\\triangleright$ D'autres ont considéré que la seule stratégie gagnante était d'enlever $n-2$ billes car 2 est une position perdante : il s'agissait certes d'une stratégie gagnante, mais pas de la seule, et formuler une telle affirmation rendait donc la preuve invalide.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle et soit $\\Gamma$ son cercle circonscrit. Soit $P$ le point d'intersection de la droite $(B C)$ et de la tangente à $\\Gamma$ en $A$. Soit $D$ et $E$ les symétriques respectifs des points $B$ et $A$ par rapport à $P$.\nSoit alors $\\omega_{1}$ le cercle circonscrit au triangle $D A C$ et soit $\\omega_{2}$ le cercle circonscrit au triangle $A P B$. On note $F$ le point d'intersection des cercles $\\omega_{1}$ et $\\omega_{2}$ autre que $A$, puis on note $G$ le point d'intersection, autre que $F$, du cercle $\\omega_{1}$ avec la droite $(B F)$.\nDémontrer que les droites $(B C)$ et $(E G)$ sont parallèles.", "solution": "Commençons par tracer une figure.\n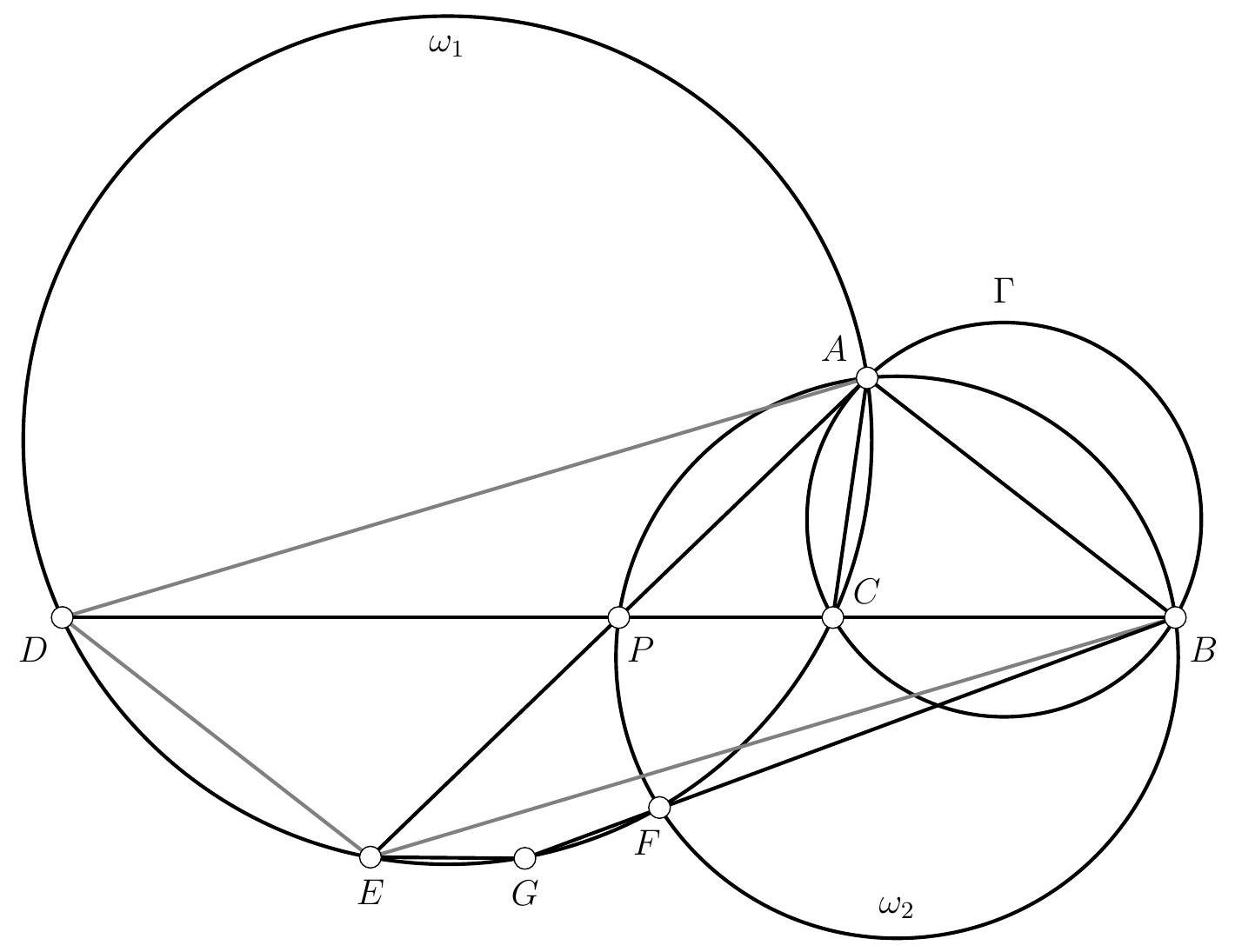\n\nUne première remarque que l'on peut formuler est que, puisque $P$ est le milieu des segments $[A E]$ et $[B D]$, le quadrilatère $A B E D$ et un parallélogramme. Les droites $(A B)$ et $(D E)$ sont donc parallèles, de même que les droites $(A D)$ et $(B E)$.\nUne seconde remarque frappante est que $E$ semble appartenir au cercle $\\omega_{1}$. Après avoir vérifié sur une deuxième figure que c'était bien le cas, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites :\n\n$$\n(E A, E D)=(E A, A B)=(C A, C B)=(C A, C D)\n$$\n\nUne chasse aux angles de droites indique alors que\n$(B C, E G)=(B C, B G)+(B G, E G)=(P B, B F)+(G F, G E)=(P A, A F)+(A F, A E)=0^{\\circ}$, ce qui signifie bien que $(B C)$ et $(E G)$ sont parallèles.\n\nCommentaire des correcteurs Une des raisons pour lesquelles on exige la présence d'une figure est qu'elle constitue un bon moyen de se forger des intuitions sur le problème; c'est alors qu'il faut démontrer que ces intuitions sont correctes. Ainsi, sur beaucoup de dessins on voyait clairement que $E$ est sur le cercle $\\omega_{1}$; cependant, peu d'élèves l'ont remarqué. Parallèlement, plusieurs élèves ont vu sur le dessin que $E$ semblait appartenir au cercle $\\omega_{1}$, et ont alors utilisé cette propriété, mais ont oublié de la démontrer!", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Soit $n$ un entier naturel non nul. On dit qu'une fonction $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ est $n$-positive si, pour tous les réels $x_{1}, \\ldots, x_{n}$ tels que $x_{1}+\\ldots+x_{n}=0$, on a $f\\left(x_{1}\\right)+\\ldots+f\\left(x_{n}\\right) \\geqslant 0$.\na) Toute fonction 2020-positive est-elle nécessairement 1010-positive?\nb) Toute fonction 1010-positive est-elle nécessairement 2020-positive?", "solution": "Dans les deux solutions, on pose $n=1010$.\na) Soit $f$ une fonction $2 n$-positive, et soit $x_{1}, \\ldots, x_{n}$ des réels tels que $x_{1}+\\ldots+x_{n}=0$. En notant que $x_{1}+\\ldots+x_{n}+x_{1}+\\ldots+x_{n}=0$ et que $f$ est $2 n$-positive, on constate que\n\n$$\n0 \\leqslant f\\left(x_{1}\\right)+\\ldots+f\\left(x_{n}\\right)+f\\left(x_{1}\\right)+\\ldots+f\\left(x_{n}\\right)=2\\left(f\\left(x_{1}\\right)+\\ldots+f\\left(x_{n}\\right)\\right),\n$$\n\nce qui montre bien que $f\\left(x_{1}\\right)+\\ldots+f\\left(x_{n}\\right) \\geqslant 0$, et donc que $f$ est $n$-positive. La réponse est donc oui!\nb) Soit $f$ la fonction définie par $f(x)=-1$ si $x$ est un entier tel que $x \\equiv 1(\\bmod 2 n)$, et par $f(x)=n$ sinon. Alors $f$ est $n$-positive. En effet, soit $x_{1}, \\ldots, x_{n}$ des réels tels que $x_{1}+\\ldots+x_{n}=0:$\n$\\triangleright$ S'il existe un entier $k$ tel que $f\\left(x_{k}\\right)=n$, et puisque $f\\left(x_{i}\\right) \\geqslant-1$ pour tout $i \\neq k$, on sait que $f\\left(x_{1}\\right)+\\ldots+f\\left(x_{k}\\right) \\geqslant f\\left(x_{k}\\right)-(n-1) \\geqslant 1$.\n$\\triangleright$ Sinon, alors $x_{k} \\equiv 1(\\bmod 2 n)$ pour tout $k$, donc $x_{1}+\\ldots+x_{n} \\equiv n \\not \\equiv 0(\\bmod 2 n)$, de sorte que ce cas est en fait impossible.\nCependant, $f$ n'est pas $2 n$-positive. En effet, si $x_{1}=1-2 n$ et $x_{2}=x_{3}=\\ldots=x_{2 n}=1$, alors $x_{1}+\\ldots+x_{2 n}=0$ mais $f\\left(x_{1}\\right)+\\ldots+f\\left(x_{2 n}\\right)=-2 n<0$. La réponse est donc non!\n\nCommentaire des correcteurs Les correcteurs ont repéré plusieurs confusions sur la notion de fonction. En effet, lafonction $f$ considérée ne change pas selon qu'il y a 1010 ou 2020 nombres réels.\nD'autre part, si l'on veut démontrer qu'une assertion est fausse (par exemple, si l'on souhaite démontrer que toute fonction $f$ qui serait $n$-positive n'est pas nécessairement $2 n$-positive), la manière la plus simple de procéder reste encore de présenter un contre-exemple.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2019", "problem_label": "4", "tier": 1, "problem": "Soit $a_{0}, a_{1}, a_{2}, \\ldots$ une suite d'entiers naturels non nuls, et soit $b_{0}, b_{1}, b_{2}, \\ldots$ la suite telle que $b_{n}=\\operatorname{PGCD}\\left(a_{n}, a_{n+1}\\right)$ pour tout entier $n \\geqslant 0$. Est-il possible que tout entier naturel non nul soit égal à exactement un des termes $b_{0}, b_{1}, b_{2}, \\ldots$ ?", "solution": "La réponse est oui!\n\nDans la suite, on dira qu'une suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ est agréable si, pour tout $k \\geqslant 0$, les entiers $b_{k}$ et $b_{k+2}$ sont premiers entre eux. Étant donnée une suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ agréable, posons $a_{0}=b_{0}$ puis $a_{k}=b_{k-1} b_{k}$ pour tout $k \\geqslant 0$. On constate alors que $\\operatorname{PGCD}\\left(a_{0}, a_{1}\\right)=b_{0}$ et que $\\operatorname{PGCD}\\left(a_{k}, a_{k+1}\\right)=b_{k} \\operatorname{PGCD}\\left(b_{k-1}, b_{k+1}\\right)=b_{k}$ pour tout $k \\geqslant 1$. Il nous suffit donc de construire une suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ agréable telle que tout entier naturel non nul soit égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \\ldots$\nÀ cette fin, et pour tout $k \\geqslant 1$, notons $p_{k}$ le $k^{\\text {ème }}$ plus petit nombre premier, et $q_{k}$ le $k^{\\text {ème }}$ plus petit entier composé et supérieur ou égal à 1 . On remarque aisément que $p_{k} \\geqslant 2 k-1$ et que $q_{k} \\leqslant 2 k$, donc que $p_{k} \\geqslant q_{k}-1$. On en déduit que $q_{k} \\leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, donc que $\\operatorname{PGCD}\\left(q_{k}, p_{k}\\right)=\\operatorname{PGCD}\\left(q_{k}, p_{k+2}\\right)=1$.\nOn pose alors $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ et $b_{4 k+3}=q_{2 k+2}$ pour tout $k \\geqslant 0$. Tout d'abord, tout entier naturel non nul est bien égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \\ldots$. En outre, pour tout $k \\geqslant 0$, et comme démontré ci-dessus :\n$\\triangleright \\operatorname{PGCD}\\left(b_{4 k}, b_{4 k+2}\\right)=\\operatorname{PGCD}\\left(p_{2 k+1}, q_{2 k+1}\\right)=1$ ,\n$\\triangleright \\operatorname{PGCD}\\left(b_{4 k+1}, b_{4 k+3}\\right)=\\operatorname{PGCD}\\left(p_{2 k+2}, q_{2 k+2}\\right)=1$ ,\n$\\triangleright \\operatorname{PGCD}\\left(b_{4 k+2}, b_{4 k+4}\\right)=\\operatorname{PGCD}\\left(p_{2 k+3}, q_{2 k+1}\\right)=1$ et\n$\\triangleright \\operatorname{PGCD}\\left(b_{4 k+3}, b_{4 k+5}\\right)=\\operatorname{PGCD}\\left(p_{2 k+4}, q_{2 k+2}\\right)=1$.\nLa suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ est donc bien une suite telle que recherchée, ce qui conclut.\nCommentaire des correcteurs Beaucoup de constructions différentes ont été trouvées, menant à des preuves plus ou moins faciles. Une idée clé était de penser à choisir la suite $\\left(a_{n}\\right)$ pour avoir une expression simple de la suite $\\left(b_{n}\\right)$.\nSouvent, une preuve par algorithme a été utilisée : après s'être ramenés à trouver une suite $\\left(b_{n}\\right)$ telle que $b_{n}$ et $b_{n+2}$ seraient premiers entre eux, certains élèves ont invoqué un algorithme glouton, où l'on choisissait à chaque fois le plus petit entier $b_{n}$ non pris qui convenait. Cet algorithme fonctionne effectivement, mais la preuve de correction de cet algorithme était très souvent incomplète :\n$\\triangleright$ il faut tout d'abord préciser que l'on peut bien choisir un tel entier $b_{n}$ à chaque étape, par exemple en invoquant l'infinité de l'ensemble des nombres premiers;\n$\\triangleright$ il faut ensuite démontrer que, dans ce cas, tous les entiers seront bien pris ; à cette fin, il suffisait par exemple de signaler qu'une infinité d'entiers $b_{n}$ seraient des nombres premiers, et en déduire que tout nombre était effectivement pris.\n\n## Exercices Senior", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2019", "problem_label": "5", "tier": 1, "problem": "Soit $a_{0}, a_{1}, a_{2}, \\ldots$ une suite d'entiers naturels non nuls, et soit $b_{0}, b_{1}, b_{2}, \\ldots$ la suite telle que $b_{n}=\\operatorname{PGCD}\\left(a_{n}, a_{n+1}\\right)$ pour tout entier $n \\geqslant 0$. Est-il possible que tout entier naturel non nul soit égal à exactement un des termes $b_{0}, b_{1}, b_{2}, \\ldots$ ?", "solution": "La réponse est oui!\n\nDans la suite, on dira qu'une suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ est agréable si, pour tout $k \\geqslant 0$, les entiers $b_{k}$ et $b_{k+2}$ sont premiers entre eux. Étant donnée une suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ agréable, posons $a_{0}=b_{0}$ puis $a_{k}=b_{k-1} b_{k}$ pour tout $k \\geqslant 0$. On constate alors que $\\operatorname{PGCD}\\left(a_{0}, a_{1}\\right)=b_{0}$ et que $\\operatorname{PGCD}\\left(a_{k}, a_{k+1}\\right)=b_{k} \\operatorname{PGCD}\\left(b_{k-1}, b_{k+1}\\right)=b_{k}$ pour tout $k \\geqslant 1$. Il nous suffit donc de construire une suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ agréable telle que tout entier naturel non nul soit égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \\ldots$\nÀ cette fin, et pour tout $k \\geqslant 1$, notons $p_{k}$ le $k^{\\text {ème }}$ plus petit nombre premier, et $q_{k}$ le $k^{\\text {ème }}$ plus petit entier composé et supérieur ou égal à 1 . On remarque aisément que $p_{k} \\geqslant 2 k-1$ et que $q_{k} \\leqslant 2 k$, donc que $p_{k} \\geqslant q_{k}-1$. On en déduit que $q_{k} \\leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, donc que $\\operatorname{PGCD}\\left(q_{k}, p_{k}\\right)=\\operatorname{PGCD}\\left(q_{k}, p_{k+2}\\right)=1$.\nOn pose alors $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ et $b_{4 k+3}=q_{2 k+2}$ pour tout $k \\geqslant 0$. Tout d'abord, tout entier naturel non nul est bien égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \\ldots$. En outre, pour tout $k \\geqslant 0$, et comme démontré ci-dessus:\n\n$$\n\\begin{aligned}\n& \\triangleright \\operatorname{PGCD}\\left(b_{4 k}, b_{4 k+2}\\right)=\\operatorname{PGCD}\\left(p_{2 k+1}, q_{2 k+1}\\right)=1, \\\\\n& \\triangleright \\operatorname{PGCD}\\left(b_{4 k+1}, b_{4 k+3}\\right)=\\operatorname{PGCD}\\left(p_{2 k+2}, q_{2 k+2}\\right)=1, \\\\\n& \\triangleright \\operatorname{PGCD}\\left(b_{4 k+2}, b_{4 k+4}\\right)=\\operatorname{PGCD}\\left(p_{2 k+3}, q_{2 k+1}\\right)=1 \\text { et } \\\\\n& \\triangleright \\operatorname{PGCD}\\left(b_{4 k+3}, b_{4 k+5}\\right)=\\operatorname{PGCD}\\left(p_{2 k+4}, q_{2 k+2}\\right)=1 .\n\\end{aligned}\n$$\n\nLa suite $\\left(b_{k}\\right)_{k \\geqslant 0}$ est donc bien une suite telle que recherchée, ce qui conclut.\nCommentaire des correcteurs Beaucoup de constructions différentes ont été trouvées, menant à des preuves plus ou moins faciles. Une idée clé était de penser à choisir la suite $\\left(a_{n}\\right)$ pour avoir une expression simple de la suite $\\left(b_{n}\\right)$.\nSouvent, une preuve par algorithme a été utilisée : après s'être ramenés à trouver une suite $\\left(b_{n}\\right)$ telle que $b_{n}$ et $b_{n+2}$ seraient premiers entre eux, certains élèves ont invoqué un algorithme glouton, où l'on choisissait à chaque fois le plus petit entier $b_{n}$ non pris qui convenait. Cet algorithme fonctionne effectivement, mais la preuve de correction de cet algorithme était très souvent incomplète :\n$\\triangleright$ il faut tout d'abord préciser que l'on peut bien choisir un tel entier $b_{n}$ à chaque étape, par exemple en invoquant l'infinité de l'ensemble des nombres premiers;\n$\\triangleright$ il faut ensuite démontrer que, dans ce cas, tous les entiers seront bien pris; à cette fin, il suffisait par exemple de signaler qu'une infinité d'entiers $b_{n}$ seraient des nombres premiers, et en déduire que tout nombre était effectivement pris.", "problem_match": "\nExercice 5.", "solution_match": "## Solution de l'exercice 5"}
|
| 6 |
+
{"year": "2019", "problem_label": "6", "tier": 1, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que\n\n$$\nf(x+f(y))+x=f(f(2 x)+y)\n$$\n\npour tous les réels $x$ et $y$.", "solution": "Tout d'abord, on constate aisément que, pour tout réel $a$, la fonction $f: x \\rightarrow x+a$ est une solution du problème. Réciproquement, on va montrer qu'il n'existe pas d'autre solution.\nDans ce qui suit, on considère une fonction solution $f$, on pose $a=f(0)$, et on notera $\\mathbf{E}(x, y)$ l'équation\n\n$$\nf(x+f(y))+x=f(f(2 x)+y)\n$$\n\nTout d'abord, les équations $\\mathbf{E}(x, 0)$ et $\\mathbf{E}(0,2 x)$ montrent que $f(f(2 x))=f(x+a)+x$ et que $f(f(2 x))=f(2 x+a)$. On en déduit que\n\n$$\nf(2 x+a)=f(f(2 x))=f(x+a)+x\n$$\n\net, si l'on pose $x=-a$, il s'ensuit même que $f(-a)=f(0)-a=0$.\nOn considère alors un réel $x$ quelconque, et on pose $y=-f(-2 x)-a$ puis $z=-x+f(y)$. Comme $f(-a)=0$, l'équation $\\mathbf{E}(-x, y)$ montre que $f(z)-x=f(-a)=0$, c'est-à-dire que $f(z)=x$. La fonction $f$ est donc surjective.\nDémontrons que $f$ est également injective. Soit $x$ et $y$ deux réels tels que $f(x)=f(y)$, et soit $d=y-x$. Soit également $t$ un réel quelconque, et soit $z$ un antécédent de $t$ par $f$. Les équations $\\mathbf{E}(z / 2, x)$ et $\\mathbf{E}(z / 2, y)$ démontrent que\n\n$$\nf(t+x)=f(f(2 z / 2)+x)=f(z / 2+f(x))+z / 2=f(z / 2+f(y))+z / 2=f(t+y)\n$$\n\nSi $d \\neq 0$, cela signifie que $f$ est $d$-périodique, ce qui prouve que $f(2 x)=f(2 x+2 d)=f(2 y)$ et que $f(x+a)=f(x+a+d)=f(y+a)$. Mais alors l'équation $\\mathbf{E}(x, 0)$ indique que\n\n$$\nx=f^{2}(2 x)-f(x+a)=f^{2}(2 y)-f(y+a)=y\n$$\n\ncontredisant le fait que $d \\neq 0$.\nLa fonction $f$ est donc bien injective. Puisque $\\mathbf{E}(0, y)$ montre que $f(f(y))=f(y+a)$, comme on l'a déjà mentionné ci-dessus, il s'ensuit que $f(y)=y+a$ pour tout réel $y$, ce qui conclut.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2019", "problem_label": "6", "tier": 1, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que\n\n$$\nf(x+f(y))+x=f(f(2 x)+y)\n$$\n\npour tous les réels $x$ et $y$.", "solution": "$n^{\\circ} 1$ Comme précédemment, constate que les fonctions de la forme $f$ : $x \\rightarrow x+a$ sont des solutions, et on va montrer que ce sont les seules. À cette fin, on pose $a=f(0)$ et on note $\\mathbf{E}(x, y)$ l'équation\n\n$$\nf(x+f(y))+x=f(f(2 x)+y)\n$$\n\nSoit alors $y$ un nombre réel quelconque, et $x=y+a-f(y)$. Alors\n\n$$\n\\begin{aligned}\nf(f(2 x)+y+a) & =f(f(f(2 x)+y)) & & \\text { d'après } \\mathbf{E}(0, f(2 x)+y) \\\\\n& =f(f(x+f(y))+x) & & \\text { d'après } \\mathbf{E}(x, y) \\\\\n& =f(f(2 x)+x+f(y))-x & & \\text { d'après } \\mathbf{E}(x, x+f(y)) \\\\\n& =f(f(2 x)+y+a)-x & & \\text { car } f(2 x)+y+a=f(2 x)+x+f(y)\n\\end{aligned}\n$$\n\nCela signifie que $x=0$, ou encore que $f(y)=y+a$, ce qui conclut.\nCommentaire des correcteurs De nombreux élèves ont fourni une solution complète. Certaines preuves étaient impressionnantes par leur efficacité! Par ailleurs, aucun élève n'a oublié de vérifier que les solutions trouvées vérifiaient bien l'équation fonctionnelle, ce qui fait très plaisir à voir. Voici, cependant, quelques erreurs qui sont revenues à plusieurs reprises:\n$\\triangleright$ Plusieurs élèves ont raisonné en utilisant la continuité ou la dérivablité de la fonction. Aucune hypothèse concernant la continuité ne figurait dans l'énoncé, et ces raisonnements ne sont donc pas valides. De même, plusieurs élèves ont supposé d'office que $f$ était un polynôme. Enfin, quelques élèves ont tenté d'interpréter, par une phrase, le comportement de $f$ à partir de l'équation de l'énoncé : cependant, comme aucune propriété « évidente » de la fonction $f$ ne se dégageait, ces tentatives se sont toutes avérées infructueuses.\n$\\triangleright$ Quelques élèves ont confondu les notions de surjectivité et d'injectivité : après avoir montré que $f$ était surjective, ils ont opéré des simplifications par $f$ de l'équation en invoquant la surjectivité, alors que cette propriété relève de l'injectivité.\n$\\triangleright$ Lorsqu'il faut composer plusieurs fois par $f$, il peut être judicieux d'employer différentes tailles ou couleurs de parenthésage : plusieurs élèves ont malheureusement fait des erreurs de calcul lors de leurs manipulations en oubliant ou en déplaçant des parenthèses.\nEnfin, dans le cadre d'une équation fonctionnelle, nous recommandons de bien écrire à chaque fois les substitutions effectuées et, si l'on combine différentes équations, de bien écrire quelles équations sont combinées. Ce souci de structure permet non seulement au correcteur de comprendre que l'élève sait ce qu'il fait et de suivre le raisonnement de celuici, mais il permet également à l'élève de ne pas se perdre dans ses équations et faire des erreurs de calcul. En particulier, cela facilite grandement le travail de relecture par l'élève, et l'aidera donc souvent à détecter puis corriger des erreurs de calcul qui lui auraient coûté des points s'il ne les avait pas vues.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 8 |
+
{"year": "2019", "problem_label": "7", "tier": 1, "problem": "Soit $k$ et $n$ deux entiers naturels non nuls, tels que $k \\leqslant 2^{n}$. Morgane a écrit, sur son cahier, l'ensemble des $n$-uplets formés de 0 et de 1 :il y en a $2^{n}$. On dit que deux $n$-uplets $\\left(x_{1}, \\ldots, x_{n}\\right)$ et $\\left(y_{1}, \\ldots, y_{n}\\right)$ sont voisins s'ils ont $n-1$ termes en commun, c'est-à-dire s'il existe un seul entier $i$ tel que $x_{i} \\neq y_{i}$. Puis Morgane choisit $k$ de ces $n$-uplets et les souligne. Elle effectue ensuite les opérations suivantes : lors de chaque opération, elle choisit un $n$-uplet dont deux voisins sont soulignés, et elle souligne également ce $n$-uplet.\nPour quelles valeurs de $k$ Morgane peut-elle parvenir à souligner l'ensemble des $n$-uplets?", "solution": "Dans toute la suite, on assimilera nos $n$-uplets à des vecteurs de $(\\mathbb{Z} / 2 \\mathbb{Z})^{n}$, c'est-à-dire des vecteurs dont les $n$ coordonnées sont des éléments de $\\mathbb{Z} / 2 \\mathbb{Z}$. Ainsi, on note\n$\\triangleright 0$ le vecteur dont toutes les coordonnées sont nulles,\n$\\triangleright \\mathbf{a}_{i}$ le vecteur dont la $i^{\\text {ème }}$ coordonnée vaut 1 et les autres valent 0\n$\\triangleright \\mathbf{b}_{i, j}$ le vecteur dont les $i$ ème et $j^{\\text {ème }}$ coordonnées valent 1 et les autres valent 0 ;\nDans un premier temps, nous allons montrer que l'entier $k=1+\\lceil n / 2\\rceil$ convient, où $\\lceil x\\rceil$ désigne la partie entière supérieure du réel $x$, c'est-à-dire le plus petit entier supérieur ou égal à $x$. Pour ce faire, on peut supposer que Morgane a d'abord souligné les vecteurs $\\mathbf{0}, \\mathbf{b}_{1,2}, \\mathbf{b}_{3,4}, \\ldots, \\mathbf{b}_{2 k-3,2 k-2}$; si $n$ est pair, ce dernier vecteur est le vecteur $\\mathbf{b}_{n-1, n}$ et, si $n$ est impair, par abus de notation, on identifiera le vecteur $\\mathbf{b}_{n, n+1}$ au vecteur $\\mathbf{a}_{n}$. Dans ces conditions:\n$\\triangleright \\operatorname{si} i$ est pair, alors $\\mathbf{a}_{i}$ est voisin des deux vecteurs $\\mathbf{0}$ et $\\mathbf{b}_{i-1, i}$;\n$\\triangleright \\operatorname{si} i$ est impair, avec $i \\leqslant n-1$, alors $\\mathbf{a}_{i}$ est voisin des deux vecteurs $\\mathbf{0}$ et $\\mathbf{b}_{i, i+1}$;\n$\\triangleright \\operatorname{si} i=n$ est impair, alors $\\mathbf{a}_{i}=\\mathbf{a}_{n}=\\mathbf{b}_{2 k-3,2 k-2}$ est déjà souligné.\nAinsi, Morgane peut souligner chacun des vecteurs $\\mathbf{a}_{i}$.\nUne récurrence immédiate sur $\\ell$ permet alors de montrer que Morgane peut souligner tout vecteur dont $\\ell$ coordonnées sont égales à 1 , et les $n-\\ell$ autres sont égales à 0 . On en conclut que tout entier $k$ compris entre $1+\\lceil n / 2\\rceil$ et $2^{n}$ convient.\nRéciproquement, soit $k$ un des entiers recherchés : démontrons que $k \\geqslant 1+\\lceil n / 2\\rceil$. Pour ce faire, on construit d'abord le graphe orienté dont les sommets sont les vecteurs de $(\\mathbb{Z} / 2 \\mathbb{Z})^{n}$ et dont les arêtes sont construites comme suit:\n$\\triangleright$ si un vecteur t était un des $k$ vecteurs que Morgane avait soulignés initialement, alors aucune arête n'arrive en $t$;\n$\\triangleright$ sinon, soit $\\mathbf{u}$ et $\\mathbf{v}$ deux voisins de $\\mathbf{t}$ que Morgane avait soulignés avant de souligner $\\mathbf{t}$ : le graphe contient une arête qui va de $\\mathbf{u}$ vers $t$, et une autre arête qui va de $\\mathbf{v}$ vers $t$.\nIntroduisons maintenant quelques notions et concepts. On dit qu'un ensemble $S$ de vecteurs est un ensemble initial si toute arête entrant en un sommet de $S$ provient d'un autre sommet de $S$. On dit également que $S$ est connexe si, quitte à prendre les arêtes dans le mauvais sens, on peut relier n'importe quel vecteur de $S$ à n'importe quel autre sans sortir de $S$. En outre, on dit que les sources de $S$ sont les vecteurs de $S$ que Morgane avait soulignés initialement, c'est-à-dire ceux en lesquels n'entre aucune arête. Enfin, on dit qu'une coordonnée $i$ est une variable de $S$ s'il existe deux vecteurs $\\mathbf{t}$ et $\\mathbf{t}^{\\prime}$ de $S$ tels que $\\mathbf{t}_{i} \\neq \\mathbf{t}_{i}^{\\prime}$.\nNous allons maintenant démontrer la propriété $\\mathcal{P}_{\\ell}$ par récurrence forte sur $\\ell$ :\nSoit $S$ un ensemble initial connexe contenant $\\ell$ vecteurs et $m$ sources. Alors $S$ a au plus $2(m-1)$ coodonnées variables.\nTout d'abord, la propriété $\\mathcal{P}_{1}$ est évidente, puisque $S$ est alors réduit à un seul vecteur, qui est lui-même une source, et n'a donc aucune coordonnée variable. Soit maintenant $\\ell \\geqslant 2$\nun entier tel que les propriétés $\\mathcal{P}_{1}, \\ldots, \\mathcal{P}_{\\ell-1}$ soient toutes vraies, et soit $S$ un ensemble initial connexe contenant $\\ell$ vecteurs, $m$ sources, et $c$ coordonnées variables.\nNotons $\\mathbf{t}$ le dernier vecteur, parmi ceux appartenant à $S$, que Morgane a souligné. Si t est une source, c'est que $S$ n'est formé que de sources, dont ne contient aucune arête, en contradiction avec le fait que $S$ soit connexe et que $\\ell \\geqslant 2$. Ainsi, il existe deux arêtes $\\mathbf{u} \\rightarrow \\mathbf{t}$ et $\\mathbf{v} \\rightarrow \\mathbf{t}$, provenant de deux autres vecteurs $\\mathbf{u}$ et $\\mathbf{v}$ de $S$. Soit $i$ et $j$ les deux coordonnées telles que $\\mathbf{t}_{i} \\neq \\mathbf{u}_{i}$ et $\\mathbf{t}_{j} \\neq \\mathbf{v}_{j}$, et soit $S^{\\prime}$ l'ensemble $\\backslash \\backslash\\{\\mathbf{t}\\}$.\n$\\triangleright$ Si $S^{\\prime}$ est connexe, on constate aisément que les coordonnées variables de $S$ sont celles de $S^{\\prime}$. Puisque $S^{\\prime}$ contient $\\ell-1$ sommets et $m$ sources, les ensembles $S$ et $S^{\\prime}$ ont donc bien $2(m-1)$ coordonnées variables au maximum.\n$\\triangleright$ Si $S^{\\prime}$ n'est pas connexe, alors on peut le couper en deux ensembles initiaux connexes, $U$ et $V$, qui contiennent respectivement les vecteurs $\\mathbf{u}$ et $\\mathbf{v}$. L'un contient $\\ell_{u}$ vecteurs, $m_{u}$ sources, et $c_{u}$ coordonées variables, tandis que l'autre contient $\\ell_{v}$ vecteurs, $m_{v}$ sources, et $c_{v}$ coordonées variables. Puisque $\\ell_{u} \\leqslant \\ell-1$ et $\\ell_{v} \\leqslant \\ell-1$, on sait que $c_{u} \\leqslant 2\\left(m_{u}-1\\right)$ et que $c_{v} \\leqslant 2\\left(m_{v}-1\\right)$.\nOr, les sources de $S$ sont celles de $U$ et de $V$, et nulle source ne peut appartenir à la fois à $U$ et à $V$, de sorte que $m=m_{u}+m_{v}$. D'un autre côté, on constate aisément que les coordonnées variables de $S$ sont soit celles de $U$, soit celles de $V$, soit $i$ et $j$. Ainsi, l'ensemble $S$ a au plus $c_{u}+c_{v}+2 \\leqslant 2\\left(m_{u}+m_{v}-1\\right)=2(m-1)$ coordonnées variables, ce qui démontre $\\mathcal{P}_{\\ell}$.\nRemarquons enfin que l'ensemble $(\\mathbb{Z} / 2 \\mathbb{Z})^{n}$ lui-même est un ensemble initial connexe, et qu'il contient $n$ variables et $k$ sources. La propriété $\\mathcal{P}_{2^{n}}$ montre donc que $n \\leqslant 2(k-1)$, c'est-à-dire que $k \\geqslant 1+\\lceil n / 2\\rceil$. Les entiers recherchés sont donc bien les entiers compris entre $1+\\lceil n / 2\\rceil$ et $2^{n}$.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 9 |
+
{"year": "2019", "problem_label": "7", "tier": 1, "problem": "Soit $k$ et $n$ deux entiers naturels non nuls, tels que $k \\leqslant 2^{n}$. Morgane a écrit, sur son cahier, l'ensemble des $n$-uplets formés de 0 et de 1 :il y en a $2^{n}$. On dit que deux $n$-uplets $\\left(x_{1}, \\ldots, x_{n}\\right)$ et $\\left(y_{1}, \\ldots, y_{n}\\right)$ sont voisins s'ils ont $n-1$ termes en commun, c'est-à-dire s'il existe un seul entier $i$ tel que $x_{i} \\neq y_{i}$. Puis Morgane choisit $k$ de ces $n$-uplets et les souligne. Elle effectue ensuite les opérations suivantes : lors de chaque opération, elle choisit un $n$-uplet dont deux voisins sont soulignés, et elle souligne également ce $n$-uplet.\nPour quelles valeurs de $k$ Morgane peut-elle parvenir à souligner l'ensemble des $n$-uplets?", "solution": "$n^{\\circ} 1$ On démontre comme ci-dessus que tout entier $k \\geqslant 1+\\lceil n / 2\\rceil$ convient, et il ne nous reste maintenant plus qu'à montrer que l'on doit nécessairement avoir $k \\geqslant 1+\\lceil n / 2\\rceil$. Pour ce faire, on va procéder par récurrence sur $n$.\nTout d'abord, pour $n=1$ et $n=2$, si Morgane ne souligne qu'un seul vecteur, aucun des autres vecteurs non soulignés ne pourra avoir deux voisins soulignés. On en déduit, dans ces cas-là, que $k \\geqslant 2$, c'est-à-dire que $k \\geqslant 1+\\lceil n / 2\\rceil$.\nSupposons maintenant que $n \\geqslant 3$, et que Morgane a souligné $k$ vecteurs, de sorte qu'elle pourra ensuite parvenir à souligner chacun des $2^{n}-k$ vecteurs restants. Morgane numérote alors les $2^{n}$ vecteurs dans l'ordre dans lequel elle les a soulignés : elle peut donc choisir les vecteurs $v_{1}, \\ldots, v_{k}$ de manière arbitraire, et elle pourra ensuite souligner les vecteurs $v_{k+1}, \\ldots, v_{2^{n}}$. En particulier, on constate que, pour tout $\\ell \\leqslant k+1$, le vecteur $v_{\\ell}$ est voisin de deux vecteurs $v_{i}$ et $v_{j}$ tels que $1 \\leqslant i<j<\\ell$.\nSoit alors $i$ et $j$ deux entiers tels que $1 \\leqslant i<j \\leqslant k$ et tels que $v_{i}$ et $v_{j}$ soient tous les deux voisins du vecteur $v_{k+1}$. Soit ensuite $s$ et $t$ les deux coordonnées en lesquelles les vecteurs $v_{i}$ et $v_{j}$ diffèrent l'un de l'autre. Morgane décide alors d'effacer les coordonnées $s$ et $t$ de l'ensemble des $2^{n}$ vecteurs.\nElle se retrouve ainsi avec $2^{n-2}$ vecteurs à $n-2$ coordonnées, chacun étant présent en quatre exemplaires. Notons $\\phi(v)$ le vecteur à $n-2$ coordonnées obtenu en effaçant les coordonnées $s$ et $t$ du vecteur $v$. Parmi les $2^{n-2}$ vecteurs obtenus, Morgane décide, initialement, de souligner les vecteurs $\\phi\\left(v_{1}\\right), \\phi\\left(v_{2}\\right), \\ldots, \\phi\\left(v_{k}\\right)$ : puisque $\\phi\\left(v_{i}\\right)=\\phi\\left(v_{j}\\right)$, elle a souligné au plus $k-1$ vecteurs.\nEn outre, si deux vecteurs $v$ et $v^{\\prime}$, à $n$ coordonnées, sont voisins l'un de l'autre, alors les vecteurs $\\phi(v)$ et $\\phi\\left(v^{\\prime}\\right)$ sont soit égaux, soit voisins. Ainsi, Morgane peut toujours souligner,\ndans cet ordre, les vecteurs $\\phi\\left(v_{k+1}\\right)$ - qui est égal à $\\phi\\left(v_{i}\\right)$ et à $\\phi\\left(v_{j}\\right)$ - puis $\\phi\\left(v_{k+2}\\right), \\ldots, \\phi\\left(v_{2^{n}}\\right)$, quitte à resouligner un vecteur déjà souligné.\nPar conséquent, en soulignant au départ $k-1$ vecteurs à $n-2$ coordonnées, Morgane est bien parvenue à souligner l'intégralité des $2^{n-2}$ vecteurs à $n-2$ coordonnées. L'hypothèse de récurrence indique donc que $k-1 \\geqslant\\lceil(n-2) / 2\\rceil+1$, c'est-à-dire que $k \\geqslant\\lceil n / 2\\rceil+1$, ce qui conclut.\n\nCommentaire des correcteurs Cet exercice très difficile se composait de deux parties :\n$\\triangleright$ Tout d'abord, il fallait constater, puis démontrer, que $k=\\lceil n / 2\\rceil+1$ convenait.\n$\\triangleright$ Puis il fallait démontrer qu'on ne pouvait pas faire mieux.\nLa première partie était déjà difficile. De nombreux élèves ont remarqué que $k=n$ convenait, sauf pour $n=1$, et ont ensuite tenté (en vain!) de démontrer qu'on ne pouvait pas faire mieux, en procédant par récurrence sur $n$. Le fait que la borne proposée, et donc le prototype de récurrence sur $n$, ne fonctionne pas pour $n=1$, aurait pu être un indice qu'il fallait rechercher une autre solution.\nPar ailleurs, les correcteurs ont constaté avec plaisir que, parmi les élèves ayant obtenu une des deux bornes $k=n$ ou bien $k=\\lceil n / 2\\rceil+1$, la quasi-totalité a réussi à démontrer que leur construction fonctionnait effectivement.\nLa seconde partie, quant à elle, était manifestement très difficile. Par conséquent, seul un élève est parvenu à démontrer que l'on ne pouvait effectivement pas faire mieux que $k=$ $\\lceil n / 2\\rceil+1$.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2019-2020-corrigé-test-novembre.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "problem_label": "1", "tier": 1, "problem": "Soit $A B C$ un triangle dont tous les angles sont aigus, avec $A B \\neq A C$. Soit $\\Gamma$ le cercle circonscrit à $A B C$, et $D$ le milieu de l'arc $\\widehat{B C}$ ne contenant pas $A$. Soit $E$ et $F$ des points appartenant respectivement aux segments $[A B]$ et $[A C]$, de sorte que $A E=A F$. Soit $P$ le point d'intersection, autre que $A$, entre $\\Gamma$ et le cercle circonscrit à $A E F$.\nSoit $G$ et $H$ les points d'intersection respectifs, autres que $P$, entre $\\Gamma$ et les droites $(P E)$ et $(P F)$. Enfin, soit $J$ le point d'intersection entre les droites $(A B)$ et $(D G)$, et soit $K$ le point d'intersection entre les droites $(A C)$ et $(D H)$.\nDémontrer que le milieu du segment $[B C]$ appartient à la droite $(J K)$.", "solution": "Commençons par tracer une figure, et notons $X$ le milieu de $[B C]$, que l'on espère être également le point d'intersection des droites $(B C)$ et $(J K)$. Sans perte de généralité, on suppose également que $A B>A C$.\n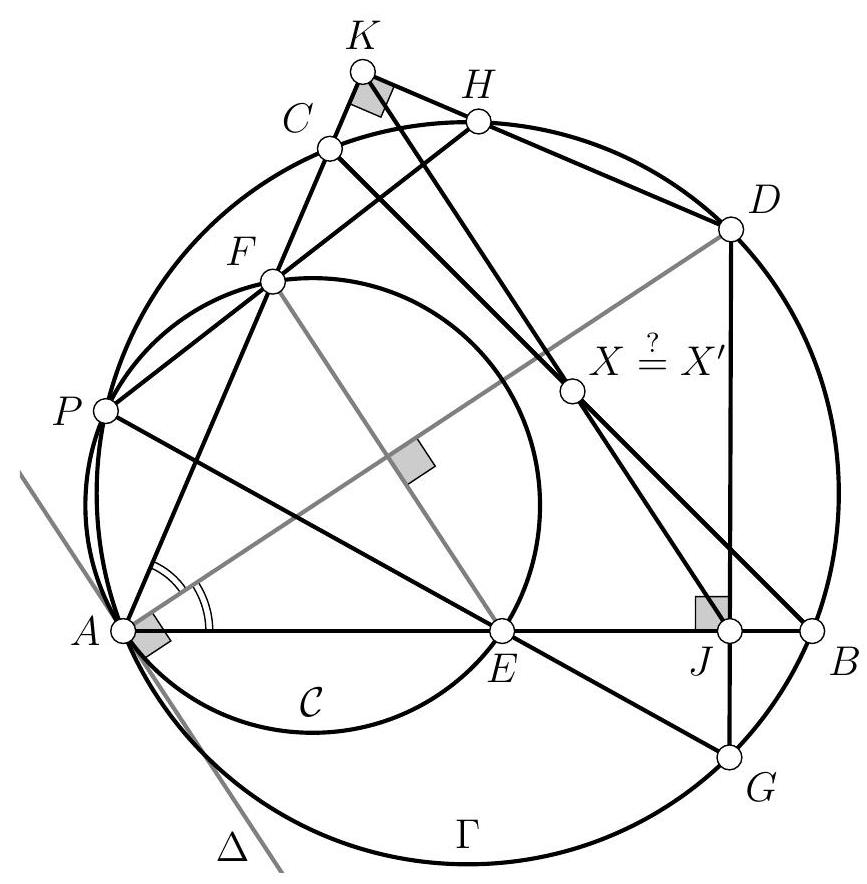\n\nUne première remarque que l'on peut formuler est que, puisque les arcs $\\widehat{B D}$ et $\\widehat{D C}$ ont même mesure, les angles $\\widehat{B A D}$ et $\\widehat{D A C}$ sont en fait égaux. Cela signifie que la droite $(A D)$ est la bissectrice de l'angle $\\widehat{B A C}$; plus précisément, le point $D$ est en fait le pôle Sud de $A$ dans le triangle $A B C$. On s'empresse donc de dessiner cette bissectrice, d'autant plus que l'égalité $A E=E F$ revient alors à dire que les points $E$ et $F$ sont en fait symétriques par rapport à la droite ( $A D$ ).\nUne seconde remarque frappante est que l'angle $\\widehat{A J D}$ semble droit. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites :\n\n$$\n(A J, D J)=(A J, P G)+(P G, D J)=(A E, P E)+(P G, D G)=(A E, P E)+(P A, A D)\n$$\n\nPour aller plus loin, on voudrait remplacer l'angle $(A E, P E)$ par un angle faisant intervenir la droite $(P A)$. On utilise alors le cas limite du théorème de l'angle au centre, comme suit.\nSoit $\\mathcal{C}$ le cercle circonscrit à $A E F$ et $\\Delta$ sa tangente en $A$. Alors on sait que $(A E, P E)=$ $(\\Delta, P A)$, et donc que $(A J, D J)=(\\Delta, A D)$. Or, la droite $(A D)$ est un axe de symétrie de $\\mathcal{C}$, et elle est donc perpendiculaire à $\\Delta$. Comme souhaité, on a donc $(A J, D J)=90^{\\circ}$.\n\nMais alors $J$ et $K$ sont les projetés orthogonaux de $D$ sur les droites $(A B)$ et $(A C)$. Puisque $D$ appartient à la bissectrice de $\\widehat{B A C}$, on a donc $D J=D K$ et $A J=A K$. Par ailleurs, comme $A$ est le milieu de l'arc $\\overparen{B C}$, on sait que $B D=C D$. Les triangles $B J D$ et $C K D$ étant respectivement rectangles en $J$ et en $K$, ils sont donc isométriques.\nPuisque $A C=|x \\pm y|, A B=|x \\pm y|$ et $A B>A C, \\mathrm{c}^{\\prime}$ est donc que $A B=x+y$ et $A C=|x-y|$. Autrement dit, on a $\\overrightarrow{A C}=(1-y / x) \\overrightarrow{A K}$ et $\\overrightarrow{A B}=(1+y / x) \\overrightarrow{A J}$. Mais alors\n\n$$\n\\overrightarrow{A X}=(\\overrightarrow{A B}+\\overrightarrow{A C}) / 2=(1-y / x) \\overrightarrow{A K} / 2+(1+y / x) \\overrightarrow{A J} / 2=\\overrightarrow{A X}+\\overrightarrow{X K}+(1+y / x) \\overrightarrow{K J} / 2\n$$\n\nce qui signifie que $\\overrightarrow{K X}=(1+y / x) \\overrightarrow{K J} / 2$, et donc que $X$ se trouve bien sur la droite $(J K)$, comme on devait le démontrer.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ On propose une autre façon de terminer le problème une fois que l'on a obtenu que les angles $\\widehat{A J D}$ et $\\widehat{A K D}$ sont droits.\nComme $(A J, D J)=90^{\\circ}=(D K, A K)$, les points $K, A, J$ et $D$ sont cocycliques. Soit alors $X^{\\prime}$ le point d'intersection des droites $(B C)$ et $(J K)$. Puisque\n\n$$\n\\left(D K, K X^{\\prime}\\right)=(D K, K J)=(D A, A J)=(D A, A B)=(D C, C B)=\\left(D C, C X^{\\prime}\\right)\n$$\n\nles points $D, C, K$ et $X^{\\prime}$ sont eux aussi cocycliques.\nMais alors $\\left(C X^{\\prime}, X^{\\prime} D\\right)=(C K, K D)=90^{\\circ}$, donc $X^{\\prime}$ est en fait le projeté orthogonal de $D$ sur la droite $(B C)$. Comme $D$ se trouve sur la médiatrice du segment $[B C]$, le point $X^{\\prime}$ est donc le milieu de ce segment, ce qui conclut.\n$\\underline{\\text { Solution alternative } n^{\\circ} 2}$ On propose une troisième façon de terminer le problème : il s'agit là d'une variante de la solution alternative $\\mathrm{n}^{\\circ} 1$.\nPuisque $B D=C D$, le point $X$ est également le projeté orthogonal de $D$ sur la droite $(B C)$. Mais alors, puisque $D$ appartient au cercle circonscrit à $A B C$, les points $J, K$ et $X$ sont en fait alignés sur la droite de Simson de $D$, ce qui conclut.\n\nCommentaire des correcteurs Le problème a été bien réussi. Cependant, quelques erreurs sont revenues fréquemment:\n$\\triangleright$ Plusieurs élèves ont introduit le point $X^{\\prime}$ avant d'avoir démontré que les droites $(J K)$ et $(B C)$ avaient effectivement un point d'intersection. Pour certaines preuves, cette omission pouvait se montrer assez pénalisante.\nUne façon efficace de traiter toutes les configurations, et donc d'éliminer ces cas pathologiques pénalisants, était d'utiliser des angles orientés, voire des angles de droites orientés, ce que peu d'élèves ont pensé à faire.\n$\\triangleright$ Plusieurs élèves ont confondu les points $X$ et $X^{\\prime}$, puisque ceux-ci apparaissaient au même endroit sur leur figure. Par exemple, après avoir défini le point $X^{\\prime}$, ils ont utilisé le fait qu'il s'agissait du milieu de $[B C]$, alors que c'est justement la propriété qu'il fallait démontrer! Une telle erreur, si elle se comprend aisément, s'est néanmoins avérée rédhibitoire dès qu'elle survenait, puisqu'elle mettait un terme à la démonstration.\nPar ailleurs, beaucoup d'élèves montrent une bonne culture, en reconnaissant dans la figure un pôle Sud, une similitude, un point de Miquel ou la droite de Simson relative au point $D$. On a également pu voir de très jolies figures! À l'inverse, un élève, qui avait pourtant fourni une solution correcte à l'exercice, n'a fourni qu'un simple schéma à main levée plutôt qu'une figure complète à la règle et au compas. Par conséquent, et au lieu des 7 points qui lui tendaient les bras, il s'est vu attribuer la note de $0 / 7$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Chaque case d'un tableau de taille $8 \\times 8$ peut être coloriée en blanc ou en noir, de telle sorte que chaque rectangle de taille $2 \\times 3$ ou $3 \\times 2$ contient deux cases noires ayant un côté en commun. Déterminer le nombre minimal de cases noires qu'il peut y avoir sur le tableau.", "solution": "Comme d'habitude dans ce genre de problèmes, on commence par rechercher des bornes supérieures (en exhibant une configuration) et inférieures (par des arguments de double comptage et/ou de pavage) sur le nombre minimal de cases noires que doit contenir le tableau.\nPar exemple, la configuration ci-dessous (à gauche) nous assure que 28 cases noires sont suffisantes; en effet, tout rectangle vertical (de taille $3 \\times 2$ ) contient deux cases sur l'une des lignes 3 ou 6 , et tout rectangle horizontal (de taille $2 \\times 3$ ) contient deux cases sur l'une des colonnes 3 ou 6. D'autre part, chacun des 10 rectangles du pavage partiel ci-dessous (à droite) doit contenir au moins 2 cases noires, de sorte que 20 cases noires ont nécessaires.\nMalheureusement, ces deux bornes ne sont pas égales l'une à l'autre. Il nous faut donc chercher à les améliorer toutes les deux jusqu'à les rendre égales.\n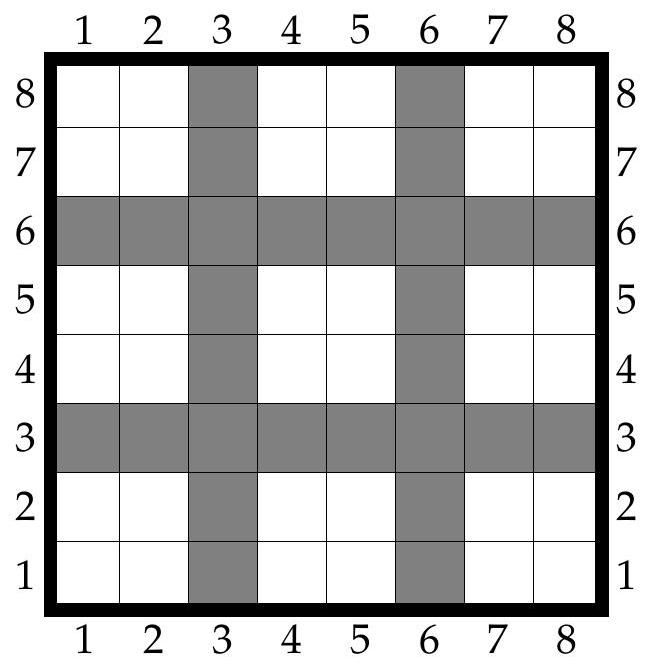\n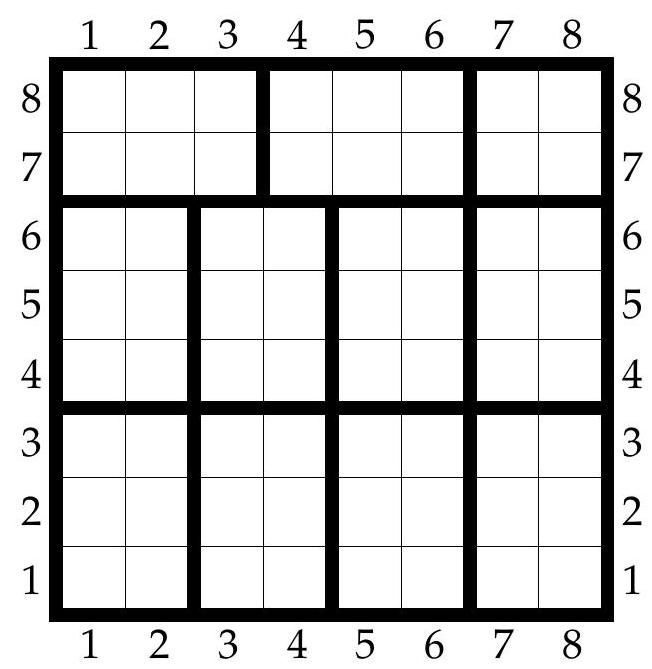\n\nEn tâtonnant, on finit par trouver une nouvelle configuration satisfaisant les conditions de l'énoncé, mais qui ne contient que 24 cases noires. Il s'agit de la configuration ci-dessous.\n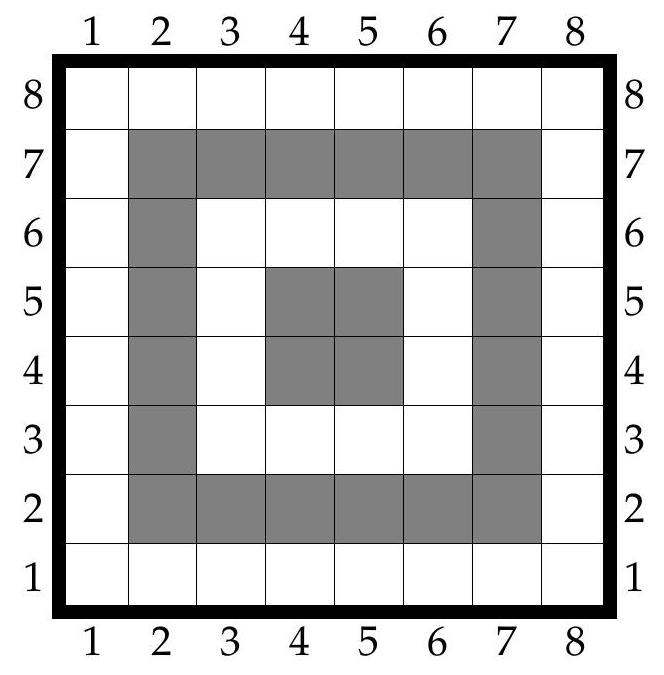\n\nD'autre part, utiliser un simple pavage par des rectangles semble un peu trop brutal pour nous indiquer la meilleure borne inférieure possible sur le nombre de cases noires nécessaires. On étudie un rectangle quelconque donné :\n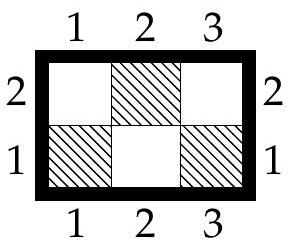\n\nOn constate ici que, parmi les 3 cases hachurées, au moins une doit être une case noire, ce sans quoi notre rectangle ne contiendra jamais deux cases noires adjacentes. En particulier, la case en ligne 1 , colonne 2 a nécessairement une voisine noire au sein de ce rectangle. De même, la case en ligne 2, colonne 2 , a aussi une voisine noire au sein de notre rectangle.\nForts de ce constat, on s'intéresse, pour chaque case $c$ de l'échiquier, au nombre minimal de voisines noires que possède la case $c$ :\n$\\triangleright$ si $c$ est un des quatre coins, a priori, elle pourrait n'avoir aucune voisine noire (c'est d'ailleurs le cas dans notre configuration précédente);\n$\\triangleright$ si $c$ est une des $2 \\times 6=12$ cases situées sur le côté haut ou bas, elle appartient à la colonne centrale d'un rectangle horizontal, donc elle a au moins une voisine noire;\n$\\triangleright$ de même, si $c$ est une des $2 \\times 6=12$ cases situées sur le côté gauche ou droit, elle appartient à la ligne centrale d'un rectangle vertical, donc elle a au moins une voisine noire;\n$\\triangleright$ enfin, si $c$ est une des $6 \\times 6=36$ cases situées au centre de l'échiquier, elle a déjà une voisine noire au minimum (disons $d$ ) ; mais alors $c$ appartient également à la colonne (respectivement, à la ligne) d'un autre rectangle horizontal (resp., vertical) ne contenant pas $d$, donc $c$ a une deuxième voisine noire.\nEn conclusion, on dispose en fait d'au moins $12+12+36 \\times 2=96$ paires $(c, d)$ de cases adjacentes telles que $d$ est une case noire. Or, chaque case noire a au plus quatre voisines, donc appartient à au plus quatre telles paires. On a donc au moins $96 / 4=24$ cases noires sur notre échiquier, ce qui rejoint la borne supérieure trouvée précédemment, et conclut donc.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2019", "problem_label": "2", "tier": 1, "problem": "Chaque case d'un tableau de taille $8 \\times 8$ peut être coloriée en blanc ou en noir, de telle sorte que chaque rectangle de taille $2 \\times 3$ ou $3 \\times 2$ contient deux cases noires ayant un côté en commun. Déterminer le nombre minimal de cases noires qu'il peut y avoir sur le tableau.", "solution": "$n^{\\circ} 1$ Voici une autre manière de démontrer que 24 cases noires sont nécessaires une fois que l'on sait que chaque case située au centre de l'échiquier a au moins deux voisines noires. En effet, cela signifie que chaque occurrence du motif représenté ci-dessous doit contenir au moins deux cases noires.\n\n\nOn peut alors placer de tels motifs à trois ou à quatre cases, sans recouvrement, dans notre échiquier $8 \\times 8$, par exemple en procédant comme suit : dans le dessin ci-dessous, on relie les centres des cases appartenant à un même motif.\n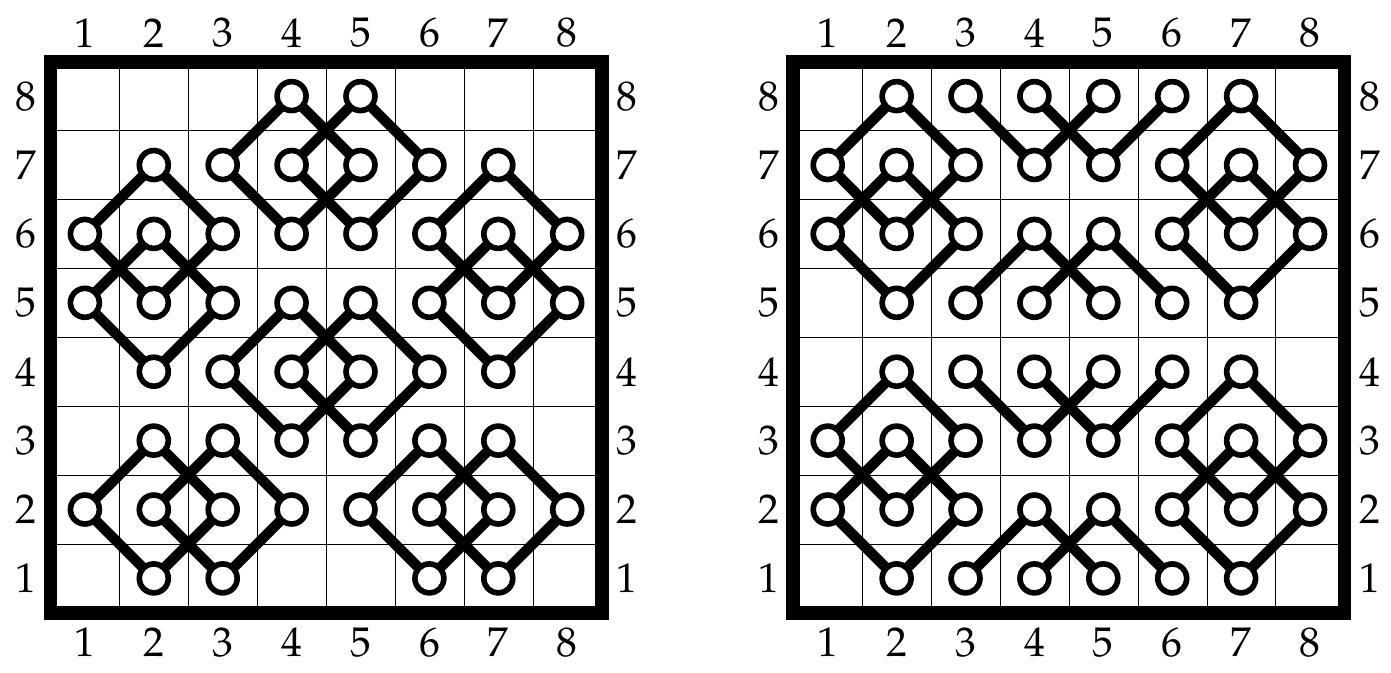\n\nOn a donc réussi à placer dans l'échiquier 12 exemplaires de notre motif à quatre cases, ou bien 8 exemplaires du motif à quatre cases et 8 exemplaires du motif à trois cases, ne se chevauchant pas. Dans chaque cas, ces motifs contiennent bien un total de 24 cases noires au minimum, ce qui conclut.\n\nCommentaire des correcteurs L'exercice a été globalement bien réussi compte tenu de son niveau de difficulté. Identifier une configuration à 24 cases noires était peu évident, et de nombreaux élèves y sont cependant parvenus. Montrer que l'on ne pouvait pas faire mieux était ensuite très difficile. Par ailleurs, de nombreux élèves ont commis plusieurs erreurs évitables, que nous récapitulons ci-dessous.\n$\\triangleright$ Ce n'est pas parce qu'une configuration adéquate (telle que tout rectangle $2 \\times 3$ ou $3 \\times 2$ contient deux cases noires adjacentes) est minimale pour l'inclusion (c'est-à-dire que, si on retire n'importe quelle case noire, notre configuration ne sera plus adéquate) qu'elle est également minimale pour le nombre de cases noires utilisées.\nOn laisse ainsi au lecteur le plaisir de vérifier que la première configuration mentionnée dans cette solution, et qui contenait 28 cases, était bien une configuration adéquate minimale pour l'inclusion, mais manifestement pas pour le nombre de cases noires utilisées.\n$\\triangleright$ Ce n'est pas parce qu'une configuration adéquate est minimale que, sur toute partie extraite de l'échiquier $8 \\times 8$, elle induit encore une configuration minimale. Un exemple évident de ce phénomène apparaît si la partie en question est un carré $2 \\times 2$, puisque aucun carré noir n'est alors nécessaire.\n$\\triangleright$ Ce n'est pas parce que l'échiquier est invariant selon certaines symétries axiales ou rotations qu'une configuration adéquate minimale est également invariante selon ces transformations. Par exemple, dans le cas d'un échiquier $3 \\times 3$, on montre aisément que la configuration ci-dessous est minimale, et elle n'est pourtant pas invariante par rotation, ou par de nombreuses symétries axiales.\n", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2019", "problem_label": "3", "tier": 1, "problem": "Soit $P_{1}, P_{2}, \\ldots, P_{2019}$ des polynômes non constants à coefficients réels tels que\n\n$$\nP_{1}\\left(P_{2}(x)\\right)=P_{2}\\left(P_{3}(x)\\right)=\\ldots=P_{2019}\\left(P_{1}(x)\\right)\n$$\n\npour tout réel $x$. Démontrer que $P_{1}=P_{2}=\\ldots=P_{2019}$.", "solution": "Nous allons en fait démontrer le résultat plus général suivant : si $P_{1}, \\ldots, P_{2 n+1}$ sont des polynômes non constants à coefficients réels et tels que $P_{1} \\circ P_{2}=$ $P_{2} \\circ P_{3}=\\ldots=P_{2 n+1} \\circ P_{1}$, alors $P_{1}=\\ldots=P_{2 n+1}$. Par commodité, dans la suite, on pose $P_{2 n+1+k}=P_{k}$ pour tout $k \\geqslant 1$.\nTout d'abord, on note $d_{k}$ le degré de $P_{k}$. Puisque $P_{k} \\circ P_{k+1}$ est un polynôme de degré $d_{k} d_{k+1}$, $c^{\\prime}$ est que $d_{k} d_{k+1}=d_{k+1} d_{k+2}$, et donc $d_{k}=d_{k+2}$, pour tout $k$. On en déduit que tous les polynômes $P_{k}$ ont degré $d_{1}$, et on pose simplement $d=d_{1}$.\nEnsuite, soit $p_{k}$ le coefficient dominant de $P_{k}$, c'est-à-dire son coefficient de degré $d$, et posons $q_{k}=p_{k} / p_{k+1}$. Le coefficient dominant de $P_{k} \\circ P_{k+1}$ est égal à $p_{k} p_{k+1}^{d}$. On en déduit que $p_{k} p_{k+1}^{d}=$ $p_{k+1} p_{k+2}^{d}$ , c'est-à-dire que $q_{k}=q_{k+1}^{-d}$. Mais alors\n\n$$\n1=\\prod_{i=k+1}^{k+2 n+1} q_{i}=q_{k}^{s}\n$$\n\noù l'on a posé\n\n$$\ns=\\sum_{i=0}^{2 n}(-d)^{i} \\equiv 1 \\quad(\\bmod 2) .\n$$\n\nPuisque $s$ est un entier impair, $\\mathrm{c}^{\\prime}$ est donc que $q_{k}=1$. Cela signifie donc que tous les polynômes $P_{k}$ sont de coefficient dominant $p_{1}$, et on pose simplement $p=p_{1}$.\nSupposons maintenant que $d=1$. Dans ce cas, on peut écrire chaque polynôme $P_{k}$ sous la forme $P_{k}(X)=p X+b_{k}$, et alors $P_{k}\\left(P_{k+1}(X)\\right)=p^{2} X+p b_{k+1}+b_{k}$. On pose alors $c_{k}=b_{k+1}-b_{k}$, et puisque l'énoncé indique entre autres que $p b_{k+1}+b_{k}=p b_{k+2}+b_{k+1}$, cela signifie en fait que $c_{k}=-p c_{k+1}$. Là encore, on en déduit que $c_{k}=(-p)^{2 n+1} c_{k}$, de sorte que $c_{k}=0$ pour tout $k$, ou bien que $p=-1$; mais, dans ce second cas, on a tout de même $c_{k}=c_{k+1}$ pour tout $k$, de sorte que $0=\\sum_{i=1}^{2 n+1} c_{i}=(2 n+1) c_{k}$ et que l'on a $c_{k}=0$ de toute façon. Ainsi, quand $d=1$, les polynômes $P_{k}$ sont bien égaux deux à deux.\nSupposons enfin que $d \\geqslant 2$. On note $p_{k, \\ell}$ le coefficient de $P_{k}$ de degré $\\ell$, et on va prouver par récurrence sur $d-\\ell$ que $p_{k, \\ell}=p_{1, \\ell}$. Tout d'abord, pour $\\ell=d$, on a bien $p_{k, d}=p=p_{1, d}$. On suppose donc maintenant que $p_{k, m}=p_{1, m}$ pour tout entier $m \\geqslant \\ell+1$, et on étudie le coefficient de degré $d^{2}-d+\\ell$ du polynôme $P_{k} \\circ P_{k+1}$. En écrivant $A \\approx B$ dès lors que deux polynômes $A$ et $B$ ont même coefficient de degré $d^{2}-d+\\ell$, on constate que\n\n$$\n\\begin{aligned}\nP_{k}\\left(P_{k+1}(X)\\right) & =\\sum_{i=0}^{d} p_{k, i}\\left(\\sum_{j=0}^{d} p_{k+1, j} X^{j}\\right)^{i} \\\\\n& \\approx p\\left(\\sum_{j=0}^{d} p_{k+1, j} X^{j}\\right)^{d}+p_{k, d-1}\\left(\\sum_{j=0}^{d} p_{k+1, j} X^{j}\\right)^{d-1} \\\\\n& \\approx p\\left(p_{k+1, \\ell} X^{\\ell}+\\sum_{j=\\ell+1}^{d} p_{1, j} X^{j}\\right)^{d}+p_{k, d-1}\\left(p X^{d}\\right)^{d-1} \\\\\n& \\approx d p_{k+1, \\ell} p^{d} X^{d^{2}-d+\\ell}+p\\left(\\sum_{j=\\ell+1}^{d} p_{1, j} X^{j}\\right)^{d}+p_{k, d-1} p^{d-1} X^{d^{2}-d}\n\\end{aligned}\n$$\n\nPour $\\ell \\geqslant 1$, on en déduit que $d p_{k+1, \\ell} p^{d}=d p_{1, \\ell} p^{d}$, ce qui signifie bien que $p_{k+1, \\ell}=p_{1, \\ell}$. Puis, pour $\\ell=0$, on en déduit aussi que $d p_{k+1,0} p^{d}+p_{k, d-1}=d p_{1,0} p^{d}+p_{2 n+1, d-1}$. Or, puisque $d \\geqslant 2$, quand on en arrive à étudier le cas $\\ell=0$, on sait déjà que $p_{k, d-1}=p_{2 n+1, d-1}$. On en déduit donc comme prévu que $p_{k+1,0}=p_{1,0}$, ce qui conclut.\n\nCommentaire des correcteurs Ce problème était extrêmement difficile, et y obtenir des points était donc ardu. Malheureusement, plusieurs élèves ont perdu ces points si durement acquis en commettant des erreurs évitables, que nous listons ci-dessous :\n$\\triangleright$ De nombreux élèves ont confondu la composée et le produit de deux polynômes. Ainsi, la composée $P \\circ Q$ de deux polynômes $P$ et $Q$ de degrés $d$ et $d^{\\prime}$ est un polynôme de degré $d \\times d^{\\prime}$, et non pas $d+d^{\\prime}$. De même, si $P$ et $Q$ sont de coefficients dominants $p$ et $q$, alors le coefficient dominant de $P \\circ Q$ est $p \\times q^{d}$, et non pas $p \\times q$. Enfin, les polynômes $P \\circ(Q+R)$ et $(P \\circ Q)+(P \\circ R)$ sont, dans le cas général, des polynômes distincts l'un de l'autre.\n$\\triangleright$ Certains élèves n'ont pas démontré que les polynômes $P_{i}$ avaient même degré, affirmant qu'il s'agissait là d'une évidence. Cependant, cette affirmation dépendait de l'imparité de 2019, ce qui la rendait nettement moins évidente : il faut éviter de perdre bêtement 1 point pour économiser une ligne de rédaction.\n$\\triangleright$ Il est recommandé de ne pas appeler $P^{\\prime}$ un polynôme que l'on introduit, car $P^{\\prime}$ désigne déjà le polynôme dérivé de $P$. Une telle notation peut donc prêter à confusion, pour le correcteur mais aussi pour l'élève lui-même !", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-1.jsonl
ADDED
|
@@ -0,0 +1,4 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Une grille de dimensions $20 \\times 20$ est divisée en 400 cases unité de dimensions $1 \\times 1$. Clara colorie chaque case en blanc ou en noir, puis Isabelle découpe la grille en rectangles dont les côtés sont contenus dans la grille. Chacun de ces rectangles doit contenir au plus 2 cases noires, et elle donne un chocolat à Clara à chaque fois qu'elle découpe un rectangle qui contient 0 ou 1 case noire.\nIsabelle choisit son découpage de manière à donner le moins de chocolats possibles à Clara, et Clara choisit son coloriage initial de manière à obtenir le plus de chocolats possibles d'Isabelle. Combien de chocolats Isabelle donnera-t-elle à Clara?", "solution": "Nous allons démontrer pour tout entier $n \\geqslant 3$ que, si Clara et Isabelle jouent sur une grille de dimensions $n \\times n$, Isabelle donnera $n$ chocolats à Clara.\nTout d'abord, pour limiter le nombre de chocolats qu'elle donnera à Clara, Isabelle peut procéder comme suit. Elle commence par découper le rectangle en $n$ lignes, et s'apprête à subdiviser chaque ligne en rectangles. Pour ce faire, elle numérote les cases noires de la ligne de gauche à droite, puis elle donne un coup de ciseaux juste à droite de chacune des cases noires $\\mathrm{n}^{\\circ} 2,4,6, \\ldots$ Ce faisant, tous les rectangles obtenus, sauf éventuellement le dernier, comptent deux cases noires. Ainsi, Isabelle donne au plus $n$ chocolats à Clara.\n\n\nRéciproquement, supposons que Clara colorie sa grille $n \\times n$ avec le coloriage suivant, où nous avons distingué avec deux niveaux de gris les cases que Clara colorie en noir, et où $k$ et $\\ell$ sont deux entiers naturels non nuls de somme $k+\\ell=n-1$.\n\n\nSi un rectangle contient exactement deux cases noires, il s'agit de cases adjacentes : une gris foncé et une gris clair. Or, il y a $(k+1)(\\ell+1)$ cases gris foncé et $k \\ell$ cases gris clair. Isabelle dessine donc au plus $k \\ell$ rectangles recouvrant exactement deux cases noires, et ces rectangles laissent de côté $k+\\ell+1=n$ cases gris foncé. Cela force donc Isabelle à donner au moins $n=20$ chocolats à Clara.\n\nCommentaire des correcteurs Les difficultés principales de cet exercice étaient les suivantes:\n\n1. se convaincre que Clara peut forcer Isabelle à lui donner au moins 2 chocolats;\n2. trouver un coloriage qui force Isabelle à donner au moins 20 chocolats;\n3. démontrer que ce coloriage force en effet Isabelle à donner au moins 20 chocolats;\n4. trouver une stratégie simple permettant à Isabelle de donner au plus $n$ chocolats.\n\nDe nombreux élèves ont été bloqués à la première difficulté, remarquant simplement qu'Isabelle donnerait au moins un chocolat si la grille était vide ou contenait un nombre impair de cases noires, mais formulant tout de go l'affirmation incorrecte suivante :\n\nSi Clara dessine un nombre pair non nul de cases noires, Isabelle peut apparier ces cases pour ne donner aucun chocolat à Clara.\nUne fois une telle propriété indûment considérée comme acquise, ces élèves n'ont donc tout simplement pas abordé les difficultés 2 à 4.\nD'un point de vue méthodologique, il est dommage que ces élèves n'aient pas pris la peine d'étudier soigneusement le cas des grilles de petites dimensions, puisque les grilles rectangulaires $2 \\times 3$ et $3 \\times 3$ fournissaient un contre-exemple manifeste à cette affirmation, comme illustré ci-dessous.\n\n\nEn outre, en cherchant des arguments aussi simples que possibles pour expliquer pourquoi de telles configurations forçaient Isabelle à donner 2 voire 3 chocolats, les élèves auraient pu avoir l'idée du coloriage entre nuances de gris; ou, au minimum, constater que deux cases noires contenues dans un même rectangle d'Isabelle étaient nécessairement contiguës.\nPar ailleurs, plusieurs élèves ont bien identifié le motif en forme de croix dans la grille $3 \\times 3$, mais n'ont ensuite pas pensé à tenter de le généraliser au cas de la grille $4 \\times 4$ : les quelques élèves qui ont suivi une telle approche sont tous parvenus à une solution complète, proposant la construction présentée ci-dessus dans le cas où $k=\\lfloor n / 2\\rfloor$ ou bien $k=1$.\nPlusieurs élèves, ayant cherché sans le trouver un coloriage qui forcerait Isabelle à donner $n$ chocolats, ont néanmoins entrepris avec succès qu'Isabelle donnerait entre $n / 2$ et $n$ chocolats à Clara. Plus généralement, les correcteurs tiennent à souligner leur satisfaction de constater que de nombreux élèves ont eu l'idée de chercher séparément des bornes inférieures et supérieures sur le nombre de chocolats que donnerait Isabelle, c'est-à-dire de chercher une bonne stratégie pour Isabelle et un bon coloriage pour Clara, puis à démontrer qu'un tel coloriage était bon. De fait, les élèves qui ont suivi une telle approche ont très souvent été récompensés par un nombre substantiel de points, et ce même quand ils ne parvenaient pas à trouver un coloriage optimal.\nEnfin, voici trois erreurs très évitables que les correcteurs ont retrouvées dans de nombreuses copies.\n$\\triangleright$ Plusieurs élèves, expliquant comment Isabelle pouvait se débrouiller pour ne pas donner plus de 20 chocolats, ont indûment écrit que, dans le cas d'une ligne avec un nombre pair de cases noires, Isabelle ne donnerait aucun chocolat. Cette assertion est incorrecte, car Isabelle doit quand même donner un chocolat si la ligne ne contient aucune case noire.\n$\\triangleright$ D'autres élèves, alors qu'ils tentaient de démontrer qu'un coloriage de Clara contraindrait Isabelle à lui donner au moins 20 chocolats, ont supposé qu'Isabelle découperait la grille en rectangles de largeur 1 . Même si de telles considérations permettaient en effet de montrer que la technique consistant à découper la grille en lamelles n'aurait pas permis à Isabelle de donner moins de 20 chocolats, cette supposition était infondée, ce sans quoi Isabelle devrait déjà donner 20 chocolats même quand la grille est vide.\n$\\triangleright$ Enfin, certains élèves, partant d'une configuration optimale, ont tenté de démontrer que celle-ci ne pouvait pas être améliorée si on changeait la couleur d'une seule case. Mais rien n'empêchait de changer la couleur de plusieurs cases, et un tel raisonnement était donc nul et non avenu : exhiber un maximum local (ce qui était fait ici) est clairement insuffisant pour démontrer qu'il s'agit en fait d'un maximum global.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "On dit qu'une suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ d'entiers naturels non nuls est sicilienne si $^{-10}$\n\n$$\nu_{n+1} \\in\\left\\{u_{n} / 2, u_{n} / 3,2 u_{n}+1,3 u_{n}+1\\right\\}\n$$\n\npour tout $n \\geqslant 0$. Démontrer que, pour tout entier $k \\geqslant 1$, il existe une suite sicilienne $\\left(u_{n}\\right)_{n \\geqslant 0}$ et un entier $\\ell \\geqslant 0$ tels que $u_{0}=k$ et $u_{\\ell}=1$.", "solution": "Nous allons démontrer, pour tout entier $k \\geqslant 2$, la propriété $\\mathcal{P}_{k}$ suivante : il existe une suite sicilienne finie $\\left(u_{0}, \\ldots, u_{\\ell}\\right)$ telle que $u_{0}=k$ et $u_{\\ell}<k$.\nLa propriété $\\mathcal{P}_{k}$ est immédiate si $k$ est pair, puisqu'il suffit de choisir $u_{1}=k / 2$. On suppose donc $k$ impair. Soit $\\alpha$ et $\\kappa$ les entiers naturels non nuls tels que $k=2^{\\alpha} \\kappa-1$, l'entier $\\kappa$ étant impair. On construit alors notre suite sicilienne comme suit.\nTout d'abord, pour tout $i \\leqslant \\alpha-1$, on pose $u_{2 i}=2^{\\alpha-i} 3^{i} \\kappa-1$ et $u_{2 i+1}=2^{\\alpha-i} 3^{i+1} \\kappa-2$. On pose ensuite $u_{2 \\alpha}=3^{\\alpha} \\kappa-1$ et $u_{2 \\alpha+1}=\\left(3^{\\alpha} \\kappa-1\\right) / 2$, qui est bien un entier puisque $\\kappa$ est impair. Enfin, pour tout $i \\leqslant \\alpha$, on pose $u_{2 \\alpha+2+i}=3^{\\alpha-i} \\kappa$. On vérifie alors aisément que la suite $\\left(u_{0}, \\ldots, u_{3 \\alpha+2}\\right)$ est sicilienne. En effet, on a $u_{2 i+1}=3 u_{2 i}+1$ et $u_{2 i+2}=u_{2 i+1} / 2$ pour tout $i \\leqslant \\alpha$, puis $u_{2 \\alpha+1}=u_{2 \\alpha} / 2$ et $u_{2 \\alpha+2}=2 u_{2 \\alpha+1}+1$, et on a également $u_{2 \\alpha+3+i}=u_{2 \\alpha+2+i} / 3$ pour tout $i \\leqslant \\alpha-1$. Puisque $u_{0}=k$ et $u_{3 \\alpha+2}=\\kappa \\leqslant(k+1) / 2<k$, cela achève de démontrer la propriété $\\mathcal{P}_{k}$.\nForts de cette propriété, on démontre enfin l'assertion de l'énoncé par récurrence sur $k$.\nCommentaire des correcteurs Sur ce problème, beaucoup d'élèves ont eu des idées pertinentes : faire une récurrence forte ou essayer de se ramener à un terme plus petit que $u_{0}$ pour s'assurer d'aboutir à 1 . Toutefois, on a constaté de nombreuses erreurs de calcul lors de la manipulation de congruences : pour diviser une égalité modulo $m$ par $k$, il faut également diviser $m$ par $\\operatorname{PGCD}(k, m)$. Par exemple, on a $6 \\equiv 2(\\bmod 4)$, donc on peut en déduire que $3 \\equiv 1(\\bmod 2)$, mais certainement pas que $3 \\equiv 1(\\bmod 4)$.\nQuelques élèves ont réussi à mettre en place des arguments rigoureux pour obtenir le résultat pour toute valeur de $k$. Certains ont traité de nombreux cas, se ramenant à des cas de plus en plus compliqués : $k \\equiv 3(\\bmod 4)$, puis $k \\equiv 7(\\bmod 8)$, et ainsi de suite. Il fallait alors se rendre compte que la bonne idée à avoir était de considérer l'entier $k+1$ et sa valuation 2 -adique.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle dont les angles sont aigus, et soit $D$ le pied de la hauteur issue du sommet $A$. Soit $X$ et $Y$ les deux points du cercle circonscrit à $A B C$ tels que $A X=A Y=A D$, et tels que $B$ et $X$ se trouvent du même côté de la droite $(A D)$. Soit $E$ le point d'intersection des droites $(B X)$ et $(C Y)$. Enfin, soit $F$ le point d'intersection, autre que $E$, entre la droite $(D E)$ et le cercle circonscrit à $E X Y$.\nDémontrer que les cercles circonscrits aux triangles $B C F$ et $E X Y$ sont tangents.", "solution": "Dans la suite, on note $\\mathcal{C}_{U V W}$ le cercle circonscrit à un triangle $U V W$. Soit $i$ l'inversion de centre $E$ qui laisse le cercle $\\mathcal{C}_{A B C}$ globalement invariant. Cette inversion échange les points $B$ et $X$, ainsi que les points $C$ et $Y$. Elle échange donc le cercle $\\mathcal{C}_{E X Y}$ et la droite $(B C)$. Puisque $i$ laisse la droite $(D E)$ globalement invariante, elle échange donc $F$ avec le point d'intersection de $(D E)$ et $(B C)$, c'est-à-dire avec le point $D$.\nPar conséquent, l'inversion $i$ échange les cercles $\\mathcal{C}_{B C F}$ et $\\mathcal{C}_{X Y D}$. Or, ce dernier cercle a pour rayon $[A D]$, et il est donc tangent à la droite ( $B C$ ). Ainsi, les cercles $\\mathcal{C}_{B C F}$ et $\\mathcal{C}_{E X Y}$ sont euxmêmes tangents.\n", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle dont les angles sont aigus, et soit $D$ le pied de la hauteur issue du sommet $A$. Soit $X$ et $Y$ les deux points du cercle circonscrit à $A B C$ tels que $A X=A Y=A D$, et tels que $B$ et $X$ se trouvent du même côté de la droite $(A D)$. Soit $E$ le point d'intersection des droites $(B X)$ et $(C Y)$. Enfin, soit $F$ le point d'intersection, autre que $E$, entre la droite $(D E)$ et le cercle circonscrit à $E X Y$.\nDémontrer que les cercles circonscrits aux triangles $B C F$ et $E X Y$ sont tangents.", "solution": "$n^{\\circ} 1$ Dans la suite, on note $\\mathcal{C}_{U V W}$ le cercle circonscrit au triangle $U V W . \\mathrm{Si}$ $A B C$ est isocèle en $A$, la droite $(A D)$ constitue un axe de symétrie de la figure et le résultat est immédiat. On suppose donc, sans perte de généralité, que $A B \\neq A C$.\nLorsque l'on trace la figure, il est évidemment important de mettre en évidence le triangle $A B C$ et départ, les triangles isocèles $A D X, A D Y$ et $A X Y$, et ce qui semble être la tangente commune aux deux cercles $\\mathcal{C}_{B C F}$ et $\\mathcal{C}_{E X Y}$. On remarque alors que ces trois droites semblent concourantes, et c'est donc ce que l'on entreprend de démontrer.\nSoit $I$ le point d'intersection des droites $(X Y)$ et $(B C)$ : ce point existe bien, car $A B C$ n'est pas isocèle en $A$. Nous allons démontrer que la droite $(I F)$ est tangente aux cercles $\\mathcal{C}_{F B C}$ et $\\mathcal{C}_{F X Y}$, ce qui donnera le résultat désiré. En considérant la puissance du point $I$ par rapport aux cercles $\\mathcal{C}_{F B C}$ et $\\mathcal{C}_{F X Y}$, il s'agit donc de démontrer que $I F^{2}$ est égal à $I X \\cdot I Y$ et à $I B \\cdot I C$. Or, puisque les droites $(B C)$ et $(A D)$ sont perpendiculaires, le cercle $\\mathcal{C}_{X Y D}$ est tangent à la droite $(B C)$. En considérant la puissance du point $I$ par rapport aux cercles $\\mathcal{C}_{X Y D}$ et $\\mathcal{C}_{A B C}$, on en déduit donc que $I D^{2}=I X \\cdot I Y=I B \\cdot I C$. Il s'agit donc de démontrer que $I F=I D$. Dès lors, on cherche des propriétés supplémentaires sur le point $D$. Si $(I F)$ est la tangente commune recherchée et si $I F D$ est isocèle en $I$, alors\n\n$$\n(F B, F D)=(F B, F I)+(F I, F D)=(C B, C F)+(F D, D I)=(F D, F C),\n$$\n\net $(F D)$ est donc la bissectrice de l'angle $\\widehat{B F C}$.\nRéciproquement, si $(F D)$ est la bissectrice de $\\widehat{B F C}$, et en notant $J$ le point d'intersection entre $(B C)$ et la tangente à $\\mathcal{C}_{B C F}$ en $F$, la chasse aux angles ci-dessus indique que $J F D$ est isocèle en $J$, donc que $J D^{2}=J F^{2}=J B \\cdot J C$. Le point $J$ a donc même puissance par rapport aux cercles $\\mathcal{C}_{B C F}$ et $\\mathcal{C}_{D X Y}$, donc il appartient à leur axe radical $(X Y)$, de sorte que $I=J$. Ainsi, notre problème est équivalent à démontrer que $(F D)$ est donc la bissectrice de l'angle $\\widehat{B F C}$.\nPour cela, on note $G$ le point d'intersection, autre que $D$, entre les cercles $\\mathcal{C}_{D B X}$ et $\\mathcal{C}_{C D Y}$. Puisque\n\n$$\n(G Y, G X)=(G Y, G D)+(G D, G X)=(C Y, C D)+(B D, B X)=(E Y, E X)\n$$\n\nles point $G$ appartient au cercle $\\mathcal{C}_{E X Y}$. En outre, $E$ est le point de concourt des axes radicaux de $\\mathcal{C}_{A B C}$ avec $\\mathcal{C}_{D B X}$ et $\\mathcal{C}_{C D Y}$. Il s'agit donc du centre radical de ces trois cercles, et $E$ appartient donc à l'axe radical de $\\mathcal{C}_{D B X}$ et $\\mathcal{C}_{C D Y}$, c'est-à-dire à la droite (GD). Cela signifie que $F=G$.\nOn conclut alors par simple chasse aux angles. En effet,\n\n$$\n\\begin{aligned}\n(F B, F D)+(F C, F D) & =(G B, G D)+(G C, G D) \\\\\n& =(X B, X D)+(Y C, Y D) \\\\\n& =(B X, B C)+(D B, D X)+(C Y, C B)+(D C, D Y) \\\\\n& =(Y X, Y C)+(Y D, Y X)+(X Y, X B)+(X D, X Y) \\\\\n& =(Y D, Y C)+(X D, X B) .\n\\end{aligned}\n$$\n\nAinsi, $2(X B, X D)+2(Y C, Y D)=0^{\\circ}$, de sorte que les angles $\\widehat{D F B}$ et $\\widehat{C F D}$ sont égaux modulo $90^{\\circ}$. Comme $\\widehat{D F B}=\\widehat{D X B} \\leqslant \\widehat{C X B}=\\widehat{C A B}<90^{\\circ}$ et, de même, $\\widehat{C F D}<90^{\\circ}$, on en déduit que $\\widehat{D F B}=\\widehat{C F D}$, ce qui conclut le problème.\n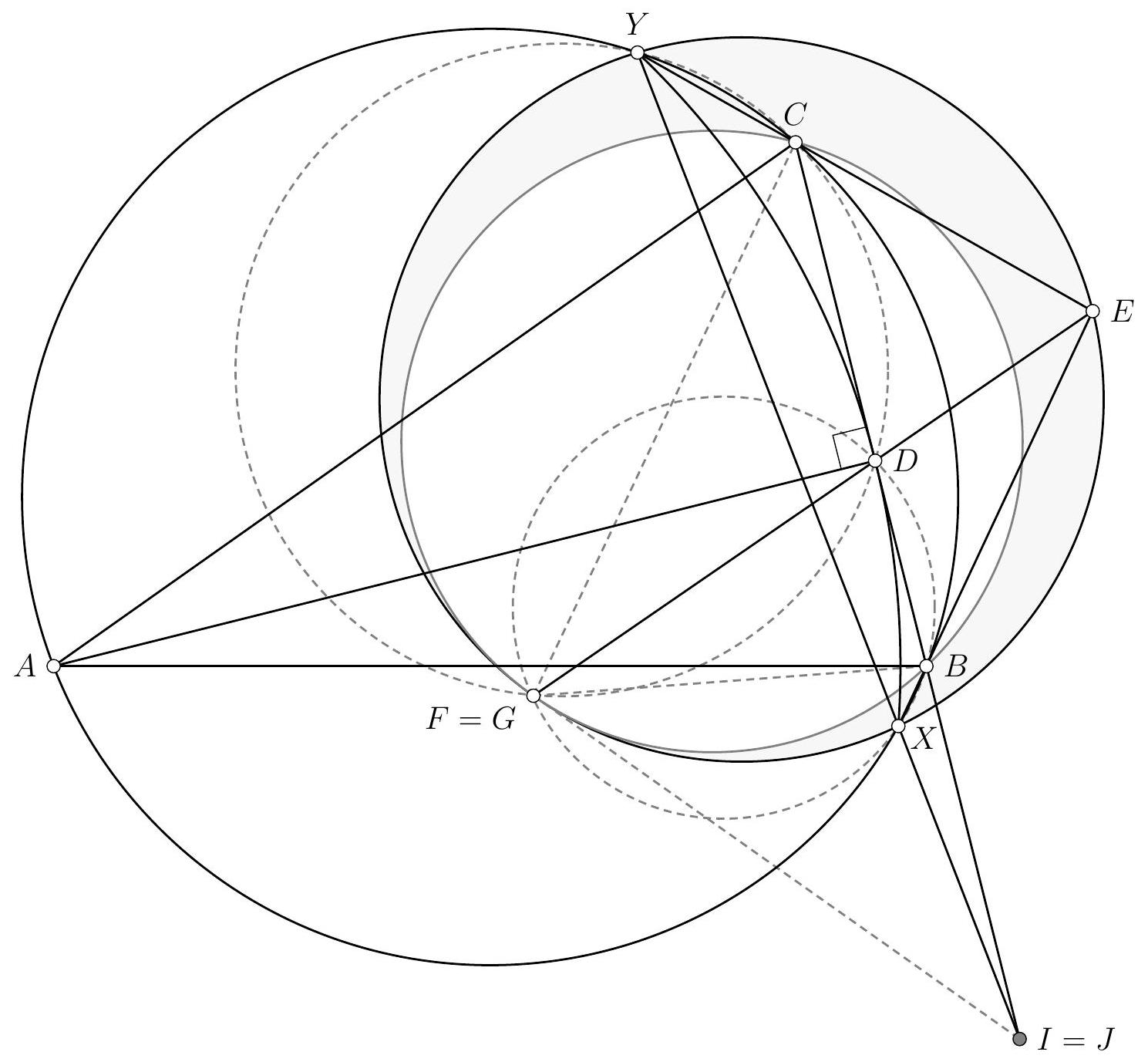\n\nCommentaire des correcteurs Pour ce problème, plusieurs élèves ont mis en évidence une solution par inversion à laquelle les correcteurs n'avaient pas pensé : il s'agit de la solution $\\mathrm{n}^{\\circ} 1$ présentée ci-dessus. Cette méthode rendait l'exercice nettement moins difficile que le niveau de difficulté estimé par l'équipe de correction.\nAinsi, on a observé une forte dichotomie entre les élèves ayant repéré cette solution par inversion et les élèves qui ne l'ont pas repérée ou qui ne sont pas adeptes de l'inversion et qui n'ont, pour la plupart, pas pu avancer de façon significative dans l'exercice. Toutefois, nous saluons les efforts et les pistes avancées par les élèves ayant tenté l'exercice et qui ont parfois pu rapporter à leur auteur 1 ou 2 points partiels.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-2.jsonl
ADDED
|
@@ -0,0 +1,16 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "On pose $n=2021$. Démontrer que le nombre $3^{2 n+1}+2^{n+2}$ est divisible par 35.", "solution": "Nous allons démontrer que le nombre $S_{n}=3^{2 n+1}+2^{n+2}$ est divisible simultanément par 5 et par 7 lorsque $n=2021$.\nOn vérifie immédiatement que\n\n$$\nS_{n} \\equiv 9^{n} \\times 3+2^{n} \\times 4 \\equiv 2^{n} \\times 3+2^{n} \\times 4 \\equiv 2^{n} \\times 7 \\equiv 0 \\quad(\\bmod 7),\n$$\n\nce qui signifie bien que $S_{n}$ est divisible par 7 .\nOn vérifie ensuite que\n\n$$\nS_{n} \\equiv 9^{n} \\times 3+2^{n} \\times 4 \\equiv(-1)^{n} \\times 3+2^{n} \\times(-1) \\equiv-3-2^{n} \\quad(\\bmod 5) .\n$$\n\nLa propriété demandée dépend donc manifestement de la valeur de $n$, puisqu'elle aurait été invalide si on avait choisi $n=3$.\nOn calcule donc les premières valeurs de $S_{n}(\\bmod 5)$ pour se donner des idées :\n\n$$\n\\begin{array}{ll}\n\\triangleright S_{0} \\equiv-3-1 \\equiv 1(\\bmod 5) ; & \\triangleright S_{4} \\equiv-3-16 \\equiv 1(\\bmod 5) ; \\\\\n\\triangleright S_{1} \\equiv-3-2 \\equiv 0(\\bmod 5) ; & \\triangleright S_{5} \\equiv-3-32 \\equiv 0(\\bmod 5) ; \\\\\n\\triangleright S_{2} \\equiv-3-4 \\equiv 3(\\bmod 5) ; & \\triangleright S_{6} \\equiv-3-64 \\equiv 3(\\bmod 5) ; \\\\\n\\triangleright S_{3} \\equiv-3-8 \\equiv 4(\\bmod 5) ; & \\triangleright S_{7} \\equiv-3-128 \\equiv 4(\\bmod 5) .\n\\end{array}\n$$\n\nIl apparaît visiblement que $S_{n} \\equiv 0(\\bmod 5)$ lorsque $n \\equiv 1(\\bmod 4)$, et on entreprend donc de le démontrer. Si l'on pose $n=4 k+1$, alors\n\n$$\nS_{n} \\equiv-3-2^{4 k+1} \\equiv-3-16^{k} \\times 2 \\equiv-3-1^{k} \\times 2 \\equiv-3-2 \\equiv 0 \\quad(\\bmod 5)\n$$\n\nAinsi, lorsque $n=2021$, on a bien $n \\equiv 1(\\bmod 4)$, et l'entier $S_{n}$ est donc divisible par 5 .\nEn conclusion, l'entier $S_{n}$ est divisible à la fois par 5 et par 7, donc il est également divisible par leur PPCM, c'est-à-dire 35.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "On pose $n=2021$. Démontrer que le nombre $3^{2 n+1}+2^{n+2}$ est divisible par 35.", "solution": "$n^{\\circ} 1$ Le petit théorème de Fermat nous assure que $2^{4} \\equiv 3^{4} \\equiv 1(\\bmod 5)$. Comme $2 n+1 \\equiv 4043 \\equiv 3(\\bmod 4)$ et $n+2 \\equiv 2023 \\equiv 3(\\bmod 4)$, on en déduit que $S_{n} \\equiv$ $3^{3}+2^{3} \\equiv 35 \\equiv 0(\\bmod 5)$.\nDe même, le petit théorème de Fermat nous assure que $2^{6} \\equiv 3^{6} \\equiv 1(\\bmod 7)$. Comme $2 n+1 \\equiv$ $4043 \\equiv-1(\\bmod 6)$ et $n+2 \\equiv 2023 \\equiv 1(\\bmod 6)$, on en déduit que $S_{n} \\equiv 3^{5}+2^{1} \\equiv 245 \\equiv 0$ $(\\bmod 7)$.\nEn conclusion, la somme $S_{n}$ est divisible par 5 et par 7, donc par 35.\nCommentaire des correcteurs Cet exercice a été globalement bien réussi, à la grande satisfaction des correcteurs. La plupart des élèves ont eu bonnes idées et de bons réflexes :\n$\\triangleright$ se ramener à étudier la divisibilité de $S_{n}$ par 5 et par 7;\n$\\triangleright$ étudier les petites valeurs de $n$;\n$\\triangleright$ considérer séparément les puissances de 2 et de 3 et étudier leur chiffre des unités, c'est-à-dire leur congruence modulo 10;\n$\\triangleright$ repérer qu'un motif se répétait.\n\nIl s'agit là de signes très encourageants!\nCertains élèves ont aussi invoqué directement le petit théorème de Fermat, qui stipule que $a^{p-1} \\equiv 1(\\bmod p)$ quand $p$ est un nombre premier qui ne divise pas $a$. Ce résultat permettait d'aboutir plus rapidement à la solution, et avait aussi le bon goût de rendre les divisibilités par 5 et par 7 symétriques.\nNéanmoins, les correcteurs ont également repéré plusieurs erreurs, mathématiques ou stratégiques, qu'ils tiennent à souligner pour éviter aux élèves de les commettre à nouveau. Voici, tout d'abord, les erreurs mathématiques les plus fréquentes:\n$\\triangleright$ Plusieurs élèves se sont trompés en manipulant les puissances, et ont écrit, à tort, des égalités de la forme $a^{k}+b^{\\ell}=(a+b)^{k+\\ell}$. Quand on « invente» une telle identité algébrique, il y a de fortes chances qu'elle soit fausse, et une étape très importante est donc de rechercher des contre-exemples éventuels : si on n'en trouve pas, on aura davantage confiance en notre identité. Ici, prendre $a=b=k=\\ell=1$ suffit à confirmer que $a^{k}+b^{\\ell}=1+1=2 \\neq 4=2^{2}=(a+b)^{k+\\ell}$.\n$\\triangleright$ Plusieurs élèves ont cru à tort que l'on pouvait réduire les exposants modulo $m$. Certes, si $a \\equiv b(\\bmod m)$, on a bien $a+c \\equiv b+c(\\bmod m)$ et $a c \\equiv b c(\\bmod m)$ pour tout $c$. En revanche, en général, $c^{a} \\not \\equiv c^{b}(\\bmod m)$. C'est le cas, par exemple, quand $a=1, b=4$, $c=2$ et $m=3$, puisque alors $c^{a} \\equiv 2^{1} \\equiv 2 \\not \\equiv 16 \\equiv 2^{4} \\equiv c^{b}(\\bmod m)$.\n$\\triangleright$ Plusieurs élèves ont affirmé, à tort, qu'un nombre est divisible par 7 si et seulement si le nombre formé par ses deux derniers chiffres est divisible par 7. Ce critère de divisibilité est manifestement incorrect, puisque 100 et 700 ont les mêmes derniers chiffres mais que seul 700 est divisible par 7 . En outre, si un tel critère existait, et au vu de sa simplicité, il serait certainement enseigné à l'école, ce qui n'est pas le cas.\n$\\triangleright$ De nombreux élèves ont confondu conditions nécessaires et suffisantes. Ils ont ainsi affirmé que « si $S_{n}$ est divisible par $35=5 \\times 7$ », il est aussi divisible par 5 et par 7 ». Cette information est certes vraie, mais elle nous est aussi inutile. On attendait des élèves qu'ils formulent l'implication réciproque, qui est d'ailleurs celle qu'ils ont utilisée : «si $S_{n}$ est divisible par 5 et par 7, il est aussi divisible par $35=5 \\times 7$ ».\nVoici, ensuite, les erreurs stratégiques les plus fréquentes :\n$\\triangleright$ Plusieurs élèves ont cru, en s'appuyant sur un raisonnement faux ou sur une erreur de calcul, démontrer que 35 ne divisait pas $S_{n}$. Dans pareil cas, au lieu de conclure au fait que l'énoncé était incorrect, il aurait été plus judicieux de se remettre d'abord en question, et revérifiant les calculs effectués et la correction des arguments invoqués.\n$\\triangleright$ De nombreux élèves, après avoir étudié le chiffre des unités de $2^{n}$ et $3^{n}$ pour en déduire que 5 divisait $S_{n}$, n'ont pas pensé à prendre du recul pour se dire qu'il suffisait de faire la même chose mais en écrivant tous nos nombres en base 7 plutôt qu'en base 10. De manière générale, quand on découpe un problème en deux sous-problèmes d'apparences analogues et que l'on résout un des deux sous-problèmes, il est très utile de prendre le temps de réfléchir à la façon dont on pourrait adapter le raisonnement utilisé pour résoudre l'autre sous-problème.\n$\\triangleright$ De nombreux élèves, après avoir repéré que les chiffres des unités de $2^{n}$ semblaient se répéter en formant le cycle $2,4,8,6,2,4,8,6, \\ldots$, ont affirmé que c'était le cas sans essayer de le démontrer. Au lieu d'une démonstration, ils se sont donc appuyés sur une simple conjecture. Puisque cette conjecture tenait un rôle central dans leur solution, il était cependant indispensable de la démontrer.\nLes correcteurs ont ici décidé de ne pas pénaliser l'absence de cette démonstration, car il s'agissait du premier test POFM en temps limité de leur vie pour la plupart des candidats.\n\nCependant, en d'autres circonstances, omettre cette démonstration aurait pu être assez lourdement sanctionné, à hauteur de 2 ou 3 points sur 7.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 3 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Soit $n$ et $k$ deux entiers, tels que $n \\geqslant 3$. Théo organise les élections des délégués de sa classe de $n$ élèves : chaque élève doit voter pour un de ses camarades (tout le monde est candidat), et nul ne vote pour lui-même. Puis Théo répartit les élèves en groupes de sorte que, si un élève est dans un groupe, l'élève pour lequel il a voté n'y soit pas.\nPour quelles valeurs de $k$ Théo est-il sûr de pouvoir répartir les élèves en au plus $k$ groupes, et ce quelle que soit la manière dont les élèves auront voté?", "solution": "Tout d'abord, si on a trois élèves (disons Anna, Martin et Vincent) tels qu'Anna a voté pour Martin, Martin a voté pour Vincent, et Vincent a voté pour Anna, il est clair que Théo aura besoin d'au moins trois groupes.\nRéciproquement, démontrons par récurrence sur $n$ que Théo peut s'en sortir avec trois groupes seulement, et ce même si certains élèves votent blanc.\nL'initialisation est claire pour $n=3$. On suppose donc que $n \\geqslant 4$. Puisqu'il y a eu au plus $n$ votes, il y a au moins un élève qui a reçu au plus un vote : on l'appelle Donald. Quitte à oublier Donald et à frauder en « oubliant» le vote que celui-ci aurait reçu pour le remplacer par un vote blanc, Théo peut répartir les $n-1$ élèves restants en au plus trois groupes.\nPuis Théo fait revenir Donald dans la classe : sur les trois groupes, il y en a au moins un qui ne contient ni la personne pour laquelle Donald a pu voter, ni l'électeur éventuel de Donald. Théo met alors Donald dans ce groupe-là, ce qui conclut la récurrence.\nEn résumé, les entiers recherchés sont les entiers $k \\geqslant 3$.\nCommentaire des correcteurs Beaucoup d'élèves ont bien compris que certains cas forçaient Théo à choisir $k \\geqslant 3$. Il fallait alors, pour tout $n$, donner un exemple de vote pour lequel 3 groupes étaient nécessaires.\nPar la suite, de nombreuses stratégies pour répartir les élèves en 3 groupes ont été proposées, mais peu étaient correctes. Dans un tel cas, essayer de prouver que la répartition convient est toujours utile : en effet, soit la répartition est correcte, et alors démontrer qu'elle l'est est nécessaire pour obtenir tous les points; soit elle ne l'est pas, et échouer dans cette tentative de preuve permet souvent de comprendre pourquoi la stratégie échoue en fait. Il ne faut pas non plus hésiter à tester la répartition qui est donnée pour certains votes : en effet, cela permet souvent facilement de voir les problèmes.\nEnfin, quelques élèves ont transformé le problème en un problème de coloriage de graphes, puis ont affirmé que, si l'on pouvait colorier toute partie de 4 sommets du graphe sans avoir deux sommets de même couleur adjacents, on pouvait colorier le graphe entier sans avoir deux sommets de même couleur adjacents. Cette affirmation est en fait invalide, comme l'illustre le contre-exemple ci-dessous. Afin d'éviter aux élèves ce genre de déconvenues, nous les encourageons encore une fois à tenter de fournir une vraie preuve des différents éléments qu'ils énoncent.\n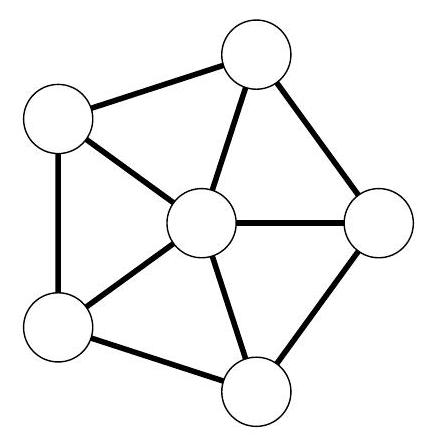", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 4 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "On définit la suite $a_{1}, a_{2}, a_{3} \\ldots$ de la façon suivante : $a_{1}=63$ et, pour tout entier $n \\geqslant 2, a_{n}$ est le plus petit multiple de $n$ qui soit supérieur ou égal à $a_{n-1}$. Démontrer que les termes de notre suite sont deux à deux distincts.", "solution": "Il est clair que la suite $\\left(a_{n}\\right)_{n \\geqslant 1}$ est croissante. Il s'agit donc de démontrer qu'elle est strictement croissante.\nOn calcule donc les premiers termes de la suite : $a_{1}=63, a_{2}=64, a_{3}=66, a_{4}=68, a_{5}=70$, $a_{6}=72, a_{7}=77, a_{8}=80, a_{9}=81, a_{10}=90, a_{11}=99, a_{12}=108, a_{13}=117 . .$.\nUne propriété se dessine alors sous nos yeux : il semble que $a_{n}=9 n$ pour tout $n \\geqslant 9$. En pratique, il est bon de vérifier cette conjecture sur quelques valeurs supplémentaires de $n$, pour se convaincre qu'elle est vraie. On entreprend donc de démontrer cette propriété par récurrence.\nTout d'abord, comme mentionné ci-dessus, on a bien $a_{9}=9^{2}$. Puis, pour tout entier $n \\geqslant 9$ tel que $a_{n}=9 n$, on constate que $8(n+1)=a_{n}-(n-8)<a_{n}<9(n+1)$, de sorte que $a_{n+1}=9(n+1)$.\nEn conclusion, la suite $\\left(a_{n}\\right)_{n \\geqslant 1}$ est strictement croissante tant que $n \\leqslant 9$, et elle l'est manifestement quand $n \\geqslant 9$. Ses termes sont donc en effet distincts deux à deux.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 5 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "On définit la suite $a_{1}, a_{2}, a_{3} \\ldots$ de la façon suivante : $a_{1}=63$ et, pour tout entier $n \\geqslant 2, a_{n}$ est le plus petit multiple de $n$ qui soit supérieur ou égal à $a_{n-1}$. Démontrer que les termes de notre suite sont deux à deux distincts.", "solution": "$n^{\\circ} 1$ Comme dans la solution précédente, il est clair que la suite $\\left(a_{n}\\right)_{n \\geqslant 1}$ est croissante. Il s'agit donc de démontrer, pour tout entier $n \\geqslant 1$, que $a_{n} \\neq a_{n+1}$, c'est-à-dire que $n(n+1)$ ne divise pas $a_{n}$.\nOn calcule alors les premiers termes de la suite, jusqu'à $a_{9}=81$, et l'on constate bien que $n(n+1)$ ne divise pas $a_{n}$ lorsque $n \\leqslant 9$. On démontre ensuite que $a_{n}<n(n+1)$ pour tout entier $n \\geqslant 9$.\nEn effet, c'est bien le cas si $n=9$. Puis, pour tout entier $n \\geqslant 9$ tel que $a_{n}<n(n+1)$, on constate que $a_{n+1} \\leqslant a_{n}+n<n(n+2)<(n+1)^{2}$, ce qui conclut.\n\nCommentaire des correcteurs De nombreux élèves ont eu des idées intéressantes et leur permettant d'avancer dans la résolution de ce problème pourtant difficile. Face à un tel énoncé, il est important de regarder comment la suite $\\left(a_{n}\\right)$ se comporte, et donc en calculer les premiers termes : on peut essayer de regarder les 10 ou 20 premiers termes pour se faire une idée de la suite. Cette idée s'avérait particulièrement fructueuse ici, puisqu'elle permettait de conjecturer que $a_{n}=9 n$ lorsque $n \\geqslant 9$, ce qui semble a priori plus facile à prouver que l'énoncé initial.\nNéanmoins, attention à la rédaction! Les élèves qui ont entamé une récurrence on souvent écrit que $a_{n}=9 n$ puisque $a_{n+1}=k(n+1)$ pour un certain $k$, et ont ensuite tenté de trouver $k$, mais ont uniquement démontré que $k \\leqslant 9$ ou que $k \\geqslant 9$, oubliant l'autre inégalité : il est important de bien justifier pourquoi $k=9$.\nPar ailleurs, dans cet exercice, il était possible de remarquer empiriquement que $a_{n}=9 n$ lorsque $n \\geqslant 9$, mais sans parvenir à le démontrer. Dans ce cas, il faut évidemment mentionner une telle conjecture, puis voir comment on pourrait l'utiliser pour résoudre l'exercice. En effet, plus le raisonnement est complet et moins il manque d'éléments à justifier, et plus il vaudra de points. Admettre un résultat coûte évidemment des points (et si le résultat que l'on admet est aussi difficile à démontrer que l'énoncé initial, cela peut même coûter l'intégralité des points), mais il est souvent possible de formuler une conjecture puis d'en déduire le résultat désiré.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution alternative"}
|
| 6 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "Dans la suite, on pose $n=2019$ et, pour tout sommet $P_{i}$, on note $a_{i}$ l'angle $\\widehat{P}_{i} / n$. Soit alors $P_{k}$, $P_{k+1}, P_{k+2}, P_{k+3}$ et $P_{k+4}$ quatre sommets consécutifs, les indices des sommets étant considérés modulo $n+2$.\nLa somme des angles d'un triangle vaut $180^{\\circ}$. En considérant respectivement les triangles $P_{i} P_{i+1} P_{i+2}, P_{i} P_{i+1} P_{i+3}$ et $P_{i} P_{i+1} P_{i+4}$, on constate que\n\n$$\n\\begin{aligned}\na_{i}+n a_{i+1}+a_{i+2} & =180^{\\circ} \\\\\n2 a_{i}+(n-1) a_{i+1}+a_{i+3} & =180^{\\circ} \\\\\n3 a_{i}+(n-2) a_{i+1}+a_{i+4} & =180^{\\circ}\n\\end{aligned}\n$$\n\nNous allons alors soustraire deux à deux ces équations :\n$\\triangleright(11)-(2)$ indique que $a_{i+1}+a_{i+2}=a_{i}+a_{i+3}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$;\n$\\triangleright(2)-(3)$ indique que $a_{i+1}+a_{i+3}=a_{i}+a_{i+4}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+4}-a_{i+3}$.\nOn constate donc que $a_{i+4}-a_{i+3}=a_{i+3}-a_{i+2}$. La différence entre deux angles $a_{j}$ et $a_{j+1}$ consécutifs est donc égale à une constante $\\mathbf{c}$.\nCela signifie que $a_{i+k}=a_{i}+k \\mathbf{c}$ pour tous les entiers $i$ et $k$. En particulier, $a_{1}=a_{n+3}=$ $a_{1}+(n+2) \\mathbf{c}$, donc $\\mathbf{c}=0^{\\circ}$. Ainsi, notre polygone a tous ses sommets égaux.\nLe triangle $P_{i} P_{i+1} P_{i+2}$ est donc isocèle en $P_{i+1}$, de sorte que $P_{i} P_{i+1}=P_{i+1} P_{i+2}$. Deux côtés consécutifs étant de même longueur, notre polygone a donc tous ses côtés de même longueur, et il s'agit bien d'un polygone régulier.\n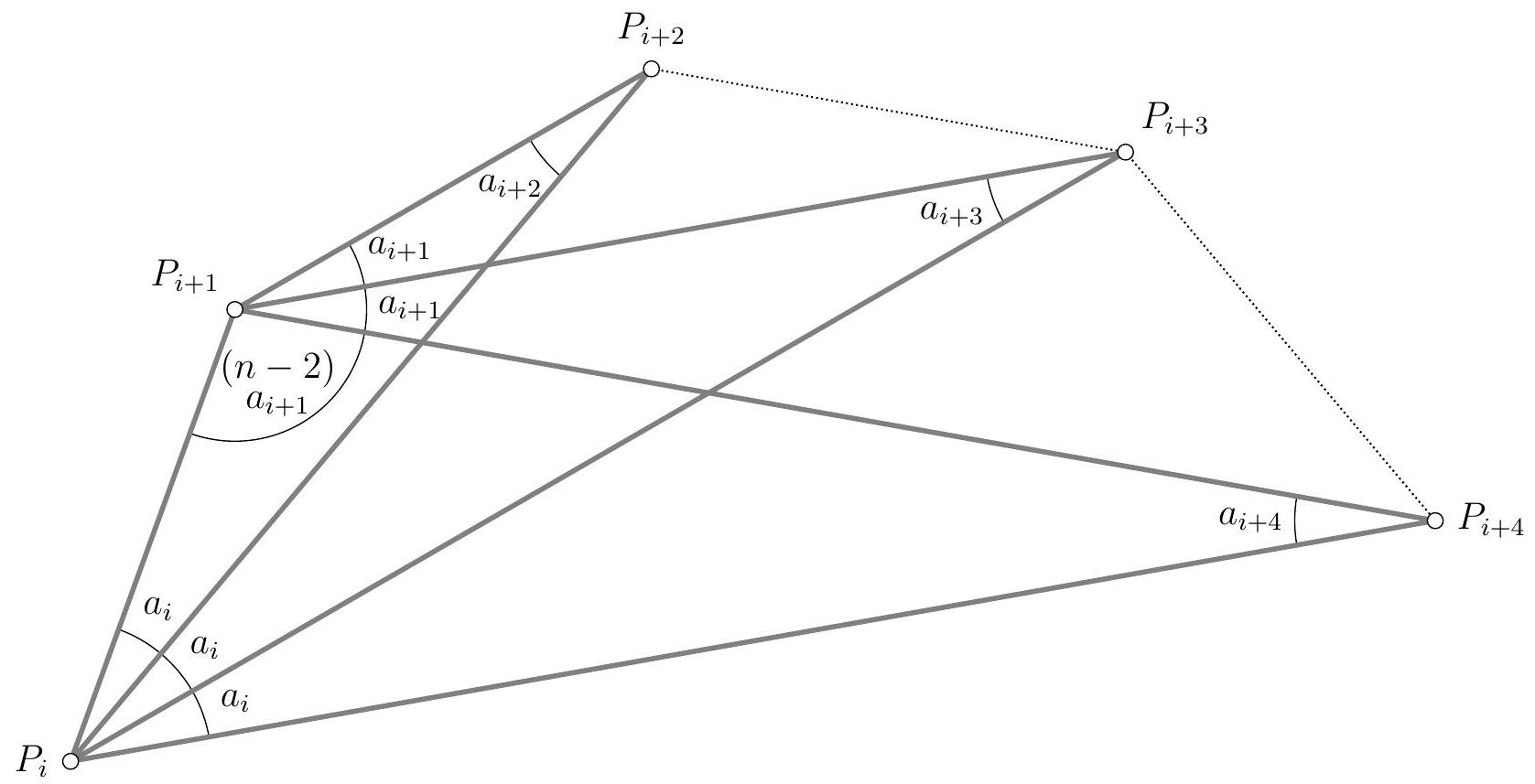", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 7 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "$n^{\\circ} 1$ Comme dans la solution précédente, on démontre les égalités (1) et (2) pour en déduire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$. Si l'on pose $\\mathbf{c}=a_{2}-a_{1}$, une récurrence immédiate démontre alors que $a_{2 k}-a_{2 k-1}=\\mathbf{c}$ pour tout entier $k \\geqslant 1$.\nOr, nos indices sont considérés modulo $n+2=2021$, qui est impair. On en déduit que $a_{i+1}-a_{i}=\\mathbf{c}$ pour tout indice $i$. On conclut alors comme précédemment.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution alternative"}
|
| 8 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "$n^{\\circ} 2$ Comme précédemment, on démontre l'égalité (1). Si l'on pose $b_{i}=a_{i}-180^{\\circ} /(n+2)$, cette égalité se réécrit comme $b_{i}+n b_{i+1}+b_{i+2}=0$.\nLa suite $\\left(b_{i}\\right)_{i \\geqslant 1}$ est donc récurrente linéaire. Si l'on note $r_{+}$et $r_{-}$les deux racines du polynôme $1+n X+X^{2}$, c'est-à-dire\n\n$$\nr_{ \\pm}=\\frac{-n \\pm \\sqrt{n^{2}-4}}{2}\n$$\n\nil existe donc deux nombres $\\lambda_{+}$et $\\lambda_{-}$tels que\n\n$$\nb_{i}=\\lambda_{+} r_{+}^{i}+\\lambda_{-} r_{-}^{i}\n$$\n\npour tout $i \\geqslant 0$.\nPuisque $n \\geqslant 5$, on sait que\n\n$$\n\\left(n^{2}-4\\right)-(n-2)^{2}=2(n-4)>0\n$$\n\ndonc que $r_{-} \\leqslant-n / 2<-1<r_{+}<0$ et que on sait que $\\left|r_{-}\\right|>1>\\left|r_{+}\\right|$. Par conséquent, on sait que, si $\\lambda_{-} \\neq 0$, la fraction $b_{i} /\\left(\\lambda_{-} r_{-}^{i}\\right)$ tend vers 1 quand $i \\rightarrow+\\infty$. Or, la suite $\\left(b_{i}\\right)_{i \\geqslant 1}$ est $(n+2)$-périodique. On en déduit que $\\lambda_{-}=0$.\nDe même, si $\\lambda_{+} \\neq 0$, la fraction $b_{i} /\\left(\\lambda_{+} r_{+}^{i}\\right)$ tend vers 1 quand $i \\rightarrow+\\infty$, en contradiction avec le caractère $(n+2)$-périodique de la suite $\\left(b_{i}\\right)_{i \\geqslant 1}$. On en déduit que $\\lambda_{+}=0$, donc que $b_{i}=0$ pour tout $i \\geqslant 1$.\nEn conclusion, tous les angles $a_{i}$ sont égaux, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution alternative"}
|
| 9 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "$n^{\\circ} 3$ Comme précédemment, on démontre l'égalité (1). En écrivant cette égalité pour deux entiers $i$ consécutifs, et en soustrayant les deux égalités obtenues, on constate que\n\n$$\na_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .\n$$\n\nLa suite $a_{i}$ est donc récurrente linéaire. Cette fois-ci, les racines du polynôme\n\n$$\n1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\\left(1+n X+X^{2}\\right)\n$$\n\nsont $r_{ \\pm}$et 1 . Puisque $n \\geqslant 5$, on sait que\n\n$$\n\\left(n^{2}-4\\right)-(n-2)^{2}=2(n-4)>0\n$$\n\ndonc que $r_{-} \\leqslant-n / 2<-1<r_{+}<0<1$ et que on sait que $\\left|r_{-}\\right|>1>\\left|r_{+}\\right|$.\nIl existe donc trois nombres $\\lambda_{+}, \\lambda_{1}$ et $\\lambda_{-}$tels que\n\n$$\na_{i}=\\lambda_{+} r_{+}^{i}+\\lambda_{1}+\\lambda_{-} r_{-}^{i}\n$$\n\npour tout $i \\in \\mathbb{Z}$. On démontre comme dans la solution précédente que $\\lambda_{-}=0$. De même, si $\\lambda_{+} \\neq 0$, alors $a_{i} /\\left(\\lambda_{+} r_{+}^{i}\\right) \\rightarrow 1$ quand $i \\rightarrow-\\infty$, en contradiction avec le caractère périodique de $\\left(a_{i}\\right)$. Ainsi, $\\lambda_{+}=0.1$\n\n[^0]En conclusion, tous les angles $a_{i}$ sont égaux à $\\lambda_{1}$, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.\n\nRemarque : Cet exercice avait été proposé en 2003, aux Olympiades mathématiques de première, dans l'académie de Versailles, mais en incluant des questions intermédiaires. Sur les 623 candidats présents dans l'académie, dont deux lauréats nationaux, aucun n'était parvenu à résoudre cet exercice, qui s'était donc révélé particulièrement difficile bien qu'abordable avec peu d'outils techniques.\n\nCommentaire des correcteurs L'exercice, difficile, n'a été complètement résolu que par très peu d'élèves. Un grand nombre d'élèves ont tout de même réussi à obtenir des points partiels en établissant des équations intéressantes entre les angles, ou bien en montrant que, si tous les angles du polygone étaient égaux, alors tous les côtés du polygone étaient également de même longueur.\n\n## Problèmes Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution alternative"}
|
| 10 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "Dans la suite, on pose $n=2019$ et, pour tout sommet $P_{i}$, on note $a_{i}$ l'angle $\\widehat{P}_{i} / n$. Soit alors $P_{k}$, $P_{k+1}, P_{k+2}, P_{k+3}$ et $P_{k+4}$ quatre sommets consécutifs, les indices des sommets étant considérés modulo $n+2$.\nLa somme des angles d'un triangle vaut $180^{\\circ}$. En considérant respectivement les triangles $P_{i} P_{i+1} P_{i+2}, P_{i} P_{i+1} P_{i+3}$ et $P_{i} P_{i+1} P_{i+4}$, on constate que\n\n$$\n\\begin{aligned}\na_{i}+n a_{i+1}+a_{i+2} & =180^{\\circ} \\\\\n2 a_{i}+(n-1) a_{i+1}+a_{i+3} & =180^{\\circ} \\\\\n3 a_{i}+(n-2) a_{i+1}+a_{i+4} & =180^{\\circ}\n\\end{aligned}\n$$\n\nNous allons alors soustraire deux à deux ces équations :\n$\\triangleright$ (1) - (2) indique que $a_{i+1}+a_{i+2}=a_{i}+a_{i+3}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$;\n$\\triangleright(2)-(3)$ indique que $a_{i+1}+a_{i+3}=a_{i}+a_{i+4}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+4}-a_{i+3}$.\nOn constate donc que $a_{i+4}-a_{i+3}=a_{i+3}-a_{i+2}$. La différence entre deux angles $a_{j}$ et $a_{j+1}$ consécutifs est donc égale à une constante $\\mathbf{c}$.\nCela signifie que $a_{i+k}=a_{i}+k \\mathbf{c}$ pour tous les entiers $i$ et $k$. En particulier, $a_{1}=a_{n+3}=$ $a_{1}+(n+2) \\mathbf{c}$, donc $\\mathbf{c}=0^{\\circ}$. Ainsi, notre polygone a tous ses sommets égaux.\nLe triangle $P_{i} P_{i+1} P_{i+2}$ est donc isocèle en $P_{i+1}$, de sorte que $P_{i} P_{i+1}=P_{i+1} P_{i+2}$. Deux côtés consécutifs étant de même longueur, notre polygone a donc tous ses côtés de même longueur, et il s'agit bien d'un polygone régulier.\n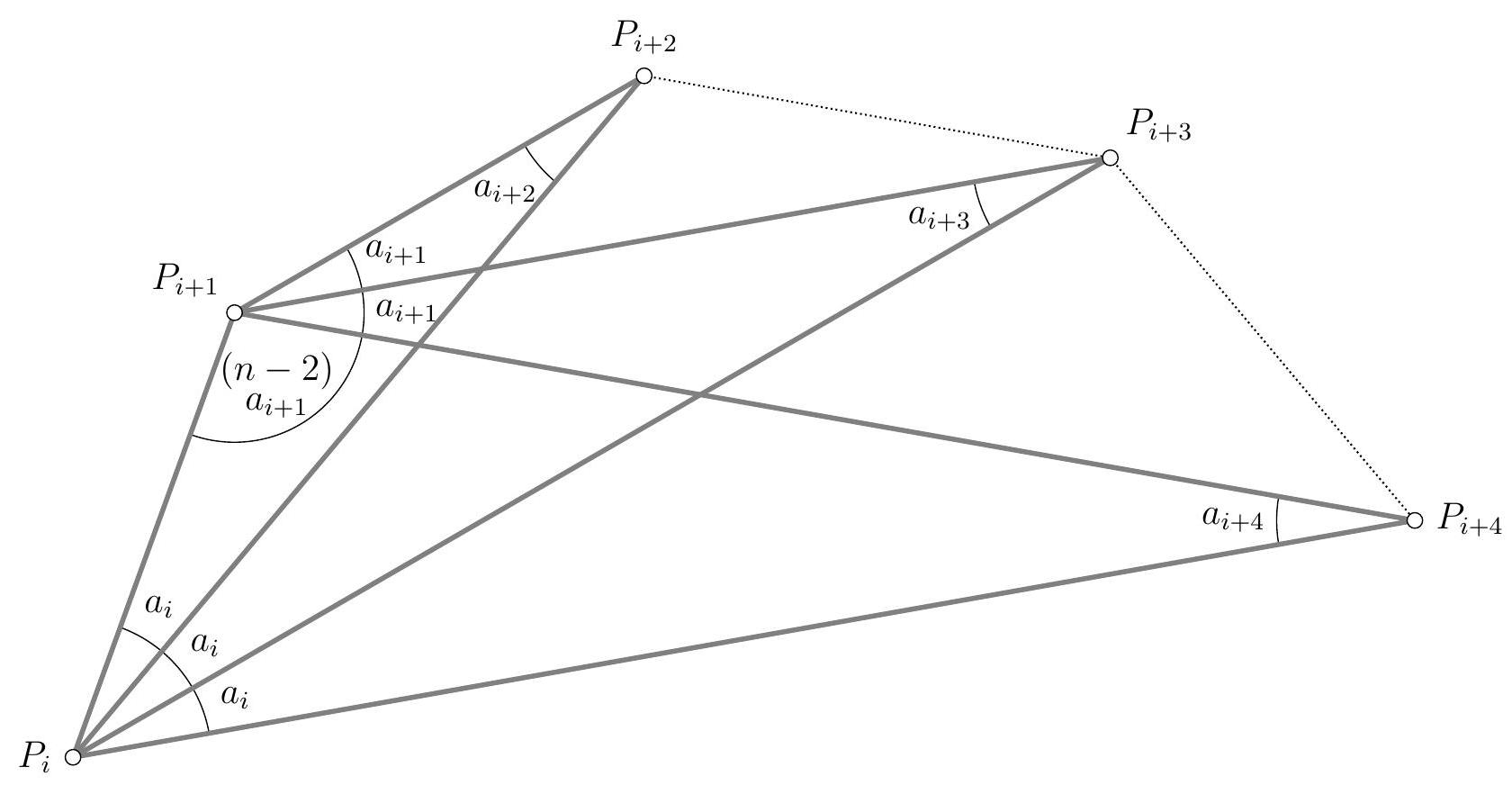", "problem_match": "\nExercice 5.", "solution_match": "## Solution de l'exercice 5"}
|
| 11 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "$n^{\\circ} 1$ Comme dans la solution précédente, on démontre les égalités (1) et (2) pour en déduire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$. Si l'on pose $\\mathbf{c}=a_{2}-a_{1}$, une récurrence immédiate démontre alors que $a_{2 k}-a_{2 k-1}=\\mathbf{c}$ pour tout entier $k \\geqslant 1$.\nOr, nos indices sont considérés modulo $n+2=2021$, qui est impair. On en déduit que $a_{i+1}-a_{i}=\\mathbf{c}$ pour tout indice $i$. On conclut alors comme précédemment.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution alternative"}
|
| 12 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "$n^{\\circ} 2$ Comme précédemment, on démontre l'égalité (1). Si l'on pose $b_{i}=a_{i}-180^{\\circ} /(n+2)$, cette égalité se réécrit comme $b_{i}+n b_{i+1}+b_{i+2}=0$.\nLa suite $\\left(b_{i}\\right)_{i \\geqslant 1}$ est donc récurrente linéaire. Si l'on note $r_{+}$et $r_{-}$les deux racines du polynôme $1+n X+X^{2}$, c'est-à-dire\n\n$$\nr_{ \\pm}=\\frac{-n \\pm \\sqrt{n^{2}-4}}{2}\n$$\n\nil existe donc deux nombres $\\lambda_{+}$et $\\lambda_{-}$tels que\n\n$$\nb_{i}=\\lambda_{+} r_{+}^{i}+\\lambda_{-} r_{-}^{i}\n$$\n\npour tout $i \\geqslant 0$.\nPuisque $n \\geqslant 5$, on sait que\n\n$$\n\\left(n^{2}-4\\right)-(n-2)^{2}=2(n-4)>0\n$$\n\ndonc que $r_{-} \\leqslant-n / 2<-1<r_{+}<0$ et que on sait que $\\left|r_{-}\\right|>1>\\left|r_{+}\\right|$. Par conséquent, on sait que, si $\\lambda_{-} \\neq 0$, la fraction $b_{i} /\\left(\\lambda_{-} r_{-}^{i}\\right)$ tend vers 1 quand $i \\rightarrow+\\infty$. Or, la suite $\\left(b_{i}\\right)_{i \\geqslant 1}$ est $(n+2)$-périodique. On en déduit que $\\lambda_{-}=0$.\nDe même, si $\\lambda_{+} \\neq 0$, la fraction $b_{i} /\\left(\\lambda_{+} r_{+}^{i}\\right)$ tend vers 1 quand $i \\rightarrow+\\infty$, en contradiction avec le caractère $(n+2)$-périodique de la suite $\\left(b_{i}\\right)_{i \\geqslant 1}$. On en déduit que $\\lambda_{+}=0$, donc que $b_{i}=0$ pour tout $i \\geqslant 1$.\nEn conclusion, tous les angles $a_{i}$ sont égaux, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution alternative"}
|
| 13 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Soit $P_{1} P_{2} \\ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\\widehat{P}_{i}$ en 2019 angles égaux.\nDémontrer que $P_{1} P_{2} \\ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.", "solution": "$n^{\\circ} 3$ Comme précédemment, on démontre l'égalité (1). En écrivant cette égalité pour deux entiers $i$ consécutifs, et en soustrayant les deux égalités obtenues, on constate que\n\n$$\na_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .\n$$\n\nLa suite $a_{i}$ est donc récurrente linéaire. Cette fois-ci, les racines du polynôme\n\n$$\n1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\\left(1+n X+X^{2}\\right)\n$$\n\nsont $r_{ \\pm}$et 1 . Puisque $n \\geqslant 5$, on sait que\n\n$$\n\\left(n^{2}-4\\right)-(n-2)^{2}=2(n-4)>0\n$$\n\ndonc que $r_{-} \\leqslant-n / 2<-1<r_{+}<0<1$ et que on sait que $\\left|r_{-}\\right|>1>\\left|r_{+}\\right|$.\nIl existe donc trois nombres $\\lambda_{+}, \\lambda_{1}$ et $\\lambda_{-}$tels que\n\n$$\na_{i}=\\lambda_{+} r_{+}^{i}+\\lambda_{1}+\\lambda_{-} r_{-}^{i}\n$$\n\npour tout $i \\in \\mathbb{Z}$. On démontre comme dans la solution précédente que $\\lambda_{-}=0$. De même, si $\\lambda_{+} \\neq 0$, alors $a_{i} /\\left(\\lambda_{+} r_{+}^{i}\\right) \\rightarrow 1$ quand $i \\rightarrow-\\infty$, en contradiction avec le caractère périodique de $\\left(a_{i}\\right)$. Ainsi, $\\lambda_{+}=0 .{ }^{2}$\n2. On pourrait aussi considérer le caractère périodique de la suite $a_{i}-\\lambda_{1}$, mais alors on retomberait dans la solution alternative $\\mathrm{n}^{\\circ} 2$.\n\nEn conclusion, tous les angles $a_{i}$ sont égaux à $\\lambda_{1}$, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.\n\nRemarque : Cet exercice avait été proposé en 2003, aux Olympiades mathématiques de première, dans l'académie de Versailles, mais en incluant des questions intermédiaires. Sur les 623 candidats présents dans l'académie, dont deux lauréats nationaux, aucun n'était parvenu à résoudre cet exercice, qui s'était donc révélé particulièrement difficile bien qu'abordable avec peu d'outils techniques.\n\nCommentaire des correcteurs L'exercice a été résolu par un grand nombre d'élèves. Pratiquement tous les élèves ont su obtenir au moins des points partiels en établissant des équations intéressantes entre les angles associés à deux ou trois sommets consécutifs. Voici cependant plusieurs erreurs rencontrées fréquemment:\n$\\triangleright$ Une partie non négligeable des élèves s'arrête après avoir montré que tous les angles sont égaux. Cela ne suffit pourtant pas à montrer que le polygone est régulier, puisqu'il faut aussi montrer que toutes les longueurs sont égales.\n$\\triangleright$ Quelques élèves ont donné le raisonnement suivant : ils partent de la configuration du polygone régulier et montrent qu'il n'est pas possible, en bougeant les sommets à partir de cette configuration de manière à respecter l'hypothèse de l'énoncé, d'obtenir un autre polygone respectant la condition. Cependant ce raisonnement repose sur des hypothèses de continuité qui n'ont aucune raison d'être, et ne permet donc pas de montrer qu'il n'existe pas d'autres polygones respectant la propriété donnée par l'énoncé. Bien souvent, les transformations proposées ne permettent pas de passer du carré au losange non carré, alors que les deux quadrilatères respectent la condition de l'énoncé.\n$\\triangleright$ Beaucoup d'élèves se contentent de traiter le cas du pentagone au lieu du 2021-gone et disent qu'on étend aisément le résultat pour le cas du 2021-gone. Si une grande partie de leurs raisonnement est effectivement utilisable pour la résolution du cas $n=2021$, l'un des aspects du problème est justement d'être capable de généraliser complètement le raisonnement sur des petits polygones. Il fallait donc, pour être parfaitement convaincant, effectuer de nouveau la preuve dans le cas général. En effet, bien souvent, le raisonnement sur le pentagone produisait des équations reliant les angles entre eux qui étaient beaucoup plus simples que le cas général.\n$\\triangleright$ Quelques élèves se contentent de signaler qu'il y a beaucoup d'équations entre les angles et qu'on a donc un système avec 2021 équations à 2021 inconnues, avant d'affirmer qu'un tel système admet toujours une unique solution (ici, la solution constante). Mais il fallait alors préciser les 2021 équations mises en jeu (trop d'élèves ne font que signaler qu'il y a bien plus que 2021 équations) et montrer que ces équations étaient indépendantes les unes des autres. Le fait qu'un système linéaire de 2021 équations à 2021 inconnues admet une unique solution n'est vrai que dans ce cadre.\nD'autres élèves, après avoir énoncé le système, affirment que « après calculs », l'unique solution est donnée par des angles tous égaux. Mais cette affirmation est loin d'être convaincante sans les calculs à l'appui.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution alternative"}
|
| 14 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Les suites $\\left(a_{n}\\right)_{n \\geqslant 0}$ et $\\left(b_{n}\\right)_{n \\geqslant 0}$ sont définies par\n\n$$\n\\left\\{\\begin{array} { l l } \n{ a _ { n } = 0 } & { \\text { si } n = 0 ; } \\\\\n{ a _ { n } = 2 a _ { \\lfloor n / 2 \\rfloor } + n } & { \\text { si } n \\geqslant 1 ; }\n\\end{array} \\quad \\text { et } \\quad \\left\\{\\begin{array}{ll}\nb_{n}=0 & \\text { si } n=0 ; \\\\\nb_{n}=3 b_{\\lfloor n / 3\\rfloor}+n & \\text { si } n \\geqslant 1 .\n\\end{array}\\right.\\right.\n$$\n\nDémontrer que la suite de terme général $2^{a_{n}}-3^{b_{n}}$ change de signe infiniment souvent.", "solution": "On montre tout d'abord, par récurrence sur $n$, que $a_{n} \\leqslant n\\left\\lfloor\\log _{2}(2 n)\\right\\rfloor$ pour tout entier $n \\geqslant 1$, avec égalité lorsque $n$ est une puissance de 2 . En effet, pour $n=1$, on a bien $a_{n}=1=n \\log _{2}(2 n)$. Puis, si $n \\geqslant 2$,\n\n$$\na_{n}=2 a_{\\lfloor n / 2\\rfloor}+n \\leqslant 2\\lfloor n / 2\\rfloor\\left\\lfloor\\log _{2}(2\\lfloor n / 2\\rfloor)\\right\\rfloor+n \\leqslant n\\left\\lfloor\\log _{2}(n)+1\\right\\rfloor=n\\left\\lfloor\\log _{2}(2 n)\\right\\rfloor \\text {, }\n$$\n\navec égalité lorsque $n / 2=\\lfloor n / 2\\rfloor$ et $n / 2$ est une puissance de 2 .\nOn montre de même que $b_{n} \\leqslant n\\left\\lfloor\\log _{3}(3 n)\\right\\rfloor$ pour tout entier $n \\geqslant 1$, avec égalité lorsque $n$ est une puissance de 3 . On en déduit déjà, si $n$ est une puissance de 3 , que\n\n$$\n2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-(3 n)^{n} \\leqslant(2 n)^{n}-(3 n)^{n}<0 .\n$$\n\nRéciproquement, soit $k$ et $\\ell$ deux entiers naturels non nuls tels que $2^{\\ell}<3^{k} \\leqslant 2^{\\ell+1}$, et soit $n=2^{\\ell}$. Alors $k \\log _{2}(3) \\leqslant \\ell+1$, donc\n\n$$\n\\log _{2}(3) b_{n} \\leqslant \\log _{2}(3) n\\left\\lfloor\\log _{3}(3 n)\\right\\rfloor=\\log _{2}(3) k n \\leqslant(\\ell+1) n=a_{n}\n$$\n\nde sorte que $2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-2^{\\log _{2}(3) b_{n}} \\geqslant 0$. Puisque $2^{a_{n}} \\neq 3^{b_{n}}$, car l'un est impair et l'autre non, on en déduit que $2^{a_{n}}-3^{b_{n}}>0$, ce qui conclut cette solution.\n\nRemarque: On pouvait en fait démontrer que, si\n\n$$\nn=\\sum_{k \\geqslant 0} \\alpha_{k} 2^{k}=\\sum_{\\ell \\geqslant 0} \\beta_{\\ell} 3^{\\ell},\n$$\n\nalors\n\n$$\na_{n}=\\sum_{k \\geqslant 0}(k+1) \\alpha_{k} 2^{k} \\text { et } b_{n}=\\sum_{\\ell \\geqslant 0}(\\ell+1) \\beta_{\\ell} 3^{\\ell} .\n$$\n\nRemarque: Il eût été tentant de démontrer que $2^{a_{n}}>3^{b_{n}}$ dès lors que $n$ est une puissance de 2 ou que $n+1$ est une puissance de 3 . Cependant, il n'en est rien : en notant $\\langle x\\rangle$ la partie fractionnaire d'un réel $x$, c'est-à-dire $\\langle x\\rangle=x-\\lfloor x\\rfloor$, on peut en fait démontrer que $2^{a_{n}}<3^{b_{n}}$ dès lors que $\\left\\langle\\log _{3}(n)\\right\\rangle<7 / 100$ ou que $\\left\\langle\\log _{2}(n)\\right\\rangle>98 / 100$.\n\nCommentaire des correcteurs Cet exercice était difficile, et seuls cinq élèves l'ont intégralement résolu. En pratique, de nombreux élèves ont eu de bonnes idées mais se sont arrêtés en cours de route, au lieu de prendre du recul pour voir comment généraliser ou exploiter leurs découvertes. Ainsi,\n$\\triangleright$ Plusieurs élèves ont remarqué empiriquement, puis démontré, que la valeur de $a_{n+1}-$ $a_{n}$ dépendait de la valuation 2-adique de $n$, en déduisant des sommes horribles pour l'expression de $a_{n}$, alors qu'en utiisant un double-comptage, ils auraient pu obtenir les expressions somme toute mignonnes obtenues ci-dessus.\n$\\triangleright$ De nombreux élèves ont remarqué empiriquement que $a_{n}$ croissait vite quand $n$ était une puissance de 2, et ont donc exprimé leur envie de démontrer que $2^{a_{n}}>3^{b_{n}}$ quand $n$ était une puissance de 2 . Cependant, ils se sont arrêtés là, ou bien se sont contentés de vérifier que $a_{n}=n\\left(1+\\log _{2}(n)\\right)$ quand $n$ est une puissance de 2, mais n'ont pas pensé à rechercher de borne supérieure pour le terme $b_{n}$ quand $n$ est un nombre quelconque.\n$\\triangleright$ Plusieurs élèves, après avoir réussi à démontrer que $3^{b_{n}}>2^{a_{n}}$ lorsque $n$ était une puissance de 3 , ont conjecturé et cherché à démontrer que $2^{a_{n}}>3^{b_{n}}$ lorsque $n$ était une puissance de 2 . Malheureusement pour eux, là résidait la difficulté principale (et particulièrement sournoise!) du problème, puisque cette conjecture pourtant très tentante était invalide, le premier contre-exemple étant $n=2^{8}$.\nC'est là qu'il aurait été utile de prendre du recul pour voir où la preuve de cette conjecture pêchait, avant de l'affiner pour se concentrer simultanément sur les entiers $n$ pour lesquels $a_{n}$ est « grand » (c'est-à-dire que $n$ n'est pas beaucoup plus grand qu'une puissance de 2) et $b_{n}$ est « petit » (c'est-à-dire que $n$ n'est pas beaucoup plus petit qu'une puissance de 3). Les élèves qui ont eu cette idée s'en sont tous tirés avec brio.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 15 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "Morgane a écrit les trois entiers 3, 4 et 12 au tableau. Elle effectue ensuite des changements successifs en procédant comme suit : elle choisit deux nombres $a$ et $b$ écrits au tableau, les efface, et les remplace par $(3 a+4 b) / 5$ et $(4 a-3 b) / 5$.\nMorgane peut-elle, après un nombre fini de tels changements,\na) parvenir à écrire le nombre 13 au tableau?\nb) parvenir à écrire le nombre - 12 au tableau?", "solution": "Nous allons démontrer que la réponse est négative dans les deux cas. Soit $\\mathcal{S}$ la somme des carrés des nombres écrits au tableau, et soit $f$ et $g$ les fonctions définies par $f:(x, y) \\rightarrow(3 x+4 y) / 5$ et $g:(x, y) \\rightarrow(4 x-3 y) / 5$. La relation\n\n$$\nf(x, y)^{2}+g(x, y)^{2}=x^{2}+y^{2}\n$$\n\nnous assure que, lorsque Morgane remplace deux nombres $a$ et $b$ par $f(a, b)$ et $g(a, b)$, elle ne change pas la valeur de $\\mathcal{S}$.\nEn outre, les égalités $f(f(x, y), g(x, y))=x$ et $g(f(x, y), g(x, y))=y$ nous indiquent que les changements qu'effectue Morgane sont réversible : si elle transforme un triplet non ordonné $\\mathbf{t}=(a, b, c)$ en un autre triplet $\\mathbf{t}^{\\prime}=\\left(a^{\\prime}, b^{\\prime}, c\\right)$ tel que $a^{\\prime}=f(a, b)$ et $b^{\\prime}=g(a, b)$, elle peut retransformer $\\mathbf{t}^{\\prime}$ en $\\mathbf{t}$.\nOn traite maintenant les deux questions séparément.\na) Si jamais elle réussit à écrire trois nombres $x, y$ et $z$ tels que $z=13$, alors\n\n$$\nx^{2}+y^{2}+13^{2}=x^{2}+y^{2}+z^{2}=\\mathcal{S}=3^{2}+4^{2}+12^{2}=13^{2}\n$$\n\nde sorte que $x=y=0$. Cela signifie que Morgane peut transformer, en plusieurs étapes, le triplet $(3,4,12)$ en $(0,0,13)$. Elle peut donc également transformer $(0,0,13)$ et $(3,4,12)$.\nOn dit alors qu'un triplet $(x, y, z)$ de nombres rationnelles est sympathique si $v_{13}(u) \\geqslant$ 1 pour tout $u \\in\\{x, y, z\\}$. Si Morgane transforme un triplet $(x, y, z)$ sympathique en un nouveau triplet $\\left(x^{\\prime}, y^{\\prime}, z^{\\prime}\\right)$, ce dernier est clairement sympathique lui aussi. Ainsi, à partir du triplet sympathique $(0,0,13)$, Morgane ne peut obtenir que des triplets sympathiques. Elle ne peut donc pas obtenir le triplet $(3,4,12)$. Ceci démontre bien qu'elle ne pouvait pas transformer le triplet $(3,4,12)$ en $(0,0,13)$.\nb) Nous allons carrément démontrer que Morgane ne peut pas écrire d'entier autre que les éléments de l'ensemble $\\Omega=\\{0, \\pm 3, \\pm 4, \\pm 5,12\\} \\cdot{ }^{3}$\nConsidérons un triplet ordonné ( $x_{1}, x_{2}, x_{3}$ ). Pour tous les entiers $i$ et $j$ distincts l'un de l'autre, on note $\\Theta_{i, j}\\left(x_{1}, x_{2}, x_{3}\\right)$ le triplet obtenu à partir de $\\left(x_{1}, x_{2}, x_{3}\\right)$ en remplaçant les nombres $x_{i}$ et $x_{j}$ par $f\\left(x_{i}, x_{j}\\right)$ et $g\\left(x_{i}, x_{j}\\right)$. Par ailleurs, on dit que $\\left(x_{1}, x_{2}, x_{3}\\right)$ est d'ordre $n$ si $\\min \\left\\{v_{5}\\left(x_{1}\\right), v_{5}\\left(x_{2}\\right), v_{5}\\left(x_{3}\\right)\\right\\}=-n$, et qu'il s'agit d'un triplet égalitaire s'il y a au moins deux indices $i$ tels qu $v_{5}\\left(x_{i}\\right)=-n$.\nTout triplet d'ordre $n \\geqslant 1$ qu'obtiendra Morgane est égalitaire. En effet, supposons que cela ne soit pas le cas. Sans perte de généralité, on a $v_{5}\\left(x_{1}\\right)=-n, v_{5}\\left(x_{2}\\right) \\geqslant 1-n$ et $v_{5}\\left(x_{3}\\right) \\geqslant 1-n$. Alors, en posant $X_{i}=5^{n} x_{i}$, on constate que $X_{1} \\not \\equiv 0(\\bmod 5)$ et que $X_{2} \\equiv X_{3} \\equiv 0(\\bmod 5)$, de sorte que\n\n$$\n0 \\equiv 5^{2 n} \\times 13^{2} \\equiv 5^{2 n}\\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\\right) \\equiv X_{1}^{2}+X_{2}^{2}+X_{3}^{2} \\equiv X_{1}^{2} \\not \\equiv 0 \\quad(\\bmod 5),\n$$\n\nce qui est absurde.\n3. Cela répondrait aussi à la question a), mais de manière nettement plus compliquée.\n\nSoit alors $n \\geqslant 0$ un entier, puis $\\left(x_{1}, x_{2}, x_{3}\\right)$ et $\\left(y_{1}, y_{2}, y_{3}\\right)$ deux triplets d'ordres $\\ell \\leqslant n$ et $n+1$ que Morgane peut obtenir successivement. Il existe deux entiers $i$ et $j$ tels que $\\Theta_{i, j}\\left(x_{1}, x_{2}, x_{3}\\right)=\\left(y_{1}, y_{2}, y_{3}\\right)$, et le triplet $\\left(y_{1}, y_{2}, y_{3}\\right)$ est égalitaire. En notant $k$ l'élément de $\\{1,2,3\\}$ autre que $i$ et $j$, puis $X_{u}=5^{n} x_{u}$ et $Y_{u}=5^{n+1} y_{u}$ pour tout $u \\in\\{1,2,3\\}$, on constate que\n\n$$\nY_{i}=3 X_{i}+4 X_{j} \\not \\equiv 0(\\bmod 5), Y_{j}=4 X_{i}-3 X_{j} \\not \\equiv 0(\\bmod 5) \\text { et } Y_{k} \\equiv 0(\\bmod 5) .\n$$\n\nOn en déduit immédiatement que les triplets $\\Theta_{i, k}\\left(y_{1}, y_{2}, y_{3}\\right)$, $\\Theta_{j, k}\\left(y_{1}, y_{2}, y_{3}\\right)$, $\\Theta_{k, i}\\left(y_{1}, y_{2}, y_{3}\\right)$ et $\\Theta_{k, j}\\left(y_{1}, y_{2}, y_{3}\\right)$ sont tous d'ordre $n+2$. De même,\n\n$$\nf\\left(y_{j}, y_{i}\\right)=\\left(24 X_{i}+7 X_{j}\\right) / 5^{n+2} \\text { et } g\\left(y_{j}, y_{i}\\right)=\\left(7 X_{i}-24 X_{j}\\right) / 5^{n+2}\n$$\n\nPuisque $24 X_{i}+7 X_{j} \\equiv Y_{j}(\\bmod 5)$ et $7 X_{i}-24 X_{j} \\equiv-Y_{i}(\\bmod 5)$, le triplet $\\Theta_{j, i}\\left(y_{1}, y_{2}, y_{3}\\right)$ est lui aussi d'ordre $n+2$. Enfin, comme dans la solution $\\mathrm{n}^{\\circ} 1$, on vérifie aisément que $\\Theta_{i, j}$ est une involution, de sorte que $\\Theta_{i, j}\\left(y_{1}, y_{2}, y_{3}\\right)$ est d'ordre $\\ell \\leqslant n$.\nPour finir, soit $\\mathbf{T}$ un triplet, avec au moins une coordonnée $x$ entière, que Morgane peut écrire. Supposons que Morgane a écrit successivement des triplets $\\mathbf{T}_{0}, \\ldots, \\mathbf{T}_{k}$ tels que $\\mathbf{T}_{0}=(3,4,12)$ et $\\mathbf{T}_{k}=\\mathbf{T}$ soit à coordonnées entières, avec $k$ minimal.\nSoit $\\mathbf{T}_{i}$ un triplet d'ordre $n$ maximal parmi les triplets $\\mathbf{T}_{0}, \\ldots, \\mathbf{T}_{k}$. Si $n \\geqslant 1$ et si $i \\leqslant k-1$, on vient de démontrer que $\\mathbf{T}_{i-1}=\\mathbf{T}_{i+1}$, ce qui vient contredire la minimalité de $k$. Si $n \\geqslant 1$ et si $i=k$, alors $\\mathbf{T}_{k}$ contient une coordonnée déjà présente dans $\\mathbf{T}_{k-1}$ et deux coordonnées de valuation 5 -adique égale à $-n$, donc distinctes de $x$. Ceci vient là encore contredire la minimalité de $k$.\nIl suffit maintenant de démontrer que, partant d'un triplet $\\mathbf{t}=\\left(x_{1}, x_{2}, x_{3}\\right)$ d'éléments de $\\Omega$ tel que $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=13^{2}$, tout triplet $\\mathbf{t}^{\\prime}=\\left(y_{1}, y_{2}, y_{3}\\right)$ à coordonnées entières que Morgane peut former est à coordonnées dans $\\Omega$. Tout d'abord, on peut supposer sans perte de généralité que $\\left|x_{1}\\right| \\leqslant\\left|x_{2}\\right| \\leqslant\\left|x_{3}\\right|$, de sorte que $3 \\times 5^{2}<13^{2} \\leqslant 3 x_{3}^{2}$, donc que $x_{3}=12$ et que $\\left(x_{1}, x_{2}\\right) \\in\\{(0, \\pm 5),( \\pm 3, \\pm 4)\\}$.\nOn suppose alors que $\\mathbf{t}^{\\prime}$ a une coordonnée entière qui n'appartient pas à $\\Omega$. Soit $i$ et $j$ les entiers tels que $\\mathbf{t}^{\\prime}=\\Theta_{i, j}(\\mathbf{t})$. Si $\\left\\{x_{i}, x_{j}\\right\\} \\subseteq\\{0, \\pm 3, \\pm 4, \\pm 5\\}$, alors $y_{i}^{2}+y_{j}^{2}=x_{i}^{2}+x_{j}^{2}=5^{2}$, donc $\\left\\{y_{i}, y_{j}\\right\\} \\subseteq \\Omega$. Ainsi, l'un des deux entiers $x_{i}$ et $x_{j}$ est égal à 12 . Or,\n\n$$\n0 \\equiv 5 y_{i} \\equiv 3 x_{i}+4 x_{j} \\equiv 3\\left(x_{i}-2 x_{j}\\right)(\\bmod 5)\n$$\n\ndonc $x_{i} \\equiv 2 x_{j}(\\bmod 5)$.\nSi $x_{i}=12$, alors $x_{j} \\equiv 1(\\bmod 5)$, donc $x_{j}=-4$, et $\\left(y_{i}, y_{j}\\right)=(4,12)$; si $x_{j}=12$, alors $x_{i} \\equiv-1(\\bmod 5)$, donc $x_{j}=4$, et $\\left(y_{i}, y_{j}\\right)=(12,-4)$. Dans les deux cas, on a bien $\\left\\{y_{i}, y_{j}\\right\\} \\subseteq \\Omega$. En conclusion, tout nombre entier que peut écrire Morgane appartient nécessairement à $\\Omega$. Elle ne peut donc pas écrire le nombre -12 au tableau.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ On peut présenter la solution à la partie a) d'une autre manière. Tout d'abord, tout nombre qu'écrira Morgane appartiendra nécessairement à l'ensemble $\\mathbb{L}=\\left\\{d / 5^{k}: d, k \\in \\mathbb{Z}\\right\\}$. Puisque 5 et 13 sont premiers entre eux, on identifie chaque élément de $\\mathbb{L}$ à son résidu modulo 13.\nMais alors, si Morgane parvient à remplacer deux nombres $a$ et $b$ par des nombres $a^{\\prime}=f(a, b)$ et $b^{\\prime}=g(a, b)$ tels que $a^{\\prime} \\equiv b^{\\prime} \\equiv 0(\\bmod 13)$, cela signifie que $3 a+4 b \\equiv 4 a-3 b \\equiv 0(\\bmod 13)$, et donc que\n\n$$\n\\begin{aligned}\na & \\equiv-25 a \\\\\nb & \\equiv-3(3 a+4 b)-4(4 a-3 b) \\\\\nb & \\equiv 0 \\quad(\\bmod 13) ; \\\\\n& \\equiv-4(3 a+4 b)+3(4 a-3 b) \\equiv 0 \\quad(\\bmod 13)\n\\end{aligned}\n$$\n\nPar conséquent, une récurrence immédiate indique que les nombres que Morgane écrira au tableau ne seront jamais tous congrus à 0 modulo 13.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 16 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "Morgane a écrit les trois entiers 3, 4 et 12 au tableau. Elle effectue ensuite des changements successifs en procédant comme suit : elle choisit deux nombres $a$ et $b$ écrits au tableau, les efface, et les remplace par $(3 a+4 b) / 5$ et $(4 a-3 b) / 5$.\nMorgane peut-elle, après un nombre fini de tels changements,\na) parvenir à écrire le nombre 13 au tableau?\nb) parvenir à écrire le nombre - 12 au tableau?", "solution": "$n^{\\circ} 2$ On peut également répondre à la partie a) avec une version simplifiée du raisonnement utilisé pour la partie b).\nEn effet, il s'agit de démontrer que l'on ne peut pas atteindre le triplet $\\mathbf{T}=(0,0,13)$, à l'ordre près des coordonnées. Si Morgane atteint ce triplet, et en raisonnant comme ci-dessus, elle a nécessairement dû écrire des triplets $\\mathbf{T}_{0}=(3,4,12), \\mathbf{T}_{1}, \\ldots, \\mathbf{T}_{k}=\\mathbf{T}$, chaque $\\mathbf{T}_{i}$ étant à coordonnées entières.\nMais alors, puisque chaque opération $\\Theta_{i, j}$ est une involution, on peut écrire $\\mathbf{T}_{k-1}$ sous la forme $\\Theta_{i, j}(\\mathbf{T})$. À l'ordre près de ses coordonnées, le triplet $\\mathbf{T}_{k-1}$ donc est égal à $\\Theta_{2,3}(0,0,13)$ ou à $\\Theta_{3,2}(0,0,13)$, c'est-à-dire à $(0,52 / 5,-39 / 5)$ ou à $(0,39 / 5,52 / 5)$. Cette contradiction démontre que Morgane ne pourra jamais écrire le nombre 13 au tableau.\n\nCommentaire des correcteurs L'exercice était très difficile, et peu d'élèves ont réussi à trouver des éléments véritablement intéressants. Plusieurs élèves ont compris l'importance de la valuation 5 adique des nombres écrits : il fallait réussir à formaliser cette idée et regarder l'évolution des valuations 5 -adiques écrites.\n\n\n[^0]: 1. On pourrait aussi considérer le caractère périodique de la suite $a_{i}-\\lambda_{1}$, mais alors on retomberait dans la solution alternative $\\mathrm{n}^{\\circ} 2$.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-3-Web.jsonl
ADDED
|
@@ -0,0 +1,21 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que\n\n$$\nx \\leqslant 2 a-b, y \\leqslant 2 b-c, z \\leqslant 2 c-d \\text { et } t \\leqslant 2 d-a .\n$$\n\nDémontrer que $a=b=c=d$.", "solution": "Pour mieux exploiter la première inégalité, que l'on réécrit comme $x+b \\leqslant 2 a$, l'idéal serait que $x$ et $b$ soient maximaux, ou bien que $a$ soit minimal. Évidemment, il se pourrait très bien que ni $a$, ni $b$, ni $x$ ne soit extrémal. Néanmoins, puisque les variables jouent des rôles cycliques, on peut tout de même espérer, au choix, que $a$ soit minimal, ou que $b$ soit maximal, ou que $x$ soit maximal.\nCependant, espérer que $b$ et $x$ seraient simultanément maximaux serait trop demander. À la place, on se contente de supposer, sans perte de généralité, que $a$ est le plus petit des quatre nombres réels. Dans ces conditions, $2 a \\leqslant b+x \\leqslant 2 a$, donc $a=b$. Mais alors $b$ est aussi le plus petit des quatre nombres réels, donc $b=c$, et on démontre de même que $c=d$.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ En sommant les quatre inégalités de l'énoncé, on obtient l'inégalité $x+y+z+t \\leqslant a+b+c+d$. Puisque $(x, y, z, t)$ est une permutation de $(a, b, c, d)$, cette dernière inégalité est en fait une égalité, donc chacune des inégalités de l'énoncé est également une égalité : $x=2 a-b, y=2 b-c, z=2 c-d$ et $t=2 d-a$.\nEn élevant chaque membre au carré et en additionnant les égalités ainsi obtenues, on constate alors que\n\n$$\na^{2}+b^{2}+c^{2}+d^{2}=x^{2}+y^{2}+z^{2}+t^{2}=5\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)-4(a b+b c+c d+d a)\n$$\n\nCela signifie que $a b+b c+c d+d a=a^{2}+b^{2}+c^{2}+d^{2}$, ou encore que\n\n$$\n0=2\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)-2(a b+b c+c d+d a)=(a-b)^{2}+(b-c)^{2}+(c-d)^{2}+(d-a)^{2},\n$$\n\nde sorte que $a=b=c=d$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que\n\n$$\nx \\leqslant 2 a-b, y \\leqslant 2 b-c, z \\leqslant 2 c-d \\text { et } t \\leqslant 2 d-a .\n$$\n\nDémontrer que $a=b=c=d$.", "solution": "$n^{\\circ} 2$ Une autre manière de conclure consiste à remarquer que l'égalité $a b+b c+c d+d a=a^{2}+b^{2}+c^{2}+d^{2}$ est un cas d'égalité de l'inégalité de Cauchy-Schwarz, qui n'est atteint que si les quadruplets $(a, b, c, d)$ et $(b, c, d, a)$ sont proportionnels l'un à l'autre. Puisque ceux-ci sont de même somme, ils sont donc égaux, ce qui conclut en effet.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 3 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que\n\n$$\nx \\leqslant 2 a-b, y \\leqslant 2 b-c, z \\leqslant 2 c-d \\text { et } t \\leqslant 2 d-a .\n$$\n\nDémontrer que $a=b=c=d$.", "solution": "$n^{\\circ} 3$ Une autre variante des deux solutions précédentes est la suivante: quitte à soustraire un réel $\\lambda$ suffisamment grand à tous nos nombres, on suppose que chaque membre de chaque inégalité est négatif. En élevant ces membres au carré et en additionnant les inégalités ainsi obtenues, on constate alors que\n\n$$\na^{2}+b^{2}+c^{2}+d^{2}=x^{2}+y^{2}+z^{2}+t^{2} \\geqslant 5\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)-4(a b+b c+c d+d a) .\n$$\n\nCela signifie une fois de plus que $a b+b c+c d+d a \\geqslant a^{2}+b^{2}+c^{2}+d^{2}$, et l'on conclut alors comme précédemment.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que\n\n$$\nx \\leqslant 2 a-b, y \\leqslant 2 b-c, z \\leqslant 2 c-d \\text { et } t \\leqslant 2 d-a .\n$$\n\nDémontrer que $a=b=c=d$.", "solution": "$n^{\\circ} 4$ On procède de manière brutale, étudiant séparément chacune des $4!=24$ permutations $(x, y, z, t)$ possibles. Dans chaque cas, nous allons exprimer les nombres $a-b, b-c, c-d$ et $d-a$ comme combinaisons linéaires, à coefficients positifs, des\nnombres $\\alpha=(2 a-b-x) / 60, \\beta=(2 b-c-y) / 60, \\gamma=(2 c-d-z) / 60$ et $\\delta=(2 d-a-t) / 60$; les dénominateurs ont été choisis a posteriori pour que tous nos coefficients soient entiers. Cela démontrera qu'il s'agit de nombres positifs ou nuls, et puisque leur somme vaut 0 , on en conclura que $a=b=c=d$.\nCependant, que l'on ne se méprenne pas! Nous présentons cette solution dans le seul but de le convaincre le lecteur que, si celle-ci est théoriquement faisable dans le temps imparti des quatre heures de l'épreuve, elle est très risquée, et intellectuellement très peu satisfaisante. En outre, on serait bien en peine d'appliquer une telle méthode si on avait 2021 variables plutôt que quatre. Pour information, les correcteurs ont eu besoin d'un programme informatique pour écrire les cases de ce tableau, qu'ils n'ont pas eu le courage de calculer à la main après y avoir passé plus de deux heures.\n\n| Cas | $(x, y, z, t)$ | $a-b$ | $b-c$ | $c-d$ | $d-a$ |\n| :---: | :---: | :---: | :---: | :---: | :---: |\n| 1 | $(a, b, c, d)$ | $60 \\alpha$ | $60 \\beta$ | $60 \\gamma$ | $60 \\delta$ |\n| 2 | $(a, b, d, c)$ | $60 \\alpha$ | $60 \\beta$ | $30 \\gamma$ | $30 \\gamma+60 \\delta$ |\n| 3 | $(a, c, b, d)$ | $60 \\alpha$ | $30 \\beta$ | $30 \\beta+60 \\gamma$ | $60 \\delta$ |\n| 4 | $(a, c, d, b)$ | $60 \\alpha$ | $30 \\beta$ | $30 \\gamma$ | $30 \\beta+30 \\gamma+60 \\delta$ |\n| 5 | $(a, d, b, c)$ | $60 \\alpha$ | $20 \\alpha+40 \\beta+20 \\delta$ | $20 \\beta+40 \\gamma$ | $20 \\beta+40 \\gamma+60 \\delta$ |\n| 6 | $(a, d, c, b)$ | $60 \\alpha$ | $30 \\alpha+60 \\beta+30 \\delta$ | $60 \\gamma$ | $30 \\beta+30 \\gamma+60 \\delta$ |\n| 7 | $(b, a, c, d)$ | $30 \\alpha$ | $30 \\alpha+60 \\beta$ | $60 \\gamma$ | $60 \\delta$ |\n| 8 | $(b, a, d, c)$ | $30 \\alpha$ | $30 \\alpha+60 \\beta$ | $30 \\gamma$ | $30 \\gamma+60 \\delta$ |\n| 9 | $(b, c, a, d)$ | $30 \\alpha$ | $30 \\beta$ | $30 \\alpha+30 \\beta+60 \\gamma$ | $60 \\delta$ |\n| 10 | $(b, c, d, a)$ | $30 \\alpha$ | $30 \\beta$ | $30 \\gamma$ | $30 \\delta$ |\n| 11 | $(b, d, a, c)$ | $30 \\alpha$ | $10 \\alpha+40 \\beta+20 \\delta$ | $20 \\alpha+20 \\beta+40 \\gamma$ | $30 \\alpha+20 \\gamma+40 \\delta$ |\n| 12 | $(b, d, c, a)$ | $30 \\alpha$ | $30 \\alpha+60 \\beta+30 \\delta$ | $60 \\gamma$ | $30 \\delta$ |\n| 13 | $(c, a, b, d)$ | $40 \\alpha+20 \\gamma+20 \\delta$ | $20 \\alpha+40 \\beta$ | $20 \\alpha+40 \\beta+60 \\gamma$ | $60 \\delta$ |\n| 14 | $(c, a, d, b)$ | $40 \\alpha+20 \\gamma+20 \\delta$ | $20 \\alpha+40 \\beta$ | $30 \\gamma$ | $20 \\beta+10 \\gamma+40 \\delta$ |\n| 15 | $(c, b, a, d)$ | $60 \\alpha+30 \\gamma+30 \\delta$ | $60 \\beta$ | $30 \\alpha+30 \\beta+60 \\gamma$ | $60 \\delta$ |\n| 16 | $(c, b, d, a)$ | $60 \\alpha+30 \\gamma+30 \\delta$ | $60 \\beta$ | $30 \\gamma$ | $30 \\delta$ |\n| 17 | $(c, d, a, b)$ | $48 \\alpha+24 \\gamma+12 \\delta$ | $12 \\alpha+48 \\beta+24 \\delta$ | $24 \\alpha+12 \\beta+48 \\delta$ | $24 \\beta+12 \\gamma+48 \\delta$ |\n| 18 | $(c, d, b, a)$ | $40 \\alpha+20 \\gamma+10 \\delta$ | $20 \\alpha+40 \\beta+20 \\delta$ | $20 \\beta+40 \\gamma$ | $30 \\delta$ |\n| 19 | $(d, a, b, c)$ | $45 \\alpha+15 \\gamma+30 \\delta$ | $30 \\alpha+45 \\beta+15 \\delta$ | $15 \\alpha+30 \\beta+45 \\gamma$ | $15 \\beta+30 \\gamma+45 \\delta$ |\n| 20 | $(d, a, c, b)$ | $40 \\alpha+20 \\delta$ | $40 \\alpha+60 \\beta+20 \\delta$ | $60 \\gamma$ | $20 \\beta+20 \\gamma+40 \\delta$ |\n| 21 | $(d, b, a, c)$ | $60 \\alpha+20 \\gamma+40 \\delta$ | $60 \\beta$ | $20 \\alpha+20 \\beta+40 \\gamma$ | $20 \\gamma+40 \\delta$ |\n| 22 | $(d, b, c, a)$ | $60 \\alpha+30 \\delta$ | $60 \\beta$ | $60 \\gamma$ | $30 \\delta$ |\n| 23 | $(d, c, a, b)$ | $40 \\alpha+20 \\delta$ | $30 \\beta$ | $20 \\alpha+10 \\beta+40 \\gamma$ | $20 \\beta+20 \\gamma+40 \\delta$ |\n| 24 | $(d, c, b, a)$ | $60 \\alpha+30 \\delta$ | $30 \\beta$ | $30 \\beta+60 \\gamma$ | $30 \\delta$ |\n\nRemarque : Les paires de variables $(a, x),(b, y),(c, z)$ et $(d, t)$ jouent des rôles cycliques. Dans la solution précédente, il est donc possible de traiter plusieurs permutations d'un coup. Par exemple, les cas où $(x, y, z, t)=(a, b, d, c)$ et $(y, z, t, x)=(b, c, a, d)$ se traitent de la même manière, puisque traiter la seconde permutation revient à traiter la première, mais en remplaçant respectivement les nombres $\\alpha, \\beta, \\gamma$ et $\\delta \\operatorname{par} \\beta, \\gamma, \\delta$ et $\\beta$. Plus généralement, si on note $\\sigma$ la fonction telle que $\\sigma(a)=b, \\sigma(b)=c, \\sigma(c)=d$ et $\\sigma(d)=a$, chaque permutation $(x, y, z, t)$ se traite de la même manière que la permutation $(\\sigma(t), \\sigma(x), \\sigma(y), \\sigma(z))$.\nCette observation permet de regrouper les cas\n$\\triangleright 2,22,7$ et 3 ,\n$\\triangleright 4,16,12$ et 9 ,\net donc de n'étudier « que » 10 permutations plutôt que 24 (par exemple les permutations sur fond gris), ce qui permet d'obtenir une solution horrible plutôt qu'inhumaine.\n\nRemarque: Alternativement, et au vu du rôle cyclique de nos variables, il est en fait suffisant de démontrer l'inégalité $a \\geqslant b$ pour chaque permutation $(x, y, z, t)$, pour en déduire ensuite les inégalités analogues $b \\geqslant c, c \\geqslant d$ et $d \\geqslant a$. Une telle approche, si elle ne permet plus le regroupement mentionné à la remarque précédente, nous permet de nous concentrer sur la première colonne du tableau.\nDe surcroît, puisque $a-b=60 \\alpha$ lorsque $x=a$, et $a-b=30 \\alpha$ lorsque $x=b$, il suffit en fait d'étudier que les 12 permutations pour lesquelles $x=c$ ou $x=d$, soit 12 cases sur les $24 \\times 4=96$ cases du tableau. Certains cas restent cependant particulièrement pénibles à traiter, par exemple le cas 17.\n\nCommentaire des correcteurs Relativement peu d'élèves ont obtenu tous les points sur le problème. Plusieurs approches étaient possibles. La stratégie la plus risquée consistait à tester les 24 cas possibles, éventuellement en invoquant des arguments de symétrie pour se débarrasser de certains cas. Parmi les élèves qui ont tenté cette approche, très peu en sont arrivés à bout. Voici quelques remarques générales à la suite de la lecture des tentatives proposées:\n$\\triangleright$ De nombreux élèves ont pensé à sommer les inégalités pour montrer qu'il s'agissait en fait d'égalités. Il s'agit là d'un excellent réflexe!\n$\\triangleright$ De nombreux élèves pensent à considérer $a$ comme le minimum et supposent par l'absurde que $a<b, a<c$ et $a<d$. Après avoir obtenu une contradiction, (par exemple en montrant que $a=b$ ), ils en déduisent immédiatement que $a=b=c=d$. Toutefois, la contradiction obtenue ici permettait simplement d'affirmer qu'au moins l'une des inégalités strictes était invalide, mais pas forcément les trois en même temps.\n$\\triangleright$ La remarque la plus importante est sans doute la suivante: De nombreux élèves affirment que l'on peut supposer sans perte de généralité que $a \\leqslant b \\leqslant c \\leqslant d$. Cette supposition n'est possible que si les inégalités sont totalement symétriques, c'est-àdire si échanger deux variables ne changent pas les inégalités. Or, ici, si on échange les variables $a$ et $b$, le système d'inégalités change complètement.\nLes inégalités possèdent toutefois une symétrie cyclique : remplacer ( $a, b, c, d$ ) par $(d, a, b, c)$ ne change pas les inégalités. Cette symétrie cyclique ne nous permet donc pas d'ordonner les variables, mais seulement de choisir une variable pour être le minimum ou le maximum des 4 réels.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 5 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle dont les angles sont aigus. On note $D$ le pied de la hauteur issue de $A$ dans le triangle $A B C$, puis $E$ le milieu du segment $[A D]$, et $\\omega$ le cercle de diamètre $[A D]$. Ensuite, soit $X$ le point d'intersection entre $\\omega$ et la droite $(B E)$, tel que $B$ et $X$ soient situés de part et d'autre de la droite $(A D)$. De même, soit $Y$ le point d'intersection entre $\\omega$ et la droite $(C E)$, tel que $C$ et $Y$ soient situés de part et d'autre de la droite $(A D)$. Enfin, on suppose qu'il existe un point $Z$, autre que $D$, appartenant à la droite $(A D)$ et aux deux cercles circonscrits à $B D X$ et à $C D Y$. Démontrer que $A B=A C$.", "solution": "Soit $\\omega^{\\prime}$ le cercle de diamètre $[E Z]$ et $\\omega_{b}$ le cercle passant par $B, D$, $X$ et $Z$. Puisque $\\widehat{B D Z}=90^{\\circ}$, on sait que $[B Z]$ est un diamètre de $\\omega_{b}$. On en déduit que $\\widehat{E X Z}=\\widehat{B X Z}=90^{\\circ}$, donc que $X$ est un point d'intersection entre $\\omega$ et $\\omega^{\\prime}$. De même, $Y$ est un point d'intersection entre $\\omega$ et $\\omega^{\\prime}$.\nSoit $s$ la symétrie d'axe $(A D)$ : elle laisse les cercles $\\omega$ et $\\omega^{\\prime}$ globalement invariants, donc elle échange $X$ et $Y$. Puisque $E=s(E)$, la symétrie $s$ échange donc les droites $(E X)$ et $(E Y)$. En outre, $s$ laisse également la droite $(B C)$ globalement invariante. Ainsi, $s$ échange $B$ et $C$. Puisque $A=s(A)$, on en conclut que $A B=A C$.\n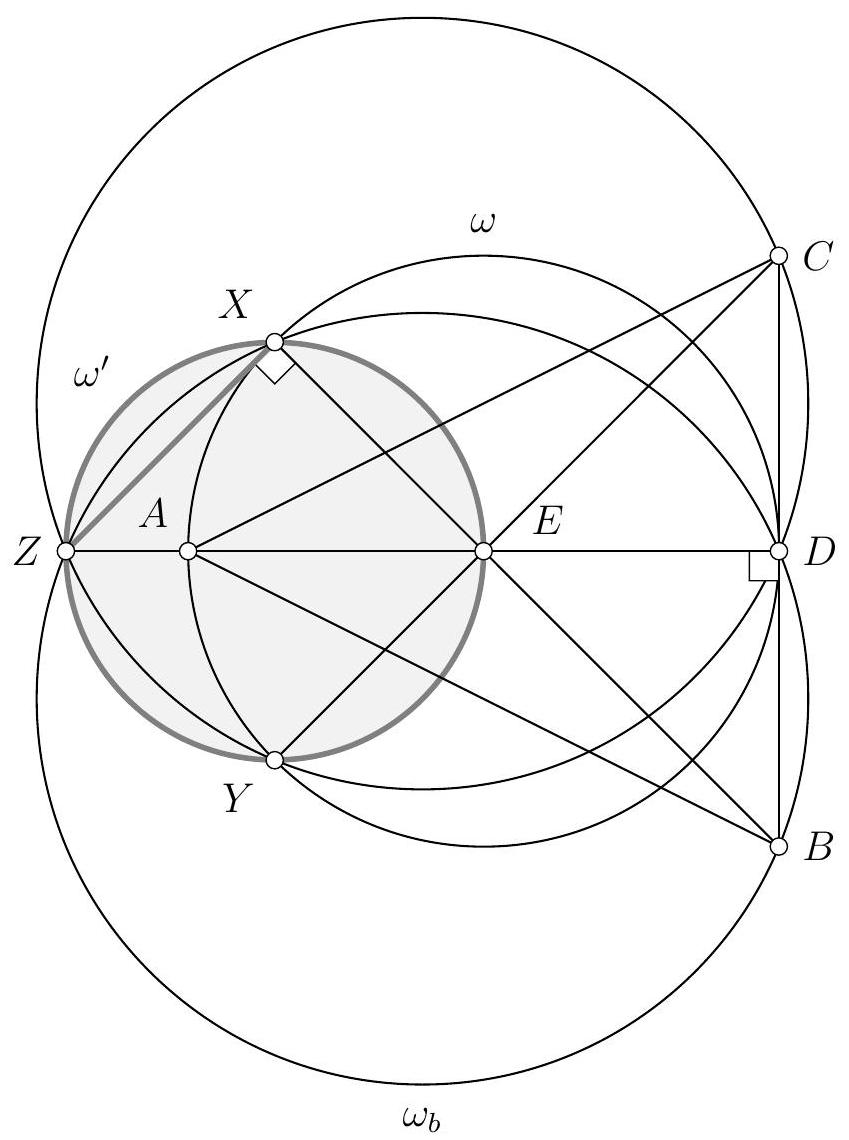", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 6 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle dont les angles sont aigus. On note $D$ le pied de la hauteur issue de $A$ dans le triangle $A B C$, puis $E$ le milieu du segment $[A D]$, et $\\omega$ le cercle de diamètre $[A D]$. Ensuite, soit $X$ le point d'intersection entre $\\omega$ et la droite $(B E)$, tel que $B$ et $X$ soient situés de part et d'autre de la droite $(A D)$. De même, soit $Y$ le point d'intersection entre $\\omega$ et la droite $(C E)$, tel que $C$ et $Y$ soient situés de part et d'autre de la droite $(A D)$. Enfin, on suppose qu'il existe un point $Z$, autre que $D$, appartenant à la droite $(A D)$ et aux deux cercles circonscrits à $B D X$ et à $C D Y$. Démontrer que $A B=A C$.", "solution": "$n^{\\circ} 1$ Notons $\\omega_{b}$ et $\\omega_{c}$ les cercles circonscrits à $B D X Z$ et à $C D Y Z$. La droite $(D Z)$ est l'axe radical de ces deux cercles. Puisque $E$ appartient à cet axe radical, il a mêmes puissances par rapport aux cercles $\\omega_{b}$ et $\\omega_{c}$, ce qui signifie que $E X \\cdot E B=E Y \\cdot E C$. Or, $E$ est le centre du cercle $\\omega$. On en déduit que $E X=E Y$, et donc que $E B=E C$.\nPar conséquent, la droite $(A D)$, qui est la perpendiculaire à $(B C)$ passant par $E$, est aussi la médiatrice de $[B C]$. On en conclut comme prévu que $A B=A C$.\n\nCommentaire des correcteurs Une première difficulté de l'exercice était de trouver comment tracer sa figure de façon pertinente. En effet, tracer d'emblée un triangle isocèle risquait\nde donner de fausses intuitions sur la figure. Cela a été dommageable pour des nombreux élèves qui, après avoir tracé la figure pour un triangle $A B C$ isocèle en $A$, ont affirmé sans les démontrer certaines égalités d'angles parce qu'elles apparaissaient comme vraies sur la figure. Après avoir tracé cette première figure, il aurait en fait fallu tracer une nouvelle figure obtenue en oubliant l'une des hypothèses, par exemple en construisant un côté $A B$ légèrement plus grand que le côté $A C$; cette nouvelle figure pouvant alors servir comme support de réflexion alternatif, pour être sûr de ne pas être trompé par son propre brouillon. De manière générale, ce conseil reste valide pour tous les exercices de géométrie ayant un format analogue à celui de l'énoncé.\nIl fallait ensuite trouver comment exploiter l'hypothèse donnée par l'énoncé. Le théorème de l'angle inscrit était de mise ici, et très peu d'élèves ont relevé l'égalité $\\widehat{Z X B}=\\widehat{Z D B}=90^{\\circ}$, qui était pourtant le point de départ du raisonnement. La plupart des élèves qui ont noté cette égalité sont parvenus à conclure l'exercice.\nVoici quelques éléments trouvés de façon récurrente dans les réponses proposées :\n$\\triangleright$ Beaucoup d'élèves prétendent donner une solution complète du problème, mais qui en réalité ne fonctionnait pas ou comportait un trou important. La plupart du temps, cela vient du fait qu'une affirmation est donnée sans démonstration, sans doute parce qu'elle apparaît visuellement sur la figure (cf la remarque plus haut). L'affirmation est souvent vraie mais la démontrer revient souvent à démontrer l'exercice.\nUne façon de ne pas tomber dans cet écueil est de se relire, de vérifier que toutes les affirmations sont justifiées, et de vérifier si toutes les hypothèses de l'énoncé ont été utilisées! Certains élèves affirment ainsi démontrer que le triangle $A B C$ est isocèle sans évoquer une seule fois le point $Z$ ou sans mentionner que le point $E$ est défini comme le milieu du segment $[A D]$.\nDe fait, tracer une figure alternative où l'on oublie telle ou telle hypothèse (par exemple les hypothèses que l'on n'a pas utilisées) permet de vérifier si ce que l'on raconte a une chance d'être vrai.\n$\\triangleright$ Beaucoup d'élèves remarquent que la droite $(A D)$ est l'axe radical de deux cercles. Cette remarque pouvait conduire à une autre façon (plutôt efficace) de résoudre l'exercice. Toutefois, il est frustrant de voir que la plupart des élèves ayant formulé cette remarque se sont arrêtés à cette remarque sans continuer leur raisonnement.\nL'intérêt de repérer un axe radical est de pouvoir ensuite regarder la puissance d'un point bien choisi sur cet axe par rapport aux deux cercles concernés. Ici, très peu d'élèves signalent que le point $E$ appartenait à l'axe radical et a donc la même puissance par rapport aux deux cercles donnés.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 7 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Soit $k \\geqslant 1$ un entier, et soit $A$ un sous-ensemble de $\\{1,2, \\ldots, 3 k\\}$ tel que, pour tous les éléments $a, b, c$ de $A$, si $a+b=2 c$, alors $a=b=c$. Pour tout entier $n \\geqslant 1$, on note $r_{k}(n)$ le plus petit entier naturel non nul tel que $3 k$ divise $n-r_{k}(n)$. En outre, on dit que $n$ est petit si $n \\leqslant k$, que $n$ est moyen si $k+1 \\leqslant n \\leqslant 2 k$, et que $n$ est grand si $2 k+1 \\leqslant n$. Enfin, on suppose que l'on dispose de deux entiers naturels non nuls $x$ et $d$ tels que $r_{k}(x), r_{k}(x+d)$ et $r_{k}(x+2 d)$ appartiennent tous trois à $A$, et tels que $r_{k}(x) \\neq r_{k}(x+d)$.\nPeut-on nécessairement affirmer, au vu des informations ci-dessus, que\na) au moins l'un des deux entiers $r_{k}(x)$ et $r_{k}(x+d)$ est moyen ou grand?\nb) au moins l'un des deux entiers $r_{k}(x)$ et $r_{k}(x+d)$ est petit ou grand?\nc) au moins l'un des deux entiers $r_{k}(x)$ et $r_{k}(x+d)$ est petit ou moyen?", "solution": "Cet énoncé peut paraître long et compliqué. Il contient donc d'en retenir les éléments saillants, pour mieux comprendre ce qui se passe. Ici, on souhaite que l'ensemble $A$ ne contienne pas de progression arithmétique ( $a, c, b$ ). Il s'agit donc de trouver deux entiers $x$ et $d$ pour lesquels, quand bien même $x, x+d$ et $x+2 d$ sont manifestement en progression arithmétique, les restes $r_{k}(x), r_{k}(x+d)$ et $r_{k}(x+2 d)$ dans la division euclidienne par $3 k$ ne seront pas en progression arithmétique.\nUne idée, pour ce faire, est de construire $x$ et $d$, éventuellement en les choisissant négatifs si ça nous arrange (il sera toujours temps d'ajouter à $x$ et à $d$ des multiples de $3 k$ arbitrairement grands) tels que $x$ et $x+d$ soient compris entre 1 et $3 k$, mais $x+2 d$ dépasse de l'intervalle $\\{1,2, \\ldots, 3 k\\}$. Une fois effectué ce travail de réflexion préparatoire, on peut maintenant traiter une à une les trois questions de l'énoncé : on cherchera à construire des entiers $x$ et $x+d$ qui sont tous deux petits, ou tous deux moyens, ou tous deux grands.\na) Cherchons à construire de petits entiers $x$ et $x+d$ tels que $x+2 d \\leqslant 0$ et $x+2 d \\geqslant 3 k+1$. Puisque $x+2 d=2(x+d)-x \\leqslant 2 k-1<2 k+1$, il nous faut faire en sorte que $x+2 d \\leqslant 0$, donc que $d<0$. La manière la plus simple de procéder est alors de choisir $d=-1, x=2$, et $k \\geqslant 2$. Évidemment, on n'a pas vraiment le droit de choisir $d=-1$; comme mentionné précédemment, on choisira donc $d=3 k-1$, ce qui revient au même mais est conforme aux contraintes de l'énoncé.\nEn pratique, si $k=2, A=\\{1,2,6\\}, x=2$ et $d=5$, alors $r_{k}(x)=2$ et $r_{k}(x+d)=1$ sont deux petits éléments de $A$, et $r_{k}(x+2 d)=6$ appartient à $A$ également. La réponse est donc négative.\n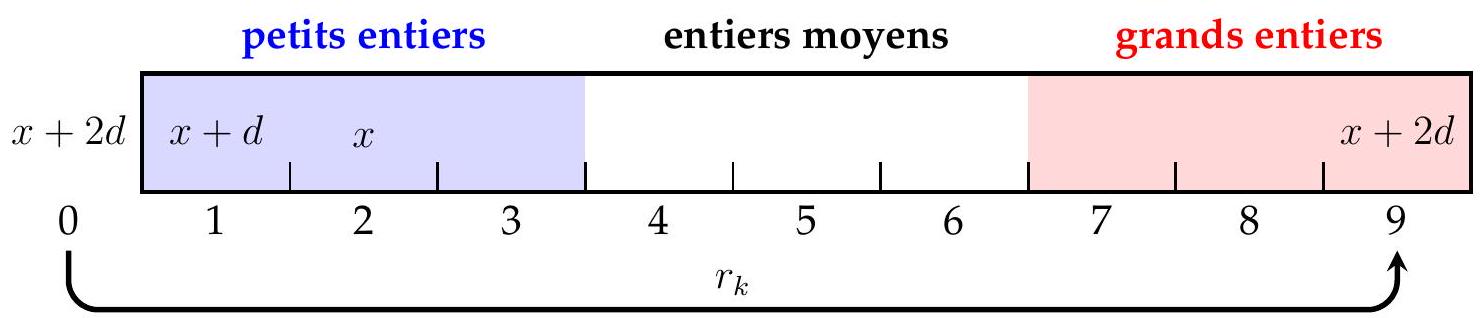\nb) Supposons que $r_{k}(x)$ et $r_{k}(x+d)$ soient tous deux moyens, puis soit $t=2 r_{k}(x+d)-r_{k}(x)$. On sait que\n\n$$\n2=2(k+1)-2 k \\leqslant t \\leqslant 2 \\times 2 k-(k+1)=3 k-1\n$$\n\net que\n\n$$\nt \\equiv 2(x+d)-x \\equiv x+2 d \\quad(\\bmod 3 k),\n$$\n\ndonc que $t=r_{k}(x+2 d)$. Mais alors $t+r_{k}(x)=2 r_{k}(x+d)$, en contradiction avec la caractérisation initiale de $A$. Ceci invalide notre supposition, et la réponse est donc positive.\nc) Au vu de la symétrie manifeste entre gauche et droite, il suffit d'adapter la construction proposée en question a), en remplaçant $x$ par $3 k+1-x$ et $d$ par $3 k-d$.\nEn pratique, si $k=2, A=\\{1,5,6\\}, x=5$ et $d=1$, alors $r_{k}(x)=5$ et $r_{k}(x+d)=6$ sont deux grands éléments de $A$, et $r_{k}(x+2 d)=1$ appartient à $A$ également. La réponse est donc négative.\n\n\nCommentaire des correcteurs Une des difficultés principales de cet exercice était d'en comprendre l'énoncé en détail, sans oublier des contraintes de ci de là. L'idée était ensuite de mettre en évidence trois entiers qui sont en progression arithmétique si on les considère modulo $3 k$, mais pas si on les considère en tant qu'entiers. Les élèves qui ont eu cette idée ont en général obtenu d'excellents résultats.\nOn peut cependant noter que plusieurs erreurs évitables ont piégé de nombreux élèves. Nous les listons ici pour éviter qu'elles ne se reproduisent:\n$\\triangleright$ Plusieurs élèves ont confondu les entiers $x, x+d$ et $x+2 d$ avec leurs restes $r_{k}(x), r_{k}(x+d)$ et $r_{k}(x+2 d)$. En particulier, ils ont cru que $x, x+d$ et $x+2 d$ devaient forcément être compris entre 1 et $3 k$.\n$\\triangleright$ Plusieurs élèves ont cru à tort que, pour que l'on puisse diviser $x$ par $3 k$, il fallait nécessairement que le quotient de cette division soit non nul.\n$\\triangleright$ Plusieurs élèves ont cru fournir des contre-exemples qui étaient en fait faux, parce qu'ils avaient oublié certaines contraintes de l'énoncé. De manière générale, une fois que l'on dispose d'un contre-exemple, il est très important de relire attentivement l'énoncé pour vérifier qu'il s'agit bien d'un contre-exemple : en effet, si on se contente d'exhiber ce contre-exemple mais que l'on s'est en fait trompé, on ne fournit plus au correcteur d'éléments qui lui permettront de donner des points, et il se retrouve donc sans autre choix que de n'en donner aucun pour la question concernée.\n$\\triangleright$ Enfin, de manière surprenante, et même s'il ne s'agit pas d'une erreur stricto sensu, plusieurs élèves on traité le cas a) mais pas le cas c), ou l'inverse, alors même que les idées mises en jeu étaient exactement les mêmes.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 8 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Soit $\\left(F_{k}\\right)_{k \\geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \\geqslant 0$. Soit ensuite $n \\geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \\ldots, n$ de manière à obtenir un $n$-uplet $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ tel que\n\n$$\na_{1} \\leqslant 2 a_{2} \\leqslant 3 a_{3} \\leqslant \\ldots \\leqslant n a_{n} .\n$$", "solution": "On dit qu'une permutation $\\mathbf{a}=\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ des entiers $1,2, \\ldots, n$ est jolie si elle satisfait les inégalités $a_{1} \\leqslant 2 a_{2} \\leqslant \\ldots \\leqslant n a_{n}$.\nTout d'abord, soit a une jolie permutation. S'il existe un entier $k$ pour lequel $a_{k} \\leqslant k-2$, on choisit $k$ minimal. Dans ces conditions, on sait que $k \\geqslant 2$ et que $a_{k-1} \\geqslant k-2 \\geqslant a_{k}$, de sorte que $a_{k-1} \\geqslant a_{k}+1$. On en conclut que\n\n$$\n(k-1) a_{k-1} \\geqslant(k-1)\\left(a_{k}+1\\right)=k a_{k}+\\left(k-a_{k}-1\\right) \\geqslant k a_{k}+1,\n$$\n\net donc que a n'est pas jolie. On en conclut donc que $a_{k} \\geqslant k-1$ pour tout $k \\leqslant n$.\nD'autre part, soit $\\ell$ l'entier tel que $a_{\\ell}=n$. Au vu du résultat obtenu précédemment, une récurrence descendante immédiate sur $k$ nous assure que $a_{k}=k-1$ pour tout entier $k$ tel que $\\ell+1 \\leqslant k \\leqslant n$. Puisque\n\n$$\n\\ell n=\\ell a_{\\ell} \\leqslant(\\ell+1) a_{\\ell+1}=(\\ell+1) \\ell\n$$\n\non en conclut que $\\ell \\in\\{n-1, n\\}$.\nAinsi, pour que a soit jolie, on dispose a priori de deux choix :\n$\\triangleright$ soit $\\ell=n$, auquel cas a est effectivement jolie si et seulement si la permutation $\\left(a_{1}, a_{2}, \\ldots, a_{n-1}\\right)$ des entiers $1,2, \\ldots, n-1$ est jolie;\n$\\triangleright$ soit $\\ell=n-1$, auquel cas $a_{n}=n-1$, et alors a est effectivement jolie si la permutation $\\left(a_{1}, a_{2}, \\ldots, a_{n-2}\\right)$ des entiers $1,2, \\ldots, n-2$ est jolie.\nPar conséquent, si on note $J_{n}$ le nombre de jolies permutations de $1,2, \\ldots, n$, on remarque bien que $J_{n}=J_{n-1}+J_{n-2}$ dès lors que $n \\geqslant 3$. On conclut en vérifiant que $J_{1}=1=F_{2}$ et que $J_{2}=2=F_{3}$ 。", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 9 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Soit $\\left(F_{k}\\right)_{k \\geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \\geqslant 0$. Soit ensuite $n \\geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \\ldots, n$ de manière à obtenir un $n$-uplet $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ tel que\n\n$$\na_{1} \\leqslant 2 a_{2} \\leqslant 3 a_{3} \\leqslant \\ldots \\leqslant n a_{n} .\n$$", "solution": "$n^{\\circ} 1$ Comme précédemment, on considère une permutation a puis l'entier $\\ell$ tel que $a_{\\ell}=n$. Puisque $n a_{k} \\geqslant k a_{k} \\geqslant \\ell a_{\\ell}=\\ell$ n pour tout $k \\geqslant \\ell$, on sait que a induit une permutation de $1,2, \\ldots, \\ell-1$ et de $\\ell, \\ell+1, \\ldots, n$.\nSi $\\ell \\leqslant n-1$, soit $m$ l'unique entier tel que $a_{m}=\\ell$. Puisque $m \\geqslant \\ell$, on sait que\n\n$$\nm \\ell=m a_{m} \\geqslant \\ell a_{\\ell}=\\ell n\n$$\n\ndonc que $m=n$. Mais alors $k a_{k}=\\ell n$ pour tout entier $k$ tel que $\\ell \\leqslant k \\leqslant n$. On en déduit en particulier que $n-1$ divise $(n-1) a_{n-1}=\\ell n$, donc divise $\\ell$ aussi, ce qui signifie que $\\ell=n-1$. Maintenant acquis le fait que $\\ell \\in\\{n-1, n\\}$, on conclut comme précédemment.\n\nCommentaire des correcteurs Cet exercice était difficile. Néanmoins, une bonne partie des élèves a eu la bonne idée d'essayer de trouver une relation de récurrence sur le nombre de permutations vérifiant l'énoncé et a réussi, en analysant la relation de récurrence, à comprendre la structure des permutations vérifiant l'énoncé.\nToutefois, très peu d'élèves ont réussi à formaliser cela, en particulier à montrer que l'entier $\\ell$ défini dans la correction était bien supérieur ou égal à $n-1$. Certains ont utilisé le fait que $n(n-2)<(n-1)^{2}$ pour conclure dans le cas général. Si cet argument fonctionnait\npour $\\ell=n-2$, il était malheureusement impossible de l'adapter directement pour des $\\ell$ quelconques.\nAttention aussi à la récurrence! Plusieurs élèves ont montré, si on note $k_{n}$ le nombre de permutations de $\\{1, \\ldots, n\\}$ vérifiant l'énoncé, que $k_{n}=k_{n-1}+k_{n-2}$. Ils ont ensuite fait une récurrence forte, initialisée à $n=1$, pour prouver que $k_{n}=F_{n+1}$. Ici pour $n=2$, la formule $k_{2}=k_{1}+k_{0}$ n'a pas de sens car $k_{0}$ n'est même pas défini. Ce raisonnement par récurrence ne permettait donc pas de prouver que $k_{2}=F_{3}$, et il aurait fallu traiter cette égalité dans le cadre de l'initialisation de notre récurrence. Ici, pour éviter cette erreur, il valait mieux faire une récurrence double, qui nécessite explicitement d'initialiser à $n=1$ et $n=2$.\n\n## Problèmes Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution alternative"}
|
| 10 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Pierre et Clara jouent au jeu suivant. Tout d'abord, Clara choisit un entier $c$. Puis Pierre choisit un nombre premier $p \\geqslant c$ et écrit deux entiers $a$ et $b$ au tableau. Clara se permet alors d'effectuer les opérations suivantes : elle choisit un des deux nombres écrits au tableau, disons $n$, l'efface, et écrit à la place un autre entier, disons $m$, tel que $p$ divise $\\left(n^{2}-m+1\\right)\\left(m^{2}-n+1\\right)$. Clara gagne si elle réussit à faire en sorte, au bout d'un nombre fini de telles opérations, que les deux entiers écrits au tableau soient identiques. Sinon, elle perd, et c'est Pierre qui gagne.\nDémontrer que Pierre peut empêcher Clara de gagner.", "solution": "Soit $p$ un nombre premier, arbitrairement grand, que Pierre est susceptible de choisir, et soit $f: \\mathbb{Z} / p \\mathbb{Z} \\mapsto \\mathbb{Z} / p \\mathbb{Z}$ la fonction définie par $f(x)=x^{2}+1$.\nLorsque Clara remplace un entier $n$ par un entier $m$, l'une des deux égalités $n=f(m)$ ou $m=f(n)$ est nécessairement vérifiée, de sorte que $m$ et $n$ appartiennent à une même orbite de $f$. On dit alors que deux résidus $u$ et $v$ modulo $p$ sont reliés s'il existe deux entiers $k \\geqslant 0$ et $\\ell \\geqslant 0$ tels que $f^{k}(u)=f^{\\ell}(v)$. Il apparaît directement que, si Clara parvient à transformer un résidu $m$ en un résidu $n$, ces deux résidus sont reliés; la réciproque est d'ailleurs vraie, même si nous n'en aurons pas besoin.\nPierre a donc pour but de trouver un nombre premier $p \\geqslant c$, puis deux résidus $a$ et $b$ modulo $p$ qui ne sont pas reliés l'un à l'autre. Pour ce faire, le plus simple est que $a$ et $b$ soient des points fixes de $f$, c'est-à-dire que $(X-a)(X-b) \\equiv X^{2}-X+1(\\bmod p)$.\nOr, si $X^{2}-X+1$ admet une racine $a$ modulo $p$, l'autre racine vaut $1 / a$ (car $a$ est non nul), ou encore $1-a$. Ces deux racines ne sont donc égales que si $1-a \\equiv a \\equiv 1 / a(\\bmod p)$, c'est-à-dire si $p \\neq 2$ et $1 / 2 \\equiv a \\equiv \\pm 1(\\bmod p)$. Or, on sait que $1 / 2 \\equiv \\pm 1(\\bmod p)$ si et seulement si $p=3$. Par conséquent, Pierre n'a qu'à choisir un nombre premier $p>\\max \\{c, 3\\}$ qui divise un nombre de la forme $n^{2}-n+1$. En pratique, pour ce faire, il lui suffit de définir $p$ comme le plus petit facteur premier du nombre $S_{m}=(m!)^{2}-m!+1$, où l'on a posé $m=\\max \\{c, 3\\}$. En effet, on sait que $S_{m} \\geqslant 2$ et que $S_{m}$ est premier avec $m!$. Ainsi, le plus petit facteur premier de $S_{m}$ existe bien, et il est premier avec $m$ !, donc strictement supérieur à $m$. Pierre s'empressera ensuite de choisir $a=m$ ! et $b=1-m$ ! pour enfin savourer une victoire amplement méritée.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ Étant donné un nombre premier $p$, nous allons construire le graphe $G$ dont les sommets sont les éléments de $\\mathbb{Z} / p \\mathbb{Z}$ et les arêtes sont les paires $(m, n)$ telles que $\\left(n^{2}-m+1\\right)\\left(m^{2}-n+1\\right) \\equiv 0(\\bmod p)$. On dira qu'une arête $(m, n)$ est utile si $m \\neq n$, et qu'elle est inutile sinon, c'est-à-dire s'il s'agit d'une boucle. Si $G$ contient au plus $p-2$ arêtes utiles, alors il n'est pas connexe, et Pierre n'a plus qu'à choisir des entiers appartenant à deux composantes connexes distinctes.\nOn dit ensuite qu'une arête $(m, n)$ est engendrée par $n$ si $m \\equiv n^{2}+1(\\bmod m)$. Toute arête est engendrée par une de ses extrémités, et chaque sommet engendre une unique arête, donc $G$ contient au plus $p$ arêtes. Par conséquent, si $G$ contient deux arêtes inutiles, c'est-à-dire s'il existe deux résidus distincts $u$ et $v$ tels que $u \\equiv u^{2}+1(\\bmod p)$ et $v \\equiv v^{2}+1(\\bmod p)$, Pierre est assuré de pouvoir gagner.\nIl lui suffit alors de procéder comme dans la solution précédente.\nRemarque: On peut en fait démontrer que tout graphe $G$ construit comme ci-dessus contient au moins $p-1$ arêtes. En effet, si ce n'est pas le cas, il existe deux arêtes $(m, n)$ et $(u, v)$, dont chacune est engendrée par ses deux extrémités, et telles que $m, n, u$ et $v$ sont deux à deux distincts modulo $p$. Ce sont là quatre racines distinctes du polynôme $P(X)=\\left(X^{2}+1\\right)^{2}+1-X$\ndans $\\mathbb{Z} / p \\mathbb{Z}$, telles que $m=f(n), n=f(m), u=f(v)$ et $v=f(u)$.\nOr, tout point fixe de $f$ est racine de $P$, ce qui signifie que $P$ est divisible par le polynôme $Q(X)=X^{2}+1-X$. On en déduit la factorisation $P(X)=\\left(X^{2}+X+2\\right) Q(X)$. Ainsi, parmi $m, n, u$ et $v$, deux sont des racines de $Q$, c'est-à-dire des points fixes de $f$, en contradiction avec notre hypothèse.\nEn particulier, s'intéresser aux points fixes de $f$, ou au minimum à ses cycles de petite taille, était donc indispensable.\n$\\underline{\\text { Solution alternative } n^{\\circ} 2}$ La solution ci-dessous fait appel à des notions plus avancées, mais cela permet une approche laxiste de la dimension combinatoire du problème. Ci-dessous, on considère directement que Pierre choisit des résidus modulo $p$ plutôt que des entiers, et on note $f: \\mathbb{Z} / p \\mathbb{Z}$ la fonction définie par $f(x)=x^{2}+1$. Lorsque $x$ et $y$ sont des résidus modulo $p$, on notera abusivement $x=y$ et $x \\neq y$ les relations $x \\equiv y(\\bmod p)$ et $x \\not \\equiv y(\\bmod p)$.\nSupposons que Pierre a choisi un nombre premier $p$ et deux résidus $a$ et $b$ tels que $b \\neq \\pm a$ tels que $a=f(a)$, mais que Clara gagne malgré tout. Puisque toute opération de Clara peut être inversée, on suppose sans perte de généralité que celle-ci a graduellement transformé $a$ en $b$, en le plus petit nombre d'étapes possibles.\nLa première étape de Clara consiste à transformer $a$ en $f(a)=a$, ce qui serait stupide, ou en un antécédent $x \\neq a$ de $a$ par $f$. Les deux antécédents de $a$ par $f$ sont opposés l'un à l'autre, et l'un est égal à $a$, donc l'autre vaut $-a$. Ainsi, Clara a transformé $a$ en $-a$.\nPuisque $b \\neq-a$, Clara a de nouveau dû transformer $-a$ en $f(-a)=a$, ce qui serait encore une fois stupide, ou bien en un antécédent $y$ de $-a$ par $f$, de sorte que $-a-1=f(y)-1=y^{2}$ est un résidu quadratique modulo $p$.\nPar conséquent, Pierre gagnera s'il trouve un nombre premier $p \\geqslant 3$ pour lequel $f$ a un point fixe $a$ tel que $-a-1$ ne soit pas un résidu quadratique modulo $p$. Or, si $a$ est un point fixe de $f$, on sait que $f(1-a)=a^{2}-2 a+2=f(a)-2 a+1=1-a$, donc que $1-a$ est aussi un point fixe de $f$. Il suffit donc que soit $-a-1$, soit $a-2$ ne soit pas un résidu quadratique (soit les deux).\nLa manière la plus simple pour s'assurer que deux nombres ne seront pas tous deux des résidus quadratiques est de faire en sorte que leur produit n'en soit pas un. Cette technique sera ici avantageuse, puisqu'elle nous permettra de ne pas devoir distinguer les résidus $-a-1$ et $a-2$, qui avaient été définis de manière symétrique. Ici, Pierre va donc choisir $p$ de sorte que $(a-2)(-a-1)=2+a-a^{2}=3$ ne soit pas un résidu quadratique.\nEnfin, il doit s'assurer que $f$ ait bien un point fixe. Or, s'il se plonge dans le corps $\\mathbb{C}$ des nombres complexes, Pierre sait bien que les racines du polynôme $f(X)-X=X^{2}-X+1$ sont $(1+\\sqrt{-3}) / 2$ et $(1-\\sqrt{-3}) / 2$. On reconnaît donc là que $a$ est un point fixe de $f$ si et seulement si $(2 a-1)^{2}=-3$, et un tel point fixe existe donc si et seulement si -3 est un résidu quadratique. Il s'agit donc, pour Pierre, de choisir un nombre premier $p$ pour lequel -3 est un résidu quadratique et -1 n'en est pas un.\nOr, s'il existe un résidu $z$ tel que $z^{2}=-1$, on sait que $z$ est d'ordre 4 , donc que $p \\equiv 1(\\bmod 4)$. Pierre va donc chercher $p$ parmi les facteurs premiers non congrus à $1(\\bmod 4) \\mathrm{d}$ 'un entier de la forme $n^{2}+3$. Choisir $n$ premier avec 3 nous assure déjà que $p \\neq 3$. Ensuite, choisir $n$ pair nous assure que $n^{2}+3 \\equiv 3(\\bmod 4)$, donc que $n$ admet nécessairement un facteur premier $p \\equiv 3(\\bmod 4)$. Il suffit donc de définir $n$ comme le PPCM des nombres premiers inférieurs ou égaux à max $\\{c, 2\\}$ et différents de $3:$ le facteur $p$ que choisira Pierre sera premier avec tous ces nombres premiers, mais aussi avec 3 , de sorte que $p>c$, et les considérations des paragraphes précédents nous assurent alors que Pierre peut choisir des entiers $a$ et $b$ de façon adéquate.\n\nRemarque: Une fois résolu à choisir un nombre premier $p$ pour lequel ni $3 \\mathrm{ni}-1$ ne sont des résidus quadratiques, Pierre peut aussi se reposer sur des théorèmes puissants mais qu'il ne sait pas nécessairement démontrer, ce qui lui laissera un léger goût d'inachevé.\n\nThéorème de la réciprocité quadratique. Soit $p$ un nombre premier et $n$ un entier non divisible par $p$. On pose $\\binom{n}{p}=1$ si $n$ est un résidu quadratique modulo $p$, et $\\binom{n}{p}=-1$ sinon.\n$\\triangleright$ Si $p$ et $q$ sont deux nombres premiers impairs distincts, $\\binom{p}{q}\\binom{q}{p}=(-1)^{(p-1)(q-1) / 4}$.\n$\\triangleright$ Pour tout nombre premier $p$ impair, $\\binom{-1}{p}=(-1)^{(p-1) / 2}$ et $\\binom{2}{p}=(-1)^{\\left(p^{2}-1\\right) / 8}$.\nThéorème de Dirichlet sur les nombres premiers. Soit $a$ et $b$ deux entiers premiers entre eux. Il existe une infinité de nombres premiers $p$ tels que $p \\equiv a(\\bmod b)$.\n\nMuni de ces deux résultats, Pierre choisit donc un nombre premier $p$ tel que $p \\equiv 3(\\bmod 4)$ et $\\binom{p}{3}=-\\binom{3}{p}=1$, c'est-à-dire $p \\equiv 1(\\bmod 3)$. Il s'agit ainsi de choisir un nombre premier $p \\geqslant c$ tel que $p \\equiv 7(\\bmod 12)$, et le théorème de Dirichlet indique qu'un tel nombre premier existe bien.\n\nCommentaire des correcteurs Très peu d'élèves ont entièrement résolu ce problème difficile, qui aurait pu faire figure de problème 1 ou 4 difficile à l'Olympiade Internationale. Il s'agit de l'étude d'un système dynamique présentée sous la forme d'un jeu à stratégie gagnante. Deux approches principales étaient possibles ici : une approche combinatoire traduisant le problème en termes d'un graphe dont les sommets appartenaient à $\\mathbb{Z} / p \\mathbb{Z}$, comme dans les deux premières solutions proposées, et une approche très arithmétique passant par une étude des carrés modulo $p$, comme dans la solution alternative $\\mathrm{n}^{\\circ} 2$. Chacune des deux approches nécessitait la mise en place de nombreuses idées, et obtenir des points nécessitait donc d'établir des résultats significatifs.\nCe problème consistait en l'étude d'un système dynamique, c'est-à-dire un système (ici, un couple d'entiers) sur lequel on agit via une opération (ici, on remplace un entier par un autre selon certaines contraintes). Dans un tel cas, il est primordial d'étudier les petits cas. De nombreux élèves ont présenté leur étude pour des $p$ particuliers, le plus souvent pour $p=7$. Même si cette initiative n'était pas récompensée par un point ici, nous l'encourageons fortement!\nUn autre réflexe important à avoir est de considérer les éventuels points fixes de l'opération. C'était ici, quelle que soit l'approche, le point de départ du problème, et plusieurs élèves ont eu ce réflexe, à la grande satisfaction des correcteurs. Quelques élèves ont cherché des invariants au système et c'est évidemment une très bonne idée. Même si elle ne permettait pas d'avancer dans ce problème, cette tentative était très pertinente. De même, plusieurs élèves ont mentionné la que les opérations de Clara étaient réversibles : ce point était certes facile à démontrer, mais il s'agit là d'une caractéristique qu'il est utile à étudier de manière générale. Nous espérons que ces rappels permettront aux élèves de progresser et d'être mieux armés la prochaine fois qu'ils tombent sur un problème similaire.\nNous listons maintenant quelques erreurs rencontrées dans les tentatives de solutions.\n$\\triangleright$ Attention à bien lire l'énoncé! Nous déplorons que plusieurs raisonnements soient voués à l'échec car l'énoncé de départ n'est pas compris correctement. Quelques élèves ont par exemple cru que les entiers $m$ et $n$ de l'hypothèse $p \\mid\\left(m^{2}-n+1\\right)\\left(n^{2}-m+1\\right)$\nétaient les deux entiers écrits au tableau. D'autres élèves font d'emblée une erreur de signe dans leur congruence, en écrivant que que $m^{2} \\equiv n+1(\\bmod p)$.\n$\\triangleright$ Une fois supposée ou acquise l'existence d'un point fixe pour l'opération de Clara, c'est-à-dire d'un entier $a$ et d'un nombre premier $p$ tels que $a^{2}+1 \\equiv a(\\bmod p)$, plusieurs élèves étudient les antécédents possibles de $a$ par l'opération, dans l'espoir de montrer que $a$ ne peut pas être obtenu à partir de tous les autres restes modulo $p$. La plupart remarquent que $-a$ est lui aussi un antécédent de $a$, car $a^{2} \\equiv b^{2}(\\bmod p)$ si et seulement si $a \\equiv \\pm b(\\bmod p)$ ). Mais certains concluent trop hâtivement qu'alors $a$ et $-a$ sont isolés et ne peuvent être atteints par d'autres entiers; il restait cependant possible que $-a$ ait plusieurs antécédents autres que $\\pm a$.\nNous terminons par avouer notre surprise devant les statistiques : de nombreux élèves ayant passé le test n'ont rien rendu pour ce problème en particulier, pourtant censé être plus abordable que les deux suivants. S'il est bon de regarder tous les problèmes, il est stratégique de passer une grande partie du temps donné sur le problème classé comme le plus abordable, puisqu'on peut plus facilement espérer y avoir des idées intéressantes et donc y récolter des points.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 11 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Trouver le plus grand entier $n \\geqslant 3$ pour lequel il existe un ensemble $\\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\\mathcal{S}$ est isocèle mais pas équilatéral.", "solution": "On dit qu'un ensemble $\\mathcal{S}$ ayant la propriété requise est mignon. Nous allons démontrer que tout ensemble mignon contient au plus 6 éléments. En outre, on notera $\\omega_{A, B}$ le cercle de centre $A$ passant par $B$, et par $\\ell_{A, B}$ la médiatrice du segment $[A B]$.\nTout d'abord, si $\\mathcal{S}$ est formé des cinq sommets $P_{1}, \\ldots, P_{5}$ d'un pentagone régulier ainsi que de son centre $O$, on vérifie aisément que $\\mathcal{S}$ est mignon.\nRéciproquement, soit $\\mathcal{S}$ un ensemble mignon à $n \\geqslant 6$ points : nous allons démontrer que $n=6$. Pour tous les points $X, Y$ et $Z$ de $\\mathcal{S}$, on sait que $Z$ appartient à un seul des trois ensembles $\\omega_{X, Y}, \\omega_{Y, X}$ et $\\ell_{X, Y}$. Cette remarque nous permet déjà de démontrer le résultat suivant.\n\nLemme 1. Trois points quelconques de $\\mathcal{S}$ ne sont jamais alignés.\nDémonstration : Supposons que $\\mathcal{S}$ contient trois points $A, B$ et $C$, alignés dans cet ordre. Puisque $A B C$ est isocèle, $B$ est le milieu de $[A C]$. Soit maintenant $D$ un autre point de $\\mathcal{S}$. Sans perte de généralité, on suppose que $A D \\leqslant C D$.\nComme $D$ ne peut appartenir ni au cercle $\\omega_{C, B}$ ni à la droite $\\ell_{B, C}$, il appartient nécessairement au cercle $\\omega_{B, C}=\\omega_{B, A}$. Mais alors $D$ ne peut appartenir ni au cercle $\\omega_{C, A}$, ni au cercle $\\omega_{A, C}$, et il appartient donc nécessairement à la droite $\\ell_{A, C}$. Cette situation se répète pour chacun des $n-3$ points de $\\mathcal{S} \\backslash\\{A, B, C\\}$, qui appartiennent donc à la fois à $\\omega_{B, C}$ et à $\\ell_{A, C}$.\nOr, une droite et un cercle ont au plus deux points d'intersection. Notre supposition initiale était donc invalide, ce qui démontre le lemme.\n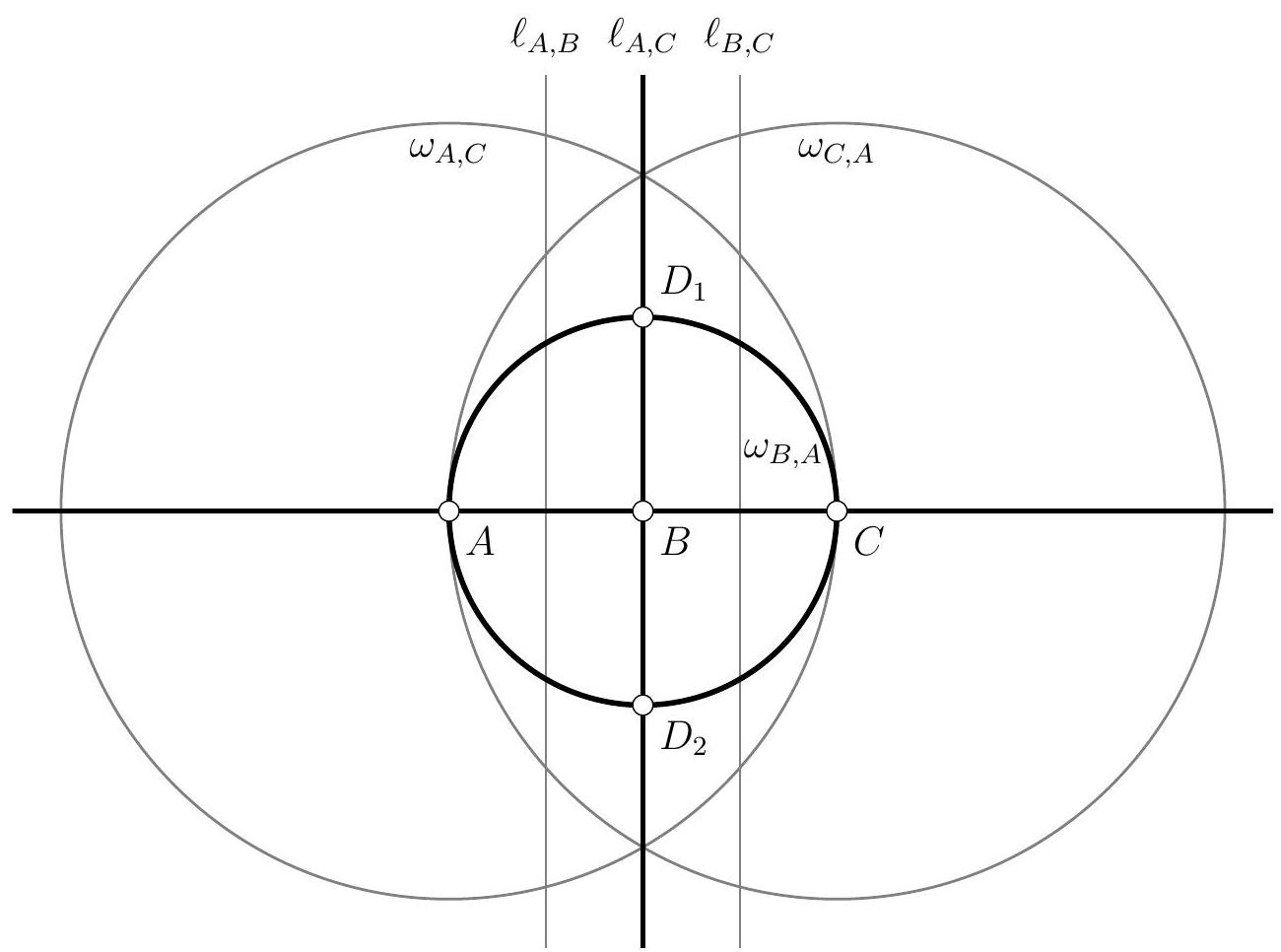\n\nOn continue alors, et on s'intéresse aux paires de cercles $\\omega_{A, B}$ et $\\omega_{B, A}$.\nLemme 2. Soit $A$ et $B$ deux points de $\\mathcal{S}$. Si $\\mathcal{S}$ contient à la fois des points de $\\omega_{A, B}$ et de $\\omega_{B, A}$ autres que $A$ et $B$, alors $n \\leqslant 6$.\n\nDémonstration : Supposons que $\\mathcal{S}$ contient deux points $C$ et $D$, distincts de $A$ et de $B$, qui appartiennent respectivement aux cercles $\\omega_{B, A}$ et $\\omega_{A, B}$. Ils ne peuvent être égaux l'un à l'autre, ce sans quoi le triangle $A B C$ serait équilatéral. Nous allons d'abord démontrer que $(A B)$ est parallèle à $(C D)$.\nEn effet, si $A B=C D$, alors $A B=B C=C D=D A$, et le quadrilatère $A B C D$ est un losange, donc $(A B)$ est bien parallèle à $(C D)$. On suppose donc que $A B \\neq C D$, c'est-à-dire que $A D \\neq C D$. Puisque $A C \\neq A D$ et que $A C D$ est isocèle, on en déduit que $A C=C D$. On démontre de même que $B D=C D$, de sorte que $A C=B D$, et donc que les triangles $A B C$ et $D A B$ sont isométriques.\nSupposons ensuite que $C$ et $D$ se trouvent de part et d'autre de la droite $(A B)$. Si l'on note $\\theta$ l'angle $\\widehat{A B C}$, on peut alors vérifier, par exemple en utilisant des coordonnées cartésiennes, que $A C^{2}=B D^{2}=(2-2 \\cos (\\theta)) A B^{2}$ et que $C D^{2}=(5-4 \\cos (\\theta)) A B^{2}$. Comme $A C=C D$, on en conclut alors que $2 \\cos (\\theta)=3$, ce qui est absurde. Notre supposition est donc invalide, de sorte que $C$ et $D$ sont nécessairement du même côté de $(A B)$, et donc que $(A B)$ est bien parallèle à $(C D)$.\nUne fois cette relation de parallélisme acquise, on conclut que tout point de $\\mathcal{S}$ appartient à la droite $(A B)$, à la médiatrice $\\ell_{A, B}$, ou encore à une parallèle à $(A B)$ passant par $C$ ou par $D$, c'est-à-dire à $(C D)$. Le lemme 1 nous assure que nulle de ces droites ne contient plus de deux points de $\\mathcal{S}$, ce qui prouve que $n \\leqslant 6$ et démontre le lemme.\n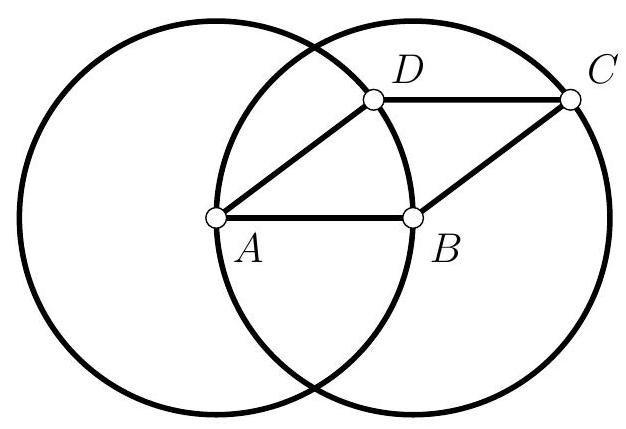\n\nCas 1: $A B=B C=C D=D A$\n\n\nCas 2: $A C=C D=D B$\n\nLemme 3. Soit $A$ et $B$ deux points de $\\mathcal{S}$. Si $n \\geqslant 7$, alors soit $\\omega_{A, B}$ contient au moins $n-2$ points de $\\mathcal{S}$, soit $B$ est le seul point de $\\mathcal{S}$ appartenant à $\\omega_{A, B}$.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 12 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Trouver le plus grand entier $n \\geqslant 3$ pour lequel il existe un ensemble $\\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\\mathcal{S}$ est isocèle mais pas équilatéral.", "solution": "Supposons que $n \\geqslant 7$ et que le cercle $\\omega_{A, B}$ contient $k \\geqslant 2$ points de $\\mathcal{S}$. Les lemmes 1 et 2 nous assurent respectivement que $\\ell_{A, B}$ contient au plus deux points de $\\mathcal{S}$, et que $A$ est le seul point de $\\mathcal{S}$ appartenant à $\\omega_{B, A}$. On en déduit que $k \\geqslant n-3$, avec égalité si et seulement si $\\ell_{A, B}$ contient exactement deux points de $\\mathcal{S}$, dont aucun n'appartient à $\\omega_{A, B}$. Si $k=n-3$, soit $C$ un autre point de $\\omega_{A, B}$. Pour les mêmes raisons que précédemment, la droite $\\ell_{A, C}$ contient deux points de $\\mathcal{S}$, dont aucun n'appartient à $\\omega_{A, C}=\\omega_{A, B}$. Or, puisque $\\ell_{A, B}$ et $\\ell_{A, C}$ ont au plus un point commun, elles contiennent donc au moins, à elles deux, trois points de $\\mathcal{S}$. Si l'on ajoute le point $A$ et les $k$ points de $\\mathcal{S}$ appartenant à $\\omega_{A, B}$, cela nous fait un total de $k+4=n+1$ points dans $\\mathcal{S}$. Notre supposition initiale était donc invalide, ce qui démontre le lemme.\n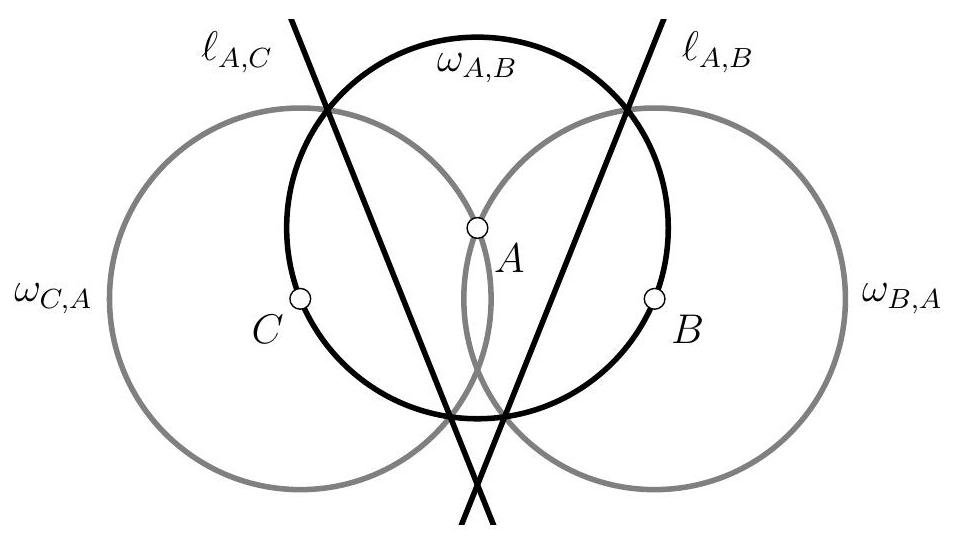\n\nEn conclusion, revenons à l'énoncé lui-même. Nous allons supposer que $n \\geqslant 7$ et aboutir à une absurdité. Soit $A, B$ et $C$ trois points de $\\mathcal{S}$. La droite $\\ell_{A, B}$ contient au plus deux points de $\\mathcal{S}$, donc l'un des cercles $\\omega_{A, B}$ et $\\omega_{B, A}$ (disons $\\omega_{A, B}$ ) en contient au moins deux. Le lemme 3 nous assure alors que $\\omega_{A, B}$ contient au moins $n-2$ points de $\\mathcal{S}$.\nDe même, l'un des cercles $\\omega_{B, C}$ et $\\omega_{C, B}$ (disons $\\omega_{X, Y}$ ) contient au moins $n-2$ points de $\\mathcal{S}$. On dispose alors de deux cercles, de centres $A$ et $X$, qui contiennent chacun $n-2$ points de $\\mathcal{S}$. Ils ont donc au moins $n-4 \\geqslant 3$ points communs, ce qui est absurde puisque leurs centres sont distincts. On tient donc ici l'absurdité tant désirée, qui conclut notre solution.", "problem_match": "\nExercice 6.", "solution_match": "\nDémonstration:"}
|
| 13 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Trouver le plus grand entier $n \\geqslant 3$ pour lequel il existe un ensemble $\\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\\mathcal{S}$ est isocèle mais pas équilatéral.", "solution": "$n^{\\circ} 1$ Réutilisons les notations de la solution ci-dessus. On démontre comme précédemment qu'il existe un ensemble mignon à 6 éléments, et on procède désormais par l'absurde, en supposant que l'on dispose d'un ensemble $\\mathcal{S}$ mignon à 7 éléments. Comme dans la solution précédente, on démontre que 3 points de $\\mathcal{S}$ ne sont jamais alignés. On démontre ensuite le résultat suivant.\nLemme 4. Soit $A$ et $B$ deux points de $\\mathcal{S}$. Si $n \\geqslant 7$, alors $\\omega_{A, B}$ contient au plus 3 points de $\\mathcal{S}$.\nDémonstration : Supposons que $\\omega_{A, B}$ contient au moins quatre points $B, C, D$ et $E$, tels que $B C=C D$. Puisque $B$ et $D$ sont les deux seuls points d'intersection de $\\omega_{A, B}$ et $\\omega_{C, B}=\\omega_{C, D}$, et que $A$ est l'unique point d'intersection de $\\omega_{B, C}$ et $\\omega_{D, C}$, on sait que $E$ est, au choix :\n\n1. $\\operatorname{sur} \\omega_{A, B}, \\ell_{C, D}$ et $\\omega_{B, C}$;\n2. sur $\\omega_{A, B}, \\ell_{B, C}$ et $\\omega_{D, C}$;\n3. $\\operatorname{sur} \\omega_{A, B}, \\omega_{B, C}$ et $\\omega_{D, C}$.\n\nDans le troisième cas, on a donc $B C=C D=D E=E B$, de sorte que $B C D E$ est un losange dont les sommets sont cocycliques, c'est-à-dire un carré, et donc que $A, B$ et $D$ sont alignés. Ce cas est donc impossible. Par ailleurs, les premier et deuxième cas sont symétriques l'un de l'autre. On suppose donc que l'on est dans le deuxième cas.\nOn observe alors que $B, C, D$ et $E$ sont quatre sommets consécutifs d'un pentagone régulier de centre $A$, et dont on note $d$ la longueur des côtés. Parmi les deux autres points de $\\mathcal{S}$, l'un n'appartient pas à $\\ell_{C, D}$, qui contient déjà $A$ : on note $X$ ce point. Chacune des droites $\\ell_{B, C}$ et $\\ell_{D, E}$ contient déjà deux points de $\\mathcal{S}$ parmi $A, B, C, D$ et $E$, et ne contient donc pas $X$. On en déduit que\n\n$$\n\\left\\{\\begin{array}{l}\nB X=d \\text { ou } C X=d \\\\\nC X=d \\text { ou } D X=d ; \\\\\nD X=d \\text { ou } E X=d\n\\end{array}\\right.\n$$\n\nPar conséquent, $X$ est sur $\\ell_{B, D}$ (si $B X=D X=d$ ) ou sur $\\ell_{C, E}$ (si $C X=E X=d$ ). Ces deux cas sont impossibles, puisque $\\ell_{B, D}$ contient déjà $A$ et $C$, tandis que $\\ell_{C, E}$ contient déjà $A$ et $D$. Note supposition initiale était donc invalide, ce qui démontre le lemme.\n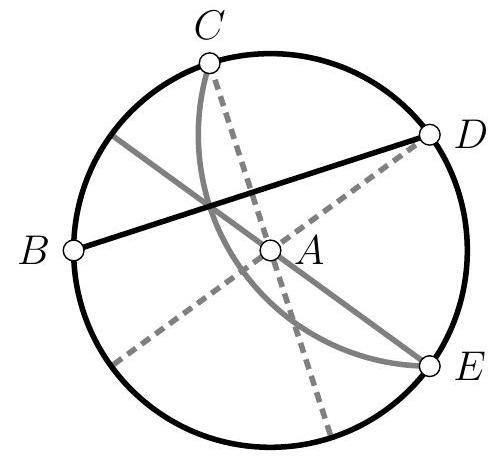\n\nCas 2: $E \\in \\ell_{B, C} \\cap \\omega_{D, C}$\n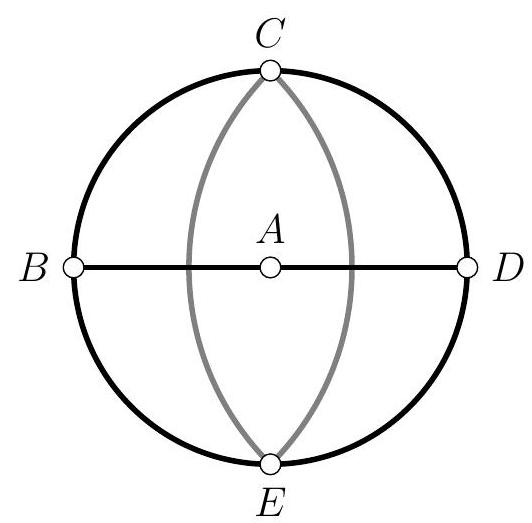\n\nCas 3: $E \\in \\omega_{B, C} \\cap \\omega_{D, C}$\n\nPour tout segment $[A, B]$ dont les extrémités sont dans $\\mathcal{S}$, on note maintenant $p_{A, B}$ le nombre de points de $\\mathcal{S}$ situés sur la médiatrice $\\ell_{A, B}$ : on dit qu'il s'agit du poids de $[A, B]$. Puisqu'il existe $\\binom{7}{3}=35$ triangles isocèles (mais pas équilatéraux) à sommets dans $\\mathcal{S}$, la somme des poids des segments vaut 35 . Or, il y a $\\binom{7}{2}=21$ segments, dont aucun n'est de poids $p_{A, B} \\geqslant 3$. Si on note $a_{i}$ le nombre de segments de poids $i$, on constate donc que\n\n$$\n35=2 a_{2}+a_{1} \\leqslant\\left(a_{0}+a_{1}+a_{2}\\right)+a_{2}=21+a_{2},\n$$\n\nde sorte que $a_{2} \\geqslant 14$. Comme $2 a_{2}=28 \\geqslant 24,5=(1-1 / 2) \\times 7^{2}$, le théorème de Turan indique qu'il existe un triangle $A B C$, isocèle en $A$, dont les trois côtés $[A, B],[B, C]$ et $[C, A]$ sont de poids 2.\nParmi $A, B$ et $C$, seul $A$ appartient à l'une des trois médiatrices $\\ell_{A, B}, \\ell_{B, C}$ ou $\\ell_{C, A}$. En outre, ces trois médiatrices concourent en $O$, le centre du cercle circonscrit à $A B C$. Par conséquent, si $O \\notin \\mathcal{S}$, on sait que $\\mathcal{S}$ contient 8 points distincts, que sont $B, C$, et deux points sur chacune des médiatrices $\\ell_{A, B}, \\ell_{B, C}$ et $\\ell_{C, A}$. On en déduit que $O \\in \\mathcal{S}$.\nSoit alors $D$ le second point de $\\mathcal{S}$ situé sur $\\ell_{A, B}$. Puisque $D \\notin \\omega_{O, B}$, on sait que $D \\in \\omega_{B, O}$, auquel cas $D$ coïncide avec le symétrique de $O$ par rapport à $(A B)$, ou bien que $D \\in \\ell_{B, O}$, auquel cas $D$ coïncide avec le centre du cercle circonscrit à $A B O$. Dans les deux cas, remarquons que $D \\notin \\omega_{A, B}=\\omega_{A, C}$ et que $D \\notin \\ell_{A, C}$, de sorte que $D \\in \\omega_{C, A}$.\nDans le premier cas, on sait en outre que $B D=B O \\neq B C$, donc que $D \\notin \\omega_{B, C}$, et que $D \\notin \\ell_{B, C}$, de sorte que $D \\in \\omega_{C, B}$. Cela signifie que $C D=C B \\neq C O$, donc que $D \\notin \\omega_{C, O}$. Puisque $D \\notin \\omega_{O, C}$, on en déduit que $D \\in \\ell_{C, O}$. Ainsi, et puisque $D \\in \\omega_{C, A}$, on sait que $O D=C D=C A=B A$, donc que $A D B O$ est un losange dont les diagonales sont de même longueur, c'est-à-dire un carré. Mais alors $\\widehat{A O B}$ est droit, et $\\widehat{A O C}$ est droit aussi, donc $B, O$ et $C$ sont alignés, ce qui contrevient au lemme 1. Ce cas est donc impossible.\nOn est donc dans le deuxième cas et, de même, $\\mathcal{S}$ contient le centre du cercle circonscrit à $A C O$, que l'on note $E$. Puisque $C D=C A \\neq C O$ et que $D \\notin \\omega_{O, C}$, on sait que $D \\in \\ell_{C, O}$. Ainsi, $D$ appartient aux deux droites $\\ell_{B, O}$ et $\\ell_{C, O}$ et, pour des raisons de symétrie, $E$ appartient également à ces deux droites. Puisque ces deux droites ne sauraient être confondues, ce second cas est lui aussi impossible, ce qui conclut.\n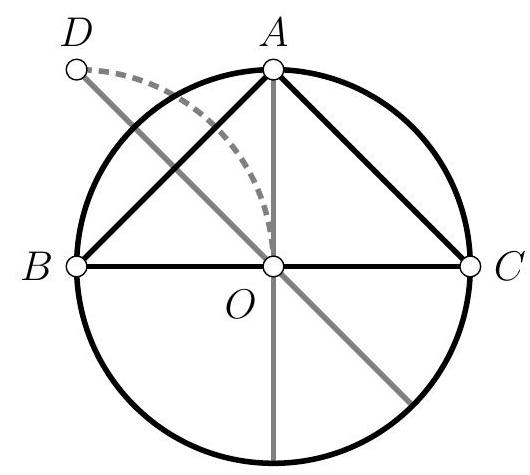\n\nCas 1: $D \\in \\ell_{A, B} \\cap \\omega_{B, O}$\n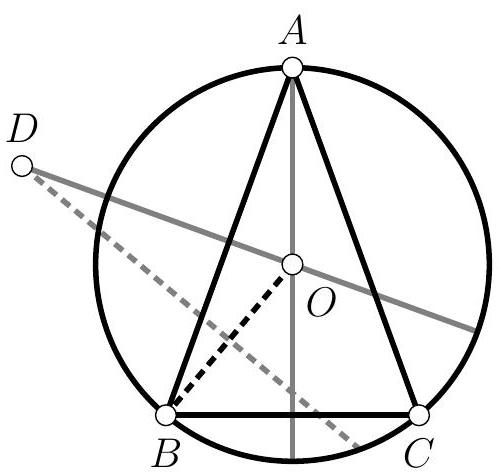\n\nCas $2: D \\in \\ell_{A, B} \\cap \\ell_{B, O}$", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 14 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Trouver le plus grand entier $n \\geqslant 3$ pour lequel il existe un ensemble $\\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\\mathcal{S}$ est isocèle mais pas équilatéral.", "solution": "$n^{\\circ} 2$ Réutilisons les notations de la solution ci-dessus. On démontre comme précédemment qu'il existe un ensemble mignon à 6 éléments, et on procède désormais par l'absurde, en supposant que l'on dispose d'un ensemble $\\mathcal{S}$ mignon à 7 éléments. Comme dans la solution précédente, on démontre que 3 points de $\\mathcal{S}$ ne sont jamais alignés.\nConsidérons maintenant un triangle $A B C$, isocèle en $A$, dont les sommets appartiennent à $\\mathcal{S}$, puis soit $D$ un autre point de $\\mathcal{S}$. Puisque les triangles $A B D, B C D$ et $C A D$ sont isocèles mais pas équilatéraux, on sait que $D$ appartient à\n$\\triangleright$ un seul des trois ensembles $\\omega_{A, B}, \\omega_{B, A}$ et $\\ell_{A, B}$;\n$\\triangleright$ un seul des trois ensembles $\\omega_{A, C}, \\omega_{C, A}$ et $\\ell_{A, C}$;\n$\\triangleright$ un seul des trois ensembles $\\omega_{B, C}, \\omega_{C, B}$ et $\\ell_{B, C}$.\nOr, les cercles et droites $\\omega_{A, B}, \\omega_{B, A}, \\omega_{B, C}, \\omega_{C, B}, \\ell_{A, B}$ et $\\ell_{B, C}$ sont deux à deux distincts et, pris deux à deux, ont au plus deux points d'intersection. On peut donc considérer un à un tous les points $D$ possibles.\n\n1. Si $D$ appartient à $\\omega_{A, B}=\\omega_{A, C}$ et à $\\omega_{B, C}, \\mathrm{c}^{\\prime}$ est le symétrique $C^{\\bullet}$ de $C$ par rapport à $(A B)$.\n2. Si $D$ appartient à $\\omega_{A, B}=\\omega_{A, C}$ et à $\\omega_{C, B}, \\mathrm{C}^{\\prime}$ est le symétrique $B^{\\bullet}$ de $B$ par rapport à $(A C)$.\n3. Si $D$ appartient à $\\omega_{A, B}=\\omega_{A, C}$ et à $\\ell_{B, C}$, c'est le milieu d'un des deux arcs de cercles $\\overline{B C}$ sur $\\omega_{A, B}$, que l'on note $M$ et $M^{\\prime}$.\n4. Si $D$ appartient à au moins deux médiatrices, c'est le centre $O$ du cercle circonscrit à $A B C$.\n5. Si $D$ appartient à $\\omega_{B, A}$ et à $\\omega_{C, A}, \\mathrm{c}^{\\prime}$ est le symétrique $A^{\\bullet}$ de $A$ par rapport à $(B C)$.\n6. Si $D$ appartient à $\\omega_{B, A}$ à $\\ell_{A, C}$, et à aucune autre médiatrice, il ne peut appartenir à $\\omega_{B, C}$, donc il appartient à $\\omega_{C, B}$. On a alors $B D=B A=C A$ et $A D=C D=B C$. Ainsi, les triangles $A B C$ et $A B D$ sont isométriques, de même que les triangles $A C D$ et $B C D$. En posant $x=\\widehat{B A C}$ et $y=\\widehat{C A D}$, on calcule aisément chacun des angles de la figure, de sorte que $3 x+2 y=x+4 y=180^{\\circ}$ (donc $x=y=36^{\\circ}$ ) si $A B C D$ est croisé. Si $A B C D$ est non croisé, on récupère une figure totalement analogue, à l'ordre près des points, de sorte que $x=108^{\\circ}$. Dans ces circonstances, on note $B^{\\boldsymbol{k}}$ le point de concours de $\\omega_{B, A}$, $\\omega_{C, B}$ et $\\ell_{A, C}$.\n7. Si $D$ appartient à $\\omega_{C, A}$, à $\\ell_{A, B}$, et à aucune autre médiatrice, la situation est totalement analogue, et $x=36^{\\circ}$ ou $108^{\\circ}$. Il coïncide alors avec le point de concours de $\\omega_{C, A}, \\omega_{B, C}$ et $\\ell_{A, B}$, que l'on note $C^{\\boldsymbol{\\alpha}}$.\n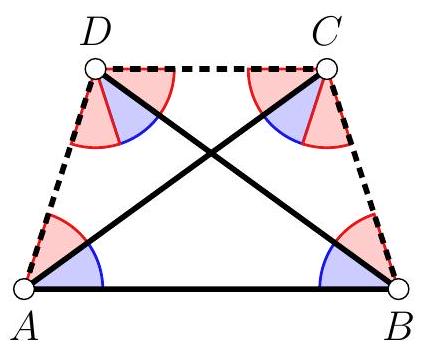\n\nCas 6: $A B C D$ croisé\n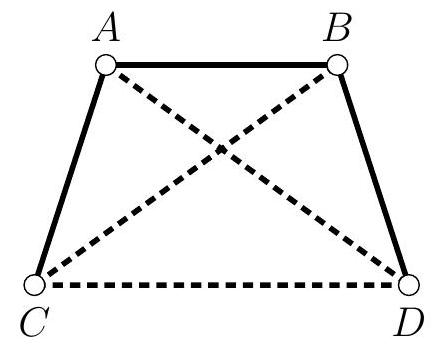\n\nCas 6 : $A B C D$ non croisé\n\nPuisque $A$ appartient déjà à $\\ell_{B, C}$, le lemme 1 nous assure que $\\mathcal{S}$ contient au plus un des points $A^{\\bullet}, O, M$ et $M^{\\prime}$. L'ensemble $\\mathcal{S}$ contient donc au moins trois des quatre points $B^{\\bullet}, C^{\\bullet}$, $B^{\\boldsymbol{\\omega}}$ et $C^{\\boldsymbol{\\omega}}$, ce qui signifie que $x=36^{\\circ}$ ou $108^{\\circ}$. En répétant ce raisonnement pour chaque triangle, on en conclut que tout triangle a pour angles $36^{\\circ}$ et $108^{\\circ}$, ou bien $36^{\\circ}$ et $72^{\\circ}$.\nMais alors, si un segment $[A B]$ est situé sur l'enveloppe convexe de $\\mathcal{S}$, les cinq autres points $P_{1}, P_{2}, \\ldots, P_{5}$ de $\\mathcal{S}$ sont situés dans un même demi-plan délimité par $(A B)$, et tout angle $\\widehat{P_{i} A B}$ vaut $36^{\\circ}, 72^{\\circ}$ ou $108^{\\circ}$. Ainsi, deux de ces angles sont égaux, donc on a trois points alignés, ce qui contrevient au lemme 1 et conclut.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 15 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Trouver le plus grand entier $n \\geqslant 3$ pour lequel il existe un ensemble $\\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\\mathcal{S}$ est isocèle mais pas équilatéral.", "solution": "$n^{\\circ} 3$ Voici une autre manière de démontrer que tout ensemble mignon compte au plus 6 éléments. Comme ci-dessus, on procède par l'absurde, et l'on suppose que l'on dispose d'un ensemble $\\mathcal{S}$ mignon à 7 éléments. Une fois de plus, on démontre que 3 points de $\\mathcal{S}$ ne sont jamais alignés.\nLe score d'un point $A$ de $\\mathcal{S}$ est le nombre de segments $[B C]$ à extrémités dans $\\mathcal{S}$ tels que $A B C$ soit isocèle en $A$. Puisqu'il existe $\\binom{7}{3}=35$ triangles isocèles (mais pas équilatéraux) à sommets dans $\\mathcal{S}$, la somme des scores des sommets vaut 35 . Comme $\\mathcal{S}$ compte 7 sommets, l'un d'entre eux, disons $O$, est de score $s \\geqslant 5$.\nOr, le score de $O$ ne peut pas être dû à $s$ segments d'extrémités deux à deux distinctes. Il existe donc trois points $A, B$ et $C$ dans $\\mathcal{S}$ tels que $A O=B O=C O$. Sans perte de généralité, on suppose même $A B=A C \\neq B C$. On pose alors $A O=x, A B=y$ et $B C=z$, et l'on sait que $x, y$ et $z$ sont deux à deux distincts.\nSupposons maintenant que $\\mathcal{S}$ contient un point $D \\neq O$ qui n'est pas sur $\\omega_{O, A}$. La médiatrice $\\ell_{B, C}$ contient déjà $A$ et $O$, donc ne contient pas $D$. Sans perte de généralité, on suppose donc que $D \\in \\omega_{B, C}$. Puisque $O B D$ est isocèle et que $O B=x \\neq O D$ et $B D=B C=z, \\mathrm{c}^{\\prime}$ est donc que $O D=z$. Par ailleurs, $B C D$ est isocèle en $C$ mais pas équilatéral, donc $C D \\neq z$. Puisque $O C D$ est isocèle, que $O D=z \\neq C D$ et que $O C=x, \\mathrm{c}^{\\prime}$ est donc que $C D=x$. Dès lors :\n$\\triangleright A B D$ est isocèle, $A B=y$ et $B D=x$, donc $A D$ vaut $x$ ou $y$;\n$\\triangleright A O D$ est isocèle, $A O=x$ et $O D=z$, donc $A D$ vaut $x$ ou $z$;\n$\\triangleright A C D$ est isocèle, $A C=y$ et $C D=z$, donc $A D$ vaut $y$ ou $z$.\nOn dispose ainsi d'une contradiction.\nAinsi, à l'exception de $O$, tout point de $\\mathcal{S}$ se trouve sur $\\omega_{O, A}$, mais également sur $\\omega_{A, B}, \\omega_{B, A}$ ou $\\ell_{A, B}$. Or, les cercles $\\omega_{A, B}$ et $\\omega_{B, A}$ ont chacun deux points d'intersection avec $\\omega_{O, A}$. Quant à la médiatrice $\\ell_{A, B}$, elle contient déjà $O$, et contient donc au plus un point de $\\omega_{O, A}$. Ainsi, $\\mathcal{S}$ est de taille au plus six, ce qui conclut.\n\nCommentaire des correcteurs Malgré sa difficulté, ce problème est celui pour lequel nous avons reçu le plus de solutions. De nombreuses approches ont été tentées : considérer l'enveloppe convexe, les points extrémaux, le nombre de points sur une médiatrice ou sur un cercle, le nombre de fois qu'un point est sommet d'un triangle isocèle,...Si ces\napproches, prises isolément, permettaient rarement de conclure, chacune donnait toutefois des informations sur la forme d'un ensemble vérifiant les contraintes de l'énoncé, et combiner ces approches permettait donc d'aboutir à une solution complète. Les solutions auxquelles nous avions pensé en proposant ce problème étaient de cette nature. Nous encourageons donc les élèves à essayer ce genre d'approche de géométrie combinatoire, et à utiliser tous les outils à leur disposition pour pouvoir croiser les informations obtenues. Cependant, la majorité des solutions était bien différente. Les deux approches les plus suivies pour résoudre le problème étaient:\n$\\triangleright$ Partir d'un triangle isocèle, et déterminer quels points peuvent être ajoutés à l'ensemble, puis exclure des choix simultanés de ces points pour montrer qu'on ne peut ajouter que 3 points, établissant ainsi la borne de 6, ou bien\n$\\triangleright$ Établir une liste de toutes les configurations possibles vérifiant l'énoncé.\nIci, ces deux approches étaient effectivement réalistes. Cependant, il était aisé d'oublier accidentellement des cas, et c'est ce que beaucoup ont fait. Par exemple, la première approche nécessitait de remarquer que, dans un triangle $A B C$ isocèle en $A$, la médiatrice de $A B$, le cercle de centre $B$ passant par $C$ et le cercle de centre $C$ passant par $A$ peuvent s'intersecter à condition que $\\hat{A}=36^{\\circ}$, ce que tout le monde n'a pas vu. Ces oublis ont été sévèrement sanctionnés, puisque la base de toute disjonction de cas consiste précisément à être suffisamment rigoureux pour n'oublier aucun cas.\nEnfin, les correcteurs ont été surpris du nombre d'élèves qui n'ont pas repéré la configuration à six points (un pentagone et son centre), qui était pourtant apparue dans le problème 1 de l'Olympiade Internationale de 2015. Nous espérons que cette configuration rejoindra le « bagage standard » des élèves à l'avenir.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 16 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "On note $\\mathbb{R}_{>0}$ l'ensemble des réels strictement positifs. Trouver toutes les fonctions $f: \\mathbb{R}_{>0} \\mapsto \\mathbb{R}_{>0}$ telles que\n\n$$\nf(x+f(x y))+y=f(x) f(y)+1\n$$\n\npour tous les réels strictement positifs $x$ et $y$.", "solution": "Soit $f$ une solution éventuelle du problème. Dans la suite, on notera $\\mathbf{E}_{x, y}$ l'égalité de l'énoncé. Soit $a$ et $b$ deux réels strictement positifs tels que $f(a)=f(b)$. Les égalités $\\mathbf{E}_{1, a}$ et $\\mathbf{E}_{1, b}$ indiquent que\n\n$$\na=f(1) f(a)+1-f(1+f(a))=f(1) f(b)+1-f(1+f(b))=b\n$$\n\nce qui signifie que $f$ est injective.\nSoit ensuite $c$ et $d$ deux réels tels que $0<c<d$, puis soit $t$ un réel strictement positif. Puisque $f$ est injective, les égalités $\\mathbf{E}_{c / t, t}$ et $\\mathbf{E}_{d / t, t}$ indiquent que\n\n$$\nf(c / t+f(c))=f(c / t) f(t)+1-t \\neq f(d / t) f(t)+1-t=f(d / t+f(d))\n$$\n\nde sorte que $c / t+f(c) \\neq d / t+f(d)$, ou encore que $f(d)-f(c) \\neq(c-d) / t$. Cette dernière inégalité étant valide pour tout $t>0$, on en déduit que $f(d) \\geqslant f(c)$, ce qui signifie que $f$ est croissante.\nOn pose alors $p=\\inf \\{f(x): x>0\\}$ et $q=\\inf \\{f(x): x>p\\}$. Puisque $f$ est croissante, on sait que $f(x) \\rightarrow p$ lorsque $x \\rightarrow 0$ et que $x>0$, et que $f(y) \\rightarrow q$ lorsque $y \\rightarrow p$ et que $y>p$. Un réel $y>0$ étant fixé, si on fait tendre $x$ vers 0 , on en déduit que $f(x) \\rightarrow p$ et que $f(x y) \\rightarrow p$, de sorte que $x+f(x y) \\rightarrow p$ et que $f(x+f(x y)) \\rightarrow q$. Par conséquent, l'égalité $\\mathbf{E}_{x, y}$ indique que\n\n$$\ny-1=f(x) f(y)-f(x+f(x y)) \\rightarrow p f(y)-q,\n$$\n\nce qui signifie que $f(y)=y+(q-1) / p$.\nLa fonction $f$ est donc une fonction affine, de la forme $f: t \\mapsto u t+v$. Réciproquement, une fois les coefficients $u$ et $v$ fixés, l'égalité $\\mathbf{E}_{x, y}$ indique que\n\n$$\nu^{2} x y+u x+u v+v+y=f(x+f(x y))+y=f(x) f(y)+1=u^{2} x y+u v x+u v y+v^{2}+1\n$$\n\nou encore que $u(v-1) x+(u v-1) y=u v+v-v^{2}-1$. Cela signifie que\n\n$$\nu v-u=u v-1=u v+v-v^{2}-1=0\n$$\n\nOn en déduit que $u-1=(u v-1)-(u v-u)=0$, c'est-à-dire que $u=1$, puis que $v-1=$ $u v-u=0$, c'est-à-dire que $v=1$. Mais alors la triple égalité\n\n$$\nu v-u=u v-1=u v+v-v^{2}-1=0\n$$\n\nest bien respectée.\nEn conclusion, la fonction $f: t \\mapsto t+1$ est l'unique solution du problème.\nCommentaire des correcteurs Cet exercice était extrêmement difficile, et aucun élève (ni encadrant de la POFM) n'est parvenu à passer l'étape cruciale qui consistait à démontrer que $f$ était croissante. Plusieurs élèves ont eu d'excellents réflexes : rechercher une solution particulière (la fonction $f: t \\mapsto t+1$ ), regarder des valeurs particulières de $x$ et $y$ (ici, $x=1$ ), s'intéresser à l'injectivité de $f$, conjecturer que $f$ était croissante (en repérant une infinité de valeurs $x<y$ telles que $f(x)<f(y)$ ), puis utiliser cette conjecture. Ces excellentes initiatives ont à peu près toutes permis à leur auteur d'obtenir quelques points.\nMentionnons cependant quelques erreurs ou maladresses évitables que les correcteurs ont repérées, dans l'espoir que les élèves les éviteront en d'autres occasions:\n$\\triangleright$ Plusieurs élèves ont regardé ce qui se passait lorsque $x=0$ ou $y=0$. Cela leur a souvent permis de repérer la fonction $f: t \\mapsto t+1$, ce qui était très positif. Cependant, on ne pouvait bien sûr pas se baser sur les égalités obtenues lorsque $x=0$ ou $y=0$ pour démontrer quoi que ce soit, puisque la fonction $f$ n'était définie que sur $\\mathbb{R}_{>0}$.\n$\\triangleright$ De nombreux élèves ont regardé ce qui se passait lorsque $y=1$, mais pas lorsque $x=1$. D'autres ont regardé le cas où $x=1$, mais n'ont pas pensé à en déduire l'injectivité de $f$, alors même qu'ils disposaient de l'égalité $f(1+f(x))+x=1+f(1) f(x)$, ce qui rendait l'injectivité de $f$ immédiate.\n$\\triangleright$ Plusieurs élèves ont regardé si l'identité ou les fonctions constantes pouvaient être solutions. Il est dommage de ne pas avoir traité directement le cas des fonctions affines, qui était aussi facile à traiter, et qui leur aurait permis d'identifier la seule solution du problème.\n\n## Problèmes EGMO", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 17 |
+
{"year": "2020", "problem_label": "8", "tier": 1, "problem": "Soit $\\left(F_{k}\\right)_{k \\geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \\geqslant 0$. Soit ensuite $n \\geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \\ldots, n$ de manière à obtenir un $n$-uplet $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ tel que\n\n$$\na_{1} \\leqslant 2 a_{2} \\leqslant 3 a_{3} \\leqslant \\ldots \\leqslant n a_{n}\n$$", "solution": "On dit qu'une permutation $\\mathbf{a}=\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ des entiers $1,2, \\ldots, n$ est jolie si elle satisfait les inégalités $a_{1} \\leqslant 2 a_{2} \\leqslant \\ldots \\leqslant n a_{n}$.\nTout d'abord, soit a une jolie permutation. S'il existe un entier $k$ pour lequel $a_{k} \\leqslant k-2$, on choisit $k$ minimal. Dans ces conditions, on sait que $k \\geqslant 2$ et que $a_{k-1} \\geqslant k-2 \\geqslant a_{k}$, de sorte que $a_{k-1} \\geqslant a_{k}+1$. On en conclut que\n\n$$\n(k-1) a_{k-1} \\geqslant(k-1)\\left(a_{k}+1\\right)=k a_{k}+\\left(k-a_{k}-1\\right) \\geqslant k a_{k}+1,\n$$\n\net donc que a n'est pas jolie. On en conclut donc que $a_{k} \\geqslant k-1$ pour tout $k \\leqslant n$.\nD'autre part, soit $\\ell$ l'entier tel que $a_{\\ell}=n$. Au vu du résultat obtenu précédemment, une récurrence descendante immédiate sur $k$ nous assure que $a_{k}=k-1$ pour tout entier $k$ tel que $\\ell+1 \\leqslant k \\leqslant n$. Puisque\n\n$$\n\\ell n=\\ell a_{\\ell} \\leqslant(\\ell+1) a_{\\ell+1}=(\\ell+1) \\ell\n$$\n\non en conclut que $\\ell \\in\\{n-1, n\\}$.\nAinsi, pour que a soit jolie, on dispose a priori de deux choix :\n$\\triangleright$ soit $\\ell=n$, auquel cas a est effectivement jolie si et seulement si la permutation $\\left(a_{1}, a_{2}, \\ldots, a_{n-1}\\right)$ des entiers $1,2, \\ldots, n-1$ est jolie;\n$\\triangleright$ soit $\\ell=n-1$, auquel cas $a_{n}=n-1$, et alors a est effectivement jolie si la permutation $\\left(a_{1}, a_{2}, \\ldots, a_{n-2}\\right)$ des entiers $1,2, \\ldots, n-2$ est jolie.\nPar conséquent, si on note $J_{n}$ le nombre de jolies permutations de $1,2, \\ldots, n$, on remarque bien que $J_{n}=J_{n-1}+J_{n-2}$ dès lors que $n \\geqslant 3$. On conclut en vérifiant que $J_{1}=1=F_{2}$ et que $J_{2}=2=F_{3}$.", "problem_match": "\nExercice 8.", "solution_match": "\nSolution de l'exercice 8"}
|
| 18 |
+
{"year": "2020", "problem_label": "8", "tier": 1, "problem": "Soit $\\left(F_{k}\\right)_{k \\geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \\geqslant 0$. Soit ensuite $n \\geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \\ldots, n$ de manière à obtenir un $n$-uplet $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ tel que\n\n$$\na_{1} \\leqslant 2 a_{2} \\leqslant 3 a_{3} \\leqslant \\ldots \\leqslant n a_{n}\n$$", "solution": "$n^{\\circ} 1$ Comme précédemment, on considère une permutation a puis l'entier $\\ell$ tel que $a_{\\ell}=n$. Puisque $n a_{k} \\geqslant k a_{k} \\geqslant \\ell a_{\\ell}=\\ell$ n pour tout $k \\geqslant \\ell$, on sait que a induit une permutation de $1,2, \\ldots, \\ell-1$ et de $\\ell, \\ell+1, \\ldots, n$.\nSi $\\ell \\leqslant n-1$, soit $m$ l'unique entier tel que $a_{m}=\\ell$. Puisque $m \\geqslant \\ell$, on sait que\n\n$$\nm \\ell=m a_{m} \\geqslant \\ell a_{\\ell}=\\ell n\n$$\n\ndonc que $m=n$. Mais alors $k a_{k}=\\ell n$ pour tout entier $k$ tel que $\\ell \\leqslant k \\leqslant n$. On en déduit en particulier que $n-1$ divise $(n-1) a_{n-1}=\\ell n$, donc divise $\\ell$ aussi, ce qui signifie que $\\ell=n-1$. Maintenant acquis le fait que $\\ell \\in\\{n-1, n\\}$, on conclut comme précédemment.\n\nCommentaire des correcteurs Cet exercice était difficile. Néanmoins, une bonne partie des élèves a eu la bonne idée d'essayer de trouver une relation de récurrence sur le nombre de permutations vérifiant l'énoncé et a réussi, en analysant la relation de récurrence, à comprendre la structure des permutations vérifiant l'énoncé.\n\nToutefois, très peu d'élèves ont réussi à formaliser cela, en particulier à montrer que l'entier $\\ell$ défini dans la correction était bien supérieur ou égal à $n-1$. Certains ont utilisé le fait que $n(n-2)<(n-1)^{2}$ pour conclure dans le cas général. Si cet argument fonctionnait pour $\\ell=n-2$, il était malheureusement impossible de l'adapter directement pour des $\\ell$ quelconques.\nAttention aussi à la récurrence! Plusieurs élèves ont montré, si on note $k_{n}$ le nombre de permutations de $\\{1, \\ldots, n\\}$ vérifiant l'énoncé, que $k_{n}=k_{n-1}+k_{n-2}$. Ils ont ensuite fait une récurrence forte, initialisée à $n=1$, pour prouver que $k_{n}=F_{n+1}$. Ici pour $n=2$, la formule $k_{2}=k_{1}+k_{0}$ n'a pas de sens car $k_{0}$ n'est même pas défini. Ce raisonnement par récurrence ne permettait donc pas de prouver que $k_{2}=F_{3}$, et il aurait fallu traiter cette égalité dans le cadre de l'initialisation de notre récurrence. Ici, pour éviter cette erreur, il valait mieux faire une récurrence double, qui nécessite explicitement d'initialiser à $n=1$ et $n=2$.", "problem_match": "\nExercice 8.", "solution_match": "\nSolution alternative"}
|
| 19 |
+
{"year": "2020", "problem_label": "9", "tier": 1, "problem": "Soit $n$ un entier naturel. Démontrer que l'écriture de l'entier $n\\left(2^{n}-1\\right)$ en base 2 compte exactement $n$ occurrences du chiffre 1.", "solution": "Notons $s_{n}$ l'entier $n\\left(2^{n}-1\\right)$. Puisque $s_{0}=0$ et $s_{1}=1$, l'énoncé est bien vérifié lorsque $n \\leqslant 1$. On suppose donc désormais que $n \\geqslant 2$.\nOn pose alors $t=2^{n}-n$ et $s=n-1$, de sorte que $n\\left(2^{n}-1\\right)=2^{n} s+t$ et que $s+t=2^{n}-1$. En vertu du binôme de Newton, on sait que $2^{n} \\geqslant(1+1)^{n} \\geqslant\\binom{ n}{0}+\\binom{n}{1}=n+1$. Ainsi, $s$ et $t$ sont deux entiers naturels de somme $2^{n}-1$. Par conséquent, ils s'écrivent respectivement comme\n\n$$\n{\\overline{a_{n-1} a_{n-2} \\ldots a_{0}}}^{2} \\text { et }{\\overline{b_{n-1} b_{n-2} \\ldots b_{0}}}^{2}\n$$\n\nen base 2 , et on est assuré que $a_{i}+b_{i}=1$ pour tout $i \\leqslant n-1$.\nEn outre, comme $t<2^{n}$, l'écriture de $2^{n} s+t$ en base 2 commence avec les $n$ chiffres de $s$ puis se termine avec les $n$ chiffres de $t$. L'entier $n\\left(2^{n}-1\\right)=2^{n} s+t$ s'écrit donc\n\n$$\n{\\overline{a_{n-1} a_{n-2} \\ldots a_{0} b_{n-1} b_{n-2} \\ldots b_{0}}}^{2}\n$$\n\nen base 2. La somme de ces chiffres vaut donc $\\left(a_{0}+b_{0}\\right)+\\left(a_{1}+b_{1}\\right)+\\ldots+\\left(a_{n-1}+b_{n-1}\\right)=n$ , ce qui conclut.\n\nCommentaire des correcteurs Cet exercice était difficile. Le point crucial consistait à repérer que les $k^{\\text {ème }}$ et $(n+k)^{\\text {ème }}$ chiffres de $n\\left(2^{n}-1\\right)$ étaient un 0 et un 1 , ce qu'une étude systématique des petits cas (disons, jusqu'à 8) aurait pu aider à constater. La seule élève qui a remarqué ce phénomène est également la seule qui a fourni une solution complète.\nPar ailleurs, il est dommage que plusieurs élèves, ayant eu la bonne idée d'écrire $2^{n}-1$ en base 2, aient ensuite prématurément affirmé que tout nombre de la forme $k\\left(2^{n}-1\\right)$ contenait $n$ occurrences du chiffre 1 quand on l'écrivait en base 2 : ceci n'est vrai que si $1 \\leqslant k \\leqslant 2^{n}$. Toute preuve censée fonctionner pour tout entier $k$ était donc vouée à l'échec, ce qui était prévisible en regardant le cas où $n=1$.", "problem_match": "\nExercice 9.", "solution_match": "\nSolution de l'exercice 9"}
|
| 20 |
+
{"year": "2020", "problem_label": "10", "tier": 1, "problem": "Soit $A B C$ un triangle. On note $H_{A}$ le pied de la hauteur de $A B C$ issue de $A$, et $A^{\\prime}$ le milieu du segment $[B C]$. On note ensuite $Q_{A}$ le symétrique de $H_{A}$ par rapport à $A^{\\prime}$. On définit de même les points $Q_{B}$ et $Q_{C}$. Enfin, on note $R$ le point d'intersection, autre que $Q_{A}$, entre les cercles circonscrits aux triangles $Q_{A} Q_{B} C$ et $Q_{A} B Q_{C}$.\nDémontrer que les droites $\\left(Q_{A} R\\right)$ et $(B C)$ sont perpendiculaires.", "solution": "Soit $H$ l'orthocentre de $A B C, O$ le centre du cercle circonscrit à $A B C$, et $R^{\\prime}$ le symétrique de $H$ par rapport à $O$. Les projetés orthogonaux de $H$ et $O \\operatorname{sur}(B C)$ sont $H_{a}$ et $A^{\\prime}$, donc le projeté orthogonal de $R^{\\prime}$ sur $(B C)$ est $Q_{A}$. De même, les projetés orthogonaux de $R^{\\prime}$ sur $(C A)$ et sur $(A B)$ sont $Q_{B}$ et $Q_{C}$.\nCela signifie entre autres que $\\widehat{C Q_{A} R^{\\prime}}=\\widehat{Q C_{B} R^{\\prime}}=90^{\\circ}$, donc que $Q_{A}$ et $Q_{B}$ appartiennent au cercle de diamètre $\\left[C R^{\\prime}\\right]$. Ce cercle coïncide donc avec le cercle circonscrit à $Q_{A} Q_{B} C$. De même, les points $Q_{A}$ et $Q_{C}$ appartiennent au cercle de diamètre [ $B R^{\\prime}$ ], qui coïncide avec le cercle circonscrit à $Q_{A} B Q_{C}$. Par conséquent, les points $R$ et $R^{\\prime}$ sont confondus, et ( $Q_{A} R$ ) est bien perpendiculaire à $(B C)$.\n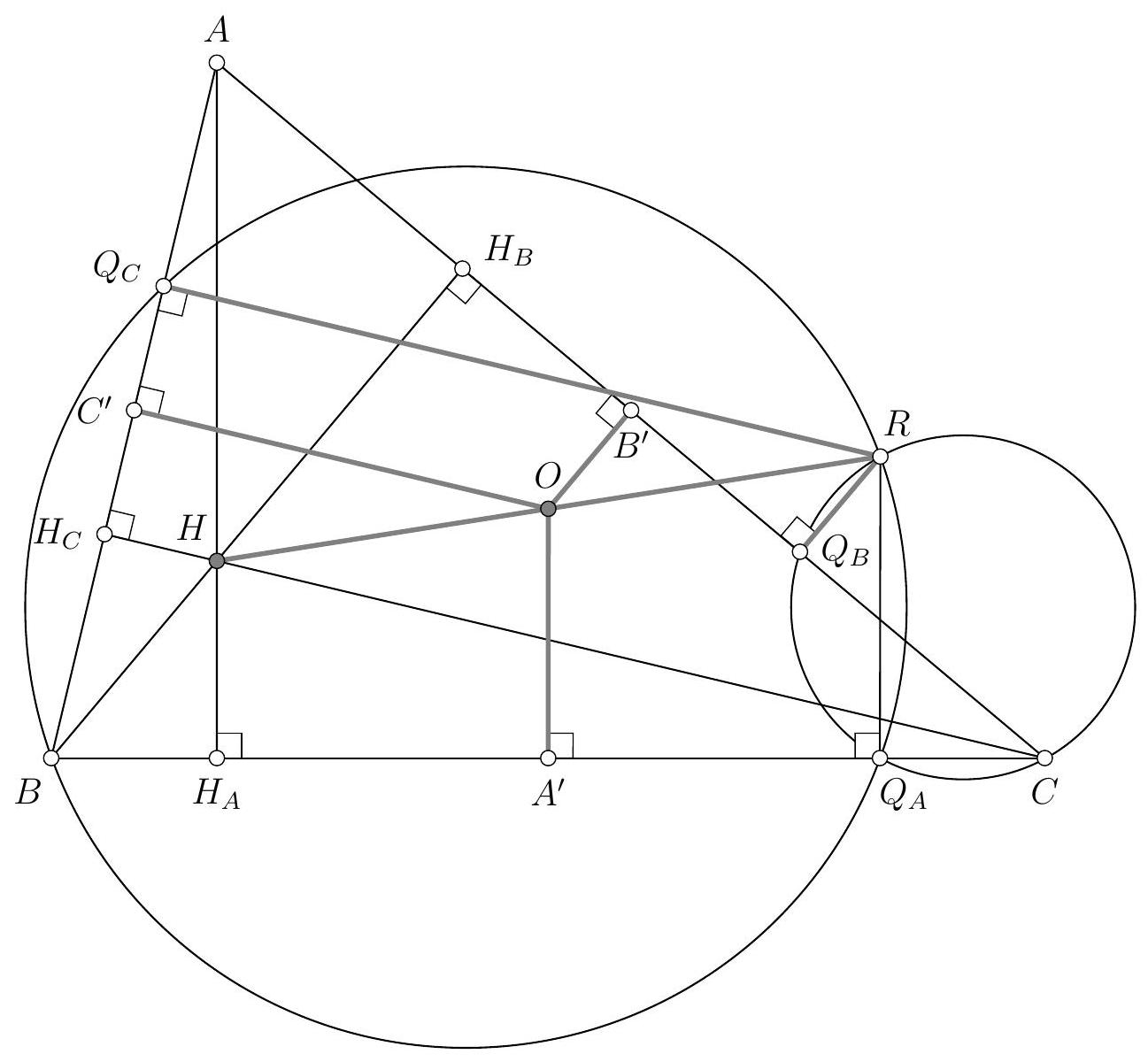\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ Ci-dessous, on note $\\Gamma_{A}, \\Gamma_{B}$ et $\\Gamma_{C}$ les cercles circonscrits respectifs à $A Q_{B} Q_{C}, Q_{A} B Q_{C}$ et $Q_{A} Q_{B} C$. Puisque $R$ appartient à $\\Gamma_{B}$ et à $\\Gamma_{C}$, on sait que\n\n$$\n\\left(Q_{C} A, Q_{C} R\\right)=\\left(Q_{C} B, Q_{C} R\\right)=\\left(Q_{A} B, Q_{A} R\\right)=\\left(Q_{A} C, Q_{A} R\\right)=\\left(Q_{B} C, Q_{B} R\\right)=\\left(Q_{B} A, Q_{B} R\\right)\n$$\n\nCela signifie que $R$ appartient aussi à $\\Gamma_{A}$, et donc que $A, B$ et $C$ jouent des rôles symétriques. Forts de ce constat, on introduit donc également le cercle circonscrit à $A B C$, que l'on note $\\Omega$. Toujours à la recherche de cercles remarquables, on remarque alors que les angles droits en $H_{A}, H_{B}$ et $H_{C}$ suggèrent aussi de tracer les cercles $\\Xi_{A}, \\Xi_{B}$ et $\\Xi_{C}$, de diamètres respectifs $[B C],[C A]$ et $[A B]$.\n\nEnfin, si l'on note $m$ la médiatrice de $[B C]$, l'énoncé nous demande de démontrer que ( $Q_{A} R$ ) et $\\left(A H_{A}\\right)$ sont symétriques l'une de l'autre par rapport à $m$. On s'intéresse donc de plus près à la symétrie d'axe $m$ et aux cercles dont $m$ est un axe de symétrie : il s'agit des cercles $\\Omega, \\Xi_{A}$ et, ne serait-ce qu'en apparence, $\\Gamma_{A}$.\nÀ défaut de démontrer que le centre de ce dernier cercle se trouve sur $m$, on peut tenter de démontrer que les axes radicaux de $\\Gamma_{A}$ avec $\\Omega$ ou $\\Xi_{A}$ sont parallèles à $(B C)$. Le premier serait alors manifestement la parallèle à $(B C)$ passant par $A$, tandis que le deuxième a l'air $d^{\\prime}$ être la droite $\\left(B^{\\prime} C^{\\prime}\\right)$.\nComme $B^{\\prime}$ est le milieu de $[A C]$ et de $\\left[H_{B} Q_{B}\\right.$, on sait que $B^{\\prime} H_{B} \\cdot B^{\\prime} C=B^{\\prime} Q_{B} \\cdot B^{\\prime} A$, ce qui signifie bien que $B^{\\prime}$ appartient à l'axe radical de $\\Gamma_{A}$ et $\\Xi_{A}$. De même, $C^{\\prime}$ appartient à cet axe radical, qui est donc confondu avec $\\left(B^{\\prime} C^{\\prime}\\right)$, de sorte que $\\Gamma_{A}$ est bien symétrique par rapport à $m$.\nPar conséquent, les cercles $\\Omega$ et $\\Gamma_{A}$ se rencontrent en un point $X$ qui n'est autre que le symétrique de $A$ par rapport à $m$. Notons alors $R^{\\prime}$ le point d'intersection entre $\\left(Q_{A} X\\right)$ et $\\Gamma_{C}$. On sait que $\\widehat{C Q_{B} R^{\\prime}}=\\widehat{C Q_{A} R^{\\prime}}=90^{\\circ}$. Puisque l'on a également $\\widehat{A X R^{\\prime}}=90^{\\circ}$, le point $R^{\\prime}$ est donc diamétralement opposé à $A$ dans le cercle circonscrit à $A Q_{B} X$. Cela démontre que $R^{\\prime}$ appartient à $\\Gamma_{A}$, donc coïncide avec $R$, ce qui conclut.\n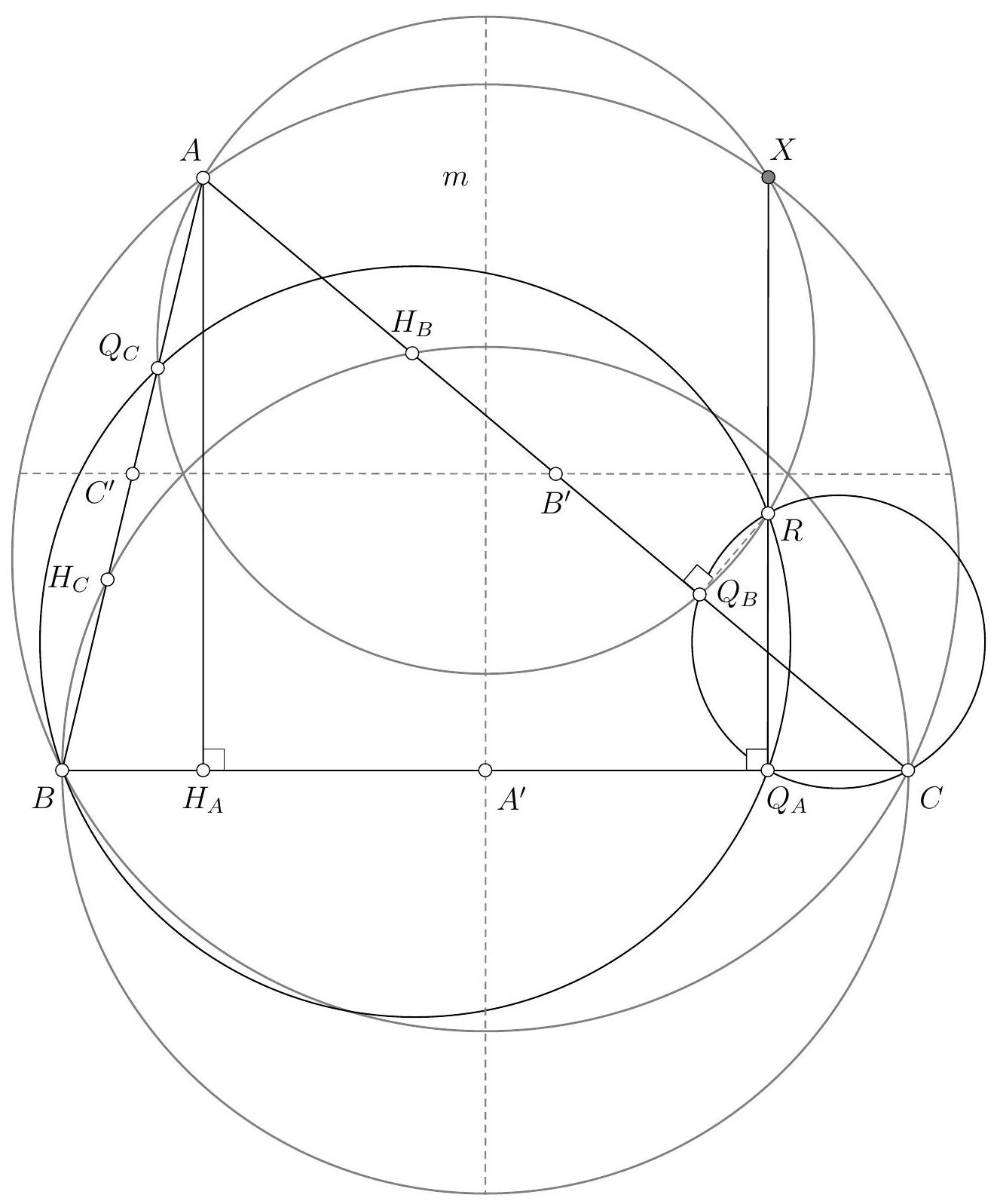", "problem_match": "\nExercice 10.", "solution_match": "\nSolution de l'exercice 10"}
|
| 21 |
+
{"year": "2020", "problem_label": "10", "tier": 1, "problem": "Soit $A B C$ un triangle. On note $H_{A}$ le pied de la hauteur de $A B C$ issue de $A$, et $A^{\\prime}$ le milieu du segment $[B C]$. On note ensuite $Q_{A}$ le symétrique de $H_{A}$ par rapport à $A^{\\prime}$. On définit de même les points $Q_{B}$ et $Q_{C}$. Enfin, on note $R$ le point d'intersection, autre que $Q_{A}$, entre les cercles circonscrits aux triangles $Q_{A} Q_{B} C$ et $Q_{A} B Q_{C}$.\nDémontrer que les droites $\\left(Q_{A} R\\right)$ et $(B C)$ sont perpendiculaires.", "solution": "$n^{\\circ} 2$ On reprend les notations de la solution précédente. Puisque la droite $\\left(Q_{A} R\\right)$ est l'axe radical des cercles $\\Gamma_{B}$ et $\\Gamma_{C}$, il est tentant de rechercher les axes radicaux de ces deux cercles avec un autre cercle. À cette fin, on pourrait considérer le cercle $\\Gamma_{A}$, et constater comme précédemment que $R$ est le centre radical des trois cercles $\\Gamma_{A}, \\Gamma_{B}$ et $\\Gamma_{C}$. Au vu de cette symétrie des rôles, on considère également le cercle $\\Omega$, et on note alors $Y$ le centre radical de $\\Gamma_{B}, \\Gamma_{C}$ et $\\Omega$.\nIl semble que $B A C Y$ soit un parallélogramme, et on entreprend donc de le démontrer. Pour ce faire, on procède comme dans la solution précédente. Puisque $A^{\\prime}$ est le milieu de $[B C]$ et de $\\left[H_{A} Q_{A}\\right]$, il a même puissance par rapport à $\\Gamma_{C}$ et $\\Xi_{C}$. De même, $B^{\\prime}$ a même puissance par rapport à $\\Gamma_{C}$ et $\\Xi_{C}$. On en déduit que $\\left(A^{\\prime} B^{\\prime}\\right)$ est l'axe radical de $\\Gamma_{C}$ et $\\Xi_{C}$. Puisque $(A B)$ est l'axe radical de $\\Xi_{C}$ et $\\Omega$ et que $(A B)$ est parallèle à $\\left(A^{\\prime} B^{\\prime}\\right)$, on en déduit que $(A B)$ est parallèle au troisième axe radical $(C Y)$ entre $\\Gamma_{C}$ et $\\Omega$. De même, $(A C)$ est parallèle à $(B Y)$.\nLa symétrie de centre $A^{\\prime}$ échange donc la droite $\\left(A H_{A}\\right)$ avec $\\left(Y Q_{A}\\right)$, c'est-à-dire avec $\\left(Q_{A} R\\right)$. La droite $\\left(Q_{A} R\\right)$ est donc bien perpendiculaire à $(B C)$.\n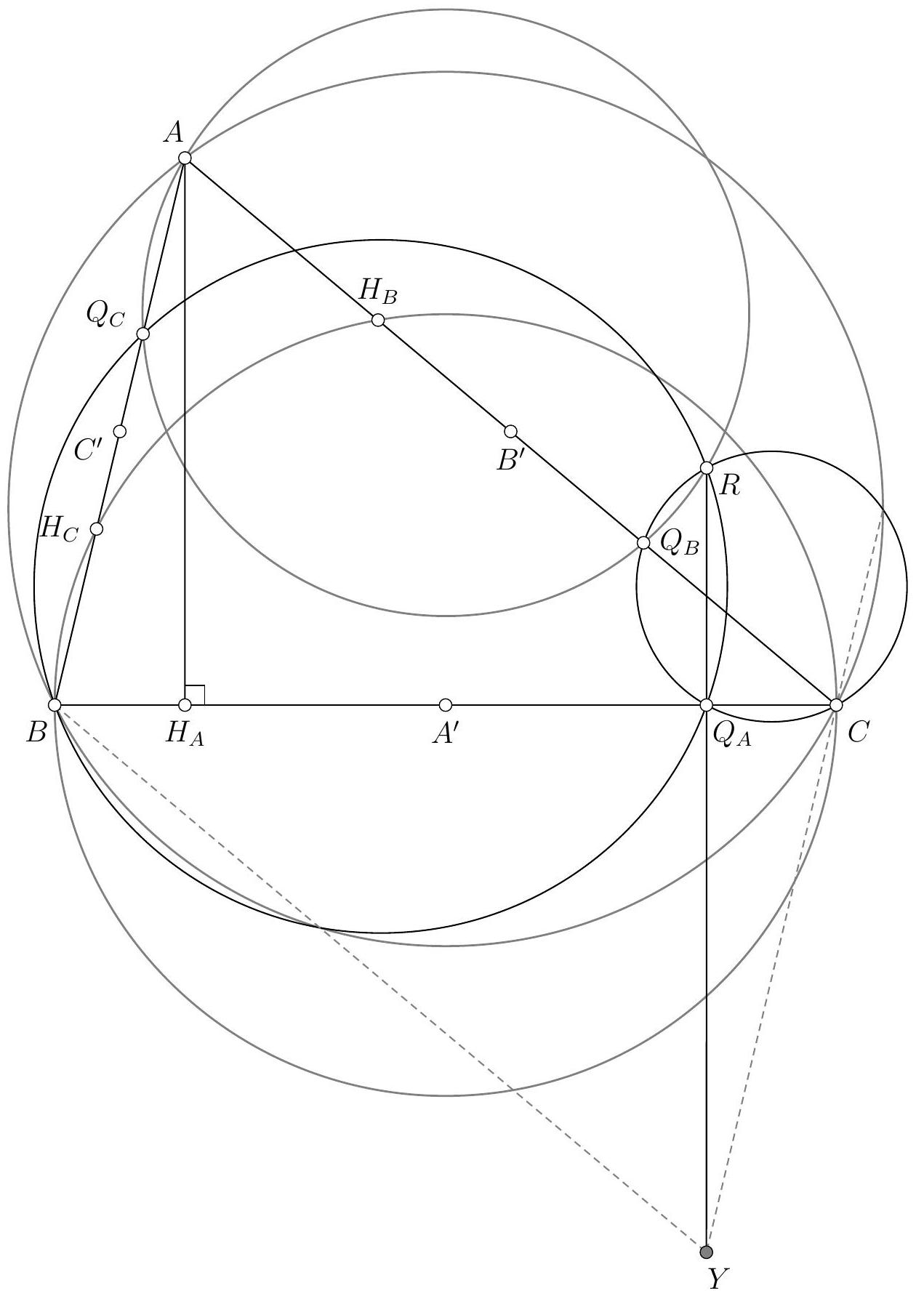\n\nCommentaire des correcteurs Très peu de points ont été distribués sur cet exercice, pour lequel aucune élève n'a proposé de solution complète. Les correcteurs tiennent toutefois à saluer les nombreuses tentatives qui ont été rendues, témoignant d'un réel effort de recherche sur le problème.\nBien souvent, les relations établies autour des points $H_{A}, H_{B}$ et $H_{C}$ sont tout à fait correctes, et nous encourageons les élèves à les retenir car elles sont vraies et applicables dans de nombreux contextes. Toutefois ici, elles ne suffisaient pas à elles seules à se rapprocher de la solution et ne rapportaient donc pas de points.\nL'exercice nécessitait un peu de recul sur la définition des points $Q_{A}, Q_{B}$ et $Q_{C}$. De rares élèves ont pu donc rajouté de la symétrie au problème en montrant que le point $R$ défini appartenait également au cercle $\\Gamma_{C}$. C'est en examinant les nombreuses symétries offertes par la figure qu'il était possible d'acquérir l'intuition des nombreuses propriétés sur le point $R$, comme le fait qu'il s'agit du symétrique de $H$ par rapport à $O$.\nVoici quelques éléments récurrents dans les solutions proposées:\n$\\triangleright$ Quelques élèves ont identifié la droite $\\left(Q_{A} R\\right)$ comme un axe radical. C'est en effet le point de départ d'une approche possible. Il aurait fallu prolonger cet axe radical pour en deviner quelques propriétés ou pour introduire d'autres points intéressants y appartenant, par exemple le symétrique du point $A$ par rapport à $A^{\\prime}$.\n$\\triangleright$ Quelques élèves ont prétendu rendre une solution complète mais qui ne fonctionnait en réalité pas. Pour éviter de tomber dans cet écueil, il est important de se relire et de vérifier que chaque affirmation est vraie et justifiée. Une autre façon de se relire est de vérifier que toutes les hypothèses de l'énoncé ont été utilisées.\nPar exemple, le fait de n'avoir utilisé l'appartenance du point $R$ qu'à un seul des deux cercles doit mettre sur la piste que l'on a été trop vite.", "problem_match": "\nExercice 10.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2020-2021-Corrigé-Test-4-Web.jsonl
ADDED
|
@@ -0,0 +1,13 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.\nBosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.", "solution": "Tout d'abord, si Morgane répartit les entiers de 1 à 8 comme suit, on constate en effet que Bosphore devra lui donner au moins 12 bonbons; on a indiqué, à côté de chaque sommet, la somme $s$ que calculerait Bosphore s'il choisissait ce sommet.\n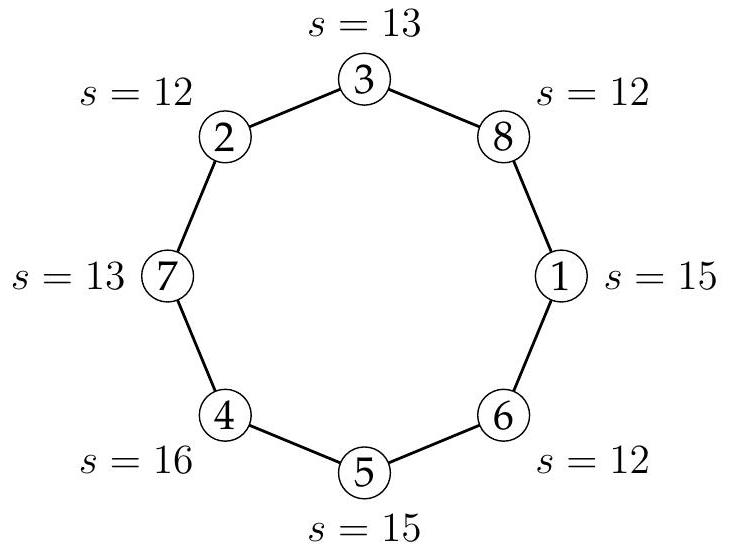\n\nRéciproquement, quel que soit la répartition que choisit Morgane, Bosphore peut procéder comme suit pour éviter de lui donner 13 bonbons ou plus. Ci-dessous, on identifie chaque sommet à l'entier que Morgane a écrit sur ce sommet.\nSi les deux voisins du sommet 8 sont les sommets 1 et 2, Bosphore n'a qu'à choisir le sommet 8 , et il ne donnera que 11 bonbons à Morgane. Sinon, l'un des deux sommets de 8 est un entier $k \\geqslant 3$. Bosphore répartit les six sommets restants en deux groupes de trois sommets consécutifs, comme illustré ci-dessous. La somme des valeurs de ces deux groupes de sommets vaut $(1+2+\\ldots+8)-(k+8)=28-k \\leqslant 25$, donc l'un des deux groupes est de somme $s \\leqslant 12$. Bosphore s'assure alors de donner au plus 12 bonbons à Morgane en choisissant le sommet au milieu de ce groupe.\n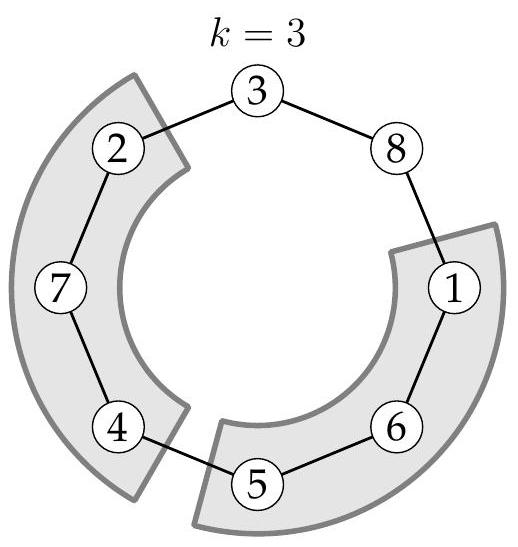", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.\nBosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.", "solution": "$n^{\\circ} 1$ Bosphore a d'autres manières de procéder, par exemple celle-ci. Regroupons les sommets en trois groupes de trois, de sorte que le sommet de valeur 1 soit le seul sommet appartenant à deux groupes. La somme des valeurs de ces groupes de sommets vaut $1+(1+2+\\ldots+8)=37<3 \\times 13$, donc l'un de ces groupes est de valeur $s \\leqslant 12$, et Bosphore n'a qu'à choisir le sommet au milieu de ce groupe.\n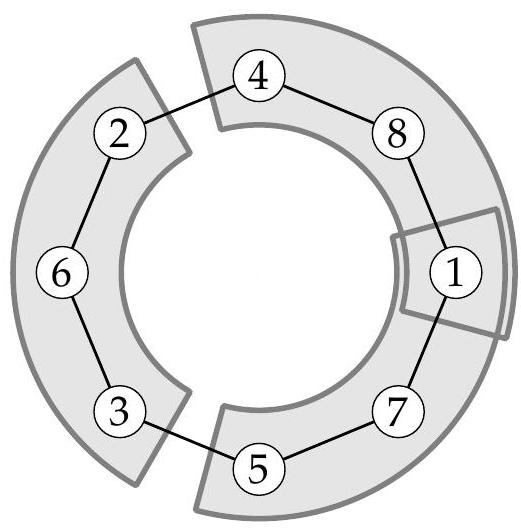", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 3 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.\nBosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.", "solution": "$n^{\\circ} 2$ Voici une troisième manière, pour Bosphore, de s'assurer qu'il donnera au plus 12 bonbons à Morgane. Soit $a$ et $b$ les deux voisins du sommet 5 , avec $a \\geqslant b$. Si $b \\leqslant 4$, alors $a \\leqslant 3$, donc $a+b+5 \\leqslant 12$ et Bosphore choisit directement le sommet 5 . Sinon, on sait que $b \\geqslant 6$. Bosphore élimine alors les sommets 5 et $b$, qui sont contigus, et répartit les six sommets restants en deux groupes de trois sommets consécutifs. Comme dans la solution précédente, la somme des valeurs de ces deux groupes de sommets vaut $(1+2+\\ldots+8)-(5+b)=31-b \\leqslant 25$, donc l'un des deux groupes est de somme $s \\leqslant 12$. Bosphore choisit alors le sommet au milieu de ce groupe.\n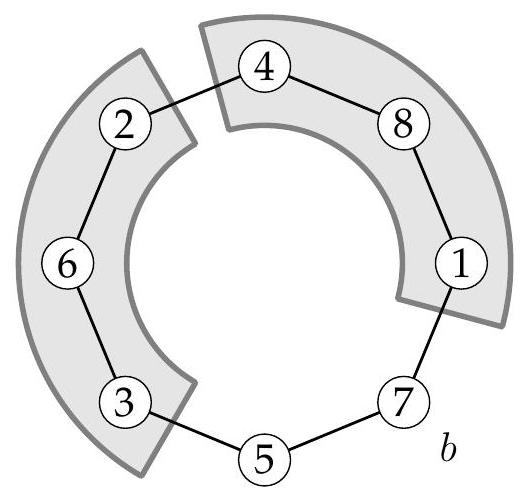", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.\nBosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.", "solution": "$n^{\\circ} 3$ Voici encore une manière de démontrer que Bosphore pourra nécessairement se débrouiller pour donner au plus 12 bonbons à Morgane. À la différence des solutions précédentes, celle-ci ne fournit pas de stratégie explicite pour Bosphore.\nSupposons que Morgane ait trouvé une configuration qui force Bosphore à lui donner au moins 13 bonbons. On numérote les sommets de l'octogone de 1 à 8 , ces numéros étant considérés modulo 8. On note alors $a_{i}$ le nombre que Morgane a écrit sur le sommet $i$, et on note $s_{i}$ la somme $a_{i-1}+a_{i}+a_{i+1}$.\nRemarquons que $s_{i+1}-s_{i}=a_{i+2}-a_{i-1} \\neq 0$, et ce quelle que soit la valeur de $i$. Ainsi, la somme de deux nombres $s_{i}$ consécutifs vaut au minimum $13+14=27$. En outre, la somme des entiers $s_{i}$ vaut $3\\left(a_{1}+a_{2}+\\ldots+a_{8}\\right)=3(1+2+\\ldots+8)=108=4 \\times 27$. Par conséquent, la\nsomme de deux nombres $s_{i}$ consécutifs vaut toujours 27 , et les $s_{i}$ alternent entre les valeurs 13 et 14 , de sorte que $s_{1}=s_{3}=s_{5}=s_{7}$ et $s_{2}=s_{4}=s_{6}=s_{8}$.\nDans ces conditions, on constate que\n\n$$\n0=\\left(s_{2}-s_{3}\\right)+\\left(s_{5}-s_{6}\\right)=\\left(a_{1}-a_{4}\\right)+\\left(a_{4}-a_{7}\\right)=a_{4}-a_{7},\n$$\n\nce qui est impossible. Ainsi, Morgane ne pourra jamais forcer Bosphore à lui donner 13 bonbons ou plus.\n\nCommentaire des correcteurs Cet exercice a été très réussi dans l'ensemble, à la grande satisfaction des correcteurs. La grande majorité des élèves avait identifié les deux enjeux, qui consistaient à démontrer, à l'aide d'un exemple de configuration possible, que Morgane pouvait forcer Bosphore à lui donner au moins 12 bonbons, puis à démontrer qu'elle ne pouvait pas faire mieux.\nUn très grand nombre d'élèves a pensé à regarder la somme des scores des huit groupes de trois, qui valait $3 \\times(1+2+\\ldots+8)=108=13 \\times 8+4$, pour en déduire instantanément que Morgane pourrait gagner au plus 13 bonbons. Cela ne répondait bien sûr pas directement à l'énoncé, mais permettait de s'en approcher, ce qui est toujours positif. Un tel résultat n'était donc certes pas valorisé, mais les éléments de raisonnement qui y avaient mené, et qui étaient réutilisables pour se ramener à 12 bonbons, l'ont bien sûr été.\nNotons néanmoins quelques bévues que l'on a retrouvé dans de multiples copies, et qui ont systématiquement coûté des points à leurs auteurs :\n$\\triangleright$ Plusieurs élèves se sont trompés dans leur contre-exemple, permettant à Bosphore de donner 11 bonbons ou moins à Morgane, ou bien écrivant deux fois un entier entre 1 et 8 et zéro fois un autre. En règle générale, il est bien sûr indispensable de se relire, d'autant plus que vérifier ces contre-exemples prenait généralement de l'ordre de 20 à 30 secondes, qui ne sont donc manifestement pas du temps perdu.\n$\\triangleright$ Plusieurs élèves se sont trompés dans leurs calculs, par exemple en indiquant que $108<13 \\times 8$, ce qui aurait permis de s'en sortir en utilisant le principe des tiroirs (ou de la moyenne, ce qui revient au même). Comme au point précédent, une fois une solution écrite, et d'autant plus si elle est simple et courte, se relire est indispensable et toujours salutaire : soit l'élève repère une erreur et a la possibilité de la corriger, soit il s'assure d'avoir très vraisemblablement une solution correcte.\n$\\triangleright$ Enfin, plusieurs élèves ont procédé par disjonction de cas, utilisant souvent des arguments de symétrie, mais sans les préciser, voire sans préciser du tout comment fonctionnait leur disjonction de cas. Dans une telle situation, ces élèves ont très souvent perdu un ou plusieurs points, car il était impossible distinguer l'élève qui a vraiment procédé à une disjonction de cas sans en oublier un seul de l'élève qui bluffe car il a confiance en l'énoncé et sait à quel résultat il souhaite aboutir.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 5 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Soit $x, y$ et $z$ trois nombres réels tels que $0 \\leqslant x \\leqslant y \\leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression\n\n$$\n(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .\n$$", "solution": "La quantité que l'on souhaite maximiser peut se récrire comme\n\n$$\n\\begin{aligned}\n\\mathcal{S} & =\\left(x^{2}+y^{2}+z^{2}\\right)+\\left((x y)^{2}+(y z)^{2}+(z x)^{2}\\right)-6 x y z \\\\\n& =(x+y+z)^{2}-2(x y+y z+z x)+(x y+y z+z x)^{2}-2 x y z(x+y+z)-6 x y z \\\\\n& =1-2(x y+y z+z x)+(x y+y z+z x)^{2}-8 x y z \\\\\n& =(x y+y z+z x-1)^{2}-8 x y z .\n\\end{aligned}\n$$\n\nPuisque $0 \\leqslant x y+y z+z x \\leqslant(x+y+z)^{2} / 2=1 / 2$, on en déduit que $\\mathcal{S} \\leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\\mathcal{S}=1$, ce qui conclut.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 6 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Soit $x, y$ et $z$ trois nombres réels tels que $0 \\leqslant x \\leqslant y \\leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression\n\n$$\n(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .\n$$", "solution": "$n^{\\circ} 1$ La quantité que l'on souhaite maximiser peut se réécrire comme\n\n$$\n\\begin{aligned}\n\\mathcal{S} & =\\left(x^{2}+y^{2}+z^{2}\\right)+\\left((x y)^{2}+(y z)^{2}+(z x)^{2}\\right)-6 x y z \\\\\n& =(x+y+z)^{2}-2(x y+y z+z x)+\\left((x y)^{2}+(y z)^{2}+(z x)^{2}\\right)-6 x y z\n\\end{aligned}\n$$\n\nOr, l'énoncé indique que $0 \\leqslant x \\leqslant y \\leqslant z \\leqslant 1$, de sorte que $0 \\leqslant x y \\leqslant x z \\leqslant y z \\leqslant 1$. Puisque tout nombre $t$ tel que $0 \\leqslant t$ satisfait l'inégalité $t^{2} \\leqslant 2 t$, on en déduit que $\\mathcal{S} \\leqslant(x+y+z)^{2}-6 x y z \\leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\\mathcal{S}=1$, ce qui conclut.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 7 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Soit $x, y$ et $z$ trois nombres réels tels que $0 \\leqslant x \\leqslant y \\leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression\n\n$$\n(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .\n$$", "solution": "$n^{\\circ} 2$ Les inégalités $0 \\leqslant x \\leqslant y \\leqslant z \\leqslant x+y+z=1$ indiquent que $z \\geqslant y \\geqslant x y$ et $y \\geqslant x \\geqslant z x$, de sorte que la quantité que l'on souhaite maximiser satisfait l'inégalité\n\n$$\n\\mathcal{S} \\leqslant \\max \\{x, y z\\}^{2}+y^{2}+z^{2}\n$$\n\nPuisque $x^{2}+y^{2}+z^{2} \\leqslant(x+y+z)^{2}=1$ et $(y z)^{2}+y^{2}+z^{2} \\leqslant 2 y z+y^{2}+z^{2}=(y+z)^{2}=(1-x)^{2} \\leqslant 1$, on en déduit que $\\mathcal{S} \\leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\\mathcal{S}=1$, ce qui conclut.\n\nCommentaire des correcteurs L'inégalité proposée était inhabituelle, en ce sens que l'optimum recherché était obtenu lorsque les variables n'étaient pas égales l'une à l'autre, ce qui est peu courant. De nombreux élèves ont eu l'intuition (correcte) selon laquelle le maximum recherché était égal à 1 , et qu'il était obtenu lorsque $x=y=0$ et $z=1$. Ils se sont ensuite attachés à démontrer que l'expression recherchée ne pouvait jamais dépasser 1, et il s'agissait là de la démarche attendue, ce qui a ravi les correcteurs.\nCependant, voici quelques erreurs évitables que plusieurs élèves ont commises:\n$\\triangleright$ Certains élèves ont simplement cherché à trouver des majorations de l'expression étudiée, sans même regarder des cas particulier, dont le cas où $x=y=0$ et $z=1$, pour se faire une idée. D'autres ont carrément dit qu'ils souhaitaient démontrer l'inégalité $\\mathcal{S} \\leqslant 1$, mais n'ont pas pensé à indiquer que $\\mathcal{S}=1$ quand $x=y=0$ et $z=1$. De telles omissions sont regrettables, car l'élève renonce ainsi purement et simplement à des points qui lui tendaient la main.\n$\\triangleright$ Plusieurs élèves ont écrit des inégalités qui étaient toutes correctes, mais qui étaient manifestement trop faibles pour conclure. Ainsi, un élève a commencé par démontrer que $\\mathcal{S} \\leqslant 3(z-x y)^{2}$. Si cette inégalité est correcte, elle est également inutile pour montrer que $\\mathcal{S} \\leqslant 1$, puisque le membre de droite vaut 3 lorsque $x=y=0$ et $z=1$.\nDe manière générale, lorsque l'on souhaite démontrer une inégalité en introduisant des inégalités intermédiaires, il est bien sûr indispensable de s'assurer, ne seraitce qu'en regardant des exemples simples, que celles-ci ont une chance d'être suffisamment précises pour aboutir. Dans notre cas, toute inégalité intermédiaire utilisable devait en fait être une égalité lorsque $x=y=0$ et $z=1$.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 8 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle tel que $90^{\\circ}>\\widehat{A B C}>\\widehat{B C A}$. Soit $D$ le point sur le segment $[B C]$ tel que $2 \\widehat{D A C}=\\widehat{A B C}-\\widehat{B C A}$. On note $E$ le point d'intersection, autre que $A$, entre $(A B)$ et le cercle circonscrit à $A C D$, puis $P$ le point d'intersection entre $(A B)$ et la bissectrice de $\\widehat{B D E}$. De même, on note $F$ le point d'intersection, autre que $A$, entre $(A C)$ et le cercle circonscrit à $A B D$, puis $Q$ le point d'intersection entre $(A C)$ et la bissectrice de $\\widehat{C D F}$.\nDémontrer que $(A B)$ et $(P Q)$ sont perpendiculaires.", "solution": "Comme d'habitude, on commence par une figure suffisamment belle et grande pour servir de support à la réflexion. À cette fin, on construit tout d'abord un triangle $A^{\\prime} B C^{\\prime}$ isométrique à $A B C$, tel que $C^{\\prime}$ se trouve sur la demi-droite $[B A)$, puis on trace la bissectrice de l'angle $\\widehat{C B A^{\\prime}}$, que l'on note $d$. On peut alors reporter en $A$ l'angle en entre les droites $(B C)$ et $d$, pour construire la demi-droite $[A D)$.\nAlternativement, la cocyclicité des points $A, B, D$ et $F$ nous assure de l'égalité\n\n$$\n\\widehat{D B F}=\\widehat{D A F}=\\widehat{D A C}=\\widehat{C B A^{\\prime}} / 2\n$$\n\nAinsi, $F$ est le point d'intersection des droites $(A C)$ et $d$, et $D$ est le point d'intersection, autre que $B$, de la droite $(B C)$ avec le cercle circonscrit à $A B F$.\n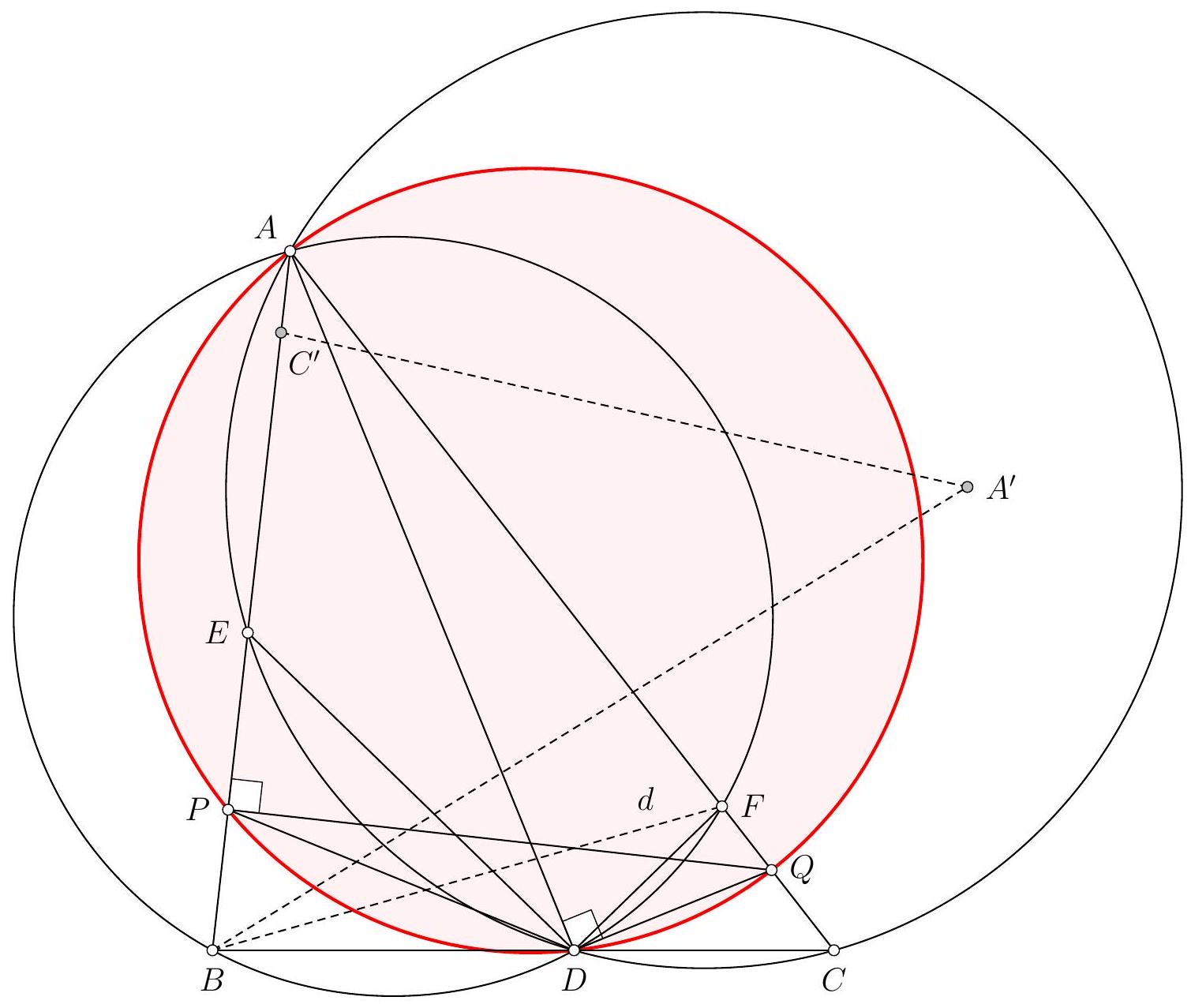\n\nAu vu de l'énoncé, une chasse aux angles s'impose. On pose donc $x=\\widehat{B C A}$ et $y=\\widehat{D A C}$, puis l'on constate que\n\n$$\n2 \\widehat{C D Q}=\\widehat{C D F}=180^{\\circ}-\\widehat{F D B}=\\widehat{B A F}=\\widehat{B A C}=180^{\\circ}-2(x+y),\n$$\n\nde sorte que $\\widehat{C D Q}=90^{\\circ}-(x+y)$. De même,\n\n$$\n2 \\widehat{P D B}=\\widehat{E D B}=180^{\\circ}-\\widehat{C D E}=\\widehat{E A C}=\\widehat{B A C}\n$$\n\nde sorte que $\\widehat{P D B}=90^{\\circ}-(x+y)$.\nOn continue notre chasse aux angles, d'où l'on déduit que\n$\\widehat{Q D A}=180^{\\circ}-\\widehat{D A Q}-\\widehat{A Q D}=180^{\\circ}-y-\\left(180^{\\circ}-\\widehat{D Q C}\\right)=\\left(180^{\\circ}-\\widehat{C D Q}-\\widehat{Q C D}\\right)-y=90^{\\circ}$.\nIl s'agit donc de démontrer que $A, P, D$ et $Q$ sont cocycliques. On vérifie alors que\n\n$$\n\\widehat{D P A}=180^{\\circ}-\\widehat{B P D}=\\widehat{P D B}+\\widehat{D B P}=\\left(90^{\\circ}-x-y\\right)+(x+2 y)=90^{\\circ}+y=180^{\\circ}-\\widehat{A Q D},\n$$\n\nce qui conclut.\nCommentaire des correcteurs L'exercice comportait deux difficultés:\n$\\triangleright$ La première difficulté était de tracer la figure. Ici il était certes possible de résoudre le problème sans avoir une figure exacte, mais il est toujours bon de s'intéresser à a construction exacte de la figure car bien souvent, trouver comment construire une figure comportant une hypothèse compliquée, c'est déjà commencer à résoudre l'exercice. De plus, une figure exacte permettait de constater visuellement que l'angle $\\widehat{Q D A}$ était droit, ce qui constituait une étape cruciale de la preuve.\n$\\triangleright$ La deuxième difficulté était d'exprimer tous les angles de la figures uniquement en fonction des angles $\\widehat{C A B}, \\widehat{A B C}$ et $\\widehat{B C A}$. Les quelques élèves ayant réussi ce travail ont pour la plupart résolu l'exercice dans la foulée.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 9 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Trouver tous les triplets d'entiers naturels non nuls $(a, b, c)$ tels que\n\n$$\n2021^{a}+4=3^{b} \\times 5^{c}\n$$", "solution": "Dans une équation diophantienne, on commence toujours par regarder de petites valeurs des paramètres. Ici, il suffit de factoriser $2021^{a}+4$ en produit de facteurs premiers, donc on regarde les petites valeurs de $a$. Ici, lorsque $a=1$, l'équation devient $2025=3^{b} \\times 5^{c}$, donc $(a, b, c)=(1,4,2)$ est solution. Par ailleurs, si $a \\geqslant 2$, personne n'a envie de factoriser $2021^{a}+4$, donc on arrête ici notre exploration des petits cas.\nDans un deuxième temps, il faudra soit procéder à des factorisations, soit regarder l'équation modulo un nombre $n$ bien choisi pour réduire l'ensemble des valeurs possibles de $a, b$ et $c$. Les nombres 3 et 5 sont manifestement des nombres premiers, et notre étude du cas $a=1$ indique que $2021=45^{2}-4=43 \\times 47$. On note donc cette relation dans un coin de notre brouillon en attendant de pouvoir en faire usage.\nEnfin, quitte à utiliser le théorème chinois, on réduit notre équation modulo $n$ lorsque $n$ est une puissance de nombre premier. Par exemple :\n$\\triangleright n=1, n=2$ et $n=5$ ne nous apportent aucune information;\n$\\triangleright n=3$ indique que $a$ est impair;\n$\\triangleright n=4$ indique que $b$ est pair;\n$\\triangleright n=7$ ne nous apporte aucune information facile à exploiter;\n$\\triangleright n=8$ indique, puisque $a$ est impair et $b$ est pair, que $c$ est pair.\nOn pose alors $\\beta=b / 2$ et $\\gamma=c / 2$. En outre, deux des trois termes de notre équation sont des carrés, ce qui nous permet d'obtenir la factorisation\n\n$$\n43^{a} \\times 47^{a}=2021^{a}=\\left(3^{\\beta} \\times 5^{\\gamma}\\right)^{2}-2^{2}=\\left(3^{\\beta} \\times 5^{\\gamma}+2\\right)\\left(3^{\\beta} \\times 5^{\\gamma}-2\\right) .\n$$\n\nPuisque $3^{\\beta} \\times 5^{\\gamma}+2$ et $3^{\\beta} \\times 5^{\\gamma}-2$ sont deux entiers impairs dont la différence vaut 4 , ils sont premiers entre eux.\nSeul l'un de ces deux facteurs est divisible par 43, et seul l'un est divisible par 47. Plusieurs cas sont donc possibles a priori :\n$\\triangleright \\operatorname{si} 47$ divise $3^{\\beta} \\times 5^{\\gamma}-2$, alors $47^{a}$ divise $3^{\\beta} \\times 5^{\\gamma}-2$, donc $3^{\\beta} \\times 5^{\\gamma}-2 \\geqslant 47^{a} \\geqslant 43^{a} \\geqslant 3^{\\beta} \\times 5^{\\gamma}+2$, ce qui est impossible;\n$\\triangleright$ si 43 et 47 divisent $3^{\\beta} \\times 5^{\\gamma}+2$, on a $3^{\\beta} \\times 5^{\\gamma}+2=43^{a} \\times 47^{a}$ et $3^{\\beta} \\times 5^{\\gamma}-2=1$, ce qui est impossible puisque $3^{\\beta} \\times 5^{\\gamma}-2 \\geqslant 3 \\times 5-2=13$.\nAinsi, 47 divise $3^{\\beta} \\times 5^{\\gamma}+2$ et 43 divise $3^{\\beta} \\times 5^{\\gamma}-2$, de sorte que $3^{\\beta} \\times 5^{\\gamma}+2=47^{a}$ et $3^{\\beta} \\times 5^{\\gamma}-2=43^{a}$. Mais alors\n\n$$\n4=\\left(3^{\\beta} \\times 5^{\\gamma}+2\\right)-\\left(3^{\\beta} \\times 5^{\\gamma}-2\\right)=47^{a}-43^{a} \\geqslant 47^{a}-43 \\times 47^{a-1}=4 \\times 47^{a-1}\n$$\n\nce qui démontre que $a \\leqslant 1$.\nEn conclusion, la seule solution du problème est $(a, b, c)=(1,4,2)$.\nCommentaire des correcteurs L'exercice était difficile, mais de nombreux élèves ont réussi à obtenir des points grâce à des réflexions intelligentes. Trouver une solution particulière est toujours une avancée, puisqu'elle permet de voir ce qu'on pourra ou non prouver : ici $(1,4,2)$ était solution, donc on pouvait s'attendre à avoir $b$ ou $c$ pair, en tout cas il était illusoire de prouver que $b$ ou $c$ était impair sans hypothèses supplémentaires sur $a$.\n\nRappelons que regarder modulo un nombre composé est très rarement intelligent : regarder modulo 15 par exemple ne sert à rien, puisqu'on peut faire les mêmes observations modulo 3 et 5 , et comme les calculs sont plus simples, cela permet de ne pas faire d'erreur.\nIci la clé du problème était de s'interroger sur les parité de $b, c$ pour obtenir un carré : obtenir des carrés en équation diophantienne est crucial, car cela permet de factoriser et donc de rendre le problème plus simple. Néanmoins, une fois l'équation factorisée, certains oublient de préciser que les deux termes sont positifs, et qu'ils sont même strictement plus grand que 1 , ce qui fait qu'on ne peut pas conclure immédiatement qu'un des facteurs vaut $47^{a}$ et l'autre $43^{a}$. De plus, il serait bien de justifier rigoureusement à la fin que $47^{a}=43^{a}+4$ implique $a=1$. Par exemple, on peut invoquer que $47^{2}>43^{2}+4$ et dire que par récurrence immédiate $47^{k}>43^{k}+4$ si $k \\geqslant 2$.\n\n## Énoncés Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 10 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "On note $\\mathbb{Z}[x, y, z]$ l'ensemble des polynômes à coefficients entiers en les trois variables $x, y$ et $z$. On dit ensuite qu'un polynôme $P \\in \\mathbb{Z}[x, y, z]$ est olympique si $\\mathbb{Z}[x, y, z]$ contient des polynômes $A, B$ et $C$ tels que\n\n$$\nP(x, y, z)=(x+y+z) A(x, y, z)+(x y+y z+z x) B(x, y, z)+x y z C(x, y, z) .\n$$\n\nTrouver le plus grand entier $n$ pour lequel il existe des entiers naturels $i, j$ et $k$ de somme $i+j+k=n$ et tels que le polynôme $x^{i} y^{j} z^{k}$ ne soit pas olympique.\nNote : Un polynôme à coefficients entiers en les variables $x, y$ et $z$ est une fonction que l'on peut écrire comme une somme de termes de la forme $\\lambda x^{i} y^{j} z^{k}$, où $\\lambda$ est un entier relatif et $i, j$ et $k$ sont des entiers naturels. Par exemple, $x-y+1$ et $x y+y z+z x$ sont de tels polynômes, mais $\\pi x y z, \\exp (x), x /\\left(y^{2}+1\\right)$ et $\\sqrt{x y+z}$ n'en sont pas.", "solution": "Posons $s_{1}=x+y+z, s_{2}=x y+y z+z x$ et $s_{3}=x y z$. On constate que\n\n$$\n\\begin{cases}x^{3} \\equiv-x^{2}(y+z) \\equiv-x(x y+x z) \\equiv x y z \\equiv 0 & \\left(\\bmod s_{1}, s_{2}, s_{3}\\right) \\\\ x^{2} y^{2} \\equiv x y(-x z-y z) \\equiv-x y z(x+y) \\equiv 0 & \\left(\\bmod s_{1}, s_{2}, s_{3}\\right)\\end{cases}\n$$\n\nce qui signifie que $x^{3}$ et $x^{2} y^{2}$ sont olympiques. Or, l'ensemble des polynômes olympiques est stable par multiplication par tout polynôme et par permutation des variables.\nPar conséquent, considérons un polynôme $x^{i} y^{j} z^{k}$, non olympique. Sans perte de généralité, on suppose que $i \\geqslant j \\geqslant k$. Si $i \\geqslant 3, j \\geqslant 2$ ou $k \\geqslant 1$, notre polynôme est un multiple de $x^{3}$, de $x^{2} y^{2}$ ou de $x y z$, donc il est olympique. On en déduit que $i \\leqslant 2, j \\leqslant 1$ et $k \\leqslant 0$, de sorte que $i+j+k \\leqslant 3$. Cela nous assure déjà que $n \\leqslant 3$.\nRéciproquement, intéressons-nous à l'ensemble $\\mathcal{E}$ des polynômes olympiques dont tous les monômes sont de degré total 3, c'est-à-dire sont des polynômes $x^{i} y^{j} z^{k}$ tels que $i+j+k=3$. Quitte à restreindre respectivement $A, B$ et $C$ à leurs monômes de degrés totaux 2,1 et 0 , chaque polynôme de $\\mathcal{E}$ s'écrit sous la forme\n\n$$\n\\begin{aligned}\nP= & (x+y+z)\\left(a x^{2}+b y^{2}+c z^{2}+d x y+e x z+f y z\\right)+(x y+y z+z x)(g x+h y+i z)+j x y z \\\\\n= & a x^{3}+b y^{2}+c z^{3}+(a+d+g) x^{2} y+(a+e+g) x^{2} z+(b+d+h) y^{2} x+(b+f+h) y^{2} z \\\\\n& \\quad+(c+e+i) z^{2} x+(c+f+i) z^{2} y+(d+e+f+g+h+i+j) x y z .\n\\end{aligned}\n$$\n\nSi $x^{2} y$ est olympique, on a alors\n\n$$\n1=(a+d+g)+(b+f+h)+(c+e+i)-(a+e+g)-(b+d+h)-(c+f+i)=0,\n$$\n\nce qui est absurde. Ainsi, le polynôme $x^{2} y$ n'est pas olympique, et le plus grand entier recherché est $n=3$.\n\nCommentaire des correcteurs L'exercice était difficile, mais de nombreux élèves ont bien avancé sur le problème, en montrant que plusieurs polynômes étaient olympiques. Attention néanmoins aux erreurs de calcul!\nCertains ont essayé de montrer que $x^{2} y$ n'était pas olympique en faisant de l'arithmétique sur les polynômes à plusieurs variables. Cette approche était risquée et, comme toute voie compliquée pour obtenir la solution, elle a mené à de nombreuses erreurs.\nIci, la la clé était de regarder les termes de degré 3 mais en deux variables, c'est-à-dire en $x^{2} y, x^{2} z, z^{2} x, z^{2} y, y^{2} x$ et $y^{2} z$. Attention, toutefois: certains élèves ont procédé par l'absurde\net, à partir de polynômes $(A, B, C)$ qui permettaient d'obtenir $x^{2} y$, ont exhibé de nouveaux $\\left(A^{\\prime}, B^{\\prime}, C^{\\prime}\\right)$ qui permettaient d'obtenir $\\pm y^{2} x$, puis en ont conclu directement que comme on se ramenait au même cas (à symétrie près) c'était impossible. Il n'y a à priori pas de raison que ce soit le cas : il pourrait y avoir de nombreux triplets $(A, B, C)$ permettant d'obtenir que $x^{2} y$ est olympique!\nEnfin, après s'être restreints aux termes de degré 3 , certains oublient les termes en $x^{2}, y^{2}$ et $z^{2}$ dans $A$, ce qui est dommage.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 11 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Soit $A B C$ un triangle isocèle en $A$, puis $D$ un point du segment $[B C]$ tel que $B D \\neq C D$. Soit $P$ et $Q$ les projetés orthogonaux de $D$ sur $(A B)$ et $(A C)$. Enfin, soit $E$ le point d'intersection, autre que $A$, entre les cercles circonscrits à $A B C$ et $A P Q$.\nDémontrer que, si les droites $(E P),(A C)$ et la médiatrice de $[P Q]$ sont concourantes, le triangle $A B C$ est rectangle en $A$.", "solution": "Un premier réflexe est de dessiner une figure où le triangle $A B C$ est isocèle rectangle, mais sans indiquer qu'il l'est. De nombreuses symétries apparaissent alors. Notons $X$ le point d'intersection des droites $(A C)$, et $(E P), \\ell$ la médiatrice de $[P Q]$, $O$ le centre du cercle circonscrit à $A B C$ et $M$ le milieu de $[B C]$ : il s'agit de démontrer que $M=O$.\nComme $P Q X$ est isocèle en $X$, la symétrie d'axe $\\ell$ échange les droites $(A Q)$ et $(P E)$, de sorte que $\\widehat{A Q P}=\\widehat{Q P E}$. Puisque $A, E, P$ et $Q$ sont cocycliques, le quadrilatère $A E P Q$ est donc un trapèze isocèle, ce qui se vérifie aisément puisque\n\n$$\n(A E, P Q)=(A E, A Q)+(A Q, P Q)=(P E, P Q)+(Q A, Q P)=0^{\\circ}\n$$\n\nLa symétrie d'axe $\\ell$ échange donc les points $A$ et $E$, et $\\ell$ est en fait la médiatrice de $[A E]$. Elle contient donc, en particulier, les centres $O$ et $O^{\\prime}$ des cercles circonscrits à $A B C$ et $A E P Q$.\nAu vu des angles droits en $P, Q$ et $M$, ce dernier cercle est en fait le cercle de diamètre $[A D]$, et il contient $D$ et $M$. En outre, $(A M)$ est la bissectrice de $\\widehat{B A C}$, donc $M$ est le pôle Sud de $A$ dans le triangle $A P Q$, et $P Q M$ est isocèle en $M$. Ainsi, $M$ appartient à $\\ell$.\nEn conclusion, $M$ et $O$ appartiennent tous deux à $(A M)$ et à $\\ell$. Puisque $D \\neq M$, on sait aussi que $O^{\\prime}$, le milieu de $[A D]$, n'est pas sur $(A M)$. Puisque $\\ell$ contient $O^{\\prime}$, elle n'est donc pas confondue avec ( $A M)$, et $M$ coïncide donc avec $O$, ce qui conclut.\n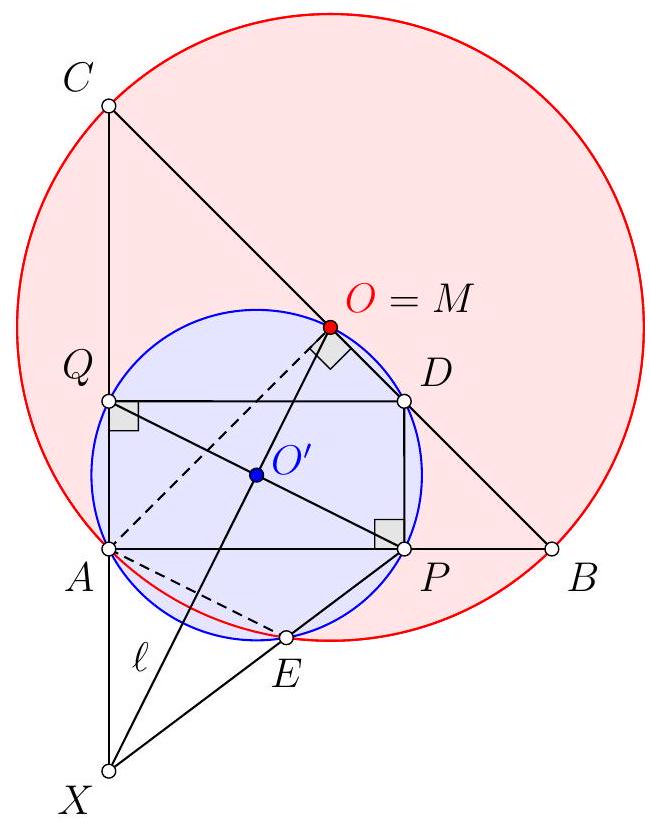\n\nCommentaire des correcteurs L'exercice a été très bien réussi. Beaucoup d'élèves arrivent, par le développement d'idées simples comme une chasse aux angles, à avancer significativement dans la résolution du problème, quand certains autres forcent l'utilisation de résultats très avancés comme le théorème de Pascal ou de Desargues mais sans en obtenir des résultats conséquents.\n\nLes figures fournies sont souvent très précises et il a été parfois frustrant de voir apparaître sur celles-ci que le milieu du segment $[B C]$ appartient au cercle passant par les points $A, P$ et $Q$ sans que l'élève n'évoque ce milieu dans sa tentative.\nNous avons noté une quantité significative de solutions erronées. Les erreurs sont souvent dues à l'utilisation d'une propriété manifeste sur la figure mais qui n'est pas encore démontrée. Bien souvent, pour éviter cet écueil, il est bon de se demander si toutes les hypothèses de l'énoncé ont été utilisées. Ainsi, plusieurs élèves croient avoir résolu l'exercice sans avoir utilisé ni que le triangle $A B C$ est isocèle, ni que le point $E$ appartient à son cercle circonscrit.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 12 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "Soit $n \\geqslant 6$ un entier. On a disposé, dans le plan, $n$ disques $D_{1}, D_{2}, \\ldots, D_{n}$ deux à deux disjoints, de rayons $r_{1} \\geqslant r_{2} \\geqslant \\ldots \\geqslant r_{n}$. Pour tout entier $i \\leqslant n$, on considère un point $P_{i}$ à l'intérieur du disque $D_{i}$. Enfin, soit $A$ un point quelconque du plan. Démontrer que\n\n$$\nA P_{1}+A P_{2}+\\ldots+A P_{n} \\geqslant r_{6}+r_{7}+\\ldots+r_{n}\n$$", "solution": "Au vu d'un tel énoncé, et ne sachant pas nécessairement par où commencer, on souhaite utiliser une récurrence sur $n$. Dans ces conditions, il s'avère que la propriété clé de notre récurrence sera la suivante.\nLemme. Si $n=6$, il existe un entier $i$ tel que $A P_{i} \\geqslant r_{6}$.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 13 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "Soit $n \\geqslant 6$ un entier. On a disposé, dans le plan, $n$ disques $D_{1}, D_{2}, \\ldots, D_{n}$ deux à deux disjoints, de rayons $r_{1} \\geqslant r_{2} \\geqslant \\ldots \\geqslant r_{n}$. Pour tout entier $i \\leqslant n$, on considère un point $P_{i}$ à l'intérieur du disque $D_{i}$. Enfin, soit $A$ un point quelconque du plan. Démontrer que\n\n$$\nA P_{1}+A P_{2}+\\ldots+A P_{n} \\geqslant r_{6}+r_{7}+\\ldots+r_{n}\n$$", "solution": "Soit $O_{i}$ le centre du disque $D_{i}$. Si $A$ coïncide avec l'un des points $O_{i}$, le résultat désiré est immédiat. Sinon, on trie les centres $O_{i}$ dans le sens horaire autour de $A$. Ceux-ci définissent six angles de somme $360^{\\circ}$, donc l'un des angles, disons $\\widehat{O_{i} A O_{j}}$, vaut au plus $60^{\\circ}$. Si l'on suppose sans perte de généralité que $A O_{i} \\geqslant A O_{j}$, le théorème d'Al-Kashi indique alors que\n\n$$\n\\begin{aligned}\n\\left(r_{i}+r_{j}\\right)^{2} & \\leqslant O_{i} O_{j}^{2}=A O_{i}^{2}+A O_{j}^{2}-2 \\cos \\left(\\widehat{O_{i} A O_{j}}\\right) A O_{i} \\cdot A O_{j} \\leqslant A O_{i}^{2}-A O_{i} \\cdot A O_{j}+A O_{j}^{2} \\\\\n& \\leqslant A O_{i}^{2} \\leqslant\\left(A P_{i}+r_{i}\\right)^{2},\n\\end{aligned}\n$$\n\nde sorte que $A P_{i} \\geqslant r_{j} \\geqslant r_{6}$.\nOn procède maintenant par récurrence sur $n$. Tout d'abord, si $n=6$, le résultat de l'énoncé est un simple corollaire de notre lemme. Puis, si $n \\geqslant 7$, on applique notre lemme aux disques $D_{1}, \\ldots, D_{6}$. Il existe donc un entier $i \\leqslant 6$ tel que $A P_{i} \\geqslant r_{6}$. On supprime maintenant le disque $D_{i}$ et on applique l'hypothèse de récurrence aux $n-1$ disques restants, de sorte que\n\n$$\nA P_{i}+\\sum_{j \\neq i} A P_{j} \\geqslant r_{6}+\\left(r_{7}+\\ldots+r_{n}\\right)\n$$\n\nce qui conclut.\nCommentaire des correcteurs Le problème proposé était très difficile, et il n'a été abordé que par une vingtaine d'élèves. Les correcteurs se sont émerveillés de constater que deux élèves l'avaient résolu avec brio.\nDe nombreux élèves ont tout d'abord formulé la remarque pertinente selon laquelle on pouvait toujours supposer que $A P_{i}=A O_{i}-r_{i}$ quand $A$ n'appartient pas à $D_{i}$, où $O_{i}$ est le centre du disque $D_{i}$. Toutefois, les correcteurs ont été surpris de découvrir des preuves parfois très compliquées pour ce résultat pourtant fort simple et géométriquement clair. Malheureusement, au vu de la difficulté de l'exercice, cette remarque ne rapportait aucun point, mais cela n'enlève rien à sa pertinence. La clé consistait donc à trouver un énoncé intermédiaire plus fort, dont on pourrait déduire la conclusion demandée.\nPlusieurs élèves ont pensé à regarder le cas $n=6$, ce qui était très bien, mais les deux seuls qui ont traité ce cas rigoureusement sont aussi les deux seuls à avoir conclu l'exercice. De manière générale, affirmer tout de go que « la pire situation est celle où les disques sont de même rayon et où leurs centres forment un hexagone régulier de centre $A$ » repose sur une heuristique bienvenue, mais nullement prouvée, et il est clair que cette affirmation ne peut pas rapporter le moindre point tant qu'elle n'est pas étayée.\nDe même, plusieurs élèves ont cherché à démontrer que lorsque $A$ n'appartient à aucun disque $D_{i}$, il existait un tel disque pour lequel $A P_{i} \\geqslant r_{i}$. Cependant, il était facile de construire un contre-exemple à cette inégalité, par exemple si $A$ et les points $P_{i}$ et $O_{i}$ sont\nalignés, avec $A O_{i}=5^{i}, r_{i}=3 \\times 5^{i-1}$ et $A P_{i}=2 \\times 5^{i-1}$. De fait, lorsque l'on formule une idée de lemme, il est très important de rechercher des contre-exemples simples à ce lemme, qui seraient de nature à l'invalider, et ce dans le but de limiter le temps perdu à tenter de démontrer quelque chose de faux. Une telle phase permet souvent, à peu de frais, d'affiner la formulation du lemme, ou bien de se rendre compte que l'idée sous-jacente est complètement fausse; quand elle n'aboutit pas, c'est-à-dire quand on n'a pas trouvé de contre-exemple, on a plus confiance dans le lemme, et c'est là aussi encourageant, donc positif.", "problem_match": "\nExercice 7.", "solution_match": "\nDémonstration."}
|
French_TST_Senior/segmented/fr-2020-2021-Corrigé-Web-Test-5.jsonl
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "problem_label": "1", "tier": 1, "problem": "Soit $A B C D E$ un pentagone convexe tel que $\\widehat{A B E}=\\widehat{A C E}=\\widehat{A D E}=90^{\\circ}$ et $B C=C D$. Enfin, soit $K$ un point sur la demi-droite $[A B]$ tel que $A K=A D$, et soit $L$ un point sur la demi-droite $[E D)$ tel que $E L=B E$. Démontrer que les points $B, D, K$ et $L$ appartiennent à un même cercle de centre $C$.", "solution": "Au vu des angles droits dont on dispose en $B, C$ et $D$, les points $A$, $B, C, D$ et $E$ appartiennent à un même demi-cercle de diamètre $[A E]$. Comme $B C=C D$, le point $C$ est donc le pôle Sud issu de $A$ dans le triangle $A B D$. Ainsi, $(A C)$ est la bissectrice de $\\widehat{D A B}$, c'est-à-dire la médiatrice de $[K D]$. De même, $(C E)$ est la médiatrice de $[B L]$. Cela signifie que $C L=B C=D C=C K$, ce qui conclut.\n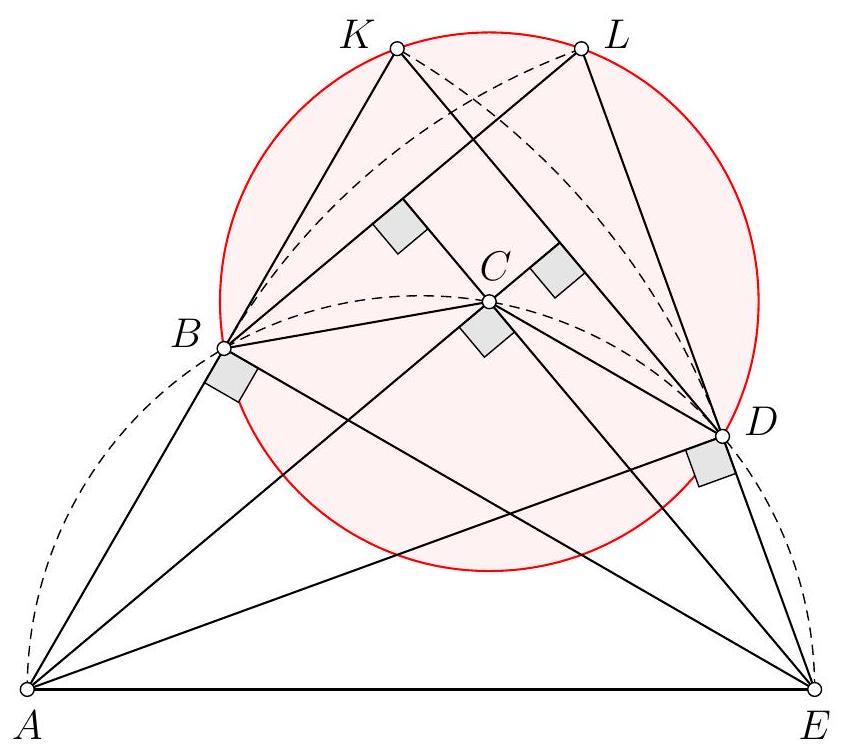\n\nCommentaire des correcteurs Le problème a été bien abordé. Une bonne partie des élèves parvient à montrer que les points $B, D, L$ et $K$ sont cocycliques. Une fois cette étape franchie, la plupart des élèves tentent de montrer que $\\widehat{B C D}=2 \\widehat{B K D}$ pour appliquer une réciproque du théorème de l'angle au centre.\nMalheureusement, l'égalité d'angle seule ne permet pas d'établir que le point $C$ est le centre du cercle circonscrit au triangle $B K D$. En effet, tout point $X$ sur l'arc $B D$ contenant $C$ dans le cercle circonscrit au triangle $B C D$ vérifie également cette égalité d'angle.\nIl fallait encore invoquer l'hypothèse donnée par l'énoncé qui est que $B C=C D$. Les égalités $B C=C D$ et $\\widehat{B C D}=2 \\widehat{B K D}$ étaient alors suffisantes pour conclure, puisque sur la médiatrice du segment $[B D]$, il n'y a qu'un seul point $X$ vérifiant $\\widehat{B X D}=2 \\widehat{B K D}$, et comme cette propriété est vérifiée par le centre du cercle circonscrit au triangle $B K D$, un tel point $X$ est bien le centre recherché. Cette erreur récurrente a empêché de nombreux élèves d'avoir la totalité des points.\nMentionnons également que très peu d'élèves ont reconnu la configuration du pôle Sud, qui est pourtant présente dans de nombreux problèmes de géométrie et qui est donc à retenir.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2020", "problem_label": "2", "tier": 1, "problem": "Trouver tous les quadruplets d'entiers relatifs $(a, b, c, p)$ tels que $p$ soit un nombre premier et pour lesquels\n\n$$\n73 p^{2}+6=9 a^{2}+17 b^{2}+17 c^{2}\n$$", "solution": "L'égalité de l'énoncé met en jeu de nombreux carrés. La première chose à faire consiste donc à l'étudier modulo un nombre $n$ pour lequel il y a peu de résidus quadratiques. On étudie donc le cas $n=8$, car les carrés modulo 8 sont 0,1 et 4 .\nEn particulier, si $p$ est impair, l'équation devient $a^{2}+b^{2}+c^{2} \\equiv-1(\\bmod 8)$, et cette équation n'a aucune solution. On en déduit que $p=2$, et il s'agit désormais de trouver les entiers $a, b$ et $c$ tels que $298=9 a^{2}+17 b^{2}+17 c^{2}$.\nSans perte de généralité, on suppose que $a, b$ et $c$ sont positifs ou nuls. Puisque $b$ et $c$ jouent des rôles symétriques, on suppose même que $b \\leqslant c$. On constate alors que $9 \\times 6^{2}=324>$ $298 \\geqslant 9 a^{2}$, de sorte que $0 \\leqslant a \\leqslant 5$. Puisque $9 a^{2}+17 b^{2}+17 c^{2} \\equiv 298 \\equiv 9(\\bmod 17)$, on en déduit en outre que 17 divise $9(a-1)(a+1)$. Cela signifie que $a=1$, et notre équation devient $17=b^{2}+c^{2}$, ce qui signifie que $b=1$ et $c=4$.\nEn conclusion, les seules solutions possibles sont\n\n$$\n(a, b, c, p)=( \\pm 1, \\pm 1, \\pm 4,2) \\text { et }( \\pm 1, \\pm 4, \\pm 1,2)\n$$\n\nRéciproquement, et en vertu de l'égalité $73 \\times 2^{2}+6=298=9 \\times 1^{2}+17 \\times 1^{2}+17 \\times 4^{2}$, ces quadruplets conviennent effectivement.\n\nCommentaire des correcteurs Beaucoup d'élèves ont abordé l'exercice mais peu ont réussi à véritablement avancer. L'exercice consistait en deux parties : regarder modulo 8 pour montrer que $p=2$, puis trouver les solutions. Il est dommage que beaucoup d'élèves aient tenté des simplifications, sans finalement chercher le cas $p=2$, qui était assez facile à traiter et aurait pu rapporter des points. Ce cas est d'ailleurs plus pertinent que des cas comme $a=b$ ou $a=b=c$, puisqu'il y a peu de chances d'aboutir à une telle égalité.\nConcernant les études modulo de la première équation, regarder modulo 8 est assez naturel en présence de carrés. Quand il y a plusieurs carrés présents, il faut étudier modulo 4, 3 puis 8 en premier, ce sont trois modulos très adaptés pour ces équations. Pour réussir, il faut ici regarder quels sont les carrés modulo 8 , qui sont 0,1 et 4 , et en déduit que $p$ ne peut pas être impair.\nRappelons aussi qu'il est inutile de regarder l'équation modulo un nombre $n$ qui a deux facteurs premiers différents, par exemple comme $n=6$ ou $n=10$. Pour $n=6$, l'équation donne autant d'information que l'équation prise modulo 2 puis modulo 3 , et les calculs sont plus simples dans ce cas.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2020", "problem_label": "3", "tier": 1, "problem": "Pour s'entraîner en prévision du dernier test POFM de l'année, Jean-Baptiste et Marie-Odile ont collecté 100 problèmes de mathématiques, et s'attellent désormais à la confection d'un programme de révisions. Pendant les 100 jours qui les séparent du test POFM, chacun devra traiter un problème par jour. On note $x$ le nombre de problèmes que Jean-Baptiste a traités strictement avant Marie-Odile, et $y$ le nombre de problèmes que Marie-Odile a traités strictement avant Jean-Baptiste. Enfin, on dit que le programme de révisions est équitable si $x=y$.\nDémontrer qu'il existe au moins $100!\\times\\left(2^{50}+(50!)^{2}\\right)$ programmes équitables.", "solution": "Tout d'abord, il existe 100! manières de choisir l'ordre dans lequel Jean-Baptiste traitera les problèmes. Ces 100! manières jouent toutes des rôles symétriques. Sans perte de généralité, on numérote les problèmes de 1 à 100, dans l'ordre où Jean-Baptiste les traite, et il s'agit de démontrer qu'il existe au moins $2^{50}+(50!)^{2}$ permutations $\\sigma$ de l'ensemble $\\{1,2, \\ldots, 100\\}$ pour lesquelles les ensembles $\\{k: \\sigma(k)<k\\}$ et $\\{k: \\sigma(k)>k\\}$ ont même cardinal. On dira que ces permutations sont équitables.\nTout d'abord, on peut construire $2^{50}$ permutations équitables comme suit : étant donné un sous-ensemble $X$ de $\\{1,2, \\ldots, 50\\}$, parmi les $2^{50}$ possibles, on construit la permutation $\\sigma_{X}$ telle que\n\n$$\n\\sigma_{X}(2 k-1)=\\left\\{\\begin{array}{ll}\n2 k & \\text { si } k \\in X \\\\\n2 k-1 & \\text { si } k \\notin X\n\\end{array} \\text { et } \\sigma_{X}(2 k)= \\begin{cases}2 k-1 & \\text { si } k \\in X \\\\\n2 k & \\text { si } k \\notin X .\\end{cases}\\right.\n$$\n\nPour une telle permutation, on constate que $\\sigma_{X}(k)<k$ si et seulement $k / 2 \\in X$, et que $\\sigma_{X}(k)>k$ si et seulement si $(k+1) / 2 \\in X$. Par conséquent, $\\sigma_{X}$ est équitable.\nOn construit ensuite (50! $)^{2}$ permutations équitables comme suit : étant données deux permutations $\\tau$ et $\\pi$ de $\\{1,2, \\ldots, 50\\}$ parmi les $(50!)^{2}$ paires de permutations possibles, on construit la permutation $\\sigma_{\\pi, \\tau}$ telle que\n\n$$\n\\sigma_{\\pi, \\tau}(k)= \\begin{cases}50+\\pi(k) & \\text { si } 1 \\leqslant k \\leqslant 50 \\\\ \\tau(k-50) & \\text { si } 51 \\leqslant k \\leqslant 100\\end{cases}\n$$\n\nPour une telle permutation, on constate que $\\sigma_{\\pi, \\tau}(k)<k$ si et seulement $51 \\leqslant k \\leqslant 100$, et que $\\sigma_{X}(k)>k$ si et seulement si $1 \\leqslant k \\leqslant 50$. Par conséquent, $\\sigma_{\\pi, \\tau}$ est équitable.\nEnfin, on vérifie bien sûr que deux permutations $\\sigma_{X}$ et $\\sigma_{\\pi, \\tau}$ ne sont jamais égales, puisque $\\sigma_{X}(1) \\leqslant 2<51 \\leqslant \\sigma_{\\pi, \\tau}(1)$.\n\nCommentaire des correcteurs L'exercice était difficile et peu d'élèves ont réussi à bien avancer dessus. Certains ont tenté d'invoquer parfois un peu au hasard des significations possibles de $100!, 2^{50}$ et $(50!)^{2}$ en espérant que cela fonctionnait. Il faut rester rigoureux : essayer d'interpréter chacune de ces quantités est évidemment une bonne idée, mais il faut bien regarder l'expression.\nIci, le terme 100! nous invitait à fixer une permutation initiale pour une des deux personnes, pour laquelle il y a 100! choix. Ensuite, on voulait trouver $2^{50}+(50!)^{2}$ permutations. Ici, le fait d'avoir un plus nous fait comprendre qu'il faut trouver deux types de permutations au moins : idéalement, un type avec (50!) $)^{2}$ permutations, et un autre avec $2^{50}$ permutations.\nCertains élèves, dans leurs justifications très vagues, n'ont pas compris cela, et essayaient de montrer qu'il y avait $2^{50}$ possibilités pour quelque chose, puis (50!) ${ }^{2}$ pour autre chose, ce qui ici aurait donné un produit. Par ailleurs, plusieurs élèves, une fois les deux ensembles de permutations créés, n'ont pas vérifié que ces ensembles étaient disjoints, chose pourtant nécessaire pour conclure : il faut évidemment le faire!", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2020", "problem_label": "4", "tier": 1, "problem": "Trouver tous les nombres réels $x$ et $y$ tels que\n\n$$\n\\left(x-\\sqrt{x^{2}+1}\\right)\\left(y-\\sqrt{y^{2}+1}\\right)=1 \\text { et }\\left(x^{2}+y+2\\right)\\left(y^{2}+x+2\\right)=8 .\n$$", "solution": "Soit $(x, y)$ une solution éventuelle. Les égalités\n\n$$\n\\left\\{\\begin{array}{l}\n\\left(x-\\sqrt{x^{2}+1}\\right)\\left(x+\\sqrt{x^{2}+1}\\right)=x^{2}-\\left(x^{2}+1\\right)=-1 \\\\\n\\left(y-\\sqrt{y^{2}+1}\\right)\\left(y+\\sqrt{y^{2}+1}\\right)=y^{2}-\\left(y^{2}+1\\right)=-1\n\\end{array}\\right.\n$$\n\nindiquent en fait que\n\n$$\n\\left\\{\\begin{array}{l}\nx+\\sqrt{x^{2}+1}=\\sqrt{y^{2}+1}-y \\\\\n\\sqrt{x^{2}+1}-x=y+\\sqrt{y^{2}+1}\n\\end{array}\\right.\n$$\n\nL'équation (1) - (2) indique que $x=-y$, et l'égalité $\\left(x^{2}+y+2\\right)\\left(y^{2}+x+2\\right)=8$ se réécrit alors comme\n\n$$\n8=\\left(x^{2}-x+2\\right)\\left(x^{2}+x+2\\right)=\\left(x^{2}+2\\right)^{2}-x^{2}\n$$\n\nSi l'on pose $z=x^{2}$, il s'agit donc de résoudre l'équation\n$0=(z+2)^{2}-z-8=z^{2}+3 z-4=(z+3 / 2)^{2}-25 / 4=(z+3 / 2)^{2}-(5 / 2)^{2}=(z+4)(z-1)$.\nOr, on sait que $z=x^{2} \\geqslant 0$. On en déduit que $z=1$, donc que $x= \\pm 1$ et $y=-x= \\pm 1$.\nRéciproquement, lorsque $(x, y)=( \\pm 1, \\mp 1)$, on vérifie aisément que les deux égalités de l'énoncé sont vérifiées. En conclusion, les deux solutions sont\n\n$$\n(x, y)=(1,-1) \\text { et }(x, y)=(-1,1)\n$$\n\nCommentaire des correcteurs Ce problème fort difficile a été assez peu abordé, et les correcteurs ont eu le plaisir de constater que cinq élèves en étaient venus à bout.\nL'idée clé pour ce problème consistait à reconnaître ce que l'on appelle les conjugués d'une différence de la forme $a-b$ où $a$ et $b$ sont deux termes dont les carrés $a^{2}$ et $b^{2}$ sont très proches. En effet, dans ces cas-là, il est souvent pertinent d'étudier également le terme $a+b$, que l'on appelle conjugué du terme $a-b$, et ce en vertu de l'identité remarquable $a^{2}-b^{2}=(a+b)(a-b)$. C'est exactement ainsi que commence la solution ci-dessus, et les élèves qui ont réussi ce problème sont peu ou prou ceux qui ont eu l'idée d'introduire ces conjugués.\nPar ailleurs, plusieurs élèves ont abusivement cru que $x$ et $y$ devaient être des entiers, voire que les termes $x-\\sqrt{x^{2}+1}$ et $y-\\sqrt{y^{2}+1}$ devaient eux aussi être des entiers. Il est important de lire attentivement l'énoncé!\nDe même, plusieurs élèves ont eu le très bon réflexe de rechercher des solutions particulières, mais beaucoup d'entre eux se sont arrêtés aux cas où $x=0$ (ou $y=0$ ), $x=y=1$, ou plus généralement au cas où $x=y$, mais sans considérer le cas pourtant analogue où $x=-y$. C'est dommage! De manière générale, dans une telle équation, il est toujours important de ne pas oublier le cas où une des deux inconnues (voire les deux) pourrait être négative.\n\n## Énoncés Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2020", "problem_label": "5", "tier": 1, "problem": "Soit $A B C D$ un quadrilatère convexe dont les angles en $B$ et en $D$ sont obtus, et dont les angles en $A$ et en $C$ sont égaux l'un à l'autre. Soit $E$ et $F$ les symétriques de $A$ par rapport à $(B C)$ et $(C D)$. Soit $K$ et $L$ les points d'intersection de $(B D)$ avec $(A E)$ et $(A F)$. Démontrer que les cercles circonscrits aux triangles $B E K$ et $D F L$ sont tangents l'un à l'autre.", "solution": "La manière la plus pratique de construire le point $A$ est d'en construire tout d'abord son symétrique $A^{\\prime}$ par rapport à $(B D)$, puisque $A^{\\prime}$ est cocyclique avec $B, C$ et $D$. Ce faisant, on constate que $A^{\\prime}$ semble appartenir aux deux cercles circonscrits aux triangles $B E K$ et $D F L$, et une chasse aux angles indique en effet que\n\n$$\n\\begin{aligned}\n\\left(K E, K A^{\\prime}\\right) & =(K E, B C)+(B C, B D)+\\left(B D, K A^{\\prime}\\right) \\\\\n& =90^{\\circ}+(B C, B D)+(K A, B D) \\\\\n& =90^{\\circ}+(B C, B D)+(K A, B C)+(B C, B D) \\\\\n& =2(B C, B D) \\\\\n\\left(B E, B A^{\\prime}\\right) & =(B E, B C)+(B C, B D)+\\left(B D, B A^{\\prime}\\right) \\\\\n& =(B C, B A)+(B C, B D)+(B A, B D) \\\\\n& =2(B C, B D) .\n\\end{aligned}\n$$\n\nCela signifie bien que $A^{\\prime}, B, K$ et $E$ appartiennent à un cercle $\\omega_{b}$ et, de même, que $A^{\\prime}, D, L$ et $F$ appartiennent à un cercle $\\omega_{d}$.\nSoit alors $t$ et $t^{\\prime}$ les tangentes à $\\omega_{b}$ et $\\omega_{d}$ en $A^{\\prime}$. Une nouvelle chasse aux angles indique que\n\n$$\n\\begin{aligned}\n(t, B D) & =\\left(t, A^{\\prime} B\\right)+\\left(A^{\\prime} B, B D\\right) \\\\\n& =\\left(K A^{\\prime}, K B\\right)+(B D, B A) \\\\\n& =(K B, K A)+(B D, B A) \\\\\n& =(B D, B C)+90^{\\circ}+(B D, B A) \\\\\n\\left(t^{\\prime}, B D\\right) & =\\left(t^{\\prime}, A^{\\prime} D\\right)+\\left(A^{\\prime} D, B D\\right) \\\\\n& =\\left(L A^{\\prime}, L D\\right)+(B D, A D) \\\\\n& =(L D, L A)+(B D, A D) \\\\\n& =(B D, D C)+90^{\\circ}+(B D, A D) .\n\\end{aligned}\n$$\n\nOn vérifie enfin que\n\n$$\n\\begin{aligned}\n(B D, B C)+(B D, B A) & =(B D, B C)+(B D, A D)+(A D, A B) \\\\\n& =(B D, B C)+(B D, A D)+(B C, C D) \\\\\n& =(B D, D C)+(B D, A D),\n\\end{aligned}\n$$\n\nce qui conclut.\n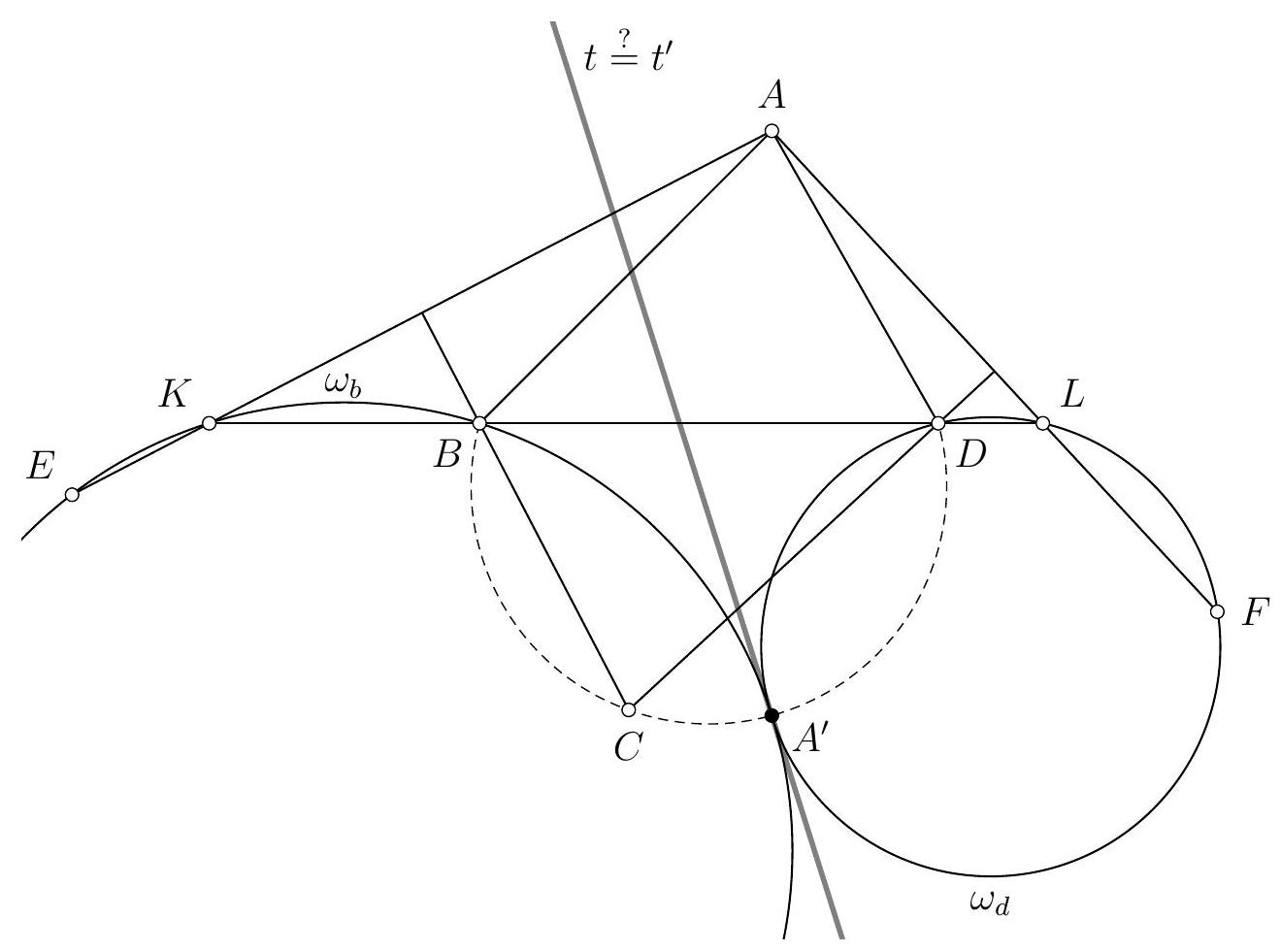\n\nCommentaire des correcteurs Seule la moitié des élèves ayant pris part au test ont abordé cet exercice. Il est très préoccupant de constater que la stratégie des élèves face à un sujet d'Olympiade ne prend pas en compte le fait que les problèmes sont classés par ordre de difficulté croissante. On encourage bien sûr les élèves à regarder chacun des problèmes du sujet. Mais, à moins d'avoir une appétence très particulière pour un domaine des olympiades, au point d'être capable de résoudre complètement des problèmes de toute difficulté portant sur ce thème, il est bien plus rentable de consacrer la majeure partie de son temps au problème classé comme le plus facile, quel que soit son thème, puisqu'on a plus de chances d'y avoir des idées intéressantes.\nIl est bien naïf de penser pouvoir faire l'impasse sur l'un des 4 thèmes des olympiades, en particulier la géométrie qui, ces 10 dernières années, a été 8 fois le thème d'un problème 1 ou 4 des Olympiades Internationales. La stratégie de ne pas réfléchir au problème de géométrie du présent test pour se consacrer aux deux autres problèmes s'est bien souvent retournée contre les élèves, puisque les problèmes 6 et 7 étaient très difficiles et demandaient de nombreuses idées pour espérer obtenir une quantité significative de points. Nous espérons donc que les élèves qui en ont l'occasion adapteront leur stratégie pour l'année prochaine.\nConcernant ce problème, trouver comment tracer la figure exacte était essentiel pour démarrer. En effet, chercher comment tracer la figure exacte poussait à introduire des points supplémentaires nécessaires dans la suite. Pour construire un point $C$ tel que $\\widehat{B C D}=\\widehat{B A D}$, il fallait trouver un point $X$ particulier qui vérifie $\\widehat{B X D}=\\widehat{B A D}$ mais tel que $X$ et $A$ soient de part et d'autre de l'axe $(B D)$, puis construire $C$ quelconque sur le cercle $\\mathcal{C}_{B X D}$. Ce raisonnement (qui peut être employé dès que l'on se retrouve face à une hypothèse d'angle à réaliser à la règle et au compas) poussait à introduire le symétrique du point $A$ par rapport à la droite $(B D)$. Une fois la figure complétée, il était alors légitime de conjecturer que ce symétrique était le point de tangence recherché. Ce travail de conjecture était la partie la plus difficile du travail, et bien souvent les élèves ayant fait cette conjecture ont réussi à la démontrer complètement.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Pour tout entier $k \\geqslant 0$, on note $F_{k}$ le $k^{\\text {ème }}$ nombre de Fibonacci, défini par $F_{0}=0$, $F_{1}=1$, et $F_{k}=F_{k-2}+F_{k-1}$ lorsque $k \\geqslant 2$. Soit $n \\geqslant 2$ un entier, et soit $S$ un ensemble d'entiers ayant la propriété suivante :\n\nPour tout entier $k$ tel que $2 \\leqslant k \\leqslant n$, l'ensemble $S$ contient deux entiers $x$ et $y$ tels que $x-y=F_{k}$.\nQuel est le plus petit nombre possible d'éléments d'un tel ensemble $S$ ?", "solution": "Tout d'abord, soit $m=\\lceil n / 2\\rceil$, et soit $S$ l'ensemble $\\left\\{F_{2 \\ell}: 0 \\leqslant \\ell \\leqslant m\\right\\}$. Pour tout entier $k$ tel que $2 \\leqslant k \\leqslant n$, on choisit $x=F_{k}$ et $y=F_{0}=0$ si $k$ est pair, ou bien $x=F_{k+1}$ et $y=F_{k-1}$ si $k$ est impair. Dans les deux cas, $x$ et $y$ sont deux éléments de $S$ tels que $x-y=F_{k}$.\nRéciproquement, soit $S$ un ensemble tel que décrit dans l'énoncé. Nous allons démontrer que $|S| \\geqslant m+1$. Pour ce faire, on construit un graphe pondéré $G$, non orienté, en procédant comme suit. Les sommets de notre graphe sont les éléments de l'ensemble $S$. Puis, pour tout entier $k$ impair tel que $1 \\leqslant k \\leqslant n$, et en se rappelant que $F_{1}=F_{2}$, on choisit deux éléments $x$ et $y$ de $S$ tels que $x-y=F_{k}$. On insère alors dans notre graphe $G$ l'arête $\\{x, y\\}$, à qui l'on affecte le poids $F_{k}$.\nLe graphe ainsi obtenu compte $m$ arêtes. En outre, supposons qu'il contienne un cycle $c=x_{0} x_{1} \\ldots x_{\\ell}$, avec $x_{0}=x_{\\ell}$, que l'on choisit de longueur $\\ell$ minimale. Sans perte de généralité, on suppose que $x_{0}>x_{1}$, et que $\\left\\{x_{0}, x_{1}\\right\\}$ est l'arête de $c$ de poids maximal. On note $F_{2 k+1}$ ce poids. Le poids cumulé des autres arêtes ne dépasse pas $F_{1}+F_{3}+\\ldots+F_{2 k-1}$ et, par construction, il est égal à\n\n$$\n\\left|x_{1}-x_{2}\\right|+\\left|x_{2}-x_{3}\\right|+\\ldots+\\left|x_{\\ell-1}-x_{\\ell}\\right| \\geqslant\\left|x_{\\ell}-x_{1}\\right|=F_{2 k+1}\n$$\n\nCependant, une récurrence immédiate sur $k$ montre que $F_{1}+F_{3}+\\ldots+F_{2 k-1}=F_{2 k}<F_{2 k+1}$. Par conséquent, notre graphe est acyclique, et puisqu'il compte $m$ arêtes, il compte au moins $m+1$ sommets.\nLe cardinal minimal recherché est donc égal à $m+1$.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2020", "problem_label": "6", "tier": 1, "problem": "Pour tout entier $k \\geqslant 0$, on note $F_{k}$ le $k^{\\text {ème }}$ nombre de Fibonacci, défini par $F_{0}=0$, $F_{1}=1$, et $F_{k}=F_{k-2}+F_{k-1}$ lorsque $k \\geqslant 2$. Soit $n \\geqslant 2$ un entier, et soit $S$ un ensemble d'entiers ayant la propriété suivante :\n\nPour tout entier $k$ tel que $2 \\leqslant k \\leqslant n$, l'ensemble $S$ contient deux entiers $x$ et $y$ tels que $x-y=F_{k}$.\nQuel est le plus petit nombre possible d'éléments d'un tel ensemble $S$ ?", "solution": "$n^{\\circ} 1$ On dit qu'un ensemble tel que décrit dans l'énoncé est $n$-mignon. Soit $S_{n}$ un ensemble $n$-mignon de cardinal aussi petit que possible. Nous allons démontrer, par récurrence sur $n$, que $\\left|S_{n}\\right| \\geqslant\\lceil n / 2\\rceil+1$. Tout d'abord, pour $n=2$, le résultat désiré est immédiat. On suppose désormais que $n \\geqslant 3$.\nCette fois-ci, on introduit le graphe pondéré $G$ dont les sommets sont les éléments de $S_{n}$ et qui contient, pour tout entier $k$ tel que $2 \\leqslant k \\leqslant n-2$, une arête $(x, y)$ de poids $F_{k}$ entre deux sommets $x$ et $y$ tels que $|x-y|=F_{k}$. Enfin, soit $u$ et $v$ deux éléments de $S_{n}$ tels que $|u-v|=F_{n}$.\nUne récurrence immédiate sur $k$ montre que $F_{2}+F_{3}+\\ldots+F_{k-2}=F_{k}-3$ pour tout entier $k \\geqslant 4$. Par conséquent, deux sommets de $S_{n}$ appartenant à une même composante connexe de $G$ sont distants d'au plus $F_{n}-3$, et $u$ et $v$ ne peuvent pas appartenir à la même composante connexe de $G$.\nSoit $U_{n}$ l'ensemble des éléments de $S_{n}$ qui appartiennent à la même composante connexe de $G$ que $u$, et soit $V_{n}$ les autres éléments de $S_{n}$. Nulle arête de $G$ n'a une extrémité dans $U_{n}$ et une autre dans $V_{n}$. Par conséquent, si l'on remplace chaque sommet $x$ de $U_{n}$ par $x+v-u$, on obtient un nouvel ensemble $S_{n}^{\\prime}=\\left\\{x+v-u: x \\in U_{n}\\right\\} \\cup V_{n}$ de cardinal $\\left|S_{n}^{\\prime}\\right| \\leqslant\\left|S_{n}\\right|-1$ et qui est $(n-2)$-mignon. On en conclut comme prévu que\n\n$$\n\\left|S_{n}\\right| \\geqslant\\left|S_{n}^{\\prime}\\right|+1 \\geqslant\\lceil(n-2) / 2\\rceil+1+2=\\lceil n / 2\\rceil+1\n$$\n\nCommentaire des correcteurs Ce problème était très difficile. La grande majorité des élèves qui l'ont abordé ont effectivement trouvé un ensemble adéquat de cardinal minimal, mais très peu ont trouvé des arguments permettant de démontrer que ce cardinal était effectivement minimal. Cette difficulté a manifestement été perçue par de nombreux élèves, et cela rend très surprenant que la moitié des élèves qui ont abordé le problème 6 n'aient pas même rendu de figure pour le problème 5.\nDe nombreux élèves ont identifié des constructions semblables à celle proposée ci-dessus, même si elles sont parfois apparues sous des formes beaucoup trop compliquées. Rappelons ici qu'il est toujours bon de commencer par regarder des cas particuliers pour de petites valeurs de $n$ (ici, $2 \\leqslant n \\leqslant 4$ ou 5 , par exemple) pour se forger une intuition sur la forme générale des objets que l'on s'apprête à construire.\nL'idée de considérer un graphe implicitement ou explicitement pondéré était ensuite cruciale, et pouvait en fait survenir naturellement lorsque l'on essayait de mettre en évidence des arêtes « indispensables » à la $n$-mignonitude des ensembles considérés. De manière générale, tenter de mettre en évidence une structure combinatoire à la fois simple et usuelle (ici, un graphe) pour caractériser une propriété est souvent une bonne idée.\nEnfin, de nombreux élèves on indûment affirmé que tout ensemble $n$-mignon de cardinal minimal contenait déjà un ensemble ( $n-2$ )-mignon de cardinal minimal. La solution alternative ci-dessus démontre qu'une telle affirmation est vraie, mais dans l'absolu, cette affirmation n'a rien d'évident, et il existe de nombreux problèmes analogues pour lesquels elle est grossièrement fausse.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 8 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "Trouver les fonctions $f: \\mathbb{N}_{\\geqslant 1} \\mapsto \\mathbb{N}_{\\geqslant 0}$ vérifiant les deux conditions suivantes :\n\n1. $f(x y)=f(x)+f(y)$ pour tous les entiers $x \\geqslant 1$ et $y \\geqslant 1$;\n2. il existe une infinité d'entiers $n \\geqslant 1$ tels que l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k$ tel que $1 \\leqslant k \\leqslant n-1$.\nOn note $\\mathbb{N}_{\\geqslant 0}$ l'ensemble des entiers supérieurs ou égaux à 0 , et $\\mathbb{N}_{\\geqslant 1}$ l'ensemble des entiers supérieurs ou égauxà 1.", "solution": "Les fonctions recherchées sont les fonctions de la forme $f: n \\mapsto c v_{p}(n)$, où $c$ est un entier naturel, $p$ est un nombre premier, et $v_{p}(n)$ et la valuation $p$-adique de $n$. Tout d'abord, il est clair que ces fonctions sont bien solutions du problème.\nRéciproquement, soit $f$ une solution non nulle du problème. On dit qu'un entier $n$ est $j o l i$ si l'égalit�� $f(k)=f(n-k)$ est vraie pour tout entier $k \\leqslant 1$. Remarquons que tout diviseur d'un joli entier est joli. En effet, si $d$ divise un joli entier $n=a d$, alors\n\n$$\nf(k)=f(a k)-f(a)=f(n-a k)-f(a)=f(a(d-k))-f(a)=f(d-k)\n$$\n\npour tout entier $k \\leqslant d-1$.\nEn outre, la condition 1 signifie que $f\\left(\\prod_{i} p_{i}^{\\alpha_{i}}\\right)=\\sum_{i} \\alpha_{i} f\\left(p_{i}\\right)$ pour toute décomposition en produit de facteurs premiers. Il s'agit donc de démontrer qu'il existe au plus un nombre premier $p$ pour lequel $f(p)>0$. On considère alors le plus petit entier $p$ tel que $f(p)>0$. La formule ci-dessus indique que $p$ est premier, et on pose $c=f(p)$.\nS'il existe un joli entier $n \\geqslant p$ que $p$ ne divise pas, posons $n=p q+r$, avec $q$ entier et $1 \\leqslant r \\leqslant p-1$. Puisque $n$ est joli, on sait que $f(r)=f(n-p q)=f(p q) \\geqslant f(p)>0$, en contradiction avec la définition de $p$. Ainsi, tout entier joli est de la forme $a p^{b}$ avec $b$ entier et $1 \\leqslant a \\leqslant p-1$. Réciproquement, puisqu'il existe une infinité d'entiers jolis et que $a$ ne peut prendre qu'un nombre fini de valeurs, toute puissance de $p$ divise un joli entier, et est donc elle-même jolie.\nPar conséquent, pour tout nombre premier $q$ distinct de $p, l^{\\prime}$ entier $p^{q-1}$ est joli. Puisque $q$ divise $p^{q-1}-1$, on en déduit en particulier que $0=f(1)=f\\left(p^{q-1}-1\\right) \\geqslant f(q)$, ce qui conclut.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 9 |
+
{"year": "2020", "problem_label": "7", "tier": 1, "problem": "Trouver les fonctions $f: \\mathbb{N}_{\\geqslant 1} \\mapsto \\mathbb{N}_{\\geqslant 0}$ vérifiant les deux conditions suivantes :\n\n1. $f(x y)=f(x)+f(y)$ pour tous les entiers $x \\geqslant 1$ et $y \\geqslant 1$;\n2. il existe une infinité d'entiers $n \\geqslant 1$ tels que l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k$ tel que $1 \\leqslant k \\leqslant n-1$.\nOn note $\\mathbb{N}_{\\geqslant 0}$ l'ensemble des entiers supérieurs ou égaux à 0 , et $\\mathbb{N}_{\\geqslant 1}$ l'ensemble des entiers supérieurs ou égauxà 1.", "solution": "$n^{\\circ} 1$ Une fois acquis le fait que tout entier joli est de la forme $a p^{b}$, avec $b$ entier et $1 \\leqslant a \\leqslant p-1$, et que tout diviseur d'un entier joli est joli, on peut aussi procéder comme suit.\nSupposons qu'il existe un nombre premier $q \\neq p$ pour lequel $f(q)>0$, et soit $q$ le plus petit tel nombre premier. On considère alors le plus petit entier joli $n>q$, puis on écrit $n$ sous la forme $n=a p^{b}=u q+v$, avec $u$ entier et $0 \\leqslant v \\leqslant q-1$.\nPuisque $n>q>p$, on sait que $b \\geqslant 1$, donc que $p$ divise $n$, et comme $q$ ne divise pas $n$, on sait que $v \\geqslant 1$. Dans ces conditions, $f(v)=f(u q)>0$, et la minimalité de $q$ indique que $p$ divise $v$. Mais alors $p$ divise aussi $u q=n-v$, et $p$ est premier avec $q$, donc $p$ divise $u$. On en déduit que $n>p q$, donc que le joli entier $n / p$ satisfait lui aussi l'inégalité $n / p>q$, en contradiction avec la minimalité de $n$. Notre supposition est ainsi invalide, ce qui conclut.\n\nCommentaire des correcteurs L'exercice était très difficile et, même s'il a été beaucoup traité, très peu d'élèves ont réussi à avoir ne serait-ce qu'un point. Dans un tel exercice, la première chose à comprendre est l'ensemble des solutions : en effet, beaucoup d'élèves ont tenté de prouver que $f$ était nulle, quand beaucoup d'autres fonctions étaient des solutions. En particulier, toute preuve qui ne prenait pas en compte cela ne pouvait pas aboutir, ni introduire les bons outils comme dans la solution donnée : ainsi il était difficile d'avoir des points sans comprendre les solutions.\n\nIl est aussi regrettable que de nombreux élèves aient cherché sans aboutir à des éléments concluant le problème 7 sans même aborder le problème 5. Comme aux Olympiades Internationales, les énoncés sont proposés par ordre de difficulté croissante. Ainsi, des remarques basiques sur les problèmes 5 et 6 ont plus de chance de rapporter des points que sur le problème 7. Cela ne veut pas dire pour autant qu'il faut « oublier » d'office de s'attaquer au problème 7 : il est évidemment conseillé de regarder au moins un peu chaque problème, mais il faut savoir consacrer ses efforts sur les problèmes plus accessibles.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-1.jsonl
ADDED
|
@@ -0,0 +1,13 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme. La bissectrice intérieure de l'angle $\\widehat{B A C}$ coupe le segment $[B C]$ en $E$ tandis que sa bissectrice extérieure coupe la droite ( $C D)$ en $F$. Soit $M$ le milieu du segment $[A E]$.\nDémontrer que les droites $(E F)$ et $(B M)$ sont parallèles.", "solution": "Soit $G$ le point d'intersection des droites $(A B)$ et $(E F)$. Le problème revient à démontrer que $(M B)$ est une droite des milieux du triangle $A E G$, c'est-à-dire que $B$ est le milieu de $[A G]$.\nDe même, soit $H$ le point d'intersection des droites $(A E)$ et $(C D)$. L'homothétie de centre $E$ qui envoie $(A B)$ sur $(C D)$ envoie les points $A, B$ et $G \\operatorname{sur} H, C$ et $F$. De manière équivalente, le problème revient donc à démontrer que $C$ est le milieu de $[H F]$.\nOr, en angles de droites,\n\n$$\n\\begin{aligned}\n(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\\\\n& =(F A, F C)\n\\end{aligned}\n$$\n\nce qui signifie que le triangle $A C F$ est isocèle en $C$. De même,\n\n$$\n(H A, H C)=(E A, C D)=(A E, A B)=(A C, A E)=(A C, A H)\n$$\n\ndonc $A C H$ est isocèle en $C$.\nOn en conclut que $C F=C A=C H$, donc que $C$ est bien le milieu de $[\\mathrm{CH}]$.\n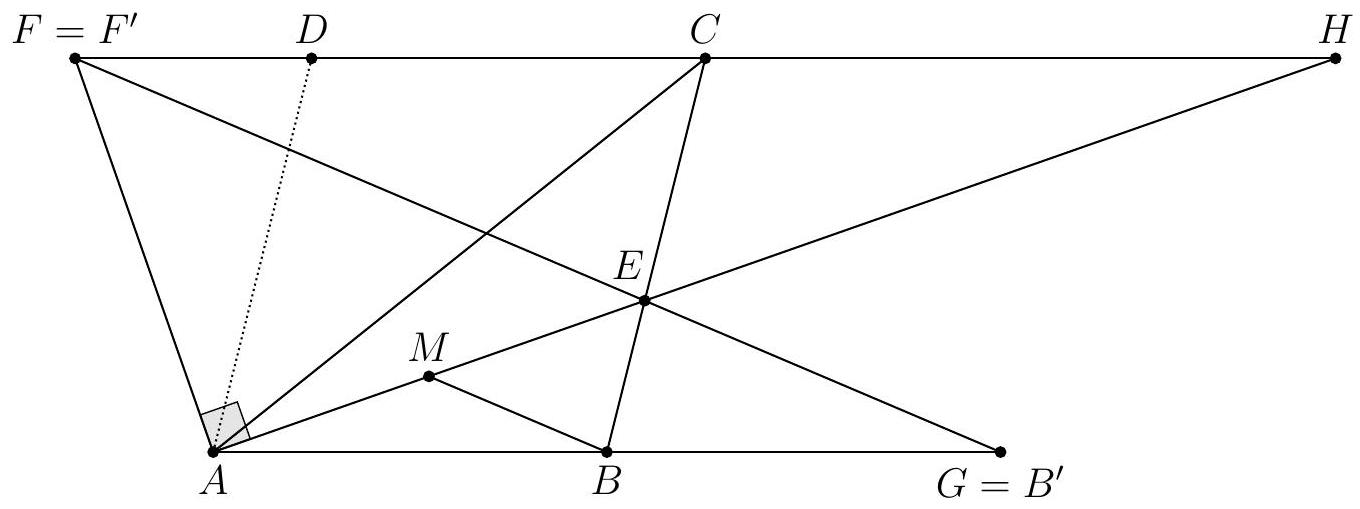", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme. La bissectrice intérieure de l'angle $\\widehat{B A C}$ coupe le segment $[B C]$ en $E$ tandis que sa bissectrice extérieure coupe la droite ( $C D)$ en $F$. Soit $M$ le milieu du segment $[A E]$.\nDémontrer que les droites $(E F)$ et $(B M)$ sont parallèles.", "solution": "$n^{\\circ} 1$ Comme dans la solution précédente, il s'agit de démontrer que $A B=B G$. Or, le théorème de la bissectrice indique que $E B / E C=A B / A C$, et le théorème de Thalès indique que $E B / E C=B G / C F$. On en conclut que\n\n$$\n\\frac{A B}{A C}=\\frac{E B}{E C}=\\frac{B G}{C F},\n$$\n\nIl reste donc à démontrer que $C A=C F$, c'est-à-dire que le triangle $A C F$ est isocèle en $C$, ce qui se déduit directement des égalités d'angles de droites\n\n$$\n\\begin{aligned}\n(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\\\\n& =(F A, F C) .\n\\end{aligned}\n$$", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 3 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme. La bissectrice intérieure de l'angle $\\widehat{B A C}$ coupe le segment $[B C]$ en $E$ tandis que sa bissectrice extérieure coupe la droite ( $C D)$ en $F$. Soit $M$ le milieu du segment $[A E]$.\nDémontrer que les droites $(E F)$ et $(B M)$ sont parallèles.", "solution": "$n^{\\circ} 2$ Nous allons utiliser les coordonnées barycentriques dans le triangle $A B C$, en notant $a, b$ et $c$ les longueurs $B C, C A$ et $A B$. Nous identifierons chaque point $X$ à ses coordonnées barycentriques normalisées $(x, y, z)$ telles que $x+y+z=1$.\n\nAvec cette convention, si quatre points $S, T, U, V$ de coordonnées $\\mathbf{s , t} \\mathbf{t}, \\mathbf{u}, \\mathbf{v}$ vérifient une relation de la forme $\\overrightarrow{U V}=\\lambda \\overrightarrow{S T}$, la relation $(\\mathbf{v}-\\mathbf{u})=\\lambda(\\mathbf{t}-\\mathbf{s})$ entre triplets de coordonnées barycentriques sera automatiquement vérifiées, et on pourra même se permettre d'écrire abusivement $V=U+\\lambda(S-T)$.\nTout d'abord, il est clair que $A=(1,0,0), B=(0,1,0)$ et $C=(0,0,1)$. Ensuite, le théorème de la bissectrice indique que $E B / E C=A B / A C=b / c$, de sorte que $E=(0, b /(b+c), c /(b+c))$. Quitte à changer d'unités de longueur, on suppose que $b+c=1$, de sorte que $E=(0, b, c)$.\nToujours mus par le souhait de démontrer que $(M B)$ est une droite des milieux, on note $B^{\\prime}$ le symétrique de $A$ par rapport à $B$, puis $F^{\\prime}$ le point d'intersection de $\\left(E B^{\\prime}\\right)$ et $(C D)$, et il s'agit dès lors de montrer que $(A E)$ et $\\left(A F^{\\prime}\\right)$ sont perpendiculaires.\nTout d'abord, on sait que $B^{\\prime}=2 B-A=(-1,2,0)$. Ensuite, il existe des réels $x$ et $y$ tels que $F=B^{\\prime}+x\\left(E-B^{\\prime}\\right)=C+y(A-B)$, donc $F$ s'identifie à ses coordonnées barycentriques $(x-1,2+x(b-2), c x)=(y,-y, 1)$. Ainsi, $x=1 / c$ et $y=x-1=(1-c) / c=b / c$.\nOn vérifie alors comme prévu que\n\n$$\n\\begin{aligned}\n\\overrightarrow{A E} \\cdot \\overrightarrow{A F} & =(b \\overrightarrow{A B}+c \\overrightarrow{A C}) \\cdot(-b / c \\overrightarrow{A B}+\\overrightarrow{A C}) \\\\\n& =-b^{2} / c \\overrightarrow{A B} \\cdot \\overrightarrow{A B}+c \\overrightarrow{A C} \\cdot \\overrightarrow{A C}+(b-b) \\overrightarrow{A B} \\cdot \\overrightarrow{A C} \\\\\n& =-b^{2} c+c b^{2}-0=0\n\\end{aligned}\n$$\n\n$\\underline{\\text { Solution alternative } n^{\\circ} 3}$ Nous allons reprendre le raisonnement précédent, mais sans introduire les points $B^{\\prime}$ et $F^{\\prime}$. Ainsi, on observe comme précédemment que $A=(1,0,0)$, $B=(0,1,0), C=(0,0,1)$ et $E=(0, b, c)$. Puisque $M$ est le milieu de $[A E]$, on sait également que $M=(A+E) / 2=(1 / 2, b / 2, c / 2)$.\nPar ailleurs, il existe un réel $y$ tel que $F=C+y(A-B)$, de sorte que $F=(y,-y, 1)$. Si l'on pose $\\theta=\\overrightarrow{A B} \\cdot \\overrightarrow{A C}$, on en déduit que\n\n$$\n\\begin{aligned}\n0=\\overrightarrow{A E} \\cdot \\overrightarrow{A F} & =(b \\overrightarrow{A B}+c \\overrightarrow{A C}) \\cdot(-y \\overrightarrow{A B}+\\overrightarrow{A C}) \\\\\n& =-b y \\overrightarrow{A B} \\cdot \\overrightarrow{A B}+c \\overrightarrow{A C} \\cdot \\overrightarrow{A C}+(b-c y) \\overrightarrow{A B} \\cdot \\overrightarrow{A C} \\\\\n& =-b y c^{2}+c b^{2}+(b-c y) \\theta=(b c+\\theta)(b-c y) .\n\\end{aligned}\n$$\n\nComme les points $A, B$ et $C$ ne sont pas alignés, on sait que $|\\theta|<b c$, de sorte que $y=b / c$. Ainsi, $F=(b / c,-b / c, 1)$. Par conséquent, $2(M-B)=(1, b-2, c)$ et\n\n$$\nc(F-E)=\\left(b,-b-b c, c-c^{2}\\right)=(b, b(b-2), b c)=2 b(M-B)\n$$\n\nce qui signifie que $c \\overrightarrow{E F}=2 b \\overrightarrow{B M}$, et donc que les droites $(B M)$ et $(E F)$ sont bien parallèles.\nCommentaire des correcteurs Ce problème a été résolu par une petite vingtaine d'élèves. Les élèves ont fourni des preuves assez différentes. La plupart ont introduit un nouveau point qui permettait d'exploiter le fait que le point $M$ était un milieu de segment. On a également pu voir plusieurs approches analytiques, mais qui nécessitaient pratiquement toutes de faire des observations géométriques préliminaires pour éviter de trop gros calculs. Cette façon de procéder est excellente : commencer par chercher l'exercice avec des outils conventionnels, puis une fois que l'on s'est ramené à un problème plus simple, on s'assure de conclure en se plaçant dans un repère adapté et en s'aidant des observations géométriques.\nMême sans avoir résolu le problème, près de la moitié des élèves ont sur voir et démontrer que le triangle $A F C$ était isocèle au point $C$, ce qui pouvait se conjecturer en faisant une\nfigure exacte. De manière générale, les élèves ont su montrer beaucoup de soin dans leurs tentatives de preuves, en définissant bien tous les points qu'ils introduisaient et en détaillant bien les étapes.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Une permutation de l'ensemble $\\{1, \\ldots, 2021\\}$ est une suite $\\sigma=\\left(\\sigma_{1}, \\ldots, \\sigma_{2021}\\right)$ telle que chaque élément de l'ensemble $\\{1, \\ldots, 2021\\}$ soit égal à exactement un terme $\\sigma_{i}$. On définit le poids d'une telle permutation $\\sigma$ comme la somme\n\n$$\n\\sum_{i=1}^{2020}\\left|\\sigma_{i+1}-\\sigma_{i}\\right|\n$$\n\nQuelle est le plus grand poids possible des permutations de $\\{1, \\ldots, 2021\\}$ ?", "solution": "Soit $n=2021$, et soit $\\sigma$ une permutation de $\\{1,2, \\ldots, n\\}$ et soit $\\mathbf{W}(\\sigma)$ son poids. Pour tout entier $k \\leqslant n$, on pose\n\n$$\n\\alpha_{k}=\\left\\{\\begin{array}{ll}\n1 & \\text { si } k \\neq n \\text { et } \\sigma(k)>\\sigma(k+1) \\\\\n0 & \\text { si } k=n \\\\\n-1 & \\text { si } k \\neq n \\text { et } \\sigma(k)<\\sigma(k+1)\n\\end{array} \\text { et } \\beta_{k}= \\begin{cases}1 & \\text { si } k \\neq 1 \\text { et } \\sigma(k)>\\sigma(k-1) \\\\\n0 & \\text { si } k=1 \\\\\n-1 & \\text { si } k \\neq 1 \\text { et } \\sigma(k)<\\sigma(k-1)\\end{cases}\\right.\n$$\n\nEnfin, on pose $\\varepsilon_{k}=\\alpha_{\\sigma^{-1}(k)}+\\beta_{\\sigma^{-1}(k)}$. On constate alors que\n\n$$\n\\mathbf{W}(\\sigma)=\\sum_{k=1}^{n}\\left(\\alpha_{k}+\\beta_{k}\\right) \\sigma(k)=\\sum_{k=1}^{n} k \\varepsilon_{k} .\n$$\n\nOn note maintenant $\\mathcal{X}$ l'ensemble des $n$-uplets $\\mathbf{x}=\\left(x_{1}, x_{2}, \\ldots, x_{n}\\right)$ tels que\n$\\triangleright x_{1}+x_{2}+\\ldots+x_{n}=0$ et\n$\\triangleright$ il existe deux indices $i$ et $j$ pour lesquels $x_{i}, x_{j} \\in\\{-1,+1\\}$, et $x_{k} \\in\\{-2,0,2\\}$ dès lors que $k \\notin\\{i, j\\}$.\nPar construction, le $n$-uplet $\\left(\\varepsilon_{1}, \\ldots, \\varepsilon_{n}\\right)$ appartient à $\\mathcal{X}$.\nPlus généralement, on pose donc $\\mathbf{W}(\\mathbf{x})=\\sum_{k=1}^{n} k x_{k}$ pour tout $n$-uplet $\\mathbf{x} \\in \\mathcal{X}$, et on considère alors un $n$-tuplet $\\mathbf{y}=\\left(y_{1}, y_{2}, \\ldots, y_{n}\\right) \\in \\mathcal{X}$ pour lequel $\\mathbf{W}(y)$ est maximal.\nL'inégalité du réordonnement indique que $y_{1} \\leqslant y_{2} \\leqslant \\ldots \\leqslant y_{n}$. Supposons en outre qu'il existe un indice $i$ pour lequel $y_{i}=0$. Si $i \\geqslant 2$ et $y_{i-1}=-1$, remplacer $y_{i}$ et $y_{i+1}$ par -2 et 1 augmente $\\mathbf{W}(\\mathbf{y})$ de 2 . De même, si $i \\leqslant n-1$ et $y_{i+1}=1$, remplacer $y_{i}$ et $y_{i+1}$ par -1 et 2 augmente $\\mathbf{W}(\\mathbf{y})$ de 2. Puisque le $n$-uplet y contient nécessairement des coordonnées égales à $\\pm 1$, ses coordonnées sont donc toutes non nulles.\nEnfin, soit $a$ le nombre d'indices $i$ pour lesquels $y_{i}=-2$, et $b$ le nombre d'indices $i$ pour lesquels $y_{i}=2$. On sait que $y_{1}=\\ldots=y_{a}=-2, y_{a+1}= \\pm 1, y_{a+2}= \\pm 1$ et $y_{a+3}=\\ldots=y_{n}=2$, de sorte que $a+b+2=n$ et que $-2 a+y_{a+1}+y_{a+2}+2 b=0$. Ainsi,\n\n$$\na=\\frac{2 n+y_{a+1}+y_{a+2}}{4}-1 \\text { et } b=\\frac{2 n-y_{a+1}-y_{a+2}}{4}-1 .\n$$\n\nOn distingue alors trois cas, en fonction de valeurs de $y_{a+1}$ et $y_{a+2}$ :\n\n1. Si $y_{a+1}=y_{a+2}=-1$, alors $a=(n-3) / 2, b=(n-1) / 2$, donc\n\n$$\n\\mathbf{W}(\\mathbf{y})=-2 \\sum_{k=1}^{a} k-(a+1)-(a+2)+2 \\sum_{k=a+3}^{n} k=\\left(n^{2}-3\\right) / 2\n$$\n\n2. Si $y_{a+1}=y_{a+2}=1$, alors $a=(n-1) / 2, b=(n-3) / 2$, donc\n\n$$\n\\mathbf{W}(\\mathbf{y})=-2 \\sum_{k=1}^{a} k+(a+1)+(a+2)+2 \\sum_{k=a+3}^{n} k=\\left(n^{2}-3\\right) / 2\n$$\n\n3. Si $y_{a+1}=-1$ et $y_{a+2}=1$, alors $a=b=(n-2) / 2$, ce qui est impossible puisque $n$ est impair.\nPar conséquent, $\\mathbf{W}(\\sigma) \\leqslant\\left(n^{2}-3\\right) / 2$.\nRéciproquement, on pose $\\ell=(n-1) / 2$, puis on note $\\sigma$ la permutation de $\\{1,2, \\ldots, n\\}$ définie par\n\n$$\n\\begin{cases}\\sigma(2 k-1)=\\ell+1+k & \\text { si } 1 \\leqslant k \\leqslant \\ell \\\\ \\sigma(2 k)=k & \\text { si } 1 \\leqslant k \\leqslant \\ell \\\\ \\sigma(n)=\\ell+1 & \\end{cases}\n$$\n\n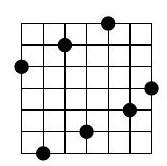\n\nCette permutation est associée au $n$-uplet $(-2, \\ldots,-2,1,1,2, \\ldots, 2)$ avec $\\ell$ coordonnées égales à -2 et $\\ell$ coordonnées égales à 2 , donc son poids vaut $\\left(n^{2}-3\\right) / 2$, comme montré dans le cas 2 ci-dessus.\nEn conclusion, le poids maximum recherché est $\\left(n^{2}-3\\right) / 2$, c'est-à-dire 2042219.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ Soit $n=2021$, et soit $\\sigma$ une permutation de $\\{1,2, \\ldots, n\\}$ de poids maximal. Ci-dessous, on pose $k=(n-1) / 2=1010$.\nSupposons qu'il existe un entier $i$ tel que $2 \\leqslant i \\leqslant n-1$ et $\\sigma_{i-1}<\\sigma_{i}<\\sigma_{i+1}$ ou $\\sigma_{i-1}>\\sigma_{i}>\\sigma_{i+1}$. On note alors $\\sigma^{\\prime}$ la permutation de $\\{1,2, \\ldots, n\\}$ définie par :\n\n$$\n\\begin{aligned}\n& \\triangleright \\sigma_{j}^{\\prime}=\\sigma_{j} \\text { lorsque } 1 \\leqslant j \\leqslant i-1 ; \\\\\n& \\triangleright \\sigma_{j}^{\\prime}=\\sigma_{j+1} \\text { lorsque } i \\leqslant j \\leqslant n-1 ; \\\\\n& \\triangleright \\sigma_{n}^{\\prime}=\\sigma_{i} .\n\\end{aligned}\n$$\n\nComme $\\left|\\sigma_{i}-\\sigma_{i+1}\\right|+\\left|\\sigma_{i+1}-\\sigma_{i+2}\\right|=\\left|\\sigma_{i}-\\sigma_{i+2}\\right|$, le poids de $\\sigma^{\\prime}$ vaut celui de $\\sigma$ auquel on ajoute $\\left|\\sigma_{n}-\\sigma_{1}\\right|$, ce qui contredit la maximalité du poids de $\\sigma$.\nEn outre, et quitte à remplacer $\\sigma$ par sa permutation « miroir horizontal », c'est-à-dire à remplacer chaque terme $\\sigma_{j}$ par $n+1-\\sigma_{j}$, ce qui ne changera rien au poids de $\\sigma$, on suppose sans perte de généralité que $\\sigma_{1}<\\sigma_{2}$. L'absence d'un entier $i$ tel que décrit au paragraphe précédent nous assure alors que $\\sigma_{2 j-1}<\\sigma_{2 j}>\\sigma_{2 j+1}$ pour tout entier $j$ tel que $1 \\leqslant j \\leqslant k$.\nLe poids de $\\sigma$ vaut alors\n\n$$\n\\sum_{j=1}^{k} 2 \\sigma_{2 j}-\\sigma_{1}-\\sigma_{n}-\\sum_{j=1}^{k-1} 2 \\sigma_{2 j+1}\n$$\n\nComme $\\sigma$ ne prend pas deux fois la même valeur, on a\n\n$$\n\\begin{aligned}\n& \\sum_{j=1}^{k} 2 \\sigma_{2 j} \\leqslant \\sum_{j=n+1-k}^{n} 2 j=n(n+1)-(n-k)(n+1-k)=3 k^{2}+3 k \\text { et } \\\\\n& \\sum_{j=1}^{k-1} 2 \\sigma_{2 j+1}+\\sigma_{1}+\\sigma_{n} \\geqslant \\sum_{j=1}^{k-1} 2 j+k+(k+1)=k(k-1)+(2 k+1)=k^{2}+k+1\n\\end{aligned}\n$$\n\nPar conséquent, le poids de $\\sigma$ ne peut pas dépasser $2 k^{2}+2 k-1=2042219$.\nRéciproquement, la permutation indiquée à la fin de la solution précédente est bien de poids 2042219, et il s'agit donc bien là du poids maximal.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 5 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Une permutation de l'ensemble $\\{1, \\ldots, 2021\\}$ est une suite $\\sigma=\\left(\\sigma_{1}, \\ldots, \\sigma_{2021}\\right)$ telle que chaque élément de l'ensemble $\\{1, \\ldots, 2021\\}$ soit égal à exactement un terme $\\sigma_{i}$. On définit le poids d'une telle permutation $\\sigma$ comme la somme\n\n$$\n\\sum_{i=1}^{2020}\\left|\\sigma_{i+1}-\\sigma_{i}\\right|\n$$\n\nQuelle est le plus grand poids possible des permutations de $\\{1, \\ldots, 2021\\}$ ?", "solution": "$n^{\\circ} 2$ Soit $n=2021$, puis $k=(n-1) / 2=1010$, et soit $\\sigma$ une permutation de $\\{1,2, \\ldots, n\\}$ de poids maximal. Le poids de $\\sigma$ vaut\n\n$$\n\\sum_{i=1}^{2 k} \\max \\left(\\sigma_{i}, \\sigma_{i+1}\\right)-\\sum_{i=1}^{2 k} \\min \\left(\\sigma_{i}, \\sigma_{i+1}\\right)\n$$\n\nOr, chaque entier compris entre 1 et 2021 apparaît au plus deux fois dans chacune de nos deux sommes, de sorte que\n\n$$\n\\begin{aligned}\n& \\sum_{i=1}^{2 k} \\max \\left(\\sigma_{i}, \\sigma_{i+1}\\right) \\leqslant \\sum_{i=n+1-k}^{n} 2 i=n(n+1)-(n-k)(n+1-k)=3 k^{2}+3 k \\mathrm{et} \\\\\n& \\sum_{i=1}^{2 k} \\min \\left(\\sigma_{i}, \\sigma_{i+1}\\right) \\geqslant \\sum_{i=1}^{k} 2 i=k(k+1) .\n\\end{aligned}\n$$\n\nAinsi, $\\sigma$ est une permutation de poids $\\mathbf{W}(\\sigma) \\leqslant 2 k^{2}+2 k$, avec égalité si et seulement si chaque terme $\\max \\left(\\sigma_{i}, \\sigma_{i+1}\\right)$ est supérieur ou égal à $n+1-k=1012$ et chaque terme $\\min \\left(\\sigma_{i}, \\sigma_{i+1}\\right)$ est inférieur ou égal à $k=1010$. Or, au moins l'un de ces termes est égal à 1011. On en conclut que $\\mathbf{W}(\\sigma) \\leqslant 2 k^{2}+2 k-1=2042219$.\nRéciproquement, la permutation indiquée à la fin des solutions précédentes est bien de poids 2042219, et il s'agit donc bien là du poids maximal.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 6 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Une permutation de l'ensemble $\\{1, \\ldots, 2021\\}$ est une suite $\\sigma=\\left(\\sigma_{1}, \\ldots, \\sigma_{2021}\\right)$ telle que chaque élément de l'ensemble $\\{1, \\ldots, 2021\\}$ soit égal à exactement un terme $\\sigma_{i}$. On définit le poids d'une telle permutation $\\sigma$ comme la somme\n\n$$\n\\sum_{i=1}^{2020}\\left|\\sigma_{i+1}-\\sigma_{i}\\right|\n$$\n\nQuelle est le plus grand poids possible des permutations de $\\{1, \\ldots, 2021\\}$ ?", "solution": "$n^{\\circ} 3$ Représentons-nous le problème d'une autre façon. On considère 2021 villes numérotées de 1 à 2021, et la ville numéro $k$ est placée sur l'axe des abscisses, au point de coordonnées $(k, 0)$. Les villes $i$ et $j$ sont donc à distance $|i-j|$. Un voyageur désire visiter toutes les villes une seule fois : il choisit sa ville de départ, puis va à pied de la ville où il est à une ville qu'il n'a pas visité, et s'arrête quand il a visité toutes les villes. Il souhaite effectuer son trajet de sorte à parcourir la plus grande distance possible. Cette distance maximale sera le poids maximal que nous recherchons.\nSoit $i$ un entier compris entre 1 et 1010. Lors des 2020 trajets qu'effectue notre voyageur, et comme il n'y a que $i$ villes situées à gauche du chemin entre les villes $i$ et $i+1$, ce chemin est emprunté au plus $2 i$ fois. De même, le passage entre les villes $2021-i$ et $2021+1-i$ est emprunté au plus $2 i$ fois. La distance totale parcourue vaut donc au plus\n\n$$\n2 \\sum_{i=1}^{1010} 2 i=2 \\times 1010 \\times 1011\n$$\n\nOr, nous ne pouvons avoir égalité : en effet, si on a égalité, alors chacun des 2020 trajets aura amené notre voyageur à traverser à la fois le chemin entre les villes 1010 et 1011, mais aussi entre les villes 1011 et 1012. Il ne prendra donc jamais le temps de visiter la ville 1011. Ainsi, la distance totale parcourue vaut au plus $2 \\times 1010^{2}-1=2042219$.\nRéciproquement, on construit une permutation de poids maximal comme dans les solutions précédentes.\n\nCommentaire des correcteurs Le problème a été peu réussi. Il était difficile mais de nombreuses remarques étaient pertinentes à faire, et permettaient de gagner des points. Quelques remarques:\n$\\triangleright$ Plusieurs élèves n'ont pas traité cet exercice, mais ont décidé de traiter le problème 3 et/ou le problème 4. C'est un très mauvais calcul, qui ne s'est pas révélé payant. Les exercices sont classés par ordre de difficulté, il est très rarement intelligent de se dire que l'exercice 4 , supposément très très dur, sera plus propice à avoir des points que l'exercice 2.\n$\\triangleright$ De nombreux élèves ont proposé une permutation de poids soi-disant optimal, dont le poids valait $1010 \\times 2021$. Penser qu'une telle permutation est optimale dans un premier temps est possible, mais après avoir examiné le cas $n=5$, on se rend compte\nque la permutation associée n'est pas optimale. La première chose dans un problème compliqué de combinatoire à faire étant de regarder les petits cas, il est dommage que des élèves se soient entêtés à prouver que c'était ce poids qui était maximal, puisque cela ne pouvait mener qu'à des preuves fausses. Regarder les petits cas est toujours crucial en combinatoire.\n$\\triangleright$ Plusieurs élèves laissent leur résultat sous forme d'une somme qu'ils ne calculent pas, font des erreurs de calcul ou ne daignent pas expliquer un minimum leur calcul : c'est dommage, et cela peut coûter des points. Il faut faire attention en cas de calcul compliqué à ne pas écrire n'importe quoi : regarder modulo 10 permet d'avoir une idée du dernier chiffre, et regarder l'ordre de grandeur que devrait avoir le résultat permet d'éviter une bête erreur de calcul.\n$\\triangleright$ Beaucoup de candidats tombent dans l'écueil des affirmations non justifiées : une affirmation doit être justifiée rigoureusement. Il n'est pas correct d'affirmer sans preuve que la meilleure configuration est celle-là (sachant qu'en plus souvent ça ne l'est pas). Il faut prouver ses différentes affirmations, et faire preuve d'honnêteté : s'il n'est pas grave de supposer quelque chose à un moment, parce qu'on sait traiter le problème sous cette supposition, il est par contre plus embêtant de fournir une fausse preuve pour se ramener à un cas particulier, puis de traiter ce cas.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution alternative"}
|
| 7 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Étant donnés deux entiers naturels non nuls $a$ et $b$, on dit que $b$ est $a$-gréable si, pour toute liste $d_{1}, d_{2}, \\ldots, d_{k}$ de diviseurs de $b$, non nécessairement distincts, telle que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k}}>a\n$$\n\nil existe un ensemble $I$ inclus dans $\\{1,2, \\ldots, k\\}$ tel que\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}}=a\n$$\n\nL'entier $a$ étant fixé, quels sont les entiers $a$-gréables?", "solution": "Tout d'abord, soit $b$ un entier qui admet au moins deux facteurs premiers distincts $p<q$. On pose alors $d_{1}=p$ et $d_{2}=d_{3}=\\ldots=d_{a q}=q$, de sorte que\n\n$$\n\\sum_{i=1}^{a q} \\frac{1}{d_{i}}=a+\\frac{1}{p}-\\frac{1}{q}>a\n$$\n\nCependant, si $1 \\notin I$, on sait que\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}}=\\frac{|I|}{q} \\leqslant \\frac{a q-1}{q}<a,\n$$\n\net si $1 \\in I$,\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}}=\\frac{1}{p}+\\frac{|I|-1}{q}=\\frac{q+(|I|-1) p}{p q}\n$$\n\nne peut être égal à $a$, car $p$ ne divise pas $q+(|I|-1) p$. Ainsi, l'entier $b$ n'est pas $a$-gréable.\nRéciproquement, supposons que $b$ est une puissance de nombre premier, disons $b=p^{\\alpha}$, et soit $d_{1}, d_{2}, \\ldots, d_{k}$ une liste de diviseurs de $b$, ordonnée dans l'ordre croissant, telle que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k}}>a\n$$\n\nSoit $\\ell$ le plus petit entier tel que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{\\ell}} \\geqslant a\n$$\n\nTous les diviseurs $d_{i}$ tels que $i \\leqslant \\ell$ divisent $d_{\\ell}$, et on pose $t_{i}=d_{\\ell} / d_{i}$. Alors\n\n$$\nt_{1}+t_{2}+\\ldots+t_{\\ell-1}<a d_{\\ell} \\leqslant t_{1}+t_{2}+\\ldots+t_{\\ell-1}+t_{\\ell}\n$$\n\net $t_{\\ell}=1$, donc l'inégalité $a d_{\\ell} \\leqslant t_{1}+t_{2}+\\ldots+t_{\\ell-1}+t_{\\ell}$ est une égalité, ce qui signifie bien que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{\\ell}}=a\n$$\n\nPar conséquent, l'entier $b$ est $a$-gréable.\nEn conclusion, les entiers $a$-gréables sont les puissances de nombres premiers.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 8 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Étant donnés deux entiers naturels non nuls $a$ et $b$, on dit que $b$ est $a$-gréable si, pour toute liste $d_{1}, d_{2}, \\ldots, d_{k}$ de diviseurs de $b$, non nécessairement distincts, telle que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k}}>a\n$$\n\nil existe un ensemble $I$ inclus dans $\\{1,2, \\ldots, k\\}$ tel que\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}}=a\n$$\n\nL'entier $a$ étant fixé, quels sont les entiers $a$-gréables?", "solution": "$n^{\\circ} 1$ Voici une manière alternative de démontrer que toute puissance de nombre premier est $a$-gréable. Nous allons démontrer par récurrence forte sur $k$ la propriété $\\mathcal{P}_{k}$ suivante:\n\nPour tout entier $a \\geqslant 0$, toute puissance de nombre premier $n=p^{\\alpha}$ et toute suite $\\left(d_{i}\\right)_{1 \\leqslant i \\leqslant k}$ formée de $k$ diviseurs de $n$ telle que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k}} \\geqslant a\n$$\n\nil existe un entier $I$ inclus dans $\\{1,2, \\ldots, k\\}$ pour lequel\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}} \\neq a\n$$\n\nTout d'abord, si $k=0$, la somme des inverses des diviseurs $d_{i}$ est nulle, donc $a=0$ et choisir $I=\\emptyset$ nous assure que\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}}=0=a\n$$\n\nAinsi, $\\mathcal{P}_{0}$ est vraie.\nOn considère maintenant un entier $k \\geqslant 1$ tel que $\\mathcal{P}_{0}, \\ldots, \\mathcal{P}_{k-1}$ soient vraies, puis un entier $a \\geqslant 0$, un nombre premier $n=p^{\\alpha}$ et une suite $\\left(d_{i}\\right)_{1 \\leqslant i \\leqslant k}$ formée de $k$ diviseurs de $n$ telle que\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k}} \\geqslant a\n$$\n\nSi l'un des diviseurs $d_{i}$ est égal à 1 , et quitte à réordonner les nombres $d_{i}$, on suppose que $i=k$. Mais alors\n\n$$\n\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k-1}} \\geqslant a-1\n$$\n\nD'après $\\mathcal{P}_{k-1}$, il existe donc un ensemble $J$ inclus dans $\\{1,2, \\ldots, k-1\\}$ tel que\n\n$$\n\\sum_{i \\in J} \\frac{1}{d_{i}}=a-1\n$$\n\nde sorte que choisir $I=J \\cup\\{k\\}$ nous permet d'obtenir l'égalité\n\n$$\n\\sum_{i \\in J} \\frac{1}{d_{i}}=a\n$$\n\nDe même, si $k \\geqslant p$ et s'il existe $p$ diviseurs $d_{i}$ égaux à un même nombre $p^{t}$, avec $t \\geqslant 1$, on suppose sans perte de généralité qu'il s'agit des diviseurs $d_{1}, d_{2}, \\ldots, d_{p}$. Quitte à remplacer ces $p$ diviseurs par un nouveau diviseur $d_{p}^{\\prime}=p^{t-1}$, et à poser $d_{i}^{\\prime}=d_{i}$ lorsque $p+1 \\leqslant i \\leqslant k$, on sait que\n\n$$\n\\frac{1}{d_{p}^{\\prime}}+\\frac{1}{d_{p+1}^{\\prime}}+\\ldots+\\frac{1}{d_{k}^{\\prime}}=\\frac{1}{d_{1}}+\\frac{1}{d_{2}}+\\ldots+\\frac{1}{d_{k}} \\geqslant a\n$$\n\nD'après $\\mathcal{P}_{k-p+1}$, il existe un ensemble $J$ inclus dans $\\{p, p+1, \\ldots, k\\}$ tel que\n\n$$\n\\sum_{i \\in J} \\frac{1}{d_{i}^{\\prime}}=a\n$$\n\nMais alors choisir $I=J$ si $p \\notin J$, ou bien $I=J \\cup\\{1,2, \\ldots, p-1\\}$ si $p \\in J$, nous permet d'obtenir l'égalité\n\n$$\n\\sum_{i \\in J} \\frac{1}{d_{i}}=a\n$$\n\n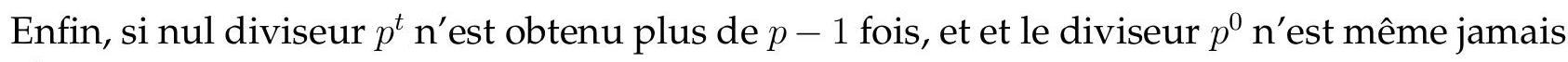 obtenu, on sait que\n\n$$\n\\sum_{i=1}^{k} \\frac{1}{d_{i}} \\leqslant \\sum_{t=1}^{\\alpha} \\frac{p-1}{p^{t}}<1\n$$\n\nde sorte que $a=0$, donc que choisir $I=\\emptyset$ permet d'obtenir l'égalité\n\n$$\n\\sum_{i \\in I} \\frac{1}{d_{i}}=0=a\n$$\n\nAinsi, $\\mathcal{P}_{k}$ est vraie. Ceci conclut notre récurrence et notre démonstration.\n\nCommentaire des correcteurs Le problème a été correctement résolu par une douzaine d'élèves et était plutôt difficile. Voici quelques remarques sur le problème et sur les solutions proposées :\n$\\triangleright$ Les élèves ont fait dans l'ensemble assez peu d'erreurs : les copies ayant perdu des points ont en général fait des oublis ou n'ont pas démontré ce qu'elles avançaient.\n$\\triangleright \\mathrm{Il}$ faut faire attention à démontrer ce que l'on affirme : plusieurs copies donnent une suite pour montrer qu'un entier n'est pas $a$-gréable sans démontrer qu'elle convient.\n$\\triangleright$ La conclusion obtenue sur les entiers $a$-gréables est parfois fausse à cause d'une mauvaise compréhension de la condition obtenue : les entiers $b$ ne possédant pas deux diviseurs (différents de 1) premiers entre eux sont les puissances de premiers.\n$\\triangleright$ Plusieurs élèves utilisent une récurrence pour montrer que les puissances de premiers sont bien $a$-gréables mais ne la rédigent pas correctement. Même si cela n'était pas pénalisé ici, il faut faire attention à bien détailler les éléments de la preuve : certains ont oublié des éléments en allant trop vite.\n$\\triangleright$ Un nombre conséquent d'élèves étudient certains cas particuliers, par exemple celui où $b$ est premier. Bien que cela soit souvent pertinent pour l'étude d'un problème, il faut être conscient que l'étude de cas particuliers est en général peu récompensée. Il faut mieux résoudre un problème entièrement que d'essayer de « grappiller » des points sur chaque problème. Enfin, et comme mentionné au problème précédent, il est beaucoup plus stratégique de traiter les problèmes dans l'ordre.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution alternative"}
|
| 9 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\\left(u_{n}\\right)_{n \\geqslant 0}$ une suite telle que $u_{n+2}=f\\left(u_{n+1}\\right)-f\\left(u_{n}\\right)$ pour tout entier $n \\geqslant 0$.\nDémontrer que la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\\varepsilon>0$, il existe un entier $N$ tel que $\\left|u_{n}\\right| \\leqslant \\varepsilon$ pour tout entier $n \\geqslant N$.", "solution": "Quitte à remplacer la fonction $f$ par la fonction $t \\mapsto f(t)-f(0)$, ce qui ne change rien à la propriété désirée, on suppose que $f(0)=0$.\nPar ailleurs, remplacer la fonction $f$ par la fonction $t \\mapsto-f(-t)$ et la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ par la suite $\\left(-u_{n}\\right)_{n \\geqslant 0}$ ne change rien non plus à la propriété désirée. On pourra donc librement supposer, sans autre forme de procès, que tel ou tel terme $u_{n}$ est positif ou nul. Ci-dessous, ces suppositions sont marquées par le symbole ( $\\star$ ).\nOn dit maintenant qu'un entier $n$ est bon si les termes $u_{n}$ et $u_{n+1}$ sont de même signe et vérifient l'inégalité $\\left|u_{n+1}\\right| \\leqslant\\left|u_{n}\\right|$. Par ailleurs, on dit qu'un entier $n$ est dominant si tout entier $k \\geqslant n$ satisfait l'inégalité $\\left|u_{k}\\right| \\leqslant\\left|u_{n}\\right|$. Démontrons quelques résultats intermédiaires.\nLemme 1 : Parmi trois entiers consécutifs, au moins un est bon.", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 10 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\\left(u_{n}\\right)_{n \\geqslant 0}$ une suite telle que $u_{n+2}=f\\left(u_{n+1}\\right)-f\\left(u_{n}\\right)$ pour tout entier $n \\geqslant 0$.\nDémontrer que la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\\varepsilon>0$, il existe un entier $N$ tel que $\\left|u_{n}\\right| \\leqslant \\varepsilon$ pour tout entier $n \\geqslant N$.", "solution": "Soit $n$ un entier naturel. Si $u_{n}$ et $u_{n+1}$ sont de signes opposés, et en supposant que $u_{n} \\geqslant 0^{(*)}$, on constate que $u_{n} \\geqslant 0 \\geqslant u_{n+1}$, donc que $u_{n+2}=f\\left(u_{n+1}\\right)-f\\left(u_{n}\\right) \\leqslant 0$ est de même signe que $u_{n+1}$. Ainsi, on peut choisir $k=n$ ou $k=n+1$ de sorte que $u_{k}$ et $u_{k+1}$ soient de même signe.\nOn démontre alors que l'un des deux entiers $k$ ou $k+1$ est bon. En effet, si $\\left|u_{k+1}\\right| \\geqslant\\left|u_{k}\\right|$, et en supposant que $u_{k} \\geqslant 0^{(*)}$, on a $u_{k+1} \\geqslant u_{k}$, et le terme $u_{k+2}=f\\left(u_{k+1}\\right)-f\\left(u_{k}\\right)$ est compris entre 0 et $u_{k+1}$, de sorte que $k+1$ est bon.\nLemme 2: Pour tout bon entier $m$, il existe un entier $n$, égal à $m+2$ ou à $m+3$, tel que\n$\\triangleright n$ est bon,\n$\\triangleright u_{m}$ et $u_{n}$ sont de signes opposés, et\n$\\triangleright\\left|u_{k}\\right| \\leqslant\\left|u_{m}\\right|$ pour tout entier $k$ tel que $m \\leqslant k \\leqslant n$.", "problem_match": "\nExercice 4.", "solution_match": "\nDémonstration."}
|
| 11 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\\left(u_{n}\\right)_{n \\geqslant 0}$ une suite telle que $u_{n+2}=f\\left(u_{n+1}\\right)-f\\left(u_{n}\\right)$ pour tout entier $n \\geqslant 0$.\nDémontrer que la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\\varepsilon>0$, il existe un entier $N$ tel que $\\left|u_{n}\\right| \\leqslant \\varepsilon$ pour tout entier $n \\geqslant N$.", "solution": "Soit $m$ un bon entier. En supposant que $u_{m} \\geqslant 0{ }^{(*)}$, l'inégalité $0 \\leqslant u_{m+1} \\leqslant u_{m}$ nous assure que $u_{m+2}=f\\left(u_{m+1}\\right)-f\\left(u_{m}\\right) \\leqslant 0 \\leqslant u_{m+1}$, puis $u_{m+3}=f\\left(u_{m+2}\\right)-f\\left(u_{m+1}\\right) \\leqslant 0$. Ainsi, $u_{m+2}$ et $u_{m+3}$ sont de signe opposé à celui de $u_{m}$, et l'un des deux entiers $m+2$ ou $m+3$ est bon.\nEnfin, $0 \\leqslant u_{m+1} \\leqslant u_{m}, u_{m+2} \\geqslant u_{m+1}-u_{m} \\geqslant-u_{m}$ et $u_{m+3} \\geqslant u_{m+2}-u_{m+1} \\geqslant-u_{m}$, de sorte que $u_{m+1}, u_{m+2}$ et $u_{m+3}$ sont tous trois compris entre $-u_{m}$ et $u_{m}$.\nLemme 3 : Tout bon entier est dominant.", "problem_match": "\nExercice 4.", "solution_match": "\nDémonstration."}
|
| 12 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\\left(u_{n}\\right)_{n \\geqslant 0}$ une suite telle que $u_{n+2}=f\\left(u_{n+1}\\right)-f\\left(u_{n}\\right)$ pour tout entier $n \\geqslant 0$.\nDémontrer que la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\\varepsilon>0$, il existe un entier $N$ tel que $\\left|u_{n}\\right| \\leqslant \\varepsilon$ pour tout entier $n \\geqslant N$.", "solution": "Pour tout bon entier $m$, on note $\\psi(m)$ le plus petit bon entier supérieur ou égal à $m+2$. Ici, le lemme 2 et une récurrence montrent que $\\left|u_{m}\\right| \\geqslant\\left|u_{\\psi^{k}(m)}\\right| \\geqslant\\left|u_{\\ell}\\right|$ pour tout entier $\\ell$ tel que $\\psi^{k}(m) \\leqslant \\ell \\leqslant \\psi^{k+1}(m)$, de sorte que $m$ est dominant.\nSoit $a$ le plus petit bon entier. On suppose que $u_{a} \\geqslant 0{ }^{(*)}$. La suite $\\left(u_{\\psi^{k}(a)}\\right)_{k \\geqslant 0}$ est formée de termes alternativement positifs et négatifs, dont les valeurs absolues décroissent. Ainsi, la suite $\\left(u_{\\psi^{2 k}(a)}\\right)_{k \\geqslant 0}$ est décroissante, et admet une limite $\\ell \\geqslant 0$, tandis que la suite $\\left(u_{\\psi^{2 k+1}(a)}\\right)_{k \\geqslant 0}$ est croissante, et admet $-\\ell$ pour limite.\nSi $\\ell=0$, puisque tous les entiers $\\psi^{k}(a)$ sont dominants, la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ converge bien vers 0 . Sinon, soit $\\varepsilon=\\min \\{\\ell / 2-f(\\ell / 2), \\ell / 2+f(\\ell / 2)-f(\\ell)\\}$. L'énoncé nous indique que $\\varepsilon>0$, et nous permet aussi d'obtenir le résultat suivant.\nLemme 4 : Soit $x$ et $y$ deux réels. Si $x \\leqslant \\ell / 2$ et $y \\geqslant \\ell$, ou bien si $x \\leqslant 0$ et $y \\geqslant \\ell / 2$, alors $f(y)-f(x) \\leqslant y-x-\\varepsilon$.", "problem_match": "\nExercice 4.", "solution_match": "\nDémonstration."}
|
| 13 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\\left(u_{n}\\right)_{n \\geqslant 0}$ une suite telle que $u_{n+2}=f\\left(u_{n+1}\\right)-f\\left(u_{n}\\right)$ pour tout entier $n \\geqslant 0$.\nDémontrer que la suite $\\left(u_{n}\\right)_{n \\geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\\varepsilon>0$, il existe un entier $N$ tel que $\\left|u_{n}\\right| \\leqslant \\varepsilon$ pour tout entier $n \\geqslant N$.", "solution": "On traite les deux cas séparément:\n$\\triangleright$ si $x \\leqslant 0$ et $y \\geqslant \\ell / 2$, alors\n\n$$\n\\begin{aligned}\nf(y)-f(x) & =f(y)-f(\\ell / 2)+f(\\ell / 2)-f(0)+f(0)-f(x) \\\\\n& \\leqslant(y-\\ell / 2)+(\\ell / 2-\\varepsilon)+(0-x)=y-x-\\varepsilon\n\\end{aligned}\n$$\n\n$\\triangleright$ si $x \\geqslant \\ell$ et $y \\leqslant \\ell / 2$, alors\n\n$$\n\\begin{aligned}\nf(y)-f(x) & =f(y)-f(\\ell)+f(\\ell)-f(\\ell / 2)+f(\\ell / 2)-f(x) \\\\\n& \\leqslant(y-\\ell)+(\\ell / 2-\\varepsilon)+(\\ell / 2-x)=y-x-x-\\varepsilon .\n\\end{aligned}\n$$\n\nDans les deux cas, on a bien l'inégalité désirée.\nOn reprend alors la construction suivie au lemme 2. Étant donné un bon entier $m$, pour lequel on aura supposé que $u_{m} \\geqslant 0^{(*)}$, on sait que $u_{m} \\geqslant \\ell$, et on distingue deux cas :\n$\\triangleright$ si $u_{m+1} \\geqslant \\ell / 2$, alors $0 \\geqslant u_{m+2} \\geqslant u_{m+1}-u_{m} \\geqslant \\ell / 2-u_{m} \\geqslant \\varepsilon-u_{m}$, et le lemme 4 indique que $0 \\geqslant u_{m+3}=f\\left(u_{m+2}\\right)-f\\left(u_{m+1}\\right) \\geqslant \\varepsilon+u_{m+2}-u_{m+1} \\geqslant \\varepsilon-u_{m}$;\n$\\triangleright$ si $u_{m+1} \\leqslant \\ell / 2$, alors le lemme 4 indique que $0 \\geqslant u_{m+2} \\geqslant \\varepsilon+u_{m+1}-u_{m} \\geqslant \\varepsilon-u_{m}$, et $0 \\geqslant u_{m+3} \\geqslant u_{m+2}-u_{m+1} \\geqslant \\varepsilon-u_{m}$.\nDans les deux cas, les termes $u_{m+2}$ et $u_{m+3}$ sont compris entre $\\varepsilon-u_{m}$ et 0 . On en déduit que $\\left|u_{\\psi(m)}\\right| \\leqslant\\left|u_{m}\\right|-\\varepsilon$, et une relation de récurrence immédiate permet de conclure que $0 \\leqslant\\left|u_{\\psi^{k}}(a)\\right| \\leqslant\\left|u_{a}\\right|-k \\varepsilon$ pour tout entier $k$, ce qui est absurde lorsque $k>\\left|u_{a}\\right| / \\varepsilon$.\n\nCommentaire des correcteurs Ce problème était très difficile : seul un élève l'a résolu, et un seul autre a réussi à avoir strictement plus qu'un point. De manière générale, cependant, plusieurs élèves ont commis des erreurs qu'ils auraient pu éviter, ce qui leur aurait permis d'avancer dans le problème :\n$\\triangleright$ supposer indûment que toute suite est soit croissante, soit décroissante : la suite $u_{n}=$ $(-1)^{n}$ est un contre-exemple;\n$\\triangleright$ supposer indûment que toute suite positive décroissante tend vers 0 : la suite $u_{n}=$ $(n+2) /(n+1)$ est un contre-exemple;\n$\\triangleright$ supposer indûment que toute fonction croissante continue est dérivable : la fonction $t \\mapsto 2 t+|t|$ est un contre-exemple;\n$\\triangleright$ remplacer des inégalités larges par des inégalités strictes;\n$\\triangleright$ oublier que les termes de la suite pouvaient changer de signe;\n$\\triangleright$ de manière analogue, invoquer l'inégalité $f(x)-f(y)<x-y$ quelles que soient les valeurs de $x$ et de $y$, alors que cette inégalité était fausse quand $x<y$ (d'après l'énoncé), et manifestement fausse quand $x=y$;\n$\\triangleright$ supposer que, si $x_{n} \\rightarrow \\ell$, alors $f\\left(x_{n}\\right) \\rightarrow f(\\ell):$ cette affirmation n'est vraie que si $f$ est continue (ce qui était le cas ici, mais aurait nécessité d'être démontré);\n$\\triangleright$ supposer indûment que, si $x_{n} \\rightarrow \\ell, y_{n} \\rightarrow \\ell^{\\prime}$ et $x_{n}<y_{n}$, alors $\\ell<\\ell^{\\prime}$ : on a simplement l'inégalité large $\\ell \\leqslant \\ell^{\\prime}$, et les suites $x_{n}=1 /(n+1)$ puis $y_{n}=2 x_{n}$ sont un contre-exemple. Enfin, et comme signalé dans les commentaires sur les problèmes précédents, il est très surprenant que, sur les 36 élèves qui ont tenté de répondre à ce problème, seuls 9 aient préalablement tenté de répondre aux problèmes 1 à 3 . Le fait que les 27 élèves ayant choisi de faire l'impasse sur un des problèmes 1 à 3 aient cumulé 8 points, à eux tous, sur le problème 4 , suggère qu'une telle impasse était une erreur stratégique particulièrement pénalisante.", "problem_match": "\nExercice 4.", "solution_match": "\nDémonstration."}
|
French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-2.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Martin a versé à la hâte $n$ litres d'eau dans $n$ bouteilles. Certaines bouteilles sont donc plus remplies que d'autres. C'est alors qu'il se rappelle que sa mission était de mettre exactement un litre d'eau dans chaque bouteille avant de refermer le bouchon de celle-ci. Comme il n'a pas encore refermé les bouchons, il est encore temps de réparer ses bêtises.\nPour ce faire, il choisit une première bouteille, verse une partie de son contenu dans une autre bouteille s'il le souhaite, puis bouche cette première bouteille. Il choisit ensuite une seconde bouteille (qui peut être celle dans laquelle il a partiellement vidé la première bouteille, ou pas), verse une partie de son contenu dans une autre bouteille (mais pas dans la première bouteille, qui est déjà bouchée) s'il le souhaite, puis la bouche. Puis il procède de même avec une troisième bouteille, et ainsi de suite, jusqu'à boucher toutes les bouteilles.\nDémontrer que, si Martin choisit astucieusement les bouteilles dont il referme le bouchon et celles dans lesquelles il les vide partiellement, il finira bien par réparer ses bêtises.\nNote : les bouteilles sont surdimensionnées, et pourraient chacune contenir jusqu'à n litres d'eau, ce qui les empêchera de déborder.", "solution": "Nous allons procéder par récurrence sur $n$. Tout d'abord, si $n=1$, il y a une seule bouteille dans laquelle se trouve un litre d'eau, donc Martin a déjà gagné.\nPuis, si $n \\geqslant 2$, Martin choisit la bouteille $\\mathrm{n}^{\\circ} i$ la plus remplie, c'est-à-dire celle pour laquelle $x_{i}$ est maximal. On constate alors que\n\n$$\nn=x_{1}+x_{2}+\\ldots+x_{n} \\leqslant x_{i}+x_{i}+\\ldots+x_{i}=n x_{i}\n$$\n\nde sorte que $x_{i} \\geqslant 1$. Si $x_{i}>1$, il la vide donc partiellement dans une autre bouteille, jusqu'à ce que la bouteille $n^{\\circ} i$ ne contienne plus qu'un litre d'eau, puis il la bouche. Il lui suffit alors de répartir harmonieusement les $n-1$ litres d'eau restants, qui se trouvent dans $n-1$ bouteilles, et l'hypothèse de récurrence lui assure qu'il pourra bien effectuer cette répartition.\n\nCommentaire des correcteurs Ce problème a été très bien réussi dans l'ensemble. Quelques élèves ont malheureusement mal compris ce qui leur était demandé, ce qui les a empêchés de résoudre ce problème. D'autres ont proposé une stratégie gagnante pour Martin, mais démontrer que cette stratégie fonctionnait nécessitait néanmoins quelques lignes d'explication : le but n'est pas simplement d'avoir une solution correcte, mais aussi de convaincre le lecteur qu'elle est correcte et, plus encore, de convaincre le correcteur que l'élève a compris que la solution était correcte.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Aline et Théo jouent au jeu suivant. Tout d'abord, Théo choisit des nombres premiers $p_{1}, p_{2}, \\ldots$ Puis Aline choisit des entiers naturels non nuls $n_{1}, n_{2}, \\ldots$ deux à deux distincts. Théo choisit ensuite deux entiers $k \\geqslant 1$ et $\\ell \\geqslant 1$. Il gagne la partie s'il existe une infinité d'entiers $n_{i}$ qui ne sont pas divisibles par $p_{k}^{\\ell}$. Sinon, $c^{\\prime}$ est Aline qui gagne.\na) Qui, d'Aline ou de Théo, dispose d'une stratégie gagnante?\nb) Pour corser encore le jeu, Aline a maintenant une contrainte supplémentaire : chaque entier $n_{i}$ ne peut diviser qu'un nombre fini d'entiers $n_{j}$. Avec ces nouvelles règles, qui, $d^{\\prime}$ Aline ou de Théo, dispose d'une stratégie gagnante?", "solution": "a) C'est Aline qui dispose d'une stratégie gagnante. Une telle stratégie consiste, par exemple, à choisir\n\n$$\nn_{i}=\\left(p_{1} \\times p_{2} \\times \\cdots \\times p_{i}\\right)^{i}\n$$\n\npour tout $i$. En effet, tout entier $p_{k}^{\\ell}$ divise chacun des entiers $\\left(p_{1} \\times p_{2} \\times \\cdots \\times p_{i}\\right)^{i}=n_{i}$ pour lesquels $i \\geqslant \\max \\{k, \\ell\\}$.\nb) Cette fois, c'est Théo qui dispose d'une stratégie gagnante. Pour ce faire, il commence par définir $p_{i}$ comme le $i^{\\text {ème }}$ nombre premier. Puis, une fois qu'Aline a choisi les entiers $n_{i}$, Théo considère la factorisation de $n_{1}$ en produits de facteurs premiers :\n\n$$\nn_{1}=p_{1}^{\\alpha_{1}} \\times p_{2}^{\\alpha_{2}} \\times \\cdots \\times p_{t}^{\\alpha_{t}}\n$$\n\noù chaque exposant $\\alpha_{i}$ est un entier naturel.\nSupposons que, pour chaque entier $j \\leqslant t$, l'ensemble $\\mathcal{E}_{j}$ des entiers $i$ pour lesquels $p_{j}^{\\alpha_{j}}$ ne divise pas $n_{i}$ soit un ensemble fini. Tout entier $i$ pour lequel $n_{1}$ ne divise pas $n_{i}$ appartient alors à l'ensemble\n\n$$\n\\mathcal{E}_{1} \\cup \\mathcal{E}_{2} \\cup \\ldots \\cup \\mathcal{E}_{t}\n$$\n\nque l'on note $\\mathcal{E}$ et qui est lui-même fini. Mais alors il existe une infinité d'entiers $i$ qui n'appartiennent pas à $\\mathcal{E}$, et donc tels que $n_{1}$ divise $n_{i}$. Ceci est absurde, ce qui invalide notre supposition.\nIl suffit donc pour Théo de choisir un entier $j \\leqslant t$ pour lequel l'ensemble $\\mathcal{E}_{j}$ est infini, puis de choisir $k=j$ et $\\ell=\\alpha_{j}+1$.\n\nCommentaire des correcteurs Ce problème a été très peu réussi dans son intégralité par les élèves, mais plusieurs élèves ont su résoudre correctement la première question, qui était difficile.\nL'erreur commise par la quasi-intégralité des élèves est de penser que les suites $\\left(p_{i}\\right)$ et $\\left(n_{i}\\right)$ respectivement choisies par Aline et Théo étaient finies. Plusieurs élèves ont alors donné une stratégie pour Aline à la première question qui aurait pu fonctionner dans le cas de suites finies, et se sont vus récompensés de quelques points pour cela. Mais la plupart du temps, cette stratégie ne permettait pas de résoudre le cas où les suites sont infinies.\nIl en va de même pour la deuxième question, où la plupart des raisonnements proposés par les élèves sont centrés sur l'idée de prendre un élément maximal dans la suite d'Aline, mais un tel élément n'existe pas dans le cas où Aline peut produire une suite infinie d'entiers.\nIl est à noter qu'une autre erreur assez fréquente, aussi due à une mauvaise lecture de l'énoncé, était d'attribuer à Aline une suite pour laquelle tout entier choisi par Théo diviserait une infinité de terme d'Aline. Si les suites données (et valorisées par les correcteurs) vérifiaient bien cette propriété, cela ne signifie pas pour autant que, pour chaque entier de Théo, il n'existe qu'une nombre fini d'entiers d'Aline divisibles par l'entier de Théo.", "problem_match": "\nExercice 2.", "solution_match": "## Solution de l'exercice 2"}
|
| 3 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\Omega$ son cercle circonscrit. Soit $D$ le pied de la hauteur issue du sommet $A$. La bissectrice issue du sommet $A$ coupe le segment $[B C]$ au point $P$ et recoupe le cercle $\\Omega$ au point $S$. Soit $A^{\\prime}$ le point diamétralement opposé au sommet $A$ dans le cercle $\\Omega$. Démontrer que les droites $(S D)$ et ( $A^{\\prime} P$ ) se coupent sur le cercle $\\Omega$.", "solution": "Soit $X$ le point où la droite $\\left(A^{\\prime} P\\right)$ recoupe le cercle $\\Omega$. Nous allons démontrer que les points $D, S$ et $X$ sont alignés.\nSoit $O$ le centre de $\\Omega$. Le point $S$ n'est autre que le pôle Sud de $A B C$ issu de $A$, donc il appartient à la médiatrice de $[B C]$, qui n'est autre que la droite $(O S)$. Par conséquent, les droites $(O S)$ et $(A D)$ sont parallèles, et les angles $\\widehat{D A P}$ et $\\widehat{O S A}$ sont alternes-internes. En outre, le triangle $A O S$ est isocèle en $O$. Ainsi, en angles de droites, on sait déjà que\n\n$$\n\\left(X A^{\\prime}, X S\\right)=\\left(A A^{\\prime}, A X\\right)=(A O, A S)=(S A, S O)=(A P, A D)\n$$\n\nIl reste donc à vérifier que\n\n$$\n(X P, X D)=\\left(X A^{\\prime}, X D\\right)=(A P, A D)\n$$\n\nc'est-à-dire que les points $X, A, D$ et $P$ sont cocycliques. Or, puisque $\\left[A A^{\\prime}\\right]$ est un diamètre de $\\Omega$, on sait que $\\widehat{A X P}=\\widehat{A X A^{\\prime}}=90^{\\circ}=\\widehat{A D P}$. Ainsi, les deux points $D$ et $X$ appartiennent au cercle de diamètre $[A P]$, et le résultat désiré en découle immédiatement.\n\n\nCommentaire des correcteurs Ce problème a été très peu réussi. La difficulté principale était de penser à montrer un énoncé différent mais équivalent à l'énoncé du problème : montrer que le second point d'intersection de la droite $\\left(A^{\\prime} P\\right.$ ) et du cercle $\\Omega$ appartient à $(S D)$. Ceci est bien équivalent à l'énoncé puisqu'il s'agit finalement de montrer que les trois objets (deux droites et un cercle) sont concourants. Une telle astuce est parfois appelée astuce du « point fantôme » et est extrêmement utile. Ici, travailler avec le point d'intersection d'une droite et d'un cercle plutôt que le point d'intersection de deux droites fournissait plus d'égalités d'angles.\nUn tel raisonnement ne doit surtout pas être confondu avec le « raisonnement», qui ne marche bien sûr pas, consistant à supposer de prime abord que le point d'intersection des deux droites est sur le cercle, c'est-à-dire précisément le résultat que l'on souhaite démontrer. Beaucoup d'élèves ont ainsi supposé que le point $X$ d'intersection de $(S D)$ et $\\left(A^{\\prime} P\\right)$ était sur $\\Omega$, ont obtenu une égalité d'angles concernant le point $X$ avec le théorème de l'angle inscrit,\net ont conclu peu de temps après que le point $I$ était sur le cercle par la réciproque du théorème de l'angle inscrit.\nComprendre la différence entre les deux raisonnements pour ne plus refaire une telle erreur est sûrement la meilleure leçon que l'on peut tirer de cet exercice.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $n$ un entier naturel non nul. Anna a écrit $4 n+2$ entiers deux à deux distincts et compris entre 0 et $5^{n}$ inclus. Démontrer que, parmi les entiers qu'elle a écrits, il en existe trois, disons $a, b$ et $c$, tels que $a<b<c$ et $c+2 a>3 b$.", "solution": "Soit $x_{1}<x_{2}<\\ldots<x_{4 n+2}$ les $4 n+2$ entiers qu'Anna a écrits. Nous allons démontrer qu'il existe un entier $k \\leqslant 4 n$ tel que $x_{4 n+2}+2 x_{k}>3 x_{k+1}$.\nEn effet, dans le cas contraire, posons $y_{k}=x_{4 n+2}-x_{k}$ pour tout entier $k$, de sorte que\n\n$$\n3 y_{k+1}=3 x_{4 n+2}-3 x_{k+1} \\leqslant 2 x_{4 n+2}-2 x_{k}=2 y_{k} .\n$$\n\nCela signifie que $y_{k} \\geqslant(3 / 2) y_{k+1}$ pour tout $k \\leqslant 4 n$, et donc que\n\n$$\n5^{n} \\geqslant y_{1} \\geqslant(3 / 2)^{4 n} y_{4 n+1} \\geqslant(3 / 2)^{4 n}=(5+1 / 16)^{n}\n$$\n\nce qui est impossible.\nCommentaire des correcteurs Ce problème, dont la solution tient certes en quelques lignes, était loin d'être facile et comportait de nombreux pièges. Typiquement il était peu intéressant de regarder le plus petit écart, et souvent toute intuition sur un «pire cas » se révélait inexacte.\nMême si le problème a été plutôt bien réussi, les solutions étaient souvent assez longues, en introduisant parfois des variables pas forcément utiles : nous invitons donc même les élèves ayant eu la note maximale à lire attentivement le corrigé.\nDe plus, il y a de nombreuses confusions entre inégalités larges et strictes : il faut faire attention à cela, qui peut mener parfois à des solutions incorrectes. De même, certains transforment des inégalités en égalités à leur bon vouloir : c'est rarement rigoureux et cela entraîne souvent des pertes bêtes de points. Attention, enfin, aux erreurs de calcul récurrentes.\nIci, une bonne piste pour commencer était de se questionner sur $a, b, c$ : une fois $a$ fixé, quels sont les $b$ et les $c$ qui auront le plus tendance à donner $2 a+c>3 b$ ? Se poser cette question et y répondre était déjà un pas en avant vers la solution et était évidemment valorisé.\n\n## Problèmes Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Soit $n$ un entier naturel non nul. Anna a écrit $4 n+2$ entiers deux à deux distincts et compris entre 0 et $5^{n}$ inclus. Démontrer que, parmi les entiers qu'elle a écrits, il en existe trois, disons $a, b$ et $c$, tels que $a<b<c$ et $c+2 a>3 b$.", "solution": "Soit $x_{1}<x_{2}<\\ldots<x_{4 n+2}$ les $4 n+2$ entiers qu'Anna a écrits. Nous allons démontrer qu'il existe un entier $k \\leqslant 4 n$ tel que $x_{4 n+2}+2 x_{k}>3 x_{k+1}$.\nEn effet, dans le cas contraire, posons $y_{k}=x_{4 n+2}-x_{k}$ pour tout entier $k$, de sorte que\n\n$$\n3 y_{k+1}=3 x_{4 n+2}-3 x_{k+1} \\leqslant 2 x_{4 n+2}-2 x_{k}=2 y_{k} .\n$$\n\nCela signifie que $y_{k} \\geqslant(3 / 2) y_{k+1}$ pour tout $k \\leqslant 4 n$, et donc que\n\n$$\n5^{n} \\geqslant y_{1} \\geqslant(3 / 2)^{4 n} y_{4 n+1} \\geqslant(3 / 2)^{4 n}=(5+1 / 16)^{n},\n$$\n\nce qui est impossible.\nCommentaire des correcteurs Ce problème, dont la solution tient certes en quelques lignes, était loin d'être facile et comportait de nombreux pièges. Typiquement il était peu intéressant de regarder le plus petit écart, et souvent toute intuition sur un «pire cas » se révélait inexacte.\nMême si le problème a été plutôt bien réussi, les solutions étaient souvent assez longues, en introduisant parfois des variables pas forcément utiles: nous invitons donc même les élèves ayant eu la note maximale à lire attentivement le corrigé.\nDe plus, il y a de nombreuses confusions entre inégalités larges et strictes : il faut faire attention à cela, qui peut mener parfois à des solutions incorrectes. De même, certains transforment des inégalités en égalités à leur bon vouloir : c'est rarement rigoureux et cela entraîne souvent des pertes bêtes de points. Attention, enfin, aux erreurs de calcul récurrentes.\nIci, une bonne piste pour commencer était de se questionner sur $a, b, c$ : une fois $a$ fixé, quels sont les $b$ et les $c$ qui auront le plus tendance à donner $2 a+c>3 b$ ? Se poser cette question et y répondre était déjà un pas en avant vers la solution et était évidemment valorisé.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2021", "problem_label": "6", "tier": 1, "problem": "Trouver tous les entiers $n \\geqslant 1$ ayant la propriété suivante : il existe une permutation $d_{1}, d_{2}, \\ldots, d_{k}$ des diviseurs positifs de $n$ telle que, pour tout $i \\leqslant k$, la somme $d_{1}+d_{2}+\\ldots+d_{i}$ soit un carré parfait.", "solution": "Soit $n$ un des entiers recherchés, et $d_{1}, d_{2}, \\ldots, d_{k}$ une permutation adéquate des diviseurs positifs de $n$. Pour tout entier $i \\leqslant k$, on pose $s_{i}=\\sqrt{d_{1}+d_{2}+\\ldots+d_{i}}$. On dit qu'un entier $\\ell$ est bon si $s_{i}=i$ et $d_{i}=2 i-1$ pour tout $i \\leqslant \\ell$. Ci-dessous, nous allons démontrer que tout entier $\\ell \\leqslant k$ est bon.\nTout d'abord, pour tout entier $i \\geqslant 2$, on remarque déjà que\n\n$$\nd_{i}=s_{i}^{2}-s_{i-1}^{2}=\\left(s_{i}-s_{i-1}\\right)\\left(s_{i}+s_{i-1}\\right) \\geqslant s_{i}+s_{i-1} \\geqslant 2 .\n$$\n\nPar conséquent, $d_{1}=s_{1}=1$.\nConsidérons maintenant un bon entier $\\ell \\leqslant k-1$. Nous allons démontrer que $\\ell+1$ est bon lui aussi. En effet, si $s_{\\ell+1}+s_{\\ell}$ divise $\\left(s_{\\ell+1}-s_{\\ell}\\right)\\left(s_{\\ell+1}+s_{\\ell}\\right)=d_{\\ell+1}$, donc divise $n$. Il existe donc un entier $m$ tel que\n\n$$\nd_{m}=s_{\\ell+1}+s_{\\ell} \\geqslant 2 s_{\\ell}+1 \\geqslant 2 \\ell+1\n$$\n\nComme $d_{m}>d_{i}$ pour tout $i \\leqslant \\ell$, on en déduit que $m \\geqslant \\ell+1$. Mais alors\n\n$$\ns_{\\ell+1}+s_{\\ell}=d_{m}=\\left(s_{m}-s_{m-1}\\right)\\left(s_{m}+s_{m-1}\\right) \\geqslant\\left(s_{m}-s_{m-1}\\right)\\left(s_{\\ell+1}+s_{\\ell}\\right) \\geqslant s_{\\ell+1}+s_{\\ell}\n$$\n\nLes inégalités sont donc des égalités, ce qui signifie que $s_{m}+s_{m-1}=s_{\\ell+1}+s_{\\ell}$, donc que que $m=\\ell+1$, et que $s_{m}-s_{m-1}=1$, c'est-à-dire que $s_{\\ell+1}=s_{\\ell}+1=\\ell+1$. On en conclut que\n\n$$\nd_{\\ell+1}=\\left(s_{\\ell+1}-s_{\\ell}\\right)\\left(s_{\\ell+1}+s_{\\ell}\\right)=2 \\ell+1\n$$\n\nce qui signifie comme prévu que $\\ell+1$ est bon.\nEn conclusion, les diviseurs de $n$ sont les entiers $1,3, \\ldots, 2 k-1$. Réciproquement, si les diviseurs de $n$ sont les entiers $1,3, \\ldots, 2 k-1$, l'entier $n$ convient assurément.\nEn particulier, si $k \\geqslant 2$, l'entier $d_{k-1}$ est un diviseur impair de $n-d_{k-1}=2$, donc $d_{k-1}=1$ et $k=2$. Ainsi, soit $k=1$, auquel cas $n=1$, soit $k=2$, auquel cas $n=3$. Dans les deux cas, ces valeurs de $n$ conviennent. Les entiers recherchés sont donc $n=1$ et $n=3$.\n\nCommentaire des correcteurs Ce problème était plutôt difficile et a été assez peu résolu dans son intégralité : seule une dizaine d'élèves ont obtenu la totalité des points.\nBeaucoup d'élèves ont cependant pu obtenir des points en montrant en essayant de trouver quels devaient être les premiers diviseurs de la permutation. Beaucoup d'élèves obtiennent par exemple $d_{1}=1, d_{2}=3, d_{3}=5$, mais « n'osent $^{2}$ pas poursuivre en tentant une récurrence pour montrer que $d_{i}=2 i-1$. Certains veulent conclure directement, ce qui n'est pas possible ici, et beaucoup de copies se terminent alors abruptement et sans aucune justifications par: «on en déduit que 1 et 3 sont les seules solutions». Il faut être conscient que ce genre de bluff est rarement payant.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2021", "problem_label": "7", "tier": 1, "problem": "Trouver tous les entiers $n \\geqslant 3$ pour lesquels tout $n$-gone convexe dont les côtés sont de longueur 1 contient un triangle équilatéral de côté 1.", "solution": "Tout d'abord, nul entier $n$ pair ne figure parmi les entiers recherchés. En effet, le cercle inscrit d'un triangle équilatéral de côté 1 a pour aire $\\mathcal{A}=\\sqrt{3} / 4$ et pour rayon $r=2 \\mathcal{A} / 3=\\sqrt{3} / 6$. Par conséquent, l'amande ci-dessous, dessinée dans le cas où $n=6$, et elle-même contenue dans une bande de largeur $r$, ne saurait contenir de tel triangle équilatéral.\n\n\nRéciproquement, soit $n \\geqslant 3$ un entier pour lequel il existe un polygone $\\mathcal{P}=A_{0} A_{1} \\ldots A_{n-1}$, convexe de côté 1 , tel que décrit dans l'énoncé, et qui ne contient aucun triangle équilatéral de côté 1 . On suppose que ses sommets ont été listés dans le sens des aiguilles d'une montre. En s'inspirant de la construction ci-dessus, on note $d$ la distance maximale entre deux points de $\\mathcal{P}$ et, sans perte de généralité, on suppose qu'il existe un point $A_{\\ell}$, avec $1 \\leqslant \\ell \\leqslant k$, situé à distance $d$ de $A_{0}$.\nSi $d=1$, le polygone $\\mathcal{P}$ est contenu dans la zone grise représentée ci-dessous, qui consiste en l'intersection de deux demi-cercles de rayon 1 . Comme $A_{2}$ est à distance 1 de $A_{1}$, il se trouve sur l'arc de cercle $\\widehat{B A_{0}}$ et, de même, $A_{n-1}$ se trouve sur l'arc de cercle $\\widehat{A_{1} B}$. Comme $\\mathcal{P}$ est convexe, on en déduit que $A_{2}=B=A_{n-1}$, donc que $\\mathcal{P}$ est un triangle équilatéral, qui se contient bien sûr lui-même.\n\n\nOn sait donc que $d>1$, de sorte que que $A_{0} A_{\\ell}$ est une diagonale de $\\mathcal{P}$. Si $\\widehat{A_{\\ell} A_{0} A_{1}} \\geqslant 60^{\\circ}$, et puisque $A_{1} A_{\\ell} \\leqslant d=A_{0} A_{\\ell}$, on sait que $\\widehat{A_{0} A_{1} A_{\\ell}} \\geqslant \\widehat{A_{\\ell} A_{0} A_{1}} \\geqslant 60^{\\circ}$, de sorte que le triangle $A_{0} A_{1} A_{\\ell}$ lui-même contient un triangle équilatéral de côté 1 , comme illustré ci-dessous.\n\n\nAinsi, $\\widehat{A_{\\ell} A_{0} A_{1}}<60^{\\circ}$ et, de même, $\\widehat{A_{\\ell-1} A_{\\ell}} A_{0}<60^{\\circ}$. On dessine alors le trapèze isocèle $\\mathcal{T}=A_{0} B_{0} B_{\\ell} A_{\\ell}$ représenté ci-dessous dans le cas où $\\ell=4$, d'angles $60^{\\circ}$ en $A_{0}$ et $A_{\\ell}$ et de côtés $A_{0} B_{0}=A_{\\ell} B_{\\ell}=1$. S'il existe un point $A_{i}$ (avec $1 \\leqslant i \\leqslant \\ell-1$ ) situé en-dehors de $\\mathcal{T}$, le polygone $\\mathcal{P}$ contient de nouveau un triangle équilatéral de côté 1 , comme illustré ci-dessous, en blanc sur fond gris.\n\n\nCe cas de figure ne survient donc pas non plus, de sorte que le polygone $A_{0} A_{1} \\ldots A_{\\ell}$ est strictement inclus dans le polygone $\\mathcal{T}$. Son périmètre $\\ell+d$ est donc strictement inférieur à celui de $\\mathcal{T}$, c'est-à-dire à $2 d+1$, donc $\\ell-1<d$, et l'inégalité triangulaire indique également que $d \\leqslant \\ell$, ce qui signifie que $\\ell=\\lceil d\\rceil$. En considérant le polygone $A_{0} A_{n} A_{n-1} \\ldots A_{\\ell}$, on constate de même que $n-\\ell=\\lceil d\\rceil$, de sorte que $n=2\\lceil d\\rceil$ est nécessairement pair.\nAinsi, les entiers recherchés sont les entiers impairs.\nRemarque: Nous avons affirmé ci-dessus que, lorsqu'un polygone convexe $\\mathcal{P}$ est strictement inclus dans un polygone $\\mathcal{Q}$, le périmètre de $\\mathcal{P}$ est strictement inférieur à celui de $\\mathcal{Q}$. Cette affirmation «classique» ce démontre comme suit.\nTout d'abord, soit $\\mathcal{C}$ l'enveloppe convexe de $\\mathcal{Q}$. Par construction, son périmètre est inférieur ou égal à celui de $\\mathcal{Q}$, et on peut donc supposer sans perte de généralité que $\\mathcal{Q}$ est convexe.\nDans la suite, on suppose $\\mathcal{Q}$ fixé, puis on note $\\mathrm{p}(\\mathcal{P})$ le périmètre d'un polygone $\\mathcal{P}$ et $\\mathrm{c}(\\mathcal{P})$ le nombre de côtés de $\\mathcal{P}$ qui ne sont pas inclus dans des côtés de $\\mathcal{Q}$. On démontre alors par récurrence sur $c(\\mathcal{P})$ que $p(\\mathcal{P}) \\leqslant p(\\mathcal{Q})$.\nÉtant donné un polygone $\\mathcal{P}$ strictement inclus dans $\\mathcal{Q}$, on sait que $c(\\mathcal{P}) \\geqslant 1$, et on considère un côté $[B C]$ de $\\mathcal{P}$ qui n'est pas inclus dans un côté de $\\mathcal{Q}$. Puisque $\\mathcal{Q}$ est convexe, ce côté est strictement inclus dans $\\mathcal{Q}$. Puis, comme illustré ci-dessous, on prolonge les demi-droites $[A B)$ et $[D C)$ jusqu'à l'infini, où jusqu'à ce qu'elles se rencontrent. On définit ainsi une zone finie ou infinie, que l'on note $\\mathcal{Z}$, et qui est susceptible d'être bornée ou non.\n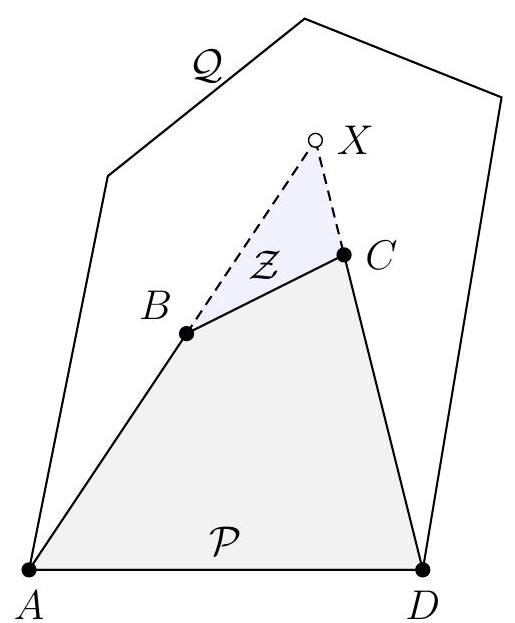\n\nCas 1\n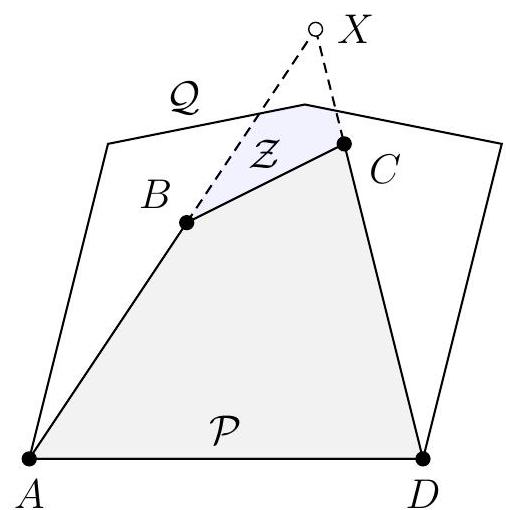\n\nCas 2\n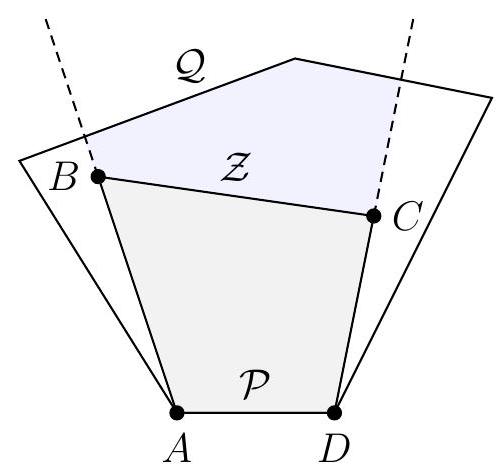\n\nCas 3\n\nOn intègre alors au polygone $\\mathcal{P}$ la portion du polygone $\\mathcal{Q}$ incluse dans la zone $\\mathcal{Z}$, que nous avons représentée en bleu. On forme ainsi un nouveau polygone convexe $\\mathcal{P}^{\\prime}$. Puisque le côté $[B C]$ de $\\mathcal{P}$ a disparu, on sait que $\\mathrm{c}\\left(\\mathcal{P}^{\\prime}\\right)<\\mathrm{c}(\\mathcal{P})$. L'hypothèse de récurrence et l'inégalité triangulaire indiquent alors que $\\mathrm{p}(\\mathcal{P})<\\mathrm{p}\\left(\\mathcal{P}^{\\prime}\\right) \\leqslant \\mathrm{p}(\\mathcal{Q})$, ce qui conclut.\n\nCommentaire des correcteurs Ce problème était extrêmement difficile, au point qu'un seul élève a eu plus de deux points (et l'a résolu). De nombreux élèves ont eu l'excellente idée d'utiliser une amande allongée pour traiter le cas $n$ pair. L'idée principale, difficile à trouver, était alors de continuer sur une construction analogue en considérant l'allongement d'un polygone, c'est-à-dire la plus grande distance entre deux sommets. Il est cependant dommage que plusieurs élèves aient prétendu avoir « magiquement» résolu le cas $n$ impair : de telles affirmations n'aideront évidemment pas à obtenir des points, et leur seul effet éventuel serait de fâcher le correcteur (ce qui n'a pas été le cas ici).", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-3.jsonl
ADDED
|
@@ -0,0 +1,14 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ des entiers naturels non nuls. On suppose que $a!+b!=c!+d!$. Démontrer que $a b=c d$.", "solution": "Supposons sans perte de généralité que $a \\leqslant b, c \\leqslant d$ et $a \\leqslant c$. Alors\n\n$$\nb!=c!-a!+d!\\geqslant d!\n$$\n\ndonc $b \\geqslant d$, de sorte que $a \\leqslant c \\leqslant d \\leqslant b$. L'entier $c$ ! divise donc $c!+d$ ! $-b$ ! $=a$ !, ce qui signifie que $c \\leqslant a$, et donc que $a=c$. On en conclut que $b!=d!$, donc que $b=d$ et que $a b=c d$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ des entiers naturels non nuls. On suppose que $a!+b!=c!+d!$. Démontrer que $a b=c d$.", "solution": "$n^{\\circ} 1$ Supposons de nouveau que $a \\leqslant b, c \\leqslant d$ et $a \\leqslant c$. Si $a=c$, on conclut comme précédemment que $b=d$ et que $a b=c d$.\nSinon, on sait que $(a+1)!\\geqslant 2 a!$ divise $c!+d!=a!+b!$, donc ne divise ni $a!$, ni $b!$. Cela signifie que $a=b$. La double inégalité\n\n$$\na!+b!\\geqslant c!+d!\\geqslant 2 \\times a!=a!+b!\n$$\n\ndevient alors une égalité, donc $a=b=c=d$, de sorte que $a b=c d$ malgré tout.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 3 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $a, b, c$ et $d$ des entiers naturels non nuls. On suppose que $a!+b!=c!+d!$. Démontrer que $a b=c d$.", "solution": "$n^{\\circ} 2$ Supposons simplement que $a \\leqslant b$ et $c \\leqslant d$. Si $b<d$, alors\n\n$$\nc!+d!>d!\\geqslant(b+1)!=(b+1) b!\\geqslant 2 b!\\geqslant a!+b!\n$$\n\nce qui est absurde. On en déduit que $b \\leqslant d$ et, de même, que $d \\leqslant b$. Ainsi, $b=d$ et $a!=c$ !, donc $a=c$ et $a b=c d$.\n\nCommentaire des correcteurs L'exercice est globalement bien résolu, et les élèves ont eu beaucoup d'idées intéressantes, même si celles-ci ne permettaient pas toujours de conclure. Les élèves ont souvent ordonné $a, b, c$ et $d$, mais parfois en faisant des erreurs de logique: par exemple, certains supposaient que $c$ était le plus petit, montraient que si $c<a, c<b$ et $c<d$ on avait une contradiction, pour en déduire que $c=a$ ou $c=b$, oubliant ainsi le cas $c=d$. Plus généralement, il faut faire attention. Ainsi, on ne pouvait pas supposer d'emblée $a \\geqslant c \\geqslant d \\geqslant b$, mais simplement $a \\geqslant b, c \\geqslant d$, et $a \\geqslant c$ : il n'y a pas de raison à priori que $d \\geqslant b$, cela restait à prouver.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution alternative"}
|
| 4 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Soit $A B C$ un triangle dont les angles sont aigus et soit $D$ un point situé à l'intérieur du triangle $A B C$. Les droites $(A D)$ et $(B D)$ recoupent le cercle circonscrit au triangle $A B C$ respectivement en les points $A_{1}$ et $B_{1}$. Le cercle circonscrit au triangle $B_{1} D A$ recoupe la droite $(A C)$ au point $P$. Le cercle circonscrit au triangle $A_{1} B D$ recoupe la droite $(B C)$ au point $Q$.\nDémontrer que le quadrilatère $C P D Q$ est un parallélogramme.", "solution": "Une chasse aux angles de droites indique que\n\n$$\n(Q D, C B)=(Q D, Q B)=\\left(A_{1} D, A_{1} B\\right)=\\left(A_{1} A, A_{1} B\\right)=(C A, C B),\n$$\n\nce qui signifie que les droites $(Q D)$ et $(A C)$ sont parallèles l'une à l'autre. On démontre de même que\n\n$$\n(P D, C A)=(P D, P A)=\\left(B_{1} D, B_{1} A\\right)=\\left(B_{1} B, B_{1} A\\right)=(C B, C A)\n$$\n\nce qui signifie que les droites $(P D)$ et $(B C)$ sont parallèles l'une à l'autre. Le quadrilatère $C P D Q$ est donc un parallélogramme.\n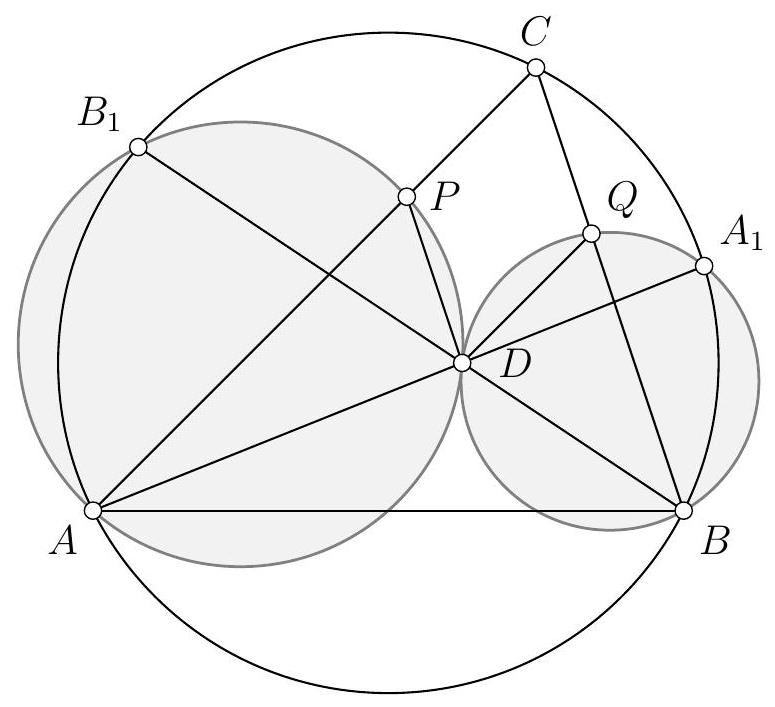\n\nCommentaire des correcteurs L'exercice est très bien résolu.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 5 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Maena et Théodore jouent à un jeu. Ils jouent sur une grille carrée formée de $99 \\times 99$ cases. On considère que deux cases sont adjacentes si elles ont un sommet ou un côté en commun.\nInitialement, Maéna numérote les cases de la grille de 1 à $99^{2}$, de façon arbitraire. Théodore place alors un jeton sur l'une des cases du carré, puis il s'autorise des mouvements de la forme suivante : il peut déplacer le jeton d'une case vers une autre uniquement si ces cases sont adjacentes et si la nouvelle case sur laquelle se retrouve le jeton a un numéro strictement plus grand que l'ancienne case.\nCombien de mouvements au minimum Théodore peut-il garantir, quelle que soit la manière avec laquelle Maena a placé ses entiers?", "solution": "Tout d'abord, Théodore peut toujours se débrouiller pour effectuer au moins trois mouvements. Pour ce faire, il lui suffit de sélectionner un carré de taille $2 \\times 2$ à l'intérieur du carré de taille $99 \\times 99$, puis d'en parcourir les quatre cases, qui sont nécessairement adjacentes puisqu'elles ont un sommet en commun.\nRéciproquement, voici comment peut procéder Maena pour empêcher Théodore d'effecuter plus de trois mouvements. Elle numérote lignes et colonnes de 1 à 99 , puis regroupe les $99 \\times 99$ cases du carré en quatre catégories :\n$\\triangleright$ la catégorie 1 contient les cases situées en une ligne et une colonne impaires;\n$\\triangleright$ la catégorie 2 contient les cases situées en une ligne impaire et une colonne paire;\n$\\triangleright$ la catégorie 3 contient les cases situées en une ligne paire et une colonne impaire;\n$\\triangleright$ la catégorie 4 contient les cases situées en une ligne et une colonne paires.\nDeux cases de la même catégorie ne sont jamais adjacentes.\nEnsuite, Maena place ses entiers, dans l'ordre croissant, dans des cases de catégorie 1, puis de catégorie 2, puis de catégorie 3, et enfin de catégorie 4. Ainsi, Théodore ne peut jamais se déplacer entre deux cases de même catégorie, et encore moins baisser de catégorie. Tout mouvement augmente donc la catégorie de la case dans laquelle se trouve le jeton de Théodore, qui se voit ainsi limité à effectuer au plus trois mouvements.\n\nCommentaire des correcteurs Dans un problème tel que celui-ci, il y a deux choses à faire:\n\n1. proposer une stratégie que pourra utiliser Maena pour empêcher Théodore de faire trop de mouvements;\n2. proposer une stratégie que pourra utiliser Théodore pour faire au moins $k$ mouvements (avec $k$ à choisir) quelle que soit la stratégie de Maena.\nParmi les élèves qui ont recherché une stratégie pour Maena, nombreux sont ceux qui ont conclu qu'elle pouvait empêcher Théodore de faire plus de trois mouvements. Parmi ceux qui ont recherché une stratégie pour Théodore, nombreux sont ceux qui ont conclu qu'il pouvait toujours faire au moins trois mouvements.\nMalheureusement, peu nombreux sont les élèves qui ont pensé à rechercher des stratégies pour Maena et pour Théodore. En particulier, démontrer que Théodore peut toujours faire au moins trois mouvements quand Maena suit la stratégie qu'elle a choisi est à peu près inutile, puisque Maena a encore $\\left(99^{2}\\right)!-1 \\approx 10^{34864}$ manières alternatives de numéroter la grille, et qu'il reste alors à démontrer que Théodore peut aussi faire au moins trois mouvements dans chacun de ces $\\left(99^{2}\\right)!-1$ cas.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 6 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $p$ et $q$ deux nombres premiers distincts, tels que $p<2 q$ et $q<2 p$. Démontrer qu'il existe deux entiers consécutifs dont l'un a $p$ pour plus grand facteur premier et l'autre a $q$ pour plus grand facteur premier.", "solution": "Supposons sans perte de généralité que $p<q$. Le théorème de Bézout indique qu'il existe des entiers $a$ et $b$ tels que $a p+b q=1$.\nOn peut toujours remplacer un tel couple $(a, b) \\operatorname{par}(a \\pm q, b \\mp p)$. Par conséquent, si on cherche un couple pour lequel la valeur de $|a|$ est minimale, on sait que $|a-q| \\geqslant|a|$ et $|a| \\leqslant|a+q|$, de sorte que $|a| \\leqslant q / 2<p$.\nEn outre, puisque $|a p+b q|=1 \\leqslant p+q$, les entiers $a$ et $b$ sont de signes opposés, ce qui signifie que les entiers $n=|a| p$ et $m=|b| q$ sont deux entiers consécutifs.\nPuisque $|a|<p$, l'entier $n$ a donc $p$ comme facteur premier maximal. En outre, $m \\leqslant n+1 \\leqslant$ $p^{2} \\leqslant q^{2}$, donc $m$ a $q$ comme facteur premier maximal. Les entiers $m$ et $n$ satisfont donc les contraintes de l'énoncé.\n\nCommentaire des correcteurs Seuls deux élèves ont résolu ce problème particulièrement difficile. L'idée était de trouver un nombre $n$, éventuellement négatif, de la forme $n=a p=$ $b q-1$, où $a$ et $b$ n'auraient que de petits facteurs premiers.\nDeux approches étaient alors a priori possibles : soit s'assurer que $a$ et $b$ seraient des puissances de $p$ et de $q$, auquel cas le petit théorème de Fermat aurait pu être pertinent, soit s'assurer qu'ils étaient petits. Or, dès que l'on impose à $a$ d'être une puissance de $p$ telle que $a p \\equiv 1(\\bmod q)$, on n'a plus aucun contrôle sur les facteurs de $b$. Il convenait donc de choisir $a, b$ et $n$ petits, ce qui exigeait de faire appel au théorème de Bézout.\nUne dernière difficulté était que l'on devait, au besoin, ne pas hésiter à chosir $n$ négatif, quitte à passer ensuite à la valeur absolue.\nEnfin, de manière surprenante, plusieurs élèves se sont contentés de regarder ce qui se passait dans certains cas particuliers, par exemple $p=2$ et $q=3$, ou encore $p=3$ et $q=5$. Regarder des petits cas est toujours une excellente chose, mais il est évidemment indispensable de s'intéresser ensuite au cas général.\n\n## Problèmes Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 7 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Soit $\\mathcal{S}$ un ensemble infini d'entiers naturels non nuls contenant quatre entiers $a, b, c, d$ deux à deux distincts tels que $\\operatorname{pgcd}(a, b) \\neq \\operatorname{pgcd}(c, d)$. Démontrer que $\\mathcal{S}$ contient trois entiers $x, y, z$ deux à deux distincts tels que $\\operatorname{pgcd}(x, y)=\\operatorname{pgcd}(y, z) \\neq \\operatorname{pgcd}(z, x)$.", "solution": "Ci-dessous, on note $m \\wedge n$ le plus grand diviseur commun à deux entiers $m$ et $n$. On considère alors le graphe colorié infini dont les sommets sont les éléments de $\\mathcal{S}$, et où chaque paire de sommets $(u, v)$ distincts l'un de l'autre est reliée par une arête de couleur $u \\wedge v$.\nSupposons que les entiers $x, y, z$ n'existent pas. Cela signifie que tout triangle est colorié en utilisant soit une seule couleur, soit exactement trois couleurs.\n\n\nSoit maintenant $u, v$ et $w$ trois éléments de $\\mathcal{S}$. Puisque $u, v$ et $w$ comptent chacun un nombre fini de diviseurs, la fonction $f: x \\mapsto(u \\wedge x, v \\wedge x, w \\wedge x)$ ne prend qu'un nombre fini de valeurs. Parmi l'infinité d'éléments de $\\mathcal{S}$ distincts de $u, v$ et $w$, il en existe donc deux, disons $s$ et $t$, tels que $f(s)=f(t)$, c'est-à-dire que\n\n$$\ns \\wedge u=t \\wedge u, s \\wedge v=t \\wedge v \\text { et } s \\wedge w=t \\wedge w\n$$\n\nLes triangles $(s, t, u),(s, t, v)$ et $(s, t, w)$ sont donc monochromes, et puisqu'ils partagent l'arête $(s, t)$, ils sont de la même couleur, disons $\\mathcal{C}$. Mais alors les triangles $(s, u, v)$ et $(s, u, w)$ ont chacun deux arêtes de couleur $\\mathcal{C}$, dont ils sont eux aussi monochromes de couleur $\\mathcal{C}$, de sorte que $u \\wedge v=u \\wedge w$.\n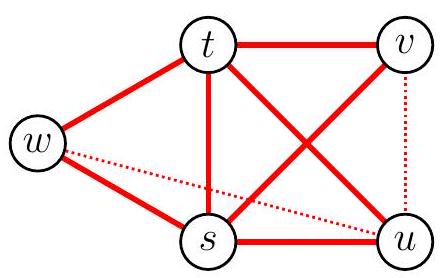\n\nAinsi, deux arêtes ayant un sommet commun sont nécessairement de la même couleur, et notre graphe est monochrome. Cela signifie en particulier que\n\n$$\na \\wedge b=c \\wedge d\n$$\n\nen contradiction avec les hypothèses de l'énoncé. Notre hypothèse initiale était donc invalide, ce qui conclut.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 8 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Soit $\\mathcal{S}$ un ensemble infini d'entiers naturels non nuls contenant quatre entiers $a, b, c, d$ deux à deux distincts tels que $\\operatorname{pgcd}(a, b) \\neq \\operatorname{pgcd}(c, d)$. Démontrer que $\\mathcal{S}$ contient trois entiers $x, y, z$ deux à deux distincts tels que $\\operatorname{pgcd}(x, y)=\\operatorname{pgcd}(y, z) \\neq \\operatorname{pgcd}(z, x)$.", "solution": "$n^{\\circ} 1$ Soit $k$ le PGCD des éléments de $\\mathcal{S}$. Si l'on divise chaque élément de $\\mathcal{S}$ par $k$, on obtient un ensemble $\\mathcal{S}^{\\prime}$ qui vérifie toujours l'énoncé et, réciproquement, si $\\mathcal{S}^{\\prime}$ vérifie l'énoncé, $\\mathcal{S}$ le vérifie aussi. On remplace donc $\\mathcal{S}$ par $\\mathcal{S}^{\\prime}$, c'est-à-dire que l'on suppose désormais que $k=1$.\nSoit $x$ et $y$ deux éléments de $\\mathcal{S}$ tels que $x \\wedge y \\neq 1$. Il suffit, par exemple, de choisir $(x, y)=(a, b)$ ou $(x, y)=(c, d)$. Si $\\mathcal{S}$ admet un élément $z$ premier avec $x$ et $y$, on a $x \\wedge z=y \\wedge z=1 \\neq x \\wedge y$, ce qui constitue le résultat souhaité.\n\nSinon, parmi les facteurs premiers de $x y$, il en existe au moins un, disons $p$, qui divise une infinité d'éléments de $\\mathcal{S}$. Notons $\\mathcal{S}_{p}$ l'ensemble des éléments de $\\mathcal{S}$ qui sont divisibles par $p$. Puisque $k=1$, il existe un élément $t$ de $\\mathcal{S}$ qui n'appartient pas à $\\mathcal{S}_{p}$. Comme $\\mathcal{S}_{p}$ est infini, et puisque la fonction $n \\mapsto t \\wedge n$ ne prend qu'un nombre fini de valeurs lorsque $n$ varie, il existe deux éléments $u$ et $v$ de $\\mathcal{S}_{p}$ tels que $t \\wedge u=t \\wedge v$. Puisque $p$ divise $u \\wedge v$ mais pas $u \\wedge v$, on en conclut que $t \\wedge u=t \\wedge v \\neq u \\wedge v$, ce qui donne de nouveau le résultat souhaité.\n\nCommentaire des correcteurs L'exercice a été assez discriminant : peu d'élèves ont eu des éléments intéressants et permettant de bien avancer sans avoir intuité et trouvé la solution. Beaucoup des élèves n'ayant pas réussi à avancer se sont focalisés sur $a, b, c$ et $d$. Cependant un élément était clé pour pouvoir avancer : l'infinité de $S$. C'est l'hypothèse la plus cruciale de l'énoncé, et il est dommage que certaines copies se retrouvent à n'utiliser nulle part ce fait, qui est pourtant le plus intéressant de l'énoncé, et incitait à appliquer le principe des tiroirs.\nDans un exercice, même si celui-ci a un aspect arithmétique apparent, il ne faut pas forcément se limiter à ce domaine et aux considérations qui y sont directement liées : l'exercice peut se situer à l'interface entre plusieurs domaines. Ici, certains ont présenté des preuves très combinatoires, d'autres plus arithmétiques:il est important de ne pas se limiter à sa première impression.\nPar ailleurs, plus d'un élève sur cinq n'a pas rendu de copies au problème : en olympiades, le premier problème est difficile, mais les problèmes sont en ordre graduel. Il est donc dangereux de faire l'impasse sur le premier problème en espérant mieux réussir après.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution alternative"}
|
| 9 |
+
{"year": "2021", "problem_label": "6", "tier": 1, "problem": "Soit $A, B, C$ et $D$ quatre points situés sur un cercle $\\Omega$. Soit $E$ et $F$ les points d'intersection des demi-droites $[B A)$ et $[B C)$ avec la tangente à $\\Omega$ en $D$. Soit $T$ un point, situé à l'intérieur du triangle $A B C$, tel que $(T E)$ soit parallèle à $(C D)$ et que $(T F)$ soit parallèle à $(A D)$. Enfin, soit $K$ le point du segment $[D F]$, autre que $D$, tel que $T D=T K$.\nDémontrer que les droites $(A C),(D T)$ et $(B K)$ sont concourantes.", "solution": "Soit $P$ et $Q$ les points d'intersection des droites (TE) et (TF) avec $(A C)$. Puisque $(E D)$ est tangente à $\\Omega$, on sait que\n\n$$\n(P A, P E)=(C A, C D)=(D A, D E)\n$$\n\ndonc que les points $A, D, E$ et $P$ sont appartiennent à un même cercle $\\alpha$. On démontre de même que les points $C, D, F$ et $Q$ appartiennent à un même cercle $\\beta$.\nCela signifie en outre que\n\n$$\n(P Q, P E)=(P A, P E)=(D A, D E)=(F Q, F E)\n$$\n\ndonc que les points $E, F, P$ et $Q$ appartiennent à un même cercle $\\gamma$. Ainsi, $T$ est le centre radical des trois cercles $\\alpha, \\beta$ et $\\gamma$. On s'intéresse donc à l'axe radical des cercles $\\alpha$ et $\\beta$, qui semble être leur tangente commune en $D$. On note donc $d$ et $d^{\\prime}$ les tangentes à $\\alpha$ et à $\\beta$ en $D$, et on vérifie que\n\n$$\n\\left(d, d^{\\prime}\\right)=(d, D E)+\\left(D F, d^{\\prime}\\right)=(A D, A E)+(C F, C D)=(A D, A B)+(C B, C D)=0^{\\circ},\n$$\n\nce qui signifie bien que les tangentes $d$ et $d^{\\prime}$ sont confondues. En particulier, cette tangente commune contient $T$.\nPar conséquent, et puisque le triangle $T D K$ est isocèle en $K$, on sait que\n\n$$\n(T P, T K)=(P E, E D)+(E D, T K)=(D P, D T)+(T D, D K)=(D P, D K)\n$$\n\nce qui signifie que $P$ appartient au cercle circonscrit à $D K T$. On démontre de même que $Q$ appartient à ce cercle circonscrit, que l'on note $\\tau$.\nForts de toutes ces relations de cocyclicité et de tangence, ensuite que\n\n$$\n(K T, K D)=(D K, D T)=(D E, d)=(A E, A D)=(A B, A D)=(B D, D K)\n$$\n\nce qui signifie que les droites $(B D)$ et $(K T)$ sont parallèles. De manière analogue,\n\n$$\n\\begin{aligned}\n(K P, K D) & =(Q P, Q D)=(Q P, Q F)+(Q F, Q D)=(E P, E F)+(C F, C D) \\\\\n& =(C D, K D)+(B C, C D)=(B C, K D)\n\\end{aligned}\n$$\n\ndonc $(K P)$ est parallèle à $(B C)$. On démontre de même que $(K Q)$ est parallèle à $(A B)$.\nCes relations de parallélisme indique qu'il existe une homothétie qui envoie $A B C D$ sur $Q K P T$, et le centre de cette homothétie appartient bien aux droites $(A Q)=(C P)=(A C)$, $(B K)$ et $(D T)$.\n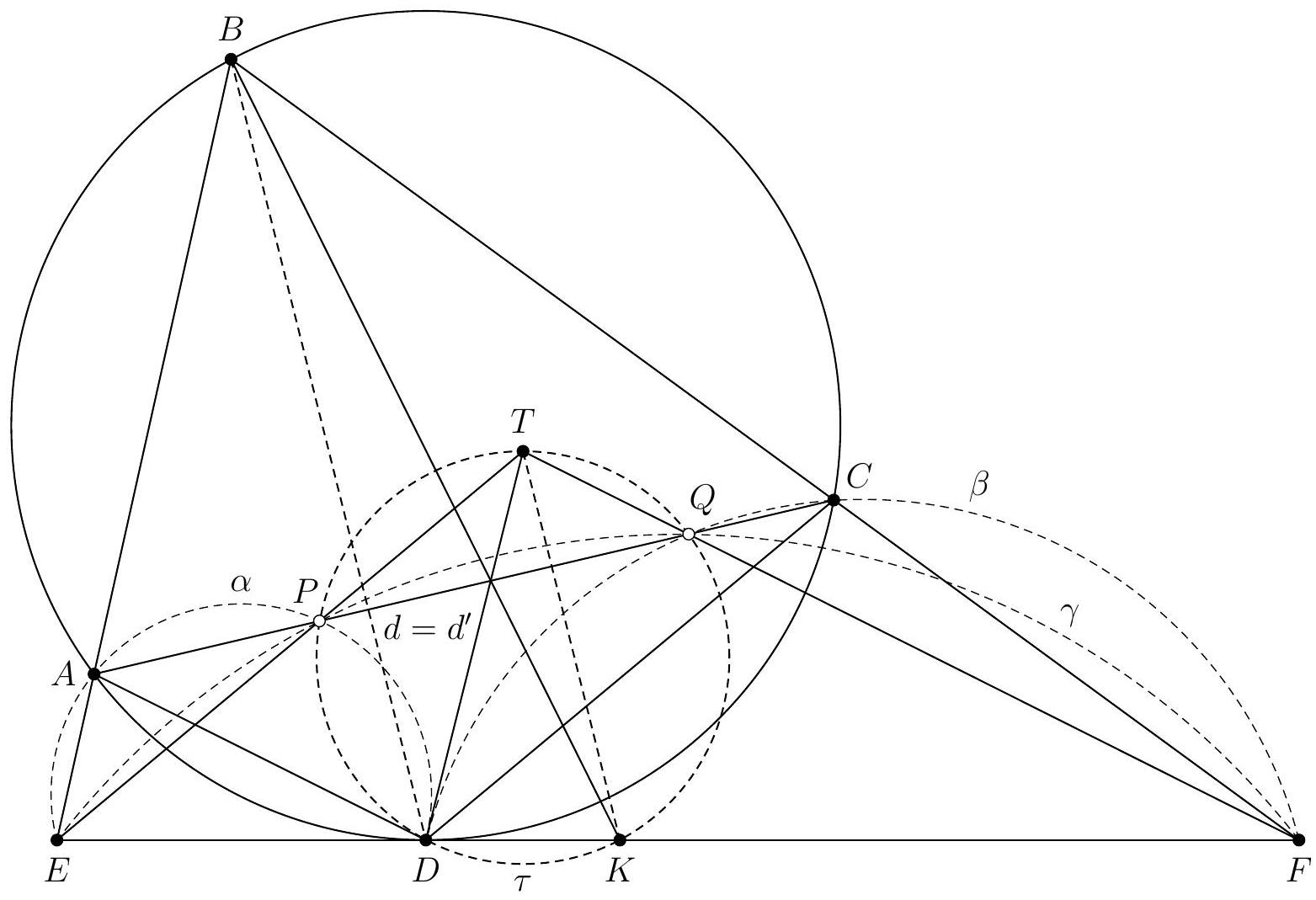\n\nCommentaire des correcteurs L'exercice était très long. Dans chacune des solutions possibles, il y avait des points à introduire et beaucoup de relations à deviner puis à démontrer. Beaucoup d'élèves ont bien su démarrer sur l'une ou l'autre des solutions et montrer les premières relations. Une poignée d'élèves est parvenue à tout démontrer.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 10 |
+
{"year": "2021", "problem_label": "7", "tier": 1, "problem": "Soit $n \\geqslant 2$ un entier. Une grenouille se déplace dans une grille de $3 n \\times 3 n$ cases, sautant chaque fois d'une case vers la case située juste au-dessus ou juste à droite. Elle souhaite aller du coin en bas à gauche, marqué d'un $S$, au coin en haut à droite, marqué d'un F. Malheureusement, certaines cases sont piégées, et si la grenouille saute sur une telle case, elle y restera prisonnière.\nOn dit qu'un ensemble de cases piégées est bloquant s'il empêche la grenouille d'aller de la case $S$ à la case $F$. On dit aussi qu'un ensemble bloquant est minimal si, dès lors que l'on retire le piège de l'une des cases de cet ensemble, notre ensemble n'est plus bloquant.\nPar exemple, les cases noires de la grille ci-dessous forment un ensemble bloquant minimal.\n\na) Démontrer qu'il existe un ensemble bloquant minimal qui contient au moins $3 n(n-1)$ cases.\nb) Démontrer que tout ensemble bloquant minimal contient au plus $3 n^{2}$ cases.", "solution": "Colorions notre grille en trois couleurs:\n$\\triangleright$ en noir, les cases piégées;\n$\\triangleright$ en rose, les cases non piégées auxquelles la grenouille peut accéder depuis la case S;\n$\\triangleright$ en vert, les cases non piégées depuis lesquelles la grenouille peut accéder à la case $F$.\nNotons que notre grille contient éventuellement des cases incolores.\nNotre ensemble de cases piégées est bloquant si et seulement si nulle case n'est à la fois rose et verte, c'est-à-dire si nulle case verte n'est située juste au-dessus ou juste à droite d'une case rose. Notre ensemble bloquant est donc minimal s'il consiste en la seule case $S$, ou bien en la seule case $F$, ou bien ne contient aucune de ces cases et si toute case noire est située juste au-dessus ou juste à droite d'une case rose, et juste en-dessous ou juste à gauche d'une case verte.\nDe la sorte, on vérifie aisément que la construction ci-dessous nous fournit un ensemble bloquant minimal composé de $n(3 n-2) \\geqslant 3 n(n-1)$ cases piégées.\n\n\nOn démontre maintenant que tout ensemble bloquant minimal contient au plus $3 n^{2}$ cases. Étant donné un tel ensemble bloquant minimal, soit $r$ le nombre de cases roses, $p$ le nombre de cases piégées et $v$ le nombre de cases vertes. Au vu de la minimalité de notre ensemble bloquant, et à part la case S , chaque case rose ou noire se trouve juste au-dessus ou juste à gauche d'une case rose. On en déduit que $r-1+p \\leqslant 2 r$, c'est-à-dire que $p \\leqslant r+1$. On démontre de même que $p \\leqslant v+1$, et on en conclut que $3 n^{2} \\geqslant(r+p+v) / 3 \\geqslant p-2 / 3$, donc que $p \\leqslant 3 n^{2}$.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ Voici une manière alternative, plus progressive mais nettement plus longue, de démontrer que tout ensemble bloquant minimal contient au plus $3 n^{2}$ cases. On suppose évidemment que cet ensemble n'est pas constitué de la seule case $S$ ou de la seule case $F$, auquel cas on aurait déjà gagné.\nOn aimerait bien découper dans la grille $3 n \\times 3 n$ des rectangles $3 \\times 1$ ou $1 \\times 3$ contenant chacun une case de chaque couleur, de sorte que les cases n'appartenant à aucun rectangle ne soient pas piégées. On disposerait alors de la borne supérieure tant désirée.\nOn commence par démontrer que la grille $3 n \\times 3 n$ ne contient aucune case incolore. En effet, si une case rose $(x, y)$ a pour voisine une case incolore, il s'agit de sa voisine de gauche ou du dessous. Quitte à effectuer une symétrie par rapport à la diagonale (SF), on suppose que c'est la voisine du dessous, c'est-à-dire $(x, y-1)$. On démontre alors par récurrence sur $k$ que les cases $(x-k, y)$ et $(x-k, y-1)$ sont rose et incolore, comme illustré ci-dessous, les cases incolores étant simplement laissées en blanc.\n\n\nEn effet,\n$\\triangleright$ la case $(x-k-1, y)$ est nécessairement rose, ce sans quoi aucune des voisines de gauche et du dessous de la case $(x-k, y)$ ne serait rose;\n$\\triangleright$ la case $(x-k-1, y-1)$ n'est ni rose (sinon sa voisine de droite serait rose), ni verte ou noire (sinon l'une de ses voisines du haut ou de droite serait verte).\nEn particulier, la case $(0, y)$ est rose tandis que la case $(0, y-1)$ est incolore, ce qui est absurde. Puis, si une case noire $(x, y)$ a pour voisine de gauche ou du dessous une case incolore, on suppose toujours, à symétrie près, que cette case incolore est $(x, y-1)$. Mais alors $(x-1, y)$ est rose et $(x-1, y-1)$ est incolore, ce qui est impossible.\nEnfin, quitte à effectuer une symétrie par rapport à la médiatrice de [SF] et à échanger les couleurs rose et verte, une case incolore ne peut pas non plus se situer en haut ou à droite d'une case noire, ni être adjacente à une case verte. Ainsi, nulle case n'est incolore.\nOn entreprend désormais de démontrer que chaque case noire, sauf les éventuels coins noirs, a soit une case rose à sa gauche et une case verte à sa droite, soit une case rose en-dessous et une case verte au-dessus. Dans les deux cas, on dira que ces trois cases forment un rectangle tricolore.\nSi une case noire est disposée sur le côté bas, sa voisine de gauche est nécessairement rose, et sa voisine de droite n'est ni rose ni noire, donc elle est verte. On traite de même les autres cases noires situées sur les côtés, et on s'intéresse désormais aux cases éloignées des côtés.\nSupposons que l'on dispose d'une case noire, disons en position $(x, y)$, dont la voisine de droite, en position $(x+1, y)$, est rose ou noire. Toute case rose ou noire a une case rose à sa\ngauche ou juste en-dessous. Par conséquent, la case $(x+1, y-1)$ est rose. De même, toute case verte ou noire a une case verte à sa droite ou juste au-dessus, donc la case ( $x, y-1$ ) est rose et la case $(x, y+1)$ est verte. La case $(x, y)$ appartient donc à un rectangle tricolore.\n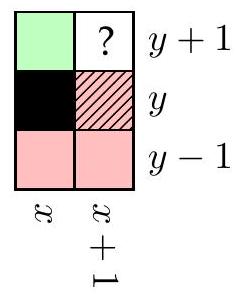\n\nQuitte à appliquer une symétrie par rapport au milieu de $[S F]$, ce qui échangera les couleurs verte et rose, on démontre de même que, si la voisine de gauche de $(x, y)$ est verte ou noire, la case $(x, y)$ appartient à un rectangle tricolore. Enfin, si la voisine de gauche de $(x, y)$ est rose et sa voisine de droite est verte, la case $(x, y)$ appartient de facto à un rectangle tricolore horizontal.\nOn peut donc, pour chaque case noire autre que les cases situées dans les coins, choisir un rectangle tricolore dont elle est la case centrale. Par ailleurs, si une case noire est située dans le coin en haut à gauche ou en bas à droite, on peut tout de même l'insérer dans un L tricolore plutôt que dans un rectangle tricolore. Il reste à étudier le cas où deux zone de notre sélection (qui seront communément des rectangles) auraient une case commune.\nSi deux rectangles tricolores partagent leur case verte, disons $(x, y)$, on est dans la situation représentée ci-dessous. Par construction, les cases $(x-1, y)$ et $(x, y-1)$ sont noires et les cases $(x-2, y)$ et $(x, y-2)$ sont roses, puis on montre que les quatre cases du carré $2 \\times 2$ situé en bas à gauche sont roses elles aussi. Cette situation est illustrée ci-dessous, à gauche, les deux rectangles étant mis en surbrillance.\n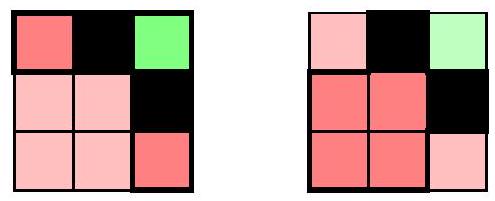\n\nOn décide alors de supprimer nos deux rectangles et les remplacer par la zone en forme de et mise en surbrillance ci-dessus, à droite. Celle-ci a certes le mauvais goût de ne plus contenir deux cases de chaque couleur, mais elle ne contient néanmoins que deux cases noires sur six. En outre, aucune case de notre motif n'appartient à un rectangle autre que ceux que nous avons supprimés, ni à un autre motif que nous aurions créé, car un tel motif est bordé par des rectangles tricolores de notre sélection sur ses côtés haut et droit.\nDe même, chaque case noire de notre motif ne sera intégrée à aucun autre motif ou rectangle, et chaque case rose du motif\nLe même phénomène peut bien sûr être mis en place si deux rectangles ont une case rose commune, auquel cas on les remplace par une zone $\\boldsymbol{\\Psi}$ formée de deux cases piégées et de quatre cases vertes n'appartenant à aucun rectangle.\nEnfin, le coin en haut à gauche est piégé, et si le L tricolore auquel il appartient partage sa case verte avec un rectangle tricolore, comme illustré ci-dessous à gauche, on le remplace par le rectangle formé des cases $(1,3 n-2),(1,3 n-1),(1,3 n)$, comme illustré ci-dessous à droite. Les autres cas d'intersection entre un L situé dans un coin et un rectangle se traitent de la même manière.\n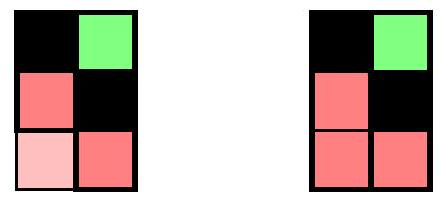\n\nEn conclusion, nous sommes parvenus à découper dans notre grille $3 n \\times 3 n$ des zones deux à deux disjointes dont chacune contient un tiers de cases piégées, et dont l'union recouvre l'ensemble des cases piégées. Ainsi, comme désiré, au plus un tiers des cases de la grille sont piégées.\n\nCommentaire des correcteurs La question a) était difficile et la question b) était très difficile, au point que seul un élève l'a résolue.\nL'idée, pour trouver la construction de la question a), était de partir d'un coloriage des lignes de la grille en rose, noir, vert, rose, noir, vert, etc, puis de le modifier à la marge pour que ce coloriage respecte les règles de l'énoncé : en-dessous ou à gauche d'une case rose ou noire se trouve une case rose, et au-dessus ou à droite d'une case noire ou verte se trouve une case verte.\nPour la question b), plusieurs élèves ont tenté des approches analogues à celle, longue et ardue, de la solution alternative. En particulier, l'affirmation selon laquelle tout carré $3 \\times 3$ de la grille contient au plus trois cases piégées est incorrecte.\nEnfin, plusieurs élèves ont eu le mauvais réflexe de regarder uniquement les cas $n=1$ et $n=2$, trouvant sans surprise des ensembles piégés minimaux à $3 n \\geqslant 3 n(n-1)$ cases. C'est bien sûr à partir de $n=3$, c'est-à-dire lorsque $3 n<3 n(n-1)$, que l'on pouvait espérer voir des ensembles bloquants minimaux pertinents.\n\n## Problèmes EGMO", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 11 |
+
{"year": "2021", "problem_label": "8", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme. Une droite $d$ passant par $C$ coupe respectivement les droites $(A B)$ et $(A D)$ en $X$ et en $Y$. Les tangentes en $X$ et en $Y$ au cercle circonscrit à $A X Y$ se coupent en un point $T$, puis la droite $(C T)$ recoupe le cercle circonscrit à $C D Y$ en un point $P$.\nDémontrer que les points $A, B, D$ et $P$ sont cocycliques.", "solution": "Dans la suite, on note $\\mathcal{C}_{\\mathcal{P}}$ le cercle circonscrit à un triangle $\\mathcal{P}$.\nPuisque $(T X)$ est tangente à $\\mathcal{C}_{A X Y}$, une chasse aux angles indique que\n\n$$\n(X T, X Y)=(A X, A Y)=(D C, D Y)=(P C, P Y)=(P T, P Y)\n$$\n\nce qui signifie que $P$ appartient à $\\mathcal{C}_{T X Y}$.\nDe même, puisque $(T Y)$ est tangente à $\\mathcal{C}_{A X Y}$, une chasse aux angles indique que\n\n$$\n(P C, P X)=(P T, P X)=(Y T, Y X)=(A Y, A X)=(B C, B X),\n$$\n\nce qui signifie que $P$ appartient à $\\mathcal{C}_{B C X}$.\nOn en conclut que\n\n$$\n(B P, B A)=(B P, B X)=(C P, C X)=(C P, C Y)=(D P, D Y)=(D P, D A)\n$$\n\nce qui signifie que $P$ appartient à $\\mathcal{C}_{A B D}$.\n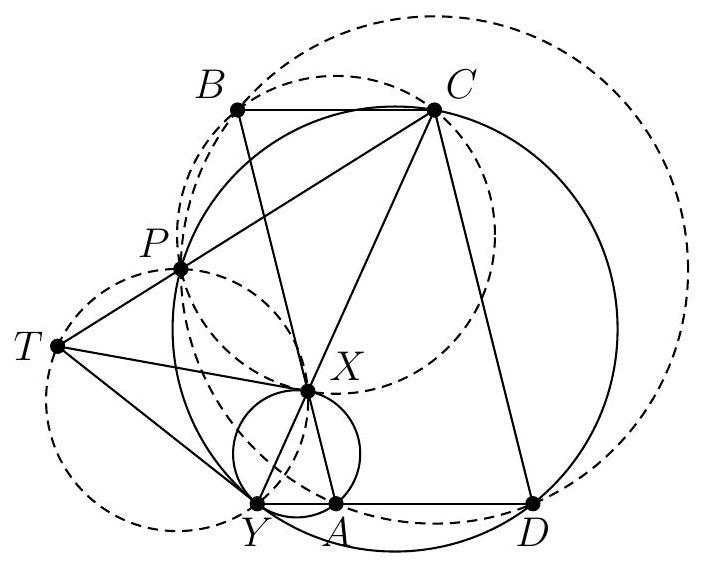", "problem_match": "\nExercice 8.", "solution_match": "\nSolution de l'exercice 8"}
|
| 12 |
+
{"year": "2021", "problem_label": "8", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme. Une droite $d$ passant par $C$ coupe respectivement les droites $(A B)$ et $(A D)$ en $X$ et en $Y$. Les tangentes en $X$ et en $Y$ au cercle circonscrit à $A X Y$ se coupent en un point $T$, puis la droite $(C T)$ recoupe le cercle circonscrit à $C D Y$ en un point $P$.\nDémontrer que les points $A, B, D$ et $P$ sont cocycliques.", "solution": "$n^{\\circ} 1$ Le tracé de la figure suggère que $(T Y)$ est tangente aux deux cercles $\\mathcal{C}_{A X Y}$ et $\\mathcal{C}_{C D Y P}$. On vérifie alors que c'est bien le cas, puisque\n\n$$\n(Y T, Y D)=(Y T, Y A)=(A Y, A X)=(D Y, D C)\n$$\n\nAinsi, $T$ est le centre radical des trois cercles $\\mathcal{C}_{A X Y}, \\mathcal{C}_{C D Y P}$ et $\\mathcal{C}_{P C X}$, et puisque l'axe radical $(T X)$ des cercles $\\mathcal{C}_{A X Y}$ et $\\mathcal{C}_{P C X}$ est tangent à $\\mathcal{C}_{A X Y}$, il est aussi tangent à $\\mathcal{C}_{P C X}$.\nOn en déduit en particulier que\n\n$$\n(P X, P C)=(X T, X C)=(X T, X Y)=(A X, A Y)=(B X, B C),\n$$\n\nde sorte que $B$ appartient à $\\mathcal{C}_{P C X}$, et que\n\n$$\n(X T, X P)=(C X, C P)=(C Y, C P)=(Y T, Y P)\n$$\n\nde sorte que $P$ appartient à $\\mathcal{C}_{T X Y}$.\nOn en conclut comme précédemment que\n\n$$\n(B P, B A)=(B P, B X)=(C P, C X)=(C P, C Y)=(D P, D Y)=(D P, D A)\n$$\n\nce qui signifie que $P$ appartient à $\\mathcal{C}_{A B D}$.\nCommentaire des correcteurs L'exercice a été bien abordé : plusieurs élèves ont proposé une solution complète et plusieurs élèves ont produit des avances significative. Le plus difficile ici était de remarquer la multitude de points cocycliques. Une bonne figure était encore une fois essentielle ici pour pouvoir effectuer des conjectures et les prouver.", "problem_match": "\nExercice 8.", "solution_match": "\nSolution alternative"}
|
| 13 |
+
{"year": "2021", "problem_label": "9", "tier": 1, "problem": "Trouver les entiers $n$ pour lesquels l'égalité\n\n$$\n\\sum_{i=1}^{n} \\sum_{j=1}^{n}\\left\\lfloor\\frac{i \\times j}{n+1}\\right\\rfloor=\\frac{n^{2}(n-1)}{4}\n$$\n\nest vérifiée.\nOn rappelle que, pour tout nombre réel $x$, la notation $\\lfloor x\\rfloor$ désigne la partie entière de $x$, c'est-à-dire le plus grand entier inférieur ou égal à $x$.", "solution": "Pour tout entier $k$, on note $r_{n+1}(k)$ le reste de la division euclidienne de $k$ par $n+1$, c'est-à-dire le plus petit entier naturel tel que $n+1$ divise $k-r_{n+1}(k)$. La double somme de gauche se réécrit alors comme\n\n$$\n\\begin{aligned}\n\\mathcal{S} & =\\sum_{i=1}^{n} \\sum_{j=0}^{n} \\frac{i j-r_{n+1}(i j)}{n+1} \\\\\n& =\\frac{1}{n+1}\\left(\\sum_{i=1}^{n} i\\right)\\left(\\sum_{j=0}^{n} j\\right)-\\frac{1}{n+1} \\sum_{i=0}^{n} \\sum_{j=0}^{n} r_{n+1}(i j) \\\\\n& =\\frac{1}{n+1} \\frac{n(n+1)}{2} \\frac{n(n+1)}{2}-\\frac{1}{n+1} \\sum_{i=0}^{n} \\sum_{j=0}^{n} r_{n+1}(i j) \\\\\n& =\\frac{n^{2}(n+1)}{4}-\\frac{1}{n+1} \\sum_{i=0}^{n} \\sum_{j=0}^{n} r_{n+1}(i j) .\n\\end{aligned}\n$$\n\nIl s'agit donc de trouver les entiers $n$ pour lesquels\n\n$$\n\\sum_{i=1}^{n} \\sum_{j=0}^{n} r_{n+1}(i j)=(n+1)\\left(\\frac{n^{2}(n+1)}{4}-\\frac{n^{2}(n-1)}{4}\\right)=\\frac{n^{2}(n+1)}{2}\n$$\n\nSoit alors $i$ un entier, puis soit $d=\\operatorname{PGCD}(i, n+1)$ et $k=(n+1) / d$ et $\\ell=i / d$. Les entiers $k$ et $\\ell$ sont premiers entre eux, donc les $k$ entiers $0, \\ell, 2 \\ell, \\ldots,(k-1) \\ell$ représentent les $k$ résidus modulo $k$, et les $k$ entiers $0, i, 2 i, \\ldots,(k-1) i$ représentent les $k$ résidus $0, d, 2 d, \\ldots,(k-1) d$ modulo $n+1=k d$. En particulier, pour tout entier $t$, on sait que\n\n$$\n\\sum_{j=k t}^{(k+1) t-1} r_{n+1}(i j)=\\sum_{j=0}^{k-1} j d=d \\frac{k(k-1)}{2}\n$$\n\nde sorte que\n\n$$\n\\sum_{j=0}^{n-1} r_{n+1}(i j)=\\sum_{t=0}^{d-1} \\sum_{j=k t}^{(k+1) t-1} r_{n+1}(i j)=d^{2} \\frac{k(k-1)}{2}=\\frac{(n+1)(n+1-d)}{2}\n$$\n\nEn particulier,\n\n$$\n\\sum_{j=0}^{n-1} r_{n+1}(i j) \\leqslant \\frac{n(n+1)}{2}\n$$\n\navec égalité si et seulement si $d=1$, donc si $i$ et $n+1$ sont premiers entre eux. Ainsi,\n\n$$\n\\sum_{i=1}^{n} \\sum_{j=0}^{n} r_{n+1}(i j) \\leqslant \\frac{n^{2}(n+1)}{2}\n$$\n\navec égalité si et seulement si $n+1$ est premier avec chacun des entiers $1,2, \\ldots, n$, c'est-à-dire si $n+1$ est un nombre premier.\nEn conclusion, les entiers recherchés sont les entiers $n$ tels que $n+1$ est premier.\n$\\underline{\\text { Solution alternative } n^{\\circ} 1}$ Dans la suite, on pose $s_{i, j}=i j /(n+1)$ et $\\mathcal{S}_{i}=\\sum_{j=1}^{n}\\left\\lfloor s_{i, j}\\right\\rfloor$. Pour tout $j \\leqslant n$, on note que $s_{i, j}+s_{i, n+1-j}=i$. Par conséquent, si l'on pose $s_{i, j}=k+x$ avec $k$ entier et $0 \\leqslant x<1$, on en déduit que\n\n$$\n\\left\\lfloor s_{i, j}\\right\\rfloor+\\left\\lfloor s_{i, n+1-j}\\right\\rfloor=\\lfloor k+x\\rfloor+\\lfloor(i-k-1)+(1-x)\\rfloor=i-1+\\lfloor 1-x\\rfloor,\n$$\n\nde sorte que $\\left\\lfloor s_{i, j}\\right\\rfloor+\\left\\lfloor s_{i, n+1-j}\\right\\rfloor \\geqslant i-1$ avec égalité si et seulement si $x \\neq 0$, c'est-à-dire si $n+1$ ne divise pas $i j$.\nOr, quand $j$ décrit l'ensemble $\\{1,2, \\ldots, n-1\\}, n+1-j$ décrit aussi cet ensemble. On en déduit que\n\n$$\n2 \\mathcal{S}_{i}=\\sum_{j=1}^{n}\\left\\lfloor s_{i, j}\\right\\rfloor+\\left\\lfloor s_{i, n+1-j}\\right\\rfloor \\geqslant \\sum_{j=1}^{n}(i-1)=n(i-1)\n$$\n\navec égalité si et seulement si $n+1$ ne divise aucun produit $i j$, c'est-à-dire si $n+1$ est premier avec $i$. On en conclut alors que\n\n$$\n\\mathcal{S}=\\sum_{i=1}^{n} \\mathcal{S}_{i} \\geqslant \\frac{n}{2} \\sum_{i=1}^{n}(i-1)=\\frac{n^{2}(n-1)}{4}\n$$\n\navec égalité si et seulement si $n+1$ est premier avec tous les entiers $i$, c'est-à-dire si $n+1$ est un nombre premier.\nAinsi, les entiers $n$ recherchés sont exactement ceux pour lesquels $n+1$ est premier.\nCommentaire des correcteurs L'exercice était difficile, et peu d'élèves ont réussi à avancer. Une vraie difficulté était de se convaincre qu'il existait des entiers $n$ arbitrairement grands pour lesquels l'énoncé était vrai. Ici, traiter les petits cas donnait une bonne intuition des $n$ solutions, mais il fallait en traiter beaucoup. Par conséquent, de de nombreuses élèves ont essayé d'utiliser des inégalités pour montrer que, lorsque $n$ était arbitrairement grand, la somme allait devenir plus grande ou plus petite que $n^{2}(n-1) / 4$. Au vu de la solution de cet exercice, cette stratégie était malheureusement vouée à l'échec.\nLes élèves ayant trouvé le problème ont fait comme dans la solution 2, dont l'astuce principale est non sans rappeler la solution du problème 16 de la coupe Animath d'automne : il est important de lire les corrigés des exercices non trouvés, car ceux-ci peuvent aider à avancer dans des problèmes très différents.", "problem_match": "\nExercice 9.", "solution_match": "\nSolution de l'exercice 9"}
|
| 14 |
+
{"year": "2021", "problem_label": "10", "tier": 1, "problem": "Soit $n$ un entier naturel. On dit qu'un ensemble fini d'entiers est $n$-équilibré s'il y a exactement $n$ manières de le partitionner en deux sous-ensembles de même somme. Par exemple, l'ensemble $\\{1,3,4,5,6,7\\}$ est 2-équilibré, car les seules manières de le partitionner en deux sous-ensembles de même somme sont de le partitionner en $\\{1,3,4,5\\}$ et $\\{6,7\\}$, ou bien en $\\{1,5,7\\}$ et $\\{3,4,6\\}$.\nTrouver tous les entiers $n \\geqslant 0$ pour lesquels il existe un ensemble $n$-équilibré.", "solution": "Tout d'abord, l'ensemble $\\{1\\}$ est 0 -équilibré et l'ensemble $\\{1,2,3\\}$ est 1-équilibré.\nÉtant donné un entier $n \\geqslant 2$, nous allons démontrer que l'ensemble\n\n$$\nE=\\{k: 3 n \\leqslant k \\leqslant 4 n-1\\} \\cup\\{k: 4 n+1 \\leqslant k \\leqslant 5 n\\} \\cup\\{8 n(n-2)\\}\n$$\n\nest $n$-équilibré. En effet, si l'on note $\\Sigma_{X}$ la somme des éléments d'un ensemble $X$, partitionner $E$ en deux sous-ensembles de même somme revient à choisir un sous-ensemble $X$ de $E$ contenant l'entier $8 n(n-2)$ et dont la somme vaut\n\n$$\n\\Sigma_{X}=\\frac{\\Sigma_{E}}{2}=\\frac{1}{2}\\left(8 n(n-2)+\\sum_{\\ell=1}^{n}((4 n-\\ell)+(4 n+\\ell))\\right)=\\frac{1}{2}\\left(8 n(n-2)+8 n^{2}\\right)=8 n(n-1)\n$$\n\nAutrement dit, cela revient à sélectionner un sous-ensemble $Y$ de $E^{\\prime}=E \\backslash\\{8 n(n-2)\\}$ pour lequel $\\Sigma_{Y}=8 n$.\nPuisque $\\max E^{\\prime}<8 n<3 \\min E^{\\prime}$, un tel ensemble $Y$ contient exactement 2 éléments. Les ensembles $Y$ recherchés sont donc les ensembles de la forme $\\{4 n-\\ell, 4 n+\\ell\\}$ avec $1 \\leqslant \\ell \\leqslant n$. Il existe $n$ tels ensembles, donc $E$ est bien $n$-équilibré, comme souhaité.\n\nCommentaire des correcteurs L'exercice était difficile, et une seule élève est parvenue à le résoudre. Une première étape consistait à étudier les petites valeurs de $n$. Ici, il est dommage que plusieurs élèves aient oublié le cas $n=0$. Une difficulté importante était ensuite de se figurer que tout entier était en fait solution. L'idée, pour le démontrer, était d'imposer l'apparition d'un ou plusieurs nombres dans l'ensemble $E$, que l'on aura préalablement choisis aussi grands que possible, de manière à se ramener à un problème légèrement plus simple : étant donné une somme $s$ et un ensemble $E$ combien y a-t-il de sous-ensembles de $E$ dont la somme vaut $s$ ?", "problem_match": "\nExercice 10.", "solution_match": "\nSolution de l'exercice 10"}
|
French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-4.jsonl
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Soit $A B C D$ un rectangle. Soit $\\omega$ le demi-cercle de diamètre $[B C]$, de sorte que le point $A$ et le demi-cercle $\\omega$ sont situés du même côté par rapport au segment $[B C]$. Le cercle de centre $B$ et de rayon $A B$ recoupe le demi-cercle $\\omega$ au point $E$. La droite $(A E)$ recoupe le demi-cercle $\\omega$ au point $F$. Montrer que $A F=B F$.", "solution": "Tout d'abord, l'énoncé nous indique que $B A=B E$, de sorte que le triangle $A B E$ est isocèle en $B$. En outre, puisque $(A B)$ est tangente à $\\omega$, on sait que\n\n$$\n\\widehat{E B A}=\\widehat{E F B}=\\widehat{A F B} .\n$$\n\nComme les triangles $A B E$ et $A F B$ ont l'angle $\\widehat{B A E}$ en commun, ils sont donc semblables. En particulier, $A F B$ est isocèle en $F$, ce qui signifie comme souhaité que $A F=B F$.\n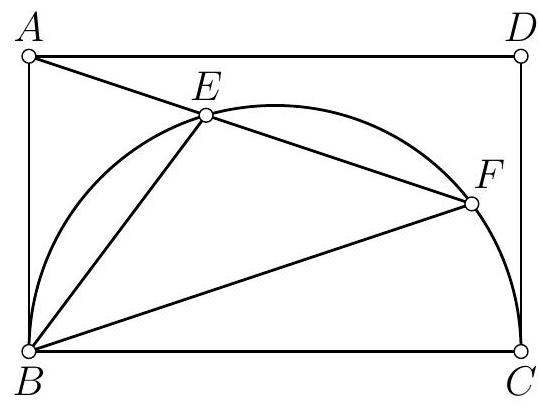\n\nCommentaire des correcteurs L'exercice est dans l'ensemble bien résolu. Toutefois, beaucoup d'élèves se sont lancés dans de grandes chasses aux angles, en introduisant beaucoup de notations et de nouveaux points. Comme le suggère le corrigé, cela n'était pas nécessaire. Systématiquement, les égalités obtenues autour de l'introduction du centre de $\\omega$ pouvaient être retrouvées en une ligne en invoquant le théorème de l'angle inscrit ou le théorème de l'angle tangentiel, puisque $(A B)$ est tangent au cercle $\\omega$.\nCertaines tentatives consistaient à regarder les symétries de la figure. Il s'agissait d'un jeu dangereux puisque, la figure semblant symétrique, on pouvait rapidement affirmer que $F$ était sur la médiatrice de $[A B]$ alors que cela était équivalent à l'énoncé. Pour ne pas tomber dans ce piège, l'étape de relecture est très importante et permet de regarder si toutes les hypothèses de l'énoncé ont bien été utilisées. Bien souvent, les tentatives infructueuses n'utilisaient tout simplement pas le point $E$.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Soit $n$ un entier tel que $n \\geqslant 3$. Lucie dispose $n$ feuilles blanches en cercle, puis elle écrit un nombre réel sur chaque feuille. Trouver tous les entiers $k$ tels que $1 \\leqslant k \\leqslant n$ pour lesquels la propriété suivante est vraie :\n\nSi au moins un des nombres qu'a écrits Lucie n'est pas nul, il existe $k$ feuilles consécutives dont la somme des nombres n'est pas nulle.", "solution": "Dans la suite, on numérote les feuilles de 1 à $n$, dans le sens des aiguilles d'une montre, et on note $x_{i}$ le nombre que Lucie écrit sur la feuille $i$. Les indices seront considérés modulo $n$. L'énoncé revient donc à trouver les entiers $k$ pour lesquels il est impossible que toute somme $\\mathcal{S}_{a}=x_{a+1}+x_{a+2}+\\ldots+x_{a+k}$ soit nulle si les $x_{i}$ ne sont pas tous nuls.\nTout d'abord, s'il existe un entier $d \\geqslant 2$ qui divise à la fois $k$ et $n$, Lucie peut choisir les nombres $x_{i}$ de sorte que $x_{i}=1$ si $i \\equiv 1(\\bmod d), x_{i}=-1$ si $i \\equiv 2(\\bmod d)$, et $x_{i}=0$ sinon. Par la suite, toute somme $\\mathcal{S}_{a}=x_{a+1}+x_{a+2}+\\ldots+x_{a+k}$ est une somme de $k / d$ nombres égaux à +1 , de $k / d$ nombres égaux à -1 , et de nombres égaux à 0 . Ainsi, $\\mathcal{S}_{a}=0$, et ce quel que soit $a$. Par conséquent, l'entier $k$ ne figure pas parmi les entiers recherchés.\nAu contraire, si $k$ est premier avec $n$, et si toute somme $\\mathcal{S}_{a}$ est nulle, nous allons démontrer que $x_{1}=x_{2}=\\ldots=x_{n}=0$. En effet, pour tout indice $a$, on constate que\n\n$$\nx_{a}=x_{a}+\\mathcal{S}_{a}=x_{a}+x_{a+1}+\\ldots+x_{a+k}=\\mathcal{S}_{a-1}+x_{a+k}=x_{a+k}\n$$\n\nOn en déduit de même que $x_{a}=x_{a+k \\ell}$ pour tous les entiers $a$ et $\\ell$. Or, puisque $k$ est premier avec $n$, le théorème de Bézout indique qu'il existe un entier $m$ tel que $k m \\equiv 1(\\bmod n)$. Par conséquent, pour tout entier $a$, on sait que\n\n$$\nx_{0}=x_{a k m}=x_{a}\n$$\n\nAinsi, les nombres $x_{i}$ sont tous égaux à $x_{0}$, et chaque somme $\\mathcal{S}_{a}$ est égale à $k x_{0}$. Si $\\mathcal{S}_{a}=0$, c'est donc que $x_{0}=0$, et que les nombres $x_{i}$ sont tous nuls.\nEn conclusion, les entiers $k$ recherchés sont les entiers premiers avec $n$.\nCommentaire des correcteurs L'exercice était accessible à condition de l'aborder sous le bon point de vue, c'est-à-dire un sous angle arithmétique. Beaucoup d'élèves ont tenté de distinguer des cas selon la positivité des termes, mais cette n'aboutit malheureusement pas. Il faut faire attention à comprendre correctement l'énoncé : un nombre non négligeable d'élèves a essayé de trouver les $k$ qui conviennent quelque soit $n$, au lieu de trouver les $k$ qui fonctionnent à $n$ fixé. Il ne faut pas non plus oublier que, dans ce genre d'exercice, il faut traiter les deux sens de l'équivalence : ici, il faut étudier le cas où $k$ et $n$ sont premiers entre eux, mais ne pas oublier le cas où ils ont un facteur commun.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Pour tout entier $n \\geqslant 1$, on note $f_{n}$ la somme de tous les restes obtenus en divisant $n$ par les nombres $1,2, \\ldots, n$. Par exemple, si on divise 5 par $1,2,3,4$ et 5 , les restes que l'on obtient sont $0,1,2,1$ et 0 , de sorte que $f_{5}=0+1+2+1+0=4$.\nTrouver tous les entiers $n \\geqslant 2$ tels que $f_{n}=f_{n-1}+n-2$.", "solution": "Pour tous les entiers $a$ et $b$ tels que $1 \\leqslant a \\leqslant b$, on note $r_{a}(b)$ le reste obtenu en divisant $b$ par $a$. Puisque\n\n$$\nf_{n}-f_{n-1}=\\sum_{i=1}^{n} r_{i}(n)-\\sum_{i=1}^{n-1} r_{i}(n-1)=\\sum_{i=2}^{n-1} r_{i}(n)-\\sum_{i=2}^{n-1} r_{i}(n-1)=\\sum_{i=2}^{n-1}\\left(r_{i}(n)-r_{i}(n-1)\\right),\n$$\n\non s'intéresse aux quantités $r_{a}(b+1)-r_{a}(b)$. On remarque alors que $r_{a}(b+1)-r_{a}(b)=1-a$ si $a$ divise $b+1$, et que $r_{a}(b+1)-r_{a}(b)=1$ sinon. Ainsi, la somme\n\n$$\nf_{n}-f_{n-1}=\\sum_{i=2}^{n-1}\\left(r_{i}(n)-r_{i}(n-1)\\right)\n$$\n\nqui est formée de $n-2$ termes inférieurs ou égaux à 1 , ne peut valoir $n-2$ que si tous ces termes valent 1 , c'est-à-dire si aucun entier $i$ tel que $2 \\leqslant i \\leqslant n-1$ ne divise $n$.\nEn conclusion, les entiers recherchés sont les nombres premiers.\nCommentaire des correcteurs Le problème pourtant difficile a été plutôt bien réussi. Néanmoins, il faut faire attention à être rigoureux : ici il fallait constater ce qui se passait pour les restes, l'énoncer rigoureusement et expliquer pourquoi cela était vrai, puis voir comment cela permettait de prouver l'énoncé. Certains se sont limités au stade du constat, et ont extrapolé que c'était vrai, ce qui est faux. Certains aussi ont constaté que l'égalité était vraie si et seulement si n est premier, et ont expliqué pourquoi si $n$ n'était pas premier c'était faux, ou ont expliqué pourquoi si $n$ est premier c'était vrai : les deux preuves sont requises pour montrer que ce sont exactement les nombres premiers les solutions.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $m$ et $n$ deux entiers tels que $m>n \\geqslant 3$. Morgane a disposé $m$ jetons en cercle, et s'apprête à les peindre en utilisant $n$ couleurs distinctes. Elle souhaite que, parmi $n+1$ jetons consécutifs, il y ait toujours au moins un jeton de chacune des $n$ couleurs. Si elle peut y parvenir, on dira que l'entier $m$ est $n$-coloriable.\nDémontrer que, pour tout entier $n \\geqslant 3$, il n'existe qu'un nombre fini non nul d'entiers $m$ qui ne sont pas $n$-coloriables, et trouver le plus grand entier $m$ qui ne soit pas $n$-coloriable.", "solution": "Tout d'abord, si $m \\geqslant n^{2}-n$, Morgane peut réaliser son souhait en procédant comme suit, montrant au passage que $m$ est $n$-coloriable.\nSoit $a$ le résidu de $m$ modulo $n$, c'est-à-dire le plus petit entier naturel tel que $a \\equiv m(\\bmod n)$. Morgane commence par placer $m-a$ jetons, qu'elle choisit de couleurs $1,2, \\ldots, n$, puis de nouveau $1,2, \\ldots, n$, etc. Ainsi, elle a placé $(m-a) / n \\geqslant n-1 \\geqslant a$ jetons de chaque couleur, comme illustré ci-dessous (à gauche) dans le cas où $n=5$ et $m=23$.\n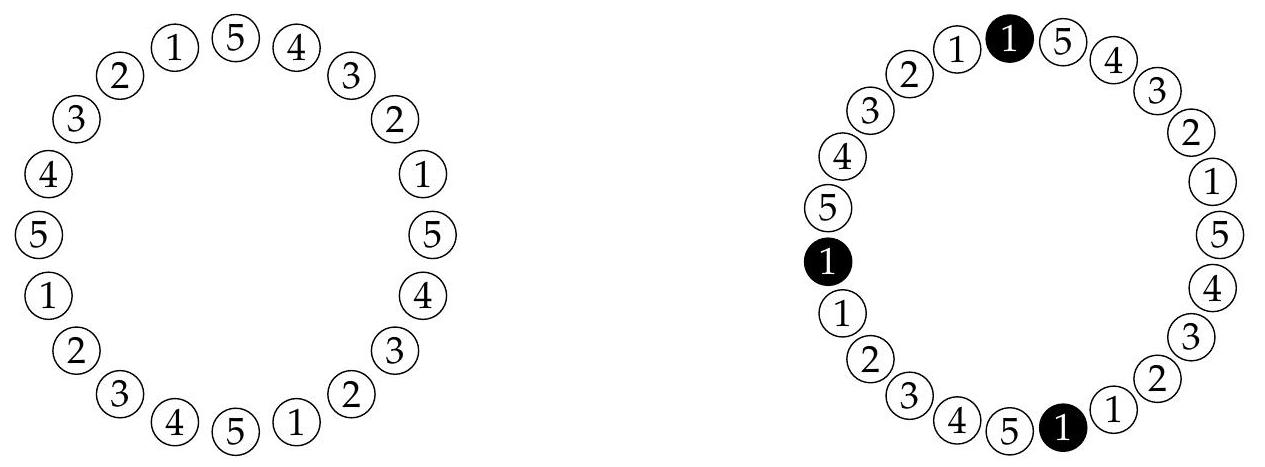\n\nPuis elle choisit $a$ jetons de couleur $m$, et insère ajoute un nouveau jeton de couleur 1 juste entre ces jetons et les jetons de couleur 1 qui suivent, comme illustré ci-dessus (à droite) dans le cas où $n=5$ et $m=23$ : nous avons dessiné en noir (avec texte blanc) les jetons ainsi insérés.\nAprès avoir procédé de la sorte, Morgane constate que toute suite de $n+1$ jetons consécutifs contient au moins $n$ jetons consécutifs de la configuration qu'elle avait obtenue avant d'insérer ses $a$ jetons surnuméraires, et ces $n$ jetons sont bien de chacune des couleurs $1,2, \\ldots, n$. Comme annoncé, l'entier $m$ est donc bien $n$-coloriable.\nRéciproquement, supposons que, partant de l'entier $m=n^{2}-n-1$, Morgane a pu parvenir a ses fins. Puisque $m / n<n-1$, l'une des couleurs, disons la couleur 1 , est représentée au plus $n-2$ fois, et au moins une fois. Morgane isole alors un jeton de couleur 1, puis sépare les $m-1=(n+1)(n-2)$ jetons restants en $n-2$ groupes de $n+1$ jetons consécutifs. Puisqu'elle est satisfaite, chacun de ces groupes contient au moins un jeton de couleur 1 : cela lui fait un minimum de $n-1$ jetons de couleur 1 en tout, ce qui est absurde!\nAinsi, l'entier $m=n^{2}-n-1$ n'est pas $n$-coloriable, et il s'agit du plus grand entier qui ne soit pas $n$-coloriable.\n\nRemarque : En adaptant le raisonnement ci-dessus, on peut démontrer qu'un entier $m$ est $n$-coloriable si et seulement s'il existe des entiers naturels $k$ et $\\ell$ tels que $m=k n+\\ell(n+1)$, c'est-à-dire si $m \\leqslant(n+1)\\lfloor m / n\\rfloor$.\n\nCommentaire des correcteurs Le problème était composé de deux parties : dans l'une, il fallait démontrer que tout entier $m \\geqslant n^{2}-n$ était de la forme $a n+b(n+1)$, donc $n$-coloriable; dans l'autre, il fallait démontrer que l'entier $m=n^{2}-n-1$ n'était pas $n$-coloriable. Chacune de ces deux parties, prise isolément, était accessible, mais beaucoup d'élèves ne sont venus à bout que de l'une ou l'autre de ces parties. En particulier, nombreux sont les élèves qui,\naprès avoir triomphé d'une des deux parties, ont prétendu réutiliser leurs arguments pour l'autre partie, alors qu'une telle stratégie échouait de manière quasi-systématique.\nAinsi, plusieurs élèves ont trouvé un algorithme de coloriage pour $m$ grand, et ont bien démontré que cet algorithme échouait pour $m=n^{2}-n-1$, mais il aurait évidemment pu être concevable que $m=n^{2}-n-1$ soit colorié d'une autre manière. De même, certains élèves ont trouvé une condition nécessaire sur $m$ pour être $n$-coloriable, démontrant ainsi que $m=n^{2}-n-1$ n'était pas $n$-coloriable, mais rien n'indiquait que cette condition était également suffisante, et donc que les entiers $m \\geqslant n^{2}-n$ étaient $n$-coloriables.\n\n## Énoncés Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Soit $m$ et $n$ deux entiers tels que $m>n \\geqslant 3$. Morgane a disposé $m$ jetons en cercle, et s'apprête à les peindre en utilisant $n$ couleurs distinctes. Elle souhaite que, parmi $n+1$ jetons consécutifs, il y ait toujours au moins un jeton de chacune des $n$ couleurs. Si elle peut y parvenir, on dira que l'entier $m$ est $n$-coloriable.\nDémontrer que, pour tout entier $n \\geqslant 3$, il n'existe qu'un nombre fini non nul d'entiers $m$ qui ne sont pas $n$-coloriables, et trouver le plus grand entier $m$ qui ne soit pas $n$-coloriable.", "solution": "Tout d'abord, si $m \\geqslant n^{2}-n$, Morgane peut réaliser son souhait en procédant comme suit, montrant au passage que $m$ est $n$-coloriable.\nSoit $a$ le résidu de $m$ modulo $n$, c'est-à-dire le plus petit entier naturel tel que $a \\equiv m(\\bmod n)$. Morgane commence par placer $m-a$ jetons, qu'elle choisit de couleurs $1,2, \\ldots, n$, puis de nouveau $1,2, \\ldots, n$, etc. Ainsi, elle a placé $(m-a) / n \\geqslant n-1 \\geqslant a$ jetons de chaque couleur, comme illustré ci-dessous (à gauche) dans le cas où $n=5$ et $m=23$.\n\n\nPuis elle choisit $a$ jetons de couleur $m$, et insère ajoute un nouveau jeton de couleur 1 juste entre ces jetons et les jetons de couleur 1 qui suivent, comme illustré ci-dessus (à droite) dans le cas où $n=5$ et $m=23$ : nous avons dessiné en noir (avec texte blanc) les jetons ainsi insérés.\nAprès avoir procédé de la sorte, Morgane constate que toute suite de $n+1$ jetons consécutifs contient au moins $n$ jetons consécutifs de la configuration qu'elle avait obtenue avant d'insérer ses $a$ jetons surnuméraires, et ces $n$ jetons sont bien de chacune des couleurs $1,2, \\ldots, n$. Comme annoncé, l'entier $m$ est donc bien $n$-coloriable.\nRéciproquement, supposons que, partant de l'entier $m=n^{2}-n-1$, Morgane a pu parvenir a ses fins. Puisque $m / n<n-1$, l'une des couleurs, disons la couleur 1 , est représentée au plus $n-2$ fois, et au moins une fois. Morgane isole alors un jeton de couleur 1, puis sépare les $m-1=(n+1)(n-2)$ jetons restants en $n-2$ groupes de $n+1$ jetons consécutifs. Puisqu'elle est satisfaite, chacun de ces groupes contient au moins un jeton de couleur 1 : cela lui fait un minimum de $n-1$ jetons de couleur 1 en tout, ce qui est absurde!\nAinsi, l'entier $m=n^{2}-n-1$ n'est pas $n$-coloriable, et il s'agit du plus grand entier qui ne soit pas $n$-coloriable.\n\nRemarque: En adaptant le raisonnement ci-dessus, on peut démontrer qu'un entier $m$ est $n$-coloriable si et seulement s'il existe des entiers naturels $k$ et $\\ell$ tels que $m=k n+\\ell(n+1)$, c'est-à-dire si $m \\leqslant(n+1)\\lfloor m / n\\rfloor$.\n\nCommentaire des correcteurs Le problème était composé de deux parties: dans l'une, il fallait démontrer que tout entier $m \\geqslant n^{2}-n$ était de la forme $a n+b(n+1)$, donc $n$-coloriable;\ndans l'autre, il fallait démontrer que l'entier $m=n^{2}-n-1$ n'était pas $n$-coloriable. Chacune de ces deux parties, prise isolément, était accessible, mais beaucoup d'élèves ne sont venus à bout que de l'une ou l'autre de ces parties. En particulier, nombreux sont les élèves qui, après avoir triomphé d'une des deux parties, ont prétendu réutiliser leurs arguments pour l'autre partie, alors qu'une telle stratégie échouait de manière quasi-systématique.\nAinsi, plusieurs élèves ont trouvé un algorithme de coloriage pour $m$ grand, et ont bien démontré que cet algorithme échouait pour $m=n^{2}-n-1$, mais il aurait évidemment pu être concevable que $m=n^{2}-n-1$ soit colorié d'une autre manière. De même, certains élèves ont trouvé une condition nécessaire sur $m$ pour être $n$-coloriable, démontrant ainsi que $m=n^{2}-n-1 \\mathrm{n}^{\\prime}$ était pas $n$-coloriable, mais rien $\\mathrm{n}^{\\prime}$ indiquait que cette condition était également suffisante, et donc que les entiers $m \\geqslant n^{2}-n$ étaient $n$-coloriables.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2021", "problem_label": "6", "tier": 1, "problem": "Une permutation des entiers 1 à 2022 est une suite $\\sigma=\\left(\\sigma_{1}, \\ldots, \\sigma_{2022}\\right)$ telle que chaque élément de l'ensemble $\\{1, \\ldots, 2022\\}$ soit égal à exactement un terme $\\sigma_{i}$. Quelle est la plus petite valeur possible que peut prendre la somme\n\n$$\n\\left\\lfloor\\frac{a_{1}}{1}\\right\\rfloor+\\left\\lfloor\\frac{a_{2}}{2}\\right\\rfloor+\\ldots+\\left\\lfloor\\frac{a_{2022}}{2022}\\right\\rfloor\n$$\n\nlorsque les entiers $a_{1}, a_{2}, \\ldots, a_{2022}$ forment une permutation des entiers de 1 à 2022 ?", "solution": "De manière générale, notons $\\mathcal{S}\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ la somme\n\n$$\n\\left\\lfloor\\frac{a_{1}}{1}\\right\\rfloor+\\left\\lfloor\\frac{a_{2}}{2}\\right\\rfloor+\\ldots+\\left\\lfloor\\frac{a_{n}}{n}\\right\\rfloor,\n$$\n\net $\\mathcal{S}_{n}$ la plus petite valeur que peut prendre $\\mathcal{S}\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ lorsque les entiers $a_{1}, a_{2}, \\ldots, a_{n}$ forment une permutation des entiers de 1 à $n$.\nÉtant donnée une telle permutation, soit $k$ l'entier tel que $a_{k}=n$. Puis, pour tout entier $i \\leqslant k$, soit $b_{i}$ le rang de l'entier $a_{i}$ au sein de l'ensemble $\\left\\{a_{1}, \\ldots, a_{k-1}\\right\\}$, c'est-à-dire le nombre d'indices $j \\leqslant k-1$ pour lesquels $a_{j} \\leqslant a_{i}$. Puisque $a_{i} \\geqslant b_{i}$, on constate alors que\n\n$$\n\\begin{aligned}\n\\mathcal{S}\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right) & \\geqslant\\left\\lfloor\\frac{a_{1}}{1}\\right\\rfloor+\\left\\lfloor\\frac{a_{2}}{2}\\right\\rfloor+\\ldots+\\left\\lfloor\\frac{a_{k}}{k}\\right\\rfloor \\\\\n& \\geqslant\\left\\lfloor\\frac{b_{1}}{1}\\right\\rfloor+\\left\\lfloor\\frac{b_{2}}{2}\\right\\rfloor+\\ldots+\\left\\lfloor\\frac{b_{k-1}}{k-1}\\right\\rfloor+\\left\\lfloor\\frac{n}{k}\\right\\rfloor \\\\\n& \\geqslant \\mathcal{S}_{k-1}+\\left\\lfloor\\frac{n}{k}\\right\\rfloor,\n\\end{aligned}\n$$\n\navec la convention selon laquelle $\\mathcal{S}_{0}=0$.\nEn outre, si $a_{1}, a_{2}, \\ldots, a_{k-1}$ est une permutation des entiers de 1 à $k-1$ pour laquelle $\\mathcal{S}\\left(a_{1}, a_{2}, \\ldots, a_{k-1}\\right)=\\mathcal{S}_{k-1}$ et si l'on pose $a_{i}=i-1$ pour tout $i \\geqslant k+1$, on a bien\n\n$$\n\\mathcal{S}\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)=\\left\\lfloor\\frac{a_{1}}{1}\\right\\rfloor+\\left\\lfloor\\frac{a_{2}}{2}\\right\\rfloor+\\ldots+\\left\\lfloor\\frac{a_{k-1}}{k-1}\\right\\rfloor+\\left\\lfloor\\frac{n}{k}\\right\\rfloor=\\mathcal{S}_{k-1}+\\left\\lfloor\\frac{n}{k}\\right\\rfloor .\n$$\n\nOn en déduit que $\\mathcal{S}_{n}=\\min \\left\\{\\mathcal{S}_{k-1}+\\lfloor n / k\\rfloor: 1 \\leqslant k \\leqslant n\\right\\}$.\nNous allons maintenant démontrer par récurrence sur $n$ que $\\mathcal{S}_{n}=\\left\\lceil\\log _{2}(n+1)\\right\\rceil$ pour tout entier $n \\geqslant 0$, ce qui nous permettra d'affirmer que $\\mathcal{S}_{2022}=\\left\\lceil\\log _{2}(2023)\\right\\rceil=11$.\nEn effet, c'est bien le cas pour $n=0$. Soit maintenant $n$ un entier naturel non nul, puis $k$ un entier tel que $1 \\leqslant k \\leqslant n$ et $\\mathcal{S}_{n}=\\mathcal{S}_{k-1}+\\lfloor n / k\\rfloor$. Si l'on pose $\\lambda=\\lfloor n / k\\rfloor$, on constate que $k>n /(\\lambda+1)$ et que\n\n$$\n2^{\\lambda}=\\sum_{i=0}^{\\lambda}\\binom{\\lambda}{i} \\geqslant\\binom{\\lambda}{0}+\\binom{\\lambda}{1}=1+\\lambda\n$$\n\nde sorte que\n\n$$\n\\mathcal{S}_{n}=\\mathcal{S}\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right) \\geqslant \\mathcal{S}_{k-1}+\\lfloor n / k\\rfloor \\geqslant \\log _{2}(k)+\\lambda>\\log _{2}\\left(2^{\\lambda} n /(\\lambda+1)\\right) \\geqslant \\log _{2}(n)\n$$\n\nCela signifie que $2^{\\mathcal{S}_{n}}>n$, ou encore que $2^{\\mathcal{S}_{n}} \\geqslant n+1$, donc que $\\mathcal{S}_{n} \\geqslant\\left\\lceil\\log _{2}(n+1)\\right\\rceil$.\nRéciproquement, soit $k=\\lceil(n+1) / 2\\rceil$ et $\\ell=\\left\\lceil\\log _{2}((n+1) / 2)\\right\\rceil$. Pusique $(n+1) / 2 \\leqslant 2^{\\ell}$, on sait aussi que $k \\leqslant 2^{\\ell}$, de sorte que\n\n$$\n\\mathcal{S}_{n} \\leqslant \\mathcal{S}_{k-1}+\\lfloor n / k\\rfloor=\\left\\lceil\\log _{2}(k)\\right\\rceil+1 \\leqslant \\ell+1=\\left\\lceil\\log _{2}(n+1)\\right\\rceil,\n$$\n\nce qui conclut la récurrence.\nCommentaire des correcteurs Le problème était difficile, et nombreux sont les élèves qui ont prétendu à tort avoir une solution complète. Beaucoup de candidats ont traité uniquement des cas particuliers, ou ne prouvent pas leurs affirmations, ce qui peut faire perdre beaucoup de points.\nAttention à bien justifier toutes ses affirmations : il vaut mieux passer un peu plus de temps sur un problème et le réussir totalement, que de tenter d'avoir des points sur un problème plus difficile (ce qui manifestement n'a pas été réussi sur le problème 7).", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2021", "problem_label": "7", "tier": 1, "problem": "Soit $\\left(a_{n}\\right)_{n \\geqslant 1}$ une suite d'entiers naturels non nuls telle que $a_{n+2 m}$ divise $a_{n}+a_{n+m}$ pour tous les entiers $m \\geqslant 1$ et $n \\geqslant 1$. Démontrer que cette suite est ultimement périodique, c'est-à-dire qu'il existe deux entiers $N \\geqslant 1$ et $d \\geqslant 1$ tels que $a_{n}=a_{n+d}$ pour tout $n \\geqslant N$.", "solution": "Supposons qu'il existe un entier $k \\geqslant 9$ tel que $a_{i}<a_{k}$ pour tout $i \\leqslant k-1$. Dans ces conditions, et pour tout entier $i<k / 2$, on sait que $a_{k-2 i}+a_{k-i}$ est un multiple de $a_{k}$ et que $a_{k-2 i}+a_{k-i}<2 a_{k}$, de sorte que $a_{k-2 i}+a_{k-i}=a_{k}$. En choisissant $i=1$, $i=2$ et $i=4$, on en déduit que\n\n$$\na_{k-8}+a_{k-4}=a_{k-4}+a_{k-2}=a_{k}=a_{k-2}+a_{k-1}\n$$\n\ndonc que $a_{k-8}=a_{k-2}$ et $a_{k-4}=a_{k-1}$.\nUne récurrence sur $\\ell$ indique alors que $a_{k-1}$ divise $a_{k-1-3 \\ell}$ pour tout $\\ell \\leqslant(k-2) / 3$, de sorte que $a_{k-1} \\leqslant \\max \\left\\{a_{1}, a_{2}, a_{3}\\right\\}$, et que $a_{k-2}$ divise $a_{k-2-6 \\ell}$ pour tout $\\ell \\leqslant(k-3) / 6$, de sorte que $a_{k-2} \\leqslant \\max \\left\\{a_{1}, a_{2}, \\ldots, a_{6}\\right\\}$. On en conclut que\n\n$$\na_{k}=a_{k-1}+a_{k-2} \\leqslant 2 \\max \\left\\{a_{1}, a_{2}, \\ldots, a_{6}\\right\\}\n$$\n\nPar conséquent, la suite $\\left(a_{n}\\right)_{n \\geqslant 1}$ est bornée.\nSoit $\\lambda$ la valeur maximale que prend infiniment souvent la suite $\\left(a_{n}\\right)_{n \\geqslant 1}$, et soit $\\kappa \\geqslant 0$ un entier tel que $a_{n} \\leqslant \\lambda$ pour tout $n \\geqslant \\kappa+1$. Quitte à oublier les $\\kappa$ premiers termes de la suite, c'est-à-dire à remplacer chaque terme $a_{n}$ par le terme $\\hat{a}_{n}=a_{n+\\kappa}$, ce qui ne change rien à l'énoncé, on suppose que $\\kappa=0$, c'est-à-dire que $a_{n} \\leqslant \\lambda$ pour tout $n \\geqslant 1$.\nConsidérons l'ensemble $\\mathcal{E}=\\left\\{k \\geqslant 1: a_{k}=\\lambda\\right\\}$, puis trois éléments consécutifs $k<\\ell<m$ de $\\mathcal{E}$. Si $k \\equiv \\ell(\\bmod 2)$, on sait que $\\lambda=a_{\\ell}$ divise $a_{k}+a_{(k+\\ell) / 2}=\\lambda+a_{(k+\\ell) / 2}$, donc que $a_{(k+\\ell) / 2}=\\lambda$, en contradiction avec le fait que $k$ et $\\ell$ étaient des éléments consécutifs de $\\mathcal{E}$.\nOn en déduit que $k \\not \\equiv \\ell(\\bmod 2)$ et, de même, que $\\ell \\not \\equiv m(\\bmod 2)$. Mais alors $\\lambda=a_{m}$ divise $a_{k}+a_{(k+m) / 2}=\\lambda+a_{(k+m) / 2}$, donc $a_{(k+m) / 2}=\\lambda$, et $(k+m) / 2$ est un élément de $\\mathcal{E}$ compris entre $k$ et $m$, de sorte que $(k+m) / 2=\\ell$. Cela signifie que $\\ell-k=m-\\ell$ et, plus généralement, que les éléments de $\\mathcal{E}$ forment une progression arithmétique infinie, dont on note $d$ la raison.\nEnfin, soit $n \\geqslant 1$ un entier quelconque, puis soit $m \\geqslant 1$ un entier tel que $m+n \\in \\mathcal{E}$. Alors $\\lambda=a_{m+n}$ divise $a_{n}+a_{m}$, et $m+n+d \\in \\mathcal{E}$, donc $\\lambda=a_{m+n+d}$ divise $a_{n+d}+a_{m}$. On en conclut que $a_{n} \\equiv-a_{m} \\equiv a_{n+d}(\\bmod \\lambda)$. Comme $a_{n}$ et $a_{n+d}$ sont compris entre 1 et $\\lambda$, cela signifie que $a_{n}=a_{n+d}$. Par conséquent, la suite $\\left(a_{n}\\right)_{n \\geqslant 1}$ est $d$-périodique, ce qui conclut.\n\nCommentaire des correcteurs Le problème était extrêmement difficile, et un seul élève a obtenu des points. Des élèves ont eu de bons réflexes pour commencer mais n'ont pas réussi à avancer suffisamment. Attention cependant aux erreurs sur les propriétés arithmétique de base : ce n'est pas parce que $a$ divise $b+c$ que $a$ divise $\\operatorname{PGCD}(b, c)$, surtout si $a=b+c$. De même, si $a$ divise $b-c$, on a certes $a \\leqslant|b-c|$, mais uniquement à condition que $b$ soit différent de $c$ !", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
French_TST_Senior/segmented/fr-2021-2022-Corrigé-Web-Test-5.jsonl
ADDED
|
@@ -0,0 +1,10 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2021", "problem_label": "1", "tier": 1, "problem": "Trouver tous les entiers naturels non nuls $a, b$ et $c$ pour lesquels il existe des entiers naturels non nuls $x, y$ et $z$ tels que $x!=a b+1, y!=b c+1$ et $z!=c a+1$.\nRemarque : Pour tout entier naturel non nul $n$, l'entier $n!$ désigne le produit $1 \\times 2 \\times \\cdots \\times n$.", "solution": "Soit $(a, b, c)$ un triplet solution éventuel. Sans perte de généralité, et puisque $a, b$ et $c$ jouent des rôles symétriques, on suppose que $a \\leqslant b \\leqslant c$, de sorte que $x \\leqslant z \\leqslant y$ et que $x$ ! divise à la fois $y!$ et $z!$.\nSoit $d$ un diviseur de $x$ !, $c^{\\prime}$ est-à-dire un diviseur commun à $x!$, $y$ ! et $z$ !. Puisque\n\n$$\na b \\equiv b c \\equiv c a \\equiv-1 \\quad(\\bmod d),\n$$\n\non sait que\n\n$$\n-1 \\equiv(a b)(b c)(c a) \\equiv(a b c)^{2} \\quad(\\bmod d)\n$$\n\nest un carré modulo $d$. Or, -1 n'est pas un carré modulo 3 . Ainsi, $d \\neq 3$, ce qui signifie que $x \\leqslant 2$.\nComme $x!=a b+1 \\geqslant 2>1$ !, on en conclut que $x=2$, de sorte que $a b=x!-1=1$, donc que $a=b=1$. Le triplet $(a, b, c)$ est donc, à permutation près, égal au triplet $(1,1, z!-1)$.\nRéciproquement, tout triplet de la forme $(1,1, z!-1)$ convient manifestement.\nCommentaire des correcteurs L'exercice a été très peu réussi : en effet, beaucoup d'élèves ont indûment supposé que le nombre $n!-1$ était un nombre premier pour tout $n \\geqslant 1$. C'est faux, par exemple pour $n=5$, car $5!-1=119=7 \\times 17$. Certains élèves ont essayé d'appliquer le théorème de Wilson, sans grand succès : ici, ce théorème ne permettait pas d'avancer, car il ne permet pas de déterminer $x, y$ et $z$ en fonction de $a, b$ et $c$ ou inversement.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2021", "problem_label": "2", "tier": 1, "problem": "Le gouvernement de Bosnie-Herzégovine a décidé de mettre en place un nouveau système de plaques d'immatriculations. Chaque plaque d'immatriculation devra contenir 8 chiffres, chacun pouvant valoir $0,1,2,3,4,5,6,7,8$ ou 9 . En outre, deux plaques d'immatriculation distinctes devront toujours avoir au moins deux chiffres différents. Par exemple, s'il met en circulation la plaque 00000000 , le gouvernement ne pourra pas mettre en circulation la plaque 00010000 .\nTrouver le nombre maximum de plaques d'immatriculation que le gouvernement peut mettre en circulation.", "solution": "Nous allons montrer que le nombre maximal de plaques disponibles est égal à $10^{7}$.\nTout d'abord, on dit que deux plaques font partie de la même famille si leur sept premiers chiffres sont différents. Chaque famille contient dix plaques, donc il y a $10^{7}$ familles distinctes. Or, le gouvernement ne peut pas mettre en circulation plus d'une plaque par famille. Il met donc en circulation au plus $10^{7}$ plaques.\nRéciproquement, il peut se débrouiller pour créer $10^{7}$ plaques en procédant comme suit : le dernier chiffre de chaque plaque est égal à l'opposé de la somme, modulo 10, des sept premiers chiffres de la plaque. Ainsi, il crée bien une plaque par famille.\nEn outre, la somme des chiffres de chaque plaque est divisible par 10. Mais si deux plaques ont exactement un chiffre de différence, les sommes de leurs chiffres ne peuvent être égales l'une à l'autre (modulo 10). Ainsi, deux plaques distinctes ont toujours au moins deux chiffres de différence, ce qui conclut.\n\nCommentaire des correcteurs Cet exercice difficile n'a été résolu intégralement que par un seul élève. Plusieurs élèves ont trouvé des constructions ou bornes inférieures intéressantes, leur permettant par exemple d'affirmer que l'on pourrait mettre en place au moins $10^{4}$ ou $8!=40320$ plaques d'immatriculation.\nCependant, très peu d'élèves ont réussi à obtenir la construction adéquate permettant d'atteindre $10^{7}$ plaques. Le moyen le plus sûr d'obtenir une telle construction consistait à regarder ce qui se passait si on avait droit à 1 chiffre, puis 2 chiffres, puis 3 chiffres, et à repérer des motifs réguliers qui apparaissaient dans toutes les copies concernées : un entier était égal à la somme des autres.\nPar ailleurs, et indépendamment, très peu d'élèves ont entrepris de trouver une borne supérieure sur le nombre de plaques possibles, alors même qu'une simple application du principe des tiroirs suffisait ici et que de nombreux élèves semblaient en avoir l'intuition. Il est toujours dommage de ne pas chercher des bornes supérieures et inférieures quand on cherche à évaluer une quantité, et même si ces bornes ne sont pas nécessairement faciles à trouver.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Soit $x, y$ et $z$ trois nombres réels tels que $x^{2}+y^{2}+z^{2}=1$. Trouver les valeurs minimale et maximale possibles du nombre réel $x y+y z-z x$.", "solution": "En vertu de l'identité\n\n$$\n(x-y+z)^{2}=x^{2}+y^{2}+z^{2}-2(x y+y z-z x)=1-2(x y+y z-z x),\n$$\n\nil s'agit ici de trouver les valeurs extrêmes que peut prendre le nombre $(x-y+z)^{2}$.\nTout d'abord, puisque $(x-y+z)^{2} \\geqslant 0$, avec égalité lorsque $x=y=1 / \\sqrt{2}$ et $z=0$, on a bien\n\n$$\nx y+y z-z x=\\frac{1-(x-y+z)^{2}}{2} \\leqslant \\frac{1}{2}\n$$\n\navec égalité lorsque $x=y=1 / \\sqrt{2}$ et $z=0$.\nEn outre, l'inégalité de Cauchy-Schwarz indique que\n\n$$\n(x-y+z)^{2} \\leqslant\\left(x^{2}+y^{2}+z^{2}\\right) \\times\\left(1^{2}+(-1)^{2}+1^{2}\\right)=3,\n$$\n\navec égalité si et seulement si les triplets $(x, y, z)$ et $(1,-1,1)$ sont colinéaires. Par conséquent, on a bien\n\n$$\n(x y+y z-z x)=\\frac{1-(x-y+z)^{2}}{2} \\geqslant \\frac{1-3}{2}=-1\n$$\n\navec égalité lorsque $x=-y=z=1 / \\sqrt{3}$.\nEn conclusion, les valeurs extrémales recherchées sont -1 et $1 / 2$.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2021", "problem_label": "3", "tier": 1, "problem": "Soit $x, y$ et $z$ trois nombres réels tels que $x^{2}+y^{2}+z^{2}=1$. Trouver les valeurs minimale et maximale possibles du nombre réel $x y+y z-z x$.", "solution": "$n^{\\circ} 1$ On peut aussi démontrer l'inégalité $x y+y z-z x \\geqslant-1$ comme suit. Il s'agit d'appliquer directement l'inégalité de Cauchy-Schwarz aux triplets $(x, y, z)$ et $(y, z,-x)$, pour constater que\n\n$$\n(x y+y z-z x)^{2} \\leqslant\\left(x^{2}+y^{2}+z^{2}\\right)^{2}=1\n$$\n\ndonc que $x y+y z-z x \\geqslant-1$.\nPar la suite, on est dans le cas d'égalité si et seulement s'il existe un réel $\\lambda$ tel que $(x, y, z)=$ $\\lambda(y, z,-x)$. Mais alors les quatre réels $x, y, z$ et $\\lambda$ sont non nuls et $x y z=-\\lambda^{3} x y z$, donc $\\lambda=-1$ et $x=-y=z= \\pm 1 / \\sqrt{3}$, auquel cas on a bien $x y+y z-z x=-1$.\n\nCommentaire des correcteurs Cet exercice a rencontré un succès mitigé. On peut distinguer quelques bons réflexes : tester des valeurs particulières de $x, y$ et $z$ pour se faire une idée, chercher à contrôler le produit de deux nombres par la somme des carrés... À l'inverse, on donne ici les deux défauts majeurs rencontrés dans les copies des élèves:\n$\\triangleright$ Beaucoup d'élèves cherchent à argumenter que l'extremum est forcément atteint dans une situation où les $x, y$ et $z$ atteindrait des valeurs extrémales. Cette argumentation est souvent constituée d'un raisonnement purement qualitatif : «il faut que $x y$ soit petit, donc on prend $x$ et $y$ tels qu'il soit le plus petit possible pour atteindre l'extremum ». Le problème de ce raisonnement est qu'il ne tient pas compte des effets possibles de compensation : choisir $x$ et $y$ de sorte que $x y$ soit minimal peut forcer $z$, et donc les termes $y z$ et $-y z$, à être très grands, ce qui compensera la minimisation de $x y$. Ainsi, chercher à minimiser les termes un par un ne permet pas en général d'obtenir le minimum de l'expression totale.\nLa façon la plus efficace, la plus fiable et la plus convaincante de montrer qu'une expression atteint un minimum est de faire des inégalités qui sont valables pour tous les $(x, y, z)$ satisfaisant l'hypothèse de départ. Plusieurs solutions contenaient des longs paragraphes explicatifs, alors qu'on attend ici des calculs.\n$\\triangleright$ Pratiquement tous les élèves qui ont réussi à obtenir une borne ont oublié de montrer que celle-ci était bien atteinte. Il est très bien de montrer que l'expression considérée est inférieure ou égale à 3 , mais si il n'existe pas de $(x, y, z)$ tels que $x y+y z-z x=3$, alors 3 n'est pas notre maximum. Cet oubli était systématiquement pénalisé d'un point, ce qui est vraiment dommage pour les élèves qui avaient fait le plus gros du travail.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution alternative"}
|
| 5 |
+
{"year": "2021", "problem_label": "4", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme tel que $A C=B C$. Soit $P$ un point situé sur le prolongement du segment $[A B]$ au-delà de $B$. Soit $Q$ le point d'intersection, autre que $D$, entre le segment $[P D]$ et le cercle circonscrit à $A C D$. Soit ensuite $R$ le point d'intersection, autre que $P$, entre le segment $[P C]$ et le cercle circonscrit à $A P Q$.\nDémontrer que les droites $(A Q),(B R)$ et $(C D)$ sont concourantes.", "solution": "Tout d'abord, on constate que\n\n$$\n(R A, R C)=(R A, R P)=(Q A, Q P)=(Q A, Q D)=(C A, C D)=(A C, A B)=(B A, B C)\n$$\n\nce qui signifie que les points $A, B, C$ et $R$ sont cocycliques.\nDe même, si l'on note $X$ le point d'intersection des droites $(A Q)$ et $(C D)$, on constate que\n\n$$\n(Q R, Q X)=(Q R, Q A)=(P R, P A)=(C R, C X)\n$$\n\nce qui signifie que les points $C, Q, R$ et $X$ sont cocycliques.\nOn en conclut que\n\n$$\n(R C, R X)=(Q C, Q X)=(Q C, Q A)=(D C, D A)=(B A, B C)=(A C, A B)=(R C, R B)\n$$\n\nce qui signifie que, comme annoncé, les points $B, R$ et $X$ sont alignés.\n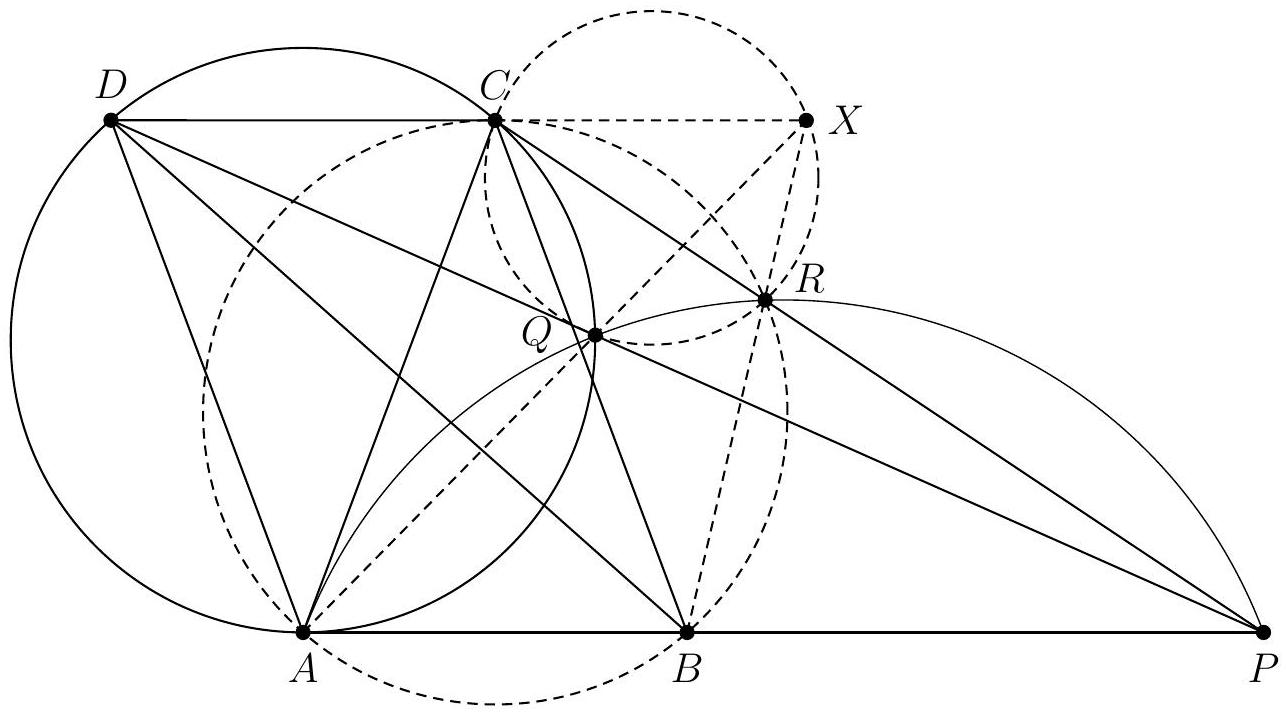\n\nCommentaire des correcteurs Si l'exercice n'a été résolu en entier par aucun élève, quelques élèves courageux ont développé des idées très intéressantes : abordé le problème sous l'angle des axes radicaux, montré que des points étaient cocycliques etc...Tous les élèves qui ont rendu une tentative ont fait preuve d'initiative, ont tracé une figure sur laquelle ils pouvaient raisonnablement effectuer des conjectures (et sur laquelle les correcteurs ont pu suivre leur raisonnement) et ont démarré un raisonnement dans le but d'aller vers la solution. Même si cela ne rapportait pas toujours des points, c'est le genre d'effort qui permettra à ces élèves de progresser sur la durée.\n\n## Énoncés Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 6 |
+
{"year": "2021", "problem_label": "5", "tier": 1, "problem": "Soit $A B C D$ un parallélogramme tel que $A C=B C$. Soit $P$ un point situé sur le prolongement du segment $[A B]$ au-delà de $B$. Soit $Q$ le point d'intersection, autre que $D$, entre le segment $[P D]$ et le cercle circonscrit à $A C D$. Soit ensuite $R$ le point d'intersection, autre que $P$, entre le segment $[P C]$ et le cercle circonscrit à $A P Q$.\nDémontrer que les droites $(A Q),(B R)$ et $(C D)$ sont concourantes.", "solution": "Tout d'abord, on constate que\n\n$$\n(R A, R C)=(R A, R P)=(Q A, Q P)=(Q A, Q D)=(C A, C D)=(A C, A B)=(B A, B C),\n$$\n\nce qui signifie que les points $A, B, C$ et $R$ sont cocycliques.\nDe même, si l'on note $X$ le point d'intersection des droites $(A Q)$ et ( $C D)$, on constate que\n\n$$\n(Q R, Q X)=(Q R, Q A)=(P R, P A)=(C R, C X)\n$$\n\nce qui signifie que les points $C, Q, R$ et $X$ sont cocycliques.\nOn en conclut que\n\n$$\n(R C, R X)=(Q C, Q X)=(Q C, Q A)=(D C, D A)=(B A, B C)=(A C, A B)=(R C, R B)\n$$\n\nce qui signifie que, comme annoncé, les points $B, R$ et $X$ sont alignés.\n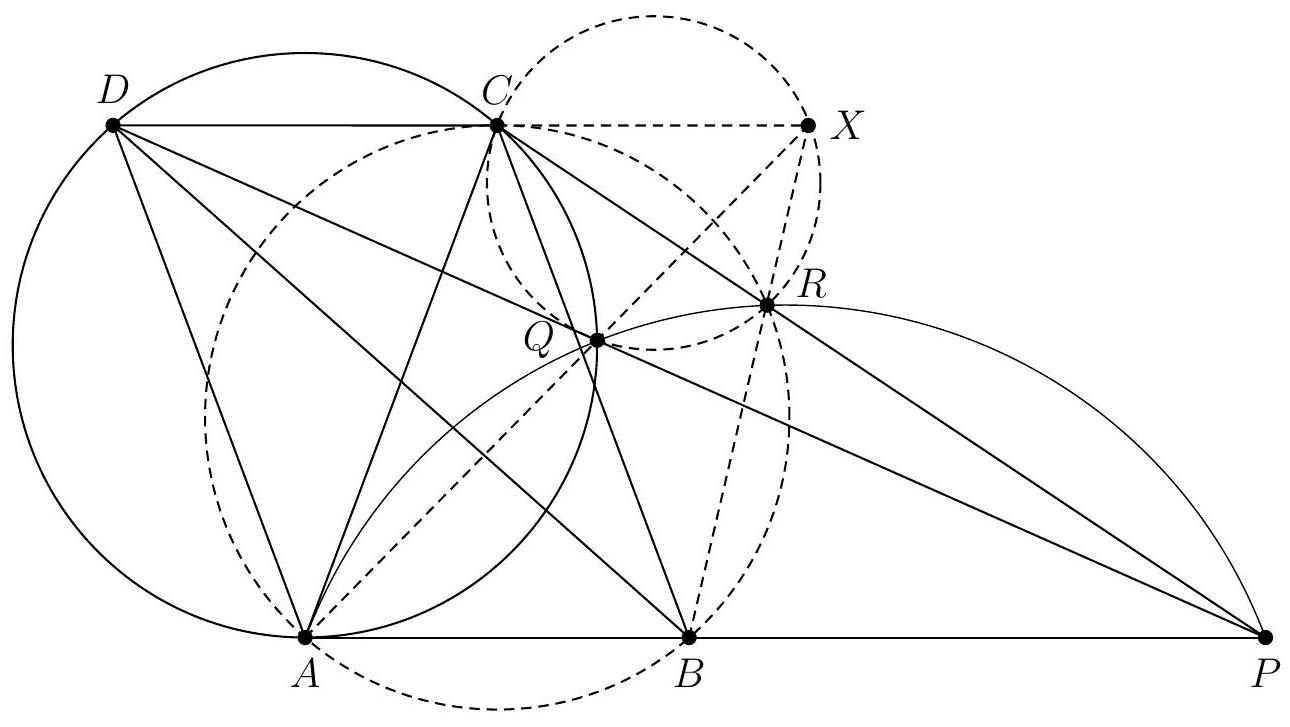\n\nCommentaire des correcteurs L'exercice est plutôt bien réussi. Il est à noter que beaucoup d'élèves ont tenté, avec plus ou moins de succès, une approche avec de la géométrie dynamique.\nDans un tel problème, où il faut montrer que trois objets concourent, il est toujours possible de faire des erreurs de raisonnement, par exemple en utilisant une propriété qui est apparente sur la figure mais que l'on n'a pas encore démontrée et qui génère un raccourci dans la solution. Ainsi, plusieurs élèves se sont retrouvés à montrer l'énoncé sans même utiliser tous les points de la figure. Pour pallier ce danger, quelques élèves ont tracé des figures volontairement inexactes (sans pour autant perdre en propreté), sur lesquelles par exemple les droites $(C D),(A Q)$ et $(B R)$ ne sont pas concourantes, en plus de leur figure de départ, pour être sûr de ne pas supposer sans le vouloir la concourance des trois droites dans leur résolution. Ces initiatives et le niveau global des élèves sur le problème nous confortent dans l'idée que les élèves sont armés pour affronter les problèmes de compétitions internationales.", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 7 |
+
{"year": "2021", "problem_label": "6", "tier": 1, "problem": "Un chasseur et un lapin invisible jouent sur une grille infinie à maille carrée, c'est-à-dire où chaque case a quatre voisines : à gauche, à droite, en haut et en bas. Tout d'abord, le chasseur colorie chaque case de la grille, mais ne peut utiliser qu'un nombre fini de couleurs. Le lapin choisit ensuite une case de la grille, qui sera son point de départ. Il commence alors à se déplacer : chaque minute, il indique au chasseur la couleur de la case sur laquelle il se trouve, puis il se déplace sur une des quatre cases adjacentes. Évidemment, comme il est invisible, les seules informations auxquelles le chasseur a accès sont les couleurs que le lapin annonce chaque minute juste avant de se déplacer.\nLe chasseur gagne si, au bout d'une durée finie,\n$\\triangleright$ il peut identifier la case que le lapin avait initialement choisie, ou bien si\n$\\triangleright$ le lapin revient en une case où il s'était déjà trouvé précédemment.\nLe chasseur dispose-t-il d'une stratégie gagnante?", "solution": "Le chasseur dispose en effet d'une stratégie gagnante, par exemple celle que nous donnons ci-dessous. Tout d'abord, il identifie la grille à l'ensemble $\\mathbb{Z}^{2}$, puis il associe à chaque case $\\mathbf{c}=(x, y)$ le triplet $\\varphi(\\mathbf{c})=(x, y, x+y)$.\nChaque fois que le lapin se déplace, deux composantes du triplet $\\varphi \\mathbf{( c )}$ varient de $\\pm 1$, et la troisième composante ne change pas. En outre, connaître deux des coordonnées de $\\varphi(\\mathbf{c})$ suffit à identifier c. En particulier, s'il existe un ensemble fini $E$ tel que, à tout moment, le lapin se trouve en une case c telle que deux des composantes (au moins) de $\\varphi(\\mathbf{c})$ soient dans $E$, on sait que lapin est contraint d'évoluer dans un ensemble fini de cases, ce qui entraînera immanquablement sa défaite et sa transformation en civet.\nOn sait donc qu'au moins deux des trois composantes de $\\varphi(\\mathbf{c})$ prendront une infinité de valeurs. Si le chasseur parvient à identifier, à un instant donné, les valeurs prises par ces composantes, il en déduira la position réelle du lapin et aura donc gagné.\nCe faisant, le chasseur s'est ramené au problème unidimensionnel suivant : étant donné un lapin invisible qui se déplace sur l'axe $\\mathbb{Z}$ par pas de $-1,0$ ou +1 et qui est contraint à passer par une infinité d'entiers, comment colorier $\\mathbb{Z}$ en usant d'un nombre fini de couleurs peut-il permettre au chasseur d'identifier la position initiale du lapin le long de cet axe? Une fois un tel coloriage col: $\\mathbb{Z} \\rightarrow\\{0,1, \\ldots, \\kappa-1\\}$ utilisant $\\kappa$ couleurs numérotées de 0 à $\\kappa-1$, le chasseur n'aura plus qu'à utiliser $\\kappa^{3}$ couleurs, identifiées aux éléments de l'ensemble $\\{0,1, \\ldots, \\kappa-1\\}^{3}$, et à colorier la case $\\mathbf{c}=(x, y)$ avec la couleur $(\\operatorname{col}(x), \\operatorname{col}(y), \\operatorname{col}(x+y))$.\nPour répondre à ce nouveau problème unidimensionnel, le chasseur colorie $\\mathbb{Z}$ en utilisant trois couleurs, numérotées de 1 et à 3 , et peint en couleur $c$ tous les entiers $n$ tels que $n \\equiv c(\\bmod 3)$. De la sorte, il sait à tout instant si le lapin se déplace vers la gauche ou vers la droite.\nPuis il repeint avec la couleur 4 les entiers, préalablement de couleur 3, qui sont de la forme $3 \\times(-3)^{n}$ avec $n$ entier naturel. Ainsi, il ne perd pas son information précédente sur la valeur des cases modulo 3 , ni sur la valeur $(-1,0$ ou +1 ) des mouvements du lapin. Par conséquent, si jamais il arrive à identifier la position du lapin à un moment donné, il connaît sa position à tout moment du jeu.\nEnfin, le lapin passera par deux éléments consécutifs de l'ensemble $\\mathcal{E}=\\left\\{3 \\times(-3)^{n}: n \\geqslant 0\\right\\}$. Si ces deux éléments sont $3 \\times(-3)^{n}$ et $3 \\times(-3)^{n+2}$, la différence entre eux, en valeur absolue, est $8 \\times 3^{n}$. Si ce sont 3 et -9 , cette différence, en valeur absolue, est égale à 12 . Par conséquent, après que le lapin est passé par deux éléments consécutifs de $\\mathcal{E}$, le chasseur identifie aisément ces deux éléments et, en fonction des variations de position du lapin, l'élément de $\\mathcal{E}$ en lequel le lapin vient d'arriver. Il en déduit alors la position initiale du lapin, ce qui lui permet de gagner le jeu unidimensionnel, donc de gagner le jeu bidimensionnel d'origine.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 8 |
+
{"year": "2021", "problem_label": "6", "tier": 1, "problem": "Un chasseur et un lapin invisible jouent sur une grille infinie à maille carrée, c'est-à-dire où chaque case a quatre voisines : à gauche, à droite, en haut et en bas. Tout d'abord, le chasseur colorie chaque case de la grille, mais ne peut utiliser qu'un nombre fini de couleurs. Le lapin choisit ensuite une case de la grille, qui sera son point de départ. Il commence alors à se déplacer : chaque minute, il indique au chasseur la couleur de la case sur laquelle il se trouve, puis il se déplace sur une des quatre cases adjacentes. Évidemment, comme il est invisible, les seules informations auxquelles le chasseur a accès sont les couleurs que le lapin annonce chaque minute juste avant de se déplacer.\nLe chasseur gagne si, au bout d'une durée finie,\n$\\triangleright$ il peut identifier la case que le lapin avait initialement choisie, ou bien si\n$\\triangleright$ le lapin revient en une case où il s'était déjà trouvé précédemment.\nLe chasseur dispose-t-il d'une stratégie gagnante?", "solution": "$n^{\\circ} 1$ Afin de suivre à la trace les mouvements du lapin, et au lieu de superposer trois pavages unidimensionnels utilisant chacun trois couleurs, le chasseur aurait tout aussi bien pu utiliser une coloration du plan en cinq couleurs, avec la fonction de coloriage $\\operatorname{col}(x, y)=x+2 y(\\bmod 5)$.\nVoici ce que donnent les deux coloriages obtenus. Dans la grille de gauche, chaque case contient trois entiers, qui représentent les couleurs (entre 0 et 2 ) associés aux jeux unidimensionnels horizontal, vertical et diagonal. Dans la grille de gauche, chaque case contient un unique entier entre 0 et 4 .\n\n| | | | | | | ${ }^{0} 0$ |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| | | | | | | ${ }^{0} 2$ |\n| $1$ | | | | | 0 | |\n| | | | | | | ${ }_{0}$ |\n| | | | | | | ${ }^{0} 2$ |\n| $1$ | | | | | | |\n| $0$ | $0$ | | 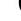 | $0_{1}$ | ${ }^{2} 0_{2}$ | ${ }^{0}$ |\n\n\n| 2 | 3 | 4 | 0 | 1 | 2 | 3 |\n| :--- | :--- | :--- | :--- | :--- | :--- | :--- |\n| 0 | 1 | 2 | 3 | 4 | 0 | 1 |\n| 3 | 4 | 0 | 1 | 2 | 3 | 4 |\n| 1 | 2 | 3 | 4 | 0 | 1 | 2 |\n| 4 | 0 | 1 | 2 | 3 | 4 | 0 |\n| 2 | 3 | 4 | 0 | 1 | 2 | 3 |\n| 0 | 1 | 2 | 3 | 4 | 0 | 1 |\n\nEn revanche, disposer de bandes orientées dans trois directions distinctes et arbitrairement espacées les unes des autres s'avérait, en pratique, nécessaire pour savoir ensuite où était passé le lapin.\n\nCommentaire des correcteurs L'exercice a été peu réussi : de nombreux élèves ont cherché à montrer que le lapin gagnait, ce qui malheureusement était faux et ne permettait pas de développer des idées intéressantes. Beaucoup d'élèves affirment que, puisque le lapin peut trouver des colonnes (ou des chemins) qui sont identiques sur un nombre aussi grand de cases que voulu, alors le lapin gagne. Cependant, cette assertion admet de nombreux contre-exemples : en effet, comme le moment où le chasseur décide d'affirmer où est le lapin dépend des premières couleurs vues, cela ne constitue en rien une contradiction. Et on peut construire très facilement (comme dans le corrigé) un système de colonnes où le lapin ne peut pas rester au sein de deux colonnes différentes sans se faire attraper.\nParmi les élèves qui n'étaient pas convaincus de qui gagnait, très peu ont essayé de donner des coloriages intelligents au chasseur : il est dangereux, dans un problème comme celui-ci, de ne traiter qu'un cas, car très souvent il est impossible d'obtenir des points en essayant de trouver une stratégie pour un joueur qui n'a pas de stratégie gagnante. Il faut donc prudemment, dans un problème de jeu complexe, essayer de trouver des stratégies pour chacun, afin de voir si la stratégie marche à coup sûr, où si l'adversaire a des moyens de la contrer. Ici, grappiller des points en donnant des informations intéressantes utilisables par le chasseur était tout à fait envisageable, même sans avoir trouvé un coloriage qui lui permettait de gagner.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 9 |
+
{"year": "2021", "problem_label": "7", "tier": 1, "problem": "Soit $n$ un entier supérieur ou égal à 2 , et soit $a_{1}, a_{2}, \\ldots, a_{n}$ des réels strictement positifs tels que $a_{1}+a_{2}+\\ldots+a_{n}=1$. Démontrer que\n\n$$\n\\sum_{k=1}^{n} \\frac{a_{k}}{1-a_{k}}\\left(a_{1}+a_{2}+\\ldots+a_{k-1}\\right)^{2}<\\frac{1}{3}\n$$", "solution": "Pour tout entier $k$, puisque $0<a_{k}<1$, on pose $s_{k}=a_{1}+a_{2}+\\ldots+a_{k}$ et $b_{k}=a_{k} s_{k-1}^{2} /\\left(1-a_{k}\\right)$, avec la convention selon laquelle $s_{0}=0$. Nous allons démontrer l'inégalité\n\n$$\nb_{k}<\\left(s_{k}^{3}-s_{k-1}^{3}\\right) / 3\n$$\n\nCelle-ci découle du fait que\n\n$$\n\\text { (1) } \\begin{aligned}\n& \\Leftrightarrow 0<\\left(1-a_{k}\\right)\\left(\\left(s_{k-1}+a_{k}\\right)^{3}-s_{k-1}^{3}\\right)-3 a_{k} s_{k-1}^{2} \\\\\n& \\Leftrightarrow 0<\\left(1-a_{k}\\right) a_{k}\\left(3 s_{k-1}^{2}+3 s_{k-1} a_{k}+a_{k}^{2}\\right)-3 a_{k} s_{k-1}^{2} \\\\\n& \\Leftrightarrow 0<3 a_{k} s_{k-1}^{2}-3 a_{k}^{2} s_{k-1}^{2}+3\\left(1-a_{k}\\right) s_{k-1} a_{k}^{2}+\\left(1-a_{k}\\right) a_{k}^{3}-3 a_{k} s_{k-1}^{2} \\\\\n& \\Leftrightarrow 0<3\\left(1-a_{k}-s_{k-1}\\right) s_{k-1} a_{k}^{2}+\\left(1-a_{k}\\right) a_{k}^{3} \\\\\n& \\Leftrightarrow 0<3\\left(1-s_{k}\\right) s_{k-1} a_{k}^{2}+\\left(1-a_{k}\\right) a_{k}^{3},\n\\end{aligned}\n$$\n\ncette dernière inégalité étant effectivement correcte. On en conclut que\n\n$$\nb_{1}+b_{2}+\\ldots+b_{n}<\\left(s_{n}^{3}-s_{0}^{3}\\right) / 3=1 / 3 .\n$$", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 10 |
+
{"year": "2021", "problem_label": "7", "tier": 1, "problem": "Soit $n$ un entier supérieur ou égal à 2 , et soit $a_{1}, a_{2}, \\ldots, a_{n}$ des réels strictement positifs tels que $a_{1}+a_{2}+\\ldots+a_{n}=1$. Démontrer que\n\n$$\n\\sum_{k=1}^{n} \\frac{a_{k}}{1-a_{k}}\\left(a_{1}+a_{2}+\\ldots+a_{k-1}\\right)^{2}<\\frac{1}{3}\n$$", "solution": "$n^{\\circ} 1$ On remarque tout d'abord que $\\left(1-a_{k}\\right) s_{k}=s_{k-1}+a_{k}\\left(1-s_{k}\\right) \\geqslant s_{k-1}$. On en conclut que\n\n$$\n\\begin{aligned}\n\\sum_{k=1}^{n} b_{k} & \\leqslant \\sum_{k=1}^{n} a_{k} s_{k-1} s_{k}=\\sum_{k=1}^{n} s_{k-1} a_{k}\\left(s_{k-1}+a_{k}\\right)=\\sum_{k=1}^{n} \\frac{\\left(s_{k-1}+a_{k}\\right)^{3}-s_{k-1}^{3}-a_{k}^{3}}{3} \\\\\n& \\leqslant \\frac{1}{3} \\sum_{k=1}^{n}\\left(s_{k}^{3}-s_{k-1}^{3}\\right)-\\frac{1}{3} \\sum_{k=1}^{n} a_{k}^{3}=1-\\frac{1}{3} \\sum_{k=1}^{n} a_{k}^{3}<1\n\\end{aligned}\n$$\n\n$\\underline{\\text { Solution alternative } n^{\\circ} 2}$ Pour tout entier $k \\geqslant 2$ et tous réels strictement positifs $x_{1}, x_{2}, \\ldots, x_{k}$ de somme 1 , on note $S\\left(x_{1}, x_{2}, \\ldots, x_{k}\\right)$ la somme\n\n$$\n\\sum_{i=1}^{n} \\frac{x_{i}}{1-x_{i}}\\left(x_{1}+x_{2}+\\ldots+x_{i-1}\\right)^{2}\n$$\n\nSoit alors $i \\leqslant n$ un entier, puis $s=a_{1}+a_{2}+\\ldots+a_{i-1}$, et soit $S$ et $S^{\\prime}$ les sommes $S\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ et $S\\left(a_{1}, a_{2}, \\ldots, a_{i-1}, a_{i} / 2, a_{i} / 2, a_{i+1}, \\ldots, a_{n}\\right)$. On remarque que\n\n$$\n\\begin{aligned}\nS^{\\prime}-S & =\\frac{a_{i} / 2}{1-a_{i} / 2}\\left(s^{2}+\\left(s+a_{i} / 2\\right)^{2}\\right)-\\frac{a_{i}}{1-a_{i}} s^{2} \\\\\n& =a_{i} \\frac{\\left(1-a_{i}\\right)\\left(2 s^{2}+s a_{i}+a_{i}^{2} / 4\\right)-\\left(2-a_{i}\\right) s^{2}}{\\left(2-a_{i}\\right)\\left(1-a_{i}\\right)} \\\\\n& =a_{i} \\frac{\\left(1-a_{i}-s\\right) s a_{i}+\\left(1-a_{i}\\right) a_{i}^{2} / 4}{\\left(2-a_{i}\\right)\\left(1-a_{i}\\right)}\n\\end{aligned}\n$$\n\nPuisque $a_{i}+s \\leqslant 1$ et $0<a_{i}<1$, on en déduit que $S^{\\prime}>S$.\nSoit $S_{\\ell}$ la $\\ell^{\\text {ème }}$ somme que l'on atteint via ce processus. En répétant celui-ci de manière à rendre chaque terme $a_{i}$ arbitrairement petit, par exemple en ciblant à chaque étape le terme $a_{i}$ le plus grand, on ne fait qu'augmenter la valeur de la somme $S_{\\ell}$. En particulier, pour tout réel $\\varepsilon>0$, il existe un moment où ce processus nous permet d'atteindre des $a_{i}$ tels que $0<a_{i} \\leqslant \\varepsilon$. Mais alors\n\n$$\nS_{0}<S_{1}<S_{\\ell} \\leqslant \\frac{1}{1-\\varepsilon} \\sum_{i=1}^{n} a_{i}\\left(a_{1}+\\ldots+a_{i-1}\\right)^{2}\n$$\n\nEn outre, si on pose $s_{i}=a_{1}+\\ldots+a_{i}$, on constate que\n\n$$\n\\sum_{i=1}^{n} a_{i} s_{i-1}^{2} \\leqslant \\frac{1}{3} \\sum_{i=1}^{n}\\left(s_{i-1}+a_{i}\\right)^{3}-s_{i-1}^{3} \\leqslant \\frac{1}{3} \\sum_{i=1}^{n} s_{i}^{3}-s_{i-1}^{3}=\\frac{1}{3}\n$$\n\nPar conséquent,\n\n$$\nS_{1} \\leqslant S_{\\ell} \\leqslant \\frac{1}{3(1-\\varepsilon)}\n$$\n\npour tout $\\varepsilon>0$, de sorte que\n\n$$\nS_{0}<S_{1} \\leqslant \\frac{1}{3}\n$$\n\nRemarque: En abusant des notations $\\mathrm{d} x$, on constate en fait que la suite $S_{\\ell}$ converge vers\n\n$$\n\\int_{0}^{1} \\frac{\\mathrm{~d} x}{1-\\mathrm{d} x} x^{2}=\\int_{0}^{1} x^{2} \\mathrm{~d} x=\\frac{1}{3} .\n$$\n\nPar conséquent, $S_{0}=\\mathcal{S}\\left(x_{1}, x_{2}, \\ldots, x_{k}\\right)$, était strictement inférieure à $1 / 3$.\nRemarque: Au lieu de découper le terme $a_{i}$ en deux termes égaux à $a_{i} / 2$, on pouvait aussi le découper en deux termes de la forme $x a_{i}$ et $(1-x) a_{i}$, avec $0<x<1$ quelconque. Munis d'un tel découpage, et quitte à poser $y=a_{i} /(1-s)$, de sorte que $0<y \\leqslant 1$, on pouvait également démontrer que $S^{\\prime}>S$, en écrivant $S^{\\prime}-S$ sous forme d'une somme de termes positifs. Cependant, l'expression obtenue avait tôt fait d'être ingérable en pratique, puisque\n\n$$\n\\begin{aligned}\nS^{\\prime}-S & =\\frac{x y^{2}(1-s)^{3}(1-x)}{\\left(1-a_{i}\\right)\\left(1-x a_{i}\\right)\\left(1-(1-x) a_{i}\\right)}\\left(\\Delta_{1}+\\Delta_{2}+\\Delta_{3}+\\Delta_{4}+\\Delta_{5}+\\Delta_{6}\\right), \\text { avec } \\\\\n\\Delta_{1} & =x y(1-y)(1-x y) \\geqslant 0 \\\\\n\\Delta_{2} & =2 s(1-y)\\left(y+(1-y)^{2}\\right) \\geqslant 0 \\\\\n\\Delta_{3} & =2 s y(1-x)(1-y-x y / 4)^{2} \\geqslant 0 \\\\\n\\Delta_{4} & =s x y^{3}(1-x)(1-x / 8)>0 \\\\\n\\Delta_{5} & =s^{2} y(1-y)^{2} \\geqslant 0 \\\\\n\\Delta_{6} & =s^{2} y^{2}(1-x)(2-y-x y)>0 .\n\\end{aligned}\n$$\n\nCommentaire des correcteurs Cet exercice, d'une difficulté redoutable, a été résolu par un seul élève. Plusieurs élèves ont eu l'idée de regarder ce qui se passait pour $n=2$, car cela faisait disparaître l'inopportun dénominateur $1-a_{i}$. L'idée, simple à exécuter mais très difficile à trouver, était effectivement de se débarrasser de celui-ci pour tout réécrire à partir des nombres $s_{k}$, par exemple en constatant que $\\left(1-a_{k}\\right) s_{k}=s_{k-1}+a_{k}\\left(1-s_{k}\\right) \\geqslant s_{k-1}$.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|
French_TST_Senior/segmented/fr-2022-2023-Corrige-Test-3.jsonl
ADDED
|
@@ -0,0 +1,11 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2022", "problem_label": "1", "tier": 1, "problem": "Trouver tous les quadruplets de réels $(a, b, c, d)$ tels que\n\n$$\na=b c+c d, b=c d+d a, c=d a+a b \\text { et } d=a b+b c\n$$", "solution": "Soit $(a, b, c, d)$ une solution éventuelle. Une première étape consiste à factoriser les membres de droite de nos égalités :\n\n$$\na=c \\times(b+d), b=d \\times(a+c), c=a \\times(b+d) \\text { et } d=b \\times(a+c) \\text {. }\n$$\n\nMaintenant, si $a=0$, l'énoncé indique que $c=0 \\times(b+d)=0$, puis que $b=d \\times 0=0$ et que $d=b \\times 0=0$. En outre, puisque les quatre nombres jouent des rôles cycliques, toute autre solution éventuelle est formée de quatre réels non nuls.\nDans ces nouvelles conditions, puisque $a c=a c \\times(b+d)^{2} \\neq 0$, on sait que $b+d= \\pm 1$. De même, $a+c= \\pm 1$. Comme $a+c=(a+c) \\times(b+d)$, on en déduit que $b+d=1 \\mathrm{et}$, de même, que $a+c=1$. Dès lors, les équations de l'énoncé se réécrivent comme $a=c$ et $b=d$, de sorte que $a=b=c=d=1 / 2$.\nEn conclusion, les deux seules solutions éventuelles sont $(0,0,0,0)$ et $(1 / 2,1 / 2,1 / 2,1 / 2)$, et on vérifie sans effort qu'il s'agit manifestement de solutions au problème.\n\nCommentaire des correcteurs L'exercice a été abordé par la grande majorité des élèves, mais n'a pourtant pas été très bien réussi, puisque plus de la moitié des copies contient une erreur grave parmi les deux suivantes :\n$\\triangleright$ De très nombreux élèves divisent des égalités par une quantité (comme $a$ ou $b+d$ le plus souvent) sans vérifier si celle-ci est non nulle, ce qui explique l'absence de la solution $(0,0,0,0)$ dans trop de copies. Diviser par 0 est une des erreurs les plus fréquentes dans toutes les copies d'algèbre et d'arithmétique, et est pourtant facilement évitable : il faut y remédier!\n$\\triangleright$ Plusieurs élèves tentent de faire des inégalités, mais se retrouvent très vite à multiplier par $b+d$ sans vérifier le signe de cette quantité. Multiplier par un nombre négatif change le sens de l'inégalité, donc la preuve entière tombe à l'eau à partir de là. Il était possible de raisonner avec des inégalités, mais cela s'avérait très laborieux, et une seule copie l'a fait parfaitement.\nEnfin, de trop nombreux élèves oublient de vérifier leurs solutions. Ici, la vérification est facile à faire, mais il faut au moins mentionner qu'elle a été faite. Une phrase comme « et on vérifie réciproquement que ces solutions conviennent » est le minimum nécessaire pour montrer que cette étape n'a pas été négligée.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2022", "problem_label": "2", "tier": 1, "problem": "Trouver tous les couples d'entiers naturels non nuls $(k, n)$ pour lesquels\n\n$$\n1!+2!+\\cdots+k!=1+2+\\cdots+n\n$$", "solution": "Dans toute la solution, on notera $A_{k}$ l'expression $1!+2!+\\cdots+k$ et $B_{n}$ l'expression $1+2+\\cdots+n$. Comme dans tout exercice de ce genre, on commence par rechercher d'éventuelles solutions pour de petites valeurs de $k$ et de $n$. À cette fin, il est pratique de reconnaître en $B_{n}$ la somme des termes d'une suite arithmétique, de sorte que $B_{n}=n(n+1) / 2$. En particulier, si $(k, n)$ est une solution, on sait que\n\n$$\nn^{2} \\leqslant 2 B_{n}=2 A_{k}<(n+1)^{2},\n$$\n\ndonc que $n=\\left\\lfloor\\sqrt{2 A_{k}}\\right\\rfloor$.\nOn calcule alors les premières valeurs de $A_{k}$ : par exemple, lorsque $k$ varie de 1 à $5, A_{k}$ vaut successivement $1,3,9,33$ et 153 , puis l'entier $n=\\left\\lfloor\\sqrt{2 A_{k}}\\right\\rfloor$ vaut alors successivement $1,2,4,8$ et 17 , de sorte que $B_{n}$ vaut $1,3,10,36$ et 153 . Cette première étude, bien que fastidieuse vers la fin, nous a permis d'identifier trois couples solutions: $(k, n)=(1,1),(2,2)$ et $(5,17)$.\nPar ailleurs, on se voit mal calculer à la main $\\left\\lfloor 2 \\sqrt{A_{\\ell}}\\right\\rfloor$ lorsque $\\ell \\geqslant 6$, et il faut donc trouver une approche plus générale lorsque $\\ell$ est grand. Par exemple, quand $\\ell \\leqslant k$, l'entier $\\ell$ ! divise l'entier $k!=A_{k}-A_{k-1}$, de sorte que $A_{k} \\equiv A_{\\ell-1}(\\bmod \\ell!)$. On entreprend donc d'étudier la suite $\\left(A_{k}\\right)$ modulo $\\ell$ ! ou $\\ell$ pour de petites valeurs de $\\ell$, par exemple lorsque $\\ell$ est un nombre premier.\nAprès une étude infructueuse des cas $\\ell=2,3$ et 5 , on constate ainsi que $k!\\equiv 1,2,6,3,1,6$ $(\\bmod 7)$ lorsque $k$ varie de 1 à 6 , et donc que $A_{k} \\equiv A_{6} \\equiv 1+2+6+3+1+6 \\equiv 5(\\bmod 7)$ lorsque $k \\geqslant 6$. D'autre part, $B_{n} \\equiv 1,3,6,3,1,0,0(\\bmod 7)$ lorsque $n$ varie de 1 à 7 . Puisque 2 est inversible modulo 7 , on sait que $B_{n}(\\bmod 7)$ ne dépend que de $n(\\bmod 7)$. Cela signifie en particulier que $B_{n} \\not \\equiv 5 \\equiv A_{k}(\\bmod 7)$ dès lors que $k \\geqslant 6$ et $n \\geqslant 1$, démontrant par la même que $(k, n)$ n'est pas une solution.\nEn conclusion, les solutions sont les couples $(k, n)=(1,1),(2,2)$ et $(5,17)$.\nCommentaire des correcteurs Le problème était plutôt difficile, et a été bien abordé. Néanmoins, certains candidats n'ont pas cherché des solutions, ou ont loupé la solution $(5,17)$ : il ne faut pas hésiter à passer du temps sur ces débuts de preuve, qui permettent aussi de se forger une intuition. Ici, une fois la solution $(5,17)$ trouvée, on pouvait constater que tout modulo divisant 5 ! ne permettrait pas d'avancer dans le sens de la solution. Il fallait donc chercher un modulo ne divisant pas 5!; ; ici 7 était le modulo le plus facile, mais 13 et 25 fonctionnaient aussi.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2022", "problem_label": "3", "tier": 1, "problem": "Soit $A B C$ un triangle et $\\Gamma$ son cercle circonscrit. Soit $A_{1}$ le milieu de l'arc $\\widehat{B C}$ ne contenant pas $A ; B_{1}$ le milieu de l'arc $\\overparen{C A}$ ne contenant pas $B ; C_{1}$ le milieu de l'arc $\\overparen{A B}$ ne contenant pas $C$. Enfin, soit $A_{2}$ le point pour lequel $A B_{1} A_{2} C_{1}$ est un parallélogramme; $B_{2}$ le point pour lequel $B C_{1} B_{2} A_{1}$ est un parallélogramme; $C_{2}$ le point pour lequel $C A_{1} C_{2} B_{1}$ est un parallélogramme.\nDémontrer que les cercles circonscrits à $A B C$ et à $A_{2} B_{2} C_{2}$ sont concentriques.", "solution": "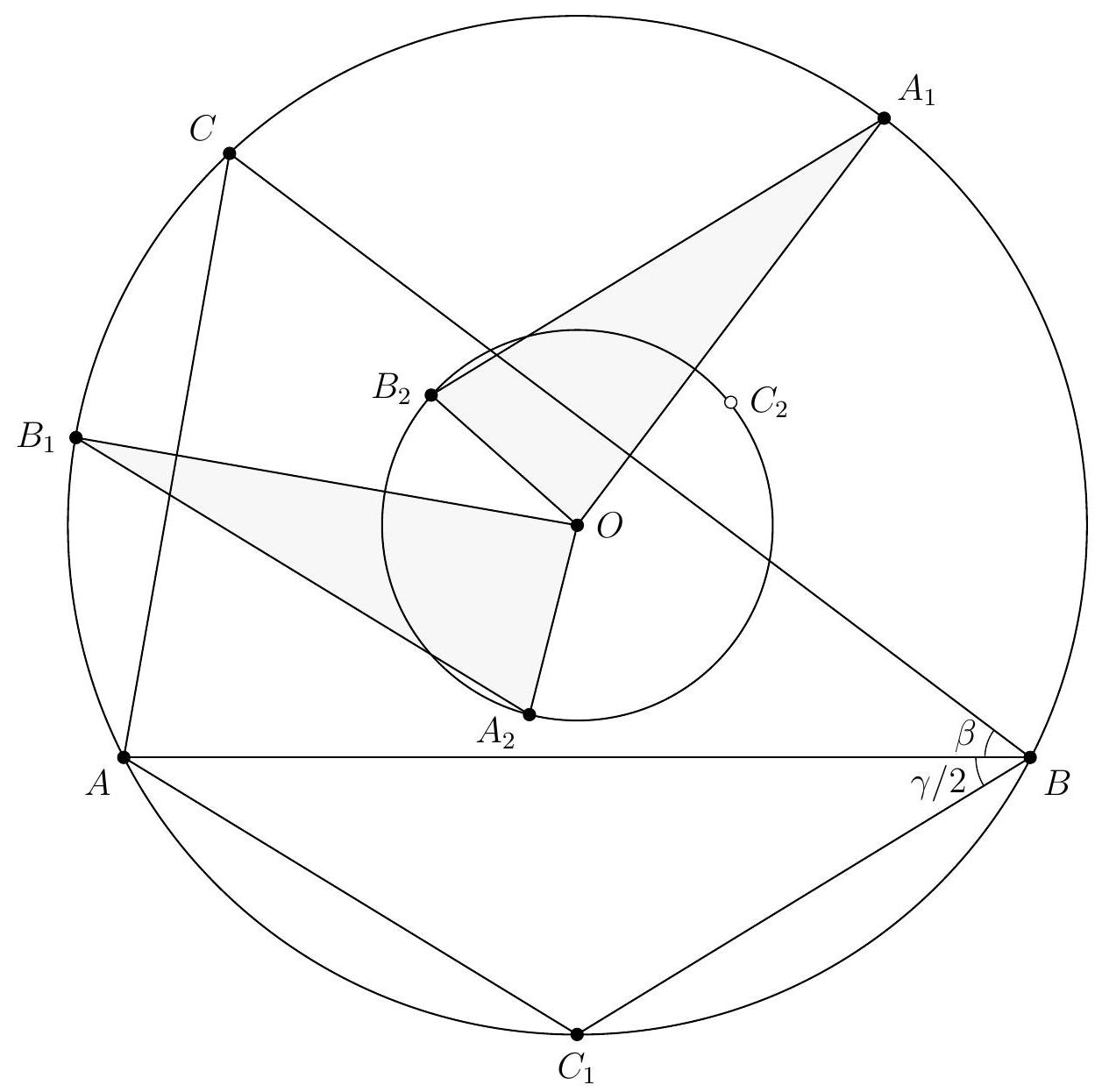\n\nOn cherche tout d'abord à démontrer que $O A_{2}=O B_{2}$. Puisque $A_{1} B_{2}=B C_{1}=A C_{1}=B_{1} A_{2}$ et que $A_{1} O=B_{1} O$, l'égalité $O A_{2}=O B_{2}$ équivaut au fait que les triangles $O A_{1} B_{2}$ et $O B_{1} A_{2}$ soient isométriques l'un de l'autre, c'est-à-dire au fait que $\\widehat{O A_{1} B}=\\widehat{O B_{1} A_{2}}$.\nOn note alors $\\alpha=\\widehat{C A B}, \\beta=\\widehat{A B C}$ et $\\gamma=\\widehat{B C A}$ les angles du triangle. Ici, vu nos relations de parallélisme et de cocyclicité, il sera plus agréable de travailler en angles de droites. Ainsi, comme ( $C C_{1}$ ) est la bissectrice de l'angle $\\widehat{B C A}$, on constate que\n\n$$\n\\begin{aligned}\n\\left(A_{1} O, A_{1} B_{2}\\right) & =\\left(A_{1} O, B C\\right)+\\left(B C, A_{1} B_{2}\\right) \\\\\n& =90^{\\circ}+\\left(B C, B C_{1}\\right) \\\\\n& =90^{\\circ}+(B C, B A)+\\left(B A, B C_{1}\\right) \\\\\n& =90^{\\circ}+\\alpha+\\gamma / 2=(\\alpha-\\beta) / 2 .\n\\end{aligned}\n$$\n\nCela signifie que $\\widehat{O A_{1} B_{2}}=|\\alpha-\\beta| / 2$. Puisque $A, B$ et $C$ jouent des rôles symétriques, on en déduit que $\\widehat{O B_{1} A_{2}}=|\\beta-\\alpha| / 2=\\widehat{O A_{1} B}$, donc que $O A_{2}=O B_{2}$. Toujours par symétrie des rôles, on en conclut même que $O B_{2}=O C_{2}$.\n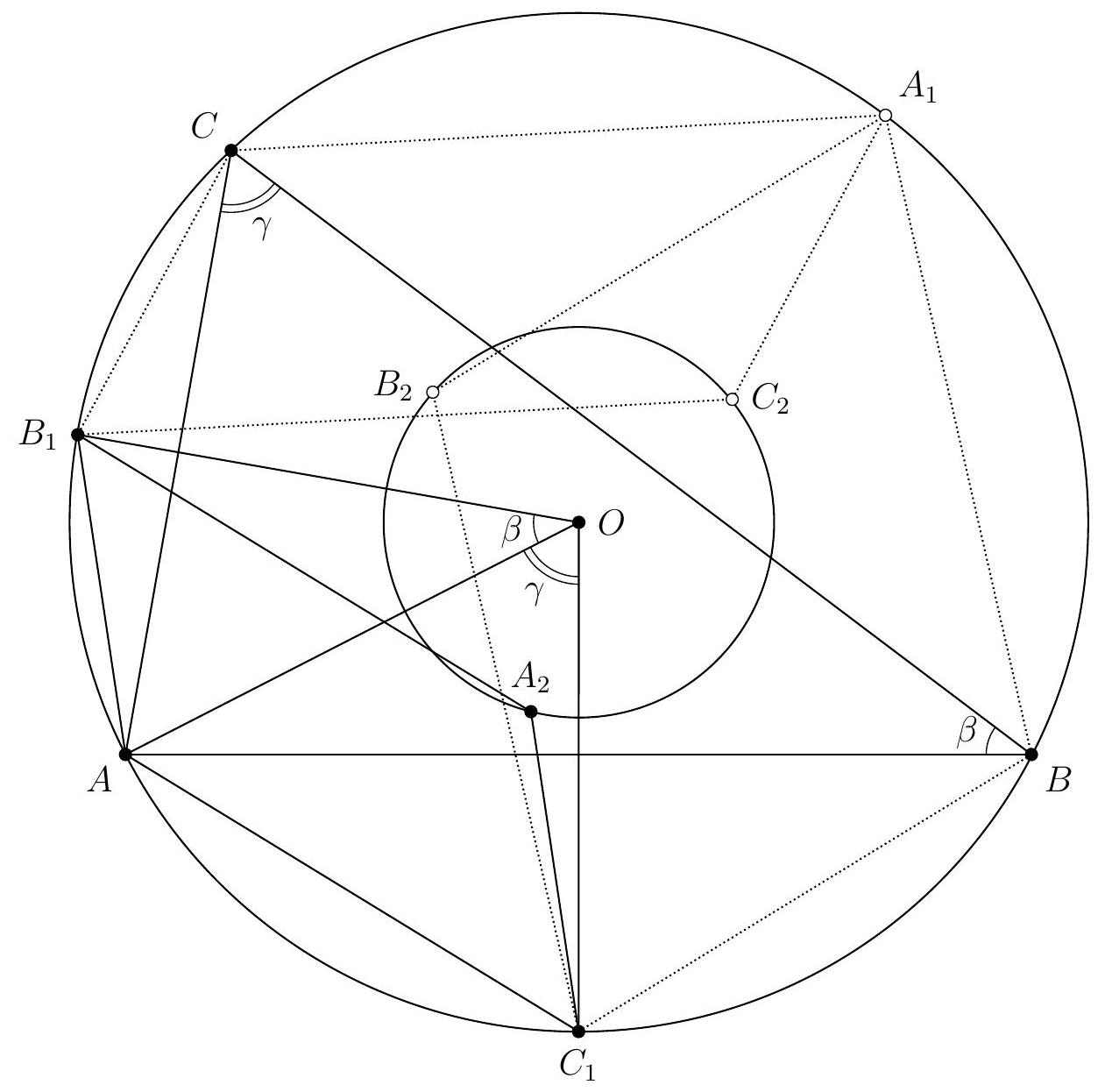\n\nNous allons calculer directement $O A_{2}$ en fonction des angles $\\alpha, \\beta, \\gamma$ et du rayon $R=O A$. Pour ce faire, on remarque d'abord que $\\widehat{A O B_{1}}=\\beta, \\widehat{C_{1} O A}=\\gamma$ et $\\widehat{C_{1} O B_{1}}=\\beta+\\gamma=180^{\\circ}-\\alpha$. En outre, la condition sur $A_{2}$ signifie que $A_{2}=\\left(B_{1}+C_{1}\\right)-A$, de sorte que\n\n$$\n\\begin{aligned}\nO A_{2}^{2} & =\\overrightarrow{O A_{2}} \\cdot \\overrightarrow{O A_{2}} \\\\\n& =\\left(\\overrightarrow{O B_{1}}+\\overrightarrow{O C_{1}}-\\overrightarrow{O A}\\right) \\cdot\\left(\\overrightarrow{O B_{1}}+\\overrightarrow{O C_{1}}-\\overrightarrow{O A}\\right) \\\\\n& ={\\overrightarrow{O B_{1}}}^{2}+{\\overrightarrow{O C_{1}}}^{2}+\\overrightarrow{O A}^{2}+2 \\overrightarrow{O B_{1}} \\cdot \\overrightarrow{O C_{1}}-2 \\overrightarrow{O A} \\cdot \\overrightarrow{O B_{1}}-2 \\overrightarrow{O C_{1}} \\cdot \\overrightarrow{O A} \\\\\n& =\\left(3+2 \\cos \\left(180^{\\circ}-\\alpha\\right)-2 \\cos (\\beta)-2 \\cos (\\gamma)\\right) R^{2} \\\\\n& =(3-2 \\cos (\\alpha)-2 \\cos (\\beta)-2 \\cos (\\gamma)) R^{2} .\n\\end{aligned}\n$$\n\nPuisque $A, B$ et $C$ jouent des rôles symétriques, on en conclut que $O A_{2}^{2}=O B_{2}^{2}=O C_{2}^{2}$.\nCommentaire des correcteurs L'exercice a été très peu réussi. Beaucoup d'élèves ont effleuré le début de la solution en exploitant les égalités de longueurs issues des parallélogrammes ou les égalités d'angles avec les pôles Sud, mais très très peu ont pensé à introduire le centre $O$ dans leurs calculs ou dans leur figure alors qu'il était la star de l'exercice.\nMentionnons également qu'il est agaçant de voir des élèves lancer des phrases du type « il existe une transformation/une similitude envoyant le triangle/le parallélogramme sur un autre » alors que le contenu de la phrase est faux et que l'issue de la phrase ne permet pas de conclure :non, l'existence d'une similitude envoyant un triangle sur un autre ne nous dit rien sur le fait que le centre des cercles est le même! Il est encore plus agaçant de voir que ces raisonnements sont les seuls apparents. Les élèves, au lieu d'essayer des choses simples\ncomme une chasse aux angles ou une chasse aux longueurs, s'entêtent à improviser des raisonnements avec des concepts dont ils ne maîtrisent ni la théorie ni la portée. Ce n'est certainement pas de cette façon que l'on progresse en géométrie.", "problem_match": "\nExercice 3.", "solution_match": "## Solution de l'exercice 3"}
|
| 4 |
+
{"year": "2022", "problem_label": "4", "tier": 1, "problem": "Un jardinier et un pivert jouent au jeu suivant, dans leur jardin dont la forme est celle d'une grille $2022 \\times 2022$ formée de $2022^{2}$ cases. Deux cases sont considérées comme voisines si elles ont un sommet ou une arête en commun. Initialement, chaque case abrite un arbre de taille 0 . Puis, à chaque tour de jeu,\n$\\triangleright$ le jardinier choisit une case; les arbres de cette case et des cases adjacentes (soit de quatre à neuf cases en tout) voient tous leur taille augmenter de 1;\n$\\triangleright$ le pivert choisit alors quatre cases; les arbres de ces cases voient tous leur taille diminuer de 1 (ou rester égale à 0 si le pivert a choisi une case avec un arbre de taille 0 ).\nOn dit qu'un arbre est resplendissant si sa taille vaut au moins $10^{6}$. Trouver le plus grand entier $A$ pour lequel le jardinier pourra s'assurer, en un nombre fini de tours de jeu, et quels que soient les choix du pivert, d'avoir fait pousser au moins $A$ arbres resplendissants.", "solution": "Nous allons démontrer que l'entier recherché est $A=5 n=2271380$, où l'on a posé $n=674^{2}=(2022 / 3)^{2}$.\nTout d'abord, voici une stratégie pour le pivert. Il numérote les lignes et les colonnes de 1 à 2022, puis colorie en noir chaque case située dans une colonne $c$ et une ligne $\\ell$ pour lesquelles 3 ne divise ni $c$, ni $\\ell$. Parmi les quatre à neuf cases sur lesquelles le jardinier agit à chaque tour, au plus quatre sont noires. Le pivert choisit alors les cases noires en question; si cela fait moins de quatre cases, il choisit d'autres cases au hasard.\nCe faisant, il s'assure, à la fin du tour de jeu, qu'aucun arbre situé dans une case noire n'aura vu sa taille augmenter. Une récurrence immédiate indique donc que nul arbre situé dans une case noire ne verra sa hauteur dépasser 1, et puisqu'il y a $4 n$ cases noires, on ne pourra jamais dépasser un total de $2022^{2}-4 n=5 n$ arbres resplendissants.\nRéciproquement, voici une stratégie pour le jardinier; on pose $m=10^{6}$. Faisant fi de la coloration imposée par le pivert, il colorie en rouge chaque case située dans une colonne $c$ et une ligne $\\ell$ pour lesquelles $c \\equiv \\ell \\equiv 2(\\bmod 3)$. Il y a $n$ cases rouges, et chaque case est soit rouge, soit adjacente à une case rouge. Le jardinier pose alors $k=(4 n+1) m+1$ puis, au cours des $k n$ premiers tours de jeu, il choisit chaque case rouge exactement $k$ fois. Il a donc fait croître de $k$ la hauteur de chaque arbre du jardin.\nSoit $a$ le nombre d'arbres qui ne sont pas resplendissants à l'issue de cette première partie du jeu : le pivert a dû choisir au moins $k-m$ fois chacun de ces $a$ arbres. Puisqu'il a choisi $4 k n$ arbres au cours des $k n$ tours de jeu, en déduit que $a(k-m) \\leqslant 4 k n$, donc que\n\n$$\n(k-m)(a-4 n-1) \\leqslant 4 k n-(k-m)(4 n+1)=(4 n+1) m-k<0 .\n$$\n\nPuisque $k \\geqslant m$, cela signifie que $a<4 n+1$, donc que $a \\leqslant 4 n=9 n-A$.\nEn conclusion, l'entier recherché est bien $A=5 n$.\nCommentaire des correcteurs Le problème était difficile et beaucoup d'élèves n'ont pas bien compris ce qui été demandé d'eux, y compris certains qui ont reçus de points pour avoir eu de bonnes idées. Beaucoup trop de copies ressemblent à ceci :\n«Le jardinier découpe la grille en carrés $3 \\times 3$ et joue dans les milieux des carrés car c'est le plus intéressant pour lui. Dans chacun de ces carrés, le pivert a le choix entre attaquer toujours les mêmes arbres ou se répartir, il a intérêt à toujours attaquer les mêmes arbres sinon tous les arbres deviennent resplendissants. Il peut en attaquer 4 par carré; par conséquent, le jardinier en jouant suffisamment de fois dans chaque milieu arrive à rendre 5 arbres par carré resplendissants, soit $5 \\times 2022^{2} / 9$ arbres.»\nUne telle copie combine essentiellement tout ce qu'il ne faut pas faire:\n$\\triangleright$ Que signifie la phrase « il est plus intéressant de jouer au milieu »? Il faut le justifier même si ça parait intuitif. De même, beaucoup d'élèves ont affirmé que le jardinier n'avait pas intérêt à jouer au bord car « il augmente moins d'arbres », mais un seul élève est parvenu à le justifier correctement. En effet, faire grandir ces arbres sur le bord sont susceptibles d'être plus intéressants que d'autres arbres déjà immenses, donc la bonne manière de justifier cette affirmation était de dire que le jardinier peut remplacer un coup sur le bord par un coup adjacent, qui va faire pousser les même arbres et d'autres en plus, et qui est donc toujours meilleur. Pour résumer : pour dire qu'un coup est mauvais, il est nécessaire de proposer un coup alternatif meilleur qui remplisse tous les objectifs atteints par le premier coup.\n$\\triangleright$ Beaucoup d'élèves ont fait des fausses dichotomies pour la stratégie du pivert : soit il attaque toujours les mêmes arbres, soit il papillonne uniformément. Des intermédiaires sont bien sûr possibles, où le pivert attaque principalement certains arbres mais va parfois sur d'autres.\n$\\triangleright$ La principale erreur est cependant celle-ci : une bonne stratégie pour un des deux joueurs étant trouvée, il est absolument interdit de s'en servir pour trouver une stratégie « par réaction » pour l'autre joueur. Même si vous êtes convaincus que le jardinier a intérêt à jouer au milieu des carrés $3 \\times 3$, il est impossible de le supposer pour décrire la stratégie du pivert. Même si vous êtes convaincus que le pivert a intérêt a choisir un certain nombre d'arbres contre lesquels il entretient une rancœur millénaire et à les attaquer dès que le jardinier essaye de les faire pousser, il est impossible de le supposer pour décrire la stratégie du jardinier. En effet, même s'il existe des stratégies optimales pour chacun des deux joueurs vérifiant ces contraintes raisonnables, il existe aussi des stratégies tout aussi performantes ne fonctionnant pas ainsi.\nVoilà comment il faut procéder pour un affrontement entre deux joueurs : il faut séparer sa preuve en deux parties totalement disjointes qui ne partageront aucun argument en commun. D'une part, il faut donner une stratégie pour le pivert qui permette d'assurer un certain score même si le jardinier joue de manière chaotique. Il est alors crucial de ne rien supposer sur la stratégie du jardinier et de ne pas faire de fausse dichotomie; il faut laisser le jardinier « mal » jouer dans cette partie s'il le souhaite, car c'est toujours plus simple que de justifier que son « mauvais » coup ne pourrait pas devenir bon dans un lointain futur. Dans la deuxième moitié de la preuve, on inverse tout, on donne une stratégie pour le jardinier qui reste valable même si le pivert ne suit pas la stratégie qu'on vient de décrire, même si lui aussi joue de manière chaotique, sans rien supposer sur sa stratégie à lui.\n\n## Problèmes Senior", "problem_match": "\nExercice 4.", "solution_match": "\nSolution de l'exercice 4"}
|
| 5 |
+
{"year": "2022", "problem_label": "5", "tier": 1, "problem": "Soit $a_{1}, a_{2}, \\ldots$ des nombres réels strictement positifs tels que\n\n$$\na_{n+1}^{2}+a_{n} a_{n+2} \\leqslant a_{n}+a_{n+2}\n$$\n\npour tout entier $n \\geqslant 1$. Démontrer que $a_{2023} \\leqslant 1$.", "solution": "L'inégalité donnée dans l'énoncé et celle qu'il nous est demandé de démontrer suggèrent de s'intéresser aux termes de la forme $b_{n}=a_{n}-1$, car alors l'équation de l'énoncé se réécrit comme\n\n$$\nb_{n+1}\\left(b_{n+1}+2\\right)+b_{n} b_{n+2} \\leqslant 0,\n$$\n\net il s'agit de démontrer que $b_{2023} \\leqslant 0$.\nSoit $n \\geqslant 2$ un entier éventuel pour lequel $b_{n}>0$. Puisque $b_{n-1} b_{n+1} \\leqslant-b_{n}\\left(b_{n}+2\\right)<0, l^{\\prime}$ un des deux termes $b_{n-1}$ et $b_{n+1}$ est strictement positif, et l'autre est strictement négatif. En posant $m=n-1$ dans le cas où $b_{n-1}>0$, et $m=n$ dans le cas où $b_{n+1}>0$, on dispose désormais d'un entier $m \\geqslant 1$ pour lequel $b_{m}>0$ et $b_{m+1}>0$. Dans ces conditions, et puisque $b_{m+2} \\geqslant-1$, on sait que\n\n$$\nb_{m} \\geqslant b_{m}+b_{m} b_{m+2}+b_{m+1}\\left(b_{m+1}+2\\right) \\geqslant b_{m+1}\\left(b_{m+1}+2\\right)>b_{m+1}\n$$\n\nDe même, puisque $b_{m-1} \\geqslant-1$, on sait que\n\n$$\nb_{m+1} \\geqslant b_{m+1}+b_{m-1} b_{m+1}+b_{m}\\left(b_{m}+2\\right) \\geqslant b_{m}\\left(b_{m}+2\\right)>b_{m},\n$$\n\nce qui contredit l'inégalité $b_{m}>b_{m+1}$ obtenue précédemment.\nOn en conclut que $b_{n} \\leqslant 0$, c'est-à-dire $a_{n} \\leqslant 1$, pour tout entier $n \\geqslant 2$, et notamment pour $n=2023$.\n\nCommentaire des correcteurs Le problème était relativement difficile, mais a été plutôt bien réussi. Attention à ne pas s'emmêler dans les implications, à bien distinguer les inégalités $<$ et $\\leqslant$, et surtout à faire attention attention lorsque l'on divise une inégalité : le terme par lequel on divise peut être nul (auquel cas on n'a pas le droit de diviser) ou négatif (auquel cas la division change le sens de l'inégalité).", "problem_match": "\nExercice 5.", "solution_match": "\nSolution de l'exercice 5"}
|
| 6 |
+
{"year": "2022", "problem_label": "6", "tier": 1, "problem": "Soit $A, B, C, D$ quatre points situés dans cet ordre sur un cercle $\\omega$. Soit $P$ et $Q$ deux points situés sur la droite $(A B)$, de sorte que les points $Q, A, B, P$ soient alignés dans cet ordre, que le cercle circonscrit à $A D Q$ soit tangent à la droite ( $A C$ ), et que le cercle circonscrit à $B C P$ soit tangent à la droite $(B D)$. Soit $M$ et $N$ les milieux respectifs des segments $[B C]$ et $[A D]$.\nDémontrer que la tangente en $A$ au cercle circonscrit à $A N Q$, la tangente en $B$ au cercle circonscrit à $B M P$ et la droite $(C D)$ sont concourantes.", "solution": "\n\nSoit $X$ le point d'intersection éventuel dont on doit démontrer l'existence : nous allons en chercher des caractérisations alternatives. Pour ce faire, et au vu des nombreuses relations de tangence et de cocyclicité dont on dispose, une chasse aux angles s'impose.\nPar exemple, $(A Q, A D)=(A B, A D)=(C B, C D)$ et $(Q A, Q D)=(A C, A D)=(B C, B D)$. Il existe donc une similitude directe qui envoie $A Q D$ sur $C B D$. Celle-ci envoie également $N$ sur le milieu de $[C D]$, que l'on notera $R$. Mais alors\n\n$$\n(A B, A X)=(A Q, A X)=(N Q, N A)=(R B, R C)=(R B, R X)\n$$\n\nce qui signifie que les points $A, B, X$ et $R$ sont cocycliques.\nOn définit donc le point $\\hat{X}$ comme étant le second point d'intersection du cercle circonscrit à $A B R$ avec la droite $(C D)$, et en reprenant le calcul précédent, on remarque que\n\n$$\n(A Q, A \\hat{X})=(A B, A \\hat{X})=(R B, R \\hat{X})=(R B, R C)=(N Q, N A)\n$$\n\nce qui signifie comme prévu que la droite $(A \\hat{X})$ est tangente au cercle circonscrit à $A N Q$. On démontre de même que $(B \\hat{X})$ est tangente au cercle circonscrit à $B M P$, ce qui conclut.", "problem_match": "\nExercice 6.", "solution_match": "## Solution de l'exercice 6"}
|
| 7 |
+
{"year": "2022", "problem_label": "6", "tier": 1, "problem": "Soit $A, B, C, D$ quatre points situés dans cet ordre sur un cercle $\\omega$. Soit $P$ et $Q$ deux points situés sur la droite $(A B)$, de sorte que les points $Q, A, B, P$ soient alignés dans cet ordre, que le cercle circonscrit à $A D Q$ soit tangent à la droite ( $A C$ ), et que le cercle circonscrit à $B C P$ soit tangent à la droite $(B D)$. Soit $M$ et $N$ les milieux respectifs des segments $[B C]$ et $[A D]$.\nDémontrer que la tangente en $A$ au cercle circonscrit à $A N Q$, la tangente en $B$ au cercle circonscrit à $B M P$ et la droite $(C D)$ sont concourantes.", "solution": "$n^{\\circ} 1$ Une fois n'est pas coutume, on peut utiliser brutalement des coordonnées cartésiennes. On identifie chaque point à ses coordonnées, puis on note $O$ et $O_{2}$ les centres des cercles circonscrits à $Q A D$ et à $Q A N$. On choisit en outre le repère de sorte que $A=(0,0)$ et $B=(1,0)$, puis on pose $C=(x, y)$ et $D=(u, v), O=(s, t)$ et $O_{2}=\\left(s_{2}, t_{2}\\right)$. Ainsi, $N=(u / 2, v / 2), Q=(2 s, 0)$ et $s_{2}=s$.\n\nLes égalités $O C^{2}=O A^{2}+A C^{2}$ et $O A^{2}=O D^{2}$ se réécrivent comme $s x+t y=0$ et $2(s u+t v)=$ $u^{2}+v^{2}$, de sorte que\n\n$$\ns=\\frac{u^{2}+v^{2}}{2 \\delta} y\n$$\n\noù l'on a posé $\\delta=u y-v x$. De même, l'égalité $O_{2} A^{2}=O_{2} N^{2}$ se réécrit comme $4\\left(u s+v t_{2}\\right)=$ $u^{2}+v^{2}$, de sorte que\n\n$$\nt_{2}=\\frac{u^{2}+v^{2}-4 u s}{4 v} .\n$$\n\nPar ailleurs, notons $Z=(z, w)$ le point de $(C D)$ pour lequel $(A Z)$ est tangente au cercle circonscrit à $A Q N$. L'alignement de $Z$ avec $C$ et $D$ indique qu'il existe un réel $\\lambda$ tel que $Z=\\lambda C+(1-\\lambda) D$; l'orthogonalité de $(A X)$ avec $\\left(A O_{2}\\right)$ indique que $\\overrightarrow{A O_{2}} \\cdot \\overrightarrow{A Z}=s z+t_{2} w=0$. On en déduit que $s(\\lambda x+u-\\lambda u)+t_{2}(\\lambda y+v-\\lambda v)=0$, c'est-à-dire\n\n$$\n\\begin{aligned}\n\\lambda & =\\frac{s u+t_{2} v}{s(u-x)+t_{2}(v-y)} \\\\\n& =\\frac{4 s u v+\\left(u^{2}+v^{2}-4 u s\\right) v}{4 s(u-x) v+\\left(u^{2}+v^{2}-4 u s\\right)(v-y)} \\\\\n& =\\frac{\\left(u^{2}+v^{2}\\right) v}{\\left(u^{2}+v^{2}\\right)(v-y)+4(u y-v x) s} \\\\\n& =\\frac{\\left(u^{2}+v^{2}\\right) v}{\\left(u^{2}+v^{2}\\right)(v-y)+2\\left(u^{2}+v^{2}\\right) y} \\\\\n& =\\frac{v}{v+y} .\n\\end{aligned}\n$$\n\nPour des raisons de symétrie, le point $Z^{\\prime}$ de $(C D)$ pour lequel $\\left(B Z^{\\prime}\\right)$ est tangente au cercle circonscrit à $B P M$ est lui aussi décrit par la relation $Z^{\\prime}=\\mu D+(1-\\mu) C$, avec $\\mu=y /(v+y)$. Mais alors $\\lambda+\\mu=1$, ce qui signifie comme prévu que $Z=Z^{\\prime}$.\n\nRemarque: Dans cette deuxième solution, on n'a même pas utilisé la cocyclicité des points $A, B, C$ et $D$, qui se traduit par l'égalité $v\\left(x^{2}+y^{2}\\right)+u y=v x+\\left(u^{2}+v^{2}\\right) y$. Ainsi, l'hypothèse de cocyclicité mentionnée dans l'énoncé avait pour but principal de rendre le problème plus accessible.\n\nPar ailleurs, une caractérisation alternative du point $X$ qui reste valide dans ce cadre plus général est la suivante : si l'on note $Y$ le point d'intersection des droites $(A C)$ et $(B D)$, puis $Z$ le point d'intersection des droites $(A D)$ et $(B C), X$ est en fait le point d'intersection des droites $(Y Z)$ et $(C D)$. Cette caractérisation se vérifie assez simplement en calculant les coordonnées des points $Y$ et $Z$.\n\nCommentaire des correcteurs L'exercice a été relativement bien trouvé. Des approches à coup de loi des sinus et de chasse aux rapports étaient possibles. En revanche, beaucoup trop d'élèves introduisent encore les centre des cercles circonscrits pour traduire les hypothèses de tangence, alors que cela est souvent très inefficace comparé à l'usage du théorème de l'angle tangentiel. Beaucoup d'élèves annoncent vouloir tenter des transformations compliquées ou introduire beaucoup de nouveaux points avant même d'essayer une chasse aux angles avec les points existant déjà. Il faut TOUJOURS commencer par tester des idées simples et à sa portée plutôt que d'essayer des méthodes conceptuelles.\nIl est également dommage de ne pas voir plus d'élèves introduire le milieu de $[C D$ ], alors que la figure présente déjà quelques milieux et que l'on sait qu'en présence de milieux de segments, introduire de nouveaux milieux peut s'avérer très utile pour obtenir des égalités d'angles.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution alternative"}
|
| 8 |
+
{"year": "2022", "problem_label": "7", "tier": 1, "problem": "Soit $n \\geqslant 1$ un entier. Morgane écrit au tableau, en base 10 , les nombres $2023,2023 \\times 2, \\ldots, 2023 \\times n$. Pour tout chiffre $c$ compris entre 1 et 9 , elle note alors $\\mathrm{d}_{c}(n)$ le nombre d'apparitions du chiffre $c$ sur le tableau. Par exemple, si $n=3$, elle écrit les nombres 2023, 4046 et 6069, donc $\\mathrm{d}_{1}(3)=\\mathrm{d}_{5}(3)=\\mathrm{d}_{7}(3)=\\mathrm{d}_{8}(3)=0, \\mathrm{~d}_{3}(3)=\\mathrm{d}_{9}(3)=1$, $\\mathrm{d}_{2}(3)=\\mathrm{d}_{4}(3)=2$ et $\\mathrm{d}_{6}(3)=3$; ces neuf nombres prennent donc exactement quatre valeurs.\nDémontrer qu'il existe une infinité d'entiers $n \\geqslant 1$ pour lesquels les neuf nombres $\\mathrm{d}_{1}(n), \\mathrm{d}_{2}(n), \\ldots, \\mathrm{d}_{9}(n)$ prennent exactement deux valeurs.", "solution": "Soit $k$ un multiple de $\\varphi(2023)$, soit $\\ell=\\left(10^{k}-1\\right) / 2023$. Nous allons démontrer que $\\ell$ est une solution. Pour ce faire, on introduit l'ensemble\n\n$$\n\\Omega=\\{2023 n: 1 \\leqslant n \\leqslant \\ell\\}\n$$\n\nLes éléments de $\\Omega$ décrivent précisément l'ensemble des résidus modulo $10^{k}-1$ qui sont des multiples de 2023, chaque résidu étant obtenu exactement une fois. Par conséquent, l'application $\\phi: x \\mapsto 10 x$, qui définit une permutation de $\\mathbb{Z} /\\left(10^{k}-1\\right) \\mathbb{Z}$, définit aussi une permutation de l'ensemble des résidus qui sont des multiples de 2023, et induit donc une permutation de $\\Omega$ lui-même. Concrètement, si l'on écrit les éléments de $\\Omega$ en base 10 avec $k$ chiffres (quitte à laisser des 0 en apparence inutiles sur la gauche), $\\phi$ envoie ${\\overline{a_{k-1} a_{k-2} \\ldots a_{1} a_{0}}}^{10}$ sur $\\overline{a_{k-2} a_{k-3} \\ldots a_{1} a_{0} a_{k-1}}{ }^{10}$ 。\nPour tout chiffre $c$ et tout entier $i$ tel que $0 \\leqslant i \\leqslant k-1$, on note $\\Omega(c, i)$ l'ensemble des éléments de $\\Omega$ dont le chiffre $a_{i}$, de poids $10^{i}$, est égal à $c$; on pose abusivement $\\Omega(c, k)=\\Omega(c, 0)$. Lorsque $0 \\leqslant i \\leqslant k-1$, la bijection $\\phi$ induit une bijection de $\\Omega(c, i)$ vers $\\Omega(c, i+1)$. Ainsi, les ensembles $\\Omega(c, 0), \\Omega(c, 1), \\ldots, \\Omega(c, k-1)$ sont tous de même cardinal, et\n\n$$\n\\mathrm{d}_{c}(\\ell)=|\\Omega(c, 0)|+|\\Omega(c, 1)|+\\cdots+|\\Omega(c, k-1)|=k|\\Omega(c, 0)| .\n$$\n\nOr, $\\Omega(c, 0)$ est formé des nombres $2023 n$ pour lesquels $1 \\leqslant n \\leqslant \\ell$ et $c \\equiv 3 n(\\bmod 10)$. Puisque $\\ell \\equiv-1 / 3 \\equiv 3(\\bmod 10)$, on en déduit que $|\\Omega(c, 0)|$ vaut $(\\ell+7) / 10$ si $c$ vaut 3,6 ou 9 , et vaut $(\\ell-3) / 10$ sinon. Cela signifie que les cardinaux $|\\Omega(c, 0)|$ prennent exactement deux valeurs lorsque $c$ varie de 1 à 9 , et donc que les entiers $\\mathrm{d}_{c}(\\ell)$ prennent eux aussi deux valeurs.\n\nCommentaire des correcteurs Le problème était très difficile. Peu d'élèves l'ont abordé et, parmi eux, plusieurs on formulé des remarques sur la périodicité qu'il était ensuite difficile de valoriser. L'idée était de se demander pourquoi 2023 marcherait et de tester des petits cas pour trouver une conjecture à prouver : la propriété remarquable pour 2023 était d'être premier avec 10 et de ne pas terminer par 1, donc le premier petit cas intéressant était 3 :il se trouve que les solutions que donne ce petit cas sont exactement des solutions générales au problème!\nUne autre approche, plus qualitative, était possible; elle consistait à se dire qu'il fallait que $2023 n$ soit une puissance de 10 moins 1, pour avoir une répartition quasi-uniforme de tous les chiffres de 1 à 9 . Une fois la forme générale des solutions trouvées, on pouvait montrer qu'il s'agissait effectivement de solutions, en dénombrant les occurrences de chaque chiffre et en montrant qu'on pouvait permuter cycliquement les chiffres des nombres.\n\n## Problèmes EGMO", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 9 |
+
{"year": "2022", "problem_label": "8", "tier": 1, "problem": "Un jardinier et un pivert jouent au jeu suivant, dans leur jardin dont la forme est celle d'une grille $2022 \\times 2022$ formée de $2022^{2}$ cases. Deux cases sont considérées comme voisines si elles ont un sommet ou une arête en commun. Initialement, chaque case abrite un arbre de taille 0 . Puis, à chaque tour de jeu,\n$\\triangleright$ le jardinier choisit une case; les arbres de cette case et des cases adjacentes (soit de quatre à neuf cases en tout) voient tous leur taille augmenter de 1;\n$\\triangleright$ le pivert choisit alors quatre cases; les arbres de ces cases voient tous leur taille diminuer de 1 (ou rester égale à 0 si le pivert a choisi une case avec un arbre de taille 0 ).\nOn dit qu'un arbre est resplendissant si sa taille vaut au moins $10^{6}$. Trouver le plus grand entier $A$ pour lequel le jardinier pourra s'assurer, en un nombre fini de tours de jeu, et quels que soient les choix du pivert, d'avoir fait pousser au moins $A$ arbres resplendissants.", "solution": "Nous allons démontrer que l'entier recherché est $A=5 n=2271380$, où l'on a posé $n=674^{2}=(2022 / 3)^{2}$.\nTout d'abord, voici une stratégie pour le pivert. Il numérote les lignes et les colonnes de 1 à 2022, puis colorie en noir chaque case située dans une colonne $c$ et une ligne $\\ell$ pour lesquelles 3 ne divise ni $c$, ni $\\ell$. Parmi les quatre à neuf cases sur lesquelles le jardinier agit à chaque tour, au plus quatre sont noires. Le pivert choisit alors les cases noires en question; si cela fait moins de quatre cases, il choisit d'autres cases au hasard.\nCe faisant, il s'assure, à la fin du tour de jeu, qu'aucun arbre situé dans une case noire n'aura vu sa taille augmenter. Une récurrence immédiate indique donc que nul arbre situé dans une case noire ne verra sa hauteur dépasser 1, et puisqu'il y a $4 n$ cases noires, on ne pourra jamais dépasser un total de $2022^{2}-4 n=5 n$ arbres resplendissants.\nRéciproquement, voici une stratégie pour le jardinier; on pose $m=10^{6}$. Faisant fi de la coloration imposée par le pivert, il colorie en rouge chaque case située dans une colonne $c$ et une ligne $\\ell$ pour lesquelles $c \\equiv \\ell \\equiv 2(\\bmod 3)$. Il y a $n$ cases rouges, et chaque case est soit rouge, soit adjacente à une case rouge. Le jardinier pose alors $k=(4 n+1) m+1$ puis, au cours des $k n$ premiers tours de jeu, il choisit chaque case rouge exactement $k$ fois. Il a donc fait croître de $k$ la hauteur de chaque arbre du jardin.\nSoit $a$ le nombre d'arbres qui ne sont pas resplendissants à l'issue de cette première partie du jeu : le pivert a dû choisir au moins $k-m$ fois chacun de ces $a$ arbres. Puisqu'il a choisi $4 k n$ arbres au cours des $k n$ tours de jeu, en déduit que $a(k-m) \\leqslant 4 k n$, donc que\n\n$$\n(k-m)(a-4 n-1) \\leqslant 4 k n-(k-m)(4 n+1)=(4 n+1) m-k<0 .\n$$\n\nPuisque $k \\geqslant m$, cela signifie que $a<4 n+1$, donc que $a \\leqslant 4 n=9 n-A$.\nEn conclusion, l'entier recherché est bien $A=5 n$.\nCommentaire des correcteurs Le problème a été beaucoup abordé mais assez mal traité dans l'ensemble. De nombreuses copies donnent des stratégies raisonnables pour les joueurs sans justifier qu'elle soient réellement optimales, ou donnent une stratégie optimale sachant que l'autre joueur joue la stratégie raisonnable précédemment décrite.\nIl y avait deux parties à ce problème, qui ont rarement été bien séparées :\n$\\triangleright$ donner une stratégie pour le pivert, valable même si le jardinier agit de manière chaotique, et\n$\\triangleright$ donner une stratégie pour le jardinier, valable même si le pivert agit de manière chaotique.\n\nUne justification de la stratégie du jardinier ne peut pas commencer par «si le pivert joue le mieux possible pour lui», car la stratégie doit marcher complètement indépendamment de l'autre joueur. Par exemple, fournir un pavage était la bonne manière de justifier la stratégie du pivert, puisque peu importe les choix du jardinier, le pivert peut s'adapter. Le lecteur est très fortement encouragé à lire les commentaires formulés à propos du problème 4 , qui présentait le même énoncé mais était destiné aux élèves du groupe Junior.\nLa plupart des élèves ont tout de même réussi à se forger une intution de la bonne borne, ce qui n'était pas évident.", "problem_match": "\nExercice 8.", "solution_match": "\nSolution de l'exercice 8"}
|
| 10 |
+
{"year": "2022", "problem_label": "9", "tier": 1, "problem": "Soit $A B C$ un triangle, et soit $E$ le milieu de $[B C]$. Soit $m$ la médiatrice de $[A C]$, et soit $D$ un point de $m$ tel que le cercle circonscrit à $A B D$ soit tangent à $m$. Enfin, soit $K$ le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B D$ et la droite $(A C)$, et soit $F$ le milieu de $[C K]$. Démontrer que les droites $(D E)$ et $(E F)$ sont perpendiculaires.", "solution": "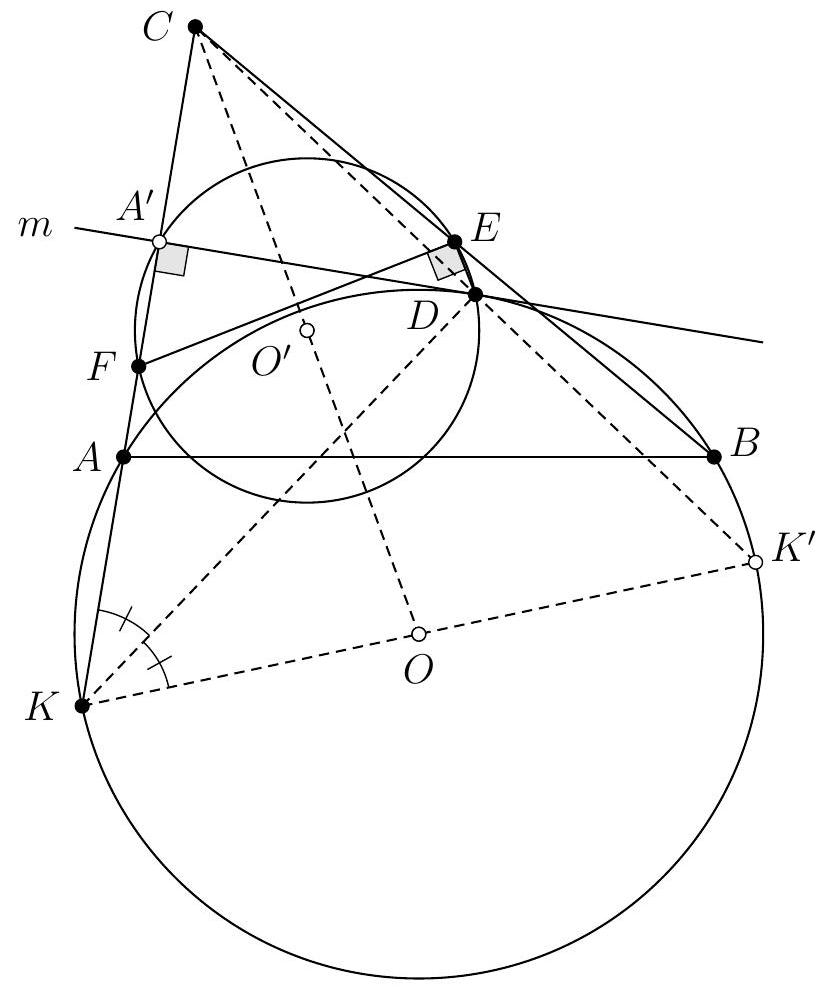\n\nUne première difficulté est de tracer la figure : comment tracer un point tangent à une droite et passant par deux points donnés? Une stratégie usuelle, en pareil cas, est d'inverser le tracé : on commence par placer les points $A, B$ et $D$, puis on en déduit la tangente $m$ et le point $C$.\nNotons maintenant $\\Omega$ et $\\Omega^{\\prime}$ les cercles circonscrits à $A B D$ et $D E F$, puis $O$ et $O^{\\prime}$ leurs centres. Notre figure chèrement acquise suggère que $\\Omega^{\\prime}, m$ et $(A C)$ sont concourantes. Ce n'est pas là une surprise : en effet, il s'agit de démontrer que $\\mathcal{C}^{\\prime}$ est le cercle de diamètre $[F D]$, ou encore que le milieu de $[A C]$, que l'on notera $A^{\\prime}$, appartient à $\\Omega^{\\prime}$.\nOr, les trois points $A^{\\prime}, E$ et $F$ sont les milieux respectifs des segments $[C A],[C B]$ et $[C K]$. Le cercle circonscrit à ces trois points, dont on souhaite démontrer qu'il s'agit de $\\Omega^{\\prime}$, est donc l'image de $\\Omega$ par l'homothétie de centre $C$ et de rayon $1 / 2$. Au vu de la figure, il s'agit donc de démontrer, si l'on note $K^{\\prime}$ le symétrique de $K$ par rapport à $O$, que cette homothétie envoie $K^{\\prime}$ sur $D$, c'est-à-dire que $D$ est le milieu de $\\left[K^{\\prime} C\\right]$. Or, par construction, on sait déjà que $\\widehat{K D K^{\\prime}}=90^{\\circ}$.\nOn va donc maintenant démontrer que $(K D)$ est la bissectrice de $\\widehat{C K K^{\\prime}}$, grâce à une chasse aux angles. Tout d'abord, puisque $A K O$ est isocèle en $O$ et que $(A K)$ et $(D O)$ sont perpendiculaires à $m$, on sait que\n\n$$\n\\left(K C, K K^{\\prime}\\right)=(K A, K O)=(A O, A K)=(O A, O D)\n$$\n\nD'autre part, puisque $m$ est tangente à $\\Omega$, on sait également que\n\n$$\n(K C, K D)=(K A, K D)=\\left(D A, D A^{\\prime}\\right)=(D A, C A)+90^{\\circ}=(D A, D O)+90^{\\circ} .\n$$\n\nPuisque $A D O$ est isocèle en $O$, on en conclut comme souhaité que\n\n$$\n2(K C, K D)=2(D A, D O)=(D A, D O)+(A O, A D)=(O A, O D)=\\left(K C, K K^{\\prime}\\right)\n$$\n\nCommentaire des correcteurs Problème convenablement traité, avec plusieurs copies qui arrivent à aller loin voire à conclure avec des remarques simples sur la figure, comme l'angle droit $\\widehat{K D C}$. Peu d'élèves ont pensé à introduire le point $K^{\\prime}$ de la solution officielle; même si introduire ce point n'était pas strictement nécessaire, tous les élèves qui l'ont fait on ensuite résolu le problème et obtenu d'excellentes notes.\nIl peut donc être judicieux d'introduire de nouveaux points mais beaucoup le font sans raison précise, simplement pour exprimer un angle d'une nouvelle façon. Ici, on a de très fortes raisons de vouloir introduire le point $K^{\\prime}$, et il est nécessaire de se convaincre de la possible utilité d'un point avant de l'introduire, au risque de se perdre dans des considérations inutiles.", "problem_match": "\nExercice 9.", "solution_match": "## Solution de l'exercice 9"}
|
| 11 |
+
{"year": "2022", "problem_label": "10", "tier": 1, "problem": "Soit $k \\geqslant 2$ un entier. Trouver le plus petit entier $n \\geqslant k+1$ pour lequel il existe un ensemble $E$ de $n$ réels, deux à deux distincts, dont chaque élément peut s'écrire comme la somme de $k$ autres éléments de $E$, qui sont eux-mêmes deux à deux distincts.", "solution": "Soit $n$ un entier et $E$ un ensemble tels que décrits dans l'énoncé. On trie les éléments de $E$ dans l'ordre croissant : ce sont $x_{1}<x_{2}<\\cdots<x_{k}$. Enfin, soit $s$ la somme de tous les éléments de $S$.\nPuisque $x_{1} \\geqslant x_{2}+x_{3}+\\cdots+x_{k+1}$ et $x_{n} \\leqslant x_{n-1-k}+x_{n-k}+\\cdots+x_{n-1}$, on sait que\n\n$$\n\\begin{aligned}\n2 x_{1}+(n-k-1) x_{n} & \\geqslant 2 x_{1}+x_{k+2}+x_{k+3}+\\cdots+x_{n} \\geqslant s \\\\\n& \\geqslant x_{1}+x_{2}+\\cdots+x_{n-2-k}+2 x_{n} \\geqslant(n-k-1) x_{1}+2 x_{n}\n\\end{aligned}\n$$\n\nla première et la dernière inégalité étant strictes si $n \\geqslant k+3$.\nLorsque $n$ vaut $k+1, k+2$ et $k+3$, on obtient respectivement les inégalités absurdes $2 x_{1} \\geqslant 2 x_{n}$, $2 x_{1}+x_{n} \\geqslant x_{1}+2 x_{n}$ et $2 x_{1}+2 x_{n}>2 x_{1}+2 x_{n}$. Par conséquent, $n \\geqslant k+4$.\nRéciproquement, si $n=k+4$, et si $E=\\left\\{x_{1}, x_{2}, \\ldots, x_{n}\\right\\}$ est un ensemble convenable, il s'agit d'identifier, pour tout entier $i \\leqslant n$, trois réels $x_{u}<x_{v}<x_{w}$ distincts de $i$ et tels que $x_{i}$ est la somme des réels $x_{j}$ lorsque $j \\neq i, u, v, w$; ou, alternativement, tels que $x_{u}+x_{v}+x_{w}=s-2 x_{i}$. On pose alors $\\ell=\\lfloor k / 2\\rfloor$, de sorte que $\\ell \\geqslant 1$, puis on procède par disjonction de cas, en fonction de la parité de $k$.\n$\\triangleright$ Si $k$ est pair, on pose $E=\\{-\\ell-2,-\\ell-1, \\ldots,-2,-1,1,2, \\ldots, \\ell+1, \\ell+2\\}$. La somme des éléments de $E$ vaut $s=0$. On choisit alors les réels $x_{u}, x_{v}$ et $x_{w}$ comme suit :\n$\\triangleright \\operatorname{si} 3 \\leqslant x_{i} \\leqslant \\ell+2$, on pose $x_{u}=-x_{i}, x_{v}=1-x_{i}$ et $x_{w}=-1$;\n$\\triangleright$ si $1 \\leqslant x_{i} \\leqslant 2$, on pose $x_{u}=-3, x_{v}=-x_{i}$ et $x_{w}=3-x_{i}$;\n$\\triangleright \\operatorname{si}-\\ell-2 \\leqslant x_{i} \\leqslant-1$, on reprend les choix de $x_{u}, x_{v}$ et $x_{w}$ effectués pour $-x_{i}$, puis on change leurs signes.\n$\\triangleright$ Si $k$ est impair, on pose $E=\\{-\\ell-2,-\\ell-1, \\ldots, \\ell+1, \\ell+2\\} ;$ il s'agit du même ensemble que précédemment, auquel on a ajouté l'entier 0 . La somme des éléments de $E$ vaut toujours $s=0$, et il suffit de traiter le cas où $x_{i}=0$, cas pour lequel on choisit $x_{u}=-2$, $x_{v}=-1$ et $x_{w}=3$.\n\nEn conclusion, l'entier recherché est $n=k+4$.\nCommentaire des correcteurs Le problème a été très peu abordé. C'est dommage, car il était possible de faire de nombreuses remarques simples mais valorisées. Certaines élèves ont traité le cas $k=2$ plus ou moins correctement, ce qui est un bon début.", "problem_match": "\nExercice 10.", "solution_match": "\nSolution de l'exercice 10"}
|
French_TST_Senior/segmented/fr-2022-2023-Corrige-Test-4.jsonl
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2022", "problem_label": "1", "tier": 1, "problem": "Soit $n \\geqslant 2$ un entier. Anna a écrit au tableau $n$ entiers $a_{1}, a_{2}, \\ldots, a_{n}$ deux à deux distincts. Elle remarque alors que, quelle que soit la manière de sélectionner $n-1$ de ces entiers, leur somme est divisible par $n$.\nDémontrer que la somme de l'ensemble des $n$ entiers est divisible par $n$.", "solution": "Soit $s$ la somme de tous les entiers. Sélectionner $n-1$ entiers revient à choisir l'entier, disons $a_{i}$, que l'on n'a pas sélectionné. La somme de nos $n-1$ entiers est alors égale à $s-a_{i}$. Ainsi, Anna a simplement remarqué que $a_{i} \\equiv s(\\bmod n)$.\nCeci étant valable pour tout $i$, on en déduit que $a_{1} \\equiv a_{2} \\equiv \\ldots \\equiv a_{n} \\equiv s(\\bmod n)$. On en conclut que $s \\equiv a_{1}+a_{2}+\\cdots+a_{n} \\equiv n s \\equiv 0(\\bmod n)$.\n\nCommentaire des correcteurs Le problème a été très réussi dans l'ensemble, mais un quart des élèves a écrit, à tort, que « si $a$ ne divise ni $b$ ni $c$, alors $a$ ne divise pas $b c$. » Ce genre de résultats n'est valide que si $a$ est premier avec $b$ ou $c$, et tout élève qui l'énonçait dans un cadre général (donc faux) a vu sa note fortement chuter. Il est dommage de réussir à avoir des idées pertinentes sur un exercice qui requiert de l'imagination, pour ensuite se fourvoyer de la sorte.", "problem_match": "\nExercice 1.", "solution_match": "\nSolution de l'exercice 1"}
|
| 2 |
+
{"year": "2022", "problem_label": "2", "tier": 1, "problem": "Soit $a, b$ et $c$ trois réels strictement positifs. Démontrer que\n\n$$\n4\\left(a^{3}+b^{3}+c^{3}+3\\right) \\geqslant 3(a+1)(b+1)(c+1) .\n$$", "solution": "Dans cette inégalité, les termes en $a, b$ et $c$ sont additionnés les uns aux autres (et de degré 3) dans le membre de gauche, tandis qu'ils sont multipliés les uns aux autres (et chacun de degré 1) dans le membre de droite. Une première idée est donc d'utiliser l'inégalité arithmético-géométrique pour se retrouver, de part et d'autre de l'inégalité, avec deux produits de termes de degré 1 , ou bien deux sommes de termes de degré 3 faisant chacun intervenir une seule des variables $a, b$ ou $c$.\nAinsi, on constate que\n\n$$\n(a+1)(b+1)(c+1)=\\sqrt[3]{(a+1)^{3}(b+1)^{3}(c+1)^{3}} \\leqslant \\frac{(a+1)^{3}+(b+1)^{3}+(c+1)^{3}}{3}\n$$\n\nEn outre, cette inégalité a le bon goût d'être une égalité lorsque $a=b=c=1$, qui est également un cas d'égalité pour l'inégalité de l'énoncé. On espère donc très fort que l'inégalité\n\n$$\n4\\left(a^{3}+b^{3}+c^{3}+3\\right) \\geqslant(a+1)^{3}+(b+1)^{3}+(c+1)^{3}\n$$\n\nest valide, et on va tenter de la démontrer.\nOn continue donc nos pérégrinations et, puisque l'on a fait tous ces efforts pour séparer les termes en les variables $a, b$ et $c$, on constate qu'il suffit désormais de démontrer que\n\n$$\n4\\left(a^{3}+1\\right) \\geqslant(a+1)^{3}\n$$\n\nIl s'agit là d'une inégalité en une seule variable, dont $a=1$ est un cas d'égalité, et qui aura le bon goût d'être démontrée (ou invalidée pour certaines valeurs de $a$ ) sans trop d'efforts.\nEn effet, si on développe chaque terme et qu'on les insère tous dans le membre de gauche, l'inégalité se réécrit comme\n\n$$\n3 a^{3}-3 a^{2}-3 a+3 \\geqslant 0\n$$\n\nPuisque l'on sait qu'il y a égalité lorsque $a=0$, et au vu de la symétrie manifeste entre les termes de petit degré et ceux de grand degré, on factorise le membre de gauche comme\n\n$$\n3 a^{3}-3 a^{2}-3 a+3=3(a-1)\\left(a^{2}-1\\right)=3(a-1)^{2}(a+1)\n$$\n\nce qui est manifestement positif ou nul, et nous permet de conclure que l'inégalité de l'énoncé est effectivement valide.\n\nCommentaire des correcteurs Le problème a été abordé de manière assez inégale. Une moitié des élèves a pensé à l'inégalité arithmético-géométrique, mais plusieurs élèves n'ont pas réussi à conclure à partir de là; il est dommage que ces élèves ne se soient pas rendus compte que, comme $a, b$ et $c$ n'apparaissent dans aucun terme de la somme, il suffisait de prouver l'inégalité sans $b$ ni $c$, surtout que certains ont l'air de penser avoir conclu en factorisant partiellement.", "problem_match": "\nExercice 2.", "solution_match": "\nSolution de l'exercice 2"}
|
| 3 |
+
{"year": "2022", "problem_label": "3", "tier": 1, "problem": "Alice a disposé 200 boîtes dans son salon. Chaque boîte contient un papier sur lequel elle a écrit un entier naturel non nul; les 200 entiers ne sont pas nécessairement distincts. Chaque minute, et tant que c'est possible, Alice effectue une action de la forme suivante : elle choisit trois boîtes, contenant des entiers $a, b$ et $c$ tels que $a+b=c$, et choisit également un entier $k \\geqslant 2$ arbitraire; elle remplace alors l'entier $c$ par l'entier $k \\times c$. Si elle ne peut plus effectuer de telle action, elle s'arrête définitivement.\nDémontrer que, quels que soient la situation initiale et les choix d'Alice, elle sera forcée de s'arrêter à un moment.", "solution": "Ci-dessous, on dira qu'un entier change si Alice remplace $c$ par un entier $k \\times c$. Elle peint en bleu les entiers qui ne changent qu'un nombre fini de fois, et en rouge ceux qui changent un nombre infini de fois. Par construction, le nombre initialement minimal ne pourra jamais changer, donc il est bleu. On suppose alors abusivement qu'il existe un nombre rouge.\nÀ partir d'un certain temps, Alice cesse complètement de changer les nombres bleus. Soit $v$ la valeur du plus grand d'entre eux à ce moment-là. Quand un nombre rouge change, sa valeur augmente d'au moins un. Il y a donc un moment à partir duquel chaque nombre rouge vaut au moins $2 v+1$, par exemple quand chaque nombre rouge a changé au moins $2 v$ fois.\nÀ ce moment-là, le plus petit nombre rouge est inférieur ou égal à tous les autres nombres rouges, et il est strictement supérieur à la somme de deux nombres bleus quelconques. Il ne pourra donc plus jamais changer de valeur, et il aurait dû être bleu. Ce constat invalide notre supposition, ce qui signifie que tout nombre est bleu et conclut le problème.\n\nCommentaire des correcteurs Le problème comportait une erreur d'énoncé. Il était donc difficile de faire des observations pertinentes dessus.", "problem_match": "\nExercice 3.", "solution_match": "\nSolution de l'exercice 3"}
|
| 4 |
+
{"year": "2022", "problem_label": "4", "tier": 1, "problem": "Soit $A B C$ un triangle isocèle en $A$ dont tous les angles sont aigus, et soit $D$ un point situé sur le segment $[B C]$. Soit $\\ell$ la droite parallèle à $(B C)$ passant par $A$, puis $X$ le point de $\\ell$ pour lequel $(X D)$ est perpendiculaire à $(B C)$, et $\\Gamma$ le cercle de centre $X$ passant par $D$. Le cercle $\\Gamma$ coupe le segment $[A B]$ en un point $E$, et on note $Y$ le point de $\\ell$ tel que $(A B)$ soit perpendiculaire à $(E Y)$; de même, $\\Gamma$ coupe le segment $[A C]$ en un point $F$, et on note $Z$ le point de $\\ell$ tel que $(A C)$ soit perpendiculaire à $(F Z)$.\nDémonter que les bissectrices des angles $\\widehat{E Y A}$ et $\\widehat{F Z A}$ se coupent en un point de la droite ( $X D$ ).", "solution": "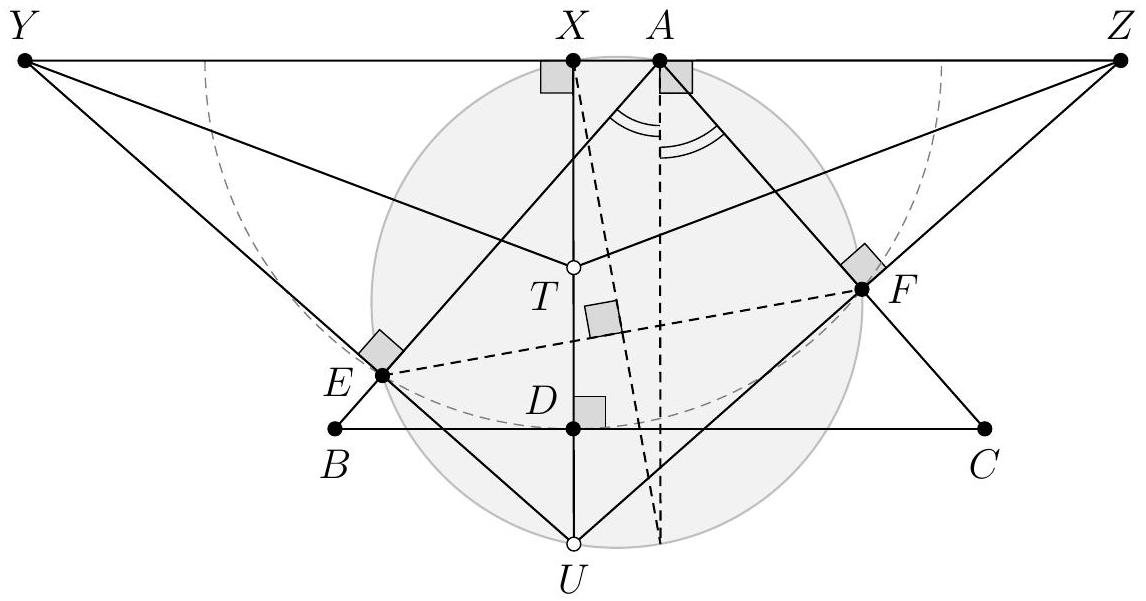\n\nNotons $T$ le point d'intersection des bissectrices de $\\widehat{E Y A}$ et $\\widehat{F Z A}, U$ le point d'intersection des droites $(E Y)$ et $(F Z)$, et $\\mathcal{C}$ le cercle de rayon $[A U]$. Puisque les angles $\\widehat{U E A}$ et $\\widehat{A F U}$ sont droits, $E$ et $F$ appartiennent à $\\mathcal{C}$.\nPar ailleurs, puisque $A B C$ est isocèle en $A$, la bissectrice des angles $\\widehat{B A C}$ et $\\widehat{E A F}$ est aussi la hauteur de $A B C$ issue de $A$. Elle est donc perpendiculaire aux droites $(B C)$ et $\\ell=(A X)$. Comme $D X=E X=F X$, le point $X$ est donc le point d'intersection de la bissectrice extérieure de $\\widehat{E A F}$ avec la médiatrice de $[E F]$, c'est-à-dire le pôle Nord de $A E F$ issu de $A$. Cela signifie en particulier que $X$ appartient au cercle circonscrit à $A E F$, c'est-à-dire à $\\mathcal{C}$.\nDans ces conditions, l'angle $\\widehat{U X A}$ est droit, donc les triangles $U X Y$ et $U X Z$ sont rectangles en $U$. Or, puisque les triangles $A F Z$ et $A E Y$ sont rectangles en $E$ et $F$ et que $A B C$ est isocèle en $A$, on sait que\n\n$$\n\\widehat{X Z U}=\\widehat{A Z F}=90^{\\circ}-\\widehat{F A Z}=90^{\\circ}-\\widehat{A C B}=90^{\\circ}-\\widehat{C B A}=90^{\\circ}-\\widehat{Y A E}=\\widehat{E Y A}=\\widehat{Y U X} .\n$$\n\nAinsi, les deux triangles rectangles $U X Y$ et $U X Z$ sont symétriques l'un de l'autre par rapport à la droite $(U X)$. Les deux bissectrices $(T Y)$ et $(T Z)$ se retrouvent elles aussi symétriques l'une de l'autre par rapport à $(U X)$, donc $T$ appartient à $(U X)$.\nEnfin, par construction, la droite $(D X)$ est perpendiculaire aux droites $(B C)$ et $\\ell$, donc elle est confondue avec $(U X)$. On en conclut donc, comme demandé dans l'énoncé, qu'elle contient le point $T$.\n\nRemarque: Lors de la recherche d'une solution, on pourra bien sûr trouver plus naturel de procéder à rebours de la solution présentée ci-dessus, par exemple en procédant comme suit:\n\n1. On remarque que les deux triangles $T X Y$ et $T X Z$ semblent symétriques, et qu'on aura gagné s'ils le sont.\n2. On démontre que $\\widehat{X Z T}=\\widehat{T Y X}$, de sorte qu'il suffit de démontrer que $X Y=X Z$.\n3. On remarque que le problème serait analogue si on remplaçait nos bissectrices par les deux droites $(Y E)$ et $(Z F)$, ce qui nous pousse à introduire le point $U$ et à chercher à démontrer que $(X U)$ est perpendiculaire à $\\ell$.\n4. On repère alors deux angles droits joignant $A$ à $U$, et un troisième dont on espère justement qu'il est droit.\n5. L'existence de ces angles droits se caractérisant par l'appartenance à un cercle de rayon [ $A U]$, il s'agit de démontrer que $E, X, A$ et $F$ sont cocycliques.\n6. Pour démontrer qu'ils le sont effectivement, on reconnaît en $X$ le pôle Nord de $A E F$ issu de $A$, et on démontre qu'il l'est effectivement.\n\nCommentaire des correcteurs Le problème, difficile, n'a été résolu entièrement que par un élève. Beaucoup d'élèves sont parvenus à réduire le problème au fait de montrer que $X Y=X Z$, ou à une propriété équivalente. Une telle réduction du problème est toujours bonne à écrire.\nEn revanche, trop d'élèves font des erreurs de raisonnements qu'il faut absolument gommer : méconnaissance du critère de similitude de deux triangles, raisonnements circulaires ou mauvaise lecture de le figure (voire de l'énoncé). Ces élèves croient alors conclure le problème en quelques lignes alors qu'ils n'ont pas utilisé certaines hypothèses cruciales de l'énoncé, ce qui devrait les amener à relire et vérifier leur preuve.\n\n## Énoncés Senior", "problem_match": "\nExercice 4.", "solution_match": "## Solution de l'exercice 4"}
|
| 5 |
+
{"year": "2022", "problem_label": "5", "tier": 1, "problem": "Soit $A B C$ un triangle dont tous les angles sont aigus. Soit $F$ le pied de la hauteur de $A B C$ issue de $A$, et soit $P$ un point situé sur le segment $[A F]$. On note $D$ le point de ( $B C)$ tel que $(P D)$ soit parallèle à $(A C)$, puis $X$ le point où se recoupent le cercle circonscrit à $A B D$ et le cercle de centre $D$ passant par $A$. De même, on note $E$ le point de $(B C)$ tel que $(P E)$ soit parallèle à $(A B)$, puis $Y$ le point où se recoupent le cercle circonscrit à $A C E$ et le cercle de centre $E$ passant par $A$.\nDémontrer que les points $B, C, X$ et $Y$ sont cocycliques.", "solution": "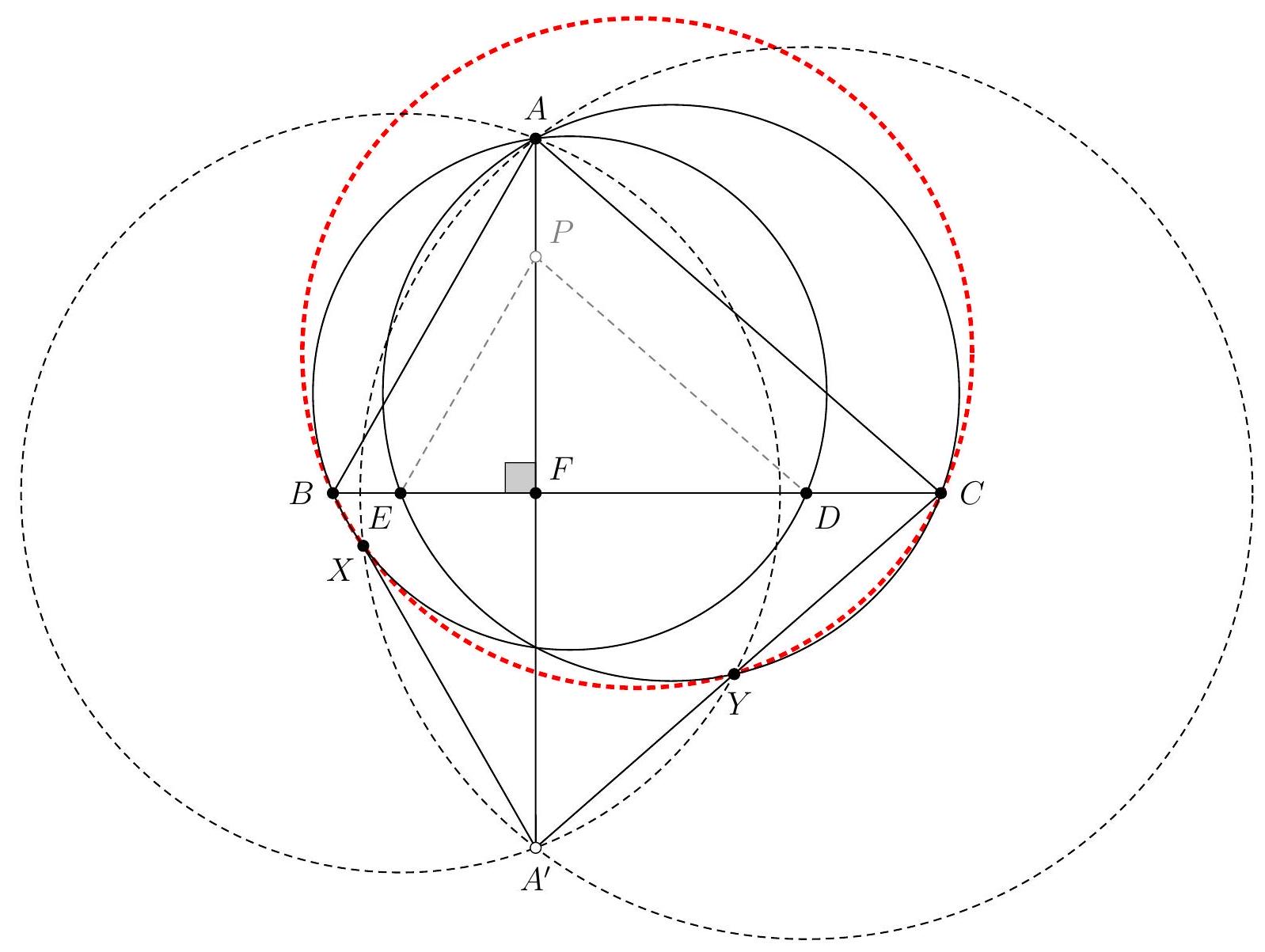\n\nDans un tel problème, le plus simple est d'essayer d'éliminer au mieux les points qui pourraient s'avérer peu utiles pour la suite. Ici, c'est par exemple le cas du point $P$, qui ne sert qu'à construire les points $D$ et $E$ en tant qu'images de $B$ et $C$ par une même homothétie de centre $F$. Ainsi, $F E \\times F C=F B \\times F D$, et $F$ a donc même puissance par rapport aux cercles circonscrits à $A B D$ et à $A C E$. Ces deux cercles ont donc $(A F)$ pour axe radical.\nOn s'intéresse donc aux axes radicaux de ces deux cercles avec l'éventuel cercle circonscrit à $B X C Y$, c'est-à-dire aux droites $(B X)$ et $(C Y)$, et au centre radical de ces trois cercles. Or, sur la figure, celui-ci semble appartenir aux cercles de centres $D$ et $E$ passant par $A$. Cela signifierait qu'il est confondu avec le symétrique de $A$ par rapport à la droite $(D E)=(B C)$; on note $A^{\\prime}$ ce symétrique.\nUne manière simple de réutiliser l'égalité $D A=D X$ consiste à dire que les arcs de cercle $\\widehat{D A}$ et $\\widehat{X D}$ ont même mesure. Ainsi,\n\n$$\n(B X, B C)=(B X, B D)=(B D, B A)=(B C, B A)=\\left(B A^{\\prime}, B C\\right)\n$$\n\nOn démontre de même que $(C Y, C B)=\\left(C A^{\\prime}, C B\\right)$, de sorte que les trois droites $(A F),(B X)$ et $(C Y)$ sont bien concourantes en $A^{\\prime}$.\nEn particulier, $A^{\\prime}$ est le centre radical des cercles circonscrits à $A B D X$, à $A C E Y$ et à $B C Y$, donc $\\left(A^{\\prime} B\\right)=(B X)$ est l'axe radical des cercles circonscrits à $A B D X$ et à $B C Y$. Puisque $X$ appartient à l'un de ces cercles, il appartient aussi à l'autre, ce qui conclut.\n\nCommentaire des correcteurs De nombreux élèves ont résolu ce problème. Se contenter de traduire les hypothèses de cocyclicité ou de parallélisme par des égalités d'angles ne suffisait pas ici pour avancer significativement. Néanmoins, plusieurs parties du problème étaient abordables, et ont été souvent abordées en pratique : montrer que $F$ est sur un axe radical par chasse aux rapports, introduire le point d'intersection de $(B X)$ et $(C Y)$ et traduire le résultat à démontrer en appartenance d'un certain point à un axe radical...\nSignalons enfin que, même devant un problème avec une preuve aux arguments aussi élémentaires, des élèves ont tenté (sans vraiment beaucoup de succès) des solutions très techniques : des inversions, de la géométrie dynamique... Il est frustrant de voir les élèves déployer un tel arsenal sans aboutir à une relation intéressante, surtout quand c'est la seule tentative dont ils laissent une trace écrite. On implore les élèves d'essayer des choses simples pour les premiers exercices.", "problem_match": "\nExercice 5.", "solution_match": "## Solution de l'exercice 5"}
|
| 6 |
+
{"year": "2022", "problem_label": "6", "tier": 1, "problem": "Soit $n \\geqslant 1$ un entier. Morgane dispose initialement de $n$ piles dont chacune contient une pièce. Elle s'autorise ensuite des opérations de la forme suivante : elle choisit deux piles, prélève autant de pièces de la première pile que de la deuxième, et forme une nouvelle pile avec les pièces qu'elle a prélevées.\nDéterminer, en fonction de $n$, le plus petit nombre de piles non vides que Morgane pourra obtenir à partir de telles opérations.", "solution": "Si $n$ est une puissance de 2, Morgane peut se débrouiller pour n'obtenir qu'une seule pile, en procédant comme suit : elle fusionne les $n$ piles de taille 1 en $n / 2$ piles de taille 2 , puis fusionne ces $n / 2$ piles en $n / 4$ piles de taille 4 , et ainsi de suite.\nRéciproquement, lorsque Morgane extrait $k$ pièces de deux piles contenant originellement $a$ et $b$ pièces pour former trois piles (éventuellement vides) de $a-k, b-k$ et $2 k$ pièces, on constate que $\\operatorname{PGCD}(a-k, b-k, 2 k)$ divise $2 a$ et $2 b$, donc divise $2 \\operatorname{PGCD}(a, b)$. Par conséquent, une récurrence immédiate montre que, si Morgane dispose de $k$ piles de tailles $t_{1}, t_{2}, \\ldots, t_{k}$, le nombre $\\operatorname{PGCD}\\left(t_{1}, t_{2}, \\ldots, t_{k}\\right)$ est une puissance de 2. En particulier, si Morgane parvient à n'avoir plus qu'une seule pile, qui contiendra $n$ pièces, c'est donc que $n$ est une puissance de 2.\nEnfin, voici comment, pour toute valeur de $n$, Morgane peut procéder pour n'obtenir que deux piles. Elle écrit $n$ comme somme de puissances de 2 croissantes, c'est-à-dire de nombres $2^{a_{1}}<2^{a_{2}}<\\cdots<2^{a_{k}}$ tels que $n=2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{k}}$. Pour chaque $i \\leqslant k$, et en procédant comme dans le cas où $n$ est une puissance de 2 , Morgane regroupe ensuite $2^{a_{i}}$ de ses pièces en une seule pile, obtenant ainsi $k$ piles.\nMorgane distingue alors sa pile de taille $2^{a_{1}}$, qu'elle appelle cible, et sa pile de taille $2^{a_{k}}$, qu'elle appelle réserve. Les $k-2$ autres piles sont vues comme des piles normales. Puis Morgane s'attelle à doubler la taille de sa pile cible tout en s'assurant qu'elle ne sera jamais plus grande qu'une pile normale, en procédant comme suit:\n$\\triangleright$ si la pile cible est de même taille qu'une pile normale, Morgane fusionne ces deux piles en une nouvelle pile cible; une pile normale disparaît au cours de cette opération;\n$\\triangleright$ sinon, la pile cible est de taille $2^{a}$ strictement plus petite que chaque pile normale, et Morgane prélève alors $2^{a}$ pièces de la réserve pour les intégrer à la pile cible, qui est désormais de taille $2^{a+1}$.\nAprès $\\ell$ telles étapes, la pile cible est désormais de taille $2^{a_{1}+\\ell}$, et elle a absorbé les piles de tailles $2^{a_{i}}<2^{a_{1}+\\ell}$, ainsi qu'au plus $2^{a_{k-1}}$ pièces issues de la réserve, qui n'est donc toujours pas vide. Ainsi, après $a_{k-1}+1-a_{1}$ étapes, la pile cible est désormais de taille $2^{a_{k-1}+1}$, et elle a absorbé toutes les piles normales, ce qui fait que l'on n'a plus que deux piles.\nEn conclusion, le nombre minimal de piles auquel pourra aboutir Morgane vaut 1 si $n$ est une puissance de 2 , et il vaut 2 sinon.\n\nCommentaire des correcteurs L'exercice était de difficulté progressive. Comme beaucoup d'exercices de combinatoire, il valorisait les élèves ayant testé les petits cas. En effet, en testant les petits cas, par exemple 2 et 4 , on voit que si $n$ est une puissance de 2, alors on peut former une seule pile. En continuant les petits cas tels que 3,5 et 6 , on voit que si $n$ est une somme de $k$ puissances de 2 , alors on peut faire $k$ piles. Mais $k$ n'est pas forcément le minimum : pour 7 , on peut obtenir une pile de 4 , une de 2 , une de 1 ; puis on peut obtenir une pile de 3 , et deux de 2 , donc une pile de 4 et une de 3 . Ainsi, on peut faire mieux que le nombre de 1 de $n$ en binaire.\nEn testant les nombres de 8 à 16 on voit qu'on peut obtenir 2 piles pour les nombres n'étant pas des puissances de 2, mais pas mieux, et que la bonne stratégie est de faire une grosse\npile de taille une puissance de 2 , puis de la vider un petit peu pour former 2 piles. Après il n'y a plus qu'à formaliser cet argument pour montrer qu'on pouvait obtenir deux piles.\nIl restait alors la partie la plus difficile de l'exercice : pourquoi, si $n$ n'est pas une puissance de 2, on ne peut pas obtenir une pile. Malheureusement, certains ont mal lu l'énoncé, et ont cru qu'il fallait retirer autant de pièces du premier tas qu'il y en avait dans le second : ce n'est pas dit dans l'énoncé. Certains ont essayé de procéder par récurrence, pour montrer que plusieurs étapes avant la fin, il y a une pile de taille $n / 2^{k}$ (ou même $2^{k}$ telles piles). Cela n'est pas vrai pour $k=3$ : en effet, on peut imaginer avoir une pile de $5 n / 8$ et une pile de $3 n / 8$, prendre $n / 8$ pièces de chaque pour avoir une pile de $n / 2$ et deux de $n / 4$, et en deux fusions obtenir une seule pile.\nL'argument était plus subtil : le plus simple était d'écrire $n=2^{k} \\times y$ avec $y$ impair, et de montrer par récurrence que $k$ étapes avant la fin, chaque pile avait une taille divisible par $y$. Ou alternativement, de montrer que les piles avaient une taille de la forme $k n / 2^{j}$ avec $k$ impair, donc ne pouvaient jamais être de taille 1.", "problem_match": "\nExercice 6.", "solution_match": "\nSolution de l'exercice 6"}
|
| 7 |
+
{"year": "2022", "problem_label": "7", "tier": 1, "problem": "Trouver tous les entiers $n \\geqslant 2$ pour lesquels il existe un nombre réel $r>0$ et $n$ nombres réels $a_{1}<a_{2}<\\cdots<a_{n}$ tels que les $n(n-1) / 2$ différences $a_{j}-a_{i}$ obtenues lorsque $1 \\leqslant i<j \\leqslant n$ sont égales, à l'ordre près, aux nombres $r^{1}, r^{2}, \\ldots, r^{n(n-1) / 2}$.", "solution": "Dans un tel problème, il est indispensable de commencer par étudier les petits cas.\n$\\triangleright$ Lorsque $n=2$, il suffit de choisir $a_{1}=0$ et $a_{2}=r=1$. Par conséquent, $n=2$ convient.\n$\\triangleright$ Lorsque $n=3$, il suffit de choisir $a_{1}=0, a_{2}=r=\\phi$ et $a_{3}=\\phi^{3}$, où $\\phi=(1+\\sqrt{5}) / 2$ est le nombre d'or et vérifie l'égalité $\\phi^{2}=1+\\phi$. En effet, on a alors $a_{2}-a_{1}=\\phi$, $a_{3}-a_{2}=\\phi\\left(\\phi^{2}-1\\right)=\\phi^{2}$ et $a_{3}-a_{1}=\\phi^{3}$, comme illustré ci-dessous à gauche. Par conséquent, $n=3$ convient.\n$\\triangleright$ Lorsque $n=4$, il suffit de choisir $a_{1}=0, a_{2}=\\lambda, a_{3}=\\lambda^{4}, a_{4}=\\lambda^{6}$ et $r=\\lambda$, où $\\lambda$ est une racine positive du polynôme $P(X)=X^{3}-X-1$, pour lequel $P(1)<0<P(2)$. En effet, on a alors $a_{2}-a_{1}=\\lambda, a_{3}-a_{2}=\\lambda\\left(\\lambda^{3}-1\\right)=\\lambda^{2}, a_{4}-a_{3}=\\lambda^{3}\\left(\\lambda^{3}-\\lambda\\right)=\\lambda^{3}, a_{3}-a_{1}=\\lambda^{4}$, $a_{4}-a_{2}=\\left(a_{4}-a_{3}\\right)=\\left(a_{3}-a_{2}\\right)=\\lambda^{3}+\\lambda^{2}=\\lambda\\left(\\left(a_{3}-a_{2}\\right)+\\left(a_{2}-a_{1}\\right)\\right)=\\lambda\\left(a_{3}-a_{1}\\right)=\\lambda^{5}$, et enfin $a_{3}-a_{1}=\\lambda^{6}$, comme illustré ci-dessous à droite. Par conséquent, $n=4$ convient.\n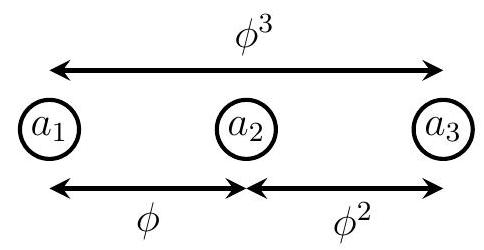\n\nCas $n=3$\n\n\nCas $n=4$\n\nEn pratique, on pouvait trouver les constructions ci-dessus par étude exhaustive des valeurs possibles pour les différences $a_{j}-a_{i}$. Cependant, lorsque $n \\geqslant 5$, on n'a guère envie de continuer sur cette lancée avec $n(n-1) / 2 \\geqslant 10$ différences à traiter. On suppose donc que l'on dispose d'une solution $n \\geqslant 5$, ainsi que de réels $r>0$ et $a_{1}<a_{2}<\\cdots<a_{n}$ adéquats.\nPosons $t=n(n-1) / 2$. Quitte à remplacer $r$ par $1 / r$ et chaque nombre $a_{i}$ par $a_{i} / r^{t+1}$, on suppose que $r \\geqslant 1$. En outre, puisque $a_{3}-a_{1}>a_{2}-a_{1}$, on sait même que $r>1$. Désormais, à chaque entier $k \\leqslant t$, on associe l'intervalle $\\mathcal{I}(k)=\\{i, i+1, \\ldots, j-1\\}$ pour lequel $a_{j}-a_{i}=r^{k}$. Lorsque l'on scinde un intervalle $\\mathcal{I}(k)$ en deux sous-intervalles $\\mathcal{I}(\\ell)$ et $\\mathcal{I}\\left(\\ell^{\\prime}\\right)$, on constate immédiatement que $r^{k}=r^{\\ell}+r^{\\ell^{\\prime}}$.\nSupposons maintenant qu'il existe un entier $k$ pour lequel l'ensemble $\\mathcal{I}(k) \\cup \\mathcal{I}(k+1)$ n'est pas un intervalle. Quitte à remplacer chaque nombre $a_{i}$ par $-a_{i}$, il existe quatre entiers $u<v<w<x$ tels que $r^{k}=a_{v}-a_{u}$ et $r^{k+1}=a_{x}-a_{w}$. Soit alors $x, y$ et $z$ les entiers tels que $r^{x}=a_{w}-a_{v}, r^{y}=a_{w}-a_{u}$ et $r^{z}=a_{x}-a_{v}$. Comme $r^{y}=r^{k}+r^{x}<r^{k+1}+r^{x}=r^{z}$, on sait que $z \\geqslant y+1$, de sorte que $r^{k+1}+r^{x}=r^{z} \\geqslant r^{y+1}=r^{k+1}+r^{x+1}$, ce qui est absurde. Ainsi, l'ensemble $\\mathcal{I}(k) \\cup \\mathcal{I}(k+1)$ est toujours un intervalle.\n\n\nPar ailleurs, la bijection réciproque $\\mathcal{I}^{-1}$ de $\\mathcal{I}$ est croissante : lorsque $\\mathcal{I}(k) \\subseteq \\mathcal{I}(\\ell)$, on sait que $k \\leqslant \\ell$. Par conséquent, et quitte à remplacer chaque terme $a_{i}$ par $-a_{i}$, les intervalles $\\mathcal{I}(1)$ et $\\mathcal{I}(2)$ sont sont des singletons voisins, de la forme $\\{k\\}$ et $\\{k+1\\}$.\n\nSoit $\\ell$ le plus grand entier pour lequel $\\mathcal{I}(\\ell+1)=\\{k+\\ell\\}$. L'intervalle $\\mathcal{I}(\\ell+2)$ ne peut contenir, parmi éventuels ses sous-intervalles stricts, que les singletons $\\{k\\},\\{k+1\\}, \\ldots,\\{k+\\ell\\}$. En outre, $\\mathcal{I}(\\ell+2)$ ne coïncide avec aucun des singletons $\\{k\\},\\{k+1\\}, \\ldots,\\{k+\\ell+1\\}$. Or, $\\mathcal{I}(\\ell+2) \\cup$ $\\{k+\\ell\\}$ est un intervalle, donc $\\mathcal{I}(\\ell+2)$ contient l'un des trois entiers $k+\\ell-1, k+\\ell$ et $k+\\ell+1$. Par conséquent, il existe un entier $a$, égal à $\\ell-2$ ou à $\\ell-1$, tel que $\\mathcal{I}(\\ell+2)=\\{k+a, k+a+1\\}$. On note alors $\\ell^{\\prime}$ l'entier $^{-1}(\\{k, k+1\\})$. Puisque $r^{1}+r^{2}=r^{\\ell^{\\prime}} \\geqslant r^{\\ell}=r^{a+1}+r^{a+2}$, on sait que $a=0$. Ainsi, $\\mathcal{I}(\\ell+2)=\\{k, k+1\\}$ et $\\ell$ est égal à 1 ou à 2 .\n$\\triangleright \\mathrm{Si} \\ell=1$, alors $r+r^{2}=r^{3}$. Cette situation est pour l'instant analogue au cas $n=2$.\nEn outre, l'intervalle $\\mathcal{I}(4)$ est un singleton $\\{k-1\\}$ ou $\\{k+2\\}$, et sa réunion disjointe avec $\\mathcal{I}(3)$ forme un intervalle $\\mathcal{I}(m)$ égal à $\\{k-1, k, k+1\\}$ ou à $\\{k, k+1, k+2\\}$, pour lequel $r^{m}=r^{3}+r^{4}=r^{2}\\left(r+r^{2}\\right)=r^{5}$. Mais alors $\\mathcal{I}(5)$ compte 6 sous-intervalles, ce qui est impossible.\n$\\triangleright \\mathrm{Si} \\ell=2$, alors $r+r^{2}=r^{4}$. On en déduit immédiatement que $r^{2}+r^{3}=r^{5}$ et $r^{3}+r^{4}=r^{6}$, donc que $\\mathcal{I}(5)=\\{k+1, k+2\\}$ et $\\mathcal{I}(6)=\\{k, k+1, k+2\\}$. Cette situation est pour l'instant analogue au cas $n=3$.\nAinsi, l'intervalle $\\mathcal{I}(7)$ est un singleton $\\{k-1\\}$ ou $\\{k+3\\}$, et sa réunion disjointe avec $\\mathcal{I}(6)$ forme un intervalle $\\mathcal{I}(m)$ égal à $\\{k-1, k, k+1, k+2\\}$ ou à $\\{k, k+1, k+2, k+3\\}$, pour lequel $r^{m}=r^{6}+r^{7}=r^{5}\\left(r+r^{2}\\right)=r^{9}$. Par conséquent, $\\mathcal{I}(9)$ compte 10 sous-intervalles, ce qui est impossible.\n\n\nEn conclusion, nul entier $n \\geqslant 5$ ne convient, et les solutions sont donc $n=2, n=3$ et $n=4$.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution de l'exercice 7"}
|
| 8 |
+
{"year": "2022", "problem_label": "7", "tier": 1, "problem": "Trouver tous les entiers $n \\geqslant 2$ pour lesquels il existe un nombre réel $r>0$ et $n$ nombres réels $a_{1}<a_{2}<\\cdots<a_{n}$ tels que les $n(n-1) / 2$ différences $a_{j}-a_{i}$ obtenues lorsque $1 \\leqslant i<j \\leqslant n$ sont égales, à l'ordre près, aux nombres $r^{1}, r^{2}, \\ldots, r^{n(n-1) / 2}$.", "solution": "$n^{\\circ} 1$ On montre comme dans la solution précédente que les entiers $n=2$, $n=3$ et $n=4$ conviennent, et que l'on peut supposer que $r>1$. On pose également $m=n(n-1) / 2$.\nOn considère maintenant une solution $n \\geqslant 4$, et des réels $a_{i}$ et $r$ adaptés. On note $\\mathrm{p}(i, j)$ l'entier pour lequel $a_{j}-a_{i}=r^{\\mathbf{p}(i, j)}$. Sous ces hypothèses, puisque $a_{n}-a_{1}$ est la plus grande des différences $a_{j}-a_{i}$, elle vaut $r^{m}$, et $\\mathrm{p}(1, n)=m$. En outre, chaque différence $a_{i}-a_{j}$ autre que $a_{n}-a_{1}$ est majorée par $a_{n}-a_{2}$ ou par $a_{n-1}-a_{1}$. Quitte à remplacer chaque entier $a_{i}$ par $-a_{i}$ et à réordonner nos nombres, on suppose que $a_{n-1}-a_{1} \\geqslant a_{n}-a_{2}$, ce qui nous assure que $p(1, n-1)=m-1$.\nOn remarque alors que $r^{m}=a_{n}-a_{1}=\\left(a_{n}-a_{j}\\right)+\\left(a_{j}-a_{1}\\right)=r^{\\mathbf{p}(j, n)}+r^{\\mathbf{p}(1, j)}$ pour chacun des entiers $j=2,3, \\ldots, n-1$. Au vu de cette égalité, on dit que deux entiers $c$ et $d$ forment un couple pivot si $1 \\leqslant c<d$ et $r^{-c}+r^{-d}=1$. Remarquons, dans ce cas-là, que $2 r^{-c}>r^{-c}+r^{-d}=$ 1 , de sorte que $c<\\log _{r}(2)$. On peut alors noter $\\left(c_{1}, d_{1}\\right), \\ldots,\\left(c_{k}, d_{k}\\right)$ les couples pivots, et les trier de sorte que $c_{1}<c_{2}<\\cdots<c_{k}$, ce qui nous conduit aux inégalités $1 \\leqslant c_{1}<c_{2}<\\cdots<$ $c_{k}<d_{k}<\\cdots<d_{2}<d_{1}$. En outre, par construction, les entiers $m-\\mathrm{p}(1, j)$ et $m-\\mathrm{p}(j, n)$ forment un couple pivot (à l'ordre près) lorsque $2 \\leqslant j \\leqslant n-1$ : il y a donc au moins $n-2$ couples pivots, ce qui nous assure que $d_{k} \\geqslant k+1 \\geqslant n-1$.\n\nSoit maintenant $\\mathrm{p}(I, J)$ le plus petit des entiers $\\mathrm{p}(i, j)$ pour lesquels $j \\geqslant i+2$. Puisque $\\mathrm{p}(I, J) \\geqslant \\mathrm{p}(I, J-1)$, on sait que $J=I+2$. En outre, parmi les $n(n-1) / 2$ entiers $\\mathrm{p}(i, j)$, il y en a $n-1$ pour lesquels $j=i+1$; ainsi, $\\mathrm{p}(I, J) \\leqslant n$. En particulier, puisque\n\n$$\nr^{\\mathbf{p}(I, J)}=a_{J}-a_{I}=\\left(a_{J}-a_{I+1}\\right)+\\left(a_{I+1}-a_{I}\\right)=r^{\\mathbf{p}(I+1, J)}+r^{\\mathbf{p}(I, I+1)}\n$$\n\nles entiers $\\mathrm{p}(I, J)-\\mathrm{p}(I+1, J)$ et $\\mathrm{p}(I, J)-\\mathrm{p}(I, I+1)$ forment, à l'ordre près, un couple pivot. Le plus grand des deux vaut donc au moins $n-1$, et puisqu'il est minoré par $n-1$, il coïncide avec $n-1$. En d'autres termes, on est assuré que $k=n-2$, que $d_{k}=n-1$; que chaque entier $c_{i}$ vaut $i$; et que les entiers $\\mathrm{p}(i, i+1)$ prennent les valeurs $1,2, \\ldots, n-1$ dans un certain ordre. Cela signifie notamment que $p(1,2) \\leqslant n-1$.\nEn outre, chacun des entiers $m-n+1, m-n+2, \\ldots, m-n$ est désormais égal à l'un des entiers $m-d_{k}, m-c_{k}, m-c_{k-1}, \\ldots, m-c_{1}$, donc coïncide avec l'un des entiers $\\mathrm{p}(1, j)$ ou $\\mathrm{p}(j, n)$ obtenus lorsque $2 \\leqslant j \\leqslant n-1$. Par conséquent, $\\mathrm{p}(2, n-1) \\leqslant m-n$. Or, l'égalité\n\n$$\nr^{\\mathbf{p}(1,2)}+r^{\\mathbf{p}(2, n-1)}=\\left(a_{2}-a_{1}\\right)+\\left(a_{n-1}-a_{2}\\right)=a_{n-1}-a_{1}=r^{m-1}\n$$\n\nnous indique que les entiers $(m-1)-\\mathrm{p}(1,2)$ et $(m-1)-\\mathrm{p}(2, n-1)$ forment, à l'ordre près, un couple pivot, disons $\\left(c_{\\ell}, d_{\\ell}\\right)$. L'inégalité $(m-1)-\\mathrm{p}(2, n-1) \\geqslant n-1>c_{\\ell}$ nous assure donc que $(m-1)-\\mathrm{p}(1,2)=c_{\\ell} \\leqslant n-1$.\nPuisque $\\mathrm{p}(1,2) \\leqslant n-1$, on en conclut que\n\n$$\nn(n-1)=2 m \\leqslant 2 p(1,2)+2 n \\leqslant 4 n-2<4 n\n$$\n\ndonc que $n-1<4$, c'est-à-dire $n \\leqslant 4$.\nRemarque: Le lecteur bien trop savant aura pu se rappeler le résultat suivant:\nSoit $a$ et $b$ deux entiers tels que $1 \\leqslant a<b$, et soit $\\delta$ leur PGCD. Posons $k=1$ si $a \\equiv 2 b(\\bmod 6 \\delta)$, et $k=0$ sinon.\nLe polynôme $P_{a, b}(X)=X^{b}-X^{a}-1$ peut s'écrire comme un produit de la forme\n\n$$\nP_{a, b}(X)=\\left(X^{2 \\delta}-X^{\\delta}+1\\right)^{k} Q_{a, b}(X)\n$$\n\noù $Q_{a, b}(X)$ est un polynôme irréductible de $\\mathbb{Z}[X]$.\nOn peut alors préciser ce résultat en invoquant le lemme suivant:\nDeux couples $(a, b)$ et $\\left(a^{\\prime}, b^{\\prime}\\right)$ satisfont l'égalité $Q_{a, b}(X)=Q_{a^{\\prime}, b^{\\prime}}(X)$ si et seulement s'ils sont égaux l'un à l'autre ou bien s'ils ont même PGCD $\\delta$ et sont égaux à $(\\delta, 3 \\delta)$ et $(4 \\delta, 5 \\delta)$.\nDémonstration : Soit $\\delta=\\operatorname{PGCD}(a, b), \\delta^{\\prime}=\\operatorname{PGCD}\\left(a^{\\prime}, b^{\\prime}\\right)$, puis $k$ et $k^{\\prime}$ définis comme ci-dessus.\n$\\triangleright \\operatorname{Si} k=k^{\\prime}=0$, alors $P_{a, b}(X)=P_{a^{\\prime}, b^{\\prime}}(X)$, donc $(a, b)=\\left(a^{\\prime}, b^{\\prime}\\right)$.\n$\\triangleright \\operatorname{Si} k=1$ et $k^{\\prime}=0$, alors $Q_{a, b}(X)=P_{a^{\\prime}, b^{\\prime}}(X)$. En outre, puisque $P_{a, b}(X)$ est un polynôme en $X^{\\delta}, Q_{a, b}(X)$ en est un aussi, donc $\\delta$ divise $a^{\\prime}$ et $b^{\\prime}$. Quitte à divise $a, b, a^{\\prime}$ et $b^{\\prime}$ par $\\delta$, on suppose donc que $\\delta=1$. On a alors\n\n$$\nX^{b}-X^{a}-1=\\left(X^{2}-X+1\\right)\\left(X^{b^{\\prime}}-X^{a^{\\prime}}-1\\right)\n$$\n\nce qui montre déjà que $b=b^{\\prime}+2$. Puisque $b \\geqslant 2$ et $b^{\\prime} \\geqslant 2$, la relation (1) indique notamment que\n\n$$\n-X^{a}-1 \\equiv X^{b}-X^{a}-1 \\equiv\\left(X^{2}-X+1\\right)\\left(X^{b^{\\prime}}-X^{a^{\\prime}}-1\\right) \\equiv-X^{a^{\\prime}}+X-1 \\quad\\left(\\bmod X^{2}\\right),\n$$\n\nde sorte que $a \\geqslant 2$ et $a^{\\prime}=1$. Mais alors (1) se réécrit comme\n\n$$\nX^{b}-X^{a}-1=\\left(X^{2}-X+1\\right)\\left(X^{b^{\\prime}}-X-1\\right)=X^{b^{\\prime}+2}-X^{b^{\\prime}+1}+X^{b^{\\prime}}-X^{3}-1,\n$$\n\net l'on est forcé d'avoir $b^{\\prime}=3$ puis $b=5$ et $a=4$.\n$\\triangleright$ Si $k=0$ et $k^{\\prime}=1$, la situation est symétrique et se traite de la même façon.\n$\\triangleright \\operatorname{Si} k=k^{\\prime}=1$, et si $\\delta^{\\prime}$ ne divise pas $\\delta$, et on pose $\\delta^{\\prime \\prime}=\\operatorname{PPCM}\\left(\\delta, \\delta^{\\prime}\\right)$. Comme mentionné précédemment, le polynôme $Q_{a, b}(X)=Q_{a^{\\prime}, b^{\\prime}}(X)$ est un polynôme en $X^{\\delta}$ et en $X^{\\delta^{\\prime}}$, donc en $X^{\\delta^{\\prime \\prime}}$. Ainsi, $Q_{a, b}(X) \\equiv-1\\left(\\bmod X^{\\delta^{\\prime \\prime}}\\right)$, et\n\n$$\nX^{b}-X^{a}-1=-X^{2 \\delta}+X^{\\delta}-1 \\quad\\left(\\bmod X^{\\delta^{\\prime \\prime}}\\right),\n$$\n\nce qui est absurde, puisque les termes de deuxième plus petit degré de ces polynômes sont de coefficients différents.\nOn en conclut que $\\delta^{\\prime}$ divise $\\delta$, et même que $\\delta=\\delta^{\\prime}$. On a donc encore $P_{a, b}(X)=P_{a^{\\prime}, b^{\\prime}}(X)$ et $(a, b)=\\left(a^{\\prime}, b^{\\prime}\\right)$.\nEn conclusion, on a bien $(a, b)=\\left(a^{\\prime}, b^{\\prime}\\right)$ ou $\\left\\{(a, b),\\left(a^{\\prime}, b^{\\prime}\\right)\\right\\}=\\{(\\delta, 3 \\delta),(4, \\delta, 5 \\delta)\\}$.\nRéciproquement, si $(a, b)=\\left(a^{\\prime}, b^{\\prime}\\right)$, on a évidemment $Q_{a, b}(X)=Q_{a^{\\prime}, b^{\\prime}}(X)$. Et , si $(a, b)=(\\delta, 3 \\delta)$ et $\\left(a^{\\prime}, b^{\\prime}\\right)=(4 \\delta, 5 \\delta)$, on a également\n\n$$\nP_{a^{\\prime}, b^{\\prime}}(X)=X^{5 \\delta}-X^{4 \\delta}-1=\\left(X^{2 \\delta}-X^{\\delta}+1\\right)\\left(X^{3 \\delta}-X^{\\delta}-1\\right)=\\left(X^{2 \\delta}-X^{\\delta}+1\\right) P_{a, b}(X),\n$$\n\nde sorte que $Q_{a, b}(X)=P_{a, b}(X)=Q_{a^{\\prime}, b^{\\prime}}(X)$.\nLa conclusion de l'exercice est désormais proche. En effet, comme on l'a vu dans la solution précédente, on sait que l'on a au moins $n-2$ couples pivots. Or, un couple $(c, d)$ est pivot si et seulement si $r$ est une racine de $P_{d-c, d}(X)$. Si l'on pose $\\delta=\\operatorname{PGCD}(c, d)$, et puisque $r^{2 \\delta}-r^{\\delta}+1 \\geqslant r^{\\delta}>0$, notre réel $r$ est même racine de $Q_{d-c, d}(X)$. Mais alors $Q_{d-c, d}(X)$ est le polynôme minimal de $r$, et ne dépend pas du couple pivot $(c, d)$ de départ. On a donc au plus deux couples pivots au total, de sorte que $n \\leqslant 4$.\n\nCommentaire des correcteurs L'exercice était très difficile. Il était important de regarder ce qui se passait pour les petites valeurs de $n$, sans négliger l'étude des cas $n=3$ et $n=$ 4 , mais également, par exemple, $n=5$, afin de se convaincre que les solutions seraient seulement $n=2,3$ et 4 . Par ailleurs, de nombreux élèves ont eu la bonne idée de regarder des phénomènes extrémaux, tels que l'apparition d'un triplet d'un couple pivot de la forme $(k, k+1)$, ou encore le fait qu'il existait au moins $n-2$ couples pivots.", "problem_match": "\nExercice 7.", "solution_match": "\nSolution alternative"}
|