m$ ). Note that for different values of $m$, we get different values of $k$, due to the different powers of 2 in the prime factorisation of $k$.
+
+Solution 2. Treat the (trivial) case when $n$ is odd as in Solution 1.
+Now assume that $n$ is even and $n>2$. Let $p$ be a prime divisor of $n-1$.
+Proceed by induction on $i$ to prove that $p^{i+1}$ is a divisor of $n^{p^{i}}-1$ for every $i \geqslant 0$. The case $i=0$ is true by the way in which $p$ is chosen. Suppose the result is true for some $i \geqslant 0$. The factorisation
+
+$$
+n^{p^{i+1}}-1=\left(n^{p^{i}}-1\right)\left[n^{p^{i}(p-1)}+n^{p^{i}(p-2)}+\cdots+n^{p^{i}}+1\right],
+$$
+
+together with the fact that each of the $p$ terms between the square brackets is congruent to 1 modulo $p$, implies that the result is also true for $i+1$.
+
+Hence $\left\lfloor\frac{n^{p^{i}}}{p^{i}}\right\rfloor=\frac{n^{p^{i}}-1}{p^{i}}$, an odd integer for each $i \geqslant 1$.
+Finally, we consider the case $n=2$. We observe that $3 \cdot 4^{i}$ is a divisor of $2^{3 \cdot 4^{i}}-4^{i}$ for every $i \geqslant 1$ : Trivially, $4^{i}$ is a divisor of $2^{3 \cdot 4^{i}}-4^{i}$, since $3 \cdot 4^{i}>2 i$. Furthermore, since $2^{3 \cdot 4^{i}}$ and $4^{i}$ are both congruent to 1 modulo 3, we have $3 \mid 2^{3 \cdot 4^{i}}-4^{i}$. Hence, $\left\lfloor\frac{2^{3 \cdot 4^{i}}}{3 \cdot 4^{i}}\right\rfloor=\frac{2^{3 \cdot 4^{i}}-4^{i}}{3 \cdot 4^{i}}=\frac{2^{3 \cdot 4^{i}-2 i}-1}{3}$, which is odd for every $i \geqslant 1$.
+
+Comment. The case $n$ even and $n>2$ can also be solved by recursively defining the sequence $\left(k_{i}\right)_{i \geqslant 1}$ by $k_{1}=1$ and $k_{i+1}=n^{k_{i}}-1$ for $i \geqslant 1$. Then $\left(k_{i}\right)$ is strictly increasing and it follows (by induction on $i$ ) that $k_{i} \mid n^{k_{i}}-1$ for all $i \geqslant 1$, so the $k_{i}$ are as desired.
+
+The case $n=2$ can also be solved as follows: Let $i \geqslant 2$. By Bertrand's postulate, there exists a prime number $p$ such that $2^{2^{i}-1}0}: 2^{i} \text { divides } a p+1\right\}
+$$
+
+Recall that there exists $a$ with $1 \leqslant a<2^{i}$ such that $a p \equiv-1\left(\bmod 2^{i}\right)$, so each $a_{i}$ satisfies $1 \leqslant a_{i}<2^{i}$. This implies that $a_{i} p+1
2$, and we let $a$ and $b$ be positive integers such that $x^{p-1}+y=p^{a}$ and $x+y^{p-1}=p^{b}$. Assume further, without loss of generality, that $x \leqslant y$, so that $p^{a}=x^{p-1}+y \leqslant x+y^{p-1}=p^{b}$, which means that $a \leqslant b$ (and thus $\left.p^{a} \mid p^{b}\right)$.
+
+Now we have
+
+$$
+p^{b}=y^{p-1}+x=\left(p^{a}-x^{p-1}\right)^{p-1}+x .
+$$
+
+We take this equation modulo $p^{a}$ and take into account that $p-1$ is even, which gives us
+
+$$
+0 \equiv x^{(p-1)^{2}}+x \quad\left(\bmod p^{a}\right)
+$$
+
+If $p \mid x$, then $p^{a} \mid x$, since $x^{(p-1)^{2}-1}+1$ is not divisible by $p$ in this case. However, this is impossible, since $x \leqslant x^{p-1}2$. Thus $a=r+1$. Now since $p^{r} \leqslant x+1$, we get
+
+$$
+x=\frac{x^{2}+x}{x+1} \leqslant \frac{x^{p-1}+y}{x+1}=\frac{p^{a}}{x+1} \leqslant \frac{p^{a}}{p^{r}}=p,
+$$
+
+so we must have $x=p-1$ for $p$ to divide $x+1$.
+It follows that $r=1$ and $a=2$. If $p \geqslant 5$, we obtain
+
+$$
+p^{a}=x^{p-1}+y>(p-1)^{4}=\left(p^{2}-2 p+1\right)^{2}>(3 p)^{2}>p^{2}=p^{a}
+$$
+
+a contradiction. So the only case that remains is $p=3$, and indeed $x=2$ and $y=p^{a}-x^{p-1}=5$ satisfy the conditions.
+
+Comment 1. In this solution, we are implicitly using a special case of the following lemma known as "lifting the exponent":
+Lemma. Let $n$ be a positive integer, let $p$ be an odd prime, and let $v_{p}(m)$ denote the exponent of the highest power of $p$ that divides $m$.
+
+If $x$ and $y$ are integers not divisible by $p$ such that $p \mid x-y$, then we have
+
+$$
+v_{p}\left(x^{n}-y^{n}\right)=v_{p}(x-y)+v_{p}(n)
+$$
+
+Likewise, if $x$ and $y$ are integers not divisible by $p$ such that $p \mid x+y$, then we have
+
+$$
+v_{p}\left(x^{n}+y^{n}\right)=v_{p}(x+y)+v_{p}(n) .
+$$
+
+Comment 2. There exist various ways of solving the problem involving the "lifting the exponent" lemma. Let us sketch another one.
+
+The cases $x=y$ and $p \mid x$ are ruled out easily, so we assume that $p>2, x2$. If $p \mid x$, then also $p \mid y$. In this case, let $p^{k}$ and $p^{\ell}$ be the highest powers of $p$ that divide $x$ and $y$ respectively, and assume without loss of generality that $k \leqslant \ell$. Then $p^{k}$ divides $x+y^{p-1}$ while $p^{k+1}$ does not, but $p^{k}p$, so $x^{p-1}+y$ and $y^{p-1}+x$ are both at least equal to $p^{2}$. Now we have
+
+$$
+x^{p-1} \equiv-y \quad\left(\bmod p^{2}\right) \quad \text { and } \quad y^{p-1} \equiv-x \quad\left(\bmod p^{2}\right)
+$$
+
+These two congruences, together with the Euler-Fermat theorem, give us
+
+$$
+1 \equiv x^{p(p-1)} \equiv(-y)^{p} \equiv-y^{p} \equiv x y \quad\left(\bmod p^{2}\right)
+$$
+
+Since $x \equiv y \equiv-1(\bmod p), x-y$ is divisible by $p$, so $(x-y)^{2}$ is divisible by $p^{2}$. This means that
+
+$$
+(x+y)^{2}=(x-y)^{2}+4 x y \equiv 4 \quad\left(\bmod p^{2}\right)
+$$
+
+so $p^{2}$ divides $(x+y-2)(x+y+2)$. We already know that $x+y \equiv-2(\bmod p)$, so $x+y-2 \equiv$ $-4 \not \equiv 0(\bmod p)$. This means that $p^{2}$ divides $x+y+2$.
+
+Using the same notation as in the first solution, we subtract the two original equations to obtain
+
+$$
+p^{b}-p^{a}=y^{p-1}-x^{p-1}+x-y=(y-x)\left(y^{p-2}+y^{p-3} x+\cdots+x^{p-2}-1\right)
+$$
+
+The second factor is symmetric in $x$ and $y$, so it can be written as a polynomial of the elementary symmetric polynomials $x+y$ and $x y$ with integer coefficients. In particular, its value modulo
+$p^{2}$ is characterised by the two congruences $x y \equiv 1\left(\bmod p^{2}\right)$ and $x+y \equiv-2\left(\bmod p^{2}\right)$. Since both congruences are satisfied when $x=y=-1$, we must have
+
+$$
+y^{p-2}+y^{p-3} x+\cdots+x^{p-2}-1 \equiv(-1)^{p-2}+(-1)^{p-3}(-1)+\cdots+(-1)^{p-2}-1 \quad\left(\bmod p^{2}\right),
+$$
+
+which simplifies to $y^{p-2}+y^{p-3} x+\cdots+x^{p-2}-1 \equiv-p\left(\bmod p^{2}\right)$. Thus the second factor in (1) is divisible by $p$, but not $p^{2}$.
+
+This means that $p^{a-1}$ has to divide the other factor $y-x$. It follows that
+
+$$
+0 \equiv x^{p-1}+y \equiv x^{p-1}+x \equiv x(x+1)\left(x^{p-3}-x^{p-4}+\cdots+1\right) \quad\left(\bmod p^{a-1}\right) .
+$$
+
+Since $x \equiv-1(\bmod p)$, the last factor is $x^{p-3}-x^{p-4}+\cdots+1 \equiv p-2(\bmod p)$ and in particular not divisible by $p$. We infer that $p^{a-1} \mid x+1$ and continue as in the first solution.
+
+Comment. Instead of reasoning by means of elementary symmetric polynomials, it is possible to provide a more direct argument as well. For odd $r,(x+1)^{2}$ divides $\left(x^{r}+1\right)^{2}$, and since $p$ divides $x+1$, we deduce that $p^{2}$ divides $\left(x^{r}+1\right)^{2}$. Together with the fact that $x y \equiv 1\left(\bmod p^{2}\right)$, we obtain
+
+$$
+0 \equiv y^{r}\left(x^{r}+1\right)^{2} \equiv x^{2 r} y^{r}+2 x^{r} y^{r}+y^{r} \equiv x^{r}+2+y^{r} \quad\left(\bmod p^{2}\right) .
+$$
+
+We apply this congruence with $r=p-2-2 k$ (where $0 \leqslant k<(p-2) / 2$ ) to find that
+
+$$
+x^{k} y^{p-2-k}+x^{p-2-k} y^{k} \equiv(x y)^{k}\left(x^{p-2-2 k}+y^{p-2-2 k}\right) \equiv 1^{k} \cdot(-2) \equiv-2 \quad\left(\bmod p^{2}\right) .
+$$
+
+Summing over all $k$ yields
+
+$$
+y^{p-2}+y^{p-3} x+\cdots+x^{p-2}-1 \equiv \frac{p-1}{2} \cdot(-2)-1 \equiv-p \quad\left(\bmod p^{2}\right)
+$$
+
+once again.
+
+N6. Let $a_{1}x_{n}
+$$
+
+holds for all integers $n \geqslant 0$, it is also strictly increasing. Since $x_{n+1}$ is by (1) coprime to $c$ for any $n \geqslant 0$, it suffices to prove that for each $n \geqslant 2$ there exists a prime number $p$ dividing $x_{n}$ but none of the numbers $x_{1}, \ldots, x_{n-1}$. Let us begin by establishing three preliminary claims.
+Claim 1. If $i \equiv j(\bmod m)$ holds for some integers $i, j \geqslant 0$ and $m \geqslant 1$, then $x_{i} \equiv x_{j}\left(\bmod x_{m}\right)$ holds as well.
+Proof. Evidently, it suffices to show $x_{i+m} \equiv x_{i}\left(\bmod x_{m}\right)$ for all integers $i \geqslant 0$ and $m \geqslant 1$. For this purpose we may argue for fixed $m$ by induction on $i$ using $x_{0}=0$ in the base case $i=0$. Now, if we have $x_{i+m} \equiv x_{i}\left(\bmod x_{m}\right)$ for some integer $i$, then the recursive equation (1) yields
+
+$$
+x_{i+m+1} \equiv c^{2}\left(x_{i+m}^{3}-4 x_{i+m}^{2}+5 x_{i+m}\right)+1 \equiv c^{2}\left(x_{i}^{3}-4 x_{i}^{2}+5 x_{i}\right)+1 \equiv x_{i+1} \quad\left(\bmod x_{m}\right),
+$$
+
+which completes the induction.
+Claim 2. If the integers $i, j \geqslant 2$ and $m \geqslant 1$ satisfy $i \equiv j(\bmod m)$, then $x_{i} \equiv x_{j}\left(\bmod x_{m}^{2}\right)$ holds as well.
+Proof. Again it suffices to prove $x_{i+m} \equiv x_{i}\left(\bmod x_{m}^{2}\right)$ for all integers $i \geqslant 2$ and $m \geqslant 1$. As above, we proceed for fixed $m$ by induction on $i$. The induction step is again easy using (1), but this time the base case $i=2$ requires some calculation. Set $L=5 c^{2}$. By (1) we have $x_{m+1} \equiv L x_{m}+1\left(\bmod x_{m}^{2}\right)$, and hence
+
+$$
+\begin{aligned}
+x_{m+1}^{3}-4 x_{m+1}^{2}+5 x_{m+1} & \equiv\left(L x_{m}+1\right)^{3}-4\left(L x_{m}+1\right)^{2}+5\left(L x_{m}+1\right) \\
+& \equiv\left(3 L x_{m}+1\right)-4\left(2 L x_{m}+1\right)+5\left(L x_{m}+1\right) \equiv 2 \quad\left(\bmod x_{m}^{2}\right)
+\end{aligned}
+$$
+
+which in turn gives indeed $x_{m+2} \equiv 2 c^{2}+1 \equiv x_{2}\left(\bmod x_{m}^{2}\right)$.
+Claim 3. For each integer $n \geqslant 2$, we have $x_{n}>x_{1} \cdot x_{2} \cdots x_{n-2}$.
+Proof. The cases $n=2$ and $n=3$ are clear. Arguing inductively, we assume now that the claim holds for some $n \geqslant 3$. Recall that $x_{2} \geqslant 3$, so by monotonicity and (2) we get $x_{n} \geqslant x_{3} \geqslant x_{2}\left(x_{2}-2\right)^{2}+x_{2}+1 \geqslant 7$. It follows that
+
+$$
+x_{n+1}>x_{n}^{3}-4 x_{n}^{2}+5 x_{n}>7 x_{n}^{2}-4 x_{n}^{2}>x_{n}^{2}>x_{n} x_{n-1}
+$$
+
+which by the induction hypothesis yields $x_{n+1}>x_{1} \cdot x_{2} \cdots x_{n-1}$, as desired.
+
+Now we direct our attention to the problem itself: let any integer $n \geqslant 2$ be given. By Claim 3 there exists a prime number $p$ appearing with a higher exponent in the prime factorisation of $x_{n}$ than in the prime factorisation of $x_{1} \cdots x_{n-2}$. In particular, $p \mid x_{n}$, and it suffices to prove that $p$ divides none of $x_{1}, \ldots, x_{n-1}$.
+
+Otherwise let $k \in\{1, \ldots, n-1\}$ be minimal such that $p$ divides $x_{k}$. Since $x_{n-1}$ and $x_{n}$ are coprime by (1) and $x_{1}=1$, we actually have $2 \leqslant k \leqslant n-2$. Write $n=q k+r$ with some integers $q \geqslant 0$ and $0 \leqslant r1$, so there exists a prime $p$ with $v_{p}(N)>0$. Since $N$ is a fraction of two odd numbers, $p$ is odd.
+
+By our lemma,
+
+$$
+0\frac{1}{2}, \quad \text { or } \quad\{x\}>\frac{1}{2}, \quad\{y\}>\frac{1}{2}, \quad\{x+y\}<\frac{1}{2},
+$$
+
+where $\{x\}$ denotes the fractional part of $x$.
+In the context of our problem, the first condition seems easier to deal with. Also, one may notice that
+
+$$
+\{x\}<\frac{1}{2} \Longleftrightarrow \varkappa(x)=0 \quad \text { and } \quad\{x\} \geqslant \frac{1}{2} \Longleftrightarrow \varkappa(x)=1,
+$$
+
+where
+
+$$
+\varkappa(x)=\lfloor 2 x\rfloor-2\lfloor x\rfloor .
+$$
+
+Now it is natural to consider the number
+
+$$
+M=\frac{\binom{2 a+2 b}{a+b}}{\binom{2 a}{a}\binom{2 b}{b}}
+$$
+
+since
+
+$$
+v_{p}(M)=\sum_{k=1}^{\infty}\left(\varkappa\left(\frac{2(a+b)}{p^{k}}\right)-\varkappa\left(\frac{2 a}{p^{k}}\right)-\varkappa\left(\frac{2 b}{p^{k}}\right)\right) .
+$$
+
+One may see that $M>1$, and that $v_{2}(M) \leqslant 0$. Thus, there exist an odd prime $p$ and a positive integer $k$ with
+
+$$
+\varkappa\left(\frac{2(a+b)}{p^{k}}\right)-\varkappa\left(\frac{2 a}{p^{k}}\right)-\varkappa\left(\frac{2 b}{p^{k}}\right)>0 .
+$$
+
+In view of (4), the last inequality yields
+
+$$
+\left\{\frac{a}{p^{k}}\right\}<\frac{1}{2}, \quad\left\{\frac{b}{p^{k}}\right\}<\frac{1}{2}, \quad \text { and } \quad\left\{\frac{a+b}{p^{k}}\right\}>\frac{1}{2}
+$$
+
+which is what we wanted to obtain.
+Comment 2. Once one tries to prove the existence of suitable $p$ and $k$ satisfying (5), it seems somehow natural to suppose that $a \leqslant b$ and to add the restriction $p^{k}>a$. In this case the inequalities (5) can be rewritten as
+
+$$
+2 ak$. We would like to mention here that Sylvester's theorem itself does not seem to suffice for solving the problem.
+
diff --git a/IMO/md/en-IMO2015SL.md b/IMO/md/en-IMO2015SL.md
new file mode 100644
index 0000000000000000000000000000000000000000..88e96b991bbdac35f5dd9fdffead6993b47498b8
--- /dev/null
+++ b/IMO/md/en-IMO2015SL.md
@@ -0,0 +1,2600 @@
+# Shortlisted Problems with Solutions
+
+## $(\sqrt{(1)}$
$56^{\text {th }}$
International Mathematical Olympiad
+
+
+
+## Shortlisted Problems with Solutions
+
+$56^{\text {th }}$ International Mathematical Olympiad
+Chiang Mai, Thailand, 4-16
+
+
+## The shortlisted problems should be kept strictly confidential until IMO 2016.
+
+## Contributing Countries
+
+The Organizing Committee and the Problem Selection Committee of IMO 2015 thank the following 53 countries for contributing 155 problem proposals:
+
+Albania, Algeria, Armenia, Australia, Austria, Brazil, Bulgaria, Canada, Costa Rica, Croatia, Cyprus, Denmark, El Salvador, Estonia, Finland, France, Georgia, Germany, Greece, Hong Kong, Hungary, India, Iran, Ireland, Israel, Italy, Japan, Kazakhstan, Lithuania, Luxembourg, Montenegro, Morocco, Netherlands, Pakistan, Poland, Romania, Russia, Saudi Arabia, Serbia, Singapore, Slovakia, Slovenia, South Africa, South Korea, Sweden, Turkey, Turkmenistan, Taiwan, Tanzania, Ukraine, United Kingdom, U.S.A., Uzbekistan
+
+## Problem Selection Committee
+
+
+
+Dungjade Shiowattana, Ilya I. Bogdanov, Tirasan Khandhawit, Wittawat Kositwattanarerk, Géza Kós, Weerachai Neeranartvong, Nipun Pitimanaaree, Christian Reiher, Nat Sothanaphan, Warut Suksompong, Wuttisak Trongsiriwat, Wijit Yangjit
+
+Assistants: Jirawat Anunrojwong, Pakawut Jiradilok
+
+## Problems
+
+## Algebra
+
+A1. Suppose that a sequence $a_{1}, a_{2}, \ldots$ of positive real numbers satisfies
+
+$$
+a_{k+1} \geqslant \frac{k a_{k}}{a_{k}^{2}+(k-1)}
+$$
+
+for every positive integer $k$. Prove that $a_{1}+a_{2}+\cdots+a_{n} \geqslant n$ for every $n \geqslant 2$.
+A2. Determine all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ with the property that
+
+$$
+f(x-f(y))=f(f(x))-f(y)-1
+$$
+
+holds for all $x, y \in \mathbb{Z}$.
+(Croatia)
+A3. Let $n$ be a fixed positive integer. Find the maximum possible value of
+
+$$
+\sum_{1 \leqslant rm \geqslant N$.
+
+C6. Let $S$ be a nonempty set of positive integers. We say that a positive integer $n$ is clean if it has a unique representation as a sum of an odd number of distinct elements from $S$. Prove that there exist infinitely many positive integers that are not clean.
+
+C7. In a company of people some pairs are enemies. A group of people is called unsociable if the number of members in the group is odd and at least 3 , and it is possible to arrange all its members around a round table so that every two neighbors are enemies. Given that there are at most 2015 unsociable groups, prove that it is possible to partition the company into 11 parts so that no two enemies are in the same part.
+
+## Geometry
+
+G1. Let $A B C$ be an acute triangle with orthocenter $H$. Let $G$ be the point such that the quadrilateral $A B G H$ is a parallelogram. Let $I$ be the point on the line $G H$ such that $A C$ bisects $H I$. Suppose that the line $A C$ intersects the circumcircle of the triangle $G C I$ at $C$ and $J$. Prove that $I J=A H$.
+(Australia)
+G2. Let $A B C$ be a triangle inscribed into a circle $\Omega$ with center $O$. A circle $\Gamma$ with center $A$ meets the side $B C$ at points $D$ and $E$ such that $D$ lies between $B$ and $E$. Moreover, let $F$ and $G$ be the common points of $\Gamma$ and $\Omega$. We assume that $F$ lies on the arc $A B$ of $\Omega$ not containing $C$, and $G$ lies on the arc $A C$ of $\Omega$ not containing $B$. The circumcircles of the triangles $B D F$ and $C E G$ meet the sides $A B$ and $A C$ again at $K$ and $L$, respectively. Suppose that the lines $F K$ and $G L$ are distinct and intersect at $X$. Prove that the points $A, X$, and $O$ are collinear.
+(Greece)
+G3. Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$.
+(Georgia)
+G4. Let $A B C$ be an acute triangle, and let $M$ be the midpoint of $A C$. A circle $\omega$ passing through $B$ and $M$ meets the sides $A B$ and $B C$ again at $P$ and $Q$, respectively. Let $T$ be the point such that the quadrilateral $B P T Q$ is a parallelogram. Suppose that $T$ lies on the circumcircle of the triangle $A B C$. Determine all possible values of $B T / B M$.
+(Russia)
+G5. Let $A B C$ be a triangle with $C A \neq C B$. Let $D, F$, and $G$ be the midpoints of the sides $A B, A C$, and $B C$, respectively. A circle $\Gamma$ passing through $C$ and tangent to $A B$ at $D$ meets the segments $A F$ and $B G$ at $H$ and $I$, respectively. The points $H^{\prime}$ and $I^{\prime}$ are symmetric to $H$ and $I$ about $F$ and $G$, respectively. The line $H^{\prime} I^{\prime}$ meets $C D$ and $F G$ at $Q$ and $M$, respectively. The line $C M$ meets $\Gamma$ again at $P$. Prove that $C Q=Q P$.
+(El Salvador)
+G6. Let $A B C$ be an acute triangle with $A B>A C$, and let $\Gamma$ be its circumcircle. Let $H$, $M$, and $F$ be the orthocenter of the triangle, the midpoint of $B C$, and the foot of the altitude from $A$, respectively. Let $Q$ and $K$ be the two points on $\Gamma$ that satisfy $\angle A Q H=90^{\circ}$ and $\angle Q K H=90^{\circ}$. Prove that the circumcircles of the triangles $K Q H$ and $K F M$ are tangent to each other.
+(Ukraine)
+G7. Let $A B C D$ be a convex quadrilateral, and let $P, Q, R$, and $S$ be points on the sides $A B, B C, C D$, and $D A$, respectively. Let the line segments $P R$ and $Q S$ meet at $O$. Suppose that each of the quadrilaterals $A P O S, B Q O P, C R O Q$, and $D S O R$ has an incircle. Prove that the lines $A C, P Q$, and $R S$ are either concurrent or parallel to each other.
+(Bulgaria)
+G8. A triangulation of a convex polygon $\Pi$ is a partitioning of $\Pi$ into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a Thaiangulation if all triangles in it have the same area.
+
+Prove that any two different Thaiangulations of a convex polygon $\Pi$ differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.)
+(Bulgaria)
+
+## Number Theory
+
+N1. Determine all positive integers $M$ for which the sequence $a_{0}, a_{1}, a_{2}, \ldots$, defined by $a_{0}=\frac{2 M+1}{2}$ and $a_{k+1}=a_{k}\left\lfloor a_{k}\right\rfloor$ for $k=0,1,2, \ldots$, contains at least one integer term.
+(Luxembourg)
+N2. Let $a$ and $b$ be positive integers such that $a!b$ ! is a multiple of $a!+b!$. Prove that $3 a \geqslant 2 b+2$.
+(United Kingdom)
+N3. Let $m$ and $n$ be positive integers such that $m>n$. Define $x_{k}=(m+k) /(n+k)$ for $k=$ $1,2, \ldots, n+1$. Prove that if all the numbers $x_{1}, x_{2}, \ldots, x_{n+1}$ are integers, then $x_{1} x_{2} \cdots x_{n+1}-1$ is divisible by an odd prime.
+(Austria)
+N4. Suppose that $a_{0}, a_{1}, \ldots$ and $b_{0}, b_{1}, \ldots$ are two sequences of positive integers satisfying $a_{0}, b_{0} \geqslant 2$ and
+
+$$
+a_{n+1}=\operatorname{gcd}\left(a_{n}, b_{n}\right)+1, \quad b_{n+1}=\operatorname{lcm}\left(a_{n}, b_{n}\right)-1
+$$
+
+for all $n \geqslant 0$. Prove that the sequence $\left(a_{n}\right)$ is eventually periodic; in other words, there exist integers $N \geqslant 0$ and $t>0$ such that $a_{n+t}=a_{n}$ for all $n \geqslant N$.
+(France)
+N5. Determine all triples $(a, b, c)$ of positive integers for which $a b-c, b c-a$, and $c a-b$ are powers of 2 .
+
+Explanation: A power of 2 is an integer of the form $2^{n}$, where $n$ denotes some nonnegative integer.
+(Serbia)
+N6. Let $\mathbb{Z}_{>0}$ denote the set of positive integers. Consider a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$. For any $m, n \in \mathbb{Z}_{>0}$ we write $f^{n}(m)=\underbrace{f(f(\ldots f}_{n}(m) \ldots))$. Suppose that $f$ has the following two properties:
+(i) If $m, n \in \mathbb{Z}_{>0}$, then $\frac{f^{n}(m)-m}{n} \in \mathbb{Z}_{>0}$;
+(ii) The set $\mathbb{Z}_{>0} \backslash\left\{f(n) \mid n \in \mathbb{Z}_{>0}\right\}$ is finite.
+
+Prove that the sequence $f(1)-1, f(2)-2, f(3)-3, \ldots$ is periodic.
+(Singapore)
+N7. Let $\mathbb{Z}_{>0}$ denote the set of positive integers. For any positive integer $k$, a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ is called $k$-good if $\operatorname{gcd}(f(m)+n, f(n)+m) \leqslant k$ for all $m \neq n$. Find all $k$ such that there exists a $k$-good function.
+(Canada)
+N8. For every positive integer $n$ with prime factorization $n=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$, define
+
+$$
+\mho(n)=\sum_{i: p_{i}>10^{100}} \alpha_{i} .
+$$
+
+That is, $\mho(n)$ is the number of prime factors of $n$ greater than $10^{100}$, counted with multiplicity.
+Find all strictly increasing functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ such that
+
+$$
+\mho(f(a)-f(b)) \leqslant \mho(a-b) \quad \text { for all integers } a \text { and } b \text { with } a>b .
+$$
+
+## Solutions
+
+## Algebra
+
+A1. Suppose that a sequence $a_{1}, a_{2}, \ldots$ of positive real numbers satisfies
+
+$$
+a_{k+1} \geqslant \frac{k a_{k}}{a_{k}^{2}+(k-1)}
+$$
+
+for every positive integer $k$. Prove that $a_{1}+a_{2}+\cdots+a_{n} \geqslant n$ for every $n \geqslant 2$.
+
+Solution. From the constraint (1), it can be seen that
+
+$$
+\frac{k}{a_{k+1}} \leqslant \frac{a_{k}^{2}+(k-1)}{a_{k}}=a_{k}+\frac{k-1}{a_{k}}
+$$
+
+and so
+
+$$
+a_{k} \geqslant \frac{k}{a_{k+1}}-\frac{k-1}{a_{k}} .
+$$
+
+Summing up the above inequality for $k=1, \ldots, m$, we obtain
+
+$$
+a_{1}+a_{2}+\cdots+a_{m} \geqslant\left(\frac{1}{a_{2}}-\frac{0}{a_{1}}\right)+\left(\frac{2}{a_{3}}-\frac{1}{a_{2}}\right)+\cdots+\left(\frac{m}{a_{m+1}}-\frac{m-1}{a_{m}}\right)=\frac{m}{a_{m+1}}
+$$
+
+Now we prove the problem statement by induction on $n$. The case $n=2$ can be done by applying (1) to $k=1$ :
+
+$$
+a_{1}+a_{2} \geqslant a_{1}+\frac{1}{a_{1}} \geqslant 2
+$$
+
+For the induction step, assume that the statement is true for some $n \geqslant 2$. If $a_{n+1} \geqslant 1$, then the induction hypothesis yields
+
+$$
+\left(a_{1}+\cdots+a_{n}\right)+a_{n+1} \geqslant n+1
+$$
+
+Otherwise, if $a_{n+1}<1$ then apply (2) as
+
+$$
+\left(a_{1}+\cdots+a_{n}\right)+a_{n+1} \geqslant \frac{n}{a_{n+1}}+a_{n+1}=\frac{n-1}{a_{n+1}}+\left(\frac{1}{a_{n+1}}+a_{n+1}\right)>(n-1)+2
+$$
+
+That completes the solution.
+Comment 1. It can be seen easily that having equality in the statement requires $a_{1}=a_{2}=1$ in the base case $n=2$, and $a_{n+1}=1$ in (3). So the equality $a_{1}+\cdots+a_{n}=n$ is possible only in the trivial case $a_{1}=\cdots=a_{n}=1$.
+
+Comment 2. After obtaining (2), there are many ways to complete the solution. We outline three such possibilities.
+
+- With defining $s_{n}=a_{1}+\cdots+a_{n}$, the induction step can be replaced by
+
+$$
+s_{n+1}=s_{n}+a_{n+1} \geqslant s_{n}+\frac{n}{s_{n}} \geqslant n+1
+$$
+
+because the function $x \mapsto x+\frac{n}{x}$ increases on $[n, \infty)$.
+
+- By applying the AM-GM inequality to the numbers $a_{1}+\cdots+a_{k}$ and $k a_{k+1}$, we can conclude
+
+$$
+a_{1}+\cdots+a_{k}+k a_{k+1} \geqslant 2 k
+$$
+
+and sum it up for $k=1, \ldots, n-1$.
+
+- We can derive the symmetric estimate
+
+$$
+\sum_{1 \leqslant ib$ with $f(a)=f(b)$. A straightforward induction using (2) in the induction step reveals that we have $f(a+n)=f(b+n)$ for all nonnegative integers $n$. Consequently, the sequence $\gamma_{n}=f(b+n)$ is periodic and thus in particular bounded, which means that the numbers
+
+$$
+\varphi=\min _{n \geqslant 0} \gamma_{n} \quad \text { and } \quad \psi=\max _{n \geqslant 0} \gamma_{n}
+$$
+
+exist.
+Let us pick any integer $y$ with $f(y)=\varphi$ and then an integer $x \geqslant a$ with $f(x-f(y))=\varphi$. Due to the definition of $\varphi$ and (3) we have
+
+$$
+\varphi \leqslant f(x+1)=f(x-f(y))+f(y)+1=2 \varphi+1
+$$
+
+whence $\varphi \geqslant-1$. The same reasoning applied to $\psi$ yields $\psi \leqslant-1$. Since $\varphi \leqslant \psi$ holds trivially, it follows that $\varphi=\psi=-1$, or in other words that we have $f(t)=-1$ for all integers $t \geqslant a$.
+
+Finally, if any integer $y$ is given, we may find an integer $x$ which is so large that $x+1 \geqslant a$ and $x-f(y) \geqslant a$ hold. Due to (3) and the result from the previous paragraph we get
+
+$$
+f(y)=f(x+1)-f(x-f(y))-1=(-1)-(-1)-1=-1 .
+$$
+
+Thereby the problem is solved.
+Solution 3. Set $d=f(0)$. By plugging $x=f(y)$ into (1) we obtain
+
+$$
+f^{3}(y)=f(y)+d+1
+$$
+
+for all $y \in \mathbb{Z}$, where the left-hand side abbreviates $f(f(f(y)))$. When we replace $x$ in (1) by $f(x)$ we obtain $f(f(x)-f(y))=f^{3}(x)-f(y)-1$ and as a consequence of (4) this simplifies to
+
+$$
+f(f(x)-f(y))=f(x)-f(y)+d
+$$
+
+Now we consider the set
+
+$$
+E=\{f(x)-d \mid x \in \mathbb{Z}\}
+$$
+
+Given two integers $a$ and $b$ from $E$, we may pick some integers $x$ and $y$ with $f(x)=a+d$ and $f(y)=b+d$; now (5) tells us that $f(a-b)=(a-b)+d$, which means that $a-b$ itself exemplifies $a-b \in E$. Thus,
+
+$$
+E \text { is closed under taking differences. }
+$$
+
+Also, the definitions of $d$ and $E$ yield $0 \in E$. If $E=\{0\}$, then $f$ is a constant function and (1) implies that the only value attained by $f$ is indeed -1 .
+
+So let us henceforth suppose that $E$ contains some number besides zero. It is known that in this case (6) entails $E$ to be the set of all integer multiples of some positive integer $k$. Indeed, this holds for
+
+$$
+k=\min \{|x| \mid x \in E \text { and } x \neq 0\}
+$$
+
+as one may verify by an argument based on division with remainder.
+Thus we have
+
+$$
+\{f(x) \mid x \in \mathbb{Z}\}=\{k \cdot t+d \mid t \in \mathbb{Z}\}
+$$
+
+Due to (5) and (7) we get
+
+$$
+f(k \cdot t)=k \cdot t+d
+$$
+
+for all $t \in \mathbb{Z}$, whence in particular $f(k)=k+d$. So by comparing the results of substituting $y=0$ and $y=k$ into (1) we learn that
+
+$$
+f(z+k)=f(z)+k
+$$
+
+holds for all integers $z$. In plain English, this means that on any residue class modulo $k$ the function $f$ is linear with slope 1.
+
+Now by (7) the set of all values attained by $f$ is such a residue class. Hence, there exists an absolute constant $c$ such that $f(f(x))=f(x)+c$ holds for all $x \in \mathbb{Z}$. Thereby (1) simplifies to
+
+$$
+f(x-f(y))=f(x)-f(y)+c-1
+$$
+
+On the other hand, considering (1) modulo $k$ we obtain $d \equiv-1(\bmod k)$ because of (7). So by (7) again, $f$ attains the value -1 .
+
+Thus we may apply (9) to some integer $y$ with $f(y)=-1$, which gives $f(x+1)=f(x)+c$. So $f$ is a linear function with slope $c$. Hence, (8) leads to $c=1$, wherefore there is an absolute constant $d^{\prime}$ with $f(x)=x+d^{\prime}$ for all $x \in \mathbb{Z}$. Using this for $x=0$ we obtain $d^{\prime}=d$ and finally (4) discloses $d=1$, meaning that $f$ is indeed the successor function.
+
+A3. Let $n$ be a fixed positive integer. Find the maximum possible value of
+
+$$
+\sum_{1 \leqslant r1$ is odd. One can modify the arguments of the last part in order to work for every (not necessarily odd) sufficiently large value of $k$; namely, when $k$ is even, one may show that the sequence $P(1), P(2), \ldots, P(k)$ has different numbers of positive and negative terms.
+
+On the other hand, the problem statement with $k$ replaced by 2 is false, since the polynomials $P(x)=T(x)-T(x-1)$ and $Q(x)=T(x-1)-T(x)$ are block-similar in this case, due to the fact that $P(2 i-1)=-P(2 i)=Q(2 i)=-Q(2 i-1)=T(2 i-1)$ for all $i=1,2, \ldots, n$. Thus, every complete solution should use the relation $k>2$.
+
+One may easily see that the condition $n \geqslant 2$ is also substantial, since the polynomials $x$ and $k+1-x$ become block-similar if we set $n=1$.
+
+It is easily seen from the solution that the result still holds if we assume that the polynomials have degree at most $n$.
+
+Solution 2. We provide an alternative argument for part (b).
+Assume again that there exist two distinct block-similar polynomials $P(x)$ and $Q(x)$ of degree $n$. Let $R(x)=P(x)-Q(x)$ and $S(x)=P(x)+Q(x)$. For brevity, we also denote the segment $[(i-1) k+1, i k]$ by $I_{i}$, and the set $\{(i-1) k+1,(i-1) k+2, \ldots, i k\}$ of all integer points in $I_{i}$ by $Z_{i}$.
+Step 1. We prove that $R(x)$ has exactly one root in each segment $I_{i}, i=1,2, \ldots, n$, and all these roots are simple.
+
+Indeed, take any $i \in\{1,2, \ldots, n\}$ and choose some points $p^{-}, p^{+} \in Z_{i}$ so that
+
+$$
+P\left(p^{-}\right)=\min _{x \in Z_{i}} P(x) \quad \text { and } \quad P\left(p^{+}\right)=\max _{x \in Z_{i}} P(x)
+$$
+
+Since the sequences of values of $P$ and $Q$ in $Z_{i}$ are permutations of each other, we have $R\left(p^{-}\right)=P\left(p^{-}\right)-Q\left(p^{-}\right) \leqslant 0$ and $R\left(p^{+}\right)=P\left(p^{+}\right)-Q\left(p^{+}\right) \geqslant 0$. Since $R(x)$ is continuous, there exists at least one root of $R(x)$ between $p^{-}$and $p^{+}$- thus in $I_{i}$.
+
+So, $R(x)$ has at least one root in each of the $n$ disjoint segments $I_{i}$ with $i=1,2, \ldots, n$. Since $R(x)$ is nonzero and its degree does not exceed $n$, it should have exactly one root in each of these segments, and all these roots are simple, as required.
+
+## Step 2. We prove that $S(x)$ is constant.
+
+We start with the following claim.
+Claim. For every $i=1,2, \ldots, n$, the sequence of values $S((i-1) k+1), S((i-1) k+2), \ldots$, $S(i k)$ cannot be strictly increasing.
+Proof. Fix any $i \in\{1,2, \ldots, n\}$. Due to the symmetry, we may assume that $P(i k) \leqslant Q(i k)$. Choose now $p^{-}$and $p^{+}$as in Step 1. If we had $P\left(p^{+}\right)=P\left(p^{-}\right)$, then $P$ would be constant on $Z_{i}$, so all the elements of $Z_{i}$ would be the roots of $R(x)$, which is not the case. In particular, we have $p^{+} \neq p^{-}$. If $p^{-}>p^{+}$, then $S\left(p^{-}\right)=P\left(p^{-}\right)+Q\left(p^{-}\right) \leqslant Q\left(p^{+}\right)+P\left(p^{+}\right)=S\left(p^{+}\right)$, so our claim holds.
+
+We now show that the remaining case $p^{-}$ $Q\left(p^{+}\right)$. Then, like in Step 1 , we have $R\left(p^{-}\right) \leqslant 0, R\left(p^{+}\right)>0$, and $R(i k) \leqslant 0$, so $R(x)$ has a root in each of the intervals $\left[p^{-}, p^{+}\right)$and $\left(p^{+}, i k\right]$. This contradicts the result of Step 1.
+
+We are left only with the case $p^{-}0$. Next, let $p^{-}, q^{+} \in I_{i}$ be some points such that $P\left(p^{-}\right)=\min _{x \in Z_{i}} P(x)$ and $Q\left(q^{+}\right)=\max _{x \in Z_{i}} Q(x)$. Notice that $P\left(p^{-}\right) \leqslant Q(r)Q(r)$, so $r$ is different from $p^{-}$and $q^{+}$.
+
+Without loss of generality, we may assume that $p^{-}r$, then, similarly, $R\left(q^{+}\right) \leqslant 0\ell_{j}>r_{i}$.
+
+Clearly, there is no town which can sweep $T_{n}$ away from the right. Then we may choose the leftmost town $T_{k}$ which cannot be swept away from the right. One can observe now that no town $T_{i}$ with $i>k$ may sweep away some town $T_{j}$ with $jm$. As we have already observed, $p$ cannot be greater than $k$. On the other hand, $T_{m}$ cannot sweep $T_{p}$ away, so a fortiori it cannot sweep $T_{k}$ away.
+
+Claim 2. Any town $T_{m}$ with $m \neq k$ can be swept away by some other town.
+
+Proof. If $mk$.
+
+Let $T_{p}$ be a town among $T_{k}, T_{k+1}, \ldots, T_{m-1}$ having the largest right bulldozer. We claim that $T_{p}$ can sweep $T_{m}$ away. If this is not the case, then $r_{p}<\ell_{q}$ for some $q$ with $p1$. Firstly, we find a town which can be swept away by each of its neighbors (each town has two neighbors, except for the bordering ones each of which has one); we call such town a loser. Such a town exists, because there are $n-1$ pairs of neighboring towns, and in each of them there is only one which can sweep the other away; so there exists a town which is a winner in none of these pairs.
+
+Notice that a loser can be swept away, but it cannot sweep any other town away (due to its neighbors' protection). Now we remove a loser, and suggest its left bulldozer to its right neighbor (if it exists), and its right bulldozer to a left one (if it exists). Surely, a town accepts a suggestion if a suggested bulldozer is larger than the town's one of the same orientation.
+
+Notice that suggested bulldozers are useless in attack (by the definition of a loser), but may serve for defensive purposes. Moreover, each suggested bulldozer's protection works for the same pairs of remaining towns as before the removal.
+
+By the induction hypothesis, the new configuration contains exactly one town which cannot be swept away. The arguments above show that the initial one also satisfies this property.
+
+Solution 3. We separately prove that $(i)$ there exists a town which cannot be swept away, and that (ii) there is at most one such town. We also make use of the two observations from the previous solutions.
+To prove ( $i$ ), assume contrariwise that every town can be swept away. Let $t_{1}$ be the leftmost town; next, for every $k=1,2, \ldots$ we inductively choose $t_{k+1}$ to be some town which can sweep $t_{k}$ away. Now we claim that for every $k=1,2, \ldots$, the town $t_{k+1}$ is to the right of $t_{k}$; this leads to the contradiction, since the number of towns is finite.
+
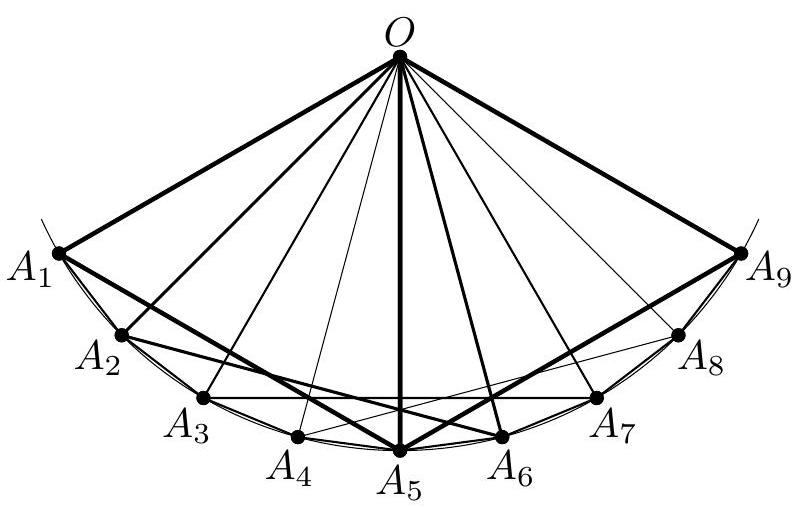
+Induction on $k$. The base case $k=1$ is clear due to the choice of $t_{1}$. Assume now that for all $j$ with $1 \leqslant jj$ and $a_{i}\frac{n}{2}$, then we have $O A_{i-n / 2+1}=A_{i} A_{i-n / 2+1}$. This completes the proof.
+
+An example of such a construction when $n=10$ is shown in Figure 1.
+
+
+Figure 1
+
+
+Figure 2
+
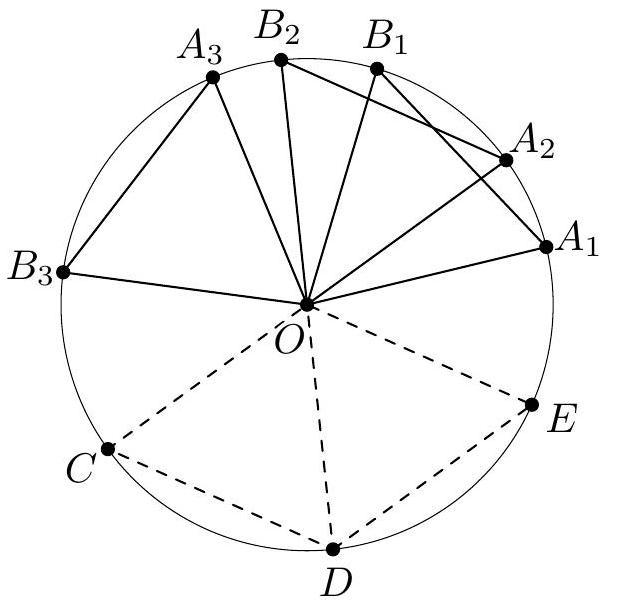
+Comment (a). There are many ways to construct an example by placing equilateral triangles in a circle. Here we present one general method.
+
+Let $O$ be the center of a circle and let $A_{1}, B_{1}, \ldots, A_{k}, B_{k}$ be distinct points on the circle such that the triangle $O A_{i} B_{i}$ is equilateral for each $i$. Then $\mathcal{V}=\left\{O, A_{1}, B_{1}, \ldots, A_{k}, B_{k}\right\}$ is balanced. To construct a set of even cardinality, put extra points $C, D, E$ on the circle such that triangles $O C D$ and $O D E$ are equilateral (see Figure 2). Then $\mathcal{V}=\left\{O, A_{1}, B_{1}, \ldots, A_{k}, B_{k}, C, D, E\right\}$ is balanced.
+
+Part (b). We now show that there exists a balanced, center-free set containing $n$ points for all odd $n \geqslant 3$, and that one does not exist for any even $n \geqslant 3$.
+
+If $n$ is odd, then let $\mathcal{V}$ be the set of vertices of a regular $n$-gon. We have shown in part ( $a$ ) that $\mathcal{V}$ is balanced. We claim that $\mathcal{V}$ is also center-free. Indeed, if $P$ is a point such that
+$P A=P B=P C$ for some three distinct vertices $A, B$ and $C$, then $P$ is the circumcenter of the $n$-gon, which is not contained in $\mathcal{V}$.
+
+Now suppose that $\mathcal{V}$ is a balanced, center-free set of even cardinality $n$. We will derive a contradiction. For a pair of distinct points $A, B \in \mathcal{V}$, we say that a point $C \in \mathcal{V}$ is associated with the pair $\{A, B\}$ if $A C=B C$. Since there are $\frac{n(n-1)}{2}$ pairs of points, there exists a point $P \in \mathcal{V}$ which is associated with at least $\left\lceil\frac{n(n-1)}{2} / n\right\rceil=\frac{n}{2}$ pairs. Note that none of these $\frac{n}{2}$ pairs can contain $P$, so that the union of these $\frac{n}{2}$ pairs consists of at most $n-1$ points. Hence there exist two such pairs that share a point. Let these two pairs be $\{A, B\}$ and $\{A, C\}$. Then $P A=P B=P C$, which is a contradiction.
+
+Comment (b). We can rephrase the argument in graph theoretic terms as follows. Let $\mathcal{V}$ be a balanced, center-free set consisting of $n$ points. For any pair of distinct vertices $A, B \in \mathcal{V}$ and for any $C \in \mathcal{V}$ such that $A C=B C$, draw directed edges $A \rightarrow C$ and $B \rightarrow C$. Then all pairs of vertices generate altogether at least $n(n-1)$ directed edges; since the set is center-free, these edges are distinct. So we must obtain a graph in which any two vertices are connected in both directions. Now, each vertex has exactly $n-1$ incoming edges, which means that $n-1$ is even. Hence $n$ is odd.
+
+C3. For a finite set $A$ of positive integers, we call a partition of $A$ into two disjoint nonempty subsets $A_{1}$ and $A_{2}$ good if the least common multiple of the elements in $A_{1}$ is equal to the greatest common divisor of the elements in $A_{2}$. Determine the minimum value of $n$ such that there exists a set of $n$ positive integers with exactly 2015 good partitions.
+(Ukraine)
+Answer. 3024.
+Solution. Let $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$, where $a_{1}1$ and $B$ can respond by choosing $a-1$ on the $k^{\text {th }}$ move instead.
+
+We now give an alternative winning strategy in the case $n$ is even and $n \geqslant 8$. We first present a winning strategy for the case when $A$ 's first pick is 1 . We consider two cases depending on $A$ 's second move.
+
+Case 1. A's second pick is 3 . Then $B$ chooses $n-3$ on the second move. On the $k^{\text {th }}$ move, $B$ chooses the number exactly 1 less than $A^{\prime}$ 's $k^{\text {th }}$ pick except that $B$ chooses 2 if $A$ 's $k^{\text {th }}$ pick is $n-2$ or $n-1$.
+
+Case 2. A's second pick is $a>3$. Then $B$ chooses $a-2$ on the second move. Afterwards on the $k^{\text {th }}$ move, $B$ picks the number exactly 1 less than $A^{\text {'s }} k^{\text {th }}$ pick.
+
+One may easily see that this strategy guarantees $B$ 's victory, when $A$ 's first pick is 1 .
+The following claim shows how to extend the strategy to the general case.
+Claim. Assume that $B$ has an explicit strategy leading to a victory after $A$ picks 1 on the first move. Then $B$ also has an explicit strategy leading to a victory after any first moves of $A$.
+Proof. Let $S$ be an optimal strategy of $B$ after $A$ picks 1 on the first move. Assume that $A$ picks some number $a>1$ on this move; we show how $B$ can make use of $S$ in order to win in this case.
+
+In parallel to the real play, $B$ starts an imaginary play. The positions in these plays differ by flipping the segment $[1, a]$; so, if a player chooses some number $x$ in the real play, then the same player chooses a number $x$ or $a+1-x$ in the imaginary play, depending on whether $x>a$ or $x \leqslant a$. Thus $A$ 's first pick in the imaginary play is 1.
+
+Clearly, a number is chosen in the real play exactly if the corresponding number is chosen in the imaginary one. Next, if an unchosen number is neighboring to one chosen by $A$ in the imaginary play, then the corresponding number also has this property in the real play, so $A$ also cannot choose it. One can easily see that a similar statement with real and imaginary plays interchanged holds for $B$ instead of $A$.
+
+Thus, when $A$ makes some move in the real play, $B$ may imagine the corresponding legal move in the imaginary one. Then $B$ chooses the response according to $S$ in the imaginary game and makes the corresponding legal move in the real one. Acting so, $B$ wins the imaginary game, thus $B$ will also win the real one.
+
+Hence, $B$ has a winning strategy for all even $n$ greater or equal to 8 .
+Notice that the claim can also be used to simplify the argument when $n$ is odd.
+Comment 2. One may also employ symmetry when $n$ is odd. In particular, $B$ could use a mirror strategy. However, additional ideas are required to modify the strategy after $A$ picks $\frac{n+1}{2}$.
+
+C5. Consider an infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers with $a_{i} \leqslant 2015$ for all $i \geqslant 1$. Suppose that for any two distinct indices $i$ and $j$ we have $i+a_{i} \neq j+a_{j}$.
+
+Prove that there exist two positive integers $b$ and $N$ such that
+
+$$
+\left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant 1007^{2}
+$$
+
+whenever $n>m \geqslant N$.
+(Australia)
+Solution 1. We visualize the set of positive integers as a sequence of points. For each $n$ we draw an arrow emerging from $n$ that points to $n+a_{n}$; so the length of this arrow is $a_{n}$. Due to the condition that $m+a_{m} \neq n+a_{n}$ for $m \neq n$, each positive integer receives at most one arrow. There are some positive integers, such as 1 , that receive no arrows; these will be referred to as starting points in the sequel. When one starts at any of the starting points and keeps following the arrows, one is led to an infinite path, called its ray, that visits a strictly increasing sequence of positive integers. Since the length of any arrow is at most 2015, such a ray, say with starting point $s$, meets every interval of the form $[n, n+2014]$ with $n \geqslant s$ at least once.
+
+Suppose for the sake of contradiction that there would be at least 2016 starting points. Then we could take an integer $n$ that is larger than the first 2016 starting points. But now the interval $[n, n+2014]$ must be met by at least 2016 rays in distinct points, which is absurd. We have thereby shown that the number $b$ of starting points satisfies $1 \leqslant b \leqslant 2015$. Let $N$ denote any integer that is larger than all starting points. We contend that $b$ and $N$ are as required.
+
+To see this, let any two integers $m$ and $n$ with $n>m \geqslant N$ be given. The sum $\sum_{i=m+1}^{n} a_{i}$ gives the total length of the arrows emerging from $m+1, \ldots, n$. Taken together, these arrows form $b$ subpaths of our rays, some of which may be empty. Now on each ray we look at the first number that is larger than $m$; let $x_{1}, \ldots, x_{b}$ denote these numbers, and let $y_{1}, \ldots, y_{b}$ enumerate in corresponding order the numbers defined similarly with respect to $n$. Then the list of differences $y_{1}-x_{1}, \ldots, y_{b}-x_{b}$ consists of the lengths of these paths and possibly some zeros corresponding to empty paths. Consequently, we obtain
+
+$$
+\sum_{i=m+1}^{n} a_{i}=\sum_{j=1}^{b}\left(y_{j}-x_{j}\right)
+$$
+
+whence
+
+$$
+\sum_{i=m+1}^{n}\left(a_{i}-b\right)=\sum_{j=1}^{b}\left(y_{j}-n\right)-\sum_{j=1}^{b}\left(x_{j}-m\right) .
+$$
+
+Now each of the $b$ rays meets the interval $[m+1, m+2015]$ at some point and thus $x_{1}-$ $m, \ldots, x_{b}-m$ are $b$ distinct members of the set $\{1,2, \ldots, 2015\}$. Moreover, since $m+1$ is not a starting point, it must belong to some ray; so 1 has to appear among these numbers, wherefore
+
+$$
+1+\sum_{j=1}^{b-1}(j+1) \leqslant \sum_{j=1}^{b}\left(x_{j}-m\right) \leqslant 1+\sum_{j=1}^{b-1}(2016-b+j)
+$$
+
+The same argument applied to $n$ and $y_{1}, \ldots, y_{b}$ yields
+
+$$
+1+\sum_{j=1}^{b-1}(j+1) \leqslant \sum_{j=1}^{b}\left(y_{j}-n\right) \leqslant 1+\sum_{j=1}^{b-1}(2016-b+j)
+$$
+
+So altogether we get
+
+$$
+\begin{aligned}
+\left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| & \leqslant \sum_{j=1}^{b-1}((2016-b+j)-(j+1))=(b-1)(2015-b) \\
+& \leqslant\left(\frac{(b-1)+(2015-b)}{2}\right)^{2}=1007^{2},
+\end{aligned}
+$$
+
+as desired.
+Solution 2. Set $s_{n}=n+a_{n}$ for all positive integers $n$. By our assumptions, we have
+
+$$
+n+1 \leqslant s_{n} \leqslant n+2015
+$$
+
+for all $n \in \mathbb{Z}_{>0}$. The members of the sequence $s_{1}, s_{2}, \ldots$ are distinct. We shall investigate the set
+
+$$
+M=\mathbb{Z}_{>0} \backslash\left\{s_{1}, s_{2}, \ldots\right\}
+$$
+
+Claim. At most 2015 numbers belong to $M$.
+Proof. Otherwise let $m_{1}m \geqslant N$. Plugging $r=n$ and $r=m$ into (3) and subtracting the estimates that result, we deduce
+
+$$
+\sum_{i=m+1}^{n}\left(a_{i}-b\right)=\sum C_{n}-\sum C_{m}
+$$
+
+Since $C_{n}$ and $C_{m}$ are subsets of $\{1,2, \ldots, 2014\}$ with $\left|C_{n}\right|=\left|C_{m}\right|=b-1$, it is clear that the absolute value of the right-hand side of the above inequality attains its largest possible value if either $C_{m}=\{1,2, \ldots, b-1\}$ and $C_{n}=\{2016-b, \ldots, 2014\}$, or the other way around. In these two cases we have
+
+$$
+\left|\sum C_{n}-\sum C_{m}\right|=(b-1)(2015-b)
+$$
+
+so in the general case we find
+
+$$
+\left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant(b-1)(2015-b) \leqslant\left(\frac{(b-1)+(2015-b)}{2}\right)^{2}=1007^{2}
+$$
+
+as desired.
+
+Comment. The sets $C_{n}$ may be visualized by means of the following process: Start with an empty blackboard. For $n \geqslant 1$, the following happens during the $n^{\text {th }}$ step. The number $a_{n}$ gets written on the blackboard, then all numbers currently on the blackboard are decreased by 1 , and finally all zeros that have arisen get swept away.
+
+It is not hard to see that the numbers present on the blackboard after $n$ steps are distinct and form the set $C_{n}$. Moreover, it is possible to complete a solution based on this idea.
+
+C6. Let $S$ be a nonempty set of positive integers. We say that a positive integer $n$ is clean if it has a unique representation as a sum of an odd number of distinct elements from $S$. Prove that there exist infinitely many positive integers that are not clean.
+
+Solution 1. Define an odd (respectively, even) representation of $n$ to be a representation of $n$ as a sum of an odd (respectively, even) number of distinct elements of $S$. Let $\mathbb{Z}_{>0}$ denote the set of all positive integers.
+
+Suppose, to the contrary, that there exist only finitely many positive integers that are not clean. Therefore, there exists a positive integer $N$ such that every integer $n>N$ has exactly one odd representation.
+
+Clearly, $S$ is infinite. We now claim the following properties of odd and even representations.
+$\underline{P r o p e r t y}$ 1. Any positive integer $n$ has at most one odd and at most one even representation.
+Proof. We first show that every integer $n$ has at most one even representation. Since $S$ is infinite, there exists $x \in S$ such that $x>\max \{n, N\}$. Then, the number $n+x$ must be clean, and $x$ does not appear in any even representation of $n$. If $n$ has more than one even representation, then we obtain two distinct odd representations of $n+x$ by adding $x$ to the even representations of $n$, which is impossible. Therefore, $n$ can have at most one even representation.
+
+Similarly, there exist two distinct elements $y, z \in S$ such that $y, z>\max \{n, N\}$. If $n$ has more than one odd representation, then we obtain two distinct odd representations of $n+y+z$ by adding $y$ and $z$ to the odd representations of $n$. This is again a contradiction.
+
+Property 2. Fix $s \in S$. Suppose that a number $n>N$ has no even representation. Then $n+2 a s$ has an even representation containing $s$ for all integers $a \geqslant 1$.
+Proof. It is sufficient to prove the following statement: If $n$ has no even representation without $s$, then $n+2 s$ has an even representation containing $s$ (and hence no even representation without $s$ by Property 1).
+
+Notice that the odd representation of $n+s$ does not contain $s$; otherwise, we have an even representation of $n$ without $s$. Then, adding $s$ to this odd representation of $n+s$, we get that $n+2 s$ has an even representation containing $s$, as desired.
+
+Property 3. Every sufficiently large integer has an even representation.
+Proof. Fix any $s \in S$, and let $r$ be an arbitrary element in $\{1,2, \ldots, 2 s\}$. Then, Property 2 implies that the set $Z_{r}=\{r+2 a s: a \geqslant 0\}$ contains at most one number exceeding $N$ with no even representation. Therefore, $Z_{r}$ contains finitely many positive integers with no even representation, and so does $\mathbb{Z}_{>0}=\bigcup_{r=1}^{2 s} Z_{r}$.
+
+In view of Properties 1 and 3 , we may assume that $N$ is chosen such that every $n>N$ has exactly one odd and exactly one even representation. In particular, each element $s>N$ of $S$ has an even representation.
+Property 4. For any $s, t \in S$ with $NN$. Then, Property 4 implies that for every $i>k$ the even representation of $s_{i}$ contains all the numbers $s_{k}, s_{k+1}, \ldots, s_{i-1}$. Therefore,
+
+$$
+s_{i}=s_{k}+s_{k+1}+\cdots+s_{i-1}+R_{i}=\sigma_{i-1}-\sigma_{k-1}+R_{i}
+$$
+
+where $R_{i}$ is a sum of some of $s_{1}, \ldots, s_{k-1}$. In particular, $0 \leqslant R_{i} \leqslant s_{1}+\cdots+s_{k-1}=\sigma_{k-1}$.
+
+Let $j_{0}$ be an integer satisfying $j_{0}>k$ and $\sigma_{j_{0}}>2 \sigma_{k-1}$. Then (1) shows that, for every $j>j_{0}$,
+
+$$
+s_{j+1} \geqslant \sigma_{j}-\sigma_{k-1}>\sigma_{j} / 2 .
+$$
+
+Next, let $p>j_{0}$ be an index such that $R_{p}=\min _{i>j_{0}} R_{i}$. Then,
+
+$$
+s_{p+1}=s_{k}+s_{k+1}+\cdots+s_{p}+R_{p+1}=\left(s_{p}-R_{p}\right)+s_{p}+R_{p+1} \geqslant 2 s_{p}
+$$
+
+Therefore, there is no element of $S$ larger than $s_{p}$ but smaller than $2 s_{p}$. It follows that the even representation $\tau$ of $2 s_{p}$ does not contain any element larger than $s_{p}$. On the other hand, inequality (2) yields $2 s_{p}>s_{1}+\cdots+s_{p-1}$, so $\tau$ must contain a term larger than $s_{p-1}$. Thus, it must contain $s_{p}$. After removing $s_{p}$ from $\tau$, we have that $s_{p}$ has an odd representation not containing $s_{p}$, which contradicts Property 1 since $s_{p}$ itself also forms an odd representation of $s_{p}$.
+
+Solution 2. We will also use Property 1 from Solution 1.
+We first define some terminology and notations used in this solution. Let $\mathbb{Z}_{\geqslant 0}$ denote the set of all nonnegative integers. All sums mentioned are regarded as sums of distinct elements of $S$. Moreover, a sum is called even or odd depending on the parity of the number of terms in it. All closed or open intervals refer to sets of all integers inside them, e.g., $[a, b]=\{x \in \mathbb{Z}: a \leqslant x \leqslant b\}$.
+
+Again, let $s_{1}$ $2^{n-1}-1+n m \geqslant \sigma_{n}$ for every sufficiently large $n$. We now claim the following.
+
+Claim 1. $\left(\sigma_{n}-s_{n+1}, s_{n+2}-s_{n+1}\right) \subseteq E_{n}$ for every sufficiently large $n$.
+Proof. For sufficiently large $n$, all elements of $\left(\sigma_{n}, s_{n+2}\right)$ are clean. Clearly, the elements of $\left(\sigma_{n}, s_{n+2}\right)$ can be in neither $O_{n}$ nor $O \backslash O_{n+1}$. So, $\left(\sigma_{n}, s_{n+2}\right) \subseteq O_{n+1} \backslash O_{n}=s_{n+1}+E_{n}$, which yields the claim.
+
+Now, Claim 1 together with inequalities (3) implies that, for all sufficiently large $n$,
+
+$$
+E \supseteq E_{n} \supseteq\left(\sigma_{n}-s_{n+1}, s_{n+2}-s_{n+1}\right) \supseteq\left(2 n m, 2^{n-1}-(n+2) m\right) .
+$$
+
+This easily yields that $\mathbb{Z}_{\geqslant 0} \backslash E$ is also finite. Since $\mathbb{Z}_{\geqslant 0} \backslash O$ is also finite, by Property 1 , there exists a positive integer $N$ such that every integer $n>N$ has exactly one even and one odd representation.
+
+Step 3. We investigate the structures of $E_{n}$ and $O_{n}$.
+Suppose that $z \in E_{2 n}$. Since $z$ can be represented as an even sum using $\left\{s_{1}, s_{2}, \ldots, s_{2 n}\right\}$, so can its complement $\sigma_{2 n}-z$. Thus, we get $E_{2 n}=\sigma_{2 n}-E_{2 n}$. Similarly, we have
+
+$$
+E_{2 n}=\sigma_{2 n}-E_{2 n}, \quad O_{2 n}=\sigma_{2 n}-O_{2 n}, \quad E_{2 n+1}=\sigma_{2 n+1}-O_{2 n+1}, \quad O_{2 n+1}=\sigma_{2 n+1}-E_{2 n+1}
+$$
+
+Claim 2. For every sufficiently large $n$, we have
+
+$$
+\left[0, \sigma_{n}\right] \supseteq O_{n} \supseteq\left(N, \sigma_{n}-N\right) \quad \text { and } \quad\left[0, \sigma_{n}\right] \supseteq E_{n} \supseteq\left(N, \sigma_{n}-N\right)
+$$
+
+Proof. Clearly $O_{n}, E_{n} \subseteq\left[0, \sigma_{n}\right]$ for every positive integer $n$. We now prove $O_{n}, E_{n} \supseteq\left(N, \sigma_{n}-N\right)$. Taking $n$ sufficiently large, we may assume that $s_{n+1} \geqslant 2^{n-1}+1-n m>\frac{1}{2}\left(2^{n-1}-1+n m\right) \geqslant \sigma_{n} / 2$. Therefore, the odd representation of every element of ( $\left.N, \sigma_{n} / 2\right]$ cannot contain a term larger than $s_{n}$. Thus, $\left(N, \sigma_{n} / 2\right] \subseteq O_{n}$. Similarly, since $s_{n+1}+s_{1}>\sigma_{n} / 2$, we also have $\left(N, \sigma_{n} / 2\right] \subseteq E_{n}$. Equations (4) then yield that, for sufficiently large $n$, the interval $\left(N, \sigma_{n}-N\right)$ is a subset of both $O_{n}$ and $E_{n}$, as desired.
+
+Step 4. We obtain a final contradiction.
+Notice that $0 \in \mathbb{Z}_{\geqslant 0} \backslash O$ and $1 \in \mathbb{Z}_{\geqslant 0} \backslash E$. Therefore, the sets $\mathbb{Z}_{\geqslant 0} \backslash O$ and $\mathbb{Z}_{\geqslant 0} \backslash E$ are nonempty. Denote $o=\max \left(\mathbb{Z}_{\geqslant 0} \backslash O\right)$ and $e=\max \left(\mathbb{Z}_{\geqslant 0} \backslash E\right)$. Observe also that $e, o \leqslant N$.
+
+Taking $k$ sufficiently large, we may assume that $\sigma_{2 k}>2 N$ and that Claim 2 holds for all $n \geqslant 2 k$. Due to (4) and Claim 2, we have that $\sigma_{2 k}-e$ is the minimal number greater than $N$ which is not in $E_{2 k}$, i.e., $\sigma_{2 k}-e=s_{2 k+1}+s_{1}$. Similarly,
+
+$$
+\sigma_{2 k}-o=s_{2 k+1}, \quad \sigma_{2 k+1}-e=s_{2 k+2}, \quad \text { and } \quad \sigma_{2 k+1}-o=s_{2 k+2}+s_{1}
+$$
+
+Therefore, we have
+
+$$
+\begin{aligned}
+s_{1} & =\left(s_{2 k+1}+s_{1}\right)-s_{2 k+1}=\left(\sigma_{2 k}-e\right)-\left(\sigma_{2 k}-o\right)=o-e \\
+& =\left(\sigma_{2 k+1}-e\right)-\left(\sigma_{2 k+1}-o\right)=s_{2 k+2}-\left(s_{2 k+2}+s_{1}\right)=-s_{1}
+\end{aligned}
+$$
+
+which is impossible since $s_{1}>0$.
+
+C7. In a company of people some pairs are enemies. A group of people is called unsociable if the number of members in the group is odd and at least 3, and it is possible to arrange all its members around a round table so that every two neighbors are enemies. Given that there are at most 2015 unsociable groups, prove that it is possible to partition the company into 11 parts so that no two enemies are in the same part.
+(Russia)
+Solution 1. Let $G=(V, E)$ be a graph where $V$ is the set of people in the company and $E$ is the set of the enemy pairs - the edges of the graph. In this language, partitioning into 11 disjoint enemy-free subsets means properly coloring the vertices of this graph with 11 colors.
+
+We will prove the following more general statement.
+Claim. Let $G$ be a graph with chromatic number $k \geqslant 3$. Then $G$ contains at least $2^{k-1}-k$ unsociable groups.
+
+Recall that the chromatic number of $G$ is the least $k$ such that a proper coloring
+
+$$
+V=V_{1} \sqcup \cdots \sqcup V_{k}
+$$
+
+exists. In view of $2^{11}-12>2015$, the claim implies the problem statement.
+Let $G$ be a graph with chromatic number $k$. We say that a proper coloring (1) of $G$ is leximinimal, if the $k$-tuple $\left(\left|V_{1}\right|,\left|V_{2}\right|, \ldots,\left|V_{k}\right|\right)$ is lexicographically minimal; in other words, the following conditions are satisfied: the number $n_{1}=\left|V_{1}\right|$ is minimal; the number $n_{2}=\left|V_{2}\right|$ is minimal, subject to the previously chosen value of $n_{1} ; \ldots$; the number $n_{k-1}=\left|V_{k-1}\right|$ is minimal, subject to the previously chosen values of $n_{1}, \ldots, n_{k-2}$.
+
+The following lemma is the core of the proof.
+Lemma 1. Suppose that $G=(V, E)$ is a graph with odd chromatic number $k \geqslant 3$, and let (1) be one of its leximinimal colorings. Then $G$ contains an odd cycle which visits all color classes $V_{1}, V_{2}, \ldots, V_{k}$.
+Proof of Lemma 1. Let us call a cycle colorful if it visits all color classes.
+Due to the definition of the chromatic number, $V_{1}$ is nonempty. Choose an arbitrary vertex $v \in V_{1}$. We construct a colorful odd cycle that has only one vertex in $V_{1}$, and this vertex is $v$.
+
+We draw a subgraph of $G$ as follows. Place $v$ in the center, and arrange the sets $V_{2}, V_{3}, \ldots, V_{k}$ in counterclockwise circular order around it. For convenience, let $V_{k+1}=V_{2}$. We will draw arrows to add direction to some edges of $G$, and mark the vertices these arrows point to. First we draw arrows from $v$ to all its neighbors in $V_{2}$, and mark all those neighbors. If some vertex $u \in V_{i}$ with $i \in\{2,3, \ldots, k\}$ is already marked, we draw arrows from $u$ to all its neighbors in $V_{i+1}$ which are not marked yet, and we mark all of them. We proceed doing this as long as it is possible. The process of marking is exemplified in Figure 1.
+
+Notice that by the rules of our process, in the final state, marked vertices in $V_{i}$ cannot have unmarked neighbors in $V_{i+1}$. Moreover, $v$ is connected to all marked vertices by directed paths.
+
+Now move each marked vertex to the next color class in circular order (see an example in Figure 3). In view of the arguments above, the obtained coloring $V_{1} \sqcup W_{2} \sqcup \cdots \sqcup W_{k}$ is proper. Notice that $v$ has a neighbor $w \in W_{2}$, because otherwise
+
+$$
+\left(V_{1} \backslash\{v\}\right) \sqcup\left(W_{2} \cup\{v\}\right) \sqcup W_{3} \sqcup \cdots \sqcup W_{k}
+$$
+
+would be a proper coloring lexicographically smaller than (1). If $w$ was unmarked, i.e., $w$ was an element of $V_{2}$, then it would be marked at the beginning of the process and thus moved to $V_{3}$, which did not happen. Therefore, $w$ is marked and $w \in V_{k}$.
+
+
+Figure 1
+Figure 2
+Since $w$ is marked, there exists a directed path from $v$ to $w$. This path moves through the sets $V_{2}, \ldots, V_{k}$ in circular order, so the number of edges in it is divisible by $k-1$ and thus even. Closing this path by the edge $w \rightarrow v$, we get a colorful odd cycle, as required.
+
+Proof of the claim. Let us choose a leximinimal coloring (1) of $G$. For every set $C \subseteq\{1,2, \ldots, k\}$ such that $|C|$ is odd and greater than 1 , we will provide an odd cycle visiting exactly those color classes whose indices are listed in the set $C$. This property ensures that we have different cycles for different choices of $C$, and it proves the claim because there are $2^{k-1}-k$ choices for the set $C$.
+
+Let $V_{C}=\bigcup_{c \in C} V_{c}$, and let $G_{C}$ be the induced subgraph of $G$ on the vertex set $V_{C}$. We also have the induced coloring of $V_{C}$ with $|C|$ colors; this coloring is of course proper. Notice further that the induced coloring is leximinimal: if we had a lexicographically smaller coloring $\left(W_{c}\right)_{c \in C}$ of $G_{C}$, then these classes, together the original color classes $V_{i}$ for $i \notin C$, would provide a proper coloring which is lexicographically smaller than (1). Hence Lemma 1, applied to the subgraph $G_{C}$ and its leximinimal coloring $\left(V_{c}\right)_{c \in C}$, provides an odd cycle that visits exactly those color classes that are listed in the set $C$.
+
+Solution 2. We provide a different proof of the claim from the previous solution.
+We say that a graph is critical if deleting any vertex from the graph decreases the graph's chromatic number. Obviously every graph contains a critical induced subgraph with the same chromatic number.
+Lemma 2. Suppose that $G=(V, E)$ is a critical graph with chromatic number $k \geqslant 3$. Then every vertex $v$ of $G$ is contained in at least $2^{k-2}-1$ unsociable groups.
+Proof. For every set $X \subseteq V$, denote by $n(X)$ the number of neighbors of $v$ in the set $X$.
+Since $G$ is critical, there exists a proper coloring of $G \backslash\{v\}$ with $k-1$ colors, so there exists a proper coloring $V=V_{1} \sqcup V_{2} \sqcup \cdots \sqcup V_{k}$ of $G$ such that $V_{1}=\{v\}$. Among such colorings, take one for which the sequence $\left(n\left(V_{2}\right), n\left(V_{3}\right), \ldots, n\left(V_{k}\right)\right)$ is lexicographically minimal. Clearly, $n\left(V_{i}\right)>0$ for every $i=2,3, \ldots, k$; otherwise $V_{2} \sqcup \ldots \sqcup V_{i-1} \sqcup\left(V_{i} \cup V_{1}\right) \sqcup V_{i+1} \sqcup \ldots V_{k}$ would be a proper coloring of $G$ with $k-1$ colors.
+
+We claim that for every $C \subseteq\{2,3, \ldots, k\}$ with $|C| \geqslant 2$ being even, $G$ contains an unsociable group so that the set of its members' colors is precisely $C \cup\{1\}$. Since the number of such sets $C$ is $2^{k-2}-1$, this proves the lemma. Denote the elements of $C$ by $c_{1}, \ldots, c_{2 \ell}$ in increasing order. For brevity, let $U_{i}=V_{c_{i}}$. Denote by $N_{i}$ the set of neighbors of $v$ in $U_{i}$.
+
+We show that for every $i=1, \ldots, 2 \ell-1$ and $x \in N_{i}$, the subgraph induced by $U_{i} \cup U_{i+1}$ contains a path that connects $x$ with another point in $N_{i+1}$. For the sake of contradiction, suppose that no such path exists. Let $S$ be the set of vertices that lie in the connected component of $x$ in the subgraph induced by $U_{i} \cup U_{i+1}$, and let $P=U_{i} \cap S$, and $Q=U_{i+1} \cap S$ (see Figure 3). Since $x$ is separated from $N_{i+1}$, the sets $Q$ and $N_{i+1}$ are disjoint. So, if we re-color $G$ by replacing $U_{i}$ and $U_{i+1}$ by $\left(U_{i} \cup Q\right) \backslash P$ and $\left(U_{i+1} \cup P\right) \backslash Q$, respectively, we obtain a proper coloring such that $n\left(U_{i}\right)=n\left(V_{c_{i}}\right)$ is decreased and only $n\left(U_{i+1}\right)=n\left(V_{c_{i+1}}\right)$ is increased. That contradicts the lexicographical minimality of $\left(n\left(V_{2}\right), n\left(V_{3}\right), \ldots, n\left(V_{k}\right)\right)$.
+
+
+Figure 3
+Next, we build a path through $U_{1}, U_{2}, \ldots, U_{2 \ell}$ as follows. Let the starting point of the path be an arbitrary vertex $v_{1}$ in the set $N_{1}$. For $i \leqslant 2 \ell-1$, if the vertex $v_{i} \in N_{i}$ is already defined, connect $v_{i}$ to some vertex in $N_{i+1}$ in the subgraph induced by $U_{i} \cup U_{i+1}$, and add these edges to the path. Denote the new endpoint of the path by $v_{i+1}$; by the construction we have $v_{i+1} \in N_{i+1}$ again, so the process can be continued. At the end we have a path that starts at $v_{1} \in N_{1}$ and ends at some $v_{2 \ell} \in N_{2 \ell}$. Moreover, all edges in this path connect vertices in neighboring classes: if a vertex of the path lies in $U_{i}$, then the next vertex lies in $U_{i+1}$ or $U_{i-1}$. Notice that the path is not necessary simple, so take a minimal subpath of it. The minimal subpath is simple and connects the same endpoints $v_{1}$ and $v_{2 \ell}$. The property that every edge steps to a neighboring color class (i.e., from $U_{i}$ to $U_{i+1}$ or $U_{i-1}$ ) is preserved. So the resulting path also visits all of $U_{1}, \ldots, U_{2 \ell}$, and its length must be odd. Closing the path with the edges $v v_{1}$ and $v_{2 \ell} v$ we obtain the desired odd cycle (see Figure 4).
+
+
+Figure 4
+Now we prove the claim by induction on $k \geqslant 3$. The base case $k=3$ holds by applying Lemma 2 to a critical subgraph. For the induction step, let $G_{0}$ be a critical $k$-chromatic subgraph of $G$, and let $v$ be an arbitrary vertex of $G_{0}$. By Lemma 2, $G_{0}$ has at least $2^{k-2}-1$ unsociable groups containing $v$. On the other hand, the graph $G_{0} \backslash\{v\}$ has chromatic number $k-1$, so it contains at least $2^{k-2}-(k-1)$ unsociable groups by the induction hypothesis. Altogether, this gives $2^{k-2}-1+2^{k-2}-(k-1)=2^{k-1}-k$ distinct unsociable groups in $G_{0}$ (and thus in $G$ ).
+
+Comment 1. The claim we proved is sharp. The complete graph with $k$ vertices has chromatic number $k$ and contains exactly $2^{k-1}-k$ unsociable groups.
+
+Comment 2. The proof of Lemma 2 works for odd values of $|C| \geqslant 3$ as well. Hence, the second solution shows the analogous statement that the number of even sized unsociable groups is at least $2^{k}-1-\binom{k}{2}$.
+
+## Geometry
+
+G1. Let $A B C$ be an acute triangle with orthocenter $H$. Let $G$ be the point such that the quadrilateral $A B G H$ is a parallelogram. Let $I$ be the point on the line $G H$ such that $A C$ bisects $H I$. Suppose that the line $A C$ intersects the circumcircle of the triangle $G C I$ at $C$ and $J$. Prove that $I J=A H$.
+(Australia)
+Solution 1. Since $H G \| A B$ and $B G \| A H$, we have $B G \perp B C$ and $C H \perp G H$. Therefore, the quadrilateral $B G C H$ is cyclic. Since $H$ is the orthocenter of the triangle $A B C$, we have $\angle H A C=90^{\circ}-\angle A C B=\angle C B H$. Using that $B G C H$ and $C G J I$ are cyclic quadrilaterals, we get
+
+$$
+\angle C J I=\angle C G H=\angle C B H=\angle H A C .
+$$
+
+Let $M$ be the intersection of $A C$ and $G H$, and let $D \neq A$ be the point on the line $A C$ such that $A H=H D$. Then $\angle M J I=\angle H A C=\angle M D H$.
+
+Since $\angle M J I=\angle M D H, \angle I M J=\angle H M D$, and $I M=M H$, the triangles $I M J$ and $H M D$ are congruent, and thus $I J=H D=A H$.
+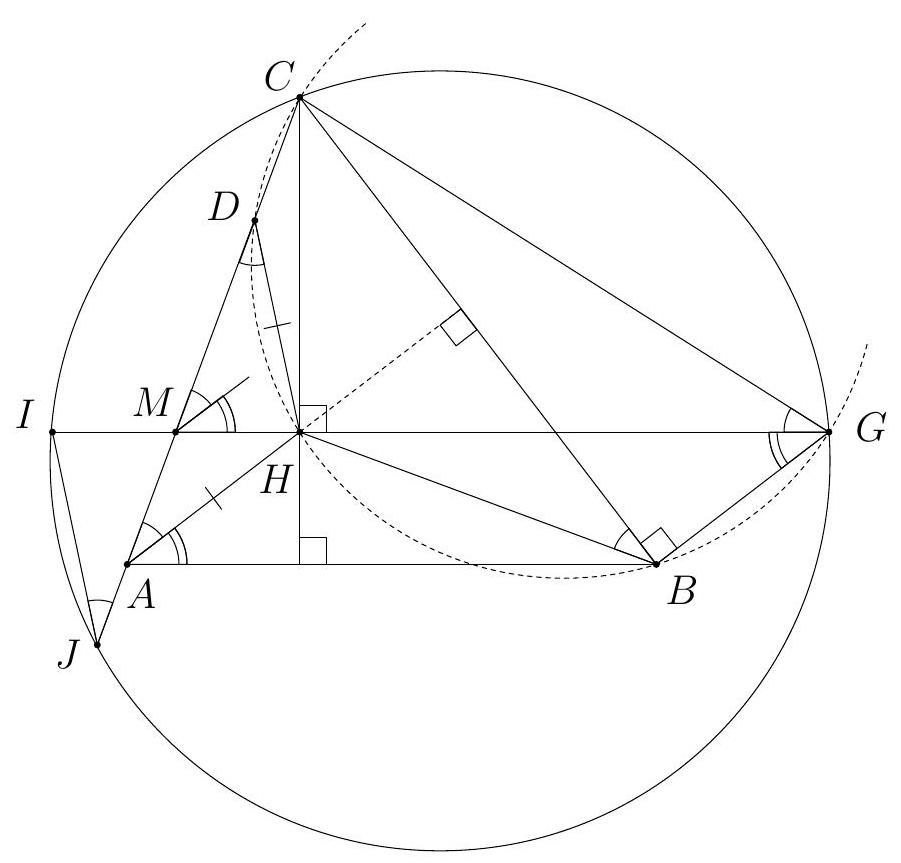
+
+Comment. Instead of introducing the point $D$, one can complete the solution by using the law of sines in the triangles $I J M$ and $A M H$, yielding
+
+$$
+\frac{I J}{I M}=\frac{\sin \angle I M J}{\sin \angle M J I}=\frac{\sin \angle A M H}{\sin \angle H A M}=\frac{A H}{M H}=\frac{A H}{I M} .
+$$
+
+Solution 2. Obtain $\angle C G H=\angle H A C$ as in the previous solution. In the parallelogram $A B G H$ we have $\angle B A H=\angle H G B$. It follows that
+
+$$
+\angle H M C=\angle B A C=\angle B A H+\angle H A C=\angle H G B+\angle C G H=\angle C G B .
+$$
+
+So the right triangles $C M H$ and $C G B$ are similar. Also, in the circumcircle of triangle $G C I$ we have similar triangles $M I J$ and $M C G$. Therefore,
+
+$$
+\frac{I J}{C G}=\frac{M I}{M C}=\frac{M H}{M C}=\frac{G B}{G C}=\frac{A H}{C G}
+$$
+
+Hence $I J=A H$.
+
+G2. Let $A B C$ be a triangle inscribed into a circle $\Omega$ with center $O$. A circle $\Gamma$ with center $A$ meets the side $B C$ at points $D$ and $E$ such that $D$ lies between $B$ and $E$. Moreover, let $F$ and $G$ be the common points of $\Gamma$ and $\Omega$. We assume that $F$ lies on the arc $A B$ of $\Omega$ not containing $C$, and $G$ lies on the arc $A C$ of $\Omega$ not containing $B$. The circumcircles of the triangles $B D F$ and $C E G$ meet the sides $A B$ and $A C$ again at $K$ and $L$, respectively. Suppose that the lines $F K$ and $G L$ are distinct and intersect at $X$. Prove that the points $A, X$, and $O$ are collinear.
+(Greece)
+Solution 1. It suffices to prove that the lines $F K$ and $G L$ are symmetric about $A O$. Now the segments $A F$ and $A G$, being chords of $\Omega$ with the same length, are clearly symmetric with respect to $A O$. Hence it is enough to show
+
+$$
+\angle K F A=\angle A G L .
+$$
+
+Let us denote the circumcircles of $B D F$ and $C E G$ by $\omega_{B}$ and $\omega_{C}$, respectively. To prove (1), we start from
+
+$$
+\angle K F A=\angle D F G+\angle G F A-\angle D F K
+$$
+
+In view of the circles $\omega_{B}, \Gamma$, and $\Omega$, this may be rewritten as
+
+$$
+\angle K F A=\angle C E G+\angle G B A-\angle D B K=\angle C E G-\angle C B G .
+$$
+
+Due to the circles $\omega_{C}$ and $\Omega$, we obtain $\angle K F A=\angle C L G-\angle C A G=\angle A G L$. Thereby the problem is solved.
+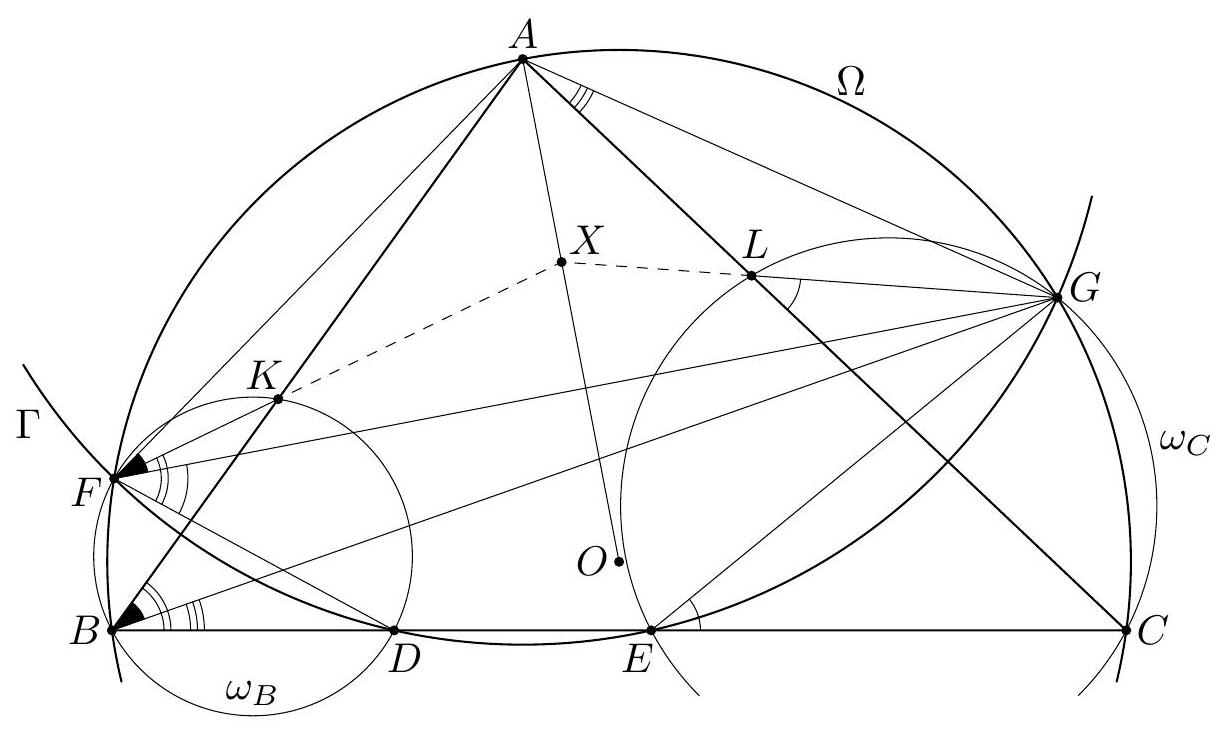
+
+Figure 1
+
+Solution 2. Again, we denote the circumcircle of $B D K F$ by $\omega_{B}$. In addition, we set $\alpha=$ $\angle B A C, \varphi=\angle A B F$, and $\psi=\angle E D A=\angle A E D$ (see Figure 2). Notice that $A F=A G$ entails $\varphi=\angle G C A$, so all three of $\alpha, \varphi$, and $\psi$ respect the "symmetry" between $B$ and $C$ of our configuration. Again, we reduce our task to proving (1).
+
+This time, we start from
+
+$$
+2 \angle K F A=2(\angle D F A-\angle D F K) .
+$$
+
+Since the triangle $A F D$ is isosceles, we have
+
+$$
+\angle D F A=\angle A D F=\angle E D F-\psi=\angle B F D+\angle E B F-\psi .
+$$
+
+Moreover, because of the circle $\omega_{B}$ we have $\angle D F K=\angle C B A$. Altogether, this yields
+
+$$
+2 \angle K F A=\angle D F A+(\angle B F D+\angle E B F-\psi)-2 \angle C B A,
+$$
+
+which simplifies to
+
+$$
+2 \angle K F A=\angle B F A+\varphi-\psi-\angle C B A .
+$$
+
+Now the quadrilateral $A F B C$ is cyclic, so this entails $2 \angle K F A=\alpha+\varphi-\psi$.
+Due to the "symmetry" between $B$ and $C$ alluded to above, this argument also shows that $2 \angle A G L=\alpha+\varphi-\psi$. This concludes the proof of (1).
+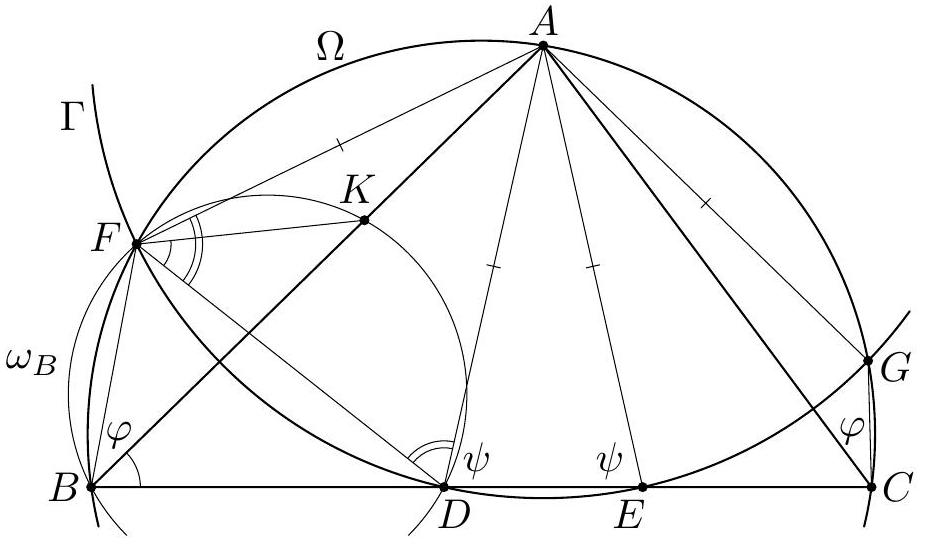
+
+Figure 2
+
+Comment 1. As the first solution shows, the assumption that $A$ be the center of $\Gamma$ may be weakened to the following one: The center of $\Gamma$ lies on the line $O A$. The second solution may be modified to yield the same result.
+
+Comment 2. It might be interesting to remark that $\angle G D K=90^{\circ}$. To prove this, let $G^{\prime}$ denote the point on $\Gamma$ diametrically opposite to $G$. Because of $\angle K D F=\angle K B F=\angle A G F=\angle G^{\prime} D F$, the points $D, K$, and $G^{\prime}$ are collinear, which leads to the desired result. Notice that due to symmetry we also have $\angle L E F=90^{\circ}$.
+
+Moreover, a standard argument shows that the triangles $A G L$ and $B G E$ are similar. By symmetry again, also the triangles $A F K$ and $C D F$ are similar.
+
+There are several ways to derive a solution from these facts. For instance, one may argue that
+
+$$
+\begin{aligned}
+\angle K F A & =\angle B F A-\angle B F K=\angle B F A-\angle E D G^{\prime}=\left(180^{\circ}-\angle A G B\right)-\left(180^{\circ}-\angle G^{\prime} G E\right) \\
+& =\angle A G E-\angle A G B=\angle B G E=\angle A G L .
+\end{aligned}
+$$
+
+Comment 3. The original proposal did not contain the point $X$ in the assumption and asked instead to prove that the lines $F K, G L$, and $A O$ are concurrent. This differs from the version given above only insofar as it also requires to show that these lines cannot be parallel. The Problem Selection Committee removed this part from the problem intending to make it thus more suitable for the Olympiad.
+
+For the sake of completeness, we would still like to sketch one possibility for proving $F K \nVdash A O$ here. As the points $K$ and $O$ lie in the angular region $\angle F A G$, it suffices to check $\angle K F A+\angle F A O<180^{\circ}$. Multiplying by 2 and making use of the formulae from the second solution, we see that this is equivalent to $(\alpha+\varphi-\psi)+\left(180^{\circ}-2 \varphi\right)<360^{\circ}$, which in turn is an easy consequence of $\alpha<180^{\circ}$.
+
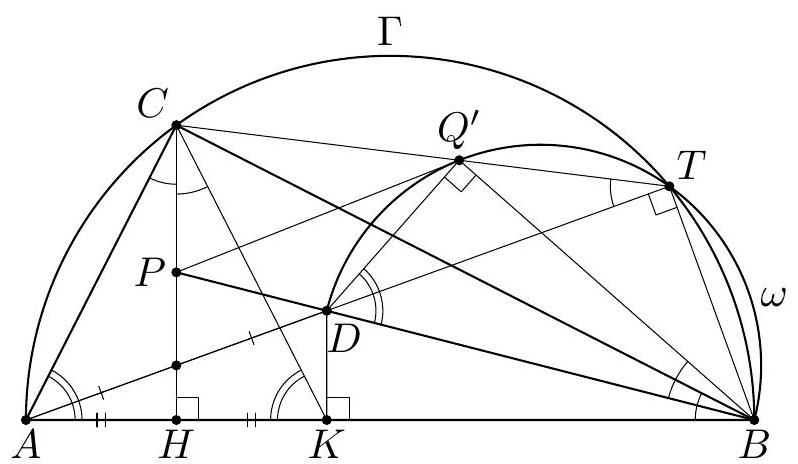
+G3. Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$.
+(Georgia)
+Solution 1. Let $K$ be the projection of $D$ onto $A B$; then $A H=H K$ (see Figure 1). Since $P H \| D K$, we have
+
+$$
+\frac{P D}{P B}=\frac{H K}{H B}=\frac{A H}{H B}
+$$
+
+Let $L$ be the projection of $Q$ onto $D B$. Since $P Q$ is tangent to $\omega$ and $\angle D Q B=\angle B L Q=$ $90^{\circ}$, we have $\angle P Q D=\angle Q B P=\angle D Q L$. Therefore, $Q D$ and $Q B$ are respectively the internal and the external bisectors of $\angle P Q L$. By the angle bisector theorem, we obtain
+
+$$
+\frac{P D}{D L}=\frac{P Q}{Q L}=\frac{P B}{B L}
+$$
+
+The relations (1) and (2) yield $\frac{A H}{H B}=\frac{P D}{P B}=\frac{D L}{L B}$. So, the spiral similarity $\tau$ centered at $B$ and sending $A$ to $D$ maps $H$ to $L$. Moreover, $\tau$ sends the semicircle with diameter $A B$ passing through $C$ to $\omega$. Due to $C H \perp A B$ and $Q L \perp D B$, it follows that $\tau(C)=Q$.
+
+Hence, the triangles $A B D$ and $C B Q$ are similar, so $\angle A D B=\angle C Q B$. This means that the lines $A D$ and $C Q$ meet at some point $T$, and this point satisfies $\angle B D T=\angle B Q T$. Therefore, $T$ lies on $\omega$, as needed.
+
+
+Figure 1
+
+
+Figure 2
+
+Comment 1. Since $\angle B A D=\angle B C Q$, the point $T$ lies also on the circumcircle of the triangle $A B C$.
+Solution 2. Let $\Gamma$ be the circumcircle of $A B C$, and let $A D$ meet $\omega$ at $T$. Then $\angle A T B=$ $\angle A C B=90^{\circ}$, so $T$ lies on $\Gamma$ as well. As in the previous solution, let $K$ be the projection of $D$ onto $A B$; then $A H=H K$ (see Figure 2).
+
+Our goal now is to prove that the points $C, Q$, and $T$ are collinear. Let $C T$ meet $\omega$ again at $Q^{\prime}$. Then, it suffices to show that $P Q^{\prime}$ is tangent to $\omega$, or that $\angle P Q^{\prime} D=\angle Q^{\prime} B D$.
+
+Since the quadrilateral $B D Q^{\prime} T$ is cyclic and the triangles $A H C$ and $K H C$ are congruent, we have $\angle Q^{\prime} B D=\angle Q^{\prime} T D=\angle C T A=\angle C B A=\angle A C H=\angle H C K$. Hence, the right triangles $C H K$ and $B Q^{\prime} D$ are similar. This implies that $\frac{H K}{C K}=\frac{Q^{\prime} D}{B D}$, and thus $H K \cdot B D=C K \cdot Q^{\prime} D$.
+
+Notice that $P H \| D K$; therefore, we have $\frac{P D}{B D}=\frac{H K}{B K}$, and so $P D \cdot B K=H K \cdot B D$. Consequently, $P D \cdot B K=H K \cdot B D=C K \cdot Q^{\prime} D$, which yields $\frac{P D}{Q^{\prime} D}=\frac{C K}{B K}$.
+
+Since $\angle C K A=\angle K A C=\angle B D Q^{\prime}$, the triangles $C K B$ and $P D Q^{\prime}$ are similar, so $\angle P Q^{\prime} D=$ $\angle C B A=\angle Q^{\prime} B D$, as required.
+
+Comment 2. There exist several other ways to prove that $P Q^{\prime}$ is tangent to $\omega$. For instance, one may compute $\frac{P D}{P B}$ and $\frac{P Q^{\prime}}{P B}$ in terms of $A H$ and $H B$ to verify that $P Q^{\prime 2}=P D \cdot P B$, concluding that $P Q^{\prime}$ is tangent to $\omega$.
+
+Another possible approach is the following. As in Solution 2, we introduce the points $T$ and $Q^{\prime}$ and mention that the triangles $A B C$ and $D B Q^{\prime}$ are similar (see Figure 3).
+
+Let $M$ be the midpoint of $A D$, and let $L$ be the projection of $Q^{\prime}$ onto $A B$. Construct $E$ on the line $A B$ so that $E P$ is parallel to $A D$. Projecting from $P$, we get $(A, B ; H, E)=(A, D ; M, \infty)=-1$. Since $\frac{E A}{A B}=\frac{P D}{D B}$, the point $P$ is the image of $E$ under the similarity transform mapping $A B C$ to $D B Q^{\prime}$. Therefore, we have $(D, B ; L, P)=(A, B ; H, E)=-1$, which means that $Q^{\prime} D$ and $Q^{\prime} B$ are respectively the internal and the external bisectors of $\angle P Q^{\prime} L$. This implies that $P Q^{\prime}$ is tangent to $\omega$, as required.
+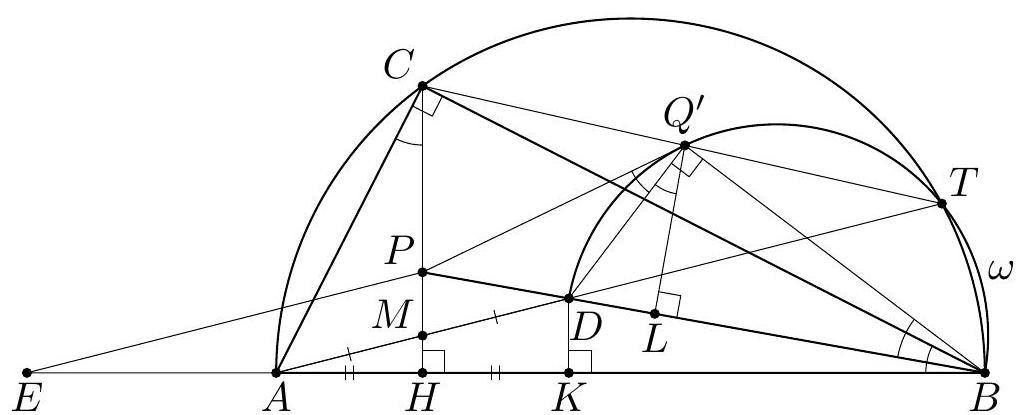
+
+Figure 3
+
+Solution 3. Introduce the points $T$ and $Q^{\prime}$ as in the previous solution. Note that $T$ lies on the circumcircle of $A B C$. Here we present yet another proof that $P Q^{\prime}$ is tangent to $\omega$.
+
+Let $\Omega$ be the circle completing the semicircle $\omega$. Construct a point $F$ symmetric to $C$ with respect to $A B$. Let $S \neq T$ be the second intersection point of $F T$ and $\Omega$ (see Figure 4).
+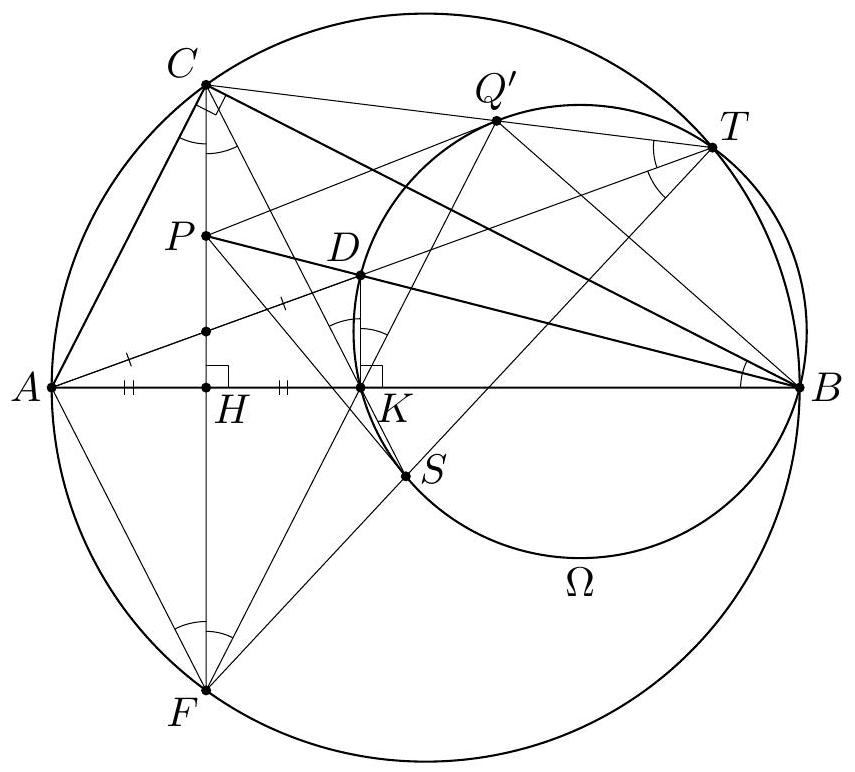
+
+Figure 4
+Since $A C=A F$, we have $\angle D K C=\angle H C K=\angle C B A=\angle C T A=\angle D T S=180^{\circ}-$ $\angle S K D$. Thus, the points $C, K$, and $S$ are collinear. Notice also that $\angle Q^{\prime} K D=\angle Q^{\prime} T D=$ $\angle H C K=\angle K F H=180^{\circ}-\angle D K F$. This implies that the points $F, K$, and $Q^{\prime}$ are collinear.
+
+Applying PASCAL's theorem to the degenerate hexagon $K Q^{\prime} Q^{\prime} T S S$, we get that the tangents to $\Omega$ passing through $Q^{\prime}$ and $S$ intersect on $C F$. The relation $\angle Q^{\prime} T D=\angle D T S$ yields that $Q^{\prime}$ and $S$ are symmetric with respect to $B D$. Therefore, the two tangents also intersect on $B D$. Thus, the two tangents pass through $P$. Hence, $P Q^{\prime}$ is tangent to $\omega$, as needed.
+
+G4. Let $A B C$ be an acute triangle, and let $M$ be the midpoint of $A C$. A circle $\omega$ passing through $B$ and $M$ meets the sides $A B$ and $B C$ again at $P$ and $Q$, respectively. Let $T$ be the point such that the quadrilateral $B P T Q$ is a parallelogram. Suppose that $T$ lies on the circumcircle of the triangle $A B C$. Determine all possible values of $B T / B M$.
+(Russia)
+Answer. $\sqrt{2}$.
+Solution 1. Let $S$ be the center of the parallelogram $B P T Q$, and let $B^{\prime} \neq B$ be the point on the ray $B M$ such that $B M=M B^{\prime}$ (see Figure 1). It follows that $A B C B^{\prime}$ is a parallelogram. Then, $\angle A B B^{\prime}=\angle P Q M$ and $\angle B B^{\prime} A=\angle B^{\prime} B C=\angle M P Q$, and so the triangles $A B B^{\prime}$ and $M Q P$ are similar. It follows that $A M$ and $M S$ are corresponding medians in these triangles. Hence,
+
+$$
+\angle S M P=\angle B^{\prime} A M=\angle B C A=\angle B T A .
+$$
+
+Since $\angle A C T=\angle P B T$ and $\angle T A C=\angle T B C=\angle B T P$, the triangles $T C A$ and $P B T$ are similar. Again, as $T M$ and $P S$ are corresponding medians in these triangles, we have
+
+$$
+\angle M T A=\angle T P S=\angle B Q P=\angle B M P .
+$$
+
+Now we deal separately with two cases.
+Case 1. $\quad S$ does not lie on $B M$. Since the configuration is symmetric between $A$ and $C$, we may assume that $S$ and $A$ lie on the same side with respect to the line $B M$.
+
+Applying (1) and (2), we get
+
+$$
+\angle B M S=\angle B M P-\angle S M P=\angle M T A-\angle B T A=\angle M T B,
+$$
+
+and so the triangles $B S M$ and $B M T$ are similar. We now have $B M^{2}=B S \cdot B T=B T^{2} / 2$, so $B T=\sqrt{2} B M$.
+Case 2. $\quad S$ lies on $B M$. It follows from (2) that $\angle B C A=\angle M T A=\angle B Q P=\angle B M P$ (see Figure 2). Thus, $P Q \| A C$ and $P M \| A T$. Hence, $B S / B M=B P / B A=B M / B T$, so $B T^{2}=2 B M^{2}$ and $B T=\sqrt{2} B M$.
+
+
+Figure 1
+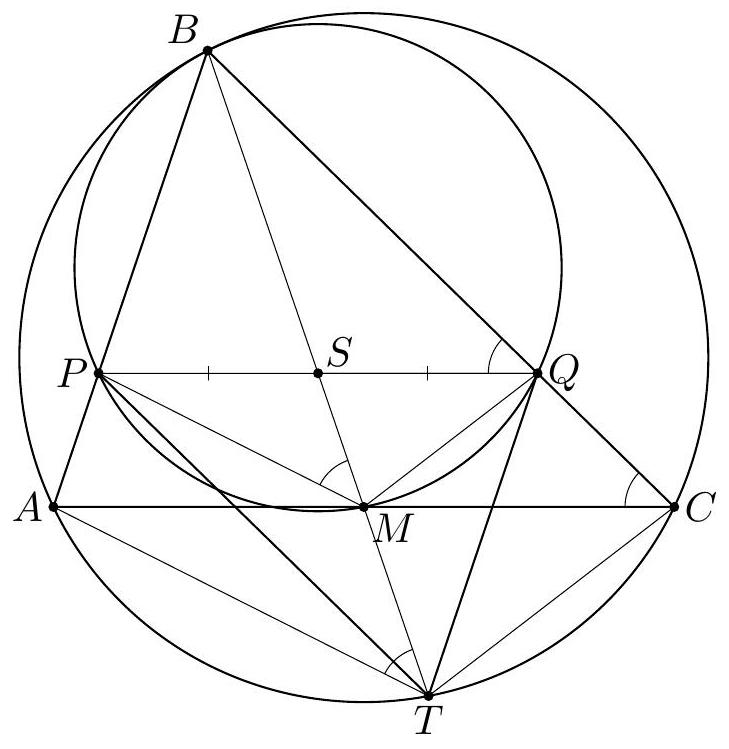
+
+Figure 2
+
+Comment 1. Here is another way to show that the triangles $B S M$ and $B M T$ are similar. Denote by $\Omega$ the circumcircle of the triangle $A B C$. Let $R$ be the second point of intersection of $\omega$ and $\Omega$, and let $\tau$ be the spiral similarity centered at $R$ mapping $\omega$ to $\Omega$. Then, one may show that $\tau$ maps each point $X$ on $\omega$ to a point $Y$ on $\Omega$ such that $B, X$, and $Y$ are collinear (see Figure 3). If we let $K$ and $L$ be the second points of intersection of $B M$ with $\Omega$ and of $B T$ with $\omega$, respectively, then it follows that the triangle $M K T$ is the image of $S M L$ under $\tau$. We now obtain $\angle B S M=\angle T M B$, which implies the desired result.
+
+
+Figure 3
+
+
+Figure 4
+
+Solution 2. Again, we denote by $\Omega$ the circumcircle of the triangle $A B C$.
+Choose the points $X$ and $Y$ on the rays $B A$ and $B C$ respectively, so that $\angle M X B=\angle M B C$ and $\angle B Y M=\angle A B M$ (see Figure 4). Then the triangles $B M X$ and $Y M B$ are similar. Since $\angle X P M=\angle B Q M$, the points $P$ and $Q$ correspond to each other in these triangles. So, if $\overrightarrow{B P}=\mu \cdot \overrightarrow{B X}$, then $\overrightarrow{B Q}=(1-\mu) \cdot \overrightarrow{B Y}$. Thus
+
+$$
+\overrightarrow{B T}=\overrightarrow{B P}+\overrightarrow{B Q}=\overrightarrow{B Y}+\mu \cdot(\overrightarrow{B X}-\overrightarrow{B Y})=\overrightarrow{B Y}+\mu \cdot \overrightarrow{Y X}
+$$
+
+which means that $T$ lies on the line $X Y$.
+Let $B^{\prime} \neq B$ be the point on the ray $B M$ such that $B M=M B^{\prime}$. Then $\angle M B^{\prime} A=$ $\angle M B C=\angle M X B$ and $\angle C B^{\prime} M=\angle A B M=\angle B Y M$. This means that the triangles $B M X$, $B A B^{\prime}, Y M B$, and $B^{\prime} C B$ are all similar; hence $B A \cdot B X=B M \cdot B B^{\prime}=B C \cdot B Y$. Thus there exists an inversion centered at $B$ which swaps $A$ with $X, M$ with $B^{\prime}$, and $C$ with $Y$. This inversion then swaps $\Omega$ with the line $X Y$, and hence it preserves $T$. Therefore, we have $B T^{2}=B M \cdot B B^{\prime}=2 B M^{2}$, and $B T=\sqrt{2} B M$.
+
+Solution 3. We begin with the following lemma.
+Lemma. Let $A B C T$ be a cyclic quadrilateral. Let $P$ and $Q$ be points on the sides $B A$ and $B C$ respectively, such that $B P T Q$ is a parallelogram. Then $B P \cdot B A+B Q \cdot B C=B T^{2}$.
+Proof. Let the circumcircle of the triangle $Q T C$ meet the line $B T$ again at $J$ (see Figure 5). The power of $B$ with respect to this circle yields
+
+$$
+B Q \cdot B C=B J \cdot B T
+$$
+
+We also have $\angle T J Q=180^{\circ}-\angle Q C T=\angle T A B$ and $\angle Q T J=\angle A B T$, and so the triangles $T J Q$ and $B A T$ are similar. We now have $T J / T Q=B A / B T$. Therefore,
+
+$$
+T J \cdot B T=T Q \cdot B A=B P \cdot B A
+$$
+
+Combining (3) and (4) now yields the desired result.
+Let $X$ and $Y$ be the midpoints of $B A$ and $B C$ respectively (see Figure 6). Applying the lemma to the cyclic quadrilaterals $P B Q M$ and $A B C T$, we obtain
+
+$$
+B X \cdot B P+B Y \cdot B Q=B M^{2}
+$$
+
+and
+
+$$
+B P \cdot B A+B Q \cdot B C=B T^{2}
+$$
+
+Since $B A=2 B X$ and $B C=2 B Y$, we have $B T^{2}=2 B M^{2}$, and so $B T=\sqrt{2} B M$.
+
+
+Comment 2. Here we give another proof of the lemma using Ptolemy's theorem. We readily have
+
+$$
+T C \cdot B A+T A \cdot B C=A C \cdot B T
+$$
+
+The lemma now follows from
+
+$$
+\frac{B P}{T C}=\frac{B Q}{T A}=\frac{B T}{A C}=\frac{\sin \angle B C T}{\sin \angle A B C}
+$$
+
+G5. Let $A B C$ be a triangle with $C A \neq C B$. Let $D, F$, and $G$ be the midpoints of the sides $A B, A C$, and $B C$, respectively. A circle $\Gamma$ passing through $C$ and tangent to $A B$ at $D$ meets the segments $A F$ and $B G$ at $H$ and $I$, respectively. The points $H^{\prime}$ and $I^{\prime}$ are symmetric to $H$ and $I$ about $F$ and $G$, respectively. The line $H^{\prime} I^{\prime}$ meets $C D$ and $F G$ at $Q$ and $M$, respectively. The line $C M$ meets $\Gamma$ again at $P$. Prove that $C Q=Q P$.
+(El Salvador)
+Solution 1. We may assume that $C A>C B$. Observe that $H^{\prime}$ and $I^{\prime}$ lie inside the segments $C F$ and $C G$, respectively. Therefore, $M$ lies outside $\triangle A B C$ (see Figure 1).
+
+Due to the powers of points $A$ and $B$ with respect to the circle $\Gamma$, we have
+
+$$
+C H^{\prime} \cdot C A=A H \cdot A C=A D^{2}=B D^{2}=B I \cdot B C=C I^{\prime} \cdot C B
+$$
+
+Therefore, $C H^{\prime} \cdot C F=C I^{\prime} \cdot C G$. Hence, the quadrilateral $H^{\prime} I^{\prime} G F$ is cyclic, and so $\angle I^{\prime} H^{\prime} C=$ $\angle C G F$.
+
+Let $D F$ and $D G$ meet $\Gamma$ again at $R$ and $S$, respectively. We claim that the points $R$ and $S$ lie on the line $H^{\prime} I^{\prime}$.
+
+Observe that $F H^{\prime} \cdot F A=F H \cdot F C=F R \cdot F D$. Thus, the quadrilateral $A D H^{\prime} R$ is cyclic, and hence $\angle R H^{\prime} F=\angle F D A=\angle C G F=\angle I^{\prime} H^{\prime} C$. Therefore, the points $R, H^{\prime}$, and $I^{\prime}$ are collinear. Similarly, the points $S, H^{\prime}$, and $I^{\prime}$ are also collinear, and so all the points $R, H^{\prime}, Q, I^{\prime}, S$, and $M$ are all collinear.
+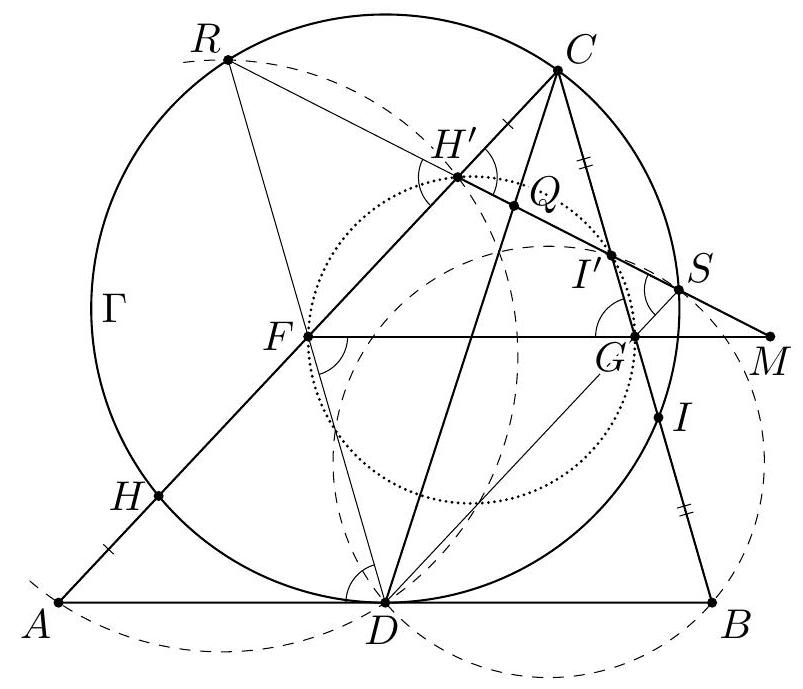
+
+Figure 1
+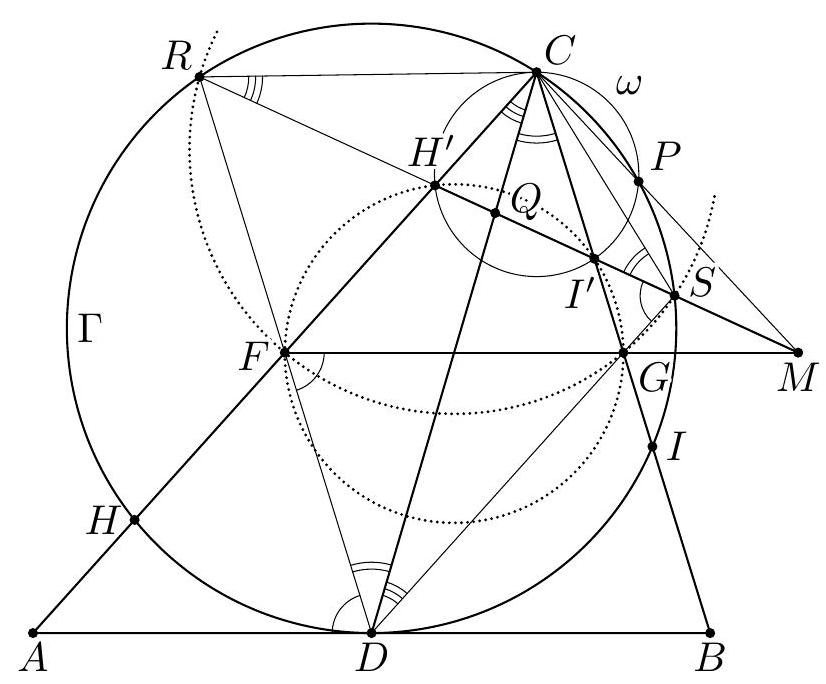
+
+Figure 2
+
+Then, $\angle R S D=\angle R D A=\angle D F G$. Hence, the quadrilateral $R S G F$ is cyclic (see Figure 2). Therefore, $M H^{\prime} \cdot M I^{\prime}=M F \cdot M G=M R \cdot M S=M P \cdot M C$. Thus, the quadrilateral $C P I^{\prime} H^{\prime}$ is also cyclic. Let $\omega$ be its circumcircle.
+
+Notice that $\angle H^{\prime} C Q=\angle S D C=\angle S R C$ and $\angle Q C I^{\prime}=\angle C D R=\angle C S R$. Hence, $\triangle C H^{\prime} Q \sim \triangle R C Q$ and $\triangle C I^{\prime} Q \sim \triangle S C Q$, and therefore $Q H^{\prime} \cdot Q R=Q C^{2}=Q I^{\prime} \cdot Q S$.
+
+We apply the inversion with center $Q$ and radius $Q C$. Observe that the points $R, C$, and $S$ are mapped to $H^{\prime}, C$, and $I^{\prime}$, respectively. Therefore, the circumcircle $\Gamma$ of $\triangle R C S$ is mapped to the circumcircle $\omega$ of $\triangle H^{\prime} C I^{\prime}$. Since $P$ and $C$ belong to both circles and the point $C$ is preserved by the inversion, we have that $P$ is also mapped to itself. We then get $Q P^{2}=Q C^{2}$. Hence, $Q P=Q C$.
+
+Comment 1. The problem statement still holds when $\Gamma$ intersects the sides $C A$ and $C B$ outside segments $A F$ and $B G$, respectively.
+
+Solution 2. Let $X=H I \cap A B$, and let the tangent to $\Gamma$ at $C$ meet $A B$ at $Y$. Let $X C$ meet $\Gamma$ again at $X^{\prime}$ (see Figure 3). Projecting from $C, X$, and $C$ again, we have $(X, A ; D, B)=$ $\left(X^{\prime}, H ; D, I\right)=(C, I ; D, H)=(Y, B ; D, A)$. Since $A$ and $B$ are symmetric about $D$, it follows that $X$ and $Y$ are also symmetric about $D$.
+
+Now, Menelaus' theorem applied to $\triangle A B C$ with the line $H I X$ yields
+
+$$
+1=\frac{C H}{H A} \cdot \frac{B I}{I C} \cdot \frac{A X}{X B}=\frac{A H^{\prime}}{H^{\prime} C} \cdot \frac{C I^{\prime}}{I^{\prime} B} \cdot \frac{B Y}{Y A} .
+$$
+
+By the converse of Menelaus' theorem applied to $\triangle A B C$ with points $H^{\prime}, I^{\prime}, Y$, we get that the points $H^{\prime}, I^{\prime}, Y$ are collinear.
+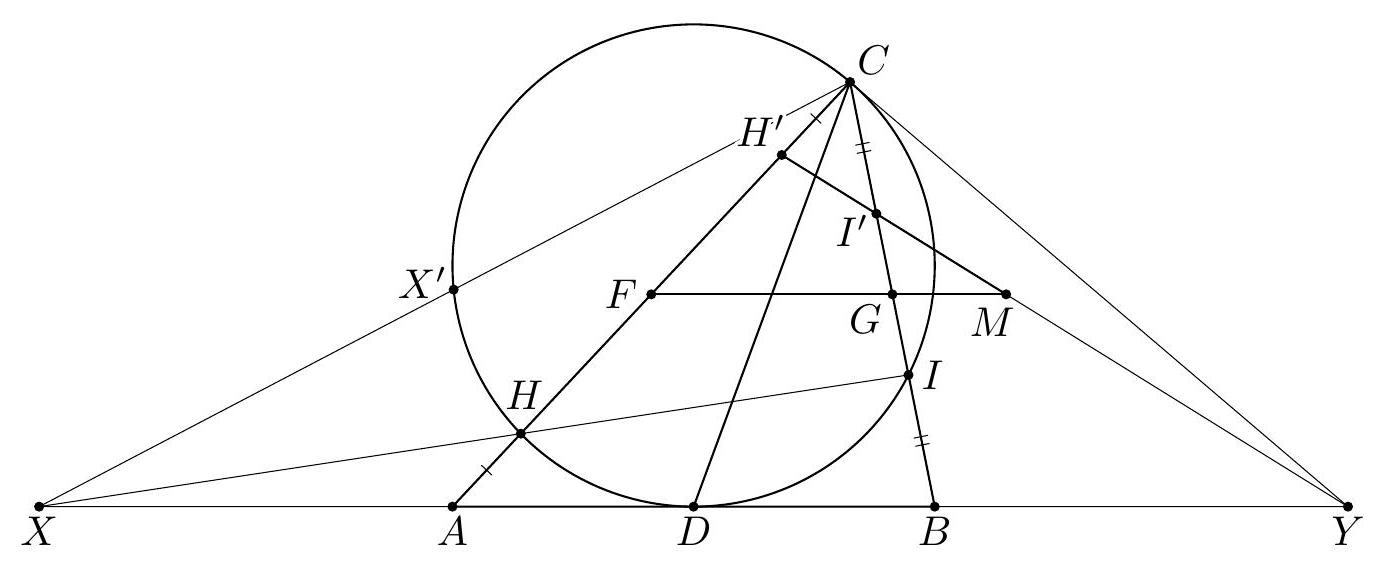
+
+Figure 3
+Let $T$ be the midpoint of $C D$, and let $O$ be the center of $\Gamma$. Let $C M$ meet $T Y$ at $N$. To avoid confusion, we clean some superfluous details out of the picture (see Figure 4).
+
+Let $V=M T \cap C Y$. Since $M T \| Y D$ and $D T=T C$, we get $C V=V Y$. Then CevA's theorem applied to $\triangle C T Y$ with the point $M$ yields
+
+$$
+1=\frac{T Q}{Q C} \cdot \frac{C V}{V Y} \cdot \frac{Y N}{N T}=\frac{T Q}{Q C} \cdot \frac{Y N}{N T}
+$$
+
+Therefore, $\frac{T Q}{Q C}=\frac{T N}{N Y}$. So, $N Q \| C Y$, and thus $N Q \perp O C$.
+Note that the points $O, N, T$, and $Y$ are collinear. Therefore, $C Q \perp O N$. So, $Q$ is the orthocenter of $\triangle O C N$, and hence $O Q \perp C P$. Thus, $Q$ lies on the perpendicular bisector of $C P$, and therefore $C Q=Q P$, as required.
+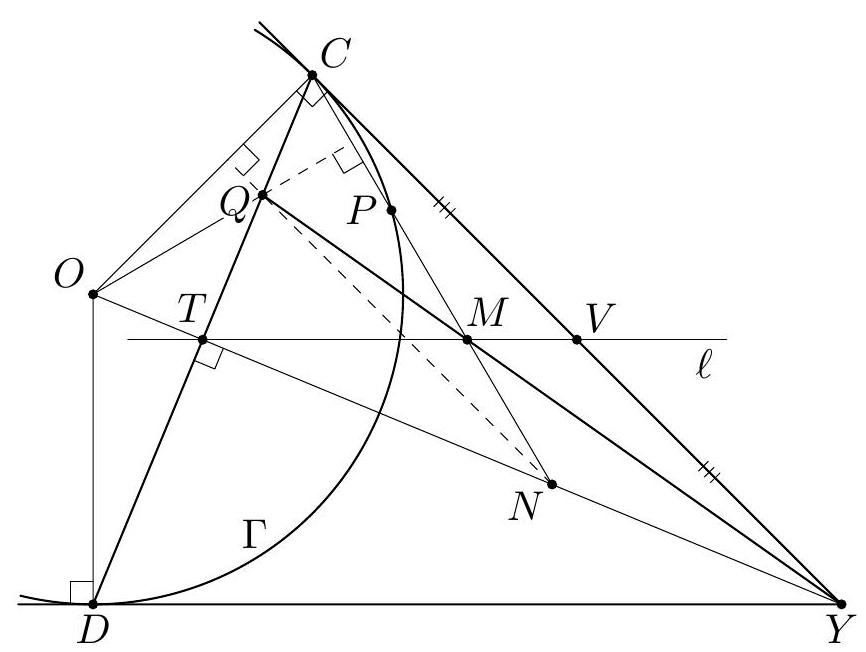
+
+Figure 4
+
+Comment 2. The second part of Solution 2 provides a proof of the following more general statement, which does not involve a specific choice of $Q$ on $C D$.
+
+Let $Y C$ and $Y D$ be two tangents to a circle $\Gamma$ with center $O$ (see Figure 4). Let $\ell$ be the midline of $\triangle Y C D$ parallel to $Y D$. Let $Q$ and $M$ be two points on $C D$ and $\ell$, respectively, such that the line $Q M$ passes through $Y$. Then $O Q \perp C M$.
+
+G6. Let $A B C$ be an acute triangle with $A B>A C$, and let $\Gamma$ be its circumcircle. Let $H$, $M$, and $F$ be the orthocenter of the triangle, the midpoint of $B C$, and the foot of the altitude from $A$, respectively. Let $Q$ and $K$ be the two points on $\Gamma$ that satisfy $\angle A Q H=90^{\circ}$ and $\angle Q K H=90^{\circ}$. Prove that the circumcircles of the triangles $K Q H$ and $K F M$ are tangent to each other.
+(Ukraine)
+Solution 1. Let $A^{\prime}$ be the point diametrically opposite to $A$ on $\Gamma$. Since $\angle A Q A^{\prime}=90^{\circ}$ and $\angle A Q H=90^{\circ}$, the points $Q, H$, and $A^{\prime}$ are collinear. Similarly, if $Q^{\prime}$ denotes the point on $\Gamma$ diametrically opposite to $Q$, then $K, H$, and $Q^{\prime}$ are collinear. Let the line $A H F$ intersect $\Gamma$ again at $E$; it is known that $M$ is the midpoint of the segment $H A^{\prime}$ and that $F$ is the midpoint of $H E$. Let $J$ be the midpoint of $H Q^{\prime}$.
+
+Consider any point $T$ such that $T K$ is tangent to the circle $K Q H$ at $K$ with $Q$ and $T$ lying on different sides of $K H$ (see Figure 1). Then $\angle H K T=\angle H Q K$ and we are to prove that $\angle M K T=\angle C F K$. Thus it remains to show that $\angle H Q K=\angle C F K+\angle H K M$. Due to $\angle H Q K=90^{\circ}-\angle Q^{\prime} H A^{\prime}$ and $\angle C F K=90^{\circ}-\angle K F A$, this means the same as $\angle Q^{\prime} H A^{\prime}=$ $\angle K F A-\angle H K M$. Now, since the triangles $K H E$ and $A H Q^{\prime}$ are similar with $F$ and $J$ being the midpoints of corresponding sides, we have $\angle K F A=\angle H J A$, and analogously one may obtain $\angle H K M=\angle J Q H$. Thereby our task is reduced to verifying
+
+$$
+\angle Q^{\prime} H A^{\prime}=\angle H J A-\angle J Q H
+$$
+
+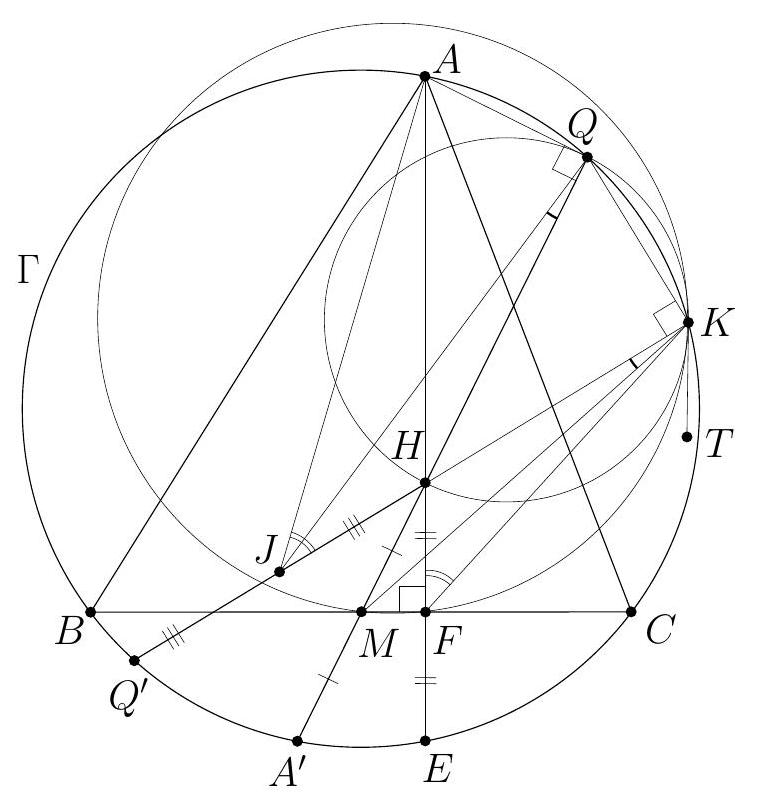
+
+Figure 1
+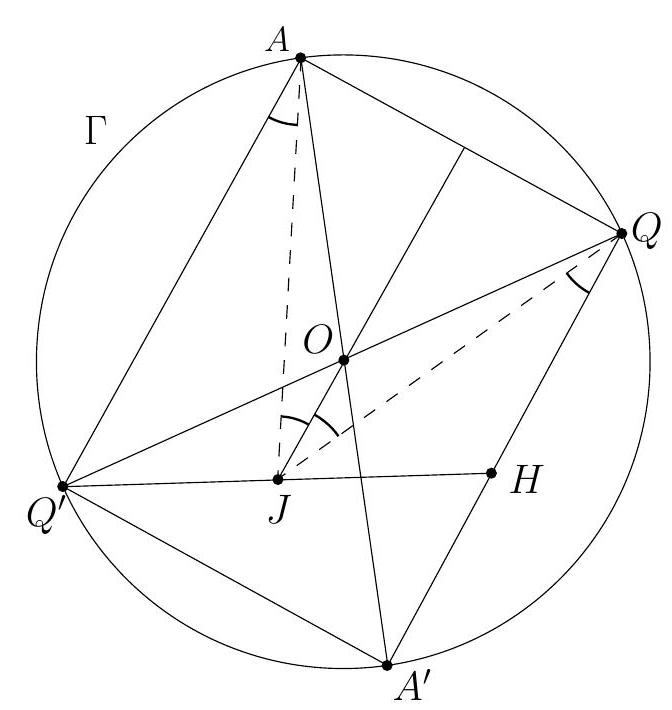
+
+Figure 2
+
+To avoid confusion, let us draw a new picture at this moment (see Figure 2). Owing to $\angle Q^{\prime} H A^{\prime}=\angle J Q H+\angle H J Q$ and $\angle H J A=\angle Q J A+\angle H J Q$, we just have to show that $2 \angle J Q H=\angle Q J A$. To this end, it suffices to remark that $A Q A^{\prime} Q^{\prime}$ is a rectangle and that $J$, being defined to be the midpoint of $H Q^{\prime}$, has to lie on the mid parallel of $Q A^{\prime}$ and $Q^{\prime} A$.
+
+Solution 2. We define the points $A^{\prime}$ and $E$ and prove that the ray $M H$ passes through $Q$ in the same way as in the first solution. Notice that the points $A^{\prime}$ and $E$ can play analogous roles to the points $Q$ and $K$, respectively: point $A^{\prime}$ is the second intersection of the line $M H$ with $\Gamma$, and $E$ is the point on $\Gamma$ with the property $\angle H E A^{\prime}=90^{\circ}$ (see Figure 3).
+
+In the circles $K Q H$ and $E A^{\prime} H$, the line segments $H Q$ and $H A^{\prime}$ are diameters, respectively; so, these circles have a common tangent $t$ at $H$, perpendicular to $M H$. Let $R$ be the radical center of the circles $A B C, K Q H$ and $E A^{\prime} H$. Their pairwise radical axes are the lines $Q K$, $A^{\prime} E$ and the line $t$; they all pass through $R$. Let $S$ be the midpoint of $H R$; by $\angle Q K H=$
+
+
+Figure 3
+$\angle H E A^{\prime}=90^{\circ}$, the quadrilateral $H E R K$ is cyclic and its circumcenter is $S$; hence we have $S K=S E=S H$. The line $B C$, being the perpendicular bisector of $H E$, passes through $S$.
+
+The circle $H M F$ also is tangent to $t$ at $H$; from the power of $S$ with respect to the circle $H M F$ we have
+
+$$
+S M \cdot S F=S H^{2}=S K^{2}
+$$
+
+So, the power of $S$ with respect to the circles $K Q H$ and $K F M$ is $S K^{2}$. Therefore, the line segment $S K$ is tangent to both circles at $K$.
+
+G7. Let $A B C D$ be a convex quadrilateral, and let $P, Q, R$, and $S$ be points on the sides $A B, B C, C D$, and $D A$, respectively. Let the line segments $P R$ and $Q S$ meet at $O$. Suppose that each of the quadrilaterals $A P O S, B Q O P, C R O Q$, and $D S O R$ has an incircle. Prove that the lines $A C, P Q$, and $R S$ are either concurrent or parallel to each other.
+(Bulgaria)
+Solution 1. Denote by $\gamma_{A}, \gamma_{B}, \gamma_{C}$, and $\gamma_{D}$ the incircles of the quadrilaterals $A P O S, B Q O P$, $C R O Q$, and $D S O R$, respectively.
+
+We start with proving that the quadrilateral $A B C D$ also has an incircle which will be referred to as $\Omega$. Denote the points of tangency as in Figure 1. It is well-known that $Q Q_{1}=O O_{1}$ (if $B C \| P R$, this is obvious; otherwise, one may regard the two circles involved as the incircle and an excircle of the triangle formed by the lines $O Q, P R$, and $B C$ ). Similarly, $O O_{1}=P P_{1}$. Hence we have $Q Q_{1}=P P_{1}$. The other equalities of segment lengths marked in Figure 1 can be proved analogously. These equalities, together with $A P_{1}=A S_{1}$ and similar ones, yield $A B+C D=A D+B C$, as required.
+
+
+Figure 1
+
+Next, let us draw the lines parallel to $Q S$ through $P$ and $R$, and also draw the lines parallel to $P R$ through $Q$ and $S$. These lines form a parallelogram; denote its vertices by $A^{\prime}, B^{\prime}, C^{\prime}$, and $D^{\prime}$ as shown in Figure 2.
+
+Since the quadrilateral $A P O S$ has an incircle, we have $A P-A S=O P-O S=A^{\prime} S-A^{\prime} P$. It is well-known that in this case there also exists a circle $\omega_{A}$ tangent to the four rays $A P$, $A S, A^{\prime} P$, and $A^{\prime} S$. It is worth mentioning here that in case when, say, the lines $A B$ and $A^{\prime} B^{\prime}$ coincide, the circle $\omega_{A}$ is just tangent to $A B$ at $P$. We introduce the circles $\omega_{B}, \omega_{C}$, and $\omega_{D}$ in a similar manner.
+
+Assume that the radii of the circles $\omega_{A}$ and $\omega_{C}$ are different. Let $X$ be the center of the homothety having a positive scale factor and mapping $\omega_{A}$ to $\omega_{C}$.
+
+Now, Monge's theorem applied to the circles $\omega_{A}, \Omega$, and $\omega_{C}$ shows that the points $A, C$, and $X$ are collinear. Applying the same theorem to the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$, we see that the points $P, Q$, and $X$ are also collinear. Similarly, the points $R, S$, and $X$ are collinear, as required.
+
+If the radii of $\omega_{A}$ and $\omega_{C}$ are equal but these circles do not coincide, then the degenerate version of the same theorem yields that the three lines $A C, P Q$, and $R S$ are parallel to the line of centers of $\omega_{A}$ and $\omega_{C}$.
+
+Finally, we need to say a few words about the case when $\omega_{A}$ and $\omega_{C}$ coincide (and thus they also coincide with $\Omega, \omega_{B}$, and $\omega_{D}$ ). It may be regarded as the limit case in the following manner.
+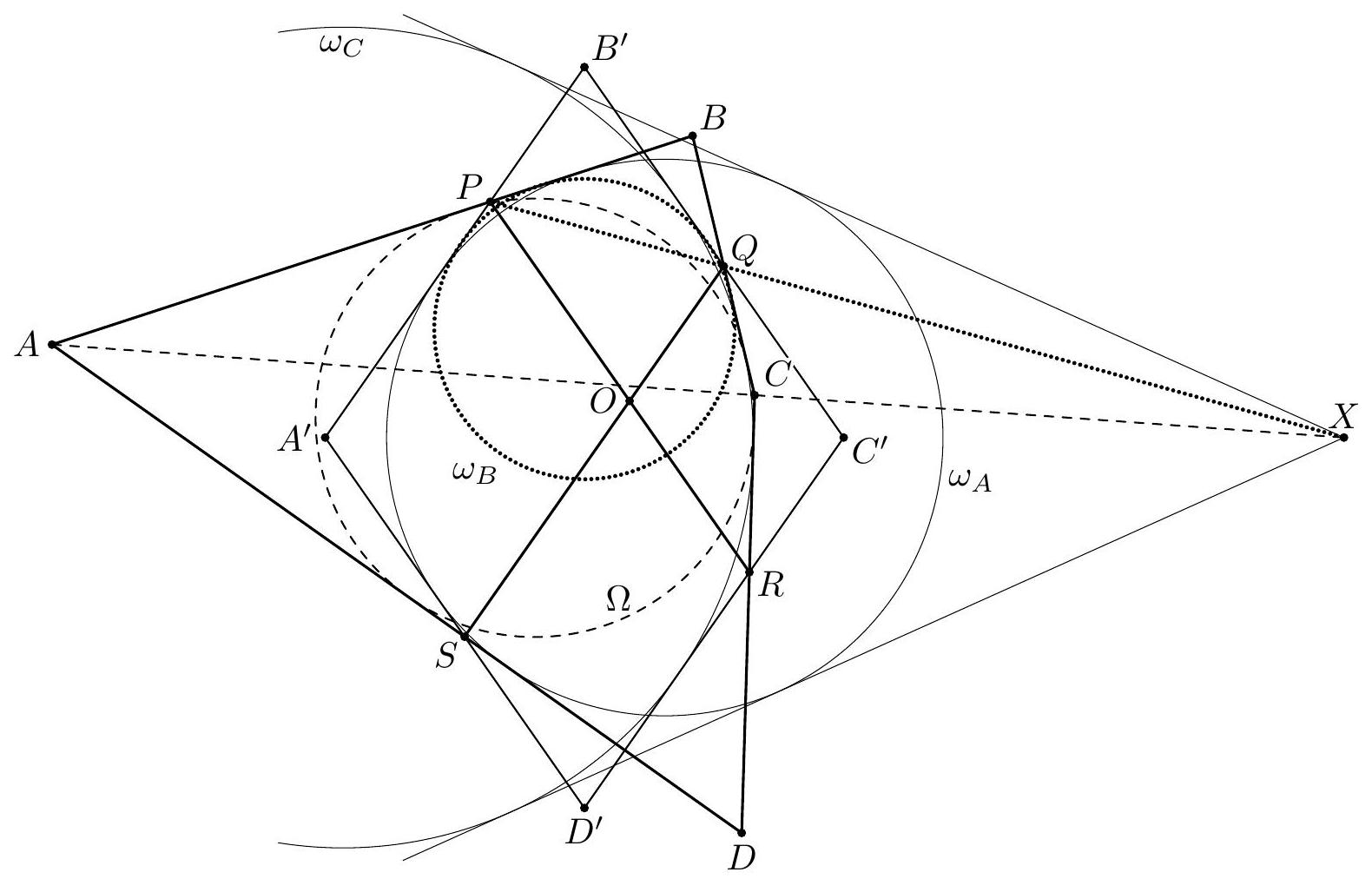
+
+Figure 2
+
+Let us fix the positions of $A, P, O$, and $S$ (thus we also fix the circles $\omega_{A}, \gamma_{A}, \gamma_{B}$, and $\gamma_{D}$ ). Now we vary the circle $\gamma_{C}$ inscribed into $\angle Q O R$; for each of its positions, one may reconstruct the lines $B C$ and $C D$ as the external common tangents to $\gamma_{B}, \gamma_{C}$ and $\gamma_{C}, \gamma_{D}$ different from $P R$ and $Q S$, respectively. After such variation, the circle $\Omega$ changes, so the result obtained above may be applied.
+
+Solution 2. Applying Menelaus' theorem to $\triangle A B C$ with the line $P Q$ and to $\triangle A C D$ with the line $R S$, we see that the line $A C$ meets $P Q$ and $R S$ at the same point (possibly at infinity) if and only if
+
+$$
+\frac{A P}{P B} \cdot \frac{B Q}{Q C} \cdot \frac{C R}{R D} \cdot \frac{D S}{S A}=1
+$$
+
+So, it suffices to prove (1).
+We start with the following result.
+Lemma 1. Let $E F G H$ be a circumscribed quadrilateral, and let $M$ be its incenter. Then
+
+$$
+\frac{E F \cdot F G}{G H \cdot H E}=\frac{F M^{2}}{H M^{2}}
+$$
+
+Proof. Notice that $\angle E M H+\angle G M F=\angle F M E+\angle H M G=180^{\circ}, \angle F G M=\angle M G H$, and $\angle H E M=\angle M E F$ (see Figure 3). By the law of sines, we get
+
+$$
+\frac{E F}{F M} \cdot \frac{F G}{F M}=\frac{\sin \angle F M E \cdot \sin \angle G M F}{\sin \angle M E F \cdot \sin \angle F G M}=\frac{\sin \angle H M G \cdot \sin \angle E M H}{\sin \angle M G H \cdot \sin \angle H E M}=\frac{G H}{H M} \cdot \frac{H E}{H M} .
+$$
+
+
+
+Figure 3
+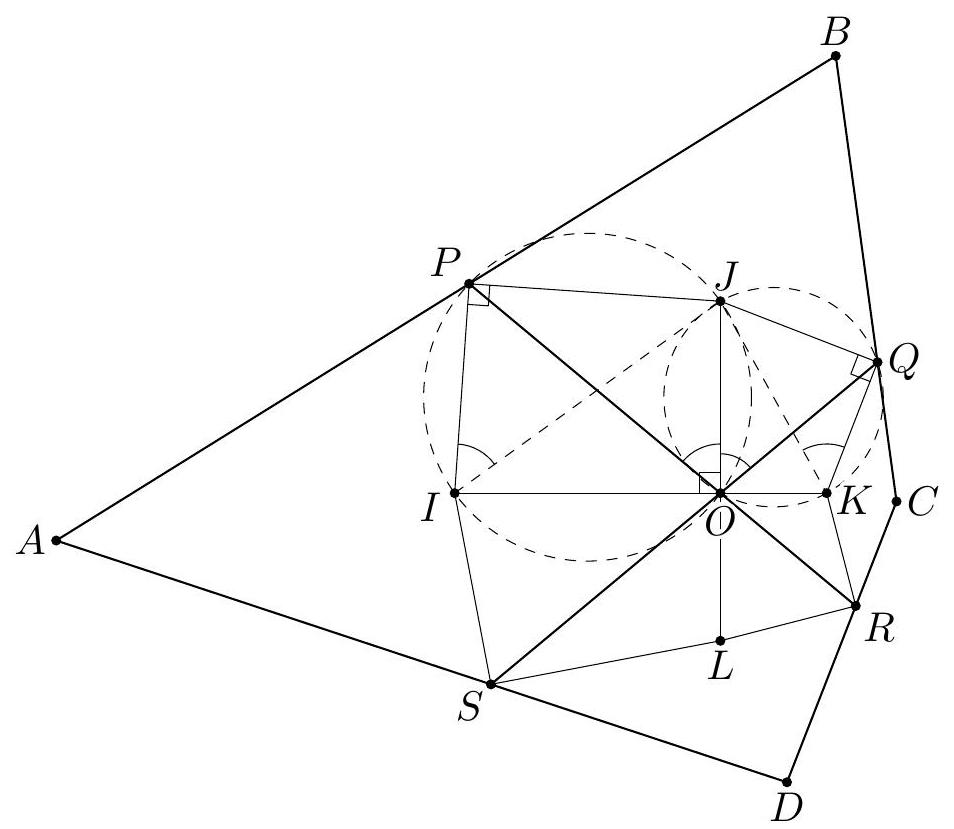
+
+Figure 4
+
+We denote by $I, J, K$, and $L$ the incenters of the quadrilaterals $A P O S, B Q O P, C R O Q$, and $D S O R$, respectively. Applying Lemma 1 to these four quadrilaterals we get
+
+$$
+\frac{A P \cdot P O}{O S \cdot S A} \cdot \frac{B Q \cdot Q O}{O P \cdot P B} \cdot \frac{C R \cdot R O}{O Q \cdot Q C} \cdot \frac{D S \cdot S O}{O R \cdot R D}=\frac{P I^{2}}{S I^{2}} \cdot \frac{Q J^{2}}{P J^{2}} \cdot \frac{R K^{2}}{Q K^{2}} \cdot \frac{S L^{2}}{R L^{2}}
+$$
+
+which reduces to
+
+$$
+\frac{A P}{P B} \cdot \frac{B Q}{Q C} \cdot \frac{C R}{R D} \cdot \frac{D S}{S A}=\frac{P I^{2}}{P J^{2}} \cdot \frac{Q J^{2}}{Q K^{2}} \cdot \frac{R K^{2}}{R L^{2}} \cdot \frac{S L^{2}}{S I^{2}}
+$$
+
+Next, we have $\angle I P J=\angle J O I=90^{\circ}$, and the line $O P$ separates $I$ and $J$ (see Figure 4). This means that the quadrilateral $I P J O$ is cyclic. Similarly, we get that the quadrilateral $J Q K O$ is cyclic with $\angle J Q K=90^{\circ}$. Thus, $\angle Q K J=\angle Q O J=\angle J O P=\angle J I P$. Hence, the right triangles $I P J$ and $K Q J$ are similar. Therefore, $\frac{P I}{P J}=\frac{Q K}{Q J}$. Likewise, we obtain $\frac{R K}{R L}=\frac{S I}{S L}$. These two equations together with (2) yield (1).
+Comment. Instead of using the sine law, one may prove Lemma 1 by the following approach.
+
+
+Figure 5
+Let $N$ be the point such that $\triangle N H G \sim \triangle M E F$ and such that $N$ and $M$ lie on different sides of the line $G H$, as shown in Figure 5. Then $\angle G N H+\angle H M G=\angle F M E+\angle H M G=180^{\circ}$. So,
+the quadrilateral $G N H M$ is cyclic. Thus, $\angle M N H=\angle M G H=\angle F G M$ and $\angle H M N=\angle H G N=$ $\angle E F M=\angle M F G$. Hence, $\triangle H M N \sim \triangle M F G$. Therefore, $\frac{H M}{H G}=\frac{H M}{H N} \cdot \frac{H N}{H G}=\frac{M F}{M G} \cdot \frac{E M}{E F}$. Similarly, we obtain $\frac{H M}{H E}=\frac{M F}{M E} \cdot \frac{G M}{G F}$. By multiplying these two equations, we complete the proof.
+
+Solution 3. We present another approach for showing (1) from Solution 2.
+Lemma 2. Let $E F G H$ and $E^{\prime} F^{\prime} G^{\prime} H^{\prime}$ be circumscribed quadrilaterals such that $\angle E+\angle E^{\prime}=$ $\angle F+\angle F^{\prime}=\angle G+\angle G^{\prime}=\angle H+\angle H^{\prime}=180^{\circ}$. Then
+
+$$
+\frac{E F \cdot G H}{F G \cdot H E}=\frac{E^{\prime} F^{\prime} \cdot G^{\prime} H^{\prime}}{F^{\prime} G^{\prime} \cdot H^{\prime} E^{\prime}}
+$$
+
+Proof. Let $M$ and $M^{\prime}$ be the incenters of $E F G H$ and $E^{\prime} F^{\prime} G^{\prime} H^{\prime}$, respectively. We use the notation [XYZ] for the area of a triangle $X Y Z$.
+
+Taking into account the relation $\angle F M E+\angle F^{\prime} M^{\prime} E^{\prime}=180^{\circ}$ together with the analogous ones, we get
+
+$$
+\begin{aligned}
+\frac{E F \cdot G H}{F G \cdot H E} & =\frac{[M E F] \cdot[M G H]}{[M F G] \cdot[M H E]}=\frac{M E \cdot M F \cdot \sin \angle F M E \cdot M G \cdot M H \cdot \sin \angle H M G}{M F \cdot M G \cdot \sin \angle G M F \cdot M H \cdot M E \cdot \sin \angle E M H} \\
+& =\frac{M^{\prime} E^{\prime} \cdot M^{\prime} F^{\prime} \cdot \sin \angle F^{\prime} M^{\prime} E^{\prime} \cdot M^{\prime} G^{\prime} \cdot M^{\prime} H^{\prime} \cdot \sin \angle H^{\prime} M^{\prime} G^{\prime}}{M^{\prime} F^{\prime} \cdot M^{\prime} G^{\prime} \cdot \sin \angle G^{\prime} M^{\prime} F^{\prime} \cdot M^{\prime} H^{\prime} \cdot M^{\prime} E^{\prime} \cdot \sin \angle E^{\prime} M^{\prime} H^{\prime}}=\frac{E^{\prime} F^{\prime} \cdot G^{\prime} H^{\prime}}{F^{\prime} G^{\prime} \cdot H^{\prime} E^{\prime}} .
+\end{aligned}
+$$
+
+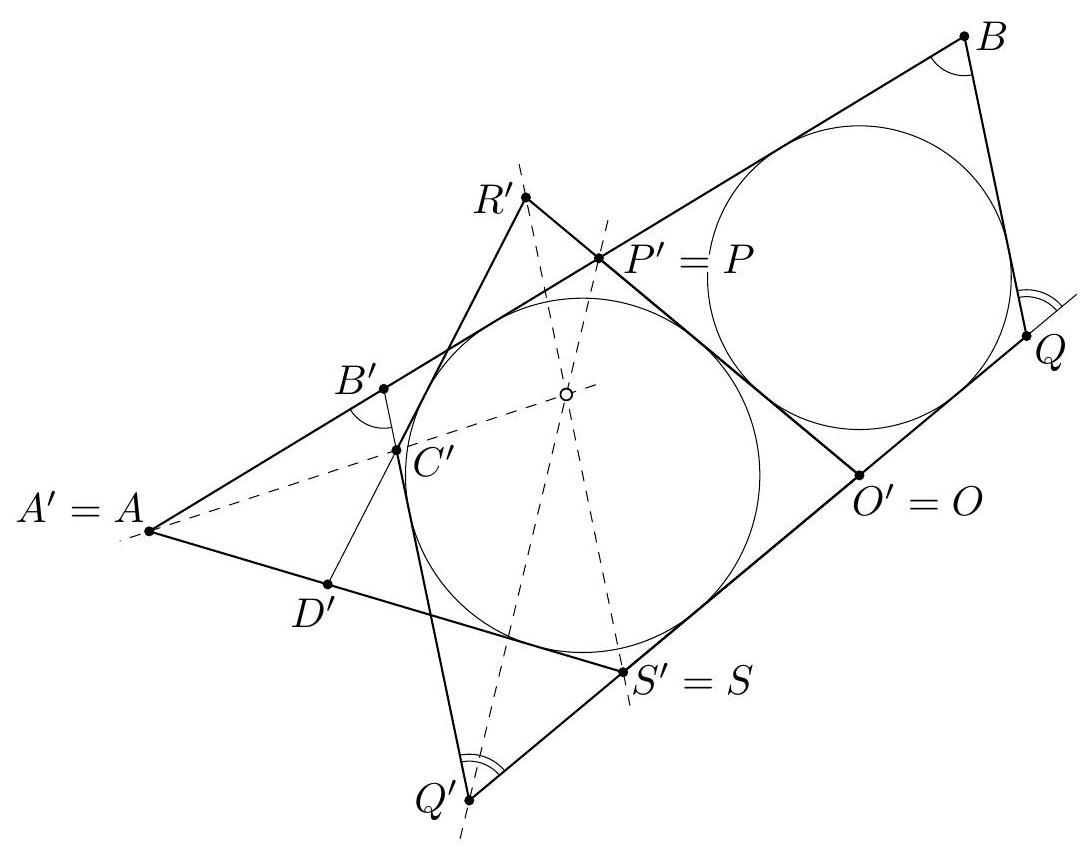
+
+Figure 6
+Denote by $h$ the homothety centered at $O$ that maps the incircle of $C R O Q$ to the incircle of $A P O S$. Let $Q^{\prime}=h(Q), C^{\prime}=h(C), R^{\prime}=h(R), O^{\prime}=O, S^{\prime}=S, A^{\prime}=A$, and $P^{\prime}=P$. Furthermore, define $B^{\prime}=A^{\prime} P^{\prime} \cap C^{\prime} Q^{\prime}$ and $D^{\prime}=A^{\prime} S^{\prime} \cap C^{\prime} R^{\prime}$ as shown in Figure 6. Then
+
+$$
+\frac{A P \cdot O S}{P O \cdot S A}=\frac{A^{\prime} P^{\prime} \cdot O^{\prime} S^{\prime}}{P^{\prime} O^{\prime} \cdot S^{\prime} A^{\prime}}
+$$
+
+holds trivially. We also have
+
+$$
+\frac{C R \cdot O Q}{R O \cdot Q C}=\frac{C^{\prime} R^{\prime} \cdot O^{\prime} Q^{\prime}}{R^{\prime} O^{\prime} \cdot Q^{\prime} C^{\prime}}
+$$
+
+by the similarity of the quadrilaterals $C R O Q$ and $C^{\prime} R^{\prime} O^{\prime} Q^{\prime}$.
+
+Next, consider the circumscribed quadrilaterals $B Q O P$ and $B^{\prime} Q^{\prime} O^{\prime} P^{\prime}$ whose incenters lie on different sides of the quadrilaterals' shared side line $O P=O^{\prime} P^{\prime}$. Observe that $B Q \| B^{\prime} Q^{\prime}$ and that $B^{\prime}$ and $Q^{\prime}$ lie on the lines $B P$ and $Q O$, respectively. It is now easy to see that the two quadrilaterals satisfy the hypotheses of Lemma 2. Thus, we deduce
+
+$$
+\frac{B Q \cdot O P}{Q O \cdot P B}=\frac{B^{\prime} Q^{\prime} \cdot O^{\prime} P^{\prime}}{Q^{\prime} O^{\prime} \cdot P^{\prime} B^{\prime}}
+$$
+
+Similarly, we get
+
+$$
+\frac{D S \cdot O R}{S O \cdot R D}=\frac{D^{\prime} S^{\prime} \cdot O^{\prime} R^{\prime}}{S^{\prime} O^{\prime} \cdot R^{\prime} D^{\prime}}
+$$
+
+Multiplying these four equations, we obtain
+
+$$
+\frac{A P}{P B} \cdot \frac{B Q}{Q C} \cdot \frac{C R}{R D} \cdot \frac{D S}{S A}=\frac{A^{\prime} P^{\prime}}{P^{\prime} B^{\prime}} \cdot \frac{B^{\prime} Q^{\prime}}{Q^{\prime} C^{\prime}} \cdot \frac{C^{\prime} R^{\prime}}{R^{\prime} D^{\prime}} \cdot \frac{D^{\prime} S^{\prime}}{S^{\prime} A^{\prime}}
+$$
+
+Finally, we apply BRIANChon's theorem to the circumscribed hexagon $A^{\prime} P^{\prime} R^{\prime} C^{\prime} Q^{\prime} S^{\prime}$ and deduce that the lines $A^{\prime} C^{\prime}, P^{\prime} Q^{\prime}$, and $R^{\prime} S^{\prime}$ are either concurrent or parallel to each other. So, by Menelaus' theorem, we obtain
+
+$$
+\frac{A^{\prime} P^{\prime}}{P^{\prime} B^{\prime}} \cdot \frac{B^{\prime} Q^{\prime}}{Q^{\prime} C^{\prime}} \cdot \frac{C^{\prime} R^{\prime}}{R^{\prime} D^{\prime}} \cdot \frac{D^{\prime} S^{\prime}}{S^{\prime} A^{\prime}}=1
+$$
+
+This equation together with (3) yield (1).
+
+G8. A triangulation of a convex polygon $\Pi$ is a partitioning of $\Pi$ into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a Thaiangulation if all triangles in it have the same area.
+
+Prove that any two different Thaiangulations of a convex polygon $\Pi$ differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.)
+(Bulgaria)
+Solution 1. We denote by [S] the area of a polygon $S$.
+Recall that each triangulation of a convex $n$-gon has exactly $n-2$ triangles. This means that all triangles in any two Thaiangulations of a convex polygon $\Pi$ have the same area.
+
+Let $\mathcal{T}$ be a triangulation of a convex polygon $\Pi$. If four vertices $A, B, C$, and $D$ of $\Pi$ form a parallelogram, and $\mathcal{T}$ contains two triangles whose union is this parallelogram, then we say that $\mathcal{T}$ contains parallelogram $A B C D$. Notice here that if two Thaiangulations $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ of $\Pi$ differ by two triangles, then the union of these triangles is a quadrilateral each of whose diagonals bisects its area, i.e., a parallelogram.
+
+We start with proving two properties of triangulations.
+Lemma 1. A triangulation of a convex polygon $\Pi$ cannot contain two parallelograms.
+Proof. Arguing indirectly, assume that $P_{1}$ and $P_{2}$ are two parallelograms contained in some triangulation $\mathcal{T}$. If they have a common triangle in $\mathcal{T}$, then we may assume that $P_{1}$ consists of triangles $A B C$ and $A D C$ of $\mathcal{T}$, while $P_{2}$ consists of triangles $A D C$ and $C D E$ (see Figure 1). But then $B C\|A D\| C E$, so the three vertices $B, C$, and $E$ of $\Pi$ are collinear, which is absurd.
+
+Assume now that $P_{1}$ and $P_{2}$ contain no common triangle. Let $P_{1}=A B C D$. The sides $A B$, $B C, C D$, and $D A$ partition $\Pi$ into several parts, and $P_{2}$ is contained in one of them; we may assume that this part is cut off from $P_{1}$ by $A D$. Then one may label the vertices of $P_{2}$ by $X$, $Y, Z$, and $T$ so that the polygon $A B C D X Y Z T$ is convex (see Figure 2; it may happen that $D=X$ and/or $T=A$, but still this polygon has at least six vertices). But the sum of the external angles of this polygon at $B, C, Y$, and $Z$ is already $360^{\circ}$, which is impossible. A final contradiction.
+
+
+Figure 1
+
+
+Figure 2
+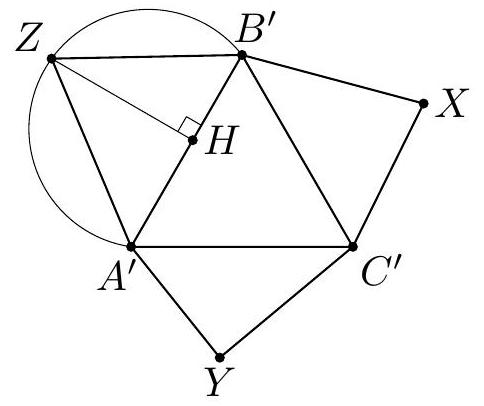
+
+Figure 3
+
+Lemma 2. Every triangle in a Thaiangulation $\mathcal{T}$ of $\Pi$ contains a side of $\Pi$.
+Proof. Let $A B C$ be a triangle in $\mathcal{T}$. Apply an affine transform such that $A B C$ maps to an equilateral triangle; let $A^{\prime} B^{\prime} C^{\prime}$ be the image of this triangle, and $\Pi^{\prime}$ be the image of $\Pi$. Clearly, $\mathcal{T}$ maps into a Thaiangulation $\mathcal{T}^{\prime}$ of $\Pi^{\prime}$.
+
+Assume that none of the sides of $\triangle A^{\prime} B^{\prime} C^{\prime}$ is a side of $\Pi^{\prime}$. Then $\mathcal{T}^{\prime}$ contains some other triangles with these sides, say, $A^{\prime} B^{\prime} Z, C^{\prime} A^{\prime} Y$, and $B^{\prime} C^{\prime} X$; notice that $A^{\prime} Z B^{\prime} X C^{\prime} Y$ is a convex hexagon (see Figure 3). The sum of its external angles at $X, Y$, and $Z$ is less than $360^{\circ}$. So one of these angles (say, at $Z$ ) is less than $120^{\circ}$, hence $\angle A^{\prime} Z B^{\prime}>60^{\circ}$. Then $Z$ lies on a circular arc subtended by $A^{\prime} B^{\prime}$ and having angular measure less than $240^{\circ}$; consequently, the altitude $Z H$ of $\triangle A^{\prime} B^{\prime} Z$ is less than $\sqrt{3} A^{\prime} B^{\prime} / 2$. Thus $\left[A^{\prime} B^{\prime} Z\right]<\left[A^{\prime} B^{\prime} C^{\prime}\right]$, and $\mathcal{T}^{\prime}$ is not a Thaiangulation. A contradiction.
+
+Now we pass to the solution. We say that a triangle in a triangulation of $\Pi$ is an ear if it contains two sides of $\Pi$. Note that each triangulation of a polygon contains some ear.
+
+Arguing indirectly, we choose a convex polygon $\Pi$ with the least possible number of sides such that some two Thaiangulations $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ of $\Pi$ violate the problem statement (thus $\Pi$ has at least five sides). Consider now any ear $A B C$ in $\mathcal{T}_{1}$, with $A C$ being a diagonal of $\Pi$. If $\mathcal{T}_{2}$ also contains $\triangle A B C$, then one may cut $\triangle A B C$ off from $\Pi$, getting a polygon with a smaller number of sides which also violates the problem statement. This is impossible; thus $\mathcal{T}_{2}$ does not contain $\triangle A B C$.
+
+Next, $\mathcal{T}_{1}$ contains also another triangle with side $A C$, say $\triangle A C D$. By Lemma 2 , this triangle contains a side of $\Pi$, so $D$ is adjacent to either $A$ or $C$ on the boundary of $\Pi$. We may assume that $D$ is adjacent to $C$.
+
+Assume that $\mathcal{T}_{2}$ does not contain the triangle $B C D$. Then it contains two different triangles $B C X$ and $C D Y$ (possibly, with $X=Y$ ); since these triangles have no common interior points, the polygon $A B C D Y X$ is convex (see Figure 4). But, since $[A B C]=[B C X]=$ $[A C D]=[C D Y]$, we get $A X \| B C$ and $A Y \| C D$ which is impossible. Thus $\mathcal{T}_{2}$ contains $\triangle B C D$.
+
+Therefore, $[A B D]=[A B C]+[A C D]-[B C D]=[A B C]$, and $A B C D$ is a parallelogram contained in $\mathcal{T}_{1}$. Let $\mathcal{T}^{\prime}$ be the Thaiangulation of $\Pi$ obtained from $\mathcal{T}_{1}$ by replacing the diagonal $A C$ with $B D$; then $\mathcal{T}^{\prime}$ is distinct from $\mathcal{T}_{2}$ (otherwise $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ would differ by two triangles). Moreover, $\mathcal{T}^{\prime}$ shares a common ear $B C D$ with $\mathcal{T}_{2}$. As above, cutting this ear away we obtain that $\mathcal{T}_{2}$ and $\mathcal{T}^{\prime}$ differ by two triangles forming a parallelogram different from $A B C D$. Thus $\mathcal{T}^{\prime}$ contains two parallelograms, which contradicts Lemma 1.
+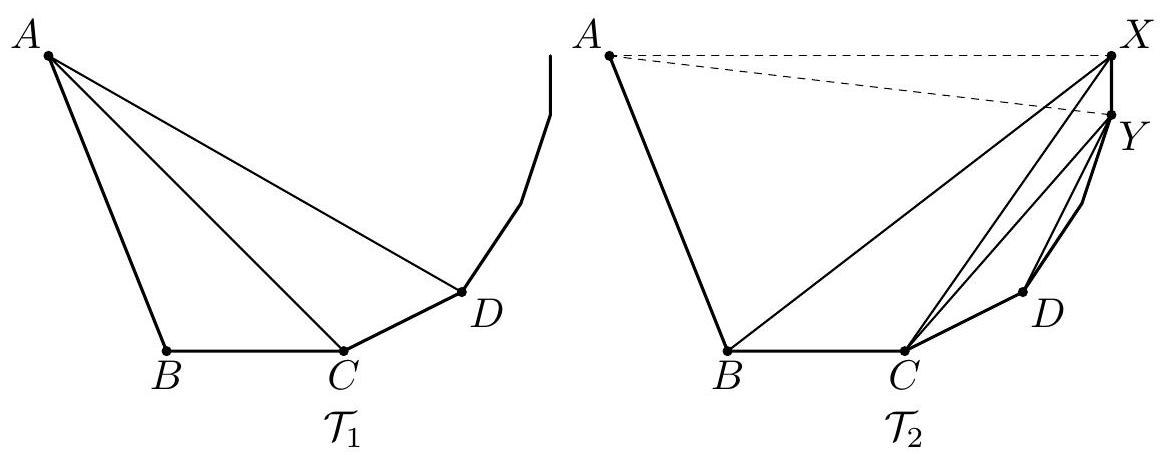
+
+Figure 4
+
+
+Figure 5
+
+Comment 1. Lemma 2 is equivalent to the well-known Erdős-Debrunner inequality stating that for any triangle $P Q R$ and any points $A, B, C$ lying on the sides $Q R, R P$, and $P Q$, respectively, we have
+
+$$
+[A B C] \geqslant \min \{[A B R],[B C P],[C A Q]\}
+$$
+
+To derive this inequality from Lemma 2, one may assume that (1) does not hold, and choose some points $X, Y$, and $Z$ inside the triangles $B C P, C A Q$, and $A B R$, respectively, so that $[A B C]=$ $[A B Z]=[B C X]=[C A Y]$. Then a convex hexagon $A Z B X C Y$ has a Thaiangulation containing $\triangle A B C$, which contradicts Lemma 2.
+
+Conversely, assume that a Thaiangulation $\mathcal{T}$ of $\Pi$ contains a triangle $A B C$ none of whose sides is a side of $\Pi$, and let $A B Z, A Y C$, and $X B C$ be other triangles in $\mathcal{T}$ containing the corresponding sides. Then $A Z B X C Y$ is a convex hexagon.
+
+Consider the lines through $A, B$, and $C$ parallel to $Y Z, Z X$, and $X Y$, respectively. They form a triangle $X^{\prime} Y^{\prime} Z^{\prime}$ similar to $\triangle X Y Z$ (see Figure 5). By (1) we have
+
+$$
+[A B C] \geqslant \min \left\{\left[A B Z^{\prime}\right],\left[B C X^{\prime}\right],\left[C A Y^{\prime}\right]\right\}>\min \{[A B Z],[B C X],[C A Y]\},
+$$
+
+so $\mathcal{T}$ is not a Thaiangulation.
+
+Solution 2. We will make use of the preliminary observations from Solution 1, together with Lemma 1.
+
+Arguing indirectly, we choose a convex polygon $\Pi$ with the least possible number of sides such that some two Thaiangulations $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ of $\Pi$ violate the statement (thus $\Pi$ has at least five sides). Assume that $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ share a diagonal $d$ splitting $\Pi$ into two smaller polygons $\Pi_{1}$ and $\Pi_{2}$. Since the problem statement holds for any of them, the induced Thaiangulations of each of $\Pi_{i}$ differ by two triangles forming a parallelogram (the Thaiangulations induced on $\Pi_{i}$ by $\mathcal{T}_{1}$ and $T_{2}$ may not coincide, otherwise $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ would differ by at most two triangles). But both these parallelograms are contained in $\mathcal{T}_{1}$; this contradicts Lemma 1. Therefore, $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ share no diagonal. Hence they also share no triangle.
+
+We consider two cases.
+Case 1. Assume that some vertex $B$ of $\Pi$ is an endpoint of some diagonal in $\mathcal{T}_{1}$, as well as an endpoint of some diagonal in $\mathcal{T}_{2}$.
+
+Let $A$ and $C$ be the vertices of $\Pi$ adjacent to $B$. Then $\mathcal{T}_{1}$ contains some triangles $A B X$ and $B C Y$, while $\mathcal{T}_{2}$ contains some triangles $A B X^{\prime}$ and $B C Y^{\prime}$. Here, some of the points $X$, $X^{\prime}, Y$, and $Y^{\prime}$ may coincide; however, in view of our assumption together with the fact that $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ share no triangle, all four triangles $A B X, B C Y, A B X^{\prime}$, and $B C Y^{\prime}$ are distinct.
+
+Since $[A B X]=[B C Y]=\left[A B X^{\prime}\right]=\left[B C Y^{\prime}\right]$, we have $X X^{\prime} \| A B$ and $Y Y^{\prime} \| B C$. Now, if $X=Y$, then $X^{\prime}$ and $Y^{\prime}$ lie on different lines passing through $X$ and are distinct from that point, so that $X^{\prime} \neq Y^{\prime}$. In this case, we may switch the two Thaiangulations. So, hereafter we assume that $X \neq Y$.
+
+In the convex pentagon $A B C Y X$ we have either $\angle B A X+\angle A X Y>180^{\circ}$ or $\angle X Y C+$ $\angle Y C B>180^{\circ}$ (or both); due to the symmetry, we may assume that the first inequality holds. Let $r$ be the ray emerging from $X$ and co-directed with $\overrightarrow{A B}$; our inequality shows that $r$ points to the interior of the pentagon (and thus to the interior of $\Pi$ ). Therefore, the ray opposite to $r$ points outside $\Pi$, so $X^{\prime}$ lies on $r$; moreover, $X^{\prime}$ lies on the "arc" $C Y$ of $\Pi$ not containing $X$. So the segments $X X^{\prime}$ and $Y B$ intersect (see Figure 6).
+
+Let $O$ be the intersection point of the rays $r$ and $B C$. Since the triangles $A B X^{\prime}$ and $B C Y^{\prime}$ have no common interior points, $Y^{\prime}$ must lie on the "arc" $C X^{\prime}$ which is situated inside the triangle $X B O$. Therefore, the line $Y Y^{\prime}$ meets two sides of $\triangle X B O$, none of which may be $X B$ (otherwise the diagonals $X B$ and $Y Y^{\prime}$ would share a common point). Thus $Y Y^{\prime}$ intersects $B O$, which contradicts $Y Y^{\prime} \| B C$.
+
+
+Figure 6
+
+Case 2. In the remaining case, each vertex of $\Pi$ is an endpoint of a diagonal in at most one of $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$. On the other hand, a triangulation cannot contain two consecutive vertices with no diagonals from each. Therefore, the vertices of $\Pi$ alternatingly emerge diagonals in $\mathcal{T}_{1}$ and in $\mathcal{T}_{2}$. In particular, $\Pi$ has an even number of sides.
+
+Next, we may choose five consecutive vertices $A, B, C, D$, and $E$ of $\Pi$ in such a way that
+
+$$
+\angle A B C+\angle B C D>180^{\circ} \text { and } \angle B C D+\angle C D E>180^{\circ} .
+$$
+
+In order to do this, it suffices to choose three consecutive vertices $B, C$, and $D$ of $\Pi$ such that the sum of their external angles is at most $180^{\circ}$. This is possible, since $\Pi$ has at least six sides.
+
+
+Figure 7
+We may assume that $\mathcal{T}_{1}$ has no diagonals from $B$ and $D$ (and thus contains the triangles $A B C$ and $C D E$ ), while $\mathcal{T}_{2}$ has no diagonals from $A, C$, and $E$ (and thus contains the triangle $B C D)$. Now, since $[A B C]=[B C D]=[C D E]$, we have $A D \| B C$ and $B E \| C D$ (see Figure 7). By (2) this yields that $A D>B C$ and $B E>C D$. Let $X=A C \cap B D$ and $Y=C E \cap B D$; then the inequalities above imply that $A X>C X$ and $E Y>C Y$.
+
+Finally, $\mathcal{T}_{2}$ must also contain some triangle $B D Z$ with $Z \neq C$; then the ray $C Z$ lies in the angle $A C E$. Since $[B C D]=[B D Z]$, the diagonal $B D$ bisects $C Z$. Together with the inequalities above, this yields that $Z$ lies inside the triangle $A C E$ (but $Z$ is distinct from $A$ and $E$ ), which is impossible. The final contradiction.
+
+Comment 2. Case 2 may also be accomplished with the use of Lemma 2. Indeed, since each triangulation of an $n$-gon contains $n-2$ triangles neither of which may contain three sides of $\Pi$, Lemma 2 yields that each Thaiangulation contains exactly two ears. But each vertex of $\Pi$ is a vertex of an ear either in $\mathcal{T}_{1}$ or in $\mathcal{T}_{2}$, so $\Pi$ cannot have more than four vertices.
+
+## Number Theory
+
+N1. Determine all positive integers $M$ for which the sequence $a_{0}, a_{1}, a_{2}, \ldots$, defined by $a_{0}=\frac{2 M+1}{2}$ and $a_{k+1}=a_{k}\left\lfloor a_{k}\right\rfloor$ for $k=0,1,2, \ldots$, contains at least one integer term.
+(Luxembourg)
+Answer. All integers $M \geqslant 2$.
+Solution 1. Define $b_{k}=2 a_{k}$ for all $k \geqslant 0$. Then
+
+$$
+b_{k+1}=2 a_{k+1}=2 a_{k}\left\lfloor a_{k}\right\rfloor=b_{k}\left\lfloor\frac{b_{k}}{2}\right\rfloor .
+$$
+
+Since $b_{0}$ is an integer, it follows that $b_{k}$ is an integer for all $k \geqslant 0$.
+Suppose that the sequence $a_{0}, a_{1}, a_{2}, \ldots$ does not contain any integer term. Then $b_{k}$ must be an odd integer for all $k \geqslant 0$, so that
+
+$$
+b_{k+1}=b_{k}\left\lfloor\frac{b_{k}}{2}\right\rfloor=\frac{b_{k}\left(b_{k}-1\right)}{2}
+$$
+
+Hence
+
+$$
+b_{k+1}-3=\frac{b_{k}\left(b_{k}-1\right)}{2}-3=\frac{\left(b_{k}-3\right)\left(b_{k}+2\right)}{2}
+$$
+
+for all $k \geqslant 0$.
+Suppose that $b_{0}-3>0$. Then equation (2) yields $b_{k}-3>0$ for all $k \geqslant 0$. For each $k \geqslant 0$, define $c_{k}$ to be the highest power of 2 that divides $b_{k}-3$. Since $b_{k}-3$ is even for all $k \geqslant 0$, the number $c_{k}$ is positive for every $k \geqslant 0$.
+
+Note that $b_{k}+2$ is an odd integer. Therefore, from equation (2), we have that $c_{k+1}=c_{k}-1$. Thus, the sequence $c_{0}, c_{1}, c_{2}, \ldots$ of positive integers is strictly decreasing, a contradiction. So, $b_{0}-3 \leqslant 0$, which implies $M=1$.
+
+For $M=1$, we can check that the sequence is constant with $a_{k}=\frac{3}{2}$ for all $k \geqslant 0$. Therefore, the answer is $M \geqslant 2$.
+
+Solution 2. We provide an alternative way to show $M=1$ once equation (1) has been reached. We claim that $b_{k} \equiv 3\left(\bmod 2^{m}\right)$ for all $k \geqslant 0$ and $m \geqslant 1$. If this is true, then we would have $b_{k}=3$ for all $k \geqslant 0$ and hence $M=1$.
+
+To establish our claim, we proceed by induction on $m$. The base case $b_{k} \equiv 3(\bmod 2)$ is true for all $k \geqslant 0$ since $b_{k}$ is odd. Now suppose that $b_{k} \equiv 3\left(\bmod 2^{m}\right)$ for all $k \geqslant 0$. Hence $b_{k}=2^{m} d_{k}+3$ for some integer $d_{k}$. We have
+
+$$
+3 \equiv b_{k+1} \equiv\left(2^{m} d_{k}+3\right)\left(2^{m-1} d_{k}+1\right) \equiv 3 \cdot 2^{m-1} d_{k}+3 \quad\left(\bmod 2^{m}\right)
+$$
+
+so that $d_{k}$ must be even. This implies that $b_{k} \equiv 3\left(\bmod 2^{m+1}\right)$, as required.
+Comment. The reason the number 3 which appears in both solutions is important, is that it is a nontrivial fixed point of the recurrence relation for $b_{k}$.
+
+N2. Let $a$ and $b$ be positive integers such that $a!b$ ! is a multiple of $a!+b!$. Prove that $3 a \geqslant 2 b+2$.
+(United Kingdom)
+Solution 1. If $a>b$, we immediately get $3 a \geqslant 2 b+2$. In the case $a=b$, the required inequality is equivalent to $a \geqslant 2$, which can be checked easily since $(a, b)=(1,1)$ does not satisfy $a!+b!\mid a!b!$. We now assume $aa$ !, which is impossible. We observe that $c!\mid M$ since $M$ is a product of $c$ consecutive integers. Thus $\operatorname{gcd}(1+M, c!)=1$, which implies
+
+$$
+1+M \left\lvert\, \frac{a!}{c!}=(c+1)(c+2) \cdots a\right.
+$$
+
+If $a \leqslant 2 c$, then $\frac{a!}{c!}$ is a product of $a-c \leqslant c$ integers not exceeding $a$ whereas $M$ is a product of $c$ integers exceeding $a$. Therefore, $1+M>\frac{a!}{c!}$, which is a contradiction.
+
+It remains to exclude the case $a=2 c+1$. Since $a+1=2(c+1)$, we have $c+1 \mid M$. Hence, we can deduce from (1) that $1+M \mid(c+2)(c+3) \cdots a$. Now $(c+2)(c+3) \cdots a$ is a product of $a-c-1=c$ integers not exceeding $a$; thus it is smaller than $1+M$. Again, we arrive at a contradiction.
+
+Comment 1. One may derive a weaker version of (1) and finish the problem as follows. After assuming $a \leqslant 2 c+1$, we have $\left\lfloor\frac{a}{2}\right\rfloor \leqslant c$, so $\left.\left\lfloor\frac{a}{2}\right\rfloor!\right\rvert\, M$. Therefore,
+
+$$
+1+M \left\lvert\,\left(\left\lfloor\frac{a}{2}\right\rfloor+1\right)\left(\left\lfloor\frac{a}{2}\right\rfloor+2\right) \cdots a\right.
+$$
+
+Observe that $\left(\left\lfloor\frac{a}{2}\right\rfloor+1\right)\left(\left\lfloor\frac{a}{2}\right\rfloor+2\right) \cdots a$ is a product of $\left\lceil\frac{a}{2}\right\rceil$ integers not exceeding $a$. This leads to a contradiction when $a$ is even since $\left\lceil\frac{a}{2}\right\rceil=\frac{a}{2} \leqslant c$ and $M$ is a product of $c$ integers exceeding $a$.
+
+When $a$ is odd, we can further deduce that $1+M \left\lvert\,\left(\frac{a+3}{2}\right)\left(\frac{a+5}{2}\right) \cdots a\right.$ since $\left.\left\lfloor\frac{a}{2}\right\rfloor+1=\frac{a+1}{2} \right\rvert\, a+1$. Now $\left(\frac{a+3}{2}\right)\left(\frac{a+5}{2}\right) \cdots a$ is a product of $\frac{a-1}{2} \leqslant c$ numbers not exceeding $a$, and we get a contradiction.
+
+Solution 2. As in Solution 1, we may assume that $aa+c$; otherwise, $a+1 \leqslant 2 c+2 \leqslant 2 p \leqslant a+c$ so $p \mid N-1$, again impossible. Thus, we have $p \in\left(\frac{a+c}{2}, a\right]$, and $p^{2} \nmid(a+c)$ ! since $2 p>a+c$. Therefore, $p^{2} \nmid N$ as well.
+
+If $a \leqslant c+2$, then the interval $\left(\frac{a+c}{2}, a\right]$ contains at most one integer and hence at most one prime number, which has to be $a$. Since $p^{2} \nmid N$, we must have $N=p=a$ or $N=1$, which is absurd since $N>a \geqslant 1$. Thus, we have $a \geqslant c+3$, and so $\frac{a+c+1}{2} \geqslant c+2$. It follows that $p$ lies in the interval $[c+2, a]$.
+
+Thus, every prime appearing in the prime factorization of $N$ lies in the interval $[c+2, a]$, and its exponent is exactly 1 . So we must have $N \mid(c+2)(c+3) \cdots a$. However, $(c+2)(c+3) \cdots a$ is a product of $a-c-1 \leqslant c$ numbers not exceeding $a$, so it is less than $N$. This is a contradiction.
+
+Comment 2. The original problem statement also asks to determine when the equality $3 a=2 b+2$ holds. It can be checked that the answer is $(a, b)=(2,2),(4,5)$.
+
+N3. Let $m$ and $n$ be positive integers such that $m>n$. Define $x_{k}=(m+k) /(n+k)$ for $k=$ $1,2, \ldots, n+1$. Prove that if all the numbers $x_{1}, x_{2}, \ldots, x_{n+1}$ are integers, then $x_{1} x_{2} \cdots x_{n+1}-1$ is divisible by an odd prime.
+(Austria)
+Solution. Assume that $x_{1}, x_{2}, \ldots, x_{n+1}$ are integers. Define the integers
+
+$$
+a_{k}=x_{k}-1=\frac{m+k}{n+k}-1=\frac{m-n}{n+k}>0
+$$
+
+for $k=1,2, \ldots, n+1$.
+Let $P=x_{1} x_{2} \cdots x_{n+1}-1$. We need to prove that $P$ is divisible by an odd prime, or in other words, that $P$ is not a power of 2 . To this end, we investigate the powers of 2 dividing the numbers $a_{k}$.
+
+Let $2^{d}$ be the largest power of 2 dividing $m-n$, and let $2^{c}$ be the largest power of 2 not exceeding $2 n+1$. Then $2 n+1 \leqslant 2^{c+1}-1$, and so $n+1 \leqslant 2^{c}$. We conclude that $2^{c}$ is one of the numbers $n+1, n+2, \ldots, 2 n+1$, and that it is the only multiple of $2^{c}$ appearing among these numbers. Let $\ell$ be such that $n+\ell=2^{c}$. Since $\frac{m-n}{n+\ell}$ is an integer, we have $d \geqslant c$. Therefore, $2^{d-c+1} \nmid a_{\ell}=\frac{m-n}{n+\ell}$, while $2^{d-c+1} \mid a_{k}$ for all $k \in\{1, \ldots, n+1\} \backslash\{\ell\}$.
+
+Computing modulo $2^{d-c+1}$, we get
+
+$$
+P=\left(a_{1}+1\right)\left(a_{2}+1\right) \cdots\left(a_{n+1}+1\right)-1 \equiv\left(a_{\ell}+1\right) \cdot 1^{n}-1 \equiv a_{\ell} \not \equiv 0 \quad\left(\bmod 2^{d-c+1}\right)
+$$
+
+Therefore, $2^{d-c+1} \nmid P$.
+On the other hand, for any $k \in\{1, \ldots, n+1\} \backslash\{\ell\}$, we have $2^{d-c+1} \mid a_{k}$. So $P \geqslant a_{k} \geqslant 2^{d-c+1}$, and it follows that $P$ is not a power of 2 .
+
+Comment. Instead of attempting to show that $P$ is not a power of 2 , one may try to find an odd factor of $P$ (greater than 1) as follows:
+
+From $a_{k}=\frac{m-n}{n+k} \in \mathbb{Z}_{>0}$, we get that $m-n$ is divisible by $n+1, n+2, \ldots, 2 n+1$, and thus it is also divisible by their least common multiple $L$. So $m-n=q L$ for some positive integer $q$; hence $x_{k}=q \cdot \frac{L}{n+k}+1$.
+
+Then, since $n+1 \leqslant 2^{c}=n+\ell \leqslant 2 n+1 \leqslant 2^{c+1}-1$, we have $2^{c} \mid L$, but $2^{c+1} \nmid L$. So $\frac{L}{n+\ell}$ is odd, while $\frac{L}{n+k}$ is even for $k \neq \ell$. Computing modulo $2 q$ yields
+
+$$
+x_{1} x_{2} \cdots x_{n+1}-1 \equiv(q+1) \cdot 1^{n}-1 \equiv q \quad(\bmod 2 q)
+$$
+
+Thus, $x_{1} x_{2} \cdots x_{n+1}-1=2 q r+q=q(2 r+1)$ for some integer $r$.
+Since $x_{1} x_{2} \cdots x_{n+1}-1 \geqslant x_{1} x_{2}-1 \geqslant(q+1)^{2}-1>q$, we have $r \geqslant 1$. This implies that $x_{1} x_{2} \cdots x_{n+1}-1$ is divisible by an odd prime.
+
+N4. Suppose that $a_{0}, a_{1}, \ldots$ and $b_{0}, b_{1}, \ldots$ are two sequences of positive integers satisfying $a_{0}, b_{0} \geqslant 2$ and
+
+$$
+a_{n+1}=\operatorname{gcd}\left(a_{n}, b_{n}\right)+1, \quad b_{n+1}=\operatorname{lcm}\left(a_{n}, b_{n}\right)-1
+$$
+
+for all $n \geqslant 0$. Prove that the sequence $\left(a_{n}\right)$ is eventually periodic; in other words, there exist integers $N \geqslant 0$ and $t>0$ such that $a_{n+t}=a_{n}$ for all $n \geqslant N$.
+(France)
+Solution 1. Let $s_{n}=a_{n}+b_{n}$. Notice that if $a_{n} \mid b_{n}$, then $a_{n+1}=a_{n}+1, b_{n+1}=b_{n}-1$ and $s_{n+1}=s_{n}$. So, $a_{n}$ increases by 1 and $s_{n}$ does not change until the first index is reached with $a_{n} \nmid s_{n}$. Define
+
+$$
+W_{n}=\left\{m \in \mathbb{Z}_{>0}: m \geqslant a_{n} \text { and } m \nmid s_{n}\right\} \quad \text { and } \quad w_{n}=\min W_{n}
+$$
+
+Claim 1. The sequence $\left(w_{n}\right)$ is non-increasing.
+Proof. If $a_{n} \mid b_{n}$ then $a_{n+1}=a_{n}+1$. Due to $a_{n} \mid s_{n}$, we have $a_{n} \notin W_{n}$. Moreover $s_{n+1}=s_{n}$; therefore, $W_{n+1}=W_{n}$ and $w_{n+1}=w_{n}$.
+
+Otherwise, if $a_{n} \nmid b_{n}$, then $a_{n} \nmid s_{n}$, so $a_{n} \in W_{n}$ and thus $w_{n}=a_{n}$. We show that $a_{n} \in W_{n+1}$; this implies $w_{n+1} \leqslant a_{n}=w_{n}$. By the definition of $W_{n+1}$, we need that $a_{n} \geqslant a_{n+1}$ and $a_{n} \nmid s_{n+1}$. The first relation holds because of $\operatorname{gcd}\left(a_{n}, b_{n}\right)\beta>\gamma .
+$$
+
+Depending on how large $a$ is, we divide the argument into two further cases.
+Case 2.1. $\quad a=2$.
+We first prove that $\gamma=0$. Assume for the sake of contradiction that $\gamma>0$. Then $c$ is even by (4) and, similarly, $b$ is even by (5) and (3). So the left-hand side of (2) is congruent to 2 modulo 4 , which is only possible if $b c=4$. As this contradicts (1), we have thereby shown that $\gamma=0$, i.e., that $c=2 b-1$.
+
+Now (3) yields $3 b-2=2^{\beta}$. Due to $b>2$ this is only possible if $\beta \geqslant 4$. If $\beta=4$, then we get $b=6$ and $c=2 \cdot 6-1=11$, which is a solution. It remains to deal with the case $\beta \geqslant 5$. Now (2) implies
+
+$$
+9 \cdot 2^{\alpha}=9 b(2 b-1)-18=(3 b-2)(6 b+1)-16=2^{\beta}\left(2^{\beta+1}+5\right)-16
+$$
+
+and by $\beta \geqslant 5$ the right-hand side is not divisible by 32 . Thus $\alpha \leqslant 4$ and we get a contradiction to (5).
+
+Case 2.2. $\quad a \geqslant 3$.
+Pick an integer $\vartheta \in\{-1,+1\}$ such that $c-\vartheta$ is not divisible by 4 . Now
+
+$$
+2^{\alpha}+\vartheta \cdot 2^{\beta}=\left(b c-a \vartheta^{2}\right)+\vartheta(c a-b)=(b+a \vartheta)(c-\vartheta)
+$$
+
+is divisible by $2^{\beta}$ and, consequently, $b+a \vartheta$ is divisible by $2^{\beta-1}$. On the other hand, $2^{\beta}=a c-b>$ $(a-1) c \geqslant 2 c$ implies in view of (1) that $a$ and $b$ are smaller than $2^{\beta-1}$. All this is only possible if $\vartheta=1$ and $a+b=2^{\beta-1}$. Now (3) yields
+
+$$
+a c-b=2(a+b)
+$$
+
+whence $4 b>a+3 b=a(c-1) \geqslant a b$, which in turn yields $a=3$.
+So (6) simplifies to $c=b+2$ and (2) tells us that $b(b+2)-3=(b-1)(b+3)$ is a power of 2 . Consequently, the factors $b-1$ and $b+3$ are powers of 2 themselves. Since their difference is 4 , this is only possible if $b=5$ and thus $c=7$. Thereby the solution is complete.
+
+Solution 2. As in the beginning of the first solution, we observe that $a, b, c \geqslant 2$. Depending on the parities of $a, b$, and $c$ we distinguish three cases.
+
+Case 1. The numbers $a, b$, and $c$ are even.
+Let $2^{A}, 2^{B}$, and $2^{C}$ be the largest powers of 2 dividing $a, b$, and $c$ respectively. We may assume without loss of generality that $1 \leqslant A \leqslant B \leqslant C$. Now $2^{B}$ is the highest power of 2 dividing $a c-b$, whence $a c-b=2^{B} \leqslant b$. Similarly, we deduce $b c-a=2^{A} \leqslant a$. Adding both estimates we get $(a+b) c \leqslant 2(a+b)$, whence $c \leqslant 2$. So $c=2$ and thus $A=B=C=1$; moreover, we must have had equality throughout, i.e., $a=2^{A}=2$ and $b=2^{B}=2$. We have thereby found the solution $(a, b, c)=(2,2,2)$.
+
+Case 2. The numbers $a, b$, and $c$ are odd.
+If any two of these numbers are equal, say $a=b$, then $a c-b=a(c-1)$ has a nontrivial odd divisor and cannot be a power of 2 . Hence $a, b$, and $c$ are distinct. So we may assume without loss of generality that $a\beta$, and thus $2^{\beta}$ divides
+
+$$
+a \cdot 2^{\alpha}-b \cdot 2^{\beta}=a(b c-a)-b(a c-b)=b^{2}-a^{2}=(b+a)(b-a)
+$$
+
+Since $a$ is odd, it is not possible that both factors $b+a$ and $b-a$ are divisible by 4 . Consequently, one of them has to be a multiple of $2^{\beta-1}$. Hence one of the numbers $2(b+a)$ and $2(b-a)$ is divisible by $2^{\beta}$ and in either case we have
+
+$$
+a c-b=2^{\beta} \leqslant 2(a+b)
+$$
+
+This in turn yields $(a-1) b\beta$ denote the integers satisfying
+
+$$
+2^{\alpha}=b c-a \quad \text { and } \quad 2^{\beta}=a c-b
+$$
+
+If $\beta=0$ it would follow that $a c-b=a b-c=1$ and hence that $b=c=1$, which is absurd. So $\beta$ and $\alpha$ are positive and consequently $a$ and $b$ are even. Substituting $c=a b-1$ into (9) we obtain
+
+$$
+\begin{aligned}
+2^{\alpha} & =a b^{2}-(a+b), \\
+\text { and } \quad 2^{\beta} & =a^{2} b-(a+b) .
+\end{aligned}
+$$
+
+The addition of both equation yields $2^{\alpha}+2^{\beta}=(a b-2)(a+b)$. Now $a b-2$ is even but not divisible by 4 , so the highest power of 2 dividing $a+b$ is $2^{\beta-1}$. For this reason, the equations (10) and (11) show that the highest powers of 2 dividing either of the numbers $a b^{2}$ and $a^{2} b$ is likewise $2^{\beta-1}$. Thus there is an integer $\tau \geqslant 1$ together with odd integers $A, B$, and $C$ such that $a=2^{\tau} A, b=2^{\tau} B, a+b=2^{3 \tau} C$, and $\beta=1+3 \tau$.
+
+Notice that $A+B=2^{2 \tau} C \geqslant 4 C$. Moreover, (11) entails $A^{2} B-C=2$. Thus $8=$ $4 A^{2} B-4 C \geqslant 4 A^{2} B-A-B \geqslant A^{2}(3 B-1)$. Since $A$ and $B$ are odd with $A0$, this may be weakened to $p^{2} q+p-q \leqslant p+q$. Hence $p^{2} q \leqslant 2 q$, which is only possible if $p=1$.
+
+Going back to (13), we get
+
+$$
+\left(d^{2} q-q-1\right) \mid d^{2}(q-1)
+$$
+
+Now $2\left(d^{2} q-q-1\right) \leqslant d^{2}(q-1)$ would entail $d^{2}(q+1) \leqslant 2(q+1)$ and thus $d=1$. But this would tell us that $a=d p=1$, which is absurd. This argument proves $2\left(d^{2} q-q-1\right)>d^{2}(q-1)$ and in the light of (14) it follows that $d^{2} q-q-1=d^{2}(q-1)$, i.e., $q=d^{2}-1$. Plugging this together with $p=1$ into (12) we infer $2^{\beta}=d^{3}\left(d^{2}-2\right)$. Hence $d$ and $d^{2}-2$ are powers of 2 . Consequently, $d=2, q=3$, $a=2, b=6$, and $c=11$, as desired.
+
+N6. Let $\mathbb{Z}_{>0}$ denote the set of positive integers. Consider a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$. For any $m, n \in \mathbb{Z}_{>0}$ we write $f^{n}(m)=\underbrace{f(f(\ldots f}_{n}(m) \ldots))$. Suppose that $f$ has the following two properties:
+(i) If $m, n \in \mathbb{Z}_{>0}$, then $\frac{f^{n}(m)-m}{n} \in \mathbb{Z}_{>0}$;
+(ii) The set $\mathbb{Z}_{>0} \backslash\left\{f(n) \mid n \in \mathbb{Z}_{>0}\right\}$ is finite.
+
+Prove that the sequence $f(1)-1, f(2)-2, f(3)-3, \ldots$ is periodic.
+(Singapore)
+Solution. We split the solution into three steps. In the first of them, we show that the function $f$ is injective and explain how this leads to a useful visualization of $f$. Then comes the second step, in which most of the work happens: its goal is to show that for any $n \in \mathbb{Z}_{>0}$ the sequence $n, f(n), f^{2}(n), \ldots$ is an arithmetic progression. Finally, in the third step we put everything together, thus solving the problem.
+$\underline{\text { Step 1. We commence by checking that } f \text { is injective. For this purpose, we consider any }}$ $m, k \in \mathbb{Z}_{>0}$ with $f(m)=f(k)$. By $(i)$, every positive integer $n$ has the property that
+
+$$
+\frac{k-m}{n}=\frac{f^{n}(m)-m}{n}-\frac{f^{n}(k)-k}{n}
+$$
+
+is a difference of two integers and thus integral as well. But for $n=|k-m|+1$ this is only possible if $k=m$. Thereby, the injectivity of $f$ is established.
+
+Now recall that due to condition (ii) there are finitely many positive integers $a_{1}, \ldots, a_{k}$ such that $\mathbb{Z}_{>0}$ is the disjoint union of $\left\{a_{1}, \ldots, a_{k}\right\}$ and $\left\{f(n) \mid n \in \mathbb{Z}_{>0}\right\}$. Notice that by plugging $n=1$ into condition $(i)$ we get $f(m)>m$ for all $m \in \mathbb{Z}_{>0}$.
+
+We contend that every positive integer $n$ may be expressed uniquely in the form $n=f^{j}\left(a_{i}\right)$ for some $j \geqslant 0$ and $i \in\{1, \ldots, k\}$. The uniqueness follows from the injectivity of $f$. The existence can be proved by induction on $n$ in the following way. If $n \in\left\{a_{1}, \ldots, a_{k}\right\}$, then we may take $j=0$; otherwise there is some $n^{\prime}0$; and $T=1$ and $A=0$ if $t=0$. For every integer $n \geqslant A$, the interval $\Delta_{n}=[n+1, n+T]$ contains exactly $T / T_{i}$
+elements of the $i^{\text {th }}$ row $(1 \leqslant i \leqslant t)$. Therefore, the number of elements from the last $(k-t)$ rows of the Table contained in $\Delta_{n}$ does not depend on $n \geqslant A$. It is not possible that none of these intervals $\Delta_{n}$ contains an element from the $k-t$ last rows, because infinitely many numbers appear in these rows. It follows that for each $n \geqslant A$ the interval $\Delta_{n}$ contains at least one member from these rows.
+
+This yields that for every positive integer $d$, the interval $[A+1, A+(d+1)(k-t) T]$ contains at least $(d+1)(k-t)$ elements from the last $k-t$ rows; therefore, there exists an index $x$ with $t+1 \leqslant x \leqslant k$, possibly depending on $d$, such that our interval contains at least $d+1$ elements from the $x^{\text {th }}$ row. In this situation we have
+
+$$
+f^{d}\left(a_{x}\right) \leqslant A+(d+1)(k-t) T .
+$$
+
+Finally, since there are finitely many possibilities for $x$, there exists an index $x \geqslant t+1$ such that the set
+
+$$
+X=\left\{d \in \mathbb{Z}_{>0} \mid f^{d}\left(a_{x}\right) \leqslant A+(d+1)(k-t) T\right\}
+$$
+
+is infinite. Thereby we have found the "dense row" promised above.
+By assumption $(i)$, for every $d \in X$ the number
+
+$$
+\beta_{d}=\frac{f^{d}\left(a_{x}\right)-a_{x}}{d}
+$$
+
+is a positive integer not exceeding
+
+$$
+\frac{A+(d+1)(k-t) T}{d} \leqslant \frac{A d+2 d(k-t) T}{d}=A+2(k-t) T
+$$
+
+This leaves us with finitely many choices for $\beta_{d}$, which means that there exists a number $T_{x}$ such that the set
+
+$$
+Y=\left\{d \in X \mid \beta_{d}=T_{x}\right\}
+$$
+
+is infinite. Notice that we have $f^{d}\left(a_{x}\right)=a_{x}+d \cdot T_{x}$ for all $d \in Y$.
+Now we are prepared to prove that the numbers in the $x^{\text {th }}$ row form an arithmetic progression, thus coming to a contradiction with our assumption. Let us fix any positive integer $j$. Since the set $Y$ is infinite, we can choose a number $y \in Y$ such that $y-j>\left|f^{j}\left(a_{x}\right)-\left(a_{x}+j T_{x}\right)\right|$. Notice that both numbers
+
+$$
+f^{y}\left(a_{x}\right)-f^{j}\left(a_{x}\right)=f^{y-j}\left(f^{j}\left(a_{x}\right)\right)-f^{j}\left(a_{x}\right) \quad \text { and } \quad f^{y}\left(a_{x}\right)-\left(a_{x}+j T_{x}\right)=(y-j) T_{x}
+$$
+
+are divisible by $y-j$. Thus, the difference between these numbers is also divisible by $y-j$. Since the absolute value of this difference is less than $y-j$, it has to vanish, so we get $f^{j}\left(a_{x}\right)=$ $a_{x}+j \cdot T_{x}$.
+
+Hence, it is indeed true that all rows of the Table are arithmetic progressions.
+Step 3. Keeping the above notation in force, we denote the step of the $i^{\text {th }}$ row of the table by $T_{i}$. Now we claim that we have $f(n)-n=f(n+T)-(n+T)$ for all $n \in \mathbb{Z}_{>0}$, where
+
+$$
+T=\operatorname{lcm}\left(T_{1}, \ldots, T_{k}\right)
+$$
+
+To see this, let any $n \in \mathbb{Z}_{>0}$ be given and denote the index of the row in which it appears in the Table by $i$. Then we have $f^{j}(n)=n+j \cdot T_{i}$ for all $j \in \mathbb{Z}_{>0}$, and thus indeed
+
+$$
+f(n+T)-f(n)=f^{1+T / T_{i}}(n)-f(n)=\left(n+T+T_{i}\right)-\left(n+T_{i}\right)=T
+$$
+
+This concludes the solution.
+
+Comment 1. There are some alternative ways to complete the second part once the index $x$ corresponding to a "dense row" is found. For instance, one may show that for some integer $T_{x}^{*}$ the set
+
+$$
+Y^{*}=\left\{j \in \mathbb{Z}_{>0} \mid f^{j+1}\left(a_{x}\right)-f^{j}\left(a_{x}\right)=T_{x}^{*}\right\}
+$$
+
+is infinite, and then one may conclude with a similar divisibility argument.
+Comment 2. It may be checked that, conversely, any way to fill out the Table with finitely many arithmetic progressions so that each positive integer appears exactly once, gives rise to a function $f$ satisfying the two conditions mentioned in the problem. For example, we may arrange the positive integers as follows:
+
+| 2 | 4 | 6 | 8 | 10 | $\ldots$ |
+| :---: | :---: | :---: | :---: | :---: | :---: |
+| 1 | 5 | 9 | 13 | 17 | $\ldots$ |
+| 3 | 7 | 11 | 15 | 19 | $\ldots$ |
+
+This corresponds to the function
+
+$$
+f(n)= \begin{cases}n+2 & \text { if } n \text { is even } \\ n+4 & \text { if } n \text { is odd }\end{cases}
+$$
+
+As this example shows, it is not true that the function $n \mapsto f(n)-n$ has to be constant.
+
+N7. Let $\mathbb{Z}_{>0}$ denote the set of positive integers. For any positive integer $k$, a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ is called $k$-good if $\operatorname{gcd}(f(m)+n, f(n)+m) \leqslant k$ for all $m \neq n$. Find all $k$ such that there exists a $k$-good function.
+(Canada)
+Answer. $k \geqslant 2$.
+Solution 1. For any function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$, let $G_{f}(m, n)=\operatorname{gcd}(f(m)+n, f(n)+m)$. Note that a $k$-good function is also $(k+1)$-good for any positive integer $k$. Hence, it suffices to show that there does not exist a 1-good function and that there exists a 2-good function.
+
+We first show that there is no 1 -good function. Suppose that there exists a function $f$ such that $G_{f}(m, n)=1$ for all $m \neq n$. Now, if there are two distinct even numbers $m$ and $n$ such that $f(m)$ and $f(n)$ are both even, then $2 \mid G_{f}(m, n)$, a contradiction. A similar argument holds if there are two distinct odd numbers $m$ and $n$ such that $f(m)$ and $f(n)$ are both odd. Hence we can choose an even $m$ and an odd $n$ such that $f(m)$ is odd and $f(n)$ is even. This also implies that $2 \mid G_{f}(m, n)$, a contradiction.
+
+We now construct a 2-good function. Define $f(n)=2^{g(n)+1}-n-1$, where $g$ is defined recursively by $g(1)=1$ and $g(n+1)=\left(2^{g(n)+1}\right)!$.
+
+For any positive integers $m>n$, set
+
+$$
+A=f(m)+n=2^{g(m)+1}-m+n-1, \quad B=f(n)+m=2^{g(n)+1}-n+m-1
+$$
+
+We need to show that $\operatorname{gcd}(A, B) \leqslant 2$. First, note that $A+B=2^{g(m)+1}+2^{g(n)+1}-2$ is not divisible by 4 , so that $4 \nmid \operatorname{gcd}(A, B)$. Now we suppose that there is an odd prime $p$ for which $p \mid \operatorname{gcd}(A, B)$ and derive a contradiction.
+
+We first claim that $2^{g(m-1)+1} \geqslant B$. This is a rather weak bound; one way to prove it is as follows. Observe that $g(k+1)>g(k)$ and hence $2^{g(k+1)+1} \geqslant 2^{g(k)+1}+1$ for every positive integer $k$. By repeatedly applying this inequality, we obtain $2^{g(m-1)+1} \geqslant 2^{g(n)+1}+(m-1)-n=B$.
+
+Now, since $p \mid B$, we have $p-11$, introduce the set $X_{m}$ like in Solution 2 and define $f(m)$ so as to satisfy
+
+$$
+\begin{array}{rll}
+f(m) \equiv f(m-p) & (\bmod p) & \text { for all } p \in X_{m} \text { with } p10^{100}} \alpha_{i} .
+$$
+
+That is, $\mho(n)$ is the number of prime factors of $n$ greater than $10^{100}$, counted with multiplicity.
+Find all strictly increasing functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ such that
+
+$$
+\mho(f(a)-f(b)) \leqslant \mho(a-b) \quad \text { for all integers } a \text { and } b \text { with } a>b .
+$$
+
+(Brazil)
+Answer. $f(x)=a x+b$, where $b$ is an arbitrary integer, and $a$ is an arbitrary positive integer with $\mho(a)=0$.
+Solution. A straightforward check shows that all the functions listed in the answer satisfy the problem condition. It remains to show the converse.
+
+Assume that $f$ is a function satisfying the problem condition. Notice that the function $g(x)=f(x)-f(0)$ also satisfies this condition. Replacing $f$ by $g$, we assume from now on that $f(0)=0$; then $f(n)>0$ for any positive integer $n$. Thus, we aim to prove that there exists a positive integer $a$ with $\mho(a)=0$ such that $f(n)=a n$ for all $n \in \mathbb{Z}$.
+
+We start by introducing some notation. Set $N=10^{100}$. We say that a prime $p$ is large if $p>N$, and $p$ is small otherwise; let $\mathcal{S}$ be the set of all small primes. Next, we say that a positive integer is large or small if all its prime factors are such (thus, the number 1 is the unique number which is both large and small). For a positive integer $k$, we denote the greatest large divisor of $k$ and the greatest small divisor of $k$ by $L(k)$ and $S(k)$, respectively; thus, $k=L(k) S(k)$.
+
+We split the proof into three steps.
+Step 1. We prove that for every large $k$, we have $k|f(a)-f(b) \Longleftrightarrow k| a-b$. In other words, $L(f(a)-f(b))=L(a-b)$ for all integers $a$ and $b$ with $a>b$.
+
+We use induction on $k$. The base case $k=1$ is trivial. For the induction step, assume that $k_{0}$ is a large number, and that the statement holds for all large numbers $k$ with $k\ell$. But then
+
+$$
+\mho(f(x)-f(y)) \geqslant \mho\left(\operatorname{lcm}\left(k_{0}, \ell\right)\right)>\mho(\ell)=\mho(x-y),
+$$
+
+which is impossible.
+Now we complete the induction step. By Claim 1, for every integer $a$ each of the sequences
+
+$$
+f(a), f(a+1), \ldots, f\left(a+k_{0}-1\right) \quad \text { and } \quad f(a+1), f(a+2), \ldots, f\left(a+k_{0}\right)
+$$
+
+forms a complete residue system modulo $k_{0}$. This yields $f(a) \equiv f\left(a+k_{0}\right)\left(\bmod k_{0}\right)$. Thus, $f(a) \equiv f(b)\left(\bmod k_{0}\right)$ whenever $a \equiv b\left(\bmod k_{0}\right)$.
+
+Finally, if $a \not \equiv b\left(\bmod k_{0}\right)$ then there exists an integer $b^{\prime}$ such that $b^{\prime} \equiv b\left(\bmod k_{0}\right)$ and $\left|a-b^{\prime}\right|N$.
+Proof. Let $d$ be the product of all small primes, and let $\alpha$ be a positive integer such that $2^{\alpha}>f(N)$. Then, for every $p \in \mathcal{S}$ the numbers $f(0), f(1), \ldots, f(N)$ are distinct modulo $p^{\alpha}$. Set $P=d^{\alpha}$ and $c=P+f(N)$.
+
+Choose any integer $t>N$. Due to the choice of $\alpha$, for every $p \in \mathcal{S}$ there exists at most one nonnegative integer $i \leqslant N$ with $p^{\alpha} \mid f(t)-f(i)$. Since $|\mathcal{S}||f(x)-a x|$. Since $n-x \equiv r-(r+1)=-1(\bmod N!)$, the number $|n-x|$ is large. Therefore, by Step 1 we have $f(x) \equiv f(n)=a n \equiv a x(\bmod n-x)$, so $n-x \mid f(x)-a x$. Due to the choice of $n$, this yields $f(x)=a x$.
+
+To complete Step 3, notice that the set $\mathcal{T}^{\prime}$ found in Step 2 contains infinitely many elements of some residue class $R_{i}$. Applying Claim 3, we successively obtain that $f(x)=a x$ for all $x \in R_{i+1}, R_{i+2}, \ldots, R_{i+N!}=R_{i}$. This finishes the solution.
+
+Comment 1. As the proposer also mentions, one may also consider the version of the problem where the condition (1) is replaced by the condition that $L(f(a)-f(b))=L(a-b)$ for all integers $a$ and $b$ with $a>b$. This allows to remove of Step 1 from the solution.
+
+Comment 2. Step 2 is the main step of the solution. We sketch several different approaches allowing to perform this step using statements which are weaker than Claim 2.
+Approach 1. Let us again denote the product of all small primes by $d$. We focus on the values $f\left(d^{i}\right)$, $i \geqslant 0$. In view of Step 1, we have $L\left(f\left(d^{i}\right)-f\left(d^{k}\right)\right)=L\left(d^{i}-d^{k}\right)=d^{i-k}-1$ for all $i>k \geqslant 0$.
+
+Acting similarly to the beginning of the proof of Claim 2, one may choose a number $\alpha \geqslant 0$ such that the residues of the numbers $f\left(d^{i}\right), i=0,1, \ldots, N$, are distinct modulo $p^{\alpha}$ for each $p \in \mathcal{S}$. Then, for every $i>N$, there exists an exponent $k=k(i) \leqslant N$ such that $S\left(f\left(d^{i}\right)-f\left(d^{k}\right)\right)N$ such that $k(i)$ attains the same value $k_{0}$ for all $i \in I$, and such that, moreover, $S\left(f\left(d^{i}\right)-f\left(d^{k_{0}}\right)\right)$ attains the same value $s_{0}$ for all $i \in I$. Therefore, for all such $i$ we have
+
+$$
+f\left(d^{i}\right)=f\left(d^{k_{0}}\right)+L\left(f\left(d^{i}\right)-f\left(d^{k_{0}}\right)\right) \cdot S\left(f\left(d^{i}\right)-f\left(d^{k_{0}}\right)\right)=f\left(d^{k_{0}}\right)+\left(d^{i-k_{0}}-1\right) s_{0},
+$$
+
+which means that $f$ is linear on the infinite set $\left\{d^{i}: i \in I\right\}$ (although with rational coefficients).
+Finally, one may implement the relation $f\left(d^{i}\right) \equiv f(1)\left(\bmod d^{i}-1\right)$ in order to establish that in fact $f\left(d^{i}\right) / d^{i}$ is a (small and fixed) integer for all $i \in I$.
+
+Approach 2. Alternatively, one may start with the following lemma.
+Lemma. There exists a positive constant $c$ such that
+
+$$
+L\left(\prod_{i=1}^{3 N}(f(k)-f(i))\right)=\prod_{i=1}^{3 N} L(f(k)-f(i)) \geqslant c(f(k))^{2 N}
+$$
+
+for all $k>3 N$.
+Proof. Let $k$ be an integer with $k>3 N$. Set $\Pi=\prod_{i=1}^{3 N}(f(k)-f(i))$.
+Notice that for every prime $p \in \mathcal{S}$, at most one of the numbers in the set
+
+$$
+\mathcal{H}=\{f(k)-f(i): 1 \leqslant i \leqslant 3 N\}
+$$
+
+is divisible by a power of $p$ which is greater than $f(3 N)$; we say that such elements of $\mathcal{H}$ are bad. Now, for each element $h \in \mathcal{H}$ which is not bad we have $S(h) \leqslant f(3 N)^{N}$, while the bad elements do not exceed $f(k)$. Moreover, there are less than $N$ bad elements in $\mathcal{H}$. Therefore,
+
+$$
+S(\Pi)=\prod_{h \in \mathcal{H}} S(h) \leqslant(f(3 N))^{3 N^{2}} \cdot(f(k))^{N} .
+$$
+
+This easily yields the lemma statement in view of the fact that $L(\Pi) S(\Pi)=\Pi \geqslant \mu(f(k))^{3 N}$ for some absolute constant $\mu$.
+
+As a corollary of the lemma, one may get a weaker version of Claim 2 stating that there exists a positive constant $C$ such that $f(k) \leqslant C k^{3 / 2}$ for all $k>3 N$. Indeed, from Step 1 we have
+
+$$
+k^{3 N} \geqslant \prod_{i=1}^{3 N} L(k-i)=\prod_{i=1}^{3 N} L(f(k)-f(i)) \geqslant c(f(k))^{2 N}
+$$
+
+so $f(k) \leqslant c^{-1 /(2 N)} k^{3 / 2}$.
+To complete Step 2 now, set $a=f(1)$. Due to the estimates above, we may choose a positive integer $n_{0}$ such that $|f(n)-a n|<\frac{n(n-1)}{2}$ for all $n \geqslant n_{0}$.
+
+Take any $n \geqslant n_{0}$ with $n \equiv 2(\bmod N!)$. Then $L(f(n)-f(0))=L(n)=n / 2$ and $L(f(n)-f(1))=$ $L(n-1)=n-1$; these relations yield $f(n) \equiv f(0)=0 \equiv a n(\bmod n / 2)$ and $f(n) \equiv f(1)=a \equiv a n$ $(\bmod n-1)$, respectively. Thus, $\left.\frac{n(n-1)}{2} \right\rvert\, f(n)-a n$, which shows that $f(n)=a n$ in view of the estimate above.
+
+Comment 3. In order to perform Step 3, it suffices to establish the equality $f(n)=a n$ for any infinite set of values of $n$. However, if this set has some good structure, then one may find easier ways to complete this step.
+
+For instance, after showing, as in Approach 2 , that $f(n)=$ an for all $n \geqslant n_{0}$ with $n \equiv 2(\bmod N!)$, one may proceed as follows. Pick an arbitrary integer $x$ and take any large prime $p$ which is greater than $|f(x)-a x|$. By the Chinese Remainder Theorem, there exists a positive integer $n>\max \left(x, n_{0}\right)$ such that $n \equiv 2(\bmod N!)$ and $n \equiv x(\bmod p)$. By Step 1 , we have $f(x) \equiv f(n)=a n \equiv a x(\bmod p)$. Due to the choice of $p$, this is possible only if $f(x)=a x$.
+
+## CHIANG MAI, THAILAND 4-16 JULY 2015
+
diff --git a/IMO/md/en-IMO2016SL.md b/IMO/md/en-IMO2016SL.md
new file mode 100644
index 0000000000000000000000000000000000000000..318e37609f72f693af2a4a947a8093982fab1325
--- /dev/null
+++ b/IMO/md/en-IMO2016SL.md
@@ -0,0 +1,2426 @@
+## Shortlisted Problems with Solutions $57^{\text {th }}$ International Mathematical Olympiad Hong Kong, 2016
+
+## Note of Confidentiality
+
+## The shortlisted problems should be kept strictly confidential until IMO 2017.
+
+## Contributing Countries
+
+The Organising Committee and the Problem Selection Committee of IMO 2016 thank the following 40 countries for contributing 121 problem proposals:
+
+Albania, Algeria, Armenia, Australia, Austria, Belarus, Belgium, Bulgaria, Colombia, Cyprus, Czech Republic, Denmark, Estonia, France, Georgia, Greece, Iceland, India, Iran, Ireland, Israel, Japan, Latvia, Luxembourg, Malaysia, Mexico, Mongolia, Netherlands, Philippines, Russia, Serbia, Slovakia, Slovenia, South Africa, Taiwan, Tanzania, Thailand, Trinidad and Tobago, Turkey, Ukraine.
+
+## Problem Selection Committee
+
+
+
+Front row from left: Yong-Gao Chen, Andy Liu, Tat Wing Leung (Chairman).
+Back row from left: Yi-Jun Yao, Yun-Hao Fu, Yi-Jie He,
+Zhongtao Wu, Heung Wing Joseph Lee, Chi Hong Chow,
+Ka Ho Law, Tak Wing Ching.
+
+## Problems
+
+## Algebra
+
+A1. Let $a, b$ and $c$ be positive real numbers such that $\min \{a b, b c, c a\} \geqslant 1$. Prove that
+
+$$
+\sqrt[3]{\left(a^{2}+1\right)\left(b^{2}+1\right)\left(c^{2}+1\right)} \leqslant\left(\frac{a+b+c}{3}\right)^{2}+1
+$$
+
+A2. Find the smallest real constant $C$ such that for any positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ (not necessarily distinct), one can always choose distinct subscripts $i, j, k$ and $l$ such that
+
+$$
+\left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leqslant C
+$$
+
+A3. Find all integers $n \geqslant 3$ with the following property: for all real numbers $a_{1}, a_{2}, \ldots, a_{n}$ and $b_{1}, b_{2}, \ldots, b_{n}$ satisfying $\left|a_{k}\right|+\left|b_{k}\right|=1$ for $1 \leqslant k \leqslant n$, there exist $x_{1}, x_{2}, \ldots, x_{n}$, each of which is either -1 or 1 , such that
+
+$$
+\left|\sum_{k=1}^{n} x_{k} a_{k}\right|+\left|\sum_{k=1}^{n} x_{k} b_{k}\right| \leqslant 1
+$$
+
+A4. Denote by $\mathbb{R}^{+}$the set of all positive real numbers. Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
+
+$$
+x f\left(x^{2}\right) f(f(y))+f(y f(x))=f(x y)\left(f\left(f\left(x^{2}\right)\right)+f\left(f\left(y^{2}\right)\right)\right)
+$$
+
+for all positive real numbers $x$ and $y$.
+
+## A5.
+
+(a) Prove that for every positive integer $n$, there exists a fraction $\frac{a}{b}$ where $a$ and $b$ are integers satisfying $0k$, and announces them to the deputy leader and a contestant. The leader then secretly tells the deputy leader an $n$-digit binary string, and the deputy leader writes down all $n$-digit binary strings which differ from the leader's in exactly $k$ positions. (For example, if $n=3$ and $k=1$, and if the leader chooses 101, the deputy leader would write down 001, 111 and 100.) The contestant is allowed to look at the strings written by the deputy leader and guess the leader's string. What is the minimum number of guesses (in terms of $n$ and $k$ ) needed to guarantee the correct answer?
+
+C2. Find all positive integers $n$ for which all positive divisors of $n$ can be put into the cells of a rectangular table under the following constraints:
+
+- each cell contains a distinct divisor;
+- the sums of all rows are equal; and
+- the sums of all columns are equal.
+
+C3. Let $n$ be a positive integer relatively prime to 6 . We paint the vertices of a regular $n$-gon with three colours so that there is an odd number of vertices of each colour. Show that there exists an isosceles triangle whose three vertices are of different colours.
+$\mathbf{C 4}$. Find all positive integers $n$ for which we can fill in the entries of an $n \times n$ table with the following properties:
+
+- each entry can be one of $I, M$ and $O$;
+- in each row and each column, the letters $I, M$ and $O$ occur the same number of times; and
+- in any diagonal whose number of entries is a multiple of three, the letters $I, M$ and $O$ occur the same number of times.
+
+C5. Let $n \geqslant 3$ be a positive integer. Find the maximum number of diagonals of a regular $n$-gon one can select, so that any two of them do not intersect in the interior or they are perpendicular to each other.
+
+C6. There are $n \geqslant 3$ islands in a city. Initially, the ferry company offers some routes between some pairs of islands so that it is impossible to divide the islands into two groups such that no two islands in different groups are connected by a ferry route.
+
+After each year, the ferry company will close a ferry route between some two islands $X$ and $Y$. At the same time, in order to maintain its service, the company will open new routes according to the following rule: for any island which is connected by a ferry route to exactly one of $X$ and $Y$, a new route between this island and the other of $X$ and $Y$ is added.
+
+Suppose at any moment, if we partition all islands into two nonempty groups in any way, then it is known that the ferry company will close a certain route connecting two islands from the two groups after some years. Prove that after some years there will be an island which is connected to all other islands by ferry routes.
+
+C7. Let $n \geqslant 2$ be an integer. In the plane, there are $n$ segments given in such a way that any two segments have an intersection point in the interior, and no three segments intersect at a single point. Jeff places a snail at one of the endpoints of each of the segments and claps his hands $n-1$ times. Each time when he claps his hands, all the snails move along their own segments and stay at the next intersection points until the next clap. Since there are $n-1$ intersection points on each segment, all snails will reach the furthest intersection points from their starting points after $n-1$ claps.
+(a) Prove that if $n$ is odd then Jeff can always place the snails so that no two of them ever occupy the same intersection point.
+(b) Prove that if $n$ is even then there must be a moment when some two snails occupy the same intersection point no matter how Jeff places the snails.
+
+C8. Let $n$ be a positive integer. Determine the smallest positive integer $k$ with the following property: it is possible to mark $k$ cells on a $2 n \times 2 n$ board so that there exists a unique partition of the board into $1 \times 2$ and $2 \times 1$ dominoes, none of which contains two marked cells.
+
+## Geometry
+
+G1. In a convex pentagon $A B C D E$, let $F$ be a point on $A C$ such that $\angle F B C=90^{\circ}$. Suppose triangles $A B F, A C D$ and $A D E$ are similar isosceles triangles with
+
+$$
+\angle F A B=\angle F B A=\angle D A C=\angle D C A=\angle E A D=\angle E D A
+$$
+
+Let $M$ be the midpoint of $C F$. Point $X$ is chosen such that $A M X E$ is a parallelogram. Show that $B D, E M$ and $F X$ are concurrent.
+
+G2. Let $A B C$ be a triangle with circumcircle $\Gamma$ and incentre $I$. Let $M$ be the midpoint of side $B C$. Denote by $D$ the foot of perpendicular from $I$ to side $B C$. The line through $I$ perpendicular to $A I$ meets sides $A B$ and $A C$ at $F$ and $E$ respectively. Suppose the circumcircle of triangle $A E F$ intersects $\Gamma$ at a point $X$ other than $A$. Prove that lines $X D$ and $A M$ meet on $\Gamma$.
+
+G3. Let $B=(-1,0)$ and $C=(1,0)$ be fixed points on the coordinate plane. A nonempty, bounded subset $S$ of the plane is said to be nice if
+(i) there is a point $T$ in $S$ such that for every point $Q$ in $S$, the segment $T Q$ lies entirely in $S$; and
+(ii) for any triangle $P_{1} P_{2} P_{3}$, there exists a unique point $A$ in $S$ and a permutation $\sigma$ of the indices $\{1,2,3\}$ for which triangles $A B C$ and $P_{\sigma(1)} P_{\sigma(2)} P_{\sigma(3)}$ are similar.
+
+Prove that there exist two distinct nice subsets $S$ and $S^{\prime}$ of the set $\{(x, y): x \geqslant 0, y \geqslant 0\}$ such that if $A \in S$ and $A^{\prime} \in S^{\prime}$ are the unique choices of points in (ii), then the product $B A \cdot B A^{\prime}$ is a constant independent of the triangle $P_{1} P_{2} P_{3}$.
+
+G4. Let $A B C$ be a triangle with $A B=A C \neq B C$ and let $I$ be its incentre. The line $B I$ meets $A C$ at $D$, and the line through $D$ perpendicular to $A C$ meets $A I$ at $E$. Prove that the reflection of $I$ in $A C$ lies on the circumcircle of triangle $B D E$.
+
+G5. Let $D$ be the foot of perpendicular from $A$ to the Euler line (the line passing through the circumcentre and the orthocentre) of an acute scalene triangle $A B C$. A circle $\omega$ with centre $S$ passes through $A$ and $D$, and it intersects sides $A B$ and $A C$ at $X$ and $Y$ respectively. Let $P$ be the foot of altitude from $A$ to $B C$, and let $M$ be the midpoint of $B C$. Prove that the circumcentre of triangle $X S Y$ is equidistant from $P$ and $M$.
+
+G6. Let $A B C D$ be a convex quadrilateral with $\angle A B C=\angle A D C<90^{\circ}$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $E$ and $F$ respectively, and meet each other at point $P$. Let $M$ be the midpoint of $A C$ and let $\omega$ be the circumcircle of triangle $B P D$. Segments $B M$ and $D M$ intersect $\omega$ again at $X$ and $Y$ respectively. Denote by $Q$ the intersection point of lines $X E$ and $Y F$. Prove that $P Q \perp A C$.
+
+G7. Let $I$ be the incentre of a non-equilateral triangle $A B C, I_{A}$ be the $A$-excentre, $I_{A}^{\prime}$ be the reflection of $I_{A}$ in $B C$, and $l_{A}$ be the reflection of line $A I_{A}^{\prime}$ in $A I$. Define points $I_{B}, I_{B}^{\prime}$ and line $l_{B}$ analogously. Let $P$ be the intersection point of $l_{A}$ and $l_{B}$.
+(a) Prove that $P$ lies on line $O I$ where $O$ is the circumcentre of triangle $A B C$.
+(b) Let one of the tangents from $P$ to the incircle of triangle $A B C$ meet the circumcircle at points $X$ and $Y$. Show that $\angle X I Y=120^{\circ}$.
+
+G8. Let $A_{1}, B_{1}$ and $C_{1}$ be points on sides $B C, C A$ and $A B$ of an acute triangle $A B C$ respectively, such that $A A_{1}, B B_{1}$ and $C C_{1}$ are the internal angle bisectors of triangle $A B C$. Let $I$ be the incentre of triangle $A B C$, and $H$ be the orthocentre of triangle $A_{1} B_{1} C_{1}$. Show that
+
+$$
+A H+B H+C H \geqslant A I+B I+C I
+$$
+
+## Number Theory
+
+N1. For any positive integer $k$, denote the sum of digits of $k$ in its decimal representation by $S(k)$. Find all polynomials $P(x)$ with integer coefficients such that for any positive integer $n \geqslant 2016$, the integer $P(n)$ is positive and
+
+$$
+S(P(n))=P(S(n))
+$$
+
+N2. Let $\tau(n)$ be the number of positive divisors of $n$. Let $\tau_{1}(n)$ be the number of positive divisors of $n$ which have remainders 1 when divided by 3 . Find all possible integral values of the fraction $\frac{\tau(10 n)}{\tau_{1}(10 n)}$.
+
+N3. Define $P(n)=n^{2}+n+1$. For any positive integers $a$ and $b$, the set
+
+$$
+\{P(a), P(a+1), P(a+2), \ldots, P(a+b)\}
+$$
+
+is said to be fragrant if none of its elements is relatively prime to the product of the other elements. Determine the smallest size of a fragrant set.
+
+N4. Let $n, m, k$ and $l$ be positive integers with $n \neq 1$ such that $n^{k}+m n^{l}+1$ divides $n^{k+l}-1$. Prove that
+
+- $m=1$ and $l=2 k$; or
+- $l \mid k$ and $m=\frac{n^{k-l}-1}{n^{l}-1}$.
+
+N5. Let $a$ be a positive integer which is not a square number. Denote by $A$ the set of all positive integers $k$ such that
+
+$$
+k=\frac{x^{2}-a}{x^{2}-y^{2}}
+$$
+
+for some integers $x$ and $y$ with $x>\sqrt{a}$. Denote by $B$ the set of all positive integers $k$ such that (1) is satisfied for some integers $x$ and $y$ with $0 \leqslant x<\sqrt{a}$. Prove that $A=B$.
+
+N6. Denote by $\mathbb{N}$ the set of all positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that for all positive integers $m$ and $n$, the integer $f(m)+f(n)-m n$ is nonzero and divides $m f(m)+n f(n)$.
+
+N7. Let $n$ be an odd positive integer. In the Cartesian plane, a cyclic polygon $P$ with area $S$ is chosen. All its vertices have integral coordinates, and all squares of its side lengths are divisible by $n$. Prove that $2 S$ is an integer divisible by $n$.
+
+N8. Find all polynomials $P(x)$ of odd degree $d$ and with integer coefficients satisfying the following property: for each positive integer $n$, there exist $n$ positive integers $x_{1}, x_{2}, \ldots, x_{n}$ such that $\frac{1}{2}<\frac{P\left(x_{i}\right)}{P\left(x_{j}\right)}<2$ and $\frac{P\left(x_{i}\right)}{P\left(x_{j}\right)}$ is the $d$-th power of a rational number for every pair of indices $i$ and $j$ with $1 \leqslant i, j \leqslant n$.
+
+## Solutions
+
+## Algebra
+
+A1. Let $a, b$ and $c$ be positive real numbers such that $\min \{a b, b c, c a\} \geqslant 1$. Prove that
+
+$$
+\sqrt[3]{\left(a^{2}+1\right)\left(b^{2}+1\right)\left(c^{2}+1\right)} \leqslant\left(\frac{a+b+c}{3}\right)^{2}+1
+$$
+
+Solution 1. We first show the following.
+
+- Claim. For any positive real numbers $x, y$ with $x y \geqslant 1$, we have
+
+$$
+\left(x^{2}+1\right)\left(y^{2}+1\right) \leqslant\left(\left(\frac{x+y}{2}\right)^{2}+1\right)^{2}
+$$
+
+Proof. Note that $x y \geqslant 1$ implies $\left(\frac{x+y}{2}\right)^{2}-1 \geqslant x y-1 \geqslant 0$. We find that $\left(x^{2}+1\right)\left(y^{2}+1\right)=(x y-1)^{2}+(x+y)^{2} \leqslant\left(\left(\frac{x+y}{2}\right)^{2}-1\right)^{2}+(x+y)^{2}=\left(\left(\frac{x+y}{2}\right)^{2}+1\right)^{2}$.
+
+Without loss of generality, assume $a \geqslant b \geqslant c$. This implies $a \geqslant 1$. Let $d=\frac{a+b+c}{3}$. Note that
+
+$$
+a d=\frac{a(a+b+c)}{3} \geqslant \frac{1+1+1}{3}=1 .
+$$
+
+Then we can apply (2) to the pair $(a, d)$ and the pair $(b, c)$. We get
+
+$$
+\left(a^{2}+1\right)\left(d^{2}+1\right)\left(b^{2}+1\right)\left(c^{2}+1\right) \leqslant\left(\left(\frac{a+d}{2}\right)^{2}+1\right)^{2}\left(\left(\frac{b+c}{2}\right)^{2}+1\right)^{2}
+$$
+
+Next, from
+
+$$
+\frac{a+d}{2} \cdot \frac{b+c}{2} \geqslant \sqrt{a d} \cdot \sqrt{b c} \geqslant 1
+$$
+
+we can apply (2) again to the pair $\left(\frac{a+d}{2}, \frac{b+c}{2}\right)$. Together with (3), we have
+
+$$
+\left(a^{2}+1\right)\left(d^{2}+1\right)\left(b^{2}+1\right)\left(c^{2}+1\right) \leqslant\left(\left(\frac{a+b+c+d}{4}\right)^{2}+1\right)^{4}=\left(d^{2}+1\right)^{4}
+$$
+
+Therefore, $\left(a^{2}+1\right)\left(b^{2}+1\right)\left(c^{2}+1\right) \leqslant\left(d^{2}+1\right)^{3}$, and (1) follows by taking cube root of both sides.
+
+Comment. After justifying the Claim, one may also obtain (1) by mixing variables. Indeed, the function involved is clearly continuous, and hence it suffices to check that the condition $x y \geqslant 1$ is preserved under each mixing step. This is true since whenever $a b, b c, c a \geqslant 1$, we have
+
+$$
+\frac{a+b}{2} \cdot \frac{a+b}{2} \geqslant a b \geqslant 1 \quad \text { and } \quad \frac{a+b}{2} \cdot c \geqslant \frac{1+1}{2}=1 .
+$$
+
+Solution 2. Let $f(x)=\ln \left(1+x^{2}\right)$. Then the inequality (1) to be shown is equivalent to
+
+$$
+\frac{f(a)+f(b)+f(c)}{3} \leqslant f\left(\frac{a+b+c}{3}\right),
+$$
+
+while (2) becomes
+
+$$
+\frac{f(x)+f(y)}{2} \leqslant f\left(\frac{x+y}{2}\right)
+$$
+
+for $x y \geqslant 1$.
+Without loss of generality, assume $a \geqslant b \geqslant c$. From the Claim in Solution 1, we have
+
+$$
+\frac{f(a)+f(b)+f(c)}{3} \leqslant \frac{f(a)+2 f\left(\frac{b+c}{2}\right)}{3} .
+$$
+
+Note that $a \geqslant 1$ and $\frac{b+c}{2} \geqslant \sqrt{b c} \geqslant 1$. Since
+
+$$
+f^{\prime \prime}(x)=\frac{2\left(1-x^{2}\right)}{\left(1+x^{2}\right)^{2}}
+$$
+
+we know that $f$ is concave on $[1, \infty)$. Then we can apply Jensen's Theorem to get
+
+$$
+\frac{f(a)+2 f\left(\frac{b+c}{2}\right)}{3} \leqslant f\left(\frac{a+2 \cdot \frac{b+c}{2}}{3}\right)=f\left(\frac{a+b+c}{3}\right) .
+$$
+
+This completes the proof.
+
+A2. Find the smallest real constant $C$ such that for any positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ (not necessarily distinct), one can always choose distinct subscripts $i, j, k$ and $l$ such that
+
+$$
+\left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leqslant C .
+$$
+
+Answer. The smallest $C$ is $\frac{1}{2}$.
+Solution. We first show that $C \leqslant \frac{1}{2}$. For any positive real numbers $a_{1} \leqslant a_{2} \leqslant a_{3} \leqslant a_{4} \leqslant a_{5}$, consider the five fractions
+
+$$
+\frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}} .
+$$
+
+Each of them lies in the interval $(0,1]$. Therefore, by the Pigeonhole Principle, at least three of them must lie in $\left(0, \frac{1}{2}\right]$ or lie in $\left(\frac{1}{2}, 1\right]$ simultaneously. In particular, there must be two consecutive terms in (2) which belong to an interval of length $\frac{1}{2}$ (here, we regard $\frac{a_{1}}{a_{2}}$ and $\frac{a_{4}}{a_{5}}$ as consecutive). In other words, the difference of these two fractions is less than $\frac{1}{2}$. As the indices involved in these two fractions are distinct, we can choose them to be $i, j, k, l$ and conclude that $C \leqslant \frac{1}{2}$.
+
+Next, we show that $C=\frac{1}{2}$ is best possible. Consider the numbers $1,2,2,2, n$ where $n$ is a large real number. The fractions formed by two of these numbers in ascending order are $\frac{1}{n}, \frac{2}{n}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{n}{2}, \frac{n}{1}$. Since the indices $i, j, k, l$ are distinct, $\frac{1}{n}$ and $\frac{2}{n}$ cannot be chosen simultaneously. Therefore the minimum value of the left-hand side of (1) is $\frac{1}{2}-\frac{2}{n}$. When $n$ tends to infinity, this value approaches $\frac{1}{2}$, and so $C$ cannot be less than $\frac{1}{2}$.
+
+These conclude that $C=\frac{1}{2}$ is the smallest possible choice.
+Comment. The conclusion still holds if $a_{1}, a_{2}, \ldots, a_{5}$ are pairwise distinct, since in the construction, we may replace the 2's by real numbers sufficiently close to 2 .
+
+There are two possible simplifications for this problem:
+(i) the answer $C=\frac{1}{2}$ is given to the contestants; or
+(ii) simply ask the contestants to prove the inequality (1) for $C=\frac{1}{2}$.
+
+A3. Find all integers $n \geqslant 3$ with the following property: for all real numbers $a_{1}, a_{2}, \ldots, a_{n}$ and $b_{1}, b_{2}, \ldots, b_{n}$ satisfying $\left|a_{k}\right|+\left|b_{k}\right|=1$ for $1 \leqslant k \leqslant n$, there exist $x_{1}, x_{2}, \ldots, x_{n}$, each of which is either -1 or 1 , such that
+
+$$
+\left|\sum_{k=1}^{n} x_{k} a_{k}\right|+\left|\sum_{k=1}^{n} x_{k} b_{k}\right| \leqslant 1
+$$
+
+Answer. $n$ can be any odd integer greater than or equal to 3 .
+Solution 1. For any even integer $n \geqslant 4$, we consider the case
+
+$$
+a_{1}=a_{2}=\cdots=a_{n-1}=b_{n}=0 \quad \text { and } \quad b_{1}=b_{2}=\cdots=b_{n-1}=a_{n}=1
+$$
+
+The condition $\left|a_{k}\right|+\left|b_{k}\right|=1$ is satisfied for each $1 \leqslant k \leqslant n$. No matter how we choose each $x_{k}$, both sums $\sum_{k=1}^{n} x_{k} a_{k}$ and $\sum_{k=1}^{n} x_{k} b_{k}$ are odd integers. This implies $\left|\sum_{k=1}^{n} x_{k} a_{k}\right| \geqslant 1$ and $\left|\sum_{k=1}^{n} x_{k} b_{k}\right| \geqslant 1$, which shows (1) cannot hold.
+
+For any odd integer $n \geqslant 3$, we may assume without loss of generality $b_{k} \geqslant 0$ for $1 \leqslant k \leqslant n$ (this can be done by flipping the pair $\left(a_{k}, b_{k}\right)$ to $\left(-a_{k},-b_{k}\right)$ and $x_{k}$ to $-x_{k}$ if necessary) and $a_{1} \geqslant a_{2} \geqslant \cdots \geqslant a_{m} \geqslant 0>a_{m+1} \geqslant \cdots \geqslant a_{n}$. We claim that the choice $x_{k}=(-1)^{k+1}$ for $1 \leqslant k \leqslant n$ will work. Define
+
+$$
+s=\sum_{k=1}^{m} x_{k} a_{k} \quad \text { and } \quad t=-\sum_{k=m+1}^{n} x_{k} a_{k} .
+$$
+
+Note that
+
+$$
+s=\left(a_{1}-a_{2}\right)+\left(a_{3}-a_{4}\right)+\cdots \geqslant 0
+$$
+
+by the assumption $a_{1} \geqslant a_{2} \geqslant \cdots \geqslant a_{m}$ (when $m$ is odd, there is a single term $a_{m}$ at the end, which is also positive). Next, we have
+
+$$
+s=a_{1}-\left(a_{2}-a_{3}\right)-\left(a_{4}-a_{5}\right)-\cdots \leqslant a_{1} \leqslant 1
+$$
+
+Similarly,
+
+$$
+t=\left(-a_{n}+a_{n-1}\right)+\left(-a_{n-2}+a_{n-3}\right)+\cdots \geqslant 0
+$$
+
+and
+
+$$
+t=-a_{n}+\left(a_{n-1}-a_{n-2}\right)+\left(a_{n-3}-a_{n-4}\right)+\cdots \leqslant-a_{n} \leqslant 1 .
+$$
+
+From the condition, we have $a_{k}+b_{k}=1$ for $1 \leqslant k \leqslant m$ and $-a_{k}+b_{k}=1$ for $m+1 \leqslant k \leqslant n$. It follows that $\sum_{k=1}^{n} x_{k} a_{k}=s-t$ and $\sum_{k=1}^{n} x_{k} b_{k}=1-s-t$. Hence it remains to prove
+
+$$
+|s-t|+|1-s-t| \leqslant 1
+$$
+
+under the constraint $0 \leqslant s, t \leqslant 1$. By symmetry, we may assume $s \geqslant t$. If $1-s-t \geqslant 0$, then we have
+
+$$
+|s-t|+|1-s-t|=s-t+1-s-t=1-2 t \leqslant 1
+$$
+
+If $1-s-t \leqslant 0$, then we have
+
+$$
+|s-t|+|1-s-t|=s-t-1+s+t=2 s-1 \leqslant 1
+$$
+
+Hence, the inequality is true in both cases.
+These show $n$ can be any odd integer greater than or equal to 3 .
+
+Solution 2. The even case can be handled in the same way as Solution 1. For the odd case, we prove by induction on $n$.
+
+Firstly, for $n=3$, we may assume without loss of generality $a_{1} \geqslant a_{2} \geqslant a_{3} \geqslant 0$ and $b_{1}=a_{1}-1$ (if $b_{1}=1-a_{1}$, we may replace each $b_{k}$ by $-b_{k}$ ).
+
+- Case 1. $b_{2}=a_{2}-1$ and $b_{3}=a_{3}-1$, in which case we take $\left(x_{1}, x_{2}, x_{3}\right)=(1,-1,1)$.
+
+Let $c=a_{1}-a_{2}+a_{3}$ so that $0 \leqslant c \leqslant 1$. Then $\left|b_{1}-b_{2}+b_{3}\right|=\left|a_{1}-a_{2}+a_{3}-1\right|=1-c$ and hence $|c|+\left|b_{1}-b_{2}+b_{3}\right|=1$.
+
+- Case 2. $b_{2}=1-a_{2}$ and $b_{3}=1-a_{3}$, in which case we take $\left(x_{1}, x_{2}, x_{3}\right)=(1,-1,1)$.
+
+Let $c=a_{1}-a_{2}+a_{3}$ so that $0 \leqslant c \leqslant 1$. Since $a_{3} \leqslant a_{2}$ and $a_{1} \leqslant 1$, we have
+
+$$
+c-1 \leqslant b_{1}-b_{2}+b_{3}=a_{1}+a_{2}-a_{3}-1 \leqslant 1-c
+$$
+
+This gives $\left|b_{1}-b_{2}+b_{3}\right| \leqslant 1-c$ and hence $|c|+\left|b_{1}-b_{2}+b_{3}\right| \leqslant 1$.
+
+- Case 3. $b_{2}=a_{2}-1$ and $b_{3}=1-a_{3}$, in which case we take $\left(x_{1}, x_{2}, x_{3}\right)=(-1,1,1)$.
+
+Let $c=-a_{1}+a_{2}+a_{3}$. If $c \geqslant 0$, then $a_{3} \leqslant 1$ and $a_{2} \leqslant a_{1}$ imply
+
+$$
+c-1 \leqslant-b_{1}+b_{2}+b_{3}=-a_{1}+a_{2}-a_{3}+1 \leqslant 1-c
+$$
+
+If $c<0$, then $a_{1} \leqslant a_{2}+1$ and $a_{3} \geqslant 0$ imply
+
+$$
+-c-1 \leqslant-b_{1}+b_{2}+b_{3}=-a_{1}+a_{2}-a_{3}+1 \leqslant 1+c
+$$
+
+In both cases, we get $\left|-b_{1}+b_{2}+b_{3}\right| \leqslant 1-|c|$ and hence $|c|+\left|-b_{1}+b_{2}+b_{3}\right| \leqslant 1$.
+
+- Case 4. $b_{2}=1-a_{2}$ and $b_{3}=a_{3}-1$, in which case we take $\left(x_{1}, x_{2}, x_{3}\right)=(-1,1,1)$.
+
+Let $c=-a_{1}+a_{2}+a_{3}$. If $c \geqslant 0$, then $a_{2} \leqslant 1$ and $a_{3} \leqslant a_{1}$ imply
+
+$$
+c-1 \leqslant-b_{1}+b_{2}+b_{3}=-a_{1}-a_{2}+a_{3}+1 \leqslant 1-c
+$$
+
+If $c<0$, then $a_{1} \leqslant a_{3}+1$ and $a_{2} \geqslant 0$ imply
+
+$$
+-c-1 \leqslant-b_{1}+b_{2}+b_{3}=-a_{1}-a_{2}+a_{3}+1 \leqslant 1+c
+$$
+
+In both cases, we get $\left|-b_{1}+b_{2}+b_{3}\right| \leqslant 1-|c|$ and hence $|c|+\left|-b_{1}+b_{2}+b_{3}\right| \leqslant 1$.
+We have found $x_{1}, x_{2}, x_{3}$ satisfying (1) in each case for $n=3$.
+Now, let $n \geqslant 5$ be odd and suppose the result holds for any smaller odd cases. Again we may assume $a_{k} \geqslant 0$ for each $1 \leqslant k \leqslant n$. By the Pigeonhole Principle, there are at least three indices $k$ for which $b_{k}=a_{k}-1$ or $b_{k}=1-a_{k}$. Without loss of generality, suppose $b_{k}=a_{k}-1$ for $k=1,2,3$. Again by the Pigeonhole Principle, as $a_{1}, a_{2}, a_{3}$ lies between 0 and 1 , the difference of two of them is at most $\frac{1}{2}$. By changing indices if necessary, we may assume $0 \leqslant d=a_{1}-a_{2} \leqslant \frac{1}{2}$.
+
+By the inductive hypothesis, we can choose $x_{3}, x_{4}, \ldots, x_{n}$ such that $a^{\prime}=\sum_{k=3}^{n} x_{k} a_{k}$ and $b^{\prime}=\sum_{k=3}^{n} x_{k} b_{k}$ satisfy $\left|a^{\prime}\right|+\left|b^{\prime}\right| \leqslant 1$. We may further assume $a^{\prime} \geqslant 0$.
+
+- Case 1. $b^{\prime} \geqslant 0$, in which case we take $\left(x_{1}, x_{2}\right)=(-1,1)$.
+
+We have $\left|-a_{1}+a_{2}+a^{\prime}\right|+\left|-\left(a_{1}-1\right)+\left(a_{2}-1\right)+b^{\prime}\right|=\left|-d+a^{\prime}\right|+\left|-d+b^{\prime}\right| \leqslant$ $\max \left\{a^{\prime}+b^{\prime}-2 d, a^{\prime}-b^{\prime}, b^{\prime}-a^{\prime}, 2 d-a^{\prime}-b^{\prime}\right\} \leqslant 1$ since $0 \leqslant a^{\prime}, b^{\prime}, a^{\prime}+b^{\prime} \leqslant 1$ and $0 \leqslant d \leqslant \frac{1}{2}$.
+
+- Case 2. $0>b^{\prime} \geqslant-a^{\prime}$, in which case we take $\left(x_{1}, x_{2}\right)=(-1,1)$.
+
+We have $\left|-a_{1}+a_{2}+a^{\prime}\right|+\left|-\left(a_{1}-1\right)+\left(a_{2}-1\right)+b^{\prime}\right|=\left|-d+a^{\prime}\right|+\left|-d+b^{\prime}\right|$. If $-d+a^{\prime} \geqslant 0$, this equals $a^{\prime}-b^{\prime}=\left|a^{\prime}\right|+\left|b^{\prime}\right| \leqslant 1$. If $-d+a^{\prime}<0$, this equals $2 d-a^{\prime}-b^{\prime} \leqslant 2 d \leqslant 1$.
+
+- Case 3. $b^{\prime}<-a^{\prime}$, in which case we take $\left(x_{1}, x_{2}\right)=(1,-1)$.
+
+We have $\left|a_{1}-a_{2}+a^{\prime}\right|+\left|\left(a_{1}-1\right)-\left(a_{2}-1\right)+b^{\prime}\right|=\left|d+a^{\prime}\right|+\left|d+b^{\prime}\right|$. If $d+b^{\prime} \geqslant 0$, this equals $2 d+a^{\prime}+b^{\prime}<2 d \leqslant 1$. If $d+b^{\prime}<0$, this equals $a^{\prime}-b^{\prime}=\left|a^{\prime}\right|+\left|b^{\prime}\right| \leqslant 1$.
+
+Therefore, we have found $x_{1}, x_{2}, \ldots, x_{n}$ satisfying (1) in each case. By induction, the property holds for all odd integers $n \geqslant 3$.
+
+A4. Denote by $\mathbb{R}^{+}$the set of all positive real numbers. Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
+
+$$
+x f\left(x^{2}\right) f(f(y))+f(y f(x))=f(x y)\left(f\left(f\left(x^{2}\right)\right)+f\left(f\left(y^{2}\right)\right)\right)
+$$
+
+for all positive real numbers $x$ and $y$.
+Answer. $f(x)=\frac{1}{x}$ for any $x \in \mathbb{R}^{+}$.
+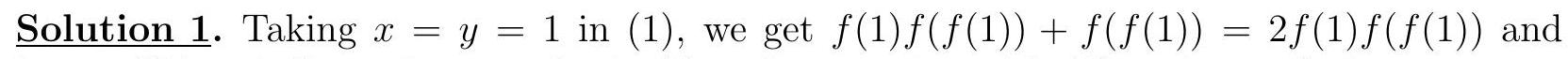 hence $f(1)=1$. Swapping $x$ and $y$ in (1) and comparing with (1) again, we find
+
+$$
+x f\left(x^{2}\right) f(f(y))+f(y f(x))=y f\left(y^{2}\right) f(f(x))+f(x f(y)) .
+$$
+
+Taking $y=1$ in (2), we have $x f\left(x^{2}\right)+f(f(x))=f(f(x))+f(x)$, that is,
+
+$$
+f\left(x^{2}\right)=\frac{f(x)}{x}
+$$
+
+Take $y=1$ in (1) and apply (3) to $x f\left(x^{2}\right)$. We get $f(x)+f(f(x))=f(x)\left(f\left(f\left(x^{2}\right)\right)+1\right)$, which implies
+
+$$
+f\left(f\left(x^{2}\right)\right)=\frac{f(f(x))}{f(x)}
+$$
+
+For any $x \in \mathbb{R}^{+}$, we find that
+
+$$
+f\left(f(x)^{2}\right) \stackrel{(3)}{=} \frac{f(f(x))}{f(x)} \stackrel{(4)}{=} f\left(f\left(x^{2}\right)\right) \stackrel{(3)}{=} f\left(\frac{f(x)}{x}\right)
+$$
+
+It remains to show the following key step.
+
+- Claim. The function $f$ is injective.
+
+Proof. Using (3) and (4), we rewrite (1) as
+
+$$
+f(x) f(f(y))+f(y f(x))=f(x y)\left(\frac{f(f(x))}{f(x)}+\frac{f(f(y))}{f(y)}\right) .
+$$
+
+Take $x=y$ in (6) and apply (3). This gives $f(x) f(f(x))+f(x f(x))=2 \frac{f(f(x))}{x}$, which means
+
+$$
+f(x f(x))=f(f(x))\left(\frac{2}{x}-f(x)\right)
+$$
+
+Using (3), equation (2) can be rewritten as
+
+$$
+f(x) f(f(y))+f(y f(x))=f(y) f(f(x))+f(x f(y))
+$$
+
+Suppose $f(x)=f(y)$ for some $x, y \in \mathbb{R}^{+}$. Then (8) implies
+
+$$
+f(y f(y))=f(y f(x))=f(x f(y))=f(x f(x))
+$$
+
+Using (7), this gives
+
+$$
+f(f(y))\left(\frac{2}{y}-f(y)\right)=f(f(x))\left(\frac{2}{x}-f(x)\right)
+$$
+
+Noting $f(x)=f(y)$, we find $x=y$. This establishes the injectivity.
+
+By the Claim and (5), we get the only possible solution $f(x)=\frac{1}{x}$. It suffices to check that this is a solution. Indeed, the left-hand side of (1) becomes
+
+$$
+x \cdot \frac{1}{x^{2}} \cdot y+\frac{x}{y}=\frac{y}{x}+\frac{x}{y},
+$$
+
+while the right-hand side becomes
+
+$$
+\frac{1}{x y}\left(x^{2}+y^{2}\right)=\frac{x}{y}+\frac{y}{x} .
+$$
+
+The two sides agree with each other.
+Solution 2. Taking $x=y=1$ in (1), we get $f(1) f(f(1))+f(f(1))=2 f(1) f(f(1))$ and hence $f(1)=1$. Putting $x=1$ in (1), we have $f(f(y))+f(y)=f(y)\left(1+f\left(f\left(y^{2}\right)\right)\right)$ so that
+
+$$
+f(f(y))=f(y) f\left(f\left(y^{2}\right)\right)
+$$
+
+Putting $y=1$ in (1), we get $x f\left(x^{2}\right)+f(f(x))=f(x)\left(f\left(f\left(x^{2}\right)\right)+1\right)$. Using (9), this gives
+
+$$
+x f\left(x^{2}\right)=f(x)
+$$
+
+Replace $y$ by $\frac{1}{x}$ in (1). Then we have
+
+$$
+x f\left(x^{2}\right) f\left(f\left(\frac{1}{x}\right)\right)+f\left(\frac{f(x)}{x}\right)=f\left(f\left(x^{2}\right)\right)+f\left(f\left(\frac{1}{x^{2}}\right)\right) .
+$$
+
+The relation (10) shows $f\left(\frac{f(x)}{x}\right)=f\left(f\left(x^{2}\right)\right)$. Also, using (9) with $y=\frac{1}{x}$ and using (10) again, the last equation reduces to
+
+$$
+f(x) f\left(\frac{1}{x}\right)=1
+$$
+
+Replace $x$ by $\frac{1}{x}$ and $y$ by $\frac{1}{y}$ in (1) and apply (11). We get
+
+$$
+\frac{1}{x f\left(x^{2}\right) f(f(y))}+\frac{1}{f(y f(x))}=\frac{1}{f(x y)}\left(\frac{1}{f\left(f\left(x^{2}\right)\right)}+\frac{1}{f\left(f\left(y^{2}\right)\right)}\right) .
+$$
+
+Clearing denominators, we can use (1) to simplify the numerators and obtain
+
+$$
+f(x y)^{2} f\left(f\left(x^{2}\right)\right) f\left(f\left(y^{2}\right)\right)=x f\left(x^{2}\right) f(f(y)) f(y f(x))
+$$
+
+Using (9) and (10), this is the same as
+
+$$
+f(x y)^{2} f(f(x))=f(x)^{2} f(y) f(y f(x))
+$$
+
+Substitute $y=f(x)$ in (12) and apply (10) (with $x$ replaced by $f(x)$ ). We have
+
+$$
+f(x f(x))^{2}=f(x) f(f(x))
+$$
+
+Taking $y=x$ in (12), squaring both sides, and using (10) and (13), we find that
+
+$$
+f(f(x))=x^{4} f(x)^{3}
+$$
+
+Finally, we combine (9), (10) and (14) to get
+
+$$
+y^{4} f(y)^{3} \stackrel{(14)}{=} f(f(y)) \stackrel{(9)}{=} f(y) f\left(f\left(y^{2}\right)\right) \stackrel{(14)}{=} f(y) y^{8} f\left(y^{2}\right)^{3} \stackrel{(10)}{=} y^{5} f(y)^{4},
+$$
+
+which implies $f(y)=\frac{1}{y}$. This is a solution by the checking in Solution 1.
+
+## A5.
+
+(a) Prove that for every positive integer $n$, there exists a fraction $\frac{a}{b}$ where $a$ and $b$ are integers satisfying $02016$ or $4 k2$ for $0 \leqslant j \leqslant 503$ in this case. So each term in the product lies strictly between 0 and 1 , and the whole product must be less than 1 , which is impossible.
+
+- Case 4. $4 k+2\frac{n+1}{2}$, we have $|l(x)|>|r(x)|$.
+
+If $n \equiv 3(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n+1}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n+3}{2}\right)\left(x-\frac{x+5}{2}\right) \cdots(x-n)$ on the right-hand side. For $x<1$ or $\frac{n+1}{2}0>r(x)$. For $1\frac{n+3}{2}$, we have $|l(x)|>|r(x)|$.
+
+If $n \equiv 1(\bmod 4)$, as the proposer mentioned, the situation is a bit more out of control. Since the construction for $n-1 \equiv 0(\bmod 4)$ works, the answer can be either $n$ or $n-1$. For $n=5$, we can leave the products $(x-1)(x-2)(x-3)(x-4)$ and $(x-5)$. For $n=9$, the only example that works is $l(x)=(x-1)(x-2)(x-9)$ and $r(x)=(x-3)(x-4) \cdots(x-8)$, while there seems to be no such partition for $n=13$.
+
+A7. Denote by $\mathbb{R}$ the set of all real numbers. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $f(0) \neq 0$ and
+
+$$
+f(x+y)^{2}=2 f(x) f(y)+\max \left\{f\left(x^{2}\right)+f\left(y^{2}\right), f\left(x^{2}+y^{2}\right)\right\}
+$$
+
+for all real numbers $x$ and $y$.
+
+## Answer.
+
+- $f(x)=-1$ for any $x \in \mathbb{R}$; or
+- $f(x)=x-1$ for any $x \in \mathbb{R}$.
+
+Solution 1. Taking $x=y=0$ in (1), we get $f(0)^{2}=2 f(0)^{2}+\max \{2 f(0), f(0)\}$. If $f(0)>0$, then $f(0)^{2}+2 f(0)=0$ gives no positive solution. If $f(0)<0$, then $f(0)^{2}+f(0)=0$ gives $f(0)=-1$. Putting $y=0$ in (1), we have $f(x)^{2}=-2 f(x)+f\left(x^{2}\right)$, which is the same as $(f(x)+1)^{2}=f\left(x^{2}\right)+1$. Let $g(x)=f(x)+1$. Then for any $x \in \mathbb{R}$, we have
+
+$$
+g\left(x^{2}\right)=g(x)^{2} \geqslant 0
+$$
+
+From (1), we find that $f(x+y)^{2} \geqslant 2 f(x) f(y)+f\left(x^{2}\right)+f\left(y^{2}\right)$. In terms of $g$, this becomes $(g(x+y)-1)^{2} \geqslant 2(g(x)-1)(g(y)-1)+g\left(x^{2}\right)+g\left(y^{2}\right)-2$. Using (2), this means
+
+$$
+(g(x+y)-1)^{2} \geqslant(g(x)+g(y)-1)^{2}-1
+$$
+
+Putting $x=1$ in (2), we get $g(1)=0$ or 1 . The two cases are handled separately.
+
+- Case 1. $g(1)=0$, which is the same as $f(1)=-1$.
+
+We put $x=-1$ and $y=0$ in (1). This gives $f(-1)^{2}=-2 f(-1)-1$, which forces $f(-1)=-1$. Next, we take $x=-1$ and $y=1$ in (1) to get $1=2+\max \{-2, f(2)\}$. This clearly implies $1=2+f(2)$ and hence $f(2)=-1$, that is, $g(2)=0$. From (2), we can prove inductively that $g\left(2^{2^{n}}\right)=g(2)^{2^{n}}=0$ for any $n \in \mathbb{N}$. Substitute $y=2^{2^{n}}-x$ in (3). We obtain
+
+$$
+\left(g(x)+g\left(2^{2^{n}}-x\right)-1\right)^{2} \leqslant\left(g\left(2^{2^{n}}\right)-1\right)^{2}+1=2
+$$
+
+For any fixed $x \geqslant 0$, we consider $n$ to be sufficiently large so that $2^{2^{n}}-x>0$. From (2), this implies $g\left(2^{2^{n}}-x\right) \geqslant 0$ so that $g(x) \leqslant 1+\sqrt{2}$. Using (2) again, we get
+
+$$
+g(x)^{2^{n}}=g\left(x^{2^{n}}\right) \leqslant 1+\sqrt{2}
+$$
+
+for any $n \in \mathbb{N}$. Therefore, $|g(x)| \leqslant 1$ for any $x \geqslant 0$.
+If there exists $a \in \mathbb{R}$ for which $g(a) \neq 0$, then for sufficiently large $n$ we must have $g\left(\left(a^{2}\right)^{\frac{1}{2^{n}}}\right)=g\left(a^{2}\right)^{\frac{1}{2^{n}}}>\frac{1}{2}$. By taking $x=-y=-\left(a^{2}\right)^{\frac{1}{2^{n}}}$ in (1), we obtain
+
+$$
+\begin{aligned}
+1 & =2 f(x) f(-x)+\max \left\{2 f\left(x^{2}\right), f\left(2 x^{2}\right)\right\} \\
+& =2(g(x)-1)(g(-x)-1)+\max \left\{2\left(g\left(x^{2}\right)-1\right), g\left(2 x^{2}\right)-1\right\} \\
+& \leqslant 2\left(-\frac{1}{2}\right)\left(-\frac{1}{2}\right)+0=\frac{1}{2}
+\end{aligned}
+$$
+
+since $|g(-x)|=|g(x)| \in\left(\frac{1}{2}, 1\right]$ by (2) and the choice of $x$, and since $g(z) \leqslant 1$ for $z \geqslant 0$. This yields a contradiction and hence $g(x)=0$ must hold for any $x$. This means $f(x)=-1$ for any $x \in \mathbb{R}$, which clearly satisfies (1).
+
+- Case 2. $g(1)=1$, which is the same as $f(1)=0$.
+
+We put $x=-1$ and $y=1$ in (1) to get $1=\max \{0, f(2)\}$. This clearly implies $f(2)=1$ and hence $g(2)=2$. Setting $x=2 n$ and $y=2$ in (3), we have
+
+$$
+(g(2 n+2)-1)^{2} \geqslant(g(2 n)+1)^{2}-1
+$$
+
+By induction on $n$, it is easy to prove that $g(2 n) \geqslant n+1$ for all $n \in \mathbb{N}$. For any real number $a>1$, we choose a large $n \in \mathbb{N}$ and take $k$ to be the positive integer such that $2 k \leqslant a^{2^{n}}<2 k+2$. From (2) and (3), we have
+
+$$
+\left(g(a)^{2^{n}}-1\right)^{2}+1=\left(g\left(a^{2^{n}}\right)-1\right)^{2}+1 \geqslant\left(g(2 k)+g\left(a^{2^{n}}-2 k\right)-1\right)^{2} \geqslant k^{2}>\frac{1}{4}\left(a^{2^{n}}-2\right)^{2}
+$$
+
+since $g\left(a^{2^{n}}-2 k\right) \geqslant 0$. For large $n$, this clearly implies $g(a)^{2^{n}}>1$. Thus,
+
+$$
+\left(g(a)^{2^{n}}\right)^{2}>\left(g(a)^{2^{n}}-1\right)^{2}+1>\frac{1}{4}\left(a^{2^{n}}-2\right)^{2}
+$$
+
+This yields
+
+$$
+g(a)^{2^{n}}>\frac{1}{2}\left(a^{2^{n}}-2\right)
+$$
+
+Note that
+
+$$
+\frac{a^{2^{n}}}{a^{2^{n}}-2}=1+\frac{2}{a^{2^{n}}-2} \leqslant\left(1+\frac{2}{2^{n}\left(a^{2^{n}}-2\right)}\right)^{2^{n}}
+$$
+
+by binomial expansion. This can be rewritten as
+
+$$
+\left(a^{2^{n}}-2\right)^{\frac{1}{2^{n}}} \geqslant \frac{a}{1+\frac{2}{2^{n}\left(a^{2^{n}}-2\right)}}
+$$
+
+Together with (4), we conclude $g(a) \geqslant a$ by taking $n$ sufficiently large.
+Consider $x=n a$ and $y=a>1$ in (3). This gives $(g((n+1) a)-1)^{2} \geqslant(g(n a)+g(a)-1)^{2}-1$. By induction on $n$, it is easy to show $g(n a) \geqslant(n-1)(g(a)-1)+a$ for any $n \in \mathbb{N}$. We choose a large $n \in \mathbb{N}$ and take $k$ to be the positive integer such that $k a \leqslant 2^{2^{n}}<(k+1) a$. Using (2) and (3), we have
+$2^{2^{n+1}}>\left(2^{2^{n}}-1\right)^{2}+1=\left(g\left(2^{2^{n}}\right)-1\right)^{2}+1 \geqslant\left(g\left(2^{2^{n}}-k a\right)+g(k a)-1\right)^{2} \geqslant((k-1)(g(a)-1)+a-1)^{2}$, from which it follows that
+
+$$
+2^{2^{n}} \geqslant(k-1)(g(a)-1)+a-1>\frac{2^{2^{n}}}{a}(g(a)-1)-2(g(a)-1)+a-1
+$$
+
+holds for sufficiently large $n$. Hence, we must have $\frac{g(a)-1}{a} \leqslant 1$, which implies $g(a) \leqslant a+1$ for any $a>1$. Then for large $n \in \mathbb{N}$, from (3) and (2) we have
+
+$$
+4 a^{2^{n+1}}=\left(2 a^{2^{n}}\right)^{2} \geqslant\left(g\left(2 a^{2^{n}}\right)-1\right)^{2} \geqslant\left(2 g\left(a^{2^{n}}\right)-1\right)^{2}-1=\left(2 g(a)^{2^{n}}-1\right)^{2}-1
+$$
+
+This implies
+
+$$
+2 a^{2^{n}}>\frac{1}{2}\left(1+\sqrt{4 a^{2^{n+1}}+1}\right) \geqslant g(a)^{2^{n}}
+$$
+
+When $n$ tends to infinity, this forces $g(a) \leqslant a$. Together with $g(a) \geqslant a$, we get $g(a)=a$ for all real numbers $a>1$, that is, $f(a)=a-1$ for all $a>1$.
+
+Finally, for any $x \in \mathbb{R}$, we choose $y$ sufficiently large in (1) so that $y, x+y>1$. This gives $(x+y-1)^{2}=2 f(x)(y-1)+\max \left\{f\left(x^{2}\right)+y^{2}-1, x^{2}+y^{2}-1\right\}$, which can be rewritten as
+
+$$
+2(x-1-f(x)) y=-x^{2}+2 x-2-2 f(x)+\max \left\{f\left(x^{2}\right), x^{2}\right\}
+$$
+
+As the right-hand side is fixed, this can only hold for all large $y$ when $f(x)=x-1$. We now check that this function satisfies (1). Indeed, we have
+
+$$
+\begin{aligned}
+f(x+y)^{2} & =(x+y-1)^{2}=2(x-1)(y-1)+\left(x^{2}+y^{2}-1\right) \\
+& =2 f(x) f(y)+\max \left\{f\left(x^{2}\right)+f\left(y^{2}\right), f\left(x^{2}+y^{2}\right)\right\} .
+\end{aligned}
+$$
+
+Solution 2. Taking $x=y=0$ in (1), we get $f(0)^{2}=2 f(0)^{2}+\max \{2 f(0), f(0)\}$. If $f(0)>0$, then $f(0)^{2}+2 f(0)=0$ gives no positive solution. If $f(0)<0$, then $f(0)^{2}+f(0)=0$ gives $f(0)=-1$. Putting $y=0$ in (1), we have
+
+$$
+f(x)^{2}=-2 f(x)+f\left(x^{2}\right)
+$$
+
+Replace $x$ by $-x$ in (5) and compare with (5) again. We get $f(x)^{2}+2 f(x)=f(-x)^{2}+2 f(-x)$, which implies
+
+$$
+f(x)=f(-x) \quad \text { or } \quad f(x)+f(-x)=-2
+$$
+
+Taking $x=y$ and $x=-y$ respectively in (1) and comparing the two equations obtained, we have
+
+$$
+f(2 x)^{2}-2 f(x)^{2}=1-2 f(x) f(-x) .
+$$
+
+Combining (6) and (7) to eliminate $f(-x)$, we find that $f(2 x)$ can be $\pm 1$ (when $f(x)=f(-x)$ ) or $\pm(2 f(x)+1)$ (when $f(x)+f(-x)=-2$ ).
+
+We prove the following.
+
+- Claim. $f(x)+f(-x)=-2$ for any $x \in \mathbb{R}$.
+
+Proof. Suppose there exists $a \in \mathbb{R}$ such that $f(a)+f(-a) \neq-2$. Then $f(a)=f(-a) \neq-1$ and we may assume $a>0$. We first show that $f(a) \neq 1$. Suppose $f(a)=1$. Consider $y=a$ in (7). We get $f(2 a)^{2}=1$. Taking $x=y=a$ in (1), we have $1=2+\max \left\{2 f\left(a^{2}\right), f\left(2 a^{2}\right)\right\}$. From (5), $f\left(a^{2}\right)=3$ so that $1 \geqslant 2+6$. This is impossible, and thus $f(a) \neq 1$.
+
+As $f(a) \neq \pm 1$, we have $f(a)= \pm\left(2 f\left(\frac{a}{2}\right)+1\right)$. Similarly, $f(-a)= \pm\left(2 f\left(-\frac{a}{2}\right)+1\right)$. These two expressions are equal since $f(a)=f(-a)$. If $f\left(\frac{a}{2}\right)=f\left(-\frac{a}{2}\right)$, then the above argument works when we replace $a$ by $\frac{a}{2}$. In particular, we have $f(a)^{2}=f\left(2 \cdot \frac{a}{2}\right)^{2}=1$, which is a contradiction. Therefore, (6) forces $f\left(\frac{a}{2}\right)+f\left(-\frac{a}{2}\right)=-2$. Then we get
+
+$$
+\pm\left(2 f\left(\frac{a}{2}\right)+1\right)= \pm\left(-2 f\left(\frac{a}{2}\right)-3\right) .
+$$
+
+For any choices of the two signs, we either get a contradiction or $f\left(\frac{a}{2}\right)=-1$, in which case $f\left(\frac{a}{2}\right)=f\left(-\frac{a}{2}\right)$ and hence $f(a)= \pm 1$ again. Therefore, there is no such real number $a$ and the Claim follows.
+
+Replace $x$ and $y$ by $-x$ and $-y$ in (1) respectively and compare with (1). We get
+
+$$
+f(x+y)^{2}-2 f(x) f(y)=f(-x-y)^{2}-2 f(-x) f(-y)
+$$
+
+Using the Claim, this simplifies to $f(x+y)=f(x)+f(y)+1$. In addition, (5) can be rewritten as $(f(x)+1)^{2}=f\left(x^{2}\right)+1$. Therefore, the function $g$ defined by $g(x)=f(x)+1$ satisfies $g(x+y)=g(x)+g(y)$ and $g(x)^{2}=g\left(x^{2}\right)$. The latter relation shows $g(y)$ is nonnegative for $y \geqslant 0$. For such a function satisfying the Cauchy Equation $g(x+y)=g(x)+g(y)$, it must be monotonic increasing and hence $g(x)=c x$ for some constant $c$.
+
+From $(c x)^{2}=g(x)^{2}=g\left(x^{2}\right)=c x^{2}$, we get $c=0$ or 1 , which corresponds to the two functions $f(x)=-1$ and $f(x)=x-1$ respectively, both of which are solutions to (1) as checked in Solution 1.
+
+Solution 3. As in Solution 2, we find that $f(0)=-1$,
+
+$$
+(f(x)+1)^{2}=f\left(x^{2}\right)+1
+$$
+
+and
+
+$$
+f(x)=f(-x) \quad \text { or } \quad f(x)+f(-x)=-2
+$$
+
+for any $x \in \mathbb{R}$. We shall show that one of the statements in (9) holds for all $x \in \mathbb{R}$. Suppose $f(a)=f(-a)$ but $f(a)+f(-a) \neq-2$, while $f(b) \neq f(-b)$ but $f(b)+f(-b)=-2$. Clearly, $a, b \neq 0$ and $f(a), f(b) \neq-1$.
+
+Taking $y=a$ and $y=-a$ in (1) respectively and comparing the two equations obtained, we have $f(x+a)^{2}=f(x-a)^{2}$, that is, $f(x+a)= \pm f(x-a)$. This implies $f(x+2 a)= \pm f(x)$ for all $x \in \mathbb{R}$. Putting $x=b$ and $x=-2 a-b$ respectively, we find $f(2 a+b)= \pm f(b)$ and $f(-2 a-b)= \pm f(-b)= \pm(-2-f(b))$. Since $f(b) \neq-1$, the term $\pm(-2-f(b))$ is distinct from $\pm f(b)$ in any case. So $f(2 a+b) \neq f(-2 a-b)$. From (9), we must have $f(2 a+b)+f(-2 a-b)=-2$. Note that we also have $f(b)+f(-b)=-2$ where $|f(b)|,|f(-b)|$ are equal to $|f(2 a+b)|,|f(-2 a-b)|$ respectively. The only possible case is $f(2 a+b)=f(b)$ and $f(-2 a-b)=f(-b)$.
+
+Applying the argument to $-a$ instead of $a$ and using induction, we have $f(2 k a+b)=f(b)$ and $f(2 k a-b)=f(-b)$ for any integer $k$. Note that $f(b)+f(-b)=-2$ and $f(b) \neq-1$ imply one of $f(b), f(-b)$ is less than -1 . Without loss of generality, assume $f(b)<-1$. We consider $x=\sqrt{2 k a+b}$ in (8) for sufficiently large $k$ so that
+
+$$
+(f(x)+1)^{2}=f(2 k a+b)+1=f(b)+1<0
+$$
+
+yields a contradiction. Therefore, one of the statements in (9) must hold for all $x \in \mathbb{R}$.
+
+- Case 1. $f(x)=f(-x)$ for any $x \in \mathbb{R}$.
+
+For any $a \in \mathbb{R}$, setting $x=y=\frac{a}{2}$ and $x=-y=\frac{a}{2}$ in (1) respectively and comparing these, we obtain $f(a)^{2}=f(0)^{2}=1$, which means $f(a)= \pm 1$ for all $a \in \mathbb{R}$. If $f(a)=1$ for some $a$, we may assume $a>0$ since $f(a)=f(-a)$. Taking $x=y=\sqrt{a}$ in (1), we get
+
+$$
+f(2 \sqrt{a})^{2}=2 f(\sqrt{a})^{2}+\max \{2, f(2 a)\}=2 f(\sqrt{a})^{2}+2
+$$
+
+Note that the left-hand side is $\pm 1$ while the right-hand side is an even integer. This is a contradiction. Therefore, $f(x)=-1$ for all $x \in \mathbb{R}$, which is clearly a solution.
+
+- Case 2. $f(x)+f(-x)=-2$ for any $x \in \mathbb{R}$.
+
+This case can be handled in the same way as in Solution 2, which yields another solution $f(x)=x-1$.
+
+A8. Determine the largest real number $a$ such that for all $n \geqslant 1$ and for all real numbers $x_{0}, x_{1}, \ldots, x_{n}$ satisfying $0=x_{0}4 \sum_{k=1}^{n} \frac{k+1}{x_{k}} .
+$$
+
+This shows (1) holds for $a=\frac{4}{9}$.
+Next, we show that $a=\frac{4}{9}$ is the optimal choice. Consider the sequence defined by $x_{0}=0$ and $x_{k}=x_{k-1}+k(k+1)$ for $k \geqslant 1$, that is, $x_{k}=\frac{1}{3} k(k+1)(k+2)$. Then the left-hand side of (1) equals
+
+$$
+\sum_{k=1}^{n} \frac{1}{k(k+1)}=\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n+1}
+$$
+
+while the right-hand side equals
+
+$$
+a \sum_{k=1}^{n} \frac{k+1}{x_{k}}=3 a \sum_{k=1}^{n} \frac{1}{k(k+2)}=\frac{3}{2} a \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+2}\right)=\frac{3}{2}\left(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right) a .
+$$
+
+When $n$ tends to infinity, the left-hand side tends to 1 while the right-hand side tends to $\frac{9}{4} a$. Therefore $a$ has to be at most $\frac{4}{9}$.
+
+Hence the largest value of $a$ is $\frac{4}{9}$.
+Solution 2. We shall give an alternative method to establish (1) with $a=\frac{4}{9}$. We define $y_{k}=x_{k}-x_{k-1}>0$ for $1 \leqslant k \leqslant n$. By the Cauchy-Schwarz Inequality, for $1 \leqslant k \leqslant n$, we have
+
+$$
+\left(y_{1}+y_{2}+\cdots+y_{k}\right)\left(\sum_{j=1}^{k} \frac{1}{y_{j}}\binom{j+1}{2}^{2}\right) \geqslant\left(\binom{2}{2}+\binom{3}{2}+\cdots+\binom{k+1}{2}\right)^{2}=\binom{k+2}{3}^{2}
+$$
+
+This can be rewritten as
+
+$$
+\frac{k+1}{y_{1}+y_{2}+\cdots+y_{k}} \leqslant \frac{36}{k^{2}(k+1)(k+2)^{2}}\left(\sum_{j=1}^{k} \frac{1}{y_{j}}\binom{j+1}{2}^{2}\right) .
+$$
+
+Summing (3) over $k=1,2, \ldots, n$, we get
+
+$$
+\frac{2}{y_{1}}+\frac{3}{y_{1}+y_{2}}+\cdots+\frac{n+1}{y_{1}+y_{2}+\cdots+y_{n}} \leqslant \frac{c_{1}}{y_{1}}+\frac{c_{2}}{y_{2}}+\cdots+\frac{c_{n}}{y_{n}}
+$$
+
+where for $1 \leqslant m \leqslant n$,
+
+$$
+\begin{aligned}
+c_{m} & =36\binom{m+1}{2}^{2} \sum_{k=m}^{n} \frac{1}{k^{2}(k+1)(k+2)^{2}} \\
+& =\frac{9 m^{2}(m+1)^{2}}{4} \sum_{k=m}^{n}\left(\frac{1}{k^{2}(k+1)^{2}}-\frac{1}{(k+1)^{2}(k+2)^{2}}\right) \\
+& =\frac{9 m^{2}(m+1)^{2}}{4}\left(\frac{1}{m^{2}(m+1)^{2}}-\frac{1}{(n+1)^{2}(n+2)^{2}}\right)<\frac{9}{4} .
+\end{aligned}
+$$
+
+From (4), the inequality (1) holds for $a=\frac{4}{9}$. This is also the upper bound as can be verified in the same way as Solution 1.
+
+## Combinatorics
+
+C1. The leader of an IMO team chooses positive integers $n$ and $k$ with $n>k$, and announces them to the deputy leader and a contestant. The leader then secretly tells the deputy leader an $n$-digit binary string, and the deputy leader writes down all $n$-digit binary strings which differ from the leader's in exactly $k$ positions. (For example, if $n=3$ and $k=1$, and if the leader chooses 101, the deputy leader would write down 001, 111 and 100.) The contestant is allowed to look at the strings written by the deputy leader and guess the leader's string. What is the minimum number of guesses (in terms of $n$ and $k$ ) needed to guarantee the correct answer?
+
+Answer. The minimum number of guesses is 2 if $n=2 k$ and 1 if $n \neq 2 k$.
+Solution 1. Let $X$ be the binary string chosen by the leader and let $X^{\prime}$ be the binary string of length $n$ every digit of which is different from that of $X$. The strings written by the deputy leader are the same as those in the case when the leader's string is $X^{\prime}$ and $k$ is changed to $n-k$. In view of this, we may assume $k \geqslant \frac{n}{2}$. Also, for the particular case $k=\frac{n}{2}$, this argument shows that the strings $X$ and $X^{\prime}$ cannot be distinguished, and hence in that case the contestant has to guess at least twice.
+
+It remains to show that the number of guesses claimed suffices. Consider any string $Y$ which differs from $X$ in $m$ digits where $02$, the deputy leader would write down the same strings if the leader's string $X$ is replaced by $X^{\prime}$ obtained by changing each digit of $X$. This shows at least 2 guesses are needed. We shall show that 2 guesses suffice in this case. Suppose the first two digits of the leader's string are the same. Then among the strings written by the deputy leader, the prefices 01 and 10 will occur $\binom{2 k-2}{k-1}$ times each, while the prefices 00 and 11 will occur $\binom{2 k-2}{k}$ times each. The two numbers are interchanged if the first two digits of the leader's string are different. Since $\binom{2 k-2}{k-1} \neq\binom{ 2 k-2}{k}$, the contestant can tell whether the first two digits of the leader's string are the same or not. He can work out the relation of the first digit and the
+other digits in the same way and reduce the leader's string to only 2 possibilities. The proof is complete.
+
+C2. Find all positive integers $n$ for which all positive divisors of $n$ can be put into the cells of a rectangular table under the following constraints:
+
+- each cell contains a distinct divisor;
+- the sums of all rows are equal; and
+- the sums of all columns are equal.
+
+Answer. 1.
+Solution 1. Suppose all positive divisors of $n$ can be arranged into a rectangular table of size $k \times l$ where the number of rows $k$ does not exceed the number of columns $l$. Let the sum of numbers in each column be $s$. Since $n$ belongs to one of the columns, we have $s \geqslant n$, where equality holds only when $n=1$.
+
+For $j=1,2, \ldots, l$, let $d_{j}$ be the largest number in the $j$-th column. Without loss of generality, assume $d_{1}>d_{2}>\cdots>d_{l}$. Since these are divisors of $n$, we have
+
+$$
+d_{l} \leqslant \frac{n}{l}
+$$
+
+As $d_{l}$ is the maximum entry of the $l$-th column, we must have
+
+$$
+d_{l} \geqslant \frac{s}{k} \geqslant \frac{n}{k} .
+$$
+
+The relations (1) and (2) combine to give $\frac{n}{l} \geqslant \frac{n}{k}$, that is, $k \geqslant l$. Together with $k \leqslant l$, we conclude that $k=l$. Then all inequalities in (1) and (2) are equalities. In particular, $s=n$ and so $n=1$, in which case the conditions are clearly satisfied.
+
+Solution 2. Clearly $n=1$ works. Then we assume $n>1$ and let its prime factorization be $n=p_{1}^{r_{1}} p_{2}^{r_{2}} \cdots p_{t}^{r_{t}}$. Suppose the table has $k$ rows and $l$ columns with $1n$. Therefore, we have
+
+$$
+\begin{aligned}
+\left(r_{1}+1\right)\left(r_{2}+1\right) \cdots\left(r_{t}+1\right) & =k l \leqslant l^{2}<\left(\frac{\sigma(n)}{n}\right)^{2} \\
+& =\left(1+\frac{1}{p_{1}}+\cdots+\frac{1}{p_{1}^{r_{1}}}\right)^{2} \cdots\left(1+\frac{1}{p_{t}}+\cdots+\frac{1}{p_{t}^{r_{t}}}\right)^{2}
+\end{aligned}
+$$
+
+This can be rewritten as
+
+$$
+f\left(p_{1}, r_{1}\right) f\left(p_{2}, r_{2}\right) \cdots f\left(p_{t}, r_{t}\right)<1
+$$
+
+where
+
+$$
+f(p, r)=\frac{r+1}{\left(1+\frac{1}{p}+\cdots+\frac{1}{p^{r}}\right)^{2}}=\frac{(r+1)\left(1-\frac{1}{p}\right)^{2}}{\left(1-\frac{1}{p^{r+1}}\right)^{2}}
+$$
+
+Direct computation yields
+
+$$
+f(2,1)=\frac{8}{9}, \quad f(2,2)=\frac{48}{49}, \quad f(3,1)=\frac{9}{8} .
+$$
+
+Also, we find that
+
+$$
+\begin{aligned}
+& f(2, r) \geqslant\left(1-\frac{1}{2^{r+1}}\right)^{-2}>1 \quad \text { for } r \geqslant 3 \\
+& f(3, r) \geqslant \frac{4}{3}\left(1-\frac{1}{3^{r+1}}\right)^{-2}>\frac{4}{3}>\frac{9}{8} \quad \text { for } r \geqslant 2, \text { and } \\
+& f(p, r) \geqslant \frac{32}{25}\left(1-\frac{1}{p^{r+1}}\right)^{-2}>\frac{32}{25}>\frac{9}{8} \quad \text { for } p \geqslant 5
+\end{aligned}
+$$
+
+From these values and bounds, it is clear that (3) holds only when $n=2$ or 4 . In both cases, it is easy to see that the conditions are not satisfied. Hence, the only possible $n$ is 1 .
+
+C3. Let $n$ be a positive integer relatively prime to 6 . We paint the vertices of a regular $n$-gon with three colours so that there is an odd number of vertices of each colour. Show that there exists an isosceles triangle whose three vertices are of different colours.
+
+Solution. For $k=1,2,3$, let $a_{k}$ be the number of isosceles triangles whose vertices contain exactly $k$ colours. Suppose on the contrary that $a_{3}=0$. Let $b, c, d$ be the number of vertices of the three different colours respectively. We now count the number of pairs $(\triangle, E)$ where $\triangle$ is an isosceles triangle and $E$ is a side of $\triangle$ whose endpoints are of different colours.
+
+On the one hand, since we have assumed $a_{3}=0$, each triangle in the pair must contain exactly two colours, and hence each triangle contributes twice. Thus the number of pairs is $2 a_{2}$ 。
+
+On the other hand, if we pick any two vertices $A, B$ of distinct colours, then there are three isosceles triangles having these as vertices, two when $A B$ is not the base and one when $A B$ is the base since $n$ is odd. Note that the three triangles are all distinct as $(n, 3)=1$. In this way, we count the number of pairs to be $3(b c+c d+d b)$. However, note that $2 a_{2}$ is even while $3(b c+c d+d b)$ is odd, as each of $b, c, d$ is. This yields a contradiction and hence $a_{3} \geqslant 1$.
+
+Comment. A slightly stronger version of this problem is to replace the condition $(n, 6)=1$ by $n$ being odd (where equilateral triangles are regarded as isosceles triangles). In that case, the only difference in the proof is that by fixing any two vertices $A, B$, one can find exactly one or three isosceles triangles having these as vertices. But since only parity is concerned in the solution, the proof goes the same way.
+
+The condition that there is an odd number of vertices of each colour is necessary, as can be seen from the following example. Consider $n=25$ and we label the vertices $A_{0}, A_{1}, \ldots, A_{24}$. Suppose colour 1 is used for $A_{0}$, colour 2 is used for $A_{5}, A_{10}, A_{15}, A_{20}$, while colour 3 is used for the remaining vertices. Then any isosceles triangle having colours 1 and 2 must contain $A_{0}$ and one of $A_{5}, A_{10}, A_{15}, A_{20}$. Clearly, the third vertex must have index which is a multiple of 5 so it is not of colour 3 .
+
+C4. Find all positive integers $n$ for which we can fill in the entries of an $n \times n$ table with the following properties:
+
+- each entry can be one of $I, M$ and $O$;
+- in each row and each column, the letters $I, M$ and $O$ occur the same number of times; and
+- in any diagonal whose number of entries is a multiple of three, the letters $I, M$ and $O$ occur the same number of times.
+
+Answer. $n$ can be any multiple of 9 .
+Solution. We first show that such a table exists when $n$ is a multiple of 9 . Consider the following $9 \times 9$ table.
+
+$$
+\left(\begin{array}{ccccccccc}
+I & I & I & M & M & M & O & O & O \\
+M & M & M & O & O & O & I & I & I \\
+O & O & O & I & I & I & M & M & M \\
+I & I & I & M & M & M & O & O & O \\
+M & M & M & O & O & O & I & I & I \\
+O & O & O & I & I & I & M & M & M \\
+I & I & I & M & M & M & O & O & O \\
+M & M & M & O & O & O & I & I & I \\
+O & O & O & I & I & I & M & M & M
+\end{array}\right)
+$$
+
+It is a direct checking that the table (1) satisfies the requirements. For $n=9 k$ where $k$ is a positive integer, we form an $n \times n$ table using $k \times k$ copies of (1). For each row and each column of the table of size $n$, since there are three $I$ 's, three $M$ 's and three $O$ 's for any nine consecutive entries, the numbers of $I, M$ and $O$ are equal. In addition, every diagonal of the large table whose number of entries is divisible by 3 intersects each copy of (1) at a diagonal with number of entries divisible by 3 (possibly zero). Therefore, every such diagonal also contains the same number of $I, M$ and $O$.
+
+Next, consider any $n \times n$ table for which the requirements can be met. As the number of entries of each row should be a multiple of 3 , we let $n=3 k$ where $k$ is a positive integer. We divide the whole table into $k \times k$ copies of $3 \times 3$ blocks. We call the entry at the centre of such a $3 \times 3$ square a vital entry. We also call any row, column or diagonal that contains at least one vital entry a vital line. We compute the number of pairs $(l, c)$ where $l$ is a vital line and $c$ is an entry belonging to $l$ that contains the letter $M$. We let this number be $N$.
+
+On the one hand, since each vital line contains the same number of $I, M$ and $O$, it is obvious that each vital row and each vital column contain $k$ occurrences of $M$. For vital diagonals in either direction, we count there are exactly
+
+$$
+1+2+\cdots+(k-1)+k+(k-1)+\cdots+2+1=k^{2}
+$$
+
+occurrences of $M$. Therefore, we have $N=4 k^{2}$.
+
+On the other hand, there are $3 k^{2}$ occurrences of $M$ in the whole table. Note that each entry belongs to exactly 1 or 4 vital lines. Therefore, $N$ must be congruent to $3 k^{2} \bmod 3$.
+
+From the double counting, we get $4 k^{2} \equiv 3 k^{2}(\bmod 3)$, which forces $k$ to be a multiple of 3. Therefore, $n$ has to be a multiple of 9 and the proof is complete.
+
+C5. Let $n \geqslant 3$ be a positive integer. Find the maximum number of diagonals of a regular $n$-gon one can select, so that any two of them do not intersect in the interior or they are perpendicular to each other.
+
+Answer. $n-2$ if $n$ is even and $n-3$ if $n$ is odd.
+
+Solution 1. We consider two cases according to the parity of $n$.
+
+- Case 1. $n$ is odd.
+
+We first claim that no pair of diagonals is perpendicular. Suppose $A, B, C, D$ are vertices where $A B$ and $C D$ are perpendicular, and let $E$ be the vertex lying on the perpendicular bisector of $A B$. Let $E^{\prime}$ be the opposite point of $E$ on the circumcircle of the regular polygon. Since $E C=E^{\prime} D$ and $C, D, E$ are vertices of the regular polygon, $E^{\prime}$ should also belong to the polygon. This contradicts the fact that a regular polygon with an odd number of vertices does not contain opposite points on the circumcircle.
+
+
+Therefore in the odd case we can only select diagonals which do not intersect. In the maximal case these diagonals should divide the regular $n$-gon into $n-2$ triangles, so we can select at most $n-3$ diagonals. This can be done, for example, by selecting all diagonals emanated from a particular vertex.
+
+- Case 2. $n$ is even.
+
+If there is no intersection, then the proof in the odd case works. Suppose there are two perpendicular diagonals selected. We consider the set $S$ of all selected diagonals parallel to one of them which intersect with some selected diagonals. Suppose $S$ contains $k$ diagonals and the number of distinct endpoints of the $k$ diagonals is $l$.
+
+Firstly, consider the longest diagonal in one of the two directions in $S$. No other diagonal in $S$ can start from either endpoint of that diagonal, since otherwise it has to meet another longer diagonal in $S$. The same holds true for the other direction. Ignoring these two longest diagonals and their four endpoints, the remaining $k-2$ diagonals share $l-4$ endpoints where each endpoint can belong to at most two diagonals. This gives $2(l-4) \geqslant 2(k-2)$, so that $k \leqslant l-2$.
+
+
+Consider a group of consecutive vertices of the regular $n$-gon so that each of the two outermost vertices is an endpoint of a diagonal in $S$, while the interior points are not. There are $l$ such groups. We label these groups $P_{1}, P_{2}, \ldots, P_{l}$ in this order. We claim that each selected diagonal outside $S$ must connect vertices of the same group $P_{i}$. Consider any diagonal $d$ joining vertices from distinct groups $P_{i}$ and $P_{j}$. Let $d_{1}$ and $d_{2}$ be two diagonals in $S$ each having one of the outermost points of $P_{i}$ as endpoint. Then $d$ must meet either $d_{1}, d_{2}$ or a diagonal in $S$ which is perpendicular to both $d_{1}$ and $d_{2}$. In any case $d$ should belong to $S$ by definition, which is a contradiction.
+
+Within the same group $P_{i}$, there are no perpendicular diagonals since the vertices belong to the same side of a diameter of the circumcircle. Hence there can be at most $\left|P_{i}\right|-2$ selected diagonals within $P_{i}$, including the one joining the two outermost points of $P_{i}$ when $\left|P_{i}\right|>2$. Therefore, the maximum number of diagonals selected is
+
+$$
+\sum_{i=1}^{l}\left(\left|P_{i}\right|-2\right)+k=\sum_{i=1}^{l}\left|P_{i}\right|-2 l+k=(n+l)-2 l+k=n-l+k \leqslant n-2
+$$
+
+This upper bound can be attained as follows. We take any vertex $A$ and let $A^{\prime}$ be the vertex for which $A A^{\prime}$ is a diameter of the circumcircle. If we select all diagonals emanated from $A$ together with the diagonal $d^{\prime}$ joining the two neighbouring vertices of $A^{\prime}$, then the only pair of diagonals that meet each other is $A A^{\prime}$ and $d^{\prime}$, which are perpendicular to each other. In total we can take $n-2$ diagonals.
+
+
+Solution 2. The constructions and the odd case are the same as Solution 1. Instead of dealing separately with the case where $n$ is even, we shall prove by induction more generally that we can select at most $n-2$ diagonals for any cyclic $n$-gon with circumcircle $\Gamma$.
+
+The base case $n=3$ is trivial since there is no diagonal at all. Suppose the upper bound holds for any cyclic polygon with fewer than $n$ sides. For a cyclic $n$-gon, if there is a selected diagonal which does not intersect any other selected diagonal, then this diagonal divides the $n$-gon into an $m$-gon and an $l$-gon (with $m+l=n+2$ ) so that each selected diagonal belongs to one of them. Without loss of generality, we may assume the $m$-gon lies on the same side of a diameter of $\Gamma$. Then no two selected diagonals of the $m$-gon can intersect, and hence we can select at most $m-3$ diagonals. Also, we can apply the inductive hypothesis to the $l$-gon. This shows the maximum number of selected diagonals is $(m-3)+(l-2)+1=n-2$.
+
+It remains to consider the case when all selected diagonals meet at least one other selected diagonal. Consider a pair of selected perpendicular diagonals $d_{1}, d_{2}$. They divide the circumference of $\Gamma$ into four arcs, each of which lies on the same side of a diameter of $\Gamma$. If there are two selected diagonals intersecting each other and neither is parallel to $d_{1}$ or $d_{2}$, then their endpoints must belong to the same arc determined by $d_{1}, d_{2}$, and hence they cannot be perpendicular. This violates the condition, and hence all selected diagonals must have the same direction as one of $d_{1}, d_{2}$.
+
+
+Take the longest selected diagonal in one of the two directions. We argue as in Solution 1 that its endpoints do not belong to any other selected diagonal. The same holds true for the longest diagonal in the other direction. Apart from these four endpoints, each of the remaining $n-4$ vertices can belong to at most two selected diagonals. Thus we can select at most $\frac{1}{2}(2(n-4)+4)=n-2$ diagonals. Then the proof follows by induction.
+
+C6. There are $n \geqslant 3$ islands in a city. Initially, the ferry company offers some routes between some pairs of islands so that it is impossible to divide the islands into two groups such that no two islands in different groups are connected by a ferry route.
+
+After each year, the ferry company will close a ferry route between some two islands $X$ and $Y$. At the same time, in order to maintain its service, the company will open new routes according to the following rule: for any island which is connected by a ferry route to exactly one of $X$ and $Y$, a new route between this island and the other of $X$ and $Y$ is added.
+
+Suppose at any moment, if we partition all islands into two nonempty groups in any way, then it is known that the ferry company will close a certain route connecting two islands from the two groups after some years. Prove that after some years there will be an island which is connected to all other islands by ferry routes.
+
+Solution. Initially, we pick any pair of islands $A$ and $B$ which are connected by a ferry route and put $A$ in set $\mathcal{A}$ and $B$ in set $\mathcal{B}$. From the condition, without loss of generality there must be another island which is connected to $A$. We put such an island $C$ in set $\mathcal{B}$. We say that two sets of islands form a network if each island in one set is connected to each island in the other set.
+
+Next, we shall included all islands to $\mathcal{A} \cup \mathcal{B}$ one by one. Suppose we have two sets $\mathcal{A}$ and $\mathcal{B}$ which form a network where $3 \leqslant|\mathcal{A} \cup \mathcal{B}|\angle C B A$. This shows $S$ and $O_{1}$ lie on different sides of $X Y$. As $S^{\prime}$ lies on ray $S O_{1}$, it follows that $S$ and $S^{\prime}$ cannot lie on the same side of $X Y$. Therefore, $S$ and $S^{\prime}$ are symmetric with respect to $X Y$.
+
+Let $d$ be the diameter of the circumcircle of triangle $X S Y$. As $S S^{\prime}$ is twice the distance from $S$ to $X Y$ and $S X=S Y$, we have $S S^{\prime}=2 \frac{S X^{2}}{d}$. It follows from (1) that $d=2 S O_{1}$. As $S O_{1}$ is the perpendicular bisector of $X Y$, point $O_{1}^{d}$ is the circumcentre of triangle $X S Y$.
+
+Solution 2. Denote the orthocentre and circumcentre of triangle $A B C$ by $H$ and $O$ respectively. Let $O_{1}$ be the circumcentre of triangle $X S Y$. Consider two other possible positions of $S$. We name them $S^{\prime}$ and $S^{\prime \prime}$ and define the analogous points $X^{\prime}, Y^{\prime}, O_{1}^{\prime}, X^{\prime \prime}, Y^{\prime \prime} O_{1}^{\prime \prime}$ accordingly. Note that $S, S^{\prime}, S^{\prime \prime}$ lie on the perpendicular bisector of $A D$.
+
+As $X X^{\prime}$ and $Y Y^{\prime}$ meet at $A$ and the circumcircles of triangles $A X Y$ and $A X^{\prime} Y^{\prime}$ meet at $D$, there is a spiral similarity with centre $D$ mapping $X Y$ to $X^{\prime} Y^{\prime}$. We find that
+
+$$
+\measuredangle S X Y=\frac{\pi}{2}-\measuredangle Y A X=\frac{\pi}{2}-\measuredangle Y^{\prime} A X^{\prime}=\measuredangle S^{\prime} X^{\prime} Y^{\prime}
+$$
+
+and similarly $\measuredangle S Y X=\measuredangle S^{\prime} Y^{\prime} X^{\prime}$. This shows triangles $S X Y$ and $S^{\prime} X^{\prime} Y^{\prime}$ are directly similar. Then the spiral similarity with centre $D$ takes points $S, X, Y, O_{1}$ to $S^{\prime}, X^{\prime}, Y^{\prime}, O_{1}^{\prime}$. Similarly, there is a spiral similarity with centre $D$ mapping $S, X, Y, O_{1}$ to $S^{\prime \prime}, X^{\prime \prime}, Y^{\prime \prime}, O_{1}^{\prime \prime}$. From these, we see that there is a spiral similarity taking the corresponding points $S, S^{\prime}, S^{\prime \prime}$ to points $O_{1}, O_{1}^{\prime}, O_{1}^{\prime \prime}$. In particular, $O_{1}, O_{1}^{\prime}, O_{1}^{\prime \prime}$ are collinear.
+
+
+It now suffices to show that $O_{1}$ lies on the perpendicular bisector of $P M$ for two special cases.
+
+Firstly, we take $S$ to be the midpoint of $A H$. Then $X$ and $Y$ are the feet of altitudes from $C$ and $B$ respectively. It is well-known that the circumcircle of triangle $X S Y$ is the nine-point circle of triangle $A B C$. Then $O_{1}$ is the nine-point centre and $O_{1} P=O_{1} M$. Indeed, $P$ and $M$ also lies on the nine-point circle.
+
+Secondly, we take $S^{\prime}$ to be the midpoint of $A O$. Then $X^{\prime}$ and $Y^{\prime}$ are the midpoints of $A B$ and $A C$ respectively. Then $X^{\prime} Y^{\prime} / / B C$. Clearly, $S^{\prime}$ lies on the perpendicular bisector of $P M$. This shows the perpendicular bisectors of $X^{\prime} Y^{\prime}$ and $P M$ coincide. Hence, we must have $O_{1}^{\prime} P=O_{1}^{\prime} M$.
+
+
+G6. Let $A B C D$ be a convex quadrilateral with $\angle A B C=\angle A D C<90^{\circ}$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $E$ and $F$ respectively, and meet each other at point $P$. Let $M$ be the midpoint of $A C$ and let $\omega$ be the circumcircle of triangle $B P D$. Segments $B M$ and $D M$ intersect $\omega$ again at $X$ and $Y$ respectively. Denote by $Q$ the intersection point of lines $X E$ and $Y F$. Prove that $P Q \perp A C$.
+
+## Solution 1.
+
+
+
+Let $\omega_{1}$ be the circumcircle of triangle $A B C$. We first prove that $Y$ lies on $\omega_{1}$. Let $Y^{\prime}$ be the point on ray $M D$ such that $M Y^{\prime} \cdot M D=M A^{2}$. Then triangles $M A Y^{\prime}$ and $M D A$ are oppositely similar. Since $M C^{2}=M A^{2}=M Y^{\prime} \cdot M D$, triangles $M C Y^{\prime}$ and $M D C$ are also oppositely similar. Therefore, using directed angles, we have
+
+$$
+\measuredangle A Y^{\prime} C=\measuredangle A Y^{\prime} M+\measuredangle M Y^{\prime} C=\measuredangle M A D+\measuredangle D C M=\measuredangle C D A=\measuredangle A B C
+$$
+
+so that $Y^{\prime}$ lies on $\omega_{1}$.
+Let $Z$ be the intersection point of lines $B C$ and $A D$. Since $\measuredangle P D Z=\measuredangle P B C=\measuredangle P B Z$, point $Z$ lies on $\omega$. In addition, from $\measuredangle Y^{\prime} B Z=\measuredangle Y^{\prime} B C=\measuredangle Y^{\prime} A C=\measuredangle Y^{\prime} A M=\measuredangle Y^{\prime} D Z$, we also know that $Y^{\prime}$ lies on $\omega$. Note that $\angle A D C$ is acute implies $M A \neq M D$ so $M Y^{\prime} \neq M D$. Therefore, $Y^{\prime}$ is the second intersection of $D M$ and $\omega$. Then $Y^{\prime}=Y$ and hence $Y$ lies on $\omega_{1}$.
+
+Next, by the Angle Bisector Theorem and the similar triangles, we have
+
+$$
+\frac{F A}{F C}=\frac{A D}{C D}=\frac{A D}{A M} \cdot \frac{C M}{C D}=\frac{Y A}{Y M} \cdot \frac{Y M}{Y C}=\frac{Y A}{Y C}
+$$
+
+Hence, $F Y$ is the internal angle bisector of $\angle A Y C$.
+Let $B^{\prime}$ be the second intersection of the internal angle bisector of $\angle C B A$ and $\omega_{1}$. Then $B^{\prime}$ is the midpoint of arc $A C$ not containing $B$. Therefore, $Y B^{\prime}$ is the external angle bisector of $\angle A Y C$, so that $B^{\prime} Y \perp F Y$.
+
+Denote by $l$ the line through $P$ parallel to $A C$. Suppose $l$ meets line $B^{\prime} Y$ at $S$. From
+
+$$
+\begin{aligned}
+\measuredangle P S Y & =\measuredangle\left(A C, B^{\prime} Y\right)=\measuredangle A C Y+\measuredangle C Y B^{\prime}=\measuredangle A C Y+\measuredangle C A B^{\prime}=\measuredangle A C Y+\measuredangle B^{\prime} C A \\
+& =\measuredangle B^{\prime} C Y=\measuredangle B^{\prime} B Y=\measuredangle P B Y
+\end{aligned}
+$$
+
+the point $S$ lies on $\omega$. Similarly, the line through $X$ perpendicular to $X E$ also passes through the second intersection of $l$ and $\omega$, which is the point $S$. From $Q Y \perp Y S$ and $Q X \perp X S$, point $Q$ lies on $\omega$ and $Q S$ is a diameter of $\omega$. Therefore, $P Q \perp P S$ so that $P Q \perp A C$.
+
+Solution 2. Denote by $\omega_{1}$ and $\omega_{2}$ the circumcircles of triangles $A B C$ and $A D C$ respectively. Since $\angle A B C=\angle A D C$, we know that $\omega_{1}$ and $\omega_{2}$ are symmetric with respect to the midpoint $M$ of $A C$.
+
+Firstly, we show that $X$ lies on $\omega_{2}$. Let $X_{1}$ be the second intersection of ray $M B$ and $\omega_{2}$ and $X^{\prime}$ be its symmetric point with respect to $M$. Then $X^{\prime}$ lies on $\omega_{1}$ and $X^{\prime} A X_{1} C$ is a parallelogram. Hence, we have
+
+$$
+\begin{aligned}
+\measuredangle D X_{1} B & =\measuredangle D X_{1} A+\measuredangle A X_{1} B=\measuredangle D C A+\measuredangle A X_{1} X^{\prime}=\measuredangle D C A+\measuredangle C X^{\prime} X_{1} \\
+& =\measuredangle D C A+\measuredangle C A B=\measuredangle(C D, A B) .
+\end{aligned}
+$$
+
+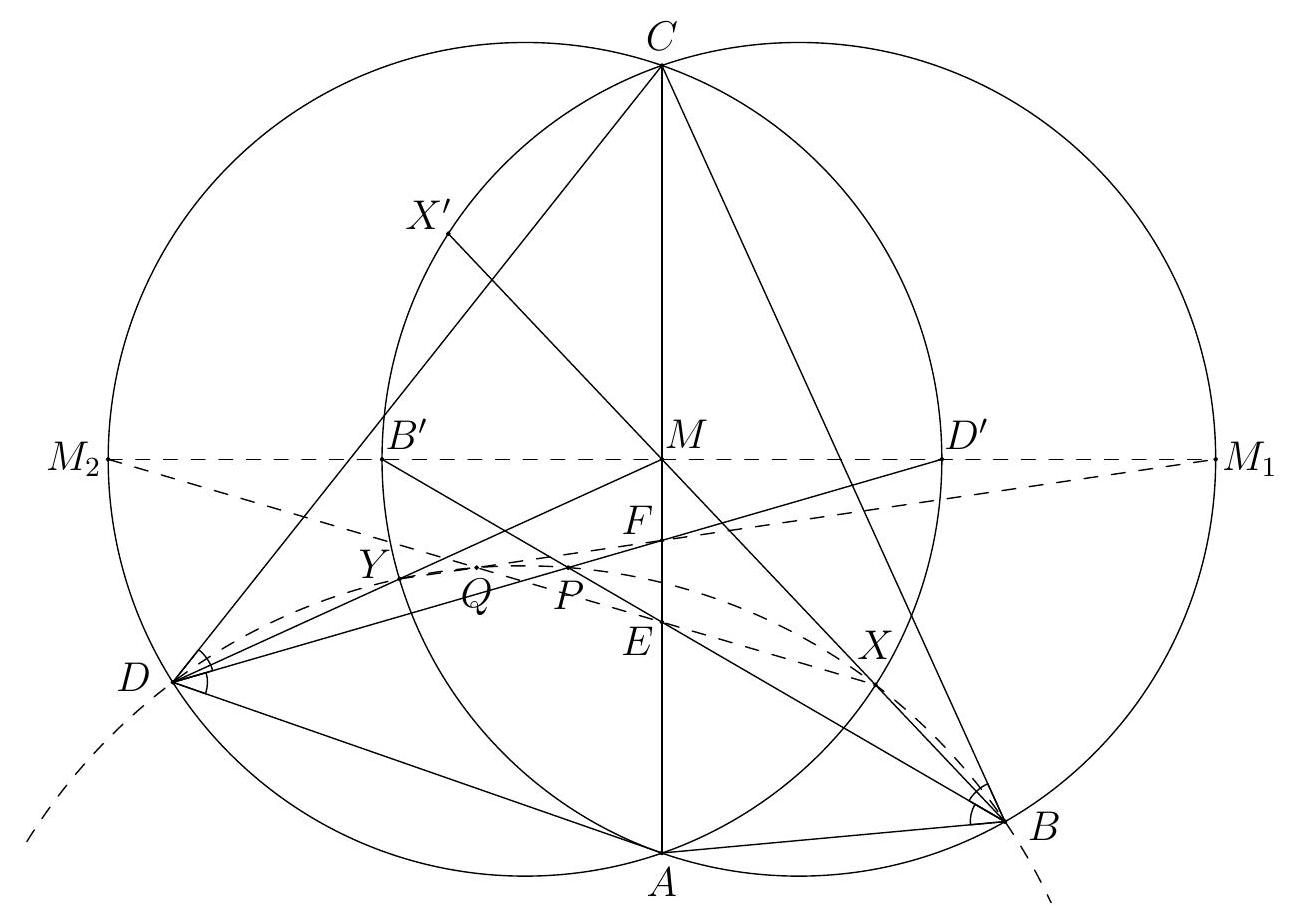
+
+Also, we have
+
+$$
+\measuredangle D P B=\measuredangle P D C+\angle(C D, A B)+\measuredangle A B P=\angle(C D, A B) .
+$$
+
+These yield $\measuredangle D X_{1} B=\measuredangle D P B$ and hence $X_{1}$ lies on $\omega$. It follows that $X_{1}=X$ and $X$ lies on $\omega_{2}$. Similarly, $Y$ lies on $\omega_{1}$.
+
+Next, we prove that $Q$ lies on $\omega$. Suppose the perpendicular bisector of $A C$ meet $\omega_{1}$ at $B^{\prime}$ and $M_{1}$ and meet $\omega_{2}$ at $D^{\prime}$ and $M_{2}$, so that $B, M_{1}$ and $D^{\prime}$ lie on the same side of $A C$. Note that $B^{\prime}$ lies on the angle bisector of $\angle A B C$ and similarly $D^{\prime}$ lies on $D P$.
+
+If we denote the area of $W_{1} W_{2} W_{3}$ by $\left[W_{1} W_{2} W_{3}\right]$, then
+
+$$
+\frac{B A \cdot X^{\prime} A}{B C \cdot X^{\prime} C}=\frac{\frac{1}{2} B A \cdot X^{\prime} A \sin \angle B A X^{\prime}}{\frac{1}{2} B C \cdot X^{\prime} C \sin \angle B C X^{\prime}}=\frac{\left[B A X^{\prime}\right]}{\left[B C X^{\prime}\right]}=\frac{M A}{M C}=1
+$$
+
+As $B E$ is the angle bisector of $\angle A B C$, we have
+
+$$
+\frac{E A}{E C}=\frac{B A}{B C}=\frac{X^{\prime} C}{X^{\prime} A}=\frac{X A}{X C}
+$$
+
+Therefore, $X E$ is the angle bisector of $\angle A X C$, so that $M_{2}$ lies on the line joining $X, E, Q$. Analogously, $M_{1}, F, Q, Y$ are collinear. Thus,
+
+$$
+\begin{aligned}
+\measuredangle X Q Y & =\measuredangle M_{2} Q M_{1}=\measuredangle Q M_{2} M_{1}+\measuredangle M_{2} M_{1} Q=\measuredangle X M_{2} D^{\prime}+\measuredangle B^{\prime} M_{1} Y \\
+& =\measuredangle X D D^{\prime}+\measuredangle B^{\prime} B Y=\measuredangle X D P+\measuredangle P B Y=\measuredangle X B P+\measuredangle P B Y=\measuredangle X B Y,
+\end{aligned}
+$$
+
+which implies $Q$ lies on $\omega$.
+Finally, as $M_{1}$ and $M_{2}$ are symmetric with respect to $M$, the quadrilateral $X^{\prime} M_{2} X M_{1}$ is a parallelogram. Consequently,
+
+$$
+\measuredangle X Q P=\measuredangle X B P=\measuredangle X^{\prime} B B^{\prime}=\measuredangle X^{\prime} M_{1} B^{\prime}=\measuredangle X M_{2} M_{1} .
+$$
+
+This shows $Q P / / M_{2} M_{1}$. As $M_{2} M_{1} \perp A C$, we get $Q P \perp A C$.
+Solution 3. We first state two results which will be needed in our proof.
+
+- Claim 1. In $\triangle X^{\prime} Y^{\prime} Z^{\prime}$ with $X^{\prime} Y^{\prime} \neq X^{\prime} Z^{\prime}$, let $N^{\prime}$ be the midpoint of $Y^{\prime} Z^{\prime}$ and $W^{\prime}$ be the foot of internal angle bisector from $X^{\prime}$. Then $\tan ^{2} \measuredangle W^{\prime} X^{\prime} Z^{\prime}=\tan \measuredangle N^{\prime} X^{\prime} W^{\prime} \tan \measuredangle Z^{\prime} W^{\prime} X^{\prime}$.
+
+Proof.
+
+
+Without loss of generality, assume $X^{\prime} Y^{\prime}>X^{\prime} Z^{\prime}$. Then $W^{\prime}$ lies between $N^{\prime}$ and $Z^{\prime}$. The signs of both sides agree so it suffices to establish the relation for ordinary angles. Let $\angle W^{\prime} X^{\prime} Z^{\prime}=\alpha, \angle N^{\prime} X^{\prime} W^{\prime}=\beta$ and $\angle Z^{\prime} W^{\prime} X^{\prime}=\gamma$. We have
+
+$$
+\frac{\sin (\gamma-\alpha)}{\sin (\alpha-\beta)}=\frac{N^{\prime} X^{\prime}}{N^{\prime} Y^{\prime}}=\frac{N^{\prime} X^{\prime}}{N^{\prime} Z^{\prime}}=\frac{\sin (\gamma+\alpha)}{\sin (\alpha+\beta)}
+$$
+
+This implies
+
+$$
+\frac{\tan \gamma-\tan \alpha}{\tan \gamma+\tan \alpha}=\frac{\sin \gamma \cos \alpha-\cos \gamma \sin \alpha}{\sin \gamma \cos \alpha+\cos \gamma \sin \alpha}=\frac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\sin \alpha \cos \beta+\cos \alpha \sin \beta}=\frac{\tan \alpha-\tan \beta}{\tan \alpha+\tan \beta}
+$$
+
+Expanding and simplifying, we get the desired result $\tan ^{2} \alpha=\tan \beta \tan \gamma$.
+
+- Claim 2. Let $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ be a quadrilateral inscribed in circle $\Gamma$. Let diagonals $A^{\prime} C^{\prime}$ and $B^{\prime} D^{\prime}$ meet at $E^{\prime}$, and $F^{\prime}$ be the intersection of lines $A^{\prime} B^{\prime}$ and $C^{\prime} D^{\prime}$. Let $M^{\prime}$ be the midpoint of $E^{\prime} F^{\prime}$. Then the power of $M^{\prime}$ with respect to $\Gamma$ is equal to $\left(M^{\prime} E^{\prime}\right)^{2}$.
+
+Proof.
+
+
+Let $O^{\prime}$ be the centre of $\Gamma$ and let $\Gamma^{\prime}$ be the circle with centre $M^{\prime}$ passing through $E^{\prime}$. Let $F_{1}$ be the inversion image of $F^{\prime}$ with respect to $\Gamma$. It is well-known that $E^{\prime}$ lies on the polar of $F^{\prime}$ with respect to $\Gamma$. This shows $E^{\prime} F_{1} \perp O^{\prime} F^{\prime}$ and hence $F_{1}$ lies on $\Gamma^{\prime}$. It follows that the inversion image of $\Gamma^{\prime}$ with respect to $\Gamma$ is $\Gamma^{\prime}$ itself. This shows $\Gamma^{\prime}$ is orthogonal to $\Gamma$, and thus the power of $M^{\prime}$ with respect to $\Gamma$ is the square of radius of $\Gamma^{\prime}$, which is $\left(M^{\prime} E^{\prime}\right)^{2}$.
+
+We return to the main problem. Let $Z$ be the intersection of lines $A D$ and $B C$, and $W$ be the intersection of lines $A B$ and $C D$. Since $\measuredangle P D Z=\measuredangle P B C=\measuredangle P B Z$, point $Z$ lies on $\omega$. Similarly, $W$ lies on $\omega$. Applying Claim 2 to the cyclic quadrilateral $Z B D W$, we know that the power of $M$ with respect to $\omega$ is $M A^{2}$. Hence, $M X \cdot M B=M A^{2}$.
+
+Suppose the line through $B$ perpendicular to $B E$ meets line $A C$ at $T$. Then $B E$ and $B T$ are the angle bisectors of $\angle C B A$. This shows $(T, E ; A, C)$ is harmonic. Thus, we have $M E \cdot M T=M A^{2}=M X \cdot M B$. It follows that $E, T, B, X$ are concyclic.
+
+
+The result is trivial for the special case $A D=C D$ since $P, Q$ lie on the perpendicular bisector of $A C$ in that case. Similarly, the case $A B=C B$ is trivial. It remains to consider the general cases where we can apply Claim 1 in the latter part of the proof.
+
+Let the projections from $P$ and $Q$ to $A C$ be $P^{\prime}$ and $Q^{\prime}$ respectively. Then $P Q \perp A C$ if and only if $P^{\prime}=Q^{\prime}$ if and only if $\frac{E P^{\prime}}{F P^{\prime}}=\frac{E Q^{\prime}}{F Q^{\prime}}$ in terms of directed lengths. Note that
+
+$$
+\frac{E P^{\prime}}{F P^{\prime}}=\frac{\tan \measuredangle E F P}{\tan \measuredangle F E P}=\frac{\tan \measuredangle A F D}{\tan \measuredangle A E B}
+$$
+
+Next, we have $\frac{E Q^{\prime}}{F Q^{\prime}}=\frac{\tan \measuredangle E F Q}{\tan \measuredangle F E Q}$ where $\measuredangle F E Q=\measuredangle T E X=\measuredangle T B X=\frac{\pi}{2}+\measuredangle E B M$ and by symmetry $\measuredangle E F Q=\frac{\pi}{2}+\measuredangle F D M$. Combining all these, it suffices to show
+
+$$
+\frac{\tan \measuredangle A F D}{\tan \measuredangle A E B}=\frac{\tan \measuredangle M B E}{\tan \measuredangle M D F}
+$$
+
+We now apply Claim 1 twice to get
+
+$$
+\tan \measuredangle A F D \tan \measuredangle M D F=\tan ^{2} \measuredangle F D C=\tan ^{2} \measuredangle E B A=\tan \measuredangle M B E \tan \measuredangle A E B .
+$$
+
+The result then follows.
+
+G7. Let $I$ be the incentre of a non-equilateral triangle $A B C, I_{A}$ be the $A$-excentre, $I_{A}^{\prime}$ be the reflection of $I_{A}$ in $B C$, and $l_{A}$ be the reflection of line $A I_{A}^{\prime}$ in $A I$. Define points $I_{B}, I_{B}^{\prime}$ and line $l_{B}$ analogously. Let $P$ be the intersection point of $l_{A}$ and $l_{B}$.
+(a) Prove that $P$ lies on line $O I$ where $O$ is the circumcentre of triangle $A B C$.
+(b) Let one of the tangents from $P$ to the incircle of triangle $A B C$ meet the circumcircle at points $X$ and $Y$. Show that $\angle X I Y=120^{\circ}$.
+
+## Solution 1.
+
+(a) Let $A^{\prime}$ be the reflection of $A$ in $B C$ and let $M$ be the second intersection of line $A I$ and the circumcircle $\Gamma$ of triangle $A B C$. As triangles $A B A^{\prime}$ and $A O C$ are isosceles with $\angle A B A^{\prime}=2 \angle A B C=\angle A O C$, they are similar to each other. Also, triangles $A B I_{A}$ and $A I C$ are similar. Therefore we have
+
+$$
+\frac{A A^{\prime}}{A I_{A}}=\frac{A A^{\prime}}{A B} \cdot \frac{A B}{A I_{A}}=\frac{A C}{A O} \cdot \frac{A I}{A C}=\frac{A I}{A O}
+$$
+
+Together with $\angle A^{\prime} A I_{A}=\angle I A O$, we find that triangles $A A^{\prime} I_{A}$ and $A I O$ are similar.
+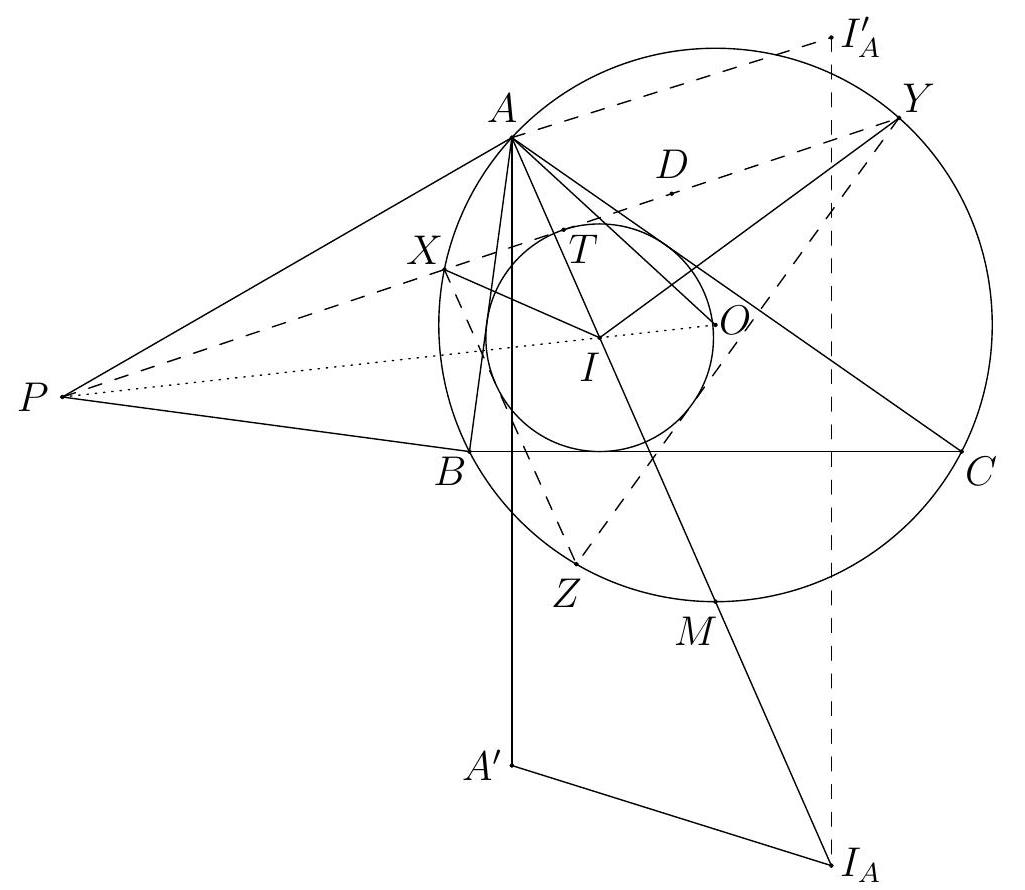
+
+Denote by $P^{\prime}$ the intersection of line $A P$ and line $O I$. Using directed angles, we have
+
+$$
+\begin{aligned}
+\measuredangle M A P^{\prime} & =\measuredangle I_{A}^{\prime} A I_{A}=\measuredangle I_{A}^{\prime} A A^{\prime}-\measuredangle I_{A} A A^{\prime}=\measuredangle A A^{\prime} I_{A}-\measuredangle(A M, O M) \\
+& =\measuredangle A I O-\measuredangle A M O=\measuredangle M O P^{\prime} .
+\end{aligned}
+$$
+
+This shows $M, O, A, P^{\prime}$ are concyclic.
+
+Denote by $R$ and $r$ the circumradius and inradius of triangle $A B C$. Then
+
+$$
+I P^{\prime}=\frac{I A \cdot I M}{I O}=\frac{I O^{2}-R^{2}}{I O}
+$$
+
+is independent of $A$. Hence, $B P$ also meets line $O I$ at the same point $P^{\prime}$ so that $P^{\prime}=P$, and $P$ lies on $O I$.
+(b) By Poncelet's Porism, the other tangents to the incircle of triangle $A B C$ from $X$ and $Y$ meet at a point $Z$ on $\Gamma$. Let $T$ be the touching point of the incircle to $X Y$, and let $D$ be the midpoint of $X Y$. We have
+
+$$
+\begin{aligned}
+O D & =I T \cdot \frac{O P}{I P}=r\left(1+\frac{O I}{I P}\right)=r\left(1+\frac{O I^{2}}{O I \cdot I P}\right)=r\left(1+\frac{R^{2}-2 R r}{R^{2}-I O^{2}}\right) \\
+& =r\left(1+\frac{R^{2}-2 R r}{2 R r}\right)=\frac{R}{2}=\frac{O X}{2}
+\end{aligned}
+$$
+
+This shows $\angle X Z Y=60^{\circ}$ and hence $\angle X I Y=120^{\circ}$.
+
+## Solution 2.
+
+(a) Note that triangles $A I_{B} C$ and $I_{A} B C$ are similar since their corresponding interior angles are equal. Therefore, the four triangles $A I_{B}^{\prime} C, A I_{B} C, I_{A} B C$ and $I_{A}^{\prime} B C$ are all similar. From $\triangle A I_{B}^{\prime} C \sim \triangle I_{A}^{\prime} B C$, we get $\triangle A I_{A}^{\prime} C \sim \triangle I_{B}^{\prime} B C$. From $\measuredangle A B P=\measuredangle I_{B}^{\prime} B C=\measuredangle A I_{A}^{\prime} C$ and $\measuredangle B A P=\measuredangle I_{A}^{\prime} A C$, the triangles $A B P$ and $A I_{A}^{\prime} C$ are directly similar.
+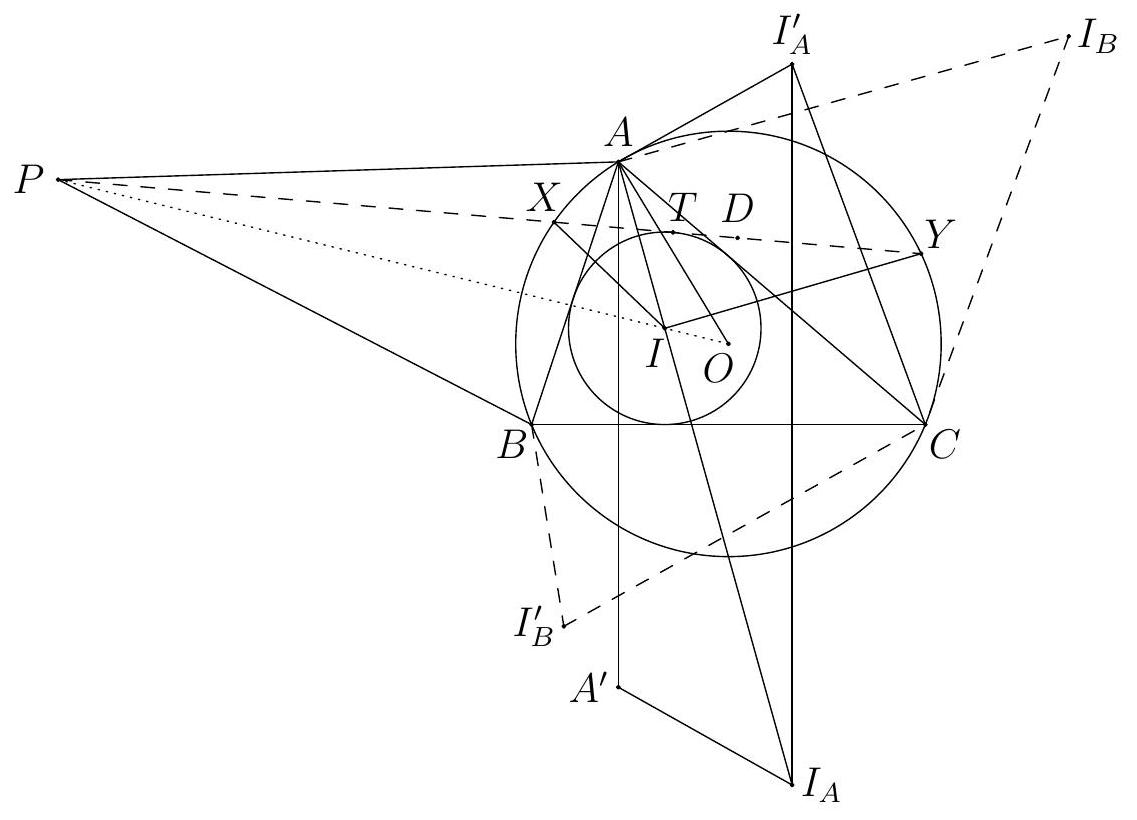
+
+Consider the inversion with centre $A$ and radius $\sqrt{A B \cdot A C}$ followed by the reflection in $A I$. Then $B$ and $C$ are mapped to each other, and $I$ and $I_{A}$ are mapped to each other.
+
+From the similar triangles obtained, we have $A P \cdot A I_{A}^{\prime}=A B \cdot A C$ so that $P$ is mapped to $I_{A}^{\prime}$ under the transformation. In addition, line $A O$ is mapped to the altitude from $A$, and hence $O$ is mapped to the reflection of $A$ in $B C$, which we call point $A^{\prime}$. Note that $A A^{\prime} I_{A} I_{A}^{\prime}$ is an isosceles trapezoid, which shows it is inscribed in a circle. The preimage of this circle is a straight line, meaning that $O, I, P$ are collinear.
+(b) Denote by $R$ and $r$ the circumradius and inradius of triangle $A B C$. Note that by the above transformation, we have $\triangle A P O \sim \triangle A A^{\prime} I_{A}^{\prime}$ and $\triangle A A^{\prime} I_{A} \sim \triangle A I O$. Therefore, we find that
+
+$$
+P O=A^{\prime} I_{A}^{\prime} \cdot \frac{A O}{A I_{A}^{\prime}}=A I_{A} \cdot \frac{A O}{A^{\prime} I_{A}}=\frac{A I_{A}}{A^{\prime} I_{A}} \cdot A O=\frac{A O}{I O} \cdot A O
+$$
+
+This shows $P O \cdot I O=R^{2}$, and it follows that $P$ and $I$ are mapped to each other under the inversion with respect to the circumcircle $\Gamma$ of triangle $A B C$. Then $P X \cdot P Y$, which is the power of $P$ with respect to $\Gamma$, equals $P I \cdot P O$. This yields $X, I, O, Y$ are concyclic.
+
+Let $T$ be the touching point of the incircle to $X Y$, and let $D$ be the midpoint of $X Y$. Then
+
+$$
+O D=I T \cdot \frac{P O}{P I}=r \cdot \frac{P O}{P O-I O}=r \cdot \frac{R^{2}}{R^{2}-I O^{2}}=r \cdot \frac{R^{2}}{2 R r}=\frac{R}{2}
+$$
+
+This shows $\angle D O X=60^{\circ}$ and hence $\angle X I Y=\angle X O Y=120^{\circ}$.
+Comment. A simplification of this problem is to ask part (a) only. Note that the question in part (b) implicitly requires $P$ to lie on $O I$, or otherwise the angle is not uniquely determined as we can find another tangent from $P$ to the incircle.
+
+G8. Let $A_{1}, B_{1}$ and $C_{1}$ be points on sides $B C, C A$ and $A B$ of an acute triangle $A B C$ respectively, such that $A A_{1}, B B_{1}$ and $C C_{1}$ are the internal angle bisectors of triangle $A B C$. Let $I$ be the incentre of triangle $A B C$, and $H$ be the orthocentre of triangle $A_{1} B_{1} C_{1}$. Show that
+
+$$
+A H+B H+C H \geqslant A I+B I+C I
+$$
+
+Solution. Without loss of generality, assume $\alpha=\angle B A C \leqslant \beta=\angle C B A \leqslant \gamma=\angle A C B$. Denote by $a, b, c$ the lengths of $B C, C A, A B$ respectively. We first show that triangle $A_{1} B_{1} C_{1}$ is acute.
+
+Choose points $D$ and $E$ on side $B C$ such that $B_{1} D / / A B$ and $B_{1} E$ is the internal angle bisector of $\angle B B_{1} C$. As $\angle B_{1} D B=180^{\circ}-\beta$ is obtuse, we have $B B_{1}>B_{1} D$. Thus,
+
+$$
+\frac{B E}{E C}=\frac{B B_{1}}{B_{1} C}>\frac{D B_{1}}{B_{1} C}=\frac{B A}{A C}=\frac{B A_{1}}{A_{1} C}
+$$
+
+Therefore, $B E>B A_{1}$ and $\frac{1}{2} \angle B B_{1} C=\angle B B_{1} E>\angle B B_{1} A_{1}$. Similarly, $\frac{1}{2} \angle B B_{1} A>\angle B B_{1} C_{1}$. It follows that
+
+$$
+\angle A_{1} B_{1} C_{1}=\angle B B_{1} A_{1}+\angle B B_{1} C_{1}<\frac{1}{2}\left(\angle B B_{1} C+\angle B B_{1} A\right)=90^{\circ}
+$$
+
+is acute. By symmetry, triangle $A_{1} B_{1} C_{1}$ is acute.
+Let $B B_{1}$ meet $A_{1} C_{1}$ at $F$. From $\alpha \leqslant \gamma$, we get $a \leqslant c$, which implies
+
+$$
+B A_{1}=\frac{c a}{b+c} \leqslant \frac{a c}{a+b}=B C_{1}
+$$
+
+and hence $\angle B C_{1} A_{1} \leqslant \angle B A_{1} C_{1}$. As $B F$ is the internal angle bisector of $\angle A_{1} B C_{1}$, this shows $\angle B_{1} F C_{1}=\angle B F A_{1} \leqslant 90^{\circ}$. Hence, $H$ lies on the same side of $B B_{1}$ as $C_{1}$. This shows $H$ lies inside triangle $B B_{1} C_{1}$. Similarly, from $\alpha \leqslant \beta$ and $\beta \leqslant \gamma$, we know that $H$ lies inside triangles $C C_{1} B_{1}$ and $A A_{1} C_{1}$.
+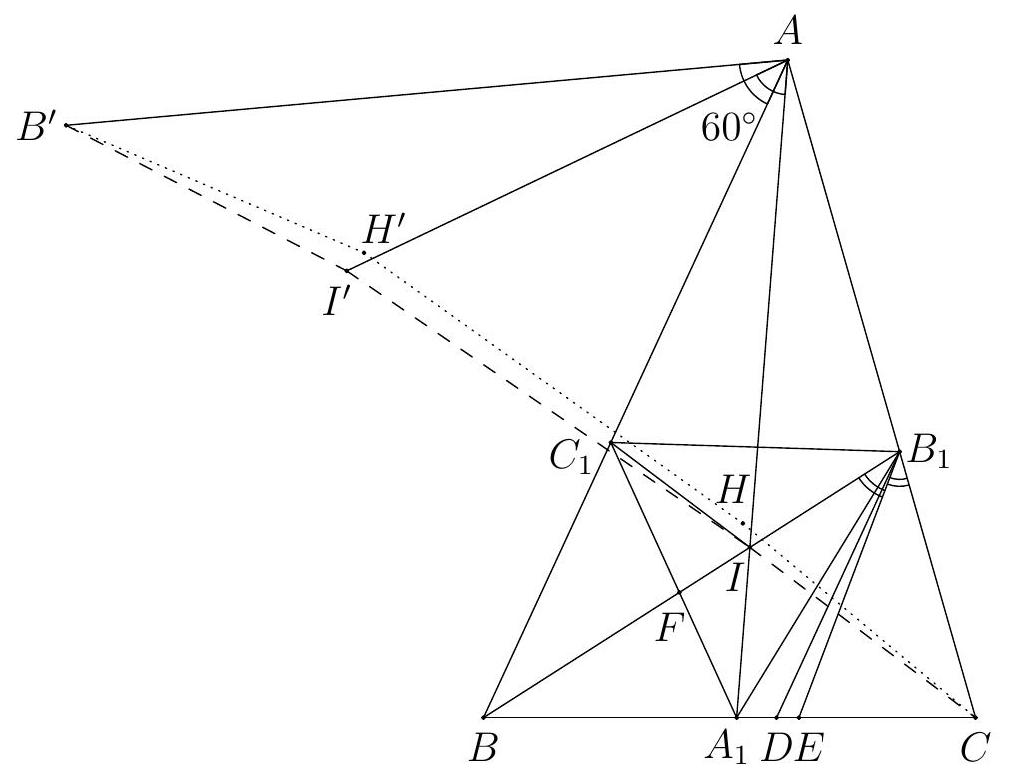
+
+As $\alpha \leqslant \beta \leqslant \gamma$, we have $\alpha \leqslant 60^{\circ} \leqslant \gamma$. Then $\angle B I C \leqslant 120^{\circ} \leqslant \angle A I B$. Firstly, suppose $\angle A I C \geqslant 120^{\circ}$.
+
+Rotate points $B, I, H$ through $60^{\circ}$ about $A$ to $B^{\prime}, I^{\prime}, H^{\prime}$ so that $B^{\prime}$ and $C$ lie on different sides of $A B$. Since triangle $A I^{\prime} I$ is equilateral, we have
+
+$$
+A I+B I+C I=I^{\prime} I+B^{\prime} I^{\prime}+I C=B^{\prime} I^{\prime}+I^{\prime} I+I C .
+$$
+
+Similarly,
+
+$$
+A H+B H+C H=H^{\prime} H+B^{\prime} H^{\prime}+H C=B^{\prime} H^{\prime}+H^{\prime} H+H C
+$$
+
+As $\angle A I I^{\prime}=\angle A I^{\prime} I=60^{\circ}, \angle A I^{\prime} B^{\prime}=\angle A I B \geqslant 120^{\circ}$ and $\angle A I C \geqslant 120^{\circ}$, the quadrilateral $B^{\prime} I^{\prime} I C$ is convex and lies on the same side of $B^{\prime} C$ as $A$.
+
+Next, since $H$ lies inside triangle $A C C_{1}, H$ lies outside $B^{\prime} I^{\prime} I C$. Also, $H$ lying inside triangle $A B I$ implies $H^{\prime}$ lies inside triangle $A B^{\prime} I^{\prime}$. This shows $H^{\prime}$ lies outside $B^{\prime} I^{\prime} I C$ and hence the convex quadrilateral $B^{\prime} I^{\prime} I C$ is contained inside the quadrilateral $B^{\prime} H^{\prime} H C$. It follows that the perimeter of $B^{\prime} I^{\prime} I C$ cannot exceed the perimeter of $B^{\prime} H^{\prime} H C$. From (1) and (2), we conclude that
+
+$$
+A H+B H+C H \geqslant A I+B I+C I
+$$
+
+For the case $\angle A I C<120^{\circ}$, we can rotate $B, I, H$ through $60^{\circ}$ about $C$ to $B^{\prime}, I^{\prime}, H^{\prime}$ so that $B^{\prime}$ and $A$ lie on different sides of $B C$. The proof is analogous to the previous case and we still get the desired inequality.
+
+## Number Theory
+
+N1. For any positive integer $k$, denote the sum of digits of $k$ in its decimal representation by $S(k)$. Find all polynomials $P(x)$ with integer coefficients such that for any positive integer $n \geqslant 2016$, the integer $P(n)$ is positive and
+
+$$
+S(P(n))=P(S(n))
+$$
+
+Answer.
+
+- $P(x)=c$ where $1 \leqslant c \leqslant 9$ is an integer; or
+- $P(x)=x$.
+
+Solution 1. We consider three cases according to the degree of $P$.
+
+- Case 1. $P(x)$ is a constant polynomial.
+
+Let $P(x)=c$ where $c$ is an integer constant. Then (1) becomes $S(c)=c$. This holds if and only if $1 \leqslant c \leqslant 9$.
+
+- Case 2. $\operatorname{deg} P=1$.
+
+We have the following observation. For any positive integers $m, n$, we have
+
+$$
+S(m+n) \leqslant S(m)+S(n)
+$$
+
+and equality holds if and only if there is no carry in the addition $m+n$.
+Let $P(x)=a x+b$ for some integers $a, b$ where $a \neq 0$. As $P(n)$ is positive for large $n$, we must have $a \geqslant 1$. The condition (1) becomes $S(a n+b)=a S(n)+b$ for all $n \geqslant 2016$. Setting $n=2025$ and $n=2020$ respectively, we get
+
+$$
+S(2025 a+b)-S(2020 a+b)=(a S(2025)+b)-(a S(2020)+b)=5 a
+$$
+
+On the other hand, (2) implies
+
+$$
+S(2025 a+b)=S((2020 a+b)+5 a) \leqslant S(2020 a+b)+S(5 a)
+$$
+
+These give $5 a \leqslant S(5 a)$. As $a \geqslant 1$, this holds only when $a=1$, in which case (1) reduces to $S(n+b)=S(n)+b$ for all $n \geqslant 2016$. Then we find that
+
+$$
+S(n+1+b)-S(n+b)=(S(n+1)+b)-(S(n)+b)=S(n+1)-S(n)
+$$
+
+If $b>0$, we choose $n$ such that $n+1+b=10^{k}$ for some sufficiently large $k$. Note that all the digits of $n+b$ are 9 's, so that the left-hand side of (3) equals $1-9 k$. As $n$ is a positive integer less than $10^{k}-1$, we have $S(n)<9 k$. Therefore, the right-hand side of (3) is at least $1-(9 k-1)=2-9 k$, which is a contradiction.
+
+The case $b<0$ can be handled similarly by considering $n+1$ to be a large power of 10 . Therefore, we conclude that $P(x)=x$, in which case (1) is trivially satisfied.
+
+- Case 3. $\operatorname{deg} P \geqslant 2$.
+
+Suppose the leading term of $P$ is $a_{d} n^{d}$ where $a_{d} \neq 0$. Clearly, we have $a_{d}>0$. Consider $n=10^{k}-1$ in (1). We get $S(P(n))=P(9 k)$. Note that $P(n)$ grows asymptotically as fast as $n^{d}$, so $S(P(n))$ grows asymptotically as no faster than a constant multiple of $k$. On the other hand, $P(9 k)$ grows asymptotically as fast as $k^{d}$. This shows the two sides of the last equation cannot be equal for sufficiently large $k$ since $d \geqslant 2$.
+
+Therefore, we conclude that $P(x)=c$ where $1 \leqslant c \leqslant 9$ is an integer, or $P(x)=x$.
+Solution 2. Let $P(x)=a_{d} x^{d}+a_{d-1} x^{d-1}+\cdots+a_{0}$. Clearly $a_{d}>0$. There exists an integer $m \geqslant 1$ such that $\left|a_{i}\right|<10^{m}$ for all $0 \leqslant i \leqslant d$. Consider $n=9 \times 10^{k}$ for a sufficiently large integer $k$ in (1). If there exists an index $0 \leqslant i \leqslant d-1$ such that $a_{i}<0$, then all digits of $P(n)$ in positions from $10^{i k+m+1}$ to $10^{(i+1) k-1}$ are all 9 's. Hence, we have $S(P(n)) \geqslant 9(k-m-1)$. On the other hand, $P(S(n))=P(9)$ is a fixed constant. Therefore, (1) cannot hold for large $k$. This shows $a_{i} \geqslant 0$ for all $0 \leqslant i \leqslant d-1$.
+
+Hence, $P(n)$ is an integer formed by the nonnegative integers $a_{d} \times 9^{d}, a_{d-1} \times 9^{d-1}, \ldots, a_{0}$ by inserting some zeros in between. This yields
+
+$$
+S(P(n))=S\left(a_{d} \times 9^{d}\right)+S\left(a_{d-1} \times 9^{d-1}\right)+\cdots+S\left(a_{0}\right) .
+$$
+
+Combining with (1), we have
+
+$$
+S\left(a_{d} \times 9^{d}\right)+S\left(a_{d-1} \times 9^{d-1}\right)+\cdots+S\left(a_{0}\right)=P(9)=a_{d} \times 9^{d}+a_{d-1} \times 9^{d-1}+\cdots+a_{0}
+$$
+
+As $S(m) \leqslant m$ for any positive integer $m$, with equality when $1 \leqslant m \leqslant 9$, this forces each $a_{i} \times 9^{i}$ to be a positive integer between 1 and 9 . In particular, this shows $a_{i}=0$ for $i \geqslant 2$ and hence $d \leqslant 1$. Also, we have $a_{1} \leqslant 1$ and $a_{0} \leqslant 9$. If $a_{1}=1$ and $1 \leqslant a_{0} \leqslant 9$, we take $n=10^{k}+\left(10-a_{0}\right)$ for sufficiently large $k$ in (1). This yields a contradiction since
+
+$$
+S(P(n))=S\left(10^{k}+10\right)=2 \neq 11=P\left(11-a_{0}\right)=P(S(n))
+$$
+
+The zero polynomial is also rejected since $P(n)$ is positive for large $n$. The remaining candidates are $P(x)=x$ or $P(x)=a_{0}$ where $1 \leqslant a_{0} \leqslant 9$, all of which satisfy (1), and hence are the only solutions.
+
+N2. Let $\tau(n)$ be the number of positive divisors of $n$. Let $\tau_{1}(n)$ be the number of positive divisors of $n$ which have remainders 1 when divided by 3 . Find all possible integral values of the fraction $\frac{\tau(10 n)}{\tau_{1}(10 n)}$.
+
+Answer. All composite numbers together with 2.
+Solution. In this solution, we always use $p_{i}$ to denote primes congruent to $1 \bmod 3$, and use $q_{j}$ to denote primes congruent to $2 \bmod 3$. When we express a positive integer $m$ using its prime factorization, we also include the special case $m=1$ by allowing the exponents to be zeros. We first compute $\tau_{1}(m)$ for a positive integer $m$.
+
+- Claim. Let $m=3^{x} p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{s}^{a_{s}} q_{1}^{b_{1}} q_{2}^{b_{2}} \cdots q_{t}^{b_{t}}$ be the prime factorization of $m$. Then
+
+$$
+\tau_{1}(m)=\prod_{i=1}^{s}\left(a_{i}+1\right)\left\lceil\frac{1}{2} \prod_{j=1}^{t}\left(b_{j}+1\right)\right\rceil .
+$$
+
+Proof. To choose a divisor of $m$ congruent to $1 \bmod 3$, it cannot have the prime divisor 3, while there is no restriction on choosing prime factors congruent to $1 \bmod 3$. Also, we have to choose an even number of prime factors (counted with multiplicity) congruent to $2 \bmod 3$.
+
+If $\prod_{j=1}^{t}\left(b_{j}+1\right)$ is even, then we may assume without loss of generality $b_{1}+1$ is even. We can choose the prime factors $q_{2}, q_{3}, \ldots, q_{t}$ freely in $\prod_{j=2}^{t}\left(b_{j}+1\right)$ ways. Then the parity of the number of $q_{1}$ is uniquely determined, and hence there are $\frac{1}{2}\left(b_{1}+1\right)$ ways to choose the exponent of $q_{1}$. Hence (1) is verified in this case.
+
+If $\prod_{j=1}^{t}\left(b_{j}+1\right)$ is odd, we use induction on $t$ to count the number of choices. When $t=1$, there are $\left\lceil\frac{b_{1}+1}{2}\right\rceil$ choices for which the exponent is even and $\left\lfloor\frac{b_{1}+1}{2}\right\rfloor$ choices for which the exponent is odd. For the inductive step, we find that there are
+
+$$
+\left\lceil\frac{1}{2} \prod_{j=1}^{t-1}\left(b_{j}+1\right)\right\rceil \cdot\left\lceil\frac{b_{t}+1}{2}\right\rceil+\left\lfloor\frac{1}{2} \prod_{j=1}^{t-1}\left(b_{j}+1\right)\right\rfloor \cdot\left\lfloor\frac{b_{t}+1}{2}\right\rfloor=\left\lceil\frac{1}{2} \prod_{j=1}^{t}\left(b_{j}+1\right)\right\rceil
+$$
+
+choices with an even number of prime factors and hence $\left\lfloor\frac{1}{2} \prod_{j=1}^{t}\left(b_{j}+1\right)\right\rfloor$ choices with an odd number of prime factors. Hence (1) is also true in this case.
+
+Let $n=3^{x} 2^{y} 5^{z} p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{s}^{a_{s}} q_{1}^{b_{1}} q_{2}^{b_{2}} \cdots q_{t}^{b_{t}}$. Using the well-known formula for computing the divisor function, we get
+
+$$
+\tau(10 n)=(x+1)(y+2)(z+2) \prod_{i=1}^{s}\left(a_{i}+1\right) \prod_{j=1}^{t}\left(b_{j}+1\right)
+$$
+
+By the Claim, we have
+
+$$
+\tau_{1}(10 n)=\prod_{i=1}^{s}\left(a_{i}+1\right)\left\lceil\frac{1}{2}(y+2)(z+2) \prod_{j=1}^{t}\left(b_{j}+1\right)\right\rceil
+$$
+
+If $c=(y+2)(z+2) \prod_{j=1}^{t}\left(b_{j}+1\right)$ is even, then (2) and (3) imply
+
+$$
+\frac{\tau(10 n)}{\tau_{1}(10 n)}=2(x+1)
+$$
+
+In this case $\frac{\tau(10 n)}{\tau_{1}(10 n)}$ can be any even positive integer as $x$ runs through all nonnegative integers.
+If $c$ is odd, which means $y, z$ are odd and each $b_{j}$ is even, then (2) and (3) imply
+
+$$
+\frac{\tau(10 n)}{\tau_{1}(10 n)}=\frac{2(x+1) c}{c+1}
+$$
+
+For this to be an integer, we need $c+1$ divides $2(x+1)$ since $c$ and $c+1$ are relatively prime. Let $2(x+1)=k(c+1)$. Then (4) reduces to
+
+$$
+\frac{\tau(10 n)}{\tau_{1}(10 n)}=k c=k(y+2)(z+2) \prod_{j=1}^{t}\left(b_{j}+1\right)
+$$
+
+Noting that $y, z$ are odd, the integers $y+2$ and $z+2$ are at least 3 . This shows the integer in this case must be composite. On the other hand, for any odd composite number $a b$ with $a, b \geqslant 3$, we may simply take $n=3^{\frac{a b-1}{2}} \cdot 2^{a-2} \cdot 5^{b-2}$ so that $\frac{\tau(10 n)}{\tau_{1}(10 n)}=a b$ from (5).
+
+We conclude that the fraction can be any even integer or any odd composite number. Equivalently, it can be 2 or any composite number.
+
+N3. Define $P(n)=n^{2}+n+1$. For any positive integers $a$ and $b$, the set
+
+$$
+\{P(a), P(a+1), P(a+2), \ldots, P(a+b)\}
+$$
+
+is said to be fragrant if none of its elements is relatively prime to the product of the other elements. Determine the smallest size of a fragrant set.
+
+Answer. 6.
+Solution. We have the following observations.
+(i) $(P(n), P(n+1))=1$ for any $n$.
+
+We have $(P(n), P(n+1))=\left(n^{2}+n+1, n^{2}+3 n+3\right)=\left(n^{2}+n+1,2 n+2\right)$. Noting that $n^{2}+n+1$ is odd and $\left(n^{2}+n+1, n+1\right)=(1, n+1)=1$, the claim follows.
+(ii) $(P(n), P(n+2))=1$ for $n \not \equiv 2(\bmod 7)$ and $(P(n), P(n+2))=7$ for $n \equiv 2(\bmod 7)$.
+
+From $(2 n+7) P(n)-(2 n-1) P(n+2)=14$ and the fact that $P(n)$ is odd, $(P(n), P(n+2))$ must be a divisor of 7 . The claim follows by checking $n \equiv 0,1, \ldots, 6(\bmod 7)$ directly.
+(iii) $(P(n), P(n+3))=1$ for $n \not \equiv 1(\bmod 3)$ and $3 \mid(P(n), P(n+3))$ for $n \equiv 1(\bmod 3)$.
+
+From $(n+5) P(n)-(n-1) P(n+3)=18$ and the fact that $P(n)$ is odd, $(P(n), P(n+3))$ must be a divisor of 9 . The claim follows by checking $n \equiv 0,1,2(\bmod 3)$ directly.
+
+Suppose there exists a fragrant set with at most 5 elements. We may assume it contains exactly 5 elements $P(a), P(a+1), \ldots, P(a+4)$ since the following argument also works with fewer elements. Consider $P(a+2)$. From (i), it is relatively prime to $P(a+1)$ and $P(a+3)$. Without loss of generality, assume $(P(a), P(a+2))>1$. From (ii), we have $a \equiv 2(\bmod 7)$. The same observation implies $(P(a+1), P(a+3))=1$. In order that the set is fragrant, $(P(a), P(a+3))$ and $(P(a+1), P(a+4))$ must both be greater than 1. From (iii), this holds only when both $a$ and $a+1$ are congruent to $1 \bmod 3$, which is a contradiction.
+
+It now suffices to construct a fragrant set of size 6. By the Chinese Remainder Theorem, we can take a positive integer $a$ such that
+
+$$
+a \equiv 7 \quad(\bmod 19), \quad a+1 \equiv 2 \quad(\bmod 7), \quad a+2 \equiv 1 \quad(\bmod 3)
+$$
+
+For example, we may take $a=197$. From (ii), both $P(a+1)$ and $P(a+3)$ are divisible by 7. From (iii), both $P(a+2)$ and $P(a+5)$ are divisible by 3 . One also checks from $19 \mid P(7)=57$ and $19 \mid P(11)=133$ that $P(a)$ and $P(a+4)$ are divisible by 19. Therefore, the set $\{P(a), P(a+1), \ldots, P(a+5)\}$ is fragrant.
+
+Therefore, the smallest size of a fragrant set is 6 .
+Comment. "Fragrant Harbour" is the English translation of "Hong Kong".
+A stronger version of this problem is to show that there exists a fragrant set of size $k$ for any $k \geqslant 6$. We present a proof here.
+
+For each even positive integer $m$ which is not divisible by 3 , since $m^{2}+3 \equiv 3(\bmod 4)$, we can find a prime $p_{m} \equiv 3(\bmod 4)$ such that $p_{m} \mid m^{2}+3$. Clearly, $p_{m}>3$.
+
+If $b=2 t \geqslant 6$, we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for each $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$. For $0 \leqslant r \leqslant t$ and $3 \mid r$, we have $a+t \pm r \equiv 1(\bmod 3)$ so that $3 \mid P(a+t \pm r)$. For $0 \leqslant r \leqslant t$ and $(r, 3)=1$, we have
+
+$$
+4 P(a+t \pm r) \equiv(-1 \pm 2 r)^{2}+2(-1 \pm 2 r)+4=4 r^{2}+3 \equiv 0 \quad\left(\bmod p_{2 r}\right) .
+$$
+
+Hence, $\{P(a), P(a+1), \ldots, P(a+b)\}$ is fragrant.
+If $b=2 t+1 \geqslant 7$ (the case $b=5$ has been done in the original problem), we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$, and that $a+b \equiv 9(\bmod 13)$. Note that $a$ exists by the Chinese Remainder Theorem since $p_{m} \neq 13$ for all $m$. The even case shows that $\{P(a), P(a+1), \ldots, P(a+b-1)\}$ is fragrant. Also, one checks from $13 \mid P(9)=91$ and $13 \mid P(3)=13$ that $P(a+b)$ and $P(a+b-6)$ are divisible by 13. The proof is thus complete.
+
+N4. Let $n, m, k$ and $l$ be positive integers with $n \neq 1$ such that $n^{k}+m n^{l}+1$ divides $n^{k+l}-1$. Prove that
+
+- $m=1$ and $l=2 k$; or
+- $l \mid k$ and $m=\frac{n^{k-l}-1}{n^{l}-1}$.
+
+Solution 1. It is given that
+
+$$
+n^{k}+m n^{l}+1 \mid n^{k+l}-1
+$$
+
+This implies
+
+$$
+n^{k}+m n^{l}+1 \mid\left(n^{k+l}-1\right)+\left(n^{k}+m n^{l}+1\right)=n^{k+l}+n^{k}+m n^{l} .
+$$
+
+We have two cases to discuss.
+
+- Case 1. $l \geqslant k$.
+
+Since $\left(n^{k}+m n^{l}+1, n\right)=1$,(2) yields
+
+$$
+n^{k}+m n^{l}+1 \mid n^{l}+m n^{l-k}+1 .
+$$
+
+In particular, we get $n^{k}+m n^{l}+1 \leqslant n^{l}+m n^{l-k}+1$. As $n \geqslant 2$ and $k \geqslant 1,(m-1) n^{l}$ is at least $2(m-1) n^{l-k}$. It follows that the inequality cannot hold when $m \geqslant 2$. For $m=1$, the above divisibility becomes
+
+$$
+n^{k}+n^{l}+1 \mid n^{l}+n^{l-k}+1 .
+$$
+
+Note that $n^{l}+n^{l-k}+12 m n^{l}+1>n^{l}+m n^{l-k}+1$, it follows that $n^{k}+m n^{l}+1=n^{l}+m n^{l-k}+1$, that is,
+
+$$
+m\left(n^{l}-n^{l-k}\right)=n^{l}-n^{k} .
+$$
+
+If $m \geqslant 2$, then $m\left(n^{l}-n^{l-k}\right) \geqslant 2 n^{l}-2 n^{l-k} \geqslant 2 n^{l}-n^{l}>n^{l}-n^{k}$ gives a contradiction. Hence $m=1$ and $l-k=k$, which means $m=1$ and $l=2 k$.
+
+- Case 2. $l2 n^{k}+m>n^{k}+n^{k-l}+m$, it follows that $n^{k}+m n^{l}+1=n^{k}+n^{k-l}+m$. This gives $m=\frac{n^{k-l}-1}{n^{l}-1}$. Note that $n^{l}-1 \mid n^{k-l}-1$ implies $l \mid k-l$ and hence $l \mid k$. The proof is thus complete.
+
+Comment. Another version of this problem is as follows: let $n, m, k$ and $l$ be positive integers with $n \neq 1$ such that $k$ and $l$ do not divide each other. Show that $n^{k}+m n^{l}+1$ does not divide $n^{k+l}-1$.
+
+N5. Let $a$ be a positive integer which is not a square number. Denote by $A$ the set of all positive integers $k$ such that
+
+$$
+k=\frac{x^{2}-a}{x^{2}-y^{2}}
+$$
+
+for some integers $x$ and $y$ with $x>\sqrt{a}$. Denote by $B$ the set of all positive integers $k$ such that (1) is satisfied for some integers $x$ and $y$ with $0 \leqslant x<\sqrt{a}$. Prove that $A=B$.
+
+Solution 1. We first prove the following preliminary result.
+
+- Claim. For fixed $k$, let $x, y$ be integers satisfying (1). Then the numbers $x_{1}, y_{1}$ defined by
+
+$$
+x_{1}=\frac{1}{2}\left(x-y+\frac{(x-y)^{2}-4 a}{x+y}\right), \quad y_{1}=\frac{1}{2}\left(x-y-\frac{(x-y)^{2}-4 a}{x+y}\right)
+$$
+
+are integers and satisfy (1) (with $x, y$ replaced by $x_{1}, y_{1}$ respectively).
+Proof. Since $x_{1}+y_{1}=x-y$ and
+
+$$
+x_{1}=\frac{x^{2}-x y-2 a}{x+y}=-x+\frac{2\left(x^{2}-a\right)}{x+y}=-x+2 k(x-y),
+$$
+
+both $x_{1}$ and $y_{1}$ are integers. Let $u=x+y$ and $v=x-y$. The relation (1) can be rewritten as
+
+$$
+u^{2}-(4 k-2) u v+\left(v^{2}-4 a\right)=0
+$$
+
+By Vieta's Theorem, the number $z=\frac{v^{2}-4 a}{u}$ satisfies
+
+$$
+v^{2}-(4 k-2) v z+\left(z^{2}-4 a\right)=0
+$$
+
+Since $x_{1}$ and $y_{1}$ are defined so that $v=x_{1}+y_{1}$ and $z=x_{1}-y_{1}$, we can reverse the process and verify (1) for $x_{1}, y_{1}$.
+
+We first show that $B \subset A$. Take any $k \in B$ so that (1) is satisfied for some integers $x, y$ with $0 \leqslant x<\sqrt{a}$. Clearly, $y \neq 0$ and we may assume $y$ is positive. Since $a$ is not a square, we have $k>1$. Hence, we get $0 \leqslant x\sqrt{a}
+$$
+
+This implies $k \in A$ and hence $B \subset A$.
+
+Next, we shall show that $A \subset B$. Take any $k \in A$ so that (1) is satisfied for some integers $x, y$ with $x>\sqrt{a}$. Again, we may assume $y$ is positive. Among all such representations of $k$, we choose the one with smallest $x+y$. Define
+
+$$
+x_{1}=\frac{1}{2}\left|x-y+\frac{(x-y)^{2}-4 a}{x+y}\right|, \quad y_{1}=\frac{1}{2}\left(x-y-\frac{(x-y)^{2}-4 a}{x+y}\right) .
+$$
+
+By the Claim, $x_{1}, y_{1}$ are integers satisfying (1). Since $k>1$, we get $x>y>\sqrt{a}$. Therefore, we have $y_{1}>\frac{4 a}{x+y}>0$ and $\frac{4 a}{x+y}\sqrt{a}$, we get a contradiction due to the minimality of $x+y$. Therefore, we must have $0 \leqslant x_{1}<\sqrt{a}$, which means $k \in B$ so that $A \subset B$.
+
+The two subset relations combine to give $A=B$.
+Solution 2. The relation (1) is equivalent to
+
+$$
+k y^{2}-(k-1) x^{2}=a
+$$
+
+Motivated by Pell's Equation, we prove the following, which is essentially the same as the Claim in Solution 1.
+
+- Claim. If $\left(x_{0}, y_{0}\right)$ is a solution to $(2)$, then $\left((2 k-1) x_{0} \pm 2 k y_{0},(2 k-1) y_{0} \pm 2(k-1) x_{0}\right)$ is also a solution to (2).
+
+Proof. We check directly that
+
+$$
+\begin{aligned}
+& k\left((2 k-1) y_{0} \pm 2(k-1) x_{0}\right)^{2}-(k-1)\left((2 k-1) x_{0} \pm 2 k y_{0}\right)^{2} \\
+= & \left(k(2 k-1)^{2}-(k-1)(2 k)^{2}\right) y_{0}^{2}+\left(k(2(k-1))^{2}-(k-1)(2 k-1)^{2}\right) x_{0}^{2} \\
+= & k y_{0}^{2}-(k-1) x_{0}^{2}=a
+\end{aligned}
+$$
+
+If (2) is satisfied for some $0 \leqslant x<\sqrt{a}$ and nonnegative integer $y$, then clearly (1) implies $y>x$. Also, we have $k>1$ since $a$ is not a square number. By the Claim, consider another solution to (2) defined by
+
+$$
+x_{1}=(2 k-1) x+2 k y, \quad y_{1}=(2 k-1) y+2(k-1) x
+$$
+
+It satisfies $x_{1} \geqslant(2 k-1) x+2 k(x+1)=(4 k-1) x+2 k>x$. Then we can replace the old solution by a new one which has a larger value in $x$. After a finite number of replacements, we must get a solution with $x>\sqrt{a}$. This shows $B \subset A$.
+
+If (2) is satisfied for some $x>\sqrt{a}$ and nonnegative integer $y$, by the Claim we consider another solution to (2) defined by
+
+$$
+x_{1}=|(2 k-1) x-2 k y|, \quad y_{1}=(2 k-1) y-2(k-1) x .
+$$
+
+From (2), we get $\sqrt{k} y>\sqrt{k-1} x$. This implies $k y>\sqrt{k(k-1)} x>(k-1) x$ and hence $(2 k-1) x-2 k yy$. Then it is clear that $(2 k-1) x-2 k y>-x$. These combine to give $x_{1}|x|$, and, in case of $x>\sqrt{a}$, another solution $\left(x_{2}, y_{2}\right)$ with $\left|x_{2}\right|<|x|$.
+
+Without loss of generality, assume $x, y \geqslant 0$. Let $u=x+y$ and $v=x-y$. Then $u \geqslant v$ and (1) becomes
+
+$$
+k=\frac{(u+v)^{2}-4 a}{4 u v}
+$$
+
+This is the same as
+
+$$
+v^{2}+(2 u-4 k u) v+u^{2}-4 a=0
+$$
+
+Let $v_{1}=4 k u-2 u-v$. Then $u+v_{1}=4 k u-u-v \geqslant 8 u-u-v>u+v$. By Vieta's Theorem, $v_{1}$ satisfies
+
+$$
+v_{1}^{2}+(2 u-4 k u) v_{1}+u^{2}-4 a=0
+$$
+
+This gives $k=\frac{\left(u+v_{1}\right)^{2}-4 a}{4 u v_{1}}$. As $k$ is an integer, $u+v_{1}$ must be even. Therefore, $x_{1}=\frac{u+v_{1}}{2}$ and $y_{1}=\frac{v_{1}-u}{2}$ are integers. By reversing the process, we can see that $\left(x_{1}, y_{1}\right)$ is a solution to (1), with $x_{1}=\frac{u+v_{1}}{2}>\frac{u+v}{2}=x \geqslant 0$. This completes the first half of the proof.
+
+Suppose $x>\sqrt{a}$. Then $u+v>2 \sqrt{a}$ and (3) can be rewritten as
+
+$$
+u^{2}+(2 v-4 k v) u+v^{2}-4 a=0 .
+$$
+
+Let $u_{2}=4 k v-2 v-u$. By Vieta's Theorem, we have $u u_{2}=v^{2}-4 a$ and
+
+$$
+u_{2}^{2}+(2 v-4 k v) u_{2}+v^{2}-4 a=0
+$$
+
+By $u>0, u+v>2 \sqrt{a}$ and (3), we have $v>0$. If $u_{2} \geqslant 0$, then $v u_{2} \leqslant u u_{2}=v^{2}-4 a0$ and $u_{2}+v\nu_{p}\left(A_{1} A_{m+1}^{2}\right)$ for $2 \leqslant m \leqslant k-1$.
+
+Proof. The case $m=2$ is obvious since $\nu_{p}\left(A_{1} A_{2}^{2}\right) \geqslant p^{t}>\nu_{p}\left(A_{1} A_{3}^{2}\right)$ by the condition and the above assumption.
+
+Suppose $\nu_{p}\left(A_{1} A_{2}^{2}\right)>\nu_{p}\left(A_{1} A_{3}^{2}\right)>\cdots>\nu_{p}\left(A_{1} A_{m}^{2}\right)$ where $3 \leqslant m \leqslant k-1$. For the induction step, we apply Ptolemy's Theorem to the cyclic quadrilateral $A_{1} A_{m-1} A_{m} A_{m+1}$ to get
+
+$$
+A_{1} A_{m+1} \times A_{m-1} A_{m}+A_{1} A_{m-1} \times A_{m} A_{m+1}=A_{1} A_{m} \times A_{m-1} A_{m+1}
+$$
+
+which can be rewritten as
+
+$$
+\begin{aligned}
+A_{1} A_{m+1}^{2} \times A_{m-1} A_{m}^{2}= & A_{1} A_{m-1}^{2} \times A_{m} A_{m+1}^{2}+A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2} \\
+& -2 A_{1} A_{m-1} \times A_{m} A_{m+1} \times A_{1} A_{m} \times A_{m-1} A_{m+1}
+\end{aligned}
+$$
+
+From this, $2 A_{1} A_{m-1} \times A_{m} A_{m+1} \times A_{1} A_{m} \times A_{m-1} A_{m+1}$ is an integer. We consider the component of $p$ of each term in (1). By the inductive hypothesis, we have $\nu_{p}\left(A_{1} A_{m-1}^{2}\right)>\nu_{p}\left(A_{1} A_{m}^{2}\right)$. Also, we have $\nu_{p}\left(A_{m} A_{m+1}^{2}\right) \geqslant p^{t}>\nu_{p}\left(A_{m-1} A_{m+1}^{2}\right)$. These give
+
+$$
+\nu_{p}\left(A_{1} A_{m-1}^{2} \times A_{m} A_{m+1}^{2}\right)>\nu_{p}\left(A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2}\right)
+$$
+
+Next, we have $\nu_{p}\left(4 A_{1} A_{m-1}^{2} \times A_{m} A_{m+1}^{2} \times A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2}\right)=\nu_{p}\left(A_{1} A_{m-1}^{2} \times A_{m} A_{m+1}^{2}\right)+$ $\nu_{p}\left(A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2}\right)>2 \nu_{p}\left(A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2}\right)$ from (2). This implies
+
+$$
+\nu_{p}\left(2 A_{1} A_{m-1} \times A_{m} A_{m+1} \times A_{1} A_{m} \times A_{m-1} A_{m+1}\right)>\nu_{p}\left(A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2}\right)
+$$
+
+Combining (1), (2) and (3), we conclude that
+
+$$
+\nu_{p}\left(A_{1} A_{m+1}^{2} \times A_{m-1} A_{m}^{2}\right)=\nu_{p}\left(A_{1} A_{m}^{2} \times A_{m-1} A_{m+1}^{2}\right)
+$$
+
+By $\nu_{p}\left(A_{m-1} A_{m}^{2}\right) \geqslant p^{t}>\nu_{p}\left(A_{m-1} A_{m+1}^{2}\right)$, we get $\nu_{p}\left(A_{1} A_{m+1}^{2}\right)<\nu_{p}\left(A_{1} A_{m}^{2}\right)$. The Claim follows by induction.
+
+From the Claim, we get a chain of inequalities
+
+$$
+p^{t}>\nu_{p}\left(A_{1} A_{3}^{2}\right)>\nu_{p}\left(A_{1} A_{4}^{2}\right)>\cdots>\nu_{p}\left(A_{1} A_{k}^{2}\right) \geqslant p^{t}
+$$
+
+which yields a contradiction. Therefore, we can show by induction that $2 S$ is divisible by $n$.
+Comment. The condition that $P$ is cyclic is crucial. As a counterexample, consider the rhombus with vertices $(0,3),(4,0),(0,-3),(-4,0)$. Each of its squares of side lengths is divisible by 5 , while $2 S=48$ is not.
+
+The proposer also gives a proof for the case $n$ is even. One just needs an extra technical step for the case $p=2$.
+
+N8. Find all polynomials $P(x)$ of odd degree $d$ and with integer coefficients satisfying the following property: for each positive integer $n$, there exist $n$ positive integers $x_{1}, x_{2}, \ldots, x_{n}$ such that $\frac{1}{2}<\frac{P\left(x_{i}\right)}{P\left(x_{j}\right)}<2$ and $\frac{P\left(x_{i}\right)}{P\left(x_{j}\right)}$ is the $d$-th power of a rational number for every pair of indices $i$ and $j$ with $1 \leqslant i, j \leqslant n$.
+
+Answer. $P(x)=a(r x+s)^{d}$ where $a, r, s$ are integers with $a \neq 0, r \geqslant 1$ and $(r, s)=1$.
+Solution. Let $P(x)=a_{d} x^{d}+a_{d-1} x^{d-1}+\cdots+a_{0}$. Consider the substitution $y=d a_{d} x+a_{d-1}$. By defining $Q(y)=P(x)$, we find that $Q$ is a polynomial with rational coefficients without the term $y^{d-1}$. Let $Q(y)=b_{d} y^{d}+b_{d-2} y^{d-2}+b_{d-3} y^{d-3}+\cdots+b_{0}$ and $B=\max _{0 \leqslant i \leqslant d}\left\{\left|b_{i}\right|\right\}$ (where $b_{d-1}=0$ ).
+
+The condition shows that for each $n \geqslant 1$, there exist integers $y_{1}, y_{2}, \ldots, y_{n}$ such that $\frac{1}{2}<\frac{Q\left(y_{i}\right)}{Q\left(y_{j}\right)}<2$ and $\frac{Q\left(y_{i}\right)}{Q\left(y_{j}\right)}$ is the $d$-th power of a rational number for $1 \leqslant i, j \leqslant n$. Since $n$ can be arbitrarily large, we may assume all $x_{i}$ 's and hence $y_{i}$ 's are integers larger than some absolute constant in the following.
+
+By Dirichlet's Theorem, since $d$ is odd, we can find a sufficiently large prime $p$ such that $p \equiv 2(\bmod d)$. In particular, we have $(p-1, d)=1$. For this fixed $p$, we choose $n$ to be sufficiently large. Then by the Pigeonhole Principle, there must be $d+1$ of $y_{1}, y_{2}, \ldots, y_{n}$ which are congruent $\bmod p$. Without loss of generality, assume $y_{i} \equiv y_{j}(\bmod p)$ for $1 \leqslant i, j \leqslant d+1$. We shall establish the following.
+
+- Claim. $\frac{Q\left(y_{i}\right)}{Q\left(y_{1}\right)}=\frac{y_{i}^{d}}{y_{1}^{d}}$ for $2 \leqslant i \leqslant d+1$.
+
+Proof. Let $\frac{Q\left(y_{i}\right)}{Q\left(y_{1}\right)}=\frac{l^{d}}{m^{d}}$ where $(l, m)=1$ and $l, m>0$. This can be rewritten in the expanded form
+
+$$
+b_{d}\left(m^{d} y_{i}^{d}-l^{d} y_{1}^{d}\right)=-\sum_{j=0}^{d-2} b_{j}\left(m^{d} y_{i}^{j}-l^{d} y_{1}^{j}\right)
+$$
+
+Let $c$ be the common denominator of $Q$, so that $c Q(k)$ is an integer for any integer $k$. Note that $c$ depends only on $P$ and so we may assume $(p, c)=1$. Then $y_{1} \equiv y_{i}(\bmod p)$ implies $c Q\left(y_{1}\right) \equiv c Q\left(y_{i}\right)(\bmod p)$.
+
+- Case 1. $p \mid c Q\left(y_{1}\right)$.
+
+In this case, there is a cancellation of $p$ in the numerator and denominator of $\frac{c Q\left(y_{i}\right)}{c Q\left(y_{1}\right)}$, so that $m^{d} \leqslant p^{-1}\left|c Q\left(y_{1}\right)\right|$. Noting $\left|Q\left(y_{1}\right)\right|<2 B y_{1}^{d}$ as $y_{1}$ is large, we get
+
+$$
+m \leqslant p^{-\frac{1}{d}}(2 c B)^{\frac{1}{d}} y_{1}
+$$
+
+For large $y_{1}$ and $y_{i}$, the relation $\frac{1}{2}<\frac{Q\left(y_{i}\right)}{Q\left(y_{1}\right)}<2$ implies
+
+$$
+\frac{1}{3}<\frac{y_{i}^{d}}{y_{1}^{d}}<3
+$$
+
+We also have
+
+$$
+\frac{1}{2}<\frac{l^{d}}{m^{d}}<2
+$$
+
+Now, the left-hand side of (1) is
+
+$$
+b_{d}\left(m y_{i}-l y_{1}\right)\left(m^{d-1} y_{i}^{d-1}+m^{d-2} y_{i}^{d-2} l y_{1}+\cdots+l^{d-1} y_{1}^{d-1}\right) .
+$$
+
+Suppose on the contrary that $m y_{i}-l y_{1} \neq 0$. Then the absolute value of the above expression is at least $\left|b_{d}\right| m^{d-1} y_{i}^{d-1}$. On the other hand, the absolute value of the right-hand side of (1) is at most
+
+$$
+\begin{aligned}
+\sum_{j=0}^{d-2} B\left(m^{d} y_{i}^{j}+l^{d} y_{1}^{j}\right) & \leqslant(d-1) B\left(m^{d} y_{i}^{d-2}+l^{d} y_{1}^{d-2}\right) \\
+& \leqslant(d-1) B\left(7 m^{d} y_{i}^{d-2}\right) \\
+& \leqslant 7(d-1) B\left(p^{-\frac{1}{d}}(2 c B)^{\frac{1}{d}} y_{1}\right) m^{d-1} y_{i}^{d-2} \\
+& \leqslant 21(d-1) B p^{-\frac{1}{d}}(2 c B)^{\frac{1}{d}} m^{d-1} y_{i}^{d-1}
+\end{aligned}
+$$
+
+by using successively (3), (4), (2) and again (3). This shows
+
+$$
+\left|b_{d}\right| m^{d-1} y_{i}^{d-1} \leqslant 21(d-1) B p^{-\frac{1}{d}}(2 c B)^{\frac{1}{d}} m^{d-1} y_{i}^{d-1},
+$$
+
+which is a contradiction for large $p$ as $b_{d}, B, c, d$ depend only on the polynomial $P$. Therefore, we have $m y_{i}-l y_{1}=0$ in this case.
+
+- Case 2. $\left(p, c Q\left(y_{1}\right)\right)=1$.
+
+From $c Q\left(y_{1}\right) \equiv c Q\left(y_{i}\right)(\bmod p)$, we have $l^{d} \equiv m^{d}(\bmod p)$. Since $(p-1, d)=1$, we use Fermat Little Theorem to conclude $l \equiv m(\bmod p)$. Then $p \mid m y_{i}-l y_{1}$. Suppose on the contrary that $m y_{i}-l y_{1} \neq 0$. Then the left-hand side of (1) has absolute value at least $\left|b_{d}\right| p m^{d-1} y_{i}^{d-1}$. Similar to Case 1, the right-hand side of (1) has absolute value at most
+
+$$
+21(d-1) B(2 c B)^{\frac{1}{d}} m^{d-1} y_{i}^{d-1}
+$$
+
+which must be smaller than $\left|b_{d}\right| p m^{d-1} y_{i}^{d-1}$ for large $p$. Again this yields a contradiction and hence $m y_{i}-l y_{1}=0$.
+
+In both cases, we find that $\frac{Q\left(y_{i}\right)}{Q\left(y_{1}\right)}=\frac{l^{d}}{m^{d}}=\frac{y_{i}^{d}}{y_{1}^{d}}$.
+From the Claim, the polynomial $Q\left(y_{1}\right) y^{d}-y_{1}^{d} Q(y)$ has roots $y=y_{1}, y_{2}, \ldots, y_{d+1}$. Since its degree is at most $d$, this must be the zero polynomial. Hence, $Q(y)=b_{d} y^{d}$. This implies $P(x)=a_{d}\left(x+\frac{a_{d-1}}{d a_{d}}\right)^{d}$. Let $\frac{a_{d-1}}{d a_{d}}=\frac{s}{r}$ with integers $r, s$ where $r \geqslant 1$ and $(r, s)=1$. Since $P$ has integer coefficients, we need $r^{d} \mid a_{d}$. Let $a_{d}=r^{d} a$. Then $P(x)=a(r x+s)^{d}$. It is obvious that such a polynomial satisfies the conditions.
+
+Comment. In the proof, the use of prime and Dirichlet's Theorem can be avoided. One can easily show that each $P\left(x_{i}\right)$ can be expressed in the form $u v_{i}^{d}$ where $u, v_{i}$ are integers and $u$ cannot be divisible by the $d$-th power of a prime (note that $u$ depends only on $P$ ). By fixing a large integer $q$ and by choosing a large $n$, we can apply the Pigeonhole Principle and assume
+$x_{1} \equiv x_{2} \equiv \cdots \equiv x_{d+1}(\bmod q)$ and $v_{1} \equiv v_{2} \equiv \cdots \equiv v_{d+1}(\bmod q)$. Then the remaining proof is similar to Case 2 of the Solution.
+
+Alternatively, we give another modification of the proof as follows.
+We take a sufficiently large $n$ and consider the corresponding positive integers $y_{1}, y_{2}, \ldots, y_{n}$. For each $2 \leqslant i \leqslant n$, let $\frac{Q\left(y_{i}\right)}{Q\left(y_{1}\right)}=\frac{l_{i}^{d}}{m_{i}^{d}}$.
+
+As in Case 1, if there are $d$ indices $i$ such that the integers $\frac{c\left|Q\left(y_{1}\right)\right|}{m_{i}^{d}}$ are bounded below by a constant depending only on $P$, we can establish the Claim using those $y_{i}$ 's and complete the proof. Similarly, as in Case 2, if there are $d$ indices $i$ such that the integers $\left|m_{i} y_{i}-l_{i} y_{1}\right|$ are bounded below, then the proof goes the same. So it suffices to consider the case where $\frac{c\left|Q\left(y_{1}\right)\right|}{m_{i}^{d}} \leqslant M$ and $\left|m_{i} y_{i}-l_{i} y_{1}\right| \leqslant N$ for all $2 \leqslant i \leqslant n^{\prime}$ where $M, N$ are fixed constants and $n^{\prime}$ is large. Since there are only finitely many choices for $m_{i}$ and $m_{i} y_{i}-l_{i} y_{1}$, by the Pigeonhole Principle, we can assume without loss of generality $m_{i}=m$ and $m_{i} y_{i}-l_{i} y_{1}=t$ for $2 \leqslant i \leqslant d+2$. Then
+
+$$
+\frac{Q\left(y_{i}\right)}{Q\left(y_{1}\right)}=\frac{l_{i}^{d}}{m^{d}}=\frac{\left(m y_{i}-t\right)^{d}}{m^{d} y_{1}^{d}}
+$$
+
+so that $Q\left(y_{1}\right)(m y-t)^{d}-m^{d} y_{1}^{d} Q(y)$ has roots $y=y_{2}, y_{3}, \ldots, y_{d+2}$. Its degree is at most $d$ and hence it is the zero polynomial. Therefore, $Q(y)=\frac{b_{d}}{m^{d}}(m y-t)^{d}$. Indeed, $Q$ does not have the term $y^{d-1}$, which means $t$ should be 0 . This gives the corresponding $P(x)$ of the desired form.
+
+The two modifications of the Solution work equally well when the degree $d$ is even.
+
diff --git a/IMO/md/en-IMO2017SL.md b/IMO/md/en-IMO2017SL.md
new file mode 100644
index 0000000000000000000000000000000000000000..672a0a9eb08ecc7bc3e4aa25377096c9154798d2
--- /dev/null
+++ b/IMO/md/en-IMO2017SL.md
@@ -0,0 +1,2968 @@
+
+
+# ImO2017
RIO DE JANEIRO - BRAZIL
+
+58 ${ }^{\text {th }}$ International Mathematical Olympiad
+
+## Shortlisted Problems (with solutions)
+
+
+
+## Shortlisted Problems (with solutions)
+
+$58^{\text {th }}$ International Mathematical Olympiad Rio de Janeiro, 12-23 July 2017
+
+## The Shortlist has to be kept strictly confidential until the conclusion of the following International Mathematical Olympiad. IMO General Regulations §6.6
+
+## Contributing Countries
+
+The Organizing Committee and the Problem Selection Committee of IMO 2017 thank the following 51 countries for contributing 150 problem proposals:
+
+Albania, Algeria, Armenia, Australia, Austria, Azerbaijan, Belarus, Belgium, Bulgaria, Cuba, Cyprus, Czech Republic, Denmark, Estonia, France, Georgia, Germany, Greece, Hong Kong, India, Iran, Ireland, Israel, Italy, Japan, Kazakhstan, Latvia, Lithuania, Luxembourg, Mexico, Montenegro, Morocco, Netherlands, Romania, Russia, Serbia, Singapore, Slovakia, Slovenia, South Africa, Sweden, Switzerland, Taiwan, Tajikistan, Tanzania, Thailand, Trinidad and Tobago, Turkey, Ukraine, United Kingdom, U.S.A.
+
+## Problem Selection Committee
+
+
+
+Carlos Gustavo Tamm de Araújo Moreira (Gugu) (chairman), Luciano Monteiro de Castro, Ilya I. Bogdanov, Géza Kós, Carlos Yuzo Shine, Zhuo Qun (Alex) Song, Ralph Costa Teixeira, Eduardo Tengan
+
+## Problems
+
+## Algebra
+
+A1. Let $a_{1}, a_{2}, \ldots, a_{n}, k$, and $M$ be positive integers such that
+
+$$
+\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=k \quad \text { and } \quad a_{1} a_{2} \ldots a_{n}=M
+$$
+
+If $M>1$, prove that the polynomial
+
+$$
+P(x)=M(x+1)^{k}-\left(x+a_{1}\right)\left(x+a_{2}\right) \cdots\left(x+a_{n}\right)
+$$
+
+has no positive roots.
+(Trinidad and Tobago)
+A2. Let $q$ be a real number. Gugu has a napkin with ten distinct real numbers written on it, and he writes the following three lines of real numbers on the blackboard:
+
+- In the first line, Gugu writes down every number of the form $a-b$, where $a$ and $b$ are two (not necessarily distinct) numbers on his napkin.
+- In the second line, Gugu writes down every number of the form $q a b$, where $a$ and $b$ are two (not necessarily distinct) numbers from the first line.
+- In the third line, Gugu writes down every number of the form $a^{2}+b^{2}-c^{2}-d^{2}$, where $a, b, c, d$ are four (not necessarily distinct) numbers from the first line.
+
+Determine all values of $q$ such that, regardless of the numbers on Gugu's napkin, every number in the second line is also a number in the third line.
+
+A3. Let $S$ be a finite set, and let $\mathcal{A}$ be the set of all functions from $S$ to $S$. Let $f$ be an element of $\mathcal{A}$, and let $T=f(S)$ be the image of $S$ under $f$. Suppose that $f \circ g \circ f \neq g \circ f \circ g$ for every $g$ in $\mathcal{A}$ with $g \neq f$. Show that $f(T)=T$.
+(India)
+A4. A sequence of real numbers $a_{1}, a_{2}, \ldots$ satisfies the relation
+
+$$
+a_{n}=-\max _{i+j=n}\left(a_{i}+a_{j}\right) \quad \text { for all } n>2017
+$$
+
+Prove that this sequence is bounded, i.e., there is a constant $M$ such that $\left|a_{n}\right| \leqslant M$ for all positive integers $n$.
+
+A5. An integer $n \geqslant 3$ is given. We call an $n$-tuple of real numbers $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ Shiny if for each permutation $y_{1}, y_{2}, \ldots, y_{n}$ of these numbers we have
+
+$$
+\sum_{i=1}^{n-1} y_{i} y_{i+1}=y_{1} y_{2}+y_{2} y_{3}+y_{3} y_{4}+\cdots+y_{n-1} y_{n} \geqslant-1
+$$
+
+Find the largest constant $K=K(n)$ such that
+
+$$
+\sum_{1 \leqslant i1
+\end{array} \quad \text { for } n=1,2, \ldots\right.
+$$
+
+Prove that at least one of the two numbers $a_{2017}$ and $a_{2018}$ must be greater than or equal to 2017 .
+(Australia)
+A8. Assume that a function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies the following condition:
+For every $x, y \in \mathbb{R}$ such that $(f(x)+y)(f(y)+x)>0$, we have $f(x)+y=f(y)+x$.
+Prove that $f(x)+y \leqslant f(y)+x$ whenever $x>y$.
+(Netherlands)
+
+## Combinatorics
+
+C1. A rectangle $\mathcal{R}$ with odd integer side lengths is divided into small rectangles with integer side lengths. Prove that there is at least one among the small rectangles whose distances from the four sides of $\mathcal{R}$ are either all odd or all even.
+(Singapore)
+C2. Let $n$ be a positive integer. Define a chameleon to be any sequence of $3 n$ letters, with exactly $n$ occurrences of each of the letters $a, b$, and $c$. Define a swap to be the transposition of two adjacent letters in a chameleon. Prove that for any chameleon $X$, there exists a chameleon $Y$ such that $X$ cannot be changed to $Y$ using fewer than $3 n^{2} / 2$ swaps.
+(Australia)
+C3. Sir Alex plays the following game on a row of 9 cells. Initially, all cells are empty. In each move, Sir Alex is allowed to perform exactly one of the following two operations:
+(1) Choose any number of the form $2^{j}$, where $j$ is a non-negative integer, and put it into an empty cell.
+(2) Choose two (not necessarily adjacent) cells with the same number in them; denote that number by $2^{j}$. Replace the number in one of the cells with $2^{j+1}$ and erase the number in the other cell.
+
+At the end of the game, one cell contains the number $2^{n}$, where $n$ is a given positive integer, while the other cells are empty. Determine the maximum number of moves that Sir Alex could have made, in terms of $n$.
+(Thailand)
+C4. Let $N \geqslant 2$ be an integer. $N(N+1)$ soccer players, no two of the same height, stand in a row in some order. Coach Ralph wants to remove $N(N-1)$ people from this row so that in the remaining row of $2 N$ players, no one stands between the two tallest ones, no one stands between the third and the fourth tallest ones, ..., and finally no one stands between the two shortest ones. Show that this is always possible.
+(Russia)
+C5. A hunter and an invisible rabbit play a game in the Euclidean plane. The hunter's starting point $H_{0}$ coincides with the rabbit's starting point $R_{0}$. In the $n^{\text {th }}$ round of the game $(n \geqslant 1)$, the following happens.
+(1) First the invisible rabbit moves secretly and unobserved from its current point $R_{n-1}$ to some new point $R_{n}$ with $R_{n-1} R_{n}=1$.
+(2) The hunter has a tracking device (e.g. dog) that returns an approximate position $R_{n}^{\prime}$ of the rabbit, so that $R_{n} R_{n}^{\prime} \leqslant 1$.
+(3) The hunter then visibly moves from point $H_{n-1}$ to a new point $H_{n}$ with $H_{n-1} H_{n}=1$.
+
+Is there a strategy for the hunter that guarantees that after $10^{9}$ such rounds the distance between the hunter and the rabbit is below 100 ?
+
+C6. Let $n>1$ be an integer. An $n \times n \times n$ cube is composed of $n^{3}$ unit cubes. Each unit cube is painted with one color. For each $n \times n \times 1$ box consisting of $n^{2}$ unit cubes (of any of the three possible orientations), we consider the set of the colors present in that box (each color is listed only once). This way, we get $3 n$ sets of colors, split into three groups according to the orientation. It happens that for every set in any group, the same set appears in both of the other groups. Determine, in terms of $n$, the maximal possible number of colors that are present.
+(Russia)
+C7. For any finite sets $X$ and $Y$ of positive integers, denote by $f_{X}(k)$ the $k^{\text {th }}$ smallest positive integer not in $X$, and let
+
+$$
+X * Y=X \cup\left\{f_{X}(y): y \in Y\right\}
+$$
+
+Let $A$ be a set of $a>0$ positive integers, and let $B$ be a set of $b>0$ positive integers. Prove that if $A * B=B * A$, then
+
+$$
+\underbrace{A *(A * \cdots *(A *(A * A)) \ldots)}_{A \text { appears } b \text { times }}=\underbrace{B *(B * \cdots *(B *(B * B)) \ldots)}_{B \text { appears } a \text { times }} .
+$$
+
+C8. Let $n$ be a given positive integer. In the Cartesian plane, each lattice point with nonnegative coordinates initially contains a butterfly, and there are no other butterflies. The neighborhood of a lattice point $c$ consists of all lattice points within the axis-aligned $(2 n+1) \times(2 n+1)$ square centered at $c$, apart from $c$ itself. We call a butterfly lonely, crowded, or comfortable, depending on whether the number of butterflies in its neighborhood $N$ is respectively less than, greater than, or equal to half of the number of lattice points in $N$.
+
+Every minute, all lonely butterflies fly away simultaneously. This process goes on for as long as there are any lonely butterflies. Assuming that the process eventually stops, determine the number of comfortable butterflies at the final state.
+
+## Geometry
+
+G1. Let $A B C D E$ be a convex pentagon such that $A B=B C=C D, \angle E A B=\angle B C D$, and $\angle E D C=\angle C B A$. Prove that the perpendicular line from $E$ to $B C$ and the line segments $A C$ and $B D$ are concurrent.
+(Italy)
+G2. Let $R$ and $S$ be distinct points on circle $\Omega$, and let $t$ denote the tangent line to $\Omega$ at $R$. Point $R^{\prime}$ is the reflection of $R$ with respect to $S$. A point $I$ is chosen on the smaller arc $R S$ of $\Omega$ so that the circumcircle $\Gamma$ of triangle $I S R^{\prime}$ intersects $t$ at two different points. Denote by $A$ the common point of $\Gamma$ and $t$ that is closest to $R$. Line $A I$ meets $\Omega$ again at $J$. Show that $J R^{\prime}$ is tangent to $\Gamma$.
+(Luxembourg)
+G3. Let $O$ be the circumcenter of an acute scalene triangle $A B C$. Line $O A$ intersects the altitudes of $A B C$ through $B$ and $C$ at $P$ and $Q$, respectively. The altitudes meet at $H$. Prove that the circumcenter of triangle $P Q H$ lies on a median of triangle $A B C$.
+(Ukraine)
+G4. In triangle $A B C$, let $\omega$ be the excircle opposite $A$. Let $D, E$, and $F$ be the points where $\omega$ is tangent to lines $B C, C A$, and $A B$, respectively. The circle $A E F$ intersects line $B C$ at $P$ and $Q$. Let $M$ be the midpoint of $A D$. Prove that the circle $M P Q$ is tangent to $\omega$.
+(Denmark)
+G5. Let $A B C C_{1} B_{1} A_{1}$ be a convex hexagon such that $A B=B C$, and suppose that the line segments $A A_{1}, B B_{1}$, and $C C_{1}$ have the same perpendicular bisector. Let the diagonals $A C_{1}$ and $A_{1} C$ meet at $D$, and denote by $\omega$ the circle $A B C$. Let $\omega$ intersect the circle $A_{1} B C_{1}$ again at $E \neq B$. Prove that the lines $B B_{1}$ and $D E$ intersect on $\omega$.
+(Ukraine)
+G6. Let $n \geqslant 3$ be an integer. Two regular $n$-gons $\mathcal{A}$ and $\mathcal{B}$ are given in the plane. Prove that the vertices of $\mathcal{A}$ that lie inside $\mathcal{B}$ or on its boundary are consecutive.
+(That is, prove that there exists a line separating those vertices of $\mathcal{A}$ that lie inside $\mathcal{B}$ or on its boundary from the other vertices of $\mathcal{A}$.)
+(Czech Republic)
+G7. A convex quadrilateral $A B C D$ has an inscribed circle with center $I$. Let $I_{a}, I_{b}, I_{c}$, and $I_{d}$ be the incenters of the triangles $D A B, A B C, B C D$, and $C D A$, respectively. Suppose that the common external tangents of the circles $A I_{b} I_{d}$ and $C I_{b} I_{d}$ meet at $X$, and the common external tangents of the circles $B I_{a} I_{c}$ and $D I_{a} I_{c}$ meet at $Y$. Prove that $\angle X I Y=90^{\circ}$.
+(Kazakhstan)
+G8. There are 2017 mutually external circles drawn on a blackboard, such that no two are tangent and no three share a common tangent. A tangent segment is a line segment that is a common tangent to two circles, starting at one tangent point and ending at the other one. Luciano is drawing tangent segments on the blackboard, one at a time, so that no tangent segment intersects any other circles or previously drawn tangent segments. Luciano keeps drawing tangent segments until no more can be drawn. Find all possible numbers of tangent segments when he stops drawing.
+(Australia)
+
+## Number Theory
+
+N1. The sequence $a_{0}, a_{1}, a_{2}, \ldots$ of positive integers satisfies
+
+$$
+a_{n+1}=\left\{\begin{array}{ll}
+\sqrt{a_{n}}, & \text { if } \sqrt{a_{n}} \text { is an integer } \\
+a_{n}+3, & \text { otherwise }
+\end{array} \quad \text { for every } n \geqslant 0\right.
+$$
+
+Determine all values of $a_{0}>1$ for which there is at least one number $a$ such that $a_{n}=a$ for infinitely many values of $n$.
+(South Africa)
+N2. Let $p \geqslant 2$ be a prime number. Eduardo and Fernando play the following game making moves alternately: in each move, the current player chooses an index $i$ in the set $\{0,1, \ldots, p-1\}$ that was not chosen before by either of the two players and then chooses an element $a_{i}$ of the set $\{0,1,2,3,4,5,6,7,8,9\}$. Eduardo has the first move. The game ends after all the indices $i \in\{0,1, \ldots, p-1\}$ have been chosen. Then the following number is computed:
+
+$$
+M=a_{0}+10 \cdot a_{1}+\cdots+10^{p-1} \cdot a_{p-1}=\sum_{j=0}^{p-1} a_{j} \cdot 10^{j}
+$$
+
+The goal of Eduardo is to make the number $M$ divisible by $p$, and the goal of Fernando is to prevent this.
+
+Prove that Eduardo has a winning strategy.
+(Morocco)
+N3. Determine all integers $n \geqslant 2$ with the following property: for any integers $a_{1}, a_{2}, \ldots, a_{n}$ whose sum is not divisible by $n$, there exists an index $1 \leqslant i \leqslant n$ such that none of the numbers
+
+$$
+a_{i}, a_{i}+a_{i+1}, \ldots, a_{i}+a_{i+1}+\cdots+a_{i+n-1}
+$$
+
+is divisible by $n$. (We let $a_{i}=a_{i-n}$ when $i>n$.)
+(Thailand)
+N4. Call a rational number short if it has finitely many digits in its decimal expansion. For a positive integer $m$, we say that a positive integer $t$ is $m$-tastic if there exists a number $c \in\{1,2,3, \ldots, 2017\}$ such that $\frac{10^{t}-1}{c \cdot m}$ is short, and such that $\frac{10^{k}-1}{c \cdot m}$ is not short for any $1 \leqslant kq$ for which the number
+
+$$
+\frac{(p+q)^{p+q}(p-q)^{p-q}-1}{(p+q)^{p-q}(p-q)^{p+q}-1}
+$$
+
+is an integer.
+
+N6. Find the smallest positive integer $n$, or show that no such $n$ exists, with the following property: there are infinitely many distinct $n$-tuples of positive rational numbers ( $a_{1}, a_{2}, \ldots, a_{n}$ ) such that both
+
+$$
+a_{1}+a_{2}+\cdots+a_{n} \quad \text { and } \quad \frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}
+$$
+
+are integers.
+(Singapore)
+N7. Say that an ordered pair $(x, y)$ of integers is an irreducible lattice point if $x$ and $y$ are relatively prime. For any finite set $S$ of irreducible lattice points, show that there is a homogenous polynomial in two variables, $f(x, y)$, with integer coefficients, of degree at least 1 , such that $f(x, y)=1$ for each $(x, y)$ in the set $S$.
+
+Note: A homogenous polynomial of degree $n$ is any nonzero polynomial of the form
+
+$$
+f(x, y)=a_{0} x^{n}+a_{1} x^{n-1} y+a_{2} x^{n-2} y^{2}+\cdots+a_{n-1} x y^{n-1}+a_{n} y^{n} .
+$$
+
+N8 Let $p$ be an odd prime number and $\mathbb{Z}_{>0}$ be the set of positive integers. Suppose that a function $f: \mathbb{Z}_{>0} \times \mathbb{Z}_{>0} \rightarrow\{0,1\}$ satisfies the following properties:
+
+- $f(1,1)=0$;
+- $f(a, b)+f(b, a)=1$ for any pair of relatively prime positive integers $(a, b)$ not both equal to 1 ;
+- $f(a+b, b)=f(a, b)$ for any pair of relatively prime positive integers $(a, b)$.
+
+Prove that
+
+$$
+\sum_{n=1}^{p-1} f\left(n^{2}, p\right) \geqslant \sqrt{2 p}-2
+$$
+
+## Solutions
+
+## Algebra
+
+A1. Let $a_{1}, a_{2}, \ldots, a_{n}, k$, and $M$ be positive integers such that
+
+$$
+\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=k \quad \text { and } \quad a_{1} a_{2} \ldots a_{n}=M
+$$
+
+If $M>1$, prove that the polynomial
+
+$$
+P(x)=M(x+1)^{k}-\left(x+a_{1}\right)\left(x+a_{2}\right) \cdots\left(x+a_{n}\right)
+$$
+
+has no positive roots.
+(Trinidad and Tobago)
+Solution 1. We first prove that, for $x>0$,
+
+$$
+a_{i}(x+1)^{1 / a_{i}} \leqslant x+a_{i},
+$$
+
+with equality if and only if $a_{i}=1$. It is clear that equality occurs if $a_{i}=1$.
+If $a_{i}>1$, the AM-GM inequality applied to a single copy of $x+1$ and $a_{i}-1$ copies of 1 yields
+
+$$
+\frac{(x+1)+\overbrace{1+1+\cdots+1}^{a_{i}-1 \text { ones }}}{a_{i}} \geqslant \sqrt[a_{i}]{(x+1) \cdot 1^{a_{i}-1}} \Longrightarrow a_{i}(x+1)^{1 / a_{i}} \leqslant x+a_{i}
+$$
+
+Since $x+1>1$, the inequality is strict for $a_{i}>1$.
+Multiplying the inequalities (1) for $i=1,2, \ldots, n$ yields
+
+$$
+\prod_{i=1}^{n} a_{i}(x+1)^{1 / a_{i}} \leqslant \prod_{i=1}^{n}\left(x+a_{i}\right) \Longleftrightarrow M(x+1)^{\sum_{i=1}^{n} 1 / a_{i}}-\prod_{i=1}^{n}\left(x+a_{i}\right) \leqslant 0 \Longleftrightarrow P(x) \leqslant 0
+$$
+
+with equality iff $a_{i}=1$ for all $i \in\{1,2, \ldots, n\}$. But this implies $M=1$, which is not possible. Hence $P(x)<0$ for all $x \in \mathbb{R}^{+}$, and $P$ has no positive roots.
+
+Comment 1. Inequality (1) can be obtained in several ways. For instance, we may also use the binomial theorem: since $a_{i} \geqslant 1$,
+
+$$
+\left(1+\frac{x}{a_{i}}\right)^{a_{i}}=\sum_{j=0}^{a_{i}}\binom{a_{i}}{j}\left(\frac{x}{a_{i}}\right)^{j} \geqslant\binom{ a_{i}}{0}+\binom{a_{i}}{1} \cdot \frac{x}{a_{i}}=1+x
+$$
+
+Both proofs of (1) mimic proofs to Bernoulli's inequality for a positive integer exponent $a_{i}$; we can use this inequality directly:
+
+$$
+\left(1+\frac{x}{a_{i}}\right)^{a_{i}} \geqslant 1+a_{i} \cdot \frac{x}{a_{i}}=1+x
+$$
+
+and so
+
+$$
+x+a_{i}=a_{i}\left(1+\frac{x}{a_{i}}\right) \geqslant a_{i}(1+x)^{1 / a_{i}}
+$$
+
+or its (reversed) formulation, with exponent $1 / a_{i} \leqslant 1$ :
+
+$$
+(1+x)^{1 / a_{i}} \leqslant 1+\frac{1}{a_{i}} \cdot x=\frac{x+a_{i}}{a_{i}} \Longrightarrow a_{i}(1+x)^{1 / a_{i}} \leqslant x+a_{i} .
+$$
+
+Solution 2. We will prove that, in fact, all coefficients of the polynomial $P(x)$ are non-positive, and at least one of them is negative, which implies that $P(x)<0$ for $x>0$.
+
+Indeed, since $a_{j} \geqslant 1$ for all $j$ and $a_{j}>1$ for some $j$ (since $a_{1} a_{2} \ldots a_{n}=M>1$ ), we have $k=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}1$, if (2) is true for a given $r-1$ and $x \neq 0$.
+
+A2. Let $q$ be a real number. Gugu has a napkin with ten distinct real numbers written on it, and he writes the following three lines of real numbers on the blackboard:
+
+- In the first line, Gugu writes down every number of the form $a-b$, where $a$ and $b$ are two (not necessarily distinct) numbers on his napkin.
+- In the second line, Gugu writes down every number of the form qab, where $a$ and $b$ are two (not necessarily distinct) numbers from the first line.
+- In the third line, Gugu writes down every number of the form $a^{2}+b^{2}-c^{2}-d^{2}$, where $a, b, c, d$ are four (not necessarily distinct) numbers from the first line.
+
+Determine all values of $q$ such that, regardless of the numbers on Gugu's napkin, every number in the second line is also a number in the third line.
+(Austria)
+Answer: -2, 0,2 .
+Solution 1. Call a number $q$ good if every number in the second line appears in the third line unconditionally. We first show that the numbers 0 and $\pm 2$ are good. The third line necessarily contains 0 , so 0 is good. For any two numbers $a, b$ in the first line, write $a=x-y$ and $b=u-v$, where $x, y, u, v$ are (not necessarily distinct) numbers on the napkin. We may now write
+
+$$
+2 a b=2(x-y)(u-v)=(x-v)^{2}+(y-u)^{2}-(x-u)^{2}-(y-v)^{2}
+$$
+
+which shows that 2 is good. By negating both sides of the above equation, we also see that -2 is good.
+
+We now show that $-2,0$, and 2 are the only good numbers. Assume for sake of contradiction that $q$ is a good number, where $q \notin\{-2,0,2\}$. We now consider some particular choices of numbers on Gugu's napkin to arrive at a contradiction.
+
+Assume that the napkin contains the integers $1,2, \ldots, 10$. Then, the first line contains the integers $-9,-8, \ldots, 9$. The second line then contains $q$ and $81 q$, so the third line must also contain both of them. But the third line only contains integers, so $q$ must be an integer. Furthermore, the third line contains no number greater than $162=9^{2}+9^{2}-0^{2}-0^{2}$ or less than -162 , so we must have $-162 \leqslant 81 q \leqslant 162$. This shows that the only possibilities for $q$ are $\pm 1$.
+
+Now assume that $q= \pm 1$. Let the napkin contain $0,1,4,8,12,16,20,24,28,32$. The first line contains $\pm 1$ and $\pm 4$, so the second line contains $\pm 4$. However, for every number $a$ in the first line, $a \not \equiv 2(\bmod 4)$, so we may conclude that $a^{2} \equiv 0,1(\bmod 8)$. Consequently, every number in the third line must be congruent to $-2,-1,0,1,2(\bmod 8)$; in particular, $\pm 4$ cannot be in the third line, which is a contradiction.
+
+Solution 2. Let $q$ be a good number, as defined in the first solution, and define the polynomial $P\left(x_{1}, \ldots, x_{10}\right)$ as
+
+$$
+\prod_{i