add EGMO 2012-2024 data files
Browse files- EGMO/download_script/download.py +120 -0
- EGMO/md/en-2012-solutions-day1.md +131 -0
- EGMO/md/en-2012-solutions-day2.md +213 -0
- EGMO/md/en-2013-solutions.md +688 -0
- EGMO/md/en-2014-solutions-day1.md +195 -0
- EGMO/md/en-2014-solutions-day2.md +167 -0
- EGMO/md/en-2015-solutions.md +423 -0
- EGMO/md/en-2016-solutions.md +139 -0
- EGMO/md/en-2017-solutions.md +444 -0
- EGMO/md/en-2018-solutions.md +455 -0
- EGMO/md/en-2019-solutions-day1.md +623 -0
- EGMO/md/en-2019-solutions-day2.md +379 -0
- EGMO/md/en-2020-solutions.md +621 -0
- EGMO/md/en-2021-solutions.md +366 -0
- EGMO/md/en-2022-solutions.md +507 -0
- EGMO/md/en-2023-solutions.md +723 -0
- EGMO/md/en-2024-solutions.md +555 -0
- EGMO/raw/en-2012-solutions-day1.pdf +3 -0
- EGMO/raw/en-2012-solutions-day2.pdf +3 -0
- EGMO/raw/en-2013-solutions.pdf +3 -0
- EGMO/raw/en-2014-solutions-day1.pdf +3 -0
- EGMO/raw/en-2014-solutions-day2.pdf +3 -0
- EGMO/raw/en-2015-solutions.pdf +3 -0
- EGMO/raw/en-2016-solutions.pdf +3 -0
- EGMO/raw/en-2017-solutions.pdf +3 -0
- EGMO/raw/en-2018-solutions.pdf +3 -0
- EGMO/raw/en-2019-solutions-day1.pdf +3 -0
- EGMO/raw/en-2019-solutions-day2.pdf +3 -0
- EGMO/raw/en-2020-solutions.pdf +3 -0
- EGMO/raw/en-2021-solutions.pdf +3 -0
- EGMO/raw/en-2022-solutions.pdf +3 -0
- EGMO/raw/en-2023-solutions.pdf +3 -0
- EGMO/raw/en-2024-solutions.pdf +3 -0
EGMO/download_script/download.py
ADDED
|
@@ -0,0 +1,120 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-11-22
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download EGMO data
|
| 7 |
+
|
| 8 |
+
Notes:
|
| 9 |
+
2012 and 2014, the pdf with solutions was downloaded to the official homepage.
|
| 10 |
+
|
| 11 |
+
To run:
|
| 12 |
+
`python EGMO/download_script/download.py`
|
| 13 |
+
'''
|
| 14 |
+
|
| 15 |
+
import requests
|
| 16 |
+
from requests.adapters import HTTPAdapter
|
| 17 |
+
from tqdm import tqdm
|
| 18 |
+
from bs4 import BeautifulSoup
|
| 19 |
+
from urllib.parse import urljoin
|
| 20 |
+
from urllib3.util.retry import Retry
|
| 21 |
+
from pathlib import Path
|
| 22 |
+
|
| 23 |
+
|
| 24 |
+
def build_session(
|
| 25 |
+
max_retries: int = 3,
|
| 26 |
+
backoff_factor: int = 2,
|
| 27 |
+
session: requests.Session = None
|
| 28 |
+
) -> requests.Session:
|
| 29 |
+
"""
|
| 30 |
+
Build a requests session with retries
|
| 31 |
+
|
| 32 |
+
Args:
|
| 33 |
+
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 34 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 35 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 36 |
+
"""
|
| 37 |
+
session = session or requests.Session()
|
| 38 |
+
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 39 |
+
session.mount("http://", adapter)
|
| 40 |
+
session.mount("https://", adapter)
|
| 41 |
+
session.headers.update({
|
| 42 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 43 |
+
})
|
| 44 |
+
|
| 45 |
+
return session
|
| 46 |
+
|
| 47 |
+
|
| 48 |
+
def main():
|
| 49 |
+
base_url = "https://www.egmo.org/egmos/"
|
| 50 |
+
|
| 51 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 52 |
+
output_dir.mkdir(parents=True, exist_ok=True)
|
| 53 |
+
|
| 54 |
+
req_session = build_session()
|
| 55 |
+
|
| 56 |
+
resp = req_session.get(base_url)
|
| 57 |
+
soup = BeautifulSoup(resp.text, "html.parser")
|
| 58 |
+
egmo_list_ele = soup.find("table", class_="egmo-list")
|
| 59 |
+
|
| 60 |
+
for year_a_ele in tqdm(egmo_list_ele.select("tr > td:nth-child(2) > a")):
|
| 61 |
+
year = year_a_ele.get_text(strip=True)
|
| 62 |
+
|
| 63 |
+
year_page_url = urljoin(base_url, year_a_ele["href"])
|
| 64 |
+
html_resp = req_session.get(year_page_url)
|
| 65 |
+
html_soup = BeautifulSoup(html_resp.text, "html.parser")
|
| 66 |
+
|
| 67 |
+
solution_pdf = html_soup.find_all("a", href=lambda h: "solutions" in h.lower() and h.lower().endswith(".pdf"))
|
| 68 |
+
problem_day1_pdf = html_soup.find("a", href=lambda h: "english" in h.lower() and "day1" in h.lower() and h.lower().endswith(".pdf"))
|
| 69 |
+
problem_day2_pdf = html_soup.find("a", href=lambda h: "english" in h.lower() and "day2" in h.lower() and h.lower().endswith(".pdf"))
|
| 70 |
+
|
| 71 |
+
# download solution pdf
|
| 72 |
+
if solution_pdf:
|
| 73 |
+
for sp in solution_pdf:
|
| 74 |
+
sp_url = urljoin(year_page_url, sp["href"])
|
| 75 |
+
|
| 76 |
+
output_file = output_dir / f"en-{year}-{sp_url.split("/")[-1]}"
|
| 77 |
+
if output_file.exists():
|
| 78 |
+
continue
|
| 79 |
+
|
| 80 |
+
sp_resp = req_session.get(sp_url)
|
| 81 |
+
if sp_resp.status_code != 200:
|
| 82 |
+
print(f"Year {year}, Failed to download {sp_url}")
|
| 83 |
+
continue
|
| 84 |
+
|
| 85 |
+
output_file.write_bytes(sp_resp.content)
|
| 86 |
+
else:
|
| 87 |
+
# if no solution pdf, download problem pdf
|
| 88 |
+
# day1 pdf
|
| 89 |
+
if problem_day1_pdf:
|
| 90 |
+
p_d1_url = urljoin(year_page_url, problem_day1_pdf["href"])
|
| 91 |
+
|
| 92 |
+
output_file = output_dir / f"en-{year}-{p_d1_url.split('/')[-1]}"
|
| 93 |
+
if output_file.exists():
|
| 94 |
+
continue
|
| 95 |
+
|
| 96 |
+
p_d1_resp = req_session.get(p_d1_url)
|
| 97 |
+
if p_d1_resp.status_code != 200:
|
| 98 |
+
print(f"Year {year}, Failed to download {p_d1_url}")
|
| 99 |
+
continue
|
| 100 |
+
|
| 101 |
+
output_file.write_bytes(p_d1_resp.content)
|
| 102 |
+
|
| 103 |
+
# day2 pdf
|
| 104 |
+
if problem_day2_pdf:
|
| 105 |
+
p_d2_url = urljoin(year_page_url, problem_day2_pdf["href"])
|
| 106 |
+
|
| 107 |
+
output_file = output_dir / f"en-{year}-{p_d2_url.split('/')[-1]}"
|
| 108 |
+
if output_file.exists():
|
| 109 |
+
continue
|
| 110 |
+
|
| 111 |
+
p_d2_resp = req_session.get(p_d2_url)
|
| 112 |
+
if p_d2_resp.status_code != 200:
|
| 113 |
+
print(f"Year {year}, Failed to download {p_d2_url}")
|
| 114 |
+
continue
|
| 115 |
+
|
| 116 |
+
output_file.write_bytes(p_d2_resp.content)
|
| 117 |
+
|
| 118 |
+
|
| 119 |
+
if __name__ == "__main__":
|
| 120 |
+
main()
|
EGMO/md/en-2012-solutions-day1.md
ADDED
|
@@ -0,0 +1,131 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# European Girls' Mathematical Olympiad 2012-Day 1 Solutions
|
| 2 |
+
|
| 3 |
+
Problem 1. Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
|
| 4 |
+
|
| 5 |
+
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
|
| 6 |
+
Origin. Netherlands (Merlijn Staps).
|
| 7 |
+
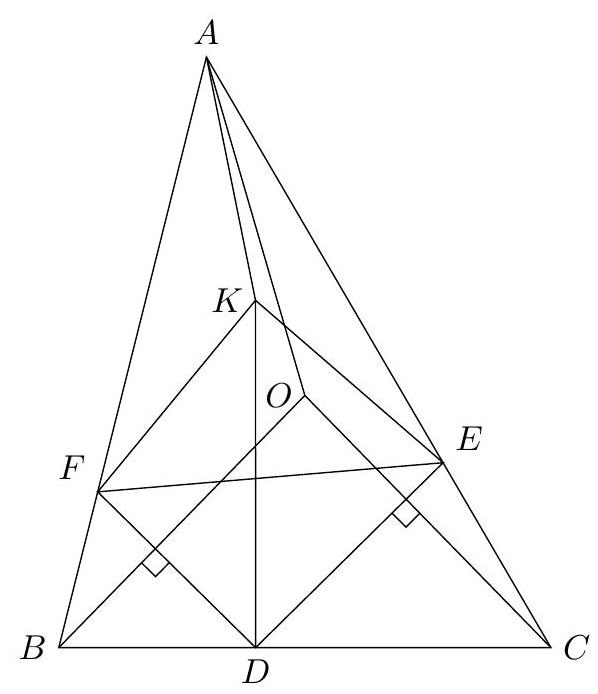
|
| 8 |
+
|
| 9 |
+
Solution 1 (submitter). Let $\ell_{C}$ be the tangent at $C$ to the circumcircle of $\triangle A B C$. As $C O \perp \ell_{C}$, the lines $D E$ and $\ell_{C}$ are parallel. Now we find that
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\angle C D E=\angle\left(B C, \ell_{C}\right)=\angle B A C,
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
hence the quadrilateral $B D E A$ is cyclic. Analogously, we find that the quadrilateral $C D F A$ is cyclic. As we now have $\angle C D E=\angle A=\angle F D B$, we conclude that the line $B C$ is the external angle bisector of $\angle E D F$. Furthermore, $\angle E D F=180^{\circ}-2 \angle A$. Since $K$ is the circumcentre of $\triangle A E F, \angle F K E=2 \angle F A E=2 \angle A$. So $\angle F K E+\angle E D F=180^{\circ}$, hence $K$ lies on the circumcircle of $\triangle D E F$. As $|K E|=|K F|$, we have that $K$ is the midpoint of the arc $E F$ of this circumcircle. It is well known that this point lies on the internal angle bisector of $\angle E D F$. We conclude that $D K$ is the internal angle bisector of $\angle E D F$. Together with the fact that $B C$ is the external angle bisector of $\angle E D F$, this yields that $D K \perp B C$, as desired.
|
| 16 |
+
|
| 17 |
+
Solution 2 (submitter). As in the previous solution, we show that the quadrilaterals $B D E A$ and $C D F A$ are both cyclic. Denote by $M$ and $L$ respectively the circumcentres of these quadrilaterals. We will show that the quadrilateral $K L O M$ is a parallelogram. The lines $K L$ and $M O$ are the perpendicular bisectors of the line segments $A F$ and $A B$, respectively. Hence both $K L$ and $M O$ are perpendicular to $A B$, which yields $K L \| M O$. In the same way we can show that the lines $K M$ and $L O$ are both perpendicular to $A C$ and hence parallel as well. We conclude that $K L O M$ is indeed a parallelogram. Now, let $K^{\prime}, L^{\prime}, O^{\prime}$ and $M^{\prime}$ be the respective projections of $K, L, O$ and $M$ to $B C$. We have to show that $K^{\prime}=D$. As $L$ lies on the perpendicular bisector of $C D$, we have that $L^{\prime}$ is the midpoint of $C D$. Similarly, $M^{\prime}$ is the midpoint of $B D$ and $O^{\prime}$ is the midpoint of $B C$. Now we are going to use directed lengths. Since $K L O M$ is a parallelogram, $M^{\prime} K^{\prime}=O^{\prime} L^{\prime}$. As
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
O^{\prime} L^{\prime}=O^{\prime} C-L^{\prime} C=\frac{1}{2} \cdot(B C-D C)=\frac{1}{2} \cdot B D=M^{\prime} D
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
we find that $M^{\prime} K^{\prime}=M^{\prime} D$, hence $K^{\prime}=D$, as desired.
|
| 24 |
+
|
| 25 |
+
Solution 3 (submitter). Denote by $\ell_{A}, \ell_{B}$ and $\ell_{C}$ the tangents at $A, B$ and $C$ to the circumcircle of $\triangle A B C$. Let $A^{\prime}$ be the point of intersection of $\ell_{B}$ and $\ell_{C}$ and define $B^{\prime}$ and $C^{\prime}$ analogously. As in the first solution, we find that $D E \| \ell_{C}$ and $D F \| \ell_{B}$. Now, let $Q$ be the point of intersection of $D E$ and $\ell_{A}$ and let $R$ be the point of intersection of $D F$ and $\ell_{A}$. We easily find $\triangle A Q E \sim \triangle A B^{\prime} C$. As $\left|B^{\prime} A\right|=\left|B^{\prime} C\right|$, we must have $|Q A|=|Q E|$, hence $\triangle A Q E$ is isosceles. Therefore the perpendicular bisector of $A E$ is the internal angle bisector of $\angle E Q A=\angle D Q R$. Analogously, the perpendicular bisector of $A F$ is the internal angle bisector of $\angle D R Q$. We conclude that $K$ is the incentre of $\triangle D Q R$, thus $D K$ is the angle bisector of $\angle Q D R$. Because the sides of the triangles $\triangle Q D R$ and $\triangle B^{\prime} A^{\prime} C^{\prime}$ are pairwise parallel, the angle bisector $D K$ of $\angle Q D R$ is parallel to the angle bisector of $\angle B^{\prime} A^{\prime} C^{\prime}$. Finally, as the angle bisector of $\angle B^{\prime} A^{\prime} C^{\prime}$ is easily seen to be perpendicular to $B C$ (as it is the perpendicular bisector of this segment), we find that $D K \perp B C$, as desired.
|
| 26 |
+
|
| 27 |
+
Remark (submitter). The fact that the quadrilateral $B D E A$ is cyclic (which is an essential part of the first two solutions) can be proven in various ways. Another possibility is as follows. Let $P$ be the midpoint of $B C$. Then, as $\angle C P O=90^{\circ}$, we have $\angle P O C=90^{\circ}-\angle O C P$. Let $X$ be the point of intersection of $D E$ and $C O$, then we have that $\angle C D E=\angle C D X=90^{\circ}-\angle X C D=90^{\circ}-\angle O C P$. Hence $\angle C D E=\angle P O C=\frac{1}{2} \angle B O C=\angle B A C$. From this we can conclude that $B D E A$ is cyclic.
|
| 28 |
+
|
| 29 |
+
Solution 4 (PSC). This is a simplified variant of Solution 1. $\angle C O B=2 \angle A$ (angle at centre of circle $A B C$ ) and $O B=O C$ so $\angle O B C=\angle B C O=90^{\circ}-\angle A$. Likewise $\angle E K F=2 \angle A$ and $\angle K F E=\angle F E K=90^{\circ}-\angle A$. Now because $D E \perp C O, \angle E D C=90^{\circ}-\angle D C O=90^{\circ}-\angle B C O=\angle A$ and similarly $\angle B D F=\angle A$, so $\angle F D E=180^{\circ}-2 \angle A$. So quadrilateral $K F D E$ is cyclic (opposite angles), so (same segment) $\angle K D E=$ $\angle K F E=90^{\circ}-\angle A$, so $\angle K D C=90^{\circ}$ and $D K$ is perpendicular to $B C$.
|
| 30 |
+
|
| 31 |
+
Problem 2. Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Origin. Poland (Tomasz Kobos).
|
| 38 |
+
Solution 1 (submitter). The largest possible $m$ is equal to $2^{n}$.
|
| 39 |
+
In order to see that the value $2^{n}$ can be indeed achieved, consider all binary vectors of length $n$ as rows of the table. We now proceed with proving that this is the maximum value.
|
| 40 |
+
|
| 41 |
+
Let $\left[a_{k}^{i}\right]$ be a feasible table, where $i=1, \ldots, m$ and $k=1, \ldots, n$. Let us define undirected graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, each with vertex set $\{1,2, \ldots, m\}$, where $i j \in E\left(G_{k}\right)$ if and only if $\left|a_{k}^{i}-a_{k}^{j}\right|=1$ (by $E\left(G_{k}\right)$ we denote the edge set of the graph $G_{k}$ ). Observe the following two properties.
|
| 42 |
+
(1) Each graph $G_{k}$ is bipartite. Indeed, if it contained a cycle of odd length, then the sum of $\pm 1$ along this cycle would need to be equal to 0 , which contradicts the length of the cycle being odd.
|
| 43 |
+
(2) For every $i \neq j, i j \in E\left(G_{k}\right)$ for some $k$. This follows directly from the problem statement.
|
| 44 |
+
|
| 45 |
+
For every graph $G_{k}$ fix some bipartition $\left(A_{k}, B_{k}\right)$ of $\{1,2, \ldots, m\}$, i.e., a partition of $\{1,2, \ldots, m\}$ into two disjoint sets $A_{k}, B_{k}$ such that the edges of $G_{k}$ traverse only between $A_{k}$ and $B_{k}$. If $m>2^{n}$, then there are two distinct indices $i, j$ such that they belong to exactly the same parts $A_{k}, B_{k}$, that is, $i \in A_{k}$ if and only if $j \in A_{k}$ for all $k=1,2, \ldots, n$. However, this means that the edge $i j$ cannot be present in any of the graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, which contradicts (2). Therefore, $m \leq 2^{n}$.
|
| 46 |
+
|
| 47 |
+
Solution 2 (PSC). In any table with the given property, the least and greatest values in a column cannot differ by more than 1 . Thus, if each value that is neither least nor greatest in its column is changed to be equal to either the least or the greatest value in its column (arbitrarily), this does not affect any $\left|a_{i}-b_{i}\right|=1$, nor does it increase any difference above 1 , so the table still has that given property. But after such a change, for any choice of what the least and greatest values in each column are, there are only two possible choices for each entry in the table (either the least or the greatest value in its column); that is, only $2^{n}$ possible distinct rows, and the given property implies that all rows must be distinct. As in the previous solution, we see that this number can be achieved.
|
| 48 |
+
|
| 49 |
+
Solution 3 (Coordinators). We prove by induction on $n$ that $m \leq 2^{n}$.
|
| 50 |
+
First suppose $n=1$. If real numbers $x$ and $y$ have $|x-y|=1$ then $\lfloor x\rfloor$ and $\lfloor y\rfloor$ have opposite parities and hence it is impossible to find three real numbers with all differences 1 . Thus $m \leq 2$.
|
| 51 |
+
|
| 52 |
+
Suppose instead $n>1$. Let $a$ be the smallest number appearing in the first column of the table; then every entry in the first column of the table lies in the interval $[a, a+1]$. Let $A$ be the collection of rows with first entry $a$ and $B$ be the collection of rows with first entry in $(a, a+1]$. No two rows in $A$ differ by 1 in their first entries, so if we list the rows in $A$ and delete their first entries we obtain a table satisfying the conditions of the problem with $n$ replaced by $n-1$; thus, by the induction hypothesis, there are at most $2^{n-1}$ rows in $A$. Similarly, there are at most $2^{n-1}$ rows in $B$. Hence $m \leq 2^{n-1}+2^{n-1}=2^{n}$. As before, this number can be achieved.
|
| 53 |
+
|
| 54 |
+
Solution 4 (Coordinators). Consider the rows of the table as points of $\mathbb{R}^{n}$. As the values in each column differ by at most 1 , these points must lie in some $n$-dimensional unit cube $C$. Consider the unit cubes centred on each of the $m$ points. The conditions of the problem imply that the interiors of these unit cubes are pairwise disjoint. But now $C$ has volume 1, and each of these cubes intersects $C$ in volume at least $2^{-n}$ : indeed, if the unit cube centred on a point of $C$ is divided into $2^{n}$ cubes of equal size then one of these cubes must lie entirely within $C$. Hence $m \leq 2^{n}$. As before, this number can be achieved.
|
| 55 |
+
|
| 56 |
+
Solution 5 (Coordinators). Again consider the rows of the table as points of $\mathbb{R}^{n}$. The conditions of the problem imply that these points must all lie in some $n$-dimensional unit cube $C$, but no two of the points lie in any smaller cube. Thus if $C$ is divided into $2^{n}$ equally-sized subcubes, each of these subcubes contains at most one row of the table, giving $m \leq 2^{n}$. As before, this number can be achieved.
|
| 57 |
+
|
| 58 |
+
Problem 3. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
f(y f(x+y)+f(x))=4 x+2 y f(x+y)
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
for all $x, y \in \mathbb{R}$.
|
| 65 |
+
|
| 66 |
+
Origin. Netherlands (Birgit van Dalen).
|
| 67 |
+
Solution 1 (submitter). Setting $y=0$ yields
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
f(f(x))=4 x
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
from which we derive that $f$ is a bijective function. Also, we find that
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
f(0)=f(4 \cdot 0)=f(f(f(0)))=4 f(0)
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
hence $f(0)=0$. Now set $x=0$ and $y=1$ in the given equation and use (1) again:
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
4=f(f(1))=2 f(1)
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
so $f(1)=2$ and therefore also $f(2)=f(f(1))=4$. Finally substitute $y=1-x$ in the equation:
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
f(2(1-x)+f(x))=4 x+4(1-x)=4=f(2) \quad \text { for all } x \in \mathbb{R}
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
As $f$ is injective, from this it follows that $f(x)=2-2(1-x)=2 x$. It is easy to see that this function satisfies the original equation. Hence the only solution is the function defined by $f(x)=2 x$ for all $x \in \mathbb{R}$.
|
| 92 |
+
|
| 93 |
+
Solution 2 (Coordinators). Setting $y=0$ in the equation we see
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
f(f(x))=4 x
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
so $f$ is a bijection. Let $\kappa=f^{-1}(2)$ and set $x+y=\kappa$ in the original equation to see
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
f(2 \kappa-2 x+f(x))=4 \kappa
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
As the right hand side is independent of $x$ and $f$ is injective, $2 \kappa-2 x+f(x)$ is constant, i.e. $f(x)=2 x+\alpha$.
|
| 106 |
+
Substituting this into the original equation, we see that $2 x+\alpha$ is a solution to the original equation if and only if $4\left(y^{2}+x y+x\right)+(3+2 y) \alpha=4\left(y^{2}+x y+x\right)+2 y \alpha$ for all $x, y$, i.e. if and only if $\alpha=0$. Thus the unique solution to the equation is $f(x)=2 x$.
|
| 107 |
+
|
| 108 |
+
Problem 4. A set $A$ of integers is called sum-full if $A \subseteq A+A$, i.e. each element $a \in A$ is the sum of some pair of (not necessarily different) elements $b, c \in A$. A set $A$ of integers is said to be zero-sum-free if 0 is the only integer that cannot be expressed as the sum of the elements of a finite nonempty subset of $A$.
|
| 109 |
+
|
| 110 |
+
Does there exist a sum-full zero-sum-free set of integers?
|
| 111 |
+
|
| 112 |
+
Origin. Romania (Dan Schwarz).
|
| 113 |
+
Remark. The original formulation of this problem had a weaker definition of zero-sum-free that did not require all nonzero integers to be sums of finite nonempty subsets of $A$.
|
| 114 |
+
|
| 115 |
+
Solution (submitter, adapted). The set $A=\left\{F_{2 n}: n=1,2, \ldots\right\} \cup\left\{-F_{2 n+1}: n=1,2, \ldots\right\}$, where $F_{k}$ is the $k^{\text {th }}$ Fibonacci number $\left(F_{1}=1, F_{2}=1, F_{k+2}=F_{k+1}+F_{k}\right.$ for $k \geq 1$ ) qualifies for an example. We then have $F_{2 n}=F_{2 n+2}+\left(-F_{2 n+1}\right)$ and $-F_{2 n+1}=\left(-F_{2 n+3}\right)+F_{2 n+2}$ for all $n \geq 1$, so $A$ is sum-full (and even with unique representations). On the other hand, we can never have
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
0=\sum_{i=1}^{s} F_{2 n_{i}}-\sum_{j=1}^{t} F_{2 n_{j}+1}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
owing to the fact that Zeckendorf representations are known to be unique.
|
| 122 |
+
It remains to be shown that all nonzero values can be represented as sums of distinct numbers $1,-2,3$, $-5,8,-13,21, \ldots$. This may be done using a greedy algorithm: when representing $n$, the number largest in magnitude that is used is the element $m= \pm F_{k}$ of $A$ that is closest to 0 subject to having the same sign as $n$ and $|m| \geq|n|$. That this algorithm terminates without using any member of $A$ twice is a straightforward induction on $k$; the base case is $k=2(m=1)$ and the induction hypothesis is that for all $n$ for which the above algorithm starts with $\pm F_{\ell}$ with $\ell \leq k$, it terminates without having used any member of $A$ twice and without having used any $\pm F_{j}$ with $j>\ell$.
|
| 123 |
+
|
| 124 |
+
Remark (James Aaronson and Adam P Goucher). Let $n$ be a positive integer, and write $u=2^{n}$; we claim that the set
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\left\{1,2,4, \ldots, 2^{n-1},-u, u+1,-(2 u+1), 3 u+2,-(5 u+3), 8 u+5, \ldots\right\}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
is a sum-full zero-sum-free set. The proof is similar to that used for the standard examples.
|
| 131 |
+
|
EGMO/md/en-2012-solutions-day2.md
ADDED
|
@@ -0,0 +1,213 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# European Girls' Mathematical Olympiad 2012-Day 2 Solutions
|
| 2 |
+
|
| 3 |
+
Problem 5. The numbers $p$ and $q$ are prime and satisfy
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
for some positive integer $n$. Find all possible values of $q-p$.
|
| 10 |
+
Origin. Luxembourg (Pierre Haas).
|
| 11 |
+
Solution 1 (submitter). Rearranging the equation, $2 q n(p+1)=(n+2)(2 p q+p+q+1)$. The left hand side is even, so either $n+2$ or $p+q+1$ is even, so either $p=2$ or $q=2$ since $p$ and $q$ are prime, or $n$ is even.
|
| 12 |
+
|
| 13 |
+
If $p=2,6 q n=(n+2)(5 q+3)$, so $(q-3)(n-10)=36$. Considering the divisors of 36 for which $q$ is prime, we find the possible solutions $(p, q, n)$ in this case are $(2,5,28)$ and $(2,7,19)$ (both of which satisfy the equation).
|
| 14 |
+
|
| 15 |
+
If $q=2,4 n(p+1)=(n+2)(5 p+3)$, so $n=p n+10 p+6$, a contradiction since $n<p n$, so there is no solution with $q=2$.
|
| 16 |
+
|
| 17 |
+
Finally, suppose that $n=2 k$ is even. We may suppose also that $p$ and $q$ are odd primes. The equation becomes $2 k q(p+1)=(k+1)(2 p q+p+q+1)$. The left hand side is even and $2 p q+p+q+1$ is odd, so $k+1$ is even, so $k=2 \ell+1$ is odd. We now have
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
q(p+1)(2 \ell+1)=(\ell+1)(2 p q+p+q+1)
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
or equivalently
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\ell q(p+1)=(\ell+1)(p q+p+1)
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
Note that $q \mid p q+p+1$ if and only if $q \mid p+1$. Furthermore, because $(p, p+1)=1$ and $q$ is prime, $(p+1, p q+p+1)=(p+1, p q)=(p+1, q)>1$ if and only if $q \mid p+1$.
|
| 30 |
+
|
| 31 |
+
Since $(\ell, \ell+1)$, we see that, if $q \nmid p+1$, then $\ell=p q+p+1$ and $\ell+1=q(p+1)$, so $q=p+2$ (and $\left(p, p+2,2\left(2 p^{2}+6 p+3\right)\right)$ satisfies the original equation). In the contrary case, suppose $p+1=r q$, so $\ell(p+1)=(\ell+1)(p+r)$, a contradiction since $\ell<\ell+1$ and $p+1 \leq p+r$.
|
| 32 |
+
|
| 33 |
+
Thus the possible values of $q-p$ are 2,3 and 5 .
|
| 34 |
+
Solution 2 (PSC). Subtracting 2 and multiplying by -1 , the condition is equivalent to
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
\frac{1}{p+1}-\frac{1}{q}=\frac{4}{n+2}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Thus $q>p+1$. Rearranging,
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
q-p-1=\frac{4(p+1) q}{n+2}
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
The expression on the right is a positive integer, and $q$ must cancel into $n+2$ else $q$ would divide $p+1<q$. Let $(n+2) / q=u$ a positive integer.
|
| 47 |
+
|
| 48 |
+
Now
|
| 49 |
+
so
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
q-p-1=\frac{4(p+1)}{u}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
u q-u(p+1)=4(p+1)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
so $p+1$ divides $u q$. However, $q$ is prime and $p+1<q$, therefore $p+1$ divides $u$. Let $v$ be the integer $u /(p+1)$. Now
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
q-p=1+\frac{4}{v} \in\{2,3,5\}
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
All three cases can occur, where $(p, q, n)$ is $(3,5,78),(2,5,28)$ or $(2,7,19)$. Note that all pairs of twin primes $q=p+2$ yield solutions $\left(p, p+2,2\left(2 p^{2}+6 p+3\right)\right)$.
|
| 66 |
+
|
| 67 |
+
Solution 3 (Coordinators). Subtract 2 from both sides to get
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\frac{1}{p+1}-\frac{1}{q}=\frac{4}{n+2}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
From this, since $n$ is positive, we have that $q>p+1$. Therefore $q$ and $p+1$ are coprime, since $q$ is prime.
|
| 74 |
+
Group the terms on the LHS to get
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\frac{q-p-1}{q(p+1)}=\frac{4}{n+2}
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
Now $(q, q-p-1)=(q, p+1)=1$ and $(p+1, q-p-1)=(p+1, q)=1$ so the fraction on the left is in lowest terms. Therefore the numerator must divide the numerator on the right, which is 4 . Since $q-p-1$ is positive, it must be 1,2 or 4 , so that $q-p$ must be 2,3 or 5 . All of these can be attained, by $(p, q, n)=(3,5,78)$, $(2,5,28)$ and $(2,7,19)$ respectively.
|
| 81 |
+
|
| 82 |
+
Problem 6. There are infinitely many people registered on the social network Mugbook. Some pairs of (different) users are registered as friends, but each person has only finitely many friends. Every user has at least one friend. (Friendship is symmetric; that is, if $A$ is a friend of $B$, then $B$ is a friend of $A$.)
|
| 83 |
+
|
| 84 |
+
Each person is required to designate one of their friends as their best friend. If $A$ designates $B$ as her best friend, then (unfortunately) it does not follow that $B$ necessarily designates $A$ as her best friend. Someone designated as a best friend is called a 1-best friend. More generally, if $n>1$ is a positive integer, then a user is an $n$-best friend provided that they have been designated the best friend of someone who is an $(n-1)$-best friend. Someone who is a $k$-best friend for every positive integer $k$ is called popular.
|
| 85 |
+
(a) Prove that every popular person is the best friend of a popular person.
|
| 86 |
+
(b) Show that if people can have infinitely many friends, then it is possible that a popular person is not the best friend of a popular person.
|
| 87 |
+
|
| 88 |
+
Origin. Romania (Dan Schwarz) (rephrasing by Geoff Smith).
|
| 89 |
+
Remark. The original formulation of this problem was:
|
| 90 |
+
Given a function $f: X \rightarrow X$, let us use the notations $f^{0}(X):=X, f^{n+1}(X):=f\left(f^{n}(X)\right)$ for $n \geq 0$, and also $f^{\omega}(X):=\bigcap_{n \geq 0} f^{n}(X)$. Let us now impose on $f$ that all its fibres $f^{-1}(y):=\{x \in X \mid f(x)=y\}$, for $y \in f(X)$, are finite. Prove that $f\left(f^{\omega}(X)\right)=f^{\omega}(X)$.
|
| 91 |
+
|
| 92 |
+
Solution 1 (submitter, adapted). For any person $A$, let $f^{0}(x)=x$, let $f(A)$ be $A$ 's best friend, and define $f^{k+1}(A)=f\left(f^{k}(A)\right)$, so any person who is a $k$-best friend is $f^{k}(A)$ for some person $A$; clearly a $k$-best friend is also an $\ell$-best friend for all $\ell<k$. Let $X$ be a popular person. For each positive integer $k$, let $x_{k}$ be a person with $f^{k}\left(x_{k}\right)=X$. Because $X$ only has finitely many friends, infinitely many of the $f^{k-1}\left(x_{k}\right)$ (all of whom designated $X$ as best friend) must be the same person, who must be popular.
|
| 93 |
+
|
| 94 |
+
If people can have infinitely many friends, consider people $X_{i}$ for positive integers $i$ and $P_{i, j}$ for $i<j$ positive integers. $X_{i}$ designates $X_{i+1}$ as her best friend; $P_{i, i}$ designates $X_{1}$ as her best friend; $P_{i, j}$ designates $P_{i+1, j}$ as her best friend if $i<j$. Then all $X_{i}$ are popular, but $X_{1}$ is not the best friend of a popular person.
|
| 95 |
+
|
| 96 |
+
Solution 2 (submitter, adapted). For any set $S$ of people, let $f^{-1}(S)$ be the set of people who designated someone in $S$ as their best friend. Since each person has only finitely many friends, if $S$ is finite then $f^{-1}(S)$ is finite.
|
| 97 |
+
|
| 98 |
+
Let $X$ be a popular person and put $V_{0}=\{X\}$ and $V_{k}=f^{-1}\left(V_{k-1}\right)$. All $V_{i}$ are finite and (since $X$ is popular) nonempty.
|
| 99 |
+
|
| 100 |
+
If any two sets $V_{i}, V_{j}$, with $0 \leq i<j$ are not disjoint, define $f^{i}(x)$ for positive integers $i$ as in Solution 1 . It follows $\emptyset \neq f^{i}\left(V_{i} \cap V_{j}\right) \subseteq f^{i}\left(V_{i}\right) \cap f^{i}\left(V_{j}\right) \subseteq V_{0} \cap V_{j-i}$, thus $X \in V_{j-i}$. But this means that $f^{j-i}(X)=X$, therefore $f^{n(j-i)}(X)=X$. Furthermore, if $Y=f^{j-i-1}(X)$, then $f(Y)=X$ and $f^{n(j-i)}(Y)=Y$, so $X$ is the best friend of $Y$, who is popular.
|
| 101 |
+
|
| 102 |
+
If all sets $V_{n}$ are disjoint, by König's infinity lemma there exists an infinite sequence of (distinct) $x_{i}, i \geq 0$, with $x_{i} \in V_{i}$ and $x_{i}=f\left(x_{i+1}\right)$ for all $i$. Now $x_{1}$ is popular and her best friend is $x_{0}=X$.
|
| 103 |
+
|
| 104 |
+
If people can have infinitely many friends, proceed as in Solution 1.
|
| 105 |
+
|
| 106 |
+
Problem 7. Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$ and orthocentre $H$. Let $K$ be a point of $\Gamma$ on the other side of $B C$ from $A$. Let $L$ be the reflection of $K$ in the line $A B$, and let $M$ be the reflection of $K$ in the line $B C$. Let $E$ be the second point of intersection of $\Gamma$ with the circumcircle of triangle $B L M$. Show that the lines $K H, E M$ and $B C$ are concurrent. (The orthocentre of a triangle is the point on all three of its altitudes.)
|
| 107 |
+
|
| 108 |
+
Origin. Luxembourg (Pierre Haas).
|
| 109 |
+
|
| 110 |
+
Solution 1 (submitter). Since the quadrilateral $B M E L$ is cyclic, we have $\angle B E M=\angle B L M$. By construction, $|B K|=|B L|=|B M|$, and so (using directed angles)
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
\begin{aligned}
|
| 114 |
+
\angle B L M & =90^{\circ}-\frac{1}{2} \angle M B L=90^{\circ}-\left(180^{\circ}-\frac{1}{2} \angle L B K-\frac{1}{2} \angle K B M\right) \\
|
| 115 |
+
& =\left(\frac{1}{2} \angle L B K+\frac{1}{2} \angle K B M\right)-90^{\circ}=\left(180^{\circ}-\angle B\right)-90^{\circ}=90^{\circ}-B .
|
| 116 |
+
\end{aligned}
|
| 117 |
+
$$
|
| 118 |
+
|
| 119 |
+
We see also that $\angle B E M=\angle B A H$, and so the point $N$ of intersection of $E M$ and $A H$ lies on $\Gamma$.
|
| 120 |
+
Let $X$ be the point of intersection of $K H$ and $B C$, and let $N^{\prime}$ be the point of intersection of $M X$ and $A H$. Since $B C$ bisects the segment $K M$ by construction, the triangle $K X M$ is isosceles; as $A H \| M K, H X N^{\prime}$ is isosceles. Since $A H \perp B C, N^{\prime}$ is the reflection of $H$ in the line $B C$. It is well known that this reflection lies on $\Gamma$, and so $N^{\prime}=N$. Thus $E, M, N$ and $M, X, N^{\prime}$ all lie on the same line $M N$; that is, $E M$ passes through $X$.
|
| 121 |
+
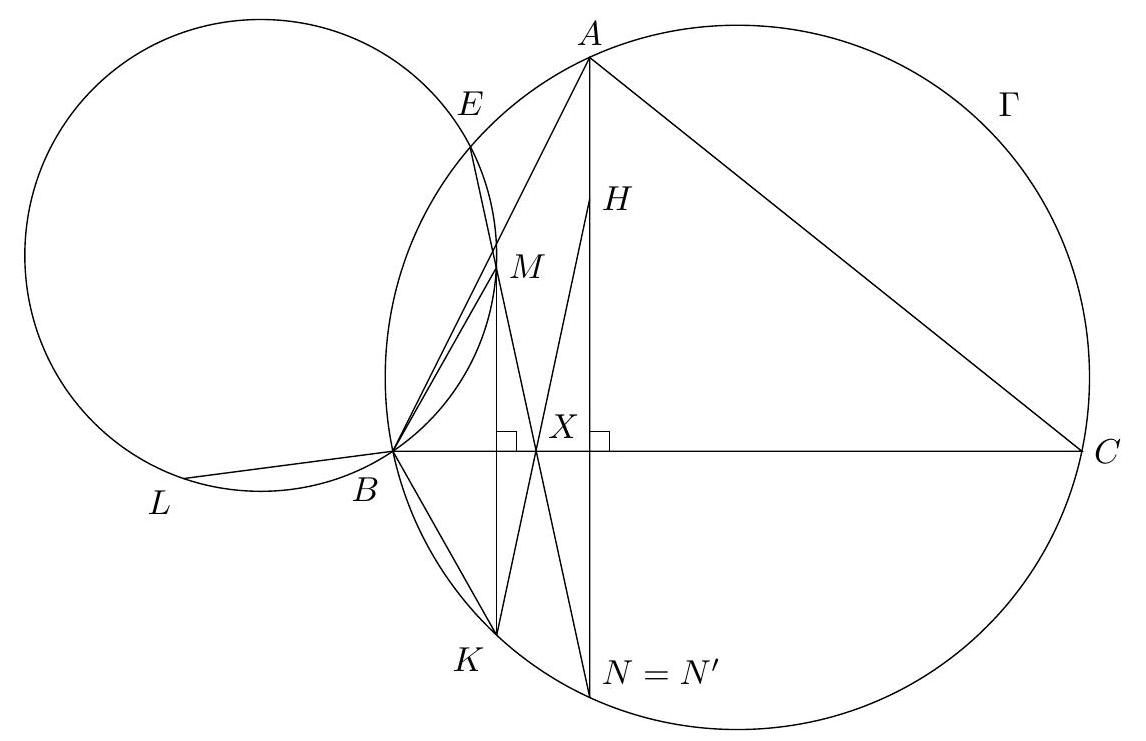
|
| 122 |
+
|
| 123 |
+
Remark (submitter). The condition that $K$ lies on the circumcircle of $A B C$ is not necessary; indeed, the solution above does not use it. However, together with the fact that the triangle $A B C$ is acute-angled, this condition implies that $M$ is in the interior of $\Gamma$, which is necessary to avoid dealing with different configurations including coincident points or the point of concurrence being at infinity.
|
| 124 |
+
|
| 125 |
+
Solution 2 (PSC). We work with directed angles. Let $H K$ meet $B C$ at $X$. Let $M X$ meet $A H$ at $H_{A}$ on $\Gamma$ (where $H_{A}$ is the reflection of $H$ in $B C$ ). Define $E^{\prime}$ to be where $H_{A} M$ meets $\Gamma$ (again). Our task is to show that $\angle M E^{\prime} B=\angle M L B$.
|
| 126 |
+
|
| 127 |
+
Observe that
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\begin{aligned}
|
| 131 |
+
\angle M E^{\prime} B & =\angle H_{A} A B & \text { (angles in same segment) } \\
|
| 132 |
+
& =B^{c} &
|
| 133 |
+
\end{aligned}
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
Now
|
| 137 |
+
|
| 138 |
+
$$
|
| 139 |
+
\begin{aligned}
|
| 140 |
+
\angle M L B & =\angle H L B \\
|
| 141 |
+
& =\angle B K H_{C} \\
|
| 142 |
+
& =\angle B C H_{C} \\
|
| 143 |
+
& =B^{c} .
|
| 144 |
+
\end{aligned}
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
(Simson line, doubled)
|
| 148 |
+
(reflecting in the line $A B$ )
|
| 149 |
+
(angles in the same segment)
|
| 150 |
+
|
| 151 |
+
Problem 8. A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
|
| 152 |
+
|
| 153 |
+
## Origin. Romania (Dan Schwarz).
|
| 154 |
+
|
| 155 |
+
Solution 1 (submitter). In this and the subsequent solutions we refer to a word with all letters identical as constant.
|
| 156 |
+
|
| 157 |
+
Let us consider a nonconstant word $W$, of length $|W|=w$, and reach a contradiction. Since the word $W$ must contain two distinct adjacent letters, be it $W=A a b B$ with $a \neq b$, we may assume $B=c C$ to be non-empty, and so $W=A a b c C$. By the proper transpositions we get the repetitive words $W^{\prime}=A b a c C=P^{w / p}$, of a period $P$ of length $p \mid w, 1<p<w$, and $W^{\prime \prime}=A a c b C=Q^{w / q}$, of a period $Q$ of length $q \mid w, 1<q<w$. However, if a word $U V$ is repetitive, then the word $V U$ is also repetitive, of a same period length; therefore we can work in the sequel with the repetitive words $W_{0}^{\prime}=C A b a c$, of a period $P^{\prime}$ of length $p$, and $W_{0}^{\prime \prime}=C A a c b$, of a period $Q^{\prime}$ of length $q$. The main idea now is that the common prefix of two repetitive words cannot be too long.
|
| 158 |
+
|
| 159 |
+
Now, if a word $a_{1} a_{2} \ldots a_{w}=T^{w / t}$ is repetitive, of a period $T$ of length $t \mid w, 1 \leq t<w$, then the word (and any subword of it) is $t$-periodic, i.e. $a_{k}=a_{k+t}$, for all $1 \leq k \leq w-t$. Therefore the word $C A$ is both $p$-periodic and $q$-periodic.
|
| 160 |
+
|
| 161 |
+
We now use the following classical result:
|
| 162 |
+
Wilf-Fine Theorem. Let $p, q$ be positive integers, and let $N$ be a word of length $n$, which is both p-periodic and $q$-periodic. If $n \geq p+q-\operatorname{gcd}(p, q)$ then the word $N$ is $\operatorname{gcd}(p, q)$-periodic (but this need not be the case if instead $n \leq p+q-\operatorname{gcd}(p, q)-1)$.
|
| 163 |
+
|
| 164 |
+
By this we need $|C A| \leq p+q-\operatorname{gcd}(p, q)-1 \leq p+q-2$, hence $w \leq p+q+1$, otherwise $W_{0}^{\prime}$ and $W_{0}^{\prime \prime}$ would be identical, absurd. Since $p \mid w$ and $1<p<w$, we have $2 p \leq w \leq p+q+1$, and so $p \leq q+1$; similarly we have $q \leq p+1$.
|
| 165 |
+
|
| 166 |
+
If $p=q$, then $|C A| \leq p+p-\operatorname{gcd}(p, p)-1=p-1$, so $2 p \leq w \leq p+2$, implying $p \leq 2$. But the three-letter suffix $a c b$ is not periodic (not even for $c=a$ or $c=b$ ), thus must be contained in $Q^{\prime}$, forcing $q \geq 3$, contradiction.
|
| 167 |
+
|
| 168 |
+
If $p \neq q$, then $\max (p, q)=\min (p, q)+1$, so $3 \min (p, q) \leq w \leq 2 \min (p, q)+2$, hence $\min (p, q) \leq 2$, forcing $\min (p, q)=2$ and $\max (p, q)=3$; by an above observation, we may even say $q=3$ and $p=2$, leading to $c=b$. It follows $6=3 \min (p, q) \leq w \leq 2 \min (p, q)+2=6$, forcing $w=6$. This leads to $C A=a b a=a b b$, contradiction.
|
| 169 |
+
|
| 170 |
+
Solution 2 (submitter). We will take over from the solution above, just before invoking the Wilf-Fine Theorem, by replacing it with a weaker lemma, also built upon a seminal result of combinatorics on words.
|
| 171 |
+
|
| 172 |
+
Lemma. Let $p, q$ be positive integers, and let $N$ be a word of length $n$, which is both $p$-periodic and $q$ periodic. If $n \geq p+q$ then the word $N$ is $\operatorname{gcd}(p, q)$-periodic.
|
| 173 |
+
|
| 174 |
+
Proof. Let us first prove that two not-null words $U, V$ commute, i.e. $U V=V U$, if and only if there exists a word $W$ with $|W|=\operatorname{gcd}(|U|,|V|)$, such that $U=W^{|U| /|W|}, V=W^{|V| /|W|}$. The "if" part being trivial, we will prove the "only if" part, by strong induction on $|U|+|V|$. Indeed, for the base step $|U|+|V|=2$ we have $|U|=|V|=1$, and so clearly we can take $W=U=V$. Now, for $|U|+|V|>2$, if $|U|=|V|$ it follows $U=V$, and so we can again take $W=U=V$. If not, assume without loss of generality $|U|<|V|$; then $V=U V^{\prime}$, so $U U V^{\prime}=U V^{\prime} U$, whence $U V^{\prime}=V^{\prime} U$. Since $\left|V^{\prime}\right|<|V|$, it follows $2 \leq|U|+\left|V^{\prime}\right|<|U|+|V|$, so by the induction hypothesis there exists a suitable word $W$ such that $U=W^{|U| /|W|}, V^{\prime}=W^{\left|V^{\prime}\right| /|W|}$, so $V=U V^{\prime}=W^{|U| /|W|} W^{\left|V^{\prime}\right| /|W|}=W^{\left(|U|+\left|V^{\prime}\right|\right) /|W|}=W^{|V| /|W|}$.
|
| 175 |
+
|
| 176 |
+
Now, assuming without loss of generality $p \leq q, q=k p+r$, we have $N=Q P S$, with $|Q|=q,|P|=p$. If $r=0$ all is clear; otherwise it follows we can write $P=U V, Q=V(U V)^{k}$, with $|V|=r$, whence $U V=V U$, implying $P Q=Q P$, and so by the above result there will exist a word $W$ of length $\operatorname{gcd}(p, q)$ such that $P=W^{p / \operatorname{gcd}(p, q)}$, $Q=W^{q / \operatorname{gcd}(p, q)}$, therefore $N$ is $\operatorname{gcd}(p, q)$-periodic.
|
| 177 |
+
|
| 178 |
+
By this we need $|C A| \leq p+q-1$, hence $w \leq p+q+2$, otherwise by the previous lemma $W_{0}^{\prime}$ and $W_{0}^{\prime \prime}$ would be identical, absurd. Since $p \mid w$ and $1<p<w$, we have $2 p \leq w \leq p+q+2$, and so $p \leq q+2$; similarly we have $q \leq p+2$. That implies $\max (p, q) \leq \min (p, q)+2$. Now, from $k \max (p, q)=w \leq p+q+2 \leq 2 \max (p, q)+2$ we will have $(k-2) \max (p, q) \leq 2$; but $\max (p, q) \leq 2$ is impossible, since the three-letter suffix $a c b$ is not periodic (not even for $c=a$ or $c=b$ ), thus must be contained in $Q^{\prime}$, forcing $q \geq 3$. Therefore $k=2$, and so $w=2 \max (p, q)$.
|
| 179 |
+
|
| 180 |
+
If $\max (p, q)=\min (p, q)$, then $w=2 p=2 q$, for a quick contradiction.
|
| 181 |
+
If $\max (p, q)=\min (p, q)+1$, it follows $3 \min (p, q) \leq w=2 \max (p, q)=2 \min (p, q)+2$, hence $\min (p, q) \leq 2$, forcing $\min (p, q)=2$ and $\max (p, q)=3$; by an above observation, we may even say $q=3$ and $p=2$, leading to $c=b$. It follows $w=2 \max (p, q)=6$, leading to $C A=a b a=a b b$, contradiction.
|
| 182 |
+
|
| 183 |
+
If $\max (p, q)=\min (p, q)+2$, it follows $3 \min (p, q) \leq w=2 \max (p, q)=2 \min (p, q)+4$, hence $\min (p, q) \leq 4$. From $\min (p, q) \mid w=2 \max (p, q)$ then follows either $\min (p, q)=2$ and $\max (p, q)=4$, thus $w=8$, clearly contradictory, or else $\min (p, q)=4$ and $\max (p, q)=6$, thus $w=12$, which also leads to contradiction, by just a little deeper analysis.
|
| 184 |
+
|
| 185 |
+
Solution 3 (PSC). We define the distance between two words of the same length to be the number of positions in which those two words have different letters. Any two words related by a transposition have distance 0 or 2 ; any two words related by a sequence of two transpositions have distance $0,2,3$ or 4 .
|
| 186 |
+
|
| 187 |
+
Say the period of a repetitive word is the least $k$ such that the word is the concatenation of two or more identical subwords of length $k$. We use the following lemma on distances between repetitive words.
|
| 188 |
+
|
| 189 |
+
Lemma. Consider a pair of distinct, nonconstant repetitive words with periods ga and gb, where $(a, b)=1$ and $a, b>1$, the first word is made up of $k b$ repetitions of the subword of length ga and the second word is made up of ka repetitions of the subword of length gb . These two words have distance at least $\max (k a, k b)$.
|
| 190 |
+
|
| 191 |
+
Proof. We may assume $k=1$, since the distance between the words is $k$ times the distance between their initial subwords of length $g a b$. Without loss of generality suppose $b>a$.
|
| 192 |
+
|
| 193 |
+
For each positive integer $m$, look at the subsequence in each word of letters in positions congruent to $m$ $(\bmod g)$. Those subsequences (of length $a b)$ have periods dividing $a$ and $b$ respectively. If they are equal, then they are constant (since each letter is equal to those $a$ and $b$ before and after it, mod $a b$, and $(a, b)=1$ ). Because $a>1$, there is some $m$ for which the first subsequence is not constant, and so is unequal to the second subsequence. Restrict attention to those subsequences.
|
| 194 |
+
|
| 195 |
+
We now have two distinct repetitive words, one (nonconstant) made up of $b$ repetitions of a subword of length $a$ and one made up of $a$ repetitions of a subword of length $b$. Looking at the first of those words, for any $1 \leq t \leq b$ consider the letters in positions $t, t+b, \ldots, t+(a-1) b$. These letters cover every position (mod $a)$; since the first word is not constant, the letters are not all equal, but the letters in the corresponding positions in the second word are all equal. At least one of these letters in the first word must change to make them all equal to those in the corresponding positions in the second word; repeating for each $t$, at least $b$ letters must change, so the words have distance at least $b$.
|
| 196 |
+
|
| 197 |
+
In the original problem, consider all the words (which we suppose to be repetitive) obtained by a transposition of two adjacent letters from the original nonconstant word; say that word has length $n$. Suppose those words include two distinct words with periods $n / a$ and $n / b$; those words have distance at most 4 . If $a>4$ or $b>4$, we have a contradiction unless $a \mid b$ or $b \mid a$. If $a>4$ is the greatest number of repetitions in any of the words ( $n / a$ is the smallest period), then unless all the numbers of repetitions divide each other there must be words with 2 or 4 repetitions, words with 3 repetitions and all larger numbers of repetitions must divide each other and be divisible by 6 .
|
| 198 |
+
|
| 199 |
+
We now divide into three cases: all the numbers of repetitions may divide either other; or there may be words with (multiples of) 2,3 and 6 repetitions; or all words may have at most 4 repetitions, with at least one word having 3 repetitions and at least one having 2 or 4 repetitions.
|
| 200 |
+
|
| 201 |
+
Case 1. Suppose all the numbers of repetitions divide each other. Let $k$ be the least number of repetitions. Consider the word as being divided into $k$ blocks, each of $\ell$ letters; any transposition of two adjacent letters leaves those blocks identical. If any two adjacent letters within a block are the same, then this means all the blocks are already identical; since the word is not constant, the letters in the first block are not all identical, so there are two distinct adjacent letters in the first block, and transposing them leaves it distinct from the other blocks, a contradiction. Otherwise, all pairs of adjacent letters within each block are distinct; transposing any adjacent pair within the first block leaves it identical to the second block. If the first block has more than two letters, this is impossible since transposing the first two letters has a different result from transposing the second two. So the blocks all have length 2 ; similarly, there are just two blocks, the arrangement is $a b b a$ but transposing the adjacent letters $b b$ does not leave the word repetitive.
|
| 202 |
+
|
| 203 |
+
Case 2. Suppose some word resulting from a transposition is made of (a multiple of) 6 repetitions, some of 3 repetitions and some of 2 repetitions (or 4 repetitions, counted as 2 ). Consider it as a sequence of 6 blocks, each of length $\ell$. If the six blocks are already identical, then as the word is not constant, there are some two distinct adjacent letters within the first block; transposing them leaves a result where the blocks form a
|
| 204 |
+
pattern $B A A A A A$, which cannot have two, three or six repetitions. So the six blocks are not already identical. If a transposition within a block results in them being identical, the blocks form a pattern (without loss of generality) $B A A A A A, A B A A A A$ or $A A B A A A$. In any of these cases, apply the same transposition (that converts between $A$ and $B$ ) to an $A$ block adjacent to the $B$ block, and the result cannot have two, three or six repetitions. Finally, consider the case where some transposition between two adjacent blocks results in all six blocks being identical. The patterns are $B C A A A A, A B C A A A$ and $A A B C A A$ (and considering the letters at the start and end of each block shows $B \neq C$ ). In all cases, transposing two adjacent distinct letters within an $A$ block produces a result that cannot have two, three or six repetitions.
|
| 205 |
+
|
| 206 |
+
Case 3. In the remaining case, all words have at most 4 repetitions, at least one has 3 repetitions and at least one has 2 or 4 repetitions. For the purposes of this case we will think of 4 -repetition words as being 2 -repetition words. The number of each letter is a multiple of 6 , so $n \geq 12$; consider the word as made of six blocks of length $\ell$.
|
| 207 |
+
|
| 208 |
+
If the word is already repetitive with 2 repetitions, pattern $A B C A B C$, any transposition between two distinct letters leaves it no longer repetitive with two repetitions, so it must instead have three repetitions after the transposition. If $A B$ is not all one letter, transposing two adjacent letters within $A B$ implies that $C A=B C$, so $A=B=C$, the word has pattern $A A A A A A$ but transposing within the initial $A A$ means it no longer has 3 repetitions. This implies that $A B$ is all one letter, but similarly $B C$ must also be all one letter and so the word is constant, a contradiction.
|
| 209 |
+
|
| 210 |
+
If the word is already repetitive with 3 repetitions, it has pattern $A B A B A B$ and any transposition leaves it no longer having 3 repetitions, so having 2 repetitions instead. $A B A$ is not made all of one letter (since the word is not constant) and any transposition between two adjacent distinct letters therein turns it into $B A B$; such a transposition affects at most two of the blocks, so $A=B$, the word has pattern $A A A A A A$ and transposing two adjacent distinct letters within the first half cannot leave it with two repetitions.
|
| 211 |
+
|
| 212 |
+
So the word is not already repetitive, and so no two adjacent letters are the same; all transpositions give distinct strings. Consider transpositions of adjacent letters within the first four letters; three different words result, of which at most one is periodic with two repetitions (it must be made of two copies of the second half of the word) and at most one is periodic with three repetitions, a contradiction.
|
| 213 |
+
|
EGMO/md/en-2013-solutions.md
ADDED
|
@@ -0,0 +1,688 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# EGMO 2013
|
| 2 |
+
|
| 3 |
+
## Problems with Solutions
|
| 4 |
+
|
| 5 |
+
## Problem Selection Committee:
|
| 6 |
+
|
| 7 |
+
Charles Leytem (chair), Pierre Haas, Jingran Lin, Christian Reiher, Gerhard Woeginger.
|
| 8 |
+
|
| 9 |
+
The Problem Selection Committee gratefully acknowledges the receipt of 38 problems proposals from 9 countries:
|
| 10 |
+
|
| 11 |
+
Belarus,
|
| 12 |
+
Bulgaria,
|
| 13 |
+
Finland,
|
| 14 |
+
the Netherlands,
|
| 15 |
+
Poland,
|
| 16 |
+
Romania,
|
| 17 |
+
|
| 18 |
+
Slovenia,
|
| 19 |
+
Turkey, the United Kingdom.
|
| 20 |
+
|
| 21 |
+
Problem 1. (Proposed by David Monk, United Kingdom)
|
| 22 |
+
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
|
| 23 |
+
|
| 24 |
+
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
| 25 |
+
|
| 26 |
+
Solution 1: Define $F$ so that $A B F D$ is a parallelogram. Then $E, A, C, F$ are collinear (as diagonals of a parallelogram bisect each other) and $B F=A D=B E$. Further, $A$ is the midpoint of $E F$, since $A F=2 A C$, and thus $A B$ is an altitude of the isosceles triangle $E B F$ with apex $B$. Therefore $A B \perp A C$.
|
| 27 |
+
|
| 28 |
+
|
| 29 |
+
A Variant. Let $P$ be the midpoint of $[A E]$, so that $A P=A B$ because $A E=2 A B$. Let $Q$ be the midpoint of $[A B]$. Then $P Q=\frac{1}{2} B E=\frac{1}{2} A D=C Q$. Hence $P A$ is a median of the isosceles triangle $C P Q$. In other words, $P A \perp A B$, which completes the proof.
|
| 30 |
+
|
| 31 |
+
|
| 32 |
+
Solution 2: Notice that $A$ is the centroid of triangle $B D E$, since $C$ is the midpoint of $[B D]$ and $A E=2 C A$. Let $M$ be the midpoint of $[B E]$. Then $M, A, D$ lie on a line, and further, $A M=\frac{1}{2} A D=\frac{1}{2} B E$. This implies that $\angle E A B=90^{\circ}$.
|
| 33 |
+
|
| 34 |
+
|
| 35 |
+
Solution 3: Let $P$ be the midpoint $[A E]$. Since $C$ is the midpoint of $[B D]$, and, moreover, $A C=E P$, we have
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
[A C D]=[A B C]=[E B P]
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
But $A D=B E$, and, as mentioned previously, $A C=E P$, so this implies that
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
\angle B E P=\angle C A D \text { or } \angle B E P=180^{\circ}-\angle C A D .
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
But $\angle B E P<\angle B A C$ and $\angle B A C+\angle C A D=\angle B A D<180^{\circ}$, so we must be in the first case, i.e. $\angle B E P=\angle C A D$. It follows that triangles $B E P$ and $D A C$ are congruent, and thus $\angle B P A=\angle A C B$. But $A P=A C$, so $B A$ is a median of the isosceles triangle $B C P$. Thus $A B \perp P C$, completing the proof.
|
| 48 |
+
|
| 49 |
+
|
| 50 |
+
Solution 4: Write $\beta=\angle E C B$, and let $x=A C, y=B C=C D, z=B E=A D$. Notice that $E C=3 x$. Then, using the cosine theorem,
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\begin{array}{ll}
|
| 54 |
+
z^{2}=x^{2}+y^{2}+2 x y \cos \beta & \text { in triangle } A C D ; \\
|
| 55 |
+
z^{2}=9 x^{2}+y^{2}-6 x y \cos \beta & \text { in triangle } B C E .
|
| 56 |
+
\end{array}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Hence $4 z^{2}=12 x^{2}+4 y^{2}$ or $z^{2}-y^{2}=3 x^{2}$. Let $H$ be the foot of the perpendicular through $B$ to $A C$, and write $h=B H$. Then
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
y^{2}-h^{2}=C H^{2}, z^{2}-h^{2}=E H^{2}
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
Hence $z^{2}-y^{2}=E H^{2}-C H^{2}$. Substituting from the above,
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
E H^{2}-C H^{2}=3 x^{2}=E A^{2}-C A^{2} .
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Thus $H=A$, and hence the triangle $A B C$ is right-angled at $A$.
|
| 72 |
+
Remark. It is possible to conclude directly from $z^{2}-y^{2}=3 x^{2}=(2 x)^{2}-x^{2}$ using Carnot's theorem.
|
| 73 |
+
|
| 74 |
+
Solution 5: Writing $a=B C, b=C A, c=A B$, we have
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\left.\begin{array}{rlrl}
|
| 78 |
+
a^{2} & =b^{2}+c^{2}-2 b c \cos \angle A \\
|
| 79 |
+
c^{2} & =a^{2}+b^{2}-2 a b \cos \angle C
|
| 80 |
+
\end{array}\right\} \quad \begin{array}{ll}
|
| 81 |
+
\text { in triangle } A B C ; \\
|
| 82 |
+
E B^{2} & =4 b^{2}+c^{2}+4 b c \cos \angle A \\
|
| 83 |
+
A D^{2} & =a^{2}+b^{2}+2 a b \cos \angle C
|
| 84 |
+
\end{array} \quad \begin{aligned}
|
| 85 |
+
& \text { in triangle } A E B ; \\
|
| 86 |
+
& \text { in triangle } A C D .
|
| 87 |
+
\end{aligned}
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Thus
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
\begin{aligned}
|
| 94 |
+
6 b^{2}+3 c^{2}-2 a^{2} & =4 b^{2}+c^{2}+4 b c \cos \angle A=E B^{2}=A D^{2} \\
|
| 95 |
+
& =a^{2}+b^{2}+2 a b \cos \angle C=2 a^{2}+2 b^{2}-c^{2}
|
| 96 |
+
\end{aligned}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
which gives $a^{2}=b^{2}+c^{2}$. Therefore $\angle B A C$ is a right angle by the converse of the theorem of Pythagoras.
|
| 100 |
+
|
| 101 |
+
Solution 6: Let $\overrightarrow{A C}=\vec{x}$ and $\overrightarrow{A B}=\vec{y}$. Now $\overrightarrow{A D}=2 \vec{x}-\vec{y}$ and $\overrightarrow{E B}=2 \vec{x}+\vec{y}$. Then
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
\overrightarrow{B E} \cdot \overrightarrow{B E}=\overrightarrow{A D} \cdot \overrightarrow{A D} \quad \Longleftrightarrow \quad(2 \vec{x}+\vec{y})^{2}=(2 \vec{x}-\vec{y})^{2} \quad \Longleftrightarrow \quad \vec{x} \cdot \vec{y}=0
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
and thus $A C \perp A B$, whence triangle $A B C$ is right-angled at $A$.
|
| 108 |
+
Remark. It is perhaps more natural to introduce $\overrightarrow{C A}=\vec{a}$ and $\overrightarrow{C B}=\vec{b}$. Then we have the equality
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
(3 \vec{a}-\vec{b})^{2}=(\vec{a}+\vec{b})^{2} \quad \Longrightarrow \quad \vec{a} \cdot(\vec{a}-\vec{b})=0
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Solution 7: Let $a, b, c, d, e$ denote the complex co-ordinates of the points $A, B, C, D$, $E$ and take the unit circle to be the circumcircle of $A B C$. We have
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
d=b+2(c-b)=2 c-b \quad \text { and } \quad e=c+3(a-c)=3 a-2 c .
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
Thus $b-e=(d-a)+2(b-a)$, and hence
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
\begin{aligned}
|
| 124 |
+
B E=A D & \Longleftrightarrow(b-e)(\overline{b-e})=(d-a)(\overline{d-a}) \\
|
| 125 |
+
& \Longleftrightarrow 2(d-a)(\overline{b-a})+2(\overline{d-a})(b-a)+4(b-a)(\overline{b-a})=0 \\
|
| 126 |
+
& \Longleftrightarrow 2(d-a)(a-b)+2(\overline{d-a})(b-a) a b+4(b-a)(a-b)=0 \\
|
| 127 |
+
& \Longleftrightarrow(d-a)-(\overline{d-a}) a b+2(b-a)=0 \\
|
| 128 |
+
& \Longleftrightarrow 2 c-b-a-2 \bar{c} a b+a+b+2(b-a)=0 \\
|
| 129 |
+
& \Longleftrightarrow c^{2}-a b+b c-a c=0 \\
|
| 130 |
+
& \Longleftrightarrow(b+c)(c-a)=0,
|
| 131 |
+
\end{aligned}
|
| 132 |
+
$$
|
| 133 |
+
|
| 134 |
+
implying $c=-b$ and that triangle $A B C$ is right-angled at $A$.
|
| 135 |
+
|
| 136 |
+
Solution 8: We use areal co-ordinates with reference to the triangle $A B C$. Recall that if $\left(x_{1}, y_{1}, z_{1}\right)$ and $\left(x_{2}, y_{2}, z_{2}\right)$ are points in the plane, then the square of the distance between these two points is $-a^{2} v w-b^{2} w u-c^{2} u v$, where $(u, v, w)=\left(x_{1}-x_{2}, y_{1}-y_{2}, z_{1}-z_{2}\right)$.
|
| 137 |
+
In our case $A=(1,0,0), B=(0,1,0), C=(0,0,1)$, so $E=(3,0,2)$ and, introducing point $F$ as in the first solution, $F=(-1,0,2)$. Then
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
B E^{2}=A D^{2} \quad \Longleftrightarrow \quad-2 a^{2}+6 b^{2}+3 c^{2}=2 a^{2}+2 b^{2}-c^{2},
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
and thus $a^{2}=b^{2}+c^{2}$. Therefore $\angle B A C$ is a right angle by the converse of the theorem of Pythagoras.
|
| 144 |
+
|
| 145 |
+
Problem 2. (Proposed by Matti Lehtinen, Finland)
|
| 146 |
+
Determine all integers $m$ for which the $m \times m$ square can be dissected into five rectangles, the side lengths of which are the integers $1,2,3, \ldots, 10$ in some order.
|
| 147 |
+
|
| 148 |
+
Solution: The solution naturally divides into three different parts: we first obtain some bounds on $m$. We then describe the structure of possible dissections, and finally, we deal with the few remaining cases.
|
| 149 |
+
|
| 150 |
+
In the first part of the solution, we get rid of the cases with $m \leqslant 10$ or $m \geqslant 14$. Let $\ell_{1}, \ldots, \ell_{5}$ and $w_{1}, \ldots, w_{5}$ be the lengths and widths of the five rectangles. Then the rearrangement inequality yields the lower bound
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
\begin{aligned}
|
| 154 |
+
\ell_{1} w_{1} & +\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5} \\
|
| 155 |
+
& =\frac{1}{2}\left(\ell_{1} w_{1}+\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5}+w_{1} \ell_{1}+w_{2} \ell_{2}+w_{3} \ell_{3}+w_{3} \ell_{4}+w_{5} \ell_{5}\right) \\
|
| 156 |
+
& \geqslant \frac{1}{2}(1 \cdot 10+2 \cdot 9+3 \cdot 8+\cdots+8 \cdot 3+9 \cdot 2+10 \cdot 1)=110
|
| 157 |
+
\end{aligned}
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
and the upper bound
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
\begin{aligned}
|
| 164 |
+
\ell_{1} w_{1} & +\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5} \\
|
| 165 |
+
& =\frac{1}{2}\left(\ell_{1} w_{1}+\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5}+w_{1} \ell_{1}+w_{2} \ell_{2}+w_{3} \ell_{3}+w_{3} \ell_{4}+w_{5} \ell_{5}\right) \\
|
| 166 |
+
& \leqslant \frac{1}{2}(1 \cdot 1+2 \cdot 2+3 \cdot 3+\cdots+8 \cdot 8+9 \cdot 9+10 \cdot 10)=192.5
|
| 167 |
+
\end{aligned}
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
As the area of the square is sandwiched between 110 and 192.5, the only possible candidates for $m$ are 11,12 , and 13 .
|
| 171 |
+
|
| 172 |
+
In the second part of the solution, we show that a dissection of the square into five rectangles must consist of a single inner rectangle and four outer rectangles that each cover one of the four corners of the square. Indeed, if one of the sides the square had three rectangles adjacent to it, removing these three rectangles would leave a polygon with eight vertices, which is clearly not the union of two rectangles. Moreover, since $m>10$, each side of the square has at least two adjacent rectangles. Hence each side of the square has precisely two adjacent rectangles, and thus the only way of partitionning the square into five rectangles is to have a single inner rectangle and four outer rectangles each covering of the four corners of the square, as claimed.
|
| 173 |
+
|
| 174 |
+
Let us now show that a square of size $12 \times 12$ cannot be dissected in the desired way. Let $R_{1}, R_{2}, R_{3}$ and $R_{4}$ be the outer rectangles (in clockwise orientation along the
|
| 175 |
+
boundary of the square). If an outer rectangle has a side of length $s$, then some adjacent outer rectangle must have a side of length $12-s$. Therefore, neither of $s=1$ or $s=6$ can be sidelengths of an outer rectangle, so the inner rectangle must have dimensions $1 \times 6$. One of the outer rectangles (say $R_{1}$ ) must have dimensions $10 \times x$, and an adjacent rectangle (say $R_{2}$ ) must thus have dimensions $2 \times y$. Rectangle $R_{3}$ then has dimensions $(12-y) \times z$, and rectangle $R_{4}$ has dimensions $(12-z) \times(12-x)$. Note that exactly one of the three numbers $x, y, z$ is even (and equals 4 or 8 ), while the other two numbers are odd. Now, the total area of all five rectangles is
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
144=6+10 x+2 y+(12-y) z+(12-z)(12-x),
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
which simplifies to $(y-x)(z-2)=6$. As exactly one of the three numbers $x, y, z$ is even, the factors $y-x$ and $z-2$ are either both even or both odd, so their product cannot equal 6 , and thus there is no solution with $m=12$.
|
| 182 |
+
|
| 183 |
+
Finally, we handle the cases $m=11$ and $m=13$, which indeed are solutions. The corresponding rectangle sets are $10 \times 5,1 \times 9,8 \times 2,7 \times 4$ and $3 \times 6$ for $m=11$, and $10 \times 5,9 \times 8,4 \times 6,3 \times 7$ and $1 \times 2$ for $m=13$. These sets can be found by trial and error. The corresponding partitions are shown in the figure below.
|
| 184 |
+
|
| 185 |
+
|
| 186 |
+
Remark. The configurations for $m=11$ and $m=13$ given above are not unique.
|
| 187 |
+
A Variant for Obtaining Bounds. We first exclude the cases $m \leqslant 9$ by the observation that one of the small rectangles has a side of length 10 and must fit into the square; hence $m \geqslant 10$.
|
| 188 |
+
|
| 189 |
+
To exclude the cases $m \geqslant 14$, we work via the perimeter: as every rectangle has at most two sides on the boundary of the $m \times m$ square, the perimeter $4 m$ of the square is bounded by $1+2+3+4+5+6+7+8+9+10=55$; hence $m \leqslant 13$.
|
| 190 |
+
|
| 191 |
+
We are left to deal with the case $m=10$ : clearly, the rectangle with side length 10 must have one its sides of length 10 along the boundary of the square. The remaining rectangle $R$ of dimensions $10 \times s$, say, would have to be divided into four rectangles with different sidelengths strictly less than 10 . If there were at least two rectangles adjacent to one of the sides of length $s$ of $R$, removing these two rectangles from $R$ would leave a polygon with at least six vertices (since the sidelengths of the rectangles partitioning $R$ are strictly less than 10). It is clearly impossible to partition such a polygon into no more than two rectangles with different sidelengths. Hence, given a side of length $s$ of $R$, there is only one rectangle adjacent to that side, so the rectangles adjacent to the sides of length $s$ of $R$ would have to have the same length $s$, a contradiction.
|
| 192 |
+
|
| 193 |
+
Remark. Note that the argument of the second part of the main solution cannot be directly applied to the case $m=10$.
|
| 194 |
+
|
| 195 |
+
A Variant for Dealing with $\boldsymbol{m}=12$. As in the previous solution, we show that the inner rectangle must have dimensions $1 \times 6$. Since the area of the square and the area of the inner rectangle are even, the areas of the four outer rectangles must sum to an even number. Now the four sides of the square are divided into segments of lengths 2 and 10, 3 and 9,4 and 8 , and 5 and 7 . Hence the sides with adjacent segments of lengths 3 and 9 , and 5 and 7 must be opposite sides of the square (otherwise, exactly one of the outer rectangles would have odd area). However, the difference of two rectangle side lengths on opposite sides of the square must be 1 or 6 (in order to accomodate the inner rectangle). This is not the case, so there is no solution with $m=12$.
|
| 196 |
+
|
| 197 |
+
Remark. In the case $m=12$, having shown that the inner rectangle must have dimensions $1 \times 6$, this case can also be dealt with by listing the remaining configurations one by one.
|
| 198 |
+
|
| 199 |
+
Problem 3. (Proposed by Dan Schwarz, Romania)
|
| 200 |
+
|
| 201 |
+
## Let $\boldsymbol{n}$ be a positive integer.
|
| 202 |
+
|
| 203 |
+
(a) Prove that there exists a set $S$ of $6 n$ pairwise different positive integers, such that the least common multiple of any two elements of $S$ is no larger than $32 n^{2}$.
|
| 204 |
+
(b) Prove that every set $T$ of $6 n$ pairwise different positive integers contains two elements the least common multiple of which is larger than $9 \boldsymbol{n}^{2}$.
|
| 205 |
+
|
| 206 |
+
Solution: (a) Let the set $A$ consist of the $4 n$ integers $1,2, \ldots, 4 n$ and let the set $B$ consist of the $2 n$ even integers $4 n+2,4 n+4, \ldots, 8 n$. We claim that the $6 n$-element set $S=A \cup B$ has the desired property.
|
| 207 |
+
|
| 208 |
+
Indeed, the least common multiple of two (even) elements of $B$ is no larger than $8 n \cdot(8 n / 2)=32 n^{2}$, and the least common multiple of some element of $A$ and some element of $A \cup B$ is at most their product, which is at most $4 n \cdot 8 n=32 n^{2}$.
|
| 209 |
+
(b) We prove the following lemma: "If a set $U$ contains $m+1$ integers, where $m \geqslant 2$, that are all not less than $m$, then some two of its elements have least common multiple strictly larger than $m^{2}$."
|
| 210 |
+
|
| 211 |
+
Let the elements of $U$ be $u_{1}>u_{2}>\cdots>u_{m+1} \geqslant m$. Note that $1 / u_{1} \leqslant 1 / u_{i} \leqslant 1 / m$ for $1 \leqslant i \leqslant m+1$. We partition the interval $\left[1 / u_{1} ; 1 / m\right]$ into $m$ subintervals of equal length. By the pigeonhole principle, there exist indices $i, j$ with $1 \leqslant i<j \leqslant m+1$ such that $1 / u_{i}$ and $1 / u_{j}$ belong to the same subinterval. Hence
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
0<\frac{1}{u_{j}}-\frac{1}{u_{i}} \leqslant \frac{1}{m}\left(\frac{1}{m}-\frac{1}{u_{1}}\right)<\frac{1}{m^{2}} .
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
Now $1 / u_{j}-1 / u_{i}$ is a positive fraction with denominator $\operatorname{lcm}\left(u_{i}, u_{j}\right)$. The above thus yields the lower bound $\operatorname{lcm}\left(u_{i}, u_{j}\right)>m^{2}$, completing the proof of the lemma.
|
| 218 |
+
|
| 219 |
+
Applying the lemma with $m=3 n$ to the $3 n+1$ largest elements of $T$, which are all not less than $3 n$, we arrive at the desired statement.
|
| 220 |
+
|
| 221 |
+
A Variant. Alternatively, for part (b), we prove the following lemma: "If a set $U$ contains $m \geqslant 2$ integers that all are greater than $m$, then some two of its elements have least common multiple strictly larger than $m^{2}$."
|
| 222 |
+
|
| 223 |
+
Let $u_{1}>u_{2}>\cdots>u_{m}$ be the elements of $U$. Since $u_{m}>m=m^{2} / m$, there exists a smallest index $k$ such that $u_{k}>m^{2} / k$. If $k=1$, then $u_{1}>m^{2}$, and the least common multiple of $u_{1}$ and $u_{2}$ is strictly larger than $m^{2}$. So let us suppose $k>1$ from now on, so that we have $u_{k}>m^{2} / k$ and $u_{k-1} \leqslant m^{2} /(k-1)$. The greatest common divisor $d$ of $u_{k-1}$ and $u_{k}$ satisfies
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
d \leqslant u_{k-1}-u_{k}<\frac{m^{2}}{k-1}-\frac{m^{2}}{k}=\frac{m^{2}}{(k-1) k}
|
| 227 |
+
$$
|
| 228 |
+
|
| 229 |
+
This implies $m^{2} /(d k)>k-1$ and $u_{k} / d>k-1$, and hence $u_{k} / d \geqslant k$. But then the least common multiple of $u_{k-1}$ and $u_{k}$ equals
|
| 230 |
+
|
| 231 |
+
$$
|
| 232 |
+
\frac{u_{k-1} u_{k}}{d} \geqslant u_{k} \cdot \frac{u_{k}}{d}>\frac{m^{2}}{k} \cdot k=m^{2}
|
| 233 |
+
$$
|
| 234 |
+
|
| 235 |
+
and the proof of the lemma is complete.
|
| 236 |
+
If we remove the $3 n$ smallest elements from set $T$ and apply the lemma with $m=3 n$ to the remaining elements, we arrive at the desired statement.
|
| 237 |
+
|
| 238 |
+
Problem 4. (Proposed by Vesna Iršič, Slovenia)
|
| 239 |
+
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
P(n)=\frac{n^{5}+a}{b}
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
## takes integer values.
|
| 246 |
+
|
| 247 |
+
Solution 1: Denote the three consecutive integers by $x-1, x$, and $x+1$, so that
|
| 248 |
+
|
| 249 |
+
$$
|
| 250 |
+
(x-1)^{5}+a \equiv 0 \quad(\bmod b), \quad x^{5}+a \equiv 0 \quad(\bmod b), \quad(x+1)^{5}+a \equiv 0 \quad(\bmod b) .
|
| 251 |
+
$$
|
| 252 |
+
|
| 253 |
+
By computing the differences of the equations in (1) we get
|
| 254 |
+
|
| 255 |
+
$$
|
| 256 |
+
\begin{aligned}
|
| 257 |
+
A & :=(x+1)^{5}-(x-1)^{5}=10 x^{4}+20 x^{2}+2 \equiv 0 \quad(\bmod b) \\
|
| 258 |
+
B & :=(x+1)^{5}-x^{5}=5 x^{4}+10 x^{3}+10 x^{2}+5 x+1 \equiv 0 \quad(\bmod b)
|
| 259 |
+
\end{aligned}
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
Adding the first and third equation in (1) and subtracting twice the second equation yields
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
C:=(x+1)^{5}+(x-1)^{5}-2 x^{5}=20 x^{3}+10 x \equiv 0 \quad(\bmod b) .
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
Next, (2) and (4) together yield
|
| 269 |
+
|
| 270 |
+
$$
|
| 271 |
+
D:=4 x A-\left(2 x^{2}+3\right) C=-22 x \equiv 0(\bmod b) .
|
| 272 |
+
$$
|
| 273 |
+
|
| 274 |
+
Finally we combine (3) and (5) to derive
|
| 275 |
+
|
| 276 |
+
$$
|
| 277 |
+
22 B+\left(5 x^{3}+10 x^{2}+10 x+5\right) D=22 \equiv 0(\bmod b) .
|
| 278 |
+
$$
|
| 279 |
+
|
| 280 |
+
As the positive integer $b$ divides 22 , we are left with the four cases $b=1, b=2, b=11$ and $b=22$.
|
| 281 |
+
|
| 282 |
+
If $b$ is even (i.e. $b=2$ or $b=22$ ), then we get a contradiction from (3), because the integer $B=2\left(5 x^{3}+5 x^{2}\right)+5\left(x^{4}+x\right)+1$ is odd, and hence not divisible by any even integer.
|
| 283 |
+
|
| 284 |
+
For $b=1$, it is trivial to see that a polynomial of the form $P(n)=n^{5}+a$, with $a$ any positive integer, has the desired property.
|
| 285 |
+
|
| 286 |
+
For $b=11$, we note that
|
| 287 |
+
|
| 288 |
+
$$
|
| 289 |
+
\begin{aligned}
|
| 290 |
+
& n \equiv 0,1,2,3,4,5,6,7,8,9,10 \quad(\bmod 11) \\
|
| 291 |
+
& \Longrightarrow \quad n^{5} \equiv 0,1,-1,1,1,1,-1,-1,-1,1,-1 \quad(\bmod 11)
|
| 292 |
+
\end{aligned}
|
| 293 |
+
$$
|
| 294 |
+
|
| 295 |
+
Hence a polynomial of the form $P(n)=\left(n^{5}+a\right) / 11$ has the desired property if and only if $a \equiv \pm 1(\bmod 11)$. This completes the proof.
|
| 296 |
+
|
| 297 |
+
A Variant. We start by following the first solution up to equation (4). We note that $b=1$ is a trivial solution, and assume from now on that $b \geqslant 2$. As $(x-1)^{5}+a$ and $x^{5}+a$ have different parity, $b$ must be odd. As $B$ in (3) is a multiple of $b$, we conclude that (i) $b$ is not divisible by 5 and that (ii) $b$ and $x$ are relatively prime. As $C=10 x\left(2 x^{2}+1\right)$ in (4) is divisible by $b$, we altogether derive
|
| 298 |
+
|
| 299 |
+
$$
|
| 300 |
+
E:=2 x^{2}+1 \equiv 0(\bmod b)
|
| 301 |
+
$$
|
| 302 |
+
|
| 303 |
+
Together with (2) this implies that
|
| 304 |
+
|
| 305 |
+
$$
|
| 306 |
+
5 E^{2}+10 E-2 A=11 \equiv 0 \quad(\bmod b)
|
| 307 |
+
$$
|
| 308 |
+
|
| 309 |
+
Hence $b=11$ is the only remaining candidate, and it is handled as in the first solution.
|
| 310 |
+
|
| 311 |
+
Solution 2: Let $p$ be a prime such that $p$ divides $b$. For some integer $x$, we have
|
| 312 |
+
|
| 313 |
+
$$
|
| 314 |
+
(x-1)^{5} \equiv x^{5} \equiv(x+1)^{5} \quad(\bmod p)
|
| 315 |
+
$$
|
| 316 |
+
|
| 317 |
+
Now, there is a primitive root $g$ modulo $p$, so there exist $u, v, w$ such that
|
| 318 |
+
|
| 319 |
+
$$
|
| 320 |
+
x-1 \equiv g^{u} \quad(\bmod p), \quad x \equiv g^{v} \quad(\bmod p), \quad x+1 \equiv g^{w} \quad(\bmod p)
|
| 321 |
+
$$
|
| 322 |
+
|
| 323 |
+
The condition of the problem is thus
|
| 324 |
+
|
| 325 |
+
$$
|
| 326 |
+
g^{5 u} \equiv g^{5 v} \equiv g^{5 w} \quad(\bmod p) \quad \Longrightarrow \quad 5 u \equiv 5 v \equiv 5 w \quad(\bmod p-1)
|
| 327 |
+
$$
|
| 328 |
+
|
| 329 |
+
If $p \not \equiv 1(\bmod 5)$, then 5 is invertible modulo $p-1$ and thus $u \equiv v \equiv w(\bmod p-1)$, i.e. $x-1 \equiv x \equiv x+1(\bmod p)$. This is a contradiction. Hence $p \equiv 1(\bmod 5)$ and thus $u \equiv v \equiv w\left(\bmod \frac{p-1}{5}\right)$. Thus, from (6), there exist integers $k, \ell$ such that
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
\left.\begin{array}{rl}
|
| 333 |
+
x-1 & \equiv g^{v+k \frac{p-1}{5}} \equiv x t^{k} \quad(\bmod p) \\
|
| 334 |
+
x+1 & \equiv g^{v+\ell \frac{p-1}{5}} \\
|
| 335 |
+
\equiv x t^{\ell} & (\bmod p)
|
| 336 |
+
\end{array}\right\} \quad \text { where } t=g^{\frac{p-1}{5}}
|
| 337 |
+
$$
|
| 338 |
+
|
| 339 |
+
Let $r=t^{k}$ and $s=t^{\ell}$. In particular, the above yields $r, s \not \equiv 1(\bmod p)$, and thus
|
| 340 |
+
|
| 341 |
+
$$
|
| 342 |
+
x \equiv-(r-1)^{-1} \equiv(s-1)^{-1} \quad(\bmod p)
|
| 343 |
+
$$
|
| 344 |
+
|
| 345 |
+
It follows that
|
| 346 |
+
|
| 347 |
+
$$
|
| 348 |
+
(r-1)^{-1}+(s-1)^{-1} \equiv 0 \quad(\bmod p) \quad \Longrightarrow \quad r+s \equiv 2 \quad(\bmod p)
|
| 349 |
+
$$
|
| 350 |
+
|
| 351 |
+
Now $t^{5} \equiv 1(\bmod p)$, so $r$ and $s$ must be congruent, modulo $p$, to some of the non-trivial fifth roots of unity $t, t^{2}, t^{3}, t^{4}$. Observe that, for any pair of these non-trivial roots of unity,
|
| 352 |
+
either one is the other's inverse, or one is the other's square. In the first case, we have $r+r^{-1} \equiv 2(\bmod p)$, implying $r \equiv 1(\bmod p)$, a contradiction. Hence
|
| 353 |
+
|
| 354 |
+
$$
|
| 355 |
+
r+r^{2} \equiv 2 \quad(\bmod p) \quad \Longrightarrow \quad(r-1)(r+2) \equiv 0 \quad(\bmod p),
|
| 356 |
+
$$
|
| 357 |
+
|
| 358 |
+
or
|
| 359 |
+
|
| 360 |
+
$$
|
| 361 |
+
s^{2}+s \equiv 2 \quad(\bmod p) \quad \Longrightarrow \quad(s-1)(s+2) \equiv 0 \quad(\bmod p)
|
| 362 |
+
$$
|
| 363 |
+
|
| 364 |
+
Thus, since $r, s \not \equiv 1(\bmod p)$, we have $r \equiv-2(\bmod p)$ or $s \equiv-2(\bmod p)$, and thus $1 \equiv r^{5} \equiv-32(\bmod p)$ or an analogous equation obtained from $s$. Hence $p \mid 33$. Since $p \equiv 1(\bmod 5)$, it follows that $p=11$, i.e. $b$ is a power of 11 .
|
| 365 |
+
|
| 366 |
+
Examining the fifth powers modulo 11 , we see that $b=11$ is indeed a solution with $a \equiv \pm 1(\bmod 11)$ and, correspondingly, $x \equiv \pm 4(\bmod 11)$. Now suppose, for the sake of contradiction, that $11^{2}$ divides $b$. Then, for some integer $m$, we must have
|
| 367 |
+
|
| 368 |
+
$$
|
| 369 |
+
(x-1, x, x+1) \equiv \pm(3+11 m, 4+11 m, 5+11 m) \quad(\bmod 121)
|
| 370 |
+
$$
|
| 371 |
+
|
| 372 |
+
and thus, substituting into the condition of the problem,
|
| 373 |
+
|
| 374 |
+
$$
|
| 375 |
+
\begin{aligned}
|
| 376 |
+
3^{5}+55 \cdot 3^{4} m & \equiv 4^{5}+55 \cdot 4^{4} m \equiv 5^{5}+55 \cdot 5^{4} m \quad(\bmod 121) \\
|
| 377 |
+
& \Longrightarrow \quad 1-22 m \equiv 56+44 m \equiv-21+11 m \quad(\bmod 121)
|
| 378 |
+
\end{aligned}
|
| 379 |
+
$$
|
| 380 |
+
|
| 381 |
+
Hence $33 m \equiv 22(\bmod 121)$ and $33 m \equiv 44(\bmod 121)$, so $22 \equiv 0(\bmod 121)$, a contradiction. It follows that $b \mid 11$.
|
| 382 |
+
|
| 383 |
+
Finally, we conclude that the positive integers satisfying the original condition are $b=11$, with $a \equiv \pm 1(\bmod 11)$, and $b=1$, for any positive integer $a$.
|
| 384 |
+
|
| 385 |
+
Solution 3: Denote the three consecutive integers by $x-1, x$, and $x+1$ as in Solution 1. By computing the differences in (1), we find
|
| 386 |
+
|
| 387 |
+
$$
|
| 388 |
+
\begin{aligned}
|
| 389 |
+
& F:=(x+1)^{5}-x^{5}=5 x^{4}+10 x^{3}+10 x^{2}+5 x+1 \equiv 0 \quad(\bmod b), \\
|
| 390 |
+
& G:=x^{5}-(x-1)^{5}=5 x^{4}-10 x^{3}+10 x^{2}-5 x+1 \equiv 0 \quad(\bmod b) .
|
| 391 |
+
\end{aligned}
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
By determining the polynomial greatest divisor of $F(x)$ and $G(x)$ using the Euclidean algorithm, we find that
|
| 395 |
+
|
| 396 |
+
$$
|
| 397 |
+
p(x) F(x)+q(x) G(x)=22
|
| 398 |
+
$$
|
| 399 |
+
|
| 400 |
+
where
|
| 401 |
+
|
| 402 |
+
$$
|
| 403 |
+
\begin{aligned}
|
| 404 |
+
& p(x)=-15 x^{3}+30 x^{2}-28 x+11 \\
|
| 405 |
+
& q(x)=15 x^{3}+30 x^{2}+28 x+11
|
| 406 |
+
\end{aligned}
|
| 407 |
+
$$
|
| 408 |
+
|
| 409 |
+
Since $b \mid F(x)$ and $b \mid G(x)$, it follows from (7) that $b \mid 22$. We now finish off the problem as in Solution 1.
|
| 410 |
+
|
| 411 |
+
Problem 5. (Proposed by Waldemar Pompe, Poland)
|
| 412 |
+
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
|
| 413 |
+
|
| 414 |
+
Prove that $\angle A C P=\angle Q C B$.
|
| 415 |
+
|
| 416 |
+
Solution 1: Assume that $\omega$ is tangent to $A C$ and $B C$ at $E$ and $F$, respectively and let $P E, P F, P Q$ meet $\Omega$ at $K, L, M$, respectively. Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$, and consider the homethety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Now $K$ is the image of $E$ under $\mathscr{H}$, and $E I \perp A C$. Hence $O K \perp A C$, and thus $K$ is the midpoint of the $\operatorname{arc} C A$. Similarly, $L$ is the midpoint of the arc $B C$ and $M$ is the midpoint of the arc $B A$. It follows that arcs $L M$ and $C K$ are equal, because
|
| 417 |
+
|
| 418 |
+
$$
|
| 419 |
+
\begin{aligned}
|
| 420 |
+
\overparen{B M}=\overparen{M A} & \Longrightarrow \overparen{B L}+\overparen{L M}=\overparen{M K}+\overparen{K A} \Longrightarrow \overparen{L C}+\overparen{L M}=\overparen{M K}+\overparen{C K} \\
|
| 421 |
+
& \Longrightarrow 2 \overparen{L M}+\overparen{M C}=\overparen{M C}+2 \overparen{C K}
|
| 422 |
+
\end{aligned}
|
| 423 |
+
$$
|
| 424 |
+
|
| 425 |
+
Thus arcs $F Q$ and $D E$ of $\omega$ are equal, too, where $D$ is the intersection of $C P$ with $\omega$. Since $C E$ and $C F$ are tangents to $\omega$, this implies that $\angle D E C=\angle C F Q$. Further, $C E=C F$, and thus triangles $C E D$ and $C F Q$ are congruent. In particular, $\angle E C D=\angle Q C F$, as required.
|
| 426 |
+
|
| 427 |
+
|
| 428 |
+
A Variant. As above, we show that $\operatorname{arcs} F Q$ and $D E$ of $\omega$ are equal, which implies that $D E F Q$ is an isoceles trapezoid, and so we have $\angle F E D=\angle Q F E$. Together with $|F Q|=|D E|$, this implies that, since $E$ and $F$ are images of each other under reflection in the angle bisector $C I$ of $\angle C$, so are the segments $[E Q]$ and $[F D]$, and, in particular, $D$ and $Q$. In turn, this yields $\angle E C D=\angle Q C F$, as required.
|
| 429 |
+
|
| 430 |
+
Remark. Let $J$ denote the incentre of $A B C$. By Sawayama's theorem, $J$ is the midpoint of $[E F]$, i.e. $P J$ is a median of $P F E$. Since $C$ is the intersection of the tangents $A C$ and $B C$ to the circumcircle of $P F E$ at $E$ and $F$, respectively, $P C$ is a symmedian of $P F E$. Thus $\angle C P E=\angle F P J$. But, since the arcs $F Q$ and $D E$ of $\omega$ are equal, $\angle C P E=\angle F P Q$. This shows that $J$ lies on the line $P Q$.
|
| 431 |
+
|
| 432 |
+
Another Variant. We show that $\operatorname{arcs} Q E$ and $F D$ are equal, and then finish as in the main solution. Let $B P$ meet $\omega$ again at $Z$. Consider the homothety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Under $\mathscr{H}, D \mapsto C$ and $Z \mapsto B$, so $D Z \| C B$. (This also follows by considering the common tangent to $\omega$ and $\Omega$, and tangential angles.) Now, by power of a point,
|
| 433 |
+
|
| 434 |
+
$$
|
| 435 |
+
B F^{2}=B Z \cdot B P, \quad C F^{2}=C D \cdot C P
|
| 436 |
+
$$
|
| 437 |
+
|
| 438 |
+
Now $D Z \| C B$ implies $B Z / B P=C D / C P$, and so, dividing the two previous equations by each other, and taking square roots, $B F / C F=B P / C P$. Hence $P F$ bissects angle $\angle B P C$. Now let $\angle B P F=\angle F P C=\beta$. By tangential angles, it follows that $\angle C F D=\beta$. Further, $\angle B A C=\angle B P C=2 \beta$. Let the tangent to $\omega$ through $Q$ and parallel to $A B$ meet $A C$ at $X$. Then $\angle Q X C=2 \beta$, so, since $X Q=X E$ by tangency, $\angle Q E X=\beta$. By tangential angles, it follows that $\operatorname{arcs} F D$ and $Q E$ are equal, as claimed.
|
| 439 |
+
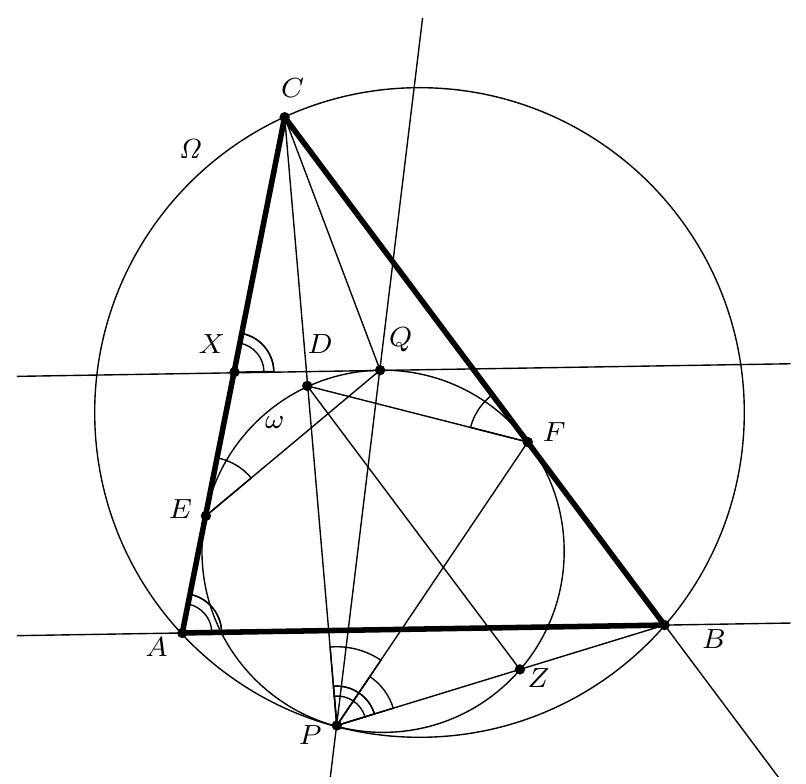
|
| 440 |
+
|
| 441 |
+
Solution 2: Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. Observe that $C I$ is the angle bisector of angle $\angle C$, because $\omega$ is tangent to $A C$ and $B C$. Consider the homethety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Let $M$ be the image of $Q$ under $\mathscr{H}$. By construction, $I Q \perp A B$, so $O M \perp A B$. Thus the diameter $O M$ of $\Omega$ passes through the midpoint of the $\operatorname{arc} A B$ of $\Omega$, which also lies on the angle bisector $C I$. This implies that $\angle I C M=90^{\circ}$. We next show that $P, I, Q, C$ lie on a circle. Notice that
|
| 442 |
+
|
| 443 |
+
$$
|
| 444 |
+
\begin{aligned}
|
| 445 |
+
\angle P Q I & =90^{\circ}-\frac{1}{2} \angle Q I P=90^{\circ}-\frac{1}{2} \angle M O P=90^{\circ}-\left(180^{\circ}-\angle P C M\right) \\
|
| 446 |
+
& =(\angle P C I+\angle I C M)-90^{\circ}=\angle P C I
|
| 447 |
+
\end{aligned}
|
| 448 |
+
$$
|
| 449 |
+
|
| 450 |
+
Hence $P, I, Q, C$ lie on a circle. But $P I=I Q$, so $C I$ is the angle bisector of $\angle P C Q$. Since $C I$ is also the angle bisector of angle $\angle C$, it follows that $\angle A C P=\angle Q C B$, as required.
|
| 451 |
+
|
| 452 |
+
|
| 453 |
+
A Variant. We show that $P I Q C$ is cyclic by chasing angles. Define $\alpha=\angle B A C$, $\beta=\angle C B A$ and $\gamma=\angle A C P$. For convenience, we consider the configuration where $A$ and $P$ lie one the same side of the angle bisector $C I$ of $\angle C$. In this configuration,
|
| 454 |
+
|
| 455 |
+
$$
|
| 456 |
+
\angle P C I=\frac{1}{2} \angle A C B-\angle A C P=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta-\gamma .
|
| 457 |
+
$$
|
| 458 |
+
|
| 459 |
+
Now notice that $\angle P B A=\angle A C P=\gamma$, and therefore $\angle C A P=180^{\circ}-\beta-\gamma$, whence $\angle P A B=180^{\circ}-\alpha-\beta-\gamma$. Further, $P O$ is a diameter of $\Omega$, and therefore $\angle A P O=90^{\circ}-\gamma$. Let $A B$ and $P O$ intersect at $T$. Then
|
| 460 |
+
|
| 461 |
+
$$
|
| 462 |
+
\angle B T O=180^{\circ}-\angle P A B-\angle A P O=\alpha+\beta+2 \gamma-90^{\circ}
|
| 463 |
+
$$
|
| 464 |
+
|
| 465 |
+
But $Q I \perp A B$ by construction, and thus
|
| 466 |
+
|
| 467 |
+
$$
|
| 468 |
+
\begin{aligned}
|
| 469 |
+
& \angle O I Q=90^{\circ}-\angle B T O=180^{\circ}-\alpha-\beta-2 \gamma \\
|
| 470 |
+
& \Longrightarrow \quad \angle Q I P=180^{\circ}-\angle O I Q=\alpha+\beta+2 \gamma \\
|
| 471 |
+
& \Longrightarrow \quad \angle P Q I=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta-\gamma .
|
| 472 |
+
\end{aligned}
|
| 473 |
+
$$
|
| 474 |
+
|
| 475 |
+
Hence $\angle I C Q=\angle P Q I$, and thus $P I Q C$ is cyclic. Since $P I=Q I$, it follows that $C I$ is the angle bisector of $\angle P C Q$, which completes the proof.
|
| 476 |
+
|
| 477 |
+
Solution 3: Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. Let $D$ be the second point of intersection of $C P$ with $\omega$, and let $\ell$ denote the tangent to $\omega$ at $D$, which meets $A C$ at $S$. Hence $I D \perp \ell$. By construction, $P, I, O$ lie one a line, and hence the isosceles triangles $P I D$ and $P O C$ are similar. In particular, it follows that $O C \perp \ell$, so $C$ is the midpoint of the arc of $\Omega$ defined by the points of intersection of $\ell$ with $\Omega$. It is easy to see that this implies that
|
| 478 |
+
|
| 479 |
+
$$
|
| 480 |
+
\angle D S C=\angle A B C
|
| 481 |
+
$$
|
| 482 |
+
|
| 483 |
+
Under reflection in the angle bisector $C I$ of $\angle C, \ell$ is thus mapped to a tangent to $\omega$ parallel to $A B$ and intersecting the interior of $A B C$, since $\omega$ is mapped to itself under this reflection. In particular, $D$ is mapped to $Q$, and thus $\angle Q C B=\angle A C D$, as required.
|
| 484 |
+
|
| 485 |
+
|
| 486 |
+
Remark. Conceptually, this solution is similar to Solution 1, but here, we proceed more directly via the reflectional symmetry. Therefore, this solution links Solution 1 to Solution 4, in which we use an inversion.
|
| 487 |
+
|
| 488 |
+
Solution 4: Let the tangent to $\omega$ at $Q$ meet $A C$ and $B C$ at $X$ and $Y$, respectively. Then $A C / X C=B C / Y C$, and thus there is a radius $r$ such that $r^{2}=A C \cdot Y C=B C \cdot X C$. Let $\Gamma$ denote the circle with centre $C$ and radius $r$, and consider the inversion $\mathscr{I}$ in the circle $\Gamma$. Under $\mathscr{I}$,
|
| 489 |
+
$A \longmapsto A^{\prime}$, the point on the ray $C A$ satisfying $C A^{\prime}=C Y$;
|
| 490 |
+
$B \longmapsto B^{\prime}$, the point on the ray $C B$ satisfying $C B^{\prime}=C X$;
|
| 491 |
+
$\Omega \longmapsto$ the line $A^{\prime} B^{\prime}$;
|
| 492 |
+
$\omega \longmapsto \omega^{\prime}$, the excircle of $C A^{\prime} B^{\prime}$ opposite $C$;
|
| 493 |
+
$P \longmapsto P^{\prime}$, the point where $\omega^{\prime}$ touches $A^{\prime} B^{\prime}$;
|
| 494 |
+
In particular, $\omega^{\prime}$, the image of $\omega$, is a circle tangent to $A C, B C$ and $A^{\prime} B^{\prime}$, so it is either the excircle of $C A^{\prime} B^{\prime}$ opposite $C$, or the incircle of $C A^{\prime} B^{\prime}$. Let $\omega$ be tangent to $B C$ at $F$, and let $F^{\prime}$ be the image of $F$ under $\mathscr{I}$. Then $C F \cdot C F^{\prime}=B C \cdot X C$. Now $C F<B C$, so $C F^{\prime}>C X=C B^{\prime}$. Hence $\omega^{\prime}$ cannot be the incircle, so $\omega^{\prime}$ is indeed the excircle of $C A^{\prime} B^{\prime}$ opposite $C$.
|
| 495 |
+
|
| 496 |
+
Now note that $\omega$ is the excircle of $C X Y$ opposite $C$. The reflection about the angle bisector of $\angle C$ maps $X$ to $B^{\prime}, Y$ to $A^{\prime}$. It thus maps the triangle $C X Y$ to $C B^{\prime} A^{\prime}, \omega$ to $\omega^{\prime}$ and, finally, $Q$ to $P^{\prime}$. It follows that $\angle A C P=\angle A C P^{\prime}=\angle Q C B$, as required.
|
| 497 |
+
|
| 498 |
+
|
| 499 |
+
Solution 5: Let $r$ be the radius such that $r^{2}=A C \cdot B C$. Let $\mathscr{J}$ denote the composition of the inversion $\mathscr{I}$ in the circle of centre $C$ and radius $r$, followed by the reflection in the
|
| 500 |
+
angle bisector of $\angle C$. Under $\mathscr{J}$,
|
| 501 |
+
$A \longmapsto B, B \mapsto A ;$
|
| 502 |
+
$\Omega \longmapsto$ the line $A B$;
|
| 503 |
+
$\omega \longmapsto \omega^{\prime}$, the excircle of $A B C$ opposite the vertex $C$;
|
| 504 |
+
$P \longmapsto Q^{\prime}$, the point where $\omega^{\prime}$ touches $A B$;
|
| 505 |
+
In particular, note that the image $\omega^{\prime}$ of $\omega$ under $\mathscr{J}$ is a circle tangent to $A C, B C$ and $A B$, so it is either the incircle of $A B C$, or the excircle opposite vertex $C$. Observe that $r \geqslant \min \{A C, B C\}$, so the image of the points of tangency of $\omega$ must lie outside $A B C$, and thus $\omega^{\prime}$ cannot be the incircle. Thus $\omega^{\prime}$ is the excircle opposite vertex $C$ as claimed. Further, the point of tangency $P$ is mapped to $Q^{\prime}$.
|
| 506 |
+
|
| 507 |
+
Now, since the line $C P$ is mapped to itself under the inversion $\mathscr{I}$, and mapped onto $C Q^{\prime}$ under $\mathscr{J}, C P$ and $C Q^{\prime}$ are images of each other under reflection in the angle bisector of $\angle C$. But $C, Q, Q^{\prime}$ lie on a line for there is a homothety with centre $C$ that maps $\omega$ onto the excircle $\omega^{\prime}$. This completes the proof.
|
| 508 |
+
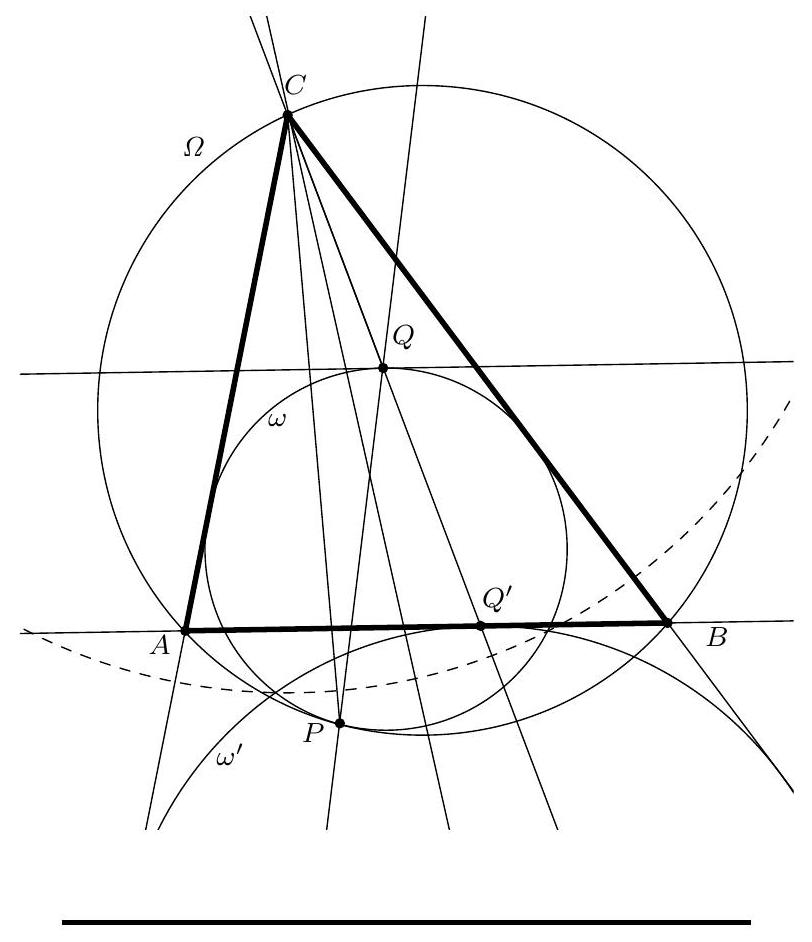
|
| 509 |
+
|
| 510 |
+
Solution 6: Assume that $\omega$ is tangent to $A C$ and $B C$ at $E$ and $F$, respectively. Assume that $C P$ meets $\omega$ at $D$. Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. To set up a solution in the complex plane, we take the circle $\omega$ as the unit circle centered at the origin of the complex plane, and let $P O$ be the real axis with $o>0$, where we use the convention that lowercase letters denote complex coordinates of corresponding points in the plane denoted by uppercase letters.
|
| 511 |
+
|
| 512 |
+
Now, a point $Z$ on the circle $\Omega$ satisfies
|
| 513 |
+
|
| 514 |
+
$$
|
| 515 |
+
|z-o|^{2}=(o+1)^{2} \quad \Longleftrightarrow \quad z z^{*}-o\left(z+z^{*}\right)-2 o-1=0
|
| 516 |
+
$$
|
| 517 |
+
|
| 518 |
+
The triangle $A B C$ is defined by the points $E$ and $F$ on $\omega$, the intersection $C$ of the corresponding tangents lying on $\Omega$. Thus $c=2 e f /(e+f)$, and further
|
| 519 |
+
|
| 520 |
+
$$
|
| 521 |
+
|c-o|^{2}=(o+1)^{2} \quad \Longleftrightarrow \quad c c^{*}-o\left(c+c^{*}\right)-2 o-1=0,
|
| 522 |
+
$$
|
| 523 |
+
|
| 524 |
+
and this is the equality defining $o$. The points $A$ and $B$ are the second intersection points of $\Omega$ with the tangents to $\omega$ at $E$ and $F$ respectively. A point $Z$ on the tangent through $E$ is given by $z=2 e-e^{2} z^{*}$, and thus $A$ and $C$ satisfy
|
| 525 |
+
|
| 526 |
+
$$
|
| 527 |
+
\begin{aligned}
|
| 528 |
+
\left(2 e-e^{2} z^{*}\right) z^{*} & -o\left(2 e-e^{2} z^{*}+z^{*}\right)-2 o-1=0 \\
|
| 529 |
+
& \Longleftrightarrow-e^{2} z^{* 2}+\left(2 e+o e^{2}-o\right) z^{*}-(2 e o+2 o+1)=0 \\
|
| 530 |
+
& \Longleftrightarrow z^{* 2}-\left(2 e^{*}+o-o e^{* 2}\right) z^{*}+\left(2 e^{*} o+2 o e^{* 2}+e^{* 2}\right)=0
|
| 531 |
+
\end{aligned}
|
| 532 |
+
$$
|
| 533 |
+
|
| 534 |
+
since $|e|=1$. Thus
|
| 535 |
+
|
| 536 |
+
$$
|
| 537 |
+
a^{*}+c^{*}=2 e^{*}+o-o e^{* 2} \quad \Longrightarrow \quad a^{*}=\frac{2 e^{*} f}{e+f}+o\left(1-e^{* 2}\right)
|
| 538 |
+
$$
|
| 539 |
+
|
| 540 |
+
and similarly
|
| 541 |
+
|
| 542 |
+
$$
|
| 543 |
+
b^{*}=\frac{2 f^{*} e}{f+e}+o\left(1-f^{* 2}\right)
|
| 544 |
+
$$
|
| 545 |
+
|
| 546 |
+
Then
|
| 547 |
+
|
| 548 |
+
$$
|
| 549 |
+
\begin{aligned}
|
| 550 |
+
b^{*}-a^{*} & =\frac{2\left(e f^{*}-e^{*} f\right)}{e+f}+o\left(e^{* 2}-f^{* 2}\right) \\
|
| 551 |
+
& =\frac{2 e f\left(f^{* 2}-e^{* 2}\right)}{e+f}+o\left(e^{* 2}-f^{* 2}\right) \\
|
| 552 |
+
& =\left(f^{* 2}-e^{* 2}\right)\left(\frac{2 e f}{e+f}-o\right)=\left(f^{* 2}-e^{* 2}\right)(c-o) .
|
| 553 |
+
\end{aligned}
|
| 554 |
+
$$
|
| 555 |
+
|
| 556 |
+
Now let $Z$ be a point on the tangent to $\omega$ parallel to $A B$ passing through $Q$. Then
|
| 557 |
+
|
| 558 |
+
$$
|
| 559 |
+
z=2 q-q^{2} z^{*} \quad \Longleftrightarrow \quad z-q=q-q^{2} z^{*}=-q^{2}\left(z^{*}-q^{*}\right)
|
| 560 |
+
$$
|
| 561 |
+
|
| 562 |
+
for $|q|=1$, and thus
|
| 563 |
+
|
| 564 |
+
$$
|
| 565 |
+
\frac{b-a}{b^{*}-a^{*}}=\frac{z-q}{z^{*}-q^{*}}=\frac{-q^{2}\left(z^{*}-q^{*}\right)}{z^{*}-q^{*}}=-q^{2} .
|
| 566 |
+
$$
|
| 567 |
+
|
| 568 |
+
It follows that
|
| 569 |
+
|
| 570 |
+
$$
|
| 571 |
+
\begin{aligned}
|
| 572 |
+
q^{2} & =-\frac{b-a}{b^{*}-a^{*}}=-\frac{\left(f^{2}-e^{2}\right)\left(c^{*}-o\right)}{\left(f^{* 2}-e^{* 2}\right)(c-o)}=e^{2} f^{2} \frac{c^{*}-o}{c-o} \\
|
| 573 |
+
& =e^{2} f^{2} \frac{\left(c^{*}-o\right)^{2}}{|c-o|^{2}}=e^{2} f^{2} \frac{\left(c^{*}-o\right)^{2}}{(1+o)^{2}}
|
| 574 |
+
\end{aligned}
|
| 575 |
+
$$
|
| 576 |
+
|
| 577 |
+
where we have used (1). In particular,
|
| 578 |
+
|
| 579 |
+
$$
|
| 580 |
+
q=e f \frac{c^{*}-o}{1+o}
|
| 581 |
+
$$
|
| 582 |
+
|
| 583 |
+
where the choice of sign is to be justified a posteriori. Further, the point $D$ satisfies
|
| 584 |
+
|
| 585 |
+
$$
|
| 586 |
+
-d p=\frac{d-p}{d^{*}-p^{*}}=\frac{c-p}{c^{*}-p^{*}} \quad \Longrightarrow \quad d=-\frac{c-p}{c^{*} p-1}=\frac{c+1}{c^{*}+1},
|
| 587 |
+
$$
|
| 588 |
+
|
| 589 |
+
using $p=-1$ to obtain the final equality.
|
| 590 |
+
Now, it suffices to show that (i) $D Q \| E F \perp C I$ and (ii) the midpoint of $[D Q]$ is on $C I$. The desired equality then follows by symmetry with respect to the angle bisector of the angle $\angle A C B$. Notice that (i) is equivalent with
|
| 591 |
+
|
| 592 |
+
$$
|
| 593 |
+
\frac{d-q}{d^{*}-q^{*}}=\frac{e-f}{e^{*}-f^{*}} \quad \Longleftrightarrow \quad d q=e f
|
| 594 |
+
$$
|
| 595 |
+
|
| 596 |
+
for $[D Q]$ and $[E F]$ are chords of $\omega$. But
|
| 597 |
+
|
| 598 |
+
$$
|
| 599 |
+
\begin{aligned}
|
| 600 |
+
d q=e f & \Longleftrightarrow \frac{c+1}{c^{*}+1} e f \frac{c^{*}-o}{1+o}=e f \quad \Longleftrightarrow \quad(c+1)\left(c^{*}-o\right)=\left(c^{*}+1\right)(1+o) \\
|
| 601 |
+
& \Longleftrightarrow c c^{*}-o\left(c+c^{*}\right)-2 o-1=0 .
|
| 602 |
+
\end{aligned}
|
| 603 |
+
$$
|
| 604 |
+
|
| 605 |
+
The last equality is precisely the defining relation for $o,(1)$. This proves (i). Further, the midpoint of $[D Q]$ is $\frac{1}{2}(d+q)$, so it remains to check that
|
| 606 |
+
|
| 607 |
+
$$
|
| 608 |
+
d q=\frac{d+q}{d^{*}+q^{*}}=\frac{c}{c^{*}}=e f
|
| 609 |
+
$$
|
| 610 |
+
|
| 611 |
+
where the first equality expresses that $[D Q]$ is a chord of $\omega$ (obviously) containing its midpoint, the second equality expresses the alignment of the midpoint of $[D Q], C$ and $I$, and the third equality follows from the expression for $c$. But we have just shown that $d q=e f$. This proves (ii), justifies the choice of sign for $q$ a posteriori, and thus completes the solution of the problem.
|
| 612 |
+
|
| 613 |
+
Problem 6. (Proposed by Emil Kolev, Bulgaria)
|
| 614 |
+
Snow White and the Seven Dwarves are living in their house in the forest. On each of 16 consecutive days, some of the dwarves worked in the diamond mine while the remaining dwarves collected berries in the forest. No dwarf performed both types of work on the same day. On any two different (not necessarily consecutive) days, at least three dwarves each performed both types of work. Further, on the first day, all seven dwarves worked in the diamond mine.
|
| 615 |
+
|
| 616 |
+
Prove that, on one of these 16 days, all seven dwarves were collecting berries.
|
| 617 |
+
|
| 618 |
+
Solution 1: We define $V$ as the set of all 128 vectors of length 7 with entries in $\{0,1\}$. Every such vector encodes the work schedule of a single day: if the $i$-th entry is 0 then the $i$-th dwarf works in the mine, and if this entry is 1 then the $i$-th dwarf collects berries. The 16 working days correspond to 16 vectors $d_{1}, \ldots, d_{16}$ in $V$, which we will call dayvectors. The condition imposed on any pair of distinct days means that any two distinct day-vectors $d_{i}$ and $d_{j}$ differ in at least three positions.
|
| 619 |
+
|
| 620 |
+
We say that a vector $x \in V$ covers some vector $y \in V$, if $x$ and $y$ differ in at most one position; note that every vector in $V$ covers exactly eight vectors. For each of the 16 day-vectors $d_{i}$ we define $B_{i} \subset V$ as the set of the eight vectors that are covered by $d_{i}$. As, for $i \neq j$, the day-vectors $d_{i}$ and $d_{j}$ differ in at least three positions, their corresponding sets $B_{i}$ and $B_{j}$ are disjoint. As the sets $B_{1}, \ldots, B_{16}$ together contain $16 \cdot 8=128=|V|$ distinct elements, they form a partition of $V$; in other words, every vector in $V$ is covered by precisely one day-vector.
|
| 621 |
+
|
| 622 |
+
The weight of a vector $v \in V$ is defined as the number of 1-entries in $v$. For $k=0,1, \ldots, 7$, the set $V$ contains $\binom{7}{k}$ vectors of weight $k$. Let us analyse the 16 dayvectors $d_{1}, \ldots, d_{16}$ by their weights, and let us discuss how the vectors in $V$ are covered by them.
|
| 623 |
+
|
| 624 |
+
1. As all seven dwarves work in the diamond mine on the first day, the first day-vector is $d_{1}=(0000000)$. This day-vector covers all vectors in $V$ with weight 0 or 1.
|
| 625 |
+
2. No day-vector can have weight 2 , as otherwise it would differ from $d_{1}$ in at most two positions. Hence each of the $\binom{7}{2}=21$ vectors of weight 2 must be covered by some day-vector of weight 3 . As every vector of weight 3 covers three vectors of weight 2 , exactly $21 / 3=7$ day-vectors have weight 3 .
|
| 626 |
+
3. How are the $\binom{7}{3}=35$ vectors of weight 3 covered by the day-vectors? Seven of them are day-vectors, and the remaining 28 ones must be covered by day-vectors of weight 4 . As every vector of weight 4 covers four vectors of weight 3 , exactly $28 / 4=7$ day-vectors have weight 4.
|
| 627 |
+
|
| 628 |
+
To summarize, one day-vector has weight 0 , seven have weight 3 , and seven have weight 4 . None of these 15 day-vectors covers any vector of weight 6 or 7 , so that the eight heavyweight vectors in $V$ must be covered by the only remaining day-vector; and this remaining vector must be (1111111). On the day corresponding to (1111111) all seven dwarves are collecting berries, and that is what we wanted to show.
|
| 629 |
+
|
| 630 |
+
Solution 2: If a dwarf $X$ performs the same type of work on three days $D_{1}, D_{2}, D_{3}$, then we say that this triple of days is monotonous for $X$. We claim that the following configuration cannot occur: There are three dwarves $X_{1}, X_{2}, X_{3}$ and three days $D_{1}, D_{2}$, $D_{3}$, such that the triple $\left(D_{1}, D_{2}, D_{3}\right)$ is monotonous for each of the dwarves $X_{1}, X_{2}, X_{3}$.
|
| 631 |
+
(Proof: Suppose that such a configuration occurs. Then among the remaining dwarves there exist three dwarves $Y_{1}, Y_{2}, Y_{3}$ that performed both types of work on day $D_{1}$ and on day $D_{2}$; without loss of generality these three dwarves worked in the mine on day $D_{1}$ and collected berries on day $D_{2}$. On day $D_{3}$, two of $Y_{1}, Y_{2}, Y_{3}$ performed the same type of work, and without loss of generality $Y_{1}$ and $Y_{2}$ worked in the mine. But then on days $D_{1}$ and $D_{3}$, each of the five dwarves $X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}$ performed only one type of work; this is in contradiction with the problem statement.)
|
| 632 |
+
|
| 633 |
+
Next we consider some fixed triple $X_{1}, X_{2}, X_{3}$ of dwarves. There are eight possible working schedules for $X_{1}, X_{2}, X_{3}$ (like mine-mine-mine, mine-mine-berries, mine-berriesmine, etc). As the above forbidden configuration does not occur, each of these eight working schedules must occur on exactly two of the sixteen days. In particular this implies that every dwarf worked exactly eight times in the mine and exactly eight times in the forest.
|
| 634 |
+
|
| 635 |
+
For $0 \leqslant k \leqslant 7$ we denote by $d(k)$ the number of days on which exactly $k$ dwarves were collecting berries. Since on the first day all seven dwarves were in the mine, on each of the remaining days at least three dwarves collected berries. This yields $d(0)=1$ and $d(1)=d(2)=0$. We assume, for the sake of contradiction, that $d(7)=0$ and hence
|
| 636 |
+
|
| 637 |
+
$$
|
| 638 |
+
d(3)+d(4)+d(5)+d(6)=15
|
| 639 |
+
$$
|
| 640 |
+
|
| 641 |
+
As every dwarf collected berries exactly eight times, we get that, further,
|
| 642 |
+
|
| 643 |
+
$$
|
| 644 |
+
3 d(3)+4 d(4)+5 d(5)+6 d(6)=7 \cdot 8=56
|
| 645 |
+
$$
|
| 646 |
+
|
| 647 |
+
Next, let us count the number $q$ of quadruples $\left(X_{1}, X_{2}, X_{3}, D\right)$ for which $X_{1}, X_{2}, X_{3}$ are three pairwise distinct dwarves that all collected berries on day $D$. As there are $7 \cdot 6 \cdot 5=210$ triples of pairwise distinct dwarves, and as every working schedule for three fixed dwarves occurs on exactly two days, we get $q=420$. As every day on which $k$ dwarves collect berries contributes $k(k-1)(k-2)$ such quadruples, we also have
|
| 648 |
+
|
| 649 |
+
$$
|
| 650 |
+
3 \cdot 2 \cdot 1 \cdot d(3)+4 \cdot 3 \cdot 2 \cdot d(4)+5 \cdot 4 \cdot 3 \cdot d(5)+6 \cdot 5 \cdot 4 \cdot d(6)=q=420
|
| 651 |
+
$$
|
| 652 |
+
|
| 653 |
+
which simplifies to
|
| 654 |
+
|
| 655 |
+
$$
|
| 656 |
+
d(3)+4 d(4)+10 d(5)+20 d(6)=70
|
| 657 |
+
$$
|
| 658 |
+
|
| 659 |
+
Finally, we count the number $r$ of quadruples $\left(X_{1}, X_{2}, X_{3}, D\right)$ for which $X_{1}, X_{2}, X_{3}$ are three pairwise distinct dwarves that all worked in the mine on day $D$. Similarly as above we see that $r=420$ and that
|
| 660 |
+
|
| 661 |
+
$$
|
| 662 |
+
7 \cdot 6 \cdot 5 \cdot d(0)+4 \cdot 3 \cdot 2 \cdot d(3)+3 \cdot 2 \cdot 1 \cdot d(4)=r=420
|
| 663 |
+
$$
|
| 664 |
+
|
| 665 |
+
which simplifies to
|
| 666 |
+
|
| 667 |
+
$$
|
| 668 |
+
4 d(3)+d(4)=35
|
| 669 |
+
$$
|
| 670 |
+
|
| 671 |
+
Multiplying (1) by -40 , multiplying (2) by 10 , multiplying (3) by -1 , multiplying (4) by 4 , and then adding up the four resulting equations yields $5 d(3)=30$ and hence $d(3)=6$. Then (4) yields $d(4)=11$. As $d(3)+d(4)=17$, the total number of days cannot be 16 . We have reached the desired contradiction.
|
| 672 |
+
|
| 673 |
+
A Variant. We follow the second solution up to equation (3). Multiplying (1) by 8 , multiplying (2) by -3 , and adding the two resulting equations to (3) yields
|
| 674 |
+
|
| 675 |
+
$$
|
| 676 |
+
3 d(5)+10 d(6)=22
|
| 677 |
+
$$
|
| 678 |
+
|
| 679 |
+
As $d(5)$ and $d(6)$ are positive integers, (5) implies $0 \leqslant d(6) \leqslant 2$. Only the case $d(6)=1$ yields an integral value $d(5)=4$. The equations (1) and (2) then yield $d(3)=10$ and $d(4)=0$.
|
| 680 |
+
|
| 681 |
+
Now let us look at the $d(3)=10$ special days on which exactly three dwarves were collecting berries. One of the dwarves collected berries on at least five special days (if every dwarf collected berries on at most four special days, this would allow at most $7 \cdot 4 / 3<10$ special days); we call this dwarf $X$. On at least two out of these five special days, some dwarf $Y$ must have collected berries together with $X$. Then these two days contradict the problem statement. We have reached the desired contradiction.
|
| 682 |
+
|
| 683 |
+
Comment. Up to permutations of the dwarves, there exists a unique set of day-vectors (as introduced in the first solution) that satisfies the conditions of the problem statement:
|
| 684 |
+
|
| 685 |
+
| 0000000 | 1110000 | 1001100 | 1000011 | 0101010 | 0100101 | 0010110 | 0011001 |
|
| 686 |
+
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
|
| 687 |
+
| 1111111 | 0001111 | 0110011 | 0111100 | 1010101 | 1011010 | 1101001 | 1100110 |
|
| 688 |
+
|
EGMO/md/en-2014-solutions-day1.md
ADDED
|
@@ -0,0 +1,195 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+

|
| 2 |
+
|
| 3 |
+
European Girls' Mathematical Olympiad Antalya - Turkey
|
| 4 |
+
|
| 5 |
+
Problems and Solutions
|
| 6 |
+
Day 1
|
| 7 |
+
|
| 8 |
+
The EGMO 2014 Problem Committee thanks the following countries for submitting problem proposals:
|
| 9 |
+
|
| 10 |
+
- Bulgaria
|
| 11 |
+
- Iran
|
| 12 |
+
- Japan
|
| 13 |
+
- Luxembourg
|
| 14 |
+
- Netherlands
|
| 15 |
+
- Poland
|
| 16 |
+
- Romania
|
| 17 |
+
- Ukraine
|
| 18 |
+
- United Kingdom
|
| 19 |
+
|
| 20 |
+
The Members of the Problem Committee:
|
| 21 |
+
|
| 22 |
+
Okan Tekman
|
| 23 |
+
Selim Bahadir
|
| 24 |
+
Şahin Emrah
|
| 25 |
+
Fehmi Emre Kadan
|
| 26 |
+
|
| 27 |
+
1. Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
|
| 28 |
+
|
| 29 |
+
Proposed by S. Khan, UNK
|
| 30 |
+
The answer is the interval $[2 / 3,2]$.
|
| 31 |
+
|
| 32 |
+
## Solution 1.
|
| 33 |
+
|
| 34 |
+
If $t<2 / 3$, take a triangle with sides $c=b=1$ and $a=2-\epsilon$. Then $b^{2}+c a t+c^{2}+$ $a b t-a^{2}-b c t=3 t-2+\epsilon(4-2 t-\epsilon) \leq 0$ for small positive $\epsilon$; for instance, for any $0<\epsilon<(2-3 t) /(4-2 t)$.
|
| 35 |
+
|
| 36 |
+
On the other hand, if $t>2$, then take a triangle with sides $b=c=1$ and $a=\epsilon$. Then $b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=2-t+\epsilon(2 t-\epsilon) \leq 0$ for small positive $\epsilon$; for instance, for any $0<\epsilon<(t-2) /(2 t)$.
|
| 37 |
+
Now assume that $2 / 3 \leq t \leq 2$ and $b+c>a$. Then using $(b+c)^{2} \geq 4 b c$ we obtain
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\begin{aligned}
|
| 41 |
+
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & =(b+c)^{2}+a t(b+c)-(2+t) b c-a^{2} \\
|
| 42 |
+
& \geq(b+c)^{2}+a t(b+c)-\frac{1}{4}(2+t)(b+c)^{2}-a^{2} \\
|
| 43 |
+
& \geq \frac{1}{4}(2-t)(b+c)^{2}+a t(b+c)-a^{2}
|
| 44 |
+
\end{aligned}
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
As $2-t \geq 0$ and $t>0$, this last expression is an increasing function of $b+c$, and hence using $b+c>a$ we obtain
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t>\frac{1}{4}(2-t) a^{2}+t a^{2}-a^{2}=\frac{3}{4}\left(t-\frac{2}{3}\right) a^{2} \geq 0
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
as $t \geq 2 / 3$. The other two inequalities follow by symmetry.
|
| 54 |
+
|
| 55 |
+
## Solution 2.
|
| 56 |
+
|
| 57 |
+
After showing that $t$ must be in the interval $[2 / 3,2]$ as in Solution 1, we let $x=$ $(c+a-b) / 2, y=(a+b-c) / 2$ and $z=(b+c-a) / 2$ so that $a=x+y, b=y+z$, $c=z+x$. Then we have:
|
| 58 |
+
$b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right) t+2\left(z^{2}+x z+y z-x y\right)$
|
| 59 |
+
Since this linear function of $t$ is positive both at $t=2 / 3$ where
|
| 60 |
+
$\frac{2}{3}\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right)+2\left(z^{2}+x z+y z-x y\right)=\frac{2}{3}\left((x-y)^{2}+4(x+y) z+2 z^{2}\right)>0$
|
| 61 |
+
and at $t=2$ where
|
| 62 |
+
$2\left(x^{2}+y^{2}-z^{2}+x y+x z-y z\right)+2\left(z^{2}+x z+y z+x y\right)=2\left(x^{2}+y^{2}\right)+4(x+y) z>0$,
|
| 63 |
+
it is positive on the entire interval $[2 / 3,2]$.
|
| 64 |
+
|
| 65 |
+
## Solution 3.
|
| 66 |
+
|
| 67 |
+
After the point in Solution 2 where we obtain
|
| 68 |
+
$b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right) t+2\left(z^{2}+x z+y z-x y\right)$
|
| 69 |
+
we observe that the right hand side can be rewritten as
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
(2-t) z^{2}+(x-y)^{2} t+(3 t-2) x y+z(x+y)(2+t)
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
As the first three terms are non-negative and the last term is positive, the result follows.
|
| 76 |
+
|
| 77 |
+
## Solution 4.
|
| 78 |
+
|
| 79 |
+
First we show that $t$ must be in the interval $[2 / 3,2]$ as in Solution 1. Then:
|
| 80 |
+
Case 1: If $a \geq b, c$, then $a b+a c-b c>0,2\left(b^{2}+c^{2}\right) \geq(b+c)^{2}>a^{2}$ and $t \geq 2 / 3$ implies:
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\begin{aligned}
|
| 84 |
+
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & =b^{2}+c^{2}-a^{2}+(a b+a c-b c) t \\
|
| 85 |
+
& \geq\left(b^{2}+c^{2}-a^{2}\right)+\frac{2}{3}(a b+a c-b c) \\
|
| 86 |
+
& \geq \frac{1}{3}\left(3 b^{2}+3 c^{2}-3 a^{2}+2 a b+2 a c-2 b c\right) \\
|
| 87 |
+
& \geq \frac{1}{3}\left[\left(2 b^{2}+2 c^{2}-a^{2}\right)+(b-c)^{2}+2 a(b+c-a)\right] \\
|
| 88 |
+
& >0
|
| 89 |
+
\end{aligned}
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
Case 2: If $b \geq a, c$, then $b^{2}+c^{2}-a^{2}>0$. If also $a b+a c-b c \geq 0$, then $b^{2}+c a t+$ $c^{2}+a b t-a^{2}-b c t>0$. If, on the other hand, $a b+a c-b c \leq 0$, then since $t \leq 2$, we have:
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\begin{aligned}
|
| 96 |
+
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & \geq b^{2}+c^{2}-a^{2}+2(a b+a c-b c) \\
|
| 97 |
+
& \geq(b-c)^{2}+a(b+c-a)+a(b+c) \\
|
| 98 |
+
& >0
|
| 99 |
+
\end{aligned}
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
By symmetry, we are done.
|
| 103 |
+
2. Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
|
| 104 |
+
|
| 105 |
+
Proposed by Danylo Khilko, UKR
|
| 106 |
+
|
| 107 |
+
# Solution 1.
|
| 108 |
+
|
| 109 |
+
As $D B=B C=C E$ we have $B I \perp C D$ and $C I \perp B E$. Hence $I$ is orthocenter of triangle $B F C$. Let $K$ be the point of intersection of the lines $B I$ and $C D$, and let $L$ be the point of intersection of the lines $C I$ and $B E$. Then we have the power relation $I B \cdot I K=I C \cdot I L$. Let $U$ and $V$ be the feet of the perpendiculars from $D$ to $E F$ and $E$ to $D F$, respectively. Now we have the power relation $D H \cdot H U=E H \cdot H V$.
|
| 110 |
+
|
| 111 |
+
|
| 112 |
+
Let $\omega_{1}$ and $\omega_{2}$ be the circles with diameters $B D$ and $C E$, respectively. From the power relations above we conclude that $I H$ is the radical axis of the circles $\omega_{1}$ and $\omega_{2}$.
|
| 113 |
+
Let $O_{1}$ and $O_{2}$ be centers of $\omega_{1}$ and $\omega_{2}$, respectively. Then $M B=M C, B O_{1}=C O_{2}$ and $\angle M B O_{1}=\angle M C O_{2}$, and the triangles $M B O_{1}$ and $M C O_{2}$ are congruent. Hence $M O_{1}=M O_{2}$. Since radii of $\omega_{1}$ and $\omega_{2}$ are equal, this implies that $M$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$ and $M, I, H$ are collinear.
|
| 114 |
+
|
| 115 |
+
## Solution 2.
|
| 116 |
+
|
| 117 |
+
Let the points $K, L, U, V$ be as in Solution 1. Le $P$ be the point of intersection of $D U$ and $E I$, and let $Q$ be the point of intersection of $E V$ and $D I$.
|
| 118 |
+
|
| 119 |
+
Since $D B=B C=C E$, the points $C I$ and $B I$ are perpendicular to $B E$ and $C D$, respectively. Hence the lines $B I$ and $E V$ are parallel and $\angle I E B=\angle I B E=$ $\angle U E H$. Similarly, the lines $C I$ and $D U$ are parallel and $\angle I D C=\angle I C D=\angle V D H$. Since $\angle U E H=\angle V D H$, the points $D, Q, F, P, E$ are concyclic. Hence $I P \cdot I E=$ $I Q \cdot I D$.
|
| 120 |
+
|
| 121 |
+
Let $R$ be the second point intersection of the circumcircle of triangle $H E P$ and the line $H I$. As $I H \cdot I R=I P \cdot I E=I Q \cdot I D$, the points $D, Q, H, R$ are also concyclic. We have $\angle D Q H=\angle E P H=\angle D F E=\angle B F C=180^{\circ}-\angle B I C=90^{\circ}-\angle B A C / 2$. Now using the concylicity of $D, Q, H, R$, and $E, P, H, R$ we obtain $\angle D R H=$ $\angle E R H=\angle 180^{\circ}-\left(90^{\circ}-\angle B A C / 2\right)=90^{\circ}+\angle B A C / 2$. Hence $R$ is inside the triangle $D E H$ and $\angle D R E=360^{\circ}-\angle D R H-\angle E R H=180^{\circ}-\angle B A C$ and it follows that the points $A, D, R, E$ are concyclic.
|
| 122 |
+
|
| 123 |
+
|
| 124 |
+
As $M B=M C, B D=C E, \angle M B D=\angle M C E$, the triangles $M B D$ and $M C E$ are congruent and $\angle M D A=\angle M E A$. Hence the points $M, D, E, A$ are concylic. Therefore the points $M, D, R, E, A$ are concylic. Now we have $\angle M R E=180^{\circ}-$ $\angle M A E=180^{\circ}-\left(90^{\circ}+\angle B A C / 2\right)=90^{\circ}-\angle B A C / 2$ and since $\angle E R H=90^{\circ}+$ $\angle B A C / 2$, we conclude that the points $I, H, R, M$ are collinear.
|
| 125 |
+
|
| 126 |
+
## Solution 3.
|
| 127 |
+
|
| 128 |
+
Suppose that we have a coordinate system and $\left(b_{x}, b_{y}\right),\left(c_{x}, c_{y}\right),\left(d_{x}, d_{y}\right),\left(e_{x}, e_{y}\right)$ are the coordinates of the points $B, C, D, E$, respectively. From $\overrightarrow{B I} \cdot \overrightarrow{C D}=0, \overrightarrow{C I} \cdot \overrightarrow{B E}=$ $0, \overrightarrow{E H} \cdot \overrightarrow{C D}=0, \overrightarrow{D H} \cdot \overrightarrow{B E}=0$ we obtain $\overrightarrow{I H} \cdot(\vec{B}-\vec{C}-\vec{E}+\vec{D})=0$. Hence the slope of the line $I H$ is $\left(c_{x}+e_{x}-b_{x}-d_{x}\right) /\left(b_{y}+d_{y}-c_{y}-e_{y}\right)$.
|
| 129 |
+
Assume that the $x$-axis lies along the line $B C$, and let $\alpha=\angle B A C, \beta=\angle A B C$, $\theta=\angle A C B$. Since $D B=B C=C E$, we have $c_{x}-b_{x}=B C, e_{x}-d_{x}=B C-$ $B C \cos \beta-B C \cos \theta, b_{y}=c_{y}=0, d_{y}-e_{y}=B C \sin \beta-B C \sin \theta$. Therefore the slope of $I H$ is $(2-\cos \beta-\cos \theta) /(\sin \beta-\sin \theta)$.
|
| 130 |
+
|
| 131 |
+
Now we will show that the slope of the line $M I$ is the same. Let $r$ and $R$ be the inradius and circumradius of the triangle $A B C$, respectively. As $\angle B M C=$ $\angle B A C=\alpha$ and $B M=M C$, we have
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
m_{y}-i_{y}=\frac{B C}{2} \cot \left(\frac{\alpha}{2}\right)-r \text { and } m_{x}-i_{x}=\frac{A C-A B}{2}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
where $\left(m_{x}, m_{y}\right)$ and $\left(i_{x}, i_{y}\right)$ are the coordinates of $M$ and $I$, respectively. Therefore the slope of $M I$ is $(B C \cot (\alpha / 2)-2 r) /(A C-A B)$.
|
| 138 |
+
|
| 139 |
+
Now the equality of these slopes follows using
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
\frac{B C}{\sin \alpha}=\frac{A C}{\sin \beta}=\frac{A B}{\sin \theta}=2 R
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
hence
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
B C \cot \left(\frac{\alpha}{2}\right)=4 R \cos ^{2}\left(\frac{\alpha}{2}\right)=2 R(1+\cos \alpha)
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
and
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
\frac{r}{R}=\cos \alpha+\cos \beta+\cos \theta-1
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
as
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\frac{B C \cot (\alpha / 2)-2 r}{A C-A B}=\frac{2 R(1+\cos \alpha)-2 r}{2 R(\sin \beta-\sin \theta)}=\frac{2-\cos \beta-\cos \theta}{\sin \beta-\sin \theta}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
giving the collinearity of the points $I, H, M$.
|
| 164 |
+
|
| 165 |
+
## Solution 4.
|
| 166 |
+
|
| 167 |
+
Let the bisectors $B I$ and $C I$ meet the circumcircle of $A B C$ again at $P$ and $Q$, respectively. Let the altitude of $D E F$ belonging to $D$ meet $B I$ at $R$ and the one belonging to $E$ meet $C I$ at $S$.
|
| 168 |
+
|
| 169 |
+
Since $B I$ is angle bisector of the iscosceles triangle $C B D, B I$ and $C D$ are perpendicular. Since $E H$ and $D F$ are also perpendicular, $H S$ and $R I$ are parallel. Similarly, $H R$ and $S I$ are parallel, and hence $H S I R$ is a parallelogram.
|
| 170 |
+
|
| 171 |
+
On the other hand, as $M$ is the midpoint of the $\operatorname{arc} B A C$, we have $\angle M P I=$ $\angle M P B=\angle M Q C=\angle M Q I$, and $\angle P I Q=(\widehat{P A}+\widehat{C B}+\widehat{A Q}) / 2=(\widehat{P C}+\widehat{C B}+$ $\widehat{B Q}) / 2=\angle P M Q$. Therefore $M P I Q$ is a parallelogram.
|
| 172 |
+
|
| 173 |
+
Since $C I$ is angle bisector of the iscosceles triangle $B C E$, the triangle $B S E$ is also isosceles. Hence $\angle F B S=\angle E B S=\angle S E B=\angle H E F=\angle H D F=\angle R D F=$ $\angle F C S$ and $B, S, F, C$ are concyclic. Similarly, $B, F, R, C$ are concyclic. Therefore $B, S, R, C$ are concyclic. As $B, Q, P, C$ are also concyclic, $S R$ an $Q P$ are parallel.
|
| 174 |
+
|
| 175 |
+
Now it follows that HSIR and MQIP are homothetic parallelograms, and therefore $M, H, I$ are collinear.
|
| 176 |
+
|
| 177 |
+
3. We denote the number of positive divisors of a positive integer $m$ by $d(m)$ and the number of distinct prime divisors of $m$ by $\omega(m)$. Let $k$ be a positive integer. Prove that there exist infinitely many positive integers $n$ such that $\omega(n)=k$ and $d(n)$ does not divide $d\left(a^{2}+b^{2}\right)$ for any positive integers $a, b$ satisfying $a+b=n$.
|
| 178 |
+
|
| 179 |
+
Proposed by JPN
|
| 180 |
+
|
| 181 |
+
## Solution.
|
| 182 |
+
|
| 183 |
+
We will show that any number of the form $n=2^{p-1} m$ where $m$ is a positive integer that has exactly $k-1$ prime factors all of which are greater than 3 and $p$ is a prime number such that $(5 / 4)^{(p-1) / 2}>m$ satisfies the given condition.
|
| 184 |
+
|
| 185 |
+
Suppose that $a$ and $b$ are positive integers such that $a+b=n$ and $d(n) \mid d\left(a^{2}+b^{2}\right)$. Then $p \mid d\left(a^{2}+b^{2}\right)$. Hence $a^{2}+b^{2}=q^{c p-1} r$ where $q$ is a prime, $c$ is a positive integer and $r$ is a positive integer not divisible by $q$. If $q \geq 5$, then
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
2^{2 p-2} m^{2}=n^{2}=(a+b)^{2}>a^{2}+b^{2}=q^{c p-1} r \geq q^{p-1} \geq 5^{p-1}
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
gives a contradiction. So $q$ is 2 or 3 .
|
| 192 |
+
If $q=3$, then $a^{2}+b^{2}$ is divisible by 3 and this implies that both $a$ and $b$ are divisible by 3 . This means $n=a+b$ is divisible by 3 , a contradiction. Hence $q=2$.
|
| 193 |
+
|
| 194 |
+
Now we have $a+b=2^{p-1} m$ and $a^{2}+b^{2}=2^{c p-1} r$. If the highest powers of 2 dividing $a$ and $b$ are different, then $a+b=2^{p-1} m$ implies that the smaller one must be $2^{p-1}$ and this makes $2^{2 p-2}$ the highest power of 2 dividing $a^{2}+b^{2}=2^{c p-1} r$, or equivalently, $c p-1=2 p-2$, which is not possible. Therefore $a=2^{t} a_{0}$ and $b=2^{t} b_{0}$ for some positive integer $t<p-1$ and odd integers $a_{0}$ and $b_{0}$. Then $a_{0}^{2}+b_{0}^{2}=2^{c p-1-2 t} r$. The left side of this equality is congruent to 2 modulo 4 , therefore $c p-1-2 t$ must be 1. But then $t<p-1$ gives $(c / 2) p=t+1<p$, which is not possible either.
|
| 195 |
+
|
EGMO/md/en-2014-solutions-day2.md
ADDED
|
@@ -0,0 +1,167 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+

|
| 2 |
+
|
| 3 |
+
European Girls' Mathematical Olympiad Antalya - Turkey
|
| 4 |
+
|
| 5 |
+
Problems and Solutions Day 2
|
| 6 |
+
|
| 7 |
+
The EGMO 2014 Problem Committee thanks the following countries for submitting problem proposals:
|
| 8 |
+
|
| 9 |
+
- Bulgaria
|
| 10 |
+
- Iran
|
| 11 |
+
- Japan
|
| 12 |
+
- Luxembourg
|
| 13 |
+
- Netherlands
|
| 14 |
+
- Poland
|
| 15 |
+
- Romania
|
| 16 |
+
- Ukraine
|
| 17 |
+
- United Kingdom
|
| 18 |
+
|
| 19 |
+
The Members of the Problem Committee:
|
| 20 |
+
|
| 21 |
+
Okan Tekman
|
| 22 |
+
Selim Bahadir
|
| 23 |
+
Şahin Emrah
|
| 24 |
+
Fehmi Emre Kadan
|
| 25 |
+
4. Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
|
| 26 |
+
|
| 27 |
+
Proposed by Merlijn Staps, NLD
|
| 28 |
+
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
| 29 |
+
|
| 30 |
+
## Solution 1.
|
| 31 |
+
|
| 32 |
+
Suppose that $n$ has one of these forms. For an integer $i$, let $x_{i}$ be the largest integer such that $2^{x_{i}}$ divides $i$. Now assume that $0<i<n, 0<j<n, i \neq j, n$ divides $2 i+j$ and $x_{i} \geq x_{j}$. Then the highest power of 2 dividing $2 i+j$ is $2^{x_{j}}$ and therefore $k \leq x_{j}$ and $2^{k} \leq j$. Since $0<j<n$, this is possible only if $n=3 \cdot 2^{k}$ and either $j=2^{k}$ or $j=2^{k+1}$. In the first case, $i \neq j$ and $x_{i} \geq x_{j}$ imply $i=2^{k+1}$ leading to the contradiction $3 \cdot 2^{k}=n \mid 2 i+j=5 \cdot 2^{k}$. The second case is not possible as $i \neq j$ and $x_{i} \geq x_{j}$ now imply $i \geq 2^{k+2}>n$.
|
| 33 |
+
|
| 34 |
+
Now suppose that $n$ does not have one of these forms and $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the given condition exist. For any positive integer $m$, let $a_{m}$ be the remainder of the division of $(-2)^{m}$ by $n$. Then none of $a_{m}$ is 0 as $n$ is not a power of 2. Also $a_{m} \neq a_{m+1}$ for any $m \geq 1$ as $a_{m}=a_{m+1}$ would lead to $n$ dividing $3 \cdot 2^{m}$. Moreover $n$ divides $2 a_{m}+a_{m+1}$. Hence we must have $x_{a_{1}}<x_{a_{2}}<x_{a_{3}}<\ldots$ which is not possible as $a_{m}$ 's can take on only finitely many values.
|
| 35 |
+
|
| 36 |
+
## Solution 2.
|
| 37 |
+
|
| 38 |
+
Let $E=\{n / 3, n / 2,2 n / 3\} \cap\{1,2, \ldots, n-1\}, D=\{1,2, \ldots, n-1\} \backslash E$, and let $f: D \rightarrow\{1,2, \ldots, n-1\}$ be the function sending $i$ in $D$ to the unique $f(i)$ in $\{1,2, \ldots, n-1\}$ such that $f(i) \equiv-2 i(\bmod n)$.
|
| 39 |
+
|
| 40 |
+
Then the condition of the problem is that $x_{i}<x_{f(i)}$ for each $i$ in $D$. Since $D$ is a finite set, the integers $x_{1}, x_{2}, \ldots, x_{n-1}$ exist if and only if for each $i$ in $D$ there exists a positive integer $k(i)$ such that $f^{k(i)}(i)$ belongs to $E$. This can be seen as follows:
|
| 41 |
+
|
| 42 |
+
- If $f^{k}(i)$ does not belong to $E$ for any $k>0$ for some $i$, then there exists $k_{2}>k_{1}>0$ such that $f^{k_{1}}(i)=f^{k_{2}}(i)$, leading to the contradiction $x_{f^{k_{1}(i)}}<$ $x_{f^{k_{2}(i)}}=x_{f^{k_{1}(i)}}$.
|
| 43 |
+
- On the other hand, if such $k(i)$ exists for each $i$ in $D$, and if $k_{0}(i)$ denotes the smallest such, then the condition of the problem is satisfied by letting $x_{i}=-k_{0}(i)$ for $i$ in $D$, and $x_{i}=0$ for $i$ in $E$.
|
| 44 |
+
|
| 45 |
+
In other words, the integers $x_{1}, x_{2}, \ldots, x_{n-1}$ exist if and only if for each $i$ in $D$ there exists a positive integer $k(i)$ such that $(-2)^{k(i)} i \equiv n / 3, n / 2$ or $2 n / 3(\bmod n)$. For $i=1$, this implies that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ with $k \geq 0$. On the other hand, if $n$ has one of these forms, letting $k(i)=k$ does the trick for all $i$ in $D$.
|
| 46 |
+
|
| 47 |
+
## Solution 3.
|
| 48 |
+
|
| 49 |
+
Suppose that $x_{1}, x_{2}, \ldots, x_{k-1}$ satisfy the condition of the problem for $n=k$. Let $y_{2 i}=x_{i}$ for $1 \leq i \leq k-1$ and choose $y_{2 i-1}$ for $1 \leq i \leq k$ to be less than $\min \left\{x_{1}, x_{2}, \ldots, x_{k-1}\right\}$. Now suppose that for $n=2 k$ we have $0<i<n, 0<j<n$, $i \neq j, n$ divides $2 i+j$. Then $j$ is even. If $i$ is also even, then $0<i / 2<k, 0<j / 2<k$ and $k$ divides $2(i / 2)+(j / 2)$; hence $y_{i}=x_{i / 2}<x_{j / 2}=y_{j}$. On the other hand, if $i$ is odd, then $y_{i}<\min \left\{x_{1}, x_{2}, \ldots, x_{k-1}\right\} \leq x_{j / 2}=y_{j}$. Therefore, $y_{1}, y_{2}, \ldots, y_{2 k-1}$ satisfy the condition of the problem for $n=2 k$.
|
| 50 |
+
|
| 51 |
+
Since the condition is vacuous for $n=2$ and $n=3$, it follows that $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition exist for all $n=2^{k}$ with $k \geq 1$ and $n=3 \cdot 2^{k}$ with $k \geq 0$.
|
| 52 |
+
|
| 53 |
+
Now suppose that $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition of the problem exist for $n=2^{k} m$ where $k$ is a nonnegative integer and $m>3$ is an odd number. Let $b_{0}=2^{k}$ and let $b_{i+1}$ be the remainder of the division of $(-2) b_{i}$ by $n$ for $i \geq 0$. No terms of this sequence is 0 and no two consecutive terms are both equal to $b_{1}$ as $m>3$. On the other hand, as $(-2)^{\phi(m)} \equiv 1(\bmod m)$, we have $b_{\phi(m)} \equiv(-2)^{\phi(m)} 2^{k} \equiv 2^{k} \equiv b_{0}$ $(\bmod n)$, and hence $b_{\phi(m)}=b_{0}$. Since $2 b_{i}+b_{i+1}$ is divisible by $n$ for all $i \geq 0$, we have $x_{b_{0}}<x_{b_{1}}<\cdots<x_{b_{\phi(m)}}=x_{b_{0}}$, a contradiction.
|
| 54 |
+
5. Let $n$ be a positive integer. We have $n$ boxes where each box contains a nonnegative number of pebbles. In each move we are allowed to take two pebbles from a box we choose, throw away one of the pebbles and put the other pebble in another box we choose. An initial configuration of pebbles is called solvable if it is possible to reach a configuration with no empty box, in a finite (possibly zero) number of moves. Determine all initial configurations of pebbles which are not solvable, but become solvable when an additional pebble is added to a box, no matter which box is chosen.
|
| 55 |
+
|
| 56 |
+
Proposed by Dan Schwarz, ROU
|
| 57 |
+
|
| 58 |
+
The answer is any configuration with $2 n-2$ pebbles which has even numbers of pebbles in each box.
|
| 59 |
+
|
| 60 |
+
Solution 1. Number the boxes from 1 through $n$ and denote a configuration by $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ where $x_{i}$ is the number of pebbles in the $i$ th box. Let
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
D(x)=\sum_{i=1}^{n}\left\lfloor\frac{x_{i}-1}{2}\right\rfloor
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
for a configuration $x$. We can rewrite this in the form
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
D(x)=\frac{1}{2} N(x)-n+\frac{1}{2} O(x)
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
where $N(x)$ is the total number of pebbles and $O(x)$ is the number of boxes with an odd number of pebbles for the configuration $x$.
|
| 73 |
+
|
| 74 |
+
Note that a move either leaves $D$ the same (if it is made into a box containing an even number of pebbles) or decreases it by 1 (if it is made into a box with an odd number of pebbles). As $D$ is nonnegative for any configuration which does not have any empty boxes, it is also nonnegative for any solvable configuration. On the other hand, if a configuration has nonnegative $D$, then making $m_{i}=\left\lfloor\left(x_{i}-1\right) / 2\right\rfloor$ moves from the $i$ th box into $m_{i}$ empty boxes for each $i$ with $m_{i}>0$ fills all boxes as $D(x) \geq 0$ means $\sum_{m_{i}>0} m_{i} \geq$ (number of empty boxes).
|
| 75 |
+
|
| 76 |
+
As $N(x)$ and $O(x)$ have the same parity, a configuration $x$ is solvable exactly when $O(x) \geq 2 n-N(x)$, and unsolvable exactly when $O(x) \leq 2 n-2-N(x)$. In particular, any configuration with $2 n-1$ pebbles is solvable, and a configuration with $2 n-2$ pebbles is unsolvable if and only if all boxes contain even numbers of pebbles.
|
| 77 |
+
|
| 78 |
+
Suppose that $x^{\prime}$ is obtained from $x$ by adding a pebble in some box. Then $O\left(x^{\prime}\right)=$ $O(x)+1$ or $O\left(x^{\prime}\right)=O(x)-1$. If $x$ is unsolvable and $x^{\prime}$ is solvable, then we must have $O(x) \leq 2 n-2-N(x)$ and $O\left(x^{\prime}\right) \geq 2 n-N\left(x^{\prime}\right)=2 n-1-N(x)$, and hence $O\left(x^{\prime}\right)=O(x)+1$. That is, the pebble must be added to a box with an even number of pebbles. This can be the case irrespective of where the pebble is added only if all boxes contain even numbers of pebbles, and $0=O(x) \leq 2 n-2-N(x)$ and $1=O\left(x^{\prime}\right) \geq 2 n-1-N(x)$; that is, $N(x)=2 n-2$.
|
| 79 |
+
|
| 80 |
+
Solution 2. Let $x$ be a configuration and $\tilde{x}$ be another configuration obtained from $x$ by removing two pebbles from a box and depositing them in another box.
|
| 81 |
+
Claim 1: $\tilde{x}$ is solvable if and only if $x$ is solvable.
|
| 82 |
+
Let us call two configurations equivalent if they have the same total number of pebbles and parities of the number of pebbles in the corresponding boxes are the same. (It does not matter whether we consider this equivalence for a fixed ordering of the boxes or up to permutation.) From Claim 1 it follows that two equivalent configurations are both solvable or both unsolvable. In particular, any configuration with $2 n-1$ or more pebbles is solvable, because it is equivalent to a configuration with no empty boxes.
|
| 83 |
+
|
| 84 |
+
Let us a call a configuration with all boxes containing two or fewer pebbles scant. Every unsolvable configuration is equivalent to a scant configuration.
|
| 85 |
+
|
| 86 |
+
Claim 2: A scant configuration is solvable if and only if it contains no empty boxes.
|
| 87 |
+
By Claim 1 and Claim 2, addition of a pebble to a scant unsolvable configuration makes it solvable if and only if the configuration has exactly one empty box and the pebble is added to the empty box or to a box containing two pebbles. Hence, the addition of a pebble makes an unsolvable scant configuration into a solvable configuration irrespective of where it is added if and only if all boxes have even numbers of pebbles and exactly one of them is empty. Therefore, the addition of a pebble makes an unsolvable configuration into a solvable one irrespective of where the pebble is added if and only if the configuration has $2 n-2$ pebbles and all boxes have even numbers of pebbles.
|
| 88 |
+
|
| 89 |
+
Proof of Claim 1: Suppose that the two pebbles were moved from box $B$ in $x$ to box $\tilde{B}$ in $\tilde{x}$, and $x$ is solvable. Then we perform exactly the same sequence of moves for $\tilde{x}$ as we did for $x$ except that instead of the first move that is made out of $B$ we make a move from $\tilde{B}$ (into the same box), and if there was no move from $B$, then at the end we make a move from $\tilde{B}$ to $B$ in case $B$ is now empty.
|
| 90 |
+
|
| 91 |
+
Proof of Claim 2: Any move from a scant configuration either leaves the number of empty boxes the same and the resulting configuration is also scant (if it is made into an empty box), or increases the number of empty boxes by one (if it is made into a nonempty box). In the second case, if the move was made into a box containing one pebble, then the resulting configuration is still scant. On the other hand, if it is made into a box containing two pebbles, then the resulting configuration is equivalent to the scant configuration which has one pebble in the box the move was made into and exactly the same number of pebbles in all other boxes as the original configuration. Therefore, any sequence of move from a scant configuration results in a configuration with more or the same number of empty boxes.
|
| 92 |
+
6. Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying the condition
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
f\left(y^{2}+2 x f(y)+f(x)^{2}\right)=(y+f(x))(x+f(y))
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
for all real numbers $x$ and $y$.
|
| 99 |
+
Proposed by Daniël Kroes, NLD
|
| 100 |
+
The answer is the functions $f(x)=x, f(x)=-x$ and $f(x)=\frac{1}{2}-x$.
|
| 101 |
+
|
| 102 |
+
## Solution.
|
| 103 |
+
|
| 104 |
+
It can be easily checked that the functions $f(x)=x, f(x)=-x$ and $f(x)=\frac{1}{2}-x$ satisfy the given condition. We will show that these are the only functions doing so. Let $y=-f(x)$ in the original equation to obtain
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
f\left(2 f(x)^{2}+2 x f(-f(x))\right)=0
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
for all $x$. In particular, 0 is a value of $f$. Suppose that $u$ and $v$ are such that $f(u)=0=f(v)$. Plugging $x=u$ or $v$ and $y=u$ or $v$ in the original equations we get $f\left(u^{2}\right)=u^{2}, f\left(u^{2}\right)=u v, f\left(v^{2}\right)=u v$ and $f\left(v^{2}\right)=v^{2}$. We conclude that $u^{2}=u v=v^{2}$ and hence $u=v$. So there is exactly one $a$ mapped to 0 , and
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
f(x)^{2}+x f(-f(x))=\frac{a}{2}
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
for all $x$.
|
| 117 |
+
Suppose that $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ for some $x_{1}$ and $x_{2}$. Using (*) we obtain $x_{1} f\left(-f\left(x_{1}\right)\right)=x_{2} f\left(-f\left(x_{2}\right)\right)=x_{2} f\left(-f\left(x_{1}\right)\right)$ and hence either $x_{1}=x_{2}$ or $f\left(x_{1}\right)=$ $f\left(x_{2}\right)=-a$. In the second case, letting $x=a$ and $y=x_{1}$ in the original equation we get $f\left(x_{1}^{2}-2 a^{2}\right)=0$, hence $x_{1}^{2}-2 a^{2}=a$. Similarly, $x_{2}^{2}-2 a^{2}=a$, and it follows that $x_{1}=x_{2}$ or $x_{1}=-x_{2}$ in this case.
|
| 118 |
+
|
| 119 |
+
Using the symmetry of the original equation we have
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
f\left(f(x)^{2}+y^{2}+2 x f(y)\right)=(x+f(y))(y+f(x))=f\left(f(y)^{2}+x^{2}+2 y f(x)\right)
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
for all $x$ and $y$. Suppose $f(x)^{2}+y^{2}+2 x f(y) \neq f(y)^{2}+x^{2}+2 y f(x)$ for some $x$ and $y$. Then by the observations above, $(x+f(y))(y+f(x)) \neq 0$ and $f(x)^{2}+y^{2}+2 x f(y)=$ $-\left(f(y)^{2}+x^{2}+2 y f(x)\right)$. But these conditions are contradictory as the second one can be rewritten as $(f(x)+y)^{2}+(f(y)+x)^{2}=0$.
|
| 126 |
+
|
| 127 |
+
Therefore from $\left({ }^{* *}\right)$ now it follows that
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
f(x)^{2}+y^{2}+2 x f(y)=f(y)^{2}+x^{2}+2 y f(x)
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
for all $x$ and $y$. In particular, letting $y=0$ we obtain $f(x)^{2}=(f(0)-x)^{2}$ for all $x$. Let $f(x)=s(x)(f(0)-x)$ where $s: \mathbf{R} \rightarrow\{1,-1\}$. Plugging this in $\left({ }^{* * *}\right)$ gives
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
x(y s(y)+f(0)(1-s(y))=y(x s(x)+f(0)(1-s(x)))
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
for all $x$ and $y$. So $s(x)+f(0)(1-s(x)) / x$ must be constant for $x \neq 0$.
|
| 140 |
+
|
| 141 |
+
If $f(0)=0$ it follows that $s(x)$ is constant for $x \neq 0$, and therefore either $f(x)=x$ for all $x$ or $f(x)=-x$ for all $x$. Suppose that $f(0) \neq 0$. If $s(x)$ is -1 for all $x \neq 0$, then $-1+2 f(0) / x$ must be constant for all $x \neq 0$, which is not possible. On the other hand, if there exist nonzero $x$ and $y$ such that $s(x)=-1$ and $s(y)=1$, then $-1+2 f(0) / x=1$. That is, there can be only one such $x$, that $x$ is $f(0)$, and hence $f(x)=f(0)-x$ for all $x$. Putting this back in the original equation gives $2 f(0)^{2}=f(0)$ and hence $f(0)=1 / 2$. We are done.
|
| 142 |
+
|
| 143 |
+
## Remark:
|
| 144 |
+
|
| 145 |
+
The following line of reasoning or a variant of it can be used between $\left({ }^{*}\right)$ and $\left({ }^{* * *}\right)$ :
|
| 146 |
+
Suppose that $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ for some $x_{1}$ and $x_{2}$. Then from $\left(^{*}\right)$ it follows that $x_{1} f\left(-f\left(x_{1}\right)\right)=x_{2} f\left(-f\left(x_{2}\right)\right)=x_{2} f\left(-f\left(x_{1}\right)\right)$ and hence either $x_{1}=x_{2}$ or $f\left(x_{1}\right)=$ $f\left(x_{2}\right)=-a$. In the second case, using $\left(^{*}\right)$ again we obtain $a^{2}=a / 2$ and therefore $a=$ $1 / 2$. Now letting $x=1 / 2$ in the original equation gives $f\left(y^{2}+f(y)\right)=y(f(y)+1 / 2)$ for all $y$. From this letting $y=0$ we obtain $f(0)=1 / 2$, and letting $f(y)=-1 / 2$ we obtain $f\left(y^{2}-1 / 2\right)=0$ and $y^{2}=1$. To summarize, $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ implies either $x_{1}=x_{2}$ or $x_{1}, x_{2} \in\{1,-1\}$ and $f(1)=f(-1)=-1 / 2, f(1 / 2)=0, f(0)=1 / 2$.
|
| 147 |
+
|
| 148 |
+
Using the symmetry of the original equation we have
|
| 149 |
+
|
| 150 |
+
$$
|
| 151 |
+
f\left(f(x)^{2}+y^{2}+2 x f(y)\right)=(x+f(y))(y+f(x))=f\left(f(y)^{2}+x^{2}+2 y f(x)\right)
|
| 152 |
+
$$
|
| 153 |
+
|
| 154 |
+
for all $x$ and $y$. Let $y=0$. Then
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
f\left(f(x)^{2}+2 x f(0)\right)=f\left(f(0)^{2}+x^{2}\right)
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
for all $x$. If $f(x)^{2}+2 x f(0) \neq f(0)^{2}+x^{2}$ for some $x$, then by the observation above we must have $f(1 / 2)=0, f(0)=1 / 2$ and $f(x)^{2}+2 x f(0)=-\left(f(0)^{2}+x^{2}\right)$. We can rewrite this as $f(x)^{2}+(f(0)+x)^{2}=0$ to obtain $x=1 / 2$ and $f(0)=-x=-1 / 2$, which contradicts $f(0)=1 / 2$. So we conclude that $f(x)^{2}+2 x f(0)=f(0)^{2}+x^{2}$ for all $x$. This implies $f(x)^{2}=(f(0)-x)^{2}$ for all $x$. In particular, the second case considered above is not possible as $(f(0)-1)^{2}=f(1)=f(-1)=(f(0)+1)^{2}$ means $f(0)=0$, contradicting $f(0)=1 / 2$. Therefore $f$ is injective and from $\left({ }^{* *}\right)$ now it follows that
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
f(x)^{2}+y^{2}+2 x f(y)=f(y)^{2}+x^{2}+2 y f(x)
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
for all $x$ and $y$.
|
| 167 |
+
|
EGMO/md/en-2015-solutions.md
ADDED
|
@@ -0,0 +1,423 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
The EGMO 2015 Problem Committee thanks the following countries for submitting problem proposals:
|
| 2 |
+
|
| 3 |
+
- Ireland
|
| 4 |
+
- Japan
|
| 5 |
+
- Luxembourg
|
| 6 |
+
- Macedonia
|
| 7 |
+
- Mexico
|
| 8 |
+
- Republic of Moldova
|
| 9 |
+
- Netherlands
|
| 10 |
+
- Poland
|
| 11 |
+
- Romania
|
| 12 |
+
- Slovenia
|
| 13 |
+
- Turkey
|
| 14 |
+
- Ukraine
|
| 15 |
+
- United States of America
|
| 16 |
+
|
| 17 |
+
The Members of the Problem Committee:
|
| 18 |
+
Yauheni Barabanov
|
| 19 |
+
Mikhail Karpuk
|
| 20 |
+
Aliaksei Vaidzelevich
|
| 21 |
+
Igor Voronovich
|
| 22 |
+
|
| 23 |
+
## PROBLEMS
|
| 24 |
+
|
| 25 |
+
## Day 1
|
| 26 |
+
|
| 27 |
+
Problem 1. Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
|
| 28 |
+
|
| 29 |
+
Problem 2. A domino is a $2 \times 1$ or $1 \times 2$ tile. Determine in how many ways exactly $n^{2}$ dominoes can be placed without overlapping on a $2 n \times 2 n$ chessboard so that every $2 \times 2$ square contains at least two uncovered unit squares which lie in the same row or column.
|
| 30 |
+
|
| 31 |
+
Problem 3. Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
| 38 |
+
|
| 39 |
+
## Day 2
|
| 40 |
+
|
| 41 |
+
Problem 4. Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
for every positive integer $n$.
|
| 48 |
+
Problem 5. Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
|
| 49 |
+
|
| 50 |
+
Problem 6. Let $H$ be the orthocentre and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
|
| 51 |
+
|
| 52 |
+
Problem 1. Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
|
| 53 |
+
(Luxembourg)
|
| 54 |
+

|
| 55 |
+
|
| 56 |
+
Solution 1: Since $\angle C D F=90^{\circ}-45^{\circ}=45^{\circ}$, the line $D F$ bisects $\angle C D A$, and so $F$ lies on the perpendicular bisector of segment $A E$, which meets $A B$ at $G$. Let $\angle A B C=2 \beta$. Since $A D E F$ is cyclic, $\angle A F E=90^{\circ}$, and hence $\angle F A E=45^{\circ}$. Further, as $B F$ bisects $\angle A B C$, we have $\angle F A B=90^{\circ}-\beta$, and thus
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
\angle E A B=\angle A E G=45^{\circ}-\beta, \quad \text { and } \quad \angle A E D=45^{\circ}+\beta,
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
so $\angle G E D=2 \beta$. This implies that right-angled triangles $\triangle E D G$ and $\triangle B D C$ are similar, and so we have $|G D| /|C D|=|D E| /|D B|$. Thus the right-angled triangles $\triangle D E B$ and $\triangle D G C$ are similar, whence $\angle G C D=\angle D B E=\beta$. But $\angle D F E=\angle D A E=45^{\circ}-$ $\beta$, then $\angle G F D=45^{\circ}-\angle D F E=\beta$. Hence $G D C F$ is cyclic, so $\angle G F C=90^{\circ}$, whence $C F$ is perpendicular to the radius $F G$ of $\omega$. It follows that $C F$ is a tangent to $\omega$, as required.
|
| 63 |
+
Solution 2: As $\angle A D F=45^{\circ}$ line $D F$ is an exterior bisector of $\angle C D B$. Since $B F$ bisects $\angle D B C$ line $C F$ is an exterior bisector of $\angle B C D$. Let $\angle A B C=2 \beta$, so $\angle E C F=(\angle D B C+\angle C D B) / 2=45^{\circ}+\beta$. Hence $\angle C F E=180^{\circ}-\angle E C F-\angle B C E-\angle E B C=180^{\circ}-\left(45^{\circ}+\beta+90^{\circ}-2 \beta+\beta\right)=45^{\circ}$. It follows that $\angle F D C=\angle C F E$, then $C F$ is tangent to $\omega$.
|
| 64 |
+
Solution 3: Note that $A E$ is diameter of circumcircle of $\triangle A B C$ since $\angle C D F=90^{\circ}$. From $\angle A E F=\angle A D F=45^{\circ}$ it follows that triangle $\triangle A F E$ is right-angled and isosceles. Without loss of generality, let points $A, E$ and $F$ have coordinates $(-1,0),(1,0)$ and $(0,1)$ respectively. Points $F, E$, $B$ are collinear, hence $B$ have coordinates $(b, 1-b)$ for some $b \neq-1$. Let point $C^{\prime}$ be intersection of line tangent to circumcircle of $\triangle A F E$ at $F$ with line $E D$. Thus $C^{\prime}$ have coordinates $(c, 1)$ and from $\overline{C^{\prime} E} \perp \overline{A B}$ we get $c=2 b /(b+1)$. Now vector $\overline{B C^{\prime}}=(2 b /(b+1)-b, b)=b /(b+1) \cdot(1-b, b+1)$, vector $\overline{B F}=(-b, b)=(-1,1) \cdot b$ and vector $\overline{B A}=(-(b+1),-(1-b))$. Its clear that $(1-b, b+1)$ and $(-(b+1),-(1-b))$ are symmetric with respect to $\overline{F E}=(-1,1)$, hence $B F$ bisects $\angle C^{\prime} B A$ and $C^{\prime}=C$ which completes the proof.
|
| 65 |
+
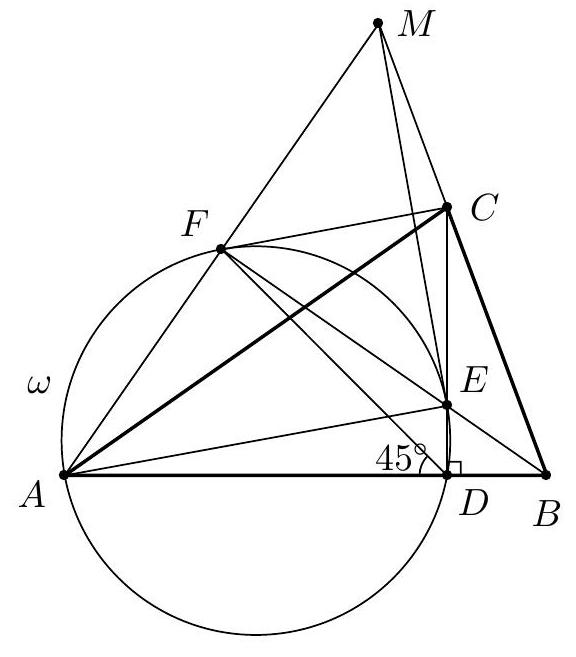
|
| 66 |
+
|
| 67 |
+
Solution 4: Again $F$ lies on the perpendicular bisector of segment
|
| 68 |
+
$A E$, so $\triangle A F E$ is right-angled and isosceles. Let $M$ be an intersection of $B C$ and $A F$. Note that $\triangle A M B$ is isosceles since $B F$ is a bisector and altitude in this triangle. Thus $B F$ is a symmetry line of $\triangle A M B$. Then $\angle F D A=\angle F E A=\angle M E F=45^{\circ}, A F=F E=F M$ and $\angle D A E=\angle E M C$. Let us show that $E C=C M$. Indeed,
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
\begin{aligned}
|
| 72 |
+
\angle C E M & =180^{\circ}-(\angle A E D+\angle F E A+\angle M E F)=90^{\circ}-\angle A E D= \\
|
| 73 |
+
& =\angle D A E=\angle E M C .
|
| 74 |
+
\end{aligned}
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
It follows that $F M C E$ is a kite, since $E F=F M$ and $M C=C E$. Hence $\angle E F C=\angle C F M=\angle E D F=45^{\circ}$, so $F C$ is tangent to $\omega$.
|
| 78 |
+
|
| 79 |
+
Solution 5: Let the tangent to $\omega$ at $F$ intersect $C D$ at $C^{\prime}$. Let $\angle A B F=$ $\angle F B C=\beta$. It follows that $\angle C^{\prime} F E=45^{\circ}$ since $C^{\prime} F$ is tangent. We have
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\frac{\sin \angle B D C}{\sin \angle C D F} \cdot \frac{\sin \angle D F C^{\prime}}{\sin \angle C^{\prime} F B} \cdot \frac{\sin \angle F B C}{\sin \angle C B D}=\frac{\sin 90^{\circ}}{\sin 45^{\circ}} \cdot \frac{\sin \left(90^{\circ}-\beta\right)}{\sin 45^{\circ}} \cdot \frac{\sin \beta}{\sin 2 \beta}=\frac{2 \sin \beta \cos \beta}{\sin 2 \beta}=1 .
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
So by trig Ceva on triangle $\triangle B D F$, lines $F C^{\prime}, D C$ and $B C$ are concurrent (at $C$ ), so $C=C^{\prime}$. Hence $C F$ is tangent to $\omega$.
|
| 86 |
+
|
| 87 |
+
Problem 2. A domino is a $2 \times 1$ or $1 \times 2$ tile. Determine in how many ways exactly $n^{2}$ dominoes can be placed without overlapping on a $2 n \times 2 n$ chessboard so that every $2 \times 2$ square contains at least two uncovered unit squares which lie in the same row or column.
|
| 88 |
+
(Turkey)
|
| 89 |
+
Solution: The answer is $\binom{2 n}{n}^{2}$.
|
| 90 |
+
Divide the schessboard into $2 \times 2$ squares. There are exactly $n^{2}$ such squares on the chessboard. Each of these squares can have at most two unit squares covered by the dominos. As the dominos cover exactly $2 n^{2}$ squares, each of them must have exactly two unit squares which are covered, and these squares must lie in the same row or column.
|
| 91 |
+
|
| 92 |
+
We claim that these two unit squares are covered by the same domino tile. Suppose that this is not the case for some $2 \times 2$ square and one of the tiles covering one of its unit squares sticks out to the left. Then considering one of the leftmost $2 \times 2$ squares in this division with this property gives a contradiction.
|
| 93 |
+
|
| 94 |
+
Now consider this $n \times n$ chessboard consisting of $2 \times 2$ squares of the original board. Define $A, B$, $C, D$ as the following configurations on the original chessboard, where the gray squares indicate the domino tile, and consider the covering this $n \times n$ chessboard with the letters $A, B, C, D$ in such a
|
| 95 |
+

|
| 96 |
+
way that the resulting configuration on the original chessboard satisfies the condition of the question.
|
| 97 |
+
Note that then a square below or to the right of one containing an $A$ or $B$ must also contain an $A$ or $B$. Therefore the (possibly empty) region consisting of all squares containing an $A$ or $B$ abuts the lower right corner of the chessboard and is separated from the (possibly empty) region consisting of all squares containing a $C$ or $D$ by a path which goes from the lower left corner to the upper right corner of this chessboard and which moves up or right at each step.
|
| 98 |
+
|
| 99 |
+
A similar reasoning shows that the (possibly empty) region consisting of all squares containing an $A$ or $D$ abuts the lower left corner of the chessboard and is separated from the (possibly empty) region consisting of all squares containing a $B$ or $C$ by a path which goes from the upper left corner to the lower right corner of this chessboard and which moves down or right at each step.
|
| 100 |
+
|
| 101 |
+
| $D$ | $D$ | $C$ | $C$ | $C$ | $C$ |
|
| 102 |
+
| :---: | :---: | :---: | :---: | :---: | :---: |
|
| 103 |
+
| $D$ | $D$ | $C$ | $C$ | $C$ | $B$ |
|
| 104 |
+
| $D$ | $D$ | $D$ | $B$ | $B$ | $B$ |
|
| 105 |
+
| $D$ | $D$ | $D$ | $A$ | $A$ | $B$ |
|
| 106 |
+
| $D$ | $D$ | $D$ | $A$ | $A$ | $B$ |
|
| 107 |
+
| $D$ | $A$ | $A$ | $A$ | $A$ | $B$ |
|
| 108 |
+
|
| 109 |
+

|
| 110 |
+
|
| 111 |
+
Therefore the $n \times n$ chessboard is divided by these two paths into four (possibly empty) regions that consist respectively of all squares containing $A$ or $B$ or $C$ or $D$. Conversely, choosing two such paths and filling the four regions separated by them with $A \mathrm{~s}, B \mathrm{~s}, C \mathrm{~s}$ and $D \mathrm{~s}$ counterclockwise starting at the bottom results in a placement of the dominos on the original board satisfying the condition of the question.
|
| 112 |
+
|
| 113 |
+
As each of these paths can be chosen in $\binom{2 n}{n}$ ways, there are $\binom{2 n}{n}^{2}$ ways the dominos can be placed.
|
| 114 |
+
|
| 115 |
+
Problem 3. Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
| 122 |
+
|
| 123 |
+
Solution 1: Suppose without loss of generality that $a_{1}$ is the smallest of the $a_{i}$. If $a_{1} \geq n^{m}-1$, then the problem is simple: either all the $a_{i}$ are equal, or $a_{1}=n^{m}-1$ and $a_{j}=n^{m}$ for some $j$. In the first case, we can take (say) $b_{1}=1, b_{2}=2$, and the rest of the $b_{i}$ can be arbitrary, and we have
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq \operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}\right)=1
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
In the second case, we can take $b_{1}=1, b_{j}=1$, and the rest of the $b_{i}$ arbitrary, and again
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq \operatorname{gcd}\left(a_{1}+b_{1}, a_{j}+b_{j}\right)=1
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
So from now on we can suppose that $a_{1} \leq n^{m}-2$.
|
| 136 |
+
Now, let us suppose the desired $b_{1}, \ldots, b_{m}$ do not exist, and seek a contradiction. Then, for any choice of $b_{1}, \ldots, b_{m} \in\{1, \ldots, n\}$, we have
|
| 137 |
+
|
| 138 |
+
$$
|
| 139 |
+
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \geq n
|
| 140 |
+
$$
|
| 141 |
+
|
| 142 |
+
Also, we have
|
| 143 |
+
|
| 144 |
+
$$
|
| 145 |
+
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq a_{1}+b_{1} \leq n^{m}+n-2
|
| 146 |
+
$$
|
| 147 |
+
|
| 148 |
+
Thus there are at most $n^{m}-1$ possible values for the greatest common divisor. However, there are $n^{m}$ choices for the $m$-tuple $\left(b_{1}, \ldots, b_{m}\right)$. Then, by the pigeonhole principle, there are two $m$-tuples that yield the same values for the greatest common divisor, say $d$. But since $d \geq n$, for each $i$ there can be at most one choice of $b_{i} \in\{1,2, \ldots, n\}$ such that $a_{i}+b_{i}$ is divisible by $d$ - and therefore there can be at most one $m$-tuple $\left(b_{1}, b_{2}, \ldots, b_{m}\right)$ yielding $d$ as the greatest common divisor. This is the desired contradiction.
|
| 149 |
+
|
| 150 |
+
Solution 2: Similarly to Solution 1 suppose that $a_{1} \leq n^{m}-2$. The gcd of $a_{1}+1, a_{2}+1, a_{3}+1, \ldots, a_{m}+1$ is co-prime with the gcd of $a_{1}+1, a_{2}+2, a_{3}+1, \ldots, a_{m}+1$, thus $a_{1}+1 \geq n^{2}$. Now change another 1 into 2 and so on. After $m-1$ changes we get $a_{1}+1 \geq n^{m}$ which gives us a contradiction.
|
| 151 |
+
Solution 3: We will prove stronger version of this problem:
|
| 152 |
+
For $m, n>1$, let $a_{1}, \ldots, a_{m}$ be positive integers with at least one $a_{i} \leq n^{2^{m-1}}$. Then there are integers $b_{1}, \ldots, b_{m}$, each equal to 1 or 2 , such that $\operatorname{gcd}\left(a_{1}+b_{1}, \ldots, a_{m}+b_{m}\right)<n$.
|
| 153 |
+
Proof: Suppose otherwise. Then the $2^{m-1}$ integers $\operatorname{gcd}\left(a_{1}+b_{1}, \ldots, a_{m}+b_{m}\right)$ with $b_{1}=1$ and $b_{i}=1$ or 2 for $i>1$ are all pairwise coprime, since for any two of them, there is some $i>1$ with $a_{i}+1$ appearing in one and $a_{i}+2$ in the other. Since each of these $2^{m-1}$ integers divides $a_{1}+1$, and each is $\geq n$ with at most one equal to $n$, it follows that $a_{1}+1 \geq n(n+1)^{2^{m-1}-1}$ so $a_{1} \geq n^{2^{m-1}}$. The same is true for each $a_{i}, i=1, \ldots, n$, a contradiction.
|
| 154 |
+
Remark: Clearly the $n^{2^{m-1}}$ bound can be strengthened as well.
|
| 155 |
+
|
| 156 |
+
Problem 4. Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
for every positive integer n.
|
| 163 |
+
(Japan)
|
| 164 |
+
Solution 1: The answer is no.
|
| 165 |
+
Suppose that there exists a sequence $\left(a_{n}\right)$ of positive integers satisfying the given condition. We will show that this will lead to a contradiction.
|
| 166 |
+
|
| 167 |
+
For each $n \geq 2$ define $b_{n}=a_{n+1}-a_{n}$. Then, by assumption, for $n \geq 2$ we get $b_{n}=\sqrt{a_{n}+a_{n-1}}$ so that we have
|
| 168 |
+
|
| 169 |
+
$$
|
| 170 |
+
b_{n+1}^{2}-b_{n}^{2}=\left(a_{n+1}+a_{n}\right)-\left(a_{n}+a_{n-1}\right)=\left(a_{n+1}-a_{n}\right)+\left(a_{n}-a_{n-1}\right)=b_{n}+b_{n-1} .
|
| 171 |
+
$$
|
| 172 |
+
|
| 173 |
+
Since each $a_{n}$ is a positive integer we see that $b_{n}$ is positive integer for $n \geq 2$ and the sequence $\left(b_{n}\right)$ is strictly increasing for $n \geq 3$. Thus $b_{n}+b_{n-1}=\left(b_{n+1}-b_{n}\right)\left(b_{n+1}+b_{n}\right) \geq b_{n+1}+b_{n}$, whence $b_{n-1} \geq b_{n+1}$ - a contradiction to increasing of the sequence $\left(b_{i}\right)$.
|
| 174 |
+
|
| 175 |
+
Thus we conclude that there exists no sequence $\left(a_{n}\right)$ of positive integers satisfying the given condition of the problem.
|
| 176 |
+
|
| 177 |
+
Solution 2: Suppose that such a sequence exists. We will calculate its members one by one and get a contradiction.
|
| 178 |
+
|
| 179 |
+
From the equality $a_{3}=a_{2}+\sqrt{a_{2}+a_{1}}$ it follows that $a_{3}>a_{2}$. Denote positive integers $\sqrt{a_{3}+a_{2}}$ by $b$ and $a_{3}$ by $a$, then we have $\sqrt{2 a}>b$. Since $a_{4}=a+b$ and $a_{5}=a+b+\sqrt{2 a+b}$ are positive integers, then $\sqrt{2 a+b}$ is positive integer.
|
| 180 |
+
|
| 181 |
+
Consider $a_{6}=a+b+\sqrt{2 a+b}+\sqrt{2 a+2 b+\sqrt{2 a+b}}$. Number $c=\sqrt{2 a+2 b+\sqrt{2 a+b}}$ must be positive integer, obviously it is greater than $\sqrt{2 a+b}$. But
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
(\sqrt{2 a+b}+1)^{2}=2 a+b+2 \sqrt{2 a+b}+1=2 a+2 b+\sqrt{2 a+b}+(\sqrt{2 a+b}-b)+1>c^{2} .
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
So $\sqrt{2 a+b}<c<\sqrt{2 a+b}+1$ which is impossible.
|
| 188 |
+
Solutions 3: We will show that there is no sequence $\left(a_{n}\right)$ of positive integers which consists of $N>5$ members and satisfies
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
for all $n=1, \ldots, N-2$. Moreover, we will describe all such sequences with five members.
|
| 195 |
+
Since every $a_{i}$ is a positive integer it follows from (1) that there exists such positive integer $k$ (obviously $k$ depends on $n$ ) that
|
| 196 |
+
|
| 197 |
+
$$
|
| 198 |
+
a_{n+1}+a_{n}=k^{2} .
|
| 199 |
+
$$
|
| 200 |
+
|
| 201 |
+
From (1) we have $\left(a_{n+2}-a_{n+1}\right)^{2}=a_{n+1}+a_{n}$, consider this equality as a quadratic equation with respect to $a_{n+1}$ :
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
a_{n+1}^{2}-\left(2 a_{n+2}+1\right) a_{n+1}+a_{n+2}^{2}-a_{n}=0 .
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
Obviously its solutions are $\left(a_{n+1}\right)_{1,2}=\frac{2 a_{n+2}+1 \pm \sqrt{D}}{2}$, where
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
D=4\left(a_{n}+a_{n+2}\right)+1
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Since $a_{n+2}>a_{n+1}$ we have
|
| 214 |
+
|
| 215 |
+
$$
|
| 216 |
+
a_{n+1}=\frac{2 a_{n+2}+1-\sqrt{D}}{2} .
|
| 217 |
+
$$
|
| 218 |
+
|
| 219 |
+
From the last equality, using that $a_{n+1}$ and $a_{n+2}$ are positive integers, we conclude that $D$ is a square of some odd number i.e. $D=(2 m+1)^{2}$ for some positive integer $m \in \mathbb{N}$, substitute this into (3):
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
a_{n}+a_{n+2}=m(m+1) \text {. }
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Now adding $a_{n}$ to both sides of (1) and using (2) and (4) we get $m(m+1)=k^{2}+k$ whence $m=k$. So
|
| 226 |
+
|
| 227 |
+
$$
|
| 228 |
+
\left\{\begin{array}{l}
|
| 229 |
+
a_{n}+a_{n+1}=k^{2}, \\
|
| 230 |
+
a_{n}+a_{n+2}=k^{2}+k
|
| 231 |
+
\end{array}\right.
|
| 232 |
+
$$
|
| 233 |
+
|
| 234 |
+
for some positive integer $k$ (recall that $k$ depends on $n$ ).
|
| 235 |
+
Write equations (5) for $n=2$ and $n=3$, then for some positive integers $k$ and $\ell$ we get
|
| 236 |
+
|
| 237 |
+
$$
|
| 238 |
+
\left\{\begin{array}{l}
|
| 239 |
+
a_{2}+a_{3}=k^{2}, \\
|
| 240 |
+
a_{2}+a_{4}=k^{2}+k, \\
|
| 241 |
+
a_{3}+a_{4}=\ell^{2} \\
|
| 242 |
+
a_{3}+a_{5}=\ell^{2}+\ell
|
| 243 |
+
\end{array}\right.
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
Solution of this linear system is
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
a_{2}=\frac{2 k^{2}-\ell^{2}+k}{2}, \quad a_{3}=\frac{\ell^{2}-k}{2}, \quad a_{4}=\frac{\ell^{2}+k}{2}, \quad a_{5}=\frac{\ell^{2}+2 \ell+k}{2} .
|
| 250 |
+
$$
|
| 251 |
+
|
| 252 |
+
From $a_{2}<a_{4}$ we obtain $k^{2}<\ell^{2}$ hence $k<\ell$.
|
| 253 |
+
Consider $a_{6}$ :
|
| 254 |
+
|
| 255 |
+
$$
|
| 256 |
+
a_{6}=a_{5}+\sqrt{a_{5}+a_{4}}=a_{5}+\sqrt{\ell^{2}+\ell+k} .
|
| 257 |
+
$$
|
| 258 |
+
|
| 259 |
+
Since $0<k<l$ we have $\ell^{2}<\ell^{2}+\ell+k<(\ell+1)^{2}$. So $a_{6}$ cannot be integer i.e. there is no such sequence with six or more members.
|
| 260 |
+
|
| 261 |
+
To find all required sequences with five members we must find positive integers $a_{2}, a_{3}, a_{4}$ and $a_{5}$ which satisfy (7) for some positive integers $k<\ell$. Its clear that $k$ and $\ell$ must be of the same parity. Vise versa, let positive integers $k, \ell$ be of the same parity and satisfy $k<\ell$ then from (7) we get integers $a_{2}, a_{3}, a_{4}$ and $a_{5}$ then $a_{1}=\left(a_{3}-a_{2}\right)^{2}-a_{2}$ and it remains to verify that $a_{1}$ and $a_{2}$ are positive i.e. $2 k^{2}+k>\ell^{2}$ and $2\left(\ell^{2}-k^{2}-k\right)^{2}>2 k^{2}-\ell^{2}+k$.
|
| 262 |
+
|
| 263 |
+
Solution 4: It is easy to see that $\left(a_{n}\right)$ is increasing for large enough $n$. Hence
|
| 264 |
+
|
| 265 |
+
$$
|
| 266 |
+
a_{n+1}<a_{n}+\sqrt{2 a_{n}}
|
| 267 |
+
$$
|
| 268 |
+
|
| 269 |
+
and
|
| 270 |
+
|
| 271 |
+
$$
|
| 272 |
+
a_{n}<a_{n-1}+\sqrt{2 a_{n-1}} .
|
| 273 |
+
$$
|
| 274 |
+
|
| 275 |
+
Lets define $b_{n}=a_{n}+a_{n-1}$. Using AM-QM inequality we have
|
| 276 |
+
|
| 277 |
+
$$
|
| 278 |
+
\frac{\sqrt{2 a_{n}}+\sqrt{2 a_{n-1}}}{2} \leq \sqrt{\frac{2 a_{n}+2 a_{n-1}}{2}}
|
| 279 |
+
$$
|
| 280 |
+
|
| 281 |
+
Adding (1), (2) and using (3):
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
b_{n+1}<b_{n}+\sqrt{2 a_{n}}+\sqrt{2 a_{n-1}} \leq b_{n}+2 \sqrt{b_{n}} .
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
Let $b_{n}=m^{2}$. Since $\left(b_{n}\right)$ is increasing for large enough $n$, we have:
|
| 288 |
+
|
| 289 |
+
$$
|
| 290 |
+
m^{2}<b_{n+1}<m^{2}+2 m<(m+1)^{2}
|
| 291 |
+
$$
|
| 292 |
+
|
| 293 |
+
So, $b_{n+1}$ can't be a perfect square, so we get contradiction.
|
| 294 |
+
|
| 295 |
+
Problem 5. Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
|
| 296 |
+
(Netherlands)
|
| 297 |
+
Solution 1A: Define the following ordered partitions:
|
| 298 |
+
|
| 299 |
+
$$
|
| 300 |
+
\begin{aligned}
|
| 301 |
+
& P_{1}=(\{1,2\},\{3,4\}, \ldots,\{2 m-1,2 m\}), \\
|
| 302 |
+
& P_{2}=(\{1, m+1\},\{2, m+2\}, \ldots,\{m, 2 m\}), \\
|
| 303 |
+
& P_{3}=(\{1,2 m\},\{2, m+1\},\{3, m+2\}, \ldots,\{m, 2 m-1\})
|
| 304 |
+
\end{aligned}
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
For each $P_{j}$ we will compute the possible values for the expression $s=a_{1}+\ldots+a_{m}$, where $a_{i} \in P_{j, i}$ are the chosen integers. Here, $P_{j, i}$ denotes the $i$-th coordinate of the ordered partition $P_{j}$.
|
| 308 |
+
We will denote by $\sigma$ the number $\sum_{i=1}^{m} i=\left(m^{2}+m\right) / 2$.
|
| 309 |
+
|
| 310 |
+
- Consider the partition $P_{1}$ and a certain choice with corresponding sum $s$. We find that
|
| 311 |
+
|
| 312 |
+
$$
|
| 313 |
+
m^{2}=\sum_{i=1}^{m}(2 i-1) \leq s \leq \sum_{i=1}^{m} 2 i=m^{2}+m
|
| 314 |
+
$$
|
| 315 |
+
|
| 316 |
+
Hence, if $n<m^{2}$ or $n>m^{2}+m$, this partition gives a positive answer.
|
| 317 |
+
|
| 318 |
+
- Consider the partition $P_{2}$ and a certain choice with corresponding $s$. We find that
|
| 319 |
+
|
| 320 |
+
$$
|
| 321 |
+
s \equiv \sum_{i=1}^{m} i \equiv \sigma \quad(\bmod m)
|
| 322 |
+
$$
|
| 323 |
+
|
| 324 |
+
Hence, if $m^{2} \leq n \leq m^{2}+m$ and $n \not \equiv \sigma(\bmod m)$, this partition solves the problem.
|
| 325 |
+
|
| 326 |
+
- Consider the partition $P_{3}$ and a certain choice with corresponding $s$. We set
|
| 327 |
+
|
| 328 |
+
$$
|
| 329 |
+
d_{i}= \begin{cases}0 & \text { if } a_{i}=i \\ 1, & \text { if } a_{i} \neq i\end{cases}
|
| 330 |
+
$$
|
| 331 |
+
|
| 332 |
+
We also put $d=\sum_{i=1}^{m} d_{i}$, and note that $0 \leq d \leq m$. Note also that if $a_{i} \neq i$, then $a_{i} \equiv i-1$ $(\bmod m)$. Hence, for all $a_{i} \in P_{3, i}$ it holds that
|
| 333 |
+
|
| 334 |
+
$$
|
| 335 |
+
a_{i} \equiv i-d_{i} \quad(\bmod m)
|
| 336 |
+
$$
|
| 337 |
+
|
| 338 |
+
Hence,
|
| 339 |
+
|
| 340 |
+
$$
|
| 341 |
+
s \equiv \sum_{i=1}^{m} a_{i} \equiv \sum_{i=1}^{m}\left(i-d_{i}\right) \equiv \sigma-d \quad(\bmod m),
|
| 342 |
+
$$
|
| 343 |
+
|
| 344 |
+
which can only be congruent to $\sigma$ modulo $m$ if all $d_{i}$ are equal, which forces $s=\left(m^{2}+m\right) / 2$ or $s=\left(3 m^{2}+m\right) / 2$. Since $m>1$, it holds that
|
| 345 |
+
|
| 346 |
+
$$
|
| 347 |
+
\frac{m^{2}+m}{2}<m^{2}<m^{2}+m<\frac{3 m^{2}+m}{2} .
|
| 348 |
+
$$
|
| 349 |
+
|
| 350 |
+
Hence if $m^{2} \leq n \leq m^{2}+m$ and $n \equiv \sigma(\bmod m)$, then $s$ cannot be equal to $n$, so partition $P_{3}$ suffices for such $n$.
|
| 351 |
+
|
| 352 |
+
Note that all $n$ are treated in one of the cases above, so we are done.
|
| 353 |
+
Common notes for solutions 1B and 1C: Given the analysis of $P_{1}$ and $P_{2}$ as in the solution 1A, we may conclude (noting that $\sigma \equiv m(m+1) / 2(\bmod m)$ ) that if $m$ is odd then $m^{2}$ and $m^{2}+m$ are the only candidates for counterexamples $n$, while if $m$ is even then $m^{2}+\frac{m}{2}$ is the only candidate.
|
| 354 |
+
|
| 355 |
+
There are now various ways to proceed as alternatives to the partition $P_{3}$.
|
| 356 |
+
Solution 1B: Consider the partition $(\{1, m+2\},\{2, m+3\}, \ldots,\{m-1,2 m\},\{m, m+1\})$. We consider possible sums mod $m+1$. For the first $m-1$ pairs, the elements of each pair are congruent mod $m+1$, so the sum of one element of each pair is $(\bmod m+1)$ congruent to $\frac{1}{2} m(m+1)-m$, which is congruent to 1 if $m+1$ is odd and $1+\frac{m+1}{2}$ if $m+1$ is even. Now the elements of the last pair are congruent to -1 and 0 , so any achievable value of $n$ is congruent to 0 or 1 if $m+1$ is odd, and to 0 or 1 plus $\frac{m+1}{2}$ if $m+1$ is even. If $m$ is even then $m^{2}+\frac{m}{2} \equiv 1+\frac{m}{2}$, which is not congruent to 0 or 1 . If $m$ is odd then $m^{2} \equiv 1$ and $m^{2}+m \equiv 0$, neither of which can equal 0 or 1 plus $\frac{m+1}{2}$.
|
| 357 |
+
Solution 1C: Similarly, consider the partition $(\{1, m\},\{2, m+1\}, \ldots,\{m-1,2 m-2\},\{2 m-1,2 m\})$, this time considering sums of elements of pairs $\bmod m-1$. If $m-1$ is odd, the sum is congruent to 1 or 2 ; if $m-1$ is even, to 1 or 2 plus $\frac{m-1}{2}$. If $m$ is even then $m^{2}+\frac{m}{2} \equiv 1+\frac{m}{2}$, and this can only be congruent to 1 or 2 when $m=2$. If $m$ is odd, $m^{2}$ and $m^{2}+m$ are congruent to 1 and 2 , and these can only be congruent to 1 or 2 plus $\frac{m-1}{2}$ when $m=3$. Now the cases of $m=2$ and $m=3$ need considering separately (by finding explicit partitions excluding each $n$ ).
|
| 358 |
+
Solution 2: This solution does not use modulo arguments. Use only $P_{1}$ from the solution 1A to conclude that $m^{2} \leq n \leq m^{2}+m$. Now consider the partition $(\{1,2 m\},\{2,3\},\{4,5\}, \ldots,\{2 m-$ $2,2 m-1\})$. If 1 is chosen from the first pair, the sum is at most $m^{2}$; if $2 m$ is chosen, the sum is at least $m^{2}+m$. So either $n=m^{2}$ or $n=m^{2}+m$. Now consider the partition ( $\{1,2 m-$ $1\},\{2,2 m\},\{3,4\},\{5,6\}, \ldots,\{2 m-3,2 m-2\})$. Sums of one element from each of the last $m-2$ pairs are in the range from $(m-2) m=m^{2}-2 m$ to $(m-2)(m+1)=m^{2}-m-2$ inclusive. Sums of one element from each of the first two pairs are $3,2 m+1$ and $4 m-1$. In the first case we have $n \leq m^{2}-m+1<m^{2}$, in the second $m^{2}+1 \leq n \leq m^{2}+m-1$ and in the third $n \geq m^{2}+2 m-1>m^{2}+m$. So these three partitions together have eliminated all $n$.
|
| 359 |
+
|
| 360 |
+
Problem 6. Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
|
| 361 |
+
(Ukraine)
|
| 362 |
+
|
| 363 |
+
|
| 364 |
+
Solution 1: Let $\omega$ be the circumcircle of $\triangle A B C$. Reflecting $\omega$ in line $B C$, we obtain circle $\omega^{\prime}$ which, obviously, contains points $H$ and $P^{\prime}$. Let $M$ be the midpoint of $B C$. As triangle $\triangle A B C$ is acute-angled, then $H$ and $O$ lie inside this triangle.
|
| 365 |
+
|
| 366 |
+
Let us assume that $\angle C A B=60^{\circ}$. Since
|
| 367 |
+
|
| 368 |
+
$$
|
| 369 |
+
\angle C O B=2 \angle C A B=120^{\circ}=180^{\circ}-60^{\circ}=180^{\circ}-\angle C A B=\angle C H B,
|
| 370 |
+
$$
|
| 371 |
+
|
| 372 |
+
hence $O$ lies on $\omega^{\prime}$. Reflecting $O$ in line $B C$, we obtain point $O^{\prime}$ which lies on $\omega$ and this point is the center of $\omega^{\prime}$. Then $O O^{\prime}=2 O M=2 R \cos \angle C A B=A H$, so $A H=O O^{\prime}=H O^{\prime}=A O=R$, where $R$ is the radius of $\omega$ and, naturally, of $\omega^{\prime}$. Then quadrilateral $A H O^{\prime} O$ is a rhombus, so $A$ and $O^{\prime}$ are symmetric to each other with respect to $H O$. As $H, G$ and $O$ are collinear (Euler line), then $\angle G A H=\angle H O^{\prime} G$. Diagonals of quadrilateral $G O P O^{\prime}$ intersects at $M$. Since $\angle B O M=60^{\circ}$, so
|
| 373 |
+
|
| 374 |
+
$$
|
| 375 |
+
O M=M O^{\prime}=\operatorname{ctg} 60^{\circ} \cdot M B=\frac{M B}{\sqrt{3}} .
|
| 376 |
+
$$
|
| 377 |
+
|
| 378 |
+
As $3 M O \cdot M O^{\prime}=M B^{2}=M B \cdot M C=M P \cdot M A=3 M G \cdot M P$, then $G O P O^{\prime}$ is a cyclic. Since $B C$ is a perpendicular bisector of $O O^{\prime}$, so the circumcircle of quadrilateral $G O P O^{\prime}$ is symmetrical with respect to $B C$. Thus $P^{\prime}$ also belongs to the circumcircle of $G O P O^{\prime}$, hence $\angle G O^{\prime} P^{\prime}=\angle G P P^{\prime}$. Note that $\angle G P P^{\prime}=\angle G A H$ since $A H \| P P^{\prime}$. And as it was proved $\angle G A H=\angle H O^{\prime} G$, then $\angle H O^{\prime} G=\angle G O^{\prime} P^{\prime}$. Thus triangles $\triangle H O^{\prime} G$ and $\triangle G O^{\prime} P^{\prime}$ are equal and hence $H G=G P^{\prime}$.
|
| 379 |
+
|
| 380 |
+
Now we will prove that if $H G=G P^{\prime}$ then $\angle C A B=60^{\circ}$. Reflecting $A$ with respect to $M$, we get $A^{\prime}$. Then, as it was said in the first part of solution, points $B, C, H$ and $P^{\prime}$ belong to $\omega^{\prime}$. Also it is clear that $A^{\prime}$ belongs to $\omega^{\prime}$. Note that $H C \perp C A^{\prime}$ since $A B \| C A^{\prime}$ and hence $H A^{\prime}$ is a diameter of $\omega^{\prime}$. Obviously, the center $O^{\prime}$ of circle $\omega^{\prime}$ is midpoint of $H A^{\prime}$. From $H G=G P^{\prime}$ it follows that $\triangle H G O^{\prime}$ is equal to $\triangle P^{\prime} G O^{\prime}$. Therefore $H$ and $P^{\prime}$ are symmetric with respect to $G O^{\prime}$. Hence $G O^{\prime} \perp H P^{\prime}$ and $G O^{\prime} \| A^{\prime} P^{\prime}$. Let $H G$ intersect $A^{\prime} P^{\prime}$ at $K$ and $K \not \equiv O$ since $A B \neq A C$. We conclude that $H G=G K$, because line $G O^{\prime}$ is midline of the triangle $\triangle H K A^{\prime}$. Note that $2 G O=H G$. since $H O$ is Euler line of triangle $A B C$. So $O$ is midpoint of segment $G K$. Because of $\angle C M P=\angle C M P^{\prime}$, then $\angle G M O=\angle O M P^{\prime}$. Line $O M$, that passes through $O^{\prime}$, is an external angle bisector of $\angle P^{\prime} M A^{\prime}$. Also we know that $P^{\prime} O^{\prime}=O^{\prime} A^{\prime}$, then $O^{\prime}$ is the midpoint of arc $P^{\prime} M A^{\prime}$ of the circumcircle of triangle $\triangle P^{\prime} M A^{\prime}$. It
|
| 381 |
+
|
| 382 |
+
follows that quadrilateral $P^{\prime} M O^{\prime} A^{\prime}$ is cyclic, then $\angle O^{\prime} M A^{\prime}=\angle O^{\prime} P^{\prime} A^{\prime}=\angle O^{\prime} A^{\prime} P^{\prime}$. Let $O M$ and $P^{\prime} A^{\prime}$ intersect at $T$. Triangles $\triangle T O^{\prime} A^{\prime}$ and $\triangle A^{\prime} O^{\prime} M$ are similar, hence $O^{\prime} A^{\prime} / O^{\prime} M=O^{\prime} T / O^{\prime} A^{\prime}$. In the other words, $O^{\prime} M \cdot O^{\prime} T=O^{\prime} A^{\prime 2}$. Using Menelaus' theorem for triangle $\triangle H K A^{\prime}$ and line $T O^{\prime}$, we obtain that
|
| 383 |
+
|
| 384 |
+
$$
|
| 385 |
+
\frac{A^{\prime} O^{\prime}}{O^{\prime} H} \cdot \frac{H O}{O K} \cdot \frac{K T}{T A^{\prime}}=3 \cdot \frac{K T}{T A^{\prime}}=1
|
| 386 |
+
$$
|
| 387 |
+
|
| 388 |
+
It follows that $K T / T A^{\prime}=1 / 3$ and $K A^{\prime}=2 K T$. Using Menelaus' theorem for triangle $T O^{\prime} A^{\prime}$ and line $H K$ we get that
|
| 389 |
+
|
| 390 |
+
$$
|
| 391 |
+
1=\frac{O^{\prime} H}{H A^{\prime}} \cdot \frac{A^{\prime} K}{K T} \cdot \frac{T O}{O O^{\prime}}=\frac{1}{2} \cdot 2 \cdot \frac{T O}{O O^{\prime}}=\frac{T O}{O O^{\prime}} .
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
It means that $T O=O O^{\prime}$, so $O^{\prime} A^{2}=O^{\prime} M \cdot O^{\prime} T=O O^{\prime 2}$. Hence $O^{\prime} A^{\prime}=O O^{\prime}$ and, consequently, $O \in \omega^{\prime}$. Finally we conclude that $2 \angle C A B=\angle B O C=180^{\circ}-\angle C A B$, so $\angle C A B=60^{\circ}$.
|
| 395 |
+
|
| 396 |
+
|
| 397 |
+
Solution 2: Let $O^{\prime}$ and $G^{\prime}$ denote the reflection of $O$ and $G$, respectively, with respect to the line $B C$. We then need to show $\angle C A B=60^{\circ}$ iff $G^{\prime} H^{\prime}=G^{\prime} P$. Note that $\triangle H^{\prime} O P$ is isosceles and hence
|
| 398 |
+
$G^{\prime} H^{\prime}=G^{\prime} P$ is equivalent to $G^{\prime}$ lying on the bisector $\angle H^{\prime} O P$. Let $\angle H^{\prime} A P=\varepsilon$. By the assumption $A B \neq A C$, we have $\varepsilon \neq 0$. Then $\angle H^{\prime} O P=2 \angle H^{\prime} A P=2 \varepsilon$, hence $G^{\prime} H^{\prime}=G^{\prime} P$ iff $\angle G^{\prime} O H^{\prime}=\varepsilon$. But $\angle G O^{\prime} H=\angle G^{\prime} O H^{\prime}$. Let $D$ be the midpoint of $O O^{\prime}$. It is known that $\angle G D O=\angle G A H=\varepsilon$. Let $F$ be the midpoint of $H G$. Then $H G=F O$ (Euler line). Let $\angle G O^{\prime} H=\delta$. We then have to show $\delta=\varepsilon$ iff $\angle C A B=60^{\circ}$. But by similarity ( $\triangle G D O \sim \triangle F O^{\prime} O$ ) we have $\angle F O^{\prime} O=\varepsilon$. Consider the circumcircles of the triangles $F O^{\prime} O$ and $G O^{\prime} H$. By the sine law and since the segments $H G$ and $F O$ are of equal length we deduce that the circumcircles of the triangles $F O^{\prime} O$ and $G O^{\prime} H$ are symmetric with respect to the perpendicular bisector of the segment $F G$ iff $\delta=\varepsilon$. Obviously, $O^{\prime}$ is the common point of these two circles. Hence $O^{\prime}$ must be fixed after the symmetry about the perpendicular bisector of the segment $F G$ iff $\delta=\varepsilon$ so we have $\varepsilon=\delta$ iff $\triangle H O O^{\prime}$ is isosceles. But $H O^{\prime}=H^{\prime} O=R$, and so
|
| 399 |
+
|
| 400 |
+
$$
|
| 401 |
+
\varepsilon=\delta \Longleftrightarrow O O^{\prime}=R \Longleftrightarrow O D=\frac{R}{2} \Longleftrightarrow \cos \angle C A B=\frac{1}{2} \Longleftrightarrow \angle C A B=60^{\circ}
|
| 402 |
+
$$
|
| 403 |
+
|
| 404 |
+
Solution 3: Let $H^{\prime}$ and $G^{\prime}$ denote the reflection of points $H$ and $G$ with respect to the line $B C$. It is known that $H^{\prime}$ belongs to the circumcircle of $\triangle A B C$. The equality $H G=G P^{\prime}$ is equivalent to $H^{\prime} G^{\prime}=G^{\prime} P$. As in the Solution 2, it is equivalent to the statement that point $G^{\prime}$ belongs to the perpendicular bisector of $H^{\prime} P$, which is equivalent to $O G^{\prime} \perp H^{\prime} P$, where $O$ is the circumcenter of $\triangle A B C$.
|
| 405 |
+
|
| 406 |
+
Let points $A(a), B(b)$, and $C(c=-\bar{b})$ belong to the unit circle in the complex plane. Point $G$ have coordinate $g=(a+b-\bar{b}) / 3$. Since $B C$ is parallel to the real axis point $H^{\prime}$ have coordinate $h^{\prime}=\bar{a}=1 / a$.
|
| 407 |
+
|
| 408 |
+
Point $P(p)$ belongs to the unit circle, so $\bar{p}=1 / p$. Since $a, p, g$ are collinear we have $\frac{p-a}{g-a}=$ $\overline{\left(\frac{p-a}{g-a}\right)}$. After computation we get $p=\frac{g-a}{1-\bar{g} a}$. Since $G^{\prime}(g)$ is the reflection of $G$ with respect to the chord $B C$, we have $g^{\prime}=b+(-\bar{b})-b(-\bar{b}) \bar{g}=b-\bar{b}+\bar{g}$. Let $b-\bar{b}=d$. We have $\bar{d}=-d$. So
|
| 409 |
+
|
| 410 |
+
$$
|
| 411 |
+
g=\frac{a+d}{3}, \quad \bar{g}=\frac{\bar{a}-d}{3}, \quad g^{\prime}=d+\bar{g}=\frac{\bar{a}+2 d}{3}, \quad \overline{g^{\prime}}=\frac{a-2 d}{3} \quad \text { and } \quad p=\frac{g-a}{1-\bar{g} a}=\frac{d-2 a}{2+a d} .
|
| 412 |
+
$$
|
| 413 |
+
|
| 414 |
+
It is easy to see that $O G^{\prime} \perp H^{\prime} P^{\prime}$ is equivalent to
|
| 415 |
+
|
| 416 |
+
$$
|
| 417 |
+
\frac{g^{\prime}}{h^{\prime}-p}=-\overline{\left(\frac{g^{\prime}}{h^{\prime}-p}\right)}=-\frac{g^{\prime}}{\frac{1}{h^{\prime}}-\frac{1}{p}}=\frac{\overline{g^{\prime}} h^{\prime} p}{h^{\prime}-p}
|
| 418 |
+
$$
|
| 419 |
+
|
| 420 |
+
since $h^{\prime}$ and $p$ belong to the unit circle (note that $H^{\prime} \neq P$ because $A B \neq A C$ ). This is equivalent to $g^{\prime}=\overline{g^{\prime}} h^{\prime} p$ and from (1), after easy computations, this is equivalent to $a^{2} g^{2}+a^{2}+d^{2}+1=$ $\left(a^{2}+1\right)\left(d^{2}+1\right)=0$.
|
| 421 |
+
|
| 422 |
+
We cannot have $a^{2}+1=0$, because then $a= \pm i$, but $A B \neq A C$. Hence $d=b-\bar{b}= \pm i$, and the pair $\{b, c=-\bar{b}\}$ is either $\{-\sqrt{3} / 2+i / 2, \sqrt{3} / 2+i / 2\}$ or $\{-\sqrt{3} / 2-i / 2, \sqrt{3} / 2-i / 2\}$. Both cases are equivalent to $\angle B A C=60^{\circ}$ which completes the proof.
|
| 423 |
+
|
EGMO/md/en-2016-solutions.md
ADDED
|
@@ -0,0 +1,139 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# EGMO 2016, Day 1 - Solutions
|
| 2 |
+
|
| 3 |
+
Problem 1. Let $n$ be an odd positive integer, and let $x_{1}, x_{2}, \ldots, x_{n}$ be non-negative real numbers. Show that
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
\min _{i=1, \ldots, n}\left(x_{i}^{2}+x_{i+1}^{2}\right) \leq \max _{j=1, \ldots, n}\left(2 x_{j} x_{j+1}\right)
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
where $x_{n+1}=x_{1}$.
|
| 10 |
+
Solution. In what follows, indices are reduced modulo $n$. Consider the $n$ differences $x_{k+1}-x_{k}, k=1, \ldots, n$. Since $n$ is odd, there exists an index $j$ such that $\left(x_{j+1}-x_{j}\right)\left(x_{j+2}-x_{j+1}\right) \geq 0$. Without loss of generality, we may and will assume both factors non-negative, so $x_{j} \leq x_{j+1} \leq x_{j+2}$. Consequently,
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
\min _{k=1, \ldots, n}\left(x_{k}^{2}+x_{k+1}^{2}\right) \leq x_{j}^{2}+x_{j+1}^{2} \leq 2 x_{j+1}^{2} \leq 2 x_{j+1} x_{j+2} \leq \max _{k=1, \ldots, n}\left(2 x_{k} x_{k+1}\right)
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
Remark. If $n \geq 3$ is odd, and one of the $x_{k}$ is negative, then the conclusion may no longer hold. This is the case if, for instance, $x_{1}=-b$, and $x_{2 k}=a$, $x_{2 k+1}=b, k=1, \ldots,(n-1) / 2$, where $0 \leq a<b$, so the string of numbers is
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
-b, b, a, b, a, \ldots, b, a
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
If $n$ is even, the conclusion may again no longer hold, as shown by any string of alternate real numbers: $a, b, a, b, \ldots, a, b$, where $a \neq b$.
|
| 23 |
+
|
| 24 |
+
Problem 2. Let $A B C D$ be a cyclic quadrilateral, and let diagonals $A C$ and $B D$ intersect at $X$. Let $C_{1}, D_{1}$ and $M$ be the midpoints of segments $C X$, $D X$ and $C D$, respectively. Lines $A D_{1}$ and $B C_{1}$ intersect at $Y$, and line $M Y$ intersects diagonals $A C$ and $B D$ at different points $E$ and $F$, respectively. Prove that line $X Y$ is tangent to the circle through $E, F$ and $X$.
|
| 25 |
+
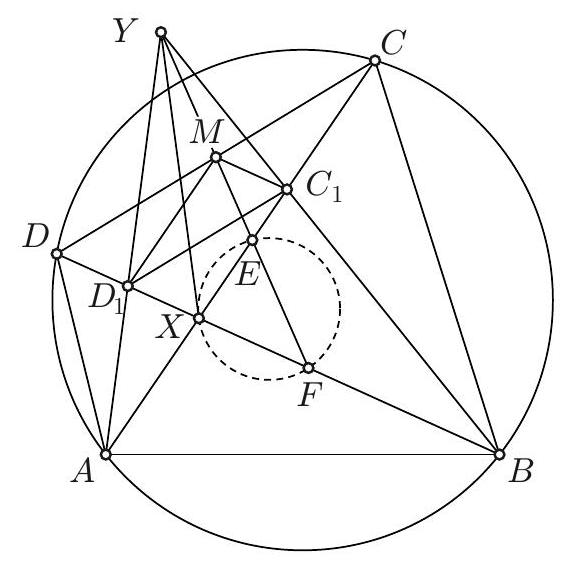
|
| 26 |
+
|
| 27 |
+
Solution. We are to prove that $\angle E X Y=\angle E F X$; alternatively, but equivalently, $\angle A Y X+\angle X A Y=\angle B Y F+\angle X B Y$.
|
| 28 |
+
|
| 29 |
+
Since the quadrangle $A B C D$ is cyclic, the triangles $X A D$ and $X B C$ are similar, and since $A D_{1}$ and $B C_{1}$ are corresponding medians in these triangles, it follows that $\angle X A Y=\angle X A D_{1}=\angle X B C_{1}=\angle X B Y$.
|
| 30 |
+
|
| 31 |
+
Finally, $\angle A Y X=\angle B Y F$, since $X$ and $M$ are corresponding points in the similar triangles $A B Y$ and $C_{1} D_{1} Y$ : indeed, $\angle X A B=\angle X D C=\angle M C_{1} D_{1}$, and $\angle X B A=\angle X C D=\angle M D_{1} C_{1}$.
|
| 32 |
+
|
| 33 |
+
Problem 3. Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
| 34 |
+
|
| 35 |
+
Solution 1 (Israel). The required minimum is 6 m and is achieved by a diagonal string of $m 4 \times 4$ blocks of the form below (bullets mark centres of blue cells):
|
| 36 |
+
|
| 37 |
+
In particular, this configuration shows that the required minimum does not exceed 6 m .
|
| 38 |
+
|
| 39 |
+
We now show that any configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m .
|
| 40 |
+
|
| 41 |
+
Fix such a configuration and let $m_{1}^{r}$ be the number of blue cells in rows containing exactly one such, let $m_{2}^{r}$ be the number of blue cells in rows containing exactly two such, and let $m_{3}^{r}$ be the number of blue cells in rows containing at least three such; the numbers $m_{1}^{c}, m_{2}^{c}$ and $m_{3}^{c}$ are defined similarly.
|
| 42 |
+
|
| 43 |
+
Begin by noticing that $m_{3}^{c} \geq m_{1}^{r}$ and, similarly, $m_{3}^{r} \geq m_{1}^{c}$. Indeed, if a blue cell is alone in its row, respectively column, then there are at least two other blue cells in its column, respectively row, and the claim follows.
|
| 44 |
+
|
| 45 |
+
Suppose now, if possible, the total number of blue cells is less than 6 m . We will show that $m_{1}^{r}>m_{3}^{r}$ and $m_{1}^{c}>m_{3}^{c}$, and reach a contradiction by the preceding: $m_{1}^{r}>m_{3}^{r} \geq m_{1}^{c}>m_{3}^{c} \geq m_{1}^{r}$.
|
| 46 |
+
|
| 47 |
+
We prove the first inequality; the other one is dealt with similarly. To this end, notice that there are no empty rows - otherwise, each column would contain at least two blue cells, whence a total of at least $8 m>6 m$ blue cells, which is a contradiction. Next, count rows to get $m_{1}^{r}+m_{2}^{r} / 2+m_{3}^{r} / 3 \geq 4 m$,
|
| 48 |
+
and count blue cells to get $m_{1}^{r}+m_{2}^{r}+m_{3}^{r}<6 m$. Subtraction of the latter from the former multiplied by $3 / 2$ yields $m_{1}^{r}-m_{3}^{r}>m_{2}^{r} / 2 \geq 0$, and the conclusion follows.
|
| 49 |
+
|
| 50 |
+
Solution 2. To prove that a minimal configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m , consider a bipartite graph whose vertex parts are the rows and the columns of the array, respectively, a row and a column being joined by an edge if and only if the two cross at a blue cell. Clearly, the number of blue cells is equal to the number of edges of this graph, and the relationship condition in the statement reads: for every row $r$ and every column $c$, $\operatorname{deg} r+\operatorname{deg} c-\epsilon(r, c) \geq 2$, where $\epsilon(r, c)=2$ if $r$ and $c$ are joined by an edge, and $\epsilon(r, c)=0$ otherwise.
|
| 51 |
+
|
| 52 |
+
Notice that there are no empty rows/columns, so the graph has no isolated vertices. By the preceding, the cardinality of every connected component of the graph is at least 4 , so there are at most $2 \cdot 4 m / 4=2 m$ such and, consequently, the graph has at least $8 m-2 m=6 m$ edges. This completes the proof.
|
| 53 |
+
|
| 54 |
+
Remarks. The argument in the first solution shows that equality to 6 m is possible only if $m_{1}^{r}=m_{3}^{r}=m_{1}^{c}=m_{3}^{c}=3 m, m_{2}^{r}=m_{2}^{c}=0$, and there are no rows, respectively columns, containing four blue cells or more.
|
| 55 |
+
|
| 56 |
+
Consider the same problem for an $n \times n$ array. The argument in the second solution shows that the corresponding minimum is $3 n / 2$ if $n$ is divisible by 4 , and $3 n / 2+1 / 2$ if $n$ is odd; if $n \equiv 2(\bmod 4)$, the minimum in question is $3 n / 2+1$. To describe corresponding minimal configurations $C_{n}$, refer to the minimal configurations $C_{2}, C_{3}, C_{4}, C_{5}$ below:
|
| 57 |
+

|
| 58 |
+
|
| 59 |
+
The case $n \equiv 0(\bmod 4)$ was dealt with above: a $C_{n}$ consists of a diagonal string of $n / 4$ blocks $C_{4}$. If $n \equiv r(\bmod 4), r=2,3$, a $C_{n}$ consists of a diagonal string of $\lfloor n / 4\rfloor$ blocks $C_{4}$ followed by a $C_{r}$, and if $n \equiv 1(\bmod 4)$, a $C_{n}$ consists of a diagonal string of $\lfloor n / 4\rfloor-1$ blocks $C_{4}$ followed by a $C_{5}$.
|
| 60 |
+
|
| 61 |
+
Minimal configurations are not necessarily unique (two configurations being equivalent if one is obtained from the other by permuting the rows and/or the columns). For instance, if $n=6$, the configurations below are both minimal:
|
| 62 |
+

|
| 63 |
+
|
| 64 |
+
## EGMO 2016, Day 2 - Solutions
|
| 65 |
+
|
| 66 |
+
Problem 4. Two circles, $\omega_{1}$ and $\omega_{2}$, of equal radius intersect at different points $X_{1}$ and $X_{2}$. Consider a circle $\omega$ externally tangent to $\omega_{1}$ at a point $T_{1}$, and internally tangent to $\omega_{2}$ at a point $T_{2}$. Prove that lines $X_{1} T_{1}$ and $X_{2} T_{2}$ intersect at a point lying on $\omega$.
|
| 67 |
+
|
| 68 |
+
Solution 1. Let the line $X_{k} T_{k}$ and $\omega$ meet again at $X_{k}^{\prime}, k=1,2$, and notice that the tangent $t_{k}$ to $\omega_{k}$ at $X_{k}$ and the tangent $t_{k}^{\prime}$ to $\omega$ at $X_{k}^{\prime}$ are parallel. Since the $\omega_{k}$ have equal radii, the $t_{k}$ are parallel, so the $t_{k}^{\prime}$ are parallel, and consequently the points $X_{1}^{\prime}$ and $X_{2}^{\prime}$ coincide (they are not antipodal, since they both lie on the same side of the line $T_{1} T_{2}$ ). The conclusion follows.
|
| 69 |
+
|
| 70 |
+
Solution 2. The circle $\omega$ is the image of $\omega_{k}$ under a homothety $h_{k}$ centred at $T_{k}, k=1,2$. The tangent to $\omega$ at $X_{k}^{\prime}=h_{k}\left(X_{k}\right)$ is therefore parallel to the tangent $t_{k}$ to $\omega_{k}$ at $X_{k}$. Since the $\omega_{k}$ have equal radii, the $t_{k}$ are parallel, so $X_{1}^{\prime}=X_{2}^{\prime}$; and since the points $X_{k}, T_{k}$ and $X_{k}^{\prime}$ are collinear, the conclusion follows.
|
| 71 |
+
|
| 72 |
+
|
| 73 |
+
Solution 3. Invert from $X_{1}$ and use an asterisk to denote images under this inversion. Notice that $\omega_{k}^{*}$ is the tangent from $X_{2}^{*}$ to $\omega^{*}$ at $T_{k}^{*}$, and the pole $X_{1}$ lies on the bisectrix of the angle formed by the $\omega_{k}^{*}$, not containing $\omega^{*}$. Letting $X_{1} T_{1}^{*}$ and $\omega^{*}$ meet again at $Y$, standard angle chase shows that $Y$ lies on the circle $X_{1} X_{2}^{*} T_{2}^{*}$, and the conclusion follows.
|
| 74 |
+
|
| 75 |
+
Remarks. The product $h_{1} h_{2}$ of the two homotheties in the first solution is reflexion across the midpoint of the segment $X_{1} X_{2}$, which lies on the line $T_{1} T_{2}$ 。
|
| 76 |
+
|
| 77 |
+
Various arguments, involving similarities, radical axes, and the like, work equally well to prove the required result.
|
| 78 |
+
|
| 79 |
+
Problem 5. Let $k$ and $n$ be integers such that $k \geq 2$ and $k \leq n \leq 2 k-1$. Place rectangular tiles, each of size $1 \times k$ or $k \times 1$, on an $n \times n$ chessboard so that each tile covers exactly $k$ cells, and no two tiles overlap. Do this until
|
| 80 |
+
no further tile can be placed in this way. For each such $k$ and $n$, determine the minimum number of tiles that such an arrangement may contain.
|
| 81 |
+
|
| 82 |
+
Solution. The required minimum is $n$ if $n=k$, and it is $\min (n, 2 n-2 k+2)$ if $k<n<2 k$.
|
| 83 |
+
|
| 84 |
+
The case $n=k$ being clear, assume henceforth $k<n<2 k$. Begin by describing maximal arrangements on the board $[0, n] \times[0, n]$, having the above mentioned cardinalities.
|
| 85 |
+
|
| 86 |
+
If $k<n<2 k-1$, then $\min (n, 2 n-2 k+2)=2 n-2 k+2$. To obtain a maximal arrangement of this cardinality, place four tiles, $[0, k] \times[0,1]$, $[0,1] \times[1, k+1],[1, k+1] \times[k, k+1]$ and $[k, k+1] \times[0, k]$ in the square $[0, k] \times[0, k]$, stack $n-k-1$ horizontal tiles in the rectangle $[1, k+1] \times[k+1, n]$, and erect $n-k-1$ vertical tiles in the rectangle $[k+1, n] \times[1, k+1]$.
|
| 87 |
+
|
| 88 |
+
If $n=2 k-1$, then $\min (n, 2 n-2 k+2)=n=2 k-1$. A maximal arrangement of $2 k-1$ tiles is obtained by stacking $k-1$ horizontal tiles in the rectangle $[0, k] \times[0, k-1]$, another $k-1$ horizontal tiles in the rectangle $[0, k] \times[k, 2 k-1]$, and adding the horizontal tile $[k-1,2 k-1] \times[k-1, k]$.
|
| 89 |
+
|
| 90 |
+
The above examples show that the required minimum does not exceed the mentioned values.
|
| 91 |
+
|
| 92 |
+
To prove the reverse inequality, consider a maximal arrangement and let $r$, respectively $c$, be the number of rows, respectively columns, not containing a tile.
|
| 93 |
+
|
| 94 |
+
If $r=0$ or $c=0$, the arrangement clearly contains at least $n$ tiles.
|
| 95 |
+
If $r$ and $c$ are both positive, we show that the arrangement contains at least $2 n-2 k+2$ tiles. To this end, we will prove that the rows, respectively columns, not containing a tile are consecutive. Assume this for the moment, to notice that these $r$ rows and $c$ columns cross to form an $r \times c$ rectangular array containing no tile at all, so $r<k$ and $c<k$ by maximality. Consequently, there are $n-r \geq n-k+1$ rows containing at least one horizontal tile each, and $n-c \geq n-k+1$ columns containing at least one vertical tile each, whence a total of at least $2 n-2 k+2$ tiles.
|
| 96 |
+
|
| 97 |
+
We now show that the rows not containing a tile are consecutive; columns are dealt with similarly. Consider a horizontal tile $T$. Since $n<2 k$, the nearest horizontal side of the board is at most $k-1$ rows away from the row containing $T$. These rows, if any, cross the $k$ columns $T$ crosses to form a rectangular array no vertical tile fits in. Maximality forces each of these rows to contain a horizontal tile and the claim follows.
|
| 98 |
+
|
| 99 |
+
Consequently, the cardinality of every maximal arrangement is at least $\min (n, 2 n-2 k+2)$, and the conclusion follows.
|
| 100 |
+
|
| 101 |
+
Remarks. (1) If $k \geq 3$ and $n=2 k$, the minimum is $n+1=2 k+1$
|
| 102 |
+
and is achieved, for instance, by the maximal arrangement consisting of the vertical tile $[0,1] \times[1, k+1]$ along with $k-1$ horizontal tiles stacked in $[1, k+1] \times[0, k-1]$, another $k-1$ horizontal tiles stacked in $[1, k+1] \times[k+1,2 k]$, and two horizontal tiles stacked in $[k, 2 k] \times[k-1, k+1]$. This example shows that the corresponding minimum does not exceed $n+1<2 n-2 k+2$. The argument in the solution also applies to the case $n=2 k$ to infer that for a maximal arrangement of minimal cardinality either $r=0$ or $c=0$, and the cardinality is at least $n$. Clearly, we may and will assume $r=0$. Suppose, if possible, such an arrangement contains exactly $n$ tiles. Then each row contains exactly one tile, and there are no vertical tiles. Since there is no room left for an additional tile, some tile $T$ must cover a cell of the leftmost column, so it covers the $k$ leftmost cells along its row, and there is then room for another tile along that row - a contradiction.
|
| 103 |
+
(2) For every pair $(r, c)$ of integers in the range $2 k-n, \ldots, k-1$, at least one of which is positive, say $c>0$, there exists a maximal arrangement of cardinality $2 n-r-c$.
|
| 104 |
+
|
| 105 |
+
Use again the board $[0, n] \times[0, n]$ to stack $k-r$ horizontal tiles in each of the rectangles $[0, k] \times[0, k-r]$ and $[k-c, 2 k-c] \times[k, 2 k-r]$, erect $k-c$ vertical tiles in each of the rectangles $[0, k-c] \times[k-r, 2 k-r]$ and $[k, 2 k-c] \times[0, k]$, then stack $n-2 k+r$ horizontal tiles in the rectangle $[k-c, 2 k-c] \times[2 k-r, n]$, and erect $n-2 k+c$ vertical tiles in the rectangle $[2 k-c, n] \times[1, k+1]$.
|
| 106 |
+
|
| 107 |
+
Problem 6. Let $S$ be the set of all positive integers $n$ such that $n^{4}$ has a divisor in the range $n^{2}+1, n^{2}+2, \ldots, n^{2}+2 n$. Prove that there are infinitely many elements of $S$ of each of the forms $7 m, 7 m+1,7 m+2,7 m+5,7 m+6$ and no elements of $S$ of the form $7 m+3$ or $7 m+4$, where $m$ is an integer.
|
| 108 |
+
|
| 109 |
+
Solution. The conclusion is a consequence of the lemma below which actually provides a recursive description of $S$. The proof of the lemma is at the end of the solution.
|
| 110 |
+
|
| 111 |
+
Lemma. The fourth power of a positive integer $n$ has a divisor in the range $n^{2}+1, n^{2}+2, \ldots, n^{2}+2 n$ if and only if at least one of the numbers $2 n^{2}+1$ and $12 n^{2}+9$ is a perfect square.
|
| 112 |
+
|
| 113 |
+
Consequently, a positive integer $n$ is a member of $S$ if and only if $m^{2}-$ $2 n^{2}=1$ or $m^{2}-12 n^{2}=9$ for some positive integer $m$.
|
| 114 |
+
|
| 115 |
+
The former is a Pell equation whose solutions are $\left(m_{1}, n_{1}\right)=(3,2)$ and
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\left(m_{k+1}, n_{k+1}\right)=\left(3 m_{k}+4 n_{k}, 2 m_{k}+3 n_{k}\right), \quad k=1,2,3, \ldots
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
In what follows, all congruences are modulo 7. Iteration shows that $\left(m_{k+3}, n_{k+3}\right) \equiv\left(m_{k}, n_{k}\right)$. Since $\left(m_{1}, n_{1}\right) \equiv(3,2),\left(m_{2}, n_{2}\right) \equiv(3,-2)$, and
|
| 122 |
+
$\left(m_{3}, n_{3}\right) \equiv(1,0)$, it follows that $S$ contains infinitely many integers from each of the residue classes 0 and $\pm 2$ modulo 7 .
|
| 123 |
+
|
| 124 |
+
The other equation is easily transformed into a Pell equation, $m^{\prime 2}-$ $12 n^{\prime 2}=1$, by noticing that $m$ and $n$ are both divisible by 3 , say $m=3 m^{\prime}$ and $n=3 n^{\prime}$. In this case, the solutions are $\left(m_{1}, n_{1}\right)=(21,6)$ and
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\left(m_{k+1}, n_{k+1}\right)=\left(7 m_{k}+24 n_{k}, 2 m_{k}+7 n_{k}\right), \quad k=1,2,3, \ldots
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
This time iteration shows that $\left(m_{k+4}, n_{k+4}\right) \equiv\left(m_{k}, n_{k}\right)$. Since $\left(m_{1}, n_{1}\right) \equiv$ $(0,-1),\left(m_{2}, n_{2}\right) \equiv(-3,0),\left(m_{3}, n_{3}\right) \equiv(0,1)$, and $\left(m_{4}, n_{4}\right) \equiv(3,0)$, it follows that $S$ contains infinitely many integers from each of the residue classes 0 and $\pm 1$ modulo 7 .
|
| 131 |
+
|
| 132 |
+
Finally, since the $n_{k}$ from the two sets of formulae exhaust $S$, by the preceding no integer in the residue classes $\pm 3$ modulo 7 is a member of $S$.
|
| 133 |
+
|
| 134 |
+
We now turn to the proof of the lemma. Let $n$ be a member of $S$, and let $d=n^{2}+m$ be a divisor of $n^{4}$ in the range $n^{2}+1, n^{2}+2, \ldots, n^{2}+2 n$, so $1 \leq m \leq 2 n$. Consideration of the square of $n^{2}=d-m$ shows $m^{2}$ divisible by $d$, so $m^{2} / d$ is a positive integer. Since $n^{2}<d<(n+1)^{2}$, it follows that $d$ is not a square; in particular, $m^{2} / d \neq 1$, so $m^{2} / d \geq 2$. On the other hand, $1 \leq m \leq 2 n$, so $m^{2} / d=m^{2} /\left(n^{2}+m\right) \leq 4 n^{2} /\left(n^{2}+1\right)<4$. Consequently, $m^{2} / d=2$ or $m^{2} / d=3$; that is, $m^{2} /\left(n^{2}+m\right)=2$ or $m^{2} /\left(n^{2}+m\right)=3$. In the former case, $2 n^{2}+1=(m-1)^{2}$, and in the latter, $12 n^{2}+9=(2 m-3)^{2}$.
|
| 135 |
+
|
| 136 |
+
Conversely, if $2 n^{2}+1=m^{2}$ for some positive integer $m$, then $1<m^{2}<$ $4 n^{2}$, so $1<m<2 n$, and $n^{4}=\left(n^{2}+m+1\right)\left(n^{2}-m+1\right)$, so the first factor is the desired divisor.
|
| 137 |
+
|
| 138 |
+
Similarly, if $12 n^{2}+9=m^{2}$ for some positive integer $m$, then $m$ is odd, $n \geq 6$, and $n^{4}=\left(n^{2}+m / 2+3 / 2\right)\left(n^{2}-m / 2+3 / 2\right)$, and again the first factor is the desired divisor.
|
| 139 |
+
|
EGMO/md/en-2017-solutions.md
ADDED
|
@@ -0,0 +1,444 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problem 1
|
| 2 |
+
|
| 3 |
+
Let $A B C D$ be a convex quadrilateral with $\angle D A B=\angle B C D=90^{\circ}$ and $\angle A B C>\angle C D A$. Let $Q$ and $R$ be points on the segments $B C$ and $C D$, respectively, such that the line $Q R$ intersects lines $A B$ and $A D$ at points $P$ and $S$, respectively. It is given that $P Q=R S$. Let the midpoint of $B D$ be $M$ and the midpoint of $Q R$ be $N$. Prove that $M, N, A$ and $C$ lie on a circle.
|
| 4 |
+
|
| 5 |
+
Mark Mordechai Etkind, Israel
|
| 6 |
+
|
| 7 |
+
## Solution 1
|
| 8 |
+
|
| 9 |
+
Note that $N$ is also the midpoint of $P S$. From right-angled triangles $P A S$ and $C Q R$ we obtain $\angle A N P=$ $2 \angle A S P, \angle C N Q=2 \angle C R Q$, hence $\angle A N C=\angle A N P+\angle C N Q=2(\angle A S P+\angle C R Q)=2(\angle R S D+\angle D R S)=$ $2 \angle A D C$.
|
| 10 |
+
Similarly, using right-angled triangles $B A D$ and $B C D$, we obtain $\angle A M C=2 \angle A D C$.
|
| 11 |
+
Thus $\angle A M C=\angle A N C$, and the required statement follows.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Solution 2
|
| 15 |
+
|
| 16 |
+
In this proof we show that we have $\angle N C M=\angle N A M$ instead. From right-angled triangles $B C D$ and $Q C R$ we get $\angle D R S=\angle C R Q=\angle R C N$ and $\angle B D C=\angle D C M$. Hence $\angle N C M=\angle D C M-\angle R C N$. From rightangled triangle $A P S$ we get $\angle P S A=\angle S A N$. From right-angled triangle $B A D$ we have $\angle M A D=\angle B D A$. Moreover, $\angle B D A=\angle D R S+\angle R S D-\angle R D B$.
|
| 17 |
+
Therefore $\angle N A M=\angle N A S-\angle M A D=\angle C D B-\angle D R S=\angle N C M$, and the required statement follows.
|
| 18 |
+
|
| 19 |
+
## Solution 3
|
| 20 |
+
|
| 21 |
+
As $N$ is also the midpoint of $P S$, we can shrink triangle $A P S$ to a triangle $A_{0} Q R$ (where $P$ is sent to $Q$ and $S$ is sent to $R$ ). Then $A_{0}, Q, R$ and $C$ lie on a circle with center $N$. According to the shrinking the line $A_{0} R$ is parallel to the line $A D$. Therefore $\angle C N A=\angle C N A_{0}=2 \angle C R A_{0}=2 \angle C D A=\angle C M A$. The required statement follows.
|
| 22 |
+
|
| 23 |
+
## Problem 2
|
| 24 |
+
|
| 25 |
+
Find the smallest positive integer $k$ for which there exist a colouring of the positive integers $\mathbb{Z}_{>0}$ with $k$ colours and a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ with the following two properties:
|
| 26 |
+
(i) For all positive integers $m, n$ of the same colour, $f(m+n)=f(m)+f(n)$.
|
| 27 |
+
(ii) There are positive integers $m, n$ such that $f(m+n) \neq f(m)+f(n)$.
|
| 28 |
+
|
| 29 |
+
In a colouring of $\mathbb{Z}_{>0}$ with $k$ colours, every integer is coloured in exactly one of the $k$ colours. In both (i) and (ii) the positive integers $m, n$ are not necessarily different.
|
| 30 |
+
|
| 31 |
+
Merlijn Staps, the Netherlands
|
| 32 |
+
|
| 33 |
+
## Solution 1:
|
| 34 |
+
|
| 35 |
+
The answer is $k=3$.
|
| 36 |
+
First we show that there is such a function and coloring for $k=3$. Consider $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ given by $f(n)=n$ for all $n \equiv 1$ or 2 modulo 3 , and $f(n)=2 n$ for $n \equiv 0$ modulo 3 . Moreover, give a positive integer $n$ the $i$-th color if $n \equiv i$ (3).
|
| 37 |
+
By construction we have $f(1+2)=6 \neq 3=f(1)+f(2)$ and hence $f$ has property (ii).
|
| 38 |
+
Now let $n, m$ be positive integers with the same color $i$. If $i=0$, then $n+m$ has color 0 , so $f(n+m)=$ $2(n+m)=2 n+2 m=f(n)+f(m)$. If $i=1$, then $n+m$ has color 2 , so $f(n+m)=n+m=f(n)+f(m)$. Finally, if $i=2$, then $n+m$ has color 1 , so $f(n+m)=n+m=f(n)+f(m)$. Therefore $f$ also satisfies condition (i).
|
| 39 |
+
|
| 40 |
+
Next we show that there is no such function and coloring for $k=2$.
|
| 41 |
+
Consider any coloring of $\mathbb{Z}_{>0}$ with 2 colors and any function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ satisfying conditions (i) and (ii). Then there exist positive integers $m$ and $n$ such that $f(m+n) \neq f(m)+f(n)$. Choose $m$ and $n$ such that their sum is minimal among all such $m, n$ and define $a=m+n$. Then in particular for every $b<a$ we have $f(b)=b f(1)$ and $f(a) \neq a f(1)$.
|
| 42 |
+
If $a$ is even, then condition (i) for $m=n=\frac{a}{2}$ implies $f(a)=f\left(\frac{a}{2}\right)+f\left(\frac{a}{2}\right)=f(1) a$, a contradiction. Hence $a$ is odd. We will prove two lemmas.
|
| 43 |
+
|
| 44 |
+
Lemma 1. Any odd integer $b<a$ has a different color than $a$.
|
| 45 |
+
Proof. Suppose that $b<a$ is an odd integer, and that $a$ and $b$ have the same color. Then on the one hand, $f(a+b)=f(a)+b f(1)$. On the other hand, we also have $f(a+b)=f\left(\frac{a+b}{2}\right)+f\left(\frac{a+b}{2}\right)=(a+b) f(1)$, as $\frac{a+b}{2}$ is a positive integer smaller than $a$. Hence $f(a)=f(a+b)-b f(1)=(a+b) f(1)-b f(1)=a f(1)$, which is again a contradiction. Therefore all odd integers smaller than $a$ have a color different from that of $a$.
|
| 46 |
+
|
| 47 |
+
Lemma 2. Any even integer $b<a$ has the same color as $a$
|
| 48 |
+
Proof. Suppose $b<a$ is an even integer, and that $a$ and $b$ have different colors. Then $a-b$ is an odd integer smaller than $a$, so it has the same color as $b$. Thus $f(a)=f(a-b)+f(b)=(a-b) f(1)+b f(1)=a f(1)$, a contradiction. Hence all even integers smaller than $a$ have the same color as $a$.
|
| 49 |
+
|
| 50 |
+
Suppose now $a+1$ has the same color as $a$. As $a>1$, we have $\frac{a+1}{2}<a$ and therefore $f(a+1)=2 f\left(\frac{a+1}{2}\right)=$ $(a+1) f(1)$. As $a-1$ is an even integer smaller than $a$, we have by Lemma 2 that $a-1$ also has the same color as $a$. Hence $2 f(a)=f(2 a)=f(a+1)+f(a-1)=(a+1) f(1)+(a-1) f(1)=2 a f(1)$, which implies that $f(a)=a f(1)$, a contradiction. So $a$ and $a+1$ have different colors.
|
| 51 |
+
Since $a-2$ is an odd integer smaller than $a$, by Lemma 1 it has a color different from that of $a$, so $a-2$ and $a+1$ have the same color. Also, we have seen by Lemma 2 that $a-1$ and $a$ have the same color. So $f(a)+f(a-1)=f(2 a-1)=f(a+1)+f(a-2)=(a+1) f(1)+(a-2) f(1)=(2 a-1) f(1)$, from which it follows that $f(a)=(2 a-1) f(1)-f(a-1)=(2 a-1) f(1)-(a-1) f(1)=a f(1)$, which contradicts our choice of $a$ and finishes the proof.
|
| 52 |
+
|
| 53 |
+
## Solution 2:
|
| 54 |
+
|
| 55 |
+
We prove that $k \leq 3$ just as in first solution.
|
| 56 |
+
Next we show that there is no such function and coloring for $k=2$.
|
| 57 |
+
Consider any coloring of $\mathbb{Z}_{>0}$ with 2 colors and any function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ satisfying conditions (i) and (ii). We first notice with $m=n$ that $f(2 n)=2 f(n)$.
|
| 58 |
+
|
| 59 |
+
Lemma 3. For every $n \in \mathbb{Z}_{>0}, f(3 n)=3 f(n)$ holds.
|
| 60 |
+
Proof. Define $c=f(n), d=f(3 n)$. Then we have the relations
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
f(2 n)=2 c, \quad f(4 n)=4 c, \quad f(6 n)=2 d
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
- If $n$ and $2 n$ have the same color, then $f(3 n)=f(n)+f(2 n)=3 c=3 f(n)$.
|
| 67 |
+
- If $n$ and $3 n$ have the same color, then $4 c=f(4 n)=f(n)+f(3 n)=c+f(3 n)$, so $f(3 n)=3 f(n)$.
|
| 68 |
+
- If $2 n$ and $4 n$ have the same color, then $2 d=f(6 n)=f(2 n)+f(4 n)=2 c+4 c=6 c$, so $f(3 n)=d=3 c$.
|
| 69 |
+
- Otherwise $n$ and $4 n$ have the same color, and $2 n$ and $3 n$ both have the opposite color to $n$. Therefore we compute $5 c=f(n)+f(4 n)=f(5 n)=f(2 n)+f(3 n)=2 c+f(3 n)$ so $f(3 n)=3 f(n)$.
|
| 70 |
+
|
| 71 |
+
Consequently, for $k=2$ we necessarily have $f(3 n)=3 f(n)$.
|
| 72 |
+
Now let $a$ be the smallest integer such that $f(a) \neq a f(1)$. In particular $a$ is odd and $a>3$. Consider the three integers $a, \frac{a-3}{2}, \frac{a+3}{2}$. By pigeonhole principle two of them have the same color.
|
| 73 |
+
|
| 74 |
+
- If $\frac{a-3}{2}$ and $\frac{a+3}{2}$ have the same color, then $f(a)=\frac{a-3}{2} f(1)+\frac{a+3}{2} f(1)=a f(1)$.
|
| 75 |
+
- If $a$ and $\frac{a-3}{2}$ have the same color, then $3 \frac{a-1}{2} f(1)=3 f\left(\frac{a-1}{2}\right)=f\left(\frac{3 a-3}{2}\right)=f(a)+f\left(\frac{a-3}{2}\right)=f(a)+$ $\frac{a-3}{2} f(1)$, so $f(a)=a f(1)$.
|
| 76 |
+
- If $a$ and $\frac{a+3}{2}$ have the same color, then $3 \frac{a+1}{2} f(1)=3 f\left(\frac{a+1}{2}\right)=f\left(\frac{3 a+3}{2}\right)=f(a)+f\left(\frac{a+3}{2}\right)=f(a)+$ $\frac{a+3}{2} f(1)$, so $f(a)=a f(1)$.
|
| 77 |
+
|
| 78 |
+
In the three cases we find a contradiction with $f(a) \neq a f(1)$, so it finishes the proof.
|
| 79 |
+
|
| 80 |
+
## Solution 3:
|
| 81 |
+
|
| 82 |
+
As before we prove that $k \leq 3$ and for any such function and colouring we have $f(2 n)=2 f(n)$.
|
| 83 |
+
Now we show that there is no such function and coloring for $k=2$.
|
| 84 |
+
Consider any coloring of $\mathbb{Z}_{>0}$ with 2 colors and any function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ satisfying conditions (i) and (ii). Say the two colors are white (W) and black (B). Pick $m, n$ any two integers such that $f(m+n)=f(m)+f(n)$. Without loss of generality we may assume that $m+n, m$ are black and $n$ is white.
|
| 85 |
+
|
| 86 |
+
Lemma 4. For all $l \in \mathbb{Z}_{>0}$ and every $x$ whose color is black, we have $x+\operatorname{lm}$ is black and $f(x+\operatorname{lm})=$ $f(x)+l f(m)$.
|
| 87 |
+
|
| 88 |
+
Proof. We proceed by induction. It is clearly true for $l=0$. If $x+\operatorname{lm}$ is black and satisfies $f(x+\operatorname{lm})=$ $f(x)+l f(m)$, then $f(x+(l+1) m)=f(x+l m)+f(m)=f(x)+(l+1) f(m)$ and $f(x+(l+1) m+n)=$ $f(x+l m)+f(m+n)=f(x)+l f(m)+f(m+n) \neq f(x)+(l+1) f(m)+f(n)=f(x+(l+1) m)+f(n)$, so $x+(l+1) m$ is not the same color of $n$, therefore $x+(l+1) m$ is black. Thjs completes the induction.
|
| 89 |
+
In particular we then must have that $2^{l} n$ is white for every $l$, because otherwise since $2^{l} m$ is black we would have $2^{l} f(m+n)=f\left(2^{l} m+2^{l} n\right)=f\left(2^{l} m\right)+f\left(2^{l} n\right)=2^{l}(f(m)+f(n))$, and consequently $f(m+n)=$ $f(m)+f(n)$.
|
| 90 |
+
Lemma 5. For every $l \geq 1,2^{l} m+2^{l-1} n$ is black.
|
| 91 |
+
|
| 92 |
+
Proof. On the one hand we have $2^{l} f(m+n)=f\left(2^{l} m+2^{l} n\right)=f\left(2^{l-1}(2 m+n)+2^{l-1} n\right)$. On the other hand we have
|
| 93 |
+
$\left.2^{l} f(m+n)=2^{l-1} \cdot 2 f(m+n) \neq 2^{l-1}(f(m+n)+f(m)+f(n))=2^{l-1}(f(2 m+n)+f(n))=f\left(2^{l} m+2^{l-1} n\right)\right)+f\left(2^{l-1} n\right)$.
|
| 94 |
+
Therefore $2^{l} m+2^{l-1} n$ and $2^{l-1} n$ have different color, which means $2^{l} m+2^{l-1} n$ is black.
|
| 95 |
+
Combining the two lemmas give $j m+2^{l-1} n$ is black for all $j \geq 2^{l}$ and every $l \geq 1$.
|
| 96 |
+
Now write $m=2^{l-1} m^{\prime}$ with $m^{\prime}$ odd. Let $t$ be a number such that $\frac{2^{t}-1}{m^{\prime}}$ is an integer and $j=\frac{2^{t}-1}{m^{\prime}} n \geq 2^{l}$, i.e. $t$ is some multiple of $\phi\left(m^{\prime}\right)$. Then we must have that $j m+2^{l-1} n$ is black, but by definition ${ }_{j m}^{m^{\prime}}+\overline{2}^{l-1} n=$ $\left(2^{t}-1\right) 2^{l-1} n+2^{l-1} n=2^{t+l-1} n$ is white. This is a contradiction, so $k=2$ is impossible.
|
| 97 |
+
|
| 98 |
+
# Problem 3
|
| 99 |
+
|
| 100 |
+
There are 2017 lines in a plane such that no 3 of them go through the same point. Turbo the snail can slide along the lines in the following fashion: she initially moves on one of the lines and continues moving on a given line until she reaches an intersection of 2 lines. At the intersection, she follows her journey on the other line turning left or right, alternating the direction she chooses at each intersection point she passes. Can it happen that she slides through a line segment for a second time in her journey but in the opposite direction as she did for the first time?
|
| 101 |
+
|
| 102 |
+
Márk Di Giovanni, Hungary
|
| 103 |
+
|
| 104 |
+
## 1. Solution
|
| 105 |
+
|
| 106 |
+
We show that this is not possible.
|
| 107 |
+
The lines divide the plane into disjoint regions. We claim that there exists an alternating 2-coloring of these regions, that is each region can be colored in black or white, such that if two regions share a line segment, they have a different color. We show this inductively.
|
| 108 |
+
If there are no lines, this is obvious. Consider now an arrangement of $n$ lines in the plane and an alternating 2-coloring of the regions. If we add a line $g$, we can simply switch the colors of all regions in one of the half planes divided by $g$ from white to black and vice versa. Any line segment not in $g$ will still be between two regions of different color. Any line segment in $g$ cuts a region determined by the $n$ lines in two, and since we switched colors on one side of $g$ this segment will also lie between two regions of different color.
|
| 109 |
+
Now without loss of generality we may assume, that Turbo starts on a line segment with a white region on her left and a black one on her right. At any intersection, if she turns right, she will keep the black tile to her right. If she turns left, she will keep the white tile to her left. Thus wherever she goes, she will always have a white tile on her left and a black tile on her right. As a consequence, she can cross every line segment only in the direction where she has a white tile to her left, and never the opposite direction where she would have a black tile to the left.
|
| 110 |
+
|
| 111 |
+
## 2. Solution
|
| 112 |
+
|
| 113 |
+
Suppose the assumption is true.
|
| 114 |
+
Let's label each segment in the snail's path with $\mathbf{L}$ or $\mathbf{R}$ depending on the direction that Turbo chose at the start point of this segment (one segment can have several labels if it has been visited several times).
|
| 115 |
+
Consider the first segment that has been visited twice in different directions, name this segment $s_{1}$. Assume without loss of generality that it is labeled with $\mathbf{L}$. Then next segment must be labeled with $\mathbf{R}$, name this one $s_{2}$.
|
| 116 |
+
Let's look at the label which $s_{1}$ can get on the second visit. If it gets $\mathbf{L}$ then the previous segment in the path must be $s_{2}$. But in this case $s_{1}$ is not the first segment that has been visited twice in different directions because $s_{2}$ has been visited earlier. So the second label of $s_{1}$ must be $\mathbf{R}$, and Turbo must have come from the opposite side of $s_{2}$.
|
| 117 |
+
|
| 118 |
+
|
| 119 |
+
Since Turbo alters directions at each point, labels in her path also alter. And because two labels of $s_{1}$ are different, the number of visited segments between these two visits must be even.
|
| 120 |
+
Now let's make the following observation: each segment in the path corresponds to exactly one line, and its previous and next segments are on opposite sides of this line.
|
| 121 |
+
|
| 122 |
+
|
| 123 |
+
Again consider the path between two visits of $s_{1}$.
|
| 124 |
+
Each line intersecting this path must be crossed an even number of times because Turbo has to return to the initial side of each line. Therefore, an even number of segments of Turbo's path are contained on each of these lines. But the line containing $s_{1}$ must be crossed an odd number times. Since each crossing corresponds to exactly one segment in the path, the number of segments must be odd.
|
| 125 |
+
Here we get the contradiction. Therefore, the assumption is false.
|
| 126 |
+
|
| 127 |
+
## 3. Solution
|
| 128 |
+
|
| 129 |
+
Suppose that the snail always slides slightly to the right of the line segments on her path. When turning to the right, she does not cross any line, whereas when turning to the left, she crosses exactly two lines. This means that at any time of her journey, she has crossed an even number of lines.
|
| 130 |
+
Assuming that at some point she slides along a segment for the second time, but in the opposite direction, we argue that she needs to cross an odd number of lines. Let $\ell$ be the line on which the revisit happens. In order to get to the other side of $\ell$, the snail has to cross $\ell$ an odd number of times. To visit the same segment of $\ell$, she must cross every other line an even number of times.
|
| 131 |
+
|
| 132 |
+
## 4. Solution
|
| 133 |
+
|
| 134 |
+
Let us color in red all intersection points of the given lines and let us choose one of two possible directions on each segment (draw an arrow on each segment). Consider a red point $R$ where two given lines $a$ and $b$ meet, and the four segments $a_{1}, a_{2}, b_{1}, b_{2}$ with endpoint $R$ (so that $a_{i} \subset a, b_{j} \subset b$ ). $R$ is called a saddle if on $a_{1}, a_{2}$ the arrows go out of $R$ while on $b_{1}, b_{2}$ the arrows enter $R$, or visa versa, on $b_{1}, b_{2}$ the arrows go out of $R$ while on $a_{1}, a_{2}$ the arrows enter $R$. The set of arrows (chosen on all segments) is said to be good if all red points are saddles. It is sufficient to prove that there exists a good set of arrows. Indeed, if initially Turbo is moving along (or opposite) the arrow, then this condition holds after she turns at a red point.
|
| 135 |
+
The given lines cut the plane into regions. Further we need the following property of the good set of arrows (this property directly follows from the definition): the boundary of any bounded region is a directed cycle of arrows; the boundary of any unbounded region is a directed chain of arrows.
|
| 136 |
+
We construct a good set of arrows by induction on $n$ with trivial base $n=1$. Now erase one of $n$ given lines and assume we have a good set of arrows for remaining $n-1$ lines. Now restore the $n$-th line $\ell$, assume that $\ell$ is horizontal. Denote by $A_{1}, \ldots, A_{n-1}$ all new red points on $\ell$ from the left to the right. Each of $A_{i}$ belongs to some old segment $m_{i}$ of the line $\ell_{i}$. Let us call $A_{i}$ ascending if the arrow on $m_{i}$ goes up, and descending if the arrow on $m_{i}$ goes down. Consider the region containing the segment $A_{i} A_{i+1}$. By the property, $A_{i}$ and $A_{i+1}$ can not be both ascending or both descending. Thus we can choose arrows on all pieces of $\ell$ so that each arrow goes from a descending to an ascending vertex.
|
| 137 |
+
|
| 138 |
+
Each of points $A_{i}$ cuts $m_{i}$ into two new pieces; the direction of new pieces supposed to be the same as on $m_{i}$. Now simultaneously change the direction of arrows on all pieces below the line $\ell$. It is easy to see that $A_{1}, \ldots, A_{n-1}$ become saddles, while the other red points remain saddles. This completes the induction step.
|
| 139 |
+
|
| 140 |
+
# Problem 4
|
| 141 |
+
|
| 142 |
+
Let $n \geq 1$ be an integer and let $t_{1}<t_{2}<\ldots<t_{n}$ be positive integers. In a group of $t_{n}+1$ people, some games of chess are played. Two people can play each other at most once. Prove that it is possible for the following conditions to hold at the same time:
|
| 143 |
+
i) The number of games played by each person is one of $t_{1}, t_{2}, \ldots, t_{n}$,
|
| 144 |
+
ii) For every $i$ with $1 \leq i \leq n$, there is someone who has played exactly $t_{i}$ games of chess.
|
| 145 |
+
|
| 146 |
+
Gerhard Wöginger, Luxembourg
|
| 147 |
+
|
| 148 |
+
## Comment
|
| 149 |
+
|
| 150 |
+
In graph theory terms the problem is to prove that for any finite nonempty set $\mathcal{T}$ of positive integers there exists a graph of size $\max \mathcal{T}+1$ such that the degree set of the graph is equal to $\mathcal{T}$.
|
| 151 |
+
|
| 152 |
+
Among graph theory specialists a generalization of this problem is known [1]. Nevertheless, the problem still suited the contest.
|
| 153 |
+
|
| 154 |
+
## 1. Solution (see also [2])
|
| 155 |
+
|
| 156 |
+
Let $\mathcal{T}=\left\{t_{1}, \ldots, t_{n}\right\}$. The proof proceeds by induction on $n=|\mathcal{T}|$. If $n=1$ and $\mathcal{T}=\{t\}$, choose a group of $t+1$ people and let every pair of two persons play against each other. Then every person has played $t$ games and the conditions of the problem are satisfied.
|
| 157 |
+
|
| 158 |
+
In the inductive step, suppose that $\mathcal{T}$ has $n \geq 2$ elements $t_{1}<t_{2}<\cdots<t_{n}$. Consider the set
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
\mathcal{T}^{\prime}=\left\{t_{n}-t_{n-1}, t_{n}-t_{n-2}, \ldots, t_{n}-t_{1}\right\} .
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
By the inductive hypothesis, there exists a group $G^{\prime}$ of $t_{n}-t_{1}+1$ people that satisfies the conditions of the problem for $T^{\prime}$.
|
| 165 |
+
|
| 166 |
+
Next construct a group $G^{\prime \prime}$ of $t_{n}+1$ people by adding $t_{1}$ people who do not know any of the other $t_{n}-t_{1}+1$ people in $G^{\prime}$. Finally, construct a group $G$ by complementing the knowledge relation in $G^{\prime \prime}$ : two persons play against each other in $G$ if and only if they do not play against each other in $G^{\prime \prime}$.
|
| 167 |
+
|
| 168 |
+
By construction $t \in \mathcal{T}$ if and only if there exists a person in $G^{\prime \prime}$ that played against exactly $t_{n}-t$ other people (if $t=t_{n}$, choose one of the $t_{1}$ people added to $\left.G^{\prime}\right)$. That person knows $t_{n}-\left(t_{n}-t\right)=t$ other students in $G$, completing the proof.
|
| 169 |
+
|
| 170 |
+
## 2. Solution
|
| 171 |
+
|
| 172 |
+
Let $\mathcal{T}=\left\{t_{1}, \ldots, t_{n}\right\}$. The proof proceeds by induction on $n=|\mathcal{T}|$. If $n=1$ and $\mathcal{T}=\{t\}$, we choose a group of $t+1$ people such that everyone plays with
|
| 173 |
+
everyone else. If $n=2$ and $\mathcal{T}=\left\{t_{1}, t_{2}\right\}$ with $t_{1}<t_{2}$, divide the $t_{2}+1$ people into groups $A$ resp. $B$ of size $t_{1}$ resp. $t_{2}-t_{1}+1$ such that everyone from group $A$ played with everyone else whereas people from group $B$ only played with the people from group $A$. Then the people from group $A$ resp. $B$ played with exactly $t_{2}$ resp. $t_{1}$ other people. In the inductive step, suppose that $T$ has $n>2$ elements $t_{1}<\ldots<t_{n}$. Consider the set
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
\mathcal{T}^{\prime}=\left(\mathcal{T} \backslash\left\{t_{1}, t_{n}\right\}\right)-t_{1}=\left\{t_{n-1}-t_{1}, t_{n-1}-t_{1}, \ldots, t_{2}-t_{1}\right\}
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
By the induction hypothesis there exists a group $C$ of $t_{n-1}-t_{1}+1$ people that satisfies the conditions of the problem for $T^{\prime}$. Next add groups $D$ resp. $E$ of $t_{1}$ resp. $t_{n}-t_{n-1}$ people such that people from group $D$ played with everyone else whereas people from group $E$ only played with the people from group $D$. Then the people from group $C$ played with $t$ other people if and only if they played with $t-t_{1}$ many people among $C$, i.e. if and only if $t \in\left\{t_{2}, \ldots, t_{n-1}\right\}=$ $\mathcal{T} \backslash\left\{t_{1}, t_{n}\right\}$. People from group $D$ resp. $E$ played with $t_{n}$ resp $t_{1}$ peoples, which completes the proof.
|
| 180 |
+
|
| 181 |
+
## 3. Solution
|
| 182 |
+
|
| 183 |
+
The proof proceeds by induction on $\left|t_{n}\right|$. If $t_{n}=1$ we have $n=1$ and we can consider two persons that play against each other. Then every player has played 1 game and the conditions of the problem are satisfied. If $t_{n}>1$ we distinguish the two cases $t_{1}>1$ and $t_{1}=1$. If $t_{1}>1$ there exists, by the induction hypothesis, a group $A$ of size $t_{n}$ that satisfies the conditions of the problem for $t_{1}^{\prime}=t_{1}-1, \ldots, t_{n}^{\prime}=t_{n}-1$. Now add a new person to $A$ and let him/her play against everyone from $A$. The new group will be of size $t_{n}+1$ and there exists a person which has played $t$ games if and only if there exists a person that has played $t-1$ games within $A$, i.e. if and only if $t \in\left\{t_{1}, \ldots, t_{n}\right\}$. Hence the conditions of the problem are satisfied.
|
| 184 |
+
|
| 185 |
+
If $t_{1}=1$ there exists, by the induction hypothesis, a group $B$ of size $t_{n-1}$ that satisfies the conditions of the problem for $t_{1}^{\prime}=t_{2}-1, \ldots, t_{n-2}^{\prime}=t_{n-1}-1$. Now add a new person $P$ and let him/her play with everyone from group $B$ and a group $C$ of size $t_{n}-t_{n-1}>0$ and let them play with $P$. The new group will be of size $t_{n-1}+1+\left(t_{n}-t_{n-1}\right)+1=t_{n}+1$. Since person $P$ has played against everyone he will have played $t_{n}$ games. The people in $C$ will have played $1=t_{1}$ games. There exists a person in $B$ that has played $t$ games if and only if there exist a person in $B$ that has played $t-1$ games within $B$, i.e. if and only if $t \in\left\{t_{2}, \ldots, t_{n-1}\right\}$. Hence the conditions of the problem are satisfied.
|
| 186 |
+
|
| 187 |
+
## 4. Solution
|
| 188 |
+
|
| 189 |
+
We generalize the construction for $\mathcal{T}=\{1, \ldots, n\}$
|
| 190 |
+
|
| 191 |
+
## Construction
|
| 192 |
+
|
| 193 |
+
Take sets of people $A_{1}, \ldots, A_{n}$. Let all people of $A_{i}$ play chess with all people in $A_{j}$ with $j \geq n-i+1$
|
| 194 |
+
|
| 195 |
+
|
| 196 |
+
Now the number of games played by anyone in $A_{i}$ is
|
| 197 |
+
$\left(\sum_{j \geq n-i+1}\left|A_{j}\right|\right)$ or $\left(\sum_{j \geq n-i+1}\left|A_{j}\right|\right)-1$ if $i \geq n-i+1$.
|
| 198 |
+
Now if we start with one person in each $A_{i}$ and two people in $A_{\left\lceil\frac{n}{2}\right\rceil}$. The number of played games for anyone in $A_{i}$ is equal to $i$. In particular this is a construction for $\mathcal{T}=\{1, . ., n\}$
|
| 199 |
+
Now to get to numbers of general sets $\mathcal{T}$ of size $n$ we can change the sizes of $A_{i}$ but keep the construction.
|
| 200 |
+
|
| 201 |
+
## Variant 1
|
| 202 |
+
|
| 203 |
+
Observation 1 Adding a person to a set $A_{i}$ increases the number of games played in $A_{j}$ for $j \geq n-i+1$, by exactly one.
|
| 204 |
+
|
| 205 |
+
Start with the construction above and then add $t_{1}-1$ people to group $A_{n}$, making the new set of games played equal to $\left\{t_{1}, t_{1}+1, \ldots, n+t_{1}-1\right\}$. Then add $t_{2}-t_{1}-1$ to $A_{n-1}$ to get set of games played to $\left\{t_{1}, t_{2}, t_{2}+1, \ldots, n+t_{2}-2\right\}$ and repeat until we get to the set $\mathcal{T}$ adding a total of $\sum_{j=1}^{n} t_{j}-t_{j-1}-1=t_{n}-n$ people (let $t_{0}=0$ ), so we get $t_{n}+1$ people in the end.
|
| 206 |
+
Clearly we can start by adding vertices to $A_{1}$ or any other set instead of $A_{n}$ first and obtain an equivalent construction with the same number of people.
|
| 207 |
+
|
| 208 |
+
## Variant 2
|
| 209 |
+
|
| 210 |
+
It is also possible to calculate the necessary sizes of $A_{i}$ 's all at once. We have by construction the number of games played in $A_{1}$ is less than the number of games played in $A_{2}$ etc. So we have that in the end we want the games played in $A_{i}$ to be exactly $t_{i}$.
|
| 211 |
+
So $\left(t_{t}, t_{2}, t_{3}, \ldots, t_{n}\right) \stackrel{!}{=}\left(\left|A_{n}\right|,\left|A_{n}\right|+\left|A_{n-1}\right|, \ldots,\left(\sum_{j=2}^{n}\left|A_{j}\right|\right)-1,\left(\sum_{j=1}^{n}\left|A_{j}\right|\right)-\right.$ 1).
|
| 212 |
+
|
| 213 |
+
This gives us by induction that $\left|A_{n}\right| \stackrel{!}{=} t_{1},\left|A_{n-1}\right| \stackrel{!}{=} t_{2}-t_{1}, \ldots,\left|A_{\left\lceil\frac{n}{2}\right\rceil}\right| \stackrel{!}{=}$ $t_{n-\left\lceil\frac{n}{2}\right\rceil+1}-t_{n-\left\lceil\frac{n}{2}\right\rceil}+1, \ldots,\left|A_{1}\right| \stackrel{!}{=} t_{n}-t_{n-1}$ and a quick calculation shows that the sum of all sets is exactly $1+\sum_{j=1}^{n}\left(t_{j}-t_{j-1}\right)=t_{n}+1$. (where the +1 comes from the set $A_{\left\lceil\frac{n}{2}\right\rceil}$ and $t_{0}=0$.)
|
| 214 |
+
|
| 215 |
+
## References
|
| 216 |
+
|
| 217 |
+
[1] Timothy A. Sipka. The orders of graphs with prescribed degree sets. Journal of Graph Theory, 4(3):301-307, 1980.
|
| 218 |
+
[2] Amitabha Tripathi and Sujith Vijay. A short proof of a theorem on degree sets of graphs. Discrete Appl. Math., 155(5):670-671, 2007.
|
| 219 |
+
|
| 220 |
+
## Problem 5
|
| 221 |
+
|
| 222 |
+
Let $n \geq 2$ be an integer. An $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of positive integers is expensive if there exists a positive integer $k$ such that
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
\left(a_{1}+a_{2}\right)\left(a_{2}+a_{3}\right) \cdots \cdots\left(a_{n-1}+a_{n}\right)\left(a_{n}+a_{1}\right)=2^{2 k-1} .
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
a) Find all positive integers $n \geq 2$ for which there exists an expensive $n$-tuple.
|
| 229 |
+
b) Prove that for every positive integer $m$ there exists an integer $n \geq 2$ such that $m$ belongs to an expensive $n$-tuple.
|
| 230 |
+
|
| 231 |
+
There are exactly $n$ factors in the product on the left hand side.
|
| 232 |
+
Harun Hindija, Bosnia and Herzegovina
|
| 233 |
+
|
| 234 |
+
## Solution 1
|
| 235 |
+
|
| 236 |
+
a) Notice that for odd integers $n>2$, the tuple $(1,1, \ldots, 1)$ is expensive. We will prove that there are no expensive $n$-tuples for even $n$.
|
| 237 |
+
|
| 238 |
+
Lemma 0.1. If an expensive $n$-tuple exists for some $n \geq 4$, then also an expensive $n-2$-tuple.
|
| 239 |
+
Proof. In what follows all indices are considered modulo $n$. Let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be an expensive $n$-tuple and $a_{t}$ the largest element of the tuple. We have the inequalities
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
\begin{aligned}
|
| 243 |
+
a_{t-1}+a_{t} & \leq 2 a_{t}<2\left(a_{t}+a_{t+1}\right) \\
|
| 244 |
+
a_{t}+a_{t+1} & \leq 2 a_{t}<2\left(a_{t-1}+a_{t}\right) .
|
| 245 |
+
\end{aligned}
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
Since both $a_{t-1}+a_{t}$ and $a_{t}+a_{t+1}$ are powers of 2 (they are divisors of a power of 2), we deduce from (1) and (2)
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
a_{t-1}+a_{t}=a_{t}+a_{t+1}=2^{r}
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
for some positive integer $r$, and in particular $a_{t-1}=a_{t+1}$.
|
| 255 |
+
Consider now the $n$-2-tuple $\left(b_{1}, \ldots, b_{n-2}\right)$ obtained by removing $a_{t}$ and $a_{t+1}$ from $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$. By what we just said we have
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
\prod_{i=1}^{n-2}\left(b_{i}+b_{i+1}\right)=\frac{\prod_{i=1}^{n}\left(a_{i}+a_{i+1}\right)}{\left(a_{t-1}+a_{t}\right)\left(a_{t}+a_{t+1}\right)}=2^{2(k-r)-1}
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
and hence $\left(b_{1}, \ldots, b_{n-2}\right)$ is again expensive.
|
| 262 |
+
From the lemma we now conclude that if there exists an expensive $n$-tuple for some even $n$, then also an expensive 2 -tuple i.e.
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
\left(a_{1}+a_{2}\right)^{2}=2^{2 k-1}
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
for some positive integers $a_{1}, a_{2}$, which is impossible since the right hand side is not a square.
|
| 269 |
+
b) We prove this by induction. In $a$ ) we saw that 1 belongs to an expensive $n$-tuple. Assume now that all odd positive integers less that $2^{k}$ belong to an expensive $n$-tuple, for some $k \geq 1$. Hence for any odd $r<2^{k}$ there is an integer $n$ and an expensive $n$-tuple $\left(a_{1}, \ldots, r, \ldots, a_{n}\right)$. We notice that then also ( $a_{1}, \ldots, r, 2^{k+1}-$ $\left.r, r, \ldots, a_{n}\right)$ is expensive. Since $2^{k+1}-r$ can take all odd values between $2^{k}$ and $2^{k+1}$ the induction step is complete.
|
| 270 |
+
|
| 271 |
+
## Solution 2
|
| 272 |
+
|
| 273 |
+
a) For odd $n$ the tuple $(1,1, \ldots, 1)$ is a solution.
|
| 274 |
+
|
| 275 |
+
Now consider $n$ even. Since the product $\prod\left(a_{i}+a_{i+1}\right)$ is a power of two, every factor needs to be a power of two. We are going to prove that for all tuples $\left(a_{1}, \ldots, a_{n}\right)$ such that $a_{i}+a_{i+1}$ is always a power of two , it is the case that $\prod\left(a_{i}+a_{i+1}\right)$ is equal to an even power of two. We are going to prove this with strong induction on $\sum a_{i}$. When all $a_{i}$ are equal to one this is certainly the case. Since $a_{i}+a_{i+1}>1$ it is even and we conclude that the $a_{i}$ are either all odd or all even. In the case they are all even, then consider the tuple $\left(b_{1}, \ldots, b_{n}\right)$ with $b_{i}=a_{i} / 2$. This tuple clearly satisfies the hypothesis as well and we have $\sum b_{i}<\sum a_{i}$. Furthermore we have $\prod\left(a_{i}+a_{i+1}\right)=2^{n} \prod\left(b_{i}+b_{i+1}\right)$ and since $n$ is even we are done in this case.
|
| 276 |
+
Now all $a_{i}$ are odd. Suppose none of are one, then consider the tuple $\left(b_{1}, \ldots, b_{n}\right)$ with $b_{i}=\left(a_{i}+(-1)^{i}\right) / 2$. Since all $a_{i}$ are odd and strictly larger than one, the $b_{i}$ are positive integers and satisfy $b_{i}+b_{i+1}=\left(a_{i}+a_{i+1}\right) / 2$, a power of two. Since $\sum b_{i}<\sum a_{i}$ and $\prod\left(a_{i}+a_{i+1}\right)=2^{n} \prod\left(b_{i}+b_{i+1}\right)$ we are done in this case again. Now there is at least one $a_{i}$ being one. We may assume $i=1$, because the condition is cyclic. Moreover we may also assume that $a_{2}>1$ since not all of the $a_{i}$ are equal to one. Let now $k$ be the smallest index larger than one such that $a_{k}$ is equal to one. We are not excluding the case $k=n+1$, yet. Now for $i=1, \ldots, k-1$ we have $a_{i}+a_{i+1}>2$ and thus divisible by four. By induction it easily follows that $a_{i} \equiv(-1)^{i+1} \bmod$ (4) for $i=1, \ldots, k-1$. In particular, since $a_{k}=1$ we find that $k$ is odd and at least three. Now consider the tuple $\left(b_{1}, \ldots, b_{n}\right)$ with $b_{i}=\left(a_{i}-(-1)^{i}\right) / 2$ for $i=1, \ldots, k$ and $b_{i}=a_{i}$ otherwise. This is again a tuple that satisfies the hypothesis, since $b_{1}=a_{1}=1=b_{k}=a_{k}$. Moreover $b_{2}<a_{2}$ and thus $\sum b_{i}<\sum a_{i}$. Finally we have $\prod\left(a_{i}+a_{i+1}\right)=2^{k-1} \prod\left(b_{i}+b_{i+1}\right)$ and since $k$ is odd we conclude the proof.
|
| 277 |
+
b) We use some of the ideas from a). Consider the operators $T_{ \pm}(n)=2 n \pm 1$. We claim that for every odd integer $m$ there is an integer $r$ and signs $\epsilon_{i} \in\{+,-\}$ for $i=1, \ldots r$ such that $T_{\epsilon_{r}} \circ \ldots \circ T_{\epsilon_{1}}(1)=m$. This is certainly true for $m=1$ and for $m>1$ we find that $m=T_{-}((m+1) / 2)$ if $m \equiv 1 \bmod (4)$ and $m=T_{+}((m-1) / 2)$ if $m \equiv 3 \bmod (4)$. Note that both $(m+1) / 2$ and $(m-1) / 2$ are odd integers in their respective cases and $(m-1) / 2 \leq(m+1) / 2<m$ for $m>1$. Therefore iterating the procedure will eventually terminate in one.
|
| 278 |
+
For the construction it is most convenient to set $n=2 l+1$ and label the tuple $\left(a_{-l}, a_{-l+1}, \ldots, a_{l}\right)$. For $m=1$ we have the expensive tuple $(1,1,1)$. For $m>1$ we will define operators $T_{ \pm}$on expensive tuples with the condition $a_{-l}=a_{l}=1$ that give rise to a new expensive tuple $\left(b_{-l^{\prime}}, \ldots, b_{l^{\prime}}\right)$ with $b_{-l^{\prime}}=b_{l^{\prime}}=1$ and $b_{0}=T_{ \pm} a_{0}$. It is then clear that $T_{\epsilon_{r}} \circ \cdots \circ T_{\epsilon_{1}}((1,1,1))$ is an expensive tuple containing $m$. We define $T_{ \pm}$as follows: set $l^{\prime}=l+1$ and $b_{-l^{\prime}}=b_{l^{\prime}}=1$ and $b_{i}=T_{ \pm(-1)^{i}}\left(a_{i}\right)$ for $i=-l, \ldots, l$. Here we identify + with +1 and - with -1 . We are left to prove that the new tuple is indeed expensive. If $\pm(-1)^{l}=-1$, then $\prod\left(b_{i}+b_{i+1}\right)=4 \cdot 2^{2 l} \prod\left(a_{i}+a_{i+1}\right)$, and if $\pm(-1)^{l}=+1$, then $\prod\left(b_{i}+b_{i+1}\right)=4 \cdot 2^{2 l+2} \prod\left(a_{i}+a_{i+1}\right)$. In both cases we end up with an expensive tuple again.
|
| 279 |
+
|
| 280 |
+
## Problem 6
|
| 281 |
+
|
| 282 |
+
Let $A B C$ be an acute-angled triangle in which no two sides have the same length. The reflections of the centroid $G$ and the circumcentre $O$ of $A B C$ in its sides $B C, C A, A B$ are denoted by $G_{1}, G_{2}, G_{3}$, and $O_{1}, O_{2}, O_{3}$, respectively. Show that the circumcircles of the triangles $G_{1} G_{2} C, G_{1} G_{3} B, G_{2} G_{3} A, O_{1} O_{2} C, O_{1} O_{3} B, O_{2} O_{3} A$ and $A B C$ have a common point.
|
| 283 |
+
|
| 284 |
+
The centroid of a triangle is the intersection point of the three medians. A median is a line connecting a vertex of the triangle to the midpoint of the opposite side.
|
| 285 |
+
|
| 286 |
+
Charles Leytem, Luxembourg
|
| 287 |
+
|
| 288 |
+
## Solution 1 (Euler lines)
|
| 289 |
+
|
| 290 |
+
Let $H$ denote the orthocenter of $A B C$, and let $e$ denote its Euler line. Let $e_{1}, e_{2}, e_{3}$ denote the respective reflections of $e$ in $B C, C A, A B$. The proof naturally divides into two parts: we first show that pairwise intersections of the circles in question correspond to pairwise intersections of $e_{1}, e_{2}, e_{3}$, and then prove that $e_{1}, e_{2}, e_{3}$ intersect in a single point on the circumcircle of $A B C$.
|
| 291 |
+
|
| 292 |
+
|
| 293 |
+
Now consider for example the circumcircles of $O_{1} O_{2} C$ and $G_{1} G_{2} C$. By construction, it is clear that $\angle O_{2} C O_{1}=\angle G_{2} C G_{1}=2 \angle A C B$. Let $G_{1} O_{1}$ and $G_{2} O_{2}$ meet at $X$, and let $e$ meet $e_{1}, e_{2}$ at $E_{1}, E_{2}$, respectively, as shown in the diagram below. Chasing angles,
|
| 294 |
+
|
| 295 |
+
$$
|
| 296 |
+
\begin{aligned}
|
| 297 |
+
\angle G_{2} X G_{1}=\angle O_{2} X O_{1} & =\angle E_{2} X E_{1}=180^{\circ}-\angle E_{1} E_{2} X-\angle X E_{1} E_{2} \\
|
| 298 |
+
& =180^{\circ}-2 \angle E_{1} E_{2} C-\left(\angle C E_{1} E_{2}-\angle C E_{1} X\right) .
|
| 299 |
+
\end{aligned}
|
| 300 |
+
$$
|
| 301 |
+
|
| 302 |
+
But $\angle C E_{1} X=\angle B E_{1} O_{1}=\angle B E_{1} O=180^{\circ}-\angle C E_{1} E_{2}$, and thus
|
| 303 |
+
|
| 304 |
+
$$
|
| 305 |
+
\angle G_{2} X G_{1}=\angle O_{2} X O_{1}=2\left(180^{\circ}-\angle E_{1} E_{2} C-\angle C E_{1} E_{2}\right)=2 \angle A C B
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+

|
| 309 |
+
|
| 310 |
+
It follows from this that $X$ lies on the circumcircles of $G_{1} G_{2} C$ and $O_{1} O_{2} C$. In other words, the second point of intersection of the circumcircles of $G_{1} G_{2} C$ and $O_{1} O_{2} C$ is the intersection of $e_{1}$ and $e_{2}$. Similarly, the circumcircles of $G_{1} G_{3} B$ and $O_{1} O_{3} B$ meet again at the intersection of $e_{1}$ and $e_{3}$, and those of $G_{2} G_{3} A$ and $O_{2} O_{3} A$ meet again at the intersection of $e_{2}$ and $e_{3}$.
|
| 311 |
+
|
| 312 |
+
|
| 313 |
+
It thus remains to show that $e_{1}, e_{2}, e_{3}$ are concurrent, and intersect on the circumcircle of $A B C$. Let $e$ meet the circumcircles of the triangles $B C H, A C H, A B H$ at $X_{1}, X_{2}, X_{3}$, respectively. It is well known that the reflections of $H$ in the sides of $A B C$ lie on the circumcircle of $A B C$. For this reason, the circumcircles of $B C H, A C H, A B H$ have the same radius as the circumcircle of $A B C$, and hence the reflections $X_{1}^{\prime}, X_{2}^{\prime}, X_{3}^{\prime}$ of $X_{1}, X_{2}, X_{3}$ in the sides $[B C],[C A],[A B]$ lie on the circumcircle of $A B C$. By definition, $X_{1}^{\prime}, X_{2}^{\prime}, X_{3}^{\prime}$ lie on $e_{1}, e_{2}, e_{3}$, respectively. It thus remains to show that they coincide.
|
| 314 |
+
To show that, for example, $X_{1}^{\prime}=X_{2}^{\prime}$, it will be sufficient to show that $\angle X_{2} A C=\angle X_{1}^{\prime} A C$, since we have already shown that $X_{1}^{\prime}$ and $X_{2}^{\prime}$ lie on the circumcircle of $A B C$. But, chasing angles in the diagram above,
|
| 315 |
+
|
| 316 |
+
$$
|
| 317 |
+
\begin{aligned}
|
| 318 |
+
\angle X_{1}^{\prime} A C & =\angle X_{1}^{\prime} A B-\angle B A C=\left(180^{\circ}-\angle X_{1}^{\prime} C B\right)-\angle B A C \\
|
| 319 |
+
& =180^{\circ}-\angle X_{1} C B-\angle B A C=\left(180^{\circ}-\angle B A C\right)-\angle X_{1} H B \\
|
| 320 |
+
& =\angle B H C-\angle X_{1} H B=\angle X_{2} H C=\angle X_{2} A C
|
| 321 |
+
\end{aligned}
|
| 322 |
+
$$
|
| 323 |
+
|
| 324 |
+
where we have used the fact that $B H C X_{1}$ and $A H X_{2} C$ are cyclic by construction, and the fact that $\angle B H C=180^{\circ}-\angle B A C$. This shows that $X_{1}^{\prime}=X_{2}^{\prime}$. Similarly, $X_{1}^{\prime}=X_{3}^{\prime}$, which completes the proof.
|
| 325 |
+
|
| 326 |
+
Remark. The statement of the problem remains true if $O$ and $G$ are replaced with two points that are aligned with the orthocenter $H$ of the triangle, and indeed, the proof above did not require any property of $G$ and $O$ other than the fact that they lie on a line through $H$, the Euler line.
|
| 327 |
+
|
| 328 |
+
## Solution 2
|
| 329 |
+
|
| 330 |
+
The proof consists of two parts. First, we show that if $P$ is any point inside the triangle $A B C$ and $P_{1}, P_{2}, P_{3}$ are its reflections in the sides $B C, C A, A B$, then the circumcircles of the triangles $P_{1} P_{2} C, P_{1} P_{3} B, P_{2} P_{3} A$ intersect in a point $T_{P}$ on the circumcircle of the triangle $A B C$. In the second part, we show that $T_{G}$ coincides with $T_{O}$.
|
| 331 |
+
Now let $P$ be any point inside the triangle $A B C$ and let $P_{1}, P_{2}, P_{3}$ be the reflections in the sides as above. Let $T_{P}$ be the second intersection of the circumcircles of the triangles $P_{1} P_{2} C$ and $A B C$. We want to show that $T_{P}$ lies on the circumcircles of the triangles $P_{1} P_{3} B$ and $P_{2} P_{3} A$.
|
| 332 |
+
|
| 333 |
+
|
| 334 |
+
By construction, we have $P_{1} C=P_{2} C$, hence
|
| 335 |
+
|
| 336 |
+
$$
|
| 337 |
+
\angle C P_{1} P_{2}=90^{\circ}-\frac{1}{2} \angle P_{2} C P_{1}=90^{\circ}-\angle A C B
|
| 338 |
+
$$
|
| 339 |
+
|
| 340 |
+
Similarly, $\angle P_{2} P_{3} A=90^{\circ}-\angle B A C$. This gives us
|
| 341 |
+
|
| 342 |
+
$$
|
| 343 |
+
\begin{aligned}
|
| 344 |
+
\angle P_{2} T_{P} A & =\angle C T_{P} A-\angle C T_{P} P_{2}=\angle C B A-\angle C P_{1} P_{2} \\
|
| 345 |
+
& =\angle C B A-90^{\circ}+\angle A C B=90^{\circ}-\angle B A C=\angle P_{2} P_{3} A,
|
| 346 |
+
\end{aligned}
|
| 347 |
+
$$
|
| 348 |
+
|
| 349 |
+
so $T_{P}$ lies on the circumcircle of the triangle $P_{2} P_{3} A$. Similarly, $T_{P}$ lies on the circumcircle of the triangle $P_{1} P_{3} B$ which completes the first part.
|
| 350 |
+
Note that if $P_{2}$ is given, then $T_{P}$ is the unique point on the circumcircle of the triangle $A B C$ with $\angle C T_{P} P_{2}=90^{\circ}-\angle A C B$. In the second part, we will use this as follows: If we can find a point $T$ on the circumcircle of the triangle $A B C$ with $\angle C T G_{2}=\angle C T O_{2}=90^{\circ}-\angle A C B$,
|
| 351 |
+
then $T=T_{G}=T_{O}$ and we are done.
|
| 352 |
+
Let $H$ be the orthocenter of the triangle $A B C$ and let $H_{2}$ be the reflection in the side $A C$. It is known that $H_{2}$ lies on the circumcircle of the triangle $A B C . G, O, H$ lie on the Euler line, so $G_{2}, O_{2}, H_{2}$ are collinear as well. Let $T$ be the second intersection of $G_{2} H_{2}$ and the circumcircle of the triangle $A B C$. We can now complete the proof by seeing that
|
| 353 |
+
|
| 354 |
+
$$
|
| 355 |
+
\angle C T G_{2}=\angle C T O_{2}=\angle C T H_{2}=\angle C B H_{2}=90^{\circ}-\angle A C B .
|
| 356 |
+
$$
|
| 357 |
+
|
| 358 |
+
|
| 359 |
+
|
| 360 |
+
## Solution 3 (complex numbers)
|
| 361 |
+
|
| 362 |
+
For every point $P$, let $p$ denote the corresponding complex number. Set $O$ to be the origin, so $o=0$, and without loss of generality we can assume that $a, b$ and $c$ lie on the unit circle. Then the centroid can be expressed as $g=\frac{a+b+c}{3}$.
|
| 363 |
+
The segments $O o_{1}$ and $b c$ have a common midpoint, so $o_{1}+o=b+c$, and then $o_{1}=b+c$. Similarly $o_{2}=a+c$ and $o_{3}=a+b$. In order to compute $g_{1}$, define $y$ to be the projection of $g$ onto $b c$. Since $b$ and $c$ are on the unit circle, it is well known that $y$ can be expressed as
|
| 364 |
+
|
| 365 |
+
$$
|
| 366 |
+
y=\frac{1}{2}(b+c+g-b c \bar{g}) .
|
| 367 |
+
$$
|
| 368 |
+
|
| 369 |
+
By using $\bar{a}=\frac{1}{a}, \bar{b}=\frac{1}{b}$ and $\bar{c}=\frac{1}{c}$ (points on the unit circle), we obtain
|
| 370 |
+
|
| 371 |
+
$$
|
| 372 |
+
g_{1}=b+c-\frac{a b+b c+c a}{3 a} .
|
| 373 |
+
$$
|
| 374 |
+
|
| 375 |
+
Similarly, we get $g_{2}=a+c-\frac{a b+b c+c a}{3 b}$ and $g_{3}=a+b-\frac{a b+b c+c a}{3 c}$.
|
| 376 |
+
|
| 377 |
+
1) Proof that circumcircles of triangles $a b c, o_{1} O_{2} c, o_{1} O_{3} b$ and $o_{2} O_{3} a$ have common point.
|
| 378 |
+
|
| 379 |
+
Let $x$ be the point of intersection of circumcircles of triangles $o_{1} O_{2} c$ and $a b c(x \neq c)$. We know that $x, o_{1}, o_{2}$ and $c$ are concyclic if and only if $\frac{x-c}{o_{1}-c}: \frac{x-o_{2}}{o_{1}-o_{2}}$ is real number, which is equivalent to
|
| 380 |
+
|
| 381 |
+
$$
|
| 382 |
+
\frac{x-c}{\bar{x}-\bar{c}} \cdot \frac{o_{1}-o_{2}}{\overline{o_{1}}-\overline{o_{2}}}=\frac{o_{1}-c}{\overline{o_{1}}-\bar{c}} \cdot \frac{x-o_{2}}{\bar{x}-\overline{o_{2}}}
|
| 383 |
+
$$
|
| 384 |
+
|
| 385 |
+
Since $x$ and $c$ are on the unit circle $\frac{x-c}{\bar{x}-\bar{c}}=-x c$. Also, $\frac{o_{1}-o_{2}}{\overline{o_{1}-\overline{o_{2}}}}=\frac{b-a}{\bar{b}-\bar{a}}=-a b$, and $\frac{o_{1}-c}{\overline{o_{1}}-\bar{c}}=\frac{b}{\bar{b}}=b^{2}$. Since $\bar{x}=\frac{1}{x}$, from (1) and previous relations, we have:
|
| 386 |
+
|
| 387 |
+
$$
|
| 388 |
+
x=\frac{a b+b c+c a}{a+b+c}
|
| 389 |
+
$$
|
| 390 |
+
|
| 391 |
+
This formula is symmetric, so we conclude that $x$ also belongs to circumcircles of $o_{1} O_{3} b$ and $o_{2} O_{3} a$.
|
| 392 |
+
2) Proof that $x$ belongs to circumcircles of $g_{1} g_{2} c, g_{1} g_{3} b$ and $g_{2} g_{3} a$.
|
| 393 |
+
|
| 394 |
+
Because of symmetry, it is enough to prove that $x$ belongs to circumcircle of $g_{1} g_{2} c$, i.e. to prove the following:
|
| 395 |
+
|
| 396 |
+
$$
|
| 397 |
+
\frac{x-c}{\bar{x}-\bar{c}} \cdot \frac{g_{1}-g_{2}}{\overline{g_{1}}-\overline{g_{2}}}=\frac{g_{1}-c}{\overline{g_{1}}-\bar{c}} \cdot \frac{x-g_{2}}{\bar{x}-\overline{g_{2}}}
|
| 398 |
+
$$
|
| 399 |
+
|
| 400 |
+
Easy computations give that
|
| 401 |
+
|
| 402 |
+
$$
|
| 403 |
+
g_{1}-g_{2}=(b-a) \frac{2 a b-b c-a c}{3 a b}, \quad \overline{g_{1}}-\overline{g_{2}}=(\bar{b}-\bar{a}) \frac{2-\frac{a}{c}-\frac{b}{c}}{3}
|
| 404 |
+
$$
|
| 405 |
+
|
| 406 |
+
and then
|
| 407 |
+
|
| 408 |
+
$$
|
| 409 |
+
\frac{g_{1}-g_{2}}{\overline{g_{1}}-\overline{g_{2}}}=\frac{c(b c+a c-2 a b)}{2 c-a-b}
|
| 410 |
+
$$
|
| 411 |
+
|
| 412 |
+
On the other hand we have
|
| 413 |
+
|
| 414 |
+
$$
|
| 415 |
+
g_{1}-c=\frac{2 a b-b c-a c}{3 a}, \quad \overline{g_{1}}-\bar{c}=\frac{2 c-a-b}{3 b c} .
|
| 416 |
+
$$
|
| 417 |
+
|
| 418 |
+
This implies
|
| 419 |
+
|
| 420 |
+
$$
|
| 421 |
+
\frac{g_{1}-c}{\overline{g_{1}-\bar{c}}}=\frac{2 a b-b c-a c}{2 c-a-b} \cdot \frac{b c}{a}
|
| 422 |
+
$$
|
| 423 |
+
|
| 424 |
+
Then (2) is equivalent to
|
| 425 |
+
|
| 426 |
+
$$
|
| 427 |
+
\begin{aligned}
|
| 428 |
+
-x c \cdot \frac{c(b c+a c-2 a b)}{2 c-a-b} & =\frac{2 a b-b c-a c}{2 c-a-b} \cdot \frac{b c}{a} \cdot \frac{x-g_{2}}{\bar{x}-\overline{g_{2}}} \\
|
| 429 |
+
\Longleftrightarrow x c a\left(\bar{x}-\bar{g}_{2}\right) & =b\left(x-g_{2}\right)
|
| 430 |
+
\end{aligned}
|
| 431 |
+
$$
|
| 432 |
+
|
| 433 |
+
which is also equivalent to
|
| 434 |
+
$\frac{a b+b c+c a}{a+b+c} \cdot c a\left(\frac{a+b+c}{a b+b c+c a}-\frac{1}{a}-\frac{1}{c}+\frac{a+b+c}{3 a c}\right)=b \cdot\left(\frac{a b+b c+c a}{a+b+c}-a-c+\frac{a b+b c+c a}{3 b}\right)$.
|
| 435 |
+
The last equality can easily be verified, which implies that $x$ belongs to circumcircle of triangle $g_{1} g_{2} c$. This concludes our proof.
|
| 436 |
+
|
| 437 |
+
## Solution 4 (rotation)
|
| 438 |
+
|
| 439 |
+
The first part of the first solution and the second part of the second solution can also be done by the following rotation argument: The rotation through $2 \angle B A C$ about $A$ takes $O_{3}$ to $O_{2}, G_{3}$ to $G_{2}$ and $H_{3}$ to $H_{2}$ (again, $H_{2}, H_{3}$ are the reflections of the orthocenter $H$ in the sides $C A, A B$ ). Let $X$ be the intersection of the Euler line reflections $e_{2}$ (going through $O_{2}, G_{2}, H_{2}$ ) and $e_{3}$ (going through $O_{3}, G_{3}, H_{3}$ ). We now use the well-known fact that if a rotation about a point $A$ takes a line $l$ and a point $P$ on $l$ to the line $l^{\prime}$ and the point $P^{\prime}$, then the quadrilateral $A P P^{\prime} X$ is cyclic, where $X$ is the intersection of $l$ and $l^{\prime}$. For this reason, $A O_{3} O_{2} X, A G_{3} G_{2} X$ and $A H_{3} H_{2} X$ are cyclic quadrilaterals. Since $H_{2}$ and $H_{3}$ lie on the circumcircle of the triangle $A B C$, the circumcircles of the triangles $A H_{3} H_{2}$ and $A B C$ are the same, hence $X$ lies on the circumcircle of $A B C$.
|
| 440 |
+
This proves the first part of the first solution as well as the second part of the second solution.
|
| 441 |
+
|
| 442 |
+
|
| 443 |
+
Remark: Problem 6 is a special case of Corollary 3 in Darij Grinberg's paper Anti-Steiner points with respect to a triangle.
|
| 444 |
+
|
EGMO/md/en-2018-solutions.md
ADDED
|
@@ -0,0 +1,455 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Problem 1 Let $A B C$ be a triangle with $C A=C B$ and $\angle A C B=120^{\circ}$, and let $M$ be the midpoint of $A B$. Let $P$ be a variable point on the circumcircle of $A B C$, and let $Q$ be the point on the segment $C P$ such that $Q P=2 Q C$. It is given that the line through $P$ and perpendicular to $A B$ intersects the line $M Q$ at a unique point $N$.
|
| 2 |
+
|
| 3 |
+
Prove that there exists a fixed circle such that $N$ lies on this circle for all possible positions of $P$.
|
| 4 |
+
(Velina Ivanova, Bulgaria)
|
| 5 |
+
Solution Let $O$ be the circumcenter of $A B C$. From the assumption that $\angle A C B=120^{\circ}$ it follows that $M$ is the midpoint of $C O$.
|
| 6 |
+
|
| 7 |
+
Let $\omega$ denote the circle with center in $C$ and radius $C O$. This circle in the image of the circumcircle of $A B C$ through the translation that sends $O$ to $C$. We claim that $N$ lies on $\omega$.
|
| 8 |
+
|
| 9 |
+
|
| 10 |
+
Let us consider the triangles $Q N P$ and $Q M C$. The angles in $Q$ are equal. Since $N P$ is parallel to $M C$ (both lines are perpendicular to $A B$ ), it turns out that $\angle Q N P=\angle Q M C$, and hence the two triangles are similar. Since $Q P=2 Q C$, it follows that
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
N P=2 M C=C O
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
which proves that $N$ lies on $\omega$.
|
| 17 |
+
Comment The possible positions of $N$ are all the points of $\omega$ with the exception of the two points lying on the line $C O$. Indeed, $P$ does not lie on the line $C O$ because otherwise the point $N$ is not well-defined, and therefore also $N$ does not lie on the same line.
|
| 18 |
+
|
| 19 |
+
Conversely, let $N$ be any point on $\omega$ and not lying on the line $C O$. Let $P$ be the corresponding point on the circumcircle of $A B C$, namely such that $N P$ is parallel and equal to $C O$. Let $Q$ be
|
| 20 |
+
the intersection of $C P$ and $N M$. As before, the triangles $Q N P$ and $Q M C$ are similar, and now from the relation $N P=2 M C$ we deduce that $Q P=2 Q C$. This proves that $N$ can be obtained from $P$ through the construction described in the statement of the problem.
|
| 21 |
+
|
| 22 |
+
Alternative solution Let $M^{\prime}$ denote the symmetric of $M$ with respect to $O$.
|
| 23 |
+
Let us consider the quadrilateral $M M^{\prime} P N$. The lines $M M^{\prime}$ and $N P$ are parallel by construction. Also the lines $P M^{\prime}$ and $N M$ are parallel (homothety from $C$ with coefficient 3). It follows that $M M^{\prime} P N$ is a parallelogram, and hence $P N=M M^{\prime}=O C$.
|
| 24 |
+
|
| 25 |
+
Computational solution There are many computation approaches to this problem. For example, we can set Cartesian coordinates so that
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
A=\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right), \quad B=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right), \quad C=(0,1), \quad M=\left(0, \frac{1}{2}\right)
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Setting $P=(a, b)$, we obtain that $Q=(a / 3,(2+b) / 3)$. The equation of the line through $P$ and perpendicular to $A B$ is $x=a$. The equation of the line $M Q$ (if $a \neq 0$ ) is
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
y-\frac{1}{2}=\frac{x}{a}\left(\frac{1}{2}+b\right) .
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
The intersection of the two lines is therefore
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
N=(a, 1+b)=P+(0,1)
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
This shows that the map $P \rightarrow N$ in the translation by the vector $(0,1)$. This result is independent of the position of $P$ (provided that $a \neq 0$, because otherwise $N$ is not well-defined).
|
| 44 |
+
|
| 45 |
+
When $P$ lies on the circumcircle of $A B C$, with the exception of the two points with $a=0$, then necessarily $N$ lies on the translated circle (which is the circle with center in $C$ and radius 1).
|
| 46 |
+
|
| 47 |
+
Problem 2 Consider the set
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
A=\left\{1+\frac{1}{k}: k=1,2,3, \ldots\right\}
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
(a) Prove that every integer $x \geq 2$ can be written as the product of one or more elements of $A$, which are not necessarily different.
|
| 54 |
+
(b) For every integer $x \geq 2$, let $f(x)$ denote the minimum integer such that $x$ can be written as the product of $f(x)$ elements of $A$, which are not necessarily different.
|
| 55 |
+
Prove that there exist infinitely many pairs $(x, y)$ of integers with $x \geq 2, y \geq 2$, and
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
f(x y)<f(x)+f(y) .
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
(Pairs $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$ are different if $x_{1} \neq x_{2}$ or $\left.y_{1} \neq y_{2}\right)$.
|
| 62 |
+
(Mihail Baluna, Romania)
|
| 63 |
+
|
| 64 |
+
Solution Every integer $x \geq 2$ can be written as the telescopic product of $x-1$ elements of $A$ as
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
x=\left(1+\frac{1}{x-1}\right) \cdot\left(1+\frac{1}{x-2}\right) \cdot \ldots \cdot\left(1+\frac{1}{2}\right) \cdot\left(1+\frac{1}{1}\right)
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
which is enough to establish part (a). We now consider part (b). Notice that for any positive integer $k$ we have
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
f\left(2^{k}+1\right) \leq k+1
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
because $2^{k}+1=\left(1+\frac{1}{2^{k}}\right) \cdot 2^{k}$ is a representation of $2^{k}+1$ as a product of $k+1$ elements of $A$. We claim that all the pairs $(x, y)$ of the form
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
x=5, \quad y=\frac{2^{4 k+2}+1}{5}
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
satisfy the required inequality. Notice that $y$ is an integer for any positive value of $k$, because $2^{4 k+2}+1 \equiv 16^{k} \cdot 4+1 \equiv 5 \equiv 0(\bmod 5)$. Furthermore, $f(x y)=f\left(2^{4 k+2}+1\right) \leq 4 k+3$ (and $f(x)=f\left(2^{2}+1\right) \leq 3$ ) by the above. We now need some lower bounds on the values of $f$. Notice that no element of $A$ exceeds 2, and therefore the product of at most $k$ elements of $A$ does not exceed $2^{k}$ : it follows that
|
| 83 |
+
|
| 84 |
+
$$
|
| 85 |
+
f(n) \geq\left\lceil\log _{2}(n)\right\rceil
|
| 86 |
+
$$
|
| 87 |
+
|
| 88 |
+
and in particular that
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
f(5)=f\left(2^{2}+1\right) \geq\left\lceil\log _{2}(5)\right\rceil=3
|
| 92 |
+
$$
|
| 93 |
+
|
| 94 |
+
We have thus proven $f(x)=f(5)=3$. We want to show $f(x y)<f(x)+f(y)$, and since we know $f(x y) \leq 4 k+3$ and $f(x)=3$ we are reduced to showing $f(y)>4 k$. Since $y>2^{4 k-1}$, from (Q2.1) we already know that $f(y) \geq 4 k$, and hence we just need to exclude that $f(y)=4 k$. Let us assume that we can represent $y$ in the form $a_{1} \cdot \ldots a_{4 k}$ with every $a_{i}$ in $A$. At least one of the $a_{i}$ is not 2 (otherwise the product would be a power of 2 , while $y$ is odd), and hence it is less than or equal to $3 / 2$. It follows that
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
a_{1} \cdot \ldots \cdot a_{4 k} \leq 2^{4 k-1} \cdot \frac{3}{2}=15 \cdot \frac{2^{4 k-2}}{5}<\frac{2^{4 k+2}}{5}<y
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
which contradicts the fact that $a_{1} \cdot \ldots \cdot a_{4 k}$ is a representation of $y$.
|
| 101 |
+
Note. Using a similar approach one can also prove that all pairs of the form
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
\left(3, \frac{2^{2 k+1}+1}{3}\right) \quad \text { and } \quad\left(11, \frac{2^{10 k+5}+1}{11}\right)
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
satisfy the required inequality.
|
| 108 |
+
Second solution As in the previous solution we obtain the lower bound (Q2.1).
|
| 109 |
+
Now we claim that all the pairs of the form
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
x=2^{k}+1, \quad y=4^{k}-2^{k}+1
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
satisfy the required inequality when $k$ is large enough. To begin with, it is easy to see that
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
2^{k}+1=\frac{2^{k}+1}{2^{k}} \cdot \underbrace{2 \cdot \ldots \cdot 2}_{k \text { terms }} \quad \text { and } \quad 2^{3 k}+1=\frac{2^{3 k}+1}{2^{3 k}} \cdot \underbrace{2 \cdot \ldots \cdot 2}_{3 k \text { terms }}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
which shows that $f\left(2^{k}+1\right) \leq k+1$ and $f\left(2^{3 k}+1\right) \leq 3 k+1$. On the other hand, from (Q2.1) we deduce that the previous inequalities are actually equalities, and therefore
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
f(x)=k+1 \quad \text { and } \quad f(x y)=3 k+1
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
Therefore, it remain to show that $f(y)>2 k$. Since $y>2^{2 k-1}$ (for $k \geq 1$ ), from (Q2.1) we already know that $f(y) \geq 2 k$, and hence we just need to exclude that $f(y)=2 k$. Let us assume that we can represent $y$ in the form $a_{1} \cdot \ldots \cdot a_{2 k}$. At least one of the factors is not 2 , and hence it is less than or equal to $3 / 2$. Thus when $k$ is large enough it follows that
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
a_{1} \cdot \ldots \cdot a_{2 k} \leq 2^{2 k-1} \cdot \frac{3}{2}=\frac{3}{4} \cdot 2^{2 k}<2^{2 k}-2^{k}<y
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
which contradicts the fact that $a_{1} \cdot \ldots \cdot a_{2 k}$ is a representation of $y$.
|
| 134 |
+
Third solution Let's start by showing that $(x, y)=(7,7)$ satisfies $f(x y)<f(x)+f(y)$. We have $f(7) \geq 4$ since 7 cannot be written as the product of 3 or fewer elements of $A$ : indeed $2^{3}>7$, and any other product of at most three elements of $A$ does not exceed $2^{2} \cdot \frac{3}{2}=6<7$. On the other hand, $f(49) \leq 7$ since $49=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot \frac{3}{2} \cdot \frac{49}{48}$.
|
| 135 |
+
|
| 136 |
+
Suppose by contradiction that there exist only finitely many pairs $(x, y)$ that satisfy $f(x y)<$ $f(x)+f(y)$. This implies that there exists $M$ large enough so that whenever $a>M$ or $b>M$ holds we have $f(a b)=f(a)+f(b)$ (indeed, it is clear that the reverse inequality $f(a b) \leq f(a)+f(b)$ is always satisfied).
|
| 137 |
+
|
| 138 |
+
Now take any pair $(x, y)$ that satisfies $f(x y)<f(x)+f(y)$ and let $n>M$ be any integer. We obtain
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
f(n)+f(x y)=f(n x y)=f(n x)+f(y)=f(n)+f(x)+f(y),
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
which contradicts $f(x y)<f(x)+f(y)$.
|
| 145 |
+
|
| 146 |
+
Problem 3 The $n$ contestants of an EGMO are named $C_{1}, \ldots, C_{n}$. After the competition they queue in front of the restaurant according to the following rules.
|
| 147 |
+
|
| 148 |
+
- The Jury chooses the initial order of the contestants in the queue.
|
| 149 |
+
- Every minute, the Jury chooses an integer $i$ with $1 \leq i \leq n$.
|
| 150 |
+
- If contestant $C_{i}$ has at least $i$ other contestants in front of her, she pays one euro to the Jury and moves forward in the queue by exactly $i$ positions.
|
| 151 |
+
- If contestant $C_{i}$ has fewer than $i$ other contestants in front of her, the restaurant opens and the process ends.
|
| 152 |
+
(a) Prove that the process cannot continue indefinitely, regardless of the Jury's choices.
|
| 153 |
+
(b) Determine for every $n$ the maximum number of euros that the Jury can collect by cunningly choosing the initial order and the sequence of moves.
|
| 154 |
+
(Hungary)
|
| 155 |
+
Solution The maximal number of euros is $2^{n}-n-1$.
|
| 156 |
+
To begin with, we show that it is possible for the Jury to collect this number of euros. We argue by induction. Let us assume that the Jury can collect $M_{n}$ euros in a configuration with $n$ contestants. Then we show that the Jury can collect at least $2 M_{n}+n$ moves in a configuration with $n+1$ contestants. Indeed, let us begin with all the contestants lined up in reverse order. In the first $M_{n}$ moves the Jury keeps $C_{n+1}$ in first position and reverses the order of the remaining contestants, then in the next $n$ moves all contestants $C_{1}, \ldots, C_{n}$ (in this order) jump over $C_{n+1}$ and end up in the first $n$ positions of the line in reverse order, and finally in the last $M_{n}$ moves the Jury rearranges the first $n$ positions.
|
| 157 |
+
|
| 158 |
+
Since $M_{1}=0$ and $M_{n+1} \geq 2 M_{n}+n$, an easy induction shows that $M_{n} \geq 2^{n}-n-1$.
|
| 159 |
+
|
| 160 |
+
Let us show now that at most $2^{n}-n-1$ moves are possible. To this end, let us identify a line of contestants with a permutation $\sigma$ of $\{1, \ldots, n\}$. To each permutation we associate the set of reverse pairs
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
R(\sigma):=\{(i, j): 1 \leq i<j \leq n \text { and } \sigma(i)>\sigma(j)\}
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
and the nonnegative integer
|
| 167 |
+
|
| 168 |
+
$$
|
| 169 |
+
W(\sigma):=\sum_{(i, j) \in R(\sigma)} 2^{i}
|
| 170 |
+
$$
|
| 171 |
+
|
| 172 |
+
which we call the total weight of the permutation. We claim that the total weight decreases after any move of the contestants. Indeed, let us assume that $C_{i}$ moves forward in the queue, let $\sigma$ be the permutation before the move, and let $\sigma^{\prime}$ denote the permutation after the move. Since $C_{i}$ jumps over exactly $i$ contestants, necessarily she jumps over at least one contestant $C_{j}$ with index
|
| 173 |
+
$j>i$. This means that the pair $(i, j)$ is reverse with respect to $\sigma$ but not with respect to $\sigma^{\prime}$, and this yields a reduction of $2^{i}$ in the total weight. On the other hand, the move by $C_{i}$ can create new reverse pairs of the form $(k, i)$ with $k<i$, but their total contribution is at most
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
2^{0}+2^{1}+\ldots+2^{i-1}=2^{i}-1
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
In conclusion, when passing from $\sigma$ to $\sigma^{\prime}$, at least one term $2^{i}$ disappears from the computation of the total weight, and the sum of all the new terms that might have been created is at most $2^{i}-1$. This shows that $W\left(\sigma^{\prime}\right) \leq W(\sigma)-1$.
|
| 180 |
+
|
| 181 |
+
We conclude by observing that the maximum possible value of $W(\sigma)$ is realized when all pairs are reverse, in which case
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
W(\sigma)=\sum_{i=1}^{n}(i-1) 2^{i}=2^{n}-n-1 .
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
This proves that the number of moves is less than or equal to $2^{n}-n-1$, and in particular it is finite.
|
| 188 |
+
|
| 189 |
+
Alternative solution As in the previous solution, the fundamental observation is again that, when a contestant $C_{i}$ moves forward, necessarily she has to jump over at least one contestant $C_{j}$ with $j>i$.
|
| 190 |
+
|
| 191 |
+
Let us show now that the process ends after a finite number of moves. Let us assume that this is not the case. Then at least one contestant moves infinitely many times. Let $i_{0}$ be the largest index such that $C_{i_{0}}$ moves infinitely many times. Then necessarily $C_{i_{0}}$ jumps infinitely many times over some fixed $C_{j_{0}}$ with $j_{0}>i_{0}$. On the other hand, we know that $C_{j_{0}}$ makes only a finite number of moves, and therefore she can precede $C_{i_{0}}$ in the line only a finite number of times, which is absurd.
|
| 192 |
+
|
| 193 |
+
In order to estimate from above the maximal number of moves, we show that the contestant $C_{i}$ can make at most $2^{n-i}-1$ moves. Indeed, let us argue by "backward extended induction". To begin with, we observe that the estimate is trivially true for $C_{n}$ because she has no legal move.
|
| 194 |
+
|
| 195 |
+
Let us assume now that the estimate has been proved for $C_{i}, C_{i+1}, \ldots, C_{n}$, and let us prove it for $C_{i-1}$. When $C_{i-1}$ moves, at least one contestant $C_{j}$ with $j>i-1$ must precede her in the line. The initial configuration can provide at most $n-i$ contestants with larger index in front of $C_{i-1}$, which means at most $n-i$ moves for $C_{i-1}$. All other moves are possible only if some contestant in the range $C_{i}, C_{i+1}, \ldots, C_{n}$ jumps over $C_{i-1}$ during her moves. As a consequence, the total number of moves of $C_{i-1}$ is at most
|
| 196 |
+
|
| 197 |
+
$$
|
| 198 |
+
n-i+\sum_{k=i}^{n}\left(2^{n-k}-1\right)=2^{n-i+1}-1
|
| 199 |
+
$$
|
| 200 |
+
|
| 201 |
+
Summing over all indices we obtain that
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\sum_{i=1}^{n}\left(2^{n-i}-1\right)=2^{n}-n-1
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
which gives an estimate for the total number of moves.
|
| 208 |
+
The same example of the first solution shows that this upper bound can actually be achieved.
|
| 209 |
+
Comment In every move of the example, the moving contestant jumps over exactly one contestant with larger index (and as a consequence over all contestants with smaller index).
|
| 210 |
+
|
| 211 |
+
Problem 4 A domino is a $1 \times 2$ or $2 \times 1$ tile.
|
| 212 |
+
Let $n \geq 3$ be an integer. Dominoes are placed on an $n \times n$ board in such a way that each domino covers exactly two cells of the board, and dominoes do not overlap.
|
| 213 |
+
|
| 214 |
+
The value of a row or column is the number of dominoes that cover at least one cell of this row or column. The configuration is called balanced if there exists some $k \geq 1$ such that each row and each column has a value of $k$.
|
| 215 |
+
|
| 216 |
+
Prove that a balanced configuration exists for every $n \geq 3$, and find the minimum number of dominoes needed in such a configuration.
|
| 217 |
+
(Merlijn Staps, The Netherlands)
|
| 218 |
+
Solution The minimal number of dominoes required in a balanced configuration is $2 n / 3$ if $n$ is a multiple of 3 , and $2 n$ otherwise.
|
| 219 |
+
|
| 220 |
+
In order to show that this number is necessary, we count in two different ways the number of elements of the set $S$ of all pairs $(\ell, d)$, where $\ell$ is a row or a column of the board, and $d$ is a domino that covers at least one cell of that row or column. On the one hand, since each row or column intersects the same number $k$ of dominoes, the set $S$ has $2 n k$ elements. On the other hand, since each domino intersects 3 rows/columns, the set $S$ has $3 D$ elements, where $D$ is the total number of dominoes on the board. This leads to the equality
|
| 221 |
+
|
| 222 |
+
$$
|
| 223 |
+
2 n k=3 D
|
| 224 |
+
$$
|
| 225 |
+
|
| 226 |
+
If $n$ is a multiple of 3 , from the trivial inequality $k \geq 1$ we obtain that $D \geq 2 n / 3$. If $n$ is not a multiple of 3 , then $k$ is a multiple of 3 , which means that $k \geq 3$ and hence $D \geq 2 n$.
|
| 227 |
+
|
| 228 |
+
Now we need to exhibit a balanced configuration with this number of dominoes. The following diagram shows a balanced configuration with $n=3$ and $k=1$.
|
| 229 |
+
|
| 230 |
+
|
| 231 |
+
If $n$ is any multiple of 3 , we can obtain a balanced configuration with $k=1$ by using $n / 3$ of these $3 \times 3$ blocks along the principal diagonal of the board.
|
| 232 |
+
|
| 233 |
+
The following diagrams show balanced configurations with $k=3$ and $n \in\{4,5,6,7\}$.
|
| 234 |
+
|
| 235 |
+
|
| 236 |
+
Any $n \geq 8$ can be written in the form $4 A+r$ where $A$ is a positive integer and $r \in\{4,5,6,7\}$. Therefore, we can obtain a balanced configuration with $n \geq 8$ and $k=3$ by using one block with size $r \times r$, and $A$ blocks with size $4 \times 4$ along the principal diagonal of the board. In particular, this construction covers all the cases where $n$ is not a multiple of 3 .
|
| 237 |
+
|
| 238 |
+
Problem 5 Let $\Gamma$ be the circumcircle of triangle $A B C$. A circle $\Omega$ is tangent to the line segment $A B$ and is tangent to $\Gamma$ at a point lying on the same side of the line $A B$ as $C$. The angle bisector of $\angle B C A$ intersects $\Omega$ at two different points $P$ and $Q$.
|
| 239 |
+
|
| 240 |
+
Prove that $\angle A B P=\angle Q B C$.
|
| 241 |
+
(Dominika Regiec, Poland)
|
| 242 |
+
Solution 1 Let $M$ be the midpoint of the arc $A B$ that does not contain $C$, let $V$ be the intersection of $\Omega$ and $\Gamma$, and let $U$ be the intersection of $\Omega$ and $A B$.
|
| 243 |
+
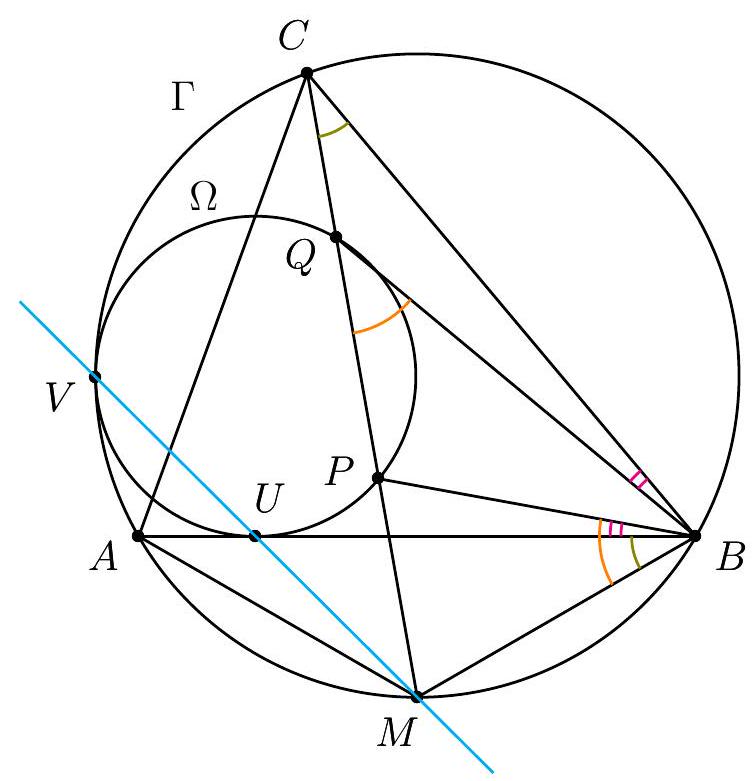
|
| 244 |
+
|
| 245 |
+
The proof can be divided in two steps:
|
| 246 |
+
|
| 247 |
+
1. Proving that $M P \cdot M Q=M B^{2}$.
|
| 248 |
+
|
| 249 |
+
It is well-known that $V, U$ and $M$ are collinear (indeed the homothety with center in $V$ that sends $\Omega$ to $\Gamma$ sends $U$ to the point of $\Gamma$ where the tangent to $\Gamma$ is parallel to $A B$, and this point is $M$ ), and
|
| 250 |
+
|
| 251 |
+
$$
|
| 252 |
+
M V \cdot M U=M A^{2}=M B^{2}
|
| 253 |
+
$$
|
| 254 |
+
|
| 255 |
+
This follows from the similitude between the triangles $\triangle M A V$ and $\triangle M U A$. Alternatively, it is a consequence of the following well-known lemma: Given a circle $\Gamma$ with a chord $A B$, let $M$ be the middle point of one of the two arcs $A B$. Take a line through $M$ which intersects $\Gamma$ again at $X$ and $A B$ at $Y$. Then $M X \cdot M Y$ is independent of the choice of the line.
|
| 256 |
+
Computing the power of $M$ with respect to $\Omega$ we obtain that
|
| 257 |
+
|
| 258 |
+
$$
|
| 259 |
+
M P \cdot M Q=M U \cdot M V=M B^{2}
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
2. Conclude the proof given that $M P \cdot M Q=M B^{2}$.
|
| 263 |
+
|
| 264 |
+
The relation $M P \cdot M Q=M B^{2}$ in turn implies that triangle $\triangle M B P$ is similar to triangle $\triangle M Q B$, and in particular $\angle M B P=\angle M Q B$. Keeping into account that $\angle M C B=$ $\angle M B A$, we finally conclude that
|
| 265 |
+
|
| 266 |
+
$$
|
| 267 |
+
\angle Q B C=\angle M Q B-\angle M C B=\angle M B P-\angle M B A=\angle P B A
|
| 268 |
+
$$
|
| 269 |
+
|
| 270 |
+
as required.
|
| 271 |
+
|
| 272 |
+
Solution 2 The second solution is in fact a different proof of the first part of Solution 1.
|
| 273 |
+
Let us consider the inversion with respect to circle with center $M$ and radius $M A=M B$. This inversion switches $A B$ and $\Gamma$, and fixes the line passing through $M, U, V$. As a consequence, it keeps $\Omega$ fixed, and therefore it switches $P$ and $Q$. This is because they are the intersections between the fixed line $M C$ and $\Omega$, and the only fixed point on the segment $M C$ is its intersection with the inversion circle (thus $P$ and $Q$ are switched). This implies that $M P \cdot M Q=M B^{2}$.
|
| 274 |
+
|
| 275 |
+
Solution 3 This solution is instead a different proof of the second step of Solution 1.
|
| 276 |
+
Let $I$ and $J$ be the incenter and the $C$-excenter of $\triangle A B C$ respectively. It is well-known that $M A=M I=M J$, therefore the relation $M P \cdot M Q=M A^{2}$ implies that $(P, Q, I, J)=-1$.
|
| 277 |
+
|
| 278 |
+
Now observe that $\angle I B J=90^{\circ}$, thus $B I$ is the angle bisector of $\angle P B Q$ as it is well-known from the theory of harmonic pencils, and this leads easily to the conclusion.
|
| 279 |
+
|
| 280 |
+
Solution 4 Let $D$ denote the intersection of $A B$ and $C M$. Let us consider an inversion with respect to $B$, and let us use primes to denote corresponding points in the transformed diagram, with the gentlemen agreement that $B^{\prime}=B$.
|
| 281 |
+
|
| 282 |
+
|
| 283 |
+
Since inversion preserves angles, it turns out that
|
| 284 |
+
|
| 285 |
+
$$
|
| 286 |
+
\angle A^{\prime} B^{\prime} M^{\prime}=\angle A^{\prime} M^{\prime} B^{\prime}=\angle A C B,
|
| 287 |
+
$$
|
| 288 |
+
|
| 289 |
+
and in particular triangle $A^{\prime} B^{\prime} M^{\prime}$ is isosceles with basis $B^{\prime} M^{\prime}$.
|
| 290 |
+
The image of $C M$ is the circumcircle of $B^{\prime} C^{\prime} M^{\prime}$, which we denote by $\omega^{\prime}$. It follows that the centers of both $\omega^{\prime}$ and the image $\Omega^{\prime}$ of $\Omega$ lie on the perpendicular bisector of $B^{\prime} M^{\prime}$. Therefore, the whole transformed diagram is symmetric with respect to the perpendicular bisector of $B^{\prime} M^{\prime}$, and in particular the $\operatorname{arcs} D^{\prime} P^{\prime}$ and $Q^{\prime} C^{\prime}$ of $\omega^{\prime}$ are equal.
|
| 291 |
+
|
| 292 |
+
This is enough to conclude that $\angle D^{\prime} B^{\prime} P^{\prime}=\angle Q^{\prime} B^{\prime} C^{\prime}$, which implies the conclusion.
|
| 293 |
+
|
| 294 |
+
## Problem 6
|
| 295 |
+
|
| 296 |
+
(a) Prove that for every real number $t$ such that $0<t<\frac{1}{2}$ there exists a positive integer $n$ with the following property: for every set $S$ of $n$ positive integers there exist two different elements $x$ and $y$ of $S$, and a non-negative integer $m$ (i.e. $m \geq 0$ ), such that
|
| 297 |
+
|
| 298 |
+
$$
|
| 299 |
+
|x-m y| \leq t y
|
| 300 |
+
$$
|
| 301 |
+
|
| 302 |
+
(b) Determine whether for every real number $t$ such that $0<t<\frac{1}{2}$ there exists an infinite set $S$ of positive integers such that
|
| 303 |
+
|
| 304 |
+
$$
|
| 305 |
+
|x-m y|>t y
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+
for every pair of different elements $x$ and $y$ of $S$ and every positive integer $m$ (i.e. $m>0$ ).
|
| 309 |
+
(Merlijn Staps, The Netherlands)
|
| 310 |
+
|
| 311 |
+
## Solution
|
| 312 |
+
|
| 313 |
+
Part (a) Let $n$ be any positive integer such that
|
| 314 |
+
|
| 315 |
+
$$
|
| 316 |
+
(1+t)^{n-1} \geq \frac{1}{t}
|
| 317 |
+
$$
|
| 318 |
+
|
| 319 |
+
(this inequality is actually true for every large enough $n$ due to Bernoulli's inequality).
|
| 320 |
+
Let $S$ be any set of $n$ distinct positive integers, which we denote by
|
| 321 |
+
|
| 322 |
+
$$
|
| 323 |
+
s_{1}<s_{2}<\ldots<s_{n}
|
| 324 |
+
$$
|
| 325 |
+
|
| 326 |
+
We distinguish two cases.
|
| 327 |
+
|
| 328 |
+
- If $s_{i+1} \leq(1+t) s_{i}$ for some $i \in\{1, \ldots, n-1\}$, then
|
| 329 |
+
|
| 330 |
+
$$
|
| 331 |
+
\left|s_{i+1}-s_{i}\right|=s_{i+1}-s_{i} \leq t s_{i}
|
| 332 |
+
$$
|
| 333 |
+
|
| 334 |
+
and therefore the required inequality is satisfied with $x=s_{i+1}, y=s_{i}$, and $m=1$.
|
| 335 |
+
|
| 336 |
+
- If $s_{i+1}>(1+t) s_{i}$ for every $i \in\{1, \ldots, n-1\}$, then by induction we obtain that
|
| 337 |
+
|
| 338 |
+
$$
|
| 339 |
+
s_{n}>(1+t)^{n-1} s_{1} .
|
| 340 |
+
$$
|
| 341 |
+
|
| 342 |
+
As a consequence, from (Q6.1) it follows that
|
| 343 |
+
|
| 344 |
+
$$
|
| 345 |
+
\left|s_{1}\right|=s_{1}<\frac{1}{(1+t)^{n-1}} \cdot s_{n} \leq t s_{n}
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
and therefore the required inequality is satisfied with $x=s_{1}, y=s_{n}$, and $m=0$.
|
| 349 |
+
|
| 350 |
+
Part (b) (Explicit formula) We claim that an infinite set with the required property exists. To this end, we rewrite the required condition in the form
|
| 351 |
+
|
| 352 |
+
$$
|
| 353 |
+
\left|\frac{x}{y}-m\right|>t
|
| 354 |
+
$$
|
| 355 |
+
|
| 356 |
+
This is equivalent to saying that the distance between the ratio $x / y$ and the set of positive integers is greater than $t$.
|
| 357 |
+
|
| 358 |
+
Now we construct an increasing sequence $s_{n}$ of odd coprime positive integers satisfying
|
| 359 |
+
|
| 360 |
+
$$
|
| 361 |
+
\frac{1}{2}-\frac{1}{2 s_{n}}>t \quad \forall n \geq 1
|
| 362 |
+
$$
|
| 363 |
+
|
| 364 |
+
and such that for every $j>i$ it turns out that
|
| 365 |
+
|
| 366 |
+
$$
|
| 367 |
+
\frac{s_{i}}{s_{j}}<\frac{1}{2} \quad \text { and } \quad t<\left\{\frac{s_{j}}{s_{i}}\right\}<\frac{1}{2}
|
| 368 |
+
$$
|
| 369 |
+
|
| 370 |
+
where $\{\alpha\}$ denotes the fractional part of $\alpha$. This is enough to show that the set $S:=\left\{s_{n}: n \geq 1\right\}$ has the required property.
|
| 371 |
+
|
| 372 |
+
To this end, we consider the sequence defined recursively by
|
| 373 |
+
|
| 374 |
+
$$
|
| 375 |
+
s_{n+1}=\frac{\left(s_{1} \cdot \ldots \cdot s_{n}\right)^{2}+1}{2}
|
| 376 |
+
$$
|
| 377 |
+
|
| 378 |
+
with $s_{1}$ large enough. An easy induction shows that this is an increasing sequence of odd positive integers. For every $i \in\{1, \ldots, n\}$ it turns out that
|
| 379 |
+
|
| 380 |
+
$$
|
| 381 |
+
\frac{s_{i}}{s_{n+1}} \leq \frac{2}{s_{i}} \leq \frac{2}{s_{1}}<\frac{1}{2}
|
| 382 |
+
$$
|
| 383 |
+
|
| 384 |
+
because $s_{1}$ is large enough, which proves the first relation in (Q6.3). Moreover, it turns out that
|
| 385 |
+
|
| 386 |
+
$$
|
| 387 |
+
\frac{s_{n+1}}{s_{i}}=\frac{\left(s_{1} \cdot \ldots \cdot s_{n}\right)^{2}}{2 s_{i}}+\frac{1}{2 s_{i}}
|
| 388 |
+
$$
|
| 389 |
+
|
| 390 |
+
The first term is a positive integer plus $1 / 2$, from which it follows that the distance of $s_{n+1} / s_{i}$ from the positive integers is greater than or equal to
|
| 391 |
+
|
| 392 |
+
$$
|
| 393 |
+
\frac{1}{2}-\frac{1}{2 s_{i}} \geq \frac{1}{2}-\frac{1}{2 s_{1}}
|
| 394 |
+
$$
|
| 395 |
+
|
| 396 |
+
which is greater than $t$ if $s_{1}$ is large enough. This proves the second relation in (Q6.3).
|
| 397 |
+
Part (b) (Arithmetic approach) We produce an increasing sequence $s_{n}$ of odd and coprime positive integers that satisfies (Q6.3) every $j>i$. As in the previous solution, this is enough to conclude.
|
| 398 |
+
|
| 399 |
+
We argue by induction. To begin with, we choose $s_{1}$ to be any odd integer satisfying the inequality in (Q6.2). Let us assume now that $s_{1}, \ldots, s_{n}$ have already been chosen, and let us choose $s_{n+1}$ in such a way that
|
| 400 |
+
|
| 401 |
+
$$
|
| 402 |
+
s_{n+1} \equiv \frac{s_{i}-1}{2} \quad\left(\bmod s_{i}\right) \quad \forall i \in\{1, \ldots, n\}
|
| 403 |
+
$$
|
| 404 |
+
|
| 405 |
+
We can solve this system because the previously chosen integers are odd and coprime. Moreover, any solution of this system is coprime with $s_{1}, \ldots, s_{n}$. Indeed, for every $1 \leq i \leq n$ it turns out that
|
| 406 |
+
|
| 407 |
+
$$
|
| 408 |
+
s_{n+1}=\frac{s_{i}-1}{2}+k_{i} s_{i}
|
| 409 |
+
$$
|
| 410 |
+
|
| 411 |
+
for some positive integer $k_{i}$. Therefore, any prime $p$ that divides both $s_{n+1}$ and $s_{i}$ divides also $\left(2 k_{i}+1\right) s_{i}-2 s_{n+1}=1$, which is absurd. Finally, we observe that we can assume that $s_{n+1}$ is odd and large enough. In this way we can guarantee that
|
| 412 |
+
|
| 413 |
+
$$
|
| 414 |
+
\frac{s_{i}}{s_{n+1}}<\frac{1}{2} \quad \forall i \in\{1, \ldots, n\}
|
| 415 |
+
$$
|
| 416 |
+
|
| 417 |
+
which is the first requirement in (Q6.3), and
|
| 418 |
+
|
| 419 |
+
$$
|
| 420 |
+
k_{i}+t<k_{i}+\frac{1}{2}-\frac{1}{2 s_{i}}=\frac{s_{n+1}}{s_{i}}<k_{i}+\frac{1}{2} \quad \forall i \in\{1, \ldots, n\}
|
| 421 |
+
$$
|
| 422 |
+
|
| 423 |
+
which implies the second requirement in (Q6.3).
|
| 424 |
+
Part (b) (Algebraic approach) Again we produce an increasing sequence $s_{n}$ of positive integers that satisfies (Q6.3) every $j>i$.
|
| 425 |
+
|
| 426 |
+
To this end, for every positive integer $x$, we define its security region
|
| 427 |
+
|
| 428 |
+
$$
|
| 429 |
+
S(x):=\bigcup_{n \geq 1}\left((n+t) x,\left(n+\frac{1}{2}\right) x\right) .
|
| 430 |
+
$$
|
| 431 |
+
|
| 432 |
+
The security region $S(x)$ is a periodic countable union of intervals of length $\left(\frac{1}{2}-t\right) x$, whose left-hand or right-hand endpoints form an arithmetic sequence. It has the property that
|
| 433 |
+
|
| 434 |
+
$$
|
| 435 |
+
t<\left\{\frac{y}{x}\right\}<\frac{1}{2} \quad \forall y \in S(x)
|
| 436 |
+
$$
|
| 437 |
+
|
| 438 |
+
Now we prove by induction that we can choose a sequence $s_{n}$ of positive integers satisfying (Q6.3) and in addition the fact that every interval of the security region $S\left(s_{n}\right)$ contains at least one interval of $S\left(s_{n-1}\right)$.
|
| 439 |
+
|
| 440 |
+
To begin with, we choose $s_{1}$ large enough so that the length of the intervals of $S\left(s_{1}\right)$ is larger than 1. This guarantees that any interval of $S\left(s_{1}\right)$ contains at least a positive integer. Now let us choose a positive integer $s_{2} \in S\left(s_{1}\right)$ that is large enough. This guarantees that $s_{1} / s_{2}$ is small enough, that the fractional part of $s_{2} / s_{1}$ is in $(t, 1 / 2)$, and that every interval of the security region $S\left(s_{2}\right)$ contains at least one interval of $S\left(s_{1}\right)$, and hence at least one positive integer.
|
| 441 |
+
|
| 442 |
+
Let us now assume that $s_{1}, \ldots, s_{n}$ have been already chosen with the required properties. We know that every interval of $S\left(s_{n}\right)$ contains at least one interval of $S\left(s_{n-1}\right)$, which in turn contains an interval in $S\left(s_{n-2}\right)$, and so on up to $S\left(s_{1}\right)$. As a consequence, we can choose a large enough positive integer $s_{n+1}$ that lies in $S\left(s_{k}\right)$ for every $k \in\{1, \ldots, n\}$. Since $s_{n+1}$ is large enough, we are sure that
|
| 443 |
+
|
| 444 |
+
$$
|
| 445 |
+
\frac{s_{k}}{s_{n+1}}<t \quad \forall k \in\{1, \ldots, n\}
|
| 446 |
+
$$
|
| 447 |
+
|
| 448 |
+
Moreover, we are sure also that all the intervals of $S\left(s_{n+1}\right)$ are large enough, and therefore they contain at least one interval of $S\left(s_{n}\right)$, which in turn contains at least one interval of $S\left(s_{n-1}\right)$, and so on. Finally, the condition
|
| 449 |
+
|
| 450 |
+
$$
|
| 451 |
+
t<\left\{\frac{s_{n-1}}{s_{n}}\right\}<\frac{1}{2}
|
| 452 |
+
$$
|
| 453 |
+
|
| 454 |
+
is guaranteed by the fact that $s_{n+1}$ was chosen in an interval that is contained in $S\left(s_{k}\right)$ for every $k \in\{1, \ldots, n\}$. This completes the induction.
|
| 455 |
+
|
EGMO/md/en-2019-solutions-day1.md
ADDED
|
@@ -0,0 +1,623 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Day 1. Solutions
|
| 2 |
+
|
| 3 |
+
Problem 1 (Netherlands). Find all triples $(a, b, c)$ of real numbers such that $a b+b c+$ $c a=1$ and
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
a^{2} b+c=b^{2} c+a=c^{2} a+b
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
Solution 1. First suppose that $a=0$. Then we have $b c=1$ and $c=b^{2} c=b$. So $b=c$, which implies $b^{2}=1$ and hence $b= \pm 1$. This leads to the solutions $(a, b, c)=(0,1,1)$ and $(a, b, c)=(0,-1,-1)$. Similarly, $b=0$ gives the solutions $(a, b, c)=(1,0,1)$ and $(a, b, c)=(-1,0,-1)$, while $c=0$ gives $(a, b, c)=(1,1,0)$ and $(a, b, c)=(-1,-1,0)$.
|
| 10 |
+
Now we may assume that $a, b, c \neq=0$. We multiply $a b+b c+c a=1$ by $a$ to find $a^{2} b+a b c+c a^{2}=a$, hence $a^{2} b=a-a b c-a^{2} c$. Substituting this in $a^{2} b+c=b^{2} c+a$ yields $a-a b c-a^{2} c+c=b^{2} c+a$, so $b^{2} c+a b c+a^{2} c=c$. As $c \neq=0$, we find $b^{2}+a b+a^{2}=1$.
|
| 11 |
+
Analogously we have $b^{2}+b c+c^{2}=1$ and $a^{2}+a c+c^{2}=1$. Adding these three equations yields $2\left(a^{2}+b^{2}+c^{2}\right)+a b+b c+c a=3$, which implies $a^{2}+b^{2}+c^{2}=1$. Combining this result with $b^{2}+a b+a^{2}=1$, we get $1-a b=1-c^{2}$, so $c^{2}=a b$.
|
| 12 |
+
Analogously we also have $b^{2}=a c$ and $a^{2}=b c$. In particular we now have that $a b, b c$ and $c a$ are all positive. This means that $a, b$ and $c$ must all be positive or all be negative. Now assume that $|c|$ is the largest among $|a|,|b|$ and $|c|$, then $c^{2} \geq|a b|=a b=c^{2}$, so we must have equality. This means that $|c|=|a|$ and $|c|=|b|$. Since $(a, b, c)$ must all have the same sign, we find $a=b=c$. Now we have $3 a^{2}=1$, hence $a= \pm \frac{1}{3} \sqrt{3}$. We find the solutions $(a, b, c)=\left(\frac{1}{3} \sqrt{3}, \frac{1}{3} \sqrt{3}, \frac{1}{3} \sqrt{3}\right)$ and $(a, b, c)=\left(-\frac{1}{3} \sqrt{3},-\frac{1}{3} \sqrt{3},-\frac{1}{3} \sqrt{3}\right)$.
|
| 13 |
+
We conclude that all possible triples $(a, b, c)$ are $(0,1,1),(0,-1,-1),(1,0,1),(-1,0,-1)$, $(1,1,0),(-1,-1,0),\left(\frac{1}{3} \sqrt{3}, \frac{1}{3} \sqrt{3}, \frac{1}{3} \sqrt{3}\right)$ and $\left(-\frac{1}{3} \sqrt{3},-\frac{1}{3} \sqrt{3},-\frac{1}{3} \sqrt{3}\right)$.
|
| 14 |
+
Solution 2. From the problem statement $a b=1-b c-c a$ and thus $b^{2} c+a=a^{2} b+c=$ $a-a b c-a^{2} c+c, c\left(b^{2}+a^{2}+a b-1\right)=0$. If $c=0$ then $a b=1$ and $a^{2} b=b$, which implies $a=b= \pm 1$. Otherwise $b^{2}+a^{2}+a b=1$. Cases $a=0$ and $b=0$ are completely analogous to $c=0$, so we may suppose that $a, b, c \neq 0$. In this case we end up with
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
\left\{\begin{array}{l}
|
| 18 |
+
a^{2}+b^{2}+a b=1 \\
|
| 19 |
+
b^{2}+c^{2}+b c=1 \\
|
| 20 |
+
c^{2}+a^{2}+c a=1 \\
|
| 21 |
+
a b+b c+c a=1
|
| 22 |
+
\end{array}\right.
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Adding first three equations and subtracting the fourth yields $2\left(a^{2}+b^{2}+c^{2}\right)=2=$ $2(a b+b c+c a)$. Consequently, $(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=0$. Now we can easily conclude that $a=b=c= \pm \frac{1}{\sqrt{3}}$.
|
| 26 |
+
Solution by Achilleas Sinefakopoulos, Greece. We have
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
c\left(1-b^{2}\right)=a(1-a b)=a(b c+c a)=c\left(a b+a^{2}\right)
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
and so
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
c\left(a^{2}+a b+b^{2}-1\right)=0
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
Similarly, we have
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
b\left(a^{2}+a c+c^{2}-1\right)=0 \quad \text { and } \quad a\left(b^{2}+b c+c^{2}-1\right)=0
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
If $c=0$, then we get $a b=1$ and $a^{2} b=a=b$, which give us $a=b=1$, or $a=b=-1$. Similarly, if $a=0$, then $b=c=1$, or $b=c=-1$, while if $b=0$, then $a=c=1$, or $a=c=-1$.
|
| 45 |
+
|
| 46 |
+
So assume that $a b c \neq 0$. Then
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
a^{2}+a b+b^{2}=b^{2}+b c+c^{2}=c^{2}+c a+a^{2}=1
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Adding these gives us
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
2\left(a^{2}+b^{2}+c^{2}\right)+a b+b c+c a=3
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
and using the fact that $a b+b c+c a=1$, we get
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
a^{2}+b^{2}+c^{2}=1=a b+b c+c a
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Hence
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=2\left(a^{2}+b^{2}+c^{2}\right)-2(a b+b c+c a)=0
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
and so $a=b=c= \pm \frac{1}{\sqrt{3}}$.
|
| 71 |
+
Therefore, the solutions $(a, b, c)$ are $(0,1,1),(0,-1,-1),(1,0,1),(-1,0,-1),(1,1,0)$, $(-1,-1,0),\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right),\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$
|
| 72 |
+
|
| 73 |
+
Solution by Eirini Miliori (HEL2). It is $a b+b c+c a=1$ and
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
a^{2} b+c=b^{2} c+a=c^{2} a+b
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
We have
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\begin{aligned}
|
| 83 |
+
a^{2} b+c=b^{2} c+a & \Longleftrightarrow a^{2} b-a=b^{2} c-c \\
|
| 84 |
+
& \Longleftrightarrow a(a b-1)=c\left(b^{2}-1\right) \\
|
| 85 |
+
& \Longleftrightarrow a(-b c-a c)=c\left(b^{2}-1\right) \\
|
| 86 |
+
& \Longleftrightarrow-a c(a+b)=c\left(b^{2}-1\right)
|
| 87 |
+
\end{aligned}
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
First, consider the case where one of $a, b, c$ is equal to 0 . Without loss of generality, assume that $a=0$. Then $b c=1$ and $b=c$ from (1), and so $b^{2}=1$ giving us $b=1$ or -1 . Hence $b=c=1$ or $b=c=-1$.
|
| 91 |
+
|
| 92 |
+
Therefore, $(a, b, c)$ equals one of the triples $(0,1,1),(0,-1,-1)$, as well as their rearrangements $(1,0,1)$ and $(-1,0,-1)$ when $b=0$, or $(1,1,0)$ and $(-1,-1,0)$ when $c=0$.
|
| 93 |
+
|
| 94 |
+
Now consider the case where $a \neq 0, b \neq 0$ and $c \neq 0$. Then (2) gives us
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
-a(a+b)=b^{2}-1 \Longleftrightarrow-a^{2}-a b=b^{2}-1 \Longleftrightarrow a^{2}+a b+b^{2}-1=0
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
The quadratic $P(x)=x^{2}+b x+b^{2}-1$ has $x=a$ as a root. Let $x_{1}$ be its second root (which could be equal to $a$ in the case where the discriminant is 0 ). From Vieta's formulas we get
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\left\{\begin{aligned}
|
| 104 |
+
x_{1}+a=-b & \Longleftrightarrow x_{1}=-b-a, \text { and } \\
|
| 105 |
+
x_{1} a=b^{2}-1 & \Longleftrightarrow x_{1}=\frac{b^{2}-1}{a} .
|
| 106 |
+
\end{aligned}\right.
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Using $a^{2} b+c=c^{2} a+b$ we obtain $b\left(a^{2}-1\right)=c(a c-1)$ yielding $a^{2}+a c+c^{2}-1=0$ in a similar way. The quadratic $Q(x)=x^{2}+c x+c^{2}-1$ has $x=a$ as a root. Let $x_{2}$ be its second root (which could be equal to $a$ in the case where the discriminant is 0 ). From Vieta's formulas we get
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\left\{\begin{aligned}
|
| 113 |
+
x_{2}+a=-c & \Longleftrightarrow x_{2}=-c-a, \text { and } \\
|
| 114 |
+
x_{2} a=c^{2}-1 & \Longleftrightarrow x_{2}=\frac{c^{2}-1}{a} .
|
| 115 |
+
\end{aligned}\right.
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
Then
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
\left\{\begin{array}{l}
|
| 122 |
+
x_{1}+x_{2}=-b-a-c-a, \text { and } \\
|
| 123 |
+
x_{1}+x_{2}=\frac{b^{2}-1}{a}+\frac{c^{2}-1}{a}
|
| 124 |
+
\end{array}\right.
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
which give us
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\begin{aligned}
|
| 131 |
+
-(2 a+b+c)=\frac{b^{2}-1}{a}+\frac{c^{2}-1}{a} & \Longleftrightarrow-2 a^{2}-b a-c a=b^{2}+c^{2}-2 \\
|
| 132 |
+
& \Longleftrightarrow b c-1-2 a^{2}=b^{2}+c^{2}-2 \\
|
| 133 |
+
& \Longleftrightarrow 2 a^{2}+b^{2}+c^{2}=1+b c .
|
| 134 |
+
\end{aligned}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
By symmetry, we get
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
\begin{aligned}
|
| 141 |
+
& 2 b^{2}+a^{2}+c^{2}=1+a c, \text { and } \\
|
| 142 |
+
& 2 c^{2}+a^{2}+b^{2}=1+b c
|
| 143 |
+
\end{aligned}
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
Adding equations (3), (4), and (5), we get
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
4\left(a^{2}+b^{2}+c^{2}\right)=3+a b+b c+c a \Longleftrightarrow 4\left(a^{2}+b^{2}+c^{2}\right)=4 \Longleftrightarrow a^{2}+b^{2}+c^{2}=1
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
From this and (3), since $a b+b c+c a=1$, we get
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
a^{2}=b c=1-a b-a c \Longleftrightarrow a(a+b+c)=1
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
Similarly, from (4) we get
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
b(a+b+c)=1
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
and from (4),
|
| 165 |
+
|
| 166 |
+
$$
|
| 167 |
+
c(a+b+c)=1
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
Clearly, it is $a+b+c \neq 0$ (for otherwise it would be $0=1$, a contradiction). Therefore,
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
a=b=c=\frac{1}{a+b+c},
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
and so $3 a^{2}=1$ giving us $a=b=c= \pm \frac{1}{\sqrt{3}}$.
|
| 177 |
+
In conclusion, the solutions $(a, b, c)$ are $(0,1,1),(0,-1,-1),(1,0,1),(-1,0,-1),(1,1,0)$, $(-1,-1,0),\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)$, and $\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$.
|
| 178 |
+
Solution by ISR5. First, homogenize the condition $a^{2} b+c=b^{2} c+a=c^{2} a+b$ by replacing $c$ by $c(a b+b c+c a)$ (etc.), yielding
|
| 179 |
+
|
| 180 |
+
$$
|
| 181 |
+
a^{2} b+c=a^{2} b+a b c+b c^{2}+c^{2} a=a b c+\sum_{c y c} a^{2} b+\left(c^{2} b-b^{2} c\right)=a b c+\sum_{c y c} a^{2} b+b c(c-b) .
|
| 182 |
+
$$
|
| 183 |
+
|
| 184 |
+
Thus, after substracting the cyclicly symmetric part $a b c+\sum_{c y c} a^{2} b$ we find the condition is eqivalent to
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
D:=b c(c-b)=c a(a-c)=a b(b-a)
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
Ending 1. It is easy to see that if e.g. $a=0$ then $b=c= \pm 1$, and if e.g. $a=b$ then either $a=b=c= \pm \frac{1}{\sqrt{3}}$ or $a=b= \pm 1, c=0$, and these are indeed solutions. So, to show that these are all solutions (up to symmetries), we may assume by contradiction that $a, b, c$ are pairwise different and non-zero. All conditions are preserved under cyclic shifts and under simultaenously switching signs on all $a, b, c$, and by applying these operations as necessary we may assume $a<b<c$. It follows that $D^{3}=a^{2} b^{2} c^{2}(c-b)(a-c)(b-a)$ must be negative (the only negative term is $a-c$, hence $D$ is negative, i.e. $b c, a b<0<a c$. But this means that $a, c$ have the same sign and $b$ has a different one, which clearly contradicts $a<b<c$ ! So, such configurations are impossible.
|
| 191 |
+
|
| 192 |
+
Ending 2. Note that $3 D=\sum c^{2} b-\sum b^{2} c=(c-b)(c-a)(b-a)$ and $D^{3}=a^{2} b^{2} c^{2}(c-$ $b)(a-c)(b-a)=-3 a^{2} b^{2} c^{2} D$. Since $3 D$ and $D^{3}$ must have the same sign, and $-3 a^{2} b^{2} c^{2}$ is non-positive, necessarily $D=0$. Thus (up to cyclic permutation) $a=b$ and from there we immediately find either $a=b= \pm 1, c=0$ or $a=b=c= \pm \frac{1}{\sqrt{3}}$.
|
| 193 |
+
|
| 194 |
+
Problem 2 (Luxembourg). Let $n$ be a positive integer. Dominoes are placed on a $2 n \times 2 n$ board in such a way that every cell of the board is adjacent to exactly one cell covered by a domino. For each $n$, determine the largest number of dominoes that can be placed in this way.
|
| 195 |
+
(A domino is a tile of size $2 \times 1$ or $1 \times 2$. Dominoes are placed on the board in such a way that each domino covers exactly two cells of the board, and dominoes do not overlap. Two cells are said to be adjacent if they are different and share a common side.)
|
| 196 |
+
|
| 197 |
+
Solution 1. Let $M$ denote the maximal number of dominoes that can be placed on the chessboard. We claim that $M=n(n+1) / 2$. The proof naturally splits into two parts: we first prove that $n(n+1) / 2$ dominoes can be placed on the board, and then show that $M \leq n(n+1) / 2$ to complete the proof.
|
| 198 |
+
|
| 199 |
+
We construct placings of the dominoes by induction. The base cases $n=1$ and $n=2$ correspond to the placings
|
| 200 |
+
|
| 201 |
+
|
| 202 |
+
Next, we add dominoes to the border of a $2 n \times 2 n$ chessboard to obtain a placing of dominoes for the $2(n+2) \times 2(n+2)$ board,
|
| 203 |
+
|
| 204 |
+
depending on whether $n$ is odd or even. In these constructions, the interior square is filled with the placing for the $2 n \times 2 n$ board. This construction adds $2 n+3$ dominoes, and therefore places, in total,
|
| 205 |
+
|
| 206 |
+
$$
|
| 207 |
+
\frac{n(n+1)}{2}+(2 n+3)=\frac{(n+2)(n+3)}{2}
|
| 208 |
+
$$
|
| 209 |
+
|
| 210 |
+
dominoes on the board. Noticing that the contour and the interior mesh together appropriately, this proves, by induction, that $n(n+1) / 2$ dominoes can be placed on the $2 n n$ board.
|
| 211 |
+
|
| 212 |
+
To prove that $M \leq n(n+1) / 2$, we border the $2 n \times 2 n$ square board up to a $(2 n+2) \times(2 n+2)$ square board; this adds $8 n+4$ cells to the $4 n^{2}$ cells that we have started with. Calling a cell covered if it belongs to a domino or is adjacent to a domino, each domino on the $2 n \times 2 n$ board is seen to cover exactly 8 cells of the $(2 n+2) \times(2 n+2)$ board (some of which may belong to the border). By construction, each of the $4 n^{2}$ cells of the $2 n \times 2 n$ board is covered by precisely one domino.
|
| 213 |
+
|
| 214 |
+
If two adjacent cells on the border, away from a corner, are covered, then there will be at least two uncovered cells on both sides of them; if one covered cell lies between uncovered cells, then again, on both sides of it there will be at least two uncovered cells; three or more adjacent cells cannot be all covered. The following diagrams, in which the borders are shaded, $\times$ marks an uncovered cell on the border, + marks a covered cell not belonging to a domino, and - marks a cell which cannot belong to a domino, summarize the two possible situations,
|
| 215 |
+
|
| 216 |
+
| $\cdots$ | $\times$ | $\times$ | + | + | $\times$ | $\times$ | $\cdots$ |
|
| 217 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 218 |
+
| | - | + | | | + | - | |
|
| 219 |
+
| | | - | + | + | - | | |
|
| 220 |
+
| | | | - | - | | | |
|
| 221 |
+
| $\vdots$ | | | | | | | $\vdots$ |
|
| 222 |
+
|
| 223 |
+
or
|
| 224 |
+
|
| 225 |
+
|
| 226 |
+
Close to a corner of the board, either the corner belongs to some domino,
|
| 227 |
+
|
| 228 |
+
| $\times$ | + | + | $\times$ | $\times$ | $\cdots$ |
|
| 229 |
+
| :---: | :---: | :---: | :---: | :---: | :---: |
|
| 230 |
+
| + | | | + | - | |
|
| 231 |
+
| $\times$ | + | + | - | | |
|
| 232 |
+
| $\times$ | - | - | | | |
|
| 233 |
+
| $\vdots$ | | | | | |
|
| 234 |
+
|
| 235 |
+
or one of the following situations, in which the corner cell of the original board is not covered by a domino, may occur:
|
| 236 |
+
|
| 237 |
+
|
| 238 |
+
It is thus seen that at most half of the cells on the border, i.e. $4 n+2$ cells, may be covered, and hence
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
M \leq\left[\frac{4 n^{2}+(4 n+2)}{8}\right]=\left[\frac{n(n+1)}{2}+\frac{1}{2}\right]=\frac{n(n+1)}{2}
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
which completes the proof of our claim.
|
| 245 |
+
Solution 2. We use the same example as in Solution 1. Let $M$ denote the maximum number of dominoes which satisfy the condition of the problem. To prove that $M \leq$ $n(n+1) / 2$, we again border the $2 n \times 2 n$ square board up to a $(2 n+2) \times(2 n+2)$ square board. In fact, we shall ignore the corner border cells as they cannot be covered anyway and consider only the $2 n$ border cells along each side. We prove that out of each four border cells next to each other at most two can be covered. Suppose three out of four cells $A, B, C, D$ are covered. Then there are two possibilities below:
|
| 246 |
+

|
| 247 |
+
|
| 248 |
+
The first option is that $A, B$ and $D$ are covered (marked with + in top row). Then the cells inside the starting square next to $A, B$ and $D$ are covered by the dominoes, but the cell in between them has now two adjacent cells with dominoes, contradiction. The second option is that $A, B$ and $C$ are covered. Then the cells inside the given square next to $A, B$ and $C$ are covered by the dominoes. But then the cell next to B has two adjacent cells with dominoes, contradiction.
|
| 249 |
+
|
| 250 |
+
Now we can split the border cells along one side in groups of 4 (leaving one group of 2 if $n$ is odd). So when $n$ is even, at most $n$ of the $2 n$ border cells along one side can be covered, and when $n$ is odd, at most $n+1$ out of the $2 n$ border cells can be covered. For all four borders together, this gives a contribution of $4 n$ when $n$ is even and $4 n+4$ when $n$ is odd. Adding $4 n^{2}$ and dividing by 8 we get the desired result.
|
| 251 |
+
|
| 252 |
+
Solution (upper bound) by ISR5. Consider the number of pairs of adjacent cells, such that one of them is covered by a domino. Since each cell is adjacent to one covered cell, the number of such pairs is exactly $4 n^{2}$. On the other hand, let $n_{2}$ be the number of covered corner cells, $n_{3}$ the number of covered edge cells (cells with 3 neighbours), and $n_{4}$ be the number of covered interior cells (cells with 4 neighbours). Thus the number of pairs is $2 n_{2}+3 n_{3}+4 n_{4}=4 n^{2}$, whereas the number of dominoes is $m=\frac{n_{2}+n_{3}+n_{4}}{2}$.
|
| 253 |
+
|
| 254 |
+
Considering only the outer frame (of corner and edge cells), observe that every covered cell dominates two others, so at most half of the cells are ccovered. The frame has a total of $4(2 n-1)$ cells, i.e. $n_{2}+n_{3} \leq 4 n-2$. Additionally $n_{2} \leq 4$ since there are only 4 corners, thus
|
| 255 |
+
$8 m=4 n_{2}+4 n_{3}+4 n_{4}=\left(2 n_{2}+3 n_{3}+4 n_{4}\right)+\left(n_{2}+n_{3}\right)+n_{2} \leq 4 n^{2}+(4 n-2)+4=4 n(n+1)+2$
|
| 256 |
+
Thus $m \leq \frac{n(n+1)}{2}+\frac{1}{4}$, so in fact $m \leq \frac{n(n+1)}{2}$.
|
| 257 |
+
Solution (upper and lower bound) by ISR5. We prove that this is the upper bound (and also the lower bound!) by proving that any two configurations, say $A$ and $B$, must contain exactly the same number of dominoes.
|
| 258 |
+
|
| 259 |
+
Colour the board in a black and white checkboard colouring. Let $W$ be the set of white cells covered by dominoes of tiling $A$. For each cell $w \in W$ let $N_{w}$ be the set of its adjacent (necessarily black) cells. Since each black cell has exactly one neighbour (necessarily white) covered by a domino of tiling $A$, it follows that each black cell is contained in exactly one $N_{w}$, i.e. the $N_{w}$ form a partition of the black cells. Since each white cell has exactly one (necessarily black) neighbour covered by a tile of $B$, each $B_{w}$ contains exactly one black tile covered by a domino of $B$. But, since each domino covers exactly one white and one black cell, we have
|
| 260 |
+
|
| 261 |
+
$$
|
| 262 |
+
|A|=|W|=\left|\left\{N_{w}: w \in W\right\}\right|=|B|
|
| 263 |
+
$$
|
| 264 |
+
|
| 265 |
+
as claimed.
|
| 266 |
+
|
| 267 |
+
Problem 3 (Poland). Let $A B C$ be a triangle such that $\angle C A B>\angle A B C$, and let $I$ be its incentre. Let $D$ be the point on segment $B C$ such that $\angle C A D=\angle A B C$. Let $\omega$ be the circle tangent to $A C$ at $A$ and passing through $I$. Let $X$ be the second point of intersection of $\omega$ and the circumcircle of $A B C$. Prove that the angle bisectors of $\angle D A B$ and $\angle C X B$ intersect at a point on line $B C$.
|
| 268 |
+
|
| 269 |
+
Solution 1. Let $S$ be the intersection point of $B C$ and the angle bisector of $\angle B A D$, and let $T$ be the intersection point of $B C$ and the angle bisector of $\angle B X C$. We will prove that both quadruples $A, I, B, S$ and $A, I, B, T$ are concyclic, which yields $S=T$.
|
| 270 |
+
|
| 271 |
+
Firstly denote by $M$ the middle of $\operatorname{arc} A B$ of the circumcenter of $A B C$ which does not contain $C$. Consider the circle centered at $M$ passing through $A, I$ and $B$ (it is well-known that $M A=M I=M B$ ); let it intersect $B C$ at $B$ and $S^{\prime}$. Since $\angle B A C>\angle C B A$ it is easy to check that $S^{\prime}$ lies on side $B C$. Denoting the angles in $A B C$ by $\alpha, \beta, \gamma$ we get
|
| 272 |
+
|
| 273 |
+
$$
|
| 274 |
+
\angle B A D=\angle B A C-\angle D A C=\alpha-\beta .
|
| 275 |
+
$$
|
| 276 |
+
|
| 277 |
+
Moreover since $\angle M B C=\angle M B A+\angle A B C=\frac{\gamma}{2}+\beta$, then
|
| 278 |
+
|
| 279 |
+
$$
|
| 280 |
+
\angle B M S^{\prime}=180^{\circ}-2 \angle M B C=180^{\circ}-\gamma-2 \beta=\alpha-\beta
|
| 281 |
+
$$
|
| 282 |
+
|
| 283 |
+
It follows that $\angle B A S^{\prime}=2 \angle B M S^{\prime}=2 \angle B A D$ which gives us $S=S^{\prime}$.
|
| 284 |
+
|
| 285 |
+
|
| 286 |
+
Secondly let $N$ be the middle of arc $B C$ of the circumcenter of $A B C$ which does not contain $A$. From $\angle B A C>\angle C B A$ we conclude that $X$ lies on the $\operatorname{arc} A B$ of circumcircle of $A B C$ not containing $C$. Obviously both $A I$ and $X T$ are passing through $N$. Since $\angle N B T=\frac{\alpha}{2}=\angle B X N$ we obtain $\triangle N B T \sim \triangle N X B$, therefore
|
| 287 |
+
|
| 288 |
+
$$
|
| 289 |
+
N T \cdot N X=N B^{2}=N I^{2}
|
| 290 |
+
$$
|
| 291 |
+
|
| 292 |
+
It follows that $\triangle N T I \sim \triangle N I X$. Keeping in mind that $\angle N B C=\angle N A C=\angle I X A$ we get
|
| 293 |
+
|
| 294 |
+
$$
|
| 295 |
+
\angle T I N=\angle I X N=\angle N X A-\angle I X A=\angle N B A-\angle N B C=\angle T B A .
|
| 296 |
+
$$
|
| 297 |
+
|
| 298 |
+
It means that $A, I, B, T$ are concyclic which ends the proof.
|
| 299 |
+
Solution 2. Let $\angle B A C=\alpha, \angle A B C=\beta, \angle B C A=\gamma \angle A C X=\phi$. Denote by $W_{1}$ and $W_{2}$ the intersections of segment $B C$ with the angle bisectors of $\angle B X C$ and $\angle B A D$ respectively. Then $B W_{1} / W_{1} C=B X / X C$ and $B W_{2} / W_{2} D=B A / A D$. We shall show that $B W_{1}=B W_{2}$.
|
| 300 |
+
|
| 301 |
+
Since $\angle D A C=\angle C B A$, triangles $A D C$ and $B A C$ are similar and therefore
|
| 302 |
+
|
| 303 |
+
$$
|
| 304 |
+
\frac{D C}{A C}=\frac{A C}{B C}
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
By the Law of sines
|
| 308 |
+
|
| 309 |
+
$$
|
| 310 |
+
\frac{B W_{2}}{W_{2} D}=\frac{B A}{A D}=\frac{B C}{A C}=\frac{\sin \alpha}{\sin \beta} .
|
| 311 |
+
$$
|
| 312 |
+
|
| 313 |
+
Consequently
|
| 314 |
+
|
| 315 |
+
$$
|
| 316 |
+
\begin{gathered}
|
| 317 |
+
\frac{B D}{B W_{2}}=\frac{W_{2} D}{B W_{2}}+1=\frac{\sin \beta}{\sin \alpha}+1, \\
|
| 318 |
+
\frac{B C}{B W_{2}}=\frac{B C}{B D} \cdot \frac{B D}{B W_{2}}=\frac{1}{1-D C / B C} \cdot \frac{B D}{B W_{2}}=\frac{1}{1-A C^{2} / B C^{2}} \cdot \frac{B D}{B W_{2}}= \\
|
| 319 |
+
\frac{\sin ^{2} \alpha}{\sin ^{2} \alpha-\sin ^{2} \beta} \cdot \frac{\sin \beta+\sin \alpha}{\sin \alpha}=\frac{\sin \alpha}{\sin \alpha-\sin \beta} .
|
| 320 |
+
\end{gathered}
|
| 321 |
+
$$
|
| 322 |
+
|
| 323 |
+
Note that $A X B C$ is cyclic and so $\angle B X C=\angle B A C=\alpha$. Hence, $\angle X B C=180^{\circ}-$ $\angle B X C-\angle B C X=180^{\circ}-\alpha-\phi$. By the Law of sines for the triangle $B X C$, we have
|
| 324 |
+
|
| 325 |
+
$$
|
| 326 |
+
\begin{gathered}
|
| 327 |
+
\frac{B C}{W_{1} B}=\frac{W_{1} C}{W_{1} B}+1=\frac{C X}{B X}+1=\frac{\sin \angle C B X}{\sin \phi}+1= \\
|
| 328 |
+
\frac{\sin (\alpha+\phi)}{\sin \phi}+1=\sin \alpha \cot \phi+\cos \alpha+1 .
|
| 329 |
+
\end{gathered}
|
| 330 |
+
$$
|
| 331 |
+
|
| 332 |
+
So, it's enough to prove that
|
| 333 |
+
|
| 334 |
+
$$
|
| 335 |
+
\frac{\sin \alpha}{\sin \alpha-\sin \beta}=\sin \alpha \cot \phi+\cos \alpha
|
| 336 |
+
$$
|
| 337 |
+
|
| 338 |
+
Since $A C$ is tangent to the circle $A I X$, we have $\angle A X I=\angle I A C=\alpha / 2$. Moreover $\angle X A I=\angle X A B+\angle B A I=\phi+\alpha / 2$ and $\angle X I A=180^{\circ}-\angle X A I-\angle A X I=180^{\circ}-\alpha-\phi$. Applying the Law of sines again $X A C, X A I, I A C$ we obtain
|
| 339 |
+
|
| 340 |
+
$$
|
| 341 |
+
\begin{gathered}
|
| 342 |
+
\frac{A X}{\sin (\alpha+\phi)}=\frac{A I}{\sin \alpha / 2}, \\
|
| 343 |
+
\frac{A X}{\sin (\gamma-\phi)}=\frac{A C}{\sin \angle A X C}=\frac{A C}{\sin \beta}, \\
|
| 344 |
+
\frac{A I}{\sin \gamma / 2}=\frac{A C}{\sin (\alpha / 2+\gamma / 2)} .
|
| 345 |
+
\end{gathered}
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
Combining the last three equalities we end up with
|
| 349 |
+
|
| 350 |
+
$$
|
| 351 |
+
\begin{gathered}
|
| 352 |
+
\frac{\sin (\gamma-\phi)}{\sin (\alpha+\phi)}=\frac{A I}{A C} \cdot \frac{\sin \beta}{\sin \alpha / 2}=\frac{\sin \beta}{\sin \alpha / 2} \cdot \frac{\sin \gamma / 2}{\sin (\alpha / 2+\gamma / 2)} \\
|
| 353 |
+
\frac{\sin (\gamma-\phi)}{\sin (\alpha+\phi)}=\frac{\sin \gamma \cot \phi-\cos \gamma}{\sin \alpha \cot \phi+\cos \alpha}=\frac{2 \sin \beta / 2 \sin \gamma / 2}{\sin \alpha / 2}
|
| 354 |
+
\end{gathered}
|
| 355 |
+
$$
|
| 356 |
+
|
| 357 |
+
$$
|
| 358 |
+
\frac{\sin \alpha \sin \gamma \cot \phi-\sin \alpha \cos \gamma}{\sin \gamma \sin \alpha \cot \phi+\sin \gamma \cos \alpha}=\frac{2 \sin \beta / 2 \cos \alpha / 2}{\cos \gamma / 2}
|
| 359 |
+
$$
|
| 360 |
+
|
| 361 |
+
Subtracting 1 from both sides yields
|
| 362 |
+
|
| 363 |
+
$$
|
| 364 |
+
\begin{gathered}
|
| 365 |
+
\frac{-\sin \alpha \cos \gamma-\sin \gamma \cos \alpha}{\sin \gamma \sin \alpha \cot \phi+\sin \gamma \cos \alpha}=\frac{2 \sin \beta / 2 \cos \alpha / 2}{\cos \gamma / 2}-1= \\
|
| 366 |
+
\frac{2 \sin \beta / 2 \cos \alpha / 2-\sin (\alpha / 2+\beta / 2)}{\cos \gamma / 2}=\frac{\sin \beta / 2 \cos \alpha / 2-\sin \alpha / 2 \cos \beta / 2}{\cos \gamma / 2}, \\
|
| 367 |
+
\frac{-\sin (\alpha+\gamma)}{\sin \gamma \sin \alpha \cot \phi+\sin \gamma \cos \alpha}=\frac{\sin (\beta / 2-\alpha / 2)}{\cos \gamma / 2}, \\
|
| 368 |
+
\frac{-\sin \beta}{\sin \alpha \cot \phi+\cos \alpha}=2 \sin \gamma / 2 \sin (\beta / 2-\alpha / 2)= \\
|
| 369 |
+
2 \cos (\beta / 2+\alpha / 2) \sin (\beta / 2-\alpha / 2)=\sin \beta-\sin \alpha
|
| 370 |
+
\end{gathered}
|
| 371 |
+
$$
|
| 372 |
+
|
| 373 |
+
and the result follows. We are left to note that none of the denominators can vanish.
|
| 374 |
+
Solution by Achilleas Sinefakopoulos, Greece. We first note that
|
| 375 |
+
|
| 376 |
+
$$
|
| 377 |
+
\angle B A D=\angle B A C-\angle D A C=\angle A-\angle B .
|
| 378 |
+
$$
|
| 379 |
+
|
| 380 |
+
Let $C X$ and $A D$ meet at $K$. Then $\angle C X A=\angle A B C=\angle K A C$. Also, we have $\angle I X A=$ $\angle A / 2$, since $\omega$ is tangent to $A C$ at $A$. Therefore,
|
| 381 |
+
|
| 382 |
+
$$
|
| 383 |
+
\angle D A I=|\angle B-\angle A / 2|=|\angle K X A-\angle I X A|=\angle K X I,
|
| 384 |
+
$$
|
| 385 |
+
|
| 386 |
+
(the absolute value depends on whether $\angle B \geq \angle A / 2$ or not) which means that $X K I A$ is cyclic, i.e. $K$ lies also on $\omega$.
|
| 387 |
+
|
| 388 |
+
Let $I K$ meet $B C$ at $E$. (If $\angle B=\angle A / 2$, then $I K$ degenerates to the tangent line to $\omega$ at I.) Note that BEIA is cyclic, because
|
| 389 |
+
|
| 390 |
+
$$
|
| 391 |
+
\angle E I A=180^{\circ}-\angle K X A=180^{\circ}-\angle A B E .
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
We have $\angle E K A=180^{\circ}-\angle A X I=180^{\circ}-\angle A / 2$ and $\angle A E I=\angle A B I=\angle B / 2$. Hence
|
| 395 |
+
|
| 396 |
+
$$
|
| 397 |
+
\begin{aligned}
|
| 398 |
+
\angle E A K & =180^{\circ}-\angle E K A-\angle A E I \\
|
| 399 |
+
& =180^{\circ}-\left(180^{\circ}-\angle A / 2\right)-\angle B / 2 \\
|
| 400 |
+
& =(\angle A-\angle B) / 2 \\
|
| 401 |
+
& =\angle B A D / 2 .
|
| 402 |
+
\end{aligned}
|
| 403 |
+
$$
|
| 404 |
+
|
| 405 |
+
This means that $A E$ is the angle bisector of $\angle B A D$. Next, let $M$ be the point of intersection of $A E$ and $B I$. Then
|
| 406 |
+
|
| 407 |
+
$$
|
| 408 |
+
\angle E M I=180^{\circ}-\angle B / 2-\angle B A D / 2=180^{\circ}-\angle A / 2
|
| 409 |
+
$$
|
| 410 |
+
|
| 411 |
+
and so, its supplement is
|
| 412 |
+
|
| 413 |
+
$$
|
| 414 |
+
\angle A M I=\angle A / 2=\angle A X I
|
| 415 |
+
$$
|
| 416 |
+
|
| 417 |
+
so $X, M, K, I, A$ all lie on $\omega$. Next, we have
|
| 418 |
+
|
| 419 |
+
$$
|
| 420 |
+
\begin{aligned}
|
| 421 |
+
\angle X M A & =\angle X K A \\
|
| 422 |
+
& =180^{\circ}-\angle A D C-\angle X C B \\
|
| 423 |
+
& =180^{\circ}-\angle A-\angle X C B \\
|
| 424 |
+
& =\angle B+\angle X C A \\
|
| 425 |
+
& =\angle B+\angle X B A \\
|
| 426 |
+
& =\angle X B E,
|
| 427 |
+
\end{aligned}
|
| 428 |
+
$$
|
| 429 |
+
|
| 430 |
+
and so $X, B, E, M$ are concyclic. Hence
|
| 431 |
+
|
| 432 |
+
$$
|
| 433 |
+
\begin{aligned}
|
| 434 |
+
\angle E X C & =\angle E X M+\angle M X C \\
|
| 435 |
+
& =\angle M B E+\angle M A K \\
|
| 436 |
+
& =\angle B / 2+\angle B A D / 2 \\
|
| 437 |
+
& =\angle A / 2 \\
|
| 438 |
+
& =\angle B X C / 2
|
| 439 |
+
\end{aligned}
|
| 440 |
+
$$
|
| 441 |
+
|
| 442 |
+
This means that $X E$ is the angle bisector of $\angle B X C$ and so we are done!
|
| 443 |
+
|
| 444 |
+
|
| 445 |
+
Solution based on that by Eirini Miliori (HEL2), edited by A. Sinefakopoulos, Greece. It is $\angle A B D=\angle D A C$, and so $\overline{A C}$ is tangent to the circumcircle of $\triangle B A D$ at $A$. Hence $C A^{2}=C D \cdot C B$.
|
| 446 |
+
|
| 447 |
+
|
| 448 |
+
Triangle $\triangle A B C$ is similar to triangle $\triangle C A D$, because $\angle C$ is a common angle and $\angle C A D=\angle A B C$, and so $\angle A D C=\angle B A C=2 \varphi$.
|
| 449 |
+
Let $Q$ be the point of intersection of $\overline{A D}$ and $\overline{C X}$. Since $\angle B X C=\angle B A C=2 \varphi$, it follows that $B D Q X$ is cyclic. Therefore, $C D \cdot C B=C Q \cdot C X=C A^{2}$ which implies that $Q$ lies on $\omega$.
|
| 450 |
+
Next let $P$ be the point of intersection of $\overline{A D}$ with the circumcircle of triangle $\triangle A B C$. Then $\angle P B C=\angle P A C=\angle A B C=\angle A P C$ yielding $C A=C P$. So, let $T$ be on the side $\overline{B C}$ such that $C T=C A=C P$. Then
|
| 451 |
+
|
| 452 |
+
$$
|
| 453 |
+
\angle T A D=\angle T A C-\angle D A C=\left(90^{\circ}-\frac{\angle C}{2}\right)-\angle B=\frac{\angle A-\angle B}{2}=\frac{\angle B A D}{2}
|
| 454 |
+
$$
|
| 455 |
+
|
| 456 |
+
that is, line $\overline{A T}$ is the angle bisector of $\angle B A D$. We want to show that $\overline{X T}$ is the angle bisector of $\angle B X C$. To this end, it suffices to show that $\angle T X C=\varphi$.
|
| 457 |
+
It is $C T^{2}=C A^{2}=C Q \cdot C X$, and so $\overline{C T}$ is tangent to the circumcircle of $\triangle X T Q$ at $T$. Since $\angle T X Q=\angle Q T C$ and $\angle Q D C=2 \varphi$, it suffices to show that $\angle T Q D=\varphi$, or, in other words, that $I, Q$, and $T$ are collinear.
|
| 458 |
+
|
| 459 |
+
Let $T^{\prime}$ is the point of intersection of $\overline{I Q}$ and $\overline{B C}$. Then $\triangle A I C$ is congruent to $\triangle T^{\prime} I C$, since they share $\overline{C I}$ as a common side, $\angle A C I=\angle T^{\prime} C I$, and
|
| 460 |
+
|
| 461 |
+
$$
|
| 462 |
+
\angle I T^{\prime} D=2 \varphi-\angle T^{\prime} Q D=2 \varphi-\angle I Q A=2 \varphi-\angle I X A=\varphi=\angle I A C .
|
| 463 |
+
$$
|
| 464 |
+
|
| 465 |
+
Therefore, $C T^{\prime}=C A=C T$, which means that $T$ coincides with $T^{\prime}$ and completes the proof.
|
| 466 |
+
|
| 467 |
+
Solution based on the work of Artemis-Chrysanthi Savva (HEL4), completed by A. Sinefakopoulos, Greece. Let $G$ be the point of intersection of $\overline{A D}$ and $\overline{C X}$. Since the quadrilateral $A X B C$ is cyclic, it is $\angle A X C=\angle A B C$.
|
| 468 |
+
|
| 469 |
+
|
| 470 |
+
Let the line $\overline{A D}$ meet $\omega$ at $K$. Then it is $\angle A X K=\angle C A D=\angle A B C$, because the angle that is formed by a chord and a tangent to the circle at an endpoint of the chord equals the inscribed angle to that chord. Therefore, $\angle A X K=\angle A X C=\angle A X G$. This means that the point $G$ coincides with the point $K$ and so $G$ belongs to the circle $\omega$.
|
| 471 |
+
|
| 472 |
+
Let $E$ be the point of intersection of the angle bisector of $\angle D A B$ with $\overline{B C}$. It suffices to show that
|
| 473 |
+
|
| 474 |
+
$$
|
| 475 |
+
\frac{C E}{B E}=\frac{X C}{X B} .
|
| 476 |
+
$$
|
| 477 |
+
|
| 478 |
+
Let $F$ be the second point of intersection of $\omega$ with $\overline{A B}$. Then we have $\angle I A F=\frac{\angle C A B}{2}=$ $\angle I X F$, where $I$ is the incenter of $\triangle A B C$, because $\angle I A F$ and $\angle I X F$ are inscribed in the same arc of $\omega$. Thus $\triangle A I F$ is isosceles with $A I=I F$. Since $I$ is the incenter of $\triangle A B C$, we have $A F=2(s-a)$, where $s=(a+b+c) / 2$ is the semiperimeter of $\triangle A B C$. Also, it is $C E=A C=b$ because in triangle $\triangle A C E$, we have
|
| 479 |
+
|
| 480 |
+
$$
|
| 481 |
+
\begin{aligned}
|
| 482 |
+
\angle A E C & =\angle A B C+\angle B A E \\
|
| 483 |
+
& =\angle A B C+\frac{\angle B A D}{2} \\
|
| 484 |
+
& =\angle A B C+\frac{\angle B A C-\angle A B C}{2} \\
|
| 485 |
+
& =90^{\circ}-\frac{\angle A C E}{2}
|
| 486 |
+
\end{aligned}
|
| 487 |
+
$$
|
| 488 |
+
|
| 489 |
+
and so $\angle C A E=180^{\circ}-\angle A E C-\angle A C E=90^{\circ}-\frac{\angle A C E}{2}=\angle A E C$. Hence
|
| 490 |
+
|
| 491 |
+
$$
|
| 492 |
+
B F=B A-A F=c-2(s-a)=a-b=C B-C E=B E .
|
| 493 |
+
$$
|
| 494 |
+
|
| 495 |
+
Moreover, triangle $\triangle C A X$ is similar to triangle $\triangle B F X$, because $\angle A C X=\angle F B X$ and
|
| 496 |
+
|
| 497 |
+
$$
|
| 498 |
+
\angle X F B=\angle X A F+\angle A X F=\angle X A F+\angle C A F=\angle C A X
|
| 499 |
+
$$
|
| 500 |
+
|
| 501 |
+
Therefore
|
| 502 |
+
|
| 503 |
+
$$
|
| 504 |
+
\frac{C E}{B E}=\frac{A C}{B F}=\frac{X C}{X B},
|
| 505 |
+
$$
|
| 506 |
+
|
| 507 |
+
as desired. The proof is complete.
|
| 508 |
+
Solution by IRL1 and IRL 5. Let $\omega$ denote the circle through $A$ and $I$ tangent to $A C$. Let $Y$ be the second point of intersection of the circle $\omega$ with the line $A D$. Let $L$
|
| 509 |
+
be the intersection of $B C$ with the angle bisector of $\angle B A D$. We will prove $\angle L X C=$ $1 / 2 \angle B A C=1 / 2 \angle B X C$.
|
| 510 |
+
|
| 511 |
+
We will refer to the angles of $\triangle A B C$ as $\angle A, \angle B, \angle C$. Thus $\angle B A D=\angle A-\angle B$.
|
| 512 |
+
On the circumcircle of $\triangle A B C$, we have $\angle A X C=\angle A B C=\angle C A D$, and since $A C$ is tangent to $\omega$, we have $\angle C A D=\angle C A Y=\angle A X Y$. Hence $C, X, Y$ are collinear.
|
| 513 |
+
Also note that $\triangle C A L$ is isosceles with $\angle C A L=\angle C L A=\frac{1}{2}(\angle B A D)+\angle A B C=\frac{1}{2}(\angle A+$ $\angle B)$ hence $A C=C L$. Moreover, $C I$ is angle bisector to $\angle A C L$ so it's the symmetry axis for the triangle, hence $\angle I L C=\angle I A C=1 / 2 \angle A$ and $\angle A L I=\angle L I A=1 / 2 \angle B$. Since $A C$ is tangent to $\omega$, we have $\angle A Y I=\angle I A C=1 / 2 \angle A=\angle L A Y+\angle A L I$. Hence $L, Y, I$ are collinear.
|
| 514 |
+
|
| 515 |
+
Since $A C$ is tangent to $\omega$, we have $\triangle C A Y \sim \triangle C X A$ hence $C A^{2}=C X \cdot C Y$. However we proved $C A=C L$ hence $C L^{2}=C X \cdot C Y$. Hence $\triangle C L Y \sim \triangle C X L$ and hence $\angle C X L=\angle C L Y=\angle C A I=1 / 2 \angle A$.
|
| 516 |
+
|
| 517 |
+
|
| 518 |
+
Solution by IRL 5. Let $M$ be the midpoint of the $\operatorname{arc} B C$. Let $\omega$ denote the circle through $A$ and $I$ tangent to $A C$. Let $N$ be the second point of intersection of $\omega$ with $A B$ and $L$ the intersection of $B C$ with the angle bisector of $\angle B A D$. We know $\frac{D L}{L B}=\frac{A D}{A B}$ and want to prove $\frac{X B}{X C}=\frac{L B}{L C}$.
|
| 519 |
+
First note that $\triangle C A L$ is isosceles with $\angle C A L=\angle C L A=\frac{1}{2}(\angle B A D)+\angle A B C$ hence $A C=C L$ and $\frac{L B}{L C}=\frac{L B}{A C}$.
|
| 520 |
+
Now we calculate $\frac{X B}{X C}$ :
|
| 521 |
+
Comparing angles on the circles $\omega$ and the circumcircle of $\triangle A B C$ we get $\triangle X I N \sim$ $\triangle X M B$ and hence also $\triangle X I M \sim \triangle X N B$ (having equal angles at $X$ and proportional adjoint sides). Hence $\frac{X B}{X M}=\frac{N B}{I M}$.
|
| 522 |
+
Also comparing angles on the circles $\omega$ and the circumcircle of $\triangle A B C$ and using the tangent $A C$ we get $\triangle X A I \sim \triangle X C M$ and hence also $\triangle X A C \sim \triangle X I M$. Hence $\frac{X C}{X M}=$ $\frac{A C}{I M}$.
|
| 523 |
+
Comparing the last two equations we get $\frac{X B}{X C}=\frac{N B}{A C}$. Comparing with $\frac{L B}{L C}=\frac{L B}{A C}$, it remains to prove $N B=L B$.
|
| 524 |
+
|
| 525 |
+
|
| 526 |
+
We prove $\triangle I N B \equiv \triangle I L B$ as follows:
|
| 527 |
+
First, we note that $I$ is the circumcentre of $\triangle A L N$. Indeed, $C I$ is angle bisector in the isosceles triangle $A C L$ so it's perpendicular bisector for $A L$. As well, $\triangle I A N$ is isosceles with $\angle I N A=\angle C A I=\angle I A B$ hence $I$ is also on the perpendicular bisector of $A N$.
|
| 528 |
+
|
| 529 |
+
Hence $I N=I L$ and also $\angle N I L=2 \angle N A L=\angle A-\angle B=2 \angle N I B$ (the last angle is calculated using that the exterior angle of $\triangle N I B$ is $\angle I N A=\angle A / 2$. Hence $\angle N I B=$ $\angle L I B$ and $\triangle I N B \equiv \triangle I L B$ by SAS.
|
| 530 |
+
|
| 531 |
+
Solution by ISR5 (with help from IRL5). Let $M, N$ be the midpoints of arcs $B C, B A$ of the circumcircle $A B C$, respectively. Let $Y$ be the second intersection of $A D$ and circle $A B C$. Let $E$ be the incenter of triangle $A B Y$ and note that $E$ lies on the angle bisectors of the triangle, which are the lines $Y N$ (immediate), $B C$ (since $\angle C B Y=\angle C A Y=\angle C A D=\angle A B C)$ and the angle bisector of $\angle D A B$; so the question reduces to showing that $E$ is also on $X M$, which is the angle bisector of $\angle C X B$.
|
| 532 |
+
|
| 533 |
+
We claim that the three lines $C X, A D Y, I E$ are concurrent at a point $D^{\prime}$. We will complete the proof using this fact, and the proof will appear at the end (and see the solution by HEL5 for an alternative proof of this fact).
|
| 534 |
+
|
| 535 |
+
To show that XEM are collinear, we construct a projective transformation which projects $M$ to $X$ through center $E$. We produce it as a composition of three other projections. Let $O$ be the intersection of lines $A D^{\prime} D Y$ and $C I N$. Projecting the points $Y N C M$ on the circle $A B C$ through the (concyclic) point $A$ to the line $C N$ yields the points $O N C I$. Projecting these points through $E$ to the line $A Y$ yields $O Y D D^{\prime}$ (here we use the facts that $D^{\prime}$ lies on $I E$ and $A Y$ ). Projecting these points to the circle $A B C$ through $C$ yields $N Y B X$ (here we use the fact that $D^{\prime}$ lies on $C X$ ). Composing, we observe that we found a projection of the circle $A B C$ to itself sending $Y N C M$ to $N Y B X$. Since the projection of the circle through $E$ also sends $Y N C$ to $N Y B$, and three points determine a projective transformation, the projection through $E$ also sends $M$ to $X$, as claimed.
|
| 536 |
+
|
| 537 |
+
|
| 538 |
+
Let $B^{\prime}, D^{\prime}$ be the intersections of $A B, A D$ with the circle $A X I$, respectively. We wish to show that this $D^{\prime}$ is the concurrency point defined above, i.e. that $C D^{\prime} X$ and $I D^{\prime} E$ are collinear. Additionally, we will show that $I$ is the circumcenter of $A B^{\prime} E$.
|
| 539 |
+
|
| 540 |
+
Consider the inversion with center $C$ and radius $C A$. The circles $A X I$ and $A B D$ are tangent to $C A$ at $A$ (the former by definition, the latter since $\angle C A D=\angle A B C$ ), so they are preserved under the inversion. In particular, the inversion transposes $D$ and $B$ and preserves $A$, so sends the circle $C A B$ to the line $A D$. Thus $X$, which is the second intersection of circles $A B C$ and $A X I$, is sent by the inversion to the second intersection of $A D$ and circle $A X I$, which is $D^{\prime}$. In particular $C D^{\prime} X$ are collinear.
|
| 541 |
+
|
| 542 |
+
In the circle $A I B^{\prime}, A I$ is the angle bisector of $B^{\prime} A$ and the tangent at $A$, so $I$ is the midpoint of the arc $A B^{\prime}$, and in particular $A I=I B^{\prime}$. By angle chasing, we find that $A C E$ is an isosceles triangle:
|
| 543 |
+
$\angle C A E=\angle C A D+\angle D A E=\angle A B C+\angle E A B=\angle A B E+\angle E A B=\angle A E B=\angle A E C$,
|
| 544 |
+
thus the angle bisector $C I$ is the perpendicular bisector of $A E$ and $A I=I E$. Thus $I$ is the circumcenter of $A B^{\prime} E$.
|
| 545 |
+
|
| 546 |
+
We can now show that $I D^{\prime} E$ are collinear by angle chasing:
|
| 547 |
+
|
| 548 |
+
$$
|
| 549 |
+
\angle E I B^{\prime}=2 \angle E A B^{\prime}=2 \angle E A B=\angle D A B=\angle D^{\prime} A B^{\prime}=\angle D^{\prime} I B^{\prime} .
|
| 550 |
+
$$
|
| 551 |
+
|
| 552 |
+
Solution inspired by ISR2. Let $W$ be the midpoint of arc $B C$, let $D^{\prime}$ be the second intersection point of $A D$ and the circle $A B C$. Let $P$ be the intersection of the angle bisector $X W$ of $\angle C X B$ with $B C$; we wish to prove that $A P$ is the angle bisector of $D A B$. Denote $\alpha=\frac{\angle C A B}{2}, \beta=\angle A B C$.
|
| 553 |
+
|
| 554 |
+
Let $M$ be the intersection of $A D$ and $X C$. Angle chasing finds:
|
| 555 |
+
|
| 556 |
+
$$
|
| 557 |
+
\begin{aligned}
|
| 558 |
+
\angle M X I & =\angle A X I-\angle A X M=\angle C A I-\angle A X C=\angle C A I-\angle A B C=\alpha-\beta \\
|
| 559 |
+
& =\angle C A I-\angle C A D=\angle D A I=\angle M A I
|
| 560 |
+
\end{aligned}
|
| 561 |
+
$$
|
| 562 |
+
|
| 563 |
+
And in particular $M$ is on $\omega$. By angle chasing we find
|
| 564 |
+
|
| 565 |
+
$$
|
| 566 |
+
\angle X I A=\angle I X A+\angle X A I=\angle I C A+\angle X A I=\angle X A C=\angle X B C=\angle X B P
|
| 567 |
+
$$
|
| 568 |
+
|
| 569 |
+
and $\angle P X B=\alpha=\angle C A I=\angle A X I$, and it follows that $\triangle X I A \sim \triangle X B P$. Let $S$ be the second intersection point of the cirumcircles of $X I A$ and $X B P$. Then by the spiral map lemma (or by the equivalent angle chasing) it follows that $I S B$ and $A S P$ are collinear.
|
| 570 |
+
|
| 571 |
+
Let $L$ be the second intersection of $\omega$ and $A B$. We want to prove that $A S P$ is the angle bisector of $\angle D A B=\angle M A L$, i.e. that $S$ is the midpoint of the $\operatorname{arc} M L$ of $\omega$. And this follows easily from chasing angular arc lengths in $\omega$ :
|
| 572 |
+
|
| 573 |
+
$$
|
| 574 |
+
\begin{aligned}
|
| 575 |
+
& \overparen{A I}=\angle C A I=\alpha \\
|
| 576 |
+
& \widehat{I L}=\angle I A L=\alpha \\
|
| 577 |
+
& \widehat{M I}=\angle M X I=\alpha-\beta \\
|
| 578 |
+
& \widehat{A I}-\widehat{S L}=\angle A B I=\frac{\beta}{2}
|
| 579 |
+
\end{aligned}
|
| 580 |
+
$$
|
| 581 |
+
|
| 582 |
+
And thus
|
| 583 |
+
|
| 584 |
+
$$
|
| 585 |
+
\widehat{M L}=\widehat{M I}+\widehat{I L}=2 \alpha-\beta=2\left(\widehat{A I}-\frac{\beta}{2}\right)=2 \widehat{S L}
|
| 586 |
+
$$
|
| 587 |
+
|
| 588 |
+
|
| 589 |
+
|
| 590 |
+
Solution by inversion, by JPN Observer A, Satoshi Hayakawa. Let $E$ be the intersection of the bisector of $\angle B A D$ and $B C$, and $N$ be the middle point of arc $B C$ of the circumcircle of $A B C$. Then it suffices to show that $E$ is on line $X N$.
|
| 591 |
+
|
| 592 |
+
We consider the inversion at $A$. Let $P^{*}$ be the image of a point denoted by $P$. Then $A, B^{*}, C^{*}, E^{*}$ are concyclic, $X^{*}, B^{*}, C^{*}$ are colinear, and $X^{*} I^{*}$ and $A C^{*}$ are parallel. Now it suffices to show that $A, X^{*}, E^{*}, N^{*}$ are concyclic. Let $Y$ be the intersection of $B^{*} C^{*}$ and $A E^{*}$. Then, by the power of a point, we get
|
| 593 |
+
|
| 594 |
+
$$
|
| 595 |
+
\begin{aligned}
|
| 596 |
+
A, X^{*}, E^{*}, N^{*} \text { are concyclic } & \Longleftrightarrow Y X^{*} \cdot Y N^{*}=Y A \cdot Y E^{*} \\
|
| 597 |
+
& \Longleftrightarrow Y X^{*} \cdot Y N^{*}=Y B^{*} \cdot Y C^{*} \\
|
| 598 |
+
& \left(A, B^{*}, C^{*}, E^{*} \text { are concyclic }\right)
|
| 599 |
+
\end{aligned}
|
| 600 |
+
$$
|
| 601 |
+
|
| 602 |
+
Here, by the property of inversion, we have
|
| 603 |
+
|
| 604 |
+
$$
|
| 605 |
+
\angle A I^{*} B^{*}=\angle A B I=\frac{1}{2} \angle A B C=\frac{1}{2} \angle C^{*} A D^{*} .
|
| 606 |
+
$$
|
| 607 |
+
|
| 608 |
+
|
| 609 |
+
|
| 610 |
+
Define $Q, R$ as described in the figure, and we get by simple angle chasing
|
| 611 |
+
|
| 612 |
+
$$
|
| 613 |
+
\angle Q A I^{*}=\angle Q I^{*} A, \quad \angle R A I^{*}=\angle B^{*} I^{*} A
|
| 614 |
+
$$
|
| 615 |
+
|
| 616 |
+
Especially, $B^{*} R$ and $A I^{*}$ are parallel, so that we have
|
| 617 |
+
|
| 618 |
+
$$
|
| 619 |
+
\frac{Y B^{*}}{Y N^{*}}=\frac{Y R}{Y A}=\frac{Y X^{*}}{Y C^{*}}
|
| 620 |
+
$$
|
| 621 |
+
|
| 622 |
+
and the proof is completed.
|
| 623 |
+
|
EGMO/md/en-2019-solutions-day2.md
ADDED
|
@@ -0,0 +1,379 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Day 2. Solutions
|
| 2 |
+
|
| 3 |
+
Problem 4 (Poland). Let $A B C$ be a triangle with incentre $I$. The circle through $B$ tangent to $A I$ at $I$ meets side $A B$ again at $P$. The circle through $C$ tangent to $A I$ at $I$ meets side $A C$ again at $Q$. Prove that $P Q$ is tangent to the incircle of $A B C$.
|
| 4 |
+
Solution 1. Let $Q X, P Y$ be tangent to the incircle of $A B C$, where $X, Y$ lie on the incircle and do not lie on $A C, A B$. Denote $\angle B A C=\alpha, \angle C B A=\beta, \angle A C B=\gamma$.
|
| 5 |
+
|
| 6 |
+
Since $A I$ is tangent to the circumcircle of $C Q I$ we get $\angle Q I A=\angle Q C I=\frac{\gamma}{2}$. Thus
|
| 7 |
+
|
| 8 |
+
$$
|
| 9 |
+
\angle I Q C=\angle I A Q+\angle Q I A=\frac{\alpha}{2}+\frac{\gamma}{2} .
|
| 10 |
+
$$
|
| 11 |
+
|
| 12 |
+
By the definition of $X$ we have $\angle I Q C=\angle X Q I$, therefore
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\angle A Q X=180^{\circ}-\angle X Q C=180^{\circ}-\alpha-\gamma=\beta
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
Similarly one can prove that $\angle A P Y=\gamma$. This means that $Q, P, X, Y$ are collinear which leads us to the conclusion that $X=Y$ and $Q P$ is tangent to the incircle at $X$.
|
| 19 |
+
|
| 20 |
+
|
| 21 |
+
Solution 2. By the power of a point we have
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
A D \cdot A C=A I^{2}=A P \cdot A B, \quad \text { which means that } \quad \frac{A Q}{A P}=\frac{A B}{A C}
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
and therefore triangles $A D P, A B C$ are similar. Let $J$ be the incenter of $A Q P$. We obtain
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\angle J P Q=\angle I C B=\angle Q C I=\angle Q I J
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
thus $J, P, I, Q$ are concyclic. Let $S$ be the intersection of $A I$ and $B C$. It follows that
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\angle I Q P=\angle I J P=\angle S I C=\angle I Q C .
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
This means that $I Q$ is the angle bisector of $\angle C Q P$, so $Q P$ is indeed tangent to the incircle of $A B C$.
|
| 40 |
+
|
| 41 |
+
Comment. The final angle chasing from the Solution 2 may simply be replaced by the observation that since $J, P, I, Q$ are concyclic, then $I$ is the $A$-excenter of triangle $A P Q$.
|
| 42 |
+
|
| 43 |
+
Solution 3. Like before, notice that $A Q \cdot A C=A P \cdot A B=A I^{2}$. Consider the positive inversion $\Psi$ with center $A$ and power $A I^{2}$. This maps $P$ to $B$ (and vice-versa), $Q$ to $C$
|
| 44 |
+
(and vice-versa), and keeps the incenter $I$ fixed. The problem statement will follow from the fact that the image of the incircle of triangle $A B C$ under $\Psi$ is the so-called mixtilinear incircle of $A B C$, which is defined to be the circle tangent to the lines $A B, A C$, and the circumcircle of $A B C$. Indeed, since the image of the line $Q P$ is the circumcircle of $A B C$, and inversion preserves tangencies, this implies that $Q P$ is tangent to the incircle of $A B C$.
|
| 45 |
+
|
| 46 |
+
We justify the claim as follows: let $\gamma$ be the incircle of $A B C$ and let $\Gamma_{A}$ be the $A$-mixtilinear incircle of $A B C$. Let $K$ and $L$ be the tangency points of $\gamma$ with the sides $A B$ and $A C$, and let $U$ and $V$ be the tangency points of $\Gamma_{A}$ with the sides $A B$ and $A C$, respectively. It is well-known that the incenter $I$ is the midpoint of segment $U V$. In particular, since also $A I \perp U V$, this implies that $A U=A V=\frac{A I}{\cos \frac{A}{2}}$. Note that $A K=A L=A I \cdot \cos \frac{A}{2}$. Therefore, $A U \cdot A K=A V \cdot A L=A I^{2}$, which means that $U$ and $V$ are the images of $K$ and $L$ under $\Psi$. Since $\Gamma_{A}$ is the unique circle simultaneously tangent to $A B$ at $U$ and to $A C$ at $V$, it follows that the image of $\gamma$ under $\Psi$ must be precisely $\Gamma_{A}$, as claimed.
|
| 47 |
+
|
| 48 |
+
Solution by Achilleas Sinefakopoulos, Greece. From the power of a point theorem, we have
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
A P \cdot A B=A I^{2}=A Q \cdot A C
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Hence $P B C Q$ is cyclic, and so, $\angle A P Q=\angle B C A$. Let $K$ be the circumcenter of $\triangle B I P$ and let $L$ be the circumcenter of $\triangle Q I C$. Then $\overline{K L}$ is perpendicular to $\overline{A I}$ at $I$.
|
| 55 |
+
|
| 56 |
+
Let $N$ be the point of intersection of line $\overline{K L}$ with $\overline{A B}$.Then in the right triangle $\triangle N I A$, we have $\angle A N I=90^{\circ}-\frac{\angle B A C}{2}$ and from the external angle theorem for triangle $\triangle B N I$, we have $\angle A N I=\frac{\angle A B C}{2}+\angle N I B$. Hence
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
\angle N I B=\angle A N I-\frac{\angle A B C}{2}=\left(90^{\circ}-\frac{\angle B A C}{2}\right)-\frac{\angle A B C}{2}=\frac{\angle B C A}{2} .
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
Since $M I$ is tangent to the circumcircle of $\triangle B I P$ at $I$, we have
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\angle B P I=\angle B I M=\angle N I M-\angle N I B=90^{\circ}-\frac{\angle B C A}{2} .
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
Also, since $\angle A P Q=\angle B C A$, we have
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
\angle Q P I=180^{\circ}-\angle A P Q-\angle B P I=180^{\circ}-\angle B C A-\left(90^{\circ}-\frac{\angle B C A}{2}\right)=90^{\circ}-\frac{\angle B C A}{2}
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
as well. Hence $I$ lies on the angle bisector of $\angle B P Q$, and so it is equidistant from its sides $\overline{P Q}$ and $\overline{P B}$. Therefore, the distance of $I$ from $\overline{P Q}$ equals the inradius of $\triangle A B C$, as desired.
|
| 75 |
+
|
| 76 |
+
|
| 77 |
+
Solution by Eirini Miliori (HEL2). Let $D$ be the point of intersection of $\overline{A I}$ and $\overline{B C}$ and let $R$ be the point of intersection of $\overline{A I}$ and $\overline{P Q}$. We have $\angle R I P=\angle P B I=\frac{\angle B}{2}$, $\angle R I Q=\angle I C Q=\frac{\angle C}{2}, \angle I Q C=\angle D I C=x$ and $\angle B P I=\angle B I D=\varphi$, since $\overline{A I}^{2}$ is tangent to both circles.
|
| 78 |
+
|
| 79 |
+
|
| 80 |
+
From the angle bisector theorem, we have
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\frac{R Q}{R P}=\frac{A Q}{A P} \quad \text { and } \quad \frac{A C}{A B}=\frac{D C}{B D}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
Since $\overline{A I}$ is tangent to both circles at $I$, we have $A I^{2}=A Q \cdot A C$ and $A I^{2}=A P \cdot A B$. Therefore,
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
\frac{R Q}{R P} \cdot \frac{D C}{B D}=\frac{A Q \cdot A C}{A B \cdot A P}=1
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
From the sine law in triangles $\triangle Q R I$ and $\triangle P R I$, it follows that $\frac{R Q}{\sin \frac{\angle C}{2}}=\frac{R I}{\sin y}$ and $\frac{R P}{\sin \frac{\angle B}{2}}=\frac{R I}{\sin \omega}$, respectively. Hence
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\frac{R Q}{R P} \cdot \frac{\sin \frac{\angle B}{2}}{\sin \frac{\angle C}{2}}=\frac{\sin \omega}{\sin y}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
Similarly, from the sine law in triangles $\triangle I D C$ and $\triangle I D B$, it is $\frac{D C}{\sin x}=\frac{I D}{\sin \frac{\angle C}{2}}$ and $\frac{B D}{\sin \varphi}=\frac{I D}{\sin \frac{\angle B}{2}}$, and so
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\frac{D C}{B D} \cdot \frac{\sin \varphi}{\sin x}=\frac{\sin \frac{\angle B}{2}}{\sin \frac{\angle C}{2}}
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
By multiplying equations (2) with (3), we obtain $\frac{R Q}{R P} \cdot \frac{D C}{B D} \cdot \frac{\sin \varphi}{\sin x}=\frac{\sin \omega}{\sin y}$, which combined with (1) and cross-multiplying yields
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\sin \varphi \cdot \sin y=\sin \omega \cdot \sin x
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Let $\theta=90^{\circ}+\frac{\angle A}{2}$. Since $I$ is the incenter of $\triangle A B C$, we have $x=90^{\circ}+\frac{\angle A}{2}-\varphi=\theta-\phi$. Also, in triangle $\triangle P I Q$, we see that $\omega+y+\frac{\angle B}{2}+\frac{\angle C}{2}=180^{\circ}$, and so $y=\theta-\omega$.
|
| 111 |
+
Therefore, equation (4) yields
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
\sin \varphi \cdot \sin (\theta-\omega)=\sin \omega \cdot \sin (\theta-\varphi)
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
or
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\frac{1}{2}(\cos (\varphi-\theta+\omega)-\cos (\varphi+\theta-\omega))=\frac{1}{2}(\cos (\omega-\theta+\varphi)-\cos (\omega+\theta-\varphi))
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
which is equivalent to
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\cos (\varphi+\theta-\omega)=\cos (\omega+\theta-\varphi)
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
So
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
\varphi+\theta-\omega=2 k \cdot 180^{\circ} \pm(\omega+\theta-\varphi), \quad(k \in \mathbb{Z} .)
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
If $\varphi+\theta-\omega=2 k \cdot 180^{\circ}+(\omega+\theta-\varphi)$, then $2(\varphi-\omega)=2 k \cdot 180^{\circ}$, with $|\varphi-\omega|<180^{\circ}$ forcing $k=0$ and $\varphi=\omega$. If $\varphi+\theta-\omega=2 k \cdot 180^{\circ}-(\omega+\theta-\varphi)$, then $2 \theta=2 k \cdot 180^{\circ}$, which contradicts the fact that $0^{\circ}<\theta<180^{\circ}$. Hence $\varphi=\omega$, and so $P I$ is the angle bisector of $\angle Q P B$.
|
| 136 |
+
|
| 137 |
+
Therefore the distance of $I$ from $\overline{P Q}$ is the same with the distance of $I$ from $A B$, which is equal to the inradius of $\triangle A B C$. Consequently, $\overline{P Q}$ is tangent to the incircle of $\triangle A B C$.
|
| 138 |
+
|
| 139 |
+
## Problem 5 (Netherlands).
|
| 140 |
+
|
| 141 |
+
Let $n \geq 2$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be positive integers. Show that there exist positive integers $b_{1}, b_{2}, \ldots, b_{n}$ satisfying the following three conditions:
|
| 142 |
+
|
| 143 |
+
1. $a_{i} \leq b_{i}$ for $i=1,2, \ldots, n$;
|
| 144 |
+
2. the remainders of $b_{1}, b_{2}, \ldots, b_{n}$ on division by $n$ are pairwise different; and
|
| 145 |
+
3. $b_{1}+\cdots+b_{n} \leq n\left(\frac{n-1}{2}+\left\lfloor\frac{a_{1}+\cdots+a_{n}}{n}\right\rfloor\right)$.
|
| 146 |
+
(Here, $\lfloor x\rfloor$ denotes the integer part of real number $x$, that is, the largest integer that does not exceed $x$.)
|
| 147 |
+
|
| 148 |
+
Solution 1. We define the $b_{i}$ recursively by letting $b_{i}$ be the smallest integer such that $b_{i} \geq a_{i}$ and such that $b_{i}$ is not congruent to any of $b_{1}, \ldots, b_{i-1}$ modulo $n$. Then $b_{i}-a_{i} \leq i-1$, since of the $i$ consecutive integers $a_{i}, a_{i}+1, \ldots, a_{i}+i-1$, at most $i-1$ are congruent to one of $b_{1}, \ldots, b_{i-1}$ modulo $n$. Since all $b_{i}$ are distinct modulo $n$, we have $\sum_{i=1}^{n} b_{i} \equiv \sum_{i=1}^{n}(i-1)=\frac{1}{2} n(n-1)$ modulo $n$, so $n$ divides $\sum_{i=1}^{n} b_{i}-\frac{1}{2} n(n-1)$. Moreover, we have $\sum_{i=1}^{n} b_{i}-\sum_{i=1}^{n} a_{i} \leq \sum_{i=1}^{n}(i-1)=\frac{1}{2} n(n-1)$, hence $\sum_{i=1}^{n} b_{i}-\frac{1}{2} n(n-1) \leq \sum_{i=1}^{n}$. As the left hand side is divisible by $n$, we have
|
| 149 |
+
|
| 150 |
+
$$
|
| 151 |
+
\frac{1}{n}\left(\sum_{i=1}^{n} b_{i}-\frac{1}{2} n(n-1)\right) \leq\left[\frac{1}{n} \sum_{i=1}^{n} a_{i}\right]
|
| 152 |
+
$$
|
| 153 |
+
|
| 154 |
+
which we can rewrite as
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
\sum_{i=1}^{n} b_{i} \leq n\left(\frac{n-1}{2}+\left[\frac{1}{n} \sum_{i=1}^{n} a_{i}\right]\right)
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
as required.
|
| 161 |
+
Solution 2. Note that the problem is invariant under each of the following operations:
|
| 162 |
+
|
| 163 |
+
- adding a multiple of $n$ to some $a_{i}$ (and the corresponding $b_{i}$ );
|
| 164 |
+
- adding the same integer to all $a_{i}$ (and all $b_{i}$ );
|
| 165 |
+
- permuting the index set $1,2, \ldots, n$.
|
| 166 |
+
|
| 167 |
+
We may therefore remove the restriction that our $a_{i}$ and $b_{i}$ be positive.
|
| 168 |
+
For each congruence class $\bar{k}$ modulo $n(\bar{k}=\overline{0}, \ldots, \overline{n-1})$, let $h(k)$ be the number of $i$ such that $a_{i}$ belongs to $\bar{k}$. We will now show that the problem is solved if we can find a $t \in \mathbb{Z}$ such that
|
| 169 |
+
|
| 170 |
+
$$
|
| 171 |
+
\begin{array}{cl}
|
| 172 |
+
h(t) & \geq 1, \\
|
| 173 |
+
h(t)+h(t+1) & \geq 2 \\
|
| 174 |
+
h(t)+h(t+1)+h(t+2) & \geq 3
|
| 175 |
+
\end{array}
|
| 176 |
+
$$
|
| 177 |
+
|
| 178 |
+
Indeed, these inequalities guarantee the existence of elements $a_{i_{1}} \in \bar{t}, a_{i_{2}} \in \bar{t} \cup \overline{t+1}$, $a_{i_{3}} \in \bar{t} \cup \overline{t+1} \cup \overline{t+2}$, et cetera, where all $i_{k}$ are different. Subtracting appropriate
|
| 179 |
+
multiples of $n$ and reordering our elements, we may assume $a_{1}=t, a_{2} \in\{t, t+1\}$, $a_{3} \in\{t, t+1, t+2\}$, et cetera. Finally subtracting $t$ from the complete sequence, we may assume $a_{1}=0, a_{2} \in\{0,1\}, a_{3} \in\{0,1,2\}$ et cetera. Now simply setting $b_{i}=i-1$ for all $i$ suffices, since $a_{i} \leq b_{i}$ for all $i$, the $b_{i}$ are all different modulo $n$, and
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\sum_{i=1}^{n} b_{i}=\frac{n(n-1)}{2} \leq \frac{n(n-1)}{2}+n\left[\frac{\sum_{i=1}^{n} a_{i}}{n}\right] .
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
Put $x_{i}=h(i)-1$ for all $i=0, \ldots, n-1$. Note that $x_{i} \geq-1$, because $h(i) \geq 0$. If we have $x_{i} \geq 0$ for all $i=0, \ldots, n-1$, then taking $t=0$ completes the proof. Otherwise, we can pick some index $j$ such that $x_{j}=-1$. Let $y_{i}=x_{i}$ where $i=0, \ldots, j-1, j+1, \ldots, n-1$ and $y_{j}=0$. For sequence $\left\{y_{i}\right\}$ we have
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
\sum_{i=0}^{n-1} y_{i}=\sum_{i=0}^{n-1} x_{i}+1=\sum_{i=0}^{n-1} h(i)-n+1=1
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
so from Raney's lemma there exists index $k$ such that $\sum_{i=k}^{k+j} y_{i}>0$ for all $j=0, \ldots, n-1$ where $y_{n+j}=y_{j}$ for $j=0, \ldots, k-1$. Taking $t=k$ we will have
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
\sum_{t=k}^{k+i} h(t)-(i+1)=\sum_{t=k}^{k+i} x(t) \geq \sum_{t=k}^{k+i} y(t)-1 \geq 0
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
for all $i=0, \ldots, n-1$ and we are done.
|
| 198 |
+
Solution 3. Choose a random permutation $c_{1}, \ldots, c_{n}$ of the integers $1,2, \ldots, n$. Let $b_{i}=a_{i}+f\left(c_{i}-a_{i}\right)$, where $f(x) \in\{0, \ldots, n-1\}$ denotes a remainder of $x$ modulo $n$. Observe, that for such defined sequence the first two conditions hold. The expected value of $B:=b_{1}+\ldots+b_{n}$ is easily seen to be equal to $a_{1}+\ldots+a_{n}+n(n-1) / 2$. Indeed, for each $i$ the random number $c_{i}-a_{i}$ has uniform distribution modulo $n$, thus the expected value of $f\left(c_{i}-a_{i}\right)$ is $(0+\ldots+(n-1)) / n=(n-1) / 2$. Therefore we may find such $c$ that $B \leq a_{1}+\ldots+a_{n}+n(n-1) / 2$. But $B-n(n-1) / 2$ is divisible by $n$ and therefore $B \leq n\left[\left(a_{1}+\ldots+a_{n}\right) / n\right]+n(n-1) / 2$ as needed.
|
| 199 |
+
|
| 200 |
+
Solution 4. We will prove the required statement for all sequences of non-negative integers $a_{i}$ by induction on $n$.
|
| 201 |
+
Case $n=1$ is obvious, just set $b_{1}=a_{1}$.
|
| 202 |
+
Now suppose that the statement is true for some $n \geq 1$; we shall prove it for $n+1$.
|
| 203 |
+
First note that, by subtracting a multiple of $n+1$ to each $a_{i}$ and possibly rearranging indices we can reduce the problem to the case where $0 \leq a_{1} \leq a_{2} \leq \cdots \leq a_{n} \leq a_{n+1}<$ $n+1$.
|
| 204 |
+
|
| 205 |
+
Now, by the induction hypothesis there exists a sequence $d_{1}, d_{2}, \ldots, d_{n}$ which satisfies the properties required by the statement in relation to the numbers $a_{1}, \ldots, a_{n}$. Set $I=\{i \mid 1 \leq$ $i \leq n$ and $\left.d_{i} \bmod n \geq a_{i}\right\}$ and construct $b_{i}$, for $i=1, \ldots, n+1$, as follows:
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
b_{i}=\left\{\begin{array}{l}
|
| 209 |
+
d_{i} \bmod n, \text { when } i \in I, \\
|
| 210 |
+
n+1+\left(d_{i} \bmod n\right), \text { when } i \in\{1, \ldots, n\} \backslash I, \\
|
| 211 |
+
n, \text { for } i=n+1
|
| 212 |
+
\end{array}\right.
|
| 213 |
+
$$
|
| 214 |
+
|
| 215 |
+
Now, $a_{i} \leq d_{i} \bmod n \leq b_{i}$ for $i \in I$, while for $i \notin I$ we have $a_{i} \leq n \leq b_{i}$. Thus the sequence $\left(b_{i}\right)_{i=1}^{n+1}$ satisfies the first condition from the problem statement.
|
| 216 |
+
By the induction hypothesis, the numbers $d_{i} \bmod n$ are distinct for $i \in\{1, \ldots, n\}$, so the values $b_{i} \bmod (n+1)$ are distinct elements of $\{0, \ldots, n-1\}$ for $i \in\{1, \ldots, n\}$. Since $b_{n+1}=n$, the second condition is also satisfied.
|
| 217 |
+
|
| 218 |
+
Denote $k=|I|$. We have
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
\begin{gathered}
|
| 222 |
+
\sum_{i=1}^{n+1} b_{i}=\sum_{i=1}^{n} b_{i}+n=\sum_{i=1}^{n} d_{i} \bmod n+(n-k)(n+1)+n= \\
|
| 223 |
+
\frac{n(n+1)}{2}+(n-k)(n+1)
|
| 224 |
+
\end{gathered}
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
hence we need to show that
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
\frac{n(n+1)}{2}+(n-k)(n+1) \leq \frac{n(n+1)}{2}+(n+1)\left[\frac{\sum_{i=1}^{n+1} a_{i}}{n+1}\right]
|
| 231 |
+
$$
|
| 232 |
+
|
| 233 |
+
equivalently, that
|
| 234 |
+
|
| 235 |
+
$$
|
| 236 |
+
n-k \leq\left[\frac{\sum_{i=1}^{n+1} a_{i}}{n+1}\right]
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
Next, from the induction hypothesis we have
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
\begin{gathered}
|
| 243 |
+
\frac{n(n-1)}{2}+n\left[\frac{\sum_{i=1}^{n} a_{i}}{n}\right] \geq \sum_{i=1}^{n} d_{i}=\sum_{i \in I} d_{i}+\sum_{i \notin I} d_{i} \geq \\
|
| 244 |
+
\sum_{i \in I} d_{i} \bmod n+\sum_{i \notin I}\left(n+d_{i} \bmod n\right)=\frac{n(n-1)}{2}+(n-k) n
|
| 245 |
+
\end{gathered}
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
or
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
n-k \leq\left[\frac{\sum_{i=1}^{n} a_{i}}{n}\right]
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
Thus, it's enough to show that
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
\frac{\sum_{i=1}^{n} a_{i}}{n} \leq \frac{\sum_{i=1}^{n+1} a_{i}}{n+1}
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
because then
|
| 261 |
+
|
| 262 |
+
$$
|
| 263 |
+
n-k \leq\left[\frac{\sum_{i=1}^{n} a_{i}}{n}\right] \leq\left[\frac{\sum_{i=1}^{n+1} a_{i}}{n+1}\right]
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
But the required inequality is equivalent to $\sum_{i=1}^{n} a_{i} \leq n a_{n+1}$, which is obvious.
|
| 267 |
+
Solution 5. We can assume that all $a_{i} \in\{0,1, \ldots, n-1\}$, as we can deduct $n$ from both $a_{i}$ and $b_{i}$ for arbitrary $i$ without violating any of the three conditions from the problem statement. We shall also assume that $a_{1} \leq \ldots \leq a_{n}$.
|
| 268 |
+
Now let us provide an algorithm for constructing $b_{1}, \ldots, b_{n}$.
|
| 269 |
+
|
| 270 |
+
We start at step 1 by choosing $f(1)$ to be the maximum $i$ in $\{1, \ldots, n\}$ such that $a_{i} \leq n-1$, that is $f(1)=n$. We set $b_{f(1)}=n-1$.
|
| 271 |
+
Having performed steps 1 through $j$, at step $j+1$ we set $f(j+1)$ to be the maximum $i$ in $\{1, \ldots, n\} \backslash\{f(1), \ldots, f(j)\}$ such that $a_{i} \leq n-j-1$, if such an index exists. If it does, we set $b_{f(j+1)}=n-j-1$. If there is no such index, then we define $T=j$ and assign to the terms $b_{i}$, where $i \notin f(\{1, \ldots, j\})$, the values $n, n+1 \ldots, 2 n-j-1$, in any order, thus concluding the run of our algorithm.
|
| 272 |
+
|
| 273 |
+
Notice that the sequence $\left(b_{i}\right)_{i=1}^{n}$ satisfies the first and second required conditions by construction. We wish to show that it also satisfies the third.
|
| 274 |
+
|
| 275 |
+
Notice that, since the values chosen for the $b_{i}$ 's are those from $n-T$ to $2 n-T-1$, we have
|
| 276 |
+
|
| 277 |
+
$$
|
| 278 |
+
\sum_{i=1}^{n} b_{i}=\frac{n(n-1)}{2}+(n-T) n
|
| 279 |
+
$$
|
| 280 |
+
|
| 281 |
+
It therefore suffices to show that
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
\left[\frac{a_{1}+\ldots+a_{n}}{n}\right] \geq n-T
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
or (since the RHS is obviously an integer) $a_{1}+\ldots+a_{n} \geq(n-T) n$.
|
| 288 |
+
First, we show that there exists $1 \leq i \leq T$ such that $n-i=b_{f(i)}=a_{f(i)}$.
|
| 289 |
+
Indeed, this is true if $a_{n}=n-1$, so we may suppose $a_{n}<n-1$ and therefore $a_{n-1} \leq n-2$, so that $T \geq 2$. If $a_{n-1}=n-2$, we are done. If not, then $a_{n-1}<n-2$ and therefore $a_{n-2} \leq n-3$ and $T \geq 3$. Inductively, we actually obtain $T=n$ and necessarily $f(n)=1$ and $a_{1}=b_{1}=0$, which gives the desired result.
|
| 290 |
+
|
| 291 |
+
Now let $t$ be the largest such index $i$. We know that $n-t=b_{f(t)}=a_{f(t)}$ and therefore $a_{1} \leq \ldots \leq a_{f(t)} \leq n-t$. If we have $a_{1}=\ldots=a_{f(t)}=n-t$, then $T=t$ and we have $a_{i} \geq n-T$ for all $i$, hence $\sum_{i} a_{i} \geq n(n-T)$. Otherwise, $T>t$ and in fact one can show $T=t+f(t+1)$ by proceeding inductively and using the fact that $t$ is the last time for which $a_{f(t)}=b_{f(t)}$.
|
| 292 |
+
|
| 293 |
+
Now we get that, since $a_{f(t+1)+1} \geq n-t$, then $\sum_{i} a_{i} \geq(n-t)(n-f(t+1))=(n-T+f(t+$ 1) $)(n-f(t+1))=n(n-T)+n f(t+1)-f(t+1)(n-T+f(t+1))=n(n-T)+t f(t+1) \geq$ $n(n-T)$.
|
| 294 |
+
|
| 295 |
+
Greedy algorithm variant $\mathbf{1}$ (ISR). Consider the residues $0, \ldots, n-1$ modulo $n$ arranged in a circle clockwise, and place each $a_{i}$ on its corresponding residue; so that on each residue there is a stack of all $a_{i}$ s congruent to it modulo $n$, and the sum of the sizes of all stacks is exactly $n$. We iteratively flatten and spread the stacks forward, in such a way that the $a_{i}$ s are placed in the nearest available space on the circle clockwise (skipping over any already flattened residue or still standing stack). We may choose the order in which the stacks are flattened. Since the total amount of numbers equals the total number of spaces, there is always an available space and at the end all spaces are covered. The $b_{i} \mathrm{~s}$ are then defined by adding to each $a_{i}$ the number of places it was moved forward, which clearly satifies (i) and (ii), and we must prove that they satisfy (iii) as well.
|
| 296 |
+
|
| 297 |
+
Suppose that we flatten a stack of $k$ numbers at a residue $i$, causing it to overtake a stack of $l$ numbers at residue $j \in(i, i+k)$ (we can allow $j$ to be larger than $n$ and identify it
|
| 298 |
+
with its residue modulo $n$ ). Then in fact in fact in whichever order we would flatten the two stacks, the total number of forward steps would be the same, and the total sum of the corresponding $b_{t}$ (such that $a_{t} \bmod n \in\{i, j\}$ ) would be the same. Moreover, we can merge the stacks to a single stack of $k+l$ numbers at residue $i$, by replacing each $a_{t} \equiv j$ $(\bmod n)$ by $a_{t}^{\prime}=a_{t}-(j-i)$, and this stack would be flattened forward into the same positions as the separate stacks would have been, so applying our algorithm to the new stacks will yield the same total sum of $\sum b_{i}-$ but the $a_{i}$ s are strictly decreased, so $\sum a_{i}$ is decreased, so $\left\lfloor\frac{\sum a_{i}}{n}\right\rfloor$ is not increased - so by merging the stacks, we can only make the inequality we wish to prove tighter.
|
| 299 |
+
|
| 300 |
+
Thus, as long as there is some stack that when flattened will overtake another stack, we may merge stacks and only make the inequality tighter. Since the amount of numbers equals the amount of places, the merging process terminates with stacks of sizes $k_{1}, \ldots, k_{m}$, such that the stack $j$, when flattened, will exactly cover the interval to the next stack. Clearly the numbers in each such stack were advanced by a total of $\sum_{t=1}^{k_{j}-1}=\frac{k_{j}\left(k_{j}-1\right)}{2}$, thus $\sum b_{i}=\sum a_{i}+\sum_{j} \frac{k_{j}\left(k_{j}-1\right)}{2}$. Writing $\sum a_{i}=n \cdot r+s$ with $0 \leq s<n$, we must therefore show
|
| 301 |
+
|
| 302 |
+
$$
|
| 303 |
+
s+\sum_{j} \frac{k_{j}\left(k_{j}-1\right)}{2} \leq \frac{n(n-1)}{2}
|
| 304 |
+
$$
|
| 305 |
+
|
| 306 |
+
Ending 1. Observing that both sides of the last inequality are congruent modulo $n$ (both are congruent to the sum of all different residues), and that $0 \leq s<n$, the inequality is eqivalent to the simpler $\sum_{j} \frac{k_{j}\left(k_{j}-1\right)}{2} \leq \frac{n(n-1)}{2}$. Since $x(x-1)$ is convex, and $k_{j}$ are nonnegative integers with $\sum_{j} k_{j}=n$, the left hand side is maximal when $k_{j^{\prime}}=n$ and the rest are 0 , and then eqaulity is achieved. (Alternatively it follows easily for any non-negative reals from AM-GM.)
|
| 307 |
+
|
| 308 |
+
Ending 2. If $m=1$ (and $k_{1}=n$ ), then all numbers are in a single stack and have the same residue, so $s=0$ and equality is attained. If $m \geq 2$, then by convexity $\sum_{j} \frac{k_{j}\left(k_{j}-1\right)}{2}$ is maximal for $m=2$ and $\left(k_{1}, k_{2}\right)=(n-1,1)$, where it equals $\frac{(n-1)(n-2)}{2}$. Since we always have $s \leq n-1$, we find
|
| 309 |
+
|
| 310 |
+
$$
|
| 311 |
+
s+\sum_{j} \frac{k_{j}\left(k_{j}-1\right)}{2} \leq(n-1)+\frac{(n-1)(n-2)}{2}=\frac{n(n-1)}{2}
|
| 312 |
+
$$
|
| 313 |
+
|
| 314 |
+
as required.
|
| 315 |
+
Greedy algorithm variant 1' (ISR). We apply the same algorithm as in the previous solution. However, this time we note that we may merge stacks not only when they overlap after flattening, but also when they merely touch front-to-back: That is, we relax the condition $j \in(i, i+k)$ to $j \in(i, i+k]$; the argument for why such merges are allowed is exactly the same (But note that this is now sharp, as merging non-touching stacks can cause the sum of $b_{i}$ s to decrease).
|
| 316 |
+
|
| 317 |
+
We now observe that as long as there at least two stacks left, at least one will spread to touch (or overtake) the next stack, so we can perform merges until there is only one stack left. We are left with verifying that the inequality indeed holds for the case of only one stack which is spread forward, and this is indeed immediate (and in fact equality is achieved).
|
| 318 |
+
|
| 319 |
+
Greedy algorithm variant 2 (ISR). Let $c_{i}=a_{i} \bmod n$. Iteratively define $b_{i}=a_{i}+l_{i}$ greedily, write $d_{i}=c_{i}+l_{i}$, and observe that $l_{i} \leq n-1$ (since all residues are present in $\left.a_{i}, \ldots, a_{i}+n-1\right)$, hence $0 \leq d_{i} \leq 2 n-2$. Let $I=\left\{i \in I: d_{i} \geq n\right\}$, and note that $d_{i}=b_{i}$ $\bmod n$ if $i \notin I$ and $d_{i}=\left(b_{i} \bmod n\right)+n$ if $i \in I$. Then we must show
|
| 320 |
+
|
| 321 |
+
$$
|
| 322 |
+
\begin{aligned}
|
| 323 |
+
& \sum\left(a_{i}+l_{i}\right)=\sum b_{i} \leq \frac{n(n-1)}{2}+n\left\lfloor\frac{\sum a_{i}}{n}\right\rfloor \\
|
| 324 |
+
\Longleftrightarrow & \sum\left(c_{i}+l_{i}\right) \leq \sum\left(b_{i} \bmod n\right)+n\left\lfloor\frac{\sum c_{i}}{n}\right\rfloor \\
|
| 325 |
+
\Longleftrightarrow & \left.n|I| \leq n\left\lfloor\frac{\sum c_{i}}{n}\right\rfloor \Longleftrightarrow|I| \leq \left\lvert\, \frac{\sum c_{i}}{n}\right.\right\rfloor \Longleftrightarrow|I| \leq \frac{\sum c_{i}}{n}
|
| 326 |
+
\end{aligned}
|
| 327 |
+
$$
|
| 328 |
+
|
| 329 |
+
Let $k=|I|$, and for each $0 \leq m<n$ let $J_{m}=\left\{i: c_{i} \geq n-m\right\}$. We claim that there must be some $m$ for which $\left|J_{m}\right| \geq m+k$ (clearly for such $m$, at least $k$ of the sums $d_{j}$ with $j \in J_{m}$ must exceed $n$, i.e. at least $k$ of the elements of $J_{m}$ must also be in $I$, so this $m$ is a "witness" to the fact $|I| \geq k$ ). Once we find such an $m$, then we clearly have
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
\sum c_{i} \geq(n-m)\left|J_{m}\right| \geq(n-m)(k+m)=n k+m(n-(k+m)) \geq n k=n|I|
|
| 333 |
+
$$
|
| 334 |
+
|
| 335 |
+
as required. We now construct such an $m$ explicitly.
|
| 336 |
+
If $k=0$, then clearly $m=n$ works (and also the original inequality is trivial). Otherwise, there are some $d_{i}$ s greater than $n$, and let $r+n=\max d_{i}$, and suppose $d_{t}=r+n$ and let $s=c_{t}$. Note that $r<s<r+n$ since $l_{t}<n$. Let $m \geq 0$ be the smallest number such that $n-m-1$ is not in $\left\{d_{1}, \ldots, d_{t}\right\}$, or equivalently $m$ is the largest such that $[n-m, n) \subset\left\{d_{1}, \ldots, d_{t}\right\}$. We claim that this $m$ satisfies the required property. More specifically, we claim that $J_{m}^{\prime}=\left\{i \leq t: d_{i} \geq n-m\right\}$ contains exactly $m+k$ elements and is a subset of $J_{m}$.
|
| 337 |
+
|
| 338 |
+
Note that by the greediness of the algorithm, it is impossible that for $\left[c_{i}, d_{i}\right)$ to contain numbers congruent to $d_{j} \bmod n$ with $j>i$ (otherwise, the greedy choice would prefer $d_{j}$ to $d_{i}$ at stage $i$ ). We call this the greedy property. In particular, it follows that all $i$ such that $d_{i} \in\left[s, d_{t}\right)=\left[c_{t}, d_{t}\right)$ must satisfy $i<t$. Additionally, $\left\{d_{i}\right\}$ is disjoint from $[n+r+1,2 n)$ (by maximality of $d_{t}$ ), but does intersect every residue class, so it contains $[r+1, n)$ and in particular also $[s, n)$. By the greedy property the latter can only be attained by $d_{i}$ with $i<t$, thus $[s, n) \subset\left\{d_{1}, \ldots, d_{t}\right\}$, and in particular $n-m \leq s$ (and in particular $m \geq 1$ ).
|
| 339 |
+
On the other hand $n-m>r$ (since $r \notin\left\{d_{i}\right\}$ at all), so $n-m-1 \geq r$. It follows that there is a time $t^{\prime} \geq t$ for which $d_{t^{\prime}} \equiv n-m-1(\bmod n)$ : If $n-m-1=r$ then this is true for $t^{\prime}=t$ with $d_{t}=n+r=2 n-m-1$; whereas if $n-m-1 \in[r+1, n)$ then there is some $t^{\prime}$ for which $d_{t^{\prime}}=n-m-1$, and by the definition of $m$ it satisfies $t^{\prime}>t$.
|
| 340 |
+
|
| 341 |
+
Therefore for all $i<t \leq t^{\prime}$ for which $d_{i} \geq n-m$, necessarily also $c_{i} \geq n-m$, since otherwise $d_{t^{\prime}} \in\left[c_{i}, d_{i}\right)$, in contradiction to the greedy property. This is also true for $i=t$, since $c_{t}=s \geq n-m$ as previously shown. Thus, $J_{m}^{\prime} \subset J_{m}$ as claimed.
|
| 342 |
+
Finally, since by definition of $m$ and greediness we have $[n-m, n) \cup\left\{d_{i}: i \in I\right\} \subset$ $\left\{d_{1}, \ldots, d_{t}\right\}$, we find that $\left\{d_{j}: j \in J_{m}^{\prime}\right\}=[n-m, n) \cup\left\{d_{i}: i \in I\right\}$ and thus $\left|J_{m}^{\prime}\right|=$ $|[n-m, n)|+|I|=m+k$ as claimed.
|
| 343 |
+
|
| 344 |
+
## Problem 6 (United Kingdom).
|
| 345 |
+
|
| 346 |
+
On a circle, Alina draws 2019 chords, the endpoints of which are all different. A point is considered marked if it is either
|
| 347 |
+
(i) one of the 4038 endpoints of a chord; or
|
| 348 |
+
(ii) an intersection point of at least two chords.
|
| 349 |
+
|
| 350 |
+
Alina labels each marked point. Of the 4038 points meeting criterion (i), Alina labels 2019 points with a 0 and the other 2019 points with a 1 . She labels each point meeting criterion (ii) with an arbitrary integer (not necessarily positive).
|
| 351 |
+
Along each chord, Alina considers the segments connecting two consecutive marked points. (A chord with $k$ marked points has $k-1$ such segments.) She labels each such segment in yellow with the sum of the labels of its two endpoints and in blue with the absolute value of their difference.
|
| 352 |
+
|
| 353 |
+
Alina finds that the $N+1$ yellow labels take each value $0,1, \ldots, N$ exactly once. Show that at least one blue label is a multiple of 3 .
|
| 354 |
+
(A chord is a line segment joining two different points on a circle.)
|
| 355 |
+
Solution 1. First we prove the following:
|
| 356 |
+
Lemma: if we color all of the points white or black, then the number of white-black edges, which we denote $E_{W B}$, is equal modulo 2 to the number of white (or black) points on the circumference, which we denote $C_{W}$, resp. $C_{B}$.
|
| 357 |
+
|
| 358 |
+
Observe that changing the colour of any interior point does not change the parity of $E_{W B}$, as each interior point has even degree, so it suffices to show the statement holds when all interior points are black. But then $E_{W B}=C_{W}$ so certainly the parities are equal.
|
| 359 |
+
|
| 360 |
+
Now returning to the original problem, assume that no two adjacent vertex labels differ by a multiple of three, and three-colour the vertices according to the residue class of the labels modulo 3. Let $E_{01}$ denote the number of edges between 0 -vertices and 1 -vertices, and $C_{0}$ denote the number of 0 -vertices on the boundary, and so on.
|
| 361 |
+
|
| 362 |
+
Then, consider the two-coloring obtained by combining the 1-vertices and 2-vertices. By applying the lemma, we see that $E_{01}+E_{02} \equiv C_{0} \bmod 2$.
|
| 363 |
+
|
| 364 |
+
$$
|
| 365 |
+
\text { Similarly } E_{01}+E_{12} \equiv C_{1}, \quad \text { and } E_{02}+E_{12} \equiv C_{2}, \quad \bmod 2
|
| 366 |
+
$$
|
| 367 |
+
|
| 368 |
+
Using the fact that $C_{0}=C_{1}=2019$ and $C_{2}=0$, we deduce that either $E_{02}$ and $E_{12}$ are even and $E_{01}$ is odd; or $E_{02}$ and $E_{12}$ are odd and $E_{01}$ is even.
|
| 369 |
+
|
| 370 |
+
But if the edge labels are the first $N$ non-negative integers, then $E_{01}=E_{12}$ unless $N \equiv 0$ modulo 3 , in which case $E_{01}=E_{02}$. So however Alina chooses the vertex labels, it is not possible that the multiset of edge labels is $\{0, \ldots, N\}$.
|
| 371 |
+
Hence in fact two vertex labels must differ by a multiple of 3 .
|
| 372 |
+
Solution 2. As before, colour vertices based on their label modulo 3.
|
| 373 |
+
Suppose this gives a valid 3-colouring of the graph with 2019 0s and 2019 1s on the
|
| 374 |
+
circumference. Identify pairs of 0-labelled vertices and pairs of 1-labelled vertices on the circumference, with one 0 and one 1 left over. The resulting graph has even degrees except these two leaves. So the connected component $\mathcal{C}$ containing these leaves has an Eulerian path, and any other component has an Eulerian cycle.
|
| 375 |
+
|
| 376 |
+
Let $E_{01}^{*}$ denote the number of edges between 0 -vertices and 1 -vertices in $\mathcal{C}$, and let $E_{01}^{\prime}$ denote the number of such edges in the other components, and so on. By studying whether a given vertex has label congruent to 0 modulo 3 or not as we go along the Eulerian path in $\mathcal{C}$, we find $E_{01}^{*}+E_{02}^{*}$ is odd, and similarly $E_{01}^{*}+E_{12}^{*}$ is odd. Since neither start nor end vertex is a 2 -vertex, $E_{02}^{*}+E_{12}^{*}$ must be even.
|
| 377 |
+
|
| 378 |
+
Applying the same argument for the Eulerian cycle in each other component and adding up, we find that $E_{01}^{\prime}+E_{02}^{\prime}, E_{01}^{\prime}+E_{12}^{\prime}, E_{02}^{\prime}+E_{12}^{\prime}$ are all even. So, again we find $E_{01}+E_{02}$, $E_{01}+E_{12}$ are odd, and $E_{02}+E_{12}$ is even, and we finish as in the original solution.
|
| 379 |
+
|
EGMO/md/en-2020-solutions.md
ADDED
|
@@ -0,0 +1,621 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Solutions of EGMO 2020
|
| 2 |
+
|
| 3 |
+
Problem 1. The positive integers $a_{0}, a_{1}, a_{2}, \ldots, a_{3030}$ satisfy
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
2 a_{n+2}=a_{n+1}+4 a_{n} \text { for } n=0,1,2, \ldots, 3028
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
Prove that at least one of the numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{3030}$ is divisible by $2^{2020}$.
|
| 10 |
+
|
| 11 |
+
Problem 2. Find all lists $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)$ of non-negative real numbers such that the following three conditions are all satisfied:
|
| 12 |
+
(i) $x_{1} \leq x_{2} \leq \ldots \leq x_{2020}$ ;
|
| 13 |
+
(ii) $x_{2020} \leq x_{1}+1$;
|
| 14 |
+
(iii) there is a permutation $\left(y_{1}, y_{2}, \ldots, y_{2020}\right)$ of $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)$ such that
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
\sum_{i=1}^{2020}\left(\left(x_{i}+1\right)\left(y_{i}+1\right)\right)^{2}=8 \sum_{i=1}^{2020} x_{i}^{3}
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
A permutation of a list is a list of the same length, with the same entries, but the entries are allowed to be in any order. For example, $(2,1,2)$ is a permutation of $(1,2,2)$, and they are both permutations of $(2,2,1)$. Note that any list is a permutation of itself.
|
| 21 |
+
|
| 22 |
+
Problem 3. Let $A B C D E F$ be a convex hexagon such that $\angle A=\angle C=\angle E$ and $\angle B=\angle D=$ $\angle F$ and the (interior) angle bisectors of $\angle A, \angle C$, and $\angle E$ are concurrent.
|
| 23 |
+
|
| 24 |
+
Prove that the (interior) angle bisectors of $\angle B, \angle D$, and $\angle F$ must also be concurrent.
|
| 25 |
+
|
| 26 |
+
Note that $\angle A=\angle F A B$. The other interior angles of the hexagon are similarly described.
|
| 27 |
+
|
| 28 |
+
Problem 4. A permutation of the integers $1,2, \ldots, m$ is called fresh if there exists no positive integer $k<m$ such that the first $k$ numbers in the permutation are $1,2, \ldots, k$ in some order. Let $f_{m}$ be the number of fresh permutations of the integers $1,2, \ldots, m$.
|
| 29 |
+
Prove that $f_{n} \geq n \cdot f_{n-1}$ for all $n \geq 3$.
|
| 30 |
+
For example, if $m=4$, then the permutation $(3,1,4,2)$ is fresh, whereas the permutation $(2,3,1,4)$ is not.
|
| 31 |
+
|
| 32 |
+
Problem 5. Consider the triangle $A B C$ with $\angle B C A>90^{\circ}$. The circumcircle $\Gamma$ of $A B C$ has radius $R$. There is a point $P$ in the interior of the line segment $A B$ such that $P B=P C$ and the length of $P A$ is $R$. The perpendicular bisector of $P B$ intersects $\Gamma$ at the points $D$ and $E$.
|
| 33 |
+
Prove that $P$ is the incentre of triangle $C D E$.
|
| 34 |
+
Problem 6. Let $m>1$ be an integer. A sequence $a_{1}, a_{2}, a_{3}, \ldots$ is defined by $a_{1}=a_{2}=1$, $a_{3}=4$, and for all $n \geq 4$,
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
a_{n}=m\left(a_{n-1}+a_{n-2}\right)-a_{n-3} .
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Determine all integers $m$ such that every term of the sequence is a square.
|
| 41 |
+
|
| 42 |
+
## Solutions to Problem 1
|
| 43 |
+
|
| 44 |
+
There are different ways of solving the problem. All of these use some induction argument. Most of these proofs use one of the following two lemmas. In many places, they can be used interchangeably.
|
| 45 |
+
|
| 46 |
+
Lemma. If $a, b, c, d$ are integers with $2 c=b+4 a$ and $2 d=c+4 b$, then $4 \mid b$.
|
| 47 |
+
Proof: From $2 d=c+4 b$ we have that $c$ is even, and then from $2 c=b+4 a$ it follows that $b$ is divisible by 4 .
|
| 48 |
+
|
| 49 |
+
Lemma:For $0 \leq n \leq 3030$, denote by $v_{n}$ the largest integer such that $2^{v_{n}}$ divides $a_{n}$. We claim the following:
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
(*) \quad v_{n+1} \geq \min \left(v_{n}+2, v_{n+2}+1\right) \quad \text { for } n=0,1, \ldots, 3028
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Proof: Let $0 \leq n \leq 3028$ and let $s=\min \left(v_{n}+2, v_{n+2}+1\right)$. Then $s \leq v_{n}+2$ implies $2^{s} \mid 4 a_{n}$ and $s \leq v_{n+2}+1$ implies $2^{s} \mid 2 a_{n+2}$. It follows that $a_{n+1}=2 a_{n+2}-4 a_{n}$ is also divisible by $2^{s}$, hence $s \leq v_{n+1}$, which proves $(*)$.
|
| 56 |
+
|
| 57 |
+
Here are different ways of working out the induction argument that is crucial in the proofs.
|
| 58 |
+
|
| 59 |
+
## Induction part, alternative A.
|
| 60 |
+
|
| 61 |
+
Statement: For $k=0,1, \ldots, 1010$, the terms $a_{k}, a_{k+1}, \ldots, a_{3030-2 k}$ are all divisible by $2^{2 k}$.
|
| 62 |
+
Reformulation of the statement using notation $v_{n}$ is the largest integer such that $2^{v_{n}}$ divides $a_{n}$ : we have $v_{n} \geq k$ for any $n$ satisfying $\left\lceil\frac{1}{2} k\right\rceil \leq n \leq 3030-k$. Here $\lceil x\rceil$ denotes the smallest integer not smaller than $x$.
|
| 63 |
+
|
| 64 |
+
Proof 1: We proceed by induction on $k$. For $k=0$ the statement is obvious, so, for the inductive step, suppose that $a_{k}, a_{k+1}, \ldots, a_{3030-2 k}$ are all divisible by $2^{2 k}$. Apply the Lemma with
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
(a, b, c, d)=\left(\frac{a_{i-1}}{2^{2 k}}, \frac{a_{i}}{2^{2 k}}, \frac{a_{i+1}}{2^{2 k}}, \frac{a_{i+2}}{2^{2 k}}\right)
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
for $i=k+1, k+2, \ldots, 3030-2 k-2$. We obtain that $\frac{a_{i}}{2^{2 k}}$ is divisible by 4 (and hence $a_{i}$ is divisible by $2^{2 k+2}$ ) for $i=k+1, k+2, \ldots, i=3030-2 k-2$. This completes the induction. For $k=1010$ we obtain that $a_{1010}$ is divisible by $2^{2020}$, and the solution is complete.
|
| 71 |
+
|
| 72 |
+
Remark. Remark, notice that by replacing 1010 with $n$ (and hence, $2 n$ with 2020 and $3 n$ with 3030, this argument works, too. Then the claim is the following: if $a_{0}, a_{1}, \ldots, a_{3 n}$ are integers that satisfy the recursion in the problem, then $a_{n}$ is divisible by $2^{2 n}$.
|
| 73 |
+
|
| 74 |
+
Proof 2: We will show by two step induction to $k \geq 0$ : we have $v_{n} \geq k$ for any $n$ satisfying $\left\lceil\frac{1}{2} k\right\rceil \leq n \leq 3030-k$. Here $\lceil x\rceil$ denotes the smallest integer not smaller than $x$. Plugging in $k=2020$ and $n=1010$ will give the desired result.
|
| 75 |
+
The case $k=0$ is trivial, since the $v_{n}$ are non-negative. For the case $k=1$, let $1 \leq n \leq 3029$, then $v_{n} \geq \min \left(v_{n-1}+2, v_{n+1}+1\right) \geq 1$.
|
| 76 |
+
Suppose we have it proven for some $k \geq 1$ and for $k-1$. Let $\left\lceil\frac{1}{2}(k+1)\right\rceil \leq n \leq 3030-(k+1)$. Then $\left\lceil\frac{1}{2}(k-1)\right\rceil \leq n-1 \leq 3030-(k-1)$ and also $\left\lceil\frac{1}{2} k\right\rceil \leq n+1 \leq 3030-k$. By induction hypothesis we have $v_{n-1} \geq k-1$ and $v_{n+1} \geq k$. Then $v_{n} \geq \min \left(v_{n-1}+2, v_{n+1}+1\right) \geq k$, finishing the induction.
|
| 77 |
+
|
| 78 |
+
Proof 3: The notation is the same as in alternative A1, but the induction step has two steps. We use the lemma stated in the beginning as the first step. Assume now that $2^{2 k} \mid a_{k}, \ldots, a_{3030-2 k}$ for some $k \geq 1$. We claim that then $2^{2 k+2} \mid a_{k+1}, \ldots, a_{3030-2(k+1)}$. Notice first that any $i$ on the interval $[k+1,3030-2 k-1]$ satisfies the equation $2 a_{i+1}=a_{i}+4 a_{i-2}$, we have $2^{2 k+1} \mid a_{i}$. Furthermore, if $i \in[k+1,3030-2 k-2]$, we have $2^{2 k+2} \mid a_{i}$ since $2^{2 k+1} \mid a_{i+1}$ and hence
|
| 79 |
+
$2^{2 k+2} \mid 2 a_{i+1}$ and $2^{2 k+2} \mid 4 a_{i-1}$.
|
| 80 |
+
|
| 81 |
+
## Induction part, alternative B.
|
| 82 |
+
|
| 83 |
+
Statement: if $a_{0}, a_{1}, \ldots, a_{3 n}$ are integers that satisfy the recursion in the problem, then $a_{n}$ is divisible by $2^{2 n}$. The problem statement follows for $n=1010$.
|
| 84 |
+
|
| 85 |
+
Proof: The base case of the induction is exactly the Lemma we just proved. Now, for the inductive step, suppose that the statement holds for $n=k-1$, and consider integers $a_{0}, a_{1}$, $\ldots, a_{3 k}$ that satisfy the recursion. By applying the induction hypothesis to the four sequences $\left(a_{0}, a_{1}, \ldots, a_{3 k-3}\right),\left(a_{1}, a_{2}, \ldots, a_{3 k-2}\right),\left(a_{2}, a_{3}, \ldots, a_{3 k-1}\right)$ and $\left(a_{3}, a_{4}, \ldots, a_{3 k}\right)$, we find that $a_{k-1}$, $a_{k}, a_{k+1}$ and $a_{k+2}$ are all divisible by $2^{2 k-2}$. If we now apply the lemma to $a_{k-1} / 2^{2 k-2}, a_{k} / 2^{2 k-2}$, $a_{k+1} / 2^{2 k-2}$ and $a_{k+2} / 2^{2 k-2}$, we find that $a_{k} / 2^{2 k-2}$ is divisible by 4 , so $a_{k}$ is divisible by $2^{2 k}$, as desired.
|
| 86 |
+
|
| 87 |
+
## Induction part, alternative C.
|
| 88 |
+
|
| 89 |
+
Statement: Given positive integers $a_{0}, a_{1}, a_{2}, \ldots, a_{3 k}$ such that
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
2 a_{n+2}=a_{n+1}+4 a_{n} \text { for } n=0,1,2, \ldots, 3 k-2
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
then $2^{2 k}$ divides at least one of the numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{3 k}$.
|
| 96 |
+
Proof: The case $k=1$ is obtained from Lemma.
|
| 97 |
+
Suppose that for some $k \geq 1$, our claim is true for any sequence of $3 k+1$ positive integers that satisfy similar defining relations. Then consider a sequence of $3(k+1)+1=3 k+4$ positive integers $a_{0}, a_{1}, a_{2}, \ldots, a_{3 k+3}$ such that
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
2 a_{n+2}=a_{n+1}+4 a_{n} \text { for } n=0,1,2, \ldots, 3 k+1
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Then, we see that all numbers $a_{1}, a_{2}, \ldots, a_{3 k+2}$ are even, and so we may set $a_{i}=2 b_{i}$ for some positive integers $b_{i}$ for $i=1,2, \ldots, 3 k+2$. Then $2 a_{2}=a_{1}+4 a_{0}$ becomes
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
2 b_{2}=b_{1}+2 a_{0}
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Note that
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
2 b_{n+2}=b_{n+1}+4 b_{n} \text { for } n=1,2, \ldots, 3 k
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Hence the positive integers $b_{1}, b_{2}, \ldots, b_{3 k+1}$ are even, and so we may write $b_{i}=2 c_{i}$ for some positive integers $c_{i}$ for $i=1,2, \ldots, 3 k+1$. Then $2 b_{2}=b_{1}+2 a_{0}$ becomes $2 c_{2}=c_{1}+a_{0}$, which does not give us anything. However, we have
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
2 c_{n+2}=c_{n+1}+4 c_{n} \text { for } n=1,2, \ldots, 3 k-1
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
So the sequence of positive integers $c_{1}, c_{2}, \ldots, c_{3 k+1}$ is a sequence of $3 k+1$ positive integers that satisfy the defining relations. By the inductive hypothesis, $2^{2 k}$ divides at least one of the numbers $c_{1}, c_{2}, \ldots, c_{3 k+1}$. Since $a_{i}=4 c_{i}$ for all $i=1,2, \ldots, 3 k+1$, it follows that $4 \cdot 2^{2 k}=2^{2(k+1)}$ divides at least one of the numbers $a_{1}, \ldots, a_{3 k+1}$. This completes the induction, and hence the proof.
|
| 122 |
+
|
| 123 |
+
## Induction part, alternative D.
|
| 124 |
+
|
| 125 |
+
Statement: If $v_{0}, v_{1}, \ldots, v_{3030}$ is a sequence of non-negative integers satisfying $(*)$, there must be a $k$ such that $v_{k} \geq 2020$. In fact, we will show that $v_{1010} \geq 2020$.
|
| 126 |
+
|
| 127 |
+
These proofs use Lemma'.
|
| 128 |
+
|
| 129 |
+
Proof 1: We will show by induction on $k$ that $v_{n} \geq 2 k$ for $k \leq n \leq 3030-2 k$ and $v_{n} \geq 2 k+1$ for $k+1 \leq n \leq 3030-2 k-1$. For $k=1010$, the first statement implies that $v_{1010} \geq 2020$.
|
| 130 |
+
For $k=0$ the first statement $v_{n} \geq 0$ is obvious, and the second statement follows using ( $*$ ): we have $v_{n} \geq v_{n+1}+1 \geq 1$ for $1 \leq n \leq 3029$.
|
| 131 |
+
Now suppose that the inductive hypothesis holds for $k=\ell$ : we have $v_{n} \geq 2 \ell$ for $\ell \leq n \leq 3030-2 \ell$ and $v_{n} \geq 2 \ell+1$ for $\ell+1 \leq n \leq 3030-2 \ell-1$. For the first statement, consider an $n$ with $\ell+1 \leq n \leq 3030-2 \ell-2$. Then using $(*)$ and the inductive hypothesis, we obtain
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
v_{n} \geq \min \left(v_{n-1}+2, v_{n+1}+1\right) \geq \min (2 \ell+2,2 \ell+2)=2 \ell+2
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
because $v_{n-1} \geq 2 \ell$ (as $\left.\ell \leq n-1 \leq 3030-2 \ell\right)$ and $v_{n+1} \geq 2 \ell+1($ as $\ell+1 \leq n+1 \leq 3030-2 \ell-1)$. Similarly, for $\ell+2 \leq n \leq 3030-2 \ell-3$ we find
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
v_{n} \geq \min \left(v_{n-1}+2, v_{n+1}+1\right) \geq \min (2 \ell+3,2 \ell+3)=2 \ell+3
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
because $v_{n-1} \geq 2 \ell+1$ (as $\left.\ell+1 \leq n-1 \leq 3030-2 \ell-1\right)$ and $v_{n+1} \geq 2 \ell+2($ as $\ell+1 \leq n \leq$ $3030-2 \ell-2$ ). This completes the induction.
|
| 144 |
+
|
| 145 |
+
Proof 2: The inequality $v_{1010} \geq \min \left(v_{1009}+2, v_{1011}+1\right)$ gives us two cases to consider: either $v_{1010} \geq v_{1009}+2$ or $v_{1010} \geq v_{1011}+1$.
|
| 146 |
+
Suppose first that $v_{1010} \geq v_{1009}+2$. In this case we will show by induction on $k$ that $v_{1010-k} \geq$ $v_{1009-k}+2$ for $0 \leq k \leq 1009$. The case $k=0$ is assumed, so suppose that $v_{1010-\ell} \geq v_{1009-\ell}+2$ holds for some $0 \leq \ell<1009$. We obtain
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
v_{1009-\ell} \geq \min \left(v_{1010-\ell}+1, v_{1008-\ell}+2\right) \geq \min \left(v_{1009-\ell}+3, v_{1008-\ell}+2\right)
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
Because $v_{1009-\ell}<v_{1009-\ell}+3$ we must have $v_{1009-\ell} \geq v_{1008-\ell}+2$, completing the induction. We conclude that
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
v_{1010} \geq v_{1009}+2 \geq v_{1008}+4 \geq \cdots \geq v_{0}+2020 \geq 2020
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
In the second case, we show by induction on $k$ that $v_{1010+k} \geq v_{1011+k}+1$ for $0 \leq k \leq 2019$. Again, the base case $k=0$ is assumed, so suppose that $v_{1010+\ell} \geq v_{1011+\ell}+1$ holds for some $0 \leq \ell<2019$. We obtain
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
v_{1011+\ell} \geq \min \left(v_{1010+\ell}+2, v_{1012+\ell}+1\right) \geq \min \left(v_{1011+\ell}+3, v_{1012+\ell}+1\right)
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
Because $v_{1011+\ell}<v_{1011+\ell}+3$, we must have $v_{1011+\ell} \geq v_{1012+\ell}+1$, completing the induction. We conclude that
|
| 165 |
+
|
| 166 |
+
$$
|
| 167 |
+
v_{1010} \geq v_{1011}+1 \geq v_{1012}+2 \geq \cdots \geq v_{3030}+2020 \geq 2020
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
as desired.
|
| 171 |
+
|
| 172 |
+
## Alternative E.
|
| 173 |
+
|
| 174 |
+
This solution is different from the other solutions. Shift the sequence so that it starts at $a_{-1010}$ and ends at $a_{2020}$. We will show that $a_{0}$ is divisible by $2^{2020}$. Consider $a_{0}$. It either has at least as many factors 2 as $2 a_{1}$, or at least as many factors 2 as $4 a_{-1}$ (this follows from $2 a_{1}=a_{0}+4 a_{-1}$ ). Consider the first case, so $e_{2}\left(a_{0}\right) \geq e_{2}\left(2 a_{1}\right)$. By multiplying the original recursion by $2^{n-1}$, we note that $b_{n}=2^{n} a_{n}$ satisfies the recursion $b_{n}=b_{n-1}+8 b_{n-2}$. Furthermore, we assumed that $e_{2}\left(b_{0}\right) \geq e_{2}\left(b_{1}\right)$. This implies that $e_{2}\left(b_{n}\right)$ is constant for $n \geq 1$. Furthermore, clearly $2^{2020} \mid b_{2020}$, so $2^{2020} \mid b_{1}$ and hence $2^{2020} \mid a_{0}$. The case where $e_{2}\left(a_{0}\right) \geq e_{2}\left(4 a_{-1}\right)$ is similar; we then look at $b_{n}=4^{n} a_{-n}$ which satisfies $b_{n}=8 b_{n-2}-b_{n-1}$ and use that $2^{2020} \mid b_{1010}$. The rest of the argument is the same.
|
| 175 |
+
|
| 176 |
+
## Solutions to Problem 2
|
| 177 |
+
|
| 178 |
+
Answer. There are two solutions: $(\underbrace{0,0, \ldots, 0}_{1010}, \underbrace{1,1, \ldots, 1}_{1010})$ and $(\underbrace{1,1, \ldots, 1}_{1010}, \underbrace{2,2, \ldots, 2}_{1010})$.
|
| 179 |
+
Solution A. We first prove the inequality
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
((x+1)(y+1))^{2} \geq 4\left(x^{3}+y^{3}\right)
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
for real numbers $x, y \geq 0$ satisfying $|x-y| \leq 1$, with equality if and only if $\{x, y\}=\{0,1\}$ or $\{x, y\}=\{1,2\}$.
|
| 186 |
+
Indeed,
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
\begin{aligned}
|
| 190 |
+
4\left(x^{3}+y^{3}\right) & =4(x+y)\left(x^{2}-x y+y^{2}\right) \\
|
| 191 |
+
& \leq\left((x+y)+\left(x^{2}-x y+y^{2}\right)\right)^{2} \\
|
| 192 |
+
& =\left(x y+x+y+(x-y)^{2}\right)^{2} \\
|
| 193 |
+
& \leq(x y+x+y+1)^{2} \\
|
| 194 |
+
& =((x+1)(y+1))^{2},
|
| 195 |
+
\end{aligned}
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
where the first inequality follows by applying the AM-GM inequality on $x+y$ and $x^{2}-x y+y^{2}$ (which are clearly nonnegative). Equality holds in the first inequality precisely if $x+y=$ $x^{2}-x y+y^{2}$ and in the second one if and only if $|x-y|=1$. Combining these equalities we have $x+y=(x-y)^{2}+x y=1+x y$ or $(x-1)(y-1)=0$, which yields the solutions $\{x, y\}=\{0,1\}$ or $\{x, y\}=\{1,2\}$. Now, let $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)$ be any sequence satisfying conditions (i) and (ii) and let $\left(y_{1}, y_{2}, \ldots, y_{2020}\right)$ be any permutation of $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)$. As $0 \leq \min \left(x_{i}, y_{i}\right) \leq$ $\max \left(x_{i}, y_{i}\right) \leq \min \left(x_{i}, y_{i}\right)+1$, we can applying inequality (1) to the pair $\left(x_{i}, y_{i}\right)$ and sum over all $1 \leq i \leq 2020$ to conclude that
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
\sum_{i=1}^{2020}\left(\left(x_{i}+1\right)\left(y_{i}+1\right)\right)^{2} \geq 4 \sum_{i=1}^{2020}\left(x_{i}^{3}+y_{i}^{3}\right)=8 \sum_{i=1}^{2020} x_{i}^{3}
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
Therefore, in order to satisfy condition (iii), every inequality must be an equality. Hence, for every $1 \leq i \leq 2020$ we must have $\left\{x_{i}, y_{i}\right\}=\{0,1\}$ or $\left\{x_{i}, y_{i}\right\}=\{1,2\}$. By condition (ii), we see that either $\left\{x_{i}, y_{i}\right\}=\{0,1\}$ for all $i$ or $\left\{x_{i}, y_{i}\right\}=\{1,2\}$ for all $i$.
|
| 205 |
+
If $\left\{x_{i}, y_{i}\right\}=\{0,1\}$ for every $1 \leq i \leq 2020$, this implies that the sequences $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)$ and $\left(y_{1}, y_{2}, \ldots, y_{2020}\right)$ together have 2020 zeroes and 2020 ones. As $\left(y_{1}, y_{2}, \ldots, y_{2020}\right)$ is a permutation of $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)$ this implies that $\left(x_{1}, x_{2}, \ldots, x_{2020}\right)=(0,0, \ldots, 0,1,1, \ldots, 1)$ with 1010 zeroes and 1010 ones. Conversely, note that this sequence satisfies conditions (i), (ii), and (iii) (in (iii), we take $\left.\left(y_{1}, y_{2}, \ldots, y_{2020}\right)=\left(x_{2020}, x_{2019}, \ldots, x_{1}\right)\right)$, showing that this sequence indeed works. The same reasoning holds for the case that $\left\{x_{i}, y_{i}\right\}=\{1,2\}$ for all $i$.
|
| 206 |
+
|
| 207 |
+
Comment. There are multiple ways to show the main inequality (1):
|
| 208 |
+
|
| 209 |
+
- Write
|
| 210 |
+
|
| 211 |
+
$$
|
| 212 |
+
\begin{aligned}
|
| 213 |
+
((x+1)(y+1))^{2} & \geq((x+1)(y+1))^{2}-((x-1)(y-1))^{2} \\
|
| 214 |
+
& =4(x+y)(x y+1) \\
|
| 215 |
+
& \geq 4(x+y)\left(x y+(x-y)^{2}\right) \\
|
| 216 |
+
& =4\left(x^{3}+y^{3}\right),
|
| 217 |
+
\end{aligned}
|
| 218 |
+
$$
|
| 219 |
+
|
| 220 |
+
where equality holds precisely if $|x-y|=1$ and $(x-1)(y-1)=0$.
|
| 221 |
+
|
| 222 |
+
- Write
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
(x+1)^{2}(y+1)^{2}-4 x^{3}-4 y^{3}=(x-1)^{2}(y-1)^{2}+4(x+y)\left(1-(x-y)^{2}\right) \geq 0
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
where equality holds precisely if $(x-1)(y-1)=0$ and $(x-y)^{2}=1$.
|
| 229 |
+
|
| 230 |
+
- One can rewrite the difference between the two sides as a sum of nonnegative expressions. One such way is to assume that $y \geq x$ and then to rewrite the difference as
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
x^{2}(y-2)^{2}+(x+1-y)\left(4 y^{2}-4 x^{2}+2 x y+x+3 y+1\right)
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
where $x^{2}(y-2)^{2} \geq 0, x+1-y \geq 0$ and $4 y^{2}-4 x^{2}+2 x y+x+3 y+1>0$, so in the equality case we must have $x+1-y=0$ and $x(y-2)=0$.
|
| 237 |
+
|
| 238 |
+
- Again assume $y \geq x$; substitute $y=x+u$ with $0 \leq u \leq 1$ and rewrite the difference as
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
x^{2}(x+u-2)^{2}+x^{2}(2-2 u)+\left(4+6 u-10 u^{2}\right) x+\left(1+2 u+u^{2}-4 u^{3}\right),
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
of which each summand is nonnegative, with equality case $u=1$ and $x \in\{0,1\}$.
|
| 245 |
+
|
| 246 |
+
- Fix $x \geq 0$. We aim to show that the function
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
f(y)=((x+1)(y+1))^{2}-4\left(x^{3}+y^{3}\right)
|
| 250 |
+
$$
|
| 251 |
+
|
| 252 |
+
viewed as polynomial in $y$, is nonnegative on the interval $[x, x+1]$. First note that for $y=x$ and $y=x+1$ the function equals
|
| 253 |
+
|
| 254 |
+
$$
|
| 255 |
+
\left(x^{2}-2 x\right)^{2}+2 x^{2}+4 x+1>0 \quad \text { and } \quad\left(x^{2}-x\right)^{2} \geq 0
|
| 256 |
+
$$
|
| 257 |
+
|
| 258 |
+
respectively. The derivative of $f$ with respect to $y$ equals
|
| 259 |
+
|
| 260 |
+
$$
|
| 261 |
+
2(x+1)^{2}+2(x+1)^{2} y-12 y^{2}
|
| 262 |
+
$$
|
| 263 |
+
|
| 264 |
+
which is a quadratic with negative leading coefficient that evaluates as $2(x+1)^{2}>0$ for $y=0$. Therefore, this quadratic has one positive and one negative root. Therefore, on $[0, \infty)$, the function $f$ will be initially increasing and eventually decreasing, hence the minimum on the interval $[x, x+1]$ will be achieved on one of the endpoints. To have equality, we must have $x^{2}-x=0$, hence $x \in\{0,1\}$.
|
| 265 |
+
|
| 266 |
+
- Observe that $((x+1)(y+1))^{2}-4\left(x^{3}+y^{3}\right)$ is the discriminant of
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
p(z)=\left(x^{2}-x y+y^{2}\right) z^{2}-(x+1)(y+1) z+(x+y)
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
Note that the leading coefficient $x^{2}-x y+y^{2}=(x-y)^{2}+x y$ is positive unless $x=y=0$, in which case $\left((0+1)^{2}(0+1)^{2}\right)>4 \cdot 0^{3}+4 \cdot 0^{3}$. Substituting $z=1$, we get
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
p(1)=\left(x^{2}-x y+y^{2}\right)-(x+1)(y+1)+(x+y)=(x-y)^{2}-1 \leq 0 .
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
It follows that the discriminant is non-negative. It equals zero if and only if $|x-y|=1$ and $p(z)$ attains its minimum at $z=1$. Without loss of generality $y=x+1$. The minimum is attained at
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
1=\frac{(x+1)(y+1)}{2\left(x^{2}-x y+y^{2}\right)}=\frac{x^{2}+3 x+2}{2 x^{2}+2 x+2}
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
which reduces to $x^{2}=x$. Therefore, the only critical points are $(x, y)=(0,1)$ and $(x, y)=$ $(1,2)$.
|
| 285 |
+
|
| 286 |
+
- Without loss of generality $y \geq x$. Let $z=\frac{x+y}{2}$ and $a=y-z$. Note that $z \geq 0$ and $0 \leq a \leq \min \left\{\frac{1}{2}, z\right\}$. We can rewrite the inequality in terms of $z$ and $a$.
|
| 287 |
+
|
| 288 |
+
$$
|
| 289 |
+
\begin{aligned}
|
| 290 |
+
((x+1)(y+1))^{2}-4 x^{3}-4 y^{3} & =((z+1+a)(z+1-a))^{2}-4(z-a)^{3}-4(z+a)^{3} \\
|
| 291 |
+
& =\left((z+1)^{2}-a^{2}\right)^{2}-8 z^{3}-24 z a^{2} \\
|
| 292 |
+
& =a^{4}-\left(24 z+2(z+1)^{2}\right) a^{2}+\left((z+1)^{4}-8 z^{3}\right)
|
| 293 |
+
\end{aligned}
|
| 294 |
+
$$
|
| 295 |
+
|
| 296 |
+
This is a quadratic in $a^{2}$. It attains its minimum at $a^{2}=12 z+(z+1)^{2} \geq 1$. Therefore it is strictly decreasing in $a$ on the interval $\left[0, \min \left\{\frac{1}{2}, z\right\}\right]$. If $a=\frac{1}{2}$, then $y=x+1$. It follows that
|
| 297 |
+
|
| 298 |
+
$$
|
| 299 |
+
((x+1)(y+1))^{2}-4 x^{3}-4 y^{3}=((x+1)(x+2))^{2}-4 x^{3}-4(x+1)^{3}=x^{2}(x-1)^{2} \geq 0
|
| 300 |
+
$$
|
| 301 |
+
|
| 302 |
+
with equality if and only if $x=0$ or $x=1$. If $a=z$, then $x=0$. It follows that
|
| 303 |
+
|
| 304 |
+
$$
|
| 305 |
+
((x+1)(y+1))^{2}-4 x^{3}-4 y^{3}=(y+1)^{2}-4 y^{3}=y^{2}(1-y)+2 y\left(1-y^{2}\right)+\left(1-y^{3}\right) \geq 0
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+
with equality if and only if $y=1$. Therefore $(0,1)$ and $(1,2)$ are the only critical points.
|
| 309 |
+
|
| 310 |
+
## Solutions to Problem 3
|
| 311 |
+
|
| 312 |
+
Solution A. Denote the angle bisector of $A$ by $a$ and similarly for the other bisectors. Thus, given that $a, c, e$ have a common point $M$, we need to prove that $b, d, f$ are concurrent. We write $\angle(x, y)$ for the value of the directed angle between the lines $x$ and $y$, i.e. the angle of the counterclockwise rotation from $x$ to $y\left(\right.$ defined $\left.\left(\bmod 180^{\circ}\right)\right)$.
|
| 313 |
+
Since the sum of the angles of a convex hexagon is $720^{\circ}$, from the angle conditions we get that the sum of any two consecutive angles is equal to $240^{\circ}$. In particular, it now follows that $\angle(b, a)=\angle(c, b)=\angle(d, c)=\angle(e, d)=\angle(f, e)=\angle(a, f)=60^{\circ}$ (assuming the hexagon is clockwise oriented).
|
| 314 |
+
Let $X=A B \cap C D, Y=C D \cap E F$ and $Z=E F \cap A B$. Similarly, let $P=B C \cap D E, Q=D E \cap F A$ and $R=F A \cap B C$. From $\angle B+\angle C=240^{\circ}$ it follows that $\angle(Z X, X Y)=\angle(B X, X C)=60^{\circ}$. Similarly we have $\angle(X Y, Y Z)=\angle(Y Z, Z X)=60^{\circ}$, so triangle $X Y Z$ (and similarly triangle $P Q R$ ) is equilateral. We see that the hexagon $A B C D E F$ is obtained by intersecting the two equilateral triangles $X Y Z$ and $P Q R$.
|
| 315 |
+
We have $\angle(A M, M C)=\angle(a, c)=\angle(a, b)+\angle(b, c)=60^{\circ}$, and since
|
| 316 |
+
|
| 317 |
+
$$
|
| 318 |
+
\angle(A M, M C)=\angle(A X, X C)=\angle(A R, R C)=60^{\circ}
|
| 319 |
+
$$
|
| 320 |
+
|
| 321 |
+
$A, C, M, X, R$ are concyclic. Because $M$ lies on the bisector of angle $\angle X A R$, we must have $M R=M X$, so triangle $M R X$ is isosceles. Moreover, we have $\angle(M R, M X)=\angle(C R, C X)=$ $\angle(B C, C D)$, which is angle $C$ of the hexagon. We now see that the triangles $M R X, M P Y$ and $M Q Z$ are isosceles and similar. This implies that there is a rotation centered at $M$ that sends $X, Y$ and $Z$ to $R, P$ and $Q$ respectively. In particular, the equilateral triangles $X Y Z$ and $P Q R$ are congruent.
|
| 322 |
+
It follows that there also exists a rotation sending $X, Y, Z$ to $P, Q, R$ respectively. Define $N$ as the center of this rotation. Triangles $N X Z$ and $N P R$ are congruent and equally oriented, hence $N$ is equidistant from $X Z$ and $P R$ and lies on the inner bisector $b$ of $\angle B$ (we know $N$ lies on the inner, not the outer bisector because the rotation centered at $N$ is clockwise). In the same way we can show that $N$ is on $d$ and on $f$, so $b, d, f$ are concurrent at $N$.
|
| 323 |
+
|
| 324 |
+
Remark. The key observation (a rotation centered at $M$ sends $\triangle X Y Z$ to $\triangle R Q P$ ) can be established in slightly different ways. E.g., since $A, M, R, X$ are concyclic and $A, M, Q, Z$ are concyclic, $M$ is the Miquel point of the lines $X Z, R Q, X R, Z Q$, hence it is the center of similitude $s$ sending $\overrightarrow{X Z}$ to $\overrightarrow{R Q}$. Repeating the same argument for the other pairs of vectors, we obtain that $s$ sends $\triangle X Y Z$ to $\triangle R Q P$. Moreover, $s$ is a rotation, since $M$ is equidistant from $X Z$ and $R Q$.
|
| 325 |
+
|
| 326 |
+
Remark. The reverse argument can be derived in a different way, e.g., defining $N$ as the common point of the circles $B X P D, D Y Q F, F Z R B$, and showing that $\triangle N X Z=\triangle N P R$, etc.
|
| 327 |
+
|
| 328 |
+
|
| 329 |
+
Solution B. As in Solution A, we prove that the hexagon $A B C D E F$ is the intersection of the equilateral triangles $P Q R$ and $X Y Z$.
|
| 330 |
+
Let $d(S, A B)$ denote the signed distance from the point $S$ to the line $A B$, where the negative sign is taken if $A B$ separates $S$ and the hexagon. We define similarly the other distances $(d(S, B C)$, etc). Since $M \in a$, we have $d(M, Z X)=d(M, Q R)$. In the same way, we have $d(M, X Y)=d(M, R P)$ and $d(M, Y Z)=d(M, P Q)$. Therefore $d(M, Z X)+d(M, X Y)+$ $d(M, Y Z)=d(M, Q R)+d(M, R P)+d(M, P Q)$.
|
| 331 |
+
We now use of the following well-known lemma (which can be easily proved using areas) to deduce that triangles $P Q R$ and $X Y Z$ are congruent.
|
| 332 |
+
|
| 333 |
+
Lemma. The sum of the signed distances from any point to the sidelines of an equilateral triangle (where the signs are taken such that all distances are positive inside the triangle) is constant and equals the length of the altitude.
|
| 334 |
+
|
| 335 |
+
For $N=b \cap d$ we now find $d(N, Z X)=d(N, R P)$ and $d(N, X Y)=d(N, P Q)$. Using again the lemma for the point $N$, we get $d(N, Z X)+d(N, X Y)+d(N, Y Z)=d(N, Q R)+d(N, R P)+$ $d(N, P Q)$. Therefore $d(N, Y Z)=d(N, Q R)$, thus $N \in f$.
|
| 336 |
+
|
| 337 |
+
Remark. Instead of using the lemma, it is possible to use some equivalent observation in terms of signed areas.
|
| 338 |
+
|
| 339 |
+
Solution C. We use the same notations as in Solution A. We will show that $a, c$ and $e$ are concurrent if and only if
|
| 340 |
+
|
| 341 |
+
$$
|
| 342 |
+
A B+C D+E F=B C+D E+F A,
|
| 343 |
+
$$
|
| 344 |
+
|
| 345 |
+
which clearly implies the problem statement by symmetry.
|
| 346 |
+
Let $\vec{a}$ be the vector of unit length parallel to $a$ directed from $A$ towards the interior of the hexagon. We define analogously $\vec{b}$, etc. The angle conditions imply that opposite bisectors of the hexagon are parallel, so we have $\vec{a}\|\vec{d}, \vec{b}\| \vec{e}$ and $\vec{c} \| \vec{f}$. Moreover, as in the previous solutions, we know that $\vec{a}, \vec{c}$ and $\vec{e}$ make angles of $120^{\circ}$ with each other. Let $M_{A}=c \cap e, M_{C}=e \cap a$ and $M_{E}=a \cap c$. Then $M_{A}, M_{C}, M_{E}$ form an equilateral triangle with side length denoted by $s$. Note that the case $s=0$ is equivalent to $a, c$ and $e$ being concurrent.
|
| 347 |
+
Projecting $\overrightarrow{M_{E}} A+\overrightarrow{A B}=\overrightarrow{M_{E}} B=\overrightarrow{M_{E}} C+\overrightarrow{C B}$ onto $\vec{e}=-\vec{b}$, we obtain
|
| 348 |
+
|
| 349 |
+
$$
|
| 350 |
+
\overrightarrow{A B} \cdot \vec{b}-\overrightarrow{C B} \cdot \vec{b}=\overrightarrow{M_{E} C} \cdot \vec{b}-\overrightarrow{M_{E} A} \cdot \vec{b}=\overrightarrow{M_{E}} A \cdot \vec{e}-\overrightarrow{M_{E}} C \cdot \vec{e}
|
| 351 |
+
$$
|
| 352 |
+
|
| 353 |
+
Writing $\varphi=\frac{1}{2} \angle B=\frac{1}{2} \angle D=\frac{1}{2} \angle F$, we know that $\overrightarrow{A B} \cdot \vec{b}=-A B \cdot \cos (\varphi)$, and similarly $\overrightarrow{C B} \cdot \vec{b}=$ $-C B \cdot \cos (\varphi)$. Because $M_{E} A$ and $M_{E} C$ intersect $e$ at $120^{\circ}$ angles, we have $\overrightarrow{M_{E}} A \cdot \vec{e}=\frac{1}{2} M_{E} A$ and $\overrightarrow{M_{E}} C \cdot \vec{e}=\frac{1}{2} M_{E} C$. We conclude that
|
| 354 |
+
|
| 355 |
+
$$
|
| 356 |
+
2 \cos (\varphi)(A B-C B)=M_{E} C-M_{E} A
|
| 357 |
+
$$
|
| 358 |
+
|
| 359 |
+
Adding the analogous equalities $2 \cos (\varphi)(C D-E D)=M_{A} E-M_{A} C$ and $2 \cos (\varphi)(E F-A F)=$ $M_{C} A-M_{C} E$, we obtain
|
| 360 |
+
$2 \cos (\varphi)(A B+C D+E F-C B-E D-A F)=M_{E} C-M_{E} A+M_{A} E-M_{A} C+M_{C} A-M_{C} E$.
|
| 361 |
+
Because $M_{A}, M_{C}$ and $M_{E}$ form an equilateral triangle with side length $s$, we have $M_{E} C-$ $M_{A} C= \pm s, M_{C} A-M_{E} A= \pm s$, and $M_{A} E-M_{C} E= \pm s$. Therefore, the right hand side $M_{E} C-M_{E} A+M_{A} E-M_{A} C+M_{C} A-M_{C} E$ equals $\pm s \pm s \pm s$, which (irrespective of the choices of the $\pm$-signs) is 0 if and only if $s=0$. Because $\cos (\varphi) \neq 0$, we conclude that
|
| 362 |
+
|
| 363 |
+
$$
|
| 364 |
+
A B+C D+E F=C B+E D+A F \Longleftrightarrow s=0 \Longleftrightarrow a, c, e \text { concurrent, }
|
| 365 |
+
$$
|
| 366 |
+
|
| 367 |
+
as desired.
|
| 368 |
+
Remark. Equalities used in the solution could appear in different forms, in particular, in terms of signed lengths.
|
| 369 |
+
|
| 370 |
+
Remark. Similar solutions could be obtained by projecting onto the line perpendicular to $b$ instead of $b$.
|
| 371 |
+
|
| 372 |
+
Solution D. We use the the same notations as in previous solutions and the fact that $a \| d$, $b \| e$ and $c \| f$ make angles of $120^{\circ}$. Also, we may assume that $E$ and $C$ are not symmetric in $a$ (if they are, the entire figure is symmetric and the conclusion is immediate).
|
| 373 |
+
We consider two mappings: the first one $s: a \rightarrow B C \rightarrow d$ sending $A^{\prime} \mapsto B^{\prime} \mapsto S$ is defined such that $A^{\prime} B^{\prime} \| A B$ and $B^{\prime} S \| b$, and the second one $t: a \rightarrow E F \rightarrow d$ sending $A^{\prime} \mapsto F^{\prime} \mapsto T$ is defined such that $A^{\prime} F^{\prime} \| A F$ and $F^{\prime} T \| f$. Both maps are affine linear since they are compositions of affine tranformations. We will prove that they coincide by finding two distinct points $A^{\prime}, A^{\prime \prime} \in a$ for which $s\left(A^{\prime}\right)=t\left(A^{\prime}\right)$ and $s\left(A^{\prime \prime}\right)=t\left(A^{\prime \prime}\right)$. Then we will obtain that $s(A)=t(A)$, which by construction implies that the bisectors of $\angle B, \angle D$ and $\angle F$ are concurrent.
|
| 374 |
+
We will choose $A^{\prime}$ to be the reflection of $C$ in $e$ and $A^{\prime \prime}$ to be the reflection of $E$ in $c$. They are distinct since otherwise $C$ and $E$ would be symmetric in $a$. Applying the above maps $a \rightarrow B C$ and $a \rightarrow E F$ to $A^{\prime}$, we get points $B^{\prime}$ and $F^{\prime}$ such that $A^{\prime} B^{\prime} C D E F^{\prime}$ satisfies the problem statement. However, this hexagon is symmetric in $e$, hence the bisectors of $\angle B^{\prime}, \angle D, \angle F^{\prime}$ are concurrent and $s\left(A^{\prime}\right)=t\left(A^{\prime}\right)$. The same reasoning yields $s\left(A^{\prime \prime}\right)=t\left(A^{\prime \prime}\right)$, which finishes the solution.
|
| 375 |
+
|
| 376 |
+
Remark. This solution is based on the fact that that two specific affine linear maps coincide. Here it was proved by exhibiting two points where they coincide. One could prove it in another way, exhibiting one such point and proving that the 'slopes' are equal.
|
| 377 |
+
|
| 378 |
+
Remark. There are similar solutions where claims and proofs could be presented in more 'elementary' terms. For example, an elementary reformulation of the 'slopes' being equal is: if $b^{\prime}$ passes through $B^{\prime}$ parallel to $b$, and $f^{\prime}$ passes through $F^{\prime}$ parallel to $f$, then the line through $b \cap f$ and $b^{\prime} \cap f^{\prime}$ is parallel to $a$ (which is parallel to $d$ ).
|
| 379 |
+
|
| 380 |
+
Solution E. We use the same notations as in previous solutions.
|
| 381 |
+
Since the sum of the angles of a convex hexagon is $720^{\circ}$, from the angle conditions we get $\angle B+\angle C=720^{\circ} / 3=240^{\circ}$. From $\angle B+\angle C=240^{\circ}$ it follows that the angle between $c$ and $b$ equals $60^{\circ}$. The same is analogously true for other pairs of bisectors of neighboring angles.
|
| 382 |
+
Consider the points $O_{a} \in a, O_{c} \in c, O_{e} \in e$, each at the same distance $d^{\prime}$ from $M$, where $d^{\prime}>\max \{M A, M C, M E\}$, and such that the rays $A O_{a}, C O_{c}, E O_{e}$ point out of the hexagon. By
|
| 383 |
+
construcion, $O_{a}$ and $O_{c}$ are symmetrical in $e$, hence $O_{a} O_{c} \perp b$. Similarly, $O_{c} O_{e} \perp d, O_{e} O_{a} \perp f$. Thus it suffices to prove that perpendiculars from $B, D, F$ to the sidelines of $\triangle O_{a} O_{c} O_{e}$ are concurrent. By a well-known criteria, this condition is equivalent to equality
|
| 384 |
+
|
| 385 |
+
$$
|
| 386 |
+
O_{a} B^{2}-O_{c} B^{2}+O_{c} D^{2}-O_{e} D^{2}+O_{e} F^{2}-O_{a} F^{2}=0
|
| 387 |
+
$$
|
| 388 |
+
|
| 389 |
+
To prove ( $*$ ) consider a circle $\omega_{a}$ centered at $O_{a}$ and tangent to $A B$ and $A F$ and define circles $\omega_{c}$ and $\omega_{e}$ in the same way. Rewrite $O_{a} B^{2}$ as $r_{a}^{2}+B_{a} B^{2}$, where $r_{a}$ is the radius of $\omega_{a}$, and $B_{a}$ is the touch point of $\omega_{a}$ with $A B$. Using similar notation for the other tangent points, transform (*) into
|
| 390 |
+
|
| 391 |
+
$$
|
| 392 |
+
B_{a} B^{2}-B_{c} B^{2}+D_{c} D^{2}-D_{e} D^{2}+F_{e} F^{2}-F_{a} F^{2}=0 .
|
| 393 |
+
$$
|
| 394 |
+
|
| 395 |
+
Furthermore, $\angle O_{c} O_{a} B_{a}=\angle M O_{a} B_{a}+\angle O_{c} O_{a} M=\left(90^{\circ}-\varphi\right)+30^{\circ}=120^{\circ}-\varphi$, where $\varphi=$ $\frac{1}{2} \angle A$. (Note that $\varphi>30^{\circ}$, since $A B C D E F$ is convex.) By analogous arguments, $\angle O_{a} O_{c} B_{c}=$ $\angle O_{e} O_{c} D_{c}=\angle O_{c} O_{e} D_{e}=\angle O_{a} O_{e} F_{e}=\angle O_{e} O_{a} F_{a}=120^{\circ}-\varphi$. It follows that rays $O_{a} B_{a}$ and $O_{c} B_{c}$ (being symmetrical in $e$ ) intersect at $U_{e} \in e$ forming an isosceles triangle $\triangle O_{a} U_{e} O_{c}$. Similarly define $\triangle O_{c} U_{a} O_{e}$ and $\triangle O_{e} U_{c} O_{a}$. These triangles are congruent (equal bases and corresponding angles). Therefore we have $O_{a} U_{c}=U_{c} O_{e}=O_{e} U_{a}=U_{a} O_{c}=O_{c} U_{e}=U_{e} O_{a}$. Moreover, we also have $B_{a} U_{e}=O_{a} U_{e}-r_{a}=O_{a} U_{c}-r_{a}=F_{a} U_{c}=x$, and thus similarly $D_{c} U_{a}=B_{c} U_{e}=y$, $F_{e} U_{c}=D_{e} U_{a}=z$.
|
| 396 |
+
Now from quadrilateral $B B_{a} U_{e} B_{c}$ with two opposite right angles $B_{a} B^{2}-B_{c} B^{2}=B_{c} U_{e}^{2}-B_{a} U_{e}^{2}=$ $y^{2}-x^{2}$. Similarly $D_{c} D^{2}-D_{e} D^{2}=D_{e} U_{a}^{2}-D_{c} U_{a}^{2}=z^{2}-y^{2}$ and $F_{e} F^{2}-F_{a} F^{2}=F_{a} U_{c}^{2}-F_{e} U_{c}^{2}=$ $x^{2}-z^{2}$. Finally, we substitute this into $(* *)$, and the claim is proved.
|
| 397 |
+
|
| 398 |
+
Remark. Circles $\omega_{a}, \omega_{c}$ and $\omega_{e}$ could be helpful in some other solutions. In particular, the movement of $A$ along $a$ in Solution D is equivalent to varying $r_{a}$.
|
| 399 |
+
|
| 400 |
+
## Solutions to Problem 4
|
| 401 |
+
|
| 402 |
+
Solution A. Let $\sigma=\left(\sigma_{1}, \ldots, \sigma_{n-1}\right)$ be a fresh permutation of the integers $1,2, \ldots, n-1$. We claim that for any $1 \leq i \leq n-1$ the permutation
|
| 403 |
+
|
| 404 |
+
$$
|
| 405 |
+
\sigma^{(i)}=\left(\sigma_{1}, \ldots, \sigma_{i-1}, n, \sigma_{i}, \ldots, \sigma_{n-1}\right)
|
| 406 |
+
$$
|
| 407 |
+
|
| 408 |
+
is a fresh permutation of the integers $1,2, \ldots, n$. Indeed, let $1 \leq k \leq n-1$. If $k \geq i$ then we have $n \in\left\{\sigma_{1}^{(i)}, \ldots, \sigma_{k}^{(i)}\right\}$, but $n \notin\{1,2, \ldots, k\}$. And if $k<i$ we have $k<n-1$, and $\left\{\sigma_{1}^{(i)}, \ldots, \sigma_{k}^{(i)}\right\}=\left\{\sigma_{1}, \ldots, \sigma_{k}\right\} \neq\{1,2, \ldots, k\}$, since $\sigma$ is fresh. Moreover, it is easy to see that when we apply this construction to all fresh permutations of $1,2, \ldots, n-1$, we obtain $(n-1) \cdot f_{n-1}$ distinct fresh permutations of $1,2, \ldots, n$.
|
| 409 |
+
Note that a fresh permutation of $1,2, \ldots, n-1$ cannot end in $n-1$, and hence none of the previously constructed fresh permutations of $1,2, \ldots, n$ will end in $n-1$ either. Therefore, we will complete the proof by finding $f_{n-1}$ fresh permutations of $1,2, \ldots, n$ that end in $n-1$. To do this, let $\sigma=\left(\sigma_{1}, \ldots, \sigma_{n-1}\right)$ be a fresh permutation of $1,2, \ldots, n-1$ and let $j$ be such that $\sigma_{j}=n-1$. Define
|
| 410 |
+
|
| 411 |
+
$$
|
| 412 |
+
\sigma^{\prime}=\left(\sigma_{1}, \ldots, \sigma_{j-1}, n, \sigma_{j+1}, \ldots, \sigma_{n-1}, n-1\right)
|
| 413 |
+
$$
|
| 414 |
+
|
| 415 |
+
then clearly $\sigma^{\prime}$ is a permutation of $1,2, \ldots, n$ that ends in $n-1$. We show that $\sigma^{\prime}$ is fresh, so let $1 \leq k \leq n-1$. If $k \geq j$ then $n \in\left\{\sigma_{1}^{\prime}, \ldots, \sigma_{k}^{\prime}\right\}$ but $n \notin\{1,2, \ldots, k\}$; if $k<j$, then $k<n-1$ and $\left\{\sigma_{1}^{\prime}, \ldots, \sigma_{k}^{\prime}\right\}=\left\{\sigma_{1}, \ldots, \sigma_{k}\right\} \neq\{1,2, \ldots, k\}$, since $\sigma$ is fresh. So we have constructed $f_{n-1}$ additional fresh permutations of $1,2, \ldots, n$ (which again are all different), and the total number $f_{n}$ of fresh permutations of $1,2, \ldots, n$ must at least be $(n-1) f_{n-1}+f_{n-1}=n f_{n-1}$, as required.
|
| 416 |
+
|
| 417 |
+
Comment. A similar way to construct $n$ fresh permutations of $1,2, \ldots, n$ for each fresh permutation $\sigma$ of $1,2, \ldots, n-1$ is as follows: increase all entries of $\sigma$ by 1 , and then add the number 1 anywhere; all these permutations are fresh, except the ones where 1 is added at the front, which can be made fresh by swapping the 1 and the 2 . It is again straightforward to check that we obtain $n f_{n-1}$ permutations that are fresh and distinct, although a little extra care is needed to account for the fact that we increased the entries of our original permutation.
|
| 418 |
+
|
| 419 |
+
Solution B. Assuming $n \geq 3$, we construct $f_{n-1} \cdot n$ different fresh permutations.
|
| 420 |
+
Consider a fresh permutation of the $n-1$ numbers $1,3,4, \ldots, n$ (the number 2 has been removed), by which we mean a permutation $\left(x_{1}, \ldots, x_{n-1}\right)$ such that $x_{1} \neq 1$ and $\left\{x_{1}, \ldots, x_{k}\right\} \neq$ $\{1,3, \ldots, k+1\}$ for all $k$ with $2 \leq k \leq n-2$. There are exactly $f_{n-1}$ such permutations.
|
| 421 |
+
By inserting 2 anywhere in such a permutation, i.e. before or after all entries, or between two entries $x_{i}, x_{i+1}$, we generate the following list of $n$ distinct permutations of $1,2, \ldots, n$, which we claim are all fresh:
|
| 422 |
+
|
| 423 |
+
$$
|
| 424 |
+
\left(2, x_{1}, \ldots, x_{n-1}\right), \quad \ldots, \quad\left(x_{1}, \ldots, x_{i-1}, 2, x_{i}, \ldots, x_{n-1}\right), \quad \ldots, \quad\left(x_{1}, \ldots, x_{n-1}, 2\right)
|
| 425 |
+
$$
|
| 426 |
+
|
| 427 |
+
In order to verify freshness, suppose that some permutation above is not fresh, that is, for some $1 \leq k \leq n-1$, the first $k$ elements are $1, \ldots, k$. If $k=1$ then the first element is 1 ; but the first element is either 2 or $x_{1}$ and $x_{1} \neq 2$, so this is not possible. If $k \geq 2$ then the first $k$ elements must contain 2 and $x_{1}, \ldots, x_{k-1}$, so $\left\{x_{1}, \ldots, x_{k-1}\right\}=\{1,3, \ldots, k\}$, in contradiction to the fact that $\left(x_{1}, \ldots, x_{n-1}\right)$ is fresh.
|
| 428 |
+
We have thus constructed $f_{n-1} \cdot n$ different fresh permutations, so $f_{n} \geq f_{n-1} \cdot n$.
|
| 429 |
+
Comment. Note that the construction from solution B can also be performed by placing $n-1$ instead of 2 , or indeed any $k$ between 2 and $n-1$ (in which case it will work for $n \geq k+1$ ).
|
| 430 |
+
Moreover, similar arguments can be made while choosing to work with non-fresh permutations rather than fresh permutations. Indeed, in order to show that $n!-f_{n} \leq n\left((n-1)!-f_{n-1}\right)$ for all $n \geq 3$, which is equivalent to the problem statement, one can argue as follows. Given a non-fresh permutation $\left(\sigma_{1}, \ldots, \sigma_{n}\right)$ of $1,2, \ldots, n$, erasing $n-1$ from it and changing $n$ to $n-1$ yields a permutation which cannot be fresh. Moreover, each non-fresh permutation of $1,2, \ldots, n-1$ can be obtained in this way from at most $n$ different non-fresh permutations of $1,2, \ldots, n$. This type of argument would essentially mirror the one carried out in Solution B.
|
| 431 |
+
|
| 432 |
+
Solution C. By considering all permutations of $1,2, \ldots, n$ and considering the smallest $k$ for which the first $k$ numbers are $1,2, \ldots, k$ in some order, one can deduce the recursion
|
| 433 |
+
|
| 434 |
+
$$
|
| 435 |
+
\sum_{k=1}^{n}(n-k)!\cdot f_{k}=n!
|
| 436 |
+
$$
|
| 437 |
+
|
| 438 |
+
which holds for any $n \geq 1$.
|
| 439 |
+
Therefore, if $n \geq 3$ we have
|
| 440 |
+
|
| 441 |
+
$$
|
| 442 |
+
\begin{aligned}
|
| 443 |
+
0 & =n!-(n+1)(n-1)!+(n-1)(n-2)! \\
|
| 444 |
+
& =\sum_{k=1}^{n}(n-k)!\cdot f_{k}-(n+1) \sum_{k=1}^{n-1}(n-1-k)!\cdot f_{k}+(n-1) \sum_{k=1}^{n-2}(n-2-k)!\cdot f_{k} \\
|
| 445 |
+
& =f_{n}-n f_{n-1}+\sum_{k=1}^{n-2}(n-2-k)!\cdot((n-k)(n-k-1)-(n+1)(n-k-1)+(n-1)) \cdot f_{k} \\
|
| 446 |
+
& =f_{n}-n f_{n-1}+\sum_{k=1}^{n-2}(n-2-k)!\cdot k(k+2-n) \cdot f_{k} \leq f_{n}-n f_{n-1}
|
| 447 |
+
\end{aligned}
|
| 448 |
+
$$
|
| 449 |
+
|
| 450 |
+
which rewrites as $f_{n} \geq n f_{n-1}$.
|
| 451 |
+
Solution D. We first show that for any $n \geq 2$ we have
|
| 452 |
+
|
| 453 |
+
$$
|
| 454 |
+
f_{n}=\sum_{k=1}^{n-1} k(n-1-k)!\cdot f_{k}
|
| 455 |
+
$$
|
| 456 |
+
|
| 457 |
+
To deduce this relation, we imagine obtaining permutations of $1,2, \ldots, n$ by inserting $n$ into a permutation of the numbers $1,2, \ldots, n-1$. Specifically, let $\left(\sigma_{1}, \ldots, \sigma_{n-1}\right)$ be any permutation of $1,2, \ldots, n-1$, and let $1 \leq k \leq n-1$ be minimal with $\left\{\sigma_{1}, \ldots, \sigma_{k}\right\}=\{1,2, \ldots, k\}$. Note that there are $(n-1-k)!\cdot f_{k}$ such permutations. Furthermore, inserting $n$ in this permutation will give a fresh permutation if and only if $n$ is inserted before $\sigma_{k}$, so there are $k$ options to do so. Consequently, if $n \geq 3$,
|
| 458 |
+
|
| 459 |
+
$$
|
| 460 |
+
\begin{aligned}
|
| 461 |
+
f_{n} & =\sum_{k=1}^{n-1} k(n-1-k)!\cdot f_{k} \\
|
| 462 |
+
& =(n-1) \cdot f_{n-1}+\sum_{k=1}^{n-2} k(n-1-k)!\cdot f_{k} \\
|
| 463 |
+
& \geq(n-1) \cdot f_{n-1}+\sum_{k=1}^{n-2} k(n-2-k)!\cdot f_{k} \\
|
| 464 |
+
& =(n-1) \cdot f_{n-1}+f_{n-1}=n \cdot f_{n-1}
|
| 465 |
+
\end{aligned}
|
| 466 |
+
$$
|
| 467 |
+
|
| 468 |
+
completing the proof.
|
| 469 |
+
Comment. Fresh permutations are known as indecomposable permutations or irreducible permutations in the literature. The problem asks to prove that the probability that a randomly chosen permutation of $1,2, \ldots, n$ is indecomposable is a non-decreasing function of $n$. In fact, it turns out that this probability goes to 1 as $n \rightarrow \infty$ : for large $n$, almost all permutations of 1 , $2, \ldots, n$ are indecomposable. More can be found in:
|
| 470 |
+
Y. Koh \& S. Ree. Connected permutation graphs. Discrete Mathematics 307 (21):2628-2635, 2007.
|
| 471 |
+
|
| 472 |
+
## Solutions to Problem 5
|
| 473 |
+
|
| 474 |
+
Solution A. The angle bisector of $\angle E C D$ intersects the circumcircle of $C D E$ (which is $\Gamma$ ) at the midpoint $M$ of arc $D B E$. It is well-known that the incentre is the intersection of the angle bisector segment $C M$ and the circle with centre at $M$ and passing through $D, E$. We will verify this property for $P$.
|
| 475 |
+
|
| 476 |
+
|
| 477 |
+
By the conditions we have $A P=O A=O B=O C=O D=O E=R$. Both lines $O M$ and $A P B$ are perpendicular to $E D$, therefore $A P \| O M$; in the quadrilateral $A O M P$ we have $A P=O A=A M=R$ and $A P \| O M$, so $A O M P$ is a rhombus and its fourth side is $P M=R$.
|
| 478 |
+
In the convex quadrilateral $O M B P$ we have $O M \| P B$, so $O M B P$ is a symmetric trapezoid; the perpendicular bisector of its bases $A O$ and $P B$ coincide. From this symmetry we obtain $M D=O D=R$ and $M E=O E=R$. (Note that the triangles $O E M$ ad $O M D$ are equilateral.) We already have $M P=M D=M E=R$, so $P$ indeed lies on the circle with center $M$ and passing through $D, E$. (Notice that this circle is the reflection of $\Gamma$ about $D E$.)
|
| 479 |
+
From $P B=P C$ and $O B=O C$ we know that $B$ and $C$ are symmetrical about $O P$; from the rhombus $A O M P$ we find that $A$ and $M$ are also symmetrical about $O P$. By reflecting the collinear points $B, P, A$ (with $P$ lying in the middle) we get that $C, P, M$ are collinear (and $P$ is in the middle). Hence, $P$ lies on the line segments $C M$.
|
| 480 |
+
|
| 481 |
+
Solution B. Let $X$ be the second intersection of $C P$ with $\Gamma$. Using the power of the point $P$ in the circle $\Gamma$ and the fact that $P B=P C$, we find that $P X=P A=R$. The quadrilateral $A O X P$ has four sides of equal length, so it is a rhombus and in particular $O X$ is parallel to $A P$. This proves that $O X B P$ is a trapezoid, and because the diagonals $P X$ and $O B$ have equal length, this is even an isosceles trapezoid. Because of that, $D E$ is not only the perpendicular bisector of $P B$, but also of $O X$.
|
| 482 |
+
|
| 483 |
+
|
| 484 |
+
In particular we have $X D=X P=X O=X E=R$, which proves that $X$ is the middle of the arc $D E$ and $P$ belongs to the circle with center $X$ going through $D$ and $E$. These properties, together with the fact that $C, P, X$ are collinear, determine uniquely the incenter of $C D E$.
|
| 485 |
+
|
| 486 |
+
Solution C. Let $Y$ be the circumcenter of triangle $B P C$. Then from $Y B=Y P$ it follows that $Y$ lies on $D E$ (we assume $D$ lies in between $Y$ and $E$ ), and from $Y B=Y C$ it follows that $Y$ lies on $O P$, where $O$ is the center of $\Gamma$.
|
| 487 |
+
From $\angle A O C=2 \angle A B C=\angle A P C$ (because $\angle P B C=\angle P C B$ ) we deduce that $A O P C$ is a cyclic quadrilateral, and from $A P=R$ it follows that $A O P C$ is an isosceles trapezoid. We now find that $\angle Y C P=\angle Y P C=180^{\circ}-\angle O P C=180^{\circ}-\angle A C P$, so $Y$ lies on $A C$.
|
| 488 |
+
|
| 489 |
+
|
| 490 |
+
Power of a point gives $Y O \cdot Y P=Y C \cdot Y A=Y D \cdot Y E$, so $D, P, O$ and $E$ are concyclic. It follows that $2 \angle D A E=\angle D O E=\angle D P E=\angle D B E=180^{\circ}-\angle D A E$, so $\angle D A E=60^{\circ}$. We can now finish the proof by angle chasing.
|
| 491 |
+
From $A B \perp D E$ we have $\angle A O D+\angle B O E=180^{\circ}$ and from $\angle D O E=2 \angle D A E=120^{\circ}$ it follows that $\angle B O D+\angle B O E=120^{\circ}$. It follows that $\angle A O D-\angle B O D=180^{\circ}-120^{\circ}=60^{\circ}$. Let $\angle O A B=\angle O B A=2 \beta$; then $\angle A O D+\angle B O D=\angle A O B=180^{\circ}-4 \beta$. Together with $\angle A O D-\angle B O D=60^{\circ}$, this yields $\angle A O D=120^{\circ}-2 \beta$ and $\angle B O D=60^{\circ}-2 \beta$. We now find $\angle A E D=\frac{1}{2} \angle A O D=60^{\circ}-\beta$, which together with $\angle D A E=60^{\circ}$ yields $\angle A D E=60^{\circ}+\beta$. From the isosceles trapezoid $A O P C$ we have $\angle C D A=\angle C B A=\frac{1}{2} \angle C P A=\frac{1}{2} \angle P A O=\beta$, so $\angle C D E=\angle C D A+\angle A D E=\beta+60^{\circ}+\beta=60^{\circ}+2 \beta$.
|
| 492 |
+
From $\angle B O D=60^{\circ}-2 \beta$ we deduce that $\angle B E D=30^{\circ}-\beta$; together with $\angle D B E=120^{\circ}$ this yields $\angle E D B=30^{\circ}+\beta$. We now see that $\angle P D E=\angle B D E=30^{\circ}+\beta=\frac{1}{2} \angle C D E$, so $P$ is on the angle bisector of $\angle C D E$. Similarly, $P$ lies on the angle bisector of $\angle C E D$, so $P$ is the incenter of $C D E$.
|
| 493 |
+
|
| 494 |
+
Solution D. We draw the lines $D P$ and $E P$ and let $D^{\prime}$ resp. $E^{\prime}$ be the second intersection point with $\Gamma$.
|
| 495 |
+
|
| 496 |
+
|
| 497 |
+
The triangles $A P D^{\prime}$ and $D P B$ are similar, and the triangles $A P E^{\prime}$ and $E P B$ are also similar, hence they are all isosceles and it follows that $E^{\prime}, O, P, D^{\prime}$ lie on a circle with center $A$. In particular $A O D^{\prime}$ and $A O E^{\prime}$ are equilateral triangles. Angle chasing gives
|
| 498 |
+
|
| 499 |
+
$$
|
| 500 |
+
\begin{gathered}
|
| 501 |
+
\angle C D P=\angle C D D^{\prime}=\frac{1}{2} \angle C O D^{\prime}=\frac{1}{2}\left(60^{\circ}+\angle C O A\right) \\
|
| 502 |
+
\angle E D P=\angle E D D^{\prime}=\angle E E^{\prime} D^{\prime}=\angle P E^{\prime} D^{\prime}=\frac{1}{2} \angle P A D^{\prime}=\frac{1}{2}\left(60^{\circ}+\angle P A O\right)
|
| 503 |
+
\end{gathered}
|
| 504 |
+
$$
|
| 505 |
+
|
| 506 |
+
Similarly we prove $\angle C E P=\frac{1}{2}\left(60^{\circ}-\angle C O A\right)$ and $\angle D E P=\frac{1}{2}\left(60^{\circ}-\angle P A O\right)$ so if we can prove that $\angle C O A=\angle P A O$, we will have proven that $P$ belongs to the angle bisector of $\angle C E D$ and to the angle bisector of $\angle C D E$, which is enough to prove that $P$ is the incenter of the triangle $C D E$.
|
| 507 |
+
Let $\beta=\angle A B C=\angle P C B$. We have $\angle A P C=2 \beta$ and $\angle A O C=2 \beta$, so $A O P C$ is an inscribed quadrilateral. Moreover, since the diagonals $A P$ and $C O$ have equal length, this is actually an isosceles trapezoid, and hence $\angle P A O=\angle C P A=\angle C O A$ which concludes the proof.
|
| 508 |
+
|
| 509 |
+
Solution E. Without loss of generality we assume that $D$ and $C$ are in the same half-plane regarding line $A B$.
|
| 510 |
+
Since $P C=B P$ and $A B C D$ is inscribed quadrilateral we have $\angle P C B=\angle C B P=\angle C E A=\alpha$. As in the other solutions, $A O P C$ is an isosceles trapezoid and $2 \alpha=\angle C P A=\angle P C O$
|
| 511 |
+
|
| 512 |
+
|
| 513 |
+
Let $K$ be intersection of $E O$ and $\Gamma$. Then $\angle K D E=90^{\circ}, A B \| D K$ and $K D B A$ is isosceles trapezoid. We obtain $D P=B D=A K$, which implies that $D P A K$ is a parallelogram and hence $D K=P A=R=O D=O K$. We see that $D O K$ is an equilateral triangle. Then $\angle E C D=\angle E K D=60^{\circ}$.
|
| 514 |
+
Further we prove that $P C$ bisects $\angle E C D$ using $\angle D C B=\angle D K B=\angle K D A$ (from isosceles trapeziod $D K A B$ ) and that $\angle K E C=\angle O E C=\angle O C E$ (from isosceles triangle $O C E$ ):
|
| 515 |
+
|
| 516 |
+
$$
|
| 517 |
+
\angle D C P=\angle D C B+\angle B C P=\angle K D A+\alpha=\angle K E C+\angle C E A+\alpha=\angle O C E+2 \alpha=\angle P C E
|
| 518 |
+
$$
|
| 519 |
+
|
| 520 |
+
Further by $\angle D C P=\angle P C E=\frac{1}{2} \angle E C D=30^{\circ}$ distances between $P$ and sides $\triangle C D E$ are $\frac{1}{2} P C=\frac{1}{2} P B$ (as ratio between cathetus and hypotenuse in right triangle with angles $60^{\circ}$ and $30^{\circ}$ ). So, we have found incentre.
|
| 521 |
+
|
| 522 |
+
Solution F. Let $F, G, H$ be the projections of $P$ on the sides $D E, D C$ resp. $C E$. If $P$ is indeed the incenter, then the three line segments $P F, P G, P H$ have the same length. This means that the problem is equivalent to proving that $P G=P H=P F=\frac{1}{2} P B=\frac{1}{2} P C$ and thus trigonometry in the right-angled triangles $C P G$ and $C P H$ tells us that it is enough to prove that $\angle D C P=\angle E C P=30^{\circ}$.
|
| 523 |
+
|
| 524 |
+
|
| 525 |
+
We introduce the point $X$ as the second intersection of the line $C P$ with $\Gamma$. Because $O$ is the center of $\Gamma$ we can reduce the problem to proving that $\angle X O D=\angle X O E=60^{\circ}$, or equivalently that $X O D$ and $X O E$ are equilateral triangles. This last condition is equivalent to $X$ being the reflection of $O$ on the line $D E$. Following the chain of equivalences, we see therefore that in order to solve the problem it is enough to prove that $X$ is the reflection of $O$ on $D E$. We prove this property as in Solution B, using the fact that $O X B P$ is an isosceles trapezoid.
|
| 526 |
+
|
| 527 |
+
Solution G. Assume $A B$ is parallel to the horizontal axis, and that $\Gamma$ is the unit circle. Write $f(\theta)$ for the point $(\cos (\theta), \sin (\theta))$ on $\Gamma$. As in Solution C, assume that $\angle A O B=180^{\circ}-4 \beta$; then we can take $B=f(2 \beta)$ and $A=f\left(180^{\circ}-2 \beta\right)$. As in Solution C, we observe that $A O P C$ is an isosceles trapezoid, which we use to deduce that $\angle A B C=\frac{1}{2} \angle A P C=\frac{1}{2} \angle O A B=\beta$. We now know that $C=f\left(180^{\circ}-4 \beta\right)$.
|
| 528 |
+
The point $P$ lies on $A B$ with $A P=R=1$, so $P=\left(\cos \left(180^{\circ}-2 \beta\right)+1, \sin (2 \beta)\right)=(1-$ $\cos (2 \beta), \sin (2 \beta))$. The midpoint of $B P$ therefore has coordinates $\left(\frac{1}{2}, \sin (2 \beta)\right)$, so $D$ and $E$ have $x$-coordinate $\frac{1}{2}$. Without loss of generality, we take $D=f\left(60^{\circ}\right)$ and $E=f\left(-60^{\circ}\right)$.
|
| 529 |
+
We have now obtained coordinates for all points in the problem, with one free parameter $(\beta)$. To show that $P$ is the incenter of $C D E$, we will show that $P$ lies on the bisector of $\angle C D E$; analogously, one can show that $P$ lies on the bisector of angle $C E D$. The bisector of angle $C D E$ passes through the midpoint $M$ of the arc $C E$ not containing $D E$; because $C=f\left(180^{\circ}-4 \beta\right)$ and $E=f\left(-60^{\circ}\right)$, we have $M=f\left(240^{\circ}-2 \beta\right)$.
|
| 530 |
+
It remains to show that $P=(1-\cos (2 \beta), \sin (2 \beta))$ lies on the line connecting the points $D=$ $\left(\cos \left(60^{\circ}\right), \sin \left(60^{\circ}\right)\right)$ and $M=\left(\cos \left(240^{\circ}-2 \beta\right), \sin \left(240^{\circ}-2 \beta\right)\right)=\left(-\cos \left(60^{\circ}-2 \beta\right),-\sin \left(60^{\circ}-2 \beta\right)\right)$. The equation for the line $D M$ is
|
| 531 |
+
$\left(Y+\sin \left(60^{\circ}-2 \beta\right)\right)\left(\cos \left(60^{\circ}\right)+\cos \left(60^{\circ}-2 \beta\right)\right)=\left(\sin \left(60^{\circ}\right)+\sin \left(60^{\circ}-2 \beta\right)\right)\left(X+\cos \left(60^{\circ}-2 \beta\right)\right)$,
|
| 532 |
+
which, using the fact that $\cos \left(60^{\circ}\right)+\cos \left(60^{\circ}-2 \beta\right)=2 \cos (\beta) \cos \left(60^{\circ}-\beta\right)$ and $\sin \left(60^{\circ}\right)+\sin \left(60^{\circ}-\right.$ $2 \beta)=2 \cos (\beta) \sin \left(60^{\circ}-\beta\right)$, simplifies to
|
| 533 |
+
|
| 534 |
+
$$
|
| 535 |
+
\left(Y+\sin \left(60^{\circ}-2 \beta\right)\right) \cos \left(60^{\circ}-\beta\right)=\left(X+\cos \left(60^{\circ}-2 \beta\right)\right) \sin \left(60^{\circ}-\beta\right)
|
| 536 |
+
$$
|
| 537 |
+
|
| 538 |
+
Because $\cos \left(60^{\circ}-2 \beta\right) \sin \left(60^{\circ}-\beta\right)-\sin \left(60^{\circ}-2 \beta\right) \cos \left(60^{\circ}-\beta\right)=\sin (\beta)$, this equation further simplifies to
|
| 539 |
+
|
| 540 |
+
$$
|
| 541 |
+
Y \cos \left(60^{\circ}-\beta\right)-X \sin \left(60^{\circ}-\beta\right)=\sin (\beta) .
|
| 542 |
+
$$
|
| 543 |
+
|
| 544 |
+
Plugging in the coordinates of $P$, i.e., $X=1-\cos (2 \beta)$ and $Y=\sin (2 \beta)$, shows that $P$ is on this line: for this choice of $X$ and $Y$, the left hand side equals $\sin \left(60^{\circ}+\beta\right)-\sin \left(60^{\circ}-\beta\right)=$ $2 \cos \left(60^{\circ}\right) \sin (\beta)$, which is indeed equal to $\sin (\beta)$. So $P$ lies on the bisector $D M$ of $\angle C D E$, as desired.
|
| 545 |
+
|
| 546 |
+
Solution H. Let $\Gamma$ be the complex unit circle and let $A B$ be parallel with the real line and $0<\varphi=\arg b<\frac{\pi}{2}$. Then
|
| 547 |
+
|
| 548 |
+
$$
|
| 549 |
+
|b|=1, \quad a=-\bar{b}, \quad p=a+1=1-\bar{b}
|
| 550 |
+
$$
|
| 551 |
+
|
| 552 |
+
From $\operatorname{Re} d=\operatorname{Re} e=\operatorname{Re} \frac{p+b}{2}=\frac{1}{2}$ we get that $d=\frac{1}{2}+\frac{\sqrt{3}}{2} i$ and $e=\frac{1}{2}-\frac{\sqrt{3}}{2} i$ are conjugate 6 th roots of unity; $d^{3}=e^{3}=-1, d+e=1, d^{2}=-e, e^{2}=-d$ etc.
|
| 553 |
+
Point $C$ is the reflection of $B$ in line $O P$. From $\arg p=\arg (1-\bar{b})=\frac{1}{2}(\pi-\varphi)$, we can get $\arg c=2 \arg p-\arg b=\pi-2 \varphi$, so $c=-\bar{b}^{2}$.
|
| 554 |
+
Now we can verify that $E P$ bisects $\angle C E D$. This happens if and only if $(p-e)^{2}(\bar{c}-\bar{e})(\bar{d}-\bar{e})$ is real. Since $\bar{d}-\bar{e}=-\sqrt{3} i$, this is equivalent with $\operatorname{Re}\left[(p-e)^{2}(\bar{c}-\bar{e})\right]=0$. Here
|
| 555 |
+
|
| 556 |
+
$$
|
| 557 |
+
\begin{aligned}
|
| 558 |
+
(p-e)^{2}(\bar{c}-\bar{e}) & =(1-\bar{b}-e)^{2}\left(-b^{2}-d\right)=(d-\bar{b})^{2}\left(-b^{2}-d\right) \\
|
| 559 |
+
& =-|b|^{4}+2 d|b|^{2} b-d^{2} b^{2}-d \bar{b}^{2}+2 d^{2} \bar{b}-d^{3} \\
|
| 560 |
+
& =-1-2 d b+\bar{d} b^{2}-d \bar{b}^{2}-2 \overline{d b}+1 \\
|
| 561 |
+
& =-2(d b-\overline{d b})+\left(\bar{d} b^{2}-d \bar{b}^{2}\right),
|
| 562 |
+
\end{aligned}
|
| 563 |
+
$$
|
| 564 |
+
|
| 565 |
+
whose real part is zero. It can be proved similarly that $D P$ bisects $\angle E D C$.
|
| 566 |
+
|
| 567 |
+
## Solutions to Problem 6
|
| 568 |
+
|
| 569 |
+
Answer. The only such $m$ are $m=2$ and $m=10$.
|
| 570 |
+
Solution A. Consider an integer $m>1$ for which the sequence defined in the problem statement contains only perfect squares. We shall first show that $m-1$ is a power of 3 .
|
| 571 |
+
Suppose that $m-1$ is even. Then $a_{4}=5 m-1$ should be divisible by 4 and hence $m \equiv 1(\bmod 4)$. But then $a_{5}=5 m^{2}+3 m-1 \equiv 3(\bmod 4)$ cannot be a square, a contradiction. Therefore $m-1$ is odd.
|
| 572 |
+
Suppose that an odd prime $p \neq 3$ divides $m-1$. Note that $a_{n}-a_{n-1} \equiv a_{n-2}-a_{n-3}(\bmod p)$. It follows that modulo $p$ the sequence takes the form $1,1,4,4,7,7,10,10, \ldots$; indeed, a simple induction shows that $a_{2 k} \equiv a_{2 k-1} \equiv 3 k-2(\bmod p)$ for $k \geq 1$. Since $\operatorname{gcd}(p, 3)=1$ we get that the sequence $a_{n}(\bmod p)$ contains all the residues modulo $p$, a contradiction since only $(p+1) / 2$ residues modulo $p$ are squares. This shows that $m-1$ is a power of 3 .
|
| 573 |
+
Let $h, k$ be integers such that $m=3^{k}+1$ and $a_{4}=h^{2}$. We then have $5 \cdot 3^{k}=(h-2)(h+2)$. Since $\operatorname{gcd}(h-2, h+2)=1$, it follows that $h-2$ equals either $1,3^{k}$ or 5 , and $h+2$ equals either $5 \cdot 3^{k}, 5$ or $3^{k}$, respectively. In the first two cases we get $k=0$ and in the last case we get $k=2$. This implies that either $m=2$ or $m=10$.
|
| 574 |
+
We now show the converse. Suppose that $m=2$ or $m=10$. Let $t=1$ or $t=3$ so that $m=t^{2}+1$. Let $b_{1}, b_{2}, b_{3}, \ldots$ be a sequence of integers defined by $b_{1}=1, b_{2}=1, b_{3}=2$, and
|
| 575 |
+
|
| 576 |
+
$$
|
| 577 |
+
b_{n}=t b_{n-1}+b_{n-2}, \quad \text { for all } n \geq 4
|
| 578 |
+
$$
|
| 579 |
+
|
| 580 |
+
Clearly, $a_{n}=b_{n}^{2}$ for $n=1,2,3$. Note that if $m=2$ then $a_{4}=9$ and $b_{4}=3$, and if $m=10$ then $a_{4}=49$ and $b_{4}=7$. In both the cases we have $a_{4}=b_{4}^{2}$.
|
| 581 |
+
If $n \geq 5$ then we have
|
| 582 |
+
|
| 583 |
+
$$
|
| 584 |
+
b_{n}^{2}+b_{n-3}^{2}=\left(t b_{n-1}+b_{n-2}\right)^{2}+\left(b_{n-1}-t b_{n-2}\right)^{2}=\left(t^{2}+1\right)\left(b_{n-1}^{2}+b_{n-2}^{2}\right)=m\left(b_{n-1}^{2}+b_{n-2}^{2}\right) .
|
| 585 |
+
$$
|
| 586 |
+
|
| 587 |
+
Therefore, it follows by induction that $a_{n}=b_{n}^{2}$ for all $n \geq 1$. This completes the solution.
|
| 588 |
+
Solution B. We present an alternate proof that $m=2$ and $m=10$ are the only possible values of $m$ with the required property.
|
| 589 |
+
Note that
|
| 590 |
+
|
| 591 |
+
$$
|
| 592 |
+
\begin{aligned}
|
| 593 |
+
& a_{4}=5 m-1 \\
|
| 594 |
+
& a_{5}=5 m^{2}+3 m-1 \\
|
| 595 |
+
& a_{6}=5 m^{3}+8 m^{2}-2 m-4
|
| 596 |
+
\end{aligned}
|
| 597 |
+
$$
|
| 598 |
+
|
| 599 |
+
Since $a_{4}$ and $a_{6}$ are squares, so is $a_{4} a_{6}$. We have
|
| 600 |
+
|
| 601 |
+
$$
|
| 602 |
+
4 a_{4} a_{6}=100 m^{4}+140 m^{3}-72 m^{2}-72 m+16
|
| 603 |
+
$$
|
| 604 |
+
|
| 605 |
+
Notice that
|
| 606 |
+
|
| 607 |
+
$$
|
| 608 |
+
\begin{aligned}
|
| 609 |
+
& \left(10 m^{2}+7 m-7\right)^{2}=100 m^{4}+140 m^{3}-91 m^{2}-98 m+49<4 a_{4} a_{6} \\
|
| 610 |
+
& \left(10 m^{2}+7 m-5\right)^{2}=100 m^{4}+140 m^{3}-51 m^{2}-70 m+25>4 a_{4} a_{6}
|
| 611 |
+
\end{aligned}
|
| 612 |
+
$$
|
| 613 |
+
|
| 614 |
+
so we must have
|
| 615 |
+
|
| 616 |
+
$$
|
| 617 |
+
4 a_{4} a_{6}=\left(10 m^{2}+7 m-6\right)^{2}=100 m^{4}+140 m^{3}-71 m^{2}-84 m+36
|
| 618 |
+
$$
|
| 619 |
+
|
| 620 |
+
This implies that $m^{2}-12 m+20=0$, so $m=2$ or $m=10$.
|
| 621 |
+
|
EGMO/md/en-2021-solutions.md
ADDED
|
@@ -0,0 +1,366 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Solutions of EGMO 2021
|
| 2 |
+
|
| 3 |
+
Problem 1. According to Anna, the number 2021 is fantabulous. She states that if any element of the set $\{m, 2 m+1,3 m\}$ is fantabulousfor a positive integer $m$, then they are all fantabulous. Is the number 2021 ${ }^{2021}$ fantabulous?
|
| 4 |
+
(Australia, Angelo Di Pasquale)
|
| 5 |
+
Answer: Yes
|
| 6 |
+
|
| 7 |
+
## Solution 1.
|
| 8 |
+
|
| 9 |
+
Consider the sequence of positive integers $m, 3 m, 6 m+1,12 m+3,4 m+1,2 m$. Since each number in the sequence is fantabulous if and only if the next one is, we deduce that $m$ is fantabulous if and only if $2 m$ is fantabulous.
|
| 10 |
+
|
| 11 |
+
Combined with the fact that $m$ is fantabulous if and only if $2 m+1$ is fantabulous, this implies that $m>1$ is fantabulous if and only if $f(m)=\left[\frac{m}{2}\right]$ is fantabulous. We can apply $f$ sufficiently many times to any positive integer $n$ to conclude that $n$ is fantabulous if and only if 1 is fantabulous. Therefore, the fact that 2021 is fantabulous implies that 1 is fantabulous, which in turn implies that $2021^{2021}$ is fantabulous.
|
| 12 |
+
|
| 13 |
+
## Solution 2.
|
| 14 |
+
|
| 15 |
+
Let $m>1$ be a fantabulous number. Note that at least one of the following four cases must hold.
|
| 16 |
+
|
| 17 |
+
- Case 1. The number $m$ is odd;
|
| 18 |
+
|
| 19 |
+
We have $m=2 a+1$ for some positive integer $a$, so $a<m$ is also fantabulous.
|
| 20 |
+
|
| 21 |
+
- Case 2. The number $m$ is a multiple of 3;
|
| 22 |
+
|
| 23 |
+
We have $m=3 a$ for some positive integer $a$, so $a<m$ is also fantabulous.
|
| 24 |
+
|
| 25 |
+
- Case 3. The number $m$ is 4 modulo 6;
|
| 26 |
+
|
| 27 |
+
We have $m=6 a-2$ for some positive integer $a$. We have the sequence of fantabulous numbers
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
(6 a-2) \rightarrow(12 a-3) \rightarrow(4 a-1)
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
so $4 a-1<m$ is also fantabulous.
|
| 34 |
+
|
| 35 |
+
## - Case 4. The number $m$ is 2 modulo 6;
|
| 36 |
+
|
| 37 |
+
We have $m=6 a+2$ for some positive integer $a$. We have the sequence of fantabulous numbers
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
(6 a+2) \rightarrow(12 a+5) \rightarrow(36 a+15) \rightarrow(18 a+7) \rightarrow(9 a+3) \rightarrow(3 a+1)
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
so $3 a+1<m$ is also fantabulous.
|
| 44 |
+
|
| 45 |
+
In all cases, we see that there is another fantabulous number less than $m$. Since 2021 is fantabulous, it follows that 1 is fantabulous.
|
| 46 |
+
|
| 47 |
+
Observe that a number $m$ is not fantabulous if and only if all of the elements of the set $\{m, 2 m+1,3 m\}$ are not fantabulous. So, the argument above shows that if there exists a positive integer that is not fantabulous, then 1 would not be fantabulous either. This is a contradiction, so all positive integers are fantabulous and, in particular, $2021^{2021}$ is fantabulous.
|
| 48 |
+
|
| 49 |
+
## Solution 3.
|
| 50 |
+
|
| 51 |
+
The following transformations show that $a$ is fantabulous if and only if $3 a, 3 a+1$ or $3 a+2$ are fantabulous.
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\begin{aligned}
|
| 55 |
+
& a \rightarrow 3 a \\
|
| 56 |
+
& a \rightarrow 2 a+1 \rightarrow 6 a+3 \rightarrow 3 a+1 \\
|
| 57 |
+
& a \rightarrow 2 a+1 \rightarrow 4 a+3 \rightarrow 12 a+9 \rightarrow 36 a+27 \rightarrow 18 a+13 \rightarrow 9 a+6 \rightarrow 3 a+2
|
| 58 |
+
\end{aligned}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
This implies that $a \geq 3$ is fantabulous if and only if $f(a)=\left[\frac{a}{3}\right]$ is fantabulous. We can use this to deduce that 1 and 2 are fantabulous from the fact that 2021 is fantabulous in the following way:
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
2021 \rightarrow 673 \rightarrow 224 \rightarrow 74 \rightarrow 24 \rightarrow 8 \rightarrow 2 \rightarrow 5 \rightarrow 1
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
We can apply $f$ sufficiently many times to any positive integer $n$ to arrive at the number 1 or 2 . It follows that every positive integer is fantabulous, so $2021^{2021}$ is fantabulous.
|
| 68 |
+
|
| 69 |
+
Problem 2. Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that the equation
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
f(x f(x)+y)=f(y)+x^{2}
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
holds for all rational numbers $x$ and $y$.
|
| 76 |
+
Here, $\mathbb{Q}$ denotes the set of rational numbers.
|
| 77 |
+
(Slovakia, Patrik Bak)
|
| 78 |
+
|
| 79 |
+
Answer: $f(x)=x$ and $f(x)=-x$.
|
| 80 |
+
|
| 81 |
+
Solution. Denote the equation from the statement by (1). Let $x f(x)=A$ and $x^{2}=B$. The equation (1) is of the form
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
f(A+y)=f(y)+B
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Also, if we put $y \rightarrow-A+y$, we have $f(A-A+y)=f(-A+y)+B$. Therefore
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
f(-A+y)=f(y)-B
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
We can easily show that for any integer $n$ we even have
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
f(n A+y)=f(y)+n B
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
Indeed, it's trivially true for $n=0$ and if this holds true for some integer $n$, then
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
f((n+1) A+y)=f(A+y+n A)=f(n y+A)+B=f(y)+n B+B=f(y)+(n+1) B
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
and
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
f((n-1) A+y)=f(-A+n A+y)=f(n A+y)-B=f(y)+n B-B=f(y)+(n-1) B .
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
So, equation (2) follows from the induction on $n$.
|
| 112 |
+
Now we can say that for any integer $k$ it holds
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
f(n x f(x)+y)=f(y)+n x^{2}
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
If $y$ is given, then $f(y)+n x^{2}$ can be any rational number, since $n x^{2}$ can be any rational number. If it is supposed to be $\frac{p}{q}$, where $q \neq 0$, then we may take $n=p q$, and $x=\frac{1}{q}$. Therefore $f$ is surjective on $\mathbb{Q}$. So there's a rational number $c$ such that $f(c)=0$. Be putting $x=c$ into (1) we immediately get $c=0$, i.e. $f(0)=0$. Therefore, $f(x)=0$ if and only if $x=0$.
|
| 119 |
+
|
| 120 |
+
For any integer $n$ and for any rational $x, y$ it holds
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
f\left(n^{2} x f(x)+y\right)=f(y)+n^{2} x^{2}=f(y)+(n x)^{2}=f(n x f(n x)+y)
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
After taking $y=-n x f(n x)$ in (4), the right-hand side becomes 0 , therefore
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
n^{2} x f(x)-n x f(n x)=0
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
This simplifies into $n f(x)=f(n x)$ for $x \neq 0$, but it also holds for $x=0$. Therefore, for any rational number $x=\frac{p}{q}$ we have,
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
f(x)=f\left(\frac{p}{q}\right)=f\left(p \cdot \frac{1}{q}\right)=p \cdot f\left(\frac{1}{p}\right)=p \cdot \frac{f\left(q \cdot \frac{1}{q}\right)}{q}=\frac{p}{q} \cdot f(1)=x f(1)
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
So, we have $f(x)=k x$, for some rational number $k$. Let's put this answer in (1) and we get $k(x k x+y)=k y+x^{2}$, thus $k^{2}=1$. Therefore $f(x)=x$ and $f(x)=-x$ are solutions.
|
| 139 |
+
|
| 140 |
+
Problem 3. Let $A B C$ be a triangle with an obtuse angle at $A$. Let $E$ and $F$ be the intersections of the external bisector of angle $A$ with the altitudes of $A B C$ through $B$ and $C$ respectively. Let $M$ and $N$ be the points on the segments $E C$ and $F B$ respectively such that $\angle E M A=\angle B C A$ and $\angle A N F=\angle A B C$. Prove that the points $E, F, N, M$ lie on a circle.
|
| 141 |
+
|
| 142 |
+
## Solution 1.
|
| 143 |
+
|
| 144 |
+
The first solution is based on the main Lemma. We present this Lemma with two different proofs.
|
| 145 |
+
Lemma: Let $A B C$ be an acute triangle with $A B=B C$. Let $P$ be any point on $A C$. Line passing through $P$ perpendicular to $A B$, intersects ray $B C$ in point $T$. If the line $A T$ intersects the circumscribed circle of the triangle $A B C$ the second time at point $K$, then $\angle A K P=\angle A B P$.
|
| 146 |
+
|
| 147 |
+
|
| 148 |
+
## Proof 1:
|
| 149 |
+
|
| 150 |
+
Let $H$ be the orthocenter of the triangle $A B P$. Then
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
\angle B H P=180^{\circ}-\angle B A C=180^{\circ}-\angle B C P
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
So $B H P C$ is cyclic. Then we get
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
T K \cdot T A=T C \cdot T B=T P \cdot T H
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
So, $A H P K$ is also cyclic. But then
|
| 163 |
+
|
| 164 |
+
$$
|
| 165 |
+
\angle A K P=180^{\circ}-\angle A H P=\angle A B P
|
| 166 |
+
$$
|
| 167 |
+
|
| 168 |
+
Proof 2:
|
| 169 |
+
Consider the symmetric points $B^{\prime}$ and $C^{\prime}$ of $B$ and $C$, respectively, with respect to the line $P T$. It is clear that
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
\mathrm{TC}^{\prime} \cdot T B^{\prime}=T C \cdot T B=T K \cdot T A
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
So $B^{\prime} C^{\prime} K A$ is cyclic. Also, because of the symmetry we have
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
\angle P C^{\prime} B^{\prime}=\angle P C B=\angle P A B
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
So $B^{\prime} C^{\prime} P A$ is also cyclic. Therefore, the points $B^{\prime}, C^{\prime}, K, P$ and $A$ all lie on the common circle. Because of this fact and because of the symmetry again we have
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\angle P K A=\angle P B^{\prime} A=\angle P B A .
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
So, lemma is proved and now return to the problem.
|
| 188 |
+
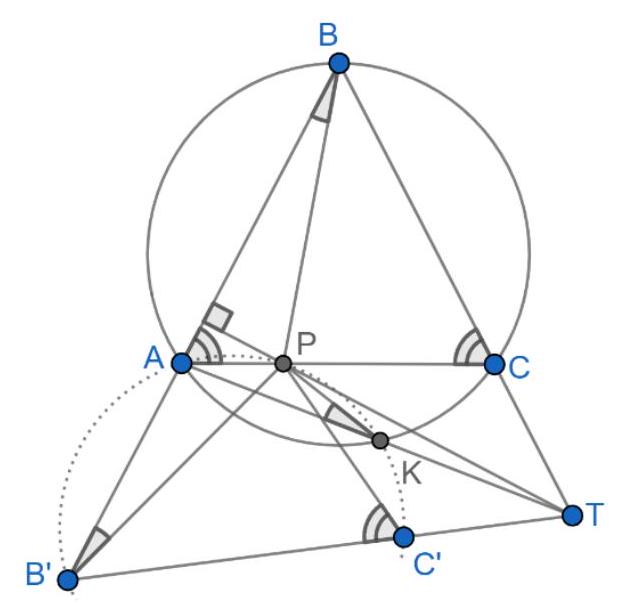
|
| 189 |
+
|
| 190 |
+
Let $H$ be intersection point of the altitudes at $B$ and $C$. Denote by $M^{\prime}$ and $N^{\prime}$ the intersection points of the circumcircle of the triangle $H E F$ with the segments $E C$ and $F B$, respectively. We are going to show that $M=M^{\prime}$ and $N=N^{\prime}$ and it will prove the points $E, F, N, M$ lie on a common circle.
|
| 191 |
+
|
| 192 |
+
Of course, $A$ is an orthocenter of the triangle $B C H$. Therefore $\angle B H A=\angle B C A, \angle C H A=\angle C B A$ and $\angle H B A=\angle H C A$. Thus
|
| 193 |
+
|
| 194 |
+
$$
|
| 195 |
+
\angle H E F=\angle H B A+\angle E A B=\angle H C A+\angle F A C=\angle H F E
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
So, the triangle $H E F$ is isosceles, $H E=H F$.
|
| 199 |
+
By using lemma, we get
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
\angle A M^{\prime} E=\angle A H E=\angle A C B
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
and
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
\angle A N^{\prime} F=\angle A H F=\angle A B C \text {. }
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
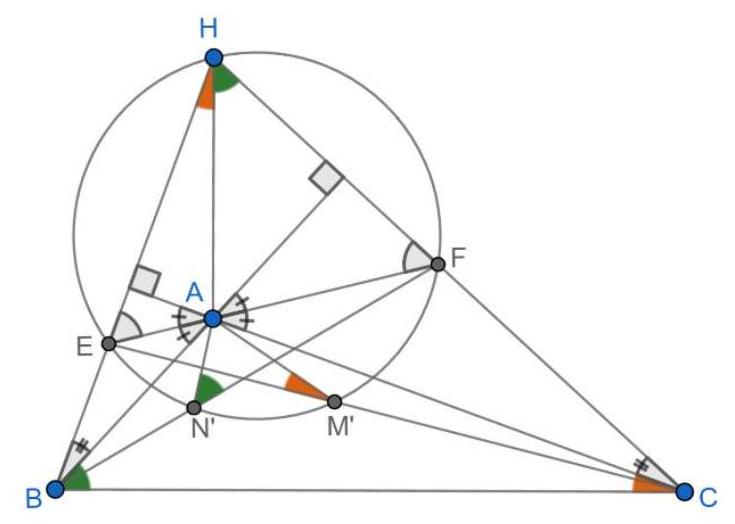
|
| 212 |
+
|
| 213 |
+
Therefore $M=M^{\prime}$ and $N=N^{\prime}$ and we are done.
|
| 214 |
+
|
| 215 |
+
## Solution 2.
|
| 216 |
+
|
| 217 |
+
Let $X, Y$ be projections of $B$ on $A C$, and $C$ on $A B$, respectively. Let $\omega$ be circumcircle of $B X Y C$. Let $Z$ be intersection of $E C$ and $\omega$ and $D$ be projection of $E$ on $B A$.
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
\angle M A C=\angle A M E-\angle M C A=\angle X C B-\angle X C E=\angle Z C B=\angle Z X B
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
Since $B X Y C$ is cyclic $\angle A C Y=\angle X B A$, and since $D E X A$ is cyclic
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
\angle E X D=\angle E A D=\angle F A C
|
| 227 |
+
$$
|
| 228 |
+
|
| 229 |
+
Therefore, we get that the quadrangles $B Z X D$ and $C M A F$ are similar. Hence $\angle F M C=\angle D Z B$. Since $Z E D B$ is cyclic,
|
| 230 |
+
|
| 231 |
+
$$
|
| 232 |
+
\angle D Z B=\angle D E B=\angle X A B .
|
| 233 |
+
$$
|
| 234 |
+
|
| 235 |
+
Thus $\angle F M C=\angle X A B$. Similarly, $\angle E N B=\angle Y A C$. We get that $\angle F M C=\angle E N B$ and it implies that the points $E, F, N, M$ lie on a circle.
|
| 236 |
+
|
| 237 |
+
|
| 238 |
+
Problem 4. Let $A B C$ be a triangle with incentre Iand let $D$ be an arbitrary point on the side $B C$. Let the line through $D$ perpendicular to $B I$ intersect $C I$ at $E$. Let the line through $D$ perpendicular to $C I$ intersect $B I$ at $F$. Prove that the reflection of $A$ in the line $E F$ lies on the line $B C$.
|
| 239 |
+
(Australia, Sampson Wong)
|
| 240 |
+
|
| 241 |
+
## Solution 1.
|
| 242 |
+
|
| 243 |
+
Let us consider the case when $I$ lies inside of triangle $E F D$. For the other cases the proof is almost the same only with the slight difference.
|
| 244 |
+
|
| 245 |
+
We are going to prove that the intersection point of the circumcircles of $A E C$ and $A F B$ (denote it by $T$ ) lies on the line $B C$ and this point is the symmetric point of $A$ with respect to $E F$. First of all we prove that $A E I F$ is cyclic, which implies that $T$ lies on the line $B C$, because
|
| 246 |
+
|
| 247 |
+
$$
|
| 248 |
+
\angle A T B+\angle A T C=\angle A F B+\angle A E C=\angle A F I+\angle A E I=180^{\circ} .
|
| 249 |
+
$$
|
| 250 |
+
|
| 251 |
+

|
| 252 |
+
|
| 253 |
+
Denote by $N$ an intersection point of the lines $D F$ and $A C$. Of course $N$ is the symmetric point with respect to $C I$. Thus, $\angle I N A=\angle I D B$. Also,
|
| 254 |
+
|
| 255 |
+
$$
|
| 256 |
+
\angle I F D=\angle N D C-\angle I B C=90^{\circ}-\angle I C B-\angle I B C=\angle I A N .
|
| 257 |
+
$$
|
| 258 |
+
|
| 259 |
+
So, we get that $A, I, N$ and $F$ lie on a common circle. Therefore, we have $\angle A F I=\angle I N A=\angle I D B$. Analogously, $\angle A E I=\angle I D C$ and we have
|
| 260 |
+
|
| 261 |
+
$$
|
| 262 |
+
\angle A F I+\angle A E I=\angle I D B+\angle I D C
|
| 263 |
+
$$
|
| 264 |
+
|
| 265 |
+
So $\angle A F I+\angle A E I=180^{\circ}$, thus $A E I F$ is cyclic and $T$ lies on the line $B C$.
|
| 266 |
+
|
| 267 |
+
Because $E C$ bisects the angle $A C B$ and $A E T C$ is cyclic we get $E A=E T$. Because of the similar reasons we have $F A=F T$. Therefore $T$ is the symmetric point of $A$ with respect to the line $E F$ and it lies on the line $B C$.
|
| 268 |
+
|
| 269 |
+
|
| 270 |
+
## Solution 2.
|
| 271 |
+
|
| 272 |
+
Like to the first solution, consider the case when $I$ lies inside of triangle $E F D$. we need to prove that $A E I F$ is cyclic. The finish of the proof is the same.
|
| 273 |
+
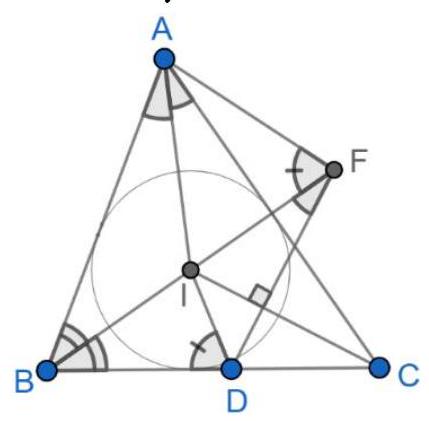
|
| 274 |
+
first note that $\triangle F D B \sim \triangle A I B$, because $\angle F B D=\angle A B I$, and
|
| 275 |
+
|
| 276 |
+
$$
|
| 277 |
+
\angle B F D=\angle F D C-\angle I B C=90^{\circ}-\angle I C D-\angle I B C=\angle I A B .
|
| 278 |
+
$$
|
| 279 |
+
|
| 280 |
+
Because of the similarity we have $\frac{A B}{A F}=\frac{B I}{B D}$. This equality of the length ratios with $\angle I B D=\angle A B F$ implies that $\triangle A B F \sim \triangle I B D$. Therefore, we have $\angle I D B=\angle A F B$. Analogously, we can get $\angle I D C=\angle A E C$, thus
|
| 281 |
+
|
| 282 |
+
$$
|
| 283 |
+
\angle A F I+\angle A E I=\angle I D B+\angle I D C=180^{\circ} .
|
| 284 |
+
$$
|
| 285 |
+
|
| 286 |
+
So, $A E I F$ is cyclic and we are done.
|
| 287 |
+
|
| 288 |
+
Problems 5. A plane has a special point $O$ called the origin. Let $P$ be a set of 2021 points in the plane, such that
|
| 289 |
+
(i) no three points in $P$ lie on a line and
|
| 290 |
+
(ii) no two points in $P$ lie on a line through the origin.
|
| 291 |
+
|
| 292 |
+
A triangle with vertices in $P$ is fat, if $O$ is strictly inside the triangle. Find the maximum number of fat triangles.
|
| 293 |
+
(Austria, Veronika Schreitter)
|
| 294 |
+
|
| 295 |
+
Answer: $2021 \cdot 505 \cdot 337$
|
| 296 |
+
|
| 297 |
+
## Solution
|
| 298 |
+
|
| 299 |
+
We will count minimal number of triangles that are not fat. Let $F$ set of fat triangles, and S set of triangles that are not fat. If triangle $X Y Z \in S$, we call $X$ and $Z$ good vertices if $O Y$ is located between $O X$ and $O Z$. For $A \in P$ let $S_{A} \subseteq S$ be set of triangles in $S$ for which $A$ is one of the good vertex.
|
| 300 |
+
|
| 301 |
+
It is easy to see that
|
| 302 |
+
|
| 303 |
+
$$
|
| 304 |
+
2|S|=\sum_{A \in P}\left|S_{A}\right|
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
For $A \in P$, let $R_{A} \subset P$ and $L_{A} \subset P$ be parts of $P \backslash\{A\}$ divided by $A O$. Suppose for $A X Y \in S$ vertex $A$ is good, then clearly $X, Y \in R_{A}$ or $X, Y \in L_{A}$. On the other hand, if $X, Y \in R_{A}$ or $X, Y \in L_{A}$ then clearly $A X Y \in S$ and $A$ is its good vertex. Therefore,
|
| 308 |
+
|
| 309 |
+
$$
|
| 310 |
+
\left|S_{A}\right|=\binom{\left|R_{A}\right|}{2}+\binom{\left|L_{A}\right|}{2}
|
| 311 |
+
$$
|
| 312 |
+
|
| 313 |
+
It is easy to show following identity:
|
| 314 |
+
|
| 315 |
+
$$
|
| 316 |
+
\frac{x(x-1)}{2}+\frac{y(y-1)}{2}-2 \cdot \frac{\frac{x+y}{2}\left(\frac{x+y}{2}-1\right)}{2}=\frac{(x-y)^{2}}{4}
|
| 317 |
+
$$
|
| 318 |
+
|
| 319 |
+
By using (2) and (3) we get
|
| 320 |
+
|
| 321 |
+
$$
|
| 322 |
+
\left|S_{A}\right| \geq 2 \cdot\binom{\frac{\left|R_{A}\right|+\left|L_{A}\right|}{2}}{2}=2 \cdot\binom{1010}{2}=1010 \cdot 1009
|
| 323 |
+
$$
|
| 324 |
+
|
| 325 |
+
and the equality holds when $\left|R_{A}\right|=\left|L_{A}\right|=1010$. Hence
|
| 326 |
+
|
| 327 |
+
$$
|
| 328 |
+
|S|=\frac{\sum_{A \in P}\left|S_{A}\right|}{2} \geq \frac{2021 \cdot 1010 \cdot 1009}{2}=2021 \cdot 505 \cdot 1009
|
| 329 |
+
$$
|
| 330 |
+
|
| 331 |
+
Therefore,
|
| 332 |
+
|
| 333 |
+
$$
|
| 334 |
+
|F|=\binom{2021}{3}-|S| \leq 2021 \cdot 1010 \cdot 673-2021 \cdot 505 \cdot 1009=2021 \cdot 505 \cdot 337
|
| 335 |
+
$$
|
| 336 |
+
|
| 337 |
+
For configuration of points on regular 2021-gon which is centered at $O$, in equalities in (4), (5), (6) become equalities. Hence $2021 \cdot 505 \cdot 337$ is indeed the answer.
|
| 338 |
+
|
| 339 |
+
Problems 6. Does there exist a nonnegative integer $a$ for which the equation
|
| 340 |
+
|
| 341 |
+
$$
|
| 342 |
+
\left\lfloor\frac{m}{1}\right\rfloor+\left\lfloor\frac{m}{2}\right\rfloor+\left\lfloor\frac{m}{3}\right\rfloor+\cdots+\left\lfloor\frac{m}{m}\right\rfloor=n^{2}+a
|
| 343 |
+
$$
|
| 344 |
+
|
| 345 |
+
has more than one million different solutions $(m, n)$ where $m$ and $n$ are positive integers? (The expression $\lfloor x\rfloor$ denotesthe integer part(or floor) of the real numberx. Thus $\lfloor\sqrt{2}\rfloor=1,\lfloor\pi\rfloor=\left\lfloor\frac{22}{7}\right\rfloor=$ $3,\lfloor 42\rfloor=42$ and $\lfloor 0\rfloor=0)$
|
| 346 |
+
|
| 347 |
+
Answer: Yes.
|
| 348 |
+
|
| 349 |
+
## Solution.
|
| 350 |
+
|
| 351 |
+
Denote the equation from the statement by (1). The left hand side of (1) depends only on $m$, and will throughout be denoted by $L(m)$. Fix an integer $q>10^{7}$ and note that for $m=q^{3}$
|
| 352 |
+
|
| 353 |
+
$$
|
| 354 |
+
L\left(q^{3}\right)=\sum_{k=1}^{q^{3}}\left[\frac{q^{3}}{k}\right] \leq \sum_{k=1}^{q^{3}} \frac{q^{3}}{k} \leq q^{3} \cdot \sum_{k=1}^{q^{3}} \frac{1}{k} \leq q^{3} \cdot q=q^{4}
|
| 355 |
+
$$
|
| 356 |
+
|
| 357 |
+
Indeed, the first inequality results from $[x] \leq x$. The second inequality can be seen (for instance) as follows. We divide the terms in the sum $\sum_{k=1}^{q^{3}} \frac{1}{k}$ into several groups: For $j \geq 0$, the $j$-th group contains the $2^{j}$ consecutive terms $\frac{1}{2^{j}}, \ldots, \frac{1}{2^{j+1}-1}$. Since every term in the $j$-th group is bounded by $\frac{1}{2^{j}}$, the overall contribution of the $j$-th group to the sum is at most 1 . Since the first $q$ groups together would contain $2^{q}-1>q^{3}$ terms, the number of groups does not exceed $q$, and hence the value of the sum under consideration is indeed bounded by $q$.
|
| 358 |
+
|
| 359 |
+
Call an integer $m$ special, if it satisfies $1 \leq L(m) \leq q^{4}$. Denote by $g(m) \geq 1$ the largest integer whose square is bounded by $L(m)$; in other words $g^{2}(m) \leq L(m)<(g(m)+1)^{2}$. Notethat $g(m) \leq$ $q^{2}$ for all special $m$, which implies
|
| 360 |
+
|
| 361 |
+
$$
|
| 362 |
+
0 \leq L(m)-g^{2}(m)<(g(m)+1)^{2}-g^{2}(m)=2 g(m)+1 \leq 2 q^{2}+1
|
| 363 |
+
$$
|
| 364 |
+
|
| 365 |
+
Finally, we do some counting. Inequality (2) and the monotonicity of $L(m)$ imply that there exist at least $q^{3}$ special integers. Because of (3), every special integer $m$ has $0 \leq L(m)-g^{2}(m) \leq 2 q^{2}+1$. By averaging, at least $\frac{q^{3}}{2 q^{2}+2}>10^{6}$ special integers must yield the same value $L(m)-g^{2}(m)$. This frequently occurring value is our choice for $\alpha$, which yields more than $10^{6}$ solutions $(m, g(m))$ to equation (1). Hence, the answer to the problem is YES.
|
| 366 |
+
|
EGMO/md/en-2022-solutions.md
ADDED
|
@@ -0,0 +1,507 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# EGMO2022 Problems
|
| 2 |
+
|
| 3 |
+
## DAY 1
|
| 4 |
+
|
| 5 |
+
## Problem 1.
|
| 6 |
+
|
| 7 |
+
Let $A B C$ be an acute-angled triangle in which $B C<A B$ and $B C<C A$. Let point $P$ lie on segment $A B$ and point $Q$ lie on segment $A C$ such that $P \neq B, Q \neq C$ and $B Q=B C=C P$. Let $T$ be the circumcentre of triangle $A P Q, H$ the orthocentre of triangle $A B C$, and $S$ the point of intersection of the lines $B Q$ and $C P$. Prove that $T, H$ and $S$ are collinear.
|
| 8 |
+
|
| 9 |
+
## Problem 2.
|
| 10 |
+
|
| 11 |
+
Let $\mathbb{N}=\{1,2,3, \ldots\}$ be the set of all positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:
|
| 12 |
+
(1) $f(a b)=f(a) f(b)$, and
|
| 13 |
+
(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.
|
| 14 |
+
|
| 15 |
+
## Problem 3.
|
| 16 |
+
|
| 17 |
+
An infinite sequence of positive integers $a_{1}, a_{2}, \ldots$ is called good if
|
| 18 |
+
(1) $a_{1}$ is a perfect square, and
|
| 19 |
+
(2) for any integer $n \geq 2, a_{n}$ is the smallest positive integer such that
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
n a_{1}+(n-1) a_{2}+\ldots+2 a_{n-1}+a_{n}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
is a perfect square.
|
| 26 |
+
Prove that for any good sequence $a_{1}, a_{2}, \ldots$, there exists a positive integer $k$ such that $a_{n}=a_{k}$ for all integers $n \geq k$.
|
| 27 |
+
|
| 28 |
+
## EGMO2022 Problems
|
| 29 |
+
|
| 30 |
+
## DAY 2
|
| 31 |
+
|
| 32 |
+
## Problem 4.
|
| 33 |
+
|
| 34 |
+
Given a positive integer $n \geq 2$, determine the largest positive integer $N$ for which there exist $N+1$ real numbers $a_{0}, a_{1}, \ldots, a_{N}$ such that
|
| 35 |
+
(1) $a_{0}+a_{1}=-\frac{1}{n}$, and
|
| 36 |
+
(2) $\left(a_{k}+a_{k-1}\right)\left(a_{k}+a_{k+1}\right)=a_{k-1}-a_{k+1}$ for $1 \leq k \leq N-1$.
|
| 37 |
+
|
| 38 |
+
## Problem 5.
|
| 39 |
+
|
| 40 |
+
For all positive integers $n, k$, let $f(n, 2 k)$ be the number of ways an $n \times 2 k$ board can be fully covered by $n k$ dominoes of size $2 \times 1$. (For example, $f(2,2)=2$ and $f(3,2)=3$.)
|
| 41 |
+
Find all positive integers $n$ such that for every positive integer $k$, the number $f(n, 2 k)$ is odd.
|
| 42 |
+
|
| 43 |
+
## Problem 6.
|
| 44 |
+
|
| 45 |
+
Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$. Let the internal angle bisectors at $A$ and $B$ meet at $X$, the internal angle bisectors at $B$ and $C$ meet at $Y$, the internal angle bisectors at $C$ and $D$ meet at $Z$, and the internal angle bisectors at $D$ and $A$ meet at $W$. Further, let $A C$ and $B D$ meet at $P$. Suppose that the points $X, Y, Z, W, O$ and $P$ are distinct.
|
| 46 |
+
|
| 47 |
+
Prove that $O, X, Y, Z$ and $W$ lie on the same circle if and only if $P, X, Y, Z$ and $W$ lie on the same circle.
|
| 48 |
+
|
| 49 |
+
## EGMO2022 Problems - Solutions
|
| 50 |
+
|
| 51 |
+
## Problem 1.
|
| 52 |
+
|
| 53 |
+
Let $A B C$ be an acute-angled triangle in which $B C<A B$ and $B C<C A$. Let point $P$ lie on segment $A B$ and point $Q$ lie on segment $A C$ such that $P \neq B, Q \neq C$ and $B Q=B C=C P$. Let $T$ be the circumcentre of triangle $A P Q, H$ the orthocentre of triangle $A B C$, and $S$ the point of intersection of the lines $B Q$ and $C P$. Prove that $T, H$ and $S$ are collinear.
|
| 54 |
+
|
| 55 |
+
Proposed by: Netherlands
|
| 56 |
+
|
| 57 |
+
## Solution 1.
|
| 58 |
+
|
| 59 |
+
|
| 60 |
+
|
| 61 |
+
We show that $T$ and $H$ are both on the angle bisector $\ell$ of $\angle B S C$.
|
| 62 |
+
We first prove that $H \in \ell$. The altitude $C H$ in triangle $A B C$ is also the altitude in isosceles triangle $P B C$ with $C P=C B$. Therefore, $C H$ is also the angle bisector of $\angle P C B$ and hence also of $\angle S C B$. Analogously, $B H$ is the angle bisector of $\angle S B C$. We conclude that $H$, as the intersection of two angle bisectors of $\triangle B S C$, is also on the third angle bisector, which is $\ell$.
|
| 63 |
+
|
| 64 |
+
We now prove that $T \in \ell$.
|
| 65 |
+
Variant 1. In the isosceles triangles $\triangle B C P$ and $\triangle C B Q$ we see that $\angle B C P=180^{\circ}-2 \angle B$ and $\angle C B Q=180^{\circ}-2 \angle C$. This yields $\angle P S Q=\angle B S C=180^{\circ}-\left(180^{\circ}-2 \angle B\right)-\left(180^{\circ}-2 \angle C\right)=$ $180^{\circ}-2 \angle A$. Furthermore, $\angle P T Q=2 \angle P A Q=2 \angle A$ ( $T$ being circumcentre of $\left.\triangle A P Q\right)$. Now $\angle P T Q+\angle P S Q=180^{\circ}$, so $P T Q S$ is a cyclic quadrilateral. From $P T=T Q$ we then obtain that $\angle P S T=\angle P Q T=\angle Q P T=\angle Q S T$, so $T$ is on the angle bisector $\angle P S Q$, which is also $\ell$.
|
| 66 |
+
|
| 67 |
+
We conclude that $T, S$ and $H$ are collinear.
|
| 68 |
+
Variant 2. Let $R$ be the second intersection of $B Q$ and $\odot A P Q$.
|
| 69 |
+
$A P R Q$ is cyclic quadrilateral, so $\angle P R S=\angle A, \angle A P R=\angle B Q C=\angle C$. On the other hand $\angle B P C=\angle B$. Therefore $\angle R P S=180^{\circ}-\angle B-\angle C=\angle A$. Hence, the triangle $P R S$ is isosceles with $S P=S R$; then $\ell$ is the perpendicular bisector of the chord $P R$ in the circle that passes through $T$.
|
| 70 |
+
|
| 71 |
+
Note that if $B Q$ is tangent to $\odot A P Q$, then $C P$ is also tangent to $\odot A P Q$ and triangle $A B C$ is isosceles, so $T, S$ and $H$ lie on the altitude from $A$.
|
| 72 |
+
|
| 73 |
+
|
| 74 |
+
Remark. The fact that $C P$ is also tangent to $\odot A P Q$ could be shown with $P T Q S$ beeing a cyclic quadrilateral like in the first variant of the solution. Otherwise we can consider $R$ the second intersection of $C P$ and $\odot A P Q$ and prove that triangle $Q R S$ is isosceles.
|
| 75 |
+
|
| 76 |
+
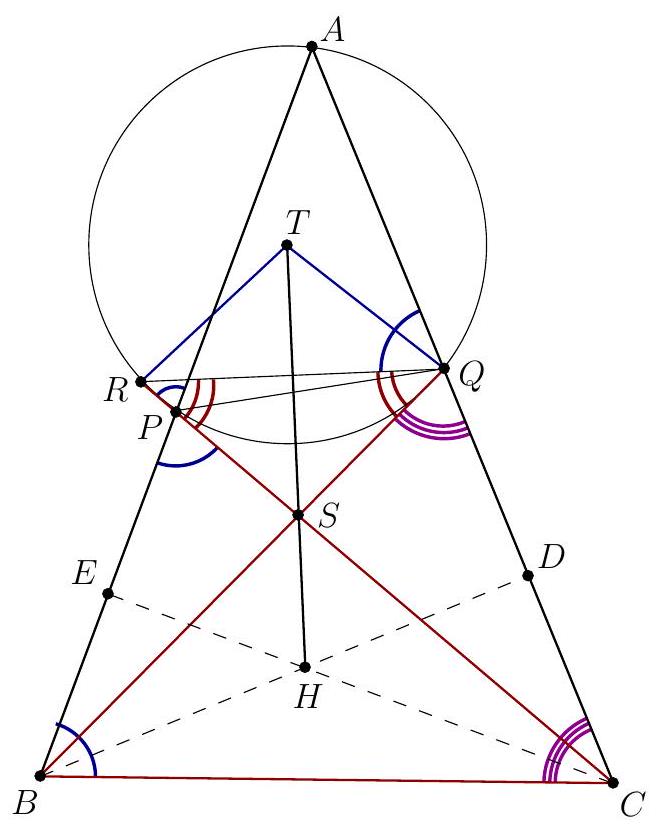
|
| 77 |
+
|
| 78 |
+
## Solution 2.
|
| 79 |
+
|
| 80 |
+
|
| 81 |
+
|
| 82 |
+
In the same way as in the previous solution, we see that $\angle P S Q=180^{\circ}-2 \angle A$, so $\angle C S Q=2 \angle A$. From the cyclic quadrilateral $A E H D$ (with $E$ and $D$ feet of the altitudes $C H$ and $B H$ ) we see that $\angle D H C=\angle D A E=\angle A$. Since $B H$ is the perpendicular bisector of $C Q$, we have $\angle D H Q=\angle A$ as well, so $\angle C H Q=2 \angle A$. From $\angle C H Q=2 \angle A=\angle C S Q$, we see $C H S Q$ is a cyclic quadrilateral. This means $\angle Q H S=\angle Q C S$.
|
| 83 |
+
|
| 84 |
+
Since triangles $P T Q$ and $C H Q$ are both isosceles with apex $2 \angle A$, we get $\triangle P T Q \sim \triangle C H Q$. We see that one can be obtained from the other by a spiral similarity centered at $Q$, so we also obtain $\triangle Q T H \sim \triangle Q P C$. This means that $\angle Q H T=\angle Q C P$. Combining this with $\angle Q H S=\angle Q C S$, we see that $\angle Q H T=\angle Q C P=\angle Q C S=\angle Q H S$. So $\angle Q H T=\angle Q H S$, which means that $T, S$ and $H$ are collinear.
|
| 85 |
+
|
| 86 |
+
## Solution 3.
|
| 87 |
+
|
| 88 |
+
|
| 89 |
+
|
| 90 |
+
Let us draw a parallel $f$ to $B C$ through $A$. Let $B^{\prime}=B Q \cap f, C^{\prime}=C P \cap f$. Then $A Q B^{\prime} \sim C Q B$ and $A P C^{\prime} \sim B P C$, therefore both $Q A B^{\prime}$ and $A P C^{\prime}$ will be isosceles.
|
| 91 |
+
|
| 92 |
+
Also, $B C S \sim B^{\prime} C^{\prime} S$ with respect to the similarity with center $S$, therefore if we take the image of the line $B H$ (which is the perpendicular bisector of the segment $C Q$ ) through this transformation, it will go through the point $B^{\prime}$, and be perpendicular to $A Q$ (as the image of $C Q$ is parallel to $C Q$ ). As $A Q B^{\prime}$ is isosceles, this line is the perpendicular bisector of the segment $A Q$. This means it goes through $T$, the circumcenter of $A P Q$. Similarly on the other side the image of $C H$ also goes through $T$. This means that the image of $H$ with respect to the similarity though $S$ will be $T$, so $T, S, H$ are collinear.
|
| 93 |
+
|
| 94 |
+
## Problem 2.
|
| 95 |
+
|
| 96 |
+
Let $\mathbb{N}=\{1,2,3, \ldots\}$ be the set of all positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:
|
| 97 |
+
(1) $f(a b)=f(a) f(b)$, and
|
| 98 |
+
(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.
|
| 99 |
+
|
| 100 |
+
Proposed by: Fedir Yudin, Ukraine
|
| 101 |
+
Answer: $f(n)=a^{v_{p}(n)}$, where $a \in \mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.
|
| 102 |
+
Solution 1. First, all such functions $f$ satisfy the conditions, as $v_{p}(a) \neq v_{p}(b)$ implies $v_{p}(a+b)=$ $\min \left(v_{p}(a), v_{p}(b)\right)$. Plugging $a, b=1$ into (1) gives $f(1)=1$. Also, a simple induction gives that $f\left(\prod_{i=1}^{k} p_{i}^{a_{i}}\right)=\prod_{i=1}^{k} f\left(p_{i}\right)^{a_{i}}$. Let $S$ be the set of all primes $p$ such that $f(p) \neq 1$. If $|S|=1$, then $S=\{p\}$ and $f(p)=a$ for some $a \neq 1$, and thus $f(n)=a^{v_{p}(n)}$ for all $n$. If $S=\emptyset$ then $f(n)=1$ for all $n$, which can be also written in the above form for $a=1$.
|
| 103 |
+
|
| 104 |
+
Now suppose that $S$ contains at least two primes. Let $p<q$ be the two smallest elements of $S$. Since all prime divisors of $q-p$ are smaller than $q$ and not equal to $p, f(q-p)=1$. Using (2) for $p$ and $q-p$ gives us that some two of $f(p) \neq 1, f(p-q)=1$ and $f(q) \neq 1$ are equal, meaning that $f(p)=f(q)$. Let $t \geq 2$ be the smallest integer such that $p^{t}>q$, and let $p^{t}=a q+b$ with $0 \leq b<q$. Since $q \geq p^{t-1}$ and $q$ is not divisible by $p$, we have $q>p^{t-1}$, so $a<p$, and thus $f(a)=1$. Therefore $a q$ is not divisible by $p$, thus neither is $b$, and since $b<q, f(b)=1$. Now using (2) for $a q$ and $b$ we get that some two of $f(a q)=f(a) f(q)=f(q)=f(p), f(b)=1$ and $f(a q+b)=f\left(p^{t}\right)=f(p)^{t}$ are equal, which is a contradiction.
|
| 105 |
+
|
| 106 |
+
## Solution 1B (for the main part).
|
| 107 |
+
|
| 108 |
+
Suppose that there are two primes, $p<q$ such that $f(p)>1$ and $f(q)>1$, and these are the two smallest such primes.
|
| 109 |
+
$1<p-q<q$ and it is not divisible by $p$ and $q$, therefore its prime factors are smaller than $q$, so we conclude $f(q-p)=1$. By (2), two of $f(q-p)=1, f(q-p)>1$ and $f(q)>1$ are equal, so $f(q)=f(p)=a$.
|
| 110 |
+
|
| 111 |
+
If $p^{2}<q$ then $q-p^{2}$ is not divisible by $p$ and $q$, so we conclude $f\left(q-p^{2}\right)=1$ in the same way. Then $f\left(p^{2}\right)=f(p)^{2}=a^{2}, f\left(q-p^{2}\right)=1$ and $f(q)=a$ are distinct, contradicting (2). Hence, $q<p^{2}$.
|
| 112 |
+
|
| 113 |
+
Let $c=\left\lfloor p^{2} / q\right\rfloor$; then $0<c<p$, so $f(c)=1$. By $0<p^{2}-c q<q$, we get $f\left(p^{2}-c q\right)=1$. Now $f\left(p^{2}-c q\right)=1, f\left(p^{2}\right)=a^{2}$ and $f(c q)=a$ are distinct, contradicting (2) again.
|
| 114 |
+
|
| 115 |
+
## Solution 2 (for the main part).
|
| 116 |
+
|
| 117 |
+
Suppose there exists a positive integer $n$ such that $f(n) \neq 1$ and $f(n+1) \neq 1$. We know that $f(1)=1$, so by $(2)$ two of $f(n) \neq 1, f(n+1) \neq 1$ and $f(1)=1$ are equal, therefore $f(n)=f(n+1)$.
|
| 118 |
+
$f\left(n^{2}\right)=f(n)^{2} \neq 1$ and $f\left(n^{2}-1\right)=f(n+1) f(n-1)=f(n) f(n-1) \neq 1$, but by (2) two of $f(1)=1, f\left(n^{2}-1\right) \neq 1$ and $f\left(n^{2}\right) \neq 1$ are equal, so $f\left(n^{2}-1\right)=f\left(n^{2}\right)$ and thus $f(n) f(n-1)=f(n)^{2}$, therefore $f(n-1)=f(n)$.
|
| 119 |
+
|
| 120 |
+
Then for $n-1$, it is also true that $f(n-1) \neq 1$ and $f(n-1+1) \neq 1$, so the same proof applies, $f(n-1-1)=f(n-1)$ and so on. By induction we get that $f(n)=f(1)$, which is a contradiction, as $f(1)=1$ and we assumed that $f(n) \neq 1$. Therefore, there can't be any $n$ for which $f(n) \neq 1$ and $f(n+1) \neq 1$.
|
| 121 |
+
|
| 122 |
+
Now suppose there are two primes, $p \neq q \in S$ such that $f(p) \neq 1$ and $f(q) \neq 1$. Then by the Chinese remainder theorem, there exists a number $n$ such that $p \mid n$ and $q \mid n+1$, so $f(p) \mid f(n)$ and $f(q) \mid f(n+1)$ thus $f(n) \neq 1$ and $f(n+1) \neq 1$. This is a contradiction, so $S$ can't have two distinct elements.
|
| 123 |
+
|
| 124 |
+
## Solution 3 (Joseph Myers) (for the second part).
|
| 125 |
+
|
| 126 |
+
Claim 3.1. If $f(m)>1$ for some $m \in \mathbb{N}$, then there are less than $m$ different prime numbers $p_{i}$ with $f\left(p_{i}\right)>1$.
|
| 127 |
+
Proof. On the one hand, if $f(m)=c>1$, then for any $n \in \mathbb{N}$, there is some $k \in\{n+1, n+2 \ldots, n+m\}$ such that $f(k) \in\{1, c\}$. To show this, it is enough to see that condition (2) implies that for any $n \in \mathbb{N}$
|
| 128 |
+
|
| 129 |
+
- if $f(n)=c$, then $f(n+1) \in\{1, c\}$;
|
| 130 |
+
- if $f(n)=1$, then $f(n+m) \in\{1, c\}$.
|
| 131 |
+
|
| 132 |
+
On the other hand, if we suppose that there are $m$ different prime numbers $p_{1}, p_{2}, \ldots, p_{m}$, then we know (by the Chinese Remainder Theorem) that for any number $t \in \mathbb{N}$, there exists a number $n_{t} \in \mathbb{N}$ such that $p_{k}^{t} \mid n_{t}+k$ for each $k \in\{1,2, \ldots, m\}$. Hence for each $k$, we have
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
f\left(n_{t}+k\right) \geq f\left(p_{i}^{t}\right)=f\left(p_{i}\right)^{t} \geq 2^{t} .
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
If $2^{t}>c$, then it means that $f(k)>c$ for all $k \in\left\{n_{t}+1, n_{t}+2 \ldots, n_{t}+m\right\}$.
|
| 139 |
+
Now we can suppose that for some $m \geq 2$, the set of primes with $f(p)>1$ is $S=\left\{p_{1}, p_{2}, \ldots, p_{m}\right\}$. Now let $S_{1}$ and $S_{2}$ be two disjoint nonempty subsets such that $S_{1} \cup S_{2}=S$. Let $a=\prod_{p_{i} \in S_{1}} p_{i}$ and $b=\prod_{p_{j} \in S_{2}} p_{j}$.
|
| 140 |
+
|
| 141 |
+
Now for any $k, \ell \in \mathbb{N}, a^{k}+b^{\ell}$ is coprime to all primes in $S$, hence $f\left(a^{k}+b^{\ell}\right)=1$. It is easy to see that we can choose $k$ and $\ell$ such that $f\left(a^{k}\right) \neq f\left(b^{\ell}\right)$, which contradicts condition (2).
|
| 142 |
+
|
| 143 |
+
Solution 4 (for the main part). Let $p$ the minimal (prime) number with $f(p)=c>1$.
|
| 144 |
+
Claim 4.1. For any $k \in \mathbb{N}, f\left(1+p+p^{2}+\ldots+p^{k}\right) \in\left\{1, c, c^{2}, \ldots, c^{k}\right\}$.
|
| 145 |
+
Proof of the claim. Use condition (2) recursively.
|
| 146 |
+
Now suppose that there exists some prime $q>p$ with $f(q)>1$, and consider the following three values of $f$ :
|
| 147 |
+
|
| 148 |
+
- $f(1)=1$.
|
| 149 |
+
- $f\left(p^{q-1}-1\right)=f(p-1) f\left(p^{q-2}+p^{q-3}+\ldots+p+1\right) \in\left\{1, c, c^{2}, \ldots, c^{q-2}\right\}$ using our claim, (note that we know $f(p-1)=1$ by the minimality of $p$ ).
|
| 150 |
+
But we also know (by Fermat's little theorem) that $q \mid p^{q-1}-1$, hence $f(q) \mid f\left(p^{q-1}-1\right)$. Therefore we have that: $f\left(p^{q-1}-1\right) \in\left\{c, c^{2}, \ldots, c^{q-2}\right\}$.
|
| 151 |
+
- $f\left(p^{q-1}\right)=c^{q-1}$.
|
| 152 |
+
|
| 153 |
+
These are three different values, hence we have a contradiction by condition (2).
|
| 154 |
+
Solution 4B (for the main part). Let $p$ the minimal (prime) number with $f(p)=c>1$.
|
| 155 |
+
Lemma 4B.1. For any $k \in \mathbb{N}, f\left(1+p+p^{2}+\ldots+p^{k}\right)=1$.
|
| 156 |
+
Proof of the Lemma, by induction. $k=0$ is trivial.
|
| 157 |
+
$k=1$ is also easy, as $p+1$ cannot be a prime, except in the case of $p=2$, which is also easy. (If $f(2)=c>1$, then $f(3) \in\{1, c\}$ by $3=1+2$ and $f(3) \in\left\{1, c^{2}\right\}$ by $2^{2}=1+3$.)
|
| 158 |
+
|
| 159 |
+
From now we suppose $k \geq 2$ and $f\left(1+p+\ldots+p^{k-1}\right)=1$. By condition (2), we have that:
|
| 160 |
+
|
| 161 |
+
- As $f\left(1+p+\ldots+p^{k-1}\right)=1$ and $f\left(p^{k}\right)=c^{k}$, we have that $f\left(1+p+\ldots+p^{k-1}\right) \in\left\{1, c^{k}\right\}$
|
| 162 |
+
- As $f(1)=1$ and $f\left(p+\ldots+p^{k}\right)=f(p) f\left(1+p+\ldots+p^{k-1}\right)=c$, we also have that $f\left(1+p+\ldots+p^{k-1}\right) \in\{1, c\}$.
|
| 163 |
+
If $k>1, c \neq c^{k}$, therefore $f\left(1+p+\ldots+p^{k}\right)=1$.
|
| 164 |
+
|
| 165 |
+
Now suppose that there exists some prime $q>p$ with $f(q)>1$. Then by condition (1),
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
f\left(p^{q-1}-1\right)=f(p-1) f\left(1+p+\ldots+p^{q-2}\right)
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
here $f(p-1)=1$ (by the minimality of $p$ ) and $f\left(1+p+\ldots+p^{q-2}\right)=1$ by the lemma. But we also know (by Fermat's little theorem) that $q \mid p^{q-1}-1$, hence $1<f(q) \leq f\left(p^{q-1}-1\right.$ ), which is a contradiction.
|
| 172 |
+
|
| 173 |
+
## Solution 5 (for the main part).
|
| 174 |
+
|
| 175 |
+
Lemma 5.1. If $f(m) \neq f(n)$, then $f(n+m)=f(n-m)$ (for all $n>m \in \mathbb{N}$ ).
|
| 176 |
+
Proof of the Lemma. By condition (2), $\{f(n+m), f(n-m)\} \subseteq\{f(n), f(m)\}$. We also have that:
|
| 177 |
+
|
| 178 |
+
$$
|
| 179 |
+
f(n-m) f(n+m)=f\left(n^{2}-m^{2}\right) \in\left\{f(n)^{2}, f(m)^{2}\right\}
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
which is only possible if $f(n-m)=f(n+m)=f(n)$ or $f(n-m)=f(n+m)=f(m)$.
|
| 183 |
+
Now let $p$ be the smallest (prime) number with $f(p)>1$.
|
| 184 |
+
Claim 5.2. If $p$ does not divide $n$, then $f(n)=1$.
|
| 185 |
+
Proof of the Claim. Let $n$ be the minimal counterexample, and and let $n=d p+r$ with $0<r<p$. Here $d \geq 1$ by the minimality of $p$.
|
| 186 |
+
|
| 187 |
+
Now $1<f(d) f(p)=f(d p) \neq f(r)=1$, hence by our lemma, $f(d p+r)=f(d p-r)=1$, contradiction.
|
| 188 |
+
|
| 189 |
+
## Problem 3.
|
| 190 |
+
|
| 191 |
+
An infinite sequence of positive integers $a_{1}, a_{2}, \ldots$ is called good if
|
| 192 |
+
(1) $a_{1}$ is a perfect square, and
|
| 193 |
+
(2) for any integer $n \geq 2, a_{n}$ is the smallest positive integer such that
|
| 194 |
+
|
| 195 |
+
$$
|
| 196 |
+
n a_{1}+(n-1) a_{2}+\ldots+2 a_{n-1}+a_{n}
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
is a perfect square.
|
| 200 |
+
Prove that for any good sequence $a_{1}, a_{2}, \ldots$, there exists a positive integer $k$ such that $a_{n}=a_{k}$ for all integers $n \geq k$.
|
| 201 |
+
|
| 202 |
+
Proposed by: Joe Benton and Dominic Yeo, United Kingdom
|
| 203 |
+
|
| 204 |
+
Solution. Define the following auxiliary sequences:
|
| 205 |
+
|
| 206 |
+
$$
|
| 207 |
+
\begin{array}{ll}
|
| 208 |
+
b_{1}=a_{1}, & b_{n}=a_{1}+a_{2}+\cdots+a_{n} \\
|
| 209 |
+
c_{1}=b_{1}, & c_{n}=b_{1}+b_{2}+\cdots+b_{n}
|
| 210 |
+
\end{array}
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Observe that
|
| 214 |
+
|
| 215 |
+
$$
|
| 216 |
+
\begin{gathered}
|
| 217 |
+
c_{n}-c_{n-1}=b_{n} \\
|
| 218 |
+
b_{n}-b_{n-1}=\left(c_{n}-c_{n-1}\right)-\left(c_{n-1}-c_{n-2}\right)=a_{n}
|
| 219 |
+
\end{gathered}
|
| 220 |
+
$$
|
| 221 |
+
|
| 222 |
+
Therefore,
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
c_{n}=\left(2 c_{n-1}-c_{n-2}\right)+a_{n}
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
is the smallest square greater than $2 c_{n-1}-c_{n-2}$.
|
| 229 |
+
Claim. $\sqrt{c_{n}}-\sqrt{c_{n-1}} \leq \sqrt{c_{n-1}}-\sqrt{c_{n-2}}$
|
| 230 |
+
Proof 1. Let $c_{n}=m_{n}^{2}, c_{n-1}=m_{n-1}^{2}, c_{n-2}=m_{n-2}^{2}$, where the value of $c_{n}$ is momentarily permitted to exceed its minimum. Any value is permitted for which
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
b_{n}=c_{n}-c_{n-1}>b_{n-1}=c_{n-1}-c_{n-2}
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
Factoring,
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
\left(m_{n}-m_{n-1}\right)\left(m_{n}+m_{n-1}\right)>\left(m_{n-1}-m_{n-2}\right)\left(m_{n-1}+m_{n-2}\right)
|
| 240 |
+
$$
|
| 241 |
+
|
| 242 |
+
In the case that $m_{n}-m_{n-1}=m_{n-1}-m_{n-2}$, this inequality clearly holds, as $m_{n}+m_{n-1}>m_{n-1}+m_{n-2}$. Thus, the minimal possible value of $m_{n}$ satisfies the claimed inequality.
|
| 243 |
+
|
| 244 |
+
Proof 2. Denote $c_{n-1}=x^{2}, c_{n-2}=(x-d)^{2}$. Then
|
| 245 |
+
|
| 246 |
+
$$
|
| 247 |
+
2 c_{n-1}-c_{n-2}=2 x^{2}-(x-d)^{2}=x^{2}+2 d x-d^{2}=(x+d)^{2}-2 d^{2}<(x+d)^{2}
|
| 248 |
+
$$
|
| 249 |
+
|
| 250 |
+
It follows that $c_{n} \leq(x+d)^{2}$.
|
| 251 |
+
And so the sequence of positive integers $\sqrt{c_{n}}-\sqrt{c_{n-1}}$ is decreasing. Any such sequence is eventually constant.
|
| 252 |
+
|
| 253 |
+
As a corollary, $c_{n}=(x+n d)^{2}$ for sufficiently large $n$, with fixed integers $x$ and $d$. Along the lines above, it becomes clear that $a_{n}=c_{n}-2 c_{n-1}+c_{n-2}=2 d^{2}$, so the sequence $\left(a_{n}\right)$ is constant.
|
| 254 |
+
|
| 255 |
+
Solution. We write:
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
s_{n}^{2}=S_{n}=a_{1}+\left(a_{1}+a_{2}\right)+\ldots+\left(a_{1}+\ldots+a_{n}\right)
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
So, setting $b_{n}:=a_{1}+\ldots+a_{n}$, we have $S_{n}=b_{1}+b_{2}+\ldots+b_{n}$ and, in particular $S_{n+1}=S_{n}+b_{n+1}$. Now, we study the quantity $S_{n} b_{n}=+b_{1}+b_{2}+\ldots+b_{n}+b_{n}$ in two different ways. Since $b_{n+1}$ is the smallest integer strictly greater than $b_{n}$ such that $b_{1}+\ldots+b_{n}+b_{n+1}$ is a perfect square, we must have
|
| 262 |
+
|
| 263 |
+
$$
|
| 264 |
+
b_{1}+b_{2}+\ldots+b_{n}+b_{n} \geq\left(s_{n+1}-1\right)^{2}
|
| 265 |
+
$$
|
| 266 |
+
|
| 267 |
+
However, we also have
|
| 268 |
+
|
| 269 |
+
$$
|
| 270 |
+
b_{1}+b_{2}+\ldots+b_{n}+b_{n}=S_{n}+b_{n}=2 S_{n}-S_{n-1}
|
| 271 |
+
$$
|
| 272 |
+
|
| 273 |
+
Combining, we obtain
|
| 274 |
+
|
| 275 |
+
$$
|
| 276 |
+
s_{n}^{2} \geq \frac{s_{n-1}^{2}+\left(s_{n+1}-1\right)^{2}}{2}>\left(\frac{s_{n-1}+s_{n+1}-1}{2}\right)^{2}
|
| 277 |
+
$$
|
| 278 |
+
|
| 279 |
+
where the final inequality is strict since the sequence $\left(s_{k}\right)$ is strictly increasing. Taking a square root, and noting that all the $\left(s_{n}\right)$ are integers, one obtains $s_{n+1}-s_{n} \leq s_{n}-s_{n-1}$.
|
| 280 |
+
Now we focus on the sequence $d_{n}=s_{n+1}-s_{n} .\left(s_{k}\right)$ is strictly increasing thus $\left(d_{k}\right)$ is positive. However we proved that $d_{n+1} \leq d_{n}$, so the sequence $\left(d_{k}\right)$ is eventually constant, so eventually $s_{n}=b n+c$ and $S_{n}=(b n+c)^{2}$ with some numbers $b, c$; then
|
| 281 |
+
|
| 282 |
+
$$
|
| 283 |
+
a_{n+2}=S_{n+2}-2 S_{n+1}+S_{n}=(b(n+2)+c)^{2}-2(b(n+1)+c)^{2}+(b n+c)^{2}=2 b^{2}
|
| 284 |
+
$$
|
| 285 |
+
|
| 286 |
+
Remark. The key idea is to use the $D$ difference operator on the space of sequences. That is a function which takes a sequence as an input and outputs another sequence the following way: if $(x)$ is the input sequence, then
|
| 287 |
+
|
| 288 |
+
$$
|
| 289 |
+
D(x)=D\left(\left(x_{1}, x_{2}, x_{3}, x_{4}, \ldots\right)\right)=\left(x_{2}-x_{1}, x_{3}-x_{2}, x_{4}-x_{3}, \ldots\right)
|
| 290 |
+
$$
|
| 291 |
+
|
| 292 |
+
Here $D D(S)=(a)$ (with some shift), $D(s)=(d)$. This $D$ operator has some nice properties; if someone studied calculus, these properties will be familiar. $D(x+y)=D(x)+D(y) ; D(\lambda x)=\lambda D(x) ;(x)$ constant iff $D x$ zero ; $(x)$ is linear iff $D x$ constant ; in general $(x)$ is a polynomial with degree $l+1$ iff $D(x)$ is a polynomial with degree $l$.
|
| 293 |
+
|
| 294 |
+
First we proved that sequence $(d)$ is eventually constant, thus $D(d)=D D(s)$ is eventually zero. Therefore the sequence $(s)$ is eventually a linear function, hence $s^{2}=S$ is eventually a quadratic polynomial, therefore $0=D D D(S)=D(a)$, so $(a)$ is constant eventually.
|
| 295 |
+
|
| 296 |
+
## Problem 4.
|
| 297 |
+
|
| 298 |
+
Given a positive integer $n \geq 2$, determine the largest positive integer $N$ for which there exist $N+1$ real numbers $a_{0}, a_{1}, \ldots, a_{N}$ such that
|
| 299 |
+
(1) $a_{0}+a_{1}=-\frac{1}{n}$, and
|
| 300 |
+
(2) $\left(a_{k}+a_{k-1}\right)\left(a_{k}+a_{k+1}\right)=a_{k-1}-a_{k+1}$ for $1 \leq k \leq N-1$.
|
| 301 |
+
|
| 302 |
+
Proposed by: Romania
|
| 303 |
+
|
| 304 |
+
Solution 1. $\left(a_{k}+a_{k-1}\right)\left(a_{k}+a_{k+1}\right)=a_{k-1}-a_{k+1}$ is equivalent to $\left(a_{k}+a_{k-1}+1\right)\left(a_{k}+a_{k+1}-1\right)=-1$. Let $b_{k}=a_{k}+a_{k+1}$. Thus we need $b_{0}, b_{1}, \ldots$ the following way: $b_{0}=-\frac{1}{n}$ and $\left(b_{k-1}+1\right)\left(b_{k}-1\right)=-1$. There is a proper sequence $b_{0}, b_{1}, \ldots, b_{N-1}$ if and only if there is proper sequence $a_{0}, a_{1}, \ldots, a_{N}$, because from a a proper $\left(a_{k}\right)$ sequence we can get a proper $\left(b_{k}\right)$ sequence with $b_{k}=a_{k}+a_{k+1}$ for $k=0,1, \ldots, N-1$ and from a proper $\left(b_{k}\right)$ sequence we can get a proper $\left(a_{k}\right)$ sequence by arbitrarily setting $a_{0}$ and then inductively defining $a_{k}=b_{k-1}-a_{k-1}$ for $k=1,2, \ldots, N$.
|
| 305 |
+
|
| 306 |
+
We prove by induction that $b_{k}=-\frac{1}{n-k}$ for $k<n$. This is true for $k=0$, as $b_{0}=-\frac{1}{n}$ and
|
| 307 |
+
|
| 308 |
+
$$
|
| 309 |
+
b_{k}=1-\frac{1}{b_{k-1}+1}=1-\frac{1}{1-\frac{1}{n-k+1}}=-\frac{1}{n-k}
|
| 310 |
+
$$
|
| 311 |
+
|
| 312 |
+
for $k<n$. Thus there is a proper sequence $b_{0}, b_{1}, \ldots, b_{n-1}$, but it can't be continued, because $b_{n-1}+1=$ 0 so there is no $b_{n}$ for which $\left(b_{n-1}+1\right)\left(b_{n}-1\right)=-1$.
|
| 313 |
+
|
| 314 |
+
Therefore the longest proper sequence $\left(b_{k}\right)$ is $n$-long, so the longest proper sequence $\left(a_{k}\right)$ is $n+1$ long, so $N=n$.
|
| 315 |
+
|
| 316 |
+
Solution 2. The required maximum is $N=n$.
|
| 317 |
+
To rule out the case $N \geq n+1$, it is clearly sufficient to rule out the case $N=n+1$.
|
| 318 |
+
Assume for contradiction that $a_{0}, a_{1}, \ldots, a_{n+1}$ are real numbers satisfying both conditions in the statement. It is sufficient to show that $a_{k}+a_{k+1}=0$ for some $k \leq n$, because then $a_{k-1}-a_{k+1}=0$ so $a_{k+1}=a_{k-1}$, therefore $a_{k-1}+a_{k}=0$ and so on, by backwards recursion we get that $a_{j}+a_{j+1}=0$ for all $0 \leq j \leq k$, but this is a contradiction with $a_{0}+a_{1}=-\frac{1}{n}$.
|
| 319 |
+
|
| 320 |
+
To prove that $a_{k}+a_{k+1}=0$ for some $k \leq n$, assume that $a_{k}+a_{k+1} \neq 0$ for all $k \leq n$, to rewrite the second condition in the statement in the form
|
| 321 |
+
|
| 322 |
+
$$
|
| 323 |
+
\frac{1}{a_{k}+a_{k+1}}-\frac{1}{a_{k-1}+a_{k}}=1, \quad k=1, \ldots, n
|
| 324 |
+
$$
|
| 325 |
+
|
| 326 |
+
and sum both sides over the full range from $k=1$ to $n$. This gives
|
| 327 |
+
|
| 328 |
+
$$
|
| 329 |
+
\frac{1}{a_{n}+a_{n+1}}-\frac{1}{a_{0}+a_{1}}=n \text {. }
|
| 330 |
+
$$
|
| 331 |
+
|
| 332 |
+
As $a_{0}+a_{1}=-\frac{1}{n}$, this means that $\frac{1}{a_{n}+a_{n+1}}=0$, which is a contradiction. Consequently, $N \leq n$.
|
| 333 |
+
To provide $n+1$ real numbers satisfying both conditions in the statement, fix $a_{0}$ and go through the telescoping procedure above to obtain
|
| 334 |
+
|
| 335 |
+
$$
|
| 336 |
+
a_{k}=(-1)^{k} a_{0}+\sum_{j=1}^{k} \frac{(-1)^{k-j+1}}{n-j+1}, \quad k=1, \ldots, n
|
| 337 |
+
$$
|
| 338 |
+
|
| 339 |
+
This concludes the proof.
|
| 340 |
+
|
| 341 |
+
## Problem 5.
|
| 342 |
+
|
| 343 |
+
For all positive integers $n, k$, let $f(n, 2 k)$ be the number of ways an $n \times 2 k$ board can be fully covered by $n k$ dominoes of size $2 \times 1$. (For example, $f(2,2)=2$ and $f(3,2)=3$.)
|
| 344 |
+
Find all positive integers $n$ such that for every positive integer $k$, the number $f(n, 2 k)$ is odd.
|
| 345 |
+
Proposed by: U.S.A.
|
| 346 |
+
|
| 347 |
+
Solution. The integers $n$ with the requested property are exactly the ones of the form $2^{k}-1$.
|
| 348 |
+
In what follows, let $f(m, n)$ denote the number of domino tilings of an $m \times n$ grid. (For convenience, we also allow $m$ and $n$ to be 0 , in which case $f(m, n)=1$.)
|
| 349 |
+
Claim. $f(m, 2 n+1) \equiv f(m, n)(\bmod 2)$ for all $n$ and even $m$
|
| 350 |
+
Proof. Consider reflecting $m \times(2 n+1)$ tilings across the central column. In this way, the tilings are grouped into singletons and pairs, so modulo $2, f(m, 2 n+1)$ is congruent to the number of singletons.
|
| 351 |
+
|
| 352 |
+
If a tiling is invariant under reflection in the central column, then every domino with one cell in that column must have both cells in that column.
|
| 353 |
+
|
| 354 |
+
In other words, the central column is filled with $\frac{m}{2}$ vertical dominoes, splitting the remainder of the grid into two $m \times n$ grids. Obeying the symmetry constraint, there are $f(m, n)$ tilings: each of the tilings of the left grid fixes the tiling of the right grid.
|
| 355 |
+
|
| 356 |
+
Claim. $f(n, n) \equiv 0(\bmod 2)$ for all even $n \geq 2$. (Recall that $f(0,0)=1$ is odd.)
|
| 357 |
+
Proof. Consider reflecting $n \times n$ tilings across the diagonal. This groups the tilings into pairs, (no tiling is grouped with itself). Hence the number of $n \times n$ tilings is even.
|
| 358 |
+
|
| 359 |
+
We are ready to complete the solution.
|
| 360 |
+
|
| 361 |
+
- If $n$ is odd, the first claim shows that $n$ satisfies the property if and only if $\frac{1}{2}(n-1)$ does.
|
| 362 |
+
- If $n \geq 2$ is even, the second claim shows that $n$ does not satisfy the property.
|
| 363 |
+
- If $n=0$, then $n$ satisfies the property, as $f(m, 0)=1$ always.
|
| 364 |
+
|
| 365 |
+
This concludes the proof that the sought numbers are the ones of the form $2^{k}-1$.
|
| 366 |
+
|
| 367 |
+
## Solution 2.
|
| 368 |
+
|
| 369 |
+
Color the board as a chessboard. Consider the bipartite graph whose vertices are the squares and the neighbors are connected by an edge. Notice that a domino tiling described in the problem corresponds to a perfect matching in this bipartite graph, so we are interested in the number of perfect matchings.
|
| 370 |
+
|
| 371 |
+
And that is the permanent of the (bipartite) adjacency matrix. However we need to compute it $\bmod 2\left(\right.$ over $\left.F_{2}\right)$, so that is the determinant of that matrix.
|
| 372 |
+
|
| 373 |
+
So our goal is to decide whether the determinant is 0 or $1 \bmod 2$, or in other world, that matrix is singular or not. From now we compute everything mod 2. Now we understand what does it mean, that a vector $v$ is in the nullspace (has eigenvalue 0 ). But each entry of $v$ is $0-1$, so in other words we choose a subset of the black squares ( $v$ is the characteristic vector of that subset). So in the language of the board, there is a nontrivial $v$ in the nullspace iff we have a subspace of black square such a way that each white square has even number of black chosen neighbors.
|
| 374 |
+
|
| 375 |
+
If $n$ is even, then we can choose a subset such a way in the $n \times n$ square: the diagonal.
|
| 376 |
+
Now we prove similar connection between $n$ and $2 n+1$ : there is a construction for $n$ iff we have one for $2 n+1 . k$ is always even. If we have a construction in $n \times k$ then we have one in $(2 n+1) \times k$ : we mirror the construction to the middle row.
|
| 377 |
+
Now we prove that from a construction in $(2 n+1) \times k$ we can make a construction in $n \times k$. First, we
|
| 378 |
+
don't have any chosen black square in the middle row. Then the chosen black squares in the upper (or lower) $n \times k$ rectangle is a construction for $n \times k$. Second, we have some chosen black square in the middle row. Because we can find a white square in the middle row such that is has only one chosen black neighbor in the middle row. Thus this construction isn't symmetric to the horizontal line the symmetric difference of the construction and its reflection (to the vertical line) is a nontrivial vector in the nullspace, thus we can use the first case.
|
| 379 |
+
|
| 380 |
+
## Problem 6.
|
| 381 |
+
|
| 382 |
+
Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$. Let the internal angle bisectors at $A$ and $B$ meet at $X$, the internal angle bisectors at $B$ and $C$ meet at $Y$, the internal angle bisectors at $C$ and $D$ meet at $Z$, and the internal angle bisectors at $D$ and $A$ meet at $W$. Further, let $A C$ and $B D$ meet at $P$. Suppose that the points $X, Y, Z, W, O$ and $P$ are distinct.
|
| 383 |
+
|
| 384 |
+
Prove that $O, X, Y, Z$ and $W$ lie on the same circle if and only if $P, X, Y, Z$ and $W$ lie on the same circle.
|
| 385 |
+
|
| 386 |
+
Proposed by: Ethan Tan, Australia
|
| 387 |
+
|
| 388 |
+
Solution 1. Let $\Omega$ be the circumcircle of the quadrilateral $A B C D$ and let $r$ be its radius.
|
| 389 |
+
First, notice that the points $X, Y, Z, W$ are concyclic. Indeed, using oriented (modulo $180^{\circ}$ ) angles,
|
| 390 |
+
|
| 391 |
+
$$
|
| 392 |
+
\angle(X W, X Y)+\angle(Z Y, Z W)=\angle(X A, X B)+\angle(Z C, Z D)=-\frac{\angle A+\angle B}{2}-\frac{\angle C+\angle D}{2}=0 .
|
| 393 |
+
$$
|
| 394 |
+
|
| 395 |
+
Let $\omega$ be the circle passing through these four points. Our goal is to prove that $O \in \omega$ occurs if and only if $P \in \omega$.
|
| 396 |
+
|
| 397 |
+
Next, we rule out the case when $A B C D$ is a trapezium. Suppose that if $A B C D$ is an isosceles trapezium; without loss of generality say $A B \| C D$. By symmetry, points $X, Z, O$ and $P$ lie on the symmetry axis (that is, the common perpendicular bisector of $A B$ and $C D$ ), therefore they are collinear. By the conditions of the problem, these four points are distinct and $X$ and $Z$ are on $\omega$, so neither $O$, nor $P$ can lie on $\omega$; therefore the problem statement is obvious. From now on we assume that $A B \nVdash C D$ and $B C \nVdash A D$.
|
| 398 |
+
|
| 399 |
+
|
| 400 |
+
Let $A B$ and $C D$ meet at $Q$, and let $B C$ and $A D$ meet at $R$. Without loss of generality, suppose that $B$ lies between $A$ and $Q$, and $D$ lies between $A$ and $R$. Now we show that line $Q R$ is the radical axis between circles $\Omega$ and $\omega$.
|
| 401 |
+
|
| 402 |
+
Point $W$ is the intersection point of the bisectors of $\angle A$ and $\angle D$, so in triangle $A D Q$, point $W$ is the incentre. Similary, $B Y$ and $C Y$ are the external bisectors of $\angle Q B C$ and $\angle B C Q$, so in triangle $B C Q$, point $Y$ is the excentre opposite to $Q$. Hence, both $Y$ and $W$ lie on the bisector of $\angle D Q A$.
|
| 403 |
+
|
| 404 |
+
By $\angle D Q A=180^{\circ}-\angle D-\angle A=\angle B-\angle A$ we get
|
| 405 |
+
|
| 406 |
+
$$
|
| 407 |
+
\angle B Y Q=\angle Y B A-\angle Y Q B=\frac{\angle B}{2}-\frac{\angle D Q A}{2}=\frac{\angle B}{2}-\frac{\angle B-\angle A}{2}=\frac{\angle A}{2}=\angle B A W
|
| 408 |
+
$$
|
| 409 |
+
|
| 410 |
+
so the points $A, B, Y, W$ are concyclic, and therefore $Q A \cdot Q B=Q Y \cdot Q W$; hence, $Q$ has equal power with respect to $\Omega$ and $\omega$. It can be seen similarly that $R$ has equal power with respect to the circles $\Omega$ and $\omega$. Hence, the radical axis of $\Omega$ and $\omega$ is line $Q R$.
|
| 411 |
+
|
| 412 |
+
Let lines $O P$ and $Q R$ meet at point $S$. It is well-known that with respect to circle $A B C D$, the diagonal triangle $P Q R$ is autopolar. As consequences we have $O P \perp Q R$, and the points $P$ and $S$ are symmetric to circle $A B C D$, so $O S \cdot O P=r^{2}$.
|
| 413 |
+
|
| 414 |
+
Notice that $P$ and $O$ lie inside $\Omega$, so the polar line $Q R$ lies entirely outside, so $S$ is different from $P$ and $O$. Moreover,
|
| 415 |
+
|
| 416 |
+
$$
|
| 417 |
+
S O \cdot S P=O S \cdot(O S-O P)=O S^{2}-O S \cdot O P=S O^{2}-r^{2}
|
| 418 |
+
$$
|
| 419 |
+
|
| 420 |
+
so $S O \cdot S P$ is equal to the power of $S$ with respect to $\Omega$. Since $S$ lies on the radical axis $Q R$, it has equal power with respect to the two circles; therefore, $S O \cdot S P$ is equal to the power of $S$ with respect to $\omega$. From this, it follows that $O \in \omega$ if and only if $P \in \omega$.
|
| 421 |
+
|
| 422 |
+
Solution 2. We will prove that the points $X, Y, Z, W, O, P$ lie on a conic section $\Gamma$. Five distinct points uniquely determine a conic section, therefore
|
| 423 |
+
|
| 424 |
+
$$
|
| 425 |
+
X, Y, Z, W, O \text { are concyclic } \Leftrightarrow \Gamma \text { is a circle } \Leftrightarrow X, Y, Z, W, P \text { are concyclic. }
|
| 426 |
+
$$
|
| 427 |
+
|
| 428 |
+
|
| 429 |
+
|
| 430 |
+
Let $\alpha=\angle A C B=\angle A D B, \beta=\angle B D C=\angle B A C, \gamma=\angle C A D=\angle C B D$ and $\delta=\angle D B A=$ $\angle D C A$, where of course $\alpha+\beta+\gamma+\delta=180^{\circ}$. For every point $\xi$ in the plane, let $a(\xi), b(\xi), c(\xi)$ and $d(\xi)$ be the signed distances between $\xi$ and the lines $A B, B C, C D$ and $D A$, respectively, such that the quadrilateral lies on the positive sides of these lines.
|
| 431 |
+
|
| 432 |
+
The equations of the bisectors of $\angle A X W, \angle B X Y, \angle C Y Z$ and $\angle D Z W$ are $a(\xi)-d(\xi)=0$, $b(\xi)-a(\xi)=0, c(\xi)-b(\xi)=0$ and $d(\xi)-c(\xi)=0$, respectively. Notice that the points $X, Y, Z, W$ satisfy the quadratic equations $(a(\xi)-d(\xi))(b(\xi)-c(\xi))=0$ and $(a(\xi)-b(\xi))(c(\xi)-d(\xi))=0$, so
|
| 433 |
+
|
| 434 |
+
$$
|
| 435 |
+
a(\xi) b(\xi)+c(\xi) d(\xi)=a(\xi) c(\xi)+b(\xi) d(\xi)=a(\xi) d(\xi)+b(\xi) c(\xi) \quad \text { for } \xi=X, Y, Z, W
|
| 436 |
+
$$
|
| 437 |
+
|
| 438 |
+
Without loss of generality, suppose that $A B C D$ is inscribed in a unit circle. Then
|
| 439 |
+
|
| 440 |
+
$$
|
| 441 |
+
a(O)=\cos \alpha, \quad b(O)=\cos \beta, \quad c(O)=\cos \gamma, \quad d(O)=\cos \delta
|
| 442 |
+
$$
|
| 443 |
+
|
| 444 |
+
By $\frac{a(P)}{b(P)}=\frac{B P \cdot \sin \delta}{B P \cdot \sin \gamma}=\frac{1 / \sin \gamma}{1 / \sin \delta}$ and the analogous relations we can see that
|
| 445 |
+
|
| 446 |
+
$$
|
| 447 |
+
a(P)=\frac{k}{\sin \gamma}, \quad b(P)=\frac{k}{\sin \delta}, \quad c(P)=\frac{k}{\sin \alpha}, \quad d(P)=\frac{k}{\sin \beta}
|
| 448 |
+
$$
|
| 449 |
+
|
| 450 |
+
with some positive number $k$.
|
| 451 |
+
Now let $s=\frac{\sin \alpha \sin \beta \sin \gamma \sin \delta}{k^{2}}$; then, by (2a) and (2b),
|
| 452 |
+
|
| 453 |
+
$$
|
| 454 |
+
\begin{aligned}
|
| 455 |
+
a(O) b(O)-s \cdot a(P) b(P) & =\cos \alpha \cos \beta-\sin \alpha \sin \beta=\cos (\alpha+\beta) \\
|
| 456 |
+
c(O) d(O)-s \cdot c(P) d(P) & =\cos (\gamma+\delta)=-\cos (\alpha+\beta) \\
|
| 457 |
+
a(O) b(O)+c(O) d(O) & =s \cdot(a(P) b(P)+c(P) d(P))
|
| 458 |
+
\end{aligned}
|
| 459 |
+
$$
|
| 460 |
+
|
| 461 |
+
analogous calculation provides
|
| 462 |
+
|
| 463 |
+
$$
|
| 464 |
+
\begin{aligned}
|
| 465 |
+
& a(O) c(O)+b(O) d(O)=s \cdot(a(P) c(P)+b(P) d(P)) \\
|
| 466 |
+
& a(O) d(O)+b(O) c(O)=s \cdot(a(P) d(P)+b(P) c(P))
|
| 467 |
+
\end{aligned}
|
| 468 |
+
$$
|
| 469 |
+
|
| 470 |
+
In order to find the equation of the curve $\Gamma$, choose real numbers $u, v, w$, not all zero, such that
|
| 471 |
+
|
| 472 |
+
$$
|
| 473 |
+
\begin{gathered}
|
| 474 |
+
u+v+w=0 \\
|
| 475 |
+
u \cdot(a(P) b(P)+c(P) d(P))+v \cdot(a(P) c(P)+b(P) d(P))+w \cdot(a(P) d(P)+b(P) c(P))=0
|
| 476 |
+
\end{gathered}
|
| 477 |
+
$$
|
| 478 |
+
|
| 479 |
+
This is always possible, because this a system of two homogeneous linear equations with three variables. Then the equation of $\Gamma$ will be
|
| 480 |
+
|
| 481 |
+
$$
|
| 482 |
+
f(\xi)=u \cdot(a(\xi) b(\xi)+c(\xi) d(\xi))+v \cdot(a(\xi) c(\xi)+b(\xi) d(\xi))+w \cdot(a(\xi) d(\xi)+b(\xi) c(\xi))=0
|
| 483 |
+
$$
|
| 484 |
+
|
| 485 |
+
As can be seen, $f(X)=f(Y)=f(Z)=f(W)=0$ follows from (1) and (4), $f(P)=0$ follows from (5), then $f(O)=s \cdot f(P)=0$ follows from $(3 a-3 c)$. So, the points $X, Y, Z, W, O, P$ all satisfy the equation $f(\xi)=0$.
|
| 486 |
+
|
| 487 |
+
Notice that $f(B)=u \cdot c(B) d(B)$ and $f(A)=w \cdot b(A) c(A)$; since at least one of $u$ and $w$ is nonzero, either $A$ or $B$ does not satisfy $(*)$. Therefore, the equation cannot degenerate to an identity.
|
| 488 |
+
|
| 489 |
+
Hence, the equation $f(\xi)=0$ is at most quadratic, it is not an identity, but satisfied by $X, Y, Z, W, O, P$, so these six points lie on a conic section.
|
| 490 |
+
|
| 491 |
+
Solution 3. Let $A^{\prime}, B^{\prime}, C^{\prime}$ and $D^{\prime}$ be the second intersection of the angle bisectors of $\angle D A C$, $\angle A B C, \angle B C D$ and $\angle C D A$ with the circumcircle of $A B C D$, respectively. Notice that $A^{\prime}$ and $C^{\prime}$ are the midpoints of the two arcs of $B D$ and $B^{\prime}$ and $D^{\prime}$ are the midpoints of arcs corresponding to $A C$ so the lines $A^{\prime} C^{\prime}$ and $B^{\prime} D^{\prime}$ intersect in $O$.
|
| 492 |
+
|
| 493 |
+
|
| 494 |
+
We will prove that the points $X, Y, Z, W, P$ and $O$ lie on a conic section. This is a more general statement because five points uniquely determine a conic sections so if $X, Y, Z, W$ and $P$ lie on a circle then this circle is the conic section so $O$ also lies on this circle. In the same way if $X, Y, Z$, $W$ and $O$ are on a circle then it also contains $P$.
|
| 495 |
+
|
| 496 |
+
Let $E$ be the intersection of the lines $A^{\prime} B$ and $C D^{\prime}$. Let $F$ be the intersection of the lines $A^{\prime} D$ and $B^{\prime} C$. Finally, let $G$ be the intesection of $X Y$ and $Z W$.
|
| 497 |
+
|
| 498 |
+
Now we use Pascal's theorem five times:
|
| 499 |
+
|
| 500 |
+
1. From $B D D^{\prime} C A A^{\prime}$ we see that the points $P, W$ and $E$ are collinear.
|
| 501 |
+
2. From $B B^{\prime} D^{\prime} C C^{\prime} A^{\prime}$ we see that the points $Y, O$ and $E$ are collinear.
|
| 502 |
+
3. From $B^{\prime} B D A^{\prime} A C$ we see that the points $X, P$ and $F$ are collinear.
|
| 503 |
+
4. From $B^{\prime} D^{\prime} D A^{\prime} C^{\prime} C$ we see that the points $O, Z$ and $F$ are collinear.
|
| 504 |
+
5. From $D^{\prime} C B^{\prime} B A^{\prime} D$ we see that the points $E, F$ and $G$ are collinear.
|
| 505 |
+
|
| 506 |
+
So the opposite sides of the hexagon $P X Y O Z W$ intersect at points $F, G$ and $E$, which are collinear, so by the converse of Pascal's theorem the points $X, Y, Z, W, P$ and $O$ indeed lie on a conic section.
|
| 507 |
+
|
EGMO/md/en-2023-solutions.md
ADDED
|
@@ -0,0 +1,723 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# EGMO 2023 - Problems and solutions
|
| 2 |
+
|
| 3 |
+
## Problems
|
| 4 |
+
|
| 5 |
+
Problem 1. There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
|
| 6 |
+
|
| 7 |
+
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
| 8 |
+
Problem 2. We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
|
| 9 |
+
|
| 10 |
+
Show that line $K L$ passes through the orthocentre of $A B C$.
|
| 11 |
+
The altitudes of a triangle meet at its orthocentre.
|
| 12 |
+
Problem 3. Let $k$ be a positive integer. Lexi has a dictionary $\mathcal{D}$ consisting of some $k$-letter strings containing only the letters $A$ and $B$. Lexi would like to write either the letter $A$ or the letter $B$ in each cell of a $k \times k$ grid so that each column contains a string from $\mathcal{D}$ when read from top-to-bottom and each row contains a string from $\mathcal{D}$ when read from left-to-right.
|
| 13 |
+
|
| 14 |
+
What is the smallest integer $m$ such that if $\mathcal{D}$ contains at least $m$ different strings, then Lexi can fill her grid in this manner, no matter what strings are in $\mathcal{D}$ ?
|
| 15 |
+
|
| 16 |
+
Problem 4. Turbo the snail sits on a point on a circle with circumference 1. Given an infinite sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$, Turbo successively crawls distances $c_{1}, c_{2}, c_{3}, \ldots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
|
| 17 |
+
For example, if the sequence $c_{1}, c_{2}, c_{3}, \ldots$ is $0.4,0.6,0.3, \ldots$, then Turbo may start crawling as follows:
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
Determine the largest constant $C>0$ with the following property: for every sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$ with $c_{i}<C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.
|
| 21 |
+
|
| 22 |
+
Problem 5. We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
|
| 23 |
+
|
| 24 |
+
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
| 25 |
+
|
| 26 |
+
Problem 6. Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
|
| 27 |
+
|
| 28 |
+
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.
|
| 29 |
+
|
| 30 |
+
## Solutions
|
| 31 |
+
|
| 32 |
+
Problem 1. There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
|
| 33 |
+
|
| 34 |
+
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
| 35 |
+
|
| 36 |
+
Solution 1. Suppose that not all $a_{i}$ are equal. Consider an index $i$ such that $a_{i}$ is maximal and $a_{i+1}<a_{i}$. Then
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}<\frac{2 a_{i}}{a_{i}}=2 .
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
But since $a_{i}$ is maximal, $b_{i}$ is also maximal, so we must have $b_{j}<2$ for all $j \in\{1,2, \ldots, n\}$. However, consider the product $b_{1} b_{2} \ldots b_{n}$. We have
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
\begin{aligned}
|
| 46 |
+
b_{1} b_{2} \ldots b_{n} & =\frac{a_{n}+a_{2}}{a_{1}} \cdot \frac{a_{1}+a_{3}}{a_{2}} \cdot \ldots \cdot \frac{a_{n-1}+a_{1}}{a_{n}} \\
|
| 47 |
+
& \geqslant 2^{n} \frac{\sqrt{a_{n} a_{2}} \sqrt{a_{1} a_{3}} \ldots \sqrt{a_{n-1} a_{1}}}{a_{1} a_{2} \ldots a_{n}} \\
|
| 48 |
+
& =2^{n}
|
| 49 |
+
\end{aligned}
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
where we used the inequality $x+y \geqslant 2 \sqrt{x y}$ for $x=a_{i-1}, y=a_{i+1}$ for all $i \in\{1,2, \ldots, n\}$ in the second row.
|
| 53 |
+
|
| 54 |
+
Since the product of all $b_{i}$ is at least $2^{n}$, at least one of them must be greater than 2 , which is a contradiction with the previous conclusion.
|
| 55 |
+
|
| 56 |
+
Thus, all $a_{i}$ must be equal.
|
| 57 |
+
|
| 58 |
+
Solution 2. This is a version of Solution 1 without use of proof by contradiction.
|
| 59 |
+
Taking $a_{i}$ such that it is maximal among $a_{1}, \ldots, a_{n}$, we obtain $b_{i} \leqslant 2$. Thus $b_{i} \leqslant 2$ for all $j \in\{1,2, \ldots, n\}$.
|
| 60 |
+
The second part of Solution 1 then gives $2^{n} \geqslant b_{1} \cdots b_{n} \geqslant 2^{n}$, which together with $b_{i} \leqslant 2$ for all $j \in\{1,2, \ldots, n\}$ implies that $b_{j}=2$ for all $j \in\{1,2, \ldots, n\}$. Since we have $b_{1}=$ $b_{2}=\cdots=b_{n}$, the condition that $a_{i} \leqslant a_{j} \Longleftrightarrow b_{i} \leqslant b_{j}$ gives that $a_{1}=a_{2}=\cdots=a_{n}$.
|
| 61 |
+
|
| 62 |
+
Solution 3. We first show that $b_{j} \leqslant 2$ for all $j$ as in Solution 2. Then
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\begin{aligned}
|
| 66 |
+
2 n & \geqslant b_{1}+\cdots+b_{n}=\frac{a_{n}}{a_{1}}+\frac{a_{2}}{a_{1}}+\frac{a_{1}}{a_{2}}+\frac{a_{3}}{a_{2}}+\cdots+\frac{a_{n-1}}{a_{n}}+\frac{a_{1}}{a_{n}} \\
|
| 67 |
+
& \geqslant 2 n \sqrt[n]{\frac{a_{n}}{a_{1}} \cdot \frac{a_{2}}{a_{1}} \cdot \frac{a_{1}}{a_{2}} \cdot \frac{a_{3}}{a_{2}} \cdots \frac{a_{n-1}}{a_{n}} \cdot \frac{a_{1}}{a_{n}}=2 n \cdot 1=2 n,}
|
| 68 |
+
\end{aligned}
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
where we used the AM-GM inequality.
|
| 72 |
+
It follows that all $b_{j}$ 's are equal which as in Solution 2 gives $a_{1}=a_{2}=\cdots=a_{n}$.
|
| 73 |
+
|
| 74 |
+
Solution 4. By assumption $a_{i} b_{i}=a_{i-1}+a_{i+1}$ for $i=\{1,2, \ldots, n\}$, hence,
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\sum_{i=1}^{n} a_{i} b_{i}=2 \sum_{i=1}^{n} a_{i} .
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
Since $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$, the Chebyshev's inequality implies
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\left(\sum_{i=1}^{n} a_{i}\right) \cdot\left(\sum_{i=1}^{n} b_{i}\right) \leqslant n \cdot \sum_{i=1}^{n} a_{i} b_{i}=2 n \cdot \sum_{i=1}^{n} a_{i}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
and so $\sum_{i=1}^{n} b_{i} \leqslant 2 n$. On the other hand, we have
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
\sum_{i=1}^{n} b_{i}=\sum_{i=1}^{n} \frac{a_{i-1}}{a_{i}}+\sum_{i=1}^{n} \frac{a_{i+1}}{a_{i}}=\sum_{i=1}^{n} \frac{a_{i-1}}{a_{i}}+\sum_{i=1}^{n} \frac{a_{i}}{a_{i-1}}=\sum_{i=1}^{n}\left(\frac{a_{i-1}}{a_{i}}+\frac{a_{i}}{a_{i-1}}\right)
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
so we can use the AM-GM inequality to estimate
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\sum_{i=1}^{n} b_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{\frac{a_{i-1}}{a_{i}} \cdot \frac{a_{i}}{a_{i-1}}}=2 n
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
We conclude that we must have equalities in all the above, which implies $\frac{a_{i-1}}{a_{i}}=\frac{a_{i}}{a_{i-1}}$ and consequently $a_{i}=a_{i-1}$ for all positive integers $i$. Hence, all $a$ 's are equal.
|
| 99 |
+
|
| 100 |
+
Solution 5. As in Solution 4 we show that $\sum_{i=1}^{n} b_{i} \leqslant 2 n$ and as in Solution 1 we show that $\prod_{i=1}^{n} b_{i} \geqslant 2^{n}$. We now use the AM-GM inequality and the first inequality to get
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\prod_{i=1}^{n} b_{i} \leqslant\left(\frac{1}{n} \sum_{i=1}^{n} b_{i}\right)^{n} \leqslant\left(\frac{1}{n} \cdot 2 n\right)^{n}=2^{n}
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
This implies that we must have equalities in all the above. In particular, we have equality in the AM-GM inequality, so all $b$ 's are equal and as in Solution 2 then all $a$ 's are equal.
|
| 107 |
+
|
| 108 |
+
Solution 6. Let $a_{i}$ to be minimal and $a_{j}$ maximal among all $a$ 's. Then
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
b_{j}=\frac{a_{j-1}+a_{j+1}}{a_{j}} \leqslant \frac{2 a_{j}}{a_{j}}=2=\frac{2 a_{i}}{a_{i}} \leqslant \frac{a_{i-1}+a_{i+1}}{a_{i}}=b_{i}
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
and by assumption $b_{i} \leqslant b_{j}$. Hence, we have equalities in the above so $b_{j}=2$ so $a_{j-1}+$ $a_{j+1}=2 a_{j}$ and therefore $a_{j-1}=a_{j}=a_{j+1}$. We have thus shown that the two neighbors of a maximal $a$ are also maximal. By an inductive argument all $a$ 's are maximal, hence equal.
|
| 115 |
+
|
| 116 |
+
Solution 7. Choose an arbitrary index $i$ and assume without loss of generality that $a_{i} \leqslant a_{i+1}$. (If the opposite inequality holds, reverse all the inequalities below.) By induction we will show that for each $k \in \mathbb{N}_{0}$ the following two inequalities hold
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
\begin{gathered}
|
| 120 |
+
a_{i+1+k} \geqslant a_{i-k} \\
|
| 121 |
+
a_{i+1+k} a_{i+1-k} \geqslant a_{i-k} a_{i+k}
|
| 122 |
+
\end{gathered}
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
(where all indices are cyclic modulo $n$ ). Both inequalities trivially hold for $k=0$.
|
| 126 |
+
Assume now that both inequalities hold for some $k \geqslant 0$. The inequality $a_{i+1+k} \geqslant a_{i-k}$ implies $b_{i+1+k} \geqslant b_{i-k}$, so
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
\frac{a_{i+k}+a_{i+2+k}}{a_{i+1+k}} \geqslant \frac{a_{i-1-k}+a_{i+1-k}}{a_{i-k}} .
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
We may rearrange this inequality by making $a_{i+2+k}$ the subject so
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
a_{i+2+k} \geqslant \frac{a_{i+1+k} a_{i-1-k}}{a_{i-k}}+\frac{a_{i+1-k} a_{i+1+k}-a_{i+k} a_{i-k}}{a_{i-k}} \geqslant \frac{a_{i+1+k} a_{i-1-k}}{a_{i-k}},
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
where the last inequality holds by (2). It follows that
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
a_{(i+1)+(k+1)} a_{(i+1)-(k+1)} \geqslant a_{i+(k+1)} a_{i-(k+1)},
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
i.e. the inequality (2) holds also for $k+1$. Using (1) we now get
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
a_{(i+1)+(k+1)} \geqslant \frac{a_{i+k+1}}{a_{i-k}} a_{i-(k+1)} \geqslant a_{i-(k+1)},
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
i.e. (1) holds for $k+1$.
|
| 151 |
+
|
| 152 |
+
Now we use the inequality (1) for $k=n-1$. We get $a_{i} \geqslant a_{i+1}$, and since at the beginning we assumed $a_{i} \leqslant a_{i+1}$, we get that any two consecutive $a$ 's are equal, so all of them are equal.
|
| 153 |
+
|
| 154 |
+
Solution 8. We first prove the following claim by induction:
|
| 155 |
+
Claim 1: If $a_{k} a_{k+2}<a_{k+1}^{2}$ and $a_{k}<a_{k+1}$, then $a_{j} a_{j+2}<a_{j+1}^{2}$ and $a_{j}<a_{j+1}$ for all $j$.
|
| 156 |
+
We assume that $a_{i} a_{i+2}<a_{i+1}^{2}$ and $a_{i}<a_{i+1}$, and then show that $a_{i-1} a_{i+1}<a_{i}^{2}$ and $a_{i-1}<a_{i}$.
|
| 157 |
+
Since $a_{i} \leq a_{i+1}$ we have that $b_{i} \leq b_{i+1}$. By plugging in the definition of $b_{i}$ and $b_{i+1}$ we have that
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
a_{i+1} a_{i-1}+a_{i+1}^{2} \leq a_{i}^{2}+a_{i+2} a_{i}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
Using $a_{i} a_{i+2}<a_{i+1}^{2}$ we get that
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
a_{i+1} a_{i-1}<a_{i}^{2} .
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
Since $a_{i}<a_{i+1}$ we have that $a_{i-1}<a_{i}$, which concludes the induction step and hence proves the claim.
|
| 170 |
+
|
| 171 |
+
We cannot have that $a_{j}<a_{j+1}$ for all indices $j$. Similar as in the above claim, one can prove that if $a_{k} a_{k+2}<a_{k+1}^{2}$ and $a_{k+2}<a_{k+1}$, then $a_{j+1}<a_{j}$ for all $j$, which also cannot be the case. Thus we have that $a_{k} a_{k+2} \geq a_{k+1}^{2}$ for all indices $k$.
|
| 172 |
+
Next observe (e.g. by taking the product over all indices) that this implies $a_{k} a_{k+2}=a_{k+1}^{2}$ for all indices $k$, which is equivalent to $b_{k}=b_{k+1}$ for all $k$ and hence $a_{k+1}=a_{k}$ for all $k$.
|
| 173 |
+
|
| 174 |
+
Solution 9. Define $c_{i}:=\frac{a_{i}}{a_{i+1}}$, then $b_{i}=c_{i-1}+1 / c_{i}$. Assume that not all $c_{i}$ are equal to 1. Since, $\prod_{i=1}^{n} c_{i}=1$ there exists a $k$ such that $c_{k} \geqslant 1$. From the condition given in the problem statement for $(i, j)=(k, k+1)$ we have
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
c_{k} \geqslant 1 \Longleftrightarrow c_{k-1}+\frac{1}{c_{k}} \geqslant c_{k}+\frac{1}{c_{k+1}} \Longleftrightarrow c_{k-1} c_{k} c_{k+1}+c_{k+1} \geqslant c_{k}^{2} c_{k+1}+c_{k}
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
Now since $c_{k+1} \leqslant c_{k}^{2} c_{k+1}$, it follows that
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
c_{i-1} c_{i} c_{i+1} \geqslant c_{i} \Longrightarrow\left(c_{i-1} \geqslant 1 \text { or } c_{i+1} \geqslant 1\right) .
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
So there exist a set of at least 2 consecutive integers, such that the corresponding $c_{i}$ are greater or equal to one. By the innitial assumption there must exist an index $\ell$, such that $c_{\ell-1}, c_{\ell} \geqslant 1$ and $c_{\ell+1}<1$. We distinguish two cases:
|
| 187 |
+
Case 1: $c_{\ell}>c_{\ell-1} \geqslant 1$
|
| 188 |
+
From $c_{\ell-1} c_{\ell} c_{\ell+1}<c_{\ell}^{2} c_{\ell+1}$ and the inequality (5), we get that $c_{\ell+1}>c_{\ell} \geqslant 1$, which is a contradiction to our choice of $\ell$.
|
| 189 |
+
|
| 190 |
+
Case 2: $c_{\ell-1} \geqslant c_{\ell} \geqslant 1$
|
| 191 |
+
Once again looking at the inequality (5) we can find that
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
c_{\ell-2} c_{\ell-1} c_{\ell} \geqslant c_{\ell-1}^{2} c_{\ell} \Longrightarrow c_{\ell-2} \geqslant c_{\ell-1} .
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Note that we only needed $c_{\ell-1} \geqslant c_{\ell} \geqslant 1$ to show $c_{\ell-2} \geqslant c_{\ell-1} \geqslant 1$. So using induction we can easily show $c_{\ell-s-1} \geqslant c_{\ell-s}$ for all $s$.
|
| 198 |
+
So
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
c_{1} \leqslant c_{2} \leqslant \cdots \leqslant c_{n} \leqslant c_{1}
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
a contradiction to our innitial assumption.
|
| 205 |
+
So our innitial assumtion must have been wrong, which implies that all the $a_{i}$ must have been equal from the start.
|
| 206 |
+
|
| 207 |
+
Problem 2. We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
|
| 208 |
+
|
| 209 |
+
Show that line $K L$ passes through the orthocentre of $A B C$.
|
| 210 |
+
The altitudes of a triangle meet at its orthocentre.
|
| 211 |
+
|
| 212 |
+
|
| 213 |
+
Figure 1: Diagram to solution 1
|
| 214 |
+
Solution 1. Let $M$ be the midpoint of $K L$. We will prove that $M$ is the orthocentre of $A B C$. Since $D K$ and $D L$ are tangent to the same circle, $|D K|=|D L|$ and hence $D M \perp K L$. The theorem of Thales in circle $A B C$ also gives $D B \perp B A$ and $D C \perp C A$. The right angles then give that quadrilaterals $B D M K$ and $D M L C$ are cyclic.
|
| 215 |
+
|
| 216 |
+
If $\angle B A C=\alpha$, then clearly $\angle D K M=\angle M L D=\alpha$ by angle in the alternate segment of circle $A K L$, and so $\angle M D K=\angle L D M=\frac{\pi}{2}-\alpha$, which thanks to cyclic quadrilaterals gives $\angle M B K=\angle L C M=\frac{\pi}{2}-\alpha$. From this, we have $B M \perp A C$ and $C M \perp A B$, and so $M$ indeed is the orthocentre of $A B C$.
|
| 217 |
+
|
| 218 |
+
## Solution 2. Preliminaries
|
| 219 |
+
|
| 220 |
+
Let $A B C$ be a triangle with circumcircle $\Gamma$. Let $X$ be a point in the plane. The Simson line (Wallace-Simson line) is defined via the following theorem. Drop perpendiculars from $X$ to each of the three side lines of $A B C$. The feet of these perpendiculars are collinear (on
|
| 221 |
+
the Simson line of $X$ ) if and only if $X$ lies of $\Gamma$. The Simson line of $X$ in the circumcircle bisects the line segment $X H$ where $H$ is the orthocentre of triangle $A B C$. See Figure 2
|
| 222 |
+
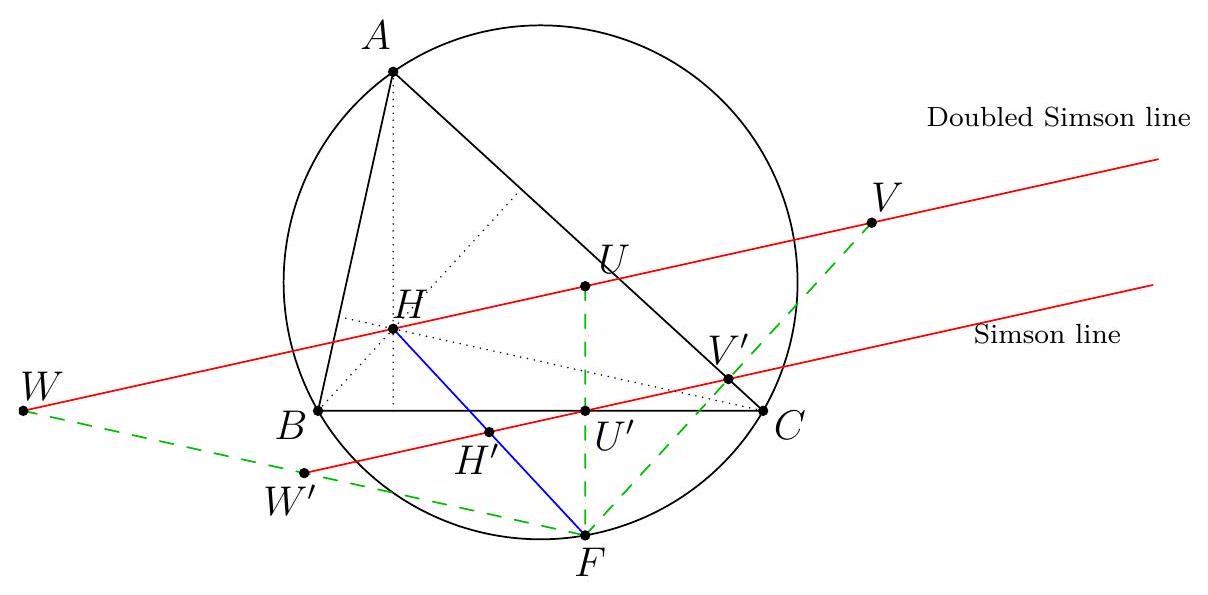
|
| 223 |
+
|
| 224 |
+
Figure 2: The Wallace-Simson configuration
|
| 225 |
+
When $X$ is on $\Gamma$, we can enlarge from $X$ with scale factor 2 (a homothety) to take the Simson line to the doubled Simson line which passes through the orthocentre $H$ and contains the reflections of $X$ in each of the three sides of $A B C$.
|
| 226 |
+
|
| 227 |
+
## Solution of the problem
|
| 228 |
+
|
| 229 |
+
|
| 230 |
+
|
| 231 |
+
Figure 3: Three circles do the work
|
| 232 |
+
Let $\Gamma$ be the circle $A B C, \Sigma$ be the circle $A K L$ with centre $O$, and $\Omega$ be the circle on diameter $O D$ so $K$ and $L$ are on this circle by converse of Thales. Let $\Omega$ and $\Gamma$ meet at $D$ and $F$. By Thales in both circles, $\angle A F D$ and $\angle O F D$ are both right angles so $A O F$ is a line. Let $A F$ meet $\Sigma$ again at $T$ so $A T$ (containing $O$ ) is a diameter of this circle and by Thales, $T L \perp A C$.
|
| 233 |
+
Let $G$ (on $\Sigma$ ) be the reflection of $K$ in $A F$. Now $A T$ is the internal angle bisector of $\angle G A K$ so, by an upmarket use of angles in the same segment (of $\Sigma$ ), $T L$ is the internal
|
| 234 |
+
angle bisector of $\angle G L K$. Thus the line $G L$ is the reflection of the line $K L$ in $T L$, and so also the reflection of $K L$ in the line $A C$ (internal and external angle bisectors).
|
| 235 |
+
|
| 236 |
+
Our next project is to show that $L G F$ are collinear. Well $\angle F L K=\angle F O K$ (angles in the same segment of $\Omega$ ) and $\angle G L K=\angle G A K$ (angles in the same segment of $\Sigma$ ) $=2 \angle O A K$ ( $A K G$ is isosceles with apex $A)=\angle T O K$ (since $O A K$ is isosceles with apex $O$, and this is an external angle at $O$ ). The point $T$ lies in the interior of the line segment $F O$ so $\angle T O K=\angle F O K$. Therefore $\angle F L K=\angle G L K$ so $L G F$ is a line.
|
| 237 |
+
|
| 238 |
+
Now from the second paragraph, $F$ is on the reflection of $K L$ in $A C$. By symmetry, $F$ is also on the reflection of $K L$ in $A B$. Therefore the reflections of $F$ in $A B$ and $A C$ are both on $K L$ which must therefore be the doubled Wallace-Simson line of $F$. Therefore the orthocentre of $A B C$ lies on $K L$.
|
| 239 |
+
|
| 240 |
+
Solution 3. Let $H$ be the orthocentre of triangle $A B C$ and $\Sigma$ the circumcircle of $A K L$ with centre $O$. Let $\Omega$ be the circle with diameter $O D$, which contains $K$ and $L$ by Thales, and let $\Gamma$ be the circumcircle of $A B C$ containing $D$. Denote the second intersection of $\Omega$ and $\Gamma$ by $F$. Since $O D$ and $A D$ are diameters of $\Omega$ and $\Gamma$ we have $\angle O F D=\frac{\pi}{2}=\angle A F D$, so the points $A, O, F$ are collinear. Let $M$ and $N$ be the second intersections of $C H$ and $B H$ with $\Gamma$, respectively. It is well-known that $M$ and $N$ are the reflections of $H$ in $A B$ and $A C$, respectively (because $\angle N C A=\angle N B A=\angle A C M=\angle A B M$ ). By collinearity of $A, O, F$ and the angles in $\Gamma$ we have
|
| 241 |
+
|
| 242 |
+
$$
|
| 243 |
+
\angle N F O=\angle N F A=\angle N B A=\frac{\pi}{2}-\angle B A C=\frac{\pi}{2}-\angle K A L
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
Since $D L$ is tangent to $\Sigma$ we obtain
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
\angle N F O=\frac{\pi}{2}-\angle K L D=\angle L D O,
|
| 250 |
+
$$
|
| 251 |
+
|
| 252 |
+
where the last equality follows from the fact that $O D$ is bisector of $\angle L D K$ since $L D$
|
| 253 |
+
|
| 254 |
+
|
| 255 |
+
Figure 4: Diagram to Solution 3
|
| 256 |
+
and $K D$ are tangent to $\Sigma$. Furthermore, $\angle L D O=\angle L F O$ since these are angles in $\Omega$. Hence, $\angle N F O=\angle L F O$, which implies that points $N, L, F$ are collinear. Similarly points $M, K, F$ are collinear. Since $N$ and $M$ are reflections of $H$ in $A C$ and $A B$ we have
|
| 257 |
+
|
| 258 |
+
$$
|
| 259 |
+
\angle L H N=\angle H N L=\angle B N F=\angle B M F=\angle B M K=\angle K H B .
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
Hence,
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
\angle L H K=\angle L H N+\angle N H K=\angle K H B+\angle N H K=\pi
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
and the points $L, H, K$ are collinear.
|
| 269 |
+
|
| 270 |
+
Solution 4. As in Solution 3 let $M$ and $N$ be the reflections of the orthocentre in $A B$ and $A C$. Let $\angle B A C=\alpha$. Then $\angle N D M=\pi-\angle M A N=\pi-2 \alpha$.
|
| 271 |
+
|
| 272 |
+
Let $M K$ and $N L$ intersect at $F$. See Figure 3.
|
| 273 |
+
Claim. $\angle N F M=\pi-2 \alpha$, so $F$ lies on the circumcircle.
|
| 274 |
+
Proof. Since $K D$ and $L D$ are tangents to circle $A K L$, we have $|D K|=|D L|$ and $\angle D K L=\angle K L D=\alpha$, so $\angle L D K=\pi-2 \alpha$.
|
| 275 |
+
By definition of $M, N$ and $D, \angle M N D=\angle A N D-\angle A N M=\frac{\pi}{2}-\left(\frac{\pi}{2}-\alpha\right)=\alpha$ and analogously $\angle D M N=\alpha$. Hence $|D M|=|D N|$.
|
| 276 |
+
|
| 277 |
+
From $\angle N D M=\angle L D K=\pi-2 \alpha$ if follows that $\angle L D N=\angle K D M$. Since $|D K|=|D L|$ and $|D M|=|D N|$, triangles $M D K$ and $N D L$ are related by a rotation about $D$ through angle $\pi-2 \alpha$, and hence the angle between $M K$ and $N L$ is $\pi-2 \alpha$, which proved the claim.
|
| 278 |
+
|
| 279 |
+
We now finish as in Solution 3:
|
| 280 |
+
|
| 281 |
+
$$
|
| 282 |
+
\begin{gathered}
|
| 283 |
+
\angle M H K=\angle K M H=\angle F M C=\angle F A C \\
|
| 284 |
+
\angle L H N=\angle H N L=\angle B N F=\angle B A F
|
| 285 |
+
\end{gathered}
|
| 286 |
+
$$
|
| 287 |
+
|
| 288 |
+
As $\angle B A F+\angle F A C=\alpha$, we have $\angle L H K=\alpha+\angle N H M=\alpha+\pi-\alpha=\pi$, so $H$ lies on $K L$.
|
| 289 |
+
|
| 290 |
+
Solution 5. Since $A D$ is a diameter, it is well known that $D B H C$ is a parallelogram (indeed, both $B D$ and $C H$ are perpendicular to $A B$, hence parallel, and similarly for $D C \| B H)$. Let $B^{\prime}, C^{\prime}$ be the reflections of $D$ in lines $A K B$ and $A L C$, respectively; since $A B D$ and $A C D$ are right angles, these are also the factor-2 homotheties of $B$ and $C$ with respect to $D$, hence $H$ is the midpoint of $B^{\prime} C^{\prime}$. We will prove that $B^{\prime} K C^{\prime} L$ is a parallelogram: it will then follow that the midpoint of $B^{\prime} C^{\prime}$, which is $H$, is also the midpoint of $K L$, and in particular is on the line, as we wanted to show.
|
| 291 |
+
|
| 292 |
+
We will prove $B^{\prime} K C^{\prime} L$ is a parallelogram by showing that $B^{\prime} K$ and $C^{\prime} L$ are the same length and direction. Indeed, for lengths we have $K B^{\prime}=K D=L D=L C^{\prime}$, where the first and last equalities arise from the reflections defining $B^{\prime}$ and $C^{\prime}$, and the middle one
|
| 293 |
+
is equality of tangents. For directions, let $\alpha, \beta, \gamma$ denote the angles of triangle $A K L$. Immediate angle chasing in the circle $A K L$, and the properties of the reflections, yield
|
| 294 |
+
|
| 295 |
+
$$
|
| 296 |
+
\begin{aligned}
|
| 297 |
+
\angle C^{\prime} L C & =\angle C L D=\angle A K L=\beta \\
|
| 298 |
+
\angle B K B^{\prime} & =\angle D K B=\angle K L A=\gamma \\
|
| 299 |
+
& \angle L D K=2 \alpha-\pi
|
| 300 |
+
\end{aligned}
|
| 301 |
+
$$
|
| 302 |
+
|
| 303 |
+
and therefore in directed angles $(\bmod 2 \pi)$ we have
|
| 304 |
+
$\angle\left(C^{\prime} L, B^{\prime} K\right)=\angle C^{\prime} L C+\angle C L D+\angle L D K+\angle D K B+\angle B K B^{\prime}=2 \alpha+2 \beta+2 \gamma-\pi=\pi$
|
| 305 |
+
and hence $C^{\prime} L$ and $B^{\prime} K$ are parallel and in opposite directions, i.e. $C^{\prime} L$ and $K B^{\prime}$ are in the same direction, as claimed.
|
| 306 |
+
|
| 307 |
+
Comment. While not necessary for the final solution, the following related observation motivates how the fact that $H$ is the midpoint of $K L$ (and therefore $B^{\prime} K C^{\prime} L$ is a parallelogram) was first conjectured. We have $A B^{\prime}=A D=A C^{\prime}$ by the reflections, i.e. $B^{\prime} A C^{\prime}$ is an isosceles triangle with $H$ being the midpoint of the base. Thus $A H$ is the median, altitude and angle bisector in $B^{\prime} A C^{\prime}$, thus $\angle B^{\prime} A K+\angle K A H=\angle H A L+\angle L A C^{\prime}$. Since from the reflections we also have $\angle B^{\prime} A K=\angle K A D$ and $\angle D A L=\angle L A C^{\prime}$ it follows that $\angle H A L=\angle K A D$ and $\angle K A H=\angle D A L$. Since $D$ is the symmedian point in $A K L$, the angle conjugation implies $A H$ is the median line of $K L$. Thus, if $H$ is indeed on $K L$ (as the problem assures us), it can only be the midpoint of $K L$.
|
| 308 |
+
|
| 309 |
+
Solution 6. There are a number of "phantom point" arguments which define $K^{\prime}$ and $L^{\prime}$ in terms of angles and then deduce that these points are actually $K$ and $L$.
|
| 310 |
+
|
| 311 |
+
Note: In these solutions it is necessary to show that $K$ and $L$ are uniquely determined by the conditions of the problem. One example of doing this is the following:
|
| 312 |
+
To prove uniqueness of $K$ and $L$, let us consider that there exist two other points $K^{\prime}$ and $L^{\prime}$ that satisfy the same properties ( $K^{\prime}$ on $A B$ and $L^{\prime}$ on $A C$ such that $D K^{\prime}$ and $D L^{\prime}$ are tangent to the circle $\left.A K^{\prime} L^{\prime}\right)$.
|
| 313 |
+
Then, we have that $D K=D L$ and $D K^{\prime}=D L^{\prime}$. We also have that $\angle K D L=\angle K^{\prime} D L^{\prime}=$ $\pi-2 \angle A$. Hence, we deduce $\angle K D K^{\prime}=\angle K D L-\angle K^{\prime} D L=\angle K^{\prime} D L^{\prime}-\angle K^{\prime} D L=\angle L D L^{\prime}$ Thus we have that $\triangle K D K^{\prime} \equiv \triangle L D L^{\prime}$, so we deduce $\angle D K A=\angle D K K^{\prime}=\angle D L L^{\prime}=$ $\pi-\angle A L D$. This implies that $A K D L$ is concyclic, which is clearly a contradiction since $\angle K A L+\angle K D L=\pi-\angle B A C$.
|
| 314 |
+
|
| 315 |
+
Solution 7. We will use the usual complex number notation, where we will use a capital letter (like $Z$ ) to denote the point associated to a complex number (like z). Consider $\triangle A K L$ on the unit circle. So, we have $a \cdot \bar{a}=k \cdot \bar{k}=l \cdot \bar{l}=1 \quad$ As point $D$ is the intersection of the tangents to the unit circle at $K$ and $L$, we have that
|
| 316 |
+
|
| 317 |
+
$$
|
| 318 |
+
d=\frac{2 k l}{k+l} \text { and } \bar{d}=\frac{2}{k+l}
|
| 319 |
+
$$
|
| 320 |
+
|
| 321 |
+
Defining $B$ as the foot of the perpendicular from $D$ on the line $A K$, and $C$ as the foot of the perpendicular from $D$ on the line $A L$, we have the formulas:
|
| 322 |
+
|
| 323 |
+
$$
|
| 324 |
+
b=\frac{1}{2}\left(d+\frac{(a-k) \bar{d}+\bar{a} k-a \bar{k}}{\bar{a}-\bar{k}}\right)
|
| 325 |
+
$$
|
| 326 |
+
|
| 327 |
+
$$
|
| 328 |
+
c=\frac{1}{2}\left(d+\frac{(a-l) \bar{d}+\bar{a} l-a \bar{l}}{\bar{a}-\bar{l}}\right)
|
| 329 |
+
$$
|
| 330 |
+
|
| 331 |
+
Simplyfing these formulas, we get:
|
| 332 |
+
|
| 333 |
+
$$
|
| 334 |
+
\begin{gathered}
|
| 335 |
+
b=\frac{1}{2}\left(d+\frac{(a-k) \frac{2}{k+l}+\frac{k}{a}-\frac{a}{k}}{\frac{1}{a}-\frac{1}{k}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-k)}{k+l}+\frac{k^{2}-a^{2}}{a k}}{\frac{k-a}{a k}}\right) \\
|
| 336 |
+
b=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a k}{k+l}+(a+k)\right)=\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a) \\
|
| 337 |
+
c=\frac{1}{2}\left(d+\frac{(a-l) \frac{2}{k+l}+\frac{l}{a}-\frac{a}{l}}{\frac{1}{a}-\frac{1}{l}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-l)}{k+l}+\frac{l^{2}-a^{2}}{a l}}{\frac{l-a}{a l}}\right) \\
|
| 338 |
+
c=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a l}{k+l}+(a+l)\right)=\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)
|
| 339 |
+
\end{gathered}
|
| 340 |
+
$$
|
| 341 |
+
|
| 342 |
+
Let $O$ be the the circumcenter of triangle $\triangle A B C$. As $A D$ is the diameter of this circle, we have that:
|
| 343 |
+
|
| 344 |
+
$$
|
| 345 |
+
o=\frac{a+d}{2}
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
Defining $H$ as the orthocentre of the $\triangle A B C$, we get that:
|
| 349 |
+
|
| 350 |
+
$$
|
| 351 |
+
\begin{gathered}
|
| 352 |
+
h=a+b+c-2 \cdot o=a+\left(\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a)\right)+\left(\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)\right)-(a+d) \\
|
| 353 |
+
h=a+\frac{2 k l}{k+l}-\frac{a(k+l)}{k+l}+\frac{1}{2} k++\frac{1}{2} l++a-\left(a+\frac{2 k l}{k+l}\right) \\
|
| 354 |
+
h=\frac{1}{2}(k+l)
|
| 355 |
+
\end{gathered}
|
| 356 |
+
$$
|
| 357 |
+
|
| 358 |
+
Hence, we conclude that $H$ is the midpoint of $K L$, so $H, K, L$ are collinear.
|
| 359 |
+
|
| 360 |
+
Solution 8. Let us employ the barycentric coordinates. Set $A(1,0,0), K(0,1,0), L(0,0,1)$.
|
| 361 |
+
The tangent at $K$ of $(A K L)$ is $a^{2} z+c^{2} x=0$, and the tangent of of $L$ at $(A K L)$ is $a^{2} y+b^{2} x=0$. Their intersection is
|
| 362 |
+
|
| 363 |
+
$$
|
| 364 |
+
D\left(-a^{2}: b^{2}: c^{2}\right)
|
| 365 |
+
$$
|
| 366 |
+
|
| 367 |
+
Since $B \in A K$, we can let $B(1-t, t, 0)$. Solving for $\overrightarrow{A B} \cdot \overrightarrow{B D}=0$ gives
|
| 368 |
+
|
| 369 |
+
$$
|
| 370 |
+
t=\frac{3 b^{2}+c^{2}-a^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)} \Longrightarrow B=\left(\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, \frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0\right)
|
| 371 |
+
$$
|
| 372 |
+
|
| 373 |
+
Likewise, $C$ has the coordinate
|
| 374 |
+
|
| 375 |
+
$$
|
| 376 |
+
C=\left(\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0, \frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right) .
|
| 377 |
+
$$
|
| 378 |
+
|
| 379 |
+
The altitude from $B$ for triangle $A B C$ is
|
| 380 |
+
|
| 381 |
+
$$
|
| 382 |
+
-b^{2}\left(x-z-\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(c^{2}-a^{2}\right)\left(y-\frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
|
| 383 |
+
$$
|
| 384 |
+
|
| 385 |
+
Also the altitude from $C$ for triangle $A B C$ is
|
| 386 |
+
|
| 387 |
+
$$
|
| 388 |
+
-c^{2}\left(x-y-\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(a^{2}-b^{2}\right)\left(z-\frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
|
| 389 |
+
$$
|
| 390 |
+
|
| 391 |
+
The intersection of these two altitudes, which is the orthocenter of triangle $A B C$, has the barycentric coordinate
|
| 392 |
+
|
| 393 |
+
$$
|
| 394 |
+
H=(0,1 / 2,1 / 2)
|
| 395 |
+
$$
|
| 396 |
+
|
| 397 |
+
which is the midpoint of the segment $K L$.
|
| 398 |
+
|
| 399 |
+
Problem 3. Let $k$ be a positive integer. Lexi has a dictionary $\mathcal{D}$ consisting of some $k$-letter strings containing only the letters $A$ and $B$. Lexi would like to write either the letter $A$ or the letter $B$ in each cell of a $k \times k$ grid so that each column contains a string from $\mathcal{D}$ when read from top-to-bottom and each row contains a string from $\mathcal{D}$ when read from left-to-right.
|
| 400 |
+
|
| 401 |
+
What is the smallest integer $m$ such that if $\mathcal{D}$ contains at least $m$ different strings, then Lexi can fill her grid in this manner, no matter what strings are in $\mathcal{D}$ ?
|
| 402 |
+
|
| 403 |
+
Solution. We claim the minimum value of $m$ is $2^{k-1}$.
|
| 404 |
+
Firstly, we provide a set $\mathcal{S}$ of size $2^{k-1}-1$ for which Lexi cannot fill her grid. Consider the set of all length- $k$ strings containing only $A$ s and $B$ shich end with a $B$, and remove the string consisting of $k B$ s. Clearly there are 2 independent choices for each of the first $k-1$ letters and 1 for the last letter, and since exactly one string is excluded, there must be exactly $2^{k-1}-1$ strings in this set.
|
| 405 |
+
|
| 406 |
+
Suppose Lexi tries to fill her grid. For each row to have a valid string, it must end in a $B$. But then the right column would necessarily contain $k B \mathrm{~s}$, and not be in our set. Thus, Lexi cannot fill her grid with our set, and we must have $m \geqslant 2^{k-1}$.
|
| 407 |
+
Now, consider any set $\mathcal{S}$ with at least $2^{k-1}$ strings. Clearly, if $\mathcal{S}$ contained either the uniform string with $k A$ s or the string with $k B \mathrm{~s}$, then Lexi could fill her grid with all of the relevant letters and each row and column would contain that string.
|
| 408 |
+
Consider the case where $\mathcal{S}$ contains neither of those strings. Among all $2^{k}$ possible length$k$ strings with $A \mathrm{~s}$ and $B \mathrm{~s}$, each has a complement which corresponds to the string with $B$ s in every position where first string had $A$ s and vice-versa. Clearly, the string with all $A$ s is paired with the string with all $B$ s. We may assume that we do not take the two uniform strings and thus applying the pigeonhole principle to the remaining set of strings, we must have two strings which are complementary.
|
| 409 |
+
Let this pair of strings be $\ell, \ell^{\prime} \in \mathcal{S}$ in some order. Define the set of indices $\mathcal{J}$ corresponding to the $A$ s in $\ell$ and thus the $B \mathrm{~s}$ in $\ell^{\prime}$, and all other indices (not in $\mathcal{J}$ ) correspond to $B \mathrm{~s}$ in $\ell$ (and thus $A$ s in $\ell^{\prime}$ ). Then, we claim that Lexi puts an $A$ in the cell in row $r$, column $c$ if $r, c \in \mathcal{J}$ or $r, c \notin \mathcal{J}$, and a $B$ otherwise, each row and column contains a string in $\mathcal{S}$.
|
| 410 |
+
We illustrate this with a simple example: If $k=6$ and we have that $A A A B A B$ and $B B B A B A$ are both in the dictionary, then Lexi could fill the table as follows:
|
| 411 |
+
|
| 412 |
+
| A | A | A | B | A | B |
|
| 413 |
+
| :---: | :---: | :---: | :---: | :---: | :---: |
|
| 414 |
+
| A | A | A | B | A | B |
|
| 415 |
+
| A | A | A | B | A | B |
|
| 416 |
+
| B | B | B | A | B | A |
|
| 417 |
+
| A | A | A | B | A | B |
|
| 418 |
+
| B | B | B | A | B | A |
|
| 419 |
+
|
| 420 |
+
Suppose we are looking at row $i$ or column $i$ for $i \in \mathcal{J}$. Then by construction the string in this row/column contains $A$ s at indices $k$ with $k \in \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell$. Suppose instead we are looking at row $i$ or column $i$ for $i \notin \mathcal{J}$. Then again
|
| 421 |
+
by construction the string in this row/column contains $A$ s at indices $k$ with $k \notin \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell^{\prime}$. So each row and column indeed contains a string in $\mathcal{S}$.
|
| 422 |
+
|
| 423 |
+
Thus, for any $\mathcal{S}$ with $|\mathcal{S}| \geqslant 2^{k-1}$, Lexi can definitely fill the grid appropriately. Since we know $m \geqslant 2^{k-1}$, $2^{k-1}$ is the minimum possible value of $m$ as claimed.
|
| 424 |
+
|
| 425 |
+
Problem 4. Turbo the snail sits on a point on a circle with circumference 1. Given an infinite sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$, Turbo successively crawls distances $c_{1}, c_{2}, c_{3}, \ldots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
|
| 426 |
+
For example, if the sequence $c_{1}, c_{2}, c_{3}, \ldots$ is $0.4,0.6,0.3, \ldots$, then Turbo may start crawling as follows:
|
| 427 |
+

|
| 428 |
+
|
| 429 |
+
Determine the largest constant $C>0$ with the following property: for every sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$ with $c_{i}<C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.
|
| 430 |
+
|
| 431 |
+
Solution 1. The largest possible $C$ is $C=\frac{1}{2}$.
|
| 432 |
+
For $0<C \leqslant \frac{1}{2}$, Turbo can simply choose an arbitrary point $P$ (different from its starting point) to avoid. When Turbo is at an arbitrary point $A$ different from $P$, the two arcs $A P$ have total length 1 ; therefore, the larger of the two the arcs (or either arc in case $A$ is diametrically opposite to $P$ ) must have length $\geqslant \frac{1}{2}$. By always choosing this larger arc (or either arc in case $A$ is diametrically opposite to $P$ ), Turbo will manage to avoid the point $P$ forever.
|
| 433 |
+
For $C>\frac{1}{2}$, we write $C=\frac{1}{2}+a$ with $a>0$, and we choose the sequence
|
| 434 |
+
|
| 435 |
+
$$
|
| 436 |
+
\frac{1}{2}, \quad \frac{1+a}{2}, \quad \frac{1}{2}, \quad \frac{1+a}{2}, \quad \frac{1}{2}, \quad \ldots
|
| 437 |
+
$$
|
| 438 |
+
|
| 439 |
+
In other words, $c_{i}=\frac{1}{2}$ if $i$ is odd and $c_{i}=\frac{1+a}{2}<C$ when $i$ is even. We claim Turbo must eventually visit all points on the circle. This is clear when it crawls in the same direction two times in a row; after all, we have $c_{i}+c_{i+1}>1$ for all $i$. Therefore, we are left with the case that Turbo alternates crawling clockwise and crawling counterclockwise. If it, without loss of generality, starts by going clockwise, then it will always crawl a distance $\frac{1}{2}$ clockwise followed by a distance $\frac{1+a}{2}$ counterclockwise. The net effect is that it crawls a distance $\frac{a}{2}$ counterclockwise. Because $\frac{a}{2}$ is positive, there exists a positive integer $N$ such that $\frac{a}{2} \cdot N>1$. After $2 N$ crawls, Turbo will have crawled a distance $\frac{a}{2}$ counterclockwise $N$ times, therefore having covered a total distance of $\frac{a}{2} \cdot N>1$, meaning that it must have crawled over all points on the circle.
|
| 440 |
+
|
| 441 |
+
Note: Every sequence of the form $c_{i}=x$ if $i$ is odd, and $c_{i}=y$ if $i$ is even, where $0<x, y<C$, such that $x+y \geqslant 1$, and $x \neq y$ satisfies the conditions with the same argument. There might be even more possible examples.
|
| 442 |
+
|
| 443 |
+
Solution 2. Alternative solution (to show that $C \leqslant \frac{1}{2}$ )
|
| 444 |
+
We consider the following related problem:
|
| 445 |
+
We assume instead that the snail Chet is moving left and right on the real line. Find the size $M$ of the smallest (closed) interval, that we cannot force Chet out of, using a sequence of real numbers $d_{i}$ with $0<d_{i}<1$ for all $i$.
|
| 446 |
+
|
| 447 |
+
Then $C=1 / M$. Indeed if for every sequence $c_{1}, c_{2}, \ldots$, with $c_{i}<C$ there exists a point that Turbo can avoid, then the circle can be cut open at the avoided point and mapped to an interval of size $M$ such that Chet can stay inside this interval for any sequence of the from $c_{1} / C, c_{2} / C, \ldots$, see Figure 5 . However, all sequences $d_{1}, d_{2}, \ldots$ with $d_{i}<1$ can be written in this form. Similarly if for every sequence $d_{1}, d_{2}, \ldots$, there exists an interval of length smaller or equal $M$ that we cannot force Chet out of, this projects to a subset of the circle, that we cannot force Turbo out of using any sequence of the form $d_{1} / M, d_{2} / M, \ldots$. These are again exactly all the sequences with elements in $[0, C)$.
|
| 448 |
+
|
| 449 |
+
|
| 450 |
+
Figure 5: Chet and Turbo equivalence
|
| 451 |
+
Claim: $M \geqslant 2$.
|
| 452 |
+
Proof. Suppose not, so $M<2$. Say $M=2-2 \varepsilon$ for some $\varepsilon>0$ and let $[-1+\varepsilon, 1-\varepsilon]$ be a minimal interval, that Chet cannot be forced out of. Then we can force Chet arbitrarily close to $\pm(1-\varepsilon)$. In partiular, we can force Chet out of $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$ by minimality of $M$. This means that there exists a sequence $d_{1}, d_{2}, \ldots$ for which Chet has to leave $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$, which means he ends up either in the interval $\left[-1+\varepsilon,-1+\frac{4}{3} \varepsilon\right)$ or in the interval $\left(1-\frac{4}{3} \varepsilon, 1-\varepsilon\right]$.
|
| 453 |
+
|
| 454 |
+
Now consider the sequence,
|
| 455 |
+
|
| 456 |
+
$$
|
| 457 |
+
d_{1}, \quad 1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, 1-\frac{7}{6} \varepsilon, \quad d_{2}, 1-\frac{7}{6} \varepsilon, 1-\frac{2}{3} \varepsilon, 1-\frac{2}{3} \varepsilon, 1-\frac{7}{6} \varepsilon, d_{3}, \ldots
|
| 458 |
+
$$
|
| 459 |
+
|
| 460 |
+
obtained by adding the sequence $1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{7}{6} \varepsilon$ in between every two steps. We claim that this sequence forces Chet to leave the larger interval $[-1+\varepsilon, 1-\varepsilon]$. Indeed no two consecutive elements in the sequence $1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{7}{6} \varepsilon$ can
|
| 461 |
+
have the same sign, because the sum of any two consecutive terms is larger than $2-2 \varepsilon$ and Chet would leave the interval $[-1+\varepsilon, 1-\varepsilon]$. It follows that the $\left(1-\frac{7}{6} \varepsilon\right.$ )'s and the ( $1-\frac{2}{3} \varepsilon$ )'s cancel out, so the position after $d_{k}$ is the same as before $d_{k+1}$. Hence, the positions after each $d_{k}$ remain the same as in the original sequence. Thus, Chet is also forced to the boundary in the new sequence.
|
| 462 |
+
If Chet is outside the interval $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$, then Chet has to move $1-\frac{7}{6} \varepsilon$ towards 0 , and ends in $\left[-\frac{1}{6} \varepsilon, \frac{1}{6} \varepsilon\right]$. Chet then has to move by $1-\frac{2}{3} \varepsilon$, which means that he has to leave the interval $[-1+\varepsilon, 1-\varepsilon]$. Indeed the absolute value of the final position is at least $1-\frac{5}{6} \varepsilon$. This contradicts the assumption, that we cannot force Chet out of $[-1+\varepsilon, 1-\varepsilon]$. Hence $M \geqslant 2$ as needed.
|
| 463 |
+
|
| 464 |
+
Problem 5. We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
|
| 465 |
+
|
| 466 |
+
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
| 467 |
+
|
| 468 |
+
Solution 1. First, we consider the difference $k-k^{\prime \prime}$. If $k=a s+b$ as in the problem statement, then $k^{\prime}=b s+a$. We write $a=l s+m$ with $m, l$ non-negative numbers and $m \leq s-1$. This gives $k^{\prime \prime}=m s+(b+l)$ and hence $k-k^{\prime \prime}=(a-m) s-l=l\left(s^{2}-1\right)$.
|
| 469 |
+
|
| 470 |
+
We conclude
|
| 471 |
+
Fact 1.1. $k \geq k^{\prime \prime}$ for every every $k \geq 1$
|
| 472 |
+
Fact 1.2. $s^{2}-1$ divides the difference $k-k^{\prime \prime}$.
|
| 473 |
+
Fact 1.2 implies that the sequences $d_{1}, d_{3}, d_{5}, \ldots$ and $d_{2}, d_{4}, d_{6}, \ldots$ are constant modulo $s^{2}-1$. Moreover, Fact 1.1 says that the sequences are (weakly) decreasing and hence eventually constant. In other words, the sequence $d_{1}, d_{2}, d_{3}, \ldots$ is 2 -periodic modulo $s^{2}-1$ (from the start) and is eventually 2-periodic.
|
| 474 |
+
|
| 475 |
+
Now, assume that some term in the sequence is equal to 1 . The next term is equal to $1^{\prime}=s$ and since the sequence is 2 -periodic from the start modulo $s^{2}-1$, we conclude that $d_{1}$ is either equal to 1 or $s$ modulo $s^{2}-1$. This proves the first implication.
|
| 476 |
+
|
| 477 |
+
To prove the other direction, assume that $d_{1}$ is congruent to 1 or $s$ modulo $s^{2}-1$. We need the observation that once one of the sequences $d_{1}, d_{3}, d_{5}, \ldots$ or $d_{2}, d_{4}, d_{6}, \ldots$ stabilises, then their value is less than $s^{2}$. This is implied by the following fact.
|
| 478 |
+
|
| 479 |
+
Fact 1.3. If $k=k^{\prime \prime}$, then $k=k^{\prime \prime}<s^{2}$.
|
| 480 |
+
Proof. We use the expression for $k-k^{\prime \prime}$ found before. If $k=k^{\prime \prime}$, then $l=0$, and so $k^{\prime \prime}=m s+b$. Both $m$ and $b$ are reminders after division by $s$, so they are both $\leq s-1$. This gives $k^{\prime \prime} \leq(s-1) s+(s-1)<s^{2}$.
|
| 481 |
+
|
| 482 |
+
Using Fact 1.2, it follows that the sequence $d_{1}, d_{3}, d_{5}, \ldots$ is constant to 1 or $s$ modulo $s^{2}-1$ and stabilises to 1 or $s$ by Fact 1.3. Since $s^{\prime}=1$, we conclude that the sequence contains a 1.
|
| 483 |
+
|
| 484 |
+
Solution 2. We make a number of initial observations. Let $k$ be a positive integer.
|
| 485 |
+
Fact 2.1. If $k \geq s^{2}$, then $k^{\prime}<k$.
|
| 486 |
+
Proof. Write $k=a s+b$, as in the problem statement. If $k \geq s^{2}$, then $a \geq s$ because $b<s$. So, $k^{\prime}=b s+a \leq(s-1) s+a \leq a s \leq a s+b=k$. Moreover, we cannot have equality since that would imply $s-1=b=0$.
|
| 487 |
+
|
| 488 |
+
Fact 2.2. If $k \leq s^{2}-1$, then $k^{\prime} \leq s^{2}-1$ and $k^{\prime \prime}=k$.
|
| 489 |
+
|
| 490 |
+
Proof. Write $k=a s+b$, as in the problem statement. If $k<s^{2}$, then it must hold $1 \leq a, b<s$, hence $k^{\prime}=b s+a<s^{2}$ and $k^{\prime \prime}=(b s+a)^{\prime}=a s+b=k$.
|
| 491 |
+
|
| 492 |
+
Fact 2.3. We have $k^{\prime} \equiv s k\left(\bmod s^{2}-1\right)\left(\right.$ or equivalently $\left.k \equiv s k^{\prime}\left(\bmod s^{2}-1\right)\right)$.
|
| 493 |
+
Proof. We write $k=a s+b$, as in the problem statement. Now,
|
| 494 |
+
|
| 495 |
+
$$
|
| 496 |
+
s k-k^{\prime}=s(a s+b)-(b s+a)=a\left(s^{2}-1\right) \equiv 0 \quad\left(\bmod s^{2}-1\right),
|
| 497 |
+
$$
|
| 498 |
+
|
| 499 |
+
as desired.
|
| 500 |
+
Combining Facts 2.1 and 2.2 , we find that the sequence $d_{1}, d_{2}, d_{3} \ldots$ is eventually periodic with period 2, starting at the first value less than $s^{2}$. From Fact 2.3, it follows that
|
| 501 |
+
|
| 502 |
+
$$
|
| 503 |
+
k^{\prime \prime} \equiv s k^{\prime} \equiv s^{2} k \equiv k \quad\left(\bmod s^{2}-1\right)
|
| 504 |
+
$$
|
| 505 |
+
|
| 506 |
+
and hence the sequence is periodic modulo $s^{2}-1$ from the start with period 2 .
|
| 507 |
+
|
| 508 |
+
Now, if the sequence contains 1 , the sequence eventually alternates between 1 and $s$ since the twist of 1 is $s$ and vice versa. Using periodicity modulo $s^{2}-1$, we must have $n \equiv 1, s$ $\left(\bmod s^{2}-1\right)$. Conversely, if $n \equiv 1, s\left(\bmod s^{2}-1\right)$ then the eventual period must contain at least one value congruent to either 1 or $s$ modulo $s^{2}-1$. Since these values must be less than $s^{2}$, this implies that the sequence eventually alternates between 1 and $s$, showing that it contains a 1 .
|
| 509 |
+
|
| 510 |
+
Solution 3. We give an alternate proof of the direct implication: if the sequence contains a 1 , then the first term is 1 or $s$ modulo $s^{2}-1$. We prove the following fact, which is a combination of Facts 2.1 and 2.3.
|
| 511 |
+
Fact 3.1. For all $k \geq s^{2}$, we have $\left(k-s^{2}+1\right)^{\prime} \in\left\{k^{\prime}, k^{\prime}-s^{2}+1\right\}$.
|
| 512 |
+
Proof. We write $k=a s+b$, as in the problem statement. Since $k \geq s^{2}$, we have $a \geq s$. If $b<s-1$, then
|
| 513 |
+
|
| 514 |
+
$$
|
| 515 |
+
\left(k-s^{2}+1\right)^{\prime}=((a-s) s+(b+1))^{\prime}=(b+1) s+(a-s)=b s+a=k^{\prime}
|
| 516 |
+
$$
|
| 517 |
+
|
| 518 |
+
On the other hand, if $b=s-1$, then
|
| 519 |
+
|
| 520 |
+
$$
|
| 521 |
+
\left(k-s^{2}+1\right)^{\prime}=((a-s+1) s+0)^{\prime}=0 s+(a-s+1)=a-s+1=k^{\prime}-s^{2}+1
|
| 522 |
+
$$
|
| 523 |
+
|
| 524 |
+
Now assume $n \geq s^{2}$ and the sequence $d_{1}, d_{2}, \ldots$ contains a 1 . Denote by $e_{1}, e_{2}, \ldots$ the sequence constructed as in the problem statement, but with initial value $e_{1}=n-s^{2}+1$. Using the above fact, we deduce that $e_{i} \equiv d_{i}\left(\bmod s^{2}-1\right)$ and $e_{i} \leq d_{i}$ for all $i \geq 1$ by induction on $i$. Hence, the sequence $e_{1}, e_{2}, \ldots$ also contains a 1 .
|
| 525 |
+
|
| 526 |
+
Since the conclusion we are trying to reach only depends on the residue of $d_{1}$ modulo $s^{2}-1$, we conclude that without loss of generality we can assume $n<s^{2}$.
|
| 527 |
+
|
| 528 |
+
Using Fact 2.2, it now follows that the sequence $d_{1}, d_{2}, \ldots$ is periodic with period two. Since 1 and $s$ are twists of each other, it follows that if this sequence contains a 1 , it must be alternating between 1 and $s$. Hence, $d_{1} \equiv 1, s\left(\bmod s^{2}-1\right)$ as desired.
|
| 529 |
+
|
| 530 |
+
For the other direction we can make a similar argument, observing that the second of the two cases in the proof of Fact 3.1 can only apply to finitely many terms of the sequence $d_{1}, d_{2}, d_{3}, \ldots$, allowing us to also go the other way.
|
| 531 |
+
|
| 532 |
+
Solution 4. First assume that $d_{k}=1$ for some $k$. Let $k$ be the smallest such index. If $k=1$ then $n=1$, so we may assume $k \geqslant 2$.
|
| 533 |
+
|
| 534 |
+
Then $d_{k-1}=a s+b$ for some non-negative integers $a, b$ satisfying $b<s$ and $b s+a=1$. The only solution is $b=0, a=1$, so $d_{k-1}=s$. So, if $k=2$, then $n=s$, so we may assume $k \geqslant 3$.
|
| 535 |
+
|
| 536 |
+
Then there exist non-negative integers $c, d$ satisfying $d_{k-2}=c s+d, d<s$ and $d s+c=s$. We have two solutions: $d=0, c=s$ and $d=1, c=0$. However, in the second case we get $d_{k-2}=1$, which contradicts the minimality of $k$. Hence, $d_{k-2}=s^{2}$. If $k=3$, then $n=d_{1}=s^{2}$, which gives remainder 1 when divided by $s^{2}-1$.
|
| 537 |
+
|
| 538 |
+
Assume now that $k \geqslant 4$. We will show that for each $m \in\{3,4, \ldots, k-1\}$ there exist $b_{1}, b_{2}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that
|
| 539 |
+
|
| 540 |
+
$$
|
| 541 |
+
d_{k-m}=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) .
|
| 542 |
+
$$
|
| 543 |
+
|
| 544 |
+
We will prove this equality by induction on $m$. If $m=3$, then $d_{k-3}=a_{1} s+b_{1}$ for some non-negative integers $a_{1}, b_{1}$ satisfying $b_{1}<s$ and $b_{1} s+a_{1}=d_{k-2}=s^{2}$. Then $a_{1}=s^{2}-b_{1} s$, so $d_{k-3}=s^{3}-b_{1}\left(s^{2}-1\right)$, which proves (9) for $m=3$.
|
| 545 |
+
Assume that (9) holds for some $m$ and consider $d_{k-(m+1)}$. There exist non-negative integers $a_{m-1}, b_{m-1}$ such that $d_{k-(m+1)}=a_{m-1} s+b_{m-1}, b_{m-1}<s$ and $d_{k-m}=b_{m-1} s+a_{m-1}$. Using the inductive assumption we get
|
| 546 |
+
|
| 547 |
+
$$
|
| 548 |
+
a_{m-1}=d_{k-m}-b_{m-1} s=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right)-b_{m-1} s,
|
| 549 |
+
$$
|
| 550 |
+
|
| 551 |
+
therefore
|
| 552 |
+
|
| 553 |
+
$$
|
| 554 |
+
\begin{aligned}
|
| 555 |
+
d_{k-(m+1)} & =a_{m-1} s+b_{m-1}=s^{m+1}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) s-b_{m-1} s^{2}+b_{m-1} \\
|
| 556 |
+
& =s^{m+1}-\sum_{i=1}^{m-1} b_{i}\left(s^{m+1-i}-s^{m-i-1}\right)
|
| 557 |
+
\end{aligned}
|
| 558 |
+
$$
|
| 559 |
+
|
| 560 |
+
which completes the proof of (9). In particular, for $m=k-1$ we get
|
| 561 |
+
|
| 562 |
+
$$
|
| 563 |
+
d_{1}=s^{k-1}-\sum_{i=1}^{k-3} b_{i}\left(s^{k-i-1}-s^{k-i-3}\right) .
|
| 564 |
+
$$
|
| 565 |
+
|
| 566 |
+
The above sum is clearly divisible by $s^{2}-1$, and it is clear that the remainder of $s^{k-1}$ when divided by $s^{2}-1$ is 1 when $k$ is odd, and $s$ when $k$ is even. It follows that the remainder when $n=d_{1}$ is divided by $s^{2}-1$ is either 1 or $s$.
|
| 567 |
+
|
| 568 |
+
To prove the other implication, assume that $n$ gives remainder 1 or $s$ when divided by $s^{2}-1$. If $n \in\left\{1, s, s^{2}\right\}$, then one of the numbers $d_{1}, d_{2}$ and $d_{3}$ is 1 . We therefore assume that $n>s^{2}$. Since the reminder when a power of $s$ is divided by $s^{2}-1$ is either 1 or $s$, there exists a positive integer $m$ such that $s^{m}-n$ is non-negative and divisible by $s^{2}-1$. By our assumption $m \geqslant 3$. We also take the smallest such $m$, so that $n>s^{m-2}$. The quotient $\frac{s^{m}-n}{s^{2}-1}$ is therefore smaller than $s^{m-2}$, so there exist $b_{1}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that $\frac{s^{m}-n}{s^{2}-1}=\sum_{i=1}^{m-2} b_{i} s^{i-1}$. It follows that
|
| 569 |
+
|
| 570 |
+
$$
|
| 571 |
+
n=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{i+1}-s^{i-1}\right) .
|
| 572 |
+
$$
|
| 573 |
+
|
| 574 |
+
We now show that
|
| 575 |
+
|
| 576 |
+
$$
|
| 577 |
+
d_{j}=s^{m+1-j}-\sum_{i=1}^{m-1-j} b_{i}\left(s^{i+1}-s^{i-1}\right)
|
| 578 |
+
$$
|
| 579 |
+
|
| 580 |
+
for $j=1,2, \ldots, m-2$ by induction on $j$. For $j=1$ this follows from $d_{1}=n$. Assume now that (10) holds for some $j<m-2$. Then
|
| 581 |
+
|
| 582 |
+
$$
|
| 583 |
+
d_{j}=\left(s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s\right) s+b_{1}
|
| 584 |
+
$$
|
| 585 |
+
|
| 586 |
+
As $d_{j}$ is positive and $b_{1} \in\{0,1, \ldots, s-1\}$, the expression $s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s$ has to be non-negative, so we can compute the twist of $d_{j}$ as
|
| 587 |
+
|
| 588 |
+
$$
|
| 589 |
+
d_{j+1}=b_{1} s+s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s=s^{m-j}-\sum_{i=1}^{m-2-j} b_{i}\left(s^{i+1}-s^{i-1}\right),
|
| 590 |
+
$$
|
| 591 |
+
|
| 592 |
+
which finishes the induction.
|
| 593 |
+
Now we use (10) for $j=m-2$ and get $d_{m-2}=s^{3}-b_{1}\left(s^{2}-1\right)=\left(s^{2}-b_{1} s\right)+b_{1}$. Then $d_{m-1}=b_{1} s+s^{2}-b_{1} s=s^{2}=s \cdot s+0, d_{m}=0 \cdot s+s=s=1 \cdot s+0$ and $d_{m+1}=0 \cdot s+1=1$.
|
| 594 |
+
|
| 595 |
+
Problem 6. Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
|
| 596 |
+
|
| 597 |
+
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.
|
| 598 |
+
|
| 599 |
+
|
| 600 |
+
Figure 6: Diagram to Solution 1
|
| 601 |
+
Solution 1. Part I: First we show that A lies on the radical axis of $\omega_{b}$ and $\omega_{c}$.
|
| 602 |
+
We first note that the line through the intersections of two circles is the radical line of the two circles. Let the tangents to $\Omega$ at $S_{b}$ and $S_{c}$ intersect at $T$. Clearly $T$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$ (and in fact is the radical centre of $\omega_{b}, \omega_{c}$ and $\Omega$ ).
|
| 603 |
+
We next show that $A$ lies on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $P_{b}$ denote the point of tangency of $\omega_{b}$ and $A B$, and let $P_{c}$ denote the point of tangency of $\omega_{c}$ and $A C$. Furthermore, let $U$ be the intersection of the tangent to $\Omega$ at $S_{b}$ with the line $A B$, and let $V$ be the intersection of the tangent to $\Omega$ at $S_{c}$ with the line $A C$. Then $T V A U$ is parallelogram. Morover, due to equality of tangent segments we have $\left|U S_{b}\right|=\left|U P_{b}\right|,\left|V P_{c}\right|=\left|V S_{c}\right|$ and $\left|T S_{b}\right|=\left|T S_{c}\right|$. It follows that
|
| 604 |
+
|
| 605 |
+
$$
|
| 606 |
+
\begin{aligned}
|
| 607 |
+
\left|A P_{b}\right| & =\left|U P_{b}\right|-|U A|=\left|U S_{b}\right|-|T V|=\left|T S_{b}\right|-|T U|-|T V| \\
|
| 608 |
+
& =\left|T S_{s}\right|-|T V|-|T U|=\left|V S_{c}\right|-|A V|=\left|V P_{c}\right|-|V A|=\left|A P_{c}\right|
|
| 609 |
+
\end{aligned}
|
| 610 |
+
$$
|
| 611 |
+
|
| 612 |
+
But $\left|A P_{b}\right|,\left|A P_{c}\right|$ are exactly the square roots of powers of $A$ with respect to $\omega_{b}$ and $\omega_{c}$, hence $A$ is indeed on their radical axis.
|
| 613 |
+
|
| 614 |
+
Thus, the radical axis of $\omega_{b}, \omega_{c}$ is $A T$.
|
| 615 |
+
Part II: Consider the triangle $A S_{b} S_{c}$. Note that since $T$ is the intersection of the tangents at $S_{b}$ and $S_{c}$ to the circumcircle of $A S_{b} S_{c}$, it follows that $A T$ is the symmedian of $A$ in this triangle. Let $X$ denote the second intersection of the symmedian $A T$ with $\Omega$. We wish to show that $X$ is also on $I N_{a}$.
|
| 616 |
+
|
| 617 |
+
Note that $A N_{a}$ is the external angle bisector of angle $A$, and therefore it is parallel to $S_{b} S_{c}$. Let $M$ denote the midpoint of $S_{b} S_{c}$, and let $Y$ be the second intersection of $A M$ with $\Omega$. Since in $A S_{b} S_{c}, A X T$ is the symmedian and $A M Y$ is the median, it follows that $X Y$ is also parallel to $S_{b} S_{c}$. Thus, reflecting in the perpendicular bisector of $S_{b} S_{c}$ sends the line $A M Y$ to line $N_{a} M X$.
|
| 618 |
+
|
| 619 |
+
Next, consider the quadrilateral $A S_{b} I S_{c}$. From the trillium theorem we have $\left|S_{b} A\right|=\left|S_{b} I\right|$ and $\left|S_{c} A\right|=\left|S_{c} I\right|$, thus the quadrilateral is a kite, from which it follows that the reflection of the line $A M$ in $S_{b} S_{c}$ is the line $I M$. But previously we have seen that this is also the line $N_{a} M X$. Thus $M, I, N_{a}$ and $X$ are collinear, as we wanted to show.
|
| 620 |
+
|
| 621 |
+
Solution 2. This is a variation of Solution 1 which avoids the theory of the symmedian point.
|
| 622 |
+
|
| 623 |
+
We begin by showing that the radical axis of $\omega_{b}, \omega_{c}$ is $A T$ as in Solution 1.
|
| 624 |
+
Part II: We introduce the point $S_{a}$ with the obvious meaning. Observe that the incentre $I$ of $A B C$ is the orthocentre of $S_{a} S_{b} S_{c}$ either because this is well-known, or because of an angle argument that $A$ reflects in $S_{b} S_{c}$ to $I$ (and similar results by cyclic change of letters). Therefore $A S_{a}$ is perpendicular to $S_{b} S_{c}$.
|
| 625 |
+
|
| 626 |
+
|
| 627 |
+
Figure 7: A reflections argument for Solution 2
|
| 628 |
+
Let $M$ denote the midpoint of $S_{b} S_{c}$. Then $A$ is the reflection of $S_{a}$ in the diameter parallel to $S_{b} S_{c}$, so the reflection of $A$ in the diameter perpendicular to $S_{b} S_{c}$ is $N_{a}$, the antipode
|
| 629 |
+
of $S_{a}$. Let the reflection of $X$ in $T M$ be $Y$, so $T Y$ passes through $N_{a}$ and is the reflection of $T X$ in $T M$.
|
| 630 |
+
|
| 631 |
+
Now $S_{b} S_{c}$ is the polar line of $T$ with respect to $\Omega$, so $A Y$ and $N_{a} X$ meet on this line, and by symmetry at its midpoint $M$. The line $N_{a} M X$ is therefore the reflection of the line $Y M A$ in $S_{b} S_{c}$, and so $N_{a} M X$ passes through $I$ (the reflection of $A$ in $S_{b} S_{c}$ ).
|
| 632 |
+
|
| 633 |
+
The triangle $A S_{c} S_{b}$ can be taken as generic, and from the argument above we can extract the fact that the symmedian point and the centroid are isogonal conjugates in that triangle.
|
| 634 |
+
|
| 635 |
+
Solution 3. Assume the notation from Solution 1, part I of Solution 1, and let $O$ be the centre of $\Omega$.
|
| 636 |
+
|
| 637 |
+
|
| 638 |
+
Figure 8: Diagram to Solution 3
|
| 639 |
+
Part II: As in Solution 1, by the trillelium theorem, $S_{c} S_{b}$ bisects $A I$, and since $N_{a} A \| S_{b} S_{c}$, then $O T$ is a bisector of $A N_{a}$. This implies $\left|M N_{a}\right|=|M A|=|M I|$, since $M$ is the midpoint of $S_{c} S_{b}$ and lies also on $O T$. Hence, $M$ is the circumcentre of triangle $I A N_{a}$. But this triangle has a right angle at $A$ (since $A I$ and $A N_{a}$ are the inner and outer angle bisector at $A$ ), hence $M$ lies on $I N_{a}$.
|
| 640 |
+
|
| 641 |
+
Again, let $X$ be the second intersection of $T A$ and $\Omega$. By the above, it suffices to prove that $X$ lies on the line $N_{a} M$. From the power of point $T$ with respect to $\Omega$ we get $|T A| \cdot|T X|=\left|T S_{c}\right|^{2}$. Since $M$ is the foot of the altitude of right triangle $T S_{c} O$, we obtain
|
| 642 |
+
$\left|T S_{c}\right|^{2}=|T M| \cdot|T O|$. Hence, $|T A| \cdot|T X|=|T M| \cdot|T O|$ so the points $O, M, A, X$ are concyclic. It follows that $\angle M X A=\angle M O A=\frac{1}{2} \angle N_{a} O A=\angle N_{a} X A$. Hence, $X$ lies on the line $N_{a} M$.
|
| 643 |
+
Remark. To show that $O M A X$ is cyclic, one can also invert the line $T A X$ in the circumcircle of the triangle $A B C$.
|
| 644 |
+
|
| 645 |
+
Solution 4. Part I is done as in solution 1.
|
| 646 |
+
|
| 647 |
+
|
| 648 |
+
Figure 9: Diagram to Solution 4
|
| 649 |
+
Part II: as in Solution 1 we show that $A N_{a} \| S_{b} S_{c}$. In particular, $\angle N_{a} O T=\angle T O A$. The conclusion of the problem trivially holds if $|A B|=|A C|$, therefore we assume without loss of generality that $|A C|>|A B|$. Let $S_{a}$ be the midpoint of the arc $B C$ which does not contain $A$. Then $N_{a} S_{a}$ is a diameter, so $\angle S_{a} B N_{a}=\frac{\pi}{2}=\angle O S_{c} T$. We also compute $\angle B N_{a} S_{a}=\angle B A S_{a}=\frac{1}{2} \angle B A C=\frac{1}{2} \angle S_{c} T S_{b}=\angle S_{c} T O$. It follows that the triangles $T S_{c} O$ and $N_{a} B S_{a}$ are similar. In particular,
|
| 650 |
+
|
| 651 |
+
$$
|
| 652 |
+
\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}
|
| 653 |
+
$$
|
| 654 |
+
|
| 655 |
+
Next we compute
|
| 656 |
+
|
| 657 |
+
$$
|
| 658 |
+
\angle I S_{a} B=\angle N_{a} S_{a} B-\angle N_{a} S_{a} I=\angle T O S_{c}-\frac{1}{2} \angle N_{a} O A=\angle T O S_{c}-\angle T O A=\angle A O S_{c}
|
| 659 |
+
$$
|
| 660 |
+
|
| 661 |
+
and
|
| 662 |
+
$\angle I B N_{a}=\angle C B N_{a}-\angle C B I=\frac{1}{2}\left(\pi-\angle B N_{a} C\right)-\frac{1}{2} \angle C B A=\frac{1}{2} \angle A C B=\angle A C S_{c}=\angle A S_{c} T$,
|
| 663 |
+
hence
|
| 664 |
+
|
| 665 |
+
$$
|
| 666 |
+
\angle S_{a} B I=\frac{\pi}{2}-\angle I B N_{a}=\frac{\pi}{2}-\angle A S_{c} T=\angle O S_{c} A
|
| 667 |
+
$$
|
| 668 |
+
|
| 669 |
+
Together with (13) it follows that the triangles $I B S_{a}$ and $A S_{c} O$ are similar, so $\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}=$ $\frac{|I B|}{\left|A S_{c}\right|}$, and (12) implies $\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{|I B|}{\left|A S_{c}\right|}$. Consequently, by (14) the triangles $T S_{c} A$ and $N_{a} B I$ are similar and therefore $\angle S_{c} T A=\angle B N_{a} I$. Now let $Q$ be the second intersection of $N_{a} I$ with $\Omega$. Then $\angle B N_{a} I=\angle B N_{a} Q=\angle B A Q$, so $\angle S_{c} T A=\angle B A Q$. Since $A B$ is parallel to $T S_{c}$, we get $A Q \| T A$, i.e. $A, T, Q$ are collinear.
|
| 670 |
+
Remark. After proving similarity of triangles $T S_{c} O$ and $N_{a} B S_{a}$ one can use spiral symmetry to show similarity of triangles $T S_{c} A$ and $N_{a} B I$.
|
| 671 |
+
|
| 672 |
+
Solution 5. Part I: First we show that $A$ lies on the radical axis between $\omega_{b}$ and $\omega_{c}$.
|
| 673 |
+
Let $T$ be the radical center of the circumcircle, $\omega_{b}$ and $\omega_{c}$; then $T S_{b}$ and $T S_{c}$ are common tangents of the circles, as shown in Figure 5a. Moreover, let $P_{b}=A B \cap S_{b} S_{c}$ and $P_{c}=$ $A C \cap S_{b} S_{c}$. The triangle $T S_{c} S_{b}$ is isosceles: $A B \| T S_{c}$ and $A C \| T S_{b}$ so
|
| 674 |
+
|
| 675 |
+
$$
|
| 676 |
+
\angle A P_{b} P_{c}=\angle T S_{c} S_{b}=\angle S_{c} S_{b} T=\angle P_{b} P_{c} A
|
| 677 |
+
$$
|
| 678 |
+
|
| 679 |
+
From these angles we can see that $\omega_{b}$ passes through $P_{b}, \omega_{c}$ passes through $P_{c}$, and finally $A P_{b}$ and $A P_{c}$ are equal tangents to $\omega_{b}$ and $\omega_{c}$, so $A$ lies on the radical axis.
|
| 680 |
+
|
| 681 |
+
|
| 682 |
+
Figure 5a
|
| 683 |
+
|
| 684 |
+
|
| 685 |
+
Figure 5b
|
| 686 |
+
|
| 687 |
+
Part II. Let the radical axis $T A$ meet the circumcircle again at $X$, let $S_{a}$ be the midpoint of the arc $B C$ opposite to $A$, and let $X I$ meet the circumcirlce again at $N$. (See Figure 2.) For solving the problem, we have prove that $N_{a}=N$.
|
| 688 |
+
|
| 689 |
+
The triples of points $A, I, S_{a} ; B, I, S_{b}$ and $C, I, S_{c}$ are collinear because they lie on the angle bisectors of the triangle $A B C$.
|
| 690 |
+
|
| 691 |
+
Notice that the quadrilateral $A S_{c} X S_{b}$ is harmonic, because the tangents at $S_{b}$ and $S_{c}$, and the line $A X$ are concurrent at $T$. This quadrilateral can be projected (or inverted) to the quadrilateral $S_{a} C N B$ through $I$. So, $S_{a} C N B$ also is a harmonic quadrilateral. Due to $S_{a} B=S_{a} C$, this implies $N B=N C$, so $N=N_{a}$. Done.
|
| 692 |
+
|
| 693 |
+
Remark. Instead of mentioning inversion and harmonic quadrilaterals, from the similar triangles $\triangle T S_{c} A \sim \triangle T X S_{c}$ and $\triangle T A S_{b} \sim \triangle T S_{b} X$ we can get
|
| 694 |
+
|
| 695 |
+
$$
|
| 696 |
+
\frac{A S_{c}}{S_{c} X}=\frac{A S_{b}}{S_{b} X}
|
| 697 |
+
$$
|
| 698 |
+
|
| 699 |
+
Then, we can apply the trigonometric form of Ceva's theorem to triangle $B C X$
|
| 700 |
+
|
| 701 |
+
$$
|
| 702 |
+
\frac{\sin \angle B X N_{a}}{\sin \angle N_{a} X C} \cdot \frac{\sin \angle C B S_{b}}{\sin \angle S_{b} B X} \cdot \frac{\sin \angle X C S_{c}}{\sin \angle S_{c} C B}=\frac{B N_{a}}{N_{a} C} \cdot \frac{-C S_{b}}{S_{b} X} \cdot \frac{X S_{c}}{-S_{c} B}=1 \cdot \frac{S_{b} A}{S_{b} N_{a}} \cdot \frac{N_{a} S_{c}}{S_{c} B}=1,
|
| 703 |
+
$$
|
| 704 |
+
|
| 705 |
+
so the Cevians $B S_{b}, C S_{c}$ and $X N_{a}$ are concurrent.
|
| 706 |
+
|
| 707 |
+
Solution 6. Part I: First let's show that this is equivalent to proving that $T A$ and $N_{a} I$ intersect in $\Omega$.
|
| 708 |
+
|
| 709 |
+
Lemma: Let's recall that if we have two circles $\omega_{1}$ and $\omega_{2}$ which are internally tangent at point $X$ and if we have a line $A B$ tangent to $\omega_{2}$ at $Y$. Let $M$ be the midpoint of the arc $A B$ not containing $Z$. We have that $Z, Y, M$ are collinear.
|
| 710 |
+
|
| 711 |
+
|
| 712 |
+
Solution 6: Lemma
|
| 713 |
+
Let $P_{b}=A B \cap \omega_{b}$ and $P_{c}=A C \cap \omega_{c}$. We can notice by the lemma that $S_{b}, P_{b}$ and $S_{c}$ are collinear, and similarly $S_{c}, P_{c}$ and $S_{b}$ are also collinear. Therefore $S_{c}, P_{b}, P_{c}$, and $S_{b}$ are collinear, and since $\angle A P_{b} P_{c}=\frac{\angle A B C}{2}+\frac{\angle A C B}{2}=\angle A P_{c} P_{b}$ then $A P_{b}=A P_{c}$ so $A$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $T$ be the intersection of the tangent lines of $\Omega$ through $S_{c}$ and $S_{b}$. Since $T S_{c}=T S_{b}$ then $A T$ is the radical axis between $\omega_{b}$ and $\omega_{c}$.
|
| 714 |
+
|
| 715 |
+
Part II: $T A$ and $N_{a} I$ intersect in $\Omega$.
|
| 716 |
+
|
| 717 |
+
Let $\omega_{a}$ the $A$-mixtilinear incircle (that is, the circle internally tangent to $\Omega$, and tangent to both $A B$ and $A C$ ), and let $X=\Omega \cap \omega_{a}$. It is known that $N_{a}, I, X$ are collinear.
|
| 718 |
+
|
| 719 |
+
Let $M_{c}$ and $M_{b}$ be the tangent points of $\omega_{A}$ to $A B$ and $A C$ respectively, then by the lemma $X, M_{c}, S_{c}$ are collinear and $X, M_{b}, S_{b}$ are collinear. We can see that $S_{c} T S_{b}$ and $M_{c} A M_{b}$ are homothetic with respect to $X$; therefore $T$ and $A$ are homothetic with respect to $X$, impying that $T, A, X$ are collinear.
|
| 720 |
+
|
| 721 |
+
|
| 722 |
+
Figure 10: Diagram to Solution 6
|
| 723 |
+
|
EGMO/md/en-2024-solutions.md
ADDED
|
@@ -0,0 +1,555 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# EGMO 2024 - Problems and Solutions
|
| 2 |
+
|
| 3 |
+
## Problems
|
| 4 |
+
|
| 5 |
+
Problem 1. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
|
| 6 |
+
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
|
| 7 |
+
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
|
| 8 |
+
|
| 9 |
+
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
| 10 |
+
|
| 11 |
+
Problem 2. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\widehat{D F}$ and $\widehat{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
| 12 |
+
|
| 13 |
+
Problem 3. We call a positive integer $n$ peculiar if, for any positive divisor $d$ of $n$, the integer $d(d+1)$ divides $n(n+1)$. Prove that for any four different peculiar positive integers $A, B, C$ and $D$, the following holds:
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\operatorname{gcd}(A, B, C, D)=1
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Here $\operatorname{gcd}(A, B, C, D)$ is the largest positive integer that divides all of $A, B, C$ and $D$.
|
| 20 |
+
Problem 4. For a sequence $a_{1}<a_{2}<\cdots<a_{n}$ of integers, a pair $\left(a_{i}, a_{j}\right)$ with $1 \leq i<$ $j \leq n$ is called interesting if there exists a pair $\left(a_{k}, a_{l}\right)$ of integers with $1 \leq k<l \leq n$ such that
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
For each $n \geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.
|
| 27 |
+
|
| 28 |
+
Problem 5. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
|
| 29 |
+
|
| 30 |
+
- $x$ and $f(x)$ have the same number of positive divisors.
|
| 31 |
+
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
| 38 |
+
Problem 6. Find all positive integers $d$ for which there exists a degree $d$ polynomial $P$ with real coefficients such that there are at most $d$ different values among $P(0), P(1), \ldots, P\left(d^{2}-\right.$ d).
|
| 39 |
+
|
| 40 |
+
## Solutions
|
| 41 |
+
|
| 42 |
+
## Problem 1 (SVK)
|
| 43 |
+
|
| 44 |
+
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
|
| 45 |
+
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
|
| 46 |
+
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
|
| 47 |
+
|
| 48 |
+
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
| 49 |
+
|
| 50 |
+
Solution 1. We will show that the answer are the integer pairs $(u, v)$ such that $u \neq 0$, $v \neq 0,\{u, v\} \neq\{-1,1\}$ and $u>0$ or $v>0$.
|
| 51 |
+
|
| 52 |
+
If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers. Hence, if $u=0$ or $v=0$, we cannot reach every possible $y$. From now on, assume $u \neq 0$ and $v \neq 0$.
|
| 53 |
+
|
| 54 |
+
If both numbers $u, v$ were negative, we will show that there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$. From now on, assume that at least one of $u, v$ is positive. Without loss of generality take $u<v$, and so $v>0$.
|
| 55 |
+
|
| 56 |
+
After one step, we can have the numbers $u, v, u+v$, which are mutually distinct due to $u, v$ being nonzero. Notice that the equation $u x^{2}+(u+v) x+v=0$ has a root -1 , and so we can have -1 on the board.
|
| 57 |
+
|
| 58 |
+
We now check two cases: case $v=1$, and case $v>1$.
|
| 59 |
+
If $v=1$, then $u<0$. Further split the case of $v=1$ based on whether $u=-1$ or $u<-1$.
|
| 60 |
+
|
| 61 |
+
If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\{a, b, c\}$ to $\{-1,0,1\}$ in any order only has solutions for $x$ in $\{-1,0,1\}$. Hence, if $\{u, v\}=\{-1,1\}$, then we cannot reach every possible $y$.
|
| 62 |
+
|
| 63 |
+
If $v=1$ and $u<-1$, we can use operation (i) on numbers $u,-1$ (and then repeat choosing the obtained result and -1 ) to get any negative number smaller than $u$, and operation (i) on numbers $(u, 1)$ (and then repeat choosing the obtained result and 1 ) to get any negative number larger than $u$, as well as 0 . Then, we set $(a, b, c)=(0,1,-2)$ and apply operation (ii) to additionally get number 2. Applying (i) on $(2,1)$ (and then repeat choosing the obtained result and 1), we can get all the remaining integers too.
|
| 64 |
+
|
| 65 |
+
From now on, assume $v>1$. Recall that we can make $u+v$ and -1 .
|
| 66 |
+
We will now apply operation (i). First, $(v,-1)$ gives $v-1$. Next, $(v, v-1)$ gives $2 v-1$. Since $v>1$, we know $v \neq 2 v-1$, so we can apply operation (i) on $(v, 2 v-1)$ to get $3 v-1$, and then continue adding $(v, k v-1)$ to get $(k+1) v-1$ for any positive $k$. Since $v>1$, we can get an arbitrarily large integer by repeating this.
|
| 67 |
+
|
| 68 |
+
If $a$ is any positive number on the board, applying (i) to $(a,-1)$ gives $a-1$. By repeating this, we have that we can get all numbers smaller than $a$ and larger than or equal to -1 . Together with previously having found a way to get an arbitrarily large integer, we have that we can get any integer $l \geq-1$ on the board.
|
| 69 |
+
|
| 70 |
+
Now, we set $(a, b, c)=(0,1,2)$ and apply operation (ii) to additionally get number -2 . Then we can repeat operation (i) on ( $-1,-2$ ) (and afterwards on -1 and the obtained result) to get any negative number.
|
| 71 |
+
|
| 72 |
+
Therefore, if $u \neq 0, v \neq 0,\{u, v\} \neq\{-1,1\}$ and $u>0$ or $v>0$, we can write every integer on the board.
|
| 73 |
+
|
| 74 |
+
Remark. There are of course many other ways to create all integers in case of $(u, v)$ that satisfies all the requirements. Basically you will always use (i) to create arbitrarily large numbers and then (ii) to create a number in a range that you didn't have before.
|
| 75 |
+
|
| 76 |
+
Solution 2. If $u=0$ or $v=0$ then we can only get $\{u, v\}$.
|
| 77 |
+
|
| 78 |
+
Proof. If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers.
|
| 79 |
+
|
| 80 |
+
If $\max (u, v)<0$, we cannot get non-negative numbers.
|
| 81 |
+
|
| 82 |
+
Proof. For $a, b, c<0$ :
|
| 83 |
+
(i) cannot generate a non-negative number as $a+b<0$.
|
| 84 |
+
(ii) cannot generate a non-negative number as for $x \geq 0$ : $a x^{2}+b x+c \leq c<0$.
|
| 85 |
+
|
| 86 |
+
If $u+v \neq 0, u, v \neq 0$ and $\max (u, v)>0$, we can get every number.
|
| 87 |
+
|
| 88 |
+
Proof. $u \neq v \rightarrow u+v$ can be written. $u \neq 0$, so $u+v \neq v \rightarrow u+2 v$ can be written. $v \neq 0$, so $u+2 v \neq u$, meaning that $2 u+2 v$ can be written. If for $n>1, n(u+v)$ can be written then $(n+1)(u+v)=n(u+v)+(u+v)$ can also be written, because $u+v \neq 0$, so $n(u+v) \neq(u+v)$. Therefore, by induction for all $n>0$ the number $n(u+v)$ can be written.
|
| 89 |
+
|
| 90 |
+
Taking $n=2,3, \ldots$ and $(u+v)(x+1)(x+n)=(u+v) x^{2}+(u+v)(n+1) x+(u+v) n=0$ gives $x=-1$ and $x=-n \rightarrow$ for all $n>0$ we can get $-n$ (we can get all the negative numbers). Additionally, we can get $u+(-u)=0$.
|
| 91 |
+
|
| 92 |
+
For $n \geq 1$ we can take $0 \cdot x^{2}+u x+(-u n)=0$ as $u \neq 0 \rightarrow u,-n u, 0$ are all distinct, therefore we can get $n$. Thus, we can get all the numbers.
|
| 93 |
+
|
| 94 |
+
If $u+v=0$ and $\max (u, v)>1$ we can get all the numbers.
|
| 95 |
+
|
| 96 |
+
Proof. We can get $0=u+v$ as $u \neq v$. Take $0 \cdot x^{2}+u x-u=0$ so we can get 1 written on the board. Take $\left(u^{\prime}, v^{\prime}\right)=(1, \max (u, v))$ and then use the result from claim 3. As $0<u^{\prime}=1<\max (u, v)=v^{\prime}$ and $u^{\prime}+v^{\prime}>0$ we can get all the numbers.
|
| 97 |
+
|
| 98 |
+
Remaining case: If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\{a, b, c\}$ to $\{-1,0,1\}$ in any order only has solutions for $x$ in $\{-1,0,1\}$. Hence, if $\{u, v\}=\{-1,1\}$, then we cannot reach every possible $y$.
|
| 99 |
+
|
| 100 |
+
Solution 3. We show none of the initial number can be 0 , as in Solution 1. Then, we split into three cases: initial numbers having different signs, both being positive, and both being negative.
|
| 101 |
+
|
| 102 |
+
Case 1. Suppose we have two numbers $u, v$ with different signs such that $\operatorname{gcd}(u, v)=k$ for some $k \in \mathbb{Z}^{+}$. Without loss of generality assume that $u>0$ and $v<0$.
|
| 103 |
+
|
| 104 |
+
Case 1.1. $v<-k$ :
|
| 105 |
+
We can generate all numbers $y$ such that $k \mid y$ and $y \leq u$.
|
| 106 |
+
|
| 107 |
+
Proof. Define $u^{\prime}=\frac{u}{k}, v^{\prime}=\frac{v}{k}$. Note that by definition, $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=1$. If starting with numbers $u^{\prime}, v^{\prime}$, we can make a sequence of applications of only the (i) rule to write a number $y=p \cdot u^{\prime}+q \cdot v^{\prime}$ on the board, then we can apply the same sequence of moves to $u, v$ to write $k \cdot y=p \cdot u+q \cdot v$ on the board.
|
| 108 |
+
|
| 109 |
+
Therefore, we will prove instead that if $v^{\prime}<-1$, we can write all numbers $y<u^{\prime}$ on the board, which is equivalent to the lemma.
|
| 110 |
+
|
| 111 |
+
We attempt to write numbers $u^{\prime}+q \cdot v^{\prime}$ for $q \in \mathbb{Z}^{+}$on the board by repeatedly adding $v^{\prime}$ to $u^{\prime}$. This process can only ever halt if we reach a point where $u^{\prime}+q \cdot v^{\prime}=v^{\prime}$. That cannot occur, as it would imply $u^{\prime}=(1-q) \cdot v^{\prime}$. Taking into account that $u^{\prime}, v^{\prime} \neq 0$, that implies $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=\left|v^{\prime}\right|$. That is a contradiction, as $\left|v^{\prime}\right|>1$.
|
| 112 |
+
|
| 113 |
+
Therefore, we can write all numbers of the form $u^{\prime}+q \cdot v^{\prime}$ on the board for $q \in \mathbb{Z}^{+}$. We will use these numbers to construct an arbitrary integer $y$.
|
| 114 |
+
|
| 115 |
+
If we want to write a number $y<u^{\prime}$ on the board, and we already have a number $n<y$ on the board such that $y \equiv n\left(\bmod u^{\prime}\right)$, then we can construct $y$ by repeatedly adding $u^{\prime}$ to $n$ until we reach $y$, skipping all numbers that are already on the board. As $y<u^{\prime}$, none of the numbers we attempt to add $u^{\prime}$ to will be equal to $u^{\prime}$.
|
| 116 |
+
|
| 117 |
+
Suppose we fix any number $y<u^{\prime}$. As $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=1, q \cdot v^{\prime}$ takes all residues modulo $u^{\prime}$ as $q$ runs through the positive integers. Therefore, we will always be able to find a number $n$ of the form $u^{\prime}+q \cdot v^{\prime}$ such that $y \equiv n \bmod u^{\prime}$. We can generate an arbitrarily small $n^{\prime}$ by taking $n^{\prime}=n+l \cdot u^{\prime} \cdot v^{\prime}=u^{\prime}+\left(q+l \cdot u^{\prime}\right) \cdot v^{\prime}$ for large enough $l$, making both $n^{\prime}<y$ and $n^{\prime} \equiv y \bmod u^{\prime}$ true.
|
| 118 |
+
|
| 119 |
+
Therefore, we can write all numbers $y<u^{\prime}$ on the board. Thus, starting from $u$ and $v$, we can get all numbers $y \leq u$ s.t. $k \mid y$.
|
| 120 |
+
|
| 121 |
+
The numbers $k, 0$ and all negative multiples of $k$ are a subset of the integers $y \leq u$ s.t. $k \mid y$. Therefore, we have all of those numbers on the board.
|
| 122 |
+
|
| 123 |
+
We can now get an arbitrary nonzero number by applying (ii) to the polynomial $k \cdot(x-$ $n)(x+n)=k \cdot x^{2}+0 \cdot x-n^{2} \cdot k$. The coefficients of this polynomial are distinct for all integers $n \neq 0$, and they are from the set $\{k, 0\} \cup\{q \cdot k \mid q<0\}$, which we have on the board. Therefore the rule application is valid.
|
| 124 |
+
|
| 125 |
+
As this works for all integers $n \in \mathbb{Z} \backslash\{0\}$, and 0 is already on the board, we have proven that we can write all integers on the board.
|
| 126 |
+
|
| 127 |
+
Case 1.2.: $v=-k$ :
|
| 128 |
+
Case 1.2.1.: $k \neq 1$.
|
| 129 |
+
If $k \neq 1$, we can generate -1 from the polynomial $u \cdot x^{2}+(u+v) x+v$. We can now repeatedly add -1 to $v=-k$ until we reach $-2 k$ on the board. Now, we can appeal to Case 1.1.
|
| 130 |
+
|
| 131 |
+
Case 1.2.2. $k=1$.
|
| 132 |
+
To restate the conditions of this sub-case, $v=-k=-1$, and $u$ is an arbitrary positive number.
|
| 133 |
+
|
| 134 |
+
Case 1.2.2.1. $u=1$.
|
| 135 |
+
If $u=1$, we are only ever able to construct the numbers $-1,0,1$, no matter how we apply the rules.
|
| 136 |
+
|
| 137 |
+
Case 1.2.2.2. $u \neq 1$.
|
| 138 |
+
We can subtract 1 from $u$ until we reach 0 . This procedure also generates 1 . We now add 1 to $u$ until we get all positive numbers.
|
| 139 |
+
|
| 140 |
+
Now, we find an arbitrary polynomial with different positive coefficients that have a negative root smaller than -1 . An example is $(x+3)^{2}$.
|
| 141 |
+
|
| 142 |
+
We will now keep adding -1 to -3 to get all the negative numbers $y \leq-3$. To get -2 , we can add -3 to 1 , generating all integers.
|
| 143 |
+
|
| 144 |
+
Case 2 Suppose that both of $u, v$ are positive.
|
| 145 |
+
We can now use any method from the previous solutions to generate a negative number, and then appeal to Case 1.
|
| 146 |
+
|
| 147 |
+
Case 3 Suppose $u<0, v<0$.
|
| 148 |
+
Then there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$.
|
| 149 |
+
|
| 150 |
+
## Problem 2 (UNK)
|
| 151 |
+
|
| 152 |
+
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
| 153 |
+
|
| 154 |
+
Solution 1. By the alternate segment theorem we have that:
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
180^{\circ}=\angle D C Y+\angle C Y D+\angle Y D C=\angle D C Y+\angle D X B+\angle Y X D=\angle D C Y+\angle Y X B
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
Therefore opposite angle of $B X Y C$ are supplementary and so $C Y X B$ cyclic.
|
| 161 |
+
One can apply power of a point at $K$ :
|
| 162 |
+
|
| 163 |
+
$$
|
| 164 |
+
K T^{2}=K B \cdot K C=K X \cdot K Y=K D^{2} \Longrightarrow K T=K D .
|
| 165 |
+
$$
|
| 166 |
+
|
| 167 |
+
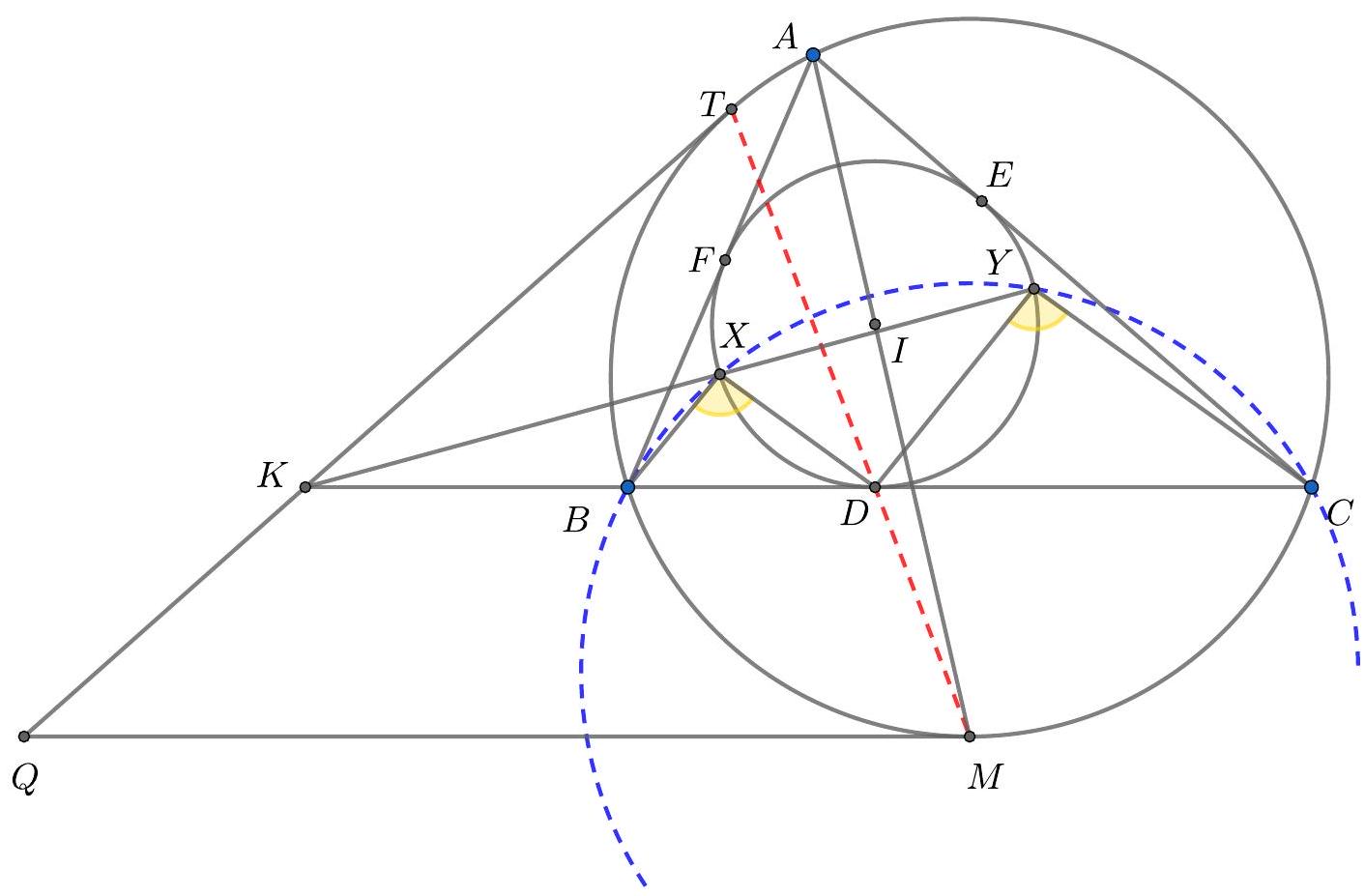
|
| 168 |
+
|
| 169 |
+
Figure 1: The proposer's solution using a new point $Q$
|
| 170 |
+
(Alternatively you can sidestep power of a point by observing that $K$ is the radical centre of the incircle $D E F$, the circumcircle $\Gamma$ and the circle $C Y X B$ and so $K T^{2}=K D^{2}$.)
|
| 171 |
+
|
| 172 |
+
Now let $A I$ meet $\Omega$ at $M$, the midpoint of $\widehat{B C}$ not containing $A$. Let the tangent at $M$ meet $K T$ at $Q$. Observe that $Q M \| K D$ so $\angle T K D=\angle T Q M$ and also $K T=K D$, $Q T=Q M$ hence $\triangle T K D \sim \triangle T Q M$. As $T, K, Q$ are collinear, this means that $T, D, M$ are collinear so $T D$ and $A I$ meet at $M$ which lies on $\Omega$.
|
| 173 |
+
|
| 174 |
+
Solution 2. The role of $X$ and $Y$ in this problem is secondary. Draw any circle through $B$ and $C$ which meets the incircle at $X$ and $Y$ and you determine the same point $K$. This is because $K$ is the radical centre of the three circles in play. Therefore $K$ is the intersection of $B C$ with the radical axis of the circumcircle $\Omega$ and the incircle $D E F$, and so is independent of the choice of circle through $B$ and $C$ which gives rise to $X$ and $Y$. In the problem as posed, this is disguised, with angle properties of $X$ and $Y$ giving rise the the circle $B X Y C$.
|
| 175 |
+
|
| 176 |
+
You can now work with the simplified diagram shown in Figure 2.
|
| 177 |
+
|
| 178 |
+
Somehow we must use a characterization of $M$ in order to finish. In the proposer's solution, we used the tangent to the circumcircle $\Omega$ at $M$ being parallel to $B C$. In this alternative, we use the fact that the internal angle bisector of angle $\angle C T B$ meets $\Omega$ again at $M$.
|
| 179 |
+
|
| 180 |
+
Triangle $T K D$ is isosceles with apex $K$ so
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
\angle K D T=\angle D T K=\angle D T B+\angle B T K .
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
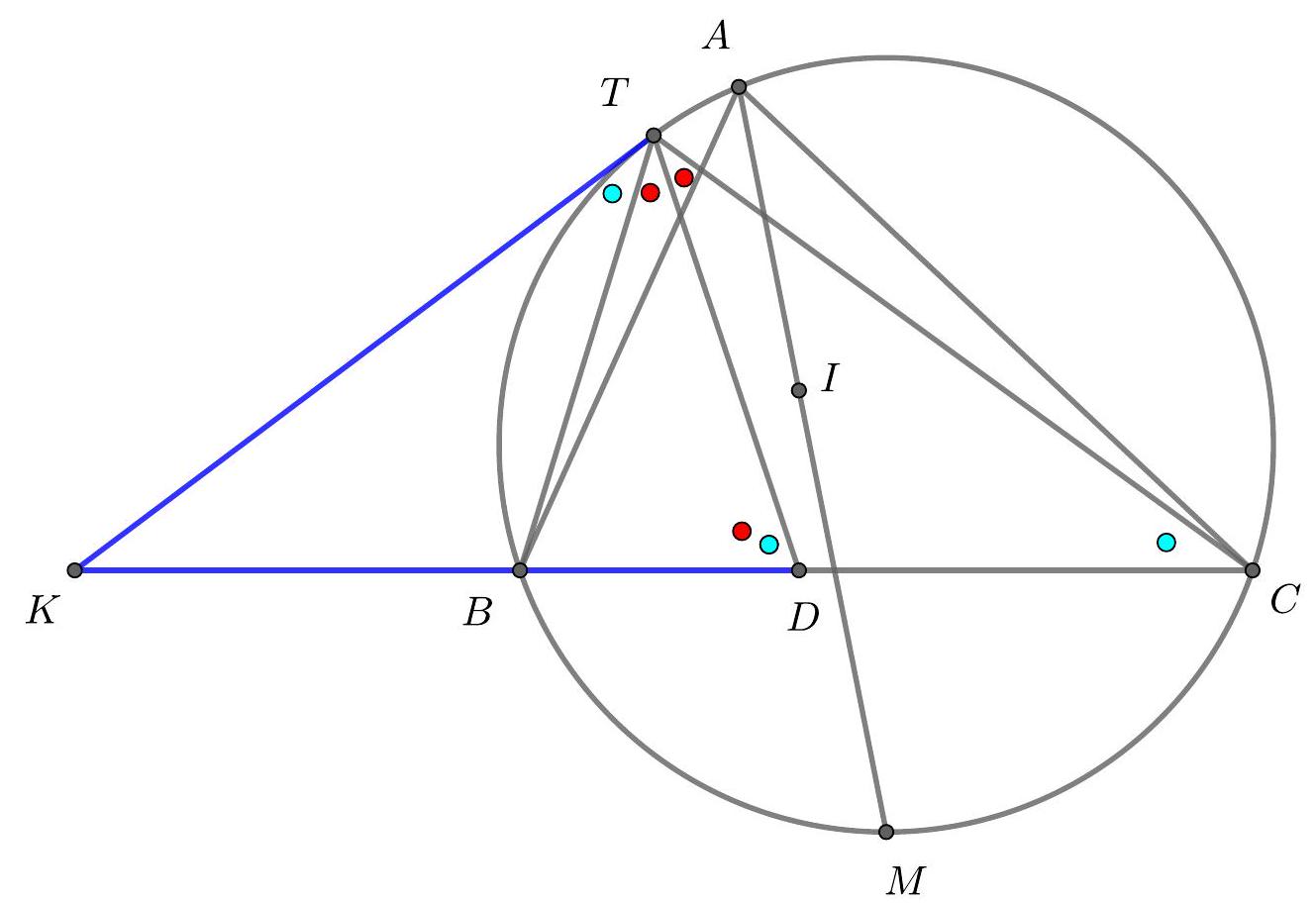
|
| 187 |
+
|
| 188 |
+
Figure 2: Illustration of an angle chase
|
| 189 |
+
|
| 190 |
+
By the alternate segment theorem, $\angle B T K=\angle B C T=\angle D C T$. Now angle $\angle K D T$ is an exterior angle of triangle $D C T$ so $\angle C T D=\angle D T B$.
|
| 191 |
+
|
| 192 |
+
Therefore the line $T D$ is the internal angle bisector of angle $\angle C T B$ and so must pass through $M$, the midpoint of the arc $\widehat{B C}$ of $\Omega$ which does not contain $T$.
|
| 193 |
+
|
| 194 |
+
Observation This affords a construction of the radical axis of the incircle and circumcircle of triangle $A B C: M$ and $D$ determine $T$ and the tangent at $T$ meets $B C$ at a point on the required radical axis. See Figure 3. Now do a cyclic change of letters of $A B C$ and find a point on $C A$ which is also on the radical axis (the dashed magenta line).
|
| 195 |
+
|
| 196 |
+
Solution 3. The centre of direct enlargement from the incircle to the circumcircle gives another way to finish the proof. This enlargement carries $D$ to $M$ since the tangent lines to their associated circles are parallel. The centre of enlargement therefore lies on the line $M D$. Let $M D$ meet the incircle again at $U$ and the circumcircle again at $V$. Draw the tangent to the incircle at $U$ to meet $B C$ at $W$ so triangle $W D U$ is isosceles with apex $W$ and has equal base angles $\angle W D U$ and $\angle D U W$. The enlargement carries the line $W U$ to the tangent line to the circumcircle at $V$ which meets $B C$ at $S$. Enlargements carry lines to parallel lines, so $\angle D V K^{\prime}=\angle D U W=\angle W D U=\angle K^{\prime} D V$. Therefore triangle $K^{\prime} D V$ is isosceles with apex $K^{\prime}$.
|
| 197 |
+
|
| 198 |
+
|
| 199 |
+
Figure 3: The three points $K$ on the radical axis.
|
| 200 |
+
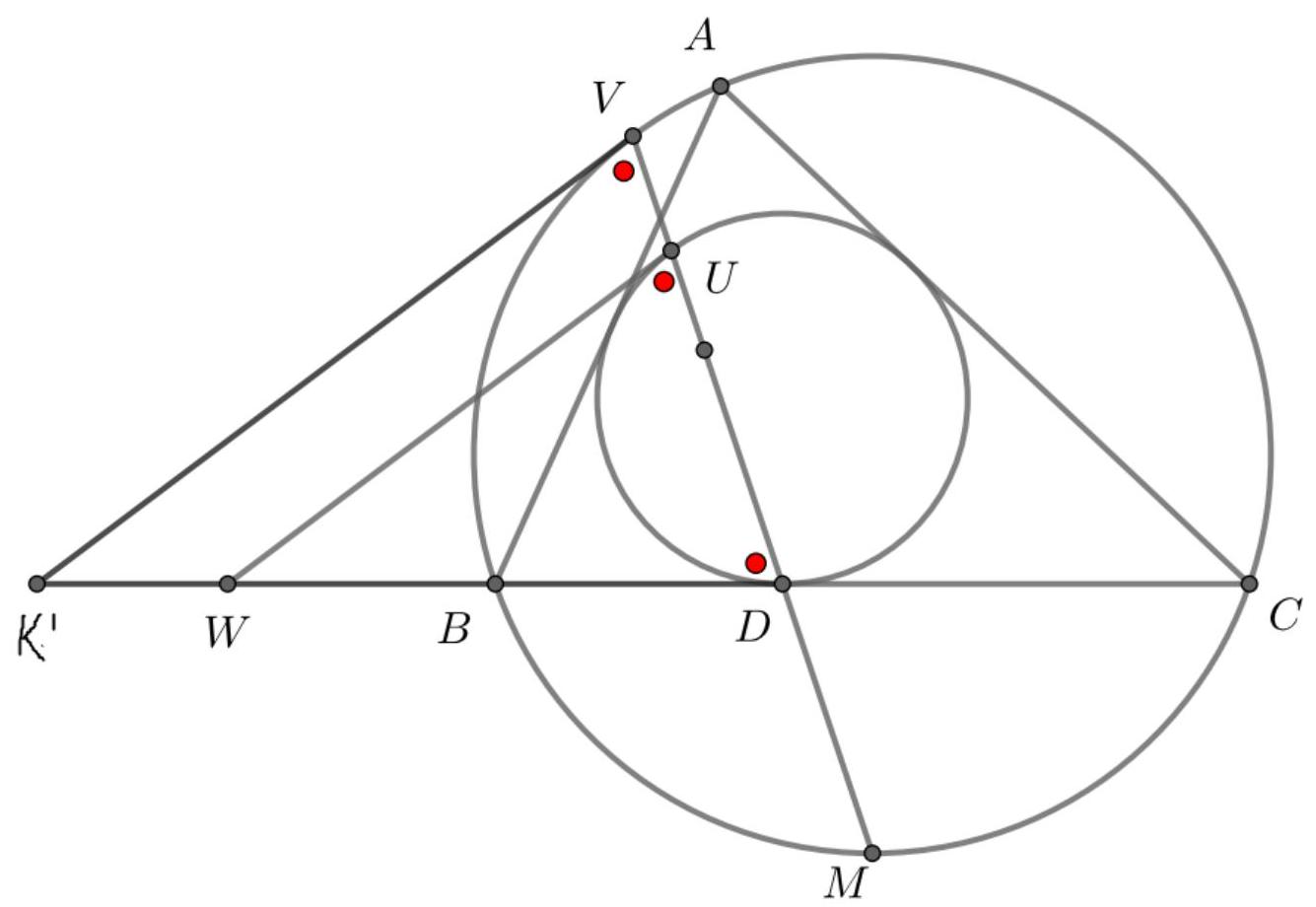
|
| 201 |
+
|
| 202 |
+
Figure 4: The enlargement of $W$ gives $K^{\prime}$.
|
| 203 |
+
|
| 204 |
+
This identifies $S$ as the intersection of the radical axis of the two circles with $B C$, so $K^{\prime}=K$ and $V=T$ and the proof is complete.
|
| 205 |
+
|
| 206 |
+
Solution 4. Let $\phi$ be the inversion with center $K$ and radius $K D$. Note that this inversion maps incirlce of $A B C$ to itself and $K, X, Y$ are collinear, hence $\phi(X)=Y$. Also $\phi(D)=D$, so $\phi$ maps circle $X B D$ to cicle $Y D B^{\prime}$, where $B^{\prime}:=\phi(B)$ is the point on $B C$ different from $B$ such that $\angle B X D=\angle D Y B^{\prime}$, hence $\phi(B)=C$. From $\phi(B)=C$ we get that $K D=K T$ as $K D^{2}=K B \cdot K C=K T^{2}$ since $K D$ is the radius of inversion.
|
| 207 |
+
|
| 208 |
+
The rest of the solutions is the same as in the other solutions.
|
| 209 |
+
|
| 210 |
+
## Problem 3 (NLD)
|
| 211 |
+
|
| 212 |
+
Problem. We call a positive integer $n$ peculiar if, for any positive divisor $d$ of $n$, the integer $d(d+1)$ divides $n(n+1)$. Prove that for any four different peculiar positive integers $A, B, C$ and $D$, the following holds:
|
| 213 |
+
|
| 214 |
+
$$
|
| 215 |
+
\operatorname{gcd}(A, B, C, D)=1
|
| 216 |
+
$$
|
| 217 |
+
|
| 218 |
+
Here $\operatorname{gcd}(A, B, C, D)$ is the largest positive integer that divides all of $A, B, C$ and $D$.
|
| 219 |
+
|
| 220 |
+
## First part of the solution, option 1
|
| 221 |
+
|
| 222 |
+
Observe that $n=1$ is peculiar and that every prime is peculiar. Consider $\frac{n}{d}$, where $d>1$
|
| 223 |
+
is a divisor of $n$. Then $\frac{n}{d}\left(\frac{n}{d}+1\right)$ divides $n(n+1)$, equivalent to $n+d$ dividing $d^{2}(n+1)$. Since $n \equiv-d(\bmod n+d)$, we obtain that $n+d$ divides $d^{3}-d^{2}$, hence $n+d \leq d^{3}-d^{2}$ and in particular $n<d^{3}$. Now taking $d$ to be the smallest prime divisor of $n$, we deduce that $n$ cannot have more than two prime factors, counting multiplicities. Hence from now on we work with $n=p q$, where $p$ and $q$ are primes. In fact, $p \neq q$, as otherwise $p+1 \mid p^{2}-p$, i.e. $p+1 \mid 2$, contradiction.
|
| 224 |
+
|
| 225 |
+
## First part of the solution, option 2
|
| 226 |
+
|
| 227 |
+
Let us first prove that $n$ is square-free. Assume that $n=p^{k} h$, where $\operatorname{gcd}(p, h)=1$. Now $p^{k-1} h\left(p^{k-1} h+1\right) \mid p^{k} h\left(k^{k} h+1\right)$, which is equivalent to $\left(p^{k-1} h+1\right) \mid p\left(p^{k} h+1\right)$. Since $\operatorname{gcd}\left(p, p^{k-1} h+1\right)=1$, we must have
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
\left(p^{k-1} h+1\right) \mid\left(p^{k} h+1\right)=p^{k} h+p-p+1
|
| 231 |
+
$$
|
| 232 |
+
|
| 233 |
+
so $\left(p^{k-1} h+1\right) \mid(p-1)$. If $k \geq 2$, this is a contradiction. Hence, $n$ is square-free.
|
| 234 |
+
Let us now show that $n$ has at most 2 different prime factors. Write $n=p_{1} p_{2} \cdots p_{k}$. Now we must have
|
| 235 |
+
|
| 236 |
+
$$
|
| 237 |
+
p_{2} \cdots p_{k}\left(p_{2} \cdots p_{k}+1\right) \mid p_{1} \cdots p_{k}\left(p_{1} \cdots p_{k}+1\right)
|
| 238 |
+
$$
|
| 239 |
+
|
| 240 |
+
which is equivalent to
|
| 241 |
+
|
| 242 |
+
$$
|
| 243 |
+
\left(p_{2} \cdots p_{k}+1\right) \mid p_{1}\left(p_{1} \cdots p_{k}+1\right)
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
Now
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
p_{1}\left(p_{1} \cdots p_{k}+1\right)-p_{1}^{2}\left(p_{2} \cdots p_{k}+1\right)=p_{1}-p_{1}^{2}
|
| 250 |
+
$$
|
| 251 |
+
|
| 252 |
+
Hence,
|
| 253 |
+
|
| 254 |
+
$$
|
| 255 |
+
\left(p_{2} \cdots p_{k}+1\right) \mid p_{1}^{2}-p_{1}
|
| 256 |
+
$$
|
| 257 |
+
|
| 258 |
+
Pick $p_{1}$ to be the smallest prime factor of $n$. Then $p_{2} \cdots p_{k}>p_{1}^{2}$ if $k>2$, which is a contradiction.
|
| 259 |
+
|
| 260 |
+
## Second part of the solution, option 1
|
| 261 |
+
|
| 262 |
+
The only relations of concern are $p(p+1) \mid n(n+1)$ and $q(q+1) \mid n(n+1)$. The former yields $p(p+1) \mid p q(p q+1)$, i.e. $p+1 \mid q(p q+1)$, that is, $p+1 \mid q(q-1)$; analogously $q+1 \mid p(p-1)$. Without loss of generality assume $p>q$. If $q$ does not divide $p+1$, then since $p+1$ and $q$ are relatively prime, we obtain from $p+1 \mid q(q-1)$ that $p+1$ divides $q-1$ and hence $p<p+1 \leq q-1<q$, contradiction. Hence $q$ divides $p+1$. Also, $p$ does not divide $q+1$ due to $p>q$ (unless $p=q+1$, i.e. $p=3, q=2$, but then $p+1 \nmid q(q-1)$ ) and now from $q+1 \mid p(p-1)$ we deduce that $q+1$ divides $p-1$.
|
| 263 |
+
|
| 264 |
+
Write $p+1=m q$ for some positive integer $m$. Then $q+1$ divides $p-1=m q-2=$ $m(q+1)-m-2$, so $q+1$ divides $m+2$. On the other hand, $p+1 \mid q(q-1)$ implies that $m$ divides $q-1$. If the ratio of the latter is greater than 1 , then $m \leq \frac{q-1}{2}$, but $q+1$ dividing $m+2$ from above insists on $q \leq m+1$, so $m \leq \frac{q-1}{2} \leq \frac{m}{2}$, contradiction. Hence $m=q-1$ and we have proven the following: if $n>1$ is composite and peculiar, then $n=p q$, where $p>q$ are primes and $p=q^{2}-q-1$.
|
| 265 |
+
|
| 266 |
+
## Second part of the solution, option 2
|
| 267 |
+
|
| 268 |
+
Hence from now on we work with $n=a b$, with $a<b$ primes. The only relations of concern are $a(a+1) \mid n(n+1)$ and $b(b+1) \mid n(n+1)$. The former yields $a(a+1) \mid a b(a b+1)$, i.e. $a+1 \mid b(a b+1)$, that is, $a+1 \mid b(b-1)$; analogously $b+1 \mid a(a-1)$. If $a$ does not divide $b+1$, then since $b+1$ and $a$ are relatively prime, we obtain from $b+1 \mid a(a-1)$ that $b+1$ divides $a-1$ and hence $b<b+1 \leq a-1<a$, contradiction. Hence $a$ divides $b+1$. Writing $b+1=a c$, from $b+1 \mid a(a-1)$ we have that $c$ divides $a-1$.
|
| 269 |
+
|
| 270 |
+
Now from $b+1=a c$ with $c \mid a-1$ and $a+1 \mid b(b-1)$ we derive that $b=a^{2}-a-1$ in a different (and longer) manner, without using the primality of $b$ until the final step. Note that since $b=a c-1 \equiv-c-2(\bmod a+1)$, we have $a+1 \mid(c+1)(c+2)$. Since $c \mid a-1$, we may write $a-1=c d$, and note that $c d \equiv-2(\bmod a+1)$. We then have
|
| 271 |
+
|
| 272 |
+
$$
|
| 273 |
+
0 \equiv-d(c+1)(c+2)=-c^{2} d-3 c d-2 d \equiv 2(c-d)+6 \quad(\bmod a+1)
|
| 274 |
+
$$
|
| 275 |
+
|
| 276 |
+
Since $1 \leq c, d \leq a-1$, we have $|2(c-d)+6| \leq 2(a-2)+6=2 a+2$. Furthermore, we have $c \geq 2$ (otherwise $b=a c-1<a$, contradiction), and so $d \leq \frac{a-1}{2}$, thus $2(c-$ d) $+6 \geq 11-a>-(a+1)$. From these inequalities and equivalence (1), we obtain $2(c-d)+6 \in\{0, a+1,2(a+1)\}$. It is immediate to verify that these three possible values correspond to the following three cases, respectively:
|
| 277 |
+
(i) $d=c+3$ and $a=c^{2}+3 c+1$;
|
| 278 |
+
(ii) $d=2, c=\frac{a-1}{2}, a=2 c+1$; and
|
| 279 |
+
(iii) $d=1, c=a-1$.
|
| 280 |
+
|
| 281 |
+
Substituting these values in $b=a c-1$, we obtain in case $(i), b=c^{3}+3 c^{2}+c-1=$ $(c+1)\left(c^{2}+2 c-1\right)$, and in case $(i i), b=2 c^{2}+c-1=(c+1)(2 c-1)$. In both cases these decompositions contradict the primality of $b$, as $c \geq 2$. Thus we are left only with case (iii), where $b=a^{2}-a+1$, as claimed.
|
| 282 |
+
|
| 283 |
+
## End of the solution (joint for different approaches)
|
| 284 |
+
|
| 285 |
+
In conclusion, a prime $p$ can only divide the peculiar numbers $p, p\left(p^{2}-p-1\right)$ (if $p^{2}-p-1$ is prime) and $p q$ where $p=q^{2}-q-1$ (if $q$ is prime). In particular, the greatest common divisor of more than three peculiar numbers must be 1. (Note that three peculiar numbers may indeed have a common divisor, e.g. $5,15=3 \cdot 5$ and $95=5 \cdot 19$ are all peculiar.)
|
| 286 |
+
|
| 287 |
+
## Problem 4 (UKR)
|
| 288 |
+
|
| 289 |
+
Problem. For a sequence $a_{1}<a_{2}<\cdots<a_{n}$ of integers, a pair $\left(a_{i}, a_{j}\right)$ with $1 \leq i<j \leq n$ is called interesting if there exists a pair $\left(a_{k}, a_{l}\right)$ of integers with $1 \leq k<l \leq n$ such that
|
| 290 |
+
|
| 291 |
+
$$
|
| 292 |
+
\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2
|
| 293 |
+
$$
|
| 294 |
+
|
| 295 |
+
For each $n \geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.
|
| 296 |
+
|
| 297 |
+
Answer. $\frac{1}{2}(n-1)(n-2)+1$.
|
| 298 |
+
|
| 299 |
+
Solution. Consider the numbers $a_{i}=2^{i}$ for $2 \leq i \leq n$ and $a_{1}=0$, and choose any pair $(i, j)$ with $1 \leq i<j \leq n$.
|
| 300 |
+
|
| 301 |
+
If $i=1$, the pair $(1, j)$ is interesting for all $2 \leq j \leq n-1$, as $\frac{a_{j+1}-a_{1}}{a_{j}-a_{1}}=\frac{2^{j+1}}{2^{j}}=2$.
|
| 302 |
+
If $i \geq 2$, the pair $(i, j)$ is also interesting for all $j$ such that $i+1 \leq j \leq n-1$, since $\frac{a_{j+1}-a_{i+1}}{a_{j}-a_{i}}=\frac{2^{j+1}-2^{i+1}}{2^{j}-2^{i}}=2$.
|
| 303 |
+
|
| 304 |
+
In addition, the pair $(n-1, n)$ is interesting, as $\frac{a_{n}-a_{0}}{a_{n}-a_{n-1}}=2$.
|
| 305 |
+
Hence, all pairs in which $j \leq n-1$, and additionally the pair $(n-1, n)$, are interesting, giving $\frac{1}{2}(n-1)(n-2)+1$ pairs in total.
|
| 306 |
+
|
| 307 |
+
Now, let's show that there can't be more interesting pairs. To this end we show that at least $\frac{1}{2} n(n-1)-\left(\frac{1}{2}(n-1)(n-2)+1\right)=n-2$ pairs are not interesting. Clearly, the pair $(1, n)$ is not interesting.
|
| 308 |
+
|
| 309 |
+
Let's make the following observation: if a pair $(i, j)$ is interesting and it's not $(1, n)$, then $a_{j}-a_{i}$ can't exceed $\frac{1}{2}\left(a_{n}-a_{1}\right)$. (Since, if $(i, j)$ is interesting then $a_{l}-a_{k}=2\left(a_{j}-a_{i}\right)$ for some pair $(k, l)$. If then $2\left(a_{j}-a_{i}\right)>a_{n}-a_{1}$ we would have $a_{l}-a_{k}>a_{n}-a_{1}$, which is not possible.)
|
| 310 |
+
|
| 311 |
+
Finally, for any $2 \leq i \leq n-1$ consider pairs $(1, i)$ and $(i, n)$. If both of them are interesting, then, following the observation above, the only possibility is $a_{i}-a_{1}=a_{n}-a_{i}=\frac{a_{n}-a_{1}}{2}$. Clearly, this is possible for at most one $i$, so for all other $n-3$ values of $i$, at least one of pairs $(1, i)$ and $(i, n)$ is not interesting. Combining with the pair $(1, n)$, we get at least $n-2$ not interesting pairs in total, as desired.
|
| 312 |
+
|
| 313 |
+
Comment: The originally proposed formulation considered a sequence $a_{1}<a_{2}<\cdots<$ $a_{n}$ of $n$ real numbers, rather than integers. The conclusion is however the same and the solution is identical.
|
| 314 |
+
|
| 315 |
+
## Problem 5 (HRV)
|
| 316 |
+
|
| 317 |
+
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
|
| 318 |
+
|
| 319 |
+
- $x$ and $f(x)$ have the same number of positive divisors.
|
| 320 |
+
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
|
| 321 |
+
|
| 322 |
+
$$
|
| 323 |
+
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
|
| 324 |
+
$$
|
| 325 |
+
|
| 326 |
+
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
| 327 |
+
Solution 1. Throughout this proof, when we write divisors we mean positive divisors.
|
| 328 |
+
Let $f$ be a function satisfying these properties. From the first one, it follows that $f(1)=1$ and for each prime number $p, f(p)=q_{p}$ for some prime number $q_{p}$. Assume $p \neq 2$, the pair $(2, p)$ in property 2 gives
|
| 329 |
+
|
| 330 |
+
$$
|
| 331 |
+
\operatorname{gcd}\left(q_{2}, q_{p}\right)=\operatorname{gcd}(f(2), f(p))>f(\operatorname{gcd}(2, p))=f(1)=1
|
| 332 |
+
$$
|
| 333 |
+
|
| 334 |
+
so $q_{p}=q_{2}$ for all $p$. Set $q=q_{2}$.
|
| 335 |
+
Denote by $d(n)$ the number of divisors of a positive integer $n$.
|
| 336 |
+
We will prove the following claim by induction on $k \geq 0$, the number of distinct prime divisors of $n$ : For a positive integer $n, f(n)$ is a power of $q$.
|
| 337 |
+
|
| 338 |
+
The claim, together with the first property, imply that $f(n)=q^{d(n)-1}$.
|
| 339 |
+
For $k=0$ the claim is already proved.
|
| 340 |
+
For $k=1$, we need to prove that $f\left(p^{m}\right)$ is a power of $q$ for all positive $m$. The case $m=1$ was already proved. Assume now the result being proved for all positive integers $\leq m$. As $d\left(p^{t}\right)=t+1$, we then know $f\left(p^{t}\right)=q^{t}$ for all $t \leq m$. Now we consider $t=m+1$.
|
| 341 |
+
|
| 342 |
+
Let $r \neq p$ be a prime. Plug the pair $\left(p^{m-1} r, p^{m}\right)$ into the second property:
|
| 343 |
+
|
| 344 |
+
$$
|
| 345 |
+
\operatorname{gcd}\left(f\left(p^{m-1} r\right), q^{m}\right)=\operatorname{gcd}\left(f\left(p^{m-1} r\right), f\left(p^{m}\right)\right)>f\left(p^{m-1}\right)=q^{m-1}
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
This implies $q^{m}$ divides $f\left(p^{m-1} r\right)$. Since $f\left(p^{m-1} r\right)$ has $2 m$ divisors, and $v_{q}\left(f\left(p^{m-1} r\right)\right) \geq m$, it follows that $f\left(p^{m-1} r\right)$ does not have prime divisors other than $q$, since it would then have at least $2 \cdot\left(v_{q}\left(f\left(p^{m-1} r\right)\right)+1\right)>2 m$ divisors. Thus, $f\left(p^{m-1} r\right)$ is a power of $q$. And since it has $2 m$ divisors, we must have $f\left(p^{m-1} r\right)=q^{2 m-1}$.
|
| 349 |
+
|
| 350 |
+
Now, plug the pair $\left(p^{m+1}, p^{m-1} r\right)$ into the second property. We have
|
| 351 |
+
|
| 352 |
+
$$
|
| 353 |
+
\operatorname{gcd}\left(f\left(p^{m+1}\right), q^{2 m-1}\right)=\operatorname{gcd}\left(f\left(p^{m+1}\right), f\left(p^{m-1} r\right)\right)>f\left(p^{m-1}\right)=q^{m-1} .
|
| 354 |
+
$$
|
| 355 |
+
|
| 356 |
+
Then $f\left(p^{m+1}\right)$ is divisible by $q^{m}$. If $f\left(p^{m+1}\right)$ had a prime factor other than $q$, it would have at least $2(m+1)$ divisors, but it has $m+2$ divisors and $2(m+1)>m+2$ since $m \geq 1$. Hence, $f\left(p^{m+1}\right)$ must also be a power of $q$. By induction, the proof is finished for $k=1$.
|
| 357 |
+
|
| 358 |
+
Suppose the claim is true for all integers $n$ with at most $k$ distinct prime factors, for some $k \geq 1$. In order to prove the claim for integers with $k+1$ distinct prime factors, it suffices
|
| 359 |
+
to show that for every positive integer $N$ with $k$ distinct prime factors, every positive integer $m$ and every prime $p$ which does not divide $N$, the number $f\left(N p^{m}\right)$ is a power of $q$. We will prove this by induction on $m$. The case $m=0$ follows from the previous induction hypothesis. Now suppose it has already been proved for a certain $m \geq 0$.
|
| 360 |
+
|
| 361 |
+
Let $s$ be a prime divisor of $N$. Consider the numbers $\left(N p^{m+1}, N s p^{m}\right)$. By the second property,
|
| 362 |
+
|
| 363 |
+
$$
|
| 364 |
+
\operatorname{gcd}\left(f\left(N p^{m+1}\right), q^{d\left(N s p^{m}\right)-1}\right)=\operatorname{gcd}\left(f\left(N p^{m+1}\right), f\left(N s p^{m}\right)\right)>f\left(N p^{m}\right)=q^{d\left(N p^{m}\right)-1}
|
| 365 |
+
$$
|
| 366 |
+
|
| 367 |
+
Then $q^{d\left(N p^{m}\right)}$ divides $f\left(N p^{m+1}\right)$. If $f\left(N p^{m+1}\right)$ has a prime factor other than $q$, it would have at least $2\left(d\left(N p^{m}\right)+1\right)=2((m+1) d(N)+1)=(2 m+2) d(N)+2$ divisors, but it has only $(m+2) d(N)$ divisors. Hence, $f\left(N p^{m+1}\right)$ must also be a power of $q$.
|
| 368 |
+
|
| 369 |
+
Finally, let us check that the function $f(n)=q^{d(n)-1}$ does satisfy the properties of the problem for any prime number $q$. The first property obviously holds. To check the second one, note that
|
| 370 |
+
|
| 371 |
+
$$
|
| 372 |
+
\operatorname{gcd}(f(x), f(y))=q^{\min (d(x), d(y))}>q^{d(\operatorname{gcd}(x, y))}=f(\operatorname{gcd}(x, y))
|
| 373 |
+
$$
|
| 374 |
+
|
| 375 |
+
whenever $x \nmid y$ and $y \nmid x$.
|
| 376 |
+
Solution 2. Firstly, one can prove that for any prime $p$ and any $m \geq 0, f\left(p^{m}\right)=q^{m}$, in the same way as in the first solution.
|
| 377 |
+
|
| 378 |
+
We will prove the claim this time by induction on $k=d(n)$. We notice again that the claim implies that $f(n)=q^{d(n)-1}$.
|
| 379 |
+
|
| 380 |
+
The cases $k=1,2,3$ are then already proved. Now suppose that for some $k \geq 3$ we have proved the claim for all positive integers $n$ with at most $k$ divisors.
|
| 381 |
+
|
| 382 |
+
Consider a positive integer $n$ with $k+1$ divisors. If $n$ is a power of a prime, then it is already proved that $f(n)$ is a power of $q$. Suppose $n$ is not a power of a prime. Consider distinct prime numbers $p_{1}$ and $p_{2}$ which divide $n$, such that $v_{p_{1}}(n) \leq v_{p_{2}}(n)$. Consider the number $\frac{n p_{2}}{p_{1}}$ : its number of divisors is $\frac{v_{p_{1}}(n)\left(v_{p_{2}}(n)+2\right)}{\left(v_{p_{1}}(n)+1\right)\left(v_{p_{2}}(n)+1\right)} d(n)$, which is strictly less than the number of divisors of $n$. Thus, by induction hypothesis, $f\left(\frac{n p_{2}}{p_{1}}\right)$ is a power of $q$.
|
| 383 |
+
|
| 384 |
+
By applying the second property to the pair $\left(n, \frac{n p_{2}}{p_{1}}\right)$, we have
|
| 385 |
+
|
| 386 |
+
$$
|
| 387 |
+
\operatorname{gcd}\left(f(n), q^{d\left(\frac{n p_{2}}{p_{1}}\right)-1}\right)=\operatorname{gcd}\left(f(n), f\left(\frac{n p_{2}}{p_{1}}\right)\right)>f\left(\frac{n}{p_{1}}\right)=q^{d\left(\frac{n}{p_{1}}\right)-1}
|
| 388 |
+
$$
|
| 389 |
+
|
| 390 |
+
This implies that $q^{d\left(\frac{n}{p_{1}}\right)}$ divides $f(n)$. Again, if other primes than $q$ divided $f(n)$, it would have at least $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)$ divisors. But $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)=2\left(\frac{v_{p_{1}}(n)}{v_{p_{1}}(n)+1} d(n)+1\right)>d(n)$. So $f(n)$ is a power of $q$ and the Claim is proved.
|
| 391 |
+
|
| 392 |
+
We finally check as in the first solution that $f(n)=q^{d(n)-1}$ satisfies the 2 properties for all prime $q$.
|
| 393 |
+
|
| 394 |
+
## Problem 6 (LUX+BEL)
|
| 395 |
+
|
| 396 |
+
Problem. Find all positive integers $d$ for which there exists a degree $d$ polynomial $P$ with real coefficients such that there are at most $d$ different values among $P(0), P(1), \ldots, P\left(d^{2}-\right.$ d).
|
| 397 |
+
|
| 398 |
+
Remark 1 You can add a constant to a polynomial satisfying the conditions and obtain another polynomial satisfying the conditions.
|
| 399 |
+
|
| 400 |
+
Remark 2 This problem is equivalent to: Find all positive integers $d$ for which there exists a polynomial $P$ of degree $d$ that takes at most $d$ different values at members of a an arithmetic progression with $d^{2}-d+1$ (different) terms.
|
| 401 |
+
The answer to this EGMO problem implies a solution to this more general problem by scaling and translating, and the general result solves the EGMO problem as a special case. This means that instead of working with $0,1, \ldots, d^{2}-d$ we have the option of working with a region that is symmetric about the origin. Irrespective of the parity of $d$ we can use the $d^{2}-d+1$ integers which run from $-\left(d^{2}-d\right) / 2$ to $\left(d^{2}-d\right) / 2$ inclusive.
|
| 402 |
+
|
| 403 |
+
The advantage of using an arithmetic progression which is symmetric about the 0 is that $P(X)$ is a polynomial which works for the problem if, and only if, $P(-X)$ is a polynomial which works for the problem. This means that working at one end of the run of integers is the reflection of the activity at the other end. T Remarks dismissing the cases at the other end of the run as similar now become obviously correct rather than having to be studied separately.
|
| 404 |
+
|
| 405 |
+
Solution. We claim that such polynomials exist if and only if $d \leq 3$. The following examples show that such polynomials do exist for $d \leq 3$ :
|
| 406 |
+
|
| 407 |
+
$$
|
| 408 |
+
\left.\begin{array}{lll}
|
| 409 |
+
d=1: & d^{2}-d=0, & P_{1}(x)=x,
|
| 410 |
+
\end{array} \begin{array}{ll}
|
| 411 |
+
& P(0)=0 ;
|
| 412 |
+
\end{array}\right\}
|
| 413 |
+
$$
|
| 414 |
+
|
| 415 |
+
We can make more examples by adding constants.
|
| 416 |
+
Now we will show that there are no examples of degree greater than 3.
|
| 417 |
+
From now on we assume (without loss of generality) that the leading coefficient of our polynomial $P$ is positive and that all values $P(i)$ are positive (by adding a constant if necessary) for integers $i$ in the range $0 \leq i \leq d^{2}-d+1$.
|
| 418 |
+
|
| 419 |
+
Assume (for contradiction) that $P$ is a polynomial of degree $d \geq 4$ that satisfies the conditions of the problem and let $P(0), \ldots, P\left(d^{2}-d\right)$ take values among $p_{1}<\cdots<p_{d}$. For $i=1, \ldots, d$, let $n_{i} \geq 0$ be the number of appearances of $p_{i}$ among $P(0), \ldots, P\left(d^{2}-d\right)$.
|
| 420 |
+
|
| 421 |
+
By definition $n_{1}+\cdots+n_{d}=d^{2}-d+1$. Since $P$ has degree $d, n_{i} \leq d$. The key observation is now the following.
|
| 422 |
+
|
| 423 |
+
Claim 1 Make the convention that $n_{0}=n_{d+1}=0$. If $n_{i}=d$ for some $i$ in the range $1 \leq i \leq d$, then $n_{i \pm 1} \leq d-2$.
|
| 424 |
+
|
| 425 |
+
Proof. Up to scaling and hence without loss of generality, $P$ has leading coefficient +1 . $\overline{\text { Since }} n_{i}=d$, there exist non-negative integers $a_{1, i}<\cdots<a_{d, i} \leq d^{2}-d$ such that
|
| 426 |
+
|
| 427 |
+
$$
|
| 428 |
+
P(X)=\left(X-a_{1, i}\right) \cdots\left(X-a_{d, i}\right)+p_{i} .
|
| 429 |
+
$$
|
| 430 |
+
|
| 431 |
+
By construction, each of the $d-1$ intervals $I_{j}=\left[a_{j, i}, a_{j+1, i}\right]$ contains at least one local extremum of $P$, so contains exactly one such extremum because $P$, having degree $d$, has at most $d-1$ such extrema. Suppose that $i \leq d-1$ and that $P(m)=p_{i+1}>p_{i}$ for some $m \in\left\{0, \ldots, d^{2}-d\right\}$. Since $P$ has positive leading coefficient,
|
| 432 |
+
|
| 433 |
+
$$
|
| 434 |
+
m \in\left(a_{d, i}, \infty\right) \cup\left(a_{d-2, i}, a_{d-1, i}\right) \cup \cdots \cup\left(a_{i, 1}, a_{2, i}\right)
|
| 435 |
+
$$
|
| 436 |
+
|
| 437 |
+
if $d$ is odd or
|
| 438 |
+
|
| 439 |
+
$$
|
| 440 |
+
m \in\left(a_{d, i}, \infty\right) \cup\left(a_{d-2, i}, a_{d-1, i}\right) \cup \cdots \cup\left(-\infty, a_{1, i}\right)
|
| 441 |
+
$$
|
| 442 |
+
|
| 443 |
+
if $d$ is even.
|
| 444 |
+
Suppose that $a_{j, i}<m<a_{j+1, i}$, for some $j \in\{1, \ldots, d-1\}$. If $a_{j, i}+1<m<a_{j+1, i}-1$, then, because $I_{j}$ contains exactly one local extremum (which is a maximum),
|
| 445 |
+
|
| 446 |
+
Either $p_{i+1}=P(m)>P\left(a_{j, i}+1\right)$ or $p_{i+1}=P(m)>P\left(a_{j+1, i}-1\right)$. Since $P\left(a_{j, i}+1\right)>$ $P\left(a_{j, i}\right)=p_{i}$ and $P\left(a_{j, i}-1\right)>P\left(a_{j+1, i}\right)=p_{i}$, this contradicts the requirement that $P\left(a_{j, i}+1\right), P\left(a_{j+1, i}-1\right) \in\left\{p_{1}, \ldots, p_{d}\right\}$. Hence $m=a_{j, i}+1$ or $m=a_{j, i}-1$. Similarly, if $m>a_{d, i}$, then $m=a_{d, i}+1$, but if $m<a_{i, 1}$ (which may arise when $d$ is even), then $m=a_{i, 1}-1$. This shows that $m$ belongs to this list:
|
| 447 |
+
|
| 448 |
+
$$
|
| 449 |
+
a_{d, i}+1, a_{d-1, i}-1, \ldots, a_{2, i}+(-1)^{d}, a_{1, i}-(-1)^{d}
|
| 450 |
+
$$
|
| 451 |
+
|
| 452 |
+
This list contains at most $d$ different integers. It follows in particular that, if $n_{i+1}>d-2$, then either
|
| 453 |
+
|
| 454 |
+
$$
|
| 455 |
+
P\left(a_{d, i}+1\right)=p_{i+1}=P\left(a_{d-1, i}-1\right)
|
| 456 |
+
$$
|
| 457 |
+
|
| 458 |
+
or
|
| 459 |
+
|
| 460 |
+
$$
|
| 461 |
+
P\left(a_{2, i}+(-1)^{d}\right)=p_{i+1}=P\left(a_{1, i}-(-1)^{d}\right)
|
| 462 |
+
$$
|
| 463 |
+
|
| 464 |
+
with, additionally, $a_{2, i}+(-1)^{d} \neq a_{1, i}-(-1)^{d}$.
|
| 465 |
+
We have
|
| 466 |
+
|
| 467 |
+
$$
|
| 468 |
+
\left|P\left(a_{1, i} \pm 1\right)-p_{i}\right|=1 \cdot\left|a_{1, i} \pm 1-a_{2, i}\right| \cdot \prod_{j=3}^{d}\left|a_{1, i} \pm 1-a_{j, i}\right|
|
| 469 |
+
$$
|
| 470 |
+
|
| 471 |
+
and
|
| 472 |
+
|
| 473 |
+
$$
|
| 474 |
+
\left|P\left(a_{2, i} \mp 1\right)-p_{i}\right|=\left|a_{2, i} \mp 1-a_{1, i}\right| \cdot 1 \cdot \prod_{j=3}^{d}\left|a_{2, i} \mp 1-a_{j, i}\right| .
|
| 475 |
+
$$
|
| 476 |
+
|
| 477 |
+
As $a_{1, i}<a_{2, i}<a_{3, i}<\ldots<a_{d, i}$ we have $\left|a_{1, i} \pm 1-a_{j, i}\right| \geq\left|a_{2, i} \mp 1-a_{j, i}\right|$ with equality possible only if $a_{1, i}+1=a_{2, i}-1$. We also have $\left|a_{1, i} \pm 1-a_{2, i}\right|=\left|a_{2, i} \mp 1-a_{1, i}\right|$, which can be zero only if $a_{1, i}+1=a_{2, i}-1$. We conclude that $\left|P\left(a_{1, i} \pm 1\right)-p_{i}\right|>\left|P\left(a_{2, i} \mp 1\right)-p_{i}\right|$ or $a_{1, i}+1=a_{2, i}-1$.
|
| 478 |
+
|
| 479 |
+
Looking at the other end of the list of $\left(a_{j, i}\right)$ as $j$ varies, we have
|
| 480 |
+
|
| 481 |
+
$$
|
| 482 |
+
\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|=1 \cdot\left|a_{d-1, i}-1-a_{d, i}\right| \cdot \prod_{j=1}^{d-2}\left|a_{d-1, i}-1-a_{j, i}\right|
|
| 483 |
+
$$
|
| 484 |
+
|
| 485 |
+
and
|
| 486 |
+
|
| 487 |
+
$$
|
| 488 |
+
\left|P\left(a_{d, i}+1\right)-p_{i}\right|=\left|a_{d, i}+1-a_{d-1, i}\right| \cdot 1 \cdot \prod_{j=1}^{d-2}\left|a_{d, i}+1-a_{j, i}\right|
|
| 489 |
+
$$
|
| 490 |
+
|
| 491 |
+
In these two formulas the shared factor outside the product is at least 2 and so is not 0 . Now look at the factors behind the product symbols. As $a_{1, i}<a_{2, i}<a_{3, i}<\ldots<a_{d, i}$, for $j \leq d-2$ we have $\left|a_{d, i}+1-a_{j, i}\right|>\left|a_{d-1, i}-1-a_{j, i}\right|$. We conclude that $\left|P\left(a_{d, i}+1\right)-p_{i}\right|>$ $\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|$. Claim 1 is proved.
|
| 492 |
+
|
| 493 |
+
For each $i \in\{1, \ldots, d-1\}$, there are three possibilities:
|
| 494 |
+
|
| 495 |
+
- $n_{i}, n_{i+1} \leq d-1$
|
| 496 |
+
- $n_{i}=d$ and $n_{i+1} \leq d-2$
|
| 497 |
+
- $n_{i+1}=d$ and $n_{i} \leq d-2$.
|
| 498 |
+
|
| 499 |
+
In all three cases, $n_{i}+n_{i+1} \leq 2(d-1)$. If $n$ is even, this leads to the contradiction
|
| 500 |
+
|
| 501 |
+
$$
|
| 502 |
+
d^{2}-d+1=\left(n_{1}+n_{2}\right)+\cdots+\left(n_{d-1}+n_{d}\right) \leq(d / 2)[2(d-1)]=d^{2}-d
|
| 503 |
+
$$
|
| 504 |
+
|
| 505 |
+
This is an important staging point in the argument because we have eliminated the possibility of a polynomial of even degree $d$ satisfying the conditions of the problem if $d \geq 4$.
|
| 506 |
+
|
| 507 |
+
From now on we assume that $d \geq 5$ is odd, and
|
| 508 |
+
$d^{2}-d+1=\left(n_{1}+n_{2}\right)+\cdots+\left(n_{d-2}+n_{d-1}\right)+n_{d} \leq[(d-1) / 2][2(d-1)]+d=d^{2}-d+1$.
|
| 509 |
+
Equality must therefore hold throughout. Since the sum can also be grouped as
|
| 510 |
+
|
| 511 |
+
$$
|
| 512 |
+
n_{1}+\left(n_{2}+n_{3}\right)+\cdots+\left(n_{d-1}+n_{d}\right)
|
| 513 |
+
$$
|
| 514 |
+
|
| 515 |
+
this requires $n_{1}=n_{d}=d, n_{i}+n_{i+1}=2(d-1)$ for $i=1,2, \ldots, d-1$ i.e. $n_{i}=d$ for odd $i$ and $n_{i}=d-2$ for even $i$.
|
| 516 |
+
|
| 517 |
+
We are interested in the degree of $P$ being $d \geq 5$ and odd, and showing that no polynomial $P$ satisfying the conditions of the problem can exist. There are $d-1 \geq 4$ extremal points points which alternate between local maxima and minima (in that order) as you read from left to right (we normalize so that $P$ is monic). For any $p_{i}$ with $i$ odd, the line $y=p_{i}$ (with
|
| 518 |
+
$i$ odd) crosses the graph of $P$ in $d$ places with $x$-coordinates in the real closed interval $\left[0, d^{2}-d\right]$ at points $\left(z, p_{i}\right)$ so each $z$ must be an integer. Suppose that $J$ is a real interval on the $x$-axis ending at adjacent local extrema. The function defined by $P$ is monotonic on each $J$. The line $y=p_{i}$ ( $i$ odd) meets the graph at most once on $J$. Therefore it meets the graph of $P$ exactly once in the interior of each $J$ (there are $d-2$ such intervals) and at the only two possible places outside the union of these intervals.
|
| 519 |
+
|
| 520 |
+
Now consider $p_{j}$ when $j$ is even (so $n_{j}=d-2$ ). These $d-2$ intervals $J$ afford $d-2$ real values at which $P$ will take $p_{j}$ as a value where $j$ is fixed and even. The question is, are the corresponding arguments integers? The proof of Claim 1 tells us that in the middle of the run $\left\{0,1, \ldots, d^{2}-d+1\right\}$ all is well: the polynomial is assuming the value $p_{j}$ at an integer where the polynomial assumes the values $p_{j-1}$ and $p_{j+1}$ at adjacent integers in some order. The problem is at the ends of the run where $\left|P\left(a_{1, i}+1\right)-p_{i}\right|>\left|P\left(a_{2, i}-1\right)-p_{i}\right|$ and $\left|P\left(a_{d, i}+1\right)-p_{i}\right|>\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|$. When $j$ is even, two of the roots of $P(x)-p_{j}$ are not integers, and we now know approximately where this trouble is happening (at the ends).
|
| 521 |
+
|
| 522 |
+
At this point we could finish if $d \geq 7$, because the run of regular behaviour in the middle is sufficiently long that we could obtain a contradiction. However we have to work a little harder to include the case $d=5$. We now show that the run of regular behaviour is slightly longer than we have currently established. We do this using Claim 2.
|
| 523 |
+
|
| 524 |
+
Claim 2. If $d$ is odd, and $n_{i}=d, n_{i \pm 1}=d-2$ for some $i$, then $P$ attains $p_{i \pm 1}$ precisely at the $d-2$ integers
|
| 525 |
+
|
| 526 |
+
$$
|
| 527 |
+
a_{2, i}-1, a_{3, i}+1, \cdots, a_{d-2, i}-1, a_{d-1, i}+1
|
| 528 |
+
$$
|
| 529 |
+
|
| 530 |
+
Proof Suppose (for contradiction) $a_{1, i}+1 \neq a_{2, i}-1$ and $P\left(a_{1, i}+1\right)=p_{i+1}$. Now $a_{1, i}<a_{2, i}$ so either $a_{1, i}+1<a_{2, i}-1$ or $a_{1, i}=a_{2, i}-1$. In the latter case, $P\left(a_{1, i}+1\right)=P\left(a_{2, i}\right)=p_{i}$, a contradiction. In the former case, the proof of Claim 1 shows that
|
| 531 |
+
|
| 532 |
+
$$
|
| 533 |
+
\left|P\left(a_{2, i}-1\right)-p_{i}\right|<\left|P\left(a_{1, i}+1\right)-p_{i}\right|=\left|p_{i+1}-p_{i}\right|=p_{i+1}-p_{i}
|
| 534 |
+
$$
|
| 535 |
+
|
| 536 |
+
so $P\left(a_{2, i}-1\right)<p_{i+1}$. The polynomial is decreasing on the interval $\left(a_{2, d}, a_{2,1}\right)$ so $p_{i}<P\left(a_{2, i}-1\right)<p_{i+1}$ which is absurd because $P\left(a_{2, i}-1\right)=p_{j}$ for some $j$. Therefore $P\left(a_{2, i}-1\right)=p_{i+1}$ for all odd $i$. A similar argument shows that $P\left(a_{d-1, i}+1\right)=p_{i+1}$ so Claim 2 is established.
|
| 537 |
+
|
| 538 |
+
Now we have n sequence of alternating falling then rising then falling etc. full runs starting at $\left(a_{2, d}, p_{d}\right)$ and ending at $\left(a_{d-1,1}, p_{1}\right)$ so the initial run of $3 d+1$ terms of this run of values is
|
| 539 |
+
|
| 540 |
+
$$
|
| 541 |
+
p_{d}, p_{d-1}, \cdots p_{1}, p_{1}, p_{2}, \ldots, p_{d}, p_{d}, p_{d-1}, \cdots p_{1}, p_{1}
|
| 542 |
+
$$
|
| 543 |
+
|
| 544 |
+
which starts at $\left(a_{2, d}, p_{d}\right)$ and ends at $\left(a_{4,1}+1, p_{1}\right)$ which is fine because $4 \leq d-1$.
|
| 545 |
+
There are now various ways we can finish.
|
| 546 |
+
(a) Consider the run of length $2 d$ consecutive values
|
| 547 |
+
|
| 548 |
+
$$
|
| 549 |
+
p_{d}, p_{d-1}, \cdots p_{1}, p_{1}, p_{2}, \ldots, p_{d}
|
| 550 |
+
$$
|
| 551 |
+
|
| 552 |
+
The first $d+1$ points determine $P(x)$. The last $d+1$ values also determine $P$ but the values are in the reverse order, so $P(X)=P(c-X)$ for some constant $c$. However, the coefficients of $X^{d}$ are have opposite signs ( $d$ is odd) so this is absurd.
|
| 553 |
+
(b) The idea in (a) can be expressed in terms of Lagrange interpolation to obtain essentially the same contradiction. Construct $P$ in two ways using Lagrange interpolation on both the first $d+1$ and the last $d+1$ points. The symmetry in the data forces the graph of $P$ to have a vertical axis of symmetry. This is absurd because the degree of $P$ is odd.
|
| 554 |
+
(c) The initial fragment length $3 d+1$ mentioned above at $(*)$ includes two identical runs of values of $P$ (in the same order) of length $d+1$. The polynomial $P$ is determined by each of them and so $P(X)=P(X+c)$ for some constant $c$ and so the polynomial defines a bounded function which is absurd.
|
| 555 |
+
|
EGMO/raw/en-2012-solutions-day1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:7af6fb30ad456584fdb879a3ffd19f1ebda7eac4b7d203e787dbb64a27e3e41d
|
| 3 |
+
size 163099
|
EGMO/raw/en-2012-solutions-day2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c04677fc8c3750d88c3b301429e39a65017c49525399ccfcdd745c2905931bbb
|
| 3 |
+
size 188147
|
EGMO/raw/en-2013-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:a424b3a76ed996208a7539cfd656a2042ba832001253e773ce94a002113c5754
|
| 3 |
+
size 364830
|
EGMO/raw/en-2014-solutions-day1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:6fdf113d212644571067b65a1a29f62031a3753889454f28377daebc06de5dbf
|
| 3 |
+
size 1371035
|
EGMO/raw/en-2014-solutions-day2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:f2087a1c703b631465e6484f424056a2438dae6686456923cf936cc83f0be80e
|
| 3 |
+
size 686064
|
EGMO/raw/en-2015-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:fce3f464522a758d577043e283698a83e3a7e53d49455dcb1c2dfe215fcb554c
|
| 3 |
+
size 137262
|
EGMO/raw/en-2016-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:5f971ec667e8d04bd0bd45912b453879d095a470bc138aaf5548b4557e095f5e
|
| 3 |
+
size 1587601
|
EGMO/raw/en-2017-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:be47094f50cf8123c9b3fa0a0f8bdd3214e53cb26440bb93925db95565b91a94
|
| 3 |
+
size 937621
|
EGMO/raw/en-2018-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:6cc7bbdafdd155d15ffc8e4e32c740506cde9406052aa146fd0829c44671668c
|
| 3 |
+
size 113499
|
EGMO/raw/en-2019-solutions-day1.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:cc22eb57da7219a3b3628c7b6a4a44df797dc1ad53c5d276fbabee0017da1ae1
|
| 3 |
+
size 590784
|
EGMO/raw/en-2019-solutions-day2.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:bc50f29dd7d2f79c728eaa1c91b2591512856c3ab8f3ab436497a35a071dd424
|
| 3 |
+
size 359162
|
EGMO/raw/en-2020-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c1edf201a1a2fa0416b908b57d052caef8756a6441de1ff9fbcf7bf8d7911fb9
|
| 3 |
+
size 1439929
|
EGMO/raw/en-2021-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3def26b50f7e7a4f0c96ea9c63249e7012147d10ddc8c5d2e6e6803bcc0a4edd
|
| 3 |
+
size 373530
|
EGMO/raw/en-2022-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:5da1f4aca14d6a000cab65f8fd8d1cfbf020add21a8a4fee536908cc5003a3cc
|
| 3 |
+
size 326694
|
EGMO/raw/en-2023-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:261dd2aa8c411f967ecd7a909b95511fc775cc382bc76036896d77f721d764c1
|
| 3 |
+
size 596918
|
EGMO/raw/en-2024-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:d6904c0f425e87b5cc557861af67a3f6fd00cb7757d8587efa2d746674596bca
|
| 3 |
+
size 337016
|