a_{j}$ si et seulement si le premier terme non nul de $a_{i}-a_{j}$ en partant de la droite est $>0$ ), avec $k=2^{d}$.\nPour passer de $a_{i}$ à $a_{i+1}$, on regarde le premier -1 en partant de la droite dans $a_{i}$, on le change par un 1 , et on remplace tous les 1 à sa droite par des -1 . Par exemple si $\\mathrm{d}=3$, les triplets sont dans l'ordre $a_{1}=(-1,-1,-1), a_{2}=(-1,-1,1), a_{3}=(-1,1,-1), a_{4}=(-1,1,1) a_{5}=(1,-1,-1), a_{6}=$ $(1,-1,1), a_{7}=(1,1,-1)$ et $a_{8}=(1,1,1)$.\nOn associe à $a_{i}=\\left(a_{i 1}, \\ldots, a_{i d}\\right)$ le polynôme $P_{i}(X)=\\sum_{j=1}^{d} a_{i j} X^{j-1}$, de telle sorte que $M:=-P_{1}(t)=$ $P_{k}(t)=1+\\ldots+t^{d-1}>d$.\nOr $\\left|P_{i+1}(t)-P_{i}(t)\\right|=2\\left|t^{\\mathrm{l}}-\\left(1+\\ldots+t^{\\mathrm{l}-1}\\right)\\right|$ pour un certain $l \\geqslant 0$ (qui dépend de $i$ ) pour tout $i$.\nMontrons $t^{\\mathrm{l}}-\\left(1+\\ldots+\\mathrm{t}^{\\mathrm{l}-1}\\right) \\leqslant 1$ : cela équivaut à $\\mathrm{t}^{\\mathrm{l}+1}-\\mathrm{t}^{\\mathrm{l}}-\\left(\\mathrm{t}^{\\mathrm{l}}-1\\right) \\leqslant \\mathrm{t}-1$ après multiplication par $t-1$, soit après réarrangement $t^{l}(2-t)+t \\geqslant 2$, ce qui est vrai car $t^{l} \\geqslant 1$.\nDès lors, $P_{i+1}(t)$ est plus grand que $P_{i}(t)$ d'au plus 2 , ce qui montre que, puisque $2019-t^{d} \\in[-M ; M]$, il existe $i$ tel que $\\left|P_{i}(t)-\\left(2019-t^{d}\\right)\\right| \\leqslant 1$, ce qui conclut en posant $P=X^{d}+P_{i}$\nCommentaire des correcteurs Les copies reçues étaient globalement bonnes. Cependant, la plupart des élèves oublient des éléments de rédactions importants. Quelques élèves ont proposé une preuve algorithmique alternative très jolie.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 16.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\n(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))\n$$", "solution": "de l'exercice 17 Clairement, $f(x)=x$ est une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\n(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))\n$$", "solution": "; on va montrer que c'est la seule. On pose dans la suite $a=f(0)$.\nAvec $y=0$ on a $\\mathbf{f}(\\mathbf{f}(\\boldsymbol{x}(\\mathrm{x}+1)))=\\mathbf{f}(\\mathrm{x})(\\mathbf{f}(\\mathrm{x})+1)(*)$ pour tout x .\nSi on prend $y=-f(x)$ on voit que la fonction $f$ admet des zéros.\nDès lors pour exploiter $(*)$ il est intéressant de choisir y tel que $f(f(x f(x+1))-y f(y-1))=f(f(x f(x+$ $1))$ ), ce qui est possible en prenant $y=z+1$ avec $f(z)=0$. On a alors $(f(x)+z+1)(f(x-z)+1)=$ $f(x)(f(x)+1)$, ce qui se simplifie avec $x=z:(z+1)(f(-1)+1)=0$.\nSi $z=-1$, on a $f(-1)=0$, donc avec $x=0, y=1$, on a $a+1=a$, une évidente contradiction.\nOn a donc montré $f(-1)=-1$. On reprend $x=0, y=1$ pour avoir $f(0)=0$. Dès lors $y=1$ dans l'équation montre que $(f(x)+1)(f(x-1)+1)=f(x)(f(x)+1)$ (1) d'après $(*)$.\n$x=0$ puis $x=-1$ dans l'équation originelle donne $y(f(-y)+1)=(y-1)(f(-y-1)+1)$ (2). Ainsi, si on avait $\\left(1^{\\prime}\\right): f(x)=f(x-1)+1$, on pourrait déduire de (2) $y(f(-y)+1)=(y-1) f(-y)$, puis $f(-y)=-y$, ce qui montrerait que $f$ est l'identité.\nPour montrer $\\left(1^{\\prime}\\right)$, commençons par prouver que $f(x)=0 \\Longleftrightarrow x=0$.\nSoit $t$ tel que $f(t)=0$; d'après (1), on a $f(t-1)=-1$. (2) donne alors, avec $y=-t, t=0$, comme voulu.\nMontrons à présent $f(x)=-1 \\Longleftrightarrow x=-1$.\nSi $f(t)=-1,(*)$ donne $f(f(t f(t+1)))=0$ donc $t f(t+1)=0$. Or $t \\neq 0$ car $f(0) \\neq-1$, donc $f(t+1)=0$ et ainsi $t=-1$ comme voulu.\nPour montrer ( $1^{\\prime}$ ) d'après (1), il suffit donc de voir que $f(-2)=f(-1)-1=-2$. Or $\\boldsymbol{f}(2)=2$ en utilisant (1) donc $(*)$ avec $x=-2$ donne $2=f(-2)+f(-2)^{2}$ et donc $f(-2) \\in\\{-2,1\\}$. Mais si $f(-2)=1$, (1) donne $f(-3)=0$, impossible d'après ce qu'on a montré. Cela conclut la preuve de ( $1^{\\prime}$ ) et donc la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\n(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))\n$$", "solution": "Commentaire des correcteurs L'exercice était assez délicat. Quelques élèves courageux ont avancé de façon substantielle dans le problème, voire même l'ont résolu complètement. Plusieurs élèves se sont contentés de vérifier que la fonction identité était", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\n(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))\n$$", "solution": ", mais cela ne rapportait aucun point. En revanche, des élèves ont montré que si f est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\n(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))\n$$", "solution": "alors f est l'identité mais ont oublié de signaler que réciproquement l'identité était", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\n(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))\n$$", "solution": "Ces élèves ont alors perdu un point, conformément à l'usage en compétition.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soient $\\mathrm{P}, \\mathrm{Q}$ deux polynômes à coefficients réels, non constants et premiers entre eux. Montrer qu'il existe au plus trois réels $\\lambda$ tels que:\n\n$$\nP+\\lambda Q=R^{2}\n$$\n\noù $R \\in \\mathbb{R}[X]$.", "solution": "de l'exercice 18 On procède par l'absurde en supposant l'existence de quatre réels distincts $\\lambda_{1}, \\ldots, \\lambda_{4}$ et quatre polynômes $R_{1}, \\ldots, R_{4}$ tels que $P+\\lambda_{i} Q=R_{i}^{2}$ pour $i=1,2,3,4$.\nOn a $P^{\\prime}+\\lambda_{i} Q^{\\prime}=2 R_{i} R_{i}^{\\prime}$ et donc $R_{i} \\mid Q^{\\prime}\\left(P+\\lambda_{i} Q\\right)-Q\\left(P^{\\prime}+\\lambda_{i} Q^{\\prime}\\right)=P Q^{\\prime}-Q^{\\prime}$.\nRemarquons que si $T \\mid R_{i}, R_{j}$ alors $T \\mid R_{i}^{2}-R_{j}^{2}=\\left(\\lambda_{i}-\\lambda_{j}\\right) Q$ puis $T \\mid R_{i}^{2}-\\lambda_{i} Q=P$ et donc $T$ est constant, car $\\mathrm{P}, \\mathrm{Q}$ sont premiers entre eux.\nDès lors les $R_{i}$ sont deux à deux premiers entre eux et ainsi $R_{1} R_{2} R_{3} R_{4} \\mid P Q^{\\prime}-P^{\\prime} Q$.\nSoient $A, B$ des polynômes non nuls ; le degré de $A+\\lambda B$, si $\\lambda \\in \\mathbb{R}$, est égal à $\\max \\{\\operatorname{deg}(A), \\operatorname{deg}(B)\\}$, sauf si $\\operatorname{deg}(A)=\\operatorname{deg}(B)$ et $\\lambda=-\\frac{a}{b}$ où $a, b$ sont les coefficients dominants de $A$ et $B$ respectivement, auquel cas il est plus petit.\nSi $A=P$ et $B=Q$, cela montre que, soit $\\operatorname{deg} R_{i}=\\frac{1}{2} \\max \\{\\operatorname{deg}(P), \\operatorname{deg}(Q)\\}$ pour tout $i$, et donc que $\\operatorname{deg}\\left(R_{1} R_{2} R_{3} R_{4}\\right)=2 \\max \\operatorname{deg}\\{P, Q\\}>\\operatorname{deg}(P)+\\operatorname{deg}(Q)-1 \\geqslant \\operatorname{deg}\\left(P Q^{\\prime}-P^{\\prime} Q\\right)$, soit il y a un $R_{i}$, tel que $\\operatorname{deg}\\left(R_{i}\\right)<\\operatorname{deg}\\left(R_{j}\\right)$ pour $j \\neq i ;$ alors pour $A=P+\\lambda_{i} Q=: P_{1}$ et $B=Q$ on voit que $\\operatorname{deg}\\left(R_{i}\\right)=\\frac{1}{2} \\operatorname{deg}\\left(P_{1}\\right)$ et $\\operatorname{deg} R_{j}=\\frac{1}{2} \\max \\left\\{\\operatorname{deg}\\left(P_{1}\\right), \\operatorname{deg}(Q)\\right\\}$ et $\\operatorname{donc} \\operatorname{deg}\\left(R_{1} R_{2} R_{3} R_{4}\\right)=\\frac{3}{2} \\max \\left\\{\\operatorname{deg}\\left(P_{1}\\right), \\operatorname{deg}(Q)\\right\\}+\\frac{1}{2} \\operatorname{deg}\\left(P_{1}\\right)>$ $\\operatorname{deg}(\\mathrm{Q})+\\operatorname{deg}\\left(\\mathrm{P}_{1}\\right)-1 \\geqslant \\operatorname{deg}\\left(\\mathrm{P}_{1} \\mathrm{Q}^{\\prime}-\\mathrm{P}_{1}^{\\prime} \\mathrm{Q}\\right)=\\operatorname{deg}\\left(\\mathrm{PQ}^{\\prime}-\\mathrm{P}^{\\prime} \\mathrm{Q}\\right)$.\nPar un argument sur les degrés, on a donc nécessairement $P Q^{\\prime}-P^{\\prime} Q=0$ et ainsi $P \\mid P^{\\prime} Q$. Or $P$ et $Q$ sont premiers entre eux donc $P \\mid P^{\\prime}$, ce qui est une évidente contradiction à $P$ non constant.\nCommentaire des correcteurs Les copies reçues étaient d'un très bon niveau (à part quelques petites erreurs). Etant donné la grande difficulté supposée de l'exercice, c'était une agréable surprise!", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": "\nSolution "}}
diff --git "a/French_STS/segmented/fr-corrig\303\251-commentaire-envoi-1.jsonl" "b/French_STS/segmented/fr-corrig\303\251-commentaire-envoi-1.jsonl"
new file mode 100644
index 0000000000000000000000000000000000000000..fedb13556cbfd989c303495ea06f64c34e1ece17
--- /dev/null
+++ "b/French_STS/segmented/fr-corrig\303\251-commentaire-envoi-1.jsonl"
@@ -0,0 +1,24 @@
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soit $A B C D$ un quadrilatère et $M, N, P, Q$ les milieux respectifs de $[A B],[B C],[C D]$, [DA].\nMontrer que le quadrilatère MNPQ est un parallélogramme.\n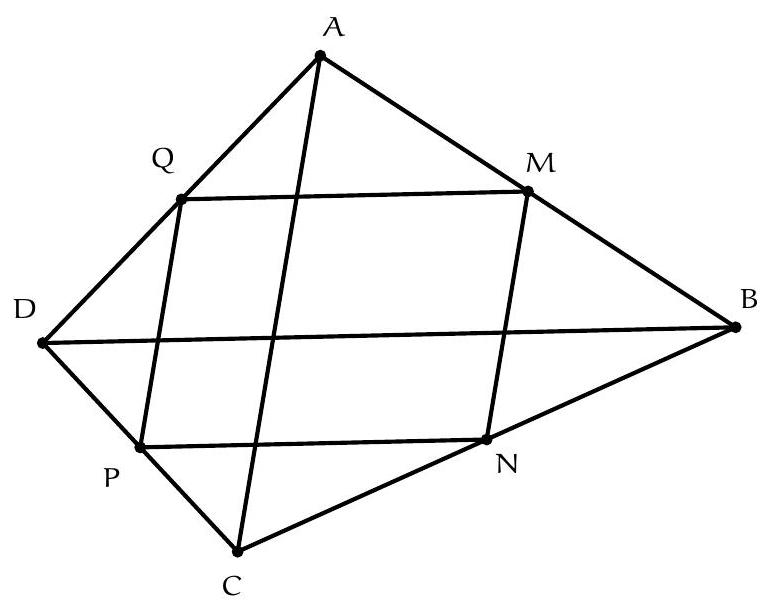", "solution": "de l'exercice 1 Puisque les points $M$ et $N$ sont les milieux respectifs des côtés $[A B]$ et $[B C]$, les droites (MN) et ( $A C$ ) sont parallèles. Puisque les points $P$ et $Q$ sont les milieux respectifs des côtés $[C D]$ et $[D A]$, les droites $(P Q)$ et ( $A C$ ) sont parallèles. Donc les droites ( $P Q)$ et $(M N)$ sont parallèles. On obtient de la même façon que les droites (NP) et (MQ) sont parallèles. Donc les côtés opposés deux à deux du quadrilatère MNPQ sont parallèles, ce qui en fait un parallélogramme.\nCommentaire des correcteurs L'exercice est bien traité.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $A B C$ un triangle rectangle en $B$. Soit $M$ le point d'intersection de la médiane issue de $B$ avec la droite (AC), et (d) la perpendiculaire à la droite (BC) passant par le point $M$. Soit $U$ le milieu du segment $[A B]$, V le milieu du segment [AM], I le point d'intersection de la droite (UV) avec la droite (d), et J le point d'instersection de la droite (UV) avec la droite (BC).\n\nMontrer que $A C=I J$.\n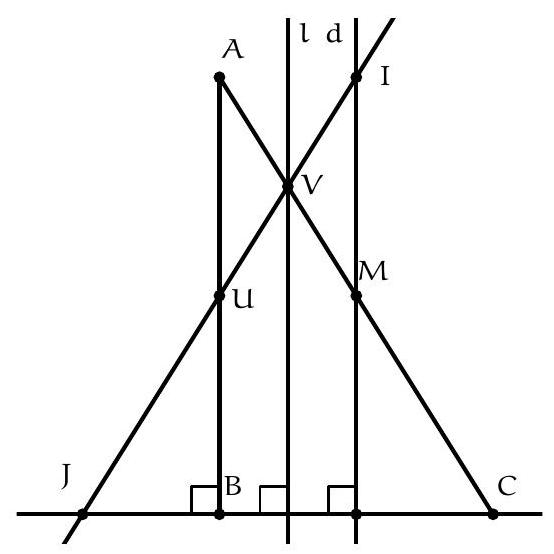", "solution": "de l'exercice 2 Les droites d et ( AB ) sont perpendiculaires à la droite ( BC ) donc elles sont parallèles. On obtient par le théorème de Thalès que $\\frac{V I}{V U}=\\frac{A V}{V M}=1$ donc $V$ est le milieu du segment [UI]. Le quadrilatère $A I M U$ a ses diagonales qui se coupent en leur milieu, c'est donc un parallélogramme. Les points $U$ et $M$ sont les milieux respectifs des segments $[A B]$ et $[A C]$ donc les droites (UM) et (BC) sont parallèles. Donc la droite (UM) est perpendiculaire au segment $[A B]$ et le quadrilatère AIMU est un rectangle.\nSoit l la droite perpendiculaire au segment [BC] passant par V. Cette droite est la médiatrice du segment $[\\mathrm{UM}]$ et du segment $[\\mathrm{AI}]$ donc le point $U$ est le symétrique du point $M$ par rapport à la droite $l$ et le point $A$ est le symétrique du point I par rapport à la droite $l$ donc la droite $(A M)$ est la symétrique de la droite (UI) par rapport à la droite $l$. Puisque la droite $(B C)$ est sa propre symétrique par rapport à la droite $l$, le point d'intersection de la droite (BC) avec la droite (UI) est le symétrique du point d'intersection de la droite $(A M)$ avec la droite $B C$ donc les points C et J sont symétriques par rapport à la droite l . La symétrie conserve les longueurs, donc $A C=I J$.\nCommentaire des correcteurs Même si l'argument semblait facile pour certains, on attendait une vraie justification, avec par exemple le théorème de Thalès. Attention à quelques confusions : une droite est bien la bissectrice d'un angle ou la médiatrice d'un segment, et non par exemple la bissectrice d'un segment.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soient $d_{1}, d_{2}, d_{3}$ des droites concourantes et $A, A^{\\prime}$ des points sur la droite $d_{1}, B, B^{\\prime}$ des points sur la droite $d_{2}, C, C^{\\prime}$ des points sur la droite $d_{3}$ tels que les droites $(A B)$ et $\\left(A^{\\prime} B^{\\prime}\\right)$ sont parallèles et les droites ( BC ) et ( $\\mathrm{B}^{\\prime} \\mathrm{C}^{\\prime}$ ) sont parallèles.\nMontrer que les droites $(A C)$ et $\\left(A^{\\prime} C^{\\prime}\\right)$ sont parallèles.\n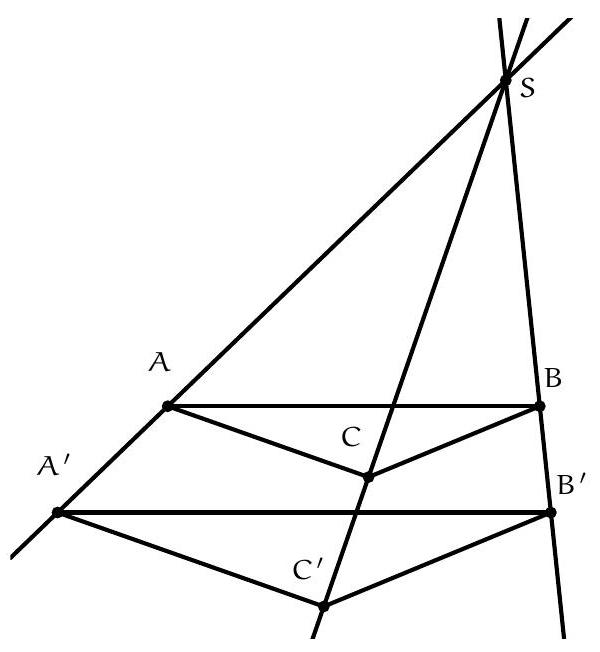", "solution": "de l'exercice 3 Soit $S$ le point de concours des trois droites. Puisque les droites $(A B)$ et $\\left(A^{\\prime} B^{\\prime}\\right)$ sont parallèles, d'après le théorème de Thalès,\n\n$$\n\\frac{A S}{A^{\\prime} S}=\\frac{B S}{B^{\\prime} S}\n$$\n\nDe même on trouve\n\n$$\n\\frac{B S}{B^{\\prime} S}=\\frac{C S}{C^{\\prime} S}\n$$\n\nOn déduit que\n\n$$\n\\frac{A S}{A^{\\prime} S}=\\frac{C S}{C^{\\prime} S}\n$$\n\nce qui signifie, d'après le théorème de Thalès, que les droites $(A C)$ et $\\left(A^{\\prime} C^{\\prime}\\right)$ sont parallèles. Commentaire des correcteurs L'exercice est bien réussi, la plupart des élèves ont remarqué l'utilisation du théorème de Thalès. attention à prendre en compte toutes les configurations, notemment les ordres possibles pour les sommets $A, B$ et $C$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C$ un triangle isocèle et obtus en $A$. Soit $\\Gamma$ le cercle de centre $B$ passant par $A$, et $\\Omega$ le cercle de centre $C$ passant par $A$. Soit $D$ le point d'intersection du cercle $\\Gamma$ avec le segment $[B C]$, E le deuxième point d'intersection de la droite (AD) avec le cercle $\\Omega$, et $F$ le point d'intersection de la droite (BC) avec le cercle $\\Omega$ qui n'est pas sur le segment $[B C]$.\nMontrer que le triangle DFE est isocèle en $F$.\n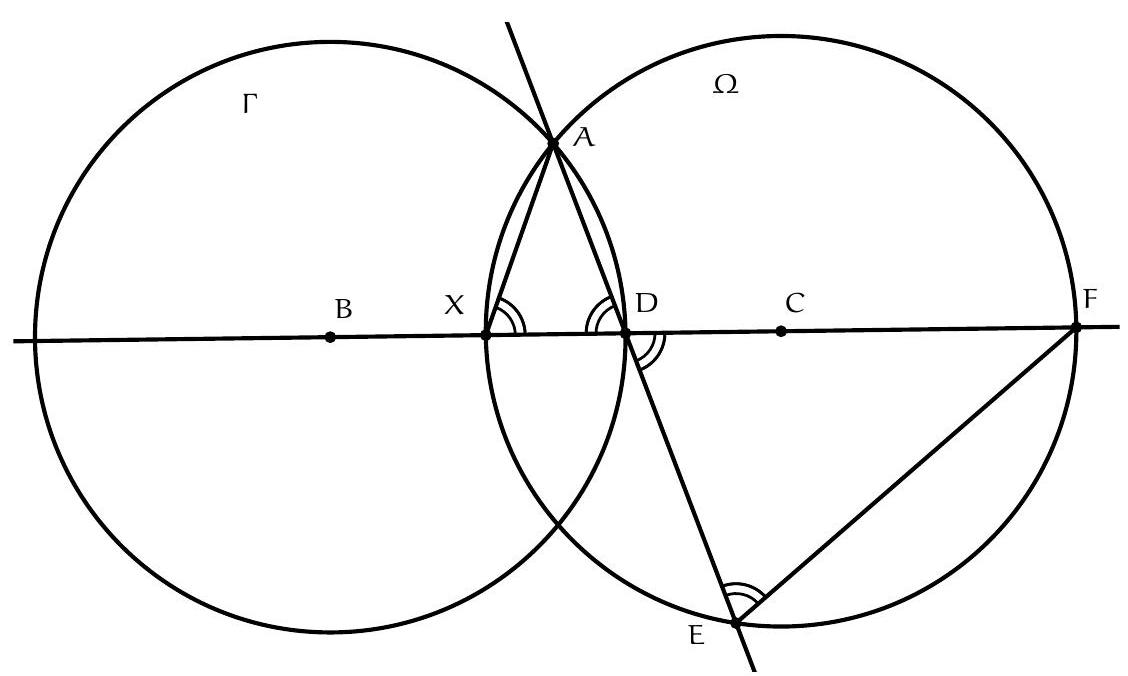", "solution": "de l'exercice 4 Soit $X$ le point d'intersection du cercle $\\Omega$ avec le segment [BC]. Les points $B$ et C sont symétriques par rapport à la médiatrice du segment $[\\mathrm{BC}]$ donc les cercles $\\Gamma$ et $\\Omega$ le sont aussi. Il vient que D et $X$ sont symétriques par rapport à la médiatrice du segment $[\\mathrm{BC}]$. Le triangle DAX est donc isocèle en $A$ et $\\widehat{A D X}=\\widehat{A X D}$.\nLes points $F, E, X$ et $A$ sont cocycliques donc $\\widehat{F E A}=\\widehat{F X A}$. On déduit\n\n$$\n\\widehat{\\mathrm{FED}}=\\widehat{\\mathrm{FEA}}=\\widehat{\\mathrm{FXA}}=\\widehat{\\mathrm{DXA}}=\\widehat{\\mathrm{XDA}}=\\widehat{\\mathrm{FDE}}\n$$\n\nCe qui donne bien que le triangle FDE est isocèle en F .\nCommentaire des correcteurs Certains élèves ont noté des symétries dans la figure, mais il fallait veiller à la justifier de façon rigoureuse.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit $\\Gamma$ un cercle, $P$ un point à l'extérieur du cercle. Les tangentes au cercle $\\Gamma$ passant par le point $P$ sont tangentes au cercle $\\Gamma$ en $A$ et $B$. Soit $M$ est le milieu du segment [BP] et $C$ le point d'intersection de la droite ( $A M$ ) et du cercle $\\Gamma$. Soit D la deuxième intersection de la droite ( PC ) et du cercle $\\Gamma$.\nMontrer que les droites $(A D)$ et $(B P)$ sont parallèles.\n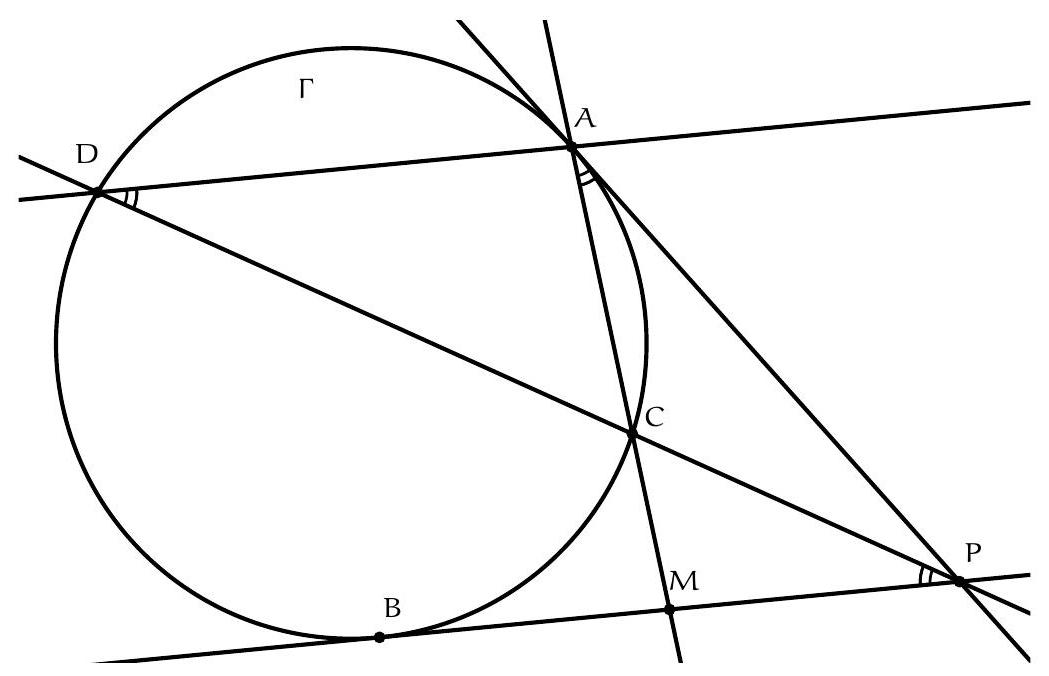", "solution": "de l'exercice 5\n En utilisant la puissance du point $M$ par rapport au cercle $\\Gamma, \\mathrm{MB}^{2}=M C \\cdot M A$. Puisque $M$ est le milieu du segment $[B P], M P^{2}=M B^{2}$ donc $M P^{2}=M C \\cdot M A$. On déduit de la réciproque de la puissance d'un point par rapport à un cercle que la droite ( PM ) est tangente au cercle circonscrit au triangle PAC. On obtient du théorème de l'angle tangent que $\\widehat{M P C}=\\widehat{P A C}$. Or la droite $(\\mathrm{PA})$ est tangente au cercle $\\Gamma$ donc à nouveau par le théorème de l'angle tangent, $\\widehat{\\mathrm{PAC}}=\\widehat{\\mathrm{ADC}}$. En résumé :\n\n$$\n\\widehat{\\mathrm{BPD}}=\\widehat{M P C}=\\widehat{\\mathrm{PAC}}=\\widehat{A D C}=\\widehat{A D P}\n$$\n\ndonc les droites $(A D)$ et (BP) sont parallèles.\nCommentaire des correcteurs Quelques démonstrations proposées étaient fausses. Une bonne façon de vérifier que sa démonstration est correcte est de vérifier qu'on a utilisé toutes les hypothèses. Plusieurs élèves n'utilisent à aucun moment que le point $M$ est le milieu du segment [PB], ce qui est pourtant une hypothèse cruciale. Attention à se relire pour éviter des erreurs typographiques comme écrire un angle ou un triangle à la place d'un autre.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $A, B, C$ et $D$ quatre points sur un cercle dans cet ordre. Soit $U$ le point d'intersection des droites $(A B)$ et (CD), et $V$ le point d'intersection des droites (BC) et ( $D A$ ). Soit $K$ le point d'intersection de la bissectrice issue de U dans le triangle AUC et de la bissectrice issue de V dans le triangle $A V C$. Soit L le point d'intersection de la médiatrice du segment $[\\mathrm{KU}]$ et de la médiatrice du segment [KV].\nMontrer que les points $\\mathrm{U}, \\mathrm{V}$ et L sont alignés.\n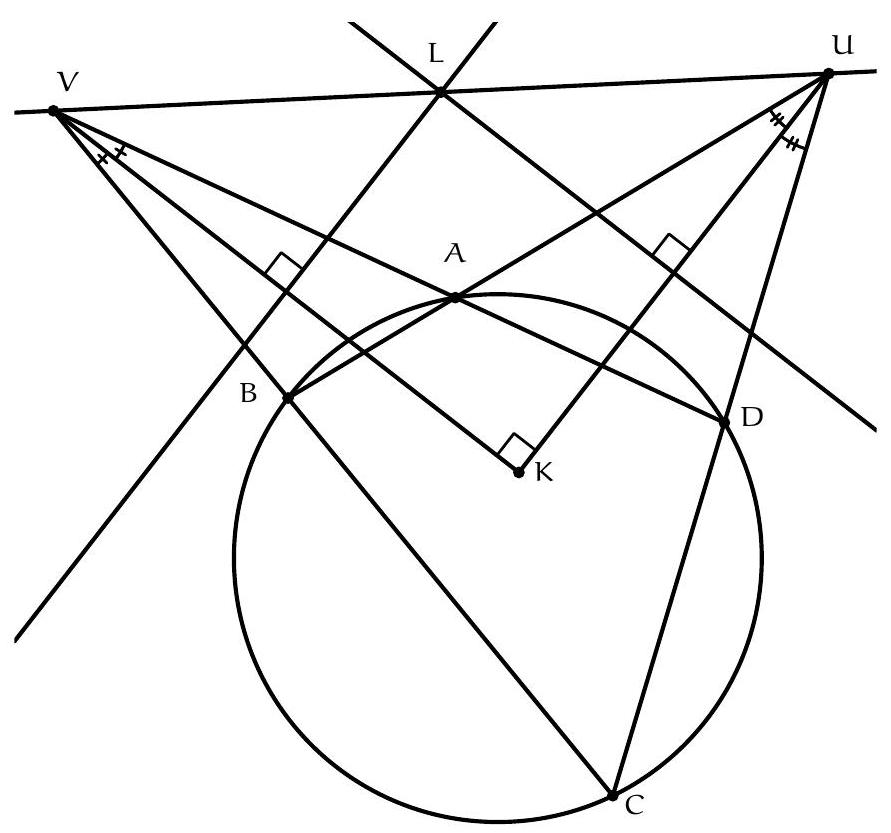", "solution": "de l'exercice 6 Le point L est le centre du cercle circonscrit au triangle UKV. Pour montrer que les points U, L et V sont alignés, il suffit de montrer que $\\widehat{U L V}=180^{\\circ}$. Par le théorème de l'angle au centre, $\\widehat{U K V}=\\frac{1}{2} \\widehat{U L V}$. Il suffit donc de montrer que $\\widehat{U K V}=90^{\\circ}$.\nLa somme des angles du triangle UKV vaut $180^{\\circ}$, donc il suffit de montrer que $\\widehat{\\mathrm{KUV}}+\\widehat{\\mathrm{KVU}}=90^{\\circ}$. D'une part $\\widehat{K U V}=\\widehat{C U V}-\\widehat{K U C}=\\widehat{C U V}-\\frac{1}{2} \\widehat{B U C}$. Or $\\widehat{B U C}=180^{\\circ}-\\widehat{U B C}-\\widehat{B C U}=\\widehat{A D C}-\\widehat{U C B}$. On déduit\n\n$$\n\\widehat{\\mathrm{KUV}}=\\widehat{\\mathrm{CUV}}-\\frac{1}{2} \\widehat{\\mathrm{ADC}}+\\frac{1}{2} \\widehat{\\mathrm{UCB}}\n$$\n\nDe la même manière, on obtient\n\n$$\n\\widehat{\\mathrm{KVU}}=\\widehat{\\mathrm{CVU}}-\\frac{1}{2} \\widehat{\\mathrm{CBA}}+\\frac{1}{2} \\widehat{\\mathrm{VCD}}\n$$\n\nOr $\\widehat{C B A}+\\widehat{A D C}=180^{\\circ}$ et\n\n$$\n\\widehat{U C B}=\\widehat{V C D}=\\widehat{U C V}=180^{\\circ}-\\widehat{C U V}-\\widehat{C V U}\n$$\n\nFinalement\n\n$$\n\\begin{aligned}\n& \\widehat{\\mathrm{KUV}}+\\widehat{\\mathrm{KVU}}=\\widehat{\\mathrm{CUV}}-\\frac{1}{2} \\widehat{\\mathrm{ADC}}+\\frac{1}{2} \\widehat{\\mathrm{UCB}}+\\widehat{\\mathrm{CVU}}-\\frac{1}{2} \\widehat{\\mathrm{CBA}}+\\frac{1}{2} \\widehat{\\mathrm{VCD}} \\\\\n& =\\widehat{\\mathrm{CUV}}+\\widehat{\\mathrm{CVU}}-\\frac{1}{2} \\cdot 180^{\\circ}+2 \\cdot \\frac{1}{2} \\cdot\\left(180^{\\circ}-\\widehat{\\mathrm{CUV}}-\\widehat{\\mathrm{CVU}}\\right)=90^{\\circ}\n\\end{aligned}\n$$\n\nce qui donne le résultat voulu.\nCommentaire des correcteurs L'exercice a été plutôt bien résolu. Attention à bien s'assurer que tout ce que l'on affirme est justifié. On a pu noté certaines affirmations fausses. Par exemple, contrairement à ce que certains élèves ont affirmé, un quadrilatère dont les deux angles opposés sont droits n'est pas forcément un rectangle.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Deux cercles de centres respectifs B et C et de rayons différents sont tangents extérieurement en un point $A$. Soit $t$ une tangente commune aux deux cercles ne contenant pas le point $A$. La perpendiculaire à la droite $t$ passant par le point $A$ coupe la médiatrice du segment $[B C]$ en un point $F$. Montrer que $B C=2 A F$.\n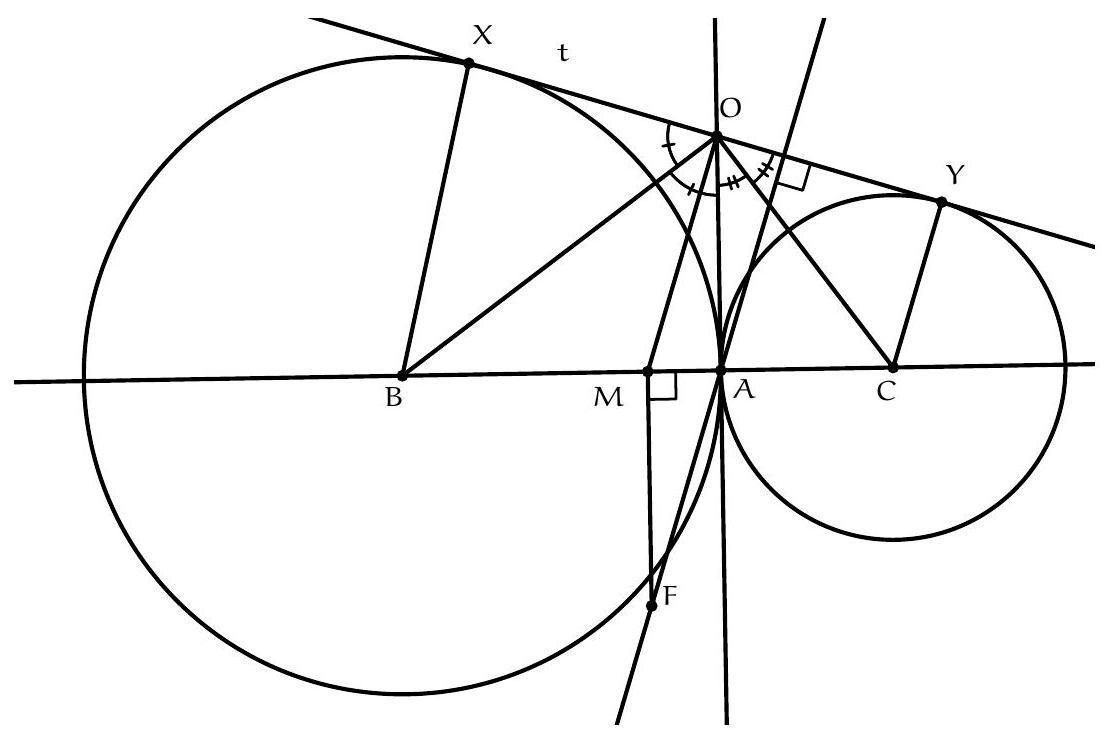", "solution": "de l'exercice 7 Soient $X$ et $Y$ les points de tangences de $t$ avec les cercles de centre B et $C$ respectivement. Soit $O$ le point d'intersection la droite $t$ avec la tangente commune au deux cercles en $A$. Les points $X$ et $A$ sont symétriques para rapport à la droite $(O B)$ et les points $Y$ et $A$ sont symétriques par rapport à la droite $(\\mathrm{OC})$. On déduit $\\widehat{\\mathrm{BOA}}=\\frac{1}{2} \\widehat{\\mathrm{XOA}}$ et $\\widehat{\\mathrm{COA}}=\\frac{1}{2} \\widehat{\\mathrm{YOA}}$. On en déduit :\n\n$$\n\\widehat{\\mathrm{BOC}}=\\widehat{\\mathrm{BOA}}+\\widehat{\\mathrm{AOC}}=\\frac{1}{2} \\widehat{\\mathrm{XOA}}+\\frac{1}{2} \\widehat{\\mathrm{AOY}}=\\frac{1}{2} \\widehat{\\mathrm{XOY}}=90^{\\circ}\n$$\n\nSoit $M$ le milieu de $[B C]$. Le triangle $B O C$ est rectangle $O$ donc $M$ est le centre du cercle circonscrit à ce triangle. Ceci donne $M O=M B=\\frac{1}{2} B C$. Comme les droites $(O A)$ et ( $M F$ ) sont perpendiculaires à la droite (BC), elles sont donc parallèles. Enfin,\n\n$$\n\\widehat{M O Y}=\\widehat{M O C}+\\widehat{C O Y}=\\widehat{M C O}+\\widehat{A O C}=90^{\\circ}\n$$\n\ndonc les droites $(\\mathrm{OM})$ et ( AF ) sont perpendiculaires à la droite $t$ donc elles sont parallèles. Donc le quadrilatère OMFA est un parallélogramme et $\\mathrm{BC}=2 \\mathrm{OM}=2 A \\mathrm{~F}$.\nCommentaire des correcteurs On a pu constaté plusieurs", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Deux cercles de centres respectifs B et C et de rayons différents sont tangents extérieurement en un point $A$. Soit $t$ une tangente commune aux deux cercles ne contenant pas le point $A$. La perpendiculaire à la droite $t$ passant par le point $A$ coupe la médiatrice du segment $[B C]$ en un point $F$. Montrer que $B C=2 A F$.\n", "solution": "s intéressantes. L'exercice nécessitait plusieurs initiatives, ainsi plusieurs", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Deux cercles de centres respectifs B et C et de rayons différents sont tangents extérieurement en un point $A$. Soit $t$ une tangente commune aux deux cercles ne contenant pas le point $A$. La perpendiculaire à la droite $t$ passant par le point $A$ coupe la médiatrice du segment $[B C]$ en un point $F$. Montrer que $B C=2 A F$.\n", "solution": "s étaient incomplètes. Quelques élèves ont tenté une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Deux cercles de centres respectifs B et C et de rayons différents sont tangents extérieurement en un point $A$. Soit $t$ une tangente commune aux deux cercles ne contenant pas le point $A$. La perpendiculaire à la droite $t$ passant par le point $A$ coupe la médiatrice du segment $[B C]$ en un point $F$. Montrer que $B C=2 A F$.\n", "solution": "calculatoire. Les calculs étaient alors souvent trop laborieux et chargés de notations un peu lourdes.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle acutangle non isocèle en $A$. Soit $M$ le milieu du segment $[B C], H$ l'orthocentre du triangle $A B C, O_{1}$ le milieu du segment $[A H]$ et $O_{2}$ le centre du cercle circonscrit au triangle CBH . Montrer que le quadrilatère $\\mathrm{O}_{1} \\mathrm{AMO}_{2}$ est un parallélogramme.\n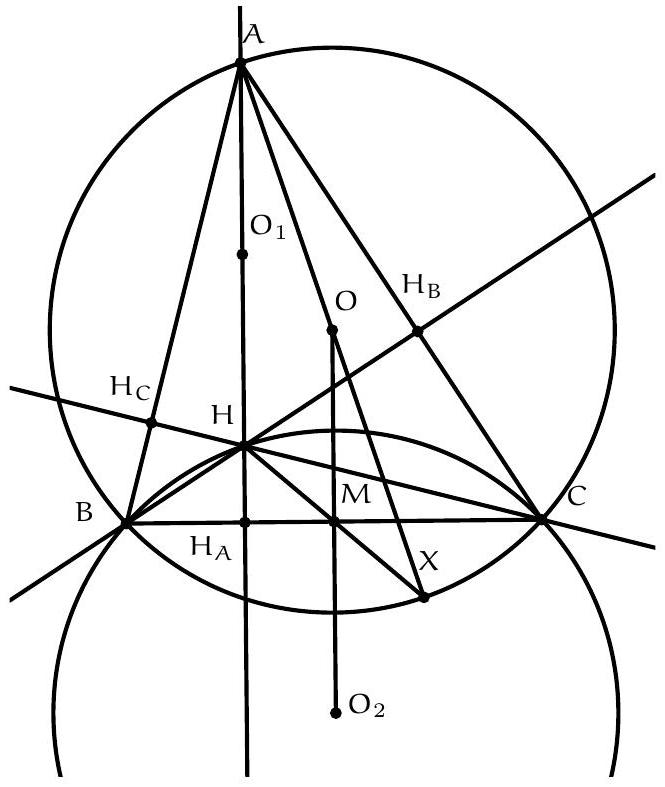", "solution": "de l'exercice 8 Soit $\\mathrm{H}_{\\mathrm{A}}$ le pied de la hauteur issue du sommet $A, \\mathrm{H}_{\\mathrm{B}}$ le pied de la hauteur issue du sommet B et O le centre du cercle circonscrit au triangle ABC .\nOn remarque déjà que $\\mathrm{O}_{2}$ est sur la médiatrice de $[\\mathrm{BC}]$ donc les droites $\\left(\\mathrm{MO}_{2}\\right)$ et $(\\mathrm{AH})$ sont parallèles car elles sont perpendiculaires à ( BC ). Il suffit donc de montrer que $\\mathrm{MO}_{2}=A \\mathrm{O}_{1}$.\nSoit $X$ le symétrique du point $H$ par rapport au point $M$. Alors $M$ est le milieu de [BC] et $[\\mathrm{XH}]$ donc BHCX est un parallélogramme et $\\widehat{\\mathrm{XBA}}=\\widehat{\\mathrm{XBC}}+\\widehat{\\mathrm{CBA}}=\\widehat{\\mathrm{HCB}}+\\widehat{\\mathrm{CBA}}=90^{\\circ}$ (car le triangle $\\mathrm{BCH}_{\\mathrm{C}}$ est rectangle en $\\mathrm{H}_{\\mathrm{C}}$ ) et de même $\\widehat{\\mathrm{XCA}}=90^{\\circ}$ donc $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$.\nLa symétrie de centre $M$ envoie $B$ sur $C, C$ sur $B$ et H sur $X$ donc elle envoie le cercle circonscrit à $B C H$ sur le cercle circonscrit à BCX donc elle envoie $\\mathrm{O}_{2}$ sur O . En particulier, $\\mathrm{MO}_{2}=\\mathrm{MO}$.\nComme les points $O$ et $M$ sont les milieux respectifs des segments $[X A]$ et $[X H]$, d'après le théorème de Thalès,\n\n$$\n\\frac{\\mathrm{OM}}{\\mathrm{AH}}=\\frac{\\mathrm{XM}}{\\mathrm{XH}}=\\frac{1}{2}\n$$\n\ndonc $\\mathrm{AH}=2 \\mathrm{OM}$ donc\n\n$$\n\\mathrm{MO}_{2}=\\mathrm{MO}=\\frac{1}{2} A \\mathrm{H}=A \\mathrm{O}_{1}\n$$\n\nce qui conclut.\nCommentaire des correcteurs Cet exercice demandait de connaître plusieurs propriétés de l'orthocentre, en particulier le fait que le symétrique de l'orthocentre H par rapport au milieu du côté [BC] appartient au cercle circonscrit au triangle $A B C$ et est également le symétrique du sommet $A$ par rapport au centre O. Plusieurs élèves ont remarqué la première étape du problème qui est que les droites $\\left(\\mathrm{MO}_{2}\\right)$ et ( AH ) sont parallèles. Ceci montre un réel effort de recherche sur un problème difficile de la part des élèves, ce qui est encourageant.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $A B C$ un triangle, $\\Gamma$ sont cercle circonscrit et $\\omega$ le cercle de même centre que $\\Gamma$ et tangent à la droite ( BC ). Les tangentes au cercle $\\omega$ passant par $A$ coupent ( BC ) en un point $X$ du côté de $B$ et en un point $Y$ du côté de $C$. La tangente au cercle $\\Gamma$ en $B$ et la parallèle à la droite $(A C)$ passant par $X$ se coupent en un point $S$ et la tangente au cercle $\\Gamma$ en $C$ et la parallèle à la droite $(A B)$ passant par $Y$ se coupent en un point $T$.\nMontrer que la droite (ST) est tangente au cercle $\\Gamma$.\n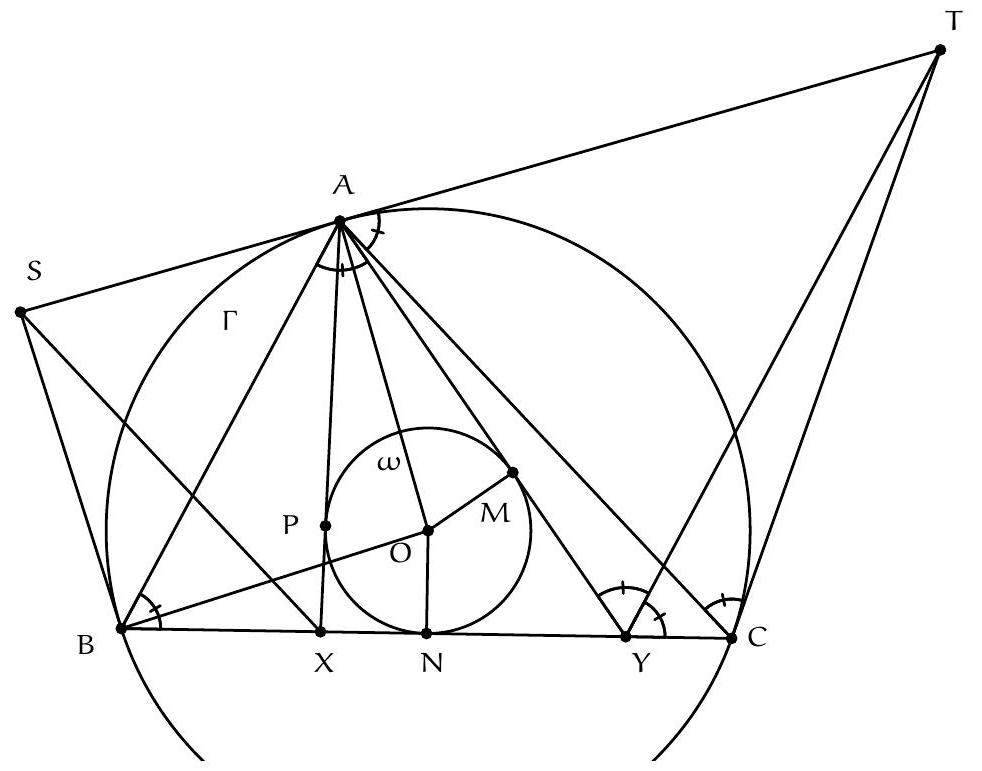", "solution": "de l'exercice 9 Afin d'éviter d'avoir à séparer les différents cas, en fonction de la position du point $Y$ par rapport au segment $[B C]$, nous allons utiliser les angles de droite orientés : ( $A B, C D$ ) désigne l'angle (relatif) dont il faut tourner la droite ( $A B$ ) pour qu'elle soit parallèle à la droite ( $C D$ ).\nNous allons montrer que la droite (TA) est tangente au cercle circonscrit au triangle $A B C$ et de même pour la droite (SA), ce qui donnera bien que la droite (ST) est tangente à ce cercle.\nPour montrer que la droite $(A T)$ est tangente au cercle $\\Gamma$, il suffit de montrer que $(A C, A T)=(B C, B A)$. Les droites $(T Y)$ et $(A B)$ sont parallèles donc $(B C, B A)=(B C, Y T)=(Y C, Y T)$, donc on est ramené à montrer que $(A C, A T)=(Y C, Y T)$, autrement dit que les points $T, A, Y$ et $C$ sont cocycliques.\nPour cela, on peut montrer que $(Y T, Y A)=(C T, C A)$. En effet, $(Y T, Y A)=(A B, A Y)$ (par parallélisme de $(A B)$ et $(Y T))$ et $(C T, C A)=(B C, B A)$ donc il ne reste plus qu'à montrer que $(A B, A Y)=$ ( $B C, B A$ ), autrement dit que le triangle $A Y B$ est isocèle en $Y$.\nSoit $O$ le centre du cercle $\\Gamma$, qui est aussi le centre du cercle $\\omega$, et soit $M$ et $N$ les points de contact respectifs du cercle $\\omega$ avec les segments [YA] et [YB]. Alors les triangles OMA et ONB sont rectangles, $\\mathrm{OA}=\\mathrm{OB}$ et $\\mathrm{OM}=\\mathrm{ON}$ donc $\\mathrm{MA}=\\sqrt{\\mathrm{OA}^{2}-\\mathrm{OM}^{2}}=\\sqrt{\\mathrm{OB}^{2}-\\mathrm{ON}}{ }^{2}=\\mathrm{NB}$ et puisque $\\mathrm{YM}=\\mathrm{YN}$, on déduit $Y A=Y B$ et le triangle $Y A B$ est isocèle en $Y$ comme voulu.\nCommentaire des correcteurs Il y avait malhreusement une imprécision dans l'énoncé puisqu'il fallait que le triangle $A B C$ ait des angles aigus. Cet oubli de notre part a provoqué quelques confusions pour certains élèves qui ont tracé une figure avec un angle obtu en $A$ et ont donc pensé que l'énoncé était faux. L'exercice restait plutôt difficile. Quelques élèves ont essayé de conclure avec les similitudes, mais les hypothèses n'étaient jamais assez fortes.\n\n## Exercices Seniors", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soient $d_{1}, d_{2}, d_{3}$ des droites concourantes et $A, A^{\\prime}$ des points sur la droite $d_{1}, B, B^{\\prime}$ des points sur la droite $d_{2}, C, C^{\\prime}$ des points sur la droite $d_{3}$ tels que les droites ( $A B$ ) et ( $A^{\\prime} B^{\\prime}$ ) sont parallèles et les droites $(B C)$ et ( $B^{\\prime} \\mathrm{C}^{\\prime}$ ) sont parallèles.\nMontrer que les droites ( $A C$ ) et ( $A^{\\prime} C^{\\prime}$ ) sont parallèles.\n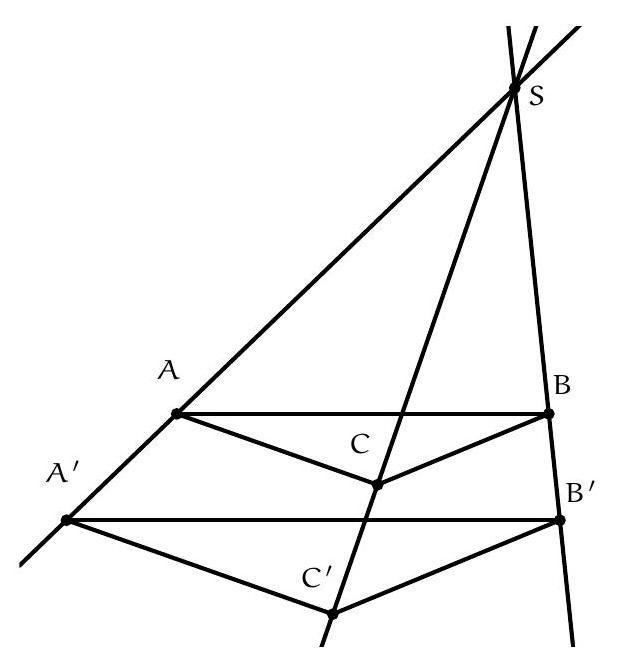", "solution": "de l'exercice 10 Soit $S$ le point de concours des trois droites. Puisque les droites ( $A B$ ) et ( $A^{\\prime} B^{\\prime}$ ) sont parallèles, d'après le théorème de Thalès,\n\n$$\n\\frac{A S}{A^{\\prime} S}=\\frac{B S}{B^{\\prime} S}\n$$\n\nDe même on trouve\n\n$$\n\\frac{B S}{B^{\\prime} S}=\\frac{C S}{C^{\\prime} S}\n$$\n\nOn déduit que\n\n$$\n\\frac{A S}{A^{\\prime} S}=\\frac{C S}{C^{\\prime} S}\n$$\n\nce qui signifie, d'après le théorème de Thalès, que les droites ( $A C$ ) et ( $A^{\\prime} \\mathrm{C}^{\\prime}$ ) sont parallèles.\nCommentaire des correcteurs L'exercice est bien réussi, la plupart des élèves ont remarqué l'utilisation du théorème de Thalès. attention à prendre en compte toutes les configurations, notemment les ordres possibles pour les sommets $A, B$ et $C$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 10.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Soit $A B C$ un triangle isocèle et obtus en $A$. Soit $\\Gamma$ le cercle de centre $B$ passant par $A$, et $\\Omega$ le cercle de centre $C$ passant par $A$. Soit $D$ le point d'intersection du cercle $\\Gamma$ avec le segment $[B C]$, E le deuxième point d'intersection de la droite (AD) avec le cercle $\\Omega$, et $F$ le point d'intersection de la droite (BC) avec le cercle $\\Omega$ qui n'est pas sur le segment $[B C]$.\nMontrer que le triangle DFE est isocèle en $F$.\n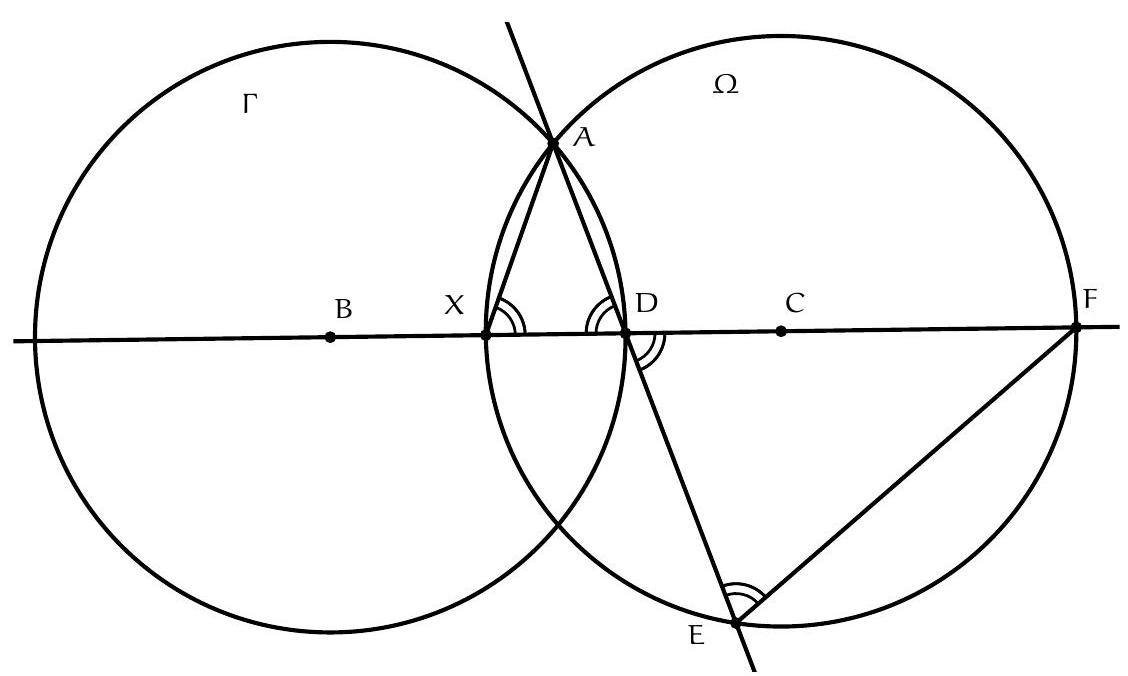", "solution": "de l'exercice 11 Soit $X$ le point d'intersection du cercle $\\Omega$ avec le segment [BC]. Les points B et C sont symétriques par rapport à la médiatrice du segment $[\\mathrm{BC}]$ donc les cercles $\\Gamma$ et $\\Omega$ le sont aussi. Il vient que D et $X$ sont symétriques par rapport à la médiatrice du segment $[\\mathrm{BC}]$. Le triangle DAX est donc isocèle en $A$ et $\\widehat{A D X}=\\widehat{A X D}$.\nLes points $F, E, X$ et $A$ sont cocycliques donc $\\widehat{F E A}=\\widehat{F X A}$. On déduit\n\n$$\n\\widehat{\\mathrm{FED}}=\\widehat{\\mathrm{FEA}}=\\widehat{\\mathrm{FXA}}=\\widehat{\\mathrm{DXA}}=\\widehat{\\mathrm{XDA}}=\\widehat{\\mathrm{FDE}}\n$$\n\nCe qui donne bien que le triangle FDE est isocèle en F .\nCommentaire des correcteurs On a observé pratiquement que des preuves complètes, même si certaines étaient très longues et calculatoires.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Soit $A B C$ un triangle, $\\Gamma$ son cercle circonscrit et $\\Omega$ un autre cercle passant par les points $A$ et $B$. La droite (AC) coupe le cercle $\\Omega$ en un point $D$ et la tangente à cercle $\\Gamma$ en B coupe $\\Omega$ en un point E .\nMontrer que les droites $(B C)$ et ( $D E$ ) sont parallèles.\n", "solution": "de l'exercice 12 La droite ( BE ) est tangente au cercle $\\Omega$ en $B$ donc par le théorème de l'angle tangent, $\\widehat{\\mathrm{EBA}}=\\widehat{\\mathrm{BCA}}$. Les points $\\mathrm{D}, \\mathrm{A}, \\mathrm{B}$ et E sont cocycliques donc $\\widehat{\\mathrm{EDA}}=180^{\\circ}-\\widehat{\\mathrm{EBA}}$. On déduit que $\\widehat{\\mathrm{EDA}}=180^{\\circ}-\\widehat{\\mathrm{BCD}}$ ce qui donne bien que les droites ( BC ) et (ED) sont parallèles.\nCommentaire des correcteurs La grande majorité des copies reçues ont fourni des preuves complètes. Cependant, beaucoup d'élèves font des chasses aux angles qui ne sont valides que dans leur cas de figure. Certains élèves ont traité tous les cas, ce qui a été récompensé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 12.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Soit $A, B, C$ et $D$ quatre points sur un cercle dans cet ordre. Soit $U$ le point d'intersection des droites $(A B$ ) et ( $C D$ ), et V le point d'intersection des droites (BC) et ( $D A$ ). Soit K le point d'intersection de la bissectrice issue de U dans le triangle AUC et de la bissectrice issue de V dans le triangle $A V C$. Soit L le point d'intersection de la médiatrice du segment $[\\mathrm{KU}]$ et de la médiatrice du segment [KV].\nMontrer que les points $\\mathrm{U}, \\mathrm{V}$ et L sont alignés.\n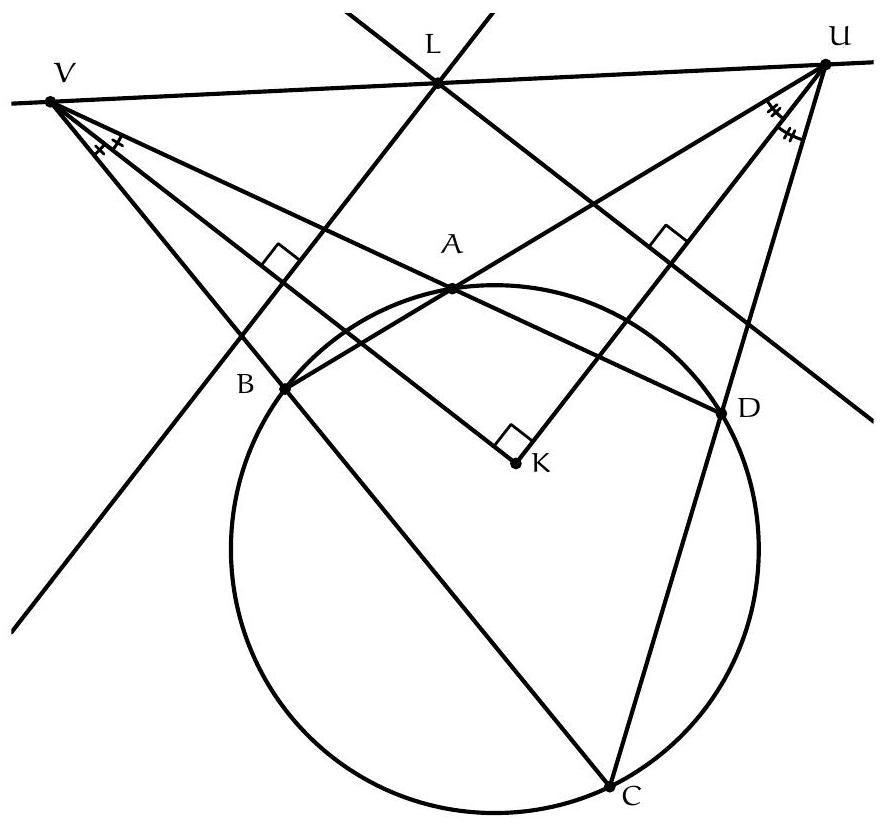", "solution": "de l'exercice 13 Le point L est le centre du cercle circonscrit au triangle UKV. Pour montrer que les points U , L et V sont alignés, il suffit de montrer que $\\widehat{\\mathrm{ULV}}=180^{\\circ}$. Par le théorème de l'angle au centre, $\\widehat{U K V}=\\frac{1}{2} \\widehat{U L V}$. Il suffit donc de montrer que $\\widehat{U K V}=90^{\\circ}$.\nLa somme des angles du triangle UKV vaut $180^{\\circ}$, donc il suffit de montrer que $\\widehat{\\mathrm{KUV}}+\\widehat{\\mathrm{KVU}}=90^{\\circ}$. D'une part $\\widehat{K U V}=\\widehat{C U V}-\\widehat{K U C}=\\widehat{C U V}-\\frac{1}{2} \\widehat{B U C}$. Or $\\widehat{B U C}=180^{\\circ}-\\widehat{U B C}-\\widehat{B C U}=\\widehat{A D C}-\\widehat{U C B}$. On déduit\n\n$$\n\\widehat{\\mathrm{KUV}}=\\widehat{\\mathrm{CUV}}-\\frac{1}{2} \\widehat{\\mathrm{ADC}}+\\frac{1}{2} \\widehat{\\mathrm{UCB}}\n$$\n\nDe la même manière, on obtient\n\n$$\n\\widehat{\\mathrm{KVU}}=\\widehat{\\mathrm{CVU}}-\\frac{1}{2} \\widehat{\\mathrm{CBA}}+\\frac{1}{2} \\widehat{\\mathrm{VCD}}\n$$\n\nOr $\\widehat{C B A}+\\widehat{A D C}=180^{\\circ}$ et\n\n$$\n\\widehat{U C B}=\\widehat{V C D}=\\widehat{U C V}=180^{\\circ}-\\widehat{C U V}-\\widehat{C V U}\n$$\n\nFinalement\n\n$$\n\\begin{aligned}\n& \\widehat{\\mathrm{KUV}}+\\widehat{\\mathrm{KVU}}=\\widehat{\\mathrm{CUV}}-\\frac{1}{2} \\widehat{\\mathrm{ADC}}+\\frac{1}{2} \\widehat{\\mathrm{UCB}}+\\widehat{\\mathrm{CVU}}-\\frac{1}{2} \\widehat{\\mathrm{CBA}}+\\frac{1}{2} \\widehat{\\mathrm{VCD}} \\\\\n& =\\widehat{\\mathrm{CUV}}+\\widehat{\\mathrm{CVU}}-\\frac{1}{2} \\cdot 180^{\\circ}+2 \\cdot \\frac{1}{2} \\cdot\\left(180^{\\circ}-\\widehat{\\mathrm{CUV}}-\\widehat{\\mathrm{CVU}}\\right)=90^{\\circ}\n\\end{aligned}\n$$\n\nce qui donne le résultat voulu.\nCommentaire des correcteurs L'exercice a été plutôt bien résolu. Attention à bien s'assurer que tout ce que l'on affirme est justifié. On a pu noté certaines affirmations fausses. Par exemple, contrairement à ce que certains élèves ont affirmé, un quadrilatère dont les deux angles opposés sont droits n'est pas forcément un rectangle. Attention également à ne pas utiliser l'énoncé pour démontrer l'énoncé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 13.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Soit BCDE un carré et soit O son centre. Soit $A$ un point situé à l'extérieur du carré $B C D E$ tel que le triangle $A B C$ est rectangle en $A$. Montrer que le point $O$ appartiant à la bissectrice de l'angle $\\widehat{B A C}$.\n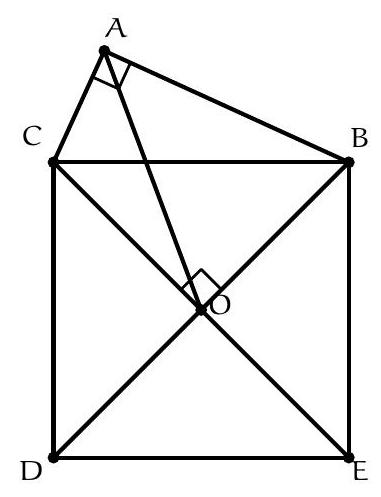", "solution": "de l'exercice 14 Les diagonales du carré BCDE se coupent perpendiculairement en O donc $\\widehat{\\mathrm{BOC}}=90^{\\circ}=\\widehat{\\mathrm{BAC}}$ donc les points $\\mathrm{A}, \\mathrm{B}, \\mathrm{O}$ et C sont cocycliques. Comme O est sur la médiatrice du segment $[B C]$, $O$ est le pôle Sud de $A$ dans le triangle $A B C$ donc $O$ est sur la bissectrice de l'angle $\\widehat{B A C}$. Commentaire des correcteurs L'exercice est plutôt bien réussi, les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Soit BCDE un carré et soit O son centre. Soit $A$ un point situé à l'extérieur du carré $B C D E$ tel que le triangle $A B C$ est rectangle en $A$. Montrer que le point $O$ appartiant à la bissectrice de l'angle $\\widehat{B A C}$.\n", "solution": "s proposées sont intéressantes mais calculatoires pour certaines.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 14.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soit $\\Omega$ et $\\Gamma$ deux cercles sécants. On note $A$ une de leurs intersections. Soit d une droite quelconque passant par le point $A$. On note $P$ et $Q$ les intersections respectives de la droite $d$ avec les cercles $\\Omega$ et $\\Gamma$ différentes de $A$.\nMontrer qu'il existe un point indépendant de la droite d choisie et qui appartient toujours à la médiatrie du segment $[\\mathrm{PQ}]$.\n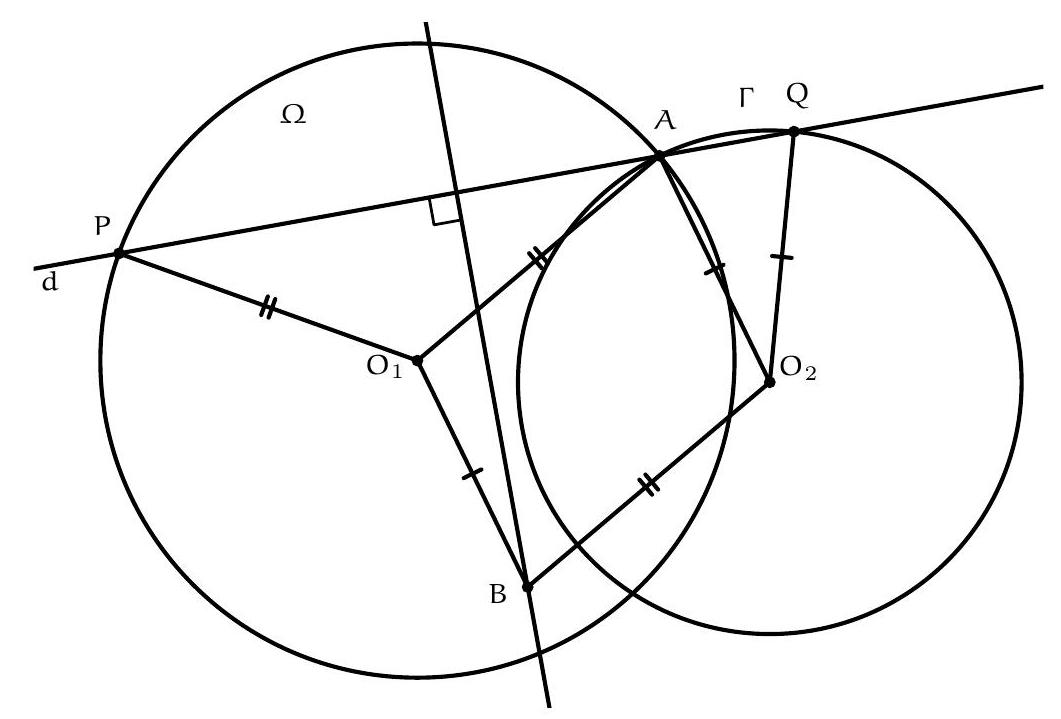", "solution": "de l'exercice 15 Par symétrie, on peut supposer que le rayon du cercle $\\Omega$ est supérieur au rayon du cercle $\\Gamma$.\nSoit $\\mathrm{O}_{1}$ le centre du cercle $\\Omega$ et $\\mathrm{O}_{2}$ le centre du cercle $\\Gamma$. Soit B le point tel que le quadrilatère $\\mathrm{AO}_{1} \\mathrm{BO}_{2}$ soit un parallélogramme. On va montrer que le point B appartient à la médiatrice du segment $[\\mathrm{PQ}]$. Comme le point B est indépendant du choix de la droite d, ceci montrera bien que les médiatrices des semgent $[\\mathrm{PQ}]$ passent par un point fixe lorsque la droite $d$ varie.\nPour montrer que $B P=B Q$, on va montrer que les triangles $\\mathrm{PO}_{1} B$ et $\\mathrm{BO}_{2} \\mathrm{Q}$ sont isométriques. On sait déjà que $\\mathrm{O}_{1} \\mathrm{P}=\\mathrm{O}_{1} \\mathrm{~A}=\\mathrm{O}_{2} \\mathrm{~B}$ et $\\mathrm{O}_{1} \\mathrm{~B}=\\mathrm{O}_{2} \\mathrm{~A}=\\mathrm{O}_{2} \\mathrm{Q}$. Il reste donc à montrer que $\\widehat{\\mathrm{BO}_{1} \\mathrm{P}}=\\widehat{\\mathrm{BO}_{2} \\mathrm{Q}}$.\nD'une part\n\n$$\n\\widehat{\\mathrm{PO}_{1} \\mathrm{~B}}=360^{\\circ}-\\widehat{\\mathrm{PO}_{1} \\mathrm{~A}}-\\widehat{\\mathrm{AO} O_{1} \\mathrm{~B}}=360^{\\circ}-\\left(180^{\\circ}-2 \\widehat{\\mathrm{O}_{1} \\mathrm{AP}}\\right)-\\widehat{\\mathrm{AO} O_{1} B}=180^{\\circ}+2 \\widehat{\\mathrm{O}_{1} \\mathrm{AP}}-\\widehat{\\mathrm{AO} \\mathrm{O}_{1} \\mathrm{~B}}\n$$\n\nD'autre part\n\n$$\n\\widehat{\\mathrm{BO}_{2} \\mathrm{Q}}=\\widehat{\\mathrm{BO}_{2} \\mathrm{~A}}+\\widehat{\\mathrm{AO}_{2} \\mathrm{Q}}=\\widehat{\\mathrm{BO}_{2} \\mathrm{~A}}+\\left(180^{\\circ}-2 \\widehat{\\mathrm{O}_{2} \\mathrm{AQ}}\\right)=180^{\\circ}+\\widehat{\\mathrm{BO}_{2} \\mathrm{~A}}-2 \\widehat{2 \\mathrm{O}_{2} \\mathrm{AQ}}\n$$\n\nMais $\\widehat{O_{1} \\mathrm{AP}}+\\widehat{\\mathrm{O}_{1} \\mathrm{AO}_{2}}+\\widehat{\\mathrm{O}_{2} \\mathrm{AQ}}=180^{\\circ}$ donc $2 \\widehat{\\mathrm{O}_{1} \\mathrm{AP}}+2 \\widehat{\\mathrm{O}_{1} \\mathrm{AO}_{2}}+2 \\widehat{\\mathrm{O}_{2} \\mathrm{AQ}}=360$ et $\\widehat{\\mathrm{O}_{1} \\mathrm{AO}_{2}}=$ $180^{\\circ}-\\widehat{\\mathrm{AO}_{1} \\mathrm{~B}}=180^{\\circ}-\\widehat{\\mathrm{BO}_{2} \\mathrm{~A}}$ donc\n\n$$\n2 \\widehat{\\mathrm{O}_{1} \\mathrm{AP}}+180^{\\circ}-\\widehat{\\mathrm{AO} O_{1} \\mathrm{~B}}+180^{\\circ}-\\widehat{\\mathrm{BO}_{2} \\mathrm{~A}}+2 \\widehat{\\mathrm{O}_{2} \\mathrm{AQ}}=360^{\\circ}\n$$\n\ndonc\n\n$$\n2 \\widehat{\\mathrm{O}_{1} \\mathrm{AP}}-\\widehat{\\mathrm{AO}_{1} \\mathrm{~B}}=\\widehat{\\mathrm{BO}_{2} \\mathrm{~A}}-2 \\widehat{\\mathrm{O}_{2} \\mathrm{AQ}}\n$$\n\nOn trouve bien $\\widehat{\\mathrm{PO}_{1} \\mathrm{~B}}=\\widehat{\\mathrm{BO}_{2} \\mathrm{Q}}$ et le point B est bien sur la médiatrice de $[\\mathrm{PQ}]$.\nCommentaire des correcteurs L'exercice est bien résolu par ceux qui l'ont traité et on a pu observé plusieurs", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 15.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soit $\\Omega$ et $\\Gamma$ deux cercles sécants. On note $A$ une de leurs intersections. Soit d une droite quelconque passant par le point $A$. On note $P$ et $Q$ les intersections respectives de la droite $d$ avec les cercles $\\Omega$ et $\\Gamma$ différentes de $A$.\nMontrer qu'il existe un point indépendant de la droite d choisie et qui appartient toujours à la médiatrie du segment $[\\mathrm{PQ}]$.\n", "solution": "s différentes. Beaucoup d'élèves font des chasses aux angles non orientés mais ils n'ont pas été pénalisés.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soit $A B C$ un triangle, $H$ son orthocentre et $M$ le milieu du segment $[B C]$. Soit $d$ une droite passant par le point $M$. On suppose que $d$ coupe le cercle de diamètre $[A H]$ en $P$ et $Q$. Montrer que l'orthocentre du triangle $A P Q$ est sur le cercle circonscrit du triangle $A B C$.\n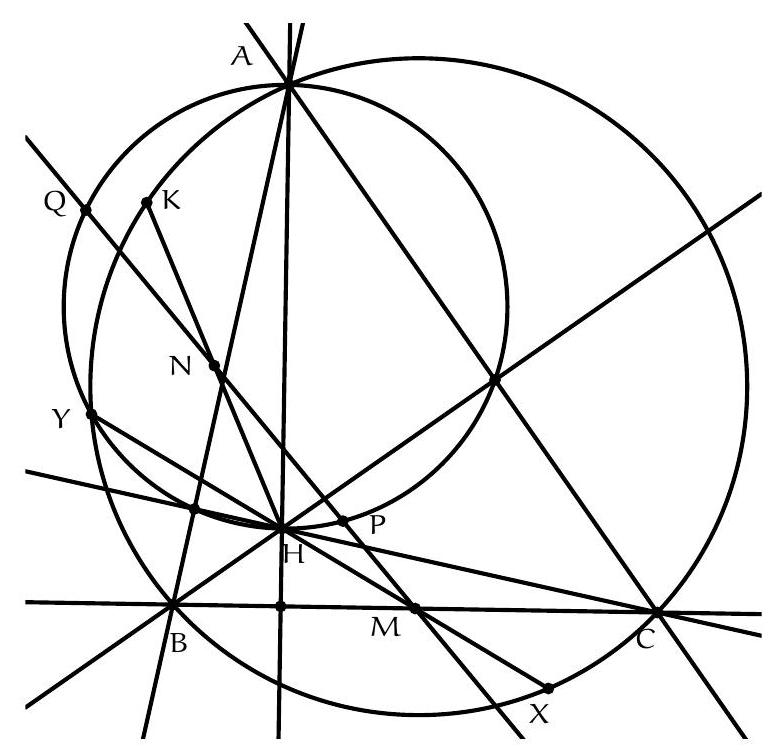", "solution": "de l'exercice 16 Soit N le milieu de $[\\mathrm{PQ}]$ et K l'orthocentre du triangle APQ . Si on appelle $\\mathrm{K}^{\\prime}$ le symétrique de K par rapport au milieu $N$ du segment $[P Q]$, alors $[P Q]$ et $\\left[K K^{\\prime}\\right]$ ont le même milieu $N$ donc $\\mathrm{PKQK}^{\\prime}$ est un parallélogramme donc $\\widehat{\\mathrm{K}^{\\prime} \\mathrm{PA}}=\\widehat{\\mathrm{K}^{\\prime} \\mathrm{PQ}}+\\widehat{\\mathrm{QPA}^{\\prime}}=\\widehat{\\mathrm{PQK}}+\\widehat{\\mathrm{QPA}^{\\prime}}=90^{\\circ}(\\mathrm{car}(\\mathrm{PA})$ et (QK) sont perpendiculaires). De même, $\\widehat{K^{\\prime} Q A}=90^{\\circ}$ donc $K^{\\prime}$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A P Q$, autrement dit $K^{\\prime}=\\mathrm{H}$ : le symétrique de K par rapport au milieu N du segment $[\\mathrm{PQ}]$ est H .\nSoit X le symétrique de H par rapport à M et Y la seconde intersection de la droite ( MH ) avec le cercle circonscrit au triangle $A B C$. Par un raisonnement analogue à celui mené précédemment, on sait que $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$ donc $\\widehat{H Y A}=\\widehat{X Y A}=90^{\\circ}$ donc $Y$ est sur le cercle de diamètre $[\\mathrm{AH}]$. Puisque $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$, il suffit de montrer que $\\widehat{X K A}=90^{\\circ}$ pour finir l'exercice.\nOn décompose l'angle en trois morceaux : $\\widehat{\\mathrm{XKA}}=360^{\\circ}-\\widehat{\\mathrm{XKH}}-\\widehat{\\mathrm{HKQ}}-\\widehat{\\mathrm{QKA}}$\nLes points $M$ et $N$ sont la milieux respectifs des segments $[H X]$ et $[H K]$ donc les droites (MN) et (KX) sont parallèles. On déduit $\\widehat{\\mathrm{XKH}}=\\widehat{\\mathrm{MNH}}=\\widehat{\\mathrm{PNH}}$.\nLes segments $[\\mathrm{PQ}]$ et $[\\mathrm{KH}]$ se coupent en leur milieu donc le quadrilatère PHQK est un parallèlogramme. $\\mathrm{D}^{\\prime}$ où $\\widehat{\\mathrm{HKQ}}=\\widehat{\\mathrm{KHP}}=\\widehat{\\mathrm{NHP}}$.\nLe point Q est l'orthocentre du triangle KPA donc $\\widehat{\\mathrm{QKA}}=180^{\\circ}-\\widehat{\\mathrm{QPA}}$.\nOn déduit\n$\\widehat{\\mathrm{XKA}}=360^{\\circ}-\\widehat{\\mathrm{PNH}}-\\widehat{\\mathrm{NHP}}-\\left(180^{\\circ}-\\widehat{\\mathrm{QPA}}\\right)=180^{\\circ}-\\widehat{\\mathrm{PNH}}-\\widehat{\\mathrm{NHP}}+\\widehat{\\mathrm{QPA}}=\\widehat{\\mathrm{NPH}}+\\widehat{\\mathrm{QPA}}=\\widehat{\\mathrm{APH}}=90^{\\circ}$\ncar $P$ est sur le cercle de diamètre $[\\mathrm{AH}]$. Ainsi, $\\widehat{X K A}=90^{\\circ}$ donc K est bien sur le cercle circonscrit à ABC.\nCommentaire des correcteurs Ce problème nécessitait un peu de culture. La plupart des élèves ayant essayé le problème ont identifié l'intérêt du cercle d'Euler et des symétriques de l'orthocentre par rapport au milieu des côtés.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 16.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $A B C$ un triangle et $I$ le centre de son cercle inscrit. La perpendiculaire à la droite ( $A \\mathrm{I}$ ) passant par le point I coupe la droite ( AB ) en un point D et la droite ( AC ) en un point E . On suppose qu'il existe deux points $F$ et $G$ sur le segment $[B C]$ tels que $B A=B F$ et $C A=C G$. Soit $T$ le point d'intersection des cercles circonscrits aux triangles ADF et AEG.\nMontrer que le centre du cercle circonscrit au triangle AIT se trouve sur la droite (BC).\n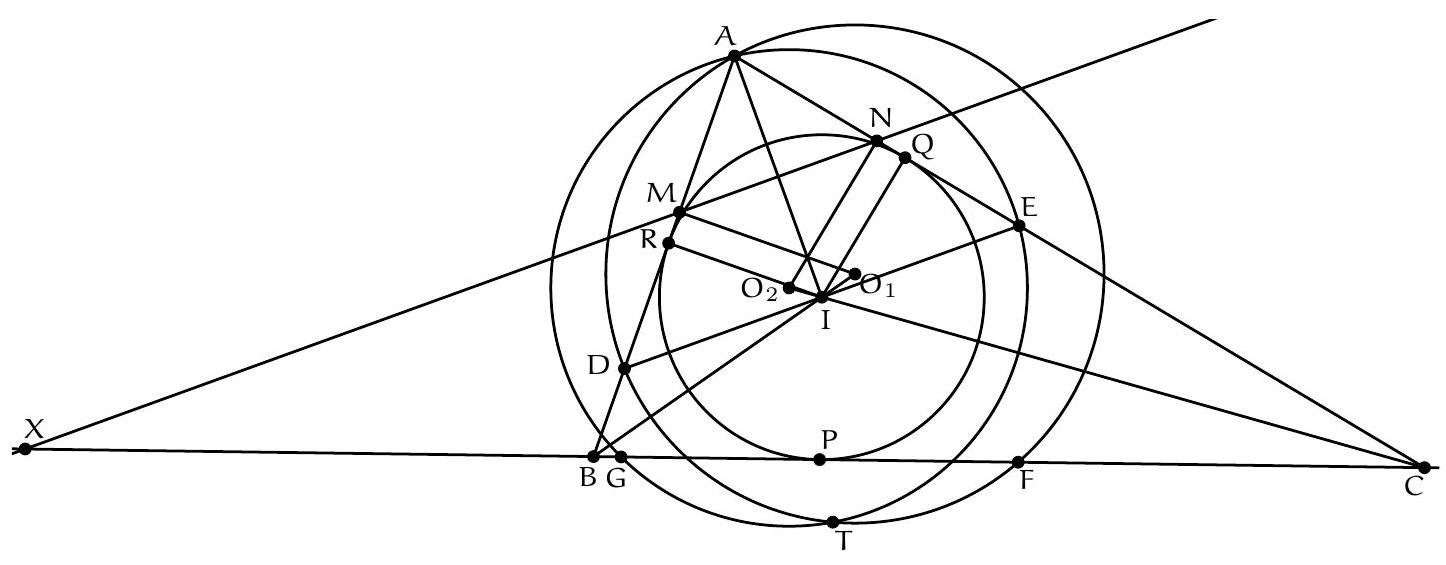", "solution": "de l'exercice 17 Soient $M$ et $N$ les milieux respectifs des segments [AD] et [AE] et soit $X$ le point d'intersection de la droite (MN) (qui est aussi la médiatrice du segment [AI]) avec la droite (BC). Soient $\\mathrm{O}_{1}$ et $\\mathrm{O}_{2}$ les centres respectifs des cercles circonscrits aus triangles ADF et AEG. On souhaite montrer que le point $X$ est le centre du cercle circonscrit à AIT donc qu'il appartient à la médiatrice du segment [AT], c'est-à-dire à la droite $\\left(\\mathrm{O}_{1} \\mathrm{O}_{2}\\right)$.\nSoient $P, Q$ et $R$ les points de contact respectifs du cercle inscrit au triangle $A B C$ avec les côtés $[B C],[A C]$ et $[A B]$. Le point $O_{1}$ est sur la médiatrice du segment $[A D]$ donc la droite $\\left(O_{1} M\\right.$ ) est perpendiculaire à la droite ( $A B$ ). Les droites $\\left(O_{1} M\\right.$ ) et (IR) sont donc parallèles. D'après le théorème de Thalès, on déduit que $\\frac{\\mathrm{O}_{1} \\mathrm{I}}{\\mathrm{O}_{1} \\mathrm{~B}}=\\frac{\\mathrm{MR}}{\\mathrm{MB}}$. On a de même $\\frac{\\mathrm{O}_{2} \\mathrm{C}}{\\mathrm{O}_{2} \\mathrm{I}}=\\frac{\\mathrm{NC}}{\\mathrm{NQ}}$. De plus, le triangles ABF est isocèle en B donc la médiatrice de $[A F]$ est la bissectrice de $\\widehat{A B F}$ donc $\\mathrm{O}_{1}$ est sur (BI) et de même $\\mathrm{O}_{2}$ est sur (CI).\nD'après le théorème de Ménélaus appliquée aux points $\\mathrm{M}, \\mathrm{N}, \\mathrm{X}$ dans le triangle $A B C$ :\n\n$$\n\\frac{X B}{X C} \\cdot \\frac{N C}{N A} \\cdot \\frac{M A}{M B}=1\n$$\n\net en l'appliquant au triangle BIC, l'alignement des points $\\mathrm{O}_{1}, \\mathrm{O}_{2}$ et $X$ équivaut à $\\frac{O_{1} \\mathrm{I}}{\\mathrm{O}_{1} \\mathrm{~B}} \\cdot \\frac{\\mathrm{XB}}{X \\mathrm{C}} \\cdot \\frac{\\mathrm{O}_{2} \\mathrm{C}}{\\mathrm{O}_{2} \\mathrm{I}}=1$. On souhaite donc montrer cette égalité.\nOn sait déjà $\\frac{\\mathrm{XB}}{\\mathrm{XC}}=\\frac{\\mathrm{NA}}{\\mathrm{NC}} \\cdot \\frac{\\mathrm{MB}}{\\mathrm{MA}}, \\frac{\\mathrm{O}_{1} \\mathrm{I}}{\\mathrm{O}_{1} \\mathrm{~B}}=\\frac{\\mathrm{MR}}{\\mathrm{MB}}, \\frac{\\mathrm{O}_{2} \\mathrm{C}}{\\mathrm{O}_{2} \\mathrm{I}}=\\frac{\\mathrm{NC}}{\\mathrm{NQ}}$ donc\n\n$$\n\\frac{\\mathrm{O}_{1} \\mathrm{I}}{\\mathrm{O}_{1} \\mathrm{~B}} \\cdot \\frac{\\mathrm{XB}}{\\mathrm{XC}} \\cdot \\frac{\\mathrm{O}_{2} \\mathrm{C}}{\\mathrm{O}_{2} \\mathrm{I}}=\\frac{\\mathrm{MR}}{\\mathrm{MB}} \\cdot \\frac{\\mathrm{NA}}{\\mathrm{NC}} \\cdot \\frac{\\mathrm{MB}}{\\mathrm{MA}} \\cdot \\frac{\\mathrm{NC}}{\\mathrm{NQ}}=\\frac{\\mathrm{MR} \\cdot \\mathrm{NA}}{\\mathrm{MA} \\cdot \\mathrm{NQ}}=1\n$$\n\ncar $M A=\\frac{1}{2} D A=\\frac{1}{2} E A=N A$ et $A R=A Q$ donc $M R=N Q$. Ainsi, $O_{1}, O_{2}, X$ sont alignés.\nCommentaire des correcteurs L'exercice était difficile et a donc été très peu abordé. Quelques élèves ont donné une reformulation intéressante de l'énoncé. Les élèves qui ont cherché l'exercice plus en profondeur ont fait preuve d'inventivité : certains ont utilise le théorème de Desargues, d'autres une inversion.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 17.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit ABC un triangle, soit O le centre de son cercle circonscrit. Soit I le centre du cercle inscrit au triangle $A B C$ et D le point de tangence de ce cercle avec le segment [AC]. Les droites (OI) et $(A B)$ se coupent en un point $P$. Soit $M$ le milieu de l'arc $A C$ ne contenant pas $B$ et $N$ le milieu de l'arc $B C$ contenant $A$.\nMontrer que les droites (MD) et (NP) se coupent sur le cercle circonscrit à ABC.\n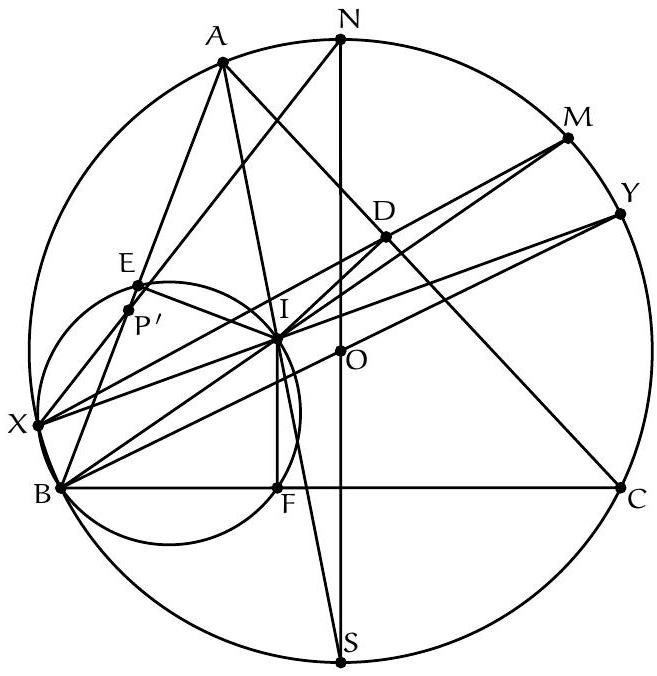", "solution": "de l'exercice 18 Soit $X$ le point d'intersection de la droite (MD) avec le cercle circonscrit au triangle $A B C$ et soit $P^{\\prime}$ le point d'intersection de la droite $(X N)$ avec le segment $[A B]$. Soit $S$ le point d'intersection de la bissectrice de l'angle $\\widehat{B A C}$ avec le cercle circonscrit au triangle $A B C$. On sait que les points $\\mathrm{N}, \\mathrm{O}$ et S sont alignés.\nSoit $E$ et $F$ les points de contact respectifs du cercle inscrit au triangles $A B C$ avec les segment $[A B]$ et [BC].\nLe point $M$ est le milieu de l'arc $C A$, il est donc sur la bissectrice de l'angle $\\widehat{A X C}$. Le point $D$ est le pied de cette bissectrice. D' après le théorème de la bissectrice, $\\frac{A X}{X C}=\\frac{D A}{D C}=\\frac{A E}{C F}$. Puisque $\\widehat{E A X}=\\widehat{B A X}=$ $\\widehat{B C X}=\\widehat{F C X}$, il vient que les triangles $A E X$ et $C F X$ sont semblables donc le point $X$ est le centre de la similitude qui envoie les points $E$ et $F$ sur les points $A$ et $C$, il est donc le point d'intersection des cercles circonscrits aux triangles $A B C$ et EFB. Puisque [BI] est un diamètre du cercle circonscrit au triangle EBF , on déduit $\\widehat{\\mathrm{IXB}}=90^{\\circ}$. Soit $Y$ le point diamétralement opposé au point B dans le cercle circonscrit au triangle ABC . Alors $\\widehat{\\mathrm{YXB}}=90=\\widehat{\\mathrm{IXB}}$. Les points $X$, I et $Y$ sont donc alignés.\nD'après le théorème de Pascal appliqué à l'hexagone SABYXN , les points $\\mathrm{O}=(\\mathrm{BY}) \\cap(\\mathrm{SN}), \\mathrm{I}=$ $(Y X) \\cap(A S)$ et $P^{\\prime}=(A B) \\cap(X N)$ sont alignés. Le point $P^{\\prime}$ correspond donc au point d'intersection des droites (OI) et ( $A B$ ) donc $P=P^{\\prime}$ ce qui donne bien que les droites (MD) et (NP) se coupent sur le cercle circonscrit au triangle $A B C$.\nCommentaire des correcteurs Des", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 18.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit ABC un triangle, soit O le centre de son cercle circonscrit. Soit I le centre du cercle inscrit au triangle $A B C$ et D le point de tangence de ce cercle avec le segment [AC]. Les droites (OI) et $(A B)$ se coupent en un point $P$. Soit $M$ le milieu de l'arc $A C$ ne contenant pas $B$ et $N$ le milieu de l'arc $B C$ contenant $A$.\nMontrer que les droites (MD) et (NP) se coupent sur le cercle circonscrit à ABC.\n", "solution": "s variées ont été proposées : utiliser une inversion de centre $M$ fixant les points $A$, I et $C$ pour montrer que les points $X$, I et $Y$ sont alignés, utiliser $Z$ le centre de l'homotétie positive envoyant le cercle inscrit sur le cercle circonscrit et considérer le cercle mixti-linéaire ou enocre utiliser les coordonnées barycentriques.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commentaire-envoi-1.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
diff --git "a/French_STS/segmented/fr-corrig\303\251-comment\303\251-envoi-3.jsonl" "b/French_STS/segmented/fr-corrig\303\251-comment\303\251-envoi-3.jsonl"
new file mode 100644
index 0000000000000000000000000000000000000000..e48009301bdd77ed1ec96be5f83b9330e705865f
--- /dev/null
+++ "b/French_STS/segmented/fr-corrig\303\251-comment\303\251-envoi-3.jsonl"
@@ -0,0 +1,51 @@
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Trouver tous les entiers $p$ tels que $p, p+2$ et $p+4$ soient tous les 3 premiers?\nUn nombre premier est un entier $\\geqslant 2$ qui n'est divisible que par 1 et lui-même.", "solution": "de l'exercice 1 Tout d'abord, on peut s'attendre à ce qu'il n'y en ait que très peu. On souhaite obtenir des informations sur ces nombres premiers.\nNotons qu'un nombre premier divisible par 3 est a fortiori égal à 3 . On considère 3 cas en fonction du reste de la division de $p$ par 3 (modulo 3 ):\n$-p=3 k: p$ est divisible par 3 donc $p=3 .\\{3,5,7\\}$ est bien un triplet de nombres premiers.\n$-p=3 k+1: p+2$ est divisible par 3 et premier donc $p=1$ (impossible).\n$-p=3 k+2: p+4$ est divisible par 3 et premier donc $p=-1$ (impossible).\nD'où $\\mathrm{p}=3$.\nCommentaire des correcteurs L'exercice est globalement très bien traité, à part quelques tentatives modulo 10 , l'argument modulo 3 a bien été compris. Attention à ne pas oublier le cas $\\mathrm{p}=2$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(n, p)$ strictement positifs où $p$ est un nombre premier et tels que $n+p$ soit une puissance de $n$.\n\nUne puissance de $n$ est de la forme $\\mathrm{n}^{\\mathrm{k}}$ pour k entier naturel.", "solution": "de l'exercice 2 Soit $(\\mathfrak{p}, \\mathfrak{n}$ ) un éventuel couple", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(n, p)$ strictement positifs où $p$ est un nombre premier et tels que $n+p$ soit une puissance de $n$.\n\nUne puissance de $n$ est de la forme $\\mathrm{n}^{\\mathrm{k}}$ pour k entier naturel.", "solution": "On dispose d'un entier naturel $k$ tel que\n\n$$\n\\mathrm{n}+\\mathrm{p}=\\mathrm{n}^{\\mathrm{k}}\n$$\n\nTout d'abord, si $k=0$, alors $n+p=1$. Or $p$ étant premier, $p>1$ et $n \\geqslant 0$ donc $n+p=12 p+1$ pour tout nombre premier $p$ car $p \\geqslant 2$. On a donc $p \\neq q$ et donc $p$ et $q$ sont premiers entre eux.\n$p^{2}$ est premier avec $q$ donc d'après le lemme de Gauss, $p^{2} \\mid q+1$. On dispose donc de $k \\in \\mathbb{N}^{*}$ tel que $\\mathrm{q}+1=\\mathrm{kp}^{2}$.\nComme q est premier avec $\\mathrm{p}^{2}, \\mathrm{q} \\mid \\mathrm{p}^{3}-1=(\\mathrm{p}-1)\\left(\\mathrm{p}^{2}+\\mathrm{p}+1\\right)$. Donc $\\mathrm{q} \\mid \\mathrm{p}-1$ ou $\\mathrm{q} \\mid \\mathrm{p}^{2}+\\mathrm{p}+1$.\nSi $q \\mid p-1$, alors\n\n$$\n\\mathrm{p}<\\mathrm{kp} \\mathrm{p}^{2}-1=\\mathrm{q} \\leqslant \\mathrm{p}-1\n$$\n\nce qui est absurde.\nOn a donc $\\mathrm{q} \\mid \\mathrm{p}^{2}+\\mathrm{p}+1$ donc $\\mathrm{kp}^{2}-1=\\mathrm{q} \\leqslant \\mathrm{p}^{2}+\\mathrm{p}+1$ soit $(\\mathrm{k}-1) \\mathrm{p}^{2} \\leqslant \\mathrm{p}+2$. Si $k=1$, alors $\\mathrm{q}=\\mathrm{p}^{2}-1=(p-1)(p+1)$ qui n'est premier que si $p=2$.\nOn a alors $q=3$ mais $2^{2}\\left(2^{3}-1\\right)=28 \\neq 12=3(3+1)$.\nOn en déduit que $k \\geqslant 2$ et $p>2$, donc $p+2i$\n- $m \\mid j p+1$ et $m>j$\n\nOn a donc $m \\mid p(j-i)$ or $\\operatorname{pgcd}(m, p)=1$ donc $m \\mid j-i$. Cependant, c'est impossible car $03$ vérifiant la propriété de l'énoncé.\nOn a $n \\left\\lvert\\, a_{1}+a_{2}+\\ldots+a_{n}=1+2+\\ldots+n=\\frac{n(n+1)}{2}\\right.$ et donc $\\frac{n+1}{2} \\in \\mathbb{Z}: n$ est impair.\nEnsuite $n-1 \\left\\lvert\\, a_{1}+a_{2}+\\ldots+a_{n-1}=\\frac{n(n+1)}{2}-a_{n}\\right.$.\n$\\operatorname{Et} n-1 \\left\\lvert\\, \\frac{(n-1)(n+1)}{2}\\right.$ donc $n-1 \\left\\lvert\\, \\frac{n+1}{2}-a_{n}\\right.$.\nCependant, il y a un \"problème de taille\" : $-(n-1)<\\frac{n+1}{2}-a_{n}3$ ) :\n$n-2 \\left\\lvert\\, \\frac{n(n+1)}{2}-\\frac{n+1}{2}-a_{n-1}=\\frac{(n-1)(n+1)}{2}-a_{n-1}\\right.$.\nEt $n-2 \\left\\lvert\\, \\frac{(n-2)(n+1)}{2}\\right.$ donc $n-2 \\left\\lvert\\, \\frac{n+1}{2}-a_{n-1}\\right.$.\nComme précédemment, $-(n-2)<\\frac{n+1}{2}-a_{n-1}q>r$. Un nombre premier est impair ou égal à 2 .\nOn suppose que $p, q$ et $r$ sont tous impairs. Alors $p-q, q-r$ et $r-p$ sont pairs. Comme leur valeur absolue est première, ces nombres valent tous 2 . Ainsi les entiers $p, p+2$ et $p+4$ sont premiers. Si $p$ est divisible par 3 , alors $\\mathrm{p}=3$ et $\\mathrm{q}=5$ et $\\mathrm{r}=7$.\nCependant, le triplet $(3,5,7)$ n'est pas", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Trouver tous les triplets ( $\\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences\n\n$$\n|p-q|,|q-r|,|r-p|\n$$\n\nsoient également des nombres premiers.", "solution": "du problème : $7-3=4$ n'est pas premier.\nSi $p$ n'est pas divisible par 3 , alors $p$ est de la forme $3 k+1$ ou $3 k+2$. Le premier cas implique que $p+2$ soit divisible par 3 donc $p+2=3$ mais $p=1$ n'est pas un nombre premier. Le deuxième cas implique que $p+4$ soit divisible par 3 , mais $p+4=3$ ne donne pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Trouver tous les triplets ( $\\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences\n\n$$\n|p-q|,|q-r|,|r-p|\n$$\n\nsoient également des nombres premiers.", "solution": "strictement positive.\nOn suppose que $r=2$. Alors $p$ et $q$ sont impaires et $p-q$ est pair et premier donc égal à 2 . Il vient que $q+2$, $q$ et $q-2$ sont tous les trois des nombres premiers. D'après le cas précédent, cela implique que $\\boldsymbol{q}-2=3$ donc $p=7$. Réciproquement, le triplet $(p, q, r)=(2,5,7)$ et ses permutations sont donc bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Trouver tous les triplets ( $\\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences\n\n$$\n|p-q|,|q-r|,|r-p|\n$$\n\nsoient également des nombres premiers.", "solution": "s au problème.\n\nLes seuls triplets", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Trouver tous les triplets ( $\\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences\n\n$$\n|p-q|,|q-r|,|r-p|\n$$\n\nsoient également des nombres premiers.", "solution": "s sont donc $(2,5,7)$ ainsi que ses permutations.\nCommentaire des correcteurs\nBeaucoup d'élèves ont les idées majeures, mais perdent bêtement des points pour la rédaction. Il faut toujours vérifier que les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Trouver tous les triplets ( $\\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences\n\n$$\n|p-q|,|q-r|,|r-p|\n$$\n\nsoient également des nombres premiers.", "solution": "s obtenues satisfont bien l'énoncé. Certains ont affirmé sans aucune justification que si $p, p+2$ et $p+4$ sont premiers alors $p=3$. De même certains ont dit qu'on ne peut pas avoir $|\\mathrm{p}-\\mathrm{q}|=|\\mathrm{q}-\\mathrm{r}|=|\\mathrm{r}-\\mathrm{p}|=2$ sans le justifier, ce qui était assez clair (on peut supposer $p>q>r$ par exemple). Il vaut mieux un peu plus détailler les points importants pour ne pas perdre de points.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "de l'exercice 11 Notons que si $(z, r)$ est un couple", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": ", $(z,-r)$ est également un couple", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "On peut donc supposer pour la suite que $r \\geqslant 0$. Etant donné que $2^{z}+z>0$, on a même $r>0$. On pose $r=\\frac{a}{b}$, avec $a$ et $b$ des entiers strictement positifs et premiers entre eux.\nSi $z \\geqslant 0$, alors $2^{z}+2$ est entier donc r est entier et $\\mathrm{b}=1$. On doit désormais résoudre l'équation $2^{z}+2=a^{2}$ dans les entiers positifs. Si $z \\geqslant 2$, alors l'équation vue modulo 4 donne $a^{2} \\equiv 2 \\bmod 4$ ce qui n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "puisqu'un carré est toujours congru à 0 ou à 1 modulo 4 . On déduit que $z=0$ ou $z=1$. Dans le premier cas, on obtient $3=\\mathfrak{a}^{2}$ qui n'admet pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "entière. Dans le deuxième cas on trouve $4=a^{2}$ soit $a=2$. Réciproquement, les couples $(1,-2)$ et $(1,2)$ satisfont bien l'équation.\n$\\mathrm{Si} z<0$, alors on pose $z^{\\prime}=-z$, avec $z^{\\prime}>0$. L'équation dévient $\\frac{1}{2^{z^{\\prime}}}+2=\\frac{a^{2}}{b^{2}}$. En supprimant les dénominateurs on obtient\n\n$$\nb^{2}\\left(1+2^{z^{\\prime}+1}\\right)=a^{2} \\cdot 2^{z^{\\prime}}\n$$\n\nPuisque $1+2^{z^{\\prime}+1}$ est premier avec $2^{z^{\\prime}}$, par le lemme de Gauss on obtient que $2^{z^{\\prime}+1}+1$ divise $a^{2}$. Comme $a$ et $b$ sont premiers entre eux, par le lemme de Gauss on obtient aussi que $a^{2}$ divise $1+2^{z^{\\prime}+1}$. On déduit que $a^{2}=2^{z^{\\prime}+1}+1$, que l'on réécrit $2^{z^{\\prime}+1}=(a-1)(a+1)$. On déduit que $a+1$ et $a-1$ sont tous les deux des puissances de 2 dont la différence vaut 2 . On déduit donc que $a+1=4$ et $a-1=2$ soit $\\mathrm{a}=3$ et $z^{\\prime}=2$. Ainsi $\\mathrm{b}=2$. Réciproquement, les couples $\\left(-2,-\\frac{3}{2}\\right)$ et $\\left(-2, \\frac{3}{2}\\right)$ sont bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "s de l'équation. Les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "s sont donc $\\left\\{\\left(-2,-\\frac{3}{2}\\right),\\left(-2, \\frac{3}{2}\\right),(1,-2),(1,2)\\right\\}$.\nCommentaire des correcteurs\nUn tiers des élèves a écrit que $x^{2}=4$ implique que $x=2$ et oublie donc la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les nombres entiers $z \\in \\mathbb{Z}$ tels que\n\n$$\n2^{z}+2=r^{2}\n$$\n\noù $r \\in \\mathbb{Q}$ est un nombre rationnel.\nUn nombre rationnel est un nombre qui s'écrit sous la forme $\\frac{\\mathrm{a}}{\\mathrm{b}}$ avec $\\mathrm{a}, \\mathrm{b}$ des entiers et $\\mathrm{b} \\neq 0$.", "solution": "$x=-2$. Quelques élèves n'ont pas vu que l'on se plaçait dans $\\mathbb{Z}$ et $\\mathbb{Q}$ et ont juste regardé l'équation sur les entiers positifs. Mis à part cela, l'exercice est assez bien réussi.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(\\mathfrak{a}, \\mathfrak{b}, \\mathfrak{n}$ ) strictement positifs vérifiant:\n\n$$\na!+b!=2^{n}\n$$", "solution": "de l'exercice 12 Les factorielles ayant beaucoup de facteurs impairs en commun, on se dit directement qu'obtenir une puissance de 2 va être très contraignant.\nSupposons que $\\mathrm{a}, \\mathrm{b} \\geqslant 3,3$ divise donc la somme des factorielles et donc $2^{\\mathrm{n}}$ : $\\mathbf{c}^{\\text {'est absurde. }}$ C'est à dire que l'un des deux est dans $\\{1,2\\}$. Par symétrie, on ne traite que deux cas :\n\n1. $a=1$ : encore deux petits cas de figure :\n$-\\mathrm{b}=1: \\mathrm{n}=1$\n$-\\mathrm{b} \\geqslant 2$ : les deux membres n'ont pas la même parité, c 'est impossible\n2. $a=2: b \\geqslant 2$ (comme vu au-dessus), quelques cas :\n$-\\mathrm{b}=2,3: \\mathbf{n}=2,3$\n$-\\mathrm{b} \\geqslant 4$ : il y a un problème modulo 4 , impossible\nD'où : les seules", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(\\mathfrak{a}, \\mathfrak{b}, \\mathfrak{n}$ ) strictement positifs vérifiant:\n\n$$\na!+b!=2^{n}\n$$", "solution": "s sont dans $\\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\\}$.\nCommentaire des correcteurs\nIl y a eu pas mal d'erreurs de logique. Ce n'est pas parce que l'on ne peut pas avoir $\\mathbf{a} \\geqslant 3$ et $\\mathbf{b} \\geqslant 3$ en même temps qu'on a forcément $\\mathrm{a}<3$ et $\\mathrm{b}<3$ (on a plutôt $\\mathrm{a}<3$ ou $\\mathrm{b}<3$ ). 1 est une puissance de 2 qu'il ne faut pas oublier et 0 n'est pas dans $\\mathbb{N}^{*}$ et 1 est un diviseur impair de 2 qu'il ne faut pas oublier non plus. Ne pas oublier de rappeller les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(\\mathfrak{a}, \\mathfrak{b}, \\mathfrak{n}$ ) strictement positifs vérifiant:\n\n$$\na!+b!=2^{n}\n$$", "solution": "s symétriques si on suppose $a \\geqslant b$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(x, y, z)$ vérifiant la propriété suivante :\n\n$$\n\\operatorname{pgcd}(x, y, z)<\\operatorname{pgcd}(x+y, y+z, z+x)\n$$", "solution": "de l'exercice 13 Notons que puisque $\\operatorname{pgcd}(x, y, z)$ divise chacun des $x, y, z$, il divise également $\\operatorname{pgcd}(x+y, y+z, z+x)$.\nOn remarque que si le triplet $(x, y, z)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 13.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(x, y, z)$ vérifiant la propriété suivante :\n\n$$\n\\operatorname{pgcd}(x, y, z)<\\operatorname{pgcd}(x+y, y+z, z+x)\n$$", "solution": ", alors les triplets $(k x, k y, k z)$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 13.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(x, y, z)$ vérifiant la propriété suivante :\n\n$$\n\\operatorname{pgcd}(x, y, z)<\\operatorname{pgcd}(x+y, y+z, z+x)\n$$", "solution": "s pour tout $k \\in \\mathbb{N}^{*}$. On peut donc supposer, quitte à diviser chaque variable par $\\operatorname{pgcd}(x, y, z)$, que les entiers $x, y, z$ sont premiers entre eux dans leur ensemble. En particulier ils ne sont pas tous pairs.\nSoit $d=\\operatorname{pgcd}(x+y, y+z, z+x)$. Alors d divise $(x+y)+(x+z)-(y+z)=2 x$ et de même $d$ divise $2 y$ et $2 z$. Donc $d$ divise $\\operatorname{pgcd}(2 x, 2 y, 2 z)=2 \\operatorname{pgcd}(x, y, z)=2$. On déduit que $d=1$ ou $d=2$. Mais comme $\\mathrm{d}>1, \\mathrm{~d}=2$ donc les entiers $x, y, z$ sont tous de même parité. Comme ils ne sont pas tous paires, ils sont tous impaires.\nRéciproquement, si $x, y$ et $z$ sont tous les trois impaires, étant donné que $\\operatorname{pgcd}(x, y, z)$ et 2 sont premiers entre eux et divisent $\\operatorname{pgcd}(x+y, y+z, z+x)$, on a bien\n\n$$\n\\operatorname{pgcd}(x, y, z)<2 \\operatorname{pgcd}(x, y, z) \\leqslant \\operatorname{pgcd}(x+y, y+z, z+x)\n$$\n\nLes triplets", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 13.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers $(x, y, z)$ vérifiant la propriété suivante :\n\n$$\n\\operatorname{pgcd}(x, y, z)<\\operatorname{pgcd}(x+y, y+z, z+x)\n$$", "solution": "s sont donc les triplets $\\left\\{(k x, k y, k z), k \\in \\mathbb{N}^{*}, x, y, z\\right.$ impaires $\\}$. Commentaire des correcteurs\nLes correcteurs étaient très satisfait des différentes approches des élèves. Quelques erreurs sont à noter : ce n'est pas parce que $2 \\mathrm{n} \\equiv k$ mod a que $k$ est pair et ce $n$ 'est pas parce que $\\operatorname{pgcd}(x, y, z)=\\operatorname{pgcd}(x+$ $y, y+z, z+x)$ que $(x, y, z)=(x+y, y+z, z+x)$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 13.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Existe-t-il des entiers $a$ et $b$ pour lesquels : $\\mathbf{a}^{5} \\mathbf{b}+3$ et $a^{5}+3$ sont tous deux des cubes parfaits?\n\nUn cube parfait est un entier $n$ pour lequel il existe $m \\in \\mathbb{Z}$ tel que : $\\mathfrak{n}=\\mathrm{m}^{3}$.", "solution": "de l'exercice 14 Nous allons montrer qu'il n'y a pas d'entiers a et b satisfaisant les conditions du problème.\nSoient $a$ et $b$ des entiers tels que $a^{5} b+3$ et $a b^{5}+3$ sont des cubes parfaits. Soit $m$ et $n$ des entiers tels que $a^{5} b+3=m^{3}$ et $a b^{5}+3=n^{3}$. Supposons que $3 \\mid n$. Alors $27 \\mid n$. De plus $3 \\mid a b^{5}$ donc $3 \\mid a$ ou $3 \\mid b^{5}$. Si $3 \\mid a$, alors $3^{5} \\mid a^{5}$ donc $3 \\mid a^{5} b+3=m^{3}$. Mais alors $27 \\mid m^{3}$ et $27 \\mid a^{5}$ donc $27 \\mid m^{3}-a^{5} b=3$ ce qui est absurde. Si $3 \\mid b$, alors $3^{5} \\mid b^{5}$ et en particulier $27 \\mid n^{3}-a b^{5}=3$ ce qui est aussi absurde. On déduit que 3 ne divise pas $n$ et de même 3 ne divise pas $m$. Si $3 \\mid a$, alors $3 \\mid \\mathrm{m}$, n ce qui est exclut. On déduit donc que 3 ne divise pas non plus $a$ et $b$. Notons que\n\n$$\nm^{3}-n^{3}=a^{5} b-a b^{5}=a b(a-b)(a+b)\\left(a^{2}+b^{2}\\right)\n$$\n\nComme $a$ et $b$ ne sont pas divisibles par $3, a^{2} \\equiv b^{2} \\equiv 1 \\bmod 3$ donc $3 \\mid a^{2}-b^{2}=(a-b)(a+b)$ et donc $3 \\mid \\mathrm{m}^{3}-\\mathrm{n}^{3}$. D'après le théorème de Fermat, $\\mathrm{m}^{3} \\equiv \\mathrm{~m} \\bmod 3$ et $\\mathrm{n}^{3} \\equiv \\mathrm{n} \\bmod 3$. On déduit que $\\mathrm{m} \\equiv \\mathrm{m}^{3} \\equiv \\mathrm{n}^{3} \\equiv \\mathrm{n} \\bmod 3$. Il vient que\n\n$$\nm^{2}+m n+n^{2} \\equiv 3 m^{2}=0 \\quad \\bmod 3\n$$\n\nOn déduit que 3 divise $m-n$ et 3 divise $m^{2}+m n+n^{2}$ donc $9 \\mid(m-n)\\left(m^{2}+m n+n^{2}\\right)=m^{3}-n^{3}$. Il vient que $9 \\mid a b(a-b)(a+b)\\left(a^{2}+b^{2}\\right)$. Mais 3 ne divise pas $a, b$ et $a^{2}+b^{2} \\equiv 2 \\bmod 3$ donc 3 ne divise pas non plus $a^{2}+b^{2}$ et donc 9 non plus. On déduit que $9 \\mid a^{2}-b^{2}$, soit $a^{2} \\equiv b^{2} \\bmod 9$. Ainsi\n\n$$\n\\mathrm{m}^{3}=\\mathrm{a}^{5} \\mathrm{~b}+3 \\equiv \\mathrm{a}^{3} \\cdot \\mathrm{a}^{2} \\cdot \\mathrm{~b}+3 \\equiv \\mathrm{a}^{3} \\mathrm{~b}^{2} \\cdot \\mathrm{~b}+3 \\equiv(\\mathrm{ab})^{3}+3 \\quad \\bmod 9\n$$\n\nOr les cubes modulo 9 prennent uniquement les valeurs $-1,0$ et 1 . On ne peut donc avoir $\\mathrm{m}^{3}-(a b)^{3} \\equiv 3$ mod 9. La condition de l'énoncé ne peut donc pas être satisfaite, comme annoncé.\nCommentaire des correcteurs\nBeaucoup d'élèves ont une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Existe-t-il des entiers $a$ et $b$ pour lesquels : $\\mathbf{a}^{5} \\mathbf{b}+3$ et $a^{5}+3$ sont tous deux des cubes parfaits?\n\nUn cube parfait est un entier $n$ pour lequel il existe $m \\in \\mathbb{Z}$ tel que : $\\mathfrak{n}=\\mathrm{m}^{3}$.", "solution": "brutale qui consiste à regarder les paires $\\left(\\mathrm{ab}^{5}, \\mathrm{ba}^{5}\\right)$ modulo 9 d 'une façon ou d'une autre, ce n'est pas forcément une mauvaise chose mais il est plus subtil d'utiliser le petit théorème de Fermat en compétition pour ne pas perdre de temps (et parce que souvent les études ne sont pas exhaustives). La plupart des élèves ont une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 14.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Existe-t-il des entiers $a$ et $b$ pour lesquels : $\\mathbf{a}^{5} \\mathbf{b}+3$ et $a^{5}+3$ sont tous deux des cubes parfaits?\n\nUn cube parfait est un entier $n$ pour lequel il existe $m \\in \\mathbb{Z}$ tel que : $\\mathfrak{n}=\\mathrm{m}^{3}$.", "solution": "légèrement différente du corrigé qui consiste à remarquer que $a^{5} b+3$ et $b^{5} a+3$ ne peuvent pas être congrus à des cubes en même temps $\\bmod 9$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 14.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soit $p$ un nombre premier impair, $hp^{2}+1>p h+1$ donc $e=2$ et le raisonnement montre que soit $a=1$, soit $N=1$ et dans tous les cas $a \\leqslant 2$ et $Np^{3}+1>p^{2} h+1=n$, contradiction\n- Si $a=1, q=1+k p, N=1+l p$ avec $k, l>0(\\operatorname{car} q \\equiv N \\equiv 1(\\bmod p))$. On a obligatoirement $k, lp^{3}+1>p^{2} h+1=n$. De plus $1+(k+l) p \\equiv n \\equiv 1$ $\\left(\\bmod p^{2}\\right)$ donc $k+l=p$. Un parmi $k$ et $l$ est donc impair, ce qui oblige $q$ ou $N$ pair, donc dans tous les cas $n$ est pair, ce qui contredit $n \\mid 2^{n-1}-1$.\n\nDans tous les cas $\\mathrm{n}=\\mathrm{q}$ est premier.\nCommentaire des correcteurs\nLes correcteurs ont noté beaucoup d'erreurs d'inattention et de mauvaises utilisations de l'ordre d'un élément modulo $n$. Certains élèves ont été surpris en train d'essayer d'arnaquer les correcteurs, ce qui est inutile et ne permettra sûrement pas de gagner des points en compétition.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-3.jsonl", "problem_match": "\nExercice 15.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soit $m, n \\geqslant 2$ des entiers vérifiant la propriété suivante:\n\n$$\na^{n} \\equiv 1 \\quad(\\bmod m) \\quad a=1, \\ldots, n\n$$\n\nProuver que $m$ est un nombre premier et que $\\mathrm{n}=\\mathrm{m}-1$.", "solution": "de l'exercice 16 Commençons par supposer que $m=p$ est un nombre premier. On doit donc montrer $n=p-1$. Si $n \\geqslant p$, on a $p^{n} \\equiv 1(\\bmod p)$, une évidente contradiction. Donc $n1$. Alice et Bob jouent au jeu suivant. 2 N cartes numérotées de 1 à 2 N sont mélangées puis disposées dans une ligne, de manière à ce que les faces numérotées soient visibles. Chacun à leur tour, Alice et Bob choisissent une carte, soit celle tout à droite soit celle soit à gauche de la ligne, et la garde pour eux, jusqu'à ce que toutes les cartes aient été prises. Alice commence. A la fin du jeu, chaque joueur calcule la somme des numéros des cartes qu'il a prises. Le joueur ayant la plus grande somme gagne. Un joueur dispose-t-il d'une façon de ne pas perdre?", "solution": "de l'exercice 13 On commence par tester le jeu pour des petites valeurs, par exemple pour un jeu composé de $2 \\cdot 3$ cartes. Après plusieurs essais, on s'aperçoit par exemple que la stratégie qui consiste à prendre toujours la plus grande carte parmi la carte située la plus à gauche et la carte située la plus à droite ne fonctionne pas toujours, pour aucun des deux joueurs.\nTestons le cas $\\mathrm{N}=2$. Chacun des deux joueurs ne pourra prendre que deux cartes. Dans ce type de problème, une première idée est d'essayer de chercher une stratégie qui permet à un joueur de jouer comme il le souhaite, quelque soit les coups de l'adversaire. Regardons donc les cartes qu'Alice et Bob peuvent s'assurer d'obtenir. On note XYZW les cartes étalées sur la rangée dans cet ordre. Supposons qu'Alice prenne la carte $X$. Si Bob choisit la carte Y, Alice a le choix entre les cartes Z et W. Si Bob choisit la carte $W$, Alice a le choix entre les cartes $Z$ et $Y$. Ainsi, en choisissant la carte X, Alice s'assure de pouvoir prendre la carte $Z$ si elle le souhaite. En revanche, avant le premier coup d'Alice, Bob ne peut pas garantir de prendre une des quatre cartes.\nOn désire désormais généraliser ce processus. On regarde alors le cas $N=3$. Les cartes sont XYZWUV. On s'aperçoit alors que si Alice prend la carte $X$ au premier tour, elle s'assure de pouvoir prendre les cartes $Z$ et $U$ si elle le veut. Ces remarques sont suffisantes pour penser qu' Alice dispose d'une stratégie gagnante en récupérant les cartes $X, Z, U$ si $X+Z+U>Y+W+V$ et en récupérant les cartes $Y, W, V$ dans le cas contraire. On prouve à présent que cette stratégie fonctionne dans le cas général.\nAlice colorie une carte sur deux en noir (la carte toute à droite est blanche, celle toute à gauche est noire). Elle calcule la somme des numéros des cartes blanches et celle de numéros des cartes noires.\nSi la somme des blanches est plus grande, elle choisit la carte blanche tout à droite. Bob prendra obligatoirement une carte noire ensuite. A chaque tour Alice peut choisir entre une carte blanche ou noire et en prenant la blanche, elle ne laisse pas la choix à Bob, qui prendra forcément une carte noire.\nAinsi à la fin Alice aura toutes les cartes blanches et Bob toutes les cartes noires. Donc elle aura un score supérieur ou égal à celui de Bob. Elle procède de même si la somme des cartes noires est plus grande.\nCommentaire des correcteurs\nLa majorité des élèves a su trouver la bonne stratégie. Parmi ceux qui ne l'ont pas trouvée, beaucoup ont proposé une stratégie \"au tour par tour\", sans justifier qu'elle permettait de ne pas perdre. Une telle approche ne peut pas permettre de résoudre l'exercice.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-4.jsonl", "problem_match": "\nExercice 13.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "On considère une grille de taille $2019 \\times 2019$. Sur cette grille sont posés des cailloux. Une configuration est dite belle s'il n'existe pas de parallélogramme formé par quatre cailloux $A B C D$, tels que $A, B, C$, et $D$ ne soient pas tous alignés.\nQuel est le plus grand nombre de cailloux qu'il est possible de mettre dans une grille?", "solution": "de l'exercice 14 Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $\\mathrm{n} \\leqslant \\mathrm{c}$ et d'autre part on va montrer que l'on peut trouver une grille possédant exactement c cailloux satisfaisant la propriété.\nOn s'empresse de tester l'énoncé pour des valeurs plus petites, par exemple pour une grille de taille $3 \\times 3$, $4 \\times 4$ ou même $5 \\times 5$, afin de deviner la valeur. On trouve dans ces petits cas que les plus grands entiers sont respectivement 5, 7 et 9 . On peut conjecturer que la valeur recherchée sera donc $2 \\times 2019-1=4037$. En testant ces petites valeurs, on a pu remarquer que la présence de cailloux sur une colonne forçait que certains emplacements soient vides. Nous allons donc essayer de formaliser ce raisonnement.\nOn considère les paires de cailloux qui sont sur la même colonne. S'il y a deux telles paires dont les cailloux sont à même distance sur des colonnes différentes alors on obtient un parallélogramme, ce que l'on veut éviter.\nSoit $n_{i}$ le nombre de cailloux dans la $i$-ième colonne. Sur la colonne $i$ il y a par conséquent au moins $n_{i}-1$ paires à distances distinctes. Puisque pour deux colonnes fixées, la distance entre deux quelconques cailloux de la première colonne doit être différente de la distance entre deux quelconques cailloux de la deuxième colonne, toutes les distances entre deux paires de cailloux appartenant à la même colonne doivent être distinctes. Cela fait en tout $\\left(n_{1}-1\\right)+\\left(n_{2}-1\\right)+\\cdots+\\left(n_{2019}-1\\right)=n-2019$ distances distinctes avec n le nombre total de cailloux. Or il y a au plus 2018 distances possibles, puisqu'il y a 2019 emplacements pour un cailloux dans une colonne. Ceci montre que $\\mathrm{n} \\leqslant 2018+2019=4037$.\nRéciproquement, si on remplit chaque case de la première ligne par un caillou et chaque case de la première colonne par un caillou et on laisse les autres cases vides, on a alors placé $2 \\times 2019-1=4037$ cailloux sans créer de parallélogrammes.\nLe plus grand entier recherché est donc 4037.\nCommentaire des correcteurs\nUne grande partie des élèves a eu la bonne idée pour résoudre l'exercice, mais beaucoup ont eu du mal à formaliser le résultat correctement. Si on tente de résoudre cet exercice par récurrence, il faut expliciter les grilles que l'on manipule et faire attention au fait qu'une sous-grille d'une grille \"maximale\" n'est pas forcément maximale.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-4.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Un lycée comporte un nombre impair de classes, et, dans chaque classe, un nombre impair d'élèves. Un élève est choisi dans chaque classe pour faire parti du comité des élèves. Si le nombre de classes avec le plus de garçons que de filles est impair, montrer que le nombre de façons de former un comité des élèves contenant un nombre impair de garçons excède le nombre de façons de former un comité d'élèves contenant un nombre impair de filles.", "solution": "de l'exercice 15 En l'absence d'idées face au problème, on peut essayer de démontrer le résultat par récurrence. Pour regarder si cela pourrait fonctionner, on peut regarder ce qu'il advient du résultat si l'on passe d'un lycée avec 3 élèves à un lycée avec 4 élèves. On vérifie également que les hypothèses de l'énoncé sont adaptées à une récurrence. On s'aperçoit que nous allons devoir distinguer plusieurs cas, selon la répartition garçon/filles dans les différentes classes. On démarre donc la récurrence.\nNous allons montrer le résultat par récurrence forte sur le nombre d'élèves au total. S'il n'y a aucun élève, alors le résultat est vrai, de même s'il n'y a qu'un élève dans le lycée.\nSupposons qu'il y ait n élèves en tout dans des classes satisfaisant l'énoncé. Supposons que l'énoncé de l'exercice est vrai dès lors qu'il y a strictement moins que n élèves. Il y a deux cas à étudier :\n\n- S'il n'y a de classe avec une fille et un garçon, alors il y a un nombre impair de classe avec que des garçons et les autres classes n'ont que des filles, donc le comité aura nécessairement un nombre impair de garçons, l'énoncé est vérifié.\n- S'il existe une classe avec une fille et un garçon, appelons-les respectivement Alice et Bob. Si on enlève Alice et Bob de la classe alors il y a plus de manières de choisir le comité avec un nombre impair de garçons. Si on considère uniquement les comités avec soit Alice soit Bob, alors on a autant de comité avec un nombre impair de garçons qu'avec un nombre impair de filles : en effet, échanger Alice et Bob change la parité du nombre de garçons et de filles. Ainsi l'énoncé est vérifié.\nPar récurrence forte, l'énoncé est vérifié quelque soit le nombre total d'élèves.\nUne", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-4.jsonl", "problem_match": "\nExercice 15.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Un lycée comporte un nombre impair de classes, et, dans chaque classe, un nombre impair d'élèves. Un élève est choisi dans chaque classe pour faire parti du comité des élèves. Si le nombre de classes avec le plus de garçons que de filles est impair, montrer que le nombre de façons de former un comité des élèves contenant un nombre impair de garçons excède le nombre de façons de former un comité d'élèves contenant un nombre impair de filles.", "solution": "un peu plus astucieuse consiste à procéder différemment : soit $n$ le nombre de classes, et soient $f_{i}$ et $g_{i}$ les nombres de filles et garçons dans la classe $i$ pour $1 \\leqslant i \\leqslant n$. Alors la quantité suivante, lorsqu'on la développ,e compte le nombre de façons de faire un comité avec un nombre impair de garçons moins celui de faire un comité avec un nombre impair de filles :\n\n$$\n\\prod_{i=1}^{n}\\left(g_{i}-f_{i}\\right)\n$$\n\nMais ce produit est positif s'il y a un nombre impair de classes avec plus de garçons que de filles, ce qui donne bien le résultat voulu.\nCommentaire des correcteurs\nLes élèves ont pour la plupart procédé par récurrence sur le nombre de classes, en utilisant l'inégalité de réordonnement. La plupart ont procédé de manière correcte, mais certains ont écrit des inégalités strictes sans justifier pourquoi le cas d'égalité ne se présente pas (qui demande de citer une des hypothèses de l'énoncé : le nombre impair d'élèves par classe).", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-4.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "On considère une grille $2019 \\times 2019$. On note $C_{i, j}$ la case sur la i-ième colonne et la j-ième ligne pour $1 \\leqslant \\mathfrak{i}, \\mathfrak{j} \\leqslant 2019$. Un coloriage de la grille est formidable s'il n'existe pas $1 \\leqslant \\mathfrak{i}<\\ell \\leqslant 2019$ et $1 \\leqslant j1$ tels qu'il est possible de paver un pavé droit de dimensions $\\mathrm{a} \\times \\mathrm{b} \\times \\mathrm{c}$ dans un grille en trois dimensions avec des super-dominos de sorte qu'il y ait autant de super-dominos de chacun des 3 types?", "solution": "de l'exercice 17 Dans ce problème, on cherche tous les entiers $a, b, c$ satisfaisant certaines propriétés. Nous allons donc établir que si $\\mathrm{a}, \\mathrm{b}$ et c satisfont la propriété alors $\\mathrm{a}, \\mathrm{b}$ et c sont d'une certaine forme, et d'autre part montrer que si $a, b$ et $c$ sont de la forme trouvée, alors ils satisfont bien la propriété.\nOn peut également noter qu'il s'agit d'un problème de pavage, nous pouvons donc nous attendre à devoir utiliser un coloriage adroit du pavé droit. Si l'on n'a à priori pas d'idée sur la forme des entiers $a, b$ et $c$, on peut commencer par effectuer quelques remarques.\nSi on parvient à paver un pavé droit $\\mathrm{a} \\times \\mathrm{b} \\times \\mathrm{c}$ avec N super-dominos de chacun des trois types, alors nécessairement il y aura $2 \\mathrm{~N}+2 \\mathrm{~N}+2 \\mathrm{~N}=\\mathrm{abc}$ cases pavées, donc 6 divise $a b c$. Ainsi une coordonnée est paire. Supposons donc sans perte de généralité que a est pair.\nPour simplifier, on supposera que le pavé est composé de abc cases de coordonnées $(i, j, k)$, où $i$ est l'abscisse, $j$ l'ordonnée de la case et $k$ la profondeur.\nOn cherche désormais un coloriage de notre pavé. Tout d'abord, les objets manipulés sont des dominos, composés de 2 cubes; On va donc chercher un coloriage à 2 couleurs, du type damier. Regardons les caractéristiques d'un éventuel coloriage. On peut commencer par se concentrer sur une face, par exemple sur les cases de profondeur 1 . Un domino $1 \\times 1 \\times 2$ occupe au maximum une case sur cette face tandis que les deux autres types de dominos occupent 0 ou 2 cases de cette face. On peut donc essayer d'adapter notre coloriage à cette remarque en appliquant le même coloriage à chacune des tranches (par tranche, on entend ici l'ensemble des cases possédant la même profondeur), c'est-à-dire un coloriage où la couleur d'une case ( $i, j, k$ ) dépend de $i$ et de $j$ mais pas de $k$. L'avantage sera que les deux cubes d'un quelconque domino $1 \\times 1 \\times 2$ seront de la même couleur. De ce constat, on peut chercher à faire en sorte que les 2 cubes des dominos $1 \\times 2 \\times 1$ et $2 \\times 1 \\times 1$ soient de couleur différentes. Ceci nous fait penser à un coloriage en damier, que l'on applique uniformément à chacune des tranches. Formalisons donc ce coloriage et voyons l'information qu'il nous apporte.\nOn colorie en blanc les cases $(i, j, k)$ telles que $i+j$ est paire, et en noir les autres. Ainsi, les cubes d'un super-domino $1 \\times 1 \\times 2$ sont de la même couleur, noir ou blanc, tandis qu'un super-domino $1 \\times 2 \\times 1$ contient exactement un cube blanc et un cube noir, de même pour un super-domino $2 \\times 1 \\times 1$. On déduit que lorsque l'on pave notre pavé droit avec le même nombre de super-domino de chaque type, le nombre total de cases blanches recouvertes est pair : en effet un super-domino $1 \\times 1 \\times 2$ en recouvre 2 ou 0 , et un super-domino d'un des deux autres type en recouvre 1 . Ainsi pour pouvoir paver le pavé droit $a \\times b \\times c$ avec autant de super-dominos de chaque type, il faut qu'il y ait un nombre pair de cases blanches. Or, la tranche constituée des cases de profondeur 1 contient exactement $\\frac{\\mathrm{ab}}{2}$ cases blanches et toutes les tranches sont coloriées de la même façon et il y a c tranches. Il y a donc $\\frac{\\mathrm{ab}}{2} \\times \\mathrm{c}$ cases blanches et ce nombre doit être pair. On déduit que 4 divise abc. Comme 6 et 4 divisent abc , on a que 12 divise abc si un pavé $a \\times b \\times c$ satisfait l'énoncé.\n\nOn s'attaque désormais à la réciproque en montrant que l'on peut paver correctement un pavé $\\mathrm{a} \\times \\mathrm{b} \\times \\mathrm{c}$ si 12 divise abc. Pour trouver un tel pavage, on commence toujours par regarder les pavés de petites dimensions, par exemple un pavé $2 \\times 2 \\times 3$. Ces essais sont plus utiles qu'on ne le croit. En effet, si l'on parvient à paver ce pavé, on pourra paver correctement des pavés plus gros en découpant ces gros pavés en petits pavés de dimension $2 \\times 2 \\times 3$ par exemple. Or, on remarque qu'avec deux dominos de chaque type, on peut paver un pavé $2 \\times 2 \\times 3$ et $3 \\times 4 \\times 3$ (voir la figure, le pavage de droite est découpé en deux parties pour être plus lisible). De plus, cela permet de paver un pavé $2 \\times 4 \\times 3$ en recollant selon\nla largeur deux pavés $2 \\times 2 \\times 3$ en recollant deux $3 \\times 2 \\times 3$ selon la largeur. Puisque tout entier $a>1$ s'écrit comme somme de 2 et de 3 , en recollant le bon nombre de pavés de la forme $2 \\times 4 \\times 3$ et $3 \\times 4 \\times 3$, on peut paver n'importe quel pavé $a \\times 4 \\times 3$ pour $a>1$. De même, on peut paver les pavés de la forme $a \\times 2 \\times 6$, avec $a>1$. Or si 12 divise $a b c$ alors il y a deux possibilités:\n\n- Une dimension du pavé droit est divisible par 6 et une autre dimension est paire. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $a \\times 2 \\times 6, a>1$.\n- Une dimension du pavé droit est divisible par 4 et une autre dimension est divisible par 3. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $\\mathbf{a} \\times 4 \\times 3$, $\\boldsymbol{a}>1$.\n- Deux dimensions du pavé sont paires, et la dernière est divisible par 3. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $2 \\times 2 \\times 3$.\n- Une dimension du pavé droit est divisible par 12 et les autres sont impaires, non divisibles par 3, supérieures ou égales à 5 . Alors on décompose le pavé droit $12 \\mathrm{a} \\times \\mathrm{b} \\times \\mathrm{c}$ en un pavé $12 \\mathrm{a} \\times 3 \\times \\mathrm{c}$ et $12 a \\times(b-3) \\times c$, et on pave chacun comme précédemment cas $b-3$ est pair.\nCeci achève la construction et montre que les pavé droits qui peuvent être ainsi pavés sont ceux tels que 12 divise abc.\n\n\n\n## Commentaire des correcteurs\n\nL'exercice était difficile et a été résolu par un faible nombre d'élèves, mais un certain nombre d'élèves a réussi à avancer sur le problème, en montrant que certains pavés étaient pavables.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-4.jsonl", "problem_match": "## Exercice 17.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "2019 élèves participent à un concours et répondent chacun à 6 questions. A la fin du concours, on remarque que, parmi les bonnes réponses données par un quelconque groupe de 3 élèves, il y a au moins une réponse correcte à au moins 5 des 6 questions du concours. Quelle est la valeur minimale du nombre total de réponses correctes aux questions du concours?", "solution": "de l'exercice 18 Dans ce problème, on cherche le plus petit entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c est bien le plus petit entier recherché, on va d'une part montrer que si un entier n satisfait la propriété, alors $n \\geqslant c$ et d'autre part on va montrer que l'on peut trouver une configuration avec exactement c réponses correctes données.\nOn peut commencer par ranger les données dans un tableau $2019 \\times 6$, où les 2019 lignes représentent les 2019 élèves et les 6 colonnes les 6 problèmes. Dans la case ( $\\boldsymbol{i}, \\mathfrak{j}$ ), on inscrit un 1 si l'élève $\\boldsymbol{i}$ a répondu correctement à la question $j$ et on inscrit un 0 sinon. Le problème nous invite à effectuer un doublecomptage, cette présentation sous forme de tableau permet de voir quel double-comptage est intéressant. Les hypothèses concernant les triplets d'élèves invitent à tenter d'effectuer un double comptage. Mais d'abord, on effectue quelques remarques simples. On peut noter que si trois élèves ont répondu tous les trois faux aux questions 5 et 6 , alors on a un triplet d'élèves dont les réponses ne sont pas correctes pour au moins 5 exercices. Ainsi, si $q_{1}$ et $\\mathrm{q}_{2}$ sont deux questions du concours, il y a au plus 2 élèves qui ont répondu faux à ces questions. Comme il y a $\\binom{6}{2}=15$ façons de choisir une paire de questions $\\left\\{\\mathbf{q}_{1}, \\mathbf{q}_{2}\\right\\}$, et pour chaque paire il y a au plus deux élèves qui ont mal répondu à ces deux questions donc il y a au plus $2 \\cdot 15=30$ paires $\\left(\\left\\{q_{1}, q_{2}\\right\\}, e\\right)$ telles que l'élève $e$ a mal répondu aux questions $q_{1}$ et $q_{2}$. Dans le tableau, cela se traduit par le fait qu'il y a au plus 30 paires de 0 tels que les deux 0 appartiennent à la même ligne. Cette majoration du nombre de paires de 0 appartenant à la même ligne nous permet de deviner le double comptage que nous allons effectuer : nous allons compter de deux façons différentes le nombre N de paires de 0 tels que les deux 0 appartiennent à la même ligne. Une telle paire sera dite mauvaise dans la suite. On a déjà compté \"selon les colonnes\", ce qui nous a donné $\\mathrm{N} \\leqslant 30$. On va chercher à présent à compter \"selon les lignes\".\nOn note El 'ensemble des élèves qui ont répondu à au plus 4 questions. A chacun des élèves de E , on peut associer au moins un couple de réponses fausses donc $|E| \\leqslant N \\leqslant 30$\nPour un élève $e \\in E$ on note $\\mathrm{n}(e)$ le nombre de questions auxquelles il a répondu faux. Alors $\\mathrm{N}=$ $\\sum_{e \\in E}\\binom{\\mathfrak{n}(e)}{2}$, puisque les seuls mauvaises paires appartiennent à des lignes associées à des éléments de E et que s'il y a $n(e) 0$ dans une lignes, il y a $\\binom{n(e)}{2}$ façons de créer des paires de 0 de cette lignes. On utilise à présent la convexité de la fonction $x \\mapsto \\frac{x(x-1)}{2}=\\binom{x}{2}$ pour appliquer l'inégalité de Jensen et obtenir une minoration de N :\n\n$$\nN=\\sum_{e \\in \\mathrm{E}}\\binom{\\mathfrak{n}(e)}{2} \\geqslant|\\mathrm{E}|\\binom{\\frac{\\sum_{e \\in \\mid} n(e)}{|E|}}{2}\n$$\n\nOn note f le nombre total de réponses fausses proposées par les élèves de E , et $v$ le nombre total de réponses justes, de telles sorte que $\\mathrm{f}+v=6|\\mathrm{E}|$. On a donc $\\sum_{e \\in \\mathrm{E}} \\mathfrak{n}(e)=\\mathrm{f}$. Ainsi :\n\n$$\n\\begin{aligned}\n& 30 \\geqslant N \\geqslant \\frac{f(f-|E|)}{2|E|} \\\\\n& \\mathbf{f}^{2}-\\mathbf{f}|\\mathrm{E}|-60|\\mathrm{E}| \\leqslant 0\n\\end{aligned}\n$$\n\nCette dernière équation fournit que $f \\leqslant \\frac{|E|+\\sqrt{|E|^{2}+240|E|}}{2}$.\nSoit $V$ le nombre total de réponses justes données par l'ensembe des élèves, alors $V$ est la somme du nombre de bonnes réponses des élèves de E et la somme des bonnes réponses des élèves qui ne sont pas\ndans E. Par définition, les élèves qui ne sont pas dans E ont répondu correctement à au moins 5 questions. Donc\n\n$$\n\\mathrm{V} \\geqslant v+(2019-|\\mathrm{E}|) 5=2019 \\times 5-5|\\mathrm{E}|+v=2019 \\times 5-5|\\mathrm{E}|+6|\\mathrm{E}|-\\mathrm{f}=5 \\times 2019+|\\mathrm{E}|-\\mathrm{f}\n$$\n\nMais en utilisant l'inégalité obtenue en f plus haut on obtient\n\n$$\n\\mathrm{V} \\geqslant 2019 \\times 5+\\frac{|\\mathrm{E}|-\\sqrt{|\\mathrm{E}|^{2}+240|\\mathrm{E}|}}{2}\n$$\n\nLe côté droit est décroissant en $|E|$ et puisque $|E| \\leqslant 30$, donc $V \\geqslant 2019 \\times 5+\\frac{30-\\sqrt{30^{2}+240 \\times 30}}{2}=10065$. Donc V $\\geqslant 10065$.\n\nRéciproquement, il est possible que 2019 - 30 élèves aient répondu à 5 problèmes, et que 30 élèves aient répondu à 4 problèmes : il suffit que pour chacun des 15 ensembles de 4 questions parmi les 6 il y ait deux élèves qui ont répondu exactement à celles là. Cette configuration satisfait l'énoncé, et est telle que le nombre de bonnes réponses est exactement 10065.\n\n## Commentaire des correcteurs\n\nL'exercice, difficile, n'a été résolu que par très peu d'élèves. Cependant, il est appréciable de voir que plusieurs élèves ont rendu quelques éléments de réponses même s'ils ne disposaient pas d'une preuve complète. Quelques erreurs à éviter :\n\n1. Ce n'est pas parce qu'on dispose d'une configuration à 10065 bonnes réponses et qu'on ne peut pas enlever de bonne réponse dans cette configuration que c'est forcément la configuration optimale et que 10065 est la valeur optimale.\n2. Ce n'est pas parce qu'on a un minimum de bonnes réponses sur les élèves qui ont répondu correctement à au plus 4 questions ET qu'on a un minimum de bonnes réponses sur les élèves ayant répondu correctement à au moins 5 questions que le minimum pour le nombre global d'élèves est la somme de ces deux minimums. Autrement dit, le minimum global n'est pas forcément la somme des deux minimums locaux, surtout lorsque les deux groupes d'élèves et leur taille ne sont pas indépendants.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-4.jsonl", "problem_match": "\nExercice 18.", "solution_match": "\nSolution "}}
diff --git "a/French_STS/segmented/fr-corrig\303\251-comment\303\251-envoi-5.jsonl" "b/French_STS/segmented/fr-corrig\303\251-comment\303\251-envoi-5.jsonl"
new file mode 100644
index 0000000000000000000000000000000000000000..434e6efa265d0b2213178119bc29bed040c2d53e
--- /dev/null
+++ "b/French_STS/segmented/fr-corrig\303\251-comment\303\251-envoi-5.jsonl"
@@ -0,0 +1,43 @@
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Martin et Théo jouent à un jeu : Martin écrit un nombre entier au tableau. Théo a ensuite le droit d'effacer le nombre et de lui ajouter 2 , ou d'effacer le nombre et de lui enlever 3 , ceci autant de fois qu'il veut. Théo gagne s'il arrive à obtenir 2020 après un nombre fini d'étapes, sinon Martin gagne. Quel joueur a une stratégie gagnante ?", "solution": "de l'exercice 1 On commence par tester l'énoncé pour des entiers proches de 2020. Par exemple, on remarque que si Martin écrit les entiers 2018, 2016, ... Théo peut écrire 2020 au tableau en rajoutant au nombre écrit par Martin un nombre suffisamment grand de 2 . On remarque aussi que si Martin écrit 2019, Théo peut aussi gagner en remplaçant 2019 par 2021 puis 2023 puis 2023 par 2020.\nCette remarque nous permet de conjecturer d'une part que Théo peut toujours gagner quelque soit le nombre écrit par Martin, d'autre part que si un nombre k est écrit au tableau, Théo peut écrire les nombres $k+1$ ou $k-1$ au bout d'un nombre fini d'opérations.\nNous montrons donc que Théo peut toujours gagner quelque soit le nombre écrit par Martin. Supposons qu'à un instant donné, le nombre $k$ est écrit au tableau. Alors en remplaçant $k$ par $k+2$ en ajoutant 2 , $k+2$ par $k+4$ en ajoutant 2 et enfin $k+4$ par $k+1$ en retranchant 3 , Théo a remplacé le nombre $k$ par le nombre $k+1$ en un nombre fini d'opération. Nous appellerons cette transformation l'opération A. D'autre part, toujours si l'entier $k$ est écrit au tableau à un instant donné, en remplaçant $k$ par $k+2$ et $k+2$ par $k-1$, Théo a remplacé l'entier $k$ par l'entier $k-1$. Nous appellerons cette transformation l'opération B.\nSupposons désormais que Martin a écrit le nombre $k_{0}$ au tableau. Si $k_{0}=2020$, Théo a déjà gagné. Si $\\mathrm{k}_{0}<2020$, alors en effectuant $2020-\\mathrm{k}_{0}$ fois l'opération $A$, Théo peut remplacer l'entier $k_{0}$ par 2020 et gagner. Si $k_{0}>2020$, en effectuant $k_{0}-2020$ fois l'opération $B$, Théo peut remplacer à nouveau l'entier $k_{0}$ par 2020. Dans tous les cas, Théo gagne!\nCommentaire des correcteurs : L'exercice a été résolu avec succès par tous les élèves qui l'ont abordé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $A B C$ un triangle tel que $\\widehat{B A C}=60^{\\circ}$. Soit $O$ le centre du cercle circonscrit au triangle $A B C, H$ son orthocentre et $I$ le point d'intersection des bissectrices. Montrer que les points B, O, I, H et C sont cocycliques.", "solution": "de l'exercice 2\n\n\n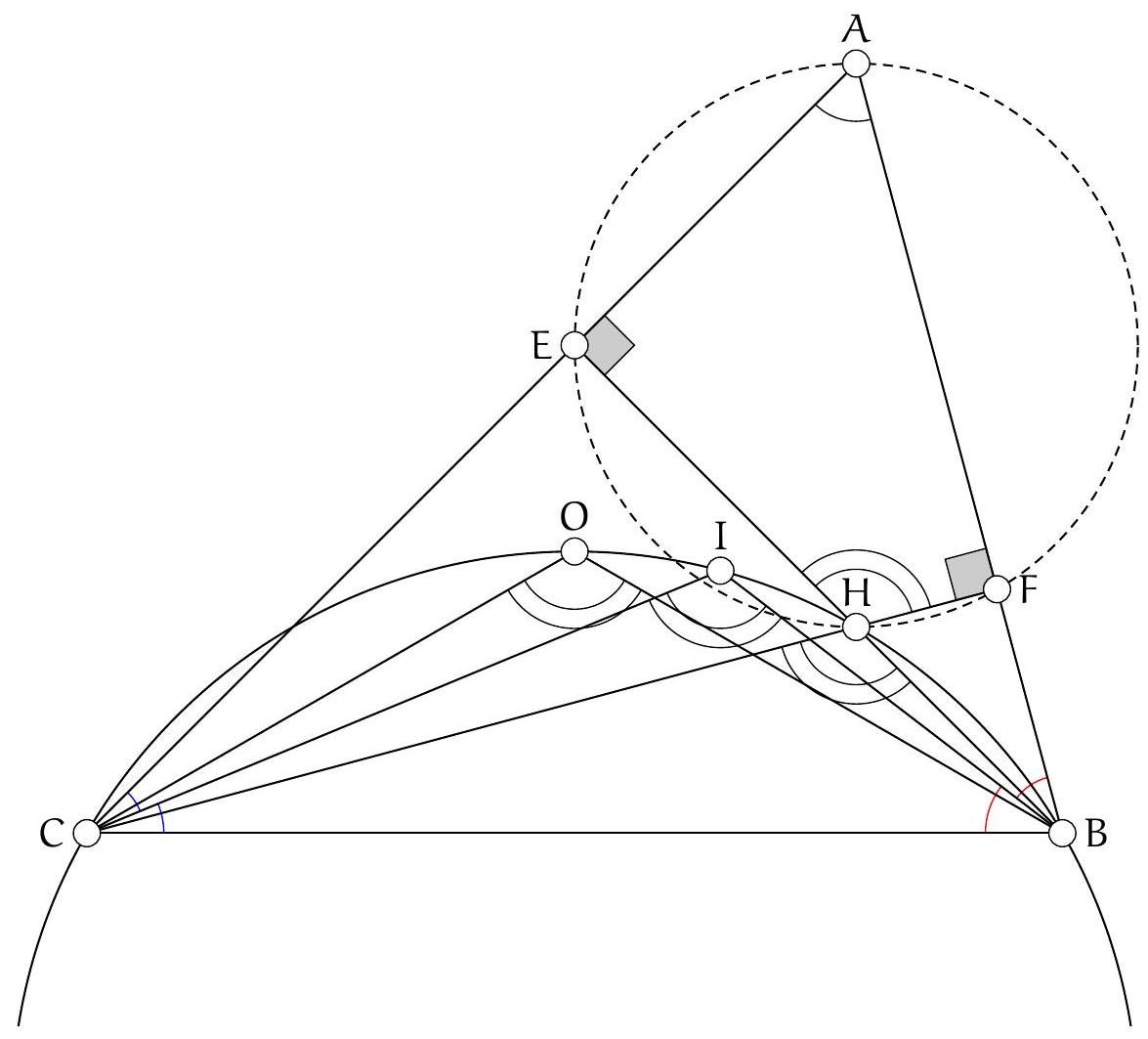\n\nOn traite le cas où les angles du triangle sont aigus.\nAvant de se lancer dans une chasse aux angles, on se demande quelles égalités d'angles nous allons déterminer pour montrer que les 5 points sont sur un même cercle. Pour cela, on note qu'on a, à priori, plus facilement accès aux angles des triangles BOC, BHC et BIC qu'aux angles du triangle BOH par exemple. Ceci nous motive à montrer que $\\widehat{\\mathrm{BOC}}=\\widehat{\\mathrm{BHC}}=\\widehat{\\mathrm{BIC}}$.\nTout d'abord, d'après le théorème de l'angle inscrit, $\\widehat{B O C}=2 \\cdot \\widehat{B A C}=120^{\\circ}$. On sait donc que nous allons devoir montrer successivement $\\widehat{\\mathrm{BHC}}=120^{\\circ}$ et $\\widehat{\\mathrm{BIC}}=120^{\\circ}$.\nPour calculer $\\widehat{\\mathrm{BHC}}$, on utilise la définition du point H comme le point d'intersection des hauteurs du triangle $A B C$. On introduit donc $D, E$ et $F$ les pieds des hauteurs respectivement issues des sommets $A, B$ et $C$. On utilise alors le fait (classique) que $\\widehat{\\mathrm{HEA}}=180^{\\circ}-\\widehat{\\mathrm{HFA}}=90^{\\circ}$ pour obtenir que les points $A, E, H$ et $F$ sont cocycliques. Ainsi $\\widehat{\\mathrm{FHE}}=180^{\\circ}-\\widehat{\\mathrm{EAF}}=120^{\\circ}$ donc $\\widehat{\\mathrm{BHC}}=\\widehat{\\mathrm{EHF}}=120^{\\circ}$\nEnfin, pour montrer que $\\widehat{\\mathrm{BIC}}=120^{\\circ}$, on se sert du fait que le point I est le point d'intersection des bissectrices du triangle. Cette définition nous donne en effet accès aux angles $\\widehat{\\mathrm{BCI}}$ et $\\widehat{\\mathrm{BCI}}$ en fonction des angles du triangle. On a donc:\n$\\widehat{\\mathrm{BIC}}=180^{\\circ}-\\widehat{\\mathrm{IBC}}-\\widehat{\\mathrm{ICB}}=180^{\\circ}-\\frac{1}{2} \\widehat{\\mathrm{ABC}}-\\frac{1}{2} \\widehat{\\mathrm{ACB}}=180^{\\circ}-\\frac{1}{2}\\left(180^{\\circ}-\\widehat{\\mathrm{BAC}}\\right)=180^{\\circ}-60^{\\circ}=120^{\\circ}$\nEn conclusion, $\\widehat{\\mathrm{BOC}}=\\widehat{\\mathrm{BHC}}=\\widehat{\\mathrm{BIC}}=120^{\\circ}$ donc les 5 points $\\mathrm{B}, \\mathrm{O}, \\mathrm{H}, \\mathrm{I}$ et C sont cocycliques.\n\nOn peut traiter de façon similaire le cas où un des angles du triangle $A B C$ est obtus.\nCommentaire des correcteurs: L'exercice est majoritairement bien réussi.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## \nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "1. Existe-t-il des nombres $a_{0}, \\ldots, a_{2020}$ valant -1 ou 1 tels que $a_{0} \\times a_{1}+a_{1} \\times a_{2}+\\cdots+a_{2019} \\times$ $a_{2020}+a_{2020} \\times a_{0}=1010 ?$\n2. Existe-t-il des nombres $a_{1}, \\ldots, a_{2020}$ valant -1 ou 1 tels que $a_{1} \\times a_{2}+a_{2} \\times a_{3}+\\cdots+a_{2019} \\times$ $a_{2020}+a_{2020} \\times a_{1}=1010 ?$", "solution": "de l'exercice 3\n\nDéjà regardons l'énoncé : on veut savoir si on peut trouver des nombres $\\left(a_{i}\\right)_{1 \\leqslant i \\leqslant n}$ valant +1 ou -1 tels que $a_{1} a_{2}+\\cdots+a_{n} a_{1}$ vaut 1010 avec dans la première question $n=2021$, dans la seconde $n=2020$. Pour cela on peut tester avec des $n$ petits quels sont les nombres qu'on peut écrire sous la forme $a_{1} a_{2}+\\cdots+a_{n} a_{1}$. Pour $n=3$, on trouve 3 (si on ne prend que des 1 ) et -1 (si on prend $a_{1}=a_{2}=1, a_{3}=-1$ ). Pour $n=4$, on trouve $4,0,-4$ (pour avoir 4 on ne prend que des 1 , pour avoir 0 il suffit de prendre trois $a_{i}$ valant 1 et un valant -1 , pour avoir -4 , il suffit d'altener les $a_{i}$ valant 1 et ceux valant -1 . On peut continuer à tester les valeurs pour des $n$ petits. On peut remarquer que déjà les nombres qu'on peut obtenir ont l'air d'être régulièrement écartés de 4 , ils sont même congrus à $n$ modulo 4.\n\nNotons également que si $a= \\pm 1$ et $b= \\pm 1$, alors $a b \\pm 1$ et que $a b=1$ si $a=b$ et $a b=-1$ si $a=-b$ 。\n\n1. Ici on est dans le cas où $n=2021$ et on veut obtenir une somme de 1010. Cela semble impossible à cause de la parité, on va donc regarder la parité de la somme. Soient $a_{0}, \\ldots, a_{2020}$ des nombres valant -1 ou 1 . Pour simplifier on pose $a_{2021}=a_{0}$. Comme on a toujours $a_{i} a_{i+1}= \\pm 1, a_{0} \\times$ $a_{1}+a_{1} \\times a_{2}+\\cdots+a_{2019} \\times a_{2020}+a_{2020} \\times a_{0}$ est une somme de 2021 nombres impairs, donc impaire. Elle ne peut donc pas valoir 1010 qui est pair. Il n'existe pas de nombres $a_{0}, \\ldots, a_{2020}$ valant -1 ou 1 tels que $a_{0} \\times a_{1}+a_{1} \\times a_{2}+\\cdots+a_{2019} \\times a_{2020}+a_{2020} \\times a_{0}=1010$.\n2. Dans ce cas $\\mathrm{n}=2020$ est divisible par 4 . A priori vu les tests effectués pour des petites valeurs, on s'attend à ce que le nombre obtenu soit divisible par 4 , or $1010=2 \\times 505$ n'est pas divisible par 4. On pourrait essayer de réutiliser l'argument de parité précédent, mais comme 2020 est pair, il prouverait que la somme est paire, or 1010 l'est aussi. Il va donc falloir plus précisément compter les moments où $a_{i} a_{i+1}=-1$ et ceux où $a_{i} a_{i+1}=1$. Or on sait que $a_{i} a_{i+1}=-1$ si et seulement si $a_{i}=-a_{i+1}$, il suffit donc de compter le nombre de changement de signes de la suite $a_{i}$ !\nSoient $a_{1}, \\ldots, a_{2020}$ des nombres valant -1 ou 1 tels que $a_{1} \\times a_{2}+a_{2} \\times a_{3}+\\cdots+a_{2019} \\times a_{2020}+$ $a_{2020} \\times a_{1}=1010$. Posons $a_{2021}=a_{1}$. On note $N$ le nombre de $i$ tels que $1 \\leqslant i \\leqslant 2020$ tels que $a_{i}=-a_{i+1}$. En particulier dans la somme $a_{1} \\times a_{2}+a_{2} \\times a_{3}+\\cdots+a_{2019} \\times a_{2020}+a_{2020} \\times a_{1}$ il y a N valeurs -1 et $(2020-\\mathrm{N})$ valeurs 1 . La somme vaut donc $2020-\\mathrm{N}-\\mathrm{N}=2020-2 \\mathrm{~N}$, on a donc $2020-2 \\mathrm{~N}=1010$ soit $2 \\mathrm{~N}=1010$ donc $\\mathrm{N}=505$. Or N est pair. En effet N est le nombre de changement de signs dans la suite $\\left(a_{1}, \\ldots, a_{2020}, a_{1}\\right)$ et cette suite commence par $a_{1}$ et termine $a_{1}$ donc elle a nécessairement un nombre pair de changements de signe puisque $a_{1}$ est du même signe que lui-même. On ne peut donc pas avoir $N=505$, ce qui fournit une contradiction. Il n'existe pas de nombres $a_{1}, \\ldots, a_{2020}$ valant -1 ou 1 tels que $a_{1} \\times a_{2}+\\cdots+a_{2019} \\times a_{2020}+a_{2020} \\times a_{1}=1010$.\nCommentaire des correcteurs: L'exercice a été bien traité : la première question a été quasiment toujours réussie, pour la seconde question, la majorité des copies mentionne qu'un nombre impair de produits valant -1 est possible mais peu trouvent un argument rigoureux pour le prouver : on pouvait vérifier que changer $a_{i}$ en $-a_{i}$ ne changeait pas la parité du nombre de produits valant -1 et dire que dans la situation où tous les $a_{i}$ valent 1 , le nombre de produits valant -1 est pair, il ne pouvait donc être impair à la fin. On pouvait également interpréter les produits -1 comme les changements de parité de la suite ( $a_{i}$ ) composée de $a_{1}, \\ldots, a_{2019}, a_{1}$. Comme elle commence à $a_{1}$ et termine à $a_{1}$, le nombre de changements de signe est forcément pair.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "## Exercice 3.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C$ un triangle dont les angles sont aigus. La hauteur issue de $A$ recoupe le cercle circonscrit au triangle $A B C$ en un point $D$. La hauteur issue de $B$ recoupe le cercle circonscrit au triangle $A B C$ en un point $E$. La droite (ED) coupe les côtés $[A C]$ et $[B C]$ respectivement en les points $P$ et $Q$. Montrer que les points $P, Q, B$ et $A$ sont cocycliques.", "solution": "de l'exercice 4\n\n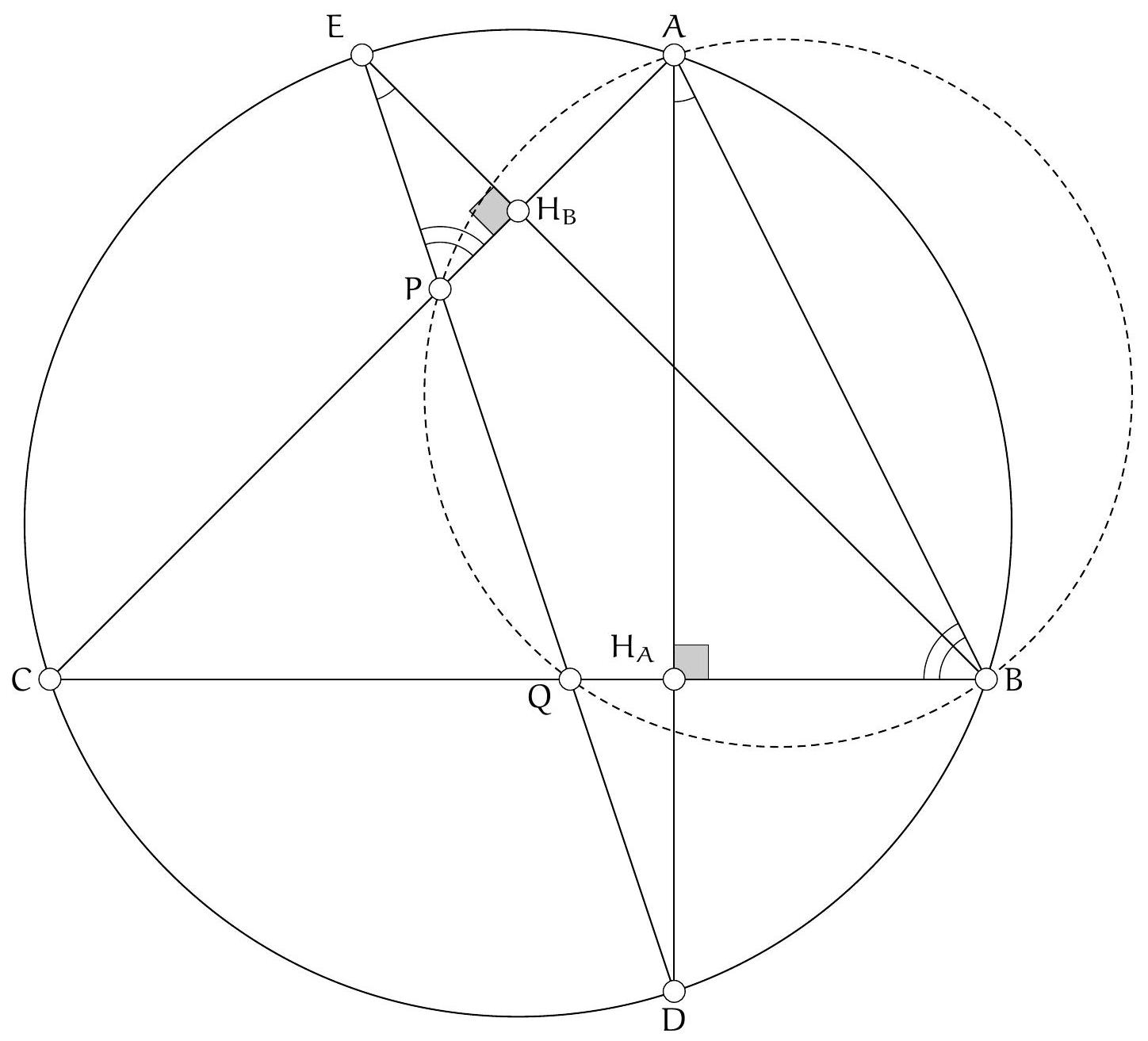\n\nDéterminons quels sont les angles qui semblent faciles d'accès. Par exemple, il semble compliqué de pouvoir obtenir l'angle $\\widehat{\\mathrm{PBQ}}$ ou l'angle $\\widehat{\\mathrm{PBA}}$. En revanche, on connait déjà l'angle $\\widehat{\\mathrm{QBA}}$ donc il semble raisonnable d'essayer de montrer que $\\widehat{\\mathrm{QPA}}=180^{\\circ}-\\widehat{\\mathrm{QBA}}$.\nOr, $180^{\\circ}-\\widehat{\\mathrm{QPA}}=\\widehat{\\mathrm{EPA}}$, on essaye donc de montrer que $\\widehat{\\mathrm{EPA}}=\\widehat{\\mathrm{QBA}}$. Deux angles droits nous sont donnés : si on pose $H_{B}$ le pied de la hauteur issue du sommet $B$ et $H_{A}$ le pied de la hauteur issue du sommet $A$, alors les angles $\\widehat{A H_{A} B}$ et $\\widehat{B H_{B} A}$ sont droits.\nOn n'a pas encore utilisé l'hypothèse que les points $E$ et $D$ étaient sur le cercle circonscrit au triangle $A B C$. Cette hypothèse se traduit par une égalité d'angle à l'aide du théorème de l'angle inscrit. Ceci donne notemment $\\widehat{\\mathrm{DEB}}=\\widehat{\\mathrm{DAB}}$.\n\nEn reportant ces différentes égalités d'angles sur la figure, on trouve donc que $\\widehat{\\mathrm{PEH}_{B}}=\\widehat{\\mathrm{H}_{\\mathrm{A}} \\mathrm{AB}}$ et $\\widehat{\\mathrm{PH}_{B} \\mathrm{E}}=\\widehat{\\mathrm{BH}_{\\mathrm{A}} \\mathrm{A}}$. Les triangles $\\mathrm{PEH}_{B}$ et $\\mathrm{BAH}_{\\mathrm{A}}$ sont donc sembables (il y a deux paires d'angles égaux deux à deux). Ainsi, $\\widehat{\\mathrm{EPH}_{\\mathrm{B}}}=\\widehat{\\mathrm{ABH}_{\\mathrm{A}}}$ qui est l'égalité que l'on souhaitait démontrer.\nCommentaire des correcteurs: L'exercice est très bien réussi et les élèves ont montré plusieurs façons efficaces de voir les choses.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Les cases d'un échiquier $8 \\times 8$ sont blanches. Un coup consiste à échanger les couleurs des cases d'un rectangle $3 \\times 1$ ou $1 \\times 3$ (les cases blanches deviennent noires et les cases noires deviennent blanches). Est-il possible d'aboutir en un nombre fini de coups à la configuration où toutes les cases de l'échiquier sont noires?", "solution": "de l'exercice 5 L'énoncé présente une suite finie d'opérations et le problème demande s'il est possible de partir de la situation initiale pour arriver à une certaine situation finale. Une première idée dans ce cas est de chercher un invariant.\nOn peut éventuellement essayer à la main de voir s'il est possible d'aboutir à une configuration où toutes les cases sont noires. Après plusieurs essais, on se rend compte qu' on n'arrive pas à aboutir la configuration désirée et on peut donc conjecturer que la réponse à l'exercice est négative.\nIci, le support de l'énoncé est un échiquier, on va donc chercher un invariant de coloriage, c'est-à-dire que nous allons chercher un coloriage astucieux de l'échiquier qui mette en évidence l'invariant. Quelles sont les caractéristiques d'un bon coloriage ? Tout d'abord, puisque les rectangles considérés possèdent 3 cases, on peut chercher un coloriage qui possède au plus 3 couleurs. Aussi, on peut chercher un coloriage tel que chaque rectangle $3 \\times 1$ ou $1 \\times 3$ possède une case de chaque couleur. On adopte donc le coloriage suivant (où on a remplacé les couleurs par des numéros, étant donné que l'exercice parle déjà de couleurs de cases).\n\n| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |\n| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |\n| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |\n| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |\n| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |\n| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |\n| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |\n| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |\n| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |\n\nQue nous apprend ce coloriage ? Chaque rectangle $3 \\times 1$ ou $1 \\times 3$ possède exactement une case de chaque numéro. Donc lorsque l'on change les couleurs d'un rectangle, exactement une case de chaque numéro change de couleur. Puisque les nombres de cases de numéro 1,2 et 3 ne sont pas identiques, ceci nous encourage à compter à chaque étape le nombre de cases blanches de chaque numéro.\nSoit $\\mathrm{N}_{1}$ le nombre de cases blanches contenant le numéro 1, dites de type $1, \\mathrm{~N}_{2}$ le nombre de cases blanches de types 2 et $\\mathrm{N}_{3}$ le nombre de cases blanches de type 3. Dans la situation initiale, $\\mathrm{N}_{1}=\\mathrm{N}_{3}=21$ et $\\mathrm{N}_{2}=22$, ces nombres ne sont pas tous égaux. On va donc s'intéresser à l'évolution de la différence entre les nombres $N_{1}$ et $N_{2}$. Changer la couleur des cases d'un rectangle $3 \\times 1$ ou $1 \\times 3$ fait en même temps diminuer ou augmenter chacun des nombres $N_{1}, N_{2}$ et $N_{3}$. En particulier, la différence $N_{1}-N_{2}$, à chaque étape, augmente de $2,0 \\mathrm{ou}-2$. En particulier, sa parité ne change pas. Or $\\mathrm{N}_{1}-\\mathrm{N}_{2}$ est impair au départ. Dans la situation finale demandée, $N_{1}-N_{2}=0.0$ est pair, donc le nombre $N_{1}-N_{2}$ ne peut être nul au bout d'un nombre fini d'étape. On ne peut donc pas arriver à un échiquier entièrement noir. Commentaire des correcteurs: L'exercice n'a pas été abordé par beaucoup d'élèves. L'exercice est cela dit un exercice d'invariant par coloriage très instructif.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "de l'exercice 6 Tout d'abord, analysons le problème : on a une équation diophantienne avec une puissance 2 , une puissance de 3 et un carré. On s'empresse donc de tester les petites valeurs de $z$ et de trouver la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "On peut remarquer que $2^{0}+3^{1}=2^{2}, 2^{3}+3^{0}=3^{2}$ et $2^{4}+3^{2}=5^{2}$. A priori comme on a quelques", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "s, on ne va pas trouver de contradictions immédiates simplement en regardant modulo quelque chose.\nNéanmoins on a un carré, donc il est naturel de regarder modulo 4 ou modulo 3 et d'essayer d'obtenir des informations sur $x$ et $y$. Idéalement, on aimerait obtenir que soit $x$ soit $y$ est pair, comme ça on aurait un autre carré dans l'équation ce qui nous permettrait de factoriser. On va donc regarder modulo 4, pour cela on a envie de traitrer en premier le cas où 4 divise $2^{\\mathrm{x}}$, i.e. le cas $x \\geqslant 2$.\nSupposons $x \\geqslant 2$. Comme un carré est congru à 0 ou 1 modulo $4, z^{2}$ est congru à 0 ou 1 modulo 4 , donc $3^{y}$ aussi. Comme il n'est pas divisible par 4 , on a forcément $3^{y} \\equiv 1(\\bmod 4)$. Comme $3^{2} \\equiv 9 \\equiv 1$ $(\\bmod 4)$, on a nécessairement $y$ pair $\\left(\\right.$ si $\\left.y=2 k+1,3^{y} \\equiv 9^{k} \\times 3 \\equiv 3(\\bmod 4)\\right)$. Posons $y=2 k$ avec $k$ entier, on obtient $2^{\\mathrm{x}}=z^{2}-\\left(3^{k}\\right)^{2}=\\left(z-3^{k}\\right)\\left(z+3^{k}\\right)$. Notons que $z+3^{k}$ est strictement positif, donc\n car elles divisent $2^{x}$.\nIci on a deux termes dont le produit vaut $2^{x}$, on aimerait montrer que l'un d'entre eux ne peut pas être très grand. Pour cela on va considérer le pgcd de $z+3^{k}$ et $z-3^{k}$ et le calculer en utilisant qu'il divise leur somme, différence et produit.\nSoit d le pgcd de $\\left(z-3^{k}\\right)$ et $\\left(z+3^{k}\\right)$, alors $d$ divise $\\left(z+3^{k}\\right)-\\left(z-3^{k}\\right)=2 \\times 3^{k}$, mais $d$ divise aussi $2^{\\mathrm{x}}$ donc $d$ divise 2 . Comme $z+3^{k} \\equiv z-3^{k}(\\bmod 2)$, si d vaut $1,\\left(z-3^{k}\\right)$ et $\\left(z+3^{k}\\right)$ sont impairs donc $2^{\\mathrm{x}}$ aussi, ce qui contredit le fait que $x \\geqslant 2$. On a donc $\\mathrm{d}=2$\nEn particulier comme $\\left(z-3^{k}\\right)$ et $\\left(z+3^{k}\\right)$ sont des puissances de 2 de pgcd 2 , le plus petit des deux vaut 2 donc comme $z+3^{k}>z-3^{k}, z=3^{k}+2$. Considérer le pgcd ici n'est pas nécessaire, on aurait pu directement aboutir à cela en posant $z+3^{\\mathrm{k}}=2^{\\mathrm{a}}, z-3^{\\mathrm{k}}=2^{\\mathrm{b}}$, observé que $\\mathrm{a}>\\mathrm{b}$ et écrit $2 \\times 3^{\\mathrm{k}}=2^{\\mathrm{a}}-2^{\\mathrm{b}}=2^{\\mathrm{b}}\\left(2^{\\mathrm{a}-\\mathrm{b}}-1\\right)$, mais un bon réflexe quand on a un produit est de regarder le pgcd des facteurs.\nDe ceci, on déduit que $z+3^{k}=2^{x-1}$ et $z-3^{k}=2$, donc en faisant la différence $2 \\times 3^{k}+2=2^{x-1}$ donc $3^{\\mathrm{k}}+1=2^{\\mathrm{x}-2}$. Cette équation est assez connue, mais si on ne la connait pas, comme on a des puissances de 2 et de 3 , il est pertinent de regarder modulo $2,4,8$ ou 3,9 . Comme $3+1=2^{2}$, regarder modulo 4 et 3 ne conclura pas tout de suite, on regarde donc modulo 8 .\nSi $x \\geqslant 5,8$ divise $2^{x-2}$ donc 8 divise $3^{x}+1$. Or les puissances de 3 modulo 8 valent 1 ou 3 donc $3^{x}-1$ vaut 2 ou 4 modulo 8 et n'est pas divisible par 8 , ce qui donne une contradiction. On a donc forcément $x=2,3$ ou 4 .\nPour $x=2,1=1+3^{k}$ donc $3^{k}=0$ ce qui est impossible. Pour $x=3,1+3^{k}=2$ donc $3^{k}=1$ donc $k=0$ et $y=0$. Pour $x=4,1+3^{k}=4$ donc $3^{k}=3$, on a donc $k=1$ soit $y=2$.\nRéciproquement, si $(x, y)=(3,0), z^{2}=2^{x}+3^{y}=9=3^{2}$ donc $z= \\pm 3$ et le triplet $(3,0,3)$ convient. Si $(x, y)=(4,2), z^{2}=2^{x}+3^{y}=25=5^{2}$ donc $z=5$ et le triplet $(4,2,5)$ convient.\nIl reste donc à traiter le cas où $x=0$ et celui où $x=1$. Pour le cas où $x=0$, on a $2^{x}=1$ qui est un carré, on va donc factoriser et réutiliser la technique du pgcd. Si $x=0$, l'équation se réécrit $3^{y}=z^{2}-1=(z-1)(z+1)$. Le pgcd de $z-1$ et $z+1$ divise $3^{y}$ et divise $z+1-(z-1)=2$ donc il vaut nécessairement 1 . Comme $3^{y}=(z-1)(z+1), z-1$ et $z+1$ sont des puissances de 3 positives (car $z+1>0$ donc $z-1>0$ leur produit étant strictement positif) de pgcd 1 , le plus petit des deux\nvaut nécessairement 1 donc $z-1=1, z=2$. On obtient $3^{y}=z^{2}-1=3$ donc $y=1$. Réciproquement $(0,1,2)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "car $1+3=2^{2}$.\nPour le cas $x=1$, on ne voit pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": ", il faut donc trouver un modulo pertinent pour évaluer l'équation, comme il y a une puissance de 3 et un carré, on peut regarder modulo 3 . $\\mathrm{Si} x=1$ l'équation devient $2+3^{y}=z^{2}$. Si $y=0$ l'équation devient $z^{2}=3$ qui n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "entière. On a donc $y>0$ donc $z^{2} \\equiv 2(\\bmod 3)$. Or un carré modulo 3 est congru à 0 ou 1 , il n'y a donc pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "pour $x=1$. Les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "s sont donc $(0,1,2),(3,0,3)$ et $(4,2,5)$.\nCommentaire des correcteurs: Exercice globalement bien réussi. Il faut néanmoins penser à vérifier les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:\n\n$$\n2^{x}+3^{y}=z^{2}\n$$", "solution": "s obtenues et justifier tout ce qui est affirmé : par exemple il faut justifier que si deux puissances de 2 sont distance de 2 ce sont forcément 2 et 4 (on peut le faire facilement en regardant modulo 4).", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Une grille de taille $\\mathrm{n} \\times \\mathrm{n}$ contient $\\mathrm{n}^{2}$ cases. Chaque case contient un entier naturel compris entre 1 et $\\boldsymbol{n}$, de telle sorte que chaque entier de l'ensemble $\\{1, \\ldots, n\\}$ apparaît exactement $n$ fois dans la grille. Montrer qu'il existe une colonne ou une ligne de la grille contenant au moins $\\sqrt{n}$ nombres différents.", "solution": "de l'exercice 7 Essayons d'abord de regarder ce qui se passe dans ce qui semble être 'le pire cas\" : si chaque ligne/colonne ne contient pas beaucoup de numéros, chaque numéro va y être beaucoup présent. En particulier, pour tout $i$, le nombre de $i$ semble être écrit dans peu de lignes et de colonnes. Mais à priori si le numéro $i$ apparait trop dans une ligne, il apparaitra dans beaucoup de colonnes et inversement. A priori, le pire cas semble être celui où chaque numéro apparaît dans autant de colonnes que de lignes et comme chaque numéro apparaît $n$ fois, le carré doit être de dimension $\\sqrt{n}$, donc $i$ apparait dans au moins $2 \\sqrt{n}$ lignes et colonnes.\nBien sûr, cette analyse ne constitue en rien une preuve, mais on voit deux idées importantes : premièrement, le nombre de numéros distincts dans chaque ligne/colonne semble avoir un lien avec le nombre de lignes/colonnes où chaque numéro apparaît. Deuxièmement, pour tout $i$ entre 1 et $n$, le nombre $i$ apparait au moins sur $2 \\sqrt{n}$ lignes et colonnes. On va donc essayer de formaliser ça.\nNotons $a_{c, i}$ pour $c$ une colonne ou une ligne et $i$ un entier entre 1 et $n$ le nombre de fois qu'apparait $i$ dans $c$, notons $c_{i}$ (resp. $l_{i}$ ) le nombre de colonnes (resp. lignes) à laquelle $i$ appartient. On note C l'ensemble des colonnes $L$ celui des lignes.\nNotons que l'hypothèse du fait que $i$ apparait $n$ fois se traduit comme $c_{i} \\times l_{i} \\geqslant n$ car $i$ apparait dans au plus $c_{i} l_{i}$ cases.\nNotons que pour tout $i$, $l_{i}+c_{i}$ étant le nombre de ligne ou de colonne où apparait $i$, il vaut $\\sum_{c \\in C \\cup L} a_{c, i}$. Le nombre d'éléments distincts dans la colonne $c$ vaut, quant à lui, $\\sum_{i=1}^{n} a_{c, i}$. En particulier, on voit bien que les $a_{c, i}$ jouent un rôle important dans le problème.\nMaintenant il reste à relier le nombre d'apparitions de i dans les différentes lignes/colonnes au nombre de numéros dans chaque ligne. Pour cela on va regarder la somme des $a_{c, i}$ (on somme sur $i$ entre 1 et $n$ et sur c colonne et ligne) et utiliser les deux interprétations précédentes.\nOn obtient ainsi $\\sum_{i=1}^{n} \\sum_{c \\in C \\cup L} a_{c, i}=\\sum_{i=1}^{n} c_{i}+l_{i} \\geqslant \\sum_{i=1}^{n} 2 \\sqrt{c_{i} l_{i}} \\geqslant 2 n \\sqrt{n}$.\nOn en déduit que $\\sum_{c \\in C \\cup L} \\sum_{i=1}^{n} a_{c, i} \\geqslant \\sum_{i=1}^{n} 2 \\sqrt{c_{i} l_{i}}=2 n \\sqrt{n}$.\nEn particulier, comme il y a $2 n$ lignes ou colonnes, il existe $c$ colonnes ou lignes telles que $\\sum_{i=1}^{n} a_{c, i} \\geqslant \\sqrt{n}$ i.e. c contient au moins $\\sqrt{\\mathrm{n}}$ numéros différents.\n\nCommentaire des correcteurs: L'exercice était très dur et seul un élève l'a réussi. Il fallait essayer de relier le nombre de numéros par ligne aux nombres de colonnes/lignes où apparait un numéro et rares sont ceux qui ont eu l'idée.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle non isocèle en $B$. Soit $D$ le pied de la bissectrice de l'angle $\\widehat{A B C}$. Soit $M$ le milieu de l'arc $\\widehat{A C}$ contenant $B$ sur le cercle circonscrit au triangle $A B C$. Le cercle circonscrit au triangle $B D M$ coupe la segment $[A B]$ en un point $K$ distinct de $B$. Soit $J$ le symétrique du point $A$ par rapport au point K . La droite (DJ) intersecte la droite ( $A M$ ) en un point O . Montrer que les points $\\mathrm{J}, \\mathrm{B}, \\mathrm{M}$ et O sont cocycliques.", "solution": "de l'exercice 8\n\n\n\nTout d'abord, on reconnaît dans la figure quelques points connus : le point $M$ est le milieu de l'arc $A C$ contenant $B$, il s'agit donc du pôle Nord du point $B$ dans le triangle $A B C$, c'est-à-dire qu'il est le point d'intersection de la bissectrice extérieure de l'angle $\\widehat{A B C}$, de la médiatrice du segment $[A C]$ et du cercle circonscrit au triangle $A B C$. On obtient donc que l'angle $\\widehat{D B M}$ est droit (par définition de la bissectrice extérieure). Le fait que $M$ appartient à la médiatrice du segment $[A C]$ nous invite également à considérer cette médiatrice. Soit N le milieu du segment $[A C]$. Alors $\\widehat{\\mathrm{DNM}}=90^{\\circ}$. On déduit donc que les points $B, M, N$ et $D$ sont cocycliques et $D$ appartient au cercle passant par les pointe $B, K$ et $D$.\nDe nouveaux points cocycliques apportent deux informations : une information sur les angles grâce au théorème de l'angle inscrit et une information sur les longueurs grâce à la puissance d'un point. Puisque la majorité des points se trouve sur deux droites se coupant en le sommet $A$, nous allons utiliser la puissance du point $A$ par rapport à divers cercles.\nNotamment, par puissance d'un point $A K \\cdot A B=A D \\cdot A N$. Donc\n\n$$\nA J \\cdot A B=2 A K \\cdot A B=2 A D \\cdot A N=A D \\cdot A C\n$$\n\ndonc les points $\\mathrm{D}, \\mathrm{C}, \\mathrm{B}$ et J sont cocycliques d'après la réciproque de la puissance d'un point. Pour conclure, nous allons utiliser les angles orientés, pour éviter d'avoir à traiter séparément les différentes configurations possibles.\nNous avons à présent tous les outils pour effectuer une chasse aux angles. Des angles difficiles d'accès sont les angles $\\widehat{\\mathrm{OMJ}}, \\widehat{\\mathrm{OBJ}}, \\widehat{M J B} \\ldots$ En revanche, les angles $\\widehat{\\mathrm{DJB}}$ et $\\widehat{\\mathrm{OMB}}$ semblent plus faciles à obtenir à l'aide des cercles présents sur la figure.\nPuisque les points D, C, B et O sont cocycliques, on trouve\n\n$$\n(J B, J O)=(J B, J D)=(C B, C D)=(C B, C A)=(M B, M A)=(M B, M O)\n$$\n\ndonc le quadrilatère JBMO est bien cyclique.\nCommentaire des correcteurs : L'exercice n'a pas été abordé par beaucoup d'élèves et il a été résolu par deux élèves. Quelques élèves ont noté que le point $M$ est le pôle Nord du point $B$, ce qui est un très bon réflexe.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Déterminer le plus petit entier $\\mathrm{n} \\geqslant 2$ tel qu'il existe des entiers strictement positifs $a_{1}, \\ldots, a_{n}$ tels que\n\n$$\na_{1}^{2}+\\ldots+a_{n}^{2} \\mid\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1\n$$", "solution": "de l'exercice 9 Analysons le problème. Dans ce problème, on cherche le plus petit entier n satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c'est bien le plus petit entier, on doit d'une part montrer que si un entier n satisfait la propriété, alors $n \\geqslant c$ et on doit montrer d'autre part que l'on peut trouver $c$ entiers satisfaisant la relation de divisibilité.\n\nPusiqu'il y a une relation de divisibilité, on peut s'attendre à utiliser divers idées :\n\n- Si $a \\mid b$ alors $a$ divise les combinaisons linéaires de $a$ et $b$\n- Si $a \\mid b$ et que $a$ et $b$ sont strictement positifs, alors $a \\mid b$\n- Si $a \\mid b$, les diviseurs de $a$ divisent également $b$\n\nUne fois cette première analyse effectuée, on peut commencer par regarder si on trouve des entiers $a_{i}$ satisfaisant la propriété pour des petites valeurs de $n$, par exemple pour $n=2,3$ ou même 4 si on est courageux, avant de se convaincre que cette méthode ne permettra pas de déterminer n .\n\nNéanmoins, avoir cherché des $a_{i}$ pour des petites valeurs de $n$ nous permet de trouver d'éventuelles propriétés que doivent satisfaire les $a_{i}$. Par exemple, on a pu remarquer que les entiers $a_{i}$ ne peuvent pas tous être pairs, puisque dans ce cas la somme des $a_{i}^{2}$ serait paire mais $\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$ est impair. On se rend alors compte que ce qui importe dans cet argument, ce n'est pas la parité des $a_{i}$ qui entre en jeu mais la parité de la somme.\n\nOn obtient que $a_{1}+a_{2}+\\ldots+a_{n}$ est impair. Dans le cas contraire, puisque $a_{1}^{2}+a_{2}^{2}+\\ldots+a_{n}^{2} \\equiv$ $a_{1}+a_{2}+\\ldots+a_{n} \\bmod 2, a_{1}+\\ldots+a_{n}$ est pair également mais alors $a_{1}^{2}+\\ldots+a_{n}^{2}$ est pair et divise $\\left(a_{1}+a_{2}+\\ldots+a_{n}\\right)^{2}-1$ qui est impair, ce qui est absurde.\n\nOn déduit que $\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$ est pair. L'argument de parité précédent nous invite à préciser cette étude. On va donc chercher si $\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$ est divisible par $4,8 \\ldots$. La présence des multiples carré nous invite à regarder chaque terme avec des modulos bien choisis.\n\nPar exemple, modulo $4,\\left(a_{1}+\\ldots+a_{n}\\right)^{2} \\equiv 1$ donc 4 divise $\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$. Ne nous arrêtons pas en si bon chemin, nous savons également que les carrés des nombres impairs ne peuvent que valoir 1 modulo 8. Ainsi, $\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$ est divisible par 8 . Or 8 est premier avec $a_{1}^{2}+\\ldots+a_{n}^{2}$ qui est impair. On déduit de tout cela que\n\n$$\n8\\left(a_{1}^{2}+\\ldots+a_{n}^{2}\\right) \\mid\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1\n$$\n\nEnfin, une autre remarque que l'on peut formuler sur l'énoncé est qu'il implique la somme des carrés de nombres d'un côté et le carré de la somme des nombres de l'autre côté. Ceci fait penser à l'inégalité de Cauchy-Schwarz, ou à l'inégalité des moyennes arithmétiques et quadratiques. On peut donc essayer de comparer les quantités $8\\left(a_{1}^{2}+\\ldots+a_{n}^{2}\\right)$ et $\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$.\n\nCette idée de comparer les termes est cohérente avec ce que l'on cherche à montrer. La divisibilité obtenue donne que $8\\left(a_{1}^{2}+\\ldots+a_{n}^{2}\\right) \\leqslant\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1$. Or, dans l'inégalité des moyennes arithmétique et quadratique, le carré de la somme est plus petit que la somme des carrés des éléments multipliée par le\nnombre de variables. On se doute donc que l'inégalité obtenue va être fausse pour n trop petit, ce qui va nous fournir la borne souhaitée. Plus précisement,\n\n$$\n8\\left(a_{1}^{2}+\\ldots+a_{n}^{2}\\right) \\leqslant\\left(a_{1}+\\ldots+a_{n}\\right)^{2}-1 \\leqslant n\\left(a_{1}^{2}+\\ldots+a_{n}^{2}\\right)-18$ donc $\\mathrm{n} \\geqslant 9$.\n\nRéciproquement, on cherche 9 entiers satisfaisant la propriété. On peut s'attendre à ce que de petits entiers fonctionnent. On peut donc chercher des $a_{i}$ valant 1 ou 2 . Finalement, on trouve qu'en prenant $a_{1}=\\cdots=a_{7}=1$ et $a_{8}=a_{9}=2$, on a bien 15 qui divise $11^{2}-1=120=15 \\times 8$.\nLa réponse attendue est donc $\\mathrm{n}=9$.\nCommentaire des correcteurs: L'exercice n'a été résolu que par un élève. C'est un exercice instructif et très complet, faisant appel à des arguments arithmétiques et des inégalités.\n\n## Exercices Seniors", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soit $\\left(x_{n}\\right)_{n \\in \\mathbb{N}}$ une suite réelle telle que $x_{0}=0$ et $x_{1}=1$ et pour tout $n \\geqslant 0, x_{n+2}=$ $3 x_{n+1}-2 x_{n}$. On pose également $y_{n}=x_{n}^{2}+2^{n+2}$ pour tout entier naturel $n$. Montrer que pour tout entier $n>0, y_{n}$ est le carré d'un entier impair.", "solution": "de l'exercice 10 On commence par tester l'énoncé pour des petites valeurs de n . On calcule donc les premières valeurs des suites $\\left(x_{n}\\right)$ et $\\left(y_{n}\\right)$. On trouve par exemple $x_{2}=3, x_{4}=7$, $x_{5}=15 \\ldots$ On peut donc conjecturer que $x_{n}=2^{n}-1$. On s'empresse de le démontrer par récurrence.\nLe résultat est déjà au rang 0 et 1 . Si on suppose $x_{n}=2^{n}-1$ et $x_{n+1}=2^{n+1}-1$, on a $x_{n+2}=$ $3 x_{n+1}-2 x_{n}=3 \\times 2^{n+1}-3-2 \\times 2^{n}+2=(3-1) \\times 2^{n+1}-1=2^{n+2}-1$ ce qui achève la récurrence. On injecte alors cette expression de $x_{n}$ dans l'expression de $y_{n}$. Il ne nous reste plus qu'à manipuler algébriquement cette nouvelle expression :\n\n$$\ny_{n}=\\left(2^{n}-1\\right)^{2}+2^{n+2}=2^{2 n}-2^{n+1}+1+2^{n+2}=2^{2 n}-2^{n+1}+1+2 \\times 2^{n+1}=2^{2 n}+2^{n+1}+1=\\left(2^{n}+1\\right)^{2}\n$$\n\nCeci montre bien que $y_{n}$ est le carré d'un entier impair.\nCommentaire des correcteurs: L'exercice a été résolu par tous les élèves qui l'ont abordé !", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 10.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver toutes les fonctions $f$ de $\\mathbb{R}$ dans $\\mathbb{R}$ telles que pour tout couple $(x, y)$ de réels :\n\n$$\nf(f(x))+f(f(y))=2 y+f(x-y)\n$$", "solution": "de l'exercice 11 Analysons le problème : ici on est face à une équation fonctionnelle, avec deux variables. La première chose à faire est d'essayer les quelques substitutions classiques : $x=y=0$, $x=0, y=0, x=y$. Ici comme on a un $f(x-y)$, il est très tentant de regarder ce que ça donne pour $x=y$. Posons donc $C=f(0)$, pour $x=y$, on obtient $2 f(f(x))=2 x+C$ soit $f(f(x))=x+\\frac{C}{2}$.\nMaintenant qu'on a une expression plus maniable de $f(f(x))$, on peut la réinjecter dans l'équation et regarder ce que ça donne.\nEn réinjectant dans l'équation initiale, on a donc $x+y+C=2 y+f(x-y)$ soit $f(x-y)=x-y+C$, pour $y=0$ on a donc $f(x)=x+C$ pour tout réel $x$. Maintenant, il faudrait déterminer $C$ avant d'effectuer la vérification, on essaie donc de voir quelle contrainte l'équation $f(f(x))=x+\\frac{C}{2}$ donne sur $C$.\nEn particulier $f(f(x))=f(x+C)=x+2 C$ donc $2 C=\\frac{C}{2}$ donc $4 C=C, 3 C=0$ donc $C=0$, on a donc $f(x)=x$ pour tout réel $x$. Maintenant on n'oublie pas de vérifier que la fonction trouvée est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver toutes les fonctions $f$ de $\\mathbb{R}$ dans $\\mathbb{R}$ telles que pour tout couple $(x, y)$ de réels :\n\n$$\nf(f(x))+f(f(y))=2 y+f(x-y)\n$$", "solution": "! Réciproquement la fonction identité convient car dans ce cas, $f(f(x))+f(f(y))=f(x)+f(y)=$ $x+y=2 y+x-y=2 y+f(x-y)$ pour tout $x, y$ réels.\nCommentaire des correcteurs: L'exercice a été très bien réussi. Il faut faire attention à ne pas conclure que $f$ est l'identité lorsque l'on trouve $f(X)=X$ avec $X$ dépendant de $x$ et $y$ (il faut vérifier que $X$ peut prendre toutes les valeurs réelles).", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Trouver tous les couples d'entiers positifs $(x, y)$ tels que $2^{x}+5^{y}+2$ est un carré parfait.", "solution": "de l'exercice 12 Ici on est face à un problème d'équation diophantienne avec un carré et une puissance de 2 . On peut se rendre compte en testant les petits cas que $(x, y)=(0,0)$ et $(1,1)$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 12.", "solution_match": " Solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Trouver tous les couples d'entiers positifs $(x, y)$ tels que $2^{x}+5^{y}+2$ est un carré parfait.", "solution": "s. Comme on a un carré et une puissance de 2 , on est très tenté de regarder modulo 4 ou 8 . Regardons déjà modulo 4 pour voir s'il y a une contradiction. Pour cela on va d'abord traiter le cas où $x \\geqslant 2$.\nDéjà notons que si $x \\geqslant 2,2^{x}+5^{y}+2 \\equiv 1+2 \\equiv 3(\\bmod 4)$ et 3 n'est pas un carré modulo 4 (les carrés sont 0 et 11 modulo 4). On a donc forcément $x=1$ ou $x=0$.\nMaintenant réécrivons l'équation dans le cas $x=1$. Pour $x=1$ soit $y$ entier positif tel que $2+5^{y}+2=$ $5^{y}+4$ est un carré parfait. Notons que comme 4 est un carré, on va pouvoir factoriser.\nSoit $k$ entier positif tel que $k^{2}=5^{y}+4$, on a donc $(k-2)(k+2)=5^{y}$. Notons que comme $k+2>0$, on a $k-2>0$ et $k+2$ et $k-2$ sont des puissances de 5 . Si $k-2>1$, alors 5 divise $k+2$ et $k-2$ donc 5 divise $k+2-(k-2)=4$ contradiction.\nAinsi $\\mathrm{k}-2=1$ donc $\\mathrm{k}=3$, donc $5^{y}+4=9$ donc $\\mathrm{y}=1$. Réciproquement si $(\\mathrm{x}, \\mathrm{y})=(1,1)$, $2^{x}+5^{y}+2=9$ est un carré parfait.\nPour $x=0$, soit $y$ tel que $1+5^{y}+2=5^{y}+3$ est un carré, soit $k \\geqslant 0$ tel que $k^{2}=5^{y}+3$. Ici comme on a des carrés et des puissances de 5 , on peut essayer de regarder modulo 5 . Si $y \\geqslant 1$, alors on a $k^{2} \\equiv 3$ $(\\bmod 5)$, or les carrés modulo 5 sont 1 et 4 , ce qui est une contradiction. On a donc forcément $y=0$.\nRéciproquement si $(\\mathrm{x}, \\mathrm{y})=(0,0), 2^{\\mathrm{x}}+5^{\\mathrm{y}}+2=4$ est un carré parfait.\nLes", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Trouver tous les couples d'entiers positifs $(x, y)$ tels que $2^{x}+5^{y}+2$ est un carré parfait.", "solution": "s sont donc les couples $(0,0)$ et $(1,1)$.\nCommentaire des correcteurs: Cet exercice a été très bien réussi dans l'ensemble. Pour le cas $x=0$, la majorité des élèves ont utilisé le fait qu'un carré n'est pas congrus à 3 modulo 5 , mais il ne fallait pas oublier de traiter à part le cas $y=0$ !", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Soit $A B C$ un triangle aux angles aigus. Soit $D$ le pied de la bissectrice de l'angle $\\widehat{B A C}$. La perpendiculaire à la droite $(A D)$ passant par le point $B$ recoupe le cercle circonscrit au triangle $A D B$ en un point $E$. Soit $O$ le centre du cercle circonscrit au triangle $A B C$. Montrer que les points $A, O$ et $E$ sont alignés.", "solution": "de l'exercice 13\n\n\n\nExaminons les angles que nous pouvons obtenir facilement. Puisque les points $A, E, D$ et $B$ sont sur un même cercle, on doit pouvoir utilise le théorème de l'angle inscrit pour avoir une égalité portant sur $\\widehat{\\mathrm{EAD}}$. Puisque la droite $(\\mathrm{BE})$ est perpendiculaire à la droite $(\\mathrm{AD})$, on doit pouvoir calculer l'angle $\\widehat{\\mathrm{EBA}}$. Enfin, on connaît bien sûr l'angle $\\widehat{O A B}$. Il semble donc raisonnable de montrer l'alignement des points $A, O$ et $E$ en montrant que $\\widehat{O A B}=\\widehat{\\mathrm{EAB}}$. On calcule séparément ces deux angles en fonction des angles du triangle $A B C$.\nD'une part, d'après le théorème de l'angle au centre et puisque le triangle $A O B$ est isocèle en O , on a\n\n$$\n\\widehat{\\mathrm{OAB}}=\\frac{1}{2}\\left(180^{\\circ}-\\widehat{\\mathrm{AOB}}\\right)=90^{\\circ}-\\widehat{\\mathrm{ACB}}\n$$\n\nD'autre part, $\\widehat{E A B}=\\widehat{\\mathrm{EAD}}+\\widehat{\\mathrm{DAB}}$. On utilise alors le théorème de l'angle inscrit et le fait que $\\widehat{\\mathrm{DAB}}=$ $\\frac{1}{2} \\widehat{\\mathrm{BAC}}$, on obtient :\n\n$$\n\\widehat{\\mathrm{EAD}}+\\widehat{\\mathrm{DAB}}=\\widehat{\\mathrm{EBD}}+\\frac{1}{2} \\widehat{\\mathrm{BAC}}=90^{\\circ}-\\widehat{\\mathrm{BDA}}+\\frac{1}{2} \\widehat{\\mathrm{BAC}}\n$$\n\nOr la somme des angles du triangle ADC fait $180^{\\circ}$ donc $\\widehat{\\mathrm{BDA}}=\\widehat{\\mathrm{DCA}}+\\widehat{\\mathrm{DAC}}=\\widehat{\\mathrm{ACB}}+\\frac{1}{2} \\widehat{\\mathrm{BAC}}$. Ainsi\n\n$$\n90^{\\circ}-\\widehat{\\mathrm{BDA}}+\\frac{1}{2} \\widehat{\\mathrm{BAC}}=90^{\\circ}-\\left(\\widehat{\\mathrm{ACB}}+\\frac{1}{2} \\widehat{\\mathrm{BAC}}\\right)+\\frac{1}{2} \\widehat{\\mathrm{BAC}}=90^{\\circ}-\\widehat{\\mathrm{ACB}}\n$$\n\net on trouve bien que $\\widehat{O A B}=90^{\\circ}-\\widehat{A C B}=\\widehat{E A B}$ donc les points $A, O$ et $E$ sont alignés. Commentaire des correcteurs: L'exercice est bien réussi. Cependant, plusieurs élèves ont rendu un preuve très compliquée.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 13.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Une grille de taille $\\mathrm{n} \\times \\mathrm{n}$ contient $\\mathrm{n}^{2}$ cases. Chaque case contient un entier naturel compris entre 1 et $\\boldsymbol{n}$, de telle sorte que chaque entier de l'ensemble $\\{1, \\ldots, n\\}$ apparaît exactement $n$ fois dans la grille. Montrer qu'il existe une colonne ou une ligne de la grille contenant au moins $\\sqrt{n}$ nombres différents.", "solution": "de l'exercice 14 Essayons d'abord de regarder ce qui se passe dans ce qui semble être 'le pire cas\" : si chaque ligne/colonne ne contient pas beaucoup de numéros, chaque numéro va y être beaucoup présent. En particulier, pour tout $i$, le nombre de $i$ semble être écrit dans peu de lignes et de colonnes. Mais à priori si le numéro $i$ apparait trop dans une ligne, il apparaitra dans beaucoup de colonnes et inversement. A priori, le pire cas semble être celui où chaque numéro apparaît dans autant de colonnes que de lignes et comme chaque numéro apparaît $n$ fois, le carré doit être de dimension $\\sqrt{n}$, donc $i$ apparait dans au moins $2 \\sqrt{n}$ lignes et colonnes.\nBien sûr, cette analyse ne constitue en rien une preuve, mais on voit deux idées importantes : premièrement, le nombre de numéros distincts dans chaque ligne/colonne semble avoir un lien avec le nombre de lignes/colonnes où chaque numéro apparaît. Deuxièmement, pour tout $i$ entre 1 et $n$, le nombre $i$ apparait au moins sur $2 \\sqrt{n}$ lignes et colonnes. On va donc essayer de formaliser ça.\nNotons $a_{c, i}$ pour $c$ une colonne ou une ligne et $i$ un entier entre 1 et $n$ le nombre de fois qu'apparait $i$ dans $c$, notons $c_{i}$ (resp. $l_{i}$ ) le nombre de colonnes (resp. lignes) à laquelle $i$ appartient. On note C l'ensemble des colonnes $L$ celui des lignes.\nNotons que l'hypothèse du fait que $i$ apparait $n$ fois se traduit comme $c_{i} \\times l_{i} \\geqslant n$ car $i$ apparait dans au plus $c_{i} l_{i}$ cases.\nNotons que pour tout $i$, $l_{i}+c_{i}$ étant le nombre de ligne ou de colonne où apparait $i$, il vaut $\\sum_{c \\in C \\cup L} a_{c, i}$. Le nombre d'éléments distincts dans la colonne $c$ vaut, quant à lui, $\\sum_{i=1}^{n} a_{c, i}$. En particulier, on voit bien que les $a_{c, i}$ jouent un rôle important dans le problème.\nMaintenant il reste à relier le nombre d'apparitions de $i$ dans les différentes lignes/colonnes au nombre de numéros dans chaque ligne. Pour cela on va regarder la somme des $a_{c, i}$ (on somme sur $i$ entre 1 et $n$ et sur c colonne et ligne) et utiliser les deux interprétations précédentes.\nOn obtient ainsi $\\sum_{i=1}^{n} \\sum_{c \\in C \\cup L} a_{c, i}=\\sum_{i=1}^{n} c_{i}+l_{i} \\geqslant \\sum_{i=1}^{n} 2 \\sqrt{c_{i} l_{i}} \\geqslant 2 n \\sqrt{n}$.\nOn en déduit que $\\sum_{c \\in C \\cup L} \\sum_{i=1}^{n} a_{c, i} \\geqslant \\sum_{i=1}^{n} 2 \\sqrt{c_{i} l_{i}}=2 n \\sqrt{n}$.\nEn particulier, comme il y a $2 n$ lignes ou colonnes, il existe $c$ colonnes ou lignes telles que $\\sum_{i=1}^{n} a_{c, i} \\geqslant \\sqrt{n}$ i.e. c contient au moins $\\sqrt{\\mathrm{n}}$ numéros différents.\n\nCommentaire des correcteurs: L'exercice a été globalement bien réussi par ceux qui l'ont traité, mais il faut faire attention à être clair dans ses explications et être précis dans les définitions des différents objets introduits.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Trouver tous les entiers $n \\geqslant 1$ tel que pour tout nombre premier $p1$ un entier vérifiant la propriété. On déduit de ceci que si $n$ n'est pas premier, si $p1$.\nEn faisant le même raisonnement $\\mathrm{n}-8$ et $\\mathrm{n}-9$ ne sont pas divisibles par $p$ si $p \\geqslant 10$.\nMaintenant analysons les facteurs premiers de $\\boldsymbol{n}-8$ et $\\mathrm{n}-9$ : ils peuvent être divisibles par 2, 3, 5, 7. Pour le facteur 3 , comme 3 divise $n-4, n \\equiv 1(\\bmod 3)$, donc $n-8 \\equiv 2(\\bmod 3)$ et $n-9 \\equiv 1$ $(\\bmod 3)$, ceux-ci ne sont pas divisibles par 3.\nDe plus $n-8$ n'est pas divisible par 2 car $n$ ne l'est pas. Comme $n-8$ et $n-9$ sont premiers entre eux, trois cas se présentent à nous : soit $\\mathrm{n}-8$ est une puissance de 5 , soit c'est une puissance de 7 , soit $\\mathrm{n}-8$ est divisible par 5 et 7 , dans ce cas $n-9$ est une puissance de 2 .\n\n- $\\operatorname{Sin}-8=5^{y}$ avec $y$ entier positif, on a $n-4=5^{y}+4=3^{x}$.\n\nIci 4 étant un carré, on aimerait montrer que $3^{x}$ est un carré pour factoriser l'équation. Pour cela, on regarde modulo 4 car on a des carrés et $5 \\equiv 1(\\bmod 4)$.\nRegardons modulo 4 , on a $3^{x} \\equiv 1^{y} \\equiv(\\bmod 4)$. Sinon comme l'ordre de 3 modulo 4 est 2 , 2 divise $x$ donc $x$ est pair. Posons $x=2 k$, on a $\\left(3^{k}-2\\right)\\left(3^{k}+2\\right)=5^{y}$ donc $3^{k}-2$ est positif et $3^{k}-2$ et $3^{k}+2$ sont des puissances de 5 . Ici on a un produit de terme valant une puissance de 2 , on essaie donc de calculer leur pgcd pour espérer borner un des termes. En particulier, le pgcd de $3^{\\mathrm{k}}+2$ et $3^{\\mathrm{k}}-2$ divise $\\left(3^{\\mathrm{k}}+2\\right)-\\left(3^{\\mathrm{k}}-2\\right)=4$ qui n'est pas divisible par 5 , et il divise leur produit c'est-à-dire $5^{y}$, il vaut donc 1 . Comme $3^{k}-2$ et $3^{k}+2$ sont des puissances de 2 de pgcd 1 , la plus petite vaut 1 , on a donc $3^{\\mathrm{k}}-2=1$ soit $\\mathrm{k}=1$ soit $\\chi=2$. On obtient $\\mathrm{n}=3^{\\mathrm{x}}+4=9+4=13$.\n\n- $\\operatorname{Sin}-8=7^{y}$ avec $y$ entier positif, on a $\\mathrm{n}-4=7^{y}+4=3^{x}$.\n\nComme 4 est un carré, on aimerait réussir à montrer que $x$ est pair pour factoriser, pour cela on regarde modulo 7 . Notons que si $y=0$, il n'y a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-commenté-envoi-5.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Trouver tous les entiers $n \\geqslant 1$ tel que pour tout nombre premier $p0$, on a égalité dans la première égalité si et seulement si on a égalité dans la première application de l'inégalité arithmético-géométrique, c'est-à-dire si $x=\\frac{2}{y}$, soit $x y=2$.\nDe même, pour avoir égalité dans la deuxième inégalité, il faut que $\\frac{y}{x}=2$. En multipliant les deux équations ensemble, on trouve $y^{2}=4$, donc $y=2$ car $y$ est positif. Ensuite, on obtient $x=1$. Réciproquement, $x=1$ et $y=2$ est un cas d'égalité, c'est le seul.\n\nCommentaire des correcteurs : Si nle problème a été bien réussi dans l'ensemble, voilà quelques pistes de progression :\n\n- Beaucoup d'élèves ne connaissent pas l'IAG et la redémontrent.\n- Le cas d'égalité a souvent été oublié.\n- Beaucoup d'élèves développent l'expression avant d'y appliquer l'IAG, plutôt que de l'appliquer directement dans les parenthèses.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "de l'exercice 2\n\nDéveloppons l'équation pour obtenir\n\n$$\nx^{2}-2 x y+2 y^{2}-4 y+4=0 .\n$$\n\nLes termes $x^{2}-2 x y$ nous font penser à l'identité remarquable $x^{2}-2 x y+y^{2}=(x-y)^{2}$. On sépare alors le $2 y^{2}$ en $y^{2}+y^{2}$ pour écrire\n\n$$\n(x-y)^{2}+y^{2}-4 y+4=0\n$$\n\nMais on reconnait alors une deuxième identité remarquable $y^{2}-4 y+4=(y-2)^{2}$. En factorisant, ceci donne\n\n$$\n(x-y)^{2}+(y-2)^{2}=0\n$$\n\nOr, une somme de carrés de nombre réels est forcément positive, et ne peut être nulle que si les deux carrés sont tous les deux nuls. Ainsi, si $x$ et $y$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "de l'équation, on a à la fois\n\n$$\nx-y=0 \\quad \\text { et } \\quad y-2=0\n$$\n\nAinsi, l'unique", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "possible de l'équation est $x=y=2$. On peut vérifier réciproquement que ceci est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": ", c'est donc la seule.\n\nCommentaire des correcteurs : Les élèves ont en général trouvé la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "avec la méthode présentée dans le", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "Malheureusement, la plupart oublient de vérifier que la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "qu'ils ont trouvé est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les réels $x, y$ tels que\n\n$$\nx(x-2 y)+y(2 y-4)+4=0\n$$", "solution": "du problème. Il suffit en effet qu'à une seule étape, l'équivalence ne soit pas justifiée pour que la vérification soit nécessaire. Certains ont considéré l'expression comme un polynôme en $x$, dont il s'agit de trouver les racines, celles-ci n'existant que pour certianes valeurs de y .", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Pour un réel $x$, on note $\\lfloor x\\rfloor$ le plus grand entier relatif inférieur ou égal à $x$ (par exemple, $\\lfloor 2,7\\rfloor=2,\\lfloor\\pi\\rfloor=3$ et $\\lfloor-1,5\\rfloor=-2)$.\nSoient $a, b$ deux réels tels que\n\n$$\na+\\lfloor a\\rfloor=b+\\lfloor b\\rfloor .\n$$\n\nMontrer que $a=b$.", "solution": "de l'exercice 3\n\nSupposons par l'absurde $a \\neq b$. Par symétrie (c'est-à-dire que $a$ et $b$ jouent le même rôle), on peut supposer $a-1\n$$\n\nMais d'après l'égalité au-dessus, $\\{b\\}-\\{a\\}$ est un entier, et il est donc nul. On a donc $\\{b\\}-\\{a\\}=0$, ce qui donne ensuite $2\\lfloor a\\rfloor-2\\lfloor b\\rfloor=0$.\nAinsi, on a\n\n$$\n\\lfloor a\\rfloor=\\lfloor b\\rfloor \\text { et } \\quad\\{a\\}=\\{b\\}\n$$\n\ndonc\n\n$$\na=\\lfloor a\\rfloor+\\{a\\}=\\lfloor b\\rfloor+\\{b\\}=b\n$$\n\nCommentaire des correcteurs : Exercice très bien réussi, avec une certaine diversité dans les approches. Quelques rares points sont perdus par étourderie. Certains élèves semblent confus sur le fonctionnement de la partie entière dans les négatifs.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $\\boldsymbol{n}$ un entier strictement positif et $x \\geqslant \\mathrm{n}$ un réel. Montrer que $x+\\frac{\\mathfrak{n}}{\\boldsymbol{x}} \\geqslant \\mathrm{n}+1$ et donner les cas d'égalité.", "solution": "de l'exercice 4\n\nLe réel $x$ est strictement positif donc on peut multiplier l'équation par $x$ pour avoir que l'équation est équivalente à\n\n$$\nx^{2}+n \\geqslant(n+1) x\n$$\n\nce qui donne, en réarrangeant les termes,\n\n$$\nx^{2}-(n+1) x+n \\geqslant 0\n$$\n\nOn reconnait alors une factorisation\n\n$$\n(x-n)(x-1) \\geqslant 0\n$$\n\nMais ceci est vrai car $x \\geqslant \\mathrm{n}$ et $x \\geqslant 1$.\nOn a égalité lorsque $x=n$ ou $x=1$. Mais si $x=1$, alors $n=1$ et $x=n$. Ainsi, dans tous les cas, le seul cas d'égalité est $x=n$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $\\boldsymbol{n}$ un entier strictement positif et $x \\geqslant \\mathrm{n}$ un réel. Montrer que $x+\\frac{\\mathfrak{n}}{\\boldsymbol{x}} \\geqslant \\mathrm{n}+1$ et donner les cas d'égalité.", "solution": "alternative de l'exercice 4\n\nOn repart de l'équation développée $x^{2}-(n+1) x+n \\geqslant 0$.\nLa condition $x \\geqslant n$ est très peu naturelle, on préfère des conditions de type $t \\geqslant 0$. On pose donc $x=n+t$ $\\operatorname{avec} t \\geqslant 0$. L'équation se réécrit alors\n\n$$\nn^{2}+2 n t+t^{2}-(n+1)(n+t)+n \\geqslant 0\n$$\n\nou encore\n\n$$\nt^{2}+(n-1) t \\geqslant 0\n$$\n\nMais cette nouvelle équation est clairement vraie car $t \\geqslant 0$ et $n \\geqslant 1$. De plus, on a égalité si et seulement si $t=0$, ou encore $x=n$.\n\nCommentaire des correcteurs : Le problème a été bien réussi par les élèves, les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $\\boldsymbol{n}$ un entier strictement positif et $x \\geqslant \\mathrm{n}$ un réel. Montrer que $x+\\frac{\\mathfrak{n}}{\\boldsymbol{x}} \\geqslant \\mathrm{n}+1$ et donner les cas d'égalité.", "solution": "s rendues étaient presque toutes abouties et suivaient le même schéma que les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $\\boldsymbol{n}$ un entier strictement positif et $x \\geqslant \\mathrm{n}$ un réel. Montrer que $x+\\frac{\\mathfrak{n}}{\\boldsymbol{x}} \\geqslant \\mathrm{n}+1$ et donner les cas d'égalité.", "solution": "s du", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $\\boldsymbol{n}$ un entier strictement positif et $x \\geqslant \\mathrm{n}$ un réel. Montrer que $x+\\frac{\\mathfrak{n}}{\\boldsymbol{x}} \\geqslant \\mathrm{n}+1$ et donner les cas d'égalité.", "solution": "En revanche, la plupart de ses copies ont été pénalisées pour des manques de justifications, notamment des justifications de signes. On rappelle que lorsqu'on multiplie ou divise une inégalité par une quantité, il faut s'assurer du signe de cette quantité : si elle est strictement positive, ça conserve le sens de l'inégalité, si elle est strictement négative, ça change le sens de l'inégalité, et si on multiplie par une quantité nulle, on n'a pas équivalence. C'est donc un détail qui a toute son importance. En ce qui concerne le cas d'égalité, plusieurs élèves ont oublié de le traiter, et d'autres ont oublié la condition $x \\geqslant \\mathrm{n}$, de sorte qu'ils considéraient que pour tout $\\mathrm{n} \\in \\mathbb{N}^{*}, x=1$ était un cas d'égalité. Ce n'était vrai que pour $\\mathrm{n}=1$, et donc c'était déjà compté dans le cas $x=\\mathrm{n}$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 4.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": "de l'exercice 5\n\nSupposons d'abord qu'un des réels est nul, sans perte de généralité $a=0$. Alors la première équation donne $\\mathrm{c}=0$ et la dernière équation donne $\\mathrm{b}=0$. Réciproquement, le triplet $\\mathrm{a}=\\mathrm{b}=\\mathrm{c}=0$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": ", on suppose à présent que les trois réels sont non nuls.\nSupposons maintenant que deux des réels soient égaux, sans perte de généralité $\\mathrm{a}=\\mathrm{b}$. On peut alors soustraire les deuxième et troisième équations pour avoir $b^{2}-c^{2}=0$. Comme $b$ et $c$ sont tous les deux positifs, on a donc $a=b=c$. Dans la première équation, on a alors $2 a^{2}=a$. Mais $a$ est non nul donc on peut diviser par $2 a$ pour avoir $a=\\frac{1}{2}$. Réciproquement, le triplet $a=b=c=\\frac{1}{2}$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": "On suppose désormais que les trois réels sont deux à deux distincts.\nFaisons le produit des équations pour obtenir\n\n$$\na(a+b) b(b+c) c(c+a)=a b c\n$$\n\nOn a supposé précédememnt que les réels étaient tous non nuls donc on peut diviser par abc pour avoir\n\n$$\n(a+b)(b+c)(c+a)=1\n$$\n\nEn faisant la différence des deux premières équations, on obtient $a^{2}-b^{2}+b a-b c=c-a$ ce qui se factorise en\n\n$$\n(a-b)(a+b)=(c-a)(b+1)\n$$\n\nEn faisant de même avec les deuxième et troisième lignes puis avec les troisième et première lignes, on obtient en plus\n\n$$\n\\left\\{\\begin{array}{l}\n(b-c)(b+c)=(a-b)(c+1) \\\\\n(c-a)(c+a)=(b-c)(a+1)\n\\end{array}\\right.\n$$\n\nEn faisant le produit de ces trois équations et en divisant par $(a-b)(b-c)(c-a)$ des deux côtés (qui est non nul car on a supposé $a, b, c$ deux à deux distincts), on obtient\n\n$$\n(1+a)(1+b)(1+c)=(a+b)(b+c)(c+a)\n$$\n\nMais on a montré précédemment que ce deuxième terme vaut 1 , ce qui est absurde car\n\n$$\n(1+a)(1+b)(1+c)>1 \\cdot 1 \\cdot 1=1\n$$\n\nAinsi, les seules", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": "s sont celles trouvées au début de la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": ", c'est-à-dire $\\mathrm{a}=\\mathrm{b}=\\mathrm{c}=0$ et $\\mathrm{a}=\\mathrm{b}=\\mathrm{c}=\\frac{1}{2}$.\nCommentaire des correcteurs : Le problème a été abordé et plutôt bien réussi. Néanmoins, plusieurs erreurs sont récurrentes :\n\n- Certains obtiennent les deux triplets", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": "s, mais ne vérifient pas qu'ils sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": "Quand on raisonne à coup d'implication, il n'est pas du tout sûr que les triplets trouvés soient", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les triplets de réels positifs ou nuls ( $\\mathrm{a}, \\mathrm{b}, \\mathrm{c})$ tels que\n\n$$\n\\left\\{\\begin{array}{l}\na^{2}+a b=c \\\\\nb^{2}+b c=a \\\\\nc^{2}+c a=b\n\\end{array}\\right.\n$$", "solution": "- Beaucoup supposent par exemple $a>b>c$. Deux problèmes : on oublie que plusieurs variables peuvent être égales. Mais surtout pour faire cela, il faut que le système soit symétrique : c'est-àdire que si on inverse deux variables, par exemple $a$ et $b$, alors le système ne change pas. Ce n'est pas du tout le cas : le système est complètement changé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Montrer que pour tous réels $\\mathrm{a}, \\mathrm{b}, \\mathrm{c}$ strictement positifs:\n\n$$\n\\frac{b c}{a^{2}+2 b c}+\\frac{c a}{b^{2}+2 c a}+\\frac{a b}{c^{2}+2 a b} \\leqslant 1 \\leqslant \\frac{a^{2}}{a^{2}+2 b c}+\\frac{b^{2}}{b^{2}+2 c a}+\\frac{c^{2}}{c^{2}+2 a b}\n$$", "solution": "de l'exercice 6\n\nCommençons par résoudre une des inégalités. Dans ce problème, l'inégalité la plus simple à étudier est celle de droite. On applique l'inégalité arithmético-géométrique sur les dénominateurs pour avoir $2 \\mathrm{bc} \\leqslant \\mathrm{b}^{2}+\\mathrm{c}^{2}$ par exemple, ce qui donne\n\n$$\n\\frac{a^{2}}{a^{2}+2 b c}+\\frac{b^{2}}{b^{2}+2 c a}+\\frac{c^{2}}{c^{2}+2 a b} \\geqslant \\frac{a^{2}}{a^{2}+b^{2}+c^{2}}+\\frac{b^{2}}{a^{2}+b^{2}+c^{2}}+\\frac{c^{2}}{a^{2}+b^{2}+c^{2}}=1 .\n$$\n\nPour le côté gauche, on remarque que celui-ci ressemble beaucoup au côté droit. Appelons $G$ et $D$ les côtés gauche et droit de l'équation respectivement. On a alors\n\n$$\n\\begin{gathered}\n\\mathrm{G}+2 \\cdot \\mathrm{D}=\\frac{\\mathrm{a}^{2}}{\\mathrm{a}^{2}+2 \\mathrm{bc}}+\\frac{\\mathrm{b}^{2}}{\\mathrm{~b}^{2}+2 \\mathrm{ca}}+\\frac{\\mathrm{c}^{2}}{\\mathrm{c}^{2}+2 \\mathrm{ab}}+\\frac{2 \\mathrm{bc}}{\\mathrm{a}^{2}+2 \\mathrm{bc}}+\\frac{2 c a}{\\mathrm{~b}^{2}+2 \\mathrm{ca}}+\\frac{2 a b}{\\mathrm{c}^{2}+2 a b} . \\\\\n\\frac{\\mathrm{a}^{2}+2 \\mathrm{bc}}{\\mathrm{a}^{2}+2 b c}+\\frac{b^{2}+2 c a}{b^{2}+2 c a}+\\frac{c^{2}+2 a b}{c^{2}+2 a b}=3 .\n\\end{gathered}\n$$\n\nOn a donc\n\n$$\n\\mathrm{G}=\\frac{1}{2}(3-\\mathrm{D}) \\leqslant \\frac{1}{2}(3-1)=1\n$$\n\npar l'inégalité de droite que l'on a montré précédemment.\nCommentaire des correcteurs : L'exercice a été bien réussi. Un certain nombre d'élève n'a trouvé qu'une seule des deux inégalités : il est important d'envoyer tout ce qui a été trouvé sur l'envoi, même si on n'a trouvé que la moitié de l'exercice. Un certain nombre d'élèves ont juste tout mis au même dénominateur, et ensuite prouvé l'inégalité, ce qui n'était pas très élégant mais fonctionnait bien.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soient $x, y, z$ des réels strictement positifs tels que $x y+y z+z x=1$. Montrer que\n\n$$\n2\\left(x^{2}+y^{2}+z^{2}\\right)+\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}+\\frac{1}{y^{2}+1}+\\frac{1}{z^{2}+1}\\right) \\geqslant 5\n$$", "solution": "de l'exercice 7\n\nDans cet exercice, on aimerait bien appliquer l'inégalité arithmético-géométrique de façon à obtenir une minoration du type $\\left(x^{2}+1\\right)+\\frac{1}{x^{2}+1} \\geqslant 2$. Mais si on s'y prend mal, on n'arrive pas à conclure. En effet, on aurait pu s'en douter en étudiant le cas d'égalité de l'équation. Au vu de la condition $x y+y z+z x=1$, on se doute que l'égalité va se produire pour $x=y=z=\\frac{1}{\\sqrt{3}}$. En introduisant ces valeurs dans l'équation, on trouve bien que l'on a égalité, mais ceci n'est pas un cas d'égalité de l'inégalité arithméticogéométrique plus tôt.\nDans le cas d'égalité $x=y=z=\\frac{1}{\\sqrt{3}}$, on a $x^{2}+1=\\frac{4}{3}$ et $\\frac{1}{x^{2}+1}=\\frac{3}{4}$. On applique donc l'inégalité arithmético-géométrique avec des coefficients appropriés pour avoir l'égalité des deux termes dans ce cas :\n\n$$\n\\frac{3}{4}\\left(x^{2}+1\\right)+\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}\\right) \\geqslant 2\n$$\n\nEn sommant ces trois équations, on a\n\n$$\n\\frac{3}{4}\\left(x^{2}+y^{2}+z^{2}+3\\right)+\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}+\\frac{1}{y^{2}+1}+\\frac{1}{z^{2}+1}\\right) \\geqslant 6\n$$\n\nqui donne\n\n$$\n\\frac{3}{4}\\left(x^{2}+y^{2}+z^{2}\\right)+\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}+\\frac{1}{y^{2}+1}+\\frac{1}{z^{2}+1}\\right) \\geqslant \\frac{15}{4}\n$$\n\nPar rapport à l'inégalité de l'énoncé, il nous reste un terme $\\frac{5}{4}\\left(x^{2}+y^{2}+z^{2}\\right)$ à minorer. Mais on a, par l'inégalité arithmético-géométrique,\n\n$$\n\\frac{5}{4}\\left(x^{2}+y^{2}+z^{2}\\right) \\geqslant \\frac{5}{4}(x y+y z+z x)=\\frac{5}{4}\n$$\n\nEn ajoutant cette inégalité à l'inégalité obtenue précédemment, on obtient bien\n\n$$\n2\\left(x^{2}+y^{2}+z^{2}\\right)+\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}+\\frac{1}{y^{2}+1}+\\frac{1}{z^{2}+1}\\right) \\geqslant \\frac{15}{4}+\\frac{5}{4}=5\n$$", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soient $x, y, z$ des réels strictement positifs tels que $x y+y z+z x=1$. Montrer que\n\n$$\n2\\left(x^{2}+y^{2}+z^{2}\\right)+\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}+\\frac{1}{y^{2}+1}+\\frac{1}{z^{2}+1}\\right) \\geqslant 5\n$$", "solution": "alternative de l'exercice 7\n\nPosons $s=x^{2}+y^{2}+z^{2}$. Notons que par l'inégalité des mauvais élèves,\n\n$$\n\\frac{4}{3}\\left(\\frac{1}{x^{2}+1}+\\frac{1}{y^{2}+1}+\\frac{1}{z^{2}+1}\\right) \\geqslant \\frac{4}{3} \\frac{(1+1+1)^{2}}{x^{2}+y^{2}+z^{2}+3}=\\frac{12}{s+3}\n$$\n\nAinsi il suffit de montrer que $2 s+\\frac{12}{s+3} \\geqslant 5$. En multipliant des deux côtés par $s+3$ qui est positif, il suffit de montrer que $2 s(s+3)+12 \\geqslant 5(s+3)$. Ceci est équivalent à $2 s^{2}+6 s+12 \\geqslant 5 s+15$ et donc à $2 s^{2}+s \\geqslant 3$. Or par le lemme du tourniquet, $s \\geqslant x y+y z+x z=1$, donc $2 s^{2}+s \\geqslant 3$. On a bien le résultat voulu.\n\nCommentaire des correcteurs : L'exercice a été bien résolu par les élèves l'ayant cherché. Attention à ne pas s'emmêler dans les inégalités. Ici on pouvait directement utiliser l'inégalité des mauvais élèves : poser $s=x^{2}+y^{2}+z^{2}$ permettait de conclure en multipliant par $s+3$. Notons qu'il n'est pas nécessaire de reprouver à chaque fois $x^{2}+y^{2}+z^{2} \\geqslant x y+y z+x z$ pour l'utiliser : c'est le lemme du tourniquet, qui est présent dans le cours de la POFM.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $a$ et $b$ deux réels. On définit les suites $\\left(a_{n}\\right)$ et $\\left(b_{n}\\right)$ par $a_{0}=a, b_{0}=b$ et pour tout $n$ entier naturel, $a_{n+1}=a_{n}+b_{n}$ et $b_{n+1}=a_{n} b_{n}$. Déterminer toutes les paires $(a, b)$ telles que $\\mathrm{a}_{2022}=\\mathrm{a}_{0}$ et $\\mathrm{b}_{2022}=\\mathrm{b}_{0}$.", "solution": "de l'exercice 8\n\nSupposons que $(a, b)$ soit une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $a$ et $b$ deux réels. On définit les suites $\\left(a_{n}\\right)$ et $\\left(b_{n}\\right)$ par $a_{0}=a, b_{0}=b$ et pour tout $n$ entier naturel, $a_{n+1}=a_{n}+b_{n}$ et $b_{n+1}=a_{n} b_{n}$. Déterminer toutes les paires $(a, b)$ telles que $\\mathrm{a}_{2022}=\\mathrm{a}_{0}$ et $\\mathrm{b}_{2022}=\\mathrm{b}_{0}$.", "solution": "de l'énoncé. On calcule\n\n$$\n\\sum_{i=1}^{2022} a_{i}=\\sum_{i=1}^{2022}\\left(a_{i-1}+b_{i-1}\\right)=\\sum_{i=0}^{2021} a_{i}+\\sum_{i=0}^{2021} b_{i}\n$$\n\nMais on a\n\n$$\n\\sum_{i=0}^{2021} a_{i}=a_{0}+\\sum_{i=1}^{2021} a_{i}=a_{2022}+\\sum_{i=1}^{2021} a_{i}=\\sum_{i=1}^{2022} a_{i}\n$$\n\ndonc on peut réécrire l'équation précédente comme\n\n$$\n\\sum_{i=0}^{2021} b_{i}=0\n$$\n\nDe la même manière, on a\n\n$$\n0=\\sum_{i=1}^{2022} b_{i}=\\sum_{i=1}^{2022} a_{i-1} b_{i-1}=\\sum_{i=0}^{2021} a_{i} b_{i}\n$$\n\nPour faire apparaître les produits $a_{i} b_{i}$, on élève l'équation $a_{i+1}=a_{i}+b_{i}$ au carré pour avoir $a_{i+1}^{2}=$ $a_{i}^{2}+b_{i}^{2}+2 a_{i} b_{i}$. On somme ceci entre $i=0$ et 2021 pour avoir\n\n$$\n\\sum_{i=1}^{2022} a_{i}^{2}=\\sum_{i=0}^{2021} a_{i}^{2}+\\sum_{i=0}^{2021} b_{i}^{2}+2 \\sum_{i=0}^{2021} a_{i} b_{i}\n$$\n\nMais encore une fois,\n\n$$\n\\sum_{i=1}^{2022} a_{i}^{2}=\\sum_{i=0}^{2021} a_{i}^{2}\n$$\n\ndonc\n\n$$\n\\sum_{i=0}^{2021} b_{i}^{2}=0\n$$\n\nUne somme de carrés de nombres réels est nécessairement positive, et ne peut être nulle que si tous les $b_{i}$ sont nuls. Ceci implique notamment $b=0$. Réciproquement, si a est un réel, le couple ( $a, 0$ ) fonctionne car on montre par récurrence que pour tout $n, a_{n}=a$ et $b_{n}=0$, et alors $a_{2022}=a=a_{0}$.\n\nCommentaire des correcteurs : L'exercice était très difficile, a été peu abordé, et encore moins réussi. Plusieurs élèves arrivent cependant à obtenir que $b_{0}+\\cdots+b_{2021}=0$ ce qui est un bon début.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soient $b_{1}, \\ldots, b_{n}$ des réels positifs ou nuls tels que $b_{1}+b_{2}+\\ldots+b_{n}=2$. Soient $a_{0}, a_{1}, \\ldots, a_{n}$ des nombres réels tels que $a_{0}=a_{n}=0$. Supposons que pour tout $i$ compris entre 1 et $n$ inclus,\n\n$$\n\\left|a_{i}-a_{i-1}\\right| \\leqslant b_{i}\n$$\n\nMontrer que l'on a\n\n$$\n\\left(a_{0}+a_{1}\\right) b_{1}+\\left(a_{1}+a_{2}\\right) b_{2}+\\ldots+\\left(a_{n-1}+a_{n}\\right) b_{n} \\leqslant 2\n$$", "solution": "de l'exercice 9\n\nPour tout indice $i$, on a deux majorations de $a_{i}$. En effet, on peut écrire\n\n$$\n\\begin{aligned}\na_{i}=a_{i}-a_{0}= & \\left(a_{i}-a_{i-1}\\right)+\\left(a_{i-1}-a_{i-2}\\right)+\\ldots+\\left(a_{1}-a_{0}\\right) \\\\\n& \\leqslant b_{i}+b_{i-1}+\\ldots+b_{1}=\\sum_{j=1}^{i} b_{j}\n\\end{aligned}\n$$\n\net\n\n$$\n\\begin{aligned}\na_{i}=a_{i}-a_{n} & =\\left(a_{i}-a_{i+1}\\right)-\\left(a_{i+1}-a_{i+2}\\right)+\\ldots+\\left(a_{n-1}-a_{n}\\right) \\\\\n& \\leqslant b_{i+1}+b_{i+2}+\\ldots+b_{n}=\\sum_{j=i+1}^{n} b_{j}\n\\end{aligned}\n$$\n\nAfin de majorer efficacement $a_{i}$, on voudrait trouver le plus petit de ces deux termes. Mais la somme des deux vaut 2 , donc il faut simplement déterminer si $\\sum_{j=1}^{i} b_{j}$ est inférieur ou supérieur à 1 .\nSoit $m$ l'entier minimal tel que $\\sum_{j=1}^{m} b_{j}>1$. On écrit alors\n\n$$\n\\sum_{i=1}^{n}\\left(a_{i-1}+a_{i}\\right) b_{i}=\\sum_{i=1}^{m-1}\\left(a_{i-1}+a_{i}\\right) b_{i}+\\left(a_{m-1}+a_{m}\\right) b_{m}+\\sum_{i=m+1}^{n}\\left(a_{i-1}+a_{i}\\right) b_{i}\n$$\n\nPour $i0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \\leqslant x0$, on en déduit $\\alpha \\geqslant 0$. Mais on a aussi\n\n$$\n\\alpha c=-Q(c)=-(c-x)(c-y)(c-z) \\leqslant 0\n$$\n\ncar $c$ est supérieur à $x, y$ et $z$. Comme $c>0$, on en déduit $\\alpha \\leqslant 0$. Ainsi, on a $\\alpha=0$ comme voulu, c'est-à-dire que $P(X)=Q(X)$.\nMais alors les deux polynômes doivent avoir les mêmes racines qui sont $a0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \\leqslant x0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \\leqslant x0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \\leqslant x0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \\leqslant xm^{2}$, ce qui donne $f(m)>m$ car $f(m)$ est positif, et donc comme $f(m)$ est entier, $f(m) \\geqslant m+1$. Par une récurrence simple, on trouve que pour tous les entiers $k$, $m$ strictement positifs, $f^{k}(m) \\geqslant m+k$.\nMais on remarque qu'à part le premier terme de l'énoncé, le reste est symétrique en $m$ et $n$, et on peut écrire que pour tous $m, n>0$,\n\n$$\nf^{f(n)}(m)+m n=f(m) f(n)=f^{f(m)}(n)+n m\n$$\n\net donc $f^{f(n)}(m)=f^{f(m)}(n)$. On veut maintenant utiliser le fait que l'on a affaire à une composée, et on pose donc $n=f(a)$ afin que $f^{f(m)}(n)=f^{f(m)+1}(a)$. En évaluant l'équation précédente avec $a=m$, on a\n\n$$\nf^{f(\\mathfrak{m})+1}(\\mathfrak{m})=f^{f(f(\\mathfrak{m}))}(\\mathfrak{m})\n$$\n\nMais ceci implique alors que $f(f(m))=f(m)+1$. En effet, sinon, soit $\\alpha=\\min (f(f(m)), f(m)+1)$ et $k=\\max (f(f(m)), f(m)+1)-\\alpha>0$ afin que l'équation s'écrive $f^{k}\\left(f^{\\alpha}(m)\\right)=f^{\\alpha}(m)$. Mais c'est absurde car $f^{k}\\left(f^{\\alpha}(m)\\right) \\geqslant f^{\\alpha}(m)+k>f^{\\alpha}(m)$.\nOn déduit que pour tout $m \\in \\mathbb{N}^{*} f(f(m))=f(m)+1$. Par une récurrence simple, pour tout $k \\geqslant 1$, $f^{k}(m)=f(m)+k-1$. Ainsi l'équation de l'énoncé donne pour tous $m, n \\in \\mathbb{N}^{*}$,\n\n$$\n\\mathbf{f}(\\mathrm{m})+\\mathrm{f}(\\mathrm{n})-1+\\mathrm{mn}=\\mathbf{f}(\\mathrm{m}) \\mathbf{f}(\\mathfrak{n})\n$$\n\nSi $n=m$, on obtient une équation liant simplement $f(n)$ et $n$ :\n\n$$\n2 \\mathrm{f}(\\mathrm{n})+\\mathrm{n}^{2}-1=\\mathrm{f}(\\mathrm{n})^{2}\n$$\n\nC'est une équation du second degré que l'on peut par exemple factoriser en $(f(n)-1)^{2}=n^{2}$, donc $\\mathrm{f}(\\mathrm{n})=\\mathrm{n}+1$ car $\\mathrm{f}(\\mathrm{n})$ est strictement positif.\nRéciproquement, si $f(n)=n+1$ pour tout $n$, alors on peut écrire pour tous $m, n$ :\n\n$$\nf^{f(n)}(m)+m n=m+f(n)+m n=m n+m+n+1=(m+1)(n+1)=f(m) f(n)\n$$\n\net cette fonction est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 15.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Pour une fonction $f$ et $n$ un entier strictement positif, on note $f^{n}$ la composée $n$-ième de f définie par $\\mathrm{f}^{\\mathrm{n}}=\\mathrm{f} \\circ \\mathrm{f} \\circ \\ldots \\circ \\mathrm{f}$ pù f apparaît n fois dans le membre de droite.\nTrouver toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ telles que\n\n$$\nf^{f(n)}(m)+m n=f(m) f(n)\n$$\n\npour tous $\\mathrm{m}, \\mathrm{n} \\in \\mathbb{N}^{*}$.", "solution": "de l'équation de l'énoncé.\nCommentaire des correcteurs: Les élèves ayant résolu le problème on tous une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Pour une fonction $f$ et $n$ un entier strictement positif, on note $f^{n}$ la composée $n$-ième de f définie par $\\mathrm{f}^{\\mathrm{n}}=\\mathrm{f} \\circ \\mathrm{f} \\circ \\ldots \\circ \\mathrm{f}$ pù f apparaît n fois dans le membre de droite.\nTrouver toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{*} \\rightarrow \\mathbb{N}^{*}$ telles que\n\n$$\nf^{f(n)}(m)+m n=f(m) f(n)\n$$\n\npour tous $\\mathrm{m}, \\mathrm{n} \\in \\mathbb{N}^{*}$.", "solution": "étudiant les antécédents du plus petit élément de l'image de f. Il est excellent d'avoir su adapter ce genre d'argument à une équation fonctionnelle. C'était d'ailleurs là que résidait la difficulté, et quelques subtilités de l'argument ont échappé à la vigilance de quelques élèves. Par ailleurs, plusieurs élèves n'ont pas hésité à proposer leur preuve de propriétés élémentaires de f, ce sur quoi il est très bon de s'entraîner : l'injectivité de f , le fait que 1 n 'est pas atteint, la symétrie de l'équation fonctionnelle en $m$ et $n$...", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soient $b_{1}, \\ldots, b_{n}$ des réels positifs ou nuls tels que $b_{1}+b_{2}+\\ldots+b_{n}=2$. Soient $a_{0}, a_{1}, \\ldots, a_{n}$ des nombres réels tels que $a_{0}=a_{n}=0$. Supposons que pour tout $i$ compris entre 1 et $n$ inclus,\n\n$$\n\\left|a_{i}-a_{i-1}\\right| \\leqslant b_{i}\n$$\n\nMontrer que l'on a\n\n$$\n\\left(a_{0}+a_{1}\\right) b_{1}+\\left(a_{1}+a_{2}\\right) b_{2}+\\ldots+\\left(a_{n-1}+a_{n}\\right) b_{n} \\leqslant 2\n$$", "solution": "de l'exercice 16\n\nPour tout indice $i$, on a deux majorations de $a_{i}$. En effet, on peut écrire\n\n$$\n\\begin{aligned}\na_{i}=a_{i}-a_{0}= & \\left(a_{i}-a_{i-1}\\right)+\\left(a_{i-1}-a_{i-2}\\right)+\\ldots+\\left(a_{1}-a_{0}\\right) \\\\\n& \\leqslant b_{i}+b_{i-1}+\\ldots+b_{1}=\\sum_{j=1}^{i} b_{j}\n\\end{aligned}\n$$\n\net\n\n$$\n\\begin{aligned}\na_{i}=a_{i}-a_{n} & =\\left(a_{i}-a_{i+1}\\right)-\\left(a_{i+1}-a_{i+2}\\right)+\\ldots+\\left(a_{n-1}-a_{n}\\right) \\\\\n& \\leqslant b_{i+1}+b_{i+2}+\\ldots+b_{n}=\\sum_{j=i+1}^{n} b_{j} .\n\\end{aligned}\n$$\n\nAfin de majorer efficacement $a_{i}$, on voudrait trouver le plus petit de ces deux termes. Mais la somme des deux vaut 2 , donc il faut simplement déterminer si $\\sum_{j=1}^{i} b_{j}$ est inférieur ou supérieur à 1 .\nSoit $m$ l'entier minimal tel que $\\sum_{j=1}^{m} b_{j}>1$. On écrit alors\n\n$$\n\\sum_{i=1}^{n}\\left(a_{i-1}+a_{i}\\right) b_{i}=\\sum_{i=1}^{m-1}\\left(a_{i-1}+a_{i}\\right) b_{i}+\\left(a_{m-1}+a_{m}\\right) b_{m}+\\sum_{i=m+1}^{n}\\left(a_{i-1}+a_{i}\\right) b_{i}\n$$\n\nPour $iy$, on a\n\n$$\nf(x)=f(y)+f(x-y)=f(y)+f\\left((\\sqrt{x-y})^{2}\\right)=f(y)+f(\\sqrt{x-y})^{2} \\geqslant f(y)\n$$\n\ndonc $f$ est linéaire sur $\\mathbb{R}$. D'après l'équation $f\\left(x^{2}\\right)=f(x)^{2}$, son coefficient dominant a vérifie $a^{2}=$ a donc $\\mathrm{a}=0$ ou $\\mathrm{a}=1$, c'est-à-dire que f est soit nulle, soit l'identité sur $\\mathbb{R}$. f étant surjective, nécessairement, c'est l'identité : pour tout $x, f(x)=x$.\nEn réinjectant dans l'équation, on obtient\n\n$$\n\\forall x, y \\in \\mathbb{R}, \\quad x^{2}+2 y=x^{2}+\\alpha y\n$$\n\ndonc avec $x=0, y=1$, on a $\\alpha=2$ nécessairement. Réciproquement, si $\\alpha=2$, l'identité est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $\\alpha \\neq 0$. Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\nf\\left(x^{2}+y+f(y)\\right)=f(x)^{2}+\\alpha y\n$$", "solution": "par le calcul précédent. Ainsi, si $\\alpha \\neq 2$, il n'y a aucune", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $\\alpha \\neq 0$. Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\nf\\left(x^{2}+y+f(y)\\right)=f(x)^{2}+\\alpha y\n$$", "solution": ", et si $\\alpha=2$, l'identité est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $\\alpha \\neq 0$. Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\nf\\left(x^{2}+y+f(y)\\right)=f(x)^{2}+\\alpha y\n$$", "solution": "Commentaire des correcteurs : L'exercice a été très peu abordé, une poignée d'élèves l'ont résolu parfaitement. Certains ont tenté des débuts de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $\\alpha \\neq 0$. Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que pour tous réels $x, y$,\n\n$$\nf\\left(x^{2}+y+f(y)\\right)=f(x)^{2}+\\alpha y\n$$", "solution": "assez naturels, en montrant notamment que f était surjective et que $f(0)=0$, mais ne sont pas allés plus loin. Attention à bien noter pour quelles valeurs les égalités obtenues sont effectivement vraies : lorsqu'on fait une substitution d'une variable en fonction d'une autre on perd de la généralité. Par exemple après avoir posé $y=f\\left(-x^{2}\\right)$, l'égalité qui en résute n'est pas vraie pour tout $x$ et pour tout $y$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 17.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "de l'exercice 18\n\nOn dit qu'un entier n fonctionne si quelque soit le polynôme P initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.\nCommençons par faire la remarque simple qu'à chaque étape, quoique choisisse Emile, le polynôme écrit au tableau sera unitaire, de degré pair, et non constant.\nOn montre les points suivants :\n\n1. $\\underline{S i n}$ fonctionne, alors $\\mathrm{n}+2$ aussi :\n\nSoit $P(X)$ un polynôme comme dans l'énoncé. Supposons qu'Emile peut trouver une suite d'opérations qui lui permet d'obtenir un polynôme $f(X)$ avec $n$ racines réelles distinctes écrit au tableau.\nOn va chercher à trouver deux constantes $a$ et $b$ telles que le polynôme $g(X)=P(f(X)+a)+b$ ait exactement $n+2$ racines réelles distinctes. Alors Emile pourra simplement ajouter $a$, composer par P , puis ajouter b au polynôme obtenu pour avoir le polynôme voulu.\nOn souhaite utiliser le fait que $f(X)$ ait exactement $n$ racines en faisant en sorte qu'une racine de $f$ soit une racine de $g(X)=P(f(X)+a)+b$, ce qui impose $b=-P(a)$. Les racines de $g(X)$ sont alors les réels $x$ tels que $f(x)+a$ soit un antécédent de $P(a)$. Pour avoir le moins de cas possibles à traiter, on choisit |a| très grand pour que l'équation $P(X)=P(a)$ ait exactement deux", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s réelles : c'est possible car pour c assez grand, l'équation $\\mathrm{P}(\\mathrm{X})=\\mathrm{c}$ a exactement deux", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s réelles.\nSoient $a, a^{\\prime}$ les deux", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s de $P(X)=P(a)$. Ainsi, les racines de $g(X)$ sont les racines de $f(X)$ et les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s de $f(x)+a=a^{\\prime}$, c'est-à-dire les antécédents par $f$ de $a^{\\prime}-a$. Encore une fois, on veut le moins d'antécédents possibles (sans pour autant en avoir aucun), donc on voudrait que $a^{\\prime}-a$ soit très grand. $f$ étant unitaire de degré pair, si $a^{\\prime}-a$ est assez grand, $a^{\\prime}-a$ exactement 2 antécédents par f , ce qui donne bien que $g(X)$ a exactement $n+2$ racines.\nVérifions que l'on peut bien choisir a comme voulu. Prenons a négatif tel que $|a|$ soit très grand. Lorsque $a$ tend vers $-\\infty, P(a)$ tend vers $+\\infty$ et $a^{\\prime}$ est la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "la plus grande de $P(X)=P(a)$ qui tend vers $+\\infty . S \\mathrm{Si}|a|$ est assez grand, $a^{\\prime}-a$ peut devenir arbitrairement grand, comme voulu.\n2. $\\underline{n}=0$ et $\\mathrm{n}=2021$ fonctionnent:\n\nSoit $P(X)$ un polynôme comme dans l'énoncé.\nLe cas de $\\mathrm{n}=0$ est simple. En effet, $\\mathrm{P}(\\mathrm{X})$ est unitaire de degré pair, donc il admet un minimum $\\operatorname{sur} \\mathbb{R}$. Si c est strictement supérieur à l'opposé de ce minimum, $\\mathrm{P}(\\mathrm{x})+\\mathrm{c}=0 \\mathrm{n}$ 'a aucune", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "sur $\\mathbb{R}$. Ainsi, si Emile remplace $P(X)$ par $P(X)+c$ au premier tour, il obtient un polynôme sans racines réelles comme voulu.\nPour $\\mathfrak{n}=2021$, c'est un peu plus subtil. Comme $x \\mapsto P(x)$ est décroissant pour $x$ assez petit et croissant pour x assez grand, P a un nombre impair d'extrema locaux. Ainsi il existe c tel qu'un nombre impair de ces extrema soient en des", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s de $\\mathrm{P}(\\mathrm{x})=\\mathrm{c}$. En effet, supposons que les valeurs prises en ces extrema soient $c_{1}, \\ldots, c_{k}$, et disons que $c_{i}$ est la valeur de $P$ en $n_{i}$ extrema distincts. Alors le nombre d'extrema de $P$ est $n_{1}+\\cdots+n_{k}$ et est impair, donc il existe $i$ tel que $n_{i}$ soit impair, et c'est ce qu'on voulait.\n\nSupposons maintenant qu'Emile remplace le polynôme $P(X)$ initial par $P(X)-c$. Celui-ci est positif en $-\\infty$ et $+\\infty$ donc change de signe un nombre pair de fois. Mais par définition de $c$, il a aussi un nombre impair de zéros qui sont des extrema locaux (c'est-à-dire où il ne change pas de signe), et donc $\\mathrm{P}(\\mathrm{X})-\\mathrm{c}$ a un nombre impair de racines réelles distinctes. Ce nombre est nécessairement inférieur à 2022, donc à 2021 car il est impair. Par la partie précédente de la démonstration, en ajoutant 2 à plusieures reprises au nombre de racines distinctes, Emile peut toujours obtenir, après un certain nombre d'étapes, un polynôme avec exactement 2021 racines réelles distinctes.\nEn combinant les deux premières parties de la démonstration, on obtient que tous les n pairs et les n impairs supérieurs ou égaux à 2021 fonctionnent. Il reste à voir que les autres ne fonctionnent pas.\n3. $\\mathrm{n} \\leqslant 2019$ impair ne fonctionne pas :\n\nSoit $n \\leqslant 2019$ impair. Dans cette partie de la démonstration, il faut exhiber un polynôme $P(X)$ qui empêche Emile d'obtenir $n$ racines réelles distinctes en un nombre fini d'étapes. D'après la preuve de la partie précédente, il faut trouver un polynôme $P(X)$ tel que si un nombre impair d'extrema locaux de $P$ vérifient $P(x)=c$, alors $P(X)-c$ a strictement plus de 2019 racines distinctes.\nConsidérons le polynôme $P(X)=X^{2}\\left(X^{2}-1\\right) \\ldots\\left(X^{2}-1010\\right)$. Il est pair donc tous ses extrema locaux vont par paires, sauf celui en 0 qui est nul. Mais le polynôme $P(X)$ a 2021 racines distinctes, et il semble donc être un bon candidat pour cette partie. Comme $P(X)$ est pair, pour tout $\\mathrm{c} \\neq 0$, l'équation $\\mathrm{P}(\\mathrm{x})=\\mathrm{c}$ a un nombre pair de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s, et l'équation $\\mathrm{P}(\\mathrm{x})=0$ a un nombre impair de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s (précisément 2021).\nSupposons par l'absurde qu'au bout d'un certain nombre d'étapes, Emile arrive à obtenir un polynôme avec $n$ racines réelles distinctes, ce polynôme sera alors de la forme $f(P(X))$, avec $f(X)$ unitaire non constant. Soient $r_{1}, \\ldots, r_{k}$ les racines de $f(X)$. Les racines de $f(P(X))$ sont exactement les réels", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s d'une équation de la forme $P(x)=r_{i}$. Soit $n_{i}$ le nombre de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "s à $P(x)=r_{i}$. On a $n_{1}+n_{2}+\\ldots+n_{k}=n$. Comme $n$ est impair, un des $n_{i}$ est forcément impair. Mais le seul réel $r_{i}$ ayant un nombre impair d'antécédents par $P$ est 0 , qui en a 2021. Ainsi, $r_{i}=0$ et $n_{i}=2021$, ce qui donne $n \\geqslant 2021$, absurde.\nPour conclure, les entiers n qui fonctionnent sont les entiers pairs et les entiers impairs supérieurs ou égaux à 2021.\n\nCommentaire des correcteurs : L'exercice n'a été abordé que par une copie qui l'a réussi parfaitement. L'exercice était très difficile, néanmoins il est dommage qu'il n'y ait pas eu plus de copies proposant au moins des pistes de recherche. Il n'est pas nécessaire d'avoir résolu entièrement un problème pour rendre quelque chose, et ici il y avait plusieurs étapes intermédiaires importantes qui pouvaient rapporter des points même si la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Soit $\\mathrm{P}(\\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :\n\n- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou\n- le polynôme $\\mathrm{P}(\\mathrm{f}(\\mathrm{X})$ ).\n\nTrouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.", "solution": "n'était pas aboutie.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-2.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution "}}
diff --git "a/French_STS/segmented/fr-corrig\303\251-envoi-3.jsonl" "b/French_STS/segmented/fr-corrig\303\251-envoi-3.jsonl"
new file mode 100644
index 0000000000000000000000000000000000000000..b7f39d40a97e4e0491ecbc8a285178079dadd05a
--- /dev/null
+++ "b/French_STS/segmented/fr-corrig\303\251-envoi-3.jsonl"
@@ -0,0 +1,51 @@
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Montrer que pour tout entier n , le nombre $\\mathrm{n}^{3}-7 \\mathrm{n}$ est divisible par 6 .", "solution": "de l'exercice 1\n Une première approche est de regarder l'expression modulo 6 :\n\n$$\n\\mathrm{n}^{3}-7 n \\equiv \\mathrm{n}^{3}-\\mathrm{n} \\equiv(\\mathrm{n}-1) \\mathrm{n}(\\mathrm{n}+1) \\quad \\bmod 6\n$$\n\ndonc il suffit de montrer que 6 divise $(n-1) \\mathfrak{n}(n+1)$. Or parmi trois nombres consécutifs, au moins un est divisible par 2 et au moins un est divisible par 3 . Ainsi comme 2 et 3 sont premiers entre eux, $6 \\mid n^{3}-n$ et donc 6 divise $n^{3}-7 n$.\n\nUne deuxième approche qui fonctionne aussi ici consiste aussi à regarder l'expression $n^{3}-7 n$ et de montrer à la main que celle-ci est toujours nulle en faisant une disjonction de cas sur les valeurs que peut prendre n modulo 6 .\n\n| n | $\\mathrm{n}^{3}-7 \\mathrm{n}$ |\n| :---: | :---: |\n| 0 | $0^{3}-7 \\cdot 0 \\equiv 0+0 \\equiv 0$ |\n| 1 | $1^{3}-7 \\cdot 1 \\equiv 1-1 \\equiv 0$ |\n| 2 | $2^{3}-7 \\cdot 2 \\equiv 8-2 \\equiv 0$ |\n| 3 | $3^{3}-7 \\cdot 3 \\equiv 3-3 \\equiv 0$ |\n| $4 \\equiv-2$ | $(-2)^{3}-7 \\cdot(-2) \\equiv-2+2 \\equiv 0$ |\n| $5 \\equiv-1$ | $(-1)^{3}-7 \\cdot(-1) \\equiv-1+1 \\equiv 0$ |\n\nAinsi, quelle que soit la valeur de n modulo $6, \\mathrm{n}^{3}-7 \\mathrm{n} \\equiv 0$.\nCommentaire des correcteurs: L'exercice est très bien résolu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soient $a, b, c$ trois entier tels que 7 divise $a^{2}+b^{2}+c^{2}$. Montrer que 7 divise $a^{4}+b^{4}+c^{4}$.", "solution": "de l'exercice 2\nLes carrés modulo 7 valent $0,1,2,4$. On cherche donc toutes les sommes de trois de ces nombres étant divisible par 7. Après avoir testé toutes les possibilités, on s'aperçoit que les seuls ensembles de trois carrés modulo 7 dont la somme est divisible par 7 sont $\\{0,0,0\\}$ et $\\{1,2,4\\}$.\nOn alors $\\mathrm{a}^{4}+\\mathrm{b}^{4}+\\mathrm{c}^{4} \\equiv 0^{2}+0^{2}+0^{2} \\equiv 0 \\bmod 7$ ou $\\mathrm{a}^{4}+\\mathrm{b}^{4}+\\mathrm{c}^{4} \\equiv 1^{2}+2^{2}+4^{2} \\equiv 1+4+16 \\equiv 0 \\bmod 7$\nDans les deux cas, $a^{4}+b^{4}+c^{4} \\equiv 0 \\bmod 7$, comme désiré.\nCommentaire des correcteurs: L'exercice est très bien résolu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 2.", "solution_match": " Solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\geqslant 1$ des entiers tels que $\\mathrm{a}^{\\mathrm{b}} \\mid \\mathrm{b}^{\\mathrm{c}}$ et $\\mathrm{a}^{\\mathrm{c}} \\mid \\mathrm{c}^{\\mathrm{b}}$. Montrer que $\\mathrm{a}^{2} \\mid \\mathrm{bc}$.", "solution": "de l'exercice 3\n\nNous allons regarder les valuations $p$-adiques de chacun des nombres premiers $a, b$ et $c$. En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{\\mathfrak{p}}(\\mathfrak{a})=v_{\\mathfrak{p}}\\left(\\mathrm{a}^{2}\\right) \\leqslant v_{\\mathfrak{p}}(\\mathrm{bc})=v_{\\mathfrak{p}}(b)+v_{\\mathfrak{p}}(\\mathfrak{c})$.\nSoit $p$ un nombre premier. Lhypothèse que $\\mathrm{a}^{\\mathrm{b}} \\mid \\mathrm{b}^{\\mathrm{c}}$ se traduit en terme de valuation p -adique par $b v_{p}(a) \\leqslant c v_{p}(b)$, ou encore $v_{p}(a) \\leqslant \\frac{c}{b} v_{p}(b)$. De même, on obtient que $v_{p}(a) \\leqslant \\frac{b}{c} v_{p}(c)$.\nEn multipliant les deux relations, on trouve que $v_{\\mathfrak{p}}(\\mathfrak{a})^{2} \\leqslant v_{\\mathfrak{p}}(\\mathrm{b}) v_{\\mathfrak{p}}(\\mathfrak{c})$. On a donc, d'après l'inégalité des moyennes:\n\n$$\nv_{p}(a) \\leqslant \\sqrt{v_{p}(b) v_{p}(c)} \\leqslant \\frac{v_{p}(b)+v_{p}(c)}{2}\n$$\n\nce qui donne bien $2 v_{\\mathfrak{p}}(\\mathrm{a}) \\leqslant v_{\\mathfrak{p}}(\\mathrm{b})+v_{\\mathfrak{p}}(\\mathrm{c})$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $\\mathrm{a}^{2} \\mid \\mathrm{bc}$.\n\nCommentaire des correcteurs: L'exercice est très bien résolu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "de l'exercice 4\n Pour $x=0$, l'équation devient $n^{2}=7$ qui n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\n\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "Supposons $x>0$, on factorise : $3 \\cdot 2^{x}=(n-2)(n+2)$. Le membre de gauche est pair donc le membre de droite est paire. Les deux facteurs du membre de droite sont de même parité donc ils sont tous les deux pairs et on a deux cas :\n\n- Cas 1: $3 \\cdot 2^{\\mathrm{a}}=\\mathrm{n}-2$ et $2^{\\mathrm{b}}=\\mathrm{n}+2$, avec $\\mathrm{a}+\\mathrm{b}=\\mathrm{x}$. On peut combiner ces deux équations pour trouver $2^{b}=3 \\cdot 2^{a}+4$. Notons que $n+2$ et $n-2$ ont pour différence 4 donc ils ne peuvent pas être tous les deux divisibles par 8 . On a donc $a \\leqslant 2$ ou $b \\leqslant 2$. Or $2^{b}>4$, donc $b>2$ et on déduit que $a \\leqslant 2$. Si $a=0,2^{b}=3+4=7$ ce qui n'est pas possible. Si $a=1,2^{b}=6+4=10$ ce qui n'est pas possible non plus. Si $\\mathbf{a}=2$, alors $2^{b}=12+4=16$ donc $b=4$. On obtient $x=6$ et $n=14$. réciproquement, on vérifie que $3 \\cdot 2^{6}+4=196=14^{2}$ et le couple $(6,14)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "- Cas 2: $3 \\cdot 2^{\\mathrm{a}}=\\mathrm{n}+2$ et $2^{\\mathrm{b}}=\\mathrm{n}-2$, avec $\\mathrm{a}+\\mathrm{b}=\\mathrm{x}$. Les deux équations combinées donnent $2^{\\mathrm{b}}+4=3 \\cdot 2^{\\mathrm{a}}$. De même que précédemment, on a $\\mathrm{a} \\leqslant 2$ ou $\\mathrm{b} \\leqslant 2$.\n\n1. Si $b \\leqslant 2$, alors $b=0,1$ ou 2 . Si $b=0$, alors $5=3 \\cdot 2^{a}$ ce qui $n$ 'est pas possible. Si $b=1$, $6=3 \\cdot 2^{\\mathrm{a}}$ et $\\mathrm{a}=1$, soit $x=2$ et $\\mathrm{n}=4$ et on vérifie que $3 \\cdot 2^{2}+4=16=4^{2}$ et $(2,4)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "Si $b=2$, alors $8=3 \\cdot 2^{a}$ ce qui n'est pas possible.\n2. Si $a \\leqslant 2$, alors $a=0,1$ ou 2 . Si $a=0,2^{b}+4=3<4$ ce qui $n$ 'est pas possible. Si $a=1$, on retombe sur le cas où $b=1$ et sur le couple $(2,4)$. Si $a=2,2^{b}+4=12$ donc $b=3$. Ceci donne $x=5$ et $\\mathfrak{n}=10$. Réciproquement, on vérifie que $3 \\cdot 2^{5}+4=100=10^{2}$ et $(5,10)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "Ainsi l'ensemble des couples ( $\\boldsymbol{x}, \\mathrm{n}$ )", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "s est $\\{(2,4),(5,10),(6,14)\\}$\nCommentaire des correcteurs: L'exercice est globalement bien résolu, mais de nombreux élèves oublient des cas, ou oublient tout simplement de vérifier les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que\n\n$$\n3 \\cdot 2^{x}+4=\\mathrm{n}^{2}\n$$", "solution": "s trouvées, chose pourtant cruciale dans une équation diophantienne.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Un ensemble E d'entiers strictement positifs est dit intéressant si pour tout $\\mathrm{n} \\geqslant 1$ et pour tous $x_{1}, \\ldots, x_{n}$ des éléments de $E$ deux à deux distincts, leur moyenne arithmétique $\\frac{1}{n}\\left(x_{1}+\\ldots+x_{n}\\right)$ et leur moyenne géométrique $\\left(x_{1} \\cdot \\ldots \\cdot x_{n}\\right)^{\\frac{1}{n}}$ sont des entiers.\n\n1. Existe-t-il un ensemble E intéressant contenant exactement 2022 éléments?\n2. Existe-t-il un ensemble E intéressant infini?", "solution": "de l'exercice 5\n\n1) Pour commencer, on peut remarquer que si $n \\geqslant 1$, alors dès que $x_{1}, \\ldots, x_{n} \\geqslant 1$ sont des entiers tous multiples de $n$, chacun des nombres $\\frac{x_{k}}{n}$ est un entier, de sorte que leur somme $\\frac{1}{n}\\left(x_{1}+\\ldots+x_{n}\\right)$ est un entier. De même, si $n \\geqslant 1$, alors dès que $x_{1}, \\ldots, x_{n} \\geqslant 1$ sont des entiers tous puissances $n$-ièmes parfaites, chacun des nombres $x_{k}^{1 / n}$ est entier, de sorte que leur produit $\\left(x_{1} \\times \\ldots \\times x_{n}\\right)^{\\frac{1}{n}}$ est un entier. Pour trouver un ensemble E intéressant contenant exactement 2022 éléments, il suffit donc que pour tout $1 \\leqslant n \\leqslant 2022$, tous les éléments de $E$ soient à la fois des multiples de $n$ et des puissances $n$-ièmes parfaites. Pour cela, il suffit que tous les éléments de E soient à la fois des multiples de 2022!, et des puissances 2022!-ièmes parfaites. Ainsi, $E=\\left\\{(2022!)^{k 2022!}, 1 \\leqslant k \\leqslant 2022\\right\\}$ convient.\n2) Nous allons montrer qu'il n'existe pas d'ensemble intéressant infini. En fait, on va montrer qu'il n'existe même pas d'ensemble infini d'entiers strictement positifs vérifiant l'hypothèse sur les moyennes arithmétiques. En effet, supposons par l'absurde qu'un tel ensemble infini E existe, c'est-à-dire que pour tout $n \\geqslant 1$ et $x_{1}, \\ldots, x_{n} \\in E$ deux à deux distincts, la moyenne arithmétique $\\frac{1}{n}\\left(x_{1}+\\ldots+x_{n}\\right)$ est un entier. Soit $a1$ alors l'ensemble $A$ des multiples de d est un ensemble admissible contenant $n$ et $m$ mais $n$ 'étant pas égal à $\\mathbb{Z}$. En effet, si $x$ et $y$ sont multiples de $d$, alors pour tout entier $k, x^{2}+k x y+y^{2}$ est bien divisible par $d$ et est dans $A$. On déduit que les couples $(m, n)$ recherchés doivent vérifier $\\operatorname{gcd}(m, n)=1$.\nRéciproquement, soient $m$ et $n$ des entiers tels que $\\operatorname{gcd}(m, n)=1$. Montrons que tout ensemble admissible contenant $m$ et $n$ est $\\mathbb{Z}$. Soit $A$ un ensemble admissible contenant $m$ et $n$. Remarquons que si $x \\in A$, alors l'hypothèse nous donne que pour tout entier $k$, l'entier $x^{2}+k x \\cdot x+x^{2}=(k+2) x^{2}$ est dans $A$. On déduit que tout multiple de $x^{2}$ est dans $A$ si $x$ est dans $A$.\nNotons que si $\\operatorname{gcd}(m, n)=1$, alors on a aussi $\\operatorname{gcd}\\left(m^{2}, n^{2}\\right)=1$. D'après le théorème de Bezout, on dispose donc d'entiers $u, v \\in \\mathbb{Z}$ tels que $u^{2}+v n^{2}=1$. Comme $u m^{2}$ et $v n^{2}$ sont dans $A$, en appliquant l'hypothèse à $x=u m^{2}, y=v n^{2}$ et $k=2$, on a\n\n$$\n\\left(u m^{2}\\right)^{2}+2 u m^{2} v n^{2}+\\left(v n^{2}\\right)^{2}=\\left(u m^{2}+v n^{2}\\right)^{2}=1^{2}=1 \\in A\n$$\n\nPar conséquent, $\\forall k \\in \\mathbb{Z}, k \\cdot 1^{2} \\in A$. Ainsi $A=\\mathbb{Z}$ et le seul ensemble admissible contenant $m$ et $n$ est $\\mathbb{Z}$.\nLes couples recherchés sont donc les couples d'entiers ( $m, n$ ) premiers entre eux.\nCommentaire des correcteurs : Parmi les élèves ayant rendu une tentatives, on trouve beaucoup de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Un ensemble $A$ d'entiers est dit admissible s'il vérifie la propriété suivante : pour tous $x, y \\in A$ (non nécessairement distincts), et pour tout $k \\in \\mathbb{Z}$, on a $x^{2}+k x y+y^{2} \\in A$.\nDéterminer tous les couples d'entiers non nuls ( $\\mathrm{m}, \\mathrm{n}$ ) tels que le seul ensemble admissible contenant à la fois $m$ et $n$ soit $\\mathbb{Z}$.", "solution": "s complètes. Parmi les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Un ensemble $A$ d'entiers est dit admissible s'il vérifie la propriété suivante : pour tous $x, y \\in A$ (non nécessairement distincts), et pour tout $k \\in \\mathbb{Z}$, on a $x^{2}+k x y+y^{2} \\in A$.\nDéterminer tous les couples d'entiers non nuls ( $\\mathrm{m}, \\mathrm{n}$ ) tels que le seul ensemble admissible contenant à la fois $m$ et $n$ soit $\\mathbb{Z}$.", "solution": "s non complètes, la plupart des élèves ont deviné la nature des couples", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Un ensemble $A$ d'entiers est dit admissible s'il vérifie la propriété suivante : pour tous $x, y \\in A$ (non nécessairement distincts), et pour tout $k \\in \\mathbb{Z}$, on a $x^{2}+k x y+y^{2} \\in A$.\nDéterminer tous les couples d'entiers non nuls ( $\\mathrm{m}, \\mathrm{n}$ ) tels que le seul ensemble admissible contenant à la fois $m$ et $n$ soit $\\mathbb{Z}$.", "solution": "s et ont réussi à montrer que si 1 est dans $A$, alors $A=\\mathbb{Z}$. Avoir été si loin dans ce problème difficile est déjà très bien!", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que\n\n$$\n\\mathrm{a}!+5^{\\mathrm{b}}=7^{\\mathrm{c}}\n$$", "solution": "de l'exercice 9\n Un premier réflexe à avoir est de regarder les petites valeurs de $\\mathrm{a}, \\mathrm{b}$ et c que l'on peut trouver dans une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que\n\n$$\n\\mathrm{a}!+5^{\\mathrm{b}}=7^{\\mathrm{c}}\n$$", "solution": "( $a, b, c$ ).\nTout d'abord, si $a=0$ ou $a=1$, alors $a!=1$, donc $0 \\equiv a!+5^{b} \\equiv 7^{c} \\equiv 1(\\bmod 2)$, ce qui est impossible. On en déduit que $a \\geqslant 2$.\nPuis, si $a \\geqslant 7$, alors $5^{b} \\equiv a!+5^{b} \\equiv 7^{c}(\\bmod 5)$ et $5^{b} \\equiv a!+5^{b} \\equiv 7^{c}(\\bmod 7)$, donc $b=c=0$. Mais alors $\\mathrm{a}!+5^{\\mathrm{b}}=\\mathrm{a}!+1 \\neq 1=7^{\\mathrm{c}}$, ce qui est impossible. On en déduit que $2 \\leqslant \\mathrm{a} \\leqslant 6$.\nSupposons maintenant que $\\mathrm{b} \\leqslant 1$. Alors\n\n$$\n7^{\\mathfrak{c}}=\\mathrm{a}!+5^{\\mathrm{b}} \\in\\{2,6,24,120,720\\}+\\{1,5\\}=\\{3,7,11,25,29,121,125,721,725\\}\n$$\n\nDans ce dernier ensemble, seul 7 lui-même est une puissance de 7 . On en déduit les deux triplets", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que\n\n$$\n\\mathrm{a}!+5^{\\mathrm{b}}=7^{\\mathrm{c}}\n$$", "solution": "s $(\\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{c})=(2,1,1)$ et $(3,0,1)$, qui sont les deux seules", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que\n\n$$\n\\mathrm{a}!+5^{\\mathrm{b}}=7^{\\mathrm{c}}\n$$", "solution": "s pour $b \\leqslant 1$.\nOn s'intéresse enfin aux cas où $b \\geqslant 2$. Alors $a!\\equiv a!+5^{b} \\equiv 7^{\\mathrm{c}}(\\bmod 25)$. Or, comme $7^{2} \\equiv-1$ $(\\bmod 25)$, on sait que $7^{\\mathrm{c}} \\equiv 1,7,-1$ ou $-7(\\bmod 25)($ selon que $\\mathrm{c} \\equiv 0,1,2$ ou $3(\\bmod 4))$ et que $\\mathrm{a}!\\equiv 2,6,-1,-5$ ou $-5(\\bmod 25)($ selon que $a$ vaut $2,3,4,5$ ou 6$)$. Cela signifie donc que $a=4$ et $\\mathrm{c} \\equiv 2(\\bmod 4)$.\nMais alors $(-3)^{\\mathrm{b}} \\equiv \\mathrm{a}!+5^{\\mathrm{b}} \\equiv(-1)^{\\mathrm{c}} \\equiv 1(\\bmod 8)$, ce qui signifie que b est pair. On pose alors $\\beta=\\mathrm{b} / 2$ et $\\gamma=\\mathrm{c} / 2$, de sorte que\n\n$$\n24=\\mathrm{a}!=7^{\\mathrm{c}}-5^{\\mathrm{b}}=\\left(7^{\\gamma}+5^{\\beta}\\right)\\left(7^{\\gamma}-5^{\\beta}\\right) .\n$$\n\nOn en déduit notamment que $7^{\\gamma}+5^{\\beta} \\leqslant 24$, donc que $\\gamma \\leqslant 1$ et $\\mathrm{c} \\leqslant 2$. Comme $\\mathrm{c} \\equiv 2(\\bmod 4)$, cela signifie que $\\mathrm{c}=2$, donc que $5^{\\mathrm{b}}=7^{\\mathrm{c}}-\\mathrm{a}!=49-24=25=5^{2}$.\nLes", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que\n\n$$\n\\mathrm{a}!+5^{\\mathrm{b}}=7^{\\mathrm{c}}\n$$", "solution": "s recherchées sont donc les triplets $(\\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{c})=(2,1,1),(3,0,1)$ et $(4,2,2)$.\nCommentaire des correcteurs: Globalement bien traité pour ceux qui l'ont rédigé, le principal souci de cet exercice consistait à bien se ramener à $a<7$, et à travailler modulo la bonne puissance de nombre premier, ici 25 , ce qui a été plutôt bien trouvé. Il faut bien faire attention aux cas limites $(\\mathrm{b}=0, \\mathrm{c}=0)$.\n\n## Exercices Seniors", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soit $a, b, c \\geqslant 1$ des entiers tels que $a^{b} \\mid b^{c}$ et $a^{c} \\mid c^{b}$. Montrer que $a^{2} \\mid b c$.", "solution": "de l'exercice 10 Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $\\mathrm{a}, \\mathrm{b}$ et c . En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{p}(a)=v_{p}\\left(a^{2}\\right) \\leqslant$ $v_{p}(b c)=v_{p}(b)+v_{p}(c)$.\nSoit $p$ un nombre premier. L'hypothèse que $a^{b} \\mid b^{c}$ se traduit en terme de valuation $p$-adique par $\\mathrm{b} v_{\\mathfrak{p}}(\\mathrm{a}) \\leqslant \\mathrm{c} v_{p}(\\mathrm{~b})$, ou encore $v_{p}(\\mathrm{a}) \\leqslant \\frac{\\mathrm{c}}{\\mathrm{b}} \\nu_{p}(\\mathrm{~b})$. De même, on obtient que $v_{p}(\\mathrm{a}) \\leqslant \\frac{\\mathrm{b}}{\\mathrm{c}} \\nu_{p}(\\mathrm{c})$.\n\nEn multipliant les deux relations, on trouve que $v_{\\mathfrak{p}}(\\mathrm{a})^{2} \\leqslant \\nu_{p}(b) v_{p}(c)$. On a donc, d'après l'inégalité des moyennes:\n\n$$\nv_{p}(a) \\leqslant \\sqrt{v_{p}(b) v_{p}(c)} \\leqslant \\frac{v_{p}(b)+v_{p}(c)}{2}\n$$\n\nce qui donne bien $2 v_{p}(a) \\leqslant v_{p}(b)+v_{p}(c)$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $a^{2} \\mid b c$.\n\nCommentaire des correcteurs : Le problème est globalement bien réussi. Une poignée d'élèves s'est trompée en affirmant que si $a$ divise $b^{c}$, alors $a$ divise $b$. Cette affirmation peut être réfutée en regardant $\\mathrm{a}=25, \\mathrm{~b}=10$ et $\\mathrm{c}=2$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 10.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Trouver tous les entiers $n \\geqslant 1$ tels que\n\n$$\n6^{n}-1 \\mid 7^{n}-1\n$$", "solution": "de l'exercice 11 Soit $n$ un éventuel entier vérifiant $6^{n}-1 \\mid 7^{n}-1$.\nOn a $5=6-1 \\mid 6^{n}-1^{n}$, donc $5 \\mid 7^{n}-1$. On calcule donc les puissances de 7 modulo 5 :\n\n| | $n$ | 0 | 1 | 2 | 3 | 4 |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $7^{\\mathrm{n}}(\\bmod 5)$ | 1 | 2 | 4 | 3 | 1 | |\n\nAinsi, si on note $n=4 q+r$ la division euclidienne de $n$ par 4 , on a $7^{n} \\equiv\\left(7^{4}\\right)^{q} \\times 7^{r} \\equiv 1^{q} 7^{r} \\equiv 7^{r}$ $(\\bmod 5)$. Donc pour que $5 \\mid 7^{n}-1$, il faut que $r=0$, autrement dit $n$ est multiple de 4 .\nEn regardant alors modulo 7 , on obtient $6^{n} \\equiv(-1)^{4 \\mathrm{q}} \\equiv 1(\\bmod 7)$, donc $7\\left|6^{n}-1\\right| 7^{n}-1$, ce qui n'est pas possible.\nIl n'y a donc aucun $n$ vérifiant $6^{n}-1 \\mid 7^{n}-1$.\nCommentaire des correcteurs: L'exercice est très bien résolu et a été traité par de nombreux élèves.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "de l'exercice 12 Remarquons que les couples $(1, \\mathfrak{n})$ et $(\\mathfrak{m}, 1)$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s pour tous les entiers strictement positifs $m$ et $n$. On suppose dans la suite que $m, n \\geqslant 2$.\nNotons que les nombres $m n-1, n^{3}-1$ sont strictement positifs. La condition de divisibilité implique donc que $\\mathrm{mn}-1 \\leqslant \\mathrm{n}^{3}-1$, donc $\\mathrm{m} \\leqslant \\mathrm{n}^{2}$.\nOn commence par ramener un peu de symétrie au problème en remarquant que $\\mathrm{mn}-1$ divise $(\\mathrm{mn})^{3}-1^{3}$, de sorte que $\\mathfrak{m n}-1$ divise $(\\mathfrak{m n})^{3}-1-\\mathfrak{m}^{3}\\left(\\mathfrak{n}^{3}-1\\right)=\\mathfrak{m}^{3}-1$.\nMaintenant que le problème est complètement symétrique en $m$ et $n$, on peut supposer sans perte de généralité que $m \\geqslant n . m \\geqslant n$. Puisque $m n-1$ divise $n^{3}-1$ et $m n-1$, il divise également $n^{3}-1-$ $(m n-1)=n\\left(n^{2}-\\mathfrak{m}\\right)$. Comme $m n-1$ et $n$ sont premiers entre eux, on a par le lemme de Gauss que $m n-1$ divise $n^{2}-m$. Mais alors, si $n^{2}-m$ est non nul, puisque $m \\geqslant n$ et $m \\geqslant 1$,\n\n$$\n0<\\mathfrak{n}^{2}-\\mathfrak{m}<\\mathrm{mn}-1 \\leqslant \\mathfrak{n}^{2}-\\mathrm{m}\n$$\n\nce qui est impossible. On a donc $n^{2}=m$. Réciproquement, le couple ( $\\left.n^{2}, n\\right)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "$\\left(n^{2}, n\\right)$.\nAinsi, les couples", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s sont $\\left\\{(1, \\mathfrak{n}),(\\mathfrak{n}, 1),\\left(\\mathfrak{n}^{2}, \\mathfrak{n}\\right),\\left(\\mathfrak{n}, \\mathfrak{n}^{2}\\right)\\right\\}$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "alternative:\n\nDe même que précédemment, on se ramène au cas où $n \\geqslant 2$.\nSoit $(m, n)$ une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "On a donc un entier a tel que $n^{3}-1=a(m n-1)$. En passant modulo $n$, on obtient $-1 \\equiv-a(\\bmod \\mathfrak{n})$, soit $a \\equiv 1(\\bmod \\mathfrak{n})$. Écrivons donc $a=k n+1$.\nEn réinjectant, on obtient $n^{3}-1=(k n+1)(m n-1)=k m n^{2}+(m-k) n-1$, ce qui se simplifie en $\\mathrm{n}^{2}=\\mathrm{kmn}+\\mathrm{m}-\\mathrm{k}$.\nRepasser modulo $n$ nous donne $m \\equiv k(\\bmod n)$, donc si $m=n p+r$ et $k=n q+r^{\\prime}$ sont les divisions euclidiennes de $m$ et $k$ par $n$, on a $r=r^{\\prime}$. On réécrit donc l'égalité sous la forme $n^{2}=$ $(n p+r)(n q+r) n+n p+r-(n q+r)$, qu'on peut encore une fois simplifier:\n\n$$\nn=p-q+n^{2} p q+n r(p+q)+r^{2}\n$$\n\nSi $p \\geqslant 1$, alors $n=p-q+n^{2} p q+n r(p+q)+r^{2} \\geqslant n^{2} q-q=q\\left(n^{2}-1\\right)$. Ainsi si $q \\geqslant 1$, il faut $n \\geqslant n^{2}-1$, impossible car $n \\geqslant 2$.\nOn vient de montrer qu'au moins un nombre parmi $p$ et $q$ doit être nul.\nSi $p=0$ et $q \\geqslant 1$, on a $n=q(n r-1)+r^{2}$. Comme $r=m \\geqslant 1, \\mathfrak{n r}-1 \\geqslant 1$ donc $\\mathbf{q}(\\mathfrak{n r}-1) \\geqslant \\mathfrak{n r}-1$ donc $n=q(n r-1)+r^{2} \\geqslant(\\mathfrak{n r}-1)+1=n r \\geqslant n$. Toutes ces inégalités sont donc des égalités, ce qui impose $\\mathrm{q}=\\mathrm{r}=1$. On obtient donc $\\mathrm{m}=1$.\nSi $q=0$ et $p \\geqslant 1$, on a $n=p(n r+1)+r^{2}$. Ainsi, si $r \\geqslant 1$, on a $n \\geqslant n+2$, donc $r=0$, puis $n=r$ et finalement $m=n^{2}$.\nSi $p=q=0$, on a $n=r^{2}$ et $m=r$.\nAinsi les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s sont les couples $(1, n)$ et $\\left(n^{2}, n\\right)$ pour tout $n \\geqslant 1$, ainsi que les couples $\\left(r, r^{2}\\right)$ avec $r \\geqslant 1$. On vérifie réciproquement que tous ces couples sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s, et que $n=1$ donne bien les mêmes", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s (puisqu'a priori ce ne sont que les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s avec $n \\geqslant 2$ ).\n\nCommentaire des correcteurs: L'exercice est globalement bien réussi. Pas mal d'élèves oublient de traiter les cas particuliers de leur raisonnement, alors que dans un tel problème c'est justement les cas particuliers/dégénérés qui donnent les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les couples d'entiers strictement positifs ( $\\mathfrak{m}, \\mathfrak{n}$ ) tels que\n\n$$\nm n-1 \\mid n^{3}-1\n$$", "solution": "s.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Soit $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ une fonction telle que pour tout entier $\\mathrm{n} \\geqslant 1, \\mathrm{f}(\\mathrm{f}(\\mathrm{n}))$ soit égal au nombre de diviseurs positifs de $n$. Montrer que si $p$ est un nombre premier, alors $f(p)$ est aussi un nombre premier.", "solution": "de l'exercice 13\n\nDans la suite, on note $d(n)$ le nombre de diviseurs positifs de $n$. Si $p$ est premier, on a $f(f(p))=2$ par définition. En appliquant f des deux côtés de l'égalité, on voit que $f(2)=d(f(p))$. On veut donc montrer que $f(2)=2$, ce qui prouvera que $f(p)$ a exactement deux diviseurs et est donc premier. Or, on a aussi $f(2)=d(f(2))$. Or, pour qu'un entier $\\boldsymbol{n} \\geqslant 2$ soit égal à son nombre de diviseurs, tous les nombres inférieurs à $n$ doivent diviser $n$, y compris $n-1$ qui est toujours premier avec $n$, donc $n-1=1$ et $n=2$. On déduit que $f(2) \\in\\{1,2\\}$. Si $f(2)=1$, alors $d(f(p))=1$ pour tout $p$ premier, donc $f(p)=1$ pour $p$ premier, puisque 1 est le seul entier à admettre un seul diviseur. Mais alors\n\n$$\n1=\\mathbf{f}(3)=\\mathbf{f}\\left(\\mathrm{d}\\left(2^{2}\\right)\\right)=\\mathbf{f}\\left(\\mathbf{f}\\left(\\mathbf{f}\\left(2^{2}\\right)\\right)\\right)=\\mathrm{d}\\left(\\mathbf{f}\\left(2^{2}\\right)\\right)\n$$\n\net l'on déduit que $f(4)=1$. Mais alors\n\n$$\n\\mathbf{f}(\\mathbf{f}(4))=\\mathbf{f}(1)=\\mathbf{f}(\\mathbf{f}(2))=\\mathrm{d}(2)=2 \\neq \\mathrm{d}(4)\n$$\n\nce qui fournit la contradiction désirée. On a donc bien $\\boldsymbol{f}(2)=2$, ce qui conclut.\nCommentaire des correcteurs : Une bonne partie des élèves ont résolu le problème, mais beaucoup d'autres sont allés bien trop vite. En effet, à partir de l'égalité $f(f(f(p)))=f(p)$, il est tentant de conclure immédiatemment que $\\boldsymbol{f}(\\mathfrak{p})=2$. Mais un autre cas possible est le cas où $f(2)=1$, puisque 1 vérifie aussi que $d(n)=n$. C'est traiter ce cas qui constituait la principale difficulté du problème. Il est donc dommage d'être passé à côté.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 13.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "On dit que deux entiers $a, b \\in \\mathbb{N}^{\\star}$ sont reliés s'il existe un nombre premier $p$ tel que $\\mathrm{a}=\\mathrm{pb}$ ou $\\mathrm{b}=\\mathrm{pa}$.\nTrouver tous les entiers $n \\geqslant 1$ ayant la propriété suivante : on peut écrire tous les diviseurs positifs de $n$ (1 et n compris) exactement une fois sur un cercle de sorte que tout diviseur soit relié avec chacun de ses deux voisins?", "solution": "de l'exercice 14 Traitons d'abord le cas où $n$ n'a qu'un seul facteur premier, donc $\\mathrm{n}=\\mathrm{p}^{\\alpha}$. Si $\\alpha \\leqslant 1$, n'importe quelle configuration marche. En revanche, si $\\alpha \\geqslant 2,1$ doit être placé à côté de deux nombres différents, et n'est relié qu'à un seul autre diviseur de $p^{\\alpha}$ (celui-ci étant $p$ ), ce n'est donc pas possible.\nRemarquons que la parité du nombre de diviseurs premiers comptés avec multiplicité change forcément entre un nombre et un nombre qui lui est relié. Ainsi, si $n$ a un nombre impair de diviseurs, l'existence d'une telle configuration impliquerait que 1 a à la fois un nombre pair et un nombre impair de diviseurs premiers, ce qui n'est pas possible. Les nombres ayant un nombre impair de diviseurs étant les carrés parfaits, ceux-ci ne vérifient pas non plus la propriété de l'énoncé.\nMaintenant, essayons de résoudre le cas où on a deux facteurs premiers, mettons $n=p^{a} q^{b}$ avec l'un des nombres $a$ ou b étant impair, et l'on suppose sans perte de généralité qu'il s'agit de $a$.\nL'arrangement suivant fonctionne :\n\n$$\n1, q, q^{2}, \\ldots, q^{b}, p q^{b}, p q^{b-1}, \\ldots, p q, p^{2} q, \\ldots, p^{a-1} q^{b}, p^{a} q^{b}, p^{a} q^{b-1}, \\ldots, p^{a} q, p^{a}, p^{a-1}, \\ldots, p, 1\n$$\n\nOn utilise le fait que a est impair pour dire qu'on a effectivement écrit $p^{a-1} q^{b}$ juste avant $p^{a} q^{b}$.\nOn procède maintenant par récurrence sur le nombre de diviseurs premiers : supposons avoir montré pour un $k \\geqslant 2$ que tous les nombres de la forme $\\prod_{i=1}^{k} p_{i}^{\\alpha_{i}}$ avec au moins l'un des $\\alpha_{i}$ impair vérifient la propriété de l'énoncé, et soit $n=\\prod_{i=1}^{k+1} p_{i}^{\\alpha_{i}}$ avec au moins l'un des $\\alpha_{i}$ impairs, disons $\\alpha_{1}$. Alors l'hypothèse de récurrence nous dit qu'on peut ordonner les diviseurs de $n^{\\prime}=\\prod_{i=1}^{k} p_{i}^{\\alpha_{i}}$ de la forme $d_{1}, \\ldots d_{m}$ de sorte que $d_{i}$ et $d_{i+1}$ soient tous reliés, de même que $d_{m}$ et $d_{1}$. Alors l'arrangement suivant fonctionne pour $m$ (car mest pair) :\n\n$$\nd_{1}, p_{k+1} d_{1}, \\ldots, p_{k+1}^{\\alpha_{k+1}} d_{1}, p_{k+1}^{\\alpha_{k+1}} d_{2}, \\ldots p_{k+1} d_{2}, d_{2}, d_{3}, \\ldots, p_{k+1}^{\\alpha_{k+1}} d_{m}, \\ldots p_{k+1} d_{m}, d_{m}, d_{1}\n$$\n\nAinsi les nombres qui ne vérifient pas cette propriété sont les carrés (différents de 1 ) et le puissances (plus grandes que 2) de nombres premiers.\n\nCommentaire des correcteurs: L'exercice, un peu combinatoire, est relativement peu traité mais globalement bien réussi par les élèves qui l'ont abordé. La plupart des élèves qui ont l'intuition de la construction à réaliser pour des nombres composés ont des difficultés à la formuler rigoureusement (par une récurrence).", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-3.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soit $m, n \\geqslant 2$ des entiers tels que $\\operatorname{PGCD}(m, n)=\\operatorname{PGCD}(m, n-1)=1$. On définit la suite $\\left(n_{k}\\right)_{k \\in \\mathbb{N}}$ par $n_{0}=m$ et $n_{k+1}=n \\cdot n_{k}+1$ pour $k \\in \\mathbb{N}$. Montrer que les entiers $n_{1}, \\ldots, n_{m-1}$ ne peuvent pas tous être des nombres premiers.", "solution": "de l'exercice 15 Tout d'abord, la suite ( $\\mathrm{n}_{\\mathrm{k}}$ ) est une suite arithmético-géométrique. On peut donc établir une formule close pour son terme général, à savoir $n_{k}=n^{k} m+\\frac{n^{k+1}-1}{n-1}$, que l'on peut aussi obtenir par récurrence à partir du calcul des premiers termes. De cette expression on déduit en particulier que $n_{k}>m$ pour tout $k>0$. On va désormais montrer que l'un des nombres $n_{1}, \\ldots, n_{m-1}$ est divisible par $m$, ce qui fera de ce nombre un nombre composé.\nEn passant modulo $m$, on déduit $n_{k} \\equiv \\frac{\\mathfrak{n}^{k+1}-1}{n-1} \\bmod m$ par récurrence, où l'on a utilisé que $n-1$ est inversible modulo $m$ car $n-1$ est premier avec $m$.\nSoit $\\omega$ l'ordre de $n \\bmod m$ (celui-ci existe car $m$ et $n$ premiers entre eux). On a $\\omega \\leqslant \\varphi(m) \\leqslant m-1$ d'après le théorème d'Euler. On déduit que $m \\mid n^{\\omega}-1$, ce qui implique que $m$ divise $n_{\\omega-1}-1$ comme voulu. Ainsi, les $n_{k}$ ne sont pas tous premiers.\n\nCommentaire des correcteurs: L'exercice est très bien résolu. Les élèves ont pratiquement tous pensé à justifier le fait que $mM$. (On utilise ici le fait que $\\left.a_{1}-a \\neq 0\\right)$.\nPour $2 \\leqslant i \\leqslant n$, on prend ensuite $p_{i}$ tel que $p_{i} \\equiv 1\\left(\\bmod 8 a_{i}\\left(a_{i}-a\\right)\\right.$ ) avec $p_{i}>p_{i-1}$ (qui existe pour les mêmes raisons que $p_{1}$ ).\nEn particulier les $p_{i}$ sont deux-à-deux distincts, et $p_{i} \\equiv 1 \\bmod 8 a_{i}$ et $p_{i} \\equiv 1 \\bmod 8\\left(a_{i}-a\\right)$, de sorte que d'après le deuxième lemme, pour tout $i,\\left(\\frac{a_{i}}{p_{i}}\\right)=\\left(\\frac{a_{i}-a}{p_{i}}\\right)=1$.\nPar définition, pour tout $i$ il existe $n_{i}$ tel que $n_{i}^{2} \\equiv a_{i}-a\\left(\\bmod p_{i}\\right)$, et quitte à remplacer $n_{i}$ par $n_{i}+p_{i}$, on peut supposer $p_{i}^{2} \\nmid n_{i}^{2}-\\left(a_{i}-a\\right)\\left(p_{i} \\neq 2\\right)$. Ainsi, on peut écrire $n_{i}^{2} \\equiv a c_{i} p_{i}+\\left(a_{i}-a\\right)\\left(\\bmod p_{i}^{2}\\right)$ avec $p_{i} \\nmid c_{i}$ puisque a et $p_{i}$ sont premiers entre eux $\\left(a\\mathrm{k}$ pour exactement une valeur de $k$.", "solution": "de l'exercice 10 À un réarrangement valide, on peut lui associer un sous-ensemble de 1, ..., 2023 de cardinal au moins $2: l$ 'ensemble des $k$ tels que $a_{k} \\neq k$.\nOn peut montrer qu'à un sous-ensemble de cardinal au moins 2 de $1, \\ldots, 2023$, on peut associer un unique réarrangement valide qui lui correspond. Si l'ensemble est $\\mathrm{E}=\\left\\{e_{1}, \\ldots, e_{n}\\right\\}$ avec $e_{1}\\mathrm{k}$ pour exactement une valeur de $k$.", "solution": "correcte. Seulement deux ont raisonné comme dans le", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Comptez le nombre de réarrangements $\\boldsymbol{a}_{1}, \\boldsymbol{a}_{2}, \\ldots, \\boldsymbol{a}_{2023}$ de la séquence $1,2, \\ldots, 2023$ telle que $\\mathrm{a}_{\\mathrm{k}}>\\mathrm{k}$ pour exactement une valeur de $k$.", "solution": "Les autres ont soit raisonné par récurrence en remplaçant 2023 par n, soit omt procédé par sommation (deux copies ont présenté la somme correcte mais n'ont pas su la calculer : peut-être qu'il ne connaissent pas la somme d'une suite géométrique)", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 10.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Un terrible groupe de bandits se prépare à se partager un butin. Chaque bandit vise deux autres bandits avec ses pistolets. Les bandits sont appelés dans un certain ordre. Lorsqu'un bandit est appelé, s'il est encore en vie, il tire sur les bandits qu'il visait. Après que tous les bandits ont été appelés, il y a eu 28 victimes. Montrez que quelque soit l'ordre dans lequel on avait appelé les bandits, il y aurait eu au moins 10 victimes.", "solution": "de l'exercice 11 Supposons par l'absurde qu'il existe un ordre qui cause 9 victimes ou moins. Il y a alors trois catégories de bandits :\n\n- Ceux qui sont morts avant de tirer\n- Ceux qui ont pu tirer puis sont morts\n- Ceux qui sont encore en vie à la fin\n\nLes bandits de 1ère et 2ème catégorie sont au total au plus 9 , car il y a au plus 9 victimes. Les bandits de 2ème et 3ème catégorie ne visent que des bandits de lère ou 2ème catégorie (s'ils ont tiré, leurs cibles sont mortes). Ils visent donc un sous-ensemble d'au plus 9 bandits. De plus, les bandits de 1ère catégorie ne visent qu'au plus $2 \\times 9=18$ bandits : il y a au plus 9 bandits de cette catégorie et chacun vise au plus 2 bandits. Il y a finalement au plus $18+9=27$ bandits visés : il existe un bandit qui n'est visé par personne. Ce bandit survit quelque soit l'ordre d'appel, ce qui contredit l'énoncé.\n\nCommentaire des correcteurs: Le principe était généralement compris mais il a été difficile pour plusieurs copies de justifier rigoureusement l'intuition. En particulier, certains considèrent les cas optimaux mais sans justifier qu'ils sont optimaux (ils peuvent par ailleurs ne pas être atteignables).", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Les nombres $0,1, \\ldots, n$ sont écrits sur un tableau. À tout moment, Thanima peut effacer un nombre s'il est la moyenne arithmétique de deux nombres encore présents sur le tableau. L'objectif de Thanima est d'effacer le plus de nombre possible, et elle joue de façon optimale. En fonction de n, combien de nombres reste t-il à la fin sur le tableau?", "solution": "de l'exercice 12 Si $n \\leqslant 2$, la réponse est $n$.\n\nSinon, à la fin du procédé, il existe toujours au moins deux nombres : on ne peut effacer ni 0 ni n .\nSi $n=2^{k}$ est une puissance de 2 , il est possible de n'avoir que deux nombres sur le tableau à la fin : on commence par effacer tous les nombres congrus à 1 modulo 2 , puis tous les nombres congrus à 2 modulo $4, \\ldots$, puis tous les nombres congrus à $2^{i}$ modulo $2^{i+1}, \\ldots$, puis $2^{k-1}$. Il ne reste alors plus que 0 et $2^{k}$.\nSi n n'est pas une puissance de 2 , on peut toujours obtenir 3 nombres : on écrit $\\mathrm{n}=2^{\\mathrm{k}}+\\mathrm{a}$ avec $0<\\mathrm{a}<2^{\\mathrm{k}}$. On efface dans l'ordre $\\boldsymbol{n}-1, \\boldsymbol{n}-2, \\ldots, 2^{\\mathrm{k}}+1$, puis on efface les nombres entre 1 et $2^{\\mathrm{k}}-1$ en utilisant la même technique qui est utilisée pour $n=2^{k}$. À la fin, il reste $0,2^{k}$ et $n$.\nMontrons maintenant que lorsque $\\mathrm{n}>2$ n'est pas une puissance de 2 , on ne peut pas finir avec seulement 0 et n . Supposons par l'absurde qu'il existe une séquence de suppressions qui permet de ne finir qu'avec 0 et $n$. Soit $p$ un nombre premier impair qui divise $n$. En prenant la séquence des suppressions à l'envers, on obtient une séquence d'insertions où l'on part de 0 et $n$, et si $x$ et $y$ sont présents, on peut ajouter $\\frac{x+y}{2}$ si c'est un nombre entier. Par récurrence, on démontre alors que tous les nombres obtenus sont divisibles par $p$, en particulier, on ne peut pas obtenir 1, ce qui est la contradiction recherchée.\n\nCommentaire des correcteurs : Exercice globalement très réussi par ceux l'ayant traité ; quelques imprécisions, notamment des", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 12.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Les nombres $0,1, \\ldots, n$ sont écrits sur un tableau. À tout moment, Thanima peut effacer un nombre s'il est la moyenne arithmétique de deux nombres encore présents sur le tableau. L'objectif de Thanima est d'effacer le plus de nombre possible, et elle joue de façon optimale. En fonction de n, combien de nombres reste t-il à la fin sur le tableau?", "solution": "s qui ne précisent pas dans quel ordre enlever les entiers entre $2^{k}$ et n , alors que celui-ci est important.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Un rectangle est divisé en dominos $1 \\times 2$ et $2 \\times 1$. Dans chaque domino, une diagonale est tracée. Deux diagonales n'ont jamais d'extrémité commune. Montrez que exactement deux coins du rectangle sont des extrémités de ces diagonales.", "solution": "de l'exercice 13 Remarquons que ce motif (ainsi que toutes ses rotations et symétries) est impossible :\n\n\nEn effet, le seul moyen de compléter le carré bas-gauche est d'ajouter ce domino :\n\n\nDe même, le seul moyen de compléter le carré bas-droite est d'ajouter ce domino :\n\n\nOn ne peut pas continuer pour toujours, car on finit par atteindre le bord du rectangle.\nCe motif aussi est impossible (ainsi que toutes ses rotations et symétries) :\n\ncar le seul moyen de compléter le carré dans le coin est en ajoutant ce domino :\n\nce qui fait apparaître le motif interdit précédent. Grâce à une analyse minutieuse, ces deux cas démontrent qu'il n'est en fait pas possible que deux dominos qui partagent un bord aient leurs diagonales dans des sens différents (montantes ou descendantes). Si on forme le graphe G dont les sommets sont les dominos et où il y a une arête entre deux dominos s'ils partagent un bord en commun, $G$ est connexe. Ainsi, tous les dominos ont leur diagonale dans le même sens; on en déduit facilement la propriété demandée.\n\nCommentaire des correcteurs: L'exercice a été peu traité. Ceux qui ont rendu une copie ont en général bien compris l'exercice et bien traité tous les cas et vu le motif du", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 13.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Un rectangle est divisé en dominos $1 \\times 2$ et $2 \\times 1$. Dans chaque domino, une diagonale est tracée. Deux diagonales n'ont jamais d'extrémité commune. Montrez que exactement deux coins du rectangle sont des extrémités de ces diagonales.", "solution": "Certains ont une argumentation différente en regardant un chemin entre les diagonales opposées, et d'autres utilisent un raisonnement de théorie des graphes.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 13.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Soit $G$ un graphe à $n$ sommets. Une arête e de $G$ est un cul-de-sac s'il est possible de partitionner $G$ en deux ensembles $A$ et $B$ tels que :\n\n- Il y a au plus 2023 arêtes de G ayant une extrémité dans A et une extrémité dans B.\n- L'arête e a l'une de ses extrémités dans $A$ et l'autre dans B.\n\nMontrez qu'il y a au plus 2023( $\\mathrm{n}-1$ ) culs-de-sac.", "solution": "de l'exercice 14 On le démontre par récurrence forte sur n . Le cas $\\mathrm{n}=1$ est immédiat. S'il n'existe aucun cul-de-sac dans G, la propriété est triviale. Sinon, soit e un cul-de-sac de G. On obtient une partition des sommets de $G$ en deux ensembles $A$, $B$ telle qu'il y a au plus 2023 arêtes entre $A$ et $B$. D'après l'hypothèse de récurrence, il y a au plus $2023(|A|-1)$ culs-de-sacs lorsque l'on ne considère que les sommets de $A$ et les arêtes qui relient ces sommets. De même, il y a au plus 2023(|B|-1) culs-de-sacs lorsque l'on ne considère que les sommets de $B$ et les arêtes qui les relient. On remarque que si une arête e n'est pas un cul-de-sac dans le graphe restreint à $A$ (de même pour $B$ ), alors elle n'est pas non plus un cul-de-sac dans G. Il y a donc au plus :\n\n$$\n2023+2023(|A|-1)+2023(|B|-1)=2023(|\\mathrm{G}|-1)\n$$\n\nculs-de-sacs dans G, ce qui termine l'hérédité.\nCommentaire des correcteurs : L'exercice est globalement bien réussi. Plusieurs élèves oublient de vérifier et même de mentionner qu'un cul-de-sac d'un graphe G appartenant à un sous-graphe $A$ de $G$ est un cul-de-sac pour $A$, c'est dommage car c'est un argument important de la preuve. En effet, être un cul-de-sac dans deux graphes différents n'est à priori pas lié.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "On place un certain nombre de segments ouverts dans le plan, aucun d'entre eux n'est parallèle aux axes $x$ et $y$. Ces segments sont disjoints. Thanima commence à se déplacer depuis $(0,0)$ parallèlement à l'axe $x$. À chaque fois qu'elle rencontre un mur, elle tourne de 90 degrés, et continue à se déplacer sans traverser le mur.\nDémontrez qu'il est impossible que Thanima visite les deux côtés de tous les murs.", "solution": "de l'exercice 15 On commence par démontrer qu'il existe un mur qui est plus bas que tous les autres (c'est à dire que l'ensemble des points sous ce segment n'intersecte aucun segment). Supposons par l'absurde que ce $n$ 'est pas le cas. On peut alors construire un cycle $A_{1}, B_{1}, A_{2}, B_{2}, \\ldots, A_{k}, B_{k}$ qui ne s'intersecte pas lui-même, où $A_{i}$ et $B_{i}$ sont sur le même mur, et $\\left[B_{i}, A_{i+1}\\right]$ est un segment vertical où $B_{i}$ est au dessus de $A_{i+1}$ (on considère les indices modulo $k$ ). On considère $l$, $r$ tel que $\\left[B_{l}, A_{l+1}\\right]$ soit le plus à gauche et $\\left[B_{r}, A_{r+1}\\right]$ soit le plus à droite. Le cycle donne une ligne brisée entre $B_{l}$ et $A_{r+1}$, et une autre entre $B_{r}$ et $A_{l+1}$. Cependant, les lignes brisées ne passent ni à gauche de $\\left[B_{l}, A_{l+1}\\right]$ ni à droite de $\\left[B_{r}, A_{r+1}\\right]$, et leurs extrémités sont \"croisées\", elles doivent donc s'intersecter. C'est une contradiction avec le fait que le cycle ne s'intersecte pas lui-même.\nSimilairement, il existe un mur plus haut que tous les autres. Si Thanima passe par le côté haut du mur le plus haut, elle continue à marcher vers l'infini en direction des y positifs. Si Thanima passe par le côté bas du mur le plus bas, elle continue à marcher vers l'infini en direction des y négatifs. Ces deux cas ne peuvent pas arriver simultanément, elle ne passe donc que par un seul de ces deux côtés. En particulier, elle ne peux pas passer par tous les côtés de tous les murs.\n\nCommentaire des correcteurs: L'exercice a été peu traité. La plupart des", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 15.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "On place un certain nombre de segments ouverts dans le plan, aucun d'entre eux n'est parallèle aux axes $x$ et $y$. Ces segments sont disjoints. Thanima commence à se déplacer depuis $(0,0)$ parallèlement à l'axe $x$. À chaque fois qu'elle rencontre un mur, elle tourne de 90 degrés, et continue à se déplacer sans traverser le mur.\nDémontrez qu'il est impossible que Thanima visite les deux côtés de tous les murs.", "solution": "s sont justes et proches de celle proposées dans le corrigé; néanmoins, elles présentaient un certain nombre d'imprécisions, auxquelles il faut être particulièrement attentif quand il s'agit de quelque chose d'aussi visuel que la géométrie combinatoire.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soit $k \\geqslant 1$ un entier. Quel est le plus petit entier $n$ tel que, quelque soit la manière de placer n points dans le plan, il est possible de choisir un sous-ensemble $S$ constitué de $k$ de ces points qui vérifie \"pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est inférieure ou égale à 2 \" ou \"pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est strictement plus grande que 1.\"", "solution": "de l'exercice 16 Commençons par montrer que $\\mathrm{n}=(k-1)^{2}+1$ est possible. Pour cela, considérons le disque de rayon 1 centré sur un point $P_{1}$ de l'ensemble. S'il y a au moins $k$ points dans ce disque, on peut prendre pour $S$ ces $k$ points (les distances entre eux sont inférieures ou égales à 2 ). On peut donc supposer qu'il y a au plus $(k-1)$ points dans le disque.\nConsidérons alors un disque de rayon 1 centré sur un $P_{2}$ de l'ensemble qui n'est pas dans le disque précédent. Par le même argument, on peut supposer qu'il y a au plus $(k-1)$ points dans ce disque.\nEn continuant à choisir des points en dehors des disques précédents, et comme on exclut au plus ( $k-1)$ points à chaque étape, on arrive à construire $S=\\left\\{P_{1}, \\ldots, P_{k}\\right\\}$ de telle manière à ce que les distances entre ces points soient toutes strictement supérieures à 1 .\nPour montrer que $\\mathrm{n}=(\\mathrm{k}-1)^{2}$ n'est pas possible, on place à distance très grande les uns des autres $k-1$ groupes, ou chaque groupe est constitué de $\\mathrm{k}-1$ points à distance très petite.\n\nCommentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont traité, avec des méthodes très variées : certains ont utilisé la même technique que la correction, d'autres ont recouru à la théorie des graphes par exemples.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 16.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $k, n \\geqslant 1$ deux entiers fixés. Thanima possédait 2 n bonbons de chaque couleur. Elle a donné deux bonbons de couleurs différentes à chacun des enfants de sa famille. Sachant que quelque soit la manière de choisir $k+1$ enfants, il y en a deux parmi eux qui ont reçu une couleur de bonbon en commun, trouvez le nombre maximum possible d'enfants.", "solution": "de l'exercice 17 On peut modéliser le problème par un graphe : chaque sommet de ce graphe est une couleur. Si Thanima a donné un bonbon d'une couleur $\\mathrm{c}_{1}$ et un bonbon d'une couleur $\\mathrm{c}_{2}$ à un enfant de sa famille, on ajoute une arête entre $\\mathrm{c}_{1}$ et $\\mathrm{c}_{2}$.\nComme Thanima n'a que 2 n bonbons de chaque couleur, le degré maximal de chaque sommet est 2 n . On sait de plus qu'il est impossible de choisir $k+1$ arêtes disjointes. On cherche le nombre maximal d'arêtes.\nOn voit qu'il est possible d'obtenir 3 kn arêtes. Pour cela, on crée un graphe dans lequel on met $k$ fois la structure suivante : on crée trois sommets, et entre chaque paire de ces trois sommets, on ajoute n arêtes. Montrons qu'il n'est pas possible de faire plus que 3 kn . Pour cela, on considère un ensemble C d'arêtes disjointes de plus grand cardinal. D'après l'énoncé, on a $|\\mathrm{C}| \\leqslant \\mathrm{k}$. Ainsi, chaque arête du graphe doit intersecter l'une des arêtes de C , sinon cela contredirait la maximalité de C . Notons $\\mathrm{V}_{\\mathrm{C}}$ l'ensemble des sommets qui apparaissent dans l'une des arêtes de C. Le nombre d'arêtes du graphe vaut :\n\n$$\n\\sum_{v \\in \\mathrm{~V}_{\\mathrm{C}}} \\mathrm{~d}_{\\text {ext }}(v)+\\frac{\\mathrm{d}_{\\mathrm{int}}(v)}{2}\n$$\n\noù $\\mathrm{d}_{\\text {ext }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets qui ne sont pas dans $V_{C}$, et $\\mathrm{d}_{\\text {int }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets de $\\mathrm{V}_{\\mathrm{C}}$. Soit $(\\mathrm{a}, \\mathrm{b}$ ) une arête de C , et soient $x, y$ deux sommets différents qui ne sont pas dans $\\mathrm{V}_{\\mathrm{C}}$, on ne peut pas à la fois avoir d'arêtes entre a et $x$ et entre $b$ et $y$, sinon remplacer $(a, b)$ par $(a, x)$ et $(b, y)$ dans $C$ donnerait un ensemble d'arêtes disjointes plus grand. Deux cas peuvent arriver :\n\n- À la fois $a$ et $b$ ont des arêtes vers le complémentaire de $\\mathrm{V}_{\\mathrm{C}}$, dans ce cas, toutes ces arêtes vont vers le même sommet, et la borne de degré sur ce sommet donnent $d_{\\text {ext }}(a)+d_{\\text {ext }}(b) \\leqslant 2 n$.\n- Soit il y a au plus un sommet parmi $a$ et $b$ qui a des arêtes vers le complémentaire de $\\mathrm{V}_{\\mathrm{C}}$, dans ce cas on a aussi $\\mathrm{d}_{\\text {ext }}(a)+\\mathrm{d}_{\\text {ext }}(b) \\leqslant 2 \\mathrm{n}$.\nComme $\\mathrm{d}_{\\mathrm{int}}(v) \\leqslant 2 \\mathrm{n}-\\mathrm{d}_{\\text {ext }}(v)$ pour tout sommet $v$, on a :\n\n$$\n\\begin{aligned}\n\\mathrm{d}_{e x t}(a)+d_{e x t}(b)+\\frac{d_{i n t}(a)+d_{i n t}(b)}{2} & \\leqslant d_{e x t}(a)+d_{e x t}(b)+\\frac{4 n-d_{e x t}(a)+d_{e x t}(b)}{2} \\\\\n& =2 n+\\frac{d_{e x t}(a)+d_{e x t}(b)}{2} \\\\\n& \\leqslant 3 n\n\\end{aligned}\n$$\n\nAinsi, en groupant les termes deux à deux, on obtient que le nombre d'arête dans le graphe est :\n\n$$\n\\sum_{v \\in \\mathrm{~V}_{\\mathrm{C}}} \\mathrm{~d}_{\\text {ext }}(v)+\\frac{\\mathrm{d}_{\\mathrm{int}}(v)}{2} \\leqslant 3 \\mathrm{kn}\n$$\n\nCommentaire des correcteurs : L'exercice a été très peu abordé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 17.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Thanima possède un magnifique collier constitué de rubis, d'émeraudes et de saphirs, que l'on représente par une suite de $\\mathrm{R}, \\mathrm{E}$ et S . En une opération magique, elle peut faire l'une des actions suivantes :\n\n- Remplacer un motif RR dans le collier par un motif ES (ou ES par RR).\n- Remplacer un motif EEE par un motif SR (ou SR par EEE).\n- Supprimer un motif SS, ou ajouter un motif SS n'importe où.\n- Supprimer un motif RES, ou ajouter un motif RES n'importe où.\n\nIl n'est pas possible de déplacer les lettres cycliquement à cause du fermoir. Elle ne peut pas non plus retourner le collier.\nEst-il possible de passer d'un collier contenant uniquement un saphir à un collier contenant uniquement une émeraude avec des opérations magiques?", "solution": "de l'exercice 18 Supposons que Thanima dispose de trois objets numérotés 1,2 et 3 sur trois supports numérotés 1,2 et 3 . Au début, chaque objet se trouve sur le support qui porte le même numéro. Thanima peut lire les lettres du collier une par une de gauche à droite et faire les opérations suivantes :\n\n- Si elle voit un E, elle échange les objets qui se trouvent sur les supports 1 et 2.\n- Si elle voit un $S$, elle échange les objets qui se trouvent sur les supports 2 et 3.\n- Si elle voit un R, elle déplace l'objet sur le support 1 sur le support 2, l'objet sur le support 2 sur le support 3 , et l'objet sur le support 3 sur le support 1 .\nOn remarque que :\n- Lorsque l'on ajoute un motif SS quelque part, on échange deux fois de suite les objets sur les supports 2 et 3 , ce qui ne change pas la position finale des objets.\n- Lorsque l'on ajoute un motif RES quelque part, l'objet qui était sur le support 1 à ce moment est déplacé sur le support 2 par $R$, puis sur le support 1 par $E$. L'objet qui était sur le support 2 est déplacé sur le support 3 par $R$, puis sur le support 2 par $S$. L'objet sur le support 3 est déplacé sur le support 1 par R, puis sur le support 2 par E puis à nouveau sur le support 3 par S . On ne change donc pas la position finale des objets.\n- Lorsque l'on applique RR, l'objet sur le support 1 est déplacé sur le support 3 , l'objet sur le support 2 est déplacé sur le support 1, et l'objet sur le support 3 est déplacé sur le support 2 . Lorsque l'on applique ES, l'objet sur le support 1 est déplacé sur le support 3, l'objet sur le support 2 est déplacé sur le support 1, et l'objet sur le support 3 est déplacé sur le support 2 . On ne change donc pas la position finale des objets en remplaçant un motif RR par un motif RES.\n- Lorsque l'on applique EEE, cela revient à échanger les objets sur les supports 1 et 2 . Lorsque l'on applique $S R$, l'objet sur le support 1 est envoyé sur le support 2 , l'objet 2 est envoyé sur le support 1 et l'objet sur le support 3 reste sur le support 3 . On ne change donc pas la position finale des objets en remplaçant un motif EEE par un motif SR.\nOn conclut qu'aucune opération magique ne permet de changer la position finale des objets. Or les colliers \"S\" et \"E\" ne donnent pas les mêmes positions finales des objets, il est donc impossible de passer de l'un à l'autre par des opérations magiques.\n\nCommentaire des correcteurs : Très peu (3) de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 18.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Thanima possède un magnifique collier constitué de rubis, d'émeraudes et de saphirs, que l'on représente par une suite de $\\mathrm{R}, \\mathrm{E}$ et S . En une opération magique, elle peut faire l'une des actions suivantes :\n\n- Remplacer un motif RR dans le collier par un motif ES (ou ES par RR).\n- Remplacer un motif EEE par un motif SR (ou SR par EEE).\n- Supprimer un motif SS, ou ajouter un motif SS n'importe où.\n- Supprimer un motif RES, ou ajouter un motif RES n'importe où.\n\nIl n'est pas possible de déplacer les lettres cycliquement à cause du fermoir. Elle ne peut pas non plus retourner le collier.\nEst-il possible de passer d'un collier contenant uniquement un saphir à un collier contenant uniquement une émeraude avec des opérations magiques?", "solution": "s rendues pour cet exercice très difficile; aucune n'a été concluante, mais les élèves ont eu de bonnes idées, ce qui est très encourageant. L'idée était effectivement de trouver un invariant, qui consistait ici en une interprétation des lettres R, E et S en tant qu'opérations sur un ensemble. Une fois cette idée en tête, une stratégie raisonnable consistait alors à chercher des simplifications produisant des mots que l'on pouvait identifier à l'opération identité.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-4.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
diff --git "a/French_STS/segmented/fr-corrig\303\251-envoi-5.jsonl" "b/French_STS/segmented/fr-corrig\303\251-envoi-5.jsonl"
new file mode 100644
index 0000000000000000000000000000000000000000..4f6b7860537a99b48bf845931516de07ff3b468d
--- /dev/null
+++ "b/French_STS/segmented/fr-corrig\303\251-envoi-5.jsonl"
@@ -0,0 +1,42 @@
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.", "solution": "de l'exercice 1 Comme souvent pour une équation diophantienne, on cherche à réarranger l'équation de sorte à avoir des produits de facteurs des deux côtés de l'égalité. Lorsque l'on est en présence de carrés parfaits, on peut utiliser l'identité remarquable $y^{2}-x^{2}=(y-x)(y+x)$. Ceci permet de réécrire l'équation sous la forme :\n\n$$\n73=(y-x)(y+x)\n$$\n\nAinsi, le nombre $y-x$ est un diviseur de 73 . Or les diviseurs de 73 sont $73,1,-1,-73$. On distingue alors quatre cas:\n\nCas $\\mathrm{n}^{\\circ} 1: \\mathrm{y}-\\mathrm{x}=73$. Alors $\\mathrm{x}+\\mathrm{y}=1$. Ceci conduit à $\\mathrm{y}=73+\\mathrm{x}=73+(1-\\mathrm{y})$, soit $\\mathrm{y}=37$ et $x=-36$. Réciproquement, on a bien $(-36)^{2}+73=37^{2}$, donc le couple $(-36,37)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.", "solution": "Cas $\\mathrm{n}^{\\circ} 2: y-x=1$. Alors $x+y=73$. Ceci conduit à $y=1+x=1+(73-y)$, soit $y=37$ et $x=36$. Réciproquement, on a bien $36^{2}+73=37^{2}$, donc le couple $(36,37)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.", "solution": "Cas $\\mathrm{n}^{\\circ} 3: \\mathrm{y}-\\mathrm{x}=-1$. Alors $\\mathrm{x}+\\mathrm{y}=-73$. Ceci conduit à $\\mathrm{y}=-1+\\mathrm{x}=-1+(-73-\\mathrm{y})$, soit $y=-37$ et $x=-36$. Réciproquement, on a bien $(-36)^{2}+73=(-37)^{2}$, donc le couple $(-36,-37)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.", "solution": "$\\underline{\\text { Cas } \\mathrm{n}^{\\circ} 4:} \\mathrm{y}-\\mathrm{x}=-73$. Alors $\\mathrm{x}+\\mathrm{y}=-1$. Ceci conduit à $\\mathrm{y}=-73+\\mathrm{x}=-73+(-1-\\mathrm{y})$, soit $y=-37$ et $x=36$. Réciproquement, on a bien $36^{2}+73=(-37)^{2}$, donc le couple $(36,-37)$ est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.", "solution": "Les couples", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.", "solution": "s sont donc $(-36,-37),(-36,37),(36,-37)$ et $(36,37)$.\n\n## Commentaires des correcteurs:\n\nExercice bien réussi dans l'ensemble, avec quelques erreurs récurrentes :\n\n- Supposer que les entiers sont positifs.\n- Oublier des cas dans la factorisation (oublier de prendre les opposés / d'échanger les facteurs)", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit a un réel strictement positif et $\\mathrm{n} \\geqslant 1$ un entier. Montrer que\n\n$$\n\\frac{a^{n}}{1+a+\\ldots+a^{2 n}}<\\frac{1}{2 n}\n$$", "solution": "de l'exercice 2 Puisque la difficulté réside dans le dénominateur du membre de droite, et pour plus de confort, on peut chercher à montrer la relation inverse, à savoir :\n\n$$\n\\frac{1+a+\\ldots+a^{2 n}}{a^{n}}>2 n\n$$\n\nL'idée derrière la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit a un réel strictement positif et $\\mathrm{n} \\geqslant 1$ un entier. Montrer que\n\n$$\n\\frac{a^{n}}{1+a+\\ldots+a^{2 n}}<\\frac{1}{2 n}\n$$", "solution": "qui suit est \"d'homogénéiser\" le numérateur du membre de gauche, c'est-àdire de comparer ce numérateur dans lequel les a sont élevés à des puissances distinctes à une expression composée uniquement de a élevés à la même puissance. Pour cela, on cherche à coupler certains termes et appliquer l'inégalité des moyennes. Voyons plutôt : pour $0 \\leqslant i \\leqslant 2 n$, on a $a^{i}+a^{2 n-i} \\geqslant 2 \\sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Ainsi :\n\n$$\n\\begin{aligned}\n\\frac{1+a+\\ldots+a^{2 n}}{a^{n}} & =\\frac{\\left(1+a^{2 n}\\right)+\\left(a+a^{2 n-1}\\right)+\\ldots+\\left(a^{n-1}+a^{n+1}\\right)+a^{n}}{a^{n}} \\\\\n& \\geqslant \\frac{\\overbrace{2 a^{n}+2 a^{n}+\\ldots+2 a^{n}}^{n \\text { termes }}+a^{n}}{a^{n}} \\\\\n& =\\frac{(2 n+1) a^{n}}{a^{n}} \\\\\n& =2 n+1 \\\\\n& >2 n\n\\end{aligned}\n$$\n\nce qui fournit l'inégalité voulue.\n\n## Commentaires des correcteurs:\n\nL'exercice est très bien résolu! Les élèves ont bien compris comment utiliser l'inégalité de la moyenne.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soient $\\omega_{1}$ et $\\omega_{2}$ deux cercles de centres respectifs $O_{1}$ et $O_{2}$. On suppose que $\\omega_{1}$ et $\\omega_{2}$ se coupent en les points $A$ et $B$. La droite $\\left(O_{1} A\\right)$ recoupe le cercle $\\omega_{2}$ en $C$ tandis que la droite $\\left(O_{2} A\\right)$ recoupe le cercle $\\omega_{1}$ en D . Montrer que les points $\\mathrm{D}, \\mathrm{O}_{1}, \\mathrm{~B}, \\mathrm{O}_{2}$ et C appartiennent à un même cercle.", "solution": "de l'exercice 3\n\n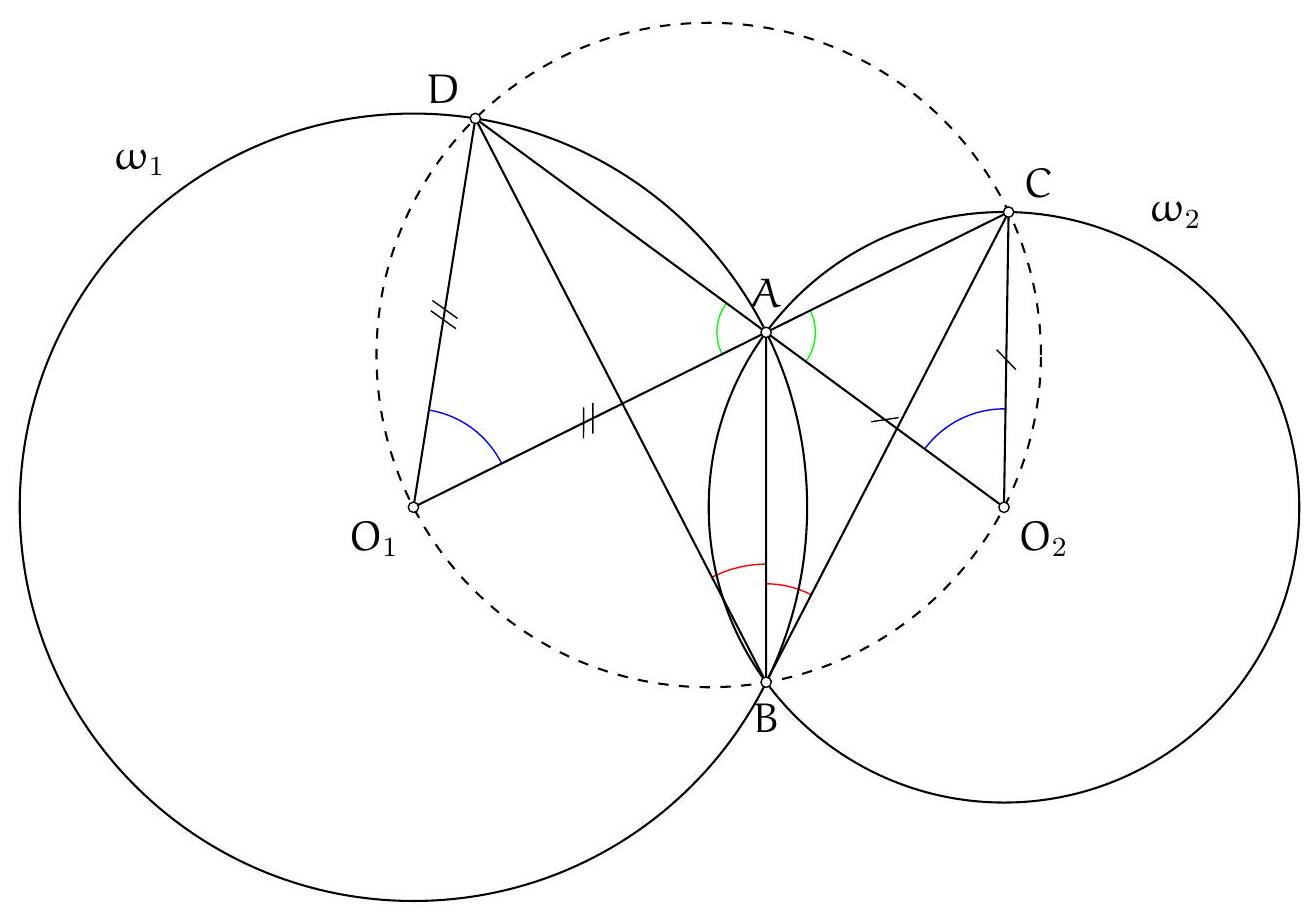\n\nNotons que puisque les angles $\\widehat{\\mathrm{DAO}_{1}}$ et $\\widehat{\\mathrm{CAO}_{2}}$ sont opposés par le sommet, ils sont égaux. D'autre part, puisque les points $A$ et $D$ appartiennent au cercle $\\omega_{1}$, le triangle $A O_{1} D$ est isocèle en $O_{1}$. De même, le triangle $\\mathrm{CO}_{2} A$ est isocèle en $\\mathrm{O}_{2}$. Les triangles $\\mathrm{DO}_{1} A$ et $\\mathrm{CO}_{2} A$ sont donc des triangels isocèle avec les mêmes angles à la base, ils sont donc semblables. Ceci implique que $\\widehat{\\mathrm{AO}_{1} \\mathrm{D}}=\\widehat{\\mathrm{CO}_{2} A}$, et donc que\n\n$$\n\\widehat{\\mathrm{CO}_{1} \\mathrm{D}}=\\widehat{\\mathrm{AO} \\mathrm{O}_{1} \\mathrm{D}}=\\widehat{\\mathrm{CO}_{2} \\mathrm{~A}}=\\widehat{\\mathrm{CO}_{2} \\mathrm{D}}\n$$\n\nsi bien que les points $\\mathrm{C}, \\mathrm{O}_{2}, \\mathrm{O}_{1}$ et D sont cocycliques.\nPar ailleurs, on peut découper l'angle $\\widehat{\\mathrm{DBC}}$ en la somme $\\widehat{\\mathrm{DBA}}+\\widehat{\\mathrm{ABC}}$. D'une part, d'après le théorème de l'angle au centre dans le cercle $\\omega_{1}$, on a $\\widehat{A B D}=\\frac{1}{2} \\widehat{\\mathrm{AO}_{1} \\mathrm{D}}$. D'autre part, d'après le théorème de l'angle au centre dans le cercle $\\omega_{1}$, on a $\\widehat{A B C}=\\frac{1}{2} \\widehat{A_{2} C}$. Ainsi\n\n$$\n\\widehat{\\mathrm{DBC}}=\\widehat{\\mathrm{DBA}}+\\widehat{A B C}=\\frac{1}{2} \\widehat{A O_{1} \\mathrm{D}}+\\frac{1}{2} \\widehat{\\mathrm{AO}_{2} \\mathrm{C}}=\\widehat{\\mathrm{AO}_{1} \\mathrm{D}}\n$$\n\nce qui permet de conclure que le point B appartient au cercle passant par les points $\\mathrm{C}, \\mathrm{O}_{2}, \\mathrm{O}_{1}$ et D .\n\n## Commentaires des correcteurs:\n\nExercice très bien résolu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Aurélien écrit 11 entiers naturels au tableau. Montrer qu'il peut choisir certains de ces entiers et placer des signes + et - entre eux de telle sorte que le résultat soit divisible par 2021.", "solution": "de l'exercice 4\n\nOn peut voir un choix de certains entiers avec des signes + et - comme un choix de certains entiers que l'on va compter positivement et de certains entiers que l'on va compter négativement. Les nombres qu'Aurélien peut obtenir sont des nombres qui s'écrivent comme la différence entre deux sommes de plusieurs entiers de départ. On peut remarquer que la réciproque est aussi vrai, si a et b s'écrivent comme somme de certains entiers, alors Aurélien peut obtenir $a-b$ en mettant un signe plus devant les entiers qui sont dans $a$ et un signe $b$ devant ceux qui sont dans $b$. Si le même entier de départ est utilisé pour obtenir à la fois a et $b$, Aurélien ne peut pas écrire devant un signe - et + , mais il peut simplement de pas écrire l'entier tout court, ce qui a le même effet que l'ajouter puis l'enlever. Toutes les différences entre deux sommes d'entiers du tableau sont donc des résultats qu'Aurélien peut obtenir. Dire qu'une différence entre deux sommes est dvisible par 2021 revient à dire que les deux sommes étaient congrues modulo 2021. On dispose de $2^{11}=2048>2021$ sommes, donc d'après le principe des tiroirs, deux sont congrues modulo 2021.\n\n## Commentaires des correcteurs:\n\nExercice extrêmement bien réussi par ceux qui l'ont traité. Les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Aurélien écrit 11 entiers naturels au tableau. Montrer qu'il peut choisir certains de ces entiers et placer des signes + et - entre eux de telle sorte que le résultat soit divisible par 2021.", "solution": "s sont presque toutes analogues à celle du", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Aurélien écrit 11 entiers naturels au tableau. Montrer qu'il peut choisir certains de ces entiers et placer des signes + et - entre eux de telle sorte que le résultat soit divisible par 2021.", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 4.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soient $x, y, z$ des réels strictement positifs tels que\n\n$$\nx+\\frac{y}{z}=y+\\frac{z}{x}=z+\\frac{x}{y}=2\n$$\n\nDéterminer toutes les valeurs possibles que peut prendre le nombre $x+y+z$.", "solution": "de l'exercice 5 Dans un tel problème, il faut chercher à examiner chaque équation séparément mais aussi à les mettre en relation. En pratique, cela consiste à regarder l'équation obtenue lorsque l'on effectue la somme ou le produit de deux ou plusieurs équations. Une autre idée est d'appliquer des inégalités connues d'un côté ou de l'autre de l'équation. En effet, souvent les égalités présentes dans les problèmes ne sont possibles que lorsque les variables vérifient le cas d'égalité d'une inégalité bien connue.\nCommençons par un examen séparé. On considère la première équation $x+\\frac{y}{z}=2$. D'après l'inégalité des moyennes, on a\n\n$$\n2=x+\\frac{y}{z} \\geqslant 2 \\sqrt{x \\cdot \\frac{y}{z}}\n$$\n\nsoit $\\sqrt{\\frac{x y}{z}} \\leqslant 1$. De même, la deuxième équation $y+\\frac{z}{x}=2$ donne $\\sqrt{\\frac{y z}{x}} \\leqslant 1$. En multipliant ces deux inégalités, on obtient\n\n$$\n1 \\geqslant \\sqrt{\\frac{x y}{z}} \\cdot \\sqrt{\\frac{y z}{x}}=y\n$$\n\nAinsi $y \\leqslant 1$, et de même on trouve que $x \\leqslant 1$ et $z \\leqslant 1$. On cherche désormais à appliquer ces estimations ou à prouver des estimations inverses (par exemple $y \\geqslant 1$, ce qui imposerait que $y=1$ ).\nNotons que la relation $x+\\frac{y}{z}=2$ se réécrit $x z+y=2 z$. On obtient de même que $y x+z=2 x$ et $y z+x=2 y$. En sommant ces trois relations, on trouve que $x z+y x+y z+x+y+z=2(x+y+z)$, ou encore $x y+y z+z x=x+y+z$. Mais alors\n\n$$\nx+y+z=x y+y z+z x \\leqslant x \\cdot 1+y \\cdot 1+z \\cdot 1=x+y+z\n$$\n\nNotre inégalité est en fait une égalité. Et puisque $x, y$ et $z$ sont non nuls, chacune des inégalités utilisées dans la ligne ci-dessus est en fait une égalité. On a donc $x=y=z=1$ et $x+y+z=3$. Cette valeur est bien atteignable puisque le triplet $(1,1,1)$ vérifie bien le système de l'énoncé, ce qui termine notre problème.\n\n## Commentaires des correcteurs:\n\nExercice plutôt bien réussi. Les méthodes de résolution sont extrêmement variées. Certains élèves ont commis l'erreur de considérer que le problème est symétrique, alors qu'il n'est que cyclique.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": "de l'exercice 6 D'une part, on peut écrire $x|x y| x^{2}+2 y-1$ donc $x \\mid 2 y-1$. Donc il existe n tel que $2 \\mathrm{y}-1=\\mathrm{nx}$. Forcément, n et $x$ sont impairs.\nD'autre part, la relation de divisibilité de l'énoncé nous donne une inégalité : on sait que $x y>0$, donc\n\n$$\nx y \\leqslant x^{2}+2 y-1\n$$\n\nEn multipliant cette relation par 2 pour simplifier les calculs et en combinant les deux, on obtient\n\n$$\nx(n x+1) \\leqslant 2 x^{2}+2(n x+1)-2\n$$\n\nEn reorganisant les termes,\n\n$$\n(n-2) x^{2} \\leqslant(2 n-1) x\n$$\n\nSoit, comme $x>0$\n\n$$\nx \\leqslant \\frac{2 n-1}{n-2}=2+\\frac{3}{n-2}\n$$\n\nEn se souvenant que n et $x$ sont forcément impairs, on distingue plusieurs cas.\nCas $\\mathrm{n}^{\\circ} 1: n \\geqslant 7$. Alors\n\n$$\nx \\leqslant 2+\\frac{3}{n-2}<3\n$$\n\nDonc $x=1$. Réciproquement, tous les couples $(1, y)$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": "Cas $\\mathrm{n}^{\\circ} 2: \\mathrm{n}=5$. Alors\n\n$$\nx \\leqslant 2+\\frac{3}{n-2}=3\n$$\n\nDonc $x=1$ ou $x=3$. Tous les couples avec $x=1$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": "s. Si $x=3$, on a $2 y-1=\\mathfrak{n} x=$ $5 \\cdot 3=15$ donc $y=8$. On vérifie $(3,8)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": ": $24 \\mid 24$.\n$\\underline{\\text { Cas } \\mathrm{n}^{\\circ} 3:} \\mathbf{n}=3$. Alors\n\n$$\nx \\leqslant 2+\\frac{3}{n-2}=5\n$$\n\nDonc $x=1$ ou $x=3$. Tous les couples avec $x=1$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": "s. Si $x=3$, on a $2 y-1=$ $\\mathrm{n} x=3 \\cdot 3=9$ donc $y=5$. On vérifie que $(3,5)$ n'est pas", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": ": $15 \\nmid 24 . \\operatorname{Si} x=5$ on a $2 \\mathrm{y}-1=\\mathrm{n} x=5 \\cdot 3=15$ donc $y=8$. On vérifie que $(5,8)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": ": $40 \\mid 40$.\nCas $\\mathrm{n}^{\\circ} 4: \\mathbf{n}=1$. Alors $x=2 y-1$. Alors\n\n$$\nx y=2 y^{2}-y \\mid 4 y^{2}-2 y=(2 y-1)^{2}+2 y-1=x^{2}+2 y+1\n$$\n\nDonc tous les couples de la forme $(2 y-1, y)$ sont", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \\mid x^{2}+2 y-1$.", "solution": "s.\n\n## Commentaires des correcteurs:\n\nL'exercice est plutôt bien réussi par les élèves qui l'ont traité. Malgré la disjonction de cas relativement fastidieuse, on relève très peu d'oublis. Certains ont encore du mal avec la notion de divisibilité, notamment comment interpréter une expression du type $a \\mid b c$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $n \\geqslant 1$ un entier strictement positif. Sur un mur, $n$ clous sont plantés. Chaque paire de clous est reliée par une corde coloriée à l'aide d'une des n couleurs. On dit que le mur est coloré si pour tout triplet de couleurs deux à deux distinctes $a, b, c$, il existe trois clous tels que les trois cordes reliant ces clous soient de couleur $a, b$ et $c$.\n\n- Existe-t-il un mur coloré pour $\\mathrm{n}=6$ ?\n- Existe-t-il un mur coloré pour $\\mathrm{n}=7$ ?", "solution": "de l'exercice 7\n\nC'est en fait la parité de n qui est cruciale.\nCas n pair : Il y a $\\frac{n(n-1)}{2}$ donc en moyenne il y a $\\frac{n-1}{2}$ cordes de chaque couleur. Ce nombre n'étant pas entier, il y a des couleurs avec plus de cordes que la moyenne et des avec moins. On pourrait tout-à-fait choisir une couleur sous-représentée et comparer le nombre de triplets de couleurs comportant cette couleur avec le nombre de triplets de cordes comportant une corde de cette couleur pour obtenir un contradiction. On va ici choisir l'approche opposée : on considère une couleur sur-représentée. Il y a au moins $\\frac{n+1}{2}$ cordes de cette couleur, donc au moins $n+1$ extrémités de cordes de cette couleur. D'après le principe des tiroirs, il existe un sommet ayant deux extrémités de cordes de cette couleur. Il existe donc un triplet de cordes comportant deux fois cette couleur, et ne correspondant donc à aucun triplet de couleur. Cependant il y a $\\binom{n}{3}$ triplets de cordes qui doivent remplir les $\\binom{n}{3}$ triplets de couleurs possibles, il n'y a aucune marge pour gâcher des triplets de cordes. Il est donc impossible d'obtenir un mur coloré pour $n$ pair.\nCas n impair : Ici le raisonnement précédent nous indique juste que pour chaque couleur il faut $\\frac{\\mathrm{n}-1}{2}$ cordes reliant $n-1$ points distincts et laissant un unique point ne relié par cette couleur. On trouve la construction suivante : on numérote les clous dans $\\mathbb{Z} / \\mathrm{n} \\mathbb{Z}$ et les couleurs aussi. Ensuite, on donne à la corde entre le clou $i$ et le clou $j$ la couleur $i+j$. Cette construction semble prometteuse car elle est totalement symétrique et vérifie la propriété voulue. En effet, on vérifie facilement que le triplet de couleur de corde $\\mathrm{a}, \\mathrm{b}, \\mathrm{c}$ est atteint en prenant les clous $\\frac{\\mathrm{a}+\\mathrm{b}}{2}, \\frac{\\mathrm{a}+\\mathrm{c}}{2}, \\frac{\\mathrm{~b}+\\mathrm{c}}{2}$\n\nCommentaires des correcteurs:\nL'exercice est bien résolu. Certains n'ont trouvé qu'un cas sur les deux, mais ont été récompensé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $\\Gamma$ un cercle et P un point à l'extérieur de $\\Gamma$. Les tangentes à $\\Gamma$ issues de P touchent $\\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle $P B K$ recoupe le cercle $\\Gamma$ au point $T$. Soit $P^{\\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\\widehat{\\mathrm{PBT}}=\\widehat{\\mathrm{P}^{\\prime} \\mathrm{KA}}$.", "solution": "de l'exercice 8\n\n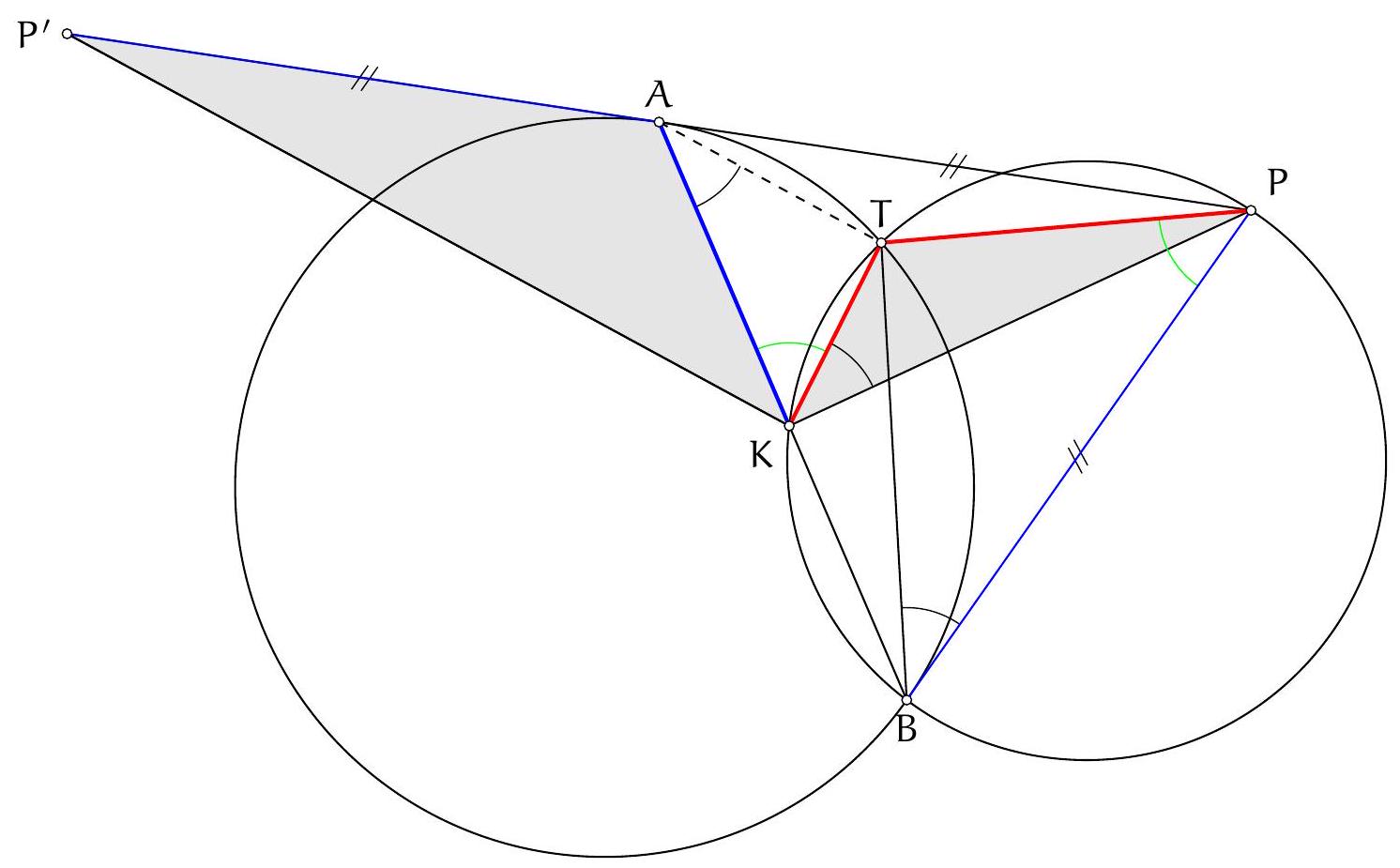\n\nD'après le théorème de l'angle inscrit, $\\widehat{\\mathrm{PBT}}=\\widehat{\\mathrm{PKT}}$. Ainsi, il suffit de montrer que $\\widehat{\\mathrm{PKT}}=\\widehat{\\mathrm{P}^{\\prime} \\mathrm{KA}}$. La figure semble suggérer que les triangles PKT et $P^{\\prime}$ KA sont semblables, nous allons donc essayer de montrer ce résultat, qui impliquera bien l'égalité d'angle voulue.\nPour montrer que $\\triangle P K T \\sim \\triangle P^{\\prime} K A$, on a plusieurs possibilités. Par exemple, on peut montrer que $\\widehat{T P K}=$ $\\widehat{K^{\\prime} A}$ et $\\widehat{\\mathrm{KTP}}=\\widehat{\\mathrm{KAP}}$. Toutefois, lorsque l'on essaye de calculer l'angle $\\widehat{\\mathrm{TPK}}$, on se rend compte que l'égalité $\\widehat{\\mathrm{TPK}}=\\widehat{\\mathrm{KP}^{\\prime} A}$ est équivalente à l'énoncé à démontrer. On va donc montrer que $\\widehat{\\mathrm{KTP}}=\\widehat{\\mathrm{P}^{\\prime} \\mathrm{AK}}$ et que $\\frac{\\mathrm{KT}}{\\mathrm{KA}}=\\frac{\\mathrm{TP}}{\\mathrm{AP}^{\\prime}}$.\nPour montrer que $\\widehat{\\mathrm{KTP}}=\\widehat{\\mathrm{P}^{\\prime} A \\mathrm{AK}}$, il faut d'abord remarquer que le triangle $A P B$ est isocèle en $P$ puisque les droites ( $A P$ ) et ( $B P$ ) sont tangentes en $A$ et $B$ au cercle $\\Gamma$. En appliquant le théorème de l'angle inscrit dans le cercle passat par $P, B, K$ et $T$, on trouve :\n\n$$\n\\widehat{\\mathrm{KTP}}=180^{\\circ}-\\widehat{\\mathrm{KBP}}=180^{\\circ}-\\widehat{\\mathrm{ABP}}=180^{\\circ}-\\widehat{\\mathrm{BAP}}=\\widehat{\\mathrm{PAK}}\n$$\n\nIl reste donc à montrer que $\\frac{K T}{K A}=\\frac{T P}{A P^{\\prime}}$. Puisque $A P^{\\prime}=A P=B P$, il suffit de montrer que $\\frac{K T}{K A}=\\frac{T P}{B P}$. Il suffit donc de montrer que les triangles AKT et BPT sont semblables. Pour cela, il suffit de montrer que les angles de ces deux triangles sont deux à deux égaux.\nD'une part, par angle inscrit, $\\widehat{A K T}=180^{\\circ}-\\widehat{\\mathrm{BKT}}=\\widehat{\\mathrm{TPB}}$. D'autre part par angle tangentiel, $\\widehat{\\mathrm{TAK}}=$ $\\widehat{\\mathrm{TAB}}=\\widehat{\\mathrm{TBP}}$.\nDonc les triangles $A K T$ et BPT sont semblables comme voulu.\n\n## Commentaires des correcteurs:\n\nUne bonne réussite relativement à la difficulté estimée de l'exercice. Quelques élèves, qui n'ont pas résolu complètement l'exercice, on tenu à partager leurs idées sur le problème, ce qui a été grandement apprécié.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soient $a_{1}, \\ldots, a_{101}$ des réels appartenant à l'intervalle $[-2 ; 10]$ tels que\n\n$$\na_{1}+\\ldots+a_{101}=0\n$$\n\nMontrer que\n\n$$\na_{1}^{2}+\\ldots+a_{101}^{2} \\leqslant 2020\n$$", "solution": "de l'exercice 9 Lorsque l'on effectue des inégalités sur des réels qui ne sont pas forcément positifs, il est essentiel de séparer les variables positives et négatives. Cette idée simple constitue souvent l'idée de départ dans la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soient $a_{1}, \\ldots, a_{101}$ des réels appartenant à l'intervalle $[-2 ; 10]$ tels que\n\n$$\na_{1}+\\ldots+a_{101}=0\n$$\n\nMontrer que\n\n$$\na_{1}^{2}+\\ldots+a_{101}^{2} \\leqslant 2020\n$$", "solution": "et peut mener à des développements intéressants, en plus de prévenir certaines erreurs lors de manipulations d'inégalités avec des nombres négatifs.\nLa deuxième idée, lorsque les variables jouent des rôles symétriques, est d'imposer un ordre aux réels. En plus de permettre, parfois, d'obtenir des résultats intéressants pour le problème, cela simplifie grandement la rédaction de la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soient $a_{1}, \\ldots, a_{101}$ des réels appartenant à l'intervalle $[-2 ; 10]$ tels que\n\n$$\na_{1}+\\ldots+a_{101}=0\n$$\n\nMontrer que\n\n$$\na_{1}^{2}+\\ldots+a_{101}^{2} \\leqslant 2020\n$$", "solution": "Quitte à renuméroter les variables, on suppose donc que $a_{1} \\leqslant a_{2} \\leqslant \\ldots \\leqslant a_{100} \\leqslant a_{101}$. Si tous les réels sont nuls, alors la somme de leur carré est nulle et donc bien inférieure à 2020. On suppose désormais que l'un des réels est non nul. Puisque la somme des $a_{i}$ est nulle, cela impose qu'au moins un réel est strictement positif et un autre strictement négatif. On note alors $p$ l'indice vérifiant $a_{p}<0 \\leqslant a_{p+1}$.\nRéécrivons dès à présent l'hypothèse de la somme nulle sous la forme\n\n$$\n-\\left(a_{1}+a_{2}+\\ldots+a_{p}\\right)=a_{p+1}+\\ldots+a_{101}\n$$\n\nOn va désormais chercher à faire apparaître cette hypothèse dans la somme à calculer. Pour cela, on va également se servir du fait que si $1 \\leqslant i \\leqslant p$, alors $a_{i} \\geqslant-2$ et que si $p+1 \\leqslant i \\leqslant 101$, alors $a_{i} \\leqslant 10$. On a :\n\n$$\n\\begin{aligned}\na_{1}^{2}+\\ldots+a_{101}^{2} & =\\underbrace{a_{1} \\cdot a_{1}}_{\\leqslant-2 a_{1}}+\\ldots+\\underbrace{a_{p} \\cdot a_{p}}_{\\leqslant-2 a_{p}}+\\underbrace{a_{p+1} \\cdot a_{p+1}}_{\\leqslant 10 a_{p+1}}+\\ldots+\\underbrace{a_{101} \\cdot a_{101}}_{\\leqslant 10 a_{101}} \\\\\n& \\leqslant-2 a_{1}+\\ldots+\\left(-2 a_{p}\\right)+10 a_{p+1}+\\ldots+10 a_{101} \\\\\n& =2\\left(-\\left(a_{1}+\\ldots+a_{p}\\right)\\right)+10\\left(a_{p+1}+\\ldots+a_{101}\\right) \\\\\n& =2(\\underbrace{a_{p+1}}_{\\leqslant 10}+\\ldots+\\underbrace{a_{101}}_{\\leqslant 10})+10(-(\\underbrace{a_{1}}_{\\geqslant-2}+\\ldots+\\underbrace{a_{p}}_{\\geqslant-2})) \\\\\n& \\leqslant 2 \\cdot 10 \\cdot(101-p)+10 \\cdot 2 \\cdot p \\\\\n& =2020\n\\end{aligned}\n$$\n\nce qui est l'inégalité voulue.\n\n## Commentaires des correcteurs :\n\nCertains élèves ont remarqué que, pour $-2 \\leqslant a_{i} \\leqslant 10$, on a $\\left(a_{i}+2\\right)\\left(a_{i}-10\\right) \\leqslant 0$, et s'en sont servi pour aboutir à une preuve de façon très efficace. D'autres ont choisi de construire les valeurs de $a_{i}$ maximisant la somme des carrés; dans ce cas, il était bien sûr indispensable de prouver l'optimalité de la construction pour obtenir la majorité des points.\n\n## Exercices Seniors", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soit a un réel strictement positif et $n \\geqslant 1$ un entier. Montrer que\n\n$$\n\\frac{a^{n}}{1+a+\\ldots+a^{2 n}}<\\frac{1}{2 n}\n$$", "solution": "de l'exercice 10 Puisque la difficulté réside dans le dénominateur du membre de droite, et pour plus de confort, on peut chercher à montrer la relation inverse, à savoir :\n\n$$\n\\frac{1+a+\\ldots+a^{2 n}}{a^{n}}>2 n\n$$\n\nL'idée derrière la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 10.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soit a un réel strictement positif et $n \\geqslant 1$ un entier. Montrer que\n\n$$\n\\frac{a^{n}}{1+a+\\ldots+a^{2 n}}<\\frac{1}{2 n}\n$$", "solution": "qui suit est \"d'homogénéiser\" le numérateur du membre de gauche, c'est-àdire de comparer ce numérateur dans lequel les a sont élevés à des puissances distinctes à une expression composée uniquement de a élevés à la même puissance. Pour cela, on cherche à coupler certains termes et appliquer l'inégalité des moyennes. Voyons plutôt : pour $0 \\leqslant i \\leqslant 2 n$, on a $a^{i}+a^{2 n-i} \\geqslant 2 \\sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Ainsi :\n\n$$\n\\begin{aligned}\n\\frac{1+a+\\ldots+a^{2 n}}{a^{n}} & =\\frac{\\left(1+a^{2 n}\\right)+\\left(a+a^{2 n-1}\\right)+\\ldots+\\left(a^{n-1}+a^{n+1}\\right)+a^{n}}{a^{n}} \\\\\n& \\geqslant \\frac{\\overbrace{2 a^{n}+2 a^{n}+\\ldots+2 a^{n}}^{n \\text { termes }}+a^{n}}{a^{n}} \\\\\n& =\\frac{(2 n+1) a^{n}}{a^{n}} \\\\\n& =2 n+1 \\\\\n& >2 n\n\\end{aligned}\n$$\n\nce qui fournit l'inégalité voulue.\nCommentaires des correcteurs:\nExercice très bien résolu dans l'ensemble. De nombreux élèves ont su appliquer l'IAG directement à $2 \\mathrm{n}+1$ termes, les autres ont pour la plupart réussi à s'en sortir avec l'IAG à deux termes.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Déterminer tous les entiers a tels que $a-3$ divise $a^{3}-3$.", "solution": "de l'exercice 11\nOn sait que $a-3 \\mid a^{3}-3^{3}$, donc il divise la différence\n\n$$\na-3 \\mid a^{3}-3-\\left(a^{3}-3^{3}\\right)=27-3=24\n$$\n\nRéciproquement, il suffit que $a-3$ divise 24 pour qu'il divise $24+a^{3}-3^{3}=a^{3}-3$. Les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Déterminer tous les entiers a tels que $a-3$ divise $a^{3}-3$.", "solution": "s sont donc exactement les diviseurs de 24 auxquels on ajoute 3 . On a donc\n\n$$\na-3 \\in\\{-24,-12,-8,-6,-4,-3,-2,-1,0,1,2,3,4,6,8,12,24\\}\n$$\n\net $a \\in\\{-21,-9,-5,-3,-1,0,1,2,3,4,5,6,9,11,15,27\\}$.\n\n## Commentaires des correcteurs:\n\nExercice très bien résolu dans l'ensemble ; l'erreur la plus fréquente est l'oubli de certains diviseurs de 24.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Soient $\\omega_{1}$ et $\\omega_{2}$ deux cercles de centres respectifs $\\mathrm{O}_{1}$ et $\\mathrm{O}_{2}$. On suppose que $\\omega_{1}$ et $\\omega_{2}$ se coupent en les points $A$ et $B$. La droite $\\left(O_{1} A\\right)$ recoupe le cercle $\\omega_{2}$ en $C$ tandis que la droite $\\left(O_{2} A\\right)$ recoupe le cercle $\\omega_{1}$ en D . Montrer que les points $\\mathrm{D}, \\mathrm{O}_{1}, \\mathrm{~B}, \\mathrm{O}_{2}$ et C appartiennent à un même cercle.", "solution": "de l'exercice 12\n\n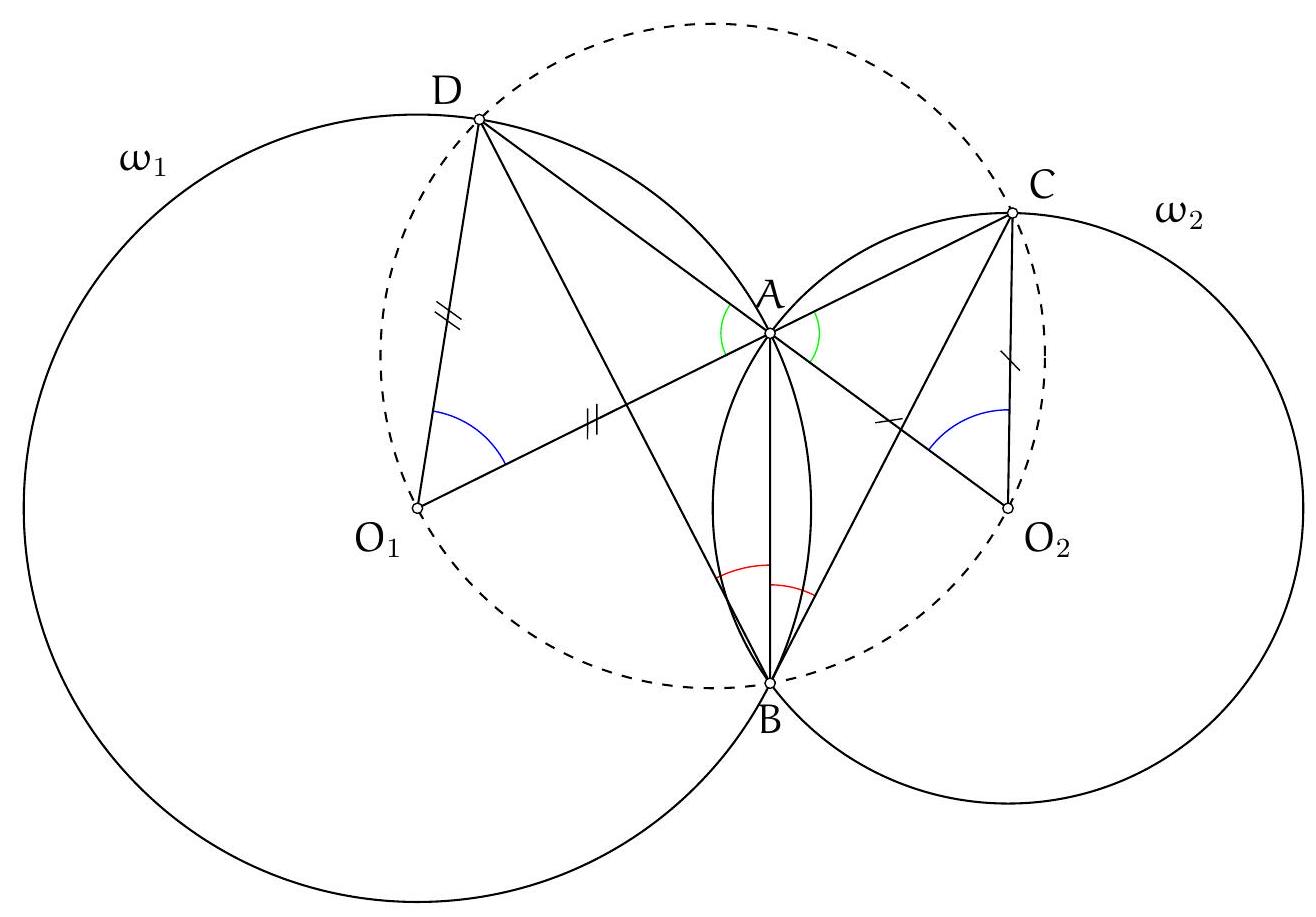\n\nNotons que puisque les angles $\\widehat{\\mathrm{DAO}_{1}}$ et $\\widehat{\\mathrm{CAO}_{2}}$ sont opposés par le sommet, ils sont égaux. D'autre part, puisque les points $A$ et $D$ appartiennent au cercle $\\omega_{1}$, le triangle $A O_{1} D$ est isocèle en $O_{1}$. De même, le triangle $\\mathrm{CO}_{2} A$ est isocèle en $\\mathrm{O}_{2}$. Les triangles $\\mathrm{DO}_{1} A$ et $\\mathrm{CO}_{2} A$ sont donc des triangels isocèle avec les mêmes angles à la base, ils sont donc semblables. Ceci implique que $\\widehat{\\mathrm{AO}_{1} \\mathrm{D}}=\\widehat{\\mathrm{CO}_{2} \\mathrm{~A}}$, et donc que\n\n$$\n\\widehat{\\mathrm{CO}_{1} \\mathrm{D}}=\\widehat{\\mathrm{AO} \\mathrm{O}_{1} \\mathrm{D}}=\\widehat{\\mathrm{CO}_{2} \\mathrm{~A}}=\\widehat{\\mathrm{CO}_{2} \\mathrm{D}}\n$$\n\nsi bien que les points $\\mathrm{C}, \\mathrm{O}_{2}, \\mathrm{O}_{1}$ et D sont cocycliques.\nPar ailleurs, on peut découper l'angle $\\widehat{\\mathrm{DBC}}$ en la somme $\\widehat{\\mathrm{DBA}}+\\widehat{\\mathrm{ABC}}$. D'une part, d'après le théorème de l'angle au centre dans le cercle $\\omega_{1}$, on a $\\widehat{A B D}=\\frac{1}{2} \\widehat{\\mathrm{AO}_{1} \\mathrm{D}}$. D'autre part, d'après le théorème de l'angle au centre dans le cercle $\\omega_{1}$, on a $\\widehat{A B C}=\\frac{1}{2} \\widehat{A O_{2} C}$. Ainsi\n\n$$\n\\widehat{\\mathrm{DBC}}=\\widehat{\\mathrm{DBA}}+\\widehat{A B C}=\\frac{1}{2} \\widehat{A O_{1} \\mathrm{D}}+\\frac{1}{2} \\widehat{\\mathrm{AO}_{2} \\mathrm{C}}=\\widehat{\\mathrm{AO}_{1} \\mathrm{D}}\n$$\n\nce qui permet de conclure que le point B appartient au cercle passant par les points $\\mathrm{C}, \\mathrm{O}_{2}, \\mathrm{O}_{1}$ et D .\n\n## Commentaires des correcteurs:\n\nExercice très bien résolu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 12.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Soit ( $a_{n}$ ) une suite strictement croissante d'entiers positifs telle que $a_{1}=1$ et pour tout $n \\geqslant 1, a_{n+1} \\leqslant 2 n$. Montrer que pour tout entier $n \\geqslant 1$, il existe deux indices $p$ et $q$ tels que $a_{p}-a_{q}=n$.", "solution": "de l'exercice 13\n\nSoit $n \\geqslant 1$ un entier. On va utiliser le principe des tiroirs. Construisons nos tiroirs deux sorte que si deux nombres sont dans un même tiroirs, ils vérifient la propriété de l'énoncé. Pour cela, on considère les tiroirs suivants : on réunit les entiers de 1 à $2 n$ en les couples de la forme $\\{i, n+i\\}$ pour $i$ entre 1 et $n$, ce qui constitue $n$ tiroirs. Ces tiroirs sont bien disjoints deux à deux, et si deux termes de la suite sont dans un même tiroir, cela donne les deux indices $p$ et $q$ tels que $a_{p}-a_{q}=n$, car tous les termes d'une suite strictement croissante sont distincts.\nOr, puisque la suite ( $a_{m}$ ) est croissante et puisque $a_{n+1} \\leqslant 2 n, a_{m} \\in \\llbracket 1,2 n \\rrbracket$ pour $m \\in \\llbracket 1, n+1 \\rrbracket$. Donc les $n+1$ premiers termes de la suites sont dans l'intervalle $\\llbracket 1,2 n \\rrbracket$. Par le principe des tiroirs, il y a deux termes distincts qui appartiennent au même ensemble $\\{i, n+i\\}$ pour un certain $i$, ce qui est le résultat voulu.\n\n## Commentaires des correcteurs :\n\nExercice très bien traité.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 13.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Soit $\\Gamma$ un cercle et $P$ un point à l'extérieur de $\\Gamma$. Les tangentes à $\\Gamma$ issues de $P$ touchent $\\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle PBK recoupe le cercle $\\Gamma$ au point $T$. Soit $\\mathrm{P}^{\\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\\widehat{\\mathrm{PBT}}=\\widehat{\\mathrm{P}^{\\prime} \\mathrm{KA}}$.", "solution": "de l'exercice 14\n\n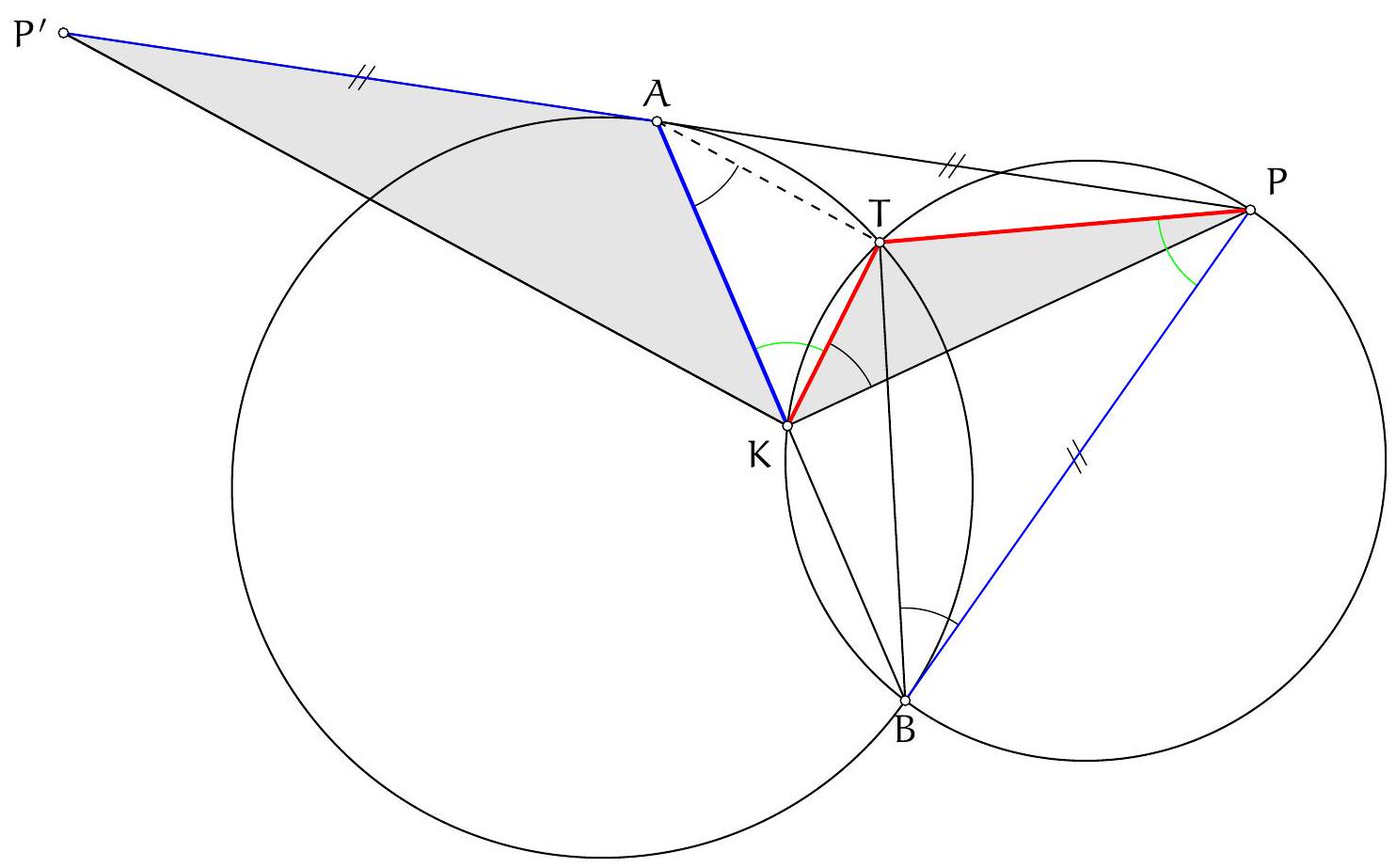\n\nD'après le théorème de l'angle inscrit, $\\widehat{\\mathrm{PBT}}=\\widehat{\\mathrm{PKT}}$. Ainsi, il suffit de montrer que $\\widehat{\\mathrm{PKT}}=\\widehat{\\mathrm{P}^{\\prime} \\mathrm{KA}}$. La figure semble suggérer que les triangles PKT et $\\mathrm{P}^{\\prime} \\mathrm{KA}$ sont semblables, nous allons donc essayer de montrer ce résultat, qui impliquera bien l'égalité d'angle voulue.\nPour montrer que $\\triangle P K T \\sim \\triangle P^{\\prime} K A$, on a plusieurs possibilités. Par exemple, on peut montrer que $\\widehat{T P K}=$ $\\widehat{K P^{\\prime} A}$ et $\\widehat{K T P}=\\widehat{K A P}$. Toutefois, lorsque l'on essaye de calculer l'angle $\\widehat{T P K}$, on se rend compte que l'égalité $\\widehat{T P K}=\\widehat{K P^{\\prime} A}$ est équivalente à l'énoncé à démontrer. On va donc montrer que $\\widehat{K T P}=\\widehat{P^{\\prime} A K}$ et que $\\frac{\\mathrm{KT}}{\\mathrm{KA}}=\\frac{\\mathrm{TP}}{\\mathrm{AP}^{\\prime}}$.\nPour montrer que $\\widehat{K T P}=\\widehat{P^{\\prime} A K}$, il faut d'abord remarquer que le triangle $A P B$ est isocèle en $P$ puisque les droites ( $A P$ ) et ( $B P$ ) sont tangentes en $A$ et $B$ au cercle $\\Gamma$. En appliquant le théorème de l'angle inscrit dans le cercle passant par $\\mathrm{P}, \\mathrm{B}, \\mathrm{K}$ et T , on trouve :\n\n$$\n\\widehat{\\mathrm{KTP}}=180^{\\circ}-\\widehat{\\mathrm{KBP}}=180^{\\circ}-\\widehat{\\mathrm{ABP}}=180^{\\circ}-\\widehat{\\mathrm{BAP}}=\\widehat{\\mathrm{PAK}}\n$$\n\nIl reste donc à montrer que $\\frac{\\mathrm{KT}}{\\mathrm{KA}}=\\frac{\\mathrm{TP}}{A \\mathrm{P}^{\\prime}}$. Puisque $A P^{\\prime}=A P=B P$, il suffit de montrer que $\\frac{\\mathrm{KT}}{\\mathrm{KA}}=\\frac{\\mathrm{TP}}{\\mathrm{BP}}$. Il suffit donc de montrer que les triangles AKT et BPT sont semblables. Pour cela, il suffit de montrer que les angles de ces deux triangles sont deux à deux égaux.\nD'une part, par angle inscrit, $\\widehat{A K T}=180^{\\circ}-\\widehat{\\mathrm{BKT}}=\\widehat{\\mathrm{TPB}}$. D' autre part, par angle tangentiel, $\\widehat{\\mathrm{TAK}}=$ $\\widehat{\\mathrm{TAB}}=\\widehat{\\mathrm{TBP}}$.\nDonc les triangles AKT et BPT sont semblables comme voulu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 14.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Soit $\\Gamma$ un cercle et $P$ un point à l'extérieur de $\\Gamma$. Les tangentes à $\\Gamma$ issues de $P$ touchent $\\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle PBK recoupe le cercle $\\Gamma$ au point $T$. Soit $\\mathrm{P}^{\\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\\widehat{\\mathrm{PBT}}=\\widehat{\\mathrm{P}^{\\prime} \\mathrm{KA}}$.", "solution": "$n^{\\circ} 2$ :\n\nEn cas d'allergie à la chasse aux angles, il est aussi possible de progresser dans le problème avec des idées avancées. Le problème se présente naturellement comme dynamique : en gardant fixe $\\Omega, P, A, B, P^{\\prime}$ on peut faire bouger K projectivement. Alors la T bouge aussi projectivement car le cercle PBK ayant deux points fixes P et B il a une intersection non fixe avec la droite $(\\mathrm{AB})$ et avec $\\Omega$, donc peut passer projectivement à $K$ ou à $T$. De plus, les angles à mesurer sont entre une droite fixe et une droite qui bouge projectivement chacun, l'égalité d'angle revient donc à dire que le point à l'infini de la première droite projective est envoyé sur le point à l'infini de la deuxième par une rotation bien choisie (ou par une symétrie si les angles avaient été dans l'autre sens). Le problème est bien projectif, cherchons trois cas particuliers.\nOn peut envoyer K à l'infini, alors par tangence $T$ se retrouve en $B$ et les deux angles qui doivent être égaux sont nuls.\nOn peut envoyer K sur $A$, alors T se retrouve aussi en $A$ et les deux angles qui doivent être égaux sont égaux car le triangle PAB est isocèle en P .\nIl nous manque encore un cas particulier utilisant le fait que $\\mathrm{P}^{\\prime}$ soit non seulement sur la droite ( $P A$ ) mais bien symétrique. On peut placer K sur le symétrique de B par rapport à $A$ pour construire un parallélogramme. La chasse aux angles n'est alors pas tout à fait immédiate, mais plus facile que dans le problème original, car elle ne nécessite pas d'idée pour utiliser la condition de milieu puisqu'il suffit de considérer le parallélogramme. Elle est laissée en exercice au lecteur.\n\n## Commentaires des correcteurs:\n\nL'exercice a été très bien réussi, et les preuves utilisant les astuces autour des milieux de segments ont été particulièrement appréciées.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 14.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soient $\\mathrm{m}, \\mathrm{n}$ et $\\times$ des entiers strictement positifs. Montrer que\n\n$$\n\\sum_{i=1}^{n} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)=\\sum_{i=1}^{m} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n\\right)\n$$", "solution": "de l'exercice 15\n\nQuitte à échanger $m$ et $n$, on peut supposer que $m \\leqslant n$. On procède alors par récurrence sur $n$ à $m$ fixé.\nInitialisation : Si $\\mathrm{m}=\\mathrm{n}$, l'égalité est triviale.\nHérédité : Supposons l'égalité vraie pour un certain $n \\geqslant m$ et cherchons à montrer que l'égalité est vraie pour $n+1$. Le membre de gauche devient\n\n$$\n\\sum_{i=1}^{n} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)+\\min \\left(\\left\\lfloor\\frac{x}{n+1}\\right\\rfloor, m\\right)\n$$\n\nExaminons les termes du membre de droite, qui sont de la forme $\\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n+1\\right)$. On a\n\n$$\n\\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n+1\\right)-\\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n\\right)= \\begin{cases}1 & \\text { si }\\left\\lfloor\\frac{x}{i}\\right\\rfloor \\geqslant n+1 \\\\ 0 & \\text { sinon }\\end{cases}\n$$\n\nOr, $\\left\\lfloor\\frac{x}{i}\\right\\rfloor \\geqslant n+1$ si et seulement si $x \\geqslant(n+1) i$, ou encore $i \\leqslant\\left\\lfloor\\frac{x}{n+1}\\right\\rfloor$. Donc le nombre de $i$ de $\\llbracket 1, m \\rrbracket$ pour lesquels $\\left\\lfloor\\frac{x}{i}\\right\\rfloor \\geqslant n+1$ est précisément $\\min \\left(\\left\\lfloor\\frac{x}{n+1}\\right\\rfloor, m\\right)$. On déduit que\n\n$$\n\\begin{aligned}\n\\sum_{i=1}^{m} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n+1\\right) & =\\sum_{i=1}^{m} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n\\right)+\\min \\left(\\left\\lfloor\\frac{x}{n+1}\\right\\rfloor, m\\right) \\\\\n& =\\sum_{i=1}^{n} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)+\\min \\left(\\left\\lfloor\\frac{x}{n+1}\\right\\rfloor, m\\right) \\\\\n& =\\sum_{i=1}^{n+1} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)\n\\end{aligned}\n$$\n\noù la deuxième égalité provient de l'hypothèse de récurrence. Ceci achève la récurrence et conclut l'exercice.\n$\\underline{\\text {", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 15.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soient $\\mathrm{m}, \\mathrm{n}$ et $\\times$ des entiers strictement positifs. Montrer que\n\n$$\n\\sum_{i=1}^{n} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)=\\sum_{i=1}^{m} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n\\right)\n$$", "solution": "alternative: }}$ Une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 15.", "solution_match": " Solution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Soient $\\mathrm{m}, \\mathrm{n}$ et $\\times$ des entiers strictement positifs. Montrer que\n\n$$\n\\sum_{i=1}^{n} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)=\\sum_{i=1}^{m} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n\\right)\n$$", "solution": "très astucieuse consiste à procéder par double comptage, en remarquant que les deux membres de l'égalité servent à compter le même objet, à savoir le nombre de paires $(a, b)$ telles que $a \\leqslant m, b \\leqslant n$ et $a b \\leqslant x$.\nCherchons en effet à compter ce nombre d'objet d'une première façon. Le choix d'une paire $(a, b) \\in$ $\\llbracket 1, \\mathrm{~m} \\rrbracket \\times \\llbracket 1, n \\rrbracket$ telle que $\\mathrm{ab} \\leqslant x$ se caractérise dans un premier temps par le choix de $a$ dans $\\llbracket 1, m \\rrbracket$. Puis, puisque $a b \\leqslant x$, on $a b \\leqslant\\left\\lfloor\\frac{x}{a}\\right\\rfloor$. Donc $b \\leqslant \\min (\\lfloor x / a\\rfloor, n)$ et il y a $\\min (\\lfloor x / a\\rfloor, n)$ choix pour $b$ si a est fixé. On a donc en tout\n\n$$\n\\sum_{i=1}^{m} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, n\\right)\n$$\n\ntelles paires $(a, b)$.\nEn commençant par choisir b plutôt que $a$, un raisonnement similaire nous permet d'affirmer qu'il y a\n\n$$\n\\sum_{i=1}^{n} \\min \\left(\\left\\lfloor\\frac{x}{i}\\right\\rfloor, m\\right)\n$$\n\ntelles paires d'entiers $(a, b)$. Les deux termes sont donc égaux.\nCommentaires des correcteurs:\nL'exercice a été bien traité et par beaucoup d'élèves, relativement à sa difficulté estimée.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 15.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soit $A B C$ un triangle dans lequel $A B2-1 / 2^{n}$ et $B<-1 / 2^{n}$, sans quoi on aurait $a_{2 n+1}>1$. On a donc $A \\leqslant 2-1 / 2^{n}$ ou $B \\geqslant-1 / 2^{n}$.\nSi $A \\leqslant 2-1 / 2^{n}$, on pose $x_{2 n}=x_{2 n-1}+a_{2 n}$ et $x_{2 n+1}=A$. On vérifie que la suite $\\left(x_{i}\\right)$ case la suite $\\left(a_{i}\\right)$ dans l'intervalle $\\left[0,2-1 / 2^{\\mathfrak{n}}\\right]$.\nOn suppose que $B \\geqslant-1 / 2^{n}$. On pose $x_{2 n}=x_{2 n-1}+a_{2 n}$ et $x_{2 n+1}=$ B. Si $x_{2 n} \\leqslant 2-1 / 2^{n-1}$, alors $B \\in\\left[-1 / 2^{n}, 2-1 / 2^{n-1}\\right]$ et la suite ( $x_{i}$ ) case la suite ( $a_{i}$ ) dans l'intervalle $\\left[-1 / 2^{n}, 2-1 / 2^{n-1}\\right]$. Si $x_{2 n}>2-1 / 2^{n-1}$, alors $B>2-1 / 2^{n-1}-1 \\geqslant 0$, si bien que la suite $\\left(x_{i}\\right)$ case la suite $\\left(a_{i}\\right)$ dans l'intervalle $\\left[0,2-1 / 2^{\\mathfrak{n}}\\right]$.\nCette disjonction de cas achève la récurrence.\n2) L'idée est la suivante : on souhaite construire des $a_{i}$ de sorte à forcer les $x_{i}$ à se trouver au centre de l'intervalle. Pour cela, on souhaite que les $a_{i}$ soient très proches de 1 , afin d'écarter deux $x_{i}$ l'un de l'autre, et on souhaite également qu'ils ne soient pas trop proches de 1 , pour éloigner les $x_{i}$ des bornes de l'intervalle. Cette discussion motive la construction qui suit.\nSoit $N=3 \\cdot 2^{n}-1$. Considérons la suite suivante :\n\n$$\n1,1-\\frac{1}{N}, 1,1-\\frac{2}{N}, 1, \\ldots, 1-\\frac{2^{2}}{N}, 1, \\ldots, 1-\\frac{2^{n}}{N}, 1, \\ldots, 1-\\frac{2}{N}, 1,1-\\frac{1}{N}, 1\n$$\n\nNous allons montrer que cette suite n'est pas casable dans l'intervalle ] $-1+1 / 2 \\mathrm{~N}, 1-1 / 2 \\mathrm{~N}$ [, qui est un intervalle de longueur $2-1 / \\mathrm{N}>2-1 / 2^{n}$, ce qui permettra de conclure. On suppose par l'absurde qu'il existe une suite ( $x_{i}$ ) qui case la suite ( $a_{i}$ ) donnée dans l'intervalle $]-1+1 / 2 \\mathrm{~N}, 1-1 / 2 \\mathrm{~N}[$ et on cherche à aboutir à une contradiction dans les estimations sur les $x_{i}$.\nQuitte à remplacer $\\left(x_{i}\\right)$ par $\\left(-x_{i}\\right)$, on peut suppose que $x_{0} \\geqslant 0$. Puisque $\\left|x_{1}-x_{0}\\right|=1$, on doit avoir $x_{1}=x_{0}-1$, et $x_{1} \\leqslant 1-1 / 2 N-1=-1 / 2 N$, soit $\\left|x_{1}\\right|>1 / 2 N$. De manière générale, on va montrer pour $i \\leqslant n$ que\n\n$$\n\\left|x_{2 i}\\right|<1-\\frac{2^{i+1}-1}{2 N} \\quad, \\quad\\left|x_{2 i+1}\\right|>\\frac{2^{i+1}-1}{2 N}\n$$\n\nLa preuve s'effectue par récurrence sur $i$. On a montré le résultat pour $i=0$. Supposons le vrai pour $i \\geqslant 0$ fixé. On a $\\left|x_{2 i+2}-x_{2 i+1}\\right|=a_{2 i+2}=1-2^{i} / N$. Si $x_{2 i+1}>0$, on a $x_{2 i+1}+\\left(1-2^{i} / N\\right)>1-\\frac{2^{i}-1}{2 N}>$ $1-\\frac{1}{2 \\mathrm{~N}}$. On a donc forcément $x_{2 i+2}=x_{2 i+1}-\\left(1-2^{i} / N\\right)$. Comme $1-2^{i} / N>\\left(2^{i+1}-1\\right) / 2 N$, on a\n\n$$\n\\left|x_{2 i+2}\\right|=1-\\frac{2^{i}}{N}-x_{2 i+1}<1-\\frac{2^{i+2}-1}{2 N}\n$$\n\nOn procède de même dans le cas où $x_{2 i+1}<0$.\nOn a ensuite $\\left|x_{2 i+3}-x_{2 i+2}\\right|=a_{2 i+3}=1$. Un raisonnement identique au précédent nous permet d'avoir, dans le cas où $x_{2 i+2}>0$ :\n\n$$\n\\left|x_{2 i+3}\\right|=1-x_{2 i+2}>1-\\left(1-\\frac{2^{i+2}-1}{2 \\mathrm{~N}}\\right)=\\frac{2^{i+2}-1}{2 \\mathrm{~N}}\n$$\n\net on procède de même dans le cas où $x_{2 i+2}<0$.\nOn procède de même pour montrer par récurrence que si $\\boldsymbol{i} \\geqslant \\mathrm{n}+1$ :\n\n$$\n\\left|x_{2 i}\\right|<\\frac{2^{2(n+1)-\\mathfrak{i}}-1}{2 N} \\quad, \\quad\\left|x_{2 i+1}\\right|>1-\\frac{2^{2(n+1)-\\mathfrak{i}}-1}{2 N}\n$$\n\nMais alors $\\left|\\mathrm{x}_{4 \\mathrm{n}+3}\\right|>1-\\frac{2-1}{2 \\mathrm{~N}}>1-\\frac{1}{2 \\mathrm{~N}}$, ce qui contredit notre hypothèse de départ et permet de conclure.\n\n## Commentaires des correcteurs:\n\nL'exercice n'a été abordé que par deux élèves, qui ont correctement résolu la question 1). La question 2) attendait cependant beaucoup de rigueur dans la preuve que la suite donnée n'était pas casable.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 17.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Un graphe G fini simple à $n$ sommets est dit divisible s'il est possible d'attribuer à chaque sommet $s$ de $G$ un numéro $n_{s}$ de sorte que deux sommets distincts possèdent toujours deux numéros distincts et deux sommets quelconques $s$ et $s^{\\prime}$ sont reliés par une arête si et seulement si $n_{s} \\mid n_{s^{\\prime}}$ ou $n_{s^{\\prime}} \\mid n_{s}$.\nUn graphe G fini simple à n sommets est dit permutable s'il est possible de numéroter les sommets de $G$ de 1 à $n$ et s'il existe une permutation $\\sigma$ de $\\{1, \\ldots, n\\}$ telle que les sommets ayant pour numéros $i$ et $j$ sont reliés par une arête si et seulement si $(\\mathfrak{i}-\\mathfrak{j})(\\sigma(\\mathfrak{i})-\\sigma(\\mathfrak{j}))<0$.\nMontrer qu'un graphe G est permutable si et seulement si G et son complémentaire sont divisibles.", "solution": "de l'exercice 18\n\nUn graphe est de divisibilité ssi on peut l'orienter (dans le sens des divisibilités) de manière à ce que s'il y a un arc (arête orientée) de A vers B et un de B vers C, il y en a un de A vers C. En effet, on peut alors attribuer à chaque sommet un nombre premier différent, et le nombre attribué pour les relations de divisibilité est alors le produit de son nombre premier par ceux de chacun ds sommets ayant un arc arrivant sur lui. On a alors les bonnes relations de divisibilité si il y a un arc de A vers B tout premier divisant le nombre attribué à A est le premier d'un sommet C avec un arc de C vers A . Il y a alors aussi un arc de C vers B donc le premier divise aussi le nombre attribué à B .\nMontrons qu'on peut orienter un graphe de permutation. On trace un arc de $a$ vers $b$ ssi $a\\sigma(b)$. On a bien les arêtes du graphe de permutation attribué et la relation est transitive, on a donc bien un graphe de divisibilité. Son complémentaire est également de divisibilité car orientable en traçant un arc de a vers b ssi $\\mathrm{a}<\\mathrm{b}$ et $\\sigma \\mathrm{a}<\\sigma \\mathrm{b}$.\n\nRéciproquement, on suppose un graphe orienté transitif dont le complémentaire est également orientable de manière transitive, montrons qu'il est de permutation. Choisir une numérotation et une permutation revient en fait à choisir librement deux numérotations des sommets, soit à ordonner deux fois les sommets. Deux sommets doivent alors être reliés si et seulement si leur position relative est différente selon les deux ordres. Pour le premier ordre, on place les éléments un à un, à chaque étape en rajoutant un élément n'ayant pas de prédécesseur selon le graphe complémentaire orienté. On considère donc tous les choix possibles, tous les sommets sans prédécesseur non choisi. Alors, tous ces éléments considérés forment une clique du graphe, il y en a donc un unique qui est sans antécédents dans cette clique pour le graphe orienté. C'est cet élément qu'on place en tout premier pour notre ordre. On l'enlève ensuite et on recommence jusqu'à ce que tous les sommets soient ordonnées. Pour le deuxième ordre, on fait presque la même chose. On rajoute aussi à chaque étape un sommet sans prédécesseur selon le graphe complémentaire, mais parmi cette clique de candidats potentiels, on va prendre celui sans successeur dans la clique.\nVérifions que cette construction fonctionne. Prenons $A$ et $B$ deux sommets non reliés. Supposons SPDG que dans le graphe complémentaire, $A$ est un prédécesseur de $B$. Si $B$ est choisi pour un des deux ordres, forcément $A$ n'a pas été considéré parmi les choix potentiels, soit il a déjà été choisi, soit il a lui-même un prédécesseur non choisi. Par transitivité, ce prédécesseur serait aussi un prédécesseur de $B$, ce qui empêcherait le choix de B. Donc pour les deux ordres, $A$ a été choisi avant B. Les deux ordres sont donc compatibles avec l'absence d'arêtes entre $A$ et $B$.\nPrenons $A$ et $B$ reliés et supposons SPDG que $A$ est un antécédent de $B$ dans le graphe. Montrons d'abords que pour le premier ordre, quand B est choisi, $A$ a déjà été choisi. À ce moment-là, si $A$ n'avait pas déjà été choisi, il n'aurait pas pu être considéré comme choix potentiel, sinon il aurait été choisi préférentiellement à $B$. Donc il avait un antécédent non choisi dans le graphe complémentaire. On remonte des antécédents successifs en partant de $A$ jusqu'à arriver jusqu'à un sommet $C$, sans antécédents encore non choisis. Par transitivité du graphe complémentaire orienté, $C$ est un antécédent de $A$ pour\nce graphe complémentaire. C a été considéré comme choix potentiel, n'ayant pas d'antécédent dans le graphe complémentaire, mais B lui a été préféré, donc B est un antécédent de C pour le graphe normal (pas complémentaire). $A$ étant lui-même un antécédent de $B$, par transitivité, $A$ doit être un antécédent de $C$ dans le graphe normal donc une arête entre $A$ et $C$ existe. Or on a construit $C$ comme un antécédent de $\\mathcal{A}$ dans le graphe complémentaire, donc une arête du graphe complémentaire existe en $\\mathcal{A}$ et C . La contradiction montre que selon le premier ordre, $A$ arrive avant $B$. On prouve identiquement que selon le deuxième ordre, $B$ arrive avant $A$. Ces deux ordres sont donc compatibles avec l'existence d'une arête entre $A$ et $B$.\n\n## Commentaires des correcteurs:\n\nL'exercice n'a été abordé que par une personne, qui l'a brillamment résolu.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé-envoi-5.jsonl", "problem_match": "\nExercice 18.", "solution_match": "## Solution "}}
diff --git "a/French_STS/segmented/fr-corrig\303\251.jsonl" "b/French_STS/segmented/fr-corrig\303\251.jsonl"
new file mode 100644
index 0000000000000000000000000000000000000000..e6707f399e4054addf7487e9a366355e187863dc
--- /dev/null
+++ "b/French_STS/segmented/fr-corrig\303\251.jsonl"
@@ -0,0 +1,63 @@
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soient $a, b$ deux entiers. Montrer que $a b(a-b)$ est divisible par 2.", "solution": "de l'exercice 1 On s'intéresse à la parité d'un produit, il est donc pertinent de faire une disjonction de cas sur la parité des entiers en jeu, ici a et $b$. On remarque alors la chose suivante :\n\n- Si $a$ ou best pair : alors $a b$ est pair (le produit d'un nombre pair par un entier quelconque étant pair) et donc $\\mathrm{ab}(\\mathrm{a}-\\mathrm{b})$ est bien divisible par 2 .\n- Sinon, si $a$ et $b$ sont tous les deux impairs, alors $a-b$ est pair (en tant que différence de deux impairs) et donc $a b(a-b)$ est divisible par 2\nFinalement, dans tous les cas, si $a$ et $b$ sont des entiers, alors $a b(a-b)$ est divisible par 2.\nCommentaire des correcteurs : Beaucoup d'élèves ont abordé cet exercice, et tous l'ont parfaitement réussi. L'idée consistait à faire des disjonctions de cas selon les parités de a et de b , ce qui pouvait se faire en deux cas : soit \" $a$ ou b pair\" et \"a et b impairs\", soit \"a et b de même parité\" et \"a et b de parité différente\". Certaines copies ont fait plus de cas, ce n'était pas nécessaire et parfois il y avait des cas qui étaient inclus dans d'autres cas déjà traités : cela rallongeait souvent les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soient $a, b$ deux entiers. Montrer que $a b(a-b)$ est divisible par 2.", "solution": "s, ce qui fait perdre en efficacité et peut faire perdre du temps qu'on aurait pu passer à chercher d'autres exercices plus difficiles.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Montrer qu'il existe une infinité de couples ( $\\mathrm{m}, \\mathfrak{n}$ ) d'entiers strictement positifs distincts tels que m ! n soit un carré parfait.", "solution": "de l'exercice 2\n On aurait envie de prendre $\\mathrm{m}=\\mathrm{n}$ pour avoir $\\mathrm{m}!\\mathrm{n}!=(\\mathrm{n}!)^{2}$ et avoir un carré parfait. Mais l'énoncé force $m \\neq n$. Malgré cela, on voit déjà un moyen de faire apparaître naturellement des carrés parfaits.\nSupposons sans perte de généralité $m>n$ (comme $m!n!=n!m!$, quitte à remplacer $(m, n) \\operatorname{par}(n, m)$, ça ne pose pas de problème). Alors $m!n!=\\mathfrak{m} \\times(m-1) \\times \\ldots \\times(n+1) \\times n!\\times n!=m \\times \\ldots \\times(n+1) \\times(n!)^{2}$. Alors $m!n!$ sera un carré parfait si et seulement si $m \\times \\ldots \\times(n+1)$ l'est. Le moyen le plus simple de le faire, c'est de choisir $m=n+1=k^{2}$ pour un certain entier $k(k \\geqslant 2$ car on veut $m, n \\geqslant 1$ ). En effet on a bien $\\left(k^{2}\\right)!\\left(k^{2}-1\\right)!=k^{2}\\left(\\left(k^{2}-1\\right)!\\right)^{2}=\\left[k\\left(k^{2}-1\\right)!\\right]^{2}$.\nFinalement, pour tout $k \\geqslant 2$ entier, $(m, n)=\\left(k^{2}, k^{2}-1\\right)$ convient, ce qui nous fournit bien une infinité de couples de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Montrer qu'il existe une infinité de couples ( $\\mathrm{m}, \\mathfrak{n}$ ) d'entiers strictement positifs distincts tels que m ! n soit un carré parfait.", "solution": "s.\n\nCommentaire des correcteurs : Le problème a été abordé par beaucoup d'élèves et une large majorité l'a parfaitement réussi. D'autres ont eu des pistes intéressantes sans forcément aboutir, comme remarquer que, dans le cas $m>n$ par exemple, il est nécessaire et suffisant d'avoir $m \\times(m-1) \\times \\ldots \\times(n+1)$ qui est un carré parfait.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "de l'exercice 3 On va montrer par descente infinie que ( $0,0,0$ ) est la seule", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "Comme un carré ne vaut que 0 ou 1 modulo 3 (une façon de le voir est de faire une disjonction de cas sur les valeurs modulo 3), il est pertinent de tenter une étude modulo 3 pour essayer de voir où ça nous mène. Pour ce faire, on remarque que si $(x, y, n)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": ", alors modulo 3 , on a\n\n$$\nn^{2} \\equiv-x^{4}-2 x^{2} y^{2}-y^{4} \\equiv-\\left(x^{2}+y^{2}\\right)^{2} \\quad(\\bmod 3)\n$$\n\nAinsi, $\\mathfrak{n}^{2}+\\left(x^{2}+y^{2}\\right)^{2}$ est divisible par 3 . Or un carré vaut 0 ou 1 modulo 3 donc la seule manière qu'une somme de carrés soit divisible par 3 , c'est que chacun des termes le soit. Donc $n$ et $x^{2}+y^{2}$ sont divisibles par 3. De même il découle que $x$ et $y$ sont divisibles par 3.\nEn réinjectant dans l'équation, on en déduit que $3^{4}=81$ divise $n^{2}$ et donc 9 divise n , donc $\\left(\\frac{x}{3}, \\frac{y}{3}, \\frac{\\mathfrak{n}}{9}\\right)$ est une autre", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "Or si on avait une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "avec $x, y$ ou n non nul (et quitte à les changer en leurs opposés, ce qui ne change pas les valeurs des carrés, positifs), on pourrait obtenir une suite strictement décroissante d'entiers naturels, ce qui est absurde (c'est le principe de la descente infinie).\nOn en déduit que la seule", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "potentielle est $(0,0,0)$. Et réciproquement, on remarque que $(x, y, \\mathfrak{n})=$ $(0,0,0)$ convient (les deux membres donnent 0 ).\nL'unique", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "de l'équation est donc $(0,0,0)$.\nCommentaire des correcteurs: Dans l'ensemble les copies qui ont abordé le problème l'ont plutôt bien réussi. Certaines ont tenté des pistes comme une étude modulo 8 ou une réécriture de l'équation, ici ça n'aboutissait pas mais c'étaient de bonnes idées qui peuvent tout de même être utiles sur d'autres problèmes similaires. Signalons des erreurs récurrentes sur le principe de la descente infinie : un certain nombre de copies concluent qu'il n'y a aucune", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "par descente infinie. En réalité la descente infinie nous permet de conclure qu'il n'y a aucune", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "non-nulle, mais rien n'exclut la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "$(0,0,0)$ a priori (et d'ailleurs elle marche). À ce sujet, un certain nombre de copies conclut que ( $0,0,0$ ) est la seule", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "possible, sans pour autant penser à la vérifier. Même si elle a l'air évidente ici, une mention de la vérification de la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "est indispensable, car la descente infinie garantit que c'est la seule", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "possible, mais pas que c'est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.", "solution": "de l'exercice 4 Comme $21=3 \\times 7$ et que 3 et 7 sont premiers entre eux, 21 divise $2^{2^{n}}+2^{n}+1$ si et seulement si 3 et 7 divisent $2^{2^{n}}+2^{n}+1$.\nÉliminons de suite le cas $n=0$, qui donne $2^{2^{0}}+2^{0}+1=4$ qui n'est pas divisible par 21. On peut donc supposer $n>0$, en particulier $2^{n}$ est pair. Alors modulo $3: 2^{2^{n}}+2^{n}+1 \\equiv(-1)^{2^{n}}+(-1)^{n}+1 \\equiv$ $(-1)^{n}+2(\\bmod 3)$. En particulier $2^{2^{n}}+2^{n}+1$ est divisible par 3 si est seulement si $n$ est pair. On suppose donc désormais que cette condition est vérifiée.\nReste à traiter le cas de la divisibilité par 7 . Modulo 7 , les puissances de 2 sont $2^{0} \\equiv 1,2^{1} \\equiv 2,2^{2} \\equiv$ $4,2^{3} \\equiv 1$ : il s'agit donc d'étudier l'exposant modulo 3. Comme $n$ est pair (par le cas précédent), on sait déjà que $2^{n} \\equiv 1(\\bmod 3)$ donc $2^{2^{n}} \\equiv 2(\\bmod 7)$. On veut donc $2^{n} \\equiv-1-2 \\equiv 4(\\bmod 3)$, et donc $n \\equiv 2(\\bmod 3)$ (et réciproquement si $n \\equiv 2(\\bmod 3)$, comme $n$ est pair alors 7 divise $\\left.2^{2^{n}}+2^{n}+1\\right)$.\nOn doit avoir $n \\equiv 0(\\bmod 2), n \\equiv 2(\\bmod 3):$ comme 2 et 3 sont premiers entre eux, le théorème des restes chinois donne qu'il existe une unique", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.", "solution": "modulo $2 \\times 3=6$, et on remarque que c'est $n \\equiv 2$ $(\\bmod 6)$.\nEn conclusion, les entiers naturels $n$ qui conviennent sont exactement ceux qui vérifient $n \\equiv 2(\\bmod 6)$.\nCommentaire des correcteurs : Les copies ont bien abordé le problème : presque tout le monde a pensé à étudier les cycles de puissances et beaucoup de gens ont pensé à se ramener à étudier la divisibilité par 3 et par 7 . Malheureusement, il y a eu beaucoup d'erreurs de calcul, raisonement, ou lecture de l'énoncé qui rendent une bonne partie de la preuve fausse, car il y a une erreur au début. Beaucoup de gens ont oublié le cas $n=0$ !", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit $n \\in \\mathbb{N}^{\\star}$. Montrer que si $2 n+1$ et $3 n+1$ sont des carrés parfaits, alors $5 n+3$ n'est pas premier.", "solution": "de l'exercice 5 Supposons que $2 \\mathrm{n}+1$ et $3 \\mathrm{n}+1$ sont des carrés parfaits : on dispose de $\\mathrm{a}, \\mathrm{b}$ deux entiers strictement positifs $(2 n+1,3 n+1>0)$ tels que $2 \\mathfrak{n}+1=a^{2}$ et $3 n+1=b^{2}$. Ici, il s'agit de remarquer que $5 \\mathfrak{n}+3=4 \\times(2 n+1)-(3 n+1)=4 a^{2}-b^{2}$. Pour trouver cette identité, on essaie d'exprimer 5 à partir de 2 et 3 : il est naturel de prendre $5=2+3$ mais cela ne donne pas $5 \\mathrm{n}+3$, en revanche on voit que $5=4 \\times 2-3$.\nOn peut donc écrire $5 n+3=(2 a-b)(2 a+b)$. Comme $a, b>02 a+b>2 a-b$, et $2 a+b>0$. Ceci force $2 a-b>0$ (sinon on aurait $5 n+3 \\leqslant 0$, ce qui est exclu). Il suffit donc de montrer que $2 a-b>1$ pour conclure : on aura alors écrit $5 \\mathrm{n}+3$ comme produit de deux entiers strictement plus grands que 1 , et il ne pourra pas être premier.\nMais si $2 \\mathrm{a}=\\mathrm{b}+1,5 \\mathrm{n}+3=2 \\mathrm{a}+\\mathrm{b}=4 \\mathrm{a}-1$ donc $\\mathrm{a}^{2}=2 \\mathrm{n}+1 \\leqslant \\frac{5 n+3}{2}<\\frac{4 \\mathrm{a}-1}{2}<2 \\mathrm{a}$ donc $\\mathrm{a}<2$. Mais $a=1$ donne $2 \\mathrm{n}+1=1$ donc $\\mathrm{n}=0$, absurde car $\\mathrm{n}>0$. Ainsi $2 a-b \\neq 1$.\nOn a donc bien montré que si $2 \\mathfrak{n}+1$ et $3 \\mathfrak{n}+1$ sont des carrés parfaits (avec $\\mathfrak{n} \\in \\mathbb{N}^{\\star}$ ), alors $5 \\mathfrak{n}+3$ n'est pas un nombre premier.\n$\\underline{\\text { Commentaire des correcteurs : Les élèves qui ont abordé le problème l'ont en général plutôt bien compris }}$ et ont trouvé la factorisation qui était intéressante ici. Néanmoins la plupart d'entre eux ont oublié de vérifier les signes de leurs termes : pour pouvoir conclure $2 \\mathrm{a}-\\mathrm{b}=1,2 \\mathrm{a}+\\mathrm{b}=5 \\mathrm{n}+3 \\mathrm{il}$ fallait avoir vérifié au préalable $2 a+b>2 a-b>0$, ce qui n'était pas très dur mais nécessaire pour que l'identification soit valide. Notons qu'un certain nombre de copies ont tenté d'exploiter des congruences : ici ça ne menait pas à grand chose d'intéressant, lorsqu'il s'agit des nombres premiers il est souvent plus intéressant de rechercher des factorisations plutôt que d'exploiter des congruences car ces dernières, à moins de trouver une divisibilité par un nombre particulier, ne nous renseignent pas sur le caractère premier ou non d'un entier.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "de l'exercice 6 Ce qu'on connaît pour des nombres premiers, c'est leurs propriétés de divisibilité. Une expression développée n'est donc pas très pratique pour étudier cela : on va d'abord chercher à factoriser.\nRemarquons que $p^{5}+p^{3}+2=p^{3}\\left(p^{2}+1\\right)+2$. On veut résoudre $p^{3}\\left(p^{2}+1\\right)=q^{2}-q-2$. Mais on reconnaît alors $q^{2}-q-2=(q-2)(q+1)$ (si on ne le voit pas directement, on peut le trouver en résolvant $\\mathrm{q}^{2}-\\mathrm{q}-2=0$ avec la méthode classique utilisant le discriminant).\nOn veut donc résoudre $p^{3}\\left(p^{2}+1\\right)=(q-2)(q+1)$. En particulier $p^{3} \\mid(q-2)(q+1)$. Alors $\\operatorname{pgcd}(q-$ $2, q+1)=\\operatorname{pgcd}(q-2, q+1-(q-2))=\\operatorname{pgcd}(q-2,3)$ vaut donc 1 ou 3. Cela suggère d'étudier d'abord le cas $p=3$ : on obtient $(q-2)(q+1)=270$, et en résolvant $q^{2}-q-2=270$ on trouve $q=17$ (qui est bien un nombre premier) et $q=-16$ (qui n'est pas", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "car ce n'est pas un nombre premier). Donc lorsque $p=3$, il y a une unique", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "$(p, q)=(3,17)$.\nOn peut donc supposer $p \\neq 3$. En particulier, il ne divise pas $\\operatorname{pgcd}(q-1, q+2)$, donc au moins un des nombres $q+1$ et $q-2$ est premier avec $p$, donc avec $p^{3}$. Or $p^{3} \\mid(q+1)(q-2)$ : donc d'après le lemme de Gauss, $q+1$ ou $q-2$ est divisible par $p^{3}$. Or, $p^{3}$ ne peut pas diviser $q-2$ parce que sinon, on aurait $(q-2)(q+1) \\geqslant p^{3} p^{3}>p^{3}\\left(p^{2}+1\\right)$, absurde. Ainsi $p^{3} \\mid q+1$, et donc $q-2 \\mid p^{2}+1$.\nMais les divisibilités qu'on vient d'obtenir montrent que $p^{3} \\leqslant q+1=(q-2)+3 \\leqslant p^{2}+1+3=p^{2}+4$, et donc $p^{2}(p-1) \\leqslant 4$. Or $p^{2}(p-1)$ est strictement croissante en $p$, et en $p=2$ on a égalité, donc le seul cas possible est $p=2$ (autrement dit, pour $p>2$, on a $p^{2}(p-1)>4$ ).\nLorsque $p=2$, l'équation devient $q^{2}-q-2=40$, en résolvant on trouve $q=7$ (qui convient car 7 est premier) et $\\mathrm{q}=-6$ (qui ne convient pas car n'est pas un nombre premier).\nFinalement, il y a deux", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "s qui sont $(\\mathbf{p}, \\mathbf{q})=(2,7)$ et $(\\mathbf{p}, \\mathbf{q})=(3,17)$.\nCommentaire des correcteurs : L'exercice a été assez abordé, mais beaucoup d'erreurs ont été commises. Quand on a une équation du type $a b=c d$, on ne peut pas conclure que $c$ vaut $a$ ou $b$, ou que $c$ divise $a$ ou b. Beaucoup d'élèves utilisent donc des affirmations arithmétiques fausses, et donc se retrouvent avec peu de points car ne traitant qu'un cas très particulier.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $n \\geqslant 2$. Montrer qu'il existe des entiers $a, b$ tels que, pour tout entier $m$, le nombre $m^{3}+a m+b$ ne soit pas un multiple de $n$.", "solution": "de l'exercice $7 \\quad \\mathrm{~m}^{3}+\\mathrm{am}+\\mathrm{b}$ est un multiple de n si et seulement si $\\mathrm{m}^{3}+\\mathrm{am} \\equiv-\\mathrm{b}(\\bmod \\mathrm{n})$. On remarque alors qu'il suffit de trouver a tel que $\\mathrm{m}^{3}+\\mathrm{am}$ ne prend pas toutes les valeurs possibles modulo $n$ (et de prendre pour $-b$ une des valeurs qui $n$ 'est pas prise). Comme $\\mathrm{m}^{3}+a m$ modulo $n$ ne dépend que de $m$ modulo $n$, on peut se restreindre à $0 \\leqslant m \\leqslant n-1$.\nIl s'agit de trouver un a tel que les $0^{3}+\\mathrm{a} \\cdot 0(\\bmod n), 1^{3}+\\mathrm{a} \\cdot 1(\\bmod n), \\ldots,(n-1)^{3}+a(n-1)$ $(\\bmod n) n$ 'atteignent pas $n$ valeurs distinctes $(\\operatorname{modulo} n)$. Alors si on trouve $m_{1} \\neq m_{2}$ entre 0 et $n-1$ tels que $m_{1}^{3}+a m_{1} \\equiv m_{2}^{3}+a m_{2}(\\bmod n)$, les $n-2$ autres valeurs de $m$ modulo $n$ donneront au plus $n-2$ valeurs de $m^{3}+$ am modulo $n$, donc au total, pour $0 \\leqslant m \\leqslant n-1, m^{3}+$ am prendra au plus $n-1$ valeurs sur mes $\\boldsymbol{n}$ possibles : il y en aura bien une qui ne sera pas atteinte. Or $0^{3}+\\mathrm{a} \\times 0 \\equiv 0(\\bmod \\mathfrak{n})$, $1^{3}+a \\times 1 \\equiv a+1(\\bmod \\mathfrak{n})$. Si $a+1 \\equiv 0(\\bmod \\boldsymbol{n})$, on sera dans la situation décrite ci-dessus.\nPosons alors $a=-1$ (ou $a=n-1$ si on veut $a>0)$. Alors $m^{3}+a m$ est nul si $m=0$ ou $m=1$. Donc il existe $c$ entier, $0 \\leqslant c \\leqslant n-1$, tel que pour tout $0 \\leqslant m \\leqslant n-1, m^{3}+a m \\not \\equiv c(\\bmod n)$. Posons alors $b=-c\\left(\\right.$ ou $b=n-c$ si on veut $b>0$ ), alors pour tout $0 \\leqslant m \\leqslant n-1, m^{3}+a m+b$ sera non nul modulo $n$, donc pour tout $m$ entier, $m^{3}+a m+b$ ne sera pas un multiple de $n$.\nAinsi, il existe bien de tels entiers $a$ et $b$.\nCommentaire des correcteurs : Le problème n'a pas beaucoup été abordé, et lorsque l'énoncé a été bien compris il a été bien réussi. Cependant, beaucoup n'ont pas compris l'énoncé, et on montré à la place que pour toute valeur de $m$ fixée, on pouvait trouver des $a$ et $b$ de sorte que $n$ ne divise pas $m^{3}+a m+b$. La différence ici est que a et bne sont pas fixés indépendamment de m , ce qui est une version sensiblement plus simple de l'exercice.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Trouver tous les entiers $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\in \\mathbb{N}$ tels que $1517^{\\mathrm{a}}+15^{\\mathrm{b}}=1532^{\\mathrm{c}}$.", "solution": "de l'exercice 8 On commence par traiter les petites valeurs de c.\nSi $c=0,1517^{a}+15^{b}=1$ n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Trouver tous les entiers $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\in \\mathbb{N}$ tels que $1517^{\\mathrm{a}}+15^{\\mathrm{b}}=1532^{\\mathrm{c}}$.", "solution": "Si $c=1$, on doit trouver $a, b$ tels que $1517^{a}+15^{b}=1532$. Si $a \\geqslant 2$ ou si $a=0$ il n'y a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Trouver tous les entiers $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\in \\mathbb{N}$ tels que $1517^{\\mathrm{a}}+15^{\\mathrm{b}}=1532^{\\mathrm{c}}$.", "solution": "Si $\\mathrm{a}=1$, alors $15^{\\mathrm{b}}=1532-1517=15$ donc $\\mathrm{b}=1$ : ceci fournit la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Trouver tous les entiers $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\in \\mathbb{N}$ tels que $1517^{\\mathrm{a}}+15^{\\mathrm{b}}=1532^{\\mathrm{c}}$.", "solution": "$(1,1,1)$.\nOn suppose maintenant $\\mathrm{c} \\geqslant 2$. En particulier $16=4^{2}$ divise $1532^{c}$ : ceci invite à étudier l'équation modulo des puissances de 2 plus petites que 16 pour éliminer la dépendance en c . On obtient alors $1+(-1)^{\\mathrm{b}} \\equiv 0(\\bmod 4)$ donc $b$ est impair (en particulier, $\\left.\\mathrm{b} \\geqslant 1\\right)$.\nEn réduisant modulo $8: 15^{b} \\equiv-1(\\bmod 8)\\left(b\\right.$ est impair). On a alors $1517^{a}-1 \\equiv 5^{a}-1 \\equiv 0(\\bmod 8)$, donc a est pair.\nEn réduisant modulo 5 (comme 5 divise 15 , cela supprime la dépendance en $b)$, on a $2^{\\mathrm{a}} \\equiv 2^{\\mathrm{c}}(\\bmod 5)$, donc $a \\equiv c(\\bmod 4)$ (l'ordre de 2 modulo 5 , est 4$)$. Puisqu'on a montré que a était pair, c est pair. Notons $a=2 e$ et $c=2 d$, alors $d$ et $e$ ont la même parité $(\\operatorname{car} 2 e \\equiv 2 \\mathrm{~d}(\\bmod 4)$ donc $e \\equiv d(\\bmod 2)$, et en réinjectant dans l'équation de départ, on obtient $15^{\\mathrm{b}}=\\left(1532^{\\mathrm{d}}-1517^{\\mathrm{e}}\\right)\\left(1532^{\\mathrm{d}}+1517^{\\mathrm{e}}\\right)$.\nRemarquons alors que\n\n$$\n\\left(1532^{\\mathrm{d}}+1517^{e}\\right)-\\left(1532^{\\mathrm{d}}-1517^{e}\\right)=2 \\times 1517^{e}=2 \\times 37^{e} \\times 41^{e}\n$$\n\nOr ni 37 ni 41 ne divisent 1532 donc $1532^{\\mathrm{d}}-1517^{e}$, et $1532^{\\mathrm{d}}-1517^{e}$ est impair. Par conséquent, $1532^{\\mathrm{d}}+1517^{e}$ et $1532^{\\mathrm{d}}-1517^{e}$ sont premiers entre eux, donc l'un d'eux est $5^{\\mathrm{b}}$ et l'autre est $3^{\\mathrm{b}}$. Puisque $1532^{\\mathrm{d}}+1517^{e}>1532^{\\mathrm{d}}-1517^{e}$, il s'ensuit que $1532^{\\mathrm{d}}+1517^{e}=5^{\\mathrm{b}}$ et $1532^{\\mathrm{d}}-1517^{e}=3^{\\mathrm{b}}$. Alors $3^{\\mathrm{b}}+5^{\\mathrm{b}}=2 \\cdot 1532^{\\mathrm{d}}$. Si $\\mathrm{d} \\geqslant 2$, le membre de droite est divisible par 16 , mais on vérifie modulo 16 que le premier membre n'est jamais divisible par $16\\left(3^{4} \\equiv 5^{4} \\equiv 1(\\bmod 16)\\right.$ donc il suffit de tester $3^{0}+5^{0} \\equiv 2(\\bmod 16), 3^{1}+5^{1} \\equiv 8(\\bmod 16), 3^{2}+5^{2} \\equiv 2(\\bmod 16)$ et $\\left.3^{3}+5^{3} \\equiv 5(\\bmod 16)\\right)$, ce qui implique que $\\mathrm{d}=1(\\operatorname{car} 2 \\mathrm{~d}=\\mathrm{c} \\geqslant 2)$ et donc e impair $(\\mathrm{d} \\equiv e(\\bmod 2))$. Comme $1532^{\\mathrm{d}}>1517^{e}, \\mathrm{il}$ s'ensuit que $e=1$, mais $1532^{\\mathrm{d}}-1517^{\\mathrm{d}}=15$ n'est pas une puissance de 3 , d'où une contradiction.\nFinalement la seule", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Trouver tous les entiers $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\in \\mathbb{N}$ tels que $1517^{\\mathrm{a}}+15^{\\mathrm{b}}=1532^{\\mathrm{c}}$.", "solution": "est $(a, b, c)=(1,1,1)$.\nCommentaire des correcteurs : Problème peu abordé mais bien compris par ceux ayant rendu une copie. Il s'agissait de trouver des propriétés sur $\\mathrm{a}, \\mathrm{b}$ et c en réduisant modulo des petits nombres jusqu'à arriver à une absurdité et de nombreux chemins ont été suivis. Attention cependant, il faut généralement traiter des petits cas à part. Par exemple ici, $15^{0}=1 \\not \\equiv 0[3]$ !", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Quentin et Timothé jouent à un jeu. D'abord, Quentin choisit un nombre premier $\\mathrm{p}>2$, puis Timothé choisit un entier strictement positif $n_{0}$. Quentin choisit alors un entier $n_{1}>n_{0}$ et calcule $s_{1}=n_{0}^{n_{1}}+n_{1}^{n_{0}}$; puis Timothé choisit un entier $n_{2}>n_{1}$ et calcule $s_{2}=n_{1}^{n_{2}}+n_{2}^{n_{1}}$. Les joueurs continuent de jouer chacun à leur tour, en choisissant au tour $k$ un entier $n_{k}>n_{k-1}$ et en calculant $s_{k}=n_{k}^{n_{k-1}}+n_{k-1}^{n_{k}}$. Le premier joueur à choisir un entier $n_{k}$ tel que $p$ divise $s_{k}\\left(s_{1}+2 s_{2}+3 s_{3}+\\ldots+k s_{k}\\right)$ gagne le jeu. Déterminer lequel de Quentin et Timothé possède une stratégie gagnante.", "solution": "de l'exercice 9 Nous allons montré que Timothé a une stratégie gagnante. Notons que Quentin va choisir les $n_{2 k+1}$ et Timothé va choisir les $n_{2 k}$. On fait d'abord quelques remarques.\n\n- Remarque 1 : Remarquons d'abord que si l'un des joueurs choisit $n_{k} \\equiv 0(\\bmod p)$ et ne gagne pas à cette étape, alors le joueur suivant gagne en choisissant $\\mathfrak{n}_{k+1} \\equiv 0(\\bmod \\mathfrak{p})$, car alors $s_{k+1} \\equiv 0(\\bmod \\mathfrak{p})$, et en particulier $p$ divise $s_{k+1}\\left(s_{1}+2 s_{2}+\\ldots+k s_{k}+(k+1) s_{k+1}\\right)$.\n- Remarque 2: Pour $a \\not \\equiv 0(\\bmod p), a^{p-1} \\equiv 1(\\bmod p)(F e r m a t)$. Alors si $a, b \\geqslant 1$ sont deux entiers tels que $a$ soit divisible par $p-1$ et congru à 1 modulo $p$ et $b$ n'est pas divisible par $p$, alors $\\mathrm{a}^{\\mathrm{b}}+\\mathrm{b}^{\\mathrm{a}} \\equiv 1^{\\mathrm{b}}+1 \\equiv 2(\\bmod \\mathrm{p})$. On va donc chercher une stratégie de ce côté-là.\n- Stratégie : On va montrer que la stratégie suivante fonctionne : pour $k \\geqslant 0$, Timothé va distinguer deux cas.\n- Si $k=0$ ou $n_{2 k-1}$ n'est pas divisible par $p$, alors Timothé choisit $n_{2 k}>n_{2 k-1}$ (resp. $n_{0}>0$ ) de telle sorte que $n_{2 k} \\equiv 0(\\bmod p-1)$ et $n_{2 k} \\equiv 1(\\bmod p)(p, p-1$ sont premiers entre eux donc par le théorème des restes chinois, il existe un unique reste modulo $p(p-1)$ qui convient, en particulier il existe bien de tels nombres aussi grands que l'on veut.)\n- Si $n_{2 k-1}$ est divisible par $p$, alors Timothé choisit $n_{2 k}>n_{2 k-1}$ divisible par $p$.\n\nPar la première remarque, dans le second cas si Quentin n'avait pas gagné, alors Timothé gagne à cet instant. Dans le premier cas, si $n_{2 k-1}$ n'est pas divisible par $p, s_{2 k} \\equiv 2(\\bmod p)$ (d'après la deuxième remarque). Donc si Timothé ne gagne pas à un instant donné, alors il a obtenu $s_{2 k} \\equiv 2(\\bmod p)$.\n\n- On s'intéresse alors aux valeurs prises par $s_{2 k+1}$. On distingue deux cas.\n- D'abord si à chaque étape, Quentin choisit $\\mathfrak{n}_{2 \\mathrm{k}+1}$ non divisible par p . Alors d'après la deuxième remarque, il obtient $s_{2 k+1} \\equiv 2(\\bmod p)$. Autrement dit, $s_{k} \\equiv 2(\\bmod p)$ pour tout $k$, et donc $1+2 s_{2}+\\ldots+k s_{k} \\equiv k(k+1)(\\bmod p)$ et donc le premier $k$ tel que cette quantité est divisible par $p$ est $k=p-1$ (lemme d'Euclide), or $p-1$ est pair ( $p>2$ ), donc c'est Timothé qui vient de choisir, et c'est donc celui-ci qui gagne.\n- Maintenant, si à un moment Quentin choisit $n_{2 k+1}$ divisible par $p$, (on considère que c'est la première fois que Quentin choisit un tel nombre), en particulier $2 k+1n$ (comme $m!n!=n!m!$, quitte à remplacer $(m, n)$ par $(n, m)$, ça ne pose pas de problème $)$. Alors $m!n!=m \\times(m-1) \\times \\ldots \\times(n+1) \\times n!\\times n!=m \\times \\ldots \\times(n+1) \\times(n!)^{2}$. Alors $m!n$ ! sera un carré parfait si et seulement si $m \\times \\ldots \\times(n+1)$ l'est. Le moyen le plus simple de le faire, c'est de choisir $m=n+1=k^{2}$ pour un certain entier $k(k \\geqslant 2$ car on veut $m, n \\geqslant 1)$. En effet on a bien $\\left(k^{2}\\right)!\\left(k^{2}-1\\right)!=k^{2}\\left(\\left(k^{2}-1\\right)!\\right)^{2}=\\left[k\\left(k^{2}-1\\right)!\\right]^{2}$.\nFinalement, pour tout $k \\geqslant 2$ entier, $(m, n)=\\left(k^{2}, k^{2}-1\\right)$ convient, ce qui nous fournit bien une infinité de couples", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 10.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Montrer qu'il existe une infinité de couples ( $\\mathrm{m}, \\mathrm{n}$ ) d'entiers distincts tels que $\\mathrm{m}!n!$ soit un carré parfait.", "solution": "s.\n\nCommentaire des correcteurs: L'ensemble des élèves ayant abordé l'exercice l'ont parfaitement réussi, même si certains détaillaient parfois plus que nécessaire.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 10.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.", "solution": "de l'exercice 11 Comme $21=3 \\times 7$ et que 3 et 7 sont premiers entre eux, 21 divise $2^{2^{n}}+2^{\\mathrm{n}}+1$ si et seulement si 3 et 7 divisent $2^{2^{n}}+2^{n}+1$.\nÉliminons de suite le cas $n=0$, qui donne $2^{2^{0}}+2^{0}+1=4$ qui n'est pas divisible par 21. On peut donc supposer $n>0$, en particulier $2^{n}$ est pair. Alors modulo $3: 2^{2^{n}}+2^{n}+1 \\equiv(-1)^{2^{n}}+(-1)^{n}+1 \\equiv$ $(-1)^{n}+2(\\bmod 3)$. En particulier $2^{2^{n}}+2^{n}+1$ est divisible par 3 si est seulement si $n$ est pair. On suppose donc désormais que cette condition est vérifiée.\nReste à traiter le cas de la divisibilité par 7 . Modulo 7 , les puissances de 2 sont $2^{0} \\equiv 1,2^{1} \\equiv 2,2^{2} \\equiv$ $4,2^{3} \\equiv 1$ : il s'agit donc d'étudier l'exposant modulo 3 . Comme n est pair (par le cas précédent), on sait déjà que $2^{n} \\equiv 1(\\bmod 3)$ donc $2^{2^{n}} \\equiv 2(\\bmod 7)$. On veut donc $2^{n} \\equiv-1-2 \\equiv 4(\\bmod 3)$, et donc $n \\equiv 2(\\bmod 3)\\left(\\right.$ et réciproquement si $n \\equiv 2(\\bmod 3)$, comme $n$ est pair alors 7 divise $\\left.2^{2^{n}}+2^{n}+1\\right)$.\nOn doit avoir $\\mathfrak{n} \\equiv 0(\\bmod 2), \\mathfrak{n} \\equiv 2(\\bmod 3):$ comme 2 et 3 sont premiers entre eux, le théorème des restes chinois donne qu'il existe une unique", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.", "solution": "modulo $2 \\times 3=6$, et on remarque que c'est $\\boldsymbol{n} \\equiv 2$ $(\\bmod 6)$.\nEn conclusion, les entiers naturels $n$ qui conviennent sont exactement ceux qui vérifient $\\mathfrak{n} \\equiv 2(\\bmod 6)$.\nCommentaire des correcteurs: Les élèves ayant abordé ce problème l'ont globalement bien compris et ont présenté des", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.", "solution": "s en général abouties. Certains ont fait une étude directement modulo 21, d'autres ont décomposé en une étude modulo 3 et modulo 7. Ceux ayant choisi cette alternative ont pour la plupart oublié de préciser que 3 et 7 sont premiers entre eux, c'est pourtant nécessaire pour que l'étude modulo 21 soit équivalent aux études modulo 3 et modulo 7 . Certains ont aussi mal lu l'énoncé et considéré $2^{2 n}+2^{n}+1$ au lieu de $2^{2^{n}}+2^{n}+1$. On rappelle que $2^{2^{n}}=2^{\\left(2^{n}\\right)}$, autrement dit c'est $2^{k}$ avec $k=2^{n}$, à différencier de $\\left(2^{2}\\right)^{n}$.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 11.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Soient $k, m, n>0$ des entiers tels que $m^{2}+n=k^{2}+k$. Montrer que $m \\leqslant n$.", "solution": "de l'exercice 12 Il y a des carrés : on aimerait faire apparaître des expressions factorisées, et plus particulièrement des carrés parfaits. Remarquons alors que $(2 k+1)^{2}=4 k^{2}+4 k+1=4 m^{2}+4 \\mathfrak{n}+1$. On a alors $4 m^{2}+n+1>4 m^{2}=(2 m)^{2}$. Alors $(2 k+1)^{2}>(2 m)^{2}$ donc $(2 k+1)^{2} \\geqslant(2 m+1)^{2}$ (il n'y a pas de carré entre deux carrés consécutifs). D'où, en redéveloppant: $4 \\mathrm{~m}^{2}+4 \\mathrm{n}+1 \\geqslant 4 \\mathrm{~m}^{2}+4 \\mathrm{~m}+1$. On obtient bien $\\mathrm{m} \\leqslant \\mathrm{n}$, comme voulu.\n\nCommentaire des correcteurs : Dans l'ensemble ce problème a été très bien réussi, à l'exception de de quelques rares exceptions relevant certainement de l'étourderie. Beaucoup ont raisonné par l'absurde en supposant $m>n$, et la plupart des autres ont fait une disjonction de cas selon si $m>k, m=k$ ou $m0$ des entiers tels que $m^{2}+n=k^{2}+k$. Montrer que $m \\leqslant n$.", "solution": "du", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 12.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Soient $k, m, n>0$ des entiers tels que $m^{2}+n=k^{2}+k$. Montrer que $m \\leqslant n$.", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 12.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "de l'exercice 13 En réarrangeant les termes et en factorisant, cela revient à résoudre $p^{3}\\left(p^{2}+\\right.$ $1)=(q-2)(q+1)$. En particulier $p^{3} \\mid(q-2)(q+1)$. Or $(q+1)-(q-2)=3$ donc $\\operatorname{pgcd}(q-2,3)$ vaut 1 ou 3. Cela suggère d'étudier d'abord le cas $p=3$ : on obtient $(q-2)(q+1)=270$, et en résolvant $\\mathrm{q}^{2}-\\mathrm{q}-2=270$ on trouve $\\mathrm{q}=17$ (qui convient) et $\\mathrm{q}=-16$ (qui ne convient pas). Donc lorsque $p=3$, il y a une unique", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 13.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "$(p, q)=(3,17)$.\nOn peut donc supposer $p \\neq 3$. En particulier, il ne divise pas $\\operatorname{pgcd}(q-1, q+2)$, donc au moins un des nombres $q+1$ et $q-2$ est premier avec $p^{3}$. Or $p^{3} \\mid(q+1)(q-2):$ donc $q+1$ ou $q-2$ est divisible par $p^{3}$ (Gauss). Or, $p^{3}$ ne peut pas diviser $q-2$ parce que sinon, on aurait $(q-2)(q+1) \\geqslant p^{3} p^{3}>p^{3}\\left(p^{2}+1\\right)$, absurde. Ainsi $p^{3} \\mid q+1$, et donc $q-2 \\mid p^{2}+1$.\nMais $\\mathrm{p}^{3} \\leqslant \\mathrm{q}+1=(\\mathrm{q}-2)+3 \\leqslant \\mathrm{p}^{2}+1+3=\\mathrm{p}^{2}+4$, et donc $\\mathrm{p}^{2}(\\mathrm{p}-1) \\leqslant 4$. Or $\\mathrm{p}^{2}(\\mathrm{p}-1)$ est strictement croissante en $p$, et en $p=2$ on a égalité, donc le seul cas possible est $p=2$ (autrement dit, pour $p>2$, on a $p^{2}(p-1)>4$ ).\nLorsque $\\mathrm{p}=2$, l'équation devient $\\mathrm{q}^{2}-\\mathrm{q}-2=40$, en résolvant on trouve $\\mathrm{q}=7$ (qui convient) et $q=-6$ (qui ne convient pas).\nFinalement, il y a deux", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 13.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "s qui sont $(\\mathbf{p}, \\mathbf{q})=(2,7)$ et $(\\mathbf{p}, \\mathbf{q})=(3,17)$.\nCommentaire des correcteurs: C'est bien réussi pour la plupart des élèves, qui ont presque tous trouvé la factorisation en $(q+1)(q-2)$ ou celle en $(x-3)(x+3)$ une fois le discriminant en $q$ considéré. En général le raisonnement a été bien mené. Attention à certaines utilisations frauduleuses du lemme de Gauss, et à vérifier rigoureusement tous les cas lors de la disjonction de cas. On peut rapidement oublier une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 13.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "13", "problem_type": null, "problem": "Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.", "solution": "!", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 13.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Anna et Elie jouent à un jeu. On leur donne à tous les deux le même ensemble $A$ composé d'un nombre fini d'entiers strictement positifs et distincts. Anna choisit un entier $a \\in A$ secrètement. Si Elie choisit un entier b (pas forcément dans $\\mathcal{A}$ ) et le donne à Anna, Anna lui donne le nombre de diviseurs strictement positifs de ab . Montrer que Elie peut choisir b de sorte à retrouver à coup sur l'entier choisi par Anna.", "solution": "de l'exercice 14 Notons P l'ensemble fini des nombres premiers divisant au moins un élément de $A$ et $n \\geqslant 1$ le plus grand entier tel qu'il existe $a \\in A$ et $p \\in P$ tels que $p^{n} \\mid a$. On peut remplacer A par l'ensemble des entiers $m$ dont les facteurs premiers sont tous dans $P$ et tels que pour tout $p \\in P$, $v_{p}(m) \\leqslant n$. Elie propose un entier $b$ de la forme $\\prod_{p \\in P} p^{b_{p}}$. Si Anna a choisi l'entier $a$, alors elle donne à Elie l'entier $\\prod_{p \\in P}\\left(b_{p}+v_{p}(a)+1\\right)$. Il suffit donc pour Elie de choisir les $b_{p}$ de sorte que tous les $\\prod_{p \\in P}\\left(b_{p}+a_{p}\\right)$ soient deux à deux distincts, pour tous les choix possibles de $a_{p}$ entre 1 et $n+1$ pour chaque $p \\in P$.\n\nOn propose deux", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 14.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "14", "problem_type": null, "problem": "Anna et Elie jouent à un jeu. On leur donne à tous les deux le même ensemble $A$ composé d'un nombre fini d'entiers strictement positifs et distincts. Anna choisit un entier $a \\in A$ secrètement. Si Elie choisit un entier b (pas forcément dans $\\mathcal{A}$ ) et le donne à Anna, Anna lui donne le nombre de diviseurs strictement positifs de ab . Montrer que Elie peut choisir b de sorte à retrouver à coup sur l'entier choisi par Anna.", "solution": "s.\n\n## Première méthode :\n\nL'idée de cette construction est de forcer les factorisations en produits de facteurs premiers des $\\prod_{p}\\left(b_{p}+a_{p}\\right)$ à être différentes pour tous les choix possibles des $a_{p}$. On veut faire en sorte que chaque $b_{p}+i$ pour $1 \\leqslant i \\leqslant n+1$ possède un diviseur premier «distinctif», qui n'apparaît que dans la décomposition en produit de facteurs premiers de $b_{p}+i$, jamais dans celle d'un autre $b_{q}+j$.\nFormellement, on choisit, pour chaque $p \\in P$ et chaque $1 \\leqslant i \\leqslant n+1$, des nombres premiers deux à deux distincts $Q_{p, i}>n+1$. On construit les $b_{p}$ grâce au théorème chinois : pour chaque $q \\in P$ distinct de $p$ et pour chaque $1 \\leqslant i \\leqslant n+1, Q_{q, i} \\mid b_{p}$, et pour chaque $1 \\leqslant i \\leqslant n+1, b_{p} \\equiv-\\mathfrak{i}\\left[Q_{p, i}\\right]$.\nAvec cette construction, si $q, p \\in P$ et $1 \\leqslant i, j \\leqslant n+1$, alors $Q_{q, j} j b_{p}+i$ si et seulement si $i=j$ et $\\mathrm{p}=\\mathrm{q}$.\nEn particulier, étant donnés des $1 \\leqslant a_{p} \\leqslant n+1$ pour chaque $p \\in P$, si $q \\in P, \\Pi=\\prod_{p \\in P}\\left(b_{p}+a_{p}\\right)$ est divisible par $Q_{q, j}$ si et seulement si $j=a_{q}$ : ainsi $\\Pi$ détermine la famille $\\left(a_{p}\\right)$.\n\n## Deuxième méthode :\n\nLa première construction était très arithmétique et utilisait des nombres premiers. Celle qu'on présente maintenant vient plus d'une idée de \"taille\". L'idée est que si l'on prend de gigantesques $b_{p}$, le produit $\\prod_{p}\\left(b_{p}+a_{p}\\right)$ ressemblera à l'écriture d'un certain nombre en une certaine base, dont les chiffres donneront les $a_{i}$.\nPassons à la construction proprement dite. Le problème tel que nous l'avons reformulé n'utilise plus le fait que $P$ soit constitué de nombres premiers : on renumérote ses éléments en $1, \\ldots, r$. Montrons que pour $N>(n+1)^{r}$, $b_{i}=N^{2^{i}}$ convient. En effet, dans ce cas, on voit que le développement de $\\Pi=\\prod_{i=1}^{r}\\left(N^{2^{i}}+a_{i}\\right)$ écrit un nombre en base $N$ dont le chiffre devant $N^{2+1}-2-2^{i}$ est exactement $a_{i}$ : ainsi $\\Pi$ détermine la famille des $\\left(a_{i}\\right)$.\n\nCommentaire des correcteurs : Le problème a été peu abordé, et peu réussi. Le principal problème est que certains montrent comment si on fixe a et $c$, choisir un $b$ pour que ba n'ait pas le même nombre de diviseur que bc de manière correcte, puis prétendent que la généralisation se fait bien en itérant. Il s'avère que cette partie est totalement fausse : s'il y a au départ trois nombres $a, c, e$, on peut choisi un b pour que $a b$ et $b c$ n'ait pas le même nombre de diviseur. Mais il est possible que $c b$ et $e b n$ 'ait pas le même nombre de diviseur, dans ce cas si on multiplie par $\\mathrm{b}^{\\prime}$ pour que $\\mathrm{cbb}^{\\prime}$ et $\\mathrm{ebb}^{\\prime}$ ait un nombre différent de diviseur, il est possible que $\\mathrm{abb}^{\\prime}$ et $\\mathrm{cbb}^{\\prime}$ ait le même nombre de diviseur. Cela montre que le procédé peut boucler et ne pas aboutir: le problème ne se résumait donc pas à ce cas particulier!", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 14.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Pour tout entier $n \\geqslant 1$, on pose $u_{n}=1!+2!+\\ldots+n!$. Montrer qu'il existe une infinité de nombres premiers divisant au moins l'un des termes de la suite ( $\\mathfrak{u}_{n}$ ).", "solution": "de l'exercice 15 Supposons l'inverse : alors il existe des nombres premiers $p_{1}<\\ldotsN, u_{n}=C \\prod_{i=1}^{s} q_{i}^{b_{i}(n)}$ et $b_{i}(n) \\geqslant$ $v_{q_{i}}((n+1)!)$.\nSoit maintenant $n>N+C+1$ tel que $n+1$ soit divisible par le produit des $q_{i}$. Alors $u_{n}=u_{n-1}+n$ ! et $v_{q_{i}}\\left(u_{n}\\right)=b_{i}(n) \\geqslant v_{q_{i}}((n+1)!)>v_{q_{i}}(n!)$, donc $v_{q_{i}}\\left(u_{n-1}\\right)=v_{q_{i}}(n!)$. D'autre part, si $p \\mid C$, $v_{p}\\left(u_{n-1}\\right)=v_{p}(C) \\leqslant v_{p}(\\mathfrak{n}!)$, donc $u_{n-1} \\mid n!$.\nIl reste à montrer que pour tout $n$ assez grand, $u_{n}$ ne divise pas $(n+1)!$.\nEn effet, si $n \\geqslant 2, n u_{n}>n \\cdot n!+n \\cdot(n-1)!=(n+1) \\cdot n!=(n+1)!$. D'autre part, si $n \\geqslant 4$,\n\n$$\n\\begin{aligned}\n(n-1) \\mathfrak{u}_{n} & =(n-1) n!+(n-1)(n-1)!+(n-1)(n-2)!+(n-1) \\sum_{k=1}^{n-3} k! \\\\\n& =n \\cdot n!+(n-1)(n-3) \\cdot(n-3)!<(n+1) \\cdot n! \\\\\n& =(n+1)!\n\\end{aligned}\n$$\n\nCommentaire des correcteurs : Le problème a été peu abordé et la majorité des copies rendues l'a résolu correctement, parfois d'une manière différente de celle du", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 15.", "solution_match": "\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "15", "problem_type": null, "problem": "Pour tout entier $n \\geqslant 1$, on pose $u_{n}=1!+2!+\\ldots+n!$. Montrer qu'il existe une infinité de nombres premiers divisant au moins l'un des termes de la suite ( $\\mathfrak{u}_{n}$ ).", "solution": "L'idée était, pour chaque diviseur premier $p$ d'un terme de la suite, de contrôler $v_{p}\\left(u_{n}\\right)$ pour $n$ assez grand en utilisant le fait que $\\mathfrak{u}_{n}-\\mathfrak{u}_{n-1}=n$ ! (ce qui est aussi apparu dans des tentatives n'ayant pas abouti) et en choisissant judicieusement la valeur de $n$ (les copies ayant remarqué cela ont toutes résolu le problème).", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 15.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soient $n \\geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \\ldots, a_{N}$ des éléments de $U$ telle que $\\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\\mathrm{p}^{\\mathrm{n}}$.", "solution": "de l'exercice 16\n\nOn commence par traiter le cas $p=3$, dont la", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 16.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soient $n \\geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \\ldots, a_{N}$ des éléments de $U$ telle que $\\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\\mathrm{p}^{\\mathrm{n}}$.", "solution": "est différente. Soit $\\mathrm{g} \\in \\mathrm{U}$ un générateur modulo $p^{n}$, on pose $a_{i}=g^{i-1}\\left(\\bmod p^{n}\\right)$. Comme $g^{2}-1$ est divisible par 3 , la somme considérée $S$ vérifie $\\left(g^{2}-1\\right) S \\equiv \\sum_{i=1}^{N}\\left(g^{2 i+1}-g^{2 i-1}\\right) \\equiv g\\left(g^{2 N}-1\\right)\\left[p^{n+1}\\right]$. Donc pour que $v_{p}(S)=n-1$, il faut et suffit que $v_{p}\\left(g^{2 N}-1\\right)=n\\left(g\\right.$ est premier avec $p$ ). Puisque $g^{N} \\equiv 1\\left[p^{n}\\right]$ (par Euler-Fermat), il suffit de montrer que $v_{p}\\left(g^{N}-1\\right)=n$. Mais par LTE, $v_{p}\\left(g^{N}-1\\right)=v_{p}\\left(g^{N / p}-1\\right)+13$ : Soient $b_{0}, \\ldots, b_{m-1} \\in U$ des entiers représentant exactement une fois chaque classe de congruence modulo $p^{n-1}$, ainsi $m=N / p=p^{n-2}(p-1)$ (et on pose $b_{m}=b_{0}$ ). On considère la permutation\n\n$$\n\\begin{aligned}\n& \\mathrm{b}_{0}, \\mathrm{~b}_{0}+\\mathrm{p}^{\\mathrm{n}-1}, \\mathrm{~b}_{0}+2 p^{n-1}, \\ldots, \\mathrm{~b}_{0}+(p-1) p^{n-1} \\\\\n& \\mathrm{~b}_{1}, \\mathrm{~b}_{1}+\\mathrm{p}^{n-1}, \\ldots, \\mathrm{~b}_{1}+(p-1) p^{n-1} \\\\\n& \\mathrm{~b}_{2}, \\ldots, b_{m-1}, \\ldots, b_{m-1}+(p-1) p^{n-1}\n\\end{aligned}\n$$\n\n(les additions sont toujours à effectuer modulo $\\mathrm{p}^{\\mathrm{n}}$ ).\nAlors la somme correspondante $S$ est congrue modulo $p^{n}$ à\n\n$$\nS_{1}=\\sum_{i=0}^{m-1} b_{i} b_{i+1}+\\sum_{i=0}^{m-1}(p-1) p^{n-1} b_{i}+\\sum_{i=0}^{m-1} \\sum_{k=0}^{p-2} b_{i} p^{n-1}(2 k+1)+(p-1) \\sum_{i=0}^{m-1} b_{i}^{2}\n$$\n\n. Comme la somme des $b_{i}$ est divisible par $p$ et la somme des $b_{i}^{2}$ par $p^{n-1}, S \\equiv S_{2}\\left[p^{n}\\right]$, où $S_{2}=$ $\\sum_{i=0}^{\\mathfrak{m}-1} b_{i} b_{i+1}-\\sum_{i=0}^{m-1} b_{i}^{2}$.\nSoit alors $g \\in U$ une racine primitive modulo $p^{n}:$ prenons $b_{i}=g^{i}\\left(\\bmod p^{n}\\right)$. Alors $(g+1) S_{2} \\equiv$ $(g+1) \\sum_{i=0}^{m-1}\\left(g^{2 i+1}-g^{2 i}\\right) \\equiv\\left(g^{2 m}-1\\right)\\left[p^{n}\\right]$. D'après LTE, $v_{p}\\left(g^{2 m}-1\\right) \\geqslant 1+v_{p}\\left(\\frac{2 m}{p-1}\\right)=n-1$ (puisque $p-1|m, p| g^{p-1}-1$ par Fermat, et $N=p^{n-1}(p-1)$, mais comme $2 m3, g+1$ est premier à $p$, et donc $v_{p}\\left(S_{2}\\right)=n-1$, d'où $\\nu_{p}(S)=n-1$.\n$\\underline{\\text { Commentaire des correcteurs : Le problème a été très peu abordé, sans doute à cause de la forme quelque }}$ peu intimidante de son énoncé. Il est important, devant de tels problèmes, de ne pas se laisser impressionner et continuer à réfléchir normalement. Tous les élèves ayant rendu une copie ont trouvé une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 16.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soient $n \\geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \\ldots, a_{N}$ des éléments de $U$ telle que $\\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\\mathrm{p}^{\\mathrm{n}}$.", "solution": "correcte, en général plus simple que la construction proposée dans le", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 16.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soient $n \\geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \\ldots, a_{N}$ des éléments de $U$ telle que $\\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\\mathrm{p}^{\\mathrm{n}}$.", "solution": "En fait, l'idée la plus naturelle (prendre les nombres dans l'ordre croissant) fournissait une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 16.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "16", "problem_type": null, "problem": "Soient $n \\geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \\ldots, a_{N}$ des éléments de $U$ telle que $\\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\\mathrm{p}^{\\mathrm{n}}$.", "solution": ", et il est étonnant qu'aussi peu d'élèves l'aient remarqué ou même essayé.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 16.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $\\left(a_{n}\\right)_{n \\geqslant 1}$ une suite d'entiers strictement positifs telle que $a_{1}$ et $a_{2}$ soient premiers entre eux et, pour tout $n \\geqslant 1, a_{n+2}=a_{n} a_{n+1}+1$. Montrer que pour tout entier $m>1$, il existe $n>m$ tel que $a_{m}^{m} \\mid a_{n}^{n}$. Le résultat est-il encore vrai lorsque $m=1$ ?", "solution": "de l'exercice 17 D'abord, $a_{n}>0$ pour tout $n>0$.\n\nOn commence par une observation : soit $n>m$ très grand (disons, $n>(m+1)\\left(a_{m}+1\\right)$ ). Alors $a_{m}^{m} \\mid a_{n}^{n}$ si et seulement si pour chaque nombre premier $p\\left|a_{m}, p\\right| a_{n}$. Cette idée justifie le lemme qui va suivre :\n\nLemme : soit $\\left(u_{n}\\right)_{n \\geqslant 0}$ la suite modulo un nombre premier $p$ telle que $u_{0}=0, u_{1}=1$ et pour tout $n \\geqslant 0$, $u_{n+2}=u_{n} u_{n+1}+1$. Alors $u$ est périodique.\n\nPreuve : soit $v_{n}=\\left(u_{n}, u_{n+1}\\right)$; alors $u$ est périodique dès que $v$ est périodique. Comme $v_{n+1}$ dépend uniquement de $\\nu_{n}, v$ est périodique dès qu'il existe $N \\geqslant 1$ tel que $\\nu_{N}=v_{0}$. Si $N \\geqslant 1$ est tel que $u_{N}=0$, alors la relation de récurrence montre que $u_{N+1}=1=u_{1}$ et donc $v_{N}=v_{0}$. Par conséquent, pour montrer que $u$ est périodique, il suffit de montrer qu'il existe $N \\geqslant 1$ tel que $u_{N}=0$.\nSupposons donc que le seul entier n tel que $u_{n}=0$ soit $n=0$. Alors comme $v$ est à valeurs dans un ensemble fini, il existe un entier $\\mathrm{n} \\geqslant 0$ minimal tel qu'il existe un entier $m>n$ tel que $v_{n}=v_{m}$. En particulier, $u_{m}=u_{n}$ et $m \\neq 0$, donc $u_{m} \\neq 0$, et donc $u_{n} \\neq 0$ et donc $n>0$. Alors $m+1>n+1 \\geqslant 2$ et $u_{n+1}=u_{m+1}$, donc $u_{n-1} u_{n}+1=u_{m-1} u_{m}+1$, donc $u_{n}\\left(u_{n-1}-u_{m-1}\\right)=0$, d'où, comme $u_{n} \\neq 0$, $u_{n-1}=u_{m-1}$, de sorte que $v_{m-1}=v_{n-1}$, ce qui contredit la minimalité de $n$.\n\nRevenons à notre preuve. Lorsque $m>1$, pour chaque facteur premier $p$ de $a_{m}, a_{m+1}=a_{m-1} a_{m}+1 \\equiv$ $1[p],\\left(a_{m+n}(\\bmod p)\\right)_{n \\geqslant 0}$ satisfait les hypothèses du lemme, donc il existe $N_{p} \\geqslant 1$ tel que que pour tout $n \\geqslant 0, a_{m+n} \\equiv a_{m+n+N_{p}}[p]$.\nSoit $N$ le produit des $N_{p}$ (où $p$ parcourt les facteurs premiers de $a_{m}$ ) : alors, si $n \\geqslant 0$, tout diviseur premier $p$ de $a_{m}$ divise $a_{m+n N}$. En particulier, si $n \\geqslant m a_{m}, a_{m}^{m} \\mid a_{m+n N}^{m+n N}$ (parce que si $p \\mid a_{m}$, $\\left.v_{p}\\left(a_{m+n N}^{m+n N}\\right) \\geqslant m+n N \\geqslant m a_{m} \\geqslant v_{p}\\left(a_{m}^{m}\\right)\\right)$.\nLe résultat est faux pour $\\mathrm{m}=1$ : prenons $\\mathrm{a}_{1}=155, \\mathrm{a}_{2}$ congru à 4 modulo 5 et congru à 29 modulo 31 . On vérifie alors que $a_{n}$ est divisible par 5 si et seulement si $n=1$ et $n \\equiv 4[7]$, alors que $a_{n}$ est divisible par 31 si et seulement si $n=1$ ou $n \\equiv 5[7]$, donc si $n>1, a_{n}$ n'est jamais divisible par 5 et 31 , et donc 155 ne divise pas $a_{n}^{n}$.\n\nCommentaire des correcteurs : Le problème a été peu abordé et toutes les copies ont su traiter le cas $\\mathrm{m}>1$, essentiellement par la méthode du", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 17.", "solution_match": "## Solution "}}
+{"year": null, "tier": "T2", "problem_label": "17", "problem_type": null, "problem": "Soit $\\left(a_{n}\\right)_{n \\geqslant 1}$ une suite d'entiers strictement positifs telle que $a_{1}$ et $a_{2}$ soient premiers entre eux et, pour tout $n \\geqslant 1, a_{n+2}=a_{n} a_{n+1}+1$. Montrer que pour tout entier $m>1$, il existe $n>m$ tel que $a_{m}^{m} \\mid a_{n}^{n}$. Le résultat est-il encore vrai lorsque $m=1$ ?", "solution": "La plupart des élèves ont détecté que le cas $m=1$ ne fonctionnait pas et exhibé des contre-exemples, mais certains ont laissé complètement implicite l'endroit où était utilisée l'hypothèse $m>1$. Dans un problème, les hypothèses doivent être utilisées; si l'énoncé attire l'attention sur l'une d'entre elles, il faut d'autant plus soigneusement relever l'endroit où l'on s'en sert.", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 17.", "solution_match": " corrigé."}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "de l'exercice 18 Soit f une", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": "\n\nSolution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "Comme les valeurs de f sont premières entre elles dans leur ensemble, si f est constante, elle égale 1 , ce qui est exclu.\nAvec $a=1$, on voit que $f(1)^{\\mathfrak{n}} \\mid \\mathbf{f}(b+1)-f(b)$ pour tout $b \\geqslant 1$ et tout $n$ assez grand. Comme $f$ est non constante, il existe $b$ tel que $f(b+1) \\neq f(b)$. Il s'ensuit que $f(1)=1$.\nSoit $a \\geqslant 2$, il existe un $t \\geqslant 0$ tel que $f(1+(t+1) a) \\neq f(1+t a)$ (car, pour $t$ assez grand, $f(1+t a) \\neq$ $1=f(1))$ : soit $b=1+$ ta. Pour tout $n \\geqslant 1$ assez grand, $f(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}$.\nSoit $p$ un nombre premier divisant $f(a)$. Alors il existe un $l \\geqslant 1$ tel que $p \\mid f(a+b)^{a^{l}}-f(b)^{a^{l}}$. Pour $n>l$, par LTE, la valuation $p$-adique de $f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}$ est $v_{p}\\left(a^{n-1-l}\\right)+C$ pour une certaine constante $C$ qui ne dépend que de $f, a, b, l$ (mais pas de $n$ ).\nDonc pour $n>l$ assez grand, $v_{p}\\left(a^{n-1-l}\\right)+C \\geqslant v_{p}\\left(f(a)^{n}\\right)$, donc $(n-1-l) v_{p}(a)+C \\geqslant n v_{p}(f(a))$, d'où $v_{p}(f(a)) \\leqslant v_{p}(a)$.\nPar conséquent, pour tout $a \\geqslant 1, f(a) \\mid a$.\nEn particulier, si a est premier, $f(a)$ vaut 1 ou $a$, et est égal à a sauf pour un nombre fini de nombres premiers.\nSoit $a$ un nombre premier tel que $f(a)=a$ : pour tout $b \\geqslant 1$ et tout $n$ assez grand, $a^{n} \\mid f(a+b)^{a^{n-1}}-$ $f(b)^{a^{n-1}}$. En particulier, $f(a+b) \\equiv f(b)[a]$ : ainsi, la classe de congruence de $f(b)$ modulo a ne dépend que de $b$ modulo $a$.\nOn va montrer que $f$ est l'identité. Soit $u \\geqslant 2$, soit $P$ l'ensemble fini des nombres premiers $p$ tels que $p \\leqslant u$ ou $f(p)=1$. Supposons qu'il existe un nombre premier $q \\notin P$ et un entier $n$ tels que $q \\mid n-u$ et $\\mathrm{f}(\\mathrm{n})=\\mathrm{n}$.\nAlors $q \\mid f(n)-f(u)$, et donc $q \\mid n-f(u)$, d'où $q \\mid u-f(u)$. Comme $0 \\leqslant u-f(u) \\leqslant u\\Pi^{N}+u$ soit congru à 1 modulo $\\Pi^{N}$ et tel que $f(n)=n$. Alors, si $p \\in P, v_{p}(n-u)<$ $N$, et $n-u>\\Pi^{N}$, de sorte que $n-u$ possède un diviseur premier $q \\notin P$, et on a gagné.\nSoit n un produit de nombres premiers deux à deux distincts, tous hors de $P$. Alors, si $\\mathrm{p} \\mid \\mathrm{n}$ est un diviseur premier, $n \\equiv p[p]$ et $f(p)=p$, donc $p \\mid f(n)-f(p)$, d'où $p \\mid f(n)$. Comme $f(n) \\mid n$, on en déduit que $\\mathrm{f}(\\mathrm{n})=\\mathrm{n}$.\nComme il existe une infinité de nombres premiers, il existe une progression arithmétique C de raison $\\Pi^{N}$ et de premier terme premier à $\\Pi$ et contenant une infinité de nombres premiers. En prenant pour n le produit de $\\varphi\\left(\\Pi^{N}\\right)$ premiers $q \\in C$ tels que $q>\\Pi^{N}+u, n$ convient.\n\nDeuxième méthode (il y a des prérequis, mais ils sont élémentaires et relativement classiques) :\nOn reprend les notations et le raisonnement de ce qui précède : on cherche à construire un entier $\\mathrm{n}>$ $\\Pi^{N}+u$ congru à 1 modulo $\\Pi^{N}$ tel que $f(n)=n$.\n\nIl est connu (du moins, classique et relativement élémentaire) que si $\\Phi_{\\Pi^{N}}$ est le $\\Pi^{\\mathrm{N}}$-ième polynôme cyclotomique, il existe une infinité de nombres premiers n divisant une valeur de $\\Phi_{\\Pi^{\\mathrm{N}}}$, et ceux qui ne sont pas dans $P$ sont congrus à 1 modulo $\\Pi^{N}$ et vérifient $f(n)=n$. On peut en choisir un qui est strictement supérieur à $\\Pi^{\\mathrm{N}}+\\mathrm{u}$.\n\nTroisième méthode (utilise un théorème relativement classique, mais dont aucune démonstration accessible au niveau olympique n'est connue) :\n\nSoit $\\mathrm{q} \\notin \\mathrm{P}$ premier : alors $\\mathrm{f}(\\mathrm{q})=\\mathrm{q}$. D’après le théorème de Dirichlet, il existe un nombre premier $p>u+q$ congru à $u$ modulo $q$ tel que $f(p)=p$. Alors le couple $(q, p)$ convient.\nAinsi, l'identité est la seule", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "potentielle. Réciproquement, l'identité vérifie la première condition et si $a, b \\geqslant 1$ et $n \\geqslant 2$, alors par LTE, pour tout nombre premier $p \\mid a, v_{p}\\left((a+b)^{a^{n-1}}-b^{a^{n-1}}\\right) \\geqslant$ $v_{p}(a)+v_{p}\\left(a^{n-1}\\right)=v_{p}\\left(a^{n}\\right)$, donc $a^{n} \\mid(a+b)^{a^{n-1}}-b^{a^{n-1}}$, et donc l'identité est", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution "}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "Commentaire des correcteurs : L'exercice a été très peu abordé. Toutes les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution."}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "s fonctionnaient en deux temps : d'abord, utiliser LTE pour montrer que $f(a) \\mid a$ pour tout entier a, éventuellement assez grand. Ensuite, utiliser cette information (souvent en conjonction avec le cas où a est un nombre premier assez grand, puisqu'alors $f(a)=a$ ) de diverses manières pour conclure. Si quelques élèves ont été hâtifs dans la deuxième partie, très peu ont songé à vérifier, en considérant la valuation $p$-adique de nombres de la forme $f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}$, que ce nombre était bien non nul. Non, ce cas n'est pas un détail! Signalons enfin que comme dans tout type d'équation, il est important de vérifier les", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "s : si un raisonnement logique montre que seule l'identité peut être", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": ", il faut déterminer si oui ou non l'identité est bien", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution"}}
+{"year": null, "tier": "T2", "problem_label": "18", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{N}^{\\star} \\rightarrow \\mathbb{N}^{\\star}$ telles que :\n(i) Les entiers $f(1), f(2), \\ldots$ sont premiers entre dans leur ensemble.\n(ii) Il existe $N \\geqslant 1$ tel que pour tout $n \\geqslant N, f(n) \\neq 1$ et pour tous $a, b \\in \\mathbb{N}^{\\star}$,\n\n$$\nf(a)^{n} \\mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}\n$$", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-corrigé.jsonl", "problem_match": "\nExercice 18.", "solution_match": " solution."}}
diff --git a/French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl b/French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..4fa700f6fc97abee0d5bf860c0c529c04e09a78d
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl
@@ -0,0 +1,11 @@
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "ABC est un triangle dont tous les angles sont aigus. À l'extérieur de ce triangle on construit les trois points $X, Y$ et $Z$ vérifiant :\n\n- Le triangle $A X B$ est isocèle de base $A B$ et l'angle $\\widehat{A X B}$ vaut $120^{\\circ}$,\n- Le triangle BYC est isocèle de base BC et l'angle $\\widehat{B Y C}$ vaut $120^{\\circ}$,\n- Le triangle CZA est isocèle de base CA et l'angle $\\widehat{C Z A}$ vaut $60^{\\circ}$.\n\nMontrer que les droites $(X Y)$ et (BZ) sont perpendiculaires.", "solution": "Traçons le cercle de centre $X$ qui passe par $A$ et $B$ et celui de centre $Y$ qui passe par $B$ et $C$ et notons K leur autre point d'intersection :\n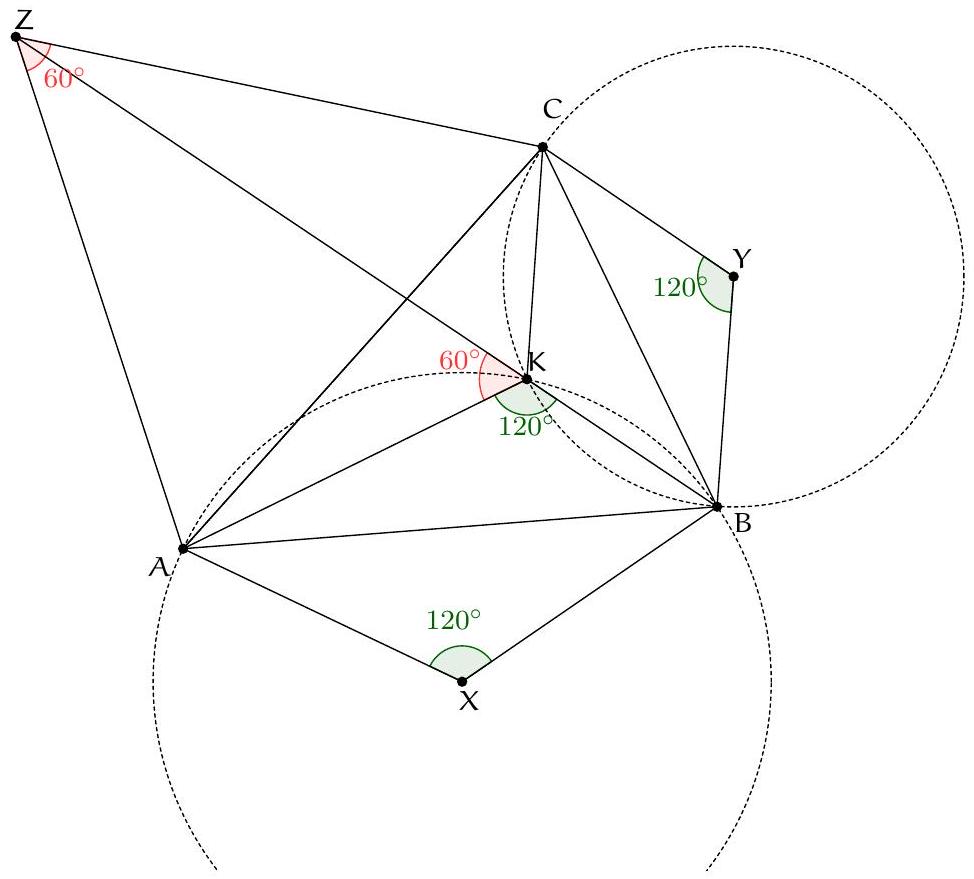\n\nL'angle $\\widehat{A K B}$ vaut la moitié de l'angle au centre, et l'angle au centre est le complémentaire de $120^{\\circ}$, donc $\\widehat{A K B}$ vaut $\\frac{240}{2}=120^{\\circ}$. De même, $\\widehat{\\mathrm{BKC}}=120^{\\circ}$ et par conséquent, l'angle restant $\\widehat{\\mathrm{CKA}}=120^{\\circ}$. Mais alors, comme $\\widehat{C K A}+\\widehat{A Z C}=120+60=180^{\\circ}$, donc les points $A, Z, C, K$ sont cocycliques. Comme $A Z=Z C$, les arcs que ces deux cordes délimitent sont égaux et les angles inscrits sont égaux. Ainsi, $\\widehat{A K Z}=\\widehat{Z K C}=60^{\\circ}$.\n\nMaintenant regardons les points $B, K$ et $Z: \\widehat{B K Z}=120+60=180^{\\circ}$, donc les trois points sont alignés, la droite ( BZ ) est la droite qui passe par les deux points d'intersection des cercles, elle est perpendiculaire au segment qui relie les deux centres, ie $[\\mathrm{XY}]$.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "$A B C D$ est un trapèze dans lequel les côtés $A D$ et $B C$ sont parallèles, $K$ est un point du côté $A B$ et $L$ un point du côté $C D$. Montrer que si les angles $\\widehat{B A L}$ et $\\widehat{C D K}$ sont égaux alors les angles $\\widehat{\\mathrm{BLA}}$ et $\\overline{\\mathrm{CKD}}$ le sont aussi.", "solution": "On suppose les angles $\\widehat{\\mathrm{BAL}}$ et $\\widehat{\\mathrm{CDK}}$ ont la même valeur. Nous allons montrer que les angles KBL et KCL sont égaux (ceci impliquera que les triangles KDC et BAL ont deux angles identiques, et donc que $\\widehat{\\mathrm{BLA}}=\\widehat{\\mathrm{KCL}}$ ).\n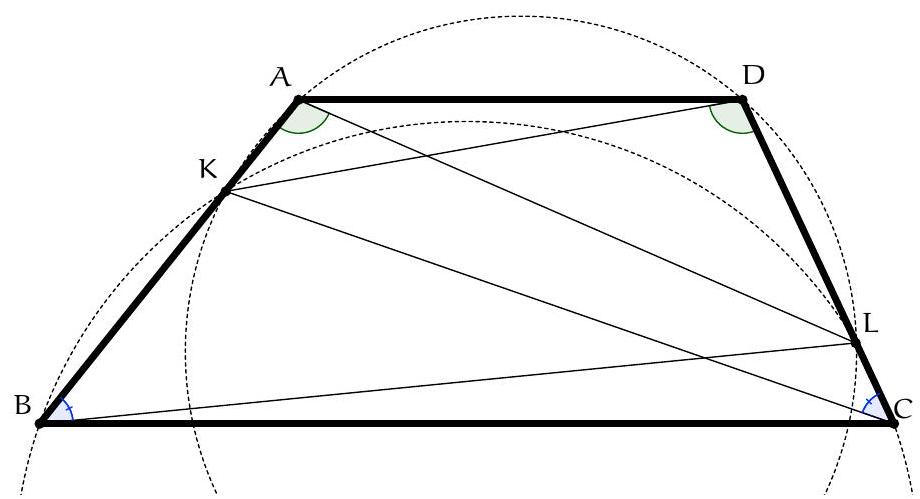\n\nJe vais d'abord montrer un point amusant sur les trapèzes : si on place des points $K$ et $L$ sur les côtés $A B$ et $C D$ tels que $A, D, K, L$ soient cocycliques, alors les points $B, C, K, L$ sont aussi cocycliques. Il suffit d'utiliser la propriété qu'un quadrilatère est inscrit dans un cercles ssi la somme des angles opposés vaut $180^{\\circ}$, et aussi que comme $A D$ et $B C$ sont parallèles, $\\widehat{A}+\\widehat{B}=\\widehat{C}+\\widehat{D}=180^{\\circ}$.\n\nL'hypothèse $\\widehat{\\mathrm{BAL}}=\\widehat{\\mathrm{CDK}}$ revient à dire que $\\mathrm{A}, \\mathrm{D}, \\mathrm{K}, \\mathrm{L}$ cocycliques par le théorème des angles inscrits, donc par le résultat précédent $\\mathrm{B}, \\mathrm{C}, \\mathrm{K}, \\mathrm{L}$ sont aussi cocycliques et les angles bleus sont égaux.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "ABC est un triangle dont tous les angles sont aigus. Soit respectivement H le pied de la hauteur de ce triangle issue de $C$ et K le milieu du côté $A C$. On suppose que $B K=C H$ et que les angles $\\widehat{\\mathrm{KBC}}$ et $\\widehat{\\mathrm{HCB}}$ sont égaux. Montrer que le triangle ABC est équilatéral.", "solution": "Voici la figure :\n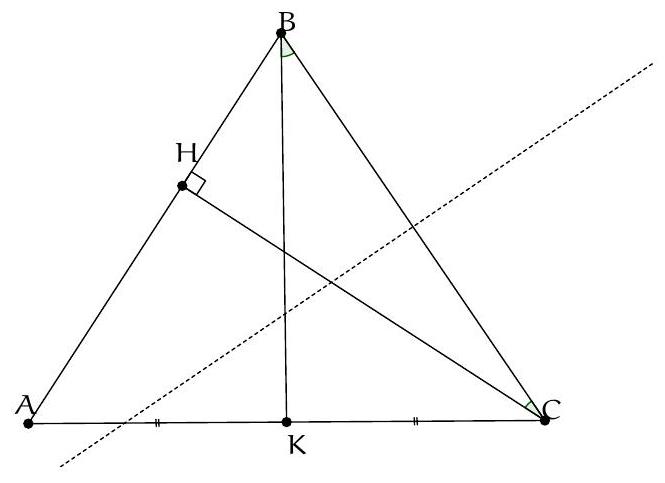\n\nMaintenant considérons la médiatrice de $[\\mathrm{BC}]$ (dessinée en pointillés sur la figure) et la symétrie par rapport à cet axe. Il est évident que par cette symétrie $B$ devient $C$ et vice-versa. Appelons $A^{\\prime}$ l'image de $A$ par la symétrie. Les hypothèses que tous les angles sont aigus, $\\mathrm{BK}=\\mathrm{CH}$ et $\\widehat{\\mathrm{KBC}}=\\widehat{\\mathrm{HCB}}$ impliquent que $K$ est l'image de $H$ par la symétrie. Mais comme $A$ est l'intersection de $B H$ et $C K$, $A^{\\prime}$ est l'intersection de l'image de $B H$ (c-à-d $C K$ ) et de l'image de $C K\\left(c-a ̀-d B H\\right.$ ), donc $A^{\\prime}=A$, $A$ est sur la médiatrice de $B C$ et le triangle est isocèle en $A$.\n\nMais nous n'avons pas fini, comme $\\mathrm{CH} \\mapsto \\mathrm{BK}$ et $\\mathrm{BA} \\mapsto \\mathrm{CA}$, l'angle droit est conservé, et BK est à la fois une hauteur et une médiane. Donc le triangle est aussi isocèle en $B$, il est donc équilatéral.\n\n## Exercices Communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\n\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "ABCD est un rectangle et $M$ un point intérieur à ce rectangle. Montrer que l'aire de ce rectangle est inférieure ou égale à la somme $A M \\times C M+B M \\times D M$ ( $A M \\times C M$ désigne le produit des longueurs des segments $A M$ et $C M$, de même pour $B M \\times D M$ )", "solution": "Nous allons travailler en analytique et tout passer aux coordonnées : $\\mathrm{A}(0,0), \\mathrm{B}(\\mathrm{a}, 0), \\mathrm{C}(\\mathrm{a}, \\mathrm{b})$, $\\mathrm{D}(0, \\mathrm{~b}), \\mathrm{M}(\\mathrm{x}, \\mathrm{y})$.\n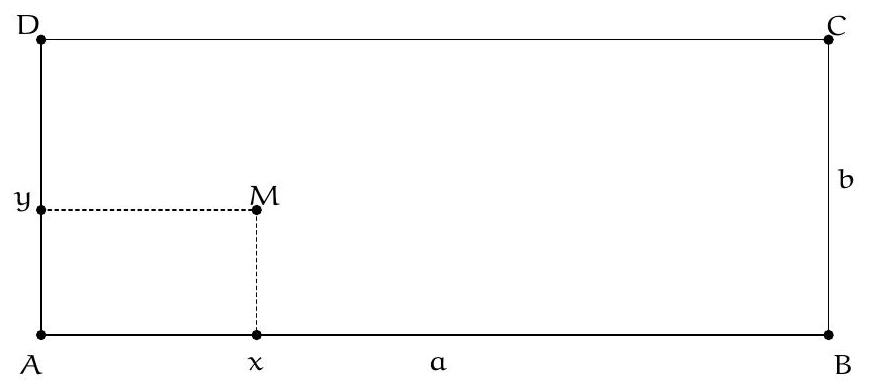\n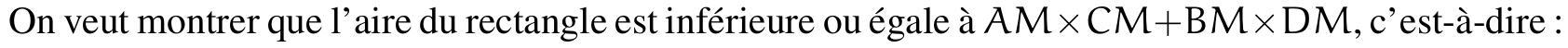\n\n$$\n\\sqrt{x^{2}+y^{2}} \\times \\sqrt{(a-x)^{2}+(b-y)^{2}}+\\sqrt{(a-x)^{2}+y^{2}} \\times \\sqrt{x^{2}+(b-y)^{2}} \\geqslant a b\n$$\n\nNous allons utiliser l'inégalité de Cauchy-Schwartz :\n\n$$\n\\begin{aligned}\n& \\sqrt{x^{2}+y^{2}} \\times \\sqrt{(b-y)^{2}+(a-x)^{2}} \\geqslant x(b-y)+y(a-x) \\\\\n& \\sqrt{(a-x)^{2}+y^{2}} \\times \\sqrt{(b-y)^{2}+x^{2}} \\geqslant(a-x)(b-y)+y x\n\\end{aligned}\n$$\n\nEt on finit en remarquant que $x(b-y)+y(a-x)+(a-x)(b-y)+y x=a b$.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\n\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit $A B C D$ un trapèze dans lequel les côtés $A B$ et $C D$ sont parallèles. On considère un point $P$ de la droite ( $A C$ ) tel que $C$ soit intérieur au segment $[A P]$ et on désigne respectivement par $X$ et $Y$ les milieux des côtés $A B$ et $C D$. La droite ( PX ) rencontre la droite (BC) en $N$ et la droite (PY) rencontre la droite (AD) en $M$. Montrer que la droite ( $M N$ ) est parallèle à la droite ( $A B$ ).", "solution": "Faisons une figure appropriée:\n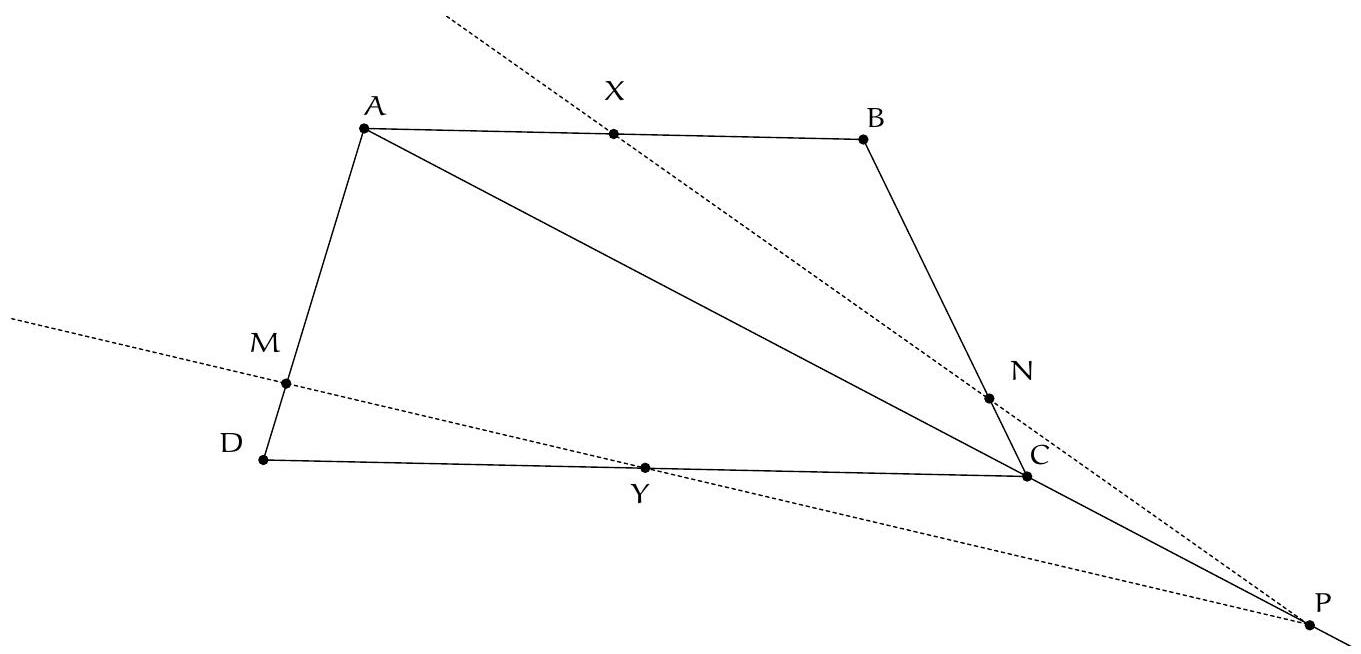\n\nTout d'abord considérez le cas où on prend $P$ \"à l'infini\", c'est au lieu de prendre $P X$ et $P Y$ on prend les droites parallèles à $A C$ passant par $X$ et $Y$. Dans ce cas, par Thalès les points $M$ et $N$ sont les milieux respectifs de $A D$ et $B C$, et par conséquent $(M N) \\|(A B)$.\n\nRevenons au cas général. Nous allons essayer de montrer que $\\frac{B N}{N C}=\\frac{A M}{M D}$, et ainsi nous aurons bien $(M N) \\|(A B)$ (je laisse en exercice la démo de ce résultat pour ceux qui ont des doutes). Comme nous avons beaucoup de points alignés et que nous voulons calculer des quotients de longueur, le théorème de Menelaus vient à l'esprit. Dans le triangle $A B C$, les points $X, N, P$ sont alignés, donc :\n\n$$\n\\frac{A X}{X B} \\cdot \\frac{B N}{N C} \\cdot \\frac{C P}{P A}=-1\n$$\n\nMais comme $X$ est le milieu de $A B, \\frac{A X}{X B}=1$, donc $\\frac{B N}{N C}=-\\frac{C P}{P A}$. Ensuite, en utilisant Menelaus dans le triangle $A D C$, on obtient $\\frac{A M}{M D}=-\\frac{C P}{P A}$, et les deux quotients sont égaux. Ensuite il n'est pas très dur de vérifier que l'on arrive bien au résultat attendu, $(M N) \\|(A B)$.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\n\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit ABC un triangle et O un point intérieur à ce triangle. D et E sont respectivement les pieds des perpendiculaires abaissées de $O$ sur les droites ( $B C$ ) et ( $A C$ ) et $F$ est le milieu du segment $A B$. Montrer que si $\\mathrm{DF}=\\mathrm{EF}$ alors les angles $\\widehat{\\mathrm{OBD}}$ et $\\widehat{\\mathrm{OAE}}$ sont égaux.", "solution": "Dans cet exercice il y a une hypothèse superflue, à savoir que le point $O$ est à l'intérieur du triangle $A B C$. Nous allons résoure l'exercice sans cette hypothèse.\n\nCommençons par tracer un angle droit $A E O$ et un segment $A B$ et plaçons $F$ au milieu du segment $A B$. Notre but maintenant est de trouver un point D tel que l'angle BDO soit droit et que l'on ait $\\mathrm{FD}=\\mathrm{FE}$.\n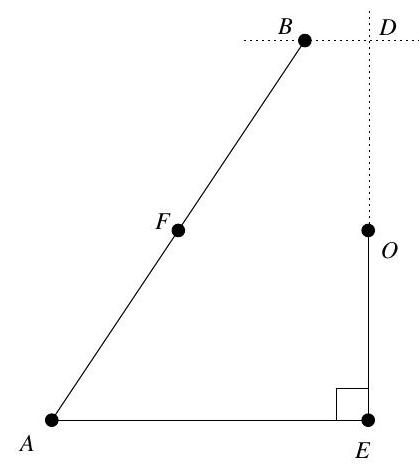\n\nComme la figure ci-dessus l'indique, il exite toujours une façon évidente de placer le point D : il suffit de tracer la droite parallèle à $A E$ passant par $B$ et de prendre le point d'intersection de cette droite avec la droite EO. L'angle BDO est alors droit par construction et on a bien $\\mathrm{FD}=\\mathrm{FE}$, car F est équidistant des deux droites parallèles. Une telle position du point $D$ ne peut pas apparaître dans l'exercice (et cela va nous servir par la suite) : en effet, l'exercice parle d'un triangle $A B C$, or ici les droites $A E$ et $B D$ ne se coupent pas et il n'y a donc pas de point $C$.\n\nRajoutons à notre figure le milieu $M$ du segment $A O$ et le milieu N du segment BO.\n\n\nOn a alors trois segments égaux représentés en gras sur la figure. En effet, $\\mathrm{ME}=\\mathrm{MO}$, car le triangle $A E O$ est rectangle en $E$; et $M O=F N$, car $F N O M$ est un parallélogramme, les lignes des mileux étant parallèles aux côtés du triangle $A O B$.\n\nRevenons maintenant à l'exercice.\n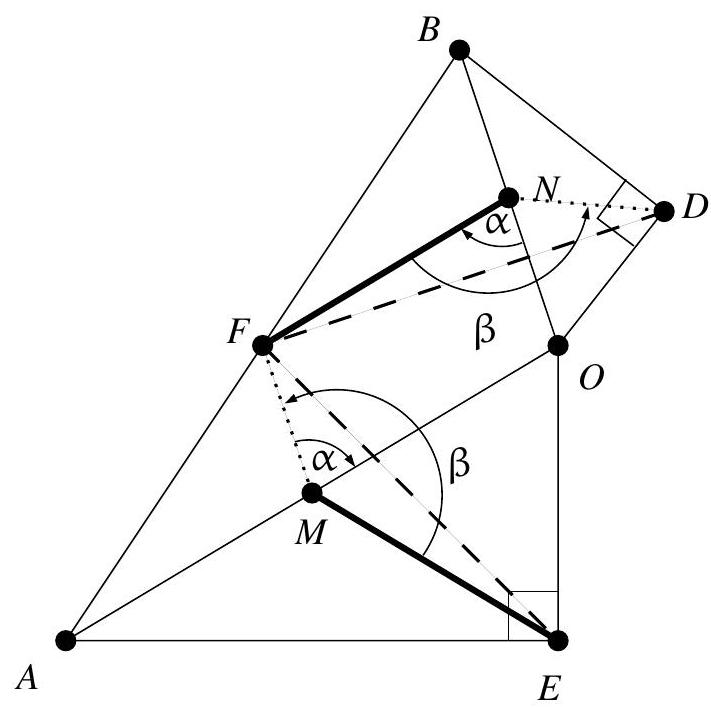\n\nNous venons de montrer que $\\mathrm{ME}=\\mathrm{FN}$ et on a de même $\\mathrm{ND}=\\mathrm{FM}$. Comme on a de plus $\\mathrm{FD}=\\mathrm{FE}$ par hypothèse, on conclut que les triangles NDF et MFE sont égaux. Il est important de distinguer deux cas : celui où ces triangles sont directement isométriques, comme sur la figure, et celui où ils sont indirectement isométrique (distinction qui n'a pas été faite correctement dans la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\n\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit ABC un triangle et O un point intérieur à ce triangle. D et E sont respectivement les pieds des perpendiculaires abaissées de $O$ sur les droites ( $B C$ ) et ( $A C$ ) et $F$ est le milieu du segment $A B$. Montrer que si $\\mathrm{DF}=\\mathrm{EF}$ alors les angles $\\widehat{\\mathrm{OBD}}$ et $\\widehat{\\mathrm{OAE}}$ sont égaux.", "solution": "initialement proposée).\n\nNous allons utiliser les angles orientés.\n\n1er cas : triangles directement isométriques. Soit\n\n$$\n\\alpha=(M F, M O)=(N O, N F), \\quad \\beta=(M E, M F)=(N F, N D)\n$$\n\nDans le triangle rectangle AEO on a\n\n$$\n(A E, A O)=\\frac{1}{2}(M E, M O) \\bmod 180^{\\circ}\n$$\n\n(L'égalité n'est vraie que modulo $180^{\\circ}$ à cause de la division par 2.) On trouve donc, modulo $180^{\\circ}$,\n\n$$\n(A E, A O)=\\frac{1}{2}(M E, M O)=\\frac{1}{2}[(M E, M F)+(M F, M O)]=\\frac{1}{2}(\\alpha+\\beta) .\n$$\n\nDe la même manière\n\n$$\n(B O, B D)=\\frac{1}{2}(N O, N D)=\\frac{1}{2}[(N O, N F)+(N F, N D)]=\\frac{1}{2}(\\alpha+\\beta) .\n$$\n\nOn a donc $(A E, A O)=(B O, B D)$ mod $180^{\\circ}$. Or les deux angles font partie de triangles rectangles et sont donc aigus, ce qui implique qu'ils sont géométriquement égaux.\n\n2ème cas : triangles indirectement isométriques. Les calculs sont exacement les mêmes que dans le cas précédent, sauf que cette fois-ci on a $(N F, N D)=-\\beta$. On trouve donc\n\n$$\n(A E, A O)=\\frac{1}{2}(\\alpha+\\beta), \\quad(B O, B D)=\\frac{1}{2}(\\alpha-\\beta)\n$$\n\nmodulo $180^{\\circ}$. Ainsi ces angles ne sont pas égaux entre eux. Avons-nous trouvé une erreur dans l'exercice ? Non : en fait nous allons prouver que dans ce cas les droites $A E$ et $B D$ sont parallèles et nous sommes donc dans la configuration interdite mentionnée au début de la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit ABC un triangle et O un point intérieur à ce triangle. D et E sont respectivement les pieds des perpendiculaires abaissées de $O$ sur les droites ( $B C$ ) et ( $A C$ ) et $F$ est le milieu du segment $A B$. Montrer que si $\\mathrm{DF}=\\mathrm{EF}$ alors les angles $\\widehat{\\mathrm{OBD}}$ et $\\widehat{\\mathrm{OAE}}$ sont égaux.", "solution": "Pour cela il suffit de prouver que $(A E, A B)+(B A, B D)=0 \\bmod 180^{\\circ}$. On a\n\n$$\n(A E, A B)+(B A, B D)=(A E, A O)+(A O, A B)+(B A, B O)+(B O, B D)\n$$\n\nNous savons déjà que, modulo $180^{\\circ}$,\n\n$$\n(A E, A O)+(B O, B D)=\\frac{1}{2}(\\alpha+\\beta)+\\frac{1}{2}(\\alpha-\\beta)=\\alpha\n$$\n\nDe plus, dans le triangle $A O B$, on a\n\n$$\n(A O, A B)+(B A, B O)=(O A, O B) \\bmod 180^{\\circ} .\n$$\n\nCe dernier angle vaut $180^{\\circ}-\\alpha=-\\alpha \\bmod 180^{\\circ}$. On trouve donc bien que $(A E, A B)+(B A, B D)=$ $\\alpha-\\alpha=0 \\bmod 180^{\\circ}$. Par conséquent $A E$ et $B D$ sont parallèles. Le cas de triangles indirectement isométrique ne peut donc pas apparaître dans un triangle $A B C$.\n\n## Exercices Olympiques", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Dans le triangle $A B C$ les bissectrices des angles en $A$ et $C$ rencontrent le cercle circonscrit au triangle $A B C$ respectivement en $A_{0}$ et $C_{0}$. La droite passant par I, centre du cercle inscrit dans le triangle $A B C$, et parallèle à la droite $(A C)$ rencontre la droite ( $A_{0} C_{0}$ ) en $P$.\n\nMontrer que la droite (PB) est tangente au cercle circonscrit au triangle $A B C$.\n$\\underline{\\text {", "solution": "Sur la figure on va rajouter } B_{0} \\text { le point d'intersection de la bissectrice de } \\widehat{A B C} \\text { avec le cercle : }}$\n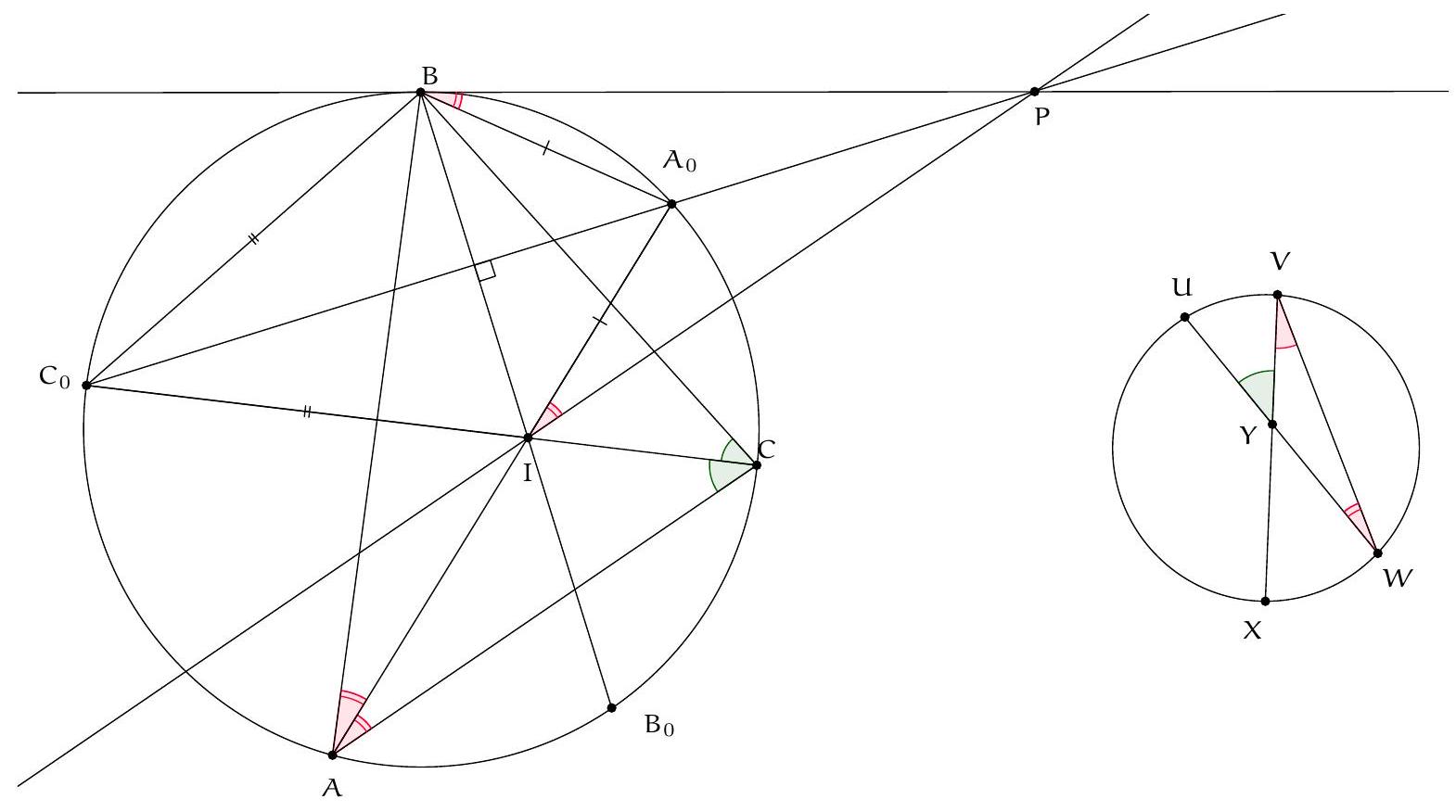\n\nAvant de commencer, je veux démontrer un petit résultat sur les arcs. Regardez la figure de droite (je vais noter $\\widehat{U V}$ l'arc délimité par U et V en radians):\n\n$$\n\\widehat{U Y V}=\\widehat{Y V W}+\\widehat{Y X W}=\\frac{1}{2} \\widehat{W X}+\\frac{1}{2} \\widehat{U V} .\n$$\n\nRevenons à nos moutons. Grâce à la formule précédente, on peut calculer :\n\n$$\n\\widehat{\\mathrm{BIC}_{0}}=\\frac{1}{2} \\widehat{\\mathrm{BC}_{0}}+\\frac{1}{2} \\widehat{\\mathrm{~B}_{0} \\mathrm{C}}=\\frac{1}{2} \\widehat{\\mathrm{C}_{0} \\mathrm{~A}}+\\frac{1}{2} \\widehat{\\mathrm{AB}_{0}}=\\widehat{\\mathrm{C}_{0} \\mathrm{BI}} .\n$$\n\nDonc le triangle $\\mathrm{BIC}_{0}$ est isocèle en $\\mathrm{C}_{0}$. On prouve de même que $A_{0} B I$ est isocèle en $A_{0}$, donc $\\left(A_{0} C_{0}\\right)$ est la médiatrice du segment BI.\n\nPar symétrie, $\\widehat{A_{0} \\mathrm{BP}}=\\widehat{A_{0} \\mathrm{IP}}$, et comme (IP) et ( AC ) sont parallèles, $\\widehat{A_{0} \\mathrm{IP}}=\\widehat{\\mathrm{A}_{\\mathrm{O}} A C}=\\widehat{\\mathrm{BAA}_{0}}$. Comme $\\widehat{A_{0} \\mathrm{BP}}=\\widehat{\\mathrm{BAA}_{0}}$, on se retrouve avec le cas extrême du théorème de l'angle inscrit, et par la réciproque du théorème ( BP ) est tangente au cercle.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": " Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle non isocèle en $A$; I et $O$ sont respectivement le centre du cercle inscrit et le centre du cercle circonscrit de ce triangle $A B C$ et le cercle inscrit touche le côté BC en D. La bissectrice intérieure de l'angle en $A$ dans le triangle $A B C$ rencontre le cercle circonscrit au point $M$ et la droite (DM) rencontre à nouveau le cercle circonscrit en P .\n\nMontrer que l'angle $\\widehat{A P I}$ est un angle droit.", "solution": "On va placer E le point diamétralement opposé à A sur le cercle circonscrit. Si on arrive à prouver que les points $\\mathrm{P}, \\mathrm{I}$ et E sont alignés, alors l'angle $\\widehat{A P I}$ sera droit.\n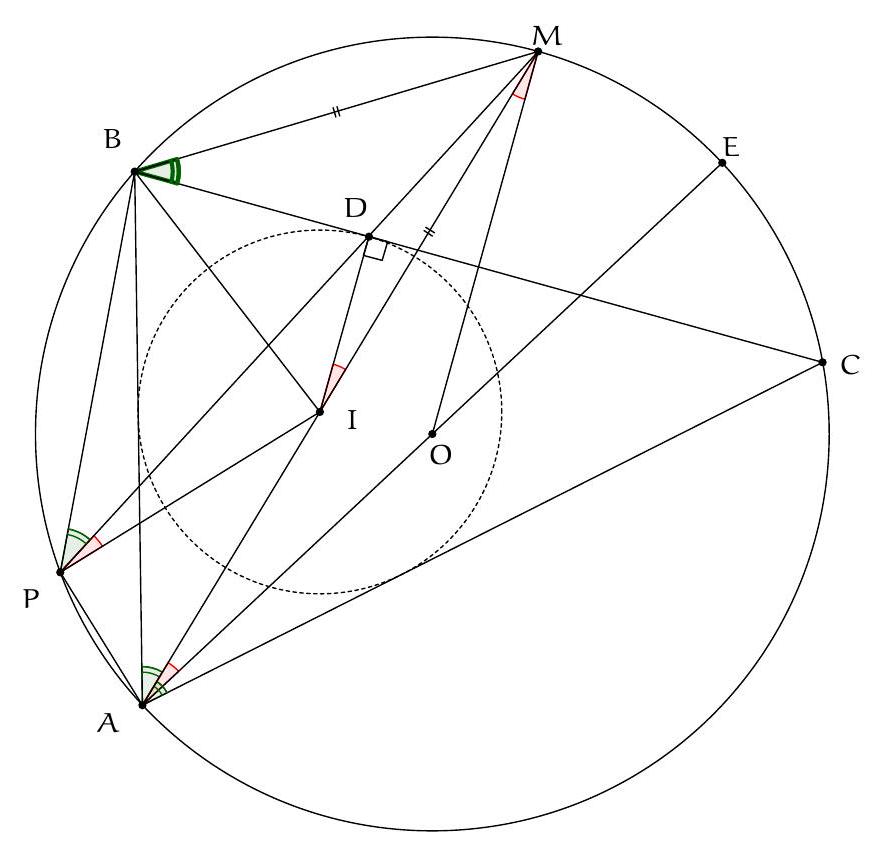\n\nTout d'abord, ramenez-vous au début de la preuve de l'exo 7 pour démontrer que $M I=M B$. Ensuite, $\\widehat{M P B}=\\widehat{C B M}$ puisque $M$ est le milieu de l'arc $\\widehat{B C}$. Les triangles MPB et MBD sont semblables (ils ont l'angle $\\widehat{M}$ en commun et ont un deuxième angle égal). Donc\n\n$$\n\\frac{M P}{M B}=\\frac{M B}{M D} \\Longrightarrow M P \\cdot M D=M B^{2}=M I^{2}\n$$\n\nLe cercle passant par les points P , I et D admet donc la droite MI comme tangente (par la théorie de la puissance d'un point part rapport à un cercle). On en déduit grâce au cas extrème du théorème de l'angle inscrit que\n\n$$\n\\widehat{\\mathrm{DPI}}=\\widehat{\\mathrm{DIM}}\n$$\n\nLe point $M$ est le milieu de l'arc $\\widehat{B C}$, donc la droite $O M$ est la médiatrice de $[B C]$, et les droites $O M$ et ID sont parallèles. De plus le triangle $A O M$ est isocèle en $O$. Ainsi\n\n$$\n\\widehat{\\mathrm{DIM}}=\\widehat{\\mathrm{IMO}}=\\widehat{\\mathrm{MAE}}=\\widehat{\\mathrm{MPE}}\n$$\n\noù la dernière égalité est simplement l'angle inscrit. On a montré que :\n\n$$\n\\widehat{\\mathrm{MPI}}=\\widehat{\\mathrm{MPE}},\n$$\n\nles points P, I, E sont bien alignés, la démonstration est achevée.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "On considère un cercle de centre $O$ et quatre points $A B C D$ de ce cercle tels que le point d'intersection $P$, autre que $O$, des cercles circonscrits aux triangles $A B O$ et $C D O$ soit intérieur au triangle OAD. On choisit un point $Q$ de la demi-droite [OP) à l'extérieur du segment $[O P]$ et on choisit un point $R$ de la demi-droite $[\\mathrm{PO})$ à l'extérieur du segment $[\\mathrm{OP}]$. Montrer que les angles $\\widehat{\\mathrm{QAP}}$ et $\\widehat{\\mathrm{OBR}}$ sont égaux si et seulement si les angles $\\widehat{\\mathrm{PDQ}}$ et $\\widehat{\\mathrm{RCO}}$ sont égaux.", "solution": "Tout d'abord on remarque que les droites $\\mathrm{AB}, \\mathrm{CD}$ et OP sont concourantes, puisque ce sont les trois axes radicaux des cercles de la figure pris deux deux. Notons $M$ leur point d'intersection.\n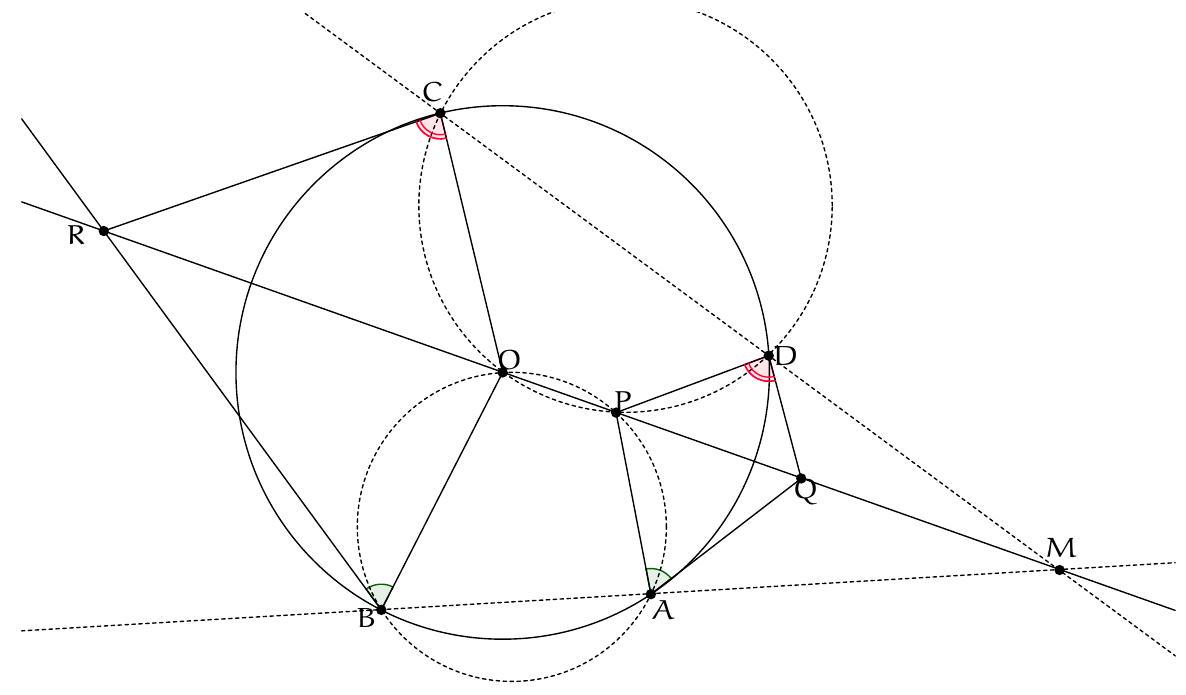\n\nComme $M$ est l'intersection des axes radicaux, on a\n\n$$\nM O \\cdot M P=M A \\cdot M B=M C \\cdot M D .\n$$\n\nNous allons travailler dans les complexes. On notera $z_{A}$ l'affixe du point $A$ etc. On peut supposer que $M$ est l'origine, que la droite ( OM ) est l'axe des réels et que $z_{\\mathrm{O}} z_{\\mathrm{P}}=1$. Considérons l'inversion de centre $M$ qui échange $O$ et $P$, qui sera d'équation : $A \\leftrightarrow A^{\\prime}$ ssi $z_{A} \\overline{z_{\\mathcal{A}^{\\prime}}}=1$. Grâce à la relation d'au dessus, cette inversion transforme $A$ en $B$ et $C$ en $D$. Plaçons un point $Q$ sur la droite $O P$ et notons $R$ son image par l'inversion. Nous allons montrer que $\\widehat{\\mathrm{QAP}}=\\widehat{\\mathrm{OBR}}$. Gardez en tête que $z_{\\mathrm{O}}, z_{\\mathrm{P}}, z_{\\mathrm{Q}}, z_{\\mathrm{R}}$ sont tous réels :\n\n$$\n\\widehat{\\mathrm{QAP}}=\\arg \\left(\\frac{z_{\\mathrm{Q}}-z_{\\mathrm{A}}}{z_{\\mathrm{P}}-z_{\\mathrm{A}}}\\right)=\\arg \\left(\\frac{\\frac{1}{z_{\\mathrm{R}}}-\\frac{1}{z_{\\mathrm{z}}}}{\\frac{1}{z_{\\mathrm{O}}}-\\frac{1}{z_{\\mathrm{B}}}}\\right)=\\arg \\left(\\frac{z_{\\mathrm{O}}}{z_{\\mathrm{R}}} \\frac{\\overline{z_{\\mathrm{B}}}-z_{\\mathrm{R}}}{\\overline{z_{\\mathrm{B}}}-z_{\\mathrm{O}}}\\right) .\n$$\n\nComme $z_{\\mathrm{O}} / z_{\\mathrm{R}}$ est réel, son argument vaut 0 à $\\pi$ près. Ensuite on utilise la formule $\\arg (\\bar{z})=-\\arg (z)$ pour finir le calcul :\n\n$$\n\\widehat{\\mathrm{QAP}}=-\\arg \\left(\\frac{z_{\\mathrm{B}}-z_{\\mathrm{R}}}{z_{\\mathrm{B}}-z_{\\mathrm{O}}}\\right)=\\widehat{\\mathrm{OBR}}\n$$\n\nDe même on montre que $\\widehat{P D Q}=\\widehat{R C O}$. Ainsi, la seule façon de placer le point $R$ telle que $\\widehat{\\mathrm{QAP}}=\\widehat{\\mathrm{OBR}}$ est de le mettre sur l'image de Q par l'inversion, et on a dans ce cas $\\widehat{\\mathrm{PDQ}}=\\widehat{\\mathrm{RCO}}$.\n\n\nFin", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi1-corrige.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution."}}
diff --git a/French_STS/segmented/fr-ofm-2012-2013-envoi2-corrige.jsonl b/French_STS/segmented/fr-ofm-2012-2013-envoi2-corrige.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..cf17897e65babaef87e930fbed90e12080d6093a
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2012-2013-envoi2-corrige.jsonl
@@ -0,0 +1,9 @@
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Peut-on numéroter les arêtes d'un cube de 1 à 12 en sorte que la somme des nombres sur les arêtes entrant dans un sommet du cube soit la même pour tous les sommets?", "solution": "Nous allons prouver par l'absurde que la réponse à la question est négative.\nSupposons qu'une telle numérotation existe et notons $k$ la somme dans chaque sommet. Sur chaque arête, écrivons son numéro deux fois : une fois à un bout de l'arête et l'autre fois à l'autre bout. Maintenant, calculons la somme des numéros ainsi écrits de deux manières différentes.\n\nPremière manière : on additionne les numéros arête par arête. On trouve alors $2(1+2+\\cdots+12)$, car chaque numéro de 1 à 12 est écrit deux fois.\n\nDeuxième manière : on additionne les numéros sommet par sommet. Par hypothèse, la somme vaut $k$ dans chaque sommet. Au total, on trouve donc 8 k .\n\nConclusion:\n\n$$\n8 k=2(1+2+\\ldots+12)=12 \\times 13=4 \\times 39\n$$\n\nd'où $k=39 / 2$, ce qui est impossible.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi2-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Les sept dixièmes de la surface de la Terre sont couverts par l'océan. Montrer qu'il existe un diamètre de la Terre dont les deux extrémités baignent dans l'océan.", "solution": "Soit $S$ la surface couverte par l'océan et $S^{\\prime}$ son symétrique par rapport au centre de la Terre. Si les surfaces $S$ et $S^{\\prime}$ étaient disjointes, elles occuperaient ensemble les 14/10 de la surface de la Terre, ce qui est impossible, car $14 / 10>1$. Donc $S$ et $S^{\\prime}$ ont au moins un point d'intersection, qu'on appellera $P$. Soit $\\mathrm{P}^{\\prime}$ le symétrique de $P$ par rapport au centre de la Terre. On a donc $P \\in S$ et $P \\in S^{\\prime}$, autrement dit $P \\in S$ et $P^{\\prime} \\in S$. Par conséquent, les deux bouts du diamètre $P P^{\\prime}$ baignent dans l'océan.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi2-corrige.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver cent entiers positifs distincts $n_{1}, \\ldots, n_{100}$ tels que\n\n$$\n1=\\frac{1}{n_{1}}+\\frac{1}{n_{2}}+\\cdots+\\frac{1}{n_{100}}\n$$", "solution": "Nous montrerons par récurrence la propriété suivante :\nPour tout entier $k \\geqslant 3$ on peut trouver $k$ entiers positifs $n_{1}25$, notre estimation montre que les ordres plutôt croissants sont beaucoup moins nombreux que tous les ordres possibles.\n\n$\\mathcal{F i n}$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi2-corrige.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution."}}
diff --git a/French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl b/French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..30c8dcb85aa219a1f12c358f5745fb5105e81284
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl
@@ -0,0 +1,22 @@
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "On appelle diviseur propre d'un entier $n$ un diviseur positif de $n$ qui est différent de 1 et de n.\n\nExiste-t-il un entier n dont le produit des diviseurs propres est égal à 2013 ?", "solution": "La décomposition en facteurs premiers de 2013 est $3 \\times 11 \\times 61$. Ainsi, si le produit des diviseurs stricts d'un entier n vaut 2013, cela implique que n est lui même divisible par 3, 11 et 61 . Or, dans ce cas, il compte parmi ses diviseurs stricts au moins les nombres suivants :\n\n$$\n3,11,61,33,671\n$$\n\ndont le produit surpasse 2013 (il vaut $2013 \\times 33 \\times 671=44573859$ ). Ainsi, un tel entier n n'existe pas.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Chaque nombre rationnel strictement positif est colorié soit en rouge, soit en noir, de telle sorte que:\n\n- les nombres $x$ et $x+1$ sont de couleurs différentes ;\n- les nombres $x$ et $\\frac{1}{x}$ sont de la même couleur;\n- le nombre 1 est colorié en rouge.\n\nQuelle est la couleur de $\\frac{2012}{2013}$ ?\n(On ne demande pas de démontrer l'existence d'un tel coloriage.)", "solution": "On remarque que $\\frac{2012}{2013}$ s'écrit:\n\n$$\n\\frac{2012}{2013}=\\frac{1}{1+\\frac{1}{2012}}\n$$\n\nAinsi, d'après les règles de l'énoncé, il a la couleur inverse de 2012. Or, ce dernier s'obtient en ajoutant 2011 fois 1 à 1 ; il a donc la couleur inverse de 1 (puisqu'on inverse 2011 fois la couleur), c'est-à-dire noir. Ainsi $\\frac{2012}{2013}$ est rouge.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "La suite de Fibonacci est construite ainsi : chaque terme est la somme des deux précédents. Ses premiers termes valent:\n\n$$\n1,1,2,3,5,8,13,21,34,55,89, \\ldots\n$$\n\nMontrer que la suite de Fibonacci contient un multiple de 1000.", "solution": "Notons $F_{n}$ le $n$-ième terme de la suite de Fibonacci ( $F_{1}=1, F_{2}=1, F_{3}=2$, etc.) et notons $u_{n}$ le reste de la division euclidienne de $F_{n}$ par 1000 ( $u_{n}$ est donc le nombre formé par les trois derniers chiffres de $F_{n}$ ). Comme il n'y a qu'un nombre fini de couples ( $x, y$ ) d'entiers compris entre 0 et 999 (il $y$ en a exactement $1000^{2}=1000000$ ), il existe des entiers $n$ et $N$ tels que $N>0$ et\n\n$$\nu_{n}=u_{n+N} \\quad ; \\quad u_{n+1}=u_{n+1+N}\n$$\n\nOr, $u_{n-1}$ (resp. $u_{n-1+N}$ ) s'obtient à partir de $u_{n}$ et $u_{n+1}$ (resp. $u_{n+N}$ et $u_{n+1+N}$ ) comme le reste de la division euclidienne de $u_{n+1}-u_{n}$ (resp. $u_{n+1+N}-u_{n+N}$ ) par 1000. Ainsi, des égalités (1), on déduit que $\\mathfrak{u}_{n-1}=u_{n-1+N}$. En continuant ainsi, on obtient $u_{N+1}=u_{1}=1$ et $u_{N+2}=u_{2}=1$, d'où il résulte enfin $u_{N}=0$. L'entier $F_{N}$ est donc multiple de 1000.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Montrer que l'équation\n\n$$\nx(x+2)=y(y+1)\n$$\n\nn'a pas de", "solution": "en nombres entiers strictement positifs.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Montrer que l'équation\n\n$$\nx(x+2)=y(y+1)\n$$\n\nn'a pas de", "solution": "Si le couple $(x, y)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Montrer que l'équation\n\n$$\nx(x+2)=y(y+1)\n$$\n\nn'a pas de", "solution": ", on a $x(x+1)x(x+2)=y(y+1)$, d'où on déduit $x+1>y$. Ainsi, une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Montrer que l'équation\n\n$$\nx(x+2)=y(y+1)\n$$\n\nn'a pas de", "solution": "( $x, y$ ) hypothétique devrait donc vérifier $xb$. Par hypothèse, $\\frac{a}{b}$ a la couleur inverse de $\\frac{a}{b}-1=\\frac{a-b}{b}$. De plus, $\\max (a-b, b)<\\max (a, b)=a$. Ainsi, la fraction $\\frac{a-b}{b}$ relève de l'hypothèse de récurrence; sa couleur est donc entièrement déterminée et, par suite, celle de $\\frac{\\mathrm{a}}{\\mathrm{b}}$ l'est également.\n\nL'existence se démontre de la même façon : en reprenant les arguments précédents, on construit le coloriage par récurrence sur $\\max (\\mathrm{a}, \\mathrm{b})$ en vérifiant que chaque identité entre couleurs est utilisée une et une seule fois lorsqu'on construit le coloriage avec cette méthode.\nRemarque. Si $a$ et $b$ sont deux entiers premiers entre eux, notons $q_{1}(a, b), \\ldots, q_{n}(a, b)$ la suite (finie) des quotients successifs obtenus lorsque l'on effectue l'algorithme d'Euclide à partir de a et b. On peut alors montrer que l'unique coloriage satisfaisant aux conditions de l'énoncé est celui qui attribue la couleur rouge (resp. bleue) à la fraction irréductible $\\frac{a}{b}$ lorsque $\\sum_{i} q_{i}(a, b)$ est impair (resp. pair).\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": "en entiers strictement positifs.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": "L'équation de l'énoncé s'écrit encore $\\left(x+\\frac{k}{2}\\right)^{2}=\\left(y+\\frac{1}{2}\\right)^{2}+\\frac{k^{2}-1}{4}$, soit, en factorisant:\n\n$$\n\\left(x-y+\\frac{k-1}{2}\\right) \\cdot\\left(x+y+\\frac{k+1}{2}\\right)=\\frac{k^{2}-1}{4} .\n$$\n\nDistinguons deux cas selon la parité de $k$. Si $k$ est impair, on écrit $k=2 a+1$ et l'équation précédente devient $(x-y+a)(x+y+a+1)=a(a+1)$. En écrivant que le premier facteur vaut 1 et le second $a(a+1)$, on obtient $x=\\frac{a(a-1)}{2}$ et $y=x+(a-1)=\\frac{(a-1)(a+2)}{2}$. Étant donné que le produit de deux entiers consécutifs est toujours pair, les valeurs que l'on vient d'obtenir forment une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": "dès que a $>1$. Pour $\\mathrm{a}=1$ (i.e. $k=3$ ), au contraire, il n'y a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": ", car l'égalité $(x-y+1)(x+y+2)=2$ ne peut être satisfaite étant donné que le deuxième facteur est toujours $>2$ lorsque $x$ et $y$ sont strictement positifs. Pour $a=0$, enfin, on a $k=1$ et, clairement, tous les couples ( $x, y$ ) conviennent.\n\nOn raisonne de manière analogue dans le cas où $k$ est pair. On pose $k=2 a$ et l'équation (2) devient $(2 x-2 y+2 a-1)(2 x+2 y+2 a+1)=4 a^{2}-1$. Comme précédemment, en demandant que le premier facteur vaille 1 , on obtient un système en $x$ et $y$ dont les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": " solution"}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": "s sont $x=a(a-1)$ et $y=$ $(a+1)(a-1)$. Cette", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": " solution"}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": "est acceptable dès que $a>1$. Pour $a=1$, l'équation à résoudre devient $(2 x-2 y+1)(2 x+2 y+3)=3$ et elle n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Trouver tous les entiers naturels $\\mathrm{k}>0$ tels que l'équation en $x$ et y :\n\n$$\nx(x+k)=y(y+1)\n$$\n\nait une", "solution": "avec $x, y>0$ étant donné que cette dernière condition implique que le deuxième facteur est $>3$.\n\nEn résumé, les entiers $k$ convenables sont $k=1$ et tous les entiers $k \\geqslant 4$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 8", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $p \\geqslant 5$ un nombre premier. Montrer que 1 et 5 sont les seuls diviseurs positifs de $2^{p}+3^{p}$ qui soient inférieurs ou égaux à $p$.", "solution": "La factorisation\n\n$$\n2^{\\mathfrak{p}}+3^{\\mathfrak{p}}=5 \\cdot \\sum_{i=0}^{p-1} 2^{\\boldsymbol{i}}(-3)^{p-1-\\mathfrak{i}}\n$$\n\nmontre que 5 est bien un diviseur de $2^{p}+3^{\\mathrm{p}}$.\nSoit à présent $\\mathrm{d} \\in\\{2, \\ldots, \\mathrm{p}\\}$ un diviseur de $2^{\\mathfrak{p}}+3^{\\mathfrak{p}}$. On souhaite démontrer que $\\mathrm{d}=5$. On considère pour cela $q$ un diviseur premier de d . Alors, manifestement, $q$ est aussi un diviseur de $2^{p}+3^{p}$ qui est $\\leqslant p$. De plus, il est clair que l'on ne peut pas avoir $\\mathbf{q}=2$. Ainsi $q$ est impair et de la congruence $2^{\\mathfrak{p}}+3^{\\mathfrak{p}} \\equiv 0$ $(\\bmod \\mathbf{q})$, on déduit que $a^{p} \\equiv 1(\\bmod q)$ où $a$ un entier est tel que $2 a \\equiv-3(\\bmod q)($ un tel entier existe bien car $q$ est impair). Par ailleurs, par le petit théorème de Fermat, on sait également que $a^{q} \\equiv a$ $(\\bmod q)$ et donc $a^{q-1} \\equiv 1(\\bmod q)\\left(\\right.$ puisque $a n^{\\prime}$ est pas un multiple de $\\left.q\\right)$. On en déduit que $a^{n} \\equiv 1$ $(\\bmod q)$ avec $n=\\operatorname{PGCD}(p, q-1)$. Or, comme $q25$, nous allons démontrer que $2^{\\mathfrak{p}}+3^{\\mathfrak{p}}$ n'est, lui-même, pas divisible par 25 (ce qui suffira à conclure). D'après l'équation (3), cela revient à prouver que $\\sum_{i=0}^{\\mathfrak{p}-1} 2^{\\boldsymbol{i}}(-3)^{p-1-\\boldsymbol{i}}$ n'est pas divisible par 5 . Or, un calcul modulo 5 montre que cette somme est congrue modulo 5 à\n\n$$\n(-3)^{\\mathrm{p}-1} \\cdot \\sum_{i=0}^{\\mathrm{p}-1} 1=(-3)^{\\mathrm{p}-1} \\cdot \\mathrm{p}\n$$\n\nOr, $(-3)^{p-1}$ est premier avec 5 et, comme $p>25$ est un nombre premier, les entiers $p$ et 5 sont premiers entre eux. On a ainsi bien démontré ce que l'on souhaitait.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 9.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soit $n \\geqslant 5$ un entier. Soient $a_{1}, \\ldots, a_{n}$ des entiers dans $\\{1, \\ldots, 2 n\\}$ deux à deux distincts. Montrer qu'il existe des indices $\\boldsymbol{i}, \\mathfrak{j} \\in\\{1, \\ldots, \\mathfrak{n}\\}$ avec $\\mathfrak{i} \\neq \\boldsymbol{j}$ tels que\n\n$$\n\\operatorname{PPCM}\\left(\\mathfrak{a}_{\\mathbf{i}}, \\mathfrak{a}_{\\mathbf{j}}\\right) \\leqslant 6\\left(\\mathrm{E}\\left(\\frac{\\mathfrak{n}}{2}\\right)+1\\right)\n$$\n\noù $\\mathrm{E}(\\mathrm{x})$ désigne la partie entière du nombre x .", "solution": "Supposons, pour commencer, qu'il existe un indice $i$ tel que $a_{i} \\leqslant n$. S'il existe $j$ tel que $a_{j}=2 a_{i}$, on a alors\n\n$$\n\\operatorname{PPCM}\\left(a_{i}, a_{j}\\right)=a_{j} \\leqslant 2 n \\leqslant 6 \\cdot\\left(E\\left(\\frac{n}{2}\\right)+1\\right)\n$$\n\net on a trouvé un couple ( $i, j)$ convenable. Si , au contraire, l'entier $2 a_{i}$ n'apparaît pas parmi les $a_{j}$, définissons les entiers $b_{1}, \\ldots, b_{n}$ en posant $b_{i}=2 a_{i}$ et $b_{j}=a_{j}$ pour $j \\neq i$. Les $b_{j}$ sont encore deux à deux distincts et compris entre 1 et 2 n . De plus, on vérifie immédiatement que $\\operatorname{PPCM}\\left(b_{i}, b_{j}\\right) \\geqslant$ $\\operatorname{PPCM}\\left(a_{i}, a_{j}\\right)$. Ainsi, il suffit de démontrer la propriété de l'énoncé pour la suite des $b_{j}$.\n\nEn appliquant à nouveau le raisonnement précédent — éventuellement plusieurs fois - on en vient à supposer que tous les $a_{j}$ sont strictement supérieurs à $n$. Autrement dit, l'ensemble des $a_{j} n^{\\prime}$ 'est autre que $\\{n+1, n+2, \\ldots, 2 n\\}$. Posons $k=E\\left(\\frac{n}{2}\\right)+1$. Comme on a supposé $n \\geqslant 5$, il est facile de vérifier que l'un des $a_{j}$ vaut $2 k$ et un autre vaut $3 k$. On conclut en remarquant que le PPCM de ces deux nombres est égal à 6 k .\n\n$\\mathcal{F i n}$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi3-corrige.jsonl", "problem_match": "\nExercice 10.", "solution_match": "## Solution."}}
diff --git a/French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl b/French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..f7558a9b2ddf7bbf4fb9123ac22b3ab4cd5e563f
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl
@@ -0,0 +1,12 @@
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soient $x_{1}, x_{2}, \\ldots, x_{5}$ des réels tels que\n\n$$\n\\left|x_{2}-x_{1}\\right|=2\\left|x_{3}-x_{2}\\right|=3\\left|x_{4}-x_{3}\\right|=4\\left|x_{5}-x_{4}\\right|=5\\left|x_{1}-x_{5}\\right| .\n$$\n\nMontrer que ces cinq réels sont égaux.", "solution": "Notons $\\alpha=\\left|x_{2}-\\chi_{1}\\right|$ et montrons par l'absurde que $\\alpha=0$. D'après l'énoncé, il existe des signes $\\varepsilon_{1}, \\ldots$, $\\varepsilon_{5}$ tels que\n\n$$\nx_{2}-x_{1}=\\varepsilon_{1} \\alpha, x_{3}-x_{2}=\\varepsilon_{2} \\frac{\\alpha}{2}, x_{4}-x_{3}=\\varepsilon_{3} \\frac{\\alpha}{3}, x_{5}-x_{4}=\\varepsilon_{4} \\frac{\\alpha}{4}, x_{1}-x_{5}=\\varepsilon_{5} \\frac{\\alpha}{5} .\n$$\n\nAlors, par télescopage,\n\n$$\n0=x_{1}-x_{5}+x_{5}-x_{4}+x_{4}-x_{3}+x_{3}-x_{2}+x_{2}-x_{1}=\\varepsilon_{1} \\alpha+\\varepsilon_{2} \\frac{\\alpha}{2}+\\varepsilon_{3} \\frac{\\alpha}{3}+\\varepsilon_{4} \\frac{\\alpha}{4}+\\varepsilon_{5} \\frac{\\alpha}{5} .\n$$\n\nSi $\\alpha \\neq 0$, il existe donc des signes $\\varepsilon_{1}^{\\prime}, \\ldots, \\varepsilon_{4}^{\\prime}$ tels que\n\n$$\n\\frac{1}{5}=\\varepsilon_{1}^{\\prime}+\\varepsilon_{2}^{\\prime} \\frac{1}{2}+\\varepsilon_{3}^{\\prime} \\frac{1}{3}+\\varepsilon_{4}^{\\prime} \\frac{1}{4}\n$$\n\ndonc un entier n tel que $\\frac{1}{5}=\\frac{\\mathfrak{n}}{12}$ ce qui est impossible car 5 ne divise par 12 .\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution."}}
+{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $\\left(u_{n}\\right)_{n}$ une suite de réels telle que, pour tout entier $n$,\n\n$$\n\\left|u_{n+1}-u_{n}\\right| \\leqslant 1 .\n$$\n\nMontrer que la moyenne des $n$ premiers termes de la suite et la moyenne des $n+1$ premiers termes de la suite sont distantes d'au plus $\\frac{1}{2}$.", "solution": "Notons, pour tout entier $n$ strictement positif $v_{n}=\\frac{1}{n}\\left(u_{1}+\\ldots+u_{n}\\right)$.\n$\\triangleright$ Soit $\\mathrm{m}>\\mathrm{n}$. Remarquons tout d'abord que, par inégalité triangulaire,\n\n$$\n\\begin{aligned}\n\\left|u_{m}-u_{n}\\right| & \\leqslant\\left|u_{m}-u_{m-1}\\right|+\\left|u_{m-1}-u_{m-2}\\right|+\\ldots+\\left|u_{n+1}-u_{n}\\right| \\\\\n& \\leqslant m-n .\n\\end{aligned}\n$$\n\n$\\triangleright$ Pour tout entier n strictement positif,\n\n$$\n\\begin{aligned}\n\\left|v_{n+1}-v_{n}\\right| & =\\left|\\frac{(n+1)\\left(u_{1}+\\ldots+u_{n}\\right)-n\\left(u_{1}+\\ldots+u_{n}+u_{n+1}\\right)}{n(n+1)}\\right| \\\\\n& \\leqslant\\left|\\frac{\\left(u_{1}-u_{n+1}\\right)+\\ldots+\\left(u_{n}-u_{n+1}\\right)}{n(n+1)}\\right| \\\\\n& \\leqslant \\frac{\\left|u_{1}-u_{n+1}\\right|+\\ldots+\\left|u_{n}-u_{n+1}\\right|}{n(n+1)} \\\\\n& \\leqslant \\frac{n+\\ldots+1}{n(n+1)}=\\frac{1}{2}\n\\end{aligned}\n$$\n\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $E$ un ensemble fini de réels strictement positifs tels que, pour tout réel $x$ strictement positif, E contient autant d'éléments strictement supérieurs à $x$ que d'éléments strictement inférieurs à $\\frac{1}{x}$. Déterminer le produit de tous les éléments de E.", "solution": "Soit $x_{0} \\in E$ tel que $x_{0}>1$. Alors, par hypothèse,\n\n- les ensembles $\\mathrm{E} \\cap$ ] - $\\infty, \\frac{1}{x_{0}}$ [et $\\left.\\mathrm{E} \\cap\\right] \\mathrm{x}_{0},+\\infty[$ ont des cardinaux de même parité,\n- les ensembles $\\mathrm{E} \\cap]-\\infty, \\mathrm{x}_{0}\\left[\\right.$ et $\\mathrm{E} \\cap \\frac{1}{\\mathrm{x}_{0}},+\\infty[$ ont des cardinaux de même parité.\n\nPar conséquent, les deux ensembles\n\n$$\n\\begin{aligned}\n\\left.\\mathrm{E} \\cap] \\frac{1}{x_{0}}, x_{0}\\right] & =(\\mathrm{E} \\cap] \\frac{1}{x_{0}},+\\infty[) \\backslash(\\mathrm{E} \\cap] \\mathrm{x}_{0},+\\infty[) \\\\\n\\mathrm{E} \\cap\\left[\\frac{1}{x_{0}}, x_{0}[ \\right. & =(\\mathrm{E} \\cap]-\\infty, \\mathrm{x}_{0}[) \\backslash(\\mathrm{E} \\cap]-\\infty, \\frac{1}{x_{0}}[)\n\\end{aligned}\n$$\n\nont des cardinaux de même parité. Or, ils sont composés des mêmes éléments, sauf éventuellement $x_{0}$ et $\\frac{1}{x_{0}}$, le premier ensemble contient $\\chi_{0}$ mais pas $\\frac{1}{x_{0}}$ : ainsi, le second ensemble contient un et un seul élément de $\\left\\{\\frac{1}{x_{0}}, x_{0}\\right\\}$ mais ne peut contenir $x_{0}:$ il contient donc $\\frac{1}{x_{0}}$.\nOn a ainsi établi que si $x_{0} \\in E$, alors $\\frac{1}{x_{0}} \\in E$. Le produit de tous les éléments de $E$ donne donc 1 .\n\n\n## Exercices Communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $x, y, z>0$ tels que $x y z=8$. Montrer que\n\n$$\n\\frac{x-2}{x+1}+\\frac{y-2}{y+1}+\\frac{z-2}{z+1} \\leqslant 0\n$$", "solution": "Commençons par remarquer que $a-2=a+1-3$ pour tout réel a donc\n\n$$\n\\frac{x-2}{x+1}+\\frac{y-2}{y+1}+\\frac{z-2}{z+1}=3-3\\left(\\frac{1}{x+1}+\\frac{1}{y+1}+\\frac{1}{z+1}\\right)\n$$\n\nL'inégalité à établir se réécrit donc\n\n$$\n\\frac{1}{x+1}+\\frac{1}{y+1}+\\frac{1}{z+1} \\geqslant 1\n$$\n\nEn mettant au même dénominateur, on obtient\n\n$$\n3+2(x+y+z)+x y+y z+z x \\geqslant 1+x+y+z+x y+y z+z x+x y z\n$$\n\nsoit\n\n$$\n\\frac{x+y+z}{3} \\geqslant 2\n$$\n\nOr, cette dernière égalité est simplement l'inégalité arithmético-géométrique.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que, pour tous $x$ et $y$,\n\n$$\nf(x y) \\leqslant x f(y)\n$$", "solution": "$\\triangleright \\operatorname{Avec}(x, y)=(0,0)$, on obtient $f(0) \\leqslant 0$ et avec $(x, y)=(2,0), f(0) \\geqslant 0$. Par conséquent, $f(0)=0$.\n$\\triangleright \\operatorname{Si} x>0$ et $y>0$, alors\n\n$$\nf(x)=f\\left(\\frac{x}{y} y\\right) \\leqslant \\frac{x}{y} f(y)\n$$\n\nD'où\n\n$$\n\\frac{f(x)}{x} \\leqslant \\frac{f(y)}{y}\n$$\n\net donc $\\frac{f(x)}{x}=\\frac{f(y)}{y}$ (par symétrie des rôles de $x$ et $y$ ).\n$\\triangleright$ De même, si $x<0$ et $y<0$, alors\n\n$$\nf(x)=f\\left(\\frac{x}{y} y\\right) \\leqslant \\frac{x}{y} f(y)\n$$\n\nD'où\n\n$$\n\\frac{f(x)}{x} \\geqslant \\frac{f(y)}{y}\n$$\n\net donc $\\frac{f(x)}{x}=\\frac{f(y)}{y}$ (par symétrie des rôles de $x$ et $y$ ).\n$\\triangleright$ Notons $\\alpha=\\mathfrak{f}(1)$ et $\\beta=-\\mathbf{f}(-1)$ les constantes exhibées aux points précédents. Avec $(x, y)=$ $(-1,-1)$, l'inéquation donne $\\alpha=f\\left((-1)^{2}\\right) \\leqslant-f(-1)=\\beta$.\n$\\triangleright$ On a obtenu qu'une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 5.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que, pour tous $x$ et $y$,\n\n$$\nf(x y) \\leqslant x f(y)\n$$", "solution": "est de la forme\n\n$$\nx \\mapsto\\left\\{\\begin{array}{cl}\n0 & \\text { si } x=0 \\\\\n\\alpha x & \\text { si } x>0 \\\\\n\\beta x & \\text { si } x<0\n\\end{array}\\right.\n$$\n\n$\\operatorname{avec} \\alpha \\leqslant \\beta$. On vérifie que ces fonctions conviennent.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soient un entier $n$ et des réels $0<\\mathfrak{u}_{1}<\\mathfrak{u}_{2}<\\ldots<\\boldsymbol{u}_{\\boldsymbol{n}}$ tels que\n\n$$\n\\mathfrak{u}_{1}+\\mathfrak{u}_{2}+\\ldots+\\mathfrak{u}_{n}=\\frac{1}{\\mathfrak{u}_{1}^{2}}+\\frac{1}{\\mathfrak{u}_{2}^{2}}+\\ldots+\\frac{1}{\\mathfrak{u}_{n}^{2}}\n$$\n\nMontrer que, pour tout entier $k$ inférieur ou égal à $n$, il existe $k$ réels parmi $\\mathfrak{u}_{1}, \\mathfrak{u}_{2}, \\ldots, \\mathfrak{u}_{n}$ dont la somme est supérieure ou égale à $k$.", "solution": "$\\triangleright$ Commençons par montrer le résultat pour $k=n$. Notons $a=\\frac{u_{1}+\\ldots+u_{n}}{n}$ et $g=\\left(u_{1} \\ldots u_{n}\\right)^{\\frac{1}{n}}$ les moyennes arithmétique et géométrique de $u_{1}, \\ldots, u_{n}$. Alors, l'inégalité classique entre moyenne arithmétique-géométrique-harmonique donne\n\n$$\n\\mathrm{a}=\\frac{\\frac{1}{\\mathbf{u}_{1}^{2}}+\\ldots+\\frac{1}{\\mathfrak{u}_{n}^{2}}}{\\mathrm{n}} \\geqslant \\frac{1}{\\mathrm{~g}^{2}} \\geqslant \\frac{1}{\\mathrm{a}^{2}}\n$$\n\nAinsi, $a \\geqslant 1$ et, donc, $u_{1}+\\ldots+u_{n} \\geqslant n$.\n$\\triangleright$ Soit $kc^{2}, \\quad b^{2}+c^{2}>a^{2}, \\quad c^{2}+a^{2}>b^{2}\n$$\n\nMontrer que\n\n$$\n\\frac{a^{2} b^{2} c^{2}}{\\left(a^{2}+b^{2}-c^{2}\\right)\\left(b^{2}+c^{2}-a^{2}\\right)\\left(c^{2}+a^{2}-b^{2}\\right)}+2 \\frac{(a+b-c)(b+c-a)(c+a-b)}{a b c} \\geqslant 3\n$$", "solution": "Notons\n\n$$\n\\begin{aligned}\n& A=\\frac{a^{2} b^{2} c^{2}}{\\left(a^{2}+b^{2}-c^{2}\\right)\\left(b^{2}+c^{2}-a^{2}\\right)\\left(c^{2}+a^{2}-b^{2}\\right)} \\\\\n& B=\\frac{(a+b-c)(b+c-a)(c+a-b)}{a b c}\n\\end{aligned}\n$$\n\nOn doit montrer que $A+2 B \\geqslant 3$. Tout d'abord, on remarque que $a+b>c$ car $c^{2}a$ et $c+a>b$, donc $a, b, c$ sont les côtés d'un triangle dont on notera $\\alpha, \\beta, \\gamma$ les angles. Le fait que $a^{2}+b^{2}>c^{2}$, etc. signifie que le triangle est acutangle.\nD'après l'inégalité arithmético-géométrique, on a $\\frac{A+2 B}{3} \\geqslant \\sqrt[3]{A B^{2}}$, donc il suffit de montrer que $A B^{2} \\geqslant$ 1, autrement dit que\n\n$$\n\\frac{(a+b-c)^{2}(b+c-a)^{2}(c+a-b)^{2}}{\\left(a^{2}+b^{2}-c^{2}\\right)\\left(b^{2}+c^{2}-a^{2}\\right)\\left(c^{2}+a^{2}-b^{2}\\right)} \\geqslant 1\n$$\n\nD'après la formule d'Al-Kashi, on a\n\n$$\na^{2}+b^{2}-c^{2}=2 a b \\cos \\alpha\n$$\n\nD'autre part,\n\n$$\n(c+a-b)(b+c-a)=c^{2}-a^{2}-b^{2}+2 a b=2 a b(1-\\cos \\alpha)\n$$\n\ndonc $\\frac{(c+a-b)(b+c-a)}{a^{2}+b^{2}-c^{2}}=\\frac{1-\\cos \\alpha}{\\cos \\alpha}$. En multipliant par les deux expressions similaires, l'inégalité à démontrer devient\n\n$$\n\\frac{(1-\\cos \\alpha)(1-\\cos \\beta)(1-\\cos \\gamma)}{\\cos \\alpha \\cos \\beta \\cos \\gamma} \\geqslant 1\n$$\n\nTraitons d'abord le cas particulier $\\alpha=\\beta$. Alors $\\gamma=\\pi-2 \\alpha$. Comme $\\gamma \\leqslant \\frac{\\pi}{2}$, on a $\\alpha \\in\\left[\\frac{\\pi}{4}, \\frac{\\pi}{2}\\right]$.\nComme $\\frac{1-\\cos \\gamma}{\\cos \\gamma}=\\frac{1+\\cos 2 \\alpha}{-\\cos 2 \\alpha}=\\frac{2 \\cos ^{2} \\alpha}{1-2 \\cos ^{2} \\alpha}$, on a\n\n$$\n\\begin{aligned}\n\\frac{(1-\\cos \\alpha)(1-\\cos \\beta)(1-\\cos \\gamma)}{\\cos \\alpha \\cos \\beta \\cos \\gamma} & =\\frac{(1-\\cos \\alpha)^{2}\\left(2 \\cos ^{2} \\alpha\\right)}{\\cos ^{2} \\alpha\\left(1-2 \\cos ^{2} \\alpha\\right)} \\\\\n& =\\frac{2(1-\\cos \\alpha)^{2}}{1-2 \\cos ^{2} \\alpha}\n\\end{aligned}\n$$\n\nCette expression est minoré par 1 si et seulement si $2(1-\\cos \\alpha)^{2} \\geqslant 1-2 \\cos ^{2} \\alpha$. On développe et on passe tout dans le membre de gauche. L'inégalité devient $(2 \\cos \\alpha-1)^{2} \\geqslant 0$, ce qui est vrai.\nTraitons maintenant le cas général. On suppose par symétrie que $\\alpha \\geqslant \\beta \\geqslant \\gamma$.\n\nPosons $f(x)=\\frac{1-\\cos x}{\\cos x}$ et $g(x)=\\log f(x)$. On veut montrer que\n\n$$\nf(\\alpha) f(\\beta) f(\\gamma) \\geqslant 1\n$$\n\nou encore que $\\frac{g(\\alpha)+g(\\beta)+g(\\gamma)}{3} \\geqslant 0=g\\left(\\frac{\\pi}{3}\\right)=g\\left(\\frac{\\alpha+\\beta+\\gamma}{3}\\right)$. La difficulté est que $g$ n'est pas convexe. En effet, on calcule que\n\n$$\ng^{\\prime \\prime}(x)=\\frac{(1-\\cos x)\\left(-\\cos ^{2} x-\\cos x+1\\right)}{\\cos ^{2} x(1-\\cos x)^{2}}\n$$\n\nest positif sur $\\left[x_{0}, \\frac{\\pi}{2}\\right]$ et négatif sur $\\left[0, x_{0}\\right]$, où $x_{0}$ satisfait l'équation $\\cos x_{0}=\\frac{-1+\\sqrt{5}}{2}$. On remarque que $x_{0}<\\frac{\\pi}{3}$ puisque $\\frac{-1+\\sqrt{5}}{2}>\\frac{1}{2}$. On en déduit que $\\alpha \\geqslant x_{0}$. En effet, dans le cas contraire on aurait $\\alpha+\\beta+\\gamma \\leqslant 3 \\alpha \\leqslant 3 x_{0}<\\pi$, ce qui est faux.\nPremier cas: $\\beta \\geqslant x_{0}$. Alors $g(\\alpha)+g(\\beta) \\geqslant 2 g\\left(\\frac{\\alpha+\\beta}{2}\\right)$ par convexité de $g$ sur $\\left[x_{0}, \\frac{\\pi}{2}\\right]$ donc on se ramène au cas particulier $\\alpha=\\beta$ traité plus haut.\nDeuxième cas: $\\betax_{0}-\\beta$. En effet, dans le cas contraire on aurait $\\alpha+\\beta+\\gamma \\leqslant$ $\\frac{\\pi}{2}+\\beta+\\left(x_{0}-\\beta\\right)=\\frac{\\pi}{2}+x_{0}<\\pi$, ce qui est faux.\nPosons $\\varphi(t)=g(\\beta+t)+g(\\gamma-t)$. Pour tout $t \\in\\left[0, x_{0}-\\beta\\right]$, on a\n\n$$\n\\varphi^{\\prime}(t)=g^{\\prime}(\\beta+t)-g^{\\prime}(\\gamma-t) \\leqslant 0\n$$\n\npuisque $0<\\gamma-t \\leqslant \\beta+t \\leqslant x_{0}$. Donc $\\varphi(0) \\geqslant \\varphi\\left(x_{0}-\\beta\\right)$, ce qui s'écrit $g(\\beta)+g(\\gamma) \\geqslant g\\left(\\beta^{\\prime}\\right)+g\\left(\\gamma^{\\prime}\\right)$ où $\\beta^{\\prime}=x_{0}$ et $\\gamma^{\\prime}=\\gamma-\\left(x_{0}-\\beta\\right)$. On est ainsi ramenés au premier cas.\n\n$\\mathcal{F i n}$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi4-corrige.jsonl", "problem_match": "\nExercice 9.", "solution_match": "## Solution."}}
diff --git a/French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl b/French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..72163109ba7fe6a2f987f1fa9c9360c0ce0b4b32
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl
@@ -0,0 +1,21 @@
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Prouver que l'équation\n\n$$\na^{3}+b^{5}+c^{7}+d^{11}=e^{13}\n$$\n\nadmet une infinité de", "solution": "s en entiers strictement positifs.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution"}}
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Prouver que l'équation\n\n$$\na^{3}+b^{5}+c^{7}+d^{11}=e^{13}\n$$\n\nadmet une infinité de", "solution": "Il convient de remarquer que si ( $a, b, c, d, e$ ) est une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Prouver que l'équation\n\n$$\na^{3}+b^{5}+c^{7}+d^{11}=e^{13}\n$$\n\nadmet une infinité de", "solution": "alors, pour tout entier $k>0$, le quintuplet\n\n$$\n\\left(a k^{5 \\times 7 \\times 11 \\times 13}, \\mathrm{bk}^{3 \\times 7 \\times 11 \\times 13}, \\mathrm{ck}^{3 \\times 5 \\times 11 \\times 13}, \\mathrm{dk}^{3 \\times 5 \\times 7 \\times 13}, e k^{3 \\times 5 \\times 7 \\times 11}\\right)\n$$\n\nen est une aussi.\nPour conclure, il suffit donc de trouver une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Prouver que l'équation\n\n$$\na^{3}+b^{5}+c^{7}+d^{11}=e^{13}\n$$\n\nadmet une infinité de", "solution": "On peut penser à en trouver une telle que\n\n$$\na^{3}=b^{5}=c^{7}=d^{11}=\\frac{1}{4} e^{13}\n$$\n\noù $e=2^{\\mathrm{t}}$ pour un certain t à déterminer. Pour cela, t doit être choisi de sorte que $13 \\mathrm{t}-2$ soit multiple commun de $3,5,7,11$ et 11 . En cherchant un peu, on voit que l'on peut prendre $13 \\mathbf{t}-2=3 \\times 5 \\times 7 \\times 11$, ou encore $\\mathrm{t}=89$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Prouver que, pour tous entiers strictement positifs a, b, c, d, on a\n\n$$\n(2 a-1)(2 b-1)(2 c-1)(2 d-1) \\geqslant 2 a b c d-1\n$$\n\net déterminer les cas d'égalité.", "solution": "Si $x$ et $y$ sont des entiers strictement positifs, on a $x \\geqslant 1$ et $y \\geqslant 1$, et ainsi $(x-1)(y-1) \\geqslant 0$. Cela conduit à $x y-x-y+1 \\geqslant 0$, et donc à $(2 x-1)(2 y-1) \\geqslant 2 x y-1$. Notons que l'égalité a lieu si et seulement si $x=1$ ou $y=1$.\n\nSi $a, b, c, d$ sont des entiers strictement positifs, on a donc $(2 a-1)(2 b-1) \\geqslant 2 a b-1$ et $(2 c-$ 1) $(2 \\mathrm{~d}-1) \\geqslant 2 \\mathrm{~cd}-1$, mais aussi $(2 a b-1)(2 c d-1) \\geqslant 2 a b c d-1$. Ainsi :\n\n$$\n(2 a-1)(2 b-1)(2 c-1)(2 d-1) \\geqslant(2 a b-1)(2 c d-1) \\geqslant 2 a b c d-1\n$$\n\nD'après ci-dessus, l'égalité a lieu si et seulement si trois des nombres $\\mathrm{a}, \\mathrm{b}, \\mathrm{c}, \\mathrm{d}$ sont égaux à 1 .\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).\n\nProuver que la droite (BP) passe par le milieu de [AL].", "solution": "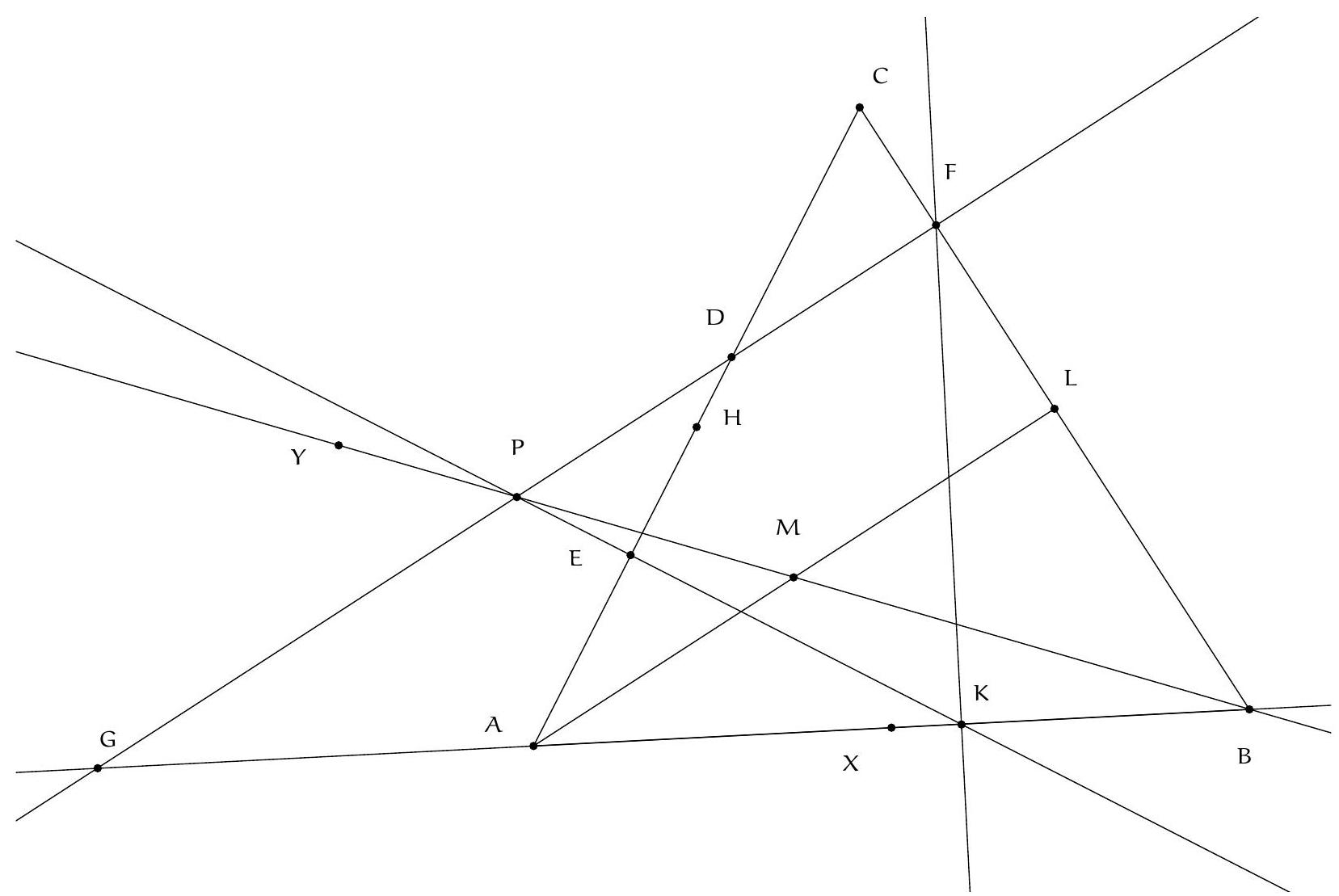\n\nPremière", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).\n\nProuver que la droite (BP) passe par le milieu de [AL].", "solution": "Comme les côtés de PKF sont perpendiculaires aux côtés de ABC , le triangle PKF a les mêmes angles intérieurs que $A B C$ et est donc équilatéral, et donc $P F=K F$.\n\nNotons $M$ l'intersection de (BP) et ( $A L$ ). Comme les triangles BLM et BFP sont semblables, on a\n\n$$\n\\frac{M L}{B L}=\\frac{P F}{B F}=\\frac{\\mathrm{KF}}{B F}=\\sin 60^{\\circ}=\\frac{\\sqrt{3}}{2}\n$$\n\nD'autre part, $\\frac{A L}{B L}=\\tan 60^{\\circ}=\\sqrt{3}$, donc $A L=2 M L$, ce qui prouve que $M$ est le milieu de [AL].\nDeuxième", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).\n\nProuver que la droite (BP) passe par le milieu de [AL].", "solution": "Posons que les côtés de $A B C$ soient de longueur 2 , et que $A D=2 a$ avec $a \\in$ $[0,1]$. On en déduit que $\\mathrm{DC}=2-2 \\mathrm{a}, \\mathrm{FC}=\\mathrm{DC} \\cos \\left(60^{\\circ}\\right)=1-\\mathrm{a}$, et $\\mathrm{BF}=1+\\mathrm{a}$ Par suite, on a\n\n$$\n\\mathrm{BK}=\\mathrm{BF} \\cos \\left(60^{\\circ}\\right)=\\frac{1+\\mathrm{a}}{2} \\quad \\text { et } \\quad \\mathrm{KF}=\\mathrm{BF} \\sin \\left(60^{\\circ}\\right)=\\frac{\\sqrt{3}}{2}(1+\\mathrm{a})\n$$\n\nPuisque les côtés de PKF sont perpendiculaires aux côtés de $A B C$, le triangle $P K F$ a les mêmes angles intérieurs que $A B C$ et est donc équilatéral. On a alors $P F=K F=\\frac{\\sqrt{3}}{2}(1+a)$.\n\nLe point $L$ étant le milieu de $[B C]$ avec $A B C$ équilatéral, les droites $(A L)$ et $(B C)$ sont donc perpendiculaires, ce qui assure que ( $M L$ ) et ( PF ) sont parallèles, où $M$ est l'intersection de ( $B P$ ) et ( $A L$ ). D'après le théorème de Thalès, il vient alors\n\n$$\n\\frac{\\mathrm{ML}}{\\mathrm{PF}}=\\frac{\\mathrm{BL}}{\\mathrm{BF}}=\\frac{1}{1+\\mathrm{a}}\n$$\n\nd'où $M L=\\frac{\\sqrt{3}}{2}=\\frac{1}{2} A L$, ce qui conclut.\nTroisième", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).\n\nProuver que la droite (BP) passe par le milieu de [AL].", "solution": "Comme ci-dessus, on remarque que PKF est équilatéral, et on note M l'intersection de (BP) et (AL). Soit Q l'intersection de (FP) et ( AB ). On a $\\widehat{\\mathrm{PKQ}}=\\widehat{\\mathrm{PQK}}=30^{\\circ}$, donc PQK est isocèle en $P$ et on a $P Q=P K$. Mais, $P K=K F$ puisque $P K F$ est équilatéral, donc $P Q=K F$ ce qui assure que $P$ est le milieu de [QF]. Ayant leurs côtés communs ou parallèles, les triangles BPQ et BMA d'une part, et les triangles BPF et BML d'autre part, sont semblables. Cela conduit à\n\n$$\n\\frac{P Q}{A M}=\\frac{P M}{B M} \\quad \\text { et } \\quad \\frac{P F}{M L}=\\frac{P M}{B M}\n$$\n\nd'où $\\frac{A M}{M L}=\\frac{P Q}{P F}=1$, et $M$ est bien le milieu de $[A L]$.\nQuatrième", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).\n\nProuver que la droite (BP) passe par le milieu de [AL].", "solution": "Soit $X$ le milieu de $[A B]$ et $Y$ tel que $A L C Y$ soit un rectangle. Alors $X C=A L=$ $C Y$ et $\\widehat{Y C X}=60^{\\circ}$, donc $X C Y$ est équilatéral. Deux de ses côtés étant perpendicualires à deux des côtés du triangle équilatéral $A B C$, il en est de même de son troisième côté. Soit $M$ l'intersection de (AL) et (BY). Puisque $(A L)$ et $(C Y)$ sont parallèles et que $B C=2 B L$, on a $A L=C Y=2 M L$, d'où $M$ est le milieu de [AL]. Comme ci-dessus, on remarque que KFP est équilatéral car ses côtés sont perpendiculaires à ceux de $A B C$. Or, il en est de même de $X Y C$, donc les triangles KFP et $X C Y$ ont leurs côtés parallèles. Puisque les points $B, F, C$ d'une part, et $B, K, X$ d'autre part sont alignés, il existe donc une homothétie de centre B qui envoie $X C Y$ sur KFP. En particulier, le point $P$ appartient à la droite (BY) qui passe par le milieu de [AL].\n\n## Exercices Communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C D$ un quadrilatère convexe. Pour tout point $M$ à l'intérieur ou sur le bord de $A B C D$, on pose\n\n$$\nf(M)=M A+M B+M C+M D .\n$$\n\nProuver que, pour tout $M$, on a\n\n$$\nf(M) \\leqslant \\max (f(A), f(B), f(C), f(D))\n$$", "solution": "Lemme. Si le point K est sur les bords ou à l'intérieur du triangle XYZ , on a\n\n$$\nX Y+X Z \\geqslant K Y+K Z .\n$$\n\nPreuve du lemme. Si $\\mathrm{K}=\\mathrm{Y}$, le résultat est immédiat d'après l'inégalité triangulaire. Sinon, on note P l'intersection de (YK) avec le côté [XZ]. D'après l'inégalité triangulaire, on a alors\n\n$$\nX Y+X Z=X Y+X P+P Z \\geqslant Y P+P Z=Y K+K P+P Z \\geqslant Y K+K Z .\n$$\n\nRevenons à l'exercice, et considérons un point $M$ à l'intérieur ou sur le bord du quadrilatère convexe $A B C D$. On va commencer par prouver que l'on peut trouver un point $P$ du bord de $A B C D$ tel que $f(M) \\leqslant f(P)$. Les diagonales $[A C]$ et $[B D]$ se coupent en $O$ et, sans perte de généralité, on peut supposer que $M$ est dans ou sur les bords du triangle $A D O$. Les droites ( $B M$ ) et ( $C M$ ) recoupent alors le côté [AD] respectivement en $X$ et $Y$. Soit $P$ un point de $[X Y]$. D'après le lemme, puisque $M$ est dans ou sur les bords du triangle BDP, on a $P B+P D \\geqslant M B+M D$. Et, puisque $M$ est dans ou sur les bords du triangle $C A P$, on a $P A+P C \\geqslant M A+M C$. En sommant, il vient $f(M) \\leqslant f(P)$, avec $P \\in[A D]$ comme désiré.\n\nToujours avec le point $P \\in[A D]$ ci-dessus, on montre maintenant que $f(P) \\leqslant f(A)$ ou $f(P) \\leqslant$ $f(D)$, ce qui terminera la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C D$ un quadrilatère convexe. Pour tout point $M$ à l'intérieur ou sur le bord de $A B C D$, on pose\n\n$$\nf(M)=M A+M B+M C+M D .\n$$\n\nProuver que, pour tout $M$, on a\n\n$$\nf(M) \\leqslant \\max (f(A), f(B), f(C), f(D))\n$$", "solution": "En effet, puisque $P \\in[A D]$, on a $P A+P D=A D$. On veut maximiser $\\mathrm{PB}+\\mathrm{PC}$. Pour cela, on construit le symétrique $\\mathrm{B}^{\\prime}$ de B par rapport à ( $A D$ ). On a donc $P B+P C=P B^{\\prime}+P C$. De plus, puisque $A B C D$ est convexe, selon que la droite ( $B^{\\prime} C$ ) rencontre ( $A D$ ) en un point de $[A D]$ ou non, le point $P$ est sur dans ou sur les bords de $A B^{\\prime} C$ ou de $D^{\\prime} C$. D'après le lemme, on a alors $\\mathrm{PB}^{\\prime}+P C \\leqslant A B^{\\prime}+A C=A B+A C$ ou $P B^{\\prime}+P C \\leqslant B^{\\prime}+D C=D B+D C$. Ainsi, on a\n\n$$\nf(P)=P A+P D+P B+P C \\leqslant A D+A B+A C=f(A)\n$$\n\nou\n\n$$\nf(P)=P A+P D+P B+P C \\leqslant A D+D B+D C=f(D),\n$$\n\ncomme annoncé.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 4.", "solution_match": " démonstration."}}
+{"year": "2013", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "On considère une grille carrée de $4 \\times 4$ cases.\n\nDeux cases distinctes ayant un côté commun sont dites voisines. Initialement, toutes les cases sont rouges. Par la suite, une case pourra éventuellement changer de couleur et être soit rouge soit bleue. Effectuer une opération sur la case c signifie que l'on change simultanément la couleur de c ainsi que celles de toutes ses voisines (les cases rouges deviennent bleues et les cases bleues deviennent rouges).\n\nDonner toutes les valeurs de $n$ pour lesquelles il existe un groupe de $n$ cases distinctes telles qu'après avoir effectué une opération sur chacune de ces n cases, on obtienne une grille entièrement bleue.", "solution": "Regroupons les cases de la grille en quatre tuiles, contenant chacune une case marquée, comme indiqué dans la figure suivante :\n\n\nIl est facile de vérifier qu'une opération quelconque change la couleur d'une et une seule de ces cases marquées et qu'une opération effectuée dans une tuile ne modifie pas la couleur des cases marquées des autres tuiles. Si l'on veut rendre la grille entièrement bleue, il faut donc que, dans chaque tuile, le nombre d'opérations effectuées soit impair. La somme de quatre nombres impairs étant paire, cela signifie que le nombre total n d'opérations doit être pair. De plus, puisque dans chaque tuile il y a quatre cases et que les opérations doivent être effectuées sur des cases distinctes, c'est que dans chaque tuile on a fait une ou trois opérations. Par suite, on a $4 \\leqslant n \\leqslant 12$.\n\nLes seules valeurs de $n$ possibles sont donc $n=4,6,8,10,12$. Il reste à prouver que ces cinq valeurs sont bien des", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "## Exercice 5.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "On considère une grille carrée de $4 \\times 4$ cases.\n\nDeux cases distinctes ayant un côté commun sont dites voisines. Initialement, toutes les cases sont rouges. Par la suite, une case pourra éventuellement changer de couleur et être soit rouge soit bleue. Effectuer une opération sur la case c signifie que l'on change simultanément la couleur de c ainsi que celles de toutes ses voisines (les cases rouges deviennent bleues et les cases bleues deviennent rouges).\n\nDonner toutes les valeurs de $n$ pour lesquelles il existe un groupe de $n$ cases distinctes telles qu'après avoir effectué une opération sur chacune de ces n cases, on obtienne une grille entièrement bleue.", "solution": "s. Pour cela, on pourra se reporter à la figure ci-dessus et ses quatre cases marquées et au figures ci-dessous (les points indiquent les cases sur lesquelles on effectue une opération).\n\n\n## Remarques.\n\nPlus généralement, on considère un graphe simple non orienté d'ordre $k$ dont chaque sommet a deux états possibles, rouge ou bleu, et on dispose d'une opération qui revient à changer simutanément l'état d'un sommet et celui de chacun de ses voisins (ici, les sommets sont les cases, deux reliées par une arête si et seulement si elles ont un côté en commun). On note que :\n\n- l'ordre dans lequel sont effectuées les opérations n'a pas d'importance,\n- si on effectue deux opérations sur un même sommet, cela revient à ne rien faire du tout. Par suite, on pourra toujours supposer qu'un sommet n'est concerné que par au plus une opération.\n\nOn dispose alors des deux théorèmes suivants :\n\n## Théorème 1.\n\nPour tout graphe fini simple et non orienté, à partir d'une configuration où tous les sommets sont rouges, il existe un ensemble de sommets $E$ tel qu'en effectuant une opération sur chaque sommet de $E$, tous les sommets soient bleus.\n\nPreuve.\nOn raisonne par récurrence sur le nombre $k$ de sommets, et on suppose directement le résultat vrai pour tout graphe de $k$ sommets. Pour un graphe d'ordre $k+1$, puisque chaque sommet peut-être soit rouge soit bleu, il y a donc $2^{k+1}$ états globaux possibles (il n'est pas ici supposé qu'ils soient tous accessibles par le jeu des opérations). De même, puisque chaque opération peut être effectuée ou non, il a $2^{k+1}$ ensembles possibles de sommets sur lesquels effectuer les opérations.\n\nRaisonnons par l'absurde en supposant qu'il soit impossible d'atteindre l'état où tous les sommets sont bleus. C'est donc qu'il existe deux ensembles de sommets, disons $T_{1}$ et $T_{2}$, distincts et qui conduisent au même état final. Il est alors facile de vérifier que l'ensemble $S=T_{1} \\Delta T_{2}$ (la différence symétrique) est un ensemble non vide de sommets pour lequel effectuer une opération sur chaque sommet de $S$ ne change pas l'état global de la configuration. En particulier, chaque sommet $L$ de $S$ doit être reliée à un nombre impair de sommets de $S$ (hors elle-même). Or, il est bien connu que, dans tout graphe simple non orienté, la somme des degrés est paire (c'est le double du nombre d'arêtes). En considérant le sous-graphe formé uniquement des sommets de $S$, on en déduit que $|S|$ est pair.\n\nPar ailleurs, puisque chaque sommet du graphe initial qui n'est pas dans $S$ doit être relié à un nombre pair de sommets de $S$, effectuer n'importe quelle opération ne change pas la parité du nombre de sommets de $S$ qui sont rouges. Fixons maintenant un sommet L dans $S$. D'après l'hypothèse de récurrence, il est possible de rendre tous les sommets bleus sauf L, qui lui se doit de rester rouge sans quoi tous les sommets seraient bleus, en contradiction avec notre hypothèse. Mais alors, entre l'état initial et l'état final, la parité du nombre de sommets de $S$ qui sont bleus n'est pas conservée, ce qui fournit la contradiction attendue.\n\n## Théorème 2.\n\nDans les conditions du théorème 1 , si deux suites d'opérations $S$ et $S^{\\prime}$ permettent chacune de rendre tous les sommets bleus, alors $|S|=\\left|S^{\\prime}\\right| \\bmod [2]$, où $|s|$ désigne le nombre d'opérations effectuées dans la suite $s$.\n\n## Preuve.\n\nComme précédemment, sans perte de généralité, on peut supposer qu'au plus une opération est effectuée par sommet (cela ne change pas la parité totale). Du coup, on peut raisonner sur l'ensemble des sommets concernés.\n\nOn reprend les notations de la preuve précédente, et on prouve un peu plus que souhaité en remarquant que si deux ensembles de sommets $\\mathrm{T}_{1}$ et $\\mathrm{T}_{2}$ distincts conduisent à un même état final (pas forcément celui où tous les sommets sont bleus), alors on a toujours $|S|$ est pair. Et, puisque $|S|=\\left|T_{1}\\right|+\\left|T_{2}\\right|-2\\left|T_{1} \\cap T_{2}\\right|$, on a directement $\\left|T_{1}\\right|=\\left|T_{2}\\right| \\bmod [2]$.\n\nOn retrouve évidemment les résultats démontrés dans le cas particulier de l'exercice.\nDéterminer la parité commune des suites d'opérations qui rendent l'ensemble des sommets bleus dépend de la strucure du graphe, pas seulement du nombre de sommets etc... et il ne semble pas qu'il soit connu de résultat simple et général.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "## Exercice 5.", "solution_match": " solution"}}
+{"year": "2013", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Pour tout entier $n \\geqslant 1$, on pose $S_{n}=x_{1}+x_{2}+\\cdots+x_{n}$, où $x_{k}=\\frac{k(k+1)}{2}$ pour tout $k \\geqslant 1$. Prouver que, pour tout $n \\geqslant 10$, il existe un entier $a_{n}$ tel que $S_{n-1}1$, car alors l'intervalle $] S_{n-1}, S_{n}[$ contiendra forcément un entier.\n\nOr, d'après le calcul ci-dessus, l'inégalité $\\sqrt{S_{n}}-\\sqrt{S_{n-1}}>1$ est équivalente à\n\n$$\n\\sqrt{\\frac{n(n+1)(n+2)}{6}}-\\sqrt{\\frac{n(n+1)(n-1)}{6}}>1\n$$\n\nou encore\n\n$$\n\\sqrt{\\frac{n(n+1)}{6}}(\\sqrt{n+2}-\\sqrt{n-1})>1\n$$\n\nPuisque\n\n$$\n\\sqrt{n+2}-\\sqrt{n-1}=\\frac{3}{\\sqrt{n+2}+\\sqrt{n-1}}\n$$\n\non veut prouver que\n\n$$\n\\sqrt{3 n(n+1)}>\\sqrt{2(n+2)}+\\sqrt{2(n-1)}\n$$\n\nPour cela, il suffit de montrer que $\\sqrt{3 n(n+1)}>2 \\sqrt{2(n+2)}$. Cette dernière inégalité s'écrit aussi $3 n^{2}-5 n-16>0$. Il est facile de vérifier qu'elle est satisfaite pour $n \\geqslant 10$.\n\n\n## Exercices Olympiques", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "On considère un ensemble fini E de garçons et de filles.\nUne partie G de garçons de E est dite populaire si chaque fille de E connaît au moins un des garçons de $G$. De même, une partie $F$ de filles est dite populaire si chaque garçon de $E$ connaît au moins une des filles de $F$. On suppose que si a connaît $b$ alors $b$ connaît $a$.\n\nProuver que le nombre de parties populaires formées par les garçons a la même parité que le nombre de parties populaires formées par les filles.", "solution": "Première", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "On considère un ensemble fini E de garçons et de filles.\nUne partie G de garçons de E est dite populaire si chaque fille de E connaît au moins un des garçons de $G$. De même, une partie $F$ de filles est dite populaire si chaque garçon de $E$ connaît au moins une des filles de $F$. On suppose que si a connaît $b$ alors $b$ connaît $a$.\n\nProuver que le nombre de parties populaires formées par les garçons a la même parité que le nombre de parties populaires formées par les filles.", "solution": "On dira qu'un ensemble X de garçons est étranger à un groupe Y de filles si aucun garçon de X n'est connu d'une des filles de Y . De même, un ensemble Y de filles sera dit étranger à un groupe $X$ de garçons si aucune fille de $Y$ n'est connue d'un des garçons de $X$. Puisque la relation 'se connaître\" est supposée symétrique, on en déduit que $X$ est étranger à $Y$ si et seulement si $Y$ est étranger à $X$. Cela ouvre la porte à un double-comptage :\n\nOn note $N$ le nombre de couples $(X, Y)$ de groupes $X$ de garçons et $Y$ de filles mutuellement étrangers. Soit $X$ un groupe de garçons. On note $Y_{X}$ le plus grand groupe de filles qui soit étranger à $X$. Clairement, tout groupe $Y$ de filles qui est étranger à $X$ est contenu dans $Y_{X}$ et, réciproquement, tout sous-ensemble de $Y_{X}$ est étranger à $X$. Par suite, le nombre de groupes $Y$ qui sont étrangers à $X$ est $2^{\\left|{ }^{\\mid}\\right|} \\mid$(où $|A|$ désigne le nombre déléments de l'ensemble $\\mathcal{A}$ ). On en déduit que\n\n$$\nN=\\sum_{X} 2^{\\left|Y_{X}\\right|}\n$$\n\nOr, pour tout groupe $X$ de garçons, on a $X$ populaire si et seulement si $Y_{X}=\\emptyset$, c.à.d. $2^{\\left|Y_{X}\\right|}=1$. Ainsi, le nombre de groupes populaires de garçons est congru à N modulo 2 .\n\nUn raisonnement analogue montre que le nombre de groupes populaires de filles est lui aussi congru à N modulo 2 , ce qui conclut.\n\nDeuxième", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "On considère un ensemble fini E de garçons et de filles.\nUne partie G de garçons de E est dite populaire si chaque fille de E connaît au moins un des garçons de $G$. De même, une partie $F$ de filles est dite populaire si chaque garçon de $E$ connaît au moins une des filles de $F$. On suppose que si a connaît $b$ alors $b$ connaît $a$.\n\nProuver que le nombre de parties populaires formées par les garçons a la même parité que le nombre de parties populaires formées par les filles.", "solution": "Soit G l'ensemble des garçons et F celui des filles. Nous allons prouver le résultat par récurrence sur $\\mathrm{n}=|\\mathrm{G}|$. On note tout d'abord que si F ou G est vide, la conclusion est immédiate (il n'existe aucun groupe populaire). Cela assure le résultat pour $\\mathrm{n}=0,1$ et on considère maintenant un groupe de $\\mathrm{n}+1 \\geqslant 2$ personnes dans lequel il y a au moins une fille et au moins un garçon.\n\nSoit $g$ un des garçons. On pose $\\mathrm{G}^{\\prime}=\\mathrm{G}-\\{\\mathrm{g}\\}$ et $\\mathrm{F}^{\\prime}$ l'ensemble des filles qui ne connaissent pas $g$. Alors :\n\n- un groupe populaire de garçons dans $G^{\\prime} \\cup F$ l'est encore dans $G \\cup F$,\n- un groupe populaire de garçons dans $G \\cup F$ qui ne l'est plus dans $G^{\\prime} \\cup F$ est la réunion d'un groupe populaire de garçons dans $G^{\\prime} \\cup F^{\\prime}$ et de $\\{g\\}$.\n\nIl en découle que le nombre $N(G, F)$ de groupes populaires de garçons dans $G \\cup F$ est la somme du nombre $N\\left(G^{\\prime}, F\\right)$ de groupes populaires de garçons dans $G^{\\prime} \\cup F$ et du nombre $N\\left(G^{\\prime}, F^{\\prime}\\right)$ de groupes populaires de garçons dans $G^{\\prime} \\cup F^{\\prime}$, soit donc $N(G, F)=N\\left(G^{\\prime}, F\\right)+N\\left(G^{\\prime}, F^{\\prime}\\right)$.\n\nD'autre part :\n\n- un groupe populaire de filles dans $G \\cup F l^{\\prime}$ est encore dans $G^{\\prime} \\cup F$,\n- un groupe populaire de filles dans $G^{\\prime} \\cup F$ qui ne l'est plus dans $G \\cup F$ est un groupe populaire de filles dans $G^{\\prime} \\cup F^{\\prime}$.\n\nPar conséquent, le nombre $M(G, F)$ de groupes populaires de filles dans $G \\cup F$ est la différence entre le nombre $M\\left(G^{\\prime}, F\\right)$ de groupes populaires de filles dans $G^{\\prime} \\cup F$ et le nombre $M\\left(G^{\\prime}, F^{\\prime}\\right)$ de groupes populaires de filles dans $G^{\\prime} \\cup F^{\\prime}$, soit donc $M(G, F)=M\\left(G^{\\prime}, F\\right)-M\\left(G^{\\prime}, F^{\\prime}\\right)$.\n\nOr, d'après l'hypothèse de récurrence, on a $N\\left(G^{\\prime}, F\\right)=M\\left(G^{\\prime}, F\\right) \\bmod [2]$ et $N\\left(G^{\\prime}, F^{\\prime}\\right)=M\\left(G^{\\prime}, F^{\\prime}\\right)=$ $-M\\left(G^{\\prime}, F^{\\prime}\\right) \\bmod [2]$, d'où $N(F, G)=M(F, G) \\bmod [2]$, ce qui achève la récurrence.\n\nTroisième", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "On considère un ensemble fini E de garçons et de filles.\nUne partie G de garçons de E est dite populaire si chaque fille de E connaît au moins un des garçons de $G$. De même, une partie $F$ de filles est dite populaire si chaque garçon de $E$ connaît au moins une des filles de $F$. On suppose que si a connaît $b$ alors $b$ connaît $a$.\n\nProuver que le nombre de parties populaires formées par les garçons a la même parité que le nombre de parties populaires formées par les filles.", "solution": "On note toujours respectivement F et G l'ensemble des filles et celui des garçons. Pour chaque fille $f$ et chaque garçon $g$, on pose $h(f, g)=0$ si $f$ et $g$ se connaissent, et $h(f, g)=1$ sinon. Alors, un ensemble $X$ de garçons est populaire si et seulement si $\\prod_{f \\in F}\\left(1-\\prod_{g \\in X} h(f, g)\\right)=1$. Par suite, le nombre N de groupes populaires de garçons est\n\n$$\n\\begin{aligned}\nN & =\\sum_{X \\subseteq G} \\prod_{f \\in F}\\left(1-\\prod_{g \\in X} h(f, g)\\right) \\\\\n& =\\sum_{X \\subseteq G} \\prod_{f \\in F}\\left(1+\\prod_{g \\in X} h(f, g)\\right) \\bmod 2 \\\\\n& =\\sum_{X \\subseteq G} \\sum_{Y \\subseteq F} \\prod_{g \\in X} \\prod_{f \\in Y} h(f, g) \\bmod 2 .\n\\end{aligned}\n$$\n\nOn a une égalité similaire pour le nombre $M$ de groupes populaires de filles, ce qui conclut.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi5-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": ". Pour tout entier $k \\geqslant 2$, on note $\\mathrm{P}(\\mathrm{k})$ le plus grand diviseur premier de $k$.\nProuver qu'il existe une infinité d'entiers $n$ tels que\n\n$$\n\\mathrm{P}(\\mathrm{n})<\\mathrm{P}(\\mathrm{n}+1)<\\mathrm{P}(\\mathrm{n}+2)\n$$", "solution": "Soit $p$ un nombre premier impair. Pour tout entier $k \\geqslant 1$, on note $n_{k}=p^{2^{k}}-1$. On a évidemment $\\mathrm{P}\\left(\\mathfrak{n}_{\\mathrm{k}}+1\\right)=\\mathrm{p}$. D'autre part, pour tout entier $i$ tel que $01$, il existe donc un nombre premier impair $q_{k}$ qui divise $n_{k}+2$ et aucun des $n_{i}+2$ pour $ip$.\n\nPour conclure, il reste à prouver que, pour ce choix de $k$, on a $P\\left(n_{k}\\right)0$, et que $B, M, N$ sont colinéaires. Déterminer la valeur de $r$.\n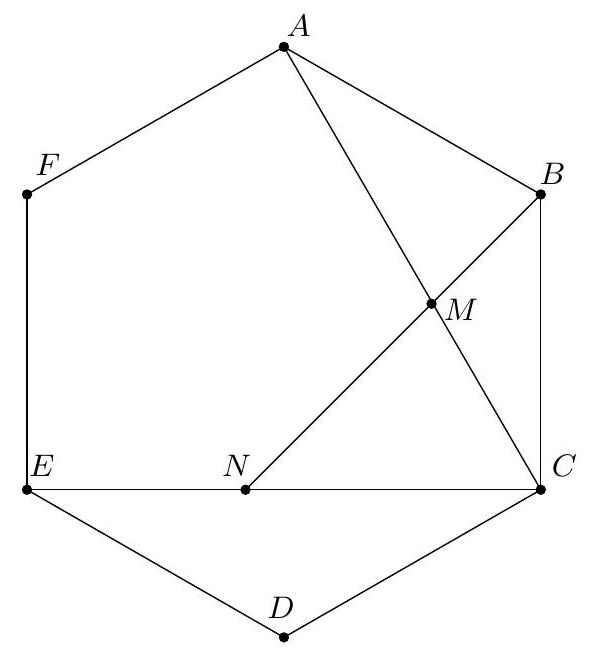", "solution": "On peut supposer que l'hexagone est inscrit dans un cercle de rayon 1. On se place dans un repère tel que les coordonnées de $A, B, C$ sont respectivement $A=(0,1), B=\\left(\\frac{\\sqrt{3}}{2}, \\frac{1}{2}\\right)$ et $C=\\left(\\frac{\\sqrt{3}}{2},-\\frac{1}{2}\\right)$.\n\nComme $C E=\\sqrt{3}$, on a $C N=r \\sqrt{3}$ donc $\\overrightarrow{C N}=(-r \\sqrt{3}, 0)$. On en déduit que\n\n$$\nN=\\left(\\frac{\\sqrt{3}}{2}-r \\sqrt{3},-\\frac{1}{2}\\right)\n$$\n\nComme $\\overrightarrow{A C}=\\left(\\frac{\\sqrt{3}}{2},-\\frac{3}{2}\\right)$, on a $\\overrightarrow{A M}=\\left(\\frac{\\sqrt{3}}{2} r,-\\frac{3 r}{2}\\right)$ donc\n\n$$\nM=\\left(\\frac{\\sqrt{3}}{2} r, 1-\\frac{3 r}{2}\\right)\n$$\n\nOn calcule aisément que\n\n$$\n\\overrightarrow{B M}=\\left(\\frac{\\sqrt{3}}{2}(r-1), \\frac{1}{2}-\\frac{3 r}{2}\\right), \\quad \\overrightarrow{B N}=(-r \\sqrt{3},-1)\n$$\n\nLe fait que $B, M, N$ sont alignés signifie que ces deux vecteurs sont colinéaires, ce qui équivaut à\n\n$$\n\\frac{\\sqrt{3}}{2}(1-r)+r \\sqrt{3}\\left(\\frac{1}{2}-\\frac{3 r}{2}\\right)=0\n$$\n\nce qui se simplifie en $r=\\frac{1}{\\sqrt{3}}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi6-corrige.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $A B C$ un triangle et $M$ un point de $[B, C]$. Soit $\\omega$ un cercle tangent à $(A B)$ en $T$ et à $(B C)$ en $K$ et tangent au cercle circonscrit à $A M C$ en $P$. Montrer que si $(K T) / /(A M)$ alors les cercles circonscrits à $K P C$ et $A P T$ sont tangents en $P$.", "solution": "\n\nRappelons d'abord que si $A, B, C$ sont trois points d'un cercle $\\Gamma$, et si $\\delta$ est la tangente en $B$ à $\\Gamma$, alors on a l'égalité d'angles de droites $(\\delta, B C)=(A B, A C)$.\n\nSoient $\\delta$ et $\\delta^{\\prime}$ les tangentes en $P$ aux cercles $(K P C)$ et $(A P T)$ respectivement. On a\n\n$$\n(\\delta, P K)=(C P, C K)=(C P, C M)=(A P, A M)\n$$\n\net\n\n$$\n\\begin{aligned}\n\\left(\\delta^{\\prime}, P K\\right) & =\\left(\\delta^{\\prime}, P T\\right)+(P T, P K)=(A P, A T)+(T B, T K) \\\\\n& =(A P, A M)+(A M, A T)+(T B, T K)=(A P, A M)\n\\end{aligned}\n$$\n\npuisque $(T B)=(A T)$ et $(A M)=(T K)$.\nOn en déduit que $\\delta$ et $\\delta^{\\prime}$ sont parallèles. Or, elles ont un point commun, donc elles sont égales.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi6-corrige.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution."}}
+{"year": "2013", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $\\omega_{1}$ et $\\omega_{2}$ deux cercles sécants en deux points $X$ et $Y$. Un cercle $\\omega$ est tangent intérieurement à $\\omega_{1}$ et $\\omega_{2}$ en $P$ et $Q$ respectivement. Le segment $[X, Y]$ coupe $\\omega$ en $M$ et $N$. Les demi-droites $[P, M)$ et $[P, N)$ coupent $\\omega_{1}$ en $A$ et $D$; les demi-droites $[Q, M)$ et $[Q, N)$ coupent $\\omega_{2}$ en $B$ et $C$. Montrer que $A B=C D$.\n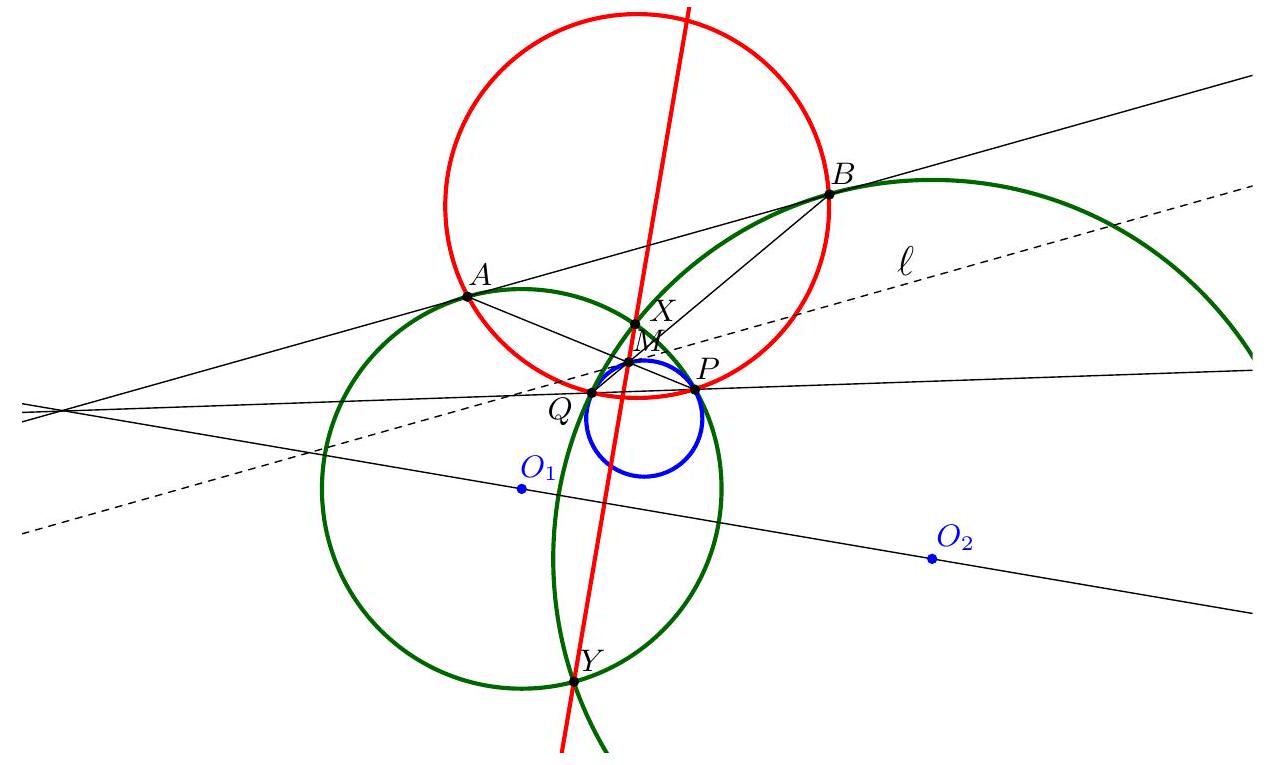\n\nSoit $\\ell$ la tangente en $M$ à $\\omega$ et $\\ell_{1}$ la tangente en $A$ à $\\omega_{1}$. Comme $\\omega$ est tangent en $P$ à $\\omega_{1}$, il existe une homothétie $h$ de centre $P$ qui envoie $\\omega \\operatorname{sur} \\omega_{1}$. Or, $P, M, A$ sont alignés donc $h(M)=A$. On en déduit que $h(\\ell)=\\ell_{1}$, et donc $\\ell / / \\ell_{1}$.\n\nD'autre part, comme $M$ est sur l'axe radical de $\\omega_{1}$ et $\\omega_{2}$, on a $\\overline{M A} \\cdot \\overline{M P}=$ $\\overline{M B} \\cdot \\overline{M Q}$ donc $A, B, P, Q$ sont cocycliques. On en déduit que\n\n$$\n(A B, A P)=(Q B, Q P)=(Q M, Q P)=(\\ell, M P)=\\left(\\ell_{1}, A P\\right)\n$$\n\nd'où $(A B)=\\ell_{1}$. Autrement dit, $(A B)$ est tangente en $A$ à $\\omega_{1}$. Mais de même, $(A B)$ est tangente en $B$ à $\\omega_{2}$, donc $(A B)$ est une tangente commune à $\\omega_{1}$ et $\\omega_{2}$. De même, $(C D)$ est une tangente commune à $\\omega_{1}$ et $\\omega_{2}$, donc $A B=C D$.\n\nExrtcice 9. Soit $A B C D$ un quadrilatère inscriptible. On note $K$ le point d'intersection des diagonales. Soient $M$ et $N$ les milieux de $[A, C]$ et $[B, D]$. Les cercles circonscrits à $A D M$ et $B C M$ se recoupent en un point $L$. Montrer que $K, L, M, N$ sont cocycliques.", "solution": "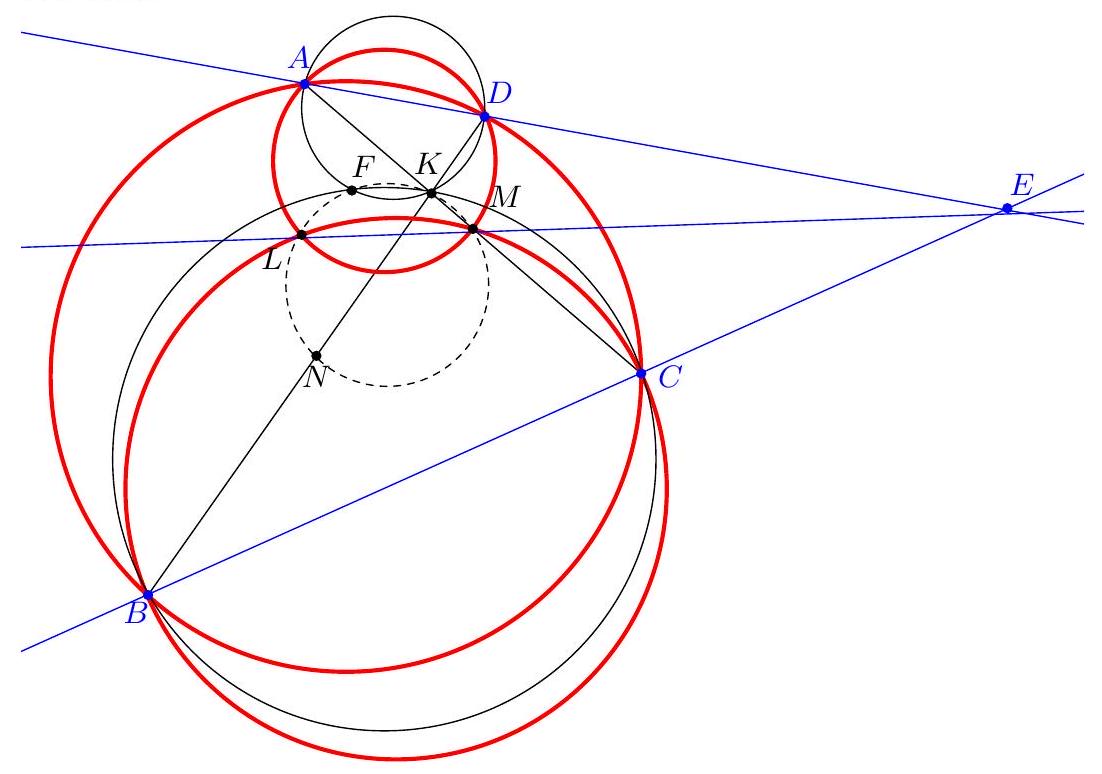\n\nNotons $E$ le centre radical des trois cercles $A B C, A D M, B C M$. Les triplets $(E, A, D),(E, L, M)$ et $(E, B, C)$ sont alignés.\n\nSoit $F$ le point où les cercles $A D K$ et $B C K$ se recoupent. On a $(F A, F D)=$ $(K A, K D)=(K C, K B)=(F C, F B)$ et $(A D, A F)=(K D, K F)=(K B, K F)=$ $(C B, C F)$, donc les triangles $F A D$ et $F C B$ sont semblables. Soit $s$ la similitude de centre $F$ qui envoie $A$ sur $D$ et $C$ sur $B$. Alors $s(M)=N$, donc l'angle de $s$ est à la fois égal à $(F M, F N)$ et à $(A C, D B)=(K M, K N)$. Par conséquent, $F, K, M, N$ sont cocycliques.\n$E$ est l'intersection de $(A D)$ et de $(B C)$, donc il est le centre radical des cercles $A B C D, A D K$ et $B C K$. Par conséquent, $E, F, K$ sont alignés. En utilisant la puissance d'un point par rapport à un cercle, on a\n\n$$\n\\overline{E K} \\cdot \\overline{E F}=\\overline{E A} \\cdot \\overline{E D}=\\overline{E B} \\cdot \\overline{E C}=\\overline{E M} \\cdot \\overline{E L},\n$$\n\ndonc $M, L, K, F$ sont cocycliques.\nFinalement, $L$ et $N$ sont sur le cercle $M K F$ donc $K, L, M, N$ sont cocycliques.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2012-2013-envoi6-corrige.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution."}}
diff --git a/French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl b/French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..185dc4727245728bff894d0bb940b9e760158bcc
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl
@@ -0,0 +1,12 @@
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soient $A, B, C, D$ quatre points sur un même cercle. Notons $A^{\\prime}$ et $C^{\\prime}$ les projetés orthogonaux de $A$ et $C$ sur $(B D)$, et $B^{\\prime}$ et $D^{\\prime}$ les projetés orthogonaux de $B$ et $D$ sur $(A C)$. Montrer que $A^{\\prime}, B^{\\prime}, C^{\\prime}, D^{\\prime}$ sont cocycliques.", "solution": "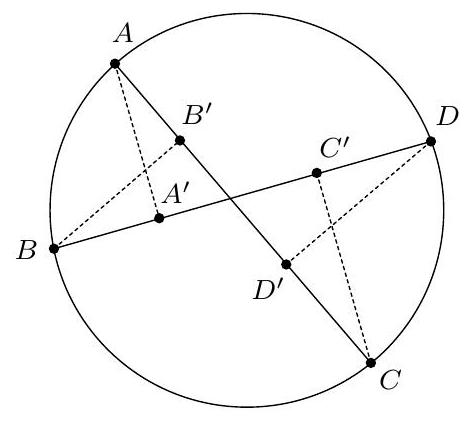\n\nComme $A, B, A^{\\prime}, B^{\\prime}$ sont cocycliques (sur le cercle de diamètre $[A B]$ ), les angles orientés de droites $\\left(B A^{\\prime}, B A\\right)$ et $\\left(B^{\\prime} A^{\\prime}, B^{\\prime} A\\right)$ sont égaux, donc $(B D, B A)=\\left(B^{\\prime} A^{\\prime}, B^{\\prime} D^{\\prime}\\right)$. De même, $(C D, C A)=\\left(C^{\\prime} A^{\\prime}, C^{\\prime} D^{\\prime}\\right)$. Or, $(C D, C A)=(B D, B A)$ puisque $A, B, C, D$ sont cocycliques, donc $\\left(B^{\\prime} A^{\\prime}, B^{\\prime} D^{\\prime}\\right)=\\left(C^{\\prime} A^{\\prime}, C^{\\prime} D^{\\prime}\\right)$, ce qui prouve que $A^{\\prime}, B^{\\prime}, C^{\\prime}, D^{\\prime}$ sont cocycliques.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "## Solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Sur la diagonale $[B D]$ d'un carré $A B C D$ on a choisi un point $E$. Soient $O_{1}$ et $O_{2}$ les centres des cercles circonscrits aux triangles $A B E$ et $A D E$ respectivement. Montrer que $A O_{1} E O_{2}$ est un carré.\n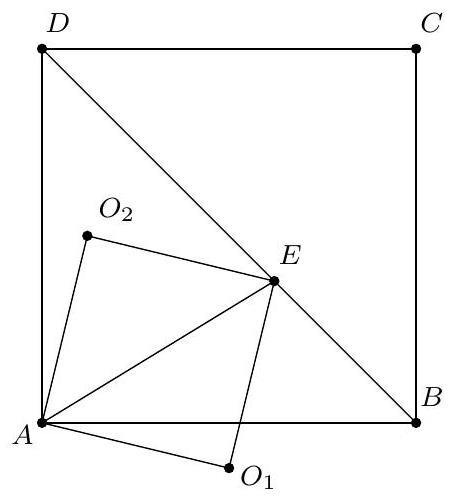", "solution": "$\\widehat{A O_{1} E}=2 \\widehat{A B E}=90^{\\circ}$ et $O_{1} A=O_{1} E$ donc $A O_{1} E$ est un triangle isocèle rectangle en $O_{1}$. De même, $A O_{2} E$ est un triangle isocèle rectangle en $O_{2}$.\n\nComme $O_{1}$ et $O_{2}$ ne sont pas dans le même demi-plan délimité par $(A E)$, on en déduit que $A O_{1} E O_{2}$ est un carré.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Un quadrilatère $A B C D$ est inscrit dans un cercle. Ses diagonales se coupent au point $K$. Le cercle passant par $A, B, K$ croise les droites $(B C)$ et $(A D)$ aux points $M$ et $N$ respectivement. Montrer que $K M=K N$.", "solution": "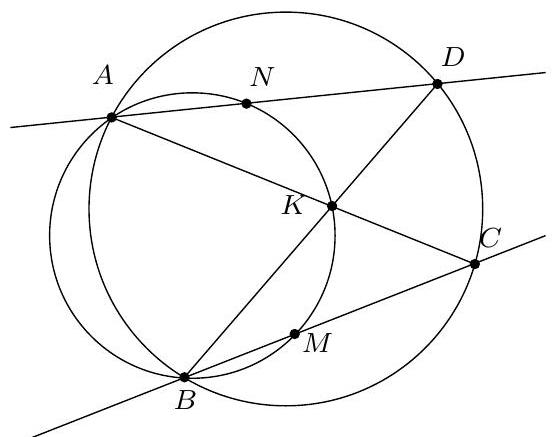\n\nOn a $(N M, N K)=(B M, B K)=(B C, B D)=(A C, A D)=(A K, A N)=(M K, M N)$ donc $M K N$ est isocèle en $K$.\n\n## Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C$ un triangle dont tous les angles sont aigus, et dont l'angle $\\widehat{B}$ est de 60 degrés ( $=\\pi / 3$ radian). Les hauteurs $[A D]$ et $[C E]$ se coupent au point $H$. Prouver que le centre du cercle circonscrit au triangle $A B C$ est situé sur la bissectrice commune des angles $\\widehat{A H E}$ et $\\widehat{C H D}$.\n", "solution": "Puisque $B, E, H, D$ sont sur le cercle de diamètre $[B H]$, on a $\\widehat{D H E}=180^{\\circ}-\\widehat{E B D}=$ $120^{\\circ}$, donc $\\widehat{A H C}=120^{\\circ}$. Comme $\\widehat{A O C}=2 \\widehat{A B C}=120^{\\circ}$, on en déduit que $A, C, O, H$ sont cocycliques.\n\nPar conséquent, $\\widehat{C H O}=\\widehat{C A O}=\\frac{1}{2}(\\widehat{C A O}+\\widehat{O C A})=\\frac{1}{2}\\left(180^{\\circ}-\\widehat{A O C}\\right)=90^{\\circ}-\\widehat{A B C}=$ $30^{\\circ}$.\n\nDe plus, comme $(C H) \\perp(A B)$ et $(A H) \\perp(B C)$, on a $\\widehat{C H D}=\\widehat{A B C}=60^{\\circ}$, donc $O$ est sur la bissectrice de $\\widehat{C H D}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "A l'extérieur du triangle $A B C$ on construit les deux points $X$ et $Y$ vérifiant :\n\n- le triangle $A X B$ est isocèle de base $[A B]$;\n- le triangle $B Y C$ est isocèle de base $[B C]$;\n$-\\widehat{A X B}+\\widehat{B Y C}=180^{\\circ}$.\nSoit $Z$ le milieu de $[A C]$. Montrer que les droites $(X Z)$ et $(Y Z)$ sont perpendiculaires.", "solution": "Notons $D$ et $E$ les milieux de $[B C]$ et $[A B]$.\n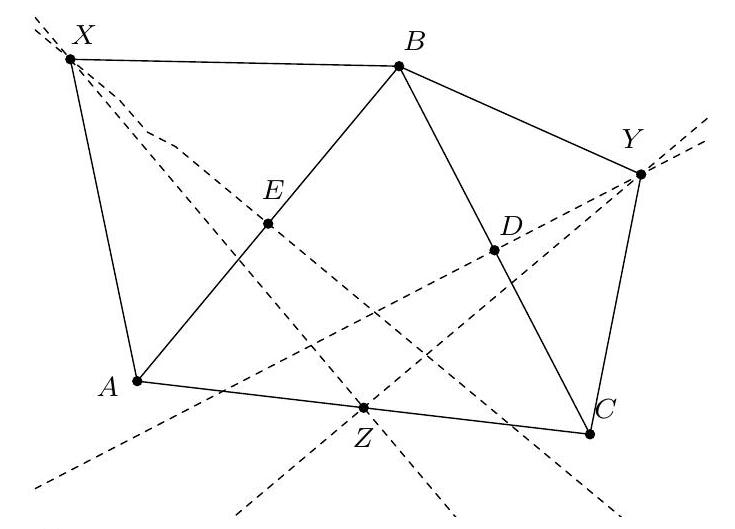\n\nOn a\n\n- $(X E) \\perp(D Z)$ car $(D Z) / /(A B)$\n- $(E Z) \\perp(D Y)$ car $(E Z) / /(B C)$\n- $\\frac{X E}{D Z}=\\frac{X E}{E A}=\\frac{C D}{D Y}=\\frac{E Z}{D Y}$ (la deuxième égalité provient du fait que les triangles rectangles $X E A$ et $C D Y$ sont semblables)\ndonc $X E Z$ et $Z D Y$ sont semblables. Comme $(X E) \\perp(D Z)$, on en déduit que $(X Z) \\perp$ $(Z Y)$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\n\nSolution."}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Le sommet $B$ d'un angle $\\widehat{A B C}$ se trouve à l'extérieur d'un cercle $\\omega$ tandis que les demi-droites $[B A)$ et $[B C)$ le traversent. Soit $K$ un point d'intersection du cercle $\\omega$ avec $[B A)$. La perpendiculaire à la bissectrice de l'angle $\\widehat{A B C}$ passant par $K$ recoupe le cercle au point $P$, et la droite $(B C)$ au point $M$. Montrer que le segment $[P M]$ est deux fois plus long que la distance entre le centre de $\\omega$ et la bissectrice de $\\widehat{A B C}$.", "solution": "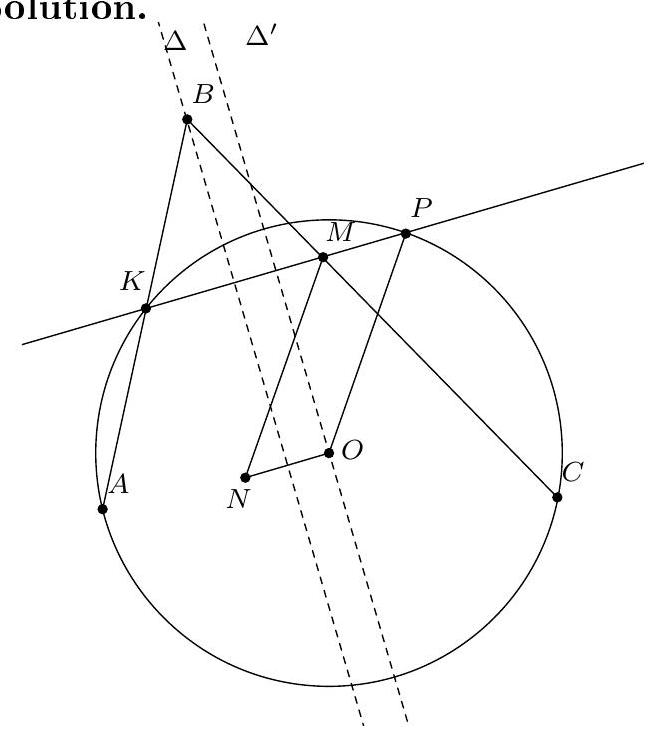\n\nSoit $O$ le centre du cercle $\\omega$. Notons $\\Delta$ la bissectrice de $\\widehat{A B C}, \\Delta^{\\prime}$ la parallèle à $\\Delta$ passant par $O$ et $N$ le symétrique de $O$ par rapport à $\\Delta$.\n\nLa symétrie $s_{\\Delta^{\\prime}}$ par rapport à $\\Delta^{\\prime}$ envoie $O$ sur $O$ et $P \\operatorname{sur} K\\left(\\operatorname{car}(P K) \\perp \\Delta^{\\prime}\\right.$ et $\\Delta^{\\prime}$ passe par $O$ ).\n\nLa symétrie $s_{\\Delta}$ par rapport à $\\Delta$ envoie $O$ sur $N$ et $K$ sur $M$.\nPar conséquent, la composée $s_{\\Delta} \\circ s_{\\Delta^{\\prime}}$ envoie $O$ sur $N$ et $P$ sur $M$. Or, $s_{\\Delta} \\circ s_{\\Delta}^{\\prime}$ est une translation, donc $M N O P$ est un parallélogramme. Il s'ensuit que $P M=O N=2 d(O, \\Delta)$.\n\n## Exercices groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## Solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $A B C D$ un quadrilatère convexe. On considère les deux quadrilatères convexes $F_{1}$ et $F_{2}$, dont chacun a deux sommets opposés qui sont les milieux des diagonales $[A C]$ et $[B D]$, et dont les deux autres sommets sont les milieux des côtés opposés du quadrilatère $A B C D$. Montrer que les aires de $F_{1}$ et de $F_{2}$ sont égales si et seulement si au moins l'une des diagonales du quadrilatère $A B C D$ le divise en triangles d'aires égales.", "solution": "Notons $I, J, K, L, M, N$ les milieux de $[A C],[B D],[A B],[B C],[C D]$ et $[D A]$.\n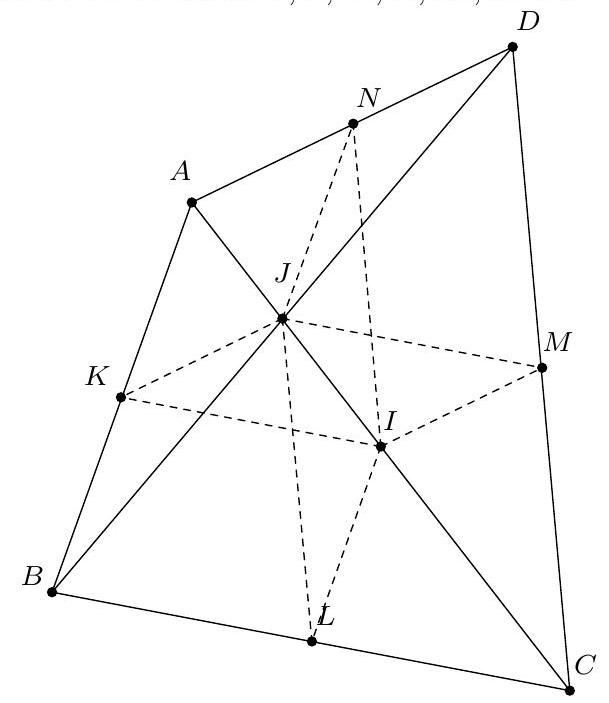\n\nOn remarque que $(I K)$ et $(J M)$ sont parallèles, puisqu'ils sont parallèles à $(B C)$. De même, $(I M) / /(J K)$. On en déduit que $I M J K$ est un parallélogramme, et de même $I N J L$ est un parallélogramme.\n\nNotons $[\\vec{u}, \\vec{v}]$ le produit mixte des vecteurs $\\vec{u}$ et $\\vec{v}$. C'est l'aire d'un parallélogramme $X Y Z T$ tel que $\\overrightarrow{X Y}=\\vec{u}$ et $\\overrightarrow{Y Z}=\\vec{v}$, affectée d'un signe + si $X Y Z T$ est parcouru dans le sens direct et d'un signe - sinon.\n\nOn vérifie facilement les propriétés suivantes:\n\n- $[\\vec{u}, \\vec{v}]=-[\\vec{v}, \\vec{u}]$\n- $[\\vec{u}, \\vec{v}+\\vec{w}]=[\\vec{u}, \\vec{v}]+[\\vec{u}, \\vec{w}]$\n- $[\\vec{v}+\\vec{w}, \\vec{u}]=[\\vec{v}, \\vec{u}]+[\\vec{w}, \\vec{u}]$.\n(La deuxième propriété dit que si un parallélogramme $P$ est la réunion de deux parallélogrammes $P_{1}$ et $P_{2}$ alors l'aire de $P$ est la somme des aires de $P_{1}$ et de $P_{2}$; la troisième propriété découle des deux précédentes.)\n\nComme $I K=B C / 2$ et $K J=A D / 2$, l'aire de $I M J K$ est égale à $\\pm \\frac{1}{4}[\\overrightarrow{A D}, \\overrightarrow{B C}]$ et de même l'aire de $I N J M$ est égale à $\\pm \\frac{1}{4}[\\overrightarrow{A B}, \\overrightarrow{C D}]$. On en déduit que les aires de $F_{1}$ et de $F_{2}$ sont égales si et seulement si\n\n$$\n[\\overrightarrow{A B}, \\overrightarrow{C D}]= \\pm[\\overrightarrow{A D}, \\overrightarrow{B C}]\n$$\n\nOn a\n\n$$\n\\begin{aligned}\n& {[\\overrightarrow{A B}, \\overrightarrow{C D}]=[\\overrightarrow{A D}, \\overrightarrow{B C}]} \\\\\n& \\quad \\Longleftrightarrow \\quad[\\overrightarrow{A B}, \\overrightarrow{A D}]-[\\overrightarrow{A B}, \\overrightarrow{A C}]=[\\overrightarrow{A D}, \\overrightarrow{A C}]-[\\overrightarrow{A D}, \\overrightarrow{A B}] \\\\\n& \\quad \\Longleftrightarrow \\quad[\\overrightarrow{A C}, \\overrightarrow{A B}]=[\\overrightarrow{A D}, \\overrightarrow{A C}] \\\\\n& \\\\\n& \\quad \\Longleftrightarrow \\quad(A C) \\text { partage le quadrilatère en deux parties d'aires égales. }\n\\end{aligned}\n$$\n\nDe même, $[\\overrightarrow{A B}, \\overrightarrow{C D}]=-[\\overrightarrow{A D}, \\overrightarrow{B C}]$ si et seulement $\\mathrm{si}(B D)$ partage le quadrilatère en deux parties d'aires égales.\n\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution."}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $A B C D$ un quadrilatère convexe. On considère les deux quadrilatères convexes $F_{1}$ et $F_{2}$, dont chacun a deux sommets opposés qui sont les milieux des diagonales $[A C]$ et $[B D]$, et dont les deux autres sommets sont les milieux des côtés opposés du quadrilatère $A B C D$. Montrer que les aires de $F_{1}$ et de $F_{2}$ sont égales si et seulement si au moins l'une des diagonales du quadrilatère $A B C D$ le divise en triangles d'aires égales.", "solution": "Comme ci-dessus, on remarque que $I M J K$ et que $I N J L$ sont des parallélogrammes.\n\nSi $(A D) / /(B C)$ on obtient que l'aire de $I M J K$ est égale à 0 . Alors l'aire de $I N J L$ est égale à 0 si et seulement si $(A B) / /(C D)$, ce qui équivaut à ce que les diagonales du quadrilatère $A B C D$ le divisent en triangles d'aires égales.\n\nOn se ramène donc à traiter le cas où $(A D)$ et $(B C)$ se croisent. De même, on peut supposer que $(A B)$ et $(C D)$ se croisent. Sans perte de généralité, on peut supposer qu'ils se croisent comment sur la figure : $X=[D A) \\cap[C B), Y=[B A) \\cap[C D)$.\n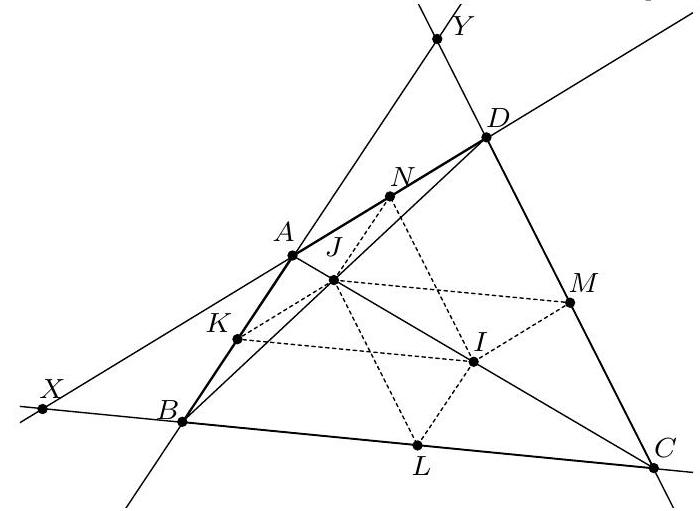\n\nL'aire de $I M J K$ est égale à\n\n$$\nK J \\cdot K I \\sin \\widehat{I K J}=\\frac{1}{4} B C \\cdot A D \\sin \\widehat{A X B}\n$$\n\nL'aire de $I N J L$ est égale à\n\n$$\nN J \\cdot N I \\sin \\widehat{J N I}=\\frac{1}{4} A B \\cdot C D \\sin \\widehat{A Y D}\n$$\n\nD'après la loi des sinus pour les triangles $A X B$ et $A Y D$, on a\n\n$$\n\\frac{\\sin \\widehat{A X B}}{\\sin \\widehat{A Y D}}=\\frac{A B \\sin \\widehat{X A B}}{B X} \\frac{D Y}{A D \\sin \\widehat{Y A D}}=\\frac{A B \\cdot D Y}{B X \\cdot A D}\n$$\n\nEn combinant (1), (2) et (3), on obtient que l'aire de $I M J K$ est égale à l'aire de $I N J L$ si et seulement si\n\n$$\n\\frac{C B}{B X}=\\frac{C D}{D Y}\n$$\n\nCette dernière égalité équivaut à dire que $(X Y) / /(B D)$.\nOn a que $(A C)$ divise $A B C D$ en triangles d'aires égales si et seulement si $J$ se trouve qur $(A C)$ (puisque l'aire de $A J B$ est égale à celle de $A J D$ et l'aire de $C J B$ est égale à celle de $C J D)$.\n\nIl ne reste plus qu'à noter que dans un quadrilatère $X B D Y$, la droite joignant $C=$ $(X B) \\cap(D Y)$ et $A=(X D) \\cap(B Y)$ passe par le milieu de $[B D]$ si et seulement si $(X Y)$ et $(B D)$ sont parallèles.\n\nEn effet, si $(X Y)$ et $(B D)$ sont parallèles, il existe une homothétie de centre $C$ qui envoie $B$ et $D$ sur $X$ et $Y$ respectivement. Cette homothétie envoie le milieu de $[B D]$ sur le milieu de $[X Y]$ donc ces deux milieux sont alignés avec $C$, et de même ils sont alignés avec $A$.\n\nRéciproquement, supposons que $(A C)$ passe par le milieu $U$ de $[B D]$. Soit $Y^{\\prime}$ le point d'intersection de $(C Y)$ avec la parallèle à $(B D)$ passant par $X$. Soit $A^{\\prime}=\\left(B Y^{\\prime}\\right) \\cap(D X)$.\n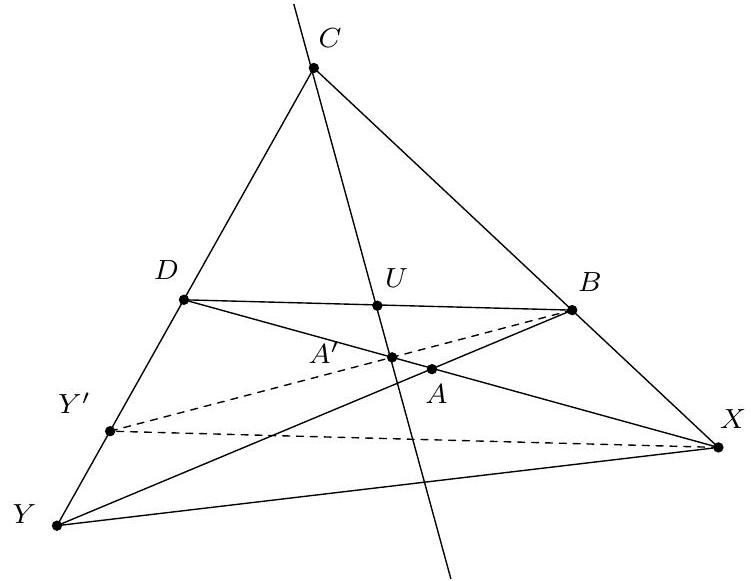\n\nD'après le paragraphe précédent, $C, A^{\\prime}$ et $U$ sont alignés, donc $A$ appartient à la droite $\\left(C A^{\\prime}\\right)$. De plus, $A$ appartient à $(D X)$, donc $A=\\left(C A^{\\prime}\\right) \\cap(D X)=A^{\\prime}$. On en déduit que $Y=Y^{\\prime}$, et que $X B D Y$ est un parallélogramme.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Le cercle $\\omega$ passe par les sommets $B$ et $C$ du triangle $A B C$ et coupe les côtés $[A B]$ et $[A C]$ aux points $D$ et $E$ respectivement. Les segments $[C D]$ et $[B E]$ se coupent en un point $O$. Soient $M$ et $N$ les centres des cercles inscrits dans les triangles $A D E$ et $O D E$ respectivement. Montrer que le milieu de l'arc $D E$ (le plus petit des deux arcs) du cercle $\\omega$ se trouve sur la droite ( $M N$ ).", "solution": "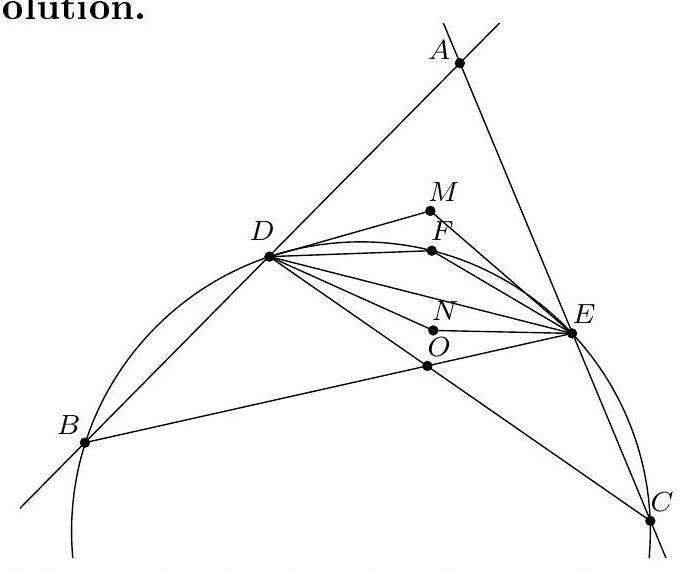\n\nNotons $\\theta=(D E, D F)=(E F, E D)$. On a $2(D F, D M)+2 \\theta=2(D E, D M)=(D E, D A)=$ $\\theta+(D F, D A)=\\theta+(D F, D B)=\\theta+(E F, E B)=2 \\theta+(E D, E O)=\\theta+2(E D, E N)$, donc $\\widehat{F D M}=\\widehat{D E N}$. De même, $\\widehat{M E F}=\\widehat{N D E}$. Notons $\\beta$ et $\\gamma$ ces angles.\n\n\nSoient $P$ et $Q$ les seconds points d'intersection des droites $(D F)$ et $(E F)$ avec le cercle circonscrit au triangle DME. On a\n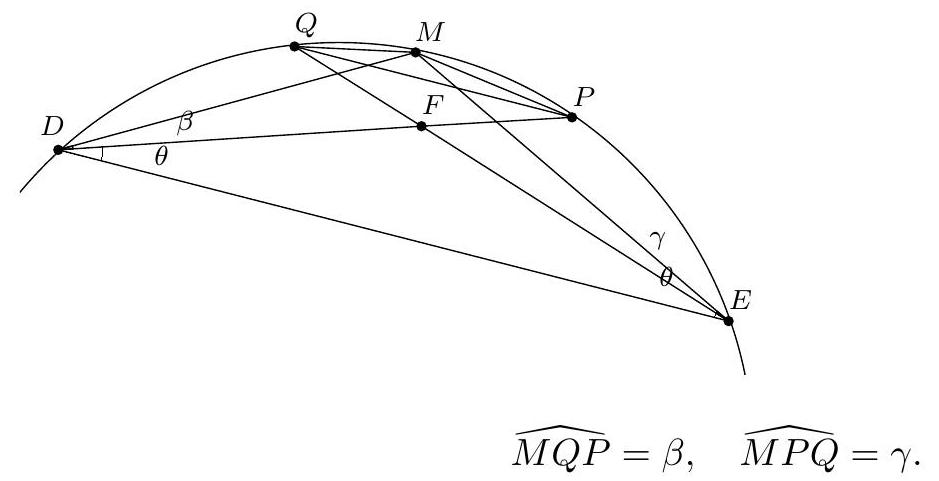\n\nComme $D F=D E$, on a $(P Q) / /(D E)$. Avec (4), cela implique que les triangles $D E N$ et $Q M P$ sont homothétiques. De plus, $F$ est le centre de l'homothétie (puisque c'est le point d'intersection des droites $(Q E)$ et $(P D)$ ). Donc la droite $(M N)$ traverse $F$.\n\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Le cercle $\\omega$ passe par les sommets $B$ et $C$ du triangle $A B C$ et coupe les côtés $[A B]$ et $[A C]$ aux points $D$ et $E$ respectivement. Les segments $[C D]$ et $[B E]$ se coupent en un point $O$. Soient $M$ et $N$ les centres des cercles inscrits dans les triangles $A D E$ et $O D E$ respectivement. Montrer que le milieu de l'arc $D E$ (le plus petit des deux arcs) du cercle $\\omega$ se trouve sur la droite ( $M N$ ).", "solution": "Si on ne pense pas à introduire les points $P$ et $Q$, on peut terminer la démonstration moyennant des calculs trigonométriques un peu pénibles.\n\nNotons $\\varphi$ l'angle $(\\overrightarrow{F M}, \\overrightarrow{E D})$. D'après la loi des sinus dans les triangles $M D F$ et $M E F$, on a\n\n$$\n\\begin{aligned}\n\\frac{M F}{\\sin \\beta} & =\\frac{D F}{\\sin (\\beta+\\varphi+\\theta)} \\\\\n\\frac{M F}{\\sin \\gamma} & =\\frac{E F}{\\sin (\\varphi-\\gamma-\\theta)}\n\\end{aligned}\n$$\n\nComme $D F=E F$, en divisant ces deux égalités on obtient\n\n$$\n\\frac{\\sin \\gamma}{\\sin \\beta}=\\frac{\\sin (\\varphi-\\gamma-\\theta)}{\\sin (\\beta+\\varphi+\\theta)}\n$$\n\nEn utilisant la formule $\\sin (x+y)=\\sin x \\cos y+\\cos x \\sin y$, on en déduit\n\n$$\n\\frac{\\sin \\gamma}{\\sin \\beta}=\\frac{\\sin (\\varphi) \\cos (\\gamma+\\theta)-\\cos \\varphi \\sin (\\gamma+\\theta)}{\\sin (\\varphi) \\cos (\\beta+\\theta)+\\cos \\varphi \\sin (\\beta+\\theta)}\n$$\n\nOn chasse les dénominateurs et on rassemble les termes en $\\sin \\varphi$ et en $\\cos \\varphi$ :\n\n$$\n\\cos \\varphi(\\sin \\gamma \\sin (\\beta+\\theta)+\\sin \\beta \\sin (\\gamma+\\theta)))=\\sin \\varphi(-\\sin \\gamma \\cos (\\beta+\\theta)+\\sin \\beta \\cos (\\gamma+\\theta))\n$$\n\nComme\n\n$$\n\\begin{aligned}\n- & \\sin \\gamma \\cos (\\beta+\\theta)+\\sin \\beta \\cos (\\gamma+\\theta) \\\\\n& =-\\sin \\gamma(\\cos \\beta \\cos \\theta-\\sin \\beta \\sin \\theta)+\\sin \\beta(\\cos \\gamma \\cos \\theta-\\sin \\gamma \\sin \\theta) \\\\\n& =\\cos \\theta \\sin (\\beta-\\gamma),\n\\end{aligned}\n$$\n\non obtient\n\n$$\n\\tan \\varphi=\\frac{\\sin \\gamma \\sin (\\beta+\\theta)+\\sin \\beta \\sin (\\gamma+\\theta)}{\\cos \\theta \\sin (\\beta-\\gamma)}\n$$\n\nSoit $\\varphi^{\\prime}=(F N, D E)$. Le calcul de $\\tan \\varphi^{\\prime}$ est identique, en remplaçant $(\\beta, \\gamma, \\theta)$ par $(\\beta+\\theta, \\gamma+\\theta,-\\theta)$. Or, l'expression de $\\tan \\varphi$ est invariante par cette transformation, donc $\\tan \\varphi^{\\prime}=\\tan \\varphi$, d'où $F, M, N$ sont alignés.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Un cercle de centre $O$ est inscrit dans un quadrilatère $A B C D$ dont les côtés ne sont pas parallèles. Montrer que le point $O$ coïncide avec le point d'intersection des lignes médianes du quadrilatère si et seulement si $O A \\cdot O C=O B \\cdot O D$. (Une ligne médiane du quadrilatère est une droite reliant les milieux des côtés opposés.)", "solution": "Soient $I$ et $J$ les milieux des côtés $[A B]$ et $[C D]$ respectivement. Les droites $(A B)$ et $(C D)$ se coupent au point $P$. Sans perte de généralité, on peut supposer que $P$ est le point d'intersection des demi-droites $[A B)$ et $[C D)$.\n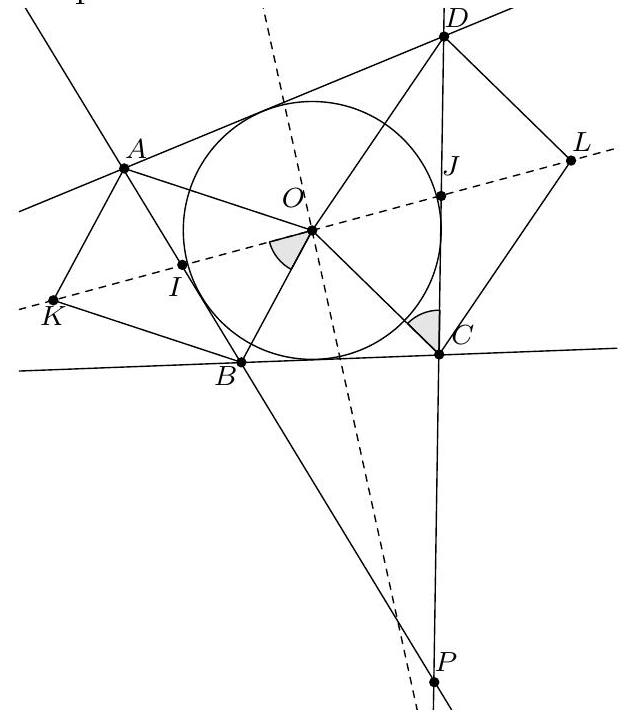\n\n1) Supposons que $O$ est le point d'intersection des lignes médianes du quadrilatère $A B C D$. Alors $O$ est le milieu du segment $[I J]$, parce que les milieux des côtés d'un quadrilatère sont les sommets d'un parallélogramme. Puis, $[P O]$ est la bissectrice et la médiane issus de $P$ du triangle $I P J$, donc $I P J$ est isocèle en $P$ et $\\widehat{B I O}=\\widehat{C J O}$. En outre,\n\n$$\n\\widehat{I B O}+\\widehat{J C O}=\\frac{1}{2}(\\widehat{A B C}+\\widehat{B C D})=\\frac{1}{2}(\\pi+\\widehat{B P C})=\\pi-\\widehat{P I J}=\\widehat{I B O}+\\widehat{I O B}\n$$\n\nAlors $\\widehat{J C O}=\\widehat{I O B}$ et les triangles $O I B$ et $C J O$ sont semblables. On obtient que $\\frac{O B}{O C}=$ $\\frac{I B}{J O}$. De même, on a $\\frac{O A}{O D}=\\frac{I A}{J O}$. Comme $I B=I A$, on obtient $O A \\cdot O C=O B \\cdot O D$.\n2) On suppose maintenant que $O A \\cdot O C=O B \\cdot O D$. On note que\n\n$$\n\\begin{aligned}\n\\widehat{A O B}+\\widehat{C O D} & =(\\pi-\\widehat{O A B}-\\widehat{O B A})+(\\pi-\\widehat{O C D}-\\widehat{O D C}) \\\\\n& =\\pi-\\frac{1}{2}(\\widehat{D A B}+\\widehat{A B C}+\\widehat{B C D}+\\widehat{C D A})=\\pi\n\\end{aligned}\n$$\n\nPar conséquent, si on construit les parallélogrammes $O A K B$ et $C O D L$ à partir des triangles $O A B$ et $O C D$, ces parallélogrammes seront semblables, parce que $\\frac{O A}{A K}=\\frac{O A}{O B}=$ $\\frac{D O}{O C}=\\frac{D O}{D L}$. En particulier, les triangles $O I B$ et $C J O$ sont également semblables, parce qu'ils se correspondent mutuellement dans les parallélogrammes semblables $O A K B$ et $C O D L . \\mathrm{Il}$ vient\n\n$$\n\\widehat{I O B}=\\widehat{O C J}=\\widehat{O C B}, \\quad \\widehat{C O J}=\\widehat{I B O}=\\widehat{O B C}\n$$\n\nOn obtient que\n\n$$\n\\widehat{I O B}+\\widehat{B O C}+\\widehat{C O J}=\\widehat{O C B}+\\widehat{B O C}+\\widehat{O B C}=\\pi,\n$$\n\ndonc $O$ se trouve sur $(I J)$. De même, $O$ se trouve sur l'autre ligne médiane du quadrilatère $A B C D$.\n\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution."}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Un cercle de centre $O$ est inscrit dans un quadrilatère $A B C D$ dont les côtés ne sont pas parallèles. Montrer que le point $O$ coïncide avec le point d'intersection des lignes médianes du quadrilatère si et seulement si $O A \\cdot O C=O B \\cdot O D$. (Une ligne médiane du quadrilatère est une droite reliant les milieux des côtés opposés.)", "solution": "On peut résoudre l'exercice par une méthode analytique utilisant les nombres complexes. Les calculs sont longs mais pas impraticables.\n\nNotons $U, V, W, X$ les points de contact des droites $(A B),(B C),(C D)$ et $(D A)$ avec le cercle. On peut supposer que le cercle est de centre 0 et de rayon 1 . Notons $a, b, c, d, u, v, w, x$ les affixes des points $A, B, C, D, U, V, W, X$.\n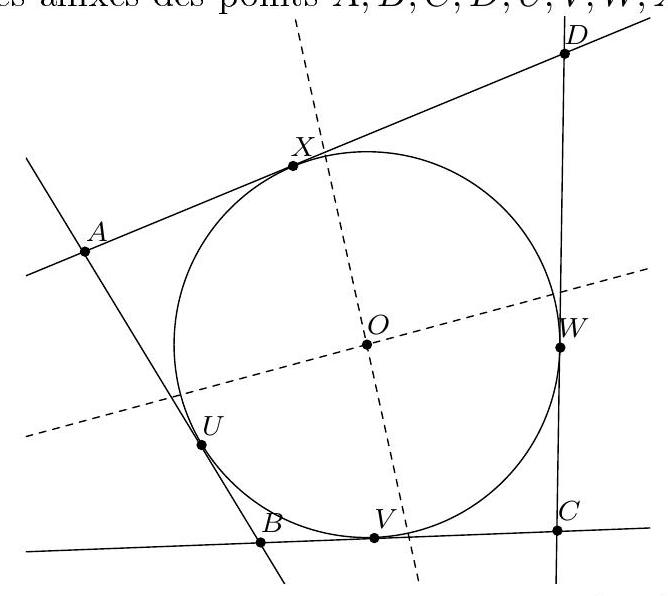\n\nUn point d'affixe $z$ appartient à $(A B)$ si et seulement si $z-u$ est perpendiculaire à $u$, ce qui s'écrit $0=\\bar{u}(z-u)+u(\\bar{z}-\\bar{u})$, ou encore $\\bar{u} z+u \\bar{z}=2$. Comme $\\bar{u}=1 / u$, ceci s'écrit encore $z+u^{2} \\bar{z}=2 u$. De même, l'équation de la droite $(A D)$ est $z+x^{2} \\bar{z}=2 x$. En combinant ces deux équations, on trouve que\n\n$$\na=\\frac{2 u x}{u+x} .\n$$\n\nDe même, on a $b=\\frac{2 u v}{u+v}, c=\\frac{2 v w}{v+w}$ et $d=\\frac{2 w x}{w+x}$.\nOn calcule que $4 O A^{-2}=|u+x|^{2}=2+u \\bar{x}+\\bar{u} x$. On a des expressions analogues pour $4 O B^{-2}$, etc. Par conséquent,\n\n$$\n\\begin{aligned}\nO A \\cdot O C & =O B \\cdot O D \\\\\n& \\Longleftrightarrow \\quad(2+u \\bar{x}+\\bar{u} x)(2+v \\bar{w}+\\bar{v} w)=(2+u \\bar{v}+\\bar{u} v)(2+w \\bar{x}+\\bar{w} x) \\\\\n& \\Longleftrightarrow \\quad u x(2+u \\bar{x}+\\bar{u} x) v w(2+v \\bar{w}+\\bar{v} w)=u v(2+u \\bar{v}+\\bar{u} v) w x(2+w \\bar{x}+\\bar{w} x) \\\\\n& \\Longleftrightarrow \\quad\\left(2 u x+u^{2}+x^{2}\\right)\\left(2 v w+v^{2}+w^{2}\\right)=\\left(2 u v+u^{2}+v^{2}\\right)\\left(2 w x+x^{2}+w^{2}\\right) \\\\\n& \\Longleftrightarrow \\quad 2 u v^{2} x+2 u w^{2} x+2 u^{2} v w+u^{2} v^{2}+2 v w x^{2}+w^{2} x^{2} \\\\\n& =2 u v x^{2}+2 u v w^{2}+2 u^{2} w x+u^{2} x^{2}+2 v^{2} w x+v^{2} w^{2} \\\\\n& \\Longleftrightarrow 2(u-w) v^{2} x-2(u-w) u w x+2(u-w) u v w \\\\\n& \\quad-2(u-w) v x^{2}+(u-w)(u+w) v^{2}-(u-w)(u+w) x^{2}=0 \\\\\n& \\Longleftrightarrow 2 v^{2} x-2 u w x+2 u v w-2 v x^{2}+u v^{2}+v^{2} w-u x^{2}-w x^{2}=0 \\\\\n& \\Longleftrightarrow \\quad 2 v x(v-x)+(v-x) w(v+x)+2 u w(v-x)+u(v+x)(v-x)=0 \\\\\n& \\Longleftrightarrow 2 v x+v w+v x+2 u w+u v+u x=0 \\\\\n& \\Longleftrightarrow 2(u w+x v)+(x+v)(u+w)=0 .\n\\end{aligned}\n$$\n\nD'autre part, $O$ appartient à la droite passant par les milieux de $[A D]$ et de $[B C]$ si et seulement si $0, \\frac{a+d}{2}$ et $\\frac{b+c}{2}$ sont alignés, ce qui se traduit par le fait que $\\frac{a+d}{b+c}$ est réel, c'est-à-dire\n\n$$\n\\frac{\\frac{u x}{u+x}+\\frac{x w}{x+w}}{\\frac{u v}{u+v}+\\frac{v w}{v+w}}=\\frac{\\frac{1}{u+x}+\\frac{1}{w+x}}{\\frac{1}{u+v}+\\frac{1}{v+w}}\n$$\n\nOn multiplie les numérateurs de chaque membre par $(u+x)(x+w)$ et les dénominateurs par $(u+v)(v+w)$, ce qui donne successivement\n\n$$\n\\begin{aligned}\n& \\frac{x[u(x+w)+w(u+x)]}{v[u(v+w)+w(u+v)]}=\\frac{2 x+(u+w)}{2 v+(u+w)} \\\\\n& \\quad \\Longleftrightarrow \\quad x[2 u w+u(u+w)][2 v+(u+w)]=v[2 u w+v(u+w)][2 x+(u+w)] \\\\\n& \\Longleftrightarrow \\quad 2 x u w(u+w)+2 x^{2} v(u+w)+x^{2}(u+w)^{2} \\\\\n& \\quad=2 v u w(u+w)+2 x v^{2}(u+w)+v^{2}(u+w)^{2} \\\\\n& \\quad \\Longleftrightarrow \\quad 2(x-v) u w(u+w)+2(x-v) x v(u+w)+(x-v)(x+v)(u+w)^{2}=0\n\\end{aligned}\n$$\n\nComme les côtés opposés ne sont pas parallèles, on a $u+w \\neq 0$. En simplifiant par $(x-v)(u+w)$, on obtient la condition $2 u w+2 x v+(x+v)(u+w)=0$ qui est la même que la précédente.\n\nOn en conclut que $O A \\cdot O C=O B \\cdot O D$ si et seulement si $O$ appartient à la droite passant par les milieux de $[A D]$ et de $[B C]$. De même, on montre que $O A \\cdot O C=O B \\cdot O D$ si et seulement si $O$ appartient à la droite passant par les milieux de $[A B]$ et de $[C D]$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-1-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution."}}
diff --git a/French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl b/French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..f75b86a23eeda51dddac8fe83e30563c73fc36c7
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl
@@ -0,0 +1,9 @@
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "On dit qu'un nombre à 9 chiffres est intéressant si chaque chiffre de 1 à 9 y apparaît une unique fois, que les chiffres de 1 à 5 y apparaissent dans l'ordre mais pas les chiffres de 1 à 6 , par exemple 189236457 .\n\nCombien y a-t-il de nombres intéressants?", "solution": "de l'exercice 1 Pour construire un nombre intéressant, on peut placer d'abord les chiffres de 1 à 5 , puis intercaler le 6 quelque part, puis le 7 , le 8 et le 9 . L'ordre des chiffres de 1 à 5 est imposé. Ensuite, le 6 peut être placé n'importe où sauf après le 5 car les chiffres de 1 à 6 ne sont pas dans l'ordre. Il y a donc 5 manières de placer le 6 . Ensuite, on peut placer le 7 n'importe où, donc il y a 7 manières de le placer, et de même 8 manières de placer le 8 et 9 pour le 9.\n\nIl y a donc $5 * 7 * 8 * 9=2520$ nombres intéressants.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 1", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Dans un pays, il y a n villes. Deux villes quelconques sont toujours reliées soit par une autoroute, soit par une ligne de train. Montrer qu'un des deux moyens de transport permet de relier n'importe quelle ville à n'importe quelle autre.", "solution": "de l'exercice 2\n On raisonne par récurrence sur $n$ : pour $n=1$ ou $n=2$, le résultat est immédiat. Supposons qu'on l'a montré au rang $n$, et considérons $n+1$ villes :\n\nOn isole une des villes, appelons-la par exemple Paris. Alors un des deux moyens de transports permet de relier entre elles toutes les villes sauf Paris. Supposons que c'est la voiture:\n\n- si Paris est relié à une ville par une autoroute par exemple Lyon, on peut en voiture aller de Paris à Lyon, puis à n'importe quelle autre ville d'après l'hypothèse de récurrence.\n- sinon, Paris est relié à toutes les villes par une ligne de train, donc on peut aller de n'importe quelle ville à n'importe quelle ville en train en passant par Paris.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "32014", "problem_type": null, "problem": "scientifiques participent à un congrès, chaque scientifique étant soit un mathématicien, soit un physicien. Bien sûr, les physiciens mentent toujours et les mathématiciens disent toujours la vérité, sauf quand ils se trompent. Lors du dîner final, tous sont assis en rond autour d'une table, et chacun prétend se trouver entre un mathématicien et un physicien. Il se trouve qu'exactement un mathématicien distrait s'est trompé. Combien y a-t-il de physiciens au congrès?", "solution": "de l'exercice 3 Si 2 physiciens sont assis côté à côté, comme ils ont menti, ils ne sont pas entre un physicien et un mathématicien, donc chacun est entre deux physiciens, et ainsi de suite, donc le congrès n'accueille que des physiciens, ce qui est absurde car il y a au moins un mathématicien (celui qui s'est trompé...). Chaque physicien est donc entre deux mathématiciens.\n\nD'autre part, chaque mathématicien est entre un mathématicien et un physicien, sauf celui qui s'est trompé. Appelons-le Thomas : si Thomas est entre deux physiciens, alors on a partout ailleurs une alternance de deux mathématiciens, un physicien... Mais alors, si il y a k paires de mathématiciens côte à côte, il y a $2 k+1$ mathématiciens et $k+1$ physiciens, donc $3 k+2$ scientifiques, ce qui est absurde car $3 k+2 \\neq 2014$.\n\nThomas est donc entre deux mathématiciens, donc on a trois mathématiciens côté à côte, et les autres par paires. Si il y a $k$ paires, alors on a $2 k+3$ mathématiciens et $k+1$ physiciens donc $3 k+4=2014$ donc $k=670$ et il y a 671 physiciens.\n\n## Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 32014", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Montrer que tout polyèdre a deux faces qui ont le même nombre de sommets.", "solution": "de l'exercice 4 Soit $n$ le nombre de faces du polyèdre, et soit $F$ une face fixée : les arêtes de $F$ séparent $F$ de faces toutes différentes, donc le nombre d'arêtes de $F$ est inférieur ou égal au nombre de faces autres que $F$. De plus, $F$ a au moins 3 arêtes. Chaque face a autant d'arêtes que de sommet, donc toute face a un nombre de sommets compris entre 3 et $n-1$, soit $n-3$ possibilités. D'après le principe des tiroirs, il existe donc deux faces qui ont le même nombre de sommets.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Sur un échiquier 5 sur 5, on a placé sur des cases différentes k cavaliers, de telle manière que chacun peut en prendre exactement 2 autres.\n\nQuelle est la plus grande valeur possible de k?", "solution": "de l'exercice 5 La configuration suivante donne un exemple avec 16 cavaliers :\n\n\nOn montre maintenant que c'est optimal : quitte à échanger les couleurs, on peut supposer le centre noir. Notons $k$ le nombre de cavaliers sur une case noire, $l$ le nombre de cavaliers sur une case blanche et $N$ le nombre de manière de choisir deux cavaliers en prise : sur deux tels cavaliers, un est sur une case noire donc il y a $k$ manières de le choisir, puis 2 manières de choisir un cavalier sur une case blanche qu'il peut prendre, donc $\\mathrm{N}=2 \\mathrm{k}$, mais le même raisonnement donne $N=2 l$ donc $k=l$.\n\nSi il y a un cavalier au centre de l'échiquier, il a accès à 8 cases blanches donc au moins 6 cases blanches sont inoccupées donc $l \\leqslant 12-6=6$ donc $k+l \\leqslant 12$. On peut donc supposer le centre vide.\n\nSi il y a un cavalier sur une case blanche qui touche le centre, il a accès à 6 cases, donc 4 d'entre elles sont inoccupées. Le centre l'est aussi, donc $k \\leqslant 13-5=8$ et $k+l \\leqslant 16$, ce qu'on veut montrer.\n\nSi enfin le centre et ses voisins immédiats sont inoccupés, alors les coins le sont aussi car il ne peuvent avoir de cavaliers en prise, ce qui ne laisse que les 16 cases de la figure ci-dessus.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": " Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $\\mathrm{n} \\in \\mathbb{N}^{*}$. Montrer qu'il est possible de partitionner $\\{1,2, \\ldots, \\mathrm{n}\\}$ en deux sousensembles $A$ et $B$ tels que la somme des éléments de $A$ soit égale au produit des éléments de B.", "solution": "de l'exercice 6 A priori, l'ensemble B doit être bien plus petit que A. On va donc chercher un $B$ avec un petit nombre d'éléments. En testant des petites valeurs de $n$, on peut penser à chercher $B$ sous la forme $\\{1, a, b\\}$ avec $a, b \\neq 1$ et $a \\neq b$.\n\nOn a alors $\\prod_{x \\in B} x=a b$, et :\n\n$$\n\\begin{aligned}\n\\sum_{x \\in \\mathcal{A}} & =\\sum_{x=1}^{n} x-1-a-b \\\\\n& =\\frac{n(n+1)}{2}-a-b-1\n\\end{aligned}\n$$\n\nOn veut donc $\\frac{n(n+1)}{2}=a b+a+b+1=(a+1)(b+1)$, donc il suffit d'écrire $\\frac{n(n+1)}{2}$ comme un produit. Or, si $n$ est pair, on peut prendre $a+1=\\frac{n}{2}$ et $b+1=n+1$, soit $a=\\frac{n}{2}-1$ et $b=n$. Si $n$ est impair, on prend $a=\\frac{n-1}{2}$ et $b=n-1$. Dans les deux cas, l'hypothèse $n \\geqslant 5$ permet de vérifier facilement que 1, a et $b$ sont deux à deux distincts.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 6", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "On se donne $n$ points du plan, tels que trois quelconques d'entre eux ne sont jamais alignés. Chacun est colorié en rouge ou en bleu. On suppose qu'il y a exactement un point bleu à l'intérieur de chaque triangle dont les sommets sont rouges, et un point rouge à l'intérieur de chaque triangle dont les sommets sont bleus.\n\nQuelle est la plus grande valeur possible de n?\n\n## Exercices groupe A", "solution": "de l'exercice 7 On montre d'abord que les points bleus forment un polygone convexe: si ce n'était pas le cas, on pourrait trouver un point bleu à l'intérieur d'un polygone bleu, donc on en découpant ce polygone en triangles, on pourrait trouver un point bleu à l'intérieur d'un triangle bleu. Le grand triangle bleu doit contenir un unique point rouge, mais on peut le découper en trois triangles qui contiennent chacun un unique point rouge, ce qui est absurde.\n\nLes points bleus forment donc un polygone convexe, de même que les rouges. De plus, il y a au maximum 2 points rouges à l'intérieur du polygone bleu, car s'il y en avait 3 ils formeraient un triangle sans point bleu à l'intérieur.\n\nEnfin, si $k$ est le nombre de points bleus, on peut découper le polygone bleu en $k-2$ triangles, qui chacun doivent contenir un point rouge, donc $k-2 \\leqslant 2$ et $k \\leqslant 4$. De même, il y a au plus 4 points rouges donc $\\mathrm{n} \\leqslant 8$. On peut alors vérifier que la configuration à 8 points suivante convient:\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "La ville de Gotham City est un grand rectangle, découpé en pâtés de maisons rectangulaires plus petits par des rues parallèles aux bords de la ville. On suppose qu'il y a au moins une rue, et qu'aucune rue ne traverse la ville de part en part.\n\nMontrer qu'il existe un pâté de maison qui ne touche pas le bord de la ville.", "solution": "de l'exercice 8\nBatman explore la ville selon le procédé suivant : il part du bord de la ville (du point rouge sur la figure) et suit jusqu'au bout une rue (l'Avenue du Joker par exemple) qui s'enfonce à l'intérieur. Comme l'Avenue de Joker ne traverse pas la ville de part en part, elle débouche sur une autre (appelons-la Boulevard Double-Face). Mais le Boulevard Double-Face ne traverse pas non plus Gotham City de part en part, donc va déboucher sur une autre rue soit à gauche, soit à droite, soit éventuellement des deux côtés. Si le Boulevard débouche sur une nouvelle rue à gauche, Batman part vers la gauche. Sinon, il part vers la droite. Il continue ainsi...\n\nIl est alors clair que Batman ne sortira jamais de Gotham. Mais le nombre de rues est fini, donc il finira forcément par passer deux fois par un même point. On suppose par exemple que le premier point où il passe deux fois de suite est la Place Ra's Al Ghul (en bleu sur la figure) : entre ses deux passages, il a fait le tour d'une certaine zone, sans toucher le bord de la ville. Tout pâté de maison dans cette zone convient, comme celui colorié en vert.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 8", "solution_match": " Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soient E un ensemble de cardinal n et $\\mathscr{F}$ un ensemble de parties de E avec $|\\mathscr{F}|=$ $2^{\\text {n-1 }}$ tel que pour tous $A, B$ et $C$ dans $\\mathscr{F}, A \\cap B \\cap C$ est non vide.\n\nMontrer que l'intersection de tous les éléments de $\\mathscr{F}$ est non vide.", "solution": "de l'exercice 9 Si $A \\subset E$, on notera $A^{c}$ son complémentaire: l'ensemble des parties de $E$ est partitionné en $2^{n-1}$ doubletons de la forme $\\left\\{A, A^{c}\\right\\}$ où $A \\subset E$. Or, il est impossible que les deux éléments d'un doubleton soient dans $\\mathscr{F}$, car leur intersection est vide, donc $\\mathscr{F}$ contient exactement un élément de chaque doubleton.\n\nSoient donc $A$ et $B$ dans $\\mathscr{F}$ : on va montrer que $A \\cap B \\in \\mathscr{F}$. D'après ce qu'on vient de dire, il suffit de montrer $(A \\cap B)^{c} \\notin \\mathscr{F}$. Or, ceci est vrai car $A \\cap B \\cap(A \\cap B)^{c}$ est vide.\n\nPar récurrence sur $k$, on en déduit que pour tous $A_{1}, A_{2}, \\ldots, A_{k}$ de $\\mathscr{F}, A_{1} \\cap A_{2} \\cap \\ldots \\cap A_{k} \\in \\mathscr{F}$. En effet, c'est vrai pour $k=2$ et si on l'a montré pour $k$, alors :\n\n$$\nA_{1} \\cap A_{2} \\cap \\ldots \\cap A_{k}=\\left(A_{1} \\cap A_{2} \\cap \\ldots \\cap A_{k-1}\\right) \\cap A_{k}\n$$\n\nest l'intersection de deux éléments de $\\mathscr{F}$, donc est dans $\\mathscr{F}$.\n\nComme $\\mathscr{F}$ est fini, l'intersection de tous les éléments de $\\mathscr{F}$ est dans $\\mathscr{F}$. Or, l'ensemble vide ne peut pas être dans $\\mathscr{F}$ car son intersection avec lui-même est vide, donc l'intersection de tous les éléments de $\\mathscr{F}$ n'est pas vide.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-2-solutions.jsonl", "problem_match": "\nExercice 9", "solution_match": "\nSolution "}}
diff --git a/French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl b/French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..ab95f23b9e846bc52157004caf248600dc1390bf
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl
@@ -0,0 +1,14 @@
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Existe-t-il des réels $\\mathrm{a}, \\mathrm{b}, \\mathrm{c}, \\mathrm{d}>0$ et $e, f, \\mathrm{~g}, \\mathrm{~h}<0$ vérifiant simultanément\n\n$$\na e+b c>0, e f+c g>0, f d+g h>0 \\text { et } d a+h b>0 ?\n$$", "solution": "de l'exercice 1 Non, il n'en existe pas. Par l'absurde : supposons qu'il existe de tels réels.On commence par réécrire les inégalités, mais avec uniquement des termes positifs. On a donc\n\n$$\nb c>a(-e) \\text { et }(-e)(-f)>c(-g) \\text { et }(-g)(-h)>(-f) d \\text { et da }>(-h) b\n$$\n\nSi l'on multiplie toutes ces inégalités membres à membres (et, comme tout est positif, il n'y a aucun danger), il vient abcdefgh > abcbdefgh, d'où la contradiction cherchée.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $a, b, c$ des réels tels que $-1 \\leqslant a x^{2}+b x+c \\leqslant 1$ pour $x=-1, x=0$ et $x=1$. Prouver que\n\n$$\n-\\frac{5}{4} \\leqslant a x^{2}+b x+c \\leqslant \\frac{5}{4} \\text { pour tout réel } x \\in[-1,1]\n$$", "solution": "de l'exercice 2 Posons $\\mathrm{P}(\\mathrm{x})=\\mathrm{ax}{ }^{2}+\\mathrm{bx}+\\mathrm{c}$. Alors $\\mathrm{P}(-1)=\\mathrm{a}-\\mathrm{b}+\\mathrm{c}, \\mathrm{P}(0)=\\mathrm{c}$ et $\\mathrm{P}(1)=$ $\\mathrm{a}+\\mathrm{b}+\\mathrm{c}$. Et, d'après l'énoncé, on a $|\\mathrm{P}(-1)| \\leqslant 1,|\\mathrm{P}(0)| \\leqslant 1$ et $|\\mathrm{P}(1)| \\leqslant 1$.\nOr, pour tout réel $\\chi$, on vérifie directement que\n\n$$\nP(x)=\\frac{x(x+1)}{2} P(1)-\\frac{x(1-x)}{2} P(-1)+\\left(1-x^{2}\\right) P(0)\n$$\n\n- Soit $x \\in[0 ; 1]$. D'après (1) et l'inégalité triangulaire, il vient\n\n$$\n\\begin{aligned}\n|\\mathrm{P}(x)| & \\leqslant \\frac{x(x+1)}{2}|\\mathrm{P}(1)|+\\frac{x(1-x)}{2}|\\mathrm{P}(-1)|+\\left(1-x^{2}\\right)|\\mathrm{P}(0)| \\\\\n& \\leqslant \\frac{x(x+1)}{2}+\\frac{x(1-x)}{2}+\\left(1-x^{2}\\right) \\\\\n& =-x^{2}+x+1 \\\\\n& =\\frac{5}{4}-\\left(x-\\frac{1}{2}\\right)^{2}\n\\end{aligned}\n$$\n\nEt ainsi $|P(x)| \\leqslant \\frac{5}{4}$.\n\n- Soit $x \\in[-1 ; 0]$. D'après (1) et l'inégalité triangulaire, il vient cette fois\n\n$$\n\\begin{aligned}\n& \\leqslant-\\frac{x(x+1)}{2}|P(1)|-\\frac{x(1-x)}{2}|P(-1)|+\\left(1-x^{2}\\right)|P(0)| \\\\\n& \\leqslant-\\frac{x(x+1)}{2}-\\frac{x(1-x)}{2}+\\left(1-x^{2}\\right) \\\\\n& =-x^{2}-x+1 \\\\\n& =\\frac{5}{4}-\\left(x+\\frac{1}{2}\\right)^{2}\n\\end{aligned}\n$$\n\nEt ainsi $|\\mathrm{P}(\\mathrm{x})| \\leqslant \\frac{5}{4}$, à nouveau.\nFinalement, pour tout $x \\in[-1 ; 1]$, on a $|\\mathrm{P}(\\mathrm{x})| \\leqslant \\frac{5}{4}$.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Prouver que, pour tout réel $a \\geqslant 0$, on a\n\n$$\na^{3}+2 \\geqslant a^{2}+2 \\sqrt{a}\n$$", "solution": "de l'exercice 3 Pour tout réel $a \\geqslant 0$, on a\n\n$$\n\\begin{aligned}\na^{3}-a^{2}-2 \\sqrt{a}+2 & =a^{2}(a-1)-2(\\sqrt{a}-1) \\\\\n& =a^{2}(\\sqrt{a}-1)(\\sqrt{a}+1)-2(\\sqrt{a}-1) \\\\\n& =(\\sqrt{a}-1)\\left(a^{2}(\\sqrt{a}+1)-2\\right) .(1)\n\\end{aligned}\n$$\n\nOr:\n\n- Si $a \\geqslant 1$ alors $\\sqrt{a} \\geqslant 1$ et $a^{2} \\geqslant 1$. Ainsi, on a $\\sqrt{a}-1 \\geqslant 0$ et $a^{2}(\\sqrt{a}+1) \\geqslant 2$. Par suite, chacun des facteurs de (1) est positif, ce qui assure que le produit est positif.\n- Si $a \\leqslant 1$ alors $\\sqrt{a} \\leqslant 1$ et $a^{2} \\leqslant 1$. Ainsi, on a $\\sqrt{a}-1 \\leqslant 0$ et $a^{2}(\\sqrt{a}+1) \\leqslant 2$. Par suite, chacun des deux facteurs de (1) est négatif, et le produit est donc encore positif.\n\nFinalement, pour tout réel $a \\geqslant 0$, on a $a^{3}-a^{2}-2 \\sqrt{a}+2 \\geqslant 0$ ou encore $a^{3}+2 \\geqslant a^{2}+2 \\sqrt{a}$.\n\n## Exercices Communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Prouver que si $n$ est un entier strictement positif, l'expression\n\n$$\n\\frac{\\sqrt{n+\\sqrt{0}}+\\sqrt{n+\\sqrt{1}}+\\sqrt{n+\\sqrt{2}}+\\cdots \\sqrt{n+\\sqrt{n^{2}-1}}+\\sqrt{n+\\sqrt{n^{2}}}}{\\sqrt{n-\\sqrt{0}}+\\sqrt{n-\\sqrt{1}}+\\sqrt{n-\\sqrt{2}}+\\cdots \\sqrt{n-\\sqrt{n^{2}-1}}+\\sqrt{n-\\sqrt{n^{2}}}}\n$$\n\nest indépendante de n .", "solution": "de l'exercice 4 En calculant le carré de chacun des deux membres, on déduit que, pour tous réels $a, b$ tels que $0 \\leqslant b \\leqslant a$, on a\n\n$$\n\\sqrt{a+\\sqrt{a^{2}-b^{2}}}=\\sqrt{\\frac{a+b}{2}}+\\sqrt{\\frac{a-b}{2}}\n$$\n\nEn particulier, pour tous entiers naturels $n$ et $m$, avec $m \\leqslant n^{2}$, on a\n\n$$\n\\sqrt{n+\\sqrt{m}}=\\sqrt{\\frac{n+\\sqrt{n^{2}-m}}{2}}+\\sqrt{\\frac{n-\\sqrt{n^{2}-m}}{2}}\n$$\n\nSoit $\\mathrm{n}>0$ un entier. On a donc\n\n$$\n\\sum_{m=0}^{n^{2}} \\sqrt{n+\\sqrt{m}}=\\sum_{m=0}^{n^{2}} \\sqrt{\\frac{n+\\sqrt{n^{2}-m}}{2}}+\\sum_{m=0}^{n^{2}} \\sqrt{\\frac{n-\\sqrt{n^{2}-m}}{2}}\n$$\n\nD'où, après réindexation :\n\n$$\n\\begin{aligned}\n\\sum_{m=0}^{n^{2}} \\sqrt{n+\\sqrt{m}} & =\\sum_{m=0}^{n^{2}} \\sqrt{\\frac{n+\\sqrt{m}}{2}}+\\sum_{m=0}^{n^{2}} \\sqrt{\\frac{n-\\sqrt{m}}{2}} \\\\\n& =\\frac{1}{\\sqrt{2}} \\sum_{m=0}^{n^{2}} \\sqrt{n+\\sqrt{m}}+\\frac{1}{\\sqrt{2}} \\sum_{m=0}^{n^{2}} \\sqrt{n-\\sqrt{m}}\n\\end{aligned}\n$$\n\n$\\operatorname{Ainsi}\\left(1-\\frac{1}{\\sqrt{2}}\\right) \\sum_{m=0}^{n^{2}} \\sqrt{n+\\sqrt{m}}=\\frac{1}{\\sqrt{2}} \\sum_{m=0}^{n^{2}} \\sqrt{n-\\sqrt{m}}$\net donc $\\frac{\\sum_{m=0}^{n^{2}} \\sqrt{n+\\sqrt{m}}}{\\sum_{m=0}^{n^{2}} \\sqrt{n-\\sqrt{m}}}=1+\\sqrt{2}$, qui est bien une valeur", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit ( $a_{n}$ ) une suite définie par $a_{1}, a_{2} \\in[0,100]$ et\n\n$$\na_{n+1}=a_{n}+\\frac{a_{n-1}}{n^{2}-1} \\quad \\text { pour tout enter } n \\geqslant 2\n$$\n\nExiste-t-il un entier $n$ tel que $a_{n}>2013$ ?", "solution": "de l'exercice 5 La réponse est non.\n\nPlus précisément, montrons par récurrence que l'on a $a_{n} \\leqslant 400$, pour tout $n \\geqslant 0$.\nL'inégalité est vraie pour $\\mathrm{n}=1$ et $\\mathrm{n}=2$, d'après l'énoncé.\nSupposons qu'elle soit vraie pour tout $k \\leqslant n$ pour un certain entier $\\mathrm{n} \\geqslant 2$.\nPour tout $k \\in\\{2, \\cdots, n\\}$, on a $a_{k+1}=a_{k}+\\frac{a_{k-1}}{k^{2}-1}$. En sommant, membre à membre, ces relations et après simplification des termes communs, il vient:\n\n$$\n\\begin{aligned}\na_{n+1} & =a_{2}+\\sum_{k=2}^{n} \\frac{a_{k-1}}{k^{2}-1} \\\\\n& \\leqslant 100+\\sum_{k=2}^{n} \\frac{400}{k^{2}-1}, \\text { d'après l'hypothèse de récurrence et l'énoncé } \\\\\n& =100+200 \\sum_{k=2}^{n}\\left(\\frac{1}{k-1}-\\frac{1}{k+1}\\right) \\\\\n& =100+200\\left(1+\\frac{1}{2}-\\frac{1}{n}-\\frac{1}{n+1}\\right) \\text { après simplification par dominos } \\\\\n& =400-\\frac{200}{n}-\\frac{200}{n+1}\n\\end{aligned}\n$$\n\net donc $a_{n+1} \\leqslant 400$, ce qui achève la récurrence.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Déterminer la plus grande valeur possible et la plus petite valeur possible de\n\n$$\n\\sqrt{4-a^{2}}+\\sqrt{4-b^{2}}+\\sqrt{4-c^{2}}\n$$\n\nlorsque $a, b, c$ sont des réels strictement positifs vérifiant $a^{2}+b^{2}+c^{2}=6$.", "solution": "de l'exercice 6 Tout d'abord, on note que si l'on veut que l'expression ait un sens, il faut $\\mathrm{a}, \\mathrm{b}, \\mathrm{c} \\in$ [0; 2].\n\nD'après l'inégalité de Cauchy-Schwarz, on a\n$\\left(\\sqrt{4-a^{2}}+\\sqrt{4-b^{2}}+\\sqrt{4-c^{2}}\\right)^{2} \\leqslant 3\\left(4-a^{2}+4-b^{2}+4-c^{2}\\right)=18$,\nc.à.d. $\\sqrt{4-\\mathrm{a}^{2}}+\\sqrt{4-\\mathrm{b}^{2}}+\\sqrt{4-\\mathrm{c}^{2}} \\leqslant 3 \\sqrt{2}$, avec égalité pour $\\mathrm{a}=\\mathrm{b}=\\mathrm{c}=\\sqrt{2}$.\n\nAinsi, la plus grande valeur possible est $3 \\sqrt{2}$.\nCherchons maintenant la valeur minimale :\nSans perte de généralité, on peut supposer que $a \\leqslant b \\leqslant c$.\nDe $a^{2}+b^{2}+c^{2}=6$, on déduit alors que $3 a^{2} \\leqslant 6$, soit donc $0 \\leqslant a^{2} \\leqslant 2$.\nD'autre part, si $x, y \\geqslant 0$, on a clairement $\\sqrt{x}+\\sqrt{y} \\leqslant \\sqrt{x+y}$, avec égalité si et seulement si $x=0$ ou $\\mathrm{y}=0$.\nIl vient alors\n$\\sqrt{4-a^{2}}+\\sqrt{4-b^{2}}+\\sqrt{4-c^{2}} \\geqslant \\sqrt{4-a^{2}}+\\sqrt{8-b^{2}-c^{2}}=\\sqrt{4-a^{2}}+\\sqrt{2+a^{2}}$,\net, puisque $0 \\leqslant 4-\\mathrm{c}^{2} \\leqslant 4-\\mathrm{b}^{2}$, égalité a lieu si et seulement si $4-\\mathrm{c}^{2}=0$, c.à $\\mathrm{d} . \\mathrm{c}=2$.\nIl reste donc à trouver le minimum de l'expression $\\mathrm{f}(\\mathrm{x})=\\sqrt{4-\\mathrm{x}}+\\sqrt{2+\\mathrm{x}}$, lorsque $x \\in[0 ; 2]$. Or, puisque tout est positif, cela revient à trouver le minimum de $(f(x))^{2}=6+2 \\sqrt{(4-x)(2+x)}$, sous les mêmes conditions.\n\nComme $(4-x)(2+x)=-x^{2}+2 x+8=9-(x-1)^{2}$, la valeur minimale de $\\sqrt{(4-x)(2+x)}$ est $\\sqrt{8}$, avec égalité pour $x=0$.\nAinsi, on a $(\\mathrm{f}(\\mathrm{x}))^{2} \\geqslant 6+2 \\sqrt{8}=(2+\\sqrt{2})^{2}$, ou encore $\\mathrm{f}(\\mathrm{x}) \\geqslant 2+\\sqrt{2}$, avec égalité pour $\\mathrm{x}=0$.\nPar suite, on a $\\sqrt{4-\\mathrm{a}^{2}}+\\sqrt{4-\\mathrm{b}^{2}}+\\sqrt{4-\\mathrm{c}^{2}} \\geqslant 2+\\sqrt{2}$, avec égalité en particulier pour $(\\mathrm{a}, \\mathrm{b}, \\mathrm{c})=$ $(0, \\sqrt{2}, 2)$.\nCela assure que la plus petite valeur cherchée est $2+\\sqrt{2}$.\n\n## Exercices du groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\longrightarrow \\mathbb{R}^{+*}$ qui vérifient les trois conditions suivantes pour tous réels $x$ et $y$ :\ni) $f\\left(x^{2}\\right)=f(x)^{2}-2 x f(x)$,\nii) $f(-x)=f(x-1)$,\niii) si $10$, on a donc $f(0)=1$.\nSoit $x$ un réel. En utilisant i) pour les valeurs $x$ et $-x$, il vient\n$f(x)^{2}-2 x f(x)=f\\left(x^{2}\\right)=f(-x)^{2}+2 x f(-x)$,\nou encore $(f(x)-f(-x))(f(x)+f(-x))=2 x(f(x)+f(-x))$.\nPuisque $f$ est à valeurs strictement positives, on a $f(x)+f(-x) \\neq 0$,\net donc $f(x)-f(-x)=2 x$.\nFinalement, et d'après ii), on a\n\n$$\nf(x)=f(x-1)+2 x \\text {, pour tout réel } x .(1)\n$$\n\nEn particulier, on déduit facilement de (1) que, pour tout entier $n \\geqslant 0$, on a\n\n$$\n\\mathrm{f}(\\mathrm{n})=\\mathrm{f}(0)+2(\\mathrm{n}+(\\mathrm{n}-1)+\\cdots+1)=\\mathrm{n}^{2}+\\mathrm{n}+1\n$$\n\nDe ii), on obtient alors que\n\n$$\nf(n)=n^{2}+n+1 \\text { pour tout entier } n\n$$\n\nSoit $x$ un réel et $\\mathrm{n} \\geqslant 0$ un entier.\nPour tout entier $k$, on a $f(x+k)=2 x+2 k+f(x+k-1)$.\nAprès sommation membre à membre de toutes ces relations pour $k=0,1, \\cdots, n$, et simplification des termes communs, il vient\n$\\mathbf{f}(\\mathrm{x}+\\mathfrak{n})=2 \\mathbf{n} x+2(\\mathfrak{n}+(\\mathfrak{n}-1)+\\cdots+1)+\\mathbf{f}(\\mathrm{x})$.\nEt ainsi :\n\n$$\nf(x+n)=f(x)+2 n x+n^{2}+n, \\text { pour tout réel } x \\text { et tout entier } n \\geqslant 0 \\text {. (2) }\n$$\n\nCela va nous permettre de conclure sur les rationnels positifs :\nSoit $x=\\frac{m}{n}$, avec $\\mathrm{m}, \\mathrm{n}>0$ entiers.\nD'après (2), on a\n\n$$\n\\begin{aligned}\n\\mathrm{f}\\left((x+\\mathrm{n})^{2}\\right) & =\\mathrm{f}\\left(x^{2}+2 \\mathrm{~m}+\\mathrm{n}^{2}\\right) \\\\\n& =\\mathrm{f}\\left(x^{2}\\right)+2\\left(2 \\mathrm{~m}+\\mathrm{n}^{2}\\right) \\mathrm{x}^{2}+\\left(2 \\mathrm{~m}+\\mathrm{n}^{2}\\right)^{2}+2 \\mathrm{~m}+\\mathrm{n}^{2} \\\\\n& =\\mathrm{f}^{2}(x)-2 \\mathrm{xf}(x)+2\\left(2 \\mathrm{~m}+\\mathrm{n}^{2}\\right) x^{2}+\\left(2 \\mathrm{~m}+\\mathrm{n}^{2}\\right)^{2}+2 \\mathrm{~m}+\\mathrm{n}^{2}\n\\end{aligned}\n$$\n\nMais, d'après i) et (2), on a également\n\n$$\n\\begin{aligned}\n\\mathbf{f}\\left((x+n)^{2}\\right) & =f^{2}(x+n)+2(x+n) f(x+n) \\\\\n& =\\left(f(x)+2 m+n^{2}+n\\right)^{2}-2(x+n)\\left(f(x)+2 m+n^{2}+n\\right)\n\\end{aligned}\n$$\n\nEn identifiant les deux dernières expressions de $f\\left((x+n)^{2}\\right)$, et après un calcul passionnant, on obtient que\n\n$$\nf(x)=x^{2}+x+1, \\text { pour tout rationnel } x>0\n$$\n\nSoit $x>1$ un réel.\nOn sait qu'il existe deux suites de rationnels positifs, $\\left(u_{n}\\right)$ et $\\left(v_{n}\\right)$, qui convergent vers $x$ et telles que $u_{n} \\leqslant w \\leqslant v_{n}$ pour tout entier $n$.\nOr, d'après iii), la fonction $f$ est strictement croissante sur $] 1 ;+\\infty\\left[\\right.$ donc, pour tout entier $n$, on a $f\\left(u_{n}\\right)<$ $\\mathrm{f}(\\mathrm{x})<\\mathrm{f}\\left(v_{\\mathrm{n}}\\right)$,\nou encore $u_{n}^{2}+u_{n}+11 \\text { (3) }\n$$\n\nDonnons maintenant le coup de grâce.\nSoit $x$ un réel.\nOn choisit un entier $\\mathrm{n}>0$ tel que $x+n>1$.\nDe (2) et (3), on déduit que\n$\\mathbf{f}(x+\\mathfrak{n})=(x+\\mathfrak{n})^{2}+(x+\\mathfrak{n})+1$ et $\\mathbf{f}(x+\\mathfrak{n})=\\mathbf{f}(\\mathrm{x})+2 \\mathfrak{n} x+\\mathfrak{n}^{2}+\\mathfrak{n}$.\nEn identifiant ces deux expressions, et après encore quelques calculs, il vient $f(x)=x^{2}+x+1$.\nEt finalement, on a $f(x)=x^{2}+x+1$, pour tout réel $x$.\nCe n'est que routine que de vérifier que cette fonction est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": " solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Déterminer toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\longrightarrow \\mathbb{R}^{+*}$ qui vérifient les trois conditions suivantes pour tous réels $x$ et $y$ :\ni) $f\\left(x^{2}\\right)=f(x)^{2}-2 x f(x)$,\nii) $f(-x)=f(x-1)$,\niii) si $10$.\n\nAlors, le polynôme $Q(P(x))-Q(Q(x))$ est de degré $n(n-1)+k$.\nD'autre part, le degré de $R(P(x))$ est $k n$, et on a $k n \\leqslant n(n-1)0$.\nEn effet, $R(x)$ peut s'écrire sous la forme $c x^{m}\\left(1+\\frac{c_{1}}{x}+\\cdots+\\frac{c_{m}}{x^{m}}\\right)$ avec $c>0$. Le terme entre parenthèses tend vers 1 lorsque $x \\rightarrow+\\infty$, donc est strictement positif pour $x$ assez grand.\n\nLemme 2. Pour tout polynôme $P$ de degré $\\geqslant 1$ ayant un coefficient dominant strictement positif, il existe a tel que P est strictement croissant sur [a, $+\\infty$ [.\nEn effet, le polynôme dérivé $P^{\\prime}$ vérifie les conditions du lemme 1 donc $P^{\\prime}(x)$ est strictement positif pour $x$ assez grand.\nRevenons à l'exercice. D'après les deux lemmes précédents, il existe a tel que sur [a, $+\\infty[, P$ et $Q$ sont strictement croissants, et $R$ et $R \\circ Q$ sont strictement positifs.\nOn a alors pour tout $x \\geqslant a$ :\n\n$$\n\\begin{aligned}\n\\mathrm{P}(\\mathrm{P}(\\mathrm{x})) & >\\mathrm{P}(\\mathrm{Q}(x)) \\quad \\text { puisque } \\mathrm{P}(\\mathrm{x})>\\mathrm{Q}(\\mathrm{x}) \\\\\n& =\\mathrm{Q}(\\mathrm{Q}(\\mathrm{x}))+\\mathrm{R}(\\mathrm{Q}(\\mathrm{x})) \\\\\n& >\\mathrm{Q}(\\mathrm{Q}(\\mathrm{x}))\n\\end{aligned}\n$$\n\nce qui contredit $\\mathrm{P}(\\mathrm{P}(\\mathrm{x}))=\\mathrm{Q}(\\mathrm{Q}(\\mathrm{x}))$.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $n>0$ un entier et $x_{1}, \\cdots, x_{n}$ des réels strictement positifs. Prouver que :\n\n$$\n\\begin{gathered}\n\\max _{x_{1}>0, \\cdots, x_{n}>0} \\min \\left(x_{1}, \\frac{1}{x_{1}}+x_{2}, \\cdots, \\frac{1}{x_{n-1}}+x_{n}, \\frac{1}{x_{n}}\\right)= \\\\\n\\min _{x_{1}>0, \\cdots, x_{n}>0} \\max \\left(x_{1}, \\frac{1}{x_{1}}+x_{2}, \\cdots, \\frac{1}{x_{n-1}}+x_{n}, \\frac{1}{x_{n}}\\right)=2 \\cos \\left(\\frac{\\pi}{n+2}\\right) .\n\\end{gathered}\n$$", "solution": "de l'exercice 9 Soit Ul'ensemble des n -uplets de réels strictement positifs. Pour $x=\\left(x_{1}, \\cdots, x_{n}\\right) \\in U$, on pose\n\n$$\n\\begin{aligned}\n& \\quad m(x)=\\min \\left(x_{1}, \\frac{1}{x_{1}}+x_{2}, \\cdots, \\frac{1}{x_{n-1}}+x_{n}, \\frac{1}{x_{n}}\\right) \\\\\n& \\text { et } M(x)=\\max \\left(x_{1}, \\frac{1}{x_{1}}+x_{2}, \\cdots, \\frac{1}{x_{n-1}}+x_{n}, \\frac{1}{x_{n}}\\right)\n\\end{aligned}\n$$\n\nNotre stratégie va consister à prouver qu'il existe $a \\in U$ tel que $m(a)=M(a)$ et que, pour tout $x \\in U$, on a $m(x) \\leqslant m(a)$ et $M(a) \\leqslant M(x)$.\n\nSoit $a=\\left(a_{1}, \\cdots, a_{n}\\right) \\in U$.\nLa condition $m(a)=M(a)$ s'écrit\n\n$$\na_{1}=\\frac{1}{a_{1}}+a_{2}=\\cdots=\\frac{1}{a_{n-1}}+a_{n}=\\frac{1}{a_{n}} .\n$$\n\nMais, admettons pour le moment que l'on ait déjà trouvé $a \\in U$ tel que $m(a)=M(a)$.\nPar l'absurde : On suppose qu'il existe $x \\in U$ tel que $m(x)>m(a)$.\nOn prouve alors par récurrence sur $k$ que $x_{k}>\\mathfrak{a}_{k}$ pour tout $k \\in\\{1, \\cdots, \\mathfrak{n}\\}$ :\nDéjà, on a $x_{1} \\geqslant m(x)>m(a)=a_{1}$.\nD'autre part, si $x_{k}>a_{k}$ pour un certain $k \\in\\{1, \\cdots, n-1\\}$, alors\n\n$$\n\\frac{1}{x_{k}}+x_{k+1} \\geqslant m(x)>m(a)=\\frac{1}{a_{k}}+a_{k+1}\n$$\n\nOr, d'après l'hypothèse de récurrence, on a $\\frac{1}{x_{k}}<\\frac{1}{a_{k}}$, d'où $x_{k+1}>a_{k+1}$, ce qui achève la récurrence.\nEn particulier, on a donc $x_{n}>a_{n}$.\nMais, $\\frac{1}{x_{n}} \\geqslant m(x)>m(a)=\\frac{1}{a_{n}}$, d'où $x_{n}0$ la valeur commune dans (1).\nOn vérifie sans difficulté qu'alors, pour tout $k$, on a $a_{k}=\\frac{b_{k}}{b_{k-1}}$, où $b_{0}=1, b_{1}=\\alpha$, et $b_{j}=\\alpha b_{j-1}-b_{j-2}$ pour $j \\geqslant 2$. (2)\n\nComme $\\alpha=\\frac{1}{a_{n}}$, on doit avoir $b_{n-1}=\\alpha b_{n}$, ce qui signifie que $b_{n+1}=0$.\nRevenons sur $\\alpha$. En fait, on a même $\\alpha<2$ :\nEn effet, supposons que $\\alpha \\geqslant 2$. Alors, $a_{1}=\\alpha \\geqslant 2$ et, par une récurrence sans difficulté, on déduit que $a_{k}=\\alpha-\\frac{1}{a_{k-1}} \\geqslant 1+\\frac{1}{k}$.\nEn particulier, on a $a_{n} \\geqslant 1+\\frac{1}{n}>1$ et $a_{n}=\\frac{1}{\\alpha}<1$, contradiction.\nOn peut donc poser $\\alpha=2 \\cos (t)$ où $t \\in] 0, \\frac{\\pi}{2}[$.\nCompte-tenu de la formule bien connue\n\n$$\n2 \\cos (a) \\sin (b)=\\sin (b+a)+\\sin (b-a)\n$$\n\nune autre récurrence sans difficulté à partir de (2) conduit alors à\n\n$$\nb_{k}=\\frac{\\sin ((k+1) t)}{\\sin (t)} \\text { pour tout } k \\geqslant 0\n$$\n\nLa condition $b_{n+1}=0$ impose alors $t=\\frac{\\pi}{n+2}$. Ainsi, on a $\\alpha=2 \\cos \\left(\\frac{\\pi}{n+2}\\right)$ et $a=\\left(a_{1}, \\cdots, a_{n}\\right)$ où $a_{k}=\\frac{\\sin \\left(\\frac{(k+1) \\pi}{n+2}\\right)}{\\sin \\left(\\frac{k \\pi}{n+2}\\right)}$.\n\nRéciproquement, on vérifie aisément que, dans ces conditions, la chaîne d'égalités (1) est vraie.\n\n$\\mathcal{F i n}$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-3-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
diff --git a/French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl b/French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..2bed106489a3e45b608fc8bbdbf49ab135caf5ee
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl
@@ -0,0 +1,17 @@
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Combien existe-t-il de couples d'entiers strictement positifs ( $a, b$ ) tels que\n\n$$\n\\frac{1}{a}+\\frac{1}{b}=\\frac{1}{2014} ?\n$$", "solution": "de l'exercice 1 Soient $a, b$ deux entiers strictement positifs tels que $1 / a+1 / b=1 / 2014$. On a en particulier $\\mathrm{a}, \\mathrm{b}>2014$. On peut donc multiplier l'équation $\\mathrm{ab}:$ on cherche en fait les entiers $\\mathrm{a}, \\mathrm{b}>2014$ tels que $\\mathrm{ab}-2014 \\mathrm{a}-2014 \\mathrm{~b}=0$ ou encore, de manière équivalente, tels que ( $a-$ $2014)(b-2014)=2014^{2}$. On en déduit que le nombre recherché est le nombre de couples d'entiers strictement positifs $(u, v)$ tels que $u v=2014^{2}$, autrement dit le nombre de diviseurs positifs de $2014^{2}$. Comme $2014^{2}=2^{2} \\cdot 19^{2} \\cdot 53^{2}, 2014^{2}$ possède $(2+1) \\cdot(2+1) \\cdot(2+1)=27$ diviseurs positifs.\n\nLa réponse est donc 27 .", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Trouver tous les entiers $\\boldsymbol{n} \\geqslant 1$ tels que $2^{n}+12^{n}+2014^{n}$ soit un carré parfait.", "solution": "de l'exercice 2 Regardons l'expression modulo $3: 2^{\\mathfrak{n}}+12^{n}+2014^{n} \\equiv(-1)^{n}+1 \\bmod 3$. Comme un carré n'est jamais congru à 2 modulo 3, on en déduit que $n$ est impair. Regardons ensuite l'expression modulo 7 :\n\n$$\n2^{n}+12^{n}+2014^{n} \\equiv 2^{n}+(-2)^{n}+5^{n} \\equiv 5^{n} \\quad \\bmod 7\n$$\n\ncar $n$ est impair. Lorsque $n$ est impair, $5^{n}$ ne peut être congru qu'à 3,5 ou 6 modulo 7 . Or un carré est congru à $0,1,2$ ou 4 modulo 7 . Il n'existe donc pas d'entiers $n \\geqslant 1$ tels que $2^{n}+12^{n}+2014^{n}$ soit un carré parfait.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver tous les couples d'entiers relatifs $(x, y)$ tels que $x^{3}+y^{3}=(x+y)^{2}$.", "solution": "de l'exercice 3 Soit $(x, y)$ un couple", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver tous les couples d'entiers relatifs $(x, y)$ tels que $x^{3}+y^{3}=(x+y)^{2}$.", "solution": "Comme $x^{3}+y^{3}=(x+y)\\left(x^{2}-x y+y^{2}\\right)$, on a donc soit $x+y=0$, soit $x^{2}-x y+y^{2}=x+y$. Dans le deuxième cas, on remarque qu'alors nécessairement\n$(x-1)^{2}+(y-1)^{2}+(x-y)^{2}=2$. Parmi les trois entiers $x-1, y-1$ et $x-y$, deux sont donc égaux à $1 \\mathrm{ou}-1$ et le troisième est nul. On vérifie que les seules possibilités sont $(2,2),(0,0),(1,2),(1,0),(2,1)$ et $(0,1)$.\n\nAinsi, les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver tous les couples d'entiers relatifs $(x, y)$ tels que $x^{3}+y^{3}=(x+y)^{2}$.", "solution": "s sont les couples $(2,2),(1,2),(1,0),(2,1),(0,1)$ et $(x,-x)$ où $x$ est un entier relatif.\n\n## Exercices Communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": " solution"}}
+{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers positifs $(m, n)$ tels que $1+(m+n) m$ divise $(m+$ $n)(n+1)-1$.", "solution": "de l'exercice 4 Soit $(m, n)$ un couple", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les couples d'entiers positifs $(m, n)$ tels que $1+(m+n) m$ divise $(m+$ $n)(n+1)-1$.", "solution": "Alors $1+(m+n) m$ divise $(m+n)(n+1)-1+$ $1+(m+n) m=(m+n)(m+n+1)$. Or, $1+(m+n) m$ est premier avec $m+n$. Ainsi, $1+(m+n) m$ divise $m+n+1$. Donc $m^{2}+m n+1 \\leqslant m+n+1$. Donc $m=0$ ou $m=1$.\n\nRéciproquement, on vérifie que les couples $(0, n)$ et $(1, n)$, où $\\boldsymbol{n} \\geqslant 0$ est un entier, conviennent.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Montrer que si la somme de tous les diviseurs positifs d'un entier $n \\geqslant 1$ est une puissance de deux, alors le nombre de diviseurs positifs de n est une puissance de deux.", "solution": "de l'exercice 5 Décomposons $n$ en produit de facteurs premiers : $n=\\prod_{i=1}^{k} p_{i}^{\\alpha_{i}}$. On voit aisément que la somme des diviseurs positifs de $n$, notée $\\sigma(n)$, vaut\n\n$$\n\\sigma(n)=\\prod_{i=1}^{k}\\left(1+p_{i}+p_{i}^{2}+\\cdots+p_{i}^{\\alpha_{i}}\\right)\n$$\n\nAinsi, si $1 \\leqslant i \\leqslant k, 1+p_{i}+p_{i}^{2}+\\cdots+p_{i}^{\\alpha_{i}}$ est une puissance de deux. Ceci implique clairement que $p_{i} \\neq 2$. Supposons ensuite par l'absurde que $\\alpha_{i}+1$ n'est pas une puissance de deux et choisissons $q$ un nombre premier impair divisant $\\alpha_{i}+1$. Alors\n\n$$\n1+p_{i}+p_{i}^{2}+\\cdots+p_{i}^{\\alpha_{i}}=\\left(1+p_{i}+p_{i}^{2}+\\cdots+p_{i}^{q-1}\\right) \\cdot\\left(1+p_{i}^{q}+p_{i}^{2 q}+\\cdots+p_{i}^{\\alpha_{i}+1-q}\\right)\n$$\n\nEn effet, cette égalité découle du fait que $\\left(p_{i}^{\\alpha_{i}+1}-1\\right) /(p-1)=\\left(p_{i}^{q}-1\\right) /(p-1) \\cdot\\left(p_{i}^{\\alpha_{i}+1}-1\\right) /\\left(p^{q}-1\\right)$. Ceci est absurde, car $1+p_{i}+p_{i}^{2}+\\cdots+p_{i}^{q-1}$ est impair. Ainsi, $\\alpha_{i}+1$ est une puissance de deux pour tout $1 \\leqslant i \\leqslant k$. Ceci conclut, car le nombre de diviseurs (positifs) de $n$ est $\\prod_{i=1}^{k}\\left(\\alpha_{i}+1\\right)$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p$ et $q$ tels que $p$ divise $5^{q}+1$ et $q$ divise $5^{p}+1$.", "solution": "de l'exercice 6 Notons $\\alpha$ l'ordre de 5 modulo $q$ et $\\beta$ l'ordre de 5 modulo $p$. Comme $5^{2 p} \\equiv 1$ $\\bmod \\mathrm{q}$, on en déduit que $\\alpha$ divise $2 p$. Donc $\\alpha=1,2, \\mathrm{p}$ ou $2 p$.\n\nSi $\\alpha=1$, alors $5 \\equiv 1 \\bmod \\mathbf{q}$, donc $\\mathbf{q}=2$. Si $\\alpha=2$, alors $25 \\equiv 1 \\bmod \\mathbf{q}$, donc $\\mathbf{q}=2$ ou $\\mathbf{q}=3$.\nSi $q=2$, alors $p$ divise $5^{2}+1$, donc $p=2$ ou $p=13$. Réciproquement, $(2,2)$ et $(13,2)$ conviennent.\nSi $q=3$, alors $p$ divise $5^{3}+1$, donc $p=2,3$ ou 7 . Réciproquement, on vérifie que $(3,3),(7,3)$ conviennent, mais que $(2,3)$ ne convient pas.\n\nDe même, on a $\\beta=1,2$, q ou 2 q. Si $\\beta=1$ ou 2 , on obtient similairement les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p$ et $q$ tels que $p$ divise $5^{q}+1$ et $q$ divise $5^{p}+1$.", "solution": "s $(2,13)$ et $(3,7)$.\n\nSupposons maintenant que $\\alpha=p$ ou $2 p$ et que $\\beta=q$ ou $2 q$. D'après le petit théorème de Fermat, $5^{p-1} \\equiv 1 \\bmod p$ et $5^{q-1} \\equiv 1 \\bmod q$. Donc $\\beta$ divise $p-1$ et $\\alpha$ divise $q-1$. Donc $q$ divise $p-1$ et $p$ divise $\\mathrm{q}-1$. Donc $\\mathrm{q} \\leqslant \\mathrm{p}-1$ et $\\mathrm{p} \\leqslant \\mathrm{q}-1$. Ainsi $\\mathrm{q} \\leqslant \\mathrm{q}-2$, ce qui est absurde.\n\nLes", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les nombres premiers $p$ et $q$ tels que $p$ divise $5^{q}+1$ et $q$ divise $5^{p}+1$.", "solution": "s sont donc $(2,2),(3,3),(13,2),(2,13),(3,7)$ et $(7,3)$.\n\n## Exercices du groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{N} \\rightarrow \\mathbb{N}$ telles que $2 m n+m f(m)+n f(n)$ est un carré parfait pour tous entiers positifs $m$ et $n$.", "solution": "de l'exercice 7 Pour simplifier, posons $F(m, n)=2 m n+m f(m)+n f(n)$. Alors $F(m, 0)=$ $\\mathrm{mf}(\\mathrm{m})$ est un carré pour tout $\\mathrm{m} \\geqslant 1$.\n\nOn peut donc écrire $f(p)=p a^{2}$ pour un nombre premier $p$. Supposons que $a \\geqslant 2$. Alors $(a p)^{2}+2 p+$ $f(1)=F(p, 1)>\\left(a p^{2}\\right)$ est un carré, donc $(a p)^{2}+2 p+f(1) \\geqslant(a p+1)^{2}$ et $2 p+f(1) \\geqslant 2 a p+1 \\geqslant 4 p+1$, de sorte que $p \\leqslant(f(1)-1) / 2$. Ainsi $f(p)=p$ pour tous nombres premiers $p$ suffisamment grands.\n\nSoit maintenant $k \\geqslant 1$ et $p$ un nombre premier suffisamment grand pour que $f(p)=p, p>k f(k)$ et $\\mathrm{p}>\\mathrm{k}^{2}+1$. Alors\n\n$$\n\\begin{gathered}\n(k+p-1)^{2}=\\left(k^{2}+1\\right)+p^{2}-2 k-2 p+2 k p0$ le plus petit entier tel que $(a, b, c)$ soit", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "(Corée 2003) Trouver tous les triplets d'entiers ( $a, b, c$ ) tels que $a \\neq 0$ et\n\n$$\n2 a^{4}+2 a^{2} b^{2}+b^{4}=c^{2}\n$$", "solution": "Si $d=\\operatorname{pgcd}(a, b)$, en divisant l'égalité par $d^{4}$ on voit que $\\left(a / d, b / d, c / d^{2}\\right)$ est également", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "(Corée 2003) Trouver tous les triplets d'entiers ( $a, b, c$ ) tels que $a \\neq 0$ et\n\n$$\n2 a^{4}+2 a^{2} b^{2}+b^{4}=c^{2}\n$$", "solution": "On a donc $\\mathrm{d}=1$.\n\nRegardons l'expression $2 a^{4}+2 a^{2} b^{2}+b^{4}$ modulo 8 , et utilisons le fait qu'un carré est congru à 0,1 ou 4 modulo 8 : si a est impair, alors $2 a^{4}+2 a^{2} b^{2}+b^{4}$ est congru à 2 ou à 5 modulo $8 ; a$ est donc forcément pair, et b es impair. Réécrivons l'égalité de l'énoncé en\n\n$$\n\\left(a^{2}\\right)^{2}+\\left(a^{2}+b^{2}\\right)^{2}=c^{2}\n$$\n\nLe triplet $\\left(a^{2}, a^{2}+b^{2}, c\\right)$ est donc pythagoricien. Comme $\\operatorname{pgcd}(a, b)=1$, il existe des entiers $u, v$ premiers entre eux tels que $a^{2}=2 u v, a^{2}+b^{2}=u^{2}-v^{2}$ et $c=u^{2}+v^{2}$.\n\nEn regardant modulo 4 , on obtient $1 \\equiv a^{2}+b^{2} \\equiv u^{2}-v^{2}$. Puisqu'un carré est congru à 0 ou 1 modulo 4 , on en déduit que $u$ est impair et que $v$ est pair. Puisque $a^{2}=2 u v$ et que $u$ et $v$ sont premiers entre eux, on peut écrire $u=m^{2}$ et $v=2 n^{2}$ avec $m, n$ premiers entre eux et $m$ impair. De $b^{2}=u^{2}-v^{2}-2 u v$ il vient $2 v^{2}=(u-v+b)(u-v-b)$. Donc\n\n$$\n2 n^{4}=\\left(\\frac{m^{2}-2 n^{2}+b}{2}\\right)\\left(\\frac{m^{2}-2 n^{2}-b}{2}\\right) .\n$$\n\nPosons $x=\\left(m^{2}-2 n^{2}+b\\right) / 2$ et $y=\\left(m^{2}-2 n^{2}-b\\right) / 2$ : ce sont des entiers car $m^{2}$ et $b$ sont impairs. En outre, $00$, donc $\\mathrm{lm} \\geqslant 1$ et $0<\\mathrm{k}<\\mathrm{a}$, ce qui contredit la minimalité de a .\nIl n'existe donc pas de triplet ( $a, b, c$ )", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "(Corée 2003) Trouver tous les triplets d'entiers ( $a, b, c$ ) tels que $a \\neq 0$ et\n\n$$\n2 a^{4}+2 a^{2} b^{2}+b^{4}=c^{2}\n$$", "solution": "lorsque $a \\neq 0$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver le nombre de suites $\\left(u_{n}\\right)_{n \\geqslant 1}$ d'entiers relatifs telles que $u_{n} \\neq-1$ pour tout entier $n \\geqslant 1$ et telles que\n\n$$\nu_{n+2}=\\frac{2014+u_{n}}{1+u_{n+1}}\n$$\n\npour tout entier $\\mathrm{n} \\geqslant 1$.", "solution": "de l'exercice 9\n La relation de l'énoncé impose que $\\left(u_{n+1}-u_{n-1}\\right)\\left(u_{n}+1\\right)=u_{n}-u_{n-2}$ pour $\\mathrm{n} \\geqslant 3$. Par récurrence, il vient\n\n$$\n\\mathbf{u}_{3}-\\mathbf{u}_{1}=\\prod_{i=3}^{n}\\left(u_{i}+1\\right)\\left(u_{n+1}-u_{n-1}\\right)\n$$\n\nSupposons par l'absurde que $u_{3} \\neq u_{1}$. Ainsi $u_{n+1} \\neq u_{n-1}$ pour tout $n \\geqslant 2$. En faisant croitre $n$, on voit qu'il ne peut pas y avoir une infinité de termes $u_{i}$ tels que $u_{i} \\neq 0,-2$. Ainsi, $u_{i}=0$ ou -2 à partir d'un certain rang (car $\\mathfrak{u}_{3}-\\mathfrak{u}_{1}$ a un nombre fini de diviseurs). On vérifie aisément à partir de la relation de récurence de l'énoncé que ceci n'est pas possible. Donc $u_{3}=u_{1}$, et par (1) on en déduit que $u_{n+2}=u_{n}$ pour tout entier $n \\geqslant 1$.\n\nSous cette hypothèse, la relation à vérifier devient $\\left(1+u_{n+1}\\right) u_{n}=2014+u_{n}$, ou encore $u_{n} u_{n+1}=$ 2014, ce qui est équivalent à $u_{1} \\mathfrak{u}_{2}=2014$. Ainsi, le nombre de suites $\\left(u_{n}\\right)_{n \\geqslant 1}$ qui conviennent est le nombre paires d'entiers $(a, b)$ telles que $a b=2014$, avec $a \\neq-1$ et $b \\neq-1$ : c'est exactement le nombre de diviseurs (positifs ou négatifs) de 2014, moins 2. Comme $2014=2 \\cdot 19 \\cdot 53$, celui-ci a $2 \\cdot(1+1) \\cdot(1+1) \\cdot(1+1)=16$ diviseurs (positifs ou négatifs), donc 14 suites conviennent.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-4-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
diff --git a/French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl b/French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..d9fae9e969d18f144a813c08fff026ba53b339d7
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl
@@ -0,0 +1,11 @@
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soit $A B C D$ un carré de côté 1. À l'intérieur du carré, on trace les arcs de cercles de centres $A, B, C, D$ et de rayon 1 . Déterminer l'aire de chaque portion délimitée à l'intérieur du carré.", "solution": "de l'exercice 1\n\nConsidérons les aires $a, b, c$ des portions indiquées sur la figure.\n\n\nComme l'aire du carré est égale à 1 , on a\n\n$$\na+4 b+4 c=1 .\n$$\n\nComme l'aire du quart de cercle $A B C$ est égale à $\\pi / 4$, on a\n\n$$\na+3 b+2 c=\\pi / 4 \\text {. }\n$$\n\nConsidérons maintenant le secteur angulaire $O M N$ de rayon 1 et d'angle $\\pi / 3$. Il a pour aire $\\pi / 6$. D'autre part, le triangle $O M N$ a pour aire $\\frac{\\sqrt{3}}{4}$, donc l'aire de la \"lune\" est égale à $\\frac{\\pi}{6}-\\frac{\\sqrt{3}}{4}$. On en déduit que\n\n$$\na+2 b+c=2\\left(\\frac{\\pi}{6}-\\frac{\\sqrt{3}}{4}\\right)+\\frac{\\sqrt{3}}{4}=\\frac{\\pi}{3}-\\frac{\\sqrt{3}}{4} .\n$$\n\nEn soustrayant les équations (1) et (2) et les équations (1) et (3), on en déduit\n\n$$\n\\begin{aligned}\nb+2 c & =1-\\frac{\\pi}{4} \\\\\n2 b+3 c & =1+\\frac{\\sqrt{3}}{4}-\\frac{\\pi}{3}\n\\end{aligned}\n$$\n\nce qui donne facilement\n\n$$\n\\begin{aligned}\nb & =-1+\\frac{\\sqrt{3}}{2}+\\frac{\\pi}{12} \\\\\nc & =1-\\frac{\\sqrt{3}}{4}-\\frac{\\pi}{6} \\\\\na & =1-\\sqrt{3}+\\frac{\\pi}{3}\n\\end{aligned}\n$$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "## Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Dans un cercle $\\mathcal{C}$ de centre $O$, on trace une corde $[C D]$. Soit $\\Gamma$ le cercle de diamètre $[C D]$ et $O^{\\prime}$ son centre. La médiatrice de $[C D]$ coupe le cercle $\\mathcal{C}$ en deux points $A$ et $B$ tels que $A$ est extérieur à $\\Gamma$. Notons $T$ et $T^{\\prime}$ les points de contact des tangentes à $\\Gamma$ passant par $A$. Soit $F$ le milieu de $\\left[T T^{\\prime}\\right]$. Montrer que $O^{\\prime}$ est le milieu de $[B F]$.", "solution": "de l'exercice 2\n\n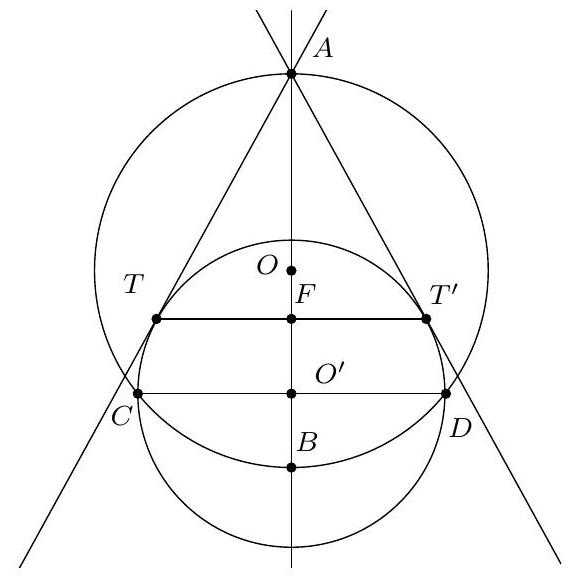\n\nComme les triangles $A F T$ et $A T O^{\\prime}$ sont semblables, on a $\\frac{A F}{A T}=\\frac{A T}{A O^{\\prime}}$. Or, $A T^{2}=A O^{\\prime 2}-O^{\\prime} T^{2}=$ $A O^{\\prime 2}-O^{\\prime} C^{2}$ donc $A F=\\frac{A O^{\\prime 2}-O^{\\prime} C^{2}}{A O^{\\prime}}$.\nComme les triangles $A C B$ et $A O^{\\prime} C$ sont semblables, on a $\\frac{A B}{A C}=\\frac{A C}{A O^{\\prime}}$. Or, $A C^{2}=A O^{\\prime 2}+O^{\\prime} C^{2}$ donc $A B=\\frac{A O^{\\prime 2}+O^{\\prime} C^{2}}{A O^{\\prime}}$.\nEn additionnant les égalités précédemment trouvées, on obtient $\\frac{A F+A B}{2}=A O^{\\prime}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $A B C$ un triangle isocèle en $A$. Soient $M$ et $N$ deux points de $[B C]$. Les droites $[A M]$ et $[A N]$ recoupent le cercle circonscrit à $A B C$ en $P$ et $Q$.\n\n1) Montrer que $M, N, P, Q$ sont cocycliques.\n2) Soient $R_{1}$ et $R_{2}$ les rayons des cercles circonscrits à $B M P$ et $C M P$. Calculer $R_{1}+R_{2}$ en fonction des longueurs $A B$ et $B C$.", "solution": "de l'exercice 3\n\n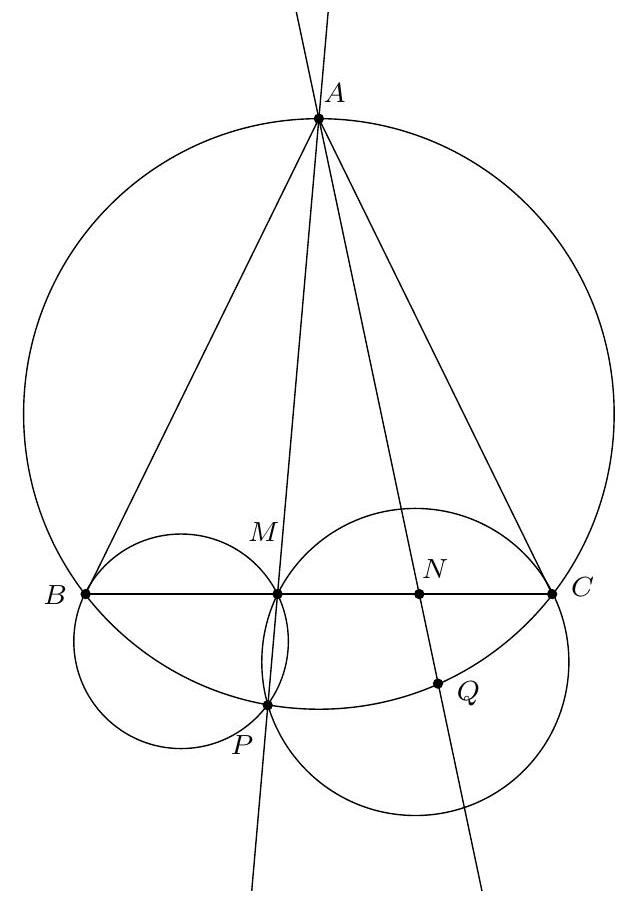\n\n1) $\\widehat{P M N}=\\widehat{P M C}=\\pi-\\widehat{M C P}-\\widehat{C P M}=\\pi-\\widehat{B C P}-\\widehat{C P A}=\\pi-\\widehat{B C P}-\\widehat{C B A}$, et $\\widehat{N Q P}=\\widehat{A Q P}=\\widehat{A C P}=\\widehat{A C B}+\\widehat{B C P}=\\widehat{C B A}+\\widehat{B C P}$,\ndonc $\\widehat{P M N}=\\pi-\\widehat{N Q P}$, ce qui prouve la cocyclicité de $M, N, P, Q$.\n2) D'après la loi des sinus, on a\n\n$$\n2\\left(R_{1}+R_{2}\\right)=\\frac{B M}{\\sin \\widehat{M P B}}+\\frac{C M}{\\sin \\widehat{C P M}}\n$$\n\nOr, $\\widehat{M P B}=\\widehat{A P B}=\\widehat{A C B}$ et de même $\\widehat{C P M}=\\widehat{A C B}$, donc\n\n$$\n2\\left(R_{1}+R_{2}\\right)=\\frac{B M+C M}{\\sin \\widehat{A C B}}=\\frac{B C}{\\sin \\widehat{A C B}} .\n$$\n\nD'autre part, soit $H$ le projeté orthogonal de $A \\operatorname{sur}(B C)$. On a $\\sin \\widehat{A C B}=\\frac{A H}{A B}=\\frac{\\sqrt{A B^{2}-(B C / 2)^{2}}}{A B}$, donc\n\n$$\nR_{1}+R_{2}=\\frac{A B \\times B C}{2 \\sqrt{A B^{2}-(B C / 2)^{2}}}\n$$\n\n## Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C$ un triangle. Les bissectrices de $\\widehat{A}, \\widehat{B}$ et $\\widehat{C}$ recoupent le cercle circonscrit en $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ respectivement. Soit $I$ le centre du cercle inscrit à $A B C$. Les cercles de diamètres $\\left[I A^{\\prime}\\right],\\left[I B^{\\prime}\\right]$ et $\\left[I C^{\\prime}\\right]$ coupent respectivement les droites $(B C),(C A)$ et $(A B)$ en $A_{1}$ et $A_{2}, B_{2}$ et $B_{2}$, $C_{1}$ et $C_{2}$. Montrer que $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ sont cocycliques.", "solution": "de l'exercice 4\n\n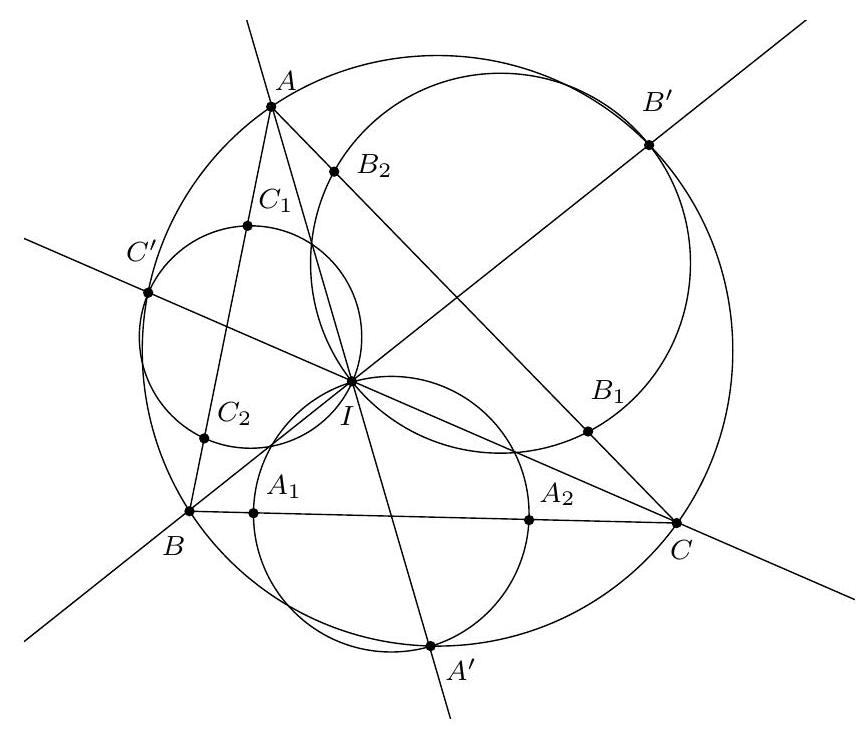\n\nNotons $\\Gamma_{A}, \\Gamma_{B}$ et $\\Gamma_{C}$ les cercles de diamètres respectifs $\\left[I A^{\\prime}\\right],\\left[I B^{\\prime}\\right]$ et $\\left[I C^{\\prime}\\right]$.\nRemarquons d'abord que $I$ est l'orthocentre de $A^{\\prime} B^{\\prime} C^{\\prime}$. Pour le voir, montrons par exemple que $\\left(A^{\\prime} C^{\\prime}\\right) \\perp\\left(B^{\\prime} I\\right)$ :\n\n$$\n\\begin{aligned}\n\\left(B^{\\prime} I, A^{\\prime} C^{\\prime}\\right) & =\\left(B B^{\\prime}, A^{\\prime} C^{\\prime}\\right)=\\left(B B^{\\prime}, B A\\right)+\\left(A B, A A^{\\prime}\\right)+\\left(A^{\\prime} A, A^{\\prime} C^{\\prime}\\right) \\\\\n& =\\left(B B^{\\prime}, B A\\right)+\\left(A B, A A^{\\prime}\\right)+\\left(C A, C C^{\\prime}\\right) \\\\\n& =\\frac{\\widehat{B}+\\widehat{A}+\\widehat{C}}{2}=\\frac{\\pi}{2} \\quad(\\bmod \\pi)\n\\end{aligned}\n$$\n\nSoit $B^{\\prime \\prime}$ le pied de la hauteur de $A^{\\prime} B^{\\prime} C^{\\prime}$ issue de $B^{\\prime}$. Alors $B, B^{\\prime \\prime}$ et $I$ sont alignés d'après ce qui précède.\nD'autre part, comme $\\left(I B^{\\prime \\prime}\\right) \\perp\\left(B^{\\prime \\prime} A^{\\prime}\\right), B^{\\prime \\prime}$ appartient à $\\Gamma_{A}$. De même, il appartient à $\\Gamma_{C}$, donc l'axe radical de ces deux cercles est $\\left(I B^{\\prime \\prime}\\right)$. On en déduit que $B$ appartient également à cet axe radical, ce qui entraîne que $B A_{1} \\cdot B A_{2}=B C_{1} \\cdot B C_{2}$ et donc $A_{1}, A_{2}, C_{1}, C_{2}$ sont cocycliques. Soit $\\Gamma_{C A}$ le cercle passant par ces points.\nOn définit de même $\\Gamma_{A B}$ et $\\Gamma_{B C}$. Si ces trois cercles étaient deux à deux distincts, alors leurs axes radicaux pris deux à deux seraient $(A B),(B C)$ et $(C A)$ et ne seraient ni concourants ni parallèles, ce qui est impossible.\nDonc deux de ces cercles sont confondus, et par conséquent $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ sont cocycliques.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit $A B C D$ un quadrilatère cyclique. Un cercle passant par $A$ et $B$ coupe $[A C]$ et $[B D]$ en $E$ et $F$. Les droites $(A F)$ et $(B E)$ coupent $[B C]$ et $[A D]$ en $P$ et $Q$ respectivement. Montrer que $(P Q)$ est parallèle à $(C D)$.", "solution": "de l'exercice 5\n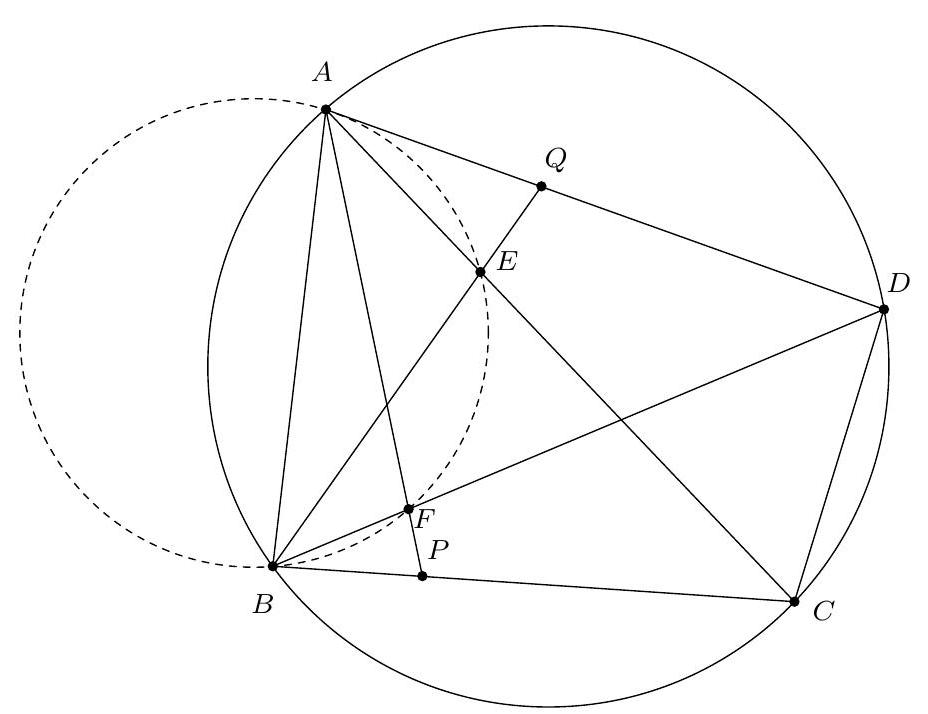\n$\\widehat{A Q B}=\\widehat{A Q E}=\\pi-\\widehat{Q E A}-\\widehat{E A Q}=\\widehat{A E B}-\\widehat{C A D}$ et de même, $\\widehat{A P B}=\\widehat{A F B}-\\widehat{C B D}$. Or, $\\widehat{A E B}=\\widehat{A F B}$ et $\\widehat{C A D}=\\widehat{C B D}$, donc $\\widehat{A Q B}=\\widehat{A P B}$. On en déduit que $A, B, P, Q$ sont cocycliques. Il vient: $(A D, P Q)=(Q A, Q P)=(B A, B P)=(B A, B C)=(D A, D C)$, donc $(P Q)$ et $(D C)$ sont parallèles.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $A$ un point extérieur à un cercle $\\Gamma$. On mène deux tangentes $[A T]$ et $\\left[A T^{\\prime}\\right]$ issues de $A$. Soient $M$ et $M^{\\prime}$ les milieux de $[A T]$ et $\\left[A T^{\\prime}\\right]$. Soit $P$ un point de $\\left(M M^{\\prime}\\right)$. Notons $[U V]$ la corde de $\\Gamma$ telle que $(P U)$ et $(P V)$ soient tangentes à $\\Gamma$. La droite $(U V)$ coupe $\\left(M M^{\\prime}\\right)$ en $Q$. Montrer que le triangle $P A Q$ est rectangle.", "solution": "de l'exercice 6\n\n\n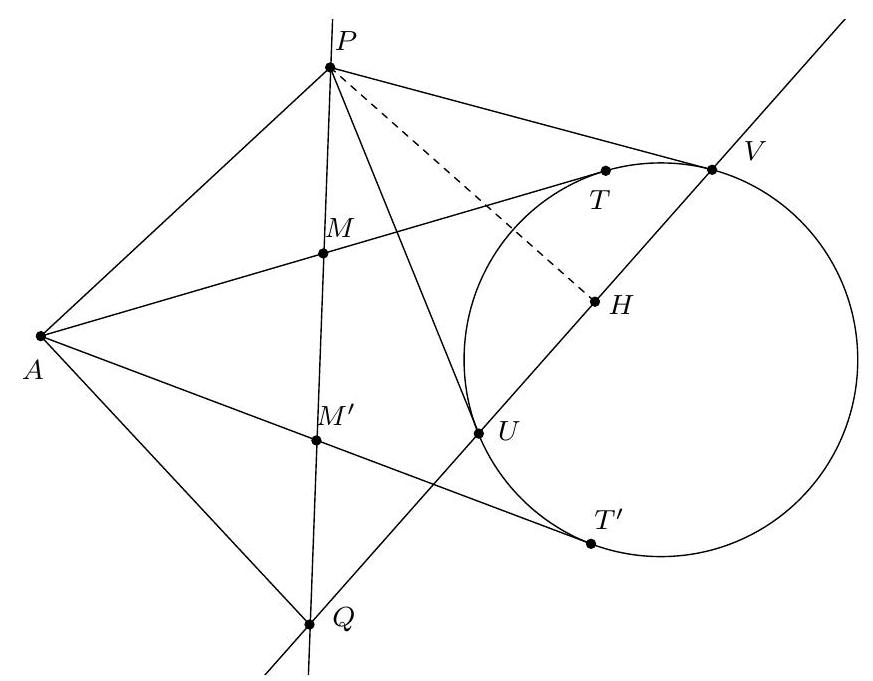\n\nComme $M A=M T, M$ appartient à l'axe radical de $A$ et $\\Gamma$ ( $A$ étant considéré comme un cercle de rayon nul). De même, $M^{\\prime}$ appartient à cet axe radical, donc $P$ et $Q$ également. On en déduit que $P A=P U=P V$ et que $Q A^{2}=Q U \\cdot Q V$.\nNotons $H$ le projeté orthogonal de $P$ sur ( $U V$ ). On a\n\n$$\n\\begin{aligned}\nP A^{2}+Q A^{2} & =P U^{2}+Q U \\cdot Q V=P H^{2}+H U^{2}+(Q H-H U)(Q H+H U) \\\\\n& =P H^{2}+H U^{2}+Q H^{2}-H U^{2}=P H^{2}+Q H^{2}=P Q^{2}\n\\end{aligned}\n$$\n\ndonc $P A Q$ est rectangle en $A$.\n\n## Exercices du groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## \nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $A B C$ un triangle et $\\omega$ son cercle inscrit. On note $P, Q, R$ les points de contact de $\\omega$ avec $(B C),(C A)$ et $(A B)$. Un cercle passant par $B$ et $C$ est tangent en $X$ à $\\omega$, un cercle passant par $C$ et $A$ est tangent en $Y$ à $\\omega$ et un cercle passant par $A$ et $B$ est tangent en $Z$ à $\\omega$. Montrer que les droites $(P X),(Q Y)$ et $(R Z)$ sont concourantes.", "solution": "de l'exercice 7\nRappelons d'abord quelques résultats sur la polarité que nous allons utiliser. Soit $\\mathcal{C}$ un cercle de centre $O$ et de rayon $R$. Si $P$ est un point distinct de $O$, la polaire de $P$ par rapport à $\\mathcal{C}$ est la droite formée des points $M$ tels que $\\overrightarrow{O P} \\cdot \\overrightarrow{O M}=R^{2}$. Le pôle par rapport à $\\mathcal{C}$ d'une droite $\\mathcal{D}$ ne passant pas par $O$ est l'unique point $P$ tel que pour tout $M$ appartenant à $\\mathcal{D}$ on a $\\overrightarrow{O P} \\cdot \\overrightarrow{O M}=R^{2}$. À partir de cette définition, il est facile de montrer les propriétés suivantes:\n(i) si $P$ est un point extérieur à $\\mathcal{C}$ et $(P T),\\left(P T^{\\prime}\\right)$ sont les deux tangentes à $\\mathcal{C}$, alors la polaire de $P$ est la droite ( $T T^{\\prime}$ );\n(ii) trois points donnés sont alignés si et seulement si leurs polaires sont concourantes.\n(Remarque : pour la propriété (ii), la droite sur laquelle se trouvent les trois points est la polaire du point de rencontre des trois droites.)\n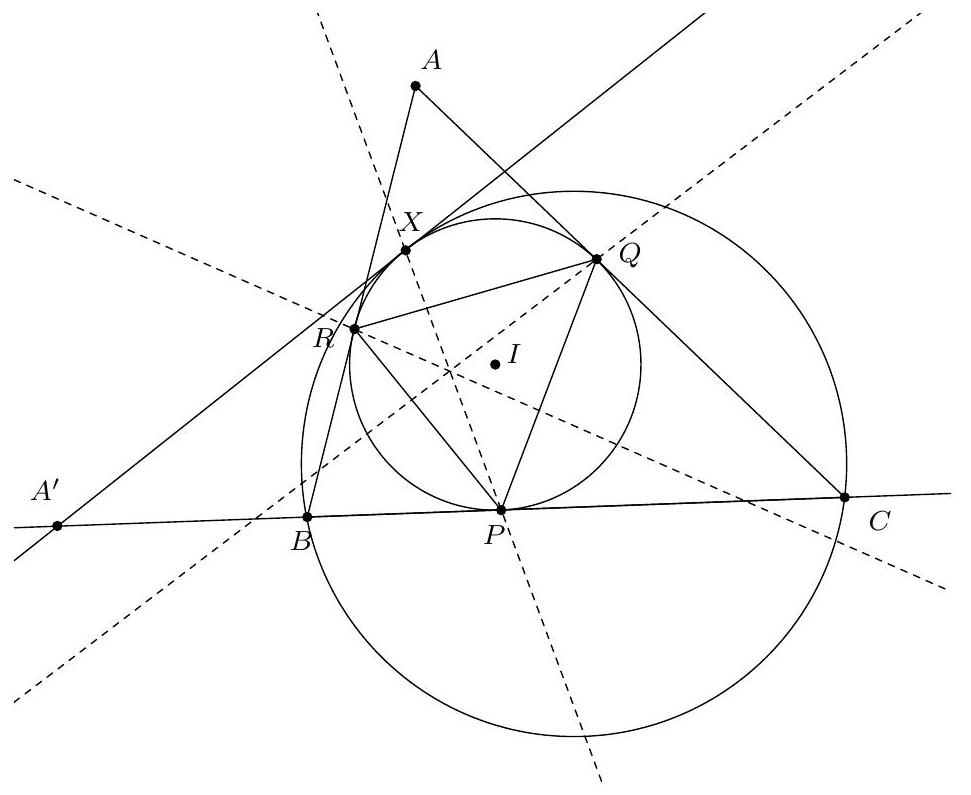\n\nRevenons à l'exercice. Notons $\\Gamma_{A}$ le cercle passant par $B, C$ et $X$. On définit de même les cercles $\\Gamma_{B}$ et $\\Gamma_{C}$. Soit $A^{\\prime}$ le point de rencontre entre la tangente commune à $\\omega$ et $\\Gamma_{X}$, et la droite $(B C)$. On définit de même les points $B^{\\prime}$ et $C^{\\prime}$.\nD'après la propriété (ii), la polaire de $A^{\\prime}$ par rapport à $\\omega$ est la droite $(P X)$. Il suffit donc d'après la propriété (i) de montrer que $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ sont alignés.\nSoit $\\Gamma$ le cercle circonscrit à $A B C$. Comme $A^{\\prime}$ appartient à l'axe radical $(B C)$ de $\\Gamma$ et $\\Gamma_{A}$, on a $\\mathcal{P}_{\\Gamma}\\left(A^{\\prime}\\right)=\\mathcal{P}_{\\Gamma_{A}}\\left(A^{\\prime}\\right)=A^{\\prime} X^{2}=\\mathcal{P}_{\\omega}\\left(A^{\\prime}\\right)$. On en déduit que $A^{\\prime}$ appartient à l'axe radical de $\\Gamma$ et $\\omega$. Il en va de même pour $B^{\\prime}$ et $C^{\\prime}$, ce qui prouve que $A^{\\prime}, B^{\\prime}$ et $C^{\\prime}$ sont alignés.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle. On note $P$ le milieu de l'arc du cercle circonscrit à $A B C$ contenant $A$. On suppose que la bissectrice de l'angle $\\widehat{B A C}$ coupe le cercle de diamètre $[P C]$ en deux points $D$ et $E$. Soit $F$ le symétrique de $E$ par rapport à $(B C)$ et $I$ le milieu de $[B C]$. Montrer que $B, D, F, I$ sont cocycliques.", "solution": "de l'exercice 8\n\n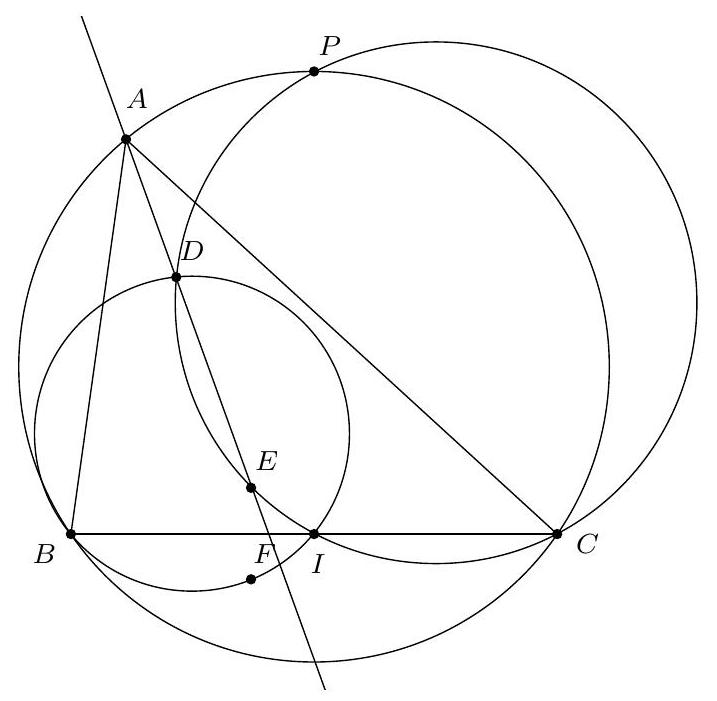\n\nOn applique l'inversion $i$ de pôle $I$ et de puissance $-I B \\cdot I C$. Soit $Q$ le point diamétralement opposé à $P$. Alors $i$ échange $P$ et $Q$ d'une part, et $B$ et $C$ d'autre part. Comme le cercle de diamètre $[P C]$ passe par $I$, son image par $i$ est une droite. Or, $i(P)=Q$ et $i(C)=B$, donc $i$ transforme le cercle de diamètre $[P C]$ en la droite $(B Q)$.\nLa bissectrice de $\\widehat{A}$ est transformée en un cercle passant par $I$ et par $P$.\nNotons $K=i(D), L=i(E)$ et $M=i(F)$. D'après ce qui précède, les points $K$ et $L$ appartiennent à $(B Q)$, et $P, I, K, L$ sont cocycliques. De plus, $L$ et $M$ sont symétriques par rapport à $(B C)$.\n\n\nEnfin, remarquons que $Q I \\cdot Q P=Q B^{2}$ car $Q B I$ et $Q P B$ sont semblables. En utilisant la puissance par rapport au cercle $P I K L$, on obtient que $Q K \\cdot Q L=Q B^{2}$, donc $K$ et $L$ sont inverses par rapport au cercle de centre $Q$ et de rayon $Q B$. On est ainsi ramenés à démontrer le lemme suivant :\nLemme: Soit $\\mathcal{C}$ un cercle de centre $Q$. Soit $[B C]$ une corde de $\\mathcal{C}$ et $L$ un point de $(Q B)$. Alors $C$, l'inverse de $L$ par rapport à $\\mathcal{C}$ et le symétrique de $L$ par rapport à $(B C)$ sont alignés.\n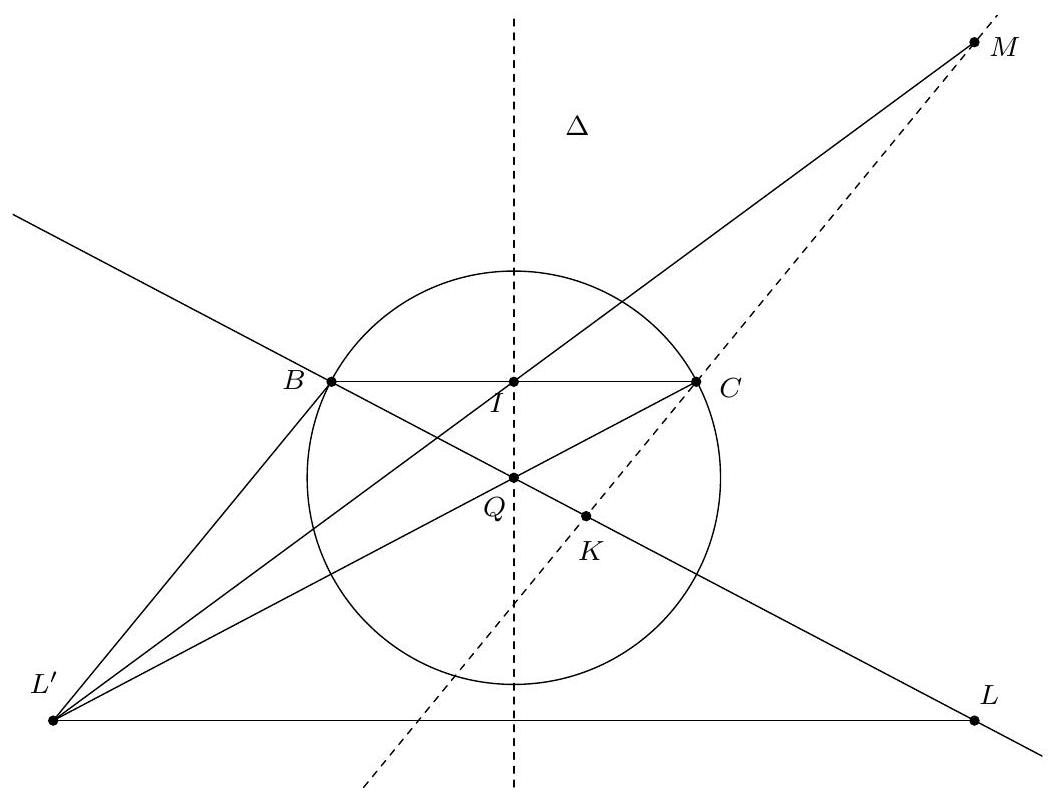", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle. On note $P$ le milieu de l'arc du cercle circonscrit à $A B C$ contenant $A$. On suppose que la bissectrice de l'angle $\\widehat{B A C}$ coupe le cercle de diamètre $[P C]$ en deux points $D$ et $E$. Soit $F$ le symétrique de $E$ par rapport à $(B C)$ et $I$ le milieu de $[B C]$. Montrer que $B, D, F, I$ sont cocycliques.", "solution": "du lemme: on note toujours $I$ le milieu de $[B C]$. Soit $\\Delta$ la médiatrice de $[B C]$ et $L^{\\prime}$ le symétrique de $L$ par rapport à $\\Delta$. On a\n\n$$\n\\left[B L^{\\prime}\\right]=\\operatorname{sym}_{\\Delta}([C L])=\\operatorname{sym}_{\\Delta} \\operatorname{sym}_{(B C)}([C M])=\\operatorname{sym}_{I}([C M]),\n$$\n\ndonc $(C M)$ et $\\left(L^{\\prime} B\\right)$ sont parallèles.\nD'autre part, $\\frac{Q B}{Q K}=\\frac{Q L}{Q B}=\\frac{Q L^{\\prime}}{Q C}$ donc $\\left(L^{\\prime} B\\right)$ et $(C K)$ sont parallèles. Finalement, $(C M)$ et $(C K)$ sont parallèles, donc $C, K, M$ sont alignés.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nPremière démonstration"}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle. On note $P$ le milieu de l'arc du cercle circonscrit à $A B C$ contenant $A$. On suppose que la bissectrice de l'angle $\\widehat{B A C}$ coupe le cercle de diamètre $[P C]$ en deux points $D$ et $E$. Soit $F$ le symétrique de $E$ par rapport à $(B C)$ et $I$ le milieu de $[B C]$. Montrer que $B, D, F, I$ sont cocycliques.", "solution": "du lemme : on conserve les notations du paragraphe précédent. On note $b, c, k, \\ell, \\ell^{\\prime}, m$ les affixes de $B, C, K, L, L^{\\prime}, M$, et on peut supposer que $Q$ est l'origine, que $|b|=1$ et que $c=\\bar{b}$.\nComme $L$ appartient à $(Q B)$, il existe $t \\in \\mathbb{R}$ tel que $\\ell=t b$.\nComme $K$ et $L$ sont inverses par rapport au cercle, on a $k=\\frac{1}{t} b$.\nOn a $\\ell^{\\prime}=\\bar{\\ell}$. Le fait que $L^{\\prime}$ est le symétrique $M$ par rapport à $I$ se traduit par $\\ell^{\\prime}+m=b+c$. Il vient $m=b+c-\\bar{\\ell}=b+c-t c$.\nOn en déduit que $\\overrightarrow{C M}=m-c=b-t c=t k-t c=t \\overrightarrow{C K}$, par conséquent $C, K, M$ sont alignés.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nDeuxième démonstration"}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $A B C$ un triangle isocèle en $A, D$ le pied de la hauteur issue de $A$ et $M$ un point intérieur à $A D C$ tel que $\\widehat{A M B}$ est obtus et $\\widehat{D B M}+\\widehat{D A M}=\\widehat{M C B}$. Les droites $(C M)$ et $(A D)$ se coupent en $P$, et les droites $(B M)$ et $(A D)$ se coupent en $Q$. Soit $S$ un point de $[A B]$ et $R$ un point de $[A M)$ qui n'est pas sur $[A M]$ tel que $\\widehat{S Q B}=\\widehat{D P C}$ et $\\widehat{M R Q}=2 \\widehat{Q A M}$. Montrer que $Q R S$ est isocèle.", "solution": "de l'exercice 9\n\n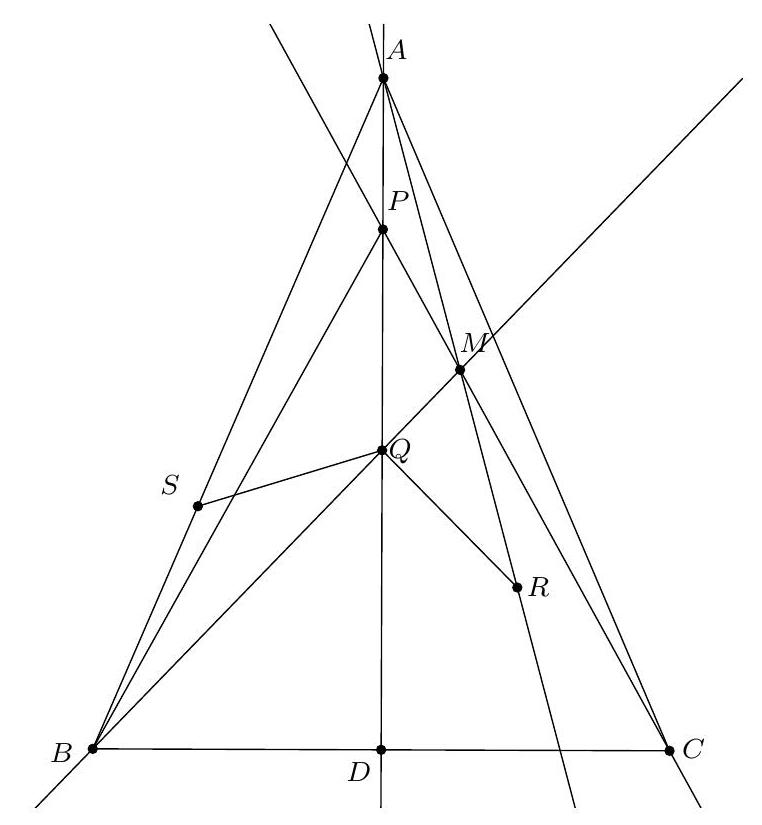\n\nNotons $\\alpha=\\widehat{B A D}, \\beta=\\widehat{C B M}, \\gamma=\\widehat{M C B}$ et $\\theta=\\widehat{D A M}$. Par hypothèse, on a $\\beta+\\theta=\\gamma$, $\\widehat{S Q B}=\\widehat{D P C}=\\frac{\\pi}{2}-\\gamma$ et $\\widehat{M R Q}=2 \\theta$.\nOn a $\\widehat{Q S A}=\\pi-\\widehat{B S Q}=\\widehat{Q B S}+\\widehat{S Q B}=\\left(\\frac{\\pi}{2}-\\alpha-\\beta\\right)+\\left(\\frac{\\pi}{2}-\\gamma\\right)=\\pi-(\\alpha+\\beta+\\gamma)$.\nD'après la loi des sinus pour les triangles $Q A S$ et $Q A R$, on a\n\n$$\n\\frac{Q S}{Q R}=\\frac{Q S}{Q A} \\times \\frac{Q A}{Q R}=\\frac{\\sin \\alpha}{\\sin (\\alpha+\\beta+\\gamma)} \\frac{\\sin 2 \\theta}{\\sin \\theta}=\\frac{2 \\sin \\alpha \\cos \\theta}{\\sin (\\alpha+\\beta+\\gamma)}\n$$\n\nOn doit montrer que ce rapport est égal à 1.\nD'après le théorème de Ceva trigonométrique appliqué au point $M$ dans le triangle $A B C$, on a\n\n$$\n\\frac{\\sin (\\alpha+\\theta)}{\\sin (\\alpha-\\theta)} \\times \\frac{\\sin \\beta}{\\sin \\left(\\frac{\\pi}{2}-\\alpha-\\beta\\right)} \\times \\frac{\\sin \\left(\\frac{\\pi}{2}-\\alpha-\\gamma\\right)}{\\sin \\gamma}=1\n$$\n\ndonc $\\sin (\\alpha+\\theta) \\sin \\beta \\cos (\\alpha+\\gamma)=\\sin (\\alpha-\\theta) \\cos (\\alpha+\\beta) \\sin \\gamma$.\nEn utilisant l'identité $2 \\sin x \\cos y=\\sin (x+y)+\\sin (x-y)$, on en déduit\n\n$$\n\\sin (\\alpha+\\theta)[\\sin (\\alpha+\\beta+\\gamma)-\\sin (\\alpha+\\gamma-\\beta)]=\\sin (\\alpha-\\theta)[\\sin (\\alpha+\\beta+\\gamma)-\\sin (\\alpha+\\beta-\\gamma)]\n$$\n\nCompte tenu de $\\gamma-\\beta=\\theta$,\n\n$$\n\\sin (\\alpha+\\theta)[\\sin (\\alpha+\\beta+\\gamma)-\\sin (\\alpha+\\theta)]=\\sin (\\alpha-\\theta)[\\sin (\\alpha+\\beta+\\gamma)-\\sin (\\alpha-\\theta)]\n$$\n\nou encore $(\\sin (\\alpha+\\theta)-\\sin (\\alpha-\\theta))[\\sin (\\alpha+\\beta+\\gamma)-(\\sin (\\alpha+\\theta)+\\sin (\\alpha-\\theta))]$.\nIl vient $\\sin (\\alpha+\\beta+\\gamma)=\\sin (\\alpha+\\theta)+\\sin (\\alpha-\\theta))=2 \\sin \\alpha \\cos \\theta$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-5-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "## Solution "}}
diff --git a/French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl b/French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..cc1acf5009e5e27920f7d5c8bef7e699b04b73dc
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl
@@ -0,0 +1,14 @@
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers $a$ et $b$ tels que $(a+1)(b-1)=a^{2} b^{2}$.", "solution": "de l'exercice 1\n\nSoit $a, b$ des entiers tels que $(a+1)(b-1)=a^{2} b^{2}$.\nPuisque d'une part $a$ et $a+1$ sont premiers entre eux, et d'autre part $b$ et $b-1$ sont premiers entre eux, c'est donc que $b-1= \\pm a^{2}$ et que $a+1= \\pm b^{2}$, où les signes sont les mêmes dans les deux relations.\n\n- Si $b-1=a^{2}$ et $a+1=b^{2}$ :\n\nAlors, $a=b^{2}-1=(b-1)(b+1)=a^{2}\\left(a^{2}+2\\right)$.\nSi $a=0$, on obtient $b=1$, et on vérifie bien que $(a, b)=(0,1)$ est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "## Solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers $a$ et $b$ tels que $(a+1)(b-1)=a^{2} b^{2}$.", "solution": "du problème.\nSi $a \\neq 0$, après division par $a$, il vient donc $a\\left(a^{2}+2\\right)=1$. Comme $a$ et $a^{2}+2$ sont des entiers, avec $a^{2}+2>2$, cette dernière égalité ne peut être satisfaite.\n\n- Si $b-1=-a^{2}$ et $a+1=-b^{2}$ :\n\nAlors, $-a-1=b^{2}$ et $-b+1=a^{2}$. Ce sont les équations obtenues au cas précédent, où $(a, b)$ a été remplacé par $(-b,-a)$. Ainsi, la seule", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers $a$ et $b$ tels que $(a+1)(b-1)=a^{2} b^{2}$.", "solution": "est $(a, b)=(-1,0)$.\n\nFinalement, les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers $a$ et $b$ tels que $(a+1)(b-1)=a^{2} b^{2}$.", "solution": "s du problème sont $(a, b)=(0,1)$ et $(a, b)=(-1,0)$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution"}}
+{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Prouver que tout ensemble de 90 nombres choisis dans $\\{1,2, \\cdots, 100\\}$ en contient 10 qui forment une progression arithmétique.", "solution": "de l'exercice 2\n\nOn dispose les entiers de 1 à 100 dans un tableau carré $10 \\times 10$ comme suit :\n\n| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |\n| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |\n| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |\n| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |\n| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |\n| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |\n| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |\n| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |\n| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |\n\nSi l'on veut éliminer 10 nombres de sorte qu'avec les 90 restants on ne puisse former de suite arithmétique de longueur 10, il faut déjà éliminer au moins un nombre dans chacune des 10 lignes, et chacune des 10 colonnes. Comme il y a justement 10 lignes, et 10 colonnes, c'est donc que l'on doit éliminer exactement un nombre par ligne et par colonne.\n\nDe plus, si pour $1 \\leqslant i \\leqslant 9$, le nombre éliminé dans la ligne $i$ appartient à la colonne $k$, alors le nombre éliminé dans la ligne $i+1$ doit appartenir à une colonne $l$, avec $l0$. On a\n\n$$\n\\begin{aligned}\n\\operatorname{pgcd}\\left(2^{a}-1,2^{b}-1\\right) & =\\operatorname{pgcd}\\left(2^{b}-1,2^{a}-1-\\left(2^{b}-1\\right)\\right) \\\\\n& =\\operatorname{pgcd}\\left(2^{b}-1,2^{b}\\left(2^{a-b}-1\\right)\\right) \\\\\n& =\\operatorname{pgcd}\\left(2^{b}-1,2^{a-b}-1\\right) \\quad \\operatorname{car} 2^{b}-1 \\text { et } 2^{b} \\text { premiers entre eux } \\\\\n& =2^{\\operatorname{pgcd}(b, a-b)}-1 \\quad \\text { par hypothèse de récurrence } \\\\\n& =2^{\\operatorname{pgcd}(a, b)}-1\n\\end{aligned}\n$$\n\nce qui démontre notre assertion.\nRevenons à l'exercice. Notons $d^{\\prime}=\\operatorname{pgcd}\\left(2^{m}-1,2^{n}+1\\right)$. Soit $d=\\operatorname{pgcd}(m, n)$, alors ce qui précède montre que $2^{d}-1=\\operatorname{pgcd}\\left(2^{m}-1,2^{2 n}-1\\right)$. Or, $2^{2 n}-1$ est un multiple de $2^{n}+1$, donc $d^{\\prime}$ divise $2^{d}-1$. Comme $2^{d}-1$ divise $2^{n}-1$, $d^{\\prime}$ divise aussi $\\left(2^{n}+1\\right)-\\left(2^{n}-1\\right)=2$. Or, $2^{m}-1$ est impair donc $d^{\\prime}$ est impair. Il vient $d^{\\prime}=1$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": " solution\n"}}
+{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "On désigne par $K$ la valeur maximale de\n\n$$\n\\left|x_{1}-x_{2}\\right| \\cdot\\left|x_{1}-x_{3}\\right| \\cdot\\left|x_{1}-x_{4}\\right| \\cdot\\left|x_{2}-x_{3}\\right| \\cdot\\left|x_{2}-x_{4}\\right| \\cdot\\left|x_{3}-x_{4}\\right|\n$$\n\noù $x_{1}, x_{2}, x_{3}, x_{4} \\in[0 ; 1]$.\na) Prouver que $\\frac{4}{243}x_{2}>x_{3}>x_{4}$. D'après l'inégalité arithmético-géométrique, on a\n\n$$\n\\sqrt[3]{\\left(x_{1}-x_{2}\\right)\\left(x_{2}-x_{3}\\right)\\left(x_{3}-x_{4}\\right)} \\leqslant \\frac{\\left(x_{1}-x_{2}\\right)+\\left(x_{2}-x_{3}\\right)+\\left(x_{3}-x_{4}\\right)}{3}=\\frac{x_{1}-x_{4}}{3} \\leqslant \\frac{1}{3}\n$$\n\net donc $\\left|x_{1}-x_{2}\\right| \\cdot\\left|x_{2}-x_{3}\\right| \\cdot\\left|x_{3}-x_{4}\\right| \\leqslant \\frac{1}{27}$.\nD'autre part, on a $\\left|x_{1}-x_{3}\\right|<1,\\left|x_{1}-x_{4}\\right| \\leqslant 1$ et $\\left|x_{2}-x_{4}\\right|<1$, d'où $f\\left(x_{1}, x_{2}, x_{3}, x_{4}\\right)<\\frac{1}{27}$.\nEt ainsi, on a $K<\\frac{1}{27}$.\nD'autre part, on vérifie facilement que $f\\left(1, \\frac{3}{4}, \\frac{1}{4}, 0\\right)=\\frac{9}{512}>\\frac{4}{243}$, d'où $K>\\frac{4}{243}$.\nb) Sans perte de généralité, on suppose toujours que $x_{1}>x_{2}>x_{3}>x_{4}$. Mais, il est facile de constater que $f\\left(x_{1}, x_{2}, x_{3}, x_{4}\\right) \\leqslant f\\left(1, x_{2}, x_{3}, 0\\right)$. Ainsi, en posant $x_{2}=y$ et $x_{3}=z$, on cherche la valeur maximale de\n\n$$\ng(x, y)=(1-y)(1-z)(y-z) y z\n$$\n\nsous la contrainte $00$ est un entier, on désigne par $d(n)$ le nombre de diviseurs strictement positifs de $n$.\na) Existe-t-il une suite $\\left(a_{i}\\right)_{i \\geqslant 1}$ strictement croissante d'entiers strictement positifs tels que, pour tout $i$ suffisamment grand, le nombre $a_{i}$ soit divisible par exactement $d(i)-1$ termes de la suite (y compris lui-même)?\nb) Existe-t-il une suite $\\left(a_{i}\\right)_{i \\geqslant 1}$ strictement croissante d'entiers strictement positifs tels que, pour tout $i$ suffisamment grand, le nombre $a_{i}$ soit divisible par exactement $d(i)+1$ termes de la suite (y compris lui-même)?", "solution": "de l'exercice 7\na) La réponse est oui.\n\nIl suffit de trouver une suite $\\left(a_{i}\\right)$ qui vérifie les deux conditions suivantes :\n\n- le nombre $a_{1}$ ne divise aucun autre terme de la suite,\n- le nombre $i$ divise $j$ si et seulement si $a_{i}$ divise $a_{j}$, pour tous $i, j \\geqslant 2$.\n\nOr, il est bien connu que, pour tous entiers $i, j \\geqslant 1$, on a $\\operatorname{pgcd}\\left(2^{i}-1,2^{j}-1\\right)=2^{d}-1$, où $d=\\operatorname{pgcd}(i, j)$. Par conséquent, la suite définie par $a_{1}=2$ et $a_{i}=2^{i}-1$ pour $i>1$ convient.\nb) La réponse est également oui.\n\nEn fait, de façon plus générale, on va prouver que si $f: \\mathbb{N}^{*} \\longrightarrow \\mathbb{N}^{*}$ est une fonction et qu'il existe un entier $N>0$ tel que $f(n) \\leqslant n$ pour tout $n \\geqslant N$, alors il existe une suite strictement croissante $\\left(a_{i}\\right)_{i \\geqslant 1}$ d'entiers strictement positifs telle que, pour tout $i$ suffisamment grand, le nombre $a_{i}$ est divisible par exactement $f(i)$ termes de la suite.\nNotons tout de suite que cela répond à la fois au a) et au b) puisque $d(n)M$, si $a_{1}, a_{2}, \\cdots, a_{k-1}$ sont définis avec $a_{1}a_{k-1}$ et on pose $a_{k}=a_{1} a_{2} \\cdots a_{f(k)-1} p_{k}$.\n\nOn a alors clairement $a_{k-1}M$, le nombre $a_{i}$ est divisible que par $a_{1}, a_{2}, \\cdots, a_{f(i)-1}$ et par lui-même. Par contre, $a_{i}$ n'est divisible par aucun autre terme $a_{j}$, avec $j>f(i)-1$ et $j \\neq i$, puisqu'un tel $a_{j}$ contient un facteur premier $p_{j}$ qui ne divise aucun des $a_{k}$ avec $k \\leqslant f(i)-1$ et tel que $p_{j} \\neq p_{i}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle. On désigne par $D$ le pied de la bissectrice de $\\widehat{B A C}$, et par $E$ le pied de la hauteur issue de $A$. La médiatrice de $[A D]$ rencontre les demi-cercles de diamètres respectifs $[A B]$ et $[A C]$ construits extérieurement à $A B C$, en $X$ et $Y$.\n\nProuver que les points $X, Y, D, E$ sont cocycliques.", "solution": "de l'exercice 8\n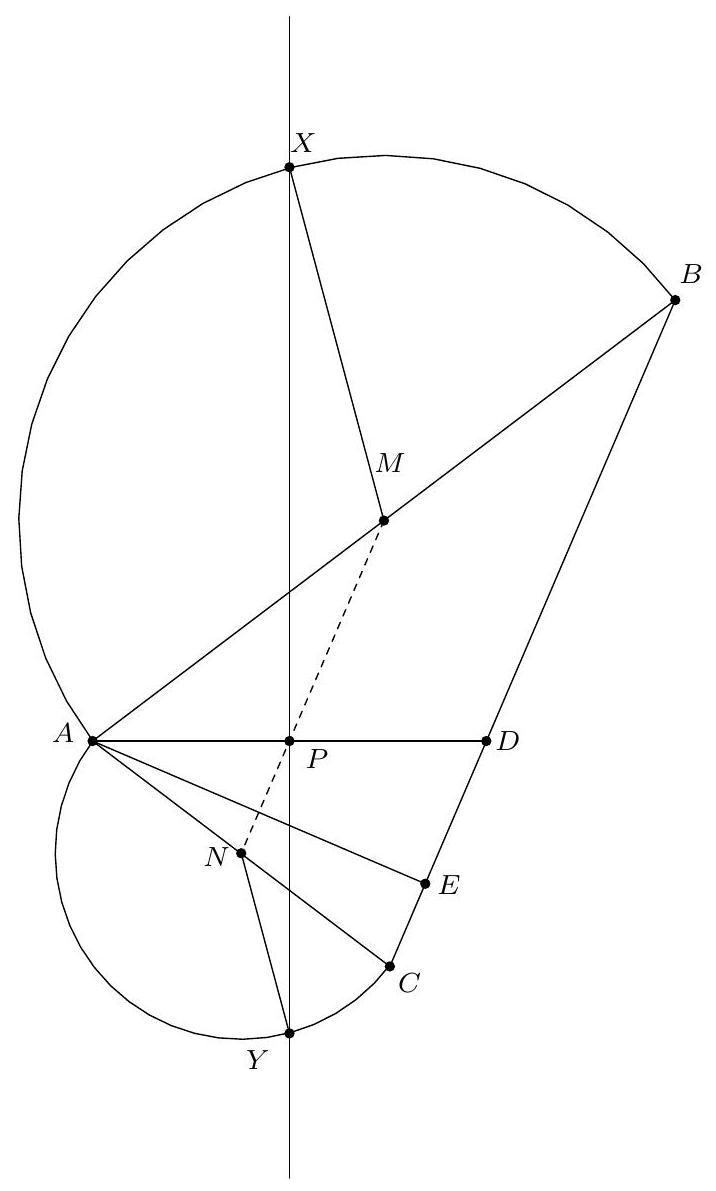\n\nOn désigne par $M, N$ et $P$ les milieux respectifs de $[A B],[A C]$ et $[A D]$. D'après le théorème des milieux, on a $N, P, M$ alignés et, compte-tenu de ce que $(A P)=(A D)$ est la bissectrice de $\\widehat{B A C}$, on a\n\n$$\n\\frac{M P}{N P}=\\frac{B D}{C D}=\\frac{A M}{A N}=\\frac{A B}{A C}=\\frac{M X}{N Y} .\n$$\n\nEn particulier, il vient $\\frac{M P}{M X}=\\frac{N P}{N Y}$. En utilisant la loi des sinus dans $M P X$ et $N P Y$, et puisque $\\widehat{N P Y}=\\widehat{M P X}$, c'est donc que $\\sin \\widehat{P X M}=\\sin \\widehat{P Y N}$. (1)\nOr, on a clairement $\\widehat{P X M}<\\widehat{B X A}=90^{\\circ}$ et $\\widehat{P Y N}<\\widehat{A Y C}=90^{\\circ}$, donc (1) donne $\\widehat{P X M}=\\widehat{P Y N}$. Comme $\\widehat{M P X}=\\widehat{N P Y}$, c'est donc que les triangles $P X M$ et $P Y N$ sont semblables, et que $\\widehat{P M X}=\\widehat{P N Y}$. (2)\n\nSans perte de généralité, on peut supposer qu'entre $M$ et $N$, c'est $N$ qui est du même côté que $A$ par rapport à $(X Y)$.\nAinsi (2) conduit à $\\widehat{P M A}+\\widehat{A M X}=\\widehat{P N C}+\\widehat{C N Y}$,\nd'où $\\widehat{C B A}+2 \\widehat{A B X}=180^{\\circ}-\\widehat{B C A}+180^{\\circ}-2 \\widehat{A C Y}$\net donc\n\n$$\n\\begin{aligned}\n\\widehat{A B X}+\\widehat{A C Y} & =180^{\\circ}-\\widehat{A B C}-\\widehat{B C A}+90^{\\circ}-\\widehat{A B X}+90^{\\circ}-\\widehat{A C Y} \\\\\n& =\\widehat{B A C}+\\widehat{X A B}+\\widehat{C A Y} \\\\\n& =\\widehat{X A Y} .\n\\end{aligned}\n$$\n\nMais, $\\widehat{A E B}=\\widehat{A E C}=90^{\\circ}$ donc $E$ appartient aux cercles de diamètres $[A B]$ et $[A C]$, soit donc aux cercles circonscrits aux triangles $A B X$ et $A C Y$. Par suite, on a $\\widehat{A B X}=\\widehat{A E X}$ et $\\widehat{A C Y}=\\widehat{A E Y}$. (4)\n\nDe (3) et (4), on déduit que\n\n$$\n\\widehat{X E Y}=\\widehat{X E A}+\\widehat{A E Y}=\\widehat{A B X}+\\widehat{A C Y}=\\widehat{X A Y}\n$$\n\nD'autre part, puisque $(X Y)$ est la médiatrice de $[A D]$, on a $\\widehat{X A Y}=\\widehat{X D Y}$, et finalement $\\widehat{X E Y}=$ $\\widehat{X D Y}$, ce qui conclut.\n\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nSolution "}}
+{"year": "2014", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle. On désigne par $D$ le pied de la bissectrice de $\\widehat{B A C}$, et par $E$ le pied de la hauteur issue de $A$. La médiatrice de $[A D]$ rencontre les demi-cercles de diamètres respectifs $[A B]$ et $[A C]$ construits extérieurement à $A B C$, en $X$ et $Y$.\n\nProuver que les points $X, Y, D, E$ sont cocycliques.", "solution": "On applique une inversion $i$ de pôle $A$. Rappelons que les cercles ne passant pas par $A$ sont transformés en des cercles ne passant pas par $A$, que les droites passant par $A$ sont conservées et que les cercles passant par $A$ sont transformés en des droites perpendiculaires à la droite reliant $A$ et le centre du cercle. D'autre part, toute inversion conserve les angles entre deux droites ou cercles sécants.\nOn en déduit que $i$ transforme le cercle de diamètre $[A B]$ en la perpendiculaire à $\\left(A B^{\\prime}\\right)$ passant par $B^{\\prime}$, transforme la droite $(B C)$ en le cercle $\\left(A B^{\\prime} C^{\\prime}\\right)$ de sorte que $D^{\\prime}$ est le milieu de l'arc $B^{\\prime} C^{\\prime}$ ne contenant pas $A$ et $E^{\\prime}$ est le point diamétralement opposé à $A$. De plus, $i$ envoie la médiatrice de $[A D]$ sur le cercle de centre $D^{\\prime}$ passant par $A$. Enfin, comme $E$ sur le cercle de diamètre $[A B]$, les points $E^{\\prime}, B, X^{\\prime}$ sont alignés et de même $E^{\\prime}, C, Y^{\\prime}$ sont alignés.\nSupposons que les angles en $B$ et en $C$ du triangle $A B C$ sont aigus (le raisonnement est analogue dans le cas contraire). Alors $E^{\\prime}$ appartient à l'arc $B^{\\prime} C^{\\prime}$ ne contenant pas $A$. Quitte à échanger les rôles de $B$ et de $C$, on peut supposer que $E^{\\prime}$ appartient à l'arc $C^{\\prime} D^{\\prime}$ comme sur la figure.\n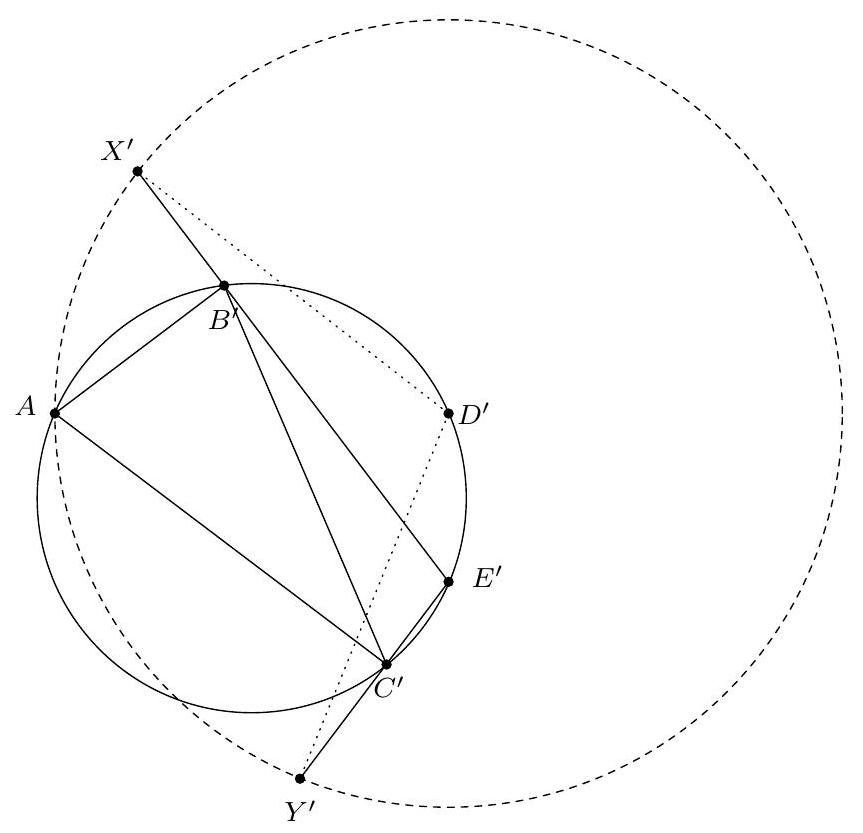\n\nLe fait que $E$ ne se trouve pas sur le même demi-cercle de diamètre $[A B]$ que $X$ implique que $B^{\\prime}$ se trouve entre $E^{\\prime}$ et $X^{\\prime}$. De même, $C^{\\prime}$ se trouve entre $E^{\\prime}$ et $Y^{\\prime}$.\nRemarquons d'abord que $\\widehat{Y^{\\prime} E^{\\prime} D^{\\prime}}$ et $\\widehat{X^{\\prime} E^{\\prime} D^{\\prime}}$ sont supplémentaires puisque $\\widehat{Y^{\\prime} E^{\\prime} D^{\\prime}}=\\widehat{C^{\\prime} E^{\\prime} D^{\\prime}}=$ $\\pi-\\widehat{C^{\\prime} A D^{\\prime}}=\\pi-\\widehat{D^{\\prime} A B^{\\prime}}=\\pi-\\widehat{D^{\\prime} E^{\\prime} B^{\\prime}}=\\pi-\\widehat{D^{\\prime} E^{\\prime} X^{\\prime}}$.\n\nAppliquons maintenant le théorème de Ceva trigonométrique pour le point $D^{\\prime}$ appartenant au triangle $E X^{\\prime} Y^{\\prime}$.\n\n$$\n\\frac{\\sin \\left(\\overrightarrow{E^{\\prime} D^{\\prime}}, \\overrightarrow{E^{\\prime} X^{\\prime}}\\right)}{\\sin \\left(\\overrightarrow{E^{\\prime} D^{\\prime}}, \\overrightarrow{E^{\\prime} Y^{\\prime}}\\right)} \\times \\frac{\\sin \\left(\\overrightarrow{X^{\\prime} D^{\\prime}}, \\overrightarrow{X^{\\prime} Y^{\\prime}}\\right)}{\\sin \\left(\\overrightarrow{X^{\\prime} D^{\\prime}}, \\overrightarrow{X^{\\prime} E^{\\prime}}\\right)} \\times \\frac{\\sin \\left(\\overrightarrow{Y^{\\prime} D^{\\prime}}, \\overrightarrow{Y^{\\prime} E^{\\prime}}\\right)}{\\sin \\left(\\overrightarrow{Y^{\\prime} D^{\\prime}}, \\overrightarrow{Y^{\\prime} X^{\\prime}}\\right)}=-1 .\n$$\n\nComme $\\left(\\overrightarrow{E^{\\prime} D^{\\prime}}, \\overrightarrow{E^{\\prime} X^{\\prime}}\\right)=\\left(\\overrightarrow{E^{\\prime} D^{\\prime}}, \\overrightarrow{E^{\\prime} B^{\\prime}}\\right)=\\left(\\overrightarrow{A D^{\\prime}}, \\overrightarrow{A B^{\\prime}}\\right)$ et $\\left(\\overrightarrow{E^{\\prime} D^{\\prime}}, \\overrightarrow{E^{\\prime} Y^{\\prime}}\\right)=\\left(\\overrightarrow{E^{\\prime} D^{\\prime}}, \\overrightarrow{E^{\\prime} C^{\\prime}}\\right)=\\left(\\overrightarrow{A D^{\\prime}}, \\overrightarrow{A C^{\\prime}}\\right)+$ $\\pi$, la première fraction est égale à 1 .\nDe plus, comme $D^{\\prime} X^{\\prime} Y^{\\prime}$ est isocèle en $D^{\\prime}$, on a $\\left(\\overrightarrow{X^{\\prime} D^{\\prime}}, \\overrightarrow{X^{\\prime} Y^{\\prime}}\\right)=-\\left(\\overrightarrow{Y^{\\prime} D^{\\prime}}, \\overrightarrow{Y^{\\prime} X^{\\prime}}\\right)$. En reportant dans (1), on en conclut que\n\n$$\n\\sin \\left(\\overrightarrow{X^{\\prime} D^{\\prime}}, \\overrightarrow{X^{\\prime} E^{\\prime}}\\right)=\\sin \\left(\\overrightarrow{Y^{\\prime} D^{\\prime}}, \\overrightarrow{Y^{\\prime} E^{\\prime}}\\right)\n$$\n\nce qui prouve que les angles $\\widehat{D^{\\prime} X^{\\prime} E^{\\prime}}$ et $\\widehat{D^{\\prime} Y^{\\prime} E^{\\prime}}$ sont égaux ou supplémentaires.\nS'ils étaient supplémentaires, on aurait $\\widehat{X^{\\prime} E^{\\prime} D^{\\prime}}+\\widehat{D^{\\prime} X^{\\prime} E^{\\prime}}+\\widehat{Y^{\\prime} E^{\\prime} D^{\\prime}}+\\widehat{D^{\\prime} Y^{\\prime} E^{\\prime}}=2 \\pi$, donc la somme des angles des triangles $D^{\\prime} X^{\\prime} E^{\\prime}$ et $D^{\\prime} Y^{\\prime} E^{\\prime}$ dépasserait $2 \\pi$, ce qui est impossible. Par conséquent, $\\widehat{D^{\\prime} X^{\\prime} E^{\\prime}}$ et $\\widehat{D^{\\prime} Y^{\\prime} E^{\\prime}}$ sont égaux. D'après $(2)$, ceci montre que $\\left(\\overrightarrow{X^{\\prime} D^{\\prime}}, \\overrightarrow{X^{\\prime} E^{\\prime}}\\right)=\\left(\\overrightarrow{Y^{\\prime} D^{\\prime}}, \\overrightarrow{Y^{\\prime} E^{\\prime}}\\right)$, d'où la cocyclicité de $D^{\\prime}, E^{\\prime}, X^{\\prime}, Y^{\\prime}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2014", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "On considère une rangée de cases numérotées $0,1, \\ldots, k$ de gauche à droite où, pour chaque $i \\geqslant 1$, la case numéro $i$ contient $x_{i}$ jetons. Il n'y a initialement aucun jeton sur la case numéro 0 . A tour de rôle, Alice et Bob jouent alors selon les règles suivantes :\n\n- Bob choisit un ensemble $S$ de jetons, pas forcément tous sur la même case.\n- Alice peut ensuite soit éliminer tous les jetons qui ne sont pas dans $S$ mais alors déplacer chaque jeton de $S$ de la case qu'il occupe à la case voisine à sa gauche (un tel jeton passe donc d'une case numéro $i$ à la case numéro $i-1$, soit éliminer tous les jetons qui sont dans $S$ mais alors déplacer chaque jeton qui n'est pas dans $S$ de la case qu'il occupe à la case voisine à sa gauche.\nBob gagne la partie s'il arrive à amener un jeton sur la case numéro 0, et Alice gagne si elle arrive à éliminer tous les jetons.\n\n1) Prouver qu'Alice possède une stratégie gagnante si $\\sum_{i=1}^{k} 2^{-i} x_{i}<1$.\n2) Est-il vrai que si $\\sum_{i=1}^{k} 2^{-i} x_{i} \\geqslant 1$ alors Bob possède une stratégie gagnante?", "solution": "de l'exercice 9\n\nDans tout ce qui suit, on peut clairement supposer que Bob ne choisit jamais $S=\\emptyset$ ou $S$ l'ensemble de tous les jetons non encore éliminés, sans quoi Alice gagne immédiatement. Du coup, le nombre de jetons diminue strictement après chaque fois qu'Alice joue, ce qui assure que le jeu se termine toujours en un nombre fini de tours, soit par élimination de tous les jetons, soit parce que l'un d'eux aura atteint la case numéro 0 . Ainsi, il n'y aura pas de partie nulle.\nDe plus, s'agissant d'un jeu à information parfaite, il est bien connu que l'un des deux joueurs a alors une stratégie gagnante. Reste à savoir lequel...\n\n1) - Approche probabiliste : Fixons une stratégie pour Bob. Alice va alors jouer de façon aléatoire. Plus précisément, à chaque tour, après que Bob ait choisi son ensemble $S$ de jetons, Alice lance une pièce équilibrée. Si elle obtient Face, elle élimine les jetons de $S$ (et déplace donc ceux qui ne sont pas dans $S$ vers la gauche) et, si elle obtient Pile, elle fait le contraire.\n\nPour chaque jeton $j$, on note $X_{j}$ la variable aléatoire égale à 1 si le jeton $j$ est sur la case numéro 0 à la fin de la partie, et égale à 0 sinon.\nSoit enfin $X=\\sum_{j} X_{j}$, la somme portant sur l'ensemble des jetons de départ.\nOn remarque que $X$ représente le nombre total de jetons qui arrivent sur la case numéro 0 à la fin du jeu, et donc qu'Alice gagne si et seulement si $X<1$.\n\nSoit $j$ un des jetons de départ. A chaque tour, Bob peut choisir $S$ de sorte que, si $j$ n'a pas encore été éliminé, on ait $j \\in S$ ou $j \\notin S$ mais, quoi qu'il en soit, la probabilité que $j$ soit alors déplacé vers la gauche est égale à $\\frac{1}{2}$. Si, au début du jeu, le jeton $j$ se trouve sur la case numéro $i$, il arrive sur la case numéro 0 à la fin du jeu si et seulement si les $i$ premiers lancers de pièces ont tous conduit à des déplacements vers la gauche, ce qui arrive donc avec une probabilité $\\frac{1}{2^{i}}$. Par suite, on a $E\\left(X_{j}\\right)=\\frac{1}{2^{i}}$ pour tout jeton $j$.\nPar linéarité de l'espérance, on a donc\n\n$$\nE(X)=\\sum_{j} E\\left(X_{j}\\right)=\\sum_{i=1}^{k} 2^{-i} x_{i}<1\n$$\n\nCela assure que l'événement $[X<1]$ se réalise avec une probabilité non nulle. Ainsi, quelle que soit la stratégie de Bob, Alice a une probabilité non nulle de gagner, ce qui prouve que Bob n'a pas de stratégie gagnante. D'après notre remarque initiale, c'est donc Alice qui en possède une.\n\n- Approche déterministe : Plaçons nous à un instant donné au cours de la partie, juste avant que ce soit à Bob de jouer, et considérons la configuration $C$ obtenue. Pour chaque $i$, on note $y_{i}$ le nombre de jetons qui sont alors sur la case numéro $i$, et on définit le poids de $C$ par $W(C)=\\sum_{i=1}^{k} y_{i} 2^{-i}$.\n\nPour faire le lien avec l'approche probabiliste, on peut noter que $W(C)=E(Y)$, où $Y$ est le nombre de jetons qui vont arriver sur la case numéro 0 si Alice joue le reste de la partie, depuis la configuration $C$, de la façon aléatoire ci-dessus.\n\nLa stratégie d'Alice va consister alors à toujours choisir des configurations afin de minimiser les poids $W$ successifs :\nSoit donc $C$ une configuration pour laquelle le jeu ne soit pas déjà terminé, de poids $W=W(C)$, et supposons que Bob choisisse l'ensemble $S$ de jetons.\nOn note $W^{+}$(resp. $W^{-}$) le poids de la configuration obtenue si Alice déplace les jetons de $S$ vers la gauche (resp. élimine les jetons de $S$ ).\nPour chaque jeton $j$, la contribution de $j$ est nulle ( $j$ a été éliminé) dans l'une des sommes $W^{+}$et $W^{-}$, et vaut le double de ce qu'elle est dans $W$ pour l'autre. Ceci étant vrai pour chaque jeton, on a donc $W=\\frac{1}{2}\\left(W^{+}+W^{-}\\right)$.\nEn particulier, Alice peut alors choisir une configuration $C^{\\prime}$ pour laquelle $W\\left(C^{\\prime}\\right) \\leqslant W(C)$. Or, puisqu'on débute le jeu avec une configuration de poids strictement inférieur à 1 , cela assure que, tout au long du jeu, Alice peut imposer des configurations de poids strictement inférieurs à 1 . Ceci empêche clairement Bob de gagner puisqu'un jeton sur la case numéro 0 donne, à lui seul, un poids égal à 1.\n2) Supposons que $\\sum_{i=1}^{k} 2^{-i} x_{i} \\geqslant 1$.\n\nOn va prouver que Bob possède une stratégie gagnante. Compte-tenu de notre remarque préliminaire, il suffit de prouver qu'Alice n'a pas de stratégie gagnante.\n\nSoit $C$ une configuration pour laquelle le jeu n'est pas encore terminé. On note $J$ l'ensemble des jetons de $C$.\nSi $A \\subset J$, on note $C_{A}$ la configuration obtenue à partir de $C$ en ne gardant que les jetons qui sont dans $A$ (sans les déplacer vers la gauche).\n\nLemme. Si $C$ est une configuration telle que $W(C) \\geqslant 1$, il existe une partie $S$ de $J$ telle que\n\n$$\nW\\left(C_{S}\\right) \\geqslant \\frac{1}{2} \\text { et } W\\left(C_{\\bar{S}}\\right) \\geqslant \\frac{1}{2} \\text {. }\n$$\n\nPreuve du lemme.\nTout d'abord, on remarque que si une configuration $C$ vérifie $W(C) \\geqslant 1$ alors il existe $i$ tel que $y_{i} \\geqslant 2$. En effet, dans le cas contraire, on aurait\n\n$$\nW(C) \\leqslant \\sum_{i=1}^{k} 2^{-i}=1-\\frac{1}{2^{k}}<1\n$$\n\nOn raisonne par récurrence sur le nombre $n$ de jetons de la configuration :\n\n- Si la configuration considérée ne possède que deux jetons alors, d'après ci-dessus, ils sont tous les deux sur la même case. De plus, si l'on veut que $W(C) \\geqslant 1$, il est facile de vérifier qu'ils sont en fait sur la case numéro 1. Ainsi, la partie $S$ formée par l'un des deux jetons convient.\n- Soit $n \\geqslant 3$ et supposons la conclusion assurée pour toute configuration de poids supérieur ou égal à 1 , et contenant $n-1$ jetons. Soit alors $C$ une configuration telle que $W(C) \\geqslant 1$ et à $n$ jetons.\nSi $y_{1} \\geqslant 2$, une partie $S$ formée uniquement d'un des jetons qui sont sur la case numéro 1 convient. Sinon, soit $i \\geqslant 2$ tel que $y_{i} \\geqslant 2$ et soit $A$ et $B$ deux jetons qui sont sur la case numéro $i$. On considère alors la configuration $C^{\\prime}$ identique à $C$ sauf pour $A$ et $B$ qui sont remplacés par un seul jeton $X$, placé sur la case numéro $i-1$. On a clairement $W\\left(C^{\\prime}\\right)=W(C) \\geqslant 1$, et $C^{\\prime}$ ne contient que $n-1$ jetons. D'après l'hypothèse de récurrence, il existe donc une partie $S^{\\prime}$ de l'ensemble des jetons de $C^{\\prime}$ telle que $W\\left(C_{S^{\\prime}}^{\\prime}\\right) \\geqslant \\frac{1}{2}$ et $W\\left(C_{\\overline{S^{\\prime}}}^{\\prime}\\right) \\geqslant \\frac{1}{2}$.\nIl est alors facile de vérifier que si $S$ est la partie formée des jetons de $S^{\\prime}$, et en remplaçant $X$ par $A$ et $B$, on a bien $W\\left(C_{S}\\right) \\geqslant \\frac{1}{2}$ et $W\\left(C_{\\bar{S}}\\right) \\geqslant \\frac{1}{2}$, ce qui achève la récurrence et la preuve.\n\nRevenons au jeu. Une fois que Bob a choisi un ensemble $S$ de jetons, quel que soit le choix d'Alice, celui-ci conduira à une configuration dont le poids sera le double de celui de la configuration formée uniquement par les jetons qui ne seront pas éliminés. Le lemme assure donc qu'à partir d'une configuration de poids supérieur ou égal à 1 , Bob peut choisir $S$ de sorte qu'après le choix d'Alice, on obtienne une configuration de poids supérieur ou égal à 1. Puisque la configuration initiale est supposée de poids supérieur ou égal à 1, Bob peut donc imposer que toute la partie se déroule sur de telles configurations. Cela empêche clairement Alice de gagner (elle cherche à obtenir une configuration de poids nul), d'où la conclusion.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2013-2014-envoi-6-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "## Solution "}}
diff --git a/French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl b/French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..2326f7e6506ca0985df451b736ca9d51258136e1
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl
@@ -0,0 +1,12 @@
+{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "On considère un échiquier classique $8 \\times 8$. Un zigzag est un chemin sur les cases blanches, qui part d'une case (quelconque) de la ligne du bas, et monte de ligne en ligne jusqu'à atteindre celle du haut (sur n'importe quelle case) : à chaque étape, on monte d'une case en diagonale. Combien y a-t-il de zigzags?", "solution": "On écrit un 1 dans chacune des quatre cases blanches du bas. Puis dans la deuxième ligne, on écrit la somme des cases blanches qui y mènent : c'est le nombre de manières d'atteindre ces cases. On recommence dans la troisième ligne, etc. jusqu'à la huitième ligne : sur chacune des quatre cases, on a le nombre de zigzags qui arrivent à cette case. Le nombre total de zigzags est donc $69+103+35+89=296$.\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 1", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "On prend 1008 entiers distincts compris (au sens large) entre 1 et 2014.\n(i) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ divise $c$ (le pgcd ou Plus Grand Diviseur Commun de deux entiers est le plus grand entier naturel qui les divise tous les deux).\n(ii) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ ne divise pas $c$.", "solution": "(i) Groupons les entiers de 1 à 2014 en paires d'entiers consécutifs : (1, 2), (3, 4),..., (2013, 2014). Il y en a 1007. Par le principe des tiroirs, si on choisit 1008 entiers, il y en aura deux d'une même paire, $a$ et $b$, avec $b=a+1$. Leur pgcd vaut 1 (puisqu'il divise leur différence), donc divise n'importe lequel des 1006 autres nombres, que l'on peut prendre pour $c$.\n(ii) Il y a 1007 entiers pairs prenables. Donc parmi 1008 nombres, il y a forcément un impair. S'il y a deux nombres pairs au moins parmi les 1008, notons-les $a$ et $b$. Soit $c$ un nombre impair parmi les 1008. Le $\\operatorname{pgcd}$ de $a$ et $b$ est multiple de 2 , puisque 2 divise à la fois $a$ et $b$. (en fait, le $\\operatorname{pgcd}$ de $a$ et $b$ vaut 2 fois le $\\operatorname{pgcd}$ de $a / 2$ et $b / 2$ ). Donc s'il divise $c$, alors 2 divise $c$, ce qui est absurde.\nS'il y a moins de 2 nombres pairs parmi les 1008, ça veut dire qu'on a pris les 1007 impairs, ainsi qu'un nombre pair, noté $c$. On peut trouver des triplets d'au moins deux manières.\n\n-", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "On prend 1008 entiers distincts compris (au sens large) entre 1 et 2014.\n(i) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ divise $c$ (le pgcd ou Plus Grand Diviseur Commun de deux entiers est le plus grand entier naturel qui les divise tous les deux).\n(ii) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ ne divise pas $c$.", "solution": "courte : on dispose du triplet $(3,9,1)$, et il est clair que $\\operatorname{pgcd}(3,9)$ ne divise pas 1.\n-", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": " Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "On prend 1008 entiers distincts compris (au sens large) entre 1 et 2014.\n(i) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ divise $c$ (le pgcd ou Plus Grand Diviseur Commun de deux entiers est le plus grand entier naturel qui les divise tous les deux).\n(ii) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ ne divise pas $c$.", "solution": "moins courte : si $c$ est divisible par tous les pgcd de couples d'entiers impairs entre 1 et 2013, ça va lui faire beaucoup de diviseurs premiers : il sera divisible par le pgcd de 3 et 9 , le pgcd de 5 et 15, celui de 7 et 21 , celui de 11 et 33 , etc. Donc il est divisible par $3,5,7,11$ déjà (et par 2 , puisqu'il est pair). Le plus petit multiple commun de ces nombres est leur produit (puisqu'ils n'ont deux-à-deux aucun facteur commun). Il vaut $2 \\times 3 \\times 5 \\times 7 \\times 11=2310$ donc $c>2014$, ce qui n'est pas possible. Donc il existe deux nombres impairs $a$ et $b$ tels que leur pged ne divise pas $c$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": " Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Combien y a-t-il de nombres à six chiffres qui ont quatre chiffres pairs, deux chiffres impairs et qui sont multiples de 5 ? Note: un nombre ne commence pas par un 0 .", "solution": "Un tel nombre termine par 0 ou 5 . Nous allons compter séparément les nombres qui se terminent par 0 et ceux qui se terminent par 5 .\nNombres dont le dernier chiffre est 0 :\n\n- Si le premier chiffre est pair, nous avons 4 possibilités pour le choisir (2,4,6,8, mais pas 0 ). Il reste à choisir les 4 chiffres du milieu. On a 6 manières de positionner les impairs :\n\n$$\n(p, p, i, i),(p, i, p, i),(p, i, i, p),(i, p, i, p),(i, i, p, p),(i, p, p, i)\n$$\n\n(où $p$ représente un chiffre pair et $i$ un chiffre impair). Ensuite, il y a 5 possibilités pour le choix de chaque chiffre. Donc $6 \\times 4 \\times 5^{4}$ possibilités.\n\n- Si le premier chiffre est impair, nous avons 5 possibilités pour le choisir . Il reste 4 manières de positionner l'impair du milieu. Et de nouveau 5 choix pour chaque chiffre du milieu. Donc $4 \\times 5^{5}$ nombres possibles.\nNombres dont le dernier chiffre est 5 :\n- Si le premier chiffre est pair, nous avons 4 possibilités pour le choisir. Il y a 4 possibilités pour la place de l'impair du milieu, 5 choix pour chacun des chiffres du milieu, donc $16 \\times 5^{4}$ possibilités.\n- Si le premier chiffre est impair il y a 5 possibilités pour le choisir. Il reste alors simplement à déterminer les pairs du milieu : 5 choix à chaque fois, donc $5^{5}$ choix en tout.\nAu total, il y a $24 \\times 5^{4}+4 \\times 5^{5}+16 \\times 5^{4}+5^{5}=13 \\times 5^{5}=40625$ possibilités.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 3", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $n$ un entier strictement positif. On considère $2 n+1$ entiers distincts compris au sens large entre $-2 n+1$ et $2 n-1$. Montrer qu'on peut en choisir 3 dont la somme soit nulle.", "solution": "On raisonne par récurrence sur $n$.\nInitialisation : Pour $n=1$, on prend $2 n+1=3$ entiers distincts parmi $-1,0,1$, donc ces trois entiers. Leur somme est bien nulle.\nHérédité : Supposons l'énoncé vrai au rang $n$ : si on prend $2 n+1$ entiers distincts compris au sens large entre $-2 n+1$ et $2 n-1$, alors on peut en choisir 3 dont la somme soit nulle. Maintenant, on veut montrer que parmi $2 n+3$ entiers distincts entre $-2 n-1$ et $2 n+1$, il y en a toujours 3 de somme nulle.\nSi parmi ces $2 n+3$ entiers, il y en a $2 n+1$ entre $-2 n+1$ et $2 n-1$, alors c'est gagné par hypothèse de récurrence. On peut donc supposer que 3 au moins de ces entiers sont parmi $\\{-2 n-1,-2 n, 2 n, 2 n+1\\}$. Par symétrie entre les positifs et les négatifs, on peut supposer qu'on dispose de $2 n$ et $2 n+1$, ainsi que de $-2 n-1$ ou $-2 n$, donc on peut supposer qu'on ne dispose pas de 0 , puisque $0+2 n+(-2 n)=0+(2 n+1)+(-2 n-1)=0$ et on aurait alors un triplet de somme nulle. Maintenant, considérons les $n$ paires\n\n$$\n\\{-k,-2 n-1+k\\}, \\quad 1 \\leq k \\leq n\n$$\n\nsi l'une d'elles est incluse dans notre sélection de $2 n+3$ entiers, alors on a encore trois nombres de somme nulle : $-k+(-2 n-1+k)+(2 n+1)=0$ et on a terminé. Supposons donc que notre sélection ne contienne qu'au plus un élément de ces $n$ paires, donc il reste au moins $n+1$ nombres à choisir parmi $(\\{1, \\ldots, 2 n-1\\}$ et $-2 n-1$ ). On pose $A=\\{1, \\ldots, 2 n-1\\}$. On distingue 2 cas.\n\n- Si on a pris $-2 n-1$, on doit prendre au moins $n$ éléments de $A$. On regarde cette fois les $n$ paires\n\n$$\n\\{k, 2 n+1-k\\}, \\quad 1 \\leq k \\leq n\n$$\n\nSi l'une d'elles est complète, on a un triplet à somme nulle avec $-2 n-1$. On a supposé au début que $2 n$ était pris, donc si on prend $1,\\{1,2 n\\}$ est complète. Sinon on prend $n$ nombres dans les $n-1$ paires restantes, donc par principe des tiroirs, on a une paire complète.\n\n- Si on n'a pas pris $-2 n-1$, on doit prendre au moins $n$ éléments de $A$. Et on a pris $-2 n$ d'après le début du raisonnement. Et $A$ peut se découper en $n-1$ paires\n\n$$\n\\{k, 2 n-k\\}, 1 \\leq k \\leq n-1\n$$\n\nDe nouveau, par le principe des tiroirs on doit prendre une paire complète, donnant un triplet à somme nulle avec $-2 n$.\nCeci clôt la récurrence.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "On considère 6 points du plan, disposés de telle sorte que le triangle formé par trois quelconques d'entre eux ait trois côtés de longueurs distinctes. Montrer qu'il existe un triangle dont le plus court côté est également le côté le plus long d'un autre triangle.", "solution": "On colorie en rouge le plus court côté de chaque triangle. Il suffit de montrer qu'on a un triangle rouge. Appelons $P_{1}, \\ldots, P_{6}$ les points. Parmi les cinq segments $P_{1} P_{2}, P_{1} P_{3}, P_{1} P_{4}, P_{1} P_{5}, P_{1} P_{6}$ ayant $P_{1}$ pour extrémité, il y en a au moins 3 rouges ou bien au moins 3 non coloriés.\n\n- Supposons qu'il y en ait 3 rouges, disons $P_{1} P_{2}, P_{1} P_{3}$ et $P_{1} P_{4}$. Le triangle $P_{2} P_{3} P_{4}$ a au moins un côté rouge, disons $P_{2} P_{3}$, donc le triangle $P_{1} P_{2} P_{3}$ est rouge.\n- Supposons qu'il y en ait 3 non coloriées, disons $P_{1} P_{2}, P_{1} P_{3}$ et $P_{1} P_{4}$. Chacun des trois triangles $P_{1} P_{2} P_{3}$, $P_{1} P_{3} P_{4}, P_{1} P_{4} P_{2}$ a au moins un côté rouge, et ce côté n'est pas l'un de ceux ayant $P_{1}$ pour extrémité, donc $P_{2} P_{3}, P_{3} P_{4}, P_{4} P_{2}$ sont rouges. Ainsi, le triangle $P_{2} P_{3} P_{4}$ est rouge.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Dans un cirque, il y a plusieurs clowns. Chacun utilise au moins 5 couleurs, parmi 12 possibles, pour se peindre. Une même couleur est utilisée par au plus 20 clowns. Deux clowns n'ont jamais exactement les mêmes couleurs. Combien y a-t-il de clowns au maximum?", "solution": "Soit $n$ le nombre de clowns et $N$ le nombre de paires $(L, c)$ où $L$ est un cLown et $c$ une couleur qu'il porte. D'une part, chaque clown ayant au moins 5 couleurs, $N \\geq 5 \\times n$. D'autre part, chacune des 12 couleurs peut apparaître dans au plus 20 paires. Donc $N \\leq 20 \\times 12$. On en déduit que $5 n \\leq 240$, donc $n \\leq 48$.\n\nMaintenant, on considère les quintuplets : $A=\\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{5}\\right), B=\\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{6}\\right), C=\\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{7}\\right)$, $D=\\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{8}\\right)$. On imagine que les 12 couleurs sont disposées dans l'ordre sur un cercle (comme les nombres sur une pendule par exemple), et on note $A_{i}$ le quintuplet obtenu en décalant les couleurs de $A$ de $i$ rangs dans le sens croissant $\\left(A_{0}=A, A_{1}=\\left(c_{1+1}, c_{2+1}, c_{3+1}, c_{4+1}, c_{5+1}\\right)=\\left(c_{2}, c_{3}, c_{4}, c_{5}, c_{6}\\right)\\right.$, $A_{9}=\\left(c_{10}, c_{11}, c_{12}, c_{1}, c_{2}\\right.$, etc. $)$, et on fait de même pour $B, C, D$. Concrètement, chaque tel quintuplet de couleurs consiste donc de quatre couleurs consécutives sur le cercle, puis fait un \"saut\" pour le numéro de la dernière couleur qui est de taille 1 pour les $A_{i}$, de 2 pour les $B_{i}$, de 3 pour les $C_{i}$ et de 4 pour les $C_{i}$.\n\nConsidérons l'ensemble des $K_{i}$ avec $K=A, B, C$ ou $D$ et $0 \\leq i \\leq 11$. Cela donne 48 paquets de 5 couleurs. Et on vérifie aisément que deux paquets ne peuvent être identiques : si pour certains $i$ et $j$ et certains $K$ et $K^{\\prime}$ on avait $K_{i}=K_{j}^{\\prime}$, alors $K=K^{\\prime}$ pour avoir le même \"saut\" entre le \"paquet\" des quatre couleurs consécutives et la cinquième ( 1 pour $A, 2$ pour $B, 3$ pour $C, 4$ pour $D$ ), donc $K_{i}=K_{j}$, et on voit bien que $i=j$, pour que les deux paquets de quatre couleurs consécutives soient les mêmes.\nEnfin, chaque couleur est utilisée exactement 20 fois. En effet, on peut remarquer que toutes les couleurs jouent ici le même rôle(puisqu'on a \"décalé\" cycliquement les ensembles $A, B, C, D$ ), donc chacune sera représentée autant que les autres. On a au total $5 \\times 48=240$ utilisations de couleur, donc chacune des 12 couleurs est utilisée $240 / 12=20$ fois. Pour s'en convaincre plus concrètement, on peut fixer une couleur : elle apparaît une et une seule fois comme \"première\" couleur d'un paquet de type $A_{i}$, puis comme \"deuxième\", etc., donc 5 paquets $A_{i}$ utilisent cette couleur, et de même pour $B, C$ et $D$. Elle est donc utilisée 20 fois. Conclusion : on peut bien avoir $n=48$ clowns, en donnant à chaque clown un des 48 paquets de couleurs qu'on vient de construire.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 6", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "On considère $n^{2}+2 n+1$ points dans un carré de côté $n$. Montrer que trois d'entre eux sont les sommets d'un triangle (éventuellement dégénéré) d'aire au plus $1 / 2$.", "solution": "On raisonne sur l'enveloppe convexe des $(n+1)^{2}$ points : si elle contient beaucoup de points, il y aura 3 sommets voisins de cette enveloppe assez proches pour faire un triangle d'aire petite. Si elle n'en contient pas beaucoup, on la triangule et on regarde les nombreux points dans les petits triangles pour en former un suffisamment petit.\n\nConcrètement, voici une démonstration : Soit $E$ l'enveloppe convexe de nos points. On vérifie aisément que son périmètre est inférieur à celui du carré, à savoir $4 n$. Si $E$ a au moins $4 n$ sommets, donc autant de côtés, il existe deux côtés consécutifs $c_{1}$ et $c_{2}$ vérifiant $c_{1}+c_{2} \\leq 2$ donc $c_{1} c_{2} \\leq 1$ par inégalité arithméticogéométrique. Si $h$ est la hauteur relative à $c_{1}$ dans le triangle formé par les extrémités de $c_{1}$ et $c_{2}, h \\leq c_{2}$, donc l'aire du triangle est bien d'au plus $1 / 2$.\nSi $E$ a $s \\leq 4 n-1$ sommets, on la triangule en $s-2$ triangles. . Maintenant, prenons un point restant et relions-le aux sommets du triangle dans lequel il se trouve (ou des triangles s'il est sur le côté commun de deux triangles de la triangulation). On prend un autre point restant et on le relie de même aux sommets des triangles de la nouvelle triangulation dans lesquels il se trouve. On continue ainsi jusqu'à ce que tous les points soient intégrés à la triangulation. Ainsi, on a obtenu ce qu'on appelle une triangulation de notre ensemble de points. On avait $s-2$ triangles initialement, on en a rajouté au moins 2 à chaque étape (voire\n3), donc on a au moins $s-2+2\\left((n+1)^{2}-s\\right) \\geq 2 n^{2}+4 n-1-s \\geq 2 n^{2}$ triangles disjoints, donc l'un d'eux est d'aire au plus $1 / 2$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "On dispose de $n$ jetons portant chacun un numéro entier (qui peut être négatif). Si on trouve parmi eux deux jetons portant le même numéro $m$, on les enlève et on met à leur place un jeton portant le numéro $m-1$, et un autre portant le numéro $m+1$. Montrer qu'au bout d'un nombre fini de tels changements, tous les jetons porteront des numéros distincts.", "solution": "On commence par montrer le lemme suivant:\nSoit $m_{0}$ le plus petit des numéros des jetons au début. On note $m_{1}^{(k)}, \\ldots, m_{j_{k}}^{(k)}$ les numéros inférieurs ou égaux à $m_{0}$ qui sont portés par des jetons après $k$ changements, comptés avec multiplicité et rangés par ordre décroissant de sorte que $m_{j_{k}}^{(k)} \\leq \\ldots \\leq m_{1}^{(k)} \\leq m_{0}^{(k)}=m_{0}$. Alors pour tout $i \\in\\left\\{0, \\ldots, j_{k}-1\\right\\}$, on a $m_{i+1}^{(k)}-m_{i}^{(k)} \\leq 2$.\n\nDémonstration : on raisonne par récurrence sur $k$. Le cas $k=0$ est clair.\nSupposons que le résultat soit vérifié pour un certain $k . \\mathrm{Au}(k+1)$-ème changement, si nous remplaçons deux jetons portant un numéro strictement plus grand que $m_{0}$, aucun des $m_{i}^{(k)}$ ne change, donc la propriété est toujours vérifiée. Supposons maintenant que nous remplaçons deux jetons portant un numéro $m_{i}^{(k)}=$ $m_{i+1}^{(k)}=m$. Alors la suite $\\left(m_{i}^{(k+1)}\\right)$ s'obtient à partir de la suite $\\left(m_{i}^{(k)}\\right)$ en remplaçant deux occurrences de $m$ par une occurrence de $m-1$ et une occurrence de $m+1$. La différence entre ces dernières est exactement 2 , donc même s'il reste encore des termes égaux à $m$, leur distance aux termes autour d'eux sera inférieure ou égale à 1 . Celle entre $m-1$ et le terme suivant est inférieure strictement à celle entre $m$ et ce même terme suivant, donc inférieure à 2 par hypothèse de récurrence. Pour ce qui est de $m+1$, nous avons deux cas à distinguer. Soit $m=m_{0}$ et alors $m+1$ est strictement supérieur à $m_{0}$ et ne nous intéresse plus. Soit $m0$, et $P_{k+1}$ s'écrit\n\n$$\nP_{k+1}=(m-1)(m+1) c=\\left(m^{2}-1\\right) cb$ alors $(a-1)^{2}+(b+1)^{2} \\leq a^{2}+b^{2} \\leq 2014^{2}$.\n- Si $a=b$, alors l'inégalité $a^{2}+b^{2}=2 a^{2} \\leq 2014^{2}$ ne peut être une égalité car la valuation 2 -adique du côté gauche est impaire alors que celle du côté droit est paire. Nous avons donc $2 a^{2}+2 \\leq 2014^{2}$, d'où $(a-1)^{2}+(a+1)^{2}=2 a^{2}+2 \\leq 2014^{2}$.\n\nOn appelle $C_{2}$ ce petit carré de centre ( $a-\\frac{3}{2}, b+\\frac{1}{2}$ ).\n2ème étape : Par des considérations de symétrie et de convexité, les petits carrés $C_{1}, \\ldots, C_{8}$ suivants appartiennent tous à la figure :\n\n\nOr chaque ligne, chaque colonne et chaque diagonale contient soit aucun, soit deux de ces huit petits carrés. Ainsi, la parité du nombre de -1 parmi ces carrés ne change pas, contradiction.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-1-solutions.jsonl", "problem_match": "\nExercice 9", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Soit $n \\in \\mathbb{N}^{*}$. On appelle $S$ l'ensemble des suites de $2 n$ chiffres comportant $n$ zéros et autant de uns. Deux suites de $S$ sont voisines lorsqu'il suffit de changer la position d'un chiffre de l'une pour obtenir l'autre. Par exemple, 11100010 et 10110010 sont voisines puisqu'en décalant le premier 0 de la deuxième suite de deux \"pas\" vers la droite, on obtient la première suite. Soit $T$ un sous-ensemble dense de cardinal minimal. Montrer que $\\frac{1}{n^{2}+1}|S| \\leq|T| \\leq \\frac{1}{n+1}|S|$. Remarque : on note $|A|$ le cardinal de $A$.", "solution": "On traite séparément les inégalités.\n\n- Montrons que $\\frac{1}{2 n^{2}+1}|S| \\leq|T|$. Soit $s$ un élément de $S$. Soit $s_{i, j}$ la suite que l'on peut obtenir à partir de $s$, en déplaçant le $i$-ème chiffre de $s$ pour le mettre en position $j$. Si $s_{i, j} \\neq s$, alors $j \\neq i$. En outre, sans perte de généralité, on suppose que le $i$-ème chiffre de $s$ est un 0 ; si $j>i$ et si le $j$-ème chiffre de $s$ est un 0 , alors $s_{i, j}=s_{i, j-1}$; si $j0$ ) : contradiction.\n$\\triangleright$ Si $n$ est impair, le pgcd de $(n+1)$ et $(n-1)$ est le pgcd de $(n+1)$ et $n+1-(n-1)=2$ donc 2 . Ainsi, ils sont égaux à 6 et $2^{\\mathrm{m}-1}$, ou bien à 2 et $3 \\cdot 2^{\\mathrm{m}-1}$.\n\n- Si $n-1=6$, alors $n=7$ et $2^{\\mathrm{m-1}}=n+1=8$ d'où $m=4$.\n- Si $n+1=6$, alors $n=5$ et $2^{\\mathrm{m}-1}=\\mathrm{n}-1=4$ d'où $m=3$.\n- Si $n-1=2$ alors $n=3$ et $3 \\cdot 2^{m}=n^{2}-1=8$, ce qui est impossible car 3 ne divise pas 8 .\n- Si $n+1=2$ alors $n=1$ et $3 \\cdot 2^{m}=n^{2}-1=0$, ce qui est impossible.\n\nEn conclusion, l'équation n'est vérifiée que pour les couples $(\\mathfrak{m}, \\mathfrak{n}) \\in\\{(4,7),(3,5)\\}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $p$ un nombre premier. Trouver tous les entiers $n \\geqslant 1$ tels que pour tout entier $a \\geqslant 1$, si $a^{n}-1$ est divisible par $p$, alors $a^{n}-1$ est aussi divisible par $p^{2}$.", "solution": "de l'exercice 3 Montrons que les entiers $n$ qui conviennent sont exactement les multiples de $p$. Pour cela, nous allons d'abord prouver que lorsque $n=p m$ pour un entier $m \\geqslant 1$, pour tout entier $a \\geqslant 1$, si $a^{n}-1$ est divisible par $p$, alors $a^{n}-1$ est aussi divisible par $p^{2}$. Puis, réciproquement, nous allons prouver que si $p$ ne divise pas $n$, alors il existe un entier $a \\geqslant 1$ tel que $a^{n}-1$ est divisible par $p$ mais tel que $a^{n}-1$ n'est pas divisible par $p^{2}$.\n$\\triangleright$ Si $n=p m$ pour un entier $m \\geqslant 1$, alors $a^{n}=a^{p m} \\equiv a^{m}(\\bmod \\mathfrak{p})$ d'après le petit théorème de Fermat pour tout entier a. Supposons dorénavant que l'entier a est tel que $a^{n}-1$ est divisible par $p$. D'après la ligne ci-dessus, $a^{\\mathrm{m}}-1$ est divisible par $p$. Par ailleurs, la factorisation suivante est vérifiée:\n\n$$\na^{n}-1=a^{p m}-1=\\left(a^{m}-1\\right)\\left(1+a^{m}+\\cdots+a^{(p-1) m}\\right)\n$$\n\nComme $p$ divise $a^{m}-1, a^{m} \\equiv 1(\\bmod p)$ donc\n\n$$\n1+a^{m}+\\cdots+a^{(\\mathfrak{p}-1) m} \\equiv 1+1+\\cdots+1 \\equiv p \\equiv 0 \\quad(\\bmod \\mathfrak{p})\n$$\n\nEn conclusion, $a^{n}-1$ est le produit de deux entiers divisibles par $p$ donc est divisible par $p^{2}$.\n$\\triangleright$ Si $p$ ne divise pas $n$, alors avec l'entier $a=p+1$, on a que $a^{n}-1 \\equiv 1^{n}-1 \\equiv 0(\\bmod \\mathfrak{p})$ donc $p$ divise $a^{n}-1$. Or\n\n$$\n1+a+\\cdots+a^{(n-1)} \\equiv 1+1+\\cdots+1^{n-1} \\equiv n \\not \\equiv 0(\\bmod p)\n$$\n\nAinsi, $p$ ne divise pas $1+a+\\cdots+a^{(n-1)}$, et donc $p^{2}$ ne divise pas $p\\left(1+a+\\cdots+a^{(n-1)}\\right)=$ $(a-1)\\left(1+a+\\cdots+a^{(n-1)}\\right)=a^{n}-1$.\n\n## Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets d'entiers strictement positifs ( $a, b, c)$ tels que $6^{a}=1+2^{b}+$ $3^{\\mathrm{c}}$.", "solution": "de l'exercice 4 Remarquons tout d'abord que 3 divise $2^{b}+1$ donc b est impair (car $2^{b}+$ $\\left.1 \\equiv(-1)^{\\mathrm{b}}+1(\\bmod 3)\\right)$.\n$\\triangleright$ Si $\\mathrm{b}=1$, l'équation se réécrit $1+3^{\\mathrm{c}-1}=2 \\cdot 6^{a-1}$ en divisant par 3 .\n\n- Si $a>1$, alors 3 divise $1+3^{\\mathrm{c}-1}$ ce qui est impossible.\n- Sinon, $\\mathrm{a}=1$ et par conséquent $\\mathrm{c}=1$.\n$\\triangleright \\mathrm{Si} \\mathrm{b} \\geqslant 3$, alors $\\mathrm{a} \\geqslant 2\\left(\\right.$ car $\\left.6<1+2^{3}\\right)$. En réduisant modulo 4 , on obtient la condition nécessaire $1+3^{c} \\equiv 0(\\bmod 4)$, et donc c est impair. En réduisant alors modulo 8 , on obtient la nouvelle condition $1+2^{\\mathrm{b}}+3^{\\mathrm{c}} \\equiv 1+0+3(\\bmod 8) \\equiv 4(\\bmod 8)$ donc $6^{\\mathrm{a}} \\equiv 4(\\bmod 8)$ ce qui entraîne immédiatement $a=2\\left(\\right.$ en effet, pour $6^{a} \\equiv 0(\\bmod 8)$ pour $\\left.a \\geqslant 3\\right)$. L'équation initiale devient alors $2^{\\mathrm{b}}+3^{\\mathrm{c}}=35$ et une étude exhaustive donne $\\mathrm{b}=3$ et $\\mathrm{c}=3$ ou $\\mathrm{b}=5$ et $\\mathrm{c}=1$.\n\nEn conclusion, les triplets", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets d'entiers strictement positifs ( $a, b, c)$ tels que $6^{a}=1+2^{b}+$ $3^{\\mathrm{c}}$.", "solution": "s sont $(\\mathbf{a}, \\boldsymbol{b}, \\boldsymbol{c}) \\in\\{(1,1,1),(2,3,3),(2,5,1)\\}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": " solution"}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit n l'entier $4 \\times 201420142014 \\ldots 2014$ (où 2014 est écrit 117819 fois). Montrer que $2014^{3}$ divise n.", "solution": "de l'exercice 5 On peut écrire\n\n$$\n4 \\times 201420142014 \\ldots 2014=4 \\cdot 2014 \\cdot \\frac{10^{4 \\cdot 117819}-1}{10^{4}-1}\n$$\n\nComme $2014=2 \\cdot 19 \\cdot 53$ et $10^{4}-1=3^{2} \\cdot 11 \\cdot 101$ sont premiers entre eux, il suffit de montrer que $19^{2}$ et $53^{2}$ divisent $10^{4 \\cdot 117819}-1$. D'après le théorème d'Euler,\n\n$$\n10^{\\Phi\\left(19^{2}\\right)} \\equiv 1 \\quad\\left(\\bmod 19^{2}\\right) \\quad \\text { et } \\quad 10^{\\Phi\\left(53^{2}\\right)} \\equiv 1 \\quad\\left(\\bmod 53^{2}\\right),\n$$\n\noù $\\phi$ désigne la fonction indicatrice d'Euler. Il suffit donc de vérifier que $\\phi\\left(19^{2}\\right)$ et $\\phi\\left(53^{2}\\right)$ divisent tous les deux $4 \\cdot 117819$. Ceci découle du fait que $\\phi\\left(19^{2}\\right)=19^{2}-19=2 \\cdot 3^{2} \\cdot 19$, $\\phi\\left(53^{2}\\right)=53^{2}-53=2^{2} \\cdot 13 \\cdot 53$ et $4 \\cdot 117819=2^{2} \\cdot 3^{2} \\cdot 13 \\cdot 19 \\cdot 53$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soient $m$ et $n$ deux entiers tels que $0 \\leqslant \\mathfrak{m} \\leqslant 2 \\boldsymbol{n}$. Prouver que le nombre entier\n\n$$\n2^{2 n+2}+2^{m+2}+1\n$$\n\nest un carré parfait $s i$, et seulement $\\mathrm{si}, \\mathrm{m}=\\mathrm{n}$.", "solution": "de l'exercice 6\n\n$\\triangleright$ Remarquons que si $\\mathrm{m}=\\mathrm{n}$, alors $2^{2 \\mathrm{n}+2}+2^{\\mathrm{m}+2}+1=\\left(2^{\\mathrm{m}+1}+1\\right)^{2}$ est bien un carré parfait.\n$\\triangleright$ Réciproquement, supposons que $2^{2 n+2}+2^{\\mathrm{m}+2}+1$ est un carré parfait. Comme il est strictement plus grand que $2^{2 \\mathrm{n}+2}=\\left(2^{\\mathrm{n}+1}\\right)^{2}$, il est supérieur ou égal au carré suivant, c'est-à-dire $2^{2 n+2}+2^{m+2}+1 \\geqslant\\left(2^{n+1}+1\\right)^{2}$.\n\nEn développant, il vient $2^{\\mathfrak{m}+2} \\geqslant 2^{\\mathfrak{n}+2}$, donc $\\mathfrak{m} \\geqslant n$. Supposons par l'absurde que $\\mathrm{m}>n$ soit $2^{m}>2^{2 n-m}$.\n\nPar hypothèse, la quantité $2^{2 n+2}+2^{m+2}+1$ est le carré d'un entier impair $2 k+1$ strictement plus grand que 1 , d'où\n\n$$\n2^{2 \\mathrm{n}+2}+2^{\\mathrm{m}+2}+1=(2 \\mathrm{k}+1)^{2}\n$$\n\npour un certain entier $k \\geqslant 1$, ce qui se réécrit sous la forme $k(k+1)=2^{2 n}+2^{m}=2^{m}\\left(2^{2 n-m}+1\\right)$. Or les entiers $k$ et $k+1$ sont premiers entre eux. On en déduit que :\n\n- soit $k=2^{m} p$ et $p(k+1)=2^{2 n-m}+1$ ce qui entraîne $(k+1) p1$.\n\nSoit $p \\geqslant 3$ un facteur premier (impair) de $q$ et vérifions que $u_{n+1}=p u_{n}$ vérifie la propriété requise. Montrons que\n\n$$\np \\quad \\text { divise } \\quad 3^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)}-2^{\\mathfrak{u}_{n}} 3^{\\mathfrak{u}_{\\mathfrak{n}}(\\mathfrak{p}-2)}+\\cdots+2^{\\mathfrak{u}_{n}(p-1)} .\n$$\n\nCeci permet de conclure, car alors, étant donné que $p u_{n}^{2}$ divise $2^{u_{n}}+3^{\\mathfrak{u}_{n}}$, il en découle que $p \\cdot p u_{n}^{2}$ divise\nce qui achève la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Montrer qu'il existe une infinité de nombres entiers strictement positifs a tels que $a^{2}$ divise $2^{a}+3^{a}$.", "solution": "Pour établir (1), on remarque que $p$ divise $2^{u_{n}}+3^{\\mathfrak{u}_{n}}$ (car $p$ divise $q$ ), de sorte qu'on a la congruence $2^{\\mathfrak{u}_{n}} \\equiv-3^{\\mathfrak{u}_{n}}(\\bmod p)$. Ainsi,\n\n$$\n\\begin{aligned}\n3^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)}-2^{\\mathfrak{u}_{n}} 3^{\\mathfrak{u}_{n}(\\mathfrak{p}-2)}+\\cdots+2^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)} & \\equiv 3^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)}+3^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)}+\\cdots+3^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)} \\quad(\\bmod p) \\\\\n& \\equiv p 3^{\\mathfrak{u}_{n}(\\mathfrak{p}-1)} \\quad(\\bmod p) \\\\\n& \\equiv 0 \\quad(\\bmod p) .\n\\end{aligned}\n$$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": " démonstration."}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $m, n \\geqslant 1$ deux entiers impairs tels que $m$ divise $n^{2}+2$ et $n$ divise $m^{2}+2$. Prouver que $m$ et $n$ sont tous les deux des termes de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ définie par\n\n$$\n\\mathfrak{u}_{1}=\\mathrm{u}_{2}=1, \\quad \\mathrm{u}_{\\mathrm{n}}=4 \\mathrm{u}_{n-1}-\\mathrm{u}_{n-2} \\quad \\text { si } n \\geqslant 3\n$$", "solution": "de l'exercice 8 La structure de la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $m, n \\geqslant 1$ deux entiers impairs tels que $m$ divise $n^{2}+2$ et $n$ divise $m^{2}+2$. Prouver que $m$ et $n$ sont tous les deux des termes de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ définie par\n\n$$\n\\mathfrak{u}_{1}=\\mathrm{u}_{2}=1, \\quad \\mathrm{u}_{\\mathrm{n}}=4 \\mathrm{u}_{n-1}-\\mathrm{u}_{n-2} \\quad \\text { si } n \\geqslant 3\n$$", "solution": "est la suivante:\n\n- On montre que mn divise $\\mathrm{m}^{2}+\\mathrm{n}^{2}+2$;\n- On montre que $\\mathrm{m}^{2}+\\mathrm{n}^{2}+2=4 \\mathrm{mn}$;\n- On montre que la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ est croissante;\n- On conclut en montrant qu'en fait $m$ et $n$ sont deux termes consécutifs de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$.\n$\\triangleright$ Soit $d$ le PGCD de $m$ et de $n$. Comme $m$ divise $n^{2}+2$, on en déduit que $d$ divise $n^{2}+2$ et donc que $d$ divise 2 . Comme $m$ et $n$ sont impairs, on en déduit que $d=1$, de sorte que $m$ et $n$ sont premiers entre eux. Ainsi, mn divise $\\mathrm{m}^{2}+\\mathrm{n}^{2}+2$.\n$\\triangleright$ Montrons que $\\mathrm{m}^{2}+\\mathrm{n}^{2}+2=4 \\mathrm{mn}$ en utilisant la technique connue en anglais sous le nom de $\\ll$ Vieta jumping $\\gg$. Plus précisément, soit $k=\\left(m^{2}+n^{2}+2\\right) /(m n)$, et considérons tous les couples d'entiers strictement positifs $(x, y)$ tels que\n\n$$\nx^{2}+y^{2}+2=k x y .\n$$\n\nParmi ces couples, choissisons-en un qui minimise la somme $x+y$. Nous allons montrer que $x=y$. Raisonnons par l'absurde en supposant, sans perte de généralité, que $x>y \\geqslant 1$. On s'intéresse alors à l'équation du second degré\n\n$$\nt^{2}-k y t+y^{2}+2=0\n$$\n\nd'inconnue $t$. On sait déjà que $t_{1}=x$ est", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $m, n \\geqslant 1$ deux entiers impairs tels que $m$ divise $n^{2}+2$ et $n$ divise $m^{2}+2$. Prouver que $m$ et $n$ sont tous les deux des termes de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ définie par\n\n$$\n\\mathfrak{u}_{1}=\\mathrm{u}_{2}=1, \\quad \\mathrm{u}_{\\mathrm{n}}=4 \\mathrm{u}_{n-1}-\\mathrm{u}_{n-2} \\quad \\text { si } n \\geqslant 3\n$$", "solution": "D'après les formules de Viète,\n\n$$\n\\mathrm{t}_{2}=\\mathrm{ky}-\\mathrm{x}=\\frac{\\mathrm{y}^{2}+2}{\\mathrm{x}}\n$$\n\nest également", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $m, n \\geqslant 1$ deux entiers impairs tels que $m$ divise $n^{2}+2$ et $n$ divise $m^{2}+2$. Prouver que $m$ et $n$ sont tous les deux des termes de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ définie par\n\n$$\n\\mathfrak{u}_{1}=\\mathrm{u}_{2}=1, \\quad \\mathrm{u}_{\\mathrm{n}}=4 \\mathrm{u}_{n-1}-\\mathrm{u}_{n-2} \\quad \\text { si } n \\geqslant 3\n$$", "solution": "L'équation (2) montre que $t_{2}$ est un entier strictement positif. Comme $1 \\leqslant y \\leqslant x-1$, on a\n\n$$\nt_{2}=\\frac{y^{2}+2}{x} \\leqslant \\frac{(x-1)^{2}+2}{x}u_{n}-u_{n-1}\n$$\n\nPar récurrence, on en déduit que, pour tout entier $\\boldsymbol{n} \\geqslant 1, \\mathfrak{u}_{n+1}-\\boldsymbol{u}_{n}>\\mathfrak{u}_{2}-\\mathfrak{u}_{1}=0$.\n$\\triangleright$ Montrons finalement que $m$ et $n$ sont deux termes consécutifs de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ par récurrence forte sur $m+n$. L'initialisation ne pose pas de soucis: si $m+n=2$, on a $m=n=1$. Soit donc $k \\geqslant 3$, supposons le résultat établi pour tous les couples ( $m, n$ ) d'entiers strictement positifs vérifiant (3) avec $m+n\\mathrm{n}$. Mais, comme dans le paragraphe précédent, si $(m, n)$ est", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient $m, n \\geqslant 1$ deux entiers impairs tels que $m$ divise $n^{2}+2$ et $n$ divise $m^{2}+2$. Prouver que $m$ et $n$ sont tous les deux des termes de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$ définie par\n\n$$\n\\mathfrak{u}_{1}=\\mathrm{u}_{2}=1, \\quad \\mathrm{u}_{\\mathrm{n}}=4 \\mathrm{u}_{n-1}-\\mathrm{u}_{n-2} \\quad \\text { si } n \\geqslant 3\n$$", "solution": ", alors $(n, 4 n-m)$ l'est également, avec $m+n>n+(4 n-m)$. D'autre part, on vérifie aisément que $2 n-\\sqrt{3 n^{2}-2}4 n-m$. Par hypothèse de récurrence, il existe un entier $i \\geqslant 2$ tel que $u_{i-1}=n$ et $u_{i-2}=4 n-m$. Mais alors $u_{i}=4 n-(4 n-m)=m$, ce qui montre bien que $m$ et $n$ sont deux termes consécutifs de la suite $\\left(u_{n}\\right)_{n \\geqslant 1}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution"}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs a tels que l'entier\n\n$$\n1-8 \\cdot 3^{a}+2^{a+2}\\left(2^{a}-1\\right)\n$$\n\nsoit un carré parfait.", "solution": "de l'exercice 9 La quantité (4) est égale à $\\left(2^{\\mathrm{a}+1}-1\\right)^{2}-2^{3} \\cdot 3^{\\mathrm{a}}$. On remarque que cette quantité est un carré pour $a=3$ (elle vaut $9=3^{2}$ ) et $a=5$ (elle vaut $2025=45^{2}$ ) mais pas pour $a \\in\\{1,2,4,6,7\\}$. On suppose dorénavant $a \\geqslant 8$.\n\nSupposons que la quantité (4) soit un carré, c'est-à-dire, puisqu'elle est impaire, qu'il existe un entier $k$ tel que\n\n$$\n\\left(2^{a+1}-1\\right)^{2}-2^{3} \\cdot 3^{a}=(2 \\mathrm{k}+1)^{2}\n$$\n\nAinsi\n\n$$\n\\left(2^{a+1}-1\\right)^{2}-(2 k+1)^{2}=2^{3} \\cdot 3^{a}\n$$\n\nsoit encore $\\left(2^{a}-k-1\\right)\\left(2^{a}+k\\right)=2 \\cdot 3^{a}$. Il existe alors un entier $b \\geqslant 0$ tel que l'une des deux situations suivantes se produit (en discutant selon la parité de $k$ ):\n\n- on a $2^{a}+\\mathrm{k}=2 \\cdot 3^{\\mathrm{b}}$ et $2^{\\mathrm{a}}-\\mathrm{k}-1=3^{\\mathrm{a}-\\mathrm{b}}$ donc $2 \\mathrm{k}+1=2 \\cdot 3^{\\mathrm{b}}-3^{\\mathrm{a}-\\mathrm{b}}$ (donc $\\mathrm{b} \\geqslant \\mathrm{a}-\\mathrm{b}$ );\n- on a $2^{\\mathrm{a}}+\\mathrm{k}=3^{\\mathrm{b}}$ et $2^{\\mathrm{a}}-\\mathrm{k}-1=2 \\cdot 3^{\\mathrm{a}-\\mathrm{b}}$ donc $2 \\mathrm{k}+1=3^{\\mathrm{b}}-2 \\cdot 3^{\\mathrm{a}-\\mathrm{b}}$ (donc $\\mathrm{b} \\geqslant \\mathrm{a}-\\mathrm{b}$ ). Ainsi, $3^{\\mathrm{a}-\\mathrm{b}}$ divise $2 \\mathrm{k}+1$, et donc $3^{2(\\mathrm{a}-\\mathrm{b})}$ divise $(2 \\mathrm{k}+1)^{2}+2^{3} \\cdot 3^{\\mathrm{a}}$. En utilisant (5), il vient $3^{\\mathrm{a}-\\mathrm{b}} \\mid 2^{\\mathrm{a}+1}-1$.\n\nDans la première situation, en additionnant les deux égalités on a $2 \\cdot 3^{\\mathbf{b}}=2^{a+1}-3^{a-b}-1<$ $2^{a+1}$ donc $3^{b}<2^{a+1}$. On montre de manière analogue que cette inégalité est valable aussi dans la deuxième situation.\n\nRemarquons que $2^{9} \\leqslant 3^{9-3}$ donc, pour tout $a \\geqslant 8$,\n\n$$\n2^{a+1}=2^{9} \\cdot 2^{a-8} \\leqslant 2^{9} \\cdot 3^{a-8} \\leqslant 3^{6} \\cdot 3^{a-8}=3^{a-2}\n$$\n\nEn combinant les deux inégalités, $3^{\\mathbf{b}}<3^{\\mathbf{a}-2}$ donc $\\mathbf{a}-\\mathrm{b} \\geqslant 3$.\nComme $3^{a-b}$ divise $2^{a+1}-1$ et $a-b \\geqslant 3$, on a $2^{a+1} \\equiv 1(\\bmod 27)$ d'où 18 divise $a+1$ (en remarquant que le plus petit entier $k>0$ tel que $2^{k} \\equiv 1(\\bmod 27)$ est 18). Fort de cette condition, réduisons la quantité de l'énoncé modulo 19 en utilisant le théorème d'Euler ( $\\chi^{18}=\\chi^{\\varphi(19)} \\equiv 1$ $(\\bmod 19)$ pour tout entier $x$ non divisible par 19$)$ et la relation $3 \\cdot 13 \\equiv 1(\\bmod 19)$ :\n\n$$\n\\left(2^{a+1}-1\\right)^{2}-2^{3} \\cdot 3^{a} \\equiv(1-1)^{2}-2^{3} \\cdot 13 \\quad(\\bmod 19) \\equiv 10 \\quad(\\bmod 19)\n$$\n\nOn conclut en remarquant alors que $(2 \\mathrm{k}+1)^{18} \\equiv 10^{9}(\\bmod 19)=18(\\bmod 19)$ ce qui contredit le théorème d'Euler. Il n'y a donc pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs a tels que l'entier\n\n$$\n1-8 \\cdot 3^{a}+2^{a+2}\\left(2^{a}-1\\right)\n$$\n\nsoit un carré parfait.", "solution": "$a \\geqslant 9$.\n\nEn conclusion, les seules", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs a tels que l'entier\n\n$$\n1-8 \\cdot 3^{a}+2^{a+2}\\left(2^{a}-1\\right)\n$$\n\nsoit un carré parfait.", "solution": "s sont 3 et 5 .", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-3-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution"}}
diff --git a/French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl b/French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..3bff6331ca266182dcdbb339bb236f4f17bda4ac
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl
@@ -0,0 +1,21 @@
+{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soit $a, b$ et $c$ des réels tels que\n\n$$\n|a-b| \\geq|c|,|b-c| \\geq|a| \\text { et }|c-a| \\geq|b| .\n$$\n\nProuver que l'un des trois nombres $a, b$ et $c$ est la somme des deux autres.", "solution": "La première inégalité s'écrit $(a-b)^{2} \\geq c^{2}$, ou encore $(a-b+c)(a-b-c) \\geq 0$. De même, les deux autre inégalités conduisent à $(b-c+a)(b-c-a) \\geq 0$ et $(c-a+b)(c-a-b) \\geq 0$.\n\nEn multipliant membre à membre ces trois inégalités, il vient\n\n$$\n(a-b+c)^{2}(-a+b+c)^{2}(a+b-c)^{2} \\leq 0\n$$\n\nOr, un carré étant toujours positif, c'est donc que l'un des facteurs est nul, ce qui conclut.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 1.", "solution_match": "## Solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soit $a, b$ et $c$ des réels tels que\n\n$$\n|a-b| \\geq|c|,|b-c| \\geq|a| \\text { et }|c-a| \\geq|b| .\n$$\n\nProuver que l'un des trois nombres $a, b$ et $c$ est la somme des deux autres.", "solution": "alternative.\n\nLes variables $a, b$ et $c$ jouent des rôles symétriques. En outre, le problème est invariant si on change simultanément les signes de $a, b$ et $c$. Ainsi, il y a au moins deux variables parmi $a, b$ et $c$ qui ont le même signe ; on peut donc supposer, sans perte de généralité, que l'on est dans un des deux cas $a \\geq b \\geq c \\geq 0$ ou $a \\geq b \\geq 0 \\geq c$.\nMontrons que la relation $b=a+c$ est vraie dans les deux cas, ce qui conclura le problème.\n\n1. Si $a \\geq b \\geq c \\geq 0$, alors $b \\geq b-c=|b-c| \\geq|a|=a$; chaque inégalité est donc une égalité, d'où la relation $b=b-c=|b-c|=|a|=a$.\n2. Si $a \\geq b \\geq 0 \\geq c$, alors $b-c=|b-c| \\geq|a|=a$ et $a-b=|a-b| \\geq|c|=-c$, d'où la relation $a+c \\geq b \\geq a+c$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 1.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Déterminer tous les nombres irrationnels $x$ pour lesquels les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.", "solution": "Soit $x$ un nombre irrationnel pour lequel les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.\n\nOn pose $x^{2}+x=a$ et $x^{3}+2 x^{2}=b$, où $a$ et $b$ sont des entiers. Alors $b-a x=x^{2}=a-x$, et ainsi $x(a-1)=b-a$. Si $a-1 \\neq 0$, on aurait $x=\\frac{b-a}{a-1}$, et $x$ serait rationnel, en contradiction avec l'énoncé.\n\nPar suite, on a $a=1$ et donc $b=a=1$. Mais alors $x^{2}+x-1=0$ et $x^{3}+2 x^{2}-1=0$. On note que, si $x^{2}+x-1=0$, alors $x^{3}=-x^{2}+x$ et $x=-x^{2}+1$, d'où $x^{3}+2 x^{2}-1=0$.\n\nAinsi, les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 2.", "solution_match": "## Solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Déterminer tous les nombres irrationnels $x$ pour lesquels les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.", "solution": "s du problème sont les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 2.", "solution_match": " solution"}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Déterminer tous les nombres irrationnels $x$ pour lesquels les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.", "solution": "s irrationnelles de l'équation du second degré $x^{2}+x-1=0$, c'est-à-dire les nombres $x_{1}=\\frac{-1-\\sqrt{5}}{2}$ et $x_{2}=\\frac{-1+\\sqrt{5}}{2}$. Puisque $\\sqrt{5}$ n'est pas rationnel, ces deux nombres sont effectivement des", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 2.", "solution_match": " solution"}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Déterminer tous les nombres irrationnels $x$ pour lesquels les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.", "solution": "s du problème.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 2.", "solution_match": " solution"}}
+{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $x$ un réel strictement positif tel que $x^{5}-x^{3}+x \\geq 3$. Prouver que $x^{6} \\geq 5$.", "solution": "La clé du problème est la factorisation $x^{6}+1=\\left(x^{2}+1\\right)\\left(x^{4}-x^{2}+1\\right)$, valable pour tout réel $x$.\n\nSoit $x>0$ tel que $x^{5}-x^{3}+x \\geq 3$. D'après l'identité ci-dessus, on a alors\n\n$$\nx^{6}+1=\\left(x^{2}+1\\right)\\left(x^{4}-x^{2}+1\\right)=\\frac{x^{2}+1}{x}\\left(x^{5}-x^{3}+x\\right)=\\left(x+\\frac{1}{x}\\right)\\left(x^{5}-x^{3}+x\\right)\n$$\n\net donc $x^{6}+1 \\geq 3\\left(x+\\frac{1}{x}\\right)$.\nOr, d'après l'inégalité arithmético-géométrique (IAG), on a $x+\\frac{1}{x} \\geq 2$, d'où $x^{6}+1 \\geq 6$, et ainsi $x^{6} \\geq 5$, comme souhaité.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 3.", "solution_match": "## Solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les réels $t$ pour lesquels le polynôme\n\n$$\nP(x)=x^{3}+3 t x^{2}+(4 t-1) x+t\n$$\n\npossède deux racines réelles dont la différence est égale à 1 .", "solution": "Si $t$ est un réel fixé, on pose $P_{t}(x)=x^{3}+3 t x^{2}+(4 t-1) x+t$.\nLa première chose à remarquer est que, pour tout $t$, on a $P_{t}(-1)=0$. Par suite, -1 est une racine du polynôme $P_{t}$, ce qui assure que $P_{t}(x)$ est factorisable par $x+1$. On trouve ainsi que\n\n$$\nP_{t}(x)=(x+1)\\left(x^{2}+(3 t-1) x+t\\right)\n$$\n\npour tout réels $x$ et $t$.\nSoit $t$ un réel pour lequel $P_{t}$ possède deux racines réelles dont la différence est égale à 1 , disons $a$ et $a+1$.\n\n- Si $a=-1$ : il faut et il suffit que 0 soit également une racine de $P_{t}$. Comme $P_{t}(0)=t$, cela signifie que $t=0$.\n- Si $a+1=-1$, il faut et il suffit que -2 soit également une racine de $P_{t}$. Comme $P_{t}(-2)=5 t-6$, cela signifie que $t=\\frac{6}{5}$.\n- Si -1 n'est ni $a$ ni $a+1$, c'est donc que $a$ et $a+1$ sont les racines de $x^{2}+(3 t-1) x+t$. On a donc $a^{2}+(3 t-1) a+t=0$ et $(a+1)^{2}+(3 t-1)(a+1)+t=0$. Par soustraction, il vient $2 a+1+3 t-1=0$, soit donc $a=-\\frac{3 t}{2}$. En reportant dans la première équation ci-dessus, il vient alors $-9 t^{2}+10 t=0$, soit $t=0$ ou $t=\\frac{10}{9}$.\nRéciproquement, on a déjà vu que $t=0$ convenait et, pour $t=\\frac{10}{9}$, les racines de $P_{t}$ sont $-1,-\\frac{2}{3}$ et $-\\frac{5}{3}$, ce qui prouve que $t=\\frac{10}{9}$ est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 4.", "solution_match": "## Solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les réels $t$ pour lesquels le polynôme\n\n$$\nP(x)=x^{3}+3 t x^{2}+(4 t-1) x+t\n$$\n\npossède deux racines réelles dont la différence est égale à 1 .", "solution": "du problème.\nFinalement, les réels $t$ cherchés sont $\\frac{10}{9}, \\frac{6}{5}$ et 0 .", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 4.", "solution_match": " solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Vietnam 2014).\n\nDéterminer toutes les fonctions $f: \\mathbb{Z} \\mapsto \\mathbb{Z}$ telles\n\n$$\nf(2 m+f(m)+f(m) f(n))=n f(m)+m\n$$\n\npour tous les entiers $m$ et $n$.", "solution": "Soit $f$ une éventuelle", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 5", "solution_match": "## Solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Vietnam 2014).\n\nDéterminer toutes les fonctions $f: \\mathbb{Z} \\mapsto \\mathbb{Z}$ telles\n\n$$\nf(2 m+f(m)+f(m) f(n))=n f(m)+m\n$$\n\npour tous les entiers $m$ et $n$.", "solution": "On note $\\mathbf{E}_{x, y}$ l'égalité de l'énoncé.\nPosons $a=f(0)$. L'égalité $\\mathbf{E}_{x, 0}$ indique que $f(2 x+(1+a) f(x))=x$, ce qui montre que $f$ est surjective. Puis, en choisissant un entier $b$ tel que $f(b)=-1$, l'égalité $\\mathbf{E}_{b, y}$ indique que $f(2 b+1-f(y))=b-y$, ce qui montre que $f$ est injective, donc bijective.\nLes égalités $\\mathbf{E}_{b, b}$ et $\\mathbf{E}_{0,0}$ indiquent respectivement que $f(2 b)=0$ et que $f\\left(a+a^{2}\\right)=0$. Il s'ensuit que $2 b=a+a^{2}$. De surcroît, l'égalité $\\mathbf{E}_{a b, 0}$ indique que $f(0)=a b$, c'est-à-dire $0=a(a-1)(a+2)$. Ainsi, $a \\in\\{-2,0,1\\}$.\nEnfin, les égalités $\\mathbf{E}_{0, y}$ et $\\mathbf{E}_{a y, 0}$ indiquent respectivement que $f(a f(y)+a)=a y$ et que $f(2 a y+(a+1) f(a y))=a y$. Il s'ensuit que $a f(y)+a=2 a y+(a+1) f(a y)$, égalité que l'on note ( $\\boldsymbol{\\phi}$ ).\n\n- Si $a=1$, alors l'égalité ( $\\boldsymbol{\\oplus}$ ) indique que $f(y)+1=2 y+2 f(y)$. Il s'ensuit que $f: y \\mapsto 1-2 y$, qui n'est manifestement pas bijective.\n- Si $a=0$, alors $b=0$, et l'égalité $\\mathbf{E}_{x, 0}$ indique que $f(2 x)=x$. Cela prouve que $f$ n'est pas injective, puisque chaque entier a déjà un antécédent pair.\n- Si $a=-2$, alors $b=1$, et l'égalité ( $\\boldsymbol{\\oplus}$ ) indique que $-2 f(y)-2=-4 y-f(-2 y)$. Or, l'égalité $\\mathbf{E}_{x, 1}$ indique que $f(2 x)=f(x)+x$. En combinant ces deux égalités, on en déduit que $f(-x)-x=f(-2 x)=2 f(x)+2-4 x$, donc que $f(-x)=2 f(x)+2-3 x$. De manière symétrique, on sait que $f(x)=2 f(-x)+2+3 x$, d'où la relation $f: x \\mapsto x-2$.\n\nRéciproquement, il on vérifie aisément que la fonction $f: n \\longmapsto n-2$ est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 5", "solution_match": " solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Vietnam 2014).\n\nDéterminer toutes les fonctions $f: \\mathbb{Z} \\mapsto \\mathbb{Z}$ telles\n\n$$\nf(2 m+f(m)+f(m) f(n))=n f(m)+m\n$$\n\npour tous les entiers $m$ et $n$.", "solution": "du problème : c'en est donc l'unique", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 5", "solution_match": " solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "(Vietnam 2014).\n\nDéterminer toutes les fonctions $f: \\mathbb{Z} \\mapsto \\mathbb{Z}$ telles\n\n$$\nf(2 m+f(m)+f(m) f(n))=n f(m)+m\n$$\n\npour tous les entiers $m$ et $n$.", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 5", "solution_match": " solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "(Pays-Bas 2014).\n\nSoit $P$ un polynôme à coefficients entiers, de degré $n$, avec $n \\leq 10$. On suppose que $|P(10)-P(0)|<1000$ et que, pour tout $k \\in\\{1, \\ldots, 10\\}$, il existe un entier $m$ tel que $P(m)=k$. Montrer que, pour tout entier $k$ il existe un entier $m$ tel que $P(m)=k$.", "solution": "Pour $i \\in\\{1, \\ldots, 10\\}$, on désigne par $c_{i}$ un entier tel que $P\\left(c_{i}\\right)=i$. Pour $i \\in\\{1, \\ldots, 9\\}$, puisque $P$ est à coefficients entiers, l'entier $c_{i+1}-c_{i}$ divise $P\\left(c_{i+1}\\right)-P\\left(c_{i}\\right)=i+1-i=1$, d'où $c_{i+1}-c_{i}= \\pm 1$. De plus, pour $i, j \\in\\{1, \\ldots, 10\\}$ distincts, on a $P\\left(c_{i}\\right)=i \\neq j=P\\left(c_{j}\\right)$, donc $c_{i} \\neq c_{j}$. Ainsi, $c_{1}, c_{2}, \\ldots, c_{10}$ sont, dans cet ordre, dix entiers consécutifs.\nQuitte à étudier le polynôme $P(10-X)$ plutôt que le polynôme $P(X)$ lui-même, on peut supposer que $c_{1}0$ est tel que $y f(y)>1$, posons $x=\\frac{1}{y f(y)-1}$. La relation de l'énoncé donne\n\n$$\nf\\left(\\frac{y}{f(x+1)}\\right)+f(y)=f(y)\n$$\n\nce qui est impossible car $f$ est à valeurs strictement positives. Ainsi, $y f(y) \\leq 1$.\nPour tous $x, y \\in \\mathbb{R}_{+}^{*}$, on a donc\n\n$$\nf(y)=f\\left(\\frac{y}{f(x+1)}\\right)+f\\left(\\frac{x+1}{x f(y)}\\right) \\leq \\frac{f(x+1)}{y}+\\frac{x f(y)}{x+1},\n$$\n\ndonc $y f(y) \\leq(x+1) f(x+1)$. En particulier, pour tous les réels $a, b>1$, on a bien $a f(a) \\leq b f(b) \\leq a f(a)$ : il existe donc un réel $c \\in] 0,1]$ tel que $x f(x)=c$ pour tout $x>1$.\nSi $y>1$, alors $y>c$ donc $\\frac{y(x+1)}{c}>x+1>1$ et $\\frac{(x+1) y}{x c}>\\frac{y}{c}>1$, et\n\n$$\n\\begin{aligned}\nc & =y \\cdot f(y)=y \\cdot f\\left(\\frac{y}{f(x+1)}\\right)+y \\cdot f\\left(\\frac{x+1}{x f(y)}\\right) \\\\\n& =y \\cdot f\\left(\\frac{(x+1) \\cdot y}{c}\\right)+y \\cdot f\\left(\\frac{(x+1) \\cdot y}{c \\cdot x}\\right) \\\\\n& =\\frac{c^{2} \\cdot y}{(x+1) \\cdot y}+\\frac{c^{2} \\cdot x \\cdot y}{(x+1) \\cdot y}=c^{2},\n\\end{aligned}\n$$\n\ndonc $c=1$. On a donc $f(x)=\\frac{1}{x}$ pour tout $x>1$.\nOn va maintenant prouver, par récurrence sur $k \\in \\mathbb{N}$, que $f(x)=\\frac{1}{x}$ pour tout $x>2^{-k}$. Le résultat est déjà connu pour $k=0$. En outre, si on suppose le résultat connu pour $k \\geq 0$, posons $x=1$. Si $y>2^{-1-k}$, alors $2 y>2^{-k}$ et $\\frac{2}{f(y)} \\geq 2 y>2^{-k}$. L'énoncé indique donc que\n\n$$\nf(y)=f(2 y)+f\\left(\\frac{2}{f(y)}\\right)=\\frac{1}{2 y}+\\frac{f(y)}{2}\n$$\n\nc'est-à-dire $f(y)=\\frac{1}{y}$. Le résultat est donc vrai aussi pour $k+1$.\nCeci montre que $f: x \\longmapsto \\frac{1}{x}$ est bien l'unique", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 8", "solution_match": " solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "(Iran 2014).\n\nDéterminer toutes les fonctions $f: \\mathbb{R}_{+}^{*} \\longmapsto \\mathbb{R}_{+}^{*}$ telles que\n\n$$\nf\\left(\\frac{y}{f(x+1)}\\right)+f\\left(\\frac{x+1}{x f(y)}\\right)=f(y)\n$$\n\npour tous $x, y \\in \\mathbb{R}_{+}^{*}$.", "solution": "du problème.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 8", "solution_match": " solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $a \\in] 0 ; 1\\left[\\right.$ et $n>0$ un entier. On note $f_{n}$ la fonction définie sur $\\mathbb{R}$ par $f_{n}(x)=x+\\frac{x^{2}}{n}$, pour tout réel $x$. Prouver que\n\n$$\n\\frac{a(1-a) n^{2}+2 a^{2} n+a^{3}}{(1-a)^{2} n^{2}+a(2-a) n+a^{2}}<\\underbrace{\\left(f_{n} \\circ f_{n} \\circ \\cdots \\circ f_{n}\\right)}_{n}(a)<\\frac{a n+a^{2}}{(1-a) n+a} .\n$$", "solution": "Pour tout entier $k \\geq 0$, posons $a_{k}=\\underbrace{\\left(f_{n} \\circ f_{n} \\circ \\cdots \\circ f_{n}\\right)}_{k}(a)$. En particulier, $a_{0}=a$.\nOn remarque que, pour tout $k \\geq 0$, on a $a_{k+1}=a_{k}+\\frac{a_{k}^{2}}{n}>a_{k}$, donc la suite $\\left(a_{k}\\right)$ est strictement croissante. En particulier, $a_{k} \\geq a>0$ pour tout $k \\geq 0$.\nDe plus, pour tout $k \\geq 0$, on a $a_{k+1}=\\frac{a_{k}\\left(a_{k}+n\\right)}{n}$ et donc\n\n$$\n\\frac{1}{a_{k+1}}=\\frac{1}{a_{k}}-\\frac{1}{a_{k}+n} .\n$$\n\nAinsi, après sommation de ces égalités pour $k=0, \\ldots, n-1$, on a\n\n$$\n\\frac{1}{a_{n}}=\\frac{1}{a}-\\sum_{k=0}^{n-1} \\frac{1}{a_{k}+n}\n$$\n\nPuisque $\\left(a_{k}\\right)$ est strictement croissante et à valeurs positives, on a\n\n$$\n\\frac{n}{a_{n}+n}<\\sum_{k=0}^{n-1} \\frac{1}{a_{k}+n}<\\frac{n}{a+n}\n$$\n\net ainsi\n\n$$\n\\frac{1}{a}-\\frac{n}{a+n}<\\frac{1}{a_{n}}<\\frac{1}{a}-\\frac{n}{a_{n}+n} .\n$$\n\nL'inégalité de gauche est équivalente à $a_{n}<\\frac{a n+a^{2}}{(1-a) n+a}$, ce qui est l'inégalité de droite de l'encadrement demandé.\n\nReportons maintenant cette dernière inégalité dans l'inégalité de droite de (1). Il vient\n\n$$\n\\frac{1}{a_{n}}<\\frac{1}{a}-\\frac{n}{\\frac{a n+a^{2}}{(1-a) n+a}+n}\n$$\n\nou encore\n\n$$\n\\frac{a(1-a) n^{2}+2 a^{2} n+a^{3}}{(1-a)^{2} n^{2}+a(2-a) n+a^{2}}0$.\nDe plus, notons que $a=\\frac{u_{1}}{u_{0}}$ est rationnel. Si $a$ n'est pas entier, soit $p$ un facteur premier tel que la valuation $p$-adique de $a$ soit strictement négative c'est-à-dire que $v_{p}(a) \\leq-1$. En posant $k=v_{p}\\left(u_{0}\\right)$, on constate alors que $v_{p}\\left(u_{k+1}\\right) \\leq-1$, ce qui contredit le fait que $u_{k+1}$ soit entier, donc que $u_{k+1} \\in P(\\mathbb{N})$. Ainsi, on sait que $a$ est un entier tel que $a>1$.\nDéveloppons alors le polynôme $P$ sous la forme $P(x)=p_{n} x^{n}+p_{n-1} x^{n-1}+\\cdots+p_{1} x+p_{0}$. Pour tout entier $b$, on a\n\n$$\n\\begin{aligned}\nP(a x+b) & =a^{n} p_{n} x^{n}+\\left(n a^{n-1} p_{n} b+a^{n-1} p_{n-1}\\right) x^{n-1}+\\cdots \\text { et } \\\\\na^{n} P(x) & =a^{n} p_{n} x^{n}+a^{n} p_{n-1} x^{n-1}+\\cdots+a^{n} p_{0} .\n\\end{aligned}\n$$\n\nLe polynôme $P(a x+b)-a^{n} P(x)$ est un polynôme de degré au plus $n-1$ et dont le coefficient de degré $n-1$ est $a^{n-1}\\left(n p_{n} b+p_{n-1}(1-a)\\right)$. Notons que $P$ est non constant, donc que $n p_{n}>0$ : ce coefficient a donc une expression affine strictement croissante en $b$. Ainsi, il existe un entier $b$ tel que\n\n$$\nn p_{n}(b+1)+p_{n-1}(1-a)>0>n p_{n}(b-1)+p_{n-1}(1-a) .\n$$\n\nPar conséquent, il existe même un entier $N \\geq 0$ tel que\n\n- $P(a x+b-1)\\sum_{i=0}^{M}|P(i)|$. Pour tout entier $k \\geq 0$, il existe donc un entier $v_{k}>M$ tel que $P\\left(v_{k}\\right)=u_{k}=u_{0} \\cdot a^{k}$.\n\nEn particulier, notons que\n\n$$\nP\\left(a v_{k}+b-1\\right)0$, on pose $x_{k}=(3 u v-1)^{2 k+1}+1$ et $y_{k}=\\frac{u}{v} x_{k}$. Alors $x_{k} \\equiv 0(\\bmod v)$, de sorte que $y_{k} \\in \\mathbb{N}$. En outre, $P\\left(y_{k}\\right)=w \\cdot u^{n} \\cdot(3 u v-1)^{(2 k+1) n}$ décrit bien une suite géométrique de raison $(3 u v-1)^{2 n} \\notin\\{-1,0,1\\}$ et de premier terme $P\\left(3 u^{2}\\right)=w \\cdot u^{n} \\cdot(3 u v-1)^{n}$ non nul.\n- Si $u \\cdot v<0$, on pose $x_{k}=1-(3 u v+1)^{2 k}$ et $y_{k}=\\frac{u}{v} x_{k}$. Alors $x_{k} \\equiv 0(\\bmod v)$, de sorte que $y_{k} \\in \\mathbb{N}$. En outre, $P\\left(y_{k}\\right)=w \\cdot(-u)^{n} \\cdot(3 u v+1)^{(2 k) n}$ décrit bien une suite géométrique de raison $(3 u v+1)^{2 n} \\notin\\{-1,0,1\\}$ et de premier terme $P(0)=w \\cdot(-u)^{n}$ non nul.\n\nLes polynômes recherchés sont donc exactement ceux de la forme $P(x)=w(v x+u)^{n}$, avec $n, u, v$ et $w$ des entiers tels que $n>0, v \\neq 0$ et $w \\neq 0$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-4-solutions.jsonl", "problem_match": "## Exercice 10", "solution_match": "## Solution."}}
diff --git a/French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl b/French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..73028c60327afb743e705c685c36db69a4f4d1dc
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl
@@ -0,0 +1,9 @@
+{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Un polyèdre a 6 sommets et 12 arêtes. Montrer que chaque face est un triangle.", "solution": "de l'exercice 1 Notons $F$ le nombre de faces, $A$ le nombre d'arêtes et $S$ le nombre de sommets. La formule d'Euler donne $F-A+S=2$, donc $F=A-S+2=8$.\n\nNotons $x_{i}(i=1,2, \\ldots, 8)$ le nombre d'arêtes de la face $i$. On a $x_{1}+\\cdots+x_{8}=2 A=24$ car chaque arête appartient à exactement deux faces. On en déduit que\n\n$$\n\\frac{x_{1}+\\cdots+x_{8}}{8}=3\n$$\n\nautrement dit le nombre moyen d'arêtes par face est 3 . Or, chaque face possède au moins 3 arêtes, donc finalement chaque face est un triangle.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Sept élèves d'une classe comparent leurs notes dans 12 épreuves, et remarquent qu'il n'existe pas deux élèves ayant des notes identiques dans chacune des 12 épreuves.\n\nMontrer que l'on peut choisir 6 épreuves telles que deux élèves quelconques aient des notes différentes à au moins l'une de ces épreuves.", "solution": "de l'exercice 2\n\nSoit $m$ le plus petit entier tel que l'on peut choisit m épreuves $E_{1}, \\ldots, E_{m}$ de sorte que deux élèves quelconques aient des notes différentes à au moins l'une de ces $m$ épreuves. On doit montrer que $m \\leqslant 6$.\n\nComme $m$ est minimal, pour tout $i=1, \\ldots, m$ il existe une paire $A_{i} d^{\\prime}$ 'élèves ayant la même note à toutes les épreuves sauf $E_{i}$.\n\nOn forme un graphe dont les sommets sont les élèves, et dont les arêtes sont $A_{1}, \\ldots, A_{m}$. Supposons que le graphe possède un cycle $\\left(A_{i_{1}}, \\ldots, A_{i_{r}}\\right)$. Notons a et b les extrémités de $A_{i_{1}}$. Par hypothèse, a et $b$ obtiennent des notes différentes à l'épreuve $i_{1}$. Cependant, le chemin $\\left(A_{i_{2}}, \\ldots, A_{i_{r}}\\right)$ montre que a et b obtiennent des notes identiques à l'épreuve $i_{1}$, ce qui est contradictoire.\n\nPar conséquent, le graphe est un arbre. Comme un arbre a strictement plus de sommets de d'arêtes, on en déduit que $\\mathrm{m}<7$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Jules et Jim, deux colocataires, reçoivent 10 autres paires de colocataires chez eux. Jules fait un petit sondage au cours de la soirée et interroge les 21 autres personnes. Parmi elles, aucune n'a serré la main de son colocataire, et il n'y en a pas deux qui ont serré le même nombre de mains. Combien de mains a serré Jim?", "solution": "de l'exercice 3 Au cours de la soirée, parmi les 21 , chaque personne serre entre 0 et 20 mains. Comme elles serrent toutes un nombre différent de mains, pour tout n compris entre 0 et 20 il existe une et une seule personne $A_{n}$ parmi les 21 qui a serré exactement n mains.\n\nComme $A_{20}$ a serré 20 mains, $A_{20}$ a serré la main à tout le monde sauf lui même et son colocataire. Or, $A_{0}$ n'a serré la main à personne, donc $A_{0}$ est le colocataire de $A_{20}$.\n\nComme $\\AA_{19}$ a serré 19 mains, $\\AA_{19}$ a serré la main à tout le monde sauf lui-même, son colocataire et $A_{0}$. Or, $A_{1}$ a serré la main à $A_{20}$ et à personne d'autre, donc n'a pas serré la main à $A_{19}$. On en déduit que $A_{1}$ est le colocataire de $A_{19}$.\n\nEn continuant le raisonnement, on montre que $A_{n}$ est le colocataire de $A_{20-n}$ pour tout $\\boldsymbol{n}=0,1, \\ldots, 9$, donc $A_{10}$ est le colocataire de Jules. Finalement, Jules a serré 10 mains.\n\n## Exercices Communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "2015 droites deux à deux distinctes sont tracées dans le plan. On suppose qu'elles délimitent moins de 8000 régions (les régions peuvent être non bornées). Montrer que le nombre de régions est égal à 2016, 4030, 6042 ou 6043, et donner un exemple de configuration dans chaque cas.", "solution": "de l'exercice 4\n\nNotons $\\mathrm{n}=2015$ le nombre de droites, f le nombre de régions, p le nombre maximal de droites parallèles et q le nombre maximal de droites concourantes.\n\nMontrons d'abord que $\\mathrm{f} \\geqslant(\\mathrm{p}+1)(\\mathrm{n}-\\mathrm{p}+1)$. En effet, plaçons d'abord les p droites parallèles. Elles forment $p+1$ régions. Il reste ensuite $n-p$ droites à placer, et chacune de ces droites crée au moins $p+1$ régions supplémentaires.\n\nDe même, montrons que $\\mathrm{g} \\geqslant \\mathrm{q}(\\mathrm{n}-\\mathrm{q}+2)$. En effet, on place d'abord q droites concourantes. Chaque nouvelle droite crée au moins $q-1$ points d'intersection, donc au moins $q$ nouvelles régions. On en déduit que $f \\geqslant(2 q)+(n-q) q=q(n-q+2)$.\n\nSupposons que $3 \\leqslant p \\leqslant n-3$. Comme l'expression $g(p)=(p+1)(n-p+1)$ est égale à $(n+2)^{2} / 4-(p-n / 2)^{2}$, la fonction $g$ croît entre 0 et $n / 2$ et décroît entre $n / 2$ et $n$, donc $\\boldsymbol{g}(\\mathrm{p}) \\geqslant \\mathrm{g}(3)=4(n-2)>8000$. Impossible. On en déduit que $p \\in\\{1,2, n-2, n-1, n\\}$ et de même $\\mathbf{q} \\in\\{1,2,3, \\mathfrak{n}-1, \\mathfrak{n}\\}$.\n\nSi $\\mathrm{p}=\\mathrm{n}$ alors toutes les droites sont parallèles, et on a $\\mathrm{f}=\\mathrm{n}+1=2016$.\nSi $p=n-1$ alors toutes les droites sauf une sont parallèles, et on a $f=2 n=4030$.\nSi $p=n-2$ et les deux droites restantes sont parallèles, ou bien sécantes sur l'une des $n-2$ premières droites, alors $\\mathrm{f}=3(\\mathrm{n}-1)=6042$.\n\nSi $p=n-2$ et les deux droites restantes sont sécantes ailleurs que sur les $n-2$ premières droites, alors $\\mathrm{f}=3 \\mathrm{n}-2=6043$.\n\nSi $q=n$ alors $f=2 n$.\nSi $\\mathrm{q}=\\mathrm{n}-1$ alors $\\mathrm{f}=3 \\mathrm{n}-3$ ou $3 \\mathrm{n}-2$ selon que la dernière droite est parallèle ou non à l'une des premières droites.\n\nIl reste à traiter le cas où $p \\leqslant 2$ et $\\mathrm{q} \\leqslant 3$. Notons $\\mathrm{D}_{1}, \\ldots, \\mathrm{D}_{2015}$ les droites. A chaque fois que l'on trace une droite $D_{i}(i>1000)$, celle-ci coupe au moins 999 des droites $D_{1}, \\ldots, D_{1000}$, et chacun de ces points d'intersection est commun à au plus deux de ces droites, donc on obtient au moins 500 points d'intersection entre $D_{i}$ et l'une des 1000 premières droites. Par conséquent, $\\mathrm{D}_{\\mathrm{i}}$ crée au moins 501 régions supplémentaires. On en déduit que $\\mathrm{f} \\geqslant 1015 \\times 501>8000$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Dans un club d'échecs de 20 personnes, 14 parties sont jouées et chaque joueur a joué au moins une partie. Montrer qu'il y a 6 parties auxquelles 12 joueurs différents ont participé.", "solution": "de l'exercice 5 Soit r le plus grand entier tel qu'il existe un ensemble $M$ de r parties faisant intervenir 2 r joueurs différents.\n\nNotons J l'ensemble des 2 r personnes qui ont joué les parties de $M$. Par maximalité de $M$, si $a$ et $b$ sont deux joueurs n'appartenant pas à $J$, alors $a$ et $b$ n'ont pas joué entre eux. Par conséquent, ils ont joué une partie contre l'un des 2 r joueurs de $M$. On en déduit que le nombre total de parties est au moins égal à $r+(20-2 r)=20-r$. Or, par hypothèse le nombre de parties est 14 , donc $14 \\geqslant 20-r$, ce qui entraîne $r \\geqslant 6$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "On considère un échiquier $2015 \\times 2015$, auquel on a retiré le carré $2 \\times 2$ en bas à droite. Montrer qu'on peut le paver par des pièces composées de 3 cases en forme de L (les pièces peuvent être pivotées).", "solution": "de l'exercice 6 Comme l'échiquier peut être décomposé en trois rectangles $2010 \\times 2015$, $5 \\times 2004$ et $5 \\times 11$, et comme 2010 et 2004 sont divisibles par 6 , il suffit de montrer que\n\n1) Pour tout $n \\geqslant 2$ et tout entier $m$, un échiquier $6 m \\times n$ peut être pavé par des pièces en forme de L;\n2) L'échiquier $5 \\times 11$ privé du carré $2 \\times 2$ en bas à droite peut être pavé par des pièces en forme de L.\n\nPour le point 1), comme un tel échiquier est réunion d'échiquiers $6 \\times \\mathrm{n}$, on se ramène à traiter le cas $\\mathrm{m}=1$.\n\nIl est clair que l'on peut paver un échiquier $3 \\times 2$, donc aussi des échiquiers $6 \\times 2$ et $6 \\times 3$. On peut donc paver tout échiquier de taille $6 \\times 2 k$ ou $6 \\times(2 k+3)$. Or, tout entier $n \\geqslant 2$ s'écrit sous la forme $2 k$ s'il est pair, et $2 k+3$ s'il est impair, ce qui conclut.\n\nLe point 2) se démontre en construisant un exemple de pavage:\n\n\n## Exercices du groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "n joueurs participent à un tournoi d'échecs. Chaque joueur fait exactement une partie avec chacun des autres joueurs. Une victoire rapporte 1 point, un match nul un demipoint et une défaite aucun point. Une partie est dite anormale si le gagnant de cette partie obtient un score au tournoi strictement plus faible que le perdant.\na) Montrer que la proportion de parties anormales est inférieure ou égale à $75 \\%$.\nb) Est-il possible qu'elle soit supérieure ou égale à $70 \\%$ ?", "solution": "de l'exercice 7\n a) Soit $m=[n / 2]$. On classe les joueurs suivant leur score (parmi les joueurs ayant le même score, on les classe arbitrairement). On dira qu'un joueur classé parmi les $m$ meilleurs est fort; sinon, on dira qu'il est faible.\n\nSoit x le nombre de parties normales entre les joueurs forts et les joueurs faibles. Les joueurs forts ont marqué au total $m(m-1) / 2$ points entre eux, et au plus $x$ lors de parties contre les joueurs faibles.\n\nNotons $S_{1}$ le score total des joueurs forts et $S_{2}$ le score total des joueurs faibles. On a donc $S_{1} \\leqslant \\mathrm{~m}(\\mathrm{~m}-1) / 2+x$ et $\\mathrm{S}_{1}+\\mathrm{S}_{2}=\\mathrm{n}(\\mathrm{n}-1) / 2$.\n\nLe score moyen des joueurs forts, $\\frac{\\mathrm{S}_{1}}{\\mathrm{~m}}$, est supérieur au score moyen de tous les joueurs: $\\frac{S_{1}}{m}>\\frac{n(n-1) / 2}{n}$, i.e. $S_{1}>m(n-1) / 2$. Par conséquent,\n\n$$\nx \\geqslant S_{1}-m(m-1) / 2>\\frac{m(n-m)}{2} \\geqslant n(n-1) / 8\n$$\n\nComme il y a au total $n(n-1) / 2$ parties, la proportion de parties normales est supérieure à $1 / 4$.\nb) Considérons un tournoi constitué de $2 k+1$ groupes de $k$ joueurs (on a donc $n=k(2 k+1)$ ). On suppose que les joueurs du groupe $i$ font match nul entre eux, perdent contre les joueurs des groupes $i+1, \\ldots, i+k$ et gagnent tous les autres matchs (ici, $i$ est pris modulo $k$ ). Alors tous les joueurs ont le même score.\n\nOn va modifier les parties des joueurs du $k+1$-ième groupe afin que les scores soient différents. Pour tout $i$, on remplace $i k$ victoires de joueurs du $(k+1)$-ième groupe contre des joueurs du $(k+1-i)$-ème groupe par des matchs nuls, de sorte que chaque joueur $\\mathrm{du}(k+1)$ ième groupe voie son score décroître de $i / 2$ tandis que chaque joueur du ( $k+1-\\mathfrak{i}$ )-ème score voie son score augmenter de $i / 2$.\n\nDe même, on remplace $i k$ défaites du $(k+1)$-ième groupe contre les $(k+1+i)$-ème groupe par des matchs nuls.\n\nAlors les premières places dans le tournoi sont prises par les joueurs du premier groupe, puis du deuxième, etc.\n\nLes joueurs des groupes $i \\leqslant k$ ont perdu $k^{3}-i k$ parties, les joueurs des groupes $i>k+1$ perdu $(2 k+1-i) k^{2}$ parties anormales, et les joueurs du $(k+1)$-ième groupe ont perdu $k^{3}-$ $k\\left(\\frac{1}{2} k(k+1)\\right)$ parties anormales. Tous calculs faits, on obtient en tout\n\n$$\n\\frac{3}{2} k^{4}-\\frac{1}{2} k^{3}-k^{2}\n$$\n\nparties anormales.\nIl y a au total $k(2 k+1)(k(2 k+1)-1) / 2$ parties. On vérifie que pour $k=100$, la proportion de parties anormales dépasse $70 \\%$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soient a et b deux entiers tels que $\\mathrm{a}+\\mathrm{b}$ n'est pas divisible par 3. Montrer que l'on ne peut pas colorier les entiers relatifs en trois couleurs de sorte que que pour tout entier $n$, les trois nombres $n, n+a$ et $n+b$ soient de couleurs différentes.", "solution": "de l'exercice 8\n Supposons par l'absurde qu'il existe un tel coloriage. On notera $x \\sim y$ si $x$ et $y$ sont de la même couleur.\n\nPour tout $n$, les entiers $(n+a)+b$ et $x+a$ ne sont pas de la même couleur, et de même $n+a+b$ n'est pas de la même couleur que $n+b$, donc $n+a+b \\sim n$. Il vient immédiatement $0 \\sim p(a+b)$ pour tout entier $p$, et en particulier $0 \\sim a(a+b)$.\n\nD'autre part, $n+a, n+2 a$ et $n+a+b$ sont de couleurs différentes, donc $n, n+a$ et $n+2 a$ sont de couleurs différentes. En appliquant ce qui précède à $n+a$, on en déduit que $n+3 a$ est de même couleur que $n$, donc pour tout entier $j$, le nombre ja est de la même couleur que ra où $r$ est le reste de la division Euclidienne de j par 3.\n\nEn appliquant ceci à $j=a+b$, on en déduit que $0 \\sim r a$ où $r$ est le reste de la division Euclidienne de $\\mathrm{a}+\\mathrm{b}$ par 3, ce qui est impossible puisque 0 , a et 2 a sont de couleurs différentes et $\\mathrm{r} \\in\\{1,2\\}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Dans tout l'exercice, on s'intéresse à des tableaux $5 \\times 5$, dont les lignes (resp. les colonnes) sont notées $\\mathrm{L}_{0}, \\mathrm{~L}_{1}, \\mathrm{~L}_{2}, \\mathrm{~L}_{3}, \\mathrm{~L}_{4}$ du bas vers le haut (resp. $\\mathrm{C}_{0}, \\mathrm{C}_{1}, \\mathrm{C}_{2}, \\mathrm{C}_{3}, \\mathrm{C}_{4}$, de gauche à droite).\n\nDans chacune des 25 cases d'un tel tableau, on écrit un nombre. Le nombre qui est dans la case située sur la ligne $L_{i}$ et la colonne $C_{j}$ est noté $f(i, j)$.\n\nUn tableau est dit cohérent lorsque, pour tous $i$ et $j$ :\nLe nombre $f(i, j)$ est le nombre de $i$ écrits dans les cases de la ligne $L_{j}$.\nDéterminer tous les tableaux cohérents de taille $5 \\times 5$.", "solution": "de l'exercice 9 On se donne un éventuel tableau cohérent. Commençons par dégager quelques unes de ses propriétés.\na) Pour tous $\\boldsymbol{i}, \\mathfrak{j}$, on a $\\boldsymbol{f}(\\mathfrak{i}, \\mathfrak{j}) \\in\\{0,1,2,3,4,5\\}$.\n\nEn effet, dans un tableau cohérent, chaque $f(i, j)$ représente le nombre de fois où $i$ apparaît sur $L_{j}$, donc $f(i, j)$ est un entier positif ou nul, et il ne peut dépasser 5 car c'est le nombre total de cases de $L_{j}$.\nb) On a $f(0,0) \\geqslant 1$.\n\nPar l'absurde : Si $f(0,0)=0$ alors, il n'y a aucun 0 sur $L_{0}$. Mais, $f(0,0)$ est lui-même sur $L_{0}$. Contradiction.\n\nAinsi, $f(0,0) \\geqslant 1$.\nPour tout $i$ (resp.j), on note $x_{i}$ (resp. $y_{j}$ ) la somme des nombres inscrits dans la colonne $C_{i}$ (resp. la ligne $\\mathrm{L}_{\\mathrm{j}}$ ).\nc) On a $x_{i} \\leqslant 5$ pour tout $i$.\n\nSoit $i$ fixé. Pour tout $j$, on note $n_{j}$ le nombre de $j$ dans $L_{i}$. Alors :\n$x_{i}=\\mathbf{f}(0, \\boldsymbol{i})+\\mathbf{f}(1, \\boldsymbol{i})+\\mathbf{f}(2, \\mathfrak{i})+\\mathbf{f}(3, \\mathfrak{i})+\\mathbf{f}(4, \\boldsymbol{i})$ $=\\mathrm{n}_{0}+\\mathrm{n}_{1}+\\mathrm{n}_{2}+\\mathrm{n}_{3}+\\mathrm{n}_{4}$ $\\leqslant$ nombre de cases de $\\mathrm{L}_{i}$ (il pourrait y avoir un 5 sur $L_{i}$ ) $=5$.\n\nAinsi, on a $x_{i} \\leqslant 5$, pour tout $i$.\nd) Pour tous $i$ et $\\mathfrak{j}$, on a $\\boldsymbol{f}(\\mathfrak{i}, \\mathfrak{j}) \\leqslant 4$.\n\nPar l'absurde : supposons qu'il existe $i$ et $j$ tels que $f(i, j) \\geqslant 5$.\nD'après a), c'est donc que $f(i, j)=5$. Cela signifie que la ligne $L_{j}$ ne contient que des $i$. En particulier, on a $f(j, j)=i$.\n\nSi $i>0$, la ligne $L_{j}$ doit donc contenir au moins un $\\boldsymbol{j}$. Comme elle ne contient que des $\\mathfrak{i}, c^{\\prime}$ est que $\\boldsymbol{i}=\\mathfrak{j}$ et que $5=\\boldsymbol{f}(\\mathfrak{i}, \\mathfrak{j})=\\mathbf{f}(\\mathfrak{j}, \\mathfrak{j})=\\mathfrak{i}$, en contradiction avec $\\mathfrak{i} \\leqslant 4$.\n\nAinsi, on a $i=0$ et il n'y a que des 0 sur la ligne $L_{j}$. Puisque $x_{j} \\leqslant 5$, il n'y a que des 0 sur $C_{j}$ sauf $f(0, j)=5$. En particulier, chaque ligne $L_{k}$ contient au moins un 0 pour $k>0$. Cela assure que $f(0, k) \\neq 0$ pour tout $k>0$. Mais, on a vu que $f(0,0)>0$ donc il doit $y$ avoir au moins un 0 sur $L_{0}$, alors qu'on vient de prouver qu'aucun des nombres sur $L_{0}$ n'est égal à 0 . Contradiction. $^{\\prime}$.\n\nFinalement, on a $f(i, j) \\leqslant 4$, pour tous $i$ et $j$.\ne) On a $x_{i}=5$ pour tout $i$.\n\nMaintenant que l'on sait qu'il n'y a pas de 5 dans le tableau, on reprend le calcul et raisonnement du c), mais il n'y a plus d'inégalité...\n\nAinsi, on a $x_{i}=5$ pour tout $i$.\nf) On a $y_{1}+2 y_{2}+3 y_{3}+4 y_{4}+5 y_{5}=25$.\n\nIl suffit de remarquer que, pour tout $i$, le nombre $y_{i}$ est le nombre de $i$ qui apparaîssent dans le tableau. Donc $0 y_{0}+y_{1}+2 y_{2}+3 y_{3}+4 y_{4}+5 y_{5}$ est la somme de tous les nombres du tableau, et on a $y_{1}+2 y_{2}+3 y_{3}+4 y_{4}+5 y_{5}=x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=25$.\ng) On a $f(0,1)=0$ et $f(0, i) \\geqslant 1$ pour tout $i \\geqslant 2$.\n\nPar l'absurde : Supposons qu'il existe $i \\geqslant 3$ tel que $f(0, i)=0$.\nAlors, il n'y a aucun 0 sur $L_{i}$, ce qui entraine que chaque ligne contient au moins un $i$. Alors, on a $y_{j} \\geqslant i \\geqslant 3$.\n\nD'après f), il vient alors $25 \\geqslant(0+1+2+3+4) \\times 3=30$. Contradiction.\nAinsi, on a $f(0,3)>0$ et $f(0,4)>0$.\nPar l'absurde: Supposons que $f(0,2)=0$.\nComme ci-dessus, cela signifie que chaque ligne contient au moins un 2. Mais alors, chacun des nombres $0,1,3,4$ ( 2 aussi, mais il va avoir un traitement particulier) apparaît au moins deux fois dans le tableau, d'où $y_{i} \\geqslant 2$ pour $i=0,1,3,4$.\n\nD'autre part, il y a 5 cases sur $\\mathrm{L}_{2}$, aucune ne contenant 0 et au moins une contenant un 2, d'où $y_{2} \\geqslant 6$. En utilisant f ), il vient\n$25 \\geqslant(0+1+3+4) \\times 2+2 \\times 6=28$. Contradiction.\nPar suite, on a $f(0,2)>0$.\nOr, on a vu que $f(0,0)>0$ et donc qu'il y a au moins un 0 sur $L_{0}$. Comme $f(0, i)>0$ pour tout $i \\neq 1$, $c^{\\prime}$ est que $f(0,1)=0$.\n\nFinalement, on a $f(0,1)=0$ et $f(0, i) \\geqslant 1$ pour tout $i \\geqslant 2$.\nIl n'y a donc qu'un seul nombre non nul sur $L_{0}$, d'où $f(0,0)=1$.\nh) On a $y_{1} \\geqslant 8$.\n\nPuisque $f(0,1)=0$, il n'y a aucun 0 sur $L_{1}$. En particulier, $f(1,1) \\geqslant 1$ donc il y a au moins un 1 sur $L_{1}$.\n\n- Il ne peut y avoir que des 1 sur $L_{1}$, car alors $f(1,1)=1$ et $f(1,1)=5$, ce qui est impossible.\n- S'il y a quatre 1 , on a $\\mathrm{f}(1,1)=4$ et tous les autres sont des 1 , d'où $y_{1}=8$.\n- S'il y a trois 1 , alors $\\mathrm{f}(1,1)=3$ et un autre des nombres est supérieur ou égal à 2 , donc $y_{1} \\geqslant 3+1+1+1+2=8$.\n- S'il y a deux 1 , le même raisonnement conduit à $y_{1} \\geqslant 2+1+1+2+2=8$.\n- S'il n'y a qu'un seul 1 , alors c'est $\\mathrm{f}(1,1)=1$ et les autres sont supérieurs ou égaux à 2 , donc $y_{1} \\geqslant 1+4 \\times 2=9$.\n\nAinsi, on a $y_{1} \\geqslant 8$.\ni) On a $f(4,2)=f(4,3)=f(4,4)=0$, et donc que $f(0,4) \\geqslant 3$.\n\nIl n'y a aucun 0 dans $L_{1}$ donc chaque ligne contient au moins un 1.\nPar l'absurde: supposons qu'il y ait un 4 sur $\\mathrm{L}_{2}, \\mathrm{~L}_{3}$ ou $\\mathrm{L}_{4}$.\n\n- S'il y a un 4 sur $L_{4}$, comme il y a aussi au moins un 1 , on a $y_{4} \\geqslant 5$. Compte-tenu de $y_{1} \\geqslant 8$, la formule du f) conduit à $25 \\geqslant 28$, ce qui est impossible. Il n'y a donc pas de 4 sur $\\mathrm{L}_{4}$.\n- S'il y a un 4 sur $L_{3}$, comme il y a aussi au moins un 1 , on a $y_{3} \\geqslant 5$. Compte-tenu de $y_{1} \\geqslant 8$ et $y_{4} \\geqslant 1$, la formule du f) conduit à $25 \\geqslant 27$, ce qui est encore impossible. Il n'y a donc pas de 4 sur $\\mathrm{L}_{3}$.\n- S'il y a un 4 sur $L_{2}$ : dans chaque colonne, sauf $C_{1}$, les lignes $L_{0}$ et $L_{1}$ ont toutes les deux un nombre non nul. Or, la somme des termes d'une colonne vaut 5 d'après e), donc le $4 \\mathrm{de} \\mathrm{L}_{2}$ ne peut être que dans $C_{1}$, c'est-à-dire $f(2,1)=4$. Il y a donc quatre 2 dans $L_{1}$, d'où $y_{1} \\geqslant 9$. Comme on a $y_{2} \\geqslant 5, y_{3} \\geqslant 1$ et $y_{4} \\geqslant 1$, la formule du f) conduit à $25 \\geqslant 26$, ce qui est encore impossible. Il n'y a donc pas de 4 sur $\\mathrm{L}_{3}$.\n\nFinalement, il n'y a aucun 4 dans les cases des lignes $L_{2}, L_{3}$ et $L_{4}$.\nCela prouve que $\\mathbf{f}(4,2)=\\mathbf{f}(4,3)=\\mathbf{f}(4,4)=0$, et donc que $\\mathbf{f}(0,4) \\geqslant 3$.\nj) On a $\\boldsymbol{f}(3,2)=\\boldsymbol{f}(3,3)=\\mathfrak{f}(3,4)=0$, et donc que $f(0,3) \\geqslant 3$.\n\nPar l'absurde : supposons qu'il y ait un 3 dans les lignes $\\mathrm{L}_{2}, \\mathrm{~L}_{3}$ ou $\\mathrm{L}_{4}$.\n\n- S'il y a un 3 sur $L_{4}$, compte-tenu des 1 sur chaque ligne et de $h$ ), on a $y_{4} \\geqslant 4$ et $y_{1} \\geqslant 8$. Comme au i), la formule du f) conduit alors à une contradiction. Il n'y a donc pas de 3 sur $\\mathrm{L}_{4}$.\n- S'il y a un 3 sur $L_{3}$, compte-tenu des 1 sur chaque ligne et de $h$ ), on a cette fois $y_{4} \\geqslant 1, y_{3} \\geqslant$ $4, y_{2} \\geqslant 1$ et $y_{1} \\geqslant 8$. Comme au i), la formule du f) conduit alors à une contradiction. Il n'y a donc pas de 3 sur $L_{3}$.\n- S'il y a un 3 sur $\\mathrm{L}_{2}$ : notons que l'on a $\\mathrm{f}(0,4) \\geqslant 3$ et $\\mathrm{f}(1,4) \\geqslant 1$. Puisque $x_{4}=5$, il est impossible que $f(2,4)=3$.\n\nDe même pour $C_{3}$, comme $\\mathrm{f}(0,3) \\geqslant 2$ et $\\mathrm{f}(1,3) \\geqslant 1$, on ne peut avoir $\\mathrm{f}(2,3)=3$.\nSi $\\mathrm{f}(2,2)=3$ alors $y_{2} \\geqslant 7$. Avec $y_{4} \\geqslant 1, y_{3} \\geqslant 1$ et $y_{1} \\geqslant 8$, on obtient le même type de contradiction que ci-dessus par utilisation de c).\n\nSi $\\mathrm{f}(2,0)=3$ alors, puisque $\\mathrm{f}(0,0)=1$ et $\\mathrm{f}(0,1)=0$, la ligne $\\mathrm{L}_{0}$ est déterminée et, en particulier, on a $f(0,4)=2$, en contradiction avec les trois 0 que l'on a déjà identifiés sur $L_{4}$.\n\nReste à étudier le cas $\\mathrm{f}(2,1)=3$.\nOn sait que $y_{4} \\geqslant 1, y_{3} \\geqslant 1, y_{2} \\geqslant 4$ et $y_{1} \\geqslant 8$. En l'état, le f) n'apporte pas de contradiction, mais permet de voir que si $y_{4} \\geqslant 2$ ou $y_{3} \\geqslant 2$, on en obtiendrait une. Donc, on doit avoir $y_{4}=y_{3}=1$, ce qui permet de remplir $L_{3}$ et donc $C_{3}$, et de savoir que $f(0,3)=f(0,4)=4$ ainsi que $\\mathrm{f}(1,4)=\\mathrm{f}(1,3)=1$. Comme $x_{4}=\\mathrm{x}_{3}=5$, les colonnes $C_{3}$ et $C_{4}$ sont complètes. Les trois 2 sur $L_{1}$ permettent de compléter $L_{1}$ et donc $C_{1}$. Ces mêmes 2 sur $L_{1}$ permettent aussi de remplir\nles trous sur $L_{0}$ et $L_{2}$ et de finir de remplir le tableau. On obtient\n\n| 1 | 0 | 0 | 0 | 0 |\n| :--- | :--- | :--- | :--- | :--- |\n| 0 | 0 | 1 | 0 | 0 |\n| 1 | 3 | 1 | 0 | 0 |\n| 2 | 2 | 2 | 1 | 1 |\n| 1 | 0 | 1 | 4 | 4 |\n\nEn particulier, on a $f(2,0)=1$ et pas de 2 sur $\\mathrm{L}_{0}$. Contradiction.\nFinalement, il n'y a aucun 3 dans les cases des lignes $\\mathrm{L}_{2}, \\mathrm{~L}_{3}$ et $\\mathrm{L}_{4}$.\nCela prouve que $\\mathbf{f}(3,2)=\\mathbf{f}(3,3)=\\mathbf{f}(3,4)=0$, et donc que $\\mathbf{f}(0,3) \\geqslant 3$.\nk) On trouve tous les tableaux cohérents.\n\nD'après ce qui précède, on part d'un tableau de la forme\n\n| . | . | 0 | 0 | 0 |\n| :--- | :--- | :--- | :--- | :--- |\n| . | . | 0 | 0 | 0 |\n| . | . | . | . | . |\n| . | . | . | . | . |\n| 1 | 0 | . | a | b |\n\navec $\\boldsymbol{a}, \\boldsymbol{b} \\geqslant 3$, et aucun terme nul sur $\\mathrm{L}_{1}$. Comme $\\boldsymbol{a}, \\boldsymbol{b} \\in\\{3,4\\}$ et que la somme par colonne doit toujours donner 5 , on tombe assez rapidement sur les deux seuls tableaux cohérents, à savoir :\n\n| 1 | 0 | 0 | 0 | 0 |\n| :--- | :--- | :--- | :--- | :--- |\n| 2 | 1 | 0 | 0 | 0 |\n| 0 | 1 | 0 | 1 | 0 |\n| 1 | 3 | 2 | 1 | 1 |\n| 1 | 0 | 3 | 3 | 4 |\n\n\n| 2 | 1 | 0 | 0 | 0 |\n| :--- | :--- | :--- | :--- | :--- |\n| 1 | 0 | 0 | 0 | 0 |\n| 0 | 0 | 0 | 0 | 1 |\n| 1 | 4 | 1 | 1 | 1 |\n| 1 | 0 | 4 | 4 | 3 |\n\nRemarque. Pour information, en affinant un peu ce qui précède, on peut prouver qu'il n'existe de tableau $n \\times n$ cohérent que pour $n=5$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-5-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\nSolution "}}
diff --git a/French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl b/French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..47e6e252e5f218a9656db1111ab3e7f0fe31952c
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl
@@ -0,0 +1,13 @@
+{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Calculer\n\n$$\n\\sqrt{1+\\frac{1}{1^{2}}+\\frac{1}{2^{2}}}+\\sqrt{1+\\frac{1}{2^{2}}+\\frac{1}{3^{2}}}+\\cdots+\\sqrt{1+\\frac{1}{2014^{2}}+\\frac{1}{2015^{2}}}\n$$", "solution": "de l'exercice 1 On réduit au même dénominateur\n\n$$\n\\begin{aligned}\n1+\\frac{1}{n^{2}}+\\frac{1}{(n+1)^{2}} & =\\frac{n^{2}(n+1)^{2}+(n+1)^{2}+n^{2}}{n^{2}(n+1)^{2}} \\\\\n& =\\frac{n^{4}+n^{2}(2 n+1)+n^{2}+(n+1)^{2}}{n^{2}(n+1)^{2}} \\\\\n& =\\frac{n^{4}+2 n^{2}(n+1)+(n+1)^{2}}{n^{2}(n+1)^{2}} \\\\\n& =\\frac{\\left(n^{2}+(n+1)\\right)^{2}}{n^{2}(n+1)^{2}}\n\\end{aligned}\n$$\n\nOn en déduit que la somme recherchée vaut\n\n$$\n\\begin{aligned}\n\\sum_{n=1}^{2014} \\frac{n^{2}+n+1}{n(n+1)} & =\\sum_{n=1}^{2014} 1+\\frac{1}{n(n+1)} \\\\\n& =2014+\\sum_{n=1}^{2014} \\frac{1}{n(n+1)} \\\\\n& =2014+\\sum_{n=1}^{2014} \\frac{1}{n}-\\frac{1}{n+1} \\\\\n& =2014+\\left(1-\\frac{1}{2}+\\frac{1}{2}-\\frac{1}{3}+\\cdots+\\frac{1}{2014}-\\frac{1}{2015}\\right)\n\\end{aligned}\n$$\n\nOn reconnaît une somme télescopique. Les termes se simplifient deux à deux, sauf 1 et $\\frac{1}{2015}$, donc la somme vaut\n\n$$\n2014+1-\\frac{1}{2015}=2015-\\frac{1}{2015}\n$$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soient $p$ et $q$ deux nombres premiers supérieurs ou égaux à 7 . Soit $x=\\frac{p^{2012}+q^{2016}}{120}$. Calculer $x-[x]$, où $[x]$ désigne la partie entière de $x$, c'est-à-dire le plus grand entier inférieur ou égal à $x$.", "solution": "de l'exercice 2 Si a est un entier non divisible par 2,3 et 5 , on vérifie facilement que a ${ }^{4}$ est congru à 1 modulo 3,5 et 8 . Autrement dit, a ${ }^{4}-1$ est divisible par 3,5 et 8 , donc par $3 \\times 5 \\times 8=$ 120 . On en déduit que $p^{4}$ et $q^{4}$ sont congrus à 1 modulo 120 , donc $p^{2012}+q^{2016} \\equiv 1+1 \\equiv 2$ $(\\bmod 120)$.\nOn en déduit que $x-[x]=\\frac{2}{120}=\\frac{1}{60}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $A B C$ un triangle. On dessine des triangles équilatéraux $A B E$ et $A C F$ à l'extérieur de $A B C$. Soit $G$ le centre de gravité de $A B E$ et K le milieu de $[E F]$. Déterminer les angles du triangle KCG.", "solution": "de l'exercice 3\n\n\n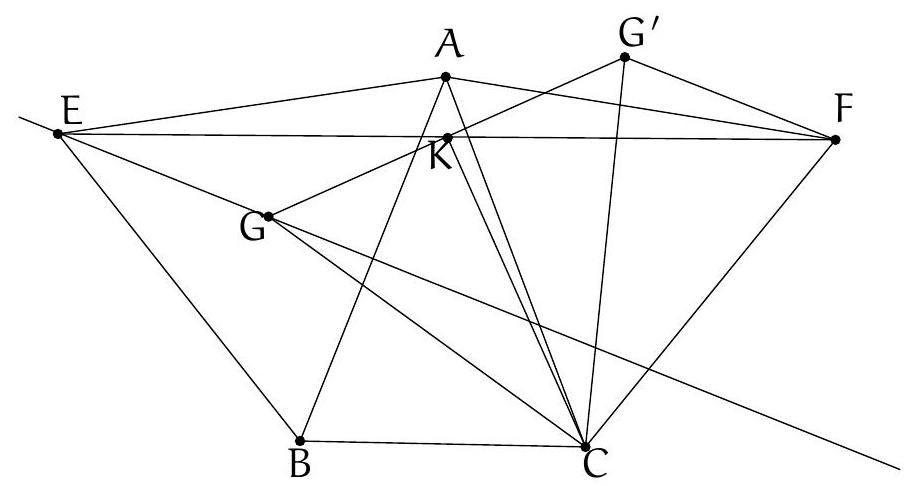\n\nMontrons que GKC est rectangle en $K$ avec $\\widehat{C G K}=60^{\\circ}$. Pour cela, considérons le symétrique $\\mathrm{G}^{\\prime}$ de $G$ par rapport à $K$ : il suffit de montrer que $\\mathrm{GCG}^{\\prime}$ est équilatéral.\nComme EGFG' est un parallélogramme, on a $G^{\\prime} F=E G$, et comme $G$ est le centre du cercle circonscrit à $A B E$, on a $G A=G E$, donc $G A=G^{\\prime} F$.\n$\\mathrm{D}^{\\prime}$ autre part, $\\mathrm{AC}=\\mathrm{FC}$ car $A F C$ est équilatéral.\nEnfin, $\\widehat{\\mathrm{GAC}}=30^{\\circ}+\\widehat{\\mathrm{BAC}}$ et $(\\overrightarrow{\\mathrm{FG}}, \\overrightarrow{\\mathrm{FC}})=(\\overrightarrow{\\mathrm{GE}}, \\overrightarrow{\\mathrm{FC}})=(\\overrightarrow{\\mathrm{GE}}, \\overrightarrow{A G})+(\\overrightarrow{A G}, \\overrightarrow{A C})+(\\overrightarrow{A C}, \\overrightarrow{F C})=$ $60^{\\circ}+(\\overrightarrow{A G}, \\overrightarrow{A C})-60^{\\circ}=(\\overrightarrow{A G}, \\overrightarrow{A C})$, donc $G A C$ et $G^{\\prime} F C$ sont isométriques.\nOr, F est obtenu à partir de $A$ en effectuant une rotation de $60^{\\circ}$ sutour de C , donc cette rotation envoie le triangle GAC sur $\\mathrm{G}^{\\prime} \\mathrm{FC}$. En particulier, $\\mathrm{GC}=\\mathrm{G}^{\\prime} \\mathrm{C}$ et $\\widehat{\\mathrm{GCG}^{\\prime}}=60^{\\circ}$, ce qui conclut.\n\nAutre méthode. Si on connaît les nombres complexes, il est facile de résoudre l'exercice par une méthode analytique systématique.\nOn prend un repère tel que $A$ soit l'origine. On nomme $b, c, e, f, g, k$ les affixes de $B, C, E, F, G, K$. On a alors $e=e^{-i \\pi / 3} \\mathrm{~b}, \\mathrm{f}=e^{i \\pi / 3} \\mathrm{c}, \\mathrm{k}=(e+\\mathrm{f}) / 2, \\mathrm{~g}=(\\mathrm{b}+\\mathrm{e}) / 3$. Il est alors facile de vérifier que $\\mathrm{c}-\\mathrm{k}=\\mathrm{i} \\sqrt{3}(\\mathrm{~g}-\\mathrm{k})$, ce qui montre que $(\\mathrm{CK}) \\perp(\\mathrm{GK})$ et que $\\mathrm{CK}=\\mathrm{GK} \\times \\sqrt{3}$, ce qui conclut.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "## \nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $\\mathrm{n} \\geqslant 1$ un entier.\nOn considère un ensemble de $4 \\mathrm{n}+5$ points du plan, trois jamais alignés, et chacun coloré soit en rouge soit en bleu.\n\nProuver qu'il existe $n$ triangles dont les sommets sont tous d'une même couleur (la même pour tous les triangles), et dont les intérieurs respectifs sont deux à deux disjoints et ne contiennent aucun point coloré.", "solution": "de l'exercice 4\n\nLemme. Soit $\\mathrm{n} \\geqslant 3$ et $\\mathrm{m} \\geqslant 1$ des entiers.\nOn considère un n-gone convexe $P$ et $m$ de ses points intérieurs, trois des $n+m$ points jamais alignés. Alors, on peut trianguler $P$ en $n+2 m-2$ triangles dont les somments sont tous parmi les $n+m$ points, aucun de ces triangles ne contenant un des $m$ points en son intérieur.\n\n## Preuve du lemme. On procède par récurrence sur m.\n\nPour $\\mathrm{m}=1$, il suffit de joindre le point intérieur à chacun des sommets, ce qui donne une triangulation adéquate de $P$ en $k$ triangles.\nSupposons que l'affirmation soit vraie pour la valeur $m$ et donnons-nous $m+1$ points intérieurs à $P$. Soit I un de ces points intérieurs. A l'aide des m autres points intérieurs, d'après l'hypothèse de récurrence, on peut trianguler $P$ de la façon souhaitée en $k+2 m-2$ triangles. Comme I est intérieur à $P$, il est donc intérieur à l'un de ces triangles. En joignant I à chacun des trois sommets de ce triangle, on obtient ainsi une triangulation adéquate en $k+2 \\mathrm{~m}-2+2=\\mathrm{k}+$ $2(m+1)-2$ triangles, ce qui achève la preuve.\n\nRevenons à l'exercice. Notons $r$ (resp. b) le nombre de points rouges (resp. bleus). On a donc $r+b=4 n+5$.\nSans perte de généralité, on peut supposer que $r \\geqslant b$ et donc $r \\geqslant 2 \\mathfrak{n}+3$.\nSoit $P$ l'enveloppe convexe des points rouges, et on suppose que $P$ est un k-gone. En particulier, il n'existe aucun point rouge en dehors de $P$, donc il y a $m$ points rouges intérieurs à $P$, avec $\\mathrm{k}+\\mathrm{m}=\\mathrm{r} \\geqslant 2 \\mathrm{n}+3$. (1)\nOn note $w$ le nombre points bleus intérieurs à $P$.\nD'après le lemme, en ne considérant que les points rouges, on peut obtenir une triangulation de $P$ en $k+2 m-2$ triangles à sommets rouges et ne contenant intérieurement aucun point rouge. Si au moins n de ces triangles ne contiennent aucun point bleu, c'est fini.\nSans quoi, au plus $n-1$ des triangles à sommets rouges ne contiennent pas de point bleu. Cela assure qu'au moins $k+2 m-2-(n-1)=k+2 m-(n+1)$ triangles à sommets rouges contiennent chacun au moins un point bleu et, ces triangles étant d'intérieurs deux à deux disjoints, on a donc $w \\geqslant k+2 m-(n+1)$.\nSoit $Q$ l'enveloppe convexe de ces $w$ points bleus intérieurs à $P$. Comme ci-dessus, on peut trianguler $Q$ en au moins $w-2$ triangles ne contenant aucun point bleu en leurs intérieurs.\nPar l'absurde : supposons qu'au plus $n-1$ de ces triangles bleus ne contiennent pas de point rouge.\nAlors, au moins $w-2-(n-1)$ triangles bleus contiennent au moins un point rouge et on a $m \\geqslant w-(n+1)$. Par suite, on a $m \\geqslant k+2 m-(n+1)-(n+1)$, d'où $k+m \\leqslant 2 n+2$, en contradiction avec (1).\n\nAinsi, au moins $n$ de ces triangles à sommets bleus ne contiennent aucun point rouge, ce qui conclut.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit $A B C$ un triangle non isocèle inscrit dans un cercle $\\Gamma$ de rayon $R$. Le cercle passant par $A$ et tangent en $C$ à $[B C]$ recoupe le cercle passant par $B$ et tangent en $C$ à $[A C]$ au point D .\na) Montrer que $C D \\leqslant R$.\nb) Montrer que lorsque $C$ se déplace sur $\\Gamma$, la droite (CD) passe par un point fixe.", "solution": "de l'exercice 5\n\n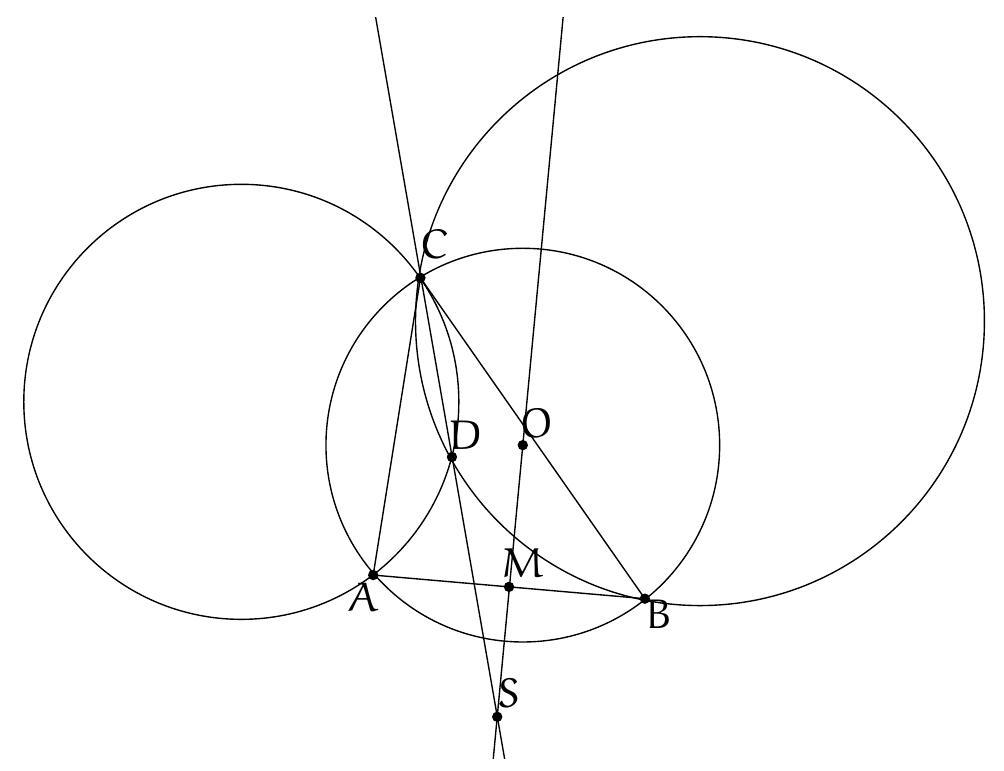\na) On observe d'abord que $(A D, A C)=(C D, C B)$ et $(B C, B D)=(C A, C D)$, donc $D A C$ et $D C B$ sont directement semblables. On en déduit que $D^{2}=D A \\cdot D B$.\nDe plus, en notant $\\gamma=(\\overrightarrow{C A}, \\overrightarrow{C B})$, on a $(\\overrightarrow{D C}, \\overrightarrow{D A})=\\pi-\\gamma$ et de même $(\\overrightarrow{D B}, \\overrightarrow{D C})=\\pi-\\gamma$, donc $(\\overrightarrow{D A}, \\overrightarrow{D B})=2 \\gamma$. Il vient\n\n$$\n\\begin{aligned}\nA^{2} & =D^{2}+D^{2}-2 D A \\cdot D B \\cos 2 \\gamma=D A^{2}+D^{2}-2 D A \\cdot D B\\left(1-2 \\sin ^{2} \\gamma\\right) \\\\\n& =(D A-D B)^{2}+4 D A \\cdot D B \\sin ^{2} \\gamma \\geqslant 4 D A \\cdot D B \\sin ^{2} \\gamma=(2 D C \\sin \\gamma)^{2} .\n\\end{aligned}\n$$\n\nOr, $2 R=\\frac{A B}{\\sin \\gamma}$, donc $R \\geqslant C D$.\nb) On va montrer que (CD) passe par le point de rencontre des tangentes en $A$ et $B$ au cercle circonscrit, que nous appellerons $S$. Il est connu que (CS) est la symédiane du triangle passant par C, donc il suffit de montrer que (CD) est une symédiane.\nNotons $M$ le milieu de $[A B]$. Comme les aires de $A C M$ et $B C M$ sont égales, on a $\\frac{1}{2} C A \\times C M \\times$ $\\sin \\widehat{A C M}=\\frac{1}{2} C B \\times C M \\times \\sin \\widehat{M C B}$, donc $C A \\sin \\widehat{A C M}=C B \\sin \\widehat{M C B}$.\nOn en déduit que si $\\Delta$ est la symédiane et $\\theta$ est l'angle entre $(C A)$ et $\\Delta$, alors $\\frac{\\sin \\theta}{\\sin (\\gamma-\\theta)}=$ $\\frac{\\sin \\widehat{M C B}}{\\sin \\widehat{A C M}}=\\frac{C A}{C B}$. Il suffit donc de montrer que $\\frac{\\sin \\widehat{A C D}}{\\sin \\widehat{D C B}}=\\frac{C A}{C B}$.\n\n$$\n\\begin{aligned}\n\\frac{\\sin \\widehat{A C D}}{\\sin \\widehat{D C B}} & =\\frac{\\sin \\widehat{A C D}}{A D} \\times \\frac{D B}{\\sin \\widehat{D C B}} \\times \\frac{D A}{D B} \\\\\n& =\\frac{\\sin \\widehat{C D A}}{A C} \\times \\frac{B C}{\\sin \\widehat{B D C}} \\times \\frac{D A}{D B}\n\\end{aligned}\n$$\n\nOr, $\\widehat{C D A}=\\widehat{B D C}=\\pi-\\gamma$ et $\\frac{B C}{A C}=\\frac{D C}{D A}=\\frac{D B}{D C}$, donc\n\n$$\n\\frac{\\sin \\widehat{A C D}}{\\sin \\widehat{D C B}}=\\frac{B C}{A C} \\times \\frac{D A}{D C} \\times \\frac{D C}{D B}=\\frac{D C}{D B}=\\frac{C A}{C B}\n$$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Existe-t-il des entiers strictement positifs $a$ et $b$ tels que $a^{n}+n^{b}$ et $b^{n}+n^{a}$ soient premiers entre eux pour tout entier $n \\geqslant 0$ ?", "solution": "de l'exercice 6\n\nPar l'absurde : supposons qu'il existe de tels entiers a et b.\nPar symétrie, on peut supposer que $a \\geqslant b$.\nSi $d=\\operatorname{pgcd}(a, b)$ alors, pour $n=d$, il est clair que $d$ divise $a^{d}+d^{b}$ et $b^{d}+d^{a}$. Or ces deux nombres étant censés être premiers entre eux, c'est que $d=1$.\n\nSoit $N=a^{a}+b^{b}$. On a $N>1$ donc il existe un nombre premier $p$ qui divise $N$. De plus, $p$ ne peut diviser a sans quoi il devrait diviser également $b$, en contradiction avec $d=1$. Ainsi, $a$ est inversible modulo $p$ et il existe un entier $k \\in\\{0, \\cdots, p-1\\}$ tel que $k a=b \\bmod [p]$.\n\nOn choisit alors $n=k+p(a-b-k+p-1)$. D'après le petit théorème de Fermat, il vient :\n\n$$\na^{n}+n^{b} \\equiv a^{k} \\cdot a^{a-b-k+p-1}+k^{b} \\equiv a^{a-b}+k^{b} \\bmod [p]\n$$\n\n$d^{\\prime}$ où $a^{b}\\left(a^{n}+n^{b}\\right) \\equiv a^{a}+b^{b} \\equiv 0 \\bmod [p]$,\net, puisque $p$ ne divise par $a$, on a alors $a^{n}+n^{b} \\equiv 0 \\bmod [p]$.\nOn prouve de même, on a $b^{n}+n^{a} \\equiv 0 \\bmod [p]$.\nMais, alors $p$ divise à la fois $a^{n}+n^{b}$ et $b^{n}+n^{a}$, ce qui contredit qu'ils soient premiers entre eux.\n\nFinalement, il n'existe pas de tels entiers.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Les Xantiens sont les habitants, en nombre éventuellement infini, de la planète Xanta. Vis-à-vis d'eux-mêmes et de leurs semblables, les Xantiens sont capables de ressentir deux types d'émotions, qu'ils appellent amour et respect. Il a été observé que:\n\n- Chaque Xantien aime un et un seul Xantien, et respecte un et un seul Xantien.\n- Si $A$ aime $B$, alors tout Xantien qui respecte $A$ aime également $B$.\n- Si $A$ respecte $B$, alors tout Xantien qui aime $A$ respecte également $B$.\n- Chaque Xantien est aimé d'au moins un Xantien.\n\nEst-il vrai que chaque Xantien respecte le Xantien qu'il aime?", "solution": "de l'exercice 7\n\nPour chaque Xantien $x$, désignons respectivement par $f(x)$ et $g(x)$ les Xantiens aimés et respectés par $x$.\nLa première condition assure que l'on a bien défini des fonctions $f$ et $g$ de l'ensemble $X$ des Xantiens sur lui-même.\nIl s'agit de savoir si, pour tout $x$, on a $f(x)=g(x)$.\nEn fait, nous allons même prouver que, pour tout $x$, on a $f(x)=g(x)=x$.\nSoit $x$ un Xantien.\nIl respecte $g(x)$ qui, de son côté, aime $f(g(x))$.\nLa seconde condition assure donc que $f(g(x))=f(x)$ pour tout $x$. (1)\nDe même, la troisième condition conduit à $g(f(x))=g(x)$ pour tout $x$. (2)\nEnfin, la quatrième condition signifie que f est surjective.\nSoit $x$ un Xantien. Il existe donc un Xantien $y$ tel que $f(y)=x$.\nOr, on a $f(g(f(y)))=f(g(y))$ d'après (2)\net ainsi, d'après (1), il vient $f(f(y))=f(y)$, ou encore $f(x)=x$.\nDe (1), on déduit alors immédiatement que $g(x)=x$.\nFinalement, pour tout $x$, on a bien $f(x)=g(x)=x$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Déterminer tous les entiers strictement positifs a et $b$ tels que $4 \\boldsymbol{a}+1$ et $4 \\boldsymbol{b}-1$ soient premiers entre eux, et tels que $a+b$ divise $16 a b+1$.", "solution": "de l'exercice 8 Notons (C) la condition de l'énoncé. Les entiers $4 \\mathbf{a}+1$ et $4 \\mathrm{~b}-1$ sont premiers entre eux si et seulement si $4 \\boldsymbol{a}+1$ est premier avec $(4 a+1)+(4 b-1)=4(a+b)$. Or, $4 \\boldsymbol{a}+1$ est impair donc il est automatiquement premier avec 4 . On en déduit que $4 \\boldsymbol{a}+1$ et $4 \\boldsymbol{b}-1$ sont premiers entre eux si et seulement si $4 a+1$ est premier avec $a+b$.\nD'autre part, $16 a b+1=16 a(a+b)+\\left(1-16 a^{2}\\right)=16 a(a+b)-(4 a-1)(1+4 a)$, donc $a+b$ divise $16 a b+1$ si et seulement si $a+b$ divise $(4 a-1)(1+4 a)$. Or, si $a+b$ est premier avec $1+4 a$ alors ceci équivaut à $a+b \\mid 4 a-1$.\nOn en déduit que (C) équivaut à ce que $\\operatorname{pgcd}(a+b, 4 a+1)=1$ et $a+b \\mid 4 a-1$.\nD'autre part, montrons que si $a+b \\mid 4 a-1$ alors on a automatiquement $\\operatorname{pgcd}(a+b, 4 a+1)=1$. En effet, si un nombre premier $p$ divise $a+b$ et $4 a+1$, alors il divise $4 a-1$ et $4 a+1$, donc il divise $(4 a+1)-(4 a-1)=2$. Il vient $p=2$, puis $2 \\mid 4 a-1$. Impossible.\nFinalement, (C) équivaut à $\\mathrm{a}+\\mathrm{b} \\mid 4 \\mathrm{a}-1$.\nOr, $\\mathrm{a}+\\mathrm{b}>\\mathrm{a}>\\frac{4 \\mathrm{a}-1}{4}$, donc $\\mathrm{a}+\\mathrm{b} \\mid 4 \\mathrm{a}-1$ ne peut se produire que si $\\mathrm{a}+\\mathrm{b}=4 \\mathrm{a}-1$ ou $\\mathrm{a}+\\mathrm{b}=\\frac{4 \\mathrm{a}-1}{2}$ ou $\\mathrm{a}+\\mathrm{b}=\\frac{4 \\mathrm{a}-1}{3}$.\nLe deuxième cas ne peut pas se produire car $4 a-1$ est impair.\n(C) équivaut donc à $\\mathrm{a}+\\mathrm{b}=4 \\mathrm{a}-1$ ou $\\mathrm{a}+\\mathrm{b}=\\frac{4 \\mathrm{a}-1}{3}$, $\\mathrm{c}^{\\prime}$ est-à-dire $\\mathrm{b}=3 \\mathrm{a}-1$ ou $\\mathrm{a}=3 \\mathrm{~b}+1$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $A B C$ un triangle tel que $\\widehat{A}=40^{\\circ}$ et $\\widehat{B}=60^{\\circ}$. Soient $D$ et $E$ des points de [AC] et $[\\mathrm{AB}]$ tels que $\\widehat{\\mathrm{CBD}}=40^{\\circ}$ et $\\widehat{\\mathrm{ECB}}=70^{\\circ}$. On note F l'intersection de (BD) et (CE). Monter que $(A F) \\perp(B C)$.", "solution": "de l'exercice 9\n\n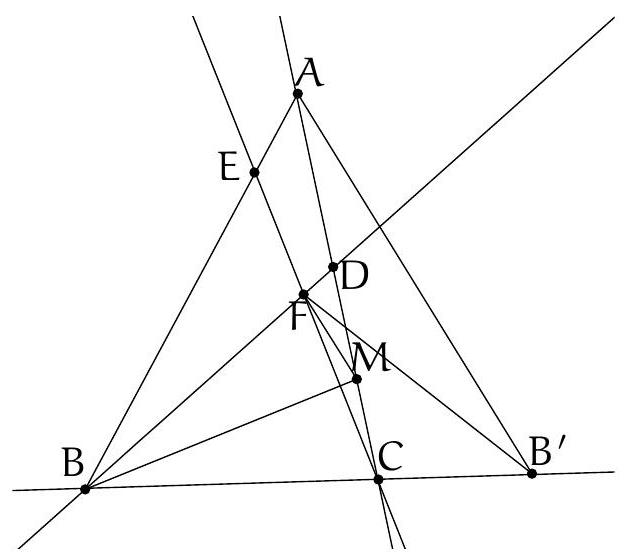\n\nOn a $\\widehat{\\mathrm{BFC}}=180^{\\circ}-\\widehat{\\mathrm{CBF}}-\\widehat{\\mathrm{FCB}}=180^{\\circ}-40^{\\circ}-70^{\\circ}=70^{\\circ}=\\widehat{\\mathrm{FCB}}$ donc BCF est isocèle en B . Il vient $B C=B F$.\nSoit $M$ le point d'intersection entre la bissectrice de $\\widehat{C B F}$ et ( $A C$ ). On a $\\widehat{B M A}=40^{\\circ}=\\widehat{B A M}$ donc $M A=M B$.\nD'autre part, $\\widehat{B M C}=180^{\\circ}-\\widehat{C B M}-\\widehat{M C B}=180^{\\circ}-20^{\\circ}-80^{\\circ}=80^{\\circ}=\\widehat{M C B}$ donc $B C=B M$.\nOn déduit de ce qui précède que $M A=B F$.\n\nSoit $\\mathrm{B}^{\\prime} \\in(\\mathrm{BC})$ tel que $A B^{\\prime}$ est équilatéral. Soit $\\Delta$ la bissectrice de $\\widehat{\\mathrm{B}^{\\prime} \\mathrm{BA}}$. Comme $\\mathrm{BF}=\\mathrm{BM}$ et $\\widehat{\\mathrm{FBA}}=\\widehat{\\mathrm{CBM}}$, les points $M$ et $F$ sont symétriques par rapport à $\\Delta$. Or, $A$ et $B^{\\prime}$ sont aussi symétriques par rapport à $\\Delta$, donc $M A=\\mathrm{FB}^{\\prime}$.\nFinalement, $\\mathrm{FB}^{\\prime}=\\mathrm{FB}$, donc $F$ appartient à la médiatrice de $\\left[\\mathrm{BB}^{\\prime}\\right]$, qui est aussi la hauteur ( $A F$ ) du triangle $A B B^{\\prime}$.\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soit $A B C$ un triangle tel que $\\widehat{A}=40^{\\circ}$ et $\\widehat{B}=60^{\\circ}$. Soient $D$ et $E$ des points de [AC] et $[\\mathrm{AB}]$ tels que $\\widehat{\\mathrm{CBD}}=40^{\\circ}$ et $\\widehat{\\mathrm{ECB}}=70^{\\circ}$. On note F l'intersection de (BD) et (CE). Monter que $(A F) \\perp(B C)$.", "solution": "Notons $H$ le projeté de $F$ sur $[B C]$ et $H^{\\prime}$ le projeté de $A$ sur [BC]. Il s'agit de montrer que $\\mathrm{H}=\\mathrm{H}^{\\prime}$. Pour cela, il suffit de voir que $\\mathrm{BH}=\\mathrm{BH}^{\\prime}$.\nOn a $B^{\\prime}=A B \\cos 60$ et $B H=B F \\cos 40=B C \\cos 40$. Comme $\\frac{A B}{B C}=\\frac{\\sin 80}{\\sin 40}$, il suffit de montrer que $\\sin 80 \\cos 60=\\sin 40 \\cos 40$, c'est-à-dire (compte tenu de $\\cos 60=\\frac{1}{2}$ ) que $\\sin 80=$ $2 \\sin 40 \\cos 40$, ce qui est vrai d'après la formule générale $\\sin 2 x=2 \\sin x \\cos x$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution."}}
+{"year": "2015", "tier": "T2", "problem_label": "10", "problem_type": null, "problem": "Pour tout entier strictement positif $x$, on note $S(x)$ la somme des chiffres de son écriture décimale.\nSoit $k>0$ un entier. On définit la suite $\\left(x_{n}\\right)$ par $x_{1}=1$ et $x_{n+1}=S\\left(k x_{n}\\right)$ pour tout $n>0$.\nProuver que $x_{n}<27 \\sqrt{k}$, pour tout $n>0$.", "solution": "de l'exercice 10\n\nLemme. Pour tout entier $s \\geqslant 0$, on a $10^{s} \\geqslant(s+1)^{3}$.\nPreuve du lemme. On raisonne par récurrence sur s.\nPour $s=0$, on a $10^{0}=1=(0+1)^{3}$.\nSupposons l'inégalité vraie pour la valeur s. Alors :\n$10^{\\mathrm{s}+1} \\geqslant 10(\\mathrm{~s}+1)^{3}$ d'après l'hypothèse de récurrence\n$=10 s^{3}+30 s^{2}+30 s+10$\n$\\geqslant \\mathrm{s}^{3}+6 \\mathrm{~s}^{2}+12 \\mathrm{~s}+8$\n$=(s+2)^{3}$, ce qui achève la preuve.\nSi $x>0$ est un entier dont l'écriture décimale utilise $s+1$ chiffres, on a $S(x) \\leqslant 9(s+1)$ et $10^{s} \\leqslant x<10^{s+1}$. Or, d'après le lemme, on a $s+1 \\leqslant 10^{\\frac{s}{3}}$, donc $s+1 \\leqslant x^{\\frac{1}{3}}$ et ainsi $S(x) \\leqslant 9 x^{\\frac{1}{3}}$.\nMontrons maintenant par récurrence que $x_{n}<27 \\sqrt{k}$ pour tout $n$. L'assertion est claire pour $n=1$. Supposons $x_{n}<27 \\sqrt{k}$, alors $x_{n+1}=S\\left(k x_{n}\\right) \\leqslant 9\\left(k x_{n}\\right)^{\\frac{1}{3}}<9(27 k \\sqrt{k})^{\\frac{1}{3}}=9 \\times 3 \\times \\sqrt{k}=$ $27 \\sqrt{\\mathrm{k}}$, d'où le résultat.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 10.", "solution_match": "## Solution "}}
+{"year": "2015", "tier": "T2", "problem_label": "11", "problem_type": null, "problem": "Soient $a, b, c$ trois nombres réels strictement positifs tels que $a+b+c=9$. Montrer que\n\n$$\n\\frac{a^{3}+b^{3}}{a b+9}+\\frac{b^{3}+c^{3}}{b c+9}+\\frac{c^{3}+a^{3}}{c a+9} \\geqslant 9\n$$", "solution": "de l'exercice 11 On cherche une minoration de la forme $\\frac{a^{3}+b^{3}}{a b+9} \\geqslant u(a+b)+v, c^{\\prime}$ est-àdire $f(a) \\geqslant 0$ où $f(a)=a^{3}+b^{3}-(u(a+b)+v)(a b+9)$.\nEn sommant les trois inégalités, on en déduirait $\\frac{a^{3}+b^{3}}{a b+9}+\\frac{b^{3}+c^{3}}{b c+9}+\\frac{c^{3}+a^{3}}{c a+9} \\geqslant 2 u(a+b+c)+3 v=$ $3(6 u+v)$, donc il suffit que $6 u+v=3$.\nD'autre part, si une telle minoration existe, comme l'inégalité devient une égalité lorsque $\\mathrm{a}=$ $\\mathrm{b}=\\mathrm{c}=3$, on doit avoir $\\mathrm{f}(3)=0$ si $\\mathrm{b}=3$. Comme de plus $\\mathrm{f}(\\mathrm{a}) \\geqslant 0$ pour tout a , on doit nécessairement avoir $\\mathrm{f}^{\\prime}(3)=0$ pour $\\mathrm{b}=3$.\nCeci impose la condition $0=f^{\\prime}(3)=27-18 \\mathbf{u}-(6 \\mathbf{u}+\\boldsymbol{v}) \\times 3=18(1-\\mathfrak{u})$, donc $\\mathbf{u}=1$ et $v=-3$.\n\nMontrons donc $\\frac{a^{3}+b^{3}}{a b+9} \\geqslant(a+b)-3$. Comme $a^{3}+b^{3} \\geqslant \\frac{(a+b)^{3}}{4}$ et $a b+9 \\leqslant\\left(\\frac{a+b}{2}\\right)^{2}+9$, il suffit de montrer que\n\n$$\n\\frac{s^{3}}{s^{2}+36} \\geqslant s-3\n$$\n\noù $s=a+b$. On réduit au même dénominateur; l'inégalité se simplifie en $3 s^{2}-36 s+108 \\geqslant 0$, ou encore en $3(s-6)^{2} \\geqslant 0$, ce qui est vrai.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 11.", "solution_match": "\n\nSolution "}}
+{"year": "2015", "tier": "T2", "problem_label": "12", "problem_type": null, "problem": "Déterminer tous les entiers $\\mathrm{n}>0$ ayant la propriété suivante: \"tout nombre strictement positif qui s'écrit comme la somme des carrés de $n$ entiers multiples de $n$ peut également s'écrire comme la somme des carrés de $n$ entiers dont aucun n'est un multiple de $\\mathrm{n}^{\\prime \\prime}$.", "solution": "de l'exercice 12\n\nUn entier n ayant la propriété désirée sera dit bon.\nSoit $\\mathrm{n} \\geqslant 2$ un entier bon. Alors 2 n est également bon : en effet, soit $\\mathrm{m}=2 \\mathrm{n}$ et soit $x_{1}, \\cdots, x_{m}$ des entiers divisibles par m. Si deux de ces entiers sont non nuls, on peut supposer sans perte de généralité qu'il s'agit de $x_{1}$ et $x_{m}$. Puisque $n$ est bon, il existe alors des entiers $y_{i}$ non divisibles par $n$ (donc non divisibles par $m$ ) tels que $\\sum_{i=1}^{n} x_{i}^{2}=\\sum_{i=1}^{n} y_{i}^{2}$ et $\\sum_{i=n+1}^{2 n} x_{i}^{2}=\\sum_{i=n+1}^{2 n} y_{i}^{2}$. Ainsi, $\\sum_{i=1}^{m} x_{i}^{2}=\\sum_{i=1}^{m} y_{i}^{2}$ avec chaque $y_{i}$ non divisible par $m$.\nSi un et un seul des $x_{i}$ est non nul, alors $\\sum_{i=1}^{m} x_{i}^{2}$ est de la forme $(2 a)^{2}=a^{2}+a^{2}+a^{2}+a^{2}$ où $a>0$ est divisible par n et on raisonne de la même manière.\n\nLemme. Soit $\\mathrm{n}>0$ un entier impair et $x_{1}, \\cdots, x_{n}$ des entiers dont au moins un n'est pas divisible par $n$. Alors il existe des entiers $y_{1}, \\cdots, y_{n}$ non divisibles par $n$ tels que $\\sum_{i=1}^{n}\\left(n x_{i}\\right)^{2}=\\sum_{i=1}^{n} y_{i}^{2}$.\n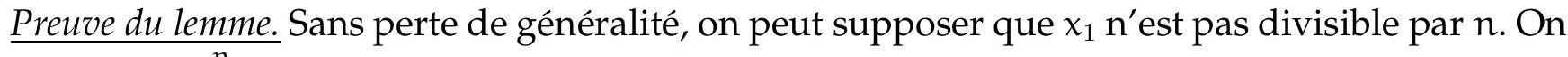 pose $X=2 \\sum_{i=1}^{n} x_{i}$.\nSi $n$ divise $X$, on remplace $x_{1}$ par $-x_{1}$. La nouvelle valeur $X^{\\prime}$ vérifie $X^{\\prime}=X-4 x_{1}$. Comme $n$ divise $X$ mais pas $4 x_{1}$ (rappelons que $n$ est supposé impair), il ne divise pas $X^{\\prime}$. Ainsi, sans perte de généralité, on peut supposer que $n$ ne divise pas $X$.\nIl est facile de vérifier que $\\sum_{i=1}^{n}\\left(n x_{i}\\right)^{2}=\\sum_{i=1}^{n}\\left(X-n x_{i}\\right)^{2}$. En posant $y_{i}=X-n x_{i}$ pour tout $i$, la conclusion souhaitée en découle.\n\nOn peut maintenant prouver que tout $n \\geqslant 3$ impair est bon. En effet, si $a>0$ est un entier qui peut s'écrire comme la somme de $n$ carrés d'entiers tous divisibles par $n$ alors, en considérant la plus grande puissance de $n$ qui divise ces entiers, il existe donc un entier $r>0$ et des entiers $x_{1}, \\cdots, x_{n}$ dont au moins un n'est pas divisible par $n$ tels que $a=\\sum_{i=1}^{n}\\left(n^{r} x_{i}\\right)^{2}$.\n\nD'après le lemme, il existe des entiers $y_{1}, \\cdots, y_{n}$ non divisibles par $n$ tels que $\\sum_{i=1}^{n}\\left(n x_{i}\\right)^{2}=\\sum_{i=1}^{n} y_{i}^{2}$, et donc $\\sum_{i=1}^{n}\\left(n^{r} x_{i}\\right)^{2}=\\sum_{i=1}^{n}\\left(n^{r-1} y_{i}\\right)^{2}$. Ainsi, en appliquant le lemme $r$ fois de suite, on est assuré de l'existence d'entiers $z_{1}, \\cdots, z_{n}$ non divisibles par $n$ tels que $a=\\sum_{i=1}^{n} z_{i}^{2}$. Cela prouve que $n$ est bon.\n\nPuisque le double de tout entier bon est bon, tout entier qui n'est pas une puissance de 2 est bon.\n\nOn prouve maintenant que 8 est bon : En effet, si a est la somme de 8 carrés d'entiers divisibles par 8 alors a est divisible par 64 . En particulier $a \\geqslant 64 \\mathrm{et}$, d'après le théorème des quatre carrés de Lagrange, il existe des entiers $x_{1}, x_{2}$, $x_{3}, x_{4}$ tels que $a=1^{2}+4^{2}+4^{2}+4^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$. Notons que, puisque $a \\equiv 0 \\bmod [8]$, on a $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2} \\equiv 7 \\bmod$ [8]. Or, un carré étant congru à 0,1 ou 4 modulo 8 , la seule façon d'obtenir une somme de quatre carrés congrue à 7 modulo 8 est d'avoir $1,1,1,4$ à l'ordre près. Ainsi, aucun des $x_{i}$ n'est divisible par 8 , ce qui conclut.\n\nEnfin, on prouve que 4 n'est pas bon. Pour cela, il suffit de constater que $32=4^{2}+4^{2}+0^{2}+0^{2}$. D'autre part, pour obtenir $32=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$, on doit avoir $\\left|x_{i}\\right| \\leqslant 5$ pour tout i. De plus, si l'on veut éviter les multiples de 4 , il ne reste plus que $\\left|x_{i}\\right|=1,2,3$ ou 5 . Or, comme ci-dessus en raisonnant modulo 8 , la seule possibilités est d'avoir $\\left|x_{i}\\right|=2$ pour tout $i$. Mais, on a $32 \\neq$ $2^{2}+2^{2}+2^{2}+2^{2}$, ce qui assure que $4 \\mathrm{n}^{\\prime}$ est pas bon.\nAinsi, tout diviseur de 4 ne peut être bon.\nFinalement, tous les entiers $\\mathrm{n}>0$ sont bons sauf 1,2 et 4 .", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2014-2015-envoi-6-solutions.jsonl", "problem_match": "\nExercice 12.", "solution_match": "## Solution "}}
diff --git a/French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl b/French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..60a819e850c7b860babbace1064c797e75817fc4
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl
@@ -0,0 +1,27 @@
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Prouver qu'il n'existe qu'un nombre fini de nombres premiers s'écrivant sous la forme $n^{3}+2 n+3$ avec $n \\in \\mathbb{N}$.", "solution": "de l'exercice 1: Remarquons que $n^{3}-n=n(n-1)(n+1)$ est un produit de trois entiers consécutifs. Puisque parmi trois entiers consécutifs il y a toujours un multiple de 3 , on obtient que $n^{3}-n$ est divisible par 3, c'est-à-dire $n^{3} \\equiv n(\\bmod 3)$. (On peut le voir aussi en utilisant le petit théorème de Fermat.) On a donc $n^{3}+2 n+3 \\equiv n+2 n+3 \\equiv 3 n+3 \\equiv 0(\\bmod 3)$, donc $n^{3}+2 n+3$ est toujours divisible par 3 . D'autre part, il ne peut être égal à 3 que pour un nombre fini de valeurs de $n$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 1", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Résoudre $x^{4}-6 x^{2}+1=7 \\times 2^{y}$ pour $x$ et $y$ entiers.", "solution": "de l'exercice 2: L'équation se réécrit $\\left(x^{2}-3\\right)^{2}=7 \\times 2^{y}+8$. Si $y \\geq 3$, alors le côté droit s'écrit $8\\left(7 \\times 2^{y-3}+1\\right)$. Le côté gauche étant un carré, sa valuation 2 -adique est paire. Ainsi, $7 \\times 2^{y-3}+1$ doit être pair, donc $y=3$. Dans ce cas $x^{2}-3=8$ donc $x^{2}=11$, impossible. Donc $y \\leq 2$. Si $y=2$, on trouve $x= \\pm 3$. Pour $y<0$, ainsi que pour $y=0$ ou $y=1$ il n'y a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Résoudre $x^{4}-6 x^{2}+1=7 \\times 2^{y}$ pour $x$ et $y$ entiers.", "solution": "Les seuls couples de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Résoudre $x^{4}-6 x^{2}+1=7 \\times 2^{y}$ pour $x$ et $y$ entiers.", "solution": "s sont donc $(x, y)=(3,2)$ et $(-3,2)$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 2", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver le plus petit entier positif qui ne s'écrit pas sous la forme $\\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ pour $a, b, c, d \\in \\mathbb{N}$.", "solution": "de l'exercice 3: Soit E l'ensemble des entiers strictement positifs s'écrivant sous cette forme. Commençons par remarquer que\n\n$$\n\\frac{2^{a}-2^{b}}{2^{c}-2^{d}}=2^{b-d} \\frac{2^{a-b}-1}{2^{c-d}-1}\n$$\n\nAinsi, si $x>0$ s'écrit $x=\\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, alors $b-d=v_{2}(x)$ et si on appelle $y$ l'entier impair tel que $x=2^{v_{2}(x)} y$, alors $y$ s'écrit sous la forme $\\frac{2^{n}-1}{2^{m}-1}$. En particulier, l'entier que nous cherchons est nécessairement impair. D'autre part, on peut tout de suite exclure les entiers de la forme $2^{n}-1$, atteints avec $m=1$.\n\nIl est classique que si $2^{m}-1$ divise $2^{n}-1$, alors $m$ divise $n$. Ainsi, en écrivant $n=m d, y$ est de la forme\n\n$$\ny=\\frac{2^{m d}-1}{2^{m}-1}=2^{(d-1) m}+2^{(d-2) m}+\\ldots+2^{m}+1\n$$\n\nAutrement dit, en notant $u=\\underbrace{0 \\ldots 0}_{m-1 \\text { zéros }} 1$, l'écriture en base 2 de $y$ est de la forme $\\overline{1 u \\ldots u}^{2}$, avec $u$ apparaissant $d-1$ fois. Les entiers impairs appartenant à $E$ sont exactement ceux ayant une telle écriture binaire pour $m$ et $d$ bien choisis. Les écritures binaires des premiers entiers impairs qui ne sont pas de la forme $2^{n}-1$ sont\n\n$$\n5=\\overline{101}^{2}, 9={\\overline{1001}^{2}}^{2}, 11={\\overline{1011}^{2}}^{2}\n$$\n\nD'après le critère ci-dessus, le plus petit entier cherché est 11.\nRemarque : cet exercice peut aussi se faire en trouvant des manières d'écrire les entiers 1 à 10 sous cette forme, puis en montrant que 11 ne s'écrit pas sous cette forme : en effet, vu que 11 est impair, on peut supposer $b=d=1$. Ensuite\n\n$$\n\\left(2^{a}-1\\right)=11\\left(2^{c}-1\\right)\n$$\n\nse réécrit\n\n$$\n10=2^{c} \\times 11-2^{a}\n$$\n\nPuisque $10=2 \\times 5$, nous avons $a=1$ ou $c=1$. Si $a=1$, on trouve $2^{c} \\times 11=12$, qui n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 3", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver le plus petit entier positif qui ne s'écrit pas sous la forme $\\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ pour $a, b, c, d \\in \\mathbb{N}$.", "solution": ", et si $c=1$, on trouve $2^{a}=12$, qui n'a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 3", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Trouver le plus petit entier positif qui ne s'écrit pas sous la forme $\\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ pour $a, b, c, d \\in \\mathbb{N}$.", "solution": "non plus. Donc 11 est l'entier cherché.\n\n## 2 Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 3", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "de l'exercice 4: Si $p=2$ alors on a $3(q+2)(r+3)=8 q r$ ce qui implique $q=3$ ou $r=3$. On a alors la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "$(2,3,5)$.\n\nSi $q=2$ et $p, r>2$ alors on a $(p+1)(r+3)=2 p r$. Puisque $p$ et $r$ sont impairs, le membre de gauche est divisible par 4 , alors que le membre de droite est divisible par 2 , mais pas par 4 , contradiction. Donc $p$ ou $r$ vaut 2 mais aucune", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "valide n'en découle.\n\nSi $r=2$ alors $5(p+1)(q+2)=8 p q$ et donc $p$ ou $q$ vaut 5 . On obtient la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "$(7,5,2)$.\nSinon, $(p+1)$ est pair et $(r+3)$ est pair. Donc on se ramène à\n\n$$\n\\left(\\frac{p+1}{2}\\right)(q+2)\\left(\\frac{r+3}{2}\\right)=p q r .\n$$\n\nNous avons donc écrit pqr comme un produit de trois facteurs strictement plus grands que 1. On en déduit que $\\left(\\frac{p+1}{2}, q+2, \\frac{r+3}{2}\\right)$ est une permutation de $(p, q, r)$.\n\nClairement, $p \\neq \\frac{p+1}{2}$ puisque $p>\\frac{p+1}{2}$.\nSi $p=\\frac{r+3}{2}$, alors puisque $q \\neq q+2$, nous avons nécessairement $q=\\frac{p+1}{2}=\\frac{r+5}{4}$. Alors $r=q+2=\\frac{r+13}{4}$, et donc $r$ n'est pas entier.\n\nSi $p=q+2$, alors il y a deux cas à considérer :\n$-r=\\frac{p+1}{2}=\\frac{q+3}{2}$ et $q=\\frac{r+3}{2}=\\frac{q+9}{4}$. Donc $q=3$ et on obtient la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "$(5,3,3)$.\n$-r=\\frac{r+3}{2}$ et $q=\\frac{p+1}{2}=\\frac{q+3}{2}$, ce qui donne $r=q=3$. On obtient alors cette même", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "$(5,3,3)$.\nFinalement, les seules", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.", "solution": "s sont $(2,3,5),(7,6,2)$ et $(5,3,3)$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 4", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.", "solution": "de l'exercice 5: On veut résoudre $2^{n-1} n+1=m^{2}$, c'est-à-dire $2^{n-1} n=(m-1)(m+1)$. Puisque $n=1$ n'est pas", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.", "solution": ", on a $n \\geq 2$, et donc $m$ est nécessairement impair, et $m-1$ et $m+1$ sont pairs (en particulier $n \\geq 3$ ). On pose $k=\\frac{m-1}{2}$. Il suffit alors de résoudre $2^{n-3} n=k(k+1)$. Parmi les entiers $k$ et $k+1$ exactement un est pair, et donc ils sont de la forme $2^{n-3} d$ et $\\frac{n}{d}$ avec $d$ un diviseur de $n$. Or un diviseur de $n$ ne peut pas être à distance 1 d'un entier supérieur à $2^{n-3}$ si $n$ est trop grand. Plus précisément, on a $2^{n-3} d \\geq 2^{n-3} \\geq n+2$ si $n \\geq 6$, donc on a nécessairement $n \\leq 5$. Pour $n=5$, on trouve $2^{4} \\times 5+1=9^{2}$, donc 5 est", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.", "solution": "On vérifie que $2,3,4$ ne sont pas", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.", "solution": "s. Donc $n=5$ est la seule", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 5", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soient $x>1$ et $y$ des entiers vérifiant $2 x^{2}-1=y^{15}$. Montrer que $x$ est divisible par 5 .", "solution": "de l'exercice 6: L'entier $y$ est clairement impair et strictement plus grand que 1. On factorise l'équation sous la forme\n\n$$\nx^{2}=\\left(\\frac{y^{5}+1}{2}\\right)\\left(y^{10}-y^{5}+1\\right)\n$$\n\nRemarquons que\n\n$$\ny^{10}-y^{5}+1 \\equiv 3\\left(\\bmod y^{5}+1\\right)\n$$\n\net que donc $\\operatorname{pgcd}\\left(y^{5}+1, y^{10}-y^{5}+1\\right)$ est égal à 1 ou à 3 . S'il valait 1 , alors $y^{10}-y^{5}+1$ serait un carré. Or pour $y>0$ nous avons\n\n$$\n\\left(y^{5}-1\\right)^{2}=y^{10}-2 y^{5}+11$, on a\n\n$$\n\\left(2 y^{2}-y\\right)^{2}=4 y^{4}-4 y^{3}+y^{2}<4\\left(y^{4}-y^{3}+y^{2}-y+1\\right)<4 y^{4}-4 y^{3}+5 y^{2}-2 y+1=\\left(2 y^{2}-y+1\\right)^{2}\n$$\n\n## 3 Exercices groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 6", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Caractériser les entiers $n \\geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\\bmod n)$.", "solution": "de l'exercice 7: Voici les $n$ vérifiant cette propriété : $2,2 \\cdot 3,2 \\cdot 3 \\cdot 7,2 \\cdot 3 \\cdot 7 \\cdot 43$.\nPour prouver que c'est exhaustif on procède de la façon suivante : on commence par remarquer que $n$ n'a pas de facteur carré. En effet, si $p^{2}$ divise $n$, alors $p^{n+1}-p$ est divisible par $p^{2}$, ce qui n'est pas possible. Ainsi, $n$ est forcément un produit $p_{1} \\ldots p_{k}$ de nombres premiers distincts. Par conséquent, par le lemme chinois la condition de l'énoncé est équivalente à $a^{n+1} \\equiv a(\\bmod p)$ pour tout entier $a$ et tout $p \\in\\left\\{p_{1}, \\ldots, p_{k}\\right\\}$. En choisissant $a$ d'ordre $p-1$ modulo $p$, on obtient que cela est équivalent à ce que $p-1$ divise $n$ pour tout $p \\in\\left\\{p_{1}, \\ldots, p_{k}\\right\\}$.\n\nEn résumé : $n$ est produit de premiers distincts $p_{1}, \\ldots, p_{k}$, et $p_{i}-1$ divise $n$ pour tout $i$. On en déduit que pour tout $i, p_{i}-1$ est sans facteur carré et $p_{i}-1=q_{1} \\ldots q_{m}$ où les $q_{j}$ sont des nombres premiers pris parmi les $p_{r}, r \\neq i$.\n\nQuitte à re-numéroter les $p_{i}$, on peut supposer que $p_{1}1$, alors $p_{2}-1$ est nécessairement égal à 2 , donc $p_{2}=3$. Si $k=2$, cela nous donne la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Caractériser les entiers $n \\geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\\bmod n)$.", "solution": "$n=6$. Si $k>2$ on continue en disant que $p_{3}-1$ ne peut être égal à 2 ou 3 , donc il est égal à $p_{1} p_{2}=6$, d'où $p_{3}=7$. Si $k=3$, cela donne la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Caractériser les entiers $n \\geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\\bmod n)$.", "solution": "$n=2 \\cdot 3 \\cdot 7=42$. Si $k>3$, on voit que de même la seule valeur possible pour $p_{4}$ est $2 \\times 3 \\times 7+1=43$. Pour $k=4$, cela donne la", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Caractériser les entiers $n \\geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\\bmod n)$.", "solution": "$n=2 \\cdot 3 \\cdot 7 \\cdot 43$. Enfin, supposons que $k>4$. Alors $p_{5}-1$ doit être pair et strictement supérieur à 43 , donc les seules valeurs possibles sont $2 \\cdot 43,2 \\cdot 3 \\cdot 43,2 \\cdot 7 \\cdot 43,2 \\cdot 3 \\cdot 7 \\cdot 43$. On vérifie qu'aucune de ces possibilités ne fournit un $p_{5}$ premier. Ainsi on a nécessairement $k \\leq 4$ et les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Caractériser les entiers $n \\geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\\bmod n)$.", "solution": "s que nous avons trouvées sont les seules.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $k \\geq 3$ un entier. On définit la suite $\\left(a_{n}\\right)_{n \\geq k}$ par $a_{k}=2 k$, et\n\n$$\na_{n}= \\begin{cases}a_{n-1}+1 & \\text { si } \\operatorname{pgcd}\\left(a_{n-1}, n\\right)=1 \\\\ 2 n & \\text { sinon. }\\end{cases}\n$$\n\nMontrer que la suite $\\left(a_{n+1}-a_{n}\\right)_{n \\geq k}$ a une infinité de termes qui sont des nombres premiers.", "solution": "de l'exercice 8: Partons d'un entier $n$ tel que $a_{n}=2 n$. Montrons par récurrence que si $p$ est le plus petit facteur premier de $n-1$, alors pour tout $i \\in\\{0, \\ldots, p-2\\}, a_{n+i}=2 n+i$. En effet, c'est vrai pour $i=0$, et si c'est vrai pour un certain $i1$ premier avec $t$ tel que pour tout entier $k \\geq 1$, l'entier $n^{k}+t$ ne soit pas une puissance (c'est-à-dire qu'il ne soit pas de la forme $m^{r}$ avec $m \\geq 1$ et $r \\geq 2$ ).", "solution": "de l'exercice 9: Pour que $n$ soit premier avec $t$, on va le chercher sous la forme $1+t s$ où $s$ est entier. On aura alors $n^{k}+t \\equiv 1+t(\\bmod s)$. En particulier, si $s$ est divisible par $(t+1)$, alors $n^{k}+t$ l'est également.\n\nOn va d'abord traiter le cas où $t+1$ n'est pas une puissance. Dans ce cas, il suffirait de s'assurer qu'on peut choisir $s$ de telle sorte que $n^{k}+t$ soit divisible par $t+1$, et que le quotient soit premier avec $t+1$. Pour cela, prenons $s=(t+1)^{2}$. Alors $n=1+t(t+1)^{2}$, et\n\n$$\nn^{k}+t=\\underbrace{\\sum_{i=1}^{k}\\binom{k}{i} t^{i}(t+1)^{2 i}}_{\\text {termes divisibles par }(t+1)^{2}}+1+t=(t+1)(a(t+1)+1)\n$$\n\npour un certain entier $a$, donc on a gagné.\n\nSupposons maintenant que $t+1$ soit une puissance : $t+1=m^{r}$ avec $m$ qui n'est pas une puissance. Si on garde le même $n$ que ci-dessus, on voit que si $n^{k}+t=b^{d}$ est une puissance (avec $d \\geq 2$ ), alors $t+1$ est nécessairement une puissance $d$-ième, et donc $d$ divise $r$. Ainsi, nous avons une borne sur les $d$ tels que $n^{k}+t$ est puissance $d$-ième pour un certain $k$. On constate alors qu'en remplaçant $n$ par sa puissance $r$-ième, c'est-à-dire en posant $n=n_{0}^{r}$ où $n_{0}=1+t(t+1)^{2}$ (ce qui ne change pas le fait que $t+1$ divise $n^{k}+t$, que le quotient soit premier avec $t+1$, et que donc $n^{k}+t=b^{d}$ implique $d \\mid r$ comme ci-dessus), on arrive à écrire $t$ comme une différence de deux puissances $d$-ièmes :\n\n$$\nt=b^{d}-\\left(n_{0}^{k e}\\right)^{d}\n$$\n\noù $e$ est l'entier naturel tel que $r=d e$. Cela n'est pas possible car $n_{0}$ est grand par rapport à $t$. Plus précisément, nous avons:\n\n$$\nt=b^{d}-\\left(n_{0}^{k e}\\right)^{d}=\\left(b-n_{0}^{k e}\\right)\\left(b^{d-1}+b^{d-2} n_{0}^{k e}+\\ldots+b n_{0}^{k e(d-2)}+n_{0}^{k e(d-1)}\\right) \\geq n_{0}>t\n$$\n\ncontradiction. Donc pour tout $k$ et pour tout $d, n^{k}+t$ n'est pas une puissance $d$-ième et nous avons terminé.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-1-solutions.jsonl", "problem_match": "\nExercice 9", "solution_match": "\n\nSolution "}}
diff --git a/French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl b/French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..2aac79c9f59e431826c9eb2198431eb6fb284eac
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl
@@ -0,0 +1,9 @@
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Soit $A$ un point extérieur à un cercle $\\mathscr{C}$ de centre $O$. Un point $P$ se déplace sur $\\mathscr{C}$. Soit $M$ le point d'intersection entre $(A P)$ et la bissectrice de $\\widehat{P O A}$. Montrer que $M$ se déplace sur un cercle que l'on décrira.", "solution": "de l'exercice 1\n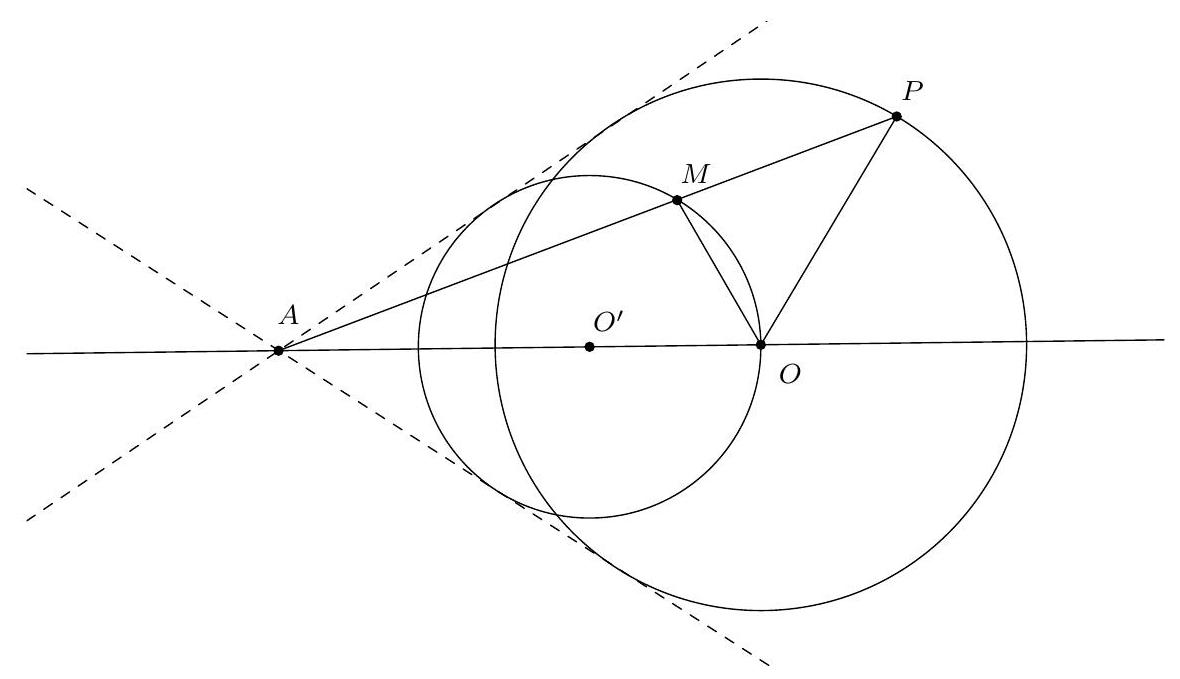\n\nNotons $d=O A$ et $R$ le rayon du cercle.\nD'après le théorème de la bissectrice, on a $M P / M A=O P / O A$, donc $\\frac{M A}{A P}=\\frac{M A}{M A+M P}=$ $\\frac{1}{1+\\frac{M P}{M A}}=\\frac{1}{1+\\frac{O P}{O A}}=\\frac{O A}{O A+O P}=\\frac{d}{d+R}$. Notons $k$ cette valeur. Soit $O^{\\prime}$ le point de $[A O]$ tel que $A O^{\\prime}=k A O$. D'après le théorème de Thalès, les droites $\\left(O^{\\prime} M\\right)$ et $(O P)$ sont parallèles, donc $\\frac{O^{\\prime} M}{O P}=\\frac{A M}{A P}=k$, donc $O^{\\prime} M=k R$. Ceci prouve que $M$ décrit le cercle de centre $O^{\\prime}$ et de rayon kR.\nRemarquons que $A O^{\\prime}+k R=k(d+R)=d$, donc ce cercle passe par $O$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $A B C$ un triangle tel que $\\widehat{A}=60^{\\circ}$. On note $O$ le centre du cercle circonscrit, $I$ le centre du cercle inscrit et $H$ l'orthocentre. Montrer que\n\n1) $B, C, O, I, H$ sont cocycliques\n2) $O I H$ est isocèle.", "solution": "de l'exercice 2\n\n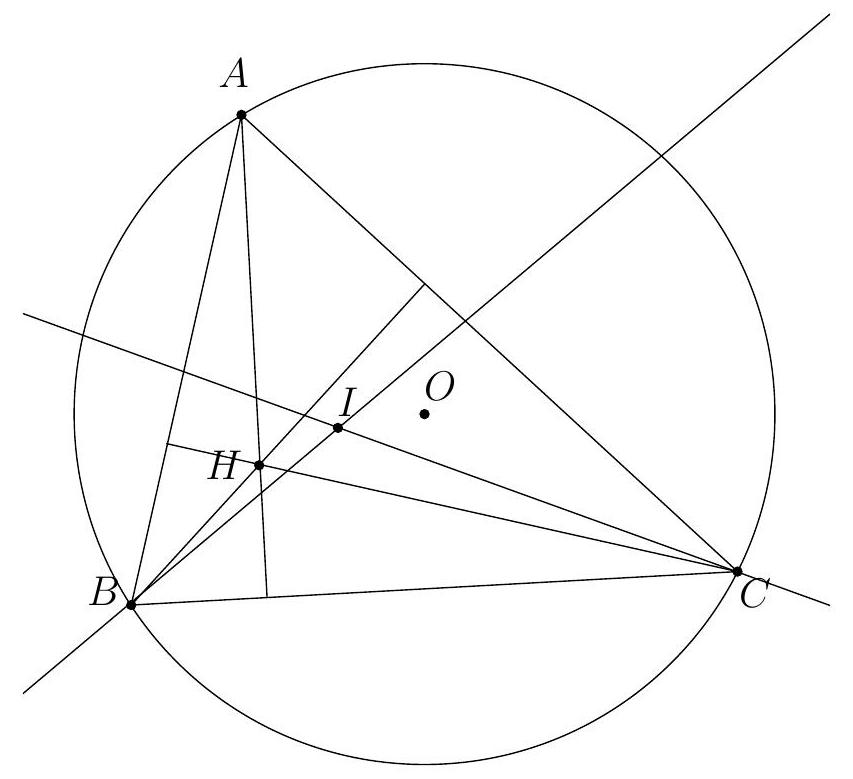\n\nOn utilise les angles de droites. Les angles sont modulo $180^{\\circ}$.\n\n1) $(H B, H C)=(H B, A C)+(A C, A B)+(A B, H C)=D-(A B, A C)+D=-(A B, A C)=-60^{\\circ}=$ $120^{\\circ}=(O B, O C)$ (où on a noté $D$ l'angle droit), donc $B, H, O, C$ sont cocycliques.\n$(I B, I C)=(I B, B C)+(B C, I C)=-\\widehat{B} / 2-\\widehat{C} / 2=-120 / 2=-60^{\\circ}=120^{\\circ}$, donc $I$ se trouve également sur ce cercle.\n2) $(C O, C I)-(C I, C H)=(C O, C B)+(C B, C I)-(C I, C B)-(C B, C H)=(C O, C B)+$ $(C H, C B)+2(C B, C I)=(90-\\widehat{A})+(90-\\widehat{B})-\\widehat{C}=0$, donc $(C O, C I)=(C I, C H)$. On a donc $(O I, O H)=(C I, C H)=(C O, C I)=(H O, H I)$, donc $O I H$ est isocèle en $I$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "## Solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Par un point $A$ d'un cercle de centre $O$, on mène une tangente à ce cercle, et on prend deux points $B$ et $C$ sur cette tangente, avec $C$ entre $A$ et $B$. De $B$ et $C$, on mène $(B D)$ et $(C E)$ tangentes au cercle. Démontrer que $\\widehat{B O C}=\\widehat{D A E}$.", "solution": "de l'exercice 3\n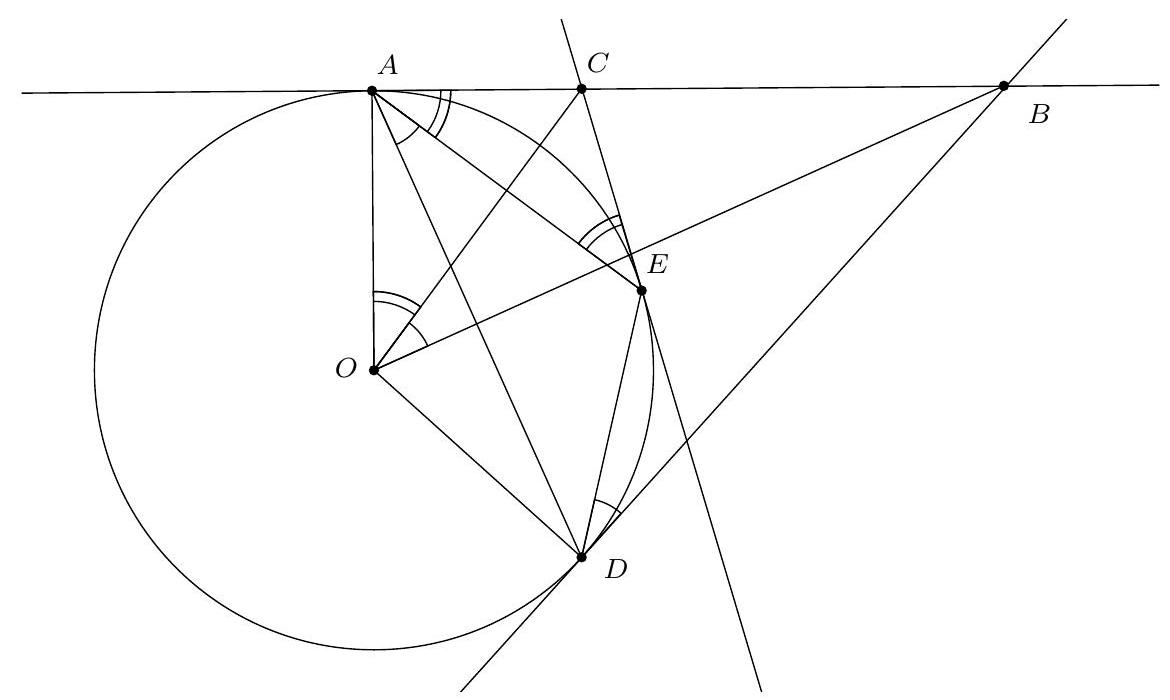\n\nNotons $\\alpha=\\widehat{B D E}$ et $\\beta=\\widehat{C E A}$. D'après le théorème de l'angle inscrit, on a $\\alpha=\\widehat{D A E}$.\nComme $(C A)$ et $(C E)$ sont les deux tangentes menées à partir de $C$, on a $\\widehat{E A C}=\\widehat{C E A}=\\beta$. $\\widehat{B O C}=\\widehat{B O A}-\\widehat{C O A} . \\mathrm{Or},(B O) \\perp(A D)$ et $(O A) \\perp(A C)$, donc $\\widehat{B O A}=\\widehat{D A C}=\\alpha+\\beta$, et de même $\\widehat{C O A}=\\beta$, donc $\\widehat{B O C}=\\alpha=\\widehat{D A E}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Soit $A B C$ un triangle. Soit $P$ appartenant au cercle circonscrit. On sait que les projetés de $P$ sur $(B C),(C A)$ et $(A B)$ sont alignés sur la droite dite de Simson. On suppose que cette droite passe par le point diamétralement opposé à $P$. Montrer qu'elle passe également par le centre de gravité de $A B C$.", "solution": "de l'exercice 4\n\n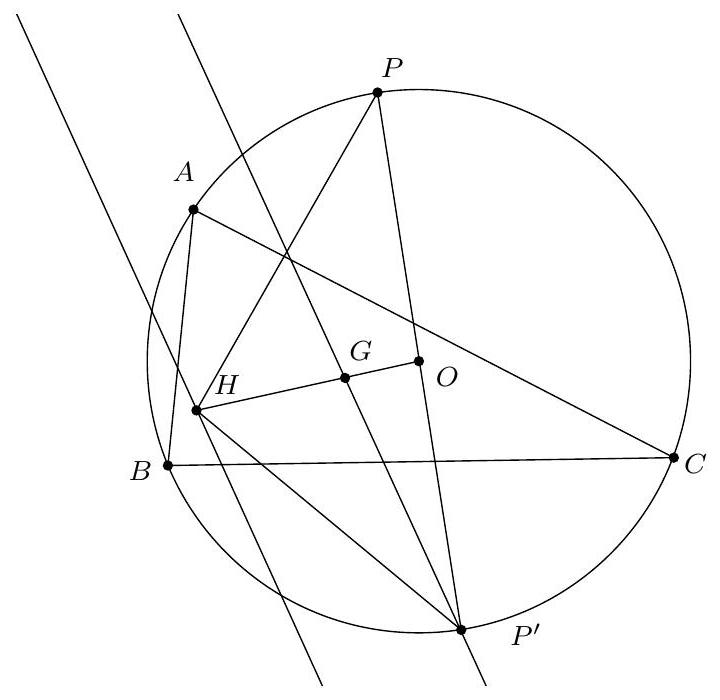\n\nNotons $P^{\\prime}$ le point diamétralement opposé à $P$. Soit $\\Delta$ la droite de Simson. Soit $h$ l'homothétie de centre $P$ et de rapport 2. Alors $h(\\Delta)$ est la droite de Steiner. On sait qu'elle passe par l'orthocentre $H$, donc $\\Delta$ passe par le milieu de $[P H]$. On en déduit que $\\Delta$ est la médiane de $P P^{\\prime} H$ issue de $P^{\\prime}$.\nPar ailleurs, (HO) est la médiane de $P P^{\\prime} H$ issue de $H$. Comme $\\overrightarrow{H G}=\\frac{2}{3} \\overrightarrow{H O}$, le point $G$ est le centre de gravité de $P H P^{\\prime}$, donc $\\Delta$ passe par $G$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "## Solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soit $A B C$ un triangle. On suppose que la médiane $(B M)$ et la bissectrice $(C D)$ se coupent en un point $J$ tel que $J B=J C$. Soit $H$ le pied de la hauteur issue de $A$. Montrer que $J M=J H$.", "solution": "de l'exercice 5\n\n\n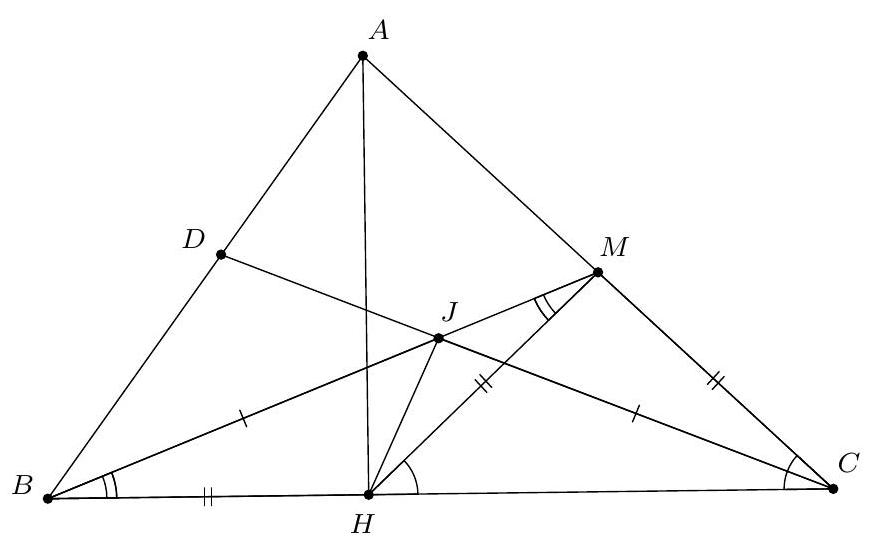\n\nNotons $\\gamma=\\widehat{A C B}$. On a $M A=M C=M H$, donc $\\widehat{C H M}=\\gamma$.\nOn a aussi $\\widehat{C H M}=180^{\\circ}-\\widehat{M H B}=\\widehat{H B M}+\\widehat{B M H}$.\nDe plus, $\\widehat{H B M}=\\widehat{D C B}=\\gamma / 2$, donc $\\widehat{B M H}=\\widehat{H M B}=\\gamma / 2$.\nOn en déduit que $B H=H M=M C$. Les triangles $B H J$ et $C M J$ vérifient $B J=C J, \\widehat{H B J}=$ $\\widehat{M C J}$ et $B H=C M$ donc sont isométriques. Par conséquent, $J H=H M$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "## \nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $A B C$ un triangle, et $D, E, F$ les pieds des hauteurs de $A, B, C$ respectivement. On définit aussi $H$ l'orthocentre de $A B C, O$ le centre de son cercle circonscrit, et $X$ le point de la droite $(E F)$ qui vérifie $X A=X D$. Montrer que les droites $(A X)$ et $(O H)$ sont perpendiculaires.", "solution": "de l'exercice 6\n\n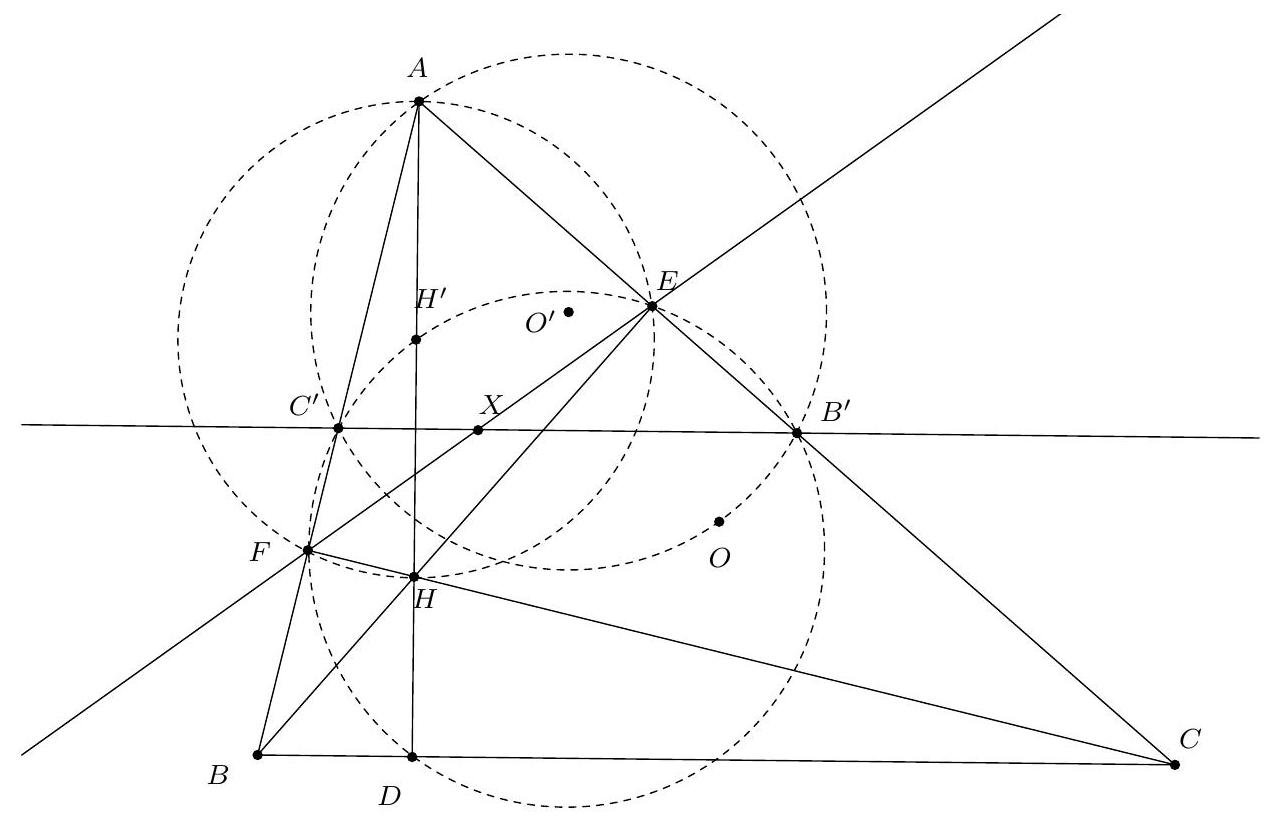\n\nOn sait que l'axe radical de deux cercles est une droite perpendiculaire à la droite passant par les centres des deux cercles.\nLa condition $X A=X D$ signifie que X est sur la médiatrice de $[A D]$, qui n'est autre que le droite des milieux $\\left(B^{\\prime} C^{\\prime}\\right)$ (avec $B^{\\prime}$ et $C^{\\prime}$ les milieux de $[A C]$ et de $[A B]$ ). On sait aussi que les points\n$A, E, F, H$ sont cocycliques d'après la réciproque du théorème de l'angle inscrit. De, plus $[A H]$ étant un diamètre du cercle passant par ces quatre points, le milieu $H^{\\prime}$ de $[A H]$ est le centre de ce cercle.\nLe centre du cercle passant par $A, B^{\\prime}, C^{\\prime}$ est le milieu $O^{\\prime}$ de $[A O]$ (par propriété de l'homothétie de centre $A$ et de rapport 1/2). On sait que $\\left(O^{\\prime} H^{\\prime}\\right)$ et $(O H)$ sont parallèles. Le problème revient donc à montrer que $(A X)$ et $\\left(O^{\\prime} H^{\\prime}\\right)$ sont perpendiculaires. Nous allons montrer ici que $(A X)$ est en fait l'axe radical des deux cercles évoqués précédemment, ce qui terminera l'exercice d'après la propriété évoquée au début de la preuve.\n$A$ étant sur les deux cercles, est bien sur leur axe radical. On sait de plus que $B^{\\prime}, C^{\\prime}, E, F$ sont cocycliques sur le cercle d'Euler du triangle $A B C$. Ainsi on a l'égalité de longueurs : $X C^{\\prime} \\times X B^{\\prime}=X E \\times X F$, ce qui signifie que $X$ est bien sur l'axe radical de nos deux cercles.\nAinsi on a bien $(A X)$ et $(O H)$ qui sont perpendiculaires.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "## Solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $A B C$ un triangle, et $\\Gamma$ son cercle circonscrit. Soit $M$ le milieu de l'arc $B C$ ne contenant pas $A$. Un cercle $\\mathscr{C}$ est tangent à $[A B),[A C)$ en $D$ et $E$ respectivement, et tangent intérieurement à $\\Gamma$ en $F$. Montrer que $(D E),(B C)$ et $(F M)$ sont concourantes.", "solution": "de l'exercice 7\n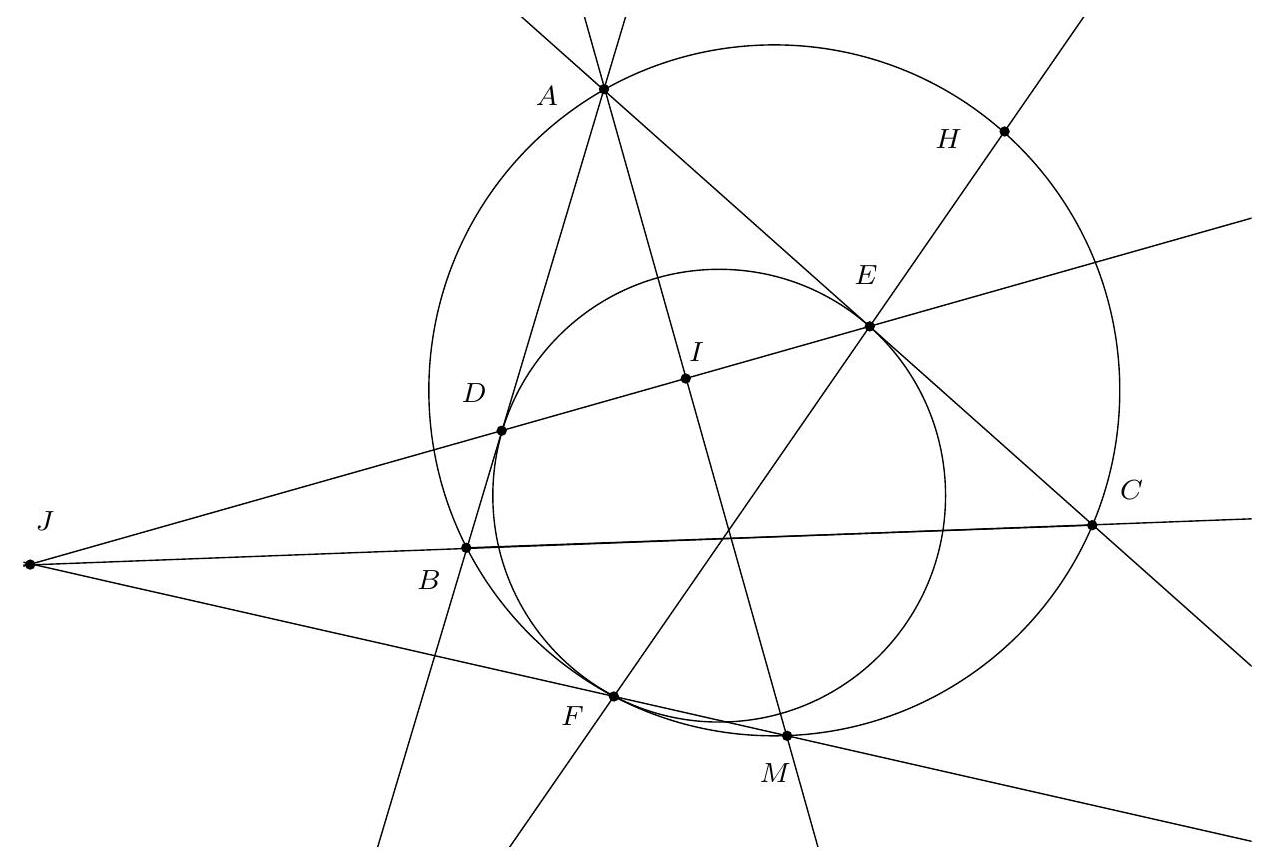\n\nSoit $I$ le centre du cercle inscrit dans $A B C$. La droite $(E F)$ recoupe $\\Gamma$ en un point $H$. Soit $J$ le point d'intersection de $(B C)$ avec $(F M)$.\nIl est facile de voir que $H$ est le milieu de l'arc $A C$ ne contenant pas $B$ : en effet, l'homothétie de centre $F$ qui envoie $\\mathscr{C}$ sur $\\Gamma$ envoie $(A C)$ sur la tangente en $H$ à $\\Gamma$; celle-ci est parallèle à $(A C)$, ce qui entraîne que $H$ est le milieu de l'arc, et par conséquent $B, I, H$ sont alignés.\nEn appliquant le théorème de Pascal à l'hexagone $A M F H B C$, on obtient que $I, E, J$ sont alignés. De même, $D, I, J$ sont alignés. Ainsi, $(D E),(B C)$ et $(F M)$ se rencontrent en $J$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle, $D, E, F$ les points de tangence du cercle inscrit sur les côtés $(B C),(A C)$ et $(A B), M$ le milieu de $[B C], I$ le centre du cercle inscrit de $A B C . G$ et $H$ sont définis comme les symétriques de $E$ et $F$ par rapport à $I$. On note $Q$ l'intersection entre les droites $(B C)$ et $(G H)$. Montrer que les droites $(I Q)$ et $(I M)$ sont perpendiculaires.", "solution": "de l'exercice 8\n\n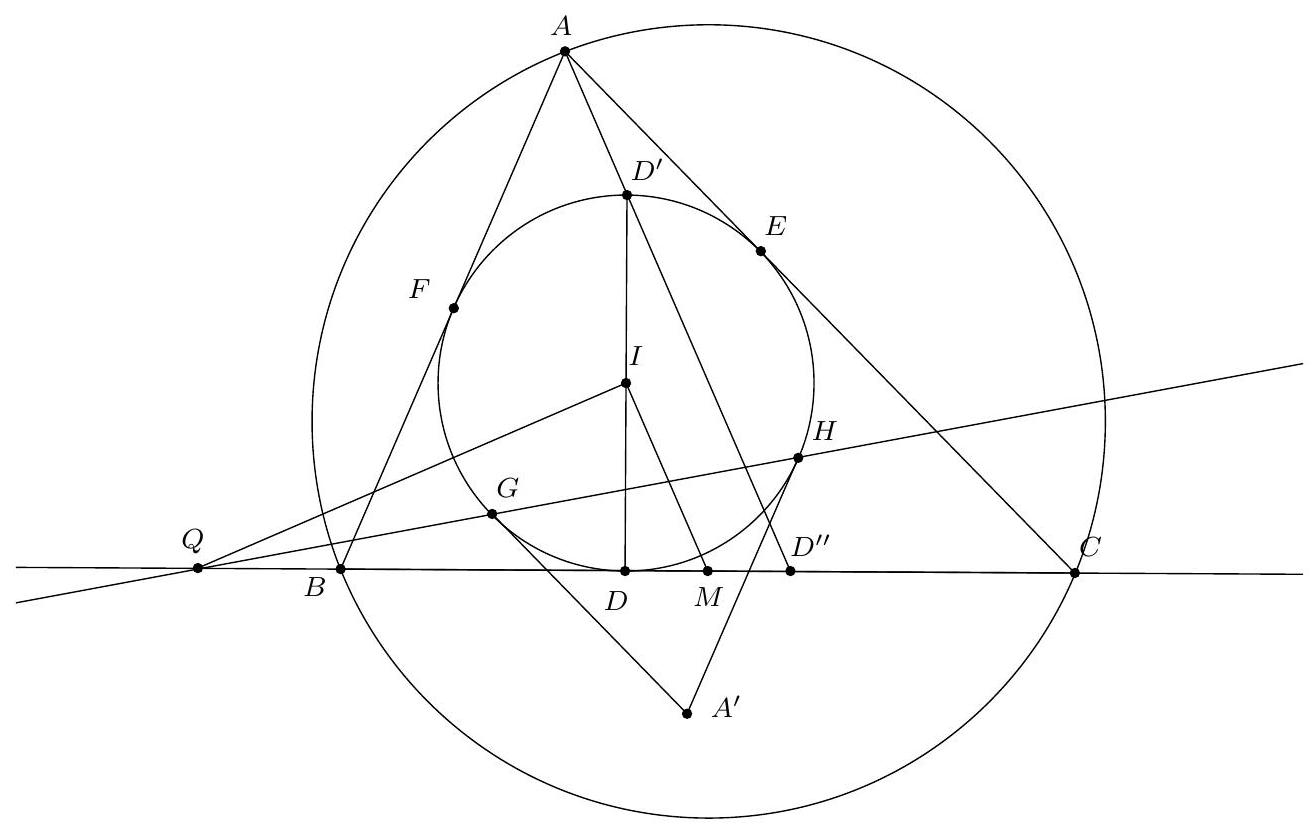\n\nSoit $\\omega$ le cercle inscrit de $A B C$.\nOn notera pour tout point $X$ du plan $p(X)$ la polaire de $X$ par rapport à $\\omega$. On sait que pour tout point $X$ du plan, $p(X)$ est une droite perpendiculaire à $(I X)$. Nous allons donc montrer que $p(Q)$ et $(I M)$ sont parallèles pour en déduire le résultat.\nOn sait que $p(D)=(B C)$, et que $Q \\in(B C)$ donc $Q \\in p(D)$. Ainsi par propriété des polaires (par rapport à un cercle fixé), on en déduit que $D \\in p(Q)$. De plus par construction de la polaire, on sait que $A^{\\prime}$ le point d'intersection des tangentes à $\\omega$ en $G$ et $H$ est aussi sur la polaire de $Q$. Ainsi on a : $p(Q)=\\left(D A^{\\prime}\\right)$. Par symétrie de la construction, on sait que $A$ et $A^{\\prime}$ sont symétriques par rapport à $I$.\nSoit maintenant $D^{\\prime}$ le symétrique de $D$ par rapport à $I$ (qui est donc sur $\\omega$ ) et $D^{\\prime \\prime}$ le point de $(B C)$ tel que $M$ soit le milieu de [ $\\left.D D^{\\prime \\prime}\\right]$. Une homothétie envoyant une droite sur une droite qui lui est parallèle, on sait que les droites $\\left(D A^{\\prime}\\right)$ et $\\left(D^{\\prime} A\\right)$ sont parallèles, ainsi que les droites $(I M)$ et $\\left(D^{\\prime} D^{\\prime \\prime}\\right)$. Or il est connu que les points $A, D^{\\prime}, D^{\\prime \\prime}$ sont alignés (se montre par une homothétie de centre $A$ ).\nAinsi les droites $\\left(D A^{\\prime}\\right)$ et $(I M)$ sont parallèles, et $\\left(D A^{\\prime}\\right)$ et $(Q I)$ étant perpendiculaires, on en déduit que $(I Q)$ et $(I M)$ sont bien perpendiculaires.\n\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "## Solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $A B C$ un triangle, $D, E, F$ les points de tangence du cercle inscrit sur les côtés $(B C),(A C)$ et $(A B), M$ le milieu de $[B C], I$ le centre du cercle inscrit de $A B C . G$ et $H$ sont définis comme les symétriques de $E$ et $F$ par rapport à $I$. On note $Q$ l'intersection entre les droites $(B C)$ et $(G H)$. Montrer que les droites $(I Q)$ et $(I M)$ sont perpendiculaires.", "solution": "Notons $\\alpha, \\beta$ et $\\gamma$ les angles de $D E F$ et $R$ le rayon du cercle circonscrit à $D E F$. On a $B D=R \\tan \\beta, C D=R \\tan \\gamma$ donc\n\n$$\n2 D M=B C-2 B D=R(\\tan \\gamma-\\tan \\beta)=R \\frac{\\sin \\gamma \\cos \\beta-\\sin \\beta \\cos \\gamma}{\\cos \\beta \\cos \\gamma}=R \\frac{\\sin (\\gamma-\\beta)}{\\cos \\beta \\cos \\gamma} .\n$$\n\nD'autre part, la loi des sinus dans $Q D H$ donne $D Q=D H \\frac{\\cos \\gamma}{\\sin (\\beta-\\gamma)}=2 R \\frac{\\cos \\beta \\cos \\gamma}{\\sin (\\beta-\\gamma)}$ donc $Q D . D M=R^{2}=D I^{2}$. Or, $[I D]$ est la hauteur de $I Q M$ issue de $I$, donc $I Q M$ est rectangle en $I$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-2-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
diff --git a/French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl b/French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..63e1e2dc2cf2c83981955f3dbb6c056b22dbb1ec
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl
@@ -0,0 +1,18 @@
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que $f(x) f(y)-f(x y)=x+y$ pour tous $x, y \\in \\mathbb{R}$.", "solution": "de l'exercice 1 Soit f une fonction vérifiant la condition de l'énoncé. En prenant $x=y=$ 0 , on obtient $f(0)(f(0)-1)=0$ donc $f(0)=0$ ou $f(0)=1$.\n\nPremier cas : supposons que $f(0)=0$. En prenant $y=0$ dans l'équation initiale, on obtient $0=\\chi$ pour tout $x \\in \\mathbb{R}$, ce qui est absurde.\n\nDeuxième cas : supposons que $f(0)=1$. En prenant $y=0$ dans l'équation initiale, on obtient $f(x)=x+1$ pour tout $x \\in \\mathbb{R}$.\nRéciproquement, on vérifie que la fonction $f(x)=x+1$ pour tout $x \\in \\mathbb{R}$ est", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que $f(x) f(y)-f(x y)=x+y$ pour tous $x, y \\in \\mathbb{R}$.", "solution": "car on a bien $(x+1)(y+1)-(x y+1)=x+y$ pour tous $x, y, \\in \\mathbb{R}$.\n\nRemarque. Il est important de vérifier que réciproquement, la fonction $f(x)=x+1$ convient. En effet, nous avons raisonné par implications successives et non pas par équivalences. Par exemple, si l'énoncé était \"Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que $f(x) f(y)-f(x y)=$ $x+y$ pour tous $x, y \\in \\mathbb{R}$ et $f(2)=2$ \", nous aurions conclu que réciproquement, la fonction $f(x)=x+1$ ne convient pas $(\\operatorname{car} f(2)=3)$ et que dans ce cas il n'y a pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que $f(x) f(y)-f(x y)=x+y$ pour tous $x, y \\in \\mathbb{R}$.", "solution": "", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $n \\geqslant 3$ un nombre entier et $a_{1}, a_{2}, \\ldots, a_{n}$ des nombres réels.\n(a) On suppose que $a_{i}<\\max \\left(a_{i-1}, a_{i+1}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$. Montrer que $a_{i}<$ $\\max \\left(a_{1}, a_{n}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$.\n(b) On suppose que $a_{i} \\leqslant \\max \\left(a_{i-1}, a_{i+1}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$. Est-il vrai que $a_{i} \\leqslant \\max \\left(a_{1}, a_{n}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$ ?\nN.B. Si $x$ et y sont deux nombres réels, on note $\\max (x, y)$ le plus grand des deux.", "solution": "de l'exercice 2 (a) Soit $i \\in\\{1,2, \\ldots, n\\}$ un entier tel que $a_{i}=\\max \\left(a_{1}, \\ldots, a_{n}\\right)$. L'énoncé indique que $i \\notin\\{2,3, \\ldots, n-1\\}$. Cela montre à la fois que $i \\in\\{1, n\\}$, donc que $a_{i}=\\max \\left(a_{1}, a_{n}\\right)$, et que $a_{k}\\max \\left(a_{1}, a_{n}\\right)$ pour tout $2 \\leqslant i \\leqslant n-1$.\n\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": "\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $n \\geqslant 3$ un nombre entier et $a_{1}, a_{2}, \\ldots, a_{n}$ des nombres réels.\n(a) On suppose que $a_{i}<\\max \\left(a_{i-1}, a_{i+1}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$. Montrer que $a_{i}<$ $\\max \\left(a_{1}, a_{n}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$.\n(b) On suppose que $a_{i} \\leqslant \\max \\left(a_{i-1}, a_{i+1}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$. Est-il vrai que $a_{i} \\leqslant \\max \\left(a_{1}, a_{n}\\right)$ pour tout $i \\in\\{2,3, \\ldots, n-1\\}$ ?\nN.B. Si $x$ et y sont deux nombres réels, on note $\\max (x, y)$ le plus grand des deux.", "solution": "pour (a). L'idée est de regarder où la suite \"remonte\" pour la première fois. Pour cela, nous allons distinguer deux cas :\n\nPremier cas : il existe un plus petit entier $1 \\leqslant \\mathfrak{i}_{0} \\leqslant n-1$ tel que $a_{i_{0}} \\leqslant a_{i_{0}+1}$. Ainsi, $a_{1}>\\cdots>a_{i_{0}}$ et $a_{i_{0}} \\leqslant a_{i_{0}+1}$. En particulier, si $i_{0}=n-1$, on remarque qu'on a bien le résultat voulu (car alors $a_{n-1}\\cdots>a_{i_{0}} \\leqslant a_{i_{0}+1}a_{2}>\\cdots>$ $a_{n}$ et on a bien le résultat voulu.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 2.", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soient $0 \\leqslant a, b, c, d, e \\leqslant 1$ des nombres réels. Montrer que\n\n$$\n(1+a+b+c+d+e)^{2} \\geqslant 4\\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\\right)\n$$", "solution": "de l'exercice 3 L'idée est d'utiliser l'inégalité $(x+y)^{2} \\geqslant 4 x y$ pour $x=1$ et une valeur particulière de $y$.\n\nPlus précisément, pour tous $x, y \\geqslant 0$, on a $(x-y)^{2} \\geqslant 0$, et donc $(x+y)^{2} \\geqslant 4 x y$ (cette inégalité est aussi l'inégalité arithmético-géométrique à deux variables). En évaluant cette inégalité avec $x=1$ et $y=a+b+c+d+e$, on obtient:\n\n$$\n(1+a+b+c+d+e)^{2} \\geqslant 4(a+b+c+d+e)\n$$\n\nOr pour tout nombre réel $x$ tel que $0 \\leqslant x \\leqslant 1$, on a $x \\geqslant x^{2}$. Donc\n\n$$\n4(a+b+c+d+e) \\geqslant 4\\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\\right)\n$$\n\nce qui montre finalement que $(1+a+b+c+d+e)^{2} \\geqslant 4\\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\\right)$.\n\n## Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 3.", "solution_match": "\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Trouver toutes les fonctions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que $f(f(x)+3 y)=12 x+f(f(y)-x)$ pour tous $x, y \\in \\mathbb{R}$.", "solution": "de l'exercice 4 Soit f une fonction satisfaisant à la condition de l'énoncé. L'idée est de montrer que f est injective en utilisant le fait qu'elle est surjective. Montrons d'abord que f est surjective. En prenant $y=-f(x) / 3$ dans l'équation fonctionnelle, on obtient $f(f(y)-x)=$ $f(0)-12 x$. En faisant varier $x$, on voit que le membre de droite de cette dernière égalité peut prendre pour valeur n'importe quel nombre réel, et donc le membre de gauche aussi, ce qui implique que f est surjective.\n\nMontrons que $f$ est injective. Soient $a, b \\in \\mathbb{R}$ tels que $f(a)=f(b)$. Nous allons montrer que $a=b$. En prenant $y=a$ et $y=b$ dans l'équation fonctionnelle, on obtient pour tout $x \\in \\mathbb{R}$\n\n$$\n\\mathbf{f}(\\mathbf{f}(\\mathrm{x})+3 \\mathbf{a})=12 x+f(f(a)-x)=12 x+f(f(b)-x)=f(f(x)+3 b)\n$$\n\noù on a utilisé le fait que $\\mathrm{f}(\\mathrm{a})=\\mathrm{f}(\\mathrm{b})$ pour la deuxième égalité. Ceci implique que pour tout $y \\in \\mathbb{R}$,\n\n$$\nf(y)=f(y+3(b-a))\n$$\n\nEn effet, si on fixe $y \\in \\mathbb{R}$, par surjectivité il existe $x$ tel que $f(x)=y-3 a$ et en injectant dans (1), ceci donne (2). En particulier, $f(0)=f(3(b-a))$. Alors\n\n$$\n\\mathbf{f}(\\mathbf{f}(0))=\\mathbf{f}(\\mathbf{f}(3(b-a))+3 \\cdot 0)=12 \\cdot 3(b-a)+\\mathbf{f}(\\mathbf{f}(0)-3(b-a))=12 \\cdot 3(b-a)+\\mathbf{f}(\\mathbf{f}(0))\n$$\n\noù pour la première égalité on utilise le fait que $f(0)=f(3(b-a))$, pour la deuxième on utilise l'équation fonctionnelle de l'énoncé (avec $x=3(b-a)$ et $y=0$ ), pour la troisième égalité on utilise (2) $(\\operatorname{avec} y=f(0)-3(b-a)$ ). Donc $3(b-a)=0$ et $a=b$.\n\nPour conclure, en prenant $x=0$ dans l'équation de départ et en utilisant l'injectivité de f , on obtient\n\n$$\nf(y)=f(0)+3 y\n$$\n\npour tout réel $y$.\nRéciproquement, on vérifie que les fonctions de la forme $f(x)=a+3 x$ pour tout $x \\in \\mathbb{R}$ avec $a \\in \\mathbb{R}$ vérifient l'équation fonctionnelle de l'énoncé.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 4.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Soient a, b, $c>0$. Montrer que\n\n$$\n\\sqrt{\\frac{a}{b+c}}+\\sqrt{\\frac{b}{c+a}}+\\sqrt{\\frac{c}{a+b}}>2 .\n$$", "solution": "de l'exercice 5 L'idée est d'utiliser inégalité arithmético-géométrique pour minorer $\\frac{1}{\\sqrt{x+y}}$. Plus précisément, on a, par inégalité arithmético-géométrique :\n\n$$\n\\sqrt{\\frac{a}{b+c}}=\\frac{a}{\\sqrt{a(b+c)}} \\geqslant \\frac{a}{(a+b+c) / 2} \\geqslant \\frac{2 a}{a+b+c}\n$$\n\nOn procède de même pour montrer que $\\sqrt{\\frac{b}{c+a}} \\geqslant \\frac{2 b}{a+b+c}$ et que $\\sqrt{\\frac{c}{a+b}} \\geqslant \\frac{2 c}{a+b+c}$. On en déduit que\n\n$$\n\\sqrt{\\frac{a}{b+c}}+\\sqrt{\\frac{b}{c+a}}+\\sqrt{\\frac{c}{a+b}} \\geqslant 2\n$$\n\nIl y a égalité seulement si et seulement si on est dans le cas d'égalité de chacune des trois inégalités arithmético-géométrique utilisées, soit : $a=b+c, b=a+c$ et $c=a+b$, ce qui est impossible.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 5.", "solution_match": "\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $n>1$ un entier. Trouver tous les polynômes $P$ non constants à coefficients réels tels que\n\n$$\nP(x) P\\left(x^{2}\\right) P\\left(x^{3}\\right) \\cdots P\\left(x^{n}\\right)=P\\left(x^{\\frac{n(n+1)}{2}}\\right)\n$$\n\npour tout nombre réel $x$.", "solution": "de l'exercice 6 Nous allons montrer que les", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $n>1$ un entier. Trouver tous les polynômes $P$ non constants à coefficients réels tels que\n\n$$\nP(x) P\\left(x^{2}\\right) P\\left(x^{3}\\right) \\cdots P\\left(x^{n}\\right)=P\\left(x^{\\frac{n(n+1)}{2}}\\right)\n$$\n\npour tout nombre réel $x$.", "solution": "s sont de la forme $\\mathrm{P}(\\mathrm{x})=\\mathrm{x}^{\\mathrm{a}}$ avec $a \\geqslant 0$ un entier si $n$ est pair, et $P(x)=x^{a}$ ou $P(x)=-x^{a}$ avec $a \\geqslant 0$ un entier si $n$ est impair. Comme $1+2+\\cdots+n=\\frac{n(n+1)}{2}$, on vérifie tout d'abord que ces polynômes vérifient l'équation de l'énoncé.\nSoit maintenant $P$ un polynôme", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Soit $n>1$ un entier. Trouver tous les polynômes $P$ non constants à coefficients réels tels que\n\n$$\nP(x) P\\left(x^{2}\\right) P\\left(x^{3}\\right) \\cdots P\\left(x^{n}\\right)=P\\left(x^{\\frac{n(n+1)}{2}}\\right)\n$$\n\npour tout nombre réel $x$.", "solution": "Écrivons d'abord $P$ sous la forme $P(x)=x^{a} Q(x)$ avec $a \\geqslant 0$ un entier et $Q$ un polynôme tel que $c=Q(0) \\neq 0$. Écrivons $Q^{\\prime}$ sous la forme $Q^{\\prime}=x^{b} S(x)$ avec $b \\geqslant 0$ un entier et $S$ un polynôme tel que $S(0) \\neq 0$ (et donc $S$ n'est pas divisible par le polynôme $x$ ), et posons\n\n$$\nR(x)=Q(x) Q\\left(x^{2}\\right) Q\\left(x^{3}\\right) \\cdots Q\\left(x^{n}\\right)\n$$\n\nL'idée est de considérer la quantité $R^{\\prime}(x) / R(x)$, où $R^{\\prime}$ est le polynôme dérivé de R. En effet, comme $1+2+\\cdots+n=\\frac{\\mathfrak{n}(\\boldsymbol{n}+1)}{2}$, Q doit aussi vérifier l'égalité\n\n$$\nQ(x) Q\\left(x^{2}\\right) Q\\left(x^{3}\\right) \\cdots Q\\left(x^{n}\\right)=Q\\left(x^{\\frac{n(n+1)}{2}}\\right) .\n$$\n\nEn faisant $x=0$, on trouve $\\boldsymbol{c}^{n-1}=1$, de sorte que $\\mathrm{c}=1$ si n est pair et $\\mathrm{c}= \\pm 1$ si n est impair. Supposons par l'absurde que $Q$ n'est pas constant (de sorte que $Q^{\\prime} n^{\\prime}$ est pas le polynôme nul), et dérivons (3) :\n\n$$\nR(x)\\left(\\frac{Q^{\\prime}(x)}{Q(x)}+2 x \\frac{Q^{\\prime}\\left(x^{2}\\right)}{Q\\left(x^{2}\\right)}+\\cdots+n x^{n-1} \\frac{Q^{\\prime}\\left(x^{n}\\right)}{Q\\left(x^{n}\\right)}\\right)=\\frac{n(n+1)}{2} x^{\\frac{n(n+1)}{2}-1} Q^{\\prime}\\left(x^{\\frac{n(n+1)}{2}}\\right) .\n$$\n\nNotons que $R(0)=c^{n} \\neq 0$ (et donc $R n^{\\prime}$ est pas divisible par le polynôme $x$ ). La plus grande puissance de $x$ qui divise le membre de droite de (4) est $x^{\\frac{n(n+1)}{2}-1+b \\frac{n(n+1)}{2}}$ tandis que la plus grande puissance de $x$ qui divise celui de gauche est $x^{b}$ (car tous les termes de la somme sont divisibles par $x^{\\mathrm{b}+1}$ sauf $\\frac{\\mathrm{Q}^{\\prime}(x)}{\\mathrm{Q}(x)}$ ). Donc\n\n$$\n\\mathrm{b}=\\frac{\\mathrm{n}(\\mathrm{n}+1)}{2}-1+\\mathrm{b} \\frac{\\mathrm{n}(\\mathrm{n}+1)}{2}\n$$\n\nOr $n \\geqslant 2$, donc\n\n$$\n\\mathrm{b}<\\mathrm{b} \\frac{\\mathrm{n}(\\mathrm{n}+1)}{2}<\\frac{\\mathrm{n}(\\mathrm{n}+1)}{2}-1+\\mathrm{b} \\frac{\\mathrm{n}(\\mathrm{n}+1)}{2}\n$$\n\nce qui est absurde. Donc $Q$ est constant, ce qui conclut.\n\n## Exercices du groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": ". Soit $n \\geqslant 2$ un nombre entier et soient $x_{1}, \\ldots, x_{n}$ des nombres réels positifs tels que $x_{1} x_{2} \\cdots x_{n}=1$. Montrer que\n\n$$\n\\frac{1}{n-1+x_{1}}+\\frac{1}{n-1+x_{2}}+\\cdots+\\frac{1}{n-1+x_{n}} \\leqslant 1\n$$", "solution": "de l'exercice 7\n En réduisant au même dénominateur, il s'agit de montrer que\n\n$$\n\\sum_{k=1}^{n} \\prod_{j \\neq k}\\left(x_{j}+n-1\\right) \\leqslant \\prod_{k=1}^{n}\\left(x_{k}+n-1\\right)\n$$\n\nOn note\n\n$$\n\\sigma_{k}=\\sum_{1 \\leqslant i_{1}<\\cdotsu_{n+1}$. Nous allons montrer que $X=F^{(n)}\\left(10^{N}-5 N\\right.$ ) (on itère $n$ fois $F$ ) est d'ordre $n$ mais pas $n+1$. Pour cela, il suffit de montrer que X n'est pas d'ordre $\\mathrm{n}+1$.\n\nOn remarque pour commencer que $F(a)-F(b)$ est toujours divisible par 9, et que si $a$ et $b$ ne différent que sur leurs $k$ derniers chiffres, alors $|a-b| \\leqslant 10^{k}$.\n\nÉtablissons maintenant une sorte de réciproque à cette remarque. Soient $a, b$ deux entiers et écrivons $a=\\sum_{i \\geqslant 0} c_{i} 10^{i}$ et $b=\\sum_{i \\geqslant 0} c_{i}^{\\prime} 10^{i}$. On a $F(a)-F(b)=\\sum_{i \\geqslant 0}\\left(c_{i}-c_{i}^{\\prime}\\right)\\left(10^{i}-1\\right)$. Si $j$ est le plus grand indice tel que $c_{j}>c_{j}^{\\prime}$, alors\n\n$$\nF(a)-F(b) \\geqslant\\left(10^{j}-1\\right)+\\sum_{i=0}^{j-1}\\left(c_{i}-c_{i}^{\\prime}\\right)\\left(10^{i}-1\\right) \\geqslant\\left(10^{j}-1\\right)-9 \\sum_{i=0}^{j-1}\\left(10^{i}-1\\right)=9 j\n$$\n\nOn en déduit que si $|F(a)-F(b)|=9 k$, alors $j \\leqslant k$, et donc\nsi $|F(a)-F(b)|=9 k, \\quad$ alors $a$ et $b$ ne peuvent différer que sur leurs $k+1$ derniers chiffres. (6)\nMontrons maintenant le lemme suivant:\nLemme. Si $F^{(n)}(a)=F^{(n)}(b)$ alors $a$ et b ne peuvent différer que sur leurs $u_{n}$ derniers chiffres.\nRevenons maintenant à la preuve du lemme en raisonnant par récurrence sur n . L'initialisation pour $n=1$ provient de (6) appliqué avec $k=0$. Pour l'hérédité, soit $n \\geqslant 1$ tel que le lemme est vrai jusqu'au rang $n$. Soient $a, b$ deux entiers tels que $F^{(n+1)}(a)=F^{(n+1)}(b)$. Alors $F^{(n)}(F(a))=$ $F^{(n)}(F(b))$, et donc $|F(a)-F(b)| \\leqslant 10^{u_{n}}$ par hypothèse de récurrence. Comme $|F(a)-F(b)|$ est divisible par 9 , écrivons $|F(a)-F(b)|=9 k$ (avec $9 k \\leqslant 10^{u_{n}}$ ). Alors d'après (6), a et b ne peuvent différer que sur leurs $k+1$ derniers chiffres. Comme $k+1 \\leqslant 10^{u_{n}} / 9+1 \\leqslant 10^{u_{n}}$, a et b ne peuvent différer que sur leurs $10^{u_{n}}=u_{n+1}$ derniers chiffres, ce qui conclut.\n\nRevenons à l'exercice. Raisonnons par l'absurde en supposant l'existence d'un entier y tel que $X=F^{(n+1)}(y)=F^{(n)}\\left(10^{N}-5 N\\right)$. Alors\n\n$$\nF^{(n)}\\left(10^{N}-5 N\\right)=F^{(n)}(F(y))\n$$\n\net donc d'après le lemme\n\n$$\n\\left|10^{\\mathrm{N}}-5 \\mathrm{~N}-\\mathrm{F}(\\mathrm{y})\\right| \\leqslant 10^{\\mathbf{u}_{\\mathrm{n}}} \\leqslant \\mathrm{~N} .\n$$\n\nDonc\n\n$$\n10^{\\mathrm{N}}-4 \\mathrm{~N} \\leqslant \\mathrm{~F}(\\mathrm{y}) \\leqslant 10^{\\mathrm{N}}-6 \\mathrm{~N}\n$$\n\nOr on constate que si $\\mathrm{y} \\geqslant 10^{\\mathrm{N}}$, alors $\\mathrm{F}(\\mathrm{y}) \\geqslant 10^{\\mathrm{N}}-1$ (en effet, on vérifie aisément que F est croissante et que $\\left.F\\left(10^{N}\\right)=10^{N}-1\\right)$. De plus, si $y \\leqslant 10^{N}-1$, alors $F(y) \\leqslant 10^{N}-9 \\mathrm{~N}-1$; en effet si $y=\\sum_{i=0}^{N-1} c_{i} 10^{i}$, alors\n\n$$\nF(y)=\\sum_{i=0}^{N-1} c_{i}\\left(10^{i}-1\\right) \\leqslant \\sum_{i=0}^{N-1} 9\\left(10^{i}-1\\right)=10^{N}-9 N-1\n$$\n\nCeci contredit (7), et $X$ vérifie bien la condition cherchée.\nAutre", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "On note $S(k)$ la somme des chiffres d'un nombre entier $k$. On dit qu'un entier a est d'ordre $n$ s'il existe une suite d'entiers $a_{0}, a_{1}, \\ldots, a_{n}$ tels que $a_{n}=a$ et $a_{i+1}=a_{i}-S\\left(a_{i}\\right)$ pour tout $i=0,1, \\ldots, n-1$. Montrer que pour tout entier $n \\geqslant 1$ il existe un entier $b$ qui soit d'ordre $n$ mais qui ne soit pas d'ordre $n+1$.", "solution": ", un peu plus courte : Comme ci-dessus, on pose $F(x)=x-S(x)$. Il vient immédiatement que $F(a+1)=F(a)$ si $a \\not \\equiv 9(\\bmod 10)$ et que $F(a+1)>F(a)$ si $a \\equiv 9(\\bmod 10)$. Par conséquent, tout entier k a au plus 10 antécédents par F , et a fortiori il a au plus $10^{\\mathrm{n}}$ antécédents par $F^{(n)}$, où $F^{(n)}$ est la $n^{\\text {ème }}$ itérée de $F$. Il s'ensuit que $F^{(n)}\\left(k+10^{n}\\right)>F^{(n)}(k)$ pour tout entier $k \\geqslant 1$ (en effet, si $F^{(n)}\\left(k+10^{n}\\right)=F^{(n)}(k)$ pour un certain entier $k \\geqslant 1$, on aurait $F^{(n)}(k)=F^{(n)}(i)$ pour tout $k \\leqslant i \\leqslant k+10^{n}$, de sorte que $l^{\\prime}$ entier $F^{(n)}(k)$ aurait au moins $10^{n}+1$ antécédents qui sont $\\left.k, k+1, k+2, \\ldots, k+10^{n}\\right)$.\n\nMaintenant, soit $\\ell$ un entier tel que $9 \\ell \\geqslant 2 \\cdot 10^{n}$. On observe que $F\\left(10^{\\ell}\\right)=10^{\\ell}-1$ et que $F\\left(10^{\\ell}-1\\right)=10^{\\ell}-1-9 \\ell$, puis on pose $a_{k}=F^{(k)}\\left(10^{\\ell}-10^{n}-1\\right)$ et $b_{k}=F^{(k)}\\left(10^{\\ell}-1\\right)$, pour $k \\geqslant 0$. Puisque $b_{0} \\geqslant a_{0}+10^{n}$, on en déduit que $b_{n}>a_{n}$. De même, puisque $a_{0} \\geqslant b_{1}+10^{n}$, on en déduit que $a_{n}>b_{n+1}$. Cela montre que $b_{0}>i>b_{1}$ pour tout entier $i$ tel que $a_{n}=F^{(n)}(i)$.\n\nOr, on a $F(k) \\geqslant b_{0}$ pour tout $k \\geqslant 10^{\\ell}$ et $F(k) \\leqslant b_{1}$ pour tout $k \\leqslant 10^{\\ell}-1$, ce qui montre que les éléments de l'ensemble $\\left\\{b_{1}+1, \\ldots, b_{0}-1\\right\\}$ sont tous d'ordre 0 mais pas d'ordre 1 . Il s'ensuit que $a_{n}$ est d'ordre $n$ mais pas d'ordre $n+1$, ce qui conclut.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que\n\n$$\nf(x) f(y f(x)-1)=x^{2} f(y)-f(x)\n$$\n\npour tous $x, y \\in \\mathbb{R}$.", "solution": "de l'exercice 9 Tout d'abord, on remarque que la fonction nulle est", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que\n\n$$\nf(x) f(y f(x)-1)=x^{2} f(y)-f(x)\n$$\n\npour tous $x, y \\in \\mathbb{R}$.", "solution": "Soit maintenant une fonction f", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-3-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Trouver toutes les fonctions $\\mathrm{f}: \\mathbb{R} \\rightarrow \\mathbb{R}$ telles que\n\n$$\nf(x) f(y f(x)-1)=x^{2} f(y)-f(x)\n$$\n\npour tous $x, y \\in \\mathbb{R}$.", "solution": "En prenant $x=0$, on obtient $f(0)(f(y f(0)-1)+1)=0$. Si $f(0) \\neq 0$, alors $f(y f(0)-1)=-1$ pour tout $y \\in \\mathbb{R}$. Comme $y f(0)-1$ parcourt $\\mathbb{R}$ quand\ny parcourt $\\mathbb{R}$, on en déduit qu'alors f est constante égale à -1 . En prenant $x=1$, on obtient $(-1)^{2}=-1^{2}+1$, ce qui est absurde. Donc $f(0)=0$.\n\nSupposons maintenant que $f n^{\\prime}$ est pas la fonction nulle. Il existe alors $a \\in \\mathbb{R}^{*}$ tel que $f(a) \\neq 0$. En prenant $x=a$ et $y=0$, on obtient $f(-1)=-1$.\n\nSi $f(x)=0$, en prenant $y=a$, on obtient $x^{2} f(a)=0$, et donc $x=0$. Ainsi, $f(x)=0$ si et seulement si $x=0$.\n\nEn prenant $x=y=1$, on obtient $f(1) f(f(1)-1)=0$, et donc, comme $f(1) \\neq 0, f(1)=1$.\nEn prenant $x=1$, on obtient $f(y-1)=f(y)-1$, et en utilisant ceci dans l'équation initiale on obtient\n\n$$\nf(x) f(y f(x))=x^{2} f(y)\n$$\n\nEn prenant $x=-1$ dans cette dernière équation, on obtient $f(-y)=-f(y)$, et donc $f$ est impaire. Combiné avec le fait que $\\mathrm{f}(\\mathrm{y}-1)=\\mathrm{f}(\\mathrm{y})-1$, on en déduit par récurrence que\n\n$$\nf(y-n)=f(y)-n\n$$\n\npour tout entier $n \\geqslant 0$, puis que $f(n)=n$ pour tout nombre entier relatif $n$. En prenant $x=n$ dans (8), on obtient\n\n$$\n\\mathrm{f}(\\mathrm{yn})=\\mathfrak{n f}(\\mathrm{y})\n$$\n\net on en déduit que $f(r)=r$ pour tout nombre rationnel $r$.\nEn prenant $y=1$ dans (8), on obtient $f(x) f(f(x))=x^{2}$. En prenant $x=y=f(x)$ dans (8), on obtient $f(f(x)) f\\left(f(x) f(f(x))=f(x)^{2} f(f(x))\\right.$. Pour $x \\neq 0, f(f(x)) \\neq 0$, et donc en simplifiant par $f(f(x))$ on obtient $f\\left(x^{2}\\right)=f\\left(f(x) f(f(x))=f(x)^{2}\\right.$. Ainsi, $f(x)>0$ pour $x>0$.\n\nSoit maintenant $z>0$ un nombre irrationnel, et supposons par l'absurde que $f(z)>z$. Soit $r=n / m$ un nombre rationnel tel que $f(z)>r>z$. Comme $m(r-z)>0$, on a $f(m(r-z))>0$. Or f est impaire (prendre $n=-1$ dans (10)), donc $m f(z)-n=f(m z)-n=f(m z-n)<0$, ce qui contredit le fait que $f(z)>r$. Le cas où $f(z)y$. On a alors $x>\\frac{x+y}{2}=2^{a-1}$, donc $2^{a-1}|\\mathrm{T}|-\\frac{1}{4}(|\\mathrm{~T}|-1)=\\frac{3}{4}(|\\mathrm{~T}|-1)+1$.\nOn peut maintenant effectuer le même raisonnement avec $x_{1}$ : il a au plus trois voisins différents de $x_{0}$ qui correspondent à trois arbres $\\mathrm{T}_{1}^{\\prime}, \\mathrm{T}_{2}^{\\prime}$ et $\\mathrm{T}_{3}^{\\prime}$, et le nombre total de sommets de ces trois arbres vaut au moins $\\frac{3}{4}(|T|-1)$. Par le principe des tiroirs il existe $i$ tel que $\\left|T_{i}^{\\prime}\\right| \\geqslant \\frac{1}{4}(|T|-1)$ donc, comme $T$ ne vérifie pas le lemme, $\\left|\\mathrm{T}_{1}^{\\prime}\\right|>\\frac{3}{4}(|\\mathrm{~T}|-1)+1$. On note $x_{2}$ le sommet par lequel $\\mathrm{T}_{1}^{\\prime}$ est relié à $x_{1}$. Comme on n'a considéré que les voisins de $x_{1}$ qui sont différents de $x_{0}$, on a $x_{2} \\neq x_{0}$. On peut alors itérer cet argument. Comme T ne vérifie pas le lemme, le procédé ne s'arrête jamais et on construit une suite $\\left(x_{n}\\right)$ de sommets telle que $x_{n+2} \\neq x_{n}$ pour tout $n$. Comme $T$ est un arbre, $\\left(x_{n}\\right)$ ne passe jamais deux fois par le même sommet donc $T$ est infini, ce qui est absurde.\n\nD'après le lemme 2, il existe donc une arête $e$ de l'arbre (en vert sur la figure) telle que, si on coupe $e$, on obtient $T_{1}$ et $T_{2}$ tels que $\\left|T_{1}\\right|,\\left|T_{2}\\right| \\geqslant \\frac{1}{4}(|T|-1)=\\frac{\\mathrm{m}^{2}-1}{2}$. Si on note $C_{1}$ et $C_{2}$ les circuits qui font le tour\nde $T_{1}$ et de $T_{2}$, on a donc d'après le lemme 1 les inégalités $\\left|C_{1}\\right|,\\left|C_{2}\\right| \\geqslant m^{2}+1$. Mais les deux parties du circuit obtenues en le coupant ont pour longueurs $\\left|C_{1}\\right|-1$ et $\\left|C_{2}\\right|-1$ (on retire l'arête orange) qui valent au moins $\\mathrm{m}^{2}$, d'où le résultat.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-4-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Soit $n \\in \\mathbb{N}^{*}$. On place des rectangles $1 \\times n$ et $n \\times 1$ sur un échiquier $2 n \\times 2 n$, de telle manière que deux rectangles ne s'intersectent jamais et que chaque rectangle recouvre exactement n cases. Un ensemble de tels rectangles est dit saturé s'il est impossible d'ajouter un rectangle sans intersecter un rectangle déjà en place.\nTrouver le plus petit $k$ tel qu'il existe un ensemble saturé de $k$ rectangles.", "solution": "de l'exercice 8 Commençons par le cas $n \\geqslant 3$ : la réponse est $k=2 n+1$. L'ensemble suivant (dans le cas $\\mathrm{n}=5$, la construction se généralisant facilement) convient :\n\n\nIl reste à montrer qu'avec 2 n rectangles il est toujours possible d'en ajouter un qui ne les intersecte pas. Si les 2 n rectangles sont orientés dans le même sens, par exemple tous horizontaux, alors il doit y en avoir exactement un sur chaque ligne (sinon il y aurait une ligne vide), et il ne peut pas être tout au bout de la ligne (s'il était tout à gauche, on pourrait ajouter un rectangle à sa droite). Par conséquent, la première et la dernière colonne sont vides, et il est possible d'ajouter un rectangle vertical.\nS'il y a des rectangles dans les deux sens, on peut supposer qu'il y a au plus n rectangles verticaux. Supposons que la configuration soit saturée. Soit $1 \\leqslant k \\leqslant n$ tel que la colonne $k$ contient un rectangle vertical noté $r$. En décalant $r$ d'une case vers la gauche, on doit intersecter un rectangle déjà en place, noté $r^{\\prime}$ (sinon on pourrait ajouter un rectangle). Cependant, si $r^{\\prime}$ était horizontal, il devrait intersecter $r$ car il n'y a pas assez de place pour un rectangle horizontal à gauche de $r$. Le rectangle $r^{\\prime}$ est donc vertical, donc la colonne $k-1$ contient un rectangle vertical et de même pour les colonnes $k-2, \\ldots, 2,1$.\nDe même, si $\\mathrm{n}+1 \\leqslant \\mathrm{k} \\leqslant 2 \\mathrm{n}$ est tel que la colonne k contient un rectangle vertical, alors toutes les colonnes à sa droite contiennent un rectangle vertical. L'ensemble des colonnes ne contenant pas de rectangle vertical est donc un ensemble d'au moins n colonnes consécutives. Il y a donc un rectangle $\\mathrm{n} \\times 2 \\mathrm{n}$ qui ne rencontre aucun des rectangles verticaux. Si la configuration est saturée, il faut donc 2 n rectangles horizontaux pour \"bloquer\" chaque ligne dans ce rectangle $\\mathrm{n} \\times 2 \\mathrm{n}$. Comme on a supposé qu'il y avait au moins un rectangle vertical, il y a donc au moins $2 \\mathrm{n}+1$ rectangles, ce qui est absurde.\nPassons aux cas $n=1$ et $n=2$ : le cas $n=1$ est trivial et la réponse est 4 (il faut tout couvrir, sinon on pourrait ajouter un carré 1 . Pour $n=2$, il n'y a pas d'ensemble saturé de 5 rectangles.\n\nPour le montrer, on peut soit effectuer une disjonction de cas un peu fastidieuse, soit adapter la preuve précédente : si tous les rectangles ont la même direction, ce n'est pas possible (une seule ligne contient 2 rectangles donc un seul rectangle peut intersecter la première colonne donc il reste la place pour un domino vertical dans la première colonne). Sinon, on peut supposer qu'il y a au plus 2 dominos verticaux. La preuve pour $n \\geqslant 3$ montre qu'il y a deux colonnes consécutives libres, donc au moins 4 dominos horizontaux, donc un seul vertical. De plus, les colonnes sans domino vertical sont consécutives donc on peut supposer que le domino vertical est dans la colonne 1. Il doit être au milieu de la colonne pour ne pas laisser une place, et il est alors facile de voir qu'il est impossible de \"boucher tous les trous\" avec 4 dominos horizontaux.\nEnfin, la configuration suivante marche avec $\\mathrm{k}=6$ :\n", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-4-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Soient $n \\geqslant 2$ et $a_{1}, \\ldots, a_{n}, b_{1}, \\ldots, b_{n}$ des réels strictement positifs. Les $a_{i}$ sont supposés deux à deux distincts, de même que les $b_{i}$. On suppose qu'il est possible de séparer les $a_{i}$ en deux sous-ensembles de même somme, et de même pour les $b_{i}$.\nMontrer qu'il existe un 2 n -gone simple ayant exactement n côtés horizontaux et n côtés verticaux, dont les longueurs des côtés horizontaux sont exactement les $a_{i}$ et dont les longueurs des côtés verticaux sont exactement les $b_{i}$.\n\nRemarque. Un polygone simple est un polygone dont les côtés ne s'intersectent pas, sauf bien sûr deux côtés consécutifs en leur extrémité commune.", "solution": "de l'exercice 9 Quitte à changer les indices et éventuellement à échanger les rôles de $a$ et $b$, on peut supposer qu'il existe $\\ell \\leqslant m \\leqslant \\frac{n}{2}$ tels que $a_{1}+\\cdots+a_{\\ell}=a_{\\ell+1}+\\cdots+a_{n}=S_{a}$ et $b_{1}+\\cdots+b_{m}=$ $b_{m+1}+\\cdots+b_{n}$, que $b_{1} \\geqslant \\cdots \\geqslant b_{m}$ et que $b_{m+1} \\leqslant \\cdots \\leqslant b_{n}$. Quand on fait le tour de notre polygone dans le sens horaire, les $a_{i}$ avec $i \\leqslant \\ell$ correspondront aux longueurs des côtés où on va vers la droite, les $a_{i}$ avec $i \\geqslant \\ell+1$ à ceux où on va vers la gauche, les $b_{i}$ avec $i \\leqslant m$ à ceux où on va vers le haut et les $b_{i}$ avec $i \\geqslant m+1$ à ceux où on va vers le bas. Il reste à placer ces côtés correctement les uns par rapport aux autres, de manière à ce qu'ils ne s'intersectent pas.\nOn note $b_{i}^{\\prime}=b_{i}$ pour $i \\leqslant m$ et $b_{i}^{\\prime}=-b_{i}$ pour $i \\geqslant m+1$, de manière à avoir $\\sum_{i=1}^{n} b_{i}^{\\prime}=0$ (ce changement de notation permettra de mesurer la variation d'ordonnée quand on passe d'un sommet du polygone à un autre). Les $b_{i}^{\\prime}$ sont alors rangés dans l'ordre décroissant.\n\nLemme. Il existe un sous-ensemble $\\mathrm{I} \\subset \\llbracket 2, n-1 \\rrbracket$ de cardinal $\\ell-1$ tel que $b_{1}^{\\prime}+\\sum_{i \\in I} b_{i}^{\\prime}>0$ et $b_{n}^{\\prime}+\\sum_{i \\in \\mathrm{I}} \\mathrm{b}_{\\mathrm{i}}^{\\prime}<0$.\n\nPreuve du lemme. L'énoncé du lemme revient à trouver I de cardinal $\\ell-1$ avec $\\left.\\sum_{i \\in I} b_{i}^{\\prime} \\in\\right]-$ $\\mathrm{b}_{1}^{\\prime},-\\mathrm{b}_{n}^{\\prime}\\left[\\right.$. Soient $\\mathrm{I}_{\\max }=\\{2, \\ldots, \\ell\\}$ et $\\mathrm{I}_{\\min }=\\{\\mathrm{n}-\\ell+1, \\ldots, \\mathrm{n}-1\\}$. Il est clair que $\\sum_{i \\in \\mathrm{I}_{\\max }} \\mathrm{b}_{\\mathrm{i}}^{\\prime}>-\\mathrm{b}_{1}^{\\prime}$ (si on a $n$ nombres de somme nulle, la somme des $\\ell$ plus grand est positive) et que $\\sum_{i \\in \\mathrm{I}_{\\mathrm{min}}} b_{i}^{\\prime}<$ $-b_{n}^{\\prime}$.\nSi on remplace un par un les éléments de $I_{\\min }$ par ceux de $I_{\\max }$, la somme augmente à chaque étape d'un nombre de la forme $b_{i}^{\\prime}-b_{j}^{\\prime}\\max \\left\\{y_{A}, y_{D}\\right\\}$. Comme il est évident que $y_{B}>y_{A}$ et $y_{C}>y_{D}$, il suffit de montrer $y_{C}>y_{A}$ et $y_{B}>y_{D}$. Or, $y_{C}-y_{A}=$ $b_{1}+\\sum_{i \\in I} b_{i}^{\\prime}$, qui est strictement positive d'après le lemme. De même, $y_{D}-y_{B}=\\sum_{i \\in I} b_{i}^{\\prime}-b_{n}^{\\prime}$ qui est strictement négative d'après le lemme. On peut donc tracer une ligne horizontale (en orange sur la figure) telle que la ligne bleue soit strictement au-dessus et la verte strictement en-dessous.\n\nRemarque. L'énoncé original omettait la condition \"les $b_{i}$ sont deux à deux distincts\". Un contre-exemple assez simple sans cette hypothèse est le suivant: $n=4$ avec $a_{1}=a_{2}=a_{3}=a_{4}$ et $b_{1}=b_{2}=b_{3}=b_{4}$. En revanche, la preuve ci-dessus peut être adaptée dès que les $a_{i}$ ne sont pas tous égaux ou que les $b_{i}$ ne sont pas tous égaux.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-4-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
diff --git a/French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl b/French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..46cb6011d4837a24f24b6dbfe1012ddcc977a35a
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl
@@ -0,0 +1,15 @@
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\\mathbf{p}, \\mathbf{q}, \\mathrm{r}$, pas forcément distincts, tels que\n\n$$\na=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}\n$$", "solution": "de l'exercice 1\n Tout d'abord, si $p=q=r$, alors on obtient $\\mathrm{a}=6$, qui est bien une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": "\n\n\nSolution "}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\\mathbf{p}, \\mathbf{q}, \\mathrm{r}$, pas forcément distincts, tels que\n\n$$\na=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}\n$$", "solution": "Montrons qu'il s'agit de la seule", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution."}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\\mathbf{p}, \\mathbf{q}, \\mathrm{r}$, pas forcément distincts, tels que\n\n$$\na=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}\n$$", "solution": ", et supposons qu'il existe une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution"}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\\mathbf{p}, \\mathbf{q}, \\mathrm{r}$, pas forcément distincts, tels que\n\n$$\na=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}\n$$", "solution": "$a=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}$ avec $p, q, r$ premiers et non tous égaux.\n\n- Si deux des nombres $p, q, r$ sont égaux, disons $p=q \\neq r$, alors:\n\n$$\n\\mathrm{a}=2\\left(\\frac{\\mathrm{p}}{\\mathrm{r}}+\\frac{\\mathrm{r}}{\\mathrm{p}}\\right)+2=\\frac{2\\left(\\mathrm{p}^{2}+\\mathrm{r}^{2}\\right)}{\\mathrm{pr}}+2\n$$\n\nAinsi, $\\frac{2\\left(\\mathfrak{p}^{2}+r^{2}\\right)}{p r}$ est un entier. On en déduit que le nombre premier $p$ divise $2 r^{2}$ tout en étant premier avec $r$, et donc que $p=2$. Le raisonnement $s^{\\prime}$ adapte mot pour mot pour prouver que $r=2$, ce qui contredit que $r \\neq p$. Il n'y a donc pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\\mathbf{p}, \\mathbf{q}, \\mathrm{r}$, pas forcément distincts, tels que\n\n$$\na=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}\n$$", "solution": "dans ce cas.\n\n- Si $p, q, r$ sont deux à deux distincts alors, sans perte de généralité, on peut supposer que $p>q>$ $r$ (on note qu'alors $p$ et $q$ sont impairs), et alors\n\n$$\n\\operatorname{apqr}=\\mathrm{pq}(\\mathrm{p}+\\mathrm{q})+\\mathrm{qr}(\\mathbf{q}+\\mathrm{r})+\\mathrm{rp}(\\mathrm{r}+\\mathrm{p})\n$$\n\nAinsi, $p$ divise $q r(q+r)$. Puisque $p$ est premier avec $q r$, il divise donc $q+r$. Mais $01$ impair. Il n'y a ainsi pas de", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\\mathbf{p}, \\mathbf{q}, \\mathrm{r}$, pas forcément distincts, tels que\n\n$$\na=\\frac{p+q}{r}+\\frac{q+r}{p}+\\frac{r+p}{q}\n$$", "solution": "dans ce cas, ce qui conclut.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2015-2016-envoi-5-solutions.jsonl", "problem_match": "\nExercice 1.", "solution_match": " solution "}}
+{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Au club théâtre d'un lycée, on a formé 14 groupes de 4 élèves afin de travailler les scènes d'une pièce. Deux groupes différents ont toujours un et un seul élève en commun.\na) Prouver qu'il existe un élève qui appartient à au moins 5 groupes.\nb) Chaque élève du club théâtre est membre d'au moins un groupe. Combien y a-t-il d'élèves dans ce club?", "solution": "de l'exercice 2\n\na) Soit G un des groupes. Chacun des 13 autres groupes a un élève en commun avec G. Or $13=3 \\times 4+1$ donc, d'après le principe des tiroirs, un des quatre élèves de G, disons $x$, appartient à au moins 4 des neuf autres groupes. Avec G, cela signifie que $x$ appartient à au moins 5 groupes.\nb) Prouvons que $x$ appartient à tous les groupes. On note $\\mathrm{G}=\\mathrm{G}_{1}, \\mathrm{G}_{2}, \\mathrm{G}_{3}, \\mathrm{G}_{4}, \\mathrm{G}_{5}$ des groupes auxquels appartient $x$, puis on procède par l'absurde : supposons qu'il existe un groupe $\\mathrm{G}^{\\prime}$ tel que $x \\notin \\mathrm{G}^{\\prime}$.\nPuisque $\\mathrm{G}^{\\prime}$ a un élève en commun avec chacun des groupes $\\mathrm{G}_{1}, \\mathrm{G}_{2}, \\mathrm{G}_{3}, \\mathrm{G}_{4}, \\mathrm{G}_{5}$ et, comme $\\mathrm{G}^{\\prime}$ ne contient que quatre élèves, c'est que l'un des membres de $G^{\\prime}$, disons $y$, appartient à deux de ces cinq groupes, disons $G_{i}$ et $G_{j}$, avec $1 \\leqslant ix_{3}+x_{4}$. Puisqu'il s'agit d'entiers, on a donc $x_{1}+x_{2}-x_{3}-x_{4} \\geqslant 1$. Soit $n=\\left\\lfloor\\sqrt{x_{1}}\\right\\rfloor$. Par définition de $S$, pour $i=1,2,3,4$, il existe donc un entier $w_{i}$ tel que $0 \\leqslant w_{i} \\leqslant 2 n$ et $x_{i}=n^{2}+w_{i}$.\n\nLes inégalités $x_{1} x_{2} \\leqslant x_{3} x_{4}$ et $x_{1}+x_{2}>x_{3}+x_{4}$ deviennent respectivement\n\n$$\nw_{1}+w_{2}-w_{3}-w_{4} \\geqslant 1 \\quad \\text { et } \\quad\\left(w_{1}+w_{2}-w_{3}+w_{4}\\right) n^{2} \\leqslant w_{3} w_{4}-w_{1} w_{2}\n$$\n\nEn particulier, on doit avoir $\\boldsymbol{w}_{3}>0$, et donc\n\n$$\n\\begin{aligned}\n\\mathrm{n}^{2} & \\leqslant\\left(w_{1}+w_{2}-w_{3}+w_{4}\\right) n^{2} \\leqslant w_{3} w_{4}-w_{1} w_{2} \\\\\n& 0$ :\n\n$$\n\\left(a_{n-1} \\vee a_{n-2}\\right)\\left(4+c_{4}-n\\right)=a_{n+1}\n$$\n\nTout d'abord, par construction, l'égalité ( $E_{4}$ ) est vraie. Supposons maintenant que l'égalités ( $E_{n-1}$ ) est vraie, et déduisons-en que, si $a_{4}, \\ldots, a_{n}>0$, alors ( $E_{n}$ ) est vraie aussi. Puisque $a_{n-3}$ divise $a_{n-1}$, on observe que\n\n$$\n\\begin{aligned}\n\\left(a_{n-1} \\wedge a_{n}\\right)\\left(a_{n-1} \\vee a_{n-2}\\right) & =\\left(a_{n-1} \\wedge\\left(a_{n-1} \\vee a_{n-2}-a_{n-2} \\vee a_{n-3}\\right)\\right) \\cdot\\left(a_{n-1} \\vee a_{n-2} \\vee a_{n-3}\\right) \\\\\n& =\\left(a_{n-1} \\wedge\\left(a_{n-2} \\vee a_{n-3}\\right)\\right) \\cdot\\left(a_{n-1} \\vee\\left(a_{n-2} \\vee a_{n-3}\\right)\\right) \\\\\n& =a_{n-1}\\left(a_{n-2} \\vee a_{n-3}\\right) .\n\\end{aligned}\n$$\n\nOr, puisque\n\n$$\n\\begin{aligned}\n\\left(E_{n}\\right) & \\Leftrightarrow \\frac{a_{n+1}}{a_{n-1} \\vee a_{n-2}}=4+c_{4}-n=\\frac{a_{n}}{a_{n-2} \\vee a_{n-3}}-1 \\\\\n& \\Leftrightarrow \\frac{a_{n} \\vee a_{n-1}}{a_{n-1} \\vee a_{n-2}}=\\frac{a_{n}}{a_{n-1} \\vee a_{n-2}}+1=\\frac{a_{n}}{a_{n-2} \\vee a_{n-3}} \\\\\n& \\Leftrightarrow\\left(a_{n-1} \\vee a_{n-2}\\right) a_{n}=\\left(a_{n-2} \\vee a_{n-3}\\right)\\left(a_{n} \\vee a_{n-1}\\right) \\\\\n& \\Leftrightarrow\\left(a_{n-1} \\vee a_{n-2}\\right) a_{n}\\left(a_{n} \\wedge a_{n-1}\\right)=\\left(a_{n-2} \\vee a_{n-3}\\right) a_{n} a_{n-1},\n\\end{aligned}\n$$\n\non en déduit que ( $E_{n}$ ) est bien vraie.\nIl s'ensuit qu'il existe un entier naturel $k$, minimal, tel que $k \\leqslant c_{4}+5$ et $a_{k} \\leqslant 0$. Si $k \\leqslant 5$, alors on a bien $k \\leqslant a_{3}+4$. Sinon, alors $00$, comme $7 \\mid 2016$, on a modulo $7 x^{2}+y^{2}=0$, ce qui donne, en écrivant la table des carrés modulo 7, $x$ et $y$ congrus modulo 7. On peut donc poser $x=7 x_{1}$ et $y=7 y_{1}$ avec $x_{1}, y_{1}$ entiers. Donc $49 \\mid x^{2}+y^{2}$, c'est-dire $49 \\mid 3 \\cdot 2016^{z}+77$ donc $z=1$. Il vient alors $x_{1}^{2}+y_{1}^{2}=125$. On teste les cas restants un par un pour voir ceux qui marchent a main : $\\left(x_{1}, y_{1}\\right)=(5,10),(2,11),(10,5),(11,2)$. Ainsi, tous les triplets", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les triplets d'entiers naturels $(x, y, z)$ tels que :\n\n$$\nx^{2}+y^{2}=3 \\cdot 2016^{z}+77 \\text {. }\n$$", "solution": "s sont dans l'ensemble :\n\n$$\n\\{(4,8,0),(8,4,0),(35,70,1),(70,35,1),(14,77,1),(77,14,1)\\}\n$$\n\net on vérifie que, réciproquement, tous ces triplets sont bien des", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": "2017", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Trouver tous les triplets d'entiers naturels $(x, y, z)$ tels que :\n\n$$\nx^{2}+y^{2}=3 \\cdot 2016^{z}+77 \\text {. }\n$$", "solution": "s.\n\n## Exercices du groupe A", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 6.", "solution_match": " solution"}}
+{"year": "2017", "tier": "T2", "problem_label": "7", "problem_type": null, "problem": "Soit $p$ un nombre premier, $m$ un entier naturel. Trouver le plus petit entier $d$ tel qu'il existe un polynôme unitaire $Q$ de degré $d$ à coefficients entiers tel que, pour tout entier $n, p^{m} \\mid Q(n)$.", "solution": "de l'exercice 7\n Montrons que $d$ est le plus petit entier tel que $p^{m} \\mid d$ !. Soit $k$ le plus petit entier tel que $p^{m} \\mid k$ !.\nTout d'abord, montrons que $k \\geq d$. On considère le polynôme $Q(x)=X(X+1) \\cdots(X+k-1)$ : il est unitaire, de degré $k$, oefficients entiers. Qui plus est, pour tout $n \\in \\mathbb{N}, Q(n)=k!\\binom{n}{k}$ (c'est une propriété des coefficients binomiaux), d'où $p^{m}|k!| Q(n)$. Donc $k$ est un entier pour lequel on dispose d'un polynôme $Q$ unitaire oefficients entiers de degré $k$ tel que pour tout $n \\in \\mathbb{N}, p^{m} \\mid Q(n)$. Donc $k \\geq d$. Reste ontrer le sens réciproque. Autrement dit, soit $Q$ un polynôme unitaire oefficients entiers de degré $l$ tel que pour tout entier $n, p^{m} \\mid Q(n)$. Montrons que $k \\leq l$. Il suffit de montrer que $p^{m} \\mid l$ ! (car, par définition, $k$ est le plus petit entier érifier cela).\n\nOn introduit la famille des polynômes $P_{i}:=X(X+1) \\cdots(X+i-1)$ pour $i \\in\\{0, \\ldots l\\}\\left(P_{0}:=1\\right)$. En effectuant les divisions euclidiennes successives de $Q$ par $P_{l}, P_{l-1}, \\ldots, P_{0}$, on montre que $Q$ s'écrit :\n\n$$\nQ=\\sum_{i=0}^{l} c_{i} P_{i}\n$$\n\noù $c_{i} \\in \\mathbb{Z}$ pour tout $i$.\nOn montre alors par récurrence sur $i \\in\\{0 \\ldots l\\}$ la propriété suivante :\n\n$$\np^{m}\\left|c_{i} P_{i}(-i)\\right| c_{i} P_{i}(n) \\text { pour tout } n \\in \\mathbb{Z}\n$$\n\n- pour $i=0$, le seul des $P_{i}$ qui ne s'annule pas en zéro est $P_{0}$, donc $Q(0)=c_{0}$, d'où $p^{m} \\mid c_{0}=$ $c_{0} P_{0}(n)$ pour tout $n \\in \\mathbb{Z}$.\n- soit $ii+1,(X+i+1) \\mid P_{j}$ donc $P_{j}(-i-1)=0$. Ainsi,\n\n$$\n\\underbrace{Q(-i-1)}_{p^{m} \\mid}=\\underbrace{\\sum_{j=0}^{i} c_{j} P_{j}(-i-1)}_{p^{m} \\mid}+c_{i+1} P_{i+1}(-i-1)\n$$\n\npar hypothèse de récurrence et par définition de $Q$. Donc $p^{m} \\mid c_{i+1} P_{i+1}(-i-1)$, et comme $P_{i+1}(-i-1)=(i+1)!$ divise tout produit de $i+1$ entiers consécutifs (on peut encore le voir grâce aux coefficients binomiaux), il divise $P_{i+1}(n)$ pour tout $n \\in \\mathbb{Z}$.\n\nAinsi, on obtient en particulier $p^{m} \\mid P_{l}(n)$ pour tout $n \\in \\mathbb{N}$, donc $p^{m} \\mid l$ !. Donc $k \\leq l$, d'où $k \\leq d$. Par double encadrement, on a donc bien montré que $k=d$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 7.", "solution_match": "\n\nSolution "}}
+{"year": "2017", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Si $n \\in \\mathbb{N}^{*}$, on note $d(n)$ son nombre de diviseurs. Quels sont les entiers strictement positifs tels que $d(n)^{3}=4 n$ ?", "solution": "de l'exercice 8 Soit $f(n):=\\frac{d(n)^{3}}{n}$, l'énoncé revient rouver les antécédents de 4 par $f$. On remarque que $f(a b)=f(a) f(b)$ si $a$ et $b$ sont premiers entre eux. Ceci nous incite écomposer $n$ en produit de facteurs premiers :\n\n$$\nn=p_{1}^{a_{1}} \\times p_{2}^{a_{2}} \\times \\cdots \\times p_{l}^{a_{l}},\n$$\n\noù les $p_{i}, 1 \\leqslant i \\leqslant l$, sont premiers et $a_{i} \\geqslant 1$. On a donc $f(n)=\\prod_{i=1}^{l} f\\left(p_{i}^{a_{i}}\\right)$.\nSoit $n \\in \\mathbb{N}^{*}$ vérifiant l'énoncé, $n^{3}=2 \\times(d(n) / 2)^{3}$ est le double d'un cube parfait ( $d(n)$ est nécessairement pair). On en déduit que $v_{p}(n) \\equiv 0(\\bmod 3)$ pour $p$ nombre premier impair, et $v_{2}(n) \\equiv 1(\\bmod 3)$. Ici, $v_{p}(n)$ désigne la valuation $p$-adique de $n$, soit le plus grand entier $k$ tel que $p^{k} \\mid n$, donc $v_{p_{i}}(n)=a_{i}$ avec nos notations. On peut écrire\n\n$$\nf(n)=\\frac{\\left(\\left(a_{1}+1\\right)\\left(a_{2}+1\\right) \\cdots\\left(a_{l}+1\\right)\\right)^{3}}{p_{1}^{a_{1}} p_{2}^{a_{2}} \\cdots p_{l}^{a_{l}}}\n$$\n\nD'après la remarque précédente, le numérateur n'est pas divisible par 3, donc aucun des $p_{i}$ ne peut valoir 3. Et $n$ est le produit de puissances de cubes de nombres premiers impairs que multplie le double d'une puissance de $2^{3}$.\nOn montre aisément que si $m$ est puissance du cube d'un nombre premier strictement plus grand que 3 , alors $f(m) \\geqslant \\frac{64}{125}$ avec égalité si et seulement si $m=5^{3}$. On prouve ette fin que pour tout premier $p \\geqslant 5$, $k \\rightarrow f\\left(p^{3 k}\\right)$ est strictement décroissante, et que pour tout $k \\geqslant 1, p \\rightarrow f\\left(p^{3 k}\\right)$ l'est aussi. Pour avoir $f(n)=4$, il faut donc utiliser des puissances de 2 . On a $f(2)=f\\left(2^{7}\\right)=4, f\\left(2^{4}\\right)=\\frac{125}{16}$ et $f\\left(2^{3 k+1}\\right)<1$ pour $k>2$.\nAinsi, 2 et 128 sont", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": "\nSolution "}}
+{"year": "2017", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Si $n \\in \\mathbb{N}^{*}$, on note $d(n)$ son nombre de diviseurs. Quels sont les entiers strictement positifs tels que $d(n)^{3}=4 n$ ?", "solution": "Et pour en avoir une autre, il faut trouver $m$ un produit de puissances de cubes de nombres premiers impairs tel que $f(m)=\\frac{64}{125}$. D'après l'étude précédente, seul $m=5^{3}$ convient. Donc il y a 3 entiers $n$", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution."}}
+{"year": "2017", "tier": "T2", "problem_label": "8", "problem_type": null, "problem": "Si $n \\in \\mathbb{N}^{*}$, on note $d(n)$ son nombre de diviseurs. Quels sont les entiers strictement positifs tels que $d(n)^{3}=4 n$ ?", "solution": "au problème : $n=2, n=2^{7}$ et $n=2^{4} \\times 5^{3}$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 8.", "solution_match": " solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Prouver qu'il existe une infinité d'entiers $n$ tels que $2^{2^{n}+1}+1$ est divisible par $n$, mais $2^{n}+1$ ne l'est pas.", "solution": "de l'exercice 9 Pour $m \\geqslant 1$, posons $a_{m}=2^{3^{m}}+1$. On a\n$a_{m}=\\left(2^{3^{m-1}}+1\\right)\\left(\\left(2^{3^{m-1}}\\right)^{2}-2^{3^{m-1}}+1\\right)=a_{m-1}\\left(\\left(2^{3^{m-1}}\\right)^{2}-2^{3^{m-1}}+1\\right)$.\nNotons que pour $a \\in \\mathbb{N}^{*}$, si $p \\mid a+1$ et $p \\mid a^{2}-a+1$, alors $p \\mid 2 a-1$ car $2 a-1=a(a+1)-\\left(a^{2}-a+1\\right)$. Et $p \\mid 2 a+2$, donc $p \\mid 3$. Donc $\\left(a_{m-1} \\wedge a_{m}\\right) \\mid 3$ pour tout $m \\in \\mathbb{N} *$. Donc $a_{m}$ possède un facteur premier impair (car $a_{m}$ impair) autre que 3 qui ne divise pas $a_{m-1}$, sauf éventuellement si $a_{m}$ est une puissance de 3 , auquel cas $a_{m+1}$ possède un facteur premier que n'a pas $a_{m}$.\nDonc pour une infinité d'entiers $m \\in \\mathbb{N}^{*}, a_{m}$ possède un facteur premier $p_{m}>3$ qui ne divise pas $a_{m-1}$. Posons $b_{m}=3^{m-1} p_{m}$. D'après le petit théorème de Fermat,\n\n$$\n2^{b_{m}}+1 \\equiv 2^{3^{m-1}}+1 \\equiv a_{m-1} \\quad(\\bmod p)_{m}\n$$\n\nDonc $p_{m} \\nmid 2^{b_{m}}+1$, donc $b_{m} \\nmid 2^{b_{m}}+1$.\nComme $p_{m}$ et 3 sont premiers entre eux, il suffit de montrer que $p_{m} \\mid 2^{2^{b m}+1}+1$ et que $3^{m_{1}} \\mid 2^{2^{b_{m}}+1}+1$. Cela se fait assez directement avec LTE mais on peut peut-être trouver une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": "\n\nSolution "}}
+{"year": "2017", "tier": "T2", "problem_label": "9", "problem_type": null, "problem": "Prouver qu'il existe une infinité d'entiers $n$ tels que $2^{2^{n}+1}+1$ est divisible par $n$, mais $2^{n}+1$ ne l'est pas.", "solution": "alternative. Recherche en cours.\nAinsi, une infinité d'entiers $b_{m}$ satisfont la condition de l'énoncé.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-1-solutions.jsonl", "problem_match": "\nExercice 9.", "solution_match": " solution "}}
diff --git a/French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl b/French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl
new file mode 100644
index 0000000000000000000000000000000000000000..55915d4da4ed7c51ade00564b3927060d16a6d76
--- /dev/null
+++ b/French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl
@@ -0,0 +1,17 @@
+{"year": "2017", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Déterminer la valeur minimale de\n\n$$\n\\left\\lfloor\\frac{\\mathrm{a}+\\mathrm{b}+\\mathrm{c}}{\\mathrm{~d}}\\right\\rfloor+\\left\\lfloor\\frac{\\mathrm{b}+\\mathrm{c}+\\mathrm{d}}{\\mathrm{a}}\\right\\rfloor+\\left\\lfloor\\frac{\\mathrm{c}+\\mathrm{d}+\\mathrm{a}}{\\mathrm{~b}}\\right\\rfloor+\\left\\lfloor\\frac{\\mathrm{d}+\\mathrm{a}+\\mathrm{b}}{\\mathrm{c}}\\right\\rfloor\n$$\n\nlorsque $\\mathrm{a}, \\mathrm{b}, \\mathrm{c}, \\mathrm{d}$ décrivent $\\mathbb{N}^{*}$.", "solution": "de l'exercice 1\n\nLe minimum cherché est 9.\nEn effet, si a, b, c, d sont des entiers naturels non nuls, on pose\n\n$$\nf(a, b, c, d)=\\left\\lfloor\\frac{a+b+c}{d}\\right\\rfloor+\\left\\lfloor\\frac{b+c+d}{a}\\right\\rfloor+\\left\\lfloor\\frac{c+d+a}{b}\\right\\rfloor+\\left\\lfloor\\frac{d+a+b}{c}\\right\\rfloor .\n$$\n\nOn rappelle que, pour tout réel $x$, on a $\\lfloor x\\rfloor>x-1$. Ainsi, pour tous entiers $a, b, c, d>0$, on a\n\n$$\n\\begin{aligned}\nf(a, b, c, d)+4 & >\\frac{a+b+c}{d}+\\frac{b+c+d}{a}+\\frac{c+d+a}{b}+\\frac{d+a+b}{c} \\\\\n& >\\left(\\frac{a}{b}+\\frac{b}{a}\\right)+\\left(\\frac{a}{c}+\\frac{c}{a}\\right)+\\left(\\frac{a}{d}+\\frac{d}{a}\\right)+\\left(\\frac{b}{c}+\\frac{c}{b}\\right)+\\left(\\frac{b}{d}+\\frac{d}{b}\\right)+\\left(\\frac{c}{d}+\\frac{d}{c}\\right) \\\\\n& >6 \\times 2 \\text { car } t+\\frac{1}{t} \\geqslant 2 \\text { pour tout réel } t>0 .\n\\end{aligned}\n$$\n\nAinsi, $f(a, b, c, d)>8$. Or, $f(a, b, c, d)$ étant clairement un entier, $c^{\\prime}$ est donc que $f(a, b, c, d) \\geqslant$ 9. Il reste à vérifier que $f(5,5,5,4)=9$ pour conclure.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 1.", "solution_match": "## Solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Soit $m$ et $n$ des entiers naturels non nuls. Prouver que\n\n$$\n\\frac{(m+n)!}{(m+n)^{m+n}}<\\frac{m!}{m^{m}} \\frac{n!}{n^{n}}\n$$", "solution": "de l'exercice 2\n\nD'après la formule du binôme, on a\n\n$$\n(m+n)^{m+n}=\\sum_{k=0}^{m+n}\\binom{m+n}{k} m^{k} n^{m+n-k}\n$$\n\nLe membre de droite étant une somme de $m+n+1$ nombres strictement positifs, elle est strictement plus grande que n'importe lequel de ces nombres. En particulier, pour $k=m$, on a donc\n\n$$\n(m+n)^{m+n}>\\binom{m+n}{m} m^{m} n^{n}\n$$\n\nPuisque $\\binom{m+n}{m}=\\frac{(m+n)!}{m!n!}$, cela conclut.\nRemarque L'inégalité demandée peut s'interpréter en termes probabilistes. En effet, considérons une urne contenant $m$ boules blanches et $n$ boules noires indiscernables au toucher, et de laquelle on tire successivement $m+n$ boules avec remise. Il est facile de vérifier que la probabilité $p_{m}$ d'obtenir exactement $m$ boules blanches au cours de ces $m+n$ tirages est\n\n$$\np_{m}=\\binom{m+n}{m}\\left(\\frac{m}{m+n}\\right)^{m}\\left(\\frac{n}{m+n}\\right)^{n}\n$$\n\nSi on note $q_{m}$ la probabilité de ne pas obtenir exactement $m$ boules blanches, on a $q_{m}>0$ et $p_{m}+q_{m}=1$, d'où $p_{m}=1-q_{m}<1$.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 2.", "solution_match": "## Solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Soit $a_{0}0$.\nD'autre part, on a $d_{n+1}=a_{0}+\\cdots+a_{n}-n a_{n+1}$, donc l'inégalité de droite est équivalente à $d_{n+1} \\leqslant 0$. Il s'agit donc de prouver qu'il existe un unique $n \\geqslant 1$ tel que $d_{n+1} \\leqslant 00$.\nAinsi, la suite ( $\\mathrm{d}_{\\mathrm{i}}$ ) est une suite strictement décroissante $\\mathrm{d}^{\\prime}$ entiers, ce qui assure qu'elle ne prendra des valeurs négatives ou nulles qu'à partir d'un certain rang, et de premier terme strictement positif. Il existe donc bien un unique indice $n$ pour lequel $d_{n+1} \\leqslant 00$.\n\nRemarque La conclusion n'est plus assurée sans l'hypothèse que les $a_{i}$ sont tous des entiers. Un contre-exemple est donné par $a_{n}=2-\\frac{1}{2^{n}}$ pour tout $n \\geqslant 0$.\n\n## Exercices communs", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 3.", "solution_match": "## Solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les entiers $n \\geqslant 3$ pour lesquels il existe $n$ polynômes $P_{1}, \\ldots, P_{n}$ à coefficients réels et tels que, pour tous $i, j, k$ distincts : $P_{i}+P_{j} n^{\\prime}$ a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.", "solution": "de l'exercice 4\n\nProuvons que seul $n=3$ a la propriété désirée.\nTout d'abord, en posant $\\mathrm{P}_{1}(x)=3 x^{2}+3$ et $\\mathrm{P}_{2}(x)=P_{3}(x)=-x^{2}-2$, on vérifie aisément que les polynômes $P_{1}(x)+P_{2}(x)=P_{1}(x)+P_{3}(x)=2 x^{2}+1$ et $P_{2}(x)+P_{3}(x)=-2 x^{2}-4$ n'ont aucune racine réelle, tandis que $P_{1}(x)+P_{2}(x)+P_{3}(x)=x^{2}-1$ admet 1 et -1 comme racines. Ainsi, $n=3$ est une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 4.", "solution_match": "## Solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les entiers $n \\geqslant 3$ pour lesquels il existe $n$ polynômes $P_{1}, \\ldots, P_{n}$ à coefficients réels et tels que, pour tous $i, j, k$ distincts : $P_{i}+P_{j} n^{\\prime}$ a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.", "solution": "du problème.\nRemarquons maintenant que si $n \\geqslant 4$ polynômes $\\mathrm{P}_{1}, \\ldots, \\mathrm{P}_{n}$ vérifient les conditions requises, alors $\\mathrm{P}_{1} \\mathrm{P}_{2}, \\mathrm{P}_{3}$ et $\\mathrm{P}_{4}$ vérifient déjà ces conditions. Pour conclure, il suffit donc de prouver que $n=4 n^{\\prime}$ est pas une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 4.", "solution_match": " solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les entiers $n \\geqslant 3$ pour lesquels il existe $n$ polynômes $P_{1}, \\ldots, P_{n}$ à coefficients réels et tels que, pour tous $i, j, k$ distincts : $P_{i}+P_{j} n^{\\prime}$ a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.", "solution": "La clé est alors de noter que si P et Q sont des polynômes tels que $\\mathrm{P}+\\mathrm{Q}$ n'a pas de racine rélle, alors $\\mathrm{P}+\\mathrm{Q}$ garde un signe constant sur $\\mathbb{R}$.\nOn procède donc par l'absurde : supposons que $\\mathrm{P}_{1}, \\mathrm{P}_{2}, \\mathrm{P}_{3}$ et $\\mathrm{P}_{4}$ soient des polynômes tels que, pour tous $i, j, k$ distincts, $P_{i}+P_{j}$ n'a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.\nTraçons alors le graphe complet dont les sommets sont les polynômes $\\mathrm{P}_{1}, \\mathrm{P}_{2}, \\mathrm{P}_{3}, \\mathrm{P}_{4}$ et colorons l'arête $P_{i} P_{j}$ en rouge si $P_{i}+P_{j}$ est strictement positif, et en vert si $P_{i}+P_{j}$ est strictement négatif. Chaque arête est nécessairement colorée. De plus, ce graphe ne peut contenir de triangles dont les trois arêtes sont de la même couleur, ce sans quoi la somme des trois polynômes qui sont les sommets de ce triangle n'aurait pas de racine réelle.\nQuitte à changer chaque $P_{i}$ en $-P_{i}$, on peut supposer que deux des trois arêtes issues de $P_{1}$ sont rouges et, quitte à renuméroter, on peut supposer que $P_{1} P_{2}$ et $P_{1} P_{4}$ sont rouges. Pour éviter le triangle rouge $P_{1} P_{2} P_{4}$, $c^{\\prime}$ est donc que $P_{2} P_{4}$ est verte. Puisque $P_{2} P_{3} P_{4}$ ne peut avoir ses trois arêtes vertes, $c^{\\prime}$ est donc que $P_{2} P_{3}$ ou $P_{4} P_{3}$ est rouge. Par symétrie des rôles, on peut supposer que $\\mathrm{P}_{2} \\mathrm{P}_{3}$ est rouge. Mais alors $\\mathrm{P}_{1} \\mathrm{P}_{3}$ est verte.\nAinsi, pour tout réel $x$, on a simultanement\n\n$$\n\\begin{aligned}\n& P_{1}(x)+P_{4}(x)>0 \\text { et } P_{2}(x)+P_{3}(x)>0 \\text {, donc } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)>0 \\text {, et } \\\\\n& P_{1}(x)+P_{3}(x)<0 \\text { et } P_{2}(x)+P_{4}(x)<0 \\text {, donc } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)<0,\n\\end{aligned}\n$$\n\nce qui est absurde. Ainsi, $n=4$ n'est pas une", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 4.", "solution_match": " solution."}}
+{"year": "2017", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Déterminer tous les entiers $n \\geqslant 3$ pour lesquels il existe $n$ polynômes $P_{1}, \\ldots, P_{n}$ à coefficients réels et tels que, pour tous $i, j, k$ distincts : $P_{i}+P_{j} n^{\\prime}$ a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.", "solution": ", ce qui conclut.", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 4.", "solution_match": " solution"}}
+{"year": "2017", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "a) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{Z}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.\nb) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{R}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.", "solution": "de l'exercice 5\n\na) Soit f une éventuelle", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 5.", "solution_match": "## Solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "a) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{Z}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.\nb) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{R}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.", "solution": "du problème. Notons $\\mathrm{P}(\\mathrm{x}, \\mathrm{y})$ l'égalité de l'énoncé pour les valeurs $x$ et $y$. On pose $c=f(0)$.\nPour tout $x$, de $P(0, x)$ on déduit que $f(f(x))^{2}+c^{2}+f(x)^{2}=f(x)+2 f(f(x)) f(x)$, d'où $f(x)=c^{2}+(f(f(x))-f(x))^{2}$. Il s'ensuit que $f(x) \\geqslant c^{2} \\geqslant 0$.\nPour $x=0$, cela donne $c=c^{2}+(f(c)-c)^{2}$, d'où $c(1-c)=(f(c)-c)^{2} \\geqslant 0$. Puisque $c$ est un entier, il vient $c=0$ ou $c=1$. Dans les deux cas, cela montre que $f(c)-c=0$. Ainsi, on sait que $f(c)=c$.\nEnfin, pour tout $x$, de $P(x, 0)$ on déduit que\n\n$$\nf(c-x)^{2}+f(x)^{2}+c^{2}=c(1+2 c)\n$$\n\n- Si $\\mathrm{c}=0$, l'égalité ci-dessus se réécrit comme $f(-x)^{2}+f(x)^{2}=0$, donc $f(x)=0$.\n- Si $\\mathrm{c}=1$, elle se réécrit comme $f(1-x)^{2}+f(x)^{2}=2$. Or, $f(1-x)$ et $f(x)$ sont entiers naturels, donc $f(x)=f(1-x)=1$.\nRéciproquement, les fonctions $\\mathrm{f}: x \\longmapsto 0$ et $\\mathrm{f}: x \\longmapsto 1$ sont clairement", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 5.", "solution_match": " solution "}}
+{"year": "2017", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "a) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{Z}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.\nb) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{R}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.", "solution": "s du problème.\nb) Soit $f$ une éventuelle", "metadata": {"resource_path": "French_STS/segmented/fr-ofm-2016-2017-envoi-2-solutions.jsonl", "problem_match": "## Exercice 5.", "solution_match": " solution"}}
+{"year": "2017", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "a) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{Z}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.\nb) Déterminer toutes les fonctions $f: \\mathbb{R} \\longrightarrow \\mathbb{R}$ telles que\n\n$$\nf(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))\n$$\n\npour tous réels $x$ et $y$.", "solution": "du problème. Notons $\\mathrm{P}(\\mathrm{x}, \\mathrm{y})$ l'égalité de l'énoncé pour les valeurs $x$ et $y$. On pose $c=f(0), d=f(c)$ et $\\mathcal{F}=\\{f(x) \\mid x \\in \\mathbb{R}\\}$.\nPour tout $x \\in \\mathbb{R}$, de $P(0, x)$ on déduit que $f(f(x))^{2}+c^{2}+f(x)^{2}=f(x)+2 f(f(x)) f(x)$, $d^{\\prime}$ où $f(x)=c^{2}+(f(f(x))-f(x))^{2}$. Par conséquent, pour tout $x \\in \\mathcal{F}$, on a $x \\geqslant c^{2} \\geqslant 0$ et $f(x)=x \\pm \\sqrt{x-c^{2}}$.\nIl s'ensuit que $c \\geqslant c^{2}$, c'est-à-dire que $c(1-c) \\geqslant 0$, donc que $0 \\leqslant c \\leqslant 1$. On procède alors par l'absurde, et on suppose que $00$ et $y_{1} \\geqslant y_{2}>0$ des réels tels que\n\n$$\nx_{1} \\geqslant y_{1} \\text { et } x_{1} x_{2} \\geqslant y_{1} y_{2}\n$$\n\nProuver que\n\n$$\nx_{1}+x_{2} \\geqslant y_{1}+y_{2}\n$$\n\nb) Soit $x_{1} \\geqslant x_{2} \\geqslant \\ldots \\geqslant x_{n}>0$ et $y_{1} \\geqslant y_{2} \\geqslant \\ldots \\geqslant y_{n}>0$ des réels tels que\n\n$$\nx_{1} x_{2} \\cdots x_{i} \\geqslant y_{1} y_{2} \\cdots y_{i} \\text { pour } i=1, \\ldots, n\n$$\n\nProuver que\n\n$$\nx_{1}+x_{2}+\\cdots+x_{n} \\geqslant y_{1}+y_{2}+\\cdots+y_{n}\n$$", "solution": "de l'exercice 6\n\na) Procédons par l'absurde: supposons que $y_{1}+y_{2}>x_{1}+x_{2}$. Alors $y_{2}>x_{1}+x_{2}-y_{1}$ et on a\n\n$$\n0 \\geqslant y_{1} y_{2}-x_{1} x_{2}>y_{1}\\left(x_{1}+x_{2}-y_{1}\\right)-x_{1} x_{2}=\\left(x_{1}-y_{1}\\right)\\left(y_{1}-x_{2}\\right)\n$$\n\nPuisque $x_{1} \\geqslant y_{1}$, alors $y_{1}0$ et $\\bar{y}_{1} \\geqslant \\ldots \\geqslant \\bar{y}_{n-\\ell}>0$. En outre, pour $i=1, \\ldots, n-\\ell$, on a\n\n$$\n\\left(x_{1} \\ldots x_{\\ell}\\right)\\left(\\bar{x}_{1} \\ldots \\bar{x}_{i}\\right)=x_{1} \\ldots x_{\\ell+i} \\geqslant y_{1}^{\\prime} \\ldots y_{\\ell+i}^{\\prime}=\\left(y_{1}^{\\prime} \\ldots y_{\\ell}^{\\prime}\\right)\\left(\\bar{y}_{1} \\ldots \\bar{y}_{i}\\right)\n$$\n\nPuisque $x_{1} \\ldots x_{\\ell}=y_{1}^{\\prime} \\ldots y_{\\ell}^{\\prime}>0$, cela montre que $\\bar{x}_{1} \\ldots \\bar{x}_{i} \\geqslant \\bar{y}_{1} \\ldots \\bar{y}_{i}$. On a $n-\\ell