{
 "cells": [
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {
    "id": "lJz6FDU1lRzc"
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Looking in indexes: https://pypi.org/simple, https://pypi.ngc.nvidia.com\n",
      "Requirement already satisfied: wget in /home/nkoluguri/miniconda3/envs/nemo/lib/python3.10/site-packages (3.2)\n",
      "E: Could not open lock file /var/lib/dpkg/lock-frontend - open (13: Permission denied)\n",
      "E: Unable to acquire the dpkg frontend lock (/var/lib/dpkg/lock-frontend), are you root?\n",
      "Looking in indexes: https://pypi.org/simple, https://pypi.ngc.nvidia.com\n",
      "Requirement already satisfied: text-unidecode in /home/nkoluguri/miniconda3/envs/nemo/lib/python3.10/site-packages (1.3)\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "'\\nRemember to restart the runtime for the kernel to pick up any upgraded packages (e.g. matplotlib)!\\nAlternatively, you can uncomment the exit() below to crash and restart the kernel, in the case\\nthat you want to use the \"Run All Cells\" (or similar) option.\\n'"
      ]
     },
     "execution_count": 1,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "\"\"\"\n",
    "You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.\n",
    "\n",
    "Instructions for setting up Colab are as follows:\n",
    "1. Open a new Python 3 notebook.\n",
    "2. Import this notebook from GitHub (File -> Upload Notebook -> \"GITHUB\" tab -> copy/paste GitHub URL)\n",
    "3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select \"GPU\" for hardware accelerator)\n",
    "4. Run this cell to set up dependencies.\n",
    "5. Restart the runtime (Runtime -> Restart Runtime) for any upgraded packages to take effect\n",
    "\n",
    "\n",
    "NOTE: User is responsible for checking the content of datasets and the applicable licenses and determining if suitable for the intended use.\n",
    "\"\"\"\n",
    "# If you're using Google Colab and not running locally, run this cell.\n",
    "\n",
    "## Install dependencies\n",
    "!pip install wget\n",
    "!apt-get install sox libsndfile1 ffmpeg\n",
    "!pip install text-unidecode\n",
    "!pip install matplotlib>=3.3.2\n",
    "\n",
    "## Install NeMo\n",
    "BRANCH = 'main'\n",
    "# !python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[all]\n",
    "\n",
    "\"\"\"\n",
    "Remember to restart the runtime for the kernel to pick up any upgraded packages (e.g. matplotlib)!\n",
    "Alternatively, you can uncomment the exit() below to crash and restart the kernel, in the case\n",
    "that you want to use the \"Run All Cells\" (or similar) option.\n",
    "\"\"\"\n",
    "# exit()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "v1Jk9etFlRzf"
   },
   "source": [
    "# Introduction to End-To-End Automatic Speech Recognition\n",
    "\n",
    "This notebook contains a basic tutorial of Automatic Speech Recognition (ASR) concepts, introduced with code snippets using the [NeMo Framework](https://github.com/NVIDIA/NeMo).\n",
    "We will first introduce the basics of the main concepts behind speech recognition, then explore concrete examples of what the data looks like and walk through putting together a simple end-to-end ASR pipeline.\n",
    "\n",
    "We assume that you are familiar with general machine learning concepts and can follow Python code, and we'll be using the [AN4 dataset from CMU](http://www.speech.cs.cmu.edu/databases/an4/) (with processing using `sox`)."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "YLln3U-IlRzg"
   },
   "source": [
    "## Conceptual Overview: What is ASR?\n",
    "\n",
    "ASR, or **Automatic Speech Recognition**, refers to the problem of getting a program to automatically transcribe spoken language (speech-to-text). Our goal is usually to have a model that minimizes the **Word Error Rate (WER)** metric when transcribing speech input. In other words, given some audio file (e.g. a WAV file) containing speech, how do we transform this into the corresponding text with as few errors as possible?\n",
    "\n",
    "Traditional speech recognition takes a generative approach, modeling the full pipeline of how speech sounds are produced in order to evaluate a speech sample. We would start from a **language model** that encapsulates the most likely orderings of words that are generated (e.g. an n-gram model), to a **pronunciation model** for each word in that ordering (e.g. a pronunciation table), to an **acoustic model** that translates those pronunciations to audio waveforms (e.g. a Gaussian Mixture Model).\n",
    "\n",
    "Then, if we receive some spoken input, our goal would be to find the most likely sequence of text that would result in the given audio according to our generative pipeline of models. Overall, with traditional speech recognition, we try to model `Pr(audio|transcript)*Pr(transcript)`, and take the argmax of this over possible transcripts.\n",
    "\n",
    "Over time, neural nets advanced to the point where each component of the traditional speech recognition model could be replaced by a neural model that had better performance and that had a greater potential for generalization. For example, we could replace an n-gram model with a neural language model, and replace a pronunciation table with a neural pronunciation model, and so on. However, each of these neural models need to be trained individually on different tasks, and errors in any model in the pipeline could throw off the whole prediction.\n",
    "\n",
    "Thus, we can see the appeal of **end-to-end ASR architectures**: discriminative models that simply take an audio input and give a textual output, and in which all components of the architecture are trained together towards the same goal. The model's encoder would be akin to an acoustic model for extracting speech features, which can then be directly piped to a decoder which outputs text. If desired, we could integrate a language model that would improve our predictions, as well.\n",
    "\n",
    "And the entire end-to-end ASR model can be trained at once--a much easier pipeline to handle! "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "0S5iZPMSlRzg"
   },
   "source": [
    "### End-To-End ASR\n",
    "\n",
    "With an end-to-end model, we want to directly learn `Pr(transcript|audio)` in order to predict the transcripts from the original audio. Since we are dealing with sequential information--audio data over time that corresponds to a sequence of letters--RNNs are the obvious choice. But now we have a pressing problem to deal with: since our input sequence (number of audio timesteps) is not the same length as our desired output (transcript length), how do we match each time step from the audio data to the correct output characters?\n",
    "\n",
    "Earlier speech recognition approaches relied on **temporally-aligned data**, in which each segment of time in an audio file was matched up to a corresponding speech sound such as a phoneme or word. However, if we would like to have the flexibility to predict letter-by-letter to prevent OOV (out of vocabulary) issues, then each time step in the data would have to be labeled with the letter sound that the speaker is making at that point in the audio file. With that information, it seems like we should simply be able to try to predict the correct letter for each time step and then collapse the repeated letters (e.g. the prediction output `LLLAAAAPPTOOOPPPP` would become `LAPTOP`). It turns out that this idea has some problems: not only does alignment make the dataset incredibly labor-intensive to label, but also, what do we do with words like \"book\" that contain consecutive repeated letters? Simply squashing repeated letters together would not work in that case!\n",
    "\n",
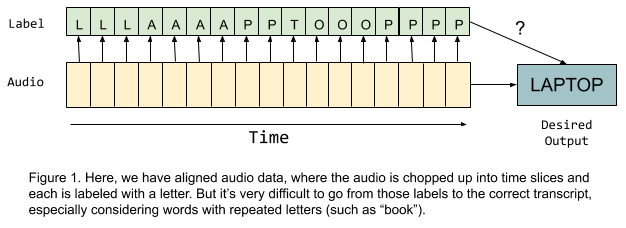    "![Alignment example](https://raw.githubusercontent.com/NVIDIA/NeMo/stable/tutorials/asr/images/alignment_example.png)\n",
    "\n",
    "Modern end-to-end approaches get around this using methods that don't require manual alignment at all, so that the input-output pairs are really just the raw audio and the transcript--no extra data or labeling required. Let's briefly go over two popular approaches that allow us to do this, Connectionist Temporal Classification (CTC) and sequence-to-sequence models with attention.\n",
    "\n",
    "#### Connectionist Temporal Classification (CTC)\n",
    "\n",
    "In normal speech recognition prediction output, we would expect to have characters such as the letters from A through Z, numbers 0 through 9, spaces (\"\\_\"), and so on. CTC introduces a new intermediate output token called the **blank token** (\"-\") that is useful for getting around the alignment issue.\n",
    "\n",
    "With CTC, we still predict one token per time segment of speech, but we use the blank token to figure out where we can and can't collapse the predictions. The appearance of a blank token helps separate repeating letters that should not be collapsed. For instance, with an audio snippet segmented into `T=11` time steps, we could get predictions that look like `BOO-OOO--KK`, which would then collapse to `\"BO-O-K\"`, and then we would remove the blank tokens to get our final output, `BOOK`.\n",
    "\n",
    "Now, we can predict one output token per time step, then collapse and clean to get sensible output without any fear of ambiguity from repeating letters! A simple way of getting predictions like this would be to apply a bidirectional RNN to the audio input, apply softmax over each time step's output, and then take the token with the highest probability. The method of always taking the best token at each time step is called **greedy decoding, or max decoding**.\n",
    "\n",
    "To calculate our loss for backprop, we would like to know the log probability of the model producing the correct transcript, `log(Pr(transcript|audio))`. We can get the log probability of a single intermediate output sequence (e.g. `BOO-OOO--KK`) by summing over the log probabilities we get from each token's softmax value, but note that the resulting sum is different from the log probability of the transcript itself (`BOOK`). This is because there are multiple possible output sequences of the same length that can be collapsed to get the same transcript (e.g. `BBO--OO-KKK` also results in `BOOK`), and so we need to **marginalize over every valid sequence of length `T` that collapses to the transcript**.\n",
    "\n",
    "Therefore, to get our transcript's log probability given our audio input, we must sum the log probabilities of every sequence of length `T` that collapses to the transcript (e.g. `log(Pr(output: \"BOOK\"|audio)) = log(Pr(BOO-OOO--KK|audio)) + log(Pr(BBO--OO-KKK|audio)) + ...`). In practice, we can use a dynamic programming approach to calculate this, accumulating our log probabilities over different \"paths\" through the softmax outputs at each time step.\n",
    "\n",
    "If you would like a more in-depth explanation of how CTC works, or how we can improve our results by using a modified beam search algorithm, feel free to check out the Further Reading section at the end of this notebook for more resources.\n",
    "\n",
    "#### Sequence-to-Sequence with Attention\n",
    "\n",
    "One problem with CTC is that predictions at different time steps are conditionally independent, which is an issue because the words in a continuous utterance tend to be related to each other in some sensible way. With this conditional independence assumption, we can't learn a language model that can represent such dependencies, though we can add a language model on top of the CTC output to mitigate this to some degree.\n",
    "\n",
    "A popular alternative is to use a sequence-to-sequence model with attention. A typical seq2seq model for ASR consists of some sort of **bidirectional RNN encoder** that consumes the audio sequence timestep-by-timestep, and where the outputs are then passed to an **attention-based decoder**. Each prediction from the decoder is based on attending to some parts of the entire encoded input, as well as the previously outputted tokens.\n",
    "\n",
    "The outputs of the decoder can be anything from word pieces to phonemes to letters, and since predictions are not directly tied to time steps of the input, we can just continue producing tokens one-by-one until an end token is given (or we reach a specified max output length). This way, we do not need to deal with audio alignment, and our predicted transcript is just the sequence of outputs given by our decoder.\n",
    "\n",
    "Now that we have an idea of what some popular end-to-end ASR models look like, let's take a look at the audio data we'll be working with for our example."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "38aYTCTIlRzh"
   },
   "source": [
    "## Taking a Look at Our Data (AN4)\n",
    "\n",
    "The AN4 dataset, also known as the Alphanumeric dataset, was collected and published by Carnegie Mellon University. It consists of recordings of people spelling out addresses, names, telephone numbers, etc., one letter or number at a time, as well as their corresponding transcripts. We choose to use AN4 for this tutorial because it is relatively small, with 948 training and 130 test utterances, and so it trains quickly.\n",
    "\n",
    "Before we get started, let's download and prepare the dataset. The utterances are available as `.sph` files, so we will need to convert them to `.wav` for later processing. If you are not using Google Colab, please make sure you have [Sox](http://sox.sourceforge.net/) installed for this step--see the \"Downloads\" section of the linked Sox homepage. (If you are using Google Colab, Sox should have already been installed in the setup cell at the beginning.)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {
    "id": "gAhsmi6HlRzh"
   },
   "outputs": [],
   "source": [
    "import os\n",
    "# This is where the an4/ directory will be placed.\n",
    "# Change this if you don't want the data to be extracted in the current directory.\n",
    "data_dir = '.'\n",
    "\n",
    "if not os.path.exists(data_dir):\n",
    "  os.makedirs(data_dir)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {
    "id": "Yb4fuUvWlRzk",
    "scrolled": true
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "******\n",
      "Tarfile already exists.\n",
      "Finished conversion.\n",
      "******\n"
     ]
    }
   ],
   "source": [
    "import glob\n",
    "import os\n",
    "import subprocess\n",
    "import tarfile\n",
    "import wget\n",
    "\n",
    "# Download the dataset. This will take a few moments...\n",
    "print(\"******\")\n",
    "if not os.path.exists(data_dir + '/an4_sphere.tar.gz'):\n",
    "    an4_url = 'https://dldata-public.s3.us-east-2.amazonaws.com/an4_sphere.tar.gz'\n",
    "    an4_path = wget.download(an4_url, data_dir)\n",
    "    print(f\"Dataset downloaded at: {an4_path}\")\n",
    "else:\n",
    "    print(\"Tarfile already exists.\")\n",
    "    an4_path = data_dir + '/an4_sphere.tar.gz'\n",
    "\n",
    "if not os.path.exists(data_dir + '/an4/'):\n",
    "    # Untar and convert .sph to .wav (using sox)\n",
    "    tar = tarfile.open(an4_path)\n",
    "    tar.extractall(path=data_dir)\n",
    "\n",
    "    print(\"Converting .sph to .wav...\")\n",
    "    sph_list = glob.glob(data_dir + '/an4/**/*.sph', recursive=True)\n",
    "    for sph_path in sph_list:\n",
    "        wav_path = sph_path[:-4] + '.wav'\n",
    "        cmd = [\"sox\", sph_path, wav_path]\n",
    "        subprocess.run(cmd)\n",
    "print(\"Finished conversion.\\n******\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "m_LFeM0elRzm"
   },
   "source": [
    "You should now have a folder called `an4` that contains `etc/an4_train.transcription`, `etc/an4_test.transcription`, audio files in `wav/an4_clstk` and `wav/an4test_clstk`, along with some other files we will not need.\n",
    "\n",
    "Now we can load and take a look at the data. As an example, file `cen2-mgah-b.wav` is a 2.6 second-long audio recording of a man saying the letters \"G L E N N\" one-by-one. To confirm this, we can listen to the file:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {
    "id": "_M_bSs3MjQlz"
   },
   "outputs": [
    {
     "data": {
      "text/html": [
       "\n",
       "                <audio  controls=\"controls\" >\n",
       "                    <source src=\"data:audio/x-wav;base64,UklGRiRFAQBXQVZFZm10IBAAAAABAAEAgD4AAAB9AAACABAAZGF0YQBFAQD3//3/BwAHAAMACQAFAAcADQAPAAcADQAJABMABQAFAAsADwANAA8ADQANAAkACwALAAsADQATABUAFwANABMABwALABEADwALAAsABQABAP///f////3/+f/9/wUAAwAFAA8ADQANAAkABwAFAAUABwADAAMA+//9//f/9//5//v/+/////H/8f/t/+3/6//r/+//9f/1//X/+f/9/wEABwAJABEACwAVABEADQAJAA8ADQAFAAMACQAJAAUAAQAJAAMA/f/1//H/7f/t/+X/6f/t/+3/6f/p/+n/8//t//H/8f/3//f////7/wMA/////wEA/f/5//n/9//3/+//7//t/+n/7//v//P/9f/3//f/////////+f/3////9//3/wEAAQALAA0ADQAPABEACQALAAUAAwD///3/9//1//H/8f/t/+X/4//j/9//4//f/+H/4f/l/93/5//j/+P/3//f/9n/5//l/+//6//r/+n/8f/t//H/9//3//P/+f8BAAcABwALAA8AFwARABMADwARAA0AEwAJAA8ACQALAAkADwAPAA8ABwALAP//AwADAP//+f/7//f/+f/z//H/6//n/+P/6//j/+f/7//v//H/8f/t/+n/6f/h/+n/6f/z/+//8f/t/+//7//v//P/+//7//n/+f/3//n/9//x//P/9f/x/+//+f/9////AwAHAAkAAwD9//n/+f8BAPn/9/////v/+f/7/wEAAwD9//n/9//z/+//8f/z/+//7//3/+//8f/p/+//9//7//f//f8BAPv/9f/z//X/9f/1//H/9//v//H/6//n/+n/6f/f/9//6//p//H/5f/p/+//8//z//H/+f/5//3//f///wEA//8BAAEACQARABUAEwAZABUAFQALAAcABQD///3/AwD7//v/+f/x//P/8//t/+//8f/r/+n/3//f/93/5//p/+//6f/n/+3/6f/p/+X/6f/x/+v/5//d/9n/2//f/9//4//b/+H/2f/f/9//5f/n/+X/4//t//P/+f/3//v/+f/5//X/AwD9/wcABQAJAAcADQALAA0ADwADAAUABQAFAP//AwD9//3/+f/1//v/9//3//X/8//1//f/+//5//v/+//5//X/9//x/+//6f/l/+f/3//b/9//3//j/9v/1//V/9P/x//L/8v/w//B/8H/xf/D/8X/yf/L/83/0f/Z/+H/7//z/wEABwALAA0AFwAXABkAFwAXABMAEQAVABUAEQATAAsADQAFAAMA/f////P/9//1//3/8//9///////7//f/+//5//f/9//3//X/+f/z//H/7//p/+P/2f/d/9//2f/X/9P/2//l/93/2f/T/9X/1f/Z/9f/3f/j/+n/7f/p//P/8//9//3//f/3////+/8BAAMAAQD5//3/AQD//wMA///5/////f/9//f/AQD//wEA9//7//X/+f/v//P/8f/5//X/9f/3//v/AQD9////AQADAPf/+f/////////9/wUACwAFAP3/9//v//H/4//l/+n/5//p//f/8//5//X////7//v//f////3//f8FAAMA//////v/8//7//X/9f/r//3////9//P/8//v/+3/5f/p/+f/7//l/+P/2//j/+H/4//r/+f/5f/t/+P/5f/h/+P/2//j/+f/6//p/+//6//r/+//9f/v/+//6//x/+v/8f/1//n/+/8BAPf/+f/1//v/+f////f//f/5////9f/z//H/8//v/+v/6f/1//X/9f/1//X/9f/7//f/7//r//H/8//5/+3/6//j/+f/4//f/9v/3f/V/9n/1//T/8f/zf/F/8v/yf/N/9f/3f/d/9P/1//X/9//2//j/+f/5//t//P/7//v//f//f/7/wEA//8DAPn////9/wcACwATAA8ADwALAAsACwAPAAcACQABAAUABwAHAAMA+//1//X/8//1/+v/6f/j//H/6//n/93/3f/Z/+H/3//f/9v/4//l/+3/8f/z//v/+f/3//X/8f/x//P/8f/x/+//7f/1//X/+//1//f/+/8BAAcAAwABAAUAAQD///////8DAP/////9//3//f/1//X/9f/z//f/9//5//n/9//5/wEABQAJAAcADQALAA0ABQALAAcACwAHAAMA/f8BAPn/8//p/+n/5f/h/+P/3//Z/9n/2f/X/9n/2f/b/+P/6f/n/+n/6f/l//H/8f/1//v/AQABAAcACwAPAA0AEQADAAcABQAJAAUACQAHAAkACwARAA8ADQAFAAUA9//3//f/9f/1//X/9f/3//f//f/5//X/6f/r/+f/6f/j/+P/5//l/+P/5f/l/+v/5//n/+n/6//t//P/7//t//f////1//P/9f/5//f/8//z//X/9//3//f/9f/5/wEA//8BAAUA//////n/AwD7////AQD5/+v/6f/l/+v/6//x/+//8//1/+//8//1//P/9f/z//n/+f/3//3///8BAAMAAwAFAP/////v/+n/5//l/9v/2//Z/9f/0//b/9//3f/d/9//1//b/+P/5//p/+f/8//7///////7//////8BAP///f8FAAsABwALAAcABwAJAAkACwATABUAGQAZAB0AHwAhABkAHQARABMAEQATABcAGQARAA0ACQAJAAMA/f/z//X/5//f/9//1//T/83/z//R/9v/2//Z/9X/1//Z/9P/0//f/+P/5f/j/+//9f/z//H/9//5//f/9f/7//n//f/5//3//f8BAP//+/8BAAUAAQD//wUADQANABUAGQAhABsAIQAXABMAEQAXABkAGwAXABEAEQAJAAMAAQADAP//+//3//f/9f/7//f/7f/t/+P/4//n/+v/7//7/wMABQD9/wEAAwD9/wMA////////AQD///3/+f///wEABwD///P/8f/j/93/3//f/+H/4//d/9n/3//r/+3/7f/x//X//f///wEAAwAJAAsACQAJAAkABwAPAAUAAwD5/wEA/f8DAAEACQD//wUA+f/3//X/9f/v//H/7//x//X/9//7//f/8//5//3/+/8BAAMAAQAFAPv/9f/3//3/9//z/+//8f/z//n/9f/z//X/9//3//3////9//f/8//z/+//7//x//P/9//3//X/8//x//X/8//x//P/9f/r/+v/4//j/9v/3f/V/9n/0//Z/83/0f/R/8v/1//d/9v/4f/n/+n/3//r/+f/6//t//X/+f/3////AwD9/wUA+/8BAPf/AQD7////8//7//X/9////wEA9//7//v/9f/7//3///8HAAsACwANAAUA+f/7//n//f/9//n/+f/z//X/8f/z/+3/8f/t/+v/4//f/9//3f/j/+H/3f/j/+v/7//r/+3/9f/5//H/8f/3//////8BAP3/+//1//f/8f/5/+//8f/3//f/9//1//P/9f/z//f/+//3//v/+f/z//P/8f/5//X/AwD7////AwALAAsADQAFAAcA//////v/+//7//v///8FAPv/+//3//n/+//7/+3/6f/p/+v/6f/j/+X/6//j/+f/4//j/+H/4//l//H/+f/1//H/8//t//H/8//r//P/9f/z//X/+/8BAAkABwAHAAcADQALAA0ADwAPAA0AEQAPAA8ADQANAAUABwAHAAMAAQD7//f/9//1/+3/5f/j/+P/4f/h/+P/2//T/9H/1f/X/+P/6//t/+3/8f/z/+//6f/t/+X/5//l/+f/5f/j/9//5//j/+X/4//n/+H/5f/j//f/8//7////BwD7//f/8f/1//n/AwABAAEAAQADAAcAAwD7//v/+f/5//3/9//z//P/8f/r/+X/5//t/+X/4f/h/+X/5f/l/+f/7//v/+3/6//r/+3/4f/d/9f/1f/X/93/3//b/9n/2//n/+X/4//f/+n/5f/r/+f/6f/n/+3/6f/z/+3/8f/z//X/7f/1//X/AQABAA0ADQALAAkACwALAA8ACQALAAcADQAJAA8ACQAPABEADwAHAAUA///5/+v/8//r/+v/5f/j/+n/6//f/9//4//h/+X/5//h/+H/6f/p/+f/7f/n/+P/2f/f/+X/5f/d/9//3//l/+X/8//z/////f8BAPn/+//5//3////9//n///8HAAkABwAJAA0ADQAJAP//AwAFAAcAAQAHAP//BwADAAsA+//9//n/AwD5////AQADAPf/8f/1/wMAAQAFAAEABQD/////+//9//3/AQD1//n/9f/z/+//7f/t//H/7//z/+//8f/7//n//f8DAP//AwAHAAkACQAHAAMABQAFAAMA/f/9//v/9f/x/+//7f/t/+n/7//v/+3/8//z/+n/6//1//f/9f/5//3/AQD//wcAEwALAAkACQADAP/////3//f/7//x//H/9f/x//P/8//1//H/8f/r/+n/4f/f/+f/6f/l/+n/6//x/+n/8//1//n/9f/9/////f/9/wUAAQAFAAMA///9/wEA//8DAAUADQALAAsAEQAJAAkABQD9/wEABwAFAAEA+f8DAAMA9//x//P/8//v/+3/6f/v/+P/4f/d/93/2f/Z/9X/4//d/9//4f/f/+P/5f/n/+3/8//3////AwAJAAcABwANAAcACQANAA8ACwANABEAEQAJAAcAAQD5/+v/6f/x/+//7//n/+P/4//h/+f/6//t//H/7f/z/+v/8f/r/+v/6f/1//n///8LAA8AEwAXAA8ADQAHAP3/AQD9//v/+f/5//X/9//3//X/8f/x//P/8f/z//H/8//1//v///8FAAcABwALAAUA///9//3/+f/7//f//f8BAAEAAwABAP//AwAFAPv/+f/1//X/9//1//f/9//9/wcADQALABEABwAHAAUACwALAA0ABwAPAA0ADQAFAAkACQAFAPv//f/5//P/7//v//P/+f/x//H/8f/z/+//9//1//f/+/8BAP//AQADAAsABQAHAAcABQAJAAkACwALAAkADwAHAA8ACwANAAMABQAJAA0ABQADAP//AwD///3/9f/z//X/9//x//P/8//5//X/+f/7//v//f/3//f/+f/3//P/6f/n/+P/6//l/+f/6f/z//P/9//3//X/+f/7//3//f8FAAEAAwD//wEA+/8FAAEABQADAAMAAQADAP3/AQAJAAsABwANAA0AEQARABcAFQAZABMAEQAHAAcABQAHAAMABwADAAEA/f/7//n///8DAP//+//1//X/8f/v/+3/6//1//H/6f/n/+n/4//n/+X/4f/b/9v/0//b/93/4//h/+P/3//n/+P/5f/p/+v/8//3//n//f8BAAkABwAJAAsAEwATABcAGwAhACcAJwApACcALwAtAC8AJwArACsAMQAlACMAHQAbAA8ADQD///v////9//v//f/5////+f/1/+n/8f/v//P/8f/5//P/6//n/+X/6f/r/+n/5f/n/+f/5f/n/+v/8f/5//n/+/8BAAEA+//7//X/7//9/////f/7//3/+f8FAAUABQAHABcAFwAXABsAJwArADEAKQApACcAJwAbABUADQAHAAcACwABAAEA9//9//3/+f/1//v/9//7//3/9f/1//v/+f/5////AQD9/wcADQANABMAEQARABMAFwATAAcACQAHAA0A/f/3//n/+//9//P/8//1//v/9//3//f//f/9//n//f/9//////8BAAMAAQAHAAkABQABAP3/+f///wUABwADAAUAAQADAP//AQD3//f/9//7//v//f8DAAEA//8FAA0ABwARABEACQAHAAMABQD//wUAAQAFAAMABQD9/wEAAQD9//v/AwD/////AQD7//3//f/5//X/9//9/wEAAwAFAAsAFQAVABMACwARAA8AEQABAAMA//////f/8//v/+//7f/3//H/7//t/+v/5f/j/+f/4//d/9n/2//f/93/2//b/93/4f/p/+n/+f/7//3/AwAJAAsAFwAPABkAFwAXAA8ADQAJAA8ADwAPAAcAEwAVABcAEQALAAUADQALAA0ABwARAA8ADQARABEABwABAAEAAQD9//f/8f/t//P/9f/3//v/9f/n/+X/6f/n/+f/6f/t//P/9f/t/+n/8f/x/+3/8//x/+v/7//x//f/+//5//3/+f/5//n/9f/1/////f/3//f/+/8BAP//BQAHAAsAAwADAAEAAwD9/wMAAwAPAAsAEwAVAB8AFwAZABUAGQAPABMADwAPAAsADQADAAMACQAJAAMACwADAAMAAQADAP3/AQD9/////f8BAAEA+/8BAPn/9//9//3/+f////X/+f/7/wEA/f/5//f///8BAP//+f/1//n/8f/1//X/9//z//n/AQABAAcACQARAA8AEQAPAA0AAQADAPv/+//9////AQD7////AQD/////9f/1//n//f/5//X/8//x/+v/6//r/+//5//n/+f/5f/Z/+f/6//1//v/AQD7/////f8DAP//AwADAAUABwADAPn/+f/5//n/9f/z/+//8//z//X/8//x/+//9f/3//v//f/7//n/9//v//f/8//t/+3/9f/p//H/8f/t/+//7//v/+v/6f/t/+//7//3//v//f///////f//////+/8BAP3/+//3//f/9//3/+//6//n/+X/7//n/+f/4f/p/+X/4//h/+f/6//n/+n/5//v//H/8//z//n//f8DAP//AwAPABEAEQAPAA8ACQADAAcABwABAP////8DAAEA+f/3//X/9f/z/+//7f/r//P/8f/t/+//9f/x/+v/6//n/+H/3f/X/9n/1f/X/9n/2f/X/9f/3//f/+H/4f/t/+3/9//x//H/9f8BAAEACQAXABsAFQAZABMAEQANABMADwATAA0ADQARAA0AAwAHAA0ABwAFAAkAAwAFAP//+f/9//3/+/////v/+//9/wEAAQD5//3/+//3/+//6//t/+3/6//f/93/3f/j/9//2f/d/93/4f/b/9n/2f/j/+f/6f/n/+P/6//p/+v/6//z//X/7f/t/+n/5//r/+n/8//1//v////9/wEA/f8BAAMAAQD9//X/8//9/wEA/////wkADwAJAAEAAQAHAAkAAwAJAA0AEQATABMACwAPAAkADQAHAAUABwD///X/7f/t/+3/5f/d/9//2//X/9f/4//p/+f/3//h/9v/3//d/9//4f/h/+f/4//n/93/6//p/+3/7f/x/+v/6//p/+//5//t/+//+//5//X/6//3/+3/9//n/+//6f/1/+//9//5//v/8f/z//H/9f/x////9//1//X/9f/z//H/8f/l/+f/4//n/+f/4//f/+P/4//t/+3/8//x//3///8HAAsACQAHAA0ADQAFAAcAAQADAAEAAQABAAMAAwD3//v/9f/1/+f/8f/v/+//6//r/+n/6f/j/93/2//f/9H/1f/T/9H/0f/R/9P/2f/d/9//2//f/+P/5//p/+n/7//p/+f/5f/d/93/6//t/+3/8//1//v/AwAHAAkABQAHAAcAFQARABUAEwATAA8AEQAVABMADQALAAsABQD///P/8//r//f/9f/x/+3/8f/t/+//6f/r/+f/5//n/+n/6f/z//v/AwD//wEACQALAAsABwAJAAcACQADAAEABwAJAP3/9f/n/+//6f/l/+H/5//j/+P/3f/n/+P/6f/p/+3/6f/t/+//9f/x//f/+/8DAPv/+//9/////f////3/AQD7/wEA+//7//n//////wMABwAFAAMABwAHAA0AEQAXABEAEQAPAA0AAQD///3////3//P/9//7//v////3//X/9f/x/+//6//p//H/7//1/+//6//n/+n/7f/v/+f/7//1//n//f/1//P/+f/9//////8DAP3/AQABAAEAAQD//wMA///9//P/8//1//f/8//3//H/7//p/+v/5//r/+P/6//r//H/6//v//P/AQD//wUAAQD//wEAAQD3//P/8//1//X/+f/7//f/9f/3/+f/7f/n/+X/6//l/+P/5//x//3//f8DAAkADwAHAA0AAwAHAP//+/8BAAEAAQADAP///f/3//3/9f/3/////f/5//f/+f/7////+/8BAAMABQAJAAcADwADAP//AwAFAP/////9//n/8//v/+//8f/x/+n/4f/h/+n/6//p/+X/7//p//P/7f/n/+f/5//n/+//8//x//P/9//z/+//9///////BQADAA0ADwALAAkAEQARABMAAwAJAAsAFQATABkAGwAXABcAEQARAAsACQAJAAsABwD9//X////1//X/8//v//v/7//x/+f/6f/r/+//8//v//X/9f/1//H/+f/1//X/8f/z//n/AQD5/wEAAwADAAcABQD9//X/9//7//v/9f/z//X/8f/9//n/AQDz//f/8//5//H////5//v/+f8BAP//AwADAAEAAQAFAAEADQAHAAkABQATAAUADQALAAcAAQABAPn/7f/r/+3/6f/r/+v/6//r/+v/3//h/+H/4//d/+f/6//1/+//9//7/wUA//8DAAUAAwABAAEA9f/1//P/7//v/+//8f/z/+//8//v/+//6f/x//P/+f/9////BQADAAUA//8HAAMAAQABAPn/9//1//n/9f/v//H/9f/t/+f/4f/j/+3/6//p/+H/4//n/9//4f/p/+f/5f/l/+P/3f/l/+X/6f/j/+n/9//1/+//8//1////9////////f/3/wMABwAJAAMABwALAAsAAwABAP//BwD//wUAAwAPAAMABQD//wEA+//7//v/+/////3/9//z/+//8//x//X/8//x/+3/6//t/+//6//l/+f/3//f/9v/3f/d/9//4f/x/+n/8//x//X/+f/9/wcABwAFAA0ABQAHAPv////7/wUA///9//H/+f/5//v/8//5//n/+//7////9/////n/+//5//f/+f/5/////f/9/wEABQAHAAsACwADAP//BQAHAAMAAwALAAsA//////v//f/7//3/8f/5//v//f/7//v/9//1//n/9//1//n/8//1//n/+f/1//X/9f/x/+//9//r/+v/7//r//P/9f//////AQAFAP///f///wMABwADAAMAAwD9/wMAAwD7/wEABwAFAAUAAQADAAEAAQABAP///f8BAAMA/f/5//f/+f/5//3/9f/v//P/8//x/+//8f/5//v////3//X/+f8BAPf/+//1/wEA+/8DAPv///8FAAUA+f/5//n/8f/x/+X/6f/r/+3/8f/p/+//6//n/+f/6f/n/+f/5f/l/+3/7f/t/+//8//z//H/6//z/+//8f/j/+P/6f/z/+3/9f/9/wMA+//7//n//f/7//X/8f/1//H/7f/1//H/7f/l/+v/5f/j/+f/6//r/+f/6//r//X/8//1//v/AQD//wEA+/8JAAcAEQAHABEAEQAbABkAGQAdACEAIwAhABcAGQANAAUA/f/7//P/9//1/+3/6//h/9//5f/f/+v/5f/v/+f/5f/n//H/6//v/+///f/9//P/8f/1////+f/v/+v/8//1//f/+f/5//v/9//5//f/9f/3//n/9f/x/+3/9f/r/+3/9//7//v///8HAAUABwADAA0ACQAVABEADwATAA0ACQAJAAUAAQD7//3//f8BAPv/9//x//P/9f/x/+3/7f/v/+//6f/5//f/BQD//wcACwAPAAsABQADAAsA//8DAAUAAQAHAA0AAQAHAA0ADwADAAkACwARAAUACQANAAsACQAJAAcABwABAP//9//3//3/AQABAAsABQANAA8AEQAFAAMA/f8DAP3////9//n/+//3//X/9f/3//f/7//p//f/8//v//H/+/8BAPX//f8FAAcAAwADAAMAAwADAAMA//8FAAcABwADAAEA/////wEAAQD/////AQD9//X/7//x/+3/6f/r/+//7f/1/+3/9f/7////CQAPAAkADQALAAsABQALAAsACQAJAAUABQALAAMA/f/3//n/9//z//P/8//z//X/6//t/+v/7f/h/+f/5f/j/+P/8f/n/+f/6//j/9//4f/n/+3/7//x/+3/9f/z//f/+f///wUACwALABMADwAPABMAFwATABsAFQANABcAEwATABMAEwAPAAsACwAFAPP/8f/t/+3/9f/1/+//9f/x//X/6//p/+3/8f/t/+3/7f/t/+v/8f/3//v/8f/3//X/8f/3//f/9f/1//X/AQADAP//AQD//wMABQD/////CwARABcAFwATABMADQANAAkABwD//wMAAQD9//X/9//9/wUA/f/3//3/8//t/+3/7//3//f/BQABAAUAAwD9/wEABQAJAAEAAwAHAA0AAwAFAP//AQD///3//f8FAPn/AQD9////+/8DAP//AwADAAMA//8DAAEAAwD5//P/9f////3/AwADAA0AEwATAA8AFwATABcAFwAPABMAEwANAA8ACQAHAAEA///3////+//7//v/AQD7/wUAAwALAP//BQABAAEABwAJAAkADQAPAA8ACQD///////8BAAUACwAPAAsAAwAFAPv/+////wUA/f/1//3/9//x//f/9f/9//v////9//v//f8DAP3/AwABAP//AQAFAAUA/f/9/wMAAQAFAPn////3/wEA/f8BAPP/9//x//n/9f////v/+//7//v/8f/x/+//8//x//X/8//5/+3/8//1//n/9f/7//X/AQD5//3/AQD9//3/+//1//X/7//x//H/7f/x//f/8//5/+3/+f/5//v///8BAP//CQD//wkACwARAA8AEQAXABcAFwATAA0ABQADAAEA/////wEA/f////n/BwAHAAUABQADAAsACwAJAAcACQABAAEAAwABAPf/7f/p/+P/5//f/+P/4//l/+P/4//j/+f/6f/z/+v/7f/x//P/+f/7////BQATABMADwANAA0AFQARAAsADQAXABMADwAJAA8AEQANAA0AEQAVABsAGwAVAA8AEwARAA8ADQALAA0ADwATAA0ACQAJAAkACwAFAP//+f8BAPv///8DAAMACQD7//v/AQD3//X/+/////3/+f/7//X/+//9/wMAAwAJAP3////9////+f/9/+//9f/3//v/+//7////AQABAAEACwANABcAGQAVABUADwAJAAsADQAHAAcA+/8BAPn///8DAAUABQAHAAcACQATABUAEQAVABUAEwAPAAkACQADAAkAAwAFAAcABQABAP//+f/z//X/8//1//3/8//1//n/9//3//3/+f/7//v//////wkAAQABAPn/8f/r/+X/5f/n/+H/5//l/+H/7f/x/+//8//v//n/+f8DAP3//f/9/wMAAwAJAAUADQAJABMADwAPAAMABQABAP//8//9//H//f/1//P/6f/p/+P/5f/V/9//3//h/93/5//r//X/+f8LAAkADwAJABEADQARABEAGwAPAAkACwAHAAUABQABAA8AAwADAP/////5//P/+f/7//P/+//5//X/8//r//P/8f/z/+n/5//p/+P/6f/j/9//6//l/+P/4//n/+3/7f/z//f/7f/x//P/7//1//X/+f/3/wEABQADAAsAEQARABUAFwARAA8ADwARABkAEwAPABEACQAJAAMAAQDt/+//6//1//H/7f/x/+n/6//1/+3/8f/x//X/9f/z//X/9//9/wEAAwALAA0ACwARAAcACQALAAcAAwAHAP//AwAFAAEA9//3//H/8//1//X/9f/3//X/9//9//v//f//////9//z/+3/+f8BAPf//f/1/wEA9//3//H/9f/9//f/+f////v/+//9//3//f/9/wkABwANAAcADwARABEAFwAZAB0AGQAdABkAGwARAAkACwAFAAUACQANAAcA+f/1//f/9//z/+//7f/p/+3/8f/z/+3/9f/5//v/+//1//f/8//5//f/9f/5//f/8//5//P/8f/v//n/9f/z/+3/8//z//n/+//1//P/7//r/+f/5//n/+v/8f/1//P//f/9/wEAAwAJAAUABQALAAUABQD9/wEA+f/5//n/9f/v//H/8//r/+3/8//p//H/6//v/+v/7f/v//H/8//j/+v/5f/r/+n/5//t/+v/8f/z/+3/6//t/+3/6f/p/+n/7//r/+v/7//t/+n/8//r/+v/8//x//H/9f/3//n/9//7//v/AwABAP//+f/7//3/8//t/+P/6f/n/+H/4//f/93/2f/b/93/4//l/+X/5//r/+f/7//5//v/9f/1//X///8BAAMAAQD3////AQD9//3/6f/p/+v/7//p/+//6f/r/+3/8//p/+f/6f/z//X/8//1//n/AwAFAAsAFQATAA0ADQARAA8ABwAFAAUAAwABAP3/+f/1//P/8//r/+3/4//b/93/1//Z/9n/1f/T/9X/2f/f/9v/4//n/+n/6//t//P/9f/5//f//f/7////+/////v/9f/p/+3/8f/z//X/9f/1//v/+f/5////AwAPABMAFQAVABcAFwAZABEAFQAfACMAHwAfACsAjwDvAqEHIQjXAfv7OfzJARkFAwL/+8/5h/1TAmMCYf5v+3f91QGxA48Anfwt/FP/EQKPAd/+sfx3/bf/OQE9AG3+tf3b/sEANwH3/8P+xf6x/2MAkQB/APX/lf85/3n/LQAzADkA5f/B/6P/4/9pANUAHQAB/xn/HQDlAJcAu//1/kH/3/93AJMAsf9J/7n/SwCNAAMAnf9l/8v/KwCnAFUA//9N/y3/FwDNAKkAe/8p/63/QwBnAHkAHwCZ/4v/GQA7AAsAof99//P/yQC9ANn/Cf+B/8EADQEdAMH+Mf+RACcBiQCN/0v/6f/tAOP/bf87AKMAfQAzAJ//R/9p//EALQCN//MAYQF1/5H+V/8XAQ8B6/7//Pv+tQGRAQEAk/4n/nv/zwD/AYf/xf4L/9H+VQG3AkkAB/5L/Of/HQQXAkn+XfuV/ZMB9wOHAPX9y/4V//P+gwC9AqcA7fsH/Q8CjQP/Aun9LfzL/30BDQFhAAcCu/7f+2MBswNH/qn9df8HAEEDYQEd/2P8m/97ATkBd/8LAL3/twDHAQX+c/17/rUDLwW//Y37k/xxA1sHQwG9+jf6/f85BNECVwGt/O39dwBxARcEff2Z+w0B3QP3A4f7VfprA7UGowGJ+KH4BwRpCf0Ce/x795H9lQYnBhP+wfmn/qMDAwSl/3/8ff8lACcByQFvAC3+ff8hAN0AH/8f/kUAvwGRARX/p/9n/9f+pwA1ABH/qf4rA30Csf4h/Hv/2QITAvH/2f19/G//1QMRA63/Cf13/A3+DQPRBRn9m/zh/IUCYwLV/5H/QQEL/7P8IQCpA8X/Q/5fAWH/zf2V/QsDuwZJ/aX6C/3jAt0Dz//r/Ff9pf+7/8cE0QEV/If9O/1FAYkDlwFH/439V/1PAJ8CZQBZ/bv9YwHRAX8A9/2z/g//+/9vAgMCL/1r/jkAnQBZANX9IfxBAVcEIQK9+2f6dQLpBF3+ffyT/d8DaQPR/ZH8vfzTAHMDbQNN/S351/4tBR0DAf91+e/9HQWbAu37Mf3d/tUCPQHFAGf8O/3TAVUD7/9L/Yf9cQEVAqUA5/2N/SMCCQIZ/gH/BwIDAQX/B/2D/48BxwHPADX+G/35/nUE8wAPABv/Jf5f/wkBgwP7AG/+n/5b/AkCbwNxApEAq/sp/WcBywMJAvH8jf59/2ECwf4X/psCQQCZADEABfxB/OECewVvANv7Yf7N/63+5QHz/9f+rwOLAKf9D/snAHkDDQYL/Yf3Q/7dBK0GNf0r+mf+IwKjAvH+NwEvAIn8o/0LAFEDbwIZAG/+/fyl/3UAxQEdAt3/B/2f/RsBYwKhAEn/7/4v/yX9bQH9BNMC8/1X+2/9LQE1Bc0A0/wp/BkB1wM/Ann9Rftn/+8CVQFnAXf+TfwFAdMCQ//1+pX/dwQFAAv+Tf6LAA0AhwGV/qH+ewJjAFX+af4BAAEBwwAp//v/gf/3/g/9CwJFAi3////p/XMAq/4bADcCwf83/mP/QQFn/2f+Of9T/vv/bQItAcf+i/2V/Wv/NQEdAV0Ck/xn/Hv+MwCXBEsCIf4B/PX7LQNlA+3+j/1t/jsB//4h/5EBhwB9+4P+6/6hA8sG5/9V+Xv4eQONBqsAQf83/Pf7jwKrAK8BF//PAJ/+Ff79/u0BxQRfACn8n/15/z0EjQMj/kX75QCBBVMAw/5l/zv+6QHvAaEAAf///YEB3QHn/u8A4/5t/mUA7QCTAh0AZf7Z/o8BWf97/UMBm/+xAPsAwf0N/W0AuwF//3f+3f7/AG0CBwFL/q38qQDPAjsAbf7L/pEA3wE3AfH+VQJ5At380/2/AKEBxQFnAYUAK/4X/Of+vwLvBHMCgfzJ+uP+qQTZBGEAw/vV+x0AxwPZAe/9Zf+HADX+Ff75AT0C8wAv/yf9cf4HAv0D6QLt+3H5AwBZBLMD+wHz+2/7ef4ZAwMFDwAp/B/+aQHJAbf9I/8LA0EAG/8D/mv/UQCDAi0BRf27/Y/+kQJzAvX+9/yZ/lMBZwG9/yH/u/7f/tX/HQFZATX/Af9/AHsB6//V/tcAOQHP/gP/VQFbAFsAHwHTAOv+ef6jAFMDsQDD/iv9+//pAYUBJQDh/c/85QAxA1kARf2b/a0BBwO9/6n8//2bAG0B0QArADn/vf6f/50BzQBnAGP+P/9nAScBWf51/mUBgwG3/rn9qf93AfcAAwCh/hH/qQCfAocAbfzf/VEChQSXAIf79/yDAfUC7QHV/vP9nf5ZABMDBQIP/9f8qf5jAMsBcQEfANv+Af5X/o8AmwHXAAv/+/31/ev/jQKbAf3+N/wX/nMCoQJ7APv9W/1t/10BWwE7AeH/2/45/n3/2wHVAbn/ff4d/5MA6wEtAYv+Mf7PAKsBVQCt/3UAWQF/ABcAJf8zAFECCQKn/yv/hwAXAt8A8/6V/gkBuwKNAu//9fy5/jsCYQJfACf+S/+FAdEB+/+F/hv/twA9Ae//xf9tABMAQf8XAKkBKQCX/gEA3QBlABkAqf+H/5f/gf81AD8BewAP/p38Xf7PAfMB3f/V/FH8uf7nARsBJ/0F/MP9KQA5/5/9p/37/m/+b/3Z/KH+GQD7/in8D/wV/gUA2/8J/q/8Af7n/6kAq/6v/bH+cQDbAM3/V//7/98AKwHTAI8AJQFBAm8CIwJZAbkBGwM3A2cCLQLLAokDbwOJAiMCuwIFBGcETQO1AQ0C0QNLBMsC6wGRAlUDxQIXAhcCuwK9AlECuwGdASECOwKHAU8BEwENAY8BewFHAbsAiQB9AB8AWwABAIH/Z//D/4P/Uf4T/jH+bf4h/rf8D/xv/Bn9D/2z+0n7e/v/++X7T/vL+t36H/s3++H6s/p5+rP6K/uP+wH7Sfud+2/7dftb+3v7K/z5/HX9x/z9+7/82f29/rX+Nf55/i0AVQKTA70CwwA3AFUCrQXNB7MGhwTPA68FZwe5B6MGiQY/BwEIjwdjBp0F7QUpBsMFBwX/BG8FfQSRAvcAOQFrAv0CuQH5/9v+J/+V/0v/e/4p/pX+Zf+X/9v+4/1f/V/+FwA9AREBtwBVAT8CVwIJAqcCDQRJBUcFGwW7BIkETQTfBHEFvQUnBakE/wMRAykCDwJRAtsBfwAj/1H+Ff3P+wf7F/sD+0P69fiL92/2Rfav9gn3rfbr9YH1a/Vd9UX1sfVT9v/2//bd9v32Xffv96/4gfnd+Qv6t/pR++H7of25AMMDLwOD/4/9kwFPCM0LWwizA40DswjlDNcLnQdvBqUJbQ3nDCkJlQadB3sJcQmTB5sGGQexBj0EgQFRAUcD+wPxAdn+T/0V/gP/O/5J/E37B/w3/fP8cftB+n/6o/tz/KH8qfyp/O38Nf2D/RX+/f5TAHMBCQIVAgECrwI9BE8GjweHB/8GDQfhB6EI7QgfCXUJWQlfCFMH4wYTB+kGLQY3BVMElQO7ArUBtQDZ/4n/Of9v/t38c/u7+rv6k/rx+Tf5t/g7+Lf3Iff59vX2A/f59tX2zfaJ9ov2l/bL9uf2I/dV9x/3v/aL9vv2U/dZ9/v2+faR92X59fyfAP0Aofw1+CH68QKlCs0JAQMX/z0DIQpZDIMIfQXvB0MNzQ4ZC/sGHQdHCgUMvQpLCVEJGwmNBjkDsQIxBU8HmwVdAT/+lf4pAPH/p/35+6P8Kf7L/Wf7T/lf+Q/7VfyP/A38Efyh/J/9ff5l//UAnwIrA6EC/QK7BSUI9QfrBTUG7QjTCqcJ5QffB+kIPwmpCO0HHwc3Bp8FZQV3BC0DMQLtAXkAf/49/Yv9c/3T+8n54fib+PH3E/d39h32jfUf9cv0mfQH9An0E/QN9Kvzt/Mf9EH0PfRb9MH0xfT99I/1ffaf9tH2lfd3+mH/XQORAof8p/hh/hMKYRBZCtUBewE5CisQ2Q3nB+UHtw3DETkPWwlTB1cKTQ3xC/cIpwhRCnEICQPH/20CwwYbBskABfzl+wX+v/5R/Pn5Afrx+3X8S/q195f3gfkR+1H7MfuR+3f7Ffv5+jX8L/4JAK0AiQCrAPUCzwVNBgEEVQP1B2cNXw0JCP8ETQg/DXEObwvtCHMIZQl/CbsIdQeVBjsGzwU/BJ0CewE9AS8A0/4h/kH+e/0t+xH58/gb+ov6S/lh91v2mfY/9y/3f/bT9RH2Y/Y39pv1ofXp9RX2t/WF9XP1p/Vz9VP1zfT99Ln14/Yz96P3z/oXADcCY/2R9pn4LwR/DuULxQEz/XcE3w39DncIRQUTCr0QUxA/Ck0GPwmzDbUNNQrBCF0K8QlzBX0BFQOnB0MIIwNr/Xn8L/+tAGH+M/vB+qv8a/1D+2X4A/jj+bP75ftJ++X6qfqP+tX6M/z7/bX/rwDFAVMCBQLFAREDTQe1CocKLQfpBeMI8wubCwEJyQi7CkMLDwn7BtMGRwf9BlcGjwVLBD8CzwBVABMA1/8x/yX+7ftN+jH60/pb+tn48/cX+PP33fbn9bH1H/aD9pX24fUV9YP00fT59DH1I/Uj9cX0NfSV9Ln1RfaB9Z30dfW598X7XwABAqf9dfaF918D7Q6PDccBg/yRA+UO8w+dCPMDHQnjEGcR2QrRBeEHwQy3De8KJQnlCdsIKwRRAdcDawhzB20Bu/wv/RMAEQAh/YP6a/tb/YP9mfoN+B34X/r/+y/8sft5+7n6U/ol+2/9f//F/3//hwCzAu8DGQPtARMESQinC7UJLQbJBEEIvwtDDNsJbwgZCDUIzwe/B4EH8QbVBRkFRQQlA9kBDQGVAGcA7f9r/4v9vfuX+qX7ffxB/Cf6ofjl9234z/ip+Nn3R/dH90P3t/ZF9nf21fan9sX1s/W/9WP1mfRN9A31lfXN9UX17fQf9SX49f29Aa3+Qffr9YP/FQuRDEsDI/1LAh0M+Q4LCY0EBwjVDiMQTQtVB40IjQsRDGUK/wmdCtEIfQQnAoEE6wcBB8kB7/1F/mcATwCt/Xn72/tr/YX9q/u3+Xn5qfo1/NH8pfz9+137OftX/O/9g/9XAHkBKQLvAS8B/QEDBjkJSwlJBucEHQdrCdcJYwhTCCEJlQgVBwcGRQZdBtcFdQUbBeUD1QGVAKcAKwHlAJ//Uf7h/B/8B/w7/B38JfuZ+nX6C/od+Zf4EfmT+Sv5efgp+BX4gfcH9xf31fed96H2ofVL9Zn1gfVl9Un1nfXd9ZH1Q/Ul9//8pwAb/ov2L/WX/ysK4QppAAP8rQKDDJUN9waLA2kICw/zDvMJnwblCCkMFQwbCoMJNQqZCI0E8wLZBXcIrQYBASX+Xf+ZASkBB/5h+wf8Pf6V/u/75fhZ+fH78/1D/X371/qr+638r/03/iv/owDvAeUBAQHtANcDhQYtB/UF9wU1BxcHWQbbBjEJnwm1B08FhQVbBmcGjQUDBbEE4QONAo8BCQHvAA0BtwCt/w/+Gf0J/ff8p/xN/C38s/vX+tX53/kd+qX6VfrJ+Qn52fij+GP4Dfhh+If45feT9hH2W/Z39qH19fSN9Sv2MfYv9cv0wfah+w0ARf7h93H06fyvB6kKvwGz+5cADQqpDOEGmQNBB50NxQ3fCZ0GcwgnC9ULZQrJCakJCQjrBNcDiQZ3CKUGjwF3/3MADQITAbv+Q/2B/Zn+K/6n/Gv6u/ov/B3+rf2P/E37l/tn/NH9w/59/38A4QEHAsUA/f/pAncHAQkvBskDwQRDB+cHawfTBxkI+wYTBbsExwWhBdkEOQRVBH8DnwErAEMAGwFRAVcAif7j/Fv8xfw//e/8Ofx1++H6p/pT+mH6Xfp1+kP63/k1+bv4s/gZ+RP54/g/+JH3AffP9tf2z/bh9cf14/XB9jv2QfVT9a/4Df6f/xv7cfVl9wkC+whXBnf9G/2zBCELeQk5BHsE3QlLDVsLjwc5B0MJPwv3ClMKaQlxCHsGBQXJBZkHYQdbBNcAbwClAQcCiQBj/s/9l/45/+/9sfvJ+kn8U/6b/vv8Tft7+/X8H/6P/uX+OwB1AXEB8f8BAM8CTwYJB1UEOwNnBOUGywY3BoEG/QZpBtUEkwQ5BXMF3wRTBA0EKwPrATEBZQHJAX0BdwA5/xn+v/27/Q/+af3D/N37f/tT+yX75foJ+xP7w/q5+S/5U/m5+W/5tfhb+E/4o/cZ9/v2V/fD9gH20fVB9nn2n/UB9aP1a/e5+pP9L/1P+Uf2XfrXA90HIQTP/LX+qwVXCgsIbwS/BZ0KYwydCaEGTwd3CukLCQuLCXUInwdNBtMF+wZJCIsGQQN1AHMBXwIZAisA+/6j/iX/h/47/Qn8E/yJ/bf+R/5p/Af7/fv9/SX/5/7d/osAyQHVAIv/twBPBW8H8QXdAtUCYwXZBjEHjQZBBqMFIQW3BAEFAQWdBIUEOQRLA9cBCQFRAZ8BkQHfAFP/3f1X/en9hf4Z/kH9T/y3+4v7w/t3+3n7Mfv/+l361flz+Zv5z/m5+dv4V/j197f3B/cj92X3VfdZ9on1y/Vh9mv2//UZ9kf4d/w5/v36ffZP99cAfQdtBYn9LfzRA4MJcwjRAxsEPQkHDLsJIQZNBmcJswsfCyMJyQdbBwUHVQabBqsH/QY5BGUBewHRAqcCLQF//xX/Xf9r/wX+g/xZ/Af+K/97/jH8Eftf/CH+Pf5T/nP+fQBlAU8Al/7D/xUE5QV7BOEBmQJ9BM8FiwXdBW8FuQRDBOEEHQU5BIcDYQSrBEcDkwFrAUsCWQLVAQ8BJwAv/7H+5f4n/7v+vf3Z/Hf8k/yH/A38pfur+4n7CftD+t/56flP+mn6cflh+LX3Pfhx+O/31/YV9m/2wfbr9ln26/Xz9W32Hfi/+y/+LfvF9hn3EwAVBy8EG/3f+z8EfQldB50CswP5CMsLdwk3BjMGgwgtC0kLoQnJB6MGsQYJB38H0weDBukDGQJFArMDBQP5AG//yf+xABsAkf0//Fn9h/+P/7P9Jfw1/CP9M/7X/rH+B/7t/SkAowIbAnH///63A+MHtQVhAasAJwUVB/sFhQSjBF8EhwMpBHsFEwWdAvEBrwNvBE8Cx/+xAHUCTwJNAN3+Uf57/tv+O/9d/uH8I/xp/An9Jf0t/FX7OfvP+437ofo7+lH6mfo7+rX5A/ll+GH4ffg3+IX3xfaB9qH2l/ad9uv2Sfcf+GP6ifxj++33V/eD/jEFIQTv/DX7MQIxCP0GjQLpAqsHdQr3BzUFRQZDCcsKfQllCOMHMQffBukGuwf3B0EG/wOjAkcD6QMfA3EBSwApAGcAAwAx/h39pf1d/33/2/0B/O/7T/3T/gP/Of49/Tn+TwB3AaEACf9lAMkD+wX1A4EA0wDHBOUHMQYDA0sCIQTfBHcEXQQXBCsDQwL3Ao8DdQKdAOcAvQKPAuP/7/27/iMAAwDX/tn9//x9/Pf82/2D/SP8Ofuj+yv84/vJ+lH6+foz+0X6P/kL+WH5F/mH+D34+/dN92n2m/YL9z/3Tfd99yv5i/sB/Lf5Efh3+oUBFQQDAef7u/2/BJMHCQX5AQkEcwgtCUsGxwTBBqEJmwqFCOkGWwZzB+UHNwfHBokGnQUZBOkCTQO9A9sClQF3ADMAMwCf/5v+I/6R/jH/l/5V/YH8Ef1v/v/+Yf6d/a/9cf+9AJUA9/99ANsCqQN9AoEB4wIPBUkF/QOXA+sDOQQzBGUEjwS9A48C+wKXAzED2QGfATECHwL7ABcAAQAxANX/V/8F/3f+q/17/c39Gf5d/V/8LfyR/Kf8Qfyp+1/7TftN+wH7lfon+sf5jfmT+U/5ifjZ94n32/en9+n2i/YL9y/4ofkh+yv7Kfnr92367QAPA4f/Mfut/VsETQatA/UAkQPbB10I/QVZBA8GgwjDCd8IEQe1BeEFYQcJCEsHnQVLBPsD8QMFBBkD9wFlAUMBOQFpABf/Af6p/t3/BwAp/p/8s/w1/jX/n/7P/ZP9r/6//8P/af+l//sAIwK1Ap0C3QFFAqcCCwWBBXsEdQK/AtkEMwXfA9cCdQPpA/sCJwJDApsC1QGXAZMBOwHT/zH/3f+lAJP/Mf6H/eH9Af7h/XP92fxt/G/8h/xT/LP7O/t/+8f7l/uR+un54fk5+j/6j/mL+An4F/if+EH4b/e79kP3+/c/+Tf6sfvP+uv4l/jb/JMCRQL3/cv7JQBRBX8FdQLRAfEECwhRB+cEhwS5BiMJqwnlB+UFJQWhBisIzwdXBhMFdQRZBPsDyQMjA5UC4QFfAesAWwBD//f+tf9pAIX/p/35/On9F/9f/5P++/1H/l//gwCFAIP/Zf/bAfMEmQPp/0n/IwRfByUFzwHxAVcEewTJAw8EMQTvAuUBRwMXBHkCUwCbAZcDkQJn/4v+RwARAQMA1/4//sn9g/0F/mn+p/19/DP81/wd/WX8f/tv+9/78fs/+2X6D/oz+qP6QfoX+VX4Y/jp+Ef4n/cZ96X3E/h1+AH52/oD/I/6pfib+a3/KwPjAFX81fzvAkUGwwRxAacCmQaJCDkGKQQ/BQsIiwlrCH0GSQXrBYMH3QfRBnkFgwQzBBUEFQRnA3MC4wGNAQsBtwDz/xX/0/6H//P/r/45/cH81/0d///+vf0h/XX+VwBhAJn+6/17AJ8DCQQ9ASMAYQJRBGEErwODBC8ExQLzAtcEYQUdA0cCzQOxBGMCZwCbAa8DDQOHAL3/YwBLAIH/xf8HAKv+Bf1N/Wf+T/4D/VP8s/wB/X38w/uR+8374fuB+yv7l/oT+u/5ffpj+lX5S/g9+K34kfjZ91n3H/ep9234n/ld+3v7n/lh+CX6PQDRAmEAM/wX/S0DMQZ3BIkBzQLRBlcILQZHBG8FDwiVCX0IvQZNBb8FaQcbCD8HgwVTBA8EXwRLBLUDbwL9Aa0BUwHhAAMAQf8z/9//KQDR/mP9Lf1T/of/af91/v39p/4TAHEAxf/j/28BgQNDA68AWQDxAiEGLwXTAjMCUwMJBC0EKwQFBP8CSwLzAosDywJbAcUBGwNjAj0AJ/9BAAMBWQAD/2H+3/2t/d397f3h/e38Nfwj/If8f/zd+6f7nfuH+wX7Z/of+lH6efrJ+cn4Lfh7+Mv45fdZ9xf3u/cP+KP3/ffr+YH8r/vP+Cn4Tf0tA1kC2/2Z+1sBtQWnBX0CawLjBQsIGQdjBc8FgwftCAMJ+Qd3BukF6QbNB68HWQZDBV8E5QPxA/kDWQNFAj0BrwC9AIcAc/+X/tP+mf8B/5v9yfwt/Zv+C//f/jv+Tf6t/iv/gwABAp8COwGpAH8BfQNNBPcDlwOzA5kDGwNzA30ErQSfA8MC7wLtAlsCKwLLAr0CmQFDAD0AlwChAB8Aqf8F/zv+zf0X/l3+9/1L/e38mfwz/BH8V/xv/Nv7+/q3+rf6q/pf+mv67/lJ+WH4qfi9+E/4Q/dv97H3m/f59kX3ffhB+t/7Xfsl+Xn4OfyPAuMC9f6B+zEAeQV3Bv0CSwJdBWEIUwdjBZkFbwcXCREJAQivBt0FvQaVB88HtQZXBT8E2QO3A8MDawORAmUBUwBdAHcAv//j/t/+a//r/q/9Ef2f/a/+Hf89///+pf7t/cX+SwG7AgUCOwAPAfUCawMXA2UDbwSDBGMDIwPBAzkEJwTPA70DPwMjAgUCxwI7A2UCRwHHALMAYwBlAEcAw/8N/2X+G/7v/dn9s/1X/S/9s/zp+7H78ft9/P/7Gftv+lH6g/qT+hf6v/nx+Gv40/cR+C/4ofe59mv22/ZV90P3q/dN+en7u/sD+YX3Gfz9Al0D6/5p+ycAiQWtBscDmwKLBU0I4wcjBhMGkwdBCa8J2QgJB9MF6QYZCCMItwZTBU0EuQO3A/UDmQOXAgEBAQCFANkAu/9H/mX+m/9X/539b/zx/Mv+5/+d/1/+h/3P/QUAzwGJAgkBAwChAcUDXwS9AvsB1QMJBkEFqwL7AQUEXQVBBDEDmwJPAscBVwIzA5sCgwCj/6kAbwEnAKH+0/6R/+H+uf1t/cX9X/0R/VX9Df0l/E37y/ut/FX8xfrf+aX6K/t7+iX5xfjB+GP4LfjN94n3f/af9vn2i/fn9qH2BfiH+/v8MfoZ9/n4wQBRBEEBE/zb/LMDJQe7BX0ChwMjB8MIWwfrBUcGBwjxCXMJxwf9BU8GgwftB18HNwbZBNEDQQPBAwEEHQNpAQ8AMwDPABUAtf4t/vP+Xf9R/j390/yn/fn+i/9L/0f+e/1R/skAzwJFAgcAn/8NAocEdQRHA6kCqQNXBG0ENwQTBOUDqwPNA7kD8QIfAlsCEQPTAlEBNQBlAPkA3QADAC3/j/5L/mf+Y/73/U39u/zP/O/8kfzh+3n7q/vR+y37a/oR+iH6Nfqh+e/4Wfgb+BH4lfdB95v2tfbb9if32fab9kn3Pfob/Zf7H/jl9l/9eQSjAzn+zfpFAeEGewedA7sC1wUHCW8IsQZtBrcHkwkFCikJ/QbfBQ0HOQgJCK0GJwUPBF8DhwMVBM0DOQJNAJv/rQDxAIn/K/5T/pv/Gf+1/en8jf0D//n/8f/v/pf9xf1lAAMD5QOfAen/vQBpA0cFFwWXA/0CcwNpBGMEzQPpAw0E1wMhA2kCNwI3AocCuwL5AXEAaf/B/+0A2QB9/yf+wf3l/eP95/3b/R/9YfwH/C38Z/wB/HX7Sftn+yH7R/qZ+Yn55fkD+n35Q/hN9+n2tffd95334fZH9l324faF+KH72/xp+if3Qfj3/40E8wFv/DX8RQMXB/MFfQI7AwsHBwm7B9kFUwbvB9MJwwmNCCkGhQXpBk0I8wcdBmUEqwNbA4sDeQP1AqUBKwC7/10APQAX/x/+q/6H/7H+U/3T/AP+nf8rAHn/j/45/jv/LwGXAv8CnwHRAG0BbwP7BLsEmwPrArMDZwRRBNED4wPjA48D0QJnAmUCWwJnAjECZwFdAJf/CQChAF8AKf89/un9C/79/QH+xf0b/Xn8I/xX/GP8Bfyr+0/7A/tj+if6Rfo7+q/58/g7+KX3o/cb+CP4D/f79UP2Y/fF94H30ff/+vv8NfsH+Cv4r/+zBPsCSf3j+2sCGQcTB1EDJwMzBqUIgQdXBq8G1wcJCdcIHQhvBtkFmwZ/B4cHYQZxBBsDyQJ/A/sD+wJfAbX/e/+LAIEAPf8n/m/+Of+P/rX9Yf15/vH/QQAz/xf+8/5LAa8CPQINAXMBxQJnA40D+QOJBHsDmQLfA0cFPQRrAsECMwTRA6UBLQGHAgcDnwFZAKEAyQABAKf/QQAfAIP+nf1Z/v/+Uf5r/Tf9b/0b/Y/8Y/yJ/HH87/tr+2P7C/vB+mX6WfoN+oX5k/gz+Bv4U/gt+Pv2D/fX9lX3tfbh9vX35/k5/Gf71/i/99P7swKBA6X/afv1/q0E5QZxBK8COwQLB0sHMwYNBhcHBwihCAsIOQfHBeUFjQaTBysHswVNA28C8wIxBAkEYQJbAFf/AQDHAP//7f6B/i//7/4R/nP9Af4d/+3/8f9j/7v+t/5RAOECswPTAfn/3QCzA6cEGQRDAysDIQMdA88DcwTnA6MCaQIlA/UC1QFfAU0ChQJVARcACwBBADMABwDf/xv/Bf6T/S/+zf5r/kv9m/yf/O382/y1/B38ffsl+0P7Ofuh+tX5s/nZ+Xv5c/in98f3P/jd9xv3v/b79v/28fbL94/5MfwD/Jf5Ffiv+s0BuwMnAVn8I/5jA6cGgQWDAwEEZQZ1B8MGUwbxBsEHoQgNCFEH3wXZBXkGGQfDBsUF2wO/Am0CjwPFA+UC+QB//4v/tQBzAJX/r/7z/vH+i/5B/k3+if5l/0MAWQCP/4X+uf85Ah8ENwP9AMcAuwK5BIUEuwMrA5sDXwNZA4cD2wNzA5UCdwK7Ak0CKQE9AR0CJQKTAGv/k/8XAPn/e/8r/5/+uf13/Q/+rf4R/tn8XfzV/B/9ufwb/PH74/t7+w/7ofqJ+j360flb+cv4q/gJ+MH3WfeF96X3D/ex9pX2u/cj+rX8iftT+P/2FfyfA6cDd//h+lH/qwShBpEEAwMvBBEGkQblBlsH6QaVBnkHeQgZCL8FNwXlBSMHuQZ3BYMDYQI5AmsD0QPtAmUAq/5N/+UAyQCV/1v+hf5v/qf+8/7B/n3+wf7f/+kAGQAF/73/XwLFA68COQHDATEDhwNjBK0EBQQJAiECEQQ1BekD9QHhAbUCvwIFAsEBxwEjAVEAkQADASUAOf89/9//Z/9V/r398/0z/lv+w/0J/Z38s/zp/AP9hfzN+w/7A/s3+xH7dfqP+Q/5Ifkt+YX4Zfcn91/3S/dh9zP3B/ej9s/3K/yd/dH6ofYz+P0AMwUdArn7r/wtA5kGZwWXA0EE9QUhBuMF8wbdBwUHvwbVBhsIDQfDBScF/wWpBocGoQS/An0BrwLTA40DdQFp//v+TQCJACUAF//v/m/+E/6P/iX/3f43/mn+yf9LAf8APf/d/qEAXwRtBI0CSwHbAaUDFQThBPsE1QMbAiEC8wP1BHsDnQERAuUCcQIBAf8AzQFfAYEAMwATAE//kf4J/9P/Y//n/c/8Mf0v/h/+ef3X/IX8Rfzx+1P8bfzV+936l/qH+nH6uflL+Tf5xfgd+D33Lfc39033d/eb90P39/cj+yX9wfpr95H4UwGpBLUBG/v3/FsDhQbfBDcDewSlBdcEJQWTB/MIrQYZBeUFdQhrB28FSQSvBTkG3QXxA6ECkwExAv0CLwOVAWP/d/6d/1sAUQBH/+X+If7f/YX+l/9//4H+O/4h/2EADQFnAREBCwCXAIECdQWvBHcCJQEJA/sE7wSpBPUDMwMbAo0CCwQjBIcCJQGdAQ0CrwGJALEA2QCtAOn/zf8f/5H+Pf4f/1n/b/73/Gn8/fy5/a/98fwh/KX7ZfvB+wH87fv5+j364fkP+tf5Wfnx+Gn4Nfiv9yv3+/Yf9+/3U/mr+5/8eflz9zH4dQCpBG0Ccfzz+h8BeQUjBg8EwQN9BJMEUwT3BQkIRQcTBhkFjwZRBlMFUQRDBc0F4wXVA/sB5wCTAfsCYQMzAqH/9/3R/iEABQE/AF3/Lf6d/XP+p/8VAGX/+f4p/wUAdQCZAJMBQQJxAhcCNwLLA9kDqQOrAxkESwSZA38DuQPHAyEDqwJfAkcC8QFZAU0BMQHNABMA5//F/4P/Hf/v/o3+I/6//cv9q/2J/Sn9s/yB/LX8s/xn/AP83fvj+7n7kftl+yP7zfqR+i36K/rv+V/5B/mx+Hf4D/g7+MX52fxh/q/7+/ff95f/3wSJA//9UfzPAKcDrwQJBBsF9QTJA9ECFwVlB88G/QS5BDEG2wVPBF0DFwTvBCMFAwQ3Ao8AfwCPAbkCrwJpAE3+P/5b/yUAHQD3/0X/Bf4j/kP/FQDZ/5n/MQC9AEUA7/9NATEDawNvAvkB5QO1Az8DIQMTBYcF+wNdArMCvQONA7sCeQJ/ArUBVwBjAGUBiQEnAGf/N/89/4P+af6z/qv+tf39/Mn8E/3J/E/8T/yp/DP8gfsf+5/76/up+zX76frB+qv6ofp7+oX6Kfp/+Xv5W/mT+V/5Cfuh/mv/v/vd99f52QLXBQ0Dsfz9/RkCTQQNBIUEXQVXBOUBeQL7BV0H+QQzAwsEGwbTBNcCSQJ5Ay8E+wOhApcBGwDr/7cAHQIpAjcAS/4r/vH+IQCZAJEANf8t/nn+9f8JAe0ASQBPAHMA/QA1AWkCTwNXA50CnQJxA48DjQMBBOMEhQQ7A0sCqwKLAz8D2QIXAnUBiQA7AL8ATwFxAHX/1f7P/of+Lf4j/jH+j/0T/a38r/xt/B38Kfxr/HP8+/tp+0/7n/sR/AH8yftB+/H6+foX+1H7P/sP+436Jfor+tP61fx3/3n/qfzJ+Q/8iQKnBNMCn/7T/+8BMwMZA2sEVQVrBKcBvwGTBOUFUwSPAj8DfQSvA+kBawExAjcDAQPrAQUBIQC5//X/ZQERAvMAQ/+t/jH/bQAPAR0BLwCz/7v/9f9nAPkASQF1AaUBgwH3AH0AfQHvAr8DBwM7ArkBgQKvAlMDkwPDA88C1wG9AVsCfQL7AasBpwEPAV0A6/8rADsAHQCp/zn/l/4F/qX93/01/hH+Ff11/DX8Xfwx/EH8QfwV/J/7V/s5+1n7b/tn+3X7jfsh+436rfox++H7i/uj+xv8j/3p/g//z/2T/Qv/OQItA3cCxwAFAT8CqQM5BI0E1wPxAksCKwMpBD8EGQORAlcCpwIdAqkBNQFPAU0BOwGbAB0AZf9V/7v/cQCXAAMAFf///pX/lwD/ALMATwA3AGsA0wBhAaEBiwE9ATcBcwGlAYEBQwFdAZUBcQH/AJkAhwBTAHkAiQCZACMAMwBxAA8Aa/8b/68AdQHxAJH/Vf9nAMEAxQDlAC8BvQAbAGkAYwGbAb8ARwDHACUBkwC7/4v/4/9//zX/yf6N/tn9Rf35/GX9af39/Nv7Z/uX+wH8+fvF+437Pfs1+zv7xfsv/EH8GfzJ/IP+4/8F/8v98f3XAOMCDQOTATkB5QFxAucC6QNlBKUDFwL7ASEDyQMbA0MCBQJLAuMBeQE1AR8B1wDDANkAAQE3AG//U/8vALsAxQAHAOv/rf/9/2cAHQFfAdsASQBbAAsBWwE7Ad8A2wDdAMEAlQCLAE8AKQAFAGkAdQDx//H+w/55//X/l//P/rv+y/6r/nH+vf5j/zX/Y/5n/kn/JQB3/8/+Af8nALUAQQDH/8n/EQBHAJMA3wALAVcA8f/t/7MAGQHpAFsAGwApAFkAgQCVAHEANwAFAEkAXQB5AAcABQAzAI8AlQB7AHMAswCjAM0A3wAJAQUByQDfAOUA/wDVAKsAmQCVAGsAWwAPAPn/uf+F/zf/Cf/N/q/+Kf7f/Y/9d/0x/QH91/yx/DP8DfwN/Hv8e/xb/EX8k/yp/Mn8Lf2L/QP+//1Z/vH+zf9JAFcAewAdAQMCtwLDApsCbwLhAmsDvwONA0ED/QK5AqUCkwKNAhsCZwEJAfMAAwGLAP//sf+z/6P/kf9j/0//Bf8B/13/s//P/6X/lf/j/yEAjQC1AO0A3wDpABUBWQFrAUUBNwE3ATMBJQHzAMEAZQBPAC8AJQDH/33/R/9X/w3/yf6t/vP+1f6P/mX+Af+d/5X/8/5B/pX+Vf8PABUAl/8d/7X+p/4L/3v/ef/R/in+D/4x/gv+zf2L/Y39Pf1j/T3+Q/8N/xv+lf0B/70AcwHjAHcA8QB1AZ0BJQKzAhMDlwL/AUECxwLLAj0CyQH/AQ8CywE1AYsAFwANADsAUwDj/z3/sf5p/qP+7/4L/7X+b/5Z/n3+sf7V/gH/Qf9h/2X/hf/v//n/4f/x/6UA7wDhAH8AbQC1AN8A1QDlABMB2wBTACUAhQCXAGsAFQAFAOn/3/+3/7f/qf+t/43/o/+h/3v/U/9t/33/j/+j/8P/of+D/5X/y//1/wcA9/////3/CwD9/xUAJwAhABkALQBDACkABwDx/w0AEwAdAOX/4f/P/8v/vf+9/9v/1f+1/6P/s//F/83/wf+//8n/yf/R/8n/3f/n/+//3f/d//H/CQD5/9//5f8TAB0A+f/Z/+P//f////3/9//l/+v//f/5/+X/y//r//n/7//3/wUAIwATAPn/BQArADUALQAZACsAJwApAB8AHwARAP//4//1/wEA7f/B/63/zf/L/7H/kf+H/4//g/9x/4f/p/+p/4X/jf+n/9f/w//D/8H/4/8BAAUAAwAdAC0AIwATACsANwAxACsALQAvACEAEwAhACEACQDf/+P/8f/f/8H/v//P/7X/g/+N/7v/xf+z/6P/z//Z/8v/x//h/wsABQDx//P/IQAxABkAAQAhAD0AMwABAO//AwAbAA0ACwAHAPf/0//b/+v/7f/Z/83/5f/t/93/z//V/9v/zf/d/+v/+//h/7//2f/5/w0A9/8BAAUAAQDt/+v/AwAXACEAGwANAAUACQANAP//CQAhAC0AFQABAP//BwANAP//+//9//n/6//Z/+P/6f/x/9//0f/J/9P/0f/H/7P/0//d/+f/1//d/9v/4f/j/+f/6f/1/wMABQDv/+3/AQAbAB0AAwALACMADwDx/+3/EQAfABcADwAPABEAHwAPABEAFQApAB8ADwD7//X/+f/7//X/7//d/93/2f/f/9H/z//f/+f/5f/N/83/2f/n/8v/uf+7/+H/4//L/63/z//z/+n/u//V////CQDJ/9H/+/8xAAsA5f/x/y8AJQD7//H/JQAxAAkA7f8XACkACwDh/+3/DQAZAGEANwDF/wkAkwC//h0Bdf6BAbH+vQAD/3kAkf9vANX/pf9L/5UAr/9bAJv/awBN/+f/AQBdAOv/AwD1/8v/HwDD/zcA6f/N/8P/FwD1//f/y//h/7P/BwADAO3/0/8XALH/sf/l/zsAJQDB/8n/+f8PAO3/v//r/wMA+//P/w8AKQDt/9n/5f8xADsAFwD//wkALQAVAAEAOwAtABkA8/8TACkADwD1/xEAFwATAAsACQARABEA3f/v////FQDv/9v/6/8DAN//5//9/yMABwDp/+v/IwAhAPf/5/8fAD8ABQDZ/wUAJwAXAN3/1f8PAAEA7//F/+//DwD1/9P/3/8DAAkA6//r//H//f/z/+3/AQD1////6f/r//n/BQD//9v/1f8BAA0A+//H/+H/CQD9/9P/0f8JABMA+f/Z/wMALwAdAPP///9HAEcAEQD7/z0AVwApAOv/IwBTAEEABQD//ysALwAFAO3/FwAZABkA6//7//P//f/p////AQAJAPf/8//n//P/8/8lAA0ADwD1//v/BwD7//3/CQANAO//4f/l/xMA8//N/8n/AwATAN3/yf/t////4f+9/+v/BwANAM//yf/v/wMA8//j/wkAEQADAOn/AQAdAB0ACQAFAAsAEQALAA0A9//r//X/EQAhAP//7f8PAB0AAQDh//P/IQAnAAUA6/8NACcACQDt/wMAKwAdAOv/5f8JAAMA6//d//v/9//h/93/7f/z/+X/2f/z//v/6f/N/9n/8f/v/9//4f8DAAcA5f/T//f/DQD5/9P/7f8NAAcA7f/l/wUA+f/p//f/DwAhAPn/9/8HAB8ADQABAAcAGQAFAO3/7/8RAAEA7//1/wEACwD5//f/BwAFAO3/7f8VABcA8f/T//f/IQAFAOH/3f8JABMA7f/V//3/GwD7/9P/7f8ZABMA6f/n/w8AJQABAOv/CwAtAB8A8f/v/xEAHwADAPn/AQAFAPf/8f/v//X/5f/N/9n/9////9//3f/x//X/1f/R//n/CQDn/9X/7/8dAA0A5//r/w0AFQD1//X/GQALAO//3f8PACMAEwD5//3/DwAHAPP/9f8HABcA+//z/wkAGwD//+3/+f8TABUAAQD7/wUA9f/7//v/EQD//+3/8f/9//n/3f/l/+n/7//x//v/DQABAPX///8HAAcA9f8DAAUADQATABMAJwAXABMA+f8HAC8AKwAFANv/BQAtABEA3f/b/xEACQDL/9P/6//1/7P/t//n//f/2f+l/8f/4f/L/7H/u//n/+f/zf/N/+H/8//d/+3///8BAPP/8f8NAAkA9//p//f/CwALAAUA9f/v/+//8////wEADQD///f/+f8HABEA8//p//v/EQABAOX/5f/z//n/7//n/+3/8f///+n/1//X//X/+f/f/9n/3//3/+//0//T/+P/+f/1//H/5//p//H/4f/p/wEAEwD1/9H/6/8hACUAqf/J//H/GQDr/9n/5f/p/+P/0//V//f/8//p/83/3f/v/wEA7f/n//P/DwAPAAkAAQD7/wUAEQAXABUAIQAdAAkA9f8FABMACwD9/wMABwD5//H/CQD5/+X/5/////v/6f/z/wkA7f/Z/+P/BQD3/9P/1//v////1f/b//n/EQDx/8n/5/8JAA0A7//l/wEA///5/+f/+f/x/9n/1f/v/wUAAQDx/+f/4f8JABsAFQDr/wMAGQALAO//8/8bABcA+//v/wsAGwD3/+X/7/8BAPf/2f/d/+P/6//P/9P/8f8BAPf/7f/t//v/7//3//X/BwADAAcACwAdAA0A+//5/xUACwAJAPv/9f/f/+3/BQABAOn/6//5//X/4f/t/wkAAwDr/+n/GwAdAPn/5/8DAAcA4//j/wcAHQD//9X/+/8NAAEAv//N/xEAIQDv/7v/4f8FAP3/y//T/wMABQDp/8X/6f8XAB8A4//N////PwAfAN3/1f8LABUA5f/D/9//+//z/8//2f//////1f/X/wcAFQDz/8f/6f8NAAMA0f/Z/xcAIQDx/+P/DwAnAOP/zf/1/yMADQDX/+X/8f/3/+H/7f8PAPP/y//V////8//D/8X/7//p/8H/yf8PAAMAt/+p/9//MQDp/8v/u/8HAN3/z//j/yUA///b/93/CwD9/9v/zf/1/wEA8//X////DQAPAO3/9/8dACMAHwAZADMAJwD7/wEAMwBFAPv/4f8lAE8ACwC1/+v/QQAnANP/y/8dAC8A1f+p/9f/IwD5/7n/1f8VAAMAq/+3/w0AFQDL/63/CQArAPP/qf/j/yUABQDN/+f/HwD3/6//w/8DACEAz/+1/+n/IwADAMf/4/8bABcA9//p/yUAGQALAPX/9/8PAA8AHwAFAAUAAwATABEA/f/x/w8AJQAbAPn/6f/3/xEAEQDp/+f/AQAXAAkA/f8JAAEA8f8HACcALQALAAUAGwAjACEAEQAVAAcADQATAAUA+f/v//n/7//f//H/9f///9f/4f/l/+v/5f/n//X/8f/d//H/8//7//P/AQAHAA0AFQAbABMABwALABMAFQARABcAIwAPAP//CwApABUA/f/x/wUA///9//n/AwDp//H/DQApAAcA8f/z/wMA8f/p//f/GwANAN3/3f8HAB0A+//l/+/////1/+n/8f/3/+X/3//z/wkABQDz//3/AwD9/+n/7f8NAB0ADQD//x8AOQAjABMAEQAVAB0AFQAbAA0ABQDp//v/AQAFAPP/9//l//H/3//v/9v/6f/l////4//h/+n////r/+X/9f8JAPn/5f/x/wkA/f/X/9//+//1/8//0//n//f/3f/h////AQD3/+//CwAbAB0A+//3/w8AJwAjAAUA+f8DABsADwD7//f///8TABUAGQAXAAMAAQD5/xEADQATAPn/AQAPABsAEQAHABEAHQAJACEAJQATAAMAEQAhAAsA9/8NACMADQDf//P/EQAHANf/3/8FAP3/z//T/wsAAwDP/8P/CwAXAOf/x//x/xkA9f/D/+H/KwArAOX/2/8PADUACQDt/w0AHwAXAPv/FQAtAB8ABQADACEAHwAJABMADwAPAA0AIQAdAAMAAQADABkAGQALAAcAAwAhAB0AEQAdABsAFwADAAkABQAHAP///f8DAPn/9f/z//v/AwD7/+X/7f8BAAEA7f/Z//X/LQApAPf/7/85AC8A+f/h/zMATwD//8f/9/9JACUA0//f/yMAMQD1/+H/JQA3AAkA5f8TADEACQDd//v/IwAZAOf/+/8VAA0A2f/n/x8AMwAFAOf/DwAtAA0A+//7/xUAEwAXAA8AEwARAAEA9/8ZACMAFQD7/xMAJwAVAPf/AwAxACUA8//t/w8ACwDp/9n/CwAPAPX/2f8JAB0A9f/X/+3/DQD1/+P/8/8RABEA5//X//f/BQDh/8P/9f8ZAPv/3f/v/yEACQDj/93/FwAlAP3/4f/3/xMABwDr////FQADAOP/5f/9////4f/d/+v/CQD5/+n/2f/z//3/+//3/+//+f8NAA8AAQDr/w8AEwALAPH/DwApABUA5f/j/zEAPwADANf/DwBNAA8A0f/j/zUAKQDl/+P/OwBLAPf/y/8NAEkAHwDN/+n/KwAnAOf/1f8HABUA5//B//H/EQDl/7X/2f8PAPv/w//F//X/CwDl/83/6f8TAAsA8f/1/wUADwD9/wsADQAFAPv/AQADAPH/7/8BAB0AFQDn/+X/DQAdAPn/2/8LACEADQDj/wcAHQAPAAEACwAnACMACQAJABcAHwABAAMAGwAjAAEA6f///yUADwD1/+f/DQAVAP3/3/8DACMAGQDp//n/FQAPAOn/7f/3//f/6//t//3/9f/f/+P/AwAHAO//4//z/wcA7//j/+3/AwDv/+f/AwADAAEA1//x/wsAIwAPAAMAIwAXAAEA/f8PABEA3f/v/xcALwD//+X/EwA9ACUA4f/p/zEALQDn/8//AwAtAPv/0f/h/xEACQDT/8X/3f/7//H/2f/p/+X/3f/f/+X/7f/L/9v/3f/p/+H/3//l/9//3//p//n/DwD5//3/+f8RAAMA7//z/w8AFQAJAPP/CQAVABMA+f8FABkAHwAHAA8AFQAXAP3/9/8FAAEA9f/h/+3/+f/x/+P/2f/5//X/zf+t/7P/2//J/7X/xf/l/9X/w//F/9n/0//N/9H/5//x/+3/3//x//X/7f/f/+v/9f/v/+f/6//5//X/6f/t////AwD1//P/AQAFAO3/5f/p/wMA9f/1/+//AwD3//P/9//9/wUACwANAB0ADQAPAAsAEQAFAAcAFwARAPP/4//t//H/8f/p/+n/6//z//P/9f/x//X/9f/r//X//f8HAPf/9f/t/+v/6//n/9//1//Z/+3/2//V/8n/5//p/9X/xf/Z/+3/8f/V/9H/2/8BAP//5//j//v/BwD3/+//+/8VABcACwADAAkAEQAPAP3/8f8BABkAGQAFAOv/+f8BAAEA4//j/+f/+f/x/+v/4//h/9n/1//n//H/8//v/+n/7f/x//f/9f/5//n///8HABMABQD//wMABwABAPv/AQAHAAsACQD3/9P/4f8BAA8A8//f//f/EwAHAO3/2//v////AQD1/+3/7//3//P/6//n//n/7f/b/83/4//v/+v/z//T/+n/9f/r/+H/2f/d/93/4f/h/+H/4f/d/+H/6f/7/wMA+//l/9n/7/8TAAsA7f/j//f/GwAVAAkA8//3//H/9f8BAP//9f/f/+P///8BAPf/4f/p//v/9//n/+//CQD7/+f/4f8HABMA8//Z//f/HwAHANn/z//3//H/0//N/+n/+//j/9H/2//p/+v/4//f/+H/1f/L/9f/6//V/7//u//j//P/6f/F/8f/2//v/+H/2f/j/+3/5f/h/+P/6//d/9P/2//5////9//x//n/DwANAO//9/8RAB0A/f/t//3/BwAFAPf/+/8DAPn/+f/3/xUACwD7////EwAdAAcA+f8FAAcACQDh/93/7/8JAPH/0//L/+//8//z/9v/9f/7//v/5//n/+n/5//f//f/7//x/+H/6f/l/9//2//n//v/7//T/9P/7/8NAP//6//j//n/BwADAPP/6//3/wUABwADAP3/DQAdAAkA3//j/wMAIQALAPP/7//1/w8AGwAnAAcA7//9/yUAKwADAPH/DwAvABcA8//7/yUAJwD5/8//7f8fAB0A6//J/+H/BwAdAAUA5f/X//P/EQAPAOP/1//p/wcA+f/x/wcAFwADAN//7f8LAAkA8//X//H/AwABAPf/+/8FAPf/6f/9/w0ADwD1//P/BQAVAAEA7f///xMABwDl/9//AwAjAAUA4f/l/wUACwDz/+X/2//r/wEA9//j/9P/7f/3/+n/3//p////6//T/9X/+/8bAAkA7//5/w8AHQAFAP//9f/1/wEAGQAhAAkA//8DABkAEQADAAEAEwANAPf/9/8PAAsA+f/t//P/8//n/+H/7//p/9P/t//B/8//1//P/8v/1//l/9n/5f/n/+//3f/x////9f/T/+P/+//5/9f/3//3/w0A8//n//P/+//3/+f/7//3////BwAFAAUA7f/r/xUAIQD9/9H/8f8nACMA4//J/+//IQAPAPP/8/8VAP//2//1/yEAFwDp/+f/DQAXAA0A//8DAAcA//8NACsALwD//8//9f8bAA8A1f/X//v/AQDb/9H/6//7/+f/yf/B/+P/8f/j/9H/v//J/8//8////+X/0//j/w8ADwD5/+P/9/8PABEABQAPABUABwDp/+n/CwAPAAUA//8DAA0ABwAZAB8AHwALAPv/HwA9ADUA9//j/wUAHQAPAPH/8f/x/wEA+f/r//H/+/8TAPP/1f/h////DQDZ/7//u//z/xEA/f/b/9X/7f8JAAEA8f/5/wkAGQALAAEACwAlABsA8f/r/xUALwAhAO3/9f8RAC0ABQD5////DwAHAPP/7f/3//n/8//b/+P/6f/9/+v/4//h//n/DQADAOf/6/8HABcA+//d/+f/AwAHAOX/0//f/wsALwD//7H/pf8BAD0ACwCn/5//+f85AAkA3//T//3/AwADABMAJQAjAPP/5/8HABkAEQD1//3/8f/j//3/GQAVANf/yf/r/xMA/f/b/+v/EwD9/+P/6/8lACMA/f/j/wEADwDz/+f/8/8FAAUA8/8BAAEA4//B/9P/BwD//9P/y//t//n/1//L/+X/9//r/9X/7//9/+v/1//Z//X//f/3/+P/6/8HAAEA6f/f//n/AwDp/+f/BQAjAAcA6f/t/wUA9f/l/wEAEQDz/9v/8/8TAPv/vf/H////FQDz/7//1f/x/xEA/f/v//P/AwAVAB0ADQDz/+X/EwAhAA8A0f/X//f/CQDf/8X/4f8DAPX/1//P/+3/AwDp/7P/t//z/xsA9//F/8v/+f8TAAMA6//p/wcAGwAPAOn/8f8lADkADwDX/+n/FwAdAPP/3f/z//v/9f/t/wkAHQD9/8//y/8RAC0ACQDf/9P/+/8BABkAEwADAOv/9/8TABsABwDr/+H/BQABAP//9f////v/1f/J/9X/9//1/9X/0//p/wkA5f+9/8//7f/1/8f/5/8FAPn/2f/V//3/CQD//w0AEQATAOn/8/8XABUA9f/L/w0ALwABAN//9/89AAcAx//X/xcAQQAVAO3/+/8dAC0A//8DABsAGwD5/+H/AQARAPn/5//N/+P/9f8LAPP/2f/f/9f/1f/X/9f/1//L/+n/1//V/9P/1//J/7//3//9//X/8//j//H/6//p/+n/6f8RAAEA6f/n//X/CQDn//f/BwAPAPf/2f/3//n//f/l/83/4//j//X/9f/n/9n/t//F/+H/+f/x/83/v//H/9n/8f/d/8f/rf/V//v/8//T/8//8//p/8f/2/8RAD0ACQDf/+n/EQAPAOf/4//7/xsAEQD3/+//5//x/+n/4f/n//X/CwDx/9n/0f/j////EQALAA8A9f/5/+H/5f/p/wEA///R/8v/4//3/+f/1//h/+//3//Z/+H/CQABAOH/sf/T/wEAFQDp/8f/z//9/wsABwDX/8v/2f8dAB0ABQDT/93/8/8FAOv/4f8BAAEA3f/H//H/KQAhAOP/qf/N/xMAHwD7/9f/8f8PADcAIQAHAO3///8VAB0A/////yEALwAHAPv/GwAvAAMA6f/r/xMAEQD//9H/x//T//H/9f/j/+f/8f/v/9n/1f/p/+n/2f/J/9H/3//z/+3/6f/j//3/CQAFAOf/6f8HABcADQD9//3/BQAPAAkAAwD///3//f/7/wMAEQAPAAkAEQAVABEABQAXAA0ACQABAB0ANQAvABcA9f8JABMAHQAFAPf/BQAVAAcA5f/j/wUAEQD//8P/zf8HACkA+f+r/7P/+/8RAO//4f8HACcA7f+v/7n/GQAvABcA7f/3/wcABwD//+X/5/8XADUABwDX/9X////v/9v/y//V/////f8BAPf/5f/n/9//9//l/+f/7f8DABkACQD9/+n/2f/d//n/HwAbAA8A///x/93/uf/T/wkAIQAHAMn/0f/x/xMA8f/J/9f/CQA7ADkAKwAdAOf/0//r/ycANwAbABMAHQA7AB0A9f/1/wEACQADACcAJwAJAAMA7f/t/9P/0f/9/xEAHwDp////BwDr/8X/vf8hACsA///r/wsAKwDx/8n/0f/v/xkAAQD3/wMAEQDr/5//uf/7/wUA5//p/wMABwDx/8n/pf/B/wMALQAdAA8ADwD5/9v/6/8BABcAIQAfAA8ABwALAAMA8//9/xUAEwANABEALwAlABcA8//X//X/GwBTADcAEQD5/w0ARwAxABEAx/8BAEsATQARAN3/8/8jADMAFwDL/+v/MQBXAA8At//3/x0A+f/T/9f/SwAzAOn/j/+t/ykALwAJANP/4/8bAAsAIQD5/9f/t//p/ycAJwDn////7f8LAOv/x//x/wMAMwD1/+n/HQAPAPf/yf/1/z8A9f8ZABEAYQA5APv/JQAPACUAGQA1AGsAIQArACcATQA9AP3/MQAxADUANwATAE0AIQAnAA8A8/8nAO//CwAPAP3/EwDD//v/BQALABsA2f8TANX/9/8PAPv/7/+R/7P/BwAdABUAjf+V/6v/7f8/ABUAIwAHAN//yf/F/3EAewAbAKn/0f9tAH8AFQDZ/83/PQANABcAAQA1ADMA///t//P/DQAfAPn/5f+5//f/JwBNAP3/xf+9//v/GQATACMABwDf/8f/1/81ADMANQADABEAGwD//wkABQANAP//6f89AEMABwDF/73/IwAFAPn/0////y0A6//p/wcAFQANANX/HQATAB0ABwAJAAUA5//X//3/8f8PAOv/CQAXAPH/4f+z/+P////r//X/8/8tABsA2//b/6//+//n/x8AOQArACEAw//p//f/CwAZAAEAOwAJAAEAGwABABcArf8DACkAXQAlANH/8//3//P/4f/5/0EAIwANABEAJQAtAMf/xf8BAGEAiwArAA0A4f8NACkAIwATAOn/8f8PAO//JwAVAEUA1/+n/7P/KwB5AFUA0f+r/7v/KQAJAP//2//z//P/8f/l//H/1f/j/9H/7f/X/xsAJwArAPn/EQADAPv/yf8dAEUAZQAFAB8APwBnAN3/pf/V/28AgQA9APP/EwC1AFsCZwPDAk8ATf/dAGUCwQKfAbUBJQHjAOkAbQExAeX/C//J/7cAIwEBAOH/DQAxAIP/S//r/zkApf81/1H/CQC//23/7f7z/h3/cf93/3X/P/99/2v/vf+h/5P/g/95/5n/if/f////y/+B/1n/nf+z/6v/of+f/9P/qf93/23/w/8XABUAHQBnAFMAAQCL/wsAdQB1ABUA9/9DAIMALwABADcAbQJBBncJuQjZBLUC6wMdBdMEYwRPBRkEdQERAIUAp/+7/Ef7yfzr/q//s/49/pn9ufxz/Pv9WwDNANX/5/8nAYcB3//t/mH/BQD7/0sAAQHDAPf+uf27/cP+9f6l/sH++/7t/m3+Vf6T/g/+2f09/kf/of9j/0v/5f5z/nv+R/8NAPH/u/9j/4n/9f87AAsAJ/8X/zX/mf/V/9v/X/9r/iX+1f5X/yn/V/47/rf+T/+J/2H/Lf/3/uf+S/8bAIcAEQBX/0X/df9r/5n//////1P/B/9t/7P/NQBtAFMAdf8z//P/UQDR/1f/6f+vAF0AEwD7/00Ao/9V/9v/9wBHAbEAKQAzAFcARwBHAIkAlQB9AIkA4QDDAHEALwBlAGUAiwDlAE8B/QB9AEcAlQAfAY8BjwEDAcMALwFBAd0AVwCXAMsArQCFAKcALwHpAI0ALwB1AD0A5f8zAKsAlwDJ/2f/g/9b//f+B/+h/5P/8/6d/u3+4/6X/vn93f0x/pf+i/7Z/Zn9Xf09/av8BfyF+9f6Z/oz+hX63/mB+eH45/fH93H4Z/i594P3/fhZ+l/7Ffxr/H/8Wfx7/S//PwCzAOEAcwJPA6kDwQObBMcFFQYpBmUH1QhtCfkH1Qc9CK0IKQi3BysIGwitBwkH7wYNBy0GgQVdBe0FCQZtBV8FbQV3BbkEPQRzBGkENwTjA/kD4QNbA98CNwL5Ab0BrwGNATsBCwHFAEMAn/9B/zf/3/55/lP+d/47/nH9n/wl/Nf7ffsR+736V/qd+cP4vffr9lf2tfXL9F/0/fSj9ZP0NfJf8FHwa/GR8h3zH/OB8+XzN/SL9CH1ffU99T/2gfjp+rn8aQD9CfMYxyTrIlsU0QiVCUURwxKZDwcOWw+3DFcFU/2t+OX0qfEf8QP3Xf9LAzsAG/ob9hn2FfqLAB8GuwivCRsLCwzxCUsGbQM5A68EQwerCR0K0QaZAMf62/jf+Yv7Kfwr/QH/kwFvAh0B+f5rAO0FAQzvDkEPQw5dDN8KlwqlCjMJywfrBjcHuQYXBdkBsf7B/N/8n/6hAOsBkQFDABX/Qf/J/+f/O/9T/4f/7/8b/1X92fo5+YH4A/l3+Zv5wfgT+F/3kfbp9QX2C/Z/9S/0D/T/85Pzw/Eh8Knv3e/z8N/xG/OX85Pz7fP99Kn2Zfff92/57/tJANUH2RJpGRkVkwpBBmkMuxMZE8cNuwrlCxEL6QYhASn9I/rJ9/33v/uV/xUA2fyp+S/4C/rR/b8BswMxBK8FSwibCSUIfwVlBL8E/QVrB5kIFwjjBLcA6/1d/bn9f/3D/bf+BwDz/xn/If9tABEC5QJBBOEGzwqNDd8MDQqPB5sHyQf/B0MJVQqHCVUFlQM9A28Cp/+1/k0A9wFBAk0CsQGHAA/+ef1n/jcAyQABAGn/p/5r/Yv7C/rn+dH55/lP+hv7xfqX+H32b/XD9en1//VL9kH24fSF8snwE/D97knu/+7F8FvxafEn8pfz0fPZ85f0f/bZ99H5fft5/k0E6w/XGXEZ5Q5FB+MKsRJZFC0QQw2XDVMM6wfXApv/z/wj+V33U/of//MAmf5X+x/5Uflp/MsA7QOnBKMFvwdxCcMIqQZPBTMFwwX9BmMI+wjPBl0Cw/6d/e39Df3T/Ff+IQDj/1X+U/5P/wEAJQGrA5UIVQyLDRMMMQovCp8JjwihCGUKYQs/CJsGrwX5A9P/X/2T/nMAvQERAg0C6wErAP/+df6p//0AMwG5ARUC7QGP/4H8Lfu7+t36A/u3++H7X/qT+AH36/bB9sf1V/Up9jH3yfVR8+XxGfH/71vub+5578fwgfHp8Zvyi/L78s/z9fXT9z34e/g7+a/7GwCFCZUVQRsnFfcJMQjJD9cUmxGPDK8MTQ27CncGNwP9/0v6y/Wx9p/8WwHrAK39u/qR+Xv62/2DArMEfQQ/BYUIBwvzCSUHTQVtBIkEFQbhCGUJBQarAK39bf2R/av8d/zt/Wv/1/8VAI0ANQHxAC8B4wK3B6sN5w+VDaMJFQn3CEsHQQcTCTEKAwenBRcGnwRNAAH9s/2v/4EB/wJ9Aw0DxQDF/jf+W/8HARUBIwGfAd8BRwBj/b/7j/rD+dH5KfuX/OH70fk39+X14/Xf9an1g/UH9v31ffTd8l3xu+8j7Qnsf+018J/x0/Ej8tPyx/KP8hfzhfXB9235b/pl/KUAJQkxFbkbwRYJCwsImQ/nFSETVQ0BDfMNNQu7BYcB8/7/+hn3I/e3+zEA3/8V/Yn6p/nF+tH9UQLTBFsFFQbhCGMLSwojB98EzwQtBmUHPwiXBzEFiwF1/kn9wfw//D38Qf2z/l3/uf+P/yv/y/7/AJcFqQpPDNsLbwsxC80KnQnrCcMJkwmxCC8Inwd3BSUCR/9D/if/4f8tAWsBpQGfAKn/cf/T/zcAiQBNAbEC4QI5AjUAV/6p/LP7bfuz+zX80/tz+in5Kfh799v1gfQp9Pn0afXf9Nfzr/L38JvvMe8h8DPwk+8j75/wc/Ix85fy6fJn9Of1e/aj9xn5p/oL/BUCow5xG/0c2xGBB5MJvxF9FZ8QUQ0tDNUMZQqDBk0BtfvF9lf1R/hp/kkBGwEz/T/64/hN+yUAqwNHBLsEpwfFC9ULAQl3BVcEfwRhBdUGDwipB1cEk//n/C38O/x9+/n71/1B/5n/a//t/03/Pf6HAIcHtw0PDj8LCwubDA0LTQjdBwEK+QgRBz8HRQiZBQ0ACf1R/ZP+g/+DAFMCcQLnADv/lf8BAcsARQADAS0D/QNNAl0Ay/5R/Zn77frX+0v8ffuL+YP4P/hx98v1gfTH9NH09/Nn873zYfMR8W3v+e4X74nud+9P8U/yj/I18zv0d/Sd9IX1SfYV9xH4h/mb/JEDqRBJG0UbVw+XBk8KxRLxFEsP8wy9DasN4wnFBOEA8fsF9zv1j/jJ/j0BfQAD/R/69fjP+r//fQN1BOcEmwe3CwkMXQnnBW8EdwQjBb8GQwgJCK0Eu/8H/WH8R/wx+3n7V/3D/hX/Zf9NAPP/M/9RAfMGKwxrDY8MUQw7DEcLNwmFCFcIXwiDBzcH1QYDBRUBrf1r/If9w/5TAHcBKQJVARcA2/9jAIMAOwDFAIcChwMRAxsBP/95/df7vfq7+mH7Efvn+c34NfhN95/1Q/Ql9E/0NfTd8wf0bfMJ8rHww+/n7ofuye/f8avy9fIR82vzj/M79LP1dfYZ9433J/nF/dsHVxV9HJMX6wsPCIcO4RQtE60Nrww1Dk0NewhRAzn/Z/rD9Uf14/mF/ykBh/9T/A36+/n1/EsBrwMXBKEFeQnJDBkM1QjFBWMELQQBBcsGFwi3BqUCsf4j/WX8Efvd+Uf6A/wp/hMATQHNACkAqwA3A1kHwwrpDAUMgQudC1kLhwlfB00HnwYXBhMGWQYDBZMB//65/RH+a/+LAKMBkwGfAV8BNQE3AdcAiQCBAJEBBQP/AvsBEQBj/rH86fv1+/H7bftj+oP5Dflf+Gv3HfYT9UX0t/PX8+vzg/NX8qvwRe9t7hXvEfAn8WvxJfIv82304/Sf9In02fQX9sP3i/mj/BsDLw8zGtkb0xG1BycJ8RCBFP8P/QvzC5cM9QrZBWMAEfvR9gv11fZj/IUAfQEd/7H7Afov+4n/SwMhBIkEHQffCz8N0wolB5kEmwNnA+8ExQYbB8MErQDR/Z38A/zj+hP6yfq1/DH/XQH3AZUBAwENAiUFzQjfC5kMsQyRDO0LgQopCDEHRQatBREFMQV9BeMDIwFv/l39Tf57/+sAdQE5AncCKwL5AWsB3QA1AHUArQF7AsUCtQEdABX+cfyT+yn79/p9+q/5L/mx+CP4e/a79MXzTfO18nPyS/Pv84fyv/BL8OnwTfA/7+Hv0fG/83f0/fQb9RH1I/Vn9bH2SfiV+7ECiw8LG/8bKxInCkEMbxFrEY8NpQy9DeEM7QmDBnECYfzP9cnyffV/+3P/VQCN/939Ffwd/EP/QwLzArEDOQf3C5sN9QsfCWcGtwMbAuEC9QS9BVEEiwE7/4H9xfv3+QH5RfkN+w/+TQGnAkECgQJnA/0EuQbhCR0MeQypDGUNHQ0pChMHywW1BO8DYwNBBKcDwwGB/zf+G/5v/v/+vf+hAA0CvQIlA9kCNQInAVMAswBvAdEBbQGJAGn/7f2d/Hv74/oV+nf4ufjB+dH4h/f59Qv1mfMb873xcfG58fnxlfJ38r3wqe/F75/wYfEr87/04/Uh9j/2Q/ZD9gv2U/ed+hEB5Qx3GGEcgxRbC08KJw9FEfkMNQqtCmcMVQvbB40D4f2n95nzKfSv+Qv+wQDBABcAY/4H/hMADwIfAtEBiQQzCusNzw2xCi8HBwSNAW0BrQLVAzsDaQEFAPP+xf29+8f5qfi1+P/6s//hA+0EQwMdA/kDUwVtB6UKiwzFCykLiQy/DHkK2QYlBTcDLQKjAjMELQS7AWv/Vf6V/l3/c/+9/1sAuQHFAn0D6wMtA5EBLQBBAGMB4wG3AacAgf8x/jv9RfwP+5f5dfgF+FP4mfhJ+P/23fW59E/zH/Lj8Vny/fFn8WXxo/HT8dvxi/K58uPyV/Nh9F31lfaf9xn4xfeX+Ef70wGvDHEXSxprE4MMiw2XERsR1wvHCGUIMQn/CKUHTQSv/rH4k/SD9Ln4VfzP/mP/8f8VAKEAwQLxAwcDmQFZA20IEQx7DHkKWQj3BXkD/QFnAQEBGwD3/qP+3/7F/j39O/v/+dv5L/sb/oUBHQPhAgkE8waBCT0K4QqfC30L/QkDCi8L2QojCKMFXwQ7A3UCCwKDAQcA9/4x/9n/twAzARMB7wCBAZ0CDQMpAxsD1QIRAmMBkQGFAYkAF/8t/vH9hf2r/IP7M/r7+PP3ifdl94X3EffJ9Vn0sfO9843zqfL38enxB/Kt8aXxMfLf8m/yCfKt8lP0afXJ9RP28/Yr+F/5vfvZAskOERkFGnsSpw1fEKsTCRBFCXcGnQdZCCEHjwVvAyH/z/ln9dX09fat+dv7+f3d/0MBMQN9BSEGJQQhAmcD5QYhCX8IBwj/CUcI/wYVBFMCvf8d/bn7Yft3/AX+tf3//Xv9T/0d/Fv9yf6dAG8BmQQFCBULowzZDQ8NaQrZCAUJTQghB38GyQYRBcsDWQPlAncA9f3L/Vn+K/8lAJUBYwK7AkEDRwP5AnEC9QFhAfsAtQEzAgMCBwEzAEn/Cf4J/U/8e/tt+pf5Q/m3+DH4dfen9qX1mfRx84PyF/Ib8mHyufLb8oHyu/GP8Sfyj/LL8kXzefSR9VH2j/ZT9wf4gfnJ/bMHlxMdGgkXCREpERkVRxQlDfEGiQVVBh8GSwVLBLsBw/35+Wn32/Zt99n4n/rD/CP/JwLnBYEIKwipBZkEAwZNB/sGxwb9B/EIuwezBVMEzQLr/9X8D/u5+g/7ifsh/M38Wf3b/f/+YQB3AcEBywIzBfMHiQrNDAkOTQ0TDLkLmwoLCFMFVwRZA+EBEwGdAYUBCQDD/sv+K/9D/0f/DQBHAYsCYQPlAyMEEwRvAz8CIwGzADsAb/+N/lf+L/6n/fH8Rfw5+/X58fh3+AP4U/eL9jv22/X59I3zkfL58Yfxw/B38KHwI/HD8b3yvfNT9K30S/XP9eH1ffUP9pP3ifr/AEsMORedGlkVXRERFCEXaRIRCYEDlwPRBNEDgwK3AVUAZf1L+nX43fdZ92H3KfkV/AX/gQLhBnMKvQqVCF8H1weJB7cFgQRTBU8G+QXfBF8EgQNpAVX+q/s1+sX5v/lB+ln7ufwR/s3/FwK7A6EDAwNdBHUHZwrdC4UMOQ1BDa8MZQvFCTUHcwTJAT8Azf8ZAAMAn/9r/xEAkQChAIcAzQD5ADsBywHXAqUD3QOPAx0DUwJTAR8AI/8z/oP9Bf0P/f/8y/w1/E/7M/oZ+ff38/b59Q/1M/TD85PzWfPj8ovyF/KR8fHw4/B/8WvyW/Mz9C31O/Yz9+X3c/h7+P34KfsHAiMNtRZDGDMT4RGvFu8YtxFrB5EC3wIXAnf/p/7l/wMAHf6/+8X6ofob+nf5v/nx+if97wDPBY8JGwoLCTMJhQrDCakGLwQRBAsEnQKnAcECiwPpAfn+Rf3L/NH7J/pJ+dv5w/q7+2/9FwDNAnsErwWTB70JowvnC10LMQstDMcLCwoHCFMHrwW9AhUAqf9f/y/+8fyD/fX+9/9XABcBAwKTAqMCnwLdAhUDxQL5AV0BTQElATsAEf+d/nf+w/3f/HP8b/zv+w/7j/pL+q/5a/gv9zP2WfU39D3zb/LT8TfxAfE78W3xT/Fh8e/x2fJD863zh/SZ9QX2MfYV91P50fyBBFEPDRiXGAcUkRTFGSEaGRHJBlMCXwKZAB/+S/0d/q39rfzX+837X/sp+lf5Ufm7+XP7R/9pBEUI/QjpCK8KEQ1XDLUIawU3BDUDLwFTACsBeQFHACn/F//H/lP9mfu3+gn6afnZ+S/8df8fAncD6QT1BwEMbQ6NDZEL4QqDC7EKiQgfB7UGAQV/Am0B/wFvARn/L/1R/Sf+nf4p/y8ANwEBAq8CZwMfBC0ERQPTAd0AkwBTAF//d/43/mX+B/63/dP98/3h/DX7J/rR+Sf50/dt9qv1L/WB9OPzp/Nb81nyPfH/8FPxXfEL8V3xX/Jb89Pzm/QL9jv3Z/eH9xn5Mf1NBR0PHxaTFjUU3RazG9EaGxINCZcEnQLp/uP79fpZ++X64fqV+8P8Z/3l/DH8H/t3+l37Tf4hAv8E3wUjB1EK/w2TDt0LrQj3BikFNQLH/+/+M/4H/Uv8Uf2J/r/+8f0x/Uf8dfsr+8370fwX/o//5wGTBNkH/wtBD/EPiQ4RDU0NbQxRCcUFvwMRAlkAYf8pAMcAif8Z/qH+5/8fAKH/Yf/p/28AHwFTAnsD6QOzAw8DawLtAVsB8f8L/pP8kfzp/NP8i/y5/M38g/zb+0/7c/ob+X/3NfY19YX04fNH86nygfJv8lPyGfI18qny2fLD8ufykfN39BP1nfUl9vH2pfiB/DsE+w2pFJEV/xN3F1Uctxu3E0kLvwYFBKH/P/y/+if6yfjh+AP7af0n/mv9M/27/P/7O/wj/psA8QFZAlsEQwhdDKkNeQzDCrUJIQhlBasClwAL/q/7p/rT+wX9Q/0j/X/91f27/aH9//19/gH/3/+/AUkE1wd7C7sNHw4TDrMOTQ5hC8cHAQWTAqn/u/3d/an+Tf7p/WP/mwF5AhECpwHHAYMB2wC5AP0ALQH3AAcBewEXAhUCTQEhAA3/Qf6N/af8B/y5+537k/vr+z38L/xt+1X6Ffmv9xn2ffQz833yH/L18SHyy/LJ84f07/SB9Q32Q/bx9Yv1jfWV9av1L/Zp9/P5g/9HCPkPPRNZEmMU/RkbHN8WmQ7LCEEGqQLd/uf7Gfqf+Of4VfvR/dH+jf7R/jn/cf5v/cv95f6f/y//+f8tA6cHYwqXCgcKUQqlCncJsQajA1kAjf3p+6/7v/tN+zv7WfzR/bv+Qf8hAN8ArwAzAA8BHQQ9B4EIVQhBCR8MIw4hDbMK3wgnB3kErwFpAKf/9/1b/P38Sf8XAcEB/wGbAj0DWwMlA3UCZwFDAHn/O/9//+v/4/9H/xf/kf8DAGf/ef65/TP9h/wF/OH7tfvt+g/6jflZ+av4afcD9vn0M/Sd8wvz5/IH8yvzMfNt8yv0+fQ19UX1kfUz9nH2g/YB9+33P/mJ/IkDkQsdEDcQcxFtF9sbiRmNEgkNewrNBo0BTf1z+iP4u/YR+Kv6kfxL/Y/+SQCdAOn/DwDXAPEAP/97/jcAhwPrBaEG7wZVCAkKkwpXCV0HvwTtAXX/3f21/PX6qfnf+RP7Sfx1/Xn/nwEfAp8BywFVBLMGOQeRBskGYQhFCu8KzQqpCTcIiwZJBS0EnwJNABv+Lf2f/ZH+k//5/4EASwGJApEDzQMtAyUCAQE3AMv/ff/Z/vn9gf3r/b/+J/8n//n+sf5j/g/+t/0D/bf7X/pl+e34U/iD92n2mfVb9Xv1c/UH9Yv0d/Q99Bf0NfSZ9L/0hfSn9Hn1PfbB9kH3Dfjt+DH6J/0hA+EJxQ0PDgEPNxQbGUUYhRI3DRcL6wjHBFEAafxj+aX3V/g7+nH7s/vh/P3+RwB3AAcB1wG9ASEAL/9fAHECuQPXAx8EfwV5B88IyQiLB8EF1QNpAhMBYf/r/Of6R/rD+nH7Jfxp/Vf/mwA1ASkClQRjB1EIhwcJB0EIQQpXCq0I+wZnBv0F7wTBA90ClQHf//H+mf9pAE8Amf+t/9sAywE7AkMCFQKlAR0B5wDXAGcAcf9T/tf9Cf5t/lH+0/2N/cH9E/4Z/tn9Z/2h/MP7//pt+pv5cfgz90v23/W99WH14/SF9Jn09fQ79UX1bfWH9Yn1d/Wz9f/1L/Y19ov2Xfej+Pn61/83BvUKZwxVDQ8SiRchGGsTew6TDAkL3Qb1Ad/9+/rl+KX49fkN+1f7W/yP/nEA0wAlAc8B/wGdAEf/uf9HARcC6wHjAYED5QWTB9kHUQeZBqMFfQQ5A3kB9/55/DH7M/td+z/7j/sZ/Qn/hQCXAd0CiwQXBj0HJwiNCKMIvQgVCdUIjQc5BnEFkwQjA78BCQFHAC//p/4h/73/tf/d/8EArQHvAe0BPQJNAqkB5wCBABEALf8//sv9nf1l/Uv9a/2R/aX9zf3z/df9b/3l/Dn8QftJ+mH5i/iR9732RfYN9sf1kfWT9bn1xfWj9Yf1efVX9Sv1KfVV9Y31yfVD9jP3k/j/+oP/YwX3CbsL5QxHEWUWOxc7E98ORw35CyMIRQPz/vf7Dfq3+VX6l/qd+sf7Nf4BADsAhwBlAfkB9wCH/4v/vwBnAQkB7wBFAokEMQbDBpkGqQZlBqcFvQQfA8EAZf4N/Y382fvv+gH7N/yh/f/+1wDRAmsEawUDB4cI3QhRCD8IYQiNBwkGbwUpBRUEYwL1ASkC1QG/AHEA/wArAasAzwBTAZUBCQHvAD8BTwHHAFEAJwD3/4H/Hf/H/mP+8/3L/cX9qf2L/Yn9lf2N/Vv9Mf3j/Ev8h/vD+iX6UflV+HX3//ap9i320fW39dX1x/Wf9aH1tfWf9Yv1lfW19cH1FfbF9qH3nfgf+2UALQZ9CS0KXwwrEr8WKxb7EeMOYQ6nDH8IowNn/0/8ZfpT+q/6M/oH+rH7af7b/wEAyQADAj8CqQDF/3cANQG9AN3/PwAJAs8DFwXJBSsGXwZ/BpcG6wX3A10Bhf+X/qP9D/zZ+v/6Dfzl/Kv9/f4bASUDwwQfBlsHCQiNCNcItQi1B5cG4wVbBUcEJwNlAv8BeQH/ANcABwHdAJkApwATAUEBFwH5AB8BHwH7AMEAmQBLANf/Zf8j/9H+Vf7j/Zn9df1R/UP9Pf0z/QH90/yZ/En8sfsd+4X6zfkB+V340/dX98v2VfY99jP2+/XN9aX1jfVX9Un1Z/V/9Wv1vfWH9rf3mfmL/f0CKwf3CJsKcw/1FDEWTxN5EN8P6w4nC9kGmwL9/gf8C/s5+6H6hflL+q381f4t/9n/KQHtAf0ABwCDADMBqQCj/2f/7wCvAvMDqwQ3BfUFqQY9Bz0H8wXPA9cB0QD1/z3+SfxX+8H7Z/zP/KX9Qf8bAWcCiwNNBRcH/wfRB4sHCQgvCF8HFwZXBQMFHwQjA6kCewLZAQkB4wAzATsBwwCXAMsA8wDfAOUA+QDfAIsAYQBRAAEAj/8Z/5/+Nf7p/dH9g/0X/en8Af0P/e38vfyv/Fn81ftZ++X6H/o1+X349/d79/v2m/ZF9iH25fW99Xf1U/Uv9Sn1CfUF9T/17/Wz9s/3J/rL/skD9QYnCM8KMxCZFGkUpRG9D8MPPQ6FCjcGUQIh/wn9Q/zv+7n6H/pd+6394/4f//n/PwF/AYkABwCRAL0A+/8v/3X/4wBTAl0DJwTHBKMFlQZRBw8HkwXTA7MC0QFlAF/+0fw//FX8Yfyf/Kf9P/+zAM8BGQMBBakGSQcRBy8HyQetB40GcwUBBakEiQOlAmECPQKZAekACQFtASUBpQCZAPUA4QCbAJEAqwCPADcAGQAZANH/Yf/x/pH+Qf71/bX9Sf0L/f38A/3F/If8efxd/AX8kfs3+9v6Nfpj+cP4S/jJ90/3A/en9kn2B/bf9dP1o/Vt9Wn1efWn9Rf29fZl+FP7vf/TAw0GqwehC/cQYRMREv0P0w/BDy8NWwm7BX0Cvf/x/V39XfwX+x37sfxN/rv+Mf9ZACEBxQALADkAnQAVACX/2/6t/9cAuQGPAlMDSwRrBVEGwwZdBlMFKwRFAz0CrwDd/nv9x/x9/Gn8w/yH/UX+Af8TANEBgQODBA0FrwWZBmMHxweXBw8HawYpBtUFQwUlBB8DXQK9AUMB1QBlAPP/nf/B/wUAMwAtACsAKwA3AE8ATwD3/3P/3/6P/kH+1/1T/dv8o/yH/H/8e/xn/D/8IfwD/Nv7kfsj+4368/lt+QX5m/gT+JP3M/cJ9/32x/Z79kn27fW/9Zn1q/XR9bn2S/l7/e8AtwIpBIcI+w2bEKEPYQ7tDpEPew1HCtMGDwR7Ad3/8f6l/Sf8JfyB/cP+0/5J/3kAUQHJAPP/KQCJAOv/wf4n/tv+zf+NACMB4QH3AjMEUwX9BdsFMwVpBNkDAQOPAc3/bf61/SP9g/yP/C395/07/uv+owA9Aq0CnQJJA5UEXQVfBVMFTwVXBW0F9wXbBQ8FTwRDBC8EcwN5AtEBDwFXANX/6f/B/zf/+f5t//v/KQARACsAEwC//2X/Nf+t/rX98fyj/IX8MfzT+737zfvX++P76/vP+337F/vH+nv6DfqF+QH5kfg7+P33zfeL9zv3B/cf90v3G/f39lX3Mfm3/L3/CwGxAeMEIQoxDbEMVwvjC1sNdwwZCl0H9wTjAmUBtQCR//v9Rf0L/h//Lf9N/wcAxQCbAOP/CQBxAPf/9/4//tf+s/8/AKEAEwH/AQ0DDQTLBM8EXQTLA5MDMwMNApMAY//Z/k3+nf2L/dn9K/4d/pH+8/8nAWEBWwHhAfECaQNhAz8DKQM9A50DNwSBBGcEcwTfBD0FLQW7BEMEhQPJAhUCiQHJANv/Lf8N//3+Df8N/0//Zf+B/4//qf9x/9H+Hf6n/Sf9p/z7+4v7O/sx+y/7O/tR+137UftR+zH7D/u/+kX6vflf+R351fiD+Dv4G/gl+DX4Vfhd+In4y/mH/Dv/jQDfAOcC6wafCX0JawjHCO0JVwmhB+MFTQS7AlcB6QBnAF3/j/7x/sf/8//V/1cAxwCfANv/9f9RAA8AJf9//vn+0f8lAEEAiwBlAUkC2wJPA3UDUwPXApECSwKbAY8An/9H/yX/y/6Z/rn+C/89/2X/9f+nAAcBFQFLAbkBHQIlAikCOQJpAm8CoQLTAhkDIwMzA4UD8QPjA4cDMQMVA60CDwJrAQEBcwDn/4n/g/9r/yP//f4b/yv/G//n/pn+Mf6n/Tf93fxp/OX7fftf+137Q/sn+zH7U/tT+0P7O/sv+/P6k/pV+jX6D/rR+Zf5gfl/+YX5q/n1+cv6mfzX/k0A5wAFAt8EOwefB5sGewZTBzcHwwVVBDsDXQIhAZsAewAtAI//df8PAKEApwCzALsA0wB5AFkAbwBPANf/X/+j/1kAxwDlAB8BzQGLAtcCAQMHA/sCfwILArcBTQGVAMn/Wf8z/+v+r/6n/un+Lf9L/6v/GwB9AIsAswD5ADUBNwExAYcBBwIhAi8CYwLnAiED+QLhAg0D8QKTAhEC8wHDAVUB6QDNAM0AowBtAG8AeQBvAEsALwARANf/g/8J/5X+Df59/ef8SfzN+4P7Q/vz+sn62/rr+uf68/od+zH7Efv9+vv6Cfvn+qf6k/q9+tv6H/t9+4H8wf03/4MAwQELAyUEMQXrBQUGrQUNBa0ELwQjAxcCJQG1AFUADwD//wMAJQA/AIUAwwDBAJ0AZwBDABMA0f+r/3//gf+1/xkAmQD/AG8B7wFlAtEC4wLVAqECWwL9AYkBGQGrAEkAAQDF/6f/jf+L/4X/gf+F/23/Xf87/w//3/7H/sv+1f7T/u3+Jf99/8X//f89AHMAjQCPAIsAiwBnADkA///r/9H/v/+p/5//of+p/7n/2//h/+//SQD1ADEB1wCJAA8BBQKdAc0ArwCJAdcBFQHHAJ8B0QFnAd8ArQEtAp8BxwD/AJ0BYwFtADkAhwC1AA8A1/8XADEACQCv/8n/8f/d/5X/Xf9p/4n/N//9/qv+yf6f/k3+0f2d/Yv9Nf27/H/8ifyJ/En8NfyR/N38Cf35/F390f0T/hn+Sf6j/uf+1/7l/in/i/+N/43/wf8ZADsALwA1AHsAkwCJAG8AqwDnAAEB9wAhAWkBmwGVAaMB2wEBAskBowGtAc0BpQF1AWsBkwGFAX8BhwG5AbkBxQHbAQECAwL7AfcB+wHxAfcB7QHfAb8BvwHLAbsBlwGFAX8BawFBARkB5wCvAGEAFQDJ/2H/6f5h/tn9U/3j/IX8G/y3+337ZftT+zf7Jfsl+zP7Tftl+4P7q/vL+/37NfyD/Pv8of1P/vH+j/9hACEBowELApkCKwNdAyUDBQMfAx0DwQItAuEB0QGfATsB+wDlAM8AmwBtAGUAYQA5AAcA7//f/9//x//D/8H/6f8DADcAQwBXAGcAlQCpALEAiwB9AHUAewBtAF0ATwBdAF8AUwBHAF8AYQA/ABEAFQAdAAUAxf+3/83/1/+9/7X/xf/V/8v/y//Z/+n/0/+3/8P/1f/L/6f/n/+1/73/rf+r/7v/yf/B/7//3//v/9f/zf/d//f/5f/H/9f/AQD5/+//7/8ZACcAFwAdADsATQBJADsASQBXAF8AVwBVAFkAZwBpAGMAXQBhAFEAQQAvAC8AIQADAN//0//V/8v/qf+X/53/l/+J/3//hf+R/3//ef+D/53/nf+b/53/u//N/8//3f/v//3/BQAdADUALwAzAEMATQBDAC8ANQA9AC0AEQAPACsAIwANAPf/AwAFAO//1//V/+n/1f/B/7//0//h/8//zf/z/wcA///3/wsAJwAbAB0AQwBhAGEAUwBjAH8AfQBjAGUAdwB1AGsASQBDAFMAQQAfAA0AEwAPAPv/3f/L/9v/2//N/8H/vf/J/8v/w/+7/8X/z//P/7P/w//d/93/uf+z/9n/9f/T/7v/1//5/+P/u//H/wEA+//V/9v/FQAzABMA9f8XAEMANwAPABkASQBNACUAEQAzAEcAHwD7/xMAOQAbAOv/8/8hACsA7f/T//f/GQD7/8//3f8TAAcAz//N/wsADwDd/8v/+f8dAPv/yf/p/xkAEQDl/+n/IwAfAPX/3//9/xcA///Z/9n/9f/7/+X/1f/d/+n/6f/Z/9P/2//n/9v/yf/N/+X/5//N/8n/5//3/+v/1//t////9//p/+3/BQANAA0ACQARABUADwAJAAUACQADAAUABQARABcAEQADAAMABQALAAcA+f///wcAAQDz/+n/AwADAOn/4//r//n/5//N/9//+f/z/+P/4f/9//n/8f/h/+v/5//b/8//4f/j/9v/z//1//X/5f/h//f/BQD5//H/DQAZABsAAQADACMAJwARAAMABwAXAAMA9f/9/wMA+//h/+P/6//r/9X/y//N/83/v//B/9P/1//N/9f/4f/p/93/0f/V/9H/1f/V/+X/6//v//v/DQAHAA0ACQAZAAsADQAHABEACwAFABEAKQAdABUADQAhABkA/f8BABUADwD//+v/BwARAP3/2//3/wcA+//X/+f/AwD//9X/1f/5/wEA4f/L/+n/AQDx/8v/0//p/+v/0f/J/+H/8//h/9f/4//3/+3/5//r//3/8f/f/9X/5f/r/+P/2f/b/+X/3f/P/9P/3f/j/9v/4//t//n/8//p/+v/9/8HAA0A9f/x/wkAFwALAP3/BwAXAAUAAQAJACcAGQD9//v/FwAfABUA7//5/wkAEwD7/+3/BQANAPn/5f/1/wkA9//b/+X///8BAOP/1//x//P/2//J/9n/6//V/7X/uf/X/9X/x/+9/8//3f/R/8n/y//d/9v/0//h/+3/6f/n/+H/8f/1/+v/7//1/wkA///1//P//f8DAPv/8//7//n/AQD9/wEA+////wMAEQAHAAUADQAZAAEA9/8FABMAAQDr//H/BwAFAOv/7/8LAP3/5//t/wkAAwDh/9v/+//5/+H/w//b/+//5f/R/+n/AQABAOH/4f/3/w8A9f/V/+X//f8JAOn/3f/1/xcA8f/x/9//7//Z/+X/yf8BAPH/2//b/9X/8//1/+n/5//h//P/7f/f/+f/4//v/93/5//3//v////n////8//1/9v/5//x//P/3//5/wMABQDn//H/CQALAP//AQANABUAAwANABcADwD5//v/FwAVAP3/9/8LABEA//8BAAkADQAFACMASwAPAJv/HwDd/6//PQADAEEAaQBFAAMAIQC3/6n/b/93/7X/1f/b/xMAHwATAOf/1/+3/5f/g/+Z/6n/0f/t/wMAAwANAAEA3f/D/7P/v/+9/8n/1f/p//X/BQAFAP//AQD9/+P/5//1//X/9f8HAB8AJQAbACUAJQAdAA8ADwAVABMADwAJABcAGQAlABUACwABAAUA+//5//H/9//5/wEABQD5//n/AwD7/+//5//9//f/5//X/+3/9//d/8f/2f/Z/9P/xf/T/93/1f/D/9H/3//h/9X/4//n/+v/3//p//n/+//p/+n/8f8DAPH/5f/n//X/8f/x//v//f/9/+3/7f/x//v/8//x//H/BQALAP//7//7/wEABQDv//3/AQARAP3//f8PAA8A6//h//n/FQD3/9//7f8HAP3/4//n/wkAAQDp/93///8DAO//4f/3////7//d//X/+//t/9H/7/8DAPX/1//Z/+v/9//d/+n/+f///+//7f/1//3/+f/1//f///8BAPn/9/8HAAEA8f/z/wkACwD9/+P/8////wcA7f/1//n/DQD5//P/7//7/+v/4f/l//n//f/x/+v/+/8LAAMA8f/n/+//+f/5//P/BQANABMA/f8DABkAHwABAPf/CwAjABMADQAVAC8AIQAJAAsAGwARAPv/6////wUAAQD3////CQD///H//f8NAA0A5//j/+v//f/p/9X/2//v/+P/1//R/+H/4f/d/9X/2//p/+v/3//f/+v/9f/v/+3/5//3//X/5//r////BQD9//P/BwAXAAsA/f8BAAsA///v//v/BwAHAP////8JAAsACwD9//3/AwD3//H/8//7//P/7//x//3/+f/z//P//f/z/+v/6//7//v/8f/v//3/CQD9/+X/7f/5////6//x//3/+//t/+P/6f/1//n/4//l/+3/7f/d/93/6/8DAO//4f/p/wMA/f/1/+n//f//////9/8JABUAFwAHAA0AFQAhAAcAAQANAB8AEwD9//f/AwAHAP3/9f/3////+f/t//P/+f8DAPn/+f/9/wcACQADAP//+f/t/93/3//h/+//5//p/+P/7f/z/+//3//d/+f/6f/j/+P/7f/v/+v/6//5/wEA/f/1/wEAEQAPAAUAAwARABMACQALABsAGwAPAA0AGQAfAB0ADQALAAsAFwAPABUAEwAVAAkACQAJABMADQAHAP//BQD9/wMA8//1//H/8//v/+3/6//t/+v/6//r//n/+//t/9//4f/T/9//9//9/wMA/f/5//n////7/+n/6f/1/+//5//z/wUAEwALAAcAEwAXAAkAAQAPABUACwD9/wsAIQAVAAEACQAvADMAFwAPACMAIwALAP//BwAPAPv/WwDPAlkFIwG7/W39F/4Z/rf+WQDFAPUBrwKDASMBjQCt/8f+U/4l/hv/TwARAb8ANQF5AKn/G/9x/5P/mf+//+n/LwBhACsA8f/R/8n/1f/7/z0ANQDv/4v/Y/+d//n/IQAvACEACQDZ/7n/qf+P/5H/t//l/xsATQA3ANP/if+D/8n/8f8nAC0AFwDv/8n/x//F/9f/3//J/+f/JwAhANX/p/+f/6f/u//n/wsA+//P/6f/nf+//9//1f/J/+P/+//d/8P/1//d/8P/u//v/yMAEwDb/63/s//N/9H/3f/z////3//F/73/2//N/7//xf/n//X/7//d/8//w//R/9X/7f8TAA0A5f/T/9f/6//t//v/9f/9//X/7//f/+P/3//X/9n/8f8DAAEA6//b/83/1f/j//3/CQALAPv/8//v//f/9////wEACQANAAUA+f/x/+P/5f/v////CQAJAP//7f/p//X/AQD7/wEAFQANAPv/9f8DAAsACQD//wcAJwAjAAkA8/8LAAsA+//5/wUABQD//+H/3f/x//f/1//X/+n/8f/X/9H/6f/3/+3/7//x/wUA+/////f/AwAHABMAEQAZAAcADQAFAAkAEQAXAB0AHwAZABsAGwATAAEADQAXAB0AFQATABEAEQANAA0ADQAhACEADwADABUAEwAHAAMADQALAAsACwAJAP//AQD3//n/+f/3//P/5//t/+v/7f/1/wMA/f/z//X/AQABAPP/9f8BAAMA//8BAAkAEwABAO//+f8NAAEA9/8BAAsA+f/l/+n/AwD5/9//5f8DAAkA5f/R/+//CwDr/9H/6/8VAAcA4f/n/xEAGwDv/+X/CwAhAAMA5f8HACcADQDn////KQATAN//6/8JABcA6//r/xMAGQD5/93/BQAfAP3/5f/7/x8ADwDx//3/FwATAPn/8/8NABUA8//Z//3/HwALAOf/8f8LAAUA5f/n/wEAAQDp/+P/+/8DAPn/4//9/wsABQDz/wEACwARAAEAAwAHAA8ACQD///P/CQAJAP3/5//z//f/+f/b/9v/5f8DAOn/3//f//f/7//h/93/9f/1/+n/2//p//v/9//r/+//AwANAPv/8/8HAA0ACwD5////CQAHAPn/8/8FABEA+f/r//f/FwAbAA0AAQALAAsA///1/wcAGQALAPn///8jABcAAQD5/wsADwABAAEABwAFAPX/4f/p//X/6f/b/9v/7//r/9//3f/r//X/7//t//n/AwALAP3/8//3/wMA9//p/+P/6f/x/+f/6f/n//P/6//n//H///8BAPH/8f/7////AwADAAcAAwD9/w8AFwATAAsAEQApACUAFwAdACkAHwAFAAkAHQAfAAMA8/8HABUAAwD1/wcAFwD//+H/4/8LAAUA8f/h//f/8//h/9f/7f8BAOX/z//j//H/7f/V/9n/6//n/9H/y//n//n/5f/V/+f//f8BAPP/9f8BAAsAAQD1//v/DwAPAPv///8ZABcAAwDz/wkADwAHAPf/AQANAAsAAQABABEAHwADAPf/+/8RAP//+f/5/wMA9f/z//v/DQD//+//6f8BAAEA9//p//f/AwANAAUADwAXABUAAwABAA8AFwAFAP//AQAPAAcA/f/3/wEAAwDx/+n/7f8BAPn/+f/5/wUADQAJAAMA//8FAAEA9////wEA/////w0ADwD//wUAEwAVAAEA8//1//3////p/+n/+f8HAPf/8f/9/wkA9f///wEACQAHABMABwAVABMAIwATABUABwALAAkACwADABUAGQAVAP//BwAdABUA8//n//n/EQABAOv/8/8VABMA+f/7/ykALQATAP3/GQAnABsA/f8HAB0AGQDx/+f///8PAPH/6//3/xUA+f/x//n/EQADAO3/7f8BAPX/3//f/wMABQDf/9v/AwAhAPv/4//z/xkAEwDx/+P/AwATAP//8/8RACMAFQD//xMAMQApAA0ACwApADcALQAhACkAOQAjABEADwApAB8ABQD//xkAJQAbAAEAEQAjAB0AAwABABEACQDx/+//BwALAPX/3f/p//v/8//V/9f/8f/5/+n/2f/p//X/8//p/+//8//1//H/7//r//P/9f///wEA9f/5/wMACQD///v/BwAVAA0AAQD9/xEAFQALAAMADwAVAAsAAwAJABEAEwADAPv//f8NABMAFQAHAPn/7f/x///////7//X//f8BAAMABQANABkAEwADAAUADwATAAsAAQADAAcAEwADAO3/4//r/wUAAQDh/8X/0f/x//f/3f/P/+P////t/9X/2f/z//P/0//Z//v/EQDz/8f/3f8NACEA+//Z//H/DwANAO3/+/8ZACEA/f/1/wcADwAFAP//BwAVAAsAAwD5/wcAHQAZAA0AAQD9/wUAFwAVAAUA8/8JABcACwD5/+3//f8DAAEA6//v//3/8f/b/+f/AQANAOn/8/8DAAsA8f/1/+//BQD///P/8/8LACEADwADAAkACwANAAcAAQAJAAEACwAJAP//+f/v//3/AQDv/+P/2//v/+3/5//b/+P/6f/1/+v/3//p/+//BwADAAMABwD9/w0AFQAnACMAAwABAAMAHwAVAP3/9f/v//3/9//3//n/9f/7//X/+//5/wEA7//p//f/AwAFAPP/7////wsAGQD9////9/8HAA0ACQARAA0ACQABAP3/BQAHABMABQABAPf/AQAVAB8AEwD3//3/DQAZAAcA6//z/wkAEwAFAPP//f/7//H/4f/h//v/+//r/8X/0//x//n/4//b/+n//f/1/+H/2f/z/wEA9f/v//X/CQAJAAEA//8DAAsAIQAbAAMA9/8JACcAFwALAAMACwAhAA0A9/8DACcALQATAAcAFQAXAAsA9//3/wkACwD9/+f/9/8LAAEA2f/l//v/EQDv/9//6f/7//v/4//h/+//2f/T/8v/2//X/73/x//d/+P/v/+f/9H/AQAPAOH/z//x/xUABwDp/wEAKQAnAPP/6/8NADEADwDn//H/EQAXAO//yf/n/xsAIwABAOP/8f8RACkAHwABABMAMQAvAPf/6f8ZAE8AOQDx/8X/8f8lACsA9f/z////AwDp/+H/8f8BAAEA5f/R/93/9f/z/+n/6f//////8f/f/+X/BQATAPP/3f/n/wMAAQD3/+n/7f/1//P/5f/f/+v/8//7//f/6f/x//n////5//X/CwARAP//7f/5/yMAJwALAOf/9f8TAB8A7//P/+n/GQARAM3/u//x/xEA+f/B/83/+f8BAN3/v//f/xMAEQDf/8X/7f8VAA8A1//L/+f/HwARAOf/4f8PAC8AIwD5/+X/+f8RAA0A+//1/wUADwD5/+v/6/8PABkAAQDT/9P/AwAZAO//1f/p/x8AEwDV/7//9f8fAA0Azf/D//f////p/7//1f/t/+//w/+n/7P/6f/v/93/t/+3/+P/AQDl/8X/1f8NABUA1/+l/8//KQBDANn/m//j/zsAJQDH/8//GQBNACUAx//D//v/RQBDAOP/uf+3////IwAFAOH/2f8RAPf/o//B/wkAQwDz/7H/u//z/xEA6/+3/9//KQARAMX/nf/p/zkANwD1/53/v/8hABsAvf+Z/+//RwABAKP/d//N/ykAFQCh/4H/sf8RAOf/w/+1/+H/+//3/6//v//b/wUA5//V/+f/8//r/+v/2f/z/wMA+f/p/9P///8FAOf/4//z/wMA/f/X/wEAGQAlAPv/z/8LAC8AFQDd/8X/EQArAPX/5f/l/yEA8//P/9P/AQADAOP/l//5/x0AHwDJ/6v/3/8FAPv/DwDd/+f/y//1/0MAFwDf/6//8/89ABEArf/J/wkATQDr/83/3/8RAA8A5//Z/w0AHwD7/9f///8VABUA8//l//f/AQAVABMA9//3/9//DQAxACMAxf+r/9//YQAVAMP/g//j/0sAKwDN/63/6f81APv/v//Z/w8AIQDN/8v/3/8vACcA///P//v/FQAZAOP/4f/b////JwAZANv/v//5/z8AKwD3/+n/7/8dABkAHwAVAPf/9f8PADkAPwDj/9v/EQBBABUAy//j/yMAMQADAOv/BQA7ABEAAwDx/w8A1f/H////YQAjAJn/c/8BAGcAKwCR/4X/5/8vAAEAy//j/+f/0f/R//3/BQDD/7X/5f8zABcA4/+p/+3/LQAxAAkA1f/P/8//5/8HAAsA9f/x/9P/5f/1/zkAKQAVANn/EQARAEcAEQAVAAcAMwAXAC0A+f8XAOv/9//7/wsA6/+9/7///f8NAPn/wf+z/+H//f/R/8n/2//1/9H/r//1/zEADwDN/6f/GwAlAOf/r//3/zcA9/+X/93/OwAxAJ//mf8LAG8A5/+D/6v/PQBDAL3/xf8FABcAy//J/0kAKwCZ/5//JQB9APv/lf+3/zMAPwDl/8X/7//7/+X/CQArAMv/Y/+1/60ApwCP/9v+m/+pAKcAxf85/6P/QwAhAOX/CQArAOH/xf/5/zcAyf/1/0sAWQDd/5f/yf9LAF0ALwDb//n/5f+d/+P/lwCFAKn/Sf/b/0sAGQDp//P/AQD7/+v/x/8HAEsAQQDd/+n/CwDr/8n/9/8fABcA///j/3v/if/z/08ARQD7/3H/Nf/T/6sAWQB3/zP/DQCNAC0AM/8X/0UANQFdAPH+t/5dADkBhQBn/wf/2/97AJUAAwCR/7v/HwBzAGUAvf+F/wsA3wB/AJ3/Yf8xAJkAPQDd/wcAJQAFAMX/KwCHAGMAkf9z/y8AkwAhAI3/w/9FACMA3//t/wEAAQCv/73/GQBBAMn/df/J/2cA7/+3/9n/MQDX/3H/n/95AFEAyf8p/63/PwBBAAEA9//n/5v/zf93AIMAwf9f/w8AvQBHAC//Tf+RAB0BRwD//jn/YQDRAEUAof+7//f/AwAjAA8AFwAbABEAJQDl/6//3/9xAK0AEwBF/2f/cwDHAEEAb/+b/y0AYwARANH/DQBZAA0A9//1/y0A7wCDAhMCf/+P/eX/4QS7BMEAS/1z/80CQwOfAbEAjwDZAGUAKQHRAfcAgf81AN8BcQHj/gf+dQADAkcB8/4n/i//TQBPAAEA0f+j/6n++f5HANMA5/8F/4n/VQBDALX/vf/DAI0B0QDB/5n/zwDNAZUBWwHpAJEAdwD/AAMCGQIVAVUAZQBLAWEB3wClAAEBHQGPAP3/OwDlAPkAvwBxACMABwDr/3sA2QCjAO//N/+//0EAWwDP/4n/bf83/+f+G/9Z/x3/l/41/kf+bf4t/tn90f3l/aH9B/3Z/NH89/zZ/Fv8wfuP+537e/tX+x377fpj+vf5/fkp+i36q/kP+Q35lfmx+an5bfnB+ef5L/vX/HH99fxL/Bv+5QDfAkkCdQG5AUsEGQb7BgkGqQUzBvsHFQl/CNEG6wbJCN8JZQgXBs0FeQcZCNkGawWjBMEEbwSVBJMEyQM5AtsBrQJfAzECAwERAfcByQHnAE8A4wBLASsBzQCRAFUAPwCHAD0BMwFRAIX/7//HAOcAIQBb/z3/af8x/8X+X/4D/r/9Wf0V/c38bfwv/An85/t3++/6sfrd+hn71/of+q/51fkB+r/58fgP+U35aflR+CP4yfgF+Zf4Sfid+BP5o/hP+JX4nfkj+wP+kwD9/kP6l/jlAV0LxQmX/037vwOpDA8MfwWNApkHpQu1CcUFtQXfByUJDQnbB2kFiwIBAzUGvweXBcEAT/5XAAED3QK//2n+kf4J/8H+D/7H/QX+A/9F/wX+Uf27/cn+8//JAEcB4/+F/nf/9QL/BBkEsQGNAdEDEwUxBd8E3QXJBZ8ERwRZBc0FJwXhBAcFPQTLAhsCDwMPBIMDeQEHAGkAEwHhAFMAFQA3/xH+q/0l/oP+Lf5D/cX8dfxp/Ov76fuD/Jv8ZftP+lH69fr3+q/6Kfqb+Zf4d/jx+JP5zfiD90P3//df+H/33fYt98/34ffj97/30/gf+z/+B/6h+vX4z/1LBVkH0wFV/QcADQcLCosH6wODBO0HhwkxCJ8GqwYNCJEJ9wjTBp0E7QR7Bp8HrQY7BKcBnQG9AsED3QKhAf3/Mf9L/20AcQCt/5/+Xf55/iX/If/j/nn+v/5X/1sARwDp/ov+qQDxA2MD1f9n/2cC7QVHBPEBiQKRBLUE5wKJA+kEVQQbAwUD/QN9AzcCIQKJA7MDlwFrAD8BbQKvAWEAGwDl/4X/Jf8f/z//df63/QX9c/3T/bv8vfvr+7n8BfyV+hf6yfol+1/6C/mz+On48fhn+CP4nfeD9/X2kffX93P3tfaL9nf3Z/gr+BX4R/p5/uP+GfpV9/v8/QaDCC0AjfrB/+EJDQuFBOcAqwWdCzUK5wQ/BAEIOQsbCi8HBwXfBAMGywfvB6kFuwKtAS0DTwQnAzUB4wB7AZkAPf8t/+f/FQBB/8v+l/4l/pv9xf1V//MA7/99/Z/8+/5BAo8C0wHz/wMA8QCpA88EpQMvAl8C6wNRBLEDLwO7A78EawSDApEBuQIBBNsDCQOlAbkAMQFrApkCawF1APn/k//R//n/l//r/pX+Uf6P/Wv9Of0l/ef81/wJ/P/6ofrr+kH7I/sb+tX4R/hX+YX5wfhT92/3Gfgd+CX3qfbp9uP3q/cN9xH3Nfhl+c37nf0J/cf5A/lP/1UG0wUz/0H8AQLXCNcIYwRXAkEGAQp/CLEFyQUhCDcJBwmnB00G7wStBSUHuwfZBTMDfQGnAk8EHQRpAff/+//rACkBCwBX/i3+m/+3APP+tfyB/GX+KQD//23+p/1n/iUAswE/AWUADQBLAdcDmQMTAjsB/wJ/BFsETwOfAoMClQNNBAkElQLbAVkCiwNzAzsCBwF1AXsCNwL/AGMAawCvAIsAHQBN/9f+P/8j/7/+J/7n/Z/9S/0n/RP9l/wR/KP7Xfsj++H6Pfrn+av5SfnJ+FP4dfg9+M33ufdH9zP31/Yh9233jfdX98f3Mfkl/YP+P/sZ9535twNXCMkCo/pl/HsGbQsbB6EAtwF5CAUMxwd1A+0Dawj1C5kKWwUjAhMEHQn1CfcF3QF1AeUDAQVJAyMBzQClAecAi/+n/9H/Zf+9/lH/kf93/q/89/wP/6MAtf91/WX9Df/LAGkB9wDZAG8AXwHVAqcDpwJBAtkCMQQrBP0COQJjA5EElQTLAvcBYQJ/A7MDIwMDAkEBbwEnAvkBXQGPAEsATwA1AMX/Nf8p/1X/Df9T/sX9y/3n/eH9Xf3F/CX83/vX+8f7k/vp+gv6b/mF+Z35a/mz+Af4w/fp98X3Wfcd9zX3P/cF97P2Sfef+H/7F/5P/Cv46fZb/hEHRwYF/l35EwENChkKAQNLAF0G8QuTCQkEzwOpCA8MYwpzBlsEhwXPB/EITwcvBS8DEQPfAxUEAwOXAVkBdwFFALf/K/+R/2f/X/8r/1v+V/0B/dX9a/91/5H+rf2Z/jf/1f+dADcBQwE9ACMB9QIfA3kC4QGjA18EsQN7AnUC/wO9BK0DewJzAv0CCwMjA98CCQJ1AbUBJQKHAe8AfwCVAIEADQBh/wP/bf+Z/7H+Wf4D/i3+7/25/X/9Cf25/Ef84fv/+wH8b/sz+vn5L/oz+k/5vfiJ+IX4N/jX9133VfdP91v37/Yh92n3pfiT+4/9hfuD96v3QwDdBokEC/yB+ukChwpBCFEBOQBbB68LgQgjA98DYQixCyMKSQa7AxcFAQh1CQUHGQSDAvUDsQTzA5EBFwEfAjEC9//9/vv++//N/2//x/4d/nX9V/0J/h3/Of9f/vX9gf7d/lX/TwArArUBIQBp/9cB7QNRBB8CCQLfAl0EMwPvAr0DpwRtA28CkwKJA1sD3wKpAs8CIwJdAS0B9wFJAkEBGQDN/x8AAQDf/73/V/+x/mP+bf6V/i3+5/27/ZX9Df1T/OX7LfyH/AX8v/rj+d35U/pF+qX5yfhT+Cn4Kfj59wP4o/dL97X2+/YF96v3FfmR/F/9E/pB9uH4ZQI/B20Cc/qb+6sEOQq7BjMB8wEpCN8KNQdVA9sENwnzC/EJvwVdAysFGwk5ChkHPwNfAjEEfwUVBPcBSQFjArkBCQAx/3v/3f+d/2P/+f7N/a/87fyt/qn/5f5B/Vf9p/45/xv/1/+PAXEBDwCh/6MBcQNpA3MCsQIpA+0CVwJNA88EcQR3AuMBKwPlAx0DaQLhAgkDDQIbAUMBIwItAjEBWQAjACMAz//X/wcApf/L/i/+Wf6J/mv+F/7J/W391fxF/Cv8rfyp/JP7X/oV+qX6p/ot+mn5D/mx+GP4ffh1+Cf4ofcf92v3cfeF94P3tfiX+8f9i/v994P35/7FBe8Etf07+kMAIQhhCesDjQDtA+kJJwrBBf0CywXvClMM/QcbA+UCgQefCq8IRwTBAeECAwXnBNsCFwFTAf0B/QCv/+X+Jf/h/zMAX//J/ZX85fxb/mn/M/8R/hP9Q/2r/u//iQAfADcAlQCBAOUAtwG/A2sDiQLtAdECJwOFA88DQQR5A6ECIQIvAwMEewOHAmUCbwLVAWUBuwFFApMBtQAZABEA6/8/AN3/wf8d/9v+K/5P/qn+0f4p/m39zfz//OP86/xL/Nv7Y/sx+7/6Yfo7+gn6r/lT+c/4jfhN+GP4L/gD+IH3X/dT98n3Ofh9+ef7Of3b+rf3GfkTAQMGmwKD+6f7cQMzCV8GcQFbARkH5QlzB7kDQwTfB90K9wlxBmcDdwQNCCEKZQdjAxUCCQSDBScEqwEtAWUCZwJJAP/+L/8XADUArf/f/tv9Kf2D/Zv+U//P/vv9f/3v/b3+Nf9pAM8A6QBjADMA6QD/AV8DrQOhAvcB+wHtArUDBwSTAwEDbwKlAuUCRQMPA70CTQI/ApUBOQFZAQcC1QHJAM//n//Z/08A6f+T//n+s/5l/ln+c/6D/i/+u/0N/bn8ofy//H38I/yv+z/7mfpV+q362fo1+l354fgN+fX42fiP+FP4D/gD+On3E/iL+LX5vftd/XH7xfjl+Nn/SQU5A9n8dfsDAgMI7Qb/AQMBFwbPCRcHNwMpBFsIkQrbCJMFwwMPBbcHvwjDBh8EmQJVA6cEYQRtAjEB1QEjAlMAWf9p/w0A8f+R/+n+Ff5R/ZP9b/5X/xX/0/37/I39Af9jAO8AJQAf/13/0wGpAjsCgQF5AiED9QJtAsUCgwNFBJkD0QJ7AsMCEQOLA3cDpQKPAa0BMwJpAscBdQH7AMkAWQA3AAsAGQDx/1n/xf7F/pv+u/6L/oP++f2D/TP9Qf0n/QH9l/w7/M37hfsn++P63frD+kP6v/lL+QX5B/kL+QP5k/j397n30fd1+Nn4DflD+qf8ufwZ+in4g/xhA8kET//v+kn++QVJCEUEgwAxAx0I3Qj9BI8D5wWLCeUJEQcRBDsEvwbPCK0HKwX9AvUCNQTZBIcD2wE9AbcBFQE5AKn/tf/l/+P/I/8//ov9uf0z/t/+0/4R/lf98/1X/jH+4/7jAA8CIQAr/ln/rwJlBO0CcwHDAeEC8wKrAosDgQStAx8CPwJHA2sD2wIzA4cDqwIpAf8AEwInA3MCwQDj/z8AgQA/ABkAPQB7/6n+Yf7F/uP+p/5R/gP+o/0p/cX85fxR/SX9Gfw9+yv7YftN+/H6m/ol+qP5K/n7+FP5Y/nv+EX4+fcT+B/4cfgN+a35Dftv/LX7w/lx+VX+qwMtAyX+n/tpAHcGGwczAwMBMQQtCOcHtwT7A5MGgQlRCX0G2wNrBEsH2wj9BjEE1wKhA7kEOwSNAp0B7wEpApcAYf9p/wUAMwCJ/6P+y/1//eP9Sf6h/in+Rf3b/NX94f6j/qH93f2t/8UBLwFX/2/+3QD3Aw0EGwKlAOsBuQNPBGMDDwM9A6EDYwNBAw0DAwMfA4sDUQNHAiUBjwHdAhMDmwEvACUAHwEzAXUAw/+D/4f/Mf/l/qf+f/5V/i/+9/1b/cX8ufwZ/f/8O/xp+0X7k/tj+6H6FfoP+j36p/kD+cH44/ix+En4Mfhj+Gn4Qfgr+Gf56ftj/Yf76fhv+an/BwSBAvH8UfzfARkHGQYlAjMBcQXTCKEHMwTxA+kG2wlZCVUG0wPjBNMH/Qi5Bs8DAQN3BHcFMQT9AWkBlwKvArUAS/9l/y0AIwBj/43+3/2D/ZP9Lf6d/iP+7fyL/H/9df6h/m/+Vf5z/rX+OQA9AfkAMwCBAEMCOQNhAgECfQLrA5kD8QLfAq0D2QOdA2EDeQMFA6cCGQOHA/kC8wGdAR8CTQKtAQ8B4wDxAKUA8//F/73/nf83/6/+l/4t/vP93f3L/W395fyJ/HH8Ufwf/Mv7f/sF+9f6nfqp+iP6pflz+W35R/mf+Bv4K/hr+JP4e/g/+PX4TfsB/dP7yfjf+Mf+2wOFApf8SftJASkHVwZzAVUAKQUfCXUHlwNvA2UHOwoDCYUFvwOBBVMIowgnBrMDkQPXBCcFqQMdAvUB5QJTAkEAL/+r/5cAJQDz/i3+7/0D/rf9sf39/Rn+df3V/PH8rf1t/pP+gf4p/oX+af/d/zEAsQD7Ac8BLwHFAHcC4QMfBNkCWQL1At8D2wOpA98DzwMTA6sCFQNrA/UCkwKHAnkCrwEfATEB5QHbAb0Anf+n/xEA3f81/w//7/6J/tH9p/29/dX9h/3h/HX8Kfzv+8X75/vx+yv7U/oV+kn6b/oL+pn5B/m9+Kv4w/it+IX4Y/if+BX5e/pF/G/8S/q3+Kf7mwG/A5f/P/u3/YcEcQfTAyMAEQI7B8kIgQXvAp0Efwj7CcEHZwTNAzsGzQhPCGMFBwNlAy8FcQVnA5EBxQGrAvcBGQAv/6n/SQADAO3+/f2Z/ZP91f0x/iP+bf2X/Kn8gf01/iP+v/2j/VX+K//p/9X/V//D/y0B6QLDAr0AZQCFAgMFZwQRAsMBYwOHBAUE/QIjA5kDhQMvAy0D1QJ5AmUCJwPFAnEBgwBPARUCtwExAKv/u/8ZALf/Hf/f/sf+Kf7P/ZH90f17/en8bfxl/Ef8Bfyb+5n7kftZ+5v6M/ox+nP6Ifqj+Qv50/jD+L34l/iX+HX40/j7+TP8k/yR+ln4x/qlAIEDFQCJ+/H8IwOjBjEEqQC9AS8GJwixBVsDcQTZB0sJ4wf/BDEEvwUZCAEI5QXBA5MDmQT3BKsDYwIXAo8CrQFlANn/KQAjAKn/Ff+9/g/+Zf1Z/Sv+q/7z/ZP8O/xJ/Y/+vf67/eP8p/1N/0kATf/Z/u3/jQHvAXUBVQHPAY0CTQMfBGUDaQJZAiUENwUPBE0CqwILBHUEDQMjAqMCJwOZAukBpQGpAUsBNwEfAb0A+f+J/5//2f9d/7P+J/4r/jX+y/03/T39F/3D/Ev8Cfz9+8/7kftD+xP74fp7+gv6G/o3+uH5Bfm3+Pf4Pfm7+G34Y/gX+Xf5Zfo5/Lv8u/rR+Gf7ywHhA93/EfvL/Y8EaQetAycAYQKRB40I9wTJAisF6wivCScHNwQnBIMGgQirBwcFYwPHA+cEqQThAuUBNwLFAj8Bp/9p/y0ARQB1/5f+Pf7t/X39Rf37/Xv+4/1z/C/8N/1p/p/+7f0j/aX9Ff83AG//rf65/+MBkwIXARUAkwHvA2sE0QIpAgcDEQQBBAcE+QOnAwcDiwMPBNEDtwKFAhEDZwNRAj8BZQEzAu8B4QApAFcAJQDh/5H/df8D/3f+Df4d/iv+0/0b/e38C/3V/Cn86/sZ/B38h/sL+/P69/qX+kH6E/oV+pf5Gfnr+Cv5F/mx+H34sfgB+Yf5HfvZ/In88fkf+Yv90QL7AiX+JfwrANcF7wVjAtsAiQTxBzMHGwTDAykG0wjRCLkGWQQ9BGkGPwhdB6kExQKRAwcFpQRhAksBIQKZAvkAYf8p//H/+f85/2X+H/6h/Tn9Uf0n/kX+Kf0d/If8o/09/gX+lf1r/TP+Gf/B/03/D/8BAJcBPQJJAXsA6QH3A3sExwLdAQsDhQSRBOMDZQN5A4EDsQO5A6ED9QKdAq0CBQN7ApMBSQHvAeUBFQEXABcAPwA7AM//Jf+t/n/+Z/5j/iX+q/3//Pf8L/0P/Uv80fvl+xn86ftj+936n/q7+sn6UfrL+Wv5c/l5+RH5x/iF+NH43/i9+Mf4kfmN+yH9Ofzh+Wn5Ef7zAhUDGf4d/DEAHwZzBr0CxQBdBCkI6QdlBHkDMwZfCTMJTwYPBOkEMQdRCI8GcwR/Az0EjwS3A2ECIQJtAu0BOQBz/6f/MwCB/6P+Hf4v/sn9J/0F/cf9Df5Z/Un8Xfw//Sv+G/7H/Xv96f31/pH/uf9b//X/WQE9Ar8BtQCdAbUDjwRvAzUC1QJRBN0EPwS5A7kDvwOlA8UDwQN5A+ECywL1Aq8C4QF1AdEB/QFZAVkA0f8tAD0A/f9N/+f+o/5l/kv+K/73/W394/zf/Nv8l/wj/O/77/vZ+2375/rn+u36z/pj+jP6C/qh+Vf5gfnH+Wn5zfjJ+FP5nfmR+cv5l/uJ/Qv9mfrx+Sv+2wIdA/f+Hf07AEkF/QU3A6EBUwR7B0MHrwT1A/8FsQj/CJUGNQRjBKsG+Qe3BoUEYwPbA0sElwNlAhUCNQKjARsAd/+z/8n/Jf+b/l/+Pf57/bP8zfzD/VP+d/0v/A/8H/11/tf+G/5j/bP9Rf9HAEcAt/8/ABsBlQJTArEBnQE7A9sEHQSzAq8C9QMlBdkE7wNrA3sD2QPnA9MDgwPLAlECtwKtAv8BOwGHAaUBKwFDAOv/vf/3/7f/Kf99/jP+D/4P/sf9wf3p/Kf8ffyz/G/8LfzV+7v7pfu3+0/7//q3+sH6ffpZ+u/51/mh+Zf5Pfn1+A/5Y/lX+Sn5LfnZ+X37L/0b/VX7DfpN/aEBdQMDAJ/9e/+TBDsGNQTDAfMDAQezB3sFYwSrBQ0IpwhTBycFxwTJBTUH6waRBZsDUwOjA+cDxwIRArMBfwFRAOH/W/+D/wH/tf5Z/kP+f/3H/Lv86/0//m39LfxL/Cn9A/5L/oP+Yf75/dv9P/+3AHMBEwAZAPUAkwKhAk0CTQJ/AzEEQQTBAi0DMQRXBZcE4QNVA7cDrwMfBOcDxQPPAjsCEQL1Ao0CswELAXsBFwFnANf/PQD7/+3/Gf/B/jn+Qf5B/lf+Af5f/Xv8tfwx/Uv9d/wH/OP7Ifz5+5f7Mfsv+z37/fpj+jX6//kp+iH6A/pv+Q35LfnN+QX62fll+dX5l/t9/Yn9C/zB+kH9MwEdAwMBuf7R/2kDjQXfBC0DrwO/Bc8GFQY9BYMF0waDBz0H0wXjBAUF7wUhBpMFKwQBA4kC5wIFA2kCWwGVAPH/CwDH/z//gf4//mn+Z/7J/fH8ofxZ/SX++/3v/HX8If2x/jn/ef5//bn9y//NAL8A//8VABkBJwL9ApUCTwLLAgsEbQSxAzsD0QP7BPcELQSXA58DswPhA9UDvwPNAgcCEwKTAmsCYwHLAMUAvwCBANn/lf9R/z3/A/97/gP+t/3f/df9sf0R/XH8dfyl/NX8d/z9+4X7dfut+8P7dfsD+4n6ofqz+o36A/q5+ev5H/rT+Vf5OfmZ+QX6E/rp+Tn62/uR/dn9N/wB+5f9xwG1A+0ARf7V/zsERwalBIsC7QN9BlkHuQXHBIkFdQfpBw8HSwXLBEkFdQZdBkEFrQMRAxMDMQOZAvkBiQEJAe//Yf8v/4//F/9R/tf97/3Z/T390/w7/en97/0J/YH85fwH/iv/M/8T/k/9t/5RAa0BDwDf/tEA2QL3Ap8BoQHBAssDWQOTA98DywPvAqEDBQXDBAEDWQJtA2MEhwNLAvcBoQKNAvcBeQGNAUcBvwChAO0AXwCV/yv/tf/X/zn/Kf7T/Vn+t/7r/Q39vfwh/Q39qfxP/CH86fuz+8P7pfs/+7P6jfrB+s36R/q/+aH5y/m7+Y/5Y/ld+W/5dfnB+f35c/pX+6/8b/31/NH7sfzj/60CgwIBAGv/ywEVBbcFLwRvA/cEgwaDBn8FRwVhBmMHYQcVBvEEswR5BRMG6QWFBAcDPQKHAskCawKhAdcA6f9t/03/R/8b/63+Nf7f/bf9Y/0J/Q/9x/1F/tf9Df33/PH96/4p//X+Sf+v/9X/df+TAPMBnQKdAfEAjQEVA3sDdwMfA3MDZQPpAlMDJwRzBHkD9QI3A2UD5QK1AssC6QJhAnEBIQGJAb8BQwGtAHkANwCl/4//tf+p/yn/af4J/hP+Sf4b/oX9W/1V/f38m/x5/Kf8m/w5/Lv7kft9+2f7J/sj+x37m/r/+ff5SfqD+vv5mfmX+e358fnj+fX50fpn+2P8I/1p/d38h/yf/n8B/QJVAaf/TwCpA8cFTQWhA8sDPQVhBhcGnwWTBVcG2wZ1Bk0FdQSvBKkFuQWrBBcDgQKdAr0CRwLhAU8BjwBx/0v/jf+v/+f+N/79/SH+2/1r/Vv9tf0P/tf9a/1f/ef9lf4x/yn/y/4d//f/JwHvAJcAzQDnAc0CVQK3Aa8CIQRhBM8CQwKpA4kEHQRlA5cDtQMHA7kCSwOnAw8D4wHDAWkCXQJTAQMBXQFVAWMA2f8FAAkAt/9P/9n+vf5f/hH+7f0x/hP+Hf2H/Nn8I/3T/C/83/v5+wX8rfs7+yX7Lfvp+o/6c/p/+vX5z/nl+SH6v/lz+ZX57/kZ+lf6p/rR+zX9mf3b/OH7O/1XANcCTQLH/33/BQLZBEcFZwQJBJ0ECwVdBQUGewZDBpkFtQUnBskFtQRrBPkEZwWRBDEDGQLZAQ8CTwIrAlcBlf+X/gX/GwANALn+lf2N/Rf+/f1t/UH9uf33/Zn9K/0f/aX9a/5P/3f/7/6n/jn/gwDbABcBSQH3AbUBRwGbASMD4wOZA5MCEwOhA5cD6wKBA3EEIwTRAn0C6QJrAwUDxQJ/AlcCZwENAVcB/wFRAWkABQBTAOv/kf9N/3v/Ff+N/vH91/3v/dX9Sf0//SX9ufwL/AP8Z/x9/Pv7Qfvt+gH7Lfv7+pX6cfoF+uf5w/nl+eX5z/m9+ZX5pflT+pH7Ef2n/Yv8Kfsf/B8AIwMhAg3/r/7HAakE8QR7A1EDhwSjBTEFFwWBBQ0GJQZBBvsFLwVpBJUEJwV5Be0EkwMTAsUBNwLhAocCcQHL/0f/1f9HAHv/1f7j/vn+Z/6j/Zv9V/67/nH+x/3h/Sn+8f3l/cv+//8VAKn+C/7f/hcB+wH1AAUAYQCxAcUBqQHzAV0CHwLtAaMCWwMJAwsCMQLLA+kD3wLlAakCXQMZA3UCbwJNAhMCqQH9ASMCrwHDAJUAAwH3ADUAr/91/43/O//Z/ln+U/4z/sH9W/0p/T/91/xj/En8Q/wv/Lv7bftf+z/7//qt+tX60fpV+uX50fkp+in65/nF+en5lfrz+8f91f23+/v51fw1AjMEfQAH/c/+mQNfBZ0DFQKZAy0FxQSfA5EE+wUJBv0E+QQ5BecEsQO3A6kEZwUXBCcCHQG/AVcCbwLZAdUAU//l/q3/bQDj/+X+c/6R/nH+M/41/q3+s/5b/hn+ef6N/hn+O/59/6MABwCF/jv+o//TAeUBEQEtAJ8ABQG1AaECdQPPApcBSwGpAjEExQNnAicCQQOdA6UCEwKhAgsDowIJAtUBvQE1Ae8AVQHNAQ8Bif///sX/FwCv/+/+of5J/tv9nf27/en9ff25/FH8k/y9/E388fsT/E385ftZ+zX7dfu3+3n7Ifv5+t36m/qz+g37a/sB/Hn9U/4z/Q377fvx/0UD8wGn/rv93wCHA7sDiwLrAnMDKQORAt8DCwXbBJEDtQNjBJ0EJQOPAk8DqwQfBIsCPwFPAYUB+QE3AtsBcQBJ/0v/SQDHAFEAV/8V/y3/Jf/v/if/df9n/xn/Af/5/sn+8/7T/6cASwAd/8X+4/8ZAR8BnwDFAPUAxwCNAGEBLQIhAmcBIwFzAfcB9wELAjECFQJ7AXcBwQEPAt0BpQFjAUkBDwHvANMA3QC/AG8A/f+5/5n/c/9n/0v/8f6L/hX+7f0F/hf+v/1B/Qf94fzD/JP8mfyX/F38A/zX++/7Efzn+6X7h/uj+7P7jfub+5f8X/65/hH9W/vR/N8ARQKzADH+J/9BAYkCJQIjAqsC3QLhARUCYQMBBP8CcQIjA90DQQMJArEBcwJPA/sC5QEhAeMAwwAxAd0BuwFZAHH/kf9HAMMAcQDj/5H/gf+r/8P////X/5f/o//z/+f/df9h/6H/6////+f/i/8f/0P/rf8fAAUAi/8R/zP/9f83AIv/D/87/0EAdQD9/1n/ff8XAIsArwC7AMEAnQBDAIEANQHBAaEBJwE5AUcBiQF7Aa8B9wH1AZsBJwEbAXsBswGPAXcBHQHFAHMAmwCzAMEAZwDx/3X/Wf9f/zf/Df/x/qH+I/6r/bX9wf29/Xn9G/0F/b/8l/yh/P/8F/27/If8l/zV/O38If1N/YX9gf2N/cH9Kf6D/t/+Y//r/9n/if+9/xEB4wEBAm8BjQHfAWsCgwLtAgkDDQN7An8C5wIpA+MCmwKJAnECCwLTAbMBuwGVAVUBEQHhAKEAVQAzAFMAYQAdAK//ef+P/7//xf+z/7P/of99/2//o//x/93/u/+9/wcALwDl/5n/w/9RAJkASQDL/5X/k//X/zsAVQDh/0n/+f41/3H/p/9R/+3+o/7X/s/+Zf7V/QX+of6b/tH9Df0L/UX9Zf2T/cP9if0V/f38y/29/mn/Wf/h/o3+a//lANMBQQGVANkA5wFvAk0CKQJvAn0CPwJFAqkChQLTAYMB/wFDAskBvwBLAK0A8wCTAP3/qf95/wf/B/9j/33///6B/oX+8/4d/w3/9f4d/0//Xf+F/8//y/+//x8AmQClADcAPwC3AAUBxwB9AK0AGQHtAGkAVwDZAN8ASQDp/y0AewAxALP/l//h//f/m/9R/2n/jf9d/y//Sf9v/3X/Of9B/3H/nf+X/4X/pf/n/+f/1//X/wEAKQAxADkANQBLAFcAXwBbAHcAgQCPAIEAcQBjAHMAjwCnAIsAVQA7AEsAfQBbADMADwAZABsABQDv//P/6//j/8X/rf+z/63/h/97/5n/qf+L/3H/ef+L/4n/c/95/6n/p/9//3X/q//P/7f/uf/R/+//5//v/wMAIQAjABUAKwBbAEsAOwBVAIcAcQBNAEMAawBZAE8AMwBHAE0ALQABAB0AJQATANX/6f/l/9n/wf/P/8//0/+3/63/w//J/8P/v/+7/73/vf/F/8f/y//r/wEA7f/1//X/GQAVABkAMwBBAC0AIwBDAGMASQAZADEAVQBNAAcAAQAhACcA5//Z//v/AwC1/4//2f8nAMv/b/+X/w0A8f+t/5//+/8DAK3/l//9/zMA4f+b//f/NQALAMH/8f8zADsAAQD7/xcAGwD7/xkAOwApAO//+/8nACEA9/8BAAMA///p/+v/8f/3/9H/w//r/wEA3//H/8n/xf/H/9f/6f/T/73/v//n/wMA9//V/93/DwALAOn/6/8DAAUA//8VAC0AFwD9//n/EwAVAAEA9f8RAAEAy//b/x8AMwDZ/6H/2f8JAO//pf+z/+n/6/+1/7v/9////7P/pf/n/xUA8f+1/8n/+//7/+X/6/8LAAEA4//p/xkAMQABAOP/9f8dAB8AAQD//wkAGQAXAAMAAwAFAAcA//8JAA0ACQD7//3/BwAJAAcA9f/5/xEAFQD7/+n/BQATAAEA/f8FAAMA9f/l//X/FQALAPP/8f8JAAsA+//5/wkAEQADAPH/7/8BABEAAQDn/+f/CwAjAP//1f/T////BQDx/+P/7f/p/83/0//5/wUA5f/L/93/+f/x/+P/4f/t//n//f/z/+//6f/r//3/EQATAA0A+f/z/wEAHwAbAPn/9/8VAA8A9//1/xUAHQADAPH/CQAtABUA8f8FACMAIQD3/+//CwAlAAsABwAVADUAFwDv//X/GQARAP3/+f8BAPf/4f/X/+f/AQD7/+n/4//l/9v/2f/p//f/3f/b/+//+//7//n/BwANAA8AAwABABEAEQAHAAMAEQAHAPn//f/3//X/4f/r/w0ADQDd/83/+f8XAO3/1f/z/ycAEwDn/+v/GQAxAA8A+f8XADEAHQD1////KwArAAkA4//z////+//t////AwDz/93/9/8RAAUA4//l/wcADwD5/+v/8f8BAP//CwAFAAUA5f/b/+//DwAPAPv/6//3/+//6//t/wMA+//d/9v///8XAPv/yf/l/xMAFwDd/9X/+f8JAPX/5f/5/x0AAQDX/83/9/8TAA0A9f/r/+v/6//h/+X/6//r/9H/y//f/+//5f/d/93/9/8LAP3/6f/z/wcADwAHAA0AGQAVAAMA+f8VADEAIwADAAcAIQA7ACkADwAPAC8AMQALAOv/AQAbAAcA7f/z/xEADwDt/9v/8/8JAPv/4f/j/wMADQD//+//7/8HAAMA8//z//v/AwDh/+X/6//7/93/0f/R/+n/7//h/9H/1f/n/9//3f/h/+f/7//l/9v/9f8JAP//7f/t/wcABwD7//H/AwANABEA//8JABcAEwARAAcACwAVAA0A+f/1/wsAFwABAPH/AwAVAAsA9//5/w8ADQABAPX///8NAPf/6/8BAAcA+//f/+X/8f8DAO3/2//X/+3/8f/n/9//9//9/+3/y//h////+//J/73/6f8PAPf/zf/T/wkACwDr/8///f8ZABMA6f/1/xMAHQD7/+X/9/8RAP//5f/r/wcADwD7/+H/7/////X/1//b//P/8//V/9f/4//z/+P/4////xMADQDx//X/EQATAPn/6f8HABcA+//f/+3/EQALANf/v//z/wEA0/+v/9n//f/x/8f/0////wUA3f/V//H/DwDz/9X/2f/3//H/4//R/+//6//b/8X/3f/p/+f/zf/b/+f/7f/T/9X/4f/r/9//4//p/+3/3//z/wUADQDr/93/8f8HAPP/3f/j////9//f/93/6f/5//H/3f/n/+f/7f/Z/+X/BQAdAAUA6f/9/x8ACQDh/+H/BwAXAPH/3//v/wEA///v//f//f/1/+f/6//n/+X/9f8RAPP/6f/v//3/+f8DAAUA+f/n//H/7f8DAPP/4//j/+v/7f/h/+v/7//j/+X/7f/t//H/5//T/83/7f8FAOf/yf/V/9//6//L/8v/zf/p/9n/yf/d/wEA6f/P/9f//f8JAPH/2f/x/xsAIQDv/+H/9/8NAAEAAQD3//n///8VAAcAAwD//wEA9f8NABMA+//p//H/+f8JAA0ABQD3////9f/3//3/AQDj/9n/5f/z/+n/2//n/+H/4f/z//n/9f/P/8X/yf/x/wcA4f+//8///f8RAO//zf/d/wcABQDd/8P/9f8PAPv/1//t/yEAHQDn/8n/5/8TAPv/1//r/xcAAwDR/+f/GQALAM//zf8NAB8A4f/H/+n/JwALAOP/+/8hAAUA0//j/yMACQDJ/7X/9f8PAOv/t//F/+X/7//R/93/4//T/8H/x//Z/+f/zf/j/9H/4//t/9//0//P//3/BwDx/9f/x//r/wEA6//n/+H/6f/Z/8X/1f/p//P/9//d//P/7f/r/+f//f8PAAEA8/8BAPn/9////wkAEQD///H///8JAA8A5//f//3/DQDv/8//yf/n/9n/y//F/9f/1f/B/73/0f/V/9v/0f/p/+X/4//X/+v////7/+P/zf/h//n/+//T/8n/9/8RAPv/v//T/wcADwDR/7v/7f8tAA8Awf+t/+H/GwAXAPP/4//1/xUAKQD3/8n/2f8lAEUA8f+3/8n/HQArAOf/yf/h/xsAAQDB/7v/2f8HAOv/y//P/9//CwD1/+H/4f/v/wUA+f/h/73/x//5//P/wf+p/9//CwDx/7//q//N/wUABQDp/8H/5/8FAAMA6//p/xMAJQDv/63/w/8NADEA8/+3/9P/GQBBABcA2//j/yEAOQD7/9X/+/8zADMA9//f/wEAIQARANP/0/8FABcA9/+v/7P/9/8vABEAn/+X//H/KQD3/53/uf8FACMAz/+H/8P/NwAvALP/a/+9/zsAKQCz/3X/2/9ZACUAqf99/wcAXwAPAJP/kf8tAHEAFQCn/7H/KwBrACcAxf+r/wsAVQAjALv/mf/v/1MAEwCb/3n/AwBtABkAe/91/wMAdQARAIn/a//x/0kAAwCf/6f/EQAtAMf/l//l/18ARQCj/3H/2/9hAEkAs/+B/7n/MwA7ANf/g/+j/yUATwDp/4H/kf8PAEUA6/+J/63/SwBhAM//Xf+n/0kAawDf/4n/qf8hACsAx/+h/9v/OQAXALH/g//L/0sAQwCz/23/zf9ZAEkAsf95/83/cQBpANf/if/B/zMAMQDb/8v/7f83AAUAo/+h/wEAXwApAKn/jf/h/10ALwCh/3X/w/83ADkA5/+9/7v//f8TABsACQANAAkAAwDz/xkAQwA1ABEA8f8fADkADQD//+//GwAJAN3/6f/1/wcA7//R/+f/4//x/9//2f/1/+n/2//h//v/CwDV/8X/6/8DAPf/1f/Z/wMA/f/V/8X/6f8hAAcA1f+3/9H/DQALAP3/0f/F//X/JwAtAP//6f/9/y8AMQAjABEAHwAtAAMADQArAEEAOQD1/xcAEQAxABcA8f8DAAkALQAtAAsA6f+x/wEANQA7AOn/q//f/wUAGwD7/+n/2f/f/9v/9f8ZAAUAy/+V/9X/HQAhAO3/sf/X//v/FQAFAPH/9f/9////DwALAAEA6f/n/x8ADQAJAM3/w/8BABkAIQDn/9//CQD7/wMA/f8TACcA+f/3/xMAKQAhAP3/DQAlAA0ABQANADUAFwDZ/wEAOQA5APv/w/8bACUAGwDr//P/CwDn//f/DQAbANf/m//H/xUAKQDZ/7f/0f/9////3//1//H/8//d/+f/FwAPAOP/vf/h/0EAMwD1/8X/1f8RACkAHQAZABMA8//R//H/TwBZACkA0//V/w8AUQBPAAMA2//v/wkAKQADAO3/4f/p/wUA8f/v/+v/2//f/9//+//x/+H/0//F/+v/EQArAP//x//D/+f/HQAvAB0A7f/d/wMAKwArABEAFQAhADkALwAbAA0AHQAfABMAGwAxACEA///l//X/IQAtABUA6f/r/wEA//8HAAUAEQANABEA/f8DACEAMQAXANH/1f8NADkAOQDn/9X/3f8VAC8A/f/1/9v/8f8VAP//9//b/xUAJwD5/8n/y/8jAEUADwC3/7v/BQBhADUA3/+1//P/VQBBAPn/0f8rAG8AMQDn////SwBvABUA5/8VAF0AOwDp//H/OQBHAAEA+/81AE8AEwDb//f/OwBBAP//AwAXAD0AFQD7/w8AFwAzABkA/f///+3/AwAJAAEABQDj////+f/V/93/2f8ZAB8A5//d/83/GQAnAAUACQDp/x0AIwAJAA0A/f8TACsAGwBLABsA6//V/+X/UwA1AAMA5f/x/yEA5f/x/zMAUQBJAOv/BQAnADcAPQATACUAGwATAC0AFwAlAPv/+f8dABEACwDn/+P////5/wsA7f/p//f/9/8BAPn/8f/9/+H//f/5/x0APwAnANP/jf/R/2kAdQAPAIn/u/8fAD0AGQADADMAJwDr/9//JQBRAC8A3////zcAIQDp/9X/CwANAO3/9/8hAB0A1f+V//H/WwBPAMn/hf/5/1UAUQDp/6//6f8ZADMADwDX/+P/BQBLACMA7f/n/yMAUwA9APv/+f8XADsAJQAPAP3/CQBVAEcBxQJhA5EClwGzAqcF2QbjBD8CQQHRAu8DWwRlAysCEQEvAJMAYwFFATcAuf+FADkBcwAd/6P+nf/NAEMBGQGlANP/+f5f/9kAswHtAKf/Xf/L/+P/lf9X/13/k/+d/2//6f4L/m/94f0V/1P/9/11/Gv8+/xR/Rn9ef2D/bP88fvZ+7n8xfw1/CP8pfyJ/An7+/kh+yv8u/sl+on5vfpf+wP75fln+lv8B/1V/KH7kfzB/Uf+kf+JATEDJwM5AiUCPwPbBH0FqwX1BXEFbQSxAzsEwQSBBCcEIwRPBOkD0QJRAs0CnQO3A00DQwMxA9cChQK/AkUDfwM9A+cCqwLTAr8CXwJdAvkCtQO/AxsDOQKfAQMCswIXA8ECMQKPAQsB9QBDAT8B5wCzAM0AxwBHAJX/S/91/5//gf8n/6n+1f37/N/8Ff3z/B38rftf+xX7N/ox+e/4Nfm7+cf5zfh/9yP2WfZb98/3D/ej9Yf1vfWZ9VH10fXb9s32V/cB+Av5A/kT+qv+oQY5DOUJiwGD/v8FLxCxEvkMmQeHB7EJxwn/BmMF4wWHBjEGKwVNAz0ACf7P/mcBqwPLA8EBkf65/If9DwBNAoUCsQAH/2f/qQBnABH/5f69AKECxwL7ANX+H/4F/3sAwwF9Ar0Bx/9V/lH/JQL9BKcEZQGP/lEA4QT9Bf0D0wG1AvEDYQSdBDsEXQNrAg0DQQXtBe8DHQGNAQcEVQVRBBcDTQLrARUC7QIzA0ECDwGxAJ8BWwJvAZH/w/7N/8UAcQAn/3f9S/wP/KH8vfzZ+x36kfgr+LP4ffgB98v1t/Wf9RX1JfQJ9HfzpfKP8h3z1fNN8+XyH/ND9JX1O/ZB9xX6Y//tBXkJEwfdAH3/WQZLEC0SSQ0XB/UGDwlRCrEIAwevBo8H0wdhB/0EywHJ/3sB8wSpBlMFgQI1ADX/2f+hAT0DLQNVAWX/Rf8zABsAhf7p/U//SwGFAa3/S/0r/FH9if8RAYcBDQJdAlkBC/9T/rMBLQY/CBcGfQQrBO0EgwS/BFUGuQctB6UFTQTFA3cCAwLTAqkE1QQXAx0BVQBfAK0AZQFvAtcC9wGvAC8AYQBhAC8AYwDhAJsARf+b/bn8efxt/Cf8z/tR+1P60/hD95/2pfbh9mv2VfWL9MHzdfOd8r/xrfGd8rXz1/PD8r/yY/MX9UX2A/cf+cn9sQVrC9MJDwKf/Q8Dzw7dE6EP/QeHBdUHzQh/B7cFCwZdB3UHuwbDBBsC2f9XAMcDSwfTBy8FewE//3//5QGbBF8FSQNnAGv/ewDhAHf/7f2j/gEBTwK3AJv9g/sB/FX+ewA7AZcAMQBxABkAhf9l/6kBKQStBN8EkQQlBd8E+QN/BG8FnwcRCNkFqwTRA2cEYwM5AxUEcwTFA2cCpQGpAUsBBQGZAfECHQObAXsAlQDBAL8A3QAVAZcARf9v/qH9N/1t/I373fq3+nH6S/nH99H2dfYH9qn1efX79F/02fLL8XHx4/FD8r3xSfLh8h3znfJ18unzCfWp9iP6ZQEHCbEL5QWP/tf/8QgNE0sS6Qx7BzkIIwpPCXcGXwUFB9MJvwlZBycDOQBBAOcCKQbXB90G9QPfAGf/pwB5At8DSQNDAmsBrQCL/9n9Vf2T/o8A7wFTAVP/1fyx+5H8B//1AJ0BXwHvAI0A6f9N/20AfwJJBR0GHQW/A6cDZQRhBDcEywXHB2cHSQVjA1MD5QKZAmkD5QTpBNUC/QDhAD8BOQFXAYMCXwO3Al8BkwCJANEAKwGjAb0BAQGJ/+X9L/05/fP8Kfxb++X6O/rP+Dv3m/an9t32bfYN9n316/Pn8XnxJ/Mb9B/zy/Ej8u/yAfPJ8unza/Ur9jP2XfdR+g//JwZrC38KdQKD/hEFkRB/E/sM2QbVB2kLgwpDBkMEUwbLCKkIYwdnBbECMQDJACsEGwcJB20EiQHp/z0AswHdAqkCJwFxAP8ASwFd/7f8k/w7/5cBewF//6X9v/z5/N/9f/85AU8CbwEBAEH/8/9JAesByQKjA88F/QY9Bi0ExwKNBGcG2QfrBykHsQWJAyMDowNBBNcDSwObA8sDrQK1AOv/1wArAu0COQPjAnMBGQDf/+0AqwGFAZUAnf8F/zX+0fxJ+8/6F/sT+yH6ffgN90X29fWh9YP1k/UZ9RH0A/Oh8gPyW/Fz8VnyEfPj8oPy0/Il83fzy/MZ9WH3E/pP/58GOQz7CXsBaf7FBd0RHRUTDzUIyweXCrMKywfLBbsGmQiBCZEI4QU7AsX/zwA9BFcHpwclBZMBK/9p/7MBcQP7AgsBPQAnAU8B/f5d/GX8If9XAasBEQAJ/lH8A/x3/dP/ZQERAgUCTwEhAKX+4f/lAZUDPwQnBfcGHQYpBIUCFwSPBn0HkwdBB10G5wNTAs0CJwQ9BJ8DnwPfA7ECpQC1/9cAgwJ5A28DKQMTAsEAGwDnAP8BHQJNAWUAsf+R/vn8z/u9+x38tfuT+i/5K/gl90/2OfbL9in3d/Yv9U/0kfPR8t/yPfN187PyMfJV8iPyBfKL8qnzffS59Mf1ifgJ/IMB2wf9CyUJjwGVAF8JoRPbE0UMUQevCVcMswpHBpkF8QeBCd8IWwdXBXcCHwBLAb8ESQebBrcD5QB5/8f/VQFPAp0BJwDb/xEBtwAX/mX7Dfw5/4sBTwF5/3X9efx//B/+BQBxASMCQQLFAaMA+f7x/10BtQN1BAcGlQdzBv0DLwJnBLUHJwjLB+EGnQZ3BMsCuQKJA8EDmQP/Ax0EXQLR/yP/ywC5AjkD8wLTAhsC+wBPAKsAYQGTAWMB5wAVAIX+e/wf+zv72/u5+5n6S/kh+Mf2E/Y19tn29fZv9h323fXL9BnzUfJ/87H0QfTD8nHyIfNp8wPz8/Lh8wX1/fWf93P65/+ZBv0KLQl/AqkALQdzEWkTkw0tCK0J0wyNC6cG0wTZBsMJ2QlTCMMF1QKLAB8B+wOzBnkGMQStAVsATQDhAGsBCwFLAGMATwE5AcX+B/yz+yn+owAZAeH/Vf57/R39cf1v/tf/fQFVA7EDdQFR/s39VQH5A0EEiwMdBT8HFwa3A4kC7QT/Bm8HswelBy8G8wK5ATMDuwRxBIEDjQNvAxsCYQALAAsBMwLjAnMDdwMZAkkA2f/5AA0C7QExAacA//+Z/uX80/vx+yn81fsP+y/6B/mB93n2h/Yb9233Cfep9iv2N/Ud9JXzEfQ/9Nnzp/MH9OvzvfIR8vXyCfSt9B/1r/Zh+MX64f+xB9sMDQmRAbUASwqnE2cSWwsHCOcLNw4rC/MF7wQHBwkJDQk9CNUFDQJr/5sA6wP7BfUE0QIVAXcAYQCdAGMAif8r/0sAGQJpARH+Ifu3+7X+1wDHAFn/G/55/Yn9Uf4H/1P/T//hAJEE8wUzAs38Ufw9A7MHewebBOsEhQZHBc0D9wOzBS8G1QWrB38IlwVZAHn/QQNzBoEFYQO1AqkClwGdAPkA0wEZAk0CfwNBBF8CHf8J/j0AlQKdAhcBzf+3/nX9jfwz/DX8s/sx+xf7o/oB+ZH2j/X79sf4G/nL9zX2jfU79Q/12fS19OX0i/RF9JfzI/Nz8nvyY/PR9H/1n/Ub9uf2yfnp/yEIyww5CXECLQLBCSUSARFRDBkKcQ2TDgULIwYdBY0GkQgJCfUInwajApf/HQDbAsMEawQRA+8BLwGdACsAWf97/uX+1QCnAoEBO/6l+wf8Df6f////m/8n/53+Tf5f/nf+h/4h/+kBOwVlBdcB9/1B/z0D9QUBBoMFjQaLBpkFZwQdBMkErwXbBjUIhwfdBI0BAwGxAiEE6QNDAxUD9wIDAs8ANQCLAHUBrQLZA+EDCQLD/z//fQChAYEB8QBFAIP/U/4J/Q/8h/tv+5X7lfsV+5X5/fdl96X39/cF+Ef4U/h792n20/Vz9Vn1I/V39UP1+fRr9MHz3/Ph83v00fTX9eP2affh9+v5G/9JB1sMRwodA8EBMQkXEX0QGws1CfcM/w6lC/sF+QOJBbEHfQipCL0GDwPn/xEAOwKHA2EDrwIBAncBAwFTADP/2/25/bv/aQJ3Ahf/2fun+7f9Xf+p/3P/L/8p/0X/Pf/J/kn+df5fABMExQbzBAMArf21ANcF5QafBQsFlQblBi0FvQPTA2cE/wSbBrcIoQcDA8v/yQCnAx8EAwOPAiED2wKpAX0ABQAhAAUB6QKlBPkDGQEN/33/BwFzAfkAkwBbAK3/a/7t/LH7Ffs5+yf81fz7+735zfeh93f43fhh+CX4Cfjv9yf3H/ZD9bP01fRX9ef1kfWX9KPzcfOx81n0LfXf9XX2E/ch+L36w/+xBicLiwmdBL8DXwnHD18P7wsNCgsNOw65C8UGOQS1BPcGlwjPCD0GpQJhAOEAOQKTAiMCDQJJAlECoQE5AGX+Mf3z/UkA9wE9AeP+G/3n/Hf9P/7L/h//Jf9V/xUAOQAD/239w/3jAJMECQb5A5sAy/+jAV8EaQTJA50EwwYfCKsGTQTJArcCpQTJBlcI1QapA5sBEwIdA5sCVQGDATUDKwQhA+MALf8R/2UAbQK7A0cDpQGbAL0A/QBXAKf/8//lAD0BSwBl/ln8Oftj+zP81fxb/B37z/lH+Tn5wfjl9w/4HfkT+jX5Z/cb9nX1XfUz9Tv1Q/Ut9df0s/Sv9In0G/SP9AP2Z/dF+Pf4XfthAKcGZQqNCKEEkwSrCY0ONw5vC1MKdwz5DH8KJQZ9BLMENwZXB4sH7QXJAosAVwBZAScCLQLDAbMB2QHXAZsAjf7z/Gf91//rAXEBE/87/UP9//1z/nv+vf5n/yEAeQALABv/S/6B/p0A3wOBBfEDQwG7ADkD7QTLBP0DgwSVBa8FtwWBBZcE6wLTAqsFCwdDBT0CAwJ3A5MDPwJpAa0BBQIlAmECNQLJAH3/+f/5AdsCuQFnAI0AOwFHAZ0ABQCV/2//e/+Z/9v+V/0H/An8n/xP/D37j/qt+p/6F/qH+ev4V/jv94H4u/gB+Kf2DfY/9tX16/Rb9Ln0WfUR9en0CfVj9c31T/al9wn5//ql/psElwnHCVsFdQMLB+cM3Q09C9kJAQxtDRsLxQYVBDcEkQXpBnkHbQYXBMMB2QADARcBXQGzAUMCTwIRAv8AMf9R/SP92f75AEkB9f+R/gH++/3J/cn9Jf7n/u//swDXANX/vf5F/vP+lQAtAw0FhQSnAg8BswIPBP0D1QNLBIkGWQYhBg0FHwTjAosCyQQfBhcF2QJZAikD2wJhAaEAUQErAosCpwJZAg0B0f8NAHkBZQK9AQ8BOQGjAR8BAQAx//f+Jf9B/1v/of5j/SH8p/v3+8n7HfuT+rn6Ffuj+pP5lfg/+Cv4Sfhr+N33Bfcn9jv2CfY39Un0f/SZ9e/1x/XL9b/28/Zt91X4U/q3/A0B7waFClsItQP9A4MJYw2NC7EICwqNDVkNCQmlBIkDYwThBQ8H+wY5Be0C3wGjAdUA2f87ALEBaQIZAqEBvwC5/o/8q/wh/w0BpQAX/6/+E//F/rn9H/21/en+NQALAfUAtf9d/iX+Bf8VABEBjQJlBOUE4wITAVkBawMnBL8DywQ5BksGfwT5AzsEswN/AnUDpwWpBW0DCQKvAqUCFQGHALsB3wI9ArUBFQLBARkAZf+9AC8C0QHRAOUAPwGJAEX/q/7H/p/+Y/5n/mH+af35+1H7Zftr+xP7+/o5+yX7v/oX+mn5r/hz+E34ZfhJ+On3Gffv9QP1WfRD9Ef00fSB9RH2TfaF9in3N/h/+Yf8rQEfBzcJFQcBBTsGjQk5C/kJbQmrCuMMZww7CXUFkwPPA2kFXQYlBtcEnwPBAs0BlwDZ/+v/vwCrAWkCRQLdAK/+N/1t/dP+s/+z/2n/af+b/zn/bf53/S/9S/4XAE8BAwH5/2H/Sf83/y3/k//5AOcCKQSNBI0DBQLPASkCaQQHBUMFCwVNBd8FCwXBA10CMQJbA0UEjQTzA80CzwEvAVcBLwHNANEA5QHVAq0CVQFbAAUAfwDpADsBXQEtAdEAgQABAOv+t/1J/bX9Jf7n/UX9KfxL+8v60/rH+m36cfrL+tX6MfoJ+Vn49/e594v3XfdJ96/2wfUx9Tf1E/XZ9O/0n/XJ9nv3Hfi3+CH6l/2TAtkGeQfnBH0ECwepCoEK0wjPCB8LbwzlCgkIzQXbBPUE4wV9Bu8FdwRnA98CPQIPAW0ASwDJACMB1QGzAWsAQ/5n/SP+Lf8T/5f+t/5b/4H/7/4j/pv9l/1h/o3/dwBdAOn/l/9z/1f/V//V/9MA3QHVAp8D7wMzAyECsQE3A2kEjwTzA00EPwUpBREE7QKPAtcCJwOjAysEuwOjArUB7wHvAQ0BZQAlAU8ClQLZATcBwQBfADUApQAVAfUAcwBvAJ8A6/9//qH9zf0F/u39yf17/bn8zfuT+6v7P/uT+r/6a/tx+3X6kfkl+d/4hfhV+Ef4fffN9rn2ifb19Qn1O/Xf9R/2mfYv9+v3qfh1+Tf8GQDvA8MFJwXtBCsGIwiJCdUI5wihCU8LSwtvCf8GlQVjBd8FCQa9BfcEQQSnA+sCxQHJACcAUwDjAF0BVwF9AEP/Kf7l/Uf+jf59/n3+0f5V/13/1/4N/pH9/f0B//f/UwAbAOn/5//7/9P/nf83APUBWwONA7MCPwLZAqcC4QLdAvEDMwTpA3EE5QRxBKUCBQIxA98DQQOtAh0DUwMnAj0BIwEzAY0AnwCfAVUCawF/AG0A0QBbAN3/FQClAJ0AUwA7AMX/n/6x/bv9F/6t/SH91/z5/IP8y/tP+wH73/rX+iX7OftF+o35HflJ+an47ffV9xf4+/cz9632V/Y/9vH1P/bn9nP3K/i/+M/5v/q7/D8AfQPbBOMDCwQfBgMICQhHBycIrwlhCosJZQgvBzkGxwX7BTUGzQUHBYcEDwRLAy8ClwEjAckAvwBlAXMBWwDl/mv+pf6B/gv++f1V/q/+zf7T/pX+C/57/cX9t/5B/0H/Rf+5/9f/h/9R/4v/MQD/AOUBNwJPAmUCjwKRAhMCuQIjA5MDfQPTA4cEEwQrA3sC3QIHA5sCiQINAx0DOwKPAYsBSQGlAHMAWQHHAXUB8wALAeEAOwDD//v/WwBVADkAQQAFADP/Y/4b/vH9mf1L/XX9g/0D/VX83/ul+y377/oR+z/7A/uR+k36+fl/+eP4j/hR+DP4Jfj996f3Jffr9u32Lfd19wv42fiv+Zv6x/vz/bEAswIBA7ECwQNpBasGmwbbBtkH7wgVCS0IVwejBl0GPQZTBkEG6QVvBfsENwRjA5MCNQLDAY0BfwGdARkBNwBL/w3/6/6l/kf+M/6D/sX+t/5n/gX+1f3X/SX+bf7B/gf/Vf9d/0X/Tf9l/43/GQAXAdMBCQLXAScCOwIBAjUCVQLjAr0CEQODA7kDPwOjAn0CuwKhAk8ChwLLAqsCCwK5AaEBAQF5AJEAEwEzAd8AwwCvAHUA9f+z/6n/uf+1/9n/9f+j//X+Z/5F/v39of2D/aP9qf07/f/8y/xj/P/7yfv1+/P7yfuf+3X7K/uz+kX68fm9+Y35j/l/+W35H/nv+Ln4q/jX+CX5rfkv+tH6fftr/BX+CwCNAf8BHQItA0kECQUDBakFhwY1By0H7wbFBnEGDQbBBc8F0wW9BWsFCwV9BOkDUQPVAjcC7QHhAeMBTQGZABUA3f9t//v+u/7F/sf+t/6r/pf+Zf4f/gH+H/49/m3+qf7z/hH/F/8z/2P/rf/9/1sAtQAbAX8BkwHFAesBZwI1Ah0CXwL1AisD0wK5AucC3QJdAhUCUQJ1AgUCxQHbAdUBMQG7AL8A2wCFAGcAjwCnAD0A9f/v/+n/hf9Z/3P/m/9H/+v+z/63/k/+/f31/QP+xf2b/a39pf1n/Rf9B/3//M38l/yN/JP8a/wl/Pn75/uz+1X7L/s9+z37B/vz+g37EfsH+wH7V/ub+9H7E/xr/AP95f0f/zEA1wALAa0BbwLHAukCewOFBAkF6wThBD8FgwUTBZMEnwT1BCEF/QTLBHcEIwTJA20D/QKlAnkCYQIBAoMBUQEnAbMA/f+j/7v/s/9r/xf/D/8V/9f+j/5p/mX+Yf51/pf+s/67/tX+I/9j/3P/if/B/w8APwAPAIUAFQFtARkBHwGbAQsCowFdAacBEQL5AcUB2QENAq8BZQFfAYcBTQH/AP0AGQHZAJEAhwCDADsABwA5AGUAJQDb/+v/DwDP/4P/df9//13/L/8n/yH/8/69/q3+sf57/j/+N/5J/h/+7/3T/b/9hf1H/S/9Hf3X/J/8h/xr/Cv89/vR+7/7gft1+4f7ofuZ+6H74fsh/Ef8p/xj/VH+9/6N/yMAqQC5AO0AbQFXArsCwwK9AjMDmwO3A2EDPwNJA8UD9wMFBMEDmQONA4MDPwMLA+kCzQKRAj0CIQIXAtkBWQH9AN8A0wCZAF0AFwD3/93/z/+P/z3/+/73/gv/A//l/uP+Ff9F/zv/P/9H/0v/O/95/9f/NwBnAP3/AQB9AK0AiQCXANcABQHLAP8AMwE9AecA0wATAVkBFQEDAQ0BFQHzAOUADQHzAKsArQDdAOsAsQCJAJkAjQBfAD0AMQALANX/s//N/63/bf8x/zX/Nf/3/s/+vf6t/ov+Y/5X/g/+vf2F/W/9Wf0d/eX8t/yN/Gn8S/wz/A384/vN+9f72fvZ++/7GfxF/Hn8z/xN/dH9a/7//ln/R/9F/+f/5wBVARsBAQGdAXkC3QKdAm0CrwI1A6MDswOjA4MDfQN9A3kDeQN1A0UD7wKdAr0C1wKjAgUCowGhAcsBmQEzAdMAswChAHsAJQDP/3//bf9Z/0f/I/8B/+X+w/63/uP++f4H/xX/I/85/+v+J/+Z/8v/b/8//63/RwBDABcAEwBTAF8AnQDPAPUAlwCLAMsAQQExAfcA5QAZARsBOwFJAVEB9wD3ACcBVQEHAbsAwQDtAMMAkQBtAFMAIQALABUABwCz/3P/a/+H/1v/Cf/P/q3+i/5n/kv+Gf7L/Yv9c/1l/Sn95fyl/In8afxV/EP8F/zv+9/72/vf++H78/v9+y/8X/y7/CX9t/03/pv+rf7L/kP/CwChAKcAkQADAc8BWwJlAj0ChQL/AokDoQORA28DhwOjA7cDlQOXA3cDZQMrAxMDDQPnAn0CMwIXAi8CBQKhATUB/wDpAMMAcQAVAMH/q/+n/4P/Qf8H/wH/C/8J/xf/Hf8N/8f+uf4Z/4n/hf8D/9n+O/+n/6n/e/+B/9//IQBVAEcARQBNAH0AtQD3APkA+wDhAAMBHwEzAScBCQEFASMBPwFFAQ8B8wD5AAMB+wDHAJMAcQBjAGUASwAfAPf/y//D/7f/if9J/w3/A//1/s3+of5d/h3+4f3H/Z/9Yf0d/ff81fyv/Hf8Ofwb/An8A/zt++f78/vr+/f7F/xD/HP8qfwT/bH9Pf6f/o/+nf4L/+P/jwClAIsA5QCfAV0CeQJFAk0CwwJjA6UDmwN5A30DmQO7A7cDvQOTA2sDKQMZAx8DDQOpAksCDQItAhUCxwFDAfUA4QDTAI0AKQDH/53/jf+F/1v/Jf/7/uP+4f7r/vf+7f69/qv+1/4v/z3/M/8X/0//g/+d/6X/0f/p/xcAFwBnAI8AkwB/AJsAzwABAfkACwEJAR8BJwE1AT0BNQEZAS0BOwE5AR8BAwEFAfUA2QC5AKEAhQBrAFsASwAPANP/pf+V/3X/Of8H/+P+w/6d/m/+Sf4R/tX9p/19/V39Lf3z/Nv8tfyV/G38Tfw3/CH8LfxF/Cn8C/wJ/DX8afx3/KH85/xh/Qn+k/7d/tf++f6j/20A7QDhANcAYQEdAo0CnwKJAr0CGQORA78DqwORA60DxQPjA80DwwOdA3kDSwM5AzEDCwOtAlsCNQIrAgMCrwFFAfkAyQCrAGMA9/+f/4X/f/9j/yv///7t/vH+//4N/wf/3/6//uf+O/9v/1X/Tf9x/6P/4f8TAB8AEQD5/2UAuQDRAJUAmwDFAAcBAQEbAQ0BJQElAVMBcQFnAScBKwFDAWkBPwEnARsBDQHzAOMAxQCPAEEAOQA9ACUA4/+l/4X/bf9F/x//8/7X/qX+jf6D/lf+Ef7Z/bn9pf1x/UP9G/0B/eH8x/yt/If8W/xD/En8Vfxd/FH8U/xh/IH8u/wF/WP97/2F/gH/Bf8R/3X/MwDZAPkA7wA3AeUBdQK7ApsCuQIBA4MDrwPBA58DrwO1A8UDrQO/A6MDfQMpAw0DEQMLA7UCSQIDAgUC7wGlATcB5wDTALkAZwAFALf/l/99/1v/N/8Z/xn/Ef8Z/xv/B//r/tv+Sf+D/3P/H/8n/4n/0f/J/9n/5/8tACEAVQB9AJsAfQCdAM0AHQH/APEA8QAjATEBPQFDAUkBIQE3AU8BWwExARkBGwEbAQEB1wCzAI0AXQBDAEMAGwDf/6n/nf+b/1n/E//r/tv+s/5//lX+N/4F/u/93/2//X/9Qf0r/Sf9+/zT/K38rfyD/GX8Y/yF/G/8afxl/K38x/zd/Pn8W/3H/V3+y/4x/yf/Uf/F/3MA6wDvAP0AcQEFAm8CawJlApUC7wJPA2sDVwNDA0sDYwNlA08DVwNHAxED1wK/AtMCnwI/AukB2QHtAb0BWQEFAdEAyQCvAGcABQC5/5//k/93/0//M/87/zn/Kf8j/wn/9f7t/hv/Z/+H/3P/Xf9Z/6X/7/8XAA0ABQAtAH0AmQCnAJMAtwDlAA0BFwEfAQ8BDwEdAUMBQwE1ARsBIwEZARMBBQH5APEA6QDjAM8AnQBXAC0AHwAVAO//r/99/1v/Rf8n/wP/1f6t/oH+df5X/i/++/3Z/an9ff1R/TH9B/3f/L38q/yd/H38Zfxj/Ff8ZfxN/HX8nfzV/AX9Yf3N/WH+xf4V/wH/Mf+R/1EArwDDAMEAMwG3ARUCCQIdAksCvQL1AiUDJQM/AyUDMQMrA08DVQM7A+0CuwK5AskCmQIvAssBywHRAZMBJQHhANEAvwB1ACcA9f/Z/7P/ef9V/0X/L/8T/9/+z/7T/uP+4f7L/uv+H/9P/zX/G/8r/1f/if+j/8X/3f/L//v/SwCbAIkAcwCPANsA8wD9AP8AJQEhAS8BWwFpAU8BNwE5AWMBawFPAUkBLwEfAf0A7wDTAKkAbwBhAFMAKQDX/7H/p/+R/23/Sf8d/+v+u/6f/oP+R/4F/tf9z/2t/YH9V/01/Q395/zX/MP8o/xz/Gv8c/xz/Gv8c/yT/NH8Jf2X/R/+if7V/tP+9f5d/+v/VwBbAGkA2QBhAbkBmwGTAe8BTQKDApUC0wIBA/EC0QL5AhUDEQPLArMCtwLBAp0CWwIVAgMC3wHLAZcBXQExAQcB4QClAF0ANQALANf/tf+r/7H/e/9P/zf/K/8V/+P+w/7P/vP+B/8R/xv/J/8l/yX/Nf9h/5P/f/97/6H/+/8VAPX/5f8pAGcAjQCLAL0A5wADAQUBJwE1ATkBHQE9AV8BawFXAU0BUQFRATEBGQEFAfUA1QDNAMkArwBrAD8AIQAHANv/p/+P/3P/S/8p/wv/1f6R/mn+U/45/gn+3f3H/av9hf1r/Un9Mf0N/ff87fzp/M38v/y5/NH85fwL/Vn9x/03/pv+3/7v/iP/ff/9/0EAVQB7AMsAFwFLAVsBgwGdAdkBBwJFAmECSwIdAiMCRQJhAk0CMwIjAhsCFQIPAgEC0wGPAXMBdwFvATsB8wDRAMMAqwBtAC8ABwDr/8//vf+n/4v/d/9n/1//T/9J/0f/Rf9f/23/ff+F/4H/lf+l/8H/t/+7/+H/9f8HABMAKwBHAE8AZQBzAIkAjwCRAKEAoQCjALUAtQCzAJ8ApQCrAK0AmwCJAHsAZQA/ACkABwDz/8//t/+j/43/Yf9B/yP/A//X/rn+m/57/mH+Qf4X/vH90f2t/Y39af1V/UH9Of09/UX9c/2//fv9L/5Z/nX+q/67/gn/a//J//H/7/83AJ0AzwDRALsABQFBAWMBbwFxAYsBgwF/AaEBvQHHAa0BkwGlAaUBpQGPAXUBZQF3AX8BaQFpAa0BZwEFAQkB1wCbAIEAiwBhACsATQAdAMn/rf+1/5f/Xf87/1f/V/9J/yX/E/8T//3+7f71/g//Hf8T/x//K/8l/x//Lf85/z//W/+J/5//nf+f/6f/tf+9/8X/5//3/wkAFwA3AEkARwA9AEkAcwCBAIMAlwCxALUAsQCzALMApQChAJ0AsQCrAKkAmwCPAHcAWwBJAEcANwAtACEAFQDr/9X/tf+j/4f/gf9//3P/Sf9B/0f/Mf8N//n+Bf8Z/wP/B/8b/zH/F/8B/x3/R/9L/03/cf+z/8X/x//N/+X/AQALABsARQBdAHEAaQBzAI0AlQCVAI8ApQCnAJ0AowCnAJsAfwCBAHkAaQBRAFMAYQBNACcAHQAPAPX/x/+1/9P/x/+z/5v/rf+n/4n/d/9//5H/kf+D/5X/n/+p/5P/lf+b/6P/q/+5/8n/1//X/9f/xf/J/9X/6f/v//X/BwAXAA0AAQADAB8AIQAhAC0ASwBPAD8AKwA3AE8AOQAXABEAKwAvAPv/9f8NABMA6//X/w0AEwDp/9H/9f8TAOv/0//d//n/9f/F/8n/8f/n/7v/rf/X/9v/uf+x/9H/8f/Z/7//x//T/9f/q/+x/9H/4//X/8H/1f/X/9H/z//d//n/8//1/+v/9f///+//8f/7/xUAFwAPAAkAEwAXAAsA8/8HABkAHQAHABEAIwApAAkAAwAXACkAEQADAA8AJQAdABEAEwAfAA0A+f/7/wUAAwDz/+f/9//t/+f/3f/t//H/4//d/9X/2//V/8n/2f/Z/+n/5f/j/+P/3//l/93/2f/x/+3/6//t////BwD1/+3/BQAXAA0A7//7/xEACwD5/wEADwABAPf//////+v/2f/v//f/+//b/9//7//x/9P/2f/1//n/0f/L//H/AQDb/8v/7f8HANv/yf/r/wkA5f/B/93//f/x/8X/z//9//n/z//T//P/9//L/83/5//v/83/1f/x/wEA4f/h////EQDt/93/6f8DAPP/7//9/xEAAQDp/+3/9//r/9f/3//t/+H/1//j//H/5f/P/9v/+//9/+3/5/8BAPv/8f/9/w8AGwADAAEAEQAJAA0A+f8NAAcA+f/1//v/9f/n/+P/6//1//P/5f/r//P/5//f/9n/7//x/+f/4f/p//P/8//d/+X/8/8LAPf/5f/v//3/+//p/+3/AQD1/+//4f/1//f/8f/t//f//f/z/+H/5//9/wcAAQADABMAGQARAP////8NAAMA8f/n//f//f/h/9f/2//v/+3/3//f/+f/6//V/9v/7//z/9//1f/l//X/+f/7/wUADQABAAMACQANAP//7//1/wEABQAPAAEA6f/P/+v////5//X/+f/9/+//2//X/+///f/9//n/+//z/9//2f/p//X/6//n//H/AwAJAPv/8/8BABUAFQARABEAGQAHAPP/9f////3/8/8JABcADQD7//f/AQD7//////8PAA8AAwD7/w0ADQABAPv/DwAVAA8AAQADAAMA9f/r//P/+//v/9v/5f/1/+v/2f/V/+n/6//r/93/5//l/+X/3//f/+n/5//p/+f/5//x/+v/5//n/+//+f/7//P/+/8HAAsA+f/3//3/+//3//H//f8DAP//7f/x//n/9//z/+//9f/r/9//3//n/+n/4//f/+X/6f/l/+P/2f/X/9//3//Z/8v/yf/J/9n/1f/H/8X/zf/d/+H/3//r/+//7//n/+//9f/z/9//6//1//3/8f/3//3/AwDz//X/9//9//H/7//7/wMA/f/z/+v/+//9//v/6f/x//f/9f/1//3/9//7//X/+f8BAP//+f/3/wkAAwD9//X/+////wEAAwABAP//7//p/+v/7//3//X/9f/v/+3/5//z//v/8//5//v//f/1/+f/7f/t//3//f/7//v/7//3//f/9//3//H/+f/7/wMA//8DAPn/9f/p/+//9f/9//X/9f/3/wcABQD5/wMAAwABAP3///8NAPX/3//t/+f/+//p/+//6f/r//v/7f/7/+/////p//H/4f/h/9//8f/1//////8PABcAGQAXAB0AIQAXAAkABQARAAcABwADAA0AFQAHAAEABQAJAAcAAQAJAAcABwD/////BwAJAAEAAQD///3/+f/7////8//n/+v/9f8DAPv/BQD///3///8BAAMAAwD/////CQALAAEAAQAFAAMAAQD9/wsAEwATAAsAEQATAAcA+f///wcA/f/5//X/BwAJAAsAAwATABMADQD1//f///8BAP3//f/9/wsACQADAP3/BwAJAAkAAQAJABEADwAJAAkABQAHAPf//f/5//P/5f/f/+X/6f/l/+f/7f/5//X/6f/f/+n/6//h/9v/4//p/+f/3f/f/+P/4//p//f//f/5//H///8LAA0A/f/3/wUAEwAXABEAEwAVAA8ACwAXAB0AGwAXABsAHQAhAA8ABwALABsAIQAVAP//+/8LABEADQALAAkADwALAAMA/f8FAAEAAQD5//X/+/////f/8f/7/wEA7//T/9X/+f8BAPP/5f/z//v/9f/x//n////5//P/+f8LAAcA/f/3/xMAJwAdAA8AEQAdABUAAwABAA0ABwD5//X/BwAFAPv/7f/3/wsADwAHAAEAAwAJAA0ACQANABMAFwARAAcAFwAZABUAAwABAAMACwAPAPv/9//5/wMAAQD5//X/CQAdABcA/////xMAGQD1/+f/+f8XAAEA6f/n/wcADQD3/9//9f8HAPP/yf/R/+X//f/r/+P/5/8BAAMA8//r//v/BQD7//P///8HAA0A8//z////GwARAP//CQAhAC0AFQD9/wcAFwAbAPv///8LAAkA6f/3/x0AGQD1/9//+f8LAPv/7f8BAAkABQD5/wEAEQAJAO3/+f8bACsABQDz/wEAIwAZAAEA+f8TAA8A9//1/xkAJwD5/8//5/8bABkA7f/Z/+n/DQAFAPv/7//r/+v//f8JAAcA6//l//n/DwD3/+X/6///////4f/f//X/9f/h/8//3//Z/9f/z//f/93/1f/V/+H/5f/p/9//6//z/wEA8//5//3/+f/3////AwADAOv/6/8BABUAEQDx//X/AQAVABcA///r/+f/CwAnAA8A///5/xEADwD7////BwAJAP3/+/8ZAB8AAQDn/+//HwAlAAcA9f/5/wMAAQABAP3/+//r/+v/+f/5/+n/3f/j/+X/6//x//H/4f/P/+v/BwABANH/x//l//X/6f/X/+f/8f/b/9P/6f8JAPn/2//t/x0ALQAJAO3/AQAjACMAEQATACcAJwAbABkAGwAbACEAFwAdACsAKQAZAP//BwAnAC8AGQD7////EQAdAAkA7f/7//f/AwANAAEA9//t////DwAHAO//6/8RAB0A9//d//P/KwAfAOn/0f/7/xUABwDz////EQD//9//5/8BAPn/0f/N/+f/CQD///X/6/////H/+f8NACsABQDd//X/PwBHAAMAx//9/zUALwD9//X/CQD//+3/7f8FAP//6f/h/+v///8TADEAFwDZ/8n//f9PADEA3//T/xkASwAVAOv/AQArAC0AAQAJACUAIQD5/+H/EQA3ADEACwDz/wsAGwA1ACUA/f/l//P/IQA3AA0A1//R/xMAPwAbANX/2/8DABkA7f/N/+P/BQABANX/zf/p/+P/4//V/+P/2//j/xEACQDT/7X/2/8TAPP/1//z/xkABwDN/9v/CwD7//P/8/8HANv/3//1/wEAzf+9/wcARwARAMn/w////wMA/f/7/wsA6//p/xEAGQDr/73/5/9JAFkAGwDH/+P/BwAjABkA///x//n/GwAnAOf/y//j/xUAFQDJ/8v/+/8RAOv/nf+1/+H/GwADAMX/j/+P/+X/LwAFAJv/Z//Z/1EAOwDD/3//4f8lABsA9//3//P/xf/L/w8AMQD3/6//5f8/ACEArf+b//X/OQAPAO3/7//z/+H/6/8ZACUA6//T//3/MwApAPH/0f/j/wkAKQAvABEAyf+p/8//DwAdAOP/yf/r/w8ABwDf/7n/2/8XAC8AGQDb/+P/5f/3/wUACQArAP//y//V/x0AOwDR/6P/yf8nACcAv/+t/9P/9//n/8v/AwAbAOn/r/+3/xsAJwD5/6n/rf8HADUAJwC3/4//1/9LAFcA8/+x/9X/HwAjANf/1//3/zMAIwDz/9H/wf/1/wcA///T/73/9/8lACcA0/+N/8v/PQBtAAkAo/+t/wkATQAdALP/lf/l/zMAKQDP/53/uf8FACkABwDP/8f/5f8ZAB8A/f/L/9f/GwBHABsA1f/v/x8AJQD3/+f/GwAnAPP/x//J/xEAIQAHANv/rf/B/+3/HwDx/4//c//H/xsABwCx/4v/y/8XAAUAyf+r/+X/FQAXAPP/2//h//H/+f/3//P//f/x/+v/y//Z/+//DQAjAPn/w/+t/9H/PwBfACcAv/+x/w0ANwAlAN//2f8BABMAOQANANH/n//P/z0AQwD1/6X/6/8lAPf/v//d/zEADQDD/7n/8/8RAPP/AQD9//H/w//Z/yMABQCx/7H/LwBXAM3/Wf+z/zMANQCn/5H/+f8vAO3/g//D/yMACQCt/6f/HQA/AOn/h/+r/xsAOQDv/7f/8f8pABEA4f/9/ysACQDV/+//SQBNAN3/mf/x/28AQQDF/8P/ZQCLAN3/U/+9/4cAgQDF/3X/5/9pAEkA0/+f/6v/7f9RAGEA9/9J/23/GQCHABUAif+f//n/JQD9/9P/1/+r/8H/GQBpABkAef9V/+X/RwA3AMv/1f/1/ykAFwDx/9P/xf8fAHEAYwDj/6P/FQBTAB0A3f8rAKsAZwDB/6H/EQBlADEAJwBNACEAk/+V/3UAbwEtAjUCWQG//0H/cwH/ApsCOQAvAEUB3wHBADMA9QCfAe8AkwAbAb8BtQCD/zUAHQJjA9cDqQNBA9EBWwERA68E1QTjAokCqwKfAlcBhQDVABUB0QCXAEcAdf8x/g3+K/8TANf/7/4//jX+hf61/r3+df4v/gv+U/5z/uP9Of1P/dv99f2H/Y/9kf0V/XX8ofxd/Z393/wt/PX75fs1+5P65fpx+/X65/mB+cf5aflF+a35lfqX+vX5V/oD+9v7ofsV/Bv9Tf6B/5MA3wG3AS0B0QHNA1EFCQVHBFMEDQWtBQ8FKwTPA1kENwUtBZkEqQMfA1MD3wNbBBkEiQMPA+sCVwObA2sD2wKxAmUDBQTzAx0DgwKhAi8DrwOvA2UDtwINAu8BPQJpAgUCvQHTAc0BSQGRAEUAawC/ABEBCwG5AN//U/95/zEAewDr/zP/vf6t/rH+o/53/hH+xf27/af9U/2Z/On7o/v3+238R/xF+2H6PfrP+rP6vflZ+YP5qfkV+On2w/aZ9xP3Y/ZH9in3L/en9m327/ZZ9+n3H/lv+mX6m/kJ+u38XQENBfsGLwcbBq8FywavCWUMBQzBCf8H6wj/CCMGlwJvAgUFlQaPBHkBR/+n/l//uQB5ApsCRwH5/83/pwD9APkALQHDAX0CjQL5AbMAh/97/98ApQIBA18BRf/n/nUAhQLPAusBTQF/AkUExwNpAlMCvwUZCM8GpQOjAnUEuQQdBDkEPwVtBP0BlwHbAiUDswEbAbMCrQOXAt0AswB1AaMBiQENAkUCQQGP/wP/w/8xAHP/N/7n/SH+1/35/F38YfwV/IX7Zfuz+3v7XfqD+WP5b/kp+aH4WfjT9932I/Yf9if2W/W99EH1s/a/9qP1GfVB9sH3e/iz+B/5J/nR+dX6Nf3T/tUAqwR1CJsIxQMxAb8F8wxnDpEJqQUzB78J1whtBWsEDQbVBosF6QQrBREE4wDj/7MCqwUrBf8BTQDbAI8BKwH1AE8BjQG/AGsAiQAFAL3+C/49/8UA+wDp/7P+C/79/d3/hQQ1B+8DZf0T/O0C5QfbBnUD/QRzBx8F0QFJAh8GGwYNBEkFuwe7Bef/if7XAiEG1QR1AnECgQIDAb//DwHNAq0CHwEJAe8BOQHH/n39E/8RAekA+f59/Q/9d/zn+z/8W/0v/Yv7P/pN+o36T/kn+FX4gfmf+QH4WfZx9V31O/VN9cn1ufXf9PHzcfRp9UP2SfZ/9lX3yfch+PH3Yfi1+U37bf2xAJUFUwlfCMcDAwJPBtkN+Q+3DBUIoQdTCXcJdwfHBWMFRwbHBs0G7wQxAisAqQDvAgkFcQXVAxMBOf/L/w8CjQOJAnUAv/+9AEsBIQBR/uH9nf7Z/5MAVwDt/uX8Xfyl/q0CkQSlAm3/M//1Af8DwQT/BMkFWwVxBUUGkwbbBAcDiQRLBxMIqwXlAvUBcwJhAwcEHwRxAy8C2wFHAqMC9wFLAYUBgQITA2sCtQBJ/0n/DwDNAK0Au//7/aH8kfwp/SH9V/yx+2X7M/vV+uH57/ih+CP5ofk5+Tf4w/YF9jX29/ZL9yn2D/WB9Av1afVD9RX1afU19n/2Vfa19t322/bx9sP4Efsj/H38y/9pBhEL7QgFA6MC1wjvD6MPuQutCJsJTQr9CPUG7QVBBtsGlQbRBQkEKwKHAKsAXwJrBPsEUwOtAEH/HQDDAUMCEwFhAMUAUQGhAK3+Z/2l/e3+MQB9APH/W/7//JX9TQETBasEVwC3/TEBewWTBW0CXQL3BKMG7wVjBdkEswP7AhUFVwgfCEkELQE5AssEGQWtA6MCmwLBAqMC0QJpAk0BYQAdAREDtwPpAZn/N/+bAIMBLQE1AGH/x/53/pX+gf6D/SH8e/sR/Kn8y/vD+Yn48fi7+dX5C/kz+Jv3Qfdz9wX4Nfhh97n1VfXL9Q/2N/W59D312fWn9QP1D/WZ9RP2kfZ59//4u/l1+dH5D/zxAPUGUwwTDA8GdwG7BY0PtRP1Do8IHQhBC4sLowdvBJcETQanBoMGKwVRAtX+Wf5lAc8EOwX7Ai8AM/+9/9kAfQE7AYsALQCxAOEAf/+B/dX8B/7J/9kAxQAf/2X9h/1xAX0F4QQdAEv99QFDB7sH5QPVAmMFBwehBusFNQVZBEkDCQV5B0EHXQMhAKsBJwXhBb8DywHxAZUC7wI1A/cCAwLNABMB0QJ/A6UBLf/7/vEACQJZAb//2/57/n3+r/7X/iX+0/z9+1f86fz3+yH6N/mt+cH6yfrl+WH4S/ev99f4xfmN+Qv4n/bB9X/2Hffd9nX1gfR/9Hn1i/UH9e/zLfQV9Wv23fY19z33T/h1+V/6Y/wPAj0LPxDTC5sC3wClCh8VQxRvDHkH1wpHDY0KQwWLAy8F4waPBgcGyQO1AGf9/f35AYMFgwU9Ahn/0f6TABcCrQGf/z3/vwCnAuMBg/7z+yn8m/7pAFkBmwAh/zX/nQG1A+MCj/8FAJ8E6wcrBlkCcQHfAl8ExQZHCcMIPwTDAJ0DVwdVB+8DEwPLBHMFTwTfAp0B6QDzADsD9wRRBAUBpf5n//sBFwMjAucA7wBrATkBgQC7/0f/Lf+9/70ApwCb/vn7EftJ/Jv9hf1P/An7R/oX+i/6U/rp+Vv5Hflx+QH6mfld+BH3FfcN+Iv4CfiT9lX1U/SB9AP1h/Ul9d/0YfU99l321fW79ef2hfhb+v368fq7+lv/5wh3EXsPuwTn/sMGtxN7FkEOZQctCQMNYwvBBWMDqwT/BQkGSwZpBYcB0/wB/WMBqQXLBRsDWQDr/o3/KwEvAksBx/8pABECYwK3/3/8DfxB/q0A6QGdAdX/mf03/SMAHQThBK8CzQAfA0kGIQZdA28C9wV1CXMJ5wZhBPkDbwMhBBMGWQd1BRMCnQGpAw0EDwKbABECAwQ7BPMCoQHJAHkA9QCFAoEDfwKDAJP/YwDZAGMAif+b/ykAJwB1/4X+v/0f/Rf94/2H/qf9k/s7+k/62/rV+iX6g/lp+Qv6Pfph+T347/dd+C/4+/cp+IX4SfcP9d/zu/RJ9jP2O/VZ9K30zfRp9cf15/Zh9134q/k3+6/71/tB/1kHpQ/tDz8IkQI9BqcPOROdD5sKFQodC30JaQZhBDcE8wO7AwsFowV3A3/+L/zF/oMDhQXxAzsB7/8hAOsAQQHHAE8AewCDAcsBkQA5/r/8B/3//hMBAwKnAIn+3/3D/4sC7wNbBAUF5QXfBRME2wITA28EKwbVBs0H9waPBHsB9QDlAwkGnwU5BPUDDQSjAnMBiQFDAskCHwO7A3UDoQGL/zn/uwB9As0CawKvAfUASQD1/0MApwAHAUEBKwGtAC//bf2P/CX9F/4L/hH91/ud+tX50/k9+pH6v/qn+mP6Gfol+n/5Tfjn9yv5g/oB+l34r/ap9ff0Q/Vr9vv2Nfbp9Kn0YfUj9jH2rfYp+L35Yfq7+kf73/sJ/Iv91QKDCxsRLw55BdMBCwiJEHsRUQzhCCEKyQqNB/MC6wEzAxsEAwTHBPUECQJn/fX7b/8rBLUFlwPHAA0A+wBXAZEAc/+H/7MANQIzAkkAm/1T/An9S/+NATUCtwDJ/oH+XQDLA7EGRwajAnUATwNDB7sGqwJTAXcDewXRBD8E8QOzAk0BcwIdBnkGMwPBAEsC0wRzBJkCnwHjAV0CXwJ9AtcBsQC1/3EALQIVA40By//p/2MBRQKrAdMARwBXAKsAzwA9AL/+V/0J/dH9Lf4f/X37sfof+737o/v5+kv6F/pN+sn64/pL+hP5bfgV+Uv6PfqF+Af3qfb59sX2xfVD9VX12fVb9rv2g/bH9Tf1S/bf+Cn7kfvV+sv6v/tN/TP/1QIzCa0OJQ7xB00DhQZ7DYkP1Qv9B6EIOQo/CIMDaQD9AD0DuQR1BV8EgwEz/lP9sf+LAusDiQOLAsUBEQFrAOX/Y/+N/90AmwLpArUA6/3H/Ln9l//bAHEBBQFHAL//3/+hAOEBFwMRBS8GSQWfAqEAMwKbA/kDcQP1A40EuwO5AjUCLwLNApsD3QRLBYcEHwOpAYsBIwK9AsMCjwI9AsMB0QAfAKv/AQClAI8BTwIdAiUBRQBfAAUBbwHFAdEBcQGzAN//7f4T/rf9x/3B/aH9j/3f/Mf70fqf+u36e/sF/Av8l/sH+7/6Gfo9+dn4n/ll+rf5L/j19sH2Lfab9cH1E/b/9Zf1J/ZD9wn3pfZF90f5H/tJ+8n7Ufw//Tn95f1pAPcEKQrLDO8Kjwa9BKsHwQvfC6EJTwhDCV8ITwUNAnUBxQELAqcCcQSdBNUBGf5//U0A4wIxAxsCAwJrAjUCwQBd/+/+5f9RAYcCRwK5AKf+wf0x/n3/gwD7AOUAnwB5AA0Akf9F/wEA6wGnA0cEbwQfBCkDoQCT//kBGwV9BU8DeQJhA5UDYwKJAY0CLwS7BNEEXQRXA1cBQwBLAR8DZQMpAkMBUwE/AXMA0/87ACMBnwEDAjUCvwFLAF//+f9XAcsBKwFTAOn/hf/d/hf+sf3P/Sf+Uf5P/u39//wH/NH7rfxz/T39bfzT+4/7Iftp+vH5cfk9+Un5sfl7+Sn4kfbL9ef1GfYZ9i/2O/YL9vf1p/ar92X46fj1+U37P/wB/W39Cf6l/1cD8welCjkKaQhPB4cHRwhxCasJTwmjB4sGXQXhA3MBAwCrAIUCkQMdAw0C6QALAJn/eQD/ARsDDwODAk0C/wHXAKP/U/9LAEkBuwFLAUMAM/+R/r3+Kf+5/1EAuwDtAH8A3f9T/0H/jf8lAO8AqwFpAtsDhQRdA38Auf8BAk0EXQT5Ag0DfQPjAlkB8QDpAacCAQO/A2UEYQMZAfv/FwGRAtMCgQKRAsUCLQI3AbcA6wBVAZ0BawIZA6UCAwHX/w0A6QBFARkBAQHxAG8Ao/8F/93+y/7d/k3/3f+R/0/+N/0X/ZX9v/2R/W/9Y/0B/Uv8lfsJ+0H6r/nX+V36HfrP+IP3pfaB9p/2+/bn9lH2B/YB9rX2K/ep9zn4T/nl+sv7AfwV/L38w/3N/t0AQwT5B7kJAQn7Bq0FkQUdB6UIvQjtB4EG6wV1BKUCewArAH8BLwPvA3ED5wG3ANP/BQDVANsBmwLRAr0CTQIrAeX/9/4B/wUAIQENAmcB+//L/q3+Nf+Z//f/dQAFAUUBzwAFADP/q/7t/u3/CQFnAbcA9//d/8EAVwGHAX0CjwRZBUMDzQBxAT0DJwOzAc8BNQPBAtkAuf9TAJsAeQCLAYUDHQSfAm8BuwHBAvUC6QJlAzMEFQTXAoMB6QCNAF8AvwD5AWsCWQH3/6H/z/+T/2H/9f/ZADMB0wA5AIn/2f5j/q3+M/91/wX/W/61/RP9m/xB/CH8S/yx/On8f/yH+236qflJ+WX5ofnP+W/5FfmX+Nn37fY/9o/2S/cx+KH4xfjv+E/5DfqZ+g/7ufun/P/9u/9VArsEyQU/BZEF5QaVB4UGhQXBBtsHOQe/BIEDYwPpAqMBQwE5AusCJwJtAXcBtQEVAZMAZQFbAlECpQGbAckBFwHf/8H/gQDNAPf/uf9ZAMsA1//N/tn+y/9RAGEAOwBTAE0ACwDF/6n/tf/H/+f/LwBxAF0A+/+d/xMA/wGbBKkF+wO5AXsB3QJdA78CkwJJA48DoQKPAbEArf8V/2EAGQONBGsDiwFDARcCUQLtAR8C6wJ5A10D/QIRApcAPf93/+UAxwElARUAr//L/7X/W/9F/6n/UwD3AFMB8wDR/6n+Z/4N/6f/b//P/l/+Jf6z/QP9Nfy/+8X7Mfxn/Pn7D/vx+Sf59/hP+WP5IfkR+SH5Bfk5+DP3e/Z39j33V/hh+R/6r/oX+wv7Lfs1+wX8Tf2F/3EC/wRFBs0FSwXVBTUGBQZ3BXEGuQefB8MFfwNrAuEBQwEHAWkBVwKPAmUCpwG5ANH/z//jACcClwJdAvMBuQEfAQkAT/+V/1kAtQC5ALMAdwBp/4n+b/5R/yMAZwB3AJkAwQBNAJn/O/9n/+n/ZwDVAO8AZwDB/1v/c//J/+cAwwM7BsUFdQI9AHcBfQJ5AskB+QLdAw0DdQFJAJn/Y/4r/lkA6QLnA9cCAQLRAbEBbQGvAbEC0QNxBDcEZwPtAVcADf91/8MAlwEhAWEAEQC//+/+Y/59/mv/dQBbAbUBHwHt/+H+tf4Z/3v/lf+J/03/6f4B/rv8m/tv+0P85fzz/I38F/wt+z/68/ld+rX6ufrd+l37Vftj+uv4Cfgp+Ln4R/m5+SH6UfoD+qv5w/k3+rv6Sftd/Kn9Mf/DAG0ChQPlA48E9wX5BlEGMwVnBW8GVwbDBBsDrwKnAk0CuwHLAeEBpwFJAXEBnwFbAekAHQHBARcC4QGXAUUB0QBTAEMAhQB3AAUAwf8FACMAs/8b/zf/z/8fAA0ACwBXAGEADwDN/+P/6f/Z/8f/AwARAOf/o/+Z/9H/pQBNAgMEmQS3A7kCJwI1AjkChwLVAj0DGQORApcBawBP/w3/zf8PASMCzwK3AkMCsQGlAbMB3QFpAisDmQMlA10CSwFlANf/x/8XAGUAZQBFAOH/ff/7/rv+8f6B/z0AswD3AL8AKwBf//n+5f4B/9/+zf65/m3+lf3B/D38B/yz+5v7t/vR+5/7Dftx+uf5zfnD+cP56fkL+hH61fl7+Vn5Qfln+Zn5N/rF+vv6ufql+jX7+/t5/Af96/1j/ysBKwPjBMEFtwVRBS8FrwUlBhcGWQUDBR8F6QR5A58BjQAHAakB4QGNAYsBmQFbAc0AlQDHAP0A+wA1AbcBxwH9AN3/Z/95/7v/t//D/7n/6f8XACsAr/8t/xP/vf93ANMAuwCRAG8ASwAFAM3/w//F/9P/PwCtAJEARQA3AYUDuQQ5A/cAHQH9AnEDQwLnAdMCCQP5AT0BDwE9AO3+Qf8rASMCFQHf/zsAVQHRAasB6QF3Av0COQNPA+cC2wHbAMEAhwHhAe0A1/+x/ykA8f85/+f+K/+J/wcAlQDXAEMAof+t/0UAdwAJAIf/g/+j/3H/mf63/QX91/zX/OP81/yV/C380fu3+5X7L/vP+gn7b/tr+//67frz+nf6m/nF+cv6c/vp+hH6efpV+4P7A/tX+138+fwZ/Zf9a/7L/tv+ZwAFA7sEVwTZA7sEeQWvBFcDoQOxBMMEwQOJA70D6wItAYEAZQE1AukBVwGhASUCqQHpAG8AfQCLANcAaQGDAfkAUQAZACcA1/+F/5P/FwBlAFkAYQBXAOv/Wf9T//f/VwA3AA0AEQAfANv/mf9x/0//Sf+b/2cAnQFlA0kElwPTAaUBYwJlAtkB8QE5A2UDswKTAd8A3//Z/kP/nQCDAXcBSQHfAQECcQGHALUAiQFRAtsCAQPfAv8BHwGNAK8AawD1/wEApwDxAGsAl/8P/+/+E/9X/9//SwBfADkAFQD3/2//6/7P/kX/n/9z/wf/hf4B/oH9Nf0X/QH9Cf0f/T/9D/2J/Ov7X/s/+1v7h/tN+/X62/qh+i36qfnz+XH6c/oR+jn6w/rl+n36mfpL+/v7Pfzr/JP+0QCRAo0D5QNhBOEEJwULBakE4QQxBbEFLwUnBAUDQwLlAXMBVQGfAeMBGwLbAc8BfQEJAacAxQBvAbUBlwFDAR8B0wBDAM3/q/+r/6///f9VAHUAEwC7/63/x/+9/73/FQB/AJ8AlQBpAC8As/9r/4H/xf8DAB8AwwBPAosDAQMxAbMABwKDAvMBjwHHAlEDfwKNAUcB5QCn/1n/pwDHAYUBgwCnABMByQAZADcAQwHtAUcCoQLfAhECBwGhACsBWwHzALEAHwF1Ae0ACwCL/0n/N/9d/w8ApwCjAFUARwCNAFEAyf+V/yEApwClAE8AAQB3/7n+Jf4P/u/9n/1n/Yv9lf0V/SX8mft1+437ifuh+9n76fu/+4n7Mfvj+pv6ufpF++P7Gfy7+5H7g/tz+0f7Yfvb+1P88fyl/Rv+E/7H/Uf+m/8fAT8CswJ3Ay8EkQQRBFsDLwNZA9ED4QPbA5ED7wI5Ap0BXwEvAfUA/wB1AQsCBQJZAbEAhwC/ALEAmwC7AC0BVQEjAcEAXwDp/4H/df/d/3EAlQBxADMAMQATAM//c/9X/6X/LQCBAHEAHwDZ/6n/hf9z/3f/9f/5AO0B+wF1AbMBvwIpA68CLwKTAtkCaQLxAc8BnwGzAF0AwQDxAGEA0f8zANcAEQETASkBgQGLAeUBCwIPAuMB1QHzAeUBmQHbAEcAJQBLAEcA/f/j/+P/3f/J/9v/6f/F/9H/LwCNAG0ABQDL/6P/e/8l//P+vf6d/nX+P/7z/YH9G/3h/M38zfy1/JH8afxD/B/85/uB+y37DfsL+zP7P/tF+xn7L/s/+3f7f/uv+/37bfzP/AP9Of2b/fv9df4P//P/GQF5AqMD7QOvA2sDuQMRBO8DnwPBA00EZQTLA9cCPQLlAbcBlQHFAe8B/wHLAbEBewENAYUAXQCVANMA1wDTALEAXwADAMn/u/+N/3X/m////zkAJwD5/8//vf/H/+f/AQAhAEcAQwArABUA8/+x/2v/ef/T/y0AhwBnAVsCOQIZAZUAPwF1Af8AAQHxAXUC3wFLARsBvQDH/4H/aQANAfcAoQD3ACUBlQDd/8v/RwB/ALcAHwFZARcBfQBNAEMAMQAHADkAtwAJAf8AywBvABkA0f/N/+P/MQBVAG0AeQCDADUAyf+Z/6P/t//F/+P/8f/T/5n/Uf8f/+P+wf7R/uv+Af/5/u3+u/6X/m3+Vf5J/lX+ef6R/p/+of5//k/+Jf4R/v/96/3X/d393f23/Wv9M/0X/d/8vfyV/Kf8j/x1/GP8d/x1/E/8d/zN/A39I/1N/an9//1v/hX/z/+BAOcAeQHJAfkBDwJTAsEC6QITA08DnwOJAw0D4QLtAv0CpQKVAtEC9QLDAl0CSQIxAu0BpwGjAesB2wG3AYUBiwFTAfcAxwDdAAEB9wDtAPcA3QCxAHcAfwB5AHUAZwCLAJcAcwBNACsAGwAPAB0AOwBZAHEAcQBlAEUALQAnADMAYQCVAMcA6wDlAMcApwCVAHkAXwBpAIkAoQCfAI0AbQA5AAsA6f/d/+f//f8VABcAFQDt/63/d/9b/0X/Nf89/0H/Mf8B/8f+i/4//g3+6/3v/fH93/23/X39K/3r/Lv8ofyJ/Jn8n/yT/FP8Pfwj/OH7x/v5+zX8Q/xv/Kf8t/yn/JX8v/zN/O/8Uf01/kX/IQDZAHMB+wFPAnEClQLXAlcDwQMhBF8EZQQtBLsDXQMHA8cCqQLLAv0CFQPrApMCKwLLAW8BJQENARUBIQEDAecAwQBvAPn/l/95/2n/bf+L/7P/uf+n/4f/Yf85/xX/K/9n/53/t//F/9f/z/+l/4n/gf+X/7H/3/8HAC8ASQA5ACMABQANABkAMwBLAIEAqQCnAI0AhQDLAEcBZwFZAVcBvwG1AUUBMwFxAa8BTQFVAYsBmwE1AeEABwH1AL0AsQDbAPMArQCFAHcAfQBdAC0AVQA5ADMA6f8RAAsAAwDT/7//wf+j/4X/d/+L/4f/ef+D/4P/d/9Z/1X/Vf9L/1f/Vf93/23/bf9Z/0//T/9J/1v/df+V/6H/pf+9/7X/sf+Z/53/tf/V/+v//f8TAAsA///r/9n/w/+r/7P/u/+1/6P/qf+X/33/Vf9J/zX/L/81/1f/U/9L/y//Jf8L/+P+2f7n/gP/F/81/1P/Tf9V/1X/Z/9n/3//p//F/+P/6/////n/+////wUAFwA1AE8AWwBdAFkATwBBADMAKwA5AEUAWQBpAIkAgQBxAGMAcQBtAGEAbwCRAJkAoQClALMAqwCRAI8AlwCRAIkAlQCXAJMAkQCHAIEAbwBjAFkAWQBFAD8AQwBPAEkAQwA5AC8AKQAdABEAEQAVABcADwAXABMAAwD1//f/+f/1//H/7//1//X/7//j/+X/2//d/+n///8HAP//+/8BAAcA8f/t//f/+f/x/+v/8f/v/93/y//L/7//qf+J/4P/hf9//2P/Vf9R/0f/Kf8p/yP/Hf8b/zX/U/9F/yv/J/8p/xv/H/81/zH/G/8b/yv/Jf8H///+Ef8T/xX/Jf8z/yf/G/8p/zf/Rf9P/2X/a/97/4//rf/L/9X/0f/T/+n/FQA7AGEAhQClALEAvQDRAOcA/QAXAScBOwFbAWcBbwFxAXEBdwFzAXkBgwGFAYEBhQGTAYsBewFvAWcBXwFFATUBOwE5AR8BCwH1AOMAywCxAKMAmwCLAIMAcQBjAEsAOQAzACkACwABAPv/8//d/8P/w/+9/63/k/+H/33/b/9h/1//af9n/1v/V/9Z/13/V/9N/0v/Tf9N/0n/Rf9B/zn/Mf8t/yn/Hf8Z/xf/Gf8R/w3/C/8L/wn/B/8F/wn/Af/1/uv+9/75/uX+yf7L/s3+x/6z/rn+u/67/rn+xf7D/qv+of6n/qP+o/6h/qn+vf7H/u/+Kf+D/83/2//D/8X/CwBRAG0AeQCzAAEBNQEpAQ8BAwEXASkBOQFZAYkBowGJAWsBcQGJAXMBMwEPATMBXwFPAQkB0wDfAAUB8QClAGEAXwB5AIUAXQAlAA0ADwALAPH/x/+p/5v/p/+v/7P/k/95/2n/Z/9l/2f/af9n/0//V/93/5n/hf9j/1v/ef+D/4v/if+d/7X/2//1//v/6f/n//v/CQD//wUALQBJAEsAPwBJAFEASwBHAE8AZQBlAGcAbwCHAJUAjQB1AGsAZQBvAG0AcQCJAJ8AiwBlAF8AdQBnAE8ANwBFAEkAQQAnACsAFQAPAAEADwD1/+n/0//f/9P/yf/D/7//o/+X/4X/k/+J/4P/e/+P/5H/d/9d/1//bf9l/2P/bf93/2//df99/3v/a/9t/3X/if+T/5n/lf+X/5P/nf+t/6//rf+t/7P/wf+7/7f/s//B/8X/z//T/9P/u//F/8n/3f/b/9X/1f/j/+P/4//X/9v/1//h/+f/8//1//P/9f/9/wcA///x/+//9//7//H/4//r//n////7//3////7//3/AwALAAcA+//1//v/BwAXAB0AGwAZABcAGQAhACkANQBDAE8AUQBNAEEAQwBDAE0ATwBVAFMAVwBJAE8ATwBBADcAQwBNAEsAOwArAC0ANQA1ADEALQArACMAGwAfABMADQANABcAGQATAAEA9f/n/+3/4//b/9H/zf/H/7v/r/+3/7n/sf+f/53/n/+f/5P/if+J/5v/i/97/33/kf+R/4v/g/+P/5X/j/9//33/hf+N/5P/if9//4X/jf+R/33/a/9n/3//kf+V/4f/j/+V/4v/gf9//3//hf+V/6//r/+n/6H/lf+P/5X/n/+l/6f/x/+1/7n/v/+f/6X/uf/h//H/5//f/+f/AwAVACcAIwAdADMAYQB5AHUAaQBtAIkAqwCnAJUAjQClAMEA0QDZAMUAvwDHAOkA5wDdANEA3wD1AAMB7wDdAM8A2wDjAOUA2wC7AKEApQChAJkAeQBpAGEAaQBXAD0AHQANAP///f/z/93/vf+1/7X/s/+Z/3n/Z/9h/2P/Wf9B/y//J/8z/zX/Mf8z/yX/H/8n/zn/M/83/zn/Q/9R/13/W/9R/1P/X/9r/2//Xf9X/1f/Zf9x/23/W/9T/03/T/9D/0H/Nf8z/zn/N/8j/wP/8f75/gn/F/8F/+/+5/7x/vf+/f7x/vH+/f4T/yX/Rf9h/3n/hf+h/8n/8/8FAAMAFwBTAKEAtQClAJkAxQD/ABkB/QDvAA8BRQFNATMBGQErAUUBRwE/ASsBJQErAS8BKQEZAf8A/QDxAPcA5wDRALkAsQC9AL8AswCXAHkAaQBrAGkASwAzAC8AOQA5ACsAFwANABcAGQARAP3/+f/9/wcA+//t/93/2//X/9v/0//P/8v/2//p//n/9f/v/+f/7/8BAA8ACQD//wMAEwAVABMAAwABAAUABQD7/+v/4f/j/+P/5f/l/9v/0//D/6//nf+X/5v/l/+H/3H/Z/9d/03/N/8r/y//L/8b/wn//f75/uP+0f6//sH+wf6//rX+p/6X/pn+jf6P/pP+if6R/qv+w/7J/rv+vf7f/hf/U/+F/6X/p/+r/+n/NQBfAGMAbQCvAPcA/wDTAMsA/QA9AVkBVQFVAW8BiQGLAW0BbwF5AZkBjwF/AV8BVwFVAUMBLQEXAQsBAQHfALsAmwCZAI8AewBjAFcASwA9AC0AFwDn/8H/y/8DAA0A6f+9/9f/9//v/8n/x//f//n//f8DAPf/5//f//X/CQAVABcAGwAnADMANQA5ADUAOwA9AFEAUQBDADUAOwBLAFUATwBPAFMAWwBfAGEAXwBdAFsAVQBFADUAJQAXAA8ADwAJAOP/y/+3/6//n/+R/3//b/9l/2P/Vf9B/xf/D/8L/wf/8f7Z/r/+uf63/r/+qf6P/n/+j/6V/ov+ff6L/qv+z/7X/s3+wf7R/uP+8/4H/yn/Sf9z/3//k/+V/6X/sf/B/9X//f8hAEsAVwBXAF0AkwC/AMcAoQCfANkAFwElAQ8BDQFBAWkBXwErASkBSQFjAVsBTQFXAVUBOQETAQsBEwETAQ0BAQH5AO8A0QC9AK0AmQCRAIcAewBtAGMAXQBTAD0ANwA5AC8AIwAVABMAHwAjACEAIwAbAA8A/f/1/+v/7f/p//P/7//1//X/8//l/+f/3f/f/9v/3//R/83/w//B/6//o/+X/5H/kf+H/3v/ef91/3v/ff97/3H/Y/9f/3H/b/9X/0n/Sf9V/1X/Pf89/zH/Jf8h/yv/Jf8X/wH/C/8Z/xn/Af/1/v3+D/8j/y3/L/8n/yX/Nf8//zn/Mf9J/2n/b/9z/3X/e/95/4H/j/+V/6H/vf/R/+f/5//1/yEASwBTAFsAYQB7AJsAvwDPAMsA2QAFASMBEQHvAOkADwE7ATkBMQEpASsBLQE5ARsBAwH1AAMBGQErAREBAQHlANcA0QDLALcAtQCvAL0AsQCxAIsAewBlAGUAWQBZAE0AUwBJAEMAJQAVAP//+f/v/+f/3//d/+H/6//x/+X/1f/L/8n/zf/H/8n/yf/V/9n/2//T/8f/w/+9/7n/s/+5/7n/wf/D/7//s/+v/5//k/+J/4f/i/+R/4n/hf+D/3v/a/9d/1X/S/8//z//Qf9F/0f/Rf89/z3/J/8b/xX/If8l/yv/Lf85/zf/Lf8b/xn/Jf8//z3/Rf9D/1H/Xf9p/13/W/9Z/3P/mf+9/7v/uf+v/8//6//7/+3/6f/t/wUAEwAdACMANwBbAJEAlQBxAFMAWQB/AKkArQCjAJ8AwwDhAN8AvQCbAKcAxQDlAOUA1QDRAOUA8QD7AO0A2QDRANsA5QDdANEA0QDZAN0A1QDBAKMAlQCZAKUAkwB7AHcAgwB/AG0AVQBBADMANQA1ACcAFQAPABMAFwARAAEA6//Z/9v/2//P/8H/u//F/8H/uf+h/5n/j/+R/43/kf+R/5P/kf+V/5f/j/+D/4P/if+L/4v/jf+J/5P/n/+f/5X/kf+L/43/hf9//3X/ff+B/3v/c/9t/1//T/9P/1H/T/8//0P/V/9p/2H/T/9H/1H/V/9f/2H/Xf9b/2v/ff+B/3H/b/9v/4H/jf+b/5v/qf+x/8X/w//F/8X/2f/f/+P/6f/p/+X/8/8HABUACwAPAB0ANQA5ADUAOQBRAFsAYQBpAG0AZQBxAGkAdwBxAH0AkwChAKMAqQCrAJsAjwCbALEAvwC9AMkA0QDXAL0ApwCfAKcArwCxAKcAowCVAIsAdwBnAFMATQBLAEcAQQA3ACsAJQATAAcA9//p/93/3f/X/83/y//L/8f/v/+1/6n/l/+T/5f/nf+n/63/sf+p/6P/o/+p/6X/rf+z/7v/vf+//8f/y//J/7v/t/+x/7H/sf+9/9P/3f/f/9n/1//P/8P/s/+t/63/tf+//8X/v/+5/63/pf+T/3//b/9r/3X/ef99/3//f/9//3n/df9t/3X/h/+f/6//wf/D/8//0f/J/7X/qf+x/7v/z//b/+v/8f/v//X/5//n/+H/5//v////BQAVAAcABwDz//f/9f8DAAUACwAPABMAFQAPAA0ABQD//w8AHQAnACUAJQAhACcAKQArACsAOwBDAEMARwBXAF0AXwBhAGMAcQBvAGkAXQBlAGUAYQBVAFMATwBTAE8ATQBBAD0AQQBFAD0AOQAxADMAKQAnAB0AHwAbABkAFwARAAcAAQD5//H/4//b/9//7f/f/9//1//Z/8//zf/H/8H/vf/F/8P/yf/H/7//t/+3/7f/tf+t/6n/s/+1/7v/tf+v/6n/nf+h/6v/uf+7/7v/uf+5/7X/sf+p/6n/qf+1/7f/wf+//7n/sf+v/6n/n/+d/6f/q/+j/6X/q/+r/6P/p/+r/7n/uf/H/83/0//L/9P/0f/P/8v/zf/J/8f/w//J/8P/uf+v/7H/tf+3/6//n/+f/6X/o/+h/5v/of+v/7//wf+1/7f/u//B/8n/yf/T/9v/4f/h/+H/4f/h/+X/6f/p/+///f8HAPv/8f/t/+//8f8BABMAIQAbAB8AIwAnACMAHQAZAB8AIQAvADUAKQAlACcAKQAlABUACwANABMAEwAHAAMAAQAFAP3/8f/b/9n/2//b/9X/x//D/8n/yf/B/7v/t/+p/6X/p/+r/6X/mf+X/6H/q/+x/6X/of+n/63/pf+j/6X/rf+x/7n/uf+7/7X/tf+x/7f/w//R/8//2//j/+n/5f/p/+f/9/8BAAcACwAPABUAEQADAAkADQATAB8AIwAZAB0AGQAZABkAIwAdACEAGwAnACMAJQAfACMAJwAdABUAEQATABMAGQAbAB8AFQAXABcAFQANAAcACQATAA0A+//9//n///8FAAEA9f/v/+///f/9//X/8f/9/xMAHwAZAAEA/f8HABcAEQALAA8AJQAzADkALwA1ADsAQwBFAEMANwAvADcARQBBAEMAMwA7ADkAQQA7AC0AHwArAD0AQwAvACEAHQAvACcAIQATAAcAAQABAPX/6f/T/9//5//x/+//6//n/+v/9f/z/+3/4//f/+f/4//V/9f/2//n//H/6//j/93/3f/n/+P/3f/n//H/BQANAAkABwABAAcAAQAJAAMAAwADAA8ABwADAP//AwABAP///f/5//H/9f/7/wUADwATAA8ADwALAA8AFQANAAsADwATAA0A///7////BwAHAAEA8//7////AQD///3/AQADAAcA///7////+f8DAAsAGwAnACcAJQAhABsAHQAZABkADwAXACUAKQAdABEACQAFAAcACQADAAkAEQAPAA8ABwD///P/5//r/+//AQD5//v/+/8DAPv/4//P/8X/x//F/8f/v/+//73/v//F/7//sf+z/7P/t/+1/73/vf/J/9X/3f/Z/83/wf+9/7P/r/+x/73/xf/T/9f/0//J/8v/yf/N/8v/0//N/9n/3//d/9v/1//V/9v/4f/n/+P/5//r//P/9f/7//v/8f/p/+n/4//f/9H/1f/P/9H/0//T/8P/vf/H/8//1f/T/83/zf/N/8//yf/J/8n/z//R/9f/0f/T/9f/4//f/9n/1//R/9v/4//b/8//zf/P/8P/v/+1/7P/tf+1/7P/u//J/9P/z/+9/6//vf/N/83/y//F/8v/0//R/83/y//F/8f/xf/P/8n/w/+1/7f/sf+x/7H/sf+p/7X/v//B/7n/wf/H/8//zf/V/93/3f/Z/+X/9//z/+v/8/8BAA8ACwAFAAkADQARABsAFwAPAAcABwAPABEACwANABcAGwAfACcAJwAhACkALQArACEAGwAfAC0AMQA1ADEAKwAxAC8AKwAvACcAHQAdACMAIwAnACsAMQAzADsAPwBFAEUARwBLAFkAXQBdAF0AcQCBAIkAhQB9AIcAhwCLAH8AfQB5AH8AhwCDAH8AeQB7AHcAcwBlAF8AWQBdAF0AYQBVAFMAUQBVAFEATwBFAEcASwBJAD0ANwA1ADsAPwA3ADMAMwArADcALQAtACcAIwAdABkACwAFAPv/+//1//P/7//1/+n/5f/Z/9n/2f/b/93/3f/d/+//+//9//P/8//v//H/8//x/+v/5//p//X/+f/x/+v/6f/r//P/7f/j/+H/5//z//f/9f/n/+v/9/8BAAEA//8FAA0AAwAFAP3/9//t/+n/7f/x/+f/3//X/9v/2f/Z/9n/2//t//X/6//t/+f/9//7////AQATABkAGQAdACEAIQAhAB8AKwAtACsAJwArAC0AKwAhABkADQAXABkAFQALAAcACwARAA8ADwANABMAFQAZABMADQADAAMABwD/////DQADAAEA///9////AQD9/wUAAQD///3/AQD5/wEACwANAAkACwAVABcAFQALABMAEwAZABcAFwATABcAGQAZABMAEwATACMAJQAjABUAGQARABEAFQAdABcAFwANAAcA/f////v/+f/v//H/+f/5//P/6f/h/+3/5//p/93/6//v//3/9//t/+n/6f/n/+n/4f/n/+f/7f/t/+v/6f/r/+3/8//z//P/8//3//3/AQABAAMABwAVAB0AHwAbABcAFQAZACEAJQAhABsAHQAXAA0ABwAHAAcABwAHABMACwANAAUABwABAAEA+f/7/+//7//p/+//5//l/93/3//f/+X/4//h/9n/0//V/9f/zf/H/7//wf+//7//xf/L/8v/0f/b/+X/4//l/+H/6//1/wEA/f/9//3/DQAPABMADQARABMAHQAdABsAFQAXABkAGwANAA0ABwAJAA0AFQADAAMACwARAAkAAQABAAMAAwD7//v/8//z//f/8//r/+f/6//x/+v/5//p/+f/5f/l/9//5//f/9v/2//Z/9n/1f/P/8f/wf/B/8n/u/+v/7X/vf+//7//vf+7/7//v/+//7f/sf+t/7H/r/+r/6P/r/+3/8P/t/+3/7n/u/+9/8X/x//N/8P/yf/J/8f/v//H/8X/y//H/8H/t/+3/63/tf+t/7f/r/+h/5f/lf+J/4f/i/+f/5v/nf+h/6n/o/+b/53/o/+j/6X/pf+x/6//sf+1/7X/s/+7/7v/tf+1/7n/wf/F/83/z//R/9X/0//H/8f/wf+//7n/w//R/9X/1f/V/9f/2//f/9//1//l/+f/6f/j/9//2f/f/9f/1f/J/8P/vf+3/7v/vf+7/7X/r/+x/7X/u/+5/7X/tf/F/73/u/+t/7v/wf/H/8H/0//T/9f/3f/p/+f/5f/l/+n/6//n/9//2//n/+3/5//f/9X/0//b/9X/1//X/9n/6//x/+3/7f/v//v/+////wEAAQABAAcADQARABsAGwAZABsAFwANAA8ACwANAAMACwANABMADwAPAA0ACQAPABkAHwAlACcAKwA1ADkAOwArACsAKQAnAB0AGQATABMAEwAfAB8AHwAXABsAHQAhABsAGwARACEAJQArAB8AIQAdACMAIQAlAB8AIQAfADEAOQA5ADUAOQA5ADsALwAhAB8AJwAvACcAGwAfAB8AJQAXAA8ADwATABMADwAJAA0ABwAFAAkA/f/3//P/7//v//X/+f/3//P/9//7//v/+f/5/wEABQAFAP3/8//n/+v/8//x//f/9f/x/+3/9f/3//P/9f/3//v/AQD5//f/7f/z//P/9//t/+v/5//t/+n/6f/b/9n/1//V/8v/zf/D/7//u//F/8n/zf/J/8v/z//T/8//0//T/93/3f/h/93/2//R/8//zf/H/8P/x//J/8//yf/H/8P/v/+7/7v/t/+5/73/u/+9/8f/yf/N/9P/0//V/9X/1f/N/8n/zf/R/9f/3f/Z/9v/3f/d/93/3f/d/+P/3f/p/+X/4//j/+P/4f/Z/8v/v//B/83/0f/T/9f/0f/N/8v/yf/F/7v/sf+z/7//wf/F/7//x//B/8f/v/+//7n/v//H/9X/zf/N/8//2f/Z/8//v//L/9P/3f/d/+f/5//l/9v/4f/f/+P/4f/l/9//4//h/9//2f/Z/9P/0f/D/8X/xf/Z/9P/0//N/9H/zf/D/7P/q/+j/63/wf/N/9X/1//b/9n/2//b/9f/1//Z/9n/3//b/9v/1f/T/9f/2f/Z/9v/3f/r//P/8f/x//v/+f////v/9f/x//f//f8FAP///f///wUABQADAPn/8f/3/+3/7f/x//P/+//5//f/AQAFAPn/+f///wcAAQAHAAkAFQAVABcACQAHAAkADwADAPn/8//z//H/7f/n/+X/5//t/+f/6//n/+v/7//9////CQAFAA0AEQALAAcABwABAAsADwAXABsAKQA1ADUANQA3ADkAOQA7AD8ARQBDAEUARQA7ADcA\" type=\"audio/x-wav\" />\n",
       "                    Your browser does not support the audio element.\n",
       "                </audio>\n",
       "              "
      ],
      "text/plain": [
       "<IPython.lib.display.Audio object>"
      ]
     },
     "execution_count": 4,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "import librosa\n",
    "import IPython.display as ipd\n",
    "\n",
    "# Load and listen to the audio file\n",
    "example_file = data_dir + '/an4/wav/an4_clstk/mgah/cen2-mgah-b.wav'\n",
    "audio, sample_rate = librosa.load(example_file)\n",
    "\n",
    "ipd.Audio(example_file, rate=sample_rate)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "qZyElgPVjQl5"
   },
   "source": [
    "In an ASR task, if this WAV file was our input, then \"G L E N N\" would be our desired output.\n",
    "\n",
    "Let's plot the waveform, which is simply a line plot of the sequence of values that we read from the file. This is a format of viewing audio that you are likely to be familiar with seeing in many audio editors and visualizers:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {
    "id": "MqIAKkqelRzm"
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAABN0AAAJwCAYAAAC9ABeBAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjAsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvlHJYcgAAAAlwSFlzAAAPYQAAD2EBqD+naQAAwLhJREFUeJzs3Xd4FNX6B/BvEkgCgVBD76igKF1QBEFEERDEAsJVQa7tp2DDBjZAL4INlSIqRb2ICnZURAUpgqgo0qRI76GTAAECyfz+OHcyZ2ZnZmd3Z3e2fD/Pk2dmpx7CZnfmnXPeN0lRFAVERERERERERETkmmSvG0BERERERERERBRvGHQjIiIiIiIiIiJyGYNuRERERERERERELmPQjYiIiIiIiIiIyGUMuhEREREREREREbmMQTciIiIiIiIiIiKXMehGRERERERERETkMgbdiIiIiIiIiIiIXMagGxERERERERERkcsYdCMiIiIymDZtGho2bIjixYujbNmyXjfHNcuWLUObNm2QkZGBpKQkrFixwusmAQCGDx+OpKQk3bI6derg9ttv96ZBMapDhw7o0KGD180gIiKi/2HQjYiIiFw3c+ZMJCUl4YsvvvBZ16RJEyQlJWH+/Pk+62rVqoU2bdpEoomW1q9fj9tvvx3169fHpEmT8M4773jaHrecOXMGvXr1wuHDh/Haa69h2rRpqF27tt/9Zs+ejaSkJFSrVg2FhYURaGl41KlTB0lJSaY/11xzjdfNIyIiojhUzOsGEBERUfxp27YtAGDx4sW4/vrri5bn5uZizZo1KFasGJYsWYIrrriiaN3OnTuxc+dO9OnTJ+LtlS1YsACFhYV44403cM4553jaFjdt3rwZ27dvx6RJk3DnnXc63m/69OmoU6cOtm3bhp9++gmdOnUKYys1GzZsQHKyu8+HmzZtikceecRnebVq1Vw9DxERERHAoBsRERGFQbVq1VC3bl0sXrxYt3zp0qVQFAW9evXyWae+VgN2Xtm/fz8AuDqsNC8vDyVLlnTteMEI5t914sQJfPXVVxg1ahTeffddTJ8+PWJBt7S0NNePWb16ddx6662uH5eIiIjIDIeXEhERUVi0bdsWf/31F06ePFm0bMmSJWjUqBG6dOmCX3/9VTdcccmSJUhKSsJll10GAHj33XfRsWNHVKpUCWlpabjgggswceJE3TmuvfZa1KtXz/T8l156KVq2bKlb9sEHH6BFixYoUaIEypcvjz59+mDnzp1F6+vUqYNhw4YBALKyspCUlIThw4cXrX/zzTfRqFEjpKWloVq1ahg4cCCOHj2qO0eHDh1w4YUX4s8//8Tll1+OkiVL4sknn8S2bduQlJSEV155BRMmTEC9evVQsmRJXH311di5cycURcHzzz+PGjVqoESJErjuuutw+PBhR7/rn376Ce3atUNGRgbKli2L6667DuvWrStaf/vtt6N9+/YAgF69eiEpKclR7q8vvvgCJ0+eRK9evdCnTx98/vnnOHXqlG4b9d/13nvv+exv/P0BIrh68cUXIz09HfXr18fbb79tem6znG5btmxBr169UL58eZQsWRKXXHIJvv32W7//Dqf279+PrKwsdOjQAYqiFC3ftGkTMjIycPPNNxct+/nnn9GrVy/UqlULaWlpqFmzJh5++GHd+x0Qv/tSpUphx44duPbaa1GqVClUr14dEyZMAACsXr0aHTt2REZGBmrXro0PP/xQt/97772HpKQkLFq0CPfccw8qVKiAzMxM9OvXD0eOHPH7bzp9+jSGDRuGc845p6idjz/+OE6fPh3Kr4qIiIgcYNCNiIiIwqJt27Y4c+YMfvvtt6JlS5YsQZs2bdCmTRvk5ORgzZo1unUNGzZEhQoVAAATJ05E7dq18eSTT+LVV19FzZo1cd999xUFKwDg5ptvxtatW7Fs2TLdubdv345ff/1VN1R15MiR6NevH84991yMGTMGDz30EObNm4fLL7+8KHD2+uuvFw2HnThxIqZNm4YbbrgBgEj2P3DgQFSrVg2vvvoqbrzxRrz99tu4+uqrcebMGd35Dx06hC5duqBp06Z4/fXXdcNop0+fjjfffBP3338/HnnkESxcuBC9e/fG008/jTlz5uCJJ57A3Xffja+//hqPPvqo39/z3Llz0blzZ+zfvx/Dhw/H4MGD8csvv+Cyyy7Dtm3bAAD33HMPnnzySQDAAw88gGnTpuGpp57ye+zp06fjiiuuQJUqVdCnTx8cO3YMX3/9td/9rKxevRpXX311UVsHDBiAYcOGmeb+M9q3bx/atGmD77//Hvfddx9GjhyJU6dOoUePHo72B0Reu4MHD/r8qIGySpUqYeLEiVi4cCHGjRsHACgsLMTtt9+O0qVL48033yw61ieffIK8vDzce++9GDduHDp37oxx48ahX79+PuctKChAly5dULNmTbz00kuoU6cOBg0ahPfeew/XXHMNWrZsiRdffBGlS5dGv379sHXrVp9jDBo0COvWrcPw4cPRr18/TJ8+HT179tQFB40KCwvRo0cPvPLKK+jevTvGjRuHnj174rXXXtMFEImIiChMFCIiIqIw+PvvvxUAyvPPP68oiqKcOXNGycjIUN5//31FURSlcuXKyoQJExRFUZTc3FwlJSVFueuuu4r2z8vL8zlm586dlXr16hW9zsnJUdLS0pRHHnlEt91LL72kJCUlKdu3b1cURVG2bdumpKSkKCNHjtRtt3r1aqVYsWK65cOGDVMAKAcOHChatn//fiU1NVW5+uqrlYKCgqLl48ePVwAoU6dOLVrWvn17BYDy1ltv6c61detWBYCSlZWlHD16tGj50KFDFQBKkyZNlDNnzhQt79u3r5KamqqcOnXK5/cga9q0qVKpUiXl0KFDRctWrlypJCcnK/369StaNn/+fAWA8sknn9geT7Vv3z6lWLFiyqRJk4qWtWnTRrnuuutM/13vvvuuzzEAKMOGDSt63bNnTyU9Pb3o/0VRFGXt2rVKSkqKYrwsrV27ttK/f/+i1w899JACQPn555+Llh07dkypW7euUqdOHd3/i5natWsrAEx/Ro0apdu2b9++SsmSJZV//vlHefnllxUAypdffqnbxuz9OWrUKN37TlEUpX///goA5YUXXihaduTIEaVEiRJKUlKS8vHHHxctX79+vc/v7N1331UAKC1atFDy8/OLlr/00ksKAOWrr74qWta+fXulffv2Ra+nTZumJCcn635niqIob731lgJAWbJkie3vjIiIiELDnm5EREQUFueffz4qVKhQlKtt5cqVOHHiRFF10jZt2mDJkiUARK63goICXT63EiVKFM3n5OTg4MGDaN++PbZs2YKcnBwAQGZmJrp06YKZM2fqevzMmDEDl1xyCWrVqgUA+Pzzz1FYWIjevXvrejhVqVIF5557rmklVdncuXORn5+Phx56SJfc/6677kJmZqbPEMe0tDQMGDDA9Fi9evVCmTJlil63bt0aAHDrrbeiWLFiuuX5+fnYvXu3Zbv27t2LFStW4Pbbb0f58uWLljdu3BhXXXUVZs+ebfvvsvPxxx8jOTkZN954Y9Gyvn374rvvvnM0rNGooKAA33//PXr27Fn0/wKI90nnzp397j979my0atVK9x4pVaoU7r77bmzbtg1r1671e4zWrVvjxx9/9Pnp27evbrvx48ejTJkyuOmmm/DMM8/gtttuw3XXXafbRn5/njhxAgcPHkSbNm2gKAr++usvn3PLxSvKli2LBg0aICMjA7179y5a3qBBA5QtWxZbtmzx2f/uu+9G8eLFi17fe++9KFasmO3/8SeffILzzz8fDRs21L3vO3bsCAB+3/dEREQUGhZSICIiorBISkpCmzZtsGjRIhQWFmLJkiWoVKlSUUXQNm3aYPz48QBQFHyTAypLlizBsGHDsHTpUuTl5emOnZOTUxS4uvnmm/Hll19i6dKlaNOmDTZv3ow///wTr7/+etH2GzduhKIoOPfcc03bKgczzGzfvh2ACIrIUlNTUa9evaL1qurVqyM1NdX0WHLACUDRv6NmzZqmy+0CXFbtAkQw6/vvv8eJEyeQkZFheQwrH3zwAVq1aoVDhw7h0KFDAIBmzZohPz8fn3zyCe6+++6AjnfgwAGcPHnS9P+gQYMGfgOE27dvLwpQys4///yi9RdeeKHtMSpWrOioEET58uUxduxY9OrVC5UrV8bYsWN9ttmxYweeffZZzJo1y+f/SA0Kq9LT05GVlaVbVqZMGdSoUQNJSUk+y83+z42/t1KlSqFq1apFQ4jNbNy4EevWrfM5t0otrkFEREThwaAbERERhU3btm3x9ddfY/Xq1UX53FRt2rTBY489ht27d2Px4sWoVq1aUVGEzZs348orr0TDhg0xZswY1KxZE6mpqZg9ezZee+01XQGG7t27o2TJkpg5cybatGmDmTNnIjk5Gb169SraprCwEElJSfjuu++QkpLi085SpUq5+u+We0EZmZ3fbrlik7MrXDZu3FiUJ88sSDZ9+vSioJsxaKQqKCgIXwMj4Pvvvwcggp67du3SVX0tKCjAVVddhcOHD+OJJ55Aw4YNkZGRgd27d+P222/XvT8B7/7PCwsLcdFFF2HMmDGm642BXiIiInIXg25EREQUNmrPtcWLF2PJkiV46KGHita1aNECaWlpWLBgAX777Td07dq1aN3XX3+N06dPY9asWbqeYWbD4TIyMnDttdfik08+wZgxYzBjxgy0a9cO1apVK9qmfv36UBQFdevWxXnnnRfwv6N27doAgA0bNuiqpebn52Pr1q2Oek+Fg9wuo/Xr16NixYpB9XKbPn06ihcvjmnTpvkEhhYvXoyxY8dix44dqFWrFsqVKwcAPlVcjb3/srKyUKJECWzcuNHnfGbtN6pdu7blv1Nd75Y5c+Zg8uTJePzxxzF9+nT0798fv/32W9Hw39WrV+Off/7B+++/ryuc8OOPP7rWBqONGzfqCnIcP34ce/fu1f3dGNWvXx8rV67ElVdeaRkcJSIiovBhTjciIiIKm5YtWyI9PR3Tp0/H7t27dT3d0tLS0Lx5c0yYMAEnTpzQDS1VAz1yj5+cnBy8++67pue5+eabsWfPHkyePBkrV670qcx4ww03ICUlBSNGjPDpRaQoStHwSSudOnVCamoqxo4dq9t/ypQpyMnJQbdu3fz8JsKjatWqaNq0Kd5//31d0GvNmjX44YcfbAMydqZPn4527drh5ptvxk033aT7eeyxxwAAH330EQCRV69ixYpYtGiR7hhypU9A/J927twZX375JXbs2FG0fN26dUW9yux07doVv//+O5YuXVq07MSJE3jnnXdQp04dXHDBBUH9W42OHj2KO++8E61atcILL7yAyZMnY/ny5XjhhRd0/xZA//5UFAVvvPGGK20w88477+iq5E6cOBFnz55Fly5dLPfp3bs3du/ejUmTJvmsO3nyJE6cOBGWthIREZHAnm5EREQUNqmpqbj44ovx888/Iy0tDS1atNCtb9OmDV599VUA+nxuV199NVJTU9G9e3fcc889OH78OCZNmoRKlSph7969Pufp2rUrSpcujUcffRQpKSm65P+A6PHzn//8B0OHDsW2bdvQs2dPlC5dGlu3bsUXX3yBu+++G48++qjlvyMrKwtDhw7FiBEjcM0116BHjx7YsGED3nzzTVx88cW49dZbQ/k1heTll19Gly5dcOmll+KOO+7AyZMnMW7cOJQpUwbDhw8P+Hi//fYbNm3ahEGDBpmur169Opo3b47p06fjiSeeACCKBIwePRp33nknWrZsiUWLFuGff/7x2XfEiBGYM2cO2rVrh/vuuw9nz57FuHHj0KhRI6xatcq2XUOGDMFHH32ELl264IEHHkD58uXx/vvvY+vWrfjss890BS6s7N69Gx988IHP8lKlSqFnz54AgAcffBCHDh3C3LlzkZKSgmuuuQZ33nkn/vOf/+C6665DkyZN0LBhQ9SvXx+PPvoodu/ejczMTHz22WdBFZhwKj8/H1deeSV69+5d9N5r27YtevToYbnPbbfdhpkzZ+L//u//MH/+fFx22WUoKCjA+vXrMXPmTHz//fdo2bJl2NpMRESU8LwpmkpERESJYujQoQoApU2bNj7rPv/8cwWAUrp0aeXs2bO6dbNmzVIaN26spKenK3Xq1FFefPFFZerUqQoAZevWrT7HuuWWWxQASqdOnSzb8tlnnylt27ZVMjIylIyMDKVhw4bKwIEDlQ0bNhRtM2zYMAWAcuDAAZ/9x48frzRs2FApXry4UrlyZeXee+9Vjhw5otumffv2SqNGjXz23bp1qwJAefnll3XL58+frwBQPvnkE93yd999VwGgLFu2zPLfo5o7d65y2WWXKSVKlFAyMzOV7t27K2vXrnV0HqP7779fAaBs3rzZcpvhw4crAJSVK1cqiqIoeXl5yh133KGUKVNGKV26tNK7d29l//79CgBl2LBhun0XLlyotGjRQklNTVXq1aunvPXWW0W/c1nt2rWV/v3765Zt3rxZuemmm5SyZcsq6enpSqtWrZRvvvnGz29HOx4A05/atWsriqIoX331lQJAefXVV3X75ubmKrVr11aaNGmi5OfnK4qiKGvXrlU6deqklCpVSqlYsaJy1113KStXrlQAKO+++27Rvv3791cyMjJ82mP1Pqldu7bSrVu3otfq+2DhwoXK3XffrZQrV04pVaqUcssttyiHDh3yOWb79u11y/Lz85UXX3xRadSokZKWlqaUK1dOadGihTJixAglJyfH0e+OiIiIgpOkKB5k5yUiIiIiIr/ee+89DBgwAMuWLWOvNCIiohjDnG5EREREREREREQuY9CNiIiIiIiIiIjIZQy6ERERERERERERuYw53YiIiIiIiIiIiFzGnm5EREREREREREQuY9CNiIiIiIiIiIjIZcW8bkC0KywsxJ49e1C6dGkkJSV53RwiIiIiIiIiIvKIoig4duwYqlWrhuRk+75sDLr5sWfPHtSsWdPrZhARERERERERUZTYuXMnatSoYbsNg25+lC5dGoD4ZWZmZnrcGiIiIiIiIiIi8kpubi5q1qxZFC+yw6CbH+qQ0szMTAbdiIiIiIiIiIjIUQoyFlIgIiIiIiIiIiJyGYNuRERERERERERELmPQjYiIiIiIiIiIyGUMuhEREREREREREbmMQTciIiIiIiIiIiKXMehGRERERERERETkMgbdiIiIiIiIiIiIXMagGxERERERERERkcsYdCMiIiIiIiIiInIZg25EREREREREREQuY9CNiIiIiIiIiIjIZTEXdJswYQLq1KmD9PR0tG7dGr///rvltp9//jlatmyJsmXLIiMjA02bNsW0adMi2FoiIiIiIiIiIkpEMRV0mzFjBgYPHoxhw4Zh+fLlaNKkCTp37oz9+/ebbl++fHk89dRTWLp0KVatWoUBAwZgwIAB+P777yPcciIiIiIiIiIiSiRJiqIoXjfCqdatW+Piiy/G+PHjAQCFhYWoWbMm7r//fgwZMsTRMZo3b45u3brh+eefd7R9bm4uypQpg5ycHGRmZgbddiIiIiIiIiIiim2BxIlipqdbfn4+/vzzT3Tq1KloWXJyMjp16oSlS5f63V9RFMybNw8bNmzA5Zdfbrnd6dOnkZubq/shIiIiIiIiIiIKRMwE3Q4ePIiCggJUrlxZt7xy5crIzs623C8nJwelSpVCamoqunXrhnHjxuGqq66y3H7UqFEoU6ZM0U/NmjVd+zcQEREREREREVFiiJmgW7BKly6NFStWYNmyZRg5ciQGDx6MBQsWWG4/dOhQ5OTkFP3s3Lkzco0lIiIiIiIiIqK4UMzrBjhVsWJFpKSkYN++fbrl+/btQ5UqVSz3S05OxjnnnAMAaNq0KdatW4dRo0ahQ4cOptunpaUhLS3NtXYTEREREREREVHiiZmebqmpqWjRogXmzZtXtKywsBDz5s3DpZde6vg4hYWFOH36dDiaSEREREREREREBCCGeroBwODBg9G/f3+0bNkSrVq1wuuvv44TJ05gwIABAIB+/fqhevXqGDVqFACRn61ly5aoX78+Tp8+jdmzZ2PatGmYOHGil/8MIiIiIiIiIiKKczEVdLv55ptx4MABPPvss8jOzkbTpk0xZ86couIKO3bsQHKy1nnvxIkTuO+++7Br1y6UKFECDRs2xAcffICbb77Zq38CERERERERERElgCRFURSvGxHNcnNzUaZMGeTk5CAzM9Pr5hARUYIbMgRYuRL47juvW0JERERElHgCiRPFVE83IiKiRPfii163gIiIiIiInIiZQgpERERERERERESxgkE3IiIiIiIiIiIilzHoRkRERERERERE5DIG3YiIiIiIiIiIiFzGoBsREREREREREZHLGHQjIiIiIiIiIiJyGYNuRERERERERERELmPQjYiIiIiIiIiIyGUMuhEREREREREREbmMQTciIiIiIiIiIiKXMehGRERERERERETkMgbdiIiIiIiIiIiIXMagGxERERERERERkcsYdCMiIiIiIiIiInIZg25EREREREREREQuY9CNiIiIiIiIiIjIZQy6ERERERERERERuYxBNyIiIiIiIiIiIpcx6EZEREREREREROQyBt2IiIiIiIiIiIhcxqAbERERERERERGRyxh0IyIiIiIiIiIichmDbkRERERERERERC5j0I2IiIiIiIiIiMhlDLoRERERERERERG5jEE3IiIiIiIiIiIilzHoRkRERERERERE5DIG3YiIiIiIiIiIiFzGoBsREREREREREZHLGHQjIiIiIiIiIiJyGYNuRERERERERERELmPQjYiIiIiIiIiIyGUMuhEREREREREREbmMQTciIiIiIiIiIiKXMehGRERERERERETkMgbdiIiIiIiIiIiIXMagGxERERERERERkcsYdCMiIiIiIiIiInIZg25EREREREREREQuY9CNiIiIiIiIiIjIZQy6ERERERERERERuYxBNyIiIiIiIiIiIpcx6EZEREREREREROQyBt2IiIiIiIiIiIhcxqAbERERERERERGRyxh0IyIiIiIiIiIichmDbkRERERERERERC5j0I2IiIiIiIiIiMhlDLoRERERERERERG5jEE3IiIiIiIiIiIilzHoRkRElECOHAE2b/a6FURERERE8Y9BNyIiogRy443AOed43QoiIiIiovjHoBsREVECmT/f6xY4t3UrsG2b160gIiIiIgoOg25EREQJ6uBB4LHHgJMnvW6JuVatgEsu8boVRERERETBYdCNiIgoQb37LvDKK8CiRV63xNzBg8C+fV63goiIiIgoOAy6ERERJahTp8S0oMB3XUGB+XIiIiIiInKGQTciIiLycc01QLduXreCiIiIiCh2MehGREREAICzZ7X5uXOB778X87t2ARMnRqYN27bp20FEREREFKsYdCMiIiKcPg2kpgJTp/que/xx4L77gGPHwtuGvDygbl1g1KjwnoeIiIiIKBIYdCMiIiKcPAkoCvDBB77rdu4UU0UBtmwBKlUCli1zvw35+WI6f777xyYiIiIiijQG3YiIiMix1auBAweAefMie96VK4G77wYKC8Xro0cje34iIiIiokAx6EZERERRb8gQYNIk4PhxEYArVw6YM8frVhERERERWWPQjYiIiKLerl3a/NatYrpihSdNISIiIiJyhEE3IiKiODdhAjB7ttetCM2hQ163gIiIiIgoMMW8bgARERGFrrBQ5Ftr3BhIStKvGzRITBUl8u1yS0aG1y0gIiIiIgoMe7oRERHFgZkzgaZNtaqiH30kCh5EuyNHRFuJiIiIiOINg25ERERxYNMmMd2/H8jNBf71L2DoUG/b5MR//iPamp0d+L7797vfHiIiIiIitzDoRkREFGcKC8VUDcQFYt06d9viz/btYlpQ4HyfcuXEVP13EhERERFFIwbdiIiIqEj58l63wL+0NDE15q4jIiIiIoomDLoRERGRK5YtA9580+tWEBERERFFBwbdiIiIKGjPPw/Mni3mb7wRGDjQ2/YQEREREUWLYl43gIiIiGLXs88CyckiJ9vOndpyRQG2bAHq1eMwUCIiIiJKTDHX023ChAmoU6cO0tPT0bp1a/z++++W206aNAnt2rVDuXLlUK5cOXTq1Ml2eyIiIgqcWUGDuXOBc84BFiwQ688/H5g5M+JNIyIiIiLyTEwF3WbMmIHBgwdj2LBhWL58OZo0aYLOnTtj//79ptsvWLAAffv2xfz587F06VLUrFkTV199NXbv3h3hlhMRESWWrVvFdNs20Qtu/XoxFJWIiIiIKFHEVNBtzJgxuOuuuzBgwABccMEFeOutt1CyZElMnTrVdPvp06fjvvvuQ9OmTdGwYUNMnjwZhYWFmDdvXoRbTkRERGY94oiIiIiI4lXMBN3y8/Px559/olOnTkXLkpOT0alTJyxdutTRMfLy8nDmzBmUL1/ecpvTp08jNzdX90NERBStFMXrFnhv40Z9PjkiIiIiomgQM0G3gwcPoqCgAJUrV9Ytr1y5MrKzsx0d44knnkC1atV0gTujUaNGoUyZMkU/NWvWDKndRERE4fL660CtWl63wntNmwJXXOF1K4iIiIiI9GIm6Baq0aNH4+OPP8YXX3yB9PR0y+2GDh2KnJycop+dfHRORERR6rnngF27vG5FaNzoqZeXB2zeHPpxiIiIiIjcVMzrBjhVsWJFpKSkYN++fbrl+/btQ5UqVWz3feWVVzB69GjMnTsXjRs3tt02LS0NaWlpIbeXiIgo3OJhaOm6dV63gIiIiIgoPGKmp1tqaipatGihK4KgFkW49NJLLfd76aWX8Pzzz2POnDlo2bJlJJpKRERENrZuBRYvFvNqmtXkmLkiISIiIiJyJmZ6ugHA4MGD0b9/f7Rs2RKtWrXC66+/jhMnTmDAgAEAgH79+qF69eoYNWoUAODFF1/Es88+iw8//BB16tQpyv1WqlQplCpVyrN/BxERUSI791ygoCA+euoREREREVmJqaDbzTffjAMHDuDZZ59FdnY2mjZtijlz5hQVV9ixYweSpUflEydORH5+Pm666SbdcYYNG4bhw4dHsulERET0PwUF4Tv2gQPA8uVA587hOwcRERERkRMxFXQDgEGDBmHQoEGm6xYsWKB7vW3btvA3iIiIiKLG/fcDM2aIwB6HrBIRERGRl3g5SkRERHFj+XKvW0BEREREJDDoRkRERERERERE5DIG3YiIiIiIiIiIiFzGoBsREVEcYCVQIiIiIqLowqAbERFRHNi0SUzT0rxtBxERERERCQy6ERERxYHMTDEtV87bdhARERERkcCgGxEREUWF48fFtKDA23YQEREREbmBQTciIiKKCmrQrWRJ9465YgVw9qx7xyMiIiIicopBNyIiIooqZcu6c5wNG4BmzYApU8TrmTOBJUvcOTYRERERkT/FvG4AERERJQa12EOkHD0qpuvWienNNwOpqcDp05FtBxERERElJvZ0IyIioojIyPC6BUB+vtctICIiim6zZgGrVnndCqL4wJ5uREREFBFJSV63gIiIiPy57jqgWjVg926vW0IU+9jTjYiIiFx34oTXLSAiIqJg7dnjdQuI4gODbkREROSYooipv6ffhw6JqZuVSN20ezcwe7bXrSAiIiKieMbhpURERORYpUpiWszPFURamphmZoa3PcG6/XZg7lwtiEhERERE5Db2dCMiIiJbcmAqJcW7drjp99+9bgEREVF0UBRg3z6vW0EUnxh0IyIiIlt//+11C4iIiChc3noLqFIFOHjQ65YQxR8G3YiIiMhWxYpet4CIiIjC5eefxfTYMW/bQRSPGHQjIiIi1yX/7wpj2zZPm0FERERE5BkG3YiIiMh1WVlimp7ubTuIiIiIiLzCoBsREVGCO3XK6xZE3tmz+ikRERERkdsYdCMiIkpQqalimoiJk9PSxDQvz9t2EFHimjgReOklMf/zz8Add3jbHiIich+DbkRERAkoLw8oX17MFy/ubVu8oA5/JSLyyn33AU88IeYHDgSmTvW2PURE5D4G3YiIiOKUovguy8wU0zNnzPdJxKGmp04BV14J/PGH1y0hokSVm+t1C4iIKBwYdCMiIopTf/8d+D5btrjfjmi3bx/w00/AmDFet4SIiIiI4gmDbkRERHGgsFBM9+/XlgUzhFIdcpqI1N8hEREREZEbGHQjIiKKAxUqiKnZkFIiIopdixcDv/7qdSuIiCgYxbxuABEREQUnJ0dMT57UqnESEVF8addOTPlQhYgo9rCnGxERUYw65xwxzc/3th1EREQUuzZv9roFRPGLQTciIqIYlZLif5ujR8PeDCIisnDyJPDmm8Dp0+L12rWJWSWaoltGhpgWL+5tO4jiEYNuREREcWzKFP/bHDoU/nYQESWKkyeBDRvE/CefAAMHAt9+C5w5AzRqBAwZ4m37iIgochh0IyIiimPHjlmvK1tWTNnrgojIPYMHAw0binn1MzgvT6uQvGCBJ80iIiIPMOhGRESUoNLTxdTJMFUiInJmzhyvW0Dk3z33AO+953UriOIfg25ERETkKrU3R6w6fRo4e9brVhBRolIUMRyVvZApnN55BxgwwP92Z8+K3pmsnksUHAbdiIiIyBWZmaHtv2ePmIYS8Nq4MbQ2AMAllwA9e4Z+HCKiYPz1F3DttcCkSV63hEjkJbziCmDhQq9bQhSbGHQjIiKiqJD8v6uSatWCP0bp0qG3Y8UK0cuEiMhO//7A55+7f9wTJ8R05073j00UqN27xZRFl4iCw6AbERERRZVkk6uTTZsi3w4iIjv//a8IvLlBHZafn+/O8YiIKDow6EZERERRr1Qpr1tAROTr+HF3jqM+bDhyxJ3jERFRdGDQjYiIiDyjJmZWh1MREcWiP/4AZswIfv/KlZ1tt307MG5c8OchIqLIYtCNiIiIPFO8uJgeO+ZtO4iIQtGlC9CnT/jP88gjwAMPAHl54T8XERGFjkE3IvKUogD79nndCiLySoUKXreAiCh0Bw9G5jy7domp2kuYiIiiG4NuROSpb74BqlQB/vrL65YQxQ81J9DJk+4cT725O33aneMRERERESUCBt2IyFNr1ojpzp3etoMonqjV72rVcud4aoLvo0fdOR4REblj3jwWXyAiimYMuhEREcWB1au1+XnzxDQlxZ1jO03wTUREkZOfD3TqBDz8sNctoXjib+jyxx8DY8dGpi1E8YBBNyKKuFOngJUrvW4FUXyRq+YNHOhdO2KRmotJ7SFIRBQL1ODI8uXetoPii7/CRn37Ag8+GJm2EMUDBt2IKCK++gq4804x/9xzQNOmwPHjnjaJKOH984/58r17I9sOr509K6ZVqnjbDiIiIiKKLwy6EVFE3HorMGWKmP/1VzE9c8a79hAR8Oij2rzaU+7MGWDpUm/a47Xixb1uARERERHFEwbdiCgi2KuNKLq98YaYskIpERERqdyqhE6UqBh0IyIiooBt3ep1C4iIiCjcsrPFNCPD23YQxSoG3YiIiBJIbq758j17nO1frJiYlijhTnuIiIgoeqnf96VLe9sOoljFoBsReaqw0OsWECUOu2HeahU8M4sXu98WIiIiIqJ4x6AbEXnq2WfFtLBQ3PTPm8ecUkThkp9vvU7twUZ669YBo0Z53QoiIqLQrFkD9Oplfy1ARO5j0I2IPKX2dCssBNavBzp1AiZO9LZNRLHi6NHIn/OHHyJ/TqPdu8U0Ej1l77sPePJJoKAg/OciIiIKl9GjgU8/1XK0+VOqlJgyhytRaBh0I6KoceKEmG7e7G07iGKF0wtnNz35ZOTPaaT2yqtSJfzncprrjojIqfXrw3PcV14BevYMz7Ep9p05E9x+JUuKaWqqe20hSiQcTEJEREQxKdnPo8ODB8WUuSOJKJqUKxee4z72WHiOS7Hrv/8FypYFevTwuiVEiYtBNyIiojiWlOR1CzRO8zUuXgx8803o5zt7VkzLlg39WERERLGmf38xtSuWBGjfl0TkPg4vJaKotW4dLwKIZGvXBrZ9djZw8mR42hIMdQi5P3/8AXTv7t55S5QIfl8vhvASERFFUriGPBMRg25E5AGzHEnFi+tfHzgAXHAB8PrrEWkSUUzYuDGw7devB158MfDzlC4d+D7xYNMm32WspkxERPEuK8vrFhDFLwbdiCji5C7uzZuLabVq+m3y8sT0jz8i0yYi0qhJk93y1VfuHs9tamEGs2Cjmng6Nzdy7SEiIooV48cDGzZ43Qqi6MWgGxFFXDEpm2Si9qghcpO/XC1ee/xxr1sQvFq1xFR9EEBERERCYSFw//3Abbd53RKi6MWgGxFFnFWA4OefxVStOEhE1urV0+b37fOuHU6ovcWA2KskmprqdQuIiIii0++/i+myZd62gyiaMehGRBG3bp358pkzxXTbtog1hShmbd3qdQucO3ZMm//zT/06eQg5//aJiDQ7dzrbbvv28LaDyAp7gRP5x6AbERER6Rw96u7x6tTR5vPz9et27NDmBwxw97xERLGoXDkxddrTlj1yiYiiF4NuREREpHPypLvHk/M4BuPll90flnrqlJju3+/ucYmIrMi9fgsKrLdLdnCHJg/bt9re7hxERBQZDLoRUdh88AFw9936ZS+/7Gxf9cJUzf924kT0J4snihdObvgAYM2a8LZD9fjj7g9hqV1bTGMtxxwRxZZDh7T5W27R5r/8MrjjqZ9Z/vLfHj0qHnh89llw56HYpCjA669Hf65XokTCoBsRhc1ttwGTJumXOa1ieOKEmKaliWmZMsDTT7vXNqJYVKlS+M8RSHD7zTf1r3NztfkXXwzsvHJuN7cdPhy+YxMRGcn5KYcN0+Z/+EGb37UruGNXrSqmSUn226mfe59/Htx5KDbt2gU8/DAwcqTXLSEiFYNuROSZjRv9b6PmNSkoAN56K7ztIYp2TnugOTFqlPlyeciSnY8/Bs6e1V7L8wCwZYv5fiVLmi839op1g3ouJnomokSiDp+nxKM+OGNPN6LowaAbEXlm3jyvW0CUWHJytPlAe6KZ+fFHbd4qWJefr1+Xnh7aOX/5BTh+3Nm2anLx4sVDOycRUSxQP1/NPo9HjQIeeyyy7SEiIiDE1MZEREQUK9zu/XDOOdowKquCBP/3f9b7B5NPrUsXoGbNwPcjIopmy5c7204NqO3ZA9SoIebVvHF2vaGffFJMnebWJSIid7CnGxF5Sr3pDja3CRGFTq6oFwg5p5A8/8471vvIgTanQ1mNdu4Mbj8iomhlHKKvys7Wv1YDbXKALZgqpXv2sEAVEVEkMOhGRK56803gjTecb68mBC5WDDh9OjxtIkokwQSwrXqpGcmFEuzce6/1ut27nR2DiChRzZypzS9cqF/nxkPKQ4eA6tWBCRNCPxYREdlj0I2IXDVwIPDQQ863l3vH7NghpmrFUiJy5sILtfl16wLfPyPDep3cG81YrTQYzK9Gbjt5UlS3PnrU65ZQonK7x9iIEdbrvvsu9OOreTEXLw79WEREZI9BNyKKGqVLiymDbkSBkYclBdLTVPXrr8Dhw+br5N5tU6cGfmyjWK6opijAJ5+wMmC0mTcPGDkS+O9/vW4JJarVq7X5/Hz/2+fmiuGdRNGGo06I3BdzQbcJEyagTp06SE9PR+vWrfH7779bbvv333/jxhtvRJ06dZCUlITXX389cg0lIr+cVDFUk7QTUfjYfJVi1Sp3z9W3r7vHi6QffwR69wbGj/e6JSRTg84nT3rbDkpcci9Lu/xqFSuK6enTWnoNgLnVyHvqyBO1KAfgvFI4EdmLqaDbjBkzMHjwYAwbNgzLly9HkyZN0LlzZ+y3SEaTl5eHevXqYfTo0ahSpUqEW0tE/jRtqn997rnaNCVFzJv1etu5EzhyJKxNI6L/GTjQet3GjZFrh1PhDMCoPQCCLQBBRPGpfHln28kpNUqW1Oates+ePQuUKhV8uwB9EEWlBgnVAOEHH/BhQqKrVElM7SrgElFwYurPasyYMbjrrrswYMAAXHDBBXjrrbdQsmRJTLUY73LxxRfj5ZdfRp8+fZDmcLza6dOnkZubq/shovCQLz4BoH17baquM24DALVqAd27h7dtRInsttu0ebsccdHYE7VECTHNyfG2HUSUOMyuVfyxy6Wp2rAh+KCb+vDyxAnfderQ1jJlxPS224D77w/uPBSb2IuNKHJiJuiWn5+PP//8E506dSpalpycjE6dOmHp0qWunWfUqFEoU6ZM0U/NmjVdOzYRBUftVSLnrVqyxJu2ECWCvDyvWxA8pz1OiIiinZPAnBW1x1Jqqu86tddu5crBH59im9rLUQ28uqWwkKNRiIxiJuh28OBBFBQUoLLh26Fy5crIzs527TxDhw5FTk5O0c/OnTtdOzYRBUd9SuskBxxRPAumN0WkfPWV1y0gIoovhYWBbe/0gYn6XRLq0FWKDooSPdWbn3ySD7+IjGIm6BYpaWlpyMzM1P0QUWhCqYQkX0SoCYhl774LzJoV/PGJYok6XCgavfKK1y0gIkosBw963QKKBq++CpQr501l7eLF9a8//DDybSCKdsW8boBTFStWREpKCvbt26dbvm/fPhZJIIpyL7/sf5trrwXq19deqxeSZgmAZf/+t5iy8heRf+G8QeNwEiIi99n1IlaHCKpJ8N1w5AjQvz8wbhxQu7Z7x6XwUR8+h/KQO1hly4pphw5iqo5OKSxkUQYiVcz8KaSmpqJFixaYN29e0bLCwkLMmzcPl156qYctIyJ/Vq40Xy7naAOAzZvFdMsW7UKyWrXwtYso0Vx+efiOHcwT9r593W8HJZ5Vq8Q03FVlJ04EunUL7zmIjENK7Ybqvfmm+T6h+Pln4OuvRUVTShz791uv+/pr//ur+QcPHxbTX38NvU1E8SJmeroBwODBg9G/f3+0bNkSrVq1wuuvv44TJ05gwIABAIB+/fqhevXqGDVqFABRfGHt2rVF87t378aKFStQqlQpnHPOOZ79O4gSzY4d5suvusp8ecmS5vP+nDol8pQ4LFZMRB774guvW0Dx4IUXxNSsZ3SfPmL407Rp+uX79gGffgrcd5+odNuzpwhgXHCBfrtDh0Qi+tKlxbZEKn898e3Y9c43DOqBXaabF18UUzd7MavprNlLKfYFUmvw77+t1wVTDfzkycD3IYpXMfVxevPNN+OVV17Bs88+i6ZNm2LFihWYM2dOUXGFHTt2YO/evUXb79mzB82aNUOzZs2wd+9evPLKK2jWrBnuvPNOr/4JRAkpmB4waq+3YtKjAbXEvZXLLwfUAseKovWWI6L4xQIOlJ9vvW7GDPMeO8OHA4MGAbt2AWvWAAsXAu+957tdkybs3Ubm1B49gG+gzIraG9OuZ1ogwS676qMffWS9bssW63Vq0aqsLOftoOj03//63yaYgBoRBSameroBwKBBgzBo0CDTdQsWLNC9rlOnDhQmeiLyXDA9z9Ru6hUqaMv8DR1atkybf/BBYNEiYMWKwM9NRIEL99A+K9995815Kbaphe8PHdICJsaUBwCwe7f4IbLj9HajRg3zKpPhyMX19NPavLF9gwdr8xs3un9uim1//eV1C4jiS8wF3Ygo9rhVkj6Qp7/jxrlzTqJosmuX1y2IPmrwRLVpkzftIO+pCbydUBPPJyVpAQk3k9ETmbEKrrlRiMZ4DLk33Zo11vtJ6bJNDR4sqsc/+WTwbaPoZnzg0L+/N+0gilcxNbyUiKJbuDuWHjtm3hOBKFEU46MyW1KGibBISRFTBvaii1qQI9hi9up3V/HiYnrllcCXX4bcLCKdvLzwVnk2ptSQr8lCGUL42mvAU08Fvz9FB0UBZs50tq2a189MXp477SFKJAy6EVHYhTrs7N13tXkG3SiReTWEM5rJOY3CMURLpvbadav3LrmjXTsxrV8/uP3V/FapqSJw+9NPwPXXu9M2IpXVg8mLLrLeJ5DctMbCDm5WNKXY8eCD5svl64ekJPu8fnZmzQpuP6JExqAbEYVdqDfCb7yhzc+fH9qxiGLZ9u1etyC6sdoeOfXOO9q8GkQtXx7IzfWmPZQYzKqMqoWjzFSt6vzYbj2UlOvNsSBV7HHSSzc5GbjxRuv1dgFbFl4gChwvT4ko7EqXDm1/OdAgJ/zlzRElGvaw0hsyRB88CZYa2GftJXLq11+Bpk35PUS+Ah1CaldsKinJfl+nDzXtrsPszv/NN86OT9EpNdV63dat1uusUlkcPOi8Ui8RaRh0IyLXuJnnSK7uVa6cNj98uDY/fXpwxz51Krj9iCi2DBtmvU4OlkybFv62UGwwqyxpZvJkYOVK+9xHFN+seoHl52vzToKygeTqPHxY/9rp+9U49NTJMYoVA/bvd3Z8ik7HjgW3n9WQ5zNnfIO0y5cHdw6iRMKgGxG55uqrzZf/9FNgxzl7FnjkEfN18hNkp0G+AweAKVPE/MyZQIkSvJAkSgQLF1qvW7nSd9mpU+ztluicPJSRgyqUuJ57zv82ctL5unVDP6cx0CfntLRj12MuPd18eYUKzoN6FJ3cfiiQlOQ7vPT228XUKufsmDH6B+ZEiYhBNyJyzbZt7hznn3/0r61ugkuW1Obtcl316ydylBw8CHz/vVhmlleFiGLbvHnW65zkOzp6FFi1yrXmUJwyGz7IpPWJ59NPA9vemB5g/XoxDSUXZbiH+p04Ed7jU3jZDSuuVMnZMYyfbVY53dTtzjlHTLOyxPSRR4ARI5ydiyheMehGRFGnQgX964wM//tMmmS+/MQJ4JdfxDxvioji27//bb1uwgRnxzD2JDE+BKD48vXXoR/j0CGgeHHgq68C22/lSn1PKIot8rVJMMP4ypYV0+LFne8TTLGEv/6yXmeXzw0AUlL0r3fuFJV9A81bR9HFbrgxoH+fGR98+3vPqKNQ/OUjJEokDLoRUdTLzDRfLg8RNd64qMMlFEW7sI0WigIcP+51K4gSx/HjziuusWdHYvn449CPceCAeKjjpGqgKj9fFGJ48snQz0/eczIM84cfAj/uli364MXnnwd+DLsAmZwz14kPPxTv80WLAm8HRQ9/wVu7YctW19Rr1/oOMd21K6BmEcUtBt2IKOqsXavNr1kD7N1rvp2cV0funbJ7t7fFEjZsALKzxfzcucBvv+nXv/yy6PJvlf+CiNylKM6H0lglRzezdq34vKHocfYscO21vp+7gOi1OH++O+dRe06bBWlfeEF89hvl5wN//inm1ffZ4sXutIciTw602VWJVBmH2B044H+f9HQtL1flyt5/3gwZ4u35KTyMQWO73pdWOQDLl/fNd2l8qHHggBhuyoJmlGgYdCOiqPPFF9p8yZL6iwH5CZtc8Uu+od68OVwtc6ZhQ6BLFzF/1VVAmzZifuBAYOJEUcwBCG6YCBFFj0aNtL91irz8fODkSf2y3Fzg22/NE3d36QJ07OjOuf/4Q0zfftt33VNPAT17+i4fPx5o2RLYscN33e7dvpUpAfFvfOYZ6zykLPwRu5wMLU5O1nLB+euVxiGfJDN+NthV0rULgqm5kINhfI9PniwKK/BhAyUaBt2IKKp9843+tdmNDKAPwJ0+bX28DRu0+exs4IEHxMXGkSNA587Axo1BN1VnxQptvrBQVHB9803gvvvcOT4RBUbuWepmL9PVq907FgXmuuuA1q3N15n9H2/Z4t651f/3Awe0B0Ny3lC1B9xHH4lCPoDouQ2Ypxdo3Ng8gPvrr8B//mMe3HvvPdG7hA9wYpPcY8iNggjsPZS4fv5ZTOWe2uvW6bcxPqBwqlu34PYDfD+f1feo+lm5dKn4HA+khzlRLGLQjYjCwmxoT6QYk7eqvQqOHgWWLNGWv/02MG6caOvy5SLfyn//G/j5li8X53zxReundwMHavNqxTI7BQX6YbaUOH75xfvemvFITe4M2Cc9d6sKM4XfnDnWQc9580IPrtpVuVZzjaanazeSZpUC//UvYMoU/+c6fBj4/Xff5erNqNkw1vHjxfeacUgXxR67HotqsNYfJq4nechy+fLBHWPbNveCYPIDcUDrbTd4sJg+/TQwa5b2+fbdd8CVV7IHL8UfBt2IKCwuuST857DrKq+Sb6CNPeDeektM5S93RREJ15s2FcG4M2eA3r2BVausz6H2ThgyRN8T75VXzNsqDxFRFPO8Lu+/L4aurV8vekXcdhsT0iaKyy4DrrnGd3njxqK3JAXHacLwEiXC2w6KnGnTtHm73mDyQ6IZM7T5QIssmAXdrKiFPayGGPKmM3YFGgQ1frcbr1UqVgytPc2ba3nhzATyvqXoZgy8yp8jck9cO716BVf0wwn1wffff4up8W9lyBAxMoQ93yjeMOhGlECGDAHGjvW6FaGRb1DkXgxWT3jtejqoxQ4A/YXJjh3AypWid8KhQ8AnnwAjR/ru//LL4gJCrqIql2F/7DFtvnp18za89prIR3f8uPhRezqovdwOHRKVwj74AJg6VSzbtMn5xRPFJrlXlmr1atGrkojMGXOiyT1G5cCaMQAnB+fkeePwLJmTfFx21N6WNWr4rhs/HqhaNfBjTp3KhzORZFXF0UmBBCM50CZfU8iCHR7dvr19YnxjbySZv4cVe/fa9wil8LMbVpyVpc0bi5KFO7BlNoze3+caC4xRvGLQjSiBvPgi8OCDXrciNOpF7rnn6pcbX6tSUpwd96qr7NerT+P++18RrDt7Fnj8ceDGG/XblSxpvr/ZjdC6dcDXX4v5U6eAhx8W+S/UHhAq9cIoMxPYulX8W50MVyJKZPJQcopv6uf88ePAc89py+VeFPKQYruAmXwjatezNNQ8ampgxazq5ejR1jm+xo4F3nnHd/np08AddwAPPRRauyh0dtcd6gO45s31y+Vgg1WAzPhe8ZcHTj2X08rNZuyG2+/dC1SrBrRtG/zxKXRWn2enT+sDqsb3pRxQDSZQ7I+T0Sjq56hZgI4onjDoRhSHFCV+h6bIT3rlPCdbt5pvH8zvwaoQw5EjQP/+QPfuwD33iGVOkx+btaN9e/0FrZqb6OhR7biff649xUxL06qTrVghhrz27Ml8PkRmevfW5nNzzXNiBapPHzG1K9ZCkZf8v6vZtDTgjTe05fL3hdw7WO4ZIif6Pn5cn2zc7RxZ6pCqjRu1G+DKle33MSY/f/BB7ftHpn7HuFksguylpfku8/eeUXs2BnNtcvw4cMEF1uuNPeRq1RLT5BDu9sqUsV43bpyYygWqKHpYjbBQyakUwjF6wsn7Ts2N6cb3M1E0Y9CNKA517QrcdZfz7devj51S83PnavNypbdSpcy3N3and0J+avv009p8165ieviwNtTTmAvF6mZc3k694Tt+XD88Rb64/fNPMf3uO604Q6lSYpgpIP5dL74IfPWVO1XPiOLZp5/qcyw2a+ZsP+PwG/XzhEG32JCRoc1bDcFq316b/7//06+Te4a78R2pPij68ENtmb+COWrKArvhgWYOH2YALppZDU31xy5I+69/afPGodbhYHXdRdHBbtiwouhHYHhVAVkNuhHFOwbdiOLQnDmBDT88/3ytB0csSU/3v43T4aUy+YZa/j3++qvvtsan2lY5MuQLbCf5T9QbrHXrtJwc5coBEyaI+S++0PJ+LVsmplZ5YCj2McjjLrWisT9M5hxbjD1u5ByIToY6yUqU0H/HzJrlfx9/ATSzXlD+KgyqN85m29kN/bv+eqB+fftjU/hZ5agyvhfcHl7HKsxkZ8cO/ffb7t2ROa9VChaieMegGxEBCF+lolgQaA+CcLj7bm3+/fett5OT0KrDUb//Hli4UDwB//ln3yeYFPtiPRcjUSQYh8LJD12cfM536KDNGxPIO3mAM2tW+FI7mBVXMRveqFq0KDztoMAcPKgF2AYOtN7u6FHz5enp2rBkAFiwwNl5g3ngGAivekaRO+6/X/8gwu6zxE3s2UaJikE3IkpIcp4cq5wl4bp5kgNnaj42uefasGHWPWysLoz++UdMN24UeeBq1hQ53yg+yMPRKLziNR8m+ScPNTWyy08kv2f++MN6OzWQZ0xL4MT48YG1icLPSWqHjh2190eFCtbbWQWF69cHKlbUXr/wgrO2HTgQ3sBYpHpGUXjw/48osvh1TURxQR5WtH27/+3lC9zsbG1efvIn5wOyShQcTPLXatW0eTWpsvF869eb73vNNf6Pr+YN2rMn8LZRdJIrL5K7jPkvmRQ8/gUzXFtOOm6kJpQH9Hm1jHr1EtPOne3Ppd4QWxUIUqk9mplaILrIQ0qterDZefRRbd6uMMO//2297oYbtNQT4RBsTjpyn1XKks8+0w95t7quDFQ4r0fUYwfzd0MUzRh0I6KQbd0KzJ/vbRvkoRRWNyq//KLNyxey8gWEnCxb7o0gV3aSc6/UqxdYO43kXm9ym8yeiP/8s357tbdeYaHo4Qawlw5RoIzD8HgzGXusbiblz1T5s9FpUQSr7xJjpb8vvtDm5WGgxptTNUec05QG/oJuKrnAkBOHD4ueUOQ+RQEuv9z/dj/9BLz8svk6NXWEPzk5ztvlJI9l2bL21dDlHvh2VU0psuT/l8GD9csXLtRe9+tnfQyr3INm5AfVbqtbV0zVwje7dzvLp0kU7Rh0IyKdU6cCr3h2ww1iCEUkGW8Y5Jsg+aZZvhmRK9PJw0LkGzA5F5rci00+ptyrwGmFMKubQjVY5sRLL+nbdP31Yjplinbxzh5RRMFbtAiYPNnZtpGoDkjOyJVpZVddpc0H80DCah+nAauJE/Wvv/5am3/vvcDb48Rff/nfpmNHoGXL8JyfrJ06Zd07PtxVyFNT9a/VhPZ2PemMjMHmQK5fKDK+/Ta4/dTrSSfC8WBK/TxUR2iogec77wSuu8798xFFGoNuRKTzyCOBVzxbsSIsTbHldFjnSy+ZL5dvpuReB/ITQzlQJl+YylXkDh1y1g6rp8LycidDhOQ8HOrQVPZuI3KPOjwbAG67zXo7p8E58o6ctHvnTm3eaaVIJ6kK7MiBlGPH9O+tt992doy8vNDaYGblSucVfMnaueeKafXq5oUujF56Sf8ekM2ZY7580yZg3rzg2qdSc77K5PfV5s1iGkgADmBS/ET01FPAp59arw/2elTNVaiOWunaVUydPEQgigUMuhGRjvwkPpqVKGF98RpMvh6VHHCU863J5AtTpwmx5X2shoQ0buz/OFYXuWqeOHn4KRGFZuZM63XGv/1XXgGGDg1ve8ieXOXRSH64YuyhYxVskB+wbNumzTsNhMn5O+32+f1363V33unsXFZ5nQBxI/zee9Z5kow9mMgZ9Tu7QwegVKnQjmU1RHjevMCGkZoxPhw0XiOpbVeHP6tSUgIf+UDxbfVq/WehUaj5JcNddZfIKwy6EVFMSk4GsrK01zNmaPOhJGBt3jyw7eUqqE5ZVRSrXFmbV4d+ONWzp5h+8422jMm1icLHWDnysceA0aO9aQsJxlyY69Zp83JgLZgbO7mQgpvD+JOSgLvv1l7bDV2Vh9Eav0fsKlVu3QoMGAC8+KLvukWLxO9DznlK8cVY9dzYG8nqASZgfy1iDF7n54f20JNiz0cf2a/31/PNreIORNGOQTeiBDRlim/y8Fhz9Cjw/vvaazkXWygCvQCwu9EJZehFt27B7ffBB9p8//7Bn5+I7DGfUfSTe6rJ3ByyGWrv4kqV9PkB7Xo1TZumzRt7IC1ebL2f+j0lpydQqb0D5QAlxRdjkFkOGhcUABUrWu9rN+RU7skJABdfLHrLqUnwKf7ZVWsGtKHLVli4iBIFg25ECejOO4FrrvG6FdHpjz+8boFgHOZBRNFF7vlEkScPiQz0AYeT3tBqvi5/OnTQv7bqRWeXKF/utb13r/V2cjVTY2BDzj+Ym6vNy3lK7RgT7ZN/TnMDeu34cevgx733Bn9cYy+4VavE9Mcfgz8mxTZjFVR/w66NPeFYDIziFYNuRAnq5Eng1Vfty4SPHQs0aRK5NkWSVRJpu9w6oQi0Z4XcI8FpsQYiokQxapQ2LweZZFZFfoxDg2U1a4qp0yGoxp5AcpDrp5+0ebthVvKwWLvzWt2QyvnqAH0BoVOngJEjrY9Jzh0/rg/2hlpoI1JmzQImTDBfZ3cNCADFigV+vuzswPeh+BBoFd4qVfSvjaNW1M9Tu568RLGAQTeiBPH6677LHn3U/ovssce0J5fxxpjjJNwCDZzJN25OkiivXRvY8YkoNOrQKicFUMh9332nzVv1DDbe0AXCjdxUofZYdhrwMPbKMw49/e9/tfn8fPtj3XMP8Nxzzs6baGrWBO67T3ttVZU8nmRkBL6Pv0AexS/jZ1YoOZbl4117rbYs2AqpRF5i0I0oQci5vmTGC3C5h5XTYSmxKNpzjshDfawSGcsJt+WeEsEUdyCiwKh/oxdc4G07SN87TK1AbSyqYMfsJi6YBzPG90KoN4flylmvk48t97arWlXrrWdUUAA884x+mRxEAoB33gGGDQusnYni6FHg7be113b5zqJZvXrB7SfnHrQTq7+XWNO+PTB4sNetsOfvofHq1fbrK1XSH+eVV0Q6Abt8ykTRiEE3ogTh9OJfHjoRz0J9+hYKudx6oMMw5K77J06Yb2NWoY7iRzDDfYjijdVDITXXntOgmVVermACB8EWwHHihhv0r3futN5WroQta9AAmDtXey335itbVv8w6tQpoGtX4LPPxOuCAj7QUQ0bpn/oFWs9zY3veadVl9mDLbosWgS89lrgQzojyV9vXzmfpZHZCJEXXxTvX/W9eOAA8MMPwbePKFIYdCNKEFZ5YozDUIy5YUjYs8e9Y8m92OSLpU2b/O8r54aL9BBZIjLnZjVMckYuZBFKMMDp/92GDcGfww3G/KpWhQ+OH7d+mJORoX+wJgfZ0tKA//s/7fX27WII7003iYd2HTsCDRsG1/Z489xz+hxpVr3RY42xiMecOd60gwITK8MtT5/WqiU7UbGi7zB/YxBv4ECgc2ftdXY28P77wbeRKFwYdCNKEGoXbaMXXtC/Vr+8Y7nrtlvDYuWKeHLhhVALG8hJvOVzOMmdIt9oOrnQWrcOGDIkdi7KiGKF/MDCjfxfFBj5c9hfnjIjq17CRuvXa/Ny/i63e0rLVUlDdeyYdY/1/Hz9Ta9xuKB8s2oMRi5aJL4H588X80lJwP33u9PmWPTpp9r8P/94145wqlpV/zcgMya8J/LnzBnfHrr+gnDGz3b1facWyfnjD/36J54Abr+dVVAp+jDoRpQgrIaFGC+s1Yt1p7k7otG6dYFtb/VvDXUYX6CBLquKenbDiPx55BHRHZ89cYhCI1eEBLQgudkwxL17gS++CH+bEplZrqCPPgLWrBHz+/frhwDK7L7f5M/bunXFVH44AgQ3zNLu+8BqiGuwrHq2b9sGlCplvU4m37Tu36/N9+2rFbEYPz7YFsY+OVhQsqQ+CBerzEY6lC1rvi3THJDRmjX6nIdmqlbVv/aXe9PqgUSPHubL1aGmfNBM0YZBN6IE4bS0vVqRL5Y5GRIhD6OwGpoUao85qydtbhVxWLlSm7fqmShX+COi4I0d63zbQYNEDq5EyZHpBX+VSc+eFT2yzNilUZAffqgB1cxM/fB/u3xvl1wips2a6QMTcm9pI3k4qBzgCvbGUf43yN8NZcpY/96Mw7bk9AXy+7hixeAqWsaz7duBpUu9bkXoCguB7793tm1ysv69JV8v2b3XKb7JlZKdCLboxsGDYqq+B9XranU0CHu6UbRh0I0oQdhVQUtEVr3KZFY3PIFUxXODVe4eOVm2v0TOTvLFEVHg1q71DXr7q8hGoXOrp42xx5zV561VDzEjNSCVmioKF6ic5uB0Iz2C/B1lHPps1fvPjnEfXk/Ep4IC6x5ERsnJ1qMKjLnhKLxCGQ0RTgcOBD70P1DqwwJ1yL+aBkANyhFFCwbdiMjUzz973YLIeewxr1sQHPlCyypnn+rJJ8PbFqJElZkZXCCDooPTnsdWPTKMQ03lXFdOHu4YbdyozRsDcE4f+Fjl2zpwwHnPEjnvHXtskhmr6w6rwDWFh1yROJrccgswdKjz7fv0Cfwcxs/E0qXF9JprAj8WUTgx6EaU4Kxy29x0k7Mn7q+/7mpzIsZJzjpjjptwkIcSyU+NrZ4gyzc/gQzh+Pln4OOPgS+/DKh5FIViuchJPEpK8g1kqIET5pWJberns13SeDWHnMpJzw677xY5f5wxmFu+vP9jA9bBvtKl9cfMzbU+htV3pFli/a1b3UubEEtCqZobCwoKgFWrAt9P/TwcPBi49lp320S+li3zugXOGfNjykP9Z8zw3d5pZeBZs8RUvT5Sh+zv2WN+XKJIY9CNiPyye8r98MORa4ebpk71v81nn4W/HfJNj1wdz2r4TrBV7ipWFAmwr78+uP2JSHPwoLNCCXJQndwRbCBz5szA91E/n42FCeSAlDHYJPfykXutyeQq1CdPivxvZux6pdmlDJDbKwcFU1P1icztCuzIN8P79mnz554LbN6s37ZePeChh6yPFa82bPC6BeH1zDO+1SED8dprwLffutce0sgB31jqaS1/9t16q9YzLVhqKod77hHT6tX16x94QPSgi/cAOUU/Bt2ISMfshsbqxoHsyUE0K3KvJfkGS57/6SdtPpinzgB73MQTq8qEFDnffGN9MyrfAPHvzl1vvCEeSATzezWrduqPmi/IWHhhzx5t3i4wZnVDKQe7tm7VP2R54glt/rbbrI8t55gz/j5eeUWbv/JKbb6wUL9tmzbWx5fJ+2zZoj+3+lDu7bcT7/3u5Ds+XhQr5pucPtH+v6PVoUNetyA406cHPqLEWPBFHgYP+H4em/XMJfJCUEG3o0ePYvLkyRg6dCgO/+9x3/Lly7F7925XG0dEkWd2Y8J8LsEJx5O1YJPS+qv0R0TusBuy57UNG4LvLRsNHnpIfEcF853UqpV5gMyux5i6/alT+p6NTs9vFZCTUzcYh3EeP67Nyz3M1qyxfgBmvPG08tpr+kqpwahYUf9afr8nWvLyRHsAoiarB8S1yIoV5tuVKQPMnh2JFiUmRQH+/FN7HcuFTdzuDe6vk8AffwAjRzJgTJEXcNBt1apVOO+88/Diiy/ilVdewdH/fQJ//vnnGBpItkQiijq7dukv+FVHj4oKaIl2QW3F6VNFY++IQASaGNf49M+fH37gsA8it8hP0+1uImbMANq3D397rDRrBlx2mXfnD5WcD0gOSDnxwQfajZb8Ge6v8nMg59u3TxtyuHmzvoqtVaDOac6iihW1yqiAPqfnjTc6O0YgjENIVcbee3J1VDkoQ/Hl7Fl9z8itW60f5qWni2sMCo+FC4FLL/W6Fd7wlzvSWGVafVCtPph45BHg6adFj12iSAo46DZ48GDcfvvt2LhxI9Klu7yuXbti0aJFrjaOiCKrZk3z5adOAf36AbVqRbY9sS7Q4UzyDVqg/HU0Nva669yZCY6J3CL36rDr/dKnD+DlpdLJk8Devd6d301mD4icWrxYTJOTgX/+0ZaPGKHd1AUzLCkvT7vpS00FsrK0dVZBrECGKMo95555Rps3Dvtzg/HmVXXqlD6XmRyM3LULGDMGaNfO/fZEo2B7nseDsmXth1bLPSLZq8hdofZW9cqzz/p/eFGjhv61PBTfWNCmb18gLU2/zNj7Ut1f/swHErPwC3mrWKA7LFu2DG+//bbP8urVqyM7Vj8FiOLc/v2hP9UxS0IdLzdv8aB2bfubRPZAIAqfRo28bgEFQh1Sahc0CCZjSokSWg/nwkLgyBFtnVXuotTU6EjhYPz3yjkLH3hAv04OJsq/w/37RU+SRJHIQbdNm/S5DY2BX7mn/+HDwNix4vc1alRk2kfR57XX/G9jV1jB2DHg449FrkFZlSr6lAHq51r37iL4qxa64cgdirSAe7qlpaUh1yRhyT///IMs+VuYiKJGs2a+eWNC9c8/QLVq7h6Tgvf99/br5V4WX36pzcu9PCg2yPmgKDaFo2dSoon257zZ2fpejW+8EdrxJk4MrXefP08+qX89aZI2b5cnSR5emmg5zhLZu+/qgxt2eQUVBXjuOWD06PC3KxHJwf1Yt25d8PsWFto/SAG0oF6HDtbbjBwJ/N//Bd8OIjMBB9169OiB5557Dmf+N1YpKSkJO3bswBNPPIEbw5FUgoiCpt6cy08j3fLJJ+4fkyLj0Ue1+Xff9a4dRIlGHdriNPE9WStRIvRjBBvAlodXyv76y/oGWK5UbRTLFcK7dfO6Bd4JpiJupPkLQrhFfn/7KyZz9izw3ntawLaggMP9KDjy+650ad/P9Pr19a+ths2rduwQOd9MBvURhSTgoNurr76K48ePo1KlSjh58iTat2+Pc845B6VLl8bIkSPD0UYiCtL27e4cx5gz4cgR8aVEsUnOkaHmWsnPZyCAKFh//+1sO+NnKQUvOeArWPd8/bU2LwcL1qxxtr/cY23uXGDnTnfaFQnbtwMTJmiv3a4+GEvY61hz4IA2v2+fdUqTvDzgp5+AAQNE/j8AuPhiLYi+Zw/QsCGwalV420vxJy/P9+FGoAXNRoxwrz1EsoAvWcqUKYMff/wRX3/9NcaOHYtBgwZh9uzZWLhwITLkskpE5Dlj8vxgGW9u/D3FpNhz441A06Zet4Io9uzdC0ye7HUryCtyAMqpRLixC2WYGMUe+ToxM9O6Km/nzlrvO/U98tdf2voNG8TPE0+I1/fdB1SunNjBXbJm7Mnprwe0v2rV8TRUl6JLwIUUVG3btkXbtm3dbAsRxQhWvYwf6vCYb74R06NHRVUyInLGODTw5EnfbS6/HLjqKm3dkSMi4TNRvHrwQeCHH7xuBUWKsViTVT+M337Tenru2OF7DDVX49y5IkfXxInidZMmokfo44+LHvpjxvgGXBQlcsNpvTRnjtctiB4pKfrebf6qQZcv77vs2DHRIy49XZ+nkMhNjoJuY8eOdXzAB4wljogorvz5p/MhNBSdsrK0yrPGC+WHH2aeN6JAlC+vL1RjVhXt55/FjyqRqx66JdBhQxRZP/7odQvcpaZiIHNXXql/bTX8+8wZ7Xe5cKG+cu/VV2sFPc6eBVav1tZlZwPvv69VwLz9duDDD0VajPHjxYPD7t2BX34BLr0U+PZb8Rlx9dWu/POiyvvv+y5LTo6OKsheU3O2VamiH/KsMgvKZWaK6ZIl5kE5Ijc4Crq9Zqjxe+DAAeTl5aHs/7pDHD16FCVLlkSlSpUYdCOKQ/IX+VVXedcOckefPlq+FGOOqWXLIt8eEn74AWjcWHu9YQPQoIF37SFnjJWhU1Otty1RwrwnHAWubFnfhwZeSkpiYEa+VvjXv0R17L59RUCkalXv2kWR57Q4iJx72Hj9Yey1JifBVxTgpZfE/NChwIIFYl59oKiOyIjHv8k77gCmTPG6FdHBmMPt0CExzc4GKlUS+QHttpd9+imHl1L4OMrptnXr1qKfkSNHomnTpli3bh0OHz6Mw4cPY926dWjevDmef/75cLeXiAIwa5Y7x7nsMm2eX0ixzy4ooF6wUOR17iwuplVuFUKh6KEGJSZN8rYdsY4J7KOTWo0SEA8NpkwBli8Hli71rk1uYaGhwMgBMrnHUbFiwK5d2mu5qIjR7t3611aFaGrU0HJ53Xijb2Dl5Eng44/jpydYVpbXLYheK1fqX8vvNbPXsqwsbXgzkdsCLqTwzDPPYNy4cWggPX5v0KABXnvtNTzNcoZEUSVW8qkkQg6OaGUsinHsmDftIOHXX71uAYVKzY9oRg0WBZN8n7Tf34EDwLZtnjbFRzz2qAmUHJgqU0b7P4qVaxE7dsGhaObF+/Kdd/TFZeRgV3q6CLyp1LyyKrWnGuA7RNXub16uIC0XXTh+HHjmGdHj8vff/TY9Jowe7bssXgKKbpP/bu+4w38PzPPPD297KHEFHHTbu3cvzpr0zSwoKMC+fftcaRQRJRberHinUSP96xIlRN6+O+/kRRxRMN55R5vnZZG7qlcX06Qk+x675A1jYOq888T07beBevX4gC1epKQEv2/Zsvr3gd1w+82b9a/lypQ7d+rX1aplfoxbbtFyw3GkRmKbOtX+PbBliz6nG6+ByU0BB92uvPJK3HPPPVi+fHnRsj///BP33nsvOnXq5GrjiCh0333ndQsompkFBQYNEsOCjE+giSgwnTt73YL4xWIU0c1YSXLrVu/aQu4KJXhqHN5nvAaRj126tPVxjEF3eTir7J9/tICc2nPOmIeTCPCtpsugG7kp4KDb1KlTUaVKFbRs2RJpaWlIS0tDq1atULlyZUyW+xITUVT480+vW0DRzFip6cQJbYgjnwpHHm8G4otZ9TSiRFC5svlys+q+FN/sgheBjHT45x/rdXKvuC1btPmDB/U983buBCpUMB+iSYlHfrjMYi8UTo6ql8qysrIwe/Zs/PPPP1i/fj0AoGHDhjhP7UNORERRzThkQ8bKitEpNdX7nj2szkhes7vppuiSlOSbkwsABg8G/vvfyLeH3GNXAdLf90Tx4sD/bh+LtneqTBlt3hjIy8jQ5uXrmKws/fnUoK+cA44SU16e/r2cmcmHzRQ+Afd0U5133nno0aMHevTowYAbEdliHpfokpenzRtzsxhzvJF3nnnG6xboMeAWnDNnvG5B/JCHm4WSV4rCr1Qp84qfv/wS+bZQ5JgFWuXejWXKiLxuVuQAmR3jw0Or68yzZ7XzDRumtaVYwN1OKN5kZABLluiXqfn/gNgtnkLRKeCPnH//+9+266dOnRp0Y4jIXcZEs17hzXp0yczU5pmMPHrJlda87uVGwdu0SZtXq29ScNQb66FD+buMRo89ps2XKmWeMzQ9PXLtochLTvb925Qf9PkjB+SMPerknFtmwT2VfP5q1YDTp8X8b79pwbaKFZ23ieLX0KHa/KpVomekmn/y+HH7ADFRIAIOuh0x9Ls8c+YM1qxZg6NHj6Jjx46uNYyIglelCpCdDfTsCRw65HVrKNqkpWnzxoCo/Do7W1ScI2/ZDQem6HfBBdo8H0CERh1SxuGJscHsYYFagZbik1n+tgEDtPlAcvpt3Kh/LQfajIE8uYfc/v3a/N9/63vIqr2XnPaoizZMAeKuPXu0+cqVge+/964tFN8CDrp98cUXPssKCwtx7733on79+q40iohCowbdqlUTT/aIVMYhGKtW6V/v3avN8+LOe/v2AceOed0KoujA4T6x44svgG3bvG4FRZpZD1RjQRk50BHIseQhofK1CqDP9yYHe7OyRO9+tffSihViGqvBX/bwddfRo9r8P/+IHrpqcQVWLyU3BZ3TTXeQ5GQMHjwYr732mhuHIyIXVavmdQsomhiHZBgrzMmdmVllzntVqgAlS3rdCnLb1Vd7e365uh9RODDgRlbkYaPGNCgbNmjzdgGm3bv1r+UHinKQLzdXv12JEmL69tsMYJHesWP6wO6FFwJPPeVdeyi+uBJ0A4DNmzfjrF05GyLyRIMGXreAoklBAfDKK9rrt94CunUz33batMi0iex98IHXLSC3HT7s7fnl3EhEkXTqlNctIK/JuWSNhWac5tAqXlz/Wu6VJAfaDh8Gdu3SXsvvv/vvd3YuSgwlSgDbt2uvjx0DXnjBfNs9e7SHV99/H1rKg7fe0r9HKT4FPLx08ODButeKomDv3r349ttv0b9/f9caRkShO3HC92kgkdHs2ebLv/02su0gc88/73ULyG3svUiJatEir1sQvZKSEi/vo7Enml3RoIkTrdetXavNT5qkzVerpk+VsXSp/nhvvumsnRT/ihUTAWEnhavU4cmKAlxzjZjv1y/wc155JfDTT8Bnn4n9BwwA5s4FOnQI/FgU3QIOuv3111+618nJycjKysKrr77qt7IpEUWGOqzjxx+13ARERBQdjLkVI00dYhULxo4FypcHbr3V65aQWwoL7atPJqpECbi98442/+qr+nVTp1qvkxl7gMuVcuUCYsZCRHIBhiFD7NtJiad48cCqxQ8frs2fPOnsu/WTT8QQ6L59RcANEL3mHnxQjEa54grgyy+B664TQ7EVxbdnJ8WegINu8+fPD0c7iMhF6sXs8ePA8uXetsULifi02AunTgGrVwMXX+x1SyiW8e818k6c8LoF/u3ZI25gHnxQvFZ7E1DsO3WKvT3JXU4LP6WkmM8TrVunz+mm2rFDFKXr1ct33YgR2nxOjv+g29mzQO/eYv7cc7Xl9evrC5upHSbUYBuvkWJfwM+ZOnbsiKNyqY//yc3NRceOHd1oExGFSM2XsWyZt+3wCr+c3CMP2TAaPRpo1UpffIEoUF7+vXrd48wrcl7HaHXhhUDXrtrrRo28a4tbEvX9ZnT77V63gBLV339r8yNHAkOHAt27e9ceih6nT5sv79dPC5QBove1GbvA79y5ohdnWpq2TC5Wtn69Pgi8eLEYeqpSe2iuXg0YBh1SjAg46LZgwQLkm/S7PHXqFH7++WdXGkVERNHBrnPzkiViumJFRJpC4E2727wK+K1b58151Tw0V1zhzfkDceQI8Ouv2uv9+907tld/R/H6QCjQ3+cnn4SnHUT+ZGXpX48eDXzzjXXAJdrIBSOMeH0QOrNe4AsXiunx42Je7X1tZJfO56qrgDvu0P//rVypzV98sb6qb16eNvQUENV2k5KAxo2B5s215ZMn6yv+UvRyHHRbtWoVVv2v3+PatWuLXq9atQp//fUXpkyZgurq1RwRUYyJ1osVr9tVrpz1uqZNxdSqEAM557T4d7zetCea/fv1OYgiRf17TvQKkvw7clcwv8/Fi91vh1NyDxNKLKtXmy+XAxzRasoUoEwZ6/X8XAuvwYOBr76yXj95svhudVod/I8/tPmVK4FKlbTX06f7nlvWqZO4P7jrLqBhQ2fnI285Dro1bdoUzZo1Q1JSEjp27IimTZsW/bRo0QL/+c9/8Oyzz4azrQCACRMmoE6dOkhPT0fr1q3x+++/227/ySefoGHDhkhPT8dFF12E2bw7JPKUMYgkv/YywBStFytet+uWW8T0wQeB99/Xd59Xu8LHwlC1aHH6tEiUW6cOMGuWWLZ5M/DYY542KyF5HdAeM0Y8NV+0SPQWtevBYObqq4FAs3qo+WaefRY4cyawfd02d67Wg0BRxM8jj4ib4oICb9tG4deuHdC+PfDpp8BDD4X/fJ9+Kv7mk5JEb6dy5fRJ9e2cPg0cOxbe9sUKrz83w6VrV+fvh3D57DPx+5U//yZMELmZmzQB7rzTu7a5LRbfR5MmAa+9Zr1+wgTxHVu7NrBzp1h2++3W/9Y1a7T5vDwxxNSpefP0r+vVA6pWdb6/FUUBunWzH+Ui8/pvJqYoDm3btk3ZunWrkpSUpCxbtkzZtm1b0c+ePXuUs2fPOj1U0D7++GMlNTVVmTp1qvL3338rd911l1K2bFll3759ptsvWbJESUlJUV566SVl7dq1ytNPP60UL15cWb16teNz5uTkKACUnJwct/4ZRGFXpYp6C8Mf/oT+M3euNj9woPY+69FDW65+RP7zj6IUFJi/L48dU5SFCxXl7FlF+f13RSks9N1m925F+fVXRVm50v49fvasopw5oz+28XinTimKxddDQE6cUJRLLlGUvXvF64IC87YriqKcPCnW5eUpyuuvK8rp02L7555TlGHDfH+3BQWR/b9MSvL+/cQf859x45y/JwsLtf2OH3e+38UX688p/w2FQ0GBonz3nfg7UG3frijnnKO14bnnFCUrS1F69xavy5b1/v/Cy59Q/0Zj9W88O1tROncWn+VuKSxUlEOHFGXZMvNzPv64+J544QVF+fFHRXnpJfHdpCjaNkuWeP+74U9kfmrVUpRFi8T1RaTk5Yn34OnTWjvatfP+d8Gf0H7eektRNm/25tz3368o6eniXvCvvxTlhhsUZcQI8/dfQYF2zX7woKL89JN2HDuFhYpy/fViu2nTrP9mzpxRlNxcRfnhh6D/RKJaIHEiP7/S6NKqVStloHTHV1BQoFSrVk0ZNWqU6fa9e/dWunXrplvWunVr5Z577nF8zkQPup0+rShduog/lv379eumTFGUP//UXss32idOKMquXYqyYIF+n4ULFWXTJv2yAwfEH+upU9btsLqJP3NGfKidOiXOF4gTJ/THV28+tm3Tr4sWhYXWN/qyI0cUpXJl779w+BPfP6VL269/6SVFmTVLfG58/LGibNmiKGlpYt0114jpsGGK8u234sfsGK+/rij5+eJve9o0RVm6VFH+/W9Fad5c22b0aEUZPFh7nZMjAnaAuOgAxN/zwIHib2P+fHHTDyhKZqaifPihoqxdK45/5Iii3HOPojRooChXXaUoycm+bcrIcPb74d8gf4L9Oe88RZkxQ7xnn35aUf71L0VZvly8Hzt2VJS33xav1e2vu05RXn1VfI/m5orv7e3bfb8v5Js6+efQIfE3oCjiolu93FH3P3tWUb76SlE2btSOtW+faMP06SLo9+WXinL77WKfM2fEd+rEiYry8MPaefr08f53y5/o/+neXXymf/mlCJY984yizJunKNWrK8pDDynKhg2K8tRTitK0qdj+nHPE+65/f0WZMMH79ifyj13AN5aCwf37K8r774v5u+8Wn3EFBeKh4qlT4nP2s88U5YsvrK/Fc3PFezUnR1xf5OSIz9m9exXl668VZfx4RbntNu//rfxJnJ/588X0scfEe/THH+23X7FCPEg+elR7X3/0kaL06mW+/ZdfKkrfvooyc6aiXHGF7/ojR8S0dGn/97KxIpA4UZKiKIq/3nCzZs1Cly5dULx4ccxSx8NY6NGjhys98Izy8/NRsmRJfPrpp+jZs2fR8v79++Po0aP4ymSQda1atTB48GA8JPVbHzZsGL788kuslLMXSk6fPo3TUjbN3Nxc1KxZEzk5OcjMzHTt3+OlkyeBatUAkyK0cSEzE8jN9boVwalQATh0yOtWEBERIIaF+L9KIiKiWMHPdeJ7wFvx8rvPzc1FmTJlHMWJijk5YM+ePZGdnY1KlSrpAl5GSUlJKAhTIo6DBw+ioKAAlStX1i2vXLky1lsMgs7OzjbdPjs72/I8o0aNwogRI0JvcBTr3z9+A25A7AbcAAbciIiiSbxcGBIRkcDPdeJ7gCLNUSGFwsJCVPpfSY3CwkLLn3AF3CJp6NChyMnJKfrZqWZCjCO33up1C4iIiIhiU6wlAY+19hIREcUTx9VLvVaxYkWkpKRg3759uuX79u1DlSpVTPepUqVKQNsDQFpaGjIzM3U/8aZHD1EZp7BQVGQ6cwZ48kng77+BTZtEb6s5c4CePfUVpfr2BY4cEdV1vvxSLGvYUFRgW7IEGDoUWLcOOHAAaNQIyMgQPz/8AIwcCZw4AVx0EXDHHcAHH4hKUEuXAvfdBwwaJM43YoSoxpaXJ9q3ejXwySfA448D//yjjQzPzwf27xflmQFg+HDx78rOFus3bBDVAA8dEj3fTp4EcnLEv+vUKVGaecAA4KWXxHaffSbO+/vvQIcOoirc8uXArl3iXDk5wJ49wKpVYpqXJ86xdq34ty1bBsyYIc5dWCh+fv1VVCd87DHxO1bbXlgozrNypTh2YSFw9qx+5PuOHeLffuaMONfOnaJ89OTJ4nd29qzYb/ducYy9e4EvvhD/vhtuiOS7iSj63Xuv1y2gRKNWSYykK64Arr0WuO028frjj0XF4aefBgYPBkaNst63TBnxvdywoXjdpYv4/u/TB7j7brHs8svFNcM//wDyZdRrrwHF/jdu4vnngQYNgClTXP/n+XDz9xvosWKtl0SstdeOzSU8hZHXgVsvz1+/PlCypJi/4gpRSVR19qy4Rr/zTuD4cXFvc/vtwHXXiSqWb77pSZPJIDlmIh6R8cMPzrd95hnghReA//wntHOOHBna/rHOUU63sWPHOj7gAw88EFKD7LRu3RqtWrXCuHHjAIhed7Vq1cKgQYMwZMgQn+1vvvlm5OXl4euvvy5a1qZNGzRu3BhvvfWWo3MGMlY3Xp09q11QU2yoWlUEIMOFuRASS9euwOzZYr52beCbb4D0dODcc7VtvvoKaNdOBOefew5o3tz3c+Onn4ArrxQB6xEjgIkTRQ5GRRHB5AsuAHr1AubOFdsfPSqCAbKCArH9r7+K9/hNN4nXzZoBt9wigtyAWPbRRyK4/eKLvv+m/fvF9H+duIvk5ooHB/Xri4D2jh0iyNCtGzBtmgjOf/YZ0LateLhQrJgIer/+uniAMHky0Ls3kJIiHjJ8/LHY5qabzH+3t94qgh3+8G8uMSxYALRvL+bVh2PFi4vX334LXHyxeM/m5wNpaWL5zp1AjRrOjt+qlXhIpFqyBGjTxrXm+zh4UDwQu+oq4NFHga1bRQBw3rzwnTNWxNrfdLjbe//9wLhx4mbwqqvstz14UDxAnT9fBDfky/OCAmDxYqBpU/Eg+cYbge3bzY9TpYoIonz0kfg8//tvEbieNYs36Yls+3agVi3x4Fv9/A2H48fFg43rrxd/W3fdFb5zUWSdd564dvTa1VdrAbaCAtHpo1Ur8fmmKOI69dFHgW3bxHX5Cy+IjjiA+ee9oojP3j/+EA/iVFddpQ/kHTsG/Pab+B389Ze47v/pJ3FNnpQk7hHiQSBxIkdBt7p16zo6cVJSErZs2eKslUGYMWMG+vfvj7fffhutWrXC66+/jpkzZ2L9+vWoXLky+vXrh+rVq2PU/x7n/vLLL2jfvj1Gjx6Nbt264eOPP8YLL7yA5cuX48ILL3R0TgbdKBaFO+hGieXkSaBECTG/ciXQuLGYHzAAeO89MR9LN4/BKCwM/Sbs0CHRY7VBA+Caa8RF2YYNwPjx4oaTEsuNN4oL09xcUUTnjTdEsNcptedHYaHzXiBy0O3330UQzwuKovWIX7YM+Pln8Rlz8cXiwv/wYfH7oNgLzgXq3HOBjRvD/280+xtZvlw8sDGzY4cY3dGkiegx+s03wKefhreN5K2ZM8WDP680awasWCECFTt3iocizz4rRgKpI4y8EO+fQeGgPkCz+26uVk2MngLEd+GJE6Gfd9Ei8cChdGlt2bFjQKlSzq4T9u4V7WrXThzLzoED4nv6uecS9yFFQHGisNZRDYNx48YptWrVUlJTU5VWrVopv/76a9G69u3bK/3799dtP3PmTOW8885TUlNTlUaNGinffvttQOcLpBQsUbSoUsX70tT8iY+ftm3Fe6qgwPd9NnSo2Oa88yL7/o4Hx48rytmz+tde/1/zx/lPUlLox/j669DeQ6tXK8rixYHt07SpOHfPnqGdO1wKC7V5r/+P+RPenx49xP/38eOKsmtX+N9b+fmKsnatojz8sKLcf7+inDgR2P5793r/O4vEjxufbbH4c911YXnbBeTIEUX56Sf9MvU64ccfvf8d8b2lKDfeaL++SxdFad5c+y7Lz1eUWbPMt61ZU5tv0UJRypcPvl1btijK9u0RfbuSElicyFFPN5uAHQDRwy1esacbxSL2dCO3vPuuyE9i5sYbgc8/F/kMe/eOaLPiUhx/lZJBxYriKXGkXXihGEL3zjvRP5SJfw/xLT8/vEP33JadLa6t4kEi91wqXlwMGzU6dAgoXz7y7QlEbi4wYYI2/I8ia/9+YNIk4KmnzNevWKHP9ycz+z7r31/0ogVEL+/jx0VudEDkF1+wQNu2YkUxrF61bZvoJXf99cCQIfoc7BQ5gcSJguoMOGXKFFx44YVIT09Heno6LrzwQkxWM9oTEcUI3tT5Z/cdkpIipl4NUSP/+B6PToEMI3XT33+L6XffeXN+4t+kKpYCbvEmUQNugD4Xraxcuci2IxiZmUxF4aUKFUSAy4pd/vMOHYCyZfXLWrXS5kuUEHmMVXXq6LddtUoUImzZEujXT+RXvvRS8TCAAbfYEHB6/GeffRZjxozB/fffj0svvRQAsHTpUjz88MPYsWMHnnvuOdcbSUSBOXvW6xaELhJPYhP5wtOp7t2t1z3zjLhxqlkzcu2hwPA9Hp3S0709fziLJ7hl7FigenXRoxYQRUn69PG2TW7g36T/XEGxKl56kMXLv8NMQYE2X7asyN136hSD4STynimKb261Dz4Q30dq3rLTp7VCRrIKFayPPX++mH74oSj6BYjcaaqjR0XuNdVFFwFbtgD16onXWVmiUBfFroCHl2ZlZWHs2LHo27evbvlHH32E+++/Hwflvo9xgMNLKRYVLy4CbzfdxMS/FJp4vfCORtF80R+rN2HR2u727fVDRyJFfY/JBVGiXZUqwPnni5uWaP4bIecKCmIv8XasDC+N1s+8aCEP23vqKeA///GyNYE7flyfJJ/cU6uWGGZsDLqZ/T2p30Xy39uBA2IYqD+XXioKZSxYoPW8bNBAnFsNo7zxBvDAA+IeLjcX+Pe/g/onUZiFdXjpmTNn0LJlS5/lLVq0wNl46F5DFAfU4rwlSwJPPOFtW4go9sXqTVystjvcDh/2ugXObdwIzJ7tdSvITQyehk8sfOb961/a/MCB+nW33abN33CD9TE6dNC/Nrk1BQCkpupflymjzc+bZ318Sjzly5vn+7Ozb5827yTgBgBLlwK7dgF162rLUlP1+eDUINtNNzHgFi8CDrrddtttmDhxos/yd955B7eo/SWJKCq0aCF6CSQSu4v5pCRe7FPsYe6j+BMLN8bRonRpke+G4ge/hxNbqVLm8wCQkaHNy0EJALj7bm2+Rg39ulOntHk571m1avocmnLuNjVpPREAFBaKAi9OjBghAsZZWSJQXLly4OdLSRHDSkuWBAYPBr75Bvj+e3F9YPy7oNgXcE43QBRS+OGHH3DJJZcAAH777Tfs2LED/fr1w+DBg4u2GzNmjDutJKKgqcnuE4XdzSxvdMX74dprga++Eq+7dweefda8GMKMGZFtG5lbs0YMPaD4kZPj7fkZyCWvXHWV1y2gaGJMPm+XpcjuerZOHfFdCejzzG7bJvJjqRo10uZ//91pKykRHD4sChRs364ts3rg8+yz2vz77+tzBQaiTBn9cNarrw7uOBT9Ag66rVmzBs2bNwcAbN68GQBQsWJFVKxYEWvUTzsASXyMRRQV4jVhMQVPrt5VpYp+WEZqqvakL9ECttHogQeCv5ij6OV10Kt1a2/PT4mLtwd06JA237Chfp1VdVEju+9FOV/g+eeLnkRGDz8MnHees3NRYihRQh8Ae+st4Ior/O+XlGRfuZQICCLoNl8tv0FEUUu9GCko0OevIDJeqBpTcdaoISomAcF1lyd3vfEGsGyZ160gt/3xh7fnj9UbhIwM3yTXFJ0efBCYMkUkfieSNWoEfPaZ+To5B5vd9Wvz5sBHH2mvs7O1efnaJSdHX3hADcDt2uW8vZQYmjYFvv5ae92tm+8wZqJgxVjtICJyYvVqMf3gA9HlnshK7dr613JXejn3CXlHTq4bCeyJ4q4XXvC6BfGDvW9jR3Iy0LGj73IGTeObWS/eYFNVGCvcykNPjd9TagExQH8dU6kScOyY9lpN1SDnjoslzG/prlq1tPmzZ/XDj4ncFHDQ7dSpU3j55ZfRtWtXtGzZEs2bN9f9EFH0YNCEzMhDOwoLrbfjxV10SE31rcAWTsx96C45qXes9jCLNlu3MgAXjW68UZsvLDQv5LRzZ+TaQ9FBDnD5q/AoF0SQAyKAPrBWoYJ+nfzZmpmpzRcW6oeRqoE8ufdbLOHnnruuvFL/Wg7m8gEkuSngy7877rgDP/zwA2666Sa0atWKuduIohj/PMmf06f1rw8f9qYd5OvNN71uAbmBVcjck5srppEMQpNzl1yiDRvcvx9o3Nh3m6ysyLaJIsss15o8RK+gwPe6Q+Z2MOzMGeDIETH/7bda0M2uYAMlhocfBoYOBd59V7yuUQPYtElbX6mSN+2i+BRw0O2bb77B7Nmzcdlll4WjPUREFGZ2Q4737o1YM8iP+vW9bgFRdKlbV/RyA1hgJBbk5fkuGzky8u0gdxUr5psPVmXWe14eJnrkiP3QTmMPNtnJk9p81ar6dfv2afNyb+3Tp7U0Gikp2vGZ75jGjNGP/CgoAM45R0vRw44L5KaAh5dWr14dpWO1Ty5RAorVvBUUPvJ7wnjhLF/wpqVFpj3kn1pRliiReV31lZxTeyUade4c2XaQ94zBC3mIaSA5/uwCZRddpM3LD6xSU/XVSxs0AB59VFQGJ5KHIh844F07KP4FHHR79dVX8cQTT2D79u3haA8RuWzAAK9bQNHMeDGclAQMHy7mOQwo8sqX97oF5Ka33/a6BfGLQ0yjm9wriRKbfJ1hHLJn16PbmF9UzlNsXCe/lvPRHjgAbN4s5s+cEYH7l18Gzj/ff7sp/skPcvbv964dFP8CDrq1bNkSp06dQr169VC6dGmUL19e90NE0aVsWa9bQNFsxw7fZc88A2Rn86aWKFRm1RspeHIuKPb+jD7GhzhqLi0AWL8eWLo0su2h8LAaWuqEsQe9cZi4XGnU+H6Se8Wlp+vXZWebn++LL7SccsyvSXY6d9YX8mDhI3JTwG+nvn37Yvfu3XjhhRdQuXJlFlIgimL+qkQRGSuUHj0q8q9UruxJcxKe8UaCYs+sWUCPHmJeHtYEaDeR554b2TbFi127xLRkSTEUXs7H47WkJFb+lXtHHzmiBUa/+EIM64tlvN1xrnt3EVz79FPfdTt3Ajk52utq1fTr5c9GY343eVvjA2X5/0f+3G3XTuRyW7IEuOACR82PenfcAUyZ4nUrYs+RI8DNNwM//GC9zapVkWsPJZaAg26//PILli5diiZNmoSjPUTkogcfdOc4Y8cy/0WiiPUbo1jWtStw553ADTeI18xfFX+KFRNDnMaN87olsSkjQ+QKK11a/ERT0I30PUPq1gVatBDzct6kWBWr6Ra8CAZXraovymT8/5cDa8k2Y66MA6hSUsy3GzVK6wX38MO+Abk2bYB//rFtckwxe6CenGxexCLRlCypL+By3nna/33ZsvqAr9GpU7zuovAJeHhpw4YNcZKJGohigpz/IhQXX6zNP/20O8ck7/z1l/U69rTyzrffAtdfr71u29a7tpBzdtX2jNSb3ypVwtOWRCIPNY0Gid7LDdCnJNi9WzxEWL0auOIK79rkFvZ0C4zcN8PYo17+XdpVUzdejxw/rn+tBkiGDNECTmqgt1Mn4KabHDc3pnzyidctiB7GIaCXXiqmlSsDo0f7BnXtHiyXLg00bepq84iKBBx0Gz16NB555BEsWLAAhw4dQm5uru6HiOLb88+zImqs++knbV7OXwGIBMMUHfjENTYYbwStgi8XXqj9vbFHQuh4yRndfvtN3PBeeGF8BKzi4d8QTt27619b/b6KFdMX2ZCvJz//XP/5Wb26fl/5AXC1asCWLcC+feL1U08BL76o9RT/8cf4DU6ZPXDgd4qgvrf27QOeeMJ3vVmF0g8/FKN5Bg4E1q4Nb/socQUcdLvmmmuwdOlSXHnllahUqRLKlSuHcuXKoWzZsijnVrcaIopqr73mdQvILcanzPHQI4EokoxP2s16sS1cKHK9qT0+jBX8iOLN5Mlet4AiSa16rjI+0FOVLKkF0/r00a+7/nqtZ1L//vohvdOniwCuooifSpVEgQT1s7RkSeDxx3171cWjYcO8bkH0snrfqcwe1vTtC7zxhnjv2PW8JApFwDnd5s+fb7lu9erVITWGiNwVruEu110H3H13eI5N3vjpJ5ZLJwpG8+ZiKN2WLdbbXH65/rVVbiKKPWlpgQ91rVLFutpivOjf3+sWkJes3t8ffqj1Dq5d23e9+tCialUx3bRJ9Fpq08b9Nsaq0qW9bkH0MFbSNevJJvOXDoIjeShcAu7p1r59e91P8+bNsWHDBjz22GN40K2s7UTkCmNVqGAZbyjKlQssjxFFvyuuEFWdiCgwSUnxmzuI/Bs0KPB9HnlEm4+1/H7VqgE9e/rfztgDlOJbWpo2n5NjXSm0WzeR761BA+19tGAB8NFHYr5VK2DpUpHKBADq12fAjZyzK8wB+M91ze9yCpeAg26qRYsWoX///qhatSpeeeUVdOzYEb/++qubbSOiELlVMcyYK6J4ceCrr9w5NkXeVVdp8+ef7107iOKF2ivDHzXfDPNDhc6NHEb+btCsPPqo+fLbbgu8gNGFF8bWsP7ixfW5tmbO9K4tXouHqqxukSuGnnee/WdczZrA+vXAJZeI1+3ba0NNk5LEcgZtyQn5fTJ9ur6YCyDeZzJ/I4D+9S/fXIJEbgjociM7OxujR4/Gueeei169eiEzMxOnT5/Gl19+idGjR+NiOcMlEUWN995z/5gXXwzcf7/7x6XApaUF9iR44kRt/tZb3W8PhVewgQKKHszpFjo5GXuwIhn8HDw4tHZ07OheW8wEW7WvYUNXmxFTYiEwFK40I6VK6V/7ew/XqBGedlDggf549a9/+d9m714xlXsbGy1bpm1H5BbHl+7du3dHgwYNsGrVKrz++uvYs2cPxo0bF862EZFL+vfXyqgHS36KCYinSWPHhnZMcsfp08CJE/bbNGmizZcsqc0zt1TsYS+p6BNofi7+H4auXr3wHr9MGeDccwPfT80xVK2ayH+qctob0kqDBr6BDjc9/LD+9dtva/OTJunXWVWOPXMGaN3a3XZFs0T+Ox46VJ+r0u5BQqlSwC+/ANu2hb1ZFOX8PTS0GpYMAM8+67vM+Dd45oz5vv/3f/rzDxhgfZ6qVWNv2D9FP8dBt++++w533HEHRowYgW7duiGFd2pEMcXJxeGMGebLCwtF5T3G2QMT6A1SKF/y/p50Git63XKLqBRGRKGT8xnZkYd2U2gOHQp+3xtuENOCAv3y++7TbsqaNg38ocShQ1oO1MOHtYTxAFCxovk+R48Gdg6VsfKj2+QE5XIvpZQU/UM4OfF4y5bAp58CixaFt23RIpGTrht70BmvMeWE9unpYkipWeEEClysBnuPHgWuvdZ+m7Vr9a/lh8QjRujXbdrkG2QzfqbXrSumQ4aI6e7dYhquHqBEVhwH3RYvXoxjx46hRYsWaN26NcaPH4+DBw+Gs21EFGG9e4un+0ZVqwLt2gWXMDoeGXv9WZFvuJzIytLmO3UKbN/8/MC2nzYN+OyzwPYhInO9e2vzxgC37LPPxI2CV0aOjO2HJ/KN0oUXBrZvhQrazap6IwboiwJkZWk5gYIZOtiokfYd2rix/vvUqqfbrl3Ojn3ypL6oUZcu2vxbbwXWTifS082Xp6XpvwPlSoqpqSJA166d++0h7912mzZ/6pR1ryKAxbbC6eqr9d85scLt/jr16/suM35uqUE7tbCc+rAi3D2liYwcB90uueQSTJo0CXv37sU999yDjz/+GNWqVUNhYSF+/PFHHDt2LJztJKIIMftSjNWnauHi9MIhmKFJwfL3f2QMyiUl8f+VyC3ykBm7oFvp0uY3CpHy5JOx/fBEDpYFqnVr894NToZ9pqdrw5MA+yIO5cuLaVKS/kGKlWbN/G8DiJ7TVt89TvOqqYnrnbAKmqxbp38tB+A4JCt+FSsGPPCA9rpOHeu/gwMHgIEDI9KshFSuHPDBB9rrWO61Jfdkc8LqYYBKTqVi5qmnxO8r0PMShSrgdMwZGRn497//jcWLF2P16tV45JFHMHr0aFSqVAk9evQIRxuJKILMvoh4IR2cjRv9byP3prC6cJKHqXbtGlxbmBSWyD2VK1uv4xP08JkzR/QWDKbHxC+/mC+3GyKofiYbP5vNeoSb2bfPfLn8PZubqx0/JUX0RlT997/afFaWGKKnkgMexop9l16qzcvDuS67TB9kdBqAlXvYXXABcOSI9lr9DqtZ0/kw63hhHMoW74zXglbDRQsLWdk1koIdoh4NAq0UeuqU/Xrjw2QWnqJoEdJbsUGDBnjppZewa9cufPTRR261iYiijF2+sFatIteOeCTnzZFv0OR5+XeckxPceVJTxZNpf/k0KPol2o1eNOrSRR8ckckX+bzxdFfVqlo+tkDdc0/g+6gFA+SgE6DvcWfseeFkCKx8vPPOA/78U8wXFDjvOWY3/PWyy7T5KVP06+QHME6q/QH6G+N16/S9NZOSRL6kRExXEGhah1jToYM2fFi+VnEqnIU/Ep38PRNLFYTlz8c9e0L/jlQDvx06iKn8QAAAhg8PLj8nkdtcif+mpKSgZ8+emDVrlhuHI6IIUofCGPXu7exL6osv3G1PpDz6qP9t7EqKu0W+WGrc2Hy5TE5oHYgzZ0TPuy+/DG5/ih68eIwuZj1U1aHlHMISPawKGdhRK+nZDWkyfofKvU6selkYe0rK1UDloLrd+8euWqRVkYk9e/TttQvqyT3p5ADf+ecDxYvrtx01Crj4YutjxSsvh4pHwtVX6yuUBmrTJi2gTO6SrwNiKbgpF9ioWtX/g+S8PPv1as/dqVPF1PiA5IYbgL/+Yo838h7fgkRkauxYZ9upyUlj2a23et0CQb6IMg4XMiP3ZvCX0+Oxx8SNEwM2sY+5+KLLoUP2edwoujnJh2QXsKtTR//6oov8H88umCYHuOQiBYCzlAWAFiw0qlEDcJqCWf5ul39H/PxJLHZD6a3+dg4f1vZt3tz9NpGe0x6rkda1q2/BB7vP2+3bgz+X8Tv4tdeCPxZRODDoRpQgAk20Gu8X1vLvw1/iVSO5V4KX5Cd6J07Yb3vXXeFtC1GiatjQN8dXMJUvyRvGoILVkEGr/Gx2PSj279fmnX4HO80XZ+fkSW3e2D4nQUEjY4qJeB9WmciuuML5tlbXHXLuQQq/88/3ugXmHnpIFLBxqlatwM+xebOYqr1vd+wQ027dAj8WUTgx6EaUIPwFZVR2VdliRfv2/rdx0h3fqlfYmTOBtcfIX/UlI7k7vky+sT/nHPNtmHOPKLzMkse/8IJIZh/vDy+8tHOnO8cx/h/J34FyoMxpsGrpUjFdu1YfqLMrMiD30pB7zgX7/jl+3PzYiqLdlBoZh2XJw1zltmdnaz2ZSHDSMz0WFC8uipU4cfasfnitHNxlMZnIiqYCJoGOpgi18qp6La9WW1YfONgNvyfyAoNuRAnCae6RPXvENNDAUDRxkrtHDrpZ5bUL9YbZrSTqVsm4nVR96ttXTI05eIgoMLt26V+rCZvNbhp69hTVMhl0Cx+z76hLLtGKHFSrBtx4o/m+dg+X5LyZ6vfhrl36/0u7YiZqDiLjME6r7xkgct+3p09b98JUb1pV8u9ILu7Qq1dsXx+EQ61awKuvet2K8Dh40Hy5sce//PfBNBaJKSnJf0EVY0EOf5VXrR52DB1qvlx9aMHvXoo2DLoRJQirp0lXXaV/rQZnYrnqnlxZzgmrgJTVMFLjzUmgrP4vsrNDO66Zhx4SN4Hx8iSeKFpY9S6lyGjQwHdZ3bpARob/fe1ykco3a/LQU7m3uJMHHoFo2dLd41l9d9WurR8aKveQKVVK/92ZlaXNy0G2sWOBJ58EliyJnlQLXrj3Xm3+1Cnv2uEmYy/+Y8e0ojBGVsspcTVqpP/cMCP3wgX8f5Yaq5GqDw2eeUZMjb38nn5aVIRmnlWKNgy6ESUINe+B0YABkW1HLJGfyF1yiXvHlYfxyMN0nOSWky9AnFZj4sUHkfvkHkNyTyCKjN27tXkngbZgyAUP/N1Mhpucpw2wfnhTtaq46TSjKPrhq8ZcbdOna/Pqgze119JvvwEffSQeUiUlAW3a+BZ6SBQpKaI3q8r4e4xVxh5q1atbD11kT6LoYew9Fq0yMkQOVJndZ8gLL/j+bRkrLr/6KtCli/a6e3dgwwaO7qDow6AbUYJwWlI81HxlscLLL2T5pqdp08D2lRPmWnXLDyZRNsWOWLnATiS8AY08tx4mOA2mOen9LRdOcNvo0frXdkM8rXqgbdyov4mVAyoHD4o8hKqqVYGtW0XPuKQkkR+0T5/A2x2P8vOBq6/WXlsFOWNFx45iasyDFeioAYq8atViJ39ZUpJv4Rq7XqJDh/p+t6q9lNXlXbsCs2e710aicGHQjShB1K7tbLtEqToV6hBRt4SS+0R+YigHS63yGBGR+4wJ6Mlba9aIqZqPzZ+kJPOgaTAJvt9/P/B97NjdkFr1rlIU3/yDqrw8YMwY7XVyMjBunJhX89QVK6Ylwq9Tx3mP6kRRu7bv7yTWctxNmaJ/7bTgkl1eQoq8BQuAuXOjO32IvyJugf7tfP018Omnsfc3R8SvUqIE8dprvssqVrQvNd62bfja4zW7RNjhEGhwTR52mpPjf3veGBFFlpqD8YsvvG1HopJ7qMl5ymRWy504dCj4fVVOq4ZbMRZjsCK3NTvb+t+dlAQ0bqxfZvxuWr0amD/feRsTydSp+r/3UCsveqV7d+fbyj2rnY4Q4IOIyGjf3v4aPhr4q2RrHC5qtHGjmKo5FCtV4oNlik28TSNKELVq+S47cMB8uWr6dODHH8PXJi+FKweQFbvE3WYuuECbN0sYHurxiSg08ZI8PVa9/LI2b5UWIZiHEWqgy5h7KBjNmmnzdgEaObARTCDHWITn//5Pm09JAX791fmxGja0vy5IZAMG6P9PnQZFvVa9uvMUI0bBBI75/klcgaZu8VeMRR3WP2FCcO0hihYMuhEloEaNgIED/W9XvTrQqVP42+OFMmXMlz/2WGTbQUSxiXncvCVXj7V6iFKjhvlyu2CcmivTaaDKbhir3BvPrtiGXOjI7oGQnK/TGJy79lptXs7Nlp4eP4n+o0209zJStW8PPPec+bpBg4I/rlWAuFGj4I9Jsc2YusXfQ4S8PP1rq78pft9SrGPQjSgBrVyp5XGJZZdd5v4xoyVPxF9/hX6Me+4J/RhEZE6uXkresuqNY9UTyUnicadFhRYscLadVeGH48f16Q7sqvnJQUS5IA8Q/He6GoCMdMoF8o5cQKNFi+CL82zYoH/93XfAt986651P8cE4XN3IX29jY1VmonjFoBtRAkpJif2nRmXL6odUPvywNh9KZVL5YtQJuxskf93mjQoLtXk1GbhTam+LmTO1ZT17BnYMInLOWIXtggti/3M11h05on/ttDKpE3JgL5QCOGbHHTBAe21XMXLyZG3eqre2mapVxbDRu+7yXTdgAPDKK8DNNzs/HsWWffv0rwO5zjlwwHpd/fr619dcI6pJUuJYudJ+vfF70oi9cClRMOhGRDpu3qSE05kz+mE48tO0UCpsyTnswpUk2epm6aefgj/ml1+KqdOKfUQUGmOA56efgO3bvWkLCcbhpPJnrfz/5TSnp/wdULWqNl+xorP9nRTBAYDhw7V5Y88Q+eGJXe5Ou5vX0qWBdeuAdu1816WmAo88Yt0Tj6wdPy6mhw6F3mOnZMnQ22OlenX9a2MvXfX9bOzxVlhoP1Q0mqtmkjcCzR3IoBslCgbdiEjn7beBIUO8boV/J044GyJk1SNB7lVmtXzvXvNt5EpxThMpy4mu5Qve/fu1eSc3cnJvC7PhQLFaTY0oGu3aZb1OzpsFiCf6NWuGtz1kz9jzWP48lAsjGHvoWH1uyp/vwQSl5ECM3feVXc+53r2dnSvQXtoUOvUh3Zw5zh72tW5tva5PH/Pl99wD3HBD4G2TnXuu/rXx/abmGzQOqVYU+967wQ5Lpdj14Yf2eQCDLVKm9ohTr6/VYjChjFwhiiYMuhGRTsuWwKhRge0zebLzGwO3GC8iZfIN1HffafNy8Qj56Zp8oSmXL2/aVJuXg2PyE2m7dsjkBNgyuUqpv6FpWVn6m8W33xbTTp1EXhaAN15EoWjXTl8V067nb/v24W8POWPVA+yXX0I7rlUvDKc3lr16afNJScDQodrrhQuDb5cdJ73VP/4YmDIlPOdPJPJDOifDfTt3tg68dejgSpNMpab69syVBTJUWcaASPxwUlwNED3ZwvH//v33YqpeEz/1lJi++ipw+eXun48o0hh0I6KQ3XEHMGOGt22Qh+RYDfO47TZtXu61IN+wyUErOQgmH1++qTHmSrFi1ZNBHZ5iZNbzYupU895t9eppRRMYdCMKXlISCyTEIqvKjHJvZfkz3OmwuAsvNF9uHEJlrNinatXK+thO2uD081zuYWlVsVV2883Av//t7NgUODlHn5WmTbWHZUD480HKPT1lxmsNu88/ed3Zs85GG1D4yf+HdjnW5AfJRl26OD+f1XVrKNSH2cbe5b17h+8BBVEkMehGRHFBHtrRrJn5NnIPtfx8bV6+cKxdW5uX86PJeU3kAFowwznlIRnyBYbcm+70afN95Z57VjdtagVWf1WjiEifxxGwHnpO8SOYvJ92n/VjxmjzL71kvd2ff4rpunX258rMFNNLLrHfTs3V1bat/XYUOUlJwN13+9+ufHmgY0fzddOmOTvXsGHW6667Th8cdhLUO3rU/rpBPoZdgQWKLLlHrnr9B4iA1b33aq/feced851zjjvHMaP2omNAl+INb8mIKC7IN1FOcu/IPQisbqbk4JrVBWswT6dXrdLm5eCf2quialWgTh3zfa0udNUAXGqq6MEweLB50myKTVY9bih0tWrpXxuTjlPisBuCl5dnvU5+D913n/V2S5aI6YoV9u1Qc9PJ30FmCe3V7x9WzfWGVQ9H2YQJgR9XDjgcOQIcPqy9loMqjRtbH+PRR63TWrjBzQq+FJp4HOHAh8YUb/iWJiIAiVeFSv5Cd1oMwS1ykE+9WZo3T2uTXVd6uWecemNWuTJw/fXAE0+Ip9tZWSIPBqvRxY+pU71uAVH0O3pU/zrQYNTYsdbrTp3yv39aWvCJxP256y7fZQcPhudc5IyToehXXKHN26XhMEsdAQC7d+uHD8+a5axt4S6qxJ5IsW3cOG/Oy57klKgYdCOKU4GUnx86FPj88/C1xUuhXnhGqgeB/MQ6NVV/86gGBc+cARo0EPMpKVpPtn79xHCk0aN9q/dRfLj4Yq9bQBT9jL0W5YrQcq9iJ+T0AoCz3qYPPxzYOQDrVAJGxsqSgHnvN9WXXwIjRwbeHnKXPPRvwwZt3nhtYlUMBPDNIehEuIK/FB+MOf4i1XNRzrNJlEgYdCOKQz//rA1jceKFF4Bu3cLXnnD5+29t3uyGBAjuwvOFF7T5pUu1eTUwmZSkDUHLzdXvaxXs3LFDm5cTXVsFBdUKTu3ba6XUs7O1yrL33AO0aSPmrSrsEZFQsqQ+1+MXXzjbz6oHMIfzRSfj568cdDMG5FTy0L077tCv+/VXbd5ffjUn1J5RctVrebigGfW9FmgOreuuA558MrB9KHKC7aVo11NIfo/WrRvc8QMR6VEC5J7y5fXDj51UPXYDhyVTomLQjSgOtW1rX6Uolg0apM3LlUOtgl3B9Py69lptXi6s0L07cP75wCOPiF4EgTCr9jRihL7SqlpIISVFnAcQ55Jv0NQLoxIlgAcfBDZtcpZXhijRyDkN+/QBevTQXl9+eXDHnDJFTNmjNHrJSb7VggSAPkAgDwuUk9Z36qQ/1oIFrjYNN9wgpn36aMv8vZfUhy7qzer559v3fGVAOHLkokgqf73r1QeE8rWFU6VL6wPBxjyD//mPNl+smDtDTK2GvQLApZeGfnwKH/ka2Z9wD0e2sn27mPJzi+Idg25ECaRECeun/bFCDUzt2KHPc2LV080pJz0CihUD1q4V1aBathS9KB580Nnx1Z5rssce0988vfmmyP9SvbqW3618eW340f79YojTffeJ86akAPXrOzs/UaL5+GP3jxnOqm0UPPXz//hxYPp0bblcYMeqwp88vLOgQD+UzzgEyy3JyVovSrPiDU2aWO+7dCnw00++y4sXF98HTzzhThvJP7uAlJXly8X0m28C3/fYMf371argkkoN0OXkBH4ulV3euh49gPHjgQ8/DP74FDqrogP+AmnZ2dp82bKuNcfx+QGtCESketoRecVBClAiihf79nn3NMstao82Yx4cq6pzck8yOx07asNK1XOcd552c9a2re8+O3eKC4Y33tCWyU+eL7wQWLNGzFsFBZ9/XtwoVagggnjqzZQ8rE19mty4sVgeTDU0IqJ4V7++PjAqf47KDyjscp7WqaN9bt9zj3WetsxM3/QCgVBvcs1yHL39NvD77+b7lSljvjwlRfR8psgxFu5QFS8e+LHkVBhWQRQ1p6vKae+g3buDf2Dgr4rkwIHBHZfcYxcwk4fPG4trye8ff8Pcg1G1qvagXGUVqGZPN4p37OlGlEBKl9YPtwmnli3Dfw4nT+bseoINGWK9z8KFwP33i3Ns2wY89JDvdunp4kJh2DDxukkTfc+3H37Q5rdt0+ZPnNDm69YVw0yNFxz33gvceSfQooXIu7F/v6hQSvHvrrtEr0ejH38Ennsu8u2JF04fOATTe4Wi07//rc3LuTSNxo/X5keM0ObDmaZBHTZqFqCpUUMbikqxJ9CUD5Ur668BjJVB1YeMwQYmpk0DqlSxXm+Xm42fh7FNLiBjFbA3uvzy8PXq9jcqRU39wCAcxRsG3YgoLJYtC/85nCRkTU/XhtTKSbUB4LLLxLRmTa1ruzqc6PLLtW7vtWvbn2v4cDHkZ9Ys4LXXtOVVq2rz//qXNu+k8EHNmsCkSdrTR3a9TxzvvCOCrkadOtlXuCN7cu9Yu54ogVR+puhVr57/4Xdm5IBJhw7W26k3jwUFWnL7Xbt8t7MqUuSvB5ET6vcVb1BjW/Hi9gUS1GuRYBUW2vdkMstNR7FJ7s1m956y8+qr+lzCblKLfUyaJKbt24up+p386qtiCDYLLlC8YdCNiKKasTv87t3+97G60EhJ0fd8uPZaMRy0fn0xdPPvv/XBsUBccokI7lnd/IwZI6atW7PaKJEX5ACMXfL6cOS2ofCYO1erKm0U7uqNahDj9GntAYtZ/qsPP9SGfVpVwwWAceOATz7xXV6vnvhe6djRd92YMcDMmb7fkxR75PyDRna91GTslUbyaJZgg25GVg8OnNi61Xy5+jD82WeBDRu0z7CMDH2lcaJ4wZxuRBTVOnQAvvtOe/3jj+bbHTyozRuHZtiRb1bMih0EY8QIrWt+376id1JaGrB5s7gguvNO4M8/3TkXEXnnqadE7kfyxpVXiulbb2nL1MCWWR7OsWOBX35x59zt2onezX36+D5sKV9eSweQmandCA8eLIo91K/ve0MsV+aW1a4tetWZ9fyoVAno1Su0fwd5R84JZ9cTzWkhhOrVQ2oOxbB27YCff9Yvq1FDP5zTbsSEXfqFr76yL6hhZ88e/Wt1hIn6UCQ1ld+hlBgYdCOiqPPUU8DIkWK+YkXg/POBdet8tzt+XJuXn/A2bhze9vnz7LPavFzVq149MX3tNRFMZO8EoshxOoQqkErI//lPcG2h8ClVCli/Xvu8ld1/v/hxg3oDa9YrY/t288/3884DPvhAzKtFfuRqqVY41Co6lS1rXUzBTIMGoleP/Nqf/fu1YNr69d4PJe7dW/SupNhjN6Q9kIfVVo4d831/Nm+uf3311cCpU6EPmSaKNRxeSkRRzW4oppzoVb4pMV5YOH1KHCl165oXZiCi8EhPF9WGnVAT3FPsatDAeQVJdZhTKNReIOow01Kl/AfK0tOBO+4AXnkl9POT95wE680K5PjTuLG+l9FNNwV+DDvGSvD+9O0rpuxVF9uMPW2Nn1cHDljva7UuK8s3J6rZ0FQG3CgRMehGRFHH2M3dLDm1kVW11PR0JkYnShQXXmi+vHhx4LbbnB1Dri5M8e+JJ0I/Rv36IjH4Y4853ycpCZg8OTKVvin87KrjqoxDSNUe+oHk3nJyHiM1eb2ZI0cCO9Z114k8XXzfxjZ/xbns8gNarTPLh+p1z0yiaMGgGxFFHXXYjcpJLonevc2XFysmboaqVxd5ddQKpm5UjiOi6PLtt9brrAJystRUMZxdxnwz8S2YwhnGnhpJSSJXJ4vkJBanvSlVxgeKau+iQIa0GzlJUxHKg0dj25KSgqsKTN44dMh8ebFizgtvGHvBGa/RreTmiukFF7DyOhFvO4nINePGmS83q7pmp25d4Kqr/G8nPx22e5rWrZvoLZeeLnoijBnDG2ki8lW+PKuXJjonvY74HiEA+O9/A9terWKrclqV1I7TXnJ2OS2t1p08CdSsGXibKHrY5WqzCsj5Ywy6qg+qjEHoU6fEdMEC4I8/gjsXUbxg0I2IXDNwoHvH6tNHm5eHP/Trp8337Bn4cStWBB5+mD3diBLBlCnW69q10+bduPml+KDmZfNHfXDD9AWJq3598+VyjzY5R6QahDBy2uMI0CrhqpzmZKtQwXqdVW85tacSxS5jz22n8vLMl5u932bMEFOr6+qsLOefq0TxiredRBT11CGhANClizZ/8cWRbwsRRY9//cv+c8Dqptho4kQxZf4ZcvoeeOABYOFC0TObSCZfszh5Px0+7PzYxqHNTgu/2AXn7Ia3miXCp9ixZ09w+8lVdmW1a/sOkyYi/xh0I6KwO3o0tP0vvVSbv+yy0I5FFMsC6RGRCBo3Bpo1C/04HEKVeDp31ubVm8hAKjmmpwOXX+5umyg+2OWhLVXKd5ldvslACh3YBUPsvjuMgcF779XmmYsrtlnlHVQU4NVXrfezGw3CXmtEgWPQjYjCrnTp0PZ/+WVt3ulTXaJ4VL261y2IPnKgJD8/vOdSjx/u81Bgjh0TU7u8VUa1a2vz6g3mkSNa78g2bdxpG5HMWMEUENVArQTyWVO+fODtMdOihTvHIW/Mnm2+XC6IUFgI3HFHcMdv3jy4/YgSGYNuRBR2oeZPkwNtgVYLI4ongQQVEsW2bdq8HEgJB7Vqm1lvFfLOiy+K6fz5we0vJxsvVkwEQX78MfR2EcnS0kSFZKMTJ9w5vvHYxqqTwcrMBM45x51jUfg1amS+PCUF6No19ONfdFHoxyBKNAy6EZFrwp0PqXx55+fgkAiKR+XKed2C6NOwoTZfvHhkbg7d6lFC7lBzYmVlOd9HzmOlzh84IKZ16rBAArmvWDHrzw5jrrZgGIssyOyG4fsbQbBihahASbHP6oGR8eH4ww+Hvy1EiYRBNyIKu127At9H7dGj9iwBAks2PGcO8O23gZ+XKJplZHjdAmte9UKVeykRObV3r5gWL65Vr2XORAqWXTECmVWONjceqBh7ul1yiTZv/O6Q8xH26GF/3Lp1mdog3hmDbs884007iOIVg25EFHZmwyn8US8Q5ZL1F1xgv8+sWcB334n5iy5ypxs9EUU3PpEnf8x6SA8aJHr41K2rBW7lXpOqKVPEdwuRkRyoUAO3/pw65W4b7HK+jR9vvW7wYG3eahhqXl5wbaLo4bSCtxEreRO5K2aCbocPH8Ytt9yCzMxMlC1bFnfccQeOHz9uu88777yDDh06IDMzE0lJSTgaaglFIgrK+eebL+/fH2jb1nf5iRPBPfXt3h245prA9yOi2MUht6RWtTZLUv/778Aff/gu79YNyM4GSpQQOZBWrABuv913u3//W3y3AEC7dm61mOJBvXravNOevmqgzi7fWiBDm9XPP7N9KlRwfhyZ2racnOD2p+gxaJD/bcqUCX87iBJdzATdbrnlFvz999/48ccf8c0332DRokW4++67bffJy8vDNddcgyeffDJCrSQiM1Y93W6/3XzIQtWqWkXCffvC1iyihHPrreE7dmFh4PvIRRCIgvXQQ2JatqzvuosvdlZtr0kT/4nnP/nEPIBHiSlcvYGMFd///tt62+nTxdTN4i5qonyrB6YUO8weRFi54grrdcFcO1x4YeD7EMWrmAi6rVu3DnPmzMHkyZPRunVrtG3bFuPGjcPHH3+MPXv2WO730EMPYciQIbhETmpARBHnJO49aBDwwANivmRJoGZNMe+vg2rz5sD114fUPKKEEc5nUFWrBr6P0yFZRHbcqtLoT+XKQIsWkTkXkapjR+t1atEotQiIG5o3BzZtAm680b1jUnh5+V2qPiSfN09M1et3fwU6iBJJTATdli5dirJly6Jly5ZFyzp16oTk5GT89ttvrp7r9OnTyM3N1f0QUWisypfLrrlGnxBdfYJ83nn2+y1dKnofECUCRfG6BdaaNPG6BURE8ccuoKIODXTzuyEpSeQCY16v2PHSS8CoUfYVbMNFvVVW8xXWqhX5NhBFu5gIumVnZ6OSoTxZsWLFUL58eWRnZ7t6rlGjRqFMmTJFPzXVcD0ReaZYMTHduNF3XWpq5Ho5EHktmqsrjhrldQuIiBKLcfhgIPnggOh+kEPO1akDDBkSHYHSSZOAV1/1uhVE0cXToNuQIUOQlJRk+7N+/fqItmno0KHIyckp+tm5c2dEz09EvtRcJcY8J0QUPZiMmYjIXWlp4Tnu2bNi6nLfBYpBbhfMOP98fXVcIgKKeXnyRx55BLeblYqS1KtXD1WqVMH+/ft1y8+ePYvDhw+jisuD2NPS0pAWrm84IrJ18KCYHjigrwpm9OSTIjk2EYXHu+8CAwaI+fLlgcOHzbdr0gRYuTJy7XJiyxYxdVpNkIjIC06Kz5w5E3xvtDNnxPT4cd91ai44NTX2FVcwAJdo3Cy+QUT2PA26ZWVlISsry+92l156KY4ePYo///wTLf6Xwfann35CYWEhWrduHe5mElGYGC/wvvpKTGfNAtQUjmY3+yNHhrddRIlOzgtzxx3Ayy+bb5cchUkqMjKAY8eAChXcP7Z68+t2zwAiim15eYHvI1/fFLO4I6tTJ/Qq7uec47tMLXyjnnf2bK33GyUGY2qW/Hxv2kGUCKLwctnX+eefj2uuuQZ33XUXfv/9dyxZsgSDBg1Cnz59UO1/j2p2796Nhg0b4vfffy/aLzs7GytWrMCmTZsAAKtXr8aKFStw2OqRPRFF1Nat+tfqDa2iaPMsWU/krSeesF5XsWLgx+vQIeimeK5FC6BhQ6BfP69bQkTR5ORJZ9vJVUZ379bmI90z15j7Kz2dPZ8SnRrcZS9xIvfFRNANAKZPn46GDRviyiuvRNeuXdG2bVu88847RevPnDmDDRs2IE961PTWW2+hWbNmuOuuuwAAl19+OZo1a4ZZs2ZFvP1E5Jw8lCIaksISxZJgcqs98IAYRmomNTW09hg9+6y7x4uk6tWBdeuACy7wuiUka9hQfFdcdpnXLaFE1by5Nm8sbmCmQgVtiCdRNFC/6+Ve4gzEErnD0+GlgShfvjw+/PBDy/V16tSBYkh6MHz4cAwfPjzMLSMiWdOmWtnwQKld248dc605RAnhzTeB++4T88OHAw8/7N6x5QIm8+eL3D9E0aRhQ5G/ipWsyStycMLJw8LkZPvtatQAdu0KvV3+yKkEiIgoPGKmpxsRxYYFC4ClS51vf/SomJ49C9SqFY4WEcW/jh21ebsiJFac5iOqXt3ZdnZ/y6xVROHAgBvFk2++0eaNNePuvjv049eoIVIHPPVU6MciIiJ7MdPTjYhiQ6BD29ReceXKud8WokQUTPAhmECdna1brdsh/61HYyEGIiKvyXm1Lr9cv05NTR1sVVNAfD6PHh38/kRE5Bwvd4koKmRkeN0CovgXyk2amZ07tXmrv+Fevaz3DyZhc+fOwJAhge9HRBTNWrUyX24chqqm4pCH/leq5P/4554LlC0bVNOIiCgEDLoRkWeMQyaIKLwqV3b3eOeco83LN4CyLl1E1U9VqIG/mTOBSy4J7RhERLHOLMm9XaqABQuAv/4KW3OIiMgCg25E5Jnu3f1vI9+gn3de+NpClAjkHhNHjoR2rBtv1Od4c9przeq8TZqE1h4zOTli6jRnHRFRPDALyFWrBtSpE/GmEBElPAbdiChsOnf2XVa+vDbvJPeUOnztrbeAd991p11EsUotPOIGq8p5qanO9i9eHGjcWH88uRJeoMXDw/H3rQbt69Z1/9hERFbk4FazZtp8MSmbtpMqp2bOnPG/TVKSdo1VrVpw56HYVK4cUKEC0K+f1y0hIhWDbkQUNjNmAJs365cdOuRsX3XoqVrp8J57gIYN3WsbUSxSC49EC7sqelWrunceOZjnlgMH3D8mEZHRHXdo8198oc3fdFNwx9u1S0zT0+23q1ULmDQJGDo0uPNQbCpdGjh4EOjWzeuWEJGK1UuJKGzKlAm8mikRec9JTwpA32sjnHJyxI3E8ePuHbOgQEzLlAGOHXPvuEREVq66SpsPtgdayZJi6q8oQlIScOedwZ2DiIjcw55uREREpFOjhrvHk6uc2rnlFnfPa0cd2lWiROTOSUTkhPqAQc1L6c/Bg+FrCxERhYZBNyKKGrVqiSlvgonii5wn7txz9etuuEGbZ68MIiLg9GkxlStE22nUKHxtISKi0DDoRkQRd8EF5ssHDrRfT0SaWbO0ebNKddGqUiWvW0BEFBuSeadGUe6ii7xuAVH040c5EUUNNU9JsBW9iBJJ9+7afLQH3dq397oFwduxw+sWEBERRaesLPEwbfx4r1tCFL0YdCOiiDt6VJtfuFBMrRKkc6gpUeQpirvHe+MNd4/ntsJCMTX7HFKHxlauHLn2EBERxYrsbG20ChH5YtCNiCKuQQPfZYcO6V9Xrw7cfTfw5JORaRNRLEhLC3wfpzmBZPv3B76PncxMd4/nNjXoZhZYy80VU/bAJSKieBXKwzZ+PxLZY9CNiKJSsWLA22/7Jl0nSmQdOwa2fYcOIngdi669NvLnNBume955kW8HERFRJOXled0CovjFoBsREVGMkKuAOnXihPvtCFb58s62e+gh4OuvQz/fmTNimp0d+rGIiIhiTevWwPXX+9+uXr3wt4UoURXzugFERERE4VC9uphy6AsRRZNwPQxp2hRYsSI8x6bY9PPPrIJL5DX+CRJR1OHFAVH0uugir1ug9WCTi7KY4WcJEUWjcuXCc9xvvgH+/DM8x6bYVLw4kJIS2jGOHBHTs2dDbw9RIuLlKBFFjYYNgS5dgHvv9bolRLGhYcPIn3PSpMif06hCBTE9dSr857rvPlHAgr3liMgt4Qq6Va8ONG8enmNT7GvTRkwzMgLbT82vrBYdIqLAMOhGRJ667TYxLVZMJDGfPdubQAIROVMsChJTlCgRuXM9+CBw/Dh7zRERUWy7/35g2zbtwZU/x4+Laag95YgSHS8hichT55/vdQuIEkfZstbr1OEjZi64wPWmxJRoCDQSERGFIjkZqF3b61YQJR4G3YiIiBJEcjKQmWm+zq6HqVx1tKBATA8fdq9dREREFN04vJQoOAy6ERERkWOKIqYNGnjbDiIiIgo/tYDC/v3etoMoVjHoRkREREVDSJ3mLmOOFyIiovhXo4bXLSCKbQy6EVFE3HyzNl+ypHftICJN27ba/EsviWnJkkBWljftISIiIiKKJwy6EVFETJ0KbN0q5l94ARgwAChTxts2ESW6xx/X5uW8bXIwLhGoeWqys71tBxERERHFFwbdiCgiSpYE6tQR840biyCc02FsROSfXGGzffvQjpWUFNr+sUbt2Zdo/24iig+pqV63gOJJWpr9+quuAs49NzJtIYoHvOUlIiKKA8OHa/Pjx7t7bLViabwqXtzrFhARBa54caBrVy09AJEb/AXdvv4aWL48Mm0higfF/G9CRBQ+6eliyqTsRO5Re73t2ePO8bZtE1P2piAiih7JycC333rdCko0aWn+A3NEpGHQjYg81b8/sG8f0LGj1y0hih8VK4qpW0O4MzLEtFw55j0jIiIiInKKQTci8lT58sDo0V63gii+FIuhb3dF8boFREREREThwZxuRERE5Jkd/9/evcdYVR94AP/eERxQmBmoPHVUBBStL0SlYtPiiyqN1aZR29AqxmK3C3SN/rHSNNrWWNKt2dpWW/sS+nLjH8bamIhVsdKiFZWq1Sitj/U9IkUYwBWEufvHLGNZZBjgzJx5fD7Jzbn33HPP/d6EHzP3O+ec38utSxOrAD3Z176WTJnS+e8zd27r5C9O7wPoGfyKCwCUZut1HYcPLzcHwJ645ppk6dLdf31Hj/qdMSNZubJnHdEM0Jcp3QCAbm/9+rITAHSe555rXTqCDaB3UboBAN3e/vuXnQBge+edV8x+6upalw0NxewPgO7BgckAQLfQ0tK6XL16++cGDuzYPjZuLC4PQHv+/vdk5MjO23+l0nn7ho7y7xD2jNINAChEc/Oevb6+vnW5adPu76O2ds9enyR33PH+UScAOzJuXOfs96ijklNOSWbO7Jz9w644//xkyZJk6tSyk0DPpHQDAAq1u38V33ffPX/vkSOTdev2bB+f+tSe5wDYXQ0NyeLFZaegLzjttJ1v09jY+scoYPco3QCAQjkVBejLhg5N/vu/y04B7XvuueRDHyo7BfR+SjcA6KNWrmxd/s//lJsDoDe56abkv/5rx887fZ3uYOzYshNA32D2UgDoxc44Y8fPbZ24YMyYrskC0BeccELyn//Zen/q1Nb/YydPTvbeO/nXf02uv77MdAB0JUe6AUAvdvLJZScA6Ls+/OHkhRfef3zjjeVlgR3ZOhHSli3l5oDeyJFuANBDvfRS2QkAgJ7uwANbl1uPgAeK40g3AOihamtbr8fm+kAAvde//Evr//fQWQYMKDsB9F5KNwDo4SqV5K23Wu9v3FhuFgCK9aMflZ0AgN3l9FIA6AW2XoflgAPeX7c7p4lUq8XkAQCAvk7pBgC9SM0//WTfvHnXX79+fXFZeoqBA1uXEyeWmwMAgN7F6aUA0Es1Nm6/busMZTsyfnznZOnOhg9PnnwymTCh7CQAAPQmjnQDgD5o8OBk06ayU3QfRx2V9O9fdgqgLznuuOSQQ1rvf/rT5WYBoHMo3QCgD6qpSVatKjtFef72t9blXnuVmwPou+67L1m2rPX+f/xH8uqr5eYBoHhOLwWAPmrr9d9GjCg3Rxnq6lpPtd1337KTAH1VQ8P79/v3T/bfv7QoAHQSR7oBAIXbsKF1uTszqAIAQG+gdAMACrd1FtStM4MCAEBfo3QDANq1J0erDRlSXA4AoHj19WUngN7LNd0AgHZt2VJ2AgCgs3z1q8nQoclBB5WdBHofR7oBAO1qbCw7QfFqa8tOAADdQ2Njcu2170+wBBTHsAIAOmzNmtblunUd2767TqTwgx8kZ5xRdgoAAHozpRsA0GHvvtu6HDu2/e02b25dvvlm5+bZXRdckPz+92WnAACgN1O6AQC7rFJp//n99+/YdgAA0FuZSAEAAABIkkyblnz842WngN5B6QYAdInVq8tOAADszN13l50Aeg+lGwDQJQ4/vJz37d+/dfnRjyaTJpWTAQCAvkfpBgB0ia6+vtvRRycXXpjMnt36eMkS15gDAKDrKN0AgG5hayH20kvF7G/gwOQXv9h+/wAA0BXMXgoAdAvDh7cuBwwoNwcAABRB6QYAvUC12rrctKncHHvCkWgAAPQmSjcA6AW2FlZmCAUAgO5B6QYAvcCIEWUnAAAA/pnSDQAAAAAKpnQDAAAAgIIp3QCAXmPvvctOAAAArZRuAECv8Z3vJNOmmQkVAIDyKd0AgF7jrLOSu+9WugEAUL4eU7qtXr06M2bMSF1dXRoaGnLJJZdk/fr17W4/d+7cHHbYYRk4cGAOPPDAfOUrX8natWu7MDUA8P/ddFMyc2bZKQAAoHP1mNJtxowZefrpp3PPPffkzjvvzJIlS3LppZfucPvXX389r7/+eq677ro89dRTWbhwYRYtWpRLLrmkC1MDAP/fl76ULFjQer+lpXVZrZaXBwAAOkO/sgN0xDPPPJNFixblkUceyfHHH58k+cEPfpDp06fnuuuuy+jRo7d7zZFHHpnbbrut7fHYsWNz7bXX5vOf/3w2b96cfv16xEcHgF5N6QYAQG/VI450e+ihh9LQ0NBWuCXJ6aefnpqamjz88MMd3s/atWtTV1fXbuG2cePGNDc3b3MDgO5o0qSyE+y5Aw4oOwEAAHSOHnG4V1NTU4YPH77Nun79+mXo0KFpamrq0D5WrVqVa665pt1TUpNk/vz5+cY3vrHbWQGgqyxYkCxfXnaK8n3rW8mwYWWnAACAbZV6pNuVV16ZSqXS7u3ZZ5/d4/dpbm7OJz/5yRxxxBH5+te/3u628+bNy9q1a9tur7zyyh6/PwB0hsbG5Jxzyk5Rvnnzki9+sewUAACwrVKPdLviiisycyfTlx1yyCEZOXJkVq5cuc36zZs3Z/Xq1Rk5cmS7r1+3bl3OPPPMDB48OLfffnv69+/f7va1tbWpra3tUH4AAAAA+CCllm7Dhg3LsA6cD3LSSSdlzZo1eeyxxzLp/y5gs3jx4rS0tGTy5Mk7fF1zc3M+8YlPpLa2Nr/73e8yYMCAwrIDADu29fKpe+2VVCqt9//p0qwAANDr9YiJFA4//PCceeaZmTVrVpYtW5alS5dmzpw5+exnP9s2c+lrr72WCRMmZNmyZUlaC7dp06Zlw4YN+fnPf57m5uY0NTWlqakpW7ZsKfPjAECv9+lPJ7Nnt57+2q9fcu+9yXe/W3YqAADoOj1iIoUk+c1vfpM5c+bktNNOS01NTT7zmc/k+9//ftvz7733XlasWJF33nknSbJ8+fK2mU3HjRu3zb5efPHFHHzwwV2WHQB6qyFDkrPO+uD1N9zw/uPTTuu6TAAA0B30mNJt6NChueWWW3b4/MEHH5xqtdr2eOrUqds8BgCK9+KLyT77tN7/6leTX/+63DwAANBd9IjTSwGA7qm+Ptk6R9G11yYvvFBuHgAA6C6UbgBAm02b9uz1e+1VTA4AAOjplG4A0EttnTV0V9TWFp+jPbuTcdWq1uX/XcYVAAC6pR5zTTcAYMf6/dNP9H33TY4+Ornyyl3fz/DhxWXqiLlzk7//PRk6NNm4sWOv2by5dTlmTOflAgCAPaV0A4Be4KKLkmefTT7+8dZrrD3xRNmJOuZjH0sef7z1fkdLNwAA6AmUbgDQC4walSxc+MHPHXpoctxxXRoHAAD6PKUbAPRyTzzx/gyjPdW6dWUnAACAXWMiBQDo5QYM6Pmzio4f//79rQXiPvuUkwUAADpC6QYAdHuf/GTrcu+9k9NOS66+OrnwwnIzAQBAe5RuAECHDR7cuhw2rGvf99//PXnrrdaj9gYMSL7+9aShoWszAADArnBNNwAglUrr8qCD2t/u4x9Pbr01+dSnOi/LB5VplUqy336d954AAFA0pRsAkPr65Oabk7PO2v65r3wleeGFZODA1mvDnX9+52W44opk1qzO2T8AAHQlpRsAkCS5+OIPXn/eea23zlapJNdd1/nvAwAAXUHpBgBs5777khpXfgUAgN2mdAMAtnPqqWUnAACAns3fsAGgjzr55NbluHHl5gAAgN7IkW4A0EedemqyaVPSv3/ZST7Y9dc7xRUAgJ5L6QYAfVh3LdyS5N/+rewEAACw+5RuANCH/O53yRNPlJ0CAAB6P6UbAPQhZ5/degMAADqXK6UAAAAAQMGUbgAAAABQMKUbAAAAABRM6QYAAAAABVO6AQAAAEDBlG4AAAAAUDClGwAAAAAUTOkGAAAAAAVTugEAAABAwZRuAAAAAFAwpRsAAAAAFEzpBgAAAAAFU7oBAAAAQMGUbgAAAABQMKUbAAAAABRM6QYAAAAABVO6AQAAAEDBlG4AAAAAUDClGwAAAAAUTOkGAAAAAAVTugEAAABAwZRuAAAAAFAwpRsAAAAAFEzpBgAAAAAFU7oBAAAAQMGUbgAAAABQMKUbAAAAABRM6QYAAAAABVO6AQAAAEDBlG4AAAAAUDClGwAAAAAUTOkGAAAAAAVTugEAAABAwZRuAAAAAFAwpRsAAAAAFEzpBgAAAAAFU7oBAAAAQMGUbgAAAABQMKUbAAAAABRM6QYAAAAABVO6AQAAAEDBlG4AAAAAUDClGwAAAAAUTOkGAAAAAAVTugEAAABAwZRuAAAAAFAwpRsAAAAAFEzpBgAAAAAFU7oBAAAAQMGUbgAAAABQMKUbAPQgjY1lJwAAADqiX9kBAICOu/fe5B//KDsFAACwM0o3AOhBDj207AQAAEBH9JjTS1evXp0ZM2akrq4uDQ0NueSSS7J+/fp2X/OlL30pY8eOzcCBAzNs2LCcc845efbZZ7soMQAAAAB9VY8p3WbMmJGnn34699xzT+68884sWbIkl156abuvmTRpUhYsWJBnnnkmd999d6rVaqZNm5YtW7Z0UWoAAAAA+qJKtVqtlh1iZ5555pkcccQReeSRR3L88ccnSRYtWpTp06fn1VdfzejRozu0nyeffDLHHHNMnnvuuYwdO7ZDr2lubk59fX3Wrl2burq63f4MAAAAAPRsu9IT9Ygj3R566KE0NDS0FW5Jcvrpp6empiYPP/xwh/axYcOGLFiwIGPGjEljO1O/bdy4Mc3NzdvcAAAAAGBX9IjSrampKcOHD99mXb9+/TJ06NA0NTW1+9of/vCHGTRoUAYNGpS77ror99xzT/bee+8dbj9//vzU19e33dor6AAAAADgg5Raul155ZWpVCrt3vZ04oMZM2bkL3/5Sx544IEceuihOf/88/Puu+/ucPt58+Zl7dq1bbdXXnllj94fAAAAgL6nX5lvfsUVV2TmzJntbnPIIYdk5MiRWbly5TbrN2/enNWrV2fkyJHtvn7rEWvjx4/PRz7ykQwZMiS33357Pve5z33g9rW1tamtrd2lzwEAAAAA/6zU0m3YsGEZNmzYTrc76aSTsmbNmjz22GOZNGlSkmTx4sVpaWnJ5MmTO/x+1Wo11Wo1Gzdu3O3MAAAAALAzPeKabocffnjOPPPMzJo1K8uWLcvSpUszZ86cfPazn22bufS1117LhAkTsmzZsiTJCy+8kPnz5+exxx7Lyy+/nAcffDDnnXdeBg4cmOnTp5f5cQAAAADo5XpE6ZYkv/nNbzJhwoScdtppmT59ej760Y/mJz/5Sdvz7733XlasWJF33nknSTJgwID88Y9/zPTp0zNu3LhccMEFGTx4cB588MHtJmUAAAAAgCJVqtVqtewQ3Vlzc3Pq6+uzdu3a1NXVlR0HAAAAgJLsSk/UY450AwAAAICeQukGAAAAAAVTugEAAABAwZRuAAAAAFAwpRsAAAAAFEzpBgAAAAAFU7oBAAAAQMGUbgAAAABQMKUbAAAAABRM6QYAAAAABetXdoDurlqtJkmam5tLTgIAAABAmbb2Q1v7ovYo3XZi3bp1SZLGxsaSkwAAAADQHaxbty719fXtblOpdqSa68NaWlry+uuvZ/DgwalUKmXHKURzc3MaGxvzyiuvpK6uruw40G0ZK9Axxgp0jLECHWe8QMcYK12vWq1m3bp1GT16dGpq2r9qmyPddqKmpiYHHHBA2TE6RV1dnUEJHWCsQMcYK9Axxgp0nPECHWOsdK2dHeG2lYkUAAAAAKBgSjcAAAAAKJjSrQ+qra3N1Vdfndra2rKjQLdmrEDHGCvQMcYKdJzxAh1jrHRvJlIAAAAAgII50g0AAAAACqZ0AwAAAICCKd0AAAAAoGBKNwAAAAAomNKtj7nxxhtz8MEHZ8CAAZk8eXKWLVtWdiQo1a6MiYULF6ZSqWxzGzBgQBemhe5lyZIlOfvsszN69OhUKpX89re/LTsSlGpXx8Qf/vCH7X6uVCqVNDU1dU1g6Gbmz5+fE044IYMHD87w4cNz7rnnZsWKFWXHgtLszpjwnaV7Ubr1Ibfeemsuv/zyXH311Vm+fHmOOeaYfOITn8jKlSvLjgal2J0xUVdXlzfeeKPt9tJLL3VhYuheNmzYkGOOOSY33nhj2VGgW9jdMbFixYptfrYMHz68kxJC9/bAAw9k9uzZ+fOf/5x77rkn7733XqZNm5YNGzaUHQ1KsbtjwneW7qNSrVarZYega0yePDknnHBCbrjhhiRJS0tLGhsbM3fu3Fx55ZUlp4Out6tjYuHChbnsssuyZs2aLk4K3V+lUsntt9+ec889t+wo0C10ZEz84Q9/yCmnnJK33347DQ0NXZYNeoq33norw4cPzwMPPJCPfexjZceB0nVkTPjO0r040q2P2LRpUx577LGcfvrpbetqampy+umn56GHHioxGZRjd8fE+vXrc9BBB6WxsTHnnHNOnn766a6IC0Avduyxx2bUqFE544wzsnTp0rLjQLexdu3aJMnQoUNLTgLdQ0fHhO8s3YfSrY9YtWpVtmzZkhEjRmyzfsSIEa4bQp+0O2PisMMOy80335w77rgjv/71r9PS0pIpU6bk1Vdf7YrIAPQyo0aNyk033ZTbbrstt912WxobGzN16tQsX7687GhQupaWllx22WU5+eSTc+SRR5YdB0rX0THhO0v30q/sAAA9xUknnZSTTjqp7fGUKVNy+OGH58c//nGuueaaEpMB0BMddthhOeyww9oeT5kyJc8//3y++93v5le/+lWJyaB8s2fPzlNPPZU//elPZUeBbqGjY8J3lu7FkW59xH777Ze99torb7755jbr33zzzYwcObKkVFCeIsZE//79M3HixDz33HOdERGAPujEE0/0c4U+b86cObnzzjtz//3354ADDig7DpRuT8aE7yzlUrr1EXvvvXcmTZqU++67r21dS0tL7rvvvm1acOgrihgTW7ZsyV//+teMGjWqs2IC0Mc8/vjjfq7QZ1Wr1cyZMye33357Fi9enDFjxpQdCUpVxJjwnaVcTi/tQy6//PJcdNFFOf7443PiiSfm+uuvz4YNG3LxxReXHQ1KsbMxceGFF2b//ffP/PnzkyTf/OY385GPfCTjxo3LmjVr8p3vfCcvvfRSvvjFL5b5MaA069ev3+avpi+++GIef/zxDB06NAceeGCJyaAcOxsT8+bNy2uvvZZf/vKXSZLrr78+Y8aMyYc//OG8++67+dnPfpbFixfn97//fVkfAUo1e/bs3HLLLbnjjjsyePDgtuvs1tfXZ+DAgSWng67XkTHhO0v3pnTrQy644IK89dZbueqqq9LU1JRjjz02ixYt2u5C8tBX7GxMvPzyy6mpef+A4LfffjuzZs1KU1NThgwZkkmTJuXBBx/MEUccUdZHgFI9+uijOeWUU9oeX3755UmSiy66KAsXLiwpFZRnZ2PijTfeyMsvv9z2/KZNm3LFFVfktddeyz777JOjjz4699577zb7gL7kRz/6UZJk6tSp26xfsGBBZs6c2fWBoGQdGRO+s3RvlWq1Wi07BAAAAAD0Jq7pBgAAAAAFU7oBAAAAQMGUbgAAAABQMKUbAAAAABRM6QYAAAAABVO6AQAAAEDBlG4AAAAAUDClGwAAAAAUTOkGAECSZObMmTn33HPLjgEA0Cv0KzsAAACdr1KptPv81Vdfne9973upVqtdlAgAoHdTugEA9AFvvPFG2/1bb701V111VVasWNG2btCgQRk0aFAZ0QAAeiWnlwIA9AEjR45su9XX16dSqWyzbtCgQdudXjp16tTMnTs3l112WYYMGZIRI0bkpz/9aTZs2JCLL744gwcPzrhx43LXXXdt815PPfVUzjrrrAwaNCgjRozIF77whaxataqLPzEAQLmUbgAA7NAvfvGL7Lffflm2bFnmzp2bL3/5yznvvPMyZcqULF++PNOmTcsXvvCFvPPOO0mSNWvW5NRTT83EiRPz6KOPZtGiRXnzzTdz/vnnl/xJAAC6ltINAIAdOuaYY/K1r30t48ePz7x58zJgwIDst99+mTVrVsaPH5+rrroq//jHP/Lkk08mSW644YZMnDgx3/rWtzJhwoRMnDgxN998c+6///787W9/K/nTAAB0Hdd0AwBgh44++ui2+3vttVc+9KEP5aijjmpbN2LEiCTJypUrkyRPPPFE7r///g+8Ptzzzz+fQw89tJMTAwB0D0o3AAB2qH///ts8rlQq26zbOitqS0tLkmT9+vU5++yz8+1vf3u7fY0aNaoTkwIAdC9KNwAACnPcccfltttuy8EHH5x+/fyqCQD0Xa7pBgBAYWbPnp3Vq1fnc5/7XB555JE8//zzufvuu3PxxRdny5YtZccDAOgySjcAAAozevToLF26NFu2bMm0adNy1FFH5bLLLktDQ0NqavzqCQD0HZVqtVotOwQAAAAA9Cb+3AgAAAAABVO6AQAAAEDBlG4AAAAAUDClGwAAAAAUTOkGAAAAAAVTugEAAABAwZRuAAAAAFAwpRsAAAAAFEzpBgAAAAAFU7oBAAAAQMGUbgAAAABQsP8FHxsgRj2Z6+AAAAAASUVORK5CYII=",
      "text/plain": [
       "<Figure size 1500x700 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "%matplotlib inline\n",
    "import librosa.display\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "# Plot our example audio file's waveform\n",
    "plt.rcParams['figure.figsize'] = (15,7)\n",
    "plt.title('Waveform of Audio Example')\n",
    "plt.ylabel('Amplitude')\n",
    "\n",
    "_ = librosa.display.waveshow(audio, color='blue')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "Gg6RR_yolRzo"
   },
   "source": [
    "We can see the activity in the waveform that corresponds to each letter in the audio, as our speaker here enunciates quite clearly!\n",
    "You can kind of tell that each spoken letter has a different \"shape,\" and it's interesting to note that last two blobs look relatively similar, which is expected because they are both the letter \"N.\"\n",
    "\n",
    "### Spectrograms and Mel Spectrograms\n",
    "\n",
    "However, since audio information is more useful in the context of frequencies of sound over time, we can get a better representation than this raw sequence of 57,330 values.\n",
    "We can apply a [Fourier Transform](https://en.wikipedia.org/wiki/Fourier_transform) on our audio signal to get something more useful: a **spectrogram**, which is a representation of the energy levels (i.e. amplitude, or \"loudness\") of each frequency (i.e. pitch) of the signal over the duration of the file.\n",
    "A spectrogram (which can be viewed as a heat map) is a good way of seeing how the *strengths of various frequencies in the audio vary over time*, and is obtained by breaking up the signal into smaller, usually overlapping chunks and performing a Short-Time Fourier Transform (STFT) on each.\n",
    "\n",
    "Let's examine what the spectrogram of our sample looks like."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {
    "id": "oCFneEs1lRzp"
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAABHIAAAJwCAYAAADlU0bdAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjAsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvlHJYcgAAAAlwSFlzAAAPYQAAD2EBqD+naQABAABJREFUeJzsvXmYnVWVNb7uPE81V8bKQCYSSAgQRgkCAYwTAqKoHdD2Q21oW9pupW3FdqJF+5P+gVN/bQv6BVEU2wFR5nkmgwmZh0oqSc1Vt+reuvO97+8PPqIRstZJV6WSwFnPw9Nt7Zt73vu+5z1nn73XXtvlOI4DCwsLCwsLCwsLCwsLCwsLC4ujHu4jfQEWFhYWFhYWFhYWFhYWFhYWFmawgRwLCwsLCwsLCwsLCwsLCwuLYwQ2kGNhYWFhYWFhYWFhYWFhYWFxjMAGciwsLCwsLCwsLCwsLCwsLCyOEdhAjoWFhYWFhYWFhYWFhYWFhcUxAhvIsbCwsLCwsLCwsLCwsLCwsDhGYAM5FhYWFhYWFhYWFhYWFhYWFscIbCDHwsLCwsLCwsLCwsLCwsLC4hiBDeRYWFhYWFhYWFhYWFhYWFhYHCOwgRwLCwsLC4ujFFdddRXa2toO+JvL5cIXv/jFI3I9FhYWFhYWFhYWRx42kGNhYWFhYfE/wHe+8x24XC4sWbLkSF/KqJDNZnHjjTdi/vz5iEQiqK+vx8KFC/HJT34S+/btO9KXhzvvvBO33HLLkb4MCwsLCwsLC4ujBt4jfQEWFhYWFhbHIlauXIm2tjY8//zz2LZtG2bOnDku4+bzeXi9Y7N9l8tlvOUtb8GmTZuwYsUKXHfddchms3j55Zdx55134pJLLsGECRPGZKz/Ke68806sX78ef/d3f3dEr8PCwsLCwsLC4miBDeRYWFhYWFgcInbu3Imnn34a99xzD6655hqsXLkSN95447iMHQwGx+y7/vu//xurV6/GypUrceWVVx5gKxQKKJVKYzbWeKBQKMDv98PtPvyE40qlglqtBr/ff9jHsrCwsLCwsLD4c9jSKgsLCwsLi0PEypUrkUqlsHz5clx22WVYuXLlaz7z6KOPwuVy4dFHHz3g7+3t7XC5XLj99tsP+Pt///d/Y/78+QgGg5g/fz5++ctfvu7Yr6eRs3r1alx88cWIx+OIRqM477zz8Oyzz8rfsX37dgDAmWee+RpbMBhEPB7f/7+vuuoqRKNR7NixAxdeeCEikQgmTJiAL33pS3Ac54B/W6vVcMstt+D4449HMBhEc3MzrrnmGgwODr5mnPvuuw/nnHMOYrEY4vE4TjnlFNx5550AgKVLl+Lee+/Frl274HK54HK59msGvXp/77rrLvzzP/8zJk6ciHA4jOHhYQDA3XffjcWLFyMUCqGhoQEf/OAHsXfv3teMf/fdd2PevHkH3Pe/1CZ69Zl985vfxC233IIZM2YgEAhgw4YNKJVK+MIXvoDFixcjkUggEong7LPPxiOPPHLAOH/+Hd/+9rcxffp0hMNhLFu2DB0dHXAcB1/+8pcxadIkhEIhvOtd78LAwIB8hhYWFhYWFhZvPlhGjoWFhYWFxSFi5cqVeM973gO/34/3v//9+O53v4sXXngBp5xyyv/o++6//35ceumlmDdvHm666Sb09/fj6quvxqRJk+S/ffnll3H22WcjHo/jH//xH+Hz+fD9738fS5cuxWOPPUY1fKZOnQoA+NGPfoR//ud/hsvlomNVq1VcdNFFOO2003DzzTfj97//PW688UZUKhV86Utf2v+5a665Brfffjuuvvpq/O3f/i127tyJ2267DatXr8ZTTz0Fn88HALj99tvx4Q9/GMcffzxuuOEGJJNJrF69Gr///e9x5ZVX4nOf+xyGhoawZ88efOtb3wIARKPRA67py1/+Mvx+Pz796U+jWCzC7/fvH/uUU07BTTfdhO7ubvz7v/87nnrqKaxevRrJZBIAcO+99+KKK67AggULcNNNN2FwcBAf+chHMHHixNf9/T/84Q9RKBTwv/7X/0IgEEBdXR2Gh4fxn//5n3j/+9+Pj370o8hkMvjBD36ACy+8EM8//zwWLlx4wHesXLkSpVIJ1113HQYGBnDzzTfjve99L9761rfi0UcfxWc+8xls27YNt956Kz796U/jv/7rv+gzsbCwsLCwsHgTwrGwsLCwsLAwxosvvugAcB544AHHcRynVqs5kyZNcj75yU8e8LlHHnnEAeA88sgjB/x9586dDgDnhz/84f6/LVy40GltbXXS6fT+v91///0OAGfq1KkH/HsAzo033rj/f7/73e92/H6/s3379v1/27dvnxOLxZy3vOUt9Lfkcjln9uzZ+8e56qqrnB/84AdOd3f3az67YsUKB4Bz3XXX7f9brVZzli9f7vj9fqe3t9dxHMd54oknHADOypUrD/j3v//97w/4ezqddmKxmLNkyRInn88f8Nlarbb//1++fPlr7oHj/On+Tp8+3cnlcvv/XiqVnKamJmf+/PkHfO9vf/tbB4DzhS98Yf/fFixY4EyaNMnJZDL7//boo4++5r6/+szi8bjT09NzwHVUKhWnWCwe8LfBwUGnubnZ+fCHP/ya72hsbDzgOd9www0OAOfEE090yuXy/r+///3vd/x+v1MoFF7z2y0sLCwsLCze3LClVRYWFhYWFoeAlStXorm5Geeeey6AV0qdrrjiCtx1112oVquH/H2dnZ1Ys2YNVqxYgUQisf/vF1xwAebNm0f/bbVaxf333493v/vdmD59+v6/t7a24sorr8STTz65v9To9RAKhfDcc8/hH/7hHwC8wpD5yEc+gtbWVlx33XUoFouv+TfXXnvt/v/f5XLh2muvRalUwoMPPgjglVKlRCKBCy64AH19ffv/W7x4MaLR6P6SowceeACZTAaf/exnX6P7o5hBf44VK1YgFArt/98vvvgienp68IlPfOKA712+fDnmzJmDe++9FwCwb98+rFu3Dn/1V391AMvnnHPOwYIFC153rEsvvRSNjY0H/M3j8ezXyanVahgYGEClUsHJJ5+MVatWveY7Lr/88gOe86uMqQ9+8IMHiFgvWbIEpVLpdcvBLCwsLCwsLN7csIEcCwsLCwsLQ1SrVdx1110499xzsXPnTmzbtg3btm3DkiVL0N3djYceeuiQv3PXrl0AgOOOO+41ttmzZ9N/29vbi1wu97qfmzt3Lmq1Gjo6Ouh3JBIJ3HzzzWhvb0d7ezt+8IMfYPbs2bjtttvw5S9/+YDPut3uAwJGADBr1iwAr2jAAMDWrVsxNDSEpqYmNDY2HvBfNptFT08PgD/p88yfP59en8K0adMO+N+v3s/Xuydz5szZb3/1/75et7GDdSD7y7FexR133IETTjgBwWAQ9fX1aGxsxL333ouhoaHXfHbKlCkH/O9XgzqTJ09+3b+/nq6QhYWFhYWFxZsbViPHwsLCwsLCEA8//DA6Oztx11134a677nqNfeXKlVi2bBmAg7NK/iesnfHC1KlT8eEPfxiXXHIJpk+fjpUrV+IrX/nKIX1HrVZDU1PT6wpAA3gNo2W0+HM2zuHG6431f//v/8VVV12Fd7/73fiHf/gHNDU1wePx4KabbtofrPpzeDye1/3ug/3d+QshaQsLCwsLCwsLG8ixsLCwsLAwxMqVK9HU1IRvf/vbr7Hdc889+OUvf4nvfe97CIVCSKVSAIB0On3A515lgryKVwWHt27d+prv3Lx5M72exsZGhMPh1/3cpk2b4Ha7X8P0MEEqlcKMGTOwfv36A/5eq9WwY8eO/SwcANiyZQsA7O/yNGPGDDz44IM488wzaZBlxowZAID169cflAEDHFqZFfCn+7l582a89a1vPcC2efPm/fZX/++2bdte8x2v97eD4ec//zmmT5+Oe+6554BrHa929BYWFhYWFhZvPtjSKgsLCwsLCwPk83ncc889ePvb347LLrvsNf9de+21yGQy+PWvfw3glUCBx+PB448/fsD3fOc73zngf7e2tmLhwoW44447DijFeeCBB7BhwwZ6TR6PB8uWLcOvfvWr/aVNANDd3Y0777wTZ5111gEtxP8Sa9euRV9f32v+vmvXLmzYsOF1y5Nuu+22/f+/4zi47bbb4PP5cN555wEA3vve96Jarb6mLAsAKpXK/sDWsmXLEIvFcNNNN6FQKBzwuT9noUQikdctUToYTj75ZDQ1NeF73/veARo/9913HzZu3Ijly5cDACZMmID58+fjRz/6EbLZ7P7PPfbYY1i3bp3xeK8yaf78mp977jk888wzxt9hYWFhYWFhYXEosIwcCwsLCwsLA/z6179GJpPBO9/5zte1n3baaWhsbMTKlStxxRVXIJFI4PLLL8ett94Kl8uFGTNm4Le//e1+jZg/x0033YTly5fjrLPOwoc//GEMDAzg1ltvxfHHH39AkOH18JWvfAUPPPAAzjrrLHziE5+A1+vF97//fRSLRdx888303z7wwAO48cYb8c53vhOnnXYaotEoduzYgf/6r/9CsVjEF7/4xQM+HwwG8fvf/x4rVqzAkiVLcN999+Hee+/FP/3TP+0vmTrnnHNwzTXX4KabbsKaNWuwbNky+Hw+bN26FXfffTf+/d//HZdddhni8Ti+9a1v4a//+q9xyimn4Morr0QqlcLatWuRy+Vwxx13AAAWL16Mn/70p7j++utxyimnIBqN4h3veMdBf5PP58PXv/51XH311TjnnHPw/ve/f3/78ba2NnzqU5/a/9mvfe1reNe73oUzzzwTV199NQYHB3Hbbbdh/vz58r6/ire//e245557cMkll2D58uXYuXMnvve972HevHnG32FhYWFhYWFhcUg4sk2zLCwsLCwsjg284x3vcILBoDMyMnLQz1x11VWOz+dz+vr6HMdxnN7eXufSSy91wuGwk0qlnGuuucZZv379a9qPO47j/OIXv3Dmzp3rBAIBZ968ec4999zjrFixQrYfdxzHWbVqlXPhhRc60WjUCYfDzrnnnus8/fTT8jft2LHD+cIXvuCcdtppTlNTk+P1ep3GxkZn+fLlzsMPP3zAZ1esWOFEIhFn+/btzrJly5xwOOw0Nzc7N954o1OtVl/z3f/xH//hLF682AmFQk4sFnMWLFjg/OM//qOzb9++Az7361//2jnjjDOcUCjkxONx59RTT3V+8pOf7Ldns1nnyiuvdJLJ5AFtwV9tP3733Xe/7m/76U9/6ixatMgJBAJOXV2d84EPfMDZs2fPaz531113OXPmzHECgYAzf/5859e//rVz6aWXOnPmzNn/mVdbh3/jG994zb+v1WrO1772NWfq1KlOIBBwFi1a5Pz2t799zbM72Hcc7Hf88Ic/dAA4L7zwwuv+PgsLCwsLC4s3L1yOY1X0LCwsLCwsLDiuuuoq/PznP39TsEwWLlyIxsZGPPDAA0f6UiwsLCwsLCwsXgOrkWNhYWFhYWHxpkS5XEalUjngb48++ijWrl2LpUuXHpmLsrCwsLCwsLAQsBo5FhYWFhYWFm9K7N27F+effz4++MEPYsKECdi0aRO+973voaWlBR/72MeO9OVZWFhYWFhYWLwubCDHwsLCwsLC4k2JVCqFxYsX4z//8z/R29uLSCSC5cuX41//9V9RX19/pC/PwsLCwsLCwuJ1YTVyLCwsLCwsLCwsLCwsLCwsLA6Cb3/72/jGN76Brq4unHjiibj11ltx6qmnHrHrsRo5FhYWFhYWFhYWFhYWFhYWFq+Dn/70p7j++utx4403YtWqVTjxxBNx4YUXoqen54hdk2XkWFhYWFhYWFhYWFhYWFhYWLwOlixZglNOOQW33XYbAKBWq2Hy5Mm47rrr8NnPfvaIXJPVyDFErVbDvn37EIvF4HK5jvTlWFhYWFhYWFhYWFhYWLzB4TgOMpkMJkyYALf7jV1QUygUUCqVxmUsx3Fec64PBAIIBAIH/K1UKuGll17CDTfcsP9vbrcb559/Pp555plxudbXgw3kGGLfvn2YPHnykb4MCwsLCwsLCwsLCwsLizcZOjo6MGnSpCN9GYcNhUIB06ZNRFfXwLiMF41Gkc1mD/jbjTfeiC9+8YsH/K2vrw/VahXNzc0H/L25uRmbNm063Jd5UNhAjiFisdj/+//cACwjx8LCwsLCwsLCwsLCwuJwwwFQ+7Pz6BsTpVIJXV0DaN/1M8Tj4cM61vBwDm1T34uOjg7E4/H9f/9LNs7RDBvIMcSfaFcu2ECOhYWFhYWFhYWFhYWFxXjhzSLvEY8GEY+GDu8gtdorY8XjBwRyXg8NDQ3weDzo7u4+4O/d3d1oaWk5bJeo8MYusrOwsLCwsLCwsLCwsLCwsLD4H8Dv92Px4sV46KGH9v+tVqvhoYcewumnn37ErssyciwsLCwsLCwsLCwsLCwsLI48arX9jJnDOsYh4Prrr8eKFStw8skn49RTT8Utt9yCkZERXH311YfpAjVsIMfCwsLCwsLCwsLCwsLCwsLidXDFFVegt7cXX/jCF9DV1YWFCxfi97///WsEkMcTNpBjYWFhYWFhYWFhYWFhYWFx5HEUMnIA4Nprr8W11157GC7mfwarkWNhYWFhYWFhYWFhYWFhYWFxjMAyciwsLCwsLCwsLCwsLCwsLI48HOeV/w73GMc4LCPHwsLCwsLCwsLCwsLCwsLC4hiBZeRYWFhYWFhYWFhYWFhYWFgcedSccdDIsYwcCwsLCwsLCwsLCwsLCwsLC4txgmXkWFhYWFhYWFhYWFhYWFhYHHkcpV2rjjZYRo6FhYWFhYWFhYWFhYWFhYXFMQLLyLGwsLCwsLCwsLCwsLCwsDjysIwcI1hGjoWFhYWFhYWFhYWFhYWFhcUxAhvIsbCwsLCwsLCwsLCwsLCwsDhGYEurLCwsLCwsLCwsLCwsLCwsjjxsaZURLCPHwsLCwsLCwsLCwsLCwsLC4hiBZeRYWFhYWFhYWFhYWFhYWFgceTjjwMhxLCPHwsLCwsLCwsLCwsLCwsLCwmKcYBk5FhYWFhYWFhYWFhYWFhYWRxwupwbXYWbMHO7vHw9YRo6FhYWFhYWFhYWFhYWFhYXFMYIjGsipVqv4/Oc/j2nTpiEUCmHGjBn48pe/DMdx9n/mnnvuwbJly1BfXw+Xy4U1a9a85nu2b9+OSy65BI2NjYjH43jve9+L7u7u/fb29nZ85CMfOWCcG2+8EaVSaTx+poWFhYWFhYWFhYWFhYWFhcKrXasO93/HOI5oIOfrX/86vvvd7+K2227Dxo0b8fWvfx0333wzbr311v2fGRkZwVlnnYWvf/3rr/sdIyMjWLZsGVwuFx5++GE89dRTKJVKeMc73oHa/3tAmzZtQq1Ww/e//328/PLL+Na3voXvfe97+Kd/+qdx+Z0WFhYWFhYWFhYWFhYWFhYWY4EjqpHz9NNP413veheWL18OAGhra8NPfvITPP/88/s/86EPfQjAK6ya18NTTz2F9vZ2rF69GvF4HABwxx13IJVK4eGHH8b555+Piy66CBdddNH+fzN9+nRs3rwZ3/3ud/HNb37zMP06CwsLCwsLCwsLCwsLCwsLY9ScV/473GMc4ziijJwzzjgDDz30ELZs2QIAWLt2LZ588klcfPHFxt9RLBbhcrkQCAT2/y0YDMLtduPJJ5886L8bGhpCXV0d/d7h4eED/rOwsLCwsLCwsLCwsLCwsLA4kjiigZzPfvazeN/73oc5c+bA5/Nh0aJF+Lu/+zt84AMfMP6O0047DZFIBJ/5zGeQy+UwMjKCT3/606hWq+js7Hzdf7Nt2zbceuutuOaaaw76vTfddBMSicT+/yZPnnzIv8/CwsLCwsLCwsLCwsLCwsIQViPHCEc0kPOzn/0MK1euxJ133olVq1bhjjvuwDe/+U3ccccdxt/R2NiIu+++G7/5zW8QjUaRSCSQTqdx0kknwe1+7c/bu3cvLrroIlx++eX46Ec/etDvveGGGzA0NLT/v46Ojv/Rb7SwsLCwsLCwsLCwsLCwsLAYKxxRjZx/+Id/2M/KAYAFCxZg165duOmmm7BixQrj71m2bBm2b9+Ovr4+eL1eJJNJtLS0YPr06Qd8bt++fTj33HNxxhln4D/+4z/odwYCgQPKtSwsLCwsLCwsLCwsLCwsLA4jxoMx8wZg5BzRQE4ul3sNa8bj8ezvNnWoaGhoAAA8/PDD6OnpwTvf+c79tr179+Lcc8/F4sWL8cMf/vB12ToWFhYWFhYWFhYWFhYWFhYWRzOOaCDnHe94B7761a9iypQpOP7447F69Wr87//9v/HhD394/2cGBgawe/du7Nu3DwCwefNmAEBLSwtaWloAAD/84Q8xd+5cNDY24plnnsEnP/lJfOpTn8Ls2bMBvBLEWbp0KaZOnYpvfvOb6O3t3f/9r36HxRsPocAkai9Xs9TeEJkrx+gZfpHaa05Zfsdo4XLx19hxKuNwDTww6vM2yO8olXtGdQ1ud4jaW+KnyO8YKu6m9pF8+6Fc0hsWfp9+njUx7yqV9Kivw+3mrMlarTjqMSzeWLBzxuJQodY7tQcDQLHURe1ul49/gdhjATt3LSws3kBwHMA5zIwZ59jvWnVEAzm33norPv/5z+MTn/gEenp6MGHCBFxzzTX4whe+sP8zv/71r3H11Vfv/9+vlmHdeOON+OIXvwjgleDODTfcgIGBAbS1teFzn/scPvWpT+3/Nw888AC2bduGbdu2YdKkAw/3zhvgIVq8PrwefrBPhaZT+wTMlmMEk3Fq35t5gdojgWZq94hDBwAMjmym9nCQB7QmhBbJMcpOjtr3ZJ6j9qbIPDnGBFxC7VnXELUHwJ/3ZDTJa+gK8ODd8/nvy+94I6AutoDaW7zHy+/oqrxM7QEP/47h4l45RmvoRGpP1PgBbNDVLcfoyDxN7eXKgPyO0SLg5wkHFawtlfvkGC64xAe43TncDhcArzcpPxMNtFK7WlMdVKm93jdTXkNVBPAzVX6ozxk8r3KFJyKiQX4fajUd4E+PbKR2jyfC7SK4DpjNzSMNFZSeFjtbfofaQ0tOntqDLu5rAMBgeSe3Z/marKASNoBeBzwe/juq1WOjQ6ya+9XqCLXPrrtMjlF0MtTePvgHalfJLQAIi/WyJNaZ0SbgLCwsRgeXYyMZRhgeHkYikQDgAZTDa3HY0RA/SX7mrxuWU3tLkP/7vdyvAgA8O5Cm9hr46zXo5k7s5uHfyGuIiECN1+2ndhc8cgy/cFrUoXtm8Bw5RrzGHbx29wZqn+/wgNT0mHZqBgr8EHdX703UHhBOEQAUivvkZxjkgRuAI+adYqs1h3WgRkEdTFpxHLU3ISXH2Ofqpfa1g1w4f3HyI3IMv8MP/s8MfYfaTbL1KuNfF55B7en8LmrPF/fIa1BOf61msCAKqLkbi8yi9mERtAaAd9V9htpbQpz5kKvwd6c6Bi7TzmKa2lfl75Hf0RTh72gMjdSeqNXJMdyiH4ZX2IuukhxjXfH31D4eLMjG+MnUXudto/aGqmZ273CtpvZZzmJqr0AHSl/M/5zaVZBFBWriwtcAAJ87TO1dwzzpc7Swivw+nviZGjuT2uPi/Zrp40k8AAh6+Hq5SjCId5Wel2Mo/zA9so3aTYK1NYc/U/Udx0Kwd3zgAKhiaGgI8bgO7B6rePW8Pbjue4gb+O2jGiuTR2rBx47pe3pEGTkWr8XRUCZzLKBqsNlvTvOs6MRWfq+ncH8EALAnG6P2oTK/hqcG76L2ean3yWuY7HDnKujmgZrtjj7kpYRTsieYoPZh8AM3AMz2TaD2ReEz+BglfsAK6ngVQl7uyE5NLaP2kWq/HENR7FUzwbFYA6IBfvCIggcWPAZbR73D50zOxQMDXS59L1Xwb0rqAmrvdLbKMfYNPU7tir0U9OiA1LAItHSmn5LfwaAOJQDQEJnDr2HoSWo3YeSoAKNJoEYhU+XBgwf6f0LtlyY+RO1hsUYAwI4Rno2Pu/jmsij8bjnGoIsfbrIOf38muibKMRS2u/jz2jX8iPwOxVwYLXxeHbCa6TqV2ucH+XcUqjq45y7w5FNbiPsSfrcO4E8P8sD0tsIgtb+U44GgYpUzRACgP7uO2n1evh76PNrxyuZ3ULti7rkNgusV8VsdEVhTgZqIwTrybIEHUUpiD704fKkcY6DMfekHavx5zkheZDAGZ4r1Z9ZQ+1gwwSws3qiwgZxxxNGiK6GgHB8VbCpXdPRcLboqOzyU4xs5AJzYyjMNIQ9nX2zJ6M1jVXULtS8Vh6OvNH2e2ocMJHbuS/N7cYJ3KrWf7p0mx1iV66T2osPpt3WuyXKMzjL/jlCJH9pVtt8kkZ6v8HkpqcxK5wBAQ4w79PkyL9VRVGdAOz7KId9bW0PtJ3jOk9eg2GgnRvh62JnTk78X/Hcc7/DSK78IcgLAqhR/ph2DD8nvUDBhWTGo0qv6MGe6AEDAFaX2lsTp1N6X5WU4gM7MqkP9hORb5BhbXX/kY9R4oGd1qZ3aF/nb5DU0+vn+tbuUpvYetw6ui9cLewXzYVpUa8ApFkjYxQP4zTHOMgGAfWkeKFVQa248NEV+h2JAzQ79NbUn/QbNMwrcvC3PS4c73e1yiJ4CZ62WKrxsSTEfxqKMJuDjc6ZY5vfBBD4PX8s8goUC6HsxLMojt9d48LyxzO8DALhdfH+aUeOs1pegS+nas49Ru0qGuA0Y3a2iFDuW4kGvjmGeRAAOf0DYZI92iXl1tLDNLN5YsIGcccR40ANVJsKk/lhpPqhD4lhExhWNf0GKZ00BYMsQD4r9qo8HJ2Z5dZnMHPCSh94Cv4afpn9F7TN8nIUCAPO83FHdXOI6IMWy8DABXJjkekIxH8/uqnIFABgs8s905vkBrOjwwFxAaCYBQKbCn1c4yO91saxZJL1CIFuJsZpABVtjQc5+qvfy5x2saUd4SpjXLhb540KXk5ZjZN3c6U9DrLkGwb0G8GeeF2WefcOr5BiKqaKgWF56Vuo5MdXNSxe9MVGritEHvUzE4+c5vEzm5CgXPd/h8H1huKwZcYoVlHXzAGTe4cwJQLO05qc+QO1FR5c9TffzpM4ucS4JuPScyEb4/pQvcjZnVfgKSkMOAFIRrof3YIEfJCfntQZcUrCwNro486HJaZNjFALcv2sM8qTNAHgAcSyC1lmRhBuLBhEmpaSjhdfF9+mMm7/DPU67HGNqjScCu9z83Wgf5kEaQPvruwcfoPZUVJdhqzPDQIbP/aMBXsEkA8ZHL+9NhZrzyn+He4xjHDaQ8wbDeDB2jgYK41ToIMsZTXzzuDTIswCdBZ1le7iT34u4j79iH09cTu0VAxqJKima5vDM0KSoXgY2pnmwJ+Nw+/SQrj2N+vj9ztW4g1fn1YcGhbCHZ5eUUGrQz3UpAGAkzzNHY5G1cbl4lKRS5Ycfvwh6DQvhTgBYPyIEst38gNWR1oeGqBAs94nfMcXHD/0AsLP0rBiD60cpJgugWQWj7aamy/n0Z+IpHugp1/ScGC26hp6Rn0mlOPvvOIcfZutFGekI9EFTMXIaRDlsX1mzd7vdPCCcdrhuWbuYUwCwXdyLOS4+t/td+kCtyunUu+Hz1VO7KiMFgFlunjBpFQK9XiEEDgAe8ZmLAry8K2xQGpyr8r1+S4azOXdW+Fo3FhiPTp5jAcWgV+LTE6uKhaxZyo8M30rty5PXU3soqkvz25211D5U6KB2EwFtxfJXCTJVqQCMXntQoVJNy89IVvgoEzYWFq8HG8h5k8Gk1lSVNSkK41iIsSp0QHeb6crzkiKlHTNS0b/j4QJn1JxVewe1N4Z4YMCk4KIs4mqpAP+dnTlBjQAwJ8GDJP1FztCoGsT+ImI1agnwebmtxHkHzW6tE+IVOgRK9Dmd05or44FEmFOug4K5t2GYz2sTZp8KskwO8iCK+veA1ko4NXkNtSccTsEHgEE/P3SrjGVcZPsBHVjLFfShm2FScqn8TLbM11SPOlALkdPxwsbBn3G7+PdnJq6l9qkBHZRWJZp7azxbvyb3CznGkhjXQ3lu+IfUPjVxrhxjSo136IoIVoLXgJGjoA7+KgBppN0U4Z+ZGOZz3yCOg83D/B1fX+HvX8The48JhtycMdAU4AwQE23C8RCnHg8oBn2Dw1nIKpjbW9Li8a0JHmC8P3s7tc+OXijHmCaaROwUr3C1phndSvdvtPvbeOBoSGC/6VCrvfLf4R7jGIcN5IwhVCeYUkXTpQ93nafJYjTaaxiLqLMKOJ0gDlcAMDnMf+uLA3yMNgO/6YokF5PbnBUZsGEeZDFhy9QHuRfZleP3oaukNVc8Qj8jJtg0qbD2dJWYo0/YU+BikQYqBigJ0cqyoPGbvF9KeLZS5eVCJowd1Ta4KbGE2hfH3k/tUUcf2ht83ANUwtJzXDqQUwjwTJ3qavXA4OjbyavAtYmA71iU0zH0jHDtDACYEV1K7U2iM0+PW7N+RgulBQQAx0W4flNYBO+63TwDvXqYdx8CgFMC76Z2H3hgQLUOB4BO93Zqn57kwuyqRToAjAgx1Z0uvs4oEW9ABzrV+6PaQJvouuwCL+2IDvP1clJIr4czRfcVX5Y/84IBKyHi4fMqVuP3qhP8HS6UdNMCtZaNBeN0tGOYtOUOCKZXvfA3hsu8dHG3R+s8zqhyjbdwjJf7eB3tP3a4+N4wlOfrYSSgu28p1k4k1Ebtb5TgoIXF4YAN5IwhxqMud7Qw6eBwNNR5qgPxmpKO4M8ocAr9tCg/tH9+uz7kvTvBs6L9bs4Sme7nrKEtQzrbsd61htpP93JNiLc2adG9rPAhnx/gwYcLo3qMsIc/j30ikJP0cVZQ0GC1U41B4j7ubJsEcjKCtaNKCUycUL+PO3i9Q7wtaUOKvzsbSw/LazjD9S5qD3i4M54K6Af2QOEFam+rce0Kk/bj7dWXqF113DCBIw7V6rCq2rf6vZp5tGOEi856I1z0subSc18F6D2ihMXk/RoGP7gnHP5uJIVI6aTAe+Q1tLt5gEN1hZuNs+UYSv9JtRfvcvFOMgAw5OZjtNR4sNVtIAK8e+hRalfBOyVcmzNITLW4uBh4WK3JBowc1TVxVpyvh6qsF9ByD905vqburvAAiN9AJ2Q8/ODRBoOUBiOgf8fqINeomuI6gdpHalozc3poPreD238xxDv0AUBDkLN31X04PnSxHKM/xf3crhwXqFf7H3D4k+AWRwDOODBy3gBMKxvIeZNhLII0SlDZa9A+crT1rBnhrL8CfhidGubRiW/P/agc4Ze7edbFLQ4u9+e5iOJpHq2v8fbQadQ+Imj+z/Zqp2Z+ih8UT63jgZqf9ujA22WNvE66OcTvZb8Qli7XtMhA2Ms/0zu8idpNtEhMAjEM6tAP6PaqpyU+Tu314Af/XECzC+u8/IC1u8AFX2NuXZbxtjB/PzpGuMP/RJprEIwFTDqZqfIR5aQqe9hAu2liiIs2K6Jld1FrJahAzFhovHVlOWMmFeVaPy0Ov1dl6FLU2Y5oSS/KektC4woAtlR4x8Rm91Jqn+/i2X4A2ArOGnArNlpF7/PqUG6ypjJMS71NfqbF4eyLBwv8QDzP0SUsLQUeBBkUGlNPDd0mxzgn8bfUPiPMA6WnukQZqAFLeXORtzAfCz0UhWqVJ8BiIV4WBQC1Gr+OqIcHfJsc7hPN9i+V16DYnrkKXydO9fNkCgB0gYu7K3+lC7qc3C/8iUKR63m5PZz9BOgkAMS6PRaBIHUNJiXpFhaHChvIsThkKGfbJNsx2gWvwdEtRbvy/OSxZYhvklOiOpsYEA754gAXtGsN80yF6uQE6I5QDUH+OxKilhsA9mT5JqiEHC9O6ec1LOITg0V+CAx6TIqnOEoi+j8hwg+7ex3OdAGAsuhspUoTTcpwVM35UIgHdEM1PsZcFz+oAkBviTvTjV5+Koj7deBNaRo1BfnvaIxrseNsUZUbcLuJuKdaD1VwvCzKdlWpnclnZtddRu1hnw4WpaVCDUcwwIMwAFAs8SB/FfyA1iXK8SZCa225xXq4R2Tje1ztcowpXq5tsde1i9p3Dj+ix4idRe01sVZN9C6UY1QiPBmiSqtUYCAKHqQB9IH5Y80r5Hco7FVadBX+jr8z9Rk5xpOV31F7Y+nt1L61xgNv7SO6DbSCKs8ySVQAfJ9WMgdDonMWoA/2Z/j4vUz6eQB/Y1EnIxvBg0F7XFxXaUR0zgKABPi6rUo0FYMRAHw1fi/KqbdS+2BBsweVXt54wAZqxhauWg2uw8zIOdzfPx6wgRyLQ4bMMJvo8NRGt+BFHB18OLWeX8f0CD9o7s1rRsDz/TybeN/Aj6h9SY4fjubHdUmSonV3C42cjiJnRgCacRMXUyJnIBzdJRzdP5Y4xTdV4xnP5rBBVkccwNrTv6d2kw5Fqm2w6pZhovbjEWVmGwbvovZ08i3UPgW63e400bq4QdQa9Kv+5NCMtydLXPui2aOFiKNh7qhmAtxuwsgpVfh6aBKIGS2UVolfrLmqHS+gS6uCfh6oCfr0ehgPiq5VLm6PCFbeS2WTDDS/VyWhPdOZ4eV8ANBR4V3dYkLw3KRMrbfIgygDLq7TMx7zVv2OfocHtABgXfrH1L7T9V5qVwLbgA7EpMTBf29Bd4Vb6l9O7TurPHiwPvNLavd7tdC3gkmib7TIC8a3Mwasn9+lv0HtE8QeOtXhZVEAEPHyOTGhyvVpdri1/mEWaWqfVeNlhz639keeLP+B2lMentBMBTm7HgDyJR7UUsy/sZgTFhZHAjaQY3HIOBraR6puGQDw7V08U37dVFF779JsGNVJ6crwh6ldCRXvyujNxSWCD/Wia1WbWwc4Nqb5JjgknLMT4kk5RlzoKbSVhdCpIHDkBXMJAHqK/HdOTHDnbE/6UTlGKno8tVeFQzFSMBAQDfGM5JQIL8dTODeps3CNQcEsEv/eJ9huALBnhN+rtuoMan848205hgpMe4VuhInYqoIKgLhEsKhOzDkACHs4cyHg8MB2yqXZMkhyIeKRCs/Wh72aXXGGlwvTTonyebVmkB+YTw/xgw0AeETcujPPWSi1+PlyjH0F3jY45ud6XjMDnG0DAB4hlroXXCg1LUcYPYqC4VgXPkd+R3PqamqvCQbIIvHvAeCR4j3UPttZSu1Rg7qml51t1N6GNmq/MMa7/L1Q0ywu1dRDdj0VZcGA1nocizVXBULn+7hmWBycYdXv4rqCANBb4fdK+cHzYLJW8cWqJLTPeqo6EZjwcn9kX46Xwx4LXa0sDgMc55X/DvcYxzhsIMfimMSgo+tZL27gddARL3emc1WdafCLbITSp0k5/FAxQfXkBpAt84VIMRv2lfRG7BNLxYJYktoHDdgVj5Y4bXuew8tgVte4AO8yj9ZKGHb4IS4tRLZV9wVAB2pMuhwp5Mu8dGpAhFFmuk6l9qAQpgZ0oEZVGjQYdC7uynMndNDAWVZIRnlL3mbvXGqPCK0EAAiJIElWZFZ3VV6k9kxBa5WEIzpIwtBRWSU/Uyjz51Gt8TXZJJCTF7oRIQ9fy85rFmVsBn6fiC8iW+bXsLmX64wAQDLC591xzkJqL4LfawAIOJzZd26AB0n2JhbLMR4b+v/kZxiSEd4ifcDhXXcAIOjiTBOfaKO+NMTXCAA4K/o+au/M8UnTXtXiuBOrnG0WFnP/vwe+Tu0z6t4pr6EQ4O+4Evv3Sq0TIBbkQeN0jfuHPq9ek+f6eblPGTyhqXyJRpe+hqmi01le+JdPldbLMVorvDRR+X573Zqh2JvjzLximQfwVfIL0H5VZoRrio1Ft10LiyMBG8gZQ6g6a7tQjB2SLi2oPCD0ZdpzPIsd9+rn1VfkzvB68Kypk+WaKw0GrZYCIv0r/EPkXbozVlnQXaoOzxaq9uQAsLDEM+nr3Pyg2OzmznTE4Bom1rhzlXPzbjKKtQAAORc/lPeL0qruYX5oB4BT/O+m9gVxzsJqGp0eMwCgXcRah0v8/Yr6dDlea5jPy+EyP/hPTPydHEMFazfUeP3+gIuLSQJAxcWZYAlwNlrcyw82AxleYgYAlTDP3iq9hoBbMx+eKnDBVpWNVwduAPAL9tI+UWparPJ56TNpUTRKXJz8tPxMWhwUkx7+EgfcmuGxrspLpx7r4SVFk5JL5RhtKS4UrLpaKbSCMysAYKLoIlYROgoGeQo0h/i8UXt9U14wUqGTNpsqXFQWLr6etg8/Jq9htILl9aLEEwBSbh6wyrg5a9Wk2cYG9wPUPjtwLrXPj3DW0FBJT5pdWc50Xu3wMu2JLl0C/WKBl9MVSvxeNcZ5V1RAd5ZTZU+qfTmg9w57/joGURuHrlVWI8fiz2EXirGD0gmJCw0QADi9gW+U/SXutPQUtcM+McyvYyjLD0cZUabWk9H15H1uns2Y4eK01npxQAOAhKjVVoLLJuxFJRztcvgB7TgXr7Muq96sAAYqPKi1ucCdO69Bp6W4EGJMCQ2PYkTrS23Cc9QeyJxJ7aqdtYmstArUqOfxxyFd3z8nxgNSBdF5ZNilmX31VT7GiT7egtlk3imRbUV/H6zygFUpqdeRrmE+ZxbGeaC16hq9xoDSKRgoa9HLqo8fBNtHeABkYkjMfYM4zrA4pKkAicdAVykAvtasdfgYsaouj2ytcVZrLMlLcTaVH5VjlEX5iDrk5Uu8lKcY1omK3hpnpc4IiJb1AT0pOkUAcW9udC21Ac1UjoMHQqeK0sf2Qa51MhboGnpGfwb8M6pl/Vgg4fB7uTbH/bKMSwsRq3XgLM9Salf+DKD12VQ5eTN4+TIAuALcY9gb4GWg3cOa7am0l1T3LcdRGjrH/oHf4o0JG8ixOCqh2qQHlQgBgP+9i2cSbpjON/tyTY+xOc0/s9PFM+ExF3emTw7obGKbi7d2VIdEE8kjxUpIiY26r6CzT5sc3nVAdR95qcYPonMLmubfLmjCMdE1Z8BA3DNX5AyNfWMgBqmEFuv9PADZKeqeHipy0WcAOMHFGRpRkaXzGoSLunN88qrSqrCjmX1Kq6ezxAMDu91ctwIAptR4eYhPZMq73XytywohSAA4PsEFXVWradWZZCzQn1kjP/M7P9dGmxFZSu2P9PLOP6dGPyivoeDm7/AI+CEuINZ0AGipcaHToBCnXlfhQWkAeDnPS0nrory8q1Di+jUAUCrrkiGGfJGzLzZV75Xf0Rrje8PWAn9eS6u6/XhDiLvbE8Jc76RgoPEWrvIxfpnmmmCRID9Qm6A+tpDaHdEG2oQ9qEqYyxWdBFBQXZDcfr4ezvBxfyVq0OUvIlip3WKfrvPqxNLF8Y9R+w7wNWBXlevbAECuxN/x8dDAGQ+RbYsxhmXkGMEGcizGHCZidSrz6hIibirjCQCXNnLmg9/Ny6LKNS22qjbaVJmzK6qizvrH3V+V16DQEOflW40efogEgIUO/0x7ht/LDmjxwTbRUr7dxTf7wWI7tcfCWuB3eoUzqB4c/q38jtFCC9tqoe/O9BPU/hNw+5zU5dRuIng+LHRddoLT/CNungUHAH+NB9aiouQva8DI2QPObBiscJbIEh/vJAMARdESuyTud8XN7Yr1AABbyvxgXxfigZ5ht2aKeb1Jaq9W+ZyZm+Rd/gAgCx486K5sovYT4pdSe9wg+NfhcBFgtVZF/DxIAwDtHu6A7hrm7/h4oGxQZqO6uil9jAXupdQ+KaBLyPwiMbQ3z5kNnRWtM5esJaldyJ0gXdZrbpfDA04LY3xdz4v1MO3T81Ix+8IBzvLyGGjkjOTbqd3t1nukwrQU19QLQ5Tmi+YNBVHCCQDrhngA5Nn096j95ORH5Rg+h/+ODUO8w+XcFN8XAGBjQTNqGJRPBFjGjMWbFzaQY3EYMPoFVUXPUwE9defGueMTcPPrbC/q8q0f999B7fUhzqiZXTuR2meKlqUAUHR4UGuzYAU1iMwuoJ+oeh4TRNcCAOjJ8+flr/EM87QgLxcKGLTJ9Bg4DIcbyiFxHJ1ZUl09GkQmPePwwFtNlCwBwB43F1pUeicqyAnoctadbs6QGijwII0JFvvfTu1K9BIA/ljiLJDmIG9Vu2OABxh1S3sgIbLcHqGTFRIMEBN4PJyJkqjxeQ0AYRcvhSt6OROzyeGZ9BerD8prSPl4madaq4ouPWcyVc48mhw7g9rDJiW1NR5MXVPi8y4W1mUXStx9ULAct8T5OtLs6O5cIVG6ODfB53a6qJkPz+V5G/TZbpV40ntTT62d2he5eFKnW7DqCkLfDQCaYnyMoQIXn54fv0SO0SO6c3WmuXZMUDBrAWCwxAP0GwM8WHRv10PU/vbEx+U1TPPx9W52y+eoPWqgC/hShpeAKWwZ1uzc0cIGad6kqDmv/He4xzjGYQM5FmMOk0VXZV3iIc5kSQpaKwC4xCHPLwI5E0P6IHl14wpqfy7Dne2scNi7oTPpc0WQZHqZC96Z0G9TooW56p6wb0R3SJkQ4YGz0ggPOPXXuJMpfHUAQE3MGVVnPR70XZNsoyNCb8rRVVnylsTp8hoibn4grgqWya78s3KMiUJvaKrDBbBDIX2YDTs8MLCh+jQfw6OZRYkAZ6MNVXj5SFwIhNZqei2r87ZRe7nKg3f9bl2+pYRQoyGuN6RKlgAgXOMMjMliXga9/PDTn14jr+EtdRdRuwq+r3b4nAKA48C7+KVF8+8KtCZL1s2ZJk1Bvrf0l0YfKA2IEhS1zjxd4QwRAJhY5gmXU+P8GgzOy2is8WCqX7B7fQaBnHf7Oeu0JFyzl7Kcrdbi6FLvZghmbUjopVR1aZVJFz4GE7HjSpX7ZqpLUqNgkm13+JoOAHNq/F6my9yvermguzbudv5I7eEgv4axKItSPo0juhkCgEd0IlNaW7b0yuJYhQ3kWBwRVKuchq9U6geiOmvjFQf3oIc704WqPjB/u+PL1K5E99qiPFv4lqBua6riyS4XDz6UqjrwFhPyF6or1fSYZjdtHeLXkROH0aqLP8/ekj647HXxcp+jYbNXDonpZygEM6kkgmYA0JPlDqKC26BEc7Obd4WLgR/A/AYskiHwjGXQwx3IRlEyCABDbk6hV/dbsRpMxD/zDnf68y4ekBqpaT0UFSBUuhSFIA9eAECXi7eZXZvnGlXHBbm204db/1legwps73D4NSTBy08A4Pnc3dReLPEkguqyCQCz6niZWV2Na6qkXZyFAui5qTRwOoXWVltQB50Hxfu3YYiX0zUFdDIk6eX+xM5imtrV/gYAM4To+e4S97uKDl9n9rp5ySAADJf4HqrKokxaTZvsDaOFCjpXvTwZ2ebibGtXTQfm1rm4Zl9KdFtrr70kx+gTQsImZU2jhfJXTNYqt4uvAy4RCD0afDuLv4DVyDGCDeSMI5QTC5hpTxxpeDw84xkXFH0ASIuDh9LQMekcorQBt2W5c3bHTr2wn574BLWXRFvhiQ7fiH+R+ZW8hhYvd3zSDs8+XRTiwrgA5Da6K8udTJ8BHaYgAkoBIfjaJYRtQzUdmCsZZPzfDFCOlXL+ACAk2DKKNZQM8vIUAGh2OINDZRvjHh3gUEGUPelHqT0T4WVsABAU2jEm95sh5NOsII/QfHAL8emkS5cr7BP7m9JXy0NnmE9x8eB4OcDXqilhfih/OK9b4Z4X5qVwM0QAJC/YTwBwev1fU7vqltZe0JpGgw5vOpB18+cxlNNC334hCquQE6U6WwWzAgAmRniAcJOLv3+bNGEAM52F1F7v5mWFWQNWwqYKDxBW3HxejeR5Se14sC9MWk2blIoebtSEj/pS9mfUfoJBMjIlWFybK1wHyysYxACQFPtT2qCBw+GGSUfgUlnrMFpYvBFhAznjiGMhSGMCFWTJlw3aKgotBMXYeaKoN/tFeR7gmBnlh9WPTNeb4H17eTBobZk7Pso5e1/i3fIaFHry06h9a04fjvoK/HeGvDzI0iDo1ABQFRmqLRn+/gw7PAPtcetAameeMzwUTDJHJk7J4YY6MKt33ATFMmeyqDK1HoMORZPi/MAcdXNGTl+RszcAoDJKdlPUQCBUBfmbErz1d1Z0QjNxxtVnQqn3UXseOjCgoOZdT17/jucD/DomuficiRT4s1ga1IyBkTIPUqq2wHs9mskynOOsnb2iA1+Li+8LAOARLuKQWHNNgjQ+kRiC0DNRZTKKmQQA5QgP4FdEa+L50KwfxR50iUCp26C0qlDjcz8nuoHWBXlgPCQ0WwAgneOsurEQ8x9tp7OxgJp3dbEF1N4J/n4CuhW76t5lEhR7s2A8fB6LMUbNGQdGzpH3x0cLG8ixOGSobL1J/bGC2uyVvgYA7M6J1o0FfpDMG3QVSJf5vVBtZqd7uJP64wHeMQAATvDx1qcBkWmfGtBdIpR2TFeRO8LdJX0ve9zc4W50eKv2nhynffdA08Ld7tEtiWMRpJEaOAYaVKrFq2a88TnjMsn0hfmhYKTEM2heg0ND1aW6PXE2TZ1fi7G6BRNsmygHGihwOwAEvFyHRzF2VKZctQQGgFKV63F1VfihwEQAe7QI+rSmUatb6CLVOOPmqerj1N7fqw9gyTAPkkxxnUDtXtFJBgA63JzVGnLxe7VPdGMDgN2DvJOZ0s8wmRP5Kg/4qhIXBdUpDQBGKnwtSno5O7BDdFQEgClVznzwikDOy86TcgwVDFIlmO6ICibp/THo5+v2eHSckp1ThUYVoPdylbRRbdTVuwMAExJcFH2kMjqhYkAzZ70evtdncno9HA8ollZVlE5VDViQFhZHI2wg5w0GVfZUFc76eFwDAESCfPNQ4pxnB3j9MQA0ibL1tjBnw/jcJody7nQ8Lpz+Z7x8I74gxDUKACDu469xZ4Fnf1+ocOcOAGKie0mjODRkRUYT0KU2O9z8IBkP8Tl1qvs8eQ19glXwfPH78jtGi1Hr2xhABUoVezAV4m3aAaAgDmARPw/MmeggBBz+/iVdnLUwDE3HjoouRvNTH6D27qp+v4pVLipbHmX9fsCgpW9CiKa3D/EuLF6DdX+0UIcjAJia4mUybnEAKwo2aFOEC/wCwCTwYNI+Fw+iZCuaRaKaCuTdPInQO/yiHENBMThcIggKAB2DfF4pqKCzifZFRTBj947we9Uc4ewLAHgh9yi/BuGbJSMz5RgJL28S4cR5R6nBEV4KFwtq7SYVqNEYvSbLeLAr3B7OUlYCvSZlauozsTAXn1ZBGkBrUB0rONwsLZNyvqOBKWbx5oMN5BwyvHAdRO8jIA4mY8FUURiPQM1YXIPKDCmUojrIItjtWJPm4miDRT3G1iyvvw+LNtA9GV57/0KCl6ABwFCGb8RZQXVWWR8A8Am688to52NAMx8m1rjTUQQvUVlbvZ/aR4ReEQBkxOFHZeGOhrIpE4y2nafJv1cts7M1HsRMefihBACCVR6tzbv4Ia7JaZNjTHDxd3gn+LruMdBGU/ozw3nu0Csn00ScOinYgRPivLxrsNguxxito2sihNrr8LbBc/y8LXd9bTm139P/r/Ia+gK8ZC8e5HO7WOGBPcCA2WAw7xRUUqYz8wK1+0QnmbGACjq7BSMVAHyCYegWYv4mZfNTYnyf9YmgdF9VM/u68+vlZxgmx3mJWMkxCIqF+D6rBM2PFtFZtdcfDb720cKGORagmF4qgWaDNEcAjvPKf4d7jGMcNpBzyKjAcV5/gR+PQI3KpKu23qOlKY8VlD5GKMAP7VWDl69U4xvxiFBDrgtovZNUgQeDuvp4jbNCf15v1GcGL6d2b4L/jnXQmdldxeep/STfxdQeFB0FAKAqGDkN4lAxx7WU2l2OzvQpanowwDOSpYrWCVH6T8cCxkJzRR3KcyKoBgCDbj4ndpZ4C/MGv26nmwM/VJdEsEgxkwAg5udBFKXTow5HwQgPqgGAT7ALI24eLEpj9EKoCiaaDycm/o7a1d6RrvB7PTf1XnkNWfAOXpkS9xXqgwbzUmTr1ftVNFirckJ7ySWCRePjEwntC4Pger/Q45qQ5A0BqtCBnH251dSuxHNNytSU4GtQ6A21D/6B2k2Cg28UrZFjJSnDcLQ0WFGCyoUK12kci3VkPJjOFhZHAjaQM4ZQ2StFtQQACKdEZStUoMas/vjwt+lT36GyjQN+vSgnVclRjm/UEdW/HEC2wp2WeGQ2tRdK3OH3G5QrPJ5bSe1TojzLdnxNt/St+jgl+/nKvdQ+z3euHGOaqK3vLfESsY3lh6ldBZsAwA1eCvBGoSGPB9ShQR3KnYhm/cT8XMy4OcDLYFQWHADiTpLa94lD+1gEvaakLqD2So2/GyZaCjEfZ5QWHR7QUgfR8cIG8OC5r8K7Wkk9sLIOJilNI6VH1JPTY3g9fAwVnBgLxo7SnRgP8XcVOJB6KdAt0BWjrVBOyzHGouOTgtIDMhF+ZhiLQ79iD/q8moVcrnAmdFmIOo9HsEklVcMiWQkAIwXubzjieXgNGHFhsYeORdeqo6Hz1WgZORZHALb9uBFsIGcMMSZUy8McHX+jLFZxr2Z4bBfs9NmCqVIwEDuu8/PryGW7qV0F3kycUNVaeOvAL6l9h4F+hiMc9gZRe9/n5pldANgmWD+qBXNLggesii4dSC0blF9ZmGG0WbQJfq2DNdHhDKn1DmfkTITWO+ly8VIdr2CyNMZ1oFRpiewZ4gK8yqGfEObvJwA013jgbUiwn3KBtBxjPA6zPUPPUfvTIb4mzwyeQ+0xt26zXnb4QXMs7oPqijOU44dVNWcAnXAxEWxVKAjWz2iDByaHdhXgGG0AZLyg/AmZbJSsoNHvj6pEpVzmgXHg6GDLqECox819w6rBvVTvn2K6eAwSt2+WzlZvlLOPhcVfwgZyDhFB/8SDljepjhrjsWCq0iu3W2c7akJ482jYRL0H0Sn6c5zdJDJ14ndsGNYZS6+bX4dPtFlXjpdfdLMBtBCqcjiMHHrxmZESPxz1FdfoMQ7zRlsRnZwAIFPT4rdHGuodfwX8M0cD/V0JMaouSQCwIcO7uikmS4/QdgJ0oCYMvu7vLejSxcN9UByu6qBa0cUP5WXwQGh/9shnXU2Qy/PW3utLPPA9L/4uOUY/+Bh+wX5SJTIAkC3wAEgizDstmTByVKlpRew9Jj6PKrM+3MktE6hrNBH6VgEMxeAYi5JclWxUzCSTvWe0Afyjwb80gfKJGoQoernGg72ADvjWRDl6yGBeJqNcmH0ww3WXTJ6XfMfF7xgL3/BoCGJaHCIc5/C3B7caOW8+FEp7gYPQhY+GsgslQvpG0OcAgEJV0+GyFT691wxyp2S6jnmhIhYZn5dvHnmxN5g4ThEfp+gWSpxmbNIdSCFf5IEck2DRaKFa0vsMRC8Tbu7IHn7FBw0zoeKjny6q2pqqlr8A0FjHSxd7Sjy4EPNpdkUQfCHoqfFOL1VR9gSYdfpjGG07eQDYI9pZe4S7EAm2yjGGR478/qMOHmqPHIHWboq4eaeznJ/bm6O6C1J3lnfwKlX4oV3pKplAlcmo0mJg9I0PxgOKGVEag3JzNe9MyuITYd7ZaijH16rxYB6pIKbPy7tBAToYezQEg3JlXs6aFUw0E0SF7zeQ588bGB8dq9HKMYxFiebRIE5tYXE4YAM5hwgXfAftWqUWkqMhC24CVc6jFtXxEE8bNMhmjFR4pjygO6NKBIWOTlk40wr5ota2GK0jrHkqxwYywiEph/S8zIOL7h0NOFoEDEcL1XFjrv+t+kuEvz4kstxR8AM1ABTA9TEURd4k8Ha4nUzVFQsAkuBBrYDDO4TV/Pp3jnatMgl4hfz8cKO0fCpVvrc4BkHSfI0He6riGroyXBgXALyi/bEK1OgsORDw8fcjGuCB77FocT4eUGuqEo4eNNAA8Yt7qQ7UDbGFcgyTch2G8WAFKbZZaRy2Lp/oJgoAURGYLleVyD33Jcai8UhP9o/U7jZoMqHKs4ZyfM022d9UEFLph45FYG60mmDj4VNp1pCDWu3IJ0PGDce4Rs5Xv/pV3HvvvVizZg38fj/S6fRrPrN79258/OMfxyOPPIJoNIoVK1bgpptugtdrHp6xgZxDhIPyQbtWvVGgAk5HPtcBNAqmCwCUxXOan+AhjP6SjvT0FvjirroYqYymKpEB9AblEw6kSfmWOnSra5iUXCrHUOjNcWc5IVr67qrpw5E6eKjDz3i0TjVxKJTQsOqAopxtJappgmqVB0gSggkDACERdA44XJ+mbHAve2q8lfRAllPPTTLpqsxstGxPk/bjERdfUwMOPxREXFyrayzgETo9gF5zJ0ZPpfZ6obu0ufiovIaZAS6oXPSOLjgIaP0LdUBTjDgAGMhw1s/RwEIeC6g1VQlHm6yHKlDTlrqQ2lMi0AoAQ26e+BkEP5TXxDqh/ZVjo02zEkMGgMGs/gyDZh7pYJIK1iqfJ13gzCUAGBYBX5doAOHz6d8hG6i4eSDHxK9SpU/jEYhR74d6nlo77Wg4fVmYolQq4fLLL8fpp5+OH/zgB6+xV6tVLF++HC0tLXj66afR2dmJv/qrv4LP58PXvvY143FsIOcog4rI1mS28M3xoj9Y4DoGADAjz9vEpkt8+mfL+l5OivDDTTDPNzlV9mRSrlAQGWJVntUc1IKvs/y8/WoTxCHOYFrucvFDwYifb5I9wtmek9DaFtkAp5arg4uJc1ZzuMMxFuyMw02XNum4oVCp8uyv24BOrToM7XTxg+heISIMAJOT51F7MMEP7X15HggCDv+BOOLlhwoA6AIXdW51ZlB72NEB4dHCb9DRxu3mQeUpNV5+MifK5+VxvsvlNayvdFB7s4eXHA2FdLeZGHi3mcYaf+ZK/wYAhpJccLzX4XNm79CTcoxjgams9tCxYFfsyXCRbpMVQmny1QtmUUBoKJqsZQqyTEYIvwPjM2dGyyJRyRATEXzF/lMJtJpBp1yfl/tuKtFXqoiuIgDKFc5QVFUAis0GjE+JmIIKYiq2mdazdOC8YTj0BjjGGTn/8i//AgC4/fbbX9d+//33Y8OGDXjwwQfR3NyMhQsX4stf/jI+85nP4Itf/CL8opnOq7CBnKMMto7zFahN9JLYZfI7zm7gm1hTiGtXdOV5KQEA/KSdOx2NQe6wD7jbqd2ktGp2jLfVrq/xTTBS04yBbvCA0zpwJkvQrQ8mDTUetMp5efAg6+VBGI+BRk5jmGex94psv2rHC4wPa0dBZY5U+Uk2r7vu1EVFRw3hvMU8+nkFPfyA1VI6jtr3OI/KMbqynMnlcfN1olTWmiqHG0UDRo56HiEh+lxwHf55PRa6Ls/4eFecJ4Z5ScR5ib+VYyRFy/qtYr1MeDgrCADyDl+LHhviQuAmUCVFTX7+jjfHT5FjdA2JdvEiOO7x8PdvLA54ZrpkHJFQG7VXxaHb5HeogJIKGCtm0Vho3alk49HCdz/c5T5jUXao/GSlmQTo4EG+zH0/n2CZALqDl/I3joYgjQlUwFetI5o19OZI1B8JDA8fuJ8GAgEEAvpsNBo888wzWLBgAZqb/3S2ufDCC/Hxj38cL7/8MhYtWmT0PTaQY3FMYqSsHasBwbgpO5xaviunD5I7RdZlpsMd4aBosRwJ61d0T0k59P8ftau6eEALIk+McYfd5+gF8dn096hdlQulQtOoPeLosoxehx94A74ktZsIR+cKPFs/HhRglTlS97oltkSOERLdnMJununziI5wgBY9L7g4g1GVnwBASFDHM0q0chyyx8qBjLo5ewMAeou87CLo53O7vnb4S6vGAhOii6l9rsOFhocdLV69HS9Ru18wH7amfyPHCPj4M1UBEJOgsxLHzYsgpckBTJWrVkQ2v1zhhxuT/a0uMovaQx4+t000qHoL/P0qibbbM+s0o7Tm8Gx9R+ZpalclRya6SqPF0cLQ8nj5/qWCZuEg7wLoN9D7SgvtJVVqqrS4AKAiAlbxAA8qmzTkKAptpeE894lMtNFUtQJEp1uflye3yhVdMjgWAV+LP0NtHLpW/b/vnzz5wDLFG2+8EV/84hcP69BdXV0HBHEA7P/fXV3mwvM2kGNxRKAyCareNVPVh910mTsdPjdfIOJevSg3ufhm/1ztYWrvHeRZmViYMwoAoCxYXPVCJNFn4JwpjY3dokTFhIWidELCqrRKZLimxXV0u87NOyV1FXj2+FhBNDSd2uuCvIxG1c0DwO7C89ReH+RzO1rSzltQiDmGhc7OBBFIBYDOMi/PUiwR1dIX0N1iRrteVqA1V4738xKyhI8HttMGpahHA7JVznLs8IjAnAFloFTh66UqAzXJpKvDz3h0qCyWeCLDSJj9MDMUTe5Df2YttbsEoyAsAt+A1jSKizV5pKYPkmpdViUsCiZ6X47o0neslP+PtlxO6Z3odh0aKvBmogWkkAHXRzxmINpMq1I4izc2Ojo6EI//Keh/MDbOZz/7WXz961+n37Vx40bMmTNnTK+PwQZyjjKoLFqlmqZ2FRE22chH28rWbRA915FrfvAYhK7L9bg45VoFcjYO63s1K86zEQ+JqKoSxJsUMAg+CC2EYTcvFVg3+GM5xoQk18jx+3jGMhbgzCRAZz27R/iBOhjgpVl+g+VO6XwcblHa8cJIoZ3ag4J51OjRB825gQuo/Y/ZX1G7N6oPDe1DD1H71MS51J6p6qxHyMtLE/PiEDcetHC1JleELhMANLg4cyHi42tdrjoGbQDHAOqwmc7xwFtfZRW1m2hbqCx3Q+wEajdh5Smdqkxu9IEcdS8VI0CxaY4WqPvtdvjcN2ElBDx8b1EJGVWCBoyeEaCSPpmCQXmXKp0SPmjCIHmlhLr7hvk7PBbtrBXUnDAJ8B8rJUXHAlTZ4FjoXFmMMZzaK/8d7jEAxOPxAwI5B8Pf//3f46qrrqKfmT6dB+VfRUtLC55//sCEZ3d3936bKWwg5yjDWETQGUxoq6PN/jqi7SIAI0E7hlmCnQEAVdG1KuThNOT5WtYF9+7lm7U62Cutkv6a7jrQVX2Z2ksl7iCq2n1AHwRVWVM6r39Hb5EzapTjE/TxB1Z0aeG/ERefu0rHIB7hmkiA1j063GsAoEuKVGBgsMbZAICel+dHVlB7wquz+XPi/HdsdfHSEOXwjwVMOtrIjhujZC10CwYIAOREyZFf7Athz9ERyFEdUmJBXiowmE1Te7GqkwhT/DzY4wNneKzLaDF/pVcyFqKyal6qQE4yqoX0R8R6OB6ZcnWv1H3IFbvlGCMO9wWOBn1E1Z1rLKB8UNW2GwBKo9TKOhpYQSZBGsXIzorSR8UkA/TcViViJt3vCiVeNqh05sYiQWYDNRZjgcbGRjQ26lJ1E5x++un46le/ip6eHjQ1vZKQf+CBBxCPxzFvnt47X4UN5LzBoBySoKh3BYCqoMaWVCDHYJP0iu4Kqk2fKHcFAKTL/ENeF7/O5qA++M+M8+v0D/BATUAwWfwuvUk2+Tg7YrcjAiQiUwgAjqi97xziHTeUM2CCstAQcPycOeESWVUA8IgAhqqTVu8OAPhE5x2XizOsTLLcKsOstC9miw5fJsLRPeBjDDk8OBGu6e0p4OaH0foaZy2YkMaVLkTQzzf1gOj6AegyGWB0gRwTxkBYdHvyiq/wGmgajRaKMQBo1kBQBNbmpni3w4yjAwsqUKO6PSUMguuZAj/cBESnF9W6GABKIrgwKDQ8Yj6DltmCIaWgfB4Tf0R9Ru1fJvdSsWUU48akzFodmEebJFAMYmD0gTeTTktKH2o8mLGjTXgqHToAqFT5uq/mrc/At1P+vCoRM9GvORqClApqnz8amlS86TCOGjmHA7t378bAwAB2796NarWKNWvWAABmzpyJaDSKZcuWYd68efjQhz6Em2++GV1dXfjnf/5n/M3f/M0hCS3bQM4bDGphLxT3jvo7FMw2KF4hrLIVkyI6m3haHV94lRjyiwP69dgyzDdBJSqrDvVxl6bX9dW4Izw8wkUWTQRfk37uyOZFfX9YHHYBoCx0JZQTqkpgytDlCjnwbKByxk30GMZDu0IxaiLiYKL0bZoMWtaf5eVlTQG3Di4o+MQhzlPl77AJGy0sWHOqVEc5wuOB1hhn2wBARgYhuWMxDnEcDAgtEwBoTZ5N7WE3D56Ha/zwMwn60N4FfphNunhCpejSXcZUEkChM/2U/ExD/CRqV4fVrqx+XvpAPLrDrCqHBQCflx9GTVosKyhdJIVMToedR6uBo1ivsaD27dIOD8QoZkSdQcBK7W8lkewYi8CCYqMpxpxXsFAAICbKxRVMAlo6OCd8HoMAhzoTjEUJmZq7SofOBmosxhpf+MIXcMcdd+z/3692oXrkkUewdOlSeDwe/Pa3v8XHP/5xnH766YhEIlixYgW+9KUvHdI4NpDzJoPLYPNwRrmgjUWnClWO8OKA3ojbInyM+QnuLIe9OiLak+cOheqYMZJvp/Z2g/rQSpUfwCanuIhpvqoZHu2Df6B2lSnvEYwdQB8a+oZ5IEcJMg8oEVMAjnBa1PMciyCNcnpUwMvkOtShoCnBu1IlwZkuALCmtp7au0b+SO3vin1QjjEpygO6tSx/XmtLOpg0LJgPqnWqiUCoErcdbfnJSEVnybd4+Doy33krtZvoTow262mSZAgKrR/VQW9r+Ulqn+fjAUoA8ArXavXgD6ndRIcn6tfsCAbFsgR06aFiiXgNSjsUaydb4QewgQzXTlPvJwBMFKLnLj9fJzYM6lbvah/OVTibxqTsKRbmIvUjYi0rlXiJWJ84DI8FCgYlMEo4WgVqxkIjZ7TsJpdBaaPq9mSSmFVQrcGVT6SSkYDu0KVE000kIVSgZiyYexbjjFrtlf8O9xiHCbfffjtuv/12+pmpU6fid7/73ajGsYGcNxlMDhXqM2NRaxoXmXC3m09NRyjQA0BVfKSrwINaJoy7qriOKfGzqL2/tJ3aT/a+TV5DTWxAjw7eQu0mhwbF2nHADwWnJq+RY3gc7thUozz763XxeTtc1QHGoPvwB2oUxkUcV73jNc6YWz3ED6IAcHbiOmr3hfn79/NB3o4eAOZV3kHtVXAHMODV4nbKkY0HecY/5tGsupJoe6/ayHo9/F6adA9qc/hhVmgdGzFyVLnPWJRE7Bj8LbVfUvdZar+wgetc9eW149db4mvV+Ynrqf3Bof8tx1iUuprah8CDf1MDvM06AIT9PPDW7uYBYZNuaSnwQE7Fw7+jLXUhtasuZQCwPcu7S06JnUntrUluB4COQS7MroLn6ncCo+8eqUowvR4tHKj8Q8Wc8BusySbBHoaxOLSrNVUlpiJuvhYCQHv6fmqfk7qc2gvQSR/lgyb8fH9LFzXjdDDL9fLGA6NtJ29hcbTCBnLeZDBZrFTnrLFAWtTWK5w24xL5GaVx0xgQtcEV/XosqOOb+Zoenq3wCCr0NjdnNQBAPfhGqxyKBS5eigAAySA/+I9U+UFzyMCh8IrWqW2+U6lddRYJg+sZAUCXmx8kFaPAMegO5HbzOTEewSJF+57g5V11pidPk2PsdXEdkAXgncyWNuv2jSrYunOEB6TSHp3RVJnwkI+vl+mKFvpWrALFBFMHMCXSDQD1ET4v1b0uG0S+y1W+DoyWHg8AFyY/Te0JP19zd2X4u1Go6ezwH9LfpPbL6m+gdhVsAoCcuI7j/TxAohIAANBR5CVFC93zqd1twHx4scZZP4phpQL0KjgPAK3Ri6l93QDv7PjWxKfkGJOT/F49n/6+/A4FFaCPihLouEEZmsKgECJWwdqCaFoAmDG9RgvFjA2KwECrm+9f8Zqel4OC8dZR4PqHJqwfxZZRbE61/wFARcwrtT+Z6C4pxo0N1Fi8UWEDOeMI1aEI0NmIkTw/HI1FpmE8uuaMFoMl/Tv7inx6l2t84e8q6Nfjjl4ekNo2zDMq8+JcVHayo7P56pmfGOasnmxZU+w317jzFYEWvFPod/PMaaNosz7g5iViLtHNBgDcIpjUJErIqgZtg4dEOV1VPI6xoIUrrZ/1gyup/eTkR+U1LBHBICVY3pPXB2b1HR4R4Kh3TZVjTE1cS+1rS5wW6zVgQY5FAIPBZRCcz9X43HVESZIJI2dKjDMUwxCd56I8MAcAbkGYifn4hU6M8ENin8G+cH3i89Q+UuHvZ29Bz/2wYK2uLfNMeb+jA4zvjp1D7Qk/v5dDBvt0S5Z3POxx8b1nqnsRtVdc+l5OFqWicxt44K2jrDstNbn43J5ddxm178nzQzug13XtP4oyGpHIALT+oUKdv01+JgyuDzXi576ESZv2suiepQI5e6s8OL/OgKWiSm7V3mLSUarVwxMqfQ4PzHUZlM2r0qjRajsBh780yqRhgMm8sjgEHONix+MFG8gZRyjhW9PPjAYmFHvV8WYsxhjtNTRpqR/MjfM6aY/oWpWr6uDEeWFecpSpCdHLWpLam0L6EFis8s3jqRJ3GKZWuSMNAKeE+YE3XRKlHwZtxsriXuSEQ763sobagx4tDto5yPUxlCbENL9mqkSjPCC1c5AHBkwcFsXgmJbgOh8RJ0ntA9B6Q34P/51xUasz4tGO02CRz4mYh69FtaoOrj8w9G/UroIwuaK+VyqTrliSKvjeGOVsAADIgh/A8mI9LKhaVgB5hwdbC+BstM7BJ+QYvtQV1B7L8/XuwSwvNXhbgpdeAYCKQT6b413KFhowIxqCIkhZ4mu2190mxwiKhP7WIb5Pq9JjABh2palddRIM1zjTUpXsAkDZxffQnAiuTxSHegB4rPwAtc9xnU7tbQEe6AGAzS4ePKgPXkDtL6V/wP+9Qde40SYCayKYBAB9NR6QUsGkgC8px1AsENX97jjwkvVUgj8LAJgcVUFlPjELKisEYJ3D/cPJ4HtH2q8DwkWhvdSc4Gxr1T0PMNOQGg3GIkijAlYmWkAWFn8JG8g5ynC4BblGG6QxgcsgazPa8pG83p8Q93O6Zl2U14v7VGoXQH+JO3D79vCa9cEAz3YEwFvhAkBEHFaj4lA+I6pLjtShoVTlzvKqMj8cAcDZIvvUX+DvRr2b/3t1HwAgF+aZPKVVsnbwDmoHtDOsAgMm7VlV9mjvyEvUfmaQz7vjvLp7ycsFIWBY4O9XHZJyjJSXO7ovVHnXnGbw7l2ALpvo8LRT+94cv9fA6DtbqeB5f26L/I5ZIV6CqUqnektaJH8gL/QYQjz4cEbib+QYUwSrdYLoeFhX4YGakEcHpRsDopOSl8+75wfTcoyuAg/+nVzP1/XBovYlesU7qjAohPgBYHP2N9SuugMNiE5K89y6dPiUej5nAh7FoJJDYMEQv45FKV7aaMJuGsrxIGUdeEc2lQBQHfpe+Q7+vBJhXt6lNJMAoCC0enqqnCWSM/A/JyWXUvtiN9c0+qPDg2qTvAvlNbyQ4Xvo2UmeLNln0Jyrocw76KnyyGlhzrIEgC3V31N7V/ppag8G+DUCujvdeLSkV1CBGrWPO44j9SjfUKg54yB2bBk5FocAtcEBY9MWkUFpfACjb8M3HhofG9P6MPsrD89in1rHva98VTMC+oUkihJ8VeVEEQN2U9DDDyZzXbyFpcuALbM5zQOAQ1X+PKYKHR8AaB/hz2NiiNOwMjlefpJwafZFTOhKKMFKE6jMkdI0KpTTcozGIK/Pn1LjQa+JIb5OhLz63Wh18YDUk1nuWE0M6LUqGeBz97TcQmr/dfZOOUZzkGck62r8/coYOKEqkKNbNPOFKGTQqjoksoVRwaBqqennBbG1THbxe31KQv+OVnEZk0LcEY54uV2V7ALA9ixfk5N+7jyeXpeUYyjWj1rVDeJRGCzxdb/H4eUnObfWRgv5eVlTVmiuFEXXnG0BrsEDAMV+Pu/2YTO1n+LWTMxGIRytShPjoiQQAKIOD96tdvED8/QE76xVdnTZVKHG/T/Vicnr6Pcr4XCh4IhopqG6hQLAQIHPuw1hvhbNceZRu8fA75oXbKT2HcP8/Xy2phmMZeHvq851Y1HqrWAShDFp5HK0Qyfaj/2gg8XYwwZyxhGHO0gD6EXVJEgzWlaQiViyYgxURH2yz6BeVTlGGSFmXOfX7CV1aEiIwNkErxAfVK1ioDUf0iKTl6/oiHdrmN+rSUKvQVR/AQBWDfOyix/3/he1J0Wmz2sg/Kc0bsaDGtuf4W25TcaYKNgVCq1hPu+SBtWTW4b5vLu0kQf3ClXtIPYJVoFikUwJcko3AGwc/Bm1Z0W3mbhB16r5qQ9Q+4ahe6hdCXOqACUApEWnsnyFB1IrBpktpfXzUomXdvidT8gxMsN871jg5ayf9RUunntmpE1eQ0VkEfsNNHAUBkT5iEfofSkmGQBMrrVR+yQvP8z2V/ThSl8Fhwr0lCo6seSJ8AWtGbytt89AICpT5nvLTwZ5kKVnZIMcIx7ia+rx4OyJbI37qLtquoxGHUZVB6PhullyjKLo8pcX5ayKeQTo4LoK0NdcfM4UTJwiQb4YqvIAfu+I1uEJB3ggdUqKl4AFXLr9+JAQJO8x0NlR8Im1aLQ6cyZQiXJ1/lL7uOPUUCwdeWbRuMFq5BjBBnLeYFBBFpOotaIyqxroqnAGACAU4FlsVY+arujuQD5x6I54Rk9RFCXKWOM8T+3NZb7ZT6xoFskjhU3U3lblY4Td+lT+86GfUntTkGefkkJMEgASQuh0UZS32twu6NRhRzMGwkpHxzn8tFbVaSIoSq9MoDrWiMY92DuindD5KR4MUvobQVHOAABCMxZbMpzlFRRrHaBLq3a4+QHLA/1+dVa4w626oamW9cXgZHkNSRfP5peEBk5f2aC+ZJTYbJBhXojzqf2ZCi91O8vHtS1ezqTlNbQF+UFRvX9KtwIABqtcJyTq4+tEEAaHWRc/eBQrfKHocHMmC6A71niFFklVJH1qBoHvoRLvXtcY4CVLOypa27C9xufdUK6d2lMRrs8G6APxY+DsClnaYcAIGC0zQgkuA4BfrFV+H2fsqPXSBIrJssG7mtqbqzzxBABVoQvYCe77TYidIscYKPBy13SJB7Qm+k+UY6jOcSqwZsLydwt/vy62gNpzpX5qN5kzXlV1Iex6jGM/6GAx9rCBnEOEyxU4aCmKorcfDTC5xtH+DpN/ny9y8TMVuW4N6kN5UfgDk6NCDNlAI8eT5tehMnk5F2/v6nfzGmgAaKzwzNDjuR9RezLMrxEAZgW5OG6ixoMwYYMSMSU4Oejm9eKTXNyhaPBohexAhTvLe0QA0qRjh8fNr0N1yyhVOHMJALYN8W5pNUGhf4ufB7QCbs0Ui3i509GV59/RHNTv3zThN82JcYe/Pcc1IwDgv/qeoXYv+MFluKbFjpu9vBQuluSB0PbBP1C7avsNALt8PNOXAj94BA06j4SDXBsmLxxZ5WwDwPqgKB9xeJcjlSlvMCiRLo0yyzfb4fMBALb5+ZraXeQBxoSfB6xMkHOLPdQgiOkWbM5KMX0ol/Q/QsLP91C1Tw/WuHg1AIwUhXiunwcfMgUebAKAySm+rqvOjbsHuSCzCqqZjFEFnzO5mt7fvC6+5o5FoEahzseDe/PBtbY8Biyu3gq/V2tFmfZ5cc1gzPq5z/PM0HeofXhEB2tbk2dSe12Es7BMgrGKCTaQ4ZpFY4HD3azmzYcacNg7gR37ncZsIOcQ4ThFOI5BcfkxDLVZez38cGSi7u5xc5FSRWs16YaxKMkzfQNCLHJVWjvsawdE8MHFA1Y7Bn9L7b1CLwUA+od55qcleQa1Rw2CRWHVscbFs/F73Dx7DACdeS5MWyhxJtj8+CXUXjGYMx0ufuieHn4Lte8p8WcBAFUR6KzW+L1UgSAAqFT5wSNR40yvzhyf1zPjeg0s1fhn1PMYqegxpif4vewr8S3ua+3cSQWAi6IfofZnqlw3qc7bJsdQB8HO9FPyOxjSBs72qYmLqT3p5xQqg6ZVyKWVFhAPjCeDul18g5sHnHYJEdJVw1up/S3hD8pr8NT4YXYdOFOzc4h3z3sFfIzWBF/3d5d0O2u/CFqpMlAT9mCxzINzoy1XqFTS8hr8ojxk88DPqf3U5DVyjD2iA+Uk8A6YPkcHxV7I8jLQGdGl1D4v9T5q765wBggADGT4Pq6wL80bRABAMsLvld/HfRrVkQrQmpZZ0ZH0l+lfUvuC1IfkNcz18VK5s2MfpfYul/6dfnBf/OQkH6NRMKkBYNjhPs1W1wvUrtNGQKYwupKjw91oxgSKmeQ4DmoGgU6LNxdsIMfiNQj6uMZNqcKzuyabpIJy3rYZZGZ35bhQ3Nw4L5M5LqqZRZkyd85+vJUHahQmejgdFAD8Se6EJoTorN+g5Givmx9uEuBjdGR1DbTfy9kRjsi4BBwe4PAZsEjCVX4vleilz0BMXAU61cHDL1gNANAc4Ye4KniGK1vm78Z9XZrhcXwsSe2L6/h9SPh0QHhABGo6cjz4sDz213KMjBDynuZezL/AIOHTWebBBZVpL9b081Aoi7JBJY7rN8gwK6hDeY9Bi9lyhH+HytyeF/krau9y6b1nbfr/UntLgreanprUrYlVm2alXVHn1+V2PbVt1K70ukzKZEbbXEGVA5l06qxzONMyleTB3D6XZsuc6HA9rpiX/469ZR6cB4CZ0bdS+67Cs9Su9q9iRV9DSJRxqiSdYm8Aem4P5XTgWiES5EGUheDv8PQEZ/4NQPvJOdE+/NQ6HkQZLOryyd/neNB4lmAwBj36GLlHiKI3gzNy9lbWyDFGy4aRshQGrHK11qhzTcjPE2yOU8VI4U0UyLEaOUawgRyL10AFaioGpR2jhXLultVrzZWhMn9B/W6+ScZ9ujMWRFmFckpUO+upIkACACeItot/FOJoLQ4PeAHAHB+nno9U+O9oDF0px1Dds3oCfKPuEbKZM12cug4As8RGWi3x31ny6jnT5+HinDlBC1dC4YCue8/7+Dt8ohByPMege1BCdOapCmbjvrzeniaGuOM0O8YPkibO2a+709SuDtQpAy2SS2KXUfvePF8PVfmk0iEBgOHYCdRegxa1VFCZcsVGUzoIABD3csHIOPh61w5+0Nxd4GwaAGhO8EN7ocrfv5pbBx8yJc4ezIkMtWLsAEDCw+/lsBDnHI8SF3V4MuoWKrRI6mt8vTs5wgNBADBc4uvEquoWam816PyoAmcn+99J7XkXT16tr94nr6FQ4ixkBZcQ6Tb5TGOca8MoViwAZItCmN3L9boWuXi7+TOTvPQKAERTKvx6aCO1z3Z02fxFon3403kezK1z8RIzAEhWk9T+xNCt8juONEwCwvI7xLlGCbdbjRyL14MN5BxlUIc0k7Kl0UIxalRXKq/BQVNFz5Vg3h4DsdWPzeLZo4AI5Lw0oCmjKgm92MUDOc/WHqT2uoA+aKoWsbOFM26CJqFMu3uE38uYh9N3Ad35o0foDM92OHtpuKzrrO/P3k7tk6L8gNZc02yZDiEWHhOMm6CBTkH3EM+8tgV5NrG7wA/UcdFKFwBEozM83q3Kt/T25BX6GtsyfE41GOhyXj2ZB/e2ZfkYnQZrVW+BB1rSQqNjUpS3P941/Ii8BgVVmWjStUoFapSoZV1c67qotr9ZIRxddHFmn0mns9YaD4SW3Xwt6vFoXaUhUY43N8mDg1FH729lh8/LueELqb0rxIMTAJAtcX8jGeDr4ZBIVER8umGA2zEp3jg4imOggT+5yn/njCgvaQeApiI/uK8DD/CHHc6KnR3izEAAWFP8sfwMQ1l0zwMAt2DXjkUXJIXZId584eR6/rySItEBAHnhspzo5vo2xyUM2ksKvFfo16gybAB4ZJgHveIRHtQyOfdkcpw1bnEMwjJyjHDUBHL+9V//FTfccAM++clP4pZbbgEAFAoF/P3f/z3uuusuFItFXHjhhfjOd76D5uY/sTEeeughfP7zn8e6desQiUSwYsUKfPWrX4XX+6ef5jgO/u3f/g3/8R//gV27dqGhoQGf+MQn8LnPfW68f6bEeARqRgvVtcokAzZalfrnizxLAABvG+GZgpYgP1RMCuks9p48P9BuFyyRs73LqH2GgRZJkwj29Bb5d2xIay+0X3iqTUF+DdmyntdeEciZXOUsrMIYtP4+K8zbQD+RuYPa97h4AAUAqiIroyjdvVmuSwFomnB9jbOTTmvi83puXN/rkOgKN0HMmVWDeoNti/DPnN3Ir7MsdHwA4P5OHsRc2f9/qP1d8avlGPNTPHhQdTgzb+sQD65no73yGiKixFJ1GYv69GHYpPsIQ0EIgQNAMsKDxqck+AFLaf3sHdEMxp4CDxZNCQr9jaIulbssuYLaVYC/B/pezvJypokqt2st6SDK9iDXTxus8oBVwMODDz7R4QgAGhzOuNno5rovs308kAro0t5OwdjpNWhZv7XGS7yOd/NAz0CF+0TPF38lr6EhtpDalXBtwsuDoAAQc/h6l4vx8kcT4VslzH5cmAdCVdfFdoNq2FXD/HcsrefvV0aw0gGgUUjuqXd8UkTvoSu876D232TWU/uOIa5DZwLV2luJdOeLo2/77RdBZSuWbPE/wVERyHnhhRfw/e9/HyeccCC1+1Of+hTuvfde3H333UgkErj22mvxnve8B0899Yrw49q1a/G2t70Nn/vc5/CjH/0Ie/fuxcc+9jFUq1V885vf3P89n/zkJ3H//ffjm9/8JhYsWICBgQEMDPBgxMHggu+gJSDx8Ez6b0tV3ZZb1Q8HhHhgscTpoCZQi406iJqgNkpNh3OjuhXnhBAfoyHEf8egEEMGgJYg/8xbozzTUBSnBtUGGgBCYqcdECxiE+bDsHAInh3iB8VlDVpQWTk+GwZVdonb9xV1pq9HdMY6I8KFTj0GtPB1Ds9OKXr8sME6opAQtdpDIob56w59aD+jid+L4TKftwtTJl2r+MEjV+HXEDZocf72iaKLUZCLQbZn9AFMMfs2pfkD6a/xOTFc0F11/CFOsVcwETtWbE6VJDDJuu7xcfbS7l5+oceFktRuIrQ/Mcz3hV9mf0ftFwQukmM8KYTVz/RxbQtfRZdHDpf5vEv5edDsuSrvggQA+QJ/5slgG7e7+QEtDx08HHb43vB2wXgziGFi1TD/nXPD/N14tLBGjrHEy8sjM6IEekKAB73Odr1HXsPvh26h9sY41xRrrOpATkmUgKlAjQrSAEBIaEX+Nsfn9kcFW60zpxOFl07gCZegZ/SJX9WUYLuQRcpX9HoY8fIxplZ50tVJ8K6pANBX5Ow/r4f7PIVymtrbUvx5AkAYfE1VzTBsIOcvUKu98t/hHuMYxxEP5GSzWXzgAx/A//k//wdf+cpX9v99aGgIP/jBD3DnnXfirW99RcDthz/8IebOnYtnn30Wp512Gn7605/ihBNOwBe+8AUAwMyZM3HzzTfjve99L2688UbEYjFs3LgR3/3ud7F+/XrMnv3KoXraNF3TeTA4KB+0a1V6hNerjgV8omOUR2xQKlAE6I43QT9nRpiMMVqYbB7bMvxe1YlATsirD2CKaNKd49+RqyrGgC5JSvq5Fzk/yS9yn2gDDQBiCJwS41lqn1s/r0e6uTMd8/BAzcYary9uhi4xaxXMB9HYAFlHBzkVq0AdVpXOCKC7kzxe+jW1p4rcYVfsKQAYKPHP1Alqucm83Jvn73iniN3VBfTvmBnlzKJzGvmh4sSk3ma3ibh23CdEncs8kBPy6UP7oDjwlmv8XptoHQd8ST6GCORMSPKucQDQ7uJtty+Nc22Ynjx/3i0hHaydIEggHwu9ndpzBvvb5UJkWz2PdEm/Xz/o+g9qf0/qY9R+lk8ffh6s/JTalbCtT+jUZaGzISHxHaJhG9JF/bxavZyF/EyBH0TP8J0ox4iLjVodWdS67nPpuT8/+X5q31ngHfi2eJ+WY6huaqoDUd5Au6k5NJ/aZaBUvF5qTQeAhzq5P9Ea4nSaQlUfUtV6tmaY63kNiOQXAFwc5wnNlgAPspSLulvhthHOFlMd2dwefh/2ltfIa2jP/oHaTfQNLSwOFUc8kPM3f/M3WL58Oc4///wDAjkvvfQSyuUyzj///P1/mzNnDqZMmYJnnnkGp512GorFIoLBAxeyUCiEQqGAl156CUuXLsVvfvMbTJ8+Hb/97W9x0UUXwXEcnH/++bj55ptRV3fwiHuxWESx+CcHfXh4dJTwsUKhzB1dk1abCkpZXS1GkVCbHGMk334IV/RaDBZ1kKU5yB3ysWgjPznMncSlrSL4MMRfweMT2kGcHOYHyYCbb+ZR0S0DAB4Q5SUniHPiVqFVAgCLUvz088QApxnXRHaqCl1C5hVaCSPgDJDNNc62AYCgl1OyC4K1YNIVrqv8MrXP8vEDcVOI34dJulpBBjnnxXmUpSOn26y/PMzn5dJmvk64DMQDe4v8Hf3MVl7OcHGSt8MGACVlMDvJn8dzfWlqb/BznQMAmCLEwD3CB60YsAfV/qVgIji5LMjntpq7p/DXD1mTJILQTVJMzI6s/p1DVb7u7/VwFtbb47yFMwB8Zuq11D4gAhi5ij64tIIHKJI1Hrh2i5IIj4Gg+cl1PFiUFPmUpwUjFdBC+h+o54ddVdoIAEnR6a9Q4/dqjXg9g2oRABAv8/2tJcS17Ao1XfLnEgGl5gRnUPUZJF3rHc4MCgmWyR8HOONmSaOel8sjIoCf59fgNmAIrxng73CTh78bDdBSCu1iPdtd5b7dtgrvrAUAk5JLqX3D4F3U7hXag9GAFjRXUBUV4yEOf0zBauQY4YgGcu666y6sWrUKL7zwwmtsXV1d8Pv9SCaTB/y9ubkZXV2vlA9deOGFuOWWW/CTn/wE733ve9HV1YUvfelLAIDOzlfEAnfs2IFdu3bh7rvvxo9+9CNUq1V86lOfwmWXXYaHH374oNd200034V/+5V/G6JeOHcYiUKNQrfL0cNnFvRqfV5/yVLBHBXrObNabYFOIZ6kLFT7900XNhlGHvJEK32jfPoEHBvqK+neqFsyKOhsxoOee28yDIMpBPF7raiIgWDvHxXi06Pk+fgJ7ML9KXsPeLO9IE/Tzw67XbcCg8vL2rNUQP6CVKkk5Rr2fl3meFuWHo1mi21PNIAi6WnRp/kEXrzn/UJPu6qEyr90F7siqrlcAkKvyMa5o5IGaXv6KAwAao+Jgn+Pv12k+LvD7UomLnALA7hp/YFNEBz0TRo7av1LR46m9zaVZCVOiIggpnnmuyv/9E93a8TsuwW/GiJh2foMDcwx8rVke44GaVq1XjoIIOCn9jNVFXdI3pcbfnzWiIUChzA/+cdGBD9CCrR4ROJjh0x0RF9TxZ/psD58UF0zQ7npY7OUPdPIHdm4Lv8a08DUAwDsouvQV+f6Xcut1fwM4625ArHeTYkvkGF6HP3PFCj+9iftuLQGdWGrP8e9QS26Xwd4TFgGpeqFlp0r7AR38jhc5y98NzcTcXuUC1y0J3uChJOQeBoWODwCERAfZRJDP/YJI8jlOFUM5Pvct3nw4YoGcjo4OfPKTn8QDDzzwGlaNKZYtW4ZvfOMb+NjHPoYPfehDCAQC+PznP48nnnhiv6p9rVZDsVjEj370I8ya9UpW8gc/+AEWL16MzZs37y+3+kvccMMNuP766/f/7+HhYUyePBkBf+tBGSkecYgbLQtlvKCyHYoRIDQWDa+BOxT9QsAXAApCHyPo5RupycFkshBE9omg16BwjJ7s1Q79eS38d8yK8YBWUIjSAsCuEZ51ebab/47FdXoM9UtfGFCOFXdiO3Nr5DUsjFxK7T6HOzXb8ZIcoyK65kz0LqT2dRndFcQV0gdeBp+Y+z6D4N/7pvKF4D01XuK6UdTmA0DCxx3Egghi9hscTESlDXZn+TWo9xPQrdgVi6QkAqmJgqCZAKi6RLBW/AyT9VJp5CR9nEKfhy5dzIvgQ2+RryOqjDRhUI4nEumYJc66cfUCAhgu872lT+yRqrUxAAwKxs0LGc5EiYouSIDWZekq8+Beo5sHpTfjtYnCv8SzZX44usLFWSSnCT0wAEj6+Av0oen8XucNymSe7VfrGb8GxZxV8wEAdpQ4refsOl6GbfAzER7hz2N9kLNIUjUtwj0/mqT2EwULeWaUr1W5qp4zqwf5Z05v4C9xVfgrALAry+fEzACfU4qVBwBxkd9qCYt5V0rKMfaBf0b5XdlCN7WrBhKAPgP2j2ymdlVa/KZrP24ZOUY4YoGcl156CT09PTjppJP2/61areLxxx/Hbbfdhj/84Q8olUpIp9MHsHK6u7vR0vKnzOD111+PT33qU+js7EQqlUJ7eztuuOEGTJ/+SpantbUVXq93fxAHAObOfSVTtXv37oMGcgKBAAKB19ZNF0ud0HHw/zlGKwY5FqjV+ILncvFpowJBJmOo7l2NQYOa9BiPsAcCvOyiYy/PEgBAd4FvlN/ZwzOS72ngmkYn1enfGRNaPkMlvrlsLhgwj4SewklCmFZlCgFgqMznzan1ql08//fvcq6S11ASXmTIy+/DwsD51A4AA+JEvL3MmRGnJq+RY2QcXtfeLaITa8Q7rA67gK69PyHBHd13T9ElZENCkDwnWHdeA+2mOr8SPedrQFdBb7MRL593qkxtn0GLc4WaUNBQgdJ9omU9AMyOXUztLw/eSe2X1n9WjtEk8kIxL3/mRRH8S/n1/i+0qaWw+2NdOvg3J8nfL7VHjhg0+Zsm4jD1QR5EebFPz4k9RZ5oSLt4ucH2/KPUPiXKM/EAcF6Y66HMjvGbFRbvLwBszvB1Yl6cP/NuEYAEgONi/Jlf3MoP/i6hJ7Qpo5OupSpnJ60Z5CW1A0jLMVpFGegcdxu1ZwxKNEdEg4feIt8EfW6+b3Tk9PM8TQRqJoX5Hpry65c87OHPtCgOumreAsA+wYzdK7Tstji8sx0A7B16nNrV2WoshIZLFVHNMA7nN4s3H45YIOe8887DunUHKstfffXVmDNnDj7zmc9g8uTJ8Pl8eOihh3Dppa9kyTdv3ozdu3fj9NMP3JhdLhcmTHhFyPQnP/kJJk+evD9AdOaZZ6JSqWD79u2YMeOV1otbtrwiKjd1qhbQOhQoEVITbQu/j6fqEuE2alcBkExB12Cq63RE+0i32MAAIBXlpR+KLv2HfToze2KC0xQnRrkD2SzakwPA7zt5EORfZ/E5MVDim2DGQGNAsXrKIts/M6a7OTWXR7dUtAhhaRM815+k9i4hLG0CVdIQF6qXAYMAhxSUFFk0r+QuAT6Hz7vpMf48l9TzQGudX3fcKAuWyAPdPBN/UklnE4ui7Kkjz5/XhKA+gE0O83UgKUQrVeAA0CKk/7WP6/BMcfHn3SRaNANafLNeTm59yOsUHfROS3yc2qM+ffhRJQt14nAzIjLlCcGsAACPiz/zJ3r53FbaaoBuLawYVGURsAKADWk+M1Xr4fkp7QvkKvwzDSNnUvumCC9X8Dh67yqI0g9VbtcY0IGBExP8Xm7M8PswOyZeHgAFcZ1FsSbvynF/pmgQL1bdIYMiEVhx6X18rWC+LqqdTO1Rt36/aoL9UBB7j5ozJh0T/ULfcOMwZx7tNggWTYvw+63mlInOnFppFAPx1IDuUhtJfITah9w8ULM9zTsJquQzoM9OjXE+L4MefmapORXsTY++FfsxA9u1yghHLJATi8Uwf/6BWZBIJIL6+vr9f//IRz6C66+/HnV1dYjH47juuutw+umn47TT/iRk9o1vfAMXXXQR3G437rnnHvzrv/4rfvazn8Hz/xTIzz//fJx00kn48Ic/jFtuuQW1Wg1/8zd/gwsuuOAAls5YwCRQo5ArcN2IUll0FjkKIr5Vg/bIQ7lt1O6IjMnpU7QOz1CZL7yZNF801w2ZdIzi9h/v5A7DCSm+0T7fpx3Ev5vDf2cqyO3DBlpAnYK1ow5H2zLc4QCAfYLd5BOHo0minqHfwAvdlucBxO1iTplgff5eap8dvoDa21yisxaAHtF5bmqE34uWkEFxvYDS0TkpxefMqkG9PXlcfIyevCq300GxbVleVjg1wk/McZ8+mNy3j8/9Fa289l7h8W69jvy4+6vUfkXjP1H7gMG7sTHzG2qfEuct0E8RGlWADoope1AcnjKiZBcAGgM80HlxK58z6sANAGFREtst1mx10ASAmhB/V2UVbXrZl23r1w/xtejMKC/RTBmUwqlGZG4XnxNusTcBOkA4JTz6RMTsBF/3N6R5onCtEL6dFNFzRglHd4hSnk0VIa4G4J1R3nluSOz1u4q6ecniWJLaz2/mfm6j2EM9Yp0BAJeYV9uEDztVJCEAoCDmpdJgHDFYR9TbMSICqb/K3CPHcLv5dfodPi/9Qucq4tfdQkvi7NOXWUPt0ZBow+7oJILFmw9HvGsVw7e+9S243W5ceumlKBaLuPDCC/Gd73zngM/cd999+OpXv4pisYgTTzwRv/rVr3DxxX+ib7vdbvzmN7/Bddddh7e85S2IRCK4+OKL8W//9m/j/XOMoNguR0OgZixgEt1maAjoTXBeih/Kk6JrzvFZnWF+qVeI34qOGZuG+O94i4Goc0M4Te31Cf47kyV9MPEZOB0MjVHN+smKgNIDnfxet4rYnsosAcDcSFJ+hqFZdHsCgBNyH6b2iBAfNNBBRSSfpHbVGrxjhCuhmgQ53zOZO+QL2nhN+jkG87KjVziyLbzEbGREMwY29nJK9u4c/45NGX2vVkznlOw+8W78fBffyrfUtOjslU08UNMa5s9jqksH1ycEr6N2VZ6lBEYBoEmwI+bU8zkRDvMgTCar58y9HTzYOjuqWF468PaPG/ih4QMT+cFji0EjzhOSfN1XT+OpHv28gkIstS3MA6nDJX6Nw5o8iCWNfG7Xi0RFiyhxASCkwoH+Avc3UgF9KA+JeTM7roTHOHPvP7brJF2PaEddEzo9S7wnyDEGi0rPi8+J40WQBtBi4PvyfB1QrLxWwQgHtHZam5APqBqw7tIl/jvUNYQNGh+0BPm8TJf43J/p4wF+AMi5+NyOOoLtIti5PUNcTHkskMltFZ849vVcLMYeLsdx7MwwwPDwMBKJBMLB6QcV4q0LzqDfUXH0RjyY57WgxVIXtavSqvFANKTb7eZL/BCnAj3fmnuDHOPtU/i9ikb4GLt7k3KMJ/v45jAhyB1Albk1gSoRGynzYNCIQdlUt9AiUZhm4LQURWZIleo82sszLsqxAoB+EV9UQow+gyBLg4gPKhHSPVn9jq8t76b28+Jt1D43zu/VrJg+uMR8fG4PFPmcUrRyE6wb4sGFk+u0onJjhAchtw0mqb3foERM0dM3CX0NRdPvMSBYqaxoQ1BR7DU2CPGYTJVP/rMaDYJFIT5vFiT54UfBbeBMq8PPl9bx53ntLL2QJPz8XqngX0ZokgFAUGibNYig2R/F+wcAeUFEUZ13BgX7or+og2LXzuLPdLI4MG8SzAgAOG0S90eyIiA8kNeJJZVwUczYlwQL8vkB3RrcN8r8cMyjA98RL5+7USHi1qcmHYCf999E7fee+o/UvnACD2h5DHQDB4b5+zOQ59Emk7Inxch5up9fw/pBzRJZIJjnv+7h96ro0htYv7OL2pXYsdKI68v8UV5Drcb9ItVlE0Kb8JXjehFDQ0OIx4Vi/jGMV8/b6R9ei3h4dGcPOVauiOTVtx3T9/SoZuQcjcgVduFgLuvR0JXKLRgg8TDXpgEAj9C4CXmS1F4VgnmAFgXze3lLAFX/DwCrBVumQZyYlfYMADQLPYaY6Iy1McM34mYhyAwAG/bxDgwnpYQAmwGN/y3TuLZSSbAnBrPaoY+Kg4miIteLQ8Pv9mpn4Iwm/jwyYmoLPVgAWrhWSf2kDIR4lni5/pf6hpSfz9uIV7/jM6ZwRs7EEb5W7egRbUGgA4xKkHKnwbx8sJtv7q0ik6e6lwBAu2BA1Qe4Qz4oGFa9BgtmV5G/H9Oi/F4FdVwAi+r5M18/yJ/XYz06CPPX0/mBt1/MmRcHub3FQGh/SQNn/dxyKr/XRSHSDeh1OzfC74NJScT2EX4dxwu/t85AT+j5YT5xdo/w4N9QlR/QTq3T+lAdogTT7eKsoLmptBzDLYTVw0H+O1f36c5zfWIfjoqAr0pULErqgJViza3Ppqm9UYjvAkBZ5J93Z/n7tRpPyzGun/p5ak+X+dyuCTZMrEEn8UIxvs9md/Cg16/3JuUYW4e5w3F2M7/X/2umZtdvGOb7WwP4QrLFxYOgALBv6BlqD/p585JcgSe/TODx8HVCyk6IigzLyLF4PdhAzhsMNaEtkx7ZOOox1GLlNRDWVG368kWuFRQxEBBVXZAUQyNg0NFGicmpMXoKogtSUm+SqnPBnhzfRH0Gv/PerVxQUtVimwSLeov8kLdXCNcq1kHKrzN9j/dw9sWilGiVq3pVA0iLDmBZ4SBOjuplOyjKsxpEkmOGyEA3Cy0GAOjp5utAYyP/jkUnaeetKA7+54v25MURHX2Y0MFLVNak+Xq4LSs4+gCmhPl7nhRZ07ToTBczoIo1BvncVq3cO3J6Hdk4zOeVW2QsPzVbs5sWtggmZoLf67NF2W6trO9lXzefE1sFi8tkTa4XpTbzU7x2KmPAFFtSL7o1ieD7v2/QuhLThbuQEYzSST4+92dE9b1UCZMhwVr1jfDnDWhfQK2HM8WaDAAFoYEzJJonhMS+MVzS93Jzll9nzs0PswGRKASAOqF7tDPD3+Fl/qVyDHUv8kLsWAXuSlm9jw8O8jVZdWWMGvjJV0zl/sYOsUemxfsJAELKDifV8z3SPfD63YX/HHVxXrzY42qn9nYRyPH7dMv60Xa+Ug1zHKeGckX7RW8Y2PbjRrCBnDFEMDCB2k3Knsqi9bBXMFWqNb5JugRjBwDiIX5oH8ysp/aigdixWhRVi/ORiibynzdhdIvq3e2N8jP7xOHljAZ+L06o51mZvMEm2SUCNS8Pc0f3lJQBbVUEHwKCxbW4QWs7zRfBoIII9LQP8WzhiwP6QL0vzx2n9gx3+E266mhnmf97k2LYvTnunA0KpkpYdE+YK8qiAKAhyAOMj27m68yv9ujt6RyeZJPCtdMNOrbNEOwKVc4wYsCuUGLinSKIGRZDRPQyIrWZvOIgqjqPAMCp9by04+b2m6l9Ssc/yDHyVe7Qn1zupfaCeF5Vg6B00MvXCXWnsgaCyqq8JFfkv2OtQdnTpBD/HTkRGFjarBmlz/WLIIm43Uojx6Rzz8wov04VppkU04Ftha4eHoQJGYimt4vfqrQFVemH6pQGAM1+Pq+8wpfYmdfiTTsFyXG3mzfTOLW6UI6hug0q1urWHs6gahEluwCQECXMc2PcZ5pen5ZjpAUb1Ovia/aevN5cdo3wefX8QJrae9wGwQuxqMbAgyRTUrzJhCrNMvlMf5afnXTDnGM/6GAx9rCBnDFEocjLT9xufZAMCPqfz8tdikyOBy8cRwdZBjJpaldRYxOUK+o6ucORE9kQAOgZ4Q6FOoA1G1Doj4vyzVxpJQyKuvd1Q7rtR8zLf8cFzdwxCojuJwDQKFqxq6xp1iD7GxCOalrcq/+7k9tb9LkFOzKiA5if/47tOe2Etvj5M00GuDM+bOBMdxWFAxjg16CGSAW0U+OIub9jhAcvLp2sqedZcZAUnd5lmQ0AZEWJpsrWP9Cl575ouIbjYvyBBEX21+/WwYfNQ/w7vOIrnh7ulGMsCvP9TWmjmXQgaovwPc4nyn0GRGB8zaCuo18q9DGmJfg60Sk6pQG6FFWxIE+v12vVSIXP3XyVv8Pq/QSAaYIxUxJMsJLwBVQbaQDIiOCd6uKnfA0AGBCsuVWipG9qWCcCz2nkc3+zKOVe1c/3jaBn9AHGsGj9/WD+53KMy5Mf4mMU5snvUFAMxDrx/k0SwtImnc5e3MPXy4QQt1Z+GQCkxf6l3mHVOAEAEuIyYm7uu+2A7mTmBX9/VMFex+CD1O7YIMr4wzJyjGADOYcIryd1ULHjWGgi/bflqmY+eAQTJSPof2MhduzxcEf1YL//VZQrPIP9ynfwld0RkW0l7mmCJpERWWZAZX6miwe1VMlDRRx2Jwi1fwCIi808X+VzKinakwO6lbSi+P5RUL4BoC4nhP2EZtG0GL9GEyHisnh/VInK4qDWENgzwgNWGSGi41M8ZQABIZq3apg7RgtTQqPKgDGg8MF5XJxQBYIAYCTH3696cbApF/Xv2LqPB3LWpPnhqCev3+FlE8Q7KoIPqiObavEMAD1CAHReiq/ZS2KqLw+wJcPXXFW2qwJzAPBMP38HL6vjAYxZM3iSoXVAsy/WdXI2Z4MIjMfEIREAtgzxNTUiAvRbDbpvzRYZ/2FRZmbCnFUei/qOnYIlWS8C4wBQdfg60pHjc9+E/av22e3ieawb0hvYDlHiVefnC8HFE/k17Mvra1g3KOa2l691V9b9lRxjoMif+WOFn1H7u/0fNBiD36uHRPnkcUK8Om+gUXVikq81yhV4olO/49Mi/HfuFGyaEb1Uyf1nF3gSIAbNjt+Ze5LaQ37u00xLLaf2wTJvRAMAg9mXqV0l850af3eO/ZCDxeGADeQcIirVQRyMw5cVeidhv16MhnOcEgoR6HGLEheTtt8qUKPqQL0iEAToNupqwTMJVwWF0LBiw5jouiQFi0QxWWYdx2n+Xq37h+4dnF3x+D4ebLqvUzPFGoU/oIROz2vVGRWVobpvLy/HaxSCsMNlfahICr2Fh3JcY+rK+rlyjKYgf4ef6eVMlC2Oot8CbW6eyTs9xoMTMVEaooKDAFARGc1fbZlC7Yq6DgBlMUZICIS2ikw7ADiCs62Cyue36nulsprP94n2yEH+71cPaCbm7PjoDoGiizQA4P6RHdR+Soxn2ifqpQqn1/POOj1pvl4+u4cHpE6o12WiMRFc/31nktovak3LMaYK5pFiDi1K6TmREwHb46LcnzAJFm0c4hMnJb7iJz28u9BftfyTvIZLJ3MmysxG/sxNxPwV0mJ/es8kzaBSPsvaIf6OP9jJ523SbyDCLZIhcdFRKuHXC4lXsHoudK6kdtWeHAB2Zfn+88Fp/DpnCx25rcNaS1J1TAyJRN+VYh8HgG3DivUtkq5yBOB5Eeec5+Vl1iZ7y7zoNGov1Pjz3Ozirb/LVd20QElCqK5WSnLiFY0c7f+9YeDUgNph7sR8FHR6Hi1sIOcQEQ5OPWigI+hN0n+bKXABX0CLFcfDvLX3WDBysqIFuqqjVkEaAGiIn0TtAyKy3RbWG9TEJHd8lBhdr3B6AH3IqxNCxJ27efb42R5+4AaAWTHukCtmQ0prAMvMz7w4/50hcbABgC+u4gGnfz6RB722igz1r/boHzolyg8u+fQMan+hTwdKGwL8OlrD3L4ppxkBm0QJ5WRHiwcyNIW0UxMV5Vc+N5/7+/L6EHjPbr7eLZ/EtzgHOjIwKDrBrE/zl+P0Bh2Q2jjEx5gZF+UlIqBlUl6i2DIxHz+sqo5uADAPs7i9jj/zvXn9O7aKFsuzRcmDasu9SQgVA8CsJA8mXTKFvxv37NbCmgsSPOCr7tTPO3TZ7iQRn5ga5g+9UXR1BIDbcvwAdYmfB8dXtHyO2hVTEwAqDg8utPfzbL7Hpf2u7gLPyqgS6A3D2h8ZEgyppI9f5wIRNRs0EDs+PsDXVNUQoEd0EAOAzlqa2lPgc7s5qDNkqpS06hi0TiVY3ML9GQAI+LmfWxFlT36DsnlVIqaE1/fltV/VGubX2V9UuoEGSR1x9inUhL6hO0ntsUCrvIYRKZjMfdy6MPcva04FPcNvokCOhRFsIOcQQduPi3+raOMmGB7ZTO2RUBu1F8tpOYYjWuB5RMDK79HZqb7hVdQuKYhSLlKL4+4WGZE5zZpFUl/jh5+d/UlqbxCBnjqxkQPA97Zyp+XCVr7BXTV3rxwjKEQvd+zjzIdHBSsIAL58cje1D4mDfbvQXDHR19gyxA9HxwtHd+uQPs3uzvOVYtjFS/qWxTTrJyRW9kcHuTNwWj1/niaBuYDoBHPSTE6nnjWkAznpMi9nXTaV65Z1GOidbM7wdULd6y/t1p0C/3ES13QYEAKhX9z6JWpvSZwur+GCwFupXen45PRSJTU2OnN8rVpX0Do8p9Zx5uuQKHc9Uxyw1OEKAF7o5Ovd9Ch/x89t0mW9Q0J3bF6crzNhg316omCsRcU68KwocwOA8yN8PVPi77kKP+SFRSkPAOwVh9GUKG1sMyjDPq2Jz111KFcaOwCwaZivmSXB2AkKdqFi3gLANvHAJopERVPIoGFAnu9PL1W2UPvDA7wMBwDeV/cRau8WYuK93Tz4d2JSM+JUaX6LSKgURLdDAPjOFj5n3jFJdcDU62HV4feqR+SF0iXtb/RBBEJLD1B7KsgZPSMGHakiQc4yzuY5IzVdEImnNwB75JBgNXKMYAM5hwgXfHAdhJ6gAiBVg25Oo0W+yJ2FlHCaACBb5ArxxRK3u6BLkupjC6m9P7OG2p/r1xtU3Jek9vmik1JNZLkB4AcbOSX0gzP48xgSWbrjDWj855zAnciKqGsf6NcBxh9t4r9TrYUTQnoD6srw6+gTnZIUNX1jWrNl6gP8cKSEhtMVPcaMiLrf3N5TMGhxXubO9Ew/Z3q9NMjfr3lJLaI4Ig6az26fRO17cnodeefENLVv6uUOv0n55Fsa+fv1/AAPpL7Xs0COoaj+D3bxgPE/TPs8tT89oHXLSuIlVsLtqqsVAPSWuMc+JcTn/plx3hkSAOr8/F6dOJUHjHv6+fMMCZF8AGiL8r2+WOPvV2NYd7RpCPHnoXSsVFkwAHTk+P40O86/43jB1ASAfJUHlJ7o4muZEvJOG4ixLkryMRQDcfWADlidLOZNJMivocFAYL7q8D1S6cSpYGzMoDOdCtbuHuG/w0SY/fnqs9ReBT/4X5r8sBwjJCg5vQV+Ly6dzNfcSc1peQ1B8X6pDpbbt2lm36AIIP5RdLe7L8217gBgWZxXEmwZ4QzGrEufneqQpPbzQpdT+yPF/6Z2t8G5JuDj/kbAyxNH6txjVXIsXg82kHOIcFA2EuF8PXgFkwUAPEK93SeyaEqHJ53bLq+hJgJSAT/XEKgKwa5XPsM3c1V6ZdLqVi27LkEZrRgIuqoM8sR5nMY/JcEd9v61+hX93B+Oo3Z17Gg10J1ICn2MlKBsnzmRH54AwCMc3Zw4lPcLP3e+ElsAMCgEDndm+NzOQ3daWpvjTklIOOMTRccpADg+wR/qJBFLmhDka0CDyPYDgF+UVZwhXmFduw88188dI3VweVmURQHABS38MyeJzGqPQav23+3la82CBF/3e0XJUc5tkkTg97IiFhKT1sSNfj4vW8L8XrcYaIbtGOEf+s0zPPN6Sh2ft6o0CwCmTRSaKgP8eeYM2BdeUTYxYtCxRqEokhl37OQBjHoDFmRalOvcn/sxtV+Rupra+woGpTqCkRPx8sBAU0AzBnqEmH9NdL7qN5gTJyT5b42KDpcrd3J7S0jPqQZB2xnJ8r3llwPflGME/JzxFhH2nw/+pxzjirqPUvtpourdJQLbQ0Pa8aqKxNCQ6EK2R8w5AHjXJD6vOvP8HVZBGgDYNMT9phEXD5T6hE4PAHS5OMvYX+O/s8HP/ejO3Bp5DekRzr6Nhvi9mpRcSu01p4J9Q4/K63jDoIZxYOQc3q8fD9hAziHC5QodlJHj94lOL6I9OQCoHJnKySjqnlpIAF1+pRg5JkhX+BiKsXNync5OzRVslkiEf0chrzePGxZxxk1pgG+CvRv4RvuIQUmSEjq9sIVnOzwGmfSpTWlq94vSKxNG6EiGH3iVgKjS+tmV1b8zKgKEg0J7Zo+blz4CQMfgQ9TelrqQ2usqi+QYe0b4b30hzVkmn5vDD8P7DEqSogEe1KoT2k4vtGt9qEsmpaldCZ7Pi+vD0Y928qhX2Mu/45eZp+UYn55wBh/Dw1+gF/v5vK2v8b0JMOuGxmDSGSsvymB+keaO8BKvbiv8zsn8Xl0xhc/9R3r43G6L6AB/uyg1nSA6Z/UatLOOi8B3SpRFmZQnTxDMoCWN/BpeHtRMlQ+s/Ta1Xzfpk9S+RwQGTAKMNZH2UWzQ40Q7eQDoEW3t20SHon0GvoBCTrAv3iqE2SNiHQKALsFU6RPlI1OT58kxEuDJxO4aL62aG71YjqFEmbdl+e88Lsb9x2REJzxLolNnVgT3DBp1yiTcXsGMnRXX71cqwP2J33XzezUzqPevqsPX3CfLL1D7vgy3hwO8gQQA+Lxce9Av5DXSRdWVeHS6TBZvTNhAziHCcfIHZeQUippGPFr4vHyx8grGTrWmGQMTY6cc0jX9JdoH/yA/4xbtxxWe7tMHsOkx7nylBAW/kNbXqEozwjn+ivlF7f2ilHYQlzTwjVjpmbS26TEGRWerDfs4E8xnUI6g7uUz/XxuKw2PrTke0AKALg8XJG8C12RRDiYAvFWIcyaEA1mvCR6yTfOEYpLaHXAnU4l4A0BeMAIe2sXLZN41ST+vxih/h3eJtvcBAzHIyybzgO8vOvgD+crUJXKMgJsfRh/vUVs1d6a3ubl4PAD4SrwEbLpLvX86MDAogkXXts6ndpNgUWOAz93ZU7gGzokncvZgJad/57ot3OnvGuC6S7Mmaz2GihDhHhGaYd0FvZBkK4LZF+Lvxp68djGrVb7//HToYWo/xXUWtXsNetYnxD48QwRqNqUNSqsmaFYqQ0xcIwD0Cd2WoAoIi2k3VTQDAIDn+nmAfmqYz6klWCzHeKTEkyGKeb4gwgPnABAQUZC2CH8eKomgOk4BgFd0blQ6dNDLCIqi41pdgD/zx7u1b+cR636jm6+HeUUHBdBe5T/2VM/J1P68aCKWLvEgCwAUy6JELMcT7Urj9E0Hq5FjBBvIGUeYiB2HA/xwUxEt8CpVfrBRrcUBIFPhDkexog/+Cm5xLwKihfmChHZqekV78bYA3xwaW7SAYaXI72dmmF9D83Q+xoTpBgGQ3fzgku3kr/mGjTrTtzbNd7mMyPQtSmrNh6SfHwomh/jBY0hcw4JYUl5DOcudq+lB7rDHBCsPAAriNKoOqyMGorItgrWtKhMf7ObzNl/lAWUAaA7y5zlTBGFM8IudvJOE8v+Oi2lnut7Pg99/N4+LoiutIEB3WqoTJSpdorSq3uF6RACQ8vODv2LuqTI2APB7hNiqKHdtNChh8bv53rBxF1/vNq/ne9N7FvKujgCwYBbfQ3/0PO9OEhadZAAgKfRn7tzO340rpunAQn+eLyRrB/m+YNK1SnWd6i/ye7G0lc9bEz897FF+ldA0MtCvUYS3fIGvE3NEJzQACAjdo/V9fN1uEsrtz/Zpn2hGlAcGGoN8DTDhBXrK/DpLQph2k2uNHGP7MJ/7s+ILqX2vYNUp/xQAZohnroTXR8R9ArT2WUgIYE80YCj+2y5eLveW2DXU3iCanwBAI7hvtqnGAzGqY3BEtAYHgHo/X9fLDvd5smW+JpuwKC3efLCBnDGEYsuYtOX2uPgjyRR1C3P6/WPQOSse4IeChiCvNQWAfdmXqL0z/QS1dxXPkWNcMINnXt3ifNW3V9Pb65r4wjz5rcIhr/KL6HxUL9z/3zp+v0+t49fw8rBmN00McYf83CYu7Ndar4N/ikacFPXeuSr/HduzmkXiEm1oV5faqb2/yO0AsAg8G6jEIqdEdWBgWAg/DwtdipPruIN49gzd6UwdXO5a30bt08KaPRjz8t+hqipeHNBzvyPLn8dZzXxehgzKEZ7sEfT1BP8h6nl7DLb6yijFjitKeRPAT3u/Ru1To1y0OerVh4Z94oC0oC5N7W8VJS4DPaPfFz6wiGdme7pFehiAW8yrS6bww+zT3fpgojRVNg/zOTErrqN7PQWeiFhYx+/37Cj/92HBjAC0Bk690ASbFNFrVVV1pcrw3/lUjw6eJwVrp0EEQqcI97ApqP3HiFiTtwxz+7N5LZ7bmX6K2lPR46l9iftUOcaUKF8z416+R04TWlqNSR0Uq1b5nOlJ8wTAHiFWDgB37+LP45RGJaouh8DsxDv4dzj8Hc5U9f613b2V2qdUuaxEe+kZajfp+BsQDVYag3OoPSTEkmtOBTqc+8aBU3PgHGbGzOH+/vGADeSMIao1flA0CaIosSzFqFHt6RyD0iqtnM5h8jtVB6/JKV4nPcPAcVJCcLmcyuTpIIrHz+93qZ1n6r73MA/CvG0iD0YBwIem8QBhSTgDZ0zWmkd100U9tzir9m7Xh5/dQk+hTjAj/mkr1yuqd7TmSsHN3+Giix/QJjh8owaAOsF8iIrSqhEDzQeT2niGsDjAFYXOAQCMiHbxV525jdq9uloBqhGgWu6Ge7Wj+xvRXausWD9Rna3/27l83il9jRf7+L1ud9bIa5jm4muuQYWKxMy6d1F7XhwKVBt2AJgc5ofZRIzf6+QU/rxELwAAwLYNfK2ZPJEHvifP0e56fzufE411/KA420A8N13kn1k+gQcGVqX1uu9z8eDcAwN8XT8ppdd1BcXi6hBdqaa606O+hm6RqGgL63VknWAAK1adYns+0q1ZlEPg8051TJzt1uzBDtF9dTDLS0nTHq5DBwAzPXyPSwk2TLtgWZpgiuh8FRJ+sNcgieCIbk8Afzeqjg6uv0Nox3Tn+XXuymux/lm1WdSeFB1Jj3Pz5HBvQDMxu7JrqH1fdRW1hwSj22rkWLwebCBnDFETgZyxgArUKLjc2nmL+nmr6bIo3ypXRh8zDrj4JqiywwAwKFp7K92WSQ36d2zfxp2S6SLI8lcn8M2hf0AHxSY08evMCa2EmIFw9N4NPEO8Z1jUOAtqOgDUC3p6h3B0z421UXvJ4NX5rdiIj3d4nXXNoD1kR5Fn6maIskLVqhoA7s09Se3lGn+HT667gNpVqQGg39HHVk+h9ojIeAJAUsyZHlEaMimms6LvmcszxOs6eKlOwMCZ7hcskod7+DpwX+6n1J7Nt8trKKfO5XbxM0z0ayJOktr7CkIzrE6v+6rMJRznh5/v3s+D6x87n2d+AZ1t/+Ufeeesd4o5BwAB0VluWBzqpwkWJQB0Cy0fVR4SEWUZAFAWh5Oyiz+vHSP8gKa0TgDgjAaeqJg1jbOb3Aa/szjC18y4j//Othb9vOaJBg2/3clL90cq/P2aG9eBud9leYB+UoSvl3tG9GE16uMaVMmU2FsMNBqHRRLgpUE+9y+ekKb2mNCXAoBCll9nTXSV220QTFKEhM0ZfkzsE50+AaBJNORYX+DJxKlersEIAGnR4evOnm9Qu+oYZaLr2RbnwaCKYB515dZR+2jPf8ccHOeV/w73GMc4bCBnDKFedFWDaQLV+rsmUtAmGjm5Ii+bqInW4WOBkqglVdkQAJg1mbNZAqJVZ3qvztY3JnimIDiRb2DhBHfuEmWdAdvzBL9OVRffu1tvUC8P8XlTEr7XOybqIKdbZAs7cvw61XrcndPv3wTwzFGHi5c2pmq6XMEnlt2gh88Zn1u/w/OKPOB0SgN38F4c4DezyaCLRLPoeNMiBJMVGwAAXhYioz6hubKnR2fzJwlnOC70TMIGAan7RJcjv/gd74ldTu2/cHigBwDcov5eTEsjqG4y54X5AewlXZ2MmVF+oeu28T30jIbRa8DVn8if+SURHsDf16npaE31PCCsxMbXGnSF6xbMu4I4SJqw1osikDPdzbV+1LwcMnC7tmV4oHRkK7+X00S5HgAURemw6jK2ZrfumlMQAfaZogzN5+bMvpcG9N7zwfoTqV3plqkST0Dv0z1op/ZCTQeL1JG5JSjY7+JneA2E9hVrfFUP9zf8Bk0mFPu2WfzO6VH9vJ7r4y+p3+Hz7mWHBwcBoD3Pk1eLUldTexpcnyZf04FUR9zvGHhAKhmcSu01p4Ke0ujkNSzeeLCBnDGEx8OzV16hfwMApXIPtavW3yrQYxLRVYEal/gdjgn3XGBQaI1kKyfJ7/AG+AaT6+O/Y5VBu8/JER7Iqctwx6nUw+/1I4K1AAAl0e0pUxbdTUQWDgBOSnGn4zjBbBiLLkfqMPtklgcgFwV5xykA6BAU342D/EBcF+NOLABERHZpcIRnTU8Lc8YcACxt5gcTFeCYF+fzUgVpAGCSyEhWRJnMpi167k8W82qS0CkwKZ9UbLOtw6KlaFkffqaG+Zqp2E39Rf6Olyr8PgCAX5yIx0LsuCfDqeV3in//9xPOl2Oo6yzVhHCtmNvPv8jfTwCY0cCd/vopfN42Fg2E9sW63iwCPQfrvvnnKNc4O3BqhN8rFSABgIlBzvL4ST9vT56r/TW1n1KvWSSqm5PHxe1hAz2vp/dyf+L84/gBLTegg+cjFT4nnhDdPhXZszOnf2elxvfxl0d4NHbAw31gAOgsc+ZCrcajd+6gTl61VhZS+07BsHLA352TDALj9aIhwCzRTa1PMFIB4L5OHkSZEuHraa9o+AEAolocu1zrqf246kI5xpn1fB1Q+9umDA+ePzp0i7wGxeoZcDjTsig6+NnSKovXgw3kjCGqVe44qUCPCfw+7gzEgtzJrBqwaZQos1tkbeoiC+UYQ4LqPznAW1DOr9epWV+cb0DbdySp/UzhWJlANBmTgZpHe3SL2Itb+SCbM9xpeftEfS/b2vhnvCIrk+3SjlO+n39mQog7Z6lakn+/QQvLF9P/h9pPT3yC2ssunf7dXn6a2md7T6B2l1IRBrAhzTd8xb44QYjr+g2yif/+7Exq//iJ7dR+yZlcENYEmS5+cPGp9q0AckJL5N5Ofli9sEUHMRuC/DMdI3yMPSN8bk+McIYWMHqx45oBRdnr4c7yia4zqV0dCACgS5TUvmUGX9dDQuh7ooHc5M4tnGFVbec/JNWgA6Wrt3CmyvT6NLWbMN525biL6BYt6bdmtYv58/R/Ufus2EXUPiPCD6vZip6XCdHtKebj67oqYwOA01o4Q1jpjk0VSSMAeElo+UwTh/Lf7OGJp6RPzxnFkHILBbf+il73J/kXyc8wmDBnTxPVPHWCiansJnuoM8rSqU7RCQ3QDOD1af7vG0RHRQDwiMTRieDi0/0unYjoyPM91CfmXbub65OqJDkAjFT4O14VSe7hkc1ihGO/DOiQYNuPG8EGcsYQiQgX2zIpaxrICOFawdjpF0GYSFBnuZMRTltVv6NPZF0BzQxyg2c7frZTL6orgnwjnXOSqHv36w1q92oenBvZxzdSxei5ZJIODGREi8kPz+dZgGBUH2bXbOb3+75Ofh/OEhoEANAYFLRvkWlf1sKdmq/sXimvoTXJD5J7XVwfIwpdrnC6923U7hXv17aMduifLf03tb8vdSW1b8nyg0lLSAcnLmrlB95vreI04vOb9Rhl4egOinKGuQntIE6ZwNkVn4zx55E16ByyfYhnb1VANyN0y3ZnOe0cABbEeacX5e+YlJqfFHkPtavSxcES32MB4G2T+B4YiPH1rmsnX8smzDKYM0Kk9MXNPOFyQkQnXOZN4oeGh7dx0djFjf1yjCUiePdoL19z6/x6UswJcz0ut+gkmBHiTfOj2u9SJUktdfyZe0W3KACoiaYDCiERbAKAs5r5M1UH/3o/X2e8BornSoz/pDhnFtVn+XwAgI0uXqK5Z+QFam8KXibHGCjx3/q7PXzeXT9XsLwMyp584pkXxf7XKnxgAAgLNlp9gO+hIwaB0j6xnK12eBeyoJvvjwAQr/H9KwPuXxaFSHd9WO89ETf3/3ZneWcsJc/hOA4cIT5t8eaDDeSMIZRSfjCgKdmKcaMCOaqsKZvX2Q6XyNaHQ/wAFhLtyQEgV9hN7QUXX1TfN513sgCA5jPURsmzSzsf0gcwlwguTBRCxHlRAz2jRTvb//4YF+c8oVUEBgy0EqrCmT69/vDrJqmSCYU5Ad6VBwDqwTOaG7GW2ptqOsC4xvUctU9weCB1skc/r7cELqX2hAhSThAOoMmhoj7Igwvv8/Dv2J7RDMaHBNNrXpLPGZXBBoD1ae5ElsVht1m0/AWA9cP8ANWZ486byjZOi3MhYwCIiNbeY9G16tn096j9nanPUPvEkHZiO7OcvVRq579zWDBVJvl1ICcyn3/H6VFeBrrlZf2Oq71lXpLT9HtGdMlRWpS7ThLPY8QgeLE4xEtefzH8S2qf4X0ntau965XP8MndK9o8m6Agyp4SQb6HPm2g56XKpNtEl6Ozm/m/7yzoe1kUr+jaAR6gf676gBxD6U22hDmrNefoJMHmIb6OrJjB79VxTTygHG/Uya1yjt/vBfU8YDwoxMgBoFjjjDYVoH+h1yDZWOXzLuXm5eKbh34jx5gbX0DtTX7uTzRWz6b2x8v3y2tods3g1xDhwaYhoX/jOFVkcpvkdbxhYBk5RrCBnHFEuaLr3j1uvvAqep/S0DGCaAdaKnMHUZVmmUB1N3l0nxb+e8dLnIniF05oZ1Y7TinhfE1oFBodXXyj/vbjPEgD6Kzn0x18zjzeo+m388WBeGaUO0bHCc0IQOuVdHTxg4fqyr2rtlpeg+oV0+zhQRYTLBA04qpgq/kMTtQhL3+mf0zzIMuZDSILJw54ABARXTlmzuJByolpXcIS8/K5fdo8fmDODenf8eMNPHCtOvM8N6Cd6TPq+fszN8bXid918jGeGOAaBABQCs2h9rEI5Ch9tfXgyZBTCrqk4ryJfM1VeiaNHr5Pd27Qh/qtTyap/fQF3GGfPkMH8Ct5PieaBYtkWzsvzQJ0U4GkKDlaldYaOc/l+aqrNMU8otR0R0Y76hNDQiRYlMHUJ3QpXJ+4F+Egn5eLUno9vK+Ts11eHuIB41X9/Hk/U+WMAgCY6HCfZU6QlzVdXFsux3i6zBMqOwZ/S+11yY/IMeYl+fs1KOSCnt3D96YT8tpPTib5vFLtxVVJE6A1FjcJ7ffZSZMOYPwz3SN8Xp6YeJ8cwyOSGXuF7lhFyFsXDXTm4i4eLEqAB5v6/UIawylhw5spkGNhBBvIGUdUhZCVyWcUY2csAj2K1aMCNR7RPhkA/F7+GVVHfbaoNwcAr58vzLlhnjX1G7QNntiSpvbCoKgHH+LBiSX12kFsEuKcKkCydKael4lZokODiGp3vKQPP1mRCVc15y/08muY5TpNXoPSjgkIIccnC3fJMRaGeAZ5qp/ra/gMNHJeKvMSsNNDnCa8VyQsj0toZkTPMH/mL3dzh76roPUY2iL8Qldt4ofViQbtx5eLEpYXevnzWlKnBUKD4qC4Qzi6QyINnivyjhwAUA3y98dAYkqiNXEGtS9w8YyliUbOiz384P+uZe3U7p3O96ZUn16TK4/yNXXndp4kmDlPB3JUJjE/wm/WRWfoFue5Hu4idnQlqb3Op8VW4zXOinOLLn07y9wfOS+umxacJDT3GlK8fPIFg6DY8U38mZaFePWM6XpOfER0XHtkB2c/1cSRIDp8uryG8Uhwe0QJSlvqQmofcvGyegB4uIsHxa6ezq/h+FSa2n0G5XjVCp/7fhFodXQVNrJijKVNo29e0iX0n3aP8PfHRH+tKgIxqltoBXyfvjisy/Eq4jo31dqpvbHG16qKc/iZ70cVLCPHCDaQc4yhWuN0zEiQL4hKDBkARoq8fKsqWpxXKpp9kS9yh8MT4lPThBYezwvNFT/fSANuvdF+70VOpby8jR+gKqI2f7FgFABAeJ7I+ItUem1Qn9Dyu/hiNyxYBx3DOrgXFKU2LiH0NjvJD/7/2cuzdACQzm6g9mkpni0M+zWLq93h2cRyeR611yEpxwiDZ4aaQ9x5i4vSqe2ikxMA5ISDqEqSTOIG393K591wma9V5zRrZp9XBA/ObU5Te1XoGADAhiF+P3tEZxCxXBolEWri/VL3wSC+CL+LH+y7a5x1MFgSCqQArpjJ96+R3fxCNzzB95aTFmpmxMTZPOi8/WUe/OvfrQMgCaE7VhVlTXc9xvcuQOuSzUsK9pNobQwAPR6+x7UPP0btJ0QvofbH+7Q/clYDZ8tE/HwdmRzVJ2bVfnxLmge0Jhd044OS8CfUoV3FSWfGR0/LWz/I/aqeoi45qrr5++USGosJA7HjE1L8HSyIFl+qRDMrWCoAEC7qsiWGboOuVXUiGBT18udVFIweAPC7+fNoDYmGArnH5Riq3G6BiycRTozywN0WA23CvW7OtPSCv8M73JyRWhuDjsAWbzzYQM4YQglVqYXGBD4vz3KXK3yxqag2SgCKZZ6BDgV4sEjp+IwFBkQnGQDY3MkP1RtF2+DFddphV4GakKBLTz2NMwI8jZqanl/Hn3nXLn5IDIlMPKBbsd8vWliumJ6WY8QC/F7tEUKNIdF94bwAZ8IAwGYfb2u/t7KG2isiyAkACS93GLIuPu9SVa3r0ipE9xSi4gAW82qHIunj82rDMD8wTzZo6XvxBL7mbhjmjuzGIX3QbBJBr2f6+PNIC9FMQPeiUEFM1frbRJ+tVOMO+1gkrtoH/0Dt4RSn0E8K6wPY3rRa70Q3GRHAzw/wQwkARKfyeaXEkJ/bxJkTAHBcJU3tq3r4vTpZdLUCdBDyRaEx1W/Qmlg1NoiK5NRsPw/Gnlinn5dLCKH2iK5xUxvScoyKCKIcL1hBz3frIGaz8DemRcTvLPI1ud+AEDBc4gtFKsCfx/OV7XKMUo37TcoXr7j0/iU0tGUp97YMnzNnTdIsyZxgpSrdpbAIwgBAUqx3u0b4HmoSrI2Iz9QH+e84o8ibUADAc7XnqX1BnM9tlYjocuvnFXb43lNy8fezyWmj9qpTgk7tvoFgGTlGsIGcQ4TLFTpo+9+m2EL6b01ocYMj26jd5+Gbw0iBR4RrNR3IUZtguaKp5aNFwOGBgVlJg6zoDP6ZBVnuWO3o0IfhRzu5c3X5op3Unmvn3//HBzWTpTnCX+OsCHrdvlXTwt8+kd/LSydzx6gurOedogn39/Ms9qY0P6C1VzWd2i8EsGs1fo2tAV4DDQCD1Q5q3zn0O2rPp3RXj4k1rlOQFN1J7tjON7drZ+vgxNQEZ4GcNIcLlg/1aW2ZPhGMvUiUDQ5ldMbyx9v5QXG3AX1d4biYoIWL271nhH/ALbRpACBu0Fp4tJieeju1L/BOp/aUTx8apooAhWLpt4tD+6p1ek1euIczVY6bxNeiWQaaYqoU58QGXopjwpKc08Kv821JfqDe2ceD1gCQLs+l9vWDfE6kS3zdz1f13G8M8QBHSGgBhWI6SSe2DlTE85yd1xodd+7i93tRUuyxwkWNqYUIOqi8WezTIceAveviSZ1h8GTicW4d2BaEG3QJ4edTUvzQrhhaAJCIcb+pLASZVVAaANYKIe+T6/geqoTCAaBU40GUPw7w96/k6N9xaZIzbtIiwPhoYQ21J6ADqZ3gJe314Hp77dWXqL1mcB8s3nywgZxDhOPk4Rxk4eoa0kJwo0UmxxfVuGgdHvfpQ3uuyh3AwYwWzhwthtxCjb+gM7OhPdxhGBJtgTeJcgcAuHgaj4+rkqMHd/PnMTWsacbFCn+N88KuSiYAYNZkztISHbMRSOkD2M4N3An1i3adC+v5QfTBfc/Ka5joXUjtU/1cqHiqo7tW5V18M3cnefeEaREdfFCaKeow+3GhidRk0H58n2BQffdhfq+ubEvLMeIBfvJ4XrxfU6JaI+fdk/ha9LJYJ1R7V0DrP20UAaf1Izyb7wgBbQAoVPmcqTp8HakaJLbK4PPm/vyvqP3kAm9fboLEVH7Aeuc0HnzPd+sF8+nNvHNjsDNJ7Q1xHR3cI7qpxUU50AzR8QYAugf5O6xEz9eLgyYArB/k7/BgjSeO6t18jO3D+vCTbuB7h1pn0v16TVZIpPi7cfzZWhz3X07ggbfdG5PU3p7jh1V1GAaAjiy/3xdM4OvI4lKbHOPZXv48fpf+GbVPjOsmEieHeSJP6Req908JFQM62PNYN09unSwEzwHgdMEmGyjypM8fRBMKAGgSOZkpUf47h0sGekLidqoAY5tIfm1z63PPcc5Cat/p2kjtIU+S2mtOBXrVfuPAcRypvzkWYxzrsIGcNxiGRzZTezmgHURVh5mI8O4mZQPWz0i+ndpz4AyQTUNtcgxFOw0IgdFGUeoDAGs7ecnRTMEcmp/gG23QgBrrEQGOhHBCP3WmFsDODPLN/HPP8VKAL56kaambxcFkiaAiB9zcCb1o8B3yGh4o8BaTPjd3Wtam75BjnJ74BLVHhY7Ii1n9vHY7f6T2htwyaj8uJsodDN4N9ZlL+FkXvQatUx/rSVK7OnK7XPqgOVXoX5w7mT8PFTAGgJcEc2HjEM961rv5gTtf5ExNAHBHxqAtlYDSCFgWeteox9jVn6R2lytN7ZkR/ryamrTe0ElirfrppinUvqCg50xSvF8dog37Y92aLRMXDKi5cR4InZ8wCEjleCD05t23U/v5kRXUPjOuA2+KPdgyje/ThUHtSqvzgjfI7/XQFj1GTbCPYqK0alGS27cL0XUAOKOB+yx9Rb7O9BT0OqTEb0+PX0PtE306SbdNdDu7oJW/f20TeOAt3KJ9O3eA34sPpHZQe3sHD/QAQH+RrzVxH/+dS+o1G+2/O7g/0V/kY8yM6/XQK6ZNSQR6wm6tWaSgOl/Vgzs920pPUrtjGTkWrwMbyBlDeETZk0uULAFARdS9jxYmDr1LdO5Rna/cbr3ZKzhiQZyf1M701BaRSe/gQRiPEHoEgEnCAYxHuWPU1MwdxEibvAT0/JFnE4dEjbOJHkO3qNU+TjjLvVmdtTlr+j5qbxddJB7u4Zt9vqIdDpeLOxyZEi8HOj9xvRxDicrucfHSqxGDnMyprnOoPeHn73hYBDkjBvo1HlEX/0wXD7w1BPTz2iPOiQ3C/3ugS69Vbhf/zCl1/F4pgVEAuHUPZ4FcP6WN2o+L8WvM1P5WXkNVHI7U8cqA2IfeAm+d6kROpPYhA72h3+zjh7S3i1+yUWg3LRWBcwCoq+cT811tfB15RpTsAkBY6FRNjPBrWJ3Wc//sJp6I6BBlaEosGQDCXv4ZJSC/Gk9T+1u9b5XX4BVrldBqRbhBa664VU8CocVV1OQK2ZXqkW7+Qw4mG/Aq8gat67IJ7itsFwGSnoLeW56p8PLjKb6Tqb27rFerM5u5/pNibKeF2PEiF18DACA2j19neBLfe8Ldeg8t1vic8In1TvkKADAjzu/F+j7OJKsr6FK4TIW/g2p/K4ogyb7sC/Ia+n28tCrs45UEKsH9RmCPHBKsRo4RbCBnDFGtcsfJpepPDKC+w+3mh3Z1jQDgSOlNjlpNawGp3+F3cWc6KkoRAKBU5NO7TYgZ1zVpLaB9HXyzb1zCN0Gh2YdVj2mHfrfo4OV18WvYV9ABxh5RDz5HaAS0iu4mAOB283n3XD9n7JzdwB3AiFcfXLK9Z1F7SWglZF16zpTBv6Pi4vaJVU0L3+zhDsVJLq7lExGHRBNtGVXff+lZPJtoIirbGk5S+/QZvEw03a0DjLeu54ejohCENVlNbz+BZ05zQpfs9h38QJ136TX5uJDWpmBQ4p8A0BrigRqv6LCX8OtBzqjna02vKBUQmun4RbvudBbksVhcPIlreMwzSFTsznIWlipFFfqiAHDQMvJXsbCFl9wqDSsAGO7lEY5TfG+j9mY///fdujoZ/SLRUJfj75/o/wAAyGwXwrQiGGSwfSEoynXOE5W/z/Zxnyno0T5sj7jf02J8Tk2M6B9a7uVzYhN4Ccvu6otyjPPLvIzz1DruS89p4+9GraqD0vntPLjgjfL1MGfQGUv5j9/axv3k5c2aLfNUL79XU9w8qWrSEdEjPrTb4Wtu2OFrVVP0BHkNDvjz6kw/Re0BP39BHaeGUpknPC3efLCBnHGEiU6BS4hSRkPTqL1U4U6sSSBHMYs8IlhUKmtRWXUvesu8RCxb0p7ThMl8Aypk+b3+4xatd5IKcq+luJsfyvds5YGgVQOaArxpmG9gxyf4Zj9S0btkXHQgmiUo9okmXW5XyXMnsSYy6YpBtTOjM0c73VxsvLXKSyLWF3lpFqAPsw1VPrcn+3TXqlNEfb+C6go3Ka4Dc1tF/X616/9n77+j7brKq2F8nn16P+f2XtR7cZNluXcDBgMhlBDi4NeEN8aEQIDQQ5Lfx88JCamYkARSgIQABtOxwd2WbdmWrN51pdvr6f2cvb8//NnGAc25xJUBW3eNwRhxnquzdll7rafMZ07+vld2ckcYAPq6ODrpO09yotRL+rRT9LZFPBn0wzH+rDc3ax4elZhOV3lwExMIK29RO/RzFR5ItgbmT4Ycs/maUNLDR4QSDABcIJZ+hyC29Vv8PpdFNfoiX+NnS0q0TiVEOywAJAQHx4SY45ouvq4BwCeq7UdES+C0QCUAwFlJ/jxthweaAZF56w5qv6u7WYsnsNHIGCCPRKLm4B6+cFdeoDlyrgwcp/aHdvRSe9LP1+2RrL7P7jDf18MCgdUwyAg3RHo8DL4uN/jXyDkOCkXD7iBPpHbMcl+7Z7P2iVxR/g3bGb4H9LSn5RwZcdb/+Sru76druqjqEYXZh6b4fpep6j33KHi3QbfD/aojovhlGcish0VCyp+8htrT1RPU7jiNMyuRs4DIMRoLiZxfs+EIfppckW82p2OoZI/d4NUpk9YqhdqJeTiUcqSoK+m9WR68RNr5IXhWm4a+VnMCWdTBq3A9ggtoleA5AACvSKwlvNwZnzBA5LxpUFQzhOzpkcOanFolas5J8uTBg9NC+lGQuQJAi80Pe7eQyu0LcDJkAFjk8GTQlJAff9rWe0Alv5hfQ4cIVgW3Uzis4e+dNt9HxsXaPjGdkHOMFPnaD4pA9Kkxja5Q47dX8eBJoRoAYNcYR959a4Tf556c4BSzee89AATrvAWl4fB9wmcAOI0KeVY1kiJhBQBPCYLeawUaRrUsmYzxEj8D56r8/FomUJQAEPby61Tikp/Zq/kzlsf581ZJyqgBx9u2FA9WH5/j+36Lh38b3UENPWo0xDneJJIPOiZHXSjLtQo+od/9Z17EA4CNzfxeV0S53zUQ4u9rcVgHPR6hlLRX+GUm5NRqDFW4sMFZsd+Uv7G+SRSWRDGyqU340Qbir646f1+1GX4NB0Z1wbNZJLb/8yhPMLZqQI4cUQ8PRQ/VdFFnkYvzzwS9/NsYrC3h1+DSZMeHM7yQ5/Nw1Gs8wBOtir90YZyZYyGR82s2VGtUT5y3fqQqQ9SeL3LEAQAko7xaUa3zA6puayxzrc4DjyA46sCkL3d4mv9Gtz1/aWJFNLznCHfYe5P8Glb16APsrAjf3BXyaMmURnjsnuMVrrESn0NV4QDgFUt4P4I/xO9T9XLn6wl5DcUUfxZp4bFPN/T3lbZ4RaUHXI43aeukWEg4LTnhDyhIdkMEywCQFdV4hRhIiDY2k5EVyIitMzoxkBSEk7uzXIUsV9NzJETLkGqD6fLx9/F4VqMkCwJdWKrzxFvZQLZq1uIoEMX/tN7eKOdo8vF94MlpHpgcyPE1sz6hk5i9Yb5PHM3xc+GuiYScY32cB3kRwftyYZvOvEVFUmu7kC5eEtbIIiVfnHTzfcIr2vG2p/T31y84iVbb/PuJNWmfR7XS+Pz8Wb9zqc4WPTbH38fDMzzB2CGC8ozBlvydac6huCP/NWq/KvJ/5Bw7wRViy1W+z0yU9bosTfEz8HW8HoNjx3midP9O3cp6zWpeJHCLmmmLgbrk3+3ja3+ZuEyPaIkHgKNFvvbvyHyB2s8LvkHOccjFeeZCNV5ECDiClsKlkyjxEPcFXKIQqJWPX/rokVMaC4gco7GQyDnl4ZGEcCcbikQYADyirelE6u5faO5TGfkyR6LUFWLHQLVKjfHqLmpvDXAIIwAsX8OdL283P6ib8hpuvfdhHhSsXcGdmkA3d6ZTe/QnuuMAbwHbK3gKntQIeykt3BLga/s3ejXnQ12QwuamuJNqidaqpQYtEY/M8CAt4eaH/ZKGRuTMWYIfw8cdqycr3LkDALeLr0uFnlB981es4RBgAAgO8kk2CVLM0h69j9y1fYDarxocpfa1SY0Q+fejCWr3iPNgVUyvO4W/WBLhf/HIDN/LVtSvktfQ50lQuzr28jWNIkk5PFl7rnU+tQcVgQ2A40WRxBSJtUURXiT44bhuF+oJ8b9Zn+CB5FLBfQFobqakj6+7EyWNxOwTyXOl7PjgjEaU3j0l1H0E2bgt3NgtCZ2wWi6k2I/PJah9Y69G79by/H2l03zPNUGKtfn52q00+Lfx0CSfY0lc+yMXxLg/0mu9k9rzts4WqYBXte5H3XrtX9TOn1VHgENqZsrcVygKFBgAlAuioCLa6g+mdZFOJWpUy/qsUCEDgIkSX5dbgm+m9seq35Rz2DZfu4tDXABiEkeofSR1n7wGNTrim6m9ObqB2m2ngVR++7yvY2G8+GNoaAh/9md/hnvuuQcTExPo6urCW9/6VnzkIx+Bz/e8f7Bz507ccsst2LZtG1pbW3HrrbfiAx/4wCnNtZDIOeVRPylUPhlZTf+l360z8KkSzyqr4fPyBIdq3QLMOG7mcw0A4PPwoNwrElrTBvKsS4U/UBsVpLOiigAAPgEdV8GPStT89z6e4Qd0kmVCxMPjJV2dur5HBS8CUWAAsS+IdoQnRCW9I8DvoyoCHwBYFuXr8nieP0yPqLgAQK/g2Zmr8HV5VWxAzrEtnab2whT/vl7RLbi2DFAm5eOCbLWXv6/QWt0++eoB3hc/t507y0oiFgD+KMoT11MiUbp1RjvT5zTx561ayP4zxSHd3dYqeQ0jVZ5sDboT1J4x4EooNdLU/oSLK4P01i6Qc2xM8utQSK9jQn68XNdJFkcUbSJiP+w0qKQfF4pRcwJVtyamezsO5fm6y4nk+7hB+8j5SY72fDDNE9+NBt8nZg14etRY3Mb3ienjOmHV0s33kXKd+wLtcc21FRdn4KOTHM35yJRI/olkFAAU6nxtLxMJ/GmB7gWAda7fpvanU/9O7fttg0LEzAC1J7yCpLuVr5nlrbqCpopbgSDfy/oies3MVRPUrkjTy7Z+XzEf94uOVfi6TfoH5BzFBn+etiAitpV0uEiyAECqwEm254o8WVSt8b3ujEPkOM4z/3ux53gRxv79+2HbNv7pn/4JS5Yswe7du3HzzTejUCjg05/+NAAgm83i6quvxpVXXonPfe5z2LVrF97+9rcjkUjgHe94h/FcC4mc0zhKNV7VOR2qVWrUG0LOOsD7SAGgVtfBDRt6M9J/4/Nwxyhf1wFzKc2XtyIftPz6A1+8gb/z8jR/5987xHtiQ0KFAgAmhaJUQvixa5Ka0+g8UbFMhDi0PCOSNACwfYZDkVVlqCrI6EZLes1kBaneo/UfUPtF3lfJOVRyT8lkjhZ1UmzW4i1517QkqP1Ejie0ujvS8hqKGR5Ipqf591mp6uMpVRKJN4EsWifWNQB0dPEER6KdR6vNos0GAB4Z58nvB6b42l4FXunbVv6WvIYrAm+k9maBuhsv6/3yLPcV1F4U3GnbMjr4ubCVJ84GBf/T6i7+7VzUoVtufzDC3+fODF+XbpeeoyvAg7gjBb7x3zepUQlB8QmuT/C9qKtNr4knU3ySJ7L/wa8h/iZqT4i2QwDIi2RPcwdPwoSh2+2UP9IQhYadE1rBMi1aSUOi3e5VPfycnhC+BgBYQrBjVuwTlYb2ecou/j4WJfk5fKKqVavOFsmDwQjf18NBvpftMHifQeH/LU6mqT0iEHMAkBNiFw2Hv8/DBgTYewW63RGcYDGXFh6xPHw/m7F5kTzp5r542DIQkBD53NncDmpX1BqO48BxdHJuYZz6yGZf6Of5/X74/QZSgScZ1157La699trn/nvRokU4cOAAbr/99ucSOV/+8pdRrVbxhS98AT6fD6tXr8aOHTvw13/91wuJnF/VKFc494XihQHMVKXYUG1N+Xkifn5ZI1+epPa6ox2KiRmOgOp08QDN49cOxa7d/DDuFrLbi0SQ96MJ7YQ2i4RTRPDTvEIo/wBAXDglubKQ9DXoo1ZBdanGD+o/38lP0XNb9TUovoVXhW+gdpPk/q4aR5Gs8nC5656ITkj1g0uUr4pxB291Gw+YA0n9bXgrfI7fv4MTmn9srXZYDgsVoz2CWPPptCY7Pku0VexI87XfZaCasyetZLf5v2/y8Oqw39YtZEr6u1X4NJtaNILqa7P7qf14mZOUXikg+ABwosjdmpjg+yrPCBSXQZX7/BZ+tjwqzqbTUSMcFq7EeoNvOOmbH/Hs02mNhpku8esI+vk3ujnMi1OHdVcvloSFAlGB/0hDICcAIF/gH1BQkFf/ZFIHFQos1iRUqXzinDbhwXpqbn4+bMjSCcYmmydKnyj8N7UviV4p56gJ7ow5kfxzzfGE8rm9vO0eAEJxnqzNzfE1sVNwPwGaU0ytqaUx7Y9MlPjZcHfxv6g9ERiQcww6XB5ccdzsLH6f2otlAxSXn+9FPi9HxOluiDMLkePYz/zvxZ4DAHp7X5jI+8QnPoE/+ZM/Oa1zZTIZNDU9X7DeunUrLr744he0Wl1zzTW47bbbkEqlkBRo1WfHQiLnNI5IkEvdegW/BgAUKjyBMd+2J5PWKq+HIyMSIX6fs3nObwNo1SrVevXNExri2xviDsE39/K2pS3tuvo7LNSzciL58G9HuTPw+8u0zHPYMz/p4v0Z3fJXEYSRQTc/YJqEvDIALEqkqV0hcs5vS1C7gQ8qx4OiktfmDMjfGGk8LX6DH/Y/mtES5zdEXkPtSqls1xSvPl0xoJ31wCKx9l/DuX6GhrSqTpdIMPaFBVJMtJ8AwC2H+Pv6o+5zqX3agENAIR/U0h0TLUup/B55DYkOvmYiXn4VJtRxtqi8Koe9U+zpANAT5GecepbTFf4yCnXdKrcizvftS9p40voJEQQCGoF4uVBlVP8eALpEi5fak03GbIW/03W+V1C7R9xG/TQEAmXBJxQM6fPtk9t58uH/dx7n2bm6QxMq/8NB/hGq/S7m5Q/TbQAqXxzhPpHiFk1VdPLQb3O/aU2U72VFl/arLNEeuXWW+1XLoyKhbICWaRIKsUptLeHTc6gWzHGBZN4nZNoBoGrzd9oR5EmYpKMLLjuq36X2riAnyu8KcfuIQexUrvLknAlP6sL41Yzh4WHEYs/HQvNB4/y8cfjwYfz93//9c2gcAJiYmMDg4AvVCNvb25+zLSRyfgWjWFGEd3rDUwkOjyCkVIgcx9EOh1uoRGRKPDPtEuSEzwzNy8LGBQaKGwoNs349T5pVMnqObEUc5v0cpr95LV8TY8e1Q//gBA/8C+KwP6CBYoiJwuqAkCVtNnAoZkQbzD2T/Fk0CwTVHoP3qSqOfhdHNuSFnDygubIOu3if9QWe6+QcZQFPfzrFn8U5QoVlakhzQrRBtCOcz5/DysG0nGPqSe6Etqzg+4xt0A70vRhPXN8rCqsFA8VQ9f1IsvE0f5YqOQ8Aikf4dDQGR2z+DRfACxUGMR6+OsQf1qIYP996BbAobaDc4wIvRCwXfCf9IX0+/nCcF4YubeN7bsyAPPerJ/i6uqiVP4zhok68/UCQd9oWn2OiyNdUu8qSApgTbZzjab7vDwZ1O/qfns39DcW1tUS00QDAu5fzZ3H/NA/Kt85wnynh0b6dIn/3WXwnEcBAAMBO+yfUXq7wc9gEXbG+5UPU3uzn99Hs5+u2YkAPMCfU7QqiUDhe0lySY2VBgD2liiV6TbQF+N8crfLrbHISco7BwBZq3z33ZWpX3J7RAEcQA0DAI1RPBYfOwvjVjVgs9oJEzsnGH//xH+O2226jf7Nv3z6sWLHiuf8eHR3Ftddeize84Q24+eab532t/3ssJHJO4zgdak1uEeTV6+l5z6FGpcr5a7wimdRoaCyzSkjFBETRRM7aFrKmopUbXqEUAwBhQZyZz/ADbGSIv+97p/TG8tQMd8jXNnGHo0t3RKAunuWIIIZerjs7pOqUUlDZn+NOzZ6MRpGELL4ouhu8j/qYdUDOYYmQuC6SnAFLO4BJP/+bNuHf2aJyFI3p6nBmjK/9sd3cHhbVYQDoWZSm9uwx/j5tA+WQ9hYe3Axm+eLO1rSj6xUtDbvnBNdW+tPUrlRcAKAqSuUKwVE2SLLsKnyH2i8Lv43a8zU9yfW9fO2H3HwfUYgBJesNAKkav4a9IjHQY5DIuUogND53iL+vsOCUAICQOGfHy/z7mizrqHzA5m2g92Q+Q+1LE2uoPWnr/VI9b5+br7sDowYtLALdlBdB+cGsbrOeFgkp1YbdF+TJJBP+msUxfg0HhYa5amkCgLMsrsL3hJtz2YViZ8k5lDqtX+zZR/J8318U06igmOAebOT4NZpQECils6u6+H0cN6BsGcrzpPJ0g/tNBbfuRPCCO7KdCZ7o8bi4U1Ssa4S+IkxWcY8ajmOj0Zgfh+lLavwayo+/733vw4033kj/ZtGi54t/Y2NjuOyyy3DBBRfg85///Av+rqOjA5OTL0zwP/vfHR2aF+rZsZDI+SUOE7JjlQRRG4Hl4tAJEyJi1X5lC7vfpxfgfImfD+W0c3aVYNsvTPDlXxRkkQDQIbgQMhleNf2LPdx+vhYAw1VdQm5XFF4N4mU4gvxFcSm0hbR8yayoHs1W+X0qJ3VjUmests6lqf3h3OepfXGCtwEAwHhxB7UnArzlb9LWntOhPF+XG2s8IZVv4UFFraK/v1SOr+1ZwaukgicAOH6EQ09LgvzzaF4HR5WGkBcXyD+T9pMfTvC1f3dxN7UrWVMl1wsAbhG4qBDORBWuOcyD9qedh6n99SHNbdEV4MHPgAigAqKSXhatQACwN8Urswdz/GxpF8TSgF5X13Tx6xwt6Y1fB9XcblJwKYnE9dmJm6j9kIt/GwMOb30EgN3inF4bF4jToE5sq+EV/souQR4PAAkfv0511sd8fN0pjh0AOJHn9/H9wlepfaPvlXKOEYur/yjhkZhQRQWAiSo/Z++f4L+h/DK/ASJODYVemhM+EwA8NMnXjEJjP57XXD+LvTzRuQnXUPs9xS/JOVpDK6h9PM3PlqVNr6X2iqX9LkVmPP9xZnHk/DqO1tZWtLbqxD3wDBLnsssuw9lnn40vfvGLsP4XGnHz5s34yEc+glqtBq/3mf397rvvxvLly43bqoCFRM4vdShnGwDqorVqOss5OqIh7ijX65rY1hEyfY0G39BMUEMuAYcZE8TRZy3WMrSWqJj4Qvw+HUe3A6lEzbRoF/rdxfwa7xjWG/dVndxxSgrnbl2TXhMH0yIwyfPTfkigFgAgJCR5ewUPgUIMHMvr7e7x0teovUVIUA4XHpNzKFL0ipdv4LbgIwI0YbJy2GdEsHpiOiGvobuJJ5MqIskyJJSzAKAsEDXDgtuiaoAi+dokf19Jh38bB6yn5BwrnA3Ufr6fy4dna8uo/aGIRqOZtDSwoVqzACBbGaX2Wp0nfKthrnoFAEcFqaxqo/nqcb6fvmOJ/v5iXr6wVBvoPVOaT+/cJr4fBsQ+cVZSn29hkUx9cIZfp7oGAOjzJaj9J5UfUntVCET4IufJa9id5td5YSt/Vo5ArJqMpEgGbWrWyL4Hpvg5LFSgkarwdXl37pC8hnabt6C0BLiPeszRHIup8hC1qzaYsoHwyLIER0OvF92qXx/mCKxNLbpQ6BP7iCp2LBIccQAwk+DfcEGoWq0O6GqjEpGYFgfxUoN9f0+aEyYrDtOxEm/xLJSG5DUoMmMV96giuuPYqNV1Mf5lM34NETmmY3R0FJdeein6+/vx6U9/GtPTz9NsPIu2ectb3oJPfvKTuOmmm/DBD34Qu3fvxt/+7d/iM5/hKNT/PRYSOadxhAJ91D4pkjAA4HHzgFclg8oiiZKI8Kw1YKAYJZJB8fBKOUeuzB36kFCqeHRWV6eOFjjqYEsLT0iZfN8HRA9zQCSTVDX/tgu1w+ERaJiiSLLsE8S2AOAS1d/BMA8qjhe103JWE38WMcGz86+HE9Q+UdLkFucEf4Paay7+G6UQD6gBoBzm6y4i+sGzBjw801X+vGs2Dwpau/mzXr6Icz8BgL+FrxnPEA8aDh3Tyb+BMA/iBiP8GmoGhK8uFw8KHpniz6rNHpBzlEXSeLbCr/O+Mq9ym6h+ZIUzrWRoVWsWoJ3hWHg5tedrurUjLo4GlfB9xxL+HAoNXeWuicA+LGSFXdBzKFLmNXH+bUwKRBwANMR9XNjCg9VjIqkGAFXRrjOT5YnQi+K3Uvt/pb8lr+E/V3LesYRocfH5NLoiX+TPoi7WpQmyTyXoi0KCaF+FB4kVl0bWjri5MqoHHH0YAQ+GAcAjOFfUiLk138kTJe6jrgcvlry2hydIHprWydo1goPRLxI5RYO9SvGv7U3z4vKF7dq3mxCsE/uKj1P7VFYn97rjF8u/YWMkfR+1B/x6zYR9PKlVrPIWsbBIQNpOA3O5MyiR8xIed999Nw4fPozDhw+jp+eFVCHPdjjE43HcdddduOWWW3D22WejpaUFH//4x09JehxYSOSc1tGwBbmgyAgDuro0md1G7S4X37gVmfLpGMWq7iW1RGba7+FB3IaELqWf3843TY9wpvfPamibcsjXJDkqIeLn7+Mb+3lyEND8Gg+JfX9pTAezgnIF3QHuyHYFdRIlKhI1R4S61iIR93+nwL8dAIhaHDIZEegLxX8DABWHJ3Jm64epPezRFbBJHKT2yyxe4XIER870hEbLxIo8+Akm+Pt+zbVDcg6nxtf+7EEeNFREMAwA60RS7OFJ/s6vbeYOPwC0irbAEwJQswMD1D5T4LLfABBsvojaFebARJFjY/J3qT1pJ6h9fZMOTMIevq4UAe9TKR48qWAYAC5s5WtiaZS/0A0tGiW5bZpDAlSiJi7krgGgIhBvoyX+bZi0b813VFz8fb9eKBgBQNzH30dRKPvMFXVQHhR8eg9O8oLKgAFv0is609Q+Iq5zpswLaA+IRA8ABBwh5W7zOfIGyaK8i/t2JzIPUHs4wDkYAaDJ10ntihdwSwt/X10hzakpOtqRq/HvTyViAWBSXMbr+viem9LAPqQq/EZ6wXmu6mG99qcKvMVSKf4qsmPb1vtlqcb5a0qVkXnZz7TWql+m/PjpHjfeeKPk0gGAdevW4cEHH5zXXAuJnNM4FP9MtcqRLoCG3ilnWf37+apFmQwTHh41Im7e114x4GPYM8cTMWkBsVfSxgCQFcoDZWE/kOHVp8OCzA4AgkJ/dX2TCHYN5JFXxfizaA9we8igHzwqnrc7y+9jTPh/F3g2yWt4rP4ktWfB+8HHRB82AMTDHLUT9HCHvs/WiLeUxZ2W/ghflxERdCjINwAMTfDv7/G9PDFXEtw0AHBJK0cnzYqKpkmVu1Vwrrx1EQ9cpkS7AqCDgq9lH6H2dtdiap92uJMLzB9hbNJatSf/PWpXLRGb66+Wc7QIWd/eMN8oLmnn7ytdMahAl3kCURG7q8QBAKxP8rX/6Az//u6Z1HOoQFIlzzuDeu3nBMkvBLen1+H/vmSQeCuKc7pV8NfcP5WQc1zVyQtc3UG+bndntQLRAxPcF3h1L/d5lsX4R5ya1mePoj88Bu4H16AzA0o9MhLkBbCIV8tZd7l4onRFlK+JiGgVzxl840oafJXYA2YqCTlHj6ALOpjja0YpfQLAaImfoWPgZMet7iVyDn+Yn8OjmYeoXfF2qkQQADRsjtBXXRsmamoLY2H877GQyDnF4XEnT/rBB3w8AKvUdEtELMgrBQ2BqEnl98g51JAS5wI1pDh2AMDj5nMMpX5E7ceadFC+V8hN94kDrEk1lAM4X1ROUxXufI0KDo/zmnUCxCecTOVQZARXCQAsjfO2pyOCA2dzh2baL5X5s1DBT6fgMlbwXkCvu9MxlARlWECEyy59IyGHv4+weOWjonLbEdPEf3GR3Gv387U9IRRxAOCpFE8GHcnzwMRAhAVuiz+LsvhEW3T8hQNC03qqwPf10TpP9JyOodx1A38e3ZFzqF0ptqnKLgAERdJ4+UreFuiN8zVTy+hrOHaQB4H/epj7Cq/r0d9Xi6joq8Tca3v0PpIUiFGl2qgI7AEgVeV7VW+SowcPNh6l9h7nankNMR+/j7AoMlzWphFUGZFUDgp0717B4wMAHsFFcs8E/41lYu3HfXpP/kmFE6sr9R/b0ejdsvCl3RZPtpogZ9WzVEeHagVXCC0AaBM+6peOchTJq7p1zFEUqLt9We4H35fmHHIA0Oni+127wwsRByscYQXo+CoskigJP7cX6rqdvFDhf1Oppaldc+g4gEF89bIZzi+BI0dVK14CYyGRc4qj3kjhZCDzWn3+snAzAs2iFKEU2XG+xPuXAcBtcefL4+YRsyJzBfSzCgcHqH1pRG9maxJCAUwkQPICtgoAJ4TqzaRo3QgLKVuTPUy1AlzWxhNvV689LuewvPxC2lI88PAFdUJK7acx4fgELP4cJio6cFnSxGH4J3LcSbWEfDlgQHYsVKmm3ENyjsX2WmpXrVMPT/OkWm9Iq340iUBTcZUEDYhSFWonbRD4q5ER3DF+N7+Pf5r4ZzlHwMfRE5eH3krtJUGS+HTjbnkN8yU7Nvn3x9P8Ol6VeC+1r0no96lQkCcEl9bDosXlhpV6v1x2Lg/sP96RpvZv7x6Uc6hA8VWDfJ/Jl/X5FhIKXvU6X/tzoi0RAP52gqO0ZnM7qf3cOFe1agnogsxjszwh7HHxczoqUGCARh4pdOBGQa4LAPcKAaGyyFz/ZIqvWz80iqTNNUDt426+pnLVcTmHbkER/15wlQDA9hj3cwczZ1N7X4j7I1WRQAGAQp0/b+Xb7Uhpnjm1basEvSL7B4C84ICrWtzuM1AZCwui4bzoiMjW+LorVgw6KkSCUKF+goKHx3FslCpD8joWxpk1FhI5p3EoxvK6QLIAgG3z4KdS5Se1spsM9Rtug011vkPxDZmMY3l+nQ/P8EOyW6tV47EpHkCd1cI37o6AqMJlteP0lkU8+deS5OsuM6v7+5+a4NwxIUG698isfpiv6+WVuoGWNLWPlvh9NHl0dfie2Tv5NSS5TOZ0mUOETUaqyDlyFL8UAEQiPBi1HR64XNXBodAxg8CltYMnpK6K8TlUaxYAVG0epG1qFsS1wlEGgDtH+dqdLfNv+NzQb8o5Bv3cGQ54uLt9f5kjdoolzVtWFR67SiqbJJ1Vgl4ooBtJnCukSizC190FDi8y7B7WbRn9WV4dbm4XHDlNaTnHlNjvIuIbjRso2iiUpBrtoi0RAN4Y53LT97p5K2qnK0HtdYOFWRLKPOPiWScM5MeVvHi5xveyzS0aXdEd5HvVvZM8sXbP3I+p3aRQ0eVZR+1n4Xxqn/HxAhwA7BTI9KXBy6i97NK+eNXhLZgx8WkczHF/wysKTwCwSfg8Kmm9K639rsM5vl8uifK171W9dAAmXRypohBSNREXAS++9Lci4gd0wilb4glI3Vr10kePnNKwoaFvp2OOl/hYSOScxtEQm41K0vy6DNlaJQ5Rt5sHiQAQDnAiObUhzlT14aE4btbE+SHoFyTCAPCqHn4d1yzmG7NXKE4NTyTkNexP8SCwTTihJuolyhceF+ilS1t1q8DAAA+g6oLLJyAc5Zm65jxSiLeJIldPqNX1fcpr8CaovTWgHYoy+HU8NsOd1EVhJeGsy8OrRMveogGeXFizTnNt1UX8VBWS8+m0TmJeIDhR/vUIrzB3CuJ2AOgK833kUEbD8NkI+3kiFtD+jELcOAZOZlkQ4R/xc0c3OjMg5+gK8rXZluf7wKhoB3pgSp8913TydXeeUDlqT+p9ZKbM1+7DIvk+GNb+SFgQIqv2kOMFHUj6xePcm/pvaq81vZbaY/VV8hoWCYSvIqb1G6hWdVg8eXD/Ee4TdRgoNR0tcJ9mZZx/5ZcUOAfVnXO3yWtYF+etcLZAHo25jsg5ukMcDXOswtvtQh59fm10baH2gTBfM2uEIqmJYqJK1oY9/Pt7Raf2ee738Dmy4uiJenSyt7/B13ZNMM4W/fobbvbx9iwlMqGSSWVbJxgzxSFqd7v52aLAAGec/PjCMBoLiZzTOByxGSmiK2D+SBSFpmmK8pYLAKjWucORLx0Vv6AdxGyBb4rqOgvab5Ljkk5eJSgYkNGNFnjCaTrNW69mBSnmvVMa/dTq5+tuqsLvY7Ksq9xPzvB1ua6JbyUXtOvApCTQR8emOELjhOAbGnVzJScASAZ5S0Pd4Y5RLKQlKkcLT1B7SBzmVUd/X53gLZZtfqHMI1qWNgk1NgCYFfxQf/V9ruL3ml7dPtkiWj+eTPFAMmDQvtUikq23LOXB01hZt3Y8Oi2U5+q8Ut7h5iSkilMCANw6p0WHCSInIhL4StGmUyS8AOBgjv9Nk+BDUS0uNy7iARoA3D/FixnWGL/PFQn9vnoifE+tNPg1TAvOFgD48hA/f27o4fuhauEEgKS4DOU3TVe4Ipvl00FgVPAqWSJJuVMkzQBgrVDRvEooTv3nsYSc43MT/0LtbxSqcR1Bfoa+KvkBeQ0pmxcJZoR/2G3zswsAqi6+7ho+/huOQRl+yuFtZodyXI0w6Oa+39Ko3kda4vxZPjTOOXIGDJK1iyPzU56zDMLIY3m+5z5U+Tq11xsa8aZiH7WPxAO91D6X0xLoAT8/35Q8eaHKkzTPJHLkZbxshmM7cF5kjpwX+/d/GWMhkXMah0LcmDCSK1Uqk6onG/my7j9W7OwKcdNo6CBPjYiHIyOUXC8A5AXsdEYQulYaOgBbIhzuvOAI2JnhgebSiN61A4IksSx6sdsDOjgaiPL7UBVNr4HKkS3aJhrCLrpPsNFaIa/hkJOg9nGbBw3TFd1apZJFqpe74dFVthY3T3opdEWPkIs3IWpU47puvqYO5HQi9fE5/jdtopvuP0Y0geG1LTzonizx78+EBPhAiaPR4h4eNOxO/Re1q957QF+nIob2GpDkhD084F0c5vvhtzOcKBwAPrein9pXigR+QOy59YreL1WLmOKuePCQTgy8ppsnckKC5H44p/lrfnuQF3Xiggx5ykCW2ysJPvnCU7wTd2T/R17D2uybqL0nwp9DsyB2B4CpLE+KRUSCcV1CJx/eUOaJGrdYmDUxRd6g0Li98m1qV2gaj1AhA4DxKg+qlaBAIqzVt9IuzoV17wxv3+oPc6T0E3OaW+baAc5zdUk39xW2Tep95LAQBLgnNUrtZ4V48gIAwm7+TstVvidHDYrgKpGj4i9lNymCu108K10T9BoLrVUL4xcZC4mcUxyWFYPrJIehIgE24a+x3NzBU2z8KglTr+tKXyTIK+UKkaNaswDdnjUq5HaLHbzPGgDqDnfwxgRsdUA4bwDgFdwwMeHoLglz+/GidrZbBSpBtYjNid58AHjncn7QNsV45agsUEEA8MgJ7hDMCOLoo8IhKTZ0MmnS4bDuueIharcF6SwAFMq8fUQlhC2XfpblGHcyazZfVz+a4PaQh1cbAQ37VqrAu1L6fcW8/BsvCu6LS5K8QgYAe1P8Pp6yeVARgH5WSXAUVk9DkN8mOc9ItqHPHt882Y5rBpUthWhTgeRvt+gA7K4Jfh8qwe8RiByVvAeAbkG0nxVoz3xdJ0DKotBQEa0b6lkDQF0kzz/0FF/b716uJ1FJr44Q51xZ6aym9l7RJgoATT6h/Cj4htyirReA1EnyCVRQV0AnURyH79vpKp9jp8MTILal9+RVAc4jlwZHHYxWn5Zz5AocXatapAsGxLVLo1zt7Ipm3p7VE+TneMmA7Hgyw7+vYp37RC6DwH9Dgr/TziAvAoxy1w8AkK3xj7wrxv35kfS9cg6VaFHF4WKDt/3OGSgCq7hGDZWUPuNUqxY4cozGrzSR86lPfQp33HEH9u/fj2AwiAsuuAC33XYbli9/ngOiXC7jfe97H/77v/8blUoF11xzDT772c+ivf1nq6Szs7NYv349RkdHkUqlkEgknrN9+ctfxl/8xV/g0KFDiMfjuO666/CXf/mXaG7mpKD/e9h2FifjeY+HeCWwZpBEUWgWFYuqJErQpzP0ajNpjm6g9nxFBw0N8SxscQCZ5KXzQlFjVZxXNE16mPfN8sP8kVkOCbiuk8Nrr23WSmh+IeM8neGVwE39GuI7OccTjN8/zGGpqt0BALqDIoCKKBg/d9jvS+nvbyzNZS6TER40eIRUNQBMZ3lrlUK8NUd0MOsVW3t/hNsvbuVOqGrrALRkb0ag1S7r0AFYR4AnWQ4I1IGJ8mQuKJTnChz9NOOoVlRg2uEE1z1u7qSOl3jwU61plKQVvJLaVcBtMpQizTaLV8EfrOh19+5O/o3mROJ6V4YnWUwCsOUikdMmgrxqSu8je7P8b9YneIS1qVmviazgPvvIGv6NH87p1uBvjfMAKmjx/XCfiwdY6/1c8h4A1sTT1J5o5s+yWag6AsDMOH8WZRGUL2vSEue/Bb4X3THM99SeAk8YT1nat5tyDVF7q83RFZ0eLRc/kuR8KGpEoP3+iM19njtmedFnQ6KH2pfGtd/14CT3L5dH+T4yVNRFn61T/Ay9vJPvd90hfTCMiJrogM3bH70JvR+2OBy1OgF+Dit+G5MkjeQXFYgc21FI5wVEzsL42fErTeTcf//9uOWWW3DuueeiXq/jwx/+MK6++mrs3bsX4fAzh94f/uEf4nvf+x6+9rWvIR6P413vehde97rX4eGHH/6Z37vpppuwbt06jI6+EAr48MMP421vexs+85nP4Prrr8fo6Cje+c534uabb8Ydd9xxStecjKyD5fr5jqBKYIRE/yQAeAVRQUpkhZWiTU4gCkyGQgSoPlFAt4gphviwAbdFkyAgnBYkv9vmtMpRSFzHWwY5kmXJOWlqdycN5KyH5tfmsm+MowEAYHeWo81UxSVncIkX9XNHtTkqVCQEVHnltL7PvQKN1hCIG7dBel+t7WyBt2dlSlr++D6b/8aaxK3Uvj3N135fVAfUhRL/vjav5Mik88SaAoCM4MBZL/LWEwaBpnuGB5IHc3xd9bp4JRAABuP8eecFfCLv2kjt5YAO2hWiRrVe1Q0qW32B86h91uFr+3zrAjlH2MMvVAGPGiK7d+eI3pMHM3zhKfL3C5o1GnSXaMv90QS3L4noFxYXLbEZQWjecPQ3vDLEg9XvFp+k9rrgZAF0IicoSJ2nJnlQ39Ki98OoUOl79CAvhrSJpDUAhAWq59J27rv5Zvh91rIacbrGy5NBChn7QI0rRwJAi+DAGcr8hNqDfq08t8nHSbTf2Ml9hbiXr0uF8gKAa3t5TJEXPFcDBjyP2908UXMgw7/hsIGwXbOfJ8+fanBfoGbACzgCjiZrAv++Rg3Q1GqoQnwkyBOQpyM+e1kNBy9+7uplkBv7lSZyfvjDH77gv//t3/4NbW1tePLJJ3HxxRcjk8ngX//1X/GVr3wFl19+OQDgi1/8IlauXIlHH30U55//PBzv9ttvRzqdxsc//nH84Ac/eMHvbt26FQMDA3j3u98NABgcHMTv/d7v4bbbNAP//x61RgGukyRyVNuTyfAKgjSFCFBJlryBdLFqAVNZYxMuINWjnPRxZ8AEDRcRHAGq9WORwQnVLyRc+wZ5cqIuijJPPazVFWzhLG8XhMsjRe1sjxf5E3+wsoPaP9izQc6hRrowP/Ut1YYDAC0B7iBa4GsiDo14m7R4Ja8e4E6L4owAgGXR66m9KpB9l7Vxh8QvAgYAGMnyoOChp3hV1ERqeomQkn46w9dMm1/DlHuD/F67A4pQWd+HWpp7yrwd4VD6m9SuWg0AIB/mAW/D4c64iAcAALaLr10lTXzI5nwNADBcHKD2LlHcVVw/B8payr09yPeBaaGEpgiZAaA9wNfu4zP8hcwakNwHhSLNoSzfq5bH9RmqyI5f4VxF7XMV/qxKBiRVin8Novt4QpBbA0BcEM8qlc3PHtQIxa4wX9wrYvxZDIou0LqdkNcwVeL75SEXR0as9fD3DQA14YMeFe3JhdKQnCMe5M97sUAItwmls7oBsk9xC6pu1q6gJgn+zX5+n9NCLfS4UEoDgKLI8gccvvAmq3vlHKoAZiUupfZogCN60kKgBTDzzdhoi2+idtupYyb72LzmWBgvv/FrxZGTyTzT+tDU9Ezw+uSTT6JWq+HKK5+HfK9YsQJ9fX3YunXrc4mcvXv34k//9E/x2GOP4ejRnz0kNm/ejA9/+MP4/ve/j+uuuw5TU1P4+te/jle84hUnvZZKpYJK5fmNOpt95iMulMdOypHjiMPFYyDLHfHxSkFWHEANAd0zGW4h/X065sgWeSuBZfGlWW5wwjwAOJLnVe51Cf6+mgX3DAD4RM94YU4oAsxyFMl2QYoJAAdz/KBVcaRJe0nQw52O5WVOJGwi5a4UvIqCE0JVfw3yOJirDlG7kqhMi9YQAIh5eM95R5BzQvihJX3bbR5ItgX5s9o6y/eqqwwCTfU+dqb5s1ykqWXwlGhBKYsAbfYkSfmfHtMi4F2d4GtbXQOgeXj2V3iF2RItfSby43Gf4lvgQ5EhA8BMje/7ISHVvsbDq6qA3u98Yi9aG+fvYnWMt68AwL2TfI5HZ3mCY21cr8uQhz/wQp2fTW1CoQgAwoJB/voevmfPGYhwHs7yZ7W3zFGtR+1t1N5rc/4oQJ89a5o1Kboa6pztFJx8q5MaPThW5JN8ZOi71P7uDl4AMOFV2tq4n9oXg/tuSUufb3vBA/veJJdAdxuEPnemP0Pt15beT+1rWvjiP5JKyGvoEi3Mjjhjj+b1s1QIxV3inM6oqhCAoyWeBJkRyb0m34CcY6n3QmrPWpymYLz8lJxDDVVIrzd4cq9mqfd9BvHjYEG1ynT82iRybNvGe97zHmzZsgVr1qwBAExMTMDn872A6wYA2tvbMTHxDGqkUqngzW9+M/7yL/8SfX19PzeRs2XLFnz5y1/GG9/4RpTLZdTrdVx//fX4x3/8x5Nez6c+9Sl88pOf/HlXipO5tI6A5plIHioOgXCA993KjaKuIcC2IKRUw+vRKJJaXXO/sFE1gfGH+H0EBFFx0iBYXdrFq7MeUVHxiWswye8fzvL7XJXgFZeSwdnQ7FfJIh5I9ojqFKATNRNlfkiqxIEJx0dA9Dhny8PUPhjizgQAeASXz3iDt0/OZLXDcSI4QO3RWa7S8u4VfO1HRfUYAKrifdZt7mTWDM5X9X3sFJGkaqMBgLCH38fRKt/LHs/8q5yjP8Gr0AOBzdS+p/QVai9WNYqk4udP0xFJTJO9yisSTklR8a/YepZyg7s1St3u8Vn+76/u0FXuKwQA6odjfE39VUajWt/RxTn5rhQdzqMlE5Ux/n3cN8EPj7hPJ6T2l7lAQwPcr7pIcKoMGCSEe0SraC7P9+x0Sbdh+xVC2Mf3qgtbNKvs98b4nvo7TTxR8y8zXGRio0GbWtLiydYsOFddxcD/PJrmCSk1AgYqfm9p+SNqXxLhPs3eGe4HD8Q0R05EEFyHRLExUdSJnKfTfG1f3s6vYVqIUABAbpQnIVP2ALWPVLXP0+Ll3EvTFa44mgwvofaA4OoCgMn8TmovVXgLmbK/LPqAFsZpH782iZxbbrkFu3fvxkMPPXRK/+5DH/oQVq5cibe+9a0n/Zu9e/fiD/7gD/Dxj38c11xzDcbHx/H+978f73znO/Gv//rznewPfehDeO973/vcf2ezWfT29iIS7Dt5a5VoW1L8NgCQCPG+W9XWpBADJm1PisNDOeMm96kqyAqiGDMgF1RkxT+e5JXVpFcHDW4XP6xVsqhQ58mJbTP6Ps9q5k7kVJn/xkqtgomVgp/GK6rcu0WLCwDkhMLQ0RyfoyvE33fUoJd7DTgHxz0VXqWb9nPEAaATMaqauLSJ9+4DmvxWJSeeTvOHtUcQrQLAlZ08QPvNPl6B/uGErkArpaWNzUL2tKGD2b8a+RdqXx28jtpVkgbQ5JsKYZVOXELtI+n75DW4YyIRKv69CeIt4uYqYaPgidKoo0lOU1W+TxwVrQC7MnyvWx7Ta78nyIOfza1CcWpCI4+OCJW+jUl+9qyN6wz+XJVf57mt3Oc5pmNV1MB9mu2Z/6D2lvgf8N+3DZBHIjHd1MuTd+0VA8GAYY42awh/ZdBALe31wt/YJkQLOjM8mM0YcJWM17mK3/WR11F7xQDadzzGE0q5CpftXhS6WM7RFDDY0MhQPHKd7fp9FnI8yaKucJnBmjmS53vyg9McVT4r/EsAyDX4N36w8CP5G2oEPdwP3uTlyLwZcBqEvSV9jfMtUKsWaMexUa3xtb0wzrzxa5HIede73oXvfve7eOCBB9DT8zzipKOjA9VqFel0+gWonMnJSXR0PLPg77nnHuzatQtf//rXATwrzwa0tLTgIx/5CD75yU/iU5/6FLZs2YL3v/8ZKOS6desQDodx0UUX4c///M/R2fmzpSu/3w+//2c30WfIqH4x+Q4TWW6FqEkXOKGXz8s3ZdU2BQCVGt/8A8GE/A01VBtaocKhzEoWFQCOCelunzgFVeUWAB4SRKhqKP6NN/drbHpHiAceM2UeeJiosGxP8984IbrtqgY8BSsT3L48zl9IQEjADhtwAU1ZnIvEJb59rToAtContMoPar9fl5i3+LmzPFnlgUmbn387F3Tz5wQATR18UfT609S+fFxzQjwxwltRl8Y5pHu8oPfDVOUmaj+Y4/fpku42sC7I76Msgps91fkRngNArs73IsWRYzKGsrztwuPmFeQDla/LOf6k+ePU7hXy4gMhvtf92wntrF8i1DAV0fCqpH7WT8zws6Hc4N9wi0BZAkBAkPkLDlPZ5gboloeN8bdRe9nhz6Fm68SbGjt38u9z3QYtZ90h1CG/8Rgv4rUbtHpHvfxvzkry5ELd4f7j3008Kq/hVWF+9oSEY1Woa1+h3+Lk7kMCXXisqAvGc16eNJ4VqourRCHDG9IJq/QEX7utCYEkE4IDALAqxmOOiIf/xhFL71VKzfON/t+j9mxNc/JlGjwZ++Pc56ldFdH9ou0XAErza2ZArc6TSY4JD8LLaSzIjxuNX2kix3Ec3HrrrfjmN7+J++67D4ODLyS4Pfvss+H1evGTn/wEr3/96wEABw4cwIkTJ7B58zNQ82984xsolZ7fiLZt24a3v/3tePDBB7F48TMbcbFYhMfzwlt1u93PXcOpDL+v86Ty3D7xoSsyLgDICv6ZpiiXoc2WeEXT49abUW+EE27NVjnqICzaOgAg6uO4byUDnTMgmF8V405Nr0iA2AYJu1d28paFSKdotxObSG5ME2g/NcydzONFfhAPF3WgqciOVaLGpLrVIWTUc3XuMBzIzr+1Km5zlFZP8nJqn8zzaiQA9ES4cs+x3A+pXSVzASCa/F1q3yiI/QJu/u2MpvU+Mp7hCSefm6+psAhKAGBtG//+dk3xgDoorgEALm7j63JUSLy2ujU/TXOAL84n50SCv8y5mUIBDjsHgKSP34dC3Jhw5NTraWofiHFkUSLIA00AcAn4uaD7QlnsZdsKvI0NANrcPDA5muUXcXGH3qw2NvN9/UuzHJW3rsQFBwCgM8TXhEI55gz6Iw/NcaLuNcnfovaVooptgrorlfk5qxI1BsrEsERMvTzGfb+yOP8A4CGhOtUuEhyKy26z51x5DcMCnTQoWlTKQtUKACbA1X1Uome38z05R1W0ca4UaJdIM18Un3uICysAwO9t5r52ZoajUBKi/QsAfiRUS4vC156r6I3fI5Czhws8IRUxEJK5L/M31P6apg9S+4jNE2+7ylpNbb7D7+W+guPYKFd1V8XCOLPGrzSRc8stt+ArX/kK7rzzTkSj0ed4b+LxOILBIOLxOG666Sa8973vRVNTE2KxGG699VZs3rz5OaLjZ5M1z46ZmWc+xpUrVz6H4rn++utx88034/bbb3+uteo973kPzjvvPHR16V7Znx6s5Ufxa0C0LAE62TOX44GialmyDYiKD8/Nb8OKhvQBVaxxxI1ib48ZtMnEhaRorqYCF31AfWPvALX/VowfxJUc/wS/sV8HYPuEPKQKTHYVNbpikU/zHrFhAMiBX1Z/+fu0BEHocFE7wm1CNe64zZ3Mhq2/rxq4c6VI0d1uzceQAkf1DEY511Z7gDuhXTHNtZUu8uv83hhPmrX451992jrNf8OE5+4SoVT7m/38+zNZd49McVTB9sZd1F6tC5Uxb0Jew3yHSaJUtQ3WHY4U8zp6439smv9Gh1CjqYpFcWH4RnkNZbFP+C2eyElVDRSlxH55lrWK2jN1nSj1Wvx5z4i2CsV/AwCXxt9D7XsaHD1xn8OVzNLjOvD5ncWcZ6cwyc/pSlm70q1rBJfdEn4Of+ZB3vYEAAURdN89zs+eC1r5+WcZlK/r4m9SAj34aIMXMgBg0M2LIUUXTyYlg1wVFQBag/ydBkWhQQE4br1eS01bQb5PeAWa5sFH+TkPAAMhfvYoMuQu8ZwA4Eie38dokRciltp67W8UxatxO03tTUhQ+4bw6+U1zFlc8bdoC8QNlEpZ/YxK5Di2Lnafjjle6uNXmsi5/fbbAQCXXnrpC/7/X/ziF3HjjTcCAD7zmc/Asiy8/vWvR6VSwTXXXIPPfvazpzTPjTfeiFwuh3/4h3/A+973PiQSCVx++eW/kPx4tTaJk7VWZU+C1Hl2mBwe/hjf/aezT1B7JMgD/0KZkykDgBs8GdRo8KChVNUKD6oyq9rQQu4rqR3QilITQqniaF5/Hq8f4JW6cpb/xsFRXg3ZI5I0APCdPIc7rwOvTpVcumqTr/FnuRucF+nN0bPkHIo0rygqq3NCJvPeGd0SkbJ44NEODrcOxDXhULquUHOaoFCNOHiV2iuWlUpiBgUHCAAUqzwIbA/wOUxkTVWyR6FIdhd1oOme4t/o1ipPvq92aSd02uaBx8lQoM+O1shqam+xOGwc0CpHtsOvwQTcOpzi6luqNbgS1gnEy5t5smhVjEe7YUFKO1PR7Xg/GecPY0edJ/jnJnUApoLuFQn+/e1PyynQIlAkfWG+kSQN1NIen+PIhlY3/37SDk9a/2biLfIaZkt8XfW1p6k96tMQ4exhfr7FFvF195ZFun3r7lH+/WRrfO1+aZbzty12dDGy2eJzWALpfJalOcXS4PtlzcWTZl4DZaySaPF6eoajPRu7+X7Zs1Tz17gEF6TQV5ECEoAWkVCqqIqLC9DIvI0WVz3d6+jkRbPN34dqcZ5zpand5+g2tc4Gj78qLu6XKWL3BqqYxMPyOhbGmTV+5a1VagQCAfzjP/4jVZj66XHppZf+3N+99dZbceutt57yNZ7OMZl5XP6NW7Q+qbYlhehpjm6Q1zCb20HtA8lrqN0FfXhUHO44leq8ZWK6olt1yg3uUChFjvObNboikeDtWVWRnNgt2k9CBl/o2S4u5+lz82e11qWDhqKAO786wpNFrQboirSoQv/JEFf/uaWTc5mcZSAbvEsk3pTy3I7M1+QcTeFl1N4S4s6yUr0CgF2Z/6H2N7ZxRY7ZCp+j24BXKR7mCcJmEfzMGnzjqpiyJsHXlMfSgea+HHe4LYGu2OdwaVUA6HFxcturAlxtpiD4bY5gSF6DammoOxzeXjc4zxWZY8TP7X6X5odSHBvTFX4+7Uhz+7KoLuFd2sHXhGeKo1anKrpXR5HYh8QxbILIqQqi4ONp/iymynqOIy6u9JKv8gSGV/D+pas6yWIJ3iR3iO8jtZRe+6EWfh3uJP++upfyAhoALM9y/zHh5XME3PwcN5EfzwpJUcV3UhHk1wDQ5+ZBe6LOn8MRiysYAcCiKH/nxTr/xtWaKqe0nxwU5NVucY2bejlCBAA+9QRPPqxNiLZ6A77KFTH+LCwhFDOe1ojwkIuv7ahHCB/UOZLzkKP5oTrcvF31YJ4TJldrqrC0wJHzoszxEh+/FmTHL5fhFn2cHXEuIQsAs8WD1K7UnNQcGSGfDBhURUUSpmYbSE1X+Ya1OMi5EkxadSrigIm5+LM0aa1Sw+vjB7GSSP/ECU3K9/oYRyc9leVJscV+neBY38QPwVkRd4Q9+lnmhGP0jnaeqFHoi7KBzHqnj1fqjtU4qqc/ZqCG4XB+KFWVGarphLDfyx1d5ZA3+/kLTec1gaiSKFdKZx0CsQMAewXXyIoY/w0T0vRhiydiem2OdikYIN4iooVFqXMdc3iy6VCet2YBwOr4/5V/w4YJIqdS5YGF38sRbRFwdBQAHMjw5z2SF0gxkT034Vxp8vF1t0y0gd47xZG3AFDMcb6885sS1H5Wk0YlzFb4S00KwuSRot50szWOElYt620WR+zUDfonVVugS7S4+OM66Tx0H98zB3r4uvX16rbC9TM86fXjgzxhrM7IgkEm579medH1xrZ3UXuHS6NaR4scEaqSQR6XLobMCZ8mIdQylApZVghIAIDHx4uJniRfuJY4YwEgJThuDuX4fbgNemqXRvnCUs9yeViviYoICjIiofto+nPUvir5JnkNJ6pq356fEtrCWBg/bywkck7jKJSG5mUHNOKmWB6hdsWVYKKgoiT0xtO8lzsS1DD+RGCA2g8VBQTf4kE9ACyPzo9CvmwCSxWqVUM5XkF+Os0diqsCnFwXAEYK3Km5sIkH9csNKsxJH3eMygKhMSmq4AAwJeJdxZsZEw6FW1TIAGCuxp9lXvTelxzeAw0Ax20ezKr2SUV4DgArQhyeHhCvQxF9m0inBlv5urq4mSeVpyc0+iIqElaLIjzp3OrXwWzh2DpqH69yVF5aKKEBwFIDQmQ2DjceoXafR6vr2aLa5xNBQcynHXrlDO9N/Te1HxBqhgCAKJeDd9vc7dlV4MFTqc7bAACgXfBGdAX5t3Fd6EI5xyFBEHpPirccbQzxhDIAxEQPpuLP6AtrPq9dBX4dmSrnwHH7+bPuCWui1Jif72f1WcF5tEQnBnrXipb0Q7+YGupPj/FpXpRZKrjNyg2+T2yd0df4h70c+Z6t8n3kaEEnvrfVvk/tvT6uDNnV4AktQBfq2/x8TXz2AN/TP7b5mLyGo0P8fFvZwguiiaUa3fT/r/Pv66AQDCgakHAfyPPv496pNLU/WuIIYwBYE+Ly4u3gqJ4lTa+hdlVENxv8NxS/qOM0kC/xYv/LaSxw5JiNhUTOaRxKmtgxgMV5BVlxa4y30aSL/HBoCWsn1BLJnlIjTe1Bd0LOUXd4kiXk44eHiaxprsYPmCbR2hHyaEj290b4dbYIlQiFInl1j65o+hUSxeb3MVbS28BBUZX5iQgaTPqLB/0Jal8WFxw6oqVid0bza3hdfM2c7R+g9qmyDo5+mP0ral/e9BvUHnK0YlTE1kkQNkp1/qyzGV1NPDjMr2GwjSe9OgZ50gwA2nr438yM8muoiaopALyqh//GN0/wZ9HrWSPn6IvwdXdMyPQ1ezkqISdIGAHNXaEg9A0DSI5qTVQjHhqQf7PKzVsFFEDj4QZXTDxR1AT0W0XB5S0e3j65OiGnQNXmLUX3V7i63WMlzXPVVRRM32KMujQn32xJCALUOKL06eK/U/vFkY/Ja6iKYFSRHXvivC0DANzNHFFTGeYLc+cJ/S7mBC9Zr2h3bQ/wNbE8rhNze9P8Pu4qPUbtccEjAgDtfs4JtnvuS9Ten+Tk1gDQXuC8flmBwtqQ5Hud42gndvkanqgZ28PPppjBuqxW+dpuD/PE9ucP6iLEmjh/Fpe1Jai9I/12Ocd0la/t+ypfpfYrg2+m9kPQibe8KNZ7PTzRajs88XZ6kkkL4+U2FhI5pzhcriBcJ6n8B3x8Q1NoGUBLC7fE+OFSrfHqb6WhVbpUIsYtdDRH0vfJOeY/bpB/URMH5aNzPADrC+lK3iu6OXopIlpUqiJgPiZ63gHgiRR3rkY5YMAoKTacF1Bml1CbgYaFr0xwZzomiP+UYkd3QKMvDlV40GBpv0iOJU03UPvR7D3UvjHyBjmHQlcIGgP0RHmCJNGsq6aOCPwfOMb3ovRBXenrEaTLOzP821ByvADgEy2W1/fy+8zW9Ae2W3CNPFrjPCKd9gC1F1x8XQNabvepGb6XqTUHAHGHV0VjQtkx5tbnV9lEB52MgGjteLLOeQ4A4HwXRwV9ZZpz2V0e0aSyPWH+fcQr8yPWBPQ7jbv5GZmsG3Bb+Hi7XKnCk2Kqir0vq7nuCkLBUiFv7YYuEiSW8yAtmBA8PSLRAwAHcvw+JgVnn0przwpBAQDYU+B7Tc3FHZK8wV7lOLzAtSF5I7UbFTrE8ZMXreAXtHCU10NH9V52oVCfbO3h6y7Qp89Q7xH+feRS3N+/cZEWkfiWKHjuS/O9KC2Q0gDgFoIAb0q+jdqHS9ynsQ2oFlbFeRGuAF68Gi/uoPYzLpHj4MXnsHkZ0A4tJHJOcThO6aSZ9GKZM6sH/ZpUVqk55cp8Y1dDERkDGlkUF6geE0JldR9eDw+6TfhO/KIVYEWUO1aHDVSrhvO8KtosEjWzZX5Ifn9cI1kUB05QkOOecGsy1gq4w1AU5NTXh18l51Dj4Ul+2LcE+LM2IRCddPFvuAUcXeETxLcAsBY8SOsO91P7pEvvAVHwyo9K3o2Ldd0q1gMAeL0CCSbUMkxa4Z5O80TNXRP8Ok2Se45Qa1JqTwbqrJiu8rU5VztC7TPgUraKBB8AjiX5urs4MkDtJrxlRwrc6a/VeVBxrKilidtjHDGzOcGDivMDHPVaqPO2DQC4c46/r/HqLmo/kNW+wqo4/0bPC/L2EdWaBQCtfn3+sDFja6WlSlW1g/PNKuzliSCTBOPeLH+W57fyQHIqpRMDYaGaKOpjiIr2ZgBYn+D7yPEiT7zdPsploFe69bpMC+XHmIujVr0G6F0v+H3EbF4AU7xnAJBu8DN0i2uA2idKvFCYrumDISOQr0XxPhMCpQIAnoAghxeCHI/PJuQcqginEKkH0zq51w1eSJ8q82/4/sJ/UntHZL28hrHKELW3+HnSeU2Qt4c1nCq2V7nox8I488ZCIucUB0PkODYv1zeEHdBJkKiHw2sbYQ45rdjaeZvKcOhruc4rDT6PRpGEhSypQv0cyOg0banBA0XVrqBUCwCgOcAdp4ZAJdw9ye/zYE7AaQC0Wvx5q+TCIYM1ka7wBMcyHyf59RhwvFUEiehMjX8/FZs7NWVHV3Vq4M/7rsIXqH1JhBNPA0DS5oGHV2zLaYf3tAPABtFqo1r6VvdzZF94mX6hvkn+vqzD8y+FJHwKMcC/r7B6EACmSjyAytvcbpJAfLrKOR+WBjj5+yw4aqHe0A79+UGeyFkqtnWxnQIACgVekSxXeZLSpCLZ50tQe5OIE8PCK1JExgBwWZXzxH0zx7/hIYsnggBgsM65shRnUVddJzFbBJnW/Tl+LtRdBspYAqmsWtKnBKdYa4LvhQCwdZqv/cEwf1YmpOlts/ycTSzhz6pN8NsAQLrCz8C+IJ9jucUTNSZKZ4fzP6b2yyO8TcYrkBUAUBR7rkremcioewU+Kezm+4DaJULi3wPAwVSC2td1cM4whaYBgFyJ/41HXGe/EOwAgF1ZgRov8GLItKPbmtrAE/QBS6gRRjiv4JyjhWIqNX6+OYJX6aksbwk0UXp+OQ3HMRNRmO8cL/WxkMg5xcEQOaEArwTGA5pgzeviDkO+wTfumexT1K6qW4AmU53L8WpieX4cwwC0TG1rUh/2ZyV54H5dJ79QE7JjNRqivatNtJzfm1VyhEBKwG+X1DmKZDE0eW48wKvQCR/fStYKdQUAqAryir4gr5qWVEuFAYprLLuV2sPiG59ucL4HAMi7eXXpROpuan918oNyDr+QnO8K8IdxaIQnm9Y16Uq7t5OviTevHaL2J45pvqGIQP2MFHn2Yayonekd9m5q91r8I56p6TWxOHARtftFlVrxSpwo8zUFAD4B00p4+bPyKOZbAGGBFFOJGsulWzT31rnDXZjm60pxBa1I6JbbHr5V4YraFmp/sPK0nOMHRa5oeKXNCZNVFRwAjuf4PrHU4u0hJxqaU+WEkB5WIyT8qrQ4HwHg6k6ewBiI8+KVCd/JyAxv2QsluW/XqXUP0FnhCfjM02q/48/hPYe1bPeVIlGzNCZQJoLrDgCGRB/1fteT1J6rau6mlT7+wKcqXN21avO96oouTdxeFxxu/gB/Dr6gdnriLbzgMjvBN7OnRNsUAFfBjWUAAQAASURBVOREe7FKGJ9bP1/O4RXnj+JGa2vw9xkQsRkApN1D1J6rc7/Jloq/L4Osw8I47WMhkXMah8fND6iZPOe/AYCwnyNulBSn2817uZNhXZ2KunlQ4EQEga9bw4wDFr/OiMiud+o9FR0BfkD53fyQO1HQTqhq/6gINaesKHDNOhzqDOjgZsLiTkvZoE1mk5sr96wUxH8GqqU4IS4jKhRUQh7uDIwJtQwA6I7z4Ef15k8VeNAPANM1XkFem/xtap+1NefDdIk/8PMFd0VVrNt9uzXB4foBXmmPr+fXuKGmk0WzGe5kbmlR7XY6MVAd45DqR2o86G7zLJNzLBfcLydDgT47vp39LrX3Jq+Q16CUzJRcvMcAlRB2eDBrCbL/oDgfAeB49XFqb/Zw/pqcUKbzZbnDDwDehJA4F3LW3aVBOceOGm8z2w3+/UyWtaRv0K04Vfg7jzkiowUzpDIbHoHeXW7rloiAQB24xdoPCJJgQKMr2qe4vxHo03NYcYFA7OKI06YTfI5UTSMjljdvpPZxIUlfEq2qAPBI5evU3hzkLSwmoxm8CKDI35dEhJy8R99npcy/P8VDt+OQJo5ev5gT4fuEKMiSiIZi7s3y/XBPiq+7rK2rw48V+Jp4dYxz5LT7+NkzLtS9AN1JoDoq3PFN1G47dcxkecfEy2ksqFaZjYVEzimOZGQ1XCdRtvFYPLvQ6dfIB5/DN5OxOkfDNBo8eKo2dBB4osArfWoOhUwCgHiIBy5lh0f1JgS9jnAyM1VeWR02UHNSfzMpEuwjorL06giv1ANATBSIZ8uqP1k/zJxIOO3P8DkyVX3YV2zu2MS93BmI+Xhw1OrRQcWOEm8VqInvZ3mEB4kAEHT4PvF46p+o/TVNGpHTKYi62/zccVKtVbG1Br1yAsrsbhM8PNfoEzZ5LE3tXSO8kj45oWW5LSFbWhzmiDeFVgOAfvENTolYd3WNr7uyaBkE9J6qktYmnEYewSAa8nO0TEgICgDAOS7e5plz+MMcF3xDtiCFBoBvHPk3ar+p6yPUfkkLRy4BwKLCb1L7njL/hsdcGhEw4PBAsFnwkgU9Wt1urfVaas+5OLdMtsED0YfKXNIeAN5a/V1qf2KSIxQ3tmoOj+VNvO3isVH+rH3jet0tivEkpMcSCUahUPSZxTfIa/j2CHcWYl6+Zp5s7JFzdIc4j1WzzQPmJgO+ypTwQQF+jk+W+RkcyGgKgt44f5/HpxLU3p/QAituwV+T6Ob75TkVvY+E3fwM9biEgIrgAgKApPut1D5W5c8y4OJzmBRVB/wcORSzefJ8THA32U4NGqO/MM60sZDIOcWRKQ6ftDqaCPG++AMZnjEGNEeOz82DH49A7JSr3JkAAEdI4CnUj8pKA8DhuW9RezLKg6NHJnVSrOFwZJAiTDbIFcEvqtjLYvyQvKpDQGMtXYVTDsOwCCSVqhUA/DjHg5uh0iPU7jLoe18k2kt21njLxLIqrwRmXNqpafXz3vmxIm9d3JXihHkmoyvBA9FH6j+Rv/E2gTqYFkiU4fEEtS+JG6ggZfkHVinxb+PHR7vlHCtFBbooyMb3CZJTAFgc4Y7sb/YrpRi9k+zj+SbkhcxYRhGM2lo9qC7iRNU5ZRu0lzya/hy1q/PPRPmx6OHnV4+PB1D+Km8jTYMHBADQk+RtGbNlvu83+TVSLCb4nXLirA8YoGWKNr9OlWAccrTs/dEKPzsU70RHhO/7yfAF8hpUEjIuWjj3zenEW69IkoQFQnhMnPMAECzwdzolCOYVckK1PwPAHocTqxcr/H2WGtpHXWKdR+0uQVBfc2mEx3CDn/XvjXEBh3UicTdR0LDyiiBEbgkbOG9qjgJ3YnPjHCn2+KROrivlx7LgRzyS1wXobTXOM9fr4/t6SfiHPlsnpTPg+92siyeDxlIPiBnOsNYqGy++atUCIufMG7adP2kiJ5XnlQSfUFcAgHRRVQP5AeQ43OFQSZhn5lB9mtyeK2pn2+vhgYVbZOj7Inrpdov+4SYBGa2K/mQAUO3cbQJynapyx+mhKe1sH8rwwGWyxqPEY5Zu+as7fN0p/qdLvZysFQBWJblD4bMGqH1EnPU7RWIBAI41+EHrtrgzHQ4OyDkKpSFqL9Z4hashvnEAmBKtVd0hvrYXDfIqeGCpbjv0V0QiZxv/94MCmg4AD0wnqL0qXvmwgR98MMcdOIV4SxgI//y4yOXFl9m8PavN4UmvGbcOqD2C70QFu0olEACWN3F51oOpO6g9EV4p55ix+PdjVXlrVAV8P22GbklKu3gR4TtZntDaYL9BznFhnCM4Lg5wdcndQkEMAFYnDHqYyTiU1QFzs58XwBp+vt8VGzypvM7NEz2ATlLWhC+QNVAgqgrOvY4Q34yKot3VZKj2yIpI1Gyf0wF11MWTWoey36H2WJCvBwDwinbyuiDE25vSKK01yd+i9jGBxh4QxNPNQd1SWKjx+/R5+LehEkEAMDfJ31dAzGGQ20PMy99He4D7Kytjeh9qKnFk312lO6ldxW/nJX5PXkPE5td5zOJJzliYFxIdp4FcUfNULYwzaywkck5xhAN9J22tUrDv6Qzv3QcAy803ApWoMQkk1SiUdCJmvsMWiYFpoUQRan2FnEMRDdeEfa6qP49vDvP38eYBHvBOV7hz9/CMfhcnLE6m2gfOi+SGrv6OZHmloEVU0kcErBUA1roS1C5ACdiZ5QmrKnQCJF3gz1JxdFRqaTnHkqbXUPtcjcNr63UdHJlUTukcAkXiMpAhcwo8IH7oOE8+tIr2LwAYCPG/OVrgzvTObFrOkbJ4wNtm88RApqozOascHnQfE5Lzs+AJyITDkzQAEBC9VSatU2rURFuTGmWRlAaAPg+/174o35Pr4tsxQWpuL/DEmULvWkIxx2QEPfxKOwyKOoo/Xu0zJmfLRJG3i7eGePJOtWWMOxo9mKvzlj4VaLoNCHrVUDw8ai8DgCURvh+qdnO/yGgNCPUuAJgq8Xe+T7RPLvNyRCoAdHp4ovRpmxdETTjD+sSe+c1RvhctjfB9phV6L/QKJEtDJBhVAhIAcqKY6Hbxazi3TX9fM0VeDCkLtIsJAfZcjftFiz0cmReLX03tTW5dvJqu80RnwebPKu7jLX+2Uz+jEjkLHDlmYyGRc4qjYdfgcv387PJMbgf9t80xXRlSTslEhqvq+IX0t0K6AFo5pFbnvcO1uq70NQTXiCLwVZUjQCdy/OKQTAjEDgBc1cWvs9jg13kwy68x79IVMCWlqeRb+0W1HwAqQvo04eJOz2K/rmKrV5oS+Ys5i0OZTdRLWqKc1Dli8WRtIKCJvveneWVodZyjFqpejVTJ1rhD3xBcXFVBsihL2ABcQf4bm7o4h8ddx7VqlaowK6WlK9p0S8Tj09yBK4sEYVm0pwBAwsuDtEUN/n3lwR3E8RoPlgEgX+MEoer7NEn0JB2eCB0RSM1ShcusA0AizvfkHhmL8rUt8iMAgDe6eVCwLcdRQzvLvE0AAGouHoxeEOFBwWBUJ1myNf5Ox4p8Uw4KHhEAKFf4vlz08URpqsCr3Guim+U1TJb5S12kgbFy7Exz3+zKPp78u3mTVr+rlnhhaM8wf5btgvF8f1qjWlVb4HuaOOls0qf3kVSVv68Dc/yFHUhpmoNIkgtunO3j++XTGZ5EOctgv7TE3wRFy19LXPuPQS8vuGyf5s/hwn6tAJYp87hjUZhfwxcmeHELABIO73goWryY2IaEnEONiov7XVNpTlQcDfE1pcQ2FsaZORYSOac4KtWpk7ZW2YJbJlvSTmhNtFWo9iwFD1RJGgDoiHPHJ+/iahj1RlrO4RKkl/JZGigQzdX4Qdoe4M5AQCR6AKAvyK9zRqB6hJ+MXktLO56w+Zo5WBNoGr9WeOh0+N8EREUlZBD9DBf4wzgk+qSbhLTxjEs7A9NZ3u8zdRrS9yuTnKS0IVo7Mg2tnpAGd9gnSrrfm43qUe0g+gZ4EJdo5Qmpiyqa1k85iLMVQaJo8BxWJngi55EUT6Lsh1YyCzX42l3n4qiEss2rw1u8r5TX0CYKjip3pxLnADDn4k5/XST4W2JnyTl2CETbAdGu2ieStV1hnQDpFMvqfDGH23m1nGN76dvUHrNvoPawQVGn2c8TjB1B/hvVos6ABPw8SemINpmEUOLMu3T/ZKuf71XdEb4ul4hgGAC2TvA9+ckJvibiszohvKGfJ4POWsG/v7ZhXnBxuTQ9wEiR7wPbZ/m+H3AL4kEAUa/wHwXxhck+si/1P9QeT7yT2leBv0+/UEoDgLJopzuW5cnBekaj7hR3U7/g4fGItikA6G7myHIlPLLCpdvtJsDnOFrkfrAVuoza0wZ+V9Xha7s1xnl6VCfCmcaR4zjP/O/FnuOlPhYSOac4HNTgnMRhVfwzfq9GJXgEfK9Y5qo6qrXKZQDZrtocfWGL9q6ggSJAQDwLlXBK+nXQEHLzL3R3lj9rBSsHAAE6QEgc1orEdL+jkw9xoapTKPMEYtI/IOdY5ed8DF4R5RnEPjgmOGxOuPmzaG0InpC85gIK+HhQoRABJoptCj0xmRfKdAZyvZ0x3qqjEqH5ggjQDhlwVK3kLz18Dt+Lmgo6WZRocMdpZIijei5v0y1/PxjnzvK0mzt4621OzAkACTd3ZD3i+/LbHAk2K/Z0ADiW59ewWChrmaQ4R/PcUfV7eeJ6JssJSAGgHExTe1tgFbXvynEOj3MbPBELAJZIKsd9/Fm2i9YRAChlOPn7Xh8nEZ7OqKABuC7xR9TeHeJnaM2gnbUjxIULyjYP0BRK2U5osuPhouDAEXwn0aBud10uFKW+MpSg9pBHt1Z1hvle1d6i9zs2HpzUX/lawXXXHeJny4wgAgeAQo1fh1IYMiloLm3inCuLBHow6jkN7XYCkbM7yzPG5yT1vp+v8XXV35Sm9oLwFQDg2FyC2kdK/Dc2NOvk3l1TgvcvxFv23CIcnsjvkNfQGllN7bPFY/I3FsbCONWxkMg5jcMRJMFFASEGgPYol1XsCvH2rNkqh99mCgflNeQFGuZ0jHKVH0CLE9dSe7MBgWjUI5ReavxwmDCgc2gR1zEqHMQjFR7U97g4iTAAVMX7uip2C7Vf2KpRCUFxjubrQnXAgGj4zgyX3X5dklfABMgLwJvkNUxaPFF6VCRyVKLV5G/8Pp40a4tqxbadWV5NvDLxXmpPl3iAtmqZlhwt7+D24CVC2vj39drHNEeiXPcId+gn9uuA+QqbL6yqzdvxhvM6MFktgp/9ab6XqUpgEHrD7ArNjyPHhJYp4OMJDreLuyTdYX4+AkB7g6+bDHgLZjTAk7nDgrASAI7meBX7laL62xfRme8r6n9I7bOi1dQV18HRrFDo8opWnqxoZwCAodSP5N+w4RZKnl5HP8u4kGDel+X7RDygEzlNIf6Nbmnl9/G9Ue2uPzLFkwvDQxwlcl0n309fpYUE8dfH+RnZKVpgVic1F4kimLeL3CcKuhNyjpDDC7Mdwilyif1SoW2emYOvmVUCBTlS1M9SiX7sFEix1oB2lANuPkebnz+LfVm9V6WUcqOToPYD9QepfW2UJ/ZMRizKC0sVh++XtlPDifRd876OhfHyGguJnNM4VDtQwKNl+sbSSn5ufkOpRQFATBC6eoXjVKhy7gtAS5Q3xLMUBRkAQEa0Vh3OClSCwSQDYX7ACIVYXNTEK9Ct+hyWz0K5Cyc08AFTJX4Q77V5pcGEo+OcME+0OAID+WiDV5jLAnoLAFMp3sOsUHeNxvyJwitVDo+vBzTizefhAXNQENt2JIRDYZDrPX6IX4O9n/eTLztPk/q5E/wImznMk5RPTOpWgYBA1V3exoO4ScHZAgBPClqxsoAHtrsWU3vFIDkfEt6A6o5UfEUA0CckYPek/4va04IPBQDaYzzh63f4ppot8URrMJKQ1zBb4GSr3xQtZJvcV8k5uoN8bd8zdTu1b4y9Rc4xAo5iLIInzY6WeHAEaBSjQk8olKTHAIUcEYkcQXWHIwYtLCuSaWrvFy0uqYpuU6vZ/CNeHuXn+HEhiT0nil8AUHTxs2NYoLTieZ3ALzZ4YWgy8yi1u4T6JACUI/wsr9l83cZFITFX1+FXTPxNRHDk7M0ZJMWq/J2ujPFEjVozgBYuCLr5+1QFUwAYrjxJ7Zu811P7erHnzgokNQCM1bmfq+IeNVQ3xMtu2K5n/vdiz/ESHwuJnF/iMGlrssSH7nFz6KxHqF65XPoa0gXuvKlg1m7oKpwi4I0IgkOTRI76E+Wc9Ue106LIVFW1oxLmm8jxog4CvzLFW442Bwep/fESh+gDQFCQ4zpC2aBQ4bxKANAW5Ws76efvY2OJ970ftTQizolxh6JU4xG3z9Mv5yhVeaVctU6ZHOZLRMU/LGDfeVHJi9V0FS4h5MN3jfPEdtM+zW0Ra+XXUSzz/XBPVjv0T83wRM2Wdv4bJnvV8Tyf40nnYWqPWbzSlzQgcpwTSmV1EUeerOX4BXM4fK9RaDSTloiixQPiuM3bejdGuPS339FrJhpREud8bTcMGver4gC7NvYuat/r4pL3ALDe4W2BdXGdujFYIxR9Xv4s1VCqjgBQtznSKyCSlPtzOkBbHOe+lyKuvarLQEpakAA/McuvoS/C7dMCCQMAbQ2+F/mFktlkVZP5VwSPXGfiImrPVTVBr8/iKKw9Wd62tDzON8yIwTeuON5igptpeUQjxUIe7vO4hK9uoHuAQ3nuP8aFH60USwEg4eeJtbrNf+TJ2veovdev0aA11ZVR1bx/bJicfwvjzBsLiZxTHE3RDbBOIj/e7OGEXMNFLT/uiMppS5j394csXgUfK26X16CGSha1RjWRXKHOWzMyZe7wZ7QyMayTkFI/OzY28QNKEREDwA/G+B9d3sGdllKDX+NnJ/T72mCtofb7ypwAe7auHd1+D6+kt9k8ANtvoGSW9CkZTP6sqjZ3SGKO5qjKu3nQoJIoPoFWA4AlQc7ZMOPinCsjeb2P7KrtoPZC88ep3S2Ivi0DziO3QLI8lebJoohXK0q1l3jQPpLjzviXZp+Wc6wVRMP/MsXJjHsbA3KOR8pfpfbB0IXUnmrw/bJbICcAoDXA9zKFyDFxMafyPHnQEdlA7c0unSjdk+cO+dta30HtST9PKBcM0Gj/Msnf57IIr/7+OPd5OcfVUXEfPp5wWlnVLZqKAycnspSLXZfIOXZXOAorEuAIYdvHUa0B6PbJJ2f5fZzdzBMcPgO1+MkCPxsGErytaY2BAtHRPPfNSg1eDHl4ms/RMAgkp9w8SXK2h6tkmpCP7hX+xKygEIgH9T7SB+5rd/h5cqIuKv0ibw4AmKrwEK3ZzxM1Jm1PSuI8XeXJpLhIQAJASCBu7hjmcyhEKgC8Msz9qpECf1YrfZdTe8VALj4rEKMu0Trcm+AFONupYaSq2/dfLmNBftxsLCRyTnE4jg3nJPKkSm0mERiQv9+weYZiIstbP5oE2Va9oavc8x2KrwEAPBY/BFtC/LAv1PVpvyfDN97NrdzpMVHGuryDe3CKV+Jonp/mW3zr5TUcEjw7IRdHUAU8G+QcfocftLao2pwbv1nOoSo7qQp3Bo5aQ9S+2ObIJACYFLL3qn0yVdJkdpEwTxbVHe5wVGsGrYsioaSetV8gyUwSOZYgG1dth6mqniQsCEDLInB5lZCbB4DtaR5gLbe4opvXraO8jYEbqN0jeHpqbr5mLJEwBoAp4acKETKj0RLmSbHxHCcz9sQ08uG66O9Se0dQqRkqbjX9LF+b+D/Uvq3OE1orY7wNAACyArnX7eFJmJaA5kZLVfiz+Hb2P6j9vMDr5BydcR6AjWceonaF2BlxdDGk2+btqukaTwapcx4AjhX4++iKcITHohaO5AQAn0ieD5e4L7AuwT/y3Wnt2w3YA9Se8Gmks5yjwQtHjfAV1K6IbQFgRijsDTqcpiAozj8TlEnN4XtVQbRePZHS3/irunlSzC3Q1rp5H3AJRFufINLfNq2z54cq/JxuAk/QKy4tEyRmJMiL+fkSxyj6XPz7s0WMuTDOzLGQyDnFYdsVOCdB5OQbPMAyaWtSylZe1TolNtX2iE4MhFy8El5zuAN5NPVdOUdSJJxyDc4TEvZwFAoAXNjGD7HjeX5A1Q0OWksR2omqzHCeb8wmEPuSiztXHod/5sOOlkdut3hiLSGI5IIiEWQyxqrc0fWJ5OBBSxN9jxZ4n7UiWz2cv1POUQjyxJtKFvUkLpVzDDq82h4TnBBHZxPU3jKoE8KRNn4f/SGeLFoc13xDRZHsUdVGxRUEAGcn+J78PxnOA9IKnUDsFLK+SgY6UuHJpGkXd3IBoMUvSGOFM24SzCpFxOWxV1C7Y4D7UVvmoSxfd1+a43vAGxJahWyNIK92p3kC8StT/4+cQ52h5eL51J5y6XbXueoRat8S4ApeXgOfR/ECrk/+DrUXXGlqDwrSWgB4TRf3q9YLzrCqSLQCwEMzfI6mVILbCxqGbIv2xsva+Pf38AxPWC2P6cTA7gyf4wfijFV+NADEPZx1OS0QiuVaWs6hgu7N7dwH/dAQ9wX+etGr5TWoAtm0UFPb1KTP6a3T3N/fmOTn8HED1aqjBX5OLw7zPdnr0kmUvxrnHInnxq+j9rCXJ1pP5LVgx2EXbytcGuAIxf2Fu6n9TGutchyXUcv2fOd4qY+FRM4pDpfLOmlCJmlx+PqBjA7yeuJcIi8OXomog1dmS9AOfURwCFRcfOM2kR8v1Xh1KeBJULvfIACzhUc/UeKO0aqEwQGV545qR5Bfg09U6w/XtLMdcXiloeHih+QqbJZzhES1IiraosIe7dCHRe/GUYu3iA3YHAqdNuDIsSy+JdZFEnMgeY2cIwrB+SCW9p7M1+UcFVHdLdS5U9MW5g5gJaXfZ6iHr/3LlnBn+/iEbq1aOsh7zsdH+V7GgczPjHuneACm2kR73XxdAoDfzQPBsIAv7RPVyIijW/4UImeJqJoadJdgncUr5fel/obaY+Hlco6wKIa01RLUPlni+8y0/1x5DR6RwFD7oUmydrbEW2KPuXgLZtpAwTISHKD2gmg3MEm8rUzyZFBN+DSqeNVqa0JzxRkWEK0hYYP2kmVCiWxHWvkb2h8RoFVc0MLf18oo94ncBgH1vix/H8dS36f2aIgnpU1GSrS4NATZOAC0xTdRu9qT393BVY58lkZXxL38hapChbIDwBLBZbc7w/3LogHaU6GPqjZ/lgIYCAB4Q4z7NAoBXBSfcMjAh11d4Wvmsep3qL01xBGrZ1pr1cIwGwuJnFMczxAB//yNqxLgVZs2A+6Y2TJXuxgu30vtLtEa4jPgnRiqcDlQddB2hHS7gkLcqGFCsKY27ks6hHKWweHhFlXqqbKQ5a7xIDDk6H6GGYsne47k76H2JgPH6UL3pdTeFuCBaNKvX1hWkBJd6OGH5MP1bdQehVaNiwb433iFM112aQcx7fCEkgpMlsd120XU4d/5wQxf3HlR6WsIRTgAgMOd0KaL+LNsDmpHt36Cr6tF/bya2DFkojLG5agLdd4+YoLsWyZAAxMiyZITUtMdYj0AQJcotkv5cTkDMOLmrYeqJTDs1UH5rOCY8tt83SkVpH+b+HN5DT5xna9NcH6b10Y5WSsAHHfx/XAXuILKYEwji9T5o4hrp11a6WWqzhNKIQ/nwHEEN1rKSshrGC1xJMqRPP+Ny9o08qE9wJMkT8xxd9wgjkRAFLj+4SD/Sl/by1EJJu1AOfAzcEnTa6jdLdYUAFii5agnxhGpSlkLAIoO31PDInrqEC2aJu+zJtACZdFapRA7AHAoz38jJ/yyVgOwdUy8UpUMOhmdxU+PQp3vA8U6/422ILdPl/Tin7b4frfaxwsZKRcvTCn6jpfbWODIMRsLiZzTOOoN7m1PZLbOew6FdlGIgkJpSM6hWsAKZe7o+j08gw8AM1nOhaDUu9wtfEMEzCrEbJhwIShgkOLZeTL9L9T+yuT75TVMiR7m5RFeqVhqcZgyAPRE+LpSz2G8qHfL/QWOKhixOMw/Au7wmwzlRGYgEpAGRI3lBr9Pr8WDp5Do9QZ0K1trgH8dc0Ito1dIlgLAXffwBMgl63hlKbRGw/g9Axx9UT/Kn3V6Vs/RF+Xopk3N3Fmeq+qdyBaOak74b00NjvLyGUQNR0RsMyAU9kz2W/V92UL1I2JpBaMBm/MUpFw8eWfNkycLAOpCuXG2yn2FtoBGUAU9/BucyHIenqYgbwMAgAczf0/t1yT+iNoTAt0LAPDwdm+v4KYYxV5qP1zhHDsAkKq8idpXxYXcdVkHzM0+vm5WxfkZ+diM9kdqNj+ALhLt5hOi8DRS0Of4CfE+ihVevDKRaFY+asDimfGwaGUFgFKDJ3LGi3xNrI7zZ3kwp8OvniB/3pMVhfzTDkl3kN/HjjKfIycSJABw7yRPdF7Qytelx6Bt1yuqu+LTkP8+oirDACJV7pudsLgisEpKn3Hy4wvDaCwkck5xuFx+uE6inhPw8apnhwE/jSK7Ktg8Y6vUnlTFE9AS55UqD2ZVkgbQzrLfK5ARAgkDAJ3igHpyTrQzGHwdMxV+HQ1xevzlyo9Se4tPO041h7cbzIrD/lheP8sfZ3m/eB58Xc4IpBmge9IVBD8pIPQpS0s/Hq/ydoRqnQdoSSH1DuhETVk4kDuKX5NztEV5RTKc4QSjb+jj1eNKVX8cfgHrfmQXb0VdMpKWc/Ru5H9Tz/K1/QePaIf+twbnR2huAj1/apbvVYpUVqEgGw2tWrVJkHB7DZxpNUZKnMfgrDgnKvY1dJB3zM1bjgYai6l9VYLvM4eLHBULAL1hjpZ5vMKVtfI53fS3JsTXruKv+XH6r+Ucl8f/kNpnwPeqI/VH5BwhcdZP5zmHW72RpvYVid+Q16DynGmBQEwZFMqjQuY5JiSY24MaqTJd5r/x4BRPlO5zcRW/blujd1stfgbaPq4YZYI6KIEnY9O149Q+kr9PztGZ2ELti6L8DEx4eUug+yRcmz89xkv8b5SP2zDg//ALX3pAiL6VG/pcGIzwRE1JtASmhJ8NAN/K85a9cy2uStUsyN/DXv0s+3w8gTjZ4A9Trf0zjezYcX4JiJz5uzW/8rGQyDnFEfJ3wnWSDbje4IfkdJFnYwEN61bydY7I2CqkCwBUq7xVx+/jPD0mIxbgyKJW95J5z6Hy58ti/AveMae/8PWiY6HZx0+ogFCZKNT1YX9YQGOHcvwaDlZ1gmMWQ9Tud/EDqiOopW7T3gS1h+bJBTRZ3y+voVDmShWNBncg3UFOCg1oTpVMkQeits0dRACYyfO9ZjzKr7MhyKtNhk8kcg7keEKrL6bXfkVQSNXK/Dfetkg7Z3eN898YFrKm65r0MesIb+L66G9T++MNnjxvgSZ8HRFdgavET5iQHZ/l422Boy7eemW7tCPbYaBOx0bI4XuZStIAQLrOCyolgUrI+tJyDtvhiRwlj3xe4vfkHAHhIrqRoPYpH0flAcBImifGFMGnKk6pNlMASAhAjWrlHjUQA+3w833EL1SO9qY12fG9Fc7BsdnDycTVOZ6zNMdiQST3VOtw1ABZWxM8japQaAlhBACYK3IEsNPMUeGK90Ul9gAgJ1AgglYQSQPuphlRlFEnZNBAhCwk/kYAvlE1KIZcF1RkxvxZTonWKYXYAQCfgKb3VTlaVJFb150KeIpyYZyJYyGRc4rDY/lPmsixLO5Q5Eq8dx/QrVNeD59DOT0Rn4amqzGefnjev1ES6lslNw+YTRyn7bP8WWxq5adLXWExARQErLTY4J+Yuo9tGc0x0OnhEdYuhxP/TdY4FBoA8iXeBtMtJGSXiCo4APiEMpZS7nm8xu+zzaWTLKEYdyJHhcJKRajyAECbjxPapfKcbHVR8lVyjrjgA1IcAbZI5AT8OqBuCvAERyHN97L7xjVa5gKR6FSKBHuzuspdERXHgCAq/szIP+s5BMrxza0fpvY14GjPhCAjB4AlIlGj4O0mvGUlF28pyjY4f1TUrYsILsGfsTjCz56gOGNnSnpdfrfCk8aRAG9rGqtyZAQAjDvcV+gXVfBzDHyBEyJJ+WT9Lmpv9/C9DgBaBHegIkw2QQCroc5xhZZpC+jFP1Tk+8TmZl4I/MhancB/T+1qat+X5QmQx2a4EtpdJd2mppIol/g4N5OJ3/WoKoYICgHVwgkAvRH+LCdF4N8heAO7RdsUAORFe79ShasJ1VSTv+kJ8mRQxWCOlEgWKUTO4axe+zvA94ElZa4y1urj++WDFb0nd4sigiXSYsct7sOatPW+nMaCapXZWEjknOKwYcN1ko8xm+fOm8ej+8U9btEravFgViVyVMUFAIp2mtrDSsnCiIeHH3JK2SAQ4zLQAHBWM3coFHHfYFR/4GPCH5gUJ5RCDaUN2oGKNi+lH0p9k9pVyxIAzIh2OzVSBvLHmyK8eqt4eLrLvH3koGu7vIbJPOeVkGu/qqVT1dpXyldJp13OcaTGWxpa/Svkb7DhEYENAERFIqfdz7+NXRld6jtLJErLItFzLKeDhmyNO7JtouVhS/3Nco6KIHb2C3U71b51km7gF4xHp/j7GAzNl3VMJxCLAh3o8ulryLgFP4Ygz00K0KplwAa0tnIltW8t/Ce1D8S4TC0A3JX5PLW/xv371N7s1+6fCjy6PRuo3US1SrWaKp/FK1pg3I7eR44L1GpNoCtMxpjglxkIcd/OI7jwACDu46idwbDgcSxz/7O3qBX4ut3cz1XIiLwBo7JbIW6EulZHXCt1nsjxgmXBzZNeNbHuIgaInGVCRWzrLL/PdYJ3CQD2ZPj7WBXn92ESBqvcXEhw+dSEcAIA+MQ+cl/us9T+ivgfUPsGiyeCAOAQdLGejU6bFzzrTgULmlUL43+PhUTOKY5yNX1SorV4mFf8CwJODehEzVyOK1GotievWydyPAK2qsjoTHh4iqInQh20zQZM+YNhvvnn6/wAO5LXR9SE0CwsNlQih8+x0uJQTADI1vlhvyX+LmqfcWkFsbiHEyLb4qDts7RilFBnlX3S+4TcbkW0RQFAe0RwjYge5XRJA187LZ5EsUXwMw7NN6TGGnBeJcsl+vsNEjnNXRydtDTPHa9DQikGAI7k+F6zIs4TB1d0GChRVPjC/OYoT1J2+PSeW6rzfb9TJFEaDj/KTarcZ7dwh90r5HJtsZ8CwFSDKxQpovy6QSW93+JIlbQgoN+T4cFuq08fPucmEtQet7hq1XGHt3gCQFeMy6A/YT9J7TNzvPoLAOsCvBWn38WRRTOO3nMPFngBzOsRvIGicJRIajL/tU08ubc+zteECRfJdi9fN38/xIsA60L6DF2b5Pthu5/7K70hvh9uTui2J8XT81Se32dGKP8AQNHm7VvVGp8jaJ0j51DEst8tcK663ggn0F6ju13R4ue+3XRJJLQSeo6lUb4f/miUP4eusEZ7Dkb4HAqRs9ukCCdio3NiN1K7z+LnV1n48gDQ7PDv48E8R+e+JnErtdcM2upfVsN2wTFAfM13jpf6WEjknMZRbXBkhDpcAMB2+Mbt83I4tILoTwk7oOXFc8X5B5KqR9kk6FZDVamVQsP2lO7f6gpwuc6QUBapmGicizErpIdr4GvKKxSOnvkN7sgWbe58BQwq6YozL1vjz0qh0TyiYgPoJIpSzUmEdNDgEUG3QtOkC5prSw1f6LXUPidkS0fGEnKOxSvnqH3FMuFsG/T3R4PcsYnG+LrtSGgZ2l3jPIAatjhJd7eLJwcBYG0T/wajomI5LL6dhgGj32HxKJYLhKJJa1WHm7faHCj+gNo9oiUXALJu/s6jNR54qHaF4xV9NsX9CWofjAiOj7zmlnmkwVswVUGmWNa13VqAJ+/Us/LbWs0pGuD3OpvbQe1ugcDKONrnKTV4cl19Pc0CfQgAy6P8WZ1T5GeLUqQCgLvH+HX0hfmaUO2VJmO0zP2mmsX9kZka54gD9JpQ7cd+6H3EEnyUF/luoHb1tsYNlM6WRPizvL5H8AKWdYj330JU4PXdnGNqrqI3/rw4yuvCDV7r8PZLAAhF+XXuyH2D/0D49dQcc3SB2i/WzOXRd1K7ShaZIJMWxpk3FhI5pzi8ntBJETlJ/wD9t7atAxMlH16tzT/BoYbqwzxZa9mzw23QQhYL8jYYhTyq2XzTBYBh0ZN+PM83xU3NeuNWwctMWRAYlnkCRCUWAKAuSH5t8PtstTVXQhT8nfrAkUNug94OJdU+WeVOzWyBV5hNYP4RP68w50SlvNmvEVTTNndUVduT2iMAwAW+9gOiT21vljuZdUE8DQD9ZZ7ICXTzwGZZK09QAkBNEJIHlvLAJZLSAVhrmicGXh3bKH9DjY4AX5sqKT1d5ffREdDJ2g1J/iyVapVBnKlVORx+HyFfn5xj3Bqi9tEGv4YlNm+Z8AsJdQA4nOPIoYEwLwB4DLJicxmeyHHEOW7SXnKoxjlR2rycvHrWBF1R5u10sTBHD0a8vNU0ZGmy44mSQGll+fva0qKJiFsEr1jAzddV2SCGUwlCNWZFUH4wy/dCADhk8fZkRXbc5tFcdjkv59IKCX/FZHRE+L4+GOFrokW8iojHoIVMKEq5RLooJAi0AeCdgzx7l6vz3zDZq5Sy1Qnhiz/a+KGcI+Li3QhtYd4aNe7iftmOgubIWR7hhMt18PNtoqb29DMrkeM4L76q1IJq1Rk4iuUTJ01kqERNRahBATqJEgpwRzYeGqB2hRoCgLCXkzm2BrhjNVXSiIEmLw94fXHejmBS/e0L8U2vSaBEThTm/4WrKppK1IxCExF3gDs+CTtB7VGLOyQAsCrBvRKFpjmW0yRte2r8+yhbfO0uiXJeiuEylz4GgCYf71FWDuJQeaucYyDAA6gKeMLKJCHsEUFBs5+v/XOb+DW0BrVD//mHObJvWYQHP5v6dXtJy6X8Pl2Cv6Y6pBM5fe08oXSTm+8z4wVd/T1W4N/gzhT/wLY7D1L7xTUuvQoA+7PcHegKzJ8nJOzw76c9yrnPFDcGAEyWuVx1f+B8an+izlFBXoPW4TmhGgeBfrowcpOc49rYu6l9J7ZRe10kzQDALSrMaYfvE2VLk78rpU7LGqB2tSaq4hoBQAFGlUTzcYNvfEmUP4uL2/izvntCIzgUarUkoA+TonPRpCDT1+Cou7zFF38OOvnXE+GEySphnLK5qhwABEUCsNnPn8WiMD/fTNrxUgIZ2+Tj9zlW1vvlmhh/6YfzHD0f82o/uc3P/2aiyD9AFS8AmtOoJ8L3fVXo6xZrDgBy4CjjExkuluH38tYshTpfGGfmWEjknOJwu2MnReREA7ytojusCXoLNq9OKeK/odSPqF1VtwBgMsO5RmIhLg1uAtkuB/jGrHhEFBQTAHKCs+Go8DGFWigA4AszXO7zjXFesRxw86TZUymtyHFxMyfGzNa4Q7E8rqt4PpE5mxH8NYdsTQI30eDBT0CQKC4SlfRpIW8O6IrJ8Qr/NhYHLpJzJG3uIG6rfkv+hhoJgVxQn49KlJqgLzoDPMHxIxGYNPub5BzhXbxtwtvEbyQ7roOjoWn+vrxCZr3c0BvJ0yl+nfkaf5aqjSbo0UmY1YIYMyASVjlBLA0AE/Pkdwq5NLrCLQoNamQF50rS4AxdEueV2bEyr+7mXbrgYotS4miWo2kswXUHAOdFfofap918X882dFuT4tSr1XkiZqbIkZhBn14zQmAIGaEeBIGABICBiAhWBVFx0oCbqSKQe7YgTVdtUUOW/n7rFj9DVzpcYW+pW7cVput8jnvz/0LtboPild/L/Y0Ted7us1aAghSaBgAmRfvV0ijfJ9bEdBLTI5KUPUG+LtM1HUZOVwycaTISBqjxePg11H6kylvWFfenaucDAJ8ogjdFeJKz272W2htOFburnCj/5TQWVKvMxkIi5xSH35s4OdmxOICGC4/J3z83wFuGdtfvofbWGCdxM2kvgZQ05Bn8tvgmOUXV4b/xdPa/qf2i6B/JOYaFSkRSoBKO5zTy4QPdPFHT5JtfkLem6f3yGioCbVkX6gmPzOkWlm1F/j5WRl5J7UFHVyxXuDhSJSS4fIYtXtnNFTgcGwASEd7yl/DzBEnQ4dUrAMhYnBxXtWgqeVcAGM3xavyMl+8TI0X+rGMi6ACAgJuvfaWa841h3b71dJonti/p4NXdqkHy4Yk5fh2PTQu0THVIzrHO20/tuTrfi9pdHEmWMOCoOiRQIu0is20SmKwEL2Y87fDkg2oTBYDlDneGw26+7pYmONJl1OYtgwAw5QxR+2rfFdQ+Ak4ADAAxi7cSvDLxXmovGyD72vw84O1s8LaMbQaInJCf+02Kk68veRW1m6iMDYvWjt4IX/szBjwhXUF+NiyK8Ge1pUUTfR8p8H37SyN8P0yKQuFiRycxp1y8GBn38PPrWxlOCAsASyIcfbs8xkm6c9DCI+kKL0g6Yr8rN/i6i3r1XuYS7ayFOt/LTNTWdgtJekX07RbXCAATZfUs+G9ssLRS584if6chL+e66xICEMkmfkYDwJG5b1N7t/CTpxze3qUIuBfGmTkWEjmnOIrl4ziZ4J4nwKF35we0zLMK8kplHnSHffyQzJV5sAsA7SIZpBI56eIROYeCCAZ8fNONerXjpCpgVXGOxrw6YLbEIaauUihxYk4gXQAgI+Q6J8q8etUQHDsAsEEQwR2p8yTlUjeHtQLAIfDWpx7wHueRKlc2aA7p3vvDc3dSu8eToPZSSCfFcmWeUGoK8aC8bEAEnghxxJtCyLcHeKIm6NWtcnFBVqwkYmM+k+CIX2dJVAsfnknIOUri81DV/GZbK71URW9iwOKTTDeOUXu6qqvcaxL8efsE8kjJ7QLAo1Xu6NYb/GyJh/V9hASH1HRdo13YCEMna8MCOZQXMuzZqm4rXOnlSbGolz+HqIH7V6jzQ/KQw1X6vAbPqsXPWzCDXo7MK9t8P1ToXgDYUecBVL9rfigvAJip8OfdK5TpeiJ63aqg+rUd3K96eo6/76NVncQcEFwl7UH+HN7o/j05x44qT7Lsz32PX4NQpwSAHj/nyAkLlOMhoXq6Jq59u2MF/qwUb1nSp327dj/f15/O8GSuIuIHgKqA8KYq/BrmqrpwpDhuoi6O6tlT4C21q4LXyGs4K/F2an8y9a/UvqSJo4oU9cbCODPHQiLnNI6QIAANGVTSazaHGbeFePtIHPwQrUZ5WxQAuIWqjuXmDns0wq8BAGYqvMrWHlhF7SZ9uc0+7pQ8Psvvo2qgKPWTQpraL2rmDn1anE8GhXTZ9tQQSbMWS0tV5G1+oWe5eYXZZPQJdR+/wwP/Hh93vFKO7ov3+/jadVv8GrxCjQ0AeiMcsdZki+/HYE0EBXrp/ipvEbtRvAufaLMBAI+Lr7sjWf4bJkpLm5rm1zPeKxJBAHC0wN95QnAldNRM5Mf5s1DcFDERPE1VNB/KaImj5rqC/BpUUAEAVwV5Qli1THhtnSx6yP4xtV/pv5ram0Rmbs6AdTZc49XbIRffizr9HFUEADmbB/aZGkd41Fx67edcInAXudaAo9d+s61ktXli2y3amvzCnwE0GXhMu25y7Ezzh9Ue4GdHu6N5yVQip0u0u86E+bM8LAQJAKAvzPfLgHgdrUIGGgDOcnFkbMTm0t9pgRoCgITN22SEXgDCIsFh0p6cEH7ulEgOKlQsAFSE/LJK7gVEux4ALBdtZgo59HRNt2gq2ommBk/kdAfeQO2B0xAub47/PrVbAsVVdyrgGpkvr+H8EuTHX3R581/CWEjknOKIhpbC5fr5h51XqFko5w0AHBH89Nu8uvRwjvcGL05cK6/hYPoOaj8/xiX0jtd4kAhodZ+yzZFJoisKgA4sVsS4fV9Gf+C76ndT+5Lib1D78RJ3xpNu3cutIPIJD3dSx+tagjllccdnb4q3Xr259cNyjqCACTcF+PcVEP3k6tsCgP4QD6BGXTwBGXDppNh0hbdNtHo419ajmdvlHFcn3sftQZ5MytV55cdjoLiR8POgfFMrTxwcyOiPfLTEv9GknwerEY8Oyu+bEBLnHr5uHYOEVNjDAyilDJKrclj5QFgn8BUvknobJuSd+2yO1iwJROoimyf4AWCTmxM7hwUMMibQngmfdpsmS3yOvSWO3As5mtflOLiyY8TigUtXg7eRAkCniwezOZFcqBgki7zCDR11c79pkT1A7Y81OG8gAAyWOZr6nGauZqiKKQCwN8WfxfEiP7/mqnrd3SOAXFfy25Bt2udENFeJQlI+Nct5W/ojuhjiFc97QijXxaCSh8ABmxPIX+i5gdpLgq/IZL/sCnLfLi94IE+INQUA907wdamELkpK6QLAlMhBhj38WQxCIzG3Oxzp3GrxQvu0zf3gkgE5fJtbtGGneNvgpbF3UbvbhBpjYZxxYyGRc4rjmZagn7/pPJr+3Lx/f2nTa6m9LjgCHLHZNNu61xRJDu/bX72f2hf5L5BTeAW6ouwSahgGKnwFkd2eFH27NVtvmu/v5u1yqmrTEAisJ2uaXLDd4Ydcsc4P6ocz/yDneEWCc/UsSn6A2r9X/Iac4/+08GcpVDDxH5N/R+1bRAISAHbUuMzlEv+F1J4SzgSge7VzLh7M9ic5ogAAygJBVazz788v2mj8BpDtvjgPVleWeZKyT0DwAWBJgj+rmSIPCtqCmnfidX0Jar97TFTBw/o+VItlRPzExPQGak+L9ksACApnuiyqpiaBiQc8KOi2eZuNCdnqgPiN6bIIAoUUdcKg5Vbxr210cfTgIQP04DKHt1bZIsB6MPdPcg7b5v7Eq8S+H7A0IueRhlCbsTlB6HEXbxfv9/BWcQB4Rw/PcGxM6nZWNeJeHuQNFfi6PCH8GQAICBTIt0f4vr2xmc8xpbdLfDXFibxXi1a343k9yY8yf8vnSHBEjoky1jqLo4zVnhwQ0t+TBgTASyP8+ztR5Bdh4idf1M59gazo5lkU0WdLQSSc9mX4bxxwaboGr+An3Nr4CbUr/pl2j27RdETMsD7xVmo/hJ3UfqZx5LzU5cdf/epXY8eOHZiamkIymcSVV16J2267DV1dz8dsO3fuxC233IJt27ahtbUVt956Kz7wAX6u/u+xkMg5xVGt509KdpwIc4ejYoB8yDR4IKgco03xd1D7pEsrSqUqnG9BSTSfqGmZZ7+bIxemc3xDc7VzIkcAsEVgofhnDAoNMnhRv7GjNkTtU/WD8hpO1DkCqk9wN61J/pacYxe4elYTeqj9ygBPUAJASASSKQHrXpTkBIfj0Gs/CM7HoJQP4j7+HACgZvMkZdbNJSwVJwQAPFn9LrV7cQO126Id4eiURgws7+Eork3ruOJNKa2Pp3Sao3rOPZeXqE3oUrJ7uaP7iJcnY5O6KIpFYe5x18Q+0x/iTmxByBIDuiqqWgFMaoUe4XIohGPEqwsRbkHWXxQIxqIohtyT5Tw/APC62G9Te2eIJ4N8FU2sOVbl/sSMNUntq+IcLQoAcyKhlBF8eVOORuQoxbWncl+l9no9Te1XxrWvoFpQlChBQiD/AGAwzNfVw1M8sT0Q1YkchQwKuvm6U4maSUUYBsAlsHvb7K3U7hgQmsfDnO/uuGgd7vZx5SwAGLK4imapwf2q0GmIrqoied4V4O9jrqaTRXXRWqLa9cYE+hAAHNGDOV3m2aK2hoCSAXgk/wVqjwZEO544WxTqHNAKfF4P7zErV1Qh8EXOaiyM0zouu+wyfPjDH0ZnZydGR0fxR3/0R/iN3/gNPPLIM3FENpvF1VdfjSuvvBKf+9znsGvXLrz97W9HIpHAO97BY/mfHguJnFMctXoarpPwFXjdPKgI+ThMGQBmsjxgDiR4AsQRhF5DaY44ADQRsc/DryHo0eSeFUHYuijOUQcGSGZJRByWhMl6EiWDXhQwEkWEWvPqloicCPzVULLfgE5CrvBtoPYlBiQDflHBmhHlJdsxKD+JURQtKvkS71AuV3Wlr1rjCY6YkDc2SRaFAglq3+NwcuqyzWXUczX9Pitl0b+f5E5otF8HDYkNPPJwtyWo3ZvRvBNLZzlPyLlZ7rxlDYporX7uyM5W+fMOCp6CCYMArCPAf8MvZGp1mQJIgycXsgUuJR2Ka0n6Ixb/DeskrdHPjnyD76cXGYgWDFf404jWeNC+KKqlpkt17m8csnkSpsfFyeMBIC64lyyRYNxT0W1NSvZXoYKaoxuofdLSCkVVmwd53xrhBbQberQ6V0QQxG9p48/hYE4HcUppMyRaOKeEMMIU0vIaCgLtony/kIH/2BDIhFyBF8D2CzsALGvifF5SLEOgo/ZlDVqrAvxvQqLF+avHdXr9VT38nK6IZNKoVjiHV5wdhQZ/n4oHCwBiwQFqb/PxQvtUlfvBJmqhlkhKe4TsvZIvdxwbtfr8/P2X0nipy4//4R/+4XP/d39/P/74j/8YN9xwA2q1GrxeL7785S+jWq3iC1/4Anw+H1avXo0dO3bgr//6rxcSOS/mcJzKSV98tc4P82JFK1G4RY+lqsaHLV4pX5HQVbiaS8A5cxwK3RXhkG8AKNrcuSrY3BkwIYpToyximwcKmlZsXZVXThUi54hLQCkN2ruUY9TnFv3/Qd6KAAAdQlFDVfOTPv3CFIQ3KvpPltc49HXExYNIQCukKPlxRToLAFmHE/eN53gyt2YAI3EEPmJd8HpqLwoodH9YX8OjI/xZjB0SihwGPFgDIb5XXXYZb7vw9PEkDAAkF/F9/cIs36smCjzgBoBdGf43BwUIa3+OX2OXX19Dusa/4a7T4PC0O/z7KcQ5d1PUrb+vpM2LGRGbPwtLkOuOGewjs+BqThscfp9iOwUALE9wqFc9xdtAf5jVLbUXR7mCkOJwW+fjKEkAmLQ4UlKR2CcFKe3BxqPyGo4XBql9ZZxH7T+a4H4bAFzZzvfMdj93SEZLOrlXF30Cak8tCDTajHhXANDpcH+ixc191LhADQHAqIcH5Q+DJ3NNRqbBEaMei19DXMiLr47rA26kxM/I1TFeiHhtr4aDztX4dRTqfDM6nNWtcA2BJImKdz7b4C3UAJApctWqoiiytYc5P2Jbkr9vkzGUf4ja3SLR4zg2FnSrXpyRzb7QyfL7/fD79Z5rOubm5vDlL38ZF1xwAbz/X3v21q1bcfHFF8Pne/47veaaa3DbbbchlUohmdTId2AhkfMLDM9JETnVGs+Unqwl66dHQwTuUxleSfcIYjLV1gEAQXXQisx3FJoQr+7lDkOpkaZ2k7anougpVyRtIQPFDSUbnPDzSkJHjTs9Xkc7Nd0+DtdUxIBrkga996IgoghdU1UdmRzMCGK/2vwQN/ty35F/o2Dh8dAAtUfdeu3PlrjD0RCJOcej16VS13ILqeiocEIV3BoAXMJ52yPIxM8xUKRSLUfZY+I+bV1Jz4/wY/LuMR5ICmVVAIDgQZXIvpDF94mxit731wjVDzVqBuoPU4LPZCrNz7dikJPkA8AhgZq7KH4rtUdEVbXk0q2NlsP3kTmBX3oqrd31tTGePPALyfq++MVyjgj4PjIh9qpDjk6iVAR6SSXXvQLR0+/wRBAATJT4R5oQ8pFtAb0fqjbssEegTGo6KPcLxSe38AU6fHwPeCzLCbYBYBJ7qL0nfC61r7J52xSgCbKV+mSlqlWQaqJtULWCKxSKBIRDJ3R9gsuuPaBb/h6Y4t+PyBfDYxDXqEBTEdAn6jpRquj4VXx2IsXbeoN+jYQuVfj51hHfTO0TGd52eKa1Vtm2C/aLrCr17O/39r6Q/P8Tn/gE/uRP/mTev//BD34Q//AP/4BisYjzzz8f3/3u87QHExMTGBx8YRGhvb39OdtCIudFGycnOw6rBIdP93kmLa4koSTOq0IlouTRTqiClvsFT0/E1ptuwxJyueW9/N8b7GeKxGpWQHIWezXEtz/KneWjoq/iwjh/DgMaMCBJ9RR6qWwQaB4T8W5JBJqjRc34PwReAQs4vJIecfjDaotwSW0AmBNJloibExUrMlcAiAf4N94eWk3tVUdXwMbSD1B7QiA0lJqTz0DtKSh4J/bk0tS+JJqQczQEafrxCX4Q9oMTMgNALquV49gw2asUt8VAlNsrDX6UT9T0fe4TqKDuoCI7llPgaIpzN6lRqmo0zKDgyrKEY/h4g8uXd7m0NPiRzPeovRLlG+qgpVGtM2X+vpJ+viZaShwdBQAJH08QWjV+1h+xdSFCtaOWRLtrW5S3Hxct7fN4hD+iWqifntOHaKdQXRwQKMfzm3Vyb0IQq98zzn9Dqef1h7WQRUCcwx6bX+NOl04WDYK3H9dqfE2pdjwASBd5Qlitibkqf5YBkegBgIx45Tmh9Bn36pbac4Sbe1D0zCq+LwCICyWzKUEwnxICEADQJt6pSpK4XPxZRgNcTRQAWkMctWOJZJNKQDqOjWpNC2osjFMfw8PDiMWepw05GRrnj//4j3HbbbfR39q3bx9WrHimQ+D9738/brrpJhw/fhyf/OQn8ba3vQ3f/e53TwoI+UXGQiLnlId98taqmuj9DeiedFtIJFfAoZRxmwcuDUs7AyGL7+x+cAdyGDwJAwDN4C1JG8KcHFepQQE6wbE8wQ8gJRcKAC0CcbO4i2/cIbcImEXFBQAKdX4NM1V+DUcNyC22FniloejiPxJ3dFJMkWQrbpiMxbmbEkLdCwBS4M6bQpuZVOsD4jrbnAFqn3Dplj+ZVPYo52v+AN6a6K2/oo3vVYrjCgC2p/hGsDHJ7ePTHM0GAEM5nrjenZ5/lUwRY0ZF+dYvOHJMXmenaJ+0XPPnoBpIXkPtJzI8Aan42wCgx+atUVmL71VNbt5mExZKgwCwOPlKaq8L2e6nC3fKOfLhS6n9AsGvtjmq29RyNb62dwkJ9KXg6AsAKEe4X5QXkvQB0SrXZ7DvdwT596V8CRPlk4xoYVFjdVNa/k1PmRcSmn38WT2ZEsijlC5GKmXVZUHho9p6XU5UeDHjrPiN1K5UUQHADvJNsyoqZD8e5/ZX6byAHEqSvsWAhDvu5Xvqndkd1P66uE46q88jW+MJp+3Zr8g5miI8idKTuJTapwq7qV35bQCwyOZFuKMWR6vV6rzgopDvL7fxy1StisViL0jknGy8733vw4033kj/ZtGi55HDLS0taGlpwbJly7By5Ur09vbi0UcfxebNm9HR0YHJyRcWp579744OvQ8+OxYSOadx1OqcFDPX0HBOJS+niAFrbl7tPzD3dXkNavQlr6J2E1WdUeEAKtLnV7d9TM5RbnDnTAm5LIppKHNW8Er0BPkkirR5sqI/0af5ssN4iaNhykLFBQB2ZP+T2jckuEpLTSDFACDgSVB7vsa/H0egRHKi/x/QLUl18N/wCQlMAJJDuwb+rNJVzVOgWsSKDf6sMjW+7rQ7DzQJJzLo5s/6vnG9Zq7v5ddZtXmScyyn39efHeLk1G/q5IHiwYz2RFTrVJOfL5qEsLeWdcJK8ZGrVjkTRM5obhu126KdYUnTa+QcrS6eaOmxFGKUr+6GQSV9d+Euag/5OLLPZOQFqexseYDa4z59tmSq/GzosPkcJkMlamoi6VUQ1fr90NyE6xtnUbtbcLytSOgkza40tzf7+F6kGzuAmNhz+0V712yVJ63vT2ty+HVBrv4TE+gMhe4FgFmBMAyJZGvY4JwOeTjHVEG4TVd28vvsDGp/pEm09Km0tlJbA4CKQCie59lA7VOiLREAZir8XpM+7gssTlwr5yjZfE1EhRBMNHI5tzu6zcUj/K4Oh7cGF8IcfWg7DaTy2+V1LIwXb7S2tqK19Rc7v5/lPK38f9/D5s2b8ZGPfOQ58mMAuPvuu7F8+XLjtipgIZFzyiPo7z0p103Mz1PsZSGTCQAlcUCp3t4Zi5PnKkUcQJOpjueepPZmkzmEw66G4mwBgG5RUUmKQ/JYQX8eZRG93LyfJ85W+vjhMeUaktfQ7HAXr+7iHsfTmX+Xc7QJElKvaHHxCzsAbHRxpaREkP9GtcEdisMOb90CAG+AVywn61zZwAQxoNQPbJGQWurlDiYAzAoukmY/v4YmH3fYExH9/boEosYSnCyrk7pNrSi+vztH+RxbWnSy6KYeHtgPF7kjPCOkVQHNYxWJc7uSkA1YBlLu4lFUhaqV4gAxGZbFA6zZKm99BICdYqu5LsBbLDsFL3TVoGe/7nBlqzHBAXfAp7mbJvJPU/v3RYtKra7bFVSVe4nFifTnXDwJCujikuKmaNh8r+qP8nMFACpiHzkdKPiRAt8H7p3kC9fl0meoSvh2B/nZ0uzj9utbdZV4xyy/z61ljShVIy3O8oTFffHRKv92AI0ATlU4yvjLxznq591L9fnWGeRre6TI90uF1gb0ftYtkJpqvwSA4QK/zu2ZNLWPG7wvlRyftvnZoYrHJkPtVUnB8Tab2yFmONMQOS9d1arHHnsM27Ztw4UXXohkMokjR47gYx/7GBYvXozNm5/hSnrLW96CT37yk7jpppvwwQ9+ELt378bf/u3f4jOf+cwpzbWQyDnF0RRcDOskvZSOkD/OG6hWBcVmdLK5nx1VAc2rN3QApgi71NCEXYBLwBIWJV9F7SaqHuoQGypye7aqN02/6PG6PvIGav/q7N9S+4WRm+Q1tHp49Wmmzt95MsLhoACQKhyi9liMO3g9Dd6uAAABQc6ZFG1sI6JENuNoB9Lj4nwovR5eua1Cf1/7Uv9D7aUAh1iFg5fIOdR9qASkGv6ARnE1e7gj2z/Hf6NQ1733a2J8jvOa+By2wSG+bY473GJZojei72O+8OEnZ/lzmDUQB1/h4pV0laI0oNpCq2ijmRRFghafJkK1hFStIrm/f5IHT5tadOSyJimC7lSCmneWTcTc+RNXiRol6w0AzR4eeMRtnigtGeyHAT9HtHWEeOLNI8ipTUaT+InBEM9ylkWSE9AJ/K9OcaTleUGOtgaA72c5v+G5UY5K6BA8WE/N6sT3IYcrtlXA96qSo/m8Olx8H0iB84hU6/r7avFxDqnZKn8Wioy8UNetqup8UoIeJqNJJO9OR5i4SPDol+ocMTpqrZJzjOQfp/aAjyMcvB5Oqm4y+sLnU3vV4Wvf7ea+vOM4sA06HhbGr36EQiHccccd+MQnPoFCoYDOzk5ce+21+OhHP/oc/048Hsddd92FW265BWeffTZaWlrw8Y9//JSkx4GFRM4pj6ArAfdJDuSIwzej5ijnhQGAnIBLWy7upAYd3uPXMCBLKAZ5Fc4lHOWTPZ+fHgWbV+rmqkeovW6gRJEXrVXjRe4IK84IAEh4eVCgWjsurPBEjUrSAEC6LlqnXDww6fRq8k6/l1demxv8kNzv0tWOVwY50qQsINeKLDlscXUhQK/LkCByTEC3sLiTv0Xtqi1KEeYBwIkcT6Ze0cbf+UiRRzZLhSwqACS6+Lq7zD1M7YsEUTEA1IU60MpFPLDJzmki4zd4+Z65P8P33PsMntXl7ToxxkZ/hFc8p/I6ONoxx53M7hB/VlUDCh11NsQEt1NbQxNLdHt5AJWu8AstOzxAmyzpNbNIkFOvElIwITdvVQWAw4IkeNTFk+9+A5WypgYP/Jv9/D5mBIcHAAQ8fM9MQCQYBQpyViQWAN2GHRIoyWaPToplatwXSNj8OZjkepf4OEpE5e+zwj30GigU9doclXDCxRNWJQMC+qfTX6L2TbGbqX3a0vLkCmW8JsH3XCn1bpCEUa1RbX7+wr47pveqazv52t3SyheNWtcAMFzk9xoWHHBDE1xRCgA6Yhw1nnDxhHHDz8/gpK39x1CDr4msSyAtY7xIZzs1HE//QF7Hy2W8lBE5a9euxT333CP/bt26dXjwwQfnNddCIucUh+VYJw2kVBtMApp0r8XhjmoRfCNQilFbM5+V13B5/A+p3RJommG35vDwunhVc7zwMLWbODVxD3fwWgN8+SveCgAQIhGSdyJq8YM2oEhMAaQbvLqUsXhyotnmjjJg1hrFxtkWP2QBICxgVgr5sLjKHciarTEDh4R8q0+oA+0Dl08GgG7w6lJEVLkDBhD7WOiN1J6t8meRqwuC7BmdZFkb4wpDsUEeHK3p5f3iAOASDqBnkO+HEaFcBwBNB0TAvI0n917Rqdddr1CsKQp1kr4wv89URX/jPWH+gVli1xW8uACAdIWfDV2B9dQ+6vDkBABYNV6t94NvysdFkBcvbpDX4Bf8T71h/rCUGiIAHJvha2Kxw5O1TR4d5LVG+BxKeaOlqveJJwu8XRU+XuUOCr6TZQZFH0VcWxTo3phPI1UGwzyx/Zpunsj5xqhOcHR6+D6gyFKVepCJP3Jn5gvU/gqRZKk5uuBZiHGCXeVXXRbgrY8A8HCNK8+9PvA6am/3833/0Vn9LJuFalyTjydyzm/W2fXpCp+jLyQKhQYJKcUnpPgq++KXyjk6HI76Dth8TeRd/AyuuHSyNutKU7sjUJSqiKfsC+PMHAuJnFMcFeRhncQRDLm40+IXGwmgkyQVwbbfDF6ROT/xTnkNbrFZNEQFbLjIIY4A0B/kztkl8XdTu4l0oxotfiGZbUDjs32WH5RLYvwTWxLjyIeRvA40Z12C+0U8qrxQnAKAWYuvu+XOUmoPuHVgEhf5ieN55WQqpJjOvCuOG1s8zF6XVqbLCN6Ip3NcoWF9/C1yjmZBzNca5M+qI8ADk5Gi3st6Z3my1iXWVEBUAgHAJVoaXCrwWMIRBwAQCPIA6oIsb0WdndaoOr+Pf+cjKY76EXEoDtZ1W2+PoFOVrVUGW7JHkImrUbTT8m8eL32N2kMCtdBtbaD2R+375DUUM1uoPSAg9GGPfphLgjzw/0GJy6hfZl0h5xgv8kBRSQ/XRLs5oJXMFDKi5OIHtUug9gCgI8iT50+l+Tm9yUBdMiGSPcqnUUgzAAgJ+fCjBf6sZly8rVe9C0AnatQ5bdJmutd+hNpX2Jup3QTpfHWQE6tHxTfaLNAym1t0+HUgx7+vzUKSvmaANjiU4+/DL/bsqECrAUCvQLc/McufZdAA6ex1+LOatHi7nWp5N6EgyBQOUrvt8PflEYIfJhyML6dhOy6j9vf5zvFSHwuJnFMcmdowXCdpb1I90BByoADgdbjDEBfwPiWtOmpraXAlsxcWCavukJYjnKzxKlxdtDPY0AGz6h++f4LPsUrxHABI+PgheCjDAzSlHrQH++U1qHYFpaS0O/VlOcc1iT+iduWcqYQWAISEY6QQO6kKP+TmGlpyNGwlqH3CzYN2j3AmACAr1Ou647zFbHvqi3KOVck3UXuiwKtXSk1tWUyTsf54hKNAegTfQuuQVkgJiYpk35I0//ev1A6iq4/vubFN/Bv3PK0TpaNDCWofLvKkWEoAAlZ7NRr00RRPWPWGBMeAQbFwkYcn8I9WH6X2oIcnYQAgGuD3OpfnErAZZ37OOACkE5zXZXuKf2C9Qa2qExMP/OIaJ9IfqWquBYVeqtncHhXIJADwQqxtF2+PHC1yXqUbYm+V1xAS8uJNooU6XdP7fkzsVf2Ch2dxTCfPD2X4HN0Bvq4apQS1q0IGADREJuZIjSMtK6IVHADCbr4PHHM40XepwQtPADDW4Mi8jTXeBhN0c3+kSSTvAY12Ua1XCa+eI1Plc+zLct9tIKwD4aJoXfyPyf+H2i+OvUvOMeHmiRpFqj6YfAW1m1BG1AQHaaHMEamdUR472U4do+mfyOtYGGfWWEjknOJIF/ZB6gefZFRDHLoHALUG/xtVTQy4ubM9mxcwZgCNBnfw/D5ObFsXrT7PzMHvM21xZxqdOpGjKgXnt/GN+ZhAgADA50b+jNo3Jn+XzyEClyUGCkVqjIE7JCpJAwBLotwBrIrm+4SQbwUAQV2BIznu4IXcfDsbtjTZsVeQBGca3FlwCzJyAKjbPKGkSNNNRlHwDEREUrksLmGuoglGw8KRvWOY/8aF4vsEgJCYo3WOJ5xC0wbEgc2iXUGQw+Rn9bP60lGODFqX4AGaSnLeV+WtqgDwxiRX9/EIxECjrs/FacWPIVQbPULVCtCE/ouElK0tvj8TMtYn0v8s/4aN8/B78m82hrkwggqod9Z+JOe4LvQb1K72/SkDX2C4zNtR20K8Er4oyNftvppGo10C3tKuFPi2zel9v0OgB6OieFWo631EJVpUgj7u5nM8JpAwAOAWyT/F09jjcI5GAGhyuDLqqJvzIhUdvS7H0w9R+0ScJ3IqIgnjFWsKAA7n+QvzWvxZRwS9AAB0Ce7243mBwNdhDZbw2jBenXw/tX8n/XdyjkiQk1OvTXLesbDgPxyFbuut1rk/4Tg8saZ8v9PhG76UhmO74BioRM53jpf6WEjknOJIhFf+wogct6UPYkX8lypyCb2akA1uNYAHzoie9bCfO5AF3UoKl3hWcUF66TY4BAMiyFNOjYnE+S29H6P2giCOyGAxtQdPQzue3+Kw8XWCtA8A+gWng4JDp3URG1OilS3u5WtGdU6taGgH8aCLJxCnMjzoaI2dI+do8nIlmKHs/dRuGewjioMqIAL/Q3l+NKyK6e9vv4CFK9nSI3kN8egK8m98apYnYWKH03IO9zT3VAt7+eK+f2hAzrGpme/bVZs/i7YAfw4XeHirAQBkhEqfkhc3kR+fyG+n9lo9Te2JgObPWO3hrToQvvBxUURQinCnY6jkOwD0lbnKSkygRS9zOMcHALQH+T4wXuSBSdnS/clLQ7zFa1fqP6ldBWjrhCqWySgIzjDxGAAAGYHaUTxZr+7Wz3KqzOfYnubf6GiJ38gKR6Oto6IVR7V/xXx639+b54psk2WOPDcpuFwdfy+1/+3xP6f2LS0fpPZWv+ZVUn7XWIk/q4RP78mHs3yOZXH+G+mqnmNUgKEXR/ma+Q3rPXKOoTpvC1T8om6Hr4k6NFKsYfN3qny3TJXTJJxpiZyFYTZ+pYmcBx54AH/5l3+JJ598EuPj4/jmN7+JG2644Tm74zj4xCc+gX/+539GOp3Gli1bcPvtt2Pp0mdgkUNDQ/izP/sz3HPPPZiYmEBXVxfe+ta34iMf+Qh8vp/dGA4fPoyNGzfC7XYjnU7/Qtcc8rScVAJcJXLSVU0CnC1oB44Nr5ColO1fAAZjl1H7SGEbtTdsveEp0q7Z3A5qLzWul3OMlvi9qsPFwJ/AugQPoOJevvFeL1rETIKjmsgoV2xO9jilXxcenOT3ma7xA8wv1NYA4OE6rxD3eDgR6liDt0wotBvwLOLu5KMlxuXHW9w8SQMAZYc7FDHxDbsN5HbHS09Te9XPE7rr4zw50RrQiyZV5e88XeMfWLam1/5RUbHM13lbVOv3NBnrOS0cgTFe4JW8sbI+Zms2/xvBTS2TziqoB4Am//wqUyYcOW1hvt9VHQNiMjEiIpCMefmzPi6Szp2ObpGOJnmxY87miIGR9H1yjhMJjkqI1fm6DIlqPqATNTN1/r7y7rScI13n6nVtcU6Uvy/3HWpf4tK8gCeKfM2UBfKo2eDb2SYU8pS70eTXFbJFUcFpJBJzMS/Prm+f1RWZjiBfV0nxrGoGG0nK4kH7Iv8F1K4UwgBgysVJ7v9P10eofajI77M/rFu9V0b59/WNYf6+mgwoyS7rUL4dPzsWhXUWc1goNx4RAClFQQAAT+W/Su22zb+flihvh/VA+10hP28n7/dz9Ve3CMkbThW7S6Jb4WU0HMeMM2u+c7zUx680kVMoFLB+/Xq8/e1vx+te97PVob/4i7/A3/3d3+Hf//3fMTg4iI997GO45pprsHfvXgQCAezfvx+2beOf/umfsGTJEuzevRs333wzCoUCPv3pT7/gt2q1Gt785jfjoosuwiOPaHjoyUbFzp80kTMniK4SIR3kBUT1qFzhrR2ZIm8fyRtA00NRTtRoC3jgyZ7PT49qjRO+Bv2CeNPg41NJEOU4zVVM+sG5PSHg0o5A0xzM6ervnKiIKGnVB2fScg6VeBuyeAKk1+ZKMgBQs7nT0uGIVgI3D2z25jiZHQBY4vs4HWRzU6JaqJKtHuFsA4Dfw7HMWdEOpIg54wEdVPSJCvT3D/F94pjNVa8A4PpmnvRqFZKiJkSNuer8CHpNEqU9Ib6RtAoOj4M5/n3+yxivHgPAKxIc3t4a4HuRUh4BgLEsR7TZYg9IhDWqrkVUd5sDfD9cmeZJzp8UOUIEALYE30ztDbeQuk1qVZ3HU/9E7aEAbzUI+bScbrOL+yzd4N+f4vQDgLjF/2bOxVujpup8TZmQ3AfF9yW44eExQAg/PsN9gYRPBIp5HUgqn2ZFlG9G3QLhiGad/EuJo+GJWZ7AWB3XPmqLzX2BPQ5vi/JYvCgEAJPOEWoPeriPqtaUSZEuLs7hZTHuC0QNWqv84joV/9p0RRcJlL9eF38wCq1gGQ3w9shChfsTIcGPaILEtIW/XxPKVzVwu2pLXBhn5viVJnKuu+46XHfddT/X5jgO/uZv/gYf/ehH8ZrXPMMe/x//8R9ob2/Ht771LbzpTW/Ctddei2uvfb7ffdGiRThw4ABuv/32n0nkfPSjH8WKFStwxRVXzCuRk69MwOX6+cflYJwjWQIOb3EBgIwgcxyrc0ip4p5pMnCEqw4/aDvDAhmR5+SDJiPi5zw8JsSaYXGIqVYeE2K/ibIim+OOT0HImo4K6CwAHMvxoCBb4/a61KMBUhYnnFRDkWYCwMU+rhIREoTKdp2vmULiKnkN6qBURKcjFd46YjJyRd6LHY7rNpmk4MAJiw9IMfkHDUgUvYJTpTXAj5/JvFYWyZtoXpNh4kwPF3hgoSDyKggEgF2CduXiNn6fQiUav9nyIXkNfqHwpZxx1aoK6ESNLGSI8w8APGLL7BZ50M4gd9hXFLkqDwDsyvAzNG7zc37axVEqANCTuJTaT9YC/ty/t3niGwB6LY5cKIvE9kEDufikiyeDRvJcBbMvyfd1hRoCAL+bt2B2BXjCd9IgmL2ryAsJqyqclFkF3IBG5h0u8GRQRMxhUkBTBbBlgm/PJCHcEP2RDYcHxBmLFxIBIOHwvSjqFQWySaFoGtYFgu4I9+eXi8Rc3eB8a5FIL75hZgSyFgDc4jK6hKrVcFGT3A+LtiVVPFaJmvYG36cAwO3mfu7R7D3Ubgk06ZmmWrUwzMavLUfOsWPHMDExgSuvvPK5/188HsemTZuwdetWvOlNP1+VJZPJoKnphb3j99xzD772ta9hx44duOOOO4zmr1QqqFSe3+Cy2WdIrCrVcZyM7NgVFo6was4HkKtyxI1K1Cj5urpwpAHgRPYJaleO0+kYiiHehCgu7uWb3llC/nHCAOWv/sYn4OvHhfjPrpwm1oyIVptd4O8zZvEECADEnAS1T9ucuyns0Ymcp50d1H6Ww1vE4kIhxW2gKOUTTstcY4jaVRIG0Ggz9Q0XhEMCABE3J8/N1fheNFflz2p5QFeGuiJ8cV/cxtdt0q/bngYEh8DuDI9sru/SH3lzkDvLDcFf0x/SFeZu8SftQg4+IIi+96a1s+0X3rZyxk2CPHV2+AS3kyoymFyHOjuCQj3PH9HBkc8tWlTmBBKzekzOEfRyjpxSlVegfR4DOd06/86bvHzP7a9qUYIxF0cRt4RXUHvQxZNNSbeupJ8Q5/Ca2Pwr4e9o+y1qVxxVoisKADArYvK7svycfm0TR87OGqCUt1a50mZfmfNcDRjslwEXX3dhDz//5mpa+CCV203tb2z5KLVf1sH33L0GaGuVyFEtzo/P6hayziA/AxdH+cexKyWYjAFMCNS4QrYPu7haKADMZJ+i9kiQowvV2TLl5vw1AJC0+bpbFeWUEOM2/3Zsp46ZGo8RX07Dxi9BfvwXFC/6dRq/tomciYlnJHrb21/Yc9je3v6c7X+Pw4cP4+///u9fgMaZnZ3FjTfeiC996UuIxfSG8+z41Kc+hU9+8pM/x+KC6yQvPm9z1EL1NHB0qFEXZJENh/dwAkCHqPgX6hzm2BTS0o4p0TM7nd9J7TaupHYAcAlETYdou7AMPo8nZniyqODngeRQnh+iU26tuGE1eOUoYXHIabOoDgPAERd/H6tcvCe9bOsk5nkezj+jIPInhJxuSvBSAEBD9FF73NrJVKNU4U5JVHw/SsISAIq+TmpPiKjAcvHAxevT77O9kze+N2X4frwiqg/YJVHufF3cwb8vE2TRaJZX630WfxYdIgkDaEWoHpEUcwn0UsKn2/EmSvydNwwSoWpI6W7xymsGiZwTRf43g1H+rE4IbguFfgKAFtEFMxDmQdy+Ik/2AoAlGmlafDxwmRPKdgDgEWdgr5efLf0u7XMdKP98f+7ZkfDwSvih9PeofXXyD+Q1KFWdNpHM7RDBMADYDp9ktMR9BYMOMZwQLuZFIY7UTItk0om87hMNuPj35QhSitmK3pOLAnEzWeDy4wGfLhL4fNxX9ovcuHpdYQOEVVXIi4fmKWkPAEfzvFOgN8T30/6wASemKDZuT/H7PFHmqDwAaIqupfa5HF8T1To/Y2s13d61rOn11N7W4H7Z2IJq1cL4BcavbSLnVMfo6CiuvfZavOENb8DNNz8Pfb755pvxlre8BRdffPEp/d6HPvQhvPe9z7PWZ7NZ9Pb2wrJCcJ3kRM1VeNDdEeQbDQBkPEPUrhI1CpruEdA9AMiUOaxbBaIuA46cxclXUnuLzTc8vwh8AN22NFHmJ/GAAYnbpaLqMiscIzXOcmtuGbdQIKpU+WE+bdA21QxeRSuJ3t45lw4ami0NXaVziPuwG7qqmi0NUbsjHEiFtgH096MO6yYD5TmFaFNtMIrbqWJA4BuIcwfvorP4PlMzUK2yBf9TpJ8nWktjOjqqCxnZO09wh/+Kdr32u9t4y5Al9rs9qQS1z5T1XhYWajJqOAatqHXx/cxUOM9cXpyxAOCL8KTyuMgFVQWkJ2dAwh0TOa9O0UpwHTjBLwAcyPPAQ7WfVFw6yKuJv/GIjcRn6W94wOJKSAWHfxtxwT2YM9j32wUBb8DDv5+wQbJ2qc2/rwM5jp6IevX3lRWs6ONlnnCKebh/mHJ0MXJOoCc8wj88bGv0RdTiyIfBKPf3Mw2NriiU+XUo/vikKHY8OqPP0MEwT4D0iXPapHX4h2P8Ri5p54m5Fp+BZJsYJ/L8Pjb6eLwAANurPKGr4hIl0uIWisIAkLX5+WSJ/bADnPqi4VQxKxD2L6fhOC44LzIi58X+/V/G+LVN5HR0PNPuMTk5ic7O54P6yclJbNiw4QV/OzY2hssuuwwXXHABPv/5z7/Ads899+Db3/72cygdx3Fg2zY8Hg8+//nP4+1vf/vPnd/v98Pv/9lNtCWy+qRkvi0WdyiUvB0A9EYFskE4NX4Xz65n6xqWVxGZZ5X5rjV0hj4sWnVqgqvE5NNrEgeMcrYnhJQnAFSFYpSq2gxEeGW2YUCpriTOK4JgrQSOZAGANkFWPGtxhYceAyRYT5g7FCr5UM1wKfeEWxNvTid4xbJs8+8vX9MEvZY1QO114VAoCDGgv9GI6O+vO3zhPniCJ1oBYIvNK+3NAzyoCHXrta8EvCxBfBvt1nuy7yD/PjYXONqlq0V/X4nl3OnPHeHv64CQelcE9YBGvKmtSMHjAWAis1X/ERk+r/6Ga4Lza6TAg+5j4GdkqwGB71GLE5q/MsLVS3rC+oQrN3iAta3CyVq7HY6mAYCqzc9hRVJaamhOh52FO6m9K8JbaiU5/GmAzh8VqLxFELI7AJoFauesJPcF7prQRTj1DR+xeOvGYJ3zJo1bfE0BQAsEybbD90s3BuQcQ6INu9Pi7XiWQdEo5+NBuU9xwAnutKs79J48VuIHXI9oe+o2UMa6uI0jxf57iN/HNV0apayelSWKACZJ59YAf+ceJf1d5IrBJvw04+mHqX1C7EUrkm+g9gWy44Xx88avbSJncHAQHR0d+MlPfvJc4iabzeKxxx7D//2///e5vxsdHcVll12Gs88+G1/84hd/JuO5detWNH5Kuu7OO+/EbbfdhkceeQTd3dqR+d8j4m49qeOgEjVPp/5d/v5KoVYxUeItLgEvzxq7xWYGAC3RDdSeLvLDvEM4XgDgEc+q6FKOkQ4k1bZ7pCA4VQz8P6HOKhWjvp1/gNrPc58vr2GskaZ2v5BNrItEDwBY4gBSwY0JR06zWJqFOr+Gp2wOnW1zabRMQvQ4z4qWI5PWSIXaUcp0JqgfCSOO30DtxwQp5pKITtZOZXlSuXyAr4mowRz+EP8Ay6KA3HadAbLoQs4htXmj+n40abOTE2oWe8V9in0mIIiMAU2KXhOtVSb75WDyFfwaRKFBtmYB2OVwMYPFDkeA9LoEabpAHwLATJlzZWW851B7Z1C/r/4IT3zXbF5YOlZJyzk8UHPwAGyyqgPJvihv5Vby5CZrQo2iQN1lhARz3Kv5Tnpi3KeJeXkyt8VA4vwp0fr0mjhf+woZ4Xd4QgsAko0Etcfd/GxJiXYiQCsMqbbDgMGeHDJIGrMRFCguk/DLJfi86uJZKSSZyRiM8ETNdEWvS0VgrcQXHp/lCn0AkBRI5ZCXK51lBVeXx63XTL3O0bcmqNWF8fxwnBefI2cBkTPPkc/ncfjw8+Rrx44dw44dO9DU1IS+vj685z3vwZ//+Z9j6dKlz8mPd3V14YYbbgDwTBLn0ksvRX9/Pz796U9jevp5JMmziJ6VK18IVXviiSdgWRbWrNEkfKc6ii5eeV3a9Fr5G4qQNSh6e1UAZ1LRVOzuqtqvyAcBoALucCiZPsuA7FjBSgOiSmCmaMN/QwU3oxmeyKkmeOUWALrcCWo/IuCeA/YqOYdS8FKEkv1RvdVEBcmoqvifZfF1+XCDP2sAcInARbWYmXxf9QYPbhRHjtugdXEgxBPCKgDbk+GO1fKork4dzXHHp5zmQUFlfP6ywZs7RLvdjA403UnhwLWL/S5nwJ8xolA7fF0uCvMgsCoImQFg+xzfc21xNpkgcoZzPMnSF72Q2ueqGhHgs3gC0Wvz72dOoCsC0EF7yMeDhskqP/9iRc1p1CeIvhOi96O5plU0e0RrR0FEaA9k/1HOoRIxKkAb8PIz0mVwjs9V+ffRKVSrHp/Tz7JTENe2CcRO3KeRD+e08L9RbYNNfv5tzOQ4WTIAJAXy9bDDSYR7odXUqo5Qv3P4czhgPyjnqNscBWLiH7LhdukztCwSjEM5vu5MEDlK+DFV4WvfLdTxAGBflq/9gTDf79Ymf1vOcbTM32lQKAInwhx1HnBrXqW5Ev8+YgGOBIs6fI6Go5FJC+PMG7/SRM4TTzyByy57XrL7WU6a3/md38G//du/4QMf+AAKhQLe8Y53IJ1O48ILL8QPf/hDBALPOFJ33303Dh8+jMOHD6On54VVakWo9osO22kAJ8n2n8jdT//tYIzLkwPAUJlDzzuDXPo7nOSIgsk8T/QAQCjAobHKUVZ9ogAQtvhhn23wtoyarfmGaqLtqSYOYhMZzJiP/0ZOFAuXJLnktkkCf7rOD0m/kFXs8ukq210lDn9fgUuo/dKwJlRWbWozAqDRGeLbWaygUVyHMz+g9kSMc1CtDYv3CaAqYMITDY7qcQzk4m3hJCqOjk1N/GGHDCp9ASHFuXWG289u0sR+w0XuRHakeZIlsdtgr8rwv3EL9S07pZ2vE9t4sihd4t+wIlTeb6CQ0uzTrRtsmKhWrYhqrgM2LL/mDFts80SoatE87uJk4gmXbhMdcDZQ+4xrjto9eQPZ4AAPfpIC4Xgwp7/hmJf/SFZwwMUEuS4A2GI/U61TMZufX4fcOvmwscr9iajQtG/3670qX+HfV0uMn+MXCpVNABgr8QTGD8f4b5Tr/H2e5b5CXkPI4nN0uTgqKCDQGQBQrvJvXCHJbNvg/BLqkWXxylPifccEvw0AeEWxsSwS9KW6XjPtQvRjdZLfh8j/AwBWxvj5pooAHQ6PawBg1MP3gWYXL8IdFPxszRG9l7WHeHv/hMPnKLoU79mZlchZ4MgxG7/SRM6ll15KEy4ulwt/+qd/ij/90z/9ufYbb7wRN9544ynN+Yv8m58elssN6yQZ6PURzlg+7Wi1Gb+H96tGBLfMya7t2eEYcCUUhSqOT0AMTdpLfF6+MfdHt8jfUCNXFzwfE/wgbQ7oz2N5nG8CHtGzvrLAA5OIV1c77v1/2XvzeDvL8tz/etc8r7XnIXtn7515IIEQIIQZRRBRS6u1arWl9UfrKT1W7WkrR6vYSavWY3t6aus5rZ20drTOAxZQEJQxQCBk3tnJnqe11zy/vz8oaGpyXW8MIWy4v/3k86nca6/nWc/7TO/z3Pd1579E7ZeEeb/cmNG/c2fXT1F7RHhGpDy8+M9UeT1U1g4VPeJFo6opMsvNNvlLgcreBQBBlx8uNP1CwNDRbekTGjeKjgjfnalsGQCwsMQ3Vv3a6UDSHeEvgffN80Jmq3xzBwDJ/XzHrlLArmjXGjlHc3zeVzezasPv5VB6qspvuTcK/TUvdydVh98Q71/4PLVfnHm7LGMeXMeqDbyto8K+p/QNWYcLI3zOPdR6gNr7fPqF+XCe98s1Kd5nrhIipgCwJIZ5sSEElRtaO2Ykxr2w2jxoEjFWNPUYL4sDjKIIXfy/R3VGmw+s47ftHSID3yoPountOXEA7+d9e3eOH/g+Oq8PhEPCDXmVyEY4rR0YkWvwg1C/8LrbEOQXTwCw6OOe6ZOinn5xgXZRu17Hc/XTW8cnxAUAoC88H5jjhwepoN5XLdX4b02HhBCxB32aC/3XUXtdZE4NxK+n9tGazpy1wv8Kai/4+XtPpMX3K00Pe1jjpYf1ilOk6hZPmpa6pJQ3PaAOSdTtU0zE/vqSOm13BfxUWNH0cFiUL3ENgQOL3AME/TpzTzLAJ/9zO/hNw4ElfcvWFItgWVw1qMOJlUIHAQA+2KHdThntHlJJ+0UoW1DYi+JFFACOCi9gdZM+V+HPOyEOULwwm+MZA462cX0NAEiDh10crT5E7UNhHW63wuXeR/NVcdMnMr61RfRb++oE3+k2hehlSbw8AcCuRd6vNqZV6KP+HUfLfJ5QW8wHD+gUzOe38xfeuAg7zNe514KXQ5bVcb52CH1sREX2PABY0+I3lv3pd1B7XOh9AUBRZMYK+3jf9oO35cURHrYIAFER/nip2PDXxEsHAMxV+e9MCu+MNg+aKzNlXo9Hhejs+ZEbZRn3Zv+c2s/L8PWt4GSpPdVql3VoC/N9lfIYUIeDADAh5pFOEWraI0KzACAU4M9LhdpMV3gdL+zS67gKWRddCmXh5QwA6Tw/3FPZ1irQbVkWiUWUjnd/hO+Dkx48ci4WQvnfm+P97qmcfl4qRFMloTic11p2vVE+b9e8xOUKnnQeofZhl0sILIEfxm714I2m9J+WxEV81OUHb40XgffIqdCC3l89F2Usd+wg5xSZKTwOxznx5DjR4i8u/SktXDsIrt2zz+EveW0Oj8FccnnIEgDkRHrktRF+m1EP6bhcdZDTnthK7V6ENSN+PkTbQnzxmK9pn9GAj2+W1yR5GZvTfAh2hLQrpTrgULf5czV9WPTwPC9kKMHtKmwKAJ7M8n6TCfJN5jcrX6X2tR6Eo/3ixtLvE+lZ64dlGSU/z/ClxkZ38NWyDNUnRBQapip8Q6L0HgCgIZ75VIX3Sy9eJEmhoR0WLxVetGPiYh5JiJen9Ul9xfx4lnu7bGvjG3ql1zBZ8nJYe3qhqDNl/cBKIsb/kQb3dtkS4AcgAHBOIkPtM2X+gtXR5GGgJUc/zzD4S7k6WEt6EIc/WucvmncV+Tq+vjQsyyiJEJQhl+uZRBwdrqcOavZV7qT2Wp2Pjdekf0nWQaEOJ67r0+6Fd03xMRgRl3h7hXg8oMVxN6b4Jd0a4RU0LdYFADhS4n330QU+T3RG9Jy8Mcw9G+6s8uxB2ar2jlcyBmq2y4nLkKpIRw8AbcLbc22CP4/ZqvbIUQdr3eIrqk0Ph+tiMR8QF5YtaH2ocI0nWcmC9+28kHOo+nSSiVKL9/1e8LVlXiR5saxVxomwg5xTpN6Yx8mSXyuR0m53WH5/TIi0qRTncy5XXs9XtSZENMhvsNRthopFBYCgyF4yWdpF7V5u0hU5MSfOQLsyu2KBGYjyQiI+vsCpGGgAmBZp0udr/AXsUF63ZaHOV/uH5/nv6IroFxP1kjcU5m39Kh/X39hT5cK3AJCM8Ex2XWGe4tIL6oZ4W4aHFToe0unu9/EQsIEq92jrEZor4ZD2uguKvh0SXTum97lwRVuow6KVMX3AkRCeffEAH+NehNk3+Xk9wuKwSCVSUoc0ADArDq7XCA+qjAeH1HiJf2hD8CpqPwR+6woAl4dfRu2DcSXazO2FhtYU27XIXxq+lP0jan95insmAUBNJARQnrV73VFZxtEavzjqifBb7rVCrwgA5sEPnJIh7l2ogre8ZGxTF0N7lvgH1ntw9qy2+DyyP88PvQoi/AsAOsUYbIqsU+1iXp8o61eGB+f4XFURriwRL7d0goiPPxB1SAMA09Unqf1wS2mmiAQQMX3I2R3ne+0eIZAdFR4iACC0jLElzfcCG0UIJwAsiRCxPfxMGkerOkRTaT0eaHKh/Az4Jfj3FrjnIKATwXQEeZ85sPDv1P5Sy3plGjneOL0ATMMwDMMwDMMwDMMwDON5wzxyTpGBzNUnzaKQBtfH2JX7nPz+a5L/jdo7Wtw1r+bnJ/QZ4XEAAIdL91B7S9zaxANcAwQAai1+W3hl9M3UrsQ9AZ1FJSuillR2IUBnLpBhTULgd7So3RL2CUXKuTp3zz3qH5VlKLdT9Tx3tLgQHQD0BLlr+ele1I25j8nP+H38Bqsh9Dfi0Ckqe8A9cpSGx1hLC2tOlh+l9lSKh3D2iZvAdJsOL2kIsfF2kZ7cG7yMTJDf/naHtavy9xe4J1iPEIbeldW/c1F4zb1pFR9/KnVxNKBd7NPCLVzNp16yVp3ujWKhpr3qomLK3JTi83o6yNe3rNAjAoB4gD/zAN4pv0ORcHkZZSFOXRcePQBwoQjjTIJ7FYyDi9ICQN3l3ksqS2Y8pLOIKdYn+TxwQdvp94nDrWlq92W1vpqiLkR+/3KWe7S9rYtnlDqQ0+O33DjzqhOjFR5Ot9oRmes8lNEZ4J5g7SLL3woRbVcQoVcAUKzxMpSnppfZdjDKn1dUhBY7HlRGZqp8X6X01VZFtQbVA1XucbPG5fpsyiO8LfPLsg55h3vxx1vcU+z8zC9Se9OtYdfSp2U9Xiy0XKB1hj1mvOxbXujYQc4pkkQX/CfZvKTEIN2U4pl/AKAlgudV6mEVQ+nzIBbZavEJrS60gGZLOmtVU5SxL8FfiOstHg8LAEp7Uy20F3rIaKMU/x9fOr2Xo/9Y4Js/APC7fEPgE9uW7qY+3Gv6xGGRyFR2IMUXWQAIN/kDuczlYYVNMXZmczxTDACEQ3wz3XJ5O4xXdWaDjhg/pNzt8rb0i3S8ANASguMqw2tIZBmLdOnNW4cIwQxP8+dVEAdBALCjg2/oVQim38OB8JY0H18BEUK2LqHFIAeS/CC0s4e3ZSTL+2VfjF8AAMDuIn/pXi2yB6lU1ACwWwhSVsWBcCa8Upah9IJUOF5YvLgMhbQ+VEyEymWC/HBwd1a35XfLXOejLLJ3NVr6IKcrtJHaU2IimSvq/cY68MODh6pfpvZ6kx8ERWJ6HmkP8bYYzvC2zJb0Qek7h/jBwEMLfJ4peQitUpcdP995AbUrvZSwyE4JADNNPoYfqX6R2n8qoJM3qDCahTp/nkGR3RUAFnz80HhHlM+pSr/3s1pOD7+0lh/Wrkrz9e+yTq1X+ZpHeKbAT6x9k/wOhbqoUHgJtxt2eWhUUxxrZX18jFccPe8nxDtgv8Mv8XJiTlYXicZLEzvIOUWaaOBkGjkFH4/jHK1+T36/KzLS9Lr89qmzxTcLOZHh4Wn4xidX3EvtgUBGltBo8Hq40NoVp8tshS8OI1oKQR68qY2ROsjpEKKZAPC95teovVjlHhyrE1fJMgrCC2RH/C3UfqS1W5axI8T1FjpFlpWm0BO6OKVTF2dFytE9i/9E7evbXy/LKIvFOlvjL2h9YR6HDQAbI1wUVnmj5YSoZb9PZ7ZLbODP48YU1/PKjuuXoymR6WXT+bzfVuf1S95gOUvtn9/DD3yvHdQC873reHsGOoRw5qP88MHLrdPKUIbalYC2sgNAoc7bojO0jtrbWlzkFACOFXlbBH38IHSyIlIXJ/XBnEpJr5itanHPzVV+w5xv8sO9gz4uqg7oF+KRJD98vzikPRTvXeTi75FghtpXRM+n9rmK9rpTFzKxGJ8w4wn9glVq8H519wz3PNpd4msTAPQIbRgID6ppsWG5v7FL1qHi8Bfic8Pcy0ulLweAfJVfNMw4vK0SIvsrABwq3kHtfd38kFNlGlyT1hcyM1W+Pg00RXbJsJ6HPrKaXyw9KfSh5qv6UmdnF2+LOTF8niwIER0AJYcfWikPxvHW49TeaGov5FpohNqTot+pi3plf7FhGjnesIOcU2ShNQbfSVKLlmr8paFQ5i8uAFAR4oFZh2+cHsl/ltovTOrbjpHkFdS+X6QGbzb0pKtoQz+1e8h0K+kXLqXTQigVADrDfIFaVC/M4hb7G7n/LeuwM3kztS8luLtnt4eXo5UOvwmfcITbuEjpCwCdUd7eveJ5hcUGsFDPyDqUmnyhDbTx8TPX0mN8GMPUfm7gWmrvcnSoTl545in396xwha7O6QEYjQtRy438d/Ru1mX0BvgO0Gnn84gHfV409/Kb2etKXEA+4eElL7SJu467Wb4hLwvB84aH/OPZOp+sHLFdiHuYlNcHLqd2JSh5Vfqdsgx1aHUgx/ulEobO1vQhy7YMn8tU6uHzMjqsNygy6P3jHPeCHJFirYBPeC+lxLTuJfNcVIzCLj+vp+Pyto4HtPfFbFV4w5R4W2c6tOfDigy/6Lu6h+/twnM6ZL0q3EC+neeXBIPgF4UrPfSZsgjZC4C3tZeDnGSAz0X7lv6D2i+KaO/43iT3+u4K887dLxIGJPxa7Pj7c7yt1om0jYmQPsTsDAtxahGutzLuJSEHt8fFm6hf9BkAaHP5IWYqwNt7feMSaj8c1KH57S6/SJ/z8XfEDT6+z1ahk8ZLE+sVp0ilvgjnJG6Z6qAmEuYvFQAwU32K2hshPiOuSvOXwHRLp7DMuVlqV94ykbAO1clE+S32EsRNekuXoTyRDxf4huFPJ/5MlvHhtVzTqE/s+eMBvgj+Yu9vyDpUxA+drXHPhr6o9nzI1fkNmHLTvyx4oSxjpTifSIvsQVMio8Y9je/LOmxx+e3uKh8fw/3CYw4Axh3+4r/Oz12Egz69cYq5vC1USERMhFYdPsJdhAGgv8TdvjMiRNPfo1+YnbBYwprCJa5dx977L+N6Cys3i4waXtxhGryetad4Wx5e4C95ys0fAGI+3pZV8TuUXhgAdDt8s32R0CGYc7Q+1DD4GpcW6dKWanye2bukG7Pp8sOJYfHmorIHAUBfhNfzZQmeGnxvTocKnN/BJ+WkmJPHy/qlfMzP901+cQkwWeV6YJdG9eGD3+Gd98k5Pt+tE1p4ANDRyb3utpT4Bdixsp5zx0u8vS+O8bXlm6WHqb3d4S+qAFASKZQhdOQaHuZLddhzRfSN1J4TukwA0CNCuZNCn6Y/zstQaywA1EWmwCWhoRMRIZ4AcKTE56L1CX4g5SUEOiR0/7J1/jw3JLUH1cMFfuGSdHlbxRzhhQw+nwLa60cdNoWCvB0cD9knX0w8rZFz5stY7thBzinidwInPcgZbuOCrjEPQqg1h7/cqNApR4SXxPz6kXc1uYdGOfNKao+IjTQApF2+KUm7/Du8iB0rrQQlsPZzXToUJyLq0RESrpJC3+YzZa3rckmQawysEAc13tJ98n6ztspdStWBFQD0iJshNeFOlHhbXxbYIevwtRKPF98Z5CnOg46HVLeiLSeaWWovtvQLWNnhL/4r3K3UHhWCr+1JvRFeWuIHMfvv5JvUVd3ckwwAYilej2PHMtS+/lVHZRm+c4UuS7+4Ka9o7wr3KV6PuQO8LR9a5G05XtQb+qdc/kLdV+cb2amyvv0ttfhnqj5+UTFWe1CWsULcih4r83kiKW7KvaRyv3uGr+NPhficfHG39hXrj/C2XCnSrE8UtUdAOsgnXaW1dSinX1YdEcpdEy/dyoOx6EF8VwlcR4Ru0pIIRQWANqHl057k83oyoPePPtE3hxLcns/z0McBh4fzAUDVEWNYJB1YXb9alnGwzsPxwuKl/SAekmX4hKdX0Mc915NCBD8W0uvCkhDRztaFt0xKj79LOvjB2yNZvhc/R6zBgPYe/JXdH6b2n2j/LVmGotTibeEKr1Wfh72dCn3a6+PhW/4a9wJrCEFm46WJHeScIvVWBc5JBnS+IcJLAjq8ZGWT3x5FTxLW9QzqxDbf1BPBId8T1K6yc+1e/IwsY237T1L7PJTILw9BA4CwOGRRMcxdET1xL4jQqLo4qKmI2PyXRbQny2iJbwCnfNwD5BIPN5b/mvtH/h2hn6D2kaR+aegRrsglkeWhL8bHxp6s3tT0hDdT+5TLN5AJDx5vKmXGgwWe3S4S1DezfdFzqT2qHFlEvwyIm3gAKItN6J4cv706UtQeOd+b5z/k7eu5B8fi93WfyFS5KqV/WLxgebjyaRzmm+n7xoep/bvT/KU+FdKu6T0t7THKyIT0duJgi89FLbERVsLtT38Hb++I8Dwab/EDxOGAHn8hIab6YJMLmrfneFY5AAiL39Ef4Yd353fq/UhfVHiKiXki6uEAv63CL46mHH7AqLQx4gGlGwOEhGB5Srx0Pzivy+hJc4+cdCc/AHlVk48dANhR4Ae6u4Wm2G8P8ouKffx+AACQq3EvR58zTO1ebsjVYVBFaDCGAtoTM+rj87rKSNoQdr/ocwDwtQl+QHhDvxB19lBGRhw4dYb4OpwX2k8A0CY8DH9v3W9T+9em9aXOjG+Uf8AdpuZFP/fo2ehy/TYAyAkxYnVo/f36V6jddc+8dqix/LCDnFOkVs+d9CCnWs/Sv62HtVhWOcgnrE6Hu3seqtxN7WkPWT9UzsKqj2+cNra9QRaRbY1T+2T2u9TeHNAHOSpjTa9wTZ/zoJFTEJfQ+4Uew6IQ7WsP6822X9wUKNd0Lxunn+vgrsqqpYZiegFqC/NFMCReXFJBfli00NDCf7MtLuS9kOc3Kt1p7fXjE15zibBKe6pvRWMu36gqL6zJEn8h6PDgkRMQbt0xccs9VdXL06Y077zvf5hvxn9+td7Qb87xbE71O3m/7epSoQbAyQT0n6FdaB3cuJL3/Qc9iDqP145Q+ybww4VKU7807ClwYfaBBBf79/s8eD4ILQTlUfNEg3tHxer6gFGxoslDi/9pibcTAKSCr6L2tUk+NtYm9CGm8mqdqfN+5XhIgLwosgPNFPnFUj3K56IdIhzWC+pg20so3LFFPtck28Q8MqQ9MduKvC3SU3wNfEyEkD04p+fkJ6vcq+eVHTwsvuIhDrSvtoHaD4MnFplZ0mHWMsyzxg9rn1jga8/2Pt7vAeAdG/lFxFieXxx5OSzq7eD9qi4OpAp1fUm3UOWfWSPmoi0l7Y2GPA+BVqjsrTNCxBsA5v3iMl94efWH+AVc061hqfSkrMeLBRM79obe3RmGYRiGYRiGYRiGYRgvCMwj5xRxHN9JPXI6YlxDYF6k7QaAQom7EVcT3Le1I8JPpfP1CVmHFcHzqH2uyesY83XIMpRnUVsbF+XzcoaaF6E4+/L8HPOPj/2xLOO9I++k9kSQ12Gqwm/hmkK0FgDGHe7ddHmMh06FPOQNvqhD6NeIvx8Wwn9emBO3Otka/x0HnF2yDEdkR2hP8tTfxZoKCQR6ItyzwRfkHlRLjWOyjJkGv7VpudwjQLlLN8TYAoCCeF4Hi7yMor7kRodISf/KFXyMz4r0rgDwdwe4h9SlndzT8t/HdFY4dQn9qn7uFdQQHgNzHrJhn+/n6XRVdFbNw016KjpA7ccK91P7zhj3DASAunAxrIrZqsvla8+4n3suAcD+Ba61pUKLq1XtxXUwx7201NqhBM8BoNwUodp13tbfr+6TZXQIgfhgjGuRJISAqOoPAFD0EB7CeHxJeyUoD8TZKe5dkUzoQRyO8UkzneZzVX+Jl3FptxadXVflHlBB4SntRYNKhTCr0Km+zKWyDKX1c6TI69kX4XafB53HdJI/r1KW9/2m8P4FgIDQcVw1wteeiaM6rLAu6lFp8fFTEAL0Xpjw8feW3tYwtc/79N5uoc7DsPsCPHS/s8X19hpuFfot8sVDCw5ant72Tq+M5Y4d5JwyPpzMkSlX5S/UiYhW/F8s8EmzUufufb1iougK6NCqgnAhTPq5Rk6q5UFDQGT1aIosEl6ExpVbuCMG8AdX/5oso19oCOzJ8QXsZb3cTd9L+tYrIzzUJizca/ujOj1yJnx6Imsesh9josTb4vNH+XTVEeGFKP0NAJjP76J2FTbY7tMv7XWXv4DNONzeFeDC0gBwDDyTS0zoQ61L8QPjoBAHBYBai7/5rxDp5OdrehN65yTfbG/r4H1qvqo7psqmlqvz39krtEoA4GCB9+2xAn9xiYsMKD0xffA2JuJEgyLziBcdnr6WWJ8S/ND5ieY9soxzmvzF/wmXf8c652Jqr7haKGRTGz9wirZ4p4qEeIgZAPzT3IeofUvzrdQe8LD9C4t1ekOkk9vFhQ0AfDn/KWq/NP5z8jsYY+JwAgCOlLj49Ko4nyeG43qM3zPHy5is8Je4w0U9vl7WzcNkRjJ8b6cyKcXFYRQAPFLk83ZYhPV2hD0ccPj4vF4ocz2hjqgOw+lq8QvJ3Yv8kGV7G7+QqXoIHY5G+ZycEJmz9ojwLkAf9nR38/mus4NrPwFArSnC0HL8eT5cPyDLeHKJawum4vyiPRTm4eT5Jg8ZBICg6JcHS9/mXxC7kpqbJnZsnAA7yDlFgoHYST1yiuVR+rdefBLaEnyjW6zyU+Eg+MZryTcn63Bg4QvU7gjB5TVtr5Fl+ITng4olrTRFphgA6SDfdPSIF//f2Pd/ZBlf3P42al+f5AtxPMjtKnsQoGM81darIRZZAMjX+KZktsr73UJNTzXqQv+cNt4nFsUaNwDucQAAC2G+YQiI8eXlsCghUoqmhRbJjKPHcH+Aew4lxeNIiIO7kMgwBmh9DHVMkxHjFwBe1sdfjpriBHFtQpdxoMDHh0h+h3mhpQAAK4WGVIfQj1IeBSLjNgAg1+DPvNrUel0KlU0t7maovduvBSc3xLnXwIXB66m9KHTPZkpaVynb4p6vi+DPO1/Rwrbx6DC1F8CF2de4ej4civEXk88u/C21/1SKHyYBwKtSN1P7qMtfoCZbT1H7Vld7X9w7w+eBwWE+yNNBPR/WxAvzV47x79jSrueRY2W+Ph0ucu+nHpEJbbys6zBa5Acc61O8T6kLOADoDItU0k1+wFht6cOHfSLDUBu459GhIr80TXs4ZNk+xPv+kLhwOSg8dgDggVl+8bpR7P3aY1r7syI8eO+Y5Pvcq+L64C3d+hVqP+LspvaFxii1qwN+AKg6Yp32871bXfx9Ezoz5IsJ1/V2CXy6ZSx37CDnFOmObITPOfHEFonwgZ4TGxJAD9TuEN98hVv8xWbW1ervoSBfBNNiAxlw9YZ/vsXd0+MiPMuLO5xyC79jkr+4vG/kFllGKshd4Fe28xswlf2nWNIu21XxEpev8e8YFZkuAGC/8Bg4nOez4cGSvsUOiuno4k6VEYrXISpulwEgFOAvgeoW+zAekWV0+vgt9aBInzzv6tAOlXEjJNy6s2U+j6RS+pa7L8k3y9+a5m3d5eFmVmUW3pzmG6N2DylgNwhB5YZ4QWv3cIgZFM/DJ8IRlkQaWi97lSL4M3Vd7kXiRTS9JbJu5MDFPesiFTUA9Inb9lXCe0IdvE2W+M0uAIyJ37Ho8AuZQISPPwDocfk80g/+gtYW0f2yKk7Xf6nn5+V3KPYtZak9CL5+rcZ2au8Na3HqqDiNDTr8RVMlVgCAyRLvd0NJvm86UtCHRUXxwqxeWubkhYysAirCa2Cv2AqsS+rnVWrwtqiIxCMBD6LpF4euovaGyxefe2f42rMh6SGdtQiZ7e7j+8+Kh5DBXIMf9twvMrKtqui5ql1cRFzXz+up+gwATImsVWEor1b+zpEQ71YAkAL/zEx4mNprYn1rCW9u46WJHeQYhmEYhmEYhmEYhnHWabkOWmc4q9SZ/v7nAzvIOUViyMB/khuiDhFTW/BxV2cAWBI6O5MlnpZ7Sxt3Ze539W1iOsE1cFoOv4lob2qdkB7hljonbjS93IApUb0Lu/hNn/IyAYBaF78Bq4rb+MWCShuckXVQgq1hcfFz36y+6QuKZ/7dOvdEcXz69ulch4cUlRr8eSg9oW8v/YmsQ0fyPGoPuvx59fl4WlQAWAQPu/A7PA3mZvcCWcaEK0IwhQfIXTMZav+5nqysQ0ik5I2L1SfjIVyhU1yszleFW7gHjxyVenimwvtER1jfoqmbdKX/qZ7nfEXPZavD3IvLL4awCmMDgEOLX6b2gcxV1F5ztRu/0m5XqaJ7IrxPJAL6Nn9vnq9vh3N8jfx8Vof1dqZE6EZIeGrW9fiqNIUXSYJ7T5Q9CGC3gXvmLYJ7HYSFx44H7Vxc3cN/50iauwRUhUccAGzK8PHVE+ELWFakegeAb09xz4cLxYRZaPDGeiqr9fSKDh+jjgibHy/p+XKywZ9HocyFbVVYIgAstrh3xBWdHlJiEwIijAYAJuf52Fjdxt8pBvqzsoyy6LsPL3KPnPVJHZ68IDy9isJ7XnmzAUDI4Z7lk1UeKpcTyWhSGS6jAABtQni91OLPq9bkGleu8Gg1XprYQc4pUsQCfDjxy0EKfBCnoA84akEejtDRxt2pH1/8O2rf7mEyqgo1n0MLfDMebPtZWUZLaASoTBRhD4r/6uVGxWKv0gkasEeItJXEC9qcOOh5ZEFv3origGOyzEMm/CfRfPph5oTA52qXH2Ak/TpEbKbJ+35bLUPtlSbfULy67TdlHaZE6GFYHOR0OzomvdsVIooOFyruc7m4NQDsL/+H+MQvUOuNIjY/1qE32/4l/jyGYvw7jpR0iOZlXSKLX5S/VKSSOkRsYo5rojRd7k6d9mudq4EYn3N72/nLbCzL3cZ7ojqT4D8sfp/arwlcSO1VMf4AoDN1PrUfy95F7UqfDQCa3ddRe13M+6rXDUT14V/Mz+vZEhmlrm78f7KMaouPH/U81MswAIyEM9QeEEvHdF73ibp4Obl/6S+oXQlLX5bQukrntGWpfeUqbm95eL/6KaF398gcD4XLe8ji98oVfH2aq/K+/4QQmjuKGVmHXvC55pB/lNpjTS3mP+vnF56KZEgnHok4vC0HY7xvR8T+U+39ACBZ5WtLo8IHoD/o4TJSJCVYJw5qvFyqHhGXHYdFkr47a3fKMkawjdqLQf7MA0lex2kclHVo+Hg20IjL9xLqIOelhvs8ZK1yLWvVS4+jue/COckVTzPFN1ZeDnKmlu6j9nPEIcmV6XdQe9LRcZ4lcQOm6jDReEyWUa7xF+ZkhHsltNxXyDLUzWxVbL4aHq7yiuI7poVHwKjIRDFd1i/M+4Wa/hR4CtjJRe7lBQDXpN9N7RM+7mVyfkAfPgyJlKHqeY5X+UFQf0hp7ABzIgPRXvD0yJtaO2UZipNpcD2Dl03sxhh/mQ2KtozHxMuqh2xq0U4+OF4RHONFeHhxibTxigT7RBr1WV3I3kn+PNRGdm2n1iXr3sgPchzxwKqP8gOpmgcBm8EWf+FVaZwn61pANOrnt9hdKe5t5hdjA9C6SaNFvmE/KmR4NqZ0528L8b5/SSef14fjWrdsVKQ/fjLLDzHrIjseAISEJ2VCZL8bTmpx3AM1Xs/eNJ9T88J714U+yMnEeR2C7byt/Rm9lR4KZ6l9ocwvhZ7M6ZulkTjvmynxYj8idHraanxfBgAF4em12eWZ6UQeDABARnh992d45rpyQ3vHR4P8mbaLMZ4SGcAqHlKDt4X5vH50XHh5iQsAAGgXlx19wmNHiXgDQKfwgmwLc4+dLc4lsoz9Qsx4XYsf9BT8fOKfc/S+qwbeljNFXset8Z+k9qZbwyPg4u7GSw87yDlFHCdw0qxVfnGXp7xQACAZ40KN8+4otfc5PCwqHtCPfCv4Qpur85e8tBBaBYDp+FFqn6/pdIMK9YKlslZ5YaV44Z0Xty7/a+IfqD0sxHcB4CLfy6l9tUgX7+vkmx4ACIu4itUB3meKdd3W2Rp/sVgR54eQ5/i5N8yRgnZlbogxOrPEvRZCGS3UqA5qCg1+MLdYeEKWMZjhfSLo47dTdXGg9fiTPPsJAKxfyV+w4sNC4Deh5yonyjeAjkiJHfQQ9nRBQ2QQEvvY0ID2RvN18TmzOcE35Op5BT1krVJi4464uer0izztAO5ZuIPaz2u7idpjIm03AMxW+MvsYo3/jqMFPqfPVXS/TAX5GH9lH5+LtqS1qHN7iM+H9Rafi47mdWasVEhlaxIHqR5CakeC3BNlosEP4McWb6f2eLd+CVQ6CeUJbo8L7wwACAlB1zVT/HBhQ0GvLcUmb+8OcfiQF/NISKQOB4BRke496PAyxhx+wA8AK9wBap8TaaBnKvql/PEgD8UBzqXWFQnuXbEkwo0AYL84vMsLj+9L/PqdIyFCSfdN8Hmm5uFSZ32Cl5Gt8b1AW0CvoWvqPOPvIR+/0FzR4p5gw67OnDXu5+81I8mr+Bd4aMuXEpa1yhsetneGYRiGYRiGYRiGYRjGCwHzyDlFHPjgnOT8a6rEQ4rWxfgtOQDERervySwPg+lt427Ej9aelHW4Kvgyai+42rNBsRlcU2UywL1IvMTl1oVIaUFEVaj05QAwGOOfSYr04j+T+Rlq312ak3VwRXLhnhgf5tMlHV7SEGEVqq2/UPgnWcZNHVzrICWiKqZKvK0PQd/0uULUWbn5dzke4vvdw9Qe83ONgcEMFzQHgIDQ4BCySpjNc8+Hrrj2GCjk+E2ee5jPI+G09pYJxPln8kd5O2TO02M8NCxuTkXMn69Dh8mo3N31aT5Gj+X5ze2xgr7qe8z9NrV3Nni4XkSpIQN4efpd1B4X3mpz0BoCWXFF3BHmt9jxALd7EQkuCuX1BeGpmQ7pvj8Y4278+QYfw0u1YVlGr3ACifl5v816yJY7V+fzwKBI0FBMcs8/L+RKfK56eIrvy67x67Ultol7FaQHeTv0TWhtprESn6sqwmPnS7PcG/Qnuvm+DAASPvE7hQh3hwq9ApCre4i7JeyM6zW0LlI954T4dDLKn2fcg9B+ROirTZT42uJ42CfHk7yel3Zmqb3a1LFwo0Vez26h+PDA0pIsIwre91UyDSW/dmf1S7IOfb4t1O4Klxuf8K1wX2K+F5a1yht2kHOKsNCqRFhke/LgNxfxcZ2Q9e2vp/Z0k4eXJHCRrEO+wRewtHBbbbr6d8b8fPLfGOIbp5o4OAD04YJa4kIeBJXVgZKqZq52+ir0cT9/+YmIdbYzqqcB9WIyVuIv9m9u4wdWALAuJdpShHZ8vfwNan9Z+FpZh6wIG1wB7tLtxTW2DRlqV67nfg8LT9jHv8MV3/F7j/GXwN/Zpvvt96e7qF2NzwUPWVqu7ub6M50p/uJfOaSzILXqvJ71Cm/r1Ea9CVUsjvGd7u4lPid/p85DAgFgLvcwtVfbuS7ZmKuFUFMiQ5FfCIwGPGxk83W+frnCl7okMjV1hrWbvwplGy/zPlVs6hCy9Uned4dj/AWt0q718vqj/EVyocb7/mMLekLsDfN6iERM2Bng8/qc1jPHfIXXYX2GC0M/vk+Hml64go+P4DAfw5c0jskyts7wvcC+Cb6v+p9hHub2hWP6ea5K8fGRCIgwNg+Zzg5keRjazuB2+R0KJZE4JYSGfWJvmOnWa09lgu/NKoXTf7FXWnab2vlB6djejCyj2FB7TCGGDJ4VFQAuCVxJ7d1RPjaWhGjmNr/eP86CX7z2tPieKCMyItZbVTwka2G81LCDnFPE7wud9CBnNvcg/dv29mH5/Y7LN0ZpkeI8LI6VD/q4NwAAtEQWiTi4nsPROm8HABhwePaSwTrX8Cg2dby4uiEOiTWwPeQh44Z4GVVphbuivBKlAj/YA4C6ODjLifjjJQ+HSdWW0EIQma9UanAA6I3wlwZ1aPaO3uup/dF5fYs34/ANYpuboXbl1QAAHQGeeU6N8QUfvzUFgM4WHz8Ldb6heP9WfvjQltAeOdt8/KF/6Sivw0hcP69pIRD6nVk+V72mrnVCjgmdgmSQHxxUxvWN5YoM18CpCg+O+Roff1EP2dSUUL46fB9saDH/L+f/hNovT95M7UmfPnxICZHSAzU+xg8076X26wKvkXXIiQlvX5GPn7VxPe/7ReKCVXF+gnFOWr9IFsT6pZRpu8X6BgBzQtPowcbXqf0cP/cgbombegCYrfIXyZBP7InEHAAAxVFuTyb4fBdepz37gn38IuLcNJ/vDuznBz3r01r/cE+WP8/hDt4nsuLgHABWB/kaqYTZl5raG6Y/wsdXf5T/ziXh5dXer9fQDqGV1V7g+lGzwmMHAAaafK0PdvLntXJ9VpaROMrnokcm+dqxFlwEHwAC4uRNeZXfXefz/jqRFQsAyg4/8G2IjG7FJp9HlJfYiw0XzhnPKvViyFr10vLTMgzDMAzDMAzDMAzDWMaYR85ziE+EHNVcfQLf466k9iVngdoLEKfrrr6d2rPI9Uwy8Y3UngqJ8BMA08291N7p8Nv6qIjNB/QpZUU4ojyV0+ecK+P8M8pL+J4Cj61f6+uXdVCZJPYXeVrgRZ9OjzwssqFlgvxGc1NGn3p3igxCyvupIjSNvGh4BJv8d8z6uOvs3CIPTwGATPsgte+p8cw+Q2EdHll2+G27Chvs6+A3S7E2faO5NMrnw1VC32a6qpenmSr3CFgT53EZcyJ2HwAqQgPgyZwOg1FMCM8ilU1mOMYns4vzXGcEAL5ZuYvaVzjcdV2lqgaAHclfoPaCw0PhHqp8WZbxKj8P4xwRt/kd4FpASyJ0CwDGHR5GkxAhZt8s61C4tvzF1N5yeZ9KB7Un5t48H4NF4TTnIcmRkoeSWfoOZ/heYafvclmHBxaEbksvH38PLOjskhc3eRnrRRr12ArtoeiEeYOHOrl9hdAi2eLBw6Mp9ph58TO8eO+q8MfxFt8nH2npUJ1el88DPWK/8vB8htpXb+R1BIDMWl7GFvB55tic9sTMjnPPoWSZr6E+oV0IAH6xXw8Ib+sNcf07HizzTGRbW3wvvUV4/TwCrk8KAJuafE5uiqyod5U/R+2uB9mKFxMtV68Pz0UZyx07yDlF/L4gnJNoWDhCqNELMw6Pg56u7Kb2NRG+2e4SYRsA0BI6PONl/rIa8ODKHBGpou8v/xu1v7b187KMkNio9svoLP1iojYdSivBy0GNIhbghVyd5pvMeku78au5riPMP7HVgxt/Z5R/ZizP3Yj3CmVNoUkLAJh1ePrIkwmdP8NI26tkGT1NfpCzNsTTXM66WnPlmMvniUqTHxgHw3zshDKyCuhq5weIAyKcYb6mX47UBnC6yudkL6Ky3aJfLtVPfxldEgc1xYZIfxzg7XC0rC8RtvsupXafcEHe39IpfWs+3pYzDZ4idmVEH2JWmnxSrorQ4XSA95lDDS1A/2SeC2NuT7yB2kda/LIEAO5f4PPAfIXP630xvV/J13m/Wqzytk6p+GUAcbFIdqd3UHu5meV2D7q4V/Wc3toR8KCn909H+PP4afEV9UO6LTNhfsA+tFIfHjBiHtJZzwtNo6LoUyEdiYpHXL4HDfv4XqFS02toWJxCqrVjYwdv66aHnCGhlXyMZtbwOsws6uf1jcMrqL1znA+g/pheWxRHhEj3CnFhCgDFBg8nn63wsVF2+e/s8fFEMgAwow7Warzfnh+5kdobbhXfr31S1sN4aWEHOYZhGIZhGIZhGIZhnHUsa5U37CDnFAkF4if1yCmUD9G/beL0haqGItx1r9flbsYRIVgJACtbQ9TeFuaCePPOtCzj0IJ2kWd4SGyABXHL/aC4WO3WesoQmb3hE74s53YIEVMPtzYj/PIJWREFc30fD6MBgExEpIoO8NsM5R0FAAsF3uCHityD47Ie4THA9WQBAIsLXAz8ZELnz5At8pBBAGhPc2+ybnGbGG5qj7eGy5+XSByChshG4wS1i6/y6lmo8t9xXpt+YAGRLl4JZDc9LOIHRWrvLnELrrKXAMD0Eg/PUo4NJRFWOBzT4V+jJR7WFBcp7fvF2gMAe52nqN0nxPoXXe4xBwANcI+3mI+X4ReimYebD8g6XBJ/C/+A6BILHsJd21tcePZQiXvEzYvxBwAZkSpaedy0hfT4OlLg88SgSBuc9PHx2RHRdUiK9Sse4Hu3zpDOZDYT5N4Ve3J83u+L6HBW5Tl05xPcE7MnwkVppyq6z+zK8nn7/Ax/XjG1OAG4yMfDYKYbvO9HwmLTBCArship1OA1kalpblzXYYUQRPaleRmZuPaEXlXmoVUzYp6YExnfACAoEh80xHw4XtT7DSVmXBR7oqIIR+92+XsPADxQ/yq1l2o8fLIuRNOb8OBeaLzksIOcUyQZ6IXvJCFUXe1ch6DY0i7Zx7J3UfuWtrdS+5jDNVdCIm4eAAKiW0xiP7X3tXhoCACk4rytUkHuJukl9l45Y6oNXs1DOOpQjE+spQavxbY2/vLUJjZWABAS7s6OeJEMh/Ti0Gzx3+EK/ZqyCHEBgKzYMKhnrl7axb4MADAQ4tnUDpXvpvZgICPLyPmEzlWLf8eCT6d57nB4ZiyVWrVU4i8mbeLFBwCCMT6A6uIQRW2UAWBMZO3oFWFRXl5mlT5NJsh/R66u+363OPRS80hZpGqPe1jp7699gdovdX6K2guunqtccfDW4+frQlocXgDAugx/sVDhQCHxNnydo8MnZ2v8pSEoVifHQwj0k7iP2s91LqP2pkjDDgAPVUep/WLfCLX71EQDYLLCx+ikw/cbQ4FLqP2Yh5fAuQQfo0EROtXuIUQz5ueD8PtzvK02pvUL8+cm+Iviq7v5fHmgIMJdq/p5VsEPnBaqvC3b9JSMkRRvy/wi/5K7F/9OlnHJivdRe0AcTsSjfA7IFvVefOkpPqemN/E6dAzrgxxVj/c+wZ/nGwb0nNwf4eND2R929Ro6Xed7acWS0D+MNvX4Gwnxi/aD4JmxFsXervkSy1pleMMOcgzDMAzDMAzDMAzDOOtY+nFv2EHOKeLADwcnvqHtbPLMPnWfvrFUKNfyRXGDFgtq90B1K9rvcnvT0Tfp3eEN1L5Q52FqQQ/hCjGhlL8kPJXTHtzClUv2xgy/JUjHeJ/w+/VtYkt4wzQa3KPAy83QviUu1Ki8FrwwW+O31MLxQXrkeJmug+A3kkNRfuNSd3QsXFur20NNTk4EOkwm3eRi4io0sb2b91tfhwd36jrv2xsyXHByTmRyAoDdOf68VJ+4a1Zf/17eyScKFZ71/QVdxucXuMjvrUPcw6okvM2iHlb67sgm/gHRZ8LQt6ZdLg97akF4cTn6RnJYDI9zRAKUlAgDLQjvKADYtciz+xwr8t9xX5W76APABj9PbNAW4GOj7iFdx0qR6WVAiJCq8QcAMZH2ZqS1ldorIoNRf0yHPXWG+VylxniHCD0GgPESn8/6Yrwt9+d1W17exsMbO0VSgqkKr8M/Zx+Vdaj6eFhTV5WHRa3wEDqsBJOPiqQhV6XfKcuIixCvhvBSros90YzoDwDQnBEi9z3z1C4iwQEAh3M81O2Dm/j4KntQbY6KfWy5ySu6MqF/SNPlv2O+yufcdIu/Gz1S+4qsw8WhG6l9SSSy2L/weVHCiyDFkvGcYwc5p8hsZe9JdTLawzwcKOjol59kjA/0mstdJUvlI9R+srCwH+ZQjYePrI7yDeTR2oOyDKU10hFaQ+1eQquSYkO+Ic3bouwhFEdlrMnUTi+T2ZKH0I9pEbeuMuJkRVgGoF/8D+T4ByZL+gWsJ8rbqjvK6xkVZ0kqmw0ABF2+6e9wuRux4yGUYM7hoVULbpba20ToFQDMi/CtoCN0eLr58/StbJd1cGJcKyG9T4Q9idh9AHjHVTzs4tB+HqLyy+1ai+SLY/yA/hV9fDN9rofQqmt6eOaQeIC/HI0keOf/pzGtx9Dp8jrMOPx3jjV1St+Qn5+y9Do8M0jGQ2hVSITBnNfGNcEyUf5SX6rpg4GYnx9874/wPuHOvUaWMdXkv0OlaJ7xkP1OpWqPissSD9FbmBLzXUocXE+Dz3XFhs4MuaaN16Gzjx9sl5b0GH95kR/uPZrl/aqshEQArE7y9UdpaVXEQn9VZIusw0RJ6LN52bwJVFigKw6EC44Ow5mv8n6Xr/PnFa3zS769eX2QEyvxNbB3nK+xCXEJAQDrxIXKA7N8rV+V0Fmr8mINnKpwu+qXXj6zy72f2s9zeEbEFdGflnWotfic6zuJvuoznNP2s9TedGvYk/0HWY8XC5Z+3BsezmsNwzAMwzAMwzAMwzCMFwLmkXOKlKtTJ711n49wd84g+I0MALguP9Ft83PX9GzwILUXy6OyDh3Jc6l9vLGL2qsNnW0mFuJujHE3Q+1eLnUiQowuGeBHsX8x/YQs4/UNfkP1VJ778XeEeB3HSvqHLgrxwIq4yftW9VuyjB4fvynfHuH98gimZBmdIuxiriLCLoTDjcqwAgBTNR7St+DjY3i4uVqWcbTF3dPzlQlq74vz8QkAMXDPhYi6SVfRkWkd3uUM8BCynjT/nd3z3AsFABpH+fg455f5Eucu6hvLXznEvX72Pci9Fi7u11n8IlHusRbv4vYj+zLU3nS1R07K5c+0IYTy+wKbZRlLYh7wuXyMVj1kfkwG+EQQE8K0fuHRkxLhsACwTYTctod4GEDQ8RDumuM35dkar8OoWMcBYJ1zDbWrLEnZul6/lNfP4Tr3BDvS4p5guRr3lAaAWIzPA9G1fB6J1LT77iV+Pt/VD3KPuBXK5RQ6+89okT+PuQr/gk4PGcBSQe5Fouro5YY8JzJR7Fn8J2pf3/56XQj4+rUgvK0HU3z8bfOQlfH+Be7Zt2eSh9Kdn+R9DgASYj6Lifn0qIcQsQWRBXNfnveraRU7DGCixttzBHyvPu5wofBBV4fE73b4XBQUa+hKl3sP1t0q9shavHgwjRxv2EHOKRIN9540LOhk2jnPUGjpbDM7wz9J7XMudyNutni4QiikU8RWGtzVsjfC04H6gnrD0dccoPa0w8OFvKQfV1lxisLN+Hz/RllGQcRqF8R7x54sXySbHnY1ET9/+ZmoctfXpJ+HjgDACqHrouKPF6E3FD6HH+SsEm7jQXFOc9hD+vFel2uRTIEf9BShX/JW+S6k9rHoY/zvW0LLBPqFV4WfVGZ5Y4ar+gAE/T3U7O7g2hdedvRqAXPDIjSxrLN6hA7ycNWNyVFqb5V0SF9ghL/YNydF+tY9fM5NeojwbA+KNLNC88iLPlQY/EBpxMfnmf0tL/MIb8ucCFe9d5ofLIzE9RhfkeChGyNpHhaVFGloAaAvyg/evjHBx/BFLR4iDQB9QgMnE+T90ot2WkTcyjRFiMo5zhXU/t3yAVkHx+FhMo6oo3+A9zkAaPPxBeiyxiS1P3iMz6cAMCuyQ3aG+e+YF1274iHcXGWF+3aVh96/Ls1DXAAgIRb7nelfofZ6S4+vtLj46YnwfVUmI/biIvQfAMJZ3q+OlfhctlXoDgJApp8/9LV53m9nPYRAFxr8M5d28jH+vXm9gM2Kg7VMQGRFFVqSM44ORY34+MHbepdLZ6yI83mo1nIBXQ3jJYYd5BiGYRiGYRiGYRiGcdYxjRxv/FgHOWNjY+jp6UH4v9x2tlotHDt2DCtXrnxOKvdCpFQ5gpPlv0lF+A3XNr+4gQYQ9PET9FKN38K1xXlGKS9ix90+LjS8weHPN+Qh7skVF3UB4bOt77iBksguslDlZbSF9W3igIgwOSY09eZr/DbkCef7sg6vjVxN7etC/BZ8sZiRZaSDvN+o51UXXkGAzhLWE+ZP3REZUmaDerob8POQpBXudmqPeAjfUtliBsDnkUxI/46ccPUPC4+cYIy3tTvGwx0AwKnwW09nNffAcuM6FBUBMUarwkskrkPE3HN4hj3/APdo8+e1sCbmuOhy6wD34Hh8kYdwOh7ch5VQ96IvS+0h4TYOABv9/EayPSLE41u8zwBAVYyveSEOvyjE3yseREoPFfkN9LkZfsvdLgSXAWCjmO/qLX6bvy+vhfQ3p/k80hMWY1xkAQSA+Spv73PAx1dQrD2bfLzPAYDrcq+72hj3QAxWtXeFf6UIs65lqb1/QXsPTgvR2J6wEMAWex4VSgfo55Fv8FDTkIdCeqL8M3dWxvnfN/U8oqoxkBFedSO8rWNFvSe6uMDXhXtm+X6lVtF7hXg/r+e6C/haPyQyawHAyDRfZ3fPcS/IjJ5GpEfpeJ3PuZviGWqvNPVeYZXLw11D4v0uK0IGvWQaNF56/FgHOcPDw9i4cSO++MUvYvXqH2hCzM7OYmRkBE2RLWE5M5x55UkPQ4YdvuFIeXiR/G6N67IMOzz04xxwN+O9zgOyDoMujynvFLls1UskAHyl9K/U/lNJrhDvRaW7KFIaHsxxd85oQJfSEeITa1rkzK40+ctqd0O7v6u5PSJ+xgVRHpsPAPNV3lZhP+8TVwX17ygKXRaVcUOdobgeUjfmGnzDrjYLfi9Zq0S6Tldk5PAyj9RafEPgE1njAiJSoH5Ix6n5F/nLqPsIDyVwYvog1dfGX5jz9/FDlNTPeLh0WCFCD9Vhkpe3nyW+qS+N8+flPAdpSVUYZ0ocDORE6AigN7JzZT4JqLUHANJB/h0+cQCikts9zt/fAGg9rmqLu+CvieswNRW+ta2dV3RFVIdEtIX5fFgQ2WhyHlK1T4hU7HExvmYqfJ55eZ8+eFPT9tIEn/djBR1qmujgnwls4rqB5yZ0hr0NY1znY36M7zdWJXi//MUnuQ4kANzcw0PSP9x5A7XH/EqgDThQ4H3iwMIXqH1l+l2yDJV+PCIOMf0d/PTBz88uAAA9x7hO3MUiBfpTU7xPAcDWCNctS6zkE2K4U689oUX+TB9c5OPrU7O3yzJeHX85tbdEevKDRT6fbk5pnTl1wTxd4u1wuMnlN5quh5D2FxEt10FLSGQ8F2WcaarVKnbs2IFHH30UjzzyCM4777xnbY899hhuueUWPPDAA+jq6sJ//+//Hb/5m795St//Y2et2rhxIy666CL8x3/8x3H/Xb2EGIZhGIZhGIZhGIZhvFj5zd/8TfT3/6iQdS6Xw7XXXouhoSE89NBD+OhHP4rbbrsNn/rUp07p+38sjxzHcfBnf/Zn+MxnPoMbbrgBH/nIR/COd7zjWduLmRQ64T+Ju3BTHGI1PLjFbXF4aFQZ/ET3odZ/UPsO/3WyDskAv2VTt6aqHQCgM8TdnQ+X+W3iykpGltERFt4ywrPcw0UegiIzVsrP7ee285ulPUvaK2F3jqufHfZxnfufTl8sy2i6fKpIibCoWlP/DnWbMSNc8BdE9q7psvYUG/XzrG8Hm/wWLtrkN5oAMAzu1l13eEuMlnU2pzEfF/gMODzDUEtEdoRWal/nOREVuHuCZ2jIhLRXwmyFexVctpV7idS/w0MqAKCRH6X28JAQSk3pEJbmOL8N/I+nuOdQe4jPyfGAXuqVaHqsyX9nzNVXzFNVHh7ycIvfvL4Mr5ZlKO8ktUOZ1d1O8sAC73eHc3xxOZTQ3jKXdfHntSbF54mhlPagKguPmxkRynP7hA4HWhkXXnUiHWHWVSEqHhZyQSzFb8I/crcO33pf+z5qD2/j84Rvrc6aExXCtX39fK8QfIh7/XywpH9nS6Q87InwtsyKPgcAPofvJ16V+Q1qVxIGAPDgPO9XTeHx3ZznE0lgld4rdO3gdfA9wJ/nZ54ckmWExngClME834vHk3rCVK+F/VE+xt/azrPnAcCBJb43G4jzfhWpcm81FfYEAHdWv0vtlwcvofb2ZobaG3gOFqdlhPuf/850GWeSr33ta/jmN7+Jf/3Xf8XXvva142yf+cxnUKvV8Fd/9VcIhULYvHkzdu3ahY9//OP4pV/6Jc9l/FgeOc943bzrXe/C5z//ebz//e/HzTffjFrtpeX2ZRiGYRiGYRiGYRjG8iOXyx33r6r0FT0wPT2Nm2++GX/3d3+HWOxHDwrvu+8+XHHFFQiFfnBJdt1112Hv3r1YXNShtM9w2lmrrr/+etx777147Wtfi/vvv/90v+4FTxVl+HHim/0vL36E/u0rMr8uvz8PfjObBBfc2u6/ltqD4iYDAEYbPMX5MXAPj5arUzuuB0/B3BXgvzMZ1OeoyjFoV4HHk8cDOlX7buExsyYh0jwL3ZeiSG8OAI44j90Z4G3tJaVoX0yJtPF6JjykP96Q4jceyqEtI1KSlj3oNfTUuLfMffn/y/8+dYEsYwgD1P5A/avU3hYakWUcXuTfoTxylCZER5se44lu8Ty5HiUWRJpoAEiJNM13Pco9WQJCLwUAVia5Z0P9Sd6vpkpatHk4xeeRwTj3bHhwgcf/q3kGALJ13pZPOI9Su8/DvdC5vvOofbvD16+vlf5BlvEz7hupXWnkKE/MLy9qj7i+EH/mo0LYtrSkhTW7I9yTpeHyG/9kQGuRFERK3pywr0/rLeYXc49Q+44ATxLR5eN9Py1SpANAqyXE+iv8d751Fde2AIBDj3Fh2jVhvu8KeNH6EemLfR38O9pWcS+ti2v6d46LlNnzYl4/VtabhSMF4X0L3pYFDzmcr05wrZ9Smbf1Jz7P9xL/41fEAgjAN5Ch9kxujtp3TGmvu/Ey7xNTwut1KKfF/HuFuPumFP+OfEPr05QawuNGTUXivf2hGvfWBoDN4Ps/Fa2wBL62NPHScpZwceY1ctz/9NEdHDx+vH7gAx/Abbfd9uN/r+vipptuwtvf/nZccMEFGB0d/ZHPTE1NYWTk+P18T0/Ps7a2Nr5mPMOPdZBz5ZVXHneCtGnTJnzve9/D6173uhe9Rk7dqaF1ko3gQOYq+reTDhcVA4CEEORS7RsUIqa3lz4j67Aj8npq7/Bxd805HJJlREQ2C+Xm72Vop8QG7tXd/KBGnAsA0DqmFbFBPCzeCR6sHpZ1uDTBX+wXRUYND0nG8OgCd9m+oFO8VHhIM7Ymwd2IQyJM7fEsX+xXJvQDna/y79iRfBu1R10Phw8h3vd3gotBfjOn42fPbft5+RnGQo6/iHZ42Aj7xJnxYZHZ55cf/z1Zxic2/Ta1+8VL+yVd+nfUxMvqhDiomRDhJwAwVeFhSbEA7/szFd63l8RBK6CFiDc3z6X2TFCH26msG2p9+/mOt8oyfA4/kKoLgdBcXbzUi/BmAKgKsfGaw98aVsR49hMAmBLhj+Mlvr17UITkAkCvnx8G5Zt8zl6X1AdSlwR5v9pT4/um9aEeaveyvpXF4UGhyOf1Oya1qOzOziy1776Pf0e+pueRjf38xT61kr8ItsTLbLWmXxn25PgzfyzLx58XbfhDQpi2x+HjJyaSTABAWWxalkT2u7edx/duzUU9Jwe6+H4kMMjtK8QBCgBEAnx/eOd0htqH9RkLjomsimpOXqrpTnFngYcuXhXnYYG5Op/XZ5s8XB0Ahn388K7Q4GUs+pTYsb5AM348jh49ilTqB+vdf83K/Qzvec978Id/+If0u/bs2YNvfvObyOfzuPXWW5/Tep6IUzrIyeWejpX8whe+cNz/BoBQKIQvfelLz2HVDMMwDMMwDMMwDMN4qdCC1s58LsoAgFQqddxBzsn49V//ddx00030M6tWrcIdd9yB++6770cOhC644AL87M/+LP7mb/4Gvb29mJ6ePs7+zP/u7RXZUn+IUzrIyWQynsSMX8zpx9OtDvidE988lsFj2kYr98nvPzf0KmovOPwG7LEKD6k4L/JaWYeww7tF1OW3GfkqTysMAJUQvxnaV+M3CeubWvhP0RQXIoMR3Y8T4qb834/y2/xeEbI0Xt8l6+AXKenXpvlNnhfPo8E4v31SAqPbMkqQEljVycdPucJv/Mcn+a2PB61xhIVXgnLjV6lyvVASKSavTWoRtKiPj2EVsTe0lj8LJ6Zvh+tHeSGdYX479f+2vleWcfskH6NvGOLj04sDabbO+/6RkuiXZT3AUiJUVAV5rozxdpgo6XVbpbWP+XnfVinvAaDunt62bEYI7QNAQYRQOgHe1jUxUfg8+IMqMdVt4T5q747+2AlFn6UiFrjNce31UxRCw6kQD8sQ+qIAtPdtrcXXevU8cnXdlosivGReeF90hvVe4Z7ZjPwMo8tDGY1x3laLh/kYXysEsCc9hIl+e5rbR5LqeelJ+XH3bmq/JsRDNOHBseFfl3gY59tbr+FF1Ph8+dS3tSvLpiQXGvb18P3Iih08xAwAYo/z/cZ1ft7vVMIPAHhgls81EeFt/blFHtYLAFdFt1D7k3netzsDfA642v8KWQe/eD/eX+dyDuOlh6jdPc310zh9urq60NWlZTf+5E/+BL/3ez/wKp+YmMB1112Hf/zHf8SOHTsAADt37sR73/te1Ot1BINPL5a333471q9f7zmsCjjFg5w777zz2f/fdV286lWvwv/7f/8PK1asOJWvMQzDMAzDMAzDMAzDOA7XdeCeaY2cM/T9K1cer8+YSDx9cLt69WoMDDytk/nmN78ZH/zgB/G2t70Nv/Vbv4Xdu3fjj//4j/G//tf/OqWyTukg58orrzzuf/v9flx88cVYtYp7BLyYiLhhBHDi25kNOJ/+7dGojqPOuTxu/Vj9YWpPR3iMppdca3WXn8A/XvkKta+OXUntADDu8LS/xRaP9Y4HXibLUAKfd87wE/p3rNV6J90ilea1QqBwXGRnvSF2o6zDvNDAWSOEVNfEtYDamozWU2C0p7RHTiTBb9vdRf48L+vkZXxtUotFPtXg3mQFJ0vtPg9p1tMtrocy5+MiiFuEUDGgPYv8jrhla+dt7fNy1S60RDa2Zal9QdySA0BfhNcjLgRdx4r6hjns45Om0uDYkNReJMkgfx7pIP+OAwWuN/T3838l63B59E3UPubjc/aR4r2yjLWxl1P7xiAXAvfiVac8MKJ+/iUBcas6HNHu19UmvzkdLfK5KuzX2jJHC3zeHk5yT7EjJZ0afFWcj8Gw6PwJDzvMo0X+PBbqXLjliJ9rkezwMF/6Hf68gmIO6A7rDCd78/yZBsU80vKwXb9/nn+mW2S1LzYy1H7Ug3ehCoYoNk5PbBwAbvJdT+0PLPC93bifz2UAsC3EteqUCGtReGrGhFc6AOQf4Z9JXcqFspS4NQAUtXY7JeRBNH17F/cM2pfl3tQXB86RZVSFB6ISoC+JSJJ8Qz+vziAfYFPYT+3dUS6w3XLrGKuOynoYy4N0Oo1vfvObuOWWW7B9+3Z0dnbi/e9//ymlHgeeg6xVhmEYhmEYhmEYhmEYxg8YHh4+YTKHrVu34u67eaiowg5yThEfnJPGZB/0PUX/dmNL3wzNIEvt0QC/za+3+E3fXEDr13Q2efz+SOwyas/BQ4rKpe9T+5UJnh3ISyaKmLh5vUbEFycC+sZyTc88tQ9kuMeAK7JavTWkbzuUzoeStYp68MgJhEW2GRG668V9cXGW35hMF/iNpspQ5OWmbyTPM6CMNfmUqW5cAMAnMssp8k39vLLidqneEp4o4nmqNLcAEB3kt4W3fZnHAP+3dfp3fvog94B631ae3SQgbtoBoCHG6EicN9ak0HYCgGmR2aonwtsyIn7Hbw7+f7IO/zbP06sezt9F7enosCzjieznqH0w/U5qrwlvUQCYr4lMLlEukNET4c/ziUVdh/3uUWo/LzxM7UtVrYWg9BgKQmtkdUJ7o7WFeBnqFrxDrBuAzlgzIzJKVV3uUuBlrxASmXs2tnNti3kP6eKPFHh7DydEtjQP8hgHcnzO3CjSwReEF3NV2AFgrsq9k5ounw/7otqrNSUcQqsiTXO6pb3jh8Lc887v4/3OJ/Yjtx/TYqZXNrlnevRAltqDK/UY71nF3xnuvHs1ta+K631yR1Sk2BNk61rUSGXs7RT5x1WmwYRPr+MNsRnvBc+cta/2HWp3Pax/LyaeT7Hj5cxpK+p5ET8+HW677TY4jnPcvw0bNjxr/9SnPoWrrroKqVQKjuMgm80e9/ejo6N429vehpGREUSjUaxevRof+MAHUKvplwTDMAzDMAzDMAzDMIwXEqfkkfNTP/VTx/3vSqWCt7/97YjHj7+N+Ld/+7fTr9kPsXnzZnzrW9969n8HAj+odqlUwitf+Uq88pWvPGG+9qeeegqtVgt/8Rd/gTVr1mD37t24+eabUSwW8bGPfeyU65LwRRB0TqydsrK1hv5txENGm2Hwm4K8y7PJpME9dg7UtY5BLMBvIgrgXih+aP2MnuR51H7A2U3txcbFsox+kXVKeUYUGvp5hWPcY6ZtA79JcHz8ILTl4Wa2yZ0O0BTh+82qPs8tZvltxFKeu7vUPGjHZKu8jO/M8pt2dZNe1M5N0rtpW4x77LjgdgA4WuK3U0edY9S+6MvKMlrinsHn8Ju6epY3RDCtb/r8Pbzv//52Po+U63oe+cRl/Duml7jXXcSvO0UmwZ/XngXuWRQUN7MA0B7lFwu9ST7I28WNZ9XDDXR4jsf374hxDZ2CuKEGgGiGt1UmqJ65h2xpYsociPEbZKV71h/V2mkT5RFqv3OK97v7mtrVutrkGW1GWhdR+7YY97wFgIK4CL+0i/8OsbwBACaF7kpIZQBzuTahlxvXxTLv+ytXZandL7JXAsCV3bzvV4TnnxfeOMzbKtfgZdw7w39Hrq4vQP1iX6U8yZQmGaAz0xV8XCMn1eKaLACQq/O+nRQaNyHhTX1OWs+X+5f4Xry5i7flWpH1CgACXXxvdqHIJjqa19m3FsQ6XBR77ZarPXKUo/N4iW+E9/sOUHvK1Vn+1vn4/m+uNUbt2wLXUXvDreK74JEfLyZarjddvNMtY7lzSgc56fTxk99b3vKW57QyJyMQCJw0p/o73/lOAMBdd911QvszhzzPsGrVKuzduxef/OQnf6yDnEwwiJDvxJvJPj9/EV0UorQAsF6E4qx1N1F7Wbg6n9+8UdZBvdZXmlxQuVDXvzMgdnhBYY95yPKsBAr7xYv/lAh3AIB6VVSkyRfzlnjrKI3rQ5aFee7WrQ5RlNAcoBfa/QU+lTw8p8Ugf2ZYiDILMWTFkD57wFKNP/M2/Q4nyYkyegPclbnuYeXR40dsQjtFv+vXBwNOB9+EDo7yDcnMXv3AMv38ACPTy+0B3fWxeIA/9PlJ/jzPa8/KMjpT/KCmY4T/joY4zA1M6+cVcflh7Po4b6xUMCPLaIGLGQdFt5st676/Jc03/b3iBSqR4m29tqq3TZPz/MUlE+Rtua2kxfz/Zu4xal8f4C8V7WF9cLAqwdu7PcTbuuLhAP/RBd7eLXG6vrmNH8KEPaRHXt3DxVgjIvFB2MPe7po6F7H/9mg/tY8Wdb/rFX1fHaytF6FXR4t6PzIhXph7Y/w7kh4OxZQ49SWxIWrP1nQZmzK870aDvK1jCb7G+hf1XDZe5u8UPvB5ZniGH8IAQHiE9+212/nYaN+nE1ksFfkYfWSOH5Jc1iNUugEcyvP2LInDv0t8/N1KHUACQHeUf2aVs4Pam2Kuq7Yq+K4+mzNeYpzSQc6nP/3pM1UPyv79+9Hf349IJIKdO3fiQx/60I+k9joVlpaW0N7OJ45qtYrqD8X65nI2egzDMAzDMAzDMAzjTOHCgXsSTdrnsozlzgte7HjHjh3467/+a6xfvx6Tk5P44Ac/iMsvvxy7d+9GMslPo0/EgQMH8L//9/+W3jgf+tCH8MEPfvBH/rvfOfnJbJu44eqJag8P5UWiwkNC4sLEiyhSQHyoPcw/UPYgiFcWvyMtRBa7w9rVstLk9dyb5zcuOzq0F8noFHeX7q/yA8Bcid807Jrj3w8AT+Z4v3oqy9vqlSt0rzhc5G0VD/B+uz6jheJ+9pHfpfav7/gNau8UgrATJQ/inmFez4i4YC4K13UAGEryaXexytsyrgYo9PhRAry+NvG8klrc0x3ht6LBFVzscSDvIS9qWYgoJoXbt0gDDQBd93MB6+vAQ+Hi7Xoeie/gHhpOTKx1D3ExVpXeHABGwrwOnZHTTzW9JKZtJUzbIeoAAF3h0wt5aIl1IxTVnoFDA/wmXHlgHVvUrmLnpjdQ+1yNt9Whgm7LWdF114jhVRJtCQBX9QoBXjGnqlC6jIe+nx7kfcY3KEJmg7rzdzSmqP28PO8z9ZYO7VB7npDwTlIeO2uSus/0RD1kFSB4CYVT++ROsVCnxProhVqDP/NAlP+S4S7tLfPkEh9gR4XHTmFa77sCKeE51Mb3lx3rtJBx4BBvi5QIIYt7kKVQ7195sfZ0ipengIcuExELmEpKUBLvTi+GQwfjuecFf5Bz/fXXP/v/b926FTt27MDQ0BD+6Z/+CW97G89s9F8ZHx/HK1/5Svz0T/80br75ZvrZW2+9Fe9+97uf/d+5XA6DgzykyDAMwzAMwzAMwzCMHw/TyPHGC/4g57+SyWSwbt06HDjAhan+KxMTE7j66qtxySWX4FOf+pT8fDgcRjj8o7Gjs9UagifxyAn7eazp0aI+uV6d5B4an1v6GrWvcbjAYZdPezEp/ZoVMX5CP1bUgnijLr+dWlvm8eKrE/qmT90uqdvfvXl9m6F0dI6V+O3UwSIvo+RBFma2wm87+uN8mO/juoAAgGPCFSwpxC283IBtansjtUf8/GY1IfQaoJ0vMC9uoCdEO6gUloBOk6loC+vbqTsXuIfGlrTw9FI6V4seQk3jwmunLUPNLRH+6gkhlAoPz8vp5voyPRfxFLGyDoC+0T/K58u6eBzqph4Avlr+IrX/bPhGXgcPV+kPLfLJpi/Eveb647rv+4W4dKXK5+x/28PXniu6srIOnUk+2aTSXHB5Q4aPXwAYEAL03x/nHm/KsxYA1sT5Wt4W5hPm4aIWFVM33bkaf54q5fbmlIe9gtC2QEWsLR48cgLreCKKwZkZaj+c03u3OdG3s3XeFh0h3tYPc7kUAEBCO56fNkeEh/BYga9f4xW9GegM8r14to/37ZVC1kUlygCAsRL/nZtSvF/umdDaaCuE52t7B/ceDHsIjKgKXbGvT/K2VEkoACAvFqCmeGOfLfM+M1rLyjqsifB9lXonqQiN03rrpZV+3PDGaacff74pFAo4ePAg+vp0xoVnGB8fx1VXXYXt27fj05/+NHxeNtaGYRiGYRiGYRiGYTxvPKORc6b/LXde8B45/+N//A+85jWvwdDQECYmJvCBD3wAfr8fb3rT06lQp6amMDU19ayHzuOPP45kMomVK1eivb392UOcoaEhfOxjH8Ps7A9uuk6WCYtxV/Hv4ZzkRv0ng79E/7Y7om+n5ir8xPWG2CupvSZumCN+fYil4jwPF/gt3B3lz8kytkZeRe33Nr9L7Zc3r5RlqNj4JXHT58HxAe2h0zshP5ATmbViepJZk+KfiftPLy4XAKbL/DMqC0Q6pBvzJ9vXUXsksETtAeGxEwvoZzUvvJsW6rzvl6G90VaGeDx4SsRqRz0Ea1+S7qL2WIDXs3aU3/QFG3tlHXxtR6jdWc11JxwPOjxQsfMN/sxd4W0DABCaD+7gCv73InMdADjzXC/BneWeLMeOZKh9sqLH3xbf1dR+pMD7zJSblWUMB7mX1e7GUWqP17juEgAkhWdetca3PesTfIz/61GtWxb08c/85AB3bRjoycoyUkLD7bLgBLWvW9Rpg5NRXoaac8/x4An25QmuB1Rs8Dm57PLxFfZrF5GWyIZWuJs/r3CXnpODW/mcHL2A95mXt/OsVwDQWORttTTB96ATC3xtArR201PCO/CSTv680kE9X1aa/HeoDEYHfLtlGdsSF1N7WWjk+BO8T0Rj2oXxLasnqX3PAu8znxvTa+jLe7hn3xd38X77G5uzsoxwgD9TNUt0KI85aP3QVanT0ybsbaqxoT3Ta8IraLTM1/mGq/X2jJceL/iDnGPHjuFNb3oT5ufn0dXVhcsuuwzf+9730NX19OTy53/+58eJEl9xxRUAns6wddNNN+H222/HgQMHcODAAQwMHJ/61PXir2cYhmEYhmEYhmEYxhnHNHK88YI/yPnc57h3x2233YbbbrvtpPabbroJN91003NWn1clb0LQd+LbgL4Yv/VUt/0A8FSDn8AXmllqf03yHGoXDj8AgPsLXI9hY7ib2l/t/1lZRiLI2ypSOl9+h0I5LqxP8xG8Oq5Pv1fEeax1TdxIXtbFA4zHy/om/b4ZfgN9QSe/kVRaQQDQL/r2A/M8znol9M3Q/fM8Fvv6vtMLiSx7uB2eq/JnHnJ4Oxz18bEDAB0N3hZNccCcr+sHtj7N67lU5/bRvRlq75zhzwoAomneJw7+M79VbbS0Dk+PKKOtj2uRRNYLIQMAvh4hAtCpb+okM1lqrj3BvdEWy9y7VDjMAQAO+/ZQu7oNbHd0MoB8g7dlP7iXlsrGBgB+R2gluPw79hd4v7xrXmgiAVgf5Z5HT4osLQfy2lvmwj6uo5Pp4H1/IJqVZTRqfM7MZrmmkdIrAoDVCb4pma+e3rw/K/Q5AKCW5X3CF+S/Y3q3ztTUG+L9RmnoBLbwfRcABIS2WWiWz5fxx3gd5yvaq3ydmC7jAb5fWajqMpQX8XyNew+ucNfKMlLCkas/IbIqiq1bcEDviQaDvAzfw7xfBhztPaj2RT+/is/7T4m5DAA2Zvj69cYh7onySFbPh/MV/jvUTJQTGjspD17ldXEqIJwLMRLlbVlrVfBdD/KExkuLF/xBjmEYhmEYhmEYhmEYL37MI8cbdpBzisSDPoR8Jz6ZFdIWUvsCAIbr/EYyHuAZNVTmEKXsDgAzzii1r27xmNnBhO5WSr096OMn8DG/h2wz4gx+rMgrscaDREdCZO0o1/m1zq4sP+Ufjnu40RRXR7vmefCw/yRZ2H4YlS2mO8w9GyaL+nltTPHb3ZbLb6f8Pt5WUQ99pvMEmep+mKUab8sVTe2VMA/uzTIS5DoEaQ/ZZnIiyUpnSOgUxHmGvXiXKADAsf38d+zL8dunbjG2ACBc5Dfhex/jt9w9B3T2kkSYezYUqiKbWljrJhWqXKegXWQzVF4m3WHd9y/yXUDtCw3eJ/bgflnG5iDXuFEaA5Ol08/aobxEEgHeVuui+pY7ItxB/+UIL2O78KIEgIif9+2hEp9nYiHdL5cqvN/tz/F1ul1lEgRQa/G2WqjwuWooxueAuape32rC8zUa5nVoNPScPPEQr2dvmXtYBfq1148vzZ+XskeGeJ84rzAt6zA+w+f96bKYs4VHHAAcEJk27yr9PbUPJnbIMgoNPr4SMb4+lcZ4v0sk9PgLrslQ+4pWltprD3rIpiZ0rh6d4+1wuKjL2NrO57uOKF9bsjM6NdakSPGqogCO1LkOVqLG96cAMO/jWneHa9+j9msiN1J73UOWTeOlhx3kGIZhGIZhGIZhGIZx1nk+skq9GLJWWR5uwzAMwzAMwzAMwzCMZYJ55Jwi5UYLDd+JXRGPFvjJnocIFil0uq/Gxej6GhlqD54kdfoPkwYXziyLlL6H89r9ryvCu96jRf47z2/XaYPDIu12O49mwERFfABArxD/U+E+l3Ry1/P9ee1ir8SKlQBbWIQzAID6SFDEyq1K6jJWRHm/6RHC0nGRNjia02lNP5/7N2rvi55L7Rt9PIU6AEAMjwUh1PhoXQsq97s8RPPSTu5mnMjwtvQylzVa/JkfKPA5oCwELQHg38d5/OPLunlb5kRIEwAczHG37jkhpqrCngAgHeRz6lYf7zQDKR5rUBKpcgHg4RYXO74guIXar3CulGU0xVx0tMRd7EcSOrwkKEIoQwHe1u0i7LAnqvvMgws8DLQKPu/fP6vjevfn+NpwbjsXXI6L9REAZkRY0uWdWvRcERFr5APNR6m9tzhM7T1RvVdoCPF3QK8dirk8D83Y823+vLzcG1+4mqecT6zkY6NVEWnY83r87c/z+fKr47ytz+PNAEDveVbHr6L2REunUe8UEV7BEJ9HXLHOtzzsR3yd/EuC6zLUPuLLyjJGH+AhzquTfG1ZraOekE7y8ORKhc9lPRH9TrEhw7/jqSyfc2Mu79uOh03PEnh45I7gDdR+b/O71N5yT38eWk64z4NGzoshebV55BiGYRiGYRiGYRiGYSwTzCPnFJlpFBFwTnwqenfuk/yPPXjDtMU3Urv/JKnPn6HqbqD2pocT3RxmqH3K5TdL0YYWq2uU+On3U/VvU7vP+SlZhmKGX/6i4ern1V7gYo+dQuh0j7hVPaa1WDEgNNh6YryMhocj78N5fvt0TR+/rUgGdL/b3jVP7e0d/Pa3VuHTWUTcxAPAG9veTO2HirwOoYDuM0mH3+jfWf13au8Lc88IAJhzuehe0McFDOVU5eEKICC8SCrC42aqotN9Hs7z8XUsyfv+YFx7FHBpd+DJHH+e65Na8DUmBCeTUe4hFYnyMsJL+kbzPN851K7Srx4p8VtXAFgEz50aEDl7g472CFD9LiQ8bpQQ/0xZz5edQS4qu9Tgv9OLAH2tyetxUAjCeiljQ4qXcaTEf2dfRAu61kVzRsDX2JDYxh7y4PlQrfHvCBdEymyxnwGAO2cy1L5WiN+GRb8GgMdHuSfm/D4+Vynvi8cXtSfL/fO8b68TXxEXYuMA0BXhZeyd+Cq1r0q/XJaRF4lH/KKe0S5uv/fbK2QddhTHqT28hTemv4uPTwAIi/nwiPBIjYi1CwDSwuNGeUXEPSSqUPneldjxsSZfv9aE+J4JAPK1AWqvuHyMvyJ6ObXXWlX8A74j6/FioQXpwP6clLHcMY8cwzAMwzAMwzAMwzCMZYJ55DyHXJX6VWovOfrGMi1un5TGzV5nP7XXXe3iMVXgMenhJK/j+uAmWcZijd9wZUIrqV3FSHshKlLErk/q20TlcbNU4zcR4lLVU/yxaouYcGwYK+sbldcM8kJ6RDusSGjPh75V/LZeeYmM78lQe8JDut2QuI5/Ejx95PnNy2QZ+3z7qH0gtI3aO5rKRwRY9PFUmgGRgrksPMXCTX3LXWvyjtcr4t6nKvqe4ScH+RLWG+GeLEs1rXfy+BJ3eRuO8bbIBLVHzkSZezE2hd6Q60GHR1ETqU3V2GgL6Lb8j4W/pfZXpP47tR8u6JT0fuG5oLQt2uU8oXXLqqIt76n+C7VfGLpRltEf4P1S6ZrVPVxF7s6KFMrilrvc1B4Bqueuc0ao/ZCP68Jcmc7IOqj04YUc/x2zIk07ANw5yV2AIyv4HJAK6gc2U+X16Ajx7ziU53u7BaklBOREx4rUeFv36qZEW4ivX69N/wq1h/x6bcmIMnxCY0o5v4+0Z2Ud9j7G9Z02+LiWZGgdf54A0LOO63kpbaddi1xjB9BeOy0xC4wLb2sAeDLL5+3hBJ+310N73CgiLu+8bX5ujwqPbn9r+WdYMp577CDHMAzDMAzDMAzDMIyzjus6z8kllSpjuWMHOadIDQ20ThKLmXCEFgm054PyuOkMi1vP6lpq/m79K7IOO2NvpPYOh5/QV5v65ige4F1vB7bL71A44Dcm6lZnfVqIDABoT3JPk5zQEJir8RQNR0v6BmwoxvvVZZ38xqUtKsSCALS1cU+uQFjEiw9oXYnAMI/3dov8xmVtkGvsjD+l3ZtmyvwabYtzCbUvutrzaL52gNoHgudTe7tfiCIBUFONWrr+fS/3iLth1TFZhbjwbMjVeS3iAd1npqt8vlwr9GlcD7lgsqKeQR8fo2nhmQQA61N8jPqEB1Wtysvwkjmr6vJOU2rwOlQ8zPsr01dRe9LH19AOoY0B6EyBSttC3R5HhCcnAIyIdfq9XW+l9pqHm1flUaPWt2xNl5EM8u/oEfN+yUPmuaR4HuMt7l3Y5XKvhZT4DYD2Hpwt8jl30kOGyw4hHbg7y+2Hitob7aYRXkh7SGj9CA/ivHYuxGyFz/sTFf6813jITOcX86HybFBZNgHgMJ+SJUr3ZSqnvWVqTf47Hnqwj9p39HCPHQAIDfO+vXqW76uiQQ/euUITbM8S35u1efBGu6CT9915MXxyNT7ve8nUedfSJ6j9Zel3UftCnu+zG66eA4yXHnaQYxiGYRiGYRiGYRjGWcfEjr1hYseGYRiGYRiGYRiGYRjLBPPIOUXm/dPwnySE6r6Fz9O/3dTGQ5YAoNTi7paHyzwMZjjKXRQvx6tlHQLC7VS5jP7T/IdkGdszb6P2FQ53ly41teBku/B2Vhq/qZgOOereyt2IO8XzWhMVAr8RD2etIn24K46c/X1xWYST4c8DITGV+Dz8jnkeytaY4m0psnqj2tDTXVuYuwA/VN5D7X4RGgIAcYeLFbe32qi95GhX5ik/D31ysYbaX7/lMLWH4jpMdG6cz2XDcf47uoSANgDcPs3dwovimZc8hD2tiPIBtGuR9+1sTcRUAIgU+GeuEuE+2Sr/+4Cj750KLh9fjRYPEw15GOMrGjz0V0SpIVfTvyMQ4G2l+m5QiCVf1e0hnbUIjfrzw1lqf3mnmG8BPDjP3fDPb1djQ4cctYuuu0mEH3sJu5gUYUsJl69PKolEe0iHoraneFsqHYWRuN4rLIjnoaJ9trTpkKOuMK/HXJWvT7uyfADmarrPdEd4pxlJiv2lCIkHgBkhhH+4ysPxev1aoPeCDl5PlXxB7bu8zMlPFfgauqWN7x+b8zoWzpfkG6fkNpGyvm9RlpE9yL8jX+f9clasbwBQFGFoSvy96YrQLBESCADXpN9N7R0hvobWRHhy3dX7lRcTLVe+3jwnZSx3zCPHMAzDMAzDMAzDMAxjmWAeOadIqbUAn3PiZtvSxgUMVzn98vsjIXEjUue31HVxvNge1h4D+8tZag+KbvP6jltlGdkGF+1qj/B6xkTqRwCoiZS9SdH7VRpbAPB38RP2wCqRKjoubtk8iPKhJm496+JWxsuRtPqMSLeLor6xbIkb5uoM/3ufuLQZL2jPo8Uqv62vulwBMeZwbxoAWOOeR+2jPu7145xEbP2HKTR4YzVc7hmRWMmfZ6Bf33J3grfVdnGD9o+He2QZ79x2hNp///4han/ryJIs445pLsJ9fhtvK+WdAQDrk7zvR4SXyYoQb+tjeS30vTHGhdeLDXVbqOfLQ84j1F5pbKD2qqPnEUckHYis4vbNvfw2f82UFhAdH81Q+zkZXodHFrTHW8Pla0e/8CTz0i9nK/wz6Qhfx9NJ7i0DAAUhsLs+wfvuFwrfp/Zc/RpZh0Q331e1beBraP+YnkeSYzy98WSZP8+9ee2VsFTnm5qK2BO1Ca/WhAehbyWs/u0Z7sV1fb8WAQ4KQfOUSMjxlHtIlrG+vF5+hqGcc1seBOhTwqPtkQXuWbTisId+WeYJGoKdvM84HvaoTbHWT1X4PnpGiPkDWpxapbVXHjfjFb5GA8CqON9j+kVTKUHzhutBbfxFhPuf/850Gcsd88gxDMMwDMMwDMMwDMNYJphHjmEYhmEYhmEYhmEYZ52nNXI8RCWcZhnLHTvIOUVivvaTih3nXR7OkAmtlN8/U+GudckA99e8p/4AtW9zzpd1aPNxt9Qpl4ubbRKCywDQc5LwtGd4LJel9u0NHu4AAEGHTwD3zXL39WtXaFfmVpG7pfpV2JNwf0dZC74iz93X3RwPR2jN8N8AAPVJ/jsaJd7WzbqejEt57tfdsYbPuOVp7mB4pORBdFZ48GZaPDwy0dL9sj3AfXzrQhB22n9UltHj527hdRFW4YrVzVnTLesQX8W/Y9UoD1H5rUXt/l48wMv4+K+MUntjVrsq39rJ3dPH57l7uxfB16G1fE4Nr+Tzfn2c/47DD2pxz7+e/iNq35x+PbVPNp+QZZzjXEHtPvB+2R/qlWVURAymLy5CBdbzvu1l07R2nvv5Nw7xvt+1W8/J2/N8nd6zxNfh/3OIh7gAwO9t5nNmKsHXFp+HEOi6CPdRbMAOal/yEI3gF0tD8Fwe5pkWoVcAsOVJ/sw7H+fPsy2kx/CeHP+OTJDvefbV+bNYndDhk0eKfBG9oJ2HTkVE2BQAVJt8nugVgsvtTS72DwBxMdBlEgkh6jzcq0WC9+7jbdUX4f3u3/bqd46BMRE2GOMhRX1teh6pN3ifUKFTx8T+EgBSQf6Zg3n+wBpiz/OU85CsQ6TE56JEgHeqqHgvqkOH3BovPewgxzAMwzAMwzAMwzCMs45p5HjDDnJOkZibhB8n9hzYFt5M/zYV0qfKeSFWp7g6fBG176loocY28Ju8foeLYgY8XLCpVIB9QX4TUffgbhcL8BP4nxjg31H18CwWuXYnUvPj1O6IW4TSMf07R4/y5xESD2Q0p0W4k0F+a7NX3A574dwMv9lJzHFvtaa4TVRpop+G95lzA6uo/VhN304Vm9xDY200Q+3n+LkdABzhjVZs8JudpnIICAtVTADo57fYzsgAtftFHQEgpYS8/fymz1/VHm89C1lunxfPXHhRAgCivC2U111zcZ7avWimw+X9crq1j9pX+LfIItoc7o0WD/DntSqlRS9Hl7hX3HCFe+w4VdGnorrvOyu46Hmwg69vK1YJ5U4APaP8mSce5H372oIWE1/TeYza0/18Tn7wkT5ZRqnB19nvlHi/izl8vxIPaA9hqdOdFOvbKi1yH+zOUPuK2Ci1z31Lr7EXdmSpfdcCr8N1vdz74nNHdAr0/hh/NfKJtWlVnPcpAJgWadT386zcmK1p0XS/w4VrK0Veh1QPn6syPl2Hi5f4fv2JBd7v0kHtQRUP8HlfefYd9pBE4uIV09R+WRf3ThoTadgBYHeOz8shoTRcEWLHtZaek4/6p6jdJ0SfL4wOijqYR47xo9hBjmEYhmEYhmEYhmEYZ52nNXLOfBnLHctaZRiGYRiGYRiGYRiGsUwwj5xTJOJGEThJaFVYeH17cW9vuvx4sNbi7n+JIK/ESLBD1kGJBKs6PrrExUEBYGOSu793RnjX7AhpF0NHRD8+tsRdY11occHZCg8VePBR7oqcE178r+jhrs4AcLTE6zBa4n0iEdBH0mEfd1vtCvPn8d1ZPdWcm+F2V4TTiW6J7e3azfihBX62vVTl33HQeVSWMeSeQ+2tihAJjmv39lqTf0fEz39HICUmq6J2C8cx7maMNjG+gh5CktRnGkpsnI8dAMCgCA9ZIQR4qzpUAHPctbw5xufUho7ok7ws9d+pvQ7eluPOEVlG3eXhPHWXj7+IB/Hc7igPQ2vl+e+Y/9cstSd7dTheaJiLrfq6eDiCk9ZjPLiV991VQ7wd3psbk2U4Yh1u5fn4W31MC7o+MdVJ7ReEuPj73ioPP2kP6XnfUVeaar4LiFgeAOjmey//y3mfOH8zD6UDAHeG12PT+GFqLwh9eb+jw/HUPncgw+vYEkLGAFCd5W15f5X/zmFHiwA/PMfnibc2hGh6Gx/Dgf6MrMMQ+Bqa2cf3h0emdMif3+FzaqXJ948PLuokEpcP8/1hfxfvE6MeQquyYlruFVPqIbEuXOh7mazDyhifkytiXyaiv6T9xUYLSuzguSljuWMeOYZhGIZhGIZhGIZhGMsE88g5RZKIIYATn0DvLXAxrDVxfaoc9vGztZk6v2VLNfkjrTS1J8tUk5fRH+K/o92vRfmeyGepvSW8aS7r0gKGQZHG8rwMP4HvCuubV3X7dFkn7xMh4Rlx75z2CkoKUefuMLc/saSP+Rvi2HpLG7+1GdB6ePLmZ2GG96twmD/PoZj2IvnoGE/tvcW/mtfB0WO8KVJIpv3c+6nu4QrhO9XHqf2V2ETtvhifh1pPCW8bAIUn+POIdPEf4ktqYVtflH+meoSP4ch6PVc56uY0JsRvazr9eEukoz56D7/pC4g5IOLX8/5AlA9SKWJfHJJlNB3xzMXfx3SXwEAf9wJx6+JWVLTldx7ggpQAEHiIl7GhW3iRDC3IMsIb+FzjdPO1w+nUa6jyRHFn+V4h2a77fvsi91jrjvKr9KVahtq7wjo1uD8p5ruDs9ReHZuQZURfvoJ/YETY1w/LMpwR/lsDQrg9vWKS2s9PcDsA+ISTpPKczY5rL8mA2ndF11G7lzW0T6yB4Yjo2yHxetXPPdEAIJDmc3JbBxcjn/2K7vttST6G01E+B2zSPwPxdr4O10TK+qmK9s4dFCLb0xX+PAeEN01cJCYBgKboV3HRcRvK4VRES7zYcF09XzwXZSx3zCPHMAzDMAzDMAzDMAxjmWAHOYZhGIZhGIZhGIZhGMsEC606RUKOH0HnxG6AwzHuAtwZ0edmg3HuOrfB5e7SWlBZP/JGSwg1Kh1U6R8I9DQy1J4SnpQ5D2WoUICCEKtbldBuqetXcZdrxeMHuFDqYFTXQQnXZmv8mXdHdLxCl9Cz6xf1PFAQ4ScAZqu8kAMTPAzm8l7+LAaSPMwNAN49yIU1F2q8z2xoXCDLUOMnIkICRWQIAKAzslWUwV2dWxXep/xRD/NIlbfVv9/BQ3G8hDb+7WHuDv37O8apfWmvFmoEuOt5rsrDllb1aMHXgBBvv2Och128coT/zraIDivsivJQnahQWuyNZmQZak5WqUBnPehGh1K87zphXol6jc+Hnz+m+8waIRZ+rMSfZ2ZChyTtnOBhLm0befijL63DFVp5Pq/P7OLzerJNP7CeNJ+XO8IZandTvA5NV88jMlbHz/tMYVqvb77v8DEazvN5Br1auBYRUY8wtzsruYhw1EOu3voof56lcd6Wk4s65K/U5N+hwmA8bHnQGxUJAxJ8jLrTXIHeCXsQ8x/qp2bfFv471wnRZwCYuIfXo9kSos5CLBkAWnVeT/UdG5I66Ue+wfck7SLUrUt0irGirALma3ztWZPibanEjCs6QvpFhQsHLZzZcDL3DH//84F55BiGYRiGYRiGYRiGYSwTzCPHMAzDMAzDMAzDMIyzjokde8MOck6RluvKjEono+bBLTUo4i48fAWl6eHvkwH+oapQZl+q6UKUm35ZeJYvCVdNAEiJ3q1quapfZw6JrRU+uuKBDS/ysIvKjE4J0Gidnmtgb+T0ZzLVLxOiTwHAoghpuKp/htrbO7jva3ZBZyjK1k/P9TUZ9OBmLD6SU27IsgTtOn6kxN2pG1mR2UeErwBAQGRLezTL69AR1svTzi5ez7fclaH2nx3S6dRUOF1HiP/OYyUecgvo8MiXD0xTezzFw0cqVe3GnxDNreZ1Lwk1Qi7/kBpfG5I65MgvmtsJnV6oQLsIzQKAAzn+PP+2NEbtP9s9LMuIHO2h9vAEr0OhoeNLOsM8NGrDMA9nDWX0fBgu8Wc6JSKOFBGfhxRFalIW+7KQhxDoQ7t5aFTHUR6SVKnqMLVohNej4xLed31tfPA0xnV8ycGH+e/cv8TlAYIeQnUqIrRqWEzrB3nUEwBA5ucSIdDFx3g4ULToIZuaynzVydvat7ZbltF+iIf8fepuHm4+FNO/41xh96u2FGFTAFAX++BUkM8zx8p8PlQZpwBgvMKfeUpk/FWIyC3jJYod5BiGYRiGYRiGYRiGcdZp/ee/M13Gcsc0cgzDMAzDMAzDMAzDMJYJ5pFzitTdJlycWDr8G+Xv079Nl3mGIgDYFBik9gcaj1F7X2uY2vfjAVmHN2eupfaCSJtzV+VxWcaloXOovS5cnXd2avdbFa4wVeXdPxjREvG+NA/XcYs85KEmMko9kdNhGYqsSNoxFNNn0hMVfubbHuJup11hHRIR9/P27urlrufBFO8TrXntGvvIPK/D3hoPcVkX5OEOABAVqXtmKtyF3u8hhiXo8DK2tPN+1yzzMlwPWeNUiMqhPO8TEb8O/UiKFextI3x8egk17RIhYhNl3tYPLuj7ktcP8viRdBt32Q6KMVyu69Cq783yOnwz/0lqX5e6QZbR0+JZWMb9R6j9ljBfNwDAEX3CES7y/gBvy6aHoHrVr16RGqZ2L5npbp/mGds6RHIt1a+90GqKMNDnYIeZFBmIvrBwkNpfP6jDS9S1rCvCYCpFPb5mSnwuUnYVOgIA7SIUbvFr/Hd0dy9Re7Wss3N9Y4KHg6usjAMewtR6InxTc6TEx8aRgs5ktkZkQ2uJMOxIj9h/3qcHR+fsKLWHd4i4w26d6Sx6Lg/3edMsDwO950ifLMMVIbWPzrZT+5GS7ner4rzvq5A9FTEb8zBfbs3wtrx3icsDjAR51rh668XgP+Kdlnv6ciJeyljumEeOYRiGYRiGYRiGYRjGMsE8cgzDMAzDMAzDMAzDOOu40Elpnosyljt2kHOKBB0/gs6JXf7Xu1vp3/o85JtZqIssEdhI7U3hPnip72pZh7IImwiIDA4X+jfLMjojwi1VpC9xoUN1FCJZBvxhPcTdEncDrk9ze6HKMzhMiRAXANiU4j+kT2SlmqzoaaDY4PWotfjzrHpwC9/YlqV2f1SETgmPbOXeCwCdIt1TyMfdiPeWdaazaI3HPKyO60xKCjV+7hVhNO8S7u8qi4sXdnbxtv6OGDsAsJTgIQ0H8zxU7sJO7bL9xCL/jst7eFu5Hub9SRGyEIhyl2oVwlKo6dCPFTEejnCl+0vU7ne1g2/9JGHJz5BwM9TuIaLvjKsXxjxkL+nmTYld87ySsxVdDzUEt7fxMoJqjAN4YonPVZsXeehvOM3DYQGgKtafxxf4nmily8P1vGQLbRZ5W7k84gjfODgsy4gHeN8viUxMXtavY2X+vNYleYhm4RifJ+YqomMDmBF9NyDCftd7yExXafK1Y/8Sf57RgA7bna2IPiHmmZZoh6bYMwHA3kd4qM36Fg/1Du+URcAZ4aGHPT/JO/9PTsv8XqiNiXDx/bwxIws6RCwostOVRJ9ZIUL6FoQMAgDURZ84P8HbuiIWOC9h9cZLDzvIMQzDMAzDMAzDMAzjrGMaOd4wjRzDMAzDMAzDMAzDMIxlgnnknCJtwRBCvhO7wYdEOMNiVbuMHm3NU3vc5a7Mg+Ektdc8qJ7fXxqn9o1BHl4S9uvzQZXVY/cid8VcEdWhAlGRBemcNM9cEEjLIlCf4N/xxCNd3L7En9eqhM6cFRNZVlToVI+HjFIDIqypJ8KfV8inf8fKVVlqL83zZx5JcddYv3C9BXRYYUMc3y/5dGhVHtzFd0lk3LggrrNEKA/cK3v4POIXGW+EdzwAoFHjH0qIfvvaAe3+7ji8X62M85ClozzSAACwpZ3XQ4VMBD2EoWVCpxcq6oo/9+KRXRWT8j2lz1D7KxO/IMtQ4cWTraeovdgYkGWokAeVca1R5897bUI/q0NF/h0REZ51tKRjq3ojfJA2RShO0IM6wGCM9+2WKKOW0xNFtsjnoqEEH8MzFV7Huoq5BdAsCnuV/85UUPeJp/L8d2SC/HkcLem2VGHW0xXeZ57M8aw7JRFiDQCfXbyP2t+YuZja6x5CjtRK3iZSEM1X9X5ErfUKtUZWPYTq7FrIULu7iz+PTXGeJQkAght4xijE+X7EN6h/R6i1yO1HeL+tewgrPJTn88juLP+OPp40DuL1DgBwIM9D1rvDfPwt1oRUg6vnshcTrvv0vzNdxnLHPHIMwzAMwzAMwzAMwzCWCeaRYxiGYRiGYRiGYRjGWaeFM5674Ix///OBHeScItEAEDqJq7xfuNA/5D4kv/8C/3Zqf8I9QO09rbXU/mhrv6zDBmc1tZcbvOvPt3i4EQDcVX2c2i/wnU/tKjTr6c/w55FvcIe0QIcO32qJzAbr1s5Se/Up7oIfFuFhALBPuEP/5Jpj1F4SGXMAHZZUa/CpZGBNVpYRu4RnaIgJV+fGKM+uUDmip7svFG+n9mKNZ4m4LvZGWUa+yd1jJ50pap8qa/da5S66JcPbIpAUfsRh3ZbBGHczVuMz6tdL7IECHz+bRLhdxK9/x1JdhMzWdAiYotjg31EvnV4Zhbqey/ZUuRv+DclfpPaOiG7LuysHqf0y5ypqn+cRnAB0Bi+FCnnYm9cFdEd4363H+NpzYYfODlQTw2NXlpexLqkdslcneIhXWIQELszrDHyLItzngTxfQ+d9fE5+bY1n+vRCrczHn5cMYCkROpUO8gfa5JEjAHSY9VyV992cWFrUbwCAmzp4qqQVIgNfwENbzpb5fBYX091dhaOyjKsSw9Tu84tshSLabtFDBrD9Yn1LBvner+MxHTucOsbDnsIdIvtdr94/topinsjzrFS3T4lYb+g9j0hIiidFdspUyItkBG+rXbUxal/v46HD/tbp7zWMFx92kGMYhmEYhmEYhmEYxlnHslZ5wzRyDMMwDMMwDMMwDMMwTpPh4WE4jnPcvw9/+MPHfeaxxx7D5ZdfjkgkgsHBQXzkIx855XLMI8cwDMMwDMMwDMMwjLOO+5//znQZZ5Lf+Z3fwc033/zs/04mf5CpOJfL4dprr8U111yDP//zP8fjjz+OX/zFX0Qmk8Ev/dIveS7DDnJOkafj0k/86KNCI+eK4EXy+6drPCZ9NUaoPS0CQa/ABlkHL+lyGTkPmhGxxjZqz4T5d6REPDkAhEWs9bemuEPaW5I6LjdwEY9pTYzy+P3zwlwPRWqVADivLUvtKh2vf1jHaqPTQy52RlSnDUZU1GNGpPY+kKXmhbIWGXht/BXUPu7otMCKtQme53K4xce4l/GZEBoBJSG9pFI0OzGtuRLu5G11xxTvmL+wSmsBhVL8OxaE3smcSCsMABuFzo7S+hkreUjPqjSoKvw7FkXq1WpTO9+uDXZRezTAvyPsIT/rtXGuVxIU1fR78CF2RD0cJaAh+KnBefmZstAMmxX6GA8u6rUnHuBj9LwMH+QLIs06AET9XNuiKVJF3zfF+xQARIQW1qUZrgPy4CLX6CgILTwACHULvbw0b4ctRd0n6lOd1J4I8Of1tXHdJy7pVho4fGyUhK5LRWdZR0hox1RavA4FoRcGAIeKQlNM7HkujAzJMopiDQzEud2f4L8zHtTrW6/Q2loQe+17x3tkGXOH+Xf0hPlD35DJyTJG1vC9272zXCPnzcO6jPESXwP/3wH+O85p43+vxgYAxHx8bel1u6m9JY4VlN144ZFMJtHb23tC22c+8xnUajX81V/9FUKhEDZv3oxdu3bh4x//+Ckd5FholWEYhmEYhmEYhmEYLylyudxx/6pVD5kVPPDhD38YHR0d2LZtGz760Y+i0fjBieB9992HK664AqHQDy4jrrvuOuzduxeLi1yE/IcxjxzDMAzDMAzDMAzDMM46z6fY8eDg4HH//QMf+ABuu+220/rud7zjHTj//PPR3t6Oe++9F7feeismJyfx8Y9/HAAwNTWFkZHjPfB7enqetbW1cU+1Z7CDnFOEdazvF3ma50FwtzoAuD37R9R+Tfrd1B4NnF5YFAAcLXCXT0cUodIrA4ArcgWOlnlI0jW+E7uq/TAqXGFIuL4iqF183dXcRdfdtpXaI68SoTo13ZZocp9Pp8Fdtt2Ah5SGKk2zit/y8DucmTn+gTmeXrzEMztiWqS5BYB0iPeJQ0URk6SzxaPp8rZUbuEzlZosoyvCXXx3dPA+U5zgfaLtspSsQ6DBf8hHL+ZhhU/O8HT0ALCti4c0VEWIS3tKp2etVHhb1kQowPldOgzU54jUxAP8dqg1JuayJf28EiKu6ViJz1UlV/fL1TFeDxVaFfIQVuiINdC3jocbrFzFn9fKxYKsQ2OUz2ULj/E+sybDwy8BIBLgY3jfAt8E3j+v5/0dHaJftpWp/doI3xMBwJ2HVlD7TFmPH8ZURfcZXxsPzwqIPjM4wFOkA0DvsSPUPreXh9u9M5ykdgB4Yol/JiPSh69NcrsKIwWAhxdPL8V5b1SHLwfFfPlIlq/1h3I6TqZPhA+rsHd/L3+eQyMiVBzA5SIM7VP726n92j79Ozck+QNZqPF2KAg7ALRESN+bLzzI6zCj58OAw+eJX1wdp/b5Gu9ThYbu+yMJPo/UWtyeFUtotdUEvDtqGKfA0aNHkUr9YH8SDp94DnnPe96DP/zDP6TftWfPHmzYsAHvfvcP3te3bt2KUCiEX/7lX8aHPvShk37/j4Md5BiGYRiGYRiGYRiGcdZx4cDF6TsnqDIAIJVKHXeQczJ+/dd/HTfddBP9zKpVq07433fs2IFGo4HR0VGsX78evb29mJ4+3mnhmf99Ml2dE2EHOYZhGIZhGIZhGIZhGCegq6sLXV1axP9E7Nq1Cz6fD93dT0fn7Ny5E+9973tRr9cRDD7t2Xb77bdj/fr1nsOqgGUgdvyhD30IF154IZLJJLq7u3HjjTdi7969x33mqquu+pFc7W9/+9t/5Lv++q//Glu3bkUkEkF3dzduueWW5+tnGIZhGIZhGIZhGIZBcPEDOZMz9e9MSfDcd999+MQnPoFHH30Uhw4dwmc+8xm8613vwlve8pZnD2ne/OY3IxQK4W1vexueeOIJ/OM//iP++I//+LiQLC+84D1yvv3tb+OWW27BhRdeiEajgf/5P/8nrr32Wjz55JOIx38Q83jzzTfjd37nd57937HY8TGVH//4x/FHf/RH+OhHP4odO3agWCxidHT0lOvTE3MQ9p34/GtzxkOKZcHW9vdTe1P0Old0y4SHJ+5zeMyrEp8K+3XMrErlN1HksaRVETsMABE/FyxZFReVEDo+ALR2TJLHrLtxHreLfF5WwSkWub0i1NfzWvMBVRW8q8rQWiStJyaovXKIx3LXyrzfRYRmEgAURZfY0cGfZ6Gu+0xK6PA0Rb8biOvY2rBIAVtt8joEQqKtunlsPgBg6wZqHriS62sMlD2kem8IHR2l/yR0XwAAU1yHpzXBtZu84OtTLr18nuiMzVB7clZrVG3O8H7VGeE6BS54+lYvBIQA22BMj2FXjcEUT2ft9nt3aT4ZgQt43+5+BZ/Xu7M63a57jGts9D52lNpX79du5J3dfG1IXch1QJqzenxFjvBnGvHzMbyzIy3+XlYBjtBDweqV3C7mOgAITXDdv75dXCckdEdWluEX2jEloRnWGeP9NiRSpANAwOFzcrnJH8gKD+msh4O8HpVWP7Uv1fUeNernc5ETFlpca7gmZjyelXUYKPC1RSUo/uqEXqev7ubt3RPje7f5Mp8DACDULtJqi+3l1x/ok2Wc18bn1K4wL+R787xP7MnquewNQ/y9Ra1ejy/wdqq3Tk8vzHj+CIfD+NznPofbbrsN1WoVIyMjeNe73nXcIU06ncY3v/lN3HLLLdi+fTs6Ozvx/ve//5RSjwPL4CDn61//+nH/+6//+q/R3d2Nhx56CFdcccWz/z0Wi500pmxxcRHve9/78KUvfQkvf/nLn/3vW7dyIVrDMAzDMAzDMAzDMJ4fns+sVc81559/Pr73ve/Jz23duhV33333aZX1gg+t+q8sLT19Qt3efvxJ82c+8xl0dnbinHPOwa233opS6QenyLfffjtarRbGx8exceNGDAwM4A1veAOOHj35jVW1Wv2RvPKGYRiGYRiGYRiGYRhnk2V1kNNqtfDOd74Tl156Kc4555xn//ub3/xm/P3f/z3uvPNO3Hrrrfi7v/s7vOUtb3nWfujQIbRaLfzBH/wBPvGJT+Bf/uVfsLCwgFe84hWo1U7sbvehD30I6XT62X//Nce8YRiGYRiGYRiGYRjPHe7z9G+584IPrfphbrnlFuzevRv33HPPcf/9h+PJtmzZgr6+Prz85S/HwYMHsXr1arRaLdTrdfzJn/wJrr32WgDAP/zDP6C3txd33nknrrvuuh8p69Zbbz0uli2Xy2FwcBBRv4Ow78Sxsb0RHrcb8qDR0XR53K0XbRiGl06bDPLzvbr4GV7KaIrv6I3yeNVkQATVAqiIWOygT9S0oZ+XMzPL7UrjRmkhjE3JOrgLXCOnMc7t+YO6Ty0ucH2MiTzXneiJa42cFSNcx8MVjyMg4uZLTX1uvZpL4CAk+kwwpnu/0jFQKB0sQLuL9ke5plFsrRCWiPP+AACuSOXodnbyL/ASD64+I+xOU4giAcAw1z5TGlROU+tKoKFEw7gGDhxu99Ln2kK8nvEAnye8jC+f6LsRP39eGTHGASB3mPfdDqHX5SjNMKW7BMANCg2OXq6fgf4eWQbW8Pkycj5fe1bPZ3UZIa41gpPshZ7B/+gRWUR7iK/lmzNcdyIR4H2mJ6L1oeDnfdcVOj1uiuv0AICb4VlIHPHMO7dOyjI61X5inveJ1iTXyMk/rufL11zKtUScKH/tcAJ6Hqke4H1mbh8vo0fLuqBdzIduQ8yp7bxPOH0680176BC1xx7i+m1FD1pA7VH+vMp13pbre3kdAMCX5OPHqfExfG5Ga0V2RHnfrQh9qPPbeKdYl9TahHWhbxgUW+1X9PMPlJsO/kU3t/ESY9kc5Pzqr/4qvvzlL+M73/kOBgb4xnrHjh0AgAMHDmD16tXo63taKGvTpk3PfqarqwudnZ0YGxs74XeEw2GEw3rgGoZhGIZhGIZhGIZx+ixnjZznkxd8aJXruvjVX/1VfP7zn8cdd9yBkZER+Te7du0CgGcPcC699FIAOC5t+cLCAubm5jA0NPTcV9owDMMwDMMwDMMwDOMM8IL3yLnlllvw2c9+Fl/4wheQTCYxNfV0qEk6nUY0GsXBgwfx2c9+Fq961avQ0dGBxx57DO9617twxRVXPJuVat26dfiJn/gJ/Nqv/Ro+9alPIZVK4dZbb8WGDRtw9dVXn82fZxiGYRiGYRiGYRgGnpYR8CIlcLplLHde8Ac5n/zkJwEAV1111XH//dOf/jRuuukmhEIhfOtb38InPvEJFItFDA4O4nWvex3e9773Hff5v/3bv8W73vUu3HDDDfD5fLjyyivx9a9/HUEVy/5fqLVcOCd58Nm60JZxtQOU0p9R31ARGjrq+wGgKeI8c0Kexu9Bxqcm/NlSIf4l+YbWKRCSDig1eGu2lrj2BQA4dz5G7UsP8vj8WDePw547FJV1qFR5H54r8VjspRrXIACA0RIPM+wVOgQtof0EAId2cU2VSzcfo/ZintfxYEGP9d2LfID0x3mfiXmI7w8IvZJKk7dVQ4xPAMiKMboqLsaP8jfNLsk6+JZEXHtE9LtTnJtPSFU0hND4AACoEFv1HQ0PGjl5rmOFBd6W2f28rSbKWhTinhned9el+e98eE7/zr4Y73epEK/DQk2Prx0l0a/meN9tPsh1XRqL+neGhrmGlLOyndrRLewA0MY1ONx2rskCZQfgnCQZxLMsZLndw3yYFzoeU1zCAx1hXsbdM3oeuT7P13rf0QlqdyanZRnuEJcEcBNCoG3tKlkGakIPqMx1RHxTXGsrvWZR1yEd53a1tixqPRT/BP8dA1Heb++Y0bIJh/K8X71hQeihiHnfHeiQdcBOrj0YSR+g9gvbeL8FgF13cq266QpfOxarem25ZB2vhy/NX0W3nKPHV73An1e1JLSZFvh8qjTkAOBAgZeRDPA+44itRNnDVsJ46fGCP8hxxUvL4OAgvv3tb8vvSaVS+Mu//Ev85V/+5XNVNcMwDMMwDMMwDMMwniNMI8cbL3iNHMMwDMMwDMMwDMMwDONpXvAeOYZhGIZhGIZhGIZhvPhx//PfmS5juWMHOafIQsVFyHfiR+8IB6dyU3cZ5SLVUOHFVR5E6VdBmABiQlymIn5HrqYDOYtNHsvd2eAxzJtT+neEfFzvJOwXMbWjIt4cQEho3LgtXsa/3MXj3gdiWqfnz/fzthpJcl2Kf1x8SJZxS+92aj8idCke9aDDc0N/Vn6GEY40qH1tUj/P8RLXU5gu8z7lZXwpDaqiELLKi7EDAB0h3t51oVmkdEB8e8dlHfLfLVD7vsM8Nn9vjusDAMDlAzx2viX0hppifAJAZzf/HZEO/rwc3fVRm+P1jAzxejYavN/2RfU8Um/x7UC+zuvYGdG6ZU8tccGTOeSo/ZZhrSvRPlCi9tY8H3+q7+/fpetQepC35bpBrhlRLs7JMnp2ijG6tpt/gdIyAYAy7zfuZJbbhfYMAPREud7Jnizvdx1h3vdDHnSwWnk+p7rfO0TtzUW+9gBAYGCU2n0b+/kXdGRkGfCLMRgSekFJMed6iUPI8fkSef683UU+fgGgvsTroTQUDyihRwBb2vi+qjjLJ/bY1Dy1O0ojDoDbyecad9Maag+E9Cvelvwotccf41paeQ97uyqXXkJQaDuV5rXO1dQc11gcWrlA7ed3cv2nb03y/QoAtId4v5yu8LmoIKaRqtBANV6aWGiVYRiGYRiGYRiGYRjGMsE8cgzDMAzDMAzDMAzDOOuY2LE3zCPHMAzDMAzDMAzDMAxjmWAeOadIrtZC0Hfi2PSBuNA50BICcCG0K7gcA7oi/Gwuq0ODURRxmjWhkTPZyMsyqg6Pne9weXx/QWhfAEC2zru3ijddmo7IMjrb+e+ItPHGjAX4A71/ISbrcE0f/46OEH/oG1PnyTLmRb8ZK3L755cekWXs7NhA7b4g73fRNI+zTga0joHj8FjsoNBbCHjQY4j5+Wd2V6aofaWvS5Zxd/371P42/3nU7k+KM341EQHw+fnz+s5smtr7heYRAOya5nHrS3U+6c5U9aR8TpbXMxnk9TxYiMoyOkP8O64Mj1F7xxqul5ItcG0aAOiOcn2MrjB/5hHRrwGg6fI5dazItWMCjtanCWZOT0egMsv7/renuWYEAKxJ8HXhT+7n2haXdGidkOpdWWpv3cn1hsp1rlUCAE2xRg708Ik/3qvHcCbK+2YqyLUvuqO8jl40clyhfeZr43uJ790r9G0A9CV4W3U9cJja947peX9lxxIv41y+kPsHktTuCo0rAFh6mD/zw+Pt1D7QqTep+QLvE3M1Na/r9aszzNcv5yRamc9Qf0Tot93L13kACO/s4R9YM8jtQyt0GTdwjZsNG/nvaB6blWUUD/Ex6K/ytvzs7mFZxpvPGaV2R2xp4kJHrjustT9zdV5IXWjyxcUbud/De8+LCdd9+t+ZLmO5Yx45hmEYhmEYhmEYhmEYywTzyDEMwzAMwzAMwzAM46zTghffudMvY7ljHjmGYRiGYRiGYRiGYRjLBPPIMQzDMAzDMAzDMAzjrGNZq7xhBzmnSK5ZR+AkglX1FhdKPZjTwn89MS7Sds8SF0i7rqOP2lNCMBYAlGZlyMcduSaqvB0AAKIaqRAvw/WgUKXEjNuFwOgD40JoDsB1w0eoXQlvDsW5AOJkhQutAsBEWQms8ecxVdGOeStjXOgtKIS+X+dsk2XszfNnulP4QPqFpmxXRAs1VptcjDUW4L9zrqIF8TqTfNp9ZQcXKJwsaWfQy5s7qD0e5P3Ol+YCiE7Yw9IhxCBFU2KmqsuoCE3Y3ghvq/6Ifl5787xPPDjHy7i4WwsUjsS5UHcwzb/DifIxHPDpPjMc589LacZ+bSory7ihN0PtrwmtpvaG60GwXHUsQVMIVlbEugIAd8zwPjMU589jrBSWZTy2xNf6XJ3X87wMF/cEgA1tXDw3nBTPw4PPd0AI/q9M8D1RXezEvfxOkWMCrhg+w+28nQDgG0f48+pc4CLa/VEtTn3HKBddPi+fpfb9S1zseE2qIOswU+YLcSbEn8dj4zzRBQDMVvn6VBaisOe06fHVJvaHkQS3N8V+ZvGYTqYRnpqn9sz5i9Tu2z4sy0CaP3NnI2/rwIAWZk+vylJ7fR//Ha9bc0yWsbTE+12tykW0cyX+PFZ4GH/TFZ4wIBPifeLRBT7R1FovhkAg47nGDnIMwzAMwzAMwzAMwzj7PA9Zq5RTwXLANHIMwzAMwzAMwzAMwzCWCeaRYxiGYRiGYRiGYRjGWceyVnnDPHIMwzAMwzAMwzAMwzCWCeaRc4r8x9Kf4GTKeFvbfpv+7fmdXLQPALI1LtJWdLiongMuqNcR1gGB7VzbDKNFXsewo39nT5ALk7WHeRldYS166Xf4b60L0cqr1h+VZQR6hLBzg5/3dsS5gFpfMS7r8JVjvC3+vzV8mPdozT3MCuHZ8TJvSy9lDMW44GtLiHf6o/x5R4O6z2zhepMoC23c3qju+787+lfU/jurfoHaU0EvYq68HskQF/5zAuKMXynfeqArzBuz0ND3DFMVXo8+0SdCHkSAx4q8LS/s4vU8prUgcU5KiBmLZ+6L8Dqkk1qoMSTEqZ9c4mW8fiAjywiKOTkeEILLsgQPHxLiuE3R7+J+vYYOiWlb6TF7EVQe43rluKqbi8oqMVcAuGOyk9rf3J2j9mBajy+/GINqz/LIvCijQ1ZBCmQ7IgNENMLXLkDvR46W+F6i6eo+sVDnc9W3p9upfXeWlzFW4n8PAAExj4zE+PgaSfM+BQCxAN8/fn6Mbzgu69GvPrNV3paOmAf8Cd6W9YbeKxw8yjckPQt8cRkpHpBl+AeE2HFaZJEI6N+h9sGNLG/LfbO637lCsTxV5nuee+d4YpENSZ0soyXq0BRLRzLIx0bNw7rwYsJ9HjRyzrgGz/OAeeQYhmEYhmEYhmEYhmEsE8wjxzAMwzAMwzAMwzCMs45p5HjDPHIMwzAMwzAMwzAMwzCWCeaRYxiGYRiGYRiGYRjGWcd1XbhnWMTmTH//84Ed5Jwi12fehaATPqFN6OFJIWMAiAgBtZ9oW0/tqkseEULFAJAQvaJbCNf624Q4GoCc0AY8WuRCqENx7UzWIwSRG6Kxoj3a6c6JnrgvPEN9lIuMjma5wJoSQASAV/Tzz9RbvB2E9icALYTqd/jzuH9Wi0EGfVxle0eB/85AnIvZFeu6LctNPj52L/I+sTal++UHhrmYsZpHZrXmHmqi604VY9S+vlzgXxDxsHQIYT4lNh7xexBKdXg9Dha4PRPSnf+cDK/HVIU/8/PbtKhsrXV6zrGuaKpSSSjYQwvw9vMuI/scAIwJUfQOPp1iTULPI1KIW0x45QqfJzqFSDcA5OpCALvMBUIjYr4FgO3tvB5RMX68zPvzVd6W1TJvq3CZCy4DgOtBxJcxlOBtOZTQ4rlOiNfBrfK2PjKjFZXD4pmGQ7yMJ3N6/dqS5mtgRAhL9wnR9JIHAfrvzfPn0Rnidi8zYcTP59SRFJ/3S3oI45IOriYe4BrBKt8AqjW9hn5qP5903zAk5vX7ZBE4tJSi9o4wH8MjfXOyjOQgf15H9mWovTeuMwaE/PyhTha4An0iwMfG/oJYnACkxXcs1ninuL30OLU3XQ/rn/GSww5yDMMwDMMwDMMwDMM467RcbxcOp1vGcsc0cgzDMAzDMAzDMAzDMJYJdpBjGIZhGIZhGIZhGIaxTLDQKsMwDMMwDMMwDMMwzjoutO7rc1HGcscOck6RRMCPoO/EglU5rjOHhwsz8vsvTHZR+7wQ3TtazVN72qeFiAfiXNQrKTT3cjU9NBbF7zjU4AJq5zd7ZRnTVd69V8W5aqxPCCACgJvnD332IBere3CR20taJxXrk/xDyQBv6wUPonv781ykLVfnz/xnhnWfeFJoUgaFeLVPaNFFAroxx5TGr1Ai3p/Tiq/9Md6WxTJvq4YHUdmA8LWcrnCRxGaOt1UgrtUi60IEOCaEAZVgLADkRb9T4rleXFIfnOefWse1IjFZ0eOrPcRFDF2lzF7hz6PeFMqb0KLNjpgOH57XfeJIfYHaR4Lt1D4Y1YKvktMMip+u6Lb8s4l91P7Wbp60wIsI95SohxKl1yXvAAA/W0lEQVTX9Tu6jE0p3i+bQhy+XtAjLFvke5IH53i/uqN6J7W/aeQ8WQeFGn9+D+LUXzrGP9MT5fNEh0gy4YVJIeQ9VuJ9akNSi62e18bn9WNl/ju3eeiXqu+qfZOXfdWRKG/wnWJ/6AjR9aWKFs9dleLPY1poiR8e75ZlDEb5HvazR3hCjpuEyDAADIUWqb23WwuSK46M87Vjb57vtfNCyPsgf7UCAKyM82f+5zO3U/sb0tdQe7VVwV8s/ruuiPGSwg5yDMMwDMMwDMMwDMM465jYsTdMI8cwDMMwDMMwDMMwDGOZYB45hmEYhmEYhmEYhmGcdcwjxxvmkWMYhmEYhmEYhmEYhrFMMI8cwzAMwzAMwzAMwzDOOk9nrTqzLjMvAoccO8g5VQqNJoLOiVXaVcao9dEO+f1FkR3hvvouam/4uIx9tzss69Db6qP2xxZ5tqc5cIV6ANgY4lmnMm6S2lVGDgCI+3n2hK6oyFoV1w5rzTxX7D8430btyq1PZQgDgKbLlfJLTf470kGddWBnB/9Mf6xE7V4ypFzUX6T2xBr+926Vt0Oxphvz68Xd1L4jsInaF2oidR2AWpPXY6HOvyPm09P2XneU2l/WM0TtTkCkKFJpsQAEQnz8ZYI8A0pvRPfL0SKfJ/qj/DuyHjJjrRFZqTpCvAyVDQMAUkH+zF2RncttcnvNQ9aqr0xlqX1LMkPtUzWR8g2AX2w5luq8T5SaOtOL7Lsim0ypysfnt6d0v3x1hmelKjV4HXI6ORACIo2Yl36nSIrMcgv5OLXX63quUmvglwr/TO3bgzdQu9/h67wXWmXeDqMF3g4AcGkPb4u0aOv9BT2GDxV5300GeGP3RngddmX181R991V9fK7z+3RaRkfsJ6piPpwoiXRPAF7VJ7JShYVdzEM+D3uirjBvi6Miy5jKaArojImXd/HfMVni2aAAYE1sntpbYkqdG0/IMlrg9eyP8N85Leb9rogef4cL/Jm+rfMV1K7mwkBLZ9I1XnrYQY5hGIZhGIZhGIZhGGcd08jxhmnkGIZhGIZhGIZhGIZhLBPMI8cwDMMwDMMwDMMwjLOO6z7970yXsdwxjxzDMAzDMAzDMAzDMIxlgnnkGIZhGIZhGIZhGIZx1nHhonXGs1Ytf5ccO8g5RabcRfgROqGt6Fuifxsu66w5XaEItV8UOI/asyLjjV8ouwPAeIlnebiz+LfUfkXsLbKM+RrPGjDhm6B2ByKFEYBuoVJ/RGSa2Nyms104cS63PyeU8N+0dpzaEyldh3qVD+NyRajxD/FsUQAQ7BTOeyLRhC+hFf99AxnxAZ6hKPf1OWqvt7QD4kZ3HbUfqeaovS+osyvM1Xnf3+s8Ru2bW+fKMs4NrqL2mF/ME318bDhtOlNFuJtn8RsY51mOclWdoei/bRmj9u8f66H2LRk9vioN3ndzdT6+BmO6jFSYP4/aAp+3yzleh4bIXAcAnX7+zENiCG9IiPReAP459wVqP9/Hs3qIZDQAACfO28IRP0Rl2HvHBv08my5v76DIzLPkIcPesfKJ9yHP8HhW1UEWgXVJkV2rxuvgBZFEDBcGX31a3+8lC5IvzeeaxiLPyrgqoTO2DSf4D31kgY+f7W0609I9s/x5VEWmpY0pvmeK+fU6/tAC71jTYr/C80I+TVBkJD1Q5M/j+5V/kWX8N7yZ2n3p0+v74YDOfqcyImbr/HnO1fTz6grz59UR4mtTX0LvH31iOmtUTj845EiB70n6RJZalbWq4mHxeSKfpfYrwzyLbVg8ruV/5GCcCewgxzAMwzAMwzAMwzCMs45p5HjDNHIMwzAMwzAMwzAMwzCWCeaRYxiGYRiGYRiGYRjGWacFqdrwnJSx3DGPHMMwDMMwDMMwDMMwjGWCHeQYhmEYhmEYhmEYhmEsEyy0yjAMwzAMwzAMwzCMs47runDPsBrxmf7+5wM7yDlFpnEQvpM1m+gPTzpT8vv9DZ4C75LADv73Ir1400MCu4LL0/TV6jPUXkdDlpFFmdonao9Su+sh/XhZpNztj/E6OHGdXtI5f5DaX3ex+IIAT0cID+k+0RRpLFvimQc9TAMhkT/Sp9KTe4hEVfU8Oqm/g+CKsQEAAZEL9xgOUvsT1aOyDAf8mYZEGugjzjFZRrw1Ij/DcJIR/oF1Q/I7Qu08ne6GzfPU7hZ1WtPWEu/7P/GyWV5GmafbBYDmIp/PypO8z/j8es4NtfPP+KJ8fM1M8PTJ1ZaeR1pibYiIr/B5GF/b/ddSe8Hlc7Lf0WnvnZhIP762n9rX9vPUxWuLOg20u8R/R3OW2ytH9HyZnY1S+9BMB7XfMSPGOICeCB8fW9fxPU0gofv+gd28ngmfSKnt6jTOCqcrQe3h9X3Ufu62rCyjOcY/M/zEArXvOtwry3jtCv687p7ja8vmtiy1e0nlXm11U/uRIp9IfI7uM9Eg/519Ib6vGvFdJstQ4Qq+tBg/bbyt12wZl3WI7OFrz/oqn/dvn8zIMjIivfihAv8ds1W9T+4r5ag92s+feW+Sz8kAcFGIt9WT053UPl/jT3xjSs8zIR/vdytj/DumRBr2gIexYbz0sIMcwzAMwzAMwzAMwzDOOi1X3+8+F2Usd0wjxzAMwzAMwzAMwzAMY5lgBzmGYRiGYRiGYRiGYZx1WnCfl39nkq985SvYsWMHotEo2tracOONNx5nHxsbww033IBYLIbu7m78xm/8BhoNLU/yw1holWEYhmEYhmEYhmEYxmnyr//6r7j55pvxB3/wB3jZy16GRqOB3bt3P2tvNpu44YYb0Nvbi3vvvReTk5P4uZ/7OQSDQfzBH/yB53LsIMcwDMMwDMMwDMMwjLOOC+BMJ5U6U1/faDTwa7/2a/joRz+Kt73tbc/+902bNj37/3/zm9/Ek08+iW9961vo6enBeeedh9/93d/Fb/3Wb+G2225DKKSFxAELrTIMwzAMwzAMwzAM4yVGLpc77l+1qrNTMh5++GGMj4/D5/Nh27Zt6Ovrw/XXX3+cR859992HLVu2oKen59n/dt111yGXy+GJJ57wXNYL3iPnO9/5Dj760Y/ioYcewuTkJD7/+c8/G2NWr9fxvve9D1/96ldx6NAhpNNpXHPNNfjwhz+M/v4fpBjdt28ffuM3fgPf/e53UavVsHXrVvzu7/4urr766lOuz1T+YTjOidOspmOr6N92BHXK7BVNntZ3opan9oMOT9sdcnjKUgBoOjw+ryt1AbUnfR7SmooUy3H3FdSuE90C+TpPc5mviZTaHtKoI8l/h5vmKZglDQ+pVUU8pSPTk3tIDa7Siyu8/I7sEreX+MSqUlhW9ukUzPEA/8yFzXOpPe9uonYAaIg7gCXwVJsHGvfKMob9g9TuV2ksxfPy0q/doZX8A9t4v3PqOjW4T8USu6IMD/0yKBb0YImnkoYafwBQE791iqcmHqxPUvv0PXyeAoBvV79I7aubr6d2v4cpYsx3hNr7mgPUHvF7mKsUGd533RU8zbOcTwE4Fd5nAlWe8jdRLMkyEsUKtQ/keb+8tqZT+iKgHmo7tTbHxJwOoPYoL6NPpJOfFyl7my0PHTMotsIrecp6dz3f+wGAX/SJtpfzFM1XL3I7AED0iSvKfB5pzfM6lh7j3w8AN53P96hOgO/e3Ia+I5/bw9NuP9DkL0E7Q+fIMvwOH6NybIysoOZwf5esw+pjM9TeOjRH7RuPzcoyDj/JU2arrD51D+OrtMTHsC/M27pV1Tv+eIp/R6+YD1eKFOdfPqaf1wVtfPzMVPk8syDODqrPwfK3nHg+NGye+f7BweP3zB/4wAdw2223/djfe+jQIQDAbbfdho9//OMYHh7GH/3RH+Gqq67Cvn370N7ejqmpqeMOcQA8+7+npqY8l/WC98gpFos499xz8X/+z//5EVupVMLDDz+M3/7t38bDDz+Mf/u3f8PevXvx2te+9rjPvfrVr0aj0cAdd9yBhx56COeeey5e/epXn1JDGYZhGIZhGIZhGIbx4uDo0aNYWlp69t+tt956ws+95z3vgeM49N9TTz2F1n9ekL/3ve/F6173Omzfvh2f/vSn4TgO/vmf//k5rfsL3iPn+uuvx/XXX39CWzqdxu23337cf/vTP/1TXHTRRRgbG8PKlSsxNzeH/fv34y//8i+xdetWAMCHP/xh/Nmf/Rl2796N3l5++2YYhmEYhmEYhmEYxpnHdc+chs0PlwEAqVQKqZT2NP/1X/913HTTTfQzq1atwuTk017SP6yJEw6HsWrVKoyNjQEAent7cf/99x/3t9PT08/avPKCP8g5VZaWluA4DjKZDACgo6MD69evx9/+7d/i/PPPRzgcxl/8xV+gu7sb27dvP+n3VKvV42LkcjkPbq2GYRiGYRiGYRiGYbxo6OrqQleXDrPbvn07wuEw9u7di8suuwzA03Iwo6OjGBp6WkJl586d+P3f/33MzMygu7sbAHD77bcjlUoddwCkeFEd5FQqFfzWb/0W3vSmNz17suY4Dr71rW/hxhtvRDKZhM/nQ3d3N77+9a+jre3ksaEf+tCH8MEPfvD5qrphGIZhGIZhGIZhvKR5PjVynmtSqRTe/va34wMf+AAGBwcxNDSEj370owCAn/7pnwYAXHvttdi0aRPe+ta34iMf+Qimpqbwvve9D7fccgvCYa4D9sO84DVyvFKv1/GGN7wBruvik5/85LP/3XVd3HLLLeju7sbdd9+N+++/HzfeeCNe85rXPOv6dCJuvfXW4+Lljh49+nz8DMMwDMMwDMMwDMMwliEf/ehH8cY3vhFvfetbceGFF+LIkSO44447nnUi8fv9+PKXvwy/34+dO3fiLW95C37u534Ov/M7v3NK5bwoPHKeOcR5ppF+OM7tjjvuwJe//GUsLi4++9//7M/+DLfffjv+5m/+Bu95z3tO+J3hcPiUTsQMwzAMwzAMwzAMw/jxabnPg0eOe+a+PxgM4mMf+xg+9rGPnfQzQ0ND+OpXv3pa5Sz7g5xnDnH279+PO++8Ex0dHcfZS6Wn03j6/kv6ZJ/P96yq9KmwIfUa+J3QCW2pVpr+ra+pU+hVHJ7e8f7cp6m9PbGZ2huOyG8HoNLIUnvYn5TfoQj4eFvETtLGz1D20JadYT5As3WeErE1y1M7AoBvgqeHdKbEdxRF6uKahxToVZ662C3ytIxuxUMZNQ8plFkZdT3Wqsd4PXwqe7jwL2y0dJ8pinTUKj35yeaGUyljBnwOCPhisoySy/vEQi1C7arv++bmZR0g2grqoFzMEU9/Rjz0puh3HspwVT2DfB5xRPrypxHpplWqW9HUxYZe6l8V/0lqj4q0wUfyeo5Y766m9oAoo+5hDLsl3vedhSy3Z58DPTy/mqwEok8BADLiM+1CuFHlFQYAlWp9nreVW9PzvkpfnBXfUWrydaPW9PAsRGpiLImU2roEPY/0Ct2FTp7qHfAw14gU6L4cT8GcWMnbAQBQF/sJsadpTeoy/H7eJ36ldyu1T4nHDQClJu+XbpX/DkesTe6KPl2J/h5q9q3n4y9yeFwWsSbOow0GJrPUXs7rucrn53PN1GH+TjFX0nueczZOU/uGSxepvb7A+9SNfr2+Hcvx33GszNsqJtY/v4f1z3jp8YI/yCkUCjhw4MCz//vw4cPYtWsX2tvb0dfXh9e//vV4+OGH8eUvfxnNZvPZlOLt7e0IhULYuXMn2tra8PM///N4//vfj2g0iv/7f/8vDh8+jBtuuOFs/SzDMAzDMAzDMAzDMH4I9z//70yXsdx5wWvkPPjgg9i2bRu2bdsGAHj3u9+Nbdu24f3vfz/Gx8fxxS9+EceOHcN5552Hvr6+Z//de++9AIDOzk58/etfR6FQwMte9jJccMEFuOeee/CFL3wB55577tn8aYZhGIZhGIZhGIZhGKfEC94j56qrroJLYtiY7RkuuOACfOMb33guq2UYhmEYhmEYhmEYxnOIC+DUBVBOvYzlzgveI8cwDMMwDMMwDMMwDMN4GjvIMQzDMAzDMAzDMAzDWCa84EOrDMMwDMMwDMMwDMN48dPC85B+/EUQXGUeOYZhGIZhGIZhGIZhGMsE88gxDMMwDMMwDMMwDOOs47rPQ/pxDwmTXujYQc4pkm6lEXDCJ7TN+Cfp3y42j8rvb7Xq1N6e2EztxeoMtbseNMCbzQq1t4K8juP+WVnGYjXOv8O3n9ovbVwky6g2HWoP+/nf18Zqsgxn6iC1P/pgD7W3RXhbPzrfLuswHFfPNEqt9ZZ2zAv6eBnTlQi15+p6qtnStkTtbYkStft8fELOeqjDXbUvU3tPayO1x9ykLGMavM+Um1lqz5XHZBmjyQy1V5rbqb30VJXa45F9sg5u4ylqd0JiAAZO32HUzfHfAR+fIwDASZ54vn/WLr7DbemNgpvn9XSLfM6tTqu+H5R1SAZ5e0f9vIz2iH5es7UmtS81+Jwb9SdkGc1ZsX595wC17/9umtqLNd2Ww72L1B7v4s/Tz6dsAECgi9fDaY9xuxp/AFzxvFpzfE4ujcoiMCvWjscbh/jft/jzrDQukXVoHOLPyzn2OLW7NT3GA8Mp/oEe3u8QDsky0ODPC67YK5TEnmeJP28AaIm5DKJPNeb0vitf4G05VuR/P10S7QTgsk5ub03zQvx7R6nd6c3LOqAjQ81ulE8UzupBWUSwnbdlMM+feVLYAQBl/kzbpwvUvmJKt5UvzNdhJ8TtgRS3J+KiXwP40lO91H5xB5/3W+KVvNw80zmcjOWIHeQYhmEYhmEYhmEYhnHWMY0cb5hGjmEYhmEYhmEYhmEYxjLBPHIMwzAMwzAMwzAMwzjrmEeON8wjxzAMwzAMwzAMwzAMY5lgHjmGYRiGYRiGYRiGYZx13P/0yTnTZSx3zCPHMAzDMAzDMAzDMAxjmWAeOYZhGIZhGIZhGIZhnHVMI8cb5pFjGIZhGIZhGIZhGIaxTDCPnFMk7oQRdMIntFVbHfRvI764/P6ik6X2sfx3qX1N4hpqj7lJWYeqU6H2Y/WHqX3aPSjLmFj6DrX3ZS6l9mLDkWXUWvyc8qm8n9o37s3IMoI+Hl85VoxR+58+laD2nxhsyjp8cypN7Z3h0z9xnqvy9u4SZczX9PM6VGyn9gvbeFsmg3Vqz9b58waAdX7e7ybA+/a8e0SWEXKi1J4M9FB7Ktkvy1AsNfjYODraRu2tw/p5KmpN/jyi4nkCwLE8Hz8DyQKvQ0P3iWI9SO0+h/f9J5Z4HQFgc5rXc7Icofa16Ty1Hy7qpX6+0qD2oQT/jpiH3cQ3sh/THyL8ovs/5WdyB/gzLZdC1L5/KUXtUxXeHwDgQJ6v9b4D/O97IjVZhiNuEnOi3056+B0bU0VqLzV4W7WHq7KMu+f481A0WmVqLzb079x7b4ban4u5Ct/j5maLj+FjBb1/PFI68d70GS5o52V0xHlbLpT42gUA35/rpPatGd6nEkHd93M13me+lTtE7fuL/yHL+InmL1D74uN8DZ24g/eJwb6nZB2Sa/kYDwzzvR96+ToOAAiJidsn1voEX5sAAK7YgwZ4WzZ4twUA5A7xvu/z8TqEInz9K4l1AwBe0cPfnUpN/jt/dffviRKWv/fIqWAeOd4wjxzDMAzDMAzDMAzDMIxlgnnkGIZhGIZhGIZhGIZx1mn95/+d6TKWO+aRYxiGYRiGYRiGYRiGsUwwjxzDMAzDMAzDMAzDMM46ruPCdc6sx4xrGjmGYRiGYRiGYRiGYRjG84Ud5BiGYRiGYRiGYRiGYSwTLLTKMAzDMAzDMAzDMIyzjvs8pB+30CrDMAzDMAzDMAzDMAzjecM8cgzDMAzDMAzDMAzDOOu00IJj6ccldpDzHLLS3/7/t3fvQVKVd/7HP909fZn7DHMHRgFFFAVEUAMkRl0Wfq6auFtlshcR2Oj+4g+xDJZVUGugylQkZH+VYCVuzCbxkhirzBY/o2VF0QU1XnBRWS+oC4qoiHKd+7Wnu8/vD+OsE4fvtwec6Wl4v6iuYvp7+jzf85znPOfMM0+fY8Z7Mml3Ha3pMjOeLukz44cyu834hNDZbg5lmXIzXlhQZcY/avmjW8bEyr+yc1CNGU8F/nS4dzsjZvzL1V1mfMP7dg7ZrKM5aefQF9idyCN77c9LUiRk10VTb8iMj4m7RajI6Sme2W/nML7EzkGSKqJ2vC1lJ9Gesuvqwy5/AmJK9jFarEozfqh3h1tGWXycGY+FSsx4bTDeLaNPdj/RmbL3R9Kpy/LCHjeHHU12XW05XGjGTyry+8txhUkz/kZThRnvy/jt8mDSbnctdgoaE/P7qv9qLjXjs8e0mfGPO4vM+CuH/br8IN1kxs9RrRlPRPy6nFa5yIy/3vwbdx2eg0328XPAqas9XXZH1JT0t3NPxl6HV1V7uv1Ls5jTnXntMplF29/bbbfLs8rtfuZgr9OpS2q3V6GPkq+a8aKofZ5uSvo5tPbZ9V0UsY+f3i67L5Okvd0xM/7wnl4zPn1Mwi2j0i5Czx6sMOPvvWfHTyp2U9AB59TwVqt9fFYl/HZZHbevm04LN5rxzuJz3DK60vYB9siOk8x4UcTO8d12ux4kqXx3yoyPL+0w44XxfW4ZZWPsHRYrtbcjbHenkqTA3gz1Hrbr+pm37LrORotzHi+P2sd4UYF/Dm1yyqiO253dndNuMePd6R59580fuHngxMJADgAAAAAAyLlP7pAz3I8fz/8ZOdwjBwAAAAAAIE8wIwcAAAAAAORcJpRRKMQ9cjzMyAEAAAAAAMgTzMgBAAAAAAA5x1OrssOMHAAAAAAAgDzBjBwAAAAAAJBzzMjJDjNyAAAAAAAA8gQzcgAAAAAAQM4FyigY5hkzw73+kcCMHAAAAAAAgDzBjBwAAAAAAJBzGaUVUnrYy8h3DOQMUehP/wbzRmaX+dmzC0511/9eqsmMnxqcYca71GvGw8HguX9WS7jFjJ+WOceMj6+wc5SkdJAy43UaY8YzgVuEGovsAzTj1MWM8qRbRlcqYsbLo3YO44rsQ/DkEjcF9Tj9UNqpq8N2k/lTGXZdfbXe/vwrzX4ZG5s/NONLCsab8UjI3tDvv3ubm8P/Kr/RjJdkis34mPjX3DJqI/ZO7QvsqZ6Hgw63jFOitWY87HQDPWm7Xfd1Frk5vN8VN+PeMdzttDlJumWH3V8uGddgxjtTfhkdzjL7uu39lQ6OfeJre1/UjHt9WXXC3p+S9GEyZsa9VcTCfqfcrgNmfEblYjMeZHH+Smfs+o6G7f21v8f+/Ied/lTsVMZepiRml5FNn5x0OvaGomNvd50pu4yYU5eJLFIYV2Q3rIbOafbnM/Z5oSftJzGhuMuM9zlt6r9aCt0yvL6mPGof49ub/UbxSPMPzfjfVK004xUx+3rkDy12PUlSbTxhxjv67AuWnrRdD5K/P3Zm9pjxqmCcW0Zbn13G7DH2ebjXaXcfdtvnR0l6u8Puk7e12Ofhviy+NXKyc53c7NTDSYV9bhmJiF3G+FK7LscWdbtltDnnr4O9drt6eK8d/0qtfw5tSNi/MzQl7TKc7taN48TEQA4AAAAAAMi5QMEI3CMn/0fHuEcOAAAAAABAnmAgBwAAAAAAIE/w1SoAAAAAAJBzmVBGodDwfrUqw+PHAQAAAAAAMFKYkQMAAAAAAHLuk8ePD+98k+Ph8ePMyAEAAAAAAMgTzMgBAAAAAACjQGbYHz8u7pEDAAAAAACAkcKMHAAAAAAAkHOZIK3hnm/ySRn5jRk5AAAAAAAAeYIZOQAAAAAAIOeCEbhHzvDfg2f4MZAzROUFUUXD0UFjFyemmJ9NRPz1j9Wko0mrXzJdZMazabJBUHFMORSES91los5csFg4ZMbHFvpbUp/oM+MF4cCMv9kec8uoitnT8koK7DwjTj0ks9hhjYUpM96Z9ibe+RPzMoFdV+0pex31hW4R+mp4vBkvitiVkXD25/dPW+Xm0JK0406zzEpB6FhXkjjmHEqddhkN2/HtLWVuGcXO/gqH7DbTlPTr6cYJdU4Zdg4fdPmdcoGTxskl9gKNhf7U3VDIbrs9aTtPr5s41OPncF5lhRn32kxvxt9f8wvPNePeGt7p8PuqaZV2XRUV2P3l/m57Oyvi/nY+0/qxGZ+XGGvGP+q0c5Sks8YMfh3yqeICu01Fs+iGIk677HL6/YIs5nw399rxC4pOM+OFzgG6u9PP4fRy+/gIp+16+Pd9+9wyzojXmvEJpfbleGfK76tuKP2uGf+w074mSjrbOb2i2M2hrc9eR8Q5/40v9hum17b/puoUM97jbKfkX7slIvYxWuj8dvVRd9zNoTtt10XMueZ5q8W/gNzebMfPqbJz2N/r/xpZ5VxKe91ELOKfv3Z12NdFm/fZdXVWpZ3Fe53+8VdSYNdFwrkmGpuw411p/7yAEw8DOQAAAAAAIOcCpRUM8x1gAnGPHAAAAAAAAIyQ42IgZ+/evbrqqqtUVVWlwsJCTZs2TS+99NKgy377299WKBTS+vXrRzZJAAAAAABwRJkR+jccnnrqKYVCoUFfL774Yv9yr732mr7yla8okUiosbFRP/zhD4dcVt5/taq5uVnz5s3TRRddpEcffVQ1NTV6++23VVlZ+bllH3zwQb3wwgsaO9b+fjoAAAAAAEC25s6dq48/HnivvO9+97vatGmTZs+eLUlqa2vTggULNH/+fN155516/fXX9Y//+I+qqKjQP/3TP2VdVt4P5Kxbt06NjY26++67+9+bOHHi55bbu3evli9fro0bN+rSSy8dyRQBAAAAAIAjUDACT63yb3x+NGKxmOrr6/t/7uvr00MPPaTly5cr9Kcbvv/2t79VMpnUXXfdpVgspjPPPFOvvPKKfvSjHw1pICfvv1r18MMPa/bs2bryyitVW1urmTNn6he/+MWAZTKZjBYtWqSbb75ZZ555Zlbr7e3tVVtb24AXAAAAAADIf3/++35vr/M4xSF6+OGHdfjwYS1durT/vS1btuiCCy5QLPY/j3VbuHChduzYoeZm53Fyn5H3Aznvvvuufvazn2ny5MnauHGjrrvuOt1www269957+5dZt26dCgoKdMMNN2S93rVr16q8vLz/1djYOBzpAwAAAAAASUGQHpGXJDU2Ng74nX/t2rVf6Lb86le/0sKFCzV+/Pj+9/bt26e6uroBy3368759+7Jed95/tSqTyWj27Nm67bbbJEkzZ87U9u3bdeedd2rx4sV6+eWXdfvtt2vbtm3905mysWrVKq1YsaL/57a2NgZzAAAAAAA4DuzZs0dlZWX9P8fj8UGXW7lypdatW2eu66233tLpp5/e//OHH36ojRs36ne/+90Xk+yfyfuBnIaGBk2dOnXAe2eccYY2bNggSXrmmWd04MABnXTSSf3xdDqtm266SevXr9d777036Hrj8fgRdyQAAAAAAPhiffJEqeG9R86nT60qKysbMJBzJDfddJOWLFliLjNp0qQBP999992qqqrS1772tQHv19fXa//+/QPe+/Tnz95fx5P3Aznz5s3Tjh07Bry3c+dOnXzyyZKkRYsWaf78+QPiCxcu1KJFiwZ8Vw0AAAAAAOCzampqVFNTk/XyQRDo7rvv1tVXX61oNDogNmfOHP3zP/+z+vr6+mNPPPGEpkyZMuiTt48k7++R853vfEcvvPCCbrvtNr3zzju6//779W//9m9atmyZJKmqqkpnnXXWgFc0GlV9fb2mTJmS4+wBAAAAAMDxYvPmzdq9e7euueaaz8X+/u//XrFYTN/61rf0xhtv6IEHHtDtt98+4LYu2cj7GTnnnnuuHnzwQa1atUq33nqrJk6cqPXr1+sf/uEfRjyX7pT9GLNUFjPECsLZ38dnMM29aTMezWL93jKHe1JmvK4oasYlKXCe+JZM2wscDPtjkIURO4/utL2d0ZD/WLq2PjuPooi900ucI7Al6e+vTGCvpCJ67I/Xe6/DXseYuJ1nRcwMS5L2d9ltd2JJxIyHnCmYh7O4Cf3hHns7K5ztzGZkvM1p28XO4eMc4pKkqJNITdw+hotifWZ8WqX/FL99XYVmvDtt789yvxvR4aS9jj6n6Vdm0S73djn7yzmGP+rxW4V3jDYn7a/5jiu099fJpXY9SdIhp+170oHfVz3XvcOMTwxONuMzxvhfd46G7X4g42zmdOcPYf950D+Rh5ye4GC3fRBPqfAbf5+TRpd9iOu/W/yO5Owqu91s/cjeznm1fpuos7sJvd5k7zCvHhoKj+2aSpIizrXAFbX+NPg2+xBVm9NZZXNu2dXeY8ajznVTScyOP9b2tpvDBcWTzbh3HZxNP7L1oF2ZY51OuSeLc+jebrsuZo6xPx+L2IW0pvw9+pN9D5vxCZFZdg6B31/Orawy4wXO7shmf3nn+pZeO8/3OorcMj7osssIArtD9I7PaeV+o6mKJc14SdQuJOPUZUfqi32S0mgXKK1Ax95/e2UMp1/96leaO3fugHvmfKq8vFyPP/64li1bplmzZqm6ulqrV68e0qPHpeNgIEeSLrvsMl122WVZL3+k++IAAAAAAAAcrfvvv9+MT58+Xc8888wxlXFcDOQAAAAAAID8FgQZBcN8s+MgGN71j4S8v0cOAAAAAADAiYIZOQAAAAAAIOdG8vHj+YwZOQAAAAAAAHmCGTkAAAAAACDngmAEnloVDO9Tq0YCM3IAAAAAAADyBDNyAAAAAABAzgUKhv+pVQqGdf0jgRk5AAAAAAAAeYIZOUPUnk4pmokMGnu443fmZxMFFe76SwvqzHilxprxFu0342n1uTkUq9KMJ1Rsxpvby90yWsOtZnx/sMuMh9v9McglVReY8bQzEDuuyB8JLonYK+lMDd5W/idur/9At5/Df3Z3mfEpZfb++l3ro24ZS6suMeOlUfvzLx3y211p1K6r5qT9XdnOsN0m3m93KlvS/2v6v2Z8Xtm3zXhzuMktY3vzb834nPL/Y8aLlXDL8EwrLzTjsYj9veHCqF+XezuLnLhdRkGJf3pKB/bx1+18/TmTxR9jIs5XtJ8/0GPGaxIxt4zGYrvtT6/wjx9LKIvvmb/V2WzGp1Xa54VoyK/MvyqfYsa9/jAe9vvDvsyx/X2qPWXX1eGkvb8lqVJlZrym0N7fb7ce2/6WpJ60XVeTy/126TRtFUftuj7U6xahZMau7129drt8P7TdjM8Y81U3h7STQ/II13yfak66Regjp7/z6vKtzha3jEkJ+9rrQK+9Q5p77RwvKpns5lDkdNvFBV5d+/1IWczeHx199jqyuetG0ulH3DYjO8futJ/FRTH7uqu60K7szj6/v2xL2nX1SLN9fTm3psQt48vVdkfS3Gv3RY99ZNelJBU454bxJfY6ypxr2PqE35mVRO1++773Ksz4VRNazHg4i3Ps8SQIMiNwjxyeWgUAAAAAAIARwowcAAAAAAAwCqRH4A42PLUKAAAAAAAAI4QZOQAAAAAAIOc+uX8N98jxMCMHAAAAAAAgTzAjBwAAAAAA5BwzcrLDjBwAAAAAAIA8wUAOAAAAAABAnuCrVQAAAAAAIOcyyig03F+tEl+tAgAAAAAAwAhhRs4QFYUjioYjg8bOj/21+dk+pdz1lwYJM96kdjNeEaoz4291bXRzmFz0F2b8zOhYu4zkPreMg8FuM14UrjTjvUGHW0Y8EpjxcYX2SGw8bH9ekkKyl3nhsH2Idafszz+bfN3N4ZvVM8x4OrDLmBb6iltGadSJOz3J1IqYW0Zvxs5zwyG7zVxUOsGMl8UGP24/65vVN5vxp/qeNuPVmuSWMa/8ejM+PlZmxh84eJtbxpL6W8x4ymkT6Yw9xt+b8v8G0JW2l5nkNJrWpH/8Pd70kRn/Rr3dV8Wz+FPGf7fZ8dnVhWZ8R6vf76edTe1N23+V6nX2V1GBX5dV4WIz3u1sRrOTgyT1OBvqreGJj/y/njUW2ufQkqi9IVUxO8fJZfb+lqS327rNeFOPvR2tqT63jGbnWuCswhoznoj4f+n8uOvY/lrZ4/QBkt/vn1ZoXws0puaZ8QM9/nb2pO1zQzqwtyOLqlR53C6jO2XX9RnFFW4ZlXE7kTMr7LZbErX3xUuH/H5kXJGdg9ciXjrk95ctqV4zPqG4yIyXxfwdVhW3t7UrZZ+/Cpzrx2zazNRK+8Ir6pRxsMc//ra32tfS0ZDdbjv6/DbxflfcjFfF7H1+VmU2x7Adb7KbjA702PFOZ39LUjxiH8NXNtp9dlOvXU+d/qFxXOFmx9lhRg4AAAAAAECeYEYOAAAAAADIuSBwplnlSRnDjRk5AAAAAAAAeYIZOQAAAAAAIOcCBdIwP1UqcO5zmg+YkQMAAAAAAJAnmJEDAAAAAABybiSeKMVTqwAAAAAAADBimJEDAAAAAAByjhk52WFGDgAAAAAAQJ5gRs4QjSuJKB4evNrqMyXmZ5NZDPx5I2sTQwkz3p2y78B9Udm33BwKnCSae+0yTk7XuGWMy1Sb8bICu2lmsrjTeMZZpCKaMuOHk/7hMSZm79TXWtvN+JllpWb8bytnuDm82ZI04zOromZ8YYPdbiWpJRky4xVRux42NO1wy/jfDVPM+LKSk814h7071Z22t0GS0oG9z0/J/IUZT0T8dhl1jq/OlJ3nDYXfdcuotbsJ90797b0xtwxPS1/EjE8qSZvxLQf9/fWN+rFmfHyhXUZXFm1iTrVdV2NidsM7p9IvIxHuM+N7uu39cbDXblRRPwVNKrPLaLK7GfWk/bafcjrl8pid6Kllfp98sNdeR0ufvQ7vPF1c4FdmccTuc9OBXQ8TSwrdMiYE9kFek7DbRNI7QUoqcRpOvZNmp9MnS9IHHfYxOqXc3l/pwO5nJjv9jCQdcvq7eNiuqwnFfl3ubLfr8vQye381OedgSWrr8/K0d0hP2s5hdrWfQ7XTH7Y654XxJf4x/kFrkxkvixab8XAW/aHXdl9vLTLjU8u6zXjSb5aaUWF3upGQvb83OecNSbpkrH3953UT77b7bX9Xh92uIqX2Pv+oyy1Ck0rtPApC9k7vydjxA71ZtMtuu9+fVWn/PvBup/P7XRZt5ngSDPMTq0aqjOHGjBwAAAAAAIA8wYwcAAAAAACQc9wjJzvMyAEAAAAAAMgTzMgBAAAAAAA5x4yc7DAjBwAAAAAAIE8wIwcAAAAAAIwCIzFbhhk5AAAAAAAAGCEM5AAAAAAAAOQJvloFAAAAAAByjpsdZ4cZOQAAAAAAAHmCGTlDVB6VEpHBY6cUp8zP9gUhd/1tffbYWmlBYMY/7LY/f6DHTUFnldkjlJ0pezt6M1G3jJakvY7fN+0y49c0THLLmFCcNONjC7vN+MQSf6S2IGIv88MZ9iHWmeoy42+1Fbo57Gx19kfajhc7bUqSIk7TrYmnzfj3T5noltHWZ9flwaTdtk8v7XXW73d321vtZSaX2tv5dvsROofPmFBsb+f4QruMj3r8MsYl7L4oHrH3+faWMjM+qcRut5J0Yf0hM97cEzfjU0r9/rK6yD6GPU3diWP6vCQd6rW3Y3r1YXcdyZTd7grCJWY8E9jbEQ75x/i4QnuZ97rsdlebRVU+tc/uk6dVxsx4dcw+NiRp62G7LqudPH+yf7MZP0tfcnOYWVlkxjvtw1MnFbtFqNHpJ1r6/HV4ejL2MbjX6QbOKPP3VzRs76+JznVVXdzeUL/lS+902MfwyUV2GROL7XOPJE2vsLej2rkeyebvxq1On9qZsq/NDvTY8fKQ3ycfq7nVzsEhaV51pRlPZux299xB/xxa5/QT3rV4T9ou49wx/jm01jm/pdL2NdF5Vf52lkftuiousPdHY6HdZ0tSMmPn+fCHdg5LT/E7s8D5/erfD9r9zBWNdg6lTj1I0sFeuy7299iN6uzKdjPemfL7meNJMAI3Ih6JMoYbM3IAAAAAAADyBDNyAAAAAABAzgVBoOF+PPgnZeQ3ZuQAAAAAAADkCWbkAAAAAACAUSAtabjvy8WMHAAAAAAAAIwQZuQAAAAAAICcC4KMhntGDvfIAQAAAAAAwIhhRg4AAAAAABgFhn9GDvfIAQAAAAAAwIhhRs4QRUKfvAZTHk2bn41HMu766+L26GMyY4+9taeiZjwa9kc3Swvs7RgTs0cwO1MRtwzJXuaSiklmvCLq1+XYwm4zXhhNmfG//q+9bhmPn19jxiuK7RxaOgvNeH3SP0SnVsbNeHGBvb8O9LhFqMRZR4VTl0UFdlyS2vrsbY05w86FzvEVDyfdHM6ptNfhHX/RL2BofEys75jiktTn5PmN135jxv9P/bfMeE3c7mckaUKi1YyXFNkNL5TFH2ISRX5dWMp6/Mbf0WkfXzXFXWa8uNhvdz2tdtv/7/aEGT+1uNct41jFI3YfcKjX7/dPLbPrMh62j7+YE5ekmZX2+WtPt53nBdGvmvGetL1+SYo4jff0Mns7auJ+GV4/UBmz+9zutN9ZtTh9clGpvZ3eNZEkVcbsZSqi9nYWO+eeN1tL3BwSTtseE7eP4cqE34+UFtrHaGGRXUYmi/3V3Wf3yy812f3IWeX29UpPFjlsOWxf09xzeIsZ//Eps9wyauJ2XbY79XBamd9XxcJ2m6iJ2+3yzXa7r5tb1e7m4F0/9jrXh35vKaWcCQljnLr2jj9JOtBtt7u/nWC3q9Isrh/DIXtDvjbe7qu8/rS4wL/WaHHaXdTJMRGxtzMV+PVwXBmBe+SIe+QAAAAAAABgpJxQAzl33HGHJkyYoEQiofPPP19bt27NdUoAAAAAAEBSMEL/8t0JM5DzwAMPaMWKFVqzZo22bdumGTNmaOHChTpw4ECuUwMAAAAAAMjKCTOQ86Mf/UjXXnutli5dqqlTp+rOO+9UUVGR7rrrrkGX7+3tVVtb24AXAAAAAAAYLpkReuW3E2IgJ5lM6uWXX9b8+fP73wuHw5o/f762bBn8xmtr165VeXl5/6uxsXGk0gUAAAAAABjUCTGQc+jQIaXTadXV1Q14v66uTvv27Rv0M6tWrVJra2v/a8+ePSORKgAAAAAAwBGdEAM5RyMej6usrGzACwAAAAAADJfgk8eDD+drGG92vHPnTn39619XdXW1ysrK9OUvf1lPPvnkgGU++OADXXrppSoqKlJtba1uvvlmpVJDe8z8CTGQU11drUgkov379w94f//+/aqvr89RVgAAAAAA4Hhx2WWXKZVKafPmzXr55Zc1Y8YMXXbZZf3fBEqn07r00kuVTCb1/PPP695779U999yj1atXD6mcE2IgJxaLadasWdq0aVP/e5lMRps2bdKcOXNymBkAAAAAAPjESDx6fHhm5Bw6dEhvv/22Vq5cqenTp2vy5Mn6wQ9+oK6uLm3fvl2S9Pjjj+vNN9/Ufffdp7PPPluXXHKJvve97+mOO+5QMpnMuqyCYdmCUWjFihVavHixZs+erfPOO0/r169XZ2enli5dmtXng+CTnd2b6T3iMl1pu+JTgX937FQmZMb7AnvsrTudNuM9aXv9ktSVtqd1RQO74XelI24ZPWl7O3qdqupO+wdfR+rI+0qS0iF7OzNBn1tGe5+9z6Oy90dHyq6HrnTMzaHHqYtIyI57dS1JBfZmqNOp60D+VMFup914bdfLIZNFf93lHD/JjNdus9lOu8I7U9l34EeScvqJwOmLejM9Ztzr6yT/2AiH7RxCflelZJ9/jFr6+vzG35GyEwk5x5ecevikDPtU3J2298cX0WY83rHR7fTpktTrnN+8ft07N32yDq8fsfPsy9htoi9wOkNJvU5n4/UBXU5ckuIpu+2nA7uue5y+TPKvJ5JOml6bkaSwc5xHQ84x7pzHu9NRNwfvcsI7t0SzOf6cfiDlxDNZHF/eNY/fj9if944dyT/GveuqrrSdg+Tn6R0/3jWTJKXd61x7O7wyvG2Q/HNob8rezu4s6jIS8q5R7XUkM/71fpdz7eb1RdnUVdg5D3e517D2/gzkX2t0pe3zeMj9fcDezk/P84HTNo8vI7Otf/5k6ng8rng8ftTrq6qq0pQpU/TrX/9a55xzjuLxuH7+85+rtrZWs2bNkiRt2bJF06ZNG3D/3oULF+q6667TG2+8oZkzZ2ZXWHAC+clPfhKcdNJJQSwWC84777zghRdeyPqze/bs+XTojhcvXrx48eLFixcvXrx48Rqx1549e4bxN+Xc6+7uDurr60esPktKSj733po1a455O/bs2RPMmjUrCIVCQSQSCRoaGoJt27b1x6+99tpgwYIFAz7T2dkZSAr+8Ic/ZF3OCTMjR5Kuv/56XX/99Uf12bFjx2rPnj0qLS1VKBRSW1ubGhsbtWfPHm6EjLxGW8bxgHaM4wVtGccL2jKOF7luy0EQqL29XWPHjh3xskdSIpHQ7t27h/T1omMRBIFCfzYF/EizcVauXKl169aZ63vrrbc0ZcoULVu2TLW1tXrmmWdUWFioX/7yl7r88sv14osvqqGh4QvL/4QayDkW4XBY48eP/9z7PNEKxwvaMo4HtGMcL2jLOF7QlnG8yGVbLi8vz0m5Iy2RSCiRSOQ6jc+56aabtGTJEnOZSZMmafPmzXrkkUfU3Nzc31b+9V//VU888YTuvfderVy5UvX19dq6deuAz376UKahPIiJgRwAAAAAAIBB1NTUqKamxl2uq6tL0ieTQD4rHA4r86f78M2ZM0ff//73deDAAdXW1kqSnnjiCZWVlWnq1KlZ53RCPLUKAAAAAABguMyZM0eVlZVavHixXn31Ve3cuVM333yzdu/erUsvvVSStGDBAk2dOlWLFi3Sq6++qo0bN+qWW27RsmXLhnSjZQZyjlI8HteaNWuO6a7WwGhAW8bxgHaM4wVtGccL2jKOF7RlZKu6ulqPPfaYOjo6dPHFF2v27Nl69tln9dBDD2nGjBmSpEgkokceeUSRSERz5szRVVddpauvvlq33nrrkMoKBcEJ9RwzAAAAAACAvMWMHAAAAAAAgDzBQA4AAAAAAECeYCAHAAAAAAAgTzCQAwAAAAAAkCcYyDkKd9xxhyZMmKBEIqHzzz9fW7duzXVKgGkobfaee+5RKBQa8EokEiOYLTA0f/zjH3X55Zdr7NixCoVC+v3vf5/rlIAjGmp7feqppz7XJ4dCIe3bt29kEgaGaO3atTr33HNVWlqq2tpaXXHFFdqxY0eu0wIGdTTtlWtljAYM5AzRAw88oBUrVmjNmjXatm2bZsyYoYULF+rAgQO5Tg0Y1NG02bKyMn388cf9r/fff38EMwaGprOzUzNmzNAdd9yR61QA19G21x07dgzol2tra4cpQ+DYPP3001q2bJleeOEFPfHEE+rr69OCBQvU2dmZ69SAzzna9sq1MnKNx48P0fnnn69zzz1XP/3pTyVJmUxGjY2NWr58uVauXJnj7IDPG2qbveeee3TjjTeqpaVlhDMFjl0oFNKDDz6oK664ItepAK5s2utTTz2liy66SM3NzaqoqBix3IAvysGDB1VbW6unn35aF1xwQa7TAUzZtFeulTEaMCNnCJLJpF5++WXNnz+//71wOKz58+dry5YtOcwMGNzRttmOjg6dfPLJamxs1Ne//nW98cYbI5EuAOAIzj77bDU0NOgv//Iv9dxzz+U6HSBrra2tkqQxY8bkOBPAl2175VoZucZAzhAcOnRI6XRadXV1A96vq6vju+oYlY6mzU6ZMkV33XWXHnroId13333KZDKaO3euPvzww5FIGQDwGQ0NDbrzzju1YcMGbdiwQY2Njbrwwgu1bdu2XKcGuDKZjG688UbNmzdPZ511Vq7TAUzZtleulTEaFOQ6AQCjy5w5czRnzpz+n+fOnaszzjhDP//5z/W9730vh5kBwIlnypQpmjJlSv/Pc+fO1a5du/TjH/9Yv/nNb3KYGeBbtmyZtm/frmeffTbXqQCubNsr18oYDZiRMwTV1dWKRCLav3//gPf379+v+vr6HGUFHNkX0Waj0ahmzpypd955ZzhSBAAM0XnnnUefjFHv+uuv1yOPPKInn3xS48ePz3U6gOlY2ivXysgFBnKGIBaLadasWdq0aVP/e5lMRps2bRowKguMFl9Em02n03r99dfV0NAwXGkCAIbglVdeoU/GqBUEga6//no9+OCD2rx5syZOnJjrlIAj+iLaK9fKyAW+WjVEK1as0OLFizV79mydd955Wr9+vTo7O7V06dJcpwYMymuzV199tcaNG6e1a9dKkm699VZ96Utf0qmnnqqWlhb9y7/8i95//31dc801udwM4Ig6OjoG/BVs9+7deuWVVzRmzBiddNJJOcwM+Dyvva5atUp79+7Vr3/9a0nS+vXrNXHiRJ155pnq6enRL3/5S23evFmPP/54rjYBMC1btkz333+/HnroIZWWlvbfk6+8vFyFhYU5zg4YKJv2yrUyRiMGcobom9/8pg4ePKjVq1dr3759Ovvss/XYY4997maywGjhtdkPPvhA4fD/TM5rbm7Wtddeq3379qmyslKzZs3S888/r6lTp+ZqEwDTSy+9pIsuuqj/5xUrVkiSFi9erHvuuSdHWQGD89rrxx9/rA8++KA/nkwmddNNN2nv3r0qKirS9OnT9R//8R8D1gGMJj/72c8kSRdeeOGA9++++24tWbJk5BMCDNm0V66VMRqFgiAIcp0EAAAAAAAAfNwjBwAAAAAAIE8wkAMAAAAAAJAnGMgBAAAAAADIEwzkAAAAAAAA5AkGcgAAAAAAAPIEAzkAAAAAAAB5goEcAAAAAACAPMFADgAAAAAAQJ5gIAcAAByzJUuW6Iorrsh1GgAAAMe9glwnAAAARrdQKGTG16xZo9tvv11BEIxQRgAAACcuBnIAAIDp448/7v//Aw88oNWrV2vHjh3975WUlKikpCQXqQEAAJxw+GoVAAAw1dfX97/Ky8sVCoUGvFdSUvK5r1ZdeOGFWr58uW688UZVVlaqrq5Ov/jFL9TZ2amlS5eqtLRUp556qh599NEBZW3fvl2XXHKJSkpKVFdXp0WLFunQoUMjvMUAAACjFwM5AABgWNx7772qrq7W1q1btXz5cl133XW68sorNXfuXG3btk0LFizQokWL1NXVJUlqaWnRxRdfrJkzZ+qll17SY489pv379+sb3/hGjrcEAABg9GAgBwAADIsZM2bolltu0eTJk7Vq1SolEglVV1fr2muv1eTJk7V69WodPnxYr732miTppz/9qWbOnKnbbrtNp59+umbOnKm77rpLTz75pHbu3JnjrQEAABgduEcOAAAYFtOnT+//fyQSUVVVlaZNm9b/Xl1dnSTpwIEDkqRXX31VTz755KD329m1a5dOO+20Yc4YAABg9GMgBwAADItoNDrg51AoNOC9T5+GlclkJEkdHR26/PLLtW7dus+tq6GhYRgzBQAAyB8M5AAAgFHhnHPO0YYNGzRhwgQVFHCJAgAAMBjukQMAAEaFZcuWqampSX/3d3+nF198Ubt27dLGjRu1dOlSpdPpXKcHAAAwKjCQAwAARoWxY8fqueeeUzqd1oIFCzRt2jTdeOONqqioUDjMJQsAAIAkhYIgCHKdBAAAAAAAAHz8eQsAAAAAACBPMJADAAAAAACQJxjIAQAAAAAAyBMM5AAAAAAAAOQJBnIAAAAAAADyBAM5AAAAAAAAeYKBHAAAAAAAgDzBQA4AAAAAAECeYCAHAAAAAAAgTzCQAwAAAAAAkCcYyAEAAAAAAMgT/x8aTjGjf+zanQAAAABJRU5ErkJggg==",
      "text/plain": [
       "<Figure size 1500x700 with 2 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "import numpy as np\n",
    "\n",
    "# Get spectrogram using Librosa's Short-Time Fourier Transform (stft)\n",
    "spec = np.abs(librosa.stft(audio))\n",
    "spec_db = librosa.amplitude_to_db(spec, ref=np.max)  # Decibels\n",
    "\n",
    "# Use log scale to view frequencies\n",
    "librosa.display.specshow(spec_db, y_axis='log', x_axis='time')\n",
    "plt.colorbar()\n",
    "plt.title('Audio Spectrogram');"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "9OPc4tcalRzs"
   },
   "source": [
    "Again, we are able to see each letter being pronounced, and that the last two blobs that correspond to the \"N\"s are pretty similar-looking. But how do we interpret these shapes and colors? Just as in the waveform plot before, we see time passing on the x-axis (all 2.6s of audio). But now, the y-axis represents different frequencies (on a log scale), and *the color on the plot shows the strength of a frequency at a particular point in time*.\n",
    "\n",
    "We're still not done yet, as we can make one more potentially useful tweak: using the **Mel Spectrogram** instead of the normal spectrogram. This is simply a change in the frequency scale that we use from linear (or logarithmic) to the mel scale, which is \"a perceptual scale of pitches judged by listeners to be equal in distance from one another\" (from [Wikipedia](https://en.wikipedia.org/wiki/Mel_scale)).\n",
    "\n",
    "In other words, it's a transformation of the frequencies to be more aligned to what humans perceive; a change of +1000Hz from 2000Hz->3000Hz sounds like a larger difference to us than 9000Hz->10000Hz does, so the mel scale normalizes this such that equal distances sound like equal differences to the human ear. Intuitively, we use the mel spectrogram because in this case we are processing and transcribing human speech, such that transforming the scale to better match what we hear is a useful procedure."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {
    "id": "7yQXVn-TlRzt"
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAABHIAAAJwCAYAAADlU0bdAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjAsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvlHJYcgAAAAlwSFlzAAAPYQAAD2EBqD+naQABAABJREFUeJzs3XmYHVWdP/53LXftvdOddBJCNhZZRDTqGBkWHQQURUdGRnFGUQZxBERhVJCfLC6DiKMgIKPfr4M64oY64wwjCoLjFxVmGCQKCJElISFJd5be71Z1q+r3R6Q1k+TzPrG703R4v54nzwM5t2/VrTp1qvrmfN7Hy7Isg4iIiIiIiIiIPOv5M70DIiIiIiIiIiLiRl/kiIiIiIiIiIjMEvoiR0RERERERERkltAXOSIiIiIiIiIis4S+yBERERERERERmSX0RY6IiIiIiIiIyCyhL3JERERERERERGYJfZEjIiIiIiIiIjJL6IscEREREREREZFZQl/kiIiIzDLHHXccjjvuuJneDRERERGZAfoiR0REZAp9+ctfhud58DwPP/vZz3Zqz7IMixYtgud5eO1rXzut+xJFEa699lq88IUvRHt7Ozo7O3HYYYfhXe96Fx599NFp3baLH/zgB7j88stnejdEREREZhV9kSMiIjINisUivv71r+/09z/96U/x9NNPo1AoTPs+nHrqqbjwwgtx+OGH45Of/CSuuOIKHHPMMbjttttw7733Tvv2mR/84Ae44oorZno3RERERGaVcKZ3QEREZF/0mte8Brfccgs+97nPIQx/f7v9+te/jhUrVmDr1q3Tuv377rsPt956Kz7xiU/gwx/+8A5t119/PYaHh6d1+1Ot2WwiTVPk8/lp31aapoiiCMVicdq3JSIiIrKnNCNHRERkGrzlLW/Btm3bcMcdd0z8XRRF+M53voPTTz99lz+TpimuueYaHHbYYSgWi5g3bx7OPvtsDA0N7fH2n3jiCQDAUUcdtVNbEASYM2fOxP9ffvnl8DwPjz76KE477TS0t7djzpw5OP/881Gv13f6+a997WtYsWIFSqUSuru78eY3vxnr16/f6XX/9V//hde85jXo6upCS0sLjjjiCFx77bUAgDPOOAM33HADAEyUonmeBwBYu3YtPM/Dpz/9aVxzzTVYvnw5CoUCfvOb3wAA7rrrLhx99NFoaWlBZ2cnXv/61+ORRx7Zafv/+Z//iRe/+MUoFotYvnw5vvCFL0x81j/keR7OPfdc3HzzzTjssMNQKBTwwx/+EADw6U9/Gi9/+csxZ84clEolrFixAt/5znd22tYz73HLLbfg0EMPRalUwsqVK/Hggw8CAL7whS/ggAMOQLFYxHHHHYe1a9fu9B4iIiIiLjQjR0REZBosWbIEK1euxDe+8Q28+tWvBgDcdtttGBkZwZvf/GZ87nOf2+lnzj77bHz5y1/GO97xDrz3ve/FmjVrcP311+OBBx7Az3/+c+RyOeftL168GABw880346ijjtphVtDunHbaaViyZAmuvPJK3Hvvvfjc5z6HoaEhfPWrX514zSc+8Ql85CMfwWmnnYa/+Zu/wZYtW3DdddfhmGOOwQMPPIDOzk4AwB133IHXvva1mD9/Ps4//3z09fXhkUcewa233orzzz8fZ599NjZu3Ig77rgD//zP/7zL/bnppptQr9fxrne9C4VCAd3d3fjxj3+MV7/61Vi2bBkuv/xy1Go1XHfddTjqqKPwy1/+EkuWLAEAPPDAAzjppJMwf/58XHHFFUiSBB/96EfR29u7y23ddddd+Pa3v41zzz0XPT09E+9z7bXX4pRTTsFb3/pWRFGEb37zm3jTm96EW2+9FSeffPIO73H33Xfj3/7t33DOOecAAK688kq89rWvxQc/+EF8/vOfx3ve8x4MDQ3hU5/6FN75znfirrvuoudEREREZCeZiIiITJmbbropA5Ddd9992fXXX5+1tbVl1Wo1y7Ise9Ob3pS94hWvyLIsyxYvXpydfPLJEz939913ZwCym2++eYf3++EPf7jT3x977LHZsccea+5HmqbZsccemwHI5s2bl73lLW/Jbrjhhuypp57a6bWXXXZZBiA75ZRTdvj797znPRmA7Fe/+lWWZVm2du3aLAiC7BOf+MQOr3vwwQezMAwn/r7ZbGZLly7NFi9enA0NDe20X88455xzsl09iqxZsyYDkLW3t2ebN2/eoe3II4/M5s6dm23btm3i7371q19lvu9nb3vb2yb+7nWve11WLpezDRs2TPzdY489loVhuNM2AWS+72cPP/zwTvvyzLl7RhRF2eGHH5698pWv3Ok9CoVCtmbNmom/+8IXvpAByPr6+rLR0dGJv7/44oszADu8VkRERMSVSqtERESmyWmnnYZarYZbb70VY2NjuPXWW3dbVnXLLbego6MDr3rVq7B169aJPytWrEBrayt+8pOf7NG2Pc/Dj370I3z84x9HV1cXvvGNb+Ccc87B4sWL8Zd/+Ze7zMh5ZibJM8477zwA20OJAeB73/se0jTFaaedtsM+9vX14cADD5zYxwceeABr1qzB+973vokZOn+4X65OPfXUHWbQbNq0CatWrcIZZ5yB7u7uib8/4ogj8KpXvWpiP5MkwY9//GO84Q1vwIIFCyZed8ABB0zMjvrfjj32WBx66KE7/X2pVJr476GhIYyMjODoo4/GL3/5y51e+2d/9mcTM3kA4E/+5E8mPkdbW9tOf//kk0+an19ERERkV1RaJSIiMk16e3tx/PHH4+tf/zqq1SqSJMFf/MVf7PK1jz32GEZGRjB37txdtm/evHmPt18oFHDJJZfgkksuwaZNm/DTn/4U1157Lb797W8jl8vha1/72g6vP/DAA3f4/+XLl8P3/Yk8l8ceewxZlu30umc8U/r1TD7P4Ycfvsf7/IeWLl26w/8/9dRTAICDDz54p9cecsgh+NGPfoRKpYLR0VHUajUccMABO71uV3+3q20949Zbb8XHP/5xrFq1Co1GY+Lvd/WF1P7777/D/3d0dAAAFi1atMu//2Oyj0RERET0RY6IiMg0Ov3003HWWWehv78fr371q3eaofKMNE0xd+5c3Hzzzbts3122i6v58+fjzW9+M0499VQcdthh+Pa3v40vf/nLZnbO//6yIk1TeJ6H2267DUEQ7PT61tbWSe3j//aHs2Gm2662dffdd+OUU07BMcccg89//vOYP38+crkcbrrppl0uLb+rY2L9fZZlk9tpEREReU7SFzkiIiLT6M///M9x9tln495778W3vvWt3b5u+fLl+PGPf4yjjjpqWr/AyOVyOOKII/DYY49NlEU947HHHtthZsrjjz+ONE0nyoWWL1+OLMuwdOlSHHTQQeZnAYCHHnoIxx9//G5ftydlVsDvA5xXr169U9ujjz6Knp4etLS0oFgsolgs4vHHH9/pdbv6u9357ne/i2KxiB/96EcoFAoTf3/TTTft0X6LiIiITCVl5IiIiEyj1tZW3Hjjjbj88svxute9brevO+2005AkCT72sY/t1NZsNneZaWN57LHHsG7dup3+fnh4GPfccw+6urp2muXzzHLgz7juuusAYCJX5o1vfCOCIMAVV1yx02ySLMuwbds2AMCLXvQiLF26FNdcc81O+/2HP9fS0jKxTy7mz5+PI488El/5yld2+JmHHnoIt99+O17zmtcA2D4D5vjjj8e//uu/YuPGjROve/zxx3Hbbbc5beuZ9/E8D0mSTPzd2rVr8a//+q/O7yEiIiIy1TQjR0REZJq9/e1vp6859thjcfbZZ+PKK6/EqlWrcMIJJyCXy+Gxxx7DLbfcgmuvvXa3+Tq78qtf/Qqnn346Xv3qV+Poo49Gd3c3NmzYgK985SvYuHEjrrnmmp1KftasWYNTTjkFJ510Eu655x587Wtfw+mnn44XvOAFALbPtPn4xz+Oiy++GGvXrsUb3vAGtLW1Yc2aNfiXf/kXvOtd78Lf/d3fwfd93HjjjXjd616HI488Eu94xzswf/58PProo3j44Yfxox/9CACwYsUKAMB73/tenHjiiQiCAG9+85vNz3X11Vfj1a9+NVauXIkzzzxzYvnxjo4OXH755ROvu/zyy3H77bfjqKOOwt/+7d8iSRJcf/31OPzww7Fq1SqnY3jyySfjM5/5DE466SScfvrp2Lx5M2644QYccMAB+PWvf+14JkRERESmlr7IEREReZb4x3/8R6xYsQJf+MIX8OEPfxhhGGLJkiX4q7/6Kxx11FF79F7HHHMMPvaxj+G2227DZz7zGWzZsgVtbW144QtfiKuuugqnnnrqTj/zrW99C5deeikuuugihGGIc889F1dfffUOr7noootw0EEH4bOf/SyuuOIKANvDfE844QSccsopE6878cQT8ZOf/ARXXHEF/uEf/gFpmmL58uU466yzJl7zxje+Eeeddx6++c1v4mtf+xqyLKNf5Bx//PH44Q9/iMsuuwyXXnopcrkcjj32WFx11VU7lIWtWLECt912G/7u7/4OH/nIR7Bo0SJ89KMfxSOPPIJHH33U6Ri+8pWvxJe+9CV88pOfxPve9z4sXboUV111FdauXasvckRERGTGeJmS9kRERJ7TLr/8clxxxRXYsmULenp6Znp3ptUb3vAGPPzww3jsscdmeldERERE/ijKyBEREZF9Uq1W2+H/H3vsMfzgBz/AcccdNzM7JCIiIjIFVFolIiIi+6Rly5bhjDPOwLJly/DUU0/hxhtvRD6fxwc/+MGZ3jURERGRP5q+yBEREZF90kknnYRvfOMb6O/vR6FQwMqVK/H3f//3OPDAA2d610RERET+aMrIERERERERERHZjRtuuAFXX301+vv78YIXvADXXXcdXvrSl87Y/igjR0RERERERERkF771rW/hggsuwGWXXYZf/vKXeMELXoATTzwRmzdvnrF90owcEREREREREZFd+JM/+RO85CUvwfXXXw8ASNMUixYtwnnnnYeLLrpoRvZJGTmO0jTFxo0b0dbWBs/zZnp3REREREREZB+XZRnGxsawYMEC+P6+XVBTr9cRRdFe2VaWZTv9Xl8oFFAoFHb4uyiKcP/99+Piiy+e+Dvf93H88cfjnnvu2Sv7uiv6IsfRxo0bsWjRopneDREREREREXmOWb9+Pfbbb7+Z3o1pU6/XsXTpQvT3D+6V7bW2tmJ8fHyHv7vssstw+eWX7/B3W7duRZIkmDdv3g5/P2/ePDz66KPTvZu7pS9yHLW1tf3uv3wAmpEjIiIiIiIi0y0DkP7B76P7piiK0N8/iLVPfRvt7eVp3dboaBVLFp+G9evXo729feLv//dsnGczfZHj6PfTrjzoixwRERERERHZW54r8R7trUW0t5amdyNpun1b7e07fJGzKz09PQiCAAMDAzv8/cDAAPr6+qZtF5l9u8hOREREREREROSPkM/nsWLFCtx5550Tf5emKe68806sXLlyxvZLM3JEREREREREZOal6cSMmWndxh644IIL8Pa3vx0vfvGL8dKXvhTXXHMNKpUK3vGOd0zTDnL6IkdEREREREREZBf+8i//Elu2bMGll16K/v5+HHnkkfjhD3+4UwDy3qQvckRERERERERk5j0LZ+QAwLnnnotzzz13Gnbmj6OMHBERERERERGRWUIzckRERERERERk5mXZ9j/TvY1ZTjNyRERERERERERmCc3IEREREREREZGZl2Z7ISNHM3JERERERERERGQv0YwcEREREREREZl5z9JVq55tNCNHRERERERERGSW0IwcEREREREREZl5mpHjRDNyRERERERERERmCX2RIyIiIiIiIiIyS6i0SkRERERERERmnkqrnGhGjoiIiIiIiIjILKEZOSIiIiIiIiIy87K9MCMn04wcERERERERERHZSzQjR0RERERERERmnJel8KZ5xsx0v//eoBk5IiIiIiIiIiKzhGbkiIiIiIiIiMjM06pVTjQjR0RERERERERkltCMHBERERERERGZeWm2/c90b2OW04wcEREREREREZFZQjNyRERERERERGTmKSPHiWbkiIiIiIiIiIjMEpqRIyIiIiIiIiIzTzNynGhGjoiIiIiIiIjILKEZOSIiIiIiIiIy87IMyKZ5xkymVatERERERERERGQv0YwcEREREREREZl5yshxohk5IiIiIiIiIiKzhL7IERERERERERGZJVRaJSIiIiIiIiIzL822/5nubcxympEjIiIiIiIiIjJLaEaOiIiIiIiIiMw8hR070YwcEREREREREZFZYka/yEmSBB/5yEewdOlSlEolLF++HB/72MeQZb+vWfve976HE044AXPmzIHneVi1atVO7/PEE0/gz//8z9Hb24v29nacdtppGBgYmGhfu3YtzjzzzB22c9lllyGKor3xMUVERERERESEydLfz8qZrj+ZZuRMylVXXYUbb7wR119/PR555BFcddVV+NSnPoXrrrtu4jWVSgV/+qd/iquuumqX71GpVHDCCSfA8zzcdddd+PnPf44oivC6170O6e+mTD366KNI0xRf+MIX8PDDD+Ozn/0s/vEf/xEf/vCH98rnFBERERERERGZCjOakfOLX/wCr3/963HyyScDAJYsWYJvfOMb+O///u+J1/z1X/81gO2zanbl5z//OdauXYsHHngA7e3tAICvfOUr6Orqwl133YXjjz8eJ510Ek466aSJn1m2bBlWr16NG2+8EZ/+9Ken6dOJiIiIiIiIiCsvTeFNc4bNdL//3jCjM3Je/vKX484778Rvf/tbAMCvfvUr/OxnP8OrX/1q5/doNBrwPA+FQmHi74rFInzfx89+9rPd/tzIyAi6u7vN9x0dHd3hj4iIiIiIiIjITJrRL3IuuugivPnNb8bznvc85HI5vPCFL8T73vc+vPWtb3V+j5e97GVoaWnBhz70IVSrVVQqFfzd3/0dkiTBpk2bdvkzjz/+OK677jqcffbZu33fK6+8Eh0dHRN/Fi1atMefT0REREREREQcZdne+TPLzWhp1be//W3cfPPN+PrXv47DDjsMq1atwvve9z4sWLAAb3/7253eo7e3F7fccgv+9m//Fp/73Ofg+z7e8pa34EUvehF8f+fvqTZs2ICTTjoJb3rTm3DWWWft9n0vvvhiXHDBBRP/Pzo6qi9znkU8ePQ1f9bxfrO9r1Ay27dEDbqNX+Mes70SbzXbk9TeRuYQxJVmTbs9tduL+S66DZ985xunNbO9ELbRbRSCdrM9Sipme1dusdl+aPY8ug9b0jGz/Z6Rz9P32Bfkc3PN9jktB9L3YH0izeI92qddyfutZnszs68vz+HfMsYb/WZ7rfE0fY/J8v2C2Z6ScWRf4fv2mA0Ac1oPM9tbA7tvN2Efy8Sh37LxcjTe9T8yPaPW2EK3kcG+N+RDezz1PN73k9ReEILdn1Ly8wAQNwfpa6Ybe57oajvcbA/98qT3ocWfY7bXsxH6HrXYPpZsTK7W7bEsI88azyXl4v52e77HbG8L+ug22P1puPkUfQ+mGm0z26PYbn+u3HtEnq1m9IucD3zgAxOzcgDg+c9/Pp566ilceeWVzl/kAMAJJ5yAJ554Alu3bkUYhujs7ERfXx+WLVu2w+s2btyIV7ziFXj5y1+OL37xi+Z7FgqFHcq1RERERERERGQaPbOy1HRvY5ab0S9yqtXqTrNmgiCYWG1qT/X0bP8G/K677sLmzZtxyimnTLRt2LABr3jFK7BixQrcdNNNu5ytIyIiIiIiIiLybDajX+S87nWvwyc+8Qnsv//+OOyww/DAAw/gM5/5DN75zndOvGZwcBDr1q3Dxo0bAQCrV68GAPT19aGvb/vUxJtuugmHHHIIent7cc899+D888/H+9//fhx88MEAtn+Jc9xxx2Hx4sX49Kc/jS1bfj9t+Zn3EBEREREREZEZpBk5Tmb0i5zrrrsOH/nIR/Ce97wHmzdvxoIFC3D22Wfj0ksvnXjNv/3bv+Ed73jHxP8/U4Z12WWX4fLLLwew/cudiy++GIODg1iyZAkuueQSvP/9v89HueOOO/D444/j8ccfx3777bfDPmT7QNDRc9H8zqPpaw5tbzHbD2yzz32lyfMY2rYeY7angb2N9px9CSYO/XMksuvWR0kNs++QN9Tq5+lrLKHPt8GORQb7WNSa9oC8rJ0Pd9vqu1/JDgAebh5stgce30alMWC2NxM7pwcOuUkeyRJZ0P4Ss70Hdv1/R9pB9yFkGRykS+QcMjzYkRjy7GOZy3J0G4PlzWb7ev9/zHaWMwIAvm/3m3LOzltokuyLxCHbohh2mu1xMm621+Ihuo24aed8lPLzzPblRT7uL8zsDJwyOdZMzmEsY/1yIKua7dWcfT5dtGf2/c/z+Oeokoyphme3xx7v+0/U7zbbx2tP0vew5Mm1AwBL244z2w/zDjDbcw4zvMdiO1up4AVme0x7FRDn7NeMZ3WzfaRoX8MDyWq6D2wsYrlKLAsPAKr1dWY7yxRzWeeFZUgtKb3cbF+QLjDb2x2eqUJyjY445P4xQyX7Htko230mdeiXI7Bz5qqJncMzUl1Lt/FsyNoSmQkz+kVOW1sbrrnmGlxzzTW7fc0ZZ5yBM844w3yfT37yk/jkJz85qfcQERERERERkRmUZtv/TPc2ZjkFxYiIiIiIiIiIzBIzOiNHRERERERERASAMnIc6YucKZQL7XyNhNQOA0CW2XXUGck6YLXBnkOGB9uG59nb8B22kTpkNlgOzV5MXzO3aLeXSH6Ni9acXdfO4hTmllhOAc8xKId2zkd3YrcXQ74NNnWPDYUtDiNNMbD3Y1tjchk5icPpjskHCUlde9MhD4UdTZ/k27CMAYBfg1mWmO0BuTWUPZ4t0xra78EyOlimBADEZBxpRdlsDxxyeEZgf1aPZFuw/BsA8EifqJNsmZjkSrTk7dwYAGj1e832ud4LzfaRHM8oWD3y72Z7nNjZMZuzx+k25mT2fbgI+3yxvBOHaBlEZCxiuWTljOezMUXS71yy0UpkHBlJ7WM16Nn5GgC/fnjGjb0PLQW7XwNAK8n8Csk9shS4TG63x5GY/ELhZ/x8BeScsjyTumfnYDVYfhuARmyPVSx7JnW4h7L3CIM2+h6TlZFjye4tkcMvkKOpfX9zuX9NFsu38ch4CgBRaverhOQ4umB9gj03BYGdKQaHz5mR3/FS8vsd/wwZAPvZTZ579EWOiIiIiIiIiMy8NNsLM3KUkSMiIiIiIiIiInuJvsgREREREREREZklVFo1hVgGTuqQkTNZKa015bWoHqud9+ypbinJEQH4sWD1rHPyJAAHwKKyXUvaFtrtG2o8B4TVOUckmKU1Z1+CDvE1CEkQD8t0KPLSX+TJV74sCyh0CJYIJ/m1MpshSSJ4nPYhIPlQccYzIRh+DfOppsXCPLOd5VIksGvzo5TXaTdIfkaBZJEUA94xC5n9mirJGBjN7EwWABjx7IyAZmKPZS4ZOSxvodbYav98ZvcZl4ycgOQeFVN7zK15PNeFjfsxyZYZbWyg29hc3Gy2F5MFdrtT3omNDXcFcv25TCaPSc5VNbXzGJIpyFpoTjJzBeDXD/v3xnzYaraHJHMM4JlgATmhLveuEvkc2/MvjG043MDi1H5NIbGfzUpZu9mekj4FAI3IHi8ZlxxHzyGjzZI45PAUcp1me09q32PbSHZhQs43ADRIv0vIc3ID/Hz5ZBs5z86Zq6VDdBvj0YDZ3kzt56bEIZvJJTvQ3oadM7c38M8w+8uA9kiWbf8z3duY5TQjR0RERERERERkltCMHBERERERERGZeVp+3Ilm5IiIiIiIiIiIzBKakTOF9kYGzl5B6vfhsVpvO5fidy/agx3a2XDMa5wrTTvTIefZ+9Ag9eYA0CTBLKwOOmJfBjt81VpguS4094Vvg+UmsfcoBvx8s1ewQ5EnO5FnQT4ACqTr53y7XtxlRC3lus32qDlqtrtkrvgkQ6ANvWZ7R9phtufZGAGgJbRfw3In2h06JsuHGmrYveY3zQfoNoYb68z2hNT3pxk/X82EZfXYeSZZZmchRA71/43QzjOpevb9re7xbfi+nTHlkzyTYthJt1HI7HGfZUKwW5PLv9+xcZ/m0DlkIdRI3l0rySzKgV/DI7D7hJfZ15fvsA2PPE+kmX2vz4ctZntHuJDuA8uOacnZ+9iac8mvsdsTdiwd7tOtpG+3JPaxao/t63OseCDdB5Z3wnhT8O/LLHMs8HnGYjFn3wOLnt1nWnN233c5n8WmfSxi8vxZSfixTGGfc4+8Rx6L6DYqBbvfjPl2zs5677/pNqp1+z4ts1CWTf/y4MrIERERERERERGRvUVf5IiIiIiIiIjIzHsmI2e6/0yTT3ziE3j5y1+OcrmMzs7OXb5m3bp1OPnkk1EulzF37lx84AMfQLPpUNXyB1RaJSIiIiIiIiIySVEU4U1vehNWrlyJL33pSzu1J0mCk08+GX19ffjFL36BTZs24W1vextyuRz+/u//3nk7+iJHdsIybjySj+F5Dt3KY9+C2pkQcWa3A0DOt2sfewp2roRLDfODoT2prUyyEMokQoC8PQCgSQ5llXy5y3J+AJ6BUyKnPMn4wWTHu0o+KPscLKPA5T3a/Llme80boduIMzsPJSZZW17KO0U5zzJw7JyentDO15hT5NkXPUVSW0+uzxq/xGnfZkeq6LXTbfQVDzfbGwU7R6SW2PX/ANAk57yZ2jkh1cZGsz1J7TwVF4XMzoTIZXbWAgCUCvPN9vaCnWfS6fG8k6XkGp3LBisichgvo8QebGKS4TGe8by9xLMvkDrJlml4PGcuJq/Jwe4TKbmPA0CWTS7PJO+3mu0daQ/dh4Bk+bAsktghT4/uA8m3qZE+tf09SCZfYrePkHGoDju/zUXg233GRULGQ9anWC4TABSDLrO9mtlj6nhsf06X50uP9AkmJsfBRYlk6OQc8vJYllaY2u8xmLfHdACoRwP2C8ixSEnOnMyAWb5q1RVXXAEA+PKXv7zL9ttvvx2/+c1v8OMf/xjz5s3DkUceiY997GP40Ic+hMsvvxz5vNtYqdIqEREREREREXlOGR0d3eFPozH5f/xi7rnnHjz/+c/HvHnzJv7uxBNPxOjoKB5++GHn99EXOSIiIiIiIiIy89Js7/wBsGjRInR0dEz8ufLKK6f94/X39+/wJQ6Aif/v7+93fh+VVskeS8k0fQ98yjZFppR2BHwaP1sRlE1tZdOUAaCVLEu6tW5PLR+N7Z93WRrcpWTI4rK6X4EsH86mlvsOxzIkZWjF0G4fichSnE2+D5XYfo1PpgjnPbI8uYO2vF1+0uXz5T7npn1m+/KyXVLUnmdLudNdQIn0GX798W2wcoQtpEJlWbqcbiNHpuEPpaRUzudTtgMyPd0P7H0YLGw22zdFD9J9KHn2crs9gb10cZDwKfZPpHYtXJPcW5ohP5Zs6W/Wr4rkqaiVLh0OBKS8uBjZ57PQ5MeSyZM+k2X2+QQcSjPYPdah5Ghb3i5hGa9vsrfh5cz2lJZxA+2e/TzBxhlSsfS797DbW+gS5nzQZX0/JSV9Nc++/lKHUh2f9H1W9lTK2WW/AFAKOs32WjJstrPyZQDo9Zaa7XNJSV97fvLLj7OSvjFSFlL0+a941dQeUxuw28dh3/8AoOHbS9Jvzh432wcrv6Xb8H27HDxJJlcWyMYZAAB5VmC/O8nMWb9+Pdrbf/9cXCjs+p5w0UUX4aqrrjLf65FHHsHznve8Kd0/i77IEREREREREZGZl6U022hKtgGgvb19hy9ydufCCy/EGWecYb5m2bJlTpvu6+vDf//3f+/wdwMDAxNtrvRFjoiIiIiIiIjILvT29qK3115MxNXKlSvxiU98Aps3b8bcudsDve+44w60t7fj0EMPdX4ffZEjIiIiIiIiIjPvDzJspnUb02TdunUYHBzEunXrkCQJVq1aBQA44IAD0NraihNOOAGHHnoo/vqv/xqf+tSn0N/fj//v//v/cM455+y2tGtX9EWOTLkMk78wfM9ecrSHBRkA6M7btb2lwM5rGPcnn1PQH9lLE7OcAlZnDfAlRaMpWF4vIdkwLCOg4bCUNEi/GSJvMpLY9cddMe8zY027T2xu8lrtyWLLYA6kj9D3yJPlw32y7HZEztdQg/epStPuMyzxwSV3IiZ9u5rYH6TgsHRqkWSN+LCvYZcVZH0SNtJI7c9RJftQzvF/QSqSsShHQj5yZAlZAGjE28z2MLD7bRjwKctDqZ3H4JFIh5CcMJZbAfBsGdY+mvHcCbb8eKFJlot3ePyLYY+H2/wtZvsQ1tNtVBr2e+RDe6zq8Owp6D0Zz1xpz9vHIk/6vkueFxvP2H3cZflxhkTo0OXmE3KPBYByni/3bmHLyQOAR8bthGVtJTwjZwz2WFVN7TG1hWSGhQ4hOUXasextVGK+DXbvIbFK7LENADDujZjtw7Wn+JsQNH+GdX72/i7Lk5NNeORYT8XvTvLscemll+IrX/nKxP+/8IUvBAD85Cc/wXHHHYcgCHDrrbfib//2b7Fy5Uq0tLTg7W9/Oz760Y/u0Xb0RY6IiIiIiIiIzLw03f5nurcxTb785S/jy1/+svmaxYsX4wc/+MGktqPlx0VEREREREREZgl9kSMiIiIiIiIiMkuotGoKqf5xO3YcAMDz7QycMLDzGnjtMC/tjVP7e0yXDCxW9z7oD5ntbYl9HPIkZwQASIQHyiTrx6VftubsjZBmp2+Mm2Q3SqH9LgE5ViyDAADqJItkpLbWbG82h+k2GM8jmSy+nSMCAJXAzp3Ykh1kthdJho7vkC2Ta9hhbU3PrjnPZTzs7WBvidkekfM57JBFEpPa+FyWM9vzDrfZiGSRjPiDZvvmxM5ucqnvr+fmmu0sb6ia8fyMXNhhts8r2is1zE8W0m2Ufft8tIR2382R7Iq6Q1ZJkJCcHfIevsOIWfUq9jZI3kkuszN0XGTkLpvzyvQ92HgX+vY4UCT5UC45WCxHLiD7WHC4wVWdcuJ2z+UeyvK42D202LDvLXND+74BACHs85XAHotYnwKAcZJfM1bfYLYHPu/7UWbnG45ndhZXR2qPQ4HvdEbN1qnIad2c2fk1/f4as72S2OcCALaNPGi2s3wbz+P3UN+3x5oUPBdpuj1XfgecMrM87Hhv0YwcEREREREREZFZQjNyRERERERERGTmpdleCDvWjBwREREREREREdlLNCNnCu2N+sdnQw6PT2rWA9+uWQd4HXQzIfX/Dh+TfUsZ+pM/Vllmv8e8tNds7yraddTtef5dK8uniUhtfsAK6wG05uzXJOQ4sNwJl/dokNwJZiCya9oBoN/bbLYnyeik9sFFltnXRkKuDZfXbIrtz1nMLzDbC2Eb3QeWfZFkdi5Ma24e3cZ4Zmem1DM7J2TMt/MBAMAjI8kYycGKSZYCAKQkN4LlEFSjrWZ7e4FnywSZ/TgwntrHctwfo9uIY/tzVFL7cyRYTLfRnrNzPgokX42NdS0pz1ypkTyuVvIetYRneIzF9ucsBiQbzeH21yAZU35mHys2BgDAeH6O2T5aW2+2P5b+1GwfKOxH92Festxsb1btsahMjjXAM6bY+RhJeAYVywNqkudDNh7WYefGAEACezxkeV1RxrNMxhub7G2k9n4mDjlXG0f/y2yP2uz9rCZ23lc55s/JiWffIxue3SeqHh+TN0a/Mtsr9XVmO8u3mQoZeVbYvh88705mGWXkONGMHBERERERERGRWUIzckRERERERETkWSAFyAz1KdnGLKcZOSIiIiIiIiIis4Rm5EyhvZFfszcycOg+ZHatd5LwulzPt+v7WQ5PJebfoo7Edr04zRAg5xMASqH9mib5tpfVxdea/HxXyEvGY/t8xQ7feOdI1kGe5E7kff6dcUheMtiw66Q3e3a+xtysh+5DPrOzKVh+zWzBPkec2BkDuZDX9xdYVlZqZwwEnp0fBQDZJOubc+BZJIXMHotYn2l49s8DQN2zj3fBb7W3EdhjbtFvp/tQyuzzNUSygAbxNN0Gy8fYMv6w2V5s66DbKEZ2NkWU2P1qW33y91gWOxaRlTiqqX2cAGCU9JmM5IAEDo9/sWfnIm0j5zwiWSUAUI/tXJaEjEUVklvWiIfpPoRt9jVabtrXRq7Jj2Xds7OyWEbVCLn+ALfxzFIh+TajzY30PWrxoNmekKytZsKzTvZGVh1ILsto3c5uqofDZns57Ka70CT5M+w+zsZbAIhJnl4Y2Hl4MTmfwF76vYX8XiKzkDJynGhGjoiIiIiIiIjILKEZOSIiIiIiIiIy8zQjx4m+yJlCnmcfzsxhmiPfhj2JyoNdLuQy1ZJhSwG6XBY+mUbMljAvk5ImAPA9e0/qiX2sxpuTn7C22rvPbH+6aZf77N9YRrfBlhwdIkuGxmTpYwDoyOzSjAI5lm0hL5MJyRLllcTud6lnTzNmxwkAcpm9n3ujfPLZoNkcNtvrHp/Cnyva5ZNToQK7XMEnk07npF10Gx6pk4mmYEyl+0BKE+uBXWqQ88p0G6zvj3t2CUyVLC3ugvW7DeP/Q9+jr7zEbG+DXZ7FyqIGm3w5+W2+fSxYKd24t5lug5awsPv0FJQi5EmJZaPJy6zrZClpl6WHLQkp4QSASnOL2b4p5OWRTC2zy5ZCv2i2u5yvlJRyV2P7cwakpN3l+bFBxwHyjPosWUaa3ctTUlLUYCWDDst2NxN7rJnstbF9P+zPkWX2fnqk3wKgIQXsdyOXz8nOl09KtTPY19e+UlYv+x59kSMiIiIiIiIiMy9Nt/+Z7m3McsrIERERERERERGZJTQjR0RERERERERmnjJynOiLnKlEMnI8l3pWUqDP6jQzUiPNMnZctjEVUlK3HpH2MYflxz1SM5vz7fcokyW1ASDv2/XeY6T+f2v8iN1e+C3dB9+f3GXcES6ir2l6dt9lWSTDMc9LKcGuz9/i28uLj6DfbK+nvXQfKr69FOe+koEzWUlqHycAGK4+yd7FbO3LHUa3kSe3sBay9HdHjmc3VZr2fm7y7H63LVtLtxE17ePJ8lBYlkJf6yF0HwpkGfV8Zl/DOX/6M5GimGfHPFD/V7N9rPwKs72HjBPsHuvymlpq56VEZElggN/Lk4RncDDsWcADX9aeIs9NmGQGFXvWAIDB8V+b7WOhvcw6y0cEgLhpZ6b4JJ8mF7TSbYSBfQ1WG/by4VORuZKS7BeWM/esQTKJcqF9PtoLC8320OPZMrXEHidKgZ3xFjvkDY02NpjtLPMomYKxio8zU9Bn2O8+mf1sx36fAFxyUlm+qJ4vZc/pixwRERERERERmXmakeNEGTkiIiIiIiIiIrOEZuSIiIiIiIiIyMzTqlVO9EXOHgvh7S7HZirqH0md5mTtjfwbF6zm1fPtvIZ6wj9HMbCPZVvOPl+1hE9YGyXl+55nZ+g0m3YNdDPXSfeBZS/Voi1me8W32wHg6TQy21sK88z2fMizFDJSk96Ixux9yPXYPw+etdAEqe+fZK33s4XP8kxIn/JJ9gwABIGdAVAMO8z2eekCuo0CqUmvknyN2CFrq5rZfaLi29dwvTlMt9Ek11dC2puJnb8RezwvpUlyXTrTTvvnfZ611Y976GssU5GVMJCsNtuTwO4z5ayNbsMjk53ZfSEftNBtsLEmIdewS6ZRTPJlfJYL6DDp2yXDZrp5ZDwLg7LZzo4DALQUeEabuQ++vQ8uGrE9VrFxhuXCAECd5fCQ5+DAqe/bfZvl9LA8ou2vsa+PuDluttd8O9fMRUD2MyC/wjUdMjFZ3w18dj7ssQwAMnIPhcOz2WSx58upyIcC6ds8Q2f6j4Pse1RaJSIiIiIiIiIyS2hGjoiIiIiIiIjMvCyb9iqVaX//vUAzckREREREREREZgnNyNljTWTZbur0HeqkGZoBQGrrp6bOc/qxOmlWW5/z+XeQY+RQFKKc2V5LeO1vQE5XR36h2d5VWGK2z8F+dB9aU7tuPc7bdbdN2LXDAJB4JDMlI+cL9rEGgIZv11FvC54226PUrll3+ZxNzz5WQcCzfhiWCcHq+6eC59nnI5frMttLpB0ACuRY5UjmQ7dvZ+wAgE/Gy20kOyYjuTAAMOhvMtuHojVme43kUgBAktbt9ib7HPZ4mjhkELBj2U1yQpDYOVlToVTkOTyLSy8z2+en9pjcQfJS6g732HFyDSe+fT7GvW10G+xRobUw12zPZTwnZBz2fjQzu9+6oHklJAsonZJcCXsbzcT+nAHJ9AOAmDxPuOQiMc20arYHZExlGThTkQHH7qEueUNxUpnUPrjcY1leSUruoUnG75FMPbLHfZqh43AsCw75hZbQn0NfU43IOJLY+Ycssw/gv/tk2Au/G7Ecnt3lq8quaflxJ5qRIyIiIiIiIiIyS2hGjoiIiIiIiIjMPM3IcaIZOSIiIiIiIiIis4Rm5EyhvZNPY9co+37JbGfZGACQkjprj+T0uMjSiLTbNek5h1rTgm8fq3Jo17NWHDJyEvJlbrvXZ7dnnWZ7B+yadQDwyaEYJ/tY8Xm9OctKYHkN7eil26h79n6MRRvN9rbcArO9NbOvDQCI0m76GotT7T3p+3sDy0oo5+26977wMLqNctZmttdhjzOhwzUekNf4if1vFZu8J+k2GiR7KZpkXgMAhCR/hvYrkufAMscAoEByrOYU7PYgmnzGB8uIi5qj9D2G0vVmexrY94XR1M62CMHvCzXfzsGqws5NYnlfANBI7GMRJ/Y++D5/FmBCkg3jkkHlkRwP9jzC35/3/VJhvtmeI89Vvs8fpZtk3G+Qvl3K8XtT3refF8bTAbOdZXWxDB1g8jlyhVwnfY1P+l0j6p/UPvxuK2Yru4/XSS5MEPAMuLhpjwNj9Q1meyG078EAEAZ232YZOuzaAPj1MU6ituLmVr4Ndg9N7HGE5cy5oO+xD6yQtFdlKZBOPpeLbmOW04wcEREREREREZFZQjNyRERERERERGTmKSPHib7IebZh5QR0ah5ZJtphGqQX2NNnk4RN+3aYqkY+p0emr5fCyS/jVwzsY9Wd59vozNuX0NYxe2nifjJtvCPky+0WSflVxbOn8btMfy96k5suPZTZZVEAEJF+1WjaS1S2Tb5SgGIlKoHD9ZWSqf4JKdVxmbrOl5m1pyGzfteV9tB96CLLi/uwSwWaDtOQ2WuCzB5HKslmvg0yhZ4tAeuynG4jHrZfQMp2WUlSLeVLoOe9A8z2rgIpY3P4nGw/2dR01q8BoJnZZWh+RkomyHg47vFSnxR22W4JHfbPk7JgAIhTu3TK8+x+6ztMyM6RJbFD0vfZfRxw6PuTfCZyWTKbLS/Oxv2peJBOyTU+Wn+avgcr709Inynk7JJaNtZt3wdWXmwfy3zISzRZv4tju6zJZcl6dix9sg+sDM1lufmQjHfs2mF9CgAC8rzBrh+XskJ2/biUP06Wx8pAHcri6TYmeX8T+WPoixwRERERERERmXkp9sKMnOl9+71BGTkiIiIiIiIiIrOEZuSIiIiIiIiIyMxTRo4TfZGzF7GaWgDwPPs1CVlyNCO1vy4Lh7P3YJ/DZYlzlqeQkFyKlhzPr2kjy4uz0vs45duIybS8JlvKnZyRFthL4QJAIbPrqGPfrv1tZmTtRwA+2U+WO+F7diYEAJQC+zWt5blme5TZx7pKa/eBGlmKnS17Gjd5Fgm9RkntfOqwNDFbspfVpLNMlbpnZy0AQEL6ZeDbfaotx0ernG9fo/XEPpYuGR4sSyQm/colV4ItuRuR8bKZ2PlRqcP84ZD0iTw51nmH+b0eyXzISIZHQK4/AOgLDjHbF2b2UtNF0i+j1L6vAMAwGYsij/QZh3toIUey7EJ7nGHZagBQyuzrp+HZ947xkC8b3NY2z2wfa9pLZtfiQbPdJX9jv9KLzfaO1M6OGfHtTBYAGEvtPC4/Z+9nPbWf/QCeIxcn/PqxuCw1ze5vTEiy1QAg9extsDwUJHwfWb9hz+ps3C/neuk+sGzCsZy9zHo15tcfy68hsS9OcmSJ86jJ+ja/hn1yPpokA8cnY25Gcs+2v2j2fykgs4++yBERERERERGRGZelGbJpnjEz3e+/NygjR0RERERERERkltCMHBERERERERGZeVk2/eVq+0A5nL7ImUKsptaldjjLHOowJ7MPDlkJWdYkL7Dfwwt4fX9G3oMdq1LAC3eTzH5NM538hLSW0N7GgvAIs53VJy/FAroPAcmuAOxa7HzIj0OU2OerTvpM4DD5j2VTVBN7G1vBMwSYxCOfg9Te5woL6TaaqZ0rETftDBxWmw8AAckyyIdtZntb0Ge2t5LsGQDIkfMZkJCqWpOPVYnPspnY9fl8uo1x2PkXMclDcTESbTDbfd++VfuZ3ScaJFsNANLQfqDJYLe7rOLZWtrf4VW7Vw676WuWwL4Gl7axjDf7/Ucj/uA3DyQLiBzL4YjcgwHEqX3EywHpMw7ZF+waDcmbjET70W1syOwcDz+0nye6covN9tHEzhEBgLmJnZvUQcbTdofxMMUis33cs8eRWsDHmW3+U2Z7TLLT2PNh6HLvCexcF/bs1+rz7JgU9vPhYPaw2e47ZP3kc3Y+YUjyvhYUX2C2dyd25h8A5DP7Gh737XypZpGPIwns16QkGyZyyMsbabL72+SymwAgbtpZWQwb1T2HsCA2rotMB5VWiYiIiIiIiIjMEpqRIyIiIiIiIiIzT8uPO9GMHBERERERERGRWUIzcqaQ77ea7fnQrh120UzsGuc0a5jtLJMFANLUfg8m9CbfrVhGTpnkOQBAdyEy21tzdvt4PPnPEZBLrJTZtdotOTtnBABKJOOmNWfX9uYcvs7NMns/PM/OMXCINKKZDcORfSyHxipme8Pj/TohtfcdRTvnIOeV6TYC2MdqOLZzDnxyrAEgH9iZDS1+j9m+MLFzJ+bn+edsJR0rJqEqiUMIXY50mnZy/S2NeQbVltTOExrx7dr84Wwj3QbD8hjS1M458B3G5AbJZ6uT+LZ6k5+vlpzd74peh9l+GA6n21jaaud4zCnafabo259jTsFhMCOSzL422ht8UGZZPmw8ZdcfwMfthJzyKOX3r1rTHrejzM4Ma4ed5zXPP4juwxGtnWZ7L+kzYzHv+9vq9msKZMyuOlxf/Q07dyXx7JO+xbfzirZmT9J9KBdIbktiZ6q0wM6mAXiWTyFn5+wkJKcOAIqhPRa9IHyV2d7r2eezp20qnpPt3ylGI36RD0T2+aiSDByXZMJSYJ/TJG8/myUJP19hYD+TRM0hs5393uP7PB+KvQfNH5UdaUaOE83IERERERERERGZJTQjR0RERERERERmnmbkONGMHBERERERERGRWUIzcqZQktjVovVkbNLbyGB/e+jBruVOSb2ry3uwfWg2R+g2gsDOnWD1qJvsqCAAwFBkZ4mUQrtetRiQUAgAnXn7WLSndg1zm2dnX4Qs6ABAS2i/huUYkGgMAACLAIjIRoouITlErWnXe0ckA6fHpfY+tbexrvJz++czXpNeyHWa7SHp+205O4MAADpIbkRfamcIHNRuZzfNs5sBAGVyd2H9sp7wPjNmRxpha93+t4rRmNes58ltMgf7fBU9no1WKNj5amNJv9keNe0cEZZRAAB+RsaRKcg0qsR2Bkcpb+9nS8gfWUrkJS0kX41l5HgO/bJGXhN4k/9XwHEyKLMht0LGU4CP6+ycjyQ8l+zp5gNme6X+tNk+mJtjtrNcMwAYjfY328skh47lRwEOz26evQ3foc8kDvcfS3tq58KM+3Y7AAQ5+7mrEdhjVejwa0kMO98wSe32uGnnmgFA3c+b7ZWc/SzdSfIPRyPeadiQmicX+WBsHwcA2BCsN9ujzH7YzjvkAhZg39/SwL6Go5ydowUAnmfncbGMHJbzmJE+BQBhYN/r6TVO+lyWpWhE9ni4T9GMHCeakSMiIiIiIiIiMktoRo6IiIiIiIiIzLgsy5BN84yZzGEm8bOdZuSIiIiIiIiIiMwSmpGzhzyvBM/bdV1qltbJD9s1nADPhmEZHFlmh0ZkGc+E8EmtqOfZ3YbVmgJAENjZMH5m14pWm/xb1Ci1v6cskowcFzEpSQ9A6nZJQA3LhQGAStN+j7HE7hOxQ0iOT3KTYtjHMucw1LBt9PsD9jY8u8/05uxrCwD8yM7o6CwvN9vHG5voNlj9fkqu0cFoLd0G7EOBBbAzcljOCMu/AYA5ebtfVZr29dlL8qcAoKXN3sZwbF9/Dw7zPvHUuN0vvcT+HKxfAkDi2ec89u2cgiFy7/Ed/s1msv+q4/IPW/XIzil4OrrXbI9becbb8NALzfbevH3OWe6ESw4Jy5kbiezz3U/y9gAg9uxxnZ3zhIzZU2GLv46+ph5tM9vZM0s92mK2NxPyXAbgAW+J2d5Xt3PJ2P0PAMY9O+cjB5ItQzLgAMAnGRypZ/fdYdj32PFkM92HkZp9zkPy7Fcv8TyUJun7acbyTPhol6b2OWVj9lhi70OO5CMCQEAyEtnzYUvAb9T7J4vN9oj8TlF2uL+NZvY1OOKTnB1+m8ZItMFsD3w7s4g9d6UkPxHg2Uvs9zuQR/F9YfbIHlFGjhPNyBERERERERERmSU0I0dEREREREREZp5m5DjRFzl7KMtqyMgyrbvjO5RWMWx6YMKm/zmU0YShXV7Cpjo3HaaFNyK7VMAnUy17S/wcdOftKaEJKb0aI8uXA7ycYMyzl5xnU53nhwvoPuTI9NswttvzvsM0Y7J0Klumlv08wEvAypm9hGWQ2ddX4DD/sESmIh/YfInZPloaodsYgb2UdD21r5+Cbx8HACjBXiY2JuUh42RZ72GH5eQDMt6xZZ7ZkvcAEKek7In8/KIWvo2W0J4OPdiwx4lqk2+kQdb2bo3tc95stcsuWJ8CsNuS4WewcruInIvt7M/ZTOyyikqTl3ZsDezyrbhhLxFbJKXDMfkMAC9XrXt2qUHF5+Uldc9exjmXOdQjEJHHS9ksocM+FPP20sOA3Z4P7Osr9Pg+LMzmm+2debt8xGE4RJTY+8nKaJIp+IWjQu6xtATT4RF23Lfvb83EfvZjz0QAkJFrsJDrNNv9vF1aDAClXLfZ3pfZ/XJpm/2s3sIfL2npfp6crshhNfpa0x7vGon9OTKHZ7t8ZHeckJQnV3x7TAeAGiuxbA6b7SxSYipk5L4QBPZ9PstSJOT6kecefZEjIiIiIiIiIjNPM3KcKCNHRERERERERGQS1q5dizPPPBNLly5FqVTC8uXLcdlllyGKdgxB//Wvf42jjz4axWIRixYtwqc+9ak93pZm5IiIiIiIiIjIzMsyt+UwJ7uNafDoo48iTVN84QtfwAEHHICHHnoIZ511FiqVCj796U8DAEZHR3HCCSfg+OOPxz/+4z/iwQcfxDvf+U50dnbiXe96l/O29EXOFAoCu/Y+Te2adgDIyNLEQc6us2Y1mC71rM0mqUclGQIhOQ4uPLKMpksaQ4ksLx74dgGx7/FjVSQ14/v5PWZ7ObDf4IB2Pmmuk6z+GKf2+RolGTrb38Nud+lXTJrZNcqjsZ2btLFiXztOS7knZAlKUpvfmrbRbSQ+WTqVLK3qOUykZMuztgT2se7I232ir8iPZU/BHovGyfLjOYfrL0dydjp8ex+683zZ4K6cff10kqCCGqn/B4AqORYdDTvzqFBZabb/1n+Q7kNI+lVAMnRcckIC315y1/ftwaw17KPbWB7MNdsXtdrnk+aeOYQ3FcnBqDTtLIQ4ZbkxfD8nm2vmgi+PzDP51uTtTL4x2LlIPlm220WZPNPMJTf6vEN2TIUMNSzvJOcwf57dp0ci+01KsZ0d05PY5woAkrJ976k07SyT1tQe6wCeo7ON5Cax50sAKPr2c+ycnJ29tJhE2bmMl+Tyok8CY/z2hpTc61kOncsw0kE6tz9ub6MfZHly8Fyk9tIis50tNx+R/DaA53Wx58d6tM1sz5CyFcrljzQ6umOOYKFQQKHwx+fMnXTSSTjppJMm/n/ZsmVYvXo1brzxxokvcm6++WZEUYR/+qd/Qj6fx2GHHYZVq1bhM5/5zB59kaPSKhERERERERGZcVm6d/4AwKJFi9DR0THx58orr5zyzzMyMoLu7t+HqN9zzz045phjkP+DMP0TTzwRq1evxtAQD/h+hmbkiIiIiIiIiMhzyvr169He/vtZeJOZjbMrjz/+OK677rqJ2TgA0N/fj6VLl+7wunnz5k20dXXxGZCAZuSIiIiIiIiIyHNMe3v7Dn9290XORRddBM/zzD+PPvroDj+zYcMGnHTSSXjTm96Es846a8r3/VkzI+eTn/wkLr74Ypx//vm45pprAAD1eh0XXnghvvnNb6LRaODEE0/E5z//+YlvrADgzjvvxEc+8hE8+OCDaGlpwdvf/nZ84hOfQBj+/qNlWYZ/+Id/wBe/+EU89dRT6OnpwXve8x5ccsklU/oZssyuDXYJVWJZI75vn7JC3s4HiGI+XSsX8hpli0v9cUqygBiW1wAACantDUgGx5xSnW5jUcP+1vb1i+zzVSQ5PYWA9ClMfvU8VgMNANsiOwSA1e+zYw0ADbIfQ5Hdvqlqv/+mmGdUsVyJEuzznThUMGekTtrzHAIXiPa0224v2P2yI2cfB56QA7BIogVFewwYjvntqUryZ0LStfPk+gOAcmC/JiT/cOMQqUJtDO3POUTGoa50Ad0GG1NZXoPDkIw0s3MI8qGdMbUgW0630Ve2+83+dowBiiR3qZLwD1ol2RTjTfYefBv1SYYltLCLA0BEbi4Nsg8s+wkAqhU7l6Xg2blKbDyNPP6ssbjNztnZj0R0uOTX+OTeUiX9ymUb5cDeRp2Mlyy3bKDG84iCsSPN9jXhU/YbOIyXLGukJbT7VAL+XHVQ+nyzvbtIcs3IPbQt5PeeJsvrIufL5Rpn2U2MU78kt/LWnP3M01fn969G8WCzPefxnB1LJbXzawAgIjmozaQ2qX14znkWLj9+4YUX4owzzjBfs2zZson/3rhxI17xilfg5S9/Ob74xS/u8Lq+vj4MDAzs8HfP/H9fH88DfMaz4ouc++67D1/4whdwxBFH7PD373//+/Ef//EfuOWWW9DR0YFzzz0Xb3zjG/Hzn/8cAPCrX/0Kr3nNa3DJJZfgq1/9KjZs2IB3v/vdSJJkh+lL559/Pm6//XZ8+tOfxvOf/3wMDg5icHBwr35GEREREREREZldent70dtrf1H8jA0bNuAVr3gFVqxYgZtuugm+v+O3nitXrsQll1yCOI6Ry23/kvyOO+7AwQcf7FxWBTwLSqvGx8fx1re+Ff/n//yfHXZ8ZGQEX/rSl/CZz3wGr3zlKycOxC9+8Qvce++9AIBvfetbOOKII3DppZfigAMOwLHHHotPfepTuOGGGzA2NgYAeOSRR3DjjTfi+9//Pk455RQsXboUK1aswKte9aoZ+bwiIiIiIiIisgvPzMiZ7j/TYMOGDTjuuOOw//7749Of/jS2bNmC/v5+9Pf3T7zm9NNPRz6fx5lnnomHH34Y3/rWt3Dttdfiggsu2KNtzfgXOeeccw5OPvlkHH/88Tv8/f333484jnf4++c973nYf//9cc899wAAGo0GisUdp92WSiXU63Xcf//9AIB///d/x7Jly3Drrbdi6dKlWLJkCf7mb/6GzshpNBoYHR3d4Y+IiIiIiIiIyP92xx134PHHH8edd96J/fbbD/Pnz5/484yOjg7cfvvtWLNmDVasWIELL7wQl1566R4tPQ7McGnVN7/5Tfzyl7/Efffdt1Nbf38/8vk8Ojs7d/j7efPmTXyjdeKJJ+Kaa67BN77xDZx22mno7+/HRz/6UQDApk2bAABPPvkknnrqKdxyyy346le/iiRJ8P73vx9/8Rd/gbvuumu3+3bllVfiiiuu2OnvPa8EbzdhAIFfMj9vQvIBAF4Z30zsIJA0bZB34HW5WWa/Js3smnPf493KI69hGTqdef4tahfJuCkW7DrpsRpPLW8L7XPakbPbmyQXJkr5d60eyXQokYwPly+ki+Q9ksz+HK0hD3SIyWdtDew+E3fb52sVL3FGnNn72fUHywTuiu+QbVGM7PfY6NmfozPtpNtoJe/RS+r7F5Xt49BJ+jUAdObta5id726HXCXW79g2XDJy6uQ9ktjeh3LokA9F8jE6SDTF/q32tTE2wqcCF0kOz1RY1nKM2R579v1rf59PN15IohA6c3bfZkchc/j3LzYOsPyMmPRrF8MkUyxH7hsA0GkPVQjIbm6p82PVSOznplrdHkdCcj68zM5dAvg5Z9kz3Xl+f2P30BwZ71xyyVjeHRsvx5osC4+fz3xgZxotTewsk/GYf9IaCWDbGtsZceMeCdQDsLBk98s+uxl9Rfv5kp1vgI8DPXn7PjwS87y9Yd9+TUKyPV0ycsZIJhi7T/c3eDaTD/s1CckwrWV2fuhg9Qm6D4WcnS/qk5HG9+0Bl/1utq/5w+XBp3Mb0+GMM86gWToAcMQRR+Duu++e1LZmbEbO+vXrcf755+Pmm2/eaVaNqxNOOAFXX3013v3ud6NQKOCggw7Ca17zGgCYqEVL0xSNRgNf/epXcfTRR+O4447Dl770JfzkJz/B6tWrd/veF198MUZGRib+rF+//o/aRxERERERERGRqTJjX+Tcf//92Lx5M170ohchDEOEYYif/vSn+NznPocwDDFv3jxEUYTh4eEdfm5gYGCHNOcLLrgAw8PDWLduHbZu3YrXv/71AH6fGj1//nyEYYiDDjpo4mcOOeQQAMC6det2u3+FQmGn5chEREREREREZJpkeyEfx2E16We7Gfsi58/+7M/w4IMPYtWqVRN/XvziF+Otb33rxH/ncjnceeedEz+zevVqrFu3DitXrtzhvTzPw4IFC1AqlfCNb3wDixYtwote9CIAwFFHHYVms4knnvj9tLjf/va3AIDFixfvhU8qIiIiIiIiIjI1Ziwjp62tDYcffvgOf9fS0oI5c+ZM/P2ZZ56JCy64AN3d3Whvb8d5552HlStX4mUve9nEz1x99dU46aST4Ps+vve97+GTn/wkvv3tbyMIttd9Hn/88XjRi16Ed77znbjmmmuQpinOOeccvOpVr9phlo6rLKsh203dqueROk6H7BiWsxMGdgBAQraRpDW6D0laMdsDv8Vs932HjBxWK0ryUFhtPoDdnidX4xGvyx0kr2E5BKxOOueQ4dFVsDMEWnJ2bXCU8DrqYszOh/05yiRLyEWOXBtbIrtEc0ELCXwAr71vITkiLv3SI/k15Xih2V4q8O/f64n9OeaTHJFe0qd6i3b+FAAUSI4O+xSsbh7gfTchmRGpQ6ZRneRGzCPHouFwfQ3H9jjCRgGWhdCb53lfwST/Wcflxxem+5nto55971nQxu8tB7bafXe/sn0PZH2i1uT70Ejso8Gyz7wpyIcaztn76bINdg+NyVskDmNVIbD7bjO1Z0OHvr2PpBkAQOLV0FOwM3DYeAkAgcey6uwdLTrkzLHnheGGfQ9k/dLl/lYht/p6k2QBOfwD+byS3bfLof2MOhLx8XBZm30snt9h53l1kOeuPMlMAvj5HGrYn2OuwzY6SGZYY5K5SwDgkV81h8nNpyPgz249if3cFHv2NZp69vlqL9r3LgAYb/Sb7ex3o5b8XLM9zRI0oqfpfuwzUriFg012G7PcjK9aZfnsZz+L1772tTj11FNxzDHHoK+vD9/73vd2eM1tt92Go48+Gi9+8YvxH//xH/j+97+PN7zhDRPtvu/j3//939HT04NjjjkGJ598Mg455BB885vf3MufRkRERERERERkcmZ01ar/7T//8z93+P9isYgbbrgBN9xww25/xlp56hkLFizAd7/73cnunoiIiIiIiIhMkyzNkLlM0ZvkNma7Z9UXObOB77fsdvnxcmGe+bNxYk8bB4AkIdP0Y7KGMlniPJebQ/eBLXGXC+26DJ+VmAHIyDLPzdQ+Dm0OS/rmA3sbOTJV2WXqKxsDWMlRN5mS3eVQwlJipVOkFMB3mGJfJKVRbFp4C1mKGgB2c1k5e6JiTzPuK/EJiKFnv4YttelQSYCUTIR8ukKWzOaVOkgz+0XsULPzmXeY5j+nw17ilWXMjZPzCfB+ySQu5VuhfSxZ6VWBjEMA0EHOCJu+Xib72OXQMWuJfUJYn2nN8Qv4gDa75GE8sssnD2jjY1UPGVNbSTsbs9sdSgki0idoyZJDv2QlYEWylK0Ll9JeCysZBIDHx+3X9BTJ9Uf6bSnk5+sFnXaZzOJW+9mt7HB/aynbr2lE9n26Uufnk41ndVLmOda0f36AP45gpGGPdzF5aCo61Hiykj6m3eEmWk9IyR75+f27Rs129vwJ8HtkS9V+9hslpXQAkJJxOyJloknGzxe7f7GohbHE/pwA4LPxMLXvLU3PHgNG67ykKW7aS5izta5r3oD94/tAMK9MPX2RIyIiIiIiIiIzTxk5Tp7VGTkiIiIiIiIiIvJ7mpEjIiIiIiIiIjMv+92f6d7GLKcvcvZQmlawu7SA8doT5s8Ggb2MJgD4ZPnwfK6Lvsdk3t/lNSnJ4Ukyu9YUAPKBnZWQkfluLrkurF48JjkGFbLktovegn0sMlLXW3FYAr1OMnBYzkHgkIPAlqpNSB0120eAZxqFJLNov5JdRz0U8XrxJqnlzpFRn6ysCgCok9L4mJwOsgK6ExIrQfsMy2UCgCAk1zA5n20OmUm1un19hKRPsawSAAga9jZYRk7Voe9XSXZFTJaALQWTzwkJyDrNZZJLxvotALST4Szv2527myxpDwBzSnaQR3vZbmdZXb7PL/Jazf6g42TZ4NTh6bIltK9Bdg27LKPeTrJf2DgQjLXSbWwK7f1gfbdI2ucV6S6gleSVsJyQwOFYFpp2321psZ8VWIYOAGwYt5+rBshYtrVBnkf4sE8zcBKS8+GSlceWQW8kdt9vYWF3AIpkTGW5LzSDscDHsmZM8tfYeOiQkTPZDBx2bwJ49lKD9JmYZGoCwKg/bLbnPJK5R4bcMOADiefZGaQsAzUM7PzRLEtRj8bpfshzi77IEREREREREZEZp1Wr3CgjR0RERERERERkltAXOSIiIiIiIiIis4RKq/aQ5xXg7aaIt1xYaP4sy30BAG+S363FSZW08/rKYt6u88xSu26+ELbRbaTkWGSZ3V5PeF0uy65g9cU95RrdBsu/KJCMjp42+3yxOmsXjYa9jyyvAXDL+bAEDrkSIMcqIjkiEclEYnX1AFAlJefsLVzqxZskI6BGAmy2Nfg4QjaBDPaxHCPnuxbz7KZ40N4Gy7mKyfkE+L9EFEnXTh3GkXGSM8CujUGHnKthkoWQsjwG8jHa+C5gjORflO1dhD2SbTfukLFh6SdjGQAsI1lYczoqZjvL6KhWee5ETMYqphjy/IyYZFuMOmSCMVtqdi5ElWSyDDvkugxF9gFnuUos72s05tc4yzsp5yeXRwQAlZo9GG0Y5hmKk8XGSxKT5ZTPxrK22KNA4BCSU4nZvWNy7QB/nmB5eINjdt5JrsL7TEvJzk3yyMF0eu4ij5gDdXscGYz4WLehZh/LTRV7J2Lw8bCU2WNRDvZAUvLt/NFGjv/uxPJD08weR+rxCN3Gc4qWH3eiGTkiIiIiIiIiIrOEZuSIiIiIiIiIyIzL0u1/pnsbs51m5IiIiIiIiIiIzBKakbOHwqAdnrfr779yQcn82UZzjL5/1Bw1233frlcNA7um3Qvsut3t+2DvJ8uvSUidKAAEHsmWITk7C0s8bKGn3c5CyOXsz+HVeX3xghY7GaKzxc7ZKZLPkblkrjTt72MjkuFRyvFjyT5HQvIagsAhH4pkppQSez+bZBORw7FkGQHjpGsH5DNMBZ8m9QCtBft8lEhgEPscoUMmRLloZ2klJIMgbvB/Z6C5SVWWPUM3gW0Ne0zdUCNjskM2E8tvqpMcg0GSM/LoMM/aasnZx7uvZG/DJbdsa92+hnuK9lgVOUSGRWQsikkeURjafTt0yC2LWD4bycCpOuQqsVwXD3bnZjlYAFAmuWXzinXyDva1AwBpxT5WNXK4WbbT3CK/yEPPPudsJGIZVgBQLNg7Opf0iU1jrXQb46TfNcg9kH3OgkP0U2fefpeQ3WQdDJAwu+GmnS3TkrOf1QEgIjeH0di+fhrkXHS0s2sHyOVI5yd9PyD9GgAGJ5mlVQ749VUkrwlIx+sN7fwbAKgkPOvRMp7Zv/cUfH79Mc3M7peFwM7JSrMm6tG6Se/HrKGMHCeakSMiIiIiIiIiMktoRo6IiIiIiIiIzDhl5LjRjBwRERERERERkVlCM3L2UNzcCm83GRWjqV3zGpB8Gxd5kh1TynWb7WnG81BYTg+TZTxDoJjrMdsTsp9jpP4YAEYqdh10T6edocNq2gGeYdOz2M7QIVFBqG/j37X6kf2acmJnlbCMHcAtA2DSP09eM9qwa6C3RPbBrDZ5LXdEvp1PSPtWFmYCICa19zmSIZBngSoAyuTyyPskA4dk5LD8GwDI5+1jEZG3cMkbSshrfNIekZwDAGgJ7XFgv5K9jUGHvJNGSrJ8SC4Sy24aa/Lcsnxg72dMxrpkCuKhWNd2uIQRkWOZkXEmIBk5OdKvAZ5tUSO5SmwfXbjkWDHs+qHtTtuw2zdU7M8xp2hvJXPIFBuN7b7fQcaJ1gIfD5lCwb5G52Ocvgc7H3WSH1VL7M/Z5fAIW/DtbYyTi7gS84t8sGk/a68P1prtnfHz6DZQsj8Hu7pa8/Z9g+bfAAhJjiMbJ5okhw4AtjTscz75kYi/x1hsH4tKwu9f7JPu7vc2VyzfBgBS0itcfv+yf94hJG5fkmH6M2ymP9Zy2mlGjoiIiIiIiIjILKEZOSIiIiIiIiIy47Js+5/p3sZspxk5IiIiIiIiIiKzhGbk7LHMKKlj9Yv8e7MwKO7h/uyoEg2Y7Z7DPnSXD7TfwyN11vEg3cZoY4PZ3llcYrYXSMYHALSV7JrWljl2XXttmF8epZL9HuzbXp9sotDFC0TDmv2aME/qdhNeO9yMSIYHyc+o13lOSJPU7ydkGyxTpdbkn3MzybhhV0/i8PU+y7gpBvZW5pb45yiRjByWS5Ej15fnkF/DsIyAFo/XpBcSkodC+ozL5xiotJjtCckpKAeTL/Kuk2uU5deMkfw2AOjK+DVqIdFPAIA8yc84oN3++TaSXwMAHil690l2TL5ExoCAf1CvTvYhsPt2m8/PFxtzK+N2phgbAwAgImMyyz4bdsigemJ0cplhy1vtn3fJ2urM2/dxloFTcsgMy5G8E3Y+E4e8k2Jg992uvJ01UiXnO84cMvtIv2oJ7RfUHIKwNvn28yPLWKymPHOF/XrUQe5fMTlficNzV0gOBeszTYfz1Uk+B+sT28izIQAMkcvDJ/k1fUV7LAOAiIS0NVL7+vPI+Sr5XXQfEpB+l2yj7yG/p1Wr3GhGjoiIiIiIiIjILKEZOSIiIiIiIiIy81JM/6pV+8CMHH2RM4V8z57+11qcR9/Dgz1Ncaz+tNnebI6Y7YU834dKvJW+xsKWQAeAKLGX/i6TaYwdOT41tnOevfR3rptNbeXbCOwVzhHOs8sVMlLKk7L1sAE06/bEunplciUTAFAo2VNGUzL91qWEZbxiXz9sGVle9kR3AYOxXfJQJrVwxYBPM2alAmzqOSubAvgyzjlysFg5QuhQ4pIjy+kGOXsbScynnsdk6VSGlcAAQCfpE3VS3sXKTwBgDillK/h2ye2jo/a6wOOePd4CQJa10ddM1saGPSZXmq1meyfpMwAvLymW7H6Zb5uKJztSvkX20UVGSjNCUjKR8QpojNTsfsfKR1iZGwAUyHiWJ+Plga12GVrBobSxhTxPtLbYYwC7PwJ8qegauU+7lFax+2yelBWysxU7XBq0xJl0/TGHjcSk7HY82WK2dxdeQLfRSm4trG/TpcHJfQMAcsnkyvFCjx9LWmZNzmfkMJQVyQNJQHaCHAYnBVLW29q073/jPi+Lysi4Xw7mmO21ZMhs9/aFbx1kyumLHBERERERERGZccrIcaOMHBERERERERGRWUIzckRERERERERkxmUZX/l3KrYx2+mLnCmUZqRut76JvkeSsmUs7YLUXM6uwQxZqAuAJLU/R9wcN9sbsZ3Tsx3JEMjs/WzP8Zp0j9T+JhX7Ck4dMjpAsi0CkoHDCpRJNAYAINdqH8smKWJOmnxiXqNm1+83InsoiWNeDx6RmvFxspTttsg+llWHZU0jsmxpmQyZlSbPVdoW2a9pCe3lrkd51wfrdr1F+1iNkGNdq9mZLABfpjkh54PlLgFAHLNsJvvnfZelict2Bgd7EIia/Da7jWSRsCVgGyQAaou3ju7DIeijr7FkDnko64O1Zvvm+uFm+0J++0Jn0b5/+SQzJSXXDrk8AQD5on0smmP2z7N9APiU8KbDmMs0Uvs9GmTMThzyoVh22UDNHi+fqpJsQoc8r1Job4PlDXkOc9t98qyQL5Bt1Pj1lSN9m+WhxGxJ+yY/nyyfjWXLNFP+OVuyTrM98e2b5JjDfbqe2P2qTsbkiLQHJK8IADzSZ1huErv/uWD3ns48P19VkucVk6XBK6QdAIq+PRblWcckGpn9ew8AFL12s9337H2MfTtDLs0mP6bLvkelVSIiIiIiIiIis4Rm5IiIiIiIiIjIzEu97X+mexuznGbkiIiIiIiIiIjMEpqRM4VK+XlmeznfS99jtL7ebI+bdv5M4NvZFSFpB4CIFPCXCvbncNlGnNi5E+WszWzvKdfoNvJzWf4MqWEu87pclnWQjNjvEY/a+zi6jYfk1Or28W5rtY91jtTmA4BHskQCkkNQGbfrzQGgFts5PMXA3s/O3ORr7yPYtfOVxK69DxzCEjxSuL61bu9DV4HXSbNtsEMRkPPtEhDHspdyeft8sj7lgmUM5EjmGADEkX28a3W737LsJ4Bn9bBsC3Y+816Z7kPqkHEzWYXM3o/VI/a4fkg7Hw9Z3w1Ldr8KyFDlhfxf8NI6uX6mYMnThGS40X5LxluAX+cZ7H2oO/xr51hsH4yBuGK2PzDUYbYvLPPrb1GZ5J007EflLHMINSLYPba1bGc/AcDwuB0i1SB5J6OkT9VZoBF4Rs5Qw36PsSYPgYs8e5zwyL9Ru9y/FpHnP5a9VMrZ9/E8uf8BPJuJ3TdqDvlsYyRLq0L6DImw2v4eJA+vkthvshVDdBtLMddsz5GbaAn2wF/2u+g+MJV0q9k+2thgtmf7wlrZe0DLj7vRjBwRERERERERkVlCM3JEREREREREZMZlmYfMYeXDyW5jttOMHBERERERERGRWUIzcqZQPR402+OkSt+D1UAWcnPsfWhsstujLXQf2DZ88v3feH2AbiMftprtucyu3/c9XpjrkZrYjNTtjq7htfW5Ijlfc+x2v0DyHBxyQooFu6acfeNcr/KshHJbZLazPJNikde9N0ktdlS16/+rCckbivk+tMDO4GDZM4lDwW1McnjGSbaMQ9QPzVTpzNtDP/uG3w/4Tvgkn4Zl6DRJOwBEkf058nn7WKcOGR7DFbvfseur6pBTUE/s17icc0szs3OyACAgfZvxSF4KAMSenfPRHpK8r5DnSpSL9ljlk2HdL07+X+g8EhMXkq6d8jgUeB7J+snZbxIEfKwKRu2ON0z2M+dwKNlVPu7ZGTnjkZ2n13DIFKMZVFOwsklG3oPlDcVN/jlSMhYlpJ31S5c8lDzfTVN7jmcseuTeMJpsNNvHvQPpNiqJvR8xOZYsq2sq+D557gr4CWsjOTw0H9EhF3CYZC8VPLvT5FOesRiQi5jd33rz9n0+iA+g+8Ce/0a8HrN9TnEJef8Ij9SfpPuxr1BGjhvNyBERERERERERmSU0I0dEREREREREZlyW7YUZOdM/cW7aaUaOiIiIiIiIiMgsoRk5e8zbbRaATwrj09Su3QeANLOLzgu5Drs9P89sD3xef5zB/go0Suya9STleQxRk2TH5FlOCK9Zr2+yt5E07G1sGbRzfACgu93OPQry9jknpxPdhzoUpZPciKxOjkOFfyWdkniZZtU+lkmFn6+QZDa05eydqCd2jXOc8XyNJun7YWZ/zhr4NZ6QfKcy7Gs0cfgnhJi8pkRyDHKk9j6OHfIaSGYRi2Rx+ZeSWmznOzXiyd/iEpJtwfJtIpL9tP09SO4YyYTIB/Y+Nsl9Bdg7/zKVz+xrNEc6xahDbhK7N/gsbmEKFrHIyLAdDZI8B5KdBgAsmiKu29eoS85VPrQ/SEtq70Q3yagCgBT2frZmLWY7HUfoHgAtoX1vKRTtz8Ey4gCekdOM7WOZc8iHaiuR58dq2WxvDe2jtbSNXxxVcsrZeDrOo+wQwB7354TLzPYyyWAEgEqTjfvkWYDcewpV/ixeIp2X9f2CQ5/pLdh9pps8i7PjAABdOft4x6l9LNqrXXQbxZDlP9ntLaE9DmUZP1/jTbvzV0m/ZdmgzYw/X+5LtGqVG83IERERERERERGZJTQjR0RERERERERmXurRmYxTsY3ZTl/k7LFst1N1fZ8s6evZSxtvZ5fzJGRdUo/Mt86H9jRlAGg0x8z2lMwbdynfmuxkMLaMJgA0a/Y2quP2frKyDYAvkZySZRebY2SJ5q18YnhEPuf4mH3Oczk+/b1jrl0ul2+zp5Z3d/Byu+pm+/qpRvb5WNJiTyO+ezOf/s6Wui1kdl1Gu8M1PkqWgo5JedccMgXYRZGWVpElR0npFQDkyLKmrFzB5Qaei+xtJKT0o97g13hAjgXI7HWXMlB2vEukDIaVRYUeX76Vlewl7DA41Gaxst1K0z6YRbZ2OIAwsN+DlYmmw/bnYGWkAC9rSkk5QjzEtxFF9njJrr8G+XmAXz9FVnpF2gFgaZt9Hx4dtNvZ0uHtOd4vS+QemC/ZxzLITz6Rs0Qem8gKzQCABuk3y8mYOhTZyyM3M95n5uTt491bsPdhjcP9bWx4vtn+KFab7XmfX18hWXZ7Ycm+j3e11sz2zjl2OwCERbtfNcbsY9WZ8m2wUrda0z7nLsuPj5Ays5GI3P9I2RQAdJF+VSf36S01+wUbYvv3IgAokbJ4j/zeU/ft85U4lO7Lc4++yBERERERERGRGZdl05/dp1WrRERERERERERkr9GMHBERERERERGZcVq1yo2+yJlC9cZGs9337aVXASAlNa0sA4dtI2qO0n1gdZyeR7KAHDJyomiL2c6WaHZBIotQbrXrTfcvDtFtsKyDYp/9816BLNs9wmvvI14GbXIZyCosp4BkeLCMAQDIl+3XsKVV2VK3B7fzfKiHRu33KHr2cXBJSmB11ClZMLee8K2UQrtfTXY6aanE14gtkNfEDbJsd8SzEliGh0uWD9NoTj6TiCmSXJfuvH0s55ftfTxg7DC6D2wpW8alS7WlHWZ7kS1165CbNDDSZraHZKloNh6GJHsG4MeyUrHHgMEqf1YISIZHUrV3IibXDgD0lO2bC8vh6cjzTIeFJfuzrmY3cqKNLKkNAK1lO+8k12r3GbqkPQA/b58Pr0RykzbzflcZZbl/LMfRfn+XbEI2ErARuRRM/her3mSh2V4u8DGdvaRIlvZua7f7VGkB75dBl30+w8329TX2KL/G2TnPB/YZG4n48/5j43a/G4vtY9nlcL421+zjWSPPTfXE3odBfzPdh4AsL173xu1txE+a7VnGxwB57lFplYiIiIiIiIjILKEZOSIiIiIiIiIy47K9sPz4tC9vvhdoRo6IiIiIiIiIyCyhGTl7Ecu/AYAgaDfbS/kesz1J7ZrZqMlzXzzPLvjOhWWzPW5W6TbSzM58aHh2HkrUtPfBRaGTZCWkPF8jIFEGNANnjNQfr+f1x8Oj9rEYbdjvUU94/XFbzj5fnSRjIF9y6BMJyRAgmRBtoZ1v05Uv0n3oDe0cHZZfM5bw7JgmSQnIefb5YDXtANBJska68vbn6CmRbIw8r9VmGTgp+ZcQlmUCADnP3o8osvehkONZXCwXgmWVhCT7CQCqJGdgKLJr7zeRy2vc49dfb2ZfHzE5HQ7RTSiQfCiW/9Rf548sFZIDUqvZ++D59vkcGuP5NQMVexxpy9n36QLJ3wB4dtNgg9zHyecEgJG6/R6tKcnBcsjhIUMVugr2+ewp2tdnziEnq1C0x4Gw3d5GFvNjmTVJptEW+5xnDrGBuZz9WUdJnxgkuWRlkpcCAAk5FNEU/At4jmRFjvkj5B266DbYeNckfTtXtN/AI5lJAJA17D7hFez3aO/gv3NsG7efH7fU7PvCMBlvAaDI8oZILtJAlT9XNVL7WLWGJKcnscfkhs/voTHs452Q8TL07XORugwC+5DZvvz4KaecglWrVmHz5s3o6urC8ccfj6uuugoLFiyYeM2vf/1rnHPOObjvvvvQ29uL8847Dx/84Af3aDuakSMiIiIiIiIiMkmveMUr8O1vfxurV6/Gd7/7XTzxxBP4i7/4i4n20dFRnHDCCVi8eDHuv/9+XH311bj88svxxS9+cY+2oxk5IiIiIiIiIjLjZvvy4+9///sn/nvx4sW46KKL8IY3vAFxHCOXy+Hmm29GFEX4p3/6J+TzeRx22GFYtWoVPvOZz+Bd73qX83Y0I0dEREREREREnlNGR0d3+NNo2PEee2pwcBA333wzXv7ylyOX214qf8899+CYY45BPv/7cu8TTzwRq1evxtAQj0F5hmbk7LEQnrfrb/ByYbf5kyxbBgByPq+/t8SJXceZD3ltMMvZccnAYdixqqNitidZK91GWCZZJHPtwt20wnMKRtfa2RWtfXZNbFC2vw1unWufC4B/oxyRDJxqkw8DG6ukjrpu11EvJBkfANDbPW62s4ycVpLjs6SFn8/+GsudsGuUM4eCW5aBs7BojwHlcPL/guCTY9mSt/tdeS6v1Q477H8n8Ip2e1p1yOHZan+Oyjb752t13i87Wuy699Gq3fcHxu28FIDnVNVIe55kEIx7Y3QfGmnnpPahQjJAAGCbb5+QLiw021OHevZhkjeEkTazmeW6uOS+sOtrhO0jH/bpfrBsmEbCP4cH+/pokD7RT+4LALCuau/H1rr9QD0c2ePhorJDrlLFzo4pbLGfR3J2tCEAILHfArVhez9HRviz4VZyn95IxqrhePL/tlsnw/ZmEtuytc7vLY9nG8z2/uQRsz0K9qfb8Mm/c7PrZ2zQ7lNZyn9R9EnmUUZyBStj9j4AwDDJUNxYt9u3RbzPsAy3jXU7Y7Hf20y3Ufft58c5zXlme0rG7Cb4+ao27fsb+/0uTuzPkGX8mWhfkqYezVKcim0AwKJFi3b4+8suuwyXX375pN//Qx/6EK6//npUq1W87GUvw6233jrR1t/fj6VLl+7w+nnz5k20dXXx39cBzcgRERERERERkeeY9evXY2RkZOLPxRdfvMvXXXTRRfA8z/zz6KOPTrz+Ax/4AB544AHcfvvtCIIAb3vb25z+wXdPaEaOiIiIiIiIiMy4vblqVXt7O9rb+dTKCy+8EGeccYb5mmXLlk38d09PD3p6enDQQQfhkEMOwaJFi3Dvvfdi5cqV6Ovrw8DAwA4/+8z/9/X1OX8GfZEjIiIiIiIiIrILvb296O3t/aN+Nk23l0o+k7+zcuVKXHLJJRPhxwBwxx134OCDD3YuqwL0Rc4fobnbTBKWgVPO9dB3H60/bbZH0YDZHoQdZnuY66T7EDVH6WssacozdDzPrr2vwA562lxbTLexdNSuHPSDydebljrsXBYWJ7T5SbvP/HYrv5irNLvCbl9UJkXrAA7oHDHb86F9LBOHOtfRUbt+v0GyfAYbdj14NAW1tjnf7lO9eZ4JsSWy68GZFh7rAhYzUPTtf+ZIpyDJP23Y9f3pCKv/59to1klOwbjdJ8LQ3gcAaGm3A0vYezRifpsdje2TurlhX8Nba/Y+VGFfvwDQlltitveQuIViwCu1u8ft8WwI9rUx7JC1FZCsg66inXUQkGwZl3r0Gjnnw5F9MGOHsYr9Q+UI2YfE4RqPJpnDU3fI4akn9iepZfZgtrxk30P5FQ7UG3a/2k0s4oR4mB/LJLZf06iTPlPj95aIHG9/ksP6YIO/QZP8Ezo53QgddnJeav8iVQkWmO1PNrfSbSyou/+L+K7E5LmrPs7HslzB7vtJ0z7flRrPyGH5bGw8TRwusLHYfo/xzH4GTTz7ORsAOlL++5Wl33tyUj8P8Aycodoasz0l+aRZ5jKa7Ttm86pV//Vf/4X77rsPf/qnf4quri488cQT+MhHPoLly5dj5cqVAIDTTz8dV1xxBc4880x86EMfwkMPPYRrr70Wn/3sZ/doW8rIERERERERERGZhHK5jO9973v4sz/7Mxx88ME488wzccQRR+CnP/0pCoXtX7B2dHTg9ttvx5o1a7BixQpceOGFuPTSS/do6XFAM3JERERERERE5FlgNs/Ief7zn4+77rqLvu6II47A3XffPalt6YucKcSW5a5kfAm9JLWnlhcL9vKs9ajf3ofmMN2HYsGellok5VvVaAvdRhTbU1uj1F6GbzOZCg0Ao2S5zmKXvR5oymdzYtsme2nhzjn2lNHWVnua/9wKL3vaRJYcjclU5S2kJMn1NZaFDuVbXUW770dkqvJW0ic2N/gExDi163lqTbt9nEyNBYD1wVqzPVdfTt6BT7HvLJBp/KR0o0ZKfRxWTkU4xz5f4Rz7fGQOy1nnInuq8cI59rLbLp9jeIN9vFdtnGu2b3JY4pxVE9TJMrNjTXuwqme8XLYltM9Hd94+1qzsEAAqnj0O5DL7WJHTDQAYI+PEpoo9XjJlUkYKAMXALonozNsdb4xcfwAwQl7D+lRISiYA/lk9UuDlUiI2UCXlWZk9pgaefT63OZQDbRi37+PlfnsfWtr4QBKT8siYlMKVcnxZ7k01+5ln9Zi9lPQ6skS6Twv6gBwZBvL2YUCOjHUAEMM+FhkpqNvm2cuXA8B4bC9XvXqMLCVNyhIP6Bqm+9BCrp9K1T6fW0l/APj9aYgsSb+NP/IgSu1+00KeaTqz/eg2tpDy4RFv0GxPM/se2iC/kwBAktnjACudSkkZ6VSvdiT7Bn2RIyIiIiIiIiIzLs28KclrZNuY7ZSRIyIiIiIiIiIyS2hGjoiIiIiIiIjMuCz1kE3BarNsG7OdvsiZQs2mvWR2OX8AfY/Wwnx7G2Rpb1YbnCR86WP2GvYOubCVboNJyecoBbxWlOXPMNE4n7BWLJBsinH7EusfbDPbk4zvQ1/Jzp1IYQ9UrJYbALbUJ5eRUw55fX+VLC28pW7XUbOlcqsOmSsbavaxHPbszJW6T9abB9DI7FrrJ/21ZnuuwTJ0gEIwubyg0YZde+9ybaRP2ddwbdQOSyi08CwSP2dvY2SznRGQOPT9RmRfw205ewyokOVdAWBNxd7GGlKeX03t64vV/wN8mWaWd1J3WC5+q7fObJ8DOwuhyA8lioH9STrzJHPFt8cJl5yQbQ17rGJLg7c5jJcFsvT3WNPeBlkRGACQsiWUyXLXWyN+fbHl3tf7v7V/fvQQs31Fl32PBYAquUardXs8ZGOEC3YfXj/Gn6sGSN5JQH5naSEfwyWho0q67iAZKCokhw4AIpKR04T97Oc5FCOQWBc6XrKsLpeQVZ+MRU3Wb8k+APycsuXFCw7LxXfkSc5Ow+54a8EzjRqe/ewVkvy1Ns/Ouqtlw3Qf2PLgQWDfFwq+3Z5lCSp1+/dMee7RFzkiIiIiIiIiMuOybPuf6d7GbKeMHBERERERERGRWUJf5IiIiIiIiIiIzBIqrdpDHnLwvF3XhLaX7Qwcz3Opy7WzDFgNJqv99Tx+yuPmoL0PtDqY83275rzg2/XgLK8BADZvs9+jvWan/YxU7HwNgGeJtBfsPIbuVjuTxSf5AQBQI/X7tdiuDa471FGHnj3/MEdquVm9OQB0kWORkJryTeQ4RA7ddnfX9jMKmZ0VlHg82yLvlc32HNnGltTO6QGA6rhda92RbzHbfXK+Xer7g5J9wDt67Gsj44cS0aC9H8USya+p8Oynp0k2xUOj9vkc5fE0yJHDybJh6pl9LKOUhOw4oFkKDtd4GV2T2oe5drcGAHSTDJyOop2fUcjbHW+0yneCjXeLynaeQynHO/9Iw+67LSRnJ+dwbxmO2H3afo8qydABgFJIXkOi7sqefX9z0Uv6BMvCCwOe6xKTXCR2n+4t8XzDItmPDTW77w6TrJ+Hh+xrCwBGEvtYNmAfy9jjA+a4P2K252A/u7k8w0ZkQGsL7fb5Jfs4uGQTDo3Y9xb2TMT6AwC0kEyxNG9vg12+ADBCus1YavftRsCzB8fTzWZ7M7XPR5LZ7bWIZ9MUQjuPi/9+5hAC9xySYi8sP04yRGcDzcgREREREREREZklNCNHRERERERERGZclnlOs78nu43ZTjNyRERERERERERmCc3I2VNeCOwmRyNKKuaP1qMt9O1bivvZmyc5OykJlmgmdm0xAIRBu9mez9ntzYTXcrOsn2Zmv0fTIY9hsGbXSY/U7YyBesIvj7acXfxbI3Xx60n+xmiT70MLqYPuK9vZM8vm8trfcrv9Of2cfUKadf6dcXXMzmMISG5LRHKThhu80zztrTfbR9Bvto9HA3QbcdMeJ+aXjzTby57dZwDQQBOWNZJk9vmK6rxf1jfYmQ/D4/b16ZHzDfB/idhUsbOA6g4ZHk3yLzZlkjHgso0B+xLFxoo9rtc8e7yMSJ8DgIysw+mSc8XEnp1DsCBdYLbnHP7pqZPkks2bb2dM+Tn7fM7x+LFcStrHt9n3nv5BO2sBABa02Z8jIRkc28j9EQAWt5NjRa7RlnH7+gOAJ8ftz5pW7PNRYdkWTZ5p1CTHin3OeoPn9LAMnCq5168dt/NSAGCsaX+OesIyVezP2Z7nGR4jZCxrkDGg4vFn1OFsg9nOnsVLQSfdRjWxn6uSzD4WxcAes13+FT1Pcq7qpM+45ItEpO+PNe33eJrH12BD1c49SskDi0umkQf7fLD3KAdzzPbI5+N+o0nGS98+XzHpt+z3pn1Nlk1/Ro5m5IiIiIiIiIiIyF6jGTkiIiIiIiIiMuOUkeNGM3JERERERERERGYJzcjZQ1lW2+03eC7ZMMx47Qmz3fdZPoZd1xsGHXQfivkus70R2zXMcZPXOBfzvfQ1lqn4FjVPsi0Auz4Z4HXty3rs/Jl52bjZ/vSQnUcE8OyYjqLdLxNSNw8AI9vsPIUmqc33Se09AHTPtYutSy129sXTVTtDoJnyHIMG7H3wyXffhYBnWzQTO0Sgltl9pp9kDABAIXue2b6tYZ/zkcg+ViNjPF9jTrfdt/frHDbbm5FDfk1k18W3lu2+P+SQO/HEqH1OWS7FcMSvr9CfXDZF2CTtvp3JsrewnIKWwO53gcOwz7J8hslYNkSym9qK/Prr6rbHkWKLnRnR45BpxPpunmSnzSmRMBMAgW+fLzau83ssx8bcvMfHdWawYeeztVfsPtHVyoNCwtA+FuNkzJ1XtO9/AOCTz1EluX+Pjdr7+HiNP9uVPXusWeh3m+0DKc/hafr29VPw+LjODDbte0ec2s/ijcT+HEHMn4likl/DVBwyFkfI/WuI3L+GGvY4AwBRaverHPlVNAC/xkPS7yLYzyMJSJ8K+bN4kvJ7gyVN+e8czyXp7/5M9zZmO83IERERERERERGZJTQjR0RERERERERmnDJy3GhGjoiIiIiIiIjILKEZOXvI80rwvF1/g+f79uHMeTyfJstYjaT93VuS2nW9LQWeTeN59jYi0u475DHUG5vM9o7iIvvnU/4t6nhsn4+Ogl3PWgx5vSrLIUhJjfO2MbuWm9VZA0AxtPfhqRG7tpdl7ABAmRwLdhx6O3jmQ6Nif9Ztg3ZN+paGXUfN6rQBoAD7fIxnW8x2lyyS9sJCsz3L7P1MSS03ALSSevFK0z7n8RT8K0X/VrvfDdXtfWR9DgBCkuHRT3KTKg7XV0zGmnaSfVHP8X8vWTNmn4+nqnaeyTZ/wGwPHPoly5ZhVw/7eYBnHfSV7PbRmPfLzTU7z6Szxb5H9nWPme2ew3i5das9Vg1U7H7p0vcLZNzfVGkx28fI/REA+kiOTiln72fTIeOjt2gfz1b0mO1xZh+HJOPnK0fGEZcMHMYn/aavzb5HPjHUSbexsWaf060kG60U2udrjm/3KQDoz4bN9iFyH2Y5WgCQZPY9cBxbzXbfIXOlAft5fVPdPlZLW+xz0ZLj93HW78arRbO94JBRVSD5bJ127BJyPr+HMmsbG8z2weZa+h7s2ctjvzvR3724PMnRaab2+YwTO8eHPRvua9IMSKd5xozLc8uznWbkiIiIiIiIiIjMEpqRIyIiIiIiIiIzThk5bvRFzh7qKC+B5+16KmEhsKfVNZLRSW+/FttLExfz8+19aNrTxgEgJVMMc4E9vTb07emeABA7vMbchsP0drakb4Ms2cuWFgf4FPhFbfY0/uctJ1OAi3yQiUfsz1nZQpYkrZK5swDGybKmESlRWbeNlxWWyLFsJ8v+LiUlEx15vmT2eG2b2V7w7ZKJHPg2xtJ+ex8adntXaRndRo1cw+05u1+1krKNYoFPC+8kr5nr2dOII7K0OACMkqnl80hpyGCDlxw9QpZa/9Wg/fMZ+FiV9+3z0RXa19/jiX1t5HzeL9leJuSBJ3GYotya2uPAlrrdb0Ofl0QM1O1jlW6xlz/eRpaBXtbKy0TbC/ZS0W2krGI44v3yqYq9n2VS7lom1zgAVJqsXNW+Rtmy3gCwgVQt7Z8tMNurpNR0QZnfQxe3289FxZK9jXyJH8tG1X6eGBmxr9EFrfZ4CfAy6SfG7fEyAzmfpJwIABamXWb7eGofy3rGl1lvenPM9hHY91B/N8/wf6jXbzPbl5Ttc95NSvdZiScAxKT8kY3JrCwY4H2mnTwGu/wa3ErKixfW7d9bUjKWAUAps38vaQb2vWVd/D9m+0j1cboPPrnPFnP2vaeUt6MvsizBeI08cMhzjr7IEREREREREZEZtz0jZ/q3MdspI0dEREREREREZJaY0S9yrrzySrzkJS9BW1sb5s6dize84Q1YvXr1Dq+p1+s455xzMGfOHLS2tuLUU0/FwMCuV+jYtm0b9ttvP3ieh+Hh4R3abr75ZrzgBS9AuVzG/Pnz8c53vhPbttllFCIiIiIiIiIizyYzWlr105/+FOeccw5e8pKXoNls4sMf/jBOOOEE/OY3v0FLy/Z6x/e///34j//4D9xyyy3o6OjAueeeize+8Y34+c9/vtP7nXnmmTjiiCOwYcOOS9n9/Oc/x9ve9jZ89rOfxete9zps2LAB7373u3HWWWfhe9/73h7tc5zUdpuRw/JrfI8f7jmlA832UmjXBkepXUftO3x310zt2t56ZH8BxpYvB4DWol0TWyRLtTcdAqqapD64nLdrtdnSxgDQ027nJRRb7W3Eo/Y+VtbxjIH1W+1j9XTVrtvtr/PciWGy7G+ZlJwf2Gr3KQBYQOqgh8iywvWE1GG38H4ZkOVbE9h11oHHj2V3uMRsz/n20sRFz87iAoA67Pr7DPZ7FMm5CB1q1gdH7c8xVLPzGgKScQUAETnng5F9/bA+AwAkToj2qwY/VNhat8eaDbGd4VH3Rsx2lzG5SYY7loHD8hoAYMS3M8GGm3a/LDhkdFTIOV1AxvXFLXau0ljMr/GHRuwsrTzp21053mlYtsVTVTtnZwtZihoAyArKaAnsfRhr8m0MNez3KAdkJ8ihKjs85ebZeJe3+0x1lN+nfXLOc+ScPzxgZ88AwMaa3TfZNdyeI/2ywLNl1lZ49oulzeP5ibWMbIN0u5QsWQ8AHXm74/QV7Syfvk57zA5D/nzpkc/RJGPdHJLTAwAl0vf76/Y4MkxyfACgQTpegWQW9aZz+TY8+3w0ybNbLrDH7I7yAXQfquR3o1xAMnTCTrM9zZoYr/2W7se+QmHHbmb0i5wf/vCHO/z/l7/8ZcydOxf3338/jjnmGIyMjOBLX/oSvv71r+OVr3wlAOCmm27CIYccgnvvvRcve9nLJn72xhtvxPDwMC699FLcdtttO7zvPffcgyVLluC9730vAGDp0qU4++yzcdVVV03zJxQRERERERERmTrPqoyckZHt/6rY3b092fv+++9HHMc4/vjjJ17zvOc9D/vvvz/uueeeib/7zW9+g49+9KP46le/Ct/f+SOtXLkS69evxw9+8ANkWYaBgQF85zvfwWte85rd7kuj0cDo6OgOf0RERERERERkeqTw9sqf2e5Z80VOmqZ43/veh6OOOgqHH344AKC/vx/5fB6dnZ07vHbevHno79++vGCj0cBb3vIWXH311dh///13+d5HHXUUbr75ZvzlX/4l8vk8+vr60NHRgRtuuGG3+3PllVeio6Nj4s+iRYum5oOKiIiIiIiIiPyRnjXLj59zzjl46KGH8LOf/WyPfu7iiy/GIYccgr/6q7/a7Wt+85vf4Pzzz8ell16KE088EZs2bcIHPvABvPvd78aXvvSl3b7vBRdcMPH/o6OjWLRoETJkAHZd21rOk/yapp2nAgD1xM46mCyXrIRyvtdsby/sZ7bXEzsrCADS1K5XjbOq2e7yHapPMgRYRkfmsJVezz6ncd2u/R0btfdhuMrrxeN0ct/HdjrkMfQV7XruHKn/jx3qUNeMt5jtWxp2/T873yyXAgCWpIeY7Y/iv8z2YsDza1IS6hB6dk16tpvx5w8VMjuz4emKvQ/jpO49dqiLnzvHzuvqzez2SsU+DgAwXLGvD5b1s63Bt/Fkxf6sv9pm1+bHGT9fcwp2354ftpntm1I7P2NLY7XZDgAgQ81U/KtPRMb1qkfyaZo8n2YkZtkwPM/EknfITust2Pe3wcjuU78e4fvYSi7Bzpy9n/OLfDysk5w51r6VR3TgV9UtZntKxrtlYY/ZnnfouO3tduZKocPeh9I8/kGjQftYNRr2CX1eJ3823K9sXx8DJGful8P2tbOpamf+AUB3zu67HSRnZ7BuXzsAsDax82dYnwlJJgsAdJKO05G3x/0cuf5KnfbPA0Aa2/vQFdrjaRjwseqxwU6znWWf+Q4P48EkJz0UPT4elmG/ppjaN7jUP8hs3+Y9Rfeh0rDHstHaWrM9K+56MsJEu0O2074ky7b/me5tzHbPii9yzj33XNx66634f//v/2G//X7/JUFfXx+iKMLw8PAOs3IGBgbQ19cHALjrrrvw4IMP4jvf+Q4AIPvdWenp6cEll1yCK664AldeeSWOOuoofOADHwAAHHHEEWhpacHRRx+Nj3/845g/f+fg3UKhgEKBP+SLiIiIiIiIiOwtM/pFTpZlOO+88/Av//Iv+M///E8sXbp0h/YVK1Ygl8vhzjvvxKmnngoAWL16NdatW4eVK1cCAL773e+iVvv9v+Ldd999eOc734m7774by5cvBwBUq1WE4Y4fNQiCiX0QERERERERkZmVZh7SaV5Varrff2+Y0S9yzjnnHHz961/H97//fbS1tU3k3nR0dKBUKqGjowNnnnkmLrjgAnR3d6O9vR3nnXceVq5cObFi1TNf1jxj69bty5secsghE7N4Xve61+Gss87CjTfeOFFa9b73vQ8vfelLsWDBgr33gUVEREREREREJmFGv8i58cYbAQDHHXfcDn9/00034YwzzgAAfPazn4Xv+zj11FPRaDRw4okn4vOf//webeeMM87A2NgYrr/+elx44YXo7OzEK1/5yj9q+fHMyDsI/bL9ww5Hu96066DTzK5RDny7HCzw+E6w1zQzux48IBkfABAE9ms8UsPM8lAAnmUQkMyUenPyqRAtfXa9d7HDzgnJ1vFtVMbs/AxW4zwY83rx/lG79n40to/lHIcqxReQmvHegt33WYZOpcm/eW8n108PltnbyHg+VN6zx4mxeKPZHvp2zgEApN5ys/3Adrtvdxbsc1Es8qyE8XEyFjlkjTClnH191RN7LHP5t5gDWu1ttIX2NgYjvpVtJGJjS90+H03PfoOO/EK6Dy5ZB5P9edb3x2FnX7Sm5B4LIErtfjdMxrsmubWMOuRD9dtRP+gleURdeX5/i0g+zS+H7Gvc5Xy15+wXlQN7P6s87gSlzD5fm/1+s72Z2dmEa+xbLACgUbfPaVtIxjuHR4XiIvtY9rTaeSdPPMzz8p6u2tdHTPpMZ84+nz1FnlFVT+xxvZna22g6zJJfkNr/AFtBt9m+wX+MbiNHzmlvi32+2ve3x2w/zy9AjxzuZMy+wGpVnqnCZiQE5Fl7Tp7fxwdJLtJoZLfnHXIgq4l9LNizXZja2aAu13hnq90vx2Bn6JQ9O+suyWKMVH/Dd2Qfke2FVaVcslCf7Wa8tIopFou44YYbzBWm/tBxxx23y/c977zzcN555+3xPoqIiIiIiIiIPFs8K8KORUREREREROS5TatWuZmKFUVFRERERERERGQv0IycPVRrrMfukhUKoZ1VUgw76fuznJ1matfl+qyo1sF4tNlsb8vvvFz7jvvAvx+MMjtEIIRdz+qSNM6yYUYj+1gVA15fnC+QGuUt9rF48mm7vv+76+2aWQAYieyvlANyqHp46T3mFe066D4S21IgeUQA0F+3z8eWBqvltt+/xsIvAOR9+3z1NeeZ7U8F9vUJADmSCTE3f4jZHmd1uo1hDJvtrWQsKvh238/l+bVRbLFzJYa22mPdUI1nAQ038mY7q39eX7N/HgB+O2b3iQY5FEMNniFQadpv0p239/OgxvPN9if939J9INEVYJ+C/TwAVFM7Q2ok3WC2ewG/t4zGLWb7/KK9oy0k96XD4ampr2j3u401+3OsGuTbmFeyt9FOHgWqTuMhyzOxfz5x6BM1ku9Uhx1y81Ri5050x/bzCgCM1ewxuW+OnXfilXinSLbZ75Hf396HgzuG6TZ6Hq6Y7Q9vsnNAHhtnz0R0F8D+fZjdp4sO13g9ITuS2Q81CzI7Qw4AWkk+1FMj7WZ72zq7X7eQPgUAOfL4F/ba/a59mD8rdA7b+xGRfJpiwO9vy1rt9ii1z+dTJAto+37Y75Ejz3bjkX0cWjL7vuKi5o2a7VFmPz+yjNR9jVatcqMZOSIiIiIiIiIis4Rm5IiIiIiIiIjIjMvgTfuqUlq1SnZQi+1p442mvbQqALQW7GnAxcCea1lrbjPbS6FdygMAxbw9ZZSVRRV8Mo8SQB522QRbptYln4pNvy2QKaEuy7MODtnTLVl5F1se+eU9fGrsYGS/B9sHF2yKfIMsa7qlwSf/seXBO8mSvGypW7ZEOgDkyEmfW7CnbLc0D6LbeDrbarYHZFguwy7hBICOtIO+xlIgy3qHBT6d2iPLlvbMt8sAemC3A0CjYl/jY6P2+SoFfKxqC+2x6skKmd6e4/UIzcy+PrbW7WM5HPF7C9MgywZHrJzBwXwcaLb/uvovZnuxjffrp8b2M9s3VNiYbB+HhWVevjyPVAWWyZPXge18zB6o2X1iE1l6uBTyMZlUXaCdLKE84lBWuMVbb7Zvqq4y2/Mt9rNCKbCXBAb4EsvxgH0s80v4o3Qwxy6PjEgpTmo3AwDqpDy5M2+/yaHt7Brnpaj9NbtPDNbtPjEe87LdrbBLVBLPvn+xeywAbGvYfWKQlOav32KPVctL9rM6AAQlcv2Q8v/SYj6OHBoOmO19/fYz7tPD9u8LADBMnlGLrN7OAQutZZvoCOzSxm0Zr3cdwkazPSalU01ykacZLzGT5x59kSMiIiIiIiIiMy7N3LL3JruN2U4ZOSIiIiIiIiIis4Rm5IiIiIiIiIjIjNOqVW70Rc4e8rwCPG/XJ973SB1ojtf3s+XlApI/kyOZDzFZvhwAMrLQrEcmclWa9vLlAF8mneXwjDftJZoBoJqQ/SSZD3mfZ0K05siSoqFdwxx49rFmtcUA8MS4/Zpxkg3TX+M16cOR3S/rpHb3iE6eRbJf2d7PiJSLj7OMnIh/zk2xvdRtb2jXiwe7GRv+0Dx0m+0JKfZOMp47MSdvZ8OEZFnh7nZ7nCjvT3cBzSF7G//zgJ0H5nKDzfn2sVg9Zp8vlsvkgtXeO0SRYOO4faweqtlLLMeePQ7FsMdTAAhJPhRbFTiYgjnKpYK9PHLisPzq7u7Pzzi4wx7Xu/P2B3WI2sIaEln0dMX+HPMdcng6SD7NvLL9OWsOy4+z8WyIZOCsaYzQbdRgZws2E3ssGknsJes313lu2VOjdu5Y8Lj9OUtP837Zc4idfxF22P2utt4h441km1Wb9rPCxprd7zbxx0c8OGp3/lbfztlxuYe2pnYuUs6z+/54xrMHB0joXqVpb4Md6/UbyNriAObV7GNZaLH3sTiPPyv4ZKgJSQ6PizFyn62TEMZKwq+vttD+IKxfbU7sZ7/Y5yFVBc9+zi159u+Aec8OV0uyCNvwP3Q/5LlFpVUiIiIiIiIiIrOEZuSIiIiIiIiIyIzT8uNuNCNHRERERERERGSW0IycPZTPdcPzdv39VznfY/5sKeA1sazGsp7aNedRc9Teh5ydzwEAoWfna7AMHA88W6Y9WGC2s5weEucAAFhQsuugA5IT0l+zjwMA1EgddCW263Z/stmuzd/Ky3JRDOzPEZMy6c48P189RZIrUbBPSGvI6/vrpBR7E4/5MI03SYgOgM3BJrN9bWrnOZQ9fo13YI7ZXsjsDAGW0wPw8zWvQLK4QtJpQn4BFg61x7KjDrXr/xOHQIaxJ+z9WDBs172vH7GvPwD45ZD9Oe7dTI6lQ+bDfq32OHKEZ2fHrKoOmO05UnsPAAtb7H/XWVK2PyfLjACAHOzxsBHb97dCwM9XhVzn2xokOyZhYxndBcwjhzsf2MehwocqrB2zX9RNxoB2krEDACQmBHlyI54X8my09an9mrbiQvoeloGIjyPjzcKktkFizbbvx0N2p+hZSnLJDuQdr4Vk8nWts+9v7b+x702VhD8/ep59jTbJraXqkN00XLMfBmKS2Vf1K3QbcWbfZ6skYzFKyfVX5jk9UWS/hx/YB7O5jv9bfbnHPlZtXSTbaYjn8LTn2GvIscrZz0QAEKf2NliGGx2rHMbkIX+r2V7O7Gtjs7fWbE/Bs4L2JVp+3I1m5IiIiIiIiIiIzBKakSMiIiIiIiIiM04ZOW40I0dEREREREREZJbQjJw9VAzb4Xm7rudkGTiew/dmAckQaGZ2vWqjaedOBD6vBR+J15vtSRqZ7W1FO/8GAGLYNc5JZteCsjwVAKiQ/BqWs+OS+bBmvGy295AskpfNsY9D1WEfhmL7NVtIJsRQxL+R3lyz64+fJnXtdYe697kl+/poIaPVKCkfDneTbfWHoszOKagndoZH5jt0TLIbQWZ/0GLC68UPJjXl7F8hwjzJqCrxW0c2RgKeAnIgHP6ZIVe2j7c3ave7nM/r+5/XZmcZdJJjPdDgH2Qsts9HjVw/LRnLwJlP96FEhpoyyWNIMj6OxKTGv5Sz76GBZ98ft7/G3o+RyP4c68ftPtVI+TVeJxkdy1rs/I15ZCwEgJbQPmFPV+z9HIx5ANvist2vSsHk/zWzA332C8gpZ89M9YxnkQD2c9GWin2fb415dkUpZ7/mkV/bOVjtBX6+Ojrs54moYef+1RNy7yG5ggAw1LBfMx7b/XJTOky30ebZ109GQou2kedPAKimJIMqb1+j+7Xa+WwpyeICgJDkH46M2NdnkTx/AkAwQu71ZB+6ivz6WprYx2qsaZ/P0YiPh1vr9ufY6jDeTVZr1mG2pyT7MyTjUPocm3uhjBw3f1SvWLduHRqNnS+KNE2xbt26Se+UiIiIiIiIiIjs7I/6ImfJkiV40YtehCeeeGKHv9+yZQuWLl06JTsmIiIiIiIiIs8daebtlT/TrdFo4Mgjj4TneVi1atUObb/+9a9x9NFHo1gsYtGiRfjUpz61x+//R8/TOuSQQ/DSl74Ud9555w5/z6Y0ioiIiIiIiIjsqz74wQ9iwYKdI0dGR0dxwgknYPHixbj//vtx9dVX4/LLL8cXv/jFPXr/Pyojx/M8fP7zn8fNN9+Mk08+GZ/61Kfw3ve+d6LtuaqR2jWxScprNCvYYrZXo61me1txodmeZby+3/fsbpF6du3w1tFf0m0U8nZdfDk/x2yPebQFtjTs7IoFJft8zMnz+uLBiBwr8m3vcGz//COj/BJ9dNg+pyOxXcNcIblLADDuVcz2fGbX9h7W0k23scCOIaC5SGvH7H65MRuk+xDDzshpC+x+65Lh4Wf29+cF2HXvj3uP0G30jh9pth/YZu8Dq4v3ulgmCwCShTD4U7tfrtnUQzcxGtvX+Ai9vvj5qpMsg4T828Vggw9WQw2777I67hT2C0qZnY0BAEWSkVMgGTlVkoPgIk7t7ArPYRvtRfucLyN9P+fb7XHK+wzL63qSvGBtxc6hA4BD2u1cif1a7BPaGfNruBTafZ+NyaNN/jm24HGzPefbN4ZKus1s7/EPp/vA7sP7t9h9vxLzPtEgeXfzOuznx1yOP7t5nj0OxORzbquTrCCHvC+WO7as3T5WR+bsrCAAqNjDJf570M6KrGGUbiPK5prtj5F8xL6i3d5d5M9dKTkfHeQZtpnwjMXhbeTBi+jqtJ+ZACAgfWKEXD8PDvFcwIRMItjs2b87LfHsZ7t5Ib+HbmzYx+Ix/9dmO8sGTUn22r4m+92f6d7GdLrttttw++2347vf/S5uu+22HdpuvvlmRFGEf/qnf0I+n8dhhx2GVatW4TOf+Qze9a53OW/jj3ryembWzfvf/378y7/8Cy699FKcddZZiCJ+0xYRERERERERmUmjo6M7/NlVDvCeGhgYwFlnnYV//ud/Rrm88xem99xzD4455hjk87//ovLEE0/E6tWrMTQ05LydSf8T2qtf/Wr84he/wE9+8hO89rWvnezbiYiIiIiIiMhzUIbpz8d5ZgXXRYsWoaOjY+LPlVdeObl9zzKcccYZePe7340Xv/jFu3xNf38/5s2bt8PfPfP//f39ztv6o0qrjj322B2+QTr00ENx77334tRTT1VGjoiIiIiIiIg8q61fvx7t7e0T/18o7Lqs8aKLLsJVV11lvtcjjzyC22+/HWNjY7j44oundD93ZY++yBkd3V5X+v3vf3+H/weAfD6Pf//3f5/CXXt2Gqtv2m0OUJY9af5sa2kJff9i2Gm2swwclsMTJXbWCQCU83aNcpzYtdwsYwcAirkOsz0kdfE5h7lkLFdinNSsJw5p5j55yca6Xdt7zxb7DVh2BgDkA/s95hbtOuvuAq/9LZN+yY5DnQWJAFhHuuZWEsgQkxPuO0xA9EnGzabqKrM9F9q5FQAwt/A8+wXkUMUZr0lf37AzAtZVu8z2+rh9HMqb+TgS7Nduts85tdVup1sAss329NPx/7GP1SEb7HEIAB4dsl/z4Ih9jbeQnBEA6Cnax3tbw+4Ua8ftvKG56KT7wLDx9Jl/2bKM+yNmez6wr59cYPcZAOhv2McCo/Z41yQftIeFCQFoz9vH4tAuu89srfN76MOj9n24I7DH/XzAx8Mh0u+6CvaxKPr8c+Rg3+vj1L6G2TPPOHjJfz2xz0dAsmfmdfDMlSp5FnhqsNPeRgsfcztJXkl7p51BdVAybLZvafD8mjSz+0SNPAvEKR9HInKNjpBxppHZ1w4AVDz7WG2q2veFx8btDKpDfP5MVAxI7t+oPR6yvCIAyAf2c1U7yfLJHM5XGNr7USb7sKDMt/HEuJ0vU/DscX+QjDMDKc/MHPft5y6PPIM2SV7lcy0jJ/3dn+neBgC0t7fv8EXO7lx44YU444wzzNcsW7YMd911F+65556dvhB68YtfjLe+9a34yle+gr6+PgwMDOzQ/sz/9/XZmU1/aI++yOns7HQKM04SHsomIiIiIiIiIvJs1tvbi95e/oX25z73OXz84x+f+P+NGzfixBNPxLe+9S38yZ/8CQBg5cqVuOSSSxDHMXK57f+Yd8cdd+Dggw9GV5f9j61/aI++yPnJT34y8d9ZluE1r3kN/u///b9YuNCeJSIiIiIiIiIiYskyD5lDZcRktzEd9t9//x3+v7V1++y55cuXY7/99gMAnH766bjiiitw5pln4kMf+hAeeughXHvttfjsZz+7R9vaoy9yjj322B3+PwgCvOxlL8OyZcv2aKOzWeAX4Hm7nh6XD+3lcgOHkqN6c9hsL4f2Ms5hYE8Ny8BnS1WiAbOdlX+VcnypaVbi1RkutveBz26n06GfGLenng/H/AKfX7Qn/nWQJUNX9tpTLbc0eJ+pNO39zJEpvC5Tmdl06CqZ8bmxwqel5kh9Vg9ZVrieTH4SZt6zp/n7pFSgELTRbdRTe9r3tuYWs70l5P8asClYR96j02yPY7tfJkO8XCEZspd7zy2xy2i8Xl5G45X4sr+W8QZf1rQrb3fuQ9vtfrst4tdwf91+j9HIHkcSj1yADtF1pEKTlk96DhsJMvtYsHtLi8+XpGdzsbc17L7rk1nHlXF+D30KdlDhwcECs709z29wy1rs62dj1Z6mvy61xxkAWOjZx3sbqWJbiw10G+OxfaxYuWujaZc1+aTMDeB9/7Exe1yvOyzzvLDTLrvoyexSnp/383HfG7CvwW4ylrWGk59N/zC5NwTk+ppb4uPlaGRf5E8nD5rtnsfPV+zbn4PtZktg7+NWh3vPohb7fLHSqS11XjbflrOfzcZjez+bI/z6KpDSKfas3uLwm2pbYO9nG+z2kcQeLxsuJZoeKdkjt8jQs38nSeHwi4/MGh0dHbj99ttxzjnnYMWKFejp6cGll166R0uPA39k2LGIiIiIiIiIiOzakiVLdrkY1BFHHIG77757Uu+tL3JEREREREREZMbtzbDj2cxh7R+bS/ixiIiIiIiIiIhM3h7NyHnjG9+4w//X63W8+93vRsv/qtX+3ve+N/k9e5bqblm+2+W12/355s9WM3upXAAYizaa7bvL53lG0bMzciJWwwmecZP3eXYFE/h2LahPapi3NRyWBp/khLOQ1O0CQJHUQbPa34jk02yyy+a3v4YE1AzHdm3vCHifKGR2fXHRs9uTjH/vfQjJfGArmNfJank94EsLNjKyjHPxUPLz/FjOw3KzfTRvp9UPxmvoNrq8RWZ7jlw+aWqPMx57AwDNUfuEPfAtexzpIsueAkBHm32BbNhmZ3zcs40vP/5bsrJwg3RMtmw3AKyv2ZlhHaT+v5jaS936LOAGPANnb2D30HLGM6hKJIvusC773tNdsE+YSxTXAfX9zfbHR+0xeXXNfg4AgIXZXLN9btH+nAvJsQaAmHzW8dgecxdlfBvVnJ0ZlsLO8GgP7byhIQzTfRiO7bFoQcn+nAMOWSSNbfYzzeJOe6A5bpGdJQQAwxV7P9ZX7Hvsr4btjLjH7JgfAECVLAe/f9neR7a0OAAMRPZ9ujc4wGwPwLPVQpLnNRrZ+znWnHyeyZNj9vlaULKPQ3fB4R5K7rNNkv9UiV1yHO3jva5qj1VDEb85deTt/WD3tw5yvmuJfY8FgGrTfv6rZ/ZY102e2xJEJH1t35Jmbs9Pk93GbLdHv+l2dOz40PtXf/VXU7ozIiIiIiIiIiKye3v0Rc5NN900XfshIiIiIiIiIs9hGTxkmOblx6f5/feGSWfkiIiIiIiIiIjI3qFVq/ZQozkCbzf5La15u2Y9B15j2VM4yGz3yHdvcVY120PPrkUFgC7frtNk+zCc8fp+JiKfoxjwwsa8P7l8moJDiXM9sY9FpWm3/2e/XXvfSHkgg0++UQ5Iexd45tGcgt1vSqG9jZ7i5L8zfmrczgKKSf78EEjYCYCKN2y2t2ZzzPbMs88nAKRkP8uZneWThPvRbbRkdm19nexmrWHXtMeD9vUJAPk++5y/5PXD9D2YrGb3ia6RLWb7fmvsmnUAeGRTr9nOciUGHer7D2pn72H//MCgPVixMcKFB3s8dcnYYRk3m7GW7QRVS+2Mt41V+7HnaTuuCL0OY1lIXrKo1c48mpvY92AAWF+18zEeqg+Y7S0Zfx4Z9+yDMd+zx8PYIRut4Nl9P0+em+pkH8uJPRYCwJy8vZ9toT3OtOXtHB8A2Fa376H/M2DnefUU+DZi8kzDcv+WtNgDjUey8ADgcZKj86uqPSYnsI81AFQ9eyNNzz5WEXj4YAX2TXJO0c5mysh4ycYIAGgL7X0YjOzz0eXQL58es5//WM7jlgbvE1XynFz07euvFEx+zO0qkOdkcm8Zi/kvBMvG7WezzbDvf+kulqf+Q0lGHgT2McrIcaMZOSIiIiIiIiIis4Rm5IiIiIiIiIjIjFNGjhvNyBERERERERERmSU0I2cPVaNBeN6uv//ait+aP9ua66Pv72X2d2sZydcYiZ422yv1TXQfhoI1Zrvv2d2mnLdrvV3egyk55Nd05uz64mFS81qN+Te1Y037Na2hXYD5qgX2+U4z/kErib0Po7FdwzzY4EWi47H9GvYOW+o8K2G4YZ+vscSu965mDbM98/g+JJm9jaFsvdle9DvoNrZm68x2lqUVeHZ+DQA0YB+LDSTiZpzU3teG+fVbJ/Ez5bn2Pubm88/pz7GPVRbZH7Ra5fX9XQU7i+R5bfY1vLHOt7G5br/HSGRfYTHJhAgdAmzYv+qwt2AZOgC/f5U8+/rpTuwcOgCISbbFlrqdM7DB22y2V+Jhug9pZu/DgdnzzPb9y0W6jaWtdt9vqdnX6BMpfxZYmNnHm2UvDXk8gyr27HGAPRMNJWxM5hk5mxtdZrvv2ce6TPJvAKC3YPc7lkXy8612lhAA1MizAMuDYNmDW+2hcPtrMGS2Nz07A4dlyG1/D3u8Y1mRLnIsu4kMiHPJ+XYxGNnXMMuFqdf4v9WzXKUNdXsf8g7TAYbJoSiTD8L6NcDzZcZIXNDcItsGv7+15uzn9Y2RfV/IZfYzT0bGwn2NMnLcPLd6hYiIiIiIiIjILKYZOSIiIiIiIiIy4zQjx41m5IiIiIiIiIiIzBKakbOH2kuL/uh8l1pi1w4DQOjZtdasfrgQtJntHe370X2IU7u+uBJvNduHq0/Sbcxte77ZHsI+DhW7zBoAUE8n9z1lleTfAEBL0f46txTY54vVJ7MMHgDYVLPbB6p2Xe5TjVG6jTXeg2Z7i2/nIi1MFtFtLG+xswzm+vZ199sxkh/l8esvI/ka4/GA2R7meVZCG3rN9jFssX8+m0O3EcMuSv/1KM+usORL9nECgPFh+1j8+Gd2n9ivzAMZDl5oH6tmbNec3/40zy3bSHIGYhLpMErypQBgiORDdRXs2vv9Qzvjg9XuA0Det/czIBlTOfLzAJCDfT5qmd0vtwa83y1Jl5ntB3XY+TNHBPub7ZXYbgeAp8bt6+8h72GzfX2tlW7jyJz9OftK9rGek/IxeZR07gGSQdX0+Y16NOk32/MknyYluWadKc8tY08KLL9ma8Svr2pi97v9y3ZW0CvmjtFtMIMk+2wVGbMfHh2n21gc2ve3zrx9H68nPCPn4XiD2b4p3Wi2s+dsAGiF/UxTT+w+MRzbn3NpC7+/jZH3GGva/Y49fwJAJbXfY0HRHnNdZjTUE4dQS8OGCv8cm+r28ewlz2YRyeFx6ZfsNa2Z/Yzb6tvXZ0wydPY1WrXKjWbkiIiIiIiIiIjMEpqRIyIiIiIiIiIzLtsLGTlksbNZQV/k7KFmUoHn7XqaYAuZUlpL7amzAMBmedXiQbM9H9hT91jZFAD4ZHnjXGBPES7kOuk24tSuB2JLRZcdem7Rt9+jSqZ7sqUdAWBL3T5hq0fsbbCSijjlU9OHm3a/imG/R5OUEwHA8uwIs71CzueCAl86dW6JLDNLlknf4m8z2ytkWVQA8GCfr57CQWY7W3YYAEpkem2OTPtOyPkEgBHY5QovLi012+tNewp96rAcaNf+9lTn1y1cY2/DYfXWwK66QDjH7jNvW/A43cZDv7aXYP7+hk6zPXCYufuC7slNPa+RKfYu+zBZWcY3UvPscWK8affbmkNJROgvN9tZKVydXMIu05iXtdtT5Oc3jzTb+2tkrVwA9zUfMdv7GnYZdc7h8Y8tL94dkmXSm3bJHwA8TZ6Lmr59xFmZTI0sb+5ibsE+Hwe18cFqsGHv5wPD9mDWmeOlHfMK9r3BIyVi84v2No7o5CV/2+r2e2yt28eylvH725Bnl061B3bJbEvWSbcRwR6r2PPIcGz3W5dfUBe22M/rGyr2c1VzCn5JZWWDbDwFgCK5vdXIKWdlUwCw3nvabB+JOs32/QJ7rKqn/NmuQZ7/EvKsXQ7YsZ7cc4Lsm/RFjoiIiIiIiIjMuPR3f6Z7G7OdMnJERERERERERGYJfZEjIiIiIiIiIjJLqLRqDzXTaLcZOTnPrlfNh7y+OIVdP5wjWSOV5mazvZHwpaZLob28cWto1x+HPs9D6fHtjI7Es4tmnZY8JMuP10jOB4mvAQCQVYFpbXBMPkjg89yJ/cv28U5ImlfRIUCjq2C/phLbS7wOR3wC45ox+5xvbNj14iWyTO2mzM7QAYCuwF6SN5/Z2wgdhlS2BGWF1OZXfX4Nl2HXe/eV2VKbdsfdPNBG96GLnK9ylz3W5efwfhkuscdUr8XOKvH8YbqNxXPt17yRLLu9sUqCfABsadi5ZGsr9vl4rDpsth/aypdgZlKHDBymkNmZKt1kSW3P4d+eHscTZvv4qJ0dk8I+n7HH82s6YPfLrtDulzmPf84DEjsL6PHAPg71jI8jC7MDzfZiSpaS9ni2BVs+3PPs8bLFt5eJrmZ8yeyx5jyz/emafb5aQp7rsqi1YrYXA/uB4yeb7eMAAA8O2/3GJVvQMlDlD0VPR/Yy6WWSaZRzuMYXpQeb7eO+vQ9Vj/f9jBRdLGyx93NZi53NVGnyk1Em/WpB2b7HslwmAJhbtPOdRiL73jQS89yWYfKa1RXyLO6Qm+Tv5veyZwz5W+32zG7PgR/LnGePE1XSL4cT+1khyRyCA/chWeY5Ze9NdhuznWbkiIiIiIiIiIjMEpqRIyIiIiIiIiIzTmHHbjQjR0RERERERERkltCMnD3keT683dSvz8kWmj/LsjEAICTfrW3wn7Z/PrTrODPwGueUfEcZklrRkNRAA0ANdo1yltn7mbhk5JAMnLpDBg7TGto7srBkH8ulrXZd77aIf9faJF8pN0lGzlCDH8ytdfs1o5F9MAdju14c4NkUHYHdr5LE3oey30n3wc/s4x15dn5Nd7KAbiOAfc5ZPlQu49cXM0pKrVk0U47kOQDAbzfa2RU//7WdI3JEB8/XeNGiAbO93GXXpI9stjNbAOCh/l6znWVx9dftjAEAeHTUPuCba3afGCW5SYWgk+6D7zkMqpPUg3azPU3twazg0Pe7SEZbS95+7Ml5/397fx5tx1VYCdy77nzfcN88apYHyaM8gbEBxyZu23yEwFrddJp0wCbEoVmGbmI6iekQ23E6OAS+hHRCB+gEO+kkHySLFcgiacDYzDYY2/Fsy5Ysa3zz/O58b9X3h7GwQNq7xNPT05P2j/XWwjr3Vp2qOnWqXr1T+4g8sIZu+zNN3nb3NGZoeTXQ/WU/eJbdeQHPEVHXBQBoy/C+Su2LKvR2rE1fRMsrAc+4KYTdtLw90nle5QbfF7N1fo7fP6nzDy/t4Xkm/S382vKLa3Q202iZZ2y8UOQZHs/M8f0Qp+1vzPFzvDOjsgt1u8xWeLtcjHi/H4e6zk6L+6aauC4UYuQqvbDIf2fY0MrbTFrktwE6A0flP9VjZIzsLfM+t1VcIjfk9e9OzTJvm6WAn38ZcbwTMcY9qHs3JRfy87cR6f70ZBJG8fJQl7qO1c4jcszMzMzMzMzMVgmPyDEzMzMzMzOzFRf96Ge517HaeUSOmZmZmZmZmdkq4RE5RymVyCMRHP793JTKvoiRT1MHf8dyIOQZHGOJA7S8PeqSdagG/P3+tpC/c14P9LvcCfFebUPsq860fo46kOP7shLyF3PrMeLMi+KV2KbIXJkSr7zO1/V2FkVFq01eXhLZMnEkwI/nYJa/+wsAvfklPlcWr8Vnm+fIRajzryyyK8YTo3IdFfDMhw3hmbS8Cr0v+xL8HK3ECZki2tr1u9qn5Xk/kEnwdjdb43kOAPDCGO/P+hb5e/Hlus6vOVDh9fi3ad5u48yK0CquxJvaxQcWeD6byjyKIxLneJztbEny7ehq8nyNbIJfY+MopEV2RYZvZyZGHRZFu3p2gS8jG+q2Lw4HaiJvKIyRkaOuP+kj5AW+7LTEoFxHJeT9QF3lJh3hfuxlpUjfjwyILnVbB88iieOpeb6StXV+bnSkdf6GyivpyvB9vbmd78uOTIx2KdRER9EWo7MKI76vsmWefZYS3weAlohnbfWJeLV9IhdmY4vuMbszvO3uWuRtKlZGTp0f83KTZ8ckj0G2WlYcc5XBGMdQwDPFFiMeHNiW0G2/Jcn35XhdZBqJvqxxio29eCkj5xjcvIh1rHanVqswMzMzMzMzM1vFPCLHzMzMzMzMzFacM3Li8YgcMzMzMzMzM7NVwiNyjlK9WURwhPcYn8f3l7z89tQALR+MNtHyjqibli8GIkgEQBEztLyW4O95JqFzJwLxDLEJ/m5wCL6fAKAe8ncrF8Sr84sx8mn6xXvSKmdn+xx/L3csnJN1CMUz5XzE33FuxEi36Erw98VbU/zd3o3i3XsAaBe5RyMipmCyWaTlKscHAKYSE7Q8EvuqCp7JAgCViB9TlXOlzh0AaEb8nfJUjWfLNMV7ycVF3qYAoLOH74uz+8b5AmL8mSHdyeuZ2tDGF1DjeWAAsOHRF2j5pmd5btl0TfeHuQRvV9M1fqmer4mcg4buy6qiv1T9qSoHgMkGP4nnEvzcCGP0VX0hz0IYK/N6vlgSOXUZ0ekDyKf4Oja08GyLtjTvbwFgtsqP6a7yPC1XeV+AzuoZSPHzS+X0AMBejNHyhMjhSYq8k8GEzgVcm+f9ZUuKlxcy/Dr+0mf4DccTs3xfPjmnMzoWZWYfL5dZJTHuiZ5b4BlwcbJGlL3g147ZgLepZKD75EyT546pbI3u9NL6dABYk+ftqjvDD/jest7XGZGjozKN1L1CHBMVvpLFUOdczSSmafmsuKGoJcXvNXFylRo8m7Ca4PcbC6Jdh+L3opPNSxk5y7+O1c4jcszMzMzMzMzMVgmPyDEzMzMzMzOzFRci3myYS13HaucHOUepVB1FEBx+KGEjxYfwtmR65fIrIR8OPSeGD7ZEampwPZw6Bf7aRCXiQ2e7oyG5jrnEJC1vRHwIYoyZU+VQ/0qTl+9a0MOlUwk+RFcNZT6tnQ99vSjTJ+ugZutUQ1/V0FpAD907wilxUJxpMNVU7lNi+K16/etF7Jd1mI/49OGZgA9/74r0K381Mf34TLhXLkOZEa8j9DYvp+VquGmtoV+V27mHv+LSIl416GjVrz0VGvwzyT6+jqAtxtDzbr4zurK8DnGGnqvXr0arfH8viFceohiRfjXRX6rtiPNq1UyCv7a7r/EYLe9Kb5DrSAX8tiYZ8eu0egVzX5W/wgkAY3X+euQZ4K9IF9K6XfbneT0bIb8X2FfVA7KHMrxPbYoL8USoX+WeF6+z5sD73P6IT3Fej3GrfqAipv2N+Ktw2YR+3W5jm3jVtMDbVXtKzJEOYEL0EwfK/JjvXuSvkD1TFa/DQr8Kl454HTvjtP06v7bsqH2XlocxpqSH2N0JMZ11p3jtqRbq82+feDVqSztvU5vFK7sA8EKRt92Suk/mtzMAgJy4XVD3yc1Ib8dcwO/dIvG6eUJEQmTFvR8A+WL9IqZo+XxtHy1X22CnJj/IMTMzMzMzM7MVF0Xx/mi/1HWsds7IMTMzMzMzMzNbJfwgx8zMzMzMzMxslfCrVUcpDMtHzMgJxDuzHam1cvnpgL+vmhHvamfEVNNx1CP+pmcbeNZPGOj3WVujTlpeA58KMIwxlbSqhZruemunfld7IMeX0ZPh77Sq7Jg4+RqLDf48dkFkzyw2YkzLXVH15N+fV3NYAthZ5fkZSkZ0Z82Efi++2OB5DX1pnm0RR2uCnz9dIS+fSvCpVQFgrPo0Le8R2TCZBD//suL9fwCYLvO+7F/38fyndIw/M3S/yM+vV73IM8W6OvR08ZOzPFPlW+PdtHxWR23J87wg+iqVl7J9Trf9apO3iarIdIiT+TADnh1TqvHstDjX0CFxHR7M8+1sEVOHL8aYgnlMxDs9j128nEflAQC2BptpeU+O94dbMzxDBwAqYtr6/RXeT6g+GQDawI9XJeAhHGoa9Rz0dbworoGVFG/b+8WU9gAQRjxv6PR2npFzdqduFE2RUzVX4/ti+wKvY3pSZ8CpfLWcOL+aMeYDXqjzZVyQvo6W14MY/WHE25XKBJus8ra/sVXnVXaKWdKLDb6Orqy++HTX+UqenhPryOi23xDvr6hDPhfoth+IcQnZBM+4aYrcpDbxOwsA9IT8XmE24H1uUeSFhadYRk6EINbvektdx2rnETlmZmZmZmZmZquER+SYmZmZmZmZ2Ypz2HE8HpFjZmZmZmZmZrZKeETOUVrTeQUSweF3Wy4o0O+q7BkAmGtO8XLx/VyC16EZ6WyLSpOvpZnky8gG/F1UAFhsjtPyRMDf280mzpTraEvxXJb+LH83Mp3QzzlFhAAOVJK0vCJeeZ3Sr1FjtMSPx3SdL2R3kuc1APr94fXh6bS8RRxPANiY6aTlbSI0ZbLC98NUpOvQmd4gP8PEyYeqiX5gPpil5b3NIbmOKMvr0Sr2ZUpkN7UXRAgIgLY23u4K4v39kWKrXEde9EWteV6H2XmeORanHlmxr+Jkxwzl+fFqS/J1zNd5P5MOdB1qIvNBbUdVfB8AEuJvR7l0By3vAM9VAoB6xPdlh8h0UNFofTm9nUMtW2n5eJnX8fkiz4UBgMcST9Ly1jLPa2gLdUaOMpjk9xujTZ6hAwB7aw/R8r4s35dzCX7PlGzycwMAkgHvB4bzvK9aq7sRPLPA8wv3lnnbH8zpfIyutMrk4+2uPcW/P9yir6H7inwdIyW+L+P8hXwu4u0qIXIvxoI9ch2D4UZaPilyA3NJ3tdt1Jc39OX4dXZfiWcaTVR0ZmZGtIkzC3w7E9AHbF5kGs2K+9zFhPrNBwhDfo8agrftJvj3K+AZVgAwH/CLRySSO4/0u+WpKoTOOj0W61jtPCLHzMzMzMzMzGyV8OM/MzMzMzMzM1txYaRnNDsW61jtPCLHzMzMzMzMzGyV8Iico9SFYSRx+PcgE5F4/z/U2RYqQ6AaiNyJkOfTTCQmZR0GExfwD4gnmPuxX66jI7mGluci/gJxMtCPUdWT1pm62Nf6lXS0iDOoJl7A3FdU+Rp6O+ca/N3eMvg76XEyV/Lg71p3pnh5d1Z3NRva+HvU83wzsSiO5xnNdbIOL0S8nv1RDy2fj5GD1RPwtp8WWT5tIs8BAPLNzbQ8Ix7hz9V4HYoi7wEAugb5vtg8PEPLT0vwcgBI5PmGJNfzHJCgSwcVnDHH80ou/7d9tHxyN88xAIBGg2/HuMjpGavyrJJkQue6qL6m3OTLqMTIyEkFOVo+lD6PlqtrLAAkRT7G7gWeq/Rggx/vs9t4lgkADLXwOpxe4OVrWvnxBICd89to+UiF54h0p/U53Jbm+TJtab4dzQWdw7MvM0zLB5tr5TKYdtHmAKAgol9akvxmoEdkmQA67+TJOb6vfjCps35UjlU+yY9XRqxivKxvimZq/ELdklS5gTq1IhTJFl0Jfh/cG5wv11EJeD9xdifvL9fn+X4Yr+i8IaU7w+/tDpR121eXhjPbeLutxMig2i3uaQoityxX1tfp/kjcx4pb6cUE7/ezke4vlapoU50pfo/ajOqYAs8UO5lEkIftmKxjtfOIHDMzMzMzMzOzVcIjcszMzMzMzMxsxTkjJx6PyDEzMzMzMzMzWyU8IucoTUQvIHGE3ZYEfw+0PdEvlx8s8dlaJN4drgX8vXlAZ9yo7VzAhFxHvcnzM9IJnvEhXvX+0TL4o1adE6JXMlnl66iL173LDf79UlO/kz6Y4+/uBuDvSffk9Hb2iNeDm+Kpdk6/Ri2SLYARET+TTfIDOlcXITsAUqJL3BvwPJREoDe0GvANKYc8G6YR8ZwsANgY8PyMKOIZAiql4IDIcwCAvTM856O3hfdFnQXdV2Vb+TvnLYkFWp4a6pTrQDvPRcqWebsqLOjtOHCA76vFOu9z45xfiuqr6iIDR/UBAJAT7W4qepGWV4IuuY6kyLlKiKyfucQ0Lf9/pWdlHXpKPNdla4rnOXRl9QHtyvL+LiGytIrqgANIi2tkQy9CakcfLZ8RxyN9hMzCl21I67yh7jS/zk5U+TpUOQCcUeAZHNu65mn5UE7nnUyLbLMXirxdPTfHD6jKXQKAQorvC3Wdbknptr9Y5jckezFGy7uauh9Ji2t5scH7kUKaXxe6s7rDfG6B56sNiD4gK+6BAeDpeX68Cmnen7Yk9TqakchXE7e5GzAo13Eg4P1EPeB5Qm0hv6eZTI7qOlQeo+WV2hQtX9P+KloeRvoe9mQSRS/9LPc6VjuPyDEzMzMzMzMzWyU8IsfMzMzMzMzMVlwIPTr8WKxjtfOIHDMzMzMzMzOzVcIjco5SPuhEIjj8e8jpgL/DPNl4QS6/0pij5bUGz3zoa9lKywuRftc0Af5u8L76I7S8EfJ3UQEgCPgzxPkMz1JoRhvlOlQaeQL8AyK+BgBwbgd/ntud4RkekUiGWajr98VVPSOxndUYj6QbIh+jJN5xVvk2ADBR4RUpi0CGpnjZdSYqyjrsx9O0vNrgOQZr0hfIdaQinmNQavL3qFuSPLMFAObU++IRz6VIBXxfZhM6u2l3uZWWPzDF30lX+RyAfr/5Nbv48Tp/ardcR6qHV2RxB//+d59bJ9ex0ODneSDO4ZYkPzdyMULF1L5U3WGMyBVMhvwaqPKfWlO9ch2np/n50S4a1vZFfh0vxcjpqQYVWv6d+v20PBDtAQAuxCW0vDfH+5nevL79U9lLsyIjbi6MkXOV4Fk+syLvpAmeG5FMDMs6FJuisxHd3WRVn1+hyIc6q4Pf220o8HIA6BdZWoM5nofSnuKZLDsXeJ8eR1c2RsChMFnl28mvoPFEokPcL+5pRlt4js/WDn5tAoAzRRTdtyd4m1qT19fp9S38HlXl2yRiHM66uHh0ZfhCFrO6r3q+yn93WhStIh3wXM5QdQIA0kl+7VjbfjUtV/mjTejfrU4mnrUqnhUdkfPtb38bb37zmzE8PIwgCPDFL37xkPIoinDrrbdiaGgI+XweV199NZ5//vmD5S+++CLe/e53Y9OmTcjn8zjttNNw2223oVY7fGPfsWMH2tvb0dnZuYxbZWZmZmZmZmanmo0bNyIIgkN+/vAP//CQzzz++ON4/etfj1wuh3Xr1uGP/uiPjno9K/ogp1gsYtu2bfjkJz952PI/+qM/wv/6X/8Ln/rUp/CDH/wAra2tuPbaa1GpvPTXrmeffRZhGOLTn/40nnrqKfzJn/wJPvWpT+F//I//8VPLqtfrePvb347Xv/71y7pNZmZmZmZmZnb0ouP0s5zuuOMOjIyMHPx5//vff7Bsfn4e11xzDTZs2ICHH34YH/vYx3D77bfjM5/5zFGtY0VfrXrjG9+IN77xjYcti6IIn/jEJ/DhD38Yb3nLWwAAf/M3f4OBgQF88YtfxH/6T/8J1113Ha677rqD39m8eTO2b9+Ov/iLv8DHP/7xQ5b34Q9/GFu3bsXP//zP4/77+bBmZr45esQphvuTZ9LvDifPkcufSvCh/iNV/lrTeJG/GhK26vHvapr0nszptHyy+pxcx1xpOy1vSw/IZShqSKgqTwV6zGhNvHKkXnmoheK1DTFVLgDM1/lnVB33LOo2sb/Mh8hPgQ9rXR/jdaCKmGq9O8OHhRcb/PuTyRFZh3YxzWU+wV+rKIJPHQ4Ai81xWl5v8tcyghjTs6ohumrYeGeGD+Fd08+PNwB0LPDtmK3xc3x3Sf+dYXMrP+azYlrgJx/nfR0A5NPi9UjRj8zEeD1Sbem6Fv7K0XiVD+NPiql0Af2Kpe5P5SrkK7UtCd5PVCM+hTOgp+4+q4NXdFsXf11hvi7edwAwJUbAPzfH+5nnol1yHc8E/DqbrfDXZIZivGbdnebtKiPeq0jHuMVMR/wcVW0mE/DtrMVomBXxatXZBX79G1TvoAF4bJZv50Kjk5a3pfR1Wr6CKZbRk+H9aalFb6d6jXq2puooVyEtyNdo9HTxlYBvyBvy/FWcWdHvF8VrcAAw0MpfB79avOI8Ja4LANCf59fpinjNc6yi19GVVtOP8/NvvMKvfwAwFfHfneYre2l5ewt/3by/uUbWoSPJX/2NIn7+zSf4K/HqNVI78bS3t2Nw8PDX2r/7u79DrVbDZz/7WWQyGZxzzjl49NFH8cd//Mf49V//9djrOGHDjnft2oXR0VFcffWP3yns6OjApZdeigceeOCI35ubm0N3d/ch/3bffffhH//xH4848udwqtUq5ufnD/kxMzMzMzMzs9XvJ3/fr1b1w8M4/vAP/xA9PT248MIL8bGPfQyNxo//MPjAAw/giiuuQOYVf6S+9tprsX37dszM6D8Kv+yEfZAzOjoKABgYOPSvtgMDAwfLftKOHTvwZ3/2Z3jPe95z8N+mpqZwww034O6770ahUIi9/jvvvBMdHR0Hf9at04GVZmZmZmZmZvazeTnseLl/AGDdunWH/M5/5513Lrn+//W//ld87nOfwze+8Q285z3vwUc+8hH81m/91sHy0dHRwz7jeLksrpNm1qr9+/fjuuuuw9ve9jbceOONB//9xhtvxC//8i/jiiuuOKrlfehDH8LNN9988L/n5+f9MMfMzMzMzMzsJLB3795DBntks4d/ZfCWW27BRz/6UbqsZ555Blu3bj3kGcL555+PTCaD97znPbjzzjuPuPyfxQn7IOfld8rGxsYwNDR08N/HxsZwwQUXHPLZAwcO4KqrrsLll1/+UyFB9913H/75n//5YGZOFEUIwxCpVAqf+cxn8Ku/+quHXX82mz3sjq7WZxEcIW+gnuJDsZJi2mEAKDdnaXk23UnLc+kOWh5G+h3LKTFN+pGmX39ZKsmnEwWA07veQss7Qv6uqXjlFgCQE/k0w3mefdEf4zxT70E/v8gX8rgYPVeJEzwh3ot/ocLzTBJiCnQACMU62sCnJW3EmONvYxufulFFFi00+PFMR/qAqikq6xF/b36+ul+uo97gOR9tuSFaXmzwjB0AyKX56MOsmI66GfHBmskYeQ396/l2/gdRHurZPpEQkQ2Zfr4dUUO3y8XdfBkvHuim5ZcPTMp1DK7nr+5WF/il+tHdPO8kk9SXenWOql0Vp6vKBjx/JhWIqb9DPdx4usIbzmKMnA8mxizr6BERHOd18b5oU2OLXMcL8zyIZybkfVUUI+ZxqsbzM87u4P1+NsnzawDgh2Xe57aC55LNhDz7IoxxuAdz/Nqxpo1nlbRk9H3Vhlbeth+e5vduY1W9Ift4NTElgrB6sryvGynpTvn5+gQt7wPfzs60zq8phXx/5xK8n5kK9HV6vMLzJjvTm2j5ujw/P/eW9H1ya5pvZ18bP8drMRr/RJm3yw6Rl9eV4efOS/Xg7Wq2xsvnI94PAUAy4Ne4hCgfbTxFy8eg9+Vw6jxaXgh5269FvN02o1Nr+vEIAaIYv58sdR0AUCgUYr2188EPfhA33HAD/czmzYfPz7r00kvRaDTw4osvYsuWLRgcHMTY2Nghn3n5v4+Uq3M4J+yDnE2bNmFwcBD33nvvwQc38/Pz+MEPfoD3vve9Bz+3f/9+XHXVVbj44otx1113IZE4tEN44IEH0HxFiOqXvvQlfPSjH8X999+PNWt0eJWZmZmZmZmZnZr6+vrQ18eDsY/k0UcfRSKRQH//S5NsXHbZZfid3/kd1Ot1pNMvDZC45557sGXLFnR18T9gvNKKPshZXFzEjh07Dv73rl278Oijj6K7uxvr16/HBz7wAfzP//k/ccYZZ2DTpk343d/9XQwPD+Otb30rgJce4lx55ZXYsGEDPv7xj2Ni4sd/CXj5adZZZ511yDofeughJBIJnHvuucu/gWZmZmZmZmYWS4QfZ9gs5zqWwwMPPIAf/OAHuOqqq9De3o4HHngAv/Ebv4Ff+ZVfOfiQ5pd/+Zfxe7/3e3j3u9+N3/7t38aTTz6JP/3TP8Wf/MmfHNW6VvRBzkMPPYSrrrrq4H+//D7Z9ddfj7vvvhu/9Vu/hWKxiF//9V/H7OwsXve61+ErX/kKcrmXhgLec8892LFjB3bs2IG1a9cesmw1va6ZmZmZmZmZ2bGQzWbxuc99Drfffjuq1So2bdqE3/iN3zgkN6ejowNf+9rXcNNNN+Hiiy9Gb28vbr311qOaehxY4Qc5V155JX3gEgQB7rjjDtxxxx2HLb/hhhvku2rH4jtmZmZmZmZmtrxeOavUcq5jOVx00UX4/ve/Lz93/vnn4zvf+c6S1nXCZuScqNbnXo1kcPgwtpaQB1UtBjx0FgDWpy6k5RPJXbT8SEHML2vECA0LRNBpFPHAu57U4YOeXqm3yYOcmgEPUMskdORkVnxmQQQVq4A2QAd81iMe1FVs8H3ZmtJ1KDb4dmbBw6mb0AGGHQkezJcUScSnF3SA4aY2vjOLDb6O6Qo/nn21flmHlqCdltcDHjbXSPPAcwBAmgd5Vxq8n0gneTghADQiXo8W0fMv1vkH9o92yjr0lHjyZnsv74uSMcLGE0sM/k+f2Sk/0/UqHtjape4EYjSJaIaHxoYP8VDLsQo/v1pjXOlnRD2boi+Lc0MUiMDIpgjjj2L0VSM1vq/CaX486yHvT+OEw9fEMja28+O1RmcEoz/Hl7GvyMv3l3RwZk+WXzvUwOfZqj5epYAHfas20RnwrMNmjIaZDPhnRor8/BwQIfgA0NfBw91fneB1eGiqU66jkuP3C6kEL5+s8DqoIGNAhxnnErwzUpMWAMBoYoSW94f8/nIh4McTAKpZfrxaknxfrWnl179aU4fnvrjIf6c4K8331YCoAwCMTPKw/h9M8wDYwZw+vyoh7zPL4pCr3wcAIB3wTnMwfz4tn6hup+W5FG/XAHCg8QQtHxM3LKeFF9NydV9npyY/yDEzMzMzMzOzFRdh+TJsXrmO1U7/ud/MzMzMzMzMzE4IHpFjZmZmZmZmZituNWfkHE8ekWNmZmZmZmZmtkp4RM5RCpBAcITnX9VAhHeK0FkAmAMPk1uLrbS8jDItH4melXVoikCtQmqYllejBbmOSZ3zRtUjHtAGABURJjdR482/rvOU5fuVszUe8jZb40GOhYwOtu3P8+3szfHAvGGeYwwAyInjlRPBf63JGKGXTf5cuSaOx9o2XsnnZ/i5AQDP1b9NyzdkXk3LtwaXyXUkReDr/txuWp6KdD/SHfJg5zbR83dkeBBqPs3bLQA8O9ZDy/fu4m27M6MDDlUg+WntPLDy7AUd3pk5ne+LoJWHykYLOqCw/AwPS50a4+fwuhbetp9f5CHeADBZ4SeYCjuOYoQAD0TraXk14PuqLTpNriMfqH6db+eB5iwtT8c4/1TA/DPzvG3P13SnvKmd7+9hEZjcnV1iUjiAvUXerz8S8vBPAIjAj0dPxMOMu8DDWOeaOtT5hSLfWcPi2vRiUe/Ly0Sgcl8n76v+XZsOVF4o83ocEOG5j8/xdteT4yHCAJBN8HaZFfcKUzHyXCfnOml5SvyNOgz0zV17wK+h03W+jpkqv751ZfXEIyqEe/tMJy3vz+t15JJL6/ef07f7MsxYzenRG/BzHACS4RZarvrkXJafG2noc7w/4hNZjASjtDwT8mtXIkbY/8kk+tH/lnsdq51H5JiZmZmZmZmZrRIekWNmZmZmZmZmK84ZOfF4RI6ZmZmZmZmZ2SrhETlmZmZmZmZmtuIi6BzSY7GO1c4Pco7SbLQfiSPsttYED7rKRDrAcF24mZaHotkFER9k1ZVcJ+tQTszR8l4RWLmQmJHrmKhvp+VtKR6ql9K5msgkeIhbQuzLx6b1KX5ZnwicLPBwsm2d/BRMBTqoUYWMlhq8TdRFmB0AVJr8M5kE31cqyBgAdhX5OtQQyJkq/0Bb1Crr0Gjy0NipiAcRJxJ6O9tCHjzbEw7Q8i7wUD4ASCd4oLI6noFoEi153S47q/wzu0s8DHJWhJEDwGSN7+9Sg4ckHrhf98nR9/jOWNPKQ0gzSX1+Feu8TXRmeQJoWvR18zXdl2VESKnSiBEOP5DooOXjTZ6c2RbowMmzOvgxbUvz7dwW9NHyeZ3zjQMiBLgqAperTb0zH53inxlu5eGe7WndJiYr/DMHKjxM9dzgHLmO3eABoHVxDdyHvbT8gtTpsg4qzL8SimtsjOvb/eN8goYL67y/68jFSAEW+vP8+naRCAEez+vzb7rGd6aaAKIgzk8A2JLjQfrPVCblMpR0xLd1v8ieHhBh4j05HUR8bu80r8M8v248NK1D7ltE+PTGVt6X1cS5AQBzdf6ZGXE7UUjre4FMk98XLTR5x60mo+kM+bULAFqSvJ5rwiFaXoG+rzL7SX61yszMzMzMzMxslfCIHDMzMzMzMzNbcQ47jscjcszMzMzMzMzMVgmPyDEzMzMzMzOzFRdFL/0s9zpWOz/IOUrtQT+SQeawZR1NHma3mOBBjgDQmeRBjbWQB4+NgwcN52IEvk42dtDy6RQPcctGLXIdKsx4c8hDEtMiXBcAUuIzKuS3JcbZoYLe8kl+vFRQ8bwIQAR04Ou8CJobK+tgzb1FHrSoQt5a03rwX00EfK5r4yGKKRHWOhMjhLs7x8PGVaB5GOl92ZXg50dSJA0XRWgfAOwO9tHy83EmLR8sLNLy7s06qLGjyD9TeJG3qfGi7kc2hrxdndbLj3mlygMOAWC+yvu7pAgIrTVFkiqAdd08YL5jgO/LtlEeHN1yQAc1jpZ5X1UP+XbEuR9qLvGu6cVgj/zMz+W20PKzC7zddWeXHjg5V+Ptam/58PcQL3t0RgeIzi7yej68MEvLG+DHGwDWJ3mo7OZWfr8yX9P9YUuN35OMJl6k5fWIp84WMryvA4BzC3wZGzrmaXm1oa/Tj0510fIvH+DllaY+d9pENYbz/Hi0JHn53rLezufmeD3nag1aPtyq16Feh+gPeH+nrrEAMBbyPlll2E+K0Oe9i/pefEuGn+PD7fx3ikqMa8+eEr++Ded4HeL06CMV3t81xSQt7THuH8sibb8lwdtVd5Off+VAh42XQ/6ZXvDJFwLxkowqt1OTH+SYmZmZmZmZ2YoLf/Sz3OtY7fx4z8zMzMzMzMxslfCIHDMzMzMzMzNbcZ61Kh6PyDEzMzMzMzMzWyU8IucYKiWKtHwq2i2X0SrCiNuhA9KYnpAHMgNAJX06Ld+18E1ankrqkFKlL7eelocRD1mMIx3wR7FrW3UgngpUfnqeh7xVmnwdT8/q4M1ayMNvZ0Ie5NifbJPriESk3UiDh+7lG3w/AMDlfbwea0RQ42iF78vNpSFZhw3gIdxTTX6O1wMdRNwUb+VWRSBsIaX3Zaa5jq9D/BmiWuOXhiDGlSO7kQe+btrC2/bmFA/FBABkeJhj0MXDBZGOsSFlXs9wgp9fcSQ6eH8Wipzu7CzfV7mk/rOTyiGui5fJ6zH+tLUY8n05l5im5UPhGrmOCZFJua/M22VVBNh3Z/Q53pPjlWhP82X0ZHgAKQC80MbbzKNTvJ+YrOvwzr4cPz/OKIhg9oYOW52e4PcLcyIgtC3ggczH4i+u7W0ixLSVXxcAoLOtTMsHxniQ/r1j+r5qvCKChuv8b7cLony8rNv+SIMHQ+fB2/ZgpO9HsiJpeCHk4fCtgT6/5oNZWn5eB7+X3iSO97gIAAaAh8Z5m7igh18Y1okw5JfqwfvDCTEhgOovAR2IrPKt4wR9V8VEMG0pcU/T5G1/MeDh1wDQE/bxD4hdNZTh57iacOCkcxxmrYqV1n2C84gcMzMzMzMzM7NVwiNyzMzMzMzMzGzFedaqeDwix8zMzMzMzMxslfCIHDMzMzMzMzNbcdFxyMhZ9gye48AjcszMzMzMzMzMVgmPyDlKU+FuJI4wZUsuwWdX6A74TDIAEC7x8WA3Oml5V1on5Tfrw7Q82XY1La8HejaMnnCAlqvZuRI6KF9qRmLmAz1BAwZz/Hita+FvYE5UeQp9Ic6sOkIP+KwDXVn9PHexzuvRXuPruKBHb8clXXz2n3ooZtSo8pkoWlM68f9AdekzfCmTYuar9iBHyxsxpmFpiij+VLC0E6i4T+/L5BifRSI3wE+wZBdvUwCQEB1BNM9nLwl6YhzPdf28DqeJmZRqMTqSkUlaXH+Mz07yzD4+I9tcjCosNPjMV+UmP4fLDd0uCwl+jtZDPkvLeGJcrmOywmf+WKzzNlNpqj5Zt8tN7by8J8PPjZakfnP/9DZ+ULvFjG6jYj8BwFCO1yOd4OXjFd1PzEe8z00GfH93h120PCdmOAJibMcM7yfaSnp2ye5+3u9f3H6Alm/u1MdrvsLPrz2LfDu2L/L7w3KMWciiiN8Hq+twnFvgophCLy1+tRnHrFxHXswg25vl59+Gbr6O9eL+EwCeneAzY40WeZvY2K1nWrqol19bds3zzqw9rWeXVPePTy/we550jBv+UsSPR0vE69Ai+pkN0VpZh0DcV81FfCazNlHH5skwfOQoOCMnHo/IMTMzMzMzMzNbJTwix8zMzMzMzMxWXBRFiJZ5FNJyL/948IgcMzMzMzMzM7NVwiNyzMzMzMzMzGzFhdFLP8u9jtXOD3KOUqU+gyA4fFhbIs0HOM0GMRInAx6cmQ55IFcoopvmGouyCuWECB8U4bnpiAfuAUADPOxxNOChlo1QB4+pEzSf5B9IJ/SAtYUG/0yNbybmRPBmD8+AAwDkRZhjTmznoAi0BID+rA60Y7qzut11ZHlI9lSZ74xckre7qZoO4X4h8TQtz4IH/7WFHXIdoQjW3I1naXkreLgnAKQCvi9en9pIyxeqPPSyu6nDB6eneFjkw0/00PI4F9h0gn+oL8tDSDeKQEoAGNy6n5anhsVJGmNDKjt529z+TB8tLzVESGKMRL9cgoeQqqDFWoztfB67aHkywa8tuUgHvtZFPVT53uoCLe+o5mUdnpnn/WVDXKeHs3o7t3Xz4zWQ5etY3yIuTtBDtmfrIoC+vPS75JS4TVX7MnkMxp03Q97fPTTGQ7oB4DwR+Dq8jgfT9q/X19DeOg9UHprnbbt/nF9bWpMixRvA3hK/drSneZtoxmgyz4gQ+2eDR2i5uk8GgDOiC2j5SIVvZ98cD5ZePzAr63De8AQt3z7Kr6FJca8BxGh31XlaPjej+6qJRf6ZDSJgfvuc/lU1Esd0TPzuowKyE9D3PLMBP7+qCd5uE+L3gUak72Ht1ONXq8zMzMzMzMzMVgmPyDEzMzMzMzOzFRf96Ge517HaeUSOmZmZmZmZmdkq4RE5ZmZmZmZmZrbiHHYcjx/kHKW2zCASweF3WybgIYjF5pRc/hi20/LZBA9QWxedTcub0KG1RczQchUqNhCtl+sIIj4YLAUeflaPdPBYRQSoLTT4MkSGMADgok4eLtjfyoOjM0keONkM9aC5ptgXDbEfVJBjnHVUxTqiGEFxI0UeiPdCkYfKlkTTno940BwAzDX20fItqdfT8mzEAxABIB3xbncw4AGGU+CBegBQDni7683yq1d3S5mWpzI6RDEUbUa1qXqMdjlR4+eHWkZ5oluu46lxfjza0zzEfl9JJ5arfXFuJw+cbEvzxt+S0vsymVD9IS9PxRjfmwMPwE6I64K69gDA2lbeF61r4W3//EYnLX9yRtdhd5WfP+WA90UPi34IAHaN9NPyTdlOWt6V5fsJ0EO21Z5oiXGH2SPuaUohD25viokTpir6eG1f4NeeLSLjty2lg6O/OcoDkU9f5PuhTfQzAFAQEwao+41UwPeVmjgBAIoN/pmE6EfaU3od61v48XqqzPdVLtCTErSAX8u/Pca3I5vgjaYzr+9Hegf4/eVZiUlaPjnL+1sAaIzyfqC9wOvZ0sInFACANhH0PTPL91U2xs14TfxuM5Hkkxa0Rp20vCfU9wqtEf8dcDLYw78f8OPViPH7m516/CDHzMzMzMzMzFacR+TE44wcMzMzMzMzM7NVwiNyzMzMzMzMzGzFvTRr1fIOmTkJBuR4RI6ZmZmZmZmZ2WrhETlHqT/YhGRw+BC03oiHYY0neTAZAExFu2l5PtHFFyAy99ojkdoHoCqCGOsBD9TLhjrwVdYBOkBNCQL+rLUpHsVmEvpZbTrBwwHbcnw7mk3+LHWuovdlpcHD6spNfpqPxVjHtAiVHa3w8tma3pfqqXJXlgfe1cTLrh0ijBwA1qcvoeUtIV9GOtABos2It5lMgi+jK9TncDPioXgFEc6pgoozBR0gOpjkAb3nNXi7jPPuckee90WFTh46GzZ1iOLoZIGWT5V5mPGZhUW5jqEuHmCda+HhnftHO+U6lqouDkgjxgGbAg/xTQU82DaEDnztzw3T8i3t/PqWFNeNM9v1bdNsnbeZ8UonLd9bGpTrGBPp7pmEuLZU9TmcEyHZZxR4+Xxdn1/7ivwzpYCfw20RD75d06r/XnlJN5/g4bTT+b2b6LIBAFv38jDjfxOh6k/N6+uXou551J56QXdl2L3I73nSAV9Lf16fXzNV3vYXa+O0PMjoA5ZL8Hq8po9/X2Q+44VZHbicy/L+rnsd78vynfo++oWdvN09Ms5Duje08kBmAKiLSTtqYlKCmu6qpFzEz78F8MloehAj7FhcvwIxictUYoyWNyN9/TuZOCMnHo/IMTMzMzMzMzNbJTwix8zMzMzMzMxWXBS99LPc61jtPCLHzMzMzMzMzGyV8IgcMzMzMzMzM1txESKEyz5r1eofkuMHOUdpb+NxJI4QaBqmttHv5iMdVlcJeUBoIeAhiIWAB/91pnWwbW+4npbPNXmAWgk8gDSOsgg4FBmMAIC0CK3MivFoqhwAxio83GxshCfi7Szy4/H4tE55UyG/mQTfWeWGXkc+JfZlki8jxiqQEvu7QwTwzopcv450WtahVONh4vuTe2n5+nCDXIe6MD2N52h5S8CDVAEgFfGuPZvkdWhv4+dwGCOLPF0QobGX8HDBRF6fgIlWvp1Bjp+fUU2kwwMoTPIgVCU5yMOQASDRzj/THOf1LC2W+PIDHmgJAFM1HpzZU2+l5Qt1fZJ3gF+/ukN+/tXAQ04BHbC7p8TbhJIX5w4A5EQI/jYRQnppj96XMzXe9p+Y4+UPT+rgzA3tfF8N5vjxyCVjhMom+Xm+2ORB4GPBHlp+XfZiWYf+Tp7imxE5p6lefV+1bjPvUzuf5NeW+57h92UAUBGTJ6gA3p2LvM2060soWmIcc2aqqvvkSsjb3UDubFqehN6QupiUYDDHz5+tnXO0XE1SAQCT87zPbbzIl9Fe4H06AAx28/NrpsqvTYt1vS8rTRHyW+N99mRZ9/ttYjKLgghFT2CIls9D78t58H4kBx643NscoOWNqIoXZC3sVOMHOWZmZmZmZma24pyRE48zcszMzMzMzMzMVgmPyDEzMzMzMzOzFRf+6Ge517HaeUSOmZmZmZmZmdkq4RE5R6kRlhEcIex4LOQhpRsDHoYMAP3JM2l5PuLhZ+mAP5tTgZYA0J3mAYf5gDebFHQSsQpdTiU6aHkjxouNdRGOG4hqJkVYMgC0pXgwnwp528Vz5jBT04GUnSLEd00rbxPzNf08ty4ClVXOaWdWt4nX9PBAu0TA9/UjM7xdLopAPQDIira9MdxIy+uRDmpUYccbw820PM75lUnwdtcU58bUHA8GjPNecU2Esba28/DPTKvel6lWHhobNXh5qk8HTgYx2i79fk5fZqMmP4HqI7wf2DnJQ9V3Leh9ORPwcM5Sg7eJZow2MRDyevZkeLBmuaG3Y1+R78vxCu/vZkTYamdG95dJcXG5tJeXD+V0mni/+Mzr0rw/PbdDh5QmA36OqnDdGBml6Mjwc3CoxAOy0xim5bUYf3KdXuBtu/YkP4d7hnnIKQC0bOX3VYVX8ePxi1v3yXU05/gOL+3nx2vXfh6K/t2JTlkHdc/TL7Lfiw3d3z47yzubVwXnyGUoWRHCXRJ9UUc7n7Bj7YCeFKQ8zdvdzhEdYq8Mbi3S8svPOEDLyyP6eE2M8pDfSsj39QPj+iTuFb+3dOd4u1T9fpwJHkIRkL0RPLC8NcX7gHoYI23cTjl+kGNmZmZmZmZmKy6KIkTLnEa83Ms/HvxqlZmZmZmZmZnZKuEROWZmZmZmZma24sLopZ/lXsdq5xE5ZmZmZmZmZmarhEfkHKVUIo/EEcKOp4rb6Xf72k+Xy2+LeMhvEzzMrhLy8qQIQwaAnY1xWl4NeGByKEJpAWC3CEEcDlWAYV6uoyYC1LIJ/ii20tQhbmMVHtqsQmVT4nAM5vnyAaAvxxeSFuu4rFcnUnZm+GfySR7y1pbWoc2t4jOTZX7MC2kRrpvWx3NntUTLE+LZ9+7gSbmOTdF5tDwvuuXFSIckVkUy33y9l5YPDc7T8pY1+s8Y87t4m3jixQFavtDQlyfV7lIBL1/TrkNKy3UeMFis83rmU/r8yotg2pkK31f7yzxBNBEjr7kfXbRc9SOlhm4TRfBrR1GE8avzDwA6Qn4NLTeWNuHoREUfz2KTf2Z/iQdvtqd4cCcAXNTL98W6PO9P0+L6BwDTIrB8oioCYWNcQ0XWMXYEz9DygYgHiFaa+l5h13w7LV/Tyq8LLz7N2xwAnDExRct7z+DrSHboYPZEnh+P1nX8mG9oztDy2aq+H5mp8Qk5IML+MzHaZSDCxGfr/Po3BTHLBIBLsv20fFMbP17FEt9XXa36Ot61iR/PC6f5vfreR3nIMACURvg6cj3iGtsSY1IQsa25Wb6Obd36HN69yPvcmkjjn6+L360inXacEfduJbGMqgjQbsS49zuZhIjk5CDHYh3L6V/+5V9wxx134PHHH0cul8PP/dzP4Ytf/OLB8j179uC9730vvvGNb6CtrQ3XX3897rzzTqRS8R/P+EGOmZmZmZmZmdkSfeELX8CNN96Ij3zkI3jDG96ARqOBJ5/88R97m80m3vSmN2FwcBD3338/RkZG8M53vhPpdBof+chHYq/HD3LMzMzMzMzMbMVFAJZ7UqnlWnyj0cB/+2//DR/72Mfw7ne/++C/n3322Qf//9e+9jU8/fTT+PrXv46BgQFccMEF+P3f/3389m//Nm6//XZkMnoEJOCMHDMzMzMzMzM7xczPzx/yU60u7TW2Rx55BPv370cikcCFF16IoaEhvPGNbzxkRM4DDzyA8847DwMDP351/tprr8X8/Dyeeuqp2OvygxwzMzMzMzMzW3EvZ+Qs9w8ArFu3Dh0dHQd/7rzzziXV/YUXXgAA3H777fjwhz+ML3/5y+jq6sKVV16J6elpAMDo6OghD3EAHPzv0dHR2Ovyq1VHqSu9Dong8OGXa1Pb6HdrKMvl78NuWj4QnEbLGxEPDctAB+Z1icDledFskpFex97gaVo+Gxyg5WF0hVxHVQQtTlZ5uchGAwBsbuXhZAUR4HtxLw/3zMcICU4EvKKhClxO6fDPKOTLCGIEFCqzRR7YOlLmwwz7s3w7xiv6uXUlwc/RhWCaliciHowLQI7lbE3yZZQaOnRviVVAIsk/kRzkxwoACiLYtnOc/8WjJ8+/DwC1Ju9r0gneJmZESDAAFBv8eKgw45mqXsdz87xtB+KIqZzhfhGCCgC7y3w7ymIlpaYOua8FS/srV1ukglSB0wt8W7szfDsKad5m4oRwPzPH28x0he+rAyJ0HQD27efbMZRpoeWFjG4TdXFpGMjz60JHWl8X9tT5Z1SY8dokD+lOiusjoK/Tqh+JE2j+uefW0fIN+3gdWkSwOwC0inoMitBm1Z9OxAg7fmaW12FNC1/HgM61xdpWvoynZ/n31aQhgA7h7sjxvqy1hV+nZ3fpfdmdF5OX9PJlrNmqQ52ff7yHlu9+nve57THavjp/6uIeNRkjrD8pArDHK/z8Wgj5/UYu0MerJMKIdwVP0PK12ErLG1j6vZ8d3t69e1EoFA7+dzZ7+AkHbrnlFnz0ox+ly3rmmWcQhi+1+d/5nd/Bv//3/x4AcNddd2Ht2rX4x3/8R7znPe85RjX3gxwzMzMzMzMzOwFE0fJl2LxyHQBQKBQOeZBzJB/84Adxww030M9s3rwZIyMjAA7NxMlms9i8eTP27NkDABgcHMSDDz54yHfHxsYOlsXlBzlmZmZmZmZmZofR19eHvr4++bmLL74Y2WwW27dvx+te9zoAQL1ex4svvogNGzYAAC677DL8wR/8AcbHx9Hf3w8AuOeee1AoFA55AKT4QY6ZmZmZmZmZrbhXZtgs5zqWQ6FQwH/5L/8Ft912G9atW4cNGzbgYx/7GADgbW97GwDgmmuuwdlnn413vOMd+KM/+iOMjo7iwx/+MG666aYjvtp1OH6QY2ZmZmZmZma2RB/72MeQSqXwjne8A+VyGZdeeinuu+8+dHW9lOuWTCbx5S9/Ge9973tx2WWXobW1Fddffz3uuOOOo1qPH+SYmZmZmZmZ2YoLo+MwIidavuWn02l8/OMfx8c//vEjfmbDhg3413/91yWtxw9yjlIlnEciOPxuG4j4rASLMSZ7zwU8bKkuUssfbXyVlufT3bIObcl+Wt4V8vK5BJ/ZBwAK4EFOHSGvZy7GDA7dGZ6mP9/g0xKMVWJE5QvtGZ6Ur2alikSaPwCUxSwq9SZveJWS7gamKnyYX1XMatWIdOMfq/DjoWY2SIvZSWKcfmgL22h5Fzppee4IfcMrzYnZ6yYbvDxzhFnzXikQ+zsjZhnLreHLT5zH+zoASFzCZ3k4/+fEzDx1PRsGQtEP5MXw1LKeRSncMUHL5/+Nn8P1qm4T7YO8X2+Kau7ayWceeX6BlwNAXrTd6Rqv41ykZ2VsJPgx7Qt5PTOBnhHxjDa+jm09s7S8Nce3s9HQPcnr+njbn6rwmcz2lviMUwDw/CLfF3sW+cxY+0t6BpQ1LXw71rXw868irgsAUG3yZXSB98kLTXH+hbq/3Do0Scu7zxV9UUJv5xbRjzy1a4CWPzOv2wTAt3X7Al/GuJjJc15PoolOMStcSUxuF2e2UPW71wTmaHl71C7Xoc7ycp3v6y5xnR+Z0sGq+7/Dj8eWLbxNpfgEtACAgW4+s9W0uPfLJvVshSV1jyr6iVSMmzd1CtbFvUJHgk+XlopxjifFTLnD2ELL+wN+wOpY2qyPdnLygxwzMzMzMzMzW3HRj/633OtY7eL8kdrMzMzMzMzMzE4AHpFjZmZmZmZmZisuAqBDNJa+jtXOI3LMzMzMzMzMzFYJj8g5SpVwAYkjBC6mAv5cbEtyWC6/EQ3R8vmGCMXMnEfLZ6P9sg49IQ/d2yQCk0PoYE0VPFbIqqapn9OqJ611sYgRnd2JzgwPg3x6npcvNHg42lhZb2c+yZehlrCvqEMvW1M8WLNVpNHtLBblOi7u5qGWZxX4liRF2HFbWnd33UkeBpkA39f5GKl8WRGyXQ15eGB/TgT4Alis82W0p3h5VBdnTy1GEHE/7weiYR54HidAFAmxv5NLv8QF5/OAwc6fn+cLKIpQZwCYnKXFzSdGaHm4gy8+LcKtAd2uRit8PzQD3SbUNbAjz8+NOH89yyV5ImtNnH/zc7wfysQI2s+l+L5Y08b7w8FW3WbO7eRte6TMwztHKzoEeFAEP2cTfF/sKvJQZwDozvHjkQx4uwxENxEnPDfbwo9XopXv66BTb2fHWt5XvebCGVp+wfO8DwCA2QO8HgdmeMDui8VWWv74rG4zfTkxKYHoi8SuBgBU0kubiCIV42/Y+RRfR39hkZb3nMf7oe7alKzDrod4+O0Pn+CzElx05gG5jo6N/By/dD1fRl1c/gBgcj/vU5+c1L8zKCIzHW0p3rDUvVs6xv1IPeR9WR96aXlGrKMm7g3t1OQHOWZmZmZmZma24kIch+nHT4KXq/xqlZmZmZmZmZnZKuEROWZmZmZmZma24qLoOEw/HnlEjpmZmZmZmZmZHScekXOUNiUuQjI4fIBtd4IHpRYyPAgLAGarPMyqkOLhuWispcWnJTbKOrQuMRSsFiNdcKLBgzMLIpi23NTPICerPJhv1yIPFlvLDycAoDfDj1cmxxPYxqp8O+drOmCt2OD7Oy121Vmdok1BB0OrdXRledgdAJzZzlfSIkJGFxuiXYa6XaoQ7oRI1kw29fHKJHk9m+IvBDVRRwBYaPKgxTbR8wcidC96flTWIXqGhyQm+niwJlp1gCgyYkNUKHNXu15HKw+NhWpXzRgBhTM8/Hb+Gf710RLvrFpiXOmTom2nRZh/d6T3ZVa0/bka31ddWX0NVf1EscGvCw9N875qrKLPcZE/j7MKvF32ZXUAfWeGf2ZjOw9j3Rij6TdDviGq3c2LMH9AhxGr0Nl5cXE6rW3pAaGVXXxfh1Xe3wJAy/m8P0us4cG2Lev5JBMA0FLm91WDUwu0/Oxnxmn51ud1KO1oifeXalKChYburCpNfs/SB74vczFC8NX9Qr6FH/NEC++rEpv1CXjGZt52N27nk5c894g+Xmtqs7Q8383rkIpxmS50VGh5Zpqfw5kYYf2FDL+2tIqb1JkqX0cqRthxQ9yaqUWMlXmbqkcxJpk4iTgjJx6PyDEzMzMzMzMzWyU8IsfMzMzMzMzMVpxH5MTjETlmZmZmZmZmZquER+SYmZmZmZmZ2YqLfjQmZ7nXsdr5Qc5RSkUppHD4sMQXohH63cliQS4/d4Qg5ZelxSCqpAikrIQ6LCshAgr3iHC0ySTfDwCwJXEGLVeBro1IDyZToXq9IqRtXV6HJLan+GfGRZjxYp3v67GyPl4Deb6Orixfx6AIZAaADS087DEh9vVgvizX0d/JwznLFRFSOt5LyztVIjOAzgxfx0xNhF7GGOSYT/DPLET8eEyoAF8AbQm+HYmAL6O5yI9nMkZwdOMADzh88AtdtHyhroNtIYbFdmT4vuxr0X3VUiUT+vyqioDPidIALR+t8OvGFM9ABaAzm1UIvgr4BXSQd+MYTAVaC/n5VVflogrb53QQsQrrf4FnzmJ9mwjYBtCZ5p/pF/16NkaAaEmEt09Uxf1GnPB3UY+JKt+OvAjQzsY4/0oLIvBfHK+90zxcFwAKe/lJuH7zGC1P9+p9qQJ25fezvLxFBGwDQGWBh4VP1/i5MVnT19Dn53mbKaT58Vyo63DqqQqv59Q0D+tPPM4bTUE1KgCJTTysOHMxP2BndUzJdYw/zO8V9hzg1+nOFn6dB4CGmJykLS3uR2JcFtS1pS6C26tiJeMiiBjQ/X5JTHywFzxsvAl9/tmpxw9yzMzMzMzMzGzFOSMnHmfkmJmZmZmZmZmtEh6RY2ZmZmZmZmYrziNy4vGIHDMzMzMzMzOzVcIjco5Sd6IV6eDwAWP5kAestSZ5qFgc400ekFYPeCBXHiLhF0Am4oF5tYCH9rVEOtR5L3iwX0+1m5anAh40BwBpEaKowjmH8zoh9Pz1fDuy7TzELRB1CEUYMgA0RDhgKAInkykdBpkQPYXK0BYZ3C8tQ9SzJkISB3P8eB0Q4YVxdGX4OR4nq3WqygPrpkUI4nCyU64jLQKVGyL4Lz3A+4DEsA73TIn03IHWEi0v1PXxSid521WB5w0RfAsAYcT31UixhZYvNnQAaYvYjtM652h5W5r3+9P1TlmHZ2b5MiohD2qsRjqEW80QsT7XTsuLKokYwIgIRe/O8vNvWwcPZl+X19fxfWXeZl5YENdYnbOPnRURzlnhbVtkCAMAujJ8O4bzfCGtMSYM2FUUQd8iJ3+mxtttM9L9iArS7x0o0vJ14OcnAHxr9xAt/84oD+vPiT4CAFIxAseZThE6e0DsJwD4Ls9rxUCet8vNbfoc39zON/T747zd1SLdLuvi+tUU14W6mOjiua/z6wYAbDxrlJZnz+b9ZWKQB08DQO/WeVq++AgPVFZBxoC+hi6Ka/2Oed320wm+DnXtaIjjnRH3VACQEb9U7KvyYOgW8N9rGjH6spNJ+KP/Lfc6VrsTfkTO7bffjiAIDvnZunXrwfLPfOYzuPLKK1EoFBAEAWZnZw/5/osvvoh3v/vd2LRpE/L5PE477TTcdtttqInZZ8zMzMzMzMzMTjSr4vHeOeecg69//esH/zv1imlQS6USrrvuOlx33XX40Ic+9FPfffbZZxGGIT796U/j9NNPx5NPPokbb7wRxWIRH//4x49L/c3MzMzMzMyMi4IIUbC8I2aikyAjZ1U8yEmlUhgcHDxs2Qc+8AEAwDe/+c3Dlr/8kOdlmzdvxvbt2/EXf/EXfpBjZmZmZmZmZqvKCf9qFQA8//zzGB4exubNm/Gf//N/xp49e5a0vLm5OXR38wyWarWK+fn5Q37MzMzMzMzMzFbSCT8i59JLL8Xdd9+NLVu2YGRkBL/3e7+H17/+9XjyySfR3s6Dvg5nx44d+LM/+zM5GufOO+/E7/3e7/3Uv/fnUsgkDh/4VjgGQagdfBGohTwQryYCu6oxQhRVYN45iWFaXuTZgwB0PdvSvBKtSb0hbSn+mb4sD5wsNXVIaSrDh/1lB5aWPlif1o2mKQNAeR1Ki6LRQQcNF2t8GXEC8WZrPFRPhQsW0jz3anOrzsVSdWhP831djzEKdH+Jt6s1TV6HpAj1A4CcaLqJgO+LoFWEWp61SdYhuIQH953x73iAKEQoNACgIfqBtLjE1XVALw5M0OKzD8zw76d02w/aRQi9Cq59gtdx3/d0sOZ3RfL6uZ15Wt4aI2m13FSBknwZFfF9ANjUytNxzxic4nXI8zahQtkBoF7lJ2C5zPvLxaruk6fKvM08u8CP+URVb8caEVa8pZ2fwwt1HY47Uub7am0bL8+IJP52cV0AgOHTecB87tIeWl6IEYT6thf4HyD3/4Afz+8f6JfrUGHFNRHuvn2RX3tma7rN9GT5OZoTgbBqGwAdPLulk58/pYY+v4Z4d4d2MRlGax9vd42GbjPf/sE6Wr5lB7/2rHkVb9cAkBzk7W7TaxdpeV0ESwPA7H6+juYsbxPbuvW+2iduJ2ZrvF12i5umOKMeenJ8OzaJ31nrYhKKaljBD06hMQXRcZh+/GR4teqEH5Hzxje+EW9729tw/vnn49prr8W//uu/YnZ2Fv/wD/9w1Mvav38/rrvuOrztbW/DjTfeSD/7oQ99CHNzcwd/9u7d+7NugpmZmZmZmZnZMXHCj8j5SZ2dnTjzzDOxY8eOo/regQMHcNVVV+Hyyy/HZz7zGfn5bDaLbJb/dcLMzMzMzMzMjo0QIQJPPy6d8CNyftLi4iJ27tyJoaGh2N/Zv38/rrzySlx88cW46667kIgxDNbMzMzMzMzM7ERzwo/I+e///b/jzW9+MzZs2IADBw7gtttuQzKZxNvf/nYAwOjoKEZHRw+O0HniiSfQ3t6O9evXo7u7++BDnA0bNuDjH/84JiZ+nCVwpJmwzMzMzMzMzOz4eikhZ7mnH1/9I3JO+Ac5+/btw9vf/nZMTU2hr68Pr3vd6/D9738ffX19AIBPfepTh4QSX3HFFQCAu+66CzfccAPuuece7NixAzt27MDatWsPWXYUJ334J8zXQqQThw/3KmT47mzEWN2iyHmbr/FGp8Ii41BRc4HYjjiBlDXxGbUVcTZThRVPVPnIrLaUDjt+ehcPICwc4IF34yWeqLdjUSTuAZgSAYSt4ixPqwMKYFdxae0qThDqdJXX4/rNs7S8TwRvlhq6u6uFPARxlOeoohwjO1ddNtKicedj9NqqH6iK0Es0RC0XRLIgALTysONIzBx4TKjRlzHOcaxbw8vLolGEMW4Uqjw4Ezt5RluzPEvLVcgpAFSavPE2Ix5cqwLsAWBWnOMJ0Rd1Z/V2DLbw4xGKQMmx0QItz6RihLFm+Gfa2iu0vLOnJNexTuyKs4q8oyiVdOBrMsnbbiCO174Zvi8BoCvDX2FfEKGwkxV1T6TPv1TPEvvDdv0afvKsAVq+fpgf87ULo3IdkbgANcb4TBTn7+B99v37deCy6mu6xbkR53gtiLBiNanHYoxZCWpiMoximR/zgX7ep/cN6llBLm3fT8uf380nPynfr28WhgZ5em62g++rKMblTfUjdTGRRRyqGiqIuCK6dRXUDwAlsQz1e0tRTFwS5xprp54T/kHO5z73OVp+++234/bbbz9i+Q033IAbbrjh2FbKzMzMzMzMzI6pMAgRBM7IURwWY2ZmZmZmZma2SpzwI3LMzMzMzMzM7OTnWavi8YgcMzMzMzMzM7NVwiNyjlJ7JoFM4vAhaCpgtB4jqGrPIk9pS4qwrDWtPKBNhXEBwK55HsQ4mOchb4WMDi5T+2qywvdVnMwvFZqXEzmnPRkeVAwAazoXaHm9zlcyWuH7Mk60mcrtm5eZevp4qbDi+RqvaSaht+R1fbxxFrI8PDDfwo9Xy5xu/CMlvjMX6vz8bMYIUE8H/Pl5pwhZTDbjHC9enhfhg6Xn+L7Mzjwh6xCKYNv0AA/PDWIEiCK1tJDSYLBDr6O9RdRBdCRxwo4n52hx/dFxWj66u52W52IEiGaPcF172T6RxF8SYckA0JfjIaWB6IvihD22iH67Kc6fZ2d5m/jOhA4JVt3Aa/t4p7yuRYcd9xd44HiL6A9b20TANoBalbeJxVKOlmdEPwMA7Snep46LLHF1/Rut8H4GAGqjfCFhcYaWl8f4+QsAbVt5X5Xo50HDiS498QH6xLVjkJ+jw108+PYNWR6+CwD7p/j5U6zzi9N0TZ9fs3W+L5+Z5+dPKdJt/+zOLlre27NIyyNxT5Rao49nx0Z+Dbx4jtehukP3I2M72nj5bt4u41jXzc+PbX1TtHyyyoPCASCX5G1C9ROTFd4PpWLMsDJS4sdc3R+qiS5OtbBjj8iJxyNyzMzMzMzMzMxWCY/IMTMzMzMzM7MVFyFEtMwjZpZ7+ceDR+SYmZmZmZmZma0SHpFjZmZmZmZmZisuRBMBeHbRsVjHaucROWZmZmZmZmZmq4RH5BylmWoT6cThk/+nRRB+I0bieCjmKVIz3jwzy2clqEf6fcDRYIKWJyo8Qb4Z6VkikgFPZ99T4mn76YSe0SYd8H0pQurRjHRKfanKt7UZ8uPVEE1isaHrMJDjC+lM8w3tSOvZZobELCoZMfNIXzefXQEACpvFARH7qjzC91Vvq57BoTXFZ9zYX+ZTqPRl+CwuAFBs8O18vihmown0rB7BAt8XV/XznSkmMEJU133ZxPN8tqcvf22YlueSeh3qLxHrWvgMfP0tYkocAHNV3meOlHlf1JfVs98BfIefNcz7mZ4+3mb6S2LmLQDpBP/MYIuYbaai/y40WuEXydYkX0dnVl9bshnen7W08ePRJ2bHA/T5Ny/Oj3tG+XYkoGdT68p20vI1eTVrY4z7EfGRgRyffatNXBcAQE0Gs6/Ez2FltKJnBypO8WOab/I2MzJakOvY9zyfHahbtLvOvN4PnZ181qlsOz83GuIcVjNSAcC/TfN9MSNmnBrO6TaTE7Ng5gPej3Sl9DmcFt2Z2pcQ94+lx3ifDQD503m7S/TyGaWy5+pf8YZb+cyreIwXz4qZ6+IIxPFsS+nfW1rFDJaz4jIsfiVBVk0ZDGBHkd/ndqf4vmpP8+MVY+Ksk0qE6Dhk5Kz+mcA8IsfMzMzMzMzMbJXwgxwzMzMzMzMzs1XCr1aZmZmZmZmZ2YoLgxBBsLyvVoWeftzMzMzMzMzMzI4Xj8g5SpPNIlLh4UPOkiKwMisC2ACgI8VDEDMJ/uwtleDrWKzrILmWaIjXIcnrUGvq8KimCF1ek+cBhWGM0OaECDtuEWGPZw9MynUMvIbvz0QP345zVNCcCHADANRE6F5NHPOMSLYFgLwIl5YpbDyUDwBQ5ml04QgPcswn+fdFhncsVfBwz5GabpcLAT/mbWJf5cQ5DgCjTb6vkoEOC6ff79BtpmuQh0v/fJUfkLmKrmNrhh+PUARONkOdHrinyAMKVSh6uan3VY8IOg1FPStFFZ6r++RApD02jsEfrubAwyB7kt20vBgjZDub4/1h63q+jAs6R2n5WRvGZR2mp/g5PLbIy5+Z1/3leJVfG9RleDRGOHUhzReyoY0HtrbJ4GggGbTT8q4Mv4aOVnlguQp9BoBsK28zCZGx3dulg2tnyrwfeWGRhyHPzehA5Q2zfH+rvmpSTN4wWtV92YiYUyCf4nXoj3FpUrmzrSlez0yM4Fr1kYTOS6ZG9+jjOf4MD6A/bWCalvdequuR2sDb3bou3qaGxvVEFnMv8p314mQnLU+LMGQAKIhzNC+abj3kH1iMce3pT/O+qi3N16GubzFuL08qL00/vrzjTTz9uJmZmZmZmZmZHTcekWNmZmZmZmZmJ4Bw2acfhzNyzMzMzMzMzMzsePGIHDMzMzMzMzNbcWHUxHKPN3lpHaubH+QcpUpQRfIIIbpnpPvod/tU2haA6Qof5iXyKBGJUMt8jPDcWigCt5q8jhvaReoYgLSoxkSZ10GF9gFAPeQryYmw4yjGOoI8P4WC4S6+gHYeZodGjE6mLAIlS6K8ygNjAQDFCi8XbSaKEbLdHOGBkZE4N5pFXoftU+JYQA+y7E3yENKZpthPAE5L9dNyFTqbVp0AgNPTfFsrTd4mMsO8r0q+7gxZh9Z2vq/OUG27FqNdNsUyVAh3jPPrfNX21fknzo04n4mKPAG0voOHW++e1G2mIvbl/hIvr4R6Xw4kOmh5JHZVby7G9UsEsqY28UDKdD8PIc2LCQcAoFME0G8Wbeo1c/x4AkBzhre72ig/HtU5fT+SaeXLSPJdifJkjHueEl9IV5YvY1ScfvUYgeb5tbzhpV+7kZa3tIodAaB3gacARwemaHljt5gYAUBtnG/H/AQPXB6f5cG3iTkd0NuX4ft7IMcnJcgl9asOu0UAfZu4wVys63WosPBIzDGRWsvv7TZ28JBuAGh/iPcTo9M8KLx5vw7h7hji7SopwqfDGJfpZIrv73YxacFohR9vQAcBV8XlqdzgB3xPSaR4Q0/Som5HZAi37srsFOQHOWZmZmZmZma24qLjkJGz/Bk8y88ZOWZmZmZmZmZmq4RH5JiZmZmZmZnZiovQRLTM400irP6MHI/IMTMzMzMzMzNbJTwi5yj1B51IB4dP/+oQoXytKZ1UFWX5szUVwCayd1GJ8fBRBU6mEnw746xD5X8WRGBenEC8dEIErIkAtpFZHiQHAKlvz9Hy3MN7aXkkNmN6igfGAsBuGUDIj9e+sghcBtAi9veRAsBftr+sA7Bf1zdLyzdtmKblkQi17MjwkEUAGMrzUL32NN+OqYruUlXQd1tahB3HePxeFAGEKgg8oUJlyzrUGUkRdNoiAgzTMS5PqrMKxQkWI7gWHaIfUOuIE1g+zfuRaIwHUobicGQTug6Ded62MyKpsawuTjGWobL4h/O6328t8PM8muXLiGb5zgxyul0GrRn+AbGhQZcOz0318GtDaitfR0ucEG4R2hyO8nbZWBSJsABaRNBpQfSHa3L8+jWc1/1+okX0VWI/IBvjHB/spcXBmgFanr44xj1PndezdYGH3w6JwOWzn90l69CY5+0qFIdDBTIDQHWETyySTPBlqABtQN/HNiriHB7upOXJXl4OAP2v4ZXo3zdBy0v36+v03AjfV6Wy6MtiGNrIw9s35Pi93eizuj/sF787LTR4eTnPy/MpfS+u5ESzS4vrY1Xct51sQoTQU5Aci3Uce9/85jdx1VVXHbbswQcfxKte9SoAwOOPP46bbroJP/zhD9HX14f3v//9+K3f+q2jWpcf5JiZmZmZmZmZLcHll1+OkZGRQ/7td3/3d3HvvffikksuAQDMz8/jmmuuwdVXX41PfepTeOKJJ/Crv/qr6OzsxK//+q/HXpcf5JiZmZmZmZnZiosQHYdZq2KMTP0ZZDIZDA4OHvzver2OL33pS3j/+9+PIHhp5NXf/d3foVar4bOf/SwymQzOOeccPProo/jjP/7jo3qQc2qN0zIzMzMzMzOzU978/PwhP9Vq9Zgu/5//+Z8xNTWFd73rXQf/7YEHHsAVV1yBTObHry9ee+212L59O2ZmZmIv2w9yzMzMzMzMzGzFRVHzuPwAwLp169DR0XHw58477zym2/JXf/VXuPbaa7F27dqD/zY6OoqBgUOz0V7+79HR0djL9qtVR6klkURahP0uRb/I9GpGPAxLhc6q7wNAPsmXURcj3cZj5KCqwFZVXhfBtoDeVpX1uGUzD5IDgNbzDx98fVCdt5WxB3j5C7Mdsg4iHw3TNR5iGsVoEwsNXs/hHE8w7IsRBjlb4/uyUeWNItfFgx7XdfNAWQDom+HBtu0ieLM3q/elos6vOANBc0lej1KT78uwxI9XsIeHYgJA5YkXafnUHh5SmsuLxGYAqTSvZ7nIgxrbe3VnlRsSoZYqGDpGqGx1H9+O0gw/h1t6+PK72sqyDsMtXbS8JvrcAnTbF81S9mUFcbwBoHUjL1dhxYuP8H31/3t4vayDug6fIY7Hhk4eDgoA/ZsWaXlmmG9nECPwNSzyPrU+zo9HdkC3iaE639bW3TzYtl+ElHbHCLlX+yIa5deO0r/sk+vIbeTHI3kGD0NGu56UQFInWAdfR7KvJFdRF2Hh5Tnel00v6O1UPepWMf/DaIx71Izo1jMdIjT9wCwtD9SxAGRANs7aSItb+jvlKnJP7aflle38/CzP6l8jm1W+rfUKP/8yYuISAFib5yMoInF9yib4/WdRhCUDwE6e/b7ksP8Y8wnYz2jv3r0oFH7ccWSzh28Pt9xyCz760Y/SZT3zzDPYunXrwf/et28fvvrVr+If/uEfjk1lf4If5JiZmZmZmZnZijues1YVCoVDHuQcyQc/+EHccMMN9DObN28+5L/vuusu9PT04Bd/8RcP+ffBwUGMjY0d8m8v//cr83UUP8gxMzMzMzMzMzuMvr4+9PXxUaKvFEUR7rrrLrzzne9EOn3oaMTLLrsMv/M7v4N6vX6w7J577sGWLVvQ1cVHSL+SM3LMzMzMzMzMzI6B++67D7t27cKv/dqv/VTZL//yLyOTyeDd7343nnrqKXz+85/Hn/7pn+Lmm28+qnV4RI6ZmZmZmZmZrbgITZltdCzWsZz+6q/+CpdffvkhmTkv6+jowNe+9jXcdNNNuPjii9Hb24tbb731qKYeB/wg56jlUglkEocfyFQTSVTPz/HgQABIizCsasjfF2xP89Cweozgzd7c0sKcF+tx1rG0IOJ0Qq9DBU6qYLH8Ot2BBBm+r5pzPGhxscSD/UrNpQdrr2/lAYUVEWQcRy7FO8Oz+3U47uAFPIEwyIg2U+LlwYisAnYu8mWotr2gkoqhz3FVnleJsQAyIrB8d4kHToZlvh3JGP2I8rXdQ7Q8zhpi7AqqvlMvoCYOaWeaf0AFSwPAaW287V9+MQ9TTeT48osVHvoMACMiD3nPIv9AZ4a3KQCoNPm+qjR5P9J7hADCQ6SWlqiswt9T4roCAEVxzP9lpJWWFyZ5OQCkd/Ly09p4WHguqfsq1XIv3XyAlrfl9T1PrczbzYzIKt5XXPqNeLgggtVF+YHdelKCXY/z/IW0CHSthTr8vZDmn1kvAv/bOnhg7OyUDiL+2t7TabkKbN3WyUO8Ad12p2v8HB4t6bZfaYp+QjS75hjvL+e+o6c3bhvi/X7mbN6mgmH9ekZiK8/iaFnPT8CWok6Obu7jgcnjP+S/itZCfQ1V2dFqgpTWGP2hEgS8npNVMRmNuK+qid//7MTz93//97T8/PPPx3e+850lrcMPcszMzMzMzMxsxUVRiGiZw46jaPU/HHNGjpmZmZmZmZnZKuEROWZmZmZmZma24o7n9OOrmUfkmJmZmZmZmZmtEh6Rc5Ta0sERw45V8GYtRuhlSYQ9NkQYViHN16GC5gCgKj6UDPiGNiO9kpES/0xW7Mw4SeYq/KwqwuxSG3mQHADgojP5MkQA6Bm/yAPvzqjrsEg0xGeaIqAwrUNKkdVhqVSMNiFNzPDyR/bQ4oWiSIQFUBEBhuNlvq9zSX2Ot4qU7Zo4x+P8/UC1/eEc345Eltcx6NFhrNkz+M78pRpPa23W9L4MRdMX2YMIRR8AAAvzvN0slGME8ArteR18yVQm+IbOVnQd1bVlMM+X0apChgE0Ix6snknyvmiyGiOAXtQj6Guj5e2v5XW84TweQAoAjXF+PMsj/HgV53V/u1ji7fLF+XZaPlXT/f7WjgVanhABobO79HbsGueBrOrSUW7wfma0ovv9RAs/5ole3t9tzuiA3jX7eNDw6C5+vHbMdMp1jInzfO8+Hmy7+CJvl+q6AgDj4hwdzPE2k4gRJr4oJmjIxJgMQ1FXn6S4BCbaeB2DGNt5/w/W0PLm9/m+ftUZe+U6Wjfz8kS76CfUrCGAnL0kKfqRITFhBwCMiYlDdhX5ubHQ4PsyxjwWaBG/UYs5QVARv9cs9wxOJ5ooOg6zVqnU8lXAI3LMzMzMzMzMzFYJj8gxMzMzMzMzsxUXIVr+WatwDN4WWGEekWNmZmZmZmZmtkp4RI6ZmZmZmZmZrbgoCo9DRs7qn7XKD3KOUk82QO4IQbxDIsQt2amXXwv5IalHvFEnxDAxkVMMAFis8w815Eg0PdCrFvJ1VETgcj6pA6paU3Va3p7mYXRo0UGN0dphXt7dwxeggooXeNgkAATlMv9AlQdvBqoOcYiQblRihLlO8jDjaN8ULa8d4Nuxf1EH9A7lefn6Vh78FycMMiNOj0ic47HCjkX5QK7GP6CCa7duknUIruij5SKCGwhjbGlziW23xvsIAOiS55fYlyKMFYDe1tl5Wpx6gAd9p3fpfXlpL+9zSyKsXwWFA/r8UOdGX0Yfr0hdoDbxPhu9vM+Oc1uZFn1qRvSXHXH6ZNF2zyyKdluu6HVABP6HPKA33D4i1/DsP/DrcLfI6f75YX6drqtEdACJYb6d0Wsv5N9v5wHaAJAXx2vzPD/HN8/wsGQAgDrmojwa5eto7i/KKiR6+AELRCcQ1XRHUtnJ7yfqP9wglqDv7TozvB9J9Yh7gdduoeXdP6d//brqwAQtbzzBz6+px3Sg+cj94qZHyKf1+bX2Ml7efS5fRv3fRLuGnjBguI3vix9OdNPycozJaja1Lu2hwLSY4KHcjIADS1qFnYT8IMfMzMzMzMzMTgDN45Bg41mrzMzMzMzMzMzsOPGIHDMzMzMzMzNbcS/l1zgjR/GIHDMzMzMzMzOzVcIjcszMzMzMzMxsxXlETjx+kHOUmhHQOMJxV6FMDTEbDRBvRhpGzWrVjLEC9ZFKU8w6oFeBWsg/lREzG9RCPZis0uTNWy0h3K9niUj84N9oeZAUM2PN81kgwt18JicAaEzz2TDKI3xfTozqGTfGinzGp4U639ddWTGzD4B13Xx/d2/ks6w0y3w7S01xLKBnU4tE61az7gAv9SG0DiJ7Tc8ap/uabJKf5Ym82FfFkqxDMD1Ny6O0mFEjEWNnitmeAjWbWpyZsRS1HXGmClQzX5V4eWNOzJiY0I1mts73d3uKL2NBzHYI6LYfimaXitEkGlP8mKf2jdPyYJy321hT02XFrDj53NK+DwA5MZ1Tq5wXTquLWcLm+KyKQavejp686NcjPdsgM1fX/X5U5OdXMD7JFyBmhgSAqI1fZ6POTr6AgphBDNCz+NZqzdEAAB9QSURBVImZs4INi7Q8NT2r6yDu7dQsfoG4JwKA9BQ/h7Oiv1P3sIDuq+pjfF+KsxPRIJ/VEQAgPpPaspGWD1zBZ/oEgP4dfOarxk4+m1qVHwoAQNQQs+228HO0o1/PWtUo84tDd563q2TAD/iT012yDguir6mLNqXuH1WbtFOTX60yMzMzMzMzM1slPCLHzMzMzMzMzFZciBDBcr9ateT3YFaeR+SYmZmZmZmZma0SHpFjZmZmZmZmZivOYcfx+EHOUdo130Q6cfhAubYUD7qKE1KqPjIrMjH7RMJaRuf+yXFaKnDrhQURuAcgivhCNhd406zGCKsrNfjG5pI8dG/hMRH0CKC9eYCWR+Kg7/wmD0B8emZI1mF/mYetrmvh21Fq6IF5TRGeq4JS52ZEuCeAy0Rg8uUb99PybD9f/mkdPLQPAJ6a4ydQVfT5cQJfVVZqRgQ1lmMFNfJldGR5OGdQEB3J3jFZh+o/PE7Lv/q9DbS80tTtclgEpYai3UYxbhJ6cnwdna08iDGR0DcKlSo/hze8nq8js5aHyg7u4aG0ANA1zcNU1bUpm9T7Mi0+UhHZ1JkY+zKzRoRPz/DQy9JDs7T8Gw+vl3VIgLeZ4RYeqFyPEeZ/5iYewNuyWQSMtov9BCCq8gMSlURwbUa3ib5Ofp3O7uuh5VNVvo5Lu2MEEc/x44VHdtDiue/p8PdUnrfdlq28z0105eU6ZBp4bmnB7NGcDp0NJ/m+COf5/WFzQd8oT+/l9xMHKnw720RwOwD0ZXg9I3EvHj60k5Yntu+TdcBwNy/vEBNVFPREFsGFp9Py9Jn8eKaLuk1gil9/Gi/M0vK5cd3202neFyXTIpxaHO9BcR8AAKUGD5hfEPfaoxVeXo1xXbBTjx/kmJmZmZmZmdmKiyLxl51Vso7l5sd7ZmZmZmZmZmarhEfkmJmZmZmZmdmKixAByzyrVCRfGj/xeUSOmZmZmZmZmdkq4RE5x9BigwfFpUWIKQCovEiRYSrr0BLj6WNGPN7rSPNlrG/TicpFkSOsQi9VYGwcrSkebtZ6ul5J0M4DCpt7ebBmrcn3VVEENgNAd0aEKIpQ52Sg28RCnddjIMfXsbFVv4eqwqdluLzYVRmx/JfqwMtLImi4JUaIotIi6hDnLwih+EhVtauGCAhVKwAQicxz1e5akvovMd+a4GGOgzl1bujteG6BBy0mJjtpeXtKb8fmNt5PbEzxoMUgxy/lyaQOoM+K69O06ANiZB1DZOPKa08uRtgx0ryeUZMvozzN92WcPlmFWu4qddJydSwA4MlH22n52u38HFb9LQBMVnmI9lVn7aXl+SG9jiji+1v1ydM1vq/ihNwjy+sQ1fh2zM/pMNbvPDXAP/AQL47zd+kuEfiaFufPQoPvh0xChOADmKj20vK1eZ4SfE7/lFzHYoW3yxcWeaPpyerza0jUM9UnGmaV97n77tUd5vOT/Bw+o3eUlg+cr4OIUwOi7caaIYWLKnxf1EZ5u83m9PVrcYG3zX2THbR812KrXIeiztEF8ftZUUyOUo1x33UyOR4zSp0Ms1Z5RI6ZmZmZmZmZ2SrhETlmZmZmZmZmtuI8Iicej8gxMzMzMzMzM1slPCLHzMzMzMzMzFZctMwzVh2vdSw3P8g5SpUwRPMIQ7GenuXhaOmEHgDVKdIeF+q80c3WeIpwNqGDy3pEcGapwevQiBHIlRH7Yl+Vh39e3NUi16HCHNszfF+l1vIwSQBADw9bTffwALVzL+bH49wUb1MAAHE8EIryTIxuQKWQBqptx1hHIs3L5wZpcf2RMVperovlA3h4ammdelOlkQNoTfF9NS/O8XSgQxIzInl2UeyLoJWHSWKwW9Yhdyk//964ngc1hmUdlHpthe+rIMX3Q1jVx7uxwMurc0sPg0y38G0NS7zNhFO8L1ss6r7sh9N8O7qzfF9OVHTbf2qe78zeFA/eHMrpczho42036OX7ovvneJv4Dxftk3VozvNwzvo031fFCXH+AVhY5OGes+UcLa80dZ+8toWHpTZqvF1Wx3WbWCzy7fjWKG/bdTE0vjUvgtsBJDr4voLos9e+Xgcq/4exF2j5/B5+zGfm9D1PRQRxl0WYcX+eh6rXmvoettLk9VRXr2SMkPt8mp9f06Jf3zmvry0XdvLy5IDYzjzvqzr7ZmQdhkSo84vTPMD3h1/tl+tY11Ki5cUG346BVn6vDgCbt/F+PynylrMtOux4TgSO10Pedushb5lTNX2dn6jydXRneH84KLohNQmMnZr8IMfMzMzMzMzMVpwzcuJxRo6ZmZmZmZmZ2SrhETlmZmZmZmZmtuI8Iicej8gxMzMzMzMzM1slPCLnKL0QHUAShw8gy4Q8mCzXEIleAObrPO0ql+CHrBjxYL9ijLCs/SW+jL14kpa/NnmFXIfKa80GfDvjPENtRnwlKvwMLTFCTM/YQIujVhFQqIKhVVAxgKAhguCa4qDHCOGWB0xRdQCAIg/dQ51vZ5DmdSzGCDtOJ1Sb4ccrTtD3WJmHd06EPBhwMSHSdwGcHa2j5amEqGcrDyCNNvHlA0C07Vz5GSbZ1AGHaIh2Jc6fOOtIiwD5ljovh/g+AKAqAllHp2hx44c8gHexqsNzJ0WSYl+O94edGd1HtCV4PULwdplR7RZAINouTuNtNzj7NF6ujjeAhGiXabGMlooOue9T9ZDnht6Xst+u8DDV8IVJuYr6fn796c/ze4H5Gj/HI3EfAADoK/Dy0/l1PsiJNgcgI/Z3n+gD+io6tBlV0W5UPzMngmsndKjzq5s8IFtNzhDO6XuFucd4vz2Q520qKyYDAIBkwPdV0M0nssA5vB9pvUzfj2xVx6so9vWoPv+iPYu0PJzjdQiLMe7Gxf2jmisjXdB91Zo23jbXpnj5OXw3YO+LXbIOI0XeJiar/JjvLfO+Lhmjyz65HI/RMh6RY2ZmZmZmZmZmx4kf5JiZmZmZmZmZrRJ+tcrMzMzMzMzMVpzDjuPxiBwzMzMzMzMzs1XCI3KO0joMIo3DB9vVRWhSFTpYcwJztHx/+DQtb0vy8MFC2C3r0AhEqGzEQy/HGiI1DEBbk4cDzkc8+HaqpoOj21O8nvUSX0b9sb1yHanFGAGERFRU4YS6zTQrIuyxLMIFKzpBLYyR10q/r7M7sTjF20QmJ9qlyC8cLfMgcQDYU+LtLi1S+RoirBUAFiMeUDiXmKblUYxwtt11vowDZR7cV3toFy3PZPSlI+jt5B+IERAqqUBXFTQc568xKolRLaMWI7R5gbe7aJwHNdaneR1eXGyTVWhP8+1sFYe8HmNX1sW+qopw3USgA0KbL/C2nzwWIcBKSrSZOAHzighmR1ocMPV9QAbMR1M8HLe6W3f8e+YHaPkLItB1BvzcmF7U9wrDT4/Q8kSF9yNBu14H8uL6kxFtO8bEB7o/FH2RWkesNiPOHxV2vKj7y8VFPomEOoXLDX2Ol5v8/jF8kQcJJ7raaXnQq8Nz5TWyg68DWR1yr67TyTK/x02qgG0AKFZocTjCz+FQhToDCMSmJlp5nxtkeLvsnRVB4AD2L/Kw4840b9sTVd7moujUSjuOc6+7Gtax3Dwix8zMzMzMzMxslfCIHDMzMzMzMzNbcS+NQFreETMnwygnj8gxMzMzMzMzM1slPCLHzMzMzMzMzE4ATQAxcrmWZPWPyPGDnKNUSKWQThx+t2VEgGFLSjfISpOHUl4Q8GDAighxU4GwANCUQ83W0NJkjJWkRWjepiQPD2zGOPeaEV9He5qHtH33W8NyHe338xDE0TLfjvuneELbaW1LH1ao9kOlufSOsjXF6zlR1YP/VFjquR18X+cSfAFPz+vgv9PadJjqUqUSPKgxgR5aHqftq6zVebGzX/y3TlqefIyHEwLAvgVe0YkqPx7tKR16WQ9VQC9fRkkEWgLAQl0EEIobjWqoz6+ONG9361p4PxKCt6nvi34G0P1+uzjHczGCUFuOcO18mbp01GPsy5EHeUBo6dt8O74zxs+/OH2Z+kRGNLvOtO730wE/XhWxr0pNvR3daR6e2yfCVNOJDrmOR2Z5CHCXOIfXpPg90V41oQCAxFd4eV2k/U9V9L6simXURF82UtG36/N1fsw3t/J92S26idl6p6zD0/O8L1ub522qKyMCmwFUxT3LvAhcjvOr23SNb8eOe3ifW/zXWVqeFpMaAMBgL7/OFtbzNpXqi3E/k13ir4EivBoAojJvd/Uxfsyn9ugw8cl5HjRcEdf6XJLXodTQ+ykj7kHVvcJwXt2v6HPDTj1+kGNmZmZmZmZmKy6KQiz3iBxn5JiZmZmZmZmZ2XHjETlmZmZmZmZmdgJY/hE5J0NGjkfkmJmZmZmZmZmtEh6Rc5TSieCIocZZEWCYjPFgsS3NPxQjT5KK8/WESJxUobStMUKdk+IRonrC2IyRAayCxSZF2GqxoYNQszW+DBXA2ybOwDjBmj0Z/kQ5JUIxSzHCjlXAbhDwesZ5YjwjMiknq3xntST5vo4T6qxCgnOiScQ5P0OxLzNiIY0Y7/SmxDncm+WherksD1FsNOKEV/M6qFDMtpS+PHWIUNhAtJnZut6O2RrfjrYUPx5t6Th/8eENK1PhgbAq+DavuzJkxQVK9WVxrm/rRJi46mcWYwRrlqtLCyxX7XakpJexc6FCy7d28OM5KiZOAICcOl5JvjNVPwQAUcQbzoLoB9T5CQAZsakdIhlaTZywtxQj5L5Dh7czD07rMNZFnd1O1WLknKp7s5ES7w8LGX7uzNd0o+kQu3vnIj+e7Wnd9tW1vF10Aeo6DgBz4tqgJpFoy/AbmgfHeag6APztrm5annuE12G8oo9Xb1bdK/BlxAlmH85XaflQK+9U56o8wB4AnprjYccvFvnx7BbbeV6B9+kA0Jfnn2mKa0tXln9/scH340nnOGTkwBk5ZmZmZmZmZmZ2vHhEjpmZmZmZmZmtuOg45Nccj3UsN4/IMTMzMzMzMzNbJU6pBzmf/OQnsXHjRuRyOVx66aV48MEHV7pKZmZmZmZmZgbgpVmrjsfP6nbKPMj5/Oc/j5tvvhm33XYbHnnkEWzbtg3XXnstxsfHV7pqZmZmZmZmZmaxnDIZOX/8x3+MG2+8Ee9617sAAJ/61KfwL//yL/jsZz+LW265JfZyBlsSyB5hRom+HH/XTs0oAADFBk/obhEzUYyLhO9GjNcB17TwclXHspp6BHr2g4kKn+Ihk9QzkyyKGTU2tPBZBQppPU1ELsk/My1mxtrUyr+/t6SnV3hugR+PHjErQZzZZtQT306xr450zrxSQRzSumhW6vTqy+oTMIzELCxihjB1bgBAQcxilBQzEI2W9TqG83xb1cw89Tpvd4GoIwC0pvg5fFEnn4GhKuoIAH1Zfg4nRD3n6kub4QgAIjF7Sb+YyQLQs1lMi9nxpmp8O3rEjByAnm1wqsbbRJy/a6kJaQb15CTSgcU2Wp5J8L4qneD7qlXMLAkA61r5hqh7ATFREwCgU/RFapajdKyZe3i5nOFSzHoFAPN1voxzOvn31aw5LSndMmfKfBYxRV3HAd2uVF8WZ5axWdGfBSIPotzkx0vdUwFAR5r3+2oZ5RizS7bEaLvMRDXOTJ3iHrXEZyprS/OTJyvu5QHg/zNUpOVq5qzH5sTNPIBCirddNRuoui4Aul1W5ttp+XRN/6qq6qmub6ofSYnzFwDKDV5Pde0piv1UijFro516TokRObVaDQ8//DCuvvrqg/+WSCRw9dVX44EHHjjsd6rVKubn5w/5MTMzMzMzM7PlEr00Pfhy/ixj2PFzzz2Ht7zlLejt7UWhUMDrXvc6fOMb3zjkM3v27MGb3vQmtLS0oL+/H7/5m7+JRoM/DP9Jp8SDnMnJSTSbTQwMDBzy7wMDAxgdHT3sd+688050dHQc/Fm3bt3xqKqZmZmZmZmZrUK/8Au/gEajgfvuuw8PP/wwtm3bhl/4hV84+Nyh2WziTW96E2q1Gu6//3789V//Ne6++27ceuutR7WeU+JBzs/iQx/6EObm5g7+7N27d6WrZGZmZmZmZnYSi5b9f8s1ImdychLPP/88brnlFpx//vk444wz8Id/+IcolUp48sknAQBf+9rX8PTTT+Nv//ZvccEFF+CNb3wjfv/3fx+f/OQnUavxV21f6ZTIyOnt7UUymcTY2Ngh/z42NobBwcHDfiebzSKb/fF77tGP3pethkfOdaiIbJg4GTkqFyIhGl1VrCNORk5FvO6t6liN8TJ3TXymHvJKVEU5oLN6ig2e0RGJvCEAaEa8HiVRh5J4J73S1M9a1TFXxzNORo54XRzlJq9EnPfeVbNRp09K5KHEqUM15PtbneOVGOvIiHet1fGIkx2jjkepyRvFQoNfROJk5BTF++KlJfYzL61jaRk5JbGf4lAZOaqfAXRGju5H+M6M1fbFZ0TEQKyMnKX2VXHy19T+roucgnKTt9s47VJd3yCuLTFiXeS+Uhk5MSI65DoSYldkYvypUO1P1eeWVXZFoHdmnHOUUddxAEiLi6jqy+Jk5Kj+bKkZOXH6kXRC3QuojBy5CoSiz1WOxTVUtpmAZ+SUmjqfTa1DZeTEuX9My2v50o4noNtlGKl16EahsgXVvljq7wuA/n2gJq49DXH/+XIfEakb8pPK8dnWn4xP+clnAEerp6cHW7Zswd/8zd/goosuQjabxac//Wn09/fj4osvBgA88MADOO+88w55W+jaa6/Fe9/7Xjz11FO48MILY63rlHiQk8lkcPHFF+Pee+/FW9/6VgBAGIa499578b73vS/WMhYWFgAAn9zz/12uatrRmFnpCpiZmZmZmR0fCwsL6OjoWOlqLJtMJoPBwcEjRp8ca21tbT8Vn3Lbbbfh9ttv/5mXGQQBvv71r+Otb30r2tvbkUgk0N/fj6985Svo6uoCAIyOjh428uXlsrhOiQc5AHDzzTfj+uuvxyWXXIJXv/rV+MQnPoFisXhwFitleHgYe/fuRXt7O4IgwPz8PNatW4e9e/eiUCgsc+3Nlo/bsp0M3I7tZOG2bCcLt2U7Wax0W46iCAsLCxgeHj7u6z6ecrkcdu3adVSvFy1FFEUIfmIGxiONxrnlllvw0Y9+lC7vmWeewZYtW3DTTTehv78f3/nOd5DP5/GXf/mXePOb34wf/vCHGBoaOmb1P2Ue5PzSL/0SJiYmcOutt2J0dBQXXHABvvKVr/zU07AjSSQSWLt27U/9e6FQ8MXJTgpuy3YycDu2k4Xbsp0s3JbtZLGSbflkHonzSrlcDrlcbqWr8VM++MEP4oYbbqCf2bx5M+677z58+ctfxszMzMG28r//9//GPffcg7/+67/GLbfcgsHBQTz44IOHfPflCJgjxb4czinzIAcA3ve+98V+lcrMzMzMzMzMTm19fX3o6+uTnyuVSgBeGgTySolEAmH4UibUZZddhj/4gz/A+Pg4+vv7AQD33HMPCoUCzj777Nh18qxVZmZmZmZmZmZLcNlll6GrqwvXX389HnvsMTz33HP4zd/8TezatQtvetObAADXXHMNzj77bLzjHe/AY489hq9+9av48Ic/jJtuuumogpb9IOdnlM1mcdttty0p1drsROC2bCcDt2M7Wbgt28nCbdlOFm7LFldvby++8pWvYHFxEW94wxtwySWX4Lvf/S6+9KUvYdu2bQCAZDKJL3/5y0gmk7jsssvwK7/yK3jnO9+JO+6446jWFUSn1jxmZmZmZmZmZmarlkfkmJmZmZmZmZmtEn6QY2ZmZmZmZma2SvhBjpmZmZmZmZnZKuEHOWZmZmZmZmZmq4Qf5PwMPvnJT2Ljxo3I5XK49NJL8eCDD650lcyoo2mzd999N4IgOOQnl8sdx9qaHZ1vf/vbePOb34zh4WEEQYAvfvGLK10lsyM62vb6zW9+86f65CAIMDo6enwqbHaU7rzzTrzqVa9Ce3s7+vv78da3vhXbt29f6WqZHdbP0l59r2wnAj/IOUqf//zncfPNN+O2227DI488gm3btuHaa6/F+Pj4SlfN7LB+ljZbKBQwMjJy8Gf37t3HscZmR6dYLGLbtm345Cc/udJVMZN+1va6ffv2Q/rl/v7+Zaqh2dJ861vfwk033YTvf//7uOeee1Cv13HNNdegWCyudNXMfsrP2l59r2wrzdOPH6VLL70Ur3rVq/Dnf/7nAIAwDLFu3Tq8//3vxy233LLCtTP7aUfbZu+++2584AMfwOzs7HGuqdnSBUGAf/qnf8Jb3/rWla6KmRSnvX7zm9/EVVddhZmZGXR2dh63upkdKxMTE+jv78e3vvUtXHHFFStdHTMqTnv1vbKdCDwi5yjUajU8/PDDuPrqqw/+WyKRwNVXX40HHnhgBWtmdng/a5tdXFzEhg0bsG7dOrzlLW/BU089dTyqa2ZmR3DBBRdgaGgI/+7f/Tt873vfW+nqmMU2NzcHAOju7l7hmphpcdur75VtpflBzlGYnJxEs9nEwMDAIf8+MDDgd9XthPSztNktW7bgs5/9LL70pS/hb//2bxGGIS6//HLs27fveFTZzMxeYWhoCJ/61KfwhS98AV/4whewbt06XHnllXjkkUdWumpmUhiG+MAHPoDXvva1OPfcc1e6OmZU3Pbqe2U7EaRWugJmdmK57LLLcNlllx3878svvxxnnXUWPv3pT+P3f//3V7BmZmanni1btmDLli0H//vyyy/Hzp078Sd/8if4v//3/65gzcy0m266CU8++SS++93vrnRVzKS47dX3ynYi8Iico9Db24tkMomxsbFD/n1sbAyDg4MrVCuzIzsWbTadTuPCCy/Ejh07lqOKZmZ2lF796le7T7YT3vve9z58+ctfxje+8Q2sXbt2patjRi2lvfpe2VaCH+QchUwmg4svvhj33nvvwX8LwxD33nvvIU9lzU4Ux6LNNptNPPHEExgaGlquapqZ2VF49NFH3SfbCSuKIrzvfe/DP/3TP+G+++7Dpk2bVrpKZkd0LNqr75VtJfjVqqN088034/rrr8cll1yCV7/61fjEJz6BYrGId73rXStdNbPDUm32ne98J9asWYM777wTAHDHHXfgNa95DU4//XTMzs7iYx/7GHbv3o1f+7VfW8nNMDuixcXFQ/4KtmvXLjz66KPo7u7G+vXrV7BmZj9NtdcPfehD2L9/P/7mb/4GAPCJT3wCmzZtwjnnnINKpYK//Mu/xH333Yevfe1rK7UJZtRNN92Ev//7v8eXvvQltLe3H8zk6+joQD6fX+HamR0qTnv1vbKdiPwg5yj90i/9EiYmJnDrrbdidHQUF1xwAb7yla/8VJis2YlCtdk9e/Ygkfjx4LyZmRnceOONGB0dRVdXFy6++GLcf//9OPvss1dqE8yohx56CFddddXB/7755psBANdffz3uvvvuFaqV2eGp9joyMoI9e/YcLK/VavjgBz+I/fv3o6WlBeeffz6+/vWvH7IMsxPJX/zFXwAArrzyykP+/a677sINN9xw/CtkRsRpr75XthNREEVRtNKVMDMzMzMzMzMzzRk5ZmZmZmZmZmarhB/kmJmZmZmZmZmtEn6QY2ZmZmZmZma2SvhBjpmZmZmZmZnZKuEHOWZmZmZmZmZmq4Qf5JiZmZmZmZmZrRJ+kGNmZmZmZmZmtkr4QY6ZmZmZmZmZ2SrhBzlmZma2ZDfccAPe+ta3rnQ1zMzMzE56qZWugJmZmZ3YgiCg5bfddhv+9E//FFEUHacamZmZmZ26/CDHzMzMqJGRkYP///Of/zxuvfVWbN++/eC/tbW1oa2tbSWqZmZmZnbK8atVZmZmRg0ODh786ejoQBAEh/xbW1vbT71adeWVV+L9738/PvCBD6CrqwsDAwP4P//n/6BYLOJd73oX2tvbcfrpp+P//b//d8i6nnzySbzxjW9EW1sbBgYG8I53vAOTk5PHeYvNzMzMTlx+kGNmZmbL4q//+q/R29uLBx98EO9///vx3ve+F29729tw+eWX45FHHsE111yDd7zjHSiVSgCA2dlZvOENb8CFF16Ihx56CF/5ylcwNjaG//gf/+MKb4mZmZnZicMPcszMzGxZbNu2DR/+8Idxxhln4EMf+hByuRx6e3tx44034owzzsCtt96KqakpPP744wCAP//zP8eFF16Ij3zkI9i6dSsuvPBCfPazn8U3vvENPPfccyu8NWZmZmYnBmfkmJmZ2bI4//zzD/7/ZDKJnp4enHfeeQf/bWBgAAAwPj4OAHjsscfwjW9847B5Ozt37sSZZ565zDU2MzMzO/H5QY6ZmZkti3Q6fch/B0FwyL+9PBtWGIYAgMXFRbz5zW/GRz/60Z9a1tDQ0DLW1MzMzGz18IMcMzMzOyFcdNFF+MIXvoCNGzcilfItipmZmdnhOCPHzMzMTgg33XQTpqen8fa3vx0//OEPsXPnTnz1q1/Fu971LjSbzZWunpmZmdkJwQ9yzMzM7IQwPDyM733ve2g2m7jmmmtw3nnn4QMf+AA6OzuRSPiWxczMzAwAgiiKopWuhJmZmZmZmZmZaf7zlpmZmZmZmZnZKuEHOWZmZmZmZmZmq4Qf5JiZmZmZmZmZrRJ+kGNmZmZmZmZmtkr4QY6ZmZmZmZmZ2SrhBzlmZmZmZmZmZquEH+SYmZmZmZmZma0SfpBjZmZmZmZmZrZK+EGOmZmZmZmZmdkq4Qc5ZmZmZmZmZmarhB/kmJmZmZmZmZmtEv9/hpyzxkdbuKgAAAAASUVORK5CYII=",
      "text/plain": [
       "<Figure size 1500x700 with 2 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Plot the mel spectrogram of our sample\n",
    "mel_spec = librosa.feature.melspectrogram(y=audio, sr=sample_rate)\n",
    "mel_spec_db = librosa.power_to_db(mel_spec, ref=np.max)\n",
    "\n",
    "librosa.display.specshow(\n",
    "    mel_spec_db, x_axis='time', y_axis='mel')\n",
    "plt.colorbar()\n",
    "plt.title('Mel Spectrogram');"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "RSCyVizDlRz1"
   },
   "source": [
    "## Convolutional ASR Models\n",
    "\n",
    "Let's take a look at the model that we will be building, and how we specify its parameters.\n",
    "\n",
    "### The Jasper Model\n",
    "\n",
    "We will be training a small [Jasper (Just Another SPeech Recognizer) model](https://arxiv.org/abs/1904.03288) from scratch (e.g. initialized randomly). \n",
    "In brief, Jasper architectures consist of a repeated block structure that utilizes 1D convolutions.\n",
    "In a Jasper_KxR model, `R` sub-blocks (consisting of a 1D convolution, batch norm, ReLU, and dropout) are grouped into a single block, which is then repeated `K` times.\n",
    "We also have a one extra block at the beginning and a few more at the end that are invariant of `K` and `R`, and we use CTC loss.\n",
    "\n",
    "### The QuartzNet Model\n",
    "\n",
    "The QuartzNet is better variant of Jasper with a key difference that it uses time-channel separable 1D convolutions. This allows it to dramatically reduce number of weights while keeping similar accuracy.\n",
    "\n",
    "A Jasper/QuartzNet models look like this (QuartzNet model is pictured):\n",
    "\n",
    "![QuartzNet with CTC](https://developer.nvidia.com/blog/wp-content/uploads/2020/05/quartznet-model-architecture-1-625x742.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "gEpNci7slRzw"
   },
   "source": [
    "# Using NeMo for Automatic Speech Recognition\n",
    "\n",
    "Now that we have an idea of what ASR is and how the audio data looks like, we can start using NeMo to do some ASR!\n",
    "\n",
    "We'll be using the **Neural Modules (NeMo) toolkit** for this part, so if you haven't already, you should download and install NeMo and its dependencies. To do so, just follow the directions on the [GitHub page](https://github.com/NVIDIA/NeMo), or in the [documentation](https://docs.nvidia.com/deeplearning/nemo/user-guide/docs/en/stable/).\n",
    "\n",
    "NeMo lets us easily hook together the components (modules) of our model, such as the data layer, intermediate layers, and various losses, without worrying too much about implementation details of individual parts or connections between modules. NeMo also comes with complete models which only require your data and hyperparameters for training."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {
    "id": "4_W0lhaQlRzx"
   },
   "outputs": [],
   "source": [
    "# NeMo's \"core\" package\n",
    "import nemo\n",
    "# NeMo's ASR collection - this collections contains complete ASR models and\n",
    "# building blocks (modules) for ASR\n",
    "import nemo.collections.asr as nemo_asr"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "v_W8EbYktZE3"
   },
   "source": [
    "## Using an Out-of-the-Box Model\n",
    "\n",
    "NeMo's ASR collection comes with many building blocks and even complete models that we can use for training and evaluation. Moreover, several models come with pre-trained weights. Let's instantiate a complete QuartzNet15x5 model."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "metadata": {
    "id": "KFZZpYult96G"
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "[NeMo I 2025-02-17 12:54:34 cloud:68] Downloading from: https://api.ngc.nvidia.com/v2/models/nvidia/nemospeechmodels/versions/1.0.0a5/files/QuartzNet15x5Base-En.nemo to /home/nkoluguri/.cache/torch/NeMo/NeMo_2.3.0rc0/QuartzNet15x5Base-En/b69977d31abaf2ab3e8f082866f6dfcb/QuartzNet15x5Base-En.nemo\n",
      "100% [........................................................................] 71087043 / 71087043[NeMo I 2025-02-17 12:54:35 common:826] Instantiating model from pre-trained checkpoint\n",
      "[NeMo I 2025-02-17 12:54:36 features:305] PADDING: 16\n",
      "[NeMo I 2025-02-17 12:54:37 save_restore_connector:275] Model EncDecCTCModel was successfully restored from /home/nkoluguri/.cache/torch/NeMo/NeMo_2.3.0rc0/QuartzNet15x5Base-En/b69977d31abaf2ab3e8f082866f6dfcb/QuartzNet15x5Base-En.nemo.\n"
     ]
    }
   ],
   "source": [
    "# This line will download pre-trained QuartzNet15x5 model from NVIDIA's NGC cloud and instantiate it for you\n",
    "quartznet = nemo_asr.models.EncDecCTCModel.from_pretrained(model_name=\"QuartzNet15x5Base-En\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "KucxoFJhum0i"
   },
   "source": [
    "Next, we'll simply add paths to files we want to transcribe into the list and pass it to our model. Note that it will work for relatively short (<25 seconds) files. "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "metadata": {
    "id": "3QCpR_93u1hp"
   },
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "Transcribing: 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00,  1.06it/s]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Audio in ./an4/wav/an4_clstk/mgah/cen2-mgah-b.wav was recognized as: Hypothesis(score=tensor(-1.5078), y_sequence=tensor([28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28,\n",
      "        28, 28, 28, 28, 28, 28, 28, 28,  7, 28, 28, 28, 28, 28, 28, 28, 28, 28,\n",
      "        28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28,  0,  0, 28, 28, 28,\n",
      "        28, 28, 28, 28, 12, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28,  0,\n",
      "         0,  0, 28, 28, 28, 28,  5, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28,\n",
      "        28, 28, 28, 28, 28,  0,  0, 28, 28, 28, 28, 14, 28, 28, 28, 28, 28, 28,\n",
      "        28, 28, 28, 28, 28,  0,  0, 28, 28, 28, 28, 28, 14, 28, 28, 28, 28, 28,\n",
      "        28, 28, 28, 28, 28]), text='g l e n n', dec_out=None, dec_state=None, timestamp=[], alignments=None, frame_confidence=None, token_confidence=None, word_confidence=None, length=0, y=None, lm_state=None, lm_scores=None, ngram_lm_state=None, tokens=None, last_token=None, token_duration=None, last_frame=None)\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n"
     ]
    }
   ],
   "source": [
    "files = [os.path.join(data_dir, 'an4/wav/an4_clstk/mgah/cen2-mgah-b.wav')]\n",
    "for fname, transcription in zip(files, quartznet.transcribe(audio=files)):\n",
    "  print(f\"Audio in {fname} was recognized as: {transcription}\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "ppUm_kuavm_f"
   },
   "source": [
    "That was easy! But there are plenty of scenarios where you would want to fine-tune the model on your own data or even train from scratch. For example, this out-of-the box model will obviously not work for Spanish and would likely perform poorly for telephone audio. So if you have collected your own data, you certainly should attempt to fine-tune or train on it!"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "ABUDaC5Js7AW"
   },
   "source": [
    "## Training from Scratch\n",
    "\n",
    "To train from scratch, you need to prepare your training data in the right format and specify your models architecture."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "RdNyw1b_zgtm"
   },
   "source": [
    "### Creating Data Manifests\n",
    "\n",
    "The first thing we need to do now is to create manifests for our training and evaluation data, which will contain the metadata of our audio files. NeMo data sets take in a standardized manifest format where each line corresponds to one sample of audio, such that the number of lines in a manifest is equal to the number of samples that are represented by that manifest. A line must contain the path to an audio file, the corresponding transcript (or path to a transcript file), and the duration of the audio sample.\n",
    "\n",
    "Here's an example of what one line in a NeMo-compatible manifest might look like:\n",
    "```\n",
    "{\"audio_filepath\": \"path/to/audio.wav\", \"duration\": 3.45, \"text\": \"this is a nemo tutorial\"}\n",
    "```\n",
    "\n",
    "We can build our training and evaluation manifests using `an4/etc/an4_train.transcription` and `an4/etc/an4_test.transcription`, which have lines containing transcripts and their corresponding audio file IDs:\n",
    "```\n",
    "...\n",
    "<s> P I T T S B U R G H </s> (cen5-fash-b)\n",
    "<s> TWO SIX EIGHT FOUR FOUR ONE EIGHT </s> (cen7-fash-b)\n",
    "...\n",
    "```"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 11,
   "metadata": {
    "id": "lVB1sG1GlRzz"
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "******\n",
      "***Done***\n"
     ]
    }
   ],
   "source": [
    "# --- Building Manifest Files --- #\n",
    "import json\n",
    "\n",
    "# Function to build a manifest\n",
    "def build_manifest(transcripts_path, manifest_path, wav_path):\n",
    "    with open(transcripts_path, 'r') as fin:\n",
    "        with open(manifest_path, 'w') as fout:\n",
    "            for line in fin:\n",
    "                # Lines look like this:\n",
    "                # <s> transcript </s> (fileID)\n",
    "                transcript = line[: line.find('(')-1].lower()\n",
    "                transcript = transcript.replace('<s>', '').replace('</s>', '')\n",
    "                transcript = transcript.strip()\n",
    "\n",
    "                file_id = line[line.find('(')+1 : -2]  # e.g. \"cen4-fash-b\"\n",
    "                audio_path = os.path.join(\n",
    "                    data_dir, wav_path,\n",
    "                    file_id[file_id.find('-')+1 : file_id.rfind('-')],\n",
    "                    file_id + '.wav')\n",
    "\n",
    "                duration = librosa.core.get_duration(filename=audio_path)\n",
    "\n",
    "                # Write the metadata to the manifest\n",
    "                metadata = {\n",
    "                    \"audio_filepath\": audio_path,\n",
    "                    \"duration\": duration,\n",
    "                    \"text\": transcript\n",
    "                }\n",
    "                json.dump(metadata, fout)\n",
    "                fout.write('\\n')\n",
    "                \n",
    "# Building Manifests\n",
    "print(\"******\")\n",
    "train_transcripts = data_dir + '/an4/etc/an4_train.transcription'\n",
    "train_manifest = data_dir + '/an4/train_manifest.json'\n",
    "if not os.path.isfile(train_manifest):\n",
    "    build_manifest(train_transcripts, train_manifest, 'an4/wav/an4_clstk')\n",
    "    print(\"Training manifest created.\")\n",
    "\n",
    "test_transcripts = data_dir + '/an4/etc/an4_test.transcription'\n",
    "test_manifest = data_dir + '/an4/test_manifest.json'\n",
    "if not os.path.isfile(test_manifest):\n",
    "    build_manifest(test_transcripts, test_manifest, 'an4/wav/an4test_clstk')\n",
    "    print(\"Test manifest created.\")\n",
    "print(\"***Done***\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "W2fShQzRzo-M"
   },
   "source": [
    "### Specifying Our Model with a YAML Config File\n",
    "\n",
    "For this tutorial, we'll build a *Jasper_4x1 model*, with `K=4` blocks of single (`R=1`) sub-blocks and a *greedy CTC decoder*, using the configuration found in `./configs/config.yaml`.\n",
    "\n",
    "If we open up this config file, we find model section which describes architecture of our model. A model contains an entry labeled `encoder`, with a field called `jasper` that contains a list with multiple entries. Each of the members in this list specifies one block in our model, and looks something like this:\n",
    "```\n",
    "- filters: 128\n",
    "  repeat: 1\n",
    "  kernel: [11]\n",
    "  stride: [2]\n",
    "  dilation: [1]\n",
    "  dropout: 0.2\n",
    "  residual: false\n",
    "  separable: true\n",
    "  se: true\n",
    "  se_context_size: -1\n",
    "```\n",
    "The first member of the list corresponds to the first block in the Jasper architecture diagram, which appears regardless of `K` and `R`.\n",
    "Next, we have four entries that correspond to the `K=4` blocks, and each has `repeat: 1` since we are using `R=1`.\n",
    "These are followed by two more entries for the blocks that appear at the end of our Jasper model before the CTC loss.\n",
    "\n",
    "There are also some entries at the top of the file that specify how we will handle training (`train_ds`) and validation (`validation_ds`) data.\n",
    "\n",
    "Using a YAML config such as this is helpful for getting a quick and human-readable overview of what your architecture looks like, and allows you to swap out model and run configurations easily without needing to change your code."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 12,
   "metadata": {
    "id": "PXVKBniMlRz5"
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "{'name': 'QuartzNet15x5', 'sample_rate': 16000, 'repeat': 1, 'dropout': 0.0, 'separable': True, 'labels': [' ', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', \"'\"], 'model': {'train_ds': {'manifest_filepath': '???', 'sample_rate': 16000, 'labels': [' ', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', \"'\"], 'batch_size': 32, 'trim_silence': True, 'max_duration': 16.7, 'shuffle': True, 'num_workers': 8, 'pin_memory': True, 'is_tarred': False, 'tarred_audio_filepaths': None, 'shuffle_n': 2048, 'bucketing_strategy': 'synced_randomized', 'bucketing_batch_size': None}, 'validation_ds': {'manifest_filepath': '???', 'sample_rate': 16000, 'labels': [' ', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', \"'\"], 'batch_size': 32, 'shuffle': False, 'num_workers': 8, 'pin_memory': True}, 'preprocessor': {'_target_': 'nemo.collections.asr.modules.AudioToMelSpectrogramPreprocessor', 'normalize': 'per_feature', 'window_size': 0.02, 'sample_rate': 16000, 'window_stride': 0.01, 'window': 'hann', 'features': 64, 'n_fft': 512, 'frame_splicing': 1, 'dither': 1e-05, 'stft_conv': False}, 'spec_augment': {'_target_': 'nemo.collections.asr.modules.SpectrogramAugmentation', 'rect_freq': 50, 'rect_masks': 5, 'rect_time': 120}, 'encoder': {'_target_': 'nemo.collections.asr.modules.ConvASREncoder', 'feat_in': 64, 'activation': 'relu', 'conv_mask': True, 'jasper': [{'filters': 128, 'repeat': 1, 'kernel': [11], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': True, 'separable': True, 'se': True, 'se_context_size': -1}, {'filters': 256, 'repeat': 1, 'kernel': [13], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': True, 'separable': True, 'se': True, 'se_context_size': -1}, {'filters': 256, 'repeat': 1, 'kernel': [15], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': True, 'separable': True, 'se': True, 'se_context_size': -1}, {'filters': 256, 'repeat': 1, 'kernel': [17], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': True, 'separable': True, 'se': True, 'se_context_size': -1}, {'filters': 256, 'repeat': 1, 'kernel': [19], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': True, 'separable': True, 'se': True, 'se_context_size': -1}, {'filters': 256, 'repeat': 1, 'kernel': [21], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': False, 'separable': True, 'se': True, 'se_context_size': -1}, {'filters': 1024, 'repeat': 1, 'kernel': [1], 'stride': [1], 'dilation': [1], 'dropout': 0.0, 'residual': False, 'separable': True, 'se': True, 'se_context_size': -1}]}, 'decoder': {'_target_': 'nemo.collections.asr.modules.ConvASRDecoder', 'feat_in': 1024, 'num_classes': 28, 'vocabulary': [' ', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', \"'\"]}, 'optim': {'name': 'novograd', 'lr': 0.01, 'betas': [0.8, 0.5], 'weight_decay': 0.001, 'sched': {'name': 'CosineAnnealing', 'monitor': 'val_loss', 'reduce_on_plateau': False, 'warmup_steps': None, 'warmup_ratio': None, 'min_lr': 0.0, 'last_epoch': -1}}}, 'trainer': {'devices': 1, 'max_epochs': 5, 'max_steps': -1, 'num_nodes': 1, 'accelerator': 'gpu', 'strategy': 'ddp', 'accumulate_grad_batches': 1, 'enable_checkpointing': False, 'logger': False, 'log_every_n_steps': 1, 'val_check_interval': 1.0, 'benchmark': False}, 'exp_manager': {'exp_dir': None, 'name': 'QuartzNet15x5', 'create_tensorboard_logger': True, 'create_checkpoint_callback': True}}\n"
     ]
    }
   ],
   "source": [
    "# --- Config Information ---#\n",
    "try:\n",
    "    from ruamel.yaml import YAML\n",
    "except ModuleNotFoundError:\n",
    "    from ruamel_yaml import YAML\n",
    "config_path = './configs/config.yaml'\n",
    "\n",
    "if not os.path.exists(config_path):\n",
    "    # Grab the config we'll use in this example\n",
    "    BRANCH = 'main'\n",
    "    !mkdir configs\n",
    "    !wget -P configs/ https://raw.githubusercontent.com/NVIDIA/NeMo/$BRANCH/examples/asr/conf/config.yaml\n",
    "\n",
    "yaml = YAML(typ='safe')\n",
    "with open(config_path) as f:\n",
    "    params = yaml.load(f)\n",
    "print(params)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "wUmq3p2Aw_5N"
   },
   "source": [
    "### Training with PyTorch Lightning\n",
    "\n",
    "NeMo models and modules can be used in any PyTorch code where torch.nn.Module is expected.\n",
    "\n",
    "However, NeMo's models are based on [PytorchLightning's](https://github.com/PyTorchLightning/pytorch-lightning) LightningModule and we recommend you use PytorchLightning for training and fine-tuning as it makes using mixed precision and distributed training very easy. So to start, let's create Trainer instance for training on GPU for 50 epochs"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 13,
   "metadata": {
    "id": "GUfR6tAK0k2u"
   },
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "GPU available: True (cuda), used: True\n",
      "TPU available: False, using: 0 TPU cores\n",
      "HPU available: False, using: 0 HPUs\n"
     ]
    }
   ],
   "source": [
    "import lightning.pytorch as pl\n",
    "trainer = pl.Trainer(devices=1, accelerator='gpu', max_epochs=50)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "IEn2RyvgxxvO"
   },
   "source": [
    "Next, we instantiate and ASR model based on our ``config.yaml`` file from the previous section.\n",
    "Note that this is a stage during which we also tell the model where our training and validation manifests are."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 14,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "lightning.pytorch.trainer.trainer.Trainer"
      ]
     },
     "execution_count": 14,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "type(trainer)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 15,
   "metadata": {
    "id": "Cbf0fsMK09lk"
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "[NeMo I 2025-02-17 12:57:54 audio_to_text_dataset:49] Model level config does not contain `sample_rate`, please explicitly provide `sample_rate` to the dataloaders.\n",
      "[NeMo I 2025-02-17 12:57:54 audio_to_text_dataset:49] Model level config does not contain `labels`, please explicitly provide `labels` to the dataloaders.\n",
      "[NeMo I 2025-02-17 12:57:54 collections:201] Dataset loaded with 948 files totalling 0.71 hours\n",
      "[NeMo I 2025-02-17 12:57:54 collections:202] 0 files were filtered totalling 0.00 hours\n",
      "[NeMo I 2025-02-17 12:57:54 audio_to_text_dataset:49] Model level config does not contain `sample_rate`, please explicitly provide `sample_rate` to the dataloaders.\n",
      "[NeMo I 2025-02-17 12:57:54 audio_to_text_dataset:49] Model level config does not contain `labels`, please explicitly provide `labels` to the dataloaders.\n",
      "[NeMo I 2025-02-17 12:57:54 collections:201] Dataset loaded with 130 files totalling 0.10 hours\n",
      "[NeMo I 2025-02-17 12:57:54 collections:202] 0 files were filtered totalling 0.00 hours\n",
      "[NeMo I 2025-02-17 12:57:54 features:305] PADDING: 16\n"
     ]
    }
   ],
   "source": [
    "from omegaconf import DictConfig\n",
    "params['model']['train_ds']['manifest_filepath'] = train_manifest\n",
    "params['model']['validation_ds']['manifest_filepath'] = test_manifest\n",
    "first_asr_model = nemo_asr.models.EncDecCTCModel(cfg=DictConfig(params['model']), trainer=trainer)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "hWtzwL5qXTYq"
   },
   "source": [
    "With that, we can start training with just one line!"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 16,
   "metadata": {
    "id": "inRJsnrz1psq"
   },
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "You are using a CUDA device ('NVIDIA RTX A6000') that has Tensor Cores. To properly utilize them, you should set `torch.set_float32_matmul_precision('medium' | 'high')` which will trade-off precision for performance. For more details, read https://pytorch.org/docs/stable/generated/torch.set_float32_matmul_precision.html#torch.set_float32_matmul_precision\n",
      "LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0,1]\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "[NeMo I 2025-02-17 12:58:00 modelPT:793] Optimizer config = Novograd (\n",
      "    Parameter Group 0\n",
      "        amsgrad: False\n",
      "        betas: [0.8, 0.5]\n",
      "        eps: 1e-08\n",
      "        grad_averaging: False\n",
      "        lr: 0.01\n",
      "        weight_decay: 0.001\n",
      "    )\n",
      "[NeMo I 2025-02-17 12:58:01 lr_scheduler:948] Scheduler \"<nemo.core.optim.lr_scheduler.CosineAnnealing object at 0x7f20f0579a20>\" \n",
      "    will be used during training (effective maximum steps = 1500) - \n",
      "    Parameters : \n",
      "    (warmup_steps: null\n",
      "    warmup_ratio: null\n",
      "    min_lr: 0.0\n",
      "    last_epoch: -1\n",
      "    max_steps: 1500\n",
      "    )\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n",
      "  | Name              | Type                              | Params | Mode \n",
      "--------------------------------------------------------------------------------\n",
      "0 | preprocessor      | AudioToMelSpectrogramPreprocessor | 0      | train\n",
      "1 | encoder           | ConvASREncoder                    | 1.2 M  | train\n",
      "2 | decoder           | ConvASRDecoder                    | 29.7 K | train\n",
      "3 | loss              | CTCLoss                           | 0      | train\n",
      "4 | spec_augmentation | SpectrogramAugmentation           | 0      | train\n",
      "5 | wer               | WER                               | 0      | train\n",
      "--------------------------------------------------------------------------------\n",
      "1.2 M     Trainable params\n",
      "0         Non-trainable params\n",
      "1.2 M     Total params\n",
      "4.836     Total estimated model params size (MB)\n",
      "135       Modules in train mode\n",
      "0         Modules in eval mode\n"
     ]
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "ea9985cc25584b448fe4056a0f6d45c3",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Sanity Checking: |                                                                                            …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "[NeMo W 2025-02-17 12:58:01 nemo_logging:361] /home/nkoluguri/miniconda3/envs/nemo/lib/python3.10/site-packages/lightning/pytorch/loops/fit_loop.py:298: The number of training batches (30) is smaller than the logging interval Trainer(log_every_n_steps=50). Set a lower value for log_every_n_steps if you want to see logs for the training epoch.\n",
      "    \n"
     ]
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "eb0a35d8955b49ed9b74403c72ba7c82",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Training: |                                                                                                   …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "ab2e0f1083c14a03ae5c4d1d32f77448",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "cd665369137e4191a89a77a7a777be6b",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "2441f6b5d7694a958a939d544d1ad110",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "231b6b86f91a46bb9acf8fe9d648b12e",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "73298d17c7ae423da3fe2a1af3405116",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "20352ccceebe4565be54282ca45beb74",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "2c8f15b7a84345539c4d114ea26d67ea",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "94dbf0be97cd48259ac0ada91d12bf31",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "6e16c648fbbe456bb84fc67d2da53c2b",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "8bc1a472840446a2a108d8ef241909f8",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "55bc372ce2784551b0983604e665fde0",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "5ff5239908b24431a1103d04d3dccad0",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "49d13ab342854668a59942ff4ab03052",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "bf65e0bff6e244b699bf2cb96f0a5e11",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "ae96cdf5e2fa4bb3b4def009673f17a3",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "5f9d01895b654d40a2b0bede6778594b",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "42e4cf9bd1884af2a6fffa13537b0bc6",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "434ae3b11a154209985a9352a094a29f",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "30eec10ba11f4fc8a8ec731db3432bf0",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "f8d3b4128caf4bbcb76a789a659aa3f2",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "3bde915452bc405489933b9596c59e7e",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "43235ccca8da412390a504b0093eb041",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "60d579d9a93040f693eaeee1f7793770",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "354f369e4a3d494f8a029ae5447783ee",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "8abe4e6e71f54d14a049a52344b75e43",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "525747ed1153483590252345094e5f60",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "0b6a6ea625be44c194bc9bcd92929c10",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "fa5d8b34dcc5486a9f3f5b620aefeec0",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "348bf4b8b15f49209bba11a7f35f4c96",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "132b827a375542f0ad1572dba2137ec0",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "20fddc95b01e4336af2f2a831726fd85",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "4ca82134bebb406ea28e5337854a180d",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "32b458fab696408eaafb313b9e26f71e",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "ad73d70fc94b460e9cfe12337989156b",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "f9e297f3832f47faa3c50c46e9a64a78",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "413f55f4e30740a8ab5f26285e5cf6d8",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "31c828462cb348f48811d896810b9473",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "f204c37d198a4ccb94d7ee16d6817099",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "c10b1c7ddbd54845ae3d7dfb09da7835",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "872f02e3230e47678ff3344a7a41eb83",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "94b3c65f49da4dda8990ef73d7318d3a",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "fedf2e6b349945a28a933caf3e66aeab",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "06d2ecb824f4432c86261a8805b3a0cb",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "ee3bcb1b21b34962a1ee0ddec8f69ca5",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "0923326246f646b5a827e26c0c634d8d",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "e52765c9a2394ab399f1dba25c360448",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "4498e3b8e11d4d98ab8ab0a57d4ca1a1",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "d06cd9912d9c4f5793dd7cf2e4e5a72d",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "f45dc7ddda414eb4982396c08d2adc46",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "6461a9e38b3e4515a6239edbd05fdcfd",
       "version_major": 2,
       "version_minor": 0
      },
      "text/plain": [
       "Validation: |                                                                                                 …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "`Trainer.fit` stopped: `max_epochs=50` reached.\n"
     ]
    }
   ],
   "source": [
    "# Start training!!!\n",
    "trainer.fit(first_asr_model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "jpYXX-GslR0E"
   },
   "source": [
    "There we go! We've put together a full training pipeline for the model and trained it for 50 epochs.\n",
    "\n",
    "If you'd like to save this model checkpoint for loading later (e.g. for fine-tuning, or for continuing training), you can simply call `first_asr_model.save_to(<checkpoint_path>)`. Then, to restore your weights, you can rebuild the model using the config (let's say you call it `first_asr_model_continued` this time) and call `first_asr_model_continued.restore_from(<checkpoint_path>)`.\n",
    "\n",
    "### After Training: Monitoring Progress and Changing Hyperparameters\n",
    "We can  now start Tensorboard to see how training went. Recall that WER stands for Word Error Rate and so the lower it is, the better."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "n_0y3stSXDX_"
   },
   "outputs": [],
   "source": [
    "try:\n",
    "  from google import colab\n",
    "  COLAB_ENV = True\n",
    "except (ImportError, ModuleNotFoundError):\n",
    "  COLAB_ENV = False\n",
    "\n",
    "# Load the TensorBoard notebook extension\n",
    "if COLAB_ENV:\n",
    "  %load_ext tensorboard\n",
    "  %tensorboard --logdir lightning_logs/\n",
    "else:\n",
    "  print(\"To use tensorboard, please use this notebook in a Google Colab environment.\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "Z0h-BME7U8yb"
   },
   "source": [
    "We could improve this model by playing with hyperparameters. We can look at the current hyperparameters with the following:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "7kdQbpohXnEd"
   },
   "outputs": [],
   "source": [
    "print(params['model']['optim'])"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "sGZzRCvIW8kE"
   },
   "source": [
    "Let's say we wanted to change the learning rate. To do so, we can create a `new_opt` dict and set our desired learning rate, then call `<model>.setup_optimization()` with the new optimization parameters."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "AbigFKUtYgvn"
   },
   "outputs": [],
   "source": [
    "import copy\n",
    "new_opt = copy.deepcopy(params['model']['optim'])\n",
    "new_opt['lr'] = 0.001\n",
    "first_asr_model.setup_optimization(optim_config=DictConfig(new_opt))\n",
    "# And then you can invoke trainer.fit(first_asr_model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "D5Kwg8Cz-aaO"
   },
   "source": [
    "## Inference\n",
    "\n",
    "Let's have a quick look at how one could run inference with NeMo's ASR model.\n",
    "\n",
    "First, ``EncDecCTCModel`` and its subclasses contain a handy ``transcribe`` method which can be used to simply obtain audio files' transcriptions. It also has batch_size argument to improve performance."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "3FT0klSV268p"
   },
   "outputs": [],
   "source": [
    "first_asr_model.cuda()\n",
    "first_asr_model.eval()\n",
    "audio = [os.path.join(data_dir, 'an4/wav/an4_clstk/mgah/cen2-mgah-b.wav'),\n",
    "                     os.path.join(data_dir, 'an4/wav/an4_clstk/fmjd/cen7-fmjd-b.wav'),\n",
    "                     os.path.join(data_dir, 'an4/wav/an4_clstk/fmjd/cen8-fmjd-b.wav'),\n",
    "                     os.path.join(data_dir, 'an4/wav/an4_clstk/fkai/cen8-fkai-b.wav')]\n",
    "print(first_asr_model.transcribe(audio=audio,\n",
    "                                 batch_size=4))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "6FiCfLX0D7py"
   },
   "source": [
    "Below is an example of a simple inference loop in pure PyTorch. It also shows how one can compute Word Error Rate (WER) metric between predictions and references."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "7mP4r1Gx_Ilt"
   },
   "outputs": [],
   "source": [
    "# Bigger batch-size = bigger throughput\n",
    "params['model']['validation_ds']['batch_size'] = 16\n",
    "\n",
    "# Setup the test data loader and make sure the model is on GPU\n",
    "first_asr_model.setup_test_data(test_data_config=params['model']['validation_ds'])\n",
    "first_asr_model.cuda()\n",
    "first_asr_model.eval()\n",
    "\n",
    "# We will be computing Word Error Rate (WER) metric between our hypothesis and predictions.\n",
    "# WER is computed as numerator/denominator.\n",
    "# We'll gather all the test batches' numerators and denominators.\n",
    "wer_nums = []\n",
    "wer_denoms = []\n",
    "\n",
    "# Loop over all test batches.\n",
    "# Iterating over the model's `test_dataloader` will give us:\n",
    "# (audio_signal, audio_signal_length, transcript_tokens, transcript_length)\n",
    "# See the AudioToCharDataset for more details.\n",
    "for test_batch in first_asr_model.test_dataloader():\n",
    "        test_batch = [x.cuda() for x in test_batch]\n",
    "        targets = test_batch[2]\n",
    "        targets_lengths = test_batch[3]        \n",
    "        log_probs, encoded_len, greedy_predictions = first_asr_model(\n",
    "            input_signal=test_batch[0], input_signal_length=test_batch[1]\n",
    "        )\n",
    "        # Notice the model has a helper object to compute WER\n",
    "        first_asr_model.wer.update(predictions=greedy_predictions, predictions_lengths=None, targets=targets, targets_lengths=targets_lengths)\n",
    "        _, wer_num, wer_denom = first_asr_model.wer.compute()\n",
    "        first_asr_model.wer.reset()\n",
    "        wer_nums.append(wer_num.detach().cpu().numpy())\n",
    "        wer_denoms.append(wer_denom.detach().cpu().numpy())\n",
    "\n",
    "        # Release tensors from GPU memory\n",
    "        del test_batch, log_probs, targets, targets_lengths, encoded_len, greedy_predictions\n",
    "\n",
    "# We need to sum all numerators and denominators first. Then divide.\n",
    "print(f\"WER = {sum(wer_nums)/sum(wer_denoms)}\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "0kM9kBNOCptf"
   },
   "source": [
    "This WER is not particularly impressive and could be significantly improved. You could train longer (try 100 epochs) to get a better number. Check out the next section on how to improve it further."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "RBcJtg5ulR0H"
   },
   "source": [
    "## Model Improvements\n",
    "\n",
    "You already have all you need to create your own ASR model in NeMo, but there are a few more tricks that you can employ if you so desire. In this section, we'll briefly cover a few possibilities for improving an ASR model.\n",
    "\n",
    "### Data Augmentation\n",
    "\n",
    "There exist several ASR data augmentation methods that can increase the size of our training set.\n",
    "\n",
    "For example, we can perform augmentation on the spectrograms by zeroing out specific frequency segments (\"frequency masking\") or time segments (\"time masking\") as described by [SpecAugment](https://arxiv.org/abs/1904.08779), or zero out rectangles on the spectrogram as in [Cutout](https://arxiv.org/pdf/1708.04552.pdf). In NeMo, we can do all three of these by simply adding in a `SpectrogramAugmentation` neural module. (As of now, it does not perform the time warping from the SpecAugment paper.)\n",
    "\n",
    "Our toy model does not do spectrogram augmentation. But the real one we got from cloud does:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "9glGogaPlR0H"
   },
   "outputs": [],
   "source": [
    "print(quartznet._cfg['spec_augment'])"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "LdwdcA_a640R"
   },
   "source": [
    "If you want to enable SpecAugment in your model, make sure your .yaml config file contains 'model/spec_augment' section which looks like the one above."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "2f142kIQc1Z2"
   },
   "source": [
    "### Transfer learning\n",
    "\n",
    "Transfer learning is an important machine learning technique that uses a model’s knowledge of one task to make it perform better on another. Fine-tuning is one of the techniques to perform transfer learning. It is an essential part of the recipe for many state-of-the-art results where a base model is first pretrained on a task with abundant training data and then fine-tuned on different tasks of interest where the training data is less abundant or even scarce.\n",
    "\n",
    "In ASR you might want to do fine-tuning in multiple scenarios, for example, when you want to improve your model's performance on a particular domain (medical, financial, etc.) or on accented speech. You can even transfer learn from one language to another! Check out [this paper](https://arxiv.org/abs/2005.04290) for examples.\n",
    "\n",
    "Transfer learning with NeMo is simple. Let's demonstrate how the model we got from the cloud could be fine-tuned on AN4 data. (NOTE: this is a toy example). And, while we are at it, we will change model's vocabulary, just to demonstrate how it's done."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "hl320dsydWX0"
   },
   "outputs": [],
   "source": [
    "# Check what kind of vocabulary/alphabet the model has right now\n",
    "print(quartznet.decoder.vocabulary)\n",
    "\n",
    "# Let's add \"!\" symbol there. Note that you can (and should!) change the vocabulary\n",
    "# entirely when fine-tuning using a different language.\n",
    "quartznet.change_vocabulary(\n",
    "    new_vocabulary=[\n",
    "        ' ', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n',\n",
    "        'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', \"'\", \"!\"\n",
    "    ]\n",
    ")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "M7lvmiMSd3Aw"
   },
   "source": [
    "After this, our decoder has completely changed, but our encoder (which is where most of the weights are) remained intact. Let's fine tune-this model for 2 epochs on AN4 dataset. We will also use the smaller learning rate from ``new_opt` (see the \"After Training\" section)`."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "_PZJIso-eDl-"
   },
   "outputs": [],
   "source": [
    "# Use the smaller learning rate we set before\n",
    "quartznet.setup_optimization(optim_config=DictConfig(new_opt))\n",
    "\n",
    "# Point to the data we'll use for fine-tuning as the training set\n",
    "quartznet.setup_training_data(train_data_config=params['model']['train_ds'])\n",
    "\n",
    "# Point to the new validation data for fine-tuning\n",
    "quartznet.setup_validation_data(val_data_config=params['model']['validation_ds'])\n",
    "\n",
    "# And now we can create a PyTorch Lightning trainer and call `fit` again.\n",
    "trainer = pl.Trainer(devices=1, accelerator='gpu', max_epochs=2)\n",
    "trainer.fit(quartznet)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "VURa1NavlR0U"
   },
   "source": [
    "### Fast Training\n",
    "\n",
    "Last but not least, we could simply speed up training our model! If you have the resources, you can speed up training by splitting the workload across multiple GPUs. Otherwise (or in addition), there's always mixed precision training, which allows you to increase your batch size.\n",
    "\n",
    "You can use [PyTorch Lightning's Trainer object](https://pytorch-lightning.readthedocs.io/en/latest/common/trainer.html?highlight=Trainer) to handle mixed-precision and distributed training for you. Below are some examples of flags you would pass to the `Trainer` to use these features:\n",
    "\n",
    "```python\n",
    "# Mixed precision:\n",
    "trainer = pl.Trainer(amp_level='O1', precision=16)\n",
    "\n",
    "# Trainer with a distributed backend:\n",
    "trainer = pl.Trainer(devices=2, num_nodes=2, accelerator='gpu', strategy='ddp')\n",
    "\n",
    "# Of course, you can combine these flags as well.\n",
    "```\n",
    "\n",
    "Finally, have a look at [example scripts in NeMo repository](https://github.com/NVIDIA/NeMo/blob/stable/examples/asr/asr_ctc/speech_to_text_ctc.py) which can handle mixed precision and distributed training using command-line arguments."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "d1ym8QT3jQnj"
   },
   "source": [
    "### Deployment\n",
    "\n",
    "Note: It is recommended to run the deployment code from the NVIDIA PyTorch container.\n",
    "\n",
    "Let's get back to our pre-trained model and see how easy it can be exported to an ONNX file\n",
    "in order to run it in an inference engine like TensorRT or ONNXRuntime.\n",
    "\n",
    "If you are running in an environment outside of the NVIDIA PyTorch container (like Google Colab for example) then you will have to build the onnxruntime and onnxruntime-gpu. The cell below gives an example of how to build those runtimes but the example may have to be adapted depending on your environment."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "I4WRcmakjQnj"
   },
   "outputs": [],
   "source": [
    "!pip install --upgrade onnxruntime # for gpu, use onnxruntime-gpu\n",
    "#!mkdir -p ort\n",
    "#%cd ort\n",
    "#!git clean -xfd\n",
    "#!git clone --depth 1 --branch v1.8.0 https://github.com/microsoft/onnxruntime.git .\n",
    "#!./build.sh --skip_tests --config Release --build_shared_lib --parallel --use_cuda --cuda_home /usr/local/cuda --cudnn_home /usr/lib/#x86_64-linux-gnu --build_wheel\n",
    "#!pip uninstall -y onnxruntime\n",
    "#!pip uninstall -y onnxruntime-gpu\n",
    "#!pip install  --upgrade --force-reinstall ./build/Linux/Release/dist/onnxruntime*.whl\n",
    "#%cd .."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "F9yO1BEbjQnm"
   },
   "source": [
    "Then run"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "HZnyWxPyjQnm"
   },
   "outputs": [],
   "source": [
    "import json\n",
    "import os\n",
    "import tempfile\n",
    "import onnxruntime\n",
    "import torch\n",
    "\n",
    "import numpy as np\n",
    "import nemo.collections.asr as nemo_asr\n",
    "from nemo.collections.asr.data.audio_to_text import AudioToCharDataset\n",
    "from nemo.collections.asr.metrics.wer import WER\n",
    "\n",
    "def to_numpy(tensor):\n",
    "    return tensor.detach().cpu().numpy() if tensor.requires_grad else tensor.cpu().numpy()\n",
    "\n",
    "def setup_transcribe_dataloader(cfg, vocabulary):\n",
    "    config = {\n",
    "        'manifest_filepath': os.path.join(cfg['temp_dir'], 'manifest.json'),\n",
    "        'sample_rate': 16000,\n",
    "        'labels': vocabulary,\n",
    "        'batch_size': min(cfg['batch_size'], len(cfg['audio'])),\n",
    "        'trim_silence': True,\n",
    "        'shuffle': False,\n",
    "    }\n",
    "    dataset = AudioToCharDataset(\n",
    "        manifest_filepath=config['manifest_filepath'],\n",
    "        labels=config['labels'],\n",
    "        sample_rate=config['sample_rate'],\n",
    "        int_values=config.get('int_values', False),\n",
    "        augmentor=None,\n",
    "        max_duration=config.get('max_duration', None),\n",
    "        min_duration=config.get('min_duration', None),\n",
    "        max_utts=config.get('max_utts', 0),\n",
    "        blank_index=config.get('blank_index', -1),\n",
    "        unk_index=config.get('unk_index', -1),\n",
    "        normalize=config.get('normalize_transcripts', False),\n",
    "        trim=config.get('trim_silence', True),\n",
    "        parser=config.get('parser', 'en'),\n",
    "    )\n",
    "    return torch.utils.data.DataLoader(\n",
    "        dataset=dataset,\n",
    "        batch_size=config['batch_size'],\n",
    "        collate_fn=dataset.collate_fn,\n",
    "        drop_last=config.get('drop_last', False),\n",
    "        shuffle=False,\n",
    "        num_workers=config.get('num_workers', 0),\n",
    "        pin_memory=config.get('pin_memory', False),\n",
    "    )\n",
    "\n",
    "quartznet = nemo_asr.models.EncDecCTCModel.from_pretrained(model_name=\"QuartzNet15x5Base-En\")\n",
    "\n",
    "quartznet.export('qn.onnx')\n",
    "\n",
    "ort_session = onnxruntime.InferenceSession('qn.onnx', providers=['TensorrtExecutionProvider', 'CUDAExecutionProvider', 'CPUExecutionProvider'])\n",
    "\n",
    "with tempfile.TemporaryDirectory() as tmpdir:\n",
    "    with open(os.path.join(tmpdir, 'manifest.json'), 'w') as fp:\n",
    "        for audio_file in files:\n",
    "            entry = {'audio_filepath': audio_file, 'duration': 100000, 'text': 'nothing'}\n",
    "            fp.write(json.dumps(entry) + '\\n')\n",
    "\n",
    "    config = {'audio': files, 'batch_size': 4, 'temp_dir': tmpdir}\n",
    "    temporary_datalayer = setup_transcribe_dataloader(config, quartznet.decoder.vocabulary)\n",
    "    for test_batch in temporary_datalayer:\n",
    "        processed_signal, processed_signal_len = quartznet.preprocessor(\n",
    "            input_signal=test_batch[0].to(quartznet.device), length=test_batch[1].to(quartznet.device)\n",
    "        )\n",
    "        ort_inputs = {ort_session.get_inputs()[0].name: to_numpy(processed_signal),}\n",
    "        ologits = ort_session.run(None, ort_inputs)\n",
    "        alogits = np.asarray(ologits)\n",
    "        logits = torch.from_numpy(alogits[0])\n",
    "        greedy_predictions = logits.argmax(dim=-1, keepdim=False)\n",
    "        wer = WER(decoding=quartznet.decoding, use_cer=False)\n",
    "        hypotheses = wer.decoding.ctc_decoder_predictions_tensor(greedy_predictions)\n",
    "        print(hypotheses)\n",
    "        break\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "wteGqroafWg1"
   },
   "source": [
    "## Under the Hood\n",
    "\n",
    "NeMo is open-source and we do all our model development in the open, so you can inspect our code if you wish.\n",
    "\n",
    "In particular, ``nemo_asr.model.EncDecCTCModel`` is an encoder-decoder model which is constructed using several ``Neural Modules`` taken from ``nemo_asr.modules.`` Here is what its forward pass looks like:\n",
    "```python\n",
    "def forward(self, input_signal, input_signal_length):\n",
    "    processed_signal, processed_signal_len = self.preprocessor(\n",
    "        input_signal=input_signal, length=input_signal_length,\n",
    "    )\n",
    "    # Spec augment is not applied during evaluation/testing\n",
    "    if self.spec_augmentation is not None and self.training:\n",
    "        processed_signal = self.spec_augmentation(input_spec=processed_signal)\n",
    "    encoded, encoded_len = self.encoder(audio_signal=processed_signal, length=processed_signal_len)\n",
    "    log_probs = self.decoder(encoder_output=encoded)\n",
    "    greedy_predictions = log_probs.argmax(dim=-1, keepdim=False)\n",
    "    return log_probs, encoded_len, greedy_predictions\n",
    "```\n",
    "Here:\n",
    "\n",
    "* ``self.preprocessor`` is an instance of ``nemo_asr.modules.AudioToMelSpectrogramPreprocessor``, which is a neural module that takes audio signal and converts it into a Mel-Spectrogram\n",
    "* ``self.spec_augmentation`` - is a neural module of type ```nemo_asr.modules.SpectrogramAugmentation``, which implements data augmentation. \n",
    "* ``self.encoder`` - is a convolutional Jasper/QuartzNet-like encoder of type ``nemo_asr.modules.ConvASREncoder``\n",
    "* ``self.decoder`` - is a ``nemo_asr.modules.ConvASRDecoder`` which simply projects into the target alphabet (vocabulary).\n",
    "\n",
    "Also, ``EncDecCTCModel`` uses the audio dataset class ``nemo_asr.data.AudioToCharDataset`` and CTC loss implemented in ``nemo_asr.losses.CTCLoss``.\n",
    "\n",
    "You can use these and other neural modules (or create new ones yourself!) to construct new ASR models."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "smzlvbhelR0U"
   },
   "source": [
    "# Further Reading/Watching:\n",
    "\n",
    "That's all for now! If you'd like to learn more about the topics covered in this tutorial, here are some resources that may interest you:\n",
    "- [Stanford Lecture on ASR](https://www.youtube.com/watch?v=3MjIkWxXigM)\n",
    "- [\"An Intuitive Explanation of Connectionist Temporal Classification\"](https://towardsdatascience.com/intuitively-understanding-connectionist-temporal-classification-3797e43a86c)\n",
    "- [Explanation of CTC with Prefix Beam Search](https://medium.com/corti-ai/ctc-networks-and-language-models-prefix-beam-search-explained-c11d1ee23306)\n",
    "- [Listen Attend and Spell Paper (seq2seq ASR model)](https://arxiv.org/abs/1508.01211)\n",
    "- [Explanation of the mel spectrogram in more depth](https://towardsdatascience.com/getting-to-know-the-mel-spectrogram-31bca3e2d9d0)\n",
    "- [Jasper Paper](https://arxiv.org/abs/1904.03288)\n",
    "- [QuartzNet paper](https://arxiv.org/abs/1910.10261)\n",
    "- [SpecAugment Paper](https://arxiv.org/abs/1904.08779)\n",
    "- [Explanation and visualization of SpecAugment](https://towardsdatascience.com/state-of-the-art-audio-data-augmentation-with-google-brains-specaugment-and-pytorch-d3d1a3ce291e)\n",
    "- [Cutout Paper](https://arxiv.org/pdf/1708.04552.pdf)\n",
    "- [Transfer Learning Blogpost](https://developer.nvidia.com/blog/jump-start-training-for-speech-recognition-models-with-nemo/)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "id": "V3ERGX86lR0V"
   },
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "accelerator": "GPU",
  "colab": {
   "collapsed_sections": [],
   "name": "ASR_with_NeMo.ipynb",
   "provenance": [],
   "toc_visible": true
  },
  "kernelspec": {
   "display_name": "Python 3 (ipykernel)",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.10.16"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}