fix: Correct C4 problem statement and solution
Browse files
IMO/md/en-IMO2010SL.md
CHANGED
|
@@ -921,7 +921,7 @@ Move 1: If stack $S_{k}$ with $1 \leq k \leq 5$ contains at least one coin, you
|
|
| 921 |
Move 2: If stack $S_{k}$ with $1 \leq k \leq 4$ contains at least one coin, then you may remove one coin from $S_{k}$ and exchange stacks $S_{k+1}$ and $S_{k+2}$.
|
| 922 |
Decide whether it is possible to achieve by a sequence of such moves that the first five stacks are empty, whereas the sixth stack $S_{6}$ contains exactly $2010^{2010^{2010}}$ coins.
|
| 923 |
|
| 924 |
-
|
| 925 |
(Netherlands)
|
| 926 |
Answer. Yes (in both variants of the problem). There exists such a sequence of moves.
|
| 927 |
Solution. Denote by $\left(a_{1}, a_{2}, \ldots, a_{n}\right) \rightarrow\left(a_{1}^{\prime}, a_{2}^{\prime}, \ldots, a_{n}^{\prime}\right)$ the following: if some consecutive stacks contain $a_{1}, \ldots, a_{n}$ coins, then it is possible to perform several allowed moves such that the stacks contain $a_{1}^{\prime}, \ldots, a_{n}^{\prime}$ coins respectively, whereas the contents of the other stacks remain unchanged.
|
|
|
|
| 921 |
Move 2: If stack $S_{k}$ with $1 \leq k \leq 4$ contains at least one coin, then you may remove one coin from $S_{k}$ and exchange stacks $S_{k+1}$ and $S_{k+2}$.
|
| 922 |
Decide whether it is possible to achieve by a sequence of such moves that the first five stacks are empty, whereas the sixth stack $S_{6}$ contains exactly $2010^{2010^{2010}}$ coins.
|
| 923 |
|
| 924 |
+
Same as Problem C4, but the constant $2010^{2010^{2010}}$ is replaced by $2010^{2010}$.
|
| 925 |
(Netherlands)
|
| 926 |
Answer. Yes (in both variants of the problem). There exists such a sequence of moves.
|
| 927 |
Solution. Denote by $\left(a_{1}, a_{2}, \ldots, a_{n}\right) \rightarrow\left(a_{1}^{\prime}, a_{2}^{\prime}, \ldots, a_{n}^{\prime}\right)$ the following: if some consecutive stacks contain $a_{1}, \ldots, a_{n}$ coins, then it is possible to perform several allowed moves such that the stacks contain $a_{1}^{\prime}, \ldots, a_{n}^{\prime}$ coins respectively, whereas the contents of the other stacks remain unchanged.
|
IMO/segmented/en-IMO2010SL.jsonl
CHANGED
|
@@ -20,8 +20,7 @@
|
|
| 20 |
{"year": "2010", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO", "problem": "On some planet, there are $2^{N}$ countries $(N \\geq 4)$. Each country has a flag $N$ units wide and one unit high composed of $N$ fields of size $1 \\times 1$, each field being either yellow or blue. No two countries have the same flag. We say that a set of $N$ flags is diverse if these flags can be arranged into an $N \\times N$ square so that all $N$ fields on its main diagonal will have the same color. Determine the smallest positive integer $M$ such that among any $M$ distinct flags, there exist $N$ flags forming a diverse set. (Croatia) Answer. $M=2^{N-2}+1$.", "solution": "When speaking about the diagonal of a square, we will always mean the main diagonal. Let $M_{N}$ be the smallest positive integer satisfying the problem condition. First, we show that $M_{N}>2^{N-2}$. Consider the collection of all $2^{N-2}$ flags having yellow first squares and blue second ones. Obviously, both colors appear on the diagonal of each $N \\times N$ square formed by these flags. We are left to show that $M_{N} \\leq 2^{N-2}+1$, thus obtaining the desired answer. We start with establishing this statement for $N=4$. Suppose that we have 5 flags of length 4 . We decompose each flag into two parts of 2 squares each; thereby, we denote each flag as $L R$, where the $2 \\times 1$ flags $L, R \\in \\mathcal{S}=\\{\\mathrm{BB}, \\mathrm{BY}, \\mathrm{YB}, \\mathrm{YY}\\}$ are its left and right parts, respectively. First, we make two easy observations on the flags $2 \\times 1$ which can be checked manually. (i) For each $A \\in \\mathcal{S}$, there exists only one $2 \\times 1$ flag $C \\in \\mathcal{S}$ (possibly $C=A$ ) such that $A$ and $C$ cannot form a $2 \\times 2$ square with monochrome diagonal (for part BB, that is YY, and for BY that is YB). (ii) Let $A_{1}, A_{2}, A_{3} \\in \\mathcal{S}$ be three distinct elements; then two of them can form a $2 \\times 2$ square with yellow diagonal, and two of them can form a $2 \\times 2$ square with blue diagonal (for all parts but BB , a pair $(\\mathrm{BY}, \\mathrm{YB})$ fits for both statements, while for all parts but BY, these pairs are $(\\mathrm{YB}, \\mathrm{YY})$ and (BB, YB)). Now, let $\\ell$ and $r$ be the numbers of distinct left and right parts of our 5 flags, respectively. The total number of flags is $5 \\leq r \\ell$, hence one of the factors (say, $r$ ) should be at least 3 . On the other hand, $\\ell, r \\leq 4$, so there are two flags with coinciding right part; let them be $L_{1} R_{1}$ and $L_{2} R_{1}\\left(L_{1} \\neq L_{2}\\right)$. Next, since $r \\geq 3$, there exist some flags $L_{3} R_{3}$ and $L_{4} R_{4}$ such that $R_{1}, R_{3}, R_{4}$ are distinct. Let $L^{\\prime} R^{\\prime}$ be the remaining flag. By (i), one of the pairs $\\left(L^{\\prime}, L_{1}\\right)$ and $\\left(L^{\\prime}, L_{2}\\right)$ can form a $2 \\times 2$ square with monochrome diagonal; we can assume that $L^{\\prime}, L_{2}$ form a square with a blue diagonal. Finally, the right parts of two of the flags $L_{1} R_{1}, L_{3} R_{3}, L_{4} R_{4}$ can also form a $2 \\times 2$ square with a blue diagonal by (ii). Putting these $2 \\times 2$ squares on the diagonal of a $4 \\times 4$ square, we find a desired arrangement of four flags. We are ready to prove the problem statement by induction on $N$; actually, above we have proved the base case $N=4$. For the induction step, assume that $N>4$, consider any $2^{N-2}+1$ flags of length $N$, and arrange them into a large flag of size $\\left(2^{N-2}+1\\right) \\times N$. This flag contains a non-monochrome column since the flags are distinct; we may assume that this column is the first one. By the pigeonhole principle, this column contains at least $\\left\\lceil\\frac{2^{N-2}+1}{2}\\right\\rceil=2^{N-3}+1$ squares of one color (say, blue). We call the flags with a blue first square good. Consider all the good flags and remove the first square from each of them. We obtain at least $2^{N-3}+1 \\geq M_{N-1}$ flags of length $N-1$; by the induction hypothesis, $N-1$ of them can form a square $Q$ with the monochrome diagonal. Now, returning the removed squares, we obtain a rectangle $(N-1) \\times N$, and our aim is to supplement it on the top by one more flag. If $Q$ has a yellow diagonal, then we can take each flag with a yellow first square (it exists by a choice of the first column; moreover, it is not used in $Q$ ). Conversely, if the diagonal of $Q$ is blue then we can take any of the $\\geq 2^{N-3}+1-(N-1)>0$ remaining good flags. So, in both cases we get a desired $N \\times N$ square.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 21 |
{"year": "2010", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO", "problem": "On some planet, there are $2^{N}$ countries $(N \\geq 4)$. Each country has a flag $N$ units wide and one unit high composed of $N$ fields of size $1 \\times 1$, each field being either yellow or blue. No two countries have the same flag. We say that a set of $N$ flags is diverse if these flags can be arranged into an $N \\times N$ square so that all $N$ fields on its main diagonal will have the same color. Determine the smallest positive integer $M$ such that among any $M$ distinct flags, there exist $N$ flags forming a diverse set. (Croatia) Answer. $M=2^{N-2}+1$.", "solution": "We present a different proof of the estimate $M_{N} \\leq 2^{N-2}+1$. We do not use the induction, involving Hall's lemma on matchings instead. Consider arbitrary $2^{N-2}+1$ distinct flags and arrange them into a large $\\left(2^{N-2}+1\\right) \\times N$ flag. Construct two bipartite graphs $G_{\\mathrm{y}}=\\left(V \\cup V^{\\prime}, E_{\\mathrm{y}}\\right)$ and $G_{\\mathrm{b}}=\\left(V \\cup V^{\\prime}, E_{\\mathrm{b}}\\right)$ with the common set of vertices as follows. Let $V$ and $V^{\\prime}$ be the set of columns and the set of flags under consideration, respectively. Next, let the edge $(c, f)$ appear in $E_{\\mathrm{y}}$ if the intersection of column $c$ and flag $f$ is yellow, and $(c, f) \\in E_{\\mathrm{b}}$ otherwise. Then we have to prove exactly that one of the graphs $G_{\\mathrm{y}}$ and $G_{\\mathrm{b}}$ contains a matching with all the vertices of $V$ involved. Assume that these matchings do not exist. By Hall's lemma, it means that there exist two sets of columns $S_{\\mathrm{y}}, S_{\\mathrm{b}} \\subset V$ such that $\\left|E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)\\right| \\leq\\left|S_{\\mathrm{y}}\\right|-1$ and $\\left|E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right| \\leq\\left|S_{\\mathrm{b}}\\right|-1$ (in the left-hand sides, $E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)$ and $E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)$ denote respectively the sets of all vertices connected to $S_{\\mathrm{y}}$ and $S_{\\mathrm{b}}$ in the corresponding graphs). Our aim is to prove that this is impossible. Note that $S_{\\mathrm{y}}, S_{\\mathrm{b}} \\neq V$ since $N \\leq 2^{N-2}+1$. First, suppose that $S_{\\mathrm{y}} \\cap S_{\\mathrm{b}} \\neq \\varnothing$, so there exists some $c \\in S_{\\mathrm{y}} \\cap S_{\\mathrm{b}}$. Note that each flag is connected to $c$ either in $G_{\\mathrm{y}}$ or in $G_{\\mathrm{b}}$, hence $E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right) \\cup E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)=V^{\\prime}$. Hence we have $2^{N-2}+1=\\left|V^{\\prime}\\right| \\leq\\left|E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)\\right|+\\left|E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right| \\leq\\left|S_{\\mathrm{y}}\\right|+\\left|S_{\\mathrm{b}}\\right|-2 \\leq 2 N-4$; this is impossible for $N \\geq 4$. So, we have $S_{\\mathrm{y}} \\cap S_{\\mathrm{b}}=\\varnothing$. Let $y=\\left|S_{\\mathrm{y}}\\right|, b=\\left|S_{\\mathrm{b}}\\right|$. From the construction of our graph, we have that all the flags in the set $V^{\\prime \\prime}=V^{\\prime} \\backslash\\left(E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right) \\cup E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right)$ have blue squares in the columns of $S_{\\mathrm{y}}$ and yellow squares in the columns of $S_{\\mathrm{b}}$. Hence the only undetermined positions in these flags are the remaining $N-y-b$ ones, so $2^{N-y-b} \\geq\\left|V^{\\prime \\prime}\\right| \\geq\\left|V^{\\prime}\\right|-\\left|E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)\\right|-\\left|E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right| \\geq$ $2^{N-2}+1-(y-1)-(b-1)$, or, denoting $c=y+b, 2^{N-c}+c>2^{N-2}+2$. This is impossible since $N \\geq c \\geq 2$.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 22 |
{"year": "2010", "tier": "T0", "problem_label": "C3", "problem_type": "Combinatorics", "exam": "IMO", "problem": "2500 chess kings have to be placed on a $100 \\times 100$ chessboard so that (i) no king can capture any other one (i.e. no two kings are placed in two squares sharing a common vertex); (ii) each row and each column contains exactly 25 kings. Find the number of such arrangements. (Two arrangements differing by rotation or symmetry are supposed to be different.) (Russia) Answer. There are two such arrangements.", "solution": "Suppose that we have an arrangement satisfying the problem conditions. Divide the board into $2 \\times 2$ pieces; we call these pieces blocks. Each block can contain not more than one king (otherwise these two kings would attack each other); hence, by the pigeonhole principle each block must contain exactly one king. Now assign to each block a letter T or B if a king is placed in its top or bottom half, respectively. Similarly, assign to each block a letter L or R if a king stands in its left or right half. So we define $T$-blocks, $B$-blocks, $L$-blocks, and $R$-blocks. We also combine the letters; we call a block a TL-block if it is simultaneously T-block and L-block. Similarly we define TR-blocks, $B L$-blocks, and BR-blocks. The arrangement of blocks determines uniquely the arrangement of kings; so in the rest of the solution we consider the $50 \\times 50$ system of blocks (see Fig. 1). We identify the blocks by their coordinate pairs; the pair $(i, j)$, where $1 \\leq i, j \\leq 50$, refers to the $j$ th block in the $i$ th row (or the $i$ th block in the $j$ th column). The upper-left block is $(1,1)$. The system of blocks has the following properties.. ( $\\left.\\mathrm{i}^{\\prime}\\right)$ If $(i, j)$ is a B-block then $(i+1, j)$ is a B-block: otherwise the kings in these two blocks can take each other. Similarly: if $(i, j)$ is a T-block then $(i-1, j)$ is a T-block; if $(i, j)$ is an L-block then $(i, j-1)$ is an L-block; if $(i, j)$ is an R-block then $(i, j+1)$ is an R-block. (ii') Each column contains exactly 25 L-blocks and 25 R-blocks, and each row contains exactly 25 T -blocks and 25 B-blocks. In particular, the total number of L-blocks (or R-blocks, or T-blocks, or B-blocks) is equal to $25 \\cdot 50=1250$. Consider any B-block of the form $(1, j)$. By ( $\\mathrm{i}^{\\prime}$ ), all blocks in the $j$ th column are B-blocks; so we call such a column $B$-column. By (ii'), we have 25 B-blocks in the first row, so we obtain 25 B-columns. These 25 B-columns contain 1250 B-blocks, hence all blocks in the remaining columns are T-blocks, and we obtain 25 T-columns. Similarly, there are exactly $25 L$-rows and exactly $25 R$-rows. Now consider an arbitrary pair of a T-column and a neighboring B-column (columns with numbers $j$ and $j+1$ ). 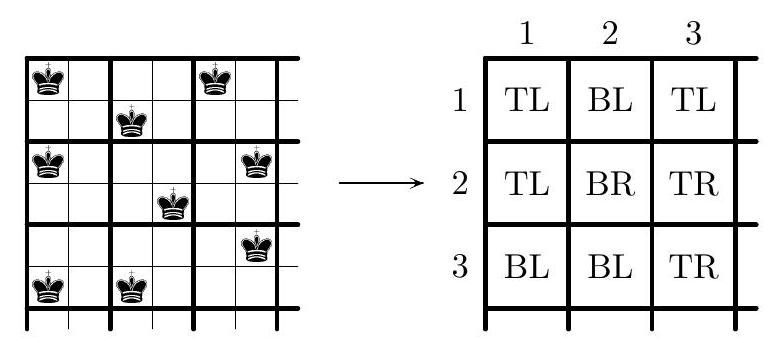 Fig. 1 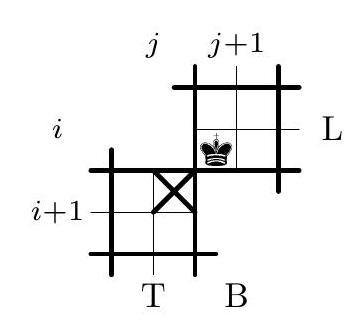 Fig. 2 Case 1. Suppose that the $j$ th column is a T-column, and the $(j+1)$ th column is a Bcolumn. Consider some index $i$ such that the $i$ th row is an L-row; then $(i, j+1)$ is a BL-block. Therefore, $(i+1, j)$ cannot be a TR-block (see Fig. 2), hence $(i+1, j)$ is a TL-block, thus the $(i+1)$ th row is an L-row. Now, choosing the $i$ th row to be the topmost L-row, we successively obtain that all rows from the $i$ th to the 50 th are L-rows. Since we have exactly 25 L-rows, it follows that the rows from the 1st to the 25 th are R-rows, and the rows from the 26 th to the 50th are L-rows. Now consider the neighboring R-row and L-row (that are the rows with numbers 25 and 26). Replacing in the previous reasoning rows by columns and vice versa, the columns from the 1 st to the 25 th are T-columns, and the columns from the 26 th to the 50 th are B-columns. So we have a unique arrangement of blocks that leads to the arrangement of kings satisfying the condition of the problem (see Fig. 3). 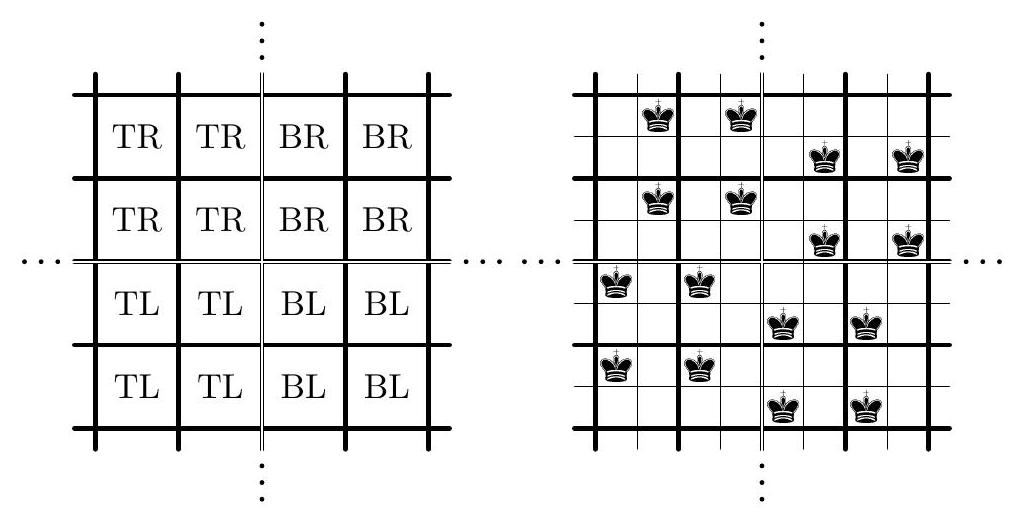 Fig. 3 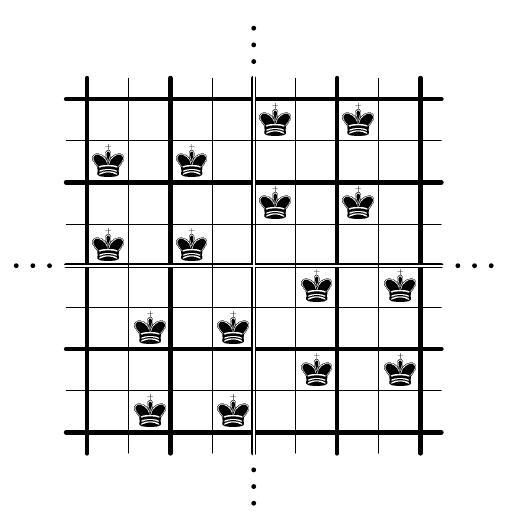 Fig. 4 Case 2. Suppose that the $j$ th column is a B-column, and the $(j+1)$ th column is a T-column. Repeating the arguments from Case 1, we obtain that the rows from the 1st to the 25th are L-rows (and all other rows are R-rows), the columns from the 1st to the 25 th are B-columns (and all other columns are T-columns), so we find exactly one more arrangement of kings (see Fig. 4).", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 23 |
-
{"year": "2010", "tier": "T0", "problem_label": "C4", "problem_type": "Combinatorics", "exam": "IMO", "problem": "Six stacks $S_{1}, \\ldots, S_{6}$ of coins are standing in a row. In the beginning every stack contains a single coin. There are two types of allowed moves: Move 1: If stack $S_{k}$ with $1 \\leq k \\leq 5$ contains at least one coin, you may remove one coin from $S_{k}$ and add two coins to $S_{k+1}$. Move 2: If stack $S_{k}$ with $1 \\leq k \\leq 4$ contains at least one coin, then you may remove one coin from $S_{k}$ and exchange stacks $S_{k+1}$ and $S_{k+2}$. Decide whether it is possible to achieve by a sequence of such moves that the first five stacks are empty, whereas the sixth stack $S_{6}$ contains exactly $2010^{2010^{2010}}$ coins.", "solution": "Denote by $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right) \\rightarrow\\left(a_{1}^{\\prime}, a_{2}^{\\prime}, \\ldots, a_{n}^{\\prime}\\right)$ the following: if some consecutive stacks contain $a_{1}, \\ldots, a_{n}$ coins, then it is possible to perform several allowed moves such that the stacks contain $a_{1}^{\\prime}, \\ldots, a_{n}^{\\prime}$ coins respectively, whereas the contents of the other stacks remain unchanged. Let $A=2010^{2010}$ or $A=2010^{2010^{2010}}$, respectively. Our goal is to show that $$ (1,1,1,1,1,1) \\rightarrow(0,0,0,0,0, A) $$ First we prove two auxiliary observations. Lemma 1. $(a, 0,0) \\rightarrow\\left(0,2^{a}, 0\\right)$ for every $a \\geq 1$. Proof. We prove by induction that $(a, 0,0) \\rightarrow\\left(a-k, 2^{k}, 0\\right)$ for every $1 \\leq k \\leq a$. For $k=1$, apply Move 1 to the first stack: $$ (a, 0,0) \\rightarrow(a-1,2,0)=\\left(a-1,2^{1}, 0\\right) $$ Now assume that $k<a$ and the statement holds for some $k<a$. Starting from $\\left(a-k, 2^{k}, 0\\right)$, apply Move 1 to the middle stack $2^{k}$ times, until it becomes empty. Then apply Move 2 to the first stack: $$ \\left(a-k, 2^{k}, 0\\right) \\rightarrow\\left(a-k, 2^{k}-1,2\\right) \\rightarrow \\cdots \\rightarrow\\left(a-k, 0,2^{k+1}\\right) \\rightarrow\\left(a-k-1,2^{k+1}, 0\\right) $$ Hence, $$ (a, 0,0) \\rightarrow\\left(a-k, 2^{k}, 0\\right) \\rightarrow\\left(a-k-1,2^{k+1}, 0\\right) $$ Lemma 2. For every positive integer $n$, let $P_{n}=\\underbrace{2^{2 \\cdot y^{2}}}_{n}$ (e.g. $\\quad P_{3}=2^{2^{2}}=16$ ). Then $(a, 0,0,0) \\rightarrow\\left(0, P_{a}, 0,0\\right)$ for every $a \\geq 1$. Proof. Similarly to Lemma 1 , we prove that $(a, 0,0,0) \\rightarrow\\left(a-k, P_{k}, 0,0\\right)$ for every $1 \\leq k \\leq a$. For $k=1$, apply Move 1 to the first stack: $$ (a, 0,0,0) \\rightarrow(a-1,2,0,0)=\\left(a-1, P_{1}, 0,0\\right) $$ Now assume that the lemma holds for some $k<a$. Starting from ( $a-k, P_{k}, 0,0$ ), apply Lemma 1, then apply Move 1 to the first stack: $$ \\left(a-k, P_{k}, 0,0\\right) \\rightarrow\\left(a-k, 0,2^{P_{k}}, 0\\right)=\\left(a-k, 0, P_{k+1}, 0\\right) \\rightarrow\\left(a-k-1, P_{k+1}, 0,0\\right) $$ Therefore, $$ (a, 0,0,0) \\rightarrow\\left(a-k, P_{k}, 0,0\\right) \\rightarrow\\left(a-k-1, P_{k+1}, 0,0\\right) $$ Now we prove the statement of the problem. First apply Move 1 to stack 5 , then apply Move 2 to stacks $S_{4}, S_{3}, S_{2}$ and $S_{1}$ in this order. Then apply Lemma 2 twice: $$ \\begin{gathered} (1,1,1,1,1,1) \\rightarrow(1,1,1,1,0,3) \\rightarrow(1,1,1,0,3,0) \\rightarrow(1,1,0,3,0,0) \\rightarrow(1,0,3,0,0,0) \\rightarrow \\\\ \\rightarrow(0,3,0,0,0,0) \\rightarrow\\left(0,0, P_{3}, 0,0,0\\right)=(0,0,16,0,0,0) \\rightarrow\\left(0,0,0, P_{16}, 0,0\\right) \\end{gathered} $$ We already have more than $A$ coins in stack $S_{4}$, since $$ A \\leq 2010^{2010^{2010}}<\\left(2^{11}\\right)^{2010^{2010}}=2^{11 \\cdot 2010^{2010}}<2^{2010^{2011}}<2^{\\left(2^{11}\\right)^{2011}}=2^{2^{11 \\cdot 2011}}<2^{2^{2^{15}}}<P_{16} $$ To decrease the number of coins in stack $S_{4}$, apply Move 2 to this stack repeatedly until its size decreases to $A / 4$. (In every step, we remove a coin from $S_{4}$ and exchange the empty stacks $S_{5}$ and $S_{6}$.) $$ \\begin{aligned} \\left(0,0,0, P_{16}, 0,0\\right) \\rightarrow & \\left(0,0,0, P_{16}-1,0,0\\right) \\rightarrow\\left(0,0,0, P_{16}-2,0,0\\right) \\rightarrow \\\\ & \\rightarrow \\cdots \\rightarrow(0,0,0, A / 4,0,0) . \\end{aligned} $$ Finally, apply Move 1 repeatedly to empty stacks $S_{4}$ and $S_{5}$ : $$ (0,0,0, A / 4,0,0) \\rightarrow \\cdots \\rightarrow(0,0,0,0, A / 2,0) \\rightarrow \\cdots \\rightarrow(0,0,0,0,0, A) $$ Comment 1. Starting with only 4 stack, it is not hard to check manually that we can achieve at most 28 coins in the last position. However, around 5 and 6 stacks the maximal number of coins explodes. With 5 stacks it is possible to achieve more than $2^{2^{14}}$ coins. With 6 stacks the maximum is greater than $P_{P_{2^{14}}}$. It is not hard to show that the numbers $2010^{2010}$ and $2010^{2010^{2010}}$ in the problem can be replaced by any nonnegative integer up to $P_{P_{214}}$. Comment 2. The simpler variant $\\mathrm{C}^{\\prime}$ of the problem can be solved without Lemma 2: $$ \\begin{aligned} (1,1,1,1,1,1) & \\rightarrow(0,3,1,1,1,1) \\rightarrow(0,1,5,1,1,1) \\rightarrow(0,1,1,9,1,1) \\rightarrow \\\\ & \\rightarrow(0,1,1,1,17,1) \\rightarrow(0,1,1,1,0,35) \\rightarrow(0,1,1,0,35,0) \\rightarrow(0,1,0,35,0,0) \\rightarrow \\\\ & \\rightarrow(0,0,35,0,0,0) \\rightarrow\\left(0,0,1,2^{34}, 0,0\\right) \\rightarrow\\left(0,0,1,0,2^{2^{34}}, 0\\right) \\rightarrow\\left(0,0,0,2^{2^{34}}, 0,0\\right) \\\\ & \\rightarrow\\left(0,0,0,2^{2^{34}}-1,0,0\\right) \\rightarrow \\ldots \\rightarrow(0,0,0, A / 4,0,0) \\rightarrow(0,0,0,0, A / 2,0) \\rightarrow(0,0,0,0,0, A) . \\end{aligned} $$ For this reason, the PSC suggests to consider the problem C4 as well. Problem C4 requires more invention and technical care. On the other hand, the problem statement in $\\mathrm{C} 4^{\\prime}$ hides the fact that the resulting amount of coins can be such incredibly huge and leaves this discovery to the students.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 24 |
-
{"year": "2010", "tier": "T0", "problem_label": "C4", "problem_type": "Combinatorics", "exam": "IMO", "problem": "${ }^{\\prime}$. Same as Problem C4, but the constant $2010^{2010^{2010}}$ is replaced by $2010^{2010}$. (Netherlands) Answer. Yes (in both variants of the problem). There exists such a sequence of moves.", "solution": "Denote by $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right) \\rightarrow\\left(a_{1}^{\\prime}, a_{2}^{\\prime}, \\ldots, a_{n}^{\\prime}\\right)$ the following: if some consecutive stacks contain $a_{1}, \\ldots, a_{n}$ coins, then it is possible to perform several allowed moves such that the stacks contain $a_{1}^{\\prime}, \\ldots, a_{n}^{\\prime}$ coins respectively, whereas the contents of the other stacks remain unchanged. Let $A=2010^{2010}$ or $A=2010^{2010^{2010}}$, respectively. Our goal is to show that $$ (1,1,1,1,1,1) \\rightarrow(0,0,0,0,0, A) $$ First we prove two auxiliary observations. Lemma 1. $(a, 0,0) \\rightarrow\\left(0,2^{a}, 0\\right)$ for every $a \\geq 1$. Proof. We prove by induction that $(a, 0,0) \\rightarrow\\left(a-k, 2^{k}, 0\\right)$ for every $1 \\leq k \\leq a$. For $k=1$, apply Move 1 to the first stack: $$ (a, 0,0) \\rightarrow(a-1,2,0)=\\left(a-1,2^{1}, 0\\right) $$ Now assume that $k<a$ and the statement holds for some $k<a$. Starting from $\\left(a-k, 2^{k}, 0\\right)$, apply Move 1 to the middle stack $2^{k}$ times, until it becomes empty. Then apply Move 2 to the first stack: $$ \\left(a-k, 2^{k}, 0\\right) \\rightarrow\\left(a-k, 2^{k}-1,2\\right) \\rightarrow \\cdots \\rightarrow\\left(a-k, 0,2^{k+1}\\right) \\rightarrow\\left(a-k-1,2^{k+1}, 0\\right) $$ Hence, $$ (a, 0,0) \\rightarrow\\left(a-k, 2^{k}, 0\\right) \\rightarrow\\left(a-k-1,2^{k+1}, 0\\right) $$ Lemma 2. For every positive integer $n$, let $P_{n}=\\underbrace{2^{2 \\cdot y^{2}}}_{n}$ (e.g. $\\quad P_{3}=2^{2^{2}}=16$ ). Then $(a, 0,0,0) \\rightarrow\\left(0, P_{a}, 0,0\\right)$ for every $a \\geq 1$. Proof. Similarly to Lemma 1 , we prove that $(a, 0,0,0) \\rightarrow\\left(a-k, P_{k}, 0,0\\right)$ for every $1 \\leq k \\leq a$. For $k=1$, apply Move 1 to the first stack: $$ (a, 0,0,0) \\rightarrow(a-1,2,0,0)=\\left(a-1, P_{1}, 0,0\\right) $$ Now assume that the lemma holds for some $k<a$. Starting from ( $a-k, P_{k}, 0,0$ ), apply Lemma 1, then apply Move 1 to the first stack: $$ \\left(a-k, P_{k}, 0,0\\right) \\rightarrow\\left(a-k, 0,2^{P_{k}}, 0\\right)=\\left(a-k, 0, P_{k+1}, 0\\right) \\rightarrow\\left(a-k-1, P_{k+1}, 0,0\\right) $$ Therefore, $$ (a, 0,0,0) \\rightarrow\\left(a-k, P_{k}, 0,0\\right) \\rightarrow\\left(a-k-1, P_{k+1}, 0,0\\right) $$ Now we prove the statement of the problem. First apply Move 1 to stack 5 , then apply Move 2 to stacks $S_{4}, S_{3}, S_{2}$ and $S_{1}$ in this order. Then apply Lemma 2 twice: $$ \\begin{gathered} (1,1,1,1,1,1) \\rightarrow(1,1,1,1,0,3) \\rightarrow(1,1,1,0,3,0) \\rightarrow(1,1,0,3,0,0) \\rightarrow(1,0,3,0,0,0) \\rightarrow \\\\ \\rightarrow(0,3,0,0,0,0) \\rightarrow\\left(0,0, P_{3}, 0,0,0\\right)=(0,0,16,0,0,0) \\rightarrow\\left(0,0,0, P_{16}, 0,0\\right) \\end{gathered} $$ We already have more than $A$ coins in stack $S_{4}$, since $$ A \\leq 2010^{2010^{2010}}<\\left(2^{11}\\right)^{2010^{2010}}=2^{11 \\cdot 2010^{2010}}<2^{2010^{2011}}<2^{\\left(2^{11}\\right)^{2011}}=2^{2^{11 \\cdot 2011}}<2^{2^{2^{15}}}<P_{16} $$ To decrease the number of coins in stack $S_{4}$, apply Move 2 to this stack repeatedly until its size decreases to $A / 4$. (In every step, we remove a coin from $S_{4}$ and exchange the empty stacks $S_{5}$ and $S_{6}$.) $$ \\begin{aligned} \\left(0,0,0, P_{16}, 0,0\\right) \\rightarrow & \\left(0,0,0, P_{16}-1,0,0\\right) \\rightarrow\\left(0,0,0, P_{16}-2,0,0\\right) \\rightarrow \\\\ & \\rightarrow \\cdots \\rightarrow(0,0,0, A / 4,0,0) . \\end{aligned} $$ Finally, apply Move 1 repeatedly to empty stacks $S_{4}$ and $S_{5}$ : $$ (0,0,0, A / 4,0,0) \\rightarrow \\cdots \\rightarrow(0,0,0,0, A / 2,0) \\rightarrow \\cdots \\rightarrow(0,0,0,0,0, A) $$ Comment 1. Starting with only 4 stack, it is not hard to check manually that we can achieve at most 28 coins in the last position. However, around 5 and 6 stacks the maximal number of coins explodes. With 5 stacks it is possible to achieve more than $2^{2^{14}}$ coins. With 6 stacks the maximum is greater than $P_{P_{2^{14}}}$. It is not hard to show that the numbers $2010^{2010}$ and $2010^{2010^{2010}}$ in the problem can be replaced by any nonnegative integer up to $P_{P_{214}}$. Comment 2. The simpler variant $\\mathrm{C}^{\\prime}$ of the problem can be solved without Lemma 2: $$ \\begin{aligned} (1,1,1,1,1,1) & \\rightarrow(0,3,1,1,1,1) \\rightarrow(0,1,5,1,1,1) \\rightarrow(0,1,1,9,1,1) \\rightarrow \\\\ & \\rightarrow(0,1,1,1,17,1) \\rightarrow(0,1,1,1,0,35) \\rightarrow(0,1,1,0,35,0) \\rightarrow(0,1,0,35,0,0) \\rightarrow \\\\ & \\rightarrow(0,0,35,0,0,0) \\rightarrow\\left(0,0,1,2^{34}, 0,0\\right) \\rightarrow\\left(0,0,1,0,2^{2^{34}}, 0\\right) \\rightarrow\\left(0,0,0,2^{2^{34}}, 0,0\\right) \\\\ & \\rightarrow\\left(0,0,0,2^{2^{34}}-1,0,0\\right) \\rightarrow \\ldots \\rightarrow(0,0,0, A / 4,0,0) \\rightarrow(0,0,0,0, A / 2,0) \\rightarrow(0,0,0,0,0, A) . \\end{aligned} $$ For this reason, the PSC suggests to consider the problem C4 as well. Problem C4 requires more invention and technical care. On the other hand, the problem statement in $\\mathrm{C} 4^{\\prime}$ hides the fact that the resulting amount of coins can be such incredibly huge and leaves this discovery to the students.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 25 |
{"year": "2010", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO", "problem": "$n \\geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3} \\geq 0 $$ (South Korea)", "solution": "For any tournament $T$ satisfying the problem condition, denote by $S(T)$ sum under consideration, namely $$ S(T)=\\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3} $$ First, we show that the statement holds if a tournament $T$ has only 4 players. Actually, let $A=\\left(a_{1}, a_{2}, a_{3}, a_{4}\\right)$ be the number of wins of the players; we may assume that $a_{1} \\geq a_{2} \\geq a_{3} \\geq a_{4}$. We have $a_{1}+a_{2}+a_{3}+a_{4}=\\binom{4}{2}=6$, hence $a_{4} \\leq 1$. If $a_{4}=0$, then we cannot have $a_{1}=a_{2}=a_{3}=2$, otherwise the company of all players is bad. Hence we should have $A=(3,2,1,0)$, and $S(T)=3^{3}+1^{3}+(-1)^{3}+(-3)^{3}=0$. On the other hand, if $a_{4}=1$, then only two possibilities, $A=(3,1,1,1)$ and $A=(2,2,1,1)$ can take place. In the former case we have $S(T)=3^{3}+3 \\cdot(-2)^{3}>0$, while in the latter one $S(T)=1^{3}+1^{3}+(-1)^{3}+(-1)^{3}=0$, as desired. Now we turn to the general problem. Consider a tournament $T$ with no bad companies and enumerate the players by the numbers from 1 to $n$. For every 4 players $i_{1}, i_{2}, i_{3}, i_{4}$ consider a \"sub-tournament\" $T_{i_{1} i_{2} i_{3} i_{4}}$ consisting of only these players and the games which they performed with each other. By the abovementioned, we have $S\\left(T_{i_{1} i_{2} i_{3} i_{4}}\\right) \\geq 0$. Our aim is to prove that $$ S(T)=\\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S\\left(T_{i_{1} i_{2} i_{3} i_{4}}\\right) $$ where the sum is taken over all 4 -tuples of distinct numbers from the set $\\{1, \\ldots, n\\}$. This way the problem statement will be established. We interpret the number $\\left(w_{i}-\\ell_{i}\\right)^{3}$ as following. For $i \\neq j$, let $\\varepsilon_{i j}=1$ if the $i$ th player wins against the $j$ th one, and $\\varepsilon_{i j}=-1$ otherwise. Then $$ \\left(w_{i}-\\ell_{i}\\right)^{3}=\\left(\\sum_{j \\neq i} \\varepsilon_{i j}\\right)^{3}=\\sum_{j_{1}, j_{2}, j_{3} \\neq i} \\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}} . $$ Hence, $$ S(T)=\\sum_{i \\notin\\left\\{j_{1}, j_{2}, j_{3}\\right\\}} \\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}} $$ To simplify this expression, consider all the terms in this sum where two indices are equal. If, for instance, $j_{1}=j_{2}$, then the term contains $\\varepsilon_{i j_{1}}^{2}=1$, so we can replace this term by $\\varepsilon_{i j_{3}}$. Make such replacements for each such term; obviously, after this change each term of the form $\\varepsilon_{i j_{3}}$ will appear $P(T)$ times, hence $$ S(T)=\\sum_{\\left|\\left\\{i, j_{1}, j_{2}, j_{3}\\right\\}\\right|=4} \\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}}+P(T) \\sum_{i \\neq j} \\varepsilon_{i j}=S_{1}(T)+P(T) S_{2}(T) $$ We show that $S_{2}(T)=0$ and hence $S(T)=S_{1}(T)$ for each tournament. Actually, note that $\\varepsilon_{i j}=-\\varepsilon_{j i}$, and the whole sum can be split into such pairs. Since the sum in each pair is 0 , so is $S_{2}(T)$. Thus the desired equality (2) rewrites as $$ S_{1}(T)=\\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S_{1}\\left(T_{i_{1} i_{2} i_{3} i_{4}}\\right) $$ Now, if all the numbers $j_{1}, j_{2}, j_{3}$ are distinct, then the set $\\left\\{i, j_{1}, j_{2}, j_{3}\\right\\}$ is contained in exactly one 4 -tuple, hence the term $\\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}}$ appears in the right-hand part of (3) exactly once, as well as in the left-hand part. Clearly, there are no other terms in both parts, so the equality is established.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 26 |
{"year": "2010", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO", "problem": "$n \\geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3} \\geq 0 $$ (South Korea)", "solution": "Similarly to the first solution, we call the subsets of players as companies, and the $k$-element subsets will be called as $k$-companies. In any company of the players, call a player the local champion of the company if he defeated all other members of the company. Similarly, if a player lost all his games against the others in the company then call him the local loser of the company. Obviously every company has at most one local champion and at most one local loser. By the condition of the problem, whenever a 4-company has a local loser, then this company has a local champion as well. Suppose that $k$ is some positive integer, and let us count all cases when a player is the local champion of some $k$-company. The $i$ th player won against $w_{i}$ other player. To be the local champion of a $k$-company, he must be a member of the company, and the other $k-1$ members must be chosen from those whom he defeated. Therefore, the $i$ th player is the local champion of $\\binom{w_{i}}{k-1} k$-companies. Hence, the total number of local champions of all $k$-companies is $\\sum_{i=1}^{n}\\binom{w_{i}}{k-1}$. Similarly, the total number of local losers of the $k$-companies is $\\sum_{i=1}^{n}\\binom{\\ell_{i}}{k-1}$. Now apply this for $k=2,3$ and 4. Since every game has a winner and a loser, we have $\\sum_{i=1}^{n} w_{i}=\\sum_{i=1}^{n} \\ell_{i}=\\binom{n}{2}$, and hence $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)=0 $$ In every 3-company, either the players defeated one another in a cycle or the company has both a local champion and a local loser. Therefore, the total number of local champions and local losers in the 3-companies is the same, $\\sum_{i=1}^{n}\\binom{w_{i}}{2}=\\sum_{i=1}^{n}\\binom{\\ell_{i}}{2}$. So we have $$ \\sum_{i=1}^{n}\\left(\\binom{w_{i}}{2}-\\binom{\\ell_{i}}{2}\\right)=0 $$ In every 4-company, by the problem's condition, the number of local losers is less than or equal to the number of local champions. Then the same holds for the total numbers of local champions and local losers in all 4-companies, so $\\sum_{i=1}^{n}\\binom{w_{i}}{3} \\geq \\sum_{i=1}^{n}\\binom{\\ell_{i}}{3}$. Hence, $$ \\sum_{i=1}^{n}\\left(\\binom{w_{i}}{3}-\\binom{\\ell_{i}}{3}\\right) \\geq 0 $$ Now we establish the problem statement (1) as a linear combination of (4), (5) and (6). It is easy check that $$ (x-y)^{3}=24\\left(\\binom{x}{3}-\\binom{y}{3}\\right)+24\\left(\\binom{x}{2}-\\binom{y}{2}\\right)-\\left(3(x+y)^{2}-4\\right)(x-y) $$ Apply this identity to $x=w_{1}$ and $y=\\ell_{i}$. Since every player played $n-1$ games, we have $w_{i}+\\ell_{i}=n-1$, and thus $$ \\left(w_{i}-\\ell_{i}\\right)^{3}=24\\left(\\binom{w_{i}}{3}-\\binom{\\ell_{i}}{3}\\right)+24\\left(\\binom{w_{i}}{2}-\\binom{\\ell_{i}}{2}\\right)-\\left(3(n-1)^{2}-4\\right)\\left(w_{i}-\\ell_{i}\\right) $$ Then $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3}=24 \\underbrace{\\sum_{i=1}^{n}\\left(\\binom{w_{i}}{3}-\\binom{\\ell_{i}}{3}\\right)}_{\\geq 0}+24 \\underbrace{\\sum_{i=1}^{n}\\left(\\binom{w_{i}}{2}-\\binom{\\ell_{i}}{2}\\right)}_{0}-\\left(3(n-1)^{2}-4\\right) \\underbrace{\\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)}_{0} \\geq 0 $$", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 27 |
{"year": "2010", "tier": "T0", "problem_label": "C6", "problem_type": "Combinatorics", "exam": "IMO", "problem": "Given a positive integer $k$ and other two integers $b>w>1$. There are two strings of pearls, a string of $b$ black pearls and a string of $w$ white pearls. The length of a string is the number of pearls on it. One cuts these strings in some steps by the following rules. In each step: (i) The strings are ordered by their lengths in a non-increasing order. If there are some strings of equal lengths, then the white ones precede the black ones. Then $k$ first ones (if they consist of more than one pearl) are chosen; if there are less than $k$ strings longer than 1 , then one chooses all of them. (ii) Next, one cuts each chosen string into two parts differing in length by at most one. (For instance, if there are strings of $5,4,4,2$ black pearls, strings of $8,4,3$ white pearls and $k=4$, then the strings of 8 white, 5 black, 4 white and 4 black pearls are cut into the parts $(4,4),(3,2),(2,2)$ and $(2,2)$, respectively.) The process stops immediately after the step when a first isolated white pearl appears. Prove that at this stage, there will still exist a string of at least two black pearls. (Canada)", "solution": "Denote the situation after the $i$ th step by $A_{i}$; hence $A_{0}$ is the initial situation, and $A_{i-1} \\rightarrow A_{i}$ is the $i$ th step. We call a string containing $m$ pearls an $m$-string; it is an $m$-w-string or a $m$-b-string if it is white or black, respectively. We continue the process until every string consists of a single pearl. We will focus on three moments of the process: (a) the first stage $A_{s}$ when the first 1 -string (no matter black or white) appears; (b) the first stage $A_{t}$ where the total number of strings is greater than $k$ (if such moment does not appear then we put $t=\\infty$ ); and (c) the first stage $A_{f}$ when all black pearls are isolated. It is sufficient to prove that in $A_{f-1}$ (or earlier), a 1-w-string appears. We start with some easy properties of the situations under consideration. Obviously, we have $s \\leq f$. Moreover, all b-strings from $A_{f-1}$ become single pearls in the $f$ th step, hence all of them are 1- or 2-b-strings. Next, observe that in each step $A_{i} \\rightarrow A_{i+1}$ with $i \\leq t-1$, all $(>1)$-strings were cut since there are not more than $k$ strings at all; if, in addition, $i<s$, then there were no 1 -string, so all the strings were cut in this step. Now, let $B_{i}$ and $b_{i}$ be the lengths of the longest and the shortest b-strings in $A_{i}$, and let $W_{i}$ and $w_{i}$ be the same for w-strings. We show by induction on $i \\leq \\min \\{s, t\\}$ that (i) the situation $A_{i}$ contains exactly $2^{i}$ black and $2^{i}$ white strings, (ii) $B_{i} \\geq W_{i}$, and (iii) $b_{i} \\geq w_{i}$. The base case $i=0$ is obvious. For the induction step, if $i \\leq \\min \\{s, t\\}$ then in the $i$ th step, each string is cut, thus the claim (i) follows from the induction hypothesis; next, we have $B_{i}=\\left\\lceil B_{i-1} / 2\\right\\rceil \\geq\\left\\lceil W_{i-1} / 2\\right\\rceil=W_{i}$ and $b_{i}=\\left\\lfloor b_{i-1} / 2\\right\\rfloor \\geq\\left\\lfloor w_{i-1} / 2\\right\\rfloor=w_{i}$, thus establishing (ii) and (iii). For the numbers $s, t, f$, two cases are possible. Case 1. Suppose that $s \\leq t$ or $f \\leq t+1$ (and hence $s \\leq t+1$ ); in particular, this is true when $t=\\infty$. Then in $A_{s-1}$ we have $B_{s-1} \\geq W_{s-1}, b_{s-1} \\geq w_{s-1}>1$ as $s-1 \\leq \\min \\{s, t\\}$. Now, if $s=f$, then in $A_{s-1}$, there is no 1 -w-string as well as no ( $>2$ )-b-string. That is, $2=B_{s-1} \\geq W_{s-1} \\geq b_{s-1} \\geq w_{s-1}>1$, hence all these numbers equal 2 . This means that in $A_{s-1}$, all strings contain 2 pearls, and there are $2^{s-1}$ black and $2^{s-1}$ white strings, which means $b=2 \\cdot 2^{s-1}=w$. This contradicts the problem conditions. Hence we have $s \\leq f-1$ and thus $s \\leq t$. Therefore, in the $s$ th step each string is cut into two parts. Now, if a 1-b-string appears in this step, then from $w_{s-1} \\leq b_{s-1}$ we see that a 1-w-string appears as well; so, in each case in the sth step a 1-w-string appears, while not all black pearls become single, as desired. Case 2. Now assume that $t+1 \\leq s$ and $t+2 \\leq f$. Then in $A_{t}$ we have exactly $2^{t}$ white and $2^{t}$ black strings, all being larger than 1 , and $2^{t+1}>k \\geq 2^{t}$ (the latter holds since $2^{t}$ is the total number of strings in $A_{t-1}$ ). Now, in the $(t+1)$ st step, exactly $k$ strings are cut, not more than $2^{t}$ of them being black; so the number of w-strings in $A_{t+1}$ is at least $2^{t}+\\left(k-2^{t}\\right)=k$. Since the number of w-strings does not decrease in our process, in $A_{f-1}$ we have at least $k$ white strings as well. Finally, in $A_{f-1}$, all b-strings are not larger than 2, and at least one 2-b-string is cut in the $f$ th step. Therefore, at most $k-1$ white strings are cut in this step, hence there exists a w-string $\\mathcal{W}$ which is not cut in the $f$ th step. On the other hand, since a 2 -b-string is cut, all $(\\geq 2)$-w-strings should also be cut in the $f$ th step; hence $\\mathcal{W}$ should be a single pearl. This is exactly what we needed. Comment. In this solution, we used the condition $b \\neq w$ only to avoid the case $b=w=2^{t}$. Hence, if a number $b=w$ is not a power of 2 , then the problem statement is also valid.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
|
|
|
| 20 |
{"year": "2010", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO", "problem": "On some planet, there are $2^{N}$ countries $(N \\geq 4)$. Each country has a flag $N$ units wide and one unit high composed of $N$ fields of size $1 \\times 1$, each field being either yellow or blue. No two countries have the same flag. We say that a set of $N$ flags is diverse if these flags can be arranged into an $N \\times N$ square so that all $N$ fields on its main diagonal will have the same color. Determine the smallest positive integer $M$ such that among any $M$ distinct flags, there exist $N$ flags forming a diverse set. (Croatia) Answer. $M=2^{N-2}+1$.", "solution": "When speaking about the diagonal of a square, we will always mean the main diagonal. Let $M_{N}$ be the smallest positive integer satisfying the problem condition. First, we show that $M_{N}>2^{N-2}$. Consider the collection of all $2^{N-2}$ flags having yellow first squares and blue second ones. Obviously, both colors appear on the diagonal of each $N \\times N$ square formed by these flags. We are left to show that $M_{N} \\leq 2^{N-2}+1$, thus obtaining the desired answer. We start with establishing this statement for $N=4$. Suppose that we have 5 flags of length 4 . We decompose each flag into two parts of 2 squares each; thereby, we denote each flag as $L R$, where the $2 \\times 1$ flags $L, R \\in \\mathcal{S}=\\{\\mathrm{BB}, \\mathrm{BY}, \\mathrm{YB}, \\mathrm{YY}\\}$ are its left and right parts, respectively. First, we make two easy observations on the flags $2 \\times 1$ which can be checked manually. (i) For each $A \\in \\mathcal{S}$, there exists only one $2 \\times 1$ flag $C \\in \\mathcal{S}$ (possibly $C=A$ ) such that $A$ and $C$ cannot form a $2 \\times 2$ square with monochrome diagonal (for part BB, that is YY, and for BY that is YB). (ii) Let $A_{1}, A_{2}, A_{3} \\in \\mathcal{S}$ be three distinct elements; then two of them can form a $2 \\times 2$ square with yellow diagonal, and two of them can form a $2 \\times 2$ square with blue diagonal (for all parts but BB , a pair $(\\mathrm{BY}, \\mathrm{YB})$ fits for both statements, while for all parts but BY, these pairs are $(\\mathrm{YB}, \\mathrm{YY})$ and (BB, YB)). Now, let $\\ell$ and $r$ be the numbers of distinct left and right parts of our 5 flags, respectively. The total number of flags is $5 \\leq r \\ell$, hence one of the factors (say, $r$ ) should be at least 3 . On the other hand, $\\ell, r \\leq 4$, so there are two flags with coinciding right part; let them be $L_{1} R_{1}$ and $L_{2} R_{1}\\left(L_{1} \\neq L_{2}\\right)$. Next, since $r \\geq 3$, there exist some flags $L_{3} R_{3}$ and $L_{4} R_{4}$ such that $R_{1}, R_{3}, R_{4}$ are distinct. Let $L^{\\prime} R^{\\prime}$ be the remaining flag. By (i), one of the pairs $\\left(L^{\\prime}, L_{1}\\right)$ and $\\left(L^{\\prime}, L_{2}\\right)$ can form a $2 \\times 2$ square with monochrome diagonal; we can assume that $L^{\\prime}, L_{2}$ form a square with a blue diagonal. Finally, the right parts of two of the flags $L_{1} R_{1}, L_{3} R_{3}, L_{4} R_{4}$ can also form a $2 \\times 2$ square with a blue diagonal by (ii). Putting these $2 \\times 2$ squares on the diagonal of a $4 \\times 4$ square, we find a desired arrangement of four flags. We are ready to prove the problem statement by induction on $N$; actually, above we have proved the base case $N=4$. For the induction step, assume that $N>4$, consider any $2^{N-2}+1$ flags of length $N$, and arrange them into a large flag of size $\\left(2^{N-2}+1\\right) \\times N$. This flag contains a non-monochrome column since the flags are distinct; we may assume that this column is the first one. By the pigeonhole principle, this column contains at least $\\left\\lceil\\frac{2^{N-2}+1}{2}\\right\\rceil=2^{N-3}+1$ squares of one color (say, blue). We call the flags with a blue first square good. Consider all the good flags and remove the first square from each of them. We obtain at least $2^{N-3}+1 \\geq M_{N-1}$ flags of length $N-1$; by the induction hypothesis, $N-1$ of them can form a square $Q$ with the monochrome diagonal. Now, returning the removed squares, we obtain a rectangle $(N-1) \\times N$, and our aim is to supplement it on the top by one more flag. If $Q$ has a yellow diagonal, then we can take each flag with a yellow first square (it exists by a choice of the first column; moreover, it is not used in $Q$ ). Conversely, if the diagonal of $Q$ is blue then we can take any of the $\\geq 2^{N-3}+1-(N-1)>0$ remaining good flags. So, in both cases we get a desired $N \\times N$ square.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 21 |
{"year": "2010", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO", "problem": "On some planet, there are $2^{N}$ countries $(N \\geq 4)$. Each country has a flag $N$ units wide and one unit high composed of $N$ fields of size $1 \\times 1$, each field being either yellow or blue. No two countries have the same flag. We say that a set of $N$ flags is diverse if these flags can be arranged into an $N \\times N$ square so that all $N$ fields on its main diagonal will have the same color. Determine the smallest positive integer $M$ such that among any $M$ distinct flags, there exist $N$ flags forming a diverse set. (Croatia) Answer. $M=2^{N-2}+1$.", "solution": "We present a different proof of the estimate $M_{N} \\leq 2^{N-2}+1$. We do not use the induction, involving Hall's lemma on matchings instead. Consider arbitrary $2^{N-2}+1$ distinct flags and arrange them into a large $\\left(2^{N-2}+1\\right) \\times N$ flag. Construct two bipartite graphs $G_{\\mathrm{y}}=\\left(V \\cup V^{\\prime}, E_{\\mathrm{y}}\\right)$ and $G_{\\mathrm{b}}=\\left(V \\cup V^{\\prime}, E_{\\mathrm{b}}\\right)$ with the common set of vertices as follows. Let $V$ and $V^{\\prime}$ be the set of columns and the set of flags under consideration, respectively. Next, let the edge $(c, f)$ appear in $E_{\\mathrm{y}}$ if the intersection of column $c$ and flag $f$ is yellow, and $(c, f) \\in E_{\\mathrm{b}}$ otherwise. Then we have to prove exactly that one of the graphs $G_{\\mathrm{y}}$ and $G_{\\mathrm{b}}$ contains a matching with all the vertices of $V$ involved. Assume that these matchings do not exist. By Hall's lemma, it means that there exist two sets of columns $S_{\\mathrm{y}}, S_{\\mathrm{b}} \\subset V$ such that $\\left|E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)\\right| \\leq\\left|S_{\\mathrm{y}}\\right|-1$ and $\\left|E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right| \\leq\\left|S_{\\mathrm{b}}\\right|-1$ (in the left-hand sides, $E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)$ and $E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)$ denote respectively the sets of all vertices connected to $S_{\\mathrm{y}}$ and $S_{\\mathrm{b}}$ in the corresponding graphs). Our aim is to prove that this is impossible. Note that $S_{\\mathrm{y}}, S_{\\mathrm{b}} \\neq V$ since $N \\leq 2^{N-2}+1$. First, suppose that $S_{\\mathrm{y}} \\cap S_{\\mathrm{b}} \\neq \\varnothing$, so there exists some $c \\in S_{\\mathrm{y}} \\cap S_{\\mathrm{b}}$. Note that each flag is connected to $c$ either in $G_{\\mathrm{y}}$ or in $G_{\\mathrm{b}}$, hence $E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right) \\cup E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)=V^{\\prime}$. Hence we have $2^{N-2}+1=\\left|V^{\\prime}\\right| \\leq\\left|E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)\\right|+\\left|E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right| \\leq\\left|S_{\\mathrm{y}}\\right|+\\left|S_{\\mathrm{b}}\\right|-2 \\leq 2 N-4$; this is impossible for $N \\geq 4$. So, we have $S_{\\mathrm{y}} \\cap S_{\\mathrm{b}}=\\varnothing$. Let $y=\\left|S_{\\mathrm{y}}\\right|, b=\\left|S_{\\mathrm{b}}\\right|$. From the construction of our graph, we have that all the flags in the set $V^{\\prime \\prime}=V^{\\prime} \\backslash\\left(E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right) \\cup E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right)$ have blue squares in the columns of $S_{\\mathrm{y}}$ and yellow squares in the columns of $S_{\\mathrm{b}}$. Hence the only undetermined positions in these flags are the remaining $N-y-b$ ones, so $2^{N-y-b} \\geq\\left|V^{\\prime \\prime}\\right| \\geq\\left|V^{\\prime}\\right|-\\left|E_{\\mathrm{y}}\\left(S_{\\mathrm{y}}\\right)\\right|-\\left|E_{\\mathrm{b}}\\left(S_{\\mathrm{b}}\\right)\\right| \\geq$ $2^{N-2}+1-(y-1)-(b-1)$, or, denoting $c=y+b, 2^{N-c}+c>2^{N-2}+2$. This is impossible since $N \\geq c \\geq 2$.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 22 |
{"year": "2010", "tier": "T0", "problem_label": "C3", "problem_type": "Combinatorics", "exam": "IMO", "problem": "2500 chess kings have to be placed on a $100 \\times 100$ chessboard so that (i) no king can capture any other one (i.e. no two kings are placed in two squares sharing a common vertex); (ii) each row and each column contains exactly 25 kings. Find the number of such arrangements. (Two arrangements differing by rotation or symmetry are supposed to be different.) (Russia) Answer. There are two such arrangements.", "solution": "Suppose that we have an arrangement satisfying the problem conditions. Divide the board into $2 \\times 2$ pieces; we call these pieces blocks. Each block can contain not more than one king (otherwise these two kings would attack each other); hence, by the pigeonhole principle each block must contain exactly one king. Now assign to each block a letter T or B if a king is placed in its top or bottom half, respectively. Similarly, assign to each block a letter L or R if a king stands in its left or right half. So we define $T$-blocks, $B$-blocks, $L$-blocks, and $R$-blocks. We also combine the letters; we call a block a TL-block if it is simultaneously T-block and L-block. Similarly we define TR-blocks, $B L$-blocks, and BR-blocks. The arrangement of blocks determines uniquely the arrangement of kings; so in the rest of the solution we consider the $50 \\times 50$ system of blocks (see Fig. 1). We identify the blocks by their coordinate pairs; the pair $(i, j)$, where $1 \\leq i, j \\leq 50$, refers to the $j$ th block in the $i$ th row (or the $i$ th block in the $j$ th column). The upper-left block is $(1,1)$. The system of blocks has the following properties.. ( $\\left.\\mathrm{i}^{\\prime}\\right)$ If $(i, j)$ is a B-block then $(i+1, j)$ is a B-block: otherwise the kings in these two blocks can take each other. Similarly: if $(i, j)$ is a T-block then $(i-1, j)$ is a T-block; if $(i, j)$ is an L-block then $(i, j-1)$ is an L-block; if $(i, j)$ is an R-block then $(i, j+1)$ is an R-block. (ii') Each column contains exactly 25 L-blocks and 25 R-blocks, and each row contains exactly 25 T -blocks and 25 B-blocks. In particular, the total number of L-blocks (or R-blocks, or T-blocks, or B-blocks) is equal to $25 \\cdot 50=1250$. Consider any B-block of the form $(1, j)$. By ( $\\mathrm{i}^{\\prime}$ ), all blocks in the $j$ th column are B-blocks; so we call such a column $B$-column. By (ii'), we have 25 B-blocks in the first row, so we obtain 25 B-columns. These 25 B-columns contain 1250 B-blocks, hence all blocks in the remaining columns are T-blocks, and we obtain 25 T-columns. Similarly, there are exactly $25 L$-rows and exactly $25 R$-rows. Now consider an arbitrary pair of a T-column and a neighboring B-column (columns with numbers $j$ and $j+1$ ).  Fig. 1  Fig. 2 Case 1. Suppose that the $j$ th column is a T-column, and the $(j+1)$ th column is a Bcolumn. Consider some index $i$ such that the $i$ th row is an L-row; then $(i, j+1)$ is a BL-block. Therefore, $(i+1, j)$ cannot be a TR-block (see Fig. 2), hence $(i+1, j)$ is a TL-block, thus the $(i+1)$ th row is an L-row. Now, choosing the $i$ th row to be the topmost L-row, we successively obtain that all rows from the $i$ th to the 50 th are L-rows. Since we have exactly 25 L-rows, it follows that the rows from the 1st to the 25 th are R-rows, and the rows from the 26 th to the 50th are L-rows. Now consider the neighboring R-row and L-row (that are the rows with numbers 25 and 26). Replacing in the previous reasoning rows by columns and vice versa, the columns from the 1 st to the 25 th are T-columns, and the columns from the 26 th to the 50 th are B-columns. So we have a unique arrangement of blocks that leads to the arrangement of kings satisfying the condition of the problem (see Fig. 3).  Fig. 3  Fig. 4 Case 2. Suppose that the $j$ th column is a B-column, and the $(j+1)$ th column is a T-column. Repeating the arguments from Case 1, we obtain that the rows from the 1st to the 25th are L-rows (and all other rows are R-rows), the columns from the 1st to the 25 th are B-columns (and all other columns are T-columns), so we find exactly one more arrangement of kings (see Fig. 4).", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 23 |
+
{"year": "2010", "tier": "T0", "problem_label": "C4", "problem_type": "Combinatorics", "exam": "IMO", "problem": "Six stacks $S_{1}, \\ldots, S_{6}$ of coins are standing in a row. In the beginning every stack contains a single coin. There are two types of allowed moves: Move 1: If stack $S_{k}$ with $1 \\leq k \\leq 5$ contains at least one coin, you may remove one coin from $S_{k}$ and add two coins to $S_{k+1}$. Move 2: If stack $S_{k}$ with $1 \\leq k \\leq 4$ contains at least one coin, then you may remove one coin from $S_{k}$ and exchange stacks $S_{k+1}$ and $S_{k+2}$. Decide whether it is possible to achieve by a sequence of such moves that the first five stacks are empty, whereas the sixth stack $S_{6}$ contains exactly $2010^{2010^{2010}}$ coins. Same as Problem C4, but the constant $2010^{2010^{2010}}$ is replaced by $2010^{2010}$. (Netherlands) Answer. Yes (in both variants of the problem). There exists such a sequence of moves.", "solution": "Denote by $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right) \\rightarrow\\left(a_{1}^{\\prime}, a_{2}^{\\prime}, \\ldots, a_{n}^{\\prime}\\right)$ the following: if some consecutive stacks contain $a_{1}, \\ldots, a_{n}$ coins, then it is possible to perform several allowed moves such that the stacks contain $a_{1}^{\\prime}, \\ldots, a_{n}^{\\prime}$ coins respectively, whereas the contents of the other stacks remain unchanged. Let $A=2010^{2010}$ or $A=2010^{2010^{2010}}$, respectively. Our goal is to show that $$ (1,1,1,1,1,1) \\rightarrow(0,0,0,0,0, A) $$ First we prove two auxiliary observations. Lemma 1. $(a, 0,0) \\rightarrow\\left(0,2^{a}, 0\\right)$ for every $a \\geq 1$. Proof. We prove by induction that $(a, 0,0) \\rightarrow\\left(a-k, 2^{k}, 0\\right)$ for every $1 \\leq k \\leq a$. For $k=1$, apply Move 1 to the first stack: $$ (a, 0,0) \\rightarrow(a-1,2,0)=\\left(a-1,2^{1}, 0\\right) $$ Now assume that $k<a$ and the statement holds for some $k<a$. Starting from $\\left(a-k, 2^{k}, 0\\right)$, apply Move 1 to the middle stack $2^{k}$ times, until it becomes empty. Then apply Move 2 to the first stack: $$ \\left(a-k, 2^{k}, 0\\right) \\rightarrow\\left(a-k, 2^{k}-1,2\\right) \\rightarrow \\cdots \\rightarrow\\left(a-k, 0,2^{k+1}\\right) \\rightarrow\\left(a-k-1,2^{k+1}, 0\\right) $$ Hence, $$ (a, 0,0) \\rightarrow\\left(a-k, 2^{k}, 0\\right) \\rightarrow\\left(a-k-1,2^{k+1}, 0\\right) $$ Lemma 2. For every positive integer $n$, let $P_{n}=\\underbrace{2^{2 \\cdot y^{2}}}_{n}$ (e.g. $\\quad P_{3}=2^{2^{2}}=16$ ). Then $(a, 0,0,0) \\rightarrow\\left(0, P_{a}, 0,0\\right)$ for every $a \\geq 1$. Proof. Similarly to Lemma 1 , we prove that $(a, 0,0,0) \\rightarrow\\left(a-k, P_{k}, 0,0\\right)$ for every $1 \\leq k \\leq a$. For $k=1$, apply Move 1 to the first stack: $$ (a, 0,0,0) \\rightarrow(a-1,2,0,0)=\\left(a-1, P_{1}, 0,0\\right) $$ Now assume that the lemma holds for some $k<a$. Starting from ( $a-k, P_{k}, 0,0$ ), apply Lemma 1, then apply Move 1 to the first stack: $$ \\left(a-k, P_{k}, 0,0\\right) \\rightarrow\\left(a-k, 0,2^{P_{k}}, 0\\right)=\\left(a-k, 0, P_{k+1}, 0\\right) \\rightarrow\\left(a-k-1, P_{k+1}, 0,0\\right) $$ Therefore, $$ (a, 0,0,0) \\rightarrow\\left(a-k, P_{k}, 0,0\\right) \\rightarrow\\left(a-k-1, P_{k+1}, 0,0\\right) $$ Now we prove the statement of the problem. First apply Move 1 to stack 5 , then apply Move 2 to stacks $S_{4}, S_{3}, S_{2}$ and $S_{1}$ in this order. Then apply Lemma 2 twice: $$ \\begin{gathered} (1,1,1,1,1,1) \\rightarrow(1,1,1,1,0,3) \\rightarrow(1,1,1,0,3,0) \\rightarrow(1,1,0,3,0,0) \\rightarrow(1,0,3,0,0,0) \\rightarrow \\\\ \\rightarrow(0,3,0,0,0,0) \\rightarrow\\left(0,0, P_{3}, 0,0,0\\right)=(0,0,16,0,0,0) \\rightarrow\\left(0,0,0, P_{16}, 0,0\\right) \\end{gathered} $$ We already have more than $A$ coins in stack $S_{4}$, since $$ A \\leq 2010^{2010^{2010}}<\\left(2^{11}\\right)^{2010^{2010}}=2^{11 \\cdot 2010^{2010}}<2^{2010^{2011}}<2^{\\left(2^{11}\\right)^{2011}}=2^{2^{11 \\cdot 2011}}<2^{2^{2^{15}}}<P_{16} $$ To decrease the number of coins in stack $S_{4}$, apply Move 2 to this stack repeatedly until its size decreases to $A / 4$. (In every step, we remove a coin from $S_{4}$ and exchange the empty stacks $S_{5}$ and $S_{6}$.) $$ \\begin{aligned} \\left(0,0,0, P_{16}, 0,0\\right) \\rightarrow & \\left(0,0,0, P_{16}-1,0,0\\right) \\rightarrow\\left(0,0,0, P_{16}-2,0,0\\right) \\rightarrow \\\\ & \\rightarrow \\cdots \\rightarrow(0,0,0, A / 4,0,0) . \\end{aligned} $$ Finally, apply Move 1 repeatedly to empty stacks $S_{4}$ and $S_{5}$ : $$ (0,0,0, A / 4,0,0) \\rightarrow \\cdots \\rightarrow(0,0,0,0, A / 2,0) \\rightarrow \\cdots \\rightarrow(0,0,0,0,0, A) $$ Comment 1. Starting with only 4 stack, it is not hard to check manually that we can achieve at most 28 coins in the last position. However, around 5 and 6 stacks the maximal number of coins explodes. With 5 stacks it is possible to achieve more than $2^{2^{14}}$ coins. With 6 stacks the maximum is greater than $P_{P_{2^{14}}}$. It is not hard to show that the numbers $2010^{2010}$ and $2010^{2010^{2010}}$ in the problem can be replaced by any nonnegative integer up to $P_{P_{214}}$. Comment 2. The simpler variant $\\mathrm{C}^{\\prime}$ of the problem can be solved without Lemma 2: $$ \\begin{aligned} (1,1,1,1,1,1) & \\rightarrow(0,3,1,1,1,1) \\rightarrow(0,1,5,1,1,1) \\rightarrow(0,1,1,9,1,1) \\rightarrow \\\\ & \\rightarrow(0,1,1,1,17,1) \\rightarrow(0,1,1,1,0,35) \\rightarrow(0,1,1,0,35,0) \\rightarrow(0,1,0,35,0,0) \\rightarrow \\\\ & \\rightarrow(0,0,35,0,0,0) \\rightarrow\\left(0,0,1,2^{34}, 0,0\\right) \\rightarrow\\left(0,0,1,0,2^{2^{34}}, 0\\right) \\rightarrow\\left(0,0,0,2^{2^{34}}, 0,0\\right) \\\\ & \\rightarrow\\left(0,0,0,2^{2^{34}}-1,0,0\\right) \\rightarrow \\ldots \\rightarrow(0,0,0, A / 4,0,0) \\rightarrow(0,0,0,0, A / 2,0) \\rightarrow(0,0,0,0,0, A) . \\end{aligned} $$ For this reason, the PSC suggests to consider the problem C4 as well. Problem C4 requires more invention and technical care. On the other hand, the problem statement in $\\mathrm{C} 4^{\\prime}$ hides the fact that the resulting amount of coins can be such incredibly huge and leaves this discovery to the students.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
|
|
|
| 24 |
{"year": "2010", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO", "problem": "$n \\geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3} \\geq 0 $$ (South Korea)", "solution": "For any tournament $T$ satisfying the problem condition, denote by $S(T)$ sum under consideration, namely $$ S(T)=\\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3} $$ First, we show that the statement holds if a tournament $T$ has only 4 players. Actually, let $A=\\left(a_{1}, a_{2}, a_{3}, a_{4}\\right)$ be the number of wins of the players; we may assume that $a_{1} \\geq a_{2} \\geq a_{3} \\geq a_{4}$. We have $a_{1}+a_{2}+a_{3}+a_{4}=\\binom{4}{2}=6$, hence $a_{4} \\leq 1$. If $a_{4}=0$, then we cannot have $a_{1}=a_{2}=a_{3}=2$, otherwise the company of all players is bad. Hence we should have $A=(3,2,1,0)$, and $S(T)=3^{3}+1^{3}+(-1)^{3}+(-3)^{3}=0$. On the other hand, if $a_{4}=1$, then only two possibilities, $A=(3,1,1,1)$ and $A=(2,2,1,1)$ can take place. In the former case we have $S(T)=3^{3}+3 \\cdot(-2)^{3}>0$, while in the latter one $S(T)=1^{3}+1^{3}+(-1)^{3}+(-1)^{3}=0$, as desired. Now we turn to the general problem. Consider a tournament $T$ with no bad companies and enumerate the players by the numbers from 1 to $n$. For every 4 players $i_{1}, i_{2}, i_{3}, i_{4}$ consider a \"sub-tournament\" $T_{i_{1} i_{2} i_{3} i_{4}}$ consisting of only these players and the games which they performed with each other. By the abovementioned, we have $S\\left(T_{i_{1} i_{2} i_{3} i_{4}}\\right) \\geq 0$. Our aim is to prove that $$ S(T)=\\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S\\left(T_{i_{1} i_{2} i_{3} i_{4}}\\right) $$ where the sum is taken over all 4 -tuples of distinct numbers from the set $\\{1, \\ldots, n\\}$. This way the problem statement will be established. We interpret the number $\\left(w_{i}-\\ell_{i}\\right)^{3}$ as following. For $i \\neq j$, let $\\varepsilon_{i j}=1$ if the $i$ th player wins against the $j$ th one, and $\\varepsilon_{i j}=-1$ otherwise. Then $$ \\left(w_{i}-\\ell_{i}\\right)^{3}=\\left(\\sum_{j \\neq i} \\varepsilon_{i j}\\right)^{3}=\\sum_{j_{1}, j_{2}, j_{3} \\neq i} \\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}} . $$ Hence, $$ S(T)=\\sum_{i \\notin\\left\\{j_{1}, j_{2}, j_{3}\\right\\}} \\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}} $$ To simplify this expression, consider all the terms in this sum where two indices are equal. If, for instance, $j_{1}=j_{2}$, then the term contains $\\varepsilon_{i j_{1}}^{2}=1$, so we can replace this term by $\\varepsilon_{i j_{3}}$. Make such replacements for each such term; obviously, after this change each term of the form $\\varepsilon_{i j_{3}}$ will appear $P(T)$ times, hence $$ S(T)=\\sum_{\\left|\\left\\{i, j_{1}, j_{2}, j_{3}\\right\\}\\right|=4} \\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}}+P(T) \\sum_{i \\neq j} \\varepsilon_{i j}=S_{1}(T)+P(T) S_{2}(T) $$ We show that $S_{2}(T)=0$ and hence $S(T)=S_{1}(T)$ for each tournament. Actually, note that $\\varepsilon_{i j}=-\\varepsilon_{j i}$, and the whole sum can be split into such pairs. Since the sum in each pair is 0 , so is $S_{2}(T)$. Thus the desired equality (2) rewrites as $$ S_{1}(T)=\\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S_{1}\\left(T_{i_{1} i_{2} i_{3} i_{4}}\\right) $$ Now, if all the numbers $j_{1}, j_{2}, j_{3}$ are distinct, then the set $\\left\\{i, j_{1}, j_{2}, j_{3}\\right\\}$ is contained in exactly one 4 -tuple, hence the term $\\varepsilon_{i j_{1}} \\varepsilon_{i j_{2}} \\varepsilon_{i j_{3}}$ appears in the right-hand part of (3) exactly once, as well as in the left-hand part. Clearly, there are no other terms in both parts, so the equality is established.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 25 |
{"year": "2010", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO", "problem": "$n \\geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3} \\geq 0 $$ (South Korea)", "solution": "Similarly to the first solution, we call the subsets of players as companies, and the $k$-element subsets will be called as $k$-companies. In any company of the players, call a player the local champion of the company if he defeated all other members of the company. Similarly, if a player lost all his games against the others in the company then call him the local loser of the company. Obviously every company has at most one local champion and at most one local loser. By the condition of the problem, whenever a 4-company has a local loser, then this company has a local champion as well. Suppose that $k$ is some positive integer, and let us count all cases when a player is the local champion of some $k$-company. The $i$ th player won against $w_{i}$ other player. To be the local champion of a $k$-company, he must be a member of the company, and the other $k-1$ members must be chosen from those whom he defeated. Therefore, the $i$ th player is the local champion of $\\binom{w_{i}}{k-1} k$-companies. Hence, the total number of local champions of all $k$-companies is $\\sum_{i=1}^{n}\\binom{w_{i}}{k-1}$. Similarly, the total number of local losers of the $k$-companies is $\\sum_{i=1}^{n}\\binom{\\ell_{i}}{k-1}$. Now apply this for $k=2,3$ and 4. Since every game has a winner and a loser, we have $\\sum_{i=1}^{n} w_{i}=\\sum_{i=1}^{n} \\ell_{i}=\\binom{n}{2}$, and hence $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)=0 $$ In every 3-company, either the players defeated one another in a cycle or the company has both a local champion and a local loser. Therefore, the total number of local champions and local losers in the 3-companies is the same, $\\sum_{i=1}^{n}\\binom{w_{i}}{2}=\\sum_{i=1}^{n}\\binom{\\ell_{i}}{2}$. So we have $$ \\sum_{i=1}^{n}\\left(\\binom{w_{i}}{2}-\\binom{\\ell_{i}}{2}\\right)=0 $$ In every 4-company, by the problem's condition, the number of local losers is less than or equal to the number of local champions. Then the same holds for the total numbers of local champions and local losers in all 4-companies, so $\\sum_{i=1}^{n}\\binom{w_{i}}{3} \\geq \\sum_{i=1}^{n}\\binom{\\ell_{i}}{3}$. Hence, $$ \\sum_{i=1}^{n}\\left(\\binom{w_{i}}{3}-\\binom{\\ell_{i}}{3}\\right) \\geq 0 $$ Now we establish the problem statement (1) as a linear combination of (4), (5) and (6). It is easy check that $$ (x-y)^{3}=24\\left(\\binom{x}{3}-\\binom{y}{3}\\right)+24\\left(\\binom{x}{2}-\\binom{y}{2}\\right)-\\left(3(x+y)^{2}-4\\right)(x-y) $$ Apply this identity to $x=w_{1}$ and $y=\\ell_{i}$. Since every player played $n-1$ games, we have $w_{i}+\\ell_{i}=n-1$, and thus $$ \\left(w_{i}-\\ell_{i}\\right)^{3}=24\\left(\\binom{w_{i}}{3}-\\binom{\\ell_{i}}{3}\\right)+24\\left(\\binom{w_{i}}{2}-\\binom{\\ell_{i}}{2}\\right)-\\left(3(n-1)^{2}-4\\right)\\left(w_{i}-\\ell_{i}\\right) $$ Then $$ \\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)^{3}=24 \\underbrace{\\sum_{i=1}^{n}\\left(\\binom{w_{i}}{3}-\\binom{\\ell_{i}}{3}\\right)}_{\\geq 0}+24 \\underbrace{\\sum_{i=1}^{n}\\left(\\binom{w_{i}}{2}-\\binom{\\ell_{i}}{2}\\right)}_{0}-\\left(3(n-1)^{2}-4\\right) \\underbrace{\\sum_{i=1}^{n}\\left(w_{i}-\\ell_{i}\\right)}_{0} \\geq 0 $$", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|
| 26 |
{"year": "2010", "tier": "T0", "problem_label": "C6", "problem_type": "Combinatorics", "exam": "IMO", "problem": "Given a positive integer $k$ and other two integers $b>w>1$. There are two strings of pearls, a string of $b$ black pearls and a string of $w$ white pearls. The length of a string is the number of pearls on it. One cuts these strings in some steps by the following rules. In each step: (i) The strings are ordered by their lengths in a non-increasing order. If there are some strings of equal lengths, then the white ones precede the black ones. Then $k$ first ones (if they consist of more than one pearl) are chosen; if there are less than $k$ strings longer than 1 , then one chooses all of them. (ii) Next, one cuts each chosen string into two parts differing in length by at most one. (For instance, if there are strings of $5,4,4,2$ black pearls, strings of $8,4,3$ white pearls and $k=4$, then the strings of 8 white, 5 black, 4 white and 4 black pearls are cut into the parts $(4,4),(3,2),(2,2)$ and $(2,2)$, respectively.) The process stops immediately after the step when a first isolated white pearl appears. Prove that at this stage, there will still exist a string of at least two black pearls. (Canada)", "solution": "Denote the situation after the $i$ th step by $A_{i}$; hence $A_{0}$ is the initial situation, and $A_{i-1} \\rightarrow A_{i}$ is the $i$ th step. We call a string containing $m$ pearls an $m$-string; it is an $m$-w-string or a $m$-b-string if it is white or black, respectively. We continue the process until every string consists of a single pearl. We will focus on three moments of the process: (a) the first stage $A_{s}$ when the first 1 -string (no matter black or white) appears; (b) the first stage $A_{t}$ where the total number of strings is greater than $k$ (if such moment does not appear then we put $t=\\infty$ ); and (c) the first stage $A_{f}$ when all black pearls are isolated. It is sufficient to prove that in $A_{f-1}$ (or earlier), a 1-w-string appears. We start with some easy properties of the situations under consideration. Obviously, we have $s \\leq f$. Moreover, all b-strings from $A_{f-1}$ become single pearls in the $f$ th step, hence all of them are 1- or 2-b-strings. Next, observe that in each step $A_{i} \\rightarrow A_{i+1}$ with $i \\leq t-1$, all $(>1)$-strings were cut since there are not more than $k$ strings at all; if, in addition, $i<s$, then there were no 1 -string, so all the strings were cut in this step. Now, let $B_{i}$ and $b_{i}$ be the lengths of the longest and the shortest b-strings in $A_{i}$, and let $W_{i}$ and $w_{i}$ be the same for w-strings. We show by induction on $i \\leq \\min \\{s, t\\}$ that (i) the situation $A_{i}$ contains exactly $2^{i}$ black and $2^{i}$ white strings, (ii) $B_{i} \\geq W_{i}$, and (iii) $b_{i} \\geq w_{i}$. The base case $i=0$ is obvious. For the induction step, if $i \\leq \\min \\{s, t\\}$ then in the $i$ th step, each string is cut, thus the claim (i) follows from the induction hypothesis; next, we have $B_{i}=\\left\\lceil B_{i-1} / 2\\right\\rceil \\geq\\left\\lceil W_{i-1} / 2\\right\\rceil=W_{i}$ and $b_{i}=\\left\\lfloor b_{i-1} / 2\\right\\rfloor \\geq\\left\\lfloor w_{i-1} / 2\\right\\rfloor=w_{i}$, thus establishing (ii) and (iii). For the numbers $s, t, f$, two cases are possible. Case 1. Suppose that $s \\leq t$ or $f \\leq t+1$ (and hence $s \\leq t+1$ ); in particular, this is true when $t=\\infty$. Then in $A_{s-1}$ we have $B_{s-1} \\geq W_{s-1}, b_{s-1} \\geq w_{s-1}>1$ as $s-1 \\leq \\min \\{s, t\\}$. Now, if $s=f$, then in $A_{s-1}$, there is no 1 -w-string as well as no ( $>2$ )-b-string. That is, $2=B_{s-1} \\geq W_{s-1} \\geq b_{s-1} \\geq w_{s-1}>1$, hence all these numbers equal 2 . This means that in $A_{s-1}$, all strings contain 2 pearls, and there are $2^{s-1}$ black and $2^{s-1}$ white strings, which means $b=2 \\cdot 2^{s-1}=w$. This contradicts the problem conditions. Hence we have $s \\leq f-1$ and thus $s \\leq t$. Therefore, in the $s$ th step each string is cut into two parts. Now, if a 1-b-string appears in this step, then from $w_{s-1} \\leq b_{s-1}$ we see that a 1-w-string appears as well; so, in each case in the sth step a 1-w-string appears, while not all black pearls become single, as desired. Case 2. Now assume that $t+1 \\leq s$ and $t+2 \\leq f$. Then in $A_{t}$ we have exactly $2^{t}$ white and $2^{t}$ black strings, all being larger than 1 , and $2^{t+1}>k \\geq 2^{t}$ (the latter holds since $2^{t}$ is the total number of strings in $A_{t-1}$ ). Now, in the $(t+1)$ st step, exactly $k$ strings are cut, not more than $2^{t}$ of them being black; so the number of w-strings in $A_{t+1}$ is at least $2^{t}+\\left(k-2^{t}\\right)=k$. Since the number of w-strings does not decrease in our process, in $A_{f-1}$ we have at least $k$ white strings as well. Finally, in $A_{f-1}$, all b-strings are not larger than 2, and at least one 2-b-string is cut in the $f$ th step. Therefore, at most $k-1$ white strings are cut in this step, hence there exists a w-string $\\mathcal{W}$ which is not cut in the $f$ th step. On the other hand, since a 2 -b-string is cut, all $(\\geq 2)$-w-strings should also be cut in the $f$ th step; hence $\\mathcal{W}$ should be a single pearl. This is exactly what we needed. Comment. In this solution, we used the condition $b \\neq w$ only to avoid the case $b=w=2^{t}$. Hence, if a number $b=w$ is not a power of 2 , then the problem statement is also valid.", "metadata": {"resource_path": "IMO/segmented/en-IMO2010SL.jsonl"}}
|