Add data for Serbia MO
#21
by
LxYxvv
- opened
- Serbia_MO/download_script/download.py +74 -0
- Serbia_MO/md/sr-2007_smo_resenja.md +178 -0
- Serbia_MO/md/sr-2008_smo_resenja.md +230 -0
- Serbia_MO/md/sr-2009_smo_resenja.md +128 -0
- Serbia_MO/md/sr-2010_smo_resenja.md +147 -0
- Serbia_MO/md/sr-2011_smo_resenja.md +109 -0
- Serbia_MO/md/sr-2012_smo_resenja.md +144 -0
- Serbia_MO/md/sr-2013_smo_resenja.md +122 -0
- Serbia_MO/md/sr-2014_smo_resenja.md +113 -0
- Serbia_MO/md/sr-2015_smo_resenja.md +113 -0
- Serbia_MO/md/sr-2016_smo_resenja.md +118 -0
- Serbia_MO/md/sr-2017_smo_resenja.md +163 -0
- Serbia_MO/md/sr-2018_smo_resenja.md +192 -0
- Serbia_MO/md/sr-2019_smo_resenja.md +262 -0
- Serbia_MO/md/sr-2020_smo_resenja.md +161 -0
- Serbia_MO/raw/sr-2007_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2008_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2009_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2010_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2011_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2012_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2013_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2014_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2015_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2016_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2017_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2018_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2019_smo_resenja.pdf +3 -0
- Serbia_MO/raw/sr-2020_smo_resenja.pdf +3 -0
- Serbia_MO/segment_script/segment.py +149 -0
- Serbia_MO/segmented/sr-2007_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2008_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2009_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2010_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2011_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2012_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2013_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2014_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2015_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2016_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2017_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2018_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2019_smo_resenja.jsonl +6 -0
- Serbia_MO/segmented/sr-2020_smo_resenja.jsonl +6 -0
Serbia_MO/download_script/download.py
ADDED
|
@@ -0,0 +1,74 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-12-24
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download script for Serbia MO
|
| 7 |
+
To run:
|
| 8 |
+
`python Serbia_MO/download_script/download.py`
|
| 9 |
+
'''
|
| 10 |
+
|
| 11 |
+
import requests
|
| 12 |
+
from bs4 import BeautifulSoup
|
| 13 |
+
from tqdm import tqdm
|
| 14 |
+
from pathlib import Path
|
| 15 |
+
from requests.adapters import HTTPAdapter
|
| 16 |
+
from urllib3.util.retry import Retry
|
| 17 |
+
from urllib.parse import urljoin
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
def build_session(
|
| 21 |
+
max_retries: int = 3,
|
| 22 |
+
backoff_factor: int = 2,
|
| 23 |
+
session: requests.Session = None
|
| 24 |
+
) -> requests.Session:
|
| 25 |
+
"""
|
| 26 |
+
Build a requests session with retries
|
| 27 |
+
|
| 28 |
+
Args:
|
| 29 |
+
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 30 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 31 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 32 |
+
"""
|
| 33 |
+
session = session or requests.Session()
|
| 34 |
+
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 35 |
+
session.mount("http://", adapter)
|
| 36 |
+
session.mount("https://", adapter)
|
| 37 |
+
session.headers.update({
|
| 38 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 39 |
+
})
|
| 40 |
+
|
| 41 |
+
return session
|
| 42 |
+
|
| 43 |
+
|
| 44 |
+
def main():
|
| 45 |
+
base_url = "https://imomath.com/srb/index.cgi?page=zadaciSaTakmichenja"
|
| 46 |
+
req_session = build_session()
|
| 47 |
+
|
| 48 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 49 |
+
output_dir.mkdir(parents=True, exist_ok=True)
|
| 50 |
+
|
| 51 |
+
resp = req_session.get(base_url)
|
| 52 |
+
soup = BeautifulSoup(resp.text, 'html.parser')
|
| 53 |
+
|
| 54 |
+
sol_list = soup.find_all('a', href=lambda x: x and x.endswith('smo_resenja.pdf'))
|
| 55 |
+
sol_url = [ele["href"] for ele in sol_list]
|
| 56 |
+
|
| 57 |
+
for url in tqdm(sol_url):
|
| 58 |
+
output_file = output_dir / f"sr-{Path(url).name}"
|
| 59 |
+
|
| 60 |
+
# Check if the file already exists
|
| 61 |
+
if output_file.exists():
|
| 62 |
+
continue
|
| 63 |
+
|
| 64 |
+
pdf_resp = req_session.get(urljoin(base_url, url))
|
| 65 |
+
|
| 66 |
+
if pdf_resp.status_code != 200:
|
| 67 |
+
print(f"Failed to download {url}")
|
| 68 |
+
continue
|
| 69 |
+
|
| 70 |
+
output_file.write_bytes(pdf_resp.content)
|
| 71 |
+
|
| 72 |
+
|
| 73 |
+
if __name__ == "__main__":
|
| 74 |
+
main()
|
Serbia_MO/md/sr-2007_smo_resenja.md
ADDED
|
@@ -0,0 +1,178 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 2 |
+
|
| 3 |
+
такмичење ученика средњих школа из математике
|
| 4 |
+
|
| 5 |
+
Београд, 02.04.2007.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Нека је $D$ тачка на страници $A C$ троугла $A B C$ у коме је $A B<B C$ таква да је $A B=B D$. Круг уписан у $\triangle A B C$ додирује $A B$ у $K$ и $A C$ у $L$, а $J$ је центар уписаног круга троугла $B C D$. Доказати да $K L$ полови дуж $A J$.
|
| 10 |
+
2. Троугао $\triangle Z C P$ је подељен на 25 „малих“ троуглова (као на слици), а затим су сва темена тих троуглова обојена са три боје на следећи начин: теме $Z$ је обојено зеленом бојом, теме $C$ црвеном, а теме $P$ плавом; свако од темена на дужи $Z C$ обојено је или зеленом или црвеном бојом, свако од темена на дужи $C P$ обојено је или црвеном или плавом бојом, а свако од темена на дужи $Z P$ обојено је или зеленом или плавом бојом. Сва темена која се налазе у унутрашњости троугла обојена су без ограничења, једном од три боје.
|
| 11 |
+
|
| 12 |
+
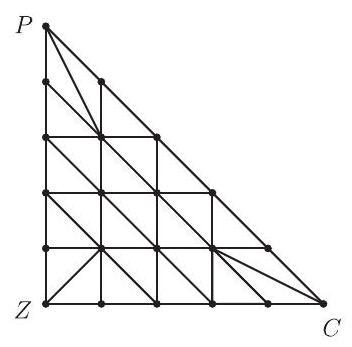
|
| 13 |
+
|
| 14 |
+
Доказати да без обзира на начин бојења, бар један од 25 „малих “ троуглова има сва три темена различите боје.
|
| 15 |
+
|
| 16 |
+
3. Одредити све парове природних бројева $(x, n)$ који су решења једначине
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
x^{3}+2 x+1=2^{n}
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Време за рад 270 минута.
|
| 23 |
+
|
| 24 |
+
Сваки задатак вреди 7 поена.
|
| 25 |
+
|
| 26 |
+
## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 27 |
+
|
| 28 |
+
такмичење ученика средњих школа из математике
|
| 29 |
+
|
| 30 |
+
Београд, 03.04.2007.
|
| 31 |
+
|
| 32 |
+
## Други дан
|
| 33 |
+
|
| 34 |
+
4. Нека је $k$ природан број. За сваку функцију $f: \mathbb{N} \rightarrow \mathbb{N}$, нека је низ функција $\left(f_{m}\right)_{m \geqslant 1}$ дефинисан са $f_{1}=f$ и $f_{m+1}=f \circ f_{m}$ за $m \geqslant 1$. Функција $f$ је $k$-фина уколико за све $n \in \mathbb{N}$ важи
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
f_{k}(n)=f(n)^{k}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
(a) За које $k$ постоји $1-1 k$-фина функција $f$ ?
|
| 41 |
+
|
| 42 |
+
(б) За које $k$ постоји на $k$-фина фунција $f$ ?
|
| 43 |
+
|
| 44 |
+
5. Дат је неједнакокраки троугао $A B C$. Нека су $A D, B E, C F$ симетрале углова овог троугла $(D \in B C, E \in A C, F \in A B)$. Нека су $K_{a}, K_{b}, K_{c}$ тачке на уписаном кругу троугла $A B C$ такве да су $D K_{a}, E K_{b}, F K_{c}$ тангенте на уписани круг и да $K_{a} \notin B C, K_{b} \notin A C, K_{c} \notin A B$. Нека су $A_{1}, B_{1}, C_{1}$ средишта страница $B C, C A, A B$. Доказати да се праве $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ секу на уписаном кругу троугла $A B C$.
|
| 45 |
+
6. Нека је $k$ природан број. Доказати да за позитивне реалне бројеве $x, y, z$ чији је збир једнак 1 , важи неједнакост
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}}+\frac{y^{k+2}}{y^{k+1}+z^{k}+x^{k}}+\frac{z^{k+2}}{z^{k+1}+x^{k}+y^{k}} \geqslant \frac{1}{7}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Када важи једнакост?
|
| 52 |
+
|
| 53 |
+
Време за рад 270 минута.
|
| 54 |
+
|
| 55 |
+
Сваки задатак вреди 7 поена.
|
| 56 |
+
|
| 57 |
+
## РЕШЕЊА
|
| 58 |
+
|
| 59 |
+
1. Нека је $M$ тачка на $A C$ таква да је $J M \| K L$. Довољно је доказати да је $A M=2 A L$.
|
| 60 |
+
|
| 61 |
+
Из $\varangle B D A=\alpha$ добијамо $\varangle J D M=90^{\circ}-\frac{\alpha}{2}=\varangle K L A=\varangle J M D$, па је $J M=$ $J D$, а додирна тачка уписаног круга $\triangle B C D$ са $C D$ је средиште $T$ дужи $M D$. Према томе, $D M=2 D T=B D+C D-B C=A B-B C+C D$, одакле je
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
A M=A D+D M=A C+A B-B C=2 A L
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
2. Посматраћемо странице малих троуглова које имају једно теме обојено црвеном, а друго плавом бојом. Такве странице ћемо звати црвено-плаве странице.
|
| 68 |
+
|
| 69 |
+
Свака црвено-плава страница која се налази у унутрашњости троугла $\triangle Z C P$ је страница тачно два мала троугла. Даље, свака црв��но-плава страница која налази на једној од страница троугла $\triangle Z C P$ по услову задатка мора припадати баш дужи $C P$. С обзиром да је теме $C$ обојено црвеном бојом а $P$ плавом, број црвено-плавих страница на дужи $C P$ је непаран.
|
| 70 |
+
|
| 71 |
+
Према томе, мора постојати бар један мали троугао који има непаран број црвено-плавих страница. Тај троугао мора да има сва три темена различите боје.
|
| 72 |
+
|
| 73 |
+
3. Провером се добија да је за $n \leqslant 2$ једино решење пар $(1,2)$. Докажимо да за $n \geqslant 3$ нема решења.
|
| 74 |
+
|
| 75 |
+
Број $x$ мора бити непаран, па је $x^{2}+2 \equiv 3(\bmod 8)$. Сада из $x\left(x^{2}+2\right) \equiv-1$ $(\bmod 8)$ следи да је $x \equiv 5(\bmod 8)$. Шта више, како $3 \mid x\left(x^{2}+2\right)$ (уколико $3 \nmid x$ тада $\left.3 \mid x^{2}+2\right)$, мора бити $2^{n} \equiv 1(\bmod 3)$, па је $n$ паран број.
|
| 76 |
+
|
| 77 |
+
Додавањем обема странама једнакости броја 2 добија се
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
(x+1)\left(x^{2}-x+3\right)=2^{n}+2
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
Како је $n$ паран, $2^{n}$ је потпун квадрат, па је број -2 квадратни остатак по сваком непарном простом делиоцу $p$ броја $(x+1)\left(x^{2}-x+3\right)$. Зато је
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
1=\left(\frac{-2}{p}\right)=\left(\frac{-1}{p}\right)\left(\frac{2}{p}\right)=(-1)^{\frac{p-1}{2}}(-1)^{\frac{p^{2}-1}{8}}=(-1)^{\frac{(p-1)(p+5)}{8}}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
одакле следи да је $p$ облика $8 k+1$ или $8 k+3$. Будући производ таквих простих бројева, и сам број $x^{2}-x+3$ мора бити тог облика. Међутим, како је $x \equiv 5(\bmod 8)$, важи $x^{2}-x+3 \equiv 7(\bmod 8)$ што је контрадикција.
|
| 90 |
+
|
| 91 |
+
Дакле, једино решење дате једначине је $(x, n)=(1,2)$.
|
| 92 |
+
|
| 93 |
+
4. Свака функција је 1-фина, па је одговор на оба дела задатка потврдан. Нека је надаље $k \geqslant 2$. Свака $k$-фина функција је 1 -1 јер из $f(m)=f(n)$ следи $m^{k}=f_{k}(m)=f_{k}(n)=n^{k}$, тј. $m=n$.
|
| 94 |
+
|
| 95 |
+
(a) Одговор: ДА. Конструишимо функцију $f$ индуктивно на следећи начин. Нека је $n$ најмањи природан број чија слика није одређена.
|
| 96 |
+
|
| 97 |
+
(1) ако је $n=1$, онда је $f(n)=1$;
|
| 98 |
+
|
| 99 |
+
(2) ако је $n=a^{k}$ за неко цело $a>1$, дефинишемо $f(n)=f(a)^{k}$;
|
| 100 |
+
|
| 101 |
+
(3) ако $n$ није потпун $k$-ти степен изаберемо најмањих $k-1$ природних бројева $n_{1}, n_{2}, \ldots, n_{k-1}$ који нису потпуни $k$-ти степени и за које до сада нису одређене слике, и дефинишемо $f\left(n_{1}\right)=n_{2}, f\left(n_{2}\right)=n_{3}$, $\ldots, f\left(n_{k-1}\right)=n_{1}^{k}$.
|
| 102 |
+
|
| 103 |
+
На овај начин функција $f$ је добро дефинисана. Покажимо да је она $k$ фина. За свако $n \in \mathbb{N}$ које није $k$-ти степен постоје бројеви $n_{1}, \ldots, n_{k-1}$ из услова (3) такви да је $n_{i}=n$ за неко $1 \leqslant i \leqslant k-1$. Тада важи $f_{k}\left(n_{i}\right)=$ $f_{i}\left(n_{1}^{k}\right)=f_{i}\left(n_{1}\right)^{k}=f\left(n_{i}\right)^{k}$. Такође, ако је $n$ потпун $k$-ти степен, тада је $n=n_{i}^{k^{s}}$ за неко $i$ и $s$, па према (2) важи $f_{k}(n)=f_{k}\left(n_{i}\right)^{k^{s}}=n_{i}^{k^{s+1}}=n^{k}$, што доказује наше тврђење.
|
| 104 |
+
|
| 105 |
+
(б) Одговор: НЕ. Заиста, ако је $f$ на и $k$-фина, за свако $a_{0}$ постоји низ природних бројева $a_{1}, a_{2}, \ldots$ таквих да је $f\left(a_{k+1}\right)=a_{k}$ за све $k$, одакле је $a_{k}^{k}=f_{k}\left(a_{k}\right)=a_{0}$, што је немогуће ако $a_{0}$ није $k$-ти степен.
|
| 106 |
+
|
| 107 |
+
5. Докажимо да су троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ хомотетични. Да бисмо то доказали, довољно је да докажемо да је $K_{a} K_{b} \| A_{1} B_{1}$, односно $K_{a} K_{b} \| A B$ (аналогно ће следити и за друге парове страница).
|
| 108 |
+
|
| 109 |
+
Означимо $M=K_{a} K_{b} \cap B C$, са $S$ означимо центар уписаног круга, и са $T$ означимо произвољну тачку на уписаном кругу. Означим�� $\alpha=\varangle B A S$, $\beta=\varangle C B S, \gamma=\varangle A C S$. Користећи оријентисане углове (по модулу $180^{\circ}$ ), добијамо $\varangle B^{\prime} E B=\beta+2 \gamma$, и аналогно $\varangle A^{\prime} D A=\alpha+2 \beta$, а одатле и $\varangle A^{\prime} D K_{a}=2 \alpha+4 \beta$. Затим, $\varangle B^{\prime} T K_{b}=\varangle B^{\prime} S E=90^{\circ}+\varangle B^{\prime} E S=\gamma-\alpha$ и аналогно $\varangle A^{\prime} T K_{a}=\beta-\gamma$. Затим, $\varangle A^{\prime} T B^{\prime}=\varangle A^{\prime} S C=90^{\circ}+\varangle A^{\prime} C S=\alpha+\beta$. И на крају добијамо $\varangle K_{a} T K_{b}=\varangle K_{a} T A^{\prime}+\varangle A^{\prime} T B^{\prime}+\varangle B^{\prime} T K_{b}=2 \gamma$.
|
| 110 |
+
|
| 111 |
+
Такође, из троугла $D K_{a} M$ добијамо $\varangle C M K_{a}=\varangle C D K_{a}+\varangle D K_{a} M=$ $\varangle A^{\prime} D K_{a}+\varangle D K_{a} K_{b}=(2 \alpha+4 \beta)+\varangle K_{a} T K_{b}=(2 \alpha+4 \beta)+2 \gamma=2 \beta$. Дакле, $\varangle C M K_{a}=\varangle C B A$, одакле следи да је $K_{a} K_{b} \| A B$, што је требало доказати. Дакле, троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ су хомотетични.
|
| 112 |
+
|
| 113 |
+
Приметимо такође да је коефицијент хомотетије позитиван: ако би био негативан, дужи $K_{a} A_{1}, K_{b} B_{1}, K_{c} C_{1}$ би се секле у једној тачки. Ако је $\alpha>$ $\beta$, онда се тачке $C_{1}$ и $K_{c}$, па и цела дуж $K_{c} C_{1}$, налазе унутар четвороугла $S F B D$. Зато, ако без умањења општости претпоставимо $\alpha>\beta>\gamma$, онда $K_{c} C_{1} \subset S F B D$, али $K_{a} A_{1} \subset S D C E$, па су ове две дужи дисјунктне.
|
| 114 |
+
|
| 115 |
+
Како су троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ хомотетични, њихови описани кругови су такође хомотетични. Али то су Ојлеров и уписани круг троугла $A B C$, респективно, и познато је да се та два круга додирују изнутра у Фојербаховој тачки троугла $A B C$. Стога (уз чињеницу да је коефицијент хомотетије позитиван), центар хомотетије је управо Фојербахова тачка. Одавде следи да се $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ секу у Фојербаховој тачки троугла $A B C$, која припада уписаном кругу троугла $A B C$, чиме је тврдјење доказано.
|
| 116 |
+
|
| 117 |
+
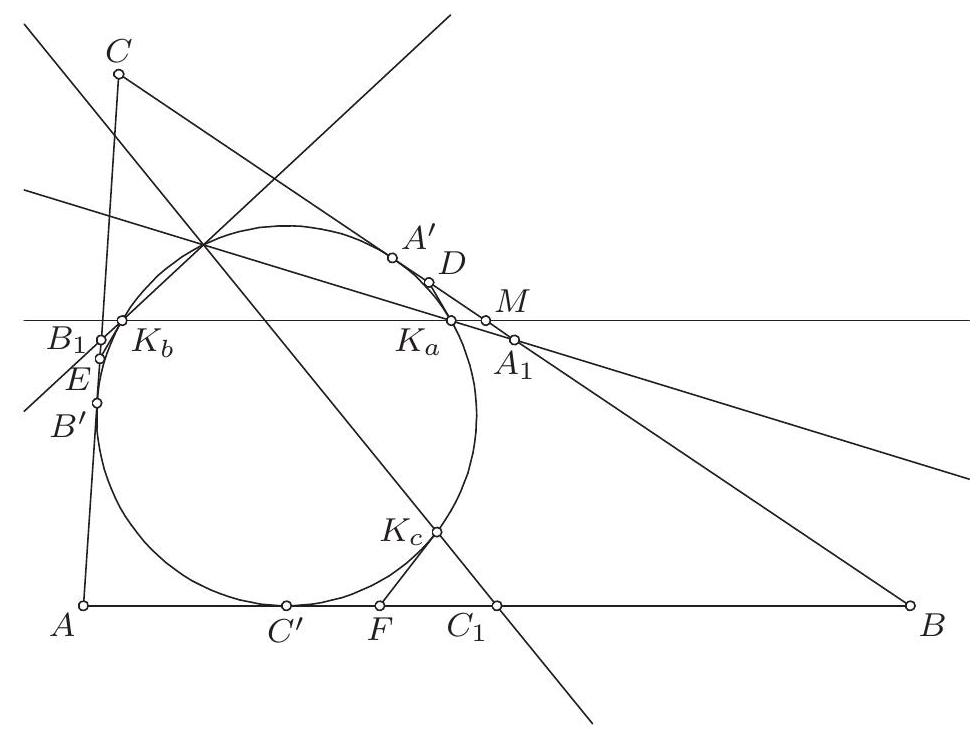
|
| 118 |
+
|
| 119 |
+
Алтернативно решење. Нека је уписани круг троугла $A B C$ јединична кружница у комплексној равни. Тада је $a=\frac{2 b^{\prime} c^{\prime}}{b^{\prime}+c^{\prime}}, b=\frac{2 a^{\prime} c^{\prime}}{a^{\prime}+c^{\prime}}, c=\frac{2 a^{\prime} b^{\prime}}{a^{\prime}+b^{\prime}}$. Затим је
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
a_{1}=\frac{b+c}{2}=\frac{a^{\prime 2} b^{\prime}+a^{\prime 2} c^{\prime}+2 a^{\prime} b^{\prime} c^{\prime}}{\left(a^{\prime}+b^{\prime}\right)\left(a^{\prime}+c^{\prime}\right)}
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
Вредност $k_{a}$ налазимо из услова $\frac{k_{a}}{a}=\overline{\left(\frac{a^{\prime}}{a}\right)}$, одакле је $k_{a}=\frac{1}{a^{\prime}} \overline{\bar{a}}=\frac{b^{\prime} c^{\prime}}{a^{\prime}}$. Сада налазимо пресечну тачку $z$ уписаног круга (одакле $|z|=1$ ) и праве $K_{a} A_{1}$ (одакле $\frac{z-k_{a}}{a_{1}-k_{a}}=\overline{\left(\frac{z-k_{a}}{a_{1}-k_{a}}\right)}$. Други услов можемо трансформисати у облик
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
\overline{\left(a_{1}-k_{a}\right)}\left(z-k_{a}\right)=\left(\frac{1}{z}-\frac{1}{k_{a}}\right)\left(a_{1}-k_{a}\right)
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
одакле (због $\left.z \neq k_{a}\right)$ следи $\overline{\left(a_{1}-k_{a}\right)}=-\frac{1}{z k_{a}}\left(a_{1}-k_{a}\right)$, па је
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
z=-\frac{1}{k_{a}} \frac{a_{1}-k_{a}}{\overline{\left(a_{1}-k_{a}\right)}}=-\frac{\left(a^{\prime 2}-b^{\prime} c^{\prime}\right)\left(a^{\prime} b^{\prime}+a^{\prime} c^{\prime}+b^{\prime} c^{\prime}\right)}{\left(b^{\prime} c^{\prime}-a^{\prime 2}\right)\left(a^{\prime}+b^{\prime}+c^{\prime}\right)}=\frac{a^{\prime} b^{\prime}+a^{\prime} c^{\prime}+b^{\prime} c^{\prime}}{a^{\prime}+b^{\prime}+c^{\prime}}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
Како је наведени израз симетричан по $a^{\prime}, b^{\prime}, c^{\prime}$, аналогно се доказује да ће праве $K_{b} B_{1}$ и $K_{c} C_{1}$ сећи уписани круг у истој тачки, чиме је тврђење доказано.
|
| 138 |
+
|
| 139 |
+
6. Дати израз је симетричан, па се без губљења општости може претпоставити да је $x \geqslant y \geqslant z$. Тада је
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
x^{k+1}+y^{k}+z^{k} \leqslant y^{k+1}+z^{k}+x^{k} \leqslant z^{k+1}+x^{k}+y^{k}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
Заиста, довољно је доказати прву неједнакост, тј. да је $x^{k+1}+y^{k} \leqslant y^{k+1}+$ $x^{k}$. Ова неједнакост је еквивалентна са $\left(\frac{y}{x}\right)^{k} \leqslant \frac{1-x}{1-y}$. Како је $y \leqslant x$, довољно је доказати да је $\frac{y}{x} \leqslant \frac{1-x}{1-y}$, што је еквивалентно тачној неједнакости $0 \leqslant$ $x-x^{2}-y+y^{2}=(x-y)(1-x-y)=(x-y) z$. Применом неједнакости Чебишева на тројке $\left(x^{k+2}, y^{k+2}, z^{k+2}\right)$ и $\left(\frac{1}{x^{k+1}+y^{k}+z^{k}}, \frac{1}{y^{k+1}+z^{k}+x^{k}}, \frac{1}{z^{k+1}+x^{k}+y^{k}}\right)$ добија се
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\sum_{\text {cyc }} \frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}} \geqslant \frac{1}{3} \sum_{\text {cyc }} x^{k+2} \sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}}=L
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
Уколико се у $L$ поново примени неједнакост Чебишева на тројке $(x, y, z)$ и $\left(x^{k+1}, y^{k+1}, z^{k+1}\right)$ добија се
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
L \geqslant \frac{1}{3} \cdot \frac{1}{3} \sum_{\text {cyc }} x \sum_{\text {cyc }} x^{k+1} \sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}}=L^{\prime}
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
Из неједнакости Коши-Шварц-Буњаковског следи
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}} \sum_{\text {cyc }}\left(x^{k+1}+y^{k}+z^{k}\right) \geqslant 9
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
па је
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
L^{\prime} \geqslant \frac{x^{k+1}+y^{k+1}+z^{k+1}}{x^{k+1}+y^{k+1}+z^{k+1}+2\left(x^{k}+y^{k}+z^{k}\right)}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
и самим тим довољно је доказати да је
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
3\left(x^{k+1}+y^{k+1}+z^{k+1}\right) \geqslant x^{k}+y^{k}+z^{k}
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
Последња неједнакост се добија поновном применом неједнакости Чебишева на тројке $(x, y, z)$ и $\left(x^{k}, y^{k}, z^{k}\right)$.
|
| 176 |
+
|
| 177 |
+
Једнакост у свим примењеним неједнакостима важи ако и само ако је $x=y=z$, тј. ако и само ако је $x=y=z=\frac{1}{3}$.
|
| 178 |
+
|
Serbia_MO/md/sr-2008_smo_resenja.md
ADDED
|
@@ -0,0 +1,230 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 2 |
+
|
| 3 |
+
такмичење ученика средњих школа из математике
|
| 4 |
+
|
| 5 |
+
Београд, 12.04.2008.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. У скупу целих бројева решити једначину
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
12^{x}+y^{4}=2008^{z} . \quad \text { (Милош Милосављевић) }
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
2. Дат је троугао $A B C$. Нека су тачке $D$ и $E$ на правој $A B$ такве да је $D-A-B-E, A D=A C$ и $B E=B C$. Симетрале унутрашњих углова код темена $A$ и $B$ секу наспрамне странице у тачкама $P$ и $Q$, редом, а описану кружницу око троугла $A B C$ у тачкама $M$ и $N$, редом. Права која спаја тачку $A$ са центром кружнице описане око троугла $B M E$ и права која спаја тачку $B$ са центром кружнице описане око троугла $A N D$ секу ce у тачки $X, X \neq C$. Доказати да је $C X \perp P Q$. (Дуиан Ђукић)
|
| 16 |
+
3. Доказати да за позитивне реалне бројеве $a, b$ и $c$, такве да је $a+b+c=1$, важи неједнакост
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\frac{1}{b c+a+\frac{1}{a}}+\frac{1}{c a+b+\frac{1}{b}}+\frac{1}{a b+c+\frac{1}{c}} \leqslant \frac{27}{31}
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
(Марко Радовановић са сараунииима)
|
| 23 |
+
|
| 24 |
+
Време за рад 270 минута.
|
| 25 |
+
|
| 26 |
+
Сваки задатак вреди 7 поена.
|
| 27 |
+
|
| 28 |
+
## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 29 |
+
|
| 30 |
+
такмичење ученика средњих школа из математике
|
| 31 |
+
|
| 32 |
+
Београд, 13.04.2008.
|
| 33 |
+
|
| 34 |
+
## Други дан
|
| 35 |
+
|
| 36 |
+
4. Свака тачка равни је обојена са једном од 3 боје. Доказати да постоји троугао за који важи:
|
| 37 |
+
|
| 38 |
+
$1^{\circ}$ сва 3 темена тог троугла су обојена истом бојом;
|
| 39 |
+
|
| 40 |
+
$2^{\circ}$ полупречник описане кружнице тог троугла је 2008;
|
| 41 |
+
|
| 42 |
+
$3^{\circ}$ један угао троугла је два или три пута већи од неког од друга два угла.
|
| 43 |
+
|
| 44 |
+
|
| 45 |
+
|
| 46 |
+
5. Нека је низ $\left(a_{n}\right)_{n \geqslant 1}$ дефинисан са $a_{1}=3, a_{2}=11$ и $a_{n}=4 a_{n-1}-a_{n-2}$, за $n \geqslant 3$. Доказати да је сваки члан овог низа облика $a^{2}+2 b^{2}$ за неке природне $a$ и $b$.
|
| 47 |
+
|
| 48 |
+
(Ђорђе Баралић)
|
| 49 |
+
|
| 50 |
+
6. Нека је $A B C D E$ конвескан петоугао у коме је $A B=1, \varangle B A E=\varangle A B C=$ $120^{\circ}, \varangle C D E=60^{\circ}$ и $\varangle A D B=30^{\circ}$. Доказати да је површина петоугла $A B C D E$ мања од $\sqrt{3}$.
|
| 51 |
+
|
| 52 |
+
(Милош Милосављевић)
|
| 53 |
+
|
| 54 |
+
## РЕШЕЊА
|
| 55 |
+
|
| 56 |
+
1. За $x<0$ или $z \leq 0$ једино решење је тривијално $(0,0,0)$. Надаље је $z>0$. Како је $2008=2^{3} \cdot 251$, обе стране једначине су дељиве са 251. Претпоставимо да је $x=2 x_{1}$ парно. Тада $\left(2^{x_{1}}\right)^{2} \equiv-\left(y^{2}\right)^{2}(\bmod 251)$, што дизанјем на 125 -ти степен даје $1 \equiv\left(2^{x_{1}}\right)^{250} \equiv-\left(y^{2}\right)^{250} \equiv-1$ по малој Фермаовој теореми, а то је немогуће. Према томе, $x$ мора бити непарно.
|
| 57 |
+
|
| 58 |
+
Очигледно је $y$ парно. Напишимо $y=2^{u} y_{1}$ за непарно $y_{1}$. Имамо
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
2^{2 x} 3^{x}+2^{4 u} y_{1}^{4}=2^{3 z} 251^{z}
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Како је $2 x \neq 4 u$ јер је $x$ непарно, највећи степен двојке који дели леву страну је $2^{2 x}$ или $2^{4 u}$, док је највећи степен двојке који дели десну страну једнак $2^{3 z}$, одакле је $3 z=2 x$ или $3 z=4 u$. Показаћемо да ни у једном од ова два случаја дата једначина нема решења.
|
| 65 |
+
|
| 66 |
+
(i) $3 z=2 x<4 u$; дакле, $2 \mid z$. Скраћивање са $2^{2 x}$ даје $3^{x}+2^{4 u-2 x} y_{1}^{4}=251^{z}$ што је немогуће јер је лева страна облика $4 k+3$ (јер $2 \nmid x$ ), а десна облика $4 k+1(k \in \mathbb{N})$.
|
| 67 |
+
|
| 68 |
+
(ii) $3 z=4 u<2 x$; опет $2 \mid z$. Скраћивање са $2^{4 u}$ даје $2^{2 x-4 u} 3^{x}+y_{1}^{4}=251^{z}$. Десна страна је облика $5 k+1$, па за $5 \nmid y_{1}$ имамо $y_{1}^{4} \equiv 1$ и $2^{2 x-4 u} 3^{x} \equiv 0$ $(\bmod 5)$ што је немогуће, док за $5 \mid y_{1}$ имамо $1 \equiv 2^{2 x-4 u} 3^{x} \equiv \pm 3^{x} \equiv \pm 3$ $(\bmod 5)$ jep $2 \nmid x$, опет немогуће.
|
| 69 |
+
|
| 70 |
+
Друго решење. За парно $x$ лева страна једначине је облика $a^{2}+b^{2}$, а за непарно $x$ лева страна је облика $a^{2}+3 b^{2}$. Међутим, како су -1 и -3 квадратни неостаци по модулу 251 , ни $a^{2}+b^{2}$ ни $a^{2}+3 b^{2}$ не могу да буду дељиви са 251 ако $251 \nmid$. Према томе, дата једначина нема целобројних решења за $z \geq 0$.
|
| 71 |
+
|
| 72 |
+
2. Означимо са $U$ центар описаног круга $\triangle B M E$. Применимо инверзију са центром $A$ и квадратом полупречника $A B \cdot A C$. Тачке $B$ и $C$ се сликају у тачке $B^{\prime}$ и $C^{\prime}$ симетричне тачкама $C$ и $B$ у односу на $A P$, тачке $P$ и $M$ се сликају једна у другу, а $E$ се слика у тачку $E^{\prime}$ симетричну $Q$ у односу на $A P$. Према томе, права $A U$ се поклапа са правом која спаја $A$ са центром круга $B^{\prime} P E^{\prime}$ (наравно, центри се не сликају један у други!). Видимо да је та права симетрична
|
| 73 |
+
|
| 74 |
+
|
| 75 |
+
правој $A Z$ у односу на симетралу угла $A$, где је $Z$ центар круга описаног око $\triangle C P Q$.
|
| 76 |
+
|
| 77 |
+
Аналогно се добија да је права $B Z$ симетрична правој која спаја $B$ са центром $V$ круга $A N D$ у односу на симетралу угла $B$. По Чевиној теореми у тригонометријском облику (или по тврђењу о изогонално спрегнутим тачкама), праве симетричне правим $A U, B V, C X$ у односу на симетрале углова $A, B, C$ редом се такође секу у једној тачки, што значи да је права $C Z$ симетрична $C X$ у односу на симетралу угла $C$. Али $Z$ је центар круга $C P Q$, одакле следи да права $C X$ садржи висину троугла $C P Q$, а то смо и желели да докажемо.
|
| 78 |
+
|
| 79 |
+
3. Тражена неједнакост је очигледно еквивалентна неједнакости
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\frac{a}{p+a^{2}}+\frac{b}{p+b^{2}}+\frac{c}{p+c^{2}} \leq \frac{27}{31}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
где је $a+b+c=1$ и $p=a b c+1$. Посматраћемо функцију
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
f(x)=\frac{3(a+b+c)}{3 x+a^{2}+b^{2}+c^{2}}-\frac{a}{x+a^{2}}-\frac{b}{x+b^{2}}-\frac{c}{x+c^{2}}
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Доказаћемо да важи $f(x) \geq 0$ за све $x \geq a b+b c+c a$. Свођење израза за $f(x)$ на заједнички именилац даје
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
f(x)=\frac{A x^{2}+B x+C}{\left(x+a^{2}\right)\left(x+b^{2}\right)\left(x+c^{2}\right)\left(3 x+a^{2}+b^{2}+c^{2}\right)}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
при чему је $A \geq 0 \geq C$. Заправо, лако се добија
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\begin{gathered}
|
| 101 |
+
A=2 a^{3}+2 b^{3}+2 c^{3}-a b(a+b)-a c(a+c)-b c(b+c) \geq 0 \\
|
| 102 |
+
C=-a b c\left[a\left(b^{3}+c^{3}\right)+b\left(c^{3}+a^{3}\right)+c\left(a^{3}+b^{3}\right)-2 a b c(a+b+c)\right] \leq 0
|
| 103 |
+
\end{gathered}
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
Приметимо да није важно колико је $B$. Према томе, полином $P(x)=$ $A x^{2}+B x+C$ (ако није константно 0 ) има две реалне нуле, једну позитивну (рецимо $x=x_{0}$ ) и једну негативну, и важи $P(x) \leq 0$ за $0 \leq x \leq x_{0}$ и $P(x) \geq 0$ за $x \geq x_{0}$. Тврдимо да је $f(a b+b c+c a) \geq 0$. Заиста,
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
\begin{aligned}
|
| 110 |
+
& f(a b+b c+c a) \\
|
| 111 |
+
& =\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)}-\frac{a}{(a+b)(a+c)}-\frac{b}{(b+c)(b+a)}-\frac{c}{(c+a)(c+b)} \\
|
| 112 |
+
& =\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)}-\frac{2(a b+b c+c a)}{(a+b)(b+c)(c+a)} \geq 0 \quad \text { jep je } \\
|
| 113 |
+
& \quad \frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)} \geq \frac{9}{4(a+b+c)} \geq \frac{2(a b+b c+c a)}{(a+b)(b+c)(c+a)},
|
| 114 |
+
\end{aligned}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
што смо и желели. Према томе, $P(a b+b c+c a) \geq 0$, тј. $x_{0} \leq a b+b c+c a$, одакле следи да је и $P(x) \geq 0$ и $f(x) \geq 0$ за све $x \geq a b+b c+c a$. Између осталог, $f(1+a b c) \geq 0$ јер је $1+a b c>1>a b+b c+c a$. Тако смо доказали
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\frac{a}{1+a b c+a^{2}}+\frac{b}{1+a b c+b^{2}}+\frac{c}{1+a b c+c^{2}} \leq \frac{3}{3+a^{2}+b^{2}+c^{2}+3 a b c}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
Остаје још само да докажемо да је $a^{2}+b^{2}+c^{2}+3 a b c \geq \frac{4}{9}$, што ће заједно са (1) дати тражену неједнакост. Хомогенизација даје $9(a+b+c)\left(a^{2}+b^{2}+\right.$ $\left.c^{2}\right)+27 a b c \geq 4(a+b+c)^{3}$, што је еквивалентно са
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
5\left(a^{3}+b^{3}+c^{3}\right)+3 a b c \geq 3(a b(a+b)+a c(a+c)+b c(b+c))
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
Последња неједнакост одмах следи из Шурове неједнакости. Овим је доказ тврђења задатка коначно завршен.
|
| 130 |
+
|
| 131 |
+
Друго решење. Након хомогенизације, свођења на заједнички именилац и скраћивања неједнакост се своди на симетричну неједнакост која се директно доказује Мјурхедовом неједнакошћу:
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\begin{aligned}
|
| 135 |
+
& \frac{23}{2} T_{900}+122 T_{810}+260 T_{720}+282 T_{630}+193 T_{540}+\frac{547}{2} T_{711}+807 T_{620}+284 T_{531} \\
|
| 136 |
+
&+91 T_{522}-98 T_{441}-1669 T_{432}-557 T_{333} \geq 0
|
| 137 |
+
\end{aligned}
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
где је $T_{i j k}$ симетрична сума $x^{i} y^{j} z^{k}+\cdots$.
|
| 141 |
+
|
| 142 |
+
4. Уочимо правилан тринаестоугао $A_{1} A_{2} \ldots A_{13}$ уписан у круг полупречника 2008. По Дирихлеовом принципу постоји пет темена која су исте боје (нпр. црвене). Разликујемо два случаја.
|
| 143 |
+
|
| 144 |
+
(i) Међу пет црвених темена не постоје два суседна. Сваком положају црвених тачака (до на ротацију) одговара композиција броја 13 на 5 сабирака већих од 1. Постоји 5 неподударних распореда и они су приказани на слици испод, са истакнутим троуглом.
|
| 145 |
+
|
| 146 |
+
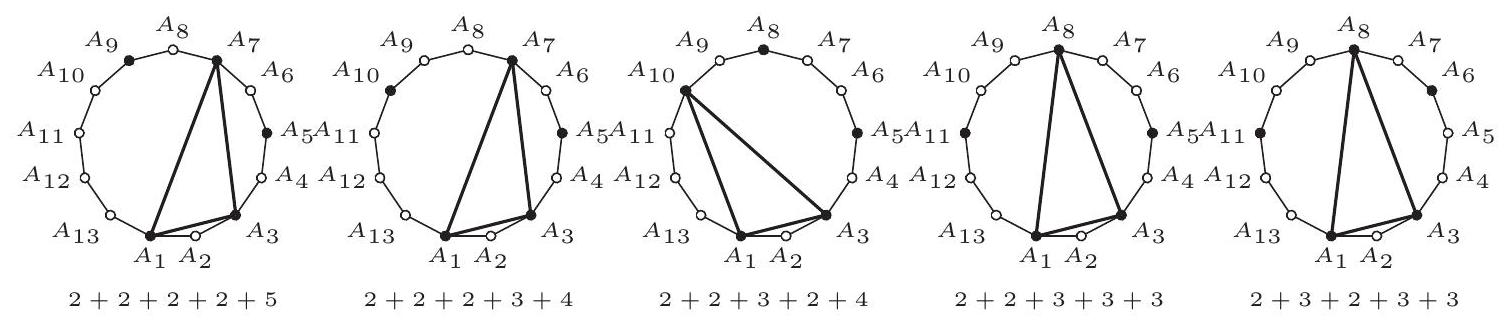
|
| 147 |
+
|
| 148 |
+
(ii) Нека два црвена темена су суседна, рецимо $A_{1}$ и $A_{2}$. Ако је црвена било која од тачака $A_{4}, A_{5}, A_{6}, A_{10}, A_{11}, A_{12}$, тражени троугао је
|
| 149 |
+
одређен том тачком и теменима $A_{1}, A_{2}$. Надаље претпостављамо да ниједна од ових 6 тачака није црвена. Тада су међу теменима $A_{3}, A_{7}$, $A_{8}, A_{9}, A_{13}$ бар три црвена. Ако је међу њима $A_{3}$ (аналогно за $A_{13}$ ), онда је бар једна од тачака $A_{7}, A_{9}, A_{13}$ црвена па бар један од троуглова одређених овом тачком и тачкама $A_{1}$ и $A_{3}$ задовољава услове. Једини преостали случај је кад су црвене тачке $A_{7}, A_{8}, A_{9}$, а онда је троугао $A_{1} A_{7} A_{9}$ тражени.
|
| 150 |
+
|
| 151 |
+
5. Имамо $a_{1}=1+2 \cdot 1^{2}, a_{2}=3^{2}+2 \cdot 1^{2}, a_{3}=3^{2}+2 \cdot 4^{2}, a_{4}=11^{2}+2 \cdot 4^{2}$, итд. Доказаћемо индукцијом по $n$ да важи
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
a_{2 n-1}=a_{n-1}^{2}+2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \quad \text { и } \quad a_{2 n}=a_{n}^{2}+2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2},
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
при чему је $a_{0}=1$. Претпоставимо да тврђење важи за $n$. Тада је
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\begin{aligned}
|
| 161 |
+
a_{2 n+1} & =4 a_{2 n}-a_{2 n-1}=4 a_{n}^{2}+8\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2}-a_{n-1}^{2}-2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \\
|
| 162 |
+
& =\frac{11}{2} a_{n}^{2}-3 a_{n} a_{n-1}+\frac{1}{2} a_{n-1}^{2}=\frac{11}{2} a_{n}^{2}-3 a_{n}\left(4 a_{n}-a_{n+1}\right)+\frac{1}{2}\left(4 a_{n}-a_{n+1}\right)^{2} \\
|
| 163 |
+
& =\frac{3}{2} a_{n}^{2}-a_{n} a_{n+1}+\frac{1}{2} a_{n+1}^{2}=a_{n}^{2}+2\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2} \\
|
| 164 |
+
a_{2 n+2} & =4 a_{2 n+1}-a_{2 n}=4 a_{n}^{2}+8\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2}-a_{n}^{2}-2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \\
|
| 165 |
+
& =3 a_{n}^{2}+8\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2}-2\left(\frac{a_{n+1}-3 a_{n}}{2}\right)^{2}=\frac{3}{2} a_{n+1}^{2}-a_{n} a_{n+1}+\frac{1}{2} a_{n}^{2} \\
|
| 166 |
+
& =a_{n+1}^{2}+2\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2},
|
| 167 |
+
\end{aligned}
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
чиме је доказ завршен.
|
| 171 |
+
|
| 172 |
+
Друго решење. Познато је да се непаран природан број $m>1$ може представити у облику $a^{2}+2 b^{2}$ за неке узајамно просте $a, b \in \mathbb{N}$ ако и само ако су сви прости делиоци $m$ облика $8 k+1$ или $8 k+3, k \in \mathbb{N}_{0}$. Лако се види да су сви чланови низа ( $a_{n}$ ) непарни; остаје да покажемо да ако прост број $p$ дели $a_{n}$, онда је $p=8 k+1$ или $8 k+3$ за неко $k \in \mathbb{N}_{0}$.
|
| 173 |
+
|
| 174 |
+
Показује се индукцијом по $n$ да је $a_{n} a_{n+2}=a_{n+1}^{2}+2$. Заиста, ово важи за $n \leq 2$, а за $n>2$, уз претпоставку да важи за $n-2$, имамо
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
\begin{aligned}
|
| 178 |
+
\frac{a_{n+1}^{2}+2}{a_{n}} & =\frac{\left(4 a_{n}-a_{n-1}\right)^{2}+2}{a_{n}}=16 a_{n}-8 a_{n-1}+\frac{a_{n-1}^{2}+2}{a_{n}} \\
|
| 179 |
+
& =16 a_{n}-8 a_{n-1}+a_{n-2}=4 a_{n+1}-a_{n}=a_{n+2}
|
| 180 |
+
\end{aligned}
|
| 181 |
+
$$
|
| 182 |
+
|
| 183 |
+
Одавде следи да је -2 квадратни остатак по сваком простом делиоцу $p$ броја $a_{n}$, па је $p \equiv 1$ или $p \equiv 3(\bmod 8)$.
|
| 184 |
+
|
| 185 |
+
6. Нека је $k$ круг описан око троугла $A B D$, и $l$ права кроз $D$ паралелна са
|
| 186 |
+
$A B$. Полупречник круга $k$ је 1 . Полуправе $B C$ и $A E$ секу $k$ у тачкама $H$ и $I$, а праву $l$ у $F$ и $G$, редом. Троуглови $F C D$ и $G D E$ су слични јер је $\angle C F D=\angle D G E=60^{\circ}$ и $\angle F C D=120^{\circ}-\angle C D F=\angle G D E$. Означимо са $k=\frac{F C}{G D}=\frac{F D}{G E}$ коефи-
|
| 187 |
+
|
| 188 |
+
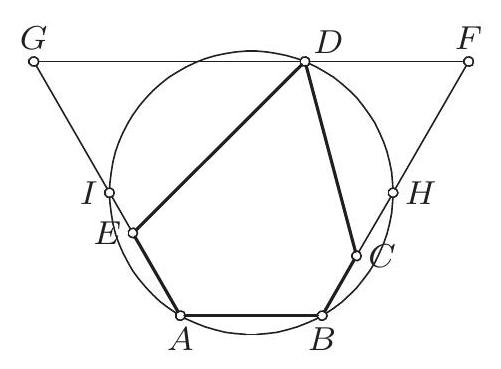
|
| 189 |
+
цијент сличности, са $h$ растојање тачке $D$ од $H I$, и $x=F D, y=G D$. Лако се налази да је $x+y=2+\frac{2}{\sqrt{3}} h$ и $x y=\frac{4}{3} h^{2}+\frac{2}{\sqrt{3}} h$ (производ $x y$ је потенција тачке $F$ у односу на $k$ и једнак је $O F^{2}-1$, где је $O$ центар круга $k$ ). Тако добијамо
|
| 190 |
+
|
| 191 |
+
$$
|
| 192 |
+
\begin{aligned}
|
| 193 |
+
& P_{A B F G}=\frac{1}{2}(1+x+y)\left(\frac{\sqrt{3}}{2}+h\right)=\frac{1}{\sqrt{3}} h^{2}+2 h+\frac{3 \sqrt{3}}{4} \\
|
| 194 |
+
& P_{F C D}+P_{G D E}=\frac{1}{2}(x \cdot F C+y \cdot G E) \sin 60^{\circ}=\frac{\sqrt{3}}{4} x y\left(k+\frac{1}{k}\right) \geq \frac{\sqrt{3}}{2} x y=\frac{2}{\sqrt{3}} h^{2}+h
|
| 195 |
+
\end{aligned}
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
па је
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
P_{A B C D E}=P_{A B F G}-\left(P_{F C D}+P_{G D E}\right) \leq-\frac{1}{\sqrt{3}} h^{2}+h+\frac{3 \sqrt{3}}{4}=f(h)
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
Квадратна функција $f(h)$ достиже максимум за $h=\frac{\sqrt{3}}{2}$, чиме је доказано да је $P_{A B C D E} \leq \sqrt{3}$. Једнакост би важила само ако је $h=\frac{\sqrt{3}}{2}$ и $k=$ 1; тада би (ако без смањења општости претпоставимо $D A \geq D B$ ) тачка $D$ била симетрична тачки $B$ у односу на $H I$, па би троугао $A D G$ био једнакостраничан и $F C=G D=G A=F B$ што је немогуће јер би се $B$ и $C$ поклапале. Зато је горња неједнакост строга.
|
| 205 |
+
|
| 206 |
+
Друго решење. Претпоставимо да троугао $A B D$ није тупоугли. Тада се тачке $C^{\prime}$ и $E^{\prime}$ симетричне тачкама $C$ и $E$ у односу на праве $B D$ и $A D$ редом налазе унутар троугла $A B D$, на истој правој кроз $D$, и важи
|
| 207 |
+
|
| 208 |
+
$S_{A B C D E}=S_{A B D}+S_{A D E}+S_{B D C}=S_{A B D}+S_{A D E^{\prime}}+S_{B D C^{\prime}} \leq 2 S_{A B D}-S_{A B F}$, при чему $F$ тачка пресека правих $A E^{\prime}$ и $B C^{\prime}$. Једнакост важи ако и само ако је $F \equiv C^{\prime} \equiv E^{\prime}$. Означимо $\angle B A D=\alpha$. Тада је $\angle A B D=150^{\circ}-\alpha$, $\angle B A F=2 \alpha-120^{\circ}, \angle A B F=180^{\circ}-2 \alpha$, па важи
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
\begin{aligned}
|
| 212 |
+
& S_{A B D}=\sin \alpha \sin \left(150^{\circ}-\alpha\right)=\frac{\sqrt{3}}{4}+\frac{1}{2} \cos \left(150^{\circ}-2 \alpha\right)=\frac{\sqrt{3}}{4}+\frac{1}{2} u \\
|
| 213 |
+
& S_{A B F}=\frac{1}{\sqrt{3}} \sin \left(2 \alpha-120^{\circ}\right) \sin 2 \alpha=-\frac{\sqrt{3}}{12}+\frac{\sqrt{3}}{6} \cos \left(300^{\circ}-4 \alpha\right)=-\frac{\sqrt{3}}{4}+\frac{1}{\sqrt{3}} u^{2}
|
| 214 |
+
\end{aligned}
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
где је $\cos \left(150^{\circ}-2 \alpha\right)=u$ и одатле $\cos \left(300^{\circ}-4 \alpha\right)=2 u^{2}-1$. Сада имамо
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
S_{A B C D E} \leq 2 S_{A B D}-S_{A B F}=\frac{3 \sqrt{3}}{4}+u-\frac{u^{2}}{\sqrt{3}} \leq \sqrt{3}
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
уз једнакост која би важила за $u=\frac{\sqrt{3}}{2}$, тј. $\alpha \in\left\{60^{\circ}, 90^{\circ}\right\}$, и $F \equiv C^{\prime} \equiv E^{\prime}$, али се никада не достиже јер се за ове вредности $\alpha$ тачка $F$ налази у темену правог угла, па је петоугао дегенерисан.
|
| 224 |
+
|
| 225 |
+
У случају тупоуглог троугла $A B D$, уз исте ознаке, тачка $F$ се налази изван троугла $A B D$, али горњи израз за површину $\triangle A B F$ узима негативне вредности, па се опет добија $S_{A B C D E} \leq \frac{3 \sqrt{3}}{4}+u-\frac{u^{2}}{\sqrt{3}}<\sqrt{3}$.
|
| 226 |
+
|
| 227 |
+
$\sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim)$
|
| 228 |
+
|
| 229 |
+
http://srb.imomath.com/
|
| 230 |
+
|
Serbia_MO/md/sr-2009_smo_resenja.md
ADDED
|
@@ -0,0 +1,128 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 2 |
+
|
| 3 |
+
такмичење ученика средњих школа из математике
|
| 4 |
+
|
| 5 |
+
Нови Сад, 13.04.2009.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Нека су $\alpha$ и $\beta$ углови неједнакокраког троугла $A B C$ код темена $A$ и $B$, редом. Нека симетрале ових углова секу наспрамне странице троугла у $D$ и $E$, редом. Доказати да оштар угао између правих $D E$ и $A B$ није већи од $\frac{|\alpha-\beta|}{3}$.
|
| 10 |
+
|
| 11 |
+
(Душан Ђукић)
|
| 12 |
+
|
| 13 |
+
2. Одредити најмањи природан број који је дељив са 2009 и коме је збир цифара једнак 2009.
|
| 14 |
+
3. Одредити највећи природан број $n$ за који постоје различити скупови $S_{1}, S_{2}, \ldots, S_{n}$ такви да је:
|
| 15 |
+
|
| 16 |
+
$1^{\circ}\left|S_{i} \cup S_{j}\right| \leqslant 2004$ за свака два цела броја $1 \leqslant i, j \leqslant n$, и
|
| 17 |
+
|
| 18 |
+
$2^{\circ} S_{i} \cup S_{j} \cup S_{k}=\{1,2, \ldots, 2008\}$ за свака три цела броја $1 \leqslant i<j<k \leqslant n$.
|
| 19 |
+
|
| 20 |
+
(Иван Матић)
|
| 21 |
+
|
| 22 |
+
## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 23 |
+
|
| 24 |
+
такмичење ученика средњих школа из математике
|
| 25 |
+
|
| 26 |
+
Нови Сад, 14.04.2009.
|
| 27 |
+
|
| 28 |
+
## Други дан
|
| 29 |
+
|
| 30 |
+
4. Нека је $n \in \mathbb{N}$ и $A_{n}$ скуп свих пермутација $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ скупа $\{1,2, \ldots, n\}$ таквих да важи
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
k \mid 2\left(a_{1}+a_{2}+\cdots+a_{k}\right) \quad \text { за свако } 1 \leqslant k \leqslant n
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
Одредити број елемената скупа $A_{n}$.
|
| 37 |
+
|
| 38 |
+
(Видан Говедарииа)
|
| 39 |
+
|
| 40 |
+
5. Нека су $x, y, z$ позитивни реални бројеви такви да је $x y+y z+z x=x+y+z$. Доказати неједнакост
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\frac{1}{x^{2}+y+1}+\frac{1}{y^{2}+z+1}+\frac{1}{z^{2}+x+1} \leqslant 1
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Када се у претходној неједнакости достиже знак једнакости?
|
| 47 |
+
|
| 48 |
+
(Марко Радовановић)
|
| 49 |
+
|
| 50 |
+
6. Нека је $k$ уписана кружница неједнакокраког $\triangle A B C$, чији је центар $S$. Кружница $k$ додирује странице $B C, C A, A B$ у тачкама $P, Q, R$, редом. Права $Q R$ сече праву $B C$ у тачки $M$. Нека кружница која садржи тачке $B$ и $C$ додирује $k$ у тачки $N$. Описана кружница $\triangle M N P$ сече праву $A P$ у тачки $L$, различитој од $P$. Доказати да су тачке $S, L$ и $M$ колинеарне.
|
| 51 |
+
|
| 52 |
+
(Ђорђе Баралић)
|
| 53 |
+
|
| 54 |
+
## РЕШЕЊА
|
| 55 |
+
|
| 56 |
+
1. Као и обично, означимо $\varangle A C B=\gamma$ и $B C=a, C A=b, A B=c$, при чему је без смањења општости $a>b$ и $\alpha>\beta$. Нека је $F$ тачка пресека правих $D E$ и $A B$, а $\varphi$ угао између ових правих. Из односа $\frac{B D}{D C}=\frac{c}{b}$ и $\frac{C E}{E A}=\frac{a}{c}$ лако налазимо $B D=\frac{a c}{b+c}, D C=\frac{a b}{b+c}$, $C E=\frac{a b}{a+c}$ и $E A=\frac{b c}{a+c}$. Менелајева теорема за праву $D E$ и троугао $A B C$ даје $A F=\frac{b c}{a-b}$ и $F B=\frac{a c}{a-b}$.
|
| 57 |
+
|
| 58 |
+
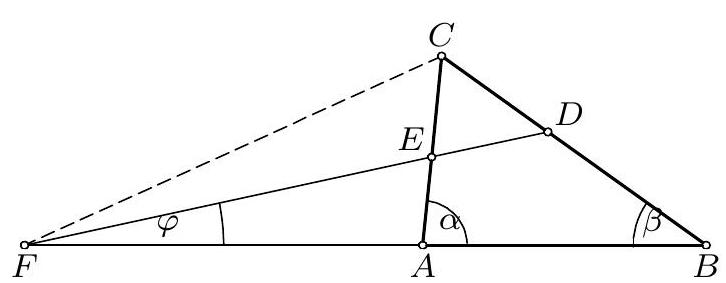
|
| 59 |
+
|
| 60 |
+
Сада на основу синусне теореме у троугловима $F E A$ и $F D B$ имамо
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
\begin{aligned}
|
| 64 |
+
& \frac{\sin (\alpha-\varphi)}{\sin \varphi}=\frac{\sin \varangle F E A}{\sin \varangle E F A}=\frac{F A}{E A}=\frac{\frac{b c}{a-b}}{\frac{b c}{a+c}}=\frac{a+c}{a-b} \\
|
| 65 |
+
& \frac{\sin (\beta+\varphi)}{\sin \varphi}=\frac{\sin \varangle F D B}{\sin \varangle D F B}=\frac{F B}{D B}=\frac{\frac{a c}{a-b}}{\frac{a c}{b+c}}=\frac{b+c}{a-b}
|
| 66 |
+
\end{aligned}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
из чега добијамо $\sin \varphi=\sin (\alpha-\varphi)-\sin (\beta+\varphi)=2 \sin \frac{\alpha-\beta-2 \varphi}{2} \cos \frac{\alpha+\beta}{2}<$ $\sin (\alpha-\beta-2 \varphi)$. Одавде је $\varphi<\alpha-\beta-2 \varphi$, тј. $3 \varphi<\alpha-\beta$.
|
| 70 |
+
|
| 71 |
+
2. Пошто је $2009=223 \cdot 9+2$, тражени број има бар 224 цифре. Посматраћемо 224 -цифрене бројеве $x=\overline{c_{223} c_{222} \ldots c_{1} c_{0}}$. Јасно је да је $c_{223} \geq 2$. Притом, ако је $c_{223}=2$ онда је $c_{222}=\cdots=c_{0}=9$ и $x=3 \cdot 10^{223}-1 \equiv 3 \cdot 10-1$, а то није дељиво са $2009=7^{2} \cdot 41$ јер је $x \equiv 1(\bmod 7)$.
|
| 72 |
+
|
| 73 |
+
Нека је сада $c_{223}=3$. Тада број $x$ има облик $399 \ldots 9899 \ldots 9=4 \cdot 10^{223}-$ $10^{i}-1$ за неко $i$. Како је $10^{5} \equiv 1(\bmod 41)$, имамо $10^{i} \equiv 1,10,18,16$ или 37 $(\bmod 41)$ за $i=0,1,2,3,4(\bmod 5)$ редом, и одатле $x \equiv 4 \cdot 10^{3}-10^{i}-1 \equiv 22-10^{i}$ $(\bmod 41)$ никад није дељиво са 41.
|
| 74 |
+
|
| 75 |
+
Нека је $c_{223}=4$. Међу цифрама $c_{222}, \ldots, c_{0}$ налазе се две осмице или једна седмица, док су све остале деветке; у сваком случају, $x=5 \cdot 10^{223}-10^{i}$ $10^{j}-1 \equiv 38-\left(10^{i}+10^{j}\right)(\bmod 41)$, где $i$ и $j$ нису обавезно различити. По претходном је $10^{i}+10^{j} \equiv 38(\bmod 41)$ ако и само ако је $(i, j) \equiv(0,4)$ или $(4,0)(\bmod 5)$. Између осталог, $i \neq j$ и $i, j \leq 220$.
|
| 76 |
+
|
| 77 |
+
Пробајмо да ставимо $j=220$ и $i \equiv 4(\bmod 5)$. Треба одабрати $i$, ако постоји, тако да $7^{2} \mid x=5 \cdot 10^{223}-10^{220}-10^{i}-1 \equiv 5 \cdot 10^{13}-10^{10}-10^{i}-1 \equiv 31-10^{i}$ $(\bmod 49)$. Лако налазимо да је $10^{i} \equiv 31(\bmod 49)$ ако и само ако је $i \equiv 7$ $(\bmod 42)$, што заједно са $i \equiv 4(\bmod 5)$ даје као једину могућност $i=49$. Према томе, тражени број је
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
4998 \underbrace{9 \ldots 99}_{170} 8 \underbrace{99 \ldots 9}_{49} .
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
3. Сваки скуп $S_{i}$ има највише 2003 елемената. Заиста, ако је $\left|S_{i}\right|=2004$, из услова $1^{\circ}$ следи да је $S_{j} \subset S_{i}$ за све $j$, противно услову $2^{\circ}$. Посматрајмо скупове
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
G_{\{i, j\}}=\{1,2, \ldots, 2008\} \backslash\left(S_{i} \cup S_{j}\right) \quad \text { за } 1 \leq i, j \leq n
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Тада је $\left|G_{\{i, j\}}\right| \geqslant 4$ и свих $\binom{n}{2}$ скупова $G_{\{i, j\}}$ су међусобно дисјунктни (у супротном, ако $x \in G_{\{i, j\}} \cap G_{\{k, l\}}$, онда $x \notin S_{i} \cup S_{j} \cup S_{k} \cup S_{l}$, што је немогуће ако су бар три међу $i, j, k, l$ различита). Следи да је $4\binom{n}{2} \leqslant 2008$, одакле je $n \leqslant 32$.
|
| 90 |
+
|
| 91 |
+
Конструисаћемо 32 скупа који задовољавају $1^{\circ}$ и $2^{\circ}$. Разложимо скуп $\{1,2, \ldots, 2008\}$ произвољно на $\binom{32}{2}=496$ (дисјунктних) скупова $G_{\{i, j\}}$, при чему је $\left|G_{\{i, j\}}\right| \geqslant 4$ за $1 \leqslant i, j \leqslant 32$, и дефинишимо
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
S_{i}=\{1,2, \ldots, 2008\} \backslash \bigcup_{j \neq i} G_{\{i, j\}} \quad \text { за } i=1, \ldots, 32
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Услов $1^{\circ}$ је аутоматски задовољен. Осим тога, свако $s \in\{1,2, \ldots, 2008\}$ припада највише једном од скупова $G_{\{p, q\}}$, што значи да постоје највише два скупа $S_{i}$ који га не садрже (то су $S_{p}$ и $S_{q}$ ), па је и услов $2^{\circ}$ задовољен. Према томе, одговор је $n=32$.
|
| 98 |
+
|
| 99 |
+
4. Означимо са $F_{n}$ број елемената скупа $A_{n}$. Имамо $F_{1}=1, F_{2}=2$ и $F_{3}=6$. За $n>3$, посматрајмо било коју пермутацију $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ у $A_{n}$. Како $n-1$ дели $2\left(a_{1}+\cdots+a_{n-1}\right)=n(n+1)-2 a_{n} \equiv 2-2 a_{n}(\bmod n-1)$, следи да је $a_{n}$ једнако $1, \frac{n+1}{2}$ или $n$.
|
| 100 |
+
|
| 101 |
+
Претпоставимо да је $a_{n}=\frac{n+1}{2}$. Тада $n-2$ дели $2\left(a_{1}+\cdots+a_{n-2}\right)=n^{2}-$ $1-2 a_{n-1} \equiv 3-2 a_{n-1}(\bmod n-2)$. Зато мора бити $2 a_{n-1}-3=n-2$, али тада је $a_{n-1}=\frac{n+1}{2}=a_{n}$, контрадикција.
|
| 102 |
+
|
| 103 |
+
Ако је $a_{n}=n$, онда је $\left(a_{1}, \ldots, a_{n}\right) \rightarrow\left(a_{1}, \ldots, a_{n-1}\right)$ бијективно пресликавање у скуп $A_{n-1}$, па оваквих пермутација има $F_{n-1}$.
|
| 104 |
+
|
| 105 |
+
Ако је $a_{n}=1$, онда је $\left(a_{1}-1, \ldots, a_{n-1}-1\right)$ пермутација на $\{1, \ldots, n-1\}$ која припада скупу $A_{n-1}$ јер је $2\left(\left(a_{1}-1\right)+\cdots+\left(a_{k}-1\right)\right)=2\left(a_{1}+\cdots+a_{k}\right)-2 k$ дељиво са $k$ за $1 \leqslant k \leqslant n-1$. Као и у претходном случају, оваквих пермутација има $F_{n-1}$.
|
| 106 |
+
|
| 107 |
+
Закључујемо да је $F_{n}=2 F_{n-1}$ за $n>3$, што заједно са $F_{3}=6$ даје $F_{n}=$ $3 \cdot 2^{n-2}$ за $n \geqslant 3$.
|
| 108 |
+
|
| 109 |
+
5. Коши-Шварцова неједнакост за тројке $(x, \sqrt{y}, 1)$ и $(1, \sqrt{y}, z)$ даје $\frac{1}{x^{2}+y+1} \leqslant$ $\frac{1+y+z^{2}}{(x+y+z)^{2}}$. Аналогно важи $\frac{1}{y^{2}+z+1} \leqslant \frac{1+z+x^{2}}{(x+y+z)^{2}}$ и $\frac{1}{z^{2}+x+1} \leqslant \frac{1+x+y^{2}}{(x+y+z)^{2}}$. Сабиранјем ових неједнакости добијамо
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\frac{1}{x^{2}+y+1}+\frac{1}{y^{2}+z+1}+\frac{1}{z^{2}+x+1} \leqslant \frac{3+x+y+z+x^{2}+y^{2}+z^{2}}{(x+y+z)^{2}}=S
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Остаје да се докаже да је $S \leqslant 1$, а то је еквивалентно са $3+x+y+z \leqslant$ $2(x y+y z+z x)=2(x+y+z)$ по услову задатка, тј. $x+y+z \geqslant 3$. Ово, међутим, следи из $x+y+z=x y+y z+z x \leqslant \frac{(x+y+z)^{2}}{3}$.
|
| 116 |
+
|
| 117 |
+
Једнакост важи само за $x=y=z=1$.
|
| 118 |
+
|
| 119 |
+
6. Посматрајмо хомотетију са центром $N$ која слика круг $k$ у круг $B C N$; нека она слика тачку $P$ у $P_{1}$. Тангента на круг $B C N$ у $P_{1}$ је паралелна тангенти на $k$ у $P$, тј. правој $B C$, што значи да је $P_{1}$ средиште лука $B C$ круга $B C N$. Дакле, $N P$ је симетрала угла $C N B$, па је $\frac{B N}{C N}=\frac{B P}{C P}$. Шта више, по Менелајевој теореми је $\frac{B M}{M C}=\frac{B R}{R A} \cdot \frac{A Q}{Q C}=\frac{B P}{P C}=\frac{B N}{N C}$, па је $N M$ спољна симетрала угла $C N B$.
|
| 120 |
+
|
| 121 |
+
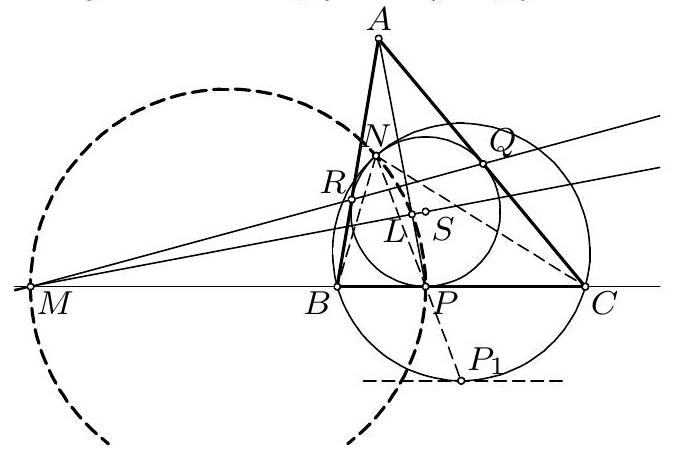
|
| 122 |
+
|
| 123 |
+
Према томе, $N$ лежи на кругу над пречником $M P$, а $L$ је подножје нормале из $M$ на $A P$. Остаје да се докаже да је $M S \perp A P$.
|
| 124 |
+
|
| 125 |
+
Нека је $L^{\prime}$ подножје нормале из $S$ на $A P$. Тачке $A, L^{\prime}, Q, R, S$ леже на кругу $\omega$ над пречником $A S$. Инверзија у односу на $k$ слика кругове $\omega$ и $S P L^{\prime}$ редом у праве $Q R$ и $B C$, па слика тачку $L^{\prime}$ у $M$. Дакле, $M$ лежи на правој $S L^{\prime}$, одакле следи тврђење (и $L^{\prime} \equiv L$ ).
|
| 126 |
+
|
| 127 |
+
Напомена. Релација $M S \perp A P$ је еквивалентна са $M P^{2}+A S^{2}=M A^{2}+P S^{2}$ и може се доказати без инверзије: $M P^{2}+A S^{2}=M P^{2}+P S^{2}+A R^{2}=$ $M S^{2}+A Q^{2}=M A^{2}+S Q^{2}$ (због $\left.M Q \perp A S\right)=M A^{2}+P S^{2}$.
|
| 128 |
+
|
Serbia_MO/md/sr-2010_smo_resenja.md
ADDED
|
@@ -0,0 +1,147 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 2 |
+
|
| 3 |
+
такмичење ученика средњих школа из математике
|
| 4 |
+
|
| 5 |
+
Ниш, 06.04.2010.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Неки од $n$ градова су повезани авионским линијама (све линије су двосмерне). Постоји тачно $m$ линија. Нека је $d_{i}$ број линија које полазе из града $i$, за $i=1,2, \ldots, n$. Ако је $1 \leqslant d_{i} \leqslant 2010$, за свако $i=1,2, \ldots, n$, доказати да важи
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\sum_{i=1}^{n} d_{i}^{2} \leqslant 4022 m-2010 n
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Одредити све $n$ за које може да се достигне једнакост.
|
| 16 |
+
|
| 17 |
+
(Александар Илић)
|
| 18 |
+
|
| 19 |
+
2. У оштроуглом $\triangle A B C$ тачка $M$ је средиште странице $B C$, а тачке $D, E$ и $F$ су подножја висина из темена $A, B$ и $C$, редом. Нека је $H$ ортоцентар $\triangle A B C, S$ средиште дужи $A H$, а $G$ пресек дужи $F E$ и $A H$. Ако је $N$ тачка пресека тежишне дужи $A M$ и описане кружнице $\triangle B C H$, доказати да је $\varangle H M A=\varangle G N S$.
|
| 20 |
+
|
| 21 |
+
(Марко Ђикић)
|
| 22 |
+
|
| 23 |
+
3. Нека је $A$ бесконачан подскуп скупа природних бројева. Одредити све природне бројеве $n$ такве да за свако $a \in A$ важи
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
a^{n}+a^{n-1}+\ldots+a^{1}+1 \mid a^{n!}+a^{(n-1)!}+\ldots+a^{1!}+1
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
(Милош Милосавлевић)
|
| 30 |
+
|
| 31 |
+
## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 32 |
+
|
| 33 |
+
такмичење ученика средњих школа из математике
|
| 34 |
+
|
| 35 |
+
Ниш, 07.04.2010.
|
| 36 |
+
|
| 37 |
+
## Други дан
|
| 38 |
+
|
| 39 |
+
4. Нека је $O$ центар описане кружнице $\triangle A B C$. Права кроз $O$ сече странице $C A$ и $C B$ у тачкама $D$ и $E$, редом, и описану кружницу $\triangle A B O$ у тачки $P$ унутар троугла (различитој од $O$ ). Тачка $Q$ на страници $A B$ је таква да је $\frac{A Q}{Q B}=\frac{D P}{P E}$. Доказати да је $\varangle A P Q=2 \cdot \varangle C A P$. (Душан Ђукић)
|
| 40 |
+
5. Таблица димензија $n \times n$, на чијим пољима су бројеви $1,2, \ldots, n^{2}$ (на сваком пољу тачно један број и сваки број на тачно једном пољу) назива се нишка ако сви производи од по $n$ бројева који се налазе на $n$ „разбацаних" поља дају исти остатак при дељењу са $n^{2}+1$. Да ли постоји нишка таблица за:
|
| 41 |
+
|
| 42 |
+
(a) $n=8$;
|
| 43 |
+
|
| 44 |
+
(б) $n=10$ ?
|
| 45 |
+
|
| 46 |
+
( $n$ поља су „разбацана" ако никоја два нису у истој врсти или у истој колони.)
|
| 47 |
+
|
| 48 |
+
(Марко Ђикић)
|
| 49 |
+
|
| 50 |
+
6. Нека су $a_{0}$ и $a_{n}$ различити делиоци природног броја $m>1$, а низ природних бројева $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ такав да задовољава
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
a_{i+1}=\left|a_{i} \pm a_{i-1}\right| \quad \text { за } 0<i<n
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
Ако је НЗД $\left(a_{0}, \ldots, a_{n}\right)=1$, доказати да у низу постоји члан који је мањи од $\sqrt{m}$.
|
| 57 |
+
|
| 58 |
+
(Душан Ђукић)
|
| 59 |
+
|
| 60 |
+
## РЕШЕЊА
|
| 61 |
+
|
| 62 |
+
1. Услов задатка нам даје $0 \leqslant\left(d_{i}-1\right)\left(2010-d_{i}\right)$ за све $i$, тј. $d_{i}^{2} \leqslant 2011 d_{i}-2010$. Користећи услов $\sum_{i=1}^{n} d_{i}=2 m$, сабирањем ових неједнакости добијамо
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\sum_{i=1}^{n} d_{i}^{2} \leqslant 2011 \cdot \sum_{i=1}^{n} d_{i}-2010 n=4022 m-2010 n
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
а једнакост важи ако и само ако је $d_{i} \in\{1,2010\}$ за свако $i \in\{1,2, \ldots, n\}$.
|
| 69 |
+
|
| 70 |
+
$1^{\circ}$ Нека је $n=2 k, k \in \mathbb{N}$. Ако успоставимо авиолинију између градова $i$ и $j$ ако и само ако је $|j-i|=k$, имамо $d_{i}=1$ за све $i$.
|
| 71 |
+
|
| 72 |
+
$2^{\circ}$ Нека је $n=2 k-1, k \in \mathbb{N}$. Не може да важи $d_{i}=1$ за све $i$ јер би иначе било $2 m=n=2 k-1$. Зато мора да буде $d_{j}=2010$ за неко $j$; отуда је $n \geqslant 2011$. С друге стране, успостављањем авиолиније између градова 1 и $i(1 \leq i \leq 2010)$ и између градова $2 i$ и $2 i+1$ $(i=1006, \ldots, k)$ даје мрежу у којој је $d_{1}=2010$ и $d_{i}=1$ за $2 \leqslant i \leqslant n$.
|
| 73 |
+
|
| 74 |
+
Према томе, једнакост се може достићи ако $2 \mid n$, или $2 \nmid n$ и $n \geq 2011$.
|
| 75 |
+
|
| 76 |
+
2. Нека је $A^{\prime}$ тачка таква да је $A B A^{\prime} C$ паралелограм. Тада важи $\varangle B A^{\prime} C=$ $\varangle B A C=180^{\circ}-\varangle B H C=180^{\circ}-$ $\varangle B N C$, па су тачке $A^{\prime}, B, C, H, N$ на истом кругу, тј. кругу над пречником $H A^{\prime}$. Одавде је $\varangle A N H=90^{\circ}$, дакле $N$ је на описаном кругу троугла $A E F$ чији је центар у $S$.
|
| 77 |
+
|
| 78 |
+
Сада имамо $\varangle S F G=90^{\circ}-\varangle E A F=$ $\varangle A C F=\varangle A D F$. Следи да су троуглови $S F G$ и $S D F$ слични, и одатле $S G \cdot S D=S F^{2}=S N^{2}$. Ово повлачи да је и $\triangle S N G \sim \triangle S D N$, и најзад $\varangle G N S=\varangle S D N=\varangle H M N$ јер је четвороугао $H D M N$ тетиван.
|
| 79 |
+
|
| 80 |
+
|
| 81 |
+
|
| 82 |
+
Друго решење. Четвороуглови $B D H F$ и $D C E H$ су тетивни и $A F \cdot A B=$ $\overline{A H \cdot A D=A E} \cdot A C$. Применимо инверзију $\mathcal{I}$ са центром $A$ и потенцијом $A F \cdot A B$. Очигледно је $\mathcal{I}(F)=B, \mathcal{I}(H)=D, \mathcal{I}(E)=C$, па $\mathcal{I}$ слика праву $B C$ у описани круг $\triangle F H E$, тј. у круг над пречником $A H$; даље, $\mathcal{I}$ слика круг $B C H$ у описани круг $\omega$ троугла $F D E$, а то је Ојлеров круг у $\triangle A B C$. Пошто је $M \in \omega \cap A M$ и $\mathcal{I}$ чува праву $A M$, имамо $\mathcal{I}(M)=N$.
|
| 83 |
+
|
| 84 |
+
Нека је $\mathcal{I}(G)=G^{*}$ и $\mathcal{I}(S)=S^{*}$. Како је $\mathcal{I}(E F)$ описани круг $\triangle A B C, S \in \omega$ и $\mathcal{I}(A H)=A H$, тачке $G^{*}$ и $S^{*}$ су други пресеци праве $A H$ са круговима $A B C$ и $H B C$, редом. Према томе, $\varangle G N S=\varangle G^{*} M S^{*}=\varangle H M A$ јер су $G^{*}$ и $S^{*}$ симетричне тачкама $H$ и $A$ у односу на $B C$.
|
| 85 |
+
|
| 86 |
+
3. Означимо $P(x)=x^{n}+x^{n-1}+\cdots+1$ и $Q(x)=x^{n!}+\cdots+x^{1!}+1$; нека је $Q(x)=C(x) P(x)+R(x)$, где су $C$ и $R$ полиноми са целим коефицијентима и $\operatorname{deg} R<\operatorname{deg} P$. По услову задатка $P(a) \mid Q(a)$, и самим тим $P(a) \mid R(a)$, за бесконачно много целих бројева $a$. Како за довољно велико $a$ важи $|R(a)|<|P(a)|$, мора бити $R(a)=0$; дакле, $R(x)$ има бесконачно много нула, па је $R(x) \equiv 0$ и $P(x) \mid Q(x)$.
|
| 87 |
+
|
| 88 |
+
Лема. Нека су $k_{0}, k_{1}, \ldots, k_{n} \in \mathbb{N}_{0}$. Полином $P(x)=x^{n}+x^{n-1}+\cdots+1$ дели $Q(x)=x^{k_{n}}+\cdots+x^{k_{1}}+x^{k_{0}}$ ако и само ако је $\left\{k_{0}, k_{1}, \ldots, k_{n}\right\}$ потпун систем остатака по модулу $n+1$.
|
| 89 |
+
|
| 90 |
+
Доказ. Нека је $r_{i}$ остатак при дељењу $k_{i}$ са $n+1$. Пошто $x^{n+1}-1$ дели $x^{k_{i}}-x^{r_{i}}$ за све $i$, следи да $P(x)=\frac{x^{n+1}-1}{x-1}$ дели $Q(x)-Q_{1}(x)$, где је $Q_{1}(x)=x^{r_{0}}+x^{r_{1}}+\cdots+x^{r_{n}}$ и притом $\operatorname{deg} Q_{1} \leqslant n$. Ако $P(x) \mid Q(x)$, онда $P(x) \mid Q_{1}(x)$, тј. $Q_{1}(x)=c P(x)$ за неку константу $c$, а то важи ако и само ако је $c=1$ и $\left\{r_{0}, r_{1}, \ldots, r_{n}\right\}=\{0,1, \ldots, n\}$.
|
| 91 |
+
|
| 92 |
+
Из леме следи да су тражени бројеви $n$ они за које је $\{0,1!, \ldots, n!\}$ потпун систем остатака по модулу $n+1$.
|
| 93 |
+
|
| 94 |
+
Ако је $n>3$ и $n+1$ је сложен број, онда је $n!\equiv 0(\bmod n+1)$, па услов није задовољен. Ако је $n+1=p>3$ прост, по Вилсоновој теореми је $(p-1)!\equiv-1(\bmod p)$, одакле је $(p-2)!\equiv 1=1!(\bmod p)$, и опет услов није задовољен. Остају случајеви $n \leqslant 3$; директном провером се добија да $n=1$ и $n=2$ задовољавају услове.
|
| 95 |
+
|
| 96 |
+
Друго решење. Доказаћемо јаче тврђење: ако $A=a^{n}+\cdots+a+1$ дели $a^{k_{n}}+\cdots+a^{k_{1}}+a^{k_{0}}$ за неко $a \in \mathbb{N} \backslash\{1\}$, онда је $\left\{k_{0}, k_{1}, \ldots, k_{n}\right\}$ потпун систем остатака по модулу $n+1$.
|
| 97 |
+
|
| 98 |
+
Нека $A \mid B=a^{k_{n}}+\cdots+a^{k_{1}}+a^{k_{0}}$. Означимо са $r_{i, j}$ остатак при дељењу $k_{i}+j$ са $n+1$ и посматрајмо бројеве $B_{j}=a^{r_{n, j}}+\cdots+a^{r_{1, j}}+a^{r_{0, j}}$. Тада је $B_{j} \equiv a^{j} B(\bmod A)$, одакле следи да $A \mid B_{j}$ за $j=0,1, \ldots, n$. С друге стране, $B_{0}+B_{1}+\cdots+B_{n}=\sum_{j} a^{r_{n, j}}+\cdots+\sum_{j} a^{r_{1, j}}+\sum_{j} a^{r_{0, j}}=(n+1) A$, па како је $B_{j}>0$, мора бити $B_{j}=A$ за све $j$. Из неједнакости $A<2 a^{n}$ закључујемо да је, за свако $j$, највише један од остатака $r_{i, j}$ једнак $n$. Али ако је $k_{i} \equiv k_{i^{\prime}} \equiv n-j(\bmod n+1)$, онда је $r_{i, j}=r_{i^{\prime}, j}=n$, што је немогуће. Према томе, $k_{0}, k_{1}, \ldots, k_{n}$ су међусобно различити по модулу $n+1$, што је и требало доказати.
|
| 99 |
+
|
| 100 |
+
4. Нека је $X$ тачка на полуправој $A P$ таква да је $E X \| A C$. По Талесовој теореми је $A P: P X=D P: P E=$ $A Q: Q B$, одакле следи $B X \| Q P$.
|
| 101 |
+
|
| 102 |
+
Права $P E$ је спољашња симетрала угла $A P B$ и полови угао $B P X$. Такође, пошто је $\varangle B E X=180-$ $\varangle A C B$ и $\varangle B P X=180^{\circ}-\varangle A P B=$ $180^{\circ}-2 \varangle A C B$, добијамо $\varangle B E X=$
|
| 103 |
+
|
| 104 |
+
|
| 105 |
+
$90^{\circ}+\frac{1}{2} \varangle B P X$. Следи да је $E$ центар уписаног круга троугла $B P X$ и одатле $\varangle A P Q=\varangle P X B=2 \varangle P X E=2 \varangle C A P$.
|
| 106 |
+
|
| 107 |
+
Друго решеъе. Конструкција из задатка је могућа само ако је $\triangle A B C$ оштроугли. Означимо $\varangle P A D=\varphi, \varangle Q P A=\psi$ и $\varangle B C A=\gamma$. Из $\varangle A P B=2 \gamma$ и $\varangle D A P+\varangle E B P=\varangle A P B-\varangle A C B=\gamma$ следи $\varangle P B E=\gamma-\varphi$ и $\varangle B P Q=2 \gamma-\psi$. Како је $\varangle A P D=\varangle B P E=90^{\circ}-\gamma$, такође имамо $\varangle A D P=90^{\circ}+\gamma-\varphi$ и $\varangle B E P=90^{\circ}+\varphi$.
|
| 108 |
+
|
| 109 |
+
Синусне теореме у троугловима $A P D$ и $P B E$ дају $\frac{D P}{P E}=\frac{D P}{P A} \cdot \frac{P A}{P B} \cdot \frac{P B}{P E}=$ $\frac{\sin \varphi \cos \varphi}{\sin (\gamma-\varphi) \cos (\gamma-\varphi)} \cdot \frac{P A}{P B}=\frac{\sin 2 \varphi}{\sin (2 \gamma-2 \varphi)} \cdot \frac{P A}{P B}$. С друге стране, $\frac{A Q}{Q B}=\frac{A Q}{A P} \cdot \frac{A P}{B P} \cdot \frac{B P}{Q B}=$ $\frac{\sin \psi}{\sin (2 \gamma-\psi)} \cdot \frac{A P}{P B}$, па се услов $\frac{A Q}{Q B}=\frac{D P}{P E}$ своди на $f(2 \varphi)=f(\psi)$, где је $f(x)=$ $\frac{\sin (2 \gamma-x)}{\sin x}=\sin 2 \gamma \operatorname{ctg} x-\cos 2 \gamma$. Јасно је да је $f$ строго опадајућа функција на $(0, \pi)$, па мора бити $\psi=2 \varphi$.
|
| 110 |
+
|
| 111 |
+
5. (a) Претпоставимо да постоји нишка таблица $8 \times 8$ и да производ ма којих 8 разбацаних бројева даје остатак $r$ по модулу $8^{2}+1=65=5 \cdot 13$. Сви бројеви у таблици се могу поделити на 8 дисјунктних осморки разбацаних бројева. Међу овим осморкама постоји једна која садржи умножак броја 13 и једна која не садржи такав умножак. Производ бројева у првој осморци је дељив са 13, а у другој није, контрадикција. Закључујемо да нишка таблица $8 \times 8$ не постоји.
|
| 112 |
+
|
| 113 |
+
(б) Број $n^{2}+1=101$ је прост. Попунимо таблицу као на слици, где је $g$ примитиван корен по модулу 101. Лако се види да је производ бројева у ма којих 10 разбацаних поља конгруентан са $g^{495}(\bmod 101)$, па је ово пример нишке таблице.
|
| 114 |
+
|
| 115 |
+
| $g^{0}$ | $g^{1}$ | $g^{2}$ | $\cdots$ | $g^{9}$ |
|
| 116 |
+
| :---: | :---: | :---: | :---: | :---: |
|
| 117 |
+
| $g^{10}$ | $g^{11}$ | $g^{12}$ | $\cdots$ | $g^{19}$ |
|
| 118 |
+
| $g^{20}$ | $g^{21}$ | $g^{22}$ | $\cdots$ | $g^{29}$ |
|
| 119 |
+
| $\vdots$ | $\vdots$ | $\vdots$ | | $\vdots$ |
|
| 120 |
+
| $g^{90}$ | $g^{91}$ | $g^{92}$ | $\cdots$ | $g^{99}$ |
|
| 121 |
+
|
| 122 |
+
6. Посматрајмо два најмања (различита) члана низа, $p$ и $q$. Ако је $\min \{p, q\}=$ 1, тврђење тривијално важи; зато надаље претпостављамо да је $p, q>1$.
|
| 123 |
+
|
| 124 |
+
Лема 1. Постоје индекси $k$ и $l$ за које је $a_{k}=p, a_{l}=q$ и $|k-l| \leq 2$.
|
| 125 |
+
|
| 126 |
+
Доказ. Нека је $a_{k}=p$ и $a_{l}=q(k<l)$. Претпоставимо да је $r=l-k>2$. Доказаћемо индукцијом по $r$ да за неко $i, k<i<l$, важи $a_{i} \in\{p, q\}$. Како је $a_{k+3} \neq\left|a_{k+2}-a_{k+1}\right|=p$, имамо $a_{k+3}=a_{k+1}+a_{k+2}$; слично је и $a_{l-3}=a_{l-2}+a_{l-1}$. Нека је $a_{m}=\max _{p<i<q} a_{i}$. Јасно је да је $k+2<m<l-2$ (дакле, $l-k \geqslant 6$ ), а такође и $a_{m+2}=a_{m}-a_{m+1}=a_{m-1}$ и $a_{m+1}=a_{m}-a_{m-1}=a_{m-2}$. То значи да низ $\left(a_{i}^{\prime}\right)$, дефинисан са $a_{i}^{\prime}=a_{i}$ за $i<m$ и $a_{i}^{\prime}=a_{i+3}$ за $i \geqslant m$, задовољава услове задатка; притом је $a_{k}^{\prime}=p$ и $a_{l-3}^{\prime}=q$, па по индуктивној претпоставци (јер је $(l-3)-k \geqslant 3$ ) важи $a_{i}^{\prime} \in\{p, q\}$ за неко $i(k<i<l-3)$. Тада је и $a_{i} \in\{p, q\}$ или $a_{i+3} \in\{p, q\}$, чиме је индукција готова.
|
| 127 |
+
|
| 128 |
+
Лема 2. За свако $i(0 \leqslant i \leqslant n)$ постоје $x_{i}, y_{i} \in \mathbb{N}_{0}$ такви да је $a_{i}=x_{i} p+y_{i} q$ и $\left(x_{i}, y_{i}\right)=1$.
|
| 129 |
+
|
| 130 |
+
Доказ. Посматрајмо векторе $v_{k}=(1,0)$ и $v_{l}=(0,1)$ и, за свако $i$, дефинишимо $v_{i+2}=\varepsilon_{i} v_{i}+\varepsilon_{i}^{\prime} v_{i+1}$ ако је $a_{i+2}=\varepsilon_{i} a_{i}+\varepsilon_{i}^{\prime} a_{i+1}\left(\varepsilon_{i}, \varepsilon_{i}^{\prime} \in\{-1,1\}\right)$. Једноставном индукцијом добијамо да за $v_{i}=\left(x_{i}, y_{i}\right)$ важи
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
a_{i}=x_{i} p+y_{i} q
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
Како је $x_{i+1} y_{i+2}-x_{i+2} y_{i+1}=x_{i+1}\left(\varepsilon_{i} y_{i}+\varepsilon_{i}^{\prime} y_{i+1}\right)-\left(\varepsilon_{i} x_{i}+\varepsilon_{i}^{\prime} x_{i+1}\right) y_{i+1}=$ $-\varepsilon_{i}\left(x_{i} y_{i+1}-x_{i+1} y_{i}\right)$ и слично $x_{i} y_{i+2}-x_{i+2} y_{i}=\varepsilon_{i}^{\prime}\left(x_{i} y_{i+1}-x_{i+1} y_{i}\right)$, имамо
|
| 137 |
+
|
| 138 |
+
$$
|
| 139 |
+
x_{i} y_{i+1}-x_{i+1} y_{i}, x_{i} y_{i+2}-x_{i+2} y_{i} \in\{-1,1\} \text { за } 0 \leqslant i<n
|
| 140 |
+
$$
|
| 141 |
+
|
| 142 |
+
и одатле $\left(x_{i}, y_{i}\right)=1$. Остаје још да покажемо да су $x_{i}, y_{i} \geqslant 0$ за све $i$.
|
| 143 |
+
|
| 144 |
+
Претпоставимо да је $x_{i}<0$ за неко $i<k$ (случај $y_{i}<0$ и/или $i>l$ је аналоган) и посматрајмо највеће такво $i$. Због $a_{i}>0$ и (1) имамо $y_{i}>0$. Из (2) и $x_{i} y_{i+1}, x_{i} y_{i+2} \leqslant 0 \leqslant x_{i+1} y_{i}, x_{i+2} y_{i}$ следи да су $v_{i+1}$, $v_{i+2} \in\{(0,1),(1,0)\}$, а тада мора бити $v_{i}= \pm(1,-1)$, тј. $a_{i}=|p-q|$. Међутим, како су $p$ и $q$ узајамно прости и већи од 1 , важи $\max \{p, q\}>$ $|p-q| \notin\{p, q\}$, противно избору $p$ и $q$.
|
| 145 |
+
|
| 146 |
+
Нека је $m=d a_{0}=e a_{n}$. По леми 2 је $m=d x_{0} p+d y_{0} q=e x_{n} p+e y_{n} q$, при чему је $\left(d x_{0}, d y_{0}\right) \neq\left(e x_{n}, e y_{n}\right)$ јер због $a_{0} \neq a_{n}$ важи $\frac{x_{0}}{y_{0}} \neq \frac{x_{n}}{y_{n}}$. Одатле следи да $p \mid d y_{0}-e y_{n}$, па је $d y_{0}>p$ или $e y_{n}>p$; коначно, $m>p q$ и према томе $\min (p, q)<\sqrt{m}$.
|
| 147 |
+
|
Serbia_MO/md/sr-2011_smo_resenja.md
ADDED
|
@@ -0,0 +1,109 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 2 |
+
|
| 3 |
+
такмичење ученика средњих школа из математике
|
| 4 |
+
|
| 5 |
+
Београд, 02.04.2011.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Нека је $n \geqslant 2$ природан број и нека позитивни реални бројеви $a_{0}, a_{1}, \ldots, a_{n}$ задовољавају једнакост
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\left(a_{k-1}+a_{k}\right)\left(a_{k}+a_{k+1}\right)=a_{k-1}-a_{k+1} \quad \text { за свако } k=1,2, \ldots, n-1 \text {. }
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Доказати да је $a_{n}<\frac{1}{n-1}$.
|
| 16 |
+
|
| 17 |
+
(Душан Ђукић)
|
| 18 |
+
|
| 19 |
+
2. Нека је $n$ непаран природан број такав да су бројеви $\varphi(n)$ и $\varphi(n+1)$ степени броја два ( $\varphi(n)$ је број природних бројева не већих од $n$ и узајамно простих са $n$ ). Доказати да је $n+1$ степен броја два или је $n=5$.
|
| 20 |
+
|
| 21 |
+
(Марко Радовановић)
|
| 22 |
+
|
| 23 |
+
3. Нека је $H$ ортоцентар, а $O$ центар описане кружнице оштроуглог троугла $A B C$. Тачке $D$ и $E$ су подножја висина из $A$ и $B$, редом. Обележимо са $K$ пресечну тачку правих $O D$ и $B E$, а са $L$ пресечну тачку правих $O E$ и $A D$. Нека је $X$ друга пресечна тачка кружница описаних око троуглова $H K D$ и $H L E$, а $M$ средиште странице $A B$. Доказати да су тачке $K, L$ и $M$ колинеарне ако и само ако је $X$ центар описане кружнице троугла $E O D$.
|
| 24 |
+
|
| 25 |
+
(Марко Ђикић)
|
| 26 |
+
|
| 27 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 28 |
+
|
| 29 |
+
такмичење ученика средњих школа из математике
|
| 30 |
+
|
| 31 |
+
Београд, 03.04.2011.
|
| 32 |
+
|
| 33 |
+
## Други дан
|
| 34 |
+
|
| 35 |
+
4. На страницама $A B, A C$ и $B C$ троугла $A B C$ дате су, редом, тачке $M, X$ и $Y$ тако да је $A X=M X$ и $B Y=M Y$. Нека су $K$ и $L$, редом, средишта дужи $A Y$ и $B X$, а $O$ центар описане кружнице троугла $A B C$. Ако су $O_{1}$ и $O_{2}$ тачке симетричне тачки $O$ у односу на $K$ и $L$, редом, доказати да тачке $X, Y, O_{1}$ и $O_{2}$ леже на истој кружници.
|
| 36 |
+
|
| 37 |
+
(Марко Ђикић)
|
| 38 |
+
|
| 39 |
+
5. Да ли постоје природни бројеви $a, b$ и $c$, већи од 2011, такви да у децималном запису важи једнакост
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
(a+\sqrt{b})^{c}=\ldots 2010,2011 \ldots ?
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
(Милош Милосављевић)
|
| 46 |
+
|
| 47 |
+
6. Скуп $T$ садржи 66 тачака, а скуп $P$ садржи 16 правих у равни. За тачку $A \in T$ и праву $l \in P$ кажемо да су иниидентни пар ако $A \in l$. Доказати да број инцидентних парова не може бити већи од 159 , као и да постоји
|
| 48 |
+
|
| 49 |
+

|
| 50 |
+
|
| 51 |
+
Време за рад 270 минута.
|
| 52 |
+
|
| 53 |
+
Сваки задатак вреди 7 поена.
|
| 54 |
+
|
| 55 |
+
## РЕШЕЊА
|
| 56 |
+
|
| 57 |
+
1. Дата једнакост је еквивалентна са
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\frac{1}{a_{k}+a_{k+1}}=1+\frac{1}{a_{k-1}+a_{k}}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
за свако $k>0$. Индукцијом следи $\frac{1}{a_{k}+a_{k+1}}=k+\frac{1}{a_{0}+a_{1}}$ за $k>0$, одакле добијамо да је $\frac{1}{a_{n-1}+a_{n}}>n-1$ и према томе $a_{n}<\frac{1}{n-1}$.
|
| 64 |
+
|
| 65 |
+
2. Ако је $n=\prod_{i=1}^{k} p_{i}^{r_{k}}$ канонска факторизација $n$, важи $\varphi(n)=\prod_{i=1}^{k} p_{i}^{r_{k}-1}\left(p_{i}-\right.$ 1), па пошто $n$ нема других простих чинилаца осим двојке, мора бити $a_{i}=1$ и $p_{i}-1=2^{b_{i}}$ за свако $i$ и неке $b_{i}$. Како $2^{b_{i}}+1$ може бити прост само ако је $b_{i}$ степен двојке, имамо $p_{i}=2^{2^{c_{i}}}+1$ за неке различите $c_{i}$.
|
| 66 |
+
|
| 67 |
+
Претпоставимо да $n+1$ није степен двојке. Из чињенице да је $\varphi(n+1)$ степен двојке добијамо да су сви непарни прости делиоци броја $n+1$ облика $2^{2^{d_{i}}}+1$. Према томе,
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
n=\prod_{i=1}^{k}\left(2^{2^{c_{i}}}+1\right), \quad n+1=2^{t} \prod_{j=1}^{l}\left(2^{2^{d_{j}}}+1\right)
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
при чему су сви $c_{i}$ и $d_{j}$ међусобно различити. Можемо узети без смањења општости да је $c_{1}<\cdots<c_{k}$ и $d_{1}<\cdots<d_{l}$.
|
| 74 |
+
|
| 75 |
+
За свако $m, M \in \mathbb{N}, m \leq M$, једноставн��м индукцијом се показује да важи
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
\frac{2^{2^{m}}+1}{2^{2^{m}}}<\prod_{i=m}^{M} \frac{2^{2^{i}}+1}{2^{2^{i}}}=\frac{2^{2^{m}}}{2^{2^{m}}-1} \cdot \frac{2^{2^{M+1}}-1}{2^{2^{M+1}}}<\frac{2^{2^{m}}}{2^{2^{m}}-1}
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
Одавде добијамо
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}} 2^{c} \leqslant n<\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c} \quad \text { и } \quad \frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{d} \leqslant n+1<\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1} 2^{d}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
где је $c=\sum_{i} 2^{c_{i}}$ и $d=t+\sum_{j} 2^{d_{i}}$. Следи да је $c=d$. Ако је $d_{1}>c_{1}$, важи $\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1}<\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}}$, па је $n+1<n$, контрадикција. Према томе, $d_{1}<c_{1}$, а тада је $n+1 \geqslant \frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{c}>\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c}>n$, па је $\frac{n+1}{n}>\frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} \cdot \frac{2^{2^{c_{1}}}-1}{2^{2^{c_{1}}}}$ и, због $n \geqslant 2^{2^{c_{1}}}+1 \geqslant a^{2}+1$ за $2^{2^{d_{1}}}=a, \frac{n+1}{n}>\frac{(a+1)\left(a^{2}-1\right)}{a^{3}}=1+\frac{a^{2}-a-1}{a^{3}}$, одакле закључујемо $a^{2}+1 \leqslant n<\frac{a^{3}}{a^{2}-a-1}$. Једина могућност је $a=2$ и $n=5$.
|
| 88 |
+
|
| 89 |
+
3. Ако је $X$ центар описаног круга $\triangle O D E$, онда је $90^{\circ}-\angle K D E=90^{\circ}-$ $\angle O D E=\angle X E O=\angle X E L=\angle X H D=\angle X K D$ (сви углови су оријентисани), одакле следи да је $X K \perp D E$; аналогно $X L \perp D E$, тј. $K$ и $L$ леже на симетрали дужи $D E$, па је $D E H O$ једнакокраки трапез, дакле $D, E, O, H$ леже на кругу.
|
| 90 |
+
|
| 91 |
+
С друге стране, ако $O$ лежи на кругу $H D E$, дакле на кругу над пречником $C H$, периферијски углови над $E H$ и $O D$ су једнаки ( $\angle E C H=$ $\angle O C D)$, па је $D E H O$ једнакокраки трапез и одатле $D L=E L$. Сада имамо $\angle E X H=\angle E L H=2 \angle E D H$
|
| 92 |
+
|
| 93 |
+
|
| 94 |
+
и аналогно $\angle D X H=2 \angle D E H$, па следи да је $X$ центар круга $D E O H$. Према томе, $X$ је центар круга $O D E$ ако и само ако $D, E, O$ и $H$ леже на кругу.
|
| 95 |
+
|
| 96 |
+
Ако су тачке $D, E, O, H$ на кругу, тада $K, L$ и $M$ леже на симетрали дужи $D E$, чиме је један смер задатка доказан. Претпоставимо сада да $O$ лежи ван круга $C D H E$ (случај када је $O$ унутар круга се разматра на исти начин). Како је $C O \perp D E$, важи $D L>L E$ и $E K>K D$, тј. $K$ и $L$ леже на разним странама симетрале дужи $D E$, а $M$ припада овој симетрали. Према томе, ако су $K, L$ и $M$ колинеарне, $M$ се мора налазити између $K$ и $L$. Следи да је једна од тачака $K$ и $L$ ван троугла $A B C$, а друга унутар троугла. Међутим, када је $O$ изван четвороугла $A B D E$, обе тачке $K$ и $L$ су ван троугла, а у супротном су обе унутар троугла. То је контрадикција са претпоставком да $M$ лежи на правој $K L$, што доказује други смер.
|
| 97 |
+
|
| 98 |
+
4. Поставимо координатни систем са почетком у тачки $M$ и $x$-осом дуж праве $A B$. Нека тачке $X$ и $Y$ имају координате $(a, b)$ и $(c, d)$ редом. Због $A X=X M$ и $B Y=Y M$, координате тачака $A$ и $B$ су $(2 a, 0)$ и $(2 c, 0)$, а тачака $K$ и $L\left(a+\frac{c}{2}, \frac{d}{2}\right)$ и $\left(c+\frac{a}{2}, \frac{b}{2}\right)$, редом. Тачка $O$ има координате $(a+c, e)$ за неко $e$, одакле добијамо $O_{1}(a, d-e)$ и $O_{2}(c, b-e)$. Према томе, тачке $O_{1}$ и $O_{2}$ су симетричне тачкама $X$ и $Y$ у односу на праву $y=\frac{b+d-e}{2}$, па су $X, Y$ и $O_{1}, O_{2}$ темена (могуће дегенерисаног) једнакокраког трапезе, и зато леже на кругу.
|
| 99 |
+
5. Показаћемо да такви бројеви $a, b$ и $c$ постоје. Број $x=(a+\sqrt{b})^{c}+(a-\sqrt{b})^{c}$ је цео. Довољно је одабрати $a, b, c$ тако да $x$ буде дељиво са $10^{4}$ и $7989,7989>$ $(a-\sqrt{b})^{c}>7989,7988$.
|
| 100 |
+
|
| 101 |
+
За непарно $c$, број $x=2 a^{c}+2\binom{c}{2} a^{c-2}+\cdots+2\binom{c}{c-1} a$ је дељив са $a$, па је довољно узети $a$ које је дељиво са $10^{4}$. Други услов постижемо избором $a$ и $b$ тако да је $1<a-\sqrt{b}<\sqrt{\frac{7989,7989}{7989,7988}}$ - на пример, $a=10^{8}$ и $b=$ $(a-1)^{2}-1$. Заиста, нека је $c$ најмањи непаран природан број за који је $(a-\sqrt{b})^{c}>7989,7988$. Такво $c$ је очигледно веће од 2011 (у овом случају $c=1797184159)$ и $(a-\sqrt{b})^{c}<7989,7989$.
|
| 102 |
+
|
| 103 |
+
6. Означимо са $A_{1}, \ldots, A_{66}$ тачке скупа $T$ и са $a_{i}$ број правих из $P$ које садрже $A_{i}$. Тада је број парова правих које се секу у $A_{i}$ једнак $\binom{a_{i}}{2}$, а број инцидентних парова $I=\sum a_{i}$. Како се сваке две праве секу у највише једној тачки, важи $\sum_{i=1}^{66}\binom{a_{i}}{2} \leqslant\binom{ 16}{2}=120$. Нека је $b_{k}$ број тачака из $T$ кроз које пролази тачно $k$ правих из $P$. Тада је $\sum b_{k}=66, \sum\binom{k}{2} b_{k} \leqslant 120$ и $I=\sum k b_{k} \leqslant \sum \frac{1}{2}\left(3+\binom{k}{2}\right) b_{k}=\frac{1}{2}(3 \cdot 66+120)=159$, јер је $3+\binom{k}{2} \geq 2 k$. Једнакост се достиже ако је $b_{k}=0$ за $k \notin\{2,3\}, b_{2}=39$ и $b_{3}=27$, другим речима, ако праве из $P$ одређују тачно 39 двоструких и 27 троструких пресека.
|
| 104 |
+
|
| 105 |
+
Пример конфигурације са 159 инцидентних парова може се конструисати нпр. помоћу Дезаргове теореме. Узмимо тачке $A_{1}, A_{2}, A_{3}$ на правој $a$ и $B_{1}, B_{2}, B_{3}$ на правој $b \| a$, затим повуцимо 9 правих $A_{i} B_{j}, i, j \in\{1,2,3\}$. Нпр. на слици је $A_{1} A_{2}: A_{2} A_{3}: B_{1} B_{2}: B_{2} B_{3}=2: 2: 3: 6$, тако да међу овим правим нема паралелних. По Дезарговој теореми, ових 9 правих одређују 18 пресечних тачака које су по три колинеарне - тако да одређују још 6 правих. Заједно са ових 6 правих, имамо слику са 15 правих и 24 трострука пресека. При том се три праве добијене Дезарговом теоремом секу у једној тачки (на слици тачка $K$ ), што нам даје и 25 -ти троструки пресек. Повуцимо још једну праву која пролази само кроз две двоструке пресечне тачке. За скуп $P 16$ нацртаних правих и скуп $T$ који се сас-
|
| 106 |
+
|
| 107 |
+
|
| 108 |
+
тоји од 27 добијених троструких и преосталих 39 двоструких пресека постиже се једнакост.
|
| 109 |
+
|
Serbia_MO/md/sr-2012_smo_resenja.md
ADDED
|
@@ -0,0 +1,144 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 2 |
+
|
| 3 |
+
ученика средњих школа
|
| 4 |
+
|
| 5 |
+
Београд, 31.03.2012.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Нека је $P$ тачка на дијагонали $B D$ паралелограма $A B C D$ таква да је $\varangle P C B=\varangle A C D$. Кружница описана око троугла $A B D$ сече праву $A C$ у тачкама $E$ и $A$. Доказати да је
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\varangle A E D=\varangle P E B . \quad \text { (Марко Ђикић) }
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
2. Наћи све природне бројеве $a$ и $b$ такве да
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
a\left|b^{2}, \quad b\right| a^{2} \quad \text { и } \quad a+1 \mid b^{2}+1 . \quad \text { (Душан Ђукић) }
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
3. У неким чворовима квадратне решетке $2012 \times 2012$ налази се мува и $k$ паукова. Један потез састоји се у следећем: мува се помера на суседан чвор или остаје на истом месту, а након тога се сваки од $k$ паукова помера на неки суседан чвор или остаје на истом месту (у једном чвору може бити више паукова). У сваком тренутку сваки паук и мува имају увид у позиције осталих.
|
| 22 |
+
|
| 23 |
+
a) Наћи најмање $k$ тако да пауци могу ухватити муву у коначном броју потеза, без обзира на почетну позицију муве и паукова.
|
| 24 |
+
|
| 25 |
+
б) Одговорити на исто питање за кубну решетку $2012 \times 2012 \times 2012$.
|
| 26 |
+
|
| 27 |
+
(Чворови су суседни ако се разликују на тачно једној координати, и то за 1. Паук хвата муву уколико се налазе у истом чвору.)
|
| 28 |
+
|
| 29 |
+
(Никола Милосављевић)
|
| 30 |
+
|
| 31 |
+
Време за рад 270 минута.
|
| 32 |
+
|
| 33 |
+
Сваки задатак вреди 7 поена.
|
| 34 |
+
|
| 35 |
+
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
|
| 36 |
+
|
| 37 |
+
ученика средњих школа
|
| 38 |
+
|
| 39 |
+
Београд, 01.04.2012.
|
| 40 |
+
|
| 41 |
+
## Други дан
|
| 42 |
+
|
| 43 |
+
4. Наћи све природне бројеве $n$ за које постоји пермутација ( $p_{1}, p_{2}, \ldots, p_{n}$ ) бројева $(1,2, \ldots, n)$ таква да скупови $\left\{p_{i}+i \mid 1 \leqslant i \leqslant n\right\}$ и $\left\{p_{i}-i \mid 1 \leqslant i \leqslant n\right\}$ чине потпуне системе остатака по модулу $n$. (Марко Ђикић)
|
| 44 |
+
5. Нека је $\mathcal{K}$ целобројна решетка. Да ли постоји бијекција $f: \mathbb{N} \rightarrow \mathcal{K}$ таква да за све међусобно различите $a, b, c \in \mathbb{N}$ важи
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
\text { НЗД }(a, b, c)>1 \quad \Longrightarrow \quad f(a), f(b), f(c) \text { нису колинеарне? }
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
(Целобројна решетка је скуп тачака у равни са целобројним координатама у Декартовом координатном систему.)
|
| 51 |
+
|
| 52 |
+
(Стеван Гајовић)
|
| 53 |
+
|
| 54 |
+
6. Нека композиција садржи $n>1$ вагона са златницима. Постоје две врсте наизглед истих златника: прави и лажни. У сваком вагону се налазе златници само једне врсте. Златници исте врсте су исте масе, док златници различитих врста немају исту масу. Маса правог златника је позната.
|
| 55 |
+
|
| 56 |
+
Одредити минималан број мерења на дигиталној ваги којима је могуће утврдити који све вагони садрже лажне златнике, као и која је маса лажног златника.
|
| 57 |
+
|
| 58 |
+
(Претпоставља се да се из сваког вагона може узети било који број златника.)
|
| 59 |
+
|
| 60 |
+
(Милош Милосављевић)
|
| 61 |
+
|
| 62 |
+
## РЕШЕЊА
|
| 63 |
+
|
| 64 |
+
1. Доказ изводимо у случају када је $\angle B A C \leq 90^{\circ}$. Други случај је аналоган.
|
| 65 |
+
|
| 66 |
+
Нека се праве $D E$ и $B C$ секу у L. Четвороугао $C D P L$ је тетиван јер је $\angle P D L=\angle P C L$, одакле имамо $\angle P L E=\angle P C D=\angle B C A=$ $\angle D A C=\angle D B E=\angle P B E$, па је и четвороугао $B P E L$ тетиван. Из ове две тетивности коначно добијамо $\angle P E B=\angle P L B=\angle P D C=$ $\angle D B A=\angle D E A$.
|
| 67 |
+
|
| 68 |
+
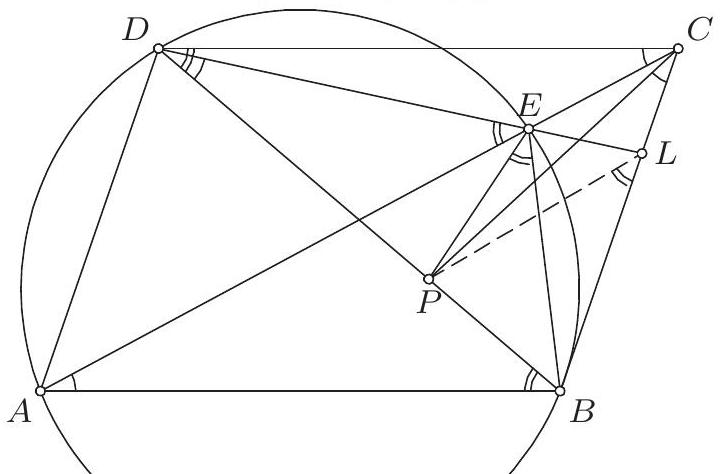
|
| 69 |
+
|
| 70 |
+
Друго решеъе. Нека је $P^{\prime}$ тачка на $B D$ таква да је $\angle D E A=\angle P E B$.
|
| 71 |
+
|
| 72 |
+
По синусној теореми је $\frac{B P}{D P}=\frac{B P}{C P} \cdot \frac{C P}{D P}=\frac{\sin \angle B C P}{\sin \angle C B D} \cdot \frac{\sin \angle C D B}{\sin \angle P C D}$. Аналогно je $\frac{B P^{\prime}}{D P^{\prime}}=\frac{\sin \angle B E P^{\prime}}{\sin \angle E B D} \cdot \frac{\sin \angle E D B}{\sin \angle P^{\prime} E D}$. Како је $\angle B C P=\angle E D B, \angle C B D=\angle P^{\prime} E D$, $\angle C D B=\angle B E P^{\prime}$ и $\angle P C D=\angle E B D$, следи $\frac{B P}{D P}=\frac{B P^{\prime}}{D P^{\prime}}$, дакле $P \equiv P^{\prime}$.
|
| 73 |
+
|
| 74 |
+
2. Нека је $b^{2}=c a$. Услови задатка дају $b^{2}=c a \mid a^{4}$ и $a+1 \mid c a+1$, а то је еквивалентно са
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
c \mid a^{3} \quad \text { и } \quad a+1 \mid c-1 .
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
Нека је $c=d(a+1)+1, d \in \mathbb{N}_{0}$. Како је $a^{3} \equiv-1(\bmod (a+1))$, имамо $\frac{a^{3}}{c} \equiv-1(\bmod (a+1))$, тј. $\frac{a^{3}}{c}=e(a+1)-1$ за неко $e \in \mathbb{N}$. Следи да је $a^{3}=(d(a+1)+1)(e(a+1)-1)$, што након множења и скраћивања са $a+1$ постаје $a^{2}-a+1=d e(a+1)+(e-d)$. Одавде имамо $e-d \equiv a^{2}-a+1 \equiv 3$ $(\bmod (a+1))$, дакле
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
e-d=k(a+1)+3 \quad \text { и } \quad d e=a-2-k \quad(k \in \mathbb{Z}) .
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
Разликујемо следеће случајеве:
|
| 87 |
+
|
| 88 |
+
(1) $k \notin\{-1,0\}$. У овом случају (*) повлачи $d e<|e-d|-1$, што је могуће само за $d=0$. Сада је $c=1$ и $b^{2}=a$, дакле $(a, b)=\left(t^{2}, t\right)$.
|
| 89 |
+
|
| 90 |
+
(2) $k=-1$. Из (*) добијамо $a=d+1$. Сада је $c=a^{2}$ и $b^{2}=a^{3}$, дакле $(a, b)=\left(t^{2}, t^{3}\right)$.
|
| 91 |
+
|
| 92 |
+
(3) $k=0$. Из (*) добијамо $a=d^{2}+3 d+2$. Сада је $c=d(a+1)+1=(d+1)^{3}$ и $b^{2}=c a=(d+1)^{4}(d+2)$. Следи да је $d+2=t^{2}$ за неко $t \in \mathbb{N}$, што даје $(a, b)=\left(t^{2}\left(t^{2}-1\right), t\left(t^{2}-1\right)^{2}\right), t \geq 2$.
|
| 93 |
+
|
| 94 |
+
Одговор: То су парови $(a, b)$ облика $\left(t^{2}, t\right),\left(t^{2}, t^{3}\right)$ и $\left(t^{2}\left(t^{2}-1\right), t\left(t^{2}-1\right)^{2}\right)$, где је $t \in \mathbb{N}$.
|
| 95 |
+
|
| 96 |
+
3. Један паук не може да ухвати муву. Довољно је да мува не мрда ако паук није на суседном пољу, односно да се помери на поље дијагонално супротно пауковом ако јесте.
|
| 97 |
+
|
| 98 |
+
Доказаћемо да су два паука довољна у оба дела задатка - означимо их са $P$ и $Q$, муву са $M$, а $x$ - и $y$-координату тачке $A$ са $A_{x}$ и $A_{y}$.
|
| 99 |
+
|
| 100 |
+
(a) Поставимо координатни почетак у доњи леви угао мреже. На почетку, крећући се дуж $x$-осе, $P$ у коначном броју потеза постиже да буде $P_{x}=$ $M_{x}$. Аналогно, $Q$ постиже да буде $Q_{y}=M_{y}$. Потом се пауци крећу на следећи начин: кад год мува промени $x$-координату, $P$ учини исто тако да остане $P_{x}=M_{x}$, у супротном приђе муви један корак дуж $y$-осе; кретање $Q$ је аналогно. На овај начин величина $\left|P_{y}-M_{y}\right|+\left|Q_{x}-M_{x}\right|$ се или смањује или остаје иста, при чему може остати иста кроз највише $2 \cdot 2010$ потеза (када се мува повлачи). Према томе, после коначног броја потеза бар један сабирак ће постати нула, тј. мува ће бити ухваћена.
|
| 101 |
+
|
| 102 |
+
(б) Занемарујући $z$-осу, на основу дела под (a), један од паукова, рецимо $P$, може постићи да буде $P_{x}=M_{x}$ и $P_{y}=M_{y}$. Надаље, кад год мува направи корак дуж $z$-осе, паук $P$ иде ка њој, а супротном се креће тако да увек буде тачно испод муве. Јасно је да мува може само коначно много пута да направи корак дуж $z$-осе или остане у месту, а да је паук $P$ не ухвати. Према томе, почев од неког момента, мува мора да се креће искључиво по својој $x y$-равни, без стајања у месту.
|
| 103 |
+
|
| 104 |
+
Сада паук $Q$ у коначно много потеза долази до $x y$-равни по којој се креће мува. Такође, стајањем у месту по потреби, $Q$ постиже да $f=\left|Q_{x}-M_{x}\right|+$ $\left|Q_{y}-M_{y}\right|$ буде парно. У сваком следећем потезу, паук $Q$ се приближава муви дуж $x$-осе ако је $\left|Q_{x}-M_{x}\right|>\left|Q_{y}-M_{y}\right|$, а дуж $y$-осе у супротном. После сваког потеза, величина $f$ се не повећава и не мења парност, при чему само коначно много пута може да остане иста (када мува бежи од паука према крају решетке). Према томе, у неком тренутку ће бити $f=0$, и мува ће бити ухваћена.
|
| 105 |
+
|
| 106 |
+
4. Претпоставимо да таква пермутација постоји. Како је $\left\{p_{i}+i \mid 1 \leq i \leq\right.$ $n\}$ потпун систем остатака по модулу $n$, важи $\sum_{k=1}^{n} k \equiv \sum_{i=1}^{n}\left(p_{i}+i\right) \equiv$ $\sum_{i=1}^{n} i+\sum_{i=1}^{n} p_{i} \equiv 2 \sum_{k=1}^{n} k(\bmod n)$, дакле $\sum_{k=1}^{n} k=\frac{n(n+1)}{2} \equiv 0(\bmod n)$, одакле следи $2 \nmid n$. Шта више, важи $2 \sum_{k=1}^{n} k^{2} \equiv \sum_{k=1}^{n}\left(\left(p_{i}+i\right)^{2}+\left(p_{i}-i\right)^{2}\right) \equiv$ $\sum_{k=1}^{n}\left(2 p_{i}^{2}+2 i^{2}\right) \equiv 4 \sum_{k=1}^{n} k^{2}$, одакле је $2 \sum_{k=1}^{n} k^{2}=\frac{n(n+1)(2 n+1)}{3} \equiv 0(\bmod n)$, дакле $3 \nmid n$. Према томе, мора бити $(n, 6)=1$.
|
| 107 |
+
|
| 108 |
+
С друге стране, ако је $(n, 6)=1$ и $p_{i} \equiv 2 i(\bmod n), p_{i} \in\{1, \ldots, n\}$, тада је $\left(p_{1}, p_{2}, \ldots, p_{n}\right.$ ) пермутација скупа $\{1, \ldots, n\}$ и задовољава услове, јер су $\left\{p_{i}+i \mid 1 \leq i \leq n\right\} \equiv\{3 i \mid 1 \leq i \leq n\}$ и $\left\{p_{i}-i \mid 1 \leq i \leq n\right\} \equiv\{i \mid 1 \leq i \leq n\}$ $(\bmod n)$ потпуни системи остатака по модулу $n$.
|
| 109 |
+
|
| 110 |
+
5. Поређајмо све тачке решетке у низ $A_{1}, A_{2}, \ldots$. Ово се може урадити нпр. спирално: $(0,0),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1), \ldots$ Конструисаћемо индуктивно пример бијекције са траженим својством.
|
| 111 |
+
|
| 112 |
+
Ставимо $f(1)=A_{1}$. Претпоставимо да су $f(1), \ldots, f(n-1)$ одређене и узмимо за $f(n)$ тачку $A_{m}$ са најмањим $m$ такву да, ни за које природне $i, j \leq n,(i, j, n)>1, A_{m}$ не лежи на правој $f(i) f(j)$. Правих $f(i) f(j)$ има коначно много, па заиста постоји тачка решетке која не лежи ни на једној од њих. Приметимо да за просто $p$ нема ограничења при избору $f(p)$, што гарантује да ће свака тачка бити слика неког природног броја.
|
| 113 |
+
|
| 114 |
+
Овако дефинисано пресликавање $f$ задовољава све услове задатка.
|
| 115 |
+
|
| 116 |
+
Друго решеъе. Ако је $n$ сложен број, узмимо за $f(n)$ тачку $\left(n, n^{2}\right)$. За прост број $p$, нека је $f(p)$ било која од дозвољених тачака на минималном растојању од тачке $(0,0)$. Покажимо да је ово пресликавање добро дефинисана бијекција са траженим својством.
|
| 117 |
+
|
| 118 |
+
За свако $p$ постоји дозвољена тачка - нпр. нека од неупотребљених тачака на параболи $y=x^{2}$. Заиста, произволна права кроз ту тачку сече ову параболу у још највише једној тачки, тј. садржи слику највише једног сложеног броја.
|
| 119 |
+
|
| 120 |
+
С друге стране, за произвољну тачку $A \in \mathcal{K} \backslash\left\{\left(n, n^{2}\right) \mid n\right.$ је сложен $\}$ постоји прост број $p$ за који је $A$ дозвољена тачка. Наиме, постоји само коначно много правих кроз $A$ које садрже две целобројне тачке на параболи $y=x^{2}$ (различите од $A$ ); означимо те праве са $p_{1}, \ldots, p_{k}$ и целобројне тачке у пресеку $p_{i}$ са параболом $y=x^{2}$ са $A_{i}, B_{i}$. Дозољно је узети $p$ које не дели $\left(f^{-1}\left(A_{i}\right), f^{-1}\left(B_{i}\right)\right)$ ни за једно $i$.
|
| 121 |
+
|
| 122 |
+
6. Доказаћемо да је минималан број мерења једнак 2. Означимо тежине правог и лажног златника са $x$ и $y$ редом, и нека је $a_{i}=1$ ако су златници у $i$-том вагону лажни, а $a_{i}=0$ у супротном.
|
| 123 |
+
|
| 124 |
+
Узмимо у првом мерењу по један златник из сваког вагона. Тада је $a_{1}+$ $a_{2}+\cdots+a_{n}=\frac{n x-m_{1}}{x-y}$, где је $m_{1}$ добијена маса. Претпостављамо да је $m_{1} \neq n x$, јер у супротном нема лажних златника. У другом мерењу, за неко $q \in \mathbb{N}$, узимамо из $i$-тог вагона $q^{i-1}$ златника. Ако је добијена маса
|
| 125 |
+
$m_{2}$, имамо $a_{1}+q a_{2}+\cdots+q^{n-1} a_{n-1}=\frac{\left(1+q+\cdots+q^{n-1}\right) x-m_{2}}{x-y}$. Одавде добијамо
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
f\left(a_{1}, a_{2}, \ldots, a_{n}\right)=\frac{a_{1}+q a_{2}+\cdots+q^{n-1} a_{n-1}}{a_{1}+a_{2}+\cdots+a_{n}}=\frac{\left(1+q+\cdots+q^{n-1}\right) x-m_{2}}{n x-m_{1}}
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
Желимо да нам вредност $f$ једнозначно одреди $a_{1}, \ldots, a_{n}$. Дакле, довољно је показати да постоји природан број $q$ такав да је функција $f:\{0,1\}^{n} \backslash$ $\{(0,0, \ldots, 0)\} \rightarrow \mathbb{R}$ инјективна.
|
| 132 |
+
|
| 133 |
+
За фиксиране $\mathfrak{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ и $\mathfrak{a}=\left(b_{1}, b_{2}, \ldots, b_{n}\right)$, једнакост $f(\mathfrak{a})=f(\mathfrak{b})$ је еквивалентна са $P_{\mathfrak{a}, \mathfrak{b}}(q)=\left(a_{n} b-b_{n} a\right) q^{n-1}+\cdots+\left(a_{2} b-b_{2} a\right) q+\left(a_{1} b-b_{1} a\right)=0$, где је $a=a_{1}+a_{2}+\ldots+a_{n} \neq 0 \neq b_{1}+b_{2}+\ldots b_{n}=b$. Према томе, ако функција $f$ није инјективна, онда је $q$ нула полинома
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
P(q)=\prod_{\mathfrak{a}, \mathfrak{b}} P_{\mathfrak{a}, \mathfrak{b}}(q)
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Како ниједан од полинома $P_{\mathfrak{a}, \mathfrak{b}}$ није идентички једнак 0 , постоји само коначно много бројева $q$ за које је $P(q)=0$, па је могуће одабрати $q$ за које је $f$ инјективна функција.
|
| 140 |
+
|
| 141 |
+
Овако у два мерења можемо да одредимо $a_{1}, \ldots, a_{n}$, тј. вагоне са лажним златницима. Најзад, $y$ одређујемо из једнакости $y=x-\frac{n x-m_{1}}{a_{1}+a_{2}+\cdots+a_{n}}$.
|
| 142 |
+
|
| 143 |
+
С друге стране, једно мерење није довољно, јер узимањем $k_{i}$ златника из $i$-тог вагона добијамо једначину $k_{1} a_{1}+\cdots+k_{n} a_{n}=\frac{k x-m}{x-y}$ (где је $k=k_{1}+$ $\cdots+k_{n}$ ) која у општем случају има више решења. На пример, два могућа решења за $\left(a_{1}, a_{2}, \ldots, a_{n}, y\right)$ су $\left(1,0, \ldots, 0, x-\frac{k x-m}{k_{1}}\right)$ и $\left(0,0, \ldots, 1, x-\frac{k x-m}{k_{n}}\right)$.
|
| 144 |
+
|
Serbia_MO/md/sr-2013_smo_resenja.md
ADDED
|
@@ -0,0 +1,122 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 2 |
+
|
| 3 |
+
Нови Сад, 5. април 2013.
|
| 4 |
+
|
| 5 |
+
## Први дан
|
| 6 |
+
|
| 7 |
+
1. Дат је природан број $k$. Нека је $f: \mathbb{Z} \rightarrow \mathbb{Z}$ бијекција таква да за свака два цела броја $i$ и $j$ за које је $|i-j| \leqslant k$ важи $|f(i)-f(j)| \leqslant k$. Доказати да за све $i, j \in \mathbb{Z}$ важи
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
|f(i)-f(j)|=|i-j|
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
(Миљан Кнежевић)
|
| 14 |
+
|
| 15 |
+
2. Нека је
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
S_{n}=\left\{\binom{n}{n},\binom{2 n}{n},\binom{3 n}{n}, \ldots,\binom{n^{2}}{n}\right\}, \quad \text { за } n \in \mathbb{N}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
a) Доказати да постоји бесконачно много сложених природних бројева $n$ таквих да $S_{n}$ није потпун систем остатака по модулу $n$.
|
| 22 |
+
|
| 23 |
+
б) Доказати да постоји бесконачно много сложених природних бројева $n$ таквих да $S_{n}$ јесте потпун систем остатака по модулу $n$.
|
| 24 |
+
|
| 25 |
+
(Милош Милосавлевић)
|
| 26 |
+
|
| 27 |
+
3. Нека су $M, N$ и $P$ средишта страница $B C, A C$ и $A B$, редом, а $O$ центар описане кружнице оштроуглог троугла $A B C$. Кружнице описане око троуглова $B O C$ и $M N P$ секу се у различитим тачкама $X$ и $Y$ унутар троугла $A B C$. Доказати да је
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\varangle B A X=\varangle C A Y
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
(Марко Ђикић)
|
| 34 |
+
|
| 35 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 36 |
+
|
| 37 |
+
Нови Сад, 6. април 2013.
|
| 38 |
+
|
| 39 |
+
## Други дан
|
| 40 |
+
|
| 41 |
+
4. Одредити све $n \in \mathbb{N}$ за које је могуће поделити скуп $\{1,2, \ldots, 3 n\}$ на $n$ дисјунктних трочланих подскупова облика $\{a, b, c\}$ у којима су $b-a$ и $c-b$ различити бројеви из скупа $\{n-1, n, n+1\}$.
|
| 42 |
+
|
| 43 |
+
(Душан Ђукић)
|
| 44 |
+
|
| 45 |
+
5. Нека су $A^{\prime}$ и $B^{\prime}$ подножја висина из темена $A$ и $B$, редом, оштроуглог троугла $A B C(A C \neq B C)$. Кружница $k$ садржи тачке $A^{\prime}$ и $B^{\prime}$ и додирује страницу $A B$ у тачки $D$. Ако троуглови $A D A^{\prime}$ и $B D B^{\prime}$ имају једнаке површине, доказати да је
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\varangle A^{\prime} D B^{\prime}=\varangle A C B .
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
(Милош Милосавлевић)
|
| 52 |
+
|
| 53 |
+
6. Наћи највећу константу $K \in \mathbb{R}$ са следећим својством: ако су $a_{1}, a_{2}, a_{3}, a_{4}>0$ такви да за све $i, j, k \in \mathbb{N}, 1 \leqslant i<j<k \leqslant 4$, важи $a_{i}^{2}+a_{j}^{2}+a_{k}^{2} \geqslant 2\left(a_{i} a_{j}+a_{j} a_{k}+a_{k} a_{i}\right)$, онда је
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2} \geqslant K\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\right)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
(Душан Ђукић)
|
| 60 |
+
|
| 61 |
+
## РЕШЕЊА
|
| 62 |
+
|
| 63 |
+
1. За $k=1$ тврђење је тривијално. Нека је зато $k>2$. Интервалом дужине $k$ зовемо скуп облика $\{x, x+1, \ldots, x+k\}, x \in \mathbb{Z}$. Два цела броја $x$ и $y$ ће бити узастопна ако и само ако постоје интервали $I_{1}$ и $I_{2}$ дужине $k$ за које је $I_{1} \cap I_{2}=\{x, y\}$. Међутим, по услову задатка су $f\left(I_{1}\right)$ и $f\left(I_{2}\right)$ такође интервали дужине $k$, па како је $\{f(x), f(y)\}=f\left(I_{1}\right) \cap f\left(I_{2}\right)$, следи да су и $f(x)$ и $f(y)$ узастопни бројеви. Одавде је $|f(x+1)-f(x)|=1$ за $x \in \mathbb{Z}$. Коначно, користећи инјективност пресликавања, једноставном индукцијом по $n$ добијамо да је $|f(x+n)-f(x)|=n$.
|
| 64 |
+
2. (а) Доказаћемо да $n=2 p$ задовољава услове, где је $p>2$ прост број. Имамо
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
\binom{2 k p}{2 p}=k \prod_{i=1}^{p-1} \frac{2 k p-i}{2 p-i} \cdot(2 k-1) \prod_{i=1}^{p-1} \frac{2 k p-p-i}{p-i} \equiv k(2 k-1) \quad(\bmod p)
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Конкретно, одавде је $\binom{2 k p}{2 p}$ дељиво са $p$ за $k \in\left\{\frac{p+1}{2}, p, 2 p\right\}$, тј. $S_{2 p}$ има три елемента дељива са $p$, па није потпун систем остатака.
|
| 71 |
+
|
| 72 |
+
(б) Доказаћемо да $n=p^{2}$ задовољава услове, где је $p>2$ прост број. Имамо $\binom{k p^{2}}{p^{2}}=\prod_{i=0}^{p^{2}-1} \frac{k p^{2}-i}{p^{2}-i}=k \prod_{j=1}^{p-1} \frac{k p^{2}-j p}{j p} \cdot \prod_{p \nmid j} \frac{k p^{2}-i}{p^{2}-i}$, па је по модулу $p^{2}$
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\binom{k n}{n} \equiv k \prod_{j=1}^{p-1} \frac{k p-j}{j}=k \prod_{j=1}^{p-1}\left(1-\frac{k p}{j}\right) \equiv k-k^{2} p \sum_{j=1}^{p-1} \frac{1}{j}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Како је $\sum_{j=1}^{p-1} \frac{1}{j}=\sum_{j=1}^{\frac{p-1}{2}}\left(\frac{1}{j}+\frac{1}{p-j}\right)=\sum_{j=1}^{\frac{p-1}{2}} \frac{p}{j(p-j)} \equiv 0(\bmod p)$, коначно следи да је $\binom{k p^{2}}{p^{2}} \equiv k\left(\bmod p^{2}\right)$.
|
| 79 |
+
|
| 80 |
+
Напомена. Има и других могућности за бројеве $n$ : на пример, (a) $n=8 k+6$ за $k \in \mathbb{N}$, односно (б) $n=p^{k}$ за прост број $p$.
|
| 81 |
+
|
| 82 |
+
3. Обележимо са $k_{1}$ и $k_{2}$ редом кругове $M N P$ и $B O C$. Круг $k_{1}$ је Ојлеров круг у $\triangle A B C$ и пролази кроз подножја висина $D, E$ из $B, C$ и средиште $O_{1}$ дужи $A H$, где је $H$ ортоцентар $\triangle A B C$.
|
| 83 |
+
|
| 84 |
+
Покажимо да друга пресечна тачка $Z$ праве $A Y$ и круга $k_{1}$ лежи на Ојлеровом кругу $k_{3}$ троугла $A D E$. Сматраћемо да
|
| 85 |
+
|
| 86 |
+
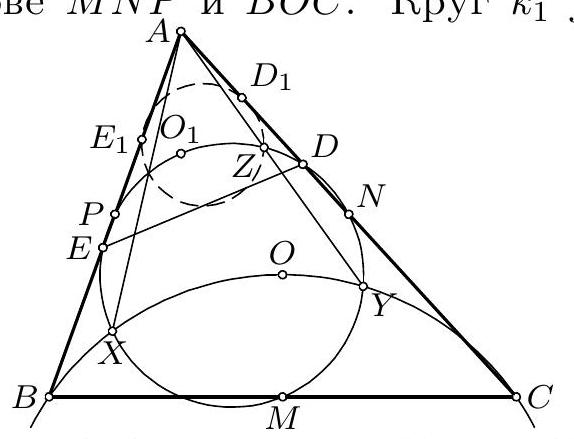
|
| 87 |
+
је $Z$ између $A$ и $Y$; доказ у другом случају је аналоган. Нека су $D_{1}$ и $E_{1}$ редом средишта дужи $A D$ и $A E$. Како је $A Y \cdot A Z=A D \cdot A N=$ $A D_{1} \cdot A C$, тачке $Y, Z, C, D_{1}$ су концикличне, па је $\varangle A Z D_{1}=\varangle A C Y$.
|
| 88 |
+
|
| 89 |
+
Аналогно је $\varangle A Z E_{1}=\varangle A B Y$, па је $\varangle D_{1} Z E_{1}=\varangle A Z D_{1}+\varangle A Z E_{1}=$ $\varangle A C Y+\varangle A B Y=\varangle B Y C-\varangle B A C=\varangle B A C$. Одавде следи да је $Z$ на $k_{3}$.
|
| 90 |
+
|
| 91 |
+
Пошто је $O_{1}$ центар описаног круга $\triangle A D E$, трансформација сличности која слика $\triangle A B C$ у $\triangle A D E$ такође слика $k_{1}$ у $k_{2}$ и $k_{2}$ у $k_{3}$, па је слика тачке $X \in k_{1} \cap k_{2}$ тачка $Z \in k_{2} \cap k_{3}$. Према томе, $\varangle B A X=\varangle D A Z=\varangle C A Y$.
|
| 92 |
+
|
| 93 |
+
Напомена. Показује се да се при инверзији са центром $A$ и квадратом полупречника $\frac{1}{2} A B \cdot A C$ кругови $k_{1}$ и $k_{2}$ сликају један у други, па се и тачке $X$ и $Y$ сликају једна у другу, одакле такође следи тврђење.
|
| 94 |
+
|
| 95 |
+
4. Тражена партиција скупа $\{1,2, \ldots, 3 n\}$ одговара партицији темена правилног $3 n$-угла $P_{1} P_{2} \ldots P_{3 n}$ на тројке $\left\{A_{i}, B_{i}, C_{i}\right\}$ такве да су углови сваког од троуглова $A_{i} B_{i} C_{i}$ једнаки $\frac{n-1}{3 n} \pi, \frac{n}{3 n} \pi$ и $\frac{n+1}{3 n} \pi$. Погодним обележавањем темена $3 n$-угла можемо постићи да темена $A_{1}, B_{1}, C_{1}$ буду управо $P_{n}, P_{2 n-1}, P_{3 n}$. Другим речима, не смањујемо општост ако претпоставимо да се међу тројкама $\{a, b, c\}$ на које је скуп $\{1,2, \ldots, 3 n\}$ подељен налази и тројка $\{n, 2 n-1,3 n\}$.
|
| 96 |
+
|
| 97 |
+
Једна од преосталих $n-1$ тројки мора да садржи два броја из интервала $[2 n, 3 n-1]$, а то могу да буду једино $2 n$ и $3 n-1$. Једина тројка која садржи ове бројеве и не садржи $n$ је $\{n-1,2 n, 3 n-1\}$.
|
| 98 |
+
|
| 99 |
+
Све остале тројке садрже тачно по један број из сваког од интервала $[1, n-2],[n+1,2 n-2]$ и $[2 n+1,3 n-2]$. Пресликавањем $(a, b, c) \rightarrow(a, b-2, c-4)$ за $a<b<c$ добијамо одговарајуће растављање скупа $\{1,2, \ldots, 3(n-2)\}$ на тројке. Како за $n=1$ овакво растављање није могуће, једноставном индукцијом показујемо да оно није могуће ни за једно непарно $n$.
|
| 100 |
+
|
| 101 |
+
С друге стране, за парно $n=2 m$ тројке ( $2 i-1,2 i+n, 2 i+2 n-1$ ) и $(2 i, 2 i+n-1,2 i+2 n)$ за $i=1, \ldots, m$ задовољавају услове.
|
| 102 |
+
|
| 103 |
+
5. Нека је без смањења општости $B C>A C$. Тада се праве $A^{\prime} B^{\prime}$ и $A B$ секу у тачки $P$, при чему је $A$ између $P$ и $B$. Из једнакости површина $A D A^{\prime}$ и $B D B^{\prime}$ следи да је $\frac{A D}{D B}=\frac{P B^{\prime}}{P A^{\prime}}$. С друге стране, важи и $P D^{2}=P A^{\prime} \cdot P B^{\prime}=P A$. $P B$, одакле је $\frac{P D}{P B}=\frac{P A}{P D}=\frac{A D}{D B}=$ $\frac{P B^{\prime}}{P A^{\prime}}$. Из последњих једнакости
|
| 104 |
+
|
| 105 |
+
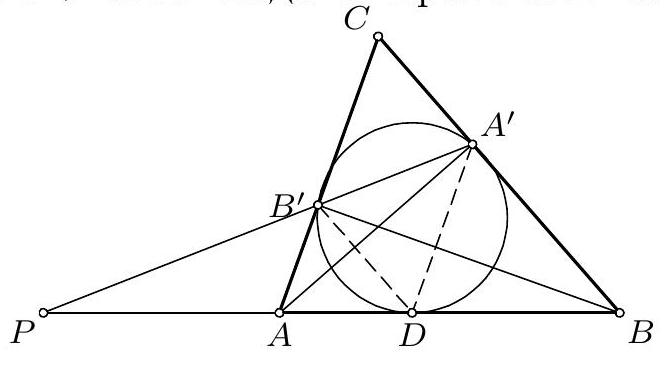
|
| 106 |
+
следи да је $B^{\prime} D \| B C$ и $A^{\prime} D \| A C$, и зато је $\varangle A^{\prime} D B^{\prime}=\varangle A C B$.
|
| 107 |
+
|
| 108 |
+
Друго решеъе. Како је $\varangle C B^{\prime} D=\alpha+\varangle A D B^{\prime}=\alpha+\varangle B^{\prime} A^{\prime} D=$ $\varangle C A^{\prime} D=x$, синусна теорема у $\triangle A^{\prime} B^{\prime} D$ и $\triangle A B^{\prime} D$ нам даје $B D=$ $\frac{B A^{\prime} \sin x}{\sin (\beta+x)}$ и $A D=\frac{A B^{\prime} \sin x}{\sin (\alpha+x)}$, па је $\frac{A D}{B D}=\frac{A B^{\prime} \sin (\beta+x)}{B A^{\prime} \sin (\alpha+x)}=\frac{\sin (\beta+x) \cos \alpha}{\sin (\alpha+x) \cos \beta}$. С
|
| 109 |
+
друге стране, из услова $\left[A D A^{\prime}\right]=\left[B D B^{\prime}\right]$ добијамо $\frac{A D}{D B}=\frac{d\left(B^{\prime}, A B\right)}{d\left(A^{\prime}, A B\right)}=$ $\frac{\sin \alpha \cos \alpha}{\sin \beta \cos \beta}$, тј. $\frac{\sin (\beta+x)}{\sin (\alpha+x)}=\frac{\sin \alpha}{\sin \beta}$. Одавде лако добијамо $\varangle A B^{\prime} D=x=\gamma$.
|
| 110 |
+
|
| 111 |
+
6. Нека је $\max \left\{a_{1}, a_{2}\right\} \leqslant a_{3} \leqslant a_{4}$. Означимо $a_{2}=\beta^{2}$ и $a_{3}=\gamma^{2}, \beta, \gamma \geqslant 0$. Из услова задатка следи $a_{1} \leqslant(\gamma-\beta)^{2}$ и $a_{4} \geqslant(\gamma+\beta)^{2}$.
|
| 112 |
+
|
| 113 |
+
Претпоставимо да су обе ове неједнакости заправо једнакости. Тада имамо $a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}=3\left(\beta^{4}+4 \beta^{2} \gamma^{2}+\gamma^{4}\right)$ и $a_{1} a_{2}+a_{1} a_{3}+$ $a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}=3\left(\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}\right)$. При том је $\gamma \leqslant 2 \beta$, па је $\frac{\beta^{4}+4 \beta^{2} \gamma^{2}+\gamma^{4}}{\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}}=1+\frac{3 \beta^{2} \gamma^{2}}{\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}}=1+\frac{3}{1+\frac{\beta^{2}}{\gamma^{2}}+\frac{\gamma^{2}}{\beta^{2}}} \geqslant \frac{11}{7}$, уз једнакост за $\gamma=2 \beta$. Према томе, у овом случају је $K \geqslant \frac{11}{7}$, а једнакост се достиже за $a_{1}: a_{2}: a_{3}: a_{4}=1: 1: 4: 9$.
|
| 114 |
+
|
| 115 |
+
Покажимо још да можемо да узмемо $a_{1}=(\gamma-\beta)^{2}$ и $a_{4}=(\gamma+\beta)^{2}$. Посматрајмо израз
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
F=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}-\frac{11}{7}\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\right)
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
За фиксирано $a_{2}, a_{3}, a_{4}, F$ је опадајућа функција по $a_{1}$ за $a_{1}<$ $\frac{11}{14}\left(a_{2}+a_{3}+a_{4}\right)$, при чему је $\frac{11}{14}\left(a_{2}+a_{3}+a_{4}\right) \geqslant \frac{11}{14}\left(\beta^{2}+\gamma^{2}+(\beta+\gamma)^{2}\right)$ $\geqslant(\gamma-\beta)^{2} \geqslant a_{1}$, па се $F$ не повећава ако $a_{1}$ заменимо са $(\gamma-\beta)^{2}$. Сада можемо да ставимо без смањења општости да је $a_{1} \leqslant a_{2}$, тј. $\beta \leqslant \gamma \leqslant 2 \beta$. Слично као горе, за фиксирано $a_{1}, a_{2}, a_{3}, F$ је растућа функција по $a_{4}$ за $a_{4}>\frac{11}{14}\left(a_{1}+a_{2}+a_{3}\right)$, и при том је $\frac{11}{14}\left(a_{1}+a_{2}+a_{3}\right)$ $\leqslant \frac{11}{14}\left(\beta^{2}+\gamma^{2}+(\gamma-\beta)^{2}\right) \leqslant(\gamma+\beta)^{2} \leqslant a_{4}$, дакле $F$ се не повећава ако $a_{4}$ заменимо са $(\gamma+\beta)^{2}$.
|
| 122 |
+
|
Serbia_MO/md/sr-2014_smo_resenja.md
ADDED
|
@@ -0,0 +1,113 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије
|
| 2 |
+
|
| 3 |
+
## 8. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 4 |
+
|
| 5 |
+
5. април 2014.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Одредити све функције $f: \mathbb{R} \rightarrow \mathbb{R}$ такве да за све $x, y \in \mathbb{R}$ важи
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
f(x f(y)-y f(x))=f(x y)-x y . \quad \text { (Душан Ђукић) }
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
2. На страницама $B C$ и $A C$ троугла $A B C$ дате су тачке $D$ и $E$, редом. Нека је $F(F \neq C)$ тачка пресека кружнице описане око троугла $C E D$ и праве која садржи тачку $C$ и паралелна је са правом $A B$. Нека је $G$ тачка пресека праве $F D$ и странице $A B$, а $H$ тачка на правој $A B$ таква да је $\varangle H D A=\varangle G E B$ и $H-A-B$. Ако је $D G=E H$, доказати да тачка пресека дужи $A D$ и $B E$ припада симетрали угла $A C B$.
|
| 16 |
+
|
| 17 |
+
(Милош Милосављевић)
|
| 18 |
+
|
| 19 |
+
3. Два играча играју следећу игру. Играчи наизменично записују по један природан број већи од један, при чему није дозвољено записати линеарну комбинацију претходно записаних бројева са ненегативним целим коефицијентима. Игру губи играч који не може да запише нови број. Да ли неко од играча има победничку стратегију и, ако има, који? (Александар Илић / "Квант”)
|
| 20 |
+
|
| 21 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије
|
| 22 |
+
|
| 23 |
+
## 8. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 24 |
+
|
| 25 |
+
## 6. април 2014.
|
| 26 |
+
|
| 27 |
+
## Други дан
|
| 28 |
+
|
| 29 |
+
4. За природан број $n$ кажемо да је шашав ако и само ако постоје природни бројеви $a>1$ и $b>1$ такви да је $n=a^{b}+b$. Да ли постоји 2014 узастопних природних бројева међу којима је тачно 2012 шашавих бројева?
|
| 30 |
+
|
| 31 |
+
(Милош Милосављевић)
|
| 32 |
+
|
| 33 |
+
5. Правилан $n$-тоугао подељен је на троуглове помоћу $n-3$ дијагонале од којих никоје две немају заједничких унутрашњих тачака. Колико највише међу овим троугловима може бити међусобно неподударних?
|
| 34 |
+
|
| 35 |
+
(Душан Ђукић)
|
| 36 |
+
|
| 37 |
+
6. Симетрале унутрашњих углова код темена $A$ и $B$ троугла $A B C$ секу наспрамне странице у тачкама $D$ и $E$, редом. Ромб је уписан у четвороугао $A B D E$ тако да се на свакој страници четвороугла налази тачно једно теме ромба. Ако је $\varangle B A C=\alpha$ и $\varangle A B C=\beta$, доказати да је барем један угао ромба не већи од $\max \{\alpha, \beta\}$.
|
| 38 |
+
|
| 39 |
+
(Душан Ђукић)
|
| 40 |
+
|
| 41 |
+
## РЕШЕЊА
|
| 42 |
+
|
| 43 |
+
1. Замена $y=0$ даје $f(x f(0))=f(0)$. Ако је $f(0) \neq 0$, израз $x f(0)$ узима све реалне вредности, па је $f$ константна функција, а она не задовољава услове. Према томе, $f(0)=0$.
|
| 44 |
+
|
| 45 |
+
Стављањем $y=x$ добијамо $f(0)=f\left(x^{2}\right)-x^{2}$, тј. $f\left(x^{2}\right)=x^{2}$. Дакле, $f(x)=x$ за све $x \geqslant 0$. Убацимо сада произвољне $x, y<0$. Како је тада $f(x y)=x y$, имамо $f(x f(y)-y f(x))=0$, што може да важи само за $x f(y)-y f(x) \leqslant 0$. Аналогно је и $y f(x)-x f(y) \leqslant 0$, па је $y f(x)=x f(y)$, тј. $f(x) / x=f(y) / y$. Следи да је $f(x)=c x$ за све $x<0$, где је $c$ нека константа. Сада за $x<0<y$ добијамо $f((1-c) x y)=f(x y)-x y=(c-1) x y$, тј. $f(z)=-z$ за $z=(1-c) x y$. Ако је $c=1$, онда је $f(x) \equiv x$, што је очигледно решење. С друге стране, за $c \neq 1$ је $z \neq 0$ и отуда $f(z) \in\{c z, z\}$, па тада мора бити $c=-1$, што даје функцију $f(x)=|x|$ за све $x$. И ова функција је решење: све случајеве осим $x>0>y$ смо већ проверили, а за $x>0>y$ је $-2 x y=f(-2 x y)=f(x f(y)-y f(x))=f(x y)-x y=-2 x y$.
|
| 46 |
+
|
| 47 |
+
Према томе, решења су функције $f(x)=x$ и $f(x)=|x|$.
|
| 48 |
+
|
| 49 |
+
2. Како је $\varangle A G D=180^{\circ}-\varangle C F D=\varangle C E D=180^{\circ}-\varangle A E D$, тачке $A$, $E, D, G$ су концикличне. Одавде је $\varangle D A G=\varangle D E G . \quad$ Међутим, тада је $\varangle D H B=\varangle D A G-\varangle H D A$ $=\varangle D E G-\varangle B E G=\varangle D E B$, па су и тачке $H, E, D, B$ концикличне. Следи да је $B H E=180^{\circ}-$ $\varangle B D E=\varangle C D E=\varangle C F E$, што
|
| 50 |
+
|
| 51 |
+
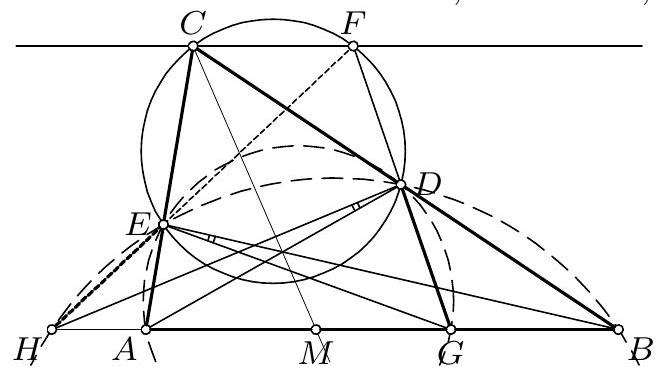
|
| 52 |
+
значи да су тачке $F, E$ и $H$ колинеарне.
|
| 53 |
+
|
| 54 |
+
Сада је $E H=E F \cdot \frac{A E}{E C}$ и $D G=D F \cdot \frac{D B}{C D}$, па услов $E H=D G$ постаје $\frac{A E}{E C} \cdot \frac{C D}{D B}=\frac{D F}{E F} . \quad$ С друге стране, из $\varangle D E F=\varangle D C F=\varangle A B C$ и $\varangle D F E=\varangle A C B$ следи да је $\triangle D E F \sim \triangle A B C$, па је $\frac{D F}{E F}=\frac{A C}{C B}=\frac{A M}{M B}$, где је $M$ пресечна тачка симетрале угла $A C B$ и странице $A B$. Према томе, $\frac{A E}{E C} \cdot \frac{C D}{D B} \cdot \frac{B M}{M A}=1$, па се по Чевиној теореми праве $A D$ и $B E$ секу на $C M$.
|
| 55 |
+
|
| 56 |
+
3. За $a, b \in \mathbb{N}$ дефинишимо $\mathcal{L}\{a, b\}=\left\{a x+b y \mid x, y \in \mathbb{N}_{0}\right\}$. Прво ћемо доказати једно помоћно тврђење.
|
| 57 |
+
|
| 58 |
+
Лема. Нека су $a>1$ и $b>1$ узајамно прости природни бројеви.
|
| 59 |
+
|
| 60 |
+
(a) $N=a b-a-b$ је највећи природан број ван скупа $\mathcal{L}\{a, b\}$.
|
| 61 |
+
|
| 62 |
+
(б) За свако $z \in \mathbb{Z}, z \in \mathcal{L}\{a, b\}$ ако и само ако $N-z \notin \mathcal{L}\{a, b\}$.
|
| 63 |
+
|
| 64 |
+
Доказ. (a) Ако је $N=(b-1) a-b=a x+b y$ за неке $x \in\{0, \ldots, b-1\}$ и $y \in \mathbb{Z}$, онда је $x \equiv b-1(\bmod b)$, па је $x \geqslant b-1$ и одатле $y<0$; дакле, $N \notin \mathcal{L}\{a, b\}$.
|
| 65 |
+
|
| 66 |
+
(б) Јасно је да из $z \in \mathcal{L}\{a, b\}$ следи $N-z \notin \mathcal{L}\{a, b\}$ (у супротном би важило $N=z+(N-z) \in \mathcal{L}\{a, b\})$. Посматрајмо сада неко $z \in \mathbb{Z} \backslash \mathcal{L}\{a, b\}$. Ако је $x \in\{0, \ldots, b-1\}$ такво да је $a x \equiv z$ $(\bmod b)$, онда је $z<a x$, тј. $a x-b y=z$ за неко $y \in \mathbb{N}$. Тада је $N-x=(b-1-x) a+b(y-1) \in \mathcal{L}\{a, b\}$.
|
| 67 |
+
|
| 68 |
+
Нека играч А започне игру уписујући прост број $a \geqslant 5$, након чега играч Б уписује природан број $b$ такав да $a \nmid b$. Само коначно много природних бројева не припада скупу $\mathcal{L}\{a, b\}$, па је игра коначна. Дакле, један од играча има победничку стратегију.
|
| 69 |
+
|
| 70 |
+
Размотримо игру у којој је други потез играча А број $N$. Ако је то губитнички потез, сада Б има победнички одговор у виду неког дозвољеног броја c. Међутим, онда играч А може да у другом потезу, уместо броја $N$, запише број с и надаље следи добитничку стратегију другог играча. Заиста, по леми, број $N-c$ није дозвољен, па након потеза $c$ ни број $N=(N-c)+c$ није дозвољен, те Б остаје управо у позицији која би за А била губитничка.
|
| 71 |
+
|
| 72 |
+
4. Прво ћемо дати пример 2012 узастопних шашавих бројева. Довољно је узети бројеве $N+2, N+3, \ldots, N+2013$, где је $N=2^{2013!}$.
|
| 73 |
+
|
| 74 |
+
За природан број $n$, означимо са $f(n)$ број шашавих бројева међу $n, n+1, \ldots, n+2013$. Како је $f(1)<2012$ (бројеви $1,2,3,4,5$ нису шашави), $f(N) \geqslant 2012$ и $|f(n+1)-f(n)| \leqslant 1$ за свако $n$, постоји $n$ такво да је $f(n)=2012$.
|
| 75 |
+
|
| 76 |
+
Друго решеъе. Означимо $N=\frac{2014!}{2011}$. Бројеви $2^{N}+i$ за $2 \leqslant i \leqslant 2010$ и $2012 \leqslant i \leqslant 2014$ су шашави; докажимо да $2^{N}+1$ и $2^{N}+2011$ то нису.
|
| 77 |
+
|
| 78 |
+
Претпоставимо да је $2^{N}+2011=a^{b}+b$ (слично се испитује и број $\left.2^{N}+1\right)$. Из $2^{b} \leqslant a^{b}<2^{N}$ следи $b<N$. Такође је $b>2011$, јер би у супротном било $2011-b=a^{b}-2^{N}=\left(a-2^{\frac{N}{b}}\right)\left(\cdots+2^{\frac{(b-1) N}{b}}\right)>2^{\frac{N}{b}}>$ 2011. Даље, ако $2 \mid a$, имамо $2^{b} \mid 2^{N}-a^{b}=b-2011<2^{b}$, што је немогуће. Најзад, за $2 \nmid a$ и $2 \mid b$ имамо $b-2011=\left(2^{\frac{N}{2}}-a^{\frac{b}{2}}\right)\left(2^{\frac{N}{2}}+a^{\frac{b}{2}}\right)>$ $2^{\frac{N}{2}}$, па је $2^{N}+2011=a^{b}+b>2^{2^{N / 2}}$, опет немогуће јер је $2^{\frac{N}{2}}>N$.
|
| 79 |
+
|
| 80 |
+
5. Одговор је $\left[\frac{3 n-7}{4}\right]$ за $n>3$, односно 1 за $n=3$.
|
| 81 |
+
|
| 82 |
+
Троуглове са по две, једном или ниједном страницом која је уједно страница $n$-тоугла ( $n>3$ ) зовемо редом уиима, танким и дебелим троугловима. Нека у подели има $a$ дебелих троуглова, $b$ танких и c ушију. Број страница $n$-тоугла које они заузимају је $b+2 c=n$. С друге стране, укупан број троуглова је $a+b+c=n-2$. Из ове две релације добијамо $c=a+2$.
|
| 83 |
+
|
| 84 |
+
Како троуглова који нису дебели има највише $\left[\frac{n-1}{2}\right]$ различитих, укупан број $N$ неподударних троуглова у подели није већи од $\frac{n-1}{2}+a$. С друге стране, у таквој подели има $a+2$ ушију, а све уши су подударне, па је $N \leqslant n-2-(a+1)=n-a-3$. Сабирањем добијамо $2 N \leqslant\left(\frac{n-1}{2}+a\right)+(n-a-3)=\frac{3 n-7}{2}$, тј. $N \leqslant\left[\frac{3 n-7}{4}\right]$.
|
| 85 |
+
|
| 86 |
+
Најзад, повлачењем дијагонала $A_{0} A_{2 i}$ и $A_{2 i-2} A_{2 i}\left(1 \leqslant i \leqslant\left[\frac{n}{4}\right]\right)$ и $A_{0} A_{j}$ $\left(2\left[\frac{n}{4}\right]<j \leqslant n-2\right)$ добијамо пример са тачно $\left[\frac{n-1}{2}\right]+\left[\frac{n}{4}\right]-1=\left[\frac{3 n-7}{4}\right]$ неподударних троуглова.
|
| 87 |
+
|
| 88 |
+
6. Нека је $K L M N$ ромб са $K \in A B, L \in B D$ и $N \in E A$. Посматрајмо трапез $P Q R S$ са $P, Q \in A B, P Q \| R S$ и $\varangle P Q R=\varangle Q P S=\varangle K N M=$ $\varphi$ такав да су $K, L, M, N$ на $P Q, Q R, R S, S P$ редом. Претпоставимо да је $\varphi>\alpha, \beta$. Тада $R$ и $S$ леже ван $\triangle A B C$.
|
| 89 |
+
|
| 90 |
+
Како је $\varangle S N M=180^{\circ}-\varphi-\varangle N M S=\angle R M L$ и $\varangle L R M=\varangle M S N$, троуглови $L R M$ и $M S N$ су подударни, па је $L R=M S$. Слично, ако је $Q^{\prime}$ тачка на $A B$ таква да је $\varangle L Q^{\prime} B=\varphi$, троуглови $L R M$ и $K Q^{\prime} L$ су подударни, па је $M R=L Q^{\prime}=L Q$. Следи да је $R Q=R L+L Q=S M+M R=R S$.
|
| 91 |
+
|
| 92 |
+
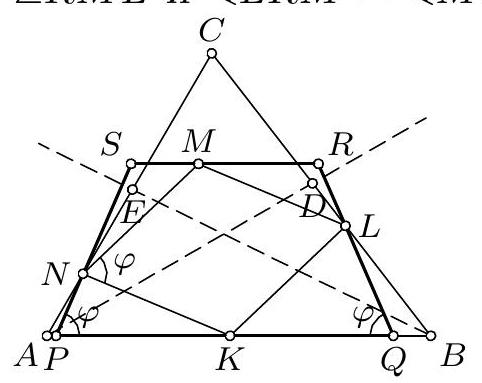
|
| 93 |
+
|
| 94 |
+
Сада је $d(R, A B)=R Q \sin \varphi>R S \sin \alpha>d(R, A C)$ и аналогно $d(S, A B)>d(S, B C)$, што значи да тачке $R$ и $S$ леже изнад правих $A D$ и $B E$ редом (тј. у полуравнима у којима је $C$ ), одакле следи да обе тачке леже изнад праве $D E$. Ово је немогуће јер се дужи $R S$ и $D E$ секу у $M$.
|
| 95 |
+
|
| 96 |
+
Друго решење. Растојање од тачке $X$ до праве $p$ означавамо $d(X, p)$.
|
| 97 |
+
|
| 98 |
+
Лема. За произвољну тачку $M$ на дужи $D E$ важи $d(M, A B)=$ $d(M, A C)+d(M, B C)$.
|
| 99 |
+
|
| 100 |
+
Доказ. Ако је $\frac{D M}{D E}=k$, важи $d(M, A B)=k d(E, A B)+(1-k) d(D, A B)$ $=k d(E, B C)+(1-k) d(D, A C)=d(M, B C)+d(M, A C)$.
|
| 101 |
+
|
| 102 |
+
Користимо исте ознаке као у првом решењу. Нека је $a$ страница ромба и $O$ његов центар. Имамо
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\begin{aligned}
|
| 106 |
+
d(M, A C)+d(M, B C) & =a(\sin \varangle M N C+\sin \varangle M L C), \\
|
| 107 |
+
\text { и } d(M, A B) & =2 d(O, A B)=d(L, A B)+d(N, A B) \\
|
| 108 |
+
& =a(\sin \varangle N K A+\sin \varangle L K B) .
|
| 109 |
+
\end{aligned}
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
Међутим, ако је $\varphi>\alpha, \beta$, онда је $\varangle N K A=\varangle M N C+\varphi-\alpha>$ $\varangle M N C$ и аналогно $\varangle L K B>\varangle M L C$, па из горњих једначина следи $d(M, A B)>d(M, A C)+d(M, B C)$, контрадикција.
|
| 113 |
+
|
Serbia_MO/md/sr-2015_smo_resenja.md
ADDED
|
@@ -0,0 +1,113 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије
|
| 2 |
+
|
| 3 |
+
## 9. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 4 |
+
|
| 5 |
+
27. март 2015.
|
| 6 |
+
|
| 7 |
+
## Први дан
|
| 8 |
+
|
| 9 |
+
1. Дат је тетивни четвороугао $A B C D$. Тачке $M, N, P$ и $Q$ су средишта страница $D A, A B, B C$ и $C D$, редом, а тачка $E$ је пресек дијагонала $A C$ и $B D$. Кружнице описане око $\triangle E M N$ и $\triangle E P Q$ секу се у тачки $F \neq E$. Доказати да важи $E F \perp A C$.
|
| 10 |
+
|
| 11 |
+
(Душан Ђукић)
|
| 12 |
+
|
| 13 |
+
2. Нека је $k$ природан број. За $n \in \mathbb{N}$ означимо са $f_{k}(n)$ најмањи природан број већи од $k n$ такав да је $n f_{k}(n)$ потпун квадрат природног броја. Ако је испуњено $f_{k}(m)=f_{k}(n)$, доказати да важи $m=n$.
|
| 14 |
+
|
| 15 |
+
(Никола Петровић)
|
| 16 |
+
|
| 17 |
+
3. Стражар предлаже затвореницима следећу игру. Сви ће бити изведени у двориште, где ће свакоме од њих бити стављен на главу шешир у једној од 5 могућих боја. Стражар ће их потом поређати у врсту тако да сваки затвореник види све шешире осим сопственог и питати првог затвореника у врсти да ли зна боју свог шешира. Затвореник гласно одговара “да" или "не". Ако одговори "не", биће одмах закључан у самицу. Ако одговори “да", стражар ће га питати које је боје његов шешир, на шта затвореник треба да одговори на такав начин да остали затвореници не чују одговор. Уколико је одговор погрешан, тај затвореник биће одмах закључан у самицу пред свима, а ако је одговор тачан, тај затвореник биће одмах ослобођен пред свима. Стражар потом прилази следећем затворенику у реду и понавља исти поступак, и тако све до последњег затвореника. Затвореници имају могућност да осмисле стратегију пре почетка игре, али кад игра почне, никаква комуникација међу затвореницима није дозвољена. Ако у затвору има 2015 затвореника, који је максималан број затвореника који ће загарантовано бити ослобођени уколико затвореници примењују оптималну стратегију?
|
| 18 |
+
|
| 19 |
+
(Бојан Башић)
|
| 20 |
+
|
| 21 |
+
Време за рад 270 минута.
|
| 22 |
+
|
| 23 |
+
Решења задатака детаљно образложити.
|
| 24 |
+
|
| 25 |
+
Сваки задатак вреди 7 бодова.
|
| 26 |
+
|
| 27 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије
|
| 28 |
+
|
| 29 |
+
## 9. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 30 |
+
|
| 31 |
+
28. март 2015.
|
| 32 |
+
|
| 33 |
+
## Други дан
|
| 34 |
+
|
| 35 |
+
4. За цео број $a, a \neq 0$, означимо са $v_{2}(a)$ највећи ненегативан цео број $k$ такав да $2^{k} \mid a$. За дато $n \in \mathbb{N}$ одредити највећу могућу кардиналност подскупа $A$ скупа $\left\{1,2,3, \ldots, 2^{n}\right\}$ са следећим својством:
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
\text { за све } x, y \in A, x \neq y, \text { број } v_{2}(x-y) \text { је паран. }
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
(Дуиан Ђукић)
|
| 42 |
+
|
| 43 |
+
5. Доказати неједнакост
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
\frac{x-y}{x y+2 y+1}+\frac{y-z}{y z+2 z+1}+\frac{z-x}{z x+2 x+1} \geqslant 0
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
где су $x, y$ и $z$ ненегативни реални бројеви.
|
| 50 |
+
|
| 51 |
+
(Душан Ђукић)
|
| 52 |
+
|
| 53 |
+
6. У скупу ненегативних целих бројева решити једначину
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
\left(2^{2015}+1\right)^{x}+2^{2015}=2^{y}+1 . \quad \text { (Бојан Баиић) }
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
## РЕШЕЊА
|
| 60 |
+
|
| 61 |
+
1. Троуглови $E A B$ и $E D C$ су слични, па су то и троуглови $E B N$ и $E C Q$. Зато у оријентисаним угловима важи $\varangle M F E=\varangle M N E=\varangle B E N=\varangle Q E C$ $=\varangle E Q M$. Аналогно важи $\varangle Q F E=$ $\varangle E M Q$, одакле следи да је $F$ ортоцентар троугла $E M Q$. Дакле, $E F \perp$ $Q M \| A C$.
|
| 62 |
+
|
| 63 |
+
Друго решеъе. Посматрајмо транслацију $\mathcal{T}$ за вектор $\frac{1}{2} \overrightarrow{A C}$. Важи $\mathcal{T}(M)=$
|
| 64 |
+
|
| 65 |
+
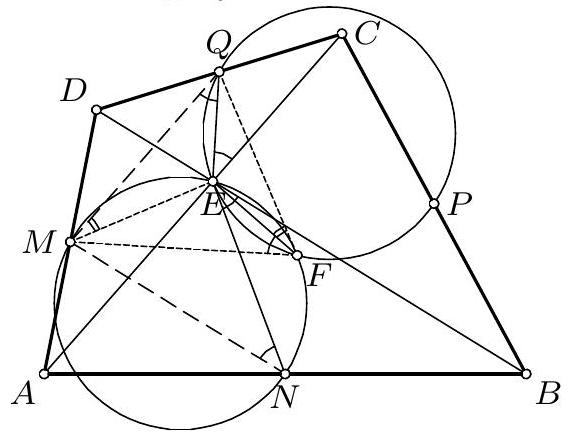
|
| 66 |
+
$Q$ и $\mathcal{T}(N)=P$; означимо $\mathcal{T}(E)=E^{\prime}$. Из сличности троуглова $A E D$ и $B E C$ следи $\triangle A E M \sim \triangle B E P$, одакле је $\varangle Q E^{\prime} E=\varangle E M Q=\varangle M E A=\varangle B E P=$ $\varangle Q P E$, па тачка $E^{\prime}$ лежи на кругу $P E Q$. Према томе, транслација $\mathcal{T}$ слика круг $M E N$ у круг $P E Q$, па је права која спаја њихове центре паралелна са $A C$, одакле следи тврђење.
|
| 67 |
+
|
| 68 |
+
2. Претпоставимо да је $f_{k}(m)=f_{k}(n)=q$. Напишимо број $q$ у облику $q=a u^{2}$, где су $a, u \in \mathbb{N}$ и $a$ није дељиво ниједним потпуним квадратом већим од 1 . Како је $m q=a m u^{2}$ потпун квадрат, то је и $a m$, па следи да је $m=a v^{2}$ за неко $v \in \mathbb{N}$. Слично је $n=a w^{2}$ за неко $w \in \mathbb{N}$.
|
| 69 |
+
|
| 70 |
+
Како је $f_{k}\left(a v^{2}\right)=a u^{2}, u$ је најмањи природан број већи од $v \sqrt{k}$. Аналогно, $u$ је најмањи природан број већи од $w \sqrt{k}$, па мора да важи $|v \sqrt{k}-w \sqrt{k}|<1$. Међутим, одавде следи $|v-w|<\frac{1}{\sqrt{k}}<1$, па мора бити $v=w$, тј. $m=n$.
|
| 71 |
+
|
| 72 |
+
3. Доделимо бојама вредности $0,1,2,3,4$ и означимо са $B$ боју шешира другог затвореника, а са $S$ збир боја шешира од трећег до последњег затвореника по модулу 5. Описаћемо стратегију прва два затвореника након које ће сви остали затвореници знати $S$, те ће, знајући боје осталих шешира, моћи да одреде своју. Овако ће за бар 2013 затвореника бити обезбеђена слобода. Први затвореник одговара "не" ако је $S \in\{0, B, B+1\}$ или $(B, S)=(4,1)$. На то други одговара "не" ако је $S=0$, а у супротном каже "да" и стражару даје одговор $S$. На овај начин, ако чују два одговора "не", остали знају да је $S=0$. Ако други каже "да" и буде ослобођен, остали знају да је $S=B$, док у супротном знају да је $S=B+1$ ако $B \neq 4$, односно $S=1$ ако $B=4$.
|
| 73 |
+
|
| 74 |
+
У осталим случајевима први затвореник каже “да" (небитно је шта ће бити с њим). На то други каже "да" ако $S \in\{2,4\}$ и стражару даје одговор $S-2$. Ако је $B=0$, онда $S \notin\{0,1\}$, па остали знају да је $S=2$ ако други буде ослобођен, $S=3$ ако каже "не", и $S=4$ ако каже "да" и промаши. Најзад, ако је $B \neq 0$, с обзиром на потврдан одговор првог важи $S \equiv B+2$ или $S \equiv B+3(\bmod 4)$, а одговор другог одређује парност $S$, што осталима омогућује да одреде $S$.
|
| 75 |
+
|
| 76 |
+
Остаје да докажемо да ниједна стратегија не гарантује слободу 2014 затвореника. Претпоставимо да таква стратегија постоји и посматрајмо скуп од
|
| 77 |
+
пет распореда који се разликују само у боји шешира другог затвореника. У највише једном од ових распореда стратегија предвиђа да први каже "не" (у супротном други не би могао да са сигурношћу одреди боју свог шешира). У бар три од преостала четири распореда први би морао да промаши, па други не би могао да одреди боју свог шешира. Овим је доказ завршен.
|
| 78 |
+
|
| 79 |
+
4. Доказаћемо индукцијом по $k$ да скуп $A$ садржи највише $2^{k}$ различитих елемената по модулу $2^{2 k}$. То тривијално важи за $k=0$. Нека је $k>0$. По индуктивној претпоставци, елементи скупа $A$ дају највише $2^{k-1}$ остатака по модулу $2^{2 k-2}$. Претпоставимо да елементи $A$ дају више од $2^{k}$ остатака по модулу $2^{2 k}$. На основу Дирихлеовог принципа, бар три од ових остатака су једнаки по модулу $2^{2 k-2}$. Али међу ова три остатка, два се разликују за $2^{2 k-1}\left(\bmod 2^{2 k}\right)$, противно услову задатка.
|
| 80 |
+
|
| 81 |
+
Следи да је $|A| \leqslant 2^{\left[\frac{n+1}{2}\right]}$. Пример скупа $A$ са $2^{\left[\frac{n+1}{2}\right]}$ елемената добијамо укључивањем бројева облика $\sum_{i \in B} 4^{i}$ за све подскупове $B$ скупа $\left\{0,1, \ldots,\left[\frac{n-1}{2}\right]\right\}$.
|
| 82 |
+
|
| 83 |
+
Друго решеъе. Кажемо да је скуп $X$ срећан ако је $v_{2}(x-y)$ парно за све $x, y \in X(x \neq y)$, а несрећан ако је $v_{2}(x-y)$ непарно за све $x, y \in X(x \neq y)$. Означимо са $a_{n}$ и $b_{n}$ редом максималне кардиналности срећног и несрећног подскупа скупа $T_{n}=\left\{1,2, \ldots, 2^{n}\right\}$.
|
| 84 |
+
|
| 85 |
+
Посматрајмо срећан скуп $A \subset T_{n}, n \geqslant 1$. Како је $v_{2}(2 x-2 y)=v_{2}(x-y)+1$, скупови $A_{0}=\left\{\frac{x}{2}|x \in A, 2| x\right\}$ и $A_{1}=\left\{\left.\frac{x-1}{2} \right\rvert\, x \in A, 2 \nmid x\right\}$ су несрећни подскупови скупа $T_{n-1}$ и имају највише по $b_{n-1}$ елемената. С друге стране, ако је $A_{0} \subset T_{n-1}$ несрећан скуп, скуп $\left\{2 x, 2 x+1 \mid x \in A_{0}\right\} \subset T_{n}$ је срећан и има $2\left|A_{0}\right|$ елемената. Следи да је $a_{n}=2 b_{n-1}$.
|
| 86 |
+
|
| 87 |
+
Слично, ако је $B \subset T_{n}$ непаран скуп, сви његови елементи су исте парности, а скуп $B^{\prime}=\left\{\left.\left\lceil\frac{x}{2}\right\rceil \right\rvert\, x \in B\right\} \subset T_{n-1}$ је срећан. С друге стране, ако је $B^{\prime} \subset T_{n-1}$ срећан, скуп $B=\left\{2 x-1 \mid x \in B^{\prime}\right\} \subset T_{n}$ је несрећан. Одавде је $b_{n}=a_{n-1}$.
|
| 88 |
+
|
| 89 |
+
Добијене релације дају $a_{n}=2 a_{n-2}$ за $n \geqslant 2$, па из $a_{0}=1$ и $a_{1}=2$ једноставном индукцијом добијамо $a_{n}=2^{\left[\frac{n+1}{2}\right]}$.
|
| 90 |
+
|
| 91 |
+
5. Означимо $a=\frac{x-y}{x y+2 y+1}, b=\frac{y-z}{y z+2 z+1}$ и $c=\frac{z-x}{z x+2 x+1}$. Тада је $1+\frac{1}{a}=\frac{x y+x+y+1}{x-y}$ и одатле $\frac{a}{a+1}=\frac{x-y}{x y+x+y+1}=\frac{1}{y+1}-\frac{1}{x+1}$; аналогно је $\frac{b}{b+1}=\frac{1}{z+1}-\frac{1}{y+1}$ и $\frac{c}{c+1}=$ $\frac{1}{x+1}-\frac{1}{z+1}$.
|
| 92 |
+
|
| 93 |
+
Из $0<\frac{1}{x+1}, \frac{1}{y+1}, \frac{1}{z+1}<1$ следи $\frac{a}{a+1}, \frac{b}{b+1}, \frac{c}{c+1}<1$, па су $a+1, b+1, c+1$ позитивни. Осим тога, имамо $\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}=0$, тј. $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=3$. Сада је по Коши-Шварцовој неједнакости $(a+1)+(b+1)+(c+1) \geqslant 3$, тј. $a+b+c \geqslant 0$.
|
| 94 |
+
|
| 95 |
+
Друго решење. Тражена неједнакост се множењем и груписањем своди на
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
\begin{aligned}
|
| 99 |
+
& 2(x-1)^{2}(y-z)^{2}+2(y-1)^{2}(z-x)^{2}+2(z-1)^{2}(x-y)^{2} \\
|
| 100 |
+
& +9\left(x y^{2}+y z^{2}+z x^{2}-3 x y z\right)+3\left(x^{2} y+y^{2} z+z^{2} x-3 x y z\right) \geqslant 0
|
| 101 |
+
\end{aligned}
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
где су сви сабирци ненегативни на основу А-Г неједнакости.
|
| 105 |
+
|
| 106 |
+
Напомена. Ако се услов $x, y, z \geqslant 0$ замени са $x, y, z \geqslant-\varepsilon$ за произвољно $\varepsilon>0$, тврђење више не мора да важи, што показује пример $(x, y, z)=\left(-\varepsilon, 1, \frac{2}{\varepsilon}\right)$.
|
| 107 |
+
|
| 108 |
+
6. За $x \leqslant 1$ једина решења су $(0,2015)$ и $(1,2016)$.
|
| 109 |
+
|
| 110 |
+
Нека је $x>1$. Како је $2^{2015}+1$ дељиво са 3 , имамо $\left(2^{2015}+1\right)^{x}+2^{2015} \equiv 2^{2015} \equiv 5$ $(\bmod 9)$, дакле $2^{y} \equiv 4(\bmod 9)$, одакле добијамо $y=6 k+2$ за неко $k \in \mathbb{N}$. Сада по модулу 13 имамо $2^{y}+1=\left(2^{6}\right)^{k} \cdot 2^{2} \equiv \pm 4$ и $2^{2015} \equiv 7(\bmod 13)$, па тако добијамо $8^{x}+7 \equiv \pm 4(\bmod 13)$. Међутим, $8^{x}$ даје један од остатака $1,5,8,12$ по модулу 13 , па је последња конгруенција немогућа.
|
| 111 |
+
|
| 112 |
+
Друго решење. За $x>1$ имамо $2^{y}=\left(2^{2015}+1\right)^{x}+2^{2015}-1=(x+1) 2^{2015}+$ $\sum_{i=2}^{x}\binom{x}{i} 2^{2015 i} \equiv(x+1) 2^{2015}\left(\bmod 2^{2019}\right)$, па због $y>2019$ следи да $16 \mid x+1$. Сада посматрајмо једначину по модулу 17 . Како је $2^{2015} \equiv 9(\bmod 17)$, добијамо $2^{y} \equiv 10^{x}+8 \equiv 10^{15}+8 \equiv 3(\bmod 17)$, што је немогуће.
|
| 113 |
+
|
Serbia_MO/md/sr-2016_smo_resenja.md
ADDED
|
@@ -0,0 +1,118 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 10. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 2 |
+
|
| 3 |
+
1. април 2016 .
|
| 4 |
+
|
| 5 |
+
## Први дан
|
| 6 |
+
|
| 7 |
+
1. Нека је $n$ природан број већи од 1. Доказати да постоји природан број $m$ већи од $n^{n}$ такав да је
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
\frac{n^{m}-m^{n}}{n+m}
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
природан број.
|
| 14 |
+
|
| 15 |
+
(Никола Петровић)
|
| 16 |
+
|
| 17 |
+
2. Дат је природан број $n$. Дефинишимо $f(0, j)=f(i, 0)=0, f(1,1)=n$ и
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
f(i, j)=\left\lfloor\frac{f(i-1, j)}{2}\right\rfloor+\left\lfloor\frac{f(i, j-1)}{2}\right\rfloor
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
за све природне бројеве $i$ и $j,(i, j) \neq(1,1)$. Колико има уређених парова природних бројева $(i, j)$ за које је $f(i, j)$ непаран број? (Душан Ђукић)
|
| 24 |
+
|
| 25 |
+
3. Нека је $O$ центар кружнице описане око $\triangle A B C$. Права $t$ додирује кружницу описану око $\triangle B O C$ и сече странице $A B$ и $A C$ у тачкама $D$ и $E$, редом $(D, E \not \equiv A)$. Тачка $A^{\prime}$ је симетрична тачки $A$ у односу на праву $t$. Доказати да се кружнице описане око $\triangle A^{\prime} D E$ и $\triangle A B C$ додирују. (Душан Ђукић)
|
| 26 |
+
|
| 27 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 10. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 28 |
+
|
| 29 |
+
## 2. април 2016 .
|
| 30 |
+
|
| 31 |
+
## Други дан
|
| 32 |
+
|
| 33 |
+
4. У $\triangle A B C(A B \neq A C)$ уписана кружница, чији је центар тачка $I$, додирује страницу $B C$ у тачки $D$. Нека је тачка $M$ средиште дужи $B C$. Доказати да се нормале из тачака $M$ и $D$ на праве $A I$ и $M I$, редом, секу на правој која садржи висину $\triangle A B C$ из темена $A$.
|
| 34 |
+
|
| 35 |
+
(Душан Ђукић)
|
| 36 |
+
|
| 37 |
+
5. Дато је $2 n-1$ двоелементних подскупова скупа $\{1,2, \ldots, n\}$. Доказати да се може одабрати $n$ од ових подскупова чија унија садржи не више од $\frac{2}{3} n+1$ елемената.
|
| 38 |
+
|
| 39 |
+
(Душан Ђукић)
|
| 40 |
+
|
| 41 |
+
6. Дати су природни бројеви $a_{1}, a_{2}, \ldots, a_{2 \text { 2016 }}$ такви да за све $n, 1 \leqslant n \leqslant 2^{2016}$, важи
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
a_{n} \leqslant 2016 \quad \text { и } \quad a_{1} a_{2} \cdots a_{n}+1 \text { је потпун квадрат. }
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
Доказати да је неки од бројева $a_{1}, a_{2}, \ldots, a_{22016}$ једнак 1. (Дуиан Ђукић)
|
| 48 |
+
|
| 49 |
+
## РЕШЕЊА
|
| 50 |
+
|
| 51 |
+
1. За почетак приметимо да за $m>n \geqslant 3$ важи $n^{m}>m^{n}$, те је $\frac{n^{m}-m^{n}}{m+n}>0$. Заиста, функција $f(x)=\frac{\ln x}{x}$ је опадајућа за $x>e$ јер је $f^{\prime}(x)=\frac{1-\ln x}{x^{2}}<0$, па је $\frac{\ln n}{n}>\frac{\ln m}{m}$, тј. $m \ln n>n \ln m$, и одатле $n^{m}=e^{m \ln n}>e^{n \ln m}=m^{n}$.
|
| 52 |
+
|
| 53 |
+
За $n=2$ се може узети $m=10$. Претпоставимо да је $n>2$. Имамо
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
n^{m}-m^{n} \equiv n^{m}-(-n)^{n}=n^{n}\left(n^{m-n}-(-1)^{n}\right) \quad(\bmod m+n)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Потражићемо $m$ у облику $m=k n^{n}-n(k \in \mathbb{N})$. Тада $m+n=k n^{n} \mid n^{m}-m^{n}$ ако и само ако $k \mid n^{m-n}-(-1)^{n}$.
|
| 60 |
+
|
| 61 |
+
$\left(1^{\circ}\right)$ Ако је $n$ непарно, онда је $n^{m-n}-(-1)^{n}$ парно, па можемо узети $k=2$, тј. $m=2 n^{n}-n$.
|
| 62 |
+
|
| 63 |
+
(2 $2^{\circ}$ Ако је $n$ парно, онда је $n^{m-n}-(-1)^{n}=n^{m-n}-1$ дељиво са $n-1$, па можемо узети $k-n-1$, тј. $m=(n-1) n^{n}-n$.
|
| 64 |
+
|
| 65 |
+
Напомена. Неједнакост $n^{m}>m^{n}$ за $m>n \geqslant 3$ се може доказати индукцијом. Могућа су и другачија решења, нпр. за $n>2$ може се узети $m=p n^{n}-n$, где је $p$ било који прост делилац броја $n^{n^{n}}-2 n-(-1)^{n}$.
|
| 66 |
+
|
| 67 |
+
2. Одговор је $n$.
|
| 68 |
+
|
| 69 |
+
За $m \geqslant 2$ означимо $s_{m}=\sum_{i+j=m} f(i, j)$. Како је остатак $f(i, j)$ при дељењу са 2 једнак $f(i, j)-2\left[\frac{f(i, j)}{2}\right]$, број непарних међу бројевима $f(i, j)$ за $i, j \geqslant 0$ и $i+j=m$ једнак је
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
\begin{aligned}
|
| 73 |
+
\sum_{i+j=m}\left(f(i, j)-2\left[\frac{f(i, j)}{2}\right]\right) & =s_{m}-\sum_{i+j=m}\left(\left[\frac{f(i-1, j+1)}{2}\right]+\left[\frac{f(i, j)}{2}\right]\right) \\
|
| 74 |
+
& =s_{m}-s_{m+1}
|
| 75 |
+
\end{aligned}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Следи да је број парова $(i, j)$ за које је $f(i, j)$ непарно и $i+j<m$ једнак $s_{2}-s_{m}=n-s_{m}$.
|
| 79 |
+
|
| 80 |
+
Остаје да покажемо да је $s_{m}=0$ за све довољно велике $m$. Јасно је да је низ $s_{m}$ ненегативан и нерастући, па постоје $N$ и $k$ такви да је $s_{m}=k$ за све $m \geqslant N$. То значи да је $f(i, j)$ парно кад год је $i+j \geqslant m$. Претпоставимо да је $k>0$ и посматрајмо најмање $i$ такво да је $f(i, m-i)>0$. Једноставном индукцијом добијамо $f(i, m+r-i)=\left[\frac{f(i, m-i)}{2^{r}}\right]$ за $r \geqslant 1$. Међутим, ако је $2^{r} \leqslant f(i, m-i)<2^{r+1}$, одавде је $f(i, m+r-i)=1$, противно претпоставци.
|
| 81 |
+
|
| 82 |
+
Друго решење (У. Динић). Поставимо $n$ жетона у тачку $(1,1)$ у координатној равни. У сваком кораку, из сваке тачке $(i, j)$ ћемо пребацити по цео део половине њених жетона у тачке $(i+1, j)$ и $(i, j+1)$. Приметимо да, ако је нека врста или колона у неком тренутку непразна, она ће увек остати непразна. Тако ниједан жетон не може изаћи из квадрата $[1, n] \times[1, n]$, па се игра завршава у коначном броју корака.
|
| 83 |
+
|
| 84 |
+
Није тешко видети да се након $i+j-2$ корака у тачки $(i, j)$ налази тачно $f(i, j)$ жетона. Шта више, број $f(i, j)$ је непаран ако након следећег корака
|
| 85 |
+
у тачки $(i, j)$ остане један жетон. Како у завршној позицији има тачно $n$ жетона, следи да међу члановима низа $f(i, j)$ има $n$ непарних бројева.
|
| 86 |
+
|
| 87 |
+
3. Означимо са $K$ додирну тачку праве $t$ и круга $B O C$. Нека се кругови описани око троуглова $B D K$ и $C E K$ секу у тачки $X \neq K$. Како је $\varangle B X C=$ $\varangle B X K+\varangle K X C=\varangle A D K+\varangle K E A=180^{\circ}-\varangle C A B$, тачка $X$ лежи на описаном кругу $k$ троугла $A B C$. Шта више, $\varangle D X E=\varangle D X K+\varangle K X E=\varangle D B K+$ $\varangle K C E=\varangle C K B-\varangle C A B=\varangle C A B=$ $\varangle D X E$, па $X$ такође лежи на описаном кругу $k_{1}$ троугла $A^{\prime} D E$. Доказаћемо да се кругови $k$ и $k_{1}$ додирују у тачки $X$.
|
| 88 |
+
|
| 89 |
+
Ако се праве $C K$ и $X D$ секу у тачки $P$, онда важи $\varangle X P C=\varangle X D E-$ $\varangle C K E=\varangle X B K-\varangle C B K=\varangle X B C$, што значи да $P$ лежи на кругу $k$. Аналогно, праве $B K$ и $X E$ се секу у тачки $Q$ на кругу $k$. Најзад, из $\varangle X P Q=\varangle X B Q=\varangle X D K$ следи да
|
| 90 |
+
|
| 91 |
+
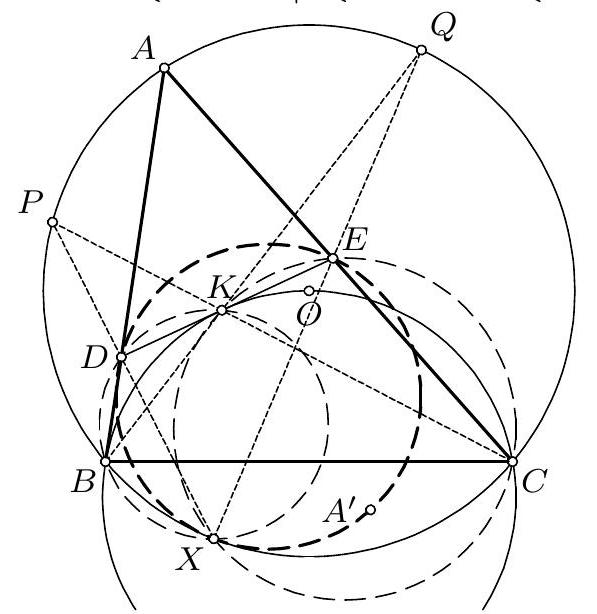
|
| 92 |
+
је $P Q \| D E$. Према томе, троуглови $X D E$ и $X P Q$ су хомотетични са центром хомотетије $X$, па се њихови описани кругови додирују у $X$.
|
| 93 |
+
|
| 94 |
+
Друго решеъе. Нека праве $B K$ и $C K$ поново секу описани круг $\triangle A B C$ редом у тачкама $Q$ и $P$. Из $\varangle C P Q=\varangle C B Q=\varangle C K E$ следи $P Q \| D E$. Нека се праве $D P$ и $E Q$ секу у тачки $X$. Како су тачке $D=P X \cap A B, K=P C \cap Q B$ и $E=A C \cap Q X$ колинеарне, по обратној Паскаловој теореми тачка $X$ лежи на истом кругу са тачкама $A, B, C, P, Q$. Према томе, троуглови $X D E$ и $X P Q$ су хомотетични, па се њихови описани кругови додирују у њиховом центру хомотетије $X$. Најзад, тачка $A^{\prime}$ лежи на описаном кругу $\triangle D E X$ јер je $\varangle D X E=\varangle P X Q=\varangle P C A+\varangle A B Q=\varangle B K C-\varangle B A C=\varangle B A C=\varangle D A^{\prime} E$.
|
| 95 |
+
|
| 96 |
+
Напомена. Важи и општије тврђење: ако је $K$ тачка у $\triangle A B C, D$ и $E$ тачке у којима тангента на круг $B K C$ у $K$ сече $A B$ и $A C$, а $X$ друга тачка пресека кругова $B D K$ и $C E K$, онда се кругови $D E X$ и $A B C$ додирују у тачки $X$.
|
| 97 |
+
|
| 98 |
+
4. Означимо са $\gamma$ уписани круг $\triangle A B C$, а са $\gamma_{a}$ и $I_{a}$ приписани круг наспрам $A$ и његов центар. Тачка $E$ симетрична тачки $D$ у односу на $M$ је додирна тачка $\gamma_{a}$ са страницом $B C$. Нормала $\ell_{1}$ из $D$ на $M I$ је радикална оса круга $\gamma$ и круга $\omega$ над пречником $D E$, док је нормала $\ell_{2}$ из $A I$ радикална оса кругова $\gamma$ и $\gamma_{a}$ (због $M D=M E$ ). Такође, радикална оса кругова $\gamma_{a}$ и $\omega$ је нормала $\ell_{3}$ из $E$ на $M I_{a}$. Праве $\ell_{1}, \ell_{2}$ и $\ell_{3}$ се секу у радикалном центру $S$ кругова $\gamma, \gamma_{a}, \omega$. С друге стране, поз-
|
| 99 |
+
|
| 100 |
+
|
| 101 |
+
нато је (по "Великом задатку") да важи $M I \| A E$ и $M I_{a} \| A D$, па праве $\ell_{1}$ и $\ell_{3}$ садрже висине из $D$ и $E$ у троуглу $A D E$. Следи да је $S$ ортоцентар $\triangle A D E$, а он лежи на висини из темена $A$.
|
| 102 |
+
|
| 103 |
+
Друго решење. Нека се нормале из $M$ и $D$ редом на $A I$ и $M I$ секу у тачки $S$ и нека је $J$ тачка у којој права $M I$ сече висину из $A$ у $\triangle A B C$. Довољно је доказати да је $A J=I D$. Заиста, тада ће следити да је $A J D I$ паралелограм, па је $M S \perp D J$, тако да је $D$ ортоцентар троугла $M S J$ и одатле $J S \perp M D$, тј. $A S \perp B C$.
|
| 104 |
+
|
| 105 |
+
Ово се директно израчунава. Означимо са $H$ и $F$ редом подножја висине и симетрале угла из темена $A$, и $a=B C, b=C A, c=A B$. Тада је $B F=\frac{a c}{b+c}$, $B D=\frac{a-b+c}{2}$ и $B H=\frac{a^{2}-b^{2}+c^{2}}{2 a}$, па је $F H=B F-B H=\frac{|b-c|\left((b+c)^{2}-a^{2}\right)}{2 a(b+c)}, F D=$ $B F-B D=\frac{|b-c|(b+c-a)}{2(b+c)}$ и најзад $\frac{A J}{A H}=\frac{F D}{F H}=\frac{a}{a+b+c}=\frac{I D}{A H}$.
|
| 106 |
+
|
| 107 |
+
5. Показаћемо индукцијом по $k\left(k \leqslant \frac{2 n-1}{3}\right)$ да се може избацити $3 k$ подскупова тако да је кардиналност уније преосталих не већа од $n-k$.
|
| 108 |
+
|
| 109 |
+
За $k=0$ то је тривијално. Претпоставимо да је $k \geqslant 1$ и да смо избацили $3(k-1)$ подскупова тако да унија преосталих не садржи више од $n-k+1$ елемената. Како је $2 n-1-3(k-1)<2(n-k+1)$, постоји елемент $x_{k}$ из уније који се налази у највише три од преосталих подскупова. Дакле, можемо да избацимо још три подскупа тако да унија преосталих $2 n-1-3 k$ не садржи елемент $x_{k}$, што завршава индуктивни корак.
|
| 110 |
+
|
| 111 |
+
Тврђење задатка следи за $k=\left[\frac{n-1}{3}\right]$ jep је $n-\left[\frac{n-1}{3}\right] \leqslant n-\frac{n-3}{3}=\frac{2}{3} n+1$.
|
| 112 |
+
|
| 113 |
+
Напомена. Пробабилистички метод даје слабију оцену $\sim \frac{n}{\sqrt{2}}$.
|
| 114 |
+
|
| 115 |
+
6. Кључна чињеница је да, ако су $a+1=u^{2}$ и $b=v^{2}$ потпуни квадрати и $a>b$, онда $a b+1$ није квадрат. Заиста, тада је $(u v-1)^{2}<a b+1=u^{2} v^{2}-v^{2}+1<(u v)^{2}$. Нека су $p_{1}, p_{2}, \ldots, p_{m}$ сви прости бројеви мањи од 2016. За $1 \leqslant n \leqslant 2^{2016}$ посматрајмо бинарни низ $\mathrm{c}_{n}=\left(r_{1}, r_{2}, \ldots, r_{m}\right)$, где је $r_{i}=0$ ако је експонент уз $p_{i}$ у производу $P_{n}=a_{1} a_{2} \cdots a_{n}$ паран, а $r_{i}=1$ у супротном. Како за низ с ${ }_{n}$ има само $2^{m}$ могућности, за свако $k \leqslant 2^{2016}-2^{m}$ међу низовима с с, c $_{k+1}, \ldots, \mathrm{c}_{k+2^{m}}$ постоје два једнака, рецимо с $s$ и $c_{t}(s<t)$, а тада је $P_{t} / P_{s}$ потпун квадрат не већи од $2016^{2^{m}}$.
|
| 116 |
+
|
| 117 |
+
Претпоставимо да у низу $\left(a_{n}\right)$ нема јединица. Узмимо $k=11 \cdot 2^{m}$; свакако је $k+2^{m}<2^{2016}$. Видели смо да постоје индекси $s, t, k \leqslant s<t \leqslant k+2^{m}$, тако да је $b=P_{t} / P_{s}$ потпун квадрат. Међутим, како је $a=P_{s} \geqslant P_{k} \geqslant 2^{k}=2048^{2^{m}}>$ $2016^{2^{m}} \geqslant b$, по чињеници са почетка, $a+1=P_{s}+1$ и $a b+1=P_{t}+1$ не могу истовремено да буду квадрати, што је контрадикција.
|
| 118 |
+
|
Serbia_MO/md/sr-2017_smo_resenja.md
ADDED
|
@@ -0,0 +1,163 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 11. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 2 |
+
|
| 3 |
+
31. март 2017 .
|
| 4 |
+
|
| 5 |
+
## Први дан
|
| 6 |
+
|
| 7 |
+
1. Нека су $a, b$ и $c$ позитивни реални бројеви за које важи $a+b+c=1$. Доказати:
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
\begin{array}{r}
|
| 11 |
+
a \sqrt{2 b+1}+b \sqrt{2 c+1}+c \sqrt{2 a+1} \leqslant \sqrt{2-\left(a^{2}+b^{2}+c^{2}\right)} \\
|
| 12 |
+
\text { (Никола Петровић) }
|
| 13 |
+
\end{array}
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
2. Дат је конвексан тетиван четвороугао $A B C D$. Нека се праве $A D$ и $B C$ секу у тачки $E$. На страницама $A D$ и $B C$ су одабране тачке $M$ и $N$, редом, такве да важи $A M: M D=B N: N C$. Кружнице описане око троугла $E M N$ и четвороугла $A B C D$ секу се у тачкама $X$ и $Y$. Доказати да се праве $A B, C D$ и $X Y$ секу у једној тачки или су све паралелне.
|
| 17 |
+
|
| 18 |
+
(Дуиан Ђукић)
|
| 19 |
+
|
| 20 |
+
3. У врсти се налази $2 n-1$ сијалица. У почетку је средња ( $n$-та) упаљена, а све остале су угашене. У једном кораку је дозвољено одабрати две несуседне угашене сијалице између којих су све сијалице упаљене, и променити стање тим двема сијалицама, као и свим сијалицама између њих (на пример, од конфигурације $\cdot$ооо $\cdot$ добија се о $\cdot$ $\cdot$ ). Колико највише корака је могуће извршити?
|
| 21 |
+
|
| 22 |
+
(Душан Ђукић)
|
| 23 |
+
|
| 24 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 11. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 25 |
+
|
| 26 |
+
## 1. април 2017 .
|
| 27 |
+
|
| 28 |
+
## Други дан
|
| 29 |
+
|
| 30 |
+
4. Нека је $a$ природан број такав да за сваки природан број $n$ број $n^{2} a-1$ има бар један делилац већи од 1 који даје остатак 1 при дељењу са $n$. Доказати да је $а$ потпун квадрат.
|
| 31 |
+
|
| 32 |
+
(Душан Ђукић)
|
| 33 |
+
|
| 34 |
+
5. Одредити колико се највише краљица може поставити на таблу $2017 \times 2017$, при чему свака краљица сме да напада највише једну од преосталих.
|
| 35 |
+
|
| 36 |
+
(Бојан Башић и комисија)
|
| 37 |
+
|
| 38 |
+
6. Нека је $k$ кружница описана око $\triangle A B C$, а $k_{a}$ приписана кружница наспрам темена $A$. Две заједничке тангенте кружница $k$ и $k_{a}$ секу праву $B C$ у тачкама $P$ и $Q$. Доказати да важи $\varangle P A B=\varangle Q A C$.
|
| 39 |
+
|
| 40 |
+
(Дуиан Ђукић)
|
| 41 |
+
|
| 42 |
+
## РЕШЕЊА
|
| 43 |
+
|
| 44 |
+
1. Квадрирањем обе стране и коришћењем једнакости $1-\left(a^{2}+b^{2}+c^{2}\right)=2(a b+$ $b c+c a)$ неједнакост из задатка се своди на
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
\begin{aligned}
|
| 48 |
+
L= & 2 a^{2} b+2 b^{2} c+2 c^{2} a+ \\
|
| 49 |
+
& 2 a b \sqrt{(2 b+1)(2 c+1)}+2 b c \sqrt{(2 c+1)(2 a+1)}+2 c a \sqrt{(2 a+1)(2 b+1)} \\
|
| 50 |
+
\leqslant D= & 4(a b+b c+c a) .
|
| 51 |
+
\end{aligned}
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
По АМ-ГМ неједнакости имамо $2 a b \sqrt{(2 b+1)(2 c+1)} \leqslant a b(2 b+2 c+2)$ и аналогно $2 b c \sqrt{(2 c+1)(2 a+1)} \leqslant b c(2 c+2 a+2)$ и $2 c a \sqrt{(2 a+1)(2 b+1)} \leqslant c a(2 a+2 b+2)$, па сабирањем добијамо
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
\begin{aligned}
|
| 58 |
+
L \leqslant & 2\left(a^{2} b+b^{2} c+c^{2} a+a b^{2}+b c^{2}+c a^{2}+3 a b c\right)+2(a b+b c+c a)= \\
|
| 59 |
+
& 2(a+b+c+1)(a b+b c+c a)=4(a b+b c+c a)=D
|
| 60 |
+
\end{aligned}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
Друго решење. Функција $f(x)=\sqrt{x}$ је конкавна јер је $f^{\prime}(x)=2 / \sqrt{x}$ опадајућа функција. Применом Јенсенове неједнакости са тежинама $a, b$ и $c$ добијамо
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\begin{aligned}
|
| 67 |
+
a \sqrt{2 b+1}+b \sqrt{2 c+1}+c \sqrt{2 a+1} & \leqslant \sqrt{a(2 b+1)+b(2 c+1)+c(2 a+1)} \\
|
| 68 |
+
& =\sqrt{1+2(a b+b c+c a)}=\sqrt{2-\left(a^{2}+b^{2}+c^{2}\right)}
|
| 69 |
+
\end{aligned}
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Напомена. Ако се допусти да неки од бројева $a, b, c$ буде нула, једнакост се достиже у случајевима $a=b=c=\frac{1}{3}$ и $(a, b, c)=(1,0,0)$ са пермутацијама.
|
| 73 |
+
|
| 74 |
+
2. У случају $A B \| C D$ тврђење је тривијално: тачке $X$ и $Y$ су симетричне у односу на симетралу дужи $A B$ и $C D$ и важи $A B\|X Y\| C D$.
|
| 75 |
+
|
| 76 |
+
Нека је $A B \nVdash C D$. Тада описани кругови $k_{1}$ и $k_{2}$ троуглова $E A B$ и $E C D$ имају другу пресечну тачку $P \neq E$. Из $\varangle P A D=\varangle P B E$ и $\varangle P D A=180^{\circ}-\varangle P D E=$ $180^{\circ}-\varangle P C E=\varangle P C B$ следи да су троуглови $P A D$ и $P B C$ слични. При овој сличности тачки $M$ у $\triangle P A D$ одговара тачка $N$ у $\triangle P B C$, па је $\varangle P M E=\varangle P N E$. Закључујемо да тачке $E, P, M$ и $N$ леже на истом кругу $k_{3}$.
|
| 77 |
+
|
| 78 |
+
Како тачка $F$ има једнаку потенцију $F A$. $F B=F C \cdot F D$ у односу на кругове $k_{1}, k_{2}$
|
| 79 |
+
|
| 80 |
+
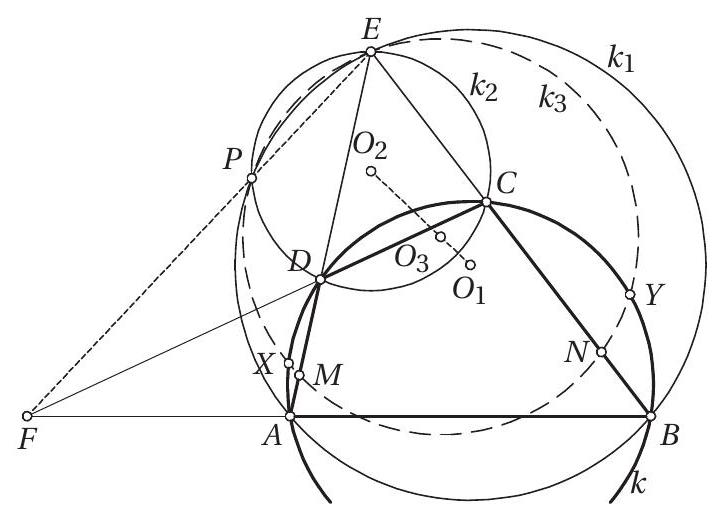
|
| 81 |
+
и круг $k$ описан око $A B C D$, она лежи на радикални оси $E P$ кругова $k_{1}$ и $k_{2}$. Сада је још $F A \cdot F B=F E \cdot F P$, па $F$ такође припада радикалној оси кругова $k_{1}$ и $k_{3}$, а то је права $X Y$.
|
| 82 |
+
|
| 83 |
+
Друго решеъе. Нека су $k, k_{1}, k_{2}$ и $k_{3}$ редом описани кругови четвороугла
|
| 84 |
+
|
| 85 |
+
|
| 86 |
+
тројки кругова ( $k, k_{1}, k_{2}$ ) и ( $k, k_{1}, k_{3}$ ) поклапају (можда у бесконачној тачки). Довољно је доказати да кругови $k_{1}, k_{2}, k_{3}$ имају заједничку радикалну осу, тј. да су њихови центри $O_{1}, O_{2}, O_{3}$ редом колинеарни.
|
| 87 |
+
|
| 88 |
+
За $i=1,2,3$, означимо са $E_{i}$ тачку симетричну тачки $E$ у односу на $O_{i}$. Доказаћемо да се тачка $E_{3}$ поклапа са тачком $E_{3}^{\prime}$ на дужи $E_{1} E_{2}$ таквом да је $E_{1} E_{3}^{\prime}: E_{3}^{\prime} E_{2}=A M: M D$. Заиста, пошто је $E_{1} A \perp A D$ и $E_{2} D \perp A D$, из Талесове теореме следи $E_{3}^{\prime} M \perp A D$; аналогно је $E_{3}^{\prime} N \perp B C$, па је $E_{3}^{\prime} \equiv E_{3}$.
|
| 89 |
+
|
| 90 |
+
3. Одговор је $\left[\frac{2^{n+1}-5}{3}\right]$.
|
| 91 |
+
|
| 92 |
+
Придружимо $i$-тој сијалици број $2^{|i-n|}$ и дефинишимо вредност конфигурације као збир бројева на упаљеним сијалицама. Вредност полазне конфигурације је 1, а при сваком кораку она се повећава за природан умножак броја 3. Корак повећава вредност за тачно 3 ако $n$-та сијалица мења стање; овакав корак зовемо добрим.
|
| 93 |
+
|
| 94 |
+
Пошто вредност не може да премаши $2^{n+1}-4$ (jep cе не могу упалити све сијалице), није могуће извршити више од $\left[\frac{2^{n+1}-5}{3}\right]$ корака. Овај број се може достићи: довољно је показати да је могуће извршити бар $\frac{2^{n+1}-7}{3}$ корака.
|
| 95 |
+
|
| 96 |
+
Доказаћемо индукцијом по $n$ да, почевши од конфигурације вредности највише 3 , можемо да низом добрих корака добијемо конфигурацију вредности бар $2^{n+1}-6$. Ово се директно проверава за $n \leqslant 2$. Нека је $n \geqslant 3$. По индуктивној претпоставци за $n-1$, могуће је доћи до конфигурације вредности бар $2^{n}-6$ са првом и последњом сијалицом угашеном. У таквој конфигурацији, осим прве и последње сијалице, могу бити угашене ( $1^{\circ}$ ) само $n$-та, $\left(2^{\circ}\right)$ само $n$-та и једна од њој суседних, или (3) само једна од две суседне. У сваком од ова три случаја, у највише три добра корака постижемо да прва и последња сијалица буду упаљене и да вредност остатка конфигурације (без ове две сијалице) буде највише 3.
|
| 97 |
+
|
| 98 |
+
|
| 99 |
+
|
| 100 |
+
$\left(1^{\circ}\right)$
|
| 101 |
+
|
| 102 |
+
|
| 103 |
+
|
| 104 |
+
$\left(2^{\circ}\right)$
|
| 105 |
+
|
| 106 |
+
|
| 107 |
+
|
| 108 |
+
$\left(3^{\circ}\right)$
|
| 109 |
+
|
| 110 |
+
Поновна примена индуктивне претпоставке за $n$ - 1 завршава индукцију.
|
| 111 |
+
|
| 112 |
+
4. Нека је $n^{2} a-1=\left(n x_{n}+1\right) d_{n}\left(x_{n}, d_{n} \in \mathbb{N}\right)$. Тада је $d_{n} \equiv-1(\bmod n)$, па је
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
n^{2} a-1=\left(n x_{n}+1\right)\left(n y_{n}-1\right) \quad \text { за неке } x_{n}, y_{n} \in \mathbb{N}
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
што се своди на $n a-n x_{n} y_{n}=y_{n}-x_{n}>-x_{n} y_{n}$. Одавде добијамо $x_{n} \leqslant x_{n} y_{n}<$ $\frac{n}{n-1} a \leqslant 2 a$. Следи да у низу $x_{1}, x_{2}, \ldots$ постоји члан који се јавља бесконачно много пута. Означимо тај члан са $X$. Тада $n X+1 \mid n^{2} a-1$ и одатле
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
n X+1 \mid X^{2}\left(n^{2} a-1\right)-a\left(n^{2} x^{2}-1\right)=a-X^{2}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
за бесконачно много бројева $n$. Ово је могуће само за $a-X^{2}=0$, тј. $X^{2}=a$.
|
| 125 |
+
|
| 126 |
+
Друго решење. Као и у првом решењу, нека је $n^{2} a-1=\left(n x_{n}+1\right)\left(n y_{n}-1\right)$, тј. $y_{n}-x_{n}=n\left(a-x_{n} y_{n}\right)=n d_{n}$. Разликујемо три случаја.
|
| 127 |
+
|
| 128 |
+
(1 ) Ако је $d_{n}>0$, онда је $a=d_{n}+x_{n}\left(x_{n}+n d_{n}\right)>n d_{n} x_{n}$, што је немогуће за $n \geqslant a$.
|
| 129 |
+
|
| 130 |
+
(2 ${ }^{\circ}$ Ако је $d_{n}<0$, онда је $a=d_{n}+y_{n}\left(y_{n}-n d_{n}\right)=y_{n}^{2}-d_{n}\left(n y_{n}-1\right)>n y_{n}-1$, што је немогуће за $n \geqslant a+1$.
|
| 131 |
+
|
| 132 |
+
$\left(3^{\circ}\right)$ Ако је $d_{n}=0$, онда је $a=x_{n}^{2}$. потпун квадрат.
|
| 133 |
+
|
| 134 |
+
5. Означимо $n=2017$. Претпоставимо да је постављено $m>n$ краљица. Ни у једној врсти нема више од две краљице, па се у бар $m-n$ врста налазе по две краљице, тако да има највише $m-2(m-n)=2 n-m$ краљица које су саме у својој врсти. Слично, највише $2 n-m$ краљица су саме у својој колони. С друге стране, свака краљица је сама у својој врсти или у својој колони, па је $m \leqslant 2(2 n-m)$, одакле је $m \leqslant\left[\frac{4 n}{3}\right]=2689$.
|
| 135 |
+
|
| 136 |
+
На слици А је приказано постављање 8 краљица на таблу $6 \times 6$ у складу са захтевом задатка. Пре конструкције примера на табли $2017 \times 2017$ размотрићемо следећи распоред краљица:
|
| 137 |
+
|
| 138 |
+
- На таблу $335 \times 335$ могуће је поставити 335 краљица које се међусобно не нападају чак ни ако се дијагонале продуже по модулу 335. Заиста, довољно је поставити краљице на сва поља $(x, y), 1 \leqslant x, y \leqslant 335$, за која је $y \equiv 2 x(\bmod 335)$, као на слици Б. Заиста, тада су сви збирови $x+y$ међусобно различити по модулу 335 , све разлике $x-y$ такође, па никоје две краљице нису у истој врсти, колони или дијагонали.
|
| 139 |
+
|
| 140 |
+
Поделимо таблу $2017 \times 2017$ на правоугаонике и квадрате страница 335, 6 и 1 , као на слици В. Квадрате обележене са Б и А попунићемо редом као на сликама Б и А, а у горње десно поље табле поставићемо још једну краљицу. Овако смо укупно поставили $8 \cdot 335+8+1=2689$ краљица. Лако се проверава да овакво постављање задовољава услове задатка.
|
| 141 |
+
|
| 142 |
+
|
| 143 |
+
Напомена. Табла $n \times n$ чије су дијагонале продужене по модулу $n$ зове се торусна табла. На торусну таблу $n \times n$ могуће је поставити $n$ краљица које се међусобно не нападају ако и само ако је $n \equiv \pm 1(\bmod 6)$. Ово је доказано у 4. задатку са СMO 2012.
|
| 144 |
+
|
| 145 |
+
6. Нека унутрашња и спољна симетрала угла $B A C$ секу праву $B C$ редом у тачкама $D$ и (можда бесконачној) $D_{1}$. Заједничке тангенте се секу у центру $T$ позитивне хомотетије $\mathscr{H}$ која слика приписани круг $\omega_{a}$ у описани круг $\Omega$. Ако је $T$ бесконачна тачка, $\mathscr{H}$ је транслација, а остатак доказа је исти.
|
| 146 |
+
|
| 147 |
+
Лема. Нека произвољна права $p$ кроз $D_{1}$ сече круг $\Omega$ у тачкама $L$ и $K$. Тангенте у $L$ и $K$ на $\Omega$ секу праву $B C$ редом у тачкама $P$ и $Q$. Тада је $\varangle P A B=\varangle C A Q$.
|
| 148 |
+
|
| 149 |
+
Доказ. Означимо $\varangle B A C=\alpha, \varangle C B A=\beta, \varangle A C B=\gamma, \varangle P A B=x$ и $\varangle C A Q=y$.
|
| 150 |
+
|
| 151 |
+
Ако је $D_{1}$ бесконачна тачка, тврђење је тривијално по симетрији. Ако није, из $\triangle P B L \sim \triangle P L C$ следи $\frac{P B}{P L}=\frac{P L}{P C}=\frac{L B}{L C}$ и одатле $\frac{P B}{P C}=\left(\frac{L B}{L C}\right)^{2}$. Слично je $\frac{Q B}{Q C}=\left(\frac{K B}{K C}\right)^{2}$. Пошто је $\frac{L B}{L C} \cdot \frac{K B}{K C}=\frac{\mid K L B]}{\mid K L C]}=\frac{D_{1} B}{D_{1} C}=\frac{A B}{A C}$, добијамо $\frac{P B}{P C} \cdot \frac{Q B}{Q C}=\left(\frac{A B}{A C}\right)^{2}$. Како је $\frac{P B}{P C}=\frac{P B}{P A} \cdot \frac{P A}{P C}=\frac{\sin x}{\sin \beta} \cdot \frac{\sin \gamma}{\sin (\alpha+x)}$ и $\frac{Q B}{Q C}=\frac{Q B}{Q A} \cdot \frac{Q A}{Q C}=\frac{\sin (\alpha+y)}{\sin \beta} \cdot \frac{\sin \gamma}{\sin y}$, множење даје $\left(\frac{\sin \gamma}{\sin \beta}\right)^{2} \cdot \frac{\sin (\alpha+y) / \sin y}{\sin (\alpha+x) / \sin x}=\left(\frac{A C}{A B}\right)^{2}=\left(\frac{\sin \gamma}{\sin \beta}\right)^{2}$, одакле је $\sin \alpha \operatorname{ctg} y+\cos \alpha=\frac{\sin (\alpha+y)}{\sin y}=$ $\frac{\sin (\alpha+x)}{\sin x}=\sin \alpha \operatorname{ctg} x+\cos \alpha$, тј. $x=y$.
|
| 152 |
+
|
| 153 |
+
Ако су $K$ и $L$ додирне тачке заједничких тангенти са $\Omega$, остаје да се покаже да тачка $D_{1}$ лежи на правој $K L$, тј. на полари тачке $T$ у односу на $\Omega$. По ставу о полу и полари, довољно је доказати да $T$ лежи на полари $d$ тачке $D_{1}$ у односу на $\Omega$.
|
| 154 |
+
|
| 155 |
+
Означимо са $N$ средиште лука $B A C$ круга $\Omega$. Слика тачке $D$ при хомотетији $\mathscr{H}$ је пресек $S$ тангенти на $\Omega$ у тачкама $A$ и $N$, па тачка $T$ лежи на правој $D S$. С друге стране, тачка $D$ је на полари $d$ јер је четворка $\left(B, C ; D_{1}, D\right)$ хармонијска, а тачка $S$ је
|
| 156 |
+
|
| 157 |
+
|
| 158 |
+
такође на $d$ јер полара тачке $S$ у односу на $\Omega$, што је права $A N$, садржи тачку $D_{1}$. Према томе, праве $D S$ и $d$ се поклапају, чиме је доказ завршен.
|
| 159 |
+
|
| 160 |
+
Друго решење. Нека заједничке тангенте додирују круг $\Omega$ у тачкама $K$ и $L$, при чему је теме $L P$ тангента ближа темену $B$. Означимо са $M$ средиште оног лука $B C$ који не садржи тачку $A$, а са $O$ и $I_{a}$ редом центре описаног и приписаног круга наспрам $A$.
|
| 161 |
+
|
| 162 |
+
Како је $\varangle L P I_{a}=90^{\circ}+\frac{1}{2} \varangle L P C$ и $\varangle L A I_{a}=\varangle L A M=\frac{1}{2} \varangle L O M=\frac{1}{2} \varangle L P D_{1}=90^{\circ}-\frac{1}{2} \varangle L P C$, следи да је $\varangle L P I_{a}+\varangle L A I_{a}=180^{\circ}$, па је четвороугао $A L P I_{a}$ тетиван. Слично, и четвороугао $A K Q I_{a}$ је тетиван. Сада имамо $\varangle P A I_{a}=\varangle P L I_{a}=\varangle Q K I_{a}=\varangle Q A I_{a}$, јер су углови $P L I_{a}$ и $Q K I_{a}$ симетрични у односу на праву $O I_{a}$, а одавде је $\varangle P A B=\varangle Q A C$.
|
| 163 |
+
|
Serbia_MO/md/sr-2018_smo_resenja.md
ADDED
|
@@ -0,0 +1,192 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 12. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 2 |
+
|
| 3 |
+
30. март 2018 .
|
| 4 |
+
|
| 5 |
+
## Први дан
|
| 6 |
+
|
| 7 |
+
1. Кружница уписана у $\triangle A B C$ има центар у тачки $I$ и додирује страницу $B C$ у тачки $D$. На дужима $B I$ и $C I$ одабране су тачке $P$ и $Q$, редом, такве да важи $\varangle B A C=2 \varangle P A Q$. Доказати: $\varangle P D Q=90^{\circ} . \quad$ (Дуиан Ђукић)
|
| 8 |
+
2. Дат је природан број $n, n>1$. Цео број $x$ зовемо красним ако је остатак броја $x^{2}$ при дељењу са $n$ непаран. Доказати да не постоји више од $1+\lfloor\sqrt{3 n}\rfloor$ узастопних красних природних бројева.
|
| 9 |
+
|
| 10 |
+
(Душан Ђукић)
|
| 11 |
+
|
| 12 |
+
3. У равни је дато $n$ правих међу којима никоје две нису паралелне и никоје три се не секу у једној тачки. Под пресечним тачкама сматрамо све тачке у којима се секу неке две од ових правих.
|
| 13 |
+
|
| 14 |
+
(a) Доказати да међу датим правим постоји једна са чије се сваке стране налази бар по
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
\left\lfloor\frac{(n-1)(n-2)}{10}\right\rfloor
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
пресечних тачака (тачке на тој правој се не рачунају).
|
| 21 |
+
|
| 22 |
+
(б) За које вредности $n$ се оцена из дела под (а) не може побољшати?
|
| 23 |
+
|
| 24 |
+
(Душан Ђукић)
|
| 25 |
+
|
| 26 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 12. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 27 |
+
|
| 28 |
+
31. март 2018 .
|
| 29 |
+
|
| 30 |
+
## Други дан
|
| 31 |
+
|
| 32 |
+
4. Доказати да постоји тачно један полином $P(x)$ с реалним коефицијентима за који је полином
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
(x+y)^{1000}-P(x)-P(y)
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
дељив полиномом $x y-x-y$.
|
| 39 |
+
|
| 40 |
+
(Душан Ђукић)
|
| 41 |
+
|
| 42 |
+
5. Нека су $a$ и $b$ непарни природни бројеви већи од 1. Посматрајмо таблу $a \times b$ којој недостају поља $(2,1),(a-2, b)$ и $(a, b)$ (под пољем $(i, j)$ подразумевамо поље у пресеку врсте $i$ и колоне $j$ ). Претпоставимо да је оваква табла поплочана помоћу $2 \times 1$ домина и $2 \times 2$ квадрата (домине се могу ротирати).
|
| 43 |
+
|
| 44 |
+
Доказати да је употребљено бар $\frac{3}{2}(a+b)-6$ домина. (Никола Петровић)
|
| 45 |
+
|
| 46 |
+
6. За задат природан број $k$, нека је $n_{k}$ најмањи природан број такав да постоји коначан скуп $A$ целих бројева са следећим особинама:
|
| 47 |
+
|
| 48 |
+
- за свако $a \in A$ постоје $x, y \in A$ (не обавезно различити) такви да
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
n_{k} \mid a-x-y
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
- не постоји подскуп $B$ скупа $A$ за који важи $|B| \leqslant k$ и $n_{k} \mid \sum_{b \in B} b$.
|
| 55 |
+
|
| 56 |
+
Доказати да за све $k, k \geqslant 3$, важи
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
n_{k}<\left(\frac{13}{8}\right)^{k+2}
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
(Бојан Bаиић)
|
| 63 |
+
|
| 64 |
+
Време за рад 270 минута.
|
| 65 |
+
|
| 66 |
+
Решења задатака детаљно образложити.
|
| 67 |
+
|
| 68 |
+
Сваки задатак вреди 7 бодова.
|
| 69 |
+
|
| 70 |
+
## РЕШЕЊА
|
| 71 |
+
|
| 72 |
+
1. Означимо са $E$ и $F$ редом подножја нормала из $P$ и $Q$ на праву $B C$, а са $M$ средиште дужи $P Q$.
|
| 73 |
+
|
| 74 |
+
Посматрајмо тачку $X$ на страници $B C$ такву да је $\varangle B A X=2 \varangle B A P$. Тада је такође $\varangle C A X=\varangle B A C-2 \varangle B A P=$ $2 \varangle C A Q$, па су $P$ и $Q$ редом центри уписаних кругова троуглова $B A X$ и $C A X$. Следи да су $X P$ и $X Q$ симетрале углова $B X A$ и $C X A$, па је $\varangle P X Q=90^{\circ}$. Услов $\varangle P D Q=90^{\circ}$ је еквивалентан са $M D=M P=M Q=$
|
| 75 |
+
|
| 76 |
+
|
| 77 |
+
$M X$, а како је $M E=M F$, довољно је доказати да је $D E=X F$. Обе дужине се једноставно рачунају на основу "великог задатка": $D E=B D-B E=$ $\frac{A B+B C-A C}{2}-\frac{A B+B X-A X}{2}=\frac{C X-A C+A X}{2}=X F$.
|
| 78 |
+
|
| 79 |
+
Друго решење. Нека права $B I$ поново сече описани круг $\triangle A P Q$ у тачки $N$. $\overline{\text { Имамо } \varangle A I N}=180^{\circ}-\varangle B I A=90^{\circ}-\frac{\gamma}{2}=\varangle D I Q$. Такође, како је $\varangle I N Q=$ $\varangle P A Q=\frac{\alpha}{2}$ и $\varangle I Q N=\varangle B I C-\varangle I N Q=\left(90^{\circ}+\frac{\alpha}{2}\right)-\frac{\alpha}{2}=90^{\circ}$, имамо $\frac{I Q}{I N}=$ $\sin \frac{\alpha}{2}=\frac{I A}{I D}$, одакле је $\frac{I A}{I N}=\frac{I D}{I Q}$. Следи да су троуглови $D I Q$ и $A I N$ слични, па је $\varangle I D Q=\varangle I A N=180^{\circ}-\varangle A I N-\varangle A N I=180^{\circ}-\left(90^{\circ}-\frac{\gamma}{2}\right)-\varangle A N P=$ $90^{\circ}+\frac{\gamma}{2}-\varangle A Q P$. Аналогно је $\varangle I D P=90^{\circ}+\frac{\beta}{2}-\varangle A P Q$, па сабирањем добијамо $\varangle P D Q=180^{\circ}+\frac{\beta+\gamma}{2}-\left(180^{\circ}-\varangle P A Q\right)=90^{\circ}$.
|
| 80 |
+
|
| 81 |
+
2. Ако је $n$ паран број, тврђење је тривијално: тада не постоје ни два узастопна красна броја, јер парни бројеви нису красни. Надаље сматрамо да је $n$ непаран.
|
| 82 |
+
|
| 83 |
+
Пошто бројеви дељиви са $n$ нису красни, можемо да се ограничимо на бројеве $x \in\{1, \ldots, n-1\}$. Претпоставимо да су бројеви $x$ и $x+1$ красни. Остаци бројева $x^{2}$ и $(x+1)^{2}$ при дељењу са $n$, који су непарни, једнаки су $x^{2}-n\left[\frac{x^{2}}{n}\right]$ и $(x+1)^{2}-n\left[\frac{(x+1)^{2}}{n}\right]$ редом, па су $\left[\frac{x^{2}}{n}\right]$ и $\left[\frac{(x+1)^{2}}{n}\right]$ различите парности. Како због $0<(x+1)^{2}-x^{2}<2 n$ важи $0 \leqslant\left[\frac{(x+1)^{2}}{n}\right]-\left[\frac{x^{2}}{n}\right] \leqslant 2$, следи да је $\left[\frac{(x+1)^{2}}{n}\right]=\left[\frac{x^{2}}{n}\right]+1$. Према томе, ако су бројеви $x, x+1, \ldots, x+k$ красни, онда је
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
m=y-\left[\frac{y^{2}}{n}\right] \quad \text { константно за све } \quad y=x, x+1, \ldots, x+k
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Како је једнакост $y-\left[\frac{y^{2}}{n}\right]=m$ еквивалентна са $y-m \leqslant \frac{y^{2}}{n}<y-m+1$, тј. са $n\left(\frac{n}{4}-m\right) \leqslant\left(y-\frac{n}{2}\right)^{2}<n\left(\frac{n}{4}-m+1\right)$, број узастопних бројева $y$ са овим својством није већи од $\left[\sqrt{n\left(\frac{n}{4}-m+1\right)}-\sqrt{n\left(\frac{n}{4}-m\right)}\right]+1 \leqslant[\sqrt{n}]+1$ ако је $m \leqslant\left[\frac{n}{4}\right]$, и није већи од $2\left[\sqrt{n\left\{\frac{n}{4}\right\}}+\frac{1}{2}\right] \leqslant[\sqrt{3 n}]+1$ за $m=\left[\frac{n}{4}\right]+1$.
|
| 90 |
+
|
| 91 |
+
Напомена. Једнакост се може достићи ако и само ако је $n \equiv 3(\bmod 8), 3 n$ није квадрат и $[\sqrt{3 n}]$ је непарно.
|
| 92 |
+
|
| 93 |
+
3. За сваку од датих правих, пресечних тачака ван ње има
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
m=\frac{(n-1)(n-2)}{2}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
Претпоставимо да, за сваку праву, с једне њене стране има не више од $k$ пресечних тачака, где је $k \leqslant \frac{n}{2}$. Пребројмо на два начина тројке $(p, A, B)$, где су $A$ и $B$ пресечне тачке са различитих страна праве $p$. По претпоставци, за сваку праву $p$ има не више од $k(m-k)$ оваквих тројки, па је њихов укупан број $N \leqslant n k(m-k)$.
|
| 100 |
+
|
| 101 |
+
Размотримо сада два типа оваквих тројки: mun 1 , када су тачке $A$ и $B$ на истој од датих правих, и mun 2 , када нису.
|
| 102 |
+
|
| 103 |
+
Свака четворка датих правих, заједно са њима одређеним пресечним тачкама, одређује тачно 4 тројке типа 1 , а свака тројка је одређена тачно једном четворком правих. Следи да има $4\binom{n}{4}$ тројки типа 1. Такође, свака петорка датих правих са њима одређеним пресечним тачкама одређује бар 5 тројки типа 2 , те тројки типа 2 има бар $5\binom{n}{5}$. Ово се директно проверава: постоји шест различитих распореда по пет правих у општем положају, као на слици.
|
| 104 |
+
|
| 105 |
+
|
| 106 |
+
Према томе, $N \geqslant 4\binom{n}{4}+5\binom{n}{5}=n\binom{n}{4}$.
|
| 107 |
+
|
| 108 |
+
Следи да је $k(m-k) \geqslant\binom{ n}{4}=\frac{m(m-1)}{6}$. Одавде се добија
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
k \geqslant k_{0}=\frac{1}{2}\left(m-\sqrt{\frac{m^{2}+2 m}{3}}\right)
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Како се неједнакост $k_{0}>\frac{m}{5}=\frac{(n-1)(n-2)}{10}$ своди на $m>25$, што важи за $n \geqslant 9$, док за $n=8$ имамо $k_{0}>\left[\frac{m}{5}\right]=4$, остаје да испитамо случајеве $n \leqslant 7$.
|
| 115 |
+
|
| 116 |
+
За $n \leqslant 4$ је тврђење тривијално, као и достизање једнакости, јер је тада $k_{0}=\left[\frac{m}{5}\right]=0$. За $n=5,6,7$ је редом $\left\lceil k_{0}\right\rceil=\left[\frac{m}{5}\right]=1,2,3$, па тврђење задатка и тада важи, а достижу се и једнакости у случајевима на слици.
|
| 117 |
+
|
| 118 |
+
|
| 119 |
+
Напомена. С друге стране, свака петорка одређује највише 7 тројки $(p, A, B)$ типа 2. Овако се може показати да увек постоји права са чије се једне стране налази мање од $\left(\frac{1}{2}-\frac{1}{2 \sqrt{15}}\right) m$ тачака.
|
| 120 |
+
|
| 121 |
+
4. Означимо $n=1000$. Сменом $x=u+1$ и $y=v+1$ добијамо да полином $u v-1$ дели полином $P(u+1)+P(v+1)-(u+v+2)^{n}$. Еквивалентан услов је да је $P(u+1)+P(v+1)-(u+v+2)^{n}=0$ кад год је $u v-1=0$ (видети напомену). Тако за $u \neq 0$ и $v=\frac{1}{u}$ имамо $P(u+1)+P\left(\frac{1}{u}+1\right)=\left(u+\frac{1}{u}+2\right)^{n}=\frac{(u+1)^{2 n}}{u^{n}}$. Полином $Q(x)=P(x+1)=\sum_{i=0}^{n} a_{i} x^{i}$ задовољава
|
| 122 |
+
|
| 123 |
+
$2 a_{0}+\sum_{i=1}^{n} a_{i}\left(u^{i}+u^{-i}\right)=Q(u)+Q\left(\frac{1}{u}\right)=\frac{(u+1)^{2 n}}{u^{n}}=\binom{2 n}{n}+\sum_{i=1}^{n}\binom{2 n}{n-i}\left(u^{i}+u^{-i}\right)$, одакле одмах следи да је $a_{0}=\frac{1}{2}\binom{2 n}{n}$ и $a_{i}=\binom{2 n}{n-i}$ за $1 \leqslant i \leqslant n$. Дакле,
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
P(x)=\frac{1}{2}\binom{2 n}{n}+\sum_{i=1}^{n}\binom{2 n}{n-i}(x-1)^{i}
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
Друго решење. Тражимо полиноме $P(x)=\sum_{i=0}^{n} p_{i} x^{i}$ и $Q(x, y)=\sum_{i, j} a_{i, j} x^{i} y^{j}$ такве да је
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
A(x, y)=(x y-x-y) Q(x, y)=(x+y)^{1000}-P(x)-P(y)
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
Приметимо да је $\operatorname{deg} Q \leqslant 998$. Заиста, ако је $a_{i, j} x^{i} y^{j}$ моном највећег степена у $Q(x, y)$, онда је коефицијент уз $x^{i+1} y^{j+1}$ у $A(x, y)$ једнак $a_{i, j} \neq 0$, па је $i+j+2 \leqslant 1000$. Следи да је $\operatorname{deg} A \leqslant 1000$, па је и $\operatorname{deg} P \leqslant 1000$.
|
| 136 |
+
|
| 137 |
+
Изједначавање коефицијената уз $x^{i} y^{j}$ у (*) даје једнакости $a_{i-1, j-1}=\binom{1000}{i}$ за $i+j=998(i, j>0), a_{i-1, j-1}=a_{i-1, j}+a_{i, j-1}$ за $i+j<998(i, j>0)$ и $a_{i-1,0}=$ $a_{0, i-1}=p_{i}$, одакле једноставном индукцијом налазимо $a_{i-1, j-1}=\binom{2000-i-j}{1000-i}$ за $i+j \leqslant 1000(i, j>0)$ и $p_{i}=\binom{1999-i}{999}$, тј.
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
P(x)=x^{1000}+\binom{1000}{999} x^{999}+\binom{1001}{999} x^{998}+\cdots+\binom{1998}{999} x
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
Из конструкције следи да овај полином задовољава услове задатка.
|
| 144 |
+
|
| 145 |
+
Tреће решење. Не постоје два различита полинома са жељеним својством. Заиста, ако $P_{1}(x) \not \equiv P_{2}(x)$ имају то својство, онда $x y-x-y$ дели разлику $P_{1}(x)+P_{1}(y)-P_{2}(x)-P_{2}(y)=(x y-x-y) U(x, y)$. Међутим, ако је $c x^{i} y^{j}$ моном највећег степена у $U(x, y)$, онда је коефицијент уз $x^{i+1} y^{j+1}$ на левој страни ове једнакости једнак $c \neq 0$, што је немогуће.
|
| 146 |
+
|
| 147 |
+
Докажимо сада да за сваки симетричан полином $Q(x, y)$ постоји полином $P(t)$ такав да $x y-x-y \mid Q(x, y)-P(x)-P(y)$. Довољно је доказати да за полиноме $Q$ облика $x^{i} y^{j}+x^{j} y^{i}(0 \leqslant i \leqslant j)$ постоји тражени полином $P_{i, j}(t)$. Тврђење је тривијално за $i=0$. За $i>0$ доказ спроводимо индукцијом по $i+j$. Наиме, $x^{i} y^{j}+x^{j} y^{i} \equiv(x+y)\left(x^{i-1} y^{j-1}+x^{j-1} y^{i-1}\right)=\left(x^{i} y^{j-1}+x^{j-1} y^{i}\right)+$ $\left(x^{i-1} y^{j}+x^{j} y^{i-1}\right)(\bmod x y-x-y)$, па можемо узети $P_{i, j}(t)=P_{i, j-1}(t)+P_{i-1, j}(t)$.
|
| 148 |
+
|
| 149 |
+
Напомена. Ако је $P(x, y)$ нерастављив полином и $Q(x, y)$ полином такав да је $\overline{Q(x, y)=0}$ кад год је $P(x, y)=0$, онда је полином $Q$ дељив полиномом $P$. Ово није потпуно тривијално. У прстену полинома $\mathbb{R}[y][x]$ Еуклидовим алгоритмом могу се наћи полиноми $A(x, y), B(x, y)$ и $C(y)$ такви да је $\operatorname{deg}_{x} B<\operatorname{deg}_{x} P$ и $A \cdot P-B \cdot Q=C(y)$. Дакле, кад год је $Q(x, y)=0$, важи $C(y)=0$, па $C$ има
|
| 150 |
+
бесконачно много нула, одакле је $C \equiv 0$ и $P \mid B \cdot Q$. Због нерастављивости полинома $P$ и јединствености факторизације у прстену $\mathbb{R}[y][x]$ следи $P \mid Q$.
|
| 151 |
+
|
| 152 |
+
5. Упишимо у поље $(i, j)$ број $(-1)^{i+j}(i+j)$. Збир уписаних бројева у читавој таблици је $\sum_{i=1}^{a}(-1)^{i} \sum_{j=1}^{b}(-1)^{j}(i+j)=\sum_{i=1}^{a}(-1)^{i+1}\left(i+\frac{b+1}{2}\right)=\frac{a+b+2}{2}$, а ако се три наведена поља избаце, збир у остатку таблице је
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
\frac{a+b+2}{2}-(-3)-(a+b-2)-(a+b)=-\frac{3}{2}(a+b)+6
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
Како је збир бројева у сваком квадрату $2 \times 2$ једнак нули, а збир у свакој домини је 1 или -1 , потребно је бар $\frac{3}{2}(a+b)-6$ домина.
|
| 159 |
+
|
| 160 |
+
Друго решеъе. Нека су врсте и колоне нумерисане одоздо нагоре и слева надесно. Можемо да сматрамо да се у поплочавању не појављује ниједна од целина означених са $L$ на слици - заиста, оне се могу заменити одговарајућим целинама означеним са $D$, притом не повећавајући број домина.
|
| 161 |
+
|
| 162 |
+
Размотримо фигуру која покрива поље $(a, 1)$. Ако је то нпр. хоризонтална домина $(a, 1)-(a, 2)$ (аналогно се испитује случај вертикалне домине), онда поље $(a-1,1)$ не може бити покривено ни квадратом ни хоризонталном домином (јер би они са горњом домином градили једну од целина $L$ ), па оно мора бити покривено вертикалном домином $(a-1,1)-(a-2,1)$. Слично, сада поље $(a-1,2)$ мора би-
|
| 163 |
+
|
| 164 |
+
ти покривено домином $(a-1,2)-(a-1,3)$, итд. до бесконачности, што је немогуће. Према томе, фигура која покрива поље $(a, 1)$ је квадрат.
|
| 165 |
+
|
| 166 |
+
На сличан начин, поља $(a, 3)$ и ( $a-2,1$ ) су такође покривена квадратима, затим поља $(a, 5),(a-2,3)$ и ( $a-4,1)$, итд. Настављајући овај поступак, закључујемо да су сва поља осим оних у врстама $1,2,3$ и оних у колонама $b-2, b-1, b$ покривена квадратима. Преостала поља се могу поплочати на једниствен начин, приказан на слици, што се директно проверава. При томе је употребљено тачно $\frac{3}{2}(a+b)-6$ домина.
|
| 167 |
+
|
| 168 |
+
Tреће решење. Обојићемо поља табле црно и бело попут шаховске табле. Праву која раздваја $i$-ту и $(i+1)$-ву врсту/колону зовемо $i$-том хоризонталом/вертикалом.
|
| 169 |
+
|
| 170 |
+
Ако је $j$ парно ( $2 \leqslant j \leqslant b-1$ ), бар једна (хоризонтална) домина сече $j$-ту вертикалу јер је број поља у првих $j$ колона непаран. С друге стране, ако је $j$ непарно $(1 \leqslant j \leqslant b-2$ ), бар две домине морају сећи $j$-ту вертикалу јер у првих $j$ колона има за два више црних поља него белих. Овако добијамо бар $\frac{3 b-3}{2}$ хоризонталних домина.
|
| 171 |
+
|
| 172 |
+
Слично, ако је $i$ парно ( $2 \leqslant i \leqslant a-3)$ или $i \in\{1, a-2\}$, бар једна (вертикална) домина сече $i$-ту хоризонталу јер је број поља у првих $i$ врста непаран. С друге стране, ако је $i$ непарно ( $3 \leqslant i \leqslant a-4$ ), број црних поља у п��вих $i$
|
| 173 |
+
врста је за два већи од броја белих, па бар две домине морају сећи $i$-ту хоризонталу. Овако добијамо бар $\frac{3 a-9}{2}$ вертикалних домина.
|
| 174 |
+
|
| 175 |
+
Дакле, укупно има бар $\frac{3 a-9}{2}+\frac{3 b-3}{2}=\frac{3}{2}(a+b)-6$ домина.
|
| 176 |
+
|
| 177 |
+
6. Са $F_{i}$ означавамо Фибоначијеве бројеве: $F_{1}=F_{2}=1, F_{i+1}=F_{i}+F_{i-1}$. Посматрајмо скуп $A=\left\{a_{1}, a_{2}, \ldots, a_{k+1}\right\}$ са $n=F_{k+2}+3$, где су
|
| 178 |
+
|
| 179 |
+
$$
|
| 180 |
+
a_{i}=(-1)^{k-1-i} F_{i+1} \text { за } i=1,2, \ldots, k-1, \quad a_{k}=F_{k}+1 \quad \text { и } \quad a_{k+1}=F_{k}+2
|
| 181 |
+
$$
|
| 182 |
+
|
| 183 |
+
У случају парног $k$ видимо да је $a_{i}=a_{i+1}+a_{i+2}(1 \leqslant i \leqslant k-3), a_{k-2} \equiv a_{k}+a_{k+1}$ $(\bmod n), a_{k-1}=a_{k+1}+a_{2}, a_{k}=a_{k-1}+a_{1}$ и $a_{k+1}=a_{k}+a_{1}$, па скуп $A$ задовољава први услов задатка. Овај услов се слично проверава и за непарно $k$.
|
| 184 |
+
|
| 185 |
+
Докажимо индукцијом по $k$ (база $k=3$ се директно проверава) да је задовољен и други услов, тј. да не постоји подскуп $B \subsetneq A$ такав да $n \mid \sum_{b \in B} b$. Како је збир елемената скупа $A$ једнак нули, можемо да сматрамо без смањења општости (заменом $B$ са $A \backslash B$ по потреби) да $B$ садржи највише један од елемената $F_{k}, F_{k}+1, F_{k}+2$. Тада је
|
| 186 |
+
|
| 187 |
+
$1-F_{k}=-\left(F_{k-1}+F_{k-3}+\cdots\right) \leqslant \sum_{b \in B} b \leqslant\left(F_{k}+2\right)+F_{k-2}+F_{k-4}+\cdots=F_{k+1}+1$,
|
| 188 |
+
|
| 189 |
+
па мора бити $\sum_{b \in B} b=0$. На основу индуктивне претпоставке за $k-1$, скуп $B$ не може бити подскуп скупа $\left\{a_{1}, a_{2}, \ldots, a_{k-2}\right\}$, тј. мора бити $a_{k-1}=F_{k} \in B$. Међутим, тада је $\sum_{b \in B} b \geqslant F_{k}-F_{k-1}-F_{k-3}-\cdots=1$, што је контрадикција. Доказ је завршен.
|
| 190 |
+
|
| 191 |
+
Према томе, $n_{k} \leqslant F_{k+2}+3<\phi^{k-3}\left(F_{5}+3\right)<\phi^{k+2}<\left(\frac{13}{8}\right)^{k+2}$, где је $\phi=\frac{1+\sqrt{5}}{2}$.
|
| 192 |
+
|
Serbia_MO/md/sr-2019_smo_resenja.md
ADDED
|
@@ -0,0 +1,262 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 13. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 2 |
+
|
| 3 |
+
## 5. април 2019 .
|
| 4 |
+
|
| 5 |
+
## Први дан
|
| 6 |
+
|
| 7 |
+
1. Одредити све природне бројеве $n(n>1)$ који имају следеће својство: ако су $a_{1}, a_{2}, a_{3}, \ldots, a_{k}$ сви природни бројеви мањи од $n$ и узајамно прости са $n$ и важи поредак $a_{1}<a_{2}<a_{3}<\cdots<a_{k}$, онда ниједан од збирова $a_{i}+a_{i+1}$ за $i=1,2, \ldots, k-1$ није дељив са 3.
|
| 8 |
+
|
| 9 |
+
(Душан Ђукић)
|
| 10 |
+
|
| 11 |
+
2. За низ ненегативних реалних бројева $a_{1}, a_{2}, \ldots, a_{k}$ кажемо да је уложсив у интервал $[b, c]$ ако постоје бројеви $x_{0}, x_{1}, \ldots, x_{k}$ из интервала $[b, c]$ такви да важи $\left|x_{i}-x_{i-1}\right|=a_{i}$ за $i=1,2, \ldots, k$. Низ је нормиран ако су сви његови чланови не већи од 1. За задат природан број $n$, доказати:
|
| 12 |
+
|
| 13 |
+
(a) сваки нормиран низ дужине $2 n+1$ је уложив у интервал $\left[0,2-\frac{1}{2^{n}}\right]$;
|
| 14 |
+
|
| 15 |
+
(б) постоји нормиран низ дужине $4 n+3$ који није уложив у $\left[0,2-\frac{1}{2^{n}}\right]$.
|
| 16 |
+
|
| 17 |
+
(Душан Ђукић)
|
| 18 |
+
|
| 19 |
+
3. Конвексан четвороугао $A B C D$ је описан око кружнице $k$. Праве $A D$ и $B C$ се секу у тачки $P$, а кружнице описане око $\triangle P A B$ и $\triangle P C D$ се секу у тачки $X$. Доказати да тангенте из тачке $X$ на кружницу $k$ граде једнаке углове са правима $A X$ и $C X$.
|
| 20 |
+
|
| 21 |
+
(Дуиан Ђукић)
|
| 22 |
+
|
| 23 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 13. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 24 |
+
|
| 25 |
+
6. април 2019 .
|
| 26 |
+
|
| 27 |
+
## Други дан
|
| 28 |
+
|
| 29 |
+
4. Дат је $\triangle A B C$. Нека је $A_{1}$ централносиметрична слика пресечне тачке симетрале $\measuredangle B A C$ и странице $B C$, где је центар симетрије средина странице $B C$. Аналогно дефинишемо тачке $B_{1}$ (на страници $C A$ ) и $C_{1}$ (на страници $A B)$. Пресек кружнице описане око $\triangle A_{1} B_{1} C_{1}$ с правом $A B$ је скуп $\left\{Z, C_{1}\right\}$, с правом $B C$ је скуп $\left\{X, A_{1}\right\}$, а с правом $C A$ је скуп $\left\{Y, B_{1}\right\}$. Ако се нормале из тачака $X, Y$ и $Z$ на $B C, C A$ и $A B$, редом, секу у једној тачки, доказати да је $\triangle A B C$ једнакокрак.
|
| 30 |
+
|
| 31 |
+
(Милош Милосављевић)
|
| 32 |
+
|
| 33 |
+
5. На планети $X$ облика лопте се налази $2 n$ бензинских пумпи. Притом је свака пумпа упарена с по једном другом пумпом и сваке две упарене пумпе се налазе на дијаметрално супротним тачкама планете. На свакој пумпи се налази одређена количина бензина. Познато је следеће: уколико аутомобил с претходно празним (довољно великим) резервоаром крене с ма које пумпе, увек може стићи до пумпе с њом упарене (уз могуће допуњавање бензина на другим пумпама током пута). Одредити све природне бројеве $n$ такве да, за ма какав распоред $2 n$ пумпи који испуњава наведени услов, увек постоји пумпа од које аутомобил може кренути с претходно празним резервоаром и обићи све остале пумпе на планети. (Сматрати да аутомобил троши константну количину бензина по јединици дужине.) (Никола Петровић)
|
| 34 |
+
6. Низови $\left(a_{n}\right)_{n=0}^{\infty}$ и $\left(b_{n}\right)_{n=0}^{\infty}$ дефинисани су рекурентним релацијама
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
a_{0}=0, \quad a_{1}=1, \quad a_{n+1}=\frac{2018}{n} a_{n}+a_{n-1} \quad \text { за } n \geqslant 1
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
и
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
b_{0}=0, \quad b_{1}=1, \quad b_{n+1}=\frac{2020}{n} b_{n}+b_{n-1} \quad \text { � } n \geqslant 1
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Доказати:
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
\frac{a_{1010}}{1010}=\frac{b_{1009}}{1009}
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
(Душан Ђукић)
|
| 53 |
+
|
| 54 |
+
Време за рад 270 минута.
|
| 55 |
+
|
| 56 |
+
Решења задатака детаљно образложити.
|
| 57 |
+
|
| 58 |
+
Сваки задатак вреди 7 бодова.
|
| 59 |
+
|
| 60 |
+
## РЕШЕЊА
|
| 61 |
+
|
| 62 |
+
1. За $n \leqslant 28$ услов задатка је задовољен само за $n \in\{2,4,10\}$. Нека је $n>28$. Приметимо да је низ $a_{i}$ симетричан у односу на $\frac{n}{2}$. Дакле, $a_{i}+a_{k+1-i}=n$. Ако $2 \nmid n$, онда је $a_{1}=1, a_{2}=2$ и $3 \mid a_{1}+a_{2}$. С друге стране, ако $3 \mid n$, одаберимо $i$ тако да је $a_{i}<\frac{n}{2}<a_{i+1}$ : тада $3 \mid a_{i}+a_{i+1}=n$. Надаље $2 \mid n$ и $3 \nmid n$, тако да је $a_{2}=3$. Одавде имамо и $a_{k-1}=n-3$ и $a_{k}=n-1$.
|
| 63 |
+
|
| 64 |
+
Ако је $n \equiv 2(\bmod 3)$, онда $3 \mid a_{k-1}+a_{k}=2 n-4$. Остаје само случај $n \equiv 1$ $(\bmod 3)$.
|
| 65 |
+
|
| 66 |
+
Даље, ако је $a_{i}+a_{i+1} \equiv 2(\bmod 3)$, онда је $a_{k-i}+a_{k+1-i}=2 n-\left(a_{i}+a_{i+1}\right) \equiv$ $0(\bmod 3)$. Зато можемо да сматрамо да је $a_{i}+a_{i+1} \equiv 1(\bmod 3)$ за $i=$ $1,2, \ldots, k-1$. Индукцијом налазимо
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
a_{1} \equiv a_{3} \equiv \cdots \equiv 1 \quad \text { и } \quad a_{2} \equiv a_{4} \equiv \cdots \equiv 0 \quad(\bmod 3)
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Како је $(n, 9)=1$, следи $a_{4}=9$, а због $a_{3} \equiv 1(\bmod 3)$ имамо и $a_{3}=7$. Одавде добијамо $(n, 7)=1$ и $(n, 5) \neq 1$, тј. $5 \mid n$.
|
| 73 |
+
|
| 74 |
+
Сада имамо $(n, 21)=(n, 27)=1$, али бројеви $22,24,25$ и 26 нису узајамно прости са $n$, а на основу $(*)$ ни број 23 се не може појавити у низу $a_{1}, \ldots, a_{k}$. Дакле, 21 и 27 су суседни у низу $a_{1}, \ldots, a_{k}$, али $3 \mid 21+27$, контрадикција.
|
| 75 |
+
|
| 76 |
+
Према томе, једина решења су 2,4 и 10 .
|
| 77 |
+
|
| 78 |
+
2. (a) Довољно је доказати да је сваки нормиран низ $a_{1}, a_{2}, \ldots, a_{2 n+1}$ уложив у неки интервал дужине $2-\frac{1}{2^{n}}$. Тврђење доказујемо индукцијом по $n$. Оно је тачно за $n=0$; нека је $n \geqslant 1$. По индуктивној претпоставци постоји низ $x_{0}, x_{1}, \ldots, x_{2 n-1} \in\left[0,2-\frac{1}{2^{n-1}}\right]$ такав да је $\left|x_{i}-x_{i-1}\right|=a_{i}$ за $i=1, \ldots, 2 n-1$. Не умањујући општост, сматраћемо да је $x_{2 n-1} \leqslant 1-\frac{1}{2^{n}}$.
|
| 79 |
+
|
| 80 |
+
(10) Ако је $a_{2 n} \geqslant \frac{1}{2^{n}}$, можемо узети $x_{2 n}=x_{2 n-1}+a_{2 n} \in\left[1,2-\frac{1}{2^{n}}\right]$ и $x_{2 n+1}=$ $x_{2 n}-a_{2 n+1} \in\left[0,2-\frac{1}{2^{n}}\right]$, чиме је низ уложен у интервал $\left[0,2-\frac{1}{2^{n}}\right]$.
|
| 81 |
+
|
| 82 |
+
$\left(2^{\circ}\right)$ Ако је $a_{2 n}<\frac{1}{2^{n}}$, узећемо $x_{2 n}=x_{2 n-1}-a_{2 n} \in\left[-\frac{1}{2^{n}}, 1-\frac{1}{2^{n}}\right]$ и $x_{2 n+1}=x_{2 n}+$ $a_{2 n+1}$, чиме је низ уложен у један од интервала $\left[0,2-\frac{1}{2^{n}}\right]$ и $\left[-\frac{1}{2^{n}}, 2-\frac{1}{2^{n-1}}\right]$.
|
| 83 |
+
|
| 84 |
+
(б) Означимо $N=3 \cdot 2^{n-1}-1$. Доказаћемо да се низ дужине $4 n-1$
|
| 85 |
+
|
| 86 |
+
$1,1-\frac{1}{N}, 1,1-\frac{2}{N}, 1,1-\frac{2^{2}}{N}, \ldots, 1,1-\frac{2^{n-1}}{N}, 1,1-\frac{2^{n-2}}{N}, 1, \ldots, 1-\frac{2}{N}, 1,1-\frac{1}{N}, 1$ не може уложити у интервал $\left(-1+\frac{1}{2 N}, 1-\frac{1}{2 N}\right)$, одакле следи твр ење.
|
| 87 |
+
|
| 88 |
+
Претпоставимо супротно. Једноставном индукцијом се доказује да је:
|
| 89 |
+
|
| 90 |
+
(i) $\left|x_{2 i}\right|<1-\frac{2^{i+1}-1}{2 N}$ и $\left|x_{2 i+1}\right|>\frac{2^{i+1}-1}{2 N}$ за $i=0, \ldots, n$;
|
| 91 |
+
|
| 92 |
+
(ii) $\left|x_{2 i}\right|<\frac{2^{2 n+2-i}-1}{2 N}$ и $\left|x_{2 i+1}\right|>1-\frac{2^{2 n+2-i}-1}{2 N}$ за $i=n+1, \ldots, 2 n+1$.
|
| 93 |
+
|
| 94 |
+
Тако за $x_{4 n+3}$ добијамо контрадикцију.
|
| 95 |
+
|
| 96 |
+
3. Пошто је $\varangle X A D=\varangle X B C$ и $\varangle X D P=\varangle X C P$, важи $\triangle X A D \sim \triangle X B C$.
|
| 97 |
+
|
| 98 |
+
Нека симетрала $s_{X}$ угла $A X C$ сече кругове $P A B$ и $P C D$ у тачкама $K$ и $R$, а симетрала $s_{P}$ угла $A P C$ сече кругове $P A B$ и $P C D$ у тачкама $L$ и $S$. Права $s_{P}$ пролази кроз центар $I$ круга $k$ и важи $L A=L B=L I$ и $S C=S D=S I$.
|
| 99 |
+
|
| 100 |
+
Како је $\varangle I L K=\varangle P X K=\varangle P X R=\varangle I S R$, важи $K L \| R S$. Даље, имамо $\varangle R X S=\varangle R X C-\varangle S P C=\frac{1}{2}(\varangle A X C-\varangle A P C)=\frac{1}{2} \varangle B X C$ и, слично, $\varangle L X K=$ $\frac{1}{2} \varangle B X C$. Следи да тетивама $K L$ и $R S$ у круговима $P A B$ и $P C D$, као и тетивама $L B$ и $S D$, одговарају једнаки периферијски углови, па је $\frac{K L}{R S}=\frac{L B}{S D}=\frac{L I}{S I}$. Следи да је $\triangle I K L \sim \triangle I R S$, па тачка $I$ лежи на правој $K R$, што је симетрала угла $A X C$. Тврђење задатка одмах следи.
|
| 101 |
+
|
| 102 |
+
Друго решење. Означимо са $U$ и $V$ редом пресеке симетрала углова $A X D$ и $B X C$ са $A D$ и $B C$. Као и у првом решењу, $\triangle X A D \sim$ $\triangle X B C$, одакле је $\varangle X U P=\varangle X V P$, па тачке $X, P, U$ и $V$ леже на истом кругу $\gamma$. Дока-
|
| 103 |
+
|
| 104 |
+
|
| 105 |
+
заћемо да је и тачка $I$ на овом кругу и да је $I U=I V$. Следиће да $I$ припада симетрали угла $U X V$, што је уједно и симетрала угла $A X C$.
|
| 106 |
+
|
| 107 |
+
Нека су $M$ и $N$ редом тачке додира круга $k$ са страницама $A D$ и $B C$. Означимо $A M=a, B N=b, C N=c$ и $D M=d$. Тада је $A B=a+b, C D=c+d$ и $A U: U D=(a+b):(c+d)$, одакле налазимо $A U=\frac{a+b}{a+b+c+d} \cdot A D=\frac{(a+b)(a+d)}{a+b+c+d}$; слично имамо $B V=\frac{(b+a)(b+c)}{a+b+c+d}$. Следи да је $A M-A U=B V-B N=\frac{a c-b d}{a+b+c+d}$, па је $M U=N V$ и троуглови $I M U$ и $I N V$ су подударни и исто оријентисани. Према томе, $I U=I V$ и $\varangle U I V=\varangle M I N=180^{\circ}-\varangle V P U$, тј. $I$ је средиште лука $U V$ круга $P X U V$.
|
| 108 |
+
|
| 109 |
+
Tреће решеъе. Познато је следеће тврђење из пројективне геометрије.
|
| 110 |
+
|
| 111 |
+
- Дезаргова теорема о инволуиији. Коника $\gamma$ је описана око четвороугла $\overline{A B C D}$. Права $\ell$ сече $A B, C D, B C, D A, A C, B D$ редом у тачкама $X_{1}$, $X_{2}, Y_{1}, Y_{2}, Z_{1}, Z_{2}$, и сече конику $\gamma$ у $W_{1}$ и $W_{2}$. Тада постоји инволуција на правој $\ell$ која слика $X_{1} \leftrightarrow X_{2}, Y_{1} \leftrightarrow Y_{2}, Z_{1} \leftrightarrow Z_{2}$ и $W_{1} \leftrightarrow W_{2}$.
|
| 112 |
+
|
| 113 |
+
Дуално тврђење (добијено поларним пресликавањем у односу на $\gamma$ ) гласи овако:
|
| 114 |
+
|
| 115 |
+
- Коника $\gamma$ је уписана у четвороугао $A B C D$ у коме је $A D \cap B C=\{P\}$ и $A B \cap C D=\{Q\}$. Праве $X U$ и $X V$ су тангенте из произвољне тачке $X$ на $\gamma$. Тада постоји инволуција на прамену правих кроз $X$ која слика $X A \leftrightarrow X C, X B \leftrightarrow X D, X P \leftrightarrow X Q$ и $X U \leftrightarrow X V$.
|
| 116 |
+
|
| 117 |
+
У нашем случају углови $A X C, B X D$ и $P X Q$ имају заједничку симетралу $s$, па је поменута инволуција управо осна симетрија у односу на $s$. Следи да су две тангенте из $X$ на круг (конику) $k$ симетричне у односу на $s$.
|
| 118 |
+
|
| 119 |
+
4. Подсетимо се да тачке $P$ и $Q$ унутар $\triangle A B C$ зовемо изогонално спрегнутим ако је $\varangle P A B=\varangle Q A C$ и $\varangle P B C=\varangle Q B A$. Тада такође важи $\varangle P C A=\varangle Q C B$.
|
| 120 |
+
|
| 121 |
+
Лема. Подножја нормала из тачака $P$ и $Q$ на праве $B C, C A$ и $A B$ леже на истом кругу.
|
| 122 |
+
|
| 123 |
+
Доказ. Нека су $P_{a}$ и $Q_{a}$ редом подножја нормала из $P$ и $Q$ на $B C$; аналогно означавамо $P_{b}, Q_{b}, P_{c}, Q_{c}$. Из $\varangle A P_{b} P_{c}=\varangle A P P_{c}=\varangle A Q Q_{b}=\varangle A Q_{c} Q_{b}$ следи $\triangle A P_{b} P_{c} \sim \triangle A Q_{c} Q_{b}$, па су тачке $P_{b}, P_{c}, Q_{b}, Q_{c}$ на истом кругу $k$, а његов центар је пресек симетрала дужи $P_{b} Q_{b}$ и $P_{c} Q_{c}$, што је управо средиште $U$ дужи $P Q$. Аналогно, и тачке $P_{c}, P_{a}, Q_{c}, Q_{a}$ су једнако удаљене од тачке $U$, па и $P_{a}$ и $Q_{a}$ леже на кругу $k$.
|
| 124 |
+
|
| 125 |
+
Претпоставимо да се нормале из $X, Y$ и $Z$ редом на $B C, C A$ и $A B$ секу у тачки $P$. Ако је тачка $Q$ изогонално спрегнута тачки $P$ у $\triangle A B C$, подножја нормала из $Q$ на $B C, C A$ и $A B$ су по Леми управо тачке $A_{1}, B_{1}$ и $C_{1}$.
|
| 126 |
+
|
| 127 |
+
Означимо са $A_{0}, B_{0}$ и $C_{0}$ редом пресеке унутрашњих симетрала углова код $A, B$ и $C$ с наспрамним страницама. Уобичајено, $B C=a, C A=b$ и $A B=c$. Из односа $B A_{0}$ : $A_{0} C=c: b$ налазимо $B A_{1}=A_{0} C=\frac{a b}{b+c}$ и, слично, $A_{1} C=\frac{a c}{b+c}, C B_{1}=\frac{b c}{c+a}, B_{1} A=\frac{b a}{c+a}$, $A C_{1}=\frac{c a}{a+b}$ и $C_{1} B=\frac{c b}{a+b}$. Сада имамо
|
| 128 |
+
|
| 129 |
+
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
\begin{aligned}
|
| 133 |
+
0 & =\left(B A_{1}^{2}-A_{1} C^{2}\right)+\left(C B_{1}^{2}-B_{1} A^{2}\right)+\left(A C_{1}^{2}-C_{1} B^{2}\right) \\
|
| 134 |
+
& =\frac{a^{2}(b-c)}{b+c}+\frac{b^{2}(c-a)}{c+a}+\frac{c^{2}(a-b)}{a+b} \\
|
| 135 |
+
& =\frac{a^{4}(b-c)+b^{4}(c-a)+c^{4}(a-b)-(b-c)(c-a)(a-b)(a b+b c+c a)}{(b+c)(c+a)(a+b)} \\
|
| 136 |
+
& =-\frac{(b-c)(c-a)(a-b)(a+b+c)^{2}}{(b+c)(c+a)(a+b)}
|
| 137 |
+
\end{aligned}
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
одакле следи $a=b$ или $a=c$ или $b=c$.
|
| 141 |
+
|
| 142 |
+
Друго решење. Као у првом решењу, $B A_{1}=A_{0} C=\frac{a b}{b+c}, A_{1} C=\frac{a c}{b+c}, C B_{1}=\frac{b c}{c+a}$, $\overline{B_{1} A=\frac{b a}{c+a}, A} C_{1}=\frac{c a}{a+b}$ и $C_{1} B=\frac{c b}{a+b}$. Означимо $B X=x, C Y=y$ и $A Z=z$. Потенција тачке $A$ даје $A B_{1} \cdot A Y=A C_{1} \cdot A Z$, тј. $\frac{b y}{c+a}+\frac{c z}{a+b}=\frac{b^{2}}{c+a}$. Слично добијамо $\frac{c z}{a+b}+\frac{a x}{b+c}=\frac{c^{2}}{a+b}$ и $\frac{a x}{b+c}+\frac{b y}{c+a}=\frac{a^{2}}{b+c}$. Одавде следи $\frac{2 a x}{b+c}=\frac{a^{2}}{b+c}+\frac{c^{2}}{a+b}-\frac{b^{2}}{c+a}$ што се своди на $x=\frac{1}{2} a-\frac{(b+c)(b-c)\left(b^{2}+c^{2}+a b+a c+b c\right)}{2 a(a+b)(a+c)}$, итд. Услов да су три нормале конкурентне је
|
| 143 |
+
|
| 144 |
+
$$
|
| 145 |
+
\begin{aligned}
|
| 146 |
+
0 & =(a+b)(a+c)(b+c)\left[x^{2}-(a-x)^{2}+y^{2}-(b-y)^{2}+z^{2}-(c-z)^{2}\right] \\
|
| 147 |
+
& =(b+c)^{2}(c-b)\left(T-a^{2}\right)+(c+a)^{2}(a-c)\left(T-b^{2}\right)+(a+b)^{2}(b-a)\left(T-c^{2}\right) \\
|
| 148 |
+
& =a^{2}(b+c)^{2}(b-c)+b^{2}(c+a)^{2}(c-a)+c^{2}(a+b)^{2}(a-b)-(a-b)(b-c)(c-a) T \\
|
| 149 |
+
& =-(a-b)(b-c)(c-a)(a+b+c)^{2}
|
| 150 |
+
\end{aligned}
|
| 151 |
+
$$
|
| 152 |
+
|
| 153 |
+
где је $T=a^{2}+b^{2}+c^{2}+a b+b c+c a$.
|
| 154 |
+
|
| 155 |
+
5. Одговор је $n \leqslant 3$.
|
| 156 |
+
|
| 157 |
+
Пумпу дијаметрално супротну пумпи $X$ означаваћемо са $X^{\prime}$.
|
| 158 |
+
|
| 159 |
+
За $n \leqslant 1$ тврђење је тривијално. Нека је $n=2$ и нека је $A B=A^{\prime} B^{\prime}$ најмање међу свим растојањима између две пумпе. Од пумпе $A$ до $A^{\prime}$ се може стићи, рецимо путем $A B^{\prime} A^{\prime}$ (случај пута $A B A^{\prime}$ је сличан), али у $B$ има довољно бензина за вожњу до њој најближе пумпе $A$, те је путања $B A B^{\prime} A^{\prime}$ могућа.
|
| 160 |
+
|
| 161 |
+
Покажимо тврђење за $n=3$ и шест пумпи $A, A^{\prime}, B, B^{\prime}, C, C^{\prime}$. Нека је $A B=$ $A^{\prime} B^{\prime}$ најмање међу растојањима између две пумпе и нека је $B$ пумпа најближа пумпи $C$. Означимо $S=\{A, B, C\}$ и $S^{\prime}=$ $\left\{A^{\prime}, B^{\prime}, C^{\prime}\right\}$. Полазећи из сваке пумпе једног скупа можемо стићи до другог скупа.
|
| 162 |
+
|
| 163 |
+
(1) Претпоставимо да се из пумпе $A$ путем $A B$ не може отићи у скуп $S^{\prime}$. До $S^{\prime}$ се не може стићи ни путем $A C$ - иначе би могло и путем $A B C$, јер је $B C \leqslant A C$, а у $B$ има довољно бензина да надокнади утрошак на путу $A B$. Дакле, полазећи из пумпе $A$, до $S^{\prime}$ можемо стићи само директно. Најбли-
|
| 164 |
+
|
| 165 |
+
|
| 166 |
+
жа тачка скупа $S^{\prime}$ је $C^{\prime}$, па је цела путања $C B A C^{\prime} B^{\prime} A^{\prime}$ могућа. Случај када се из $A^{\prime}$ путем $A^{\prime} B^{\prime}$ не може стићи до $S$ је аналоган.
|
| 167 |
+
|
| 168 |
+
$\left(2^{\circ}\right)$ Ако не важи случај $\left(1^{\circ}\right)$, кренимо из $A$ право у $B$. Како нам је скуп $S^{\prime}$ у домету, а $B C \leqslant d\left(B, S^{\prime}\right)=B C^{\prime}$, из $B$ можемо продужити у $C$. Ту ћемо надокнадити бензин потрошен ��а путу $B C$, а $d\left(C, S^{\prime}\right)=C A^{\prime}<d\left(B, S^{\prime}\right)$, па још увек можемо у $S^{\prime}$, и то у пумпу $A^{\prime}$. Даље се може ићи у $B^{\prime}$ и одатле (као малопре) у $C^{\prime}$. Добијамо путању $A B C A^{\prime} B^{\prime} C^{\prime}$.
|
| 169 |
+
|
| 170 |
+
Остаје да конструишемо контрапример за $n \geqslant 4$. Сматраћемо да је полуобим лопте 1. Распоредимо пумпе $A_{2}, A_{3}, \ldots, A_{n}$ по великом кругу тако да је $A_{2} A_{3}=A_{3} A_{4}=\cdots=A_{n-1} A_{n}=d<\frac{1}{n-1}$ и пумпу $A_{1}$ тако да је $A_{1} A_{3}=d$ и $A_{1} A_{2}=A_{1} A_{4}$. Опет означавамо $S=\left\{A_{1}, \ldots, A_{n}\right\}$ и $S^{\prime}=\left\{A_{1}^{\prime}, \ldots, A_{n}^{\prime}\right\}$. Снабдимо пумпе $A_{1}, A_{1}^{\prime}, \ldots, A_{n-1}, A_{n-1}^{\prime}$ бензином довољним за прелазак раздаљине $d$, а пумпе $A_{n}$ и $A_{n}^{\prime}$ бензином за прелазак раздаљине $1-(n-1) d$. Из сваке пумпе се може стићи до дијаметрално супротне: заиста, за $2 \leqslant i \leqslant n$ могућа је путања $A_{i} A_{i+1} \ldots A_{n} A_{2}^{\prime} A_{3}^{\prime} \ldots A_{i}^{\prime}$, а могућа је и путања $A_{1} A_{3} A_{4} \ldots A_{n} A_{2}^{\prime} A_{3}^{\prime} A_{1}^{\prime}$. С друге стране, у свакој од пумпи $A_{1}, \ldots, A_{n-1}$ има тек толико бензина да се дође до најближе пумпе, а у $A_{n}$ и $A_{n}^{\prime}$ таман довољно за прелаз у други скуп. Зато, да
|
| 171 |
+
|
| 172 |
+
|
| 173 |
+
би се обишле све пумпе, бар један од скупова, рецимо $S$, морао би се обићи цео без коришћења горива у $A_{n}$, али за то је потребно прећи пут дужи од $(n-1) d$, а бензина има само за пут дужине $(n-1) d$.
|
| 174 |
+
|
| 175 |
+
6. Дефинишимо низ $\left(c_{m, n}\right)\left(m, n \in \mathbb{N}_{0}\right)$ условима
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
c_{m, 0}=0, \quad c_{m, 1}=1, \quad c_{m, n+1}=\frac{2 m}{n} c_{m, n}+c_{m, n-1} \quad \text { за } n \geqslant 1
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
Тада је $a_{n}=c_{1010, n}$ и $b_{n}=c_{1009, n}$.
|
| 182 |
+
|
| 183 |
+
Видимо да је нпр. $c_{1, n}=n, c_{2, n}=n^{2}$ и $c_{3, n}=\frac{2 n^{3}+n}{3}$. Тврдимо да за свако $m \in \mathbb{N}$ постоји моничан полином $P_{m}(x)$ такав да је
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
P_{m}(x+1)=\frac{2 m}{x} P_{m}(x)+P_{m}(x-1)
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
пошто је очигледно $P_{m}(0)=0$, индукцијом ће следити $c_{m, n}=P_{m}(n) / P_{m}(1)$.
|
| 190 |
+
|
| 191 |
+
Лема. Дефинишимо низ полинома $P_{k}$ условима $P_{0}(x)=0, P_{1}(x)=x$ и
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
P_{k+1}(x)=x P_{k}(x)+\frac{k(k-1)}{4} \cdot P_{k-1}(x)
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Тада полиноми $P_{k}$ задовољавају (1).
|
| 198 |
+
|
| 199 |
+
Шта више, важи $P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)=\frac{k(k-1)}{x} \cdot P_{k-1}(x)$.
|
| 200 |
+
|
| 201 |
+
Доказ. Ако означимо
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\begin{aligned}
|
| 205 |
+
& A_{k}(x)=P_{k+1}(x)-x P_{k}(x)-\frac{k(k-1)}{4} P_{k-1}(x) \equiv 0 \\
|
| 206 |
+
& B_{k}(x)=P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)-\frac{k(k-1)}{x} P_{k-1}(x) \\
|
| 207 |
+
& C_{k}(x)=P_{k}(x+1)-P_{k}(x-1)-\frac{2 k}{x} P_{k}(x)
|
| 208 |
+
\end{aligned}
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
и претпоставимо да је $B_{i}(x) \equiv C_{i}(x) \equiv 0$ за све $i \leqslant k$, тада је
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
\begin{aligned}
|
| 215 |
+
& B_{k+1}(x)-x B_{k}(x)-\frac{k(k-1)}{4} B_{k-1}(x)= \\
|
| 216 |
+
& C_{k}(x)+A_{k}(x+1)+A_{k}(x-1)-2 A_{k}(x)-\frac{k(k-1)}{x} A_{k-1}(x)=0
|
| 217 |
+
\end{aligned}
|
| 218 |
+
$$
|
| 219 |
+
|
| 220 |
+
па је $B_{k+1} \equiv 0$. С друге стране,
|
| 221 |
+
|
| 222 |
+
$$
|
| 223 |
+
\begin{aligned}
|
| 224 |
+
& C_{k+1}(x)-x C_{k}(x)-\frac{k(k-1)}{4} C_{k-1}(x)= \\
|
| 225 |
+
& B_{k}(x)+A_{k}(x+1)-A_{k}(x-1)-\frac{2(k+1)}{x} A_{k}(x)=0
|
| 226 |
+
\end{aligned}
|
| 227 |
+
$$
|
| 228 |
+
|
| 229 |
+
па је и $C_{k+1} \equiv 0$.
|
| 230 |
+
|
| 231 |
+
Из (2) следи да полиноми $Q_{0}(x)=0$ и $Q_{k}(x)=\frac{2^{k-1}}{(k-1)!} P_{k}(x)$ задовољавају везу $Q_{k+1}(x)=\frac{2 x}{k} Q_{k}(x)+Q_{k-1}(x)$, па индукцијом добијамо $Q_{k}(x)=x c_{x, k}$ за све $x \in \mathbb{N}$. Одавде је $P_{k}(x)=\frac{(k-1)!}{2^{k-1}} \cdot x c_{x, k}$ и
|
| 232 |
+
|
| 233 |
+
$$
|
| 234 |
+
\frac{c_{m, n}}{n}=\frac{1}{n} \cdot \frac{P_{m}(n)}{P_{m}(1)}=\frac{c_{n, m}}{c_{1, m}}=\frac{c_{n, m}}{m}
|
| 235 |
+
$$
|
| 236 |
+
|
| 237 |
+
Тврђење задатка се добија за $m=1010$ и $n=1009$.
|
| 238 |
+
|
| 239 |
+
Друго решење. За дато $m \geqslant 0$ посматрајмо генераторску функцију низа $c_{m, n}$ датог условима $(*)$ :
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
f_{m}(x)=\frac{1}{2 m}+\sum_{n=1}^{\infty} \frac{c_{m, n}}{n} x^{n}
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
Из рекурентне везе $(*)$ следи да функција $f_{m}$ задовољава диференцијалну једначину $\left(1-x^{2}\right) f_{m}^{\prime}(x)=2 m \cdot f_{m}(x)$. Ова једначина се лако решава: ако је запишемо као $\frac{f_{m}^{\prime}(x)}{f_{m}(x)}=\frac{2 m}{1-x^{2}}$, интеграција по $x$ даје $\ln \left|f_{m}(x)\right|=\int \frac{2 m}{1-x^{2}} d x=$
|
| 246 |
+
$m \ln \frac{1+x}{1-x}+$ const, тј. $f_{m}(x)=C \cdot\left(\frac{1+x}{1-x}\right)^{m}$. Услов $f_{m}(0)=\frac{1}{2 m}$ најзад даје $C=1$, те је
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
\begin{aligned}
|
| 250 |
+
f_{m}(x) & =\frac{1}{2 m}\left(\frac{1+x}{1-x}\right)^{m}=\frac{1}{2 m}(1+x)^{m}(1-x)^{-m}= \\
|
| 251 |
+
& =\frac{1}{2 m} \sum_{i=0}^{m}\binom{m}{i} x^{i} \cdot \sum_{j=1}^{\infty}\binom{m-1+j}{m-1} x^{j}
|
| 252 |
+
\end{aligned}
|
| 253 |
+
$$
|
| 254 |
+
|
| 255 |
+
Коефицијент уз $x^{n}$ је
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
\frac{c_{m, n}}{n}=\frac{1}{2 m} \sum_{i=0}^{m}\binom{m}{i}\binom{m+n-1-i}{m-1}=\frac{1}{2} \sum_{i} \frac{(m+n-1-i)!}{i!(m-i)!(n-i)!}
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
Овај израз је симетричан по $m$ и $n$, па је $\frac{c_{m, n}}{n}=\frac{c_{n, m}}{m}$.
|
| 262 |
+
|
Serbia_MO/md/sr-2020_smo_resenja.md
ADDED
|
@@ -0,0 +1,161 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 14. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 2 |
+
|
| 3 |
+
## Први дан
|
| 4 |
+
|
| 5 |
+
1. Наћи све моничне полиноме $P(x)$ такве да је полином $P(x)^{2}-1$ дељив полиномом $P(x+1)$.
|
| 6 |
+
|
| 7 |
+
(Дуиан Ђукић)
|
| 8 |
+
|
| 9 |
+
2. Дат је конвексан полиедар са бар 5 темена у чијем се сваком темену састају тачно по три ивице. Доказати да је могуће доделити сваком темену тог полиедра неки рационалан број тако да буду задовољени следећи услови:
|
| 10 |
+
|
| 11 |
+
(i) бар један од додељених бројева је једнак 2020;
|
| 12 |
+
|
| 13 |
+
(ii) за сваку страну полиедра, производ бројева у свим теменима те стране је једнак 1 .
|
| 14 |
+
|
| 15 |
+
(Бојан Баиић са сараднииима)
|
| 16 |
+
|
| 17 |
+
3. Дат је троугао $A B C$. Тачке $D$ и $E$ на правој $A B$ су такве да је $A D=A C$ и $B E=B C$, уз распоред $D-A-B-E$. Описане кружнице троуглова $D B C$ и $E A C$ секу се у тачки $X \neq C$, а описане кружнице троуглова $D E C$ и $A B C$ секу се у тачки $Y \neq C$. Ако важи $D Y+E Y=2 X Y$, одредити $\varangle A C B$.
|
| 18 |
+
|
| 19 |
+
(Милош Милосављевић)
|
| 20 |
+
|
| 21 |
+
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 14. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
|
| 22 |
+
|
| 23 |
+
## Други дан
|
| 24 |
+
|
| 25 |
+
4. У трапезу $A B C D$ чији унутрашњи углови нису прави, дијагонале $A C$ и $B D$ секу се у тачки $E$. Нека су $P$ и $Q$ редом подножја нормала из темена $A$ и $B$ на праве $B C$ и $A D$. Описане кружнице троуглова $C E Q$ и $D E P$ секу се у тачки $F \neq E$. Доказати да се праве $A P, B Q$ и $E F$ секу у једној тачки или су паралелне.
|
| 26 |
+
|
| 27 |
+
(Душан Ђукић)
|
| 28 |
+
|
| 29 |
+
5. За природан број $n$, са $v_{2}(n)$ означавамо највећи цео број $k \geqslant 0$ такав да $2^{k} \mid n$. Претпоставимо да функција $f: \mathbb{N} \rightarrow \mathbb{N}$ задовољава услове:
|
| 30 |
+
|
| 31 |
+
(i) $f(x) \leqslant 3 x$ за све $x \in \mathbb{N}$;
|
| 32 |
+
|
| 33 |
+
(ii) $v_{2}(f(x)+f(y))=v_{2}(x+y)$ за све $x, y \in \mathbb{N}$.
|
| 34 |
+
|
| 35 |
+
Доказати да за сваки природан број $a$ постоји тачно један природан број $x$ такав да је $f(x)=3 a$.
|
| 36 |
+
|
| 37 |
+
(Душан Ђукић)
|
| 38 |
+
|
| 39 |
+
6. Дат је природан број $k$. Посматрајмо следећу игру на бесконачној једнодимензионалној табли. На почетку игре, на поља постављамо укупно $n$ жетона, при чему може бити више жетона на истом пољу. Након тога, у сваком потезу извршавамо једну од следећих операција:
|
| 40 |
+
|
| 41 |
+
$\left(1^{\circ}\right)$ бирамо два суседна поља која су оба непразна и са једног од њих преносимо све жетоне на друго;
|
| 42 |
+
|
| 43 |
+
$\left(2^{\circ}\right)$ бирамо поље са бар два жетона и са њега премештамо по један жетон $k$ поља улево и $k$ поља удесно.
|
| 44 |
+
|
| 45 |
+
(a) Ако је $n \leqslant k+1$, доказати да ће се извршити само коначно много потеза.
|
| 46 |
+
|
| 47 |
+
(б) За које вредности $k$ се може одабрати $n$ и поставити $n$ жетона тако да буде могућ бесконачан низ потеза?
|
| 48 |
+
|
| 49 |
+
(Никола Пеш̄ровић)
|
| 50 |
+
|
| 51 |
+
## РЕШЕЊА
|
| 52 |
+
|
| 53 |
+
1. Једина решења су полиноми $P(x)=1$ и $P(x)=x-c$, где је $c$ константа.
|
| 54 |
+
|
| 55 |
+
Претпоставимо да је $P(x)=(x-c)\left(x-x_{2}\right) \cdots\left(x-x_{n}\right)$ неконстантан полином, при чему је $c$ његова комплексна нула чији је реални део најмањи.
|
| 56 |
+
|
| 57 |
+
По услову задатка, $x+1-c$ дели $P(x)^{2}-1$, одакле је $P(c-1)= \pm 1$. С друге стране, за $2 \leqslant i \leqslant n$ важи $\left|c-1-x_{i}\right| \geqslant 1$, па је $|P(c-1)|=\prod_{i=2}^{n}\left|c-1-x_{i}\right| \geqslant 1$, а то је могуће само ако је $\left|c-1-x_{i}\right|=1$, тј. $x_{i}=c$ за све $i$.
|
| 58 |
+
|
| 59 |
+
Следи да је $P(x)=(x-c)^{n}$. Међутим, $P(x+c)^{2}-1=x^{2 n}-1$ није дељиво са $P(x+c+1)=(x+1)^{n}$ ако је $n \geqslant 2$, па је једина могућност $n=1$.
|
| 60 |
+
|
| 61 |
+
Найомена. Ако се искључи услов моничности, има и нетривијалних решења. На пример, до на замену променљиве $x$ са $x+c$, (једина) решења степена 3 и 4 су $P(x)=\frac{\sqrt{3}}{6}\left(x^{3}-3 x^{2}+8 x\right)$, односно $P(x)=\frac{1}{36}\left(x^{4}-2 x^{3}-x^{2}-10 x-12\right)$ и $P(x)=\frac{i \sqrt{2}}{36}\left(x^{4}-2 x^{3}+8 x^{2}-x+\frac{33}{4}\right)$, док решења степена 2 нема.
|
| 62 |
+
|
| 63 |
+
2. Означимо $c=$ 2020. Прво размотримо случај када постоји страна $\mathcal{F}$ са парним бројем темена. Тада је довољно доделити теменима стране $\mathcal{F}$ наизменично бројеве $c$ и $\frac{1}{c}$, а свим осталим теменима полиедра број 1. Заиста, производ бројева на страни $\mathcal{F}$ је једнак 1 , а свака друга страна или дели ивицу са страном $\mathcal{F}$ (а на њој је производ 1) или нема
|
| 64 |
+
|
| 65 |
+
|
| 66 |
+
ниједно заједничко теме са $\mathcal{F}$ (тада су сви бројеви на њој јединице).
|
| 67 |
+
|
| 68 |
+
Надаље сматрамо да све стране имају непаран број темена. Посматрајмо две дисјунктне стране полиедра $\mathcal{F}_{A}$ и $\mathcal{F}_{B}$ и темена $A$ и $B$ на њима, редом, тако да је $A B$ ивица полиедра. Теменима ових двеју страна, изузев $A$ и $B$, доделићемо наизменично бројеве $c$ и $\frac{1}{c}$ као на слици, а свим осталим теменима полиедра број 1. И у овом случају се лако види да је услов задатка испуњен.
|
| 69 |
+
|
| 70 |
+
Најзад, уверимо се да се овакве стране $\mathcal{F}_{A}$ и $\mathcal{F}_{B}$ увек могу наћи. Постоји страна $\mathcal{F}$ која није троугао (иначе би дати полиедар био тетраедар). Посматрајмо чети-
|
| 71 |
+
|
| 72 |
+
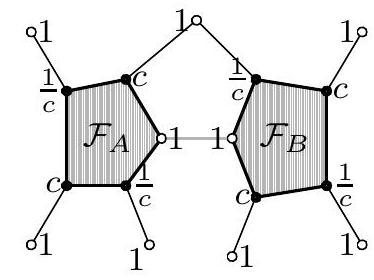
|
| 73 |
+
ри узастопне њој суседне стране $\mathcal{F}_{1}, \mathcal{F}_{2}, \mathcal{F}_{3}$ и $\mathcal{F}_{4}$. Ако су стране $\mathcal{F}_{1}$ и $\mathcal{F}_{3}$ дисјунктне, узмимо њих, а ако нису, онда оне имају заједничку целу ивицу, па три стране $\mathcal{F}_{1}, \mathcal{F}_{3}$ и $\mathcal{F}$ чине појас који раздваја $\mathcal{F}_{2}$ од $\mathcal{F}_{4}$, те у том случају можемо узети $\mathcal{F}_{2}$ и $\mathcal{F}_{4}$.
|
| 74 |
+
|
| 75 |
+
Найомена. Делује примамљиво поставити систем линеарних једначина по логаритмима уписаних бројева, јер он има више једначина него непознатих, што гарантује постојање нетривијалног целобројног решења. Ипак, да би уписани бројеви били рационални, једна од променљивих у том решењу мора бити једнака $\pm 1$, што није јасно зашто се може постићи.
|
| 76 |
+
|
| 77 |
+
3. Нека је $I_{c}$ центар приписаног круга $\triangle A B C$ наспрам темена $C$. Тада је $A I_{c}$ симетрала угла $C A D$, одакле је $\triangle I_{c} A D \cong \triangle I_{c} A C$. Следи да је $\varangle I_{c} D B=$ $\varangle I_{c} D A=\varangle I_{c} C A=\varangle I_{c} C B$, па $I_{c}$ лежи на кругу $B C D$. Слично, $I_{c}$ лежи на кругу $A C E$, што значи да је $X \equiv I_{c}$. Такође, како је $X D=X C$ и аналогно $X E=X C$, тачка $X$ је центар круга $C D E Y$.
|
| 78 |
+
|
| 79 |
+
Даље, $\varangle D Y A=\varangle C Y A-\varangle C Y D=\varangle C B A-$ $\varangle C E D=\varangle C E D=\varangle C X A=\varangle D X A$ и слично $\varangle E Y B=\varangle E X B$. Зато посматрајмо тачку $X^{\prime}$ симетричну тачки $X$ у односу на $A B$. Због $\varangle D X^{\prime} A=\varangle D Y A$ ова тачка лежи на кругу $A D Y$, а аналогно и на кругу $B E Y$.
|
| 80 |
+
|
| 81 |
+
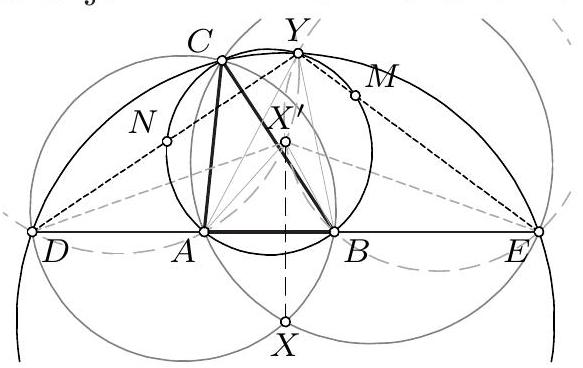
|
| 82 |
+
|
| 83 |
+
Ако је $\varangle C<60^{\circ}$, онда је $\varangle A X^{\prime} B=\varangle A X B=90^{\circ}-\frac{1}{2} \varangle C>\varangle C=\varangle A Y B$, па тачка $X^{\prime}$ лежи унутар $\triangle A B Y$, а самим тим и унутар $\triangle D E Y$. Следи да је $D Y+E Y>D X^{\prime}+E X^{\prime}=D X+E X=2 X Y$. Слично, ако је $\varangle C>60^{\circ}$, тачка $Y$ лежи унутар $\triangle D E X$, те је тада $D Y+E Y<2 X Y$. Према томе, ако је $D Y+E Y=2 X Y$, мора бити $\varangle C=60^{\circ}$, а тада је $X^{\prime} \equiv Y$ па заиста важи једнакост.
|
| 84 |
+
|
| 85 |
+
Друйо решење. Углове троугла $A B C$ означавамо уобичајено са $\alpha, \beta, \gamma$. Као у првом решењу, тачке $C, D, E, Y$ леже на кругу са центром $X$. Такође, због $\varangle C Y D=\varangle C E D=\frac{\beta}{2}$, права $D Y$ садржи средиште $N$ лука $A C$ круга $A B C$.
|
| 86 |
+
|
| 87 |
+
Означимо $\varangle Y D E=x$ и $\varangle Y E D=y$. Услов $D Y+E Y=2 X Y$ даје $\sin x+\sin y=$ $\sin x+\sin \left(90^{\circ}-\frac{\gamma}{2}-x\right)=1, \mathrm{rj}$.
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\left(1-\sin \frac{\gamma}{2}\right) \sin x+\cos \frac{\gamma}{2} \cos x=1
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
С друге стране, синусна теорема у $\triangle A D N$ даје $2 \sin x \sin \frac{\alpha+\gamma}{2}=\cos \left(\frac{\alpha-\gamma}{2}-x\right)$, одакле следи $\operatorname{tg} x=\frac{\cos \frac{\alpha-\gamma}{2}}{2 \sin \frac{\alpha+\gamma}{2}-\sin \frac{\alpha-\gamma}{2}}$. Одавде налазимо
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
\sin x=\frac{\cos \frac{\alpha-\gamma}{2}}{\sqrt{3-2 \cos \gamma+4 \sin \frac{\gamma}{2} \cos \varphi}}, \quad \cos x=\frac{2 \sin \frac{\alpha+\gamma}{2}-\sin \frac{\alpha-\gamma}{2}}{\sqrt{3-2 \cos \gamma+4 \sin \frac{\gamma}{2} \cos \varphi}}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
где је $\varphi=\alpha+\frac{\gamma}{2}-90^{\circ}=\frac{\alpha-\beta}{2}$. Заменом у једначину (*) добијамо
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
2 \cos \frac{3 \gamma-180^{\circ}}{4} \cos \frac{\varphi}{2}=\sqrt{3-2 \cos \gamma+4 \sin \frac{\gamma}{2} \cos \varphi}
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
што се након квадрирања своди на
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
\cos \varphi=\frac{2-2 \cos \gamma-\sin \frac{3 \gamma}{2}}{1-4 \sin \frac{\gamma}{2}+\sin \frac{3 \gamma}{2}}=\frac{-3 t+4 t^{2}+4 t^{3}}{1-t-4 t^{3}}, \quad \text { где је } \quad t=\sin \frac{\gamma}{2}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
Ако је $\gamma \neq 60^{\circ}$, скраћивање $2 t-1 \neq 0$ даје $\cos \varphi=-\frac{2 t^{2}+3 t}{2 t^{2}+t+1}<0$, што је немогуће. Према томе, мора бити $\gamma=60^{\circ}$.
|
| 112 |
+
|
| 113 |
+
4. Случај када је $A D \| B C$ је једноставан. Наиме, тада је $E$ средиште дијагонале $A C$, те је $E A=E C=E P$, а слично важи и $E B=E D=E Q$. Одатле следи да су кругови $C E Q$ и $D E P$ симетрични у односу на симетралу дужи $C P$ и $D Q$, те је $E F \perp C P$, тј. $E F\|A P\| B Q$.
|
| 114 |
+
|
| 115 |
+
Означимо са $O$ тачку пресека правих $A D$ и $B C$. Троуглови $O A P$ и $O B Q$ су
|
| 116 |
+
слични, па је $\frac{O P}{O Q}=\frac{O A}{O B}=\frac{O D}{O C}$, тј. $O C \cdot O P=O D \cdot O Q$, одакле следи да тачке $C, D, P$ и $Q$ леже на неком кругу $\gamma$.
|
| 117 |
+
|
| 118 |
+
Нека се праве $A P$ и $B Q$ секу у тачки $H$, а праве $D P$ и $C Q$ у тачки $G$. Како је $G C \cdot G Q=G D \cdot G P$, тачка $G$ има једнаку потенцију у односу на кругове $C E Q$ и $D E P$, па она лежи на њиховој радикалној оси $E F$. С друге стране, тачке $E, G$ и $H$ су колинеарне на
|
| 119 |
+
|
| 120 |
+
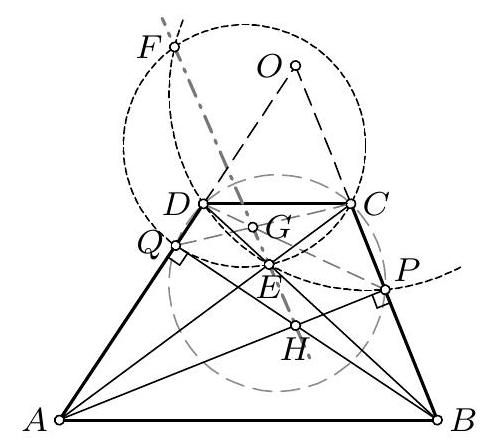
|
| 121 |
+
основу Папосове теореме за тројке тачака $B, C, P$ и $A, D, Q$. Следи да су све четири тачке $H, E, G$ и $F$ колинеарне.
|
| 122 |
+
|
| 123 |
+
5. Заменом $x=y$ добијамо $v_{2}(f(x))=v_{2}(x)$. Ако је $v_{2}(a)=k>0$, посматрањем функције $g(x)=f\left(2^{k} x\right) / 2^{k}$ тврђење сводимо на случај непарног $a$. Зато надаље сматрамо да $2 \nmid a$.
|
| 124 |
+
|
| 125 |
+
Приметимо да, ако је $x \not \equiv y\left(\bmod 2^{k}\right)$, онда је $f(x) \not \equiv f(y)\left(\bmod 2^{k}\right)$. Заиста, ако је $z \equiv-x\left(\bmod 2^{k}\right)$, онда $2^{k} \nmid z+y$, па је $f(y) \not \equiv-f(z) \equiv f(x)\left(\bmod 2^{k}\right)$. Одавде такође следи да је функција $f$ инјективна.
|
| 126 |
+
|
| 127 |
+
Нека је $2^{k-1}<3 a<2^{k}$, где је $k \in \mathbb{N}$. Како су $f(1), f(3), \ldots, f\left(2^{k}-1\right)$ међусобно различити по модулу $2^{k}$, постоји непаран број $x<2^{k}$ такав да је $f(x) \equiv 3 a$ $\left(\bmod 2^{k}\right)$. Претпоставимо да је $f(x) \neq 3 a$. Тада је $f(x)>2^{k}$, па из $f(x)+$ $f\left(2^{k}-x\right) \equiv 2^{k}\left(\bmod 2^{k+1}\right)$ следи да је $f(x)+f\left(2^{k}-x\right) \geqslant 3 \cdot 2^{k}$. Међутим, с друге стране је $f(x)+f\left(2^{k}-x\right) \leqslant 3\left(x+\left(2^{k}-x\right)\right)=3 \cdot 2^{k}$, па је то могуће једино ако је $f(x)=3 x$. Одавде је $x \equiv a\left(\bmod 2^{k}\right)$, па је $x=a$, тј. опет је $f(x)=3 a$.
|
| 128 |
+
|
| 129 |
+
6. (a) Потезе врсте $\left(1^{\circ}\right)$ зваћемо скуйљаљем, а потезе врсте $\left(2^{\circ}\right)$ сејаъем. Поља нумеришемо редом бројевима ..., $-1,0,1,2, \ldots$. Поља се могу поделити на $k$ класа по модулу $k$, тако да при сејању жетони не мењају своју класу.
|
| 130 |
+
|
| 131 |
+
Претпоставимо прво да у једној од класа нема ниједног жетона. Поља ове класе деле таблу на блокове дужине $k-1$, које опет нумеришемо целим бројевима. Како приликом скупљања ниједан жетон не излази из свог блока, унутар сваког блока може се извршити само коначно много узастопних скупљања. С друге стране, при сваком сејању се из неког блока $i$ пребацује по један жетон у блокове $i-1$ и $i+1$. Овако се задатак своди на следећи.
|
| 132 |
+
|
| 133 |
+
Лема. Нека се у сваком кораку бира $i$ и из блока $i$ премешта по један жетон у блокове $i-1$ и $i+1$. Тада се игра завршава у коначно много корака.
|
| 134 |
+
|
| 135 |
+
Доказ. Кад год нека два суседна блока $x$ и $x+1$ по први пут размене жетон, доделимо овом жетону број $x$. Приликом сваке следеће размене између ових двају блокова можемо сматрати да се размењује тај исти жетон. Овако сваки жетон само циркулише између два суседна блока. Следи да ће највише $n$ парова блокова икада разменити жетоне. Међутим, ако неки блок сеје жетоне бесконачно много пута, онда то мора да важи и за суседне блокове (иначе би се у њима гомилало бесконачно много жетона), а индукцијом и за све блокове, што је немогуће.
|
| 136 |
+
|
| 137 |
+
Остаје случај када се ниједна класа поља никад не испразни. Тада се увек у једној класи налазе два жетона, а у осталима по један. Сејања и скупљања
|
| 138 |
+
се врше из класе са два жетона. Нека се у неком тренутку сеје са поља $p$ у $i$-тој класи (на коме су два жетона) на поља $p-k$ и $p+k$. Следи скупљање, и то без смањења општости удесно ка ( $i+1$ )-тој класи - са поља $p \pm k$ на поље $p \pm k+1$. Затим се из овог поља сеје на поља $p+1$ и $p \pm 2 k+1$. Следи скупљање из ( $i+1$ )-те класе, али не у $i$-ту, јер је у њој једини жетон остао на пољу $p \mp k$. Дакле, сада се скупља у $(i+2)$-ту класу. Закључујемо да се наизменично сеје и скупља, при чему се класа из које се сеје и скупља циклично помера за један удесно. Може се сматрати без умањења општости да је жетон који се скупља увек исти - назовимо га ирним. Црни жетон периодично учествује у сејању из сваке класе, дакле са свим осталим жетонима.
|
| 139 |
+
|
| 140 |
+
При сваком сејању црни жетон баца други жетон $k$ поља на једну страну, а себе $k$ поља на другу. Тако се у сваком циклусу од $k$ сејања позиција најлевљег жетона помера бар $k$ поља улево, а најдешњег бар $k$ поља удесно, те се опсег игре увећава за бар $2 k$. Међутим, у току једног циклуса црни жетон не може прећи пут дужи од $k(k+1)$, па након $\frac{k+1}{2}$ циклуса он више не може стићи од најлевљег до најдешњег, што је коначна контрадикција.
|
| 141 |
+
|
| 142 |
+
(б) За свако $k$ даћемо пример периодичне (и самим тим бесконачне) игре. Посматрајмо $5 k$ узастопних поља означених редом бројевима $1,2, \ldots, 5 k$, свако са по једним жетоном. Делимо их на групе од по $k$ поља:
|
| 143 |
+
|
| 144 |
+
$$
|
| 145 |
+
1,1, \cdots, 1,1 \quad 1,1, \cdots, 1,1 \quad 1,1, \cdots, 1,1 \quad 1,1, \cdots, 1,1 \quad 1,1, \cdots, 1,1
|
| 146 |
+
$$
|
| 147 |
+
|
| 148 |
+
Почињемо скупљањем жетона са поља $1, \ldots, k$ на поље $k+1$. Затим, за $i=$ $1,2, \ldots, k$, са поља $k+i$ једном сејемо, а преостале жетоне с тог поља скупљамо на поље $k+i+1$ (осим за $i=k$ ). Након $i$-тог циклуса стање је овакво:
|
| 149 |
+
|
| 150 |
+
$$
|
| 151 |
+
\underbrace{1,1, \ldots, 1}_{i}, 0,0, \ldots, 0 \quad \underbrace{0,0, \ldots, 0}_{i}, k+1-i, 1,1, \ldots, 1 \quad \underbrace{2,2, \ldots, 2}_{i}, 1,1, \ldots, 1 \quad 1,1, \cdots, 1,1 \quad 1,1, \cdots, 1,1
|
| 152 |
+
$$
|
| 153 |
+
|
| 154 |
+
Када аналогне потезе одиграмо и здесна, добићемо стање
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
1,1, \cdots, 1,1 \quad 0,0, \cdots, 0,0 \quad 3,3, \cdots, 3,3 \quad 0,0, \cdots, 0,0 \quad 1,1, \cdots, 1,1
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
Најзад, ако сада посејемо по једном са сваког од поља $2 k+1, \ldots, 3 k$, добијамо конфигурацију идентичну полазној.
|
| 161 |
+
|
Serbia_MO/raw/sr-2007_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:8b68b05279621195c3d45f7f24f99f63d4d72cd2e3c227d0639307a371ba7816
|
| 3 |
+
size 91662
|
Serbia_MO/raw/sr-2008_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:593f6bbd9648ee4db663849e541c8475b3f648c4848ca2178444b6233060918a
|
| 3 |
+
size 111703
|
Serbia_MO/raw/sr-2009_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:fb765423492d761253cee09f0e8db4cffc3f0fb0af9ba573aa7a7caa1e675e9b
|
| 3 |
+
size 93407
|
Serbia_MO/raw/sr-2010_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3225ee3110d4c133c5ff9ea3a259a209a2a4d2576e1c01fd27ca10285a9b8abd
|
| 3 |
+
size 112247
|
Serbia_MO/raw/sr-2011_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:74dd8afb5013090b75d28b195fbe947f49a3fff83fcb92103567ae87d05baad9
|
| 3 |
+
size 84390
|
Serbia_MO/raw/sr-2012_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:2f5302dfa5d5798781d8f40228e8be84d9017e5c0946d6c60c7b9365d09c4722
|
| 3 |
+
size 87199
|
Serbia_MO/raw/sr-2013_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:37ccc48022fbb933fc3ec90536e52eb5d179ba86343e9dd745f27a38ebeb1cfe
|
| 3 |
+
size 89826
|
Serbia_MO/raw/sr-2014_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:30160e0a7f0b36d30f5e983fadcb362abd74792570ca461c34bcf575daac13e0
|
| 3 |
+
size 92995
|
Serbia_MO/raw/sr-2015_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:e234fc16813650da1274f984f1fdc082e170fd047e778eb3ce520ca9617ae282
|
| 3 |
+
size 88953
|
Serbia_MO/raw/sr-2016_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:479a0d3a1210ddbef6c3abdbdc5e916746d5c4ffb1f7888a009602686b7de0e4
|
| 3 |
+
size 103823
|
Serbia_MO/raw/sr-2017_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:260946b7cd2fdfd314cfc56411a23a0c332d817fb0abbd744d23b4c7c427382b
|
| 3 |
+
size 92579
|
Serbia_MO/raw/sr-2018_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:033e6d106b0737211ba3e667b24cc3a3c5f02387a98b86b59894f770407a0638
|
| 3 |
+
size 124563
|
Serbia_MO/raw/sr-2019_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:023e2aedaad92e14ca1e7f87e30629763b62a773fef24a22e6fa2722e680bec5
|
| 3 |
+
size 136695
|
Serbia_MO/raw/sr-2020_smo_resenja.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:77ae0d5844a872525335728e17fb20964e0cb50e821e02f43fea943487ed774d
|
| 3 |
+
size 115600
|
Serbia_MO/segment_script/segment.py
ADDED
|
@@ -0,0 +1,149 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
project_root = Path(__file__).parent.parent.parent
|
| 12 |
+
|
| 13 |
+
problem_tag = 'Problem'
|
| 14 |
+
solution_tag = 'Solution'
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
def clean(text: str) -> str:
|
| 18 |
+
text = text.replace('28. март 2015.', '')
|
| 19 |
+
text = text.replace('31. март 2018 .', '')
|
| 20 |
+
text = text.replace('6. април 2019 .', '')
|
| 21 |
+
|
| 22 |
+
return text
|
| 23 |
+
|
| 24 |
+
|
| 25 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 26 |
+
"""
|
| 27 |
+
Analyze the text and return the tags and problem number.
|
| 28 |
+
Args:
|
| 29 |
+
text (str): The markdown text to analyze.
|
| 30 |
+
Returns:
|
| 31 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 32 |
+
"""
|
| 33 |
+
tag_pattern = re.compile(r'\n(\d+)\.\s+', re.IGNORECASE)
|
| 34 |
+
|
| 35 |
+
problem_start_pattern = re.compile(r'## Први дан', re.IGNORECASE)
|
| 36 |
+
problem_start_position = problem_start_pattern.search(text).start()
|
| 37 |
+
separator_pattern = re.compile(r'## РЕШЕЊА', re.IGNORECASE)
|
| 38 |
+
separator_position = separator_pattern.search(text).start()
|
| 39 |
+
|
| 40 |
+
tags = []
|
| 41 |
+
tags.extend([(x, problem_tag) for x in tag_pattern.finditer(text, problem_start_position, separator_position)])
|
| 42 |
+
problem_num = len(tags)
|
| 43 |
+
|
| 44 |
+
tags.extend([(x, solution_tag) for x in tag_pattern.finditer(text, separator_position)])
|
| 45 |
+
solution_num = len(tags) - problem_num
|
| 46 |
+
|
| 47 |
+
tags.sort(key=lambda x: x[0].start())
|
| 48 |
+
return tags, problem_num, solution_num
|
| 49 |
+
|
| 50 |
+
|
| 51 |
+
def segment(text: str, tags):
|
| 52 |
+
starts = []
|
| 53 |
+
ends = []
|
| 54 |
+
|
| 55 |
+
for i in range(len(tags)):
|
| 56 |
+
starts.append(tags[i][0].end())
|
| 57 |
+
if i + 1 < len(tags):
|
| 58 |
+
ends.append(tags[i + 1][0].start())
|
| 59 |
+
else:
|
| 60 |
+
ends.append(len(text))
|
| 61 |
+
|
| 62 |
+
return [text[start:end].strip() for start, end in zip(starts, ends)]
|
| 63 |
+
|
| 64 |
+
|
| 65 |
+
def join(tags, segments):
|
| 66 |
+
problem, solution = '', ''
|
| 67 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 68 |
+
pairs = []
|
| 69 |
+
|
| 70 |
+
problems_tags = [
|
| 71 |
+
(tag, segment)
|
| 72 |
+
for tag, segment in zip(tags, segments)
|
| 73 |
+
if tag[1] == 'Problem'
|
| 74 |
+
]
|
| 75 |
+
solution_tags = {
|
| 76 |
+
tag[0].group(1): (tag, segment)
|
| 77 |
+
for tag, segment in zip(tags, segments)
|
| 78 |
+
if tag[1] == 'Solution'
|
| 79 |
+
}
|
| 80 |
+
|
| 81 |
+
for problem_tag, problem in problems_tags:
|
| 82 |
+
problem_label = problem_tag[0].group(1)
|
| 83 |
+
problem_match = problem_tag[0].group(0)
|
| 84 |
+
|
| 85 |
+
solution_tag, solution = solution_tags[problem_label]
|
| 86 |
+
solution_match = solution_tag[0].group(0)
|
| 87 |
+
|
| 88 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 89 |
+
|
| 90 |
+
return pairs
|
| 91 |
+
|
| 92 |
+
|
| 93 |
+
def write_pairs(output_file: Path, pairs):
|
| 94 |
+
year = re.search(r'(\d{4})', output_file.stem).group(1)
|
| 95 |
+
|
| 96 |
+
output_jsonl_text = ""
|
| 97 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 98 |
+
output_jsonl_text += json.dumps(
|
| 99 |
+
{
|
| 100 |
+
'year': year,
|
| 101 |
+
'tier': "T2",
|
| 102 |
+
'problem_label': problem_label,
|
| 103 |
+
'problem_type': None,
|
| 104 |
+
'problem': problem,
|
| 105 |
+
'solution': solution,
|
| 106 |
+
'metadata': {
|
| 107 |
+
'resource_path': output_file.relative_to(project_root).as_posix(),
|
| 108 |
+
'problem_match': problem_match,
|
| 109 |
+
'solution_match': solution_match
|
| 110 |
+
}
|
| 111 |
+
},
|
| 112 |
+
ensure_ascii=False
|
| 113 |
+
) + '\n'
|
| 114 |
+
|
| 115 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 116 |
+
|
| 117 |
+
|
| 118 |
+
def main():
|
| 119 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 120 |
+
compet_md_path = compet_base_path / "md"
|
| 121 |
+
seg_output_path = compet_base_path / "segmented"
|
| 122 |
+
|
| 123 |
+
total_problem_count = 0
|
| 124 |
+
total_solution_count = 0
|
| 125 |
+
|
| 126 |
+
for smo_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 127 |
+
output_file = seg_output_path / smo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 128 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 129 |
+
|
| 130 |
+
text = '\n' + clean(smo_md.read_text(encoding="utf-8"))
|
| 131 |
+
|
| 132 |
+
tags, problem_num, solution_num = analyze(text)
|
| 133 |
+
|
| 134 |
+
segments = segment(text, tags)
|
| 135 |
+
pairs = join(tags, segments)
|
| 136 |
+
if pairs and problem_num > 0:
|
| 137 |
+
write_pairs(output_file, pairs)
|
| 138 |
+
|
| 139 |
+
total_problem_count += problem_num
|
| 140 |
+
total_solution_count += len(pairs)
|
| 141 |
+
else:
|
| 142 |
+
logger.warning(f"No problem found in {smo_md}")
|
| 143 |
+
|
| 144 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 145 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 146 |
+
|
| 147 |
+
|
| 148 |
+
if __name__ == '__main__':
|
| 149 |
+
main()
|
Serbia_MO/segmented/sr-2007_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2007", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Нека је $D$ тачка на страници $A C$ троугла $A B C$ у коме је $A B<B C$ таква да је $A B=B D$. Круг уписан у $\\triangle A B C$ додирује $A B$ у $K$ и $A C$ у $L$, а $J$ је центар уписаног круга троугла $B C D$. Доказати да $K L$ полови дуж $A J$.", "solution": "Нека је $M$ тачка на $A C$ таква да је $J M \\| K L$. Довољно је доказати да је $A M=2 A L$.\n\nИз $\\varangle B D A=\\alpha$ добијамо $\\varangle J D M=90^{\\circ}-\\frac{\\alpha}{2}=\\varangle K L A=\\varangle J M D$, па је $J M=$ $J D$, а додирна тачка уписаног круга $\\triangle B C D$ са $C D$ је средиште $T$ дужи $M D$. Према томе, $D M=2 D T=B D+C D-B C=A B-B C+C D$, одакле je\n\n$$\nA M=A D+D M=A C+A B-B C=2 A L\n$$", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2007", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Троугао $\\triangle Z C P$ је подељен на 25 „малих“ троуглова (као на слици), а затим су сва темена тих троуглова обојена са три боје на следећи начин: теме $Z$ је обојено зеленом бојом, теме $C$ црвеном, а теме $P$ плавом; свако од темена на дужи $Z C$ обојено је или зеленом или црвеном бојом, свако од темена на дужи $C P$ обојено је или црвеном или плавом бојом, а свако од темена на дужи $Z P$ обојено је или зеленом или плавом бојом. Сва темена која се налазе у унутрашњости троугла обојена су без ограничења, једном од три боје.\n\n\n\nДоказати да без обзира на начин бојења, бар један од 25 „малих “ троуглова има сва три темена различите боје.", "solution": "Посматраћемо странице малих троуглова које имају једно теме обојено црвеном, а друго плавом бојом. Такве странице ћемо звати црвено-плаве странице.\n\nСвака црвено-плава страница која се налази у унутрашњости троугла $\\triangle Z C P$ је страница тачно два мала троугла. Даље, свака црвено-плава страница која налази на једној од страница троугла $\\triangle Z C P$ по услову задатка мора припадати баш дужи $C P$. С обзиром да је теме $C$ обојено црвеном бојом а $P$ плавом, број црвено-плавих страница на дужи $C P$ је непаран.\n\nПрема томе, мора постојати бар један мали троугао који има непаран број црвено-плавих страница. Тај троугао мора да има сва три темена различите боје.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2007", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Одредити све парове природних бројева $(x, n)$ који су решења једначине\n\n$$\nx^{3}+2 x+1=2^{n}\n$$\n\nВреме за рад 270 минута.\n\nСваки задатак вреди 7 поена.\n\n## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА\n\nтакмичење ученика средњих школа из математике\n\nБеоград, 03.04.2007.\n\n## Други дан", "solution": "Провером се добија да је за $n \\leqslant 2$ једино решење пар $(1,2)$. Докажимо да за $n \\geqslant 3$ нема решења.\n\nБрој $x$ мора бити непаран, па је $x^{2}+2 \\equiv 3(\\bmod 8)$. Сада из $x\\left(x^{2}+2\\right) \\equiv-1$ $(\\bmod 8)$ следи да је $x \\equiv 5(\\bmod 8)$. Шта више, како $3 \\mid x\\left(x^{2}+2\\right)$ (уколико $3 \\nmid x$ тада $\\left.3 \\mid x^{2}+2\\right)$, мора бити $2^{n} \\equiv 1(\\bmod 3)$, па је $n$ паран број.\n\nДодавањем обема странама једнакости броја 2 добија се\n\n$$\n(x+1)\\left(x^{2}-x+3\\right)=2^{n}+2\n$$\n\nКако је $n$ паран, $2^{n}$ је потпун квадрат, па је број -2 квадратни остатак по сваком непарном простом делиоцу $p$ броја $(x+1)\\left(x^{2}-x+3\\right)$. Зато је\n\n$$\n1=\\left(\\frac{-2}{p}\\right)=\\left(\\frac{-1}{p}\\right)\\left(\\frac{2}{p}\\right)=(-1)^{\\frac{p-1}{2}}(-1)^{\\frac{p^{2}-1}{8}}=(-1)^{\\frac{(p-1)(p+5)}{8}}\n$$\n\nодакле следи да је $p$ облика $8 k+1$ или $8 k+3$. Будући производ таквих простих бројева, и сам број $x^{2}-x+3$ мора бити тог облика. Међутим, како је $x \\equiv 5(\\bmod 8)$, важи $x^{2}-x+3 \\equiv 7(\\bmod 8)$ што је контрадикција.\n\nДакле, једино решење дате једначине је $(x, n)=(1,2)$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2007", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Нека је $k$ природан број. За сваку функцију $f: \\mathbb{N} \\rightarrow \\mathbb{N}$, нека је низ функција $\\left(f_{m}\\right)_{m \\geqslant 1}$ дефинисан са $f_{1}=f$ и $f_{m+1}=f \\circ f_{m}$ за $m \\geqslant 1$. Функција $f$ је $k$-фина уколико за све $n \\in \\mathbb{N}$ важи\n\n$$\nf_{k}(n)=f(n)^{k}\n$$\n\n(a) За које $k$ постоји $1-1 k$-фина функција $f$ ?\n\n(б) За које $k$ постоји на $k$-фина фунција $f$ ?", "solution": "Свака функција је 1-фина, па је одговор на оба дела задатка потврдан. Нека је надаље $k \\geqslant 2$. Свака $k$-фина функција је 1 -1 јер из $f(m)=f(n)$ следи $m^{k}=f_{k}(m)=f_{k}(n)=n^{k}$, тј. $m=n$.\n\n(a) Одговор: ДА. Конструишимо функцију $f$ индуктивно на следећи начин. Нека је $n$ најмањи природан број чија слика није одређена.\n\n(1) ако је $n=1$, онда је $f(n)=1$;\n\n(2) ако је $n=a^{k}$ за неко цело $a>1$, дефинишемо $f(n)=f(a)^{k}$;\n\n(3) ако $n$ није потпун $k$-ти степен изаберемо најмањих $k-1$ природних бројева $n_{1}, n_{2}, \\ldots, n_{k-1}$ који нису потпуни $k$-ти степени и за које до сада нису одређене слике, и дефинишемо $f\\left(n_{1}\\right)=n_{2}, f\\left(n_{2}\\right)=n_{3}$, $\\ldots, f\\left(n_{k-1}\\right)=n_{1}^{k}$.\n\nНа овај начин функција $f$ је добро дефинисана. Покажимо да је она $k$ фина. За свако $n \\in \\mathbb{N}$ које није $k$-ти степен постоје бројеви $n_{1}, \\ldots, n_{k-1}$ из услова (3) такви да је $n_{i}=n$ за неко $1 \\leqslant i \\leqslant k-1$. Тада важи $f_{k}\\left(n_{i}\\right)=$ $f_{i}\\left(n_{1}^{k}\\right)=f_{i}\\left(n_{1}\\right)^{k}=f\\left(n_{i}\\right)^{k}$. Такође, ако је $n$ потпун $k$-ти степен, тада је $n=n_{i}^{k^{s}}$ за неко $i$ и $s$, па према (2) важи $f_{k}(n)=f_{k}\\left(n_{i}\\right)^{k^{s}}=n_{i}^{k^{s+1}}=n^{k}$, што доказује наше тврђење.\n\n(б) Одговор: НЕ. Заиста, ако је $f$ на и $k$-фина, за свако $a_{0}$ постоји низ природних бројева $a_{1}, a_{2}, \\ldots$ таквих да је $f\\left(a_{k+1}\\right)=a_{k}$ за све $k$, одакле је $a_{k}^{k}=f_{k}\\left(a_{k}\\right)=a_{0}$, што је немогуће ако $a_{0}$ није $k$-ти степен.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2007", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Дат је неједнакокраки троугао $A B C$. Нека су $A D, B E, C F$ симетрале углова овог троугла $(D \\in B C, E \\in A C, F \\in A B)$. Нека су $K_{a}, K_{b}, K_{c}$ тачке на уписаном кругу троугла $A B C$ такве да су $D K_{a}, E K_{b}, F K_{c}$ тангенте на уписани круг и да $K_{a} \\notin B C, K_{b} \\notin A C, K_{c} \\notin A B$. Нека су $A_{1}, B_{1}, C_{1}$ средишта страница $B C, C A, A B$. Доказати да се праве $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ секу на уписаном кругу троугла $A B C$.", "solution": "Докажимо да су троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ хомотетични. Да бисмо то доказали, довољно је да докажемо д�� је $K_{a} K_{b} \\| A_{1} B_{1}$, односно $K_{a} K_{b} \\| A B$ (аналогно ће следити и за друге парове страница).\n\nОзначимо $M=K_{a} K_{b} \\cap B C$, са $S$ означимо центар уписаног круга, и са $T$ означимо произвољну тачку на уписаном кругу. Означимо $\\alpha=\\varangle B A S$, $\\beta=\\varangle C B S, \\gamma=\\varangle A C S$. Користећи оријентисане углове (по модулу $180^{\\circ}$ ), добијамо $\\varangle B^{\\prime} E B=\\beta+2 \\gamma$, и аналогно $\\varangle A^{\\prime} D A=\\alpha+2 \\beta$, а одатле и $\\varangle A^{\\prime} D K_{a}=2 \\alpha+4 \\beta$. Затим, $\\varangle B^{\\prime} T K_{b}=\\varangle B^{\\prime} S E=90^{\\circ}+\\varangle B^{\\prime} E S=\\gamma-\\alpha$ и аналогно $\\varangle A^{\\prime} T K_{a}=\\beta-\\gamma$. Затим, $\\varangle A^{\\prime} T B^{\\prime}=\\varangle A^{\\prime} S C=90^{\\circ}+\\varangle A^{\\prime} C S=\\alpha+\\beta$. И на крају добијамо $\\varangle K_{a} T K_{b}=\\varangle K_{a} T A^{\\prime}+\\varangle A^{\\prime} T B^{\\prime}+\\varangle B^{\\prime} T K_{b}=2 \\gamma$.\n\nТакође, из троугла $D K_{a} M$ добијамо $\\varangle C M K_{a}=\\varangle C D K_{a}+\\varangle D K_{a} M=$ $\\varangle A^{\\prime} D K_{a}+\\varangle D K_{a} K_{b}=(2 \\alpha+4 \\beta)+\\varangle K_{a} T K_{b}=(2 \\alpha+4 \\beta)+2 \\gamma=2 \\beta$. Дакле, $\\varangle C M K_{a}=\\varangle C B A$, одакле следи да је $K_{a} K_{b} \\| A B$, што је требало доказати. Дакле, троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ су хомотетични.\n\nПриметимо такође да је коефицијент хомотетије позитиван: ако би био негативан, дужи $K_{a} A_{1}, K_{b} B_{1}, K_{c} C_{1}$ би се секле у једној тачки. Ако је $\\alpha>$ $\\beta$, онда се тачке $C_{1}$ и $K_{c}$, па и цела дуж $K_{c} C_{1}$, налазе унутар четвороугла $S F B D$. Зато, ако без умањења општости претпоставимо $\\alpha>\\beta>\\gamma$, онда $K_{c} C_{1} \\subset S F B D$, али $K_{a} A_{1} \\subset S D C E$, па су ове две дужи дисјунктне.\n\nКако су троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ хомотетични, њихови описани кругови су такође хомотетични. Али то су Ојлеров и уписани круг троугла $A B C$, респективно, и познато је да се та два круга додирују изнутра у Фојербаховој тачки троугла $A B C$. Стога (уз чињеницу да је коефицијент хомотетије позитиван), центар хомотетије је управо Фојербахова тачка. Одавде следи да се $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ секу у Фојербаховој тачки троугла $A B C$, која припада уписаном кругу троугла $A B C$, чиме је тврдјење доказано.\n\n\n\nАлтернативно решење. Нека је уписани круг троугла $A B C$ јединична кружница у комплексној равни. Тада је $a=\\frac{2 b^{\\prime} c^{\\prime}}{b^{\\prime}+c^{\\prime}}, b=\\frac{2 a^{\\prime} c^{\\prime}}{a^{\\prime}+c^{\\prime}}, c=\\frac{2 a^{\\prime} b^{\\prime}}{a^{\\prime}+b^{\\prime}}$. Затим је\n\n$$\na_{1}=\\frac{b+c}{2}=\\frac{a^{\\prime 2} b^{\\prime}+a^{\\prime 2} c^{\\prime}+2 a^{\\prime} b^{\\prime} c^{\\prime}}{\\left(a^{\\prime}+b^{\\prime}\\right)\\left(a^{\\prime}+c^{\\prime}\\right)}\n$$\n\nВредност $k_{a}$ налазимо из услова $\\frac{k_{a}}{a}=\\overline{\\left(\\frac{a^{\\prime}}{a}\\right)}$, одакле је $k_{a}=\\frac{1}{a^{\\prime}} \\overline{\\bar{a}}=\\frac{b^{\\prime} c^{\\prime}}{a^{\\prime}}$. Сада налазимо пресечну тачку $z$ уписаног круга (одакле $|z|=1$ ) и праве $K_{a} A_{1}$ (одакле $\\frac{z-k_{a}}{a_{1}-k_{a}}=\\overline{\\left(\\frac{z-k_{a}}{a_{1}-k_{a}}\\right)}$. Други услов можемо трансформисати у облик\n\n$$\n\\overline{\\left(a_{1}-k_{a}\\right)}\\left(z-k_{a}\\right)=\\left(\\frac{1}{z}-\\frac{1}{k_{a}}\\right)\\left(a_{1}-k_{a}\\right)\n$$\n\nодакле (због $\\left.z \\neq k_{a}\\right)$ следи $\\overline{\\left(a_{1}-k_{a}\\right)}=-\\frac{1}{z k_{a}}\\left(a_{1}-k_{a}\\right)$, па је\n\n$$\nz=-\\frac{1}{k_{a}} \\frac{a_{1}-k_{a}}{\\overline{\\left(a_{1}-k_{a}\\right)}}=-\\frac{\\left(a^{\\prime 2}-b^{\\prime} c^{\\prime}\\right)\\left(a^{\\prime} b^{\\prime}+a^{\\prime} c^{\\prime}+b^{\\prime} c^{\\prime}\\right)}{\\left(b^{\\prime} c^{\\prime}-a^{\\prime 2}\\right)\\left(a^{\\prime}+b^{\\prime}+c^{\\prime}\\right)}=\\frac{a^{\\prime} b^{\\prime}+a^{\\prime} c^{\\prime}+b^{\\prime} c^{\\prime}}{a^{\\prime}+b^{\\prime}+c^{\\prime}}\n$$\n\nКако је наведени израз симетричан по $a^{\\prime}, b^{\\prime}, c^{\\prime}$, аналогно се доказује да ће праве $K_{b} B_{1}$ и $K_{c} C_{1}$ сећи уписани круг у истој тачки, чиме је тврђење доказано.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2007", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Нека је $k$ природан број. Доказати да за позитивне реалне бројеве $x, y, z$ чији је збир једнак 1 , важи неједнакост\n\n$$\n\\frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}}+\\frac{y^{k+2}}{y^{k+1}+z^{k}+x^{k}}+\\frac{z^{k+2}}{z^{k+1}+x^{k}+y^{k}} \\geqslant \\frac{1}{7}\n$$\n\nКада важи једнакост?\n\nВреме за рад 270 минута.\n\nСваки задатак вреди 7 поена.\n\n## РЕШЕЊА", "solution": "Дати израз је симетричан, па се без губљења општости може претпоставити да је $x \\geqslant y \\geqslant z$. Тада је\n\n$$\nx^{k+1}+y^{k}+z^{k} \\leqslant y^{k+1}+z^{k}+x^{k} \\leqslant z^{k+1}+x^{k}+y^{k}\n$$\n\nЗаиста, довољно је доказати прву неједнакост, тј. да је $x^{k+1}+y^{k} \\leqslant y^{k+1}+$ $x^{k}$. Ова неједнакост је еквивалентна са $\\left(\\frac{y}{x}\\right)^{k} \\leqslant \\frac{1-x}{1-y}$. Како је $y \\leqslant x$, довољно је доказати да је $\\frac{y}{x} \\leqslant \\frac{1-x}{1-y}$, што је еквивалентно тачној неједнакости $0 \\leqslant$ $x-x^{2}-y+y^{2}=(x-y)(1-x-y)=(x-y) z$. Применом неједнакости Чебишева на тројке $\\left(x^{k+2}, y^{k+2}, z^{k+2}\\right)$ и $\\left(\\frac{1}{x^{k+1}+y^{k}+z^{k}}, \\frac{1}{y^{k+1}+z^{k}+x^{k}}, \\frac{1}{z^{k+1}+x^{k}+y^{k}}\\right)$ добија се\n\n$$\n\\sum_{\\text {cyc }} \\frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}} \\geqslant \\frac{1}{3} \\sum_{\\text {cyc }} x^{k+2} \\sum_{\\text {cyc }} \\frac{1}{x^{k+1}+y^{k}+z^{k}}=L\n$$\n\nУколико се у $L$ поново примени неједнакост Чебишева на тројке $(x, y, z)$ и $\\left(x^{k+1}, y^{k+1}, z^{k+1}\\right)$ добија се\n\n$$\nL \\geqslant \\frac{1}{3} \\cdot \\frac{1}{3} \\sum_{\\text {cyc }} x \\sum_{\\text {cyc }} x^{k+1} \\sum_{\\text {cyc }} \\frac{1}{x^{k+1}+y^{k}+z^{k}}=L^{\\prime}\n$$\n\nИз неједнакости Коши-Шварц-Буњаковског следи\n\n$$\n\\sum_{\\text {cyc }} \\frac{1}{x^{k+1}+y^{k}+z^{k}} \\sum_{\\text {cyc }}\\left(x^{k+1}+y^{k}+z^{k}\\right) \\geqslant 9\n$$\n\nпа је\n\n$$\nL^{\\prime} \\geqslant \\frac{x^{k+1}+y^{k+1}+z^{k+1}}{x^{k+1}+y^{k+1}+z^{k+1}+2\\left(x^{k}+y^{k}+z^{k}\\right)}\n$$\n\nи самим тим довољно је доказати да је\n\n$$\n3\\left(x^{k+1}+y^{k+1}+z^{k+1}\\right) \\geqslant x^{k}+y^{k}+z^{k}\n$$\n\nПоследња неједнакост се добија поновном применом неједнакости Чебишева на тројке $(x, y, z)$ и $\\left(x^{k}, y^{k}, z^{k}\\right)$.\n\nЈеднакост у свим примењеним неједнакостима важи ако и само ако је $x=y=z$, тј. ако и само ако је $x=y=z=\\frac{1}{3}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2008_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2008", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "У скупу целих бројева решити једначину\n\n$$\n12^{x}+y^{4}=2008^{z} . \\quad \\text { (Милош Милосављевић) }\n$$", "solution": "За $x<0$ или $z \\leq 0$ једино решење је тривијално $(0,0,0)$. Надаље је $z>0$. Како је $2008=2^{3} \\cdot 251$, обе стране једначине су дељиве са 251. Претпоставимо да је $x=2 x_{1}$ парно. Тада $\\left(2^{x_{1}}\\right)^{2} \\equiv-\\left(y^{2}\\right)^{2}(\\bmod 251)$, што дизанјем на 125 -ти степен даје $1 \\equiv\\left(2^{x_{1}}\\right)^{250} \\equiv-\\left(y^{2}\\right)^{250} \\equiv-1$ по малој Фермаовој теореми, а то је немогуће. Према томе, $x$ мора бити непарно.\n\nОчигледно је $y$ парно. Напишимо $y=2^{u} y_{1}$ за непарно $y_{1}$. Имамо\n\n$$\n2^{2 x} 3^{x}+2^{4 u} y_{1}^{4}=2^{3 z} 251^{z}\n$$\n\nКако је $2 x \\neq 4 u$ јер је $x$ непарно, највећи степен двојке који дели леву страну је $2^{2 x}$ или $2^{4 u}$, док је највећи степен двојке који дели десну страну једнак $2^{3 z}$, одакле је $3 z=2 x$ или $3 z=4 u$. Показаћемо да ни у једном од ова два случаја дата једначина нема решења.\n\n(i) $3 z=2 x<4 u$; дакле, $2 \\mid z$. Скраћивање са $2^{2 x}$ даје $3^{x}+2^{4 u-2 x} y_{1}^{4}=251^{z}$ што је немогуће јер је лева страна облика $4 k+3$ (јер $2 \\nmid x$ ), а десна облика $4 k+1(k \\in \\mathbb{N})$.\n\n(ii) $3 z=4 u<2 x$; опет $2 \\mid z$. Скраћивање са $2^{4 u}$ даје $2^{2 x-4 u} 3^{x}+y_{1}^{4}=251^{z}$. Десна страна је облика $5 k+1$, па за $5 \\nmid y_{1}$ имамо $y_{1}^{4} \\equiv 1$ и $2^{2 x-4 u} 3^{x} \\equiv 0$ $(\\bmod 5)$ што је немогуће, док за $5 \\mid y_{1}$ имамо $1 \\equiv 2^{2 x-4 u} 3^{x} \\equiv \\pm 3^{x} \\equiv \\pm 3$ $(\\bmod 5)$ jep $2 \\nmid x$, опет немогуће.\n\nДруго решење. За парно $x$ лева страна једначине је облика $a^{2}+b^{2}$, а за непарно $x$ лева страна је облика $a^{2}+3 b^{2}$. Међутим, како су -1 и -3 квадратни неостаци по модулу 251 , ни $a^{2}+b^{2}$ ни $a^{2}+3 b^{2}$ не могу да буду дељиви са 251 ако $251 \\nmid$. Према томе, дата једначина нема целобројних решења за $z \\geq 0$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2008", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Дат је троугао $A B C$. Нека су тачке $D$ и $E$ на правој $A B$ такве да је $D-A-B-E, A D=A C$ и $B E=B C$. Симетрале унутрашњих углова код темена $A$ и $B$ секу наспрамне странице у тачкама $P$ и $Q$, редом, а описану кружницу око троугла $A B C$ у тачкама $M$ и $N$, редом. Права која спаја тачку $A$ са центром кружнице описане око троугла $B M E$ и права која спаја тачку $B$ са центром кружнице описане око троугла $A N D$ секу ce у тачки $X, X \\neq C$. Доказати да је $C X \\perp P Q$. (Дуиан Ђукић)", "solution": "Означимо са $U$ центар описаног круга $\\triangle B M E$. Применимо инверзију са центром $A$ и квадратом полупречника $A B \\cdot A C$. Тачке $B$ и $C$ се сликају у тачке $B^{\\prime}$ и $C^{\\prime}$ симетричне тачкама $C$ и $B$ у односу на $A P$, тачке $P$ и $M$ се сликају једна у другу, а $E$ се слика у тачку $E^{\\prime}$ симетричну $Q$ у односу на $A P$. Према томе, права $A U$ се поклапа са правом која спаја $A$ са центром круга $B^{\\prime} P E^{\\prime}$ (наравно, центри се не сликају један у други!). Видимо да је та права симетрична\n\n\nправој $A Z$ у односу на симетралу угла $A$, где је $Z$ центар круга описаног око $\\triangle C P Q$.\n\nАналогно се добија да је права $B Z$ симетрична правој која спаја $B$ са центром $V$ круга $A N D$ у односу на симетралу угла $B$. По Чевиној теореми у тригонометријском облику (или по тврђењу о изогонално спрегнутим тачкама), праве симетричне правим $A U, B V, C X$ у односу на симетрале углова $A, B, C$ редом се такође секу у једној тачки, што значи да је права $C Z$ симетрична $C X$ у односу на симетралу угла $C$. Али $Z$ је центар круга $C P Q$, одакле следи да права $C X$ садржи висину троугла $C P Q$, а то смо и желели да докажемо.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2008", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Доказати да за позитивне реалне бројеве $a, b$ и $c$, такве да је $a+b+c=1$, важи неједнакост\n\n$$\n\\frac{1}{b c+a+\\frac{1}{a}}+\\frac{1}{c a+b+\\frac{1}{b}}+\\frac{1}{a b+c+\\frac{1}{c}} \\leqslant \\frac{27}{31}\n$$\n\n(Марко Радовановић са сараунииима)\n\nВреме за рад 270 минута.\n\nСваки задатак вреди 7 поена.\n\n## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА\n\nтакмичење ученика средњих школа из математике\n\nБеоград, 13.04.2008.\n\n## Други дан", "solution": "Тражена неједнакост је очигледно еквивалентна неједнакости\n\n$$\n\\frac{a}{p+a^{2}}+\\frac{b}{p+b^{2}}+\\frac{c}{p+c^{2}} \\leq \\frac{27}{31}\n$$\n\nгде је $a+b+c=1$ и $p=a b c+1$. Посматраћемо функцију\n\n$$\nf(x)=\\frac{3(a+b+c)}{3 x+a^{2}+b^{2}+c^{2}}-\\frac{a}{x+a^{2}}-\\frac{b}{x+b^{2}}-\\frac{c}{x+c^{2}}\n$$\n\nДоказаћемо да важи $f(x) \\geq 0$ за све $x \\geq a b+b c+c a$. Свођење израза за $f(x)$ на заједнички именилац даје\n\n$$\nf(x)=\\frac{A x^{2}+B x+C}{\\left(x+a^{2}\\right)\\left(x+b^{2}\\right)\\left(x+c^{2}\\right)\\left(3 x+a^{2}+b^{2}+c^{2}\\right)}\n$$\n\nпри чему је $A \\geq 0 \\geq C$. Заправо, лако се добија\n\n$$\n\\begin{gathered}\nA=2 a^{3}+2 b^{3}+2 c^{3}-a b(a+b)-a c(a+c)-b c(b+c) \\geq 0 \\\\\nC=-a b c\\left[a\\left(b^{3}+c^{3}\\right)+b\\left(c^{3}+a^{3}\\right)+c\\left(a^{3}+b^{3}\\right)-2 a b c(a+b+c)\\right] \\leq 0\n\\end{gathered}\n$$\n\nПриметимо да није важно колико је $B$. Према томе, полином $P(x)=$ $A x^{2}+B x+C$ (ако није константно 0 ) има две реалне нуле, једну позитивну (рецимо $x=x_{0}$ ) и једну негативну, и важи $P(x) \\leq 0$ за $0 \\leq x \\leq x_{0}$ и $P(x) \\geq 0$ за $x \\geq x_{0}$. Тврдимо да је $f(a b+b c+c a) \\geq 0$. Заиста,\n\n$$\n\\begin{aligned}\n& f(a b+b c+c a) \\\\\n& =\\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)}-\\frac{a}{(a+b)(a+c)}-\\frac{b}{(b+c)(b+a)}-\\frac{c}{(c+a)(c+b)} \\\\\n& =\\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)}-\\frac{2(a b+b c+c a)}{(a+b)(b+c)(c+a)} \\geq 0 \\quad \\text { jep je } \\\\\n& \\quad \\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)} \\geq \\frac{9}{4(a+b+c)} \\geq \\frac{2(a b+b c+c a)}{(a+b)(b+c)(c+a)},\n\\end{aligned}\n$$\n\nшто смо и желели. Према томе, $P(a b+b c+c a) \\geq 0$, тј. $x_{0} \\leq a b+b c+c a$, одакле следи да је и $P(x) \\geq 0$ и $f(x) \\geq 0$ за све $x \\geq a b+b c+c a$. Између осталог, $f(1+a b c) \\geq 0$ јер је $1+a b c>1>a b+b c+c a$. Тако смо доказали\n\n$$\n\\frac{a}{1+a b c+a^{2}}+\\frac{b}{1+a b c+b^{2}}+\\frac{c}{1+a b c+c^{2}} \\leq \\frac{3}{3+a^{2}+b^{2}+c^{2}+3 a b c}\n$$\n\nОстаје још само да докажемо да је $a^{2}+b^{2}+c^{2}+3 a b c \\geq \\frac{4}{9}$, што ће заједно са (1) дати тражену неједнакост. Хомогенизација даје $9(a+b+c)\\left(a^{2}+b^{2}+\\right.$ $\\left.c^{2}\\right)+27 a b c \\geq 4(a+b+c)^{3}$, што је еквивалентно са\n\n$$\n5\\left(a^{3}+b^{3}+c^{3}\\right)+3 a b c \\geq 3(a b(a+b)+a c(a+c)+b c(b+c))\n$$\n\nПоследња неједнакост одмах следи из Шурове неједнакости. Овим је доказ тврђења задатка коначно завршен.\n\nДруго решење. Након хомогенизације, свођења на заједнички именилац и скраћивања неједнакост се своди на симетричну неједнакост која се директно доказује Мјурхедовом неједнакошћу:\n\n$$\n\\begin{aligned}\n& \\frac{23}{2} T_{900}+122 T_{810}+260 T_{720}+282 T_{630}+193 T_{540}+\\frac{547}{2} T_{711}+807 T_{620}+284 T_{531} \\\\\n&+91 T_{522}-98 T_{441}-1669 T_{432}-557 T_{333} \\geq 0\n\\end{aligned}\n$$\n\nгде је $T_{i j k}$ симетрична сума $x^{i} y^{j} z^{k}+\\cdots$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2008", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Свака тачка равни је обојена са једном од 3 боје. Доказати да постоји троугао за који важи:\n\n$1^{\\circ}$ сва 3 темена тог троугла су обојена истом бојом;\n\n$2^{\\circ}$ полупречник описане кружнице тог троугла је 2008;\n\n$3^{\\circ}$ један угао троугла је два или три пута већи од неког од друга два угла.\n\n", "solution": "Уочимо правилан тринаестоугао $A_{1} A_{2} \\ldots A_{13}$ уписан у круг полупречника 2008. По Дирихлеовом принципу постоји пет темена која су исте боје (нпр. црвене). Разликујемо два случаја.\n\n(i) Међу пет црвених темена не постоје два суседна. Сваком положају црвених тачака (до на ротацију) одговара композиција броја 13 на 5 сабирака већих од 1. Постоји 5 неподударних распореда и они су приказани на слици испод, са истакнутим троуглом.\n\n\n\n(ii) Нека два црвена темена су суседна, рецимо $A_{1}$ и $A_{2}$. Ако је црвена било која од тачака $A_{4}, A_{5}, A_{6}, A_{10}, A_{11}, A_{12}$, тражени троугао је\nодређен том тачком и теменима $A_{1}, A_{2}$. Надаље претпостављамо да ниједна од ових 6 тачака није црвена. Тада су међу теменима $A_{3}, A_{7}$, $A_{8}, A_{9}, A_{13}$ бар три црвена. Ако је међу њима $A_{3}$ (аналогно за $A_{13}$ ), онда је бар једна од тачака $A_{7}, A_{9}, A_{13}$ црвена па бар један од троуглова одређених овом тачком и тачкама $A_{1}$ и $A_{3}$ задовољава услове. Једини преостали случај је кад су црвене тачке $A_{7}, A_{8}, A_{9}$, а онда је троугао $A_{1} A_{7} A_{9}$ тражени.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2008", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Нека је низ $\\left(a_{n}\\right)_{n \\geqslant 1}$ дефинисан са $a_{1}=3, a_{2}=11$ и $a_{n}=4 a_{n-1}-a_{n-2}$, за $n \\geqslant 3$. Доказати да је сваки члан овог низа облика $a^{2}+2 b^{2}$ за неке природне $a$ и $b$.\n\n(Ђорђе Баралић)", "solution": "Имамо $a_{1}=1+2 \\cdot 1^{2}, a_{2}=3^{2}+2 \\cdot 1^{2}, a_{3}=3^{2}+2 \\cdot 4^{2}, a_{4}=11^{2}+2 \\cdot 4^{2}$, итд. Доказаћемо индукцијом по $n$ да важи\n\n$$\na_{2 n-1}=a_{n-1}^{2}+2\\left(\\frac{a_{n}-a_{n-1}}{2}\\right)^{2} \\quad \\text { и } \\quad a_{2 n}=a_{n}^{2}+2\\left(\\frac{a_{n}-a_{n-1}}{2}\\right)^{2},\n$$\n\nпри чему је $a_{0}=1$. Претпоставимо да тврђење важи за $n$. Тада је\n\n$$\n\\begin{aligned}\na_{2 n+1} & =4 a_{2 n}-a_{2 n-1}=4 a_{n}^{2}+8\\left(\\frac{a_{n}-a_{n-1}}{2}\\right)^{2}-a_{n-1}^{2}-2\\left(\\frac{a_{n}-a_{n-1}}{2}\\right)^{2} \\\\\n& =\\frac{11}{2} a_{n}^{2}-3 a_{n} a_{n-1}+\\frac{1}{2} a_{n-1}^{2}=\\frac{11}{2} a_{n}^{2}-3 a_{n}\\left(4 a_{n}-a_{n+1}\\right)+\\frac{1}{2}\\left(4 a_{n}-a_{n+1}\\right)^{2} \\\\\n& =\\frac{3}{2} a_{n}^{2}-a_{n} a_{n+1}+\\frac{1}{2} a_{n+1}^{2}=a_{n}^{2}+2\\left(\\frac{a_{n+1}-a_{n}}{2}\\right)^{2} \\\\\na_{2 n+2} & =4 a_{2 n+1}-a_{2 n}=4 a_{n}^{2}+8\\left(\\frac{a_{n+1}-a_{n}}{2}\\right)^{2}-a_{n}^{2}-2\\left(\\frac{a_{n}-a_{n-1}}{2}\\right)^{2} \\\\\n& =3 a_{n}^{2}+8\\left(\\frac{a_{n+1}-a_{n}}{2}\\right)^{2}-2\\left(\\frac{a_{n+1}-3 a_{n}}{2}\\right)^{2}=\\frac{3}{2} a_{n+1}^{2}-a_{n} a_{n+1}+\\frac{1}{2} a_{n}^{2} \\\\\n& =a_{n+1}^{2}+2\\left(\\frac{a_{n+1}-a_{n}}{2}\\right)^{2},\n\\end{aligned}\n$$\n\nчиме је доказ завршен.\n\nДруго решење. Познато је да се непаран природан број $m>1$ може представити у облику $a^{2}+2 b^{2}$ за неке узајамно просте $a, b \\in \\mathbb{N}$ ако и само ако су сви прости делиоци $m$ облика $8 k+1$ или $8 k+3, k \\in \\mathbb{N}_{0}$. Лако се види да су сви чланови низа ( $a_{n}$ ) непарни; остаје да покажемо да ако прост број $p$ дели $a_{n}$, онда је $p=8 k+1$ или $8 k+3$ за неко $k \\in \\mathbb{N}_{0}$.\n\nПоказује се индукцијом по $n$ да је $a_{n} a_{n+2}=a_{n+1}^{2}+2$. Заиста, ово важи за $n \\leq 2$, а за $n>2$, уз претпоставку да важи за $n-2$, имамо\n\n$$\n\\begin{aligned}\n\\frac{a_{n+1}^{2}+2}{a_{n}} & =\\frac{\\left(4 a_{n}-a_{n-1}\\right)^{2}+2}{a_{n}}=16 a_{n}-8 a_{n-1}+\\frac{a_{n-1}^{2}+2}{a_{n}} \\\\\n& =16 a_{n}-8 a_{n-1}+a_{n-2}=4 a_{n+1}-a_{n}=a_{n+2}\n\\end{aligned}\n$$\n\nОдавде следи да је -2 квадратни остатак по сваком простом делиоцу $p$ броја $a_{n}$, па је $p \\equiv 1$ или $p \\equiv 3(\\bmod 8)$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2008", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Нека је $A B C D E$ конвескан петоугао у коме је $A B=1, \\varangle B A E=\\varangle A B C=$ $120^{\\circ}, \\varangle C D E=60^{\\circ}$ и $\\varangle A D B=30^{\\circ}$. Доказати да је површина петоугла $A B C D E$ мања од $\\sqrt{3}$.\n\n(Милош Милосављевић)\n\n## РЕШЕЊА", "solution": "Нека је $k$ круг описан око троугла $A B D$, и $l$ права кроз $D$ паралелна са\n$A B$. Полупречник круга $k$ је 1 . Полуправе $B C$ и $A E$ секу $k$ у тачкама $H$ и $I$, а праву $l$ у $F$ и $G$, редом. Троуглови $F C D$ и $G D E$ су слични јер је $\\angle C F D=\\angle D G E=60^{\\circ}$ и $\\angle F C D=120^{\\circ}-\\angle C D F=\\angle G D E$. Означимо са $k=\\frac{F C}{G D}=\\frac{F D}{G E}$ коефи-\n\n\nцијент сличности, са $h$ растојање тачке $D$ од $H I$, и $x=F D, y=G D$. Лако се налази да је $x+y=2+\\frac{2}{\\sqrt{3}} h$ и $x y=\\frac{4}{3} h^{2}+\\frac{2}{\\sqrt{3}} h$ (производ $x y$ је потенција тачке $F$ у односу на $k$ и једнак је $O F^{2}-1$, где је $O$ центар круга $k$ ). Тако добијамо\n\n$$\n\\begin{aligned}\n& P_{A B F G}=\\frac{1}{2}(1+x+y)\\left(\\frac{\\sqrt{3}}{2}+h\\right)=\\frac{1}{\\sqrt{3}} h^{2}+2 h+\\frac{3 \\sqrt{3}}{4} \\\\\n& P_{F C D}+P_{G D E}=\\frac{1}{2}(x \\cdot F C+y \\cdot G E) \\sin 60^{\\circ}=\\frac{\\sqrt{3}}{4} x y\\left(k+\\frac{1}{k}\\right) \\geq \\frac{\\sqrt{3}}{2} x y=\\frac{2}{\\sqrt{3}} h^{2}+h\n\\end{aligned}\n$$\n\nпа је\n\n$$\nP_{A B C D E}=P_{A B F G}-\\left(P_{F C D}+P_{G D E}\\right) \\leq-\\frac{1}{\\sqrt{3}} h^{2}+h+\\frac{3 \\sqrt{3}}{4}=f(h)\n$$\n\nКвадратна функција $f(h)$ достиже максимум за $h=\\frac{\\sqrt{3}}{2}$, чиме је доказано да је $P_{A B C D E} \\leq \\sqrt{3}$. Једнакост би важила само ако је $h=\\frac{\\sqrt{3}}{2}$ и $k=$ 1; тада би (ако без смањења општости претпоставимо $D A \\geq D B$ ) тачка $D$ била симетрична тачки $B$ у односу на $H I$, па би троугао $A D G$ био једнакостраничан и $F C=G D=G A=F B$ што је немогуће јер би се $B$ и $C$ поклапале. Зато је горња неједнакост строга.\n\nДруго решење. Претпоставимо да троугао $A B D$ није тупоугли. Тада се тачке $C^{\\prime}$ и $E^{\\prime}$ симетричне тачкама $C$ и $E$ у односу на праве $B D$ и $A D$ редом налазе унутар троугла $A B D$, на истој правој кроз $D$, и важи\n\n$S_{A B C D E}=S_{A B D}+S_{A D E}+S_{B D C}=S_{A B D}+S_{A D E^{\\prime}}+S_{B D C^{\\prime}} \\leq 2 S_{A B D}-S_{A B F}$, при чему $F$ тачка пресека правих $A E^{\\prime}$ и $B C^{\\prime}$. Једнакост важи ако и само ако је $F \\equiv C^{\\prime} \\equiv E^{\\prime}$. Означимо $\\angle B A D=\\alpha$. Тада је $\\angle A B D=150^{\\circ}-\\alpha$, $\\angle B A F=2 \\alpha-120^{\\circ}, \\angle A B F=180^{\\circ}-2 \\alpha$, па важи\n\n$$\n\\begin{aligned}\n& S_{A B D}=\\sin \\alpha \\sin \\left(150^{\\circ}-\\alpha\\right)=\\frac{\\sqrt{3}}{4}+\\frac{1}{2} \\cos \\left(150^{\\circ}-2 \\alpha\\right)=\\frac{\\sqrt{3}}{4}+\\frac{1}{2} u \\\\\n& S_{A B F}=\\frac{1}{\\sqrt{3}} \\sin \\left(2 \\alpha-120^{\\circ}\\right) \\sin 2 \\alpha=-\\frac{\\sqrt{3}}{12}+\\frac{\\sqrt{3}}{6} \\cos \\left(300^{\\circ}-4 \\alpha\\right)=-\\frac{\\sqrt{3}}{4}+\\frac{1}{\\sqrt{3}} u^{2}\n\\end{aligned}\n$$\n\nгде је $\\cos \\left(150^{\\circ}-2 \\alpha\\right)=u$ и одатле $\\cos \\left(300^{\\circ}-4 \\alpha\\right)=2 u^{2}-1$. Сада имамо\n\n$$\nS_{A B C D E} \\leq 2 S_{A B D}-S_{A B F}=\\frac{3 \\sqrt{3}}{4}+u-\\frac{u^{2}}{\\sqrt{3}} \\leq \\sqrt{3}\n$$\n\nуз једнакост која би важила за $u=\\frac{\\sqrt{3}}{2}$, тј. $\\alpha \\in\\left\\{60^{\\circ}, 90^{\\circ}\\right\\}$, и $F \\equiv C^{\\prime} \\equiv E^{\\prime}$, али се никада не достиже јер се за ове вредности $\\alpha$ тачка $F$ налази у темену правог угла, па је петоугао дегенерисан.\n\nУ случају тупоуглог троугла $A B D$, уз исте ознаке, тачка $F$ се налази изван троугла $A B D$, али горњи израз за површину $\\triangle A B F$ узима негативне вредности, па се опет добија $S_{A B C D E} \\leq \\frac{3 \\sqrt{3}}{4}+u-\\frac{u^{2}}{\\sqrt{3}}<\\sqrt{3}$.\n\n$\\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim \\sim)$\n\nhttp://srb.imomath.com/", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2009_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2009", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Нека су $\\alpha$ и $\\beta$ углови неједнакокраког троугла $A B C$ код темена $A$ и $B$, редом. Нека симетрале ових углова секу наспрамне странице троугла у $D$ и $E$, редом. Доказати да оштар угао између правих $D E$ и $A B$ није већи од $\\frac{|\\alpha-\\beta|}{3}$.\n\n(Душан Ђукић)", "solution": "Као и обично, означимо $\\varangle A C B=\\gamma$ и $B C=a, C A=b, A B=c$, при чему је без смањења општости $a>b$ и $\\alpha>\\beta$. Нека је $F$ тачка пресека правих $D E$ и $A B$, а $\\varphi$ угао између ових правих. Из односа $\\frac{B D}{D C}=\\frac{c}{b}$ и $\\frac{C E}{E A}=\\frac{a}{c}$ лако налазимо $B D=\\frac{a c}{b+c}, D C=\\frac{a b}{b+c}$, $C E=\\frac{a b}{a+c}$ и $E A=\\frac{b c}{a+c}$. Менелајева теорема за праву $D E$ и троугао $A B C$ даје $A F=\\frac{b c}{a-b}$ и $F B=\\frac{a c}{a-b}$.\n\n\n\nСада на основу синусне теореме у троугловима $F E A$ и $F D B$ имамо\n\n$$\n\\begin{aligned}\n& \\frac{\\sin (\\alpha-\\varphi)}{\\sin \\varphi}=\\frac{\\sin \\varangle F E A}{\\sin \\varangle E F A}=\\frac{F A}{E A}=\\frac{\\frac{b c}{a-b}}{\\frac{b c}{a+c}}=\\frac{a+c}{a-b} \\\\\n& \\frac{\\sin (\\beta+\\varphi)}{\\sin \\varphi}=\\frac{\\sin \\varangle F D B}{\\sin \\varangle D F B}=\\frac{F B}{D B}=\\frac{\\frac{a c}{a-b}}{\\frac{a c}{b+c}}=\\frac{b+c}{a-b}\n\\end{aligned}\n$$\n\nиз чега добијамо $\\sin \\varphi=\\sin (\\alpha-\\varphi)-\\sin (\\beta+\\varphi)=2 \\sin \\frac{\\alpha-\\beta-2 \\varphi}{2} \\cos \\frac{\\alpha+\\beta}{2}<$ $\\sin (\\alpha-\\beta-2 \\varphi)$. Одавде је $\\varphi<\\alpha-\\beta-2 \\varphi$, тј. $3 \\varphi<\\alpha-\\beta$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2009", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Одредити најмањи природан број који је дељив са 2009 и коме је збир цифара једнак 2009.", "solution": "Пошто је $2009=223 \\cdot 9+2$, тражени број има бар 224 цифре. Посматраћемо 224 -цифрене бројеве $x=\\overline{c_{223} c_{222} \\ldots c_{1} c_{0}}$. Јасно је да је $c_{223} \\geq 2$. Притом, ако је $c_{223}=2$ онда је $c_{222}=\\cdots=c_{0}=9$ и $x=3 \\cdot 10^{223}-1 \\equiv 3 \\cdot 10-1$, а то није дељиво са $2009=7^{2} \\cdot 41$ јер је $x \\equiv 1(\\bmod 7)$.\n\nНека је сада $c_{223}=3$. Тада број $x$ има облик $399 \\ldots 9899 \\ldots 9=4 \\cdot 10^{223}-$ $10^{i}-1$ за неко $i$. Како је $10^{5} \\equiv 1(\\bmod 41)$, имамо $10^{i} \\equiv 1,10,18,16$ или 37 $(\\bmod 41)$ за $i=0,1,2,3,4(\\bmod 5)$ редом, и одатле $x \\equiv 4 \\cdot 10^{3}-10^{i}-1 \\equiv 22-10^{i}$ $(\\bmod 41)$ никад није дељиво са 41.\n\nНека је $c_{223}=4$. Међу цифрама $c_{222}, \\ldots, c_{0}$ налазе се две осмице или једна седмица, док су све остале деветке; у сваком случају, $x=5 \\cdot 10^{223}-10^{i}$ $10^{j}-1 \\equiv 38-\\left(10^{i}+10^{j}\\right)(\\bmod 41)$, где $i$ и $j$ нису обавезно различити. По претходном је $10^{i}+10^{j} \\equiv 38(\\bmod 41)$ ако и само ако је $(i, j) \\equiv(0,4)$ или $(4,0)(\\bmod 5)$. Између осталог, $i \\neq j$ и $i, j \\leq 220$.\n\nПробајмо да ставимо $j=220$ и $i \\equiv 4(\\bmod 5)$. Треба одабрати $i$, ако постоји, тако да $7^{2} \\mid x=5 \\cdot 10^{223}-10^{220}-10^{i}-1 \\equiv 5 \\cdot 10^{13}-10^{10}-10^{i}-1 \\equiv 31-10^{i}$ $(\\bmod 49)$. Лако налазимо да је $10^{i} \\equiv 31(\\bmod 49)$ ако и само ако је $i \\equiv 7$ $(\\bmod 42)$, што заједно са $i \\equiv 4(\\bmod 5)$ даје као једину могућност $i=49$. Према томе, тражени број је\n\n$$\n4998 \\underbrace{9 \\ldots 99}_{170} 8 \\underbrace{99 \\ldots 9}_{49} .\n$$", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2009", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Одредити највећи природан број $n$ за који постоје различити скупови $S_{1}, S_{2}, \\ldots, S_{n}$ такви да је:\n\n$1^{\\circ}\\left|S_{i} \\cup S_{j}\\right| \\leqslant 2004$ за свака два цела броја $1 \\leqslant i, j \\leqslant n$, и\n\n$2^{\\circ} S_{i} \\cup S_{j} \\cup S_{k}=\\{1,2, \\ldots, 2008\\}$ за свака три цела броја $1 \\leqslant i<j<k \\leqslant n$.\n\n(Иван Матић)\n\n## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА\n\nтакмичење ученика средњих школа из математике\n\nНови Сад, 14.04.2009.\n\n## Други дан", "solution": "Сваки скуп $S_{i}$ има највише 2003 елемената. Заиста, ако је $\\left|S_{i}\\right|=2004$, из услова $1^{\\circ}$ следи да је $S_{j} \\subset S_{i}$ за све $j$, противно услову $2^{\\circ}$. Посматрајмо скупове\n\n$$\nG_{\\{i, j\\}}=\\{1,2, \\ldots, 2008\\} \\backslash\\left(S_{i} \\cup S_{j}\\right) \\quad \\text { за } 1 \\leq i, j \\leq n\n$$\n\nТада је $\\left|G_{\\{i, j\\}}\\right| \\geqslant 4$ и свих $\\binom{n}{2}$ скупова $G_{\\{i, j\\}}$ су међусобно дисјунктни (у супротном, ако $x \\in G_{\\{i, j\\}} \\cap G_{\\{k, l\\}}$, онда $x \\notin S_{i} \\cup S_{j} \\cup S_{k} \\cup S_{l}$, што је немогуће ако су бар три међу $i, j, k, l$ различита). Следи да је $4\\binom{n}{2} \\leqslant 2008$, одакле je $n \\leqslant 32$.\n\nКонструисаћемо 32 скупа који задовољавају $1^{\\circ}$ и $2^{\\circ}$. Разложимо скуп $\\{1,2, \\ldots, 2008\\}$ произвољно на $\\binom{32}{2}=496$ (дисјунктних) скупова $G_{\\{i, j\\}}$, при чему је $\\left|G_{\\{i, j\\}}\\right| \\geqslant 4$ за $1 \\leqslant i, j \\leqslant 32$, и дефинишимо\n\n$$\nS_{i}=\\{1,2, \\ldots, 2008\\} \\backslash \\bigcup_{j \\neq i} G_{\\{i, j\\}} \\quad \\text { за } i=1, \\ldots, 32\n$$\n\nУслов $1^{\\circ}$ је аутоматски задовољен. Осим тога, свако $s \\in\\{1,2, \\ldots, 2008\\}$ припада највише једном од скупова $G_{\\{p, q\\}}$, што значи да постоје највише два скупа $S_{i}$ који га не садрже (то су $S_{p}$ и $S_{q}$ ), па је и услов $2^{\\circ}$ задовољен. Према томе, одговор је $n=32$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2009", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Нека је $n \\in \\mathbb{N}$ и $A_{n}$ скуп свих пермутација $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ скупа $\\{1,2, \\ldots, n\\}$ таквих да важи\n\n$$\nk \\mid 2\\left(a_{1}+a_{2}+\\cdots+a_{k}\\right) \\quad \\text { за свако } 1 \\leqslant k \\leqslant n\n$$\n\nОдредити број елемената скупа $A_{n}$.\n\n(Видан Говедарииа)", "solution": "Означимо са $F_{n}$ број елемената скупа $A_{n}$. Имамо $F_{1}=1, F_{2}=2$ и $F_{3}=6$. За $n>3$, посматрајмо било коју пермутацију $\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ у $A_{n}$. Како $n-1$ дели $2\\left(a_{1}+\\cdots+a_{n-1}\\right)=n(n+1)-2 a_{n} \\equiv 2-2 a_{n}(\\bmod n-1)$, следи да је $a_{n}$ једнако $1, \\frac{n+1}{2}$ или $n$.\n\nПретпоставимо да је $a_{n}=\\frac{n+1}{2}$. Тада $n-2$ дели $2\\left(a_{1}+\\cdots+a_{n-2}\\right)=n^{2}-$ $1-2 a_{n-1} \\equiv 3-2 a_{n-1}(\\bmod n-2)$. Зато мора бити $2 a_{n-1}-3=n-2$, али тада је $a_{n-1}=\\frac{n+1}{2}=a_{n}$, контрадикција.\n\nАко је $a_{n}=n$, онда је $\\left(a_{1}, \\ldots, a_{n}\\right) \\rightarrow\\left(a_{1}, \\ldots, a_{n-1}\\right)$ бијективно пресликавање у скуп $A_{n-1}$, па оваквих пермутација има $F_{n-1}$.\n\nАко је $a_{n}=1$, онда је $\\left(a_{1}-1, \\ldots, a_{n-1}-1\\right)$ пермутација на $\\{1, \\ldots, n-1\\}$ која припада скупу $A_{n-1}$ јер је $2\\left(\\left(a_{1}-1\\right)+\\cdots+\\left(a_{k}-1\\right)\\right)=2\\left(a_{1}+\\cdots+a_{k}\\right)-2 k$ дељиво са $k$ за $1 \\leqslant k \\leqslant n-1$. Као и у претходном случају, оваквих пермутација има $F_{n-1}$.\n\nЗакључујемо да је $F_{n}=2 F_{n-1}$ за $n>3$, што заједно са $F_{3}=6$ даје $F_{n}=$ $3 \\cdot 2^{n-2}$ за $n \\geqslant 3$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2009", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Нека су $x, y, z$ позитивни реални бројеви такви да је $x y+y z+z x=x+y+z$. Доказати неједнакост\n\n$$\n\\frac{1}{x^{2}+y+1}+\\frac{1}{y^{2}+z+1}+\\frac{1}{z^{2}+x+1} \\leqslant 1\n$$\n\nКада се у претходној неједнакости достиже знак једнакости?\n\n(Марко Радовановић)", "solution": "Коши-Шварцова неједнакост за тројке $(x, \\sqrt{y}, 1)$ и $(1, \\sqrt{y}, z)$ даје $\\frac{1}{x^{2}+y+1} \\leqslant$ $\\frac{1+y+z^{2}}{(x+y+z)^{2}}$. Аналогно важи $\\frac{1}{y^{2}+z+1} \\leqslant \\frac{1+z+x^{2}}{(x+y+z)^{2}}$ и $\\frac{1}{z^{2}+x+1} \\leqslant \\frac{1+x+y^{2}}{(x+y+z)^{2}}$. Сабиранјем ових неједнакости добијамо\n\n$$\n\\frac{1}{x^{2}+y+1}+\\frac{1}{y^{2}+z+1}+\\frac{1}{z^{2}+x+1} \\leqslant \\frac{3+x+y+z+x^{2}+y^{2}+z^{2}}{(x+y+z)^{2}}=S\n$$\n\nОстаје да се докаже да је $S \\leqslant 1$, а то је еквивалентно са $3+x+y+z \\leqslant$ $2(x y+y z+z x)=2(x+y+z)$ по услову задатка, тј. $x+y+z \\geqslant 3$. Ово, међутим, следи из $x+y+z=x y+y z+z x \\leqslant \\frac{(x+y+z)^{2}}{3}$.\n\nЈеднакост важи само за $x=y=z=1$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2009", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Нека је $k$ уписана кружница неједнакокраког $\\triangle A B C$, чији је центар $S$. Кружница $k$ додирује странице $B C, C A, A B$ у тачкама $P, Q, R$, редом. Права $Q R$ сече праву $B C$ у тачки $M$. Нека кружница која садржи тачке $B$ и $C$ додирује $k$ у тачки $N$. Описана кружница $\\triangle M N P$ сече праву $A P$ у тачки $L$, различитој од $P$. Доказати да су тачке $S, L$ и $M$ колинеарне.\n\n(Ђорђе Баралић)\n\n## РЕШЕЊА", "solution": "Посматрајмо хомотетију са центром $N$ која слика круг $k$ у круг $B C N$; нека она слика тачку $P$ у $P_{1}$. Тангента на круг $B C N$ у $P_{1}$ је паралелна тангенти на $k$ у $P$, тј. правој $B C$, што значи да је $P_{1}$ средиште лука $B C$ круга $B C N$. Дакле, $N P$ је симетрала угла $C N B$, па је $\\frac{B N}{C N}=\\frac{B P}{C P}$. Шта више, по Менелајевој теореми је $\\frac{B M}{M C}=\\frac{B R}{R A} \\cdot \\frac{A Q}{Q C}=\\frac{B P}{P C}=\\frac{B N}{N C}$, па је $N M$ спољна симетрала угла $C N B$.\n\n\n\nПрема томе, $N$ лежи на кругу над пречником $M P$, а $L$ је подножје нормале из $M$ на $A P$. Остаје да се докаже да је $M S \\perp A P$.\n\nНека је $L^{\\prime}$ подножје нормале из $S$ на $A P$. Тачке $A, L^{\\prime}, Q, R, S$ леже на кругу $\\omega$ над пречником $A S$. Инверзија у односу на $k$ слика кругове $\\omega$ и $S P L^{\\prime}$ редом у праве $Q R$ и $B C$, па слика тачку $L^{\\prime}$ у $M$. Дакле, $M$ лежи на правој $S L^{\\prime}$, одакле следи тврђење (и $L^{\\prime} \\equiv L$ ).\n\nНапомена. Релација $M S \\perp A P$ је еквивалентна са $M P^{2}+A S^{2}=M A^{2}+P S^{2}$ и може се доказати без инверзије: $M P^{2}+A S^{2}=M P^{2}+P S^{2}+A R^{2}=$ $M S^{2}+A Q^{2}=M A^{2}+S Q^{2}$ (због $\\left.M Q \\perp A S\\right)=M A^{2}+P S^{2}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2010_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2010", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Неки од $n$ градова су повезани авионским линијама (све линије су двосмерне). Постоји тачно $m$ линија. Нека је $d_{i}$ број линија које полазе из града $i$, за $i=1,2, \\ldots, n$. Ако је $1 \\leqslant d_{i} \\leqslant 2010$, за свако $i=1,2, \\ldots, n$, доказати да важи\n\n$$\n\\sum_{i=1}^{n} d_{i}^{2} \\leqslant 4022 m-2010 n\n$$\n\nОдредити све $n$ за које може да се достигне једнакост.\n\n(Александар Илић)", "solution": "Услов задатка нам даје $0 \\leqslant\\left(d_{i}-1\\right)\\left(2010-d_{i}\\right)$ за све $i$, тј. $d_{i}^{2} \\leqslant 2011 d_{i}-2010$. Користећи услов $\\sum_{i=1}^{n} d_{i}=2 m$, сабирањем ових неједнакости добијамо\n\n$$\n\\sum_{i=1}^{n} d_{i}^{2} \\leqslant 2011 \\cdot \\sum_{i=1}^{n} d_{i}-2010 n=4022 m-2010 n\n$$\n\nа једнакост важи ако и само ако је $d_{i} \\in\\{1,2010\\}$ за свако $i \\in\\{1,2, \\ldots, n\\}$.\n\n$1^{\\circ}$ Нека је $n=2 k, k \\in \\mathbb{N}$. Ако успоставимо авиолинију између градова $i$ и $j$ ако и само ако је $|j-i|=k$, имамо $d_{i}=1$ за све $i$.\n\n$2^{\\circ}$ Нека је $n=2 k-1, k \\in \\mathbb{N}$. Не може да важи $d_{i}=1$ за све $i$ јер би иначе било $2 m=n=2 k-1$. Зато мора да буде $d_{j}=2010$ за неко $j$; отуда је $n \\geqslant 2011$. С друге стране, успостављањем авиолиније између градова 1 и $i(1 \\leq i \\leq 2010)$ и између градова $2 i$ и $2 i+1$ $(i=1006, \\ldots, k)$ даје мрежу у којој је $d_{1}=2010$ и $d_{i}=1$ за $2 \\leqslant i \\leqslant n$.\n\nПрема томе, једнакост се може достићи ако $2 \\mid n$, или $2 \\nmid n$ и $n \\geq 2011$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2010", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "У оштроуглом $\\triangle A B C$ тачка $M$ је средиште странице $B C$, а тачке $D, E$ и $F$ су подножја висина из темена $A, B$ и $C$, редом. Нека је $H$ ортоцентар $\\triangle A B C, S$ средиште дужи $A H$, а $G$ пресек дужи $F E$ и $A H$. Ако је $N$ тачка пресека тежишне дужи $A M$ и описане кружнице $\\triangle B C H$, доказати да је $\\varangle H M A=\\varangle G N S$.\n\n(Марко Ђикић)", "solution": "Нека је $A^{\\prime}$ тачка таква да је $A B A^{\\prime} C$ паралелограм. Тада важи $\\varangle B A^{\\prime} C=$ $\\varangle B A C=180^{\\circ}-\\varangle B H C=180^{\\circ}-$ $\\varangle B N C$, па су тачке $A^{\\prime}, B, C, H, N$ на истом кругу, тј. кругу над пречником $H A^{\\prime}$. Одавде је $\\varangle A N H=90^{\\circ}$, дакле $N$ је на описаном кругу троугла $A E F$ чији је центар у $S$.\n\nСада имамо $\\varangle S F G=90^{\\circ}-\\varangle E A F=$ $\\varangle A C F=\\varangle A D F$. Следи да су троуглови $S F G$ и $S D F$ слични, и одатле $S G \\cdot S D=S F^{2}=S N^{2}$. Ово повлачи да је и $\\triangle S N G \\sim \\triangle S D N$, и најзад $\\varangle G N S=\\varangle S D N=\\varangle H M N$ јер је четвороугао $H D M N$ тетиван.\n\n\n\nДруго решење. Четвороуглови $B D H F$ и $D C E H$ су тетивни и $A F \\cdot A B=$ $\\overline{A H \\cdot A D=A E} \\cdot A C$. Применимо инверзију $\\mathcal{I}$ са центром $A$ и потенцијом $A F \\cdot A B$. Очигледно је $\\mathcal{I}(F)=B, \\mathcal{I}(H)=D, \\mathcal{I}(E)=C$, па $\\mathcal{I}$ слика праву $B C$ у описани круг $\\triangle F H E$, тј. у круг над пречником $A H$; даље, $\\mathcal{I}$ слика круг $B C H$ у описани круг $\\omega$ троугла $F D E$, а то је Ојлеров круг у $\\triangle A B C$. Пошто је $M \\in \\omega \\cap A M$ и $\\mathcal{I}$ чува праву $A M$, имамо $\\mathcal{I}(M)=N$.\n\nНека је $\\mathcal{I}(G)=G^{*}$ и $\\mathcal{I}(S)=S^{*}$. Како је $\\mathcal{I}(E F)$ описани круг $\\triangle A B C, S \\in \\omega$ и $\\mathcal{I}(A H)=A H$, тачке $G^{*}$ и $S^{*}$ су други пресеци праве $A H$ са круговима $A B C$ и $H B C$, редом. Према томе, $\\varangle G N S=\\varangle G^{*} M S^{*}=\\varangle H M A$ јер су $G^{*}$ и $S^{*}$ симетричне тачкама $H$ и $A$ у односу на $B C$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2010", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Нека је $A$ бесконачан подскуп скупа природних бројева. Одредити све природне бројеве $n$ такве да за свако $a \\in A$ важи\n\n$$\na^{n}+a^{n-1}+\\ldots+a^{1}+1 \\mid a^{n!}+a^{(n-1)!}+\\ldots+a^{1!}+1\n$$\n\n(Милош Милосавлевић)\n\n## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА\n\nтакмичење ученика средњих школа из математике\n\nНиш, 07.04.2010.\n\n## Други дан", "solution": "Означимо $P(x)=x^{n}+x^{n-1}+\\cdots+1$ и $Q(x)=x^{n!}+\\cdots+x^{1!}+1$; нека је $Q(x)=C(x) P(x)+R(x)$, где су $C$ и $R$ полиноми са целим коефицијентима и $\\operatorname{deg} R<\\operatorname{deg} P$. По услову задатка $P(a) \\mid Q(a)$, и самим тим $P(a) \\mid R(a)$, за бесконачно много целих бројева $a$. Како за довољно велико $a$ важи $|R(a)|<|P(a)|$, мора бити $R(a)=0$; дакле, $R(x)$ има бесконачно много нула, па је $R(x) \\equiv 0$ и $P(x) \\mid Q(x)$.\n\nЛема. Нека су $k_{0}, k_{1}, \\ldots, k_{n} \\in \\mathbb{N}_{0}$. Полином $P(x)=x^{n}+x^{n-1}+\\cdots+1$ дели $Q(x)=x^{k_{n}}+\\cdots+x^{k_{1}}+x^{k_{0}}$ ако и само ако је $\\left\\{k_{0}, k_{1}, \\ldots, k_{n}\\right\\}$ потпун систем остатака по модулу $n+1$.\n\nДоказ. Нека је $r_{i}$ остатак при дељењу $k_{i}$ са $n+1$. Пошто $x^{n+1}-1$ дели $x^{k_{i}}-x^{r_{i}}$ за све $i$, следи да $P(x)=\\frac{x^{n+1}-1}{x-1}$ дели $Q(x)-Q_{1}(x)$, где је $Q_{1}(x)=x^{r_{0}}+x^{r_{1}}+\\cdots+x^{r_{n}}$ и притом $\\operatorname{deg} Q_{1} \\leqslant n$. Ако $P(x) \\mid Q(x)$, онда $P(x) \\mid Q_{1}(x)$, тј. $Q_{1}(x)=c P(x)$ за неку константу $c$, а то важи ако и само ако је $c=1$ и $\\left\\{r_{0}, r_{1}, \\ldots, r_{n}\\right\\}=\\{0,1, \\ldots, n\\}$.\n\nИз леме следи да су тражени бројеви $n$ они за које је $\\{0,1!, \\ldots, n!\\}$ потпун систем остатака по модулу $n+1$.\n\nАко је $n>3$ и $n+1$ је сложен број, онда је $n!\\equiv 0(\\bmod n+1)$, па услов није задовољен. Ако је $n+1=p>3$ прост, по Вилсоновој теореми је $(p-1)!\\equiv-1(\\bmod p)$, одакле је $(p-2)!\\equiv 1=1!(\\bmod p)$, и опет услов није задовољен. Остају случајеви $n \\leqslant 3$; директном провером се добија да $n=1$ и $n=2$ задовољавају услове.\n\nДруго решење. Доказаћемо јаче тврђење: ако $A=a^{n}+\\cdots+a+1$ дели $a^{k_{n}}+\\cdots+a^{k_{1}}+a^{k_{0}}$ за неко $a \\in \\mathbb{N} \\backslash\\{1\\}$, онда је $\\left\\{k_{0}, k_{1}, \\ldots, k_{n}\\right\\}$ потпун систем остатака по модулу $n+1$.\n\nНека $A \\mid B=a^{k_{n}}+\\cdots+a^{k_{1}}+a^{k_{0}}$. Означимо са $r_{i, j}$ остатак при дељењу $k_{i}+j$ са $n+1$ и посматрајмо бројеве $B_{j}=a^{r_{n, j}}+\\cdots+a^{r_{1, j}}+a^{r_{0, j}}$. Тада је $B_{j} \\equiv a^{j} B(\\bmod A)$, одакле следи да $A \\mid B_{j}$ за $j=0,1, \\ldots, n$. С друге стране, $B_{0}+B_{1}+\\cdots+B_{n}=\\sum_{j} a^{r_{n, j}}+\\cdots+\\sum_{j} a^{r_{1, j}}+\\sum_{j} a^{r_{0, j}}=(n+1) A$, па како је $B_{j}>0$, мора бити $B_{j}=A$ за све $j$. Из неједнакости $A<2 a^{n}$ закључујемо да је, за свако $j$, највише један од остатака $r_{i, j}$ једнак $n$. Али ако је $k_{i} \\equiv k_{i^{\\prime}} \\equiv n-j(\\bmod n+1)$, онда је $r_{i, j}=r_{i^{\\prime}, j}=n$, што је немогуће. Према томе, $k_{0}, k_{1}, \\ldots, k_{n}$ су међусобно различити по модулу $n+1$, што је и требало доказати.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2010", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Нека је $O$ центар описане кружнице $\\triangle A B C$. Права кроз $O$ сече странице $C A$ и $C B$ у тачкама $D$ и $E$, редом, и описану кружницу $\\triangle A B O$ у тачки $P$ унутар троугла (различитој од $O$ ). Тачка $Q$ на страници $A B$ је таква да је $\\frac{A Q}{Q B}=\\frac{D P}{P E}$. Доказати да је $\\varangle A P Q=2 \\cdot \\varangle C A P$. (Душан Ђукић)", "solution": "Нека је $X$ тачка на полуправој $A P$ таква да је $E X \\| A C$. По Талесовој теореми је $A P: P X=D P: P E=$ $A Q: Q B$, одакле следи $B X \\| Q P$.\n\nПрава $P E$ је спољашња симетрала угла $A P B$ и полови угао $B P X$. Такође, пошто је $\\varangle B E X=180-$ $\\varangle A C B$ и $\\varangle B P X=180^{\\circ}-\\varangle A P B=$ $180^{\\circ}-2 \\varangle A C B$, добијамо $\\varangle B E X=$\n\n\n$90^{\\circ}+\\frac{1}{2} \\varangle B P X$. Следи да је $E$ центар уписаног круга троугла $B P X$ и одатле $\\varangle A P Q=\\varangle P X B=2 \\varangle P X E=2 \\varangle C A P$.\n\nДруго решеъе. Конструкција из задатка је могућа само ако је $\\triangle A B C$ оштроугли. Означимо $\\varangle P A D=\\varphi, \\varangle Q P A=\\psi$ и $\\varangle B C A=\\gamma$. Из $\\varangle A P B=2 \\gamma$ и $\\varangle D A P+\\varangle E B P=\\varangle A P B-\\varangle A C B=\\gamma$ следи $\\varangle P B E=\\gamma-\\varphi$ и $\\varangle B P Q=2 \\gamma-\\psi$. Како је $\\varangle A P D=\\varangle B P E=90^{\\circ}-\\gamma$, такође имамо $\\varangle A D P=90^{\\circ}+\\gamma-\\varphi$ и $\\varangle B E P=90^{\\circ}+\\varphi$.\n\nСинусне теореме у троугловима $A P D$ и $P B E$ дају $\\frac{D P}{P E}=\\frac{D P}{P A} \\cdot \\frac{P A}{P B} \\cdot \\frac{P B}{P E}=$ $\\frac{\\sin \\varphi \\cos \\varphi}{\\sin (\\gamma-\\varphi) \\cos (\\gamma-\\varphi)} \\cdot \\frac{P A}{P B}=\\frac{\\sin 2 \\varphi}{\\sin (2 \\gamma-2 \\varphi)} \\cdot \\frac{P A}{P B}$. С друге стране, $\\frac{A Q}{Q B}=\\frac{A Q}{A P} \\cdot \\frac{A P}{B P} \\cdot \\frac{B P}{Q B}=$ $\\frac{\\sin \\psi}{\\sin (2 \\gamma-\\psi)} \\cdot \\frac{A P}{P B}$, па се услов $\\frac{A Q}{Q B}=\\frac{D P}{P E}$ своди на $f(2 \\varphi)=f(\\psi)$, где је $f(x)=$ $\\frac{\\sin (2 \\gamma-x)}{\\sin x}=\\sin 2 \\gamma \\operatorname{ctg} x-\\cos 2 \\gamma$. Јасно је да је $f$ строго опадајућа функција на $(0, \\pi)$, па мора бити $\\psi=2 \\varphi$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2010", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Таблица димензија $n \\times n$, на чијим пољима су бројеви $1,2, \\ldots, n^{2}$ (на сваком пољу тачно један број и сваки број на тачно једном пољу) назива се нишка ако сви производи од по $n$ бројева који се налазе на $n$ „разбацаних\" поља дају исти остатак при дељењу са $n^{2}+1$. Да ли постоји нишка таблица за:\n\n(a) $n=8$;\n\n(б) $n=10$ ?\n\n( $n$ поља су „разбацана\" ако никоја два нису у истој врсти или у истој колони.)\n\n(Марко Ђикић)", "solution": "(a) Претпоставимо да постоји нишка таблица $8 \\times 8$ и да производ ма којих 8 разбацаних бројева даје остатак $r$ по модулу $8^{2}+1=65=5 \\cdot 13$. Сви бројеви у таблици се могу поделити на 8 дисјунктних осморки разбацаних бројева. Међу овим осморкама постоји једна која садржи умножак броја 13 и једна која не садржи такав умножак. Производ бројева у првој осморци је дељив са 13, а у другој није, контрадикција. Закључујемо да нишка таблица $8 \\times 8$ не постоји.\n\n(б) Број $n^{2}+1=101$ је прост. Попунимо таблицу као на слици, где је $g$ примитиван корен по модулу 101. Лако се види да је производ бројева у ма којих 10 разбацаних поља конгруентан са $g^{495}(\\bmod 101)$, па је ово пример нишке таблице.\n\n| $g^{0}$ | $g^{1}$ | $g^{2}$ | $\\cdots$ | $g^{9}$ |\n| :---: | :---: | :---: | :---: | :---: |\n| $g^{10}$ | $g^{11}$ | $g^{12}$ | $\\cdots$ | $g^{19}$ |\n| $g^{20}$ | $g^{21}$ | $g^{22}$ | $\\cdots$ | $g^{29}$ |\n| $\\vdots$ | $\\vdots$ | $\\vdots$ | | $\\vdots$ |\n| $g^{90}$ | $g^{91}$ | $g^{92}$ | $\\cdots$ | $g^{99}$ |", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2010", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Нека су $a_{0}$ и $a_{n}$ различити делиоци природног броја $m>1$, а низ природних бројева $a_{0}, a_{1}, a_{2}, \\ldots, a_{n}$ такав да задовољава\n\n$$\na_{i+1}=\\left|a_{i} \\pm a_{i-1}\\right| \\quad \\text { за } 0<i<n\n$$\n\nАко је НЗД $\\left(a_{0}, \\ldots, a_{n}\\right)=1$, доказати да у низу постоји члан који је мањи од $\\sqrt{m}$.\n\n(Душан Ђукић)\n\n## РЕШЕЊА", "solution": "Посматрајмо два најмања (различита) члана низа, $p$ и $q$. Ако је $\\min \\{p, q\\}=$ 1, тврђење тривијално важи; зато надаље претпостављамо да је $p, q>1$.\n\nЛема 1. Постоје индекси $k$ и $l$ за које је $a_{k}=p, a_{l}=q$ и $|k-l| \\leq 2$.\n\nДоказ. Нека је $a_{k}=p$ и $a_{l}=q(k<l)$. Претпоставимо да је $r=l-k>2$. Доказаћемо индукцијом по $r$ да за неко $i, k<i<l$, важи $a_{i} \\in\\{p, q\\}$. Како је $a_{k+3} \\neq\\left|a_{k+2}-a_{k+1}\\right|=p$, имамо $a_{k+3}=a_{k+1}+a_{k+2}$; слично је и $a_{l-3}=a_{l-2}+a_{l-1}$. Нека је $a_{m}=\\max _{p<i<q} a_{i}$. Јасно је да је $k+2<m<l-2$ (дакле, $l-k \\geqslant 6$ ), а такође и $a_{m+2}=a_{m}-a_{m+1}=a_{m-1}$ и $a_{m+1}=a_{m}-a_{m-1}=a_{m-2}$. То значи да низ $\\left(a_{i}^{\\prime}\\right)$, дефинисан са $a_{i}^{\\prime}=a_{i}$ за $i<m$ и $a_{i}^{\\prime}=a_{i+3}$ за $i \\geqslant m$, задовољава услове задатка; притом је $a_{k}^{\\prime}=p$ и $a_{l-3}^{\\prime}=q$, па по индуктивној претпоставци (јер је $(l-3)-k \\geqslant 3$ ) важи $a_{i}^{\\prime} \\in\\{p, q\\}$ за неко $i(k<i<l-3)$. Тада је и $a_{i} \\in\\{p, q\\}$ или $a_{i+3} \\in\\{p, q\\}$, чиме је индукција готова.\n\nЛема 2. За свако $i(0 \\leqslant i \\leqslant n)$ постоје $x_{i}, y_{i} \\in \\mathbb{N}_{0}$ такви да је $a_{i}=x_{i} p+y_{i} q$ и $\\left(x_{i}, y_{i}\\right)=1$.\n\nДоказ. Посматрајмо векторе $v_{k}=(1,0)$ и $v_{l}=(0,1)$ и, за свако $i$, дефинишимо $v_{i+2}=\\varepsilon_{i} v_{i}+\\varepsilon_{i}^{\\prime} v_{i+1}$ ако је $a_{i+2}=\\varepsilon_{i} a_{i}+\\varepsilon_{i}^{\\prime} a_{i+1}\\left(\\varepsilon_{i}, \\varepsilon_{i}^{\\prime} \\in\\{-1,1\\}\\right)$. Једноставном индукцијом добијамо да за $v_{i}=\\left(x_{i}, y_{i}\\right)$ важи\n\n$$\na_{i}=x_{i} p+y_{i} q\n$$\n\nКако је $x_{i+1} y_{i+2}-x_{i+2} y_{i+1}=x_{i+1}\\left(\\varepsilon_{i} y_{i}+\\varepsilon_{i}^{\\prime} y_{i+1}\\right)-\\left(\\varepsilon_{i} x_{i}+\\varepsilon_{i}^{\\prime} x_{i+1}\\right) y_{i+1}=$ $-\\varepsilon_{i}\\left(x_{i} y_{i+1}-x_{i+1} y_{i}\\right)$ и слично $x_{i} y_{i+2}-x_{i+2} y_{i}=\\varepsilon_{i}^{\\prime}\\left(x_{i} y_{i+1}-x_{i+1} y_{i}\\right)$, имамо\n\n$$\nx_{i} y_{i+1}-x_{i+1} y_{i}, x_{i} y_{i+2}-x_{i+2} y_{i} \\in\\{-1,1\\} \\text { за } 0 \\leqslant i<n\n$$\n\nи одатле $\\left(x_{i}, y_{i}\\right)=1$. Остаје још да покажемо да су $x_{i}, y_{i} \\geqslant 0$ за све $i$.\n\nПретпоставимо да је $x_{i}<0$ за неко $i<k$ (случај $y_{i}<0$ и/или $i>l$ је аналоган) и посматрајмо највеће такво $i$. Због $a_{i}>0$ и (1) имамо $y_{i}>0$. Из (2) и $x_{i} y_{i+1}, x_{i} y_{i+2} \\leqslant 0 \\leqslant x_{i+1} y_{i}, x_{i+2} y_{i}$ следи да су $v_{i+1}$, $v_{i+2} \\in\\{(0,1),(1,0)\\}$, а тада мора бити $v_{i}= \\pm(1,-1)$, тј. $a_{i}=|p-q|$. Међутим, како су $p$ и $q$ узајамно прости и већи од 1 , важи $\\max \\{p, q\\}>$ $|p-q| \\notin\\{p, q\\}$, противно избору $p$ и $q$.\n\nНека је $m=d a_{0}=e a_{n}$. По леми 2 је $m=d x_{0} p+d y_{0} q=e x_{n} p+e y_{n} q$, при чему је $\\left(d x_{0}, d y_{0}\\right) \\neq\\left(e x_{n}, e y_{n}\\right)$ јер због $a_{0} \\neq a_{n}$ важи $\\frac{x_{0}}{y_{0}} \\neq \\frac{x_{n}}{y_{n}}$. Одатле следи да $p \\mid d y_{0}-e y_{n}$, па је $d y_{0}>p$ или $e y_{n}>p$; коначно, $m>p q$ и према томе $\\min (p, q)<\\sqrt{m}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2011_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2011", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Нека је $n \\geqslant 2$ природан број и нека позитивни реални бројеви $a_{0}, a_{1}, \\ldots, a_{n}$ задовољавају једнакост\n\n$$\n\\left(a_{k-1}+a_{k}\\right)\\left(a_{k}+a_{k+1}\\right)=a_{k-1}-a_{k+1} \\quad \\text { за свако } k=1,2, \\ldots, n-1 \\text {. }\n$$\n\nДоказати да је $a_{n}<\\frac{1}{n-1}$.\n\n(Душан Ђукић)", "solution": "Дата једнакост је еквивалентна са\n\n$$\n\\frac{1}{a_{k}+a_{k+1}}=1+\\frac{1}{a_{k-1}+a_{k}}\n$$\n\nза свако $k>0$. Индукцијом следи $\\frac{1}{a_{k}+a_{k+1}}=k+\\frac{1}{a_{0}+a_{1}}$ за $k>0$, одакле добијамо да је $\\frac{1}{a_{n-1}+a_{n}}>n-1$ и према томе $a_{n}<\\frac{1}{n-1}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2011", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Нека је $n$ непаран природан број такав да су бројеви $\\varphi(n)$ и $\\varphi(n+1)$ степени броја два ( $\\varphi(n)$ је број природних бројева не већих од $n$ и узајамно простих са $n$ ). Доказати да је $n+1$ степен броја два или је $n=5$.\n\n(Марко Радовановић)", "solution": "Ако је $n=\\prod_{i=1}^{k} p_{i}^{r_{k}}$ канонска факторизација $n$, важи $\\varphi(n)=\\prod_{i=1}^{k} p_{i}^{r_{k}-1}\\left(p_{i}-\\right.$ 1), па пошто $n$ нема других простих чинилаца осим двојке, мора бити $a_{i}=1$ и $p_{i}-1=2^{b_{i}}$ за свако $i$ и неке $b_{i}$. Како $2^{b_{i}}+1$ може бити прост само ако је $b_{i}$ степен двојке, имамо $p_{i}=2^{2^{c_{i}}}+1$ за неке различите $c_{i}$.\n\nПретпоставимо да $n+1$ није степен двојке. Из чињенице да је $\\varphi(n+1)$ степен двојке добијамо да су сви непарни прости делиоци броја $n+1$ облика $2^{2^{d_{i}}}+1$. Према томе,\n\n$$\nn=\\prod_{i=1}^{k}\\left(2^{2^{c_{i}}}+1\\right), \\quad n+1=2^{t} \\prod_{j=1}^{l}\\left(2^{2^{d_{j}}}+1\\right)\n$$\n\nпри чему су сви $c_{i}$ и $d_{j}$ међусобно различити. Можемо узети без смањења општости да је $c_{1}<\\cdots<c_{k}$ и $d_{1}<\\cdots<d_{l}$.\n\nЗа свако $m, M \\in \\mathbb{N}, m \\leq M$, једноставном индукцијом се показује да важи\n\n$$\n\\frac{2^{2^{m}}+1}{2^{2^{m}}}<\\prod_{i=m}^{M} \\frac{2^{2^{i}}+1}{2^{2^{i}}}=\\frac{2^{2^{m}}}{2^{2^{m}}-1} \\cdot \\frac{2^{2^{M+1}}-1}{2^{2^{M+1}}}<\\frac{2^{2^{m}}}{2^{2^{m}}-1}\n$$\n\nОдавде добијамо\n\n$$\n\\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}} 2^{c} \\leqslant n<\\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c} \\quad \\text { и } \\quad \\frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{d} \\leqslant n+1<\\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1} 2^{d}\n$$\n\nгде је $c=\\sum_{i} 2^{c_{i}}$ и $d=t+\\sum_{j} 2^{d_{i}}$. Следи да је $c=d$. Ако је $d_{1}>c_{1}$, важи $\\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1}<\\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}}$, па је $n+1<n$, контрадикција. Према томе, $d_{1}<c_{1}$, а тада је $n+1 \\geqslant \\frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{c}>\\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c}>n$, па је $\\frac{n+1}{n}>\\frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} \\cdot \\frac{2^{2^{c_{1}}}-1}{2^{2^{c_{1}}}}$ и, због $n \\geqslant 2^{2^{c_{1}}}+1 \\geqslant a^{2}+1$ за $2^{2^{d_{1}}}=a, \\frac{n+1}{n}>\\frac{(a+1)\\left(a^{2}-1\\right)}{a^{3}}=1+\\frac{a^{2}-a-1}{a^{3}}$, одакле закључујемо $a^{2}+1 \\leqslant n<\\frac{a^{3}}{a^{2}-a-1}$. Једина могућност је $a=2$ и $n=5$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2011", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Нека је $H$ ортоцентар, а $O$ центар описане кружнице оштроуглог троугла $A B C$. Тачке $D$ и $E$ су подножја висина из $A$ и $B$, редом. Обележимо са $K$ пресечну тачку правих $O D$ и $B E$, а са $L$ пресечну тачку правих $O E$ и $A D$. Нека је $X$ друга пресечна тачка кружница описаних око троуглова $H K D$ и $H L E$, а $M$ средиште странице $A B$. Доказати да су тачке $K, L$ и $M$ колинеарне ако и само ако је $X$ центар описане кружнице троугла $E O D$.\n\n(Марко Ђикић)\n\n# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА \n\nтакмичење ученика средњих школа из математике\n\nБеоград, 03.04.2011.\n\n## Други дан", "solution": "Ако је $X$ центар описаног круга $\\triangle O D E$, онда је $90^{\\circ}-\\angle K D E=90^{\\circ}-$ $\\angle O D E=\\angle X E O=\\angle X E L=\\angle X H D=\\angle X K D$ (сви углови су оријентисани), одакле следи да је $X K \\perp D E$; аналогно $X L \\perp D E$, тј. $K$ и $L$ леже на симетрали дужи $D E$, па је $D E H O$ једнакокраки трапез, дакле $D, E, O, H$ леже на кругу.\n\nС друге стране, ако $O$ лежи на кругу $H D E$, дакле на кругу над пречником $C H$, периферијски углови над $E H$ и $O D$ су једнаки ( $\\angle E C H=$ $\\angle O C D)$, па је $D E H O$ једнакокраки трапез и одатле $D L=E L$. Сада имамо $\\angle E X H=\\angle E L H=2 \\angle E D H$\n\n\nи аналогно $\\angle D X H=2 \\angle D E H$, па следи да је $X$ центар круга $D E O H$. Према томе, $X$ је центар круга $O D E$ ако и само ако $D, E, O$ и $H$ леже на кругу.\n\nАко су тачке $D, E, O, H$ на кругу, тада $K, L$ и $M$ леже на симетрали дужи $D E$, чиме је један смер задатка доказан. Претпоставимо сада да $O$ лежи ван круга $C D H E$ (случај када је $O$ унутар круга се разматра на исти начин). Како је $C O \\perp D E$, важи $D L>L E$ и $E K>K D$, тј. $K$ и $L$ леже на разним странама симетрале дужи $D E$, а $M$ припада овој симетрали. Према томе, ако су $K, L$ и $M$ колинеарне, $M$ се мора налазити између $K$ и $L$. Следи да је једна од тачака $K$ и $L$ ван троугла $A B C$, а друга унутар троугла. Међутим, када је $O$ изван четвороугла $A B D E$, обе тачке $K$ и $L$ су ван троугла, а у супротном су обе унутар троугла. То је контрадикција са претпоставком да $M$ лежи на правој $K L$, што доказује други смер.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2011", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "На страницама $A B, A C$ и $B C$ троугла $A B C$ дате су, редом, тачке $M, X$ и $Y$ тако да је $A X=M X$ и $B Y=M Y$. Нека су $K$ и $L$, редом, средишта дужи $A Y$ и $B X$, а $O$ центар описане кружнице троугла $A B C$. Ако су $O_{1}$ и $O_{2}$ тачке симетричне тачки $O$ у односу на $K$ и $L$, редом, доказати да тачке $X, Y, O_{1}$ и $O_{2}$ леже на истој кружници.\n\n(Марко Ђикић)", "solution": "Поставимо координатни систем са почетком у тачки $M$ и $x$-осом дуж праве $A B$. Нека тачке $X$ и $Y$ имају координате $(a, b)$ и $(c, d)$ редом. Због $A X=X M$ и $B Y=Y M$, координате тачака $A$ и $B$ су $(2 a, 0)$ и $(2 c, 0)$, а тачака $K$ и $L\\left(a+\\frac{c}{2}, \\frac{d}{2}\\right)$ и $\\left(c+\\frac{a}{2}, \\frac{b}{2}\\right)$, редом. Тачка $O$ има координате $(a+c, e)$ за неко $e$, одакле добијамо $O_{1}(a, d-e)$ и $O_{2}(c, b-e)$. Према томе, тачке $O_{1}$ и $O_{2}$ су симетричне тачкама $X$ и $Y$ у односу на праву $y=\\frac{b+d-e}{2}$, па су $X, Y$ и $O_{1}, O_{2}$ темена (могуће дегенерисаног) једнакокраког трапезе, и зато леже на кругу.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2011", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Да ли постоје природни бројеви $a, b$ и $c$, већи од 2011, такви да у децималном запису важи једнакост\n\n$$\n(a+\\sqrt{b})^{c}=\\ldots 2010,2011 \\ldots ?\n$$\n\n(Милош Милосављевић)", "solution": "Показаћемо да такви број��ви $a, b$ и $c$ постоје. Број $x=(a+\\sqrt{b})^{c}+(a-\\sqrt{b})^{c}$ је цео. Довољно је одабрати $a, b, c$ тако да $x$ буде дељиво са $10^{4}$ и $7989,7989>$ $(a-\\sqrt{b})^{c}>7989,7988$.\n\nЗа непарно $c$, број $x=2 a^{c}+2\\binom{c}{2} a^{c-2}+\\cdots+2\\binom{c}{c-1} a$ је дељив са $a$, па је довољно узети $a$ које је дељиво са $10^{4}$. Други услов постижемо избором $a$ и $b$ тако да је $1<a-\\sqrt{b}<\\sqrt{\\frac{7989,7989}{7989,7988}}$ - на пример, $a=10^{8}$ и $b=$ $(a-1)^{2}-1$. Заиста, нека је $c$ најмањи непаран природан број за који је $(a-\\sqrt{b})^{c}>7989,7988$. Такво $c$ је очигледно веће од 2011 (у овом случају $c=1797184159)$ и $(a-\\sqrt{b})^{c}<7989,7989$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2011", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Скуп $T$ садржи 66 тачака, а скуп $P$ садржи 16 правих у равни. За тачку $A \\in T$ и праву $l \\in P$ кажемо да су иниидентни пар ако $A \\in l$. Доказати да број инцидентних парова не може бити већи од 159 , као и да постоји\n\n\n\nВреме за рад 270 минута.\n\nСваки задатак вреди 7 поена.\n\n## РЕШЕЊА", "solution": "Означимо са $A_{1}, \\ldots, A_{66}$ тачке скупа $T$ и са $a_{i}$ број правих из $P$ које садрже $A_{i}$. Тада је број парова правих које се секу у $A_{i}$ једнак $\\binom{a_{i}}{2}$, а број инцидентних парова $I=\\sum a_{i}$. Како се сваке две праве секу у највише једној тачки, важи $\\sum_{i=1}^{66}\\binom{a_{i}}{2} \\leqslant\\binom{ 16}{2}=120$. Нека је $b_{k}$ број тачака из $T$ кроз које пролази тачно $k$ правих из $P$. Тада је $\\sum b_{k}=66, \\sum\\binom{k}{2} b_{k} \\leqslant 120$ и $I=\\sum k b_{k} \\leqslant \\sum \\frac{1}{2}\\left(3+\\binom{k}{2}\\right) b_{k}=\\frac{1}{2}(3 \\cdot 66+120)=159$, јер је $3+\\binom{k}{2} \\geq 2 k$. Једнакост се достиже ако је $b_{k}=0$ за $k \\notin\\{2,3\\}, b_{2}=39$ и $b_{3}=27$, другим речима, ако праве из $P$ одређују тачно 39 двоструких и 27 троструких пресека.\n\nПример конфигурације са 159 инцидентних парова може се конструисати нпр. помоћу Дезаргове теореме. Узмимо тачке $A_{1}, A_{2}, A_{3}$ на правој $a$ и $B_{1}, B_{2}, B_{3}$ на правој $b \\| a$, затим повуцимо 9 правих $A_{i} B_{j}, i, j \\in\\{1,2,3\\}$. Нпр. на слици је $A_{1} A_{2}: A_{2} A_{3}: B_{1} B_{2}: B_{2} B_{3}=2: 2: 3: 6$, тако да међу овим правим нема паралелних. По Дезарговој теореми, ових 9 правих одређују 18 пресечних тачака које су по три колинеарне - тако да одређују још 6 правих. Заједно са ових 6 правих, имамо слику са 15 правих и 24 трострука пресека. При том се три праве добијене Дезарговом теоремом секу у једној тачки (на слици тачка $K$ ), што нам даје и 25 -ти троструки пресек. Повуцимо још једну праву која пролази само кроз две двоструке пресечне тачке. За скуп $P 16$ нацртаних правих и скуп $T$ који се сас-\n\n\nтоји од 27 добијених троструких и преосталих 39 двоструких пресека постиже се једнакост.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2012_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2012", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Нека је $P$ тачка на дијагонали $B D$ паралелограма $A B C D$ таква да је $\\varangle P C B=\\varangle A C D$. Кружница описана око троугла $A B D$ сече праву $A C$ у тачкама $E$ и $A$. Доказати да је\n\n$$\n\\varangle A E D=\\varangle P E B . \\quad \\text { (Марко Ђикић) }\n$$", "solution": "Доказ изводимо у случају када је $\\angle B A C \\leq 90^{\\circ}$. Други случај је аналоган.\n\nНека се праве $D E$ и $B C$ секу у L. Четвороугао $C D P L$ је тетиван јер је $\\angle P D L=\\angle P C L$, одакле имамо $\\angle P L E=\\angle P C D=\\angle B C A=$ $\\angle D A C=\\angle D B E=\\angle P B E$, па је и четвороугао $B P E L$ тетиван. Из ове две тетивности коначно добијамо $\\angle P E B=\\angle P L B=\\angle P D C=$ $\\angle D B A=\\angle D E A$.\n\n\n\nДруго решеъе. Нека је $P^{\\prime}$ тачка на $B D$ таква да је $\\angle D E A=\\angle P E B$.\n\nПо синусној теореми је $\\frac{B P}{D P}=\\frac{B P}{C P} \\cdot \\frac{C P}{D P}=\\frac{\\sin \\angle B C P}{\\sin \\angle C B D} \\cdot \\frac{\\sin \\angle C D B}{\\sin \\angle P C D}$. Аналогно je $\\frac{B P^{\\prime}}{D P^{\\prime}}=\\frac{\\sin \\angle B E P^{\\prime}}{\\sin \\angle E B D} \\cdot \\frac{\\sin \\angle E D B}{\\sin \\angle P^{\\prime} E D}$. Како је $\\angle B C P=\\angle E D B, \\angle C B D=\\angle P^{\\prime} E D$, $\\angle C D B=\\angle B E P^{\\prime}$ и $\\angle P C D=\\angle E B D$, следи $\\frac{B P}{D P}=\\frac{B P^{\\prime}}{D P^{\\prime}}$, дакле $P \\equiv P^{\\prime}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2012", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Наћи све природне бројеве $a$ и $b$ такве да\n\n$$\na\\left|b^{2}, \\quad b\\right| a^{2} \\quad \\text { и } \\quad a+1 \\mid b^{2}+1 . \\quad \\text { (Душан Ђукић) }\n$$", "solution": "Нека је $b^{2}=c a$. Услови задатка дају $b^{2}=c a \\mid a^{4}$ и $a+1 \\mid c a+1$, а то је еквивалентно са\n\n$$\nc \\mid a^{3} \\quad \\text { и } \\quad a+1 \\mid c-1 .\n$$\n\nНека је $c=d(a+1)+1, d \\in \\mathbb{N}_{0}$. Како је $a^{3} \\equiv-1(\\bmod (a+1))$, имамо $\\frac{a^{3}}{c} \\equiv-1(\\bmod (a+1))$, тј. $\\frac{a^{3}}{c}=e(a+1)-1$ за неко $e \\in \\mathbb{N}$. Следи да је $a^{3}=(d(a+1)+1)(e(a+1)-1)$, што након множења и скраћивања са $a+1$ постаје $a^{2}-a+1=d e(a+1)+(e-d)$. Одавде имамо $e-d \\equiv a^{2}-a+1 \\equiv 3$ $(\\bmod (a+1))$, дакле\n\n$$\ne-d=k(a+1)+3 \\quad \\text { и } \\quad d e=a-2-k \\quad(k \\in \\mathbb{Z}) .\n$$\n\nРазликујемо следеће случајеве:\n\n(1) $k \\notin\\{-1,0\\}$. У овом случају (*) повлачи $d e<|e-d|-1$, што је могуће само за $d=0$. Сада је $c=1$ и $b^{2}=a$, дакле $(a, b)=\\left(t^{2}, t\\right)$.\n\n(2) $k=-1$. Из (*) добијамо $a=d+1$. Сада је $c=a^{2}$ и $b^{2}=a^{3}$, дакле $(a, b)=\\left(t^{2}, t^{3}\\right)$.\n\n(3) $k=0$. Из (*) добијамо $a=d^{2}+3 d+2$. Сада је $c=d(a+1)+1=(d+1)^{3}$ и $b^{2}=c a=(d+1)^{4}(d+2)$. Следи да је $d+2=t^{2}$ за неко $t \\in \\mathbb{N}$, што даје $(a, b)=\\left(t^{2}\\left(t^{2}-1\\right), t\\left(t^{2}-1\\right)^{2}\\right), t \\geq 2$.\n\nОдговор: То су парови $(a, b)$ облика $\\left(t^{2}, t\\right),\\left(t^{2}, t^{3}\\right)$ и $\\left(t^{2}\\left(t^{2}-1\\right), t\\left(t^{2}-1\\right)^{2}\\right)$, где је $t \\in \\mathbb{N}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2012", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "У неким чворовима квадратне решетке $2012 \\times 2012$ налази се мува и $k$ паукова. Један потез састоји се у следећем: мува се помера на суседан чвор или остаје на истом месту, а након тога се сваки од $k$ паукова помера на неки суседан чвор или остаје на истом месту (у једном чвору може бити више паукова). У сваком тренутку сваки паук и мува имају увид у позиције осталих.\n\na) Наћи најмање $k$ тако да пауци могу ухватити муву у коначном броју потеза, без обзира на почетну позицију муве и паукова.\n\nб) Одговорити на исто питање за кубну решетку $2012 \\times 2012 \\times 2012$.\n\n(Чворови су суседни ако се разликују на тачно једној координати, и то за 1. Паук хвата муву уколико се налазе у истом чвору.)\n\n(Никола Милосављевић)\n\nВреме за рад 270 минута.\n\nСваки задатак вреди 7 поена.\n\n# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА \n\nученика средњих школа\n\nБеоград, 01.04.2012.\n\n## Други дан", "solution": "Један паук не може да ухвати муву. Довољно је да мува не мрда ако паук није на суседном пољу, односно да се помери на поље дијагонално супротно пауковом ако јесте.\n\nДоказаћемо да су два паука довољна у оба дела задатка - означимо их са $P$ и $Q$, муву са $M$, а $x$ - и $y$-координату тачке $A$ са $A_{x}$ и $A_{y}$.\n\n(a) Поставимо координатни почетак у доњи леви угао мреже. На почетку, крећући се дуж $x$-осе, $P$ у коначном броју потеза постиже да буде $P_{x}=$ $M_{x}$. Аналогно, $Q$ постиже да буде $Q_{y}=M_{y}$. Потом се пауци крећу на следећи начин: кад год мува промени $x$-координату, $P$ учини исто тако да остане $P_{x}=M_{x}$, у супротном приђе муви један корак дуж $y$-осе; кретање $Q$ је аналогно. На овај начин величина $\\left|P_{y}-M_{y}\\right|+\\left|Q_{x}-M_{x}\\right|$ се или смањује или остаје иста, при чему може остати иста кроз највише $2 \\cdot 2010$ потеза (када се мува повлачи). Према томе, после коначног броја потеза бар један сабирак ће постати нула, тј. мува ће бити ухваћена.\n\n(б) Занемарујући $z$-осу, на основу дела под (a), један од паукова, рецимо $P$, може постићи да буде $P_{x}=M_{x}$ и $P_{y}=M_{y}$. Надаље, кад год мува направи корак дуж $z$-осе, паук $P$ иде ка њој, а супротном се креће тако да увек буде тачно испод муве. Јасно је да мува може само коначно много пута да направи корак дуж $z$-осе или остане у месту, а да је паук $P$ не ухвати. Према томе, почев од неког момента, мува мора да се креће искључиво по својој $x y$-равни, без стајања у месту.\n\nСада паук $Q$ у коначно много потеза долази до $x y$-равни по којој се креће мува. Такође, стајањем у месту по потреби, $Q$ постиже да $f=\\left|Q_{x}-M_{x}\\right|+$ $\\left|Q_{y}-M_{y}\\right|$ буде парно. У сваком следећем потезу, паук $Q$ се приближава муви дуж $x$-осе ако је $\\left|Q_{x}-M_{x}\\right|>\\left|Q_{y}-M_{y}\\right|$, а дуж $y$-осе у супротном. После сваког потеза, величина $f$ се не повећава и не мења парност, при чему само коначно много пута може да остане иста (када мува бежи од паука према крају решетке). Према томе, у неком тренутку ће бити $f=0$, и мува ће бити ухваћена.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2012", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Наћи све природне бројеве $n$ за које постоји пермутација ( $p_{1}, p_{2}, \\ldots, p_{n}$ ) бројева $(1,2, \\ldots, n)$ таква да скупови $\\left\\{p_{i}+i \\mid 1 \\leqslant i \\leqslant n\\right\\}$ и $\\left\\{p_{i}-i \\mid 1 \\leqslant i \\leqslant n\\right\\}$ чине потпуне системе остатака по модулу $n$. (Марко Ђикић)", "solution": "Претпоставимо да таква пермутација постоји. Како је $\\left\\{p_{i}+i \\mid 1 \\leq i \\leq\\right.$ $n\\}$ потпун систем остатака по модулу $n$, важи $\\sum_{k=1}^{n} k \\equiv \\sum_{i=1}^{n}\\left(p_{i}+i\\right) \\equiv$ $\\sum_{i=1}^{n} i+\\sum_{i=1}^{n} p_{i} \\equiv 2 \\sum_{k=1}^{n} k(\\bmod n)$, дакле $\\sum_{k=1}^{n} k=\\frac{n(n+1)}{2} \\equiv 0(\\bmod n)$, одакле следи $2 \\nmid n$. Шта више, важи $2 \\sum_{k=1}^{n} k^{2} \\equiv \\sum_{k=1}^{n}\\left(\\left(p_{i}+i\\right)^{2}+\\left(p_{i}-i\\right)^{2}\\right) \\equiv$ $\\sum_{k=1}^{n}\\left(2 p_{i}^{2}+2 i^{2}\\right) \\equiv 4 \\sum_{k=1}^{n} k^{2}$, одакле је $2 \\sum_{k=1}^{n} k^{2}=\\frac{n(n+1)(2 n+1)}{3} \\equiv 0(\\bmod n)$, дакле $3 \\nmid n$. Према томе, мора бити $(n, 6)=1$.\n\nС друге стране, ако је $(n, 6)=1$ и $p_{i} \\equiv 2 i(\\bmod n), p_{i} \\in\\{1, \\ldots, n\\}$, тада је $\\left(p_{1}, p_{2}, \\ldots, p_{n}\\right.$ ) пермутација скупа $\\{1, \\ldots, n\\}$ и задовољава услове, јер су $\\left\\{p_{i}+i \\mid 1 \\leq i \\leq n\\right\\} \\equiv\\{3 i \\mid 1 \\leq i \\leq n\\}$ и $\\left\\{p_{i}-i \\mid 1 \\leq i \\leq n\\right\\} \\equiv\\{i \\mid 1 \\leq i \\leq n\\}$ $(\\bmod n)$ потпуни системи остатака по модулу $n$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2012", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Нека је $\\mathcal{K}$ целобројна решетка. Да ли постоји бијекција $f: \\mathbb{N} \\rightarrow \\mathcal{K}$ таква да за све међусобно различите $a, b, c \\in \\mathbb{N}$ важи\n\n$$\n\\text { НЗД }(a, b, c)>1 \\quad \\Longrightarrow \\quad f(a), f(b), f(c) \\text { нису колинеарне? }\n$$\n\n(Целобројна решетка је скуп тачака у равни са целобројним координатама у Декартовом координатном систему.)\n\n(Стеван Гајовић)", "solution": "Поређајмо све тачке решетке у низ $A_{1}, A_{2}, \\ldots$. Ово се може урадити нпр. спирално: $(0,0),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1), \\ldots$ Конструисаћемо индуктивно пример бијекције са траженим својством.\n\nСтавимо $f(1)=A_{1}$. Претпоставимо да су $f(1), \\ldots, f(n-1)$ одређене и узмимо за $f(n)$ тачку $A_{m}$ са најмањим $m$ такву да, ни за које природне $i, j \\leq n,(i, j, n)>1, A_{m}$ не лежи на правој $f(i) f(j)$. Правих $f(i) f(j)$ има коначно много, па заиста постоји тачка решетке која не лежи ни на једној од њих. Приметимо да за просто $p$ нема ограничења при избору $f(p)$, што гарантује да ће свака тачка бити слика неког природног броја.\n\nОвако дефинисано пресликавање $f$ задовољава све услове задатка.\n\nДруго решеъе. Ако је $n$ сложен број, узмимо за $f(n)$ тачку $\\left(n, n^{2}\\right)$. За прост број $p$, нека је $f(p)$ било која од дозвољених тачака на минималном растојању од тачке $(0,0)$. Покажимо да је ово пресликавање добро дефинисана бијекција са траженим својством.\n\nЗа свако $p$ постоји дозвољена тачка - нпр. нека од неупотребљених тачака на параболи $y=x^{2}$. Заиста, произволна права кроз ту тачку сече ову параболу у још највише једној тачки, тј. садржи слику највише једног сложеног броја.\n\nС друге стране, за произвољну тачку $A \\in \\mathcal{K} \\backslash\\left\\{\\left(n, n^{2}\\right) \\mid n\\right.$ је сложен $\\}$ постоји прост број $p$ за који је $A$ дозвољена тачка. Наиме, постоји само коначно много правих кроз $A$ које садрже две целобројне тачке на параболи $y=x^{2}$ (различите од $A$ ); означимо те праве са $p_{1}, \\ldots, p_{k}$ и целобројне тачке у пресеку $p_{i}$ са параболом $y=x^{2}$ са $A_{i}, B_{i}$. Дозољно је узети $p$ које не дели $\\left(f^{-1}\\left(A_{i}\\right), f^{-1}\\left(B_{i}\\right)\\right)$ ни за једно $i$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2012", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Нека композиција садржи $n>1$ вагона са златницима. Постоје две врсте наизглед истих златника: прави и лажни. У сваком вагону се налазе златници само једне врсте. Златници исте врсте су исте масе, док златници различитих врста немају исту масу. Маса правог златника је позната.\n\nОдредити минималан број мерења на дигиталној ваги којима је могуће утврдити који све вагони садрже лажне златнике, као и која је маса лажног златника.\n\n(Претпоставља се да се из сваког вагона може узети било који број златника.)\n\n(Милош Милосављевић)\n\n## РЕШЕЊА", "solution": "Доказаћемо да је минималан број мерења једнак 2. Означимо тежине правог и лажног златника са $x$ и $y$ редом, и нека је $a_{i}=1$ ако су златници у $i$-том вагону лажни, а $a_{i}=0$ у супротном.\n\nУзмимо у првом мерењу по један златник из сваког вагона. Тада је $a_{1}+$ $a_{2}+\\cdots+a_{n}=\\frac{n x-m_{1}}{x-y}$, где је $m_{1}$ добијена маса. Претпостављамо да је $m_{1} \\neq n x$, јер у супротном нема лажних златника. У другом мерењу, за неко $q \\in \\mathbb{N}$, узимамо из $i$-тог вагона $q^{i-1}$ златника. Ако је добијена маса\n$m_{2}$, имамо $a_{1}+q a_{2}+\\cdots+q^{n-1} a_{n-1}=\\frac{\\left(1+q+\\cdots+q^{n-1}\\right) x-m_{2}}{x-y}$. Одавде добијамо\n\n$$\nf\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)=\\frac{a_{1}+q a_{2}+\\cdots+q^{n-1} a_{n-1}}{a_{1}+a_{2}+\\cdots+a_{n}}=\\frac{\\left(1+q+\\cdots+q^{n-1}\\right) x-m_{2}}{n x-m_{1}}\n$$\n\nЖелимо да нам вредност $f$ једнозначно одреди $a_{1}, \\ldots, a_{n}$. Дакле, довољно је показати да постоји природан број $q$ такав да је функција $f:\\{0,1\\}^{n} \\backslash$ $\\{(0,0, \\ldots, 0)\\} \\rightarrow \\mathbb{R}$ инјективна.\n\nЗа фиксиране $\\mathfrak{a}=\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ и $\\mathfrak{a}=\\left(b_{1}, b_{2}, \\ldots, b_{n}\\right)$, једнакост $f(\\mathfrak{a})=f(\\mathfrak{b})$ је еквивалентна са $P_{\\mathfrak{a}, \\mathfrak{b}}(q)=\\left(a_{n} b-b_{n} a\\right) q^{n-1}+\\cdots+\\left(a_{2} b-b_{2} a\\right) q+\\left(a_{1} b-b_{1} a\\right)=0$, где је $a=a_{1}+a_{2}+\\ldots+a_{n} \\neq 0 \\neq b_{1}+b_{2}+\\ldots b_{n}=b$. Према томе, ако функција $f$ није инјективна, онда је $q$ нула полинома\n\n$$\nP(q)=\\prod_{\\mathfrak{a}, \\mathfrak{b}} P_{\\mathfrak{a}, \\mathfrak{b}}(q)\n$$\n\nКако ниједан од полинома $P_{\\mathfrak{a}, \\mathfrak{b}}$ није идентички једнак 0 , постоји само коначно много бројева $q$ за које је $P(q)=0$, па је могуће одабрати $q$ за које је $f$ инјективна функција.\n\nОвако у два мерења можемо да одредимо $a_{1}, \\ldots, a_{n}$, тј. вагоне са лажним златницима. Најзад, $y$ одређујемо из једнакости $y=x-\\frac{n x-m_{1}}{a_{1}+a_{2}+\\cdots+a_{n}}$.\n\nС друге стране, једно мерење није довољно, јер узимањем $k_{i}$ златника из $i$-тог вагона добијамо једначину $k_{1} a_{1}+\\cdots+k_{n} a_{n}=\\frac{k x-m}{x-y}$ (где је $k=k_{1}+$ $\\cdots+k_{n}$ ) која у општем случају има више решења. На пример, два могућа решења за $\\left(a_{1}, a_{2}, \\ldots, a_{n}, y\\right)$ су $\\left(1,0, \\ldots, 0, x-\\frac{k x-m}{k_{1}}\\right)$ и $\\left(0,0, \\ldots, 1, x-\\frac{k x-m}{k_{n}}\\right)$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2013_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2013", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Дат је природан број $k$. Нека је $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ бијекција таква да за свака два цела броја $i$ и $j$ за које је $|i-j| \\leqslant k$ важи $|f(i)-f(j)| \\leqslant k$. Доказати да за све $i, j \\in \\mathbb{Z}$ важи\n\n$$\n|f(i)-f(j)|=|i-j|\n$$\n\n(Миљан Кнежевић)", "solution": "За $k=1$ тврђење је тривијално. Нека је зато $k>2$. Интервалом дужине $k$ зовемо скуп облика $\\{x, x+1, \\ldots, x+k\\}, x \\in \\mathbb{Z}$. Два цела броја $x$ и $y$ ће бити узастопна ако и само ако постоје интервали $I_{1}$ и $I_{2}$ дужине $k$ за које је $I_{1} \\cap I_{2}=\\{x, y\\}$. Међутим, по услову задатка су $f\\left(I_{1}\\right)$ и $f\\left(I_{2}\\right)$ такође интервали дужине $k$, па како је $\\{f(x), f(y)\\}=f\\left(I_{1}\\right) \\cap f\\left(I_{2}\\right)$, следи да су и $f(x)$ и $f(y)$ узастопни бројеви. Одавде је $|f(x+1)-f(x)|=1$ за $x \\in \\mathbb{Z}$. Коначно, користећи инјективност пресликавања, једноставном индукцијом по $n$ добијамо да је $|f(x+n)-f(x)|=n$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2013", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Нека је\n\n$$\nS_{n}=\\left\\{\\binom{n}{n},\\binom{2 n}{n},\\binom{3 n}{n}, \\ldots,\\binom{n^{2}}{n}\\right\\}, \\quad \\text { за } n \\in \\mathbb{N}\n$$\n\na) Доказати да постоји бесконачно много сложених природних бројева $n$ таквих да $S_{n}$ није потпун систем остатака по модулу $n$.\n\nб) Доказати да постоји бесконачно много сложених природних бројева $n$ таквих да $S_{n}$ јесте потпун систем остатака по модулу $n$.\n\n(Милош Милосавлевић)", "solution": "(а) Доказаћемо да $n=2 p$ задовољава услове, где је $p>2$ прост број. Имамо\n\n$$\n\\binom{2 k p}{2 p}=k \\prod_{i=1}^{p-1} \\frac{2 k p-i}{2 p-i} \\cdot(2 k-1) \\prod_{i=1}^{p-1} \\frac{2 k p-p-i}{p-i} \\equiv k(2 k-1) \\quad(\\bmod p)\n$$\n\nКонкретно, одавде је $\\binom{2 k p}{2 p}$ дељиво са $p$ за $k \\in\\left\\{\\frac{p+1}{2}, p, 2 p\\right\\}$, тј. $S_{2 p}$ има три елемента дељива са $p$, па није потпун систем остатака.\n\n(б) Доказаћемо да $n=p^{2}$ задовољава услове, где је $p>2$ прост број. Имамо $\\binom{k p^{2}}{p^{2}}=\\prod_{i=0}^{p^{2}-1} \\frac{k p^{2}-i}{p^{2}-i}=k \\prod_{j=1}^{p-1} \\frac{k p^{2}-j p}{j p} \\cdot \\prod_{p \\nmid j} \\frac{k p^{2}-i}{p^{2}-i}$, па је по модулу $p^{2}$\n\n$$\n\\binom{k n}{n} \\equiv k \\prod_{j=1}^{p-1} \\frac{k p-j}{j}=k \\prod_{j=1}^{p-1}\\left(1-\\frac{k p}{j}\\right) \\equiv k-k^{2} p \\sum_{j=1}^{p-1} \\frac{1}{j}\n$$\n\nКако је $\\sum_{j=1}^{p-1} \\frac{1}{j}=\\sum_{j=1}^{\\frac{p-1}{2}}\\left(\\frac{1}{j}+\\frac{1}{p-j}\\right)=\\sum_{j=1}^{\\frac{p-1}{2}} \\frac{p}{j(p-j)} \\equiv 0(\\bmod p)$, коначно следи да је $\\binom{k p^{2}}{p^{2}} \\equiv k\\left(\\bmod p^{2}\\right)$.\n\nНапомена. Има и других могућности за бројеве $n$ : на пример, (a) $n=8 k+6$ за $k \\in \\mathbb{N}$, односно (б) $n=p^{k}$ за прост број $p$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2013", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Нека су $M, N$ и $P$ средишта страница $B C, A C$ и $A B$, редом, а $O$ центар описане кружнице оштроуглог троугла $A B C$. Кружнице описане око троуглова $B O C$ и $M N P$ секу се у различитим тачкама $X$ и $Y$ унутар троугла $A B C$. Доказати да је\n\n$$\n\\varangle B A X=\\varangle C A Y\n$$\n\n(Марко Ђикић)\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\nНови Сад, 6. април 2013.\n\n## Други дан", "solution": "Обележимо са $k_{1}$ и $k_{2}$ редом кругове $M N P$ и $B O C$. Круг $k_{1}$ је Ојлеров круг у $\\triangle A B C$ и пролази кроз подножја висина $D, E$ из $B, C$ и средиште $O_{1}$ дужи $A H$, где је $H$ ортоцентар $\\triangle A B C$.\n\nПокажимо да друга пресечна тачка $Z$ праве $A Y$ и круга $k_{1}$ лежи на Ојлеровом кругу $k_{3}$ троугла $A D E$. Сматраћемо да\n\n\nје $Z$ између $A$ и $Y$; доказ у другом случају је аналоган. Нека су $D_{1}$ и $E_{1}$ редом средишта дужи $A D$ и $A E$. Како је $A Y \\cdot A Z=A D \\cdot A N=$ $A D_{1} \\cdot A C$, тачке $Y, Z, C, D_{1}$ су концикличне, па је $\\varangle A Z D_{1}=\\varangle A C Y$.\n\nАналогно је $\\varangle A Z E_{1}=\\varangle A B Y$, па је $\\varangle D_{1} Z E_{1}=\\varangle A Z D_{1}+\\varangle A Z E_{1}=$ $\\varangle A C Y+\\varangle A B Y=\\varangle B Y C-\\varangle B A C=\\varangle B A C$. Одавде следи да је $Z$ на $k_{3}$.\n\nПошто је $O_{1}$ центар описаног круга $\\triangle A D E$, трансформација сличности која слика $\\triangle A B C$ у $\\triangle A D E$ такође слика $k_{1}$ у $k_{2}$ и $k_{2}$ у $k_{3}$, па је слика тачке $X \\in k_{1} \\cap k_{2}$ тачка $Z \\in k_{2} \\cap k_{3}$. Према томе, $\\varangle B A X=\\varangle D A Z=\\varangle C A Y$.\n\nНапомена. Показује се да се при инверзији са центром $A$ и квадратом полупречника $\\frac{1}{2} A B \\cdot A C$ кругови $k_{1}$ и $k_{2}$ сликају један у други, па се и тачке $X$ и $Y$ сликају једна у другу, одакле такође следи тврђење.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2013", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Одредити све $n \\in \\mathbb{N}$ за које је могуће поделити скуп $\\{1,2, \\ldots, 3 n\\}$ на $n$ дисјунктних трочланих подскупова облика $\\{a, b, c\\}$ у којима су $b-a$ и $c-b$ различити бројеви из скупа $\\{n-1, n, n+1\\}$.\n\n(Душан Ђукић)", "solution": "Тражена партиција скупа $\\{1,2, \\ldots, 3 n\\}$ одговара партицији темена правилног $3 n$-угла $P_{1} P_{2} \\ldots P_{3 n}$ на тројке $\\left\\{A_{i}, B_{i}, C_{i}\\right\\}$ такве да су углови сваког од троуглова $A_{i} B_{i} C_{i}$ једнаки $\\frac{n-1}{3 n} \\pi, \\frac{n}{3 n} \\pi$ и $\\frac{n+1}{3 n} \\pi$. Погодним обележавањем темена $3 n$-угла можемо постићи да темена $A_{1}, B_{1}, C_{1}$ буду управо $P_{n}, P_{2 n-1}, P_{3 n}$. Другим речима, не смањујемо општост ако претпоставимо да се међу тројкама $\\{a, b, c\\}$ на које је скуп $\\{1,2, \\ldots, 3 n\\}$ подељен налази и тројка $\\{n, 2 n-1,3 n\\}$.\n\nЈедна од преосталих $n-1$ тројки мора да садржи два броја из интервала $[2 n, 3 n-1]$, а то могу да буду једино $2 n$ и $3 n-1$. Једина тројка која садржи ове бројеве и не садржи $n$ је $\\{n-1,2 n, 3 n-1\\}$.\n\nСве остале тројке садрже тачно по један број из сваког од интервала $[1, n-2],[n+1,2 n-2]$ и $[2 n+1,3 n-2]$. Пресликавањем $(a, b, c) \\rightarrow(a, b-2, c-4)$ за $a<b<c$ добијамо одговарајуће растављање скупа $\\{1,2, \\ldots, 3(n-2)\\}$ на тројке. Како за $n=1$ овакво растављање није могуће, једноставном индукцијом показујемо да оно није могуће ни за једно непарно $n$.\n\nС друге стране, за парно $n=2 m$ тројке ( $2 i-1,2 i+n, 2 i+2 n-1$ ) и $(2 i, 2 i+n-1,2 i+2 n)$ за $i=1, \\ldots, m$ задовољавају услове.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2013", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Нека су $A^{\\prime}$ и $B^{\\prime}$ подножја висина из темена $A$ и $B$, редом, оштроуглог троугла $A B C(A C \\neq B C)$. Кружница $k$ садржи тачке $A^{\\prime}$ и $B^{\\prime}$ и дод��рује страницу $A B$ у тачки $D$. Ако троуглови $A D A^{\\prime}$ и $B D B^{\\prime}$ имају једнаке површине, доказати да је\n\n$$\n\\varangle A^{\\prime} D B^{\\prime}=\\varangle A C B .\n$$\n\n(Милош Милосавлевић)", "solution": "Нека је без смањења општости $B C>A C$. Тада се праве $A^{\\prime} B^{\\prime}$ и $A B$ секу у тачки $P$, при чему је $A$ између $P$ и $B$. Из једнакости површина $A D A^{\\prime}$ и $B D B^{\\prime}$ следи да је $\\frac{A D}{D B}=\\frac{P B^{\\prime}}{P A^{\\prime}}$. С друге стране, важи и $P D^{2}=P A^{\\prime} \\cdot P B^{\\prime}=P A$. $P B$, одакле је $\\frac{P D}{P B}=\\frac{P A}{P D}=\\frac{A D}{D B}=$ $\\frac{P B^{\\prime}}{P A^{\\prime}}$. Из последњих једнакости\n\n\nследи да је $B^{\\prime} D \\| B C$ и $A^{\\prime} D \\| A C$, и зато је $\\varangle A^{\\prime} D B^{\\prime}=\\varangle A C B$.\n\nДруго решеъе. Како је $\\varangle C B^{\\prime} D=\\alpha+\\varangle A D B^{\\prime}=\\alpha+\\varangle B^{\\prime} A^{\\prime} D=$ $\\varangle C A^{\\prime} D=x$, синусна теорема у $\\triangle A^{\\prime} B^{\\prime} D$ и $\\triangle A B^{\\prime} D$ нам даје $B D=$ $\\frac{B A^{\\prime} \\sin x}{\\sin (\\beta+x)}$ и $A D=\\frac{A B^{\\prime} \\sin x}{\\sin (\\alpha+x)}$, па је $\\frac{A D}{B D}=\\frac{A B^{\\prime} \\sin (\\beta+x)}{B A^{\\prime} \\sin (\\alpha+x)}=\\frac{\\sin (\\beta+x) \\cos \\alpha}{\\sin (\\alpha+x) \\cos \\beta}$. С\nдруге стране, из услова $\\left[A D A^{\\prime}\\right]=\\left[B D B^{\\prime}\\right]$ добијамо $\\frac{A D}{D B}=\\frac{d\\left(B^{\\prime}, A B\\right)}{d\\left(A^{\\prime}, A B\\right)}=$ $\\frac{\\sin \\alpha \\cos \\alpha}{\\sin \\beta \\cos \\beta}$, тј. $\\frac{\\sin (\\beta+x)}{\\sin (\\alpha+x)}=\\frac{\\sin \\alpha}{\\sin \\beta}$. Одавде лако добијамо $\\varangle A B^{\\prime} D=x=\\gamma$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2013", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Наћи највећу константу $K \\in \\mathbb{R}$ са следећим својством: ако су $a_{1}, a_{2}, a_{3}, a_{4}>0$ такви да за све $i, j, k \\in \\mathbb{N}, 1 \\leqslant i<j<k \\leqslant 4$, важи $a_{i}^{2}+a_{j}^{2}+a_{k}^{2} \\geqslant 2\\left(a_{i} a_{j}+a_{j} a_{k}+a_{k} a_{i}\\right)$, онда је\n\n$$\na_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2} \\geqslant K\\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\\right)\n$$\n\n(Душан Ђукић)\n\n## РЕШЕЊА", "solution": "Нека је $\\max \\left\\{a_{1}, a_{2}\\right\\} \\leqslant a_{3} \\leqslant a_{4}$. Означимо $a_{2}=\\beta^{2}$ и $a_{3}=\\gamma^{2}, \\beta, \\gamma \\geqslant 0$. Из услова задатка следи $a_{1} \\leqslant(\\gamma-\\beta)^{2}$ и $a_{4} \\geqslant(\\gamma+\\beta)^{2}$.\n\nПретпоставимо да су обе ове неједнакости заправо једнакости. Тада имамо $a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}=3\\left(\\beta^{4}+4 \\beta^{2} \\gamma^{2}+\\gamma^{4}\\right)$ и $a_{1} a_{2}+a_{1} a_{3}+$ $a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}=3\\left(\\beta^{4}+\\beta^{2} \\gamma^{2}+\\gamma^{4}\\right)$. При том је $\\gamma \\leqslant 2 \\beta$, па је $\\frac{\\beta^{4}+4 \\beta^{2} \\gamma^{2}+\\gamma^{4}}{\\beta^{4}+\\beta^{2} \\gamma^{2}+\\gamma^{4}}=1+\\frac{3 \\beta^{2} \\gamma^{2}}{\\beta^{4}+\\beta^{2} \\gamma^{2}+\\gamma^{4}}=1+\\frac{3}{1+\\frac{\\beta^{2}}{\\gamma^{2}}+\\frac{\\gamma^{2}}{\\beta^{2}}} \\geqslant \\frac{11}{7}$, уз једнакост за $\\gamma=2 \\beta$. Према томе, у овом случају је $K \\geqslant \\frac{11}{7}$, а једнакост се достиже за $a_{1}: a_{2}: a_{3}: a_{4}=1: 1: 4: 9$.\n\nПокажимо још да можемо да узмемо $a_{1}=(\\gamma-\\beta)^{2}$ и $a_{4}=(\\gamma+\\beta)^{2}$. Посматрајмо израз\n\n$$\nF=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}-\\frac{11}{7}\\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\\right)\n$$\n\nЗа фиксирано $a_{2}, a_{3}, a_{4}, F$ је опадајућа функција по $a_{1}$ за $a_{1}<$ $\\frac{11}{14}\\left(a_{2}+a_{3}+a_{4}\\right)$, при чему је $\\frac{11}{14}\\left(a_{2}+a_{3}+a_{4}\\right) \\geqslant \\frac{11}{14}\\left(\\beta^{2}+\\gamma^{2}+(\\beta+\\gamma)^{2}\\right)$ $\\geqslant(\\gamma-\\beta)^{2} \\geqslant a_{1}$, па се $F$ не повећава ако $a_{1}$ заменимо са $(\\gamma-\\beta)^{2}$. Сада можемо да ставимо без смањења општости да је $a_{1} \\leqslant a_{2}$, тј. $\\beta \\leqslant \\gamma \\leqslant 2 \\beta$. Слично као горе, за фиксирано $a_{1}, a_{2}, a_{3}, F$ је растућа функција по $a_{4}$ за $a_{4}>\\frac{11}{14}\\left(a_{1}+a_{2}+a_{3}\\right)$, и при том је $\\frac{11}{14}\\left(a_{1}+a_{2}+a_{3}\\right)$ $\\leqslant \\frac{11}{14}\\left(\\beta^{2}+\\gamma^{2}+(\\gamma-\\beta)^{2}\\right) \\leqslant(\\gamma+\\beta)^{2} \\leqslant a_{4}$, дакле $F$ се не повећава ако $a_{4}$ заменимо са $(\\gamma+\\beta)^{2}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2014_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2014", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Одредити све функције $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ такве да за све $x, y \\in \\mathbb{R}$ важи\n\n$$\nf(x f(y)-y f(x))=f(x y)-x y . \\quad \\text { (Душан Ђукић) }\n$$", "solution": "Замена $y=0$ даје $f(x f(0))=f(0)$. Ако је $f(0) \\neq 0$, израз $x f(0)$ узима све реалне вредности, па је $f$ константна функција, а она не задовољава услове. Према томе, $f(0)=0$.\n\nСтављањем $y=x$ добијамо $f(0)=f\\left(x^{2}\\right)-x^{2}$, тј. $f\\left(x^{2}\\right)=x^{2}$. Дакле, $f(x)=x$ за све $x \\geqslant 0$. Убацимо сада произвољне $x, y<0$. Како је тада $f(x y)=x y$, имамо $f(x f(y)-y f(x))=0$, што може да важи само за $x f(y)-y f(x) \\leqslant 0$. Аналогно је и $y f(x)-x f(y) \\leqslant 0$, па је $y f(x)=x f(y)$, тј. $f(x) / x=f(y) / y$. Следи да је $f(x)=c x$ за све $x<0$, где је $c$ нека константа. Сада за $x<0<y$ добијамо $f((1-c) x y)=f(x y)-x y=(c-1) x y$, тј. $f(z)=-z$ за $z=(1-c) x y$. Ако је $c=1$, онда је $f(x) \\equiv x$, што је очигледно решење. С друге стране, за $c \\neq 1$ је $z \\neq 0$ и отуда $f(z) \\in\\{c z, z\\}$, па тада мора бити $c=-1$, што даје функцију $f(x)=|x|$ за све $x$. И ова функција је решење: све случајеве осим $x>0>y$ смо већ проверили, а за $x>0>y$ је $-2 x y=f(-2 x y)=f(x f(y)-y f(x))=f(x y)-x y=-2 x y$.\n\nПрема томе, решења су функције $f(x)=x$ и $f(x)=|x|$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2014", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "На страницама $B C$ и $A C$ троугла $A B C$ дате су тачке $D$ и $E$, редом. Нека је $F(F \\neq C)$ тачка пресека кружнице описане око троугла $C E D$ и праве која садржи тачку $C$ и паралелна је са правом $A B$. Нека је $G$ тачка пресека праве $F D$ и странице $A B$, а $H$ тачка на правој $A B$ таква да је $\\varangle H D A=\\varangle G E B$ и $H-A-B$. Ако је $D G=E H$, доказати да тачка пресека дужи $A D$ и $B E$ припада симетрали угла $A C B$.\n\n(Милош Милосављевић)", "solution": "Како је $\\varangle A G D=180^{\\circ}-\\varangle C F D=\\varangle C E D=180^{\\circ}-\\varangle A E D$, тачке $A$, $E, D, G$ су концикличне. Одавде је $\\varangle D A G=\\varangle D E G . \\quad$ Међутим, тада је $\\varangle D H B=\\varangle D A G-\\varangle H D A$ $=\\varangle D E G-\\varangle B E G=\\varangle D E B$, па су и тачке $H, E, D, B$ концикличне. Следи да је $B H E=180^{\\circ}-$ $\\varangle B D E=\\varangle C D E=\\varangle C F E$, што\n\n\nзначи да су тачке $F, E$ и $H$ колинеарне.\n\nСада је $E H=E F \\cdot \\frac{A E}{E C}$ и $D G=D F \\cdot \\frac{D B}{C D}$, па услов $E H=D G$ постаје $\\frac{A E}{E C} \\cdot \\frac{C D}{D B}=\\frac{D F}{E F} . \\quad$ С друге стране, из $\\varangle D E F=\\varangle D C F=\\varangle A B C$ и $\\varangle D F E=\\varangle A C B$ следи да је $\\triangle D E F \\sim \\triangle A B C$, па је $\\frac{D F}{E F}=\\frac{A C}{C B}=\\frac{A M}{M B}$, где је $M$ пресечна тачка симетрале угла $A C B$ и странице $A B$. Према томе, $\\frac{A E}{E C} \\cdot \\frac{C D}{D B} \\cdot \\frac{B M}{M A}=1$, па се по Чевиној теореми праве $A D$ и $B E$ секу на $C M$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2014", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Два играча играју следећу игру. Играчи наизменично записују по један природан број већи од један, при чему није дозвољено записати линеарну комбинацију претходно записаних бројева са ненегативним целим коефицијентима. Игру губи играч који не може да запише нови број. Да ли неко од играча има победничку стратегију и, ако има, који? (Александар Илић / \"Квант”)\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије\n\n## 8. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\n## 6. април 2014.\n\n## Други дан", "solution": "За $a, b \\in \\mathbb{N}$ дефинишимо $\\mathcal{L}\\{a, b\\}=\\left\\{a x+b y \\mid x, y \\in \\mathbb{N}_{0}\\right\\}$. Прво ћемо доказати једно помоћно тврђење.\n\nЛема. Нека су $a>1$ и $b>1$ узајамно прости природни бројеви.\n\n(a) $N=a b-a-b$ је највећи природан број ван скупа $\\mathcal{L}\\{a, b\\}$.\n\n(б) За свако $z \\in \\mathbb{Z}, z \\in \\mathcal{L}\\{a, b\\}$ ако и само ако $N-z \\notin \\mathcal{L}\\{a, b\\}$.\n\nДоказ. (a) Ако је $N=(b-1) a-b=a x+b y$ за неке $x \\in\\{0, \\ldots, b-1\\}$ и $y \\in \\mathbb{Z}$, онда је $x \\equiv b-1(\\bmod b)$, па је $x \\geqslant b-1$ и одатле $y<0$; дакле, $N \\notin \\mathcal{L}\\{a, b\\}$.\n\n(б) Јасно је да из $z \\in \\mathcal{L}\\{a, b\\}$ следи $N-z \\notin \\mathcal{L}\\{a, b\\}$ (у супротном би важило $N=z+(N-z) \\in \\mathcal{L}\\{a, b\\})$. Посматрајмо сада неко $z \\in \\mathbb{Z} \\backslash \\mathcal{L}\\{a, b\\}$. Ако је $x \\in\\{0, \\ldots, b-1\\}$ такво да је $a x \\equiv z$ $(\\bmod b)$, онда је $z<a x$, тј. $a x-b y=z$ за неко $y \\in \\mathbb{N}$. Тада је $N-x=(b-1-x) a+b(y-1) \\in \\mathcal{L}\\{a, b\\}$.\n\nНека играч А започне игру уписујући прост број $a \\geqslant 5$, након чега играч Б уписује природан број $b$ такав да $a \\nmid b$. Само коначно много природних бројева не припада скупу $\\mathcal{L}\\{a, b\\}$, па је игра коначна. Дакле, један од играча има победничку стратегију.\n\nРазмотримо игру у којој је други потез играча А број $N$. Ако је то губитнички потез, сада Б има победнички одговор у виду неког дозвољеног броја c. Међутим, онда играч А може да у другом потезу, уместо броја $N$, запише број с и надаље следи добитничку стратегију другог играча. Заиста, по леми, број $N-c$ није дозвољен, па након потеза $c$ ни број $N=(N-c)+c$ није дозвољен, те Б остаје управо у позицији која би за А била губитничка.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2014", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "За природан број $n$ кажемо да је шашав ако и само ако постоје природни бројеви $a>1$ и $b>1$ такви да је $n=a^{b}+b$. Да ли постоји 2014 узастопних природних бројева међу којима је тачно 2012 шашавих бројева?\n\n(Милош Милосављевић)", "solution": "Прво ћемо дати пример 2012 узастопних шашавих бројева. Довољно је узети бројеве $N+2, N+3, \\ldots, N+2013$, где је $N=2^{2013!}$.\n\nЗа природан број $n$, означимо са $f(n)$ број шашавих бројева међу $n, n+1, \\ldots, n+2013$. Како је $f(1)<2012$ (бројеви $1,2,3,4,5$ нису шашави), $f(N) \\geqslant 2012$ и $|f(n+1)-f(n)| \\leqslant 1$ за свако $n$, постоји $n$ такво да је $f(n)=2012$.\n\nДруго решеъе. Означимо $N=\\frac{2014!}{2011}$. Бројеви $2^{N}+i$ за $2 \\leqslant i \\leqslant 2010$ и $2012 \\leqslant i \\leqslant 2014$ су шашави; докажимо да $2^{N}+1$ и $2^{N}+2011$ то нису.\n\nПретпоставимо да је $2^{N}+2011=a^{b}+b$ (слично се испитује и број $\\left.2^{N}+1\\right)$. Из $2^{b} \\leqslant a^{b}<2^{N}$ следи $b<N$. Такође је $b>2011$, јер би у супротном било $2011-b=a^{b}-2^{N}=\\left(a-2^{\\frac{N}{b}}\\right)\\left(\\cdots+2^{\\frac{(b-1) N}{b}}\\right)>2^{\\frac{N}{b}}>$ 2011. Даље, ако $2 \\mid a$, имамо $2^{b} \\mid 2^{N}-a^{b}=b-2011<2^{b}$, што је немогуће. Најзад, за $2 \\nmid a$ и $2 \\mid b$ имамо $b-2011=\\left(2^{\\frac{N}{2}}-a^{\\frac{b}{2}}\\right)\\left(2^{\\frac{N}{2}}+a^{\\frac{b}{2}}\\right)>$ $2^{\\frac{N}{2}}$, па ��е $2^{N}+2011=a^{b}+b>2^{2^{N / 2}}$, опет немогуће јер је $2^{\\frac{N}{2}}>N$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2014", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Правилан $n$-тоугао подељен је на троуглове помоћу $n-3$ дијагонале од којих никоје две немају заједничких унутрашњих тачака. Колико највише међу овим троугловима може бити међусобно неподударних?\n\n(Душан Ђукић)", "solution": "Одговор је $\\left[\\frac{3 n-7}{4}\\right]$ за $n>3$, односно 1 за $n=3$.\n\nТроуглове са по две, једном или ниједном страницом која је уједно страница $n$-тоугла ( $n>3$ ) зовемо редом уиима, танким и дебелим троугловима. Нека у подели има $a$ дебелих троуглова, $b$ танких и c ушију. Број страница $n$-тоугла које они заузимају је $b+2 c=n$. С друге стране, укупан број троуглова је $a+b+c=n-2$. Из ове две релације добијамо $c=a+2$.\n\nКако троуглова који нису дебели има највише $\\left[\\frac{n-1}{2}\\right]$ различитих, укупан број $N$ неподударних троуглова у подели није већи од $\\frac{n-1}{2}+a$. С друге стране, у таквој подели има $a+2$ ушију, а све уши су подударне, па је $N \\leqslant n-2-(a+1)=n-a-3$. Сабирањем добијамо $2 N \\leqslant\\left(\\frac{n-1}{2}+a\\right)+(n-a-3)=\\frac{3 n-7}{2}$, тј. $N \\leqslant\\left[\\frac{3 n-7}{4}\\right]$.\n\nНајзад, повлачењем дијагонала $A_{0} A_{2 i}$ и $A_{2 i-2} A_{2 i}\\left(1 \\leqslant i \\leqslant\\left[\\frac{n}{4}\\right]\\right)$ и $A_{0} A_{j}$ $\\left(2\\left[\\frac{n}{4}\\right]<j \\leqslant n-2\\right)$ добијамо пример са тачно $\\left[\\frac{n-1}{2}\\right]+\\left[\\frac{n}{4}\\right]-1=\\left[\\frac{3 n-7}{4}\\right]$ неподударних троуглова.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2014", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Симетрале унутрашњих углова код темена $A$ и $B$ троугла $A B C$ секу наспрамне странице у тачкама $D$ и $E$, редом. Ромб је уписан у четвороугао $A B D E$ тако да се на свакој страници четвороугла налази тачно једно теме ромба. Ако је $\\varangle B A C=\\alpha$ и $\\varangle A B C=\\beta$, доказати да је барем један угао ромба не већи од $\\max \\{\\alpha, \\beta\\}$.\n\n(Душан Ђукић)\n\n## РЕШЕЊА", "solution": "Нека је $K L M N$ ромб са $K \\in A B, L \\in B D$ и $N \\in E A$. Посматрајмо трапез $P Q R S$ са $P, Q \\in A B, P Q \\| R S$ и $\\varangle P Q R=\\varangle Q P S=\\varangle K N M=$ $\\varphi$ такав да су $K, L, M, N$ на $P Q, Q R, R S, S P$ редом. Претпоставимо да је $\\varphi>\\alpha, \\beta$. Тада $R$ и $S$ леже ван $\\triangle A B C$.\n\nКако је $\\varangle S N M=180^{\\circ}-\\varphi-\\varangle N M S=\\angle R M L$ и $\\varangle L R M=\\varangle M S N$, троуглови $L R M$ и $M S N$ су подударни, па је $L R=M S$. Слично, ако је $Q^{\\prime}$ тачка на $A B$ таква да је $\\varangle L Q^{\\prime} B=\\varphi$, троуглови $L R M$ и $K Q^{\\prime} L$ су подударни, па је $M R=L Q^{\\prime}=L Q$. Следи да је $R Q=R L+L Q=S M+M R=R S$.\n\n\n\nСада је $d(R, A B)=R Q \\sin \\varphi>R S \\sin \\alpha>d(R, A C)$ и аналогно $d(S, A B)>d(S, B C)$, што значи да тачке $R$ и $S$ леже изнад правих $A D$ и $B E$ редом (тј. у полуравнима у којима је $C$ ), одакле следи да обе тачке леже изнад праве $D E$. Ово је немогуће јер се дужи $R S$ и $D E$ секу у $M$.\n\nДруго решење. Растојање од тачке $X$ до праве $p$ означавамо $d(X, p)$.\n\nЛема. За произвољну тачку $M$ на дужи $D E$ важи $d(M, A B)=$ $d(M, A C)+d(M, B C)$.\n\nДоказ. Ако је $\\frac{D M}{D E}=k$, важи $d(M, A B)=k d(E, A B)+(1-k) d(D, A B)$ $=k d(E, B C)+(1-k) d(D, A C)=d(M, B C)+d(M, A C)$.\n\nКористимо исте ознаке као у првом решењу. Нека је $a$ страница ромба и $O$ његов центар. Имамо\n\n$$\n\\begin{aligned}\nd(M, A C)+d(M, B C) & =a(\\sin \\varangle M N C+\\sin \\varangle M L C), \\\\\n\\text { и } d(M, A B) & =2 d(O, A B)=d(L, A B)+d(N, A B) \\\\\n& =a(\\sin \\varangle N K A+\\sin \\varangle L K B) .\n\\end{aligned}\n$$\n\nМеђутим, ако је $\\varphi>\\alpha, \\beta$, онда је $\\varangle N K A=\\varangle M N C+\\varphi-\\alpha>$ $\\varangle M N C$ и аналогно $\\varangle L K B>\\varangle M L C$, па из горњих једначина следи $d(M, A B)>d(M, A C)+d(M, B C)$, контрадикција.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2015_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2015", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Дат је тетивни четвороугао $A B C D$. Тачке $M, N, P$ и $Q$ су средишта страница $D A, A B, B C$ и $C D$, редом, а тачка $E$ је пресек дијагонала $A C$ и $B D$. Кружнице описане око $\\triangle E M N$ и $\\triangle E P Q$ секу се у тачки $F \\neq E$. Доказати да важи $E F \\perp A C$.\n\n(Душан Ђукић)", "solution": "Троуглови $E A B$ и $E D C$ су слични, па су то и троуглови $E B N$ и $E C Q$. Зато у оријентисаним угловима важи $\\varangle M F E=\\varangle M N E=\\varangle B E N=\\varangle Q E C$ $=\\varangle E Q M$. Аналогно важи $\\varangle Q F E=$ $\\varangle E M Q$, одакле следи да је $F$ ортоцентар троугла $E M Q$. Дакле, $E F \\perp$ $Q M \\| A C$.\n\nДруго решеъе. Посматрајмо транслацију $\\mathcal{T}$ за вектор $\\frac{1}{2} \\overrightarrow{A C}$. Важи $\\mathcal{T}(M)=$\n\n\n$Q$ и $\\mathcal{T}(N)=P$; означимо $\\mathcal{T}(E)=E^{\\prime}$. Из сличности троуглова $A E D$ и $B E C$ следи $\\triangle A E M \\sim \\triangle B E P$, одакле је $\\varangle Q E^{\\prime} E=\\varangle E M Q=\\varangle M E A=\\varangle B E P=$ $\\varangle Q P E$, па тачка $E^{\\prime}$ лежи на кругу $P E Q$. Према томе, транслација $\\mathcal{T}$ слика круг $M E N$ у круг $P E Q$, па је права која спаја њихове центре паралелна са $A C$, одакле следи тврђење.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2015", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Нека је $k$ природан број. За $n \\in \\mathbb{N}$ означимо са $f_{k}(n)$ најмањи природан број већи од $k n$ такав да је $n f_{k}(n)$ потпун квадрат природног броја. Ако је испуњено $f_{k}(m)=f_{k}(n)$, доказати да важи $m=n$.\n\n(Никола Петровић)", "solution": "Претпоставимо да је $f_{k}(m)=f_{k}(n)=q$. Напишимо број $q$ у облику $q=a u^{2}$, где су $a, u \\in \\mathbb{N}$ и $a$ није дељиво ниједним потпуним квадратом већим од 1 . Како је $m q=a m u^{2}$ потпун квадрат, то је и $a m$, па следи да је $m=a v^{2}$ за неко $v \\in \\mathbb{N}$. Слично је $n=a w^{2}$ за неко $w \\in \\mathbb{N}$.\n\nКако је $f_{k}\\left(a v^{2}\\right)=a u^{2}, u$ је најмањи природан број већи од $v \\sqrt{k}$. Аналогно, $u$ је најмањи природан број већи од $w \\sqrt{k}$, па мора да важи $|v \\sqrt{k}-w \\sqrt{k}|<1$. Међутим, одавде следи $|v-w|<\\frac{1}{\\sqrt{k}}<1$, па мора бити $v=w$, тј. $m=n$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2015", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Стражар предлаже затвореницима следећу игру. Сви ће бити изведени у двориште, где ће свакоме од њих бити стављен на главу шешир у једној од 5 могућих боја. Стражар ће их потом поређати у врсту тако да сваки затвореник види све шешире осим сопственог и питати првог затвореника у врсти да ли зна боју свог шешира. Затвореник гласно одговара “да\" или \"не\". Ако одговори \"не\", биће одмах закључан у самицу. Ако одговори “да\", стражар ће га питати које је боје његов шешир, на шта затвореник треба да одговори на такав начин да остали затвореници не чују одговор. Уколико је одговор погрешан, тај затвореник биће одмах закључан у самицу пред свима, а ако је одговор тачан, тај затвореник биће одмах ослобођен пред свима. Стражар потом прилази следећем затворенику у реду и понавља исти поступак, и тако све ��о последњег затвореника. Затвореници имају могућност да осмисле стратегију пре почетка игре, али кад игра почне, никаква комуникација међу затвореницима није дозвољена. Ако у затвору има 2015 затвореника, који је максималан број затвореника који ће загарантовано бити ослобођени уколико затвореници примењују оптималну стратегију?\n\n(Бојан Башић)\n\nВреме за рад 270 минута.\n\nРешења задатака детаљно образложити.\n\nСваки задатак вреди 7 бодова.\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије\n\n## 9. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\n\n\n## Други дан", "solution": "Доделимо бојама вредности $0,1,2,3,4$ и означимо са $B$ боју шешира другог затвореника, а са $S$ збир боја шешира од трећег до последњег затвореника по модулу 5. Описаћемо стратегију прва два затвореника након које ће сви остали затвореници знати $S$, те ће, знајући боје осталих шешира, моћи да одреде своју. Овако ће за бар 2013 затвореника бити обезбеђена слобода. Први затвореник одговара \"не\" ако је $S \\in\\{0, B, B+1\\}$ или $(B, S)=(4,1)$. На то други одговара \"не\" ако је $S=0$, а у супротном каже \"да\" и стражару даје одговор $S$. На овај начин, ако чују два одговора \"не\", остали знају да је $S=0$. Ако други каже \"да\" и буде ослобођен, остали знају да је $S=B$, док у супротном знају да је $S=B+1$ ако $B \\neq 4$, односно $S=1$ ако $B=4$.\n\nУ осталим случајевима први затвореник каже “да\" (небитно је шта ће бити с њим). На то други каже \"да\" ако $S \\in\\{2,4\\}$ и стражару даје одговор $S-2$. Ако је $B=0$, онда $S \\notin\\{0,1\\}$, па остали знају да је $S=2$ ако други буде ослобођен, $S=3$ ако каже \"не\", и $S=4$ ако каже \"да\" и промаши. Најзад, ако је $B \\neq 0$, с обзиром на потврдан одговор првог важи $S \\equiv B+2$ или $S \\equiv B+3(\\bmod 4)$, а одговор другог одређује парност $S$, што осталима омогућује да одреде $S$.\n\nОстаје да докажемо да ниједна стратегија не гарантује слободу 2014 затвореника. Претпоставимо да таква стратегија постоји и посматрајмо скуп од\nпет распореда који се разликују само у боји шешира другог затвореника. У највише једном од ових распореда стратегија предвиђа да први каже \"не\" (у супротном други не би могао да са сигурношћу одреди боју свог шешира). У бар три од преостала четири распореда први би морао да промаши, па други не би могао да одреди боју свог шешира. Овим је доказ завршен.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2015", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "За цео број $a, a \\neq 0$, означимо са $v_{2}(a)$ највећи ненегативан цео број $k$ такав да $2^{k} \\mid a$. За дато $n \\in \\mathbb{N}$ одредити највећу могућу кардиналност подскупа $A$ скупа $\\left\\{1,2,3, \\ldots, 2^{n}\\right\\}$ са следећим својством:\n\n$$\n\\text { за све } x, y \\in A, x \\neq y, \\text { број } v_{2}(x-y) \\text { је паран. }\n$$\n\n(Дуиан Ђукић)", "solution": "Доказаћемо индукцијом по $k$ да скуп $A$ садржи највише $2^{k}$ различитих елемената по модулу $2^{2 k}$. То тривијално важи за $k=0$. Нека је $k>0$. По индуктивној претпост��вци, елементи скупа $A$ дају највише $2^{k-1}$ остатака по модулу $2^{2 k-2}$. Претпоставимо да елементи $A$ дају више од $2^{k}$ остатака по модулу $2^{2 k}$. На основу Дирихлеовог принципа, бар три од ових остатака су једнаки по модулу $2^{2 k-2}$. Али међу ова три остатка, два се разликују за $2^{2 k-1}\\left(\\bmod 2^{2 k}\\right)$, противно услову задатка.\n\nСледи да је $|A| \\leqslant 2^{\\left[\\frac{n+1}{2}\\right]}$. Пример скупа $A$ са $2^{\\left[\\frac{n+1}{2}\\right]}$ елемената добијамо укључивањем бројева облика $\\sum_{i \\in B} 4^{i}$ за све подскупове $B$ скупа $\\left\\{0,1, \\ldots,\\left[\\frac{n-1}{2}\\right]\\right\\}$.\n\nДруго решеъе. Кажемо да је скуп $X$ срећан ако је $v_{2}(x-y)$ парно за све $x, y \\in X(x \\neq y)$, а несрећан ако је $v_{2}(x-y)$ непарно за све $x, y \\in X(x \\neq y)$. Означимо са $a_{n}$ и $b_{n}$ редом максималне кардиналности срећног и несрећног подскупа скупа $T_{n}=\\left\\{1,2, \\ldots, 2^{n}\\right\\}$.\n\nПосматрајмо срећан скуп $A \\subset T_{n}, n \\geqslant 1$. Како је $v_{2}(2 x-2 y)=v_{2}(x-y)+1$, скупови $A_{0}=\\left\\{\\frac{x}{2}|x \\in A, 2| x\\right\\}$ и $A_{1}=\\left\\{\\left.\\frac{x-1}{2} \\right\\rvert\\, x \\in A, 2 \\nmid x\\right\\}$ су несрећни подскупови скупа $T_{n-1}$ и имају највише по $b_{n-1}$ елемената. С друге стране, ако је $A_{0} \\subset T_{n-1}$ несрећан скуп, скуп $\\left\\{2 x, 2 x+1 \\mid x \\in A_{0}\\right\\} \\subset T_{n}$ је срећан и има $2\\left|A_{0}\\right|$ елемената. Следи да је $a_{n}=2 b_{n-1}$.\n\nСлично, ако је $B \\subset T_{n}$ непаран скуп, сви његови елементи су исте парности, а скуп $B^{\\prime}=\\left\\{\\left.\\left\\lceil\\frac{x}{2}\\right\\rceil \\right\\rvert\\, x \\in B\\right\\} \\subset T_{n-1}$ је срећан. С друге стране, ако је $B^{\\prime} \\subset T_{n-1}$ срећан, скуп $B=\\left\\{2 x-1 \\mid x \\in B^{\\prime}\\right\\} \\subset T_{n}$ је несрећан. Одавде је $b_{n}=a_{n-1}$.\n\nДобијене релације дају $a_{n}=2 a_{n-2}$ за $n \\geqslant 2$, па из $a_{0}=1$ и $a_{1}=2$ једноставном индукцијом добијамо $a_{n}=2^{\\left[\\frac{n+1}{2}\\right]}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2015", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Доказати неједнакост\n\n$$\n\\frac{x-y}{x y+2 y+1}+\\frac{y-z}{y z+2 z+1}+\\frac{z-x}{z x+2 x+1} \\geqslant 0\n$$\n\nгде су $x, y$ и $z$ ненегативни реални бројеви.\n\n(Душан Ђукић)", "solution": "Означимо $a=\\frac{x-y}{x y+2 y+1}, b=\\frac{y-z}{y z+2 z+1}$ и $c=\\frac{z-x}{z x+2 x+1}$. Тада је $1+\\frac{1}{a}=\\frac{x y+x+y+1}{x-y}$ и одатле $\\frac{a}{a+1}=\\frac{x-y}{x y+x+y+1}=\\frac{1}{y+1}-\\frac{1}{x+1}$; аналогно је $\\frac{b}{b+1}=\\frac{1}{z+1}-\\frac{1}{y+1}$ и $\\frac{c}{c+1}=$ $\\frac{1}{x+1}-\\frac{1}{z+1}$.\n\nИз $0<\\frac{1}{x+1}, \\frac{1}{y+1}, \\frac{1}{z+1}<1$ следи $\\frac{a}{a+1}, \\frac{b}{b+1}, \\frac{c}{c+1}<1$, па су $a+1, b+1, c+1$ позитивни. Осим тога, имамо $\\frac{a}{a+1}+\\frac{b}{b+1}+\\frac{c}{c+1}=0$, тј. $\\frac{1}{a+1}+\\frac{1}{b+1}+\\frac{1}{c+1}=3$. Сада је по Коши-Шварцовој неједнакости $(a+1)+(b+1)+(c+1) \\geqslant 3$, тј. $a+b+c \\geqslant 0$.\n\nДруго решење. Тражена неједнакост се множењем и груписањем своди на\n\n$$\n\\begin{aligned}\n& 2(x-1)^{2}(y-z)^{2}+2(y-1)^{2}(z-x)^{2}+2(z-1)^{2}(x-y)^{2} \\\\\n& +9\\left(x y^{2}+y z^{2}+z x^{2}-3 x y z\\right)+3\\left(x^{2} y+y^{2} z+z^{2} x-3 x y z\\right) \\geqslant 0\n\\end{aligned}\n$$\n\nгде су сви сабирци ненегативни на основу А-Г неједнакости.\n\nНапомена. Ако се услов $x, y, z \\geqslant 0$ замени са $x, y, z \\geqslant-\\varepsilon$ за произвољно $\\varepsilon>0$, тврђење више не мора да важи, што показује пример $(x, y, z)=\\left(-\\varepsilon, 1, \\frac{2}{\\varepsilon}\\right)$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2015", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "У скупу ненегативних целих бројева решити једначину\n\n$$\n\\left(2^{2015}+1\\right)^{x}+2^{2015}=2^{y}+1 . \\quad \\text { (Бојан Баиић) }\n$$\n\n## РЕШЕЊА", "solution": "За $x \\leqslant 1$ једина решења су $(0,2015)$ и $(1,2016)$.\n\nНека је $x>1$. Како је $2^{2015}+1$ дељиво са 3 , имамо $\\left(2^{2015}+1\\right)^{x}+2^{2015} \\equiv 2^{2015} \\equiv 5$ $(\\bmod 9)$, дакле $2^{y} \\equiv 4(\\bmod 9)$, одакле добијамо $y=6 k+2$ за неко $k \\in \\mathbb{N}$. Сада по модулу 13 имамо $2^{y}+1=\\left(2^{6}\\right)^{k} \\cdot 2^{2} \\equiv \\pm 4$ и $2^{2015} \\equiv 7(\\bmod 13)$, па тако добијамо $8^{x}+7 \\equiv \\pm 4(\\bmod 13)$. Међутим, $8^{x}$ даје један од остатака $1,5,8,12$ по модулу 13 , па је последња конгруенција немогућа.\n\nДруго решење. За $x>1$ имамо $2^{y}=\\left(2^{2015}+1\\right)^{x}+2^{2015}-1=(x+1) 2^{2015}+$ $\\sum_{i=2}^{x}\\binom{x}{i} 2^{2015 i} \\equiv(x+1) 2^{2015}\\left(\\bmod 2^{2019}\\right)$, па због $y>2019$ следи да $16 \\mid x+1$. Сада посматрајмо једначину по модулу 17 . Како је $2^{2015} \\equiv 9(\\bmod 17)$, добијамо $2^{y} \\equiv 10^{x}+8 \\equiv 10^{15}+8 \\equiv 3(\\bmod 17)$, што је немогуће.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2016_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2016", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Нека је $n$ природан број већи од 1. Доказати да постоји природан број $m$ већи од $n^{n}$ такав да је\n\n$$\n\\frac{n^{m}-m^{n}}{n+m}\n$$\n\nприродан број.\n\n(Никола Петровић)", "solution": "За почетак приметимо да за $m>n \\geqslant 3$ важи $n^{m}>m^{n}$, те је $\\frac{n^{m}-m^{n}}{m+n}>0$. Заиста, функција $f(x)=\\frac{\\ln x}{x}$ је опадајућа за $x>e$ јер је $f^{\\prime}(x)=\\frac{1-\\ln x}{x^{2}}<0$, па је $\\frac{\\ln n}{n}>\\frac{\\ln m}{m}$, тј. $m \\ln n>n \\ln m$, и одатле $n^{m}=e^{m \\ln n}>e^{n \\ln m}=m^{n}$.\n\nЗа $n=2$ се може узети $m=10$. Претпоставимо да је $n>2$. Имамо\n\n$$\nn^{m}-m^{n} \\equiv n^{m}-(-n)^{n}=n^{n}\\left(n^{m-n}-(-1)^{n}\\right) \\quad(\\bmod m+n)\n$$\n\nПотражићемо $m$ у облику $m=k n^{n}-n(k \\in \\mathbb{N})$. Тада $m+n=k n^{n} \\mid n^{m}-m^{n}$ ако и само ако $k \\mid n^{m-n}-(-1)^{n}$.\n\n$\\left(1^{\\circ}\\right)$ Ако је $n$ непарно, онда је $n^{m-n}-(-1)^{n}$ парно, па можемо узети $k=2$, тј. $m=2 n^{n}-n$.\n\n(2 $2^{\\circ}$ Ако је $n$ парно, онда је $n^{m-n}-(-1)^{n}=n^{m-n}-1$ дељиво са $n-1$, па можемо узети $k-n-1$, тј. $m=(n-1) n^{n}-n$.\n\nНапомена. Неједнакост $n^{m}>m^{n}$ за $m>n \\geqslant 3$ се може доказати индукцијом. Могућа су и другачија решења, нпр. за $n>2$ може се узети $m=p n^{n}-n$, где је $p$ било који прост делилац броја $n^{n^{n}}-2 n-(-1)^{n}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2016", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Дат је природан број $n$. Дефинишимо $f(0, j)=f(i, 0)=0, f(1,1)=n$ и\n\n$$\nf(i, j)=\\left\\lfloor\\frac{f(i-1, j)}{2}\\right\\rfloor+\\left\\lfloor\\frac{f(i, j-1)}{2}\\right\\rfloor\n$$\n\nза све природне бројеве $i$ и $j,(i, j) \\neq(1,1)$. Колико има уређених парова природних бројева $(i, j)$ за које је $f(i, j)$ непаран број? (Душан Ђукић)", "solution": "Одговор је $n$.\n\nЗа $m \\geqslant 2$ означимо $s_{m}=\\sum_{i+j=m} f(i, j)$. Како је остатак $f(i, j)$ при дељењу са 2 једнак $f(i, j)-2\\left[\\frac{f(i, j)}{2}\\right]$, број непарних међу бројевима $f(i, j)$ за $i, j \\geqslant 0$ и $i+j=m$ једнак је\n\n$$\n\\begin{aligned}\n\\sum_{i+j=m}\\left(f(i, j)-2\\left[\\frac{f(i, j)}{2}\\right]\\right) & =s_{m}-\\sum_{i+j=m}\\left(\\left[\\frac{f(i-1, j+1)}{2}\\right]+\\left[\\frac{f(i, j)}{2}\\right]\\right) \\\\\n& =s_{m}-s_{m+1}\n\\end{aligned}\n$$\n\nСледи да је број парова $(i, j)$ за које је $f(i, j)$ непарно и $i+j<m$ једнак $s_{2}-s_{m}=n-s_{m}$.\n\nОстаје да покажемо да је $s_{m}=0$ за све довољно велике $m$. Јасно је да је низ $s_{m}$ ненегативан и нерастући, па постоје $N$ и $k$ такви да је $s_{m}=k$ за све $m \\geqslant N$. То значи да је $f(i, j)$ парно кад год је $i+j \\geqslant m$. Претпоставимо да је $k>0$ и посматрајмо најмање $i$ такво да је $f(i, m-i)>0$. Једноставном индукцијом добијамо $f(i, m+r-i)=\\left[\\frac{f(i, m-i)}{2^{r}}\\right]$ за $r \\geqslant 1$. Међутим, ако је $2^{r} \\leqslant f(i, m-i)<2^{r+1}$, одавде је $f(i, m+r-i)=1$, противно претпоставци.\n\nДруго решење (У. Динић). Поставимо $n$ жетона у тачку $(1,1)$ у координатној равни. У сваком кораку, из сваке тачке $(i, j)$ ћемо пребацити по цео део половине њених жетона у тачке $(i+1, j)$ и $(i, j+1)$. Приметимо да, ако је нека врста или колона у неком тренутку непразна, она ће увек остати непразна. Тако ниједан жетон не може изаћи из квадрата $[1, n] \\times[1, n]$, па се игра завршава у коначном броју корака.\n\nНије тешко видети да се након $i+j-2$ корака у тачки $(i, j)$ налази тачно $f(i, j)$ жетона. Шта више, број $f(i, j)$ је непаран ако након следећег корака\nу тачки $(i, j)$ остане један жетон. Како у завр��ној позицији има тачно $n$ жетона, следи да међу члановима низа $f(i, j)$ има $n$ непарних бројева.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2016", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Нека је $O$ центар кружнице описане око $\\triangle A B C$. Права $t$ додирује кружницу описану око $\\triangle B O C$ и сече странице $A B$ и $A C$ у тачкама $D$ и $E$, редом $(D, E \\not \\equiv A)$. Тачка $A^{\\prime}$ је симетрична тачки $A$ у односу на праву $t$. Доказати да се кружнице описане око $\\triangle A^{\\prime} D E$ и $\\triangle A B C$ додирују. (Душан Ђукић)\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 10. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\n## 2. април 2016 .\n\n## Други дан", "solution": "Означимо са $K$ додирну тачку праве $t$ и круга $B O C$. Нека се кругови описани око троуглова $B D K$ и $C E K$ секу у тачки $X \\neq K$. Како је $\\varangle B X C=$ $\\varangle B X K+\\varangle K X C=\\varangle A D K+\\varangle K E A=180^{\\circ}-\\varangle C A B$, тачка $X$ лежи на описаном кругу $k$ троугла $A B C$. Шта више, $\\varangle D X E=\\varangle D X K+\\varangle K X E=\\varangle D B K+$ $\\varangle K C E=\\varangle C K B-\\varangle C A B=\\varangle C A B=$ $\\varangle D X E$, па $X$ такође лежи на описаном кругу $k_{1}$ троугла $A^{\\prime} D E$. Доказаћемо да се кругови $k$ и $k_{1}$ додирују у тачки $X$.\n\nАко се праве $C K$ и $X D$ секу у тачки $P$, онда важи $\\varangle X P C=\\varangle X D E-$ $\\varangle C K E=\\varangle X B K-\\varangle C B K=\\varangle X B C$, што значи да $P$ лежи на кругу $k$. Аналогно, праве $B K$ и $X E$ се секу у тачки $Q$ на кругу $k$. Најзад, из $\\varangle X P Q=\\varangle X B Q=\\varangle X D K$ следи да\n\n\nје $P Q \\| D E$. Према томе, троуглови $X D E$ и $X P Q$ су хомотетични са центром хомотетије $X$, па се њихови описани кругови додирују у $X$.\n\nДруго решеъе. Нека праве $B K$ и $C K$ поново секу описани круг $\\triangle A B C$ редом у тачкама $Q$ и $P$. Из $\\varangle C P Q=\\varangle C B Q=\\varangle C K E$ следи $P Q \\| D E$. Нека се праве $D P$ и $E Q$ секу у тачки $X$. Како су тачке $D=P X \\cap A B, K=P C \\cap Q B$ и $E=A C \\cap Q X$ колинеарне, по обратној Паскаловој теореми тачка $X$ лежи на истом кругу са тачкама $A, B, C, P, Q$. Према томе, троуглови $X D E$ и $X P Q$ су хомотетични, па се њихови описани кругови додирују у њиховом центру хомотетије $X$. Најзад, тачка $A^{\\prime}$ лежи на описаном кругу $\\triangle D E X$ јер je $\\varangle D X E=\\varangle P X Q=\\varangle P C A+\\varangle A B Q=\\varangle B K C-\\varangle B A C=\\varangle B A C=\\varangle D A^{\\prime} E$.\n\nНапомена. Важи и општије тврђење: ако је $K$ тачка у $\\triangle A B C, D$ и $E$ тачке у којима тангента на круг $B K C$ у $K$ сече $A B$ и $A C$, а $X$ друга тачка пресека кругова $B D K$ и $C E K$, онда се кругови $D E X$ и $A B C$ додирују у тачки $X$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2016", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "У $\\triangle A B C(A B \\neq A C)$ уписана кружница, чији је центар тачка $I$, додирује страницу $B C$ у тачки $D$. Нека је тачка $M$ средиште дужи $B C$. Доказати да се нормале из тачака $M$ и $D$ на праве $A I$ и $M I$, редом, секу на правој која садржи висину $\\triangle A B C$ из темена $A$.\n\n(Душан Ђукић)", "solution": "Означимо са $\\gamma$ уписани круг $\\triangle A B C$, а са $\\gamma_{a}$ и $I_{a}$ приписани круг наспрам $A$ и његов центар. Тачка $E$ симетрична тачки $D$ у односу на $M$ је додирна тачка $\\gamma_{a}$ са страницом $B C$. Нормала $\\ell_{1}$ из $D$ на $M I$ је радикална оса круга $\\gamma$ и круга $\\omega$ над пречником $D E$, док је нормала $\\ell_{2}$ из $A I$ радикална оса кругова $\\gamma$ и $\\gamma_{a}$ (због $M D=M E$ ). Такође, радикална оса кругова $\\gamma_{a}$ и $\\omega$ је нормала $\\ell_{3}$ из $E$ на $M I_{a}$. Праве $\\ell_{1}, \\ell_{2}$ и $\\ell_{3}$ се секу у радикалном центру $S$ кругова $\\gamma, \\gamma_{a}, \\omega$. С друге стране, поз-\n\n\nнато је (по \"Великом задатку\") да важи $M I \\| A E$ и $M I_{a} \\| A D$, па праве $\\ell_{1}$ и $\\ell_{3}$ садрже висине из $D$ и $E$ у троуглу $A D E$. Следи да је $S$ ортоцентар $\\triangle A D E$, а он лежи на висини из темена $A$.\n\nДруго решење. Нека се нормале из $M$ и $D$ редом на $A I$ и $M I$ секу у тачки $S$ и нека је $J$ тачка у којој права $M I$ сече висину из $A$ у $\\triangle A B C$. Довољно је доказати да је $A J=I D$. Заиста, тада ће следити да је $A J D I$ паралелограм, па је $M S \\perp D J$, тако да је $D$ ортоцентар троугла $M S J$ и одатле $J S \\perp M D$, тј. $A S \\perp B C$.\n\nОво се директно израчунава. Означимо са $H$ и $F$ редом подножја висине и симетрале угла из темена $A$, и $a=B C, b=C A, c=A B$. Тада је $B F=\\frac{a c}{b+c}$, $B D=\\frac{a-b+c}{2}$ и $B H=\\frac{a^{2}-b^{2}+c^{2}}{2 a}$, па је $F H=B F-B H=\\frac{|b-c|\\left((b+c)^{2}-a^{2}\\right)}{2 a(b+c)}, F D=$ $B F-B D=\\frac{|b-c|(b+c-a)}{2(b+c)}$ и најзад $\\frac{A J}{A H}=\\frac{F D}{F H}=\\frac{a}{a+b+c}=\\frac{I D}{A H}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2016", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Дато је $2 n-1$ двоелементних подскупова скупа $\\{1,2, \\ldots, n\\}$. Доказати да се може одабрати $n$ од ових подскупова чија унија садржи не више од $\\frac{2}{3} n+1$ елемената.\n\n(Душан Ђукић)", "solution": "Показаћемо индукцијом по $k\\left(k \\leqslant \\frac{2 n-1}{3}\\right)$ да се може избацити $3 k$ подскупова тако да је кардиналност уније преосталих не већа од $n-k$.\n\nЗа $k=0$ то је тривијално. Претпоставимо да је $k \\geqslant 1$ и да смо избацили $3(k-1)$ подскупова тако да унија преосталих не садржи више од $n-k+1$ елемената. Како је $2 n-1-3(k-1)<2(n-k+1)$, постоји елемент $x_{k}$ из уније који се налази у највише три од преосталих подскупова. Дакле, можемо да избацимо још три подскупа тако да унија преосталих $2 n-1-3 k$ не садржи елемент $x_{k}$, што завршава индуктивни корак.\n\nТврђење задатка следи за $k=\\left[\\frac{n-1}{3}\\right]$ jep је $n-\\left[\\frac{n-1}{3}\\right] \\leqslant n-\\frac{n-3}{3}=\\frac{2}{3} n+1$.\n\nНапомена. Пробабилистички метод даје слабију оцену $\\sim \\frac{n}{\\sqrt{2}}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2016", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Дати су природни бројеви $a_{1}, a_{2}, \\ldots, a_{2 \\text { 2016 }}$ такви да за све $n, 1 \\leqslant n \\leqslant 2^{2016}$, важи\n\n$$\na_{n} \\leqslant 2016 \\quad \\text { и } \\quad a_{1} a_{2} \\cdots a_{n}+1 \\text { је потпун квадрат. }\n$$\n\nДоказати да је неки од бројева $a_{1}, a_{2}, \\ldots, a_{22016}$ једнак 1. (Дуиан Ђукић)\n\n## РЕШЕЊА", "solution": "Кључна чињеница је да, ако су $a+1=u^{2}$ и $b=v^{2}$ потпуни квадрати и $a>b$, онда $a b+1$ није квадрат. Заиста, тада је $(u v-1)^{2}<a b+1=u^{2} v^{2}-v^{2}+1<(u v)^{2}$. Нека су $p_{1}, p_{2}, \\ldots, p_{m}$ сви прости бројеви мањи од 2016. За $1 \\leqslant n \\leqslant 2^{2016}$ посматрајмо бинарни низ $\\mathrm{c}_{n}=\\left(r_{1}, r_{2}, \\ldots, r_{m}\\right)$, где је $r_{i}=0$ ако је експонент уз $p_{i}$ у производу $P_{n}=a_{1} a_{2} \\cdots a_{n}$ паран, а $r_{i}=1$ у супротном. Како за низ с ${ }_{n}$ има само $2^{m}$ могућности, за свако $k \\leqslant 2^{2016}-2^{m}$ међу низовима с с, c $_{k+1}, \\ldots, \\mathrm{c}_{k+2^{m}}$ постоје два једнака, рецимо с $s$ и $c_{t}(s<t)$, а тада је $P_{t} / P_{s}$ потпун квадрат не већи од $2016^{2^{m}}$.\n\nПретпоставимо да у низу $\\left(a_{n}\\right)$ нема јединица. Узмимо $k=11 \\cdot 2^{m}$; свакако је $k+2^{m}<2^{2016}$. Видели смо да постоје индекси $s, t, k \\leqslant s<t \\leqslant k+2^{m}$, тако да је $b=P_{t} / P_{s}$ потпун квадрат. Међутим, како је $a=P_{s} \\geqslant P_{k} \\geqslant 2^{k}=2048^{2^{m}}>$ $2016^{2^{m}} \\geqslant b$, по чињеници са почетка, $a+1=P_{s}+1$ и $a b+1=P_{t}+1$ не могу истовремено да буду квадрати, што је контрадикција.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2017_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2017", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Нека су $a, b$ и $c$ позитивни реални бројеви за које важи $a+b+c=1$. Доказати:\n\n$$\n\\begin{array}{r}\na \\sqrt{2 b+1}+b \\sqrt{2 c+1}+c \\sqrt{2 a+1} \\leqslant \\sqrt{2-\\left(a^{2}+b^{2}+c^{2}\\right)} \\\\\n\\text { (Никола Петровић) }\n\\end{array}\n$$", "solution": "Квадрирањем обе стране и коришћењем једнакости $1-\\left(a^{2}+b^{2}+c^{2}\\right)=2(a b+$ $b c+c a)$ неједнакост из задатка се своди на\n\n$$\n\\begin{aligned}\nL= & 2 a^{2} b+2 b^{2} c+2 c^{2} a+ \\\\\n& 2 a b \\sqrt{(2 b+1)(2 c+1)}+2 b c \\sqrt{(2 c+1)(2 a+1)}+2 c a \\sqrt{(2 a+1)(2 b+1)} \\\\\n\\leqslant D= & 4(a b+b c+c a) .\n\\end{aligned}\n$$\n\nПо АМ-ГМ неједнакости имамо $2 a b \\sqrt{(2 b+1)(2 c+1)} \\leqslant a b(2 b+2 c+2)$ и аналогно $2 b c \\sqrt{(2 c+1)(2 a+1)} \\leqslant b c(2 c+2 a+2)$ и $2 c a \\sqrt{(2 a+1)(2 b+1)} \\leqslant c a(2 a+2 b+2)$, па сабирањем добијамо\n\n$$\n\\begin{aligned}\nL \\leqslant & 2\\left(a^{2} b+b^{2} c+c^{2} a+a b^{2}+b c^{2}+c a^{2}+3 a b c\\right)+2(a b+b c+c a)= \\\\\n& 2(a+b+c+1)(a b+b c+c a)=4(a b+b c+c a)=D\n\\end{aligned}\n$$\n\nДруго решење. Функција $f(x)=\\sqrt{x}$ је конкавна јер је $f^{\\prime}(x)=2 / \\sqrt{x}$ опадајућа функција. Применом Јенсенове неједнакости са тежинама $a, b$ и $c$ добијамо\n\n$$\n\\begin{aligned}\na \\sqrt{2 b+1}+b \\sqrt{2 c+1}+c \\sqrt{2 a+1} & \\leqslant \\sqrt{a(2 b+1)+b(2 c+1)+c(2 a+1)} \\\\\n& =\\sqrt{1+2(a b+b c+c a)}=\\sqrt{2-\\left(a^{2}+b^{2}+c^{2}\\right)}\n\\end{aligned}\n$$\n\nНапомена. Ако се допусти да неки од бројева $a, b, c$ буде нула, једнакост се достиже у случајевима $a=b=c=\\frac{1}{3}$ и $(a, b, c)=(1,0,0)$ са пермутацијама.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2017", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Дат је конвексан тетиван четвороугао $A B C D$. Нека се праве $A D$ и $B C$ секу у тачки $E$. На страницама $A D$ и $B C$ су одабране тачке $M$ и $N$, редом, такве да важи $A M: M D=B N: N C$. Кружнице описане око троугла $E M N$ и четвороугла $A B C D$ секу се у тачкама $X$ и $Y$. Доказати да се праве $A B, C D$ и $X Y$ секу у једној тачки или су све паралелне.\n\n(Дуиан Ђукић)", "solution": "У случају $A B \\| C D$ тврђење је тривијално: тачке $X$ и $Y$ су симетричне у односу на симетралу дужи $A B$ и $C D$ и важи $A B\\|X Y\\| C D$.\n\nНека је $A B \\nVdash C D$. Тада описани кругови $k_{1}$ и $k_{2}$ троуглова $E A B$ и $E C D$ имају другу пресечну тачку $P \\neq E$. Из $\\varangle P A D=\\varangle P B E$ и $\\varangle P D A=180^{\\circ}-\\varangle P D E=$ $180^{\\circ}-\\varangle P C E=\\varangle P C B$ следи да су троуглови $P A D$ и $P B C$ слични. При овој сличности тачки $M$ у $\\triangle P A D$ одговара тачка $N$ у $\\triangle P B C$, па је $\\varangle P M E=\\varangle P N E$. Закључујемо да тачке $E, P, M$ и $N$ леже на истом кругу $k_{3}$.\n\nКако тачка $F$ има једнаку потенцију $F A$. $F B=F C \\cdot F D$ у односу на кругове $k_{1}, k_{2}$\n\n\nи круг $k$ описан око $A B C D$, она лежи на радикални оси $E P$ кругова $k_{1}$ и $k_{2}$. Сада је још $F A \\cdot F B=F E \\cdot F P$, па $F$ такође припада радикалној оси кругова $k_{1}$ и $k_{3}$, а то је права $X Y$.\n\nДруго решеъе. Нека су $k, k_{1}, k_{2}$ и $k_{3}$ редом описани кругови четвороугла\n\n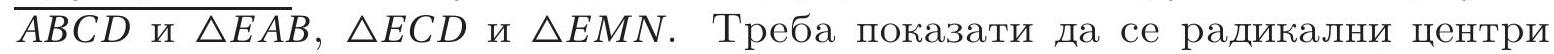\nтројки кругова ( $k, k_{1}, k_{2}$ ) и ( $k, k_{1}, k_{3}$ ) поклапају (можда у бесконачној тачки). Довољно је доказати да кругови $k_{1}, k_{2}, k_{3}$ имају заједничку радикалну осу, тј. да су њихови центри $O_{1}, O_{2}, O_{3}$ редом колинеарни.\n\nЗа $i=1,2,3$, означимо ��а $E_{i}$ тачку симетричну тачки $E$ у односу на $O_{i}$. Доказаћемо да се тачка $E_{3}$ поклапа са тачком $E_{3}^{\\prime}$ на дужи $E_{1} E_{2}$ таквом да је $E_{1} E_{3}^{\\prime}: E_{3}^{\\prime} E_{2}=A M: M D$. Заиста, пошто је $E_{1} A \\perp A D$ и $E_{2} D \\perp A D$, из Талесове теореме следи $E_{3}^{\\prime} M \\perp A D$; аналогно је $E_{3}^{\\prime} N \\perp B C$, па је $E_{3}^{\\prime} \\equiv E_{3}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2017", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "У врсти се налази $2 n-1$ сијалица. У почетку је средња ( $n$-та) упаљена, а све остале су угашене. У једном кораку је дозвољено одабрати две несуседне угашене сијалице између којих су све сијалице упаљене, и променити стање тим двема сијалицама, као и свим сијалицама између њих (на пример, од конфигурације $\\cdot$ооо $\\cdot$ добија се о $\\cdot$ $\\cdot$ ). Колико највише корака је могуће извршити?\n\n(Душан Ђукић)\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 11. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\n## 1. април 2017 .\n\n## Други дан", "solution": "Одговор је $\\left[\\frac{2^{n+1}-5}{3}\\right]$.\n\nПридружимо $i$-тој сијалици број $2^{|i-n|}$ и дефинишимо вредност конфигурације као збир бројева на упаљеним сијалицама. Вредност полазне конфигурације је 1, а при сваком кораку она се повећава за природан умножак броја 3. Корак повећава вредност за тачно 3 ако $n$-та сијалица мења стање; овакав корак зовемо добрим.\n\nПошто вредност не може да премаши $2^{n+1}-4$ (jep cе не могу упалити све сијалице), није могуће извршити више од $\\left[\\frac{2^{n+1}-5}{3}\\right]$ корака. Овај број се може достићи: довољно је показати да је могуће извршити бар $\\frac{2^{n+1}-7}{3}$ корака.\n\nДоказаћемо индукцијом по $n$ да, почевши од конфигурације вредности највише 3 , можемо да низом добрих корака добијемо конфигурацију вредности бар $2^{n+1}-6$. Ово се директно проверава за $n \\leqslant 2$. Нека је $n \\geqslant 3$. По индуктивној претпоставци за $n-1$, могуће је доћи до конфигурације вредности бар $2^{n}-6$ са првом и последњом сијалицом угашеном. У таквој конфигурацији, осим прве и последње сијалице, могу бити угашене ( $1^{\\circ}$ ) само $n$-та, $\\left(2^{\\circ}\\right)$ само $n$-та и једна од њој суседних, или (3) само једна од две суседне. У сваком од ова три случаја, у највише три добра корака постижемо да прва и последња сијалица буду упаљене и да вредност остатка конфигурације (без ове две сијалице) буде највише 3.\n\n\n\n$\\left(1^{\\circ}\\right)$\n\n\n\n$\\left(2^{\\circ}\\right)$\n\n\n\n$\\left(3^{\\circ}\\right)$\n\nПоновна примена индуктивне претпоставке за $n$ - 1 завршава индукцију.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2017", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Нека је $a$ природан број такав да за сваки природан број $n$ број $n^{2} a-1$ има бар један делилац већи од 1 који даје остатак 1 при дељењу са $n$. Доказати да је $а$ потпун квадрат.\n\n(Душан Ђукић)", "solution": "Нека је $n^{2} a-1=\\left(n x_{n}+1\\right) d_{n}\\left(x_{n}, d_{n} \\in \\mathbb{N}\\right)$. Тада је $d_{n} \\equiv-1(\\bmod n)$, па је\n\n$$\nn^{2} a-1=\\left(n x_{n}+1\\right)\\left(n y_{n}-1\\right) \\quad \\text { за неке } x_{n}, y_{n} \\in \\mathbb{N}\n$$\n\nшто се своди на $n a-n x_{n} y_{n}=y_{n}-x_{n}>-x_{n} y_{n}$. Одавде добијамо $x_{n} \\leqslant x_{n} y_{n}<$ $\\frac{n}{n-1} a \\leqslant 2 a$. Следи да у низу $x_{1}, x_{2}, \\ldots$ постоји члан који се јавља бесконачно много пута. Означимо тај члан са $X$. Тада $n X+1 \\mid n^{2} a-1$ и одатле\n\n$$\nn X+1 \\mid X^{2}\\left(n^{2} a-1\\right)-a\\left(n^{2} x^{2}-1\\right)=a-X^{2}\n$$\n\nза бесконачно много бројева $n$. Ово је могуће само за $a-X^{2}=0$, тј. $X^{2}=a$.\n\nДруго решење. Као и у првом решењу, нека је $n^{2} a-1=\\left(n x_{n}+1\\right)\\left(n y_{n}-1\\right)$, тј. $y_{n}-x_{n}=n\\left(a-x_{n} y_{n}\\right)=n d_{n}$. Разликујемо три случаја.\n\n(1 ) Ако је $d_{n}>0$, онда је $a=d_{n}+x_{n}\\left(x_{n}+n d_{n}\\right)>n d_{n} x_{n}$, што је немогуће за $n \\geqslant a$.\n\n(2 ${ }^{\\circ}$ Ако је $d_{n}<0$, онда је $a=d_{n}+y_{n}\\left(y_{n}-n d_{n}\\right)=y_{n}^{2}-d_{n}\\left(n y_{n}-1\\right)>n y_{n}-1$, што је немогуће за $n \\geqslant a+1$.\n\n$\\left(3^{\\circ}\\right)$ Ако је $d_{n}=0$, онда је $a=x_{n}^{2}$. потпун квадрат.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2017", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Одредити колико се највише краљица може поставити на таблу $2017 \\times 2017$, при чему свака краљица сме да напада највише једну од преосталих.\n\n(Бојан Башић и комисија)", "solution": "Означимо $n=2017$. Претпоставимо да је постављено $m>n$ краљица. Ни у једној врсти нема више од две краљице, па се у бар $m-n$ врста налазе по две краљице, тако да има највише $m-2(m-n)=2 n-m$ краљица које су саме у својој врсти. Слично, највише $2 n-m$ краљица су саме у својој колони. С друге стране, свака краљица је сама у својој врсти или у својој колони, па је $m \\leqslant 2(2 n-m)$, одакле је $m \\leqslant\\left[\\frac{4 n}{3}\\right]=2689$.\n\nНа слици А је приказано постављање 8 краљица на таблу $6 \\times 6$ у складу са захтевом задатка. Пре конструкције примера на табли $2017 \\times 2017$ размотрићемо следећи распоред краљица:\n\n- На таблу $335 \\times 335$ могуће је поставити 335 краљица које се међусобно не нападају чак ни ако се дијагонале продуже по модулу 335. Заиста, довољно је поставити краљице на сва поља $(x, y), 1 \\leqslant x, y \\leqslant 335$, за која је $y \\equiv 2 x(\\bmod 335)$, као на слици Б. Заиста, тада су сви збирови $x+y$ међусобно различити по модулу 335 , све разлике $x-y$ такође, па никоје две краљице нису у истој врсти, колони или дијагонали.\n\nПоделимо таблу $2017 \\times 2017$ на правоугаонике и квадрате страница 335, 6 и 1 , као на слици В. Квадрате обележене са Б и А попунићемо редом као на сликама Б и А, а у горње десно поље табле поставићемо још једну краљицу. Овако смо укупно поставили $8 \\cdot 335+8+1=2689$ краљица. Лако се проверава да овакво постављање задовољава услове задатка.\n\n\nНапомена. Табла $n \\times n$ чије су дијагонале продужене по модулу $n$ зове се торусна табла. На торусну таблу $n \\times n$ могуће је поставити $n$ краљица које се међусобно не нападају ако и само ако је $n \\equiv \\pm 1(\\bmod 6)$. Ово је доказано у 4. задатку са СMO 2012.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2017", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Нека је $k$ кружница описана око $\\triangle A B C$, а $k_{a}$ приписана кружница наспрам темена $A$. Две заједничке тангенте кружница $k$ и $k_{a}$ секу праву $B C$ у тачкама $P$ и $Q$. Доказати да важи $\\varangle P A B=\\varangle Q A C$.\n\n(Дуиан Ђукић)\n\n## РЕШЕЊА", "solution": "Нека унутрашња и спољна симетрала угла $B A C$ секу праву $B C$ редом у тачкама $D$ и (можда бесконачној) $D_{1}$. Заједничке тангенте се секу у центру $T$ позитивне хомотетије $\\mathscr{H}$ која слика приписани круг $\\omega_{a}$ у описани круг $\\Omega$. Ако је $T$ бесконачна тачка, $\\mathscr{H}$ је транслација, а остатак доказа је исти.\n\nЛема. Нека произвољна права $p$ кроз $D_{1}$ сече круг $\\Omega$ у тачкама $L$ и $K$. Тангенте у $L$ и $K$ на $\\Omega$ секу праву $B C$ редом у тачкама $P$ и $Q$. Тада је $\\varangle P A B=\\varangle C A Q$.\n\nДоказ. Означимо $\\varangle B A C=\\alpha, \\varangle C B A=\\beta, \\varangle A C B=\\gamma, \\varangle P A B=x$ и $\\varangle C A Q=y$.\n\nАко је $D_{1}$ бесконачна тачка, тврђење је тривијално по симетрији. Ако није, из $\\triangle P B L \\sim \\triangle P L C$ следи $\\frac{P B}{P L}=\\frac{P L}{P C}=\\frac{L B}{L C}$ и одатле $\\frac{P B}{P C}=\\left(\\frac{L B}{L C}\\right)^{2}$. Слично je $\\frac{Q B}{Q C}=\\left(\\frac{K B}{K C}\\right)^{2}$. Пошто је $\\frac{L B}{L C} \\cdot \\frac{K B}{K C}=\\frac{\\mid K L B]}{\\mid K L C]}=\\frac{D_{1} B}{D_{1} C}=\\frac{A B}{A C}$, добијамо $\\frac{P B}{P C} \\cdot \\frac{Q B}{Q C}=\\left(\\frac{A B}{A C}\\right)^{2}$. Како је $\\frac{P B}{P C}=\\frac{P B}{P A} \\cdot \\frac{P A}{P C}=\\frac{\\sin x}{\\sin \\beta} \\cdot \\frac{\\sin \\gamma}{\\sin (\\alpha+x)}$ и $\\frac{Q B}{Q C}=\\frac{Q B}{Q A} \\cdot \\frac{Q A}{Q C}=\\frac{\\sin (\\alpha+y)}{\\sin \\beta} \\cdot \\frac{\\sin \\gamma}{\\sin y}$, множење даје $\\left(\\frac{\\sin \\gamma}{\\sin \\beta}\\right)^{2} \\cdot \\frac{\\sin (\\alpha+y) / \\sin y}{\\sin (\\alpha+x) / \\sin x}=\\left(\\frac{A C}{A B}\\right)^{2}=\\left(\\frac{\\sin \\gamma}{\\sin \\beta}\\right)^{2}$, одакле је $\\sin \\alpha \\operatorname{ctg} y+\\cos \\alpha=\\frac{\\sin (\\alpha+y)}{\\sin y}=$ $\\frac{\\sin (\\alpha+x)}{\\sin x}=\\sin \\alpha \\operatorname{ctg} x+\\cos \\alpha$, тј. $x=y$.\n\nАко су $K$ и $L$ додирне тачке заједничких тангенти са $\\Omega$, остаје да се покаже да тачка $D_{1}$ лежи на правој $K L$, тј. на полари тачке $T$ у односу на $\\Omega$. По ставу о полу и полари, довољно је доказати да $T$ лежи на полари $d$ тачке $D_{1}$ у односу на $\\Omega$.\n\nОзначимо са $N$ средиште лука $B A C$ круга $\\Omega$. Слика тачке $D$ при хомотетији $\\mathscr{H}$ је пресек $S$ тангенти на $\\Omega$ у тачкама $A$ и $N$, па тачка $T$ лежи на правој $D S$. С друге стране, тачка $D$ је на полари $d$ јер је четворка $\\left(B, C ; D_{1}, D\\right)$ хармонијска, а тачка $S$ је\n\n\nтакође на $d$ јер полара тачке $S$ у односу на $\\Omega$, што је права $A N$, садржи тачку $D_{1}$. Према томе, праве $D S$ и $d$ се поклапају, чиме је доказ завршен.\n\nДруго решење. Нека заједничке тангенте додирују круг $\\Omega$ у тачкама $K$ и $L$, при чему је теме $L P$ тангента ближа темену $B$. Означимо са $M$ средиште оног лука $B C$ који не садржи тачку $A$, а са $O$ и $I_{a}$ редом центре описаног и приписаног круга наспрам $A$.\n\nКако је $\\varangle L P I_{a}=90^{\\circ}+\\frac{1}{2} \\varangle L P C$ и $\\varangle L A I_{a}=\\varangle L A M=\\frac{1}{2} \\varangle L O M=\\frac{1}{2} \\varangle L P D_{1}=90^{\\circ}-\\frac{1}{2} \\varangle L P C$, следи да је $\\varangle L P I_{a}+\\varangle L A I_{a}=180^{\\circ}$, па је четвороугао $A L P I_{a}$ тетиван. Слично, и четвороугао $A K Q I_{a}$ је тетиван. Сада имамо $\\varangle P A I_{a}=\\varangle P L I_{a}=\\varangle Q K I_{a}=\\varangle Q A I_{a}$, јер су углови $P L I_{a}$ и $Q K I_{a}$ симетрични у односу на праву $O I_{a}$, а одавде је $\\varangle P A B=\\varangle Q A C$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2018_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2018", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Кружница уписана у $\\triangle A B C$ има центар у тачки $I$ и додирује страницу $B C$ у тачки $D$. На дужима $B I$ и $C I$ одабране су тачке $P$ и $Q$, редом, такве да важи $\\varangle B A C=2 \\varangle P A Q$. Доказати: $\\varangle P D Q=90^{\\circ} . \\quad$ (Дуиан Ђукић)", "solution": "Означимо са $E$ и $F$ редом подножја нормала из $P$ и $Q$ на праву $B C$, а са $M$ средиште дужи $P Q$.\n\nПосматрајмо тачку $X$ на страници $B C$ такву да је $\\varangle B A X=2 \\varangle B A P$. Тада је такође $\\varangle C A X=\\varangle B A C-2 \\varangle B A P=$ $2 \\varangle C A Q$, па су $P$ и $Q$ редом центри уписаних кругова троуглова $B A X$ и $C A X$. Следи да су $X P$ и $X Q$ симетрале углова $B X A$ и $C X A$, па је $\\varangle P X Q=90^{\\circ}$. Услов $\\varangle P D Q=90^{\\circ}$ је еквивалентан са $M D=M P=M Q=$\n\n\n$M X$, а како је $M E=M F$, довољно је доказати да је $D E=X F$. Обе дужине се једноставно рачунају на основу \"великог задатка\": $D E=B D-B E=$ $\\frac{A B+B C-A C}{2}-\\frac{A B+B X-A X}{2}=\\frac{C X-A C+A X}{2}=X F$.\n\nДруго решење. Нека права $B I$ поново сече описани круг $\\triangle A P Q$ у тачки $N$. $\\overline{\\text { Имамо } \\varangle A I N}=180^{\\circ}-\\varangle B I A=90^{\\circ}-\\frac{\\gamma}{2}=\\varangle D I Q$. Такође, како је $\\varangle I N Q=$ $\\varangle P A Q=\\frac{\\alpha}{2}$ и $\\varangle I Q N=\\varangle B I C-\\varangle I N Q=\\left(90^{\\circ}+\\frac{\\alpha}{2}\\right)-\\frac{\\alpha}{2}=90^{\\circ}$, имамо $\\frac{I Q}{I N}=$ $\\sin \\frac{\\alpha}{2}=\\frac{I A}{I D}$, одакле је $\\frac{I A}{I N}=\\frac{I D}{I Q}$. Следи да су троуглови $D I Q$ и $A I N$ слични, па је $\\varangle I D Q=\\varangle I A N=180^{\\circ}-\\varangle A I N-\\varangle A N I=180^{\\circ}-\\left(90^{\\circ}-\\frac{\\gamma}{2}\\right)-\\varangle A N P=$ $90^{\\circ}+\\frac{\\gamma}{2}-\\varangle A Q P$. Аналогно је $\\varangle I D P=90^{\\circ}+\\frac{\\beta}{2}-\\varangle A P Q$, па сабирањем добијамо $\\varangle P D Q=180^{\\circ}+\\frac{\\beta+\\gamma}{2}-\\left(180^{\\circ}-\\varangle P A Q\\right)=90^{\\circ}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2018", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Дат је природан број $n, n>1$. Цео број $x$ зовемо красним ако је остатак броја $x^{2}$ при дељењу са $n$ непаран. Доказати да не постоји више од $1+\\lfloor\\sqrt{3 n}\\rfloor$ узастопних красних природних бројева.\n\n(Душан Ђукић)", "solution": "Ако је $n$ паран број, тврђење је тривијално: тада не постоје ни два узастопна красна броја, јер парни бројеви нису красни. Надаље сматрамо да је $n$ непаран.\n\nПошто бројеви дељиви са $n$ нису красни, можемо да се ограничимо на бројеве $x \\in\\{1, \\ldots, n-1\\}$. Претпоставимо да су бројеви $x$ и $x+1$ красни. Остаци бројева $x^{2}$ и $(x+1)^{2}$ при дељењу са $n$, који су непарни, једнаки су $x^{2}-n\\left[\\frac{x^{2}}{n}\\right]$ и $(x+1)^{2}-n\\left[\\frac{(x+1)^{2}}{n}\\right]$ редом, па су $\\left[\\frac{x^{2}}{n}\\right]$ и $\\left[\\frac{(x+1)^{2}}{n}\\right]$ различите парности. Како због $0<(x+1)^{2}-x^{2}<2 n$ важи $0 \\leqslant\\left[\\frac{(x+1)^{2}}{n}\\right]-\\left[\\frac{x^{2}}{n}\\right] \\leqslant 2$, следи да је $\\left[\\frac{(x+1)^{2}}{n}\\right]=\\left[\\frac{x^{2}}{n}\\right]+1$. Према томе, ако су бројеви $x, x+1, \\ldots, x+k$ красни, онда је\n\n$$\nm=y-\\left[\\frac{y^{2}}{n}\\right] \\quad \\text { константно за све } \\quad y=x, x+1, \\ldots, x+k\n$$\n\nКако је једнакост $y-\\left[\\frac{y^{2}}{n}\\right]=m$ еквивалентна са $y-m \\leqslant \\frac{y^{2}}{n}<y-m+1$, тј. са $n\\left(\\frac{n}{4}-m\\right) \\leqslant\\left(y-\\frac{n}{2}\\right)^{2}<n\\left(\\frac{n}{4}-m+1\\right)$, број узастопних бројева $y$ с�� овим својством није већи од $\\left[\\sqrt{n\\left(\\frac{n}{4}-m+1\\right)}-\\sqrt{n\\left(\\frac{n}{4}-m\\right)}\\right]+1 \\leqslant[\\sqrt{n}]+1$ ако је $m \\leqslant\\left[\\frac{n}{4}\\right]$, и није већи од $2\\left[\\sqrt{n\\left\\{\\frac{n}{4}\\right\\}}+\\frac{1}{2}\\right] \\leqslant[\\sqrt{3 n}]+1$ за $m=\\left[\\frac{n}{4}\\right]+1$.\n\nНапомена. Једнакост се може достићи ако и само ако је $n \\equiv 3(\\bmod 8), 3 n$ није квадрат и $[\\sqrt{3 n}]$ је непарно.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2018", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "У равни је дато $n$ правих међу којима никоје две нису паралелне и никоје три се не секу у једној тачки. Под пресечним тачкама сматрамо све тачке у којима се секу неке две од ових правих.\n\n(a) Доказати да међу датим правим постоји једна са чије се сваке стране налази бар по\n\n$$\n\\left\\lfloor\\frac{(n-1)(n-2)}{10}\\right\\rfloor\n$$\n\nпресечних тачака (тачке на тој правој се не рачунају).\n\n(б) За које вредности $n$ се оцена из дела под (а) не може побољшати?\n\n(Душан Ђукић)\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 12. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\n\n\n## Други дан", "solution": "За сваку од датих правих, пресечних тачака ван ње има\n\n$$\nm=\\frac{(n-1)(n-2)}{2}\n$$\n\nПретпоставимо да, за сваку праву, с једне њене стране има не више од $k$ пресечних тачака, где је $k \\leqslant \\frac{n}{2}$. Пребројмо на два начина тројке $(p, A, B)$, где су $A$ и $B$ пресечне тачке са различитих страна праве $p$. По претпоставци, за сваку праву $p$ има не више од $k(m-k)$ оваквих тројки, па је њихов укупан број $N \\leqslant n k(m-k)$.\n\nРазмотримо сада два типа оваквих тројки: mun 1 , када су тачке $A$ и $B$ на истој од датих правих, и mun 2 , када нису.\n\nСвака четворка датих правих, заједно са њима одређеним пресечним тачкама, одређује тачно 4 тројке типа 1 , а свака тројка је одређена тачно једном четворком правих. Следи да има $4\\binom{n}{4}$ тројки типа 1. Такође, свака петорка датих правих са њима одређеним пресечним тачкама одређује бар 5 тројки типа 2 , те тројки типа 2 има бар $5\\binom{n}{5}$. Ово се директно проверава: постоји шест различитих распореда по пет правих у општем положају, као на слици.\n\n\nПрема томе, $N \\geqslant 4\\binom{n}{4}+5\\binom{n}{5}=n\\binom{n}{4}$.\n\nСледи да је $k(m-k) \\geqslant\\binom{ n}{4}=\\frac{m(m-1)}{6}$. Одавде се добија\n\n$$\nk \\geqslant k_{0}=\\frac{1}{2}\\left(m-\\sqrt{\\frac{m^{2}+2 m}{3}}\\right)\n$$\n\nКако се неједнакост $k_{0}>\\frac{m}{5}=\\frac{(n-1)(n-2)}{10}$ своди на $m>25$, што важи за $n \\geqslant 9$, док за $n=8$ имамо $k_{0}>\\left[\\frac{m}{5}\\right]=4$, остаје да испитамо случајеве $n \\leqslant 7$.\n\nЗа $n \\leqslant 4$ је тврђење тривијално, као и достизање једнакости, јер је тада $k_{0}=\\left[\\frac{m}{5}\\right]=0$. За $n=5,6,7$ је редом $\\left\\lceil k_{0}\\right\\rceil=\\left[\\frac{m}{5}\\right]=1,2,3$, па тврђење задатка и тада важи, а достижу се и једнакости у случајевима на слици.\n\n\nНапомена. С друге стране, свака петорка одређује највише 7 тројки $(p, A, B)$ типа 2. Овако се може показати да увек постоји права са чије се једне стране налази мање од $\\left(\\frac{1}{2}-\\frac{1}{2 \\sqrt{15}}\\right) m$ тачака.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2018", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Доказати да постоји тачно један полином $P(x)$ с реалним коефицијентима за који је полином\n\n$$\n(x+y)^{1000}-P(x)-P(y)\n$$\n\nдељив полиномом $x y-x-y$.\n\n(Душан Ђукић)", "solution": "Означимо $n=1000$. Сменом $x=u+1$ и $y=v+1$ добијамо да полином $u v-1$ дели полином $P(u+1)+P(v+1)-(u+v+2)^{n}$. Еквивалентан услов је да је $P(u+1)+P(v+1)-(u+v+2)^{n}=0$ кад год је $u v-1=0$ (видети напомену). Тако за $u \\neq 0$ и $v=\\frac{1}{u}$ имамо $P(u+1)+P\\left(\\frac{1}{u}+1\\right)=\\left(u+\\frac{1}{u}+2\\right)^{n}=\\frac{(u+1)^{2 n}}{u^{n}}$. Полином $Q(x)=P(x+1)=\\sum_{i=0}^{n} a_{i} x^{i}$ задовољава\n\n$2 a_{0}+\\sum_{i=1}^{n} a_{i}\\left(u^{i}+u^{-i}\\right)=Q(u)+Q\\left(\\frac{1}{u}\\right)=\\frac{(u+1)^{2 n}}{u^{n}}=\\binom{2 n}{n}+\\sum_{i=1}^{n}\\binom{2 n}{n-i}\\left(u^{i}+u^{-i}\\right)$, одакле одмах следи да је $a_{0}=\\frac{1}{2}\\binom{2 n}{n}$ и $a_{i}=\\binom{2 n}{n-i}$ за $1 \\leqslant i \\leqslant n$. Дакле,\n\n$$\nP(x)=\\frac{1}{2}\\binom{2 n}{n}+\\sum_{i=1}^{n}\\binom{2 n}{n-i}(x-1)^{i}\n$$\n\nДруго решење. Тражимо полиноме $P(x)=\\sum_{i=0}^{n} p_{i} x^{i}$ и $Q(x, y)=\\sum_{i, j} a_{i, j} x^{i} y^{j}$ такве да је\n\n$$\nA(x, y)=(x y-x-y) Q(x, y)=(x+y)^{1000}-P(x)-P(y)\n$$\n\nПриметимо да је $\\operatorname{deg} Q \\leqslant 998$. Заиста, ако је $a_{i, j} x^{i} y^{j}$ моном највећег степена у $Q(x, y)$, онда је коефицијент уз $x^{i+1} y^{j+1}$ у $A(x, y)$ једнак $a_{i, j} \\neq 0$, па је $i+j+2 \\leqslant 1000$. Следи да је $\\operatorname{deg} A \\leqslant 1000$, па је и $\\operatorname{deg} P \\leqslant 1000$.\n\nИзједначавање коефицијената уз $x^{i} y^{j}$ у (*) даје једнакости $a_{i-1, j-1}=\\binom{1000}{i}$ за $i+j=998(i, j>0), a_{i-1, j-1}=a_{i-1, j}+a_{i, j-1}$ за $i+j<998(i, j>0)$ и $a_{i-1,0}=$ $a_{0, i-1}=p_{i}$, одакле једноставном индукцијом налазимо $a_{i-1, j-1}=\\binom{2000-i-j}{1000-i}$ за $i+j \\leqslant 1000(i, j>0)$ и $p_{i}=\\binom{1999-i}{999}$, тј.\n\n$$\nP(x)=x^{1000}+\\binom{1000}{999} x^{999}+\\binom{1001}{999} x^{998}+\\cdots+\\binom{1998}{999} x\n$$\n\nИз конструкције следи да овај полином задовољава услове задатка.\n\nTреће решење. Не постоје два различита полинома са жељеним својством. Заиста, ако $P_{1}(x) \\not \\equiv P_{2}(x)$ имају то својство, онда $x y-x-y$ дели разлику $P_{1}(x)+P_{1}(y)-P_{2}(x)-P_{2}(y)=(x y-x-y) U(x, y)$. Међутим, ако је $c x^{i} y^{j}$ моном највећег степена у $U(x, y)$, онда је коефицијент уз $x^{i+1} y^{j+1}$ на левој страни ове једнакости једнак $c \\neq 0$, што је немогуће.\n\nДокажимо сада да за сваки симетричан полином $Q(x, y)$ постоји полином $P(t)$ такав да $x y-x-y \\mid Q(x, y)-P(x)-P(y)$. Довољно је доказати да за полиноме $Q$ облика $x^{i} y^{j}+x^{j} y^{i}(0 \\leqslant i \\leqslant j)$ постоји тражени полином $P_{i, j}(t)$. Тврђење је тривијално за $i=0$. За $i>0$ доказ спроводимо индукцијом по $i+j$. Наиме, $x^{i} y^{j}+x^{j} y^{i} \\equiv(x+y)\\left(x^{i-1} y^{j-1}+x^{j-1} y^{i-1}\\right)=\\left(x^{i} y^{j-1}+x^{j-1} y^{i}\\right)+$ $\\left(x^{i-1} y^{j}+x^{j} y^{i-1}\\right)(\\bmod x y-x-y)$, па можемо узети $P_{i, j}(t)=P_{i, j-1}(t)+P_{i-1, j}(t)$.\n\nНапомена. Ако је $P(x, y)$ нерастављив полином и $Q(x, y)$ полином такав да је $\\overline{Q(x, y)=0}$ кад год је $P(x, y)=0$, онда је полином $Q$ дељив полиномом $P$. Ово није потпуно тривијално. У прстену полинома $\\mathbb{R}[y][x]$ Еуклидовим алгоритмом могу се наћи полиноми $A(x, y), B(x, y)$ и $C(y)$ такви да је $\\operatorname{deg}_{x} B<\\operatorname{deg}_{x} P$ и $A \\cdot P-B \\cdot Q=C(y)$. Дакле, кад год је $Q(x, y)=0$, важи $C(y)=0$, па $C$ има\nбесконачно много нула, одакле је $C \\equiv 0$ и $P \\mid B \\cdot Q$. Због нерастављивости полинома $P$ и јединствености факторизације у прстену $\\mathbb{R}[y][x]$ следи $P \\mid Q$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2018", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "Нека су $a$ и $b$ непарни природни бројеви већи од 1. Посматрајмо таблу $a \\times b$ којој недостају поља $(2,1),(a-2, b)$ и $(a, b)$ (под пољем $(i, j)$ подразумевамо поље у пресеку врсте $i$ и колоне $j$ ). Претпоставимо да је оваква табла поплочана помоћу $2 \\times 1$ домина и $2 \\times 2$ квадрата (домине се могу ротирати).\n\nДоказати да је употребљено бар $\\frac{3}{2}(a+b)-6$ домина. (Никола Петровић)", "solution": "Упишимо у поље $(i, j)$ број $(-1)^{i+j}(i+j)$. Збир уписаних бројева у читавој таблици је $\\sum_{i=1}^{a}(-1)^{i} \\sum_{j=1}^{b}(-1)^{j}(i+j)=\\sum_{i=1}^{a}(-1)^{i+1}\\left(i+\\frac{b+1}{2}\\right)=\\frac{a+b+2}{2}$, а ако се три наведена поља избаце, збир у остатку таблице је\n\n$$\n\\frac{a+b+2}{2}-(-3)-(a+b-2)-(a+b)=-\\frac{3}{2}(a+b)+6\n$$\n\nКако је збир бројева у сваком квадрату $2 \\times 2$ једнак нули, а збир у свакој домини је 1 или -1 , потребно је бар $\\frac{3}{2}(a+b)-6$ домина.\n\nДруго решеъе. Нека су врсте и колоне нумерисане одоздо нагоре и слева надесно. Можемо да сматрамо да се у поплочавању не појављује ниједна од целина означених са $L$ на слици - заиста, оне се могу заменити одговарајућим целинама означеним са $D$, притом не повећавајући број домина.\n\nРазмотримо фигуру која покрива поље $(a, 1)$. Ако је то нпр. хоризонтална домина $(a, 1)-(a, 2)$ (аналогно се испитује случај вертикалне домине), онда поље $(a-1,1)$ не може бити покривено ни квадратом ни хоризонталном домином (јер би они са горњом домином градили једну од целина $L$ ), па оно мора бити покривено вертикалном домином $(a-1,1)-(a-2,1)$. Слично, сада поље $(a-1,2)$ мора би-\n\nти покривено домином $(a-1,2)-(a-1,3)$, итд. до бесконачности, што је немогуће. Према томе, фигура која покрива поље $(a, 1)$ је квадрат.\n\nНа сличан начин, поља $(a, 3)$ и ( $a-2,1$ ) су такође покривена квадратима, затим поља $(a, 5),(a-2,3)$ и ( $a-4,1)$, итд. Настављајући овај поступак, закључујемо да су сва поља осим оних у врстама $1,2,3$ и оних у колонама $b-2, b-1, b$ покривена квадратима. Преостала поља се могу поплочати на једниствен начин, приказан на слици, што се директно проверава. При томе је употребљено тачно $\\frac{3}{2}(a+b)-6$ домина.\n\nTреће решење. Обојићемо поља табле црно и бело попут шаховске табле. Праву која раздваја $i$-ту и $(i+1)$-ву врсту/колону зовемо $i$-том хоризонталом/вертикалом.\n\nАко је $j$ парно ( $2 \\leqslant j \\leqslant b-1$ ), бар једна (хоризонтална) домина сече $j$-ту вертикалу јер је број поља у првих $j$ колона непаран. С друге стране, ако је $j$ непарно $(1 \\leqslant j \\leqslant b-2$ ), бар две домине морају сећи $j$-ту вертикалу јер у првих $j$ колона има за два више црних поља него белих. Овако добијамо бар $\\frac{3 b-3}{2}$ хоризонталних домина.\n\nСлично, ако је $i$ парно ( $2 \\leqslant i \\leqslant a-3)$ или $i \\in\\{1, a-2\\}$, бар једна (вертикална) домина сече $i$-ту хоризонталу јер је број поља у првих $i$ врста непаран. С друге стране, ако је $i$ непарно ( $3 \\leqslant i \\leqslant a-4$ ), број црних поља у првих $i$\nврста је за два већи од броја белих, па бар две домине морају сећи $i$-ту хоризонталу. Овако добијамо бар $\\frac{3 a-9}{2}$ вертикалних домина.\n\nДакле, укупно има бар $\\frac{3 a-9}{2}+\\frac{3 b-3}{2}=\\frac{3}{2}(a+b)-6$ домина.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2018", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "За задат природан број $k$, нека је $n_{k}$ најмањи природан број такав да постоји коначан скуп $A$ целих бројева са следећим особинама:\n\n- за свако $a \\in A$ постоје $x, y \\in A$ (не обавезно различити) такви да\n\n$$\nn_{k} \\mid a-x-y\n$$\n\n- не постоји подскуп $B$ скупа $A$ за који важи $|B| \\leqslant k$ и $n_{k} \\mid \\sum_{b \\in B} b$.\n\nДоказати да за све $k, k \\geqslant 3$, важи\n\n$$\nn_{k}<\\left(\\frac{13}{8}\\right)^{k+2}\n$$\n\n(Бојан Bаиић)\n\nВреме за рад 270 минута.\n\nРешења задатака детаљно образложити.\n\nСваки задатак вреди 7 бодова.\n\n## РЕШЕЊА", "solution": "Са $F_{i}$ означавамо Фибоначијеве бројеве: $F_{1}=F_{2}=1, F_{i+1}=F_{i}+F_{i-1}$. Посматрајмо скуп $A=\\left\\{a_{1}, a_{2}, \\ldots, a_{k+1}\\right\\}$ са $n=F_{k+2}+3$, где су\n\n$$\na_{i}=(-1)^{k-1-i} F_{i+1} \\text { за } i=1,2, \\ldots, k-1, \\quad a_{k}=F_{k}+1 \\quad \\text { и } \\quad a_{k+1}=F_{k}+2\n$$\n\nУ случају парног $k$ видимо да је $a_{i}=a_{i+1}+a_{i+2}(1 \\leqslant i \\leqslant k-3), a_{k-2} \\equiv a_{k}+a_{k+1}$ $(\\bmod n), a_{k-1}=a_{k+1}+a_{2}, a_{k}=a_{k-1}+a_{1}$ и $a_{k+1}=a_{k}+a_{1}$, па скуп $A$ задовољава први услов задатка. Овај услов се слично проверава и за непарно $k$.\n\nДокажимо индукцијом по $k$ (база $k=3$ се директно проверава) да је задовољен и други услов, тј. да не постоји подскуп $B \\subsetneq A$ такав да $n \\mid \\sum_{b \\in B} b$. Како је збир елемената скупа $A$ једнак нули, можемо да сматрамо без смањења општости (заменом $B$ са $A \\backslash B$ по потреби) да $B$ садржи највише један од елемената $F_{k}, F_{k}+1, F_{k}+2$. Тада је\n\n$1-F_{k}=-\\left(F_{k-1}+F_{k-3}+\\cdots\\right) \\leqslant \\sum_{b \\in B} b \\leqslant\\left(F_{k}+2\\right)+F_{k-2}+F_{k-4}+\\cdots=F_{k+1}+1$,\n\nпа мора бити $\\sum_{b \\in B} b=0$. На основу индуктивне претпоставке за $k-1$, скуп $B$ не може бити подскуп скупа $\\left\\{a_{1}, a_{2}, \\ldots, a_{k-2}\\right\\}$, тј. мора бити $a_{k-1}=F_{k} \\in B$. Међутим, тада је $\\sum_{b \\in B} b \\geqslant F_{k}-F_{k-1}-F_{k-3}-\\cdots=1$, што је контрадикција. Доказ је завршен.\n\nПрема томе, $n_{k} \\leqslant F_{k+2}+3<\\phi^{k-3}\\left(F_{5}+3\\right)<\\phi^{k+2}<\\left(\\frac{13}{8}\\right)^{k+2}$, где је $\\phi=\\frac{1+\\sqrt{5}}{2}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2019_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2019", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Одредити све природне бројеве $n(n>1)$ који имају следеће својство: ако су $a_{1}, a_{2}, a_{3}, \\ldots, a_{k}$ сви природни бројеви мањи од $n$ и узајамно прости са $n$ и важи поредак $a_{1}<a_{2}<a_{3}<\\cdots<a_{k}$, онда ниједан од збирова $a_{i}+a_{i+1}$ за $i=1,2, \\ldots, k-1$ није дељив са 3.\n\n(Душан Ђукић)", "solution": "За $n \\leqslant 28$ услов задатка је задовољен само за $n \\in\\{2,4,10\\}$. Нека је $n>28$. Приметимо да је низ $a_{i}$ симетричан у односу на $\\frac{n}{2}$. Дакле, $a_{i}+a_{k+1-i}=n$. Ако $2 \\nmid n$, онда је $a_{1}=1, a_{2}=2$ и $3 \\mid a_{1}+a_{2}$. С друге стране, ако $3 \\mid n$, одаберимо $i$ тако да је $a_{i}<\\frac{n}{2}<a_{i+1}$ : тада $3 \\mid a_{i}+a_{i+1}=n$. Надаље $2 \\mid n$ и $3 \\nmid n$, тако да је $a_{2}=3$. Одавде имамо и $a_{k-1}=n-3$ и $a_{k}=n-1$.\n\nАко је $n \\equiv 2(\\bmod 3)$, онда $3 \\mid a_{k-1}+a_{k}=2 n-4$. Остаје само случај $n \\equiv 1$ $(\\bmod 3)$.\n\nДаље, ако је $a_{i}+a_{i+1} \\equiv 2(\\bmod 3)$, онда је $a_{k-i}+a_{k+1-i}=2 n-\\left(a_{i}+a_{i+1}\\right) \\equiv$ $0(\\bmod 3)$. Зато можемо да сматрамо да је $a_{i}+a_{i+1} \\equiv 1(\\bmod 3)$ за $i=$ $1,2, \\ldots, k-1$. Индукцијом налазимо\n\n$$\na_{1} \\equiv a_{3} \\equiv \\cdots \\equiv 1 \\quad \\text { и } \\quad a_{2} \\equiv a_{4} \\equiv \\cdots \\equiv 0 \\quad(\\bmod 3)\n$$\n\nКако је $(n, 9)=1$, следи $a_{4}=9$, а због $a_{3} \\equiv 1(\\bmod 3)$ имамо и $a_{3}=7$. Одавде добијамо $(n, 7)=1$ и $(n, 5) \\neq 1$, тј. $5 \\mid n$.\n\nСада имамо $(n, 21)=(n, 27)=1$, али бројеви $22,24,25$ и 26 нису узајамно прости са $n$, а на основу $(*)$ ни број 23 се не може појавити у низу $a_{1}, \\ldots, a_{k}$. Дакле, 21 и 27 су суседни у низу $a_{1}, \\ldots, a_{k}$, али $3 \\mid 21+27$, контрадикција.\n\nПрема томе, једина решења су 2,4 и 10 .", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2019", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "За низ ненегативних реалних бројева $a_{1}, a_{2}, \\ldots, a_{k}$ кажемо да је уложсив у интервал $[b, c]$ ако постоје бројеви $x_{0}, x_{1}, \\ldots, x_{k}$ из интервала $[b, c]$ такви да важи $\\left|x_{i}-x_{i-1}\\right|=a_{i}$ за $i=1,2, \\ldots, k$. Низ је нормиран ако су сви његови чланови не већи од 1. За задат природан број $n$, доказати:\n\n(a) сваки нормиран низ дужине $2 n+1$ је уложив у интервал $\\left[0,2-\\frac{1}{2^{n}}\\right]$;\n\n(б) постоји нормиран низ дужине $4 n+3$ који није уложив у $\\left[0,2-\\frac{1}{2^{n}}\\right]$.\n\n(Душан Ђукић)", "solution": "(a) Довољно је доказати да је сваки нормиран низ $a_{1}, a_{2}, \\ldots, a_{2 n+1}$ уложив у неки интервал дужине $2-\\frac{1}{2^{n}}$. Тврђење доказујемо индукцијом по $n$. Оно је тачно за $n=0$; нека је $n \\geqslant 1$. По индуктивној претпоставци постоји низ $x_{0}, x_{1}, \\ldots, x_{2 n-1} \\in\\left[0,2-\\frac{1}{2^{n-1}}\\right]$ такав да је $\\left|x_{i}-x_{i-1}\\right|=a_{i}$ за $i=1, \\ldots, 2 n-1$. Не умањујући општост, сматраћемо да је $x_{2 n-1} \\leqslant 1-\\frac{1}{2^{n}}$.\n\n(10) Ако је $a_{2 n} \\geqslant \\frac{1}{2^{n}}$, можемо узети $x_{2 n}=x_{2 n-1}+a_{2 n} \\in\\left[1,2-\\frac{1}{2^{n}}\\right]$ и $x_{2 n+1}=$ $x_{2 n}-a_{2 n+1} \\in\\left[0,2-\\frac{1}{2^{n}}\\right]$, чиме је низ уложен у интервал $\\left[0,2-\\frac{1}{2^{n}}\\right]$.\n\n$\\left(2^{\\circ}\\right)$ Ако је $a_{2 n}<\\frac{1}{2^{n}}$, узећемо $x_{2 n}=x_{2 n-1}-a_{2 n} \\in\\left[-\\frac{1}{2^{n}}, 1-\\frac{1}{2^{n}}\\right]$ и $x_{2 n+1}=x_{2 n}+$ $a_{2 n+1}$, чиме је низ уложен у један од интервала $\\left[0,2-\\frac{1}{2^{n}}\\right]$ и $\\left[-\\frac{1}{2^{n}}, 2-\\frac{1}{2^{n-1}}\\right]$.\n\n(б) Означимо $N=3 \\cdot 2^{n-1}-1$. Доказаћемо да се низ дужине $4 n-1$\n\n$1,1-\\frac{1}{N}, 1,1-\\frac{2}{N}, 1,1-\\frac{2^{2}}{N}, \\ldots, 1,1-\\frac{2^{n-1}}{N}, 1,1-\\frac{2^{n-2}}{N}, 1, \\ldots, 1-\\frac{2}{N}, 1,1-\\frac{1}{N}, 1$ не може уложити у интервал $\\left(-1+\\frac{1}{2 N}, 1-\\frac{1}{2 N}\\right)$, одакле следи твр ење.\n\nПретпоставимо супротно. Једноставном индукцијом се доказује да је:\n\n(i) $\\left|x_{2 i}\\right|<1-\\frac{2^{i+1}-1}{2 N}$ и $\\left|x_{2 i+1}\\right|>\\frac{2^{i+1}-1}{2 N}$ за $i=0, \\ldots, n$;\n\n(ii) $\\left|x_{2 i}\\right|<\\frac{2^{2 n+2-i}-1}{2 N}$ и $\\left|x_{2 i+1}\\right|>1-\\frac{2^{2 n+2-i}-1}{2 N}$ за $i=n+1, \\ldots, 2 n+1$.\n\nТако за $x_{4 n+3}$ добијамо контрадикцију.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2019", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Конвексан четвороугао $A B C D$ је описан око кружнице $k$. Праве $A D$ и $B C$ се секу у тачки $P$, а кружнице описане око $\\triangle P A B$ и $\\triangle P C D$ се секу у тачки $X$. Доказати да тангенте из тачке $X$ на кружницу $k$ граде једнаке углове са правима $A X$ и $C X$.\n\n(Дуиан Ђукић)\n\n# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 13. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА \n\n\n\n## Други дан", "solution": "Пошто је $\\varangle X A D=\\varangle X B C$ и $\\varangle X D P=\\varangle X C P$, важи $\\triangle X A D \\sim \\triangle X B C$.\n\nНека симетрала $s_{X}$ угла $A X C$ сече кругове $P A B$ и $P C D$ у тачкама $K$ и $R$, а симетрала $s_{P}$ угла $A P C$ сече кругове $P A B$ и $P C D$ у тачкама $L$ и $S$. Права $s_{P}$ пролази кроз центар $I$ круга $k$ и важи $L A=L B=L I$ и $S C=S D=S I$.\n\nКако је $\\varangle I L K=\\varangle P X K=\\varangle P X R=\\varangle I S R$, важи $K L \\| R S$. Даље, имамо $\\varangle R X S=\\varangle R X C-\\varangle S P C=\\frac{1}{2}(\\varangle A X C-\\varangle A P C)=\\frac{1}{2} \\varangle B X C$ и, слично, $\\varangle L X K=$ $\\frac{1}{2} \\varangle B X C$. Следи да тетивама $K L$ и $R S$ у круговима $P A B$ и $P C D$, као и тетивама $L B$ и $S D$, одговарају једнаки периферијски углови, па је $\\frac{K L}{R S}=\\frac{L B}{S D}=\\frac{L I}{S I}$. Следи да је $\\triangle I K L \\sim \\triangle I R S$, па тачка $I$ лежи на правој $K R$, што је симетрала угла $A X C$. Тврђење задатка одмах следи.\n\nДруго решење. Означимо са $U$ и $V$ редом пресеке симетрала углова $A X D$ и $B X C$ са $A D$ и $B C$. Као и у првом решењу, $\\triangle X A D \\sim$ $\\triangle X B C$, одакле је $\\varangle X U P=\\varangle X V P$, па тачке $X, P, U$ и $V$ леже на истом кругу $\\gamma$. Дока-\n\n\nзаћемо да је и тачка $I$ на овом кругу и да је $I U=I V$. Следиће да $I$ припада симетрали угла $U X V$, што је уједно и симетрала угла $A X C$.\n\nНека су $M$ и $N$ редом тачке додира круга $k$ са страницама $A D$ и $B C$. Означимо $A M=a, B N=b, C N=c$ и $D M=d$. Тада је $A B=a+b, C D=c+d$ и $A U: U D=(a+b):(c+d)$, одакле налазимо $A U=\\frac{a+b}{a+b+c+d} \\cdot A D=\\frac{(a+b)(a+d)}{a+b+c+d}$; слично имамо $B V=\\frac{(b+a)(b+c)}{a+b+c+d}$. Следи да је $A M-A U=B V-B N=\\frac{a c-b d}{a+b+c+d}$, па је $M U=N V$ и троуглови $I M U$ и $I N V$ су подударни и исто оријентисани. Према томе, $I U=I V$ и $\\varangle U I V=\\varangle M I N=180^{\\circ}-\\varangle V P U$, тј. $I$ је средиште лука $U V$ круга $P X U V$.\n\nTреће решеъе. Познато је следеће тврђење из пројективне геометрије.\n\n- Дезаргова теорема о инволуиији. Коника $\\gamma$ је описана око четвороугла $\\overline{A B C D}$. Права $\\ell$ сече $A B, C D, B C, D A, A C, B D$ редом у тачкама $X_{1}$, $X_{2}, Y_{1}, Y_{2}, Z_{1}, Z_{2}$, и сече конику $\\gamma$ у $W_{1}$ и $W_{2}$. Тада постоји инволуција на правој $\\ell$ која слика $X_{1} \\leftrightarrow X_{2}, Y_{1} \\leftrightarrow Y_{2}, Z_{1} \\leftrightarrow Z_{2}$ и $W_{1} \\leftrightarrow W_{2}$.\n\nДуално тврђење (добијено поларним пресликавањем у односу на $\\gamma$ ) гласи овако:\n\n- Коника $\\gamma$ је уписана у четвороугао $A B C D$ у коме је $A D \\cap B C=\\{P\\}$ и $A B \\cap C D=\\{Q\\}$. Праве $X U$ и $X V$ су тангенте из произвољне тачке $X$ на $\\gamma$. Тада постоји инволуција на прамену правих кроз $X$ која слика $X A \\leftrightarrow X C, X B \\leftrightarrow X D, X P \\leftrightarrow X Q$ и $X U \\leftrightarrow X V$.\n\nУ нашем случају углови $A X C, B X D$ и $P X Q$ имају заједничку симетралу $s$, па је поменута инволуција управо осна симетрија у односу на $s$. Следи да су две тангенте из $X$ на круг (конику) $k$ симетричне у односу на $s$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2019", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "Дат је $\\triangle A B C$. Нека је $A_{1}$ централносиметрична слика пресечне тачке симетрале $\\measuredangle B A C$ и странице $B C$, где је центар симетрије средина странице $B C$. Аналогно дефинишемо тачке $B_{1}$ (на страници $C A$ ) и $C_{1}$ (на страници $A B)$. Пресек кружнице описане око $\\triangle A_{1} B_{1} C_{1}$ с правом $A B$ је скуп $\\left\\{Z, C_{1}\\right\\}$, с правом $B C$ је скуп $\\left\\{X, A_{1}\\right\\}$, а с правом $C A$ је скуп $\\left\\{Y, B_{1}\\right\\}$. Ако се нормале из тачака $X, Y$ и $Z$ на $B C, C A$ и $A B$, редом, секу у једној тачки, доказати да је $\\triangle A B C$ једнакокрак.\n\n(Милош Милосављевић)", "solution": "Подсетимо се да тачке $P$ и $Q$ унутар $\\triangle A B C$ зовемо изогонално спрегнутим ако је $\\varangle P A B=\\varangle Q A C$ и $\\varangle P B C=\\varangle Q B A$. Тада такође важи $\\varangle P C A=\\varangle Q C B$.\n\nЛема. Подножја нормала из тачака $P$ и $Q$ на праве $B C, C A$ и $A B$ леже на истом кругу.\n\nДоказ. Нека су $P_{a}$ и $Q_{a}$ редом подножја нормала из $P$ и $Q$ на $B C$; аналогно означавамо $P_{b}, Q_{b}, P_{c}, Q_{c}$. Из $\\varangle A P_{b} P_{c}=\\varangle A P P_{c}=\\varangle A Q Q_{b}=\\varangle A Q_{c} Q_{b}$ следи $\\triangle A P_{b} P_{c} \\sim \\triangle A Q_{c} Q_{b}$, па су тачке $P_{b}, P_{c}, Q_{b}, Q_{c}$ на истом кругу $k$, а његов центар је пресек симетрала дужи $P_{b} Q_{b}$ и $P_{c} Q_{c}$, што је управо средиште $U$ дужи $P Q$. Аналогно, и тачке $P_{c}, P_{a}, Q_{c}, Q_{a}$ су једнако удаљене од тачке $U$, па и $P_{a}$ и $Q_{a}$ леже на кругу $k$.\n\nПретпоставимо да се нормале из $X, Y$ и $Z$ редом на $B C, C A$ и $A B$ секу у тачки $P$. Ако је тачка $Q$ изогонално спрегнута тачки $P$ у $\\triangle A B C$, подножја нормала из $Q$ на $B C, C A$ и $A B$ су по Леми управо тачке $A_{1}, B_{1}$ и $C_{1}$.\n\nОзначимо са $A_{0}, B_{0}$ и $C_{0}$ редом пресеке унутрашњих симетрала углова код $A, B$ и $C$ с наспрамним страницама. Уобичајено, $B C=a, C A=b$ и $A B=c$. Из односа $B A_{0}$ : $A_{0} C=c: b$ налазимо $B A_{1}=A_{0} C=\\frac{a b}{b+c}$ и, слично, $A_{1} C=\\frac{a c}{b+c}, C B_{1}=\\frac{b c}{c+a}, B_{1} A=\\frac{b a}{c+a}$, $A C_{1}=\\frac{c a}{a+b}$ и $C_{1} B=\\frac{c b}{a+b}$. Сада имамо\n\n\n\n$$\n\\begin{aligned}\n0 & =\\left(B A_{1}^{2}-A_{1} C^{2}\\right)+\\left(C B_{1}^{2}-B_{1} A^{2}\\right)+\\left(A C_{1}^{2}-C_{1} B^{2}\\right) \\\\\n& =\\frac{a^{2}(b-c)}{b+c}+\\frac{b^{2}(c-a)}{c+a}+\\frac{c^{2}(a-b)}{a+b} \\\\\n& =\\frac{a^{4}(b-c)+b^{4}(c-a)+c^{4}(a-b)-(b-c)(c-a)(a-b)(a b+b c+c a)}{(b+c)(c+a)(a+b)} \\\\\n& =-\\frac{(b-c)(c-a)(a-b)(a+b+c)^{2}}{(b+c)(c+a)(a+b)}\n\\end{aligned}\n$$\n\nодакле следи $a=b$ или $a=c$ или $b=c$.\n\nДруго решење. Као у првом решењу, $B A_{1}=A_{0} C=\\frac{a b}{b+c}, A_{1} C=\\frac{a c}{b+c}, C B_{1}=\\frac{b c}{c+a}$, $\\overline{B_{1} A=\\frac{b a}{c+a}, A} C_{1}=\\frac{c a}{a+b}$ и $C_{1} B=\\frac{c b}{a+b}$. Означимо $B X=x, C Y=y$ и $A Z=z$. Потенција тачке $A$ даје $A B_{1} \\cdot A Y=A C_{1} \\cdot A Z$, тј. $\\frac{b y}{c+a}+\\frac{c z}{a+b}=\\frac{b^{2}}{c+a}$. Слично добијамо $\\frac{c z}{a+b}+\\frac{a x}{b+c}=\\frac{c^{2}}{a+b}$ и $\\frac{a x}{b+c}+\\frac{b y}{c+a}=\\frac{a^{2}}{b+c}$. Одавде следи $\\frac{2 a x}{b+c}=\\frac{a^{2}}{b+c}+\\frac{c^{2}}{a+b}-\\frac{b^{2}}{c+a}$ што се своди на $x=\\frac{1}{2} a-\\frac{(b+c)(b-c)\\left(b^{2}+c^{2}+a b+a c+b c\\right)}{2 a(a+b)(a+c)}$, итд. Услов да су три нормале конкурентне је\n\n$$\n\\begin{aligned}\n0 & =(a+b)(a+c)(b+c)\\left[x^{2}-(a-x)^{2}+y^{2}-(b-y)^{2}+z^{2}-(c-z)^{2}\\right] \\\\\n& =(b+c)^{2}(c-b)\\left(T-a^{2}\\right)+(c+a)^{2}(a-c)\\left(T-b^{2}\\right)+(a+b)^{2}(b-a)\\left(T-c^{2}\\right) \\\\\n& =a^{2}(b+c)^{2}(b-c)+b^{2}(c+a)^{2}(c-a)+c^{2}(a+b)^{2}(a-b)-(a-b)(b-c)(c-a) T \\\\\n& =-(a-b)(b-c)(c-a)(a+b+c)^{2}\n\\end{aligned}\n$$\n\nгде је $T=a^{2}+b^{2}+c^{2}+a b+b c+c a$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2019", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "На планети $X$ облика лопте се налази $2 n$ бензинских пумпи. Притом је свака пумпа упарена с по једном другом пумпом и сваке две упарене пумпе се налазе на дијаметрално супротним тачкама планете. На свакој пумпи се налази одређена количина бензина. Познато је следеће: уколико аутомобил с претходно празним (довољно великим) резервоаром крене с ма које пумпе, увек може стићи до пумпе с њом упарене (уз могуће допуњавање бензина на другим пумпама током пута). Одредити све природне бројеве $n$ такве да, за ма какав распоред $2 n$ пумпи који испуњава наведени услов, увек постоји пумпа од које аутомобил може кренути с претходно празним резервоаром и обићи све остале пумпе на планети. (Сматрати да аутомобил троши константну количину бензина по јединици дужине.) (Никола Петровић)", "solution": "Одговор је $n \\leqslant 3$.\n\nПумпу дијаметрално супротну пумпи $X$ означаваћемо са $X^{\\prime}$.\n\nЗа $n \\leqslant 1$ тврђење је тривијално. Нека је $n=2$ и нека је $A B=A^{\\prime} B^{\\prime}$ најмање међу свим растојањима између две пумпе. Од пумпе $A$ до $A^{\\prime}$ се може стићи, рецимо путем $A B^{\\prime} A^{\\prime}$ (случај пута $A B A^{\\prime}$ је сличан), али у $B$ има довољно бензина за вожњу до њој најближе пумпе $A$, те је путања $B A B^{\\prime} A^{\\prime}$ могућа.\n\nПокажимо тврђење за $n=3$ и шест пумпи $A, A^{\\prime}, B, B^{\\prime}, C, C^{\\prime}$. Нека је $A B=$ $A^{\\prime} B^{\\prime}$ најмање међу растојањима између две пумпе и нека је $B$ пумпа најближа пумпи $C$. Означимо $S=\\{A, B, C\\}$ и $S^{\\prime}=$ $\\left\\{A^{\\prime}, B^{\\prime}, C^{\\prime}\\right\\}$. Полазећи из сваке пумпе једног скупа можемо стићи до другог скупа.\n\n(1) Претпоставимо да се из пумпе $A$ путем $A B$ не може отићи у скуп $S^{\\prime}$. До $S^{\\prime}$ се не може стићи ни путем $A C$ - иначе би могло и путем $A B C$, јер је $B C \\leqslant A C$, а у $B$ има довољно бензина да надокнади утрошак на путу $A B$. Дакле, полазећи из пумпе $A$, до $S^{\\prime}$ можемо стићи само директно. Најбли-\n\n\nжа тачка скупа $S^{\\prime}$ је $C^{\\prime}$, па је цела путања $C B A C^{\\prime} B^{\\prime} A^{\\prime}$ могућа. Случај када се из $A^{\\prime}$ путем $A^{\\prime} B^{\\prime}$ не може стићи до $S$ је аналоган.\n\n$\\left(2^{\\circ}\\right)$ Ако не важи случај $\\left(1^{\\circ}\\right)$, кренимо из $A$ право у $B$. Како нам је скуп $S^{\\prime}$ у домету, а $B C \\leqslant d\\left(B, S^{\\prime}\\right)=B C^{\\prime}$, из $B$ можемо продужити у $C$. Ту ћемо надокнадити бензин потрошен на путу $B C$, а $d\\left(C, S^{\\prime}\\right)=C A^{\\prime}<d\\left(B, S^{\\prime}\\right)$, па још увек можемо у $S^{\\prime}$, и то у пумпу $A^{\\prime}$. Даље се може ићи у $B^{\\prime}$ и одатле (као малопре) у $C^{\\prime}$. Добијамо путању $A B C A^{\\prime} B^{\\prime} C^{\\prime}$.\n\nОстаје да конструишемо контрапример за $n \\geqslant 4$. Сматраћемо да је полуобим лопте 1. Распоредимо пумпе $A_{2}, A_{3}, \\ldots, A_{n}$ по великом кругу тако да је $A_{2} A_{3}=A_{3} A_{4}=\\cdots=A_{n-1} A_{n}=d<\\frac{1}{n-1}$ и пумпу $A_{1}$ тако да је $A_{1} A_{3}=d$ и $A_{1} A_{2}=A_{1} A_{4}$. Опет означавамо $S=\\left\\{A_{1}, \\ldots, A_{n}\\right\\}$ и $S^{\\prime}=\\left\\{A_{1}^{\\prime}, \\ldots, A_{n}^{\\prime}\\right\\}$. Снабдимо пумпе $A_{1}, A_{1}^{\\prime}, \\ldots, A_{n-1}, A_{n-1}^{\\prime}$ бензином довољним за прелазак раздаљине $d$, а пумпе $A_{n}$ и $A_{n}^{\\prime}$ бензином за прелазак раздаљине $1-(n-1) d$. Из сваке пумпе се може стићи до дијаметрално супротне: заиста, за $2 \\leqslant i \\leqslant n$ могућа је путања $A_{i} A_{i+1} \\ldots A_{n} A_{2}^{\\prime} A_{3}^{\\prime} \\ldots A_{i}^{\\prime}$, а могућа је и путања $A_{1} A_{3} A_{4} \\ldots A_{n} A_{2}^{\\prime} A_{3}^{\\prime} A_{1}^{\\prime}$. С друге стране, у свакој од пумпи $A_{1}, \\ldots, A_{n-1}$ има тек толико бензина да се дође до најближе пумпе, а у $A_{n}$ и $A_{n}^{\\prime}$ таман довољно за прелаз у други скуп. Зато, да\n\n\nби се обишле све пумпе, бар један од скупова, рецимо $S$, морао би се обићи цео без коришћења горива у $A_{n}$, али за то је потребно прећи пут дужи од $(n-1) d$, а бензина има само за пут дужине $(n-1) d$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2019", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Низови $\\left(a_{n}\\right)_{n=0}^{\\infty}$ и $\\left(b_{n}\\right)_{n=0}^{\\infty}$ дефинисани су рекурентним релацијама\n\n$$\na_{0}=0, \\quad a_{1}=1, \\quad a_{n+1}=\\frac{2018}{n} a_{n}+a_{n-1} \\quad \\text { за } n \\geqslant 1\n$$\n\nи\n\n$$\nb_{0}=0, \\quad b_{1}=1, \\quad b_{n+1}=\\frac{2020}{n} b_{n}+b_{n-1} \\quad \\text { за } n \\geqslant 1\n$$\n\nДоказати:\n\n$$\n\\frac{a_{1010}}{1010}=\\frac{b_{1009}}{1009}\n$$\n\n(Душан Ђукић)\n\nВреме за рад 270 минута.\n\nРешења задатака детаљно образложити.\n\nСваки задатак вреди 7 бодова.\n\n## РЕШЕЊА", "solution": "Дефинишимо низ $\\left(c_{m, n}\\right)\\left(m, n \\in \\mathbb{N}_{0}\\right)$ условима\n\n$$\nc_{m, 0}=0, \\quad c_{m, 1}=1, \\quad c_{m, n+1}=\\frac{2 m}{n} c_{m, n}+c_{m, n-1} \\quad \\text { за } n \\geqslant 1\n$$\n\nТада је $a_{n}=c_{1010, n}$ и $b_{n}=c_{1009, n}$.\n\nВидимо да је нпр. $c_{1, n}=n, c_{2, n}=n^{2}$ и $c_{3, n}=\\frac{2 n^{3}+n}{3}$. Тврдимо да за свако $m \\in \\mathbb{N}$ постоји моничан полином $P_{m}(x)$ такав да је\n\n$$\nP_{m}(x+1)=\\frac{2 m}{x} P_{m}(x)+P_{m}(x-1)\n$$\n\nпошто је очигледно $P_{m}(0)=0$, индукцијом ће следити $c_{m, n}=P_{m}(n) / P_{m}(1)$.\n\nЛема. Дефинишимо низ полинома $P_{k}$ условима $P_{0}(x)=0, P_{1}(x)=x$ и\n\n$$\nP_{k+1}(x)=x P_{k}(x)+\\frac{k(k-1)}{4} \\cdot P_{k-1}(x)\n$$\n\nТада полиноми $P_{k}$ задовољавају (1).\n\nШта више, важи $P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)=\\frac{k(k-1)}{x} \\cdot P_{k-1}(x)$.\n\nДоказ. Ако означимо\n\n$$\n\\begin{aligned}\n& A_{k}(x)=P_{k+1}(x)-x P_{k}(x)-\\frac{k(k-1)}{4} P_{k-1}(x) \\equiv 0 \\\\\n& B_{k}(x)=P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)-\\frac{k(k-1)}{x} P_{k-1}(x) \\\\\n& C_{k}(x)=P_{k}(x+1)-P_{k}(x-1)-\\frac{2 k}{x} P_{k}(x)\n\\end{aligned}\n$$\n\nи претпоставимо да је $B_{i}(x) \\equiv C_{i}(x) \\equiv 0$ за све $i \\leqslant k$, тада је\n\n$$\n\\begin{aligned}\n& B_{k+1}(x)-x B_{k}(x)-\\frac{k(k-1)}{4} B_{k-1}(x)= \\\\\n& C_{k}(x)+A_{k}(x+1)+A_{k}(x-1)-2 A_{k}(x)-\\frac{k(k-1)}{x} A_{k-1}(x)=0\n\\end{aligned}\n$$\n\nпа је $B_{k+1} \\equiv 0$. С друге стране,\n\n$$\n\\begin{aligned}\n& C_{k+1}(x)-x C_{k}(x)-\\frac{k(k-1)}{4} C_{k-1}(x)= \\\\\n& B_{k}(x)+A_{k}(x+1)-A_{k}(x-1)-\\frac{2(k+1)}{x} A_{k}(x)=0\n\\end{aligned}\n$$\n\nпа је и $C_{k+1} \\equiv 0$.\n\nИз (2) следи да полиноми $Q_{0}(x)=0$ и $Q_{k}(x)=\\frac{2^{k-1}}{(k-1)!} P_{k}(x)$ задовољавају везу $Q_{k+1}(x)=\\frac{2 x}{k} Q_{k}(x)+Q_{k-1}(x)$, па индукцијом добијамо $Q_{k}(x)=x c_{x, k}$ за све $x \\in \\mathbb{N}$. Одавде је $P_{k}(x)=\\frac{(k-1)!}{2^{k-1}} \\cdot x c_{x, k}$ и\n\n$$\n\\frac{c_{m, n}}{n}=\\frac{1}{n} \\cdot \\frac{P_{m}(n)}{P_{m}(1)}=\\frac{c_{n, m}}{c_{1, m}}=\\frac{c_{n, m}}{m}\n$$\n\nТврђење задатка се добија за $m=1010$ и $n=1009$.\n\nДруго решење. За дато $m \\geqslant 0$ посматрајмо генераторску функцију низа $c_{m, n}$ датог условима $(*)$ :\n\n$$\nf_{m}(x)=\\frac{1}{2 m}+\\sum_{n=1}^{\\infty} \\frac{c_{m, n}}{n} x^{n}\n$$\n\nИз рекурентне везе $(*)$ следи да функција $f_{m}$ задовољава диференцијалну једначину $\\left(1-x^{2}\\right) f_{m}^{\\prime}(x)=2 m \\cdot f_{m}(x)$. Ова једначина се лако решава: ако је запишемо као $\\frac{f_{m}^{\\prime}(x)}{f_{m}(x)}=\\frac{2 m}{1-x^{2}}$, интеграција по $x$ даје $\\ln \\left|f_{m}(x)\\right|=\\int \\frac{2 m}{1-x^{2}} d x=$\n$m \\ln \\frac{1+x}{1-x}+$ const, тј. $f_{m}(x)=C \\cdot\\left(\\frac{1+x}{1-x}\\right)^{m}$. Услов $f_{m}(0)=\\frac{1}{2 m}$ најзад даје $C=1$, те је\n\n$$\n\\begin{aligned}\nf_{m}(x) & =\\frac{1}{2 m}\\left(\\frac{1+x}{1-x}\\right)^{m}=\\frac{1}{2 m}(1+x)^{m}(1-x)^{-m}= \\\\\n& =\\frac{1}{2 m} \\sum_{i=0}^{m}\\binom{m}{i} x^{i} \\cdot \\sum_{j=1}^{\\infty}\\binom{m-1+j}{m-1} x^{j}\n\\end{aligned}\n$$\n\nКоефицијент уз $x^{n}$ је\n\n$$\n\\frac{c_{m, n}}{n}=\\frac{1}{2 m} \\sum_{i=0}^{m}\\binom{m}{i}\\binom{m+n-1-i}{m-1}=\\frac{1}{2} \\sum_{i} \\frac{(m+n-1-i)!}{i!(m-i)!(n-i)!}\n$$\n\nОвај израз је симетричан по $m$ и $n$, па је $\\frac{c_{m, n}}{n}=\\frac{c_{n, m}}{m}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|
Serbia_MO/segmented/sr-2020_smo_resenja.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2020", "tier": "T2", "problem_label": "1", "problem_type": null, "problem": "Наћи све моничне полиноме $P(x)$ такве да је полином $P(x)^{2}-1$ дељив полиномом $P(x+1)$.\n\n(Дуиан Ђукић)", "solution": "Једина решења су полиноми $P(x)=1$ и $P(x)=x-c$, где је $c$ константа.\n\nПретпоставимо да је $P(x)=(x-c)\\left(x-x_{2}\\right) \\cdots\\left(x-x_{n}\\right)$ неконстантан полином, при чему је $c$ његова комплексна нула чији је реални део најмањи.\n\nПо услову задатка, $x+1-c$ дели $P(x)^{2}-1$, одакле је $P(c-1)= \\pm 1$. С друге стране, за $2 \\leqslant i \\leqslant n$ важи $\\left|c-1-x_{i}\\right| \\geqslant 1$, па је $|P(c-1)|=\\prod_{i=2}^{n}\\left|c-1-x_{i}\\right| \\geqslant 1$, а то је могуће само ако је $\\left|c-1-x_{i}\\right|=1$, тј. $x_{i}=c$ за све $i$.\n\nСледи да је $P(x)=(x-c)^{n}$. Међутим, $P(x+c)^{2}-1=x^{2 n}-1$ није дељиво са $P(x+c+1)=(x+1)^{n}$ ако је $n \\geqslant 2$, па је једина могућност $n=1$.\n\nНайомена. Ако се искључи услов моничности, има и нетривијалних решења. На пример, до на замену променљиве $x$ са $x+c$, (једина) решења степена 3 и 4 су $P(x)=\\frac{\\sqrt{3}}{6}\\left(x^{3}-3 x^{2}+8 x\\right)$, односно $P(x)=\\frac{1}{36}\\left(x^{4}-2 x^{3}-x^{2}-10 x-12\\right)$ и $P(x)=\\frac{i \\sqrt{2}}{36}\\left(x^{4}-2 x^{3}+8 x^{2}-x+\\frac{33}{4}\\right)$, док решења степена 2 нема.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl", "problem_match": "\n1. ", "solution_match": "\n1. "}}
|
| 2 |
+
{"year": "2020", "tier": "T2", "problem_label": "2", "problem_type": null, "problem": "Дат је конвексан полиедар са бар 5 темена у чијем се сваком темену састају тачно по три ивице. Доказати да је могуће доделити сваком темену тог полиедра неки рационалан број тако да буду задовољени следећи услови:\n\n(i) бар један од додељених бројева је једнак 2020;\n\n(ii) за сваку страну полиедра, производ бројева у свим теменима те стране је једнак 1 .\n\n(Бојан Баиић са сараднииима)", "solution": "Означимо $c=$ 2020. Прво размотримо случај када постоји страна $\\mathcal{F}$ са парним бројем темена. Тада је довољно доделити теменима стране $\\mathcal{F}$ наизменично бројеве $c$ и $\\frac{1}{c}$, а свим осталим теменима полиедра број 1. Заиста, производ бројева на страни $\\mathcal{F}$ је једнак 1 , а свака друга страна или дели ивицу са страном $\\mathcal{F}$ (а на њој је производ 1) или нема\n\n\nниједно заједничко теме са $\\mathcal{F}$ (тада су сви бројеви на њој јединице).\n\nНадаље сматрамо да све стране имају непаран број темена. Посматрајмо две дисјунктне стране полиедра $\\mathcal{F}_{A}$ и $\\mathcal{F}_{B}$ и темена $A$ и $B$ на њима, редом, тако да је $A B$ ивица полиедра. Теменима ових двеју страна, изузев $A$ и $B$, доделићемо наизменично бројеве $c$ и $\\frac{1}{c}$ као на слици, а свим осталим теменима полиедра број 1. И у овом случају се лако види да је услов задатка испуњен.\n\nНајзад, уверимо се да се овакве стране $\\mathcal{F}_{A}$ и $\\mathcal{F}_{B}$ увек могу наћи. Постоји страна $\\mathcal{F}$ која није троугао (иначе би дати полиедар био тетраедар). Посматрајмо чети-\n\n\nри узастопне њој суседне стране $\\mathcal{F}_{1}, \\mathcal{F}_{2}, \\mathcal{F}_{3}$ и $\\mathcal{F}_{4}$. Ако су стране $\\mathcal{F}_{1}$ и $\\mathcal{F}_{3}$ дисјунктне, узмимо њих, а ако нису, онда оне имају заједничк�� целу ивицу, па три стране $\\mathcal{F}_{1}, \\mathcal{F}_{3}$ и $\\mathcal{F}$ чине појас који раздваја $\\mathcal{F}_{2}$ од $\\mathcal{F}_{4}$, те у том случају можемо узети $\\mathcal{F}_{2}$ и $\\mathcal{F}_{4}$.\n\nНайомена. Делује примамљиво поставити систем линеарних једначина по логаритмима уписаних бројева, јер он има више једначина него непознатих, што гарантује постојање нетривијалног целобројног решења. Ипак, да би уписани бројеви били рационални, једна од променљивих у том решењу мора бити једнака $\\pm 1$, што није јасно зашто се може постићи.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl", "problem_match": "\n2. ", "solution_match": "\n2. "}}
|
| 3 |
+
{"year": "2020", "tier": "T2", "problem_label": "3", "problem_type": null, "problem": "Дат је троугао $A B C$. Тачке $D$ и $E$ на правој $A B$ су такве да је $A D=A C$ и $B E=B C$, уз распоред $D-A-B-E$. Описане кружнице троуглова $D B C$ и $E A C$ секу се у тачки $X \\neq C$, а описане кружнице троуглова $D E C$ и $A B C$ секу се у тачки $Y \\neq C$. Ако важи $D Y+E Y=2 X Y$, одредити $\\varangle A C B$.\n\n(Милош Милосављевић)\n\n## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 14. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА\n\n## Други дан", "solution": "Нека је $I_{c}$ центар приписаног круга $\\triangle A B C$ наспрам темена $C$. Тада је $A I_{c}$ симетрала угла $C A D$, одакле је $\\triangle I_{c} A D \\cong \\triangle I_{c} A C$. Следи да је $\\varangle I_{c} D B=$ $\\varangle I_{c} D A=\\varangle I_{c} C A=\\varangle I_{c} C B$, па $I_{c}$ лежи на кругу $B C D$. Слично, $I_{c}$ лежи на кругу $A C E$, што значи да је $X \\equiv I_{c}$. Такође, како је $X D=X C$ и аналогно $X E=X C$, тачка $X$ је центар круга $C D E Y$.\n\nДаље, $\\varangle D Y A=\\varangle C Y A-\\varangle C Y D=\\varangle C B A-$ $\\varangle C E D=\\varangle C E D=\\varangle C X A=\\varangle D X A$ и слично $\\varangle E Y B=\\varangle E X B$. Зато посматрајмо тачку $X^{\\prime}$ симетричну тачки $X$ у односу на $A B$. Због $\\varangle D X^{\\prime} A=\\varangle D Y A$ ова тачка лежи на кругу $A D Y$, а аналогно и на кругу $B E Y$.\n\n\n\nАко је $\\varangle C<60^{\\circ}$, онда је $\\varangle A X^{\\prime} B=\\varangle A X B=90^{\\circ}-\\frac{1}{2} \\varangle C>\\varangle C=\\varangle A Y B$, па тачка $X^{\\prime}$ лежи унутар $\\triangle A B Y$, а самим тим и унутар $\\triangle D E Y$. Следи да је $D Y+E Y>D X^{\\prime}+E X^{\\prime}=D X+E X=2 X Y$. Слично, ако је $\\varangle C>60^{\\circ}$, тачка $Y$ лежи унутар $\\triangle D E X$, те је тада $D Y+E Y<2 X Y$. Према томе, ако је $D Y+E Y=2 X Y$, мора бити $\\varangle C=60^{\\circ}$, а тада је $X^{\\prime} \\equiv Y$ па заиста важи једнакост.\n\nДруйо решење. Углове троугла $A B C$ означавамо уобичајено са $\\alpha, \\beta, \\gamma$. Као у првом решењу, тачке $C, D, E, Y$ леже на кругу са центром $X$. Такође, због $\\varangle C Y D=\\varangle C E D=\\frac{\\beta}{2}$, права $D Y$ садржи средиште $N$ лука $A C$ круга $A B C$.\n\nОзначимо $\\varangle Y D E=x$ и $\\varangle Y E D=y$. Услов $D Y+E Y=2 X Y$ даје $\\sin x+\\sin y=$ $\\sin x+\\sin \\left(90^{\\circ}-\\frac{\\gamma}{2}-x\\right)=1, \\mathrm{rj}$.\n\n$$\n\\left(1-\\sin \\frac{\\gamma}{2}\\right) \\sin x+\\cos \\frac{\\gamma}{2} \\cos x=1\n$$\n\nС друге стране, синусна теорема у $\\triangle A D N$ даје $2 \\sin x \\sin \\frac{\\alpha+\\gamma}{2}=\\cos \\left(\\frac{\\alpha-\\gamma}{2}-x\\right)$, одакле следи $\\operatorname{tg} x=\\frac{\\cos \\frac{\\alpha-\\gamma}{2}}{2 \\sin \\frac{\\alpha+\\gamma}{2}-\\sin \\frac{\\alpha-\\gamma}{2}}$. Одавде налазимо\n\n$$\n\\sin x=\\frac{\\cos \\frac{\\alpha-\\gamma}{2}}{\\sqrt{3-2 \\cos \\gamma+4 \\sin \\frac{\\gamma}{2} \\cos \\varphi}}, \\quad \\cos x=\\frac{2 \\sin \\frac{\\alpha+\\gamma}{2}-\\sin \\frac{\\alpha-\\gamma}{2}}{\\sqrt{3-2 \\cos \\gamma+4 \\sin \\frac{\\gamma}{2} \\cos \\varphi}}\n$$\n\nгде је $\\varphi=\\alpha+\\frac{\\gamma}{2}-90^{\\circ}=\\frac{\\alpha-\\beta}{2}$. Заменом у једначину (*) добијамо\n\n$$\n2 \\cos \\frac{3 \\gamma-180^{\\circ}}{4} \\cos \\frac{\\varphi}{2}=\\sqrt{3-2 \\cos \\gamma+4 \\sin \\frac{\\gamma}{2} \\cos \\varphi}\n$$\n\nшто се након квадрирања своди на\n\n$$\n\\cos \\varphi=\\frac{2-2 \\cos \\gamma-\\sin \\frac{3 \\gamma}{2}}{1-4 \\sin \\frac{\\gamma}{2}+\\sin \\frac{3 \\gamma}{2}}=\\frac{-3 t+4 t^{2}+4 t^{3}}{1-t-4 t^{3}}, \\quad \\text { где је } \\quad t=\\sin \\frac{\\gamma}{2}\n$$\n\nАко је $\\gamma \\neq 60^{\\circ}$, скраћивање $2 t-1 \\neq 0$ даје $\\cos \\varphi=-\\frac{2 t^{2}+3 t}{2 t^{2}+t+1}<0$, што је немогуће. Према томе, мора бити $\\gamma=60^{\\circ}$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl", "problem_match": "\n3. ", "solution_match": "\n3. "}}
|
| 4 |
+
{"year": "2020", "tier": "T2", "problem_label": "4", "problem_type": null, "problem": "У трапезу $A B C D$ чији унутрашњи углови нису прави, дијагонале $A C$ и $B D$ секу се у тачки $E$. Нека су $P$ и $Q$ редом подножја нормала из темена $A$ и $B$ на праве $B C$ и $A D$. Описане кружнице троуглова $C E Q$ и $D E P$ секу се у тачки $F \\neq E$. Доказати да се праве $A P, B Q$ и $E F$ секу у једној тачки или су паралелне.\n\n(Душан Ђукић)", "solution": "Случај када је $A D \\| B C$ је једноставан. Наиме, тада је $E$ средиште дијагонале $A C$, те је $E A=E C=E P$, а слично важи и $E B=E D=E Q$. Одатле следи да су кругови $C E Q$ и $D E P$ симетрични у односу на симетралу дужи $C P$ и $D Q$, те је $E F \\perp C P$, тј. $E F\\|A P\\| B Q$.\n\nОзначимо са $O$ тачку пресека правих $A D$ и $B C$. Троуглови $O A P$ и $O B Q$ су\nслични, па је $\\frac{O P}{O Q}=\\frac{O A}{O B}=\\frac{O D}{O C}$, тј. $O C \\cdot O P=O D \\cdot O Q$, одакле следи да тачке $C, D, P$ и $Q$ леже на неком кругу $\\gamma$.\n\nНека се праве $A P$ и $B Q$ секу у тачки $H$, а праве $D P$ и $C Q$ у тачки $G$. Како је $G C \\cdot G Q=G D \\cdot G P$, тачка $G$ има једнаку потенцију у односу на кругове $C E Q$ и $D E P$, па она лежи на њиховој радикалној оси $E F$. С друге стране, тачке $E, G$ и $H$ су колинеарне на\n\n\nоснову Папосове теореме за тројке тачака $B, C, P$ и $A, D, Q$. Следи да су све четири тачке $H, E, G$ и $F$ колинеарне.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl", "problem_match": "\n4. ", "solution_match": "\n4. "}}
|
| 5 |
+
{"year": "2020", "tier": "T2", "problem_label": "5", "problem_type": null, "problem": "За природан број $n$, са $v_{2}(n)$ означавамо највећи цео број $k \\geqslant 0$ такав да $2^{k} \\mid n$. Претпоставимо да функција $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ задовољава услове:\n\n(i) $f(x) \\leqslant 3 x$ за све $x \\in \\mathbb{N}$;\n\n(ii) $v_{2}(f(x)+f(y))=v_{2}(x+y)$ за све $x, y \\in \\mathbb{N}$.\n\nДоказати да за сваки природан број $a$ постоји тачно један природан број $x$ такав да је $f(x)=3 a$.\n\n(Душан Ђукић)", "solution": "Заменом $x=y$ добијамо $v_{2}(f(x))=v_{2}(x)$. Ако је $v_{2}(a)=k>0$, посматрањем функције $g(x)=f\\left(2^{k} x\\right) / 2^{k}$ тврђење сводимо на случај непарног $a$. Зато надаље сматрамо да $2 \\nmid a$.\n\nПриметимо да, ако је $x \\not \\equiv y\\left(\\bmod 2^{k}\\right)$, онда је $f(x) \\not \\equiv f(y)\\left(\\bmod 2^{k}\\right)$. Заиста, ако је $z \\equiv-x\\left(\\bmod 2^{k}\\right)$, онда $2^{k} \\nmid z+y$, па је $f(y) \\not \\equiv-f(z) \\equiv f(x)\\left(\\bmod 2^{k}\\right)$. Одавде такође следи да је функција $f$ инјективна.\n\nНека је $2^{k-1}<3 a<2^{k}$, где је $k \\in \\mathbb{N}$. Како су $f(1), f(3), \\ldots, f\\left(2^{k}-1\\right)$ међусобно различити по модулу $2^{k}$, постоји непаран број $x<2^{k}$ такав да је $f(x) \\equiv 3 a$ $\\left(\\bmod 2^{k}\\right)$. Претпоставимо да је $f(x) \\neq 3 a$. Тада је $f(x)>2^{k}$, па из $f(x)+$ $f\\left(2^{k}-x\\right) \\equiv 2^{k}\\left(\\bmod 2^{k+1}\\right)$ следи да је $f(x)+f\\left(2^{k}-x\\right) \\geqslant 3 \\cdot 2^{k}$. Међутим, с друге стране је $f(x)+f\\left(2^{k}-x\\right) \\leqslant 3\\left(x+\\left(2^{k}-x\\right)\\right)=3 \\cdot 2^{k}$, па је то могуће једино ако је $f(x)=3 x$. Одавде је $x \\equiv a\\left(\\bmod 2^{k}\\right)$, па је $x=a$, тј. опет је $f(x)=3 a$.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl", "problem_match": "\n5. ", "solution_match": "\n5. "}}
|
| 6 |
+
{"year": "2020", "tier": "T2", "problem_label": "6", "problem_type": null, "problem": "Дат је природан број $k$. Посматрајмо следећу игру на бесконачној једнодимензионалној табли. На почетку игре, на поља постављамо укупно $n$ жетона, при чему може бити више жетона на истом пољу. Након тога, у сваком потезу извршавамо једну од следећих операција:\n\n$\\left(1^{\\circ}\\right)$ бирамо два суседна поља која су оба непразна и са једног од њих преносимо све жетоне на друго;\n\n$\\left(2^{\\circ}\\right)$ бирамо поље са бар два жетона и са њега премештамо по један жетон $k$ поља улево и $k$ поља удесно.\n\n(a) Ако је $n \\leqslant k+1$, доказати да ће се извршити само коначно много потеза.\n\n(б) За које вредности $k$ се може одабрати $n$ и поставити $n$ жетона тако да буде могућ бесконачан низ потеза?\n\n(Никола Пеш̄ровић)\n\n## РЕШЕЊА", "solution": "(a) Потезе врсте $\\left(1^{\\circ}\\right)$ зваћемо скуйљаљем, а потезе врсте $\\left(2^{\\circ}\\right)$ сејаъем. Поља нумеришемо редом бројевима ..., $-1,0,1,2, \\ldots$. Поља се могу поделити на $k$ класа по модулу $k$, тако да при сејању жетони не мењају своју класу.\n\nПретпоставимо прво да у једној од класа нема ниједног жетона. Поља ове класе деле таблу на блокове дужине $k-1$, које опет нумеришемо целим бројевима. Како приликом скупљања ниједан жетон не излази из свог блока, унутар сваког блока може се извршити само коначно много узастопних скупљања. С друге стране, при сваком сејању се из неког блока $i$ пребацује по један жетон у блокове $i-1$ и $i+1$. Овако се задатак своди на следећи.\n\nЛема. Нека се у сваком кораку бира $i$ и из блока $i$ премешта по један жетон у блокове $i-1$ и $i+1$. Тада се игра завршава у коначно много корака.\n\nДоказ. Кад год нека два суседна блока $x$ и $x+1$ по први пут размене жетон, доделимо овом жетону број $x$. Приликом сваке следеће размене између ових двају блокова можемо сматрати да се размењује тај исти жетон. Овако сваки жетон само циркулише између два суседна блока. Следи да ће највише $n$ парова блокова икада разменити жетоне. Међутим, ако неки блок сеје жетоне бесконачно много пута, онда то мора да важи и за суседне блокове (иначе би се у њима гомилало бесконачно много жетона), а индукцијом и за све блокове, што је немогуће.\n\nОстаје случај када се ниједна класа поља никад не испразни. Тада се увек у једној класи налазе два жетона, а у осталима по један. Сејања и скупљања\nсе врше из класе са два жетона. Нека се у неком тренутку сеје са поља $p$ у $i$-тој класи (на коме су два жетона) на поља $p-k$ и $p+k$. Следи скупљање, и то без смањења општос��и удесно ка ( $i+1$ )-тој класи - са поља $p \\pm k$ на поље $p \\pm k+1$. Затим се из овог поља сеје на поља $p+1$ и $p \\pm 2 k+1$. Следи скупљање из ( $i+1$ )-те класе, али не у $i$-ту, јер је у њој једини жетон остао на пољу $p \\mp k$. Дакле, сада се скупља у $(i+2)$-ту класу. Закључујемо да се наизменично сеје и скупља, при чему се класа из које се сеје и скупља циклично помера за један удесно. Може се сматрати без умањења општости да је жетон који се скупља увек исти - назовимо га ирним. Црни жетон периодично учествује у сејању из сваке класе, дакле са свим осталим жетонима.\n\nПри сваком сејању црни жетон баца други жетон $k$ поља на једну страну, а себе $k$ поља на другу. Тако се у сваком циклусу од $k$ сејања позиција најлевљег жетона помера бар $k$ поља улево, а најдешњег бар $k$ поља удесно, те се опсег игре увећава за бар $2 k$. Међутим, у току једног циклуса црни жетон не може прећи пут дужи од $k(k+1)$, па након $\\frac{k+1}{2}$ циклуса он више не може стићи од најлевљег до најдешњег, што је коначна контрадикција.\n\n(б) За свако $k$ даћемо пример периодичне (и самим тим бесконачне) игре. Посматрајмо $5 k$ узастопних поља означених редом бројевима $1,2, \\ldots, 5 k$, свако са по једним жетоном. Делимо их на групе од по $k$ поља:\n\n$$\n1,1, \\cdots, 1,1 \\quad 1,1, \\cdots, 1,1 \\quad 1,1, \\cdots, 1,1 \\quad 1,1, \\cdots, 1,1 \\quad 1,1, \\cdots, 1,1\n$$\n\nПочињемо скупљањем жетона са поља $1, \\ldots, k$ на поље $k+1$. Затим, за $i=$ $1,2, \\ldots, k$, са поља $k+i$ једном сејемо, а преостале жетоне с тог поља скупљамо на поље $k+i+1$ (осим за $i=k$ ). Након $i$-тог циклуса стање је овакво:\n\n$$\n\\underbrace{1,1, \\ldots, 1}_{i}, 0,0, \\ldots, 0 \\quad \\underbrace{0,0, \\ldots, 0}_{i}, k+1-i, 1,1, \\ldots, 1 \\quad \\underbrace{2,2, \\ldots, 2}_{i}, 1,1, \\ldots, 1 \\quad 1,1, \\cdots, 1,1 \\quad 1,1, \\cdots, 1,1\n$$\n\nКада аналогне потезе одиграмо и здесна, добићемо стање\n\n$$\n1,1, \\cdots, 1,1 \\quad 0,0, \\cdots, 0,0 \\quad 3,3, \\cdots, 3,3 \\quad 0,0, \\cdots, 0,0 \\quad 1,1, \\cdots, 1,1\n$$\n\nНајзад, ако сада посејемо по једном са сваког од поља $2 k+1, \\ldots, 3 k$, добијамо конфигурацију идентичну полазној.", "metadata": {"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl", "problem_match": "\n6. ", "solution_match": "\n6. "}}
|