Add data for Germany TST
#8
by
LxYxvv
- opened
This view is limited to 50 files because it contains too many changes.
See the raw diff here.
- Germany_TST/download_script/download.py +88 -0
- Germany_TST/md/de-2000-aufgaben_awb_00.md +46 -0
- Germany_TST/md/de-2001-aufgaben_awb_01.md +40 -0
- Germany_TST/md/de-2002-loes_awkl1_02.md +88 -0
- Germany_TST/md/de-2002-loes_awkl2_02.md +55 -0
- Germany_TST/md/de-2003-loes_awkl1_03.md +65 -0
- Germany_TST/md/de-2003-loes_awkl2_03.md +56 -0
- Germany_TST/md/de-2004-loes_awkl1_04.md +87 -0
- Germany_TST/md/de-2004-loes_awkl2_04.md +44 -0
- Germany_TST/md/de-2005-loes_awkl1_05.md +52 -0
- Germany_TST/md/de-2005-loes_awkl2_05.md +44 -0
- Germany_TST/md/de-2006-loes_awkl1_06.md +64 -0
- Germany_TST/md/de-2006-loes_awkl2_06.md +61 -0
- Germany_TST/md/de-2007-loes_awkl1_07.md +114 -0
- Germany_TST/md/de-2007-loes_awkl2_07.md +44 -0
- Germany_TST/md/de-2008-loes_awkl1_08.md +67 -0
- Germany_TST/md/de-2008-loes_awkl2_08.md +54 -0
- Germany_TST/md/de-2009-loes_awkl1_09.md +30 -0
- Germany_TST/md/de-2009-loes_awkl2_09.md +61 -0
- Germany_TST/md/de-2010-loes_awkl1_10.md +79 -0
- Germany_TST/md/de-2010-loes_awkl2_10.md +42 -0
- Germany_TST/md/de-2011-loes_awkl1_11.md +95 -0
- Germany_TST/md/de-2011-loes_awkl2_11.md +49 -0
- Germany_TST/md/de-2012-loes_awkl1_12.md +81 -0
- Germany_TST/md/de-2012-loes_awkl2_12.md +57 -0
- Germany_TST/md/de-2013-loes_awkl_13.md +140 -0
- Germany_TST/md/de-2014-loes_awkl_14.md +121 -0
- Germany_TST/md/de-2015-loes_awkl_15.md +120 -0
- Germany_TST/md/de-2016-loes_awkl_16.md +41 -0
- Germany_TST/md/de-2017-loes_awkl_17.md +76 -0
- Germany_TST/md/de-2018-loes_awkl_18.md +115 -0
- Germany_TST/md/de-2019-loes_awkl_19.md +145 -0
- Germany_TST/md/de-2020-loes_awkl_20.md +176 -0
- Germany_TST/md/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.md +131 -0
- Germany_TST/md/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.md +220 -0
- Germany_TST/raw/de-2000-aufgaben_awb_00.pdf +3 -0
- Germany_TST/raw/de-2001-aufgaben_awb_01.pdf +3 -0
- Germany_TST/raw/de-2002-loes_awkl1_02.pdf +3 -0
- Germany_TST/raw/de-2002-loes_awkl2_02.pdf +3 -0
- Germany_TST/raw/de-2003-loes_awkl1_03.pdf +3 -0
- Germany_TST/raw/de-2003-loes_awkl2_03.pdf +3 -0
- Germany_TST/raw/de-2004-loes_awkl1_04.pdf +3 -0
- Germany_TST/raw/de-2004-loes_awkl2_04.pdf +3 -0
- Germany_TST/raw/de-2005-loes_awkl1_05.pdf +3 -0
- Germany_TST/raw/de-2005-loes_awkl2_05.pdf +3 -0
- Germany_TST/raw/de-2006-loes_awkl1_06.pdf +3 -0
- Germany_TST/raw/de-2006-loes_awkl2_06.pdf +3 -0
- Germany_TST/raw/de-2007-loes_awkl1_07.pdf +3 -0
- Germany_TST/raw/de-2007-loes_awkl2_07.pdf +3 -0
- Germany_TST/raw/de-2008-loes_awkl1_08.pdf +3 -0
Germany_TST/download_script/download.py
ADDED
|
@@ -0,0 +1,88 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-12-5
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download script for Germany TST
|
| 7 |
+
To run:
|
| 8 |
+
`python Germany_TST/download_script/download.py`
|
| 9 |
+
'''
|
| 10 |
+
|
| 11 |
+
import requests
|
| 12 |
+
from bs4 import BeautifulSoup
|
| 13 |
+
from tqdm import tqdm
|
| 14 |
+
from pathlib import Path
|
| 15 |
+
from requests.adapters import HTTPAdapter
|
| 16 |
+
from urllib3.util.retry import Retry
|
| 17 |
+
|
| 18 |
+
|
| 19 |
+
def build_session(
|
| 20 |
+
max_retries: int = 3,
|
| 21 |
+
backoff_factor: int = 2,
|
| 22 |
+
session: requests.Session = None
|
| 23 |
+
) -> requests.Session:
|
| 24 |
+
"""
|
| 25 |
+
Build a requests session with retries
|
| 26 |
+
|
| 27 |
+
Args:
|
| 28 |
+
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 29 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 30 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 31 |
+
"""
|
| 32 |
+
session = session or requests.Session()
|
| 33 |
+
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 34 |
+
session.mount("http://", adapter)
|
| 35 |
+
session.mount("https://", adapter)
|
| 36 |
+
session.headers.update({
|
| 37 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 38 |
+
})
|
| 39 |
+
|
| 40 |
+
return session
|
| 41 |
+
|
| 42 |
+
|
| 43 |
+
def main():
|
| 44 |
+
"""
|
| 45 |
+
Download Germany TST (https://www.mathe-wettbewerbe.de/aufgaben#t-internationale-mathematik-olympiade)
|
| 46 |
+
"""
|
| 47 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 48 |
+
output_dir.mkdir(parents=True, exist_ok=True)
|
| 49 |
+
|
| 50 |
+
# Build a requests session with retries
|
| 51 |
+
req_session = build_session()
|
| 52 |
+
|
| 53 |
+
# Get all year list
|
| 54 |
+
resp = req_session.get('https://www.mathe-wettbewerbe.de/aufgaben#t-internationale-mathematik-olympiade')
|
| 55 |
+
soup = BeautifulSoup(resp.text, 'html.parser')
|
| 56 |
+
germ_tst_list_ele = soup.find_all('article')[1]
|
| 57 |
+
|
| 58 |
+
for sec_ele in tqdm(germ_tst_list_ele.find_all('section')):
|
| 59 |
+
year = sec_ele.find('button').get_text(strip=True)
|
| 60 |
+
resources = sec_ele.find_all('a')
|
| 61 |
+
|
| 62 |
+
with_problems = [_['href'] for _ in resources if "Auswahlklausuren" in _.get_text(strip=True)]
|
| 63 |
+
with_solutions = [_['href'] for _ in resources if "Lösungen" in _.get_text(strip=True)]
|
| 64 |
+
|
| 65 |
+
# Give priority to download those with solution.
|
| 66 |
+
if len(with_solutions) != 0:
|
| 67 |
+
download_pdfs = with_solutions
|
| 68 |
+
else:
|
| 69 |
+
download_pdfs = with_problems
|
| 70 |
+
|
| 71 |
+
for uri in download_pdfs:
|
| 72 |
+
output_file = output_dir / f"de-{year}-{Path(uri).name}"
|
| 73 |
+
|
| 74 |
+
# Skip if already downloaded
|
| 75 |
+
if output_file.exists():
|
| 76 |
+
continue
|
| 77 |
+
|
| 78 |
+
pdf_resp = req_session.get("https://www.mathe-wettbewerbe.de" + uri)
|
| 79 |
+
|
| 80 |
+
if pdf_resp.status_code != 200:
|
| 81 |
+
print(f"Year {year} Failed to download: {uri}")
|
| 82 |
+
continue
|
| 83 |
+
|
| 84 |
+
output_file.write_bytes(pdf_resp.content)
|
| 85 |
+
|
| 86 |
+
|
| 87 |
+
if __name__ == "__main__":
|
| 88 |
+
main()
|
Germany_TST/md/de-2000-aufgaben_awb_00.md
ADDED
|
@@ -0,0 +1,46 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2000
|
| 2 |
+
|
| 3 |
+
## 1. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Gegeben sei ein hinreichend großer Vorrat von gleichseitigen Dreiecken und Quadraten, alle mit der gleichen Seitenlänge. Aus diesen Bausteinen lassen sich konvexe* Polygone bilden, indem man sie in der Ebene lückenlos und überschneidungsfrei aneinander legt. (Die Figur zeigt drei Möglichkeiten für ein Sechseck.)
|
| 8 |
+

|
| 9 |
+
a) Welches ist die größtmögliche Anzahl $m$ von Seitenkanten für ein so gebildetes konvexes Polygon? (Die Antwort ist zu begründen.)
|
| 10 |
+
b) Man gebe für alle möglichen Anzahlen von Seitenkanten $\leq m$ jeweils ein Beispiel an.
|
| 11 |
+
*) Eine Figur heißt konvex, wenn für je zwei ihrer Punkte auch alle Punkte der Verbindungsstrecke zu der Figur gehören.
|
| 12 |
+
|
| 13 |
+
## Aufgabe 2
|
| 14 |
+
|
| 15 |
+
Wir betrachten - mit 1 beginnend - alle positiven Teiler einer natürlichen Zahl $n$ der Größ̉e nach geordnet: $1=d_{1}<d_{2}<d_{3}<\ldots<n$.
|
| 16 |
+
Man bestimme alle natürlichen Zahlen $n$ mit den Eigenschaften:
|
| 17 |
+
(1) $n=d_{13}+d_{14}+d_{15}$
|
| 18 |
+
und
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
\left(d_{5}+1\right)^{3}=d_{15}+1
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
## Aufgabe 3
|
| 25 |
+
|
| 26 |
+
Die natürlichen Zahlen von 1 bis $n^{2}$ werden zufällig auf die Felder eines $n \times n$-Quadrats verteilt ( $n \geq 2$ ). Für jedes Paar von Zahlen innerhalb einer Reihe bzw. einer Spalte dividieren wir die größere durch die kleinere Zahl. Der kleinste dieser $n^{2}(n-1)$ Quotienten werde als Charakteristik C der zufälligen Anordnung bezeichnet.
|
| 27 |
+
Welches ist der größtmögliche Wert für C ? (Die Antwort ist zu begründen.)
|
| 28 |
+
|
| 29 |
+
## 2. Auswahlklausur
|
| 30 |
+
|
| 31 |
+
## Aufgabe 1
|
| 32 |
+
|
| 33 |
+
In einem $10 \times 17$-Rechteck werden 74 Punkte markiert.
|
| 34 |
+
Man beweise, dass es dabei stets zwei markierte Punkte gibt, deren Abstand 2 nicht überschreitet.
|
| 35 |
+
|
| 36 |
+
## Aufgabe 2
|
| 37 |
+
|
| 38 |
+
Zwei Sehnen $A C$ und $B D$ eines Kreises mit Mittelpunkt $M$ schneiden sich in $P$. Die Umkreise der Dreiecke PBC und PDA haben ihre Mittelpunkte in $E$ bzw. $F$ und schneiden sich ein zweites Mal in $Q$.
|
| 39 |
+
Man beweise, dass $\overline{M F}=\overline{Q E}$ gilt.
|
| 40 |
+
|
| 41 |
+
## Aufgabe 3
|
| 42 |
+
|
| 43 |
+
Gegeben ist die Summe $S=\frac{1}{n}+\frac{1}{n+1}+\ldots+\frac{1}{n+m}$ mit $n, m \in\{1,2,3, \ldots\}$.
|
| 44 |
+
a) Man beweise, dass $S$ keine natürliche Zahl sein kann.
|
| 45 |
+
b) Man ermittle (mit Begründung!) für $m=2 \cdot(n-1)$ ein $k \in \operatorname{IN}$ so, dass $S \in] k, k+1[$.
|
| 46 |
+
|
Germany_TST/md/de-2001-aufgaben_awb_01.md
ADDED
|
@@ -0,0 +1,40 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Auswahlwettbewerb zur IMO 2001
|
| 2 |
+
|
| 3 |
+
## 1. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
In einem Schritt kann man vom Punkt $A(i|j| k)$, mit $i, j k \in\{0,1,2,3\}$, zu einem weiteren Punkt des Würfelgitters gelangen, indem man stets genau eine der Koordinaten um 1 vergrößert.
|
| 8 |
+
Man ermittle die Anzahl aller kürzesten Wege, die vom Ursprung $\mathrm{O}(0|0| 0)$ in den Punkt $\mathrm{P}(3|3| 3)$ führen.
|
| 9 |
+
|
| 10 |
+
## Aufgabe 2
|
| 11 |
+
|
| 12 |
+
Man beweise: Für die positiven reellen Zahlen a, b, c gilt die Ungleichung
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
\frac{a}{\sqrt{(a+b)(a+c)}}+\frac{b}{\sqrt{(b+a)(b+c)}}+\frac{c}{\sqrt{(c+a)(c+b)}} \leq \frac{3}{2} .
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
## Aufgabe 3
|
| 19 |
+
|
| 20 |
+
Im regulären 18-Eck $\quad \mathrm{A}_{1} \mathrm{~A}_{2} . \mathrm{A}_{18}$ mit den Umkreismittelpunkt M ist P der Schnitt von $A_{1} A_{7}$ mit $M A_{2}$ und $Q$ der Schnitt von $A_{2} A_{13}$ mit $M A_{1}$. Man berechne den Winkel $\angle \mathrm{MPQ}$.
|
| 21 |
+
|
| 22 |
+
## 2. Auswahlklausur
|
| 23 |
+
|
| 24 |
+
## Aufgabe 1
|
| 25 |
+
|
| 26 |
+
Gegeben seien positive ganze Zahlen $a, b, c$ mit der Eigenschaft $b>2 a$ und $c>2 b$.
|
| 27 |
+
Man zeige, dass es dann stets eine reelle Zahl $r$ mit folgender Eigenschaft gibt:
|
| 28 |
+
Die gebrochenen Teile der Zahlen $r a, r b, r c$ liegen alle im Intervall $\left.\rfloor \frac{1}{3} ; \frac{2}{3}\right\rfloor$.
|
| 29 |
+
(Hinweis: Der gebrochene Teil einer Zahl ist die Differenz zwischen der Zahl und ihrem ganzen Teil.)
|
| 30 |
+
|
| 31 |
+
## Aufgabe 2
|
| 32 |
+
|
| 33 |
+
Wir betrachten zwei Kreise in der Ebene, welche sich in den beiden verschiedenen Punkten $X$ und $Y$ schneiden.
|
| 34 |
+
Man beweise, dass es in dieser Ebene vier feste Punkte mit folgender Eigenschaft gibt: Für jeden Kreis, der im Durchschnitt der beiden gegebenen Kreise liegt und diese in den Punkten $A$ und $B$ berührt sowie die Gerade $X Y$ in den Punkten $C$ und $D$ schneidet, geht jede der Geraden $A C, A D, B C$ und $B D$ durch einen dieser vier Punkte.
|
| 35 |
+
|
| 36 |
+
## Aufgabe 3
|
| 37 |
+
|
| 38 |
+
Für jede positive ganze Zahl $n$ bezeichne $d(n)$ die Anzahl aller positiver Teiler von $n$. (Beispiele: $d(2)=2, d(6)=4, d(9)=3$.)
|
| 39 |
+
Man bestimme alle positiven ganzen Zahlen $n$ mit der Eigenschaft $(d(n))^{3}=4 n$.
|
| 40 |
+
|
Germany_TST/md/de-2002-loes_awkl1_02.md
ADDED
|
@@ -0,0 +1,88 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2002
|
| 2 |
+
|
| 3 |
+
Lösungen zur 1. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Man ermittle die Anzahl aller Zahlen der Form $x^{2}+y^{2}(x, y \in\{1,2,3, \ldots, 1000\})$, die durch 121 teilbar sind.
|
| 8 |
+
|
| 9 |
+
## Lösung
|
| 10 |
+
|
| 11 |
+
Die Reste, die eine Quadratzahl bei der Division durch 11 haben kann, sind 0, 1, 4, 9, 5 und 3. Da aber, außer zur Null, keine komplementären Reste modulo 11 auftreten, müssen sowohl $x^{2}$ als auch $y^{2}$ und folglich auch $x$ und $y$ durch 11 teilbar sein.
|
| 12 |
+
Unter den Zahlen von 1 bis 1000 gibt es genau [1000/11] = 90 Vielfache von 11. Es gibt demnach höchstens 90.89/2 = 4005 durch 121 teilbare Zahlen der Form $x^{2}+y^{2}$ mit $x \neq y$, und genau 90 durch 121 teilbare Zahlen der Form $x^{2}+x^{2}$. Folglich kann es höchstens 4095 Zahlen der genannten Form geben. Ihre Anzahl ist allerdings geringer, da es viele Zahlen gibt, die unterschiedliche Darstellungen als Summe zweier Quadrate erlauben. Leider hatte das der Aufgabensteller bei der Formulierung der Aufgabe nicht bedacht. Umso erfreulicher war die Tatsache, dass einige Teilnehmer sehr interessante Lösungsansätze lieferten.
|
| 13 |
+
|
| 14 |
+
## Aufgabe 2
|
| 15 |
+
|
| 16 |
+
Man beweise: Sind x, y, z die Längen der Winkelhalbierenden eines Dreiecks mit dem Umfang 6, dann gilt
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\frac{1}{\mathrm{x}^{2}}+\frac{1}{\mathrm{y}^{2}}+\frac{1}{\mathrm{z}^{2}} \geq 1
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
## Lösung
|
| 23 |
+
|
| 24 |
+
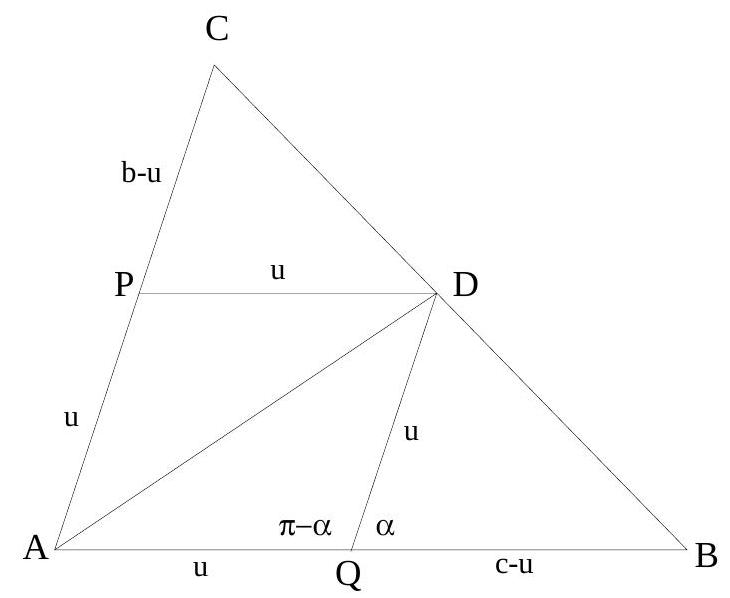
Man beachte nebenstehende Figur.
|
| 25 |
+
DP und DQ sind die Parallelen durch D zu AB und
|
| 26 |
+
AC. Da $A D=x$ die Winkelhalbierende von $\alpha$ ist, ist AQDP eine Raute, deren Seitenlänge mit $u$ bezeichnet wurde.
|
| 27 |
+
|
| 28 |
+
Aus der Ähnlichkeit der Dreiecke PDC mit QBD folgt $\frac{\mathrm{u}}{\mathrm{c}-\mathrm{u}}=\frac{\mathrm{b}-\mathrm{u}}{\mathrm{u}}$, woraus man $u=\frac{b c}{b+c}$ erhält.
|
| 29 |
+
|
| 30 |
+
Der Kosinussatz im Dreieck AQD führt zu
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
\begin{aligned}
|
| 34 |
+
\mathrm{x}^{2}=2 \mathrm{u}^{2}-2 \mathrm{u}^{2} \cos (\pi-\alpha) & =2 \mathrm{u}^{2}(1+\cos \alpha) \\
|
| 35 |
+
=2 u^{2}\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)=2 u^{2} & \frac{(b+c)^{2}-a^{2}}{2 b c}= \\
|
| 36 |
+
& =\frac{b c}{(b+c)^{2}}(a+b+c)(-a+b+c)
|
| 37 |
+
\end{aligned}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
|
| 41 |
+
|
| 42 |
+
Mit $(b+c)^{2} \geq 4 b c$ und $a+b+c=6$ folgt $x^{2} \leq 1,5(-a+b+c)$.
|
| 43 |
+
Ähnlich ergibt sich $y^{2} \leq 1,5(a-b+c)$ und $z^{2} \leq 1,5(a+b-c)$.
|
| 44 |
+
|
| 45 |
+
Aus der Ungleichung zwischen dem arithmetischen und geometrischen Mittel dreier positiver Zahlen, ergibt sich $\left(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}}\right)\left(x^{2}+y^{2}+z^{2}\right) \geq 9$ und hieraus schließlich
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}} \geq \frac{9}{x^{2}+y^{2}+z^{2}} \geq \frac{9}{1,5 \cdot 6}=1
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
wobei das Gleichheitszeichen nur für $x=y=z$ gilt.
|
| 52 |
+
|
| 53 |
+
## Aufgabe 3
|
| 54 |
+
|
| 55 |
+
Man ermittle alle Lösungen der Gleichung $\quad x^{2 y}+(x+1)^{2 y}=(x+2)^{2 y}$ mit $x, y \in N$.
|
| 56 |
+
|
| 57 |
+
## Lösung
|
| 58 |
+
|
| 59 |
+
Man erkennt leicht, dass weder $x$, noch $y$, Null sein können.
|
| 60 |
+
Für $y=1$ erhält man aus $x^{2}+(x+1)^{2}=(x+2)^{2}$ die Gleichung $x^{2}-2 x-3=0$, von der nur die Lösung $x=3$ in Frage kommt.
|
| 61 |
+
Sei nun $y>1$.
|
| 62 |
+
Da $x$ und $x+2$ dieselbe Parität haben, ist $x+1$ eine gerade und demnach $x$ eine ungerade Zahl.
|
| 63 |
+
Mit $x=2 k-1(k \in N)$ ergibt sich die Gleichung
|
| 64 |
+
(\#) $\quad(2 k-1)^{2 y}+(2 k)^{2 y}=(2 k+1)^{2 y}$
|
| 65 |
+
woraus man durch Ausmultiplizieren folgendes erhält:
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
(2 \mathrm{k})^{2 \mathrm{y}}-2 \mathrm{y}(2 \mathrm{k})^{2 \mathrm{y}-1}+\ldots-2 \mathrm{y} 2 \mathrm{~h}+1+(2 \mathrm{k})^{2 \mathrm{y}}=(2 \mathrm{k})^{2 \mathrm{y}}+2 \mathrm{y}(2 \mathrm{k})^{2 \mathrm{y}-1}+\ldots+2 \mathrm{y} 2 \mathrm{k}+1
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Da $y>1$, ist auch $2 \mathrm{y} \geq 3$. Lässt man nun alle Glieder in yk auf einer Seite und faktorisiert auf der anderen Seite (2k) ${ }^{3}$, dann erhält man:
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
8 \mathrm{yk}=(2 \mathrm{k})^{3}\left[2\binom{2 \mathrm{y}}{3}+2\binom{2 \mathrm{y}}{5}(2 \mathrm{k})^{2}+\ldots-(2 \mathrm{k})^{2 \mathrm{y}-3}\right]
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
woraus folgt, dass y ein Vielfaches von k ist.
|
| 78 |
+
Durch Division der Gleichung (\#) durch (2k) ${ }^{2 y}$ ergibt sich:
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\left(1-\frac{1}{2 k}\right)^{2 y}+1=\left(1+\frac{1}{2 k}\right)^{2 y}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
wobei die linke Seite kleiner als 2 ist. Die rechte Seite ist allerdings größer als $1+\frac{2 y}{2 k} \geq 2$, was nicht sein kann, da y ein Vielfaches von $k$ ist.
|
| 85 |
+
|
| 86 |
+
Die gegebene Gleichung hat demnach nur die Lösung $x=3$ und $\mathrm{y}=1$.
|
| 87 |
+
Dass es für y > 1 keine Lösungen geben kann, war den meisten Teilnehmern klar, da sich ein Sonderfall für den großen Satz von Fermat ergibt, der mittlerweile bewiesen ist. Leider gelang nur wenigen ein vollständiger Beweis dieses Sonderfalles.
|
| 88 |
+
|
Germany_TST/md/de-2002-loes_awkl2_02.md
ADDED
|
@@ -0,0 +1,55 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2002
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Es sei $P$ die Menge aller geordneter Paare $(p, q)$ von nichtnegativen ganzen Zahlen. Man bestimme alle Funktionen $f: P \rightarrow \mathrm{IR}$ mit der Eigenschaft
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
f(p, q)=\left\{\begin{array}{c}
|
| 11 |
+
0 \quad \text { wenn } p q=0 \\
|
| 12 |
+
1+\frac{1}{2} f(p+1, q-1)+\frac{1}{2} f(p-1, q+1) \text { sonst }
|
| 13 |
+
\end{array} .\right.
|
| 14 |
+
$$
|
| 15 |
+
|
| 16 |
+
## Lösung
|
| 17 |
+
|
| 18 |
+
Die einzige solche Funktion ist $f(p, q)=p \cdot q$.
|
| 19 |
+
Diese Funktion erfüllt offensichtlich für $p=0$ oder $q=0$ die erste Bedingung. Für $p q \neq 0$ gilt $1+\frac{1}{2} f(p+1, q-1)+\frac{1}{2} f(p-1, q+1)=1+\frac{1}{2}(p+1)(q-1)+\frac{1}{2}(p-1)(q+1)=p q$, so dass auch die zweite Bedingung erfültt ist.
|
| 20 |
+
Nun muss noch gezeigt werden, dass es keine andere Funktion mit diesen Eigenschaften gibt. Dazu setzen wir $f(p, q)=p q+g(p, q)$. Für $p q \neq 0$ ergibt sich aus der zweiten
|
| 21 |
+
Bedingung $p q+g(p, q)=1+\frac{1}{2}((p+1)(q-1)+g(p+1, q-1)+(p-1)(q+1)+g(p-1, q+1))$, also $g(p, q)=\frac{1}{2}(g(p+1, q-1)+g(p-1, q+1))$. Daher bilden die Zahlen $g(0, p+q)$, $g(1, p+q-1), g(2, p+q-2), \ldots, g(p+q-1,1), g(p+q, 0)$ eine arithmetische Folge. Da ihre Außenglieder $g(0, p+q)$ und $g(p+q, 0)$ gleich Null sind, hat jedes Folgenglied den Wert Null. Folglich ist $g(p, q)=0$ für alle nichtnegativen ganzen Zahlen und daher $f(p, q)=p \cdot q$ die einzige Lösung.
|
| 22 |
+
Anmerkung: Der zweite Teil des Beweises ist der bedeutendere. Dabei reicht es nicht, nur bestimmte Typen von Funktionen auszuschließen, wie es einige Teilnehmer versucht haben.
|
| 23 |
+
|
| 24 |
+
## Aufgabe 2
|
| 25 |
+
|
| 26 |
+
In ein spitzwinkliges Dreieck $A B C$ wird ein Quadrat mit Mittelpunkt $A_{1}$ so einbeschrieben, dass zwei Ecken auf $B C$ und je eine auf $A B$ bzw. $A C$ liegen. Analog sind die Quadrate mit den Mittelpunkten $B_{1}$ bzw. $C_{1}$ definiert.
|
| 27 |
+
Man beweise, dass die Geraden $A A_{1}, B B_{1}$ und $C C_{1}$ einen gemeinsamen Schnittpunkt haben.
|
| 28 |
+
|
| 29 |
+
## Lösung
|
| 30 |
+
|
| 31 |
+
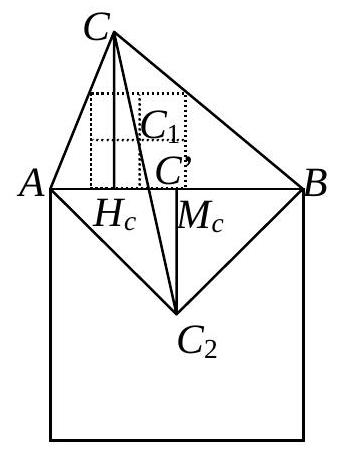
Zusätzlich zur gegebenen Figur betrachten wir das nach außen errichtete Quadrat über der Seite $A B$ mit dem Mittelpunkt $C_{2}$. Da es eine zentrische Streckung gibt, welche das einbeschriebene Quadrat mit Mittelpunkt $C_{1}$ in das nach außen errichtete Quadrat überführt, liegen $C, C_{1}$ und $C_{2}$ auf einer Geraden.
|
| 32 |
+
Die Höhe $h_{c}$ schneidet $A B$ in $H_{c}$ und es sei $\left|A H_{c}\right|=p,\left|H_{c} B\right|=q$. Ferner sei $M_{c}$ der Mittelpunkt von $A B$ und $C^{\prime}$ der Schnittpunkt von $C C_{2}$ mit $A B$. Schließlich setzen wir $\left|A C^{\prime}\right|=c_{1}$ und $\left|C^{\prime} B\right|=c_{2}$. Alle Teilstrecken von $A B$ existieren wegen der Spitzwinkligkeit des Dreiecks $A B C$. Für die anderen Dreiecksseiten seien entsprechende
|
| 33 |
+
|
| 34 |
+
|
| 35 |
+
Punkte und Abschnitte analog definiert.
|
| 36 |
+
|
| 37 |
+
Nach den Strahlensätzen gilt $\frac{\left|H_{c} C^{\prime}\right|}{\left|C H_{c}\right|}=\frac{\left|C^{\prime} M_{c}\right|}{\left|M_{c} C_{2}\right|}$, d.h. $\frac{c_{1}-p}{h_{c}}=\frac{\frac{1}{2} c-c_{1}}{\frac{1}{2} c} \Rightarrow c_{1}=\frac{c\left(p+h_{c}\right)}{c+2 h_{c}}$.
|
| 38 |
+
Analog ist $c_{2}=\frac{c\left(q+h_{c}\right)}{c+2 h_{c}}$ und wir erhalten $\frac{c_{1}}{c_{2}}=\frac{\frac{p}{h_{c}}+1}{\frac{q}{h_{c}}+1}$. (Für $\alpha=\beta$ ist $\frac{c_{1}}{c_{2}}=1$. )
|
| 39 |
+
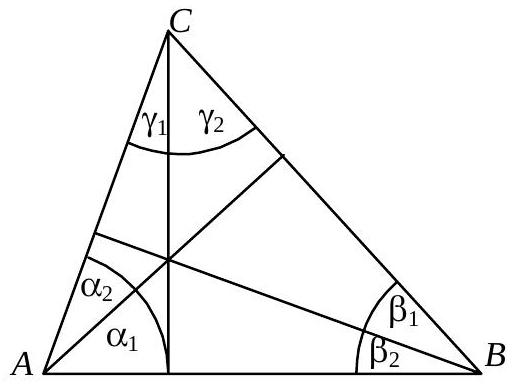
Die Winkel zwischen den Höhen und den jeweils anliegenden beiden Seiten seien zyklisch mit $\gamma_{1}, \gamma_{2}$ bzw. $\alpha_{1}, \alpha_{2}$ bzw. $\beta_{1}, \beta_{2}$ bezeichnet. Dann gilt $\alpha_{1}=\gamma_{2}\left(=90^{\circ}-\beta\right), \quad \beta_{1}=\alpha_{2}\left(=90^{\circ}-\gamma\right)$ und $\gamma_{1}=\beta_{2}\left(=90^{\circ}-\alpha\right)$. Ferner ist $\frac{p}{h_{c}}=\tan \gamma_{1}$ und $\frac{q}{h_{c}}=\tan \gamma_{2}$, also $\frac{c_{1}}{c_{2}}=\frac{\tan \gamma_{1}+1}{\tan \gamma_{2}+1}$. Analog gilt $\frac{a_{1}}{a_{2}}=\frac{\tan \alpha_{1}+1}{\tan \alpha_{2}+1}$ und $\frac{b_{1}}{b_{2}}=\frac{\tan \beta_{1}+1}{\tan \beta_{2}+1}$. Damit ist
|
| 40 |
+
|
| 41 |
+
$\frac{a_{1}}{a_{2}} \cdot \frac{b_{1}}{b_{2}} \cdot \frac{c_{1}}{c_{2}}=\frac{\left(\tan \alpha_{1}+1\right)\left(\tan \beta_{1}+1\right)\left(\tan \gamma_{1}+1\right)}{\left(\tan \alpha_{2}+1\right)\left(\tan \beta_{2}+1\right)\left(\tan \gamma_{2}+1\right)}=\frac{\tan \alpha_{1}+1}{\tan \gamma_{2}+1} \cdot \frac{\tan \beta_{1}+1}{\tan \alpha_{2}+1} \cdot \frac{\tan \gamma_{1}+1}{\tan \beta_{2}+1}=1 \cdot 1 \cdot 1=1$.
|
| 42 |
+
Nach der Umkehrung des Satzes von Ceva schneiden sich daher die Geraden $A A^{\prime}=A A_{1}$, $B B^{\prime}=B B_{1}$ und $C C^{\prime}=C C_{1}$ in einem Punkt.
|
| 43 |
+
Anmerkung: Einige Teilnehmer haben vermutet, die Geraden $A A_{1}$ etc. seien die Winkelhalbierenden des gegebenen Dreiecks. Diese Vermutung ist falsch, wie man an einem sehr spitzen, fast rechtwinkligen Dreieck sieht. Der Satz von Ceva ist zum Beweis nicht notwendig; es gibt andere Lösungsmöglichkeiten, z.B. mit Drehstreckungen.
|
| 44 |
+
|
| 45 |
+
## Aufgabe 3
|
| 46 |
+
|
| 47 |
+
Man beweise, dass es keine positive ganze Zahl $n$ mit der folgenden Eigenschaft gibt: Für $k=1,2, \ldots, 9$ ist die - in dezimaler Schreibweise - linke Ziffer von $(n+k)$ ! gleich $k$.
|
| 48 |
+
|
| 49 |
+
## Lösung
|
| 50 |
+
|
| 51 |
+
Wir nehmen an, dass es eine Zahl $n$ mit der verlangten Eigenschaft gibt. Dann kann keine der Fakultäten eine Zehnerpotenz sein, weil ab 3! alle Fakultäten durch 3 teilbar sind und die ersten Fakultäten offensichtlich nicht die verlangte Eigenschaft haben. Es kann auch keine der Zahlen $n+2, \ldots, n+9$ eine Zehnerpotenz sein, weil sonst die Anfangsziffer zweier aufeinanderfolgender Fakultäten in der betrachteten Folge dieselbe wäre. Somit gibt es ein $j$ mit $10^{j}<n+2<\ldots<n+9<10^{j+1}$ (1). Weil $(n+8)$ ! mit einer 8 und $(n+9)$ ! mit einer 9 endet, gibt es natürliche Zahlen a und $b$ mit $9 \cdot 10^{a}<(n+9)!<10^{a+1}$ und $8 \cdot 10^{b}<(n+8)!<9 \cdot 10^{b}$, was auf $10^{a-b}<n+9<\frac{5}{4} \cdot 10^{a-b}$ führt.
|
| 52 |
+
Mit (1) folgt $j=a-b$ und $10^{j}<n+2<\ldots<n+9<\frac{5}{4} \cdot 10^{j}$ (2).
|
| 53 |
+
Da $(n+1)$ ! mit 1 anfängt, gibt es ein $m$ mit $10^{m}<(n+1)!<2 \cdot 10^{m}$, während aus (2) folgt: $10^{3 j}<(n+2)(n+3)(n+4)<\left(\frac{5}{4}\right)^{3} \cdot 10^{3 j}$. Multiplikation der beiden letzten Ungleichungen liefert $10^{3 j+m}<(n+4)!<2 \cdot \frac{125}{64} \cdot 10^{3 j+m}$, was wegen $\frac{250}{64}<4 \mathrm{zu} 10^{3 j+m}<(n+4)!<4 \cdot 10^{3 j+m}$ abgeschwächt werden kann. Daraus folgt, dass die Zahl $(n+4)$ ! nicht mit 4, sondern mit 1, 2 oder 3 beginnen würde - im Widerspruch zur Voraussetzung.
|
| 54 |
+
Anmerkung: Die meisten Teilnehmer, die sich auf diese oder ähnliche Abschätzungen eingelassen hatten, waren dann auch erfolgreich. Allerdings gab es gerade bei dieser Aufgabe z.T. sehr unübersichtliche Darstellungen.
|
| 55 |
+
|
Germany_TST/md/de-2003-loes_awkl1_03.md
ADDED
|
@@ -0,0 +1,65 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2003
|
| 2 |
+
|
| 3 |
+
Lösungen zur 1. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Beim Schachspiel erhält der Sieger 1 Punkt und der Besiegte 0 Punkte. Bei Unentschieden (Remis) erhält jeder der Spieler $1 / 2$ Punkt.
|
| 8 |
+
Vierzehn Schachspieler, von denen keine zwei gleich alt waren, trugen einen Wettbewerb aus, in dem jeder gegen jeden spielte. Nach Abschluss des Wettbewerbs wurde eine Rangliste erstellt. Von zwei Spielern mit gleicher Punktezahl, erhält der Jüngere eine bessere Platzierung.
|
| 9 |
+
Nach dem Wettbewerb stellte Jan fest, dass die drei Bestplatzierten insgesamt genau so viele Punkte erhielten wie die Gesamtzahl der Punkte der letzten neun Spieler. Jörg bemerkte dazu, dass dabei die Zahl der unentschieden ausgegangenen Spiele maximal war. Man ermittle die Anzahl der unentschiedenen Spiele.
|
| 10 |
+
|
| 11 |
+
## Lösung
|
| 12 |
+
|
| 13 |
+
Die Gesamtzahl der Punkte der letzten neun Spieler beträgt mindestens (9.8):2 = 36 Punkte (denn wenn nur jeder der neun gegen einen anderen der neun spielen würde, dann wären es, da in jeder Partie ein Punkt vergeben wird, insgesamt schon 36 Punkte). Die Gesamtzahl der drei Erstplatzierten ist aber höchstens $13+12+11=36$ Punkte, falls sie alle Spiele gegen die restlichen 13 Spieler gewinnen würden.
|
| 14 |
+
Es folgt also, dass die letzten neun Spieler keines der Spiele mit den anderen gewinnen und die drei ersten, alle, wobei sie untereinander durchaus unentschieden spielen können.
|
| 15 |
+
Die Anzahl der unentschieden gespielten Partien (die ja gemäß Jörg maximal ist!) muss also $3+1+36=40$ sein.
|
| 16 |
+
|
| 17 |
+
## Aufgabe 2
|
| 18 |
+
|
| 19 |
+
Gegeben ist ein Dreieck ABC und ein Punkt M so, dass die Geraden MA, MB, MC die Geraden BC, CA, AB (in dieser Reihenfolge) in D, E beziehungsweise F schneiden.
|
| 20 |
+
Man beweise, dass es dann stets die Zahlen $\varepsilon_{1}, \varepsilon_{2}, \varepsilon_{3}$ aus $\{-1,1\}$ gibt, so dass gilt:
|
| 21 |
+
$\varepsilon_{1} \cdot \frac{M D}{A D}+\varepsilon_{2} \cdot \frac{M E}{B E}+\varepsilon_{3} \cdot \frac{M F}{C F}=1$
|
| 22 |
+
|
| 23 |
+
## Lösung
|
| 24 |
+
|
| 25 |
+
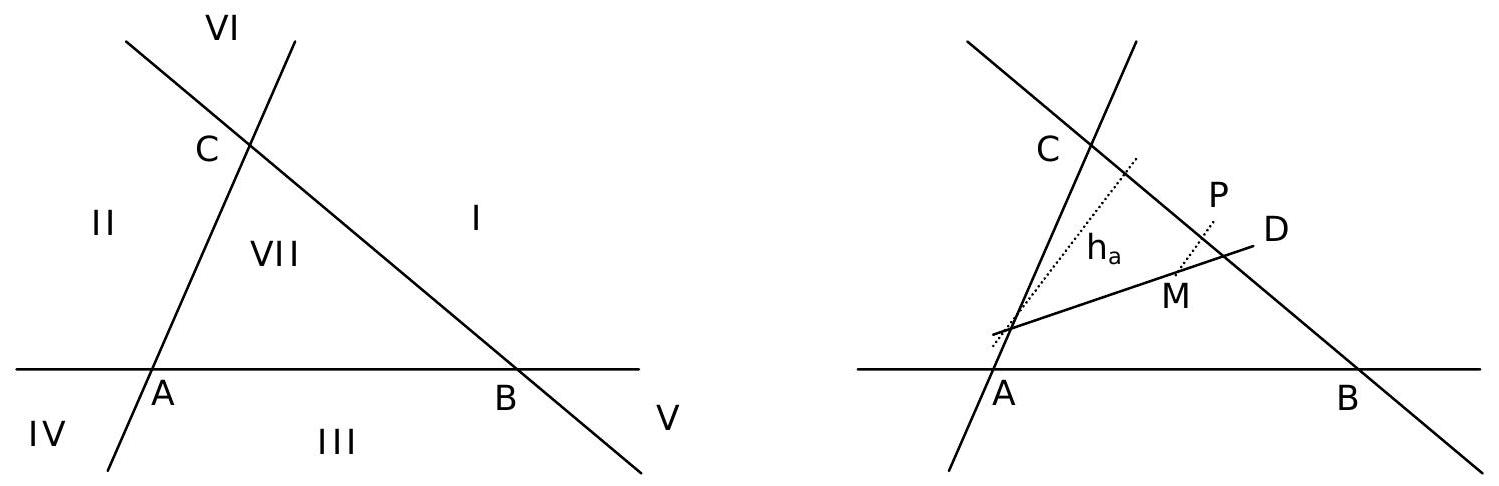
Punkt $M$ ( $M \notin\{A, B, C\})$ kann entweder auf einer der vorgegebenen Geraden, oder in einer der sieben Gebiete liegen, in denen die Ebene des Dreiecks ABC durch die Geraden $A B, B C, C A$ geteilt wird.
|
| 26 |
+
|
| 27 |
+
|
| 28 |
+
Es ist stets
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
\begin{aligned}
|
| 32 |
+
& \frac{M D}{A D}=\frac{M P}{h_{a}}=\frac{0,5 \cdot M P \cdot B C}{0,5 \cdot h_{a} \cdot B C}=\frac{F(M B C)}{F(A B C)}, \\
|
| 33 |
+
& \text { (Strahlensatz) }
|
| 34 |
+
\end{aligned}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
wobei $P \in B C$ und $M P \perp B C$ und $F(X Y Z)$ der Inhalt des Dreiecks XYZ ist. Ähnliches gilt für die anderen Verhältnisse.
|
| 38 |
+
Liegt M im Inneren oder am Rande des Dreiecks $A B C$, dann ist also:
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
\frac{M D}{A D}+\frac{M E}{B E}+\frac{M F}{C F}=\frac{F(M B C)}{F(A B C)}+\frac{F(M C A)}{F(A B C)}+\frac{F(M A B)}{F(A B C)}=1
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
woraus $\varepsilon_{1}=\varepsilon_{2}=\varepsilon_{3}=1$ folgt.
|
| 45 |
+
Ähnliche Überlegungen führen auch dann ans Ziel, wenn M außerhalb des Dreiecks ABC liegt, nur dass $\varepsilon_{1}, \varepsilon_{2}$ bzw. $\varepsilon_{3}=-1$, falls $M$ im Bereich I, II bzw. III liegt. Sollte $M$ in den Bereichen IV, V bzw. VI liegen, dann sind genau zwei der $\varepsilon_{i}$ gleich -1 .
|
| 46 |
+
Etwas eleganter und straffer lässt sich der Beweis führen, falls man orientierte Strecken oder Flächen verwendet.
|
| 47 |
+
|
| 48 |
+
## Aufgabe 3
|
| 49 |
+
|
| 50 |
+
Sei N eine natürliche Zahl und $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ weitere natürliche Zahlen kleiner als N und so, dass das kleinste gemeinsame Vielfache von beliebigen zwei dieser n Zahlen größer als N ist.
|
| 51 |
+
Man beweise, dass die Summe der Kehrwerte dieser n Zahlen stets kleiner 2 ist; also
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<2
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
## Lösung
|
| 58 |
+
|
| 59 |
+
Da das kgV von $\mathrm{x}_{\mathrm{i}}$ und $\mathrm{x}_{\mathrm{j}}$ größer als N ist, gibt es unter den Zahlen $1,2, \ldots, \mathrm{~N}$ keine zwei, die sowohl Vielfache von $\mathrm{x}_{\mathrm{i}}$, als auch von $\mathrm{x}_{\mathrm{j}}$ sind.
|
| 60 |
+
Unter den Vielfachen der natürlichen Zahl $x$ gibt es zwei so, dass $k x \leq N<(k+1) x$, woraus $\mathrm{k} \leq \frac{N}{x}<\mathrm{k}+1$ folgt. Die Anzahl der Vielfachen von x , die kleiner N sind, ist demnach der ganzzahlige Teil von $\frac{N}{X}$, also gleich $\left[\frac{N}{x}\right]$.
|
| 61 |
+
Für die Zahlen $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ gilt folglich $\left[\frac{N}{x_{1}}\right]+\left[\frac{N}{x_{2}}\right]+\cdots+\left[\frac{N}{x_{n}}\right]<N$.
|
| 62 |
+
Andrerseits ist $\left[\frac{N}{x_{i}}\right]>\frac{N}{x_{i}}-1$ und demnach $\frac{N}{x_{1}}+\frac{N}{x_{2}}+\cdots+\frac{N}{x_{n}}-n<N$.
|
| 63 |
+
Da aber $\mathrm{n}<\mathrm{N}$ ist folgt:
|
| 64 |
+
$\frac{N}{x_{1}}+\frac{N}{x_{2}}+\cdots+\frac{N}{x_{n}}<2 N$, was schließlich zu $\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<2$ führt.
|
| 65 |
+
|
Germany_TST/md/de-2003-loes_awkl2_03.md
ADDED
|
@@ -0,0 +1,56 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Auswahlwettbewerb zur IMO 2003
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Man bestimme alle Funktionen $f: \mathbb{R} \rightarrow \mathbb{R}$ mit der Eigenschaft
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
f(f(x)+y)=2 x+f(f(y)-x)
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
für alle $x, y \in \mathbb{R}$.
|
| 14 |
+
|
| 15 |
+
## Lösung
|
| 16 |
+
|
| 17 |
+
Für eine beliebige reelle Zahl $z$ setzen wir $a=f(z), b=z+f(0), n=f\left(\frac{a+b}{2}\right)$ und $m=f(0)-\frac{a+b}{2}$. Wegen $\mathbb{D}_{f}=\mathbb{R}$ sind $a, b, n$ und $m$ wohlbestimmt. Einsetzen von $x=0$, $y=z$ in $(*)$ liefert $f(z+f(0))=f(f(z))$, also $f(a)=f(b)$ (I).
|
| 18 |
+
Einsetzen von $x=m$ und $y=a$ bzw. $y=b$ in $\left(^{*}\right)$ liefert $\left\{\begin{array}{l}f(f(m)+a)=2 m+f(f(a)-m) \\ f(f(m)+b)=2 m+f(f(b)-m)\end{array}\right.$, was wir wegen (I) zu $f(f(m)+a)=f(f(m)+b$ ) (II) zusammenfassen können.
|
| 19 |
+
Einsetzen von $x=a$ bzw. $x=b$ und $y=n$ in $\left(^{*}\right.$ )liefert $\left\{\begin{array}{l}f(f(a)+n)=2 a+f(f(n)-a) \\ f(f(b)+n)=2 b+f(f(n)-b)\end{array}\right.$, was wir wegen (I) zu $2 a+f(f(n)-a)=2 b+f(f(n)-b$ ) (III) zusammenfassen können. Einsetzen von $x=\frac{a+b}{2}, y=0$ in (*) liefert $f\left(f\left(\frac{a+b}{2}\right)\right)=a+b+f\left(f(0)-\frac{a+b}{2}\right)$, also $f(n)=a+b+f(m)$ oder, anders formuliert, $f(n)-a=f(m)+b$ bzw. $f(n)-b=f(m)+a$. Dies liefert mit (III) sofort $2 a+f(f(m)+b))=2 b+f(f(m)+a)$, woraus mit (II) nun $a=b$ folgt, also $f(z)=z+f(0)$. Damit ist gezeigt, dass jede Funktion $f$, die (*) erfüllt, die Form $f(x)=x+c \quad(c=$ konst. ) haben muss. Einsetzen in (*) bestätigt, dass jedes $f$ dieser Form die gegebene Gleichung tatsächlich erfüllt: $f(f(x)+y)=x+y+2 c=2 x+f(f(y)-x)$.
|
| 20 |
+
Anmerkung: Zusätzliche Eigenschaften von $f$, wie etwa Injektivität, Monotonie oder Differenzierbarkeit, dürfen nicht vorausgesetzt, sondern müssen bewiesen werden.
|
| 21 |
+
|
| 22 |
+
## Aufgabe 2
|
| 23 |
+
|
| 24 |
+
Es sei $B$ ein beliebiger Punkt auf einem Kreis $k_{1}$ und es sei $A$ ein von $B$ verschiedener Punkt auf der Tangente an $k_{1}$ in $B$. Ferner sei $C$ ein Punkt außerhalb von $k_{1}$ mit der Eigenschaft, dass die Strecke $A C$ den Kreis $k_{1}$ in zwei verschiedenen Punkten schneidet. Schließlich sei $k_{2}$ der Kreis, der die Gerade ( $A C$ ) in $C$ berührt und den Kreis $k_{1}$ in einem Punkt $D$ berührt, welcher auf der anderen Seite von ( $A C$ ) liegt wie $B$.
|
| 25 |
+
Man beweise, dass der Umkreismittelpunkt des Dreiecks BCD auf dem Umkreis des Dreiecks $A B C$ liegt.
|
| 26 |
+
|
| 27 |
+
## Lösung
|
| 28 |
+
|
| 29 |
+
Wir bezeichnen die Mittelpunkte der Kreise $k_{1}$ und $k_{2}$ mit $O_{1}$ bzw. $O_{2}$. Die Lösung setzt nun voraus, dass $\angle C D B$ stumpf ist (siehe Fig.); andernfalls sind lediglich einige Winkel modulo $180^{\circ}$ zu vertauschen.
|
| 30 |
+
Es sei $P$ der Umkreismittelpunkt des Dreiecks BDC; dann ist nach dem Satz vom Mittelpunktswinkel
|
| 31 |
+
$\angle B P C=2 \cdot\left(180^{\circ}-\angle C D B\right)=360^{\circ}-2 \cdot \angle C D B$ (1).
|
| 32 |
+
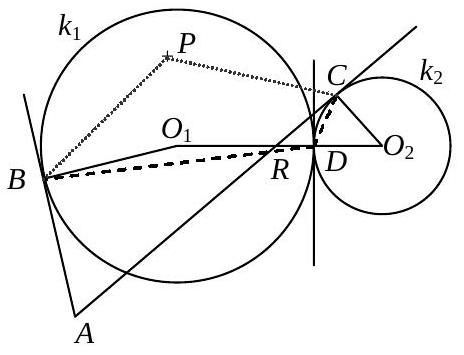
|
| 33 |
+
$P$ liegt dann auf dem Umkreis von Dreieck $A B C$, wenn $A C P B$ ein Sehnenviereck ist; dies gilt dann, wenn $\angle B P C=180^{\circ}-\angle C A B$ ist.
|
| 34 |
+
|
| 35 |
+
Um dies zu beweisen, berechnen wir $\angle C D B$. Da $k_{1}$ und $k_{2}$ sich in $D$ berühren, liegt $D$ auf der Strecke $O_{1} O_{2}$ und es gilt $\angle C D B=180^{\circ}+\angle O_{1} D B-\angle O_{2} D C$ (2). Da $k_{1}$ die Gerade ( $A B$ ) berührt, ist $\angle A B O_{1}=90^{\circ}$, also $\angle A B D+\angle D B O_{1}=90^{\circ}$. Da $B$ und $D$ auf $k_{1}$ liegen, ist das Dreieck $B D O_{1}$ gleichschenklig mit $\angle O_{1} D B=\angle D B O_{1}$. Somit ist $\angle O_{1} D B=90^{\circ}-\angle A B D$ (3). Da $k_{2}$ die Gerade ( $A C$ ) berührt, ist $\angle A C O_{2}=90^{\circ}$, also $\angle A C D+\angle D C O_{2}=90^{\circ}$. Da $C$ und $D$ auf $k_{2}$ liegen, ist das Dreieck $\mathrm{CDO}_{2}$ gleichschenklig mit $\angle \mathrm{O}_{2} D C=\angle D C O_{2}$. Somit ist $\angle O_{2} D C=90^{\circ}-\angle A C D$ (4). Einsetzen von (3) und (4) in (2) liefert $\angle C D B=180^{\circ}+\left(90^{\circ}-\angle A B D\right)-\left(90^{\circ}-\angle A C D\right)=180^{\circ}-\angle A B D+\angle A C D$ (5).
|
| 36 |
+
Nun betrachten wir den Schnittpunkt $R$ von $(A C)$ und ( $B D$ ) und folgern
|
| 37 |
+
$\angle A B D=\angle A B R=180^{\circ}-\angle R A B-\angle B R A=180^{\circ}-\angle C A B-\angle B R A$ sowie
|
| 38 |
+
$\angle A C D=\angle R C D=180^{\circ}-\angle C D R-\angle D R C=180^{\circ}-\angle C D B-\angle B R A$. Aus (5) ergibt sich
|
| 39 |
+
$\angle C D B=180^{\circ}+\angle C A B-\angle C D B$, also $2 \cdot \angle C D B=180^{\circ}+\angle C A B$. Einsetzen in (1) liefert $\angle B P C=360^{\circ}-\left(180^{\circ}+\angle C A B\right)=180^{\circ}-\angle C A B$. Damit ist alles gezeigt.
|
| 40 |
+
Anmerkung: Da $k_{1}$ von der Strecke $A C$ geschnitten wird, kann $k_{2}$ die Gerade ( $\left.A C\right)$ nicht - von $A$ aus vor dem Schnitt mit $k_{1}$ berühren. Auch darf $C$ nicht speziell gewählt werden.
|
| 41 |
+
|
| 42 |
+
## Aufgabe 3
|
| 43 |
+
|
| 44 |
+
Es sei $n$ eine ungerade natürliche Zahl. Die Felder eines $n \times n$-Schachbretts seien abwechselnd schwarz und weiß gefärbt, wobei die Eckfelder schwarz sind. Ferner sei ein Trimino definiert als eine L-förmige Figur aus drei verbundenen Einheitsquadraten.
|
| 45 |
+
a) Für welche Werte von $n$ ist es möglich, alle schwarzen Felder des Schachbretts durch nicht überlappende Triminos zu überdecken?
|
| 46 |
+
b) Welches ist bei möglicher Überdeckung die minimale Anzahl der jeweils benötigten Triminos?
|
| 47 |
+
Hinweis: Zwei Triminos überlappen sich, wenn sie wenigstens ein Einheitsquadrat gemeinsam bedecken.
|
| 48 |
+
|
| 49 |
+
## Lösung
|
| 50 |
+
|
| 51 |
+
a) und b): Wir zählen die Reihen des Schachbretts von oben. Das $n \times n$-Schachbrett hat $\frac{n+1}{2}$ Reihen mit ungerader Nummer und in jeder dieser Reihen $\frac{n+1}{2}$ schwarze Felder. Jedes dieser $\left(\frac{n+1}{2}\right)^{2}$ schwarzen Quadrate muss von einem anderen Trimino überdeckt werden, daher sind wenigstens $\left(\frac{n+1}{2}\right)^{2}$ Triminos erforderlich. Da jedes aus 3 Quadraten besteht, muss wegen des Überlappungsverbots gelten: $3\left(\frac{n+1}{2}\right)^{2} \leq n^{2}$. Für 1,3 und 5 folgt $3 \leq 1$, $12 \leq 9,27 \leq 25$. Also ist für $n<7$ eine verlangte Überdeckung nicht möglich.
|
| 52 |
+
Die Figur zeigt als Verankerung eine Überdeckung für $n=7$ mit $\left(\frac{n+1}{2}\right)^{2}=16$ Triminos und den Schritt $n \rightarrow n+2$, mit dem für jedes $n \geq 7$ die Existenz einer Überdeckung bewiesen ist. Bei diesem Schritt wird dem $n \times n$-Schachbrett, dessen Überdeckung mit $\left(\frac{n+1}{2}\right)^{2}$ Steinen vorausgesetzt ist, in der rechten unteren Ecke ein „L" angesetzt, das 5 Felder breit und hoch ist, und anschließend durch $2 \times 2$-Felder mit je einem passenden Trimino ergänzt. Das „L" enthält 5 Triminos und die beiden $2 \times(n-5)$-Rechtecke zusammen $n-3$ Triminos. Es
|
| 53 |
+
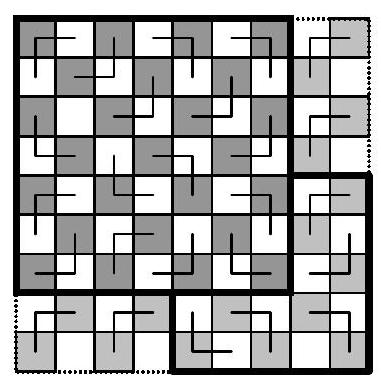
|
| 54 |
+
ergeben sich also $\left(\frac{n+1}{2}\right)^{2}+n-3+5=\frac{n^{2}+6 n+9}{4}=\left(\frac{n+3}{2}\right)^{2}$ Triminos, die Mindestzahl für das $(n+2) \times(n+2)-$ Schachbrett. Mit vollständiger Induktion folgt die Behauptung.
|
| 55 |
+
Anmerkung: Nur alle schwarzen Felder sollten überdeckt werden; es können also weiße Felder frei bleiben. Selbstverständlich ragen die Triminos nicht über das Schachbrett hinaus. Zu einer vollständigen Lösung gehört auch der Nachweis, dass beim Schritt $n \rightarrow n+2$ die hinzugefügten Triminos mit der minimalen Anzahl verträglich sind, sowie die Erwähnung von $n=1$.
|
| 56 |
+
|
Germany_TST/md/de-2004-loes_awkl1_04.md
ADDED
|
@@ -0,0 +1,87 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Auswahlwettbewerb zur IMO 2004
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 1. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Eine Funktion $f$ ist gegeben durch $f(x)+f\left(1-\frac{1}{x}\right)=1+x$ für $x \in \mathbb{R} \backslash\{0,1\}$.
|
| 8 |
+
Man ermittle eine Formel für $f$.
|
| 9 |
+
|
| 10 |
+
## Lösung
|
| 11 |
+
|
| 12 |
+
Sei $x \in \mathbb{R} \backslash\{0,1\}$ und $y=1-\frac{1}{x}$ und $z=\frac{1}{1-x}$. Es ist leicht einzusehen, dass zusammen mit $x$ auch $y$ und damit auch $z$ zu $\mathbb{R} \backslash\{0,1\}$ gehören. Einsetzen von $y$ und $z$ in die Ausgangsgleichung führt zu:
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
f\left(1-\frac{1}{x}\right)+f\left(\frac{1}{1-x}\right)=2-\frac{1}{x} \text { und } f\left(\frac{1}{1-x}\right)+f(x)=1+\frac{1}{1-x}
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
Durch Subtraktion der beiden letzten Beziehungen erhält man:
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
f(x)-f\left(1-\frac{1}{x}\right)=\frac{1}{1-x}+\frac{1}{x}-1
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
und nach Addition zur Ausgangsgleichung führt das schließlich zu
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
f(x)=\frac{1}{2}\left(\frac{1}{1-x}+\frac{1}{x}+x\right)=\frac{-x^{3}+x^{2}+1}{2 x(1-x)}
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
## Aufgabe 2
|
| 31 |
+
|
| 32 |
+
Im Dreieck $A B C$ ist $A D(D \in B C)$ eine Seitenhalbierende, $E$ ein Punkt auf $A C$ und $F$ der Schnittpunkt von $B E$ mit $A D$.
|
| 33 |
+
|
| 34 |
+
Man beweise: Falls $\frac{B F}{F E}=\frac{B C}{A B}+1$, dann ist $B E$ eine Winkelhalbierende.
|
| 35 |
+
|
| 36 |
+
## Lösung
|
| 37 |
+
|
| 38 |
+
Seien $B^{\prime}, C^{\prime}, E^{\prime}$ die Projektionen von $B, C$ und $E$ auf die Gerade $A D$. Die rechtwinkligen Dreiecke $\triangle D B B^{\prime}$ und $\triangle D C C^{\prime}$ sind kongruent, da $D$ der Mittelpunkt von $B C$ ist und die spitzen Winkel bei $D$ gleich groß sind. Daraus folgt, dass $B B^{\prime}=C C^{\prime}$.
|
| 39 |
+
Im Dreieck $\triangle A C^{\prime} C$ ist $E E^{\prime}$ parallel zu $C C^{\prime}$ und folglich
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\frac{A C}{A E}=\frac{C C^{\prime}}{E E^{\prime}}=\frac{B B^{\prime}}{E E^{\prime}} .
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Die rechtwinkligen Dreiecke $\triangle B B^{\prime} F$ und $\triangle E E^{\prime} F$ sind ähnlich, da die Winkel bei $F$ gleich sind. Daraus folgt $\frac{B B^{\prime}}{E E^{\prime}}=\frac{B F}{F E}$, was zusammen mit der vorletzten Beziehung zu $\frac{A C}{A E}=\frac{B F}{E F}$ führt.
|
| 46 |
+
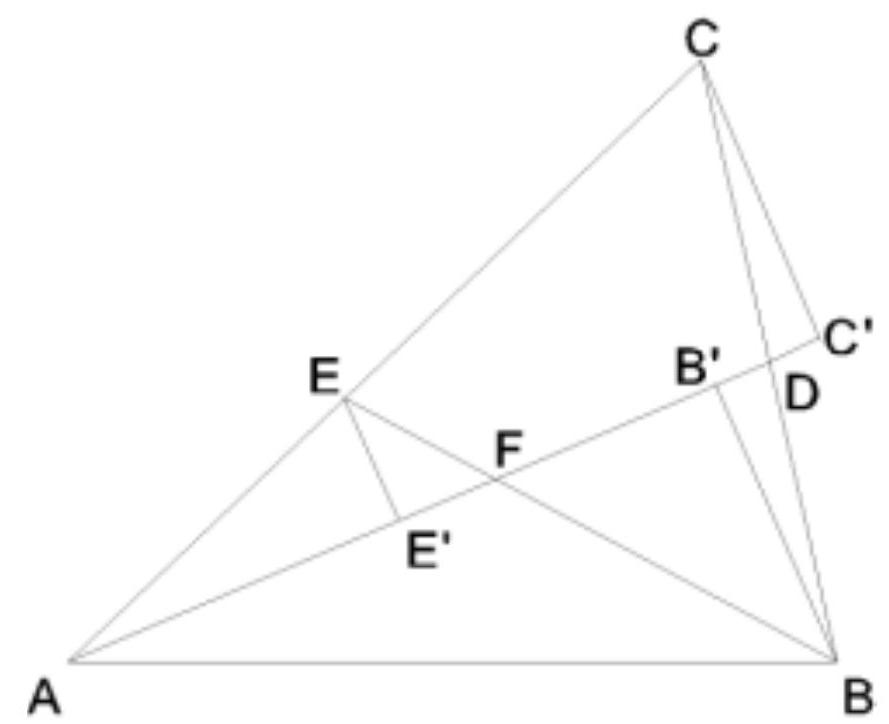
|
| 47 |
+
|
| 48 |
+
Ersetzt man nun $\frac{B F}{E F}$ in der Ausgangsbeziehung durch $\frac{A C}{A E}$, ergibt sich:
|
| 49 |
+
$\frac{B C}{A B}+1=\frac{A C}{A E}=\frac{B C+A B}{A B}$, was zu $\frac{A C-A E}{A E}=\frac{B C}{A B}$ und schließlich zu $\frac{E C}{A E}=\frac{B C}{A B}$ führt.
|
| 50 |
+
Gemäß der Umkehrung des Satzes der Winkelhalbierenden ist $B E=w_{\beta}$.
|
| 51 |
+
|
| 52 |
+
## Aufgabe 3
|
| 53 |
+
|
| 54 |
+
Gegeben sind die sechs reellen Zahlen $a, b, c$ und $x, y, z$ so, dass
|
| 55 |
+
a) $0<b-c<a<b+c$
|
| 56 |
+
b) $a x+b y+c z=0$
|
| 57 |
+
|
| 58 |
+
Man ermittle (mit Begründung!) das Vorzeichen von $a y z+b x z+c x y$.
|
| 59 |
+
|
| 60 |
+
## Lösung
|
| 61 |
+
|
| 62 |
+
Aus $0<b-c<a<b+c$ folgt, dass $a, b$ und $c$ positiv sind. Außerdem kann man mit Strecken dieser Längen ein Dreieck konstruieren. Daraus folgt, dass die Zahlen $-a+b+c, \quad a-b+c$ und $a+b-c$ positiv sind.
|
| 63 |
+
Aus $a x+b y+c z=0$ folgt $x=-\frac{b y+c z}{a}$.
|
| 64 |
+
Es ergibt sich
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
a y z+b z x+c x y=a y z-\frac{1}{a}(b y+c z)(b z+c y)=-\frac{1}{a}\left(b^{2} y z+b c y^{2}+c b z^{2}+c^{2} y z-a^{2} y z\right)
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Es reicht zu zeigen, dass der Term in der letzten Klammer nicht negativ ist.
|
| 71 |
+
Eine einfache Umformung ergibt
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
b^{2} y z+b c y^{2}+c b z^{2}+c^{2} y z-a^{2} y z=b c y^{2}+b c z^{2}+\left(b^{2}+c^{2}-a^{2}\right) y z
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
Da $a$ und $c$ positiv sind, kann man den Term mit $4 b c$ multiplizieren, ohne dass sich das Vorzeichen ändert. Es ist also das Vorzeichen von $4 b^{2} c^{2} y^{2}+4 b^{2} c^{2} z^{2}+4 b c\left(b^{2}+c^{2}-a^{2}\right) y z$ zu untersuchen. Durch Addition und Subtraktion von $\left(b^{2}+c^{2}-a^{2}\right)^{2} z^{2}$ ergibt sich der Reihe nach:
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
\begin{aligned}
|
| 81 |
+
& 4 b^{2} c^{2} y^{2}+4 b c y z\left(b^{2}+c^{2}-a^{2}\right)+\left(b^{2}+c^{2}-a^{2}\right) z^{2}+\left[4 b^{2} c^{2}-\left(b^{2}+c^{2}-a^{2}\right)^{2}\right] z^{2}= \\
|
| 82 |
+
& =\left[2 b c y+\left(b^{2}+c^{2}-a^{2}\right) z\right]^{2}+\left[4 b^{2} c^{2}-\left(b^{2}+c^{2}-a^{2}\right)^{2}\right] z^{2}
|
| 83 |
+
\end{aligned}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
Das Vorzeichen des letzten Terms ist nicht negativ, da der erste Teil ein Quadrat ist und im zweiten Teil $4 b^{2} c^{2}-\left(b^{2}+c^{2}-a^{2}\right)^{2}=(a+b+c)(-a+b+c)(a-b+c)(a+b-c)$ positiv ist. Die Zahl $a y z+b z x+c x y$ ist folglich nicht positiv.
|
| 87 |
+
|
Germany_TST/md/de-2004-loes_awkl2_04.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2004
|
| 2 |
+
|
| 3 |
+
Lösungen zur 2. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
In der Ebene liegen n abgeschlossene Kreisscheiben $\mathrm{K}_{1}, \mathrm{~K}_{2}, \ldots ; \mathrm{K}_{\mathrm{n}}$ mit gleichem Radius r . Jeder Punkt der Ebene ist dabei in höchstens 2003 dieser Kreisscheiben enthalten. Man beweise, dass jede Kreisscheibe $K_{\mathrm{i}}$ höchstens 14020 andere Kreisscheiben schneidet.
|
| 8 |
+
|
| 9 |
+
## Lösung
|
| 10 |
+
|
| 11 |
+
Wir führen einen Beweis durch Widerspruch. Dazu nehmen wir zusätzlich zur Voraussetzung an, dass eine Kreisscheibe (oBdA sei dies $K_{1}$ ) mindestens 14021 andere Kreisscheiben schneidet. Die Mittelpunkte dieser Scheiben liegen dann offensichtlich alle in einer Kreisscheibe mit Radius $2 r$ um den Mittelpunkt $M_{1}$ von $K_{1}$. Lägen 2003 oder mehr der Mittelpunkte dieser anderen Kreisscheiben in oder auf dem Rand von $K_{1}$, so würden diese Scheiben alle $M_{1}$ enthalten. Damit würde $M_{1}$ in mehr als 2003 Kreisscheiben enthalten sein, da $M_{1}$ auch in $K_{1}$ enthalten ist. Also müssen mindestens 14021 - 2002 $=12019$ Mittelpunkte der anderen Kreisscheiben in einem Kreisring mit innerem Radius r und äußerem Radius $2 r$ um $M_{1}$ liegen. Teilen wir diesen Ring in 6 gleich große Sektoren mit Innenwinkel $60^{\circ}$, so liegen nach dem Schubfachprinzip in mindestens einem Sektor wenigstens 2004 dieser Mittelpunkte.
|
| 12 |
+
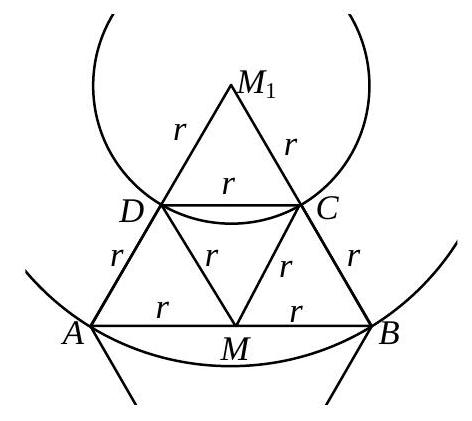
In der Zeichnung ist dieser Sektor mit dem Mittelpunkt $M$ der Strecke $A B$ dargestellt. Aus $\left|A M_{1}\right|=\left|B M_{1}\right|=2 r$ und $\angle A M_{1} B=$ $60^{\circ}$ folgt, dass $\triangle A B M_{1}$ gleichseitig ist. Also sind $M D$ und MC seine Mittelparallelen und es folgt
|
| 13 |
+
$|M A|=|M B|=|M C|=|M D|=r$. Daher liegt der Sektor vollständig in einem Kreis um M mit Radius r. Jede der wenigstens 2004 Kreisscheiben mit Mittelpunkten in diesem Sektor enthält also den Punkt M. Damit ist M aber in
|
| 14 |
+
|
| 15 |
+
wenigstens 2004 Kreisscheiben enthalten - ein Widerspruch zur Annahme.
|
| 16 |
+
|
| 17 |
+
## Aufgabe 2
|
| 18 |
+
|
| 19 |
+
Gegeben seien jeweils n reelle Zahlen $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ bzw. $\mathrm{y}_{1}, \mathrm{y}_{2}, \ldots, \mathrm{y}_{\mathrm{n}}$. Die Elemente einer $\mathrm{n} \times \mathrm{n}$-Matrix A seien folgendermaßen definiert: ( $1 \leq \mathrm{i}, \mathrm{j} \leq \mathrm{n}$ )
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
a_{i j}= \begin{cases}1 & \text { wenn } x_{i}+y_{j} \geq 0 \\ 0 & \text { wenn } x_{i}+y_{j}<0\end{cases}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Weiter sei B eine $\mathrm{n} \times \mathrm{n}$-Matrix mit Elementen 0 oder 1, so dass die Summe der Elemente in jeder Zeile und jeder Spalte von B gleich der Summe der Elemente in der entsprechenden Zeile bzw. Spalte von A ist.
|
| 26 |
+
Man beweise, dass dann $\mathrm{A}=\mathrm{B}$ gilt.
|
| 27 |
+
|
| 28 |
+
## Lösung
|
| 29 |
+
|
| 30 |
+
Wir nehmen an, dass es eine Matrix $B$ der geforderten Art gebe mit $B \neq A$. Nun betrachten wir in A nur noch diejenigen Elemente $a_{i j}$, die sich von den entsprechenden Elementen $b_{i j}$ unterscheiden. Es muss mindestens ein solches Element geben. Alle anderen Elemente von A werden gestrichen. Dann ist innerhalb jeder Zeile bzw. Spalte die Anzahl der verbleibenden Nullen gleich der Anzahl der verbleibenden Einsen, da diese
|
| 31 |
+
|
| 32 |
+
Anzahlen in B bei gleicher Zeilen- bzw. Spaltensumme gerade vertauscht sind. Also tritt jede Zahl $x_{i}$ in der verbleibenden Anordnung genauso oft als Summand einer Summe $x_{i}+y_{j}<0$ auf wie als Summand einer Summe $x_{i}+y_{j} \geq 0$. Das Gleiche gilt für jede Zahl $y_{j}$.
|
| 33 |
+
Nun addieren wir alle Summen $x_{i}+y_{j}<0$ mit $a_{i j} \neq b_{i j}$. Die Summe dieser Summen ist zwangsläufig $<0$. Ebenso addieren wir alle Summen $x_{i}+y_{j} \geq 0$ mit $a_{i j} \neq b_{i j}$. Die Summe dieser Summen ist zwangsläufig $\geq 0$. Da aber jede der Zahlen $x_{i}$ und $y_{j}$ gleich häufig in beiden Summen auftritt, müssen diese Summen den gleichen Wert haben Widerspruch! Daher kann es keine verschiedenen Elemente in A und B geben und es gilt $A=B$.
|
| 34 |
+
|
| 35 |
+
## Aufgabe 3
|
| 36 |
+
|
| 37 |
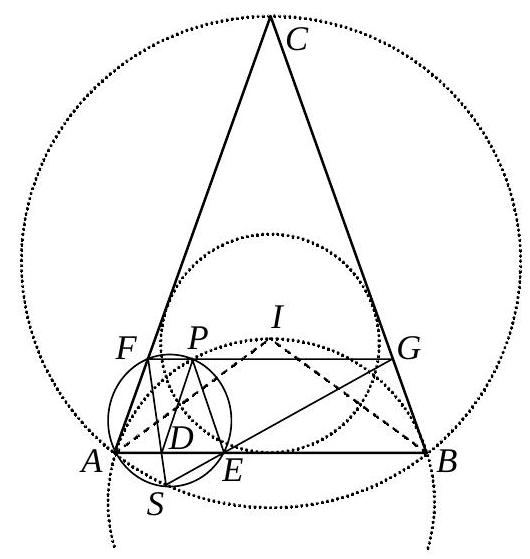
+
Es sei $A B C$ ein gleichschenkliges Dreieck mit $\overline{A C}=\overline{B C}$ und Inkreismittelpunkt I. Ferner sei $P$ ein Punkt im Inneren von ABC auf dem Umkreis des Dreiecks BIA. Die Parallelen zu $C A$ und $C B$ durch $P$ schneiden $A B$ in $D$ bzw. E. Die Parallele zu AB durch P schneidet CA und $C B$ in $F$ bzw. G.
|
| 38 |
+
Man zeige, dass sich die Geraden DF und EG auf dem Umkreis des Dreiecks ABC schneiden.
|
| 39 |
+
|
| 40 |
+
Lösung: Wegen $\angle F P E=\angle F G B=180^{\circ}-\angle C B A=180^{\circ}-\angle B A C=180^{\circ}-\angle F A E$ (Parallelität und Gleichschenkligkeit) ist FAEP ein Sehnenviereck. Analog erweist sich GPDB als Sehnenviereck. Ihre beiden Umkreise schneiden sich in P und einem weiteren Punkt, den wir mit S bezeichnen. Nun folgt weiter $\angle E S P=\angle E A P=\angle B A P=180^{\circ}-\angle A P B-\angle P B A$ $=180^{\circ}-\angle A I B-\angle P B A=\angle B A I+\angle I B A-\angle P B A=2 \cdot \frac{1}{2} \angle C B A-\angle P B A=\angle C B P=\angle G B P$ $=\angle G S P$ (Umfangswinkel und Symmetrie). Also liegt S auf der Geraden EG; entsprechend sind S, D und F kollinear. Deshalb ist S der Schnittpunkt von DF und EG. Es bleibt zu beweisen, dass dieser Punkt auf dem Umkreis von ABC liegt.
|
| 41 |
+
In der Tat gilt
|
| 42 |
+
$\angle B S A=\angle P S A+\angle B S P=180^{\circ}-\angle A F P+180^{\circ}-\angle P G B=$ $\angle G F C+\angle C G F=180^{\circ}-\angle F C G=180^{\circ}-\angle A C B$. Somit ist ASBC ein Sehnenviereck, was zu beweisen war.
|
| 43 |
+
|
| 44 |
+
|
Germany_TST/md/de-2005-loes_awkl1_05.md
ADDED
|
@@ -0,0 +1,52 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2005
|
| 2 |
+
|
| 3 |
+
Lösungen zur 1. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Gegeben sind die positiven reellen Zahle $a$ und $b$ und die natürliche Zahl $n$.
|
| 8 |
+
Man ermittle in Abhängigkeit von $a, b$ und $n$ das größte der $n+1$ Glieder in der Entwicklung von $(a+b)^{n}$.
|
| 9 |
+
|
| 10 |
+
## Lösung
|
| 11 |
+
|
| 12 |
+
Das $k$-te Glied $\mathrm{G}(\mathrm{k})$ in der Entwicklung von $(\mathrm{a}+\mathrm{b})^{\mathrm{n}}$ ist gegeben durch die Formel: $G(k)=\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1}$, wobei $\binom{n}{0}=1$ und $1 \leq \mathrm{k} \leq \mathrm{n}+1$.
|
| 13 |
+
Da es endlich viele Glieder gibt und jede endliche Zahlenmenge (mindestens) ein maximales Element enthält, wird untersucht unter welchen Bedingungen das k-te Element maximal ist. Dafür müssen die folgenden Beziehungen gleichzeitig erfüllt sein: $\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1} \geq\binom{ n}{k} \cdot a^{n-k} \cdot b^{k}$ und $\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1} \geq\binom{ n}{k-2} \cdot a^{n-k+2} \cdot b^{k-2}$, wobei im letzten Fall $k \geq 2$ sein muss und eine dieser Ungleichungen streng ist (einfacher Nachweis!).
|
| 14 |
+
Das führt einerseits $\mathrm{zu} \frac{1}{n-k+1} \cdot a \geq \frac{1}{k} \cdot b$ und andererseits $\mathrm{zu} \frac{1}{k-1} \cdot b \geq \frac{1}{n-k+2} \cdot a$, woraus sowohl $\mathrm{n}+1 \geq \mathrm{k} \geq \frac{n b+b}{a+b}$, als auch $1 \leq \mathrm{k} \leq \frac{n b+2 b+a}{a+b}=\frac{n b+b}{a+b}+1$ folgt.
|
| 15 |
+
Falls $\mathrm{i}=\frac{n b+b}{a+b}$ nicht ganzzahlig ist, ist $\mathrm{G}(\mathrm{i})$ das größte Glied, andernfalls sind $\mathrm{G}(\mathrm{i})$ und $\mathrm{G}(\mathrm{i}+1)$ maximal.
|
| 16 |
+
Weitere maximale Glieder kann es nicht geben.
|
| 17 |
+
|
| 18 |
+
## Aufgabe 2
|
| 19 |
+
|
| 20 |
+
Sei $E=\{-1,0,1\}$ und $M$ eine Menge von Gitterpunkten der Ebene. Die Punkte aus $M$ sind so durch ein Streckennetz (S) miteinander verbunden, dass man von jedem Punkt aus M zu jedem anderen Punkt aus M gelangen kann ohne ( S ) zu verlassen. Dabei können die Strecken des Streckennetzes außer den Gitterpunkten auch andere Endpunkte enthalten.
|
| 21 |
+
Man ermittle die kürzeste Gesamtlänge des Streckennetzes, falls:
|
| 22 |
+
a) $M=\{(i, j) \mid i, j \in E$ und $i \cdot j=0\}$
|
| 23 |
+
b) $M=\{(i, j) \mid i, j \in E\}$
|
| 24 |
+
|
| 25 |
+
## Lösung
|
| 26 |
+
|
| 27 |
+
Teil a): Aus Symmetriegründen reicht es zunächst das günstigste Streckennetz für die Punkte $O(0,0)$, $A(1,0)$ und $C(0,1)$ zu finden. Durch Spiegelung an O erhält man dann das gewünschte Netz für die Punkte aus M. Durch eine Drehung der Ebene $x O y$ um O mit Drehwinkel $60^{\circ}$ (Fig. 1) wird das Dreieck $\triangle O A C$ in das Dreieck $\triangle O A^{\prime} C^{\prime}$ überführt, wobei die Strecke P'C' das Bild von PC ist. Das kürzeste Streckensystem, das die Punkte O, A und $C$ wie gefordert verbindet, hat also eine Gesamtlänge, die gleich jener der Strecke $A C^{\prime}$ ist.
|
| 28 |
+
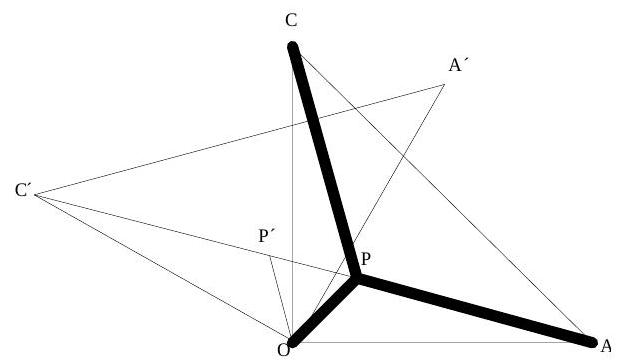
|
| 29 |
+
|
| 30 |
+
Fig. 1
|
| 31 |
+
|
| 32 |
+
Im Dreieck $\triangle \mathrm{OAC}^{\prime}$ ist aber $\mathrm{AC}^{\prime}=\sqrt{2-2 \cos 150^{\circ}}=\sqrt{2+\sqrt{3}}$ (Kosinussatz). Durch Spiegelung am Ursprung O erhält man ein für Teil a) kürzestes Streckensystem mit einer Gesamtlänge von $2 \sqrt{2+\sqrt{3}}=\sqrt{2}+\sqrt{6}$.
|
| 33 |
+
|
| 34 |
+
Teil b): Ebenfalls aus Symmetriegründen reicht es zunächst das kürzeste Streckensystem für die Punkte $D(-1 \mid 1), O(0 \mid 0), A(1 \mid 0), B(1 \mid 1)$ und $C(0 \mid 1)$ zu finden. Da die Entfernung von D zu den restlichen vier Punkten mindestens 1 beträgt, hat ein solches System eine Gesamtlänge von $1+\frac{\sqrt{2}+\sqrt{6}}{\sqrt{2}}=1+1+\sqrt{3}=2+\sqrt{3}$ (siehe Fig. 2).
|
| 35 |
+
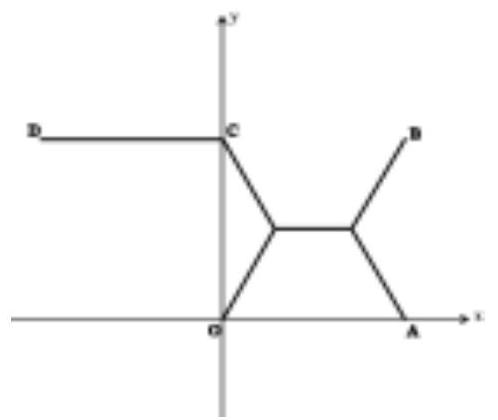
|
| 36 |
+
|
| 37 |
+
Fig. 2
|
| 38 |
+
|
| 39 |
+
Damit ergibt
|
| 40 |
+
(nach Spiegelung an 0 ) für b) eine Gesamtlänge von $2(2+\sqrt{3})=4+2 \sqrt{3}$.
|
| 41 |
+
Bemerkung: Der Punkt $P$ aus Teil a) ist der Fermat-Punkt des Dreiecks $\triangle \mathrm{OAC}$; die Summe seiner Abstände zu den Eckpunkten O, A und C ist minimal. Jedes Dreieck, in dem kein Winkel größer-gleich $120^{\circ}$ ist, enthält im Inneren einen solchen Punkt. Ist aber z.B. in einem Dreieck $\triangle A B C \alpha \geq 120^{\circ}$, dann ist dort $A B+A C$ minimal. Diese Eigenschaften wurden wohl zum ersten Mal von Evangelista Torricelli (1608 - 1647) entdeckt und von Pierre Fermat (1601 - 1665) weiter untersucht.
|
| 42 |
+
|
| 43 |
+
## Aufgabe 3
|
| 44 |
+
|
| 45 |
+
Man beweise: Ist $4^{n} \cdot 7=a^{2}+b^{2}+c^{2}+d^{2}$ mit $n, a, b, c, d \in N \backslash\{0\}$, dann kann keine der Quadratzahlen die Zahl $4^{\mathrm{n}-1}$ unterschreiten.
|
| 46 |
+
|
| 47 |
+
## Lösung
|
| 48 |
+
|
| 49 |
+
Ist $n=1$, dann ist die Behauptung richtig; die einzigen Lösungen für $a, b, c, d$ sind, abgesehen von der Reihenfolge, die Quadrupel $(1,1,1,5)$, $(1,3,3,3)$ und $(2,2,2,4)$. Für jedes $n \geq 1$ ist $4^{n} .7$ durch 4 teilbar. Da das Quadrat einer natürlichen Zahl bei der Division durch 4 nur die Reste 0 oder 1 haben kann, kommen für $a, b, c, d$ nur Zahlen gleicher Restklasse modulo 4 in Frage.
|
| 50 |
+
Sind a, b, c, d (alle) ungerade, dann ist die rechte Seite zwar durch 4, nicht aber durch 8 und erst recht nicht durch 16 teilbar. In diesem Fall kommt also nur $\mathrm{n}=1$ in Frage. Sollte $n>1$ sein, dann müssen die vier Zahlen auf der rechten Seite demnach alle gerade sein.
|
| 51 |
+
Vorausgesetzt die Eigenschaft, dass alle Quadratzahlen $4^{n-1}$ überschreiten, gilt nicht für alle $n$, dann gibt es ein kleinstes $k(k \in N)$ für das sie nicht gilt. Da sie für $n=1$ gilt, muss $k$ größer 1 sein. Dann sind aber (siehe oben) a, b, c, d alle gerade. Man könnte also beide Seiten durch 4 teilen und die Eigenschaft dürfte auch für k-1 nicht gelten, was aber wegen der Minimalität von $k$ nicht sein kann. Die Behauptung stimmt also für alle natürlichen Zahlen $\mathrm{n}, \mathrm{n} \geq 1$.
|
| 52 |
+
|
Germany_TST/md/de-2005-loes_awkl2_05.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur IMO 2005
|
| 2 |
+
|
| 3 |
+
Lösungen zur 2. Auswahlklausur
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Eine unendliche Folge $a_{0}, a_{1}, a_{2}, \ldots$ reeller Zahlen erfüllt die Bedingung $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ für alle $n \geq 0$, wobei $a_{0}$ und $a_{1}$ verschiedene positive Zahlen sind.
|
| 8 |
+
Kann diese Folge beschränkt sein? Die Antwort ist zu begründen.
|
| 9 |
+
|
| 10 |
+
## Lösung
|
| 11 |
+
|
| 12 |
+
Zunächst beweisen wir, dass zwei aufeinander folgende Glieder niemals gleich sein können. Aus $a_{n}=a_{n+1}=c$ folgte nämlich sofort $a_{n-1}=0$ und $a_{n-2}=a_{n-3}=c \quad(n>2)$. Schließlich müsste $a_{0}=a_{1}$ oder $a_{0}=0$ bzw. $a_{1}=0$ sein, was ausgeschlossen ist. Daher gilt auch $a_{n}>0$ für alle n.
|
| 13 |
+
Auflösen der Bedingung liefert $a_{n+2}=a_{n+1}+a_{n}$ falls $a_{n+2}>a_{n+1}$ ist, sowie $a_{n+2}=a_{n+1}-a_{n}$ falls $a_{n+2}<a_{n+1}$ ist. Aus $a_{n+1}<a_{n}$ folgt also $a_{n+2}>a_{n}$ und $a_{n+2}>a_{n+1}$. Daher ist diejenige Teilfolge $b_{0}, b_{1}, b_{2}, \ldots$ streng monoton wachsend, die durch Weglassen aller Glieder entsteht, die kleiner als ihr Vorgänger und ihr Nachfolger sind.
|
| 14 |
+
Wenn wir nun zeigen, dass $b_{m+1}-b_{m} \geq b_{m}-b_{m-1}$ für alle $m \geq 2$ gilt, so haben wir für diese Teilfolge eine arithmetische Folge mit positiver Differenz als Minorante, woraus die Unbeschränktheit direkt folgt. Dazu setzen wir $b_{m+1}=a_{n+2}$, wobei $a_{n+2}>a_{n+1}$ gelten soll. Für $a_{n+1}>a_{n}$ haben wir $b_{m}=a_{n+1}$ und $b_{m-1} \geq a_{n-1}$ (weil entweder $b_{m-1}=a_{n-1}$ oder $b_{m-1}=$ $a_{n}>a_{n-1}$ gilt). So ist $b_{m+1}-b_{m}=a_{n}=a_{n+1}-a_{n-1} \geq b_{m}-b_{m-1}$. Für $a_{n+1}<a_{n}$ haben wir dagegen $b_{m}=a_{n}$ und $b_{m-1} \geq a_{n-1}$ (weil entweder $b_{m-1}=a_{n-1}$ oder $b_{m-1}=a_{n-2}>a_{n-1}$ gilt). So ist hier $b_{m+1}-b_{m}=a_{n+1}=a_{n}-a_{n-1} \geq b_{m}-b_{m-1}$.
|
| 15 |
+
|
| 16 |
+
## Aufgabe 2
|
| 17 |
+
|
| 18 |
+
Gegeben seien ein Kreis K und eine Gerade g , die keinen gemeinsamen Punkt haben.
|
| 19 |
+
Ferner sei $\overline{A B}$ der Durchmesser von K , der orthogonal zu g ist, wobei B näher an g liegt als $A$. Weiter sei ein beliebiger Punkt $C$, verschieden von $A$ und $B$, auf $K$ gegeben. Die Gerade AC schneidet g in D; die Gerade DE berührt K in E, wobei B und E auf derselben Seite von AC liegen. Schließlich schneidet BE die Gerade g im Punkt F und AF den Kreis K außer in A im Punkt G.
|
| 20 |
+
Man beweise, dass der Spiegelpunkt von G bezüglich der Achse AB auf der Geraden CF liegt.
|
| 21 |
+
|
| 22 |
+
## Lösung
|
| 23 |
+
|
| 24 |
+
Wir bezeichnen den zweiten Schnittpunkt von CF und K mit H sowie den Schnittpunkt von AB und g mit X . Wegen $A B \perp g$ reicht es zu zeigen, dass $G H \| g$. Dies ist genau dann der Fall, wenn $\angle A G H=\angle A F D$. Umfangswinkelsatz und Scheitelwinkel liefern $\angle A G H=\angle A C H=\angle D C F$; also muss $\angle D C F=\angle A F D$ gezeigt werden. Da die Dreiecke DFC und ADF bei D einen Winkel gemeinsam haben, braucht nur deren (gegensinnige) Ähnlichkeit nachgewiesen zu werden. Diese ist genau dann erfültt, wenn $\frac{|D C|}{|D F|}=\frac{|D F|}{|D A|}$,
|
| 25 |
+
d.h. $|D F|^{2}=|D A| \cdot|D C|$ gilt. Nach dem TangentenSekantensatz gilt allerdings $|D E|^{2}=|D A| \cdot|D C|$, so dass nur $|D E|=|D F|$ zu zeigen bleibt, was mit $\angle D E F=\angle E F D$ gleichbedeutend ist.
|
| 26 |
+
Wegen $\angle F X B=\angle A E B=90^{\circ}$ ist AEXF ein Sehnenviereck und es gilt $\angle E F X=\angle E A B$. Die Gleichheit der Sehnen-Tangentenwinkel liefert
|
| 27 |
+
$\angle D E F=\angle E A B$, woraus $\angle D E F=\angle E F D$ folgt.
|
| 28 |
+
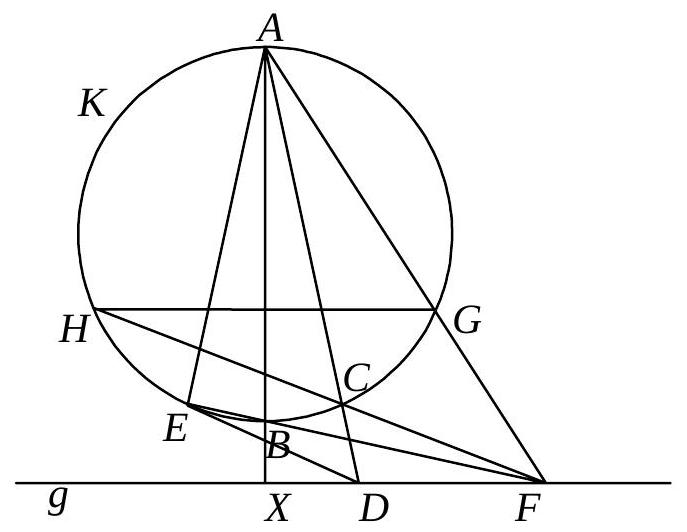
|
| 29 |
+
|
| 30 |
+
## Aufgabe 3
|
| 31 |
+
|
| 32 |
+
Gegeben seien zwei positive ganze Zahlen $n$ und $k$. In der Ebene liegen $n$ Kreise ( $\mathrm{n} \geq 2$ ), so dass jeder Kreis jeden anderen zweimal schneidet und alle diese Schnittpunkte paarweise verschieden sind.
|
| 33 |
+
Jeder Schnittpunkt wird mit einer von n Farben so gefärbt, dass jede Farbe wenigstens einmal verwendet wird und auf jedem der Kreise die gleiche Anzahl k von Farben vertreten ist.
|
| 34 |
+
Man bestimme alle Werte von $n$ und $k$, für die eine solche Färbung möglich ist.
|
| 35 |
+
|
| 36 |
+
## Lösung
|
| 37 |
+
|
| 38 |
+
Die Antwort lautet: $2 \leq k \leq n \leq 3$ oder $3 \leq k \leq n$.
|
| 39 |
+
Offensichtlich gilt $k \leq n$ nach Aufgabenstellung sowie $k \geq 2$, weil für $k=1$ alle Punkte dieselbe Farbe hätten, während die Anzahl $n$ der Farben $\geq 2$ sein soll. Wir nummerieren die Kreise und die Farben von 1 bis n und bezeichnen mit $F(i, j)$ die Menge der Farben der Schnittpunkte der Kreise i und j. F $(i, j)$ enthält ein oder zwei Elemente.
|
| 40 |
+
Sei $k=2$. Für $n=2$ ist $F(1,2)=\{1,2\}$ eine erlaubte Färbung. Für $n=3$ ist $F(1,2)=\{3\}$, $F(2,3)=\{1\}, F(3,1)=\{2\}$ ein Beispiel für eine erlaubte Färbung. Sei nun $n \geq 4$. Jedem der n Kreise ordnen wir die Menge $\{i, j\}$ der beiden auf ihm vorkommenden Farben zu. Jede dieser Mengen besteht aus zwei Elementen und jede der n Farben muss in wenigstens zwei Mengen vorkommen, da sich in jedem gefärbten Punkt zwei Kreise schneiden. Also kommt jede Farbe in genau zwei Mengen vor. Zum Kreis 1 mit der Menge $\{i, j\}$ gibt es daher noch höchstens zwei weitere Kreise, in deren Farbmengen i oder j vorkommen. Wegen $n \geq 4$ finden wir stets einen Kreis 2 mit der Menge $\{k, l\}$ und $\{k, l\} \cap\{i, j\}=\{ \}$. Die Schnittpunkte der Kreise 1 und 2 sind dann nicht erlaubt färbbar Widerspruch!
|
| 41 |
+
Nun beweisen wir mit vollständiger Induktion einen etwas stärkeren Satz als verlangt: Für $n \geq k \geq 3$ existiert stets eine erlaubte Färbung, bei der auf dem Kreis i die Farbe i für alle $i=1, \ldots, n$ vorkommt. Zur Verankerung geben wir für $k=n=3 \operatorname{mit} F(1,2)=\{1,2\}$, $F(1,3)=\{1,3\}, F(2,3)=\{2,3\}$ ein Beispiel und für $k=3, n>3$ folgendes Beispiel für eine erlaubte Färbung mit Zusatzbedingung:
|
| 42 |
+
$F(1,2)=\{1,2\}, F(i, i+1)=\{i\}$ für $1<i<n-1, F(n-1, n)=\{n-2, n-1\}$ und $F(i, j)=\{n\}$ für die restlichen Paare $(i, j)$ mit $1 \leq i<j \leq n$.
|
| 43 |
+
Nun nehmen wir an, dass der stärkere Satz für ein $k \geq 3$ erfüllt ist, und wählen $n \geq k+1$. Wegen $n-1 \geq k \geq 3$ gibt es eine erlaubte Färbung mit Zusatzbedingung für die Kreise bzw. Farben 1,2,..., n-1. Jetzt färben wir die Schnittpunkte des Kreises n: Für jedes $i=1, \ldots, n-1$ erhält ein Schnittpunkt der Kreise i und n die Farbe n . Damit kommen auf jedem der Kreise i mit $i=1, \ldots, n-1$ genau $k+1$ Farben vor; darunter i und $n$. Für $i=1, \ldots, k$ erhält der zweite Schnittpunkt der Kreise i und n die Farbe i, so dass nun auch auf dem Kreis $n$ genau $k+1$ Farben liegen, nämlich 1 bis $k$ und $n$. Alle übrigen neuen Schnittpunkte erhalten die Farbe n, so dass auf keinem Kreis weitere Farben dazukommen. Diese Färbung erfüllt alle Bedingungen.
|
| 44 |
+
|
Germany_TST/md/de-2006-loes_awkl1_06.md
ADDED
|
@@ -0,0 +1,64 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Intemationalen Mathematik-Olympiade ம̈sungen zur 1. IMO-Auswahlklausur 2006
|
| 2 |
+
|
| 3 |
+
## 1. Aufgabe
|
| 4 |
+
|
| 5 |
+
Es seien $A, B, C, D, E, F$ Punkte auf einem Kreis mit $A E \| B D$ und $B C \| D F$. Durch Spiegelung an der Geraden $C E$ gehe der Punkt $D$ in $X$ über. Zeige, dass $X$ so weit von der Geraden $E F$ entfernt ist wie $B$ von $A C$.
|
| 6 |
+
|
| 7 |
+
Lösung. Alle im folgenden auftretenden Winkel sind als orientiert und modulo $180^{\circ} \mathrm{zu}$ verstehen; dadurch wird eine Betrachtung der Lage der involvierten Punkte zueinander entbehrlich. Die Fußpunkte der Lote von $B, X$ auf $A C, E F$ seien mit $P, Q$ bezeichnet.
|
| 8 |
+
Strategie. Zeige die Kongruenz der Dreiecke ABP, EXQ. (*)
|
| 9 |
+
Hieraus wird sich sofort $B P=X Q$ und damit die Behauptung ergeben. Der Beweis von (*) selbst erfolgt vermittelst eines bekannten Kongruenzsatzes in drei Schritten.
|
| 10 |
+
I. Wegen $\varangle B P A \equiv \varangle E Q X \equiv 90^{\circ}$ sind beide Dreiecke rechtwinklig.
|
| 11 |
+
II. Da $A E \| B D$ ist das Sehnenviereck $A B D E$ ein gleichschenkeliges Trapez und demnach $A B=D E$. Weiterhin ist $D E=X E$ nach Konstruktion von $X$ und mithin $A B=X E$, d.h. die Hypotenusen stimmen überein.
|
| 12 |
+
III. Wie vorhin schließen wir aus $B C \| D F$, daß auch $B C D F$ ein gleichschenkliges Trapez ist. Durch wiederholte Verwendung des Peripheriewinkelsatzes erhalten wir nun $\varangle D E C+$ $\varangle C A B \equiv \varangle D A C+\varangle C A B \equiv \varangle D A B \equiv \varangle D F B \equiv \varangle C D F \equiv \varangle C E F \equiv \varangle C E X+\varangle X E F$. Infolge $\varangle D E C \equiv \varangle C E X$ ergibt sich hieraus $\varangle C A B \equiv \varangle X E F$, oder - anders formuliert $-\varangle P A B \equiv \varangle X E Q$.
|
| 13 |
+
|
| 14 |
+
Bemerkung. Diskussionen der Lagebeziehungen sind weder positiv noch negativ in die Bewertung eingegangen.
|
| 15 |
+
|
| 16 |
+
## 2. Aufgabe
|
| 17 |
+
|
| 18 |
+
In einem Raum stehen 2005 Obstkisten, von denen jede eine oder mehrere Sorten Obst enthält, von jeder Obstsorte ganzzahlig viele Früchte.
|
| 19 |
+
a) Man zeige, dass man stets 669 Obstkisten auswählen kann, die zusammen sowohl mindestens ein Drittel aller Äpfel als auch mindestens ein Drittel aller Birnen enthalten.
|
| 20 |
+
b) Können die Kisten in Teil a) stets so gewählt werden, dass sie außerdem mindestens ein Drittel aller Pfirsiche enthalten?
|
| 21 |
+
|
| 22 |
+
Lösung. a) Es sei $N$ eine Kiste, die eine maximale Anzahl von Äpfeln enthält, sagen wir $n$ Stück. Sie werde zunächst beiseite gestellt. Wir betrachten nun alle Möglichkeiten, die verbleibenden $2004=3 \cdot 668$ Kisten in drei Haufen, $A, B$ und $C$ zu je 668 Kisten aufzuteilen. Die Gesamtzahl an Äpfeln in diesen Kisten sei $a, b, c$. Indem wir mit einer beliebigen solchen Aufteilung beginnen und die gebildeten Haufen gegebenenfalls umbenennen, sehen wir, daß es Aufteilungen mit $a \leqq$ $b \leqq c$ gibt. Unter allen diesen fixieren wir für den Rest der Beweisführung eine solche, für die $c-a$ minimal ist. Wäre nun $c-a>n$, so könnten wir eine Kiste aus $A$ mit darin maximaler Anzahl von Äpfeln gegen eine Kiste aus $C$ mit darin minimaler Anzahl vertauschen und erhielten infolge der Maximalität von $n$ nach eventueller Umbenennung der Haufen einen Widerspruch zur Minimalität von $c-a$. Demnach ist $c-a \leqq n$, also $a+n \geqq c \geqq b$, woraus sofort
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
a+n=\frac{(a+n)+(a+n)+a+n}{3} \geqq \frac{c+b+a+n}{3}
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
folgt. Sollten wir uns also letzten Endes entschließen, die 669 Kisten $A \cup\{N\}$ zu nehmen, d.h. die Kisten des Haufens $A$ zusammen mit der Kiste $N$, so hätten wir zumindest die Bedingung über die Anzahl der zu nehmenden Äpfel erfüllt. Dies gilt natürlich erst recht für $B \cup\{N\}$ und $C \cup\{N\}$. Nun sei (nach Schubfachprinzip) $T$ ein solcher der drei Haufen, der mindestens ein Drittel der in ihnen zusammen vorkommenden Birnen enthält. Damit erfüllt die Auswahl
|
| 29 |
+
$T \cup\{N\}$ sicher die Anforderung an die zu wählende Anzahl von Birnen und ist folglich nach obigem wie gewünscht.
|
| 30 |
+
b) Hier genügt die Angabe eines Gegenbeispiels. Es enthalte eine der Kisten nichts außer einem Apfel, eine weitere bloß eine Birne und in den übrigen 2003 Kisten möge jeweils ein Pfirsich liegen. Wollte man nun den gestellten Bedingungen genügen, müßte man die Kiste mit dem Apfel, die Kiste mit der Birne und 668 Kisten mit einem Pfirsich auswählen, bräuchte also insgesamt 670 Kisten.
|
| 31 |
+
Bemerkung. In Teilaufgabe (a) ist es instruktiv, den Fall zu betrachten, daß es 1002 Kisten mit jeweil $2 m$ Äpfeln aber keiner Birne, 1002 Kisten mit jeweils $2 m$ Birnen aber keinem Apfel und eine Kiste, $(H)$, mit $m$ Äpfeln und $m$ Birnen gibt, wobei $m$ für eine womöglich große natürliche Zahl (z.B. 100000) steht. Man überzeugt sich leicht, daß Kiste $H$ genommen werden muß. Dies ist auch dann noch der Fall, wenn die beschriebene Konfiguration geringfügig, d.h. um im Vergleich zu $m$ sehr kleine Anzahlen von Früchten (z.B. 1, 2, 3) geändert wird. Nun führen die meisten vorgeschlagenen algorithmischen Ansätze der Form „Man nehme solange Kisten mit maximal vielen Früchten/Äpfeln/Birnen, bis . . . und danach immer Kisten mit maximal vielen ..." nicht immer darauf, in den beschriebenen Situationen die Kiste $H$ zu nehmen. Daher lösen sie ohne weiteres die Aufgabe nicht.
|
| 32 |
+
|
| 33 |
+
## 3. Aufgabe
|
| 34 |
+
|
| 35 |
+
Lassen sich für jede positive ganze Zahl $n$ nicht-negative ganze Zahlen $a, b, c, d, e, f, g$, $h$ mit
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
n=\frac{2^{a}-2^{b}}{2^{c}-2^{d}} \cdot \frac{2^{e}-2^{f}}{2^{g}-2^{h}}
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
finden? Die Antwort ist zu begründen.
|
| 42 |
+
Vorbemerkung: Im Folgenden sei $n$ ungerade. Ohne Einschränkung ist $a>b, c>d, e>f$, $g>h$. Die Bedingungsgleichung ist dann äquivalent zu $n 2^{d+h-b-f}\left(2^{c-d}-1\right)\left(2^{g-h}-1\right)=$ $\left(2^{a-b}-1\right)\left(2^{e-f}-1\right)$. Da $n$ ungerade ist, gilt $d+h-b-f=0$, und man kann ohne Einschränkung $d=h=b=f=0$ setzen:
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
n\left(2^{c}-1\right)\left(2^{g}-1\right)=\left(2^{a}-1\right)\left(2^{c}-1\right)
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
1. Lösung (skizziert): Die Zahlen der Form $n=19+64 k$ mit ganzzahligem $k \geqq 0$ lassen sich nicht darstellen. Für $x>1$ liefert $2^{x}-1$ Rest 3 bei Division durch 4, für $x=1$ Rest 1. Nur wenn eine ungerade Anzahl der Variablen $a, c, e, g$ Wert 1 hat, kann Gleichung (*) erfüllt sein. Haben drei der Variablen Wert 1, kann die Gleichung nicht gelten, da $n$ ncht die Form $2^{x}-1$ hat. Also hat genau eine der Klammern in $\left(^{*}\right)$ Wert 1. Durch entsprechende Überlegungen und Fallunterscheidungen zu Resten bei Division durch 8, 16, 32, 64 kann man die Werte der restlichen Klammern festlegen und jeweils zum Widerspruch führen.
|
| 49 |
+
2. Lösung (skizziert): Die Zahl $n=19$ ist nicht darstellbar. Man nutzt die Beziehung ggT( $2^{x}-1$, $\left.2^{y}-1\right)=2^{\operatorname{ggT}(x, y)}-1$, um zu zeigen: Aus $\left(2^{x}-1\right) \mid\left(2^{y}-1\right)\left(2^{z}-1\right)$ folgt $x \mid y$ oder $x \mid z$.
|
| 50 |
+
Hieraus folgt mit (*), dass sich 19 als
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
19=\frac{2^{a}-1}{2^{c}-1} \cdot \frac{2^{e}-1}{2^{g}-1} \quad \text { oder } \quad 19=\frac{2^{a}-1}{\left(2^{c}-1\right)\left(2^{g}-1\right)} \cdot\left(2^{e}-1\right)
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
als Produkt zweier ganzzahliger Faktoren schreiben lässt. Da 19 eine Primzahl ist und nicht die Form $2^{e}-1$ hat, genügt es zu zeigen, dass die Gleichung
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
19=\frac{2^{a}-1}{\left(2^{c}-1\right)\left(2^{g}-1\right)}
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
(damit auch $19=\left(2^{a}-1\right) /\left(2^{c}-1\right)=\left(2^{a}-1\right) /\left(\left(2^{c}-1\right)\left(2^{1}-1\right)\right)$ nicht gelten kann. Der Zähler enthält den Primfaktor 19, was nur für $a \geq 18$ möglich ist. Die Zahlen $c$ und $g$ teilen $a$, ohne Einschränkung ist $c \geq g$. Für $c=g=a / 2$ hat der Bruch den nichtganzzahligen Wert $1+2 /\left(2^{a / 2}-1\right)$, für $c \leq a / 3, g \leq a / 3$ oder für $c=a / 2, g \leq a / 4$ ist der Wert zu groß. Damit ist $c=a / 2, g=a / 3$, und der Bruch hat den nicht ganzzahligen Wert $2^{a / 6}+1 /\left(2^{a / 6}-1\right)$.
|
| 63 |
+
Bemerkung: Nicht immer ist $n$ Produkt zweier ganzzahliger Faktoren der Form $\left(2^{x}-1\right) /\left(2^{y}-1\right)$. Beispielsweise ist $13=\frac{\left(2^{12}-1\right)\left(2^{2}-1\right)}{\left(2^{6}-1\right)\left(2^{4}-1\right)}$, aber man kann wie bei der 2. Lösung zeigen, dass 13 nicht in der Form $\left(2^{x}-1\right) /\left(2^{y}-1\right)$ darstellbar ist.
|
| 64 |
+
|
Germany_TST/md/de-2006-loes_awkl2_06.md
ADDED
|
@@ -0,0 +1,61 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Auswahlwettbewerb zur Internationalen Mathematik-Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. IMO-Auswahlklausur 2006
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Man bestimme mit Beweis alle Funktionen $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$mit der Eigenschaft
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
f(x) f(y)=2 f(x+y f(x))
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
für alle positiven reellen Zahlen $x, y$.
|
| 14 |
+
Lösung: Offensichtlich erfüllt die Funktion $f(x)=2$ für alle $x \in \mathbb{R}^{+}$die gegebene Funktionalgleichung. Wir werden zeigen, dass dies die einzige Lösung ist.
|
| 15 |
+
Lemma 1: Für alle $x \in \mathbb{R}^{+}$gilt $f(x) \geq 1$.
|
| 16 |
+
Zum Beweis nehmen wir $f(x)<1$ für ein geeignetes $x$ an und setzen $y=\frac{x}{1-f(x)}$. Dann ist $x>0$ und es folgt $y=x+y f(x)$. Aus (I) erhalten wir $f(x) f(x+y f(x))=2 f(x+y f(x))$ und wegen $f(x+y f(x))>0$ folgt $f(x)=2$, Widerspruch!
|
| 17 |
+
Lemma 2: Für alle $x \in \mathbb{R}^{+}$gilt $f(x) \geq 2$.
|
| 18 |
+
Zum Beweis setzen wir in (I) $x=y$ und erhalten (II): $f^{2}(x)=2 f(x+x f(x))$. Sei $f\left(x_{1}\right)<2$ für ein geeignetes $x_{1}$. Dann ist $f\left(x_{1}+x_{1} f\left(x_{1}\right)\right)=\frac{f^{2}\left(x_{1}\right)}{2}<f\left(x_{1}\right)$. Mit $x_{k+1}=x_{k}+x_{k} f\left(x_{k}\right)$ für $k=1,2, \ldots$ entsteht eine monoton fallende Folge $\left(f\left(x_{1}\right)=a ; \frac{a^{2}}{2} ; \frac{a^{4}}{2^{3}} ; \ldots ; \frac{a^{2 t}}{2^{2 t-1}}, \ldots\right.$ ) von
|
| 19 |
+
Funktionswerten. Für $t>\frac{1}{2-2 \log _{2} a}$ sind die Werte dieser Folge kleiner als 1, Widerspruch!
|
| 20 |
+
Lemma 3: $f$ ist monoton steigend.
|
| 21 |
+
Zum Beweis nehmen wir an, es gibt $s, \varepsilon>0$ mit $f(s)>f(s+\varepsilon)$. Einsetzen von $x=s$ und $y=\frac{\varepsilon}{f(s)}$ in (I) liefert $f(s) f\left(\frac{\varepsilon}{f(s)}\right)=2 f(s+\varepsilon)$, woraus $f\left(\frac{\varepsilon}{f(s)}\right)<2$ folgt, Widerspruch!
|
| 22 |
+
Lemma 4: Wenn es ein $z \in \mathbb{R}^{+}$gibt mit $f(z)>2$, dann gilt $f(x)>2$ für alle $x \in \mathbb{R}^{+}$.
|
| 23 |
+
Wieder setzen wir $x=z$ und $y=\frac{\varepsilon}{f(z)}$ in (I) ein und haben $f(z) f\left(\frac{\varepsilon}{f(z)}\right)=2 f(z+\varepsilon)$, woraus jetzt mit Lemma 2 folgt: $f(z) \leq f(z+\varepsilon)$ für alle $\varepsilon>0$. Also existiert ein $z_{0} \geq 0$ mit $f(z)>2$ für alle $z>z_{0}$. Nehmen wir an, dass $z_{0}>0$ gilt. Dann folgt mit $x=y=z_{0}-\varepsilon>0$ aus (I) $f(x) f(y)=4$, und wegen $x+y f(x)=\left(z_{0}-\varepsilon\right)\left(1+f\left(z_{0}-\varepsilon\right)\right)=3\left(z_{0}-\varepsilon\right)$ gilt für hinreichend kleines $\varepsilon$, dass $3\left(z_{0}-\varepsilon\right)>z_{0}$ und daher $2 f(x+y f(x))>4$, Widerspruch!
|
| 24 |
+
Lemma 5: Wenn $f(x)>2$ für alle $x \in \mathbb{R}^{+}$, dann ist $f$ injektiv.
|
| 25 |
+
Angenommen, es gäbe $s, \varepsilon>0$ mit $f(s)=f(s+\varepsilon)$. Wir setzen $x=s$ und $y=\frac{\varepsilon}{f(s)}$ in (I) ein und haben $f(s) f\left(\frac{\varepsilon}{f(s)}\right)=2 f(s+\varepsilon)$, woraus nun $f(s)<f(s+\varepsilon)$ folgt, Widerspruch!
|
| 26 |
+
Hauptbeweis: Wegen der Symmetrie der linken Seite von (I) gilt auch $x+y f(x)=y+x f(y)$. Für $y=1$ folgt $f(x)=(f(1)-1) x+1=m x+1$. Durch Einsetzen wird jedoch leicht gezeigt, dass keine lineare Funktion Lösung von (I) sein kann.
|
| 27 |
+
|
| 28 |
+
Anmerkung: Wegen $\mathbb{D}=\mathbb{R}^{+}$darf nicht mit $f(0)$ operiert werden. $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$bedeutet nicht, dass jede positive reelle Zahl Funktionswert sein muss. Zusätzliche Annahmen über $f$ wie z.B. Stetigkeit sind nicht zulässig.
|
| 29 |
+
|
| 30 |
+
## Aufgabe 2
|
| 31 |
+
|
| 32 |
+
Gegeben sei ein Dreieck $A B C$ mit $\overline{A B}+\overline{B C}=3 \overline{A C}$. Sein Inkreis habe den Mittelpunkt $I$ und berühre die Seiten $A B$ in $D$ bzw. $B C$ in $E$. Weiter seien $K$ und $L$ die Spiegelpunkte von $D$ bzw. $E$ bezüglich $I$.
|
| 33 |
+
Man beweise, dass das Viereck $A C K L$ ein Sehnenviereck ist.
|
| 34 |
+
|
| 35 |
+
Lösung: Zu den in der Aufgabenstellung genannten Punkten bezeichnen wir den Berührpunkt des Inkreises mit $A C$ mit $F$, den Mittelpunkt von AC mit $S$, den Schnittpunkt von $w_{\beta}$ und der Mittelsenkrechten $m_{A C}$ mit $P$, den Spiegelpunkt von $B$ an $I$ mit $R$, den Mittelpunkt von $B I$ mit $T$ und die paarweise gleichen Abschnitte auf den Dreiecksseiten mit $x, y$ bzw. $z$ (siehe Figur).
|
| 36 |
+
Aus $\overline{A B}+\overline{B C}=3 \overline{A C}$ folgt
|
| 37 |
+
$x+z+z+y=3(x+y)$, also (I) $z=x+y$. Bekanntlich liegt $P$ auf dem Umkreis von $A B C$. Daher gilt $\angle C A P=\angle C B P=\angle P B A=\angle P C A=\frac{\beta}{2}$ und $\overline{A P}=\overline{C P}$. Die Dreiecke $A S P$ und $B E I$ sind ähnlich, und wegen $\overline{A S}=\frac{1}{2} \overline{A C}=\frac{x+y}{2}=\frac{z}{2}=\frac{1}{2} \overline{B E}$ gilt mit der Bezeichnung $r$ für den Inkreisradius
|
| 38 |
+
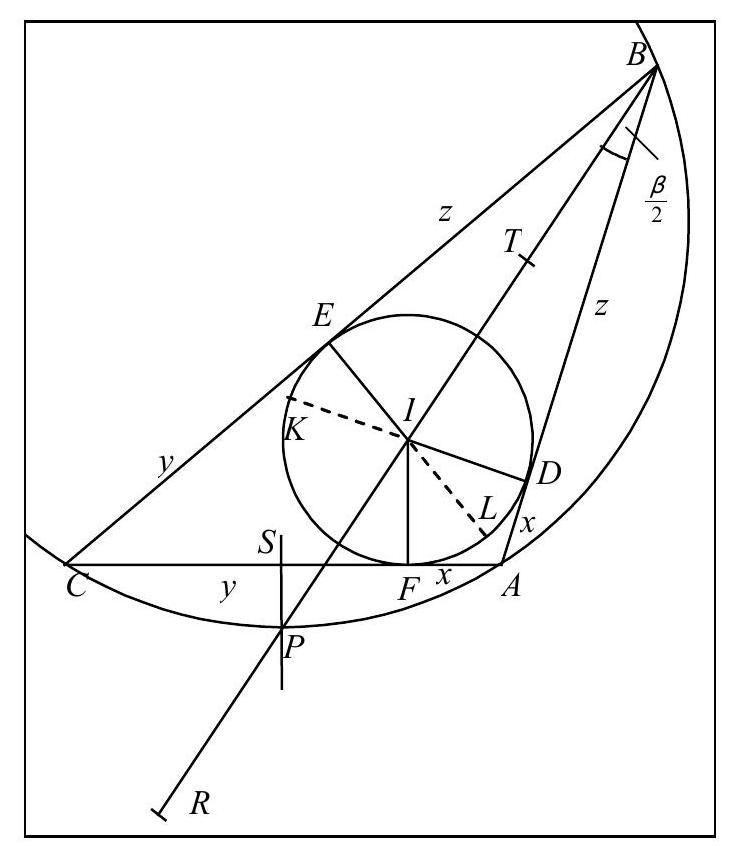
|
| 39 |
+
(II) $\overline{S P}=\frac{1}{2} \overline{E I}=\frac{r}{2}$ sowie $\overline{A P}=\frac{1}{2} \overline{B I}$.
|
| 40 |
+
|
| 41 |
+
Für den Flächeninhalt $F$ des Dreiecks $A B C$ gilt $F=r s=\sqrt{s(s-a)(s-b)(s-c)}$, wobei $s=\frac{a+b+c}{2}=x+y+z$ ist. Daher ist $r(x+y+z)=\sqrt{(x+y+z) x y z}$ und mit (I) folgt $2 r z=\sqrt{2 z x y z} \Leftrightarrow 4 r^{2}=2 x y \Leftrightarrow 8 r^{2}=4 x y \Leftrightarrow 9 r^{2}+(x-y)^{2}=r^{2}+(x+y)^{2}=r^{2}+z^{2}$. Wegen $\angle B D I=90^{\circ}$ ist (III) $\overline{B I}^{2}=r^{2}+z^{2}$. Wegen $P S \perp A C \perp F I$ gilt $\overline{P I}^{2}=\overline{S F}^{2}+(\overline{P S}+\overline{F I})^{2}$.
|
| 42 |
+
Aber $\overline{S F}=\frac{1}{2} \overline{A C}-x=\frac{x+y}{2}-x=\frac{y-x}{2}$ und $\overline{F I}=r$. Daher und mit (II) ist $\overline{P I}^{2}=\left(\frac{y-x}{2}\right)^{2}+\left(\frac{3}{2} r\right)^{2}$ $=\frac{(y-x)^{2}+9 r^{2}}{4}$. Mit (III) folgt $\overline{P I}^{2}=\frac{1}{4} \overline{B I}^{2}$, also $\overline{P I}=\frac{1}{2} \overline{B I}$. So gilt (IV) $\overline{P I}=\overline{P A}=\overline{P C}=\overline{P R}$.
|
| 43 |
+
Außerdem wird $T$ bei Spiegelung an $I$ auf $P$ abgebildet. Daher ist auch $\overline{I T}=\overline{P I} . \overline{B I}$ ist der Durchmesser des Kreises durch $B, I, D$ und $E$ (rechte Winkel bei $D$ und $E$ ). Dieser Kreis hat $T$ als Mittelpunkt. Bei Spiegelung dieses Kreises an $I$ wird $I$ auf $I, T$ auf $P, D$ auf $K, E$ auf $L$ abgebildet und der Radius bleibt erhalten. Mit (IV) folgt, dass $A, L, I, K, C$ und $R$ auf einem Kreis um $P$ liegen; also ist $A C K L$ ein Sehnenviereck.
|
| 44 |
+
|
| 45 |
+
Anmerkung: Öfters wurden Lagebeziehungen oder Kongruenzen unbewiesen verwendet.
|
| 46 |
+
|
| 47 |
+
## Aufgabe 3
|
| 48 |
+
|
| 49 |
+
Wir betrachten ein $m \times n$-Rechteck aus $m n$ Einheitsquadraten. Zwei seiner Einheitsquadrate heißen benachbart, wenn sie eine gemeinsame Seitenkante haben, und ein Pfad ist eine Folge von Einheitsquadraten, in der je zwei aufeinander folgende Elemente benachbart sind.
|
| 50 |
+
Jedes Einheitsquadrat des Rechtecks kann entweder weiß oder schwarz gefärbt werden. Sind alle Quadrate gefärbt, so liegt eine Färbung des Rechtecks vor.
|
| 51 |
+
Es sei $N$ die Anzahl aller solcher Färbungen, bei denen es wenigstens einen schwarzen Pfad von der linken zur rechten Seitenkante des Rechtecks gibt. Ferner sei $M$ die Anzahl aller Färbungen, bei denen es wenigstens zwei schwarze Pfade von der linken zur rechten Seitenkante des Rechtecks gibt, die kein gemeinsames Quadrat enthalten.
|
| 52 |
+
Man beweise, dass $N^{2} \geq M \cdot 2^{m n}$.
|
| 53 |
+
Lösung: Wir werden die Behauptung verallgemeinern. Dazu lassen wir zu, dass das $m \times n$ Rechteck auf beiden Seiten gefärbt wird und dass einige der Einheitsquadrate transparent sind. Solche Felder brauchen nur auf einer Seite gefärbt zu werden und sehen dann auf beiden Seiten gleich aus. Ein nicht transparentes Einheitsquadrat muss dagegen auf beiden Seiten gefärbt werden, allerdings nicht notwendigerweise mit der gleichen Farbe.
|
| 54 |
+
|
| 55 |
+
Nun sei $A$ die Anzahl aller solcher Färbungen der Oberseite, bei denen es wenigstens einen schwarzen Pfad von der linken zur rechten Seitenkante des Rechtecks gibt. Entsprechend sei $B$ für die Unterseite definiert. Ferner sei $C$ die Anzahl aller Färbungen, bei denen es zwei schwarze Pfade von der linken zur rechten Seitenkante des Rechtecks gibt, und zwar einen auf der Ober- und einen auf der Unterseite, die kein gemeinsames transparentes Quadrat enthalten. Schließlich sei $D$ die Anzahl aller Färbungen dieses Rechtecks. Wir werden (I) $A \cdot B \geq C \cdot D$ beweisen und haben damit die ursprüngliche Behauptung als Spezialfall gezeigt, in dem alle Felder transparent sind. Hier gilt nämlich $A=B=N, C=M, D=2^{m n}$. Den Beweis von (I) führen wir mit vollständiger Induktion nach der Anzahl $k$ der transparenten Felder. Für $k=0$ ist $A=B=N \cdot 2^{m n}, C=N^{2}$ und $D=\left(2^{m n}\right)^{2}$, so dass in (I) Gleichheit gilt. Nun nehmen wir an, dass die Behauptung für $k$ erfüllt ist, und betrachten ein Rechteck mit $k+1$ transparenten Feldern. Die Anzahlen $A, B, C, D$ gelten nun für dieses Rechteck. Wir wählen ein transparentes Einheitsquadrat $t$ und machen es undurchsichtig. Für das so entstandene Rechteck seien die jeweiligen Anzahlen mit $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ bezeichnet und nach Induktionsannahme gilt $A^{\prime} \cdot B^{\prime} \geq C^{\prime \prime} \cdot D^{\prime}$.
|
| 56 |
+
Nun ist offensichtlich $D^{\prime}=2 \cdot D$. Für jede in $A$ gezählte Färbung existieren genau zwei Färbungen von $A^{\prime}$, nämlich dadurch unterschieden, dass $t$ von unten schwarz oder weiß gefärbt wird. Umgekehrt kann man zwei in $A^{\prime}$ gezählten Färbungen, die sich nur in der Farbe der Unterseite eines Quadrats unterscheiden, eine in $A$ gezählte Färbung zuordnen. Also ist $A^{\prime}=2 \cdot A$ und entsprechend $B^{\prime}=2 \cdot B$. Zum Beweis von (I) für $k+1$ genügt also der Nachweis von $C^{\prime} \geq 2 \cdot C$.
|
| 57 |
+
Dazu sei $t$ wieder transparent. Weil in $C$ nur solche Färbungen gezählt werden, die wenigstens einen schwarzen Pfad oben und unten enthalten, wobei diese sich nicht in einem transparenten Quadrat schneiden, kann $t$ höchstens auf einem dieser Pfade, oBdA auf dem oberen, liegen. Machen wir also $t$ undurchsichtig und behalten seine Farbe oben bei, können wir seine Unterseite schwarz oder weiß färben, so dass beide Färbungen in $C^{\prime}$ gezählt werden. Dabei liefern verschiedene in $C$ gezählte F��rbungen stets verschiedene Paare von Färbungen, die in $C^{\prime}$ gezählt werden. Damit ist alles gezeigt.
|
| 58 |
+
|
| 59 |
+
[^0]
|
| 60 |
+
[^0]: Anmerkung: Ein Beweis mit vollständiger Induktion auf einer Brettseite ist heikel, da beim Abschätzen der Fortsetzungen der Pfade häufig Zählfehler auftreten. In der Regel wurden mögliche Fälle übersehen. Die Anzahl schwarzer Felder in einem schwarzen Pfad kann größer sein als die Breite des Rechtecks.
|
| 61 |
+
|
Germany_TST/md/de-2007-loes_awkl1_07.md
ADDED
|
@@ -0,0 +1,114 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwetthewerb zur Intemationalen Mathematik-Olympiade Lقsungen zur 1. IMO-Auswahlklausur 2007
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
#### Abstract
|
| 5 |
+
|
| 6 |
+
1. Aufgabe
|
| 7 |
+
|
| 8 |
+
Es seien $n$ eine positive ganze Zahl größer als Eins und $B=\left\{1,2, \ldots, 2^{n}\right\}$. Eine Teilmenge $A$ von $B$ heiße ulkig, wenn sie von je zwei verschiedenen Elementen $x, y$ von $B$, deren Summe eine Zweierpotenz ist, genau eines enthält. Wie viele ulkige Teilmengen hat $B$ ?
|
| 9 |
+
|
| 10 |
+
Lösung. Die Anzahl ist $2^{n+1}$. Wir argumentieren mit vollständiger Induktion nach $n$ und setzen hierzu $B_{n}=\left\{1,2, \ldots, 2^{n}\right\}$. Induktionsanfang, $n=1$. Dieser Fall ist klar: alle vier Teilmengen von $B_{1}=\{1,2\}$ sind ulkig. Induktionsschritt, $n \longrightarrow n+1$. Es sei also bereits bekannt, daß $B_{n}$ genau $2^{n+1}$ viele ulkige Teilmengen hat. Für jede ulkige Menge $A$ von $B_{n}$ konstruiere die Mengen $C_{n}(A)=\left\{2^{n+1}-m \mid\right.$ $\left.m \in B_{n} \backslash A, m<2^{n}\right\}, M_{n}(A)=A \cup C_{n}(A)$ und $N_{n}(A)=M_{n}(A) \cup\left\{2^{n+1}\right\}$. Offenbar sind $A, C_{n}(A)$ und $\left\{2^{n+1}\right\}$ paarweise elementfremd. Die Mengen $M_{n}(A)$ und $N_{n}(A)$ sind ulkig: Hierzu seien $x, y$ verschiedene Elemente von $B_{n+1}$, deren Summe eine Zweierpotenz ist; ohne Einschränkung gelte $x<y$. $\operatorname{Im}$ Fall $1 \leq x<y \leq 2^{n}$, also $x, y \in B_{n}$, ist genau eines von beiden in $M_{n}(A)$ bzw. $N_{n}(A)$ enthalten, da $A$ ulkig ist. Im Fall $1 \leq x \leq 2^{n}<y \leq 2^{n+1}$ ist $2^{n}<x+y<2^{n+2}$, also $x+y=2^{n+1}$; wegen $x \geq 1$ ist $y \neq 2^{n+1}$. Nach Wahl von $C_{n}(A)$ liegt entweder $x$ in $A$ oder $y$ in $C_{n}(A)$. Der Fall $2^{n}<x<y \leq 2^{n+1}$ kann nicht auftreten, da dann $2^{n+1}<x+y<2^{n+2}$. - Ist andererseits $M$ ulkige Teilmenge von $B_{n+1}$, so ist offenbar $A:=M \cap B_{n}$ ulkige Teilmenge von $B_{n}$. Das Element $y=2^{n+1}-x$ von $B_{n+1}$ mit $1 \leq x<2^{n}$ ist genau dann in $M$ enthalten, wenn $x \in B_{n}$ nicht in $A$ enthalten ist, da $x+y=2^{n+1}$ Zweierpotenz ist. Die Ulkigkeit von $M$ legt also bei Kenntnis von $M \cap B_{n}$ für alle Elemente $y$ von $B_{n+1}$ mit $2^{n}<y<2^{n+1}$ fest, ob sie in $M$ enthalten sind; es steht nur noch frei, ob $2^{n+1}$ Element ist. Damit gleicht $M$ entweder $M_{n}(A)$ oder $N_{n}(A)$, und es lassen sich jeder ulkigen Teilmenge von $B_{n}$ genau zwei ulkige Teilmengen von $B_{n+1}$ zuordnen. Das beendet den Beweis.
|
| 11 |
+
|
| 12 |
+
|
| 13 |
+
Bemerkung. Oft wurde irrtümlich angenommen, die Zahlen $2^{n-1}$ und $2^{n}$ könnten gar nicht Elemente einer ulkigen Teilmenge von $B_{n}$ sein, da für kein $x \in B_{n}$ mit $x \neq 2^{n-1}$ die Zahl $2^{n-1}+x$ eine Zweierpotenz ist und das gleiche Phänomen bei $2^{n}$ auftritt. Diese Sachlage zeigt allerdings nur, daß für jedes $X \subseteq B_{n}-\left\{2^{n-1}, 2^{n}\right\}$ die vier Mengen $X, X \cup\left\{2^{n-1}\right\}, X \cup\left\{2^{n}\right\}, X \cup\left\{2^{n-1}, 2^{n}\right\}$ entweder gleichzeitig ulkige oder gleichzeitig unulkige Teilmengen von $B_{n}$ sind.
|
| 14 |
+
|
| 15 |
+
## 2. Aufgabe
|
| 16 |
+
|
| 17 |
+
Man finde alle Quadrupel positiver ganzer Zahlen ( $m, n, p, q$ ) mit der Eigenschaft
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
p^{m} q^{n}=(p+q)^{2}+1
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
1. Lösung. Hilfssatz: Sind $k, l, a$ positive ganze Zahlen mit $a=\left(k^{2}+l^{2}+1\right) /(k l)$, folgt $a=3$. Beweis des Hilfssatzes: Zu gegebenem Wert von $a$ betrachten wir ein Paar $(k, l)$ mit $k^{2}+l^{2}+1=a k l$ und minimaler Summe $k+l$ unter allen derartigen Paaren. Ohne Einschränkung ist $k \leq l$.
|
| 24 |
+
Zunächst sei $k<l$. Nach Voraussetzung genügt $k$ der quadratischen Gleichung
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
x^{2}+l^{2}+1-a x l=0,
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
für deren 2. Lösung $k^{\prime}$ nach Satz von Vieta folgt: $k+k^{\prime}=a l$ und $k k^{\prime}=l^{2}+1$. Also ist $k^{\prime}=a l-k$ ganzzahlig, wegen $k^{\prime}=\left(l^{2}+1\right) / k$ positiv, wegen $k \geq l+1$ und $k k^{\prime}=l^{2}+1<(l+1)^{2}$ ist $k^{\prime} \leq l$, also ist $\left(l, k^{\prime}\right)$ Paar mit kleinerer Summe $l+k^{\prime}<k+l$ entgegen der Wahl von $(k, l)$.
|
| 31 |
+
Somit gilt $k=l$, also $k^{2}(a-2)=1$, woraus sich $k=1$ und $a=3$ ergeben.
|
| 32 |
+
Es ist wegen $m \geq 1$ und $n \geq 1$ der Ausdruck $p^{m-1} q^{n-1}=\left(p^{2}+q^{2}+1\right) /(p q)+2$ ganzzahlig, also nach Hilfssatz $p^{m-1} q^{n-1}=5$ und somit $p^{m-1}=1, q^{n-1}=5$ oder $p^{m-1}=5, q^{n-1}=1$. Im ersten Fall ist $n=2$ und $q=5 ; p$ genügt der Gleichung (1) für $l=5, a=3$ mit Lösungen 2 und 13, aus $p^{m-1}=1$ folgt jeweils $m=1$, und durch Einsetzen bestätigt man die Lösungsquadrupel ( $\left.1,2,2,5\right)$ und $(1,2,13,5)$. Der zweite Fall liefert entsprechend $(2,1,5,2)$ und $(2,1,5,13)$.
|
| 33 |
+
2. Lösung. Alle Summanden der Ausgangsgleichung bis auf $q^{2}+1$ sind Vielfache von $p$, daher gilt $p \mid q^{2}+1$. Damit lassen sich die Fälle $q=1,2, \ldots, 6$ mittels Durchprobieren behandeln, man erhält Lösungsquadrupel aus 1. Lösung. Für $p \geq q \geq 7$ (analog: $p \geq p \geq 7$ ) gibt es keine Lösungen:
|
| 34 |
+
|
| 35 |
+
1. Fall: $m>1$ : Dann ist $p^{m} q^{n} \geq p^{2} q>6 p^{2} \geq(p+q)^{2}+1$.
|
| 36 |
+
2. Fall: $n>2$ : Dann ist wegen $p \leq q^{2}+1: p^{m} q^{n} \geq p q^{3} \geq p^{2} q-p q>5 p^{2}>(p+q)^{2}+1$.
|
| 37 |
+
3. Fall: $m=n=1$ : Hierzu müsste $p^{2}+p q+q^{2}+1=0$ sein - unmöglich für $p>0, q>0$.
|
| 38 |
+
4. Fall: $m=1, n=2$ : Die quadratische Gleichung $p q^{2}=(p+q)^{2}+1$ für $p$ hat Diskriminante $D=q^{4}-4 q^{3}-4$, die für $q \geq 7$ zwischen den aufeinander folgenden Quadratzahlen $\left(q^{2}-2 q-3\right)^{2}$ und $\left(q^{2}-2 q-2\right)^{2}$ liegt, also ist $\sqrt{D}$, somit auch $p$ nicht ganzzahlig.
|
| 39 |
+
Bemerkung: Es gab Trugschlüsse: z. B. sind Fälle $m \geq 2, n \geq 3$ und $m \geq 3, n \geq 2$ behandelt, folgt nicht notwendig $m \leq 2$ und $n \leq 2$; sind $p, q$ teilerfremd, haben $p$ und $q$ nicht notwendig unterschiedliche Parität. Manchmal wurden nicht alle Lösungen auf Grund zu starker Einschränkungen gefunden (z. B. Voraussetzung $m \geq n$ und $p \geq q$ ).
|
| 40 |
+
|
| 41 |
+
## 3. Aufgabe
|
| 42 |
+
|
| 43 |
+
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Man beweise, dass dann gilt:
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
| 56 |
+
|
| 57 |
+
1. Lösung. Die Verlängerungen von $A P, B P, C P$ mögen den Umkreis des Dreiecks $A B C$ erneut in $A^{\prime}, B^{\prime}, C^{\prime}$ treffen. Mit Hilfe des Peripheriewinkelsatzes und einem einfachen Winkelsummenargument finden wir $\varangle B^{\prime} A^{\prime} C^{\prime}=\varangle B^{\prime} A^{\prime} A+\varangle A A^{\prime} C^{\prime}=\varangle B^{\prime} B A+\varangle A C C^{\prime}=\varangle B P C-\varangle B A C=60^{\circ}$. Ebenso $\varangle A^{\prime} C^{\prime} B^{\prime}=60^{\circ}$ und folglich ist das Dreieck $A^{\prime} B^{\prime} C^{\prime}$ gleichseitig, d.h. $A^{\prime} B^{\prime}=B^{\prime} C^{\prime}=C^{\prime} A^{\prime}$. Wie üblich haben wir $A P B \sim B^{\prime} P A^{\prime}$ und $A P C \sim C^{\prime} P A^{\prime}$; hieraus ergibt sich $\frac{A P}{A C}=\frac{C^{\prime} P}{C^{\prime} A^{\prime}}$ und $\frac{B P}{B C}=\frac{C^{\prime} P}{C^{\prime} B^{\prime}}$. In Verbindung mit vorigem lehrt dies $\frac{A P}{A C}=\frac{B P}{B C}$ und somit in der Tat $A B \cdot P C=$ $A C \cdot P B$.
|
| 58 |
+
2. Lösung. Wähle den Punkt $J$ so, daß die Dreiecke $A B C, P B J$ (gleichorientiert) ähnlich sind. Sodann ist $\frac{A B}{B P}=\frac{B C}{B J}$ und $\varangle P B A=\varangle J B C$, weshalb auch die Dreiecke $A B P, C B J$ (gleichorientiert) ähnlich sein müssen. Folglich gilt $\varangle C J P=\varangle C J B-\varangle P J B=\left(60^{\circ}+\gamma\right)-\gamma=60^{\circ}$. Da auch $\varangle J P C=\varangle B P C-\varangle B P J=\left(60^{\circ}+\alpha\right)-\alpha=60^{\circ}$ ist das Dreieck $P C J$ gleichseitig und mithin $P C=P J$. Nach Wahl von $J$ haben wir $\frac{A B}{A C}=\frac{P B}{P J}$ und hieraus folgt mit Hilfe des vorigen wie gewünscht $A C \cdot P B=A B \cdot P J=A B \cdot P C$.
|
| 59 |
+
3. Lösung. Über der Strecke $B P$ werde das gleichseitige Dreieck $B P T$ errichtet. Der Schnittpunkt von $P T$ mit $A B$ heiße $G$. Außerdem werde auf $A C$ der Punkt $H$ mit $\varangle C P H=60^{\circ}$ gewählt. Wegen $\varangle A P G=\gamma$ und $\varangle H P A=\beta$ muss $\varangle H P G+\varangle G A H=180^{\circ}$ sein, d.h. das Viereck $G A H P$ ist einem Kreis einbeschrieben. Demnach $\varangle H G A=\varangle H P A=\beta$, woraus sofort $G H \| B C$ geschlossen wird. Aus diesem Grund gilt $\frac{A B}{A C}=\frac{B G}{C H} \quad$ (1). Ferner zeigen einfache Winkelbetrachtungen $\varangle H C P=$ $60^{\circ}-\varangle P B G=\varangle G B T$, was zusammen mit $\varangle C P H=\varangle B T G\left[=60^{\circ}\right]$ die Ähnlichkeit der Dreiecke $P C H$ und $T B G$ lehrt. Mithin haben wir $\frac{B G}{C H}=\frac{B T}{C P} \quad$ (2). Nachdem das Dreieck BPT nach Konstruktion gleichseitig ist, gilt insbsondere $B T=B P$. Zusammen mit (1) und (2) erhalten wir hieraus $\frac{A B}{A C}=\frac{B P}{C P}$ und damit in der Tat $A B \cdot P C=A C \cdot P B$.
|
| 60 |
+
4. Lösung. Wähle den Punkt $G$ so, daß die Dreiecke $A G C, P B C$ (gleichorientiert) ähnlich sind. Wie in der zweiten Lösung sehen wir, daß dann auch die Dreiecke GBC und $A P C$ (gleichorientiert) ähnlich sind. Ferner ist $\varangle B A G=\varangle C A G-\varangle C A B=\left(60^{\circ}+\alpha\right)-\alpha=60^{\circ}$ und ebenso $\varangle G B A=60^{\circ}$. Das Dreieck $A G B$ ist also gleichseitig und mithin $A G=A B$. Nach $A G C \sim P B C$ haben wir also $P B: P C=A G: A C=A B: A C$. Daher wie behauptet $A B \cdot P C=A C \cdot P B$.
|
| 61 |
+
5. Lösung. Die Fußpunkte der Lote von $P$ auf die Seiten $B C, C A, A B$ mögen $X, Y, Z$ genannte werden. Nach Satz von Thales besitzen die Vierecke $P X C Y, P Y A Z, P Z B X$ jeweils einen Umkreis. Wir finden nun $\varangle Z X Y=\varangle Z X P+\varangle P X Y=\varangle Z B P+\varangle P C Y=60^{\circ}$ und analog
|
| 62 |
+
$\varangle X Y Z=\varangle Y Z X=60^{\circ}$. Das Dreieck $X Y Z$ ist also gleichseitig. Für die Länge der Seite $X Y$ finden wir durch zweimalige Verwendung des Sinussatzes $X Y=P C \cdot \sin \gamma=\frac{A B \cdot P C}{2 R}$, wobei $R$ den Radius des Umkreises des Dreiecks $A B C$ bezeichnet. Ebenso $X Z=\frac{A C \cdot P B}{2 R}$. Aus $X Y=X Z$ folgt nunmehr wie verlangt $A B \cdot P C=A C \cdot P B$.
|
| 63 |
+
6. Lösung. Der Umkreis des Dreiecks $A B P$ schneide $A C$ zum zweiten Mal in $Q$. Wir erhalten $\varangle B Q A=\varangle B P A=\gamma+60^{\circ}$ und hieraus nach Außenwinkelsatz $\varangle Q B C=60^{\circ}$. Außerdem ergibt sich aus $\varangle B P Q=180^{\circ}-\alpha$ und $\varangle C P B=60^{\circ}+\alpha$ sofort $\varangle Q P C=120^{\circ}$. Ferner erhalten wir, wenn wir $\varangle A B P=\varphi$ setzen, sofort $\varangle C Q P=\varphi$. Durch mehrmalige Verwendung des Sinussatzes erhalten wir nun
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\frac{P C}{P A}=\frac{P C}{C Q} \cdot \frac{C Q}{Q B} \cdot \frac{Q B}{A P}=\frac{\sin \varphi}{\sin 120^{\circ}} \cdot \frac{\sin 60^{\circ}}{\sin \gamma} \cdot \frac{\sin \alpha}{\sin \varphi}=\frac{\sin \alpha}{\sin \gamma}=\frac{B C}{A B}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Hieraus folgt sofort $A B \cdot P C=A P \cdot B C$.
|
| 70 |
+
7. Lösung. Über der Seite $A B$ errichte man das gleichseitige Dreieck $A B Q$ nach innen. Einfache Winkelbetrachtungen zeigen nun $\varangle Q A P=60^{\circ}-\varangle P A B=\varangle B C P$ und ebenso $\varangle P B Q=\varangle P C A$. Indem wir also den Schnittpunkt von $A C$ mit $B Q$ als $T$ in die Überlegung einführen, wird das Viereck $B C T P$ wegen $\varangle P B T=\varangle P B Q=\varangle P C A=\varangle P C T$ ein Sehnenviereck sein. Folglich $\varangle B T P=\varangle B C P=\varangle Q A P$, also $\varangle P T Q+\varangle Q A P=180^{\circ}$ und somit ist auch $P T Q A$ ein Sehnenviereck. Aus diesem Grund gilt $\varangle B Q P=\varangle T Q P=\varangle T A P=\varangle C A P$, woraus in Verbindung mit $\varangle P B Q=\varangle P C A$ die Ähnlichkeit der Dreiecke $B Q P, C A P$ folgt. Hieraus erhellt $P C: A C=P B: B Q=P B: A B$, also wie gewünscht $A B \cdot P C=A C \cdot P B$.
|
| 71 |
+
8. Lösung. Setze $\varangle A C P=\gamma^{\prime}, \varangle P B C=\gamma^{\prime \prime}, \varangle P B A=\beta^{\prime \prime}$. Nun ist nach Sinussatz
|
| 72 |
+
$\frac{\sin \beta^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \beta^{\prime \prime}}{A P} \cdot \frac{A P}{\sin \gamma^{\prime}}=\frac{\sin \left(60^{\circ}+\gamma\right)}{c} \cdot \frac{b}{\sin \left(60^{\circ}+\beta\right)}=\frac{\sin \left(60^{\circ}+\gamma\right)}{\sin \gamma} \cdot \frac{\sin \beta}{\sin \left(60^{\circ}+\beta\right)}=\frac{1+\sqrt{3} \cot \gamma}{1+\sqrt{3} \cot \beta}$.
|
| 73 |
+
Da jedoch $\beta^{\prime \prime}+\gamma^{\prime}=60^{\circ}$ haben wir auch
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\frac{\sin \beta^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \left(60^{\circ}-\gamma^{\prime}\right)}{\sin \gamma^{\prime}}=\frac{\sqrt{3}}{2} \cot \gamma^{\prime}-\frac{1}{2} .
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Diese beiden Gleichungen liefern zusammengenommen
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\cot \gamma^{\prime}=\frac{\sqrt{3}+\cot \beta+2 \cot \gamma}{1+\sqrt{3} \cot \beta}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
Weiterhin
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
\frac{\sin \gamma^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \left(\gamma-\gamma^{\prime}\right)}{\sin \gamma^{\prime}}=\sin \gamma \cot \gamma^{\prime}-\cos \gamma
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Hierin setzen wir die zuvor gefundene Gleichung ein und erhalten
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
\begin{gathered}
|
| 95 |
+
\frac{\sin \gamma^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{(\sqrt{3} \sin \beta \sin \gamma+\cos \beta \sin \gamma+2 \sin \beta \cos \gamma)-(\sin \beta \cos \gamma+\sqrt{3} \cos \beta \cos \gamma)}{\sin \beta+\sqrt{3} \cos \beta} \\
|
| 96 |
+
=\frac{\sin \alpha+\sqrt{3} \cos \alpha}{\sin \beta+\sqrt{3} \cos \beta}=\frac{\sin \left(60^{\circ}+\alpha\right)}{\sin \left(60^{\circ}+\beta\right)}
|
| 97 |
+
\end{gathered}
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
Daher nach Sinussatz
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\frac{A P}{A C}=\frac{\sin \gamma^{\prime}}{\sin \left(\beta+60^{\circ}\right)}=\frac{\sin \gamma^{\prime \prime}}{\sin \left(\alpha+60^{\circ}\right)}=\frac{B P}{B C}
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
d.h. wie gewünscht $A P \cdot B C=B P \cdot A C$.
|
| 107 |
+
9. Lösung. Der Umkreis des Dreiecks $A P B$ treffe die Gerade $C P$ zum zweiten Mal in $J$. Sodann ist $\varangle A J P=\varangle A B P$. Zusammen mit $\varangle A B P+\varangle P C A=60^{\circ}$ lehrt dies $\varangle C A J=120^{\circ}$. Ebenso sehen wir $\varangle J B C=120^{\circ}$ ein. Damit haben wir
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\frac{A C}{B C}=\frac{A C}{J C} \cdot \frac{J C}{B C}=\frac{\sin \varangle A J C}{\sin \varangle C A J} \cdot \frac{\sin \varangle J B C}{\sin \varangle C J B}=\frac{\sin \varangle A J P}{\sin \varangle P J B}=\frac{\sin \varangle A B P}{\sin \varangle P A B}=\frac{A P}{B P},
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
d.h. wie behauptet $A C \cdot B P=B C \cdot A P$.
|
| 114 |
+
|
Germany_TST/md/de-2007-loes_awkl2_07.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade <br> Lösungen zur 2. IMO-Auswahlklausur 2007
|
| 2 |
+
|
| 3 |
+
## Aufgabe 1
|
| 4 |
+
|
| 5 |
+
Eine $F$ olge $a_{0}, a_{1}, a_{2}, \ldots$ reeller Zahlen ist rekursiv definiert durch
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
a_{0}=-1, \quad \sum_{k=0}^{n} \frac{a_{n-k}}{k+1}=0 \quad \text { für } n \geq 1 .
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
$M$ an beweise, dass $a_{n}>0$ für alle $n \geq 1$ gilt.
|
| 12 |
+
|
| 13 |
+
Lösung: Für $n=1$ gilt $a_{1}+\frac{1}{2} a_{0}=0$, also $a_{1}=\frac{1}{2}>0$. Nun gelte $a_{i}>0$ für $1 \leq i<n$. A us dem Gegebenen folgt $\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}+\frac{a_{n}}{1}+\frac{a_{0}}{n+1}=0 \Leftrightarrow a_{n}=\frac{1}{n+1}-\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}(*)$ und ebenso $0=\sum_{k=0}^{n-1} \frac{a_{(n-1)-k}}{k+1}=\sum_{k=1}^{n} \frac{a_{n-k}}{k}=\sum_{k=1}^{n-1} \frac{a_{n-k}}{k}+\frac{a_{0}}{n} \Leftrightarrow \frac{1}{n}=\sum_{k=1}^{n-1} \frac{a_{n-k}}{k}$. Dies führt auf $\frac{1}{n+1}=\sum_{k=1}^{n-1}\left(\frac{a_{n-k}}{k} \cdot \frac{n}{n+1}\right)$ und wegen $n>k \Leftrightarrow \frac{n}{n+1}>\frac{k}{k+1} \Leftrightarrow \frac{n}{k(n+1)}>\frac{1}{k+1}$ auf $\frac{1}{n+1}>\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}$. Mit (*) ergibt sich $a_{n}>\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}-\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}=0$. Mit vollständiger Induktion gilt daher $a_{n}>0$ für alle $n \geq 1$.
|
| 14 |
+
|
| 15 |
+
## Aufgabe 2
|
| 16 |
+
|
| 17 |
+
Für ein konvexes Fünfeck $A B C D E$ gilt
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\varangle B A C=\varangle C A D=\varangle D A E \quad \text { sowie } \quad \varangle C B A=\varangle D C A=\varangle E D A .
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Der Schnittpunkt der Diagonalen BD und CE wird mit $P$ bezeichnet.
|
| 24 |
+
M an beweise, dass die Gerade $A P$ durch den Mittelpunkt der Seite $C D$ verläuft.
|
| 25 |
+
|
| 26 |
+
Lösung: W egen jeweils zweier gleicher Winkel sind die Dreiecke $A B C, A C D$ und $A D E$ ähnlich und wegen der Lage der W inkel gilt $\frac{|B C|}{|C D|}=\frac{|C D|}{|D E|}$. W eil gilt $\varangle D C B=\varangle E D C$ (Summe zweier gleicher Winkel), sind auch die Dreiecke $B C D$ und $C D E$ ähnlich. Daraus folgt $\varangle B D C=\varangle C E D=: \varepsilon$ sowie $\varangle C B D=\varangle D C E=: \delta$. Somit sind die Dreiecke $B C D$ und $D P C$ ähnlich, woraus $\varangle A E P=\gamma-\varepsilon=\varangle A D P$ folgt. Daher ist $A P D E$ ein Sehnenviereck. Völlig analog folgt, dass auch $A B C P$ ein Sehnenviereck ist. In der Figur sind die sich daraus ergebenden Winkel mit den Scheiteln $A$ und $P$ eingetragen. Insbesondere folgt daraus, dass die Dreiecke $A F D$ und $P F D$ sowie $A C F$ und $P C F$ ähnlich sind, wobei $F$ der Schnittpunkt von $A P$ und $C D$ ist. A us diesen
|
| 27 |
+
|
| 28 |
+
Ähnlichkeiten folgt $\frac{|D F|}{|F P|}=\frac{|A F|}{|D F|}$ sowie $\frac{|C F|}{|F P|}=\frac{|A F|}{|C F|}$, woraus sich einerseits $|A F| \cdot|F P|=|D F|^{2}$, andererseits $|A F| \cdot|F P|=|C F|^{2}$ ergibt. Dies liefert $|C F|=|D F|$, was zu beweisen war.
|
| 29 |
+
Anmerkung: Eine weitere, sehr elegante Lösung ergibt sich bei Verwendung des Satzes von Ceva im Dreieck $A C D$.
|
| 30 |
+
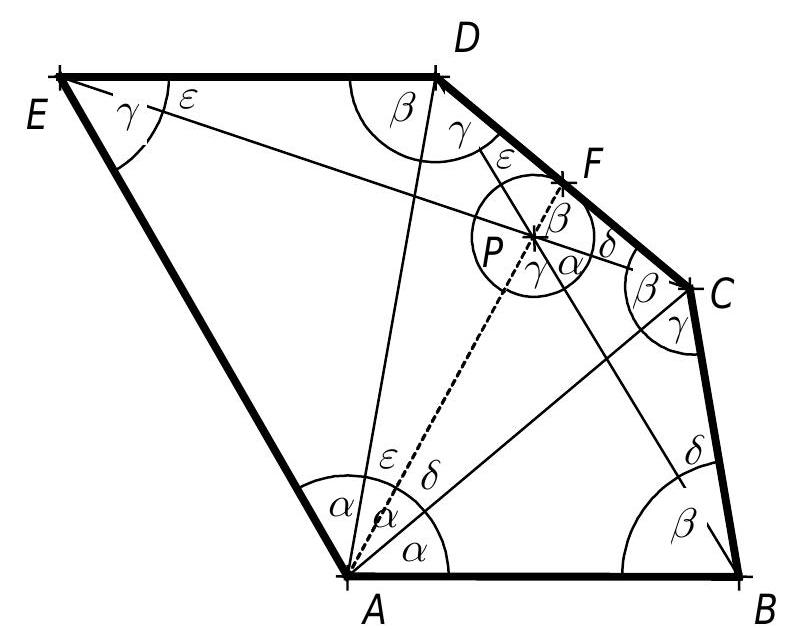
|
| 31 |
+
|
| 32 |
+
## Aufgabe 3
|
| 33 |
+
|
| 34 |
+
Für jede reelle Zahl $x$ mit $0<x<1$ sei $y \in] 0 ; 1[$ diejenige Zahl, deren $n$-te Nachkommastelle die (2n)-te Nachkommastelle von $x$ ist. $M$ an beweise: Wenn $x$ rational ist, dann ist auch $y$ rational.
|
| 35 |
+
|
| 36 |
+
Lösung: Eine rationale Zahl besitzt eine abbrechende oder eine periodische Dezimalbruchentwicklung. Eine abbrechende Dezimalbruchentwicklung lässt sich durch Anhängen von Nullen ins U nendliche fortsetzen und entspricht daher einer periodischen Dezimalbruchentwicklung mit der Periodenlänge 1.
|
| 37 |
+
Im Folgenden betrachten wir nur die Stellen hinter einer evtl. auftretenden
|
| 38 |
+
Vorperiode der Länge $v$. Die erste Zweierpotenz größer als $v$ sei mit $2^{s}$ bezeichnet, die P eriodenlänge des Dezimalbruchs mit $d$.
|
| 39 |
+
W eil es nur endlich viele Restklassen mod $d$ gibt, existieren zwei Zahlen $2^{t}$ und $2^{t+m}$, die den gleichen Rest $r$ mod $d$ lassen, d.h. $2^{t} \equiv 2^{t+m} \bmod d$ mit $m \geq 1$. Dies bedeutet, dass die $t$. und die $(t+m)$. Nachkommastelle von $y$ gleich sind.
|
| 40 |
+
Dann gilt aber auch $2 \cdot 2^{t} \equiv 2 \cdot 2^{t+m} \bmod d \Leftrightarrow 2^{t+1} \equiv 2^{t+m+1} \operatorname{modd}$, d.h. die ( $t+1$ ). und die $(t+m+1)$. Nachkommastelle von $y$ sind gleich. Entsprechend sind alle $(t+k)$. und $(t+m+k)$. Nachkommastellen von $y$ jeweils gleich $(0 \leq k \leq m)$. Daher ist $y$ periodisch mit der P eriodenlänge $m$.
|
| 41 |
+
A uch y kann eine Vorperiode - höchstens von der Länge $s$ - besitzen.
|
| 42 |
+
Diese Überlegungen sind unabhängig von der Basis $b \geq 2$ des Zahlsystems.
|
| 43 |
+
Anmerkung: Der bloße Hinweis auf das DIRICHLETsche Schubfachprinzip reicht nicht aus. Ein Zugang mit dem kleinen Satz von Fermat liefert genauere Informationen z.B. über die P eriodenlänge von $y$.
|
| 44 |
+
|
Germany_TST/md/de-2008-loes_awkl1_08.md
ADDED
|
@@ -0,0 +1,67 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwetthewerb zur Intemationalen Mathematik-Olympiade
|
| 2 |
+
|
| 3 |
+
## lösungen zur 1. IMO-Auswahlklausur 2008
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Man zeige, dass es in der Dezimaldarstellung von $\sqrt[3]{3}$ zwischen der 1000000. und 3141592. Nachkommastelle eine von 2 verschiedene Ziffer gibt.
|
| 8 |
+
|
| 9 |
+
Lösung: Hätte $\sqrt[3]{3}$ zwischen der 1000000. und 3141592. Nachkommastelle nur die Ziffer 2, wäre mit $a=\left[10^{1000000} \sqrt[3]{3}\right]<10^{1000001}$ also $\left|\sqrt[3]{3}-(a+2 / 9) 10^{-1000000}\right|<10^{-3141592}$ oder äquivalent
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\left|\sqrt[3]{3\left(9 \cdot 10^{1000000}\right)^{3}}-(9 a+2)\right|<9 \cdot 10^{-2141592}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Nun ist sicher $(9 a+2)^{3} \neq 3\left(9 \cdot 10^{1000000}\right)^{3}$, da die rechte Seite den Primfaktor 3 in nicht durch 3 teilbarer Vielfachheit enthält. Allgemein gilt für $m, n \in \mathbb{N}$ mit $m \neq n^{3}$ :
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
|\sqrt[3]{m}-n| \geq \frac{\left|m-n^{3}\right|}{\sqrt[3]{m^{2}}+\sqrt[3]{m} n+n^{2}} \geq \frac{1}{3 \cdot(\max (\sqrt[3]{m}, n))^{2}}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Daraus folgt aber - im Widerspruch zu (1):
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\left|\sqrt[3]{3\left(9 \cdot 10^{1000000}\right)^{3}}-(9 a+2)\right|>\frac{1}{3\left(10^{1000001}\right)^{2}}>10^{-2000003}
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
Bemerkungen:
|
| 28 |
+
|
| 29 |
+
1. Man konnte als bekannt voraussetzen, dass $\sqrt[3]{3}$ irrational ist.
|
| 30 |
+
2. Viele Teilnehmer haben versucht, ziffernweise zu argumentieren, dass die Ziffern von $\sqrt[3]{3}$ nach Erheben in die dritte Potenz nicht alle Null sein können, indem man $\sqrt[3]{3}$ in der Dezimaldarstellung als eine Potenzreihe $\sqrt[3]{3}=1+a_{1} x+a_{2} x^{2}+\ldots$ mit $a_{1}, a_{2}, \ldots \in\{0,1, \ldots, 9\}$ und $x=1 / 10$ betrachtet hat. Hier kann man leicht Überträge übersehen: Tatsächlich ist nämlich $\sqrt[3]{3}=1,442 \ldots$, und $\left(1+4 x+4 x^{2}+\right.$ $\left.2 x^{3}+\ldots\right)^{3}=1+12 x+60 x^{2}+166 x^{3}+\ldots$.
|
| 31 |
+
3. Manche Teilnehmer haben die binomischen Reihe $(1+x)^{1 / 3}=\sum_{k=0}^{\infty}\binom{1 / 3}{k} x^{k}$ mit $\binom{1 / 3}{k}=\frac{1}{3} \cdot\left(\frac{1}{3}-1\right)\left(\frac{1}{3}-2\right) \cdots\left(\frac{1}{3}-k+1\right) / k!$ für $k \in \mathbb{N}_{0}$, die für $|x| \leq 1$ konvergiert, an der Stelle $x=2$ betrachtet - hier konvergiert die Reihe nicht.
|
| 32 |
+
|
| 33 |
+
## Aufgabe 2
|
| 34 |
+
|
| 35 |
+
Es sei $A B C D$ ein gleichschenkliges Trapez mit $A B \| C D$ und $\overline{B C}=\overline{A D}$. Die Parallele zu $A D$ durch $B$ treffe die Senkrechte zu $A D$ durch $D$ im Punkt $X$. Ferner treffe die durch $A$ gezogene Parallele zu $B D$ die Senkrechte zu $B D$ durch $D$ im Punkt $Y$. Man beweise, dass die Punkte $C, X, D$ und $Y$ auf einem gemeinsamen Kreis liegen.
|
| 36 |
+
Erste Lösung. Es sei $M$ der Mittelpunkt der Strecke $A B$. Die durch $M$ gezogene Parallele zu $D Y$ treffe $B D$ in $G$ und die durch $A$ gezogene Parallele zu $B D$ in $H$. Aus $\overline{A M}=\overline{M B}$ schließt man leicht $\overline{H M}=\overline{M G}$, und da $D Y \perp D B$ vorausgesetzt ist, ist das Viereck $D G H Y$ ein Rechteck. Beides zusammen lehrt $\overline{D M}=\overline{M Y}$, und in gleicher
|
| 37 |
+
|
| 38 |
+
Weise zeigt man $\overline{D M}=\overline{M X}$. Da das Trapez $A B C D$ gleichschenklig ist, gilt ferner $\overline{D M}=\overline{M C}$, und aus der Kombination der drei letzten Gleichungen ergibt sich sofort, daß die vier Punkte $C, D, X, Y$ auf einem gemeinsamen Kreis um $M$ liegen.
|
| 39 |
+
Zweite Lösung. Man ergänze das Dreieck $D A B$ zu einem Parallelogramm $D A Z B$. Nach Konstruktion von $X$ und $Y$ liegen diese beiden Punkte auf $Z B$ bzw. $Z A$, und es gilt $\varangle D X Z=\varangle Z Y D=90^{\circ}$. Der Satz des Thales liefert nunmehr, daß $X$ und $Y$ auf dem Kreis mit Durchmesser $D Z$ liegen. Der Mittelpunkt dieses Kreises ist gleichzeitig der Mittelpunkt der Strecke $D Z$ und, da sich in Parallelogrammen die Diagonalen gegenseitig halbieren, fällt dieser mit dem Mittelpunkt der Strecke $A B$ zusammen. Nachdem nun das Trapez $A B C D$ als gleichschenklig vorausgesetzt ist, gilt folglich $\overline{D M}=\overline{M C}$, womit gezeigt ist, daß auch der Punkt $C$ auf dem vorhin betrachteten Kreis liegt.
|
| 40 |
+
Dritte Lösung (skizziert, nach einer Idee von Andreas Gross). Es sei $F=(A B D)$ der Flächeninhalt des Dreiecks $A B D$. Wir ziehen um $D$ einen Kreis $\omega$ mit Radius $\sqrt{2 F}$ und invertieren an diesem. Kundige können sich leicht überlegen, daß $\overline{D X^{\prime}}=\overline{D A}$ sowie $\overline{D Y^{\prime}}=\overline{D B}$ gilt und daß hieraus $\left(D X^{\prime} Y^{\prime}\right)=F$ folgt. Es sei nun $C^{*}$ der Schnittpunkt der Geraden $D C$ und $X^{\prime} Y^{\prime}$ sowie $H$ der Fußpunkt des aus $D$ auf $A B$ gefällten Lotes. Nun haben die Punkte $X^{\prime}, Y^{\prime}$ von der Geraden $C D$ die Abstände $\overline{A H}, \overline{B H}$, und hieraus ergibt sich $\left(D X^{\prime} Y^{\prime}\right)=\left(D C^{*} Y^{\prime}\right)-\left(D C^{*} X^{\prime}\right)=\frac{1}{2} \overline{D C^{*}} \cdot(\overline{H B}-\overline{A H})=\frac{1}{2} \overline{D C^{*}} \cdot \overline{D C}$. Im Zusammenhang mit einer bereits angegebenen Gleichung folgt hieraus $\overline{D C^{*}} \cdot \overline{D C}=2 F$, woraus sich mit Hilfe einer kleinen Lagebetrachtung $C^{*}=C^{\prime}$ ergibt. Demnach liegen die drei Punkte $C^{\prime}, X^{\prime}, Y^{\prime}$ auf einer gemeinsamen Geraden, und von dieser überzeugt man sich leicht, daß sie nicht durch $D$ gehen kann. Dies impliziert die Behauptung.
|
| 41 |
+
|
| 42 |
+
## Aufgabe 3
|
| 43 |
+
|
| 44 |
+
Man zeige, dass es eine ganze Zahl $a$ gibt, für die $a^{3}-36 a^{2}+51 a-97$ ein Vielfaches von $3^{2008}$ ist.
|
| 45 |
+
|
| 46 |
+
1. Lösung: Definiere das Polynom $P(x)=x^{3}-36 x^{2}+51 x-97$. Ausgehend von $P_{0}(x)=\frac{1}{81} P(9 x+1)=9 x^{3}-33 x^{2}-2 x-1$, definiere rekursiv Polynome $P_{k}(x)=$ $3 a_{k} x^{3}+3 b_{k} x^{2}+c_{k} x+d_{k}$ mit ganzen Zahlen $a_{k}, b_{k}, c_{k}, d_{k}$, wobei $c_{k}$ nicht durch 3 teilbar ist, und $P_{k+1}(x)=\frac{1}{3} P_{k}\left(3 x+\varepsilon_{k}\right)$ mit $\varepsilon_{k} \in\{-1,0,1\}$ für alle $k$ : Da $c_{k}$ nicht durch 3 teilbar ist, kann man $\varepsilon_{k}$ so wählen, dass $\varepsilon_{k} c_{k}+d_{k}$ durch 3 teilbar ist; dann ist $\frac{1}{3} P_{k}\left(3 x+\varepsilon_{k}\right)=3 a_{k+1} x^{3}+3 b_{k+1} x^{2}+c_{k+1}+d_{k+1}$ mit $a_{k+1}=9 a_{k}, b_{k+1}=9 \varepsilon_{k} a_{k}+3 b_{k}$, $c_{k+1}=3\left(3 \varepsilon_{k}^{2} a_{k}+2 \varepsilon_{k} b_{k}\right)+c_{k}, d_{k+1}=\varepsilon_{k}^{3} a_{k}+\varepsilon_{k}^{2} b_{k}+\left(\varepsilon_{k} c_{k}+d_{k}\right) / 3$, somit ist auch $c_{k+1}$ nicht durch 3 teilbar.
|
| 47 |
+
Setzt man $x_{2004}=0$ und rekursiv $x_{k}=3 x_{k+1}+\varepsilon_{k}$, also $P_{k}\left(x_{k}\right)=3 P_{k}\left(x_{k+1}\right)$ für $k=2003, \ldots, 0$, so ist für $a=9 x_{0}+1$ die Zahl $P(a)=81 \cdot 3^{2004} P_{2004}\left(x_{2004}\right)$ ein Vielfaches von $3^{2008}$.
|
| 48 |
+
2. Lösung: Definiere das Polynom $P(x)=x^{3}-36 x^{2}+51 x-97$. Für $k \geq 4$ werden induktiv ganze Zahlen $a_{k}$ mit $a_{k} \equiv 1 \bmod 9$ und $3^{k} \mid P\left(a_{k}\right)$ konstruiert; die Aufgabenstellung erfüllt dann $a=a_{2008}$ :
|
| 49 |
+
Verankerung $k=4$ : Für $a_{4}=1$ ist $3^{4} \mid P\left(a_{4}\right)$.
|
| 50 |
+
Induktionsschritt $k \rightarrow k+1$ : Für $k \geq 4$ ist $2 k-3 \geq k+1$ und $3 k-6>k+1$, also für
|
| 51 |
+
alle ganzzahligen $x$ :
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\begin{aligned}
|
| 55 |
+
P\left(x+3^{k-2}\right)-P(x) & \equiv 3^{k-1} x^{2}+3^{2 k-3} x+3^{3 k-6}-36\left(2 \cdot 3^{k-2} x+3^{2 k-4}\right)+51 \cdot 3^{k-2} \\
|
| 56 |
+
& \equiv 3^{k-1}\left(x^{2}-24 x+17\right) \bmod 3^{k+1}
|
| 57 |
+
\end{aligned}
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Für $x \equiv 1 \bmod 9$ ist $x^{2}-24 x+17 \equiv 1-24+17 \equiv 3 \bmod 9$. Wegen $k \geq 4$ ist auch $x \equiv x+3^{k-2} \bmod 9$. Daher enthält die Differenz $3^{k-1}\left(x^{2}-24 x+17\right)$ den Primfaktor 3 genau $k$-mal, also ist $P(u)$ für $u=a_{k}$ oder $u=a_{k}+3^{k-2}$ oder $u=a_{k}+2 \cdot 3^{k-2}$ durch $3^{k+1}$ teilbar, setze $a_{k+1}$ auf diesen Wert von $u$. Nach Konstruktion ist $a_{k+1} \equiv 1 \bmod 9$.
|
| 61 |
+
|
| 62 |
+
Bemerkungen:
|
| 63 |
+
|
| 64 |
+
1. Manche Teilnehmer versuchten, mittels Schubfachprinzip zu argumentieren: Wäre $P(m) \not \equiv P(n) \bmod 3^{2008}$ für $m \not \equiv n \bmod 3^{2008}$, gäbe es zwangsläufig auch ein $a \operatorname{mit} P(a) \equiv 0 \bmod 3^{2008}$. Die zweite Lösung zeigt aber, dass $P\left(x+3^{2006}\right) \equiv$ $P(x) \bmod 3^{2008}$.
|
| 65 |
+
2. Ist $P$ ein Polynom mit ganzzahligen Koeffizienten und $p$ eine Primzahl, hat die Gleichung $P(a) \equiv 0 \bmod p^{m}$ eine Lösung für alle $m \geq 0$, wenn es ein $u$ mit $P(u) \equiv 0 \bmod p$ und $P^{\prime}(u) \not \equiv 0 \bmod p$ gibt (Hensel-Lemma, siehe E. J. Barbeau, Polynomials, Springer-Verlag New York 1989, Seite 100), hierbei ist für ein Polynom $P(x)=b_{n} x^{n}+\ldots b_{0}$ die Ableitung $P^{\prime}(x)=n b_{n} x^{n-1}+\ldots+b_{1}$. Für $P(x)=x^{3}-36 x^{2}+51 x-97$ ist jedoch $3 \mid P^{\prime}(a)$ für alle $a$, so dass das HenselLemma hier nicht anwendbar ist. Es führt jedoch für $Q(x)=P(3 x+1) / 27=$ $x^{3}-11 x^{2}-2 x-3$ an der Stelle $u=0$ zum Ziel.
|
| 66 |
+
3. Die Aufgabe ist nicht für alle Polynome lösbar: es gibt zwar ganze Zahlen $a$ mit $3 \mid 1+a+a^{2}$, aber keine ganze Zahl mit $9 \mid 1+a+a^{2}$.
|
| 67 |
+
4. Die ersten Werte für die Zahlen $\varepsilon_{k}$ in der ersten Lösung lauten $1,0,0,1,-1$, $0,0,1,1,1,-1,-1,0,-1,1,-1,-1,0,1-$ es ist also keine (offensichtliche) Regelmäßigkeit erkennbar.
|
Germany_TST/md/de-2008-loes_awkl2_08.md
ADDED
|
@@ -0,0 +1,54 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Intemationalen Mathematik-Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. IMO-Auswahlklausur 2008
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Man bestimme alle positiven ganzen Zahlen $k$ und $n$ mit folgender Eigenschaft:
|
| 8 |
+
Die Zahl $k^{4}+n^{2}$ ist ohne Rest durch die Zahl $7^{k}-3^{n}$ teilbar.
|
| 9 |
+
|
| 10 |
+
Lösung: Das einzige Lösungspaar ist $(k ; n)=(2 ; 4)$. Für jedes Lösungspaar sind $k^{4}+n^{2}$ und $7^{k}-3^{n}$ ganzzahlig, wobei $7^{k}-3^{n}$ nicht notwendig positiv sein muss. Weil $7^{k}$ und $3^{n}$ ungerade sind, gilt $2 \mid 7^{k}-3^{n}$ und daher $2 \mid k^{4}+n^{2}$. Deshalb müssen $k$ und $n$ entweder beide gerade oder beide ungerade sein. Im letzten Fall gilt $k^{4}+n^{2} \equiv 2 \bmod 4$, wogegen $7^{k}-3^{n} \equiv(-1)^{k}-(-1)^{n} \equiv 0 \bmod 4$ ist. Daher sind $k$ und $n$ beide gerade und wir setzen $k=2 a$ bzw. $n=2 b$ mit positiven ganzen Zahlen $a, b$. Es folgt $7^{2 a}-3^{2 b} \mid(2 a)^{4}+(2 b)^{2}$ und weiter $49^{a}-9^{b} \mid 16 a^{4}+4 b^{2}$. Nun ist $49^{a}-9^{b} \equiv 1^{a}-1^{b} \equiv 0 \bmod 8$, so dass auch $16 a^{4}+4 b^{2}$ durch 8 teilbar sein muss.
|
| 11 |
+
|
| 12 |
+
Deshalb muss $b$ gerade sein und ist als $b=2 c$ mit einer geeigneten positiven ganzen Zahl c darstellbar. Es folgt $7^{2 a}-9^{2 c}=\left(7^{a}+9^{c}\right)\left(7^{a}-9^{c}\right) \mid 16\left(a^{4}+c^{2}\right)$. Weil stets $7^{a} \neq 9^{c}$ gilt und beide Potenzen ungerade sind, ist $\left|7^{a}-9^{c}\right| \geq 2$, so dass $7^{a}+9^{c} \mid 8\left(a^{4}+c^{2}\right)$ gelten muss.
|
| 13 |
+
Lemma 1: Für alle $a \geq 4$ ist $7^{a}>8 a^{4}$.
|
| 14 |
+
Beweis durch vollständige Induktion nach $a$ :
|
| 15 |
+
Für $a=4$ ist $2401=7^{4}>8 \cdot 4^{4}=2^{11}=2048$ wahr. Nun sei $7^{a}>8 a^{4}$ vorausgesetzt.
|
| 16 |
+
Dann ist $7^{a+1}=7 \cdot 7^{a}>7 \cdot 8 a^{4}=8(a+1)^{4} \cdot \frac{7 a^{4}}{(a+1)^{4}}>8(a+1)^{4} \cdot 7 \cdot\left(\frac{4}{5}\right)^{4}>8(a+1)^{4}$.
|
| 17 |
+
Lemma 2: Für alle $c \geq 1$ ist $9^{c}>8 c^{2}$.
|
| 18 |
+
Beweis durch vollständige Induktion nach $c$ :
|
| 19 |
+
Für $c=1$ ist $9>8$ wahr. Nun sei $9^{c}>8 c^{2}$ vorausgesetzt. Dann ist
|
| 20 |
+
$9^{c+1}=9 \cdot 9^{c}>9 \cdot 8 c^{2}=8(c+1)^{2} \cdot \frac{9 c^{2}}{(c+1)^{2}}>8(c+1)^{2} \cdot 9 \cdot\left(\frac{1}{2}\right)^{2}>8(c+1)^{2}$.
|
| 21 |
+
Aus den Lemmata folgt, dass für $a \geq 4$ wegen $7^{a}+9^{c}>8\left(a^{4}+c^{2}\right)$ keine verlangten Zahlen $k$ und $n$ existieren. Also müssen nur noch $a=1,2,3$ untersucht werden.
|
| 22 |
+
|
| 23 |
+
Lemma 3: Für alle $c \geq 3$ ist $9^{c}>305+8 c^{2}$.
|
| 24 |
+
Beweis durch vollständige Induktion nach $c$ :
|
| 25 |
+
Für $c=3$ ist $9^{3}=729>305+8 \cdot 3^{2}=377$ wahr. Nun sei $9^{c}>305+8 c^{2}$ vorausgesetzt. Dann ist $9^{c+1}>9\left(305+8 c^{2}\right)=305+8 \cdot\left(305+9 c^{2}\right)$. Wegen
|
| 26 |
+
$305+9 c^{2}=(c+1)^{2}+8 c^{2}-2 c+304>(c+1)^{2}+c(c-2)>(c+1)^{2}$ für $c>2$ folgt die Behauptung.
|
| 27 |
+
Fall 1: $a=1$. Für $c=1$ gilt $49-81=-32 \mid 32=16(1+1)$. Daher ist $(k ; n)=(2 ; 4)$ eine Lösung. Für $c=2$ gilt $7+81=88 \nmid 8(1+4)=40$. Für $c>2$ muss $7+9^{c} \leq 8+8 c^{2}$ gelten, also $9^{c}<1+8 c^{2}$. Dies widerspricht Lemma 3.
|
| 28 |
+
Fall 2: $a=2$. Für $c=1$ gilt $7^{2}+9^{1}=58 X \quad 8\left(2^{4}+1^{2}\right)=136$. Für $c=2$ gilt $49+81=130 \nmid 8(16+4)=160$. Für $c>2$ muss $49+9^{c} \leq 8\left(16+c^{2}\right)$ gelten, also $9^{c} \leq 79+8 c^{2}$. Dies widerspricht Lemma 3.
|
| 29 |
+
Fall 3: $a=3$. Für $c=1$ gilt $343+9=352 \chi 656=8\left(3^{4}+1\right)$. Für $c=2$ gilt $343+81=424 \chi \quad 680=8\left(3^{4}+4\right)$. Für $c>2$ muss $343+9^{c} \leq 8\left(81+c^{2}\right)$ gelten, also $9^{c} \leq 305+8 c^{2}$. Dies widerspricht Lemma 3.
|
| 30 |
+
|
| 31 |
+
## Aufgabe 2
|
| 32 |
+
|
| 33 |
+
Gegeben ist ein (allgemeines) Trapez $A B C D$, dessen Diagonalen sich im Punkt $P$ schneiden. Ein Punkt $Q$ liegt so zwischen den Parallelen $A B$ und $D C$, dass $\varangle A Q B=\varangle C Q D$ gilt und die Gerade $B C$ zwischen $P$ und $Q$ verläuft.
|
| 34 |
+
Man beweise, dass $\varangle D Q P=\varangle B A Q$ gilt.
|
| 35 |
+
|
| 36 |
+
Lösung: Wegen $A B \| C D$ bildet die zentrische Streckung $\sigma$ am Schnittpunkt $P$ der Diagonalen mit Streckfaktor $k=-\frac{|C D|}{|A B|}=-\frac{|C P|}{|A P|}=-\frac{|D P|}{|B P|}$ den Punkt $C$ auf $A$ und $D$ auf $B$ ab. Es sei $Q^{\prime}$ der Bildpunkt von $Q$ unter $\boldsymbol{\sigma}$. Weil
|
| 37 |
+
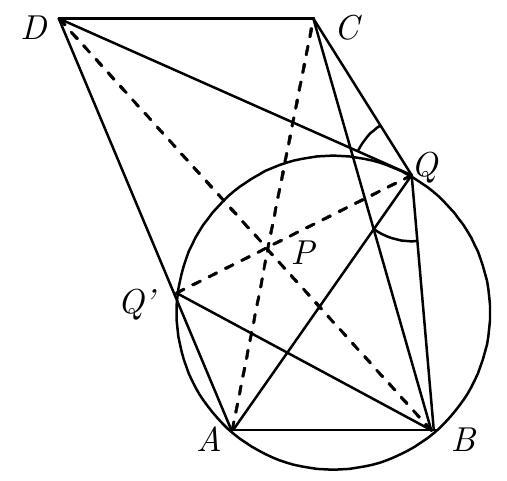
|
| 38 |
+
das Dreieck $D Q C$ unter $\sigma$ auf das Dreieck $B Q^{\prime} A$ abgebildet wird, sind beide Dreiecke ähnlich und mit der Voraussetzung gilt $\varangle A Q^{\prime} B=\varangle C Q D=\varangle A Q B$. Somit liegen $A, B, Q$ und $Q^{\prime}$ auf einem Kreis und es gilt $\varangle B A Q=\varangle B Q^{\prime} Q$. Das Dreieck $B Q^{\prime} Q$ wird unter $\sigma$ auf das Dreieck $D Q Q^{\prime}$ abgebildet. Daher sind diese Dreiecke ähnlich und es folgt, da $P, Q$ und $Q^{\prime}$ auf einer Geraden liegen, $\varangle B Q^{\prime} Q=\varangle D Q Q^{\prime}=\varangle D Q P$.
|
| 39 |
+
Also ist $\varangle B A Q=\varangle B Q^{\prime} Q=\varangle D Q P$, was zu beweisen war.
|
| 40 |
+
|
| 41 |
+
## Aufgabe 3
|
| 42 |
+
|
| 43 |
+
Ein Quadrat wird so in $n>1$ Rechtecke zerlegt, dass die Seiten der Rechtecke parallel zu den Seiten des gegebenen Quadrats verlaufen. Jede Gerade, die parallel zu einer der Seiten des Quadrats verläuft und das Innere des Quadrats schneidet, soll dabei auch im Inneren wenigstens eines der Rechtecke verlaufen.
|
| 44 |
+
|
| 45 |
+
Man beweise, dass es dann in dieser Zerlegung stets ein Rechteck gibt, das keinen Punkt mit dem Rand des Quadrats gemeinsam hat.
|
| 46 |
+
|
| 47 |
+
Lösung: Wir beweisen die Kontraposition und nehmen dazu an, dass jedes Rechteck der Zerlegung mindestens einen Punkt mit dem Rand des Quadrates gemeinsam hat. Nach den Voraussetzungen hat es dann wenigstens eine seiner Seiten mit dem Rand des Quadrates gemeinsam. Daher lässt sich der Rand des Quadrates abschnittweise eindeutig den Rechtecken der Zerlegung zuordnen. Zwei nicht zusammenhängende Abschnitte können nicht zu demselben Rechteck gehören; sie müssten sonst einander gegenüberliegen und auf den anderen Seiten dieses Rechtecks schneiden Geraden das Innere des Quadrates, ohne im Inneren eines Rechtecks zu verlaufen.
|
| 48 |
+
|
| 49 |
+
Die Anzahl $n$ dieser Abschnitte stimmt also mit der Anzahl $n$ der Rechtecke überein. In den $n$ Endpunkten der Abschnitte treffen auf dem Rand des Quadrates jeweils zwei Rechtecke zusammen und haben dort jeweils eine Ecke. Vier weitere Ecken der Rechtecke fallen mit den Ecken des Quadrates zusammen, so dass insgesamt $2 n+4$ Rechtecksecken auf dem Rand des Quadrates liegen. Somit verbleiben $4 n-(2 n+4)=2 n-4$ Ecken für das Innere des Quadrates. Nun betrachten wir einen der $n$ Punkte auf dem Rand des Quadrates, in denen zwei Rechtecke zusammenstoßen. Die Gerade senkrecht zur jeweiligen Quadratseite durch diesen Punkt $P$
|
| 50 |
+

|
| 51 |
+
verläuft im Inneren des Quadrats zunächst auf je einer Seite der beiden Rechtecke. Damit diese Gerade innerhalb des Quadrates auch im Inneren eines Rechtecks verlaufen kann, muss sie eine Rechtecksseite schneiden, die parallel zur Quadratseite verläuft, von der wir ausgegangen sind. In diesem Verzweigungspunkt $Q$ haben die zwei Rechtecke, deren Rand die Gerade vorher war (das müssen nicht mehr die beiden Rechtecke mit Eckpunkt $P$ sein), jeweils einen Eckpunkt. Ein solcher Punkt $Q$ existiert für jeden Ausgangspunkt $P$, und zwei verschiedene Ausgangspunkte können nicht denselben Verzweigungspunkt $Q$ haben. Daher müssen wenigstens $2 n$ Rechtecksecken im Inneren des Quadrates liegen, im Widerspruch zur oben bestimmten Höchstzahl $2 n-4$. Also gibt es stets ein Rechteck, das keinen Punkt mit dem Rand des Quadrats gemeinsam hat.
|
| 52 |
+
|
| 53 |
+
Anmerkungen: Das äußere Rechteck wurde nur deshalb zum Quadrat erhoben, damit die Abfassung der Lösung einfacher ist. Die häufig vorgelegten Lösungen über die Konstruktion von unmöglichen Fällen ließen leicht Lücken entstehen, wenn mit der gegenseitigen Lage von Rechtecken oder dem Verlauf von Pfaden argumentiert wurde.
|
| 54 |
+
|
Germany_TST/md/de-2009-loes_awkl1_09.md
ADDED
|
@@ -0,0 +1,30 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## ம̈sungen zur 1. IMO-Auswahlklausur 2009
|
| 2 |
+
|
| 3 |
+
## Aufgabe 1
|
| 4 |
+
|
| 5 |
+
Es sei $p>7$ eine Primzahl, die bei Division durch 6 den Rest 1 lässt. Setze $m=2^{p}-1$. Man beweise, dass $2^{m-1}-1$ ohne Rest durch $127 m$ teilbar ist.
|
| 6 |
+
Lösung: Die Lösung besteht aus drei Schritten:
|
| 7 |
+
|
| 8 |
+
1. $2^{m-1}-1$ ist durch 127 teilbar.
|
| 9 |
+
2. $2^{m-1}-1$ ist durch $m$ teilbar.
|
| 10 |
+
3. 127 und $m$ sind teilerfremd.
|
| 11 |
+
|
| 12 |
+
Zu 1: Es gilt $2^{6} \equiv 1 \bmod 7$. Aus $p \equiv 1 \bmod 6$ folgt $2^{p} \equiv 2 \bmod 7$, also $7 \mid m-1$. Mit $2^{7} \equiv 1 \bmod 127$ folgt daraus $2^{m-1} \equiv 1 \bmod 127$.
|
| 13 |
+
Zu 2 : Es gilt $2^{p} \equiv 2 \bmod p$ (kleiner Satz von Fermat), d. h. $p \mid m-1$. Aus $2^{p} \equiv 1 \bmod m$ folgt damit $2^{m-1} \equiv 1 \bmod m$.
|
| 14 |
+
Zu 3 : Es gilt $2^{p} \equiv 1 \bmod 127$ genau dann, wenn $p$ durch 7 teilbar ist (schreibe $p=7 k+r$ mit $0 \leq r<7$ und verwende $2^{7} \equiv 1 \bmod 127$ ). Wegen $p>7$ ist das nicht der Fall, also ist $m$ nicht durch 127 teilbar, und da 127 eine Primzahl ist, sind 127 und $m$ teilerfremd.
|
| 15 |
+
Bemerkungen: Die Beziehung $\operatorname{ggT}\left(2^{a}-1,2^{b}-1\right)=2^{\operatorname{ggT}(a, b)}-1$ erlaubt eine Verkürzung der Lösung. Statt Kongruenzrechnung kann teilweise auch die Teilbarkeitsaussage $a-b \mid a^{n}-b^{n}$ verwendet werden. Einige Teilnehmer verwendeten eine fehlerhafte Fassung des Satzes von Euler-Fermat: er lautet $a^{\phi(m)} \equiv 1 \bmod m$ für $\operatorname{ggT}(a, m)=1$ doch nur für $m$ Primzahl gilt $\phi(m)=m-1$.
|
| 16 |
+
|
| 17 |
+
## Aufgabe 2
|
| 18 |
+
|
| 19 |
+
Das Dreieck $A B C$ sei bei $A$ rechtwinklig. Es bezeichne $M$ den Mittelpunkt der Strecke $B C$. Der Punkt $D$ liege auf der Seite $A C$ und erfülle $\overline{A D}=\overline{A M}$. Der von $C$ verschiedene Schnittpunkt der Umkreise der Dreiecke $A M C$ und $B D C$ heiße $P$. Man beweise, dass $C P$ den bei $C$ gelegenen Winkel des Dreiecks $A B C$ halbiert.
|
| 20 |
+
|
| 21 |
+
Lösung 1: Der Winkel $\varangle P D C$ ist einerseits Nebenwinkel von $\varangle A D P$, andererseits liegt er im Sehnenviereck $B P D C$ dem Winkel $\varangle C B P$ gegenüber. Folglich $\varangle A D P=$ $\varangle C B P$. Analog ist der Winkel $\varangle C M P$ Nebenwinkel von $\varangle P M B$ und liegt im Sehnenviereck $A P M C$ dem Winkel $\varangle P A C$ gegenüber, also $\varangle P M B=\varangle P A C$. Die Dreiecke $P B M$ und $P D A$ stimmen somit in den Innenwinkeln bei $B$ und $D$ sowie bei $M$ und $A$ überein, außerdem ist nach Voraussetzung $\overline{A D}=\overline{A M}=\overline{M B}$ (die letzte Gleichheit ergibt sich aus dem Satz des Thales). Nach dem Kongruenzsatz wsw sind die Dreicke $P B M$ und $P D A$ kongruent, insbesondere sind ihre von $P$ ausgehenden Höhen gleich lang. Sie sind aber die Lote von $P$ auf die Dreiecksseiten $C A$ bzw. $C B$, also liegt $P$ auf der Winkelhalbierenden.
|
| 22 |
+
Lösung 2 (Skizze, nach M. Krebs): Bezeichne mit $m_{X Y}$ die Mittelsenkrechte der Strecke $X Y$. Dann sind sowohl $m_{C D}$ und $m_{C A}$ also auch $m_{C M}$ und $m_{C B}$ Paare paralleler Geraden im Abstand $\frac{1}{4} \overline{B C}$, also begrenzen sie eine Raute. Die Mittelpunkte $M_{1}, M_{2}$ der beiden in der Aufgabe genannten Umkreise sind die Schnittpunkte von $m_{C A}$ mit $m_{C M}$ bzw. von $m_{C D}$ mit $m_{C B}$. Die Gerade $(C P)$ steht senkrecht auf der Verbindungsgeraden $\left(M_{1} M_{2}\right)$, ist also parallel zur zweiten Diagonalen in der Raute. Man überlegt sich nun leicht, dass die zweite Diagonale parallel zur Winkelhalbierenden ist.
|
| 23 |
+
|
| 24 |
+
## Aufgabe 3
|
| 25 |
+
|
| 26 |
+
Auf einer Tafel stehe am Anfang eine positive ganze Zahl. Wenn eine Zahl $x$ auf der Tafel steht, darf man die Zahlen $2 x+1$ und $\frac{x}{x+2}$ dazuschreiben. Irgendwann stehe auch die Zahl 2008 auf der Tafel. Man beweise, dass sie von Anfang an dastand.
|
| 27 |
+
Lösungsskizze: Anfangs stehe die Zahl $a$ auf der Tafel. Der Übergang von $x$ zu $2 x+1$ oder $\frac{x}{x+2}$ werde als Transformation bezeichnet. Alle Zahlen auf der Tafel sind positiv. 1. Variante: Aus der Zahl $a$ entstehen durch $k$ Transformationen stets Zahlen der Form $\frac{m a+m-1}{\left(2^{k}-m\right) a+2^{k}-m+1}$ mit ganzzahligem $0<m \leq 2^{k}$ (Beweis durch vollständige Induktion nach $k$ ). Steht also irgendwann 2008 an der Tafel, gibt es somit $k \geq 0$ und $0<m \leq 2^{k}$ mit $\frac{m a+m-1}{\left(2^{k}-m\right) a+2^{k}-m+1}=2008$ bzw. $2009=(a+1)\left(2009 m-2008 \cdot 2^{k}\right)$. Da der zweite Faktor teilerfremd zu 2009 ist (da 2008 und $2^{k}$ teilerfremd zu 2009), folgt $a+1=2009$. 2. Variante: Schreibe auf ein Blatt Papier zu jeder Zahl $t$ der Tafel die Zahl $f(t)=\frac{2009}{t+1}$. Irgendwann steht 1 auf dem Blatt. Eine Transformation einer Zahl auf der Tafel bildet eine Zahl $z$ auf dem Blatt auf $z / 2$ oder $\frac{2009+z}{2}$ ab. Ist also die Anfangszahl $f(a)$ auf dem Blatt nicht ganzzahlig oder nicht teilerfremd zu 2009, können daraus nicht irgendwann ganzzahlige oder zu 2009 teilerfremde Zahlen entstehen. Somit ist $f(a)$ ganzzahlig und teilerfremd zu 2009. Da $f(a)=\frac{2009}{a+1}$ zudem 2009 teilt, folgt $f(a)=1$ und $a=2008$. 3. Variante: Jede Transformation bildet die gekürzte rationale Zahl $p / q$ auf die gekürzte Zahl $p^{\prime} / q^{\prime}$ ab, wobei $p, q, p^{\prime}, q^{\prime}$ positive ganze Zahlen sind und $p^{\prime}+q^{\prime} \in\{p+q, 2(p+q)\}$. Anfangs hat man die gekürzte Darstellung $\frac{a}{1}$, am Ende $\frac{2008}{1}$, es gibt also $k \geq 0$ mit $2^{k}(a+1)=2008+1$. Da 2009 ungerade ist, folgt $k=0$ und $a+1=2009$.
|
| 28 |
+
4. Variante: Bilde die Zahlenfolge $a_{0}=a, a_{1}, \ldots, a_{k}=2008$ aus Zahlen auf der Tafel, wobei $a_{j+1}$ für $0 \leq j<k$ durch eine der beiden Transformationen aus $a_{j}$ entsteht. Aus $a_{k}$ lassen sich $a_{k-1}, \ldots, a_{0}$ eindeutig rekonstruieren, da für alle $x>0$ gilt: $2 x+1>1$, $0<\frac{x}{x+2}<1$. Mit Induktion nach $n$ für $n=0, \ldots, k$ zeigt man, dass $a_{k-n}=\frac{2009-b_{n}}{b_{n}}$ mit $0<b_{n}<2009$ und $b_{n} \equiv 2^{n} \bmod 2009$. Damit ist $a_{k-n}$ ganzzahlig (mit Wert 2008) genau dann, wenn $2^{n} \equiv 1 \bmod 2009$ bzw. wenn $420 \mid n$.
|
| 29 |
+
Bemerkungen: Einige Teilnehmer betrachteten nur spezielle Abfolgen der beiden Transformationen oder versuchten (fehlerhaft) zu beweisen, dass in der 4. Variante die Zahl $a_{k-n}$ nur für $n=0$ ganzzahlig sein kann. 2009 ist keine Primzahl: $2009=7^{2} \cdot 41$.
|
| 30 |
+
|
Germany_TST/md/de-2009-loes_awkl2_09.md
ADDED
|
@@ -0,0 +1,61 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. IMO-Auswahlklausur 2009
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Es sei $p$ eine Primzahl. Weiter seien $a, b, c$ ganze Zahlen, welche die Gleichungen $a^{2}+p b=b^{2}+p c=c^{2}+p a$ erfüllen.
|
| 8 |
+
Man beweise, dass dann $a=b=c$ gilt.
|
| 9 |
+
Lösung: Wenn zwei der drei Zahlen $a, b, c$ gleich sind, können wir wegen der zyklischen Vertauschbarkeit oBdA $a=b$ annehmen. Damit wird die linke gegebene Gleichung zu $a^{2}+p b=a^{2}+p c$, woraus wegen $p \neq 0$ direkt $b=c$ folgt, so dass die Behauptung erfüllt ist. Im Folgenden können wir daher $a \neq b \neq c \neq a$ voraussetzen. Umformen der Gleichungen liefert $p=\frac{b^{2}-a^{2}}{b-c}=\frac{c^{2}-b^{2}}{c-a}=\frac{a^{2}-c^{2}}{a-b}$. Multiplizieren der drei Terme und Kürzen ergibt $p^{3}=-(a+b)(b+c)(c+a)(1)$.
|
| 10 |
+
Von den drei gegebenen Zahlen sind nach dem Schubfachprinzip wenigstens zwei gerade oder wenigstens zwei ungerade; deren Summe ist also durch 2 teilbar. Deshalb ist das Produkt auf der rechten Seite von (1) gerade. Es folgt $p=2$ und daher $(a+b)(b+c)(c+a)=-8$. (2) Sind zwei der Klammern in (2) gleich, so sei oBdA $a+b=b+c$. Es folgt direkt $a=c$ und daher die Gleichheit aller drei gegeben Zahlen.
|
| 11 |
+
Ist genau eine der Klammern ungerade (gleich $\pm 1$ ), so ist $(a+b)+(b+c)+(c+a)$ einerseits ungerade, andererseits gleich $2(a+b+c)$, also gerade - Widerspruch!
|
| 12 |
+
Es bleiben daher (bis auf zyklische Vertauschbarkeit) die Fälle ( $\pm ; \mp 1 ; 8$ ) zu untersuchen.
|
| 13 |
+
Aus $a+b=1, b+c=-1, c+a=8$ folgt $a=5, b=-4, c=3$, was mit $25-8 \neq 16+6$ einen Widerspruch zur ersten gegebenen Gleichung liefert.
|
| 14 |
+
Aus $a+b=-1, b+c=1, c+a=8$ folgt $a=3, b=-4, c=5$, was mit $9-8 \neq 16+10$ einen Widerspruch zur ersten gegebenen Gleichung liefert.
|
| 15 |
+
Daher ist nur $a=b=c$ möglich. In der Tat gilt $a^{2}+p a=a^{2}+p a$.
|
| 16 |
+
Hinweise: Aus $a>b$ folgt nicht $a^{2}>b^{2}$ und umgekehrt, denn $a$ oder $b$ können negativ sein.
|
| 17 |
+
Die gegebenen Gleichungen sind nicht symmetrisch in $a, b$ und $c$, sondern nur zyklisch. Daher darf nicht oBdA $a>b>c$ verwendet werden.
|
| 18 |
+
Die Behauptung lässt sich auf alle positiven natürlichen Exponenten $n$ verallgemeinern.
|
| 19 |
+
|
| 20 |
+
## Aufgabe 2
|
| 21 |
+
|
| 22 |
+
Ausgehend von einem konvexen Viereck $A B C D$ ohne ein Paar paralleler Seiten seien $P$ und $Q$ Punkte innerhalb $A B C D$, so dass $P Q D A$ und $Q P B C$ beides Sehnenvierecke sind. Wir nehmen außerdem an, dass es einen Punkt $E$ auf der Strecke $P Q$ mit der Eigenschaft gibt, dass $\varangle P A E=\varangle E D Q$ und $\varangle E B P=\varangle Q C E$ ist.
|
| 23 |
+
Man beweise, dass dann $A B C D$ ebenfalls ein Sehnenviereck ist.
|
| 24 |
+
Lösung: Es sei $F$ der Schnittpunkt der Parallelen zu $A P$ durch $E$ mit $A D$. Dann ist wegen $\Varangle E F D=\Varangle P A D$ auch $E Q D F$ ein Sehnenviereck und es folgt $\Varangle E F Q=\Varangle E D Q=\Varangle P A E$.
|
| 25 |
+
Somit sind die Dreiecke $A P E$ und $F E Q$ ähnlich. Für $\overline{P E} \neq \overline{E Q}$ lassen sie sich durch eine zentrische Streckung vom Schnittpunkt $X$ der Geraden $A D$ und $P Q$ aus aufeinander abbilden. Für $\overline{P E}=\overline{E Q}$ werden sie durch eine Verschiebung aufeinander abgebildet. (Falls $F$ nicht zwischen $A$ und $D$ liegt, verläuft der Beweis völlig analog.) Für den Schnittpunkt $G$ der
|
| 26 |
+
|
| 27 |
+
Parallelen zu BP durch $E$ mit $B C$ folgt entsprechend, dass EGCQ ein Sehnenviereck ist, woraus sich die Ähnlichkeit der Dreiecke BEP und GQE ergibt. Diese werden durch dieselbe Streckung bzw. Verschiebung wie vorher aufeinander abgebildet, weil sie die Seiten $P E$ bzw. $E Q$ gemeinsam haben. Somit schneiden sich $B C$ und $P Q$ ebenfalls im Punkt $X$ bzw. sind parallel.
|
| 28 |
+
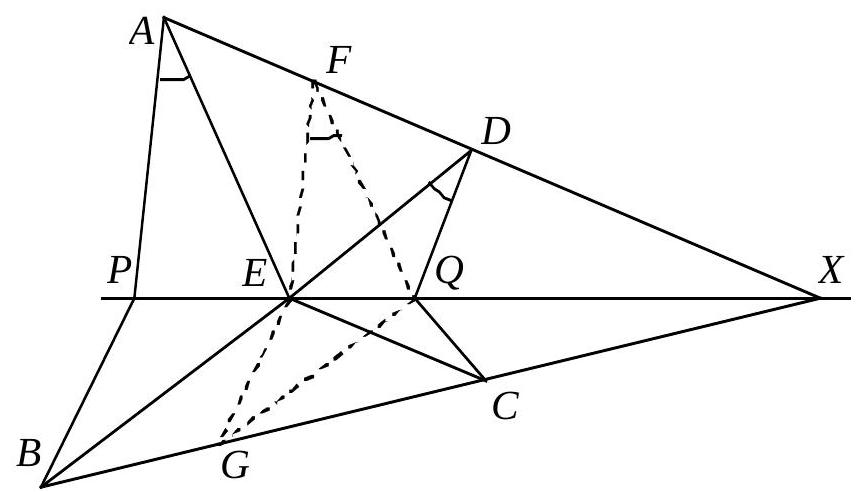
|
| 29 |
+
|
| 30 |
+
Für $\overline{P E} \neq \overline{E Q}$ folgt aus der Voraussetzung
|
| 31 |
+
$\overline{X D} \cdot \overline{X A}=\overline{X Q} \cdot \overline{X P}=\overline{X C} \cdot \overline{X B}$, woraus sich ergibt, dass $A B C D$ ein Sehnenviereck ist. Für
|
| 32 |
+
$\overline{P E}=\overline{E Q}$ sind $B C Q P$ und $P Q D A$ zwei Trapeze mit einer gemeinsamen Parallelen; daher ist auch $A B C D$ ein Trapez und somit ein Sehnenviereck.
|
| 33 |
+
Hinweise: Mit der Methode der Inversion am Einheitskreis um $E$ ergibt sich ein besonders eleganter Beweis.
|
| 34 |
+
|
| 35 |
+
## Aufgabe 3
|
| 36 |
+
|
| 37 |
+
Die 16 Felder eines 4x4-Schachbretts lassen sich wie folgt in 18 Linien ordnen: die vier Zeilen, die vier Spalten, fünf Diagonalen von Nordwest nach Südost und fünf Diagonalen von Nordost nach Südwest. Dabei bestehen diese Diagonalen aus 2, 3 oder 4 über Eck benachbarten Feldern jeweils gleicher Farbe; die Eckfelder des Schachbretts alleine bilden also keine Diagonale.
|
| 38 |
+
Nun wird in 10 der 16 Felder je ein Spielstein gesetzt. Jede der 18 Linien, die dann eine gerade Anzahl von Steinen enthält, zählt einen
|
| 39 |
+

|
| 40 |
+
|
| 41 |
+
Punkt.
|
| 42 |
+
Welches ist die größtmögliche durch Setzen der 10 Spielsteine erreichbare Punktzahl? Die Antwort ist zu begründen.
|
| 43 |
+
|
| 44 |
+
Lösung: Die größtmögliche erreichbare Punktzahl ist 17, wie das abgebildete Beispiel zeigt. Es bleibt zu zeigen, dass die Maximalpunktzahl 18 nicht erreicht werden kann. Dazu nehmen wir die Existenz einer Belegung mit 18 Punkten an und betrachten zunächst die Zeilen bzw. Spalten. Weder in einer Zeile noch in einer Spalte kann dann eine ungerade Anzahl von Steinen liegen, so dass wegen der Summe 10 nur (bis auf Permutationen) die Möglichkeiten $(4 ; 2 ; 2 ; 2)$ oder $(4 ; 4 ; 2 ; 0)$ vorkommen können. Gibt es jedoch eine Zeile (Spalte) mit 0 Steinen, so können alle Spalten (Zeilen) wegen der erforderlichen Geradzahligkeit höchstens 2 Steine enthalten, womit die Summe 10 nicht erreicht wird. Daher gibt es genau eine Zeile und eine Spalte mit 4 Steinen. Der Schnittpunkt dieser
|
| 45 |
+

|
| 46 |
+
|
| 47 |
+
17 Punkte
|
| 48 |
+

|
| 49 |
+
|
| 50 |
+
Fall a)
|
| 51 |
+

|
| 52 |
+
|
| 53 |
+
Fall b)
|
| 54 |
+

|
| 55 |
+
|
| 56 |
+
Fall c)
|
| 57 |
+
beiden Linien kann nun a) in einer Ecke, b) auf dem Rand, aber nicht in einer Ecke, c) im Inneren des Quadrats liegen. Wegen der Symmetrie genügt die Betrachtung je eines Beispiels. Fall a): Hier enthalten die fünf NW-SO-Linien erst je einen Stein. Weil aber nur noch drei Steine zu setzen sind, ist die Punktzahl 18 nicht mehr erreichbar.
|
| 58 |
+
Fall b): Hier enthalten vier der NW-SO-Linien erst je einen Stein. Weil aber nur noch drei Steine zu setzen sind, ist die Punktzahl 18 nicht mehr erreichbar.
|
| 59 |
+
Fall c): Die beiden NW-SO-Linien mit genau 2 Feldern enthalten erst einen Stein. Wenn sie mit einem zweiten Stein besetzt werden, zählt die obere SW-NO-Linie mit 3 Steinen keinen Punkt. Auch hier wird die Punktzahl 18 nicht erreicht.
|
| 60 |
+
Hinweis: Es gibt Belegungen mit 8 Steinen und 18 Punkten. Allerdings ist es unzulässig zu argumentieren, eine solche Anordnung der 8 Steine müsse in der optimalen Anordnung von 10 Steinen enthalten sein.
|
| 61 |
+
|
Germany_TST/md/de-2010-loes_awkl1_10.md
ADDED
|
@@ -0,0 +1,79 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Auswahlwettbewerb zur Internationalen Mathematik-Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 1. IMO-Auswahlklausur 2010
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Das Viereck $A B C D$ sei eine Raute mit spitzem Winkel bei $A$. Die Punkte $M$ und $N$ mögen so auf den Strecken $A C$ und $B C$ gelegen sein, dass $|D M|=|M N|$. Ferner sei $P$ der Schnittpunkt von $A C$ und $D N$ sowie $R$ der Schnittpunkt von $A B$ und $D M$. Man beweise, dass $|R P|=|P D|$.
|
| 8 |
+
|
| 9 |
+
Anmerkung: Für $M=A$ und $N=B$ gilt $|D M|=|M N|$, aber $|R P| \neq|P D|$. Unter der zusätzlichen Voraussetzung, dass $M$ bzw. $N$ im Inneren der Strecken $A C$ bzw. $B C$ liegen, ist die Behauptung jedoch korrekt. Den Fehler zu bemerken, zählte nicht als Lösung.
|
| 10 |
+
|
| 11 |
+
Lösung: Der Fall $N=B$ sei im Folgenden ausgeschlossen. Dann ist $D N$ nicht orthogonal zu $A C$, und $M$ ist eindeutig charakterisiert als Schnittpunkt der Mittelsenkrechte von $D N$ mit $A C$. Im Dreieck $D N C$ ist $A C$ die Winkelhalbierende bei $C$, und in jedem Dreieck schneiden sich die Winkelhalbierende und die gegenüberliegende Mittelsenkrechte auf dem zugehörigen Umkreisbogen, also ist $D M N C$ ein Sehnenviereck, insbesondere ist $\varangle M D N=\varangle M C N$. Nun ist $\varangle M D N=\varangle R D P$ und $\varangle M C N=\varangle A C B=\varangle B A C=\varangle R A P$, also ist nach dem Satz vom Umfangswinkel auch $A R P D$ ein Sehnenviereck. In seinem Umkreis sind wegen $\varangle R A P=\varangle B A C=\varangle C A D=\varangle P A D$ die Sehnen $R P$ und $P D$ gleich lang (Sinussatz oder Umfangswinkel).
|
| 12 |
+
|
| 13 |
+
Bemerkungen: Diese Aufgabe erforderte eine genaue Analyse der relativen Lage der verschiedenen Punkte. Häufig war das angegebene Argument deshalb nur in bestimmten Fällen anwendbar, beispielsweise im Kontext des Sehnenfünfecks $M R B N P$ bzw. MBRNP. Die meisten Versuche, die Aufgabe durch Verwendung von Koordinaten rechnerisch zu lösen, scheiterten an Rechenfehlern. Relativ häufig wurde auch das Sehnenviereck $B N P M$ erkannt.
|
| 14 |
+
|
| 15 |
+
## Aufgabe 2
|
| 16 |
+
|
| 17 |
+
Man beweise oder widerlege, dass für alle positiven reellen Zahlen $a, b$ und $c$ die Ungleichung
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
3 \leq \frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}<\frac{33}{4}
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Lösung:
|
| 24 |
+
Beweis von $3 \leq \frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}$ :
|
| 25 |
+
|
| 26 |
+
1. Variante: Multiplizieren mit Hauptnenner und Vereinfachen führt zur äquivalenten Ungleichung $45 a b c \leq 7\left(a^{2} b+b^{2} c+c^{2} a\right)+8\left(a b^{2}+b c^{2}+c a^{2}\right)$. Dies folgt aus der Ungleichung zwischen arithmetischem und geometrischem Mittel (z. B. $a^{2} b+b^{2} c+c^{2} a \geq 3 \sqrt[3]{a^{2} b \cdot b^{2} c \cdot c^{2} a}=3 a b c$ ).
|
| 27 |
+
2. Variante: Für $n \geq 1$ und reelle Zahlen $a_{1}, \ldots, a_{n}, b_{1}, \ldots, b_{n}$ gilt die Cauchy-Schwarz-Ungleichung $\sqrt{a_{1}^{2}+\ldots+a_{n}^{2}} \sqrt{b_{1}^{2}+\ldots+b_{n}^{2}} \geq a_{1} b_{1}+\ldots+a_{n} b_{n}$. Für $n=3, a_{1}^{2}=\frac{4 a+b}{a+4 b}, a_{2}^{2}=\frac{4 b+c}{b+4 c}, a_{3}^{2}=\frac{4 c+a}{c+4 a}$, $b_{1}^{2}=(4 a+b)(a+4 b), b_{2}^{2}=(4 b+c)(b+4 c), b_{3}^{2}=(4 c+a)(c+4 a)$ ergibt sich
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\left(\frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}\right)((4 a+b)(a+4 b)+(4 b+c)(b+4 c)+(4 c+a)(c+4 a)) \geq(5(a+b+c))^{2}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Der zweite Faktor ist wegen $2(a+b+c)^{2}-6(a b+b c+c a)=(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \geq 0$ kleiner als $\frac{25}{3}(a+b+c)^{2}$, woraus die Behauptung folgt.
|
| 34 |
+
Beweis von $\frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}<\frac{33}{4}$ :
|
| 35 |
+
|
| 36 |
+
1. Variante: Multiplizieren mit Hauptnenner und Vereinfachen liefert die äquivalente (triviale) Ungleichung $0<127 a b c+16\left(a^{2} b+b^{2} c+c^{2} a\right)$.
|
| 37 |
+
2. Variante: Die Ungleichung ist äquivalent $\mathrm{zu} \frac{b}{a+4 b}+\frac{c}{b+4 c}+\frac{a}{c+4 a}>\frac{1}{4}$; Letzteres gilt wegen
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\frac{b}{a+4 b}+\frac{c}{b+4 c}+\frac{a}{c+4 a}>\frac{b}{4 a+4 b+4 c}+\frac{c}{4 a+4 b+4 c}+\frac{a}{4 a+4 b+4 c}=\frac{1}{4}
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Bemerkungen: 1. Die Ungleichung geht zwar bei zyklischer Vertauschung $a$ nach $b, b$ nach $c, c$ nach $a$ in sich über, nicht aber bei beliebigem Permutatieren von $a, b, c$. Daher kann man zwar ohne Einschränkung $a \geq b$ und $a \geq c$ voraussetzen, nicht jedoch $a \geq b \geq c$. Viele Lösungsansätze funktionierten nur unter letzterer Voraussetzung.
|
| 44 |
+
2. Manche Teilnehmer untersuchten den Grenzwert für $a \rightarrow \infty$ bei festem $b$ und $c$ und schätzten dann $\frac{4 b+c}{b+4 c}$ ab. Das ist kein Beweis für die rechte Ungleichung, da die Summe für endliche Werte von $a$ größer als für $a \rightarrow \infty$ sein kann.
|
| 45 |
+
3. Die Zahl $\frac{33}{4}$ wird für $a=1, b=\varepsilon, c=\varepsilon^{2}$ für $\varepsilon \rightarrow 0$ beliebig angenähert.
|
| 46 |
+
|
| 47 |
+
## Aufgabe 3
|
| 48 |
+
|
| 49 |
+
Man bestimme alle Paare $(m, n)$ nicht-negativer ganzer Zahlen, die der Gleichung
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
3^{m}-7^{n}=2
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
genügen.
|
| 56 |
+
Lösung: Die Paare $(1,0)$ und $(2,1)$ sind Lösungen. Es sei $(m, n)$ eine Lösung mit $m, n \geq 2$. Die Lösung besteht aus drei Schritten:
|
| 57 |
+
|
| 58 |
+
1. Es ist $7^{n} \equiv-2 \bmod 9 \Longleftrightarrow n \equiv 1 \bmod 3$.
|
| 59 |
+
2. Es ist $3^{m} \equiv 2 \bmod 49 \Longleftrightarrow m \equiv 26 \bmod 42$.
|
| 60 |
+
3. Die Bedingungen aus 1 und 2 ergeben einen Widerspruch modulo 43.
|
| 61 |
+
|
| 62 |
+
Schritt 1: Es gilt $7^{1} \equiv 7,7^{2} \equiv 4$ und $7^{3} \equiv 1 \bmod 9$, ab dann sind die Reste periodisch mit Periode 3. Aus der Ausgangsgleichung folgt $7^{n} \equiv 7 \bmod 9$, also $n \equiv 1 \bmod 3$.
|
| 63 |
+
Schritt 2: Zeige zunächst $m \equiv 2 \bmod 6$ analog zu Schritt 1. Nach dem Satz von Euler-Fermat ist $3^{42} \equiv 1 \bmod 49$, die Periode ist also höchstens 42 . Unter Verwendung von $3^{6} \equiv-6 \bmod 49$ erhält man:
|
| 64 |
+
|
| 65 |
+
| $m$ | 2 | 8 | 14 | 20 | 26 | 32 | 38 |
|
| 66 |
+
| :--- | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
|
| 67 |
+
| $3^{m} \bmod 49$ | 9 | 44 | 30 | 16 | 2 | 37 | 23 |
|
| 68 |
+
|
| 69 |
+
Es gilt also $3^{m} \equiv 2 \bmod 49$ genau dann, wenn $m \equiv 26 \bmod 42$.
|
| 70 |
+
Schritt 3: Schreibe $m=42 m^{\prime}+26$ und $n=3 n^{\prime}+1$. Betrachtet man nun die ursprüngliche Gleichung modulo 43 , erhält man mit dem kleinen Satz von Fermat und $7^{3} \equiv-1 \bmod 43$
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
3^{42 m^{\prime}+26}-7^{3 n^{\prime}+1} \equiv 3^{26}-(-1)^{n^{\prime}} \cdot 7 \equiv 15-(-1)^{n^{\prime}} \cdot 7 \not \equiv 2 \quad \bmod 43
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
Es gibt also keine weiteren Lösungen.
|
| 77 |
+
Bemerkungen: Diese Aufgabe wurde von keinem Teilnehmer gelöst. Eine häufige Lücke in den Ansätzen war die folgende: Aus $a^{b} \equiv a^{c} \bmod M$ folgt nicht $b \equiv c \bmod \varphi(M)$, wie das für die Aufgabe relevante Beispiel $a=7, b=4, c=1, M=9$ zeigt.
|
| 78 |
+
Aufgrund der Periodizität der Potenzreste ist es nicht möglich, direkt aus $3^{m}-7^{n}=2$ einen Widerspruch modulo 43 oder einer anderen Primzahl $\neq 3,7$ herzuleiten, denn die Gleichung besitzt ja Lösungen. Erst mit zusätzlichen, mit Hilfe der Primzahlen 3 und 7 gewonnenen Einschränkungen erhält man den gewünschten Widerspruch.
|
| 79 |
+
|
Germany_TST/md/de-2010-loes_awkl2_10.md
ADDED
|
@@ -0,0 +1,42 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Internationalen Mathematik- Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. IMO-Auswahlklausur 2010
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Auf einem Tisch liegen nebeneinander 2009 Karten in einer Reihe. Zunächst ist bei allen Karten die Oberseite weiß und die Unterseite schwarz. Die Karten seien von 1 bis 2009 nummeriert.
|
| 8 |
+
Zwei Spieler $A$ und $B$ führend abwechselnd einen Spielzug aus, wobei $A$ beginnt. Jeder Spielzug besteht darin, dass der Spieler eine Karte mit der Nummer $k(k<1969)$ wählt, deren weiße Seite oben liegt, und anschließend die Karten mit den Nummern $k, k+1, k+2, \ldots, k+40$ auf ihren Plätzen umdreht. Der letzte Spieler, der einen gültigen Spielzug machen konnte, gewinnt das Spiel.
|
| 9 |
+
a) Man entscheide, ob dieses Spiel notwendigerweise endet.
|
| 10 |
+
b) Für welchen der beiden Spieler existiert eine Gewinnstrategie?
|
| 11 |
+
|
| 12 |
+
Lösung: a) Wenn das Spiel nicht endet, dann muss wegen der höchstens $2^{2008}$ verschiedenen möglichen Spielzustände eine sich periodisch wiederholende Folge von Zuständen existieren. Dabei sei $k$ die kleinste Nummer der Karten, die innerhalb dieser Periode umgedreht werden. Um die Karte mit der Nummer $k$ von schwarz auf weiß umzudrehen, ist jedoch eine Karte mit einer kleineren Nummer als $k$ auszuwählen - Widerspruch zur Minimalität! Also muss das Spiel nach endlich vielen Zügen enden.
|
| 13 |
+
b) Wir betrachten die Karten mit den Nummern $41 k$, wobei $1 \leq k \leq 48$. Die höchste dieser Karten mit der Nummer 1968 ist die letzte, die ausgewählt werden kann. Bei jedem Spielzug wird genau eine dieser Karten umgedreht. Weil das Spiel endet, wenn alle Karten bis zur Nummer 1968 schwarz sind, und weil diese Karten zu Beginn alle weiß sind, ist nach jedem Doppelzug von $A$ und $B$ wieder eine gerade Anzahl von ihnen weiß; $B$ findet also stets eine ungerade Anzahl weißer Karten aus dieser Menge vor und kann stets ziehen. Daher gewinnt $B$ zwangsläufig das Spiel, egal wie er zieht.
|
| 14 |
+
Hinweise: Die Endlichkeit kann auch mit der Übersetzung der Spielzustände in eine monoton sich verändernde Binärzahl gezeigt werden. Würde in der Aufgabenstellung die Karte mit der Nummer 1969 auch zur Auswahl zugelassen, so hätte $A$ eine Gewinnstrategie. Für Teil a) wurden 4 P. und für Teil b) 6 P. vergeben.
|
| 15 |
+
|
| 16 |
+
## Aufgabe 2
|
| 17 |
+
|
| 18 |
+
Gegeben sei ein Sehnenviereck $A B C D$, dessen Diagonalen $A C$ und $B D$ sich im Punkt $E$ schneiden und dessen Seiten $A D$ und $B C$ auf Geraden liegen, die sich im Punkt $F$ schneiden. Die Mittelpunkte der Strecken $A B$ und $C D$ seien mit $G$ bzw. $H$ bezeichnet. Man beweise, dass die Gerade $E F$ in $E$ den Kreis durch $E, G$ und $H$ berührt.
|
| 19 |
+
|
| 20 |
+
Lösung: Eine zentrische Streckung mit Zentrum $E$ und Streckfaktor 2 bildet $G$ auf $G^{\prime}$ und $H$ auf $H^{\prime}$ ab. Dann ist (1) $\Varangle G H E=\Varangle G^{\prime} H^{\prime} E$. Wegen $\Varangle A B F=180^{\circ}-\Varangle C B A=\Varangle A D C$ und $\Varangle F A B=180^{\circ}-\Varangle B A D=\Varangle D C B$ (Sehnenviereck $A B C D$ ) sind die Dreiecke $F B A$ und $F D C$ ähnlich und werden durch eine Streckspiegelung mit Zentrum $F$ an der Winkelhalbierenden von $\Varangle B F A$ aufeinander abgebildet. Bei dieser Abbildung gilt insbesondere $A \rightarrow C, B \rightarrow D, G \rightarrow H$ (Mittelpunkte!). Aufgrund der Definition von $H^{\prime}$ halbieren sich die Diagonalen $E H^{\prime}$ und $C D$; daher ist $D E C H^{\prime}$ ein Parallelogramm und es gilt $\Varangle H^{\prime} C D=\Varangle E D C=\Varangle B D C=\Varangle B A C=\Varangle B A E$. Analog gilt $\Varangle C D H^{\prime}=\Varangle E B A$. Damit sind die Dreiecke $A B E$ und $C D H^{\prime}$
|
| 21 |
+
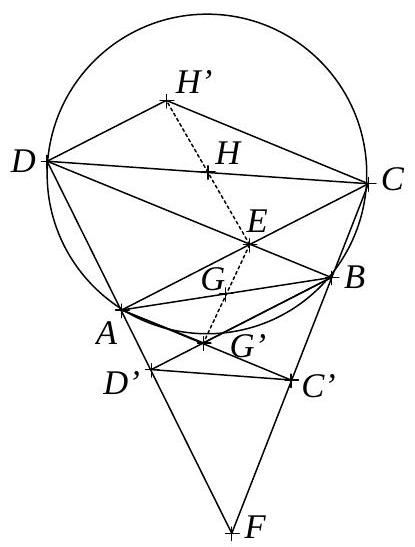
|
| 22 |
+
ähnlich. Wegen der Ähnlichkeit von FBA und FDC sind auch die
|
| 23 |
+
|
| 24 |
+
Vierecke FBEA und FDH 'C ähnlich, so dass bei der betrachteten Streckspiegelung E auf $H^{\prime}$ abgebildet wird. Damit sind die Dreiecke FGE und FHH ' ähnlich, und es gilt (2) $\Varangle G E F=\Varangle H H^{\prime} F=\Varangle E H^{\prime} F$.
|
| 25 |
+
Es seien $C^{\prime}$ und $D^{\prime}$ die Urbilder von $A$ bzw. $B$ bei der betrachteten Streckspiegelung. Dann ist wegen der Ähnlichkeit der Dreiecke $F C^{\prime} D^{\prime}$ und $F A B$ sowie wegen
|
| 26 |
+
$|F B| /\left|F D^{\prime}\right|=|F D| /|F B|$ das Viereck $D^{\prime} C^{\prime} B A$ ein zu $B A D C$ ähnliches Sehnenviereck. Sein
|
| 27 |
+
Diagonalenschnittpunkt sei $G^{\prime \prime}$. Dann gilt $\Varangle G^{\prime \prime} A B=\Varangle C^{\prime} A B=\Varangle C^{\prime} D^{\prime} B=\Varangle A B D=\Varangle A B E$ und es folgt $G^{"} A \| B E$ sowie analog $G " B \| A E$. Also ist $A G " B E$ ein Parallelogramm und nach Definition von $G^{\prime}$ gilt $G^{\prime}=G^{\prime \prime}$. Folglich geht $G^{\prime}$ bei der betrachteten Streckspiegelung in $E$ über. Weil aber $E$ in $H^{\prime}$ übergeht, wird $G^{\prime}$ bei der zweifachen
|
| 28 |
+
Hintereinanderausführung in $H^{\prime}$ abgebildet. Bei dieser Hintereinanderausführung heben sich die beiden Spiegelungen auf und es bleibt eine zentrische Streckung an $F$. Deshalb sind $F, G^{\prime}$ und $H^{\prime}$ kollinear. Daraus folgt (3) $\Varangle F H^{\prime} E=\Varangle G^{\prime} H^{\prime} E$.
|
| 29 |
+
Aus (1), (2) und (3) folgt nun $\Varangle G H E=\Varangle G^{\prime} H^{\prime} E=\Varangle F H^{\prime} E=\Varangle F E G$.
|
| 30 |
+
Aus der Umkehrung des Sehnen-Tangentenwinkelsatzes ergibt sich daher, dass FE Tangente an den Kreis durch $E, G$ und $H$ ist.
|
| 31 |
+
Hinweise: Weitere Beweisideen verwenden die Polare und den Satz vom vollständigen Vierseit oder Inversion am Kreis. Ansätze mit analytischer Geometrie konnten nur mit wenigen Teilpunkten bedacht werden.
|
| 32 |
+
|
| 33 |
+
## Aufgabe 3
|
| 34 |
+
|
| 35 |
+
Wir nennen eine natürliche Zahl $n$ ausgeglichen, wenn $n=1$ gilt oder wenn $n$ als Produkt einer geraden Anzahl von (nicht notwendigerweise verschiedenen) Primfaktoren geschrieben werden kann. Zu jedem Paar $(a, b)$ positiver ganzer Zahlen sei $P(x)=(x+a)(x+b)$.
|
| 36 |
+
a) Gibt es zwei verschiedene positive ganze Zahlen $a$ und $b$, für die alle Zahlen $P(1), P(2), \ldots, P(50)$ ausgeglichen sind?
|
| 37 |
+
b) Man beweise: Wenn $P(m)$ für alle positiven ganzen Zahlen $m$ ausgeglichen ist, dann gilt $a=b$.
|
| 38 |
+
|
| 39 |
+
Lösung: a) Die Antwort lautet „Ja". Damit $P(x)$ ausgeglichen ist, müssen $x+a$ und $x+b$ entweder beide eine gerade oder beide eine ungerade Anzahl von Primfaktoren besitzen. Hinsichtlich dieser Eigenschaft gibt es aber nur $2^{50}$, also endlich viele verschiedene Muster bei 50 aufeinanderfolgenden natürlichen Zahlen. Daher existieren zwei natürliche Zahlen $m$ und $n$, so dass sie Startzahlen zweier identischer solcher Muster sind. Mit $a=m-1$ und $b=n-1$ folgt die Ausgeglichenheit von $P(1), P(2), \ldots, P(50)$.
|
| 40 |
+
b) Wir nehmen an, dass es unter der gegebenen Voraussetzung zwei verschiedene natürliche Zahlen $a$ und $b$ gebe; oBdA sei $b>a$. Dann gilt für jede natürliche Zahl $m>a$, dass $P(m-a)=m(m+b-a)$ ausgeglichen ist. Die Geradzahligkeit bzw. Ungeradzahligkeit der Anzahl der Primfaktoren tritt also für natürliche Zahlen größer als $a$ mit der Periodenlänge $b-a$ periodisch auf. Insbesondere sind auch alle Vielfachen von $b-a$ vom gleichen Typ, sobald sie größer sind als $a$. Ein solches Vielfaches $k(b-a)$ hat jedoch einen Primfaktor weniger als $2 k(b-a)$, Widerspruch zur Annahme. Also gilt $a=b$.
|
| 41 |
+
Hinweis: Der Widerspruch kann auf verschiedenste Art und Weise hergeleitet werden. Häufig wurden Sätze über Primzahlen in arithmetischen Folgen oder geeignete Quadratzahlen verwendet. Für Teil a) wurden 4 P. und für Teil b) 6 P. vergeben.
|
| 42 |
+
|
Germany_TST/md/de-2011-loes_awkl1_11.md
ADDED
|
@@ -0,0 +1,95 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Internationalen Mathematik- Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 1. IMO-Auswahlklausur 2011
|
| 4 |
+
|
| 5 |
+
|
| 6 |
+
#### Abstract
|
| 7 |
+
|
| 8 |
+
Aufgabe 1 Zwei Kreise $\Gamma$ und $\Gamma^{\prime}$ mögen sich in den beiden voneinander verschiedenen Punkten $A$ und $B$ schneiden. Eine Gerade durch $B$ schneide $\Gamma$ und $\Gamma^{\prime}$ so in $C$ bzw. $D$, dass $B$ zwischen $C$ und $D$ liege. Eine weitere Gerade durch $B$ schneide $\Gamma$ und $\Gamma^{\prime}$ derart in $E$ bzw. $F$, dass $E$ zwischen $B$ und $F$ liege. Es möge sich ergeben, dass $|C D|=|E F|$ gilt. Das Innere der Strecke $C F$ treffe $\Gamma$ und $\Gamma^{\prime}$ ind $P$ bzw. $Q$. Weiterhin seien $M$ und $N$ die Mittelpunkte der $C$ bzw. $F$ nicht enthaltenden Bögen $P B$ bzw. $B Q$ von $\Gamma$ und $\Gamma^{\prime}$. Man beweise, dass $C N M F$ ein Sehnenviereck ist.
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
Lösung: (1) Die Dreiecke $A C D$ und $A E F$ gleichsinnig kongruent: Wir arbeiten mit orientierten Winkeln modulo $\pi$. Es ist $\varangle A D C=\varangle A D B=\varangle A F B=\varangle A F E$ und $\varangle D C A=\varangle B C A=\varangle B E A=\varangle F E A$ (für das mittlere Gleichheitszeichen wurde beide Male der Satz vom Umfangswinkel benutzt). Da außerdem nach Voraussetzung $|C D|=|E F|$ gilt, folgt die Behauptung mit dem Kongruenzsatz wsw.
|
| 12 |
+
(2) $A$ liegt auf derselben Seite der Geraden $C D$ wie $F$ : Der Überlappungsbereich der beiden Kreise enthält die Strecke $B E$ und trifft die Gerade $C D$ nur im Punkt $B$.
|
| 13 |
+
(3) Die Dreiecke $C D Q$ und EFP sind gleichsinnig kongruent: Wie bei (1), $\varangle Q D C=\varangle Q D B=\varangle Q F B=$ $\varangle P F B$ usw.
|
| 14 |
+
(4) Es gibt eine Drehung um $A$, die die Punkte $C, D, Q$ in die Punkte $E, F, P$ überführt: folgt aus (1) und (3).
|
| 15 |
+
(5) $A$ liegt auf derselben Seite der Geraden $B F$ wie $C$ : Aus (2) folgt, dass $A$ und $Q$ auf derselben Seite der Geraden $C D$ liegen, und zusammen mit (4) ergibt sich, dass $A$ und $P$ auf derselben Seite der Geraden $E F=B F$ liegen, also auch $A$ und $C$.
|
| 16 |
+
(6) $B A$ ist die Winkelhalbierende des Innenwinkels des Dreiecks $B F C$ bei $B$ : Wegen (1) sind die Abstände von $A$ zu den verlängerten Seiten gleich, und wegen (2) und (5) handelt es sich um eine innere Winkelhalbierende.
|
| 17 |
+
(7) $C M$ ist die Winkelhalbierende des Innenwinkels des Dreiecks $B F C$ bei $C$ : Das folgt aus dem Umfangswinkelsatz.
|
| 18 |
+
(8) Analog ist $F N$ ist die Winkelhalbierende des Innenwinkels des Dreiecks $B F C$ bei $F$. Es sei $I$ der Inkreismittelpunkt des Dreiecks BFC.
|
| 19 |
+
(9) $M$ liegt auf dem $C$ nicht enthaltenden Kreisbogen $B A$ von $\Gamma$ : Aus (2) und (5) folgt, dass die Punkte auf $\Gamma$ die zyklische Reihenfolge $B, E, A, C$ bzw. $B, P, C$ (gleich orientiert) haben. Die orientierten Bögen $E A$ und $A C$ sind nach (4) gleich groß, also ist $\frac{1}{2} B C<B A$ und damit $B M=\frac{1}{2} B P<\frac{1}{2} B C<B A$.
|
| 20 |
+
(10) $N$ liegt auf dem $F$ nicht enthaltenden Kreisbogen $A B$ von $\Gamma^{\prime}$ : analog zu (9).
|
| 21 |
+
(11) $I$ ist ein innerer Punkt von $C M$ und $F N$ : $I$ liegt auf der Geraden $A B$, damit folgt die Behauptung aus (9) bzw. (10).
|
| 22 |
+
(12) $I$ ist ein innerer Punkt von $B A$ : folgt aus (9) oder (10).
|
| 23 |
+
(13) Es gilt $|C I| \cdot|I M|=|F I| \cdot|I N|$ : Nach dem Sehnensatz in $\Gamma$ ist $|C I| \cdot|I M|=|B I| \cdot|I A|$, nach dem Sehnensatz in $\Gamma^{\prime}$ ist $|B I| \cdot|I A|=|F I| \cdot|I N|$.
|
| 24 |
+
(14) Nach der Umkehrung des Sehnensatzes folgt mit (11) und (13), dass CNMF ein Sehnenviereck ist.
|
| 25 |
+
|
| 26 |
+
Bemerkungen: Die Teilergebnisse (1) oder (3) wurden mit 3 Punkten, (7) oder (8) mit 1 Punkt honoriert.
|
| 27 |
+
|
| 28 |
+
## Aufgabe 2
|
| 29 |
+
|
| 30 |
+
Es sei $n$ eine positive ganze Zahl und $b$ die größte ganze Zahl, die kleiner als $(\sqrt[3]{28}-3)^{-n}$ ist. Man beweise, dass $b$ nicht durch 6 teilbar sein kann.
|
| 31 |
+
Lösung: Die komplexe Zahl $\omega=\frac{-1+\sqrt{3} i}{2}$ ist bekanntlich eine dritte Einheitswurzel und erfüllt $\omega^{2}=\frac{-1-\sqrt{3} i}{2}$, $\omega^{3}=1$ und $\omega^{2}+\omega+1=0$, insbesondere gilt
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
1+\omega^{j}+\omega^{2 j}= \begin{cases}3, & \text { falls } j \text { durch drei teilbar ist } \\ 0 & \text { sonst. }\end{cases}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Setze $r_{k}=\sqrt[3]{28} \omega^{k}-3$ für $k=0,1,2$. Nach Definition von $b$ ist $\left|r_{0}^{-n}-b\right|<1$; da die Realteile von $\omega$ und $\omega^{2}$ negativ sind, gilt $\left|r_{1}\right|>1$ und $\left|r_{2}\right|>1$. Damit ist
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\left|b-\left(r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}\right)\right|<\left|b-r_{0}^{-n}\right|+\left|r_{1}^{-n}\right|+\left|r_{2}^{-n}\right|<3 .
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Wegen $\left(\sqrt[3]{28} \omega^{k}\right)^{3}=28$ ist
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
r_{k}^{-1}=\frac{1}{\sqrt[3]{28} \omega^{k}-3}=\frac{\left(\sqrt[3]{28} \omega^{k}\right)^{3}-3^{3}}{\sqrt[3]{28} \omega^{k}-3}=\sqrt[3]{28}^{2} \omega^{2 k}+3 \sqrt[3]{28} \omega^{k}+9
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Erhebt man das Polynom $X^{2}+3 X+9$ in seine $n$-te Potenz, gibt es ganze Zahlen $c_{0}, \ldots, c_{2 n}$ mit $\left(X^{2}+3 X+\right.$ $9)^{n}=c_{2 n} X^{2 n}+c_{2 n-1} X^{2 n-1}+\ldots+c_{0}$, hierbei ist $c_{0}=9^{n}$ ungerade. Durch Einsetzen $X=\sqrt[3]{28} \omega^{k}$ folgt $r_{k}^{-n}=\sum_{j=0}^{2 n} c_{j} \sqrt[3]{28}^{j} \omega^{k j}$; daraus ergibt sich mit (1):
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}=\sum_{j=0}^{2 n} c_{j} \sqrt[3]{28}^{j}\left(1+\omega^{j}+\omega^{2 j}\right)=3 \sum_{0 \leq \ell \leq 2 n / 3} c_{3 \ell} 28^{\ell}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Die Summe ist offenbar ein Vielfaches von 3 und außerdem ungerade, da der Summand $c_{3 \ell} 28^{\ell}$ für $\ell=0$ ungerade, für $\ell>0$ gerade ist. Wäre $b$ durch 6 teilbar, wäre der Betrag $\left|b-\left(r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}\right)\right|$ mindestens 3 im Widerspruch zu (2).
|
| 56 |
+
Bemerkungen: 1. Manche Teilnehmer versuchten, den Wert von $(\sqrt[3]{28}-3)^{-1}$ und damit von $b$ numerisch abzuschätzen. Das ist ein Irrweg, weil für alle reellen Zahlen $m, M$ mit $1<m<(\sqrt[3]{28}-3)^{-1}<M$ eine positive ganze Zahl $n$ existiert mit $M^{n}-m^{n}>6$.
|
| 57 |
+
2. Manche dachten, zu $\sqrt[3]{28}-3$ sei $-\sqrt[3]{28}-3$ „konjugierte Zahl". Das funktioniert so nur bei Quadratwurzeln, hier benötigt man $\omega \sqrt[3]{28}-3$ und $\omega^{2} \sqrt[3]{28}-3$.
|
| 58 |
+
3. Die Summen $s_{n}=r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}$ genügen der linearen Rekursion $s_{t+3}=27 s_{t+2}+9 s_{t+1}+s_{t}$ für alle $t$, da aus $28=\left(r_{k}+3\right)^{3}$, also $1=27 r_{k}+9 r_{k}^{2}+r_{k}^{3}$ und $r_{k}^{-t-3}=27 r_{k}^{-t-2}+9 r_{k}^{-t-1}+r_{k}^{-t}$ die Rekursion durch Summation über $k=0,1,2$ folgt.
|
| 59 |
+
|
| 60 |
+
## Aufgabe 3
|
| 61 |
+
|
| 62 |
+
Es bezeichne $\mathbb{Q}^{+}$die Menge der positiven rationalen Zahlen. Eine Funktion $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$heiße elastisch, wenn für alle $x, y \in \mathbb{Q}^{+}$die Ungleichung
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
f(x)+f(y) \geq 4 f(x+y)
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
gilt.
|
| 69 |
+
(a) [5 Punkte] Man zeige: Ist $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$elastisch und sind $x, y, z$ positive rationale Zahlen, so ist $f(x)+$ $f(y)+f(z) \geq 8 f(x+y+z)$.
|
| 70 |
+
(b) [5 Punkte] Gibt es eine elastische Funktion $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$zusammen mit positiven rationalen Zahlen $x, y, z$, für die $f(x)+f(y)+f(z)<9 f(x+y+z)$ der Fall ist?
|
| 71 |
+
Lösung: (a) Es gilt
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
4 f(x)+f(y)+f(z) \stackrel{(*)}{\geq} 4(f(x)+f(y+z)) \stackrel{(*)}{\geq} 16 f(x+y+z) .
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
Addiert man dazu die zyklisch vertauschten Versionen $f(x)+4 f(y)+f(z) \geq \ldots$ und $f(x)+f(y)+4 f(z) \geq \ldots$, erhält man $6(f(x)+f(y)+f(z)) \geq 48 f(x+y+z)$ und nach Division durch 6 die Behauptung.
|
| 78 |
+
(b) Ja, es gibt solche $f, x, y, z$. Betrachte die stückweise affin-lineare Funktion $f$ mit den Knickpunkten $\left(2^{k}, 2^{-k}\right)$ für $k \in \mathbb{Z}$, explizit: Für jedes $k \in \mathbb{Z}$ sei $f$ auf dem Intervall $\left[2^{k}, 2^{k+1}[\right.$ definiert durch
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
f(x)=-\frac{x}{2^{2 k+1}}+\frac{3}{2^{k+1}} \quad \text { für } 2^{k} \leq x<2^{k+1} .
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Damit ist $f$ für alle $x \in \mathbb{Q}^{+}$definiert. Für alle $x$ gilt $f(2 x)=\frac{1}{2} f(x)$, damit wird (*) äquivalent zur Konvexitätsungleichung $\frac{1}{2}(f(x)+f(y)) \geq f\left(\frac{x+y}{2}\right)$. Die Funktion $f$ ist konvex, also auch elastisch. Mit $x=y=z=1$ gilt
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
f(x)+f(y)+f(z)=3<9 \cdot \frac{3}{8}=9 f(x+y+z) .
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Bemerkung: Entgegen einer häufig geäußerten Behauptung sind elastische Funktionen nicht notwendigerweise monoton, Beispiel:
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
f(x)= \begin{cases}\frac{1}{x^{2}} ; & x \neq 1 \\ 2 ; & x=1\end{cases}
|
| 94 |
+
$$
|
| 95 |
+
|
Germany_TST/md/de-2011-loes_awkl2_11.md
ADDED
|
@@ -0,0 +1,49 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Auswahlwettbewerb zur Internationalen Mathematik-Olympiade
|
| 2 |
+
|
| 3 |
+
## Lösungen zur 2. IMO-Auswahlklausur für 2011
|
| 4 |
+
|
| 5 |
+
## Aufgabe 1
|
| 6 |
+
|
| 7 |
+
Eine Folge $x_{1}, x_{2}, \ldots$ ist definiert durch $x_{1}=1$ und $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ für alle $k \geq 1$. Man zeige, dass für alle $n \geq 1$ gilt: $x_{1}+x_{2}+\ldots+x_{n} \geq 0$.
|
| 8 |
+
|
| 9 |
+
Lösung: Wir bezeichnen $S_{n}=x_{1}+\ldots+x_{n}$ und führen einen Induktionsbeweis. Nachrechnen ergibt $x_{1}=1, x_{2}=-1, x_{3}=1, x_{4}=1$ und damit $S_{n} \geq 0$ für $1 \leq n \leq 4$.
|
| 10 |
+
Nun nehmen wir an, dass $S_{k} \geq 0$ für alle natürlichen $k<n$ gilt, und behaupten $S_{n} \geq 0$.
|
| 11 |
+
Dazu unterscheiden wir vier Fälle.
|
| 12 |
+
Fall 1: $n=4 m$. Es gilt $S_{n}=\sum_{i=1}^{m}\left(x_{4 i-3}+x_{4 i-2}+x_{4 i-1}+x_{4 i}\right)=\sum_{i=1}^{m}\left(x_{2 i-1}-x_{2 i-1}-x_{2 i}-x_{2 i}\right)$
|
| 13 |
+
$=-2 \sum_{i=1}^{m} x_{2 i}=2 \sum_{i=1}^{m} x_{i}=2 S_{m} \geq 0$.
|
| 14 |
+
Fall 2: $n=4 m+1$. Es gilt $S_{n}=2 S_{m}+x_{4 m+1}=2 S_{m}+x_{2 m+1}=2 S_{m}+(-1)^{m} x_{m+1}$.
|
| 15 |
+
Fall 2.1: $m$ ist ungerade. Dann ist auch $S_{m}$ ungerade, also $2 S_{m} \geq 2$ und $S_{n} \geq 1>0$.
|
| 16 |
+
Fall 2.2: $m$ ist gerade. Es gilt $S_{n}=2 S_{m}+x_{m+1}=S_{m}+S_{m+1} \geq 0$.
|
| 17 |
+
Fall 3: $n=4 m+2$. Es gilt $S_{n}=S_{n-2}+x_{4 m+1}+x_{4 m+2}=S_{n-2}+x_{2 m+1}-x_{2 m+1}=S_{n-2} \geq 0$.
|
| 18 |
+
Fall 4: $n=4 m+3$. Es gilt $S_{n}=S_{n+1}-x_{n+1}=2 S_{m+1}+x_{2 m+2}=2 S_{m+1}-x_{m+1}=S_{m}+S_{m+1} \geq 0$.
|
| 19 |
+
Hinweise: Bei dieser oder anderen Fallunterscheidungen wurden manchmal nicht alle Möglichkeiten abgedeckt oder sorgfältig genug behandelt. Eine Bilanzierung derart, dass jedes Element auf lange Sicht gleich viele positive und negative Nachfolger erzeugt und die Behauptung folgt, weil das erste Glied positiv ist, reicht nicht.
|
| 20 |
+
|
| 21 |
+
## Aufgabe 2
|
| 22 |
+
|
| 23 |
+
Gegeben sei ein konvexes Fünfeck $A B C D E$ mit den Eigenschaften $B C \| A E$ und $\overline{A B}=\overline{A E}$. Weiter sei $F$ ein Punkt auf der Strecke $A E$, so dass $\overline{A B}=\overline{B C}+\overline{A F}$ sowie $\Varangle C B A=\Varangle F D C$ erfüllt ist. Schließlich sei $M$ der Mittelpunkt der Strecke $C F$ und $O$ der Umkreismittelpunkt des Dreiecks $B C D$.
|
| 24 |
+
Man beweise: Wenn $D M \perp M O$, dann gilt $\Varangle F D C=2 \cdot \Varangle A D B$.
|
| 25 |
+
Lösung: Aus den Bedingungen folgt $\overline{F E}=\overline{A E}-\overline{A F}=\overline{A B}-(\overline{A B}-\overline{B C})=\overline{B C}$.
|
| 26 |
+
Daher ist $B C E F$ ein Parallelogramm, dessen beide Diagonalen $C F$ und $B E$ einander in $M$ halbieren.
|
| 27 |
+
Wegen der Punktsymmetrie an M gilt $\Varangle C B E=\Varangle A E B$, und da $A B E$ ein gleichschenkliges Dreieck ist, gilt $\Varangle A E B=\Varangle E B A$. Also ist $E B$ die Winkelhalbierende von $\Varangle C B A$. Es folgt $\Varangle F D C=\Varangle C B A=2 \cdot \Varangle A E B$, so dass nur noch $\Varangle A E B=\Varangle A D B$ zu zeigen ist.
|
| 28 |
+
Es sei $D^{\prime}$ der Spiegelpunkt von $D$ an $M$. Wegen $D M \perp M O$ ist dann
|
| 29 |
+
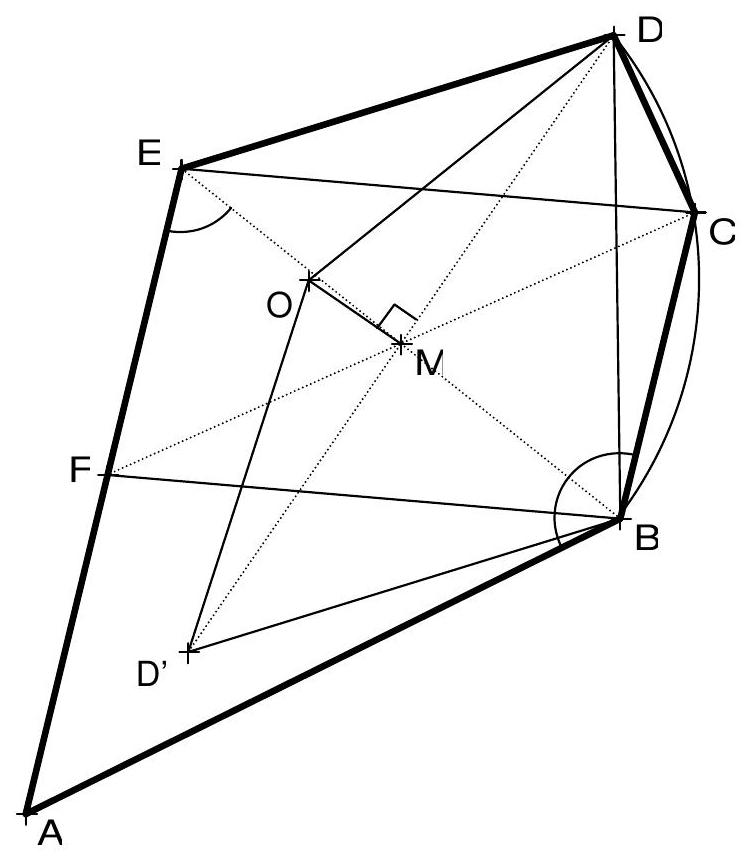
|
| 30 |
+
$\overline{O D^{\prime}}=\overline{O D}=\overline{O B}=\overline{O C}$ und $D^{\prime} B C D$ ist ein Sehnenviereck. Deshalb ist $\Varangle B D C=\Varangle B D^{\prime} C$, und weil $B C D E F D^{\prime}$ sogar ein zu $M$ punktsymmetrisches Sechseck ist, folgt weiter $\Varangle E D F=\Varangle B D^{\prime} C=\Varangle B D C$. Also ist $\Varangle E D B=\Varangle F D C$, während andererseits $\Varangle B A E=180^{\circ}-2 \cdot \Varangle A E B=180^{\circ}-\Varangle F D C$ gilt. Somit ist $A B D E$ ein Sehnenviereck, und die Behauptung folgt aus dem Umfangswinkelsatz.
|
| 31 |
+
|
| 32 |
+
Hinweis: Hier gab es mehrere unvollständige, aber wenig falsche Lösungen. Die Aufgabe war zwar elementar zu lösen, wirkte aber sperrig durch die Fülle der Informationen und Schwierigkeiten bei der Anfertigung einer befriedigenden Skizze.
|
| 33 |
+
|
| 34 |
+
## Aufgabe 3
|
| 35 |
+
|
| 36 |
+
Die Ecken und Kanten eines regulären $n$-Ecks seien im Uhrzeigersinn jeweils so von 1 bis $n$ nummeriert, dass die Kante Nr. $i$ auf die Ecke Nr. $i$ folgt ( $1 \leq i \leq n$ ).
|
| 37 |
+
Nun werden die Ecken mit nichtnegativen ganzen Zahlen $e_{i}$ und die Kanten mit nichtnegativen ganzen Zahlen $k_{i}$ so belegt, dass gilt:
|
| 38 |
+
(1) Das $n$-Tupel $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ ist eine Permutation des $n$-Tupels $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$.
|
| 39 |
+
(2) Für jedes $i \in \mathbb{N}$ mit $1 \leq i \leq n$ gilt $k_{i}=\left|e_{i+1}-e_{i}\right|$, wobei $e_{n+1}=e_{1}$ ist.
|
| 40 |
+
a) Man beweise, dass für alle natürlichen Zahlen $n, n \geq 3$, solche $n$-Tupel existieren, die von $(0, \ldots, 0)$ verschieden sind.
|
| 41 |
+
b) Man bestimme zu jeder positiven natürlichen Zahl $m$ die kleinste natürliche Zahl $n$ mit folgender Eigenschaft: In den $n$-Tupeln $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ und $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$ kommen jeweils alle natürlichen Zahlen von 0 bis $m$ vor.
|
| 42 |
+
|
| 43 |
+
Lösung: a) Ein mögliches Beispiel für $n \geq 3$ ist $e_{1}=e_{2}=1, e_{i}=0$ für $3 \leq i \leq n$. Dies bedingt $k_{2}=k_{n}=1$ und $k_{i}=0$ sonst. Offensichtlich sind alle Bedingungen erfüllt.
|
| 44 |
+
b) Wir beweisen, dass stets $n=m+2$ gilt. Der Beweis erfolgt in zwei Schritten.
|
| 45 |
+
i) Es gilt $n \geq m+2$ : Weil die Zahl 0 in $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$ vorkommt, müssen zwei Elemente von $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ gleich sein. Da außerdem jede der $m+1$ natürlichen Zahlen von 0 bis $m$ wenigstens einmal vorkommen muss, folgt $n \geq m+2$.
|
| 46 |
+
ii) Wir geben ein Beispiel für $n=m+2 \geq 3$ : Es sei $\left(e_{1}, e_{2}, \ldots, e_{n}\right)=(0, m, 1, m-1, \ldots)$. In dem $n$-Tupel werden die Zahlen alternierend bis zur Differenz 0 absteigend fortgesetzt, so dass $e_{n-1}=e_{n}$ gilt. Damit tritt jede natürliche Zahl von 0 bis $m$ genau einmal, die Zahl $e_{n}$ genau zweimal auf. Die Beträge der Differenzen treten von $m$ abwärts bis zur 0 offensichtlich je einmal auf; die Differenz $\left|e_{n}-0\right|=e_{n}$ tritt zweimal auf, weil $e_{n}<m$ ist. Damit sind die Eigenschaften (1) und (2) gezeigt.
|
| 47 |
+
|
| 48 |
+
Hinweis: Für Teil a) wurden 3 P . und für Teil b) 7 P . vergeben. Weder das Beispiel für a) noch das Beispiel für b) sind die einzig möglichen.
|
| 49 |
+
|
Germany_TST/md/de-2012-loes_awkl1_12.md
ADDED
|
@@ -0,0 +1,81 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2011/2012
|
| 2 |
+
|
| 3 |
+
Aufgabe 1 Man bestimme die kleinste positive Zahl $k$, für die folgendes der Fall ist: Wenn Kain in solcher Weise ganze Zahlen in die Zellen eines $2011 \times 2011$-Schachbrettes schreibt, dass die 4022 Summen, die man durch Addition aller Zahlen einer Zeile oder Spalte erhalten kann, paarweise übereinstimmen, so ist es für Abel möglich, durch Abänderung der Einträge aus nur $k$ der Zellen zu erreichen, dass diese 4022 Summen paarweise verschieden werden.
|
| 4 |
+
Lösung: $k=2681$. Beweis von $k \geq 2681$ : Abel muss mindestens 4021 der Summen ändern, o. B. d. A. alle Spaltensummen und alle bis auf höchstens eine Zeilensumme. Um die Spaltensummen zu ändern, muss Abel in jeder Spalte mindestens einen Eintrag abändern. Dies erledige Abel o. B. d. A. zuerst und pausiere dann. Zum Zeitpunkt dieser Pause seien $n$ Zeilen unverändert. Somit muss Abel in $n-1$ dieser Zeilen einen Eintrag abändern, damit sich die Zeilensummen unterscheiden können. Dies erledige Abel o. B. d. A. im Anschluss und pausiere wieder. Für $n \geq 671$ sind nun bereits mindestens 2681 Einträge abgeändert. Nun sei $n \leq 670$. Eine Zelle heiße unzureichend, wenn Abel ihren Eintrag geändert hat, aber keinen weiteren Eintrag einer Zelle in derselben Zeile oder Spalte. Da die Zeilen- und Spaltensumme einer unzureichenden Zelle gleich sind, darf am Ende keine Zelle unzureichend sein. Es gibt während Abels erster Pause mindestens 2011 - $2 n$ unzureichende Zellen. Durch jede Änderung bis zur zweiten Pause kann Abel höchstens eine dieser unzureichenden Zellen (durch Ändern eines Eintrags in derselben Spalte) eliminieren, durch jede Änderung nach der zweiten Pause höchstens zwei unzureichende Zellen. Daher sind nach der zweiten Pause mindestens $\frac{1}{2}(2011-2 n-(n-1))$ Einträge abzuändern, also zusammen mindestens $2011+(n-1)+\frac{1}{2}(2011-2 n-(n-1))=3016-\frac{n}{2} \geq 2681$.
|
| 5 |
+
Beweisidee zu $k \leq 2681$ : Für $1 \leq m, n \leq 2011$ sei die Zelle in Zeile $m$ und Spalte $n$ mit $\langle m ; n\rangle$ bezeichnet. Abel erhöht den Eintrag von 2681 Zellen $\langle m ; n\rangle$ jeweils um $2(m+n)+1$, und zwar von $\langle 2 ; 1\rangle$ sowie für $l=1, \ldots, 670$ von $\langle 3 l-1 ; 3 l-1\rangle,\langle 3 l ; 3 l-1\rangle,\langle 3 l+1 ; 3 l\rangle$ und $\langle 3 l+1 ; 3 l+1\rangle$.
|
| 6 |
+
|
| 7 |
+
Bemerkungen: Manchmal wurde argumentiert, dass mit Abändern zweier Einträge in derselben Zeile (oder Spalte) Abel drei Summen ändern könne und dies optimal sei, und daraus $k \geq 2681$ gefolgert. Dabei wurde aber implizit angenommen, dass eine Anordnung der Zellen mit geänderten Einträgen nach der Art wie der im Beweis von $k \leq 2681$ bereits optimal ist.
|
| 8 |
+
|
| 9 |
+
Aufgabe 2 Es sei $\Gamma$ der Umkreis des bei $C$ gleichschenkligen Dreiecks $A B C$. Im Inneren der Seite $\overline{B C}$ liege der Punkt $M$. Es gebe einen Punkt $N$ auf dem Strahl $A M$, für den $M$ zwischen $A$ und $N$ liegt und der $|A N|=|A C|$ erfüllt. Der Umkreis des Dreiecks $C M N$ schneide $\Gamma$ in den beiden verschiedenen Punkten $C$ und $P$. Die Geraden $A B$ und $C P$ mögen sich in einem Punkt $Q$ treffen. Man beweise, dass $\measuredangle B M Q=\measuredangle Q M N$.
|
| 10 |
+
|
| 11 |
+
Lösung: Die Idee zur Lösung geht von der Beobachtung aus, dass die Forderung $|A N|=|A C|=|B C|$ unverändert bleibt, wenn man $A$ und $C$ sowie $N$ und $B$ miteinander vertauscht. Dies legt nahe, dass man auch den Umkreis des Dreiecks $A M B$ betrachten sollte. Der zweite Schnittpunkt der Umkreise von $A M B$ und $C M N$ lässt sich schließlich als Inkreismittelpunkt von $A M C$ identifizieren.
|
| 12 |
+
Es sei $I$ der Inkreismittelpunkt des Dreiecks $A M C$. Bekanntlich ist $\measuredangle M I C=\frac{\pi}{2}+\frac{1}{2} \measuredangle M A C=\frac{\pi}{2}+\frac{1}{2} \measuredangle N A C$, und weil das Dreieck $A N C$ bei $A$ gleichschenklig ist, ist $\measuredangle N A C=\pi-2 \measuredangle C N A$, also ist $\measuredangle M I C=\pi-\measuredangle C N A=$ $\pi-\measuredangle C N M$, und weil $I$ und $N$ bezüglich der Geraden $C M$ in verschiedenen Halbebenen liegen, folgt aus dem Satz vom Sehnenviereck, dass $I M N C$ ein Sehnenviereck ist, d. h., dass $I$ auf dem Umkreis von $C M N$ liegt. Auf Grund der eingangs angesprochenen Symmetrie liegt $I$ auch auf dem Umkreis von $A B M$. Da $I$ als Inkreismittelpunkt ein innerer Punkt des Dreiecks $A M C$ ist, ist insbesondere $I \neq M$, und damit ist die Gerade $I M$ die Potenzgerade der Umkreise von $A B M$ und $C M N$. Da weiterhin die Gerade $A B$ die Potenzgerade der Umkreise von $A B C$ und $A B M$ und die Gerade $C P$ die Potenzgerade der Umkreise von $A B C$ und $C M N$ ist, schneiden sich die Geraden $I M, A B$ und $C P$ in einem Punkt. Dieser Punkt ist nach Definition $Q$, d.h. $Q$ liegt auf der Winkelhalbierenden $I M$ des Winkels $C M A$, aber diese ist identisch mit der Winkelhalbierenden des Winkels $B M N$, folglich ist $\measuredangle B M Q=\measuredangle Q M N$.
|
| 13 |
+
|
| 14 |
+
## Aufgabe 3
|
| 15 |
+
|
| 16 |
+
Es seien $a, b$ und $c$ drei positive reelle Zahlen mit $a^{2}+b^{2}+c^{2} \geq 3$. Man beweise, dass
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\frac{(a+1)(b+2)}{(b+1)(b+5)}+\frac{(b+1)(c+2)}{(c+1)(c+5)}+\frac{(c+1)(a+2)}{(a+1)(a+5)} \geq \frac{3}{2}
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Lösung: Die Funktion $f:(0, \infty) \rightarrow \mathbb{R}, f(x)=\frac{x+2}{(x+1)(x+5)}$ ist streng monoton fallend und konvex, denn die erste Ableitung
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
f^{\prime}(x)=-\frac{x^{2}+4 x+7}{(x+1)^{2}(x+5)^{2}}
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
ist negativ, und die zweite Ableitung
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
f^{\prime \prime}(x)=\frac{2\left(x^{3}+6 x^{2}+21 x+32\right)}{(x+1)^{3}(x+5)^{3}}
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
ist positiv. Die Ungleichung von Jensen liefert für das mit den Gewichten $a+1, b+1, c+1$ gewichtete Mittel der Argumente $b, c, a$ :
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
\frac{(a+1) f(b)+(b+1) f(c)+(c+1) f(a)}{(a+1)+(b+1)+(c+1)} \geq f\left(\frac{(a+1) b+(b+1) c+(c+1) a}{(a+1)+(b+1)+(c+1)}\right)
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Multipliziert man mit dem Nenner der linken Seite, erhält man
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\frac{(a+1)(b+2)}{(b+1)(b+5)}+\frac{(b+1)(c+2)}{(c+1)(c+5)}+\frac{(c+1)(a+2)}{(a+1)(a+5)} \geq(a+b+c+3) f\left(\frac{(a+1) b+(b+1) c+(c+1) a}{a+b+c+3}\right)
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Nun ist
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
\begin{aligned}
|
| 50 |
+
2((a+1) b+(b+1) c+(c+1) a) & =(a+b+c+3)^{2}-4(a+b+c)-\left(a^{2}+b^{2}+c^{2}\right)-9 \\
|
| 51 |
+
& \leq(a+b+c+3)^{2}-4(a+b+c+3)
|
| 52 |
+
\end{aligned}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
(im letzten Schritt wurde die Voraussetzung $a^{2}+b^{2}+c^{2} \geq 3$ verwendet), also
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\frac{(a+1) b+(b+1) c+(c+1) a}{a+b+c+3} \leq \frac{a+b+c-1}{2}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Mit der Monotonie von $f$ kann man die rechte Seite von (*) also weiter abschätzen als
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\geq(a+b+c+3) f\left(\frac{a+b+c-1}{2}\right)
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Dieser Ausdruck hängt nur noch von $s=a+b+c$ ab:
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
=(s+3) \cdot \frac{\frac{s-1}{2}+2}{\left(\frac{s-1}{2}+1\right)\left(\frac{s-1}{2}+5\right)}=\frac{2(s+3)^{2}}{(s+1)(s+9)}=2-\frac{8}{10+s+\frac{9}{s}} \geq 2-\frac{8}{10+6}=\frac{3}{2}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
(im vorletzten Schritt wurde die Ungleichung zwischen arithmetischem und geometrischem Mittel in der Form $s+\frac{9}{s} \geq 2 \sqrt{s \cdot \frac{9}{s}}=6$ angewendet).
|
| 74 |
+
Bemerkung: Diese Aufgabe wurde von keinem Teilnehmer gelöst. Die häufig behauptete Ungleichung
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\frac{b+2}{b+5}+\frac{c+2}{c+5}+\frac{a+2}{a+5} \geq \frac{3}{2}
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
ist falsch, wie das aus Stetigkeitsgründen immer noch gültige Gegenbeispiel $a=2, b=c=0$ zeigt.
|
| 81 |
+
|
Germany_TST/md/de-2012-loes_awkl2_12.md
ADDED
|
@@ -0,0 +1,57 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 2. Auswahlklausur 2011/2012
|
| 2 |
+
|
| 3 |
+
## Aufgabe 1
|
| 4 |
+
|
| 5 |
+
Für neun verschiedene positive ganze Zahlen $d_{1}, d_{2}, \ldots, d_{9}$ betrachten wir das Polynom $P(n)=\left(n+d_{1}\right)\left(n+d_{2}\right) \cdot \ldots \cdot\left(n+d_{9}\right)$.
|
| 6 |
+
Man zeige, dass eine ganze Zahl $N$ mit folgender Eigenschaft existiert:
|
| 7 |
+
Für alle ganzen Zahlen $n \geq N$ ist die Zahl $P(n)$ durch eine Primzahl größer als 20 teilbar.
|
| 8 |
+
Lösung: Wir können der Aufgabenstellung gemäß $N>0$ und $d_{1}<d_{2}<\ldots<d_{9}$ annehmen. Dann ist $k=d_{9}-d_{1}=\max _{1 \leq q<r \leq 9}\left(d_{r}-d_{q}\right)$. Es sei $z \in \mathbb{N}$ so gewählt, dass $2^{z}>k$.
|
| 9 |
+
Behauptung: Mit $N=2^{z} \cdot 3^{z} \cdot 5^{z} \cdot 7^{z} \cdot 11^{z} \cdot 13^{z} \cdot 17^{z} \cdot 19^{z}$ ist eine Lösung für $N$ gefunden.
|
| 10 |
+
Beweis: Wir nehmen an, dass für $n \geq N$ keiner der Faktoren von $P(n)$ einen Primfaktor größer als 20 besitzt und betrachten zunächst $n+d_{1}=2^{e_{1}^{(1)}} \cdot 3^{e_{2}^{(1)}} \cdot \ldots \cdot 19^{e_{8}^{(1)}}$. Wegen $n \geq N$ muss es dann wenigstens ein $e_{j}^{(1)}$ mit $e_{j}^{(1)} \geq z$ geben $(1 \leq j \leq 8)$. Der zugehörige Primfaktor sei $p$. Somit ist $n+d_{1}$ durch $p^{e_{j}^{(1)}}$ teilbar. Wegen $p^{e_{j}^{(1)}} \geq 2^{\ell_{j}^{(1)}} \geq 2^{z}>k=\max _{1 \leq q<r \leq 9}\left(d_{r}-d_{q}\right)$ ist keine weitere der Zahlen $n+d_{i}$ durch $p^{e_{j}^{(1)}}$ teilbar $(2 \leq i \leq 9)$, weil sonst $d_{i}-d_{1}$ durch $p_{j}^{e_{j}^{(1)}}$ teilbar wäre. Es ist also $e_{j}^{(1)}=\max _{1 \leq i \leq 9}\left(e_{j}^{(i)}\right)$. Betrachten wir nun $n+d_{2}$, so finden wird dort wegen $d_{2}>d_{1}$ wenigstens ein $e_{j}^{(2)}$ mit $e_{j}^{(2)}>e_{j}^{(1)}$ sowie $e_{j}^{(2)} \geq z$. Daher besitzt auch $n+d_{2}$ ein im Bezug auf alle Faktoren maximales $e_{j}^{(2)}$. Dies gilt entsprechend für die anderen Faktoren $n+d_{i}$.
|
| 11 |
+
Da es für die 9 Faktoren des Polynoms jedoch nur 8 Primfaktoren kleiner als 20 gibt, entsteht hier nach dem Schubfachprinzip ein Widerspruch. Daher muss ein weiterer Primfaktor auftreten, durch den $P(n)$ teilbar ist.
|
| 12 |
+
|
| 13 |
+
Hinweise: Das hier angegebene $N$ ist nicht das einzig mögliche. Häufig waren Beweise nicht streng genug. Man argumentierte etwa mit immer mehr dazukommenden Primzahlen, wenn $n$ immer größer wird.
|
| 14 |
+
|
| 15 |
+
## Aufgabe 2
|
| 16 |
+
|
| 17 |
+
Es sei $A B C$ ein spitzwinkliges Dreieck mit dem Umkreismittelpunkt $O$. Ferner sei $k$ ein Kreis mit folgenden Eigenschaften:
|
| 18 |
+
(1) Der Mittelpunkt $K$ von $k$ liegt im Inneren der Seite $B C$.
|
| 19 |
+
(2) $k$ berührt $A B$ in $B^{\prime}$ und $A C$ in $C^{\prime}$.
|
| 20 |
+
(3) $O$ liegt auf dem kürzeren der beiden Bogenstücke $B^{\prime} C^{\prime}$ von $k$.
|
| 21 |
+
|
| 22 |
+
Man beweise: Der Umkreis von $A B C$ und $k$ schneiden einander in zwei verschiedenen Punkten.
|
| 23 |
+
Lösung: Der Punkt $O^{\prime}$ ist Bildpunkt von $O$ bei der Spiegelung an der Geraden $B C$. $S$ ist der Schnittpunkt von $K O^{\prime}$ mit dem Umkreis $u$ (siehe Figur).
|
| 24 |
+
|
| 25 |
+
Nach dem Satz vom Mittelpunktswinkel ist $\Varangle B O C=2 \alpha$. Weil $C^{\prime}$ und $B^{\prime}$ im Inneren der Strecken $A C$ bzw. $A B$ liegen und $O$ wegen der Spitzwinkligkeit innerhalb von $A B C$ liegt, ist $\Varangle B^{\prime} O C^{\prime}>2 \alpha$. Im Viereck $A B^{\prime} K C^{\prime}$ gilt: $360^{\circ}=2 \cdot 90^{\circ}+\alpha+\Varangle C^{\prime} K B^{\prime}$, da die Winkel in den Berührpunkten $C^{\prime}$ und $B^{\prime}$ Rechte sind. Es folgt $\Varangle C^{\prime} K B^{\prime}=180^{\circ}-\alpha$.
|
| 26 |
+
Damit gilt im Sehnenviereck $B^{\prime} O^{\prime} C^{\prime} O$ :
|
| 27 |
+
$\Varangle B^{\prime} O C^{\prime}=180^{\circ}-\Varangle C^{\prime} O^{\prime} B^{\prime}=180^{\circ}-\frac{1}{2} \Varangle C^{\prime} K B^{\prime}$
|
| 28 |
+
$=\frac{1}{2}\left(180^{\circ}+\alpha\right)$. Somit ist $\frac{1}{2}\left(180^{\circ}+\alpha\right)>2 \alpha$ und daher
|
| 29 |
+
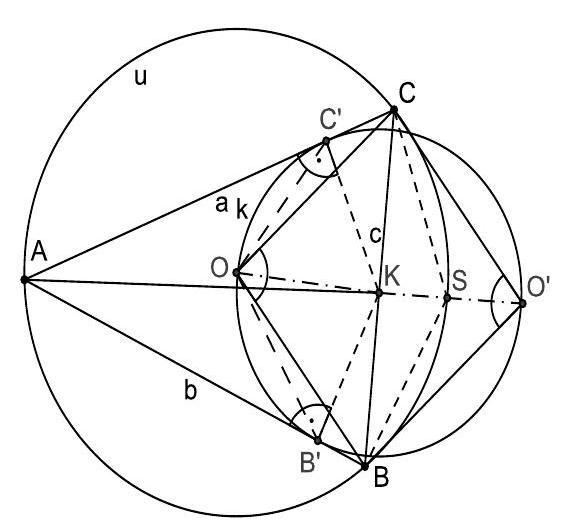
|
| 30 |
+
$\alpha<60^{\circ}$.
|
| 31 |
+
Im Sehnenviereck $A B S C$ folgt daraus $\Varangle C S B=180^{\circ}-\alpha>120^{\circ}$.
|
| 32 |
+
Aufgrund der Achsensymmetrie an $B C$ ist $B O^{\prime} C O$ ein Drachenviereck und es gilt:
|
| 33 |
+
$\Varangle C O^{\prime} B=\Varangle B O C=2 \alpha<120^{\circ}$. Also ist $\Varangle C S B>\Varangle C O^{\prime} B$.
|
| 34 |
+
Da $S$ auf $u$ liegt, ist $\Varangle C S B$ ein Umfangswinkel über der Sehne $B C$. Aus der letzten Ungleichung folgt dann, dass $O^{\prime}$ außerhalb von $u$ liegt. Weil die Spiegelachse $B C$ Durchmesser von $k$ ist, liegt $O^{\prime}$ auf $k$. Somit gibt es mit $O$ und $O^{\prime}$ je einen Punkt auf $k$, der innerhalb bzw. außerhalb von $u$ liegt. Daraus folgt die Behauptung.
|
| 35 |
+
|
| 36 |
+
Hinweis: Die Behauptung gilt nicht für jedes spitzwinklige Dreieck, was den Zugang zu der Aufgabe deutlich erschwert hat. Eine einfache Lösung ist unter Verwendung von Inversion an $u$ möglich.
|
| 37 |
+
|
| 38 |
+
## Aufgabe 3
|
| 39 |
+
|
| 40 |
+
Es seien $f$ und $g$ zwei reelle Funktionen, die für jede reelle Zahl definiert sind. Ferner soll für alle reellen Zahlen $x$ und $y$ die Gleichung gelten:
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
g(f(x+y))=f(x)+(2 x+y) g(y)
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Man bestimme alle möglichen Paare $(f, g)$.
|
| 47 |
+
Lösung: Aus der gegebenen Gleichung (1) erhalten wir für $y=-2 x: g(f(-x))=f(x)$ (2). Damit wird (1) zu $f(-x-y)=f(x)+(2 x+y) g(y)$ (3) und mit $x=0$ zu $f(-y)=f(0)+y g(y)$ (4).
|
| 48 |
+
Ersetzen von $f$ in (3) gemäß (4) liefert nach Subtraktion von $f(0)$ :
|
| 49 |
+
$(x+y) g(x+y)=(2 x+y) g(y)-x g(-x)$ (5). Mit $y=0$ ergibt sich für $x \neq 0: g(x)+g(-x)=2 g(0)$ (6), was aber auch für $x=0$, also für alle $x \in \mathbb{R}$ erfüllt ist.
|
| 50 |
+
|
| 51 |
+
Wir setzen $h(x):=g(x)-g(0)$. Dann gilt $h(0)=0$ sowie nach (6): $h(-x)=-h(x)$ (6*) sowie mit (5) und (6*): $(x+y) h(x+y)=(2 x+y) h(y)+x h(x)$ (7). Vertauschen von $x$ und $y$ in (7) und Gleichsetzen liefert $x h(y)=y h(x)$ (8). Für $x, y \neq 0$ folgt daraus $h(x) / x=h(y) / y=$ const. Also ist $h(x)=c \cdot x$, was offensichtlich auch für $x=0$ erfüllt ist. Mit $g(0)=b$ ergibt sich $g(x)=c x+b$ für alle $x \in \mathbb{R}$.
|
| 52 |
+
Mit $f(0)=a$ folgt aus (4): $f(x)=a-b x+c x^{2}$. (2) liefert $c\left(c x^{2}+b x+a\right)+b=c x^{2}-b x+a$, und nach Koeffizientenvergleich muss $c^{2}=c, b c=-b$ sowie $a c+b=a$ gelten.
|
| 53 |
+
Fall 1: $c=0$. Es ergibt sich $b=a=0$ und $f(x)=0, g(x)=0$, womit (1) erfüllt ist.
|
| 54 |
+
Fall 2: $c=1$. Dann ist $b=-b$, also $b=0$, und $a$ beliebig. Es ergibt sich $f(x)=x^{2}+a, g(x)=x$. Auch für dieses Funktionspaar liefert Einsetzen in (1) eine wahre Aussage. Also existieren die beiden Lösungspaare $(f, g)=(0,0)$ bzw. $(f, g)=\left(x^{2}+a, x\right)$ mit $a \in \mathbb{R}$.
|
| 55 |
+
|
| 56 |
+
Hinweis: Sehr häufig wurden nur spezielle Lösungen erraten und für diese die Probe durch Einsetzen durchgeführt.
|
| 57 |
+
|
Germany_TST/md/de-2013-loes_awkl_13.md
ADDED
|
@@ -0,0 +1,140 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2012/2013
|
| 2 |
+
|
| 3 |
+
1. Aufgabe. Es sei $n$ eine ungerade natürliche Zahl und $x$ und $y$ seien zwei rationale Zahlen mit
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
x^{n}+2 y=y^{n}+2 x
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
Man zeige, dass $x=y$.
|
| 10 |
+
Lösung. Wir überlegen uns zuerst
|
| 11 |
+
( $\boxtimes)$ Es sei $n \geqslant 3$ eine ungerade natürliche Zahl. Weiterhin seien $a, b$ und $c$ drei ganze Zahlen mit
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
a^{n-1}+a^{n-2} b+\ldots+b^{n-1}=2 c^{n-1}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
Sodann ist $a=b=c=0$.
|
| 18 |
+
Wenn dies bei einem gewissen $n$ falsch wäre, könnten wir zu diesem ein Gegenbeispiel ( $a, b, c$ ) wählen, bei dem der Ausdruck $|a|+|b|+|c|$ seinen kleinstmöglichen positiven Wert annimmt. Wären $a$ und $b$ beide ungerade, so wäre die linke Seite die Summe einer ungeraden Anzahl ungerader Summanden und mithin selbst ungerade, während die rechte Seite gerade ist. Also ist mindestens eine der beiden Zahlen $a$ und $b$ gerade. Ist etwa $a$ gerade, so hat die linke Seite dieselbe Parität wie $b^{n-1}$ und die rechte Seite ist gerade, sodass $b$ ebenfalls gerade ist. Ebenso sieht man, dass $a$ gerade sein muss, falls $b$ als gerade vorausgesetzt wird. Insgesamt sind also $a$ und $b$ beide gerade. Folglich ist die linke Seite durch $2^{n-1}$ und damit insbesondere durch 4 teilbar, womit sich $c^{n-1}$ und demnach auch $c$ als gerade erwiesen hat. Führt man nun drei ganze Zahlen $a^{\prime}, b^{\prime}$ und $c^{\prime}$ mit $a=2 a^{\prime}, b=2 b^{\prime}$ und $c=2 c^{\prime}$ in die Betrachtung ein, so ist erstens
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
a^{\prime n-1}+a^{\prime n-2} b^{\prime}+\ldots+b^{\prime n-1}=2 c^{\prime n-1}
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
und zweitens
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
0<\left|a^{\prime}\right|+\left|b^{\prime}\right|+\left|c^{\prime}\right|<|a|+|b|+|c| .
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
Das Tripel $\left(a^{\prime}, b^{\prime}, c^{\prime}\right)$ widerspricht also der Wahl von $(a, b, c)$ und damit ist $(\boxtimes)$ bewiesen.
|
| 31 |
+
Wir wenden und nunmehr der eigentlichen Aufgabe zu. $\operatorname{Im}$ Fall $n=1$ ist die Behauptung trivial und wir konzentrieren uns von jetzt an nur noch auf den Fall $n \geqslant 3$. Es seien $x$ und $y$ zwei rationale Zahlen mit $x^{n}+2 x=y^{n}+2 y$. Indem wir alles auf eine Seite bringen und anschließend faktorisieren, erhalten wir
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
(x-y)\left(x^{n-1}+x^{n-2} y+\ldots+y^{n-1}-2\right)=0
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Wenn $x$ und $y$ also verschieden wären, was wir von jetzt an annehmen wollen, müsste
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
x^{n-1}+x^{n-2} y+\ldots+y^{n-1}=2
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
sein. Da man je zwei rationale Zahlen auf einen gemeinsamen Nenner bringen kann, gibt es drei ganze Zahlen $a, b$ und $c$ mit $c \neq 0, x=a / c$ und $y=b / c$. Wer diese Brüche in (1) einsetzt und daraufhin mit $c^{n-1}$ multipliziert, erhält
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
a^{n-1}+a^{n-2} b+\ldots+b^{n-1}=2 c^{n-1}
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Aus $(\boxtimes)$ folgt nun allerdings insbesondere $c=0$. Dieser Widerspruch zeigt, dass $x$ und $y$ doch gleich sein müssen, womit die Aufgabe gelöst ist.
|
| 50 |
+
2. Aufgabe. Es seien $m, n \geqslant 4$ zwei ganze Zahlen. Wir betrachten ein $m \times n$-Gitterrechtteck, das von $m+1$ horizontalen und $n+1$ vertikalen Strecken gebildet wird. Die Schnittpunkte dieser Strecken heißen Ecken. Es sei $P$ ein von Selbstüberschneidungen freier, geschlossener Weg, der durch jede der $(m-1)(n-1)$ inneren Ecken aber keine der äußeren Ecken geht. Es bezeichne $A$ die Anzahl der inneren Ecken, durch die $P$ geradlinig hindurchgeht, $B$ die Anzahl der Gitterquadrate, von denen $P$ genau zwei Seiten benutzt, die sich zudem gegenüber liegen, und $C$ die Anzahl der Gitterquadrate,
|
| 51 |
+
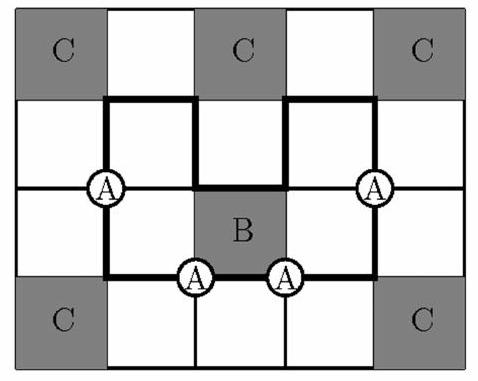
|
| 52 |
+
von denen $P$ keine Seite benutzt. Man beweise, dass $A=B-C+m+n-1$.
|
| 53 |
+
(Die Abbildung zeigt eine Situation mit $m=4, n=5, A=4, B=1$ und $C=5$.)
|
| 54 |
+
Lösung. Es sei $D$ die Anzahl der Gitterquadrate, von denen genau eine Seite zu $P$ gehört, $E$ die Anzahl der Gitterquadrate, von denen genau zwei Seiten zu $P$ gehören, die zudem benachbart sind, und schließlich $F$ die Anzahl der Gitterquadrate von denen genau drei Seiten zu $P$ gehören. Wegen $m, n \geqslant 4$ ist unter den $m n$ Gitterquadraten keines, dessen gesamter Rand in $P$ enthalten ist und folglich gibt es für den Schnitt eines solchen Randes mit $P$ nur die fünf Möglichkeiten, die in den Definitionen von $B, C, D, E$ und $F$ angesprochen sind. Wir haben also
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
m n=B+C+D+E+F
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Nun wollen wir die Paare ( $Q, S$ ), die aus einem Gitterquadrat $Q$ und einer $P$ angehörigen Seite $S$ von $Q$ bestehen, auf zwei Arten abzählen. Einerseits gibt es zu den Quadraten vom Typ $B, C$, $D, E$ und $F$ jeweils genau 2, 0, 1, 2 und 3 mögliche Wahlen für $S$ und daher beträgt diese Anzahl $2 B+D+2 E+3 F$. Andererseits ist $P$ aus $(m-1)(n-1)$ Einheitsstrecken zusammengesetzt, die alle als $S$ fungieren können und jede derselben hat zwei Seiten auf auf denen jeweils ein Gitterquadrat liegt. Insgesamt erhalten wir also
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
2(m-1)(n-1)=2 B+D+2 E+3 F
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
Bei jeder der $(m-1)(n-1)$ inneren Ecken unseres Rechtecks geht $P$ entweder geradeaus hindurch, und dies passiert genau $A$ mal, oder $P$ knickt ab. Wann immer dies geschieht, schließen die beiden zugehörigen Einheitsteilstrecken von $P$ ein Gitterquadrat ein und dieses muss entweder von Typ $E$ oder vom Typ $F$ sein. Umgekehrt gehören zu jedem Quadrat vom Typ $E$ ein und zu jedem Quadrat vom Typ $F$ zwei dieser Abknickpunkte von $P$. Alles in allem gilt also auch
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
(m-1)(n-1)=A+E+2 F
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Aus (2) $-(3)+(1)$ erhalten wir nunmehr
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
m+n-1=A-B-C
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
und dies wiederum impliziert
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
A=B-C+m-n-1
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Damit ist die Aufgabe gelöst.
|
| 85 |
+
|
| 86 |
+
## 3. Aufgabe
|
| 87 |
+
|
| 88 |
+
Es sei $A B C$ ein spitzwinkliges Dreieck mit Umkreis $\omega$. Man beweise, dass es einen Punkt $J$ mit der folgenden Eigenschaft gibt: Ist $X$ cin innerer Punkt von $A B C$, treffen die Strahlen $A X$, $B X$ und $C X$ den Kreis $w$ erneut in den Punkten $A_{1}, B_{1}$ und $C_{1}$ und liegen die Punkte $A_{2}$, $B_{2}$ und $C_{2}$ symmetrisch zu $A_{1}, B_{1}$ und $C_{1}$ bezüglich der Mittelpunkte der Strecken $\overline{B C}, \overline{C^{\prime} A}$ beziehungsweise $\overline{A B}$, so liegen die vier Punkte $A_{2}, B_{2}, C_{2}$ und $J$ auf einem gemeinsamen Kreis.
|
| 89 |
+
|
| 90 |
+
Lösung. Wir zeigen, dass der normalerweise $H$ genannte Höhenschnittpunkt $J$ des Dreiecks $A B C$ die beschriebene Eigenschaft aufweisi. Hierzu sei a die durch $A$ gezogene Parallele zu $B C$ und dic Geraden $b$ und $c$ seien analog definiert. Keine zwei der drei Geraden $a, b$ und $c$ sind parallel und folglich existieren der Schnittpunkt $A^{\prime}$ von $b$ mit $c$ sowie die beiden analog definierten Punkte $B^{\prime}$ und $C^{\prime}$.
|
| 91 |
+
Das Viereck $A^{\prime} C J B$ besitzt bei $B$ und $C$ rechte Winkel und ist daher ein Sehnenviereck. Da die Spiegelung am Mittelpunkt der Strecke $\overline{B C}$ den Punkt $A$ auf $A^{\prime}$ abbildet und $B$ mit $C$ vertauscht, führt sie $\omega$ in den Umkreis des gerade gefundenen Sehnenvierecks über. Demnach liegt $A_{2}$ auf diesom Krcis und $\Lambda^{\prime} A_{2}$ ist zu $A X$ parallel.
|
| 92 |
+
Der Schwerpunkt des Dreiecks $A B C$ heiße $S$. Die zentrische Streckung $\sigma$ mit Zentrum $S$ und Faktor -2 bildet $A$ auf $A^{\prime}$ ab; der Bildpunkt von $X$ heiBe $X^{\prime}$. Sodann sind die beiden Geraden $A X$ und $A^{\prime} X^{\prime \prime}$ parallel und daher liegt $X^{\prime}$ auf der Geraden $A^{\prime} A_{2}$. Ähnliche Argumente lassen sich auch mit $B$ und $C$ an der Stelle von $A$ ausführen und wir lernen insgesamt: Die drei Geraden $A^{\prime} A_{2}, B^{\prime} B_{2}$ und $C^{\prime \prime} C_{2}$ schneiden sich in $X^{\prime}$.
|
| 93 |
+
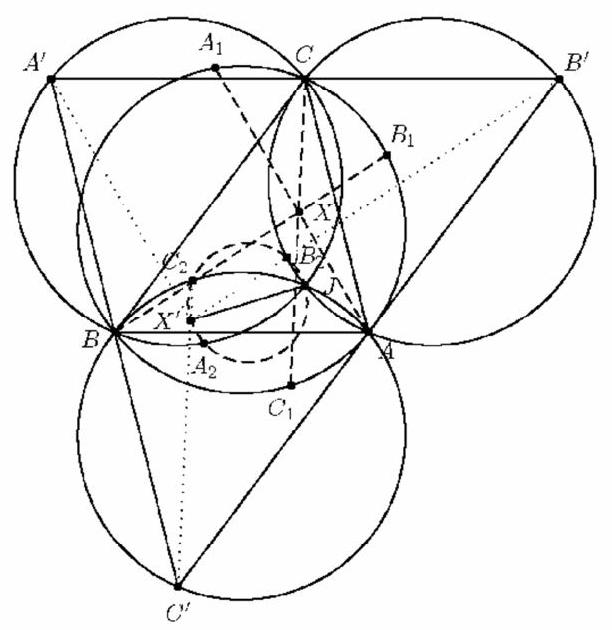
|
| 94 |
+
|
| 95 |
+
Falls $X^{\prime}=J$ fallen auch die Punkte $A_{2}, B_{2}$ und $C_{2}$ mit $J$ zusammen und die Behauptung ist trivial. Von nun ab sei daher $X^{\prime} \neq J$.
|
| 96 |
+
Wegen $\varangle A^{\prime} C J=90^{\circ}$ ist die Strecke $\overline{A^{\prime} J}$ nach Satz des Thales ein Durchmesser des Umkreises des Viereck $A^{\prime} C J B$. Wieder um nach Satz des Thales ist daher $\varangle J A_{2} A^{\prime}=90^{\circ}$ und folglich auch $\varangle J A_{2} X^{\prime}=90^{\circ}$. Der Punkt $A_{2}$ liegt demnach, abermals nach Satz des 'l'haces, auf dem Kreis mit Durchmesser $J X^{-1}$. Aus analogen Gründen liegen auch die beiden Punkte $B_{2}$ und $C_{2}$ auf diesem Kreis und insbesondere haben wir nunmehr einen Kreis gefunden, auf dem alle vier der Punkte $A_{2}, B_{2}, C_{2}$ und $J$ liegen.
|
| 97 |
+
|
| 98 |
+
## Aufgabe 1
|
| 99 |
+
|
| 100 |
+
In der Ebene liegen zwei konzentrische Kreise mit den Radien $r_{1}=13$ und $r_{2}=8$.
|
| 101 |
+
Es sei $A B$ ein Durchmesser des größeren Kreises und $B C$ eine seiner Sehnen, die den kleineren Kreis im Punkt $D$ berührt.
|
| 102 |
+
Man berechne die Länge der Strecke $A D$.
|
| 103 |
+
Lösung: Die beiden möglichen Lagen von $D$ sind symmetrisch zur Geraden $(A B)$, so dass es ausreicht, den Fall zu betrachten, bei dem das Dreieck $A B D$ gegen den Uhrzeigersinn orientiert ist (siehe Figur). Der gemeinsame Mittelpunkt der beiden Kreise sei mit $M$ bezeichnet. Weil der Berührradius MD auf der Tangente $B C$ senkrecht steht, ist $M B D$ rechtwinklig, so dass aus dem Satz des Pythagoras
|
| 104 |
+
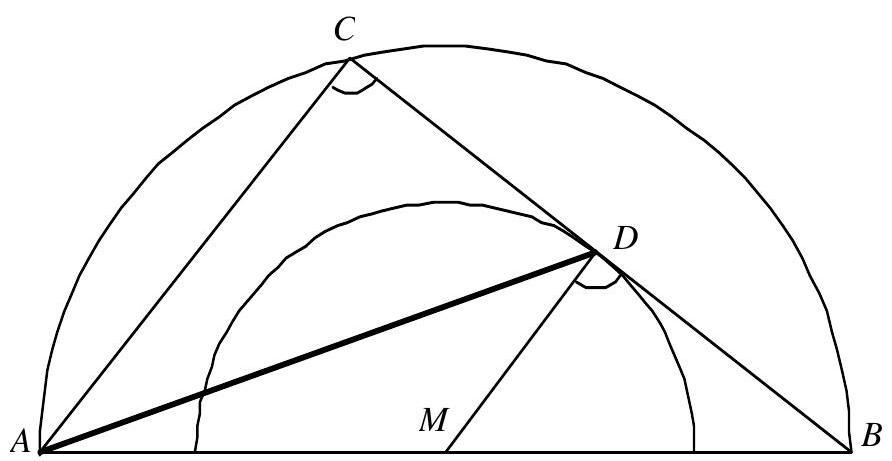
|
| 105 |
+
$|B D|^{2}=|M B|^{2}-|M D|^{2}=r_{1}^{2}-r_{2}^{2}=169-64=105$ folgt.
|
| 106 |
+
Nach dem Satz des Thales ist $\Varangle A C B=90^{\circ}$. Da wegen $\Varangle A C B=\Varangle M D B=90^{\circ}$ und des gemeinsamen Winkels $\Varangle D B M=\Varangle C B A$ die Dreiecke $A B C$ und $M B D$ ähnlich sind, und da $|M B|=r_{1}=|M A|$ gilt, ist auch $|D C|=|B D|=\sqrt{105}$ sowie $|C A|=2 \cdot|D M|=16$. Damit sind die Längen der Katheten im rechtwinkligen Dreieck $A D C$ bekannt und es folgt $|A D|=\sqrt{105+16^{2}}=\sqrt{361}=19$. Die Seite $A D$ hat also die Länge 19.
|
| 107 |
+
|
| 108 |
+
Hinweise: Zahlreiche andere Lösungswege sind möglich. Weil die Aufgabe recht einfach ist, mussten auch für Fehler im letzten Rechenschritt (Beispiele: $\sqrt{360}, \sqrt{461}$ oder sogar $\sqrt{361} \approx 18,5$ ) Punkte abgezogen werden.
|
| 109 |
+
|
| 110 |
+
## Aufgabe 2
|
| 111 |
+
|
| 112 |
+
Eine Menge $A$ von ganzen Zahlen heißt zulässig, wenn sie folgende Eigenschaft hat:
|
| 113 |
+
Für $x, y \in A\left(x=y\right.$ ist erlaubt) gilt $x^{2}+k x y+y^{2} \in A$ für jede ganze Zahl $k$.
|
| 114 |
+
Man bestimme alle Paare $m, n$ von Null verschiedener ganzer Zahlen, für welche die einzige zulässige Menge, die sowohl $m$ als auch $n$ enthält, die Menge $\mathbb{Z}$ aller ganzer Zahlen ist.
|
| 115 |
+
|
| 116 |
+
Lösung: Für ein Paar $m, n$ mit $\operatorname{ggT}(|m|,|n|)=d>1$ ist $m^{2}+k m n+n^{2}$ durch $d$ teilbar, so dass als Menge $A$ auch die Menge aller ganzzahligen Vielfachen von $d$ in Frage kommt, die das Element 1 nicht enthält und daher von $\mathbb{Z}$ verschieden ist.
|
| 117 |
+
Nun betrachten wir Zahlen $m, n$ mit $\operatorname{ggT}(|m|,|n|)=1$. Für diese gilt auch $\operatorname{ggT}\left(m^{2}, n^{2}\right)=1$. Daher folgt aus dem erweiterten Euklidischen Algorithmus oder aus dem kleinen Satz von Fermat, dass es ganze Zahlen $r$ und $s$ gibt mit $r m^{2}+s n^{2}=1$. Außerdem ist für $x=y=m$ ersichtlich, dass $(2+k) m^{2} \in A$, d.h. jedes ganzzahlige Vielfache von $m^{2}$ in $A$ liegt - entsprechend liegt jedes ganzzahlige Vielfache von $n^{2}$ in $A$. Und für $k=2$ ergibt sich, dass für alle $x, y \in A$ auch $(x+y)^{2}$ in $A$ liegt. Also liegen $r m^{2}, s n^{2}$ und folglich $\left(r m^{2}+s n^{2}\right)^{2}=1^{2}=1$ in $A$.
|
| 118 |
+
|
| 119 |
+
## Aufgabe 3
|
| 120 |
+
|
| 121 |
+
Es sei $n$ eine positive natürliche Zahl. Im Folgenden betrachten wir Paare von Elementen der Menge $\{1,2, \ldots, n\}$, die jeweils kein gemeinsames Element haben.
|
| 122 |
+
Man bestimme mit Beweis die größtmögliche Anzahl solcher Paare, für welche die Summen ihrer Elemente paarweise verschieden und nicht größer als $n$ sind.
|
| 123 |
+
(Zum Beispiel sind $(1 ; 9),(2 ; 7)$ und $(3 ; 5)$ für $n=10$ drei mögliche Paare.)
|
| 124 |
+
Lösung: Es sei $k$ die Anzahl möglicher Paare. Dann lässt sich die Summe $S$ der in ihnen vorkommenden $2 k$ Zahlen in zwei Richtungen abschätzen:
|
| 125 |
+
$S \geq 1+2+\ldots+2 k=k(2 k+1)$ (alle Zahlen sind verschieden) und
|
| 126 |
+
$S \leq n+(n-1)+\ldots+(n-k+1)=n k-\frac{1}{2} k(k-1)$ (alle Summen sind verschieden und $\left.\leq n\right)$.
|
| 127 |
+
Dies liefert für $n \geq 3$ wegen $k>0$ nach Division durch $k$ die Ungleichung $2 k+1 \leq n-\frac{1}{2}(k-1)$, aus der $k \leq \frac{2 n-1}{5}$ folgt. Es gibt also höchstens $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ mögliche Paare
|
| 128 |
+
( $\lfloor x\rfloor$ bezeichnet die größte ganze Zahl $\leq x$ ). Für $n<3$ ist offensichtlich $k=0$.
|
| 129 |
+
Nun geben wir für $n \geq 3$ eine Konstruktion mit genau $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ Paaren an. Dazu sei zunächst $n=5 m+3$, also $k=2 m+1$. Die folgende Tabelle zeigt die Paare und ihre Summen, wobei für kleine $m$ manche Spalten wegen Doppeldeutigkeit der Terme gestrichen werden müssen:
|
| 130 |
+
|
| 131 |
+
| Paar | $3 m+1$ | $3 m$ | $\ldots$ | $2 m+2$ | $4 m+2$ | $4 m+1$ | $\ldots$ | $3 m+3$ | $3 m+2$ |
|
| 132 |
+
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 133 |
+
| | 2 | 4 | $\ldots$ | $2 m$ | 1 | 3 | $\ldots$ | $2 m-1$ | $2 m+1$ |
|
| 134 |
+
| Summe | $3 m+3$ | $3 m+4$ | $\ldots$ | $4 m+2$ | $4 m+3$ | $4 m+4$ | $\ldots$ | $5 m+2$ | $5 m+3$ |
|
| 135 |
+
|
| 136 |
+
Die $2 m+1$ Paare enthalten alle Zahlen von 1 bis $4 m+2$; ihre Summen gehen von $3 m+3$ bis $5 m+3$ und sind offensichtlich verschieden und nicht größer als $n$.
|
| 137 |
+
Dieselbe Konstruktion funktioniert auch für $n=5 m+4$ und $n=5 m+5 \quad(m \geq 0)$, weil hier wieder $k=2 m+1$ ist. Für $n=5 m+2$ ist $k=2 m$ ausreichend. Daher kann hier die letze Spalte der Tabelle einfach weggelassen werden. Für $n=5 m+1$ ist ebenfalls $k=2 m$ und wir lassen wieder die letzte Spalte der Tabelle weg und vermindern außerdem jede obere Zahl in der ersten Reihe um 1. So sind wiederum alle Bedingungen erfüllt.
|
| 138 |
+
|
| 139 |
+
Hinweis: Viele Teilnehmer haben sich von dem Beispiel verleiten lassen, $k=\lfloor n / 3\rfloor$ als maximale Anzahl anzunehmen. Wer allerdings für $n=8$ die drei(!) Paare (2;4), (1;6), (3;5) oder (1;5), (3;4), (2;6) entdeckt hatte, war gegen diese Abschätzung immun. Das selten aufgetretene Missverständnis der Formulierung, ,jeweils kein gemeinsames Element" in dem Sinne, dass Paare ( $x ; x)$ erlaubt seien, führt auf ein triviales Problem, dessen Lösung nur mit einer bescheidenen Punktzahl honoriert worden ist.
|
| 140 |
+
|
Germany_TST/md/de-2014-loes_awkl_14.md
ADDED
|
@@ -0,0 +1,121 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2013/2014
|
| 2 |
+
|
| 3 |
+
Aufgabe 1. Die Zentralbank von Sikinien prägt Münzen im Wert von 11 und 12 Kulotnik. Bei einem Einbruch haben 11 sikinische Ganoven einen Tresor geknackt und Münzen im Gesamtwert von 5940 Kulotnik erbeutet. Sie versuchen für eine Weile, die Beute gerecht unter sich aufzuteilen - also so, dass jeder gleich viel erhält - aber es will ihnen nicht gelingen; nach einer Weile behauptet ihr Anführer, sich überlegt zu haben, dass dies tatsächlich nicht möglich ist.
|
| 4 |
+
Man beweise, dass sie keine Münze im Wert von 12 Kulotnik erbeutet haben.
|
| 5 |
+
Lösung. Die Ganoven mögen $a$ Münzen im Wert von 11 Kulotnik und $b$ Münzen im Wert von 12 Kulotnik erbeutet haben. Dabei sind $a$ und $b$ zwei nichtnegative ganze Zahlen mit
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
11 a+12 b=5940=11 \cdot 540=12 \cdot 495
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
Wir nehmen nun $b>0$ an und versuchen, eine gerechte Aufteilung der Beute auf die Ganoven zu finden.
|
| 12 |
+
Nach (1) ist $11 a=12 \cdot(495-b)$, d.h. $11 a$ ist durch 12 teilbar. Nachdem 11 und 12 teilerfremd sind, ist folglich auch $a$ ein Vielfaches von 12 und demnach können die Ganoven die erbeuteten 11-Kulotnik-Stücke in $\frac{a}{12}$ Säckchen verteilen, von denen jedes $12 \cdot 11=132$ Kulotnik enthält. Analog impliziert (1) die Gleichung $12 b=11 \cdot(540-a)$ und mithin ist $12 b$ durch 11 teilbar. Wie vorhin zeigt dies, dass auch $b$ durch 11 teilbar ist. Da wir $b>0$ angenommen haben, kann sich jeder der Ganoven eine Münze im Wert von 12 Kulotnik nehmen, und die Anzahl $b-11$ der übrigen 12-Kulotnik-Stücke ist immer noch durch 11 teilbar, weshalb sich diese in $\frac{b}{11}-1$ Säckchen aufteilen lassen, die ebenfalls je $11 \cdot 12=132$ Kulotnik enthalten.
|
| 13 |
+
Wegen
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
5940-11 \cdot 12=5808=132 \cdot 44
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
befindet sich der noch nicht verteilte Rest der Beute nunmehr in $44=11 \cdot 4$ Säckchen zu je 132 Kulotnik. Wenn sich nun jeder der 11 Ganoven 4 dieser Säckchen nimmt haben sie insgesamt die Beute gerecht geteilt. Doch da ihr Anführer beweisen konnte, dass dies gar nicht möglich ist, muss unsere Annahme $b>0$ falsch gewesen sein: Anders ausgedrückt lag tatsächlich keine Münze im Wert von 12 Kulotnik im Tresor.
|
| 20 |
+
|
| 21 |
+
Bemerkung. Manche Teilnehmer ersannen für die Ganoven äußerst findige Spitznamen: Bankräuber, Piraten, Gangster, Banditen, Gauner, Kriminelle, Straftäter, Diebe.
|
| 22 |
+
|
| 23 |
+
Aufgabe 2. Es sei $A B C D$ ein konvexes Sehnenviereck mit $|A D|=|B D|$. Seine Diagonalen $\overline{A C}$ und $\overline{B D}$ mögen sich in E schneiden. Der Mittelpunkt des Inkreises des Dreiecks BCE heiße I. Der Umkreis des Dreiecks BIE schneide das Innere der Strecke $\overline{A E}$ im Punkt $N$.
|
| 24 |
+
Man beweise, dass
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
|A N| \cdot|N C|=|C D| \cdot|B N|
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
Lösung. Setzt man $\varphi=\Varangle D A B$, so muss auch $\Varangle A B D=\varphi$ sein, denn das Dreieck $A B D$ wurde als gleichschenklig vorausgesetzt. Hieraus ergibt sich $\Varangle B D A=180^{\circ}-2 \varphi$ und mit Hilfe des Peripheriewinkelsatzes folgt $\Varangle B C E=\Varangle B C A=180^{\circ}-2 \varphi$.
|
| 31 |
+
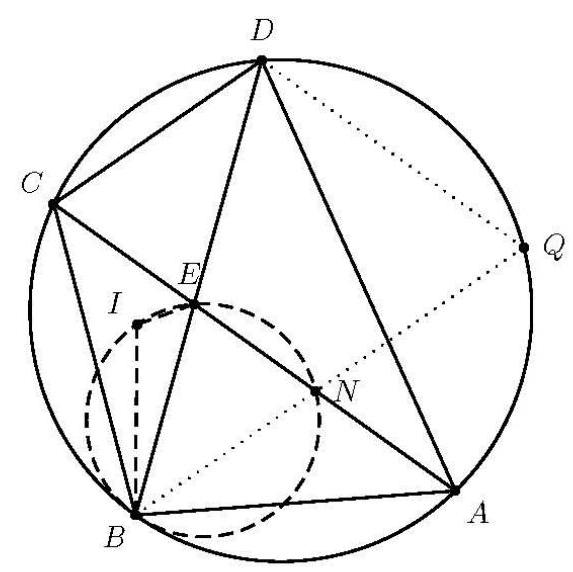
|
| 32 |
+
|
| 33 |
+
Als nächstes wollen wir den Winkel $B I E$ durch $\varphi$ ausdrücken: Da die Geraden $B I$ und $E I$ Winkelhalbierende im Dreieck $B C E$ sind, ist
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\Varangle B I E=180^{\circ}-(\Varangle I E B+\Varangle E B I)=90^{\circ}+\frac{1}{2}\left(180^{\circ}-\Varangle C E B+\Varangle E B C\right)=90^{\circ}+\frac{1}{2} \Varangle B C E,
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
was mit vorigem verbunden
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\Varangle B I E=90^{\circ}+\frac{1}{2}\left(180^{\circ}-2 \varphi\right)=180^{\circ}-\varphi
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
liefert.
|
| 46 |
+
Nachdem BIEN ein konvexes Sehnenviereck ist, impliziert dies $\Varangle C N B=\varphi$. Da nach Peripheriewinkelsatz über der Sehne $\overline{A D}$ auch $\Varangle A C D=\varphi$ gilt, muss demnach $C D \| B N$ sein.
|
| 47 |
+
Man verlängere nun die Strecke $\overline{B N}$ über $N$ hinaus, bis sie den Umkreis des Vierecks $A B C D$ erneut in $Q$ schneidet. Indem wir den Peripheriewinkelsatz über der Sehne $\overline{B D}$ anwenden, erhalten wir $\Varangle D Q B=\varphi$, was wiederum $C N \| Q D$ nach sich zieht.
|
| 48 |
+
Da die beiden Paare gegenüberliegender Seiten des Vierecks $C N Q D$ also jeweils parallel sind, muss es sich bei diesem um ein Parallelogramm handeln. Mithin ist $|C D|=|N Q|$ und sobald man dies in die aus dem Sehnensatz folgende Gleichung
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
|A N| \cdot|N C|=|B N| \cdot|N Q|
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
einträgt hat man die Behauptung bewiesen.
|
| 55 |
+
|
| 56 |
+
Bemerkung. Man kann beweisen, dass sich in der Figur die beiden Kreise berühren.
|
| 57 |
+
|
| 58 |
+
Aufgabe 3. Es sei $a_{1} \leqslant a_{2} \leqslant \ldots$ eine monoton steigende Folge positiver ganzer Zahlen. Eine positive ganze Zahl $n$ heißt verlässlich, wenn es einen positiven ganzzahligen Index i mit $n=\frac{i}{a_{i}}$ gibt.
|
| 59 |
+
Man beweise: Wenn 2013 verlässlich ist, dann ist auch 20 verlässlich.
|
| 60 |
+
Lösung. Wenn 2013 verlässlich ist, gibt es einen positiven ganzzahligen Index $i$ mit $i=2013 a_{i} \geqslant$ $20 a_{i}$. Insbesondere ist die Menge $S$ aller positiven ganzen Zahlen $s$, für die $s \geqslant 20 a_{s}$ gilt, nicht leer. Somit enthält $S$ ein kleinstes Element $j$, und dieses erfüllt einerseits
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
j \geqslant 20 a_{j}
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
und andererseits $(j-1) \notin S$. Letzteres bedeutet, dass entweder $j=1$ sein muss, oder $j>1$ und $j-1<20 a_{j-1}$. Wegen $a_{j} \geqslant 1$ folgt aus (2) jedoch $j \geqslant 20$, was die erste dieser beiden Alternativen ausschließt; demnach muss $j \leqslant 20 a_{j-1}$ sein und in Verbindung mit (2) erhalten wir die Ungleichungskette
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
j \geqslant 20 a_{j} \geqslant 20 a_{j-1} \geqslant j .
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Diese kann nicht anders bestehen als dass überall Gleichheit gilt. Wegen $j=20 a_{j}$ bezeugt der Index $j$, dass 20 wie behauptet verlässlich ist.
|
| 73 |
+
|
| 74 |
+
Bemerkung. Es ändert sich nichts, wenn man in der Aufgabenstellung die Zahlen 2013 und 20 durch zwei beliebige positive ganze Zahlen $r$ und $s$ mit $r>s$ ersetzt.
|
| 75 |
+
|
| 76 |
+
## Lösungen zur 2. Auswahlklausur 2013/2014
|
| 77 |
+
|
| 78 |
+
## Aufgabe 1
|
| 79 |
+
|
| 80 |
+
Eine natürliche Zahl $n$ habe die folgende Eigenschaft:
|
| 81 |
+
Für beliebige reelle Zahlen $a_{1}, a_{2}, \ldots, a_{d}$, die sowohl $a_{1}+a_{2}+\ldots+a_{d}=2013$ als auch $0 \leq a_{i} \leq 1$ für $i=1,2, \ldots, d$ erfüllen, existiert eine Zerlegung der Menge dieser reeller Zahlen in $n$ paarweise disjunkte Teilmengen (von denen einige leer sein dürfen), so dass die Summe der Zahlen in jeder Teilmenge höchstens 1 beträgt.
|
| 82 |
+
Man bestimme die kleinste Zahl $n$ mit dieser Eigenschaft.
|
| 83 |
+
Lösung: Die kleinste Zahl $n$ mit dieser Eigenschaft ist 4025.
|
| 84 |
+
Wir zeigen zunächst $n \geq 4025$. Dazu wählen wir $d=4025$ sowie $a_{1}=\ldots=a_{4025}=\frac{2013}{4025}>\frac{1}{2}$. Dann ist $a_{1}+\ldots+a_{4025}=2013$ und wegen $a_{i}+a_{j}=\frac{4026}{4025}>1$ für alle $1 \leq i \neq j \leq 4025$ werden hier 4025 Teilmengen benötigt.
|
| 85 |
+
Nun zeigen wir $n \leq 4025$. Dazu führen wir eine Fallunterscheidung nach $d$ durch.
|
| 86 |
+
Für $d \leq 4025$ erhält jedes $a_{i}$ seine eigene Teilmenge. Damit sind alle Teilmengen, von denen einige leer sein dürfen, disjunkt und haben Elementsummen von höchstens 1.
|
| 87 |
+
Für $d>4025$ müssen zwei Zahlen $a_{x}$ und $a_{y}$ existieren mit $a_{x}+a_{y} \leq 1$. Andernfalls wäre schon in der Summe $\left(a_{1}+a_{2}\right)+\left(a_{3}+a_{4}\right)+\ldots+\left(a_{4025}+a_{4026}\right)$ jede Klammer größer als 1 und die Summe aller $a_{i}$ größer als 2013, Widerspruch! Somit können wir $a_{x}$ und $a_{y}$ durch $a_{z}=a_{x}+a_{y}$ ersetzen und erhalten eine Menge mit $d-1$ Elementen, die alle Bedingungen erfüllt. Dieser Schritt kann wiederholt werden, bis die Ersetzung eine Menge mit 4025 Elementen liefert. Für diese und damit auch für die Ausgangsmenge existiert die gewünschte Aufteilung. Damit ist alles gezeigt.
|
| 88 |
+
|
| 89 |
+
Hinweis: Einige der $a_{i}$ dürfen durchaus gleich sein; zwei Teilmengen sind dann disjunkt, wenn sie nicht dasselbe Element (bezogen auf die Nummerierung) enthalten. Die Aufgabenstellung ließ viele Lösungswege zu.
|
| 90 |
+
|
| 91 |
+
## Aufgabe 2
|
| 92 |
+
|
| 93 |
+
Es sei $\mathbb{Z}^{+}$die Menge der positiven ganzen Zahlen.
|
| 94 |
+
Man bestimme alle Funktionen $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$mit der Eigenschaft, dass für alle positiven ganzen Zahlen $m$ und $n$ gilt: $m^{2}+f(n) \mid m f(m)+n$.
|
| 95 |
+
|
| 96 |
+
Lösung: Für eine beliebige positive ganze Zahl $n$ wählen wir $m$ so, dass $f(n) \mid m$ gilt. Dann folgt $f(n) \mid m^{2}+f(n)$ und $f(n) \mid m f(m)+n$. Weil $m$ durch $f(n)$ teilbar ist, muss auch $n$ durch $f(n)$ teilbar sein. Es gilt also $f(n) \mid n$, das bedeutet $f(n) \leq n$ für alle $n \in \mathbb{Z}^{+}$.
|
| 97 |
+
Daraus folgt insbesondere $f(1) \mid 1$, also $f(1)=1$.
|
| 98 |
+
Wir nehmen weiter an, es gäbe ein $m \in \mathbb{Z}^{+}$mit $f(m)<m$. Mit $n=1$ erhalten wir $m^{2}+1 \mid m f(m)+1$, andererseits gilt dann $0<m f(m)+1<m^{2}+1$, so dass $m^{2}+1$ kein Teiler von $m f(m)+1$ sein kann - Widerspruch! Also gilt $f(m) \geq m$ und mit dem oberen folgt $f(n)=n$ für alle $n \in \mathbb{Z}^{+}$. Einsetzen bestätigt über $n^{2}+n=n^{2}+f(n) \mid n f(n)+n=n^{2}+n$, dass diese Funktion tatsächlich die - daher - einzige Lösung ist.
|
| 99 |
+
|
| 100 |
+
Hinweis: Eine häufige Fehlerquelle war die Annahme spezieller Voraussetzungen (z.B. $m$ prim oder $n>2$ usw.), die im späteren Beweisgang zugunsten von $m, n \in \mathbb{Z}^{+}$„vergessen" wurden.
|
| 101 |
+
|
| 102 |
+
GEFÖRDERT VOM
|
| 103 |
+
Bundesministerium für Bildung und Forschung
|
| 104 |
+
|
| 105 |
+
## Aufgabe 3
|
| 106 |
+
|
| 107 |
+
In einem spitzwinkligen Dreieck $A B C$ seien die Innenwinkel $\alpha, \beta, \gamma$ wie üblich bezeichnet. Ferner seien der Schnittpunkt der Winkelhalbierenden von $\alpha$ und $B C$ mit $D$ sowie der Schnittpunkt der Winkelhalbierenden von $\beta$ und $A C$ mit $E$ bezeichnet.
|
| 108 |
+
Nun wird dem Viereck $A B D E$ eine Raute so einbeschrieben, dass alle Eckpunkte dieser Raute auf verschiedenen Seiten des Vierecks liegen. In dieser Raute seien die nicht-stumpfen Innenwinkel mit $\varphi$ bezeichnet. Man beweise, dass $\varphi \leq \max (\alpha, \beta)$ gilt.
|
| 109 |
+
|
| 110 |
+
Lösung: Die Ecken der Raute werden mit $K(K \in A E), L$ $(L \in A B), M(M \in B D)$ und $N(N \in D E)$ benannt. Mit $d(X, Y Z)$ sei der Abstand eines Punktes $X$ von einer Geraden $Y Z$ bezeichnet. Weil $D$ und $E$ auf den jeweiligen Winkelhalbierenden liegen, gilt $d(D, A B)=d(D, A C)$, $d(E, A B)=d(E, B C)$ und $d(D, B C)=d(E, A C)=0$, woraus $d(D, A C)+d(D, B C)=d(D, A B)$ und $d(E, A C)+d(E, B C)=d(E, A B)$ folgt.
|
| 111 |
+
Weil $N$ auf der Strecke $D E$ liegt und weil sich in der Gleichung $d(X, A C)+d(X, B C)=d(X, A B)$, wenn $X$ längs der Strecke $D E$ wandert, alle Terme nur linear ändern, folgt
|
| 112 |
+
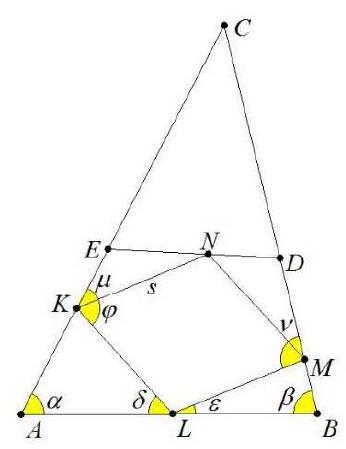
|
| 113 |
+
aus den beiden oberen Beziehungen auch für $N$ :
|
| 114 |
+
$d(N, A C)+d(N, B C)=d(N, A B)(1)$.
|
| 115 |
+
Mit den Bezeichnungen der Figur gilt $d(N, A C)=s \cdot \sin \mu$ und $d(N, B C)=s \cdot \sin v$. Weil die Raute $K L M N$ ganz in einer der Halbebenen bezüglich $A B$ liegt, erhalten wir aus ihrer Parallelogrammeigenschaft
|
| 116 |
+
$d(N, A B)=d(N, A B)+d(L, A B)=d(K, A B)+d(M, A B)=s(\sin \delta+\sin \varepsilon)$.
|
| 117 |
+
Mit (1) folgt $\sin \mu+\sin v=\sin \delta+\sin \varepsilon$ (2).
|
| 118 |
+
Aus der Annahme $\varphi>\max (\alpha, \beta)$ würde wegen $\mu+\varphi=\Varangle C K L=\alpha+\delta$ direkt $\mu=\alpha-\varphi+\delta<\delta$ und analog $v<\varepsilon$ folgen. Wegen $K L \| M N$ gilt $\beta=\delta+v$, also $\delta<\beta<90^{\circ}$. Entsprechend folgt $\varepsilon<90^{\circ}$. So erhalten wir $\sin \mu<\sin \delta$ und $\sin v<\sin \varepsilon$, im Widerspruch zu (2). Also gilt $\varphi \leq \max (\alpha, \beta)$.
|
| 119 |
+
|
| 120 |
+
Hinweis: Eine reine Winkeljagd führt nicht zum Ziel. Die Lage der Raute ist - entgegen der Meinung einiger Teilnehmer - nicht eindeutig bestimmt. Gleichheit gilt nur für $\alpha=\beta$.
|
| 121 |
+
|
Germany_TST/md/de-2015-loes_awkl_15.md
ADDED
|
@@ -0,0 +1,120 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2014/2015
|
| 2 |
+
|
| 3 |
+
## Aufgabe 1
|
| 4 |
+
|
| 5 |
+
Man bestimme die kleinste positive ganze Zahl $n$, für die es ein Polynom
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
P(X)=a_{2 n} X^{2 n}+a_{2 n-1} X^{2 n-1}+\ldots+a_{1} X+a_{0}
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
mit reellen Koeffizienten gibt, das die beiden folgenden Eigenschaften aufweist:
|
| 12 |
+
|
| 13 |
+
- Für $i=0,1, \ldots, 2 n$ gilt $2014 \leq a_{i} \leq 2015$.
|
| 14 |
+
- Es gibt eine reelle Zahl $\xi$ mit $P(\xi)=0$.
|
| 15 |
+
|
| 16 |
+
Lösung: Es ist $n=2014$. Zunächst definiere für eine spezielle Wahl der Koeffizienten $a_{k}$, nämlich 2014 für gerades $k$ und 2015 für ungerades $k$, das Polynom $Q_{n}(X)=2014 X^{2 n}+2015 X^{2 n-1}+2014 X^{2 n-2}+\ldots+2015 X+2014$. Es ist $Q_{2014}(-1)=0$, die gesuchte Zahl ist also höchstens 2014. Es bleibt zu zeigen, dass $P(X)$ für $n \leq 2013$ keine reelle Nullstelle hat. Für $x \geq 0$ ist $P(x) \geq a_{0}>0$, da die Koeffizienten positiv sind; für $x<0$ ist $P(x) \geq Q_{n}(x)$, da $x^{k}$ für gerades $k$ positiv ist, also $a_{k} x^{k} \geq 2014 x^{k}$, und $x^{k}$ für ungerades $k$ negativ ist, also $a_{k} x^{k} \geq 2015 x^{k}$. Es bleibt zu zeigen, dass $Q_{m}(x)>0$ für $m \leq 2013$.
|
| 17 |
+
|
| 18 |
+
1. Beweis: Man rechnet nach, dass für reelles $x$ gilt
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
Q_{m}(x)=1007\left(\sum_{\nu=0}^{m-1}\left(x^{\nu}+x^{\nu+1}\right)^{2}\right)+\frac{1}{2}\left(\sum_{\nu=0}^{m-1}\left(x^{2 \nu+1}+1\right)\left(x^{2 m-2 \nu-1}+1\right)\right)+\left(1007-\frac{m}{2}\right)\left(x^{2 m}+1\right)
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
Die Summanden der ersten Summe sind als Quadrate nicht negativ. Da $x^{2 k+1}+1$ für alle $k \geq 0$ positiv bzw. 0 bzw. negativ ist für $x>-1$ bzw. $x=-1$ bzw. $x<-1$, sind die Summanden in der zweiten Summe nicht negativ. Damit ist für $x<0$ und $m \leq 2013$ :
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
P(x) \geq Q_{m}(x) \geq\left(1007-\frac{m}{2}\right)\left(x^{2 m}+1\right)>\frac{1}{2}
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
2. Beweis (mit Analysis): Definiere für $x<0$ die reelle Funktion $f_{m}(x)=\left(x^{2}-1\right) Q_{m}(x)=2014\left(x^{2 m+2}-\right.$ $1)+2015 x\left(x^{2 m}-1\right)$. Die zweite Ableitung $f_{m}^{\prime \prime}(x)=2(2 m+1)\left(2014(m+1) x^{2 m}+2015 m x^{2 m-1}\right)$ hat die einzige negative Nullstelle $x_{m}=-\frac{2015 m}{2014(m+1)}>-1$ für $m \leq 2013$, und es ist
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
\begin{aligned}
|
| 34 |
+
f_{m}^{\prime}\left(x_{m}\right) & =2014(2 m+2) x_{m}^{2 m+1}+2015(2 m+1) x_{m}^{2 m}-2015= \\
|
| 35 |
+
& =\left(2014(2 m+2) x_{m}+2015(2 m+1)\right) x_{m}^{2 m}-2015=2015 \cdot x_{m}^{2 m}-2015<0
|
| 36 |
+
\end{aligned}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
Für $x<x_{m}$ bzw. $x_{m}<x<0$ wächst bzw. fällt $f_{m}^{\prime}$ streng monoton, da die Ableitung $f_{m}^{\prime \prime}$ positiv bzw. negativ ist; daher hat $f_{m}^{\prime}$ für $x<0$ ein globales Maximum bei $x=x_{m}$ und ist negativ für alle $x<0$. Daher fällt $f_{m}$ streng monoton, ist also wegen $f_{m}(-1)=0$ positiv für $x>-1$ und negativ für $x<-1$. Somit ist $Q_{m}(x)$ positiv für $x \neq-1$; für $x=-1$ ergibt sich direkt $Q_{m}(-1)=2014-m>0$.
|
| 40 |
+
|
| 41 |
+
## Bemerkungen:
|
| 42 |
+
|
| 43 |
+
1. Die Polynomfunktion $P(x)$ kann keine reellen Nullstellen außerhalb des Intervalls ] $-\frac{2015}{2014},-\frac{2014}{2015}$ [haben.
|
| 44 |
+
2. Oftmals wurden Summanden $g_{k}(x)=2014 x^{2 k}+2015 x^{2 k-1}$ von $Q_{m}(x)$ für einzelne $k$ isoliert betrachtet und fehlerhaft gegen $g_{k}(-1)$ abgeschätzt. Wie man durch Ableiten zeigt, wächst bzw. fällt $g_{k}$ streng monoton für $0>x>-\frac{2015(2 k-1)}{2014 \cdot 2 k}$ bzw. $x<-\frac{2015(2 k-1)}{2014 \cdot 2 k}$. Daraus folgt $g_{k}(x)>g_{k}(-1)$ für $k \leq 1007$ und $x<-1$ oder für $k>1007$ und $-1>x>0$. Damit kann man auf diese Weise $Q_{m}(x) \geq Q_{m}(-1)$ nur für $x<-1$ und $m \leq 1007$ nachweisen.
|
| 45 |
+
|
| 46 |
+
## » BILDUNG \& BEGABUNG GEMEINNÜTZIGE GMBH
|
| 47 |
+
|
| 48 |
+
Kortrijker Straße 1, 53177 Bonn | Postfach 2002 01, 53132 Bonn | Tel.: (02 28) 9 59 15-0, Fax: (02 28) 959 15-19 info@bildung-und-begabung.de, www.bildung-und-begabung.de I Registergericht: Amtsgericht Essen, HRB 22445 Steuer-Nr.: 206/5887/1089 | USt.-IDNr.: DE217481695 | Bankverbindung: IBAN: DE27 370501980029002250 BIC: COLSDE33XXX, Sparkasse KölnBonn I Geschäftsführung: Dr. Elke Völmicke, Prof. Dr. Andreas Schlüter
|
| 49 |
+
|
| 50 |
+
## Aufgabe 2
|
| 51 |
+
|
| 52 |
+
Eine positive ganze Zahl $n$ heißt neckisch, wenn man sie in der Form $n=a^{b}+b$ mit zwei ganzen Zahlen $a, b \geq 2$ schreiben kann.
|
| 53 |
+
Man entscheide, ob es 102 aufeinanderfolgende positive ganze Zahlen gibt, von denen genau 100 neckisch sind.
|
| 54 |
+
Lösung: Es gibt solche Zahlen. Für eine positive ganze Zahl $m$ sei $f(m)$ die Anzahl der neckischen Zahlen unter den 102 aufeinander folgenden Zahlen $m, m+1, m+2, \ldots, m+101$. Es sei $N$ das kleinste gemeinsame Vielfache der Zahlen $2,3,4, \ldots, 101$. Dann ist $f\left(2^{N}\right) \geq 100$, da für alle $b=2,3, \ldots, 101$ gilt: $2^{N}+b=\left(2^{N / b}\right)^{b}+b$ ist neckisch. Somit gibt es auch eine kleinste positive Zahl $M$ mit $f(M) \geq 100$. Offenbar ist $M \leq 2^{N}$. Andererseits gilt $M>1$ (und $M-1$ ist positive ganze Zahl), weil jede neckische Zahl größer als 5 ist, da für $a, b \geq 2$ gilt: $a^{b}+b \geq 2^{b}+b \geq 2^{2}+2=6$, und somit unter den Zahlen von 1 bis 102 höchstens 97 neckisch sind. Nun wird $f(M)=100$ bewiesen: Wäre $f(M)>100$, gäbe es unter den Zahlen von $M$ bis $M+101$ mindestens 101 neckische, also unter denen von $M$ bis $M+100$ mindestens 100 neckische ebenso wie unter denen von $M-1$ bis $M+100$. Dann wäre $f(M-1) \geq 100 \mathrm{im}$ Widerspruch zur Minimalität von $M$. Daher ist $f(M)=100$. Die Zahlen von $M$ bis $M+101$ erfüllen also die Bedingung.
|
| 55 |
+
Bemerkung: Manchmal wurde ohne Beweis vermutet, dass gewisse Zahlen $m$, z. B. $m=2^{N}$, nicht neckisch sind. Dies ist aber nicht offensichtlich, da wirklich auszuschließen ist, dass es irgendwelche Zahlen $a, b \geq 2$ mit $m=a^{b}+b$ geben kann.
|
| 56 |
+
|
| 57 |
+
## Aufgabe 3
|
| 58 |
+
|
| 59 |
+
Es sei $A B C$ ein spitzwinkliges Dreieck mit $|A B| \neq|A C|$. Die Mittelpunkte der Seiten $\overline{A B}$ und $\overline{A C}$ seien $D$ beziehungsweise $E$. Die Umkreise der Dreiecke $B C D$ und $B C E$ mögen den Umkreis des Dreiecks $A D E$ in $P$ beziehungsweise $Q$ schneiden, wobei $P \neq D$ und $Q \neq E$.
|
| 60 |
+
Man beweise, dass $|A P|=|A Q|$.
|
| 61 |
+
|
| 62 |
+
1. Lösung: Ohne Einschränkung sei $|A C|>|A B|$. Da $D$ und $E$ Mitten der Seiten $\overline{A B}$ und $\overline{A C}$ sind, ist nach Strahlensatz $D E$ parallel zu $B C$. Im Falle $E=P$ oder $D=Q$ wäre $C E D B$ Sehnenviereck mit parallelen Seiten $B C$ und $D E$, also gleichschenkliges Trapez mit $|B D|=|E C|$, somit $|A B|=|A C|$, was aber ausgeschlossen ist. Kann man zeigen, dass die (nicht ausgearteten) Dreiecke $A P C$ und $B Q A$ ähnlich sind, folgt die Behauptung, da wegen $\angle P Q A=\measuredangle P D A=180^{\circ}-\measuredangle B D P=\measuredangle P C B=\measuredangle P C A+\gamma=\measuredangle B A Q+\measuredangle A E D=\measuredangle D P Q+\measuredangle A P D=$ $\measuredangle A P Q$ (unter Benutzung des Umfangswinkelsatzes) das Dreieck $A P Q$ gleichschenklig ist mit $|A P|=|A Q| .-$ Beweis, dass Dreiecke $A P C$ und $B Q A$ ähnlich sind: Zunächst gilt mit Umfangswinkelsatz
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\measuredangle D Q B=360^{\circ}-\measuredangle E Q D-\measuredangle B Q E=\measuredangle D A E+\measuredangle E C B=\alpha+\gamma=180^{\circ}-\beta=180^{\circ}-\measuredangle E D A=\measuredangle A P E,
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
$\measuredangle E P C=\measuredangle D P C-\measuredangle D P E=\left(180^{\circ}-\beta\right)-\alpha=\gamma=\measuredangle A E D=\measuredangle A Q D$.
|
| 69 |
+
Hieraus folgt die Ähnlichkeit der Dreiecke $A P C$ und $B Q A$ :
|
| 70 |
+
|
| 71 |
+
1. Beweis: Es sei $Q^{\prime}$ der eindeutig bestimmte Punkt auf derselben Seite von $A C$ wie $P$, so dass Dreieck $A Q^{\prime} C$ ähnlich zu Dreieck $B Q A$ ist. Da $D$ und $E$ Mitten der Seiten $\overline{A B}$ und $\overline{A C}$ sind, sind auch die Teildreiecke $A Q^{\prime} E$ und $B Q D$ sowie $C E Q^{\prime}$ und $A D Q$ ähnlich. Damit liegt $Q^{\prime}$ wegen (1) und (2), also $\measuredangle A P E=\measuredangle B Q D=\measuredangle A Q^{\prime} E$ und $\measuredangle E P C=\measuredangle D Q A=\measuredangle E Q^{\prime} C$, auf den Umkreisen von $A E P$ und $C E P$, die sich in $E$ und $P$ schneiden. $Q^{\prime}=E$ ist wegen $Q \neq D$ ausgeschlossen. Damit ist $Q^{\prime}=P$, und die Dreiecke $A P C$ und $B Q A$ sind ähnlich. 2. Beweis: Mit Sinussatz in $A D Q$ und $B Q D$ gilt $|A Q|:|A D|=\sin \measuredangle Q D A: \sin \measuredangle A Q D,|B Q|:|B D|=$ $\sin \measuredangle B D Q: \sin \measuredangle D Q B$. Mit $\measuredangle B D Q=180^{\circ}-\measuredangle Q D A$ folgt $|A Q|:|B Q|=\sin \measuredangle D Q B: \sin \measuredangle A Q D$. Analog ist $|C P|:|P A|=\sin \measuredangle A P E: \sin \measuredangle E P C$. Wegen (1) und (2) sind $A P C$ und $B Q A$ ähnlich nach Merkmal sws.
|
| 72 |
+
2. Lösung (mit Inversion am Kreis): Man invertiere an einem Kreis mit Mittelpunkt $A$ und Radius 1. Der Bildpunkt eines Punkts $X$ sei mit $X^{\prime}$ bezeichnet. Da $D$ und $E$ die Mitten der Seiten $\overline{A B}$ und $\overline{A C}$ sind, sind $B^{\prime}$ und $C^{\prime}$ die Mitten der Seiten $\overline{A D^{\prime}}$ und $\overline{A E^{\prime}}$. Die Inversion bildet den Umkreis des Dreiecks $A D E$ auf die Gerade $D^{\prime} E^{\prime}$ ab, damit sind $P^{\prime} \neq D^{\prime}$ und $Q^{\prime} \neq E^{\prime}$ die zweiten Schnittpunkte der Umkreise der Dreiecke $B^{\prime} C^{\prime} D^{\prime}$ und $B^{\prime} C^{\prime} E^{\prime}$ mit der Geraden $D^{\prime} E^{\prime}$. Da die Geraden $D^{\prime} E^{\prime}$ und $B^{\prime} C^{\prime}$ parallel sind, liegen die Umkreise der Dreiecke $B^{\prime} C^{\prime} D^{\prime}$ und $B^{\prime} C^{\prime} E^{\prime}$ symmetrisch zur Mittelsenkrechten der Strecke $\overline{B^{\prime} C^{\prime}}$, insbesondere gehen die Punkte $Q^{\prime}$ bzw. $B^{\prime}$ bzw. $P^{\prime}$ in $E^{\prime}$ bzw. $C^{\prime}$ bzw. $D^{\prime}$ über. Damit ist $\left|P^{\prime} C^{\prime}\right|=\left|B^{\prime} D^{\prime}\right|=\left|A B^{\prime}\right|$ (da $B^{\prime}$ Mitte von $\overline{A D^{\prime}}$ ) sowie $\left|B^{\prime} Q^{\prime}\right|=\left|C^{\prime} E^{\prime}\right|=\left|A C^{\prime}\right|$ (da $C^{\prime}$ Mitte von $\overline{A E^{\prime}}$ ) und $\measuredangle Q^{\prime} B^{\prime} D^{\prime}=\measuredangle P^{\prime} C^{\prime} E^{\prime}$. Daraus folgt $\measuredangle A B^{\prime} Q^{\prime}=180^{\circ}-\measuredangle Q^{\prime} B^{\prime} D^{\prime}=180^{\circ}-\measuredangle P^{\prime} C^{\prime} E^{\prime}=\measuredangle A C^{\prime} P^{\prime}$. Damit sind die Dreiecke $A P^{\prime} C^{\prime}$ und $A Q^{\prime} B^{\prime}$ nach Kongruenzsatz sws kongruent. Somit ist $\left|A P^{\prime}\right|=\left|A Q^{\prime}\right|$ und $|A P|=1 /\left|A P^{\prime}\right|=1 /\left|A Q^{\prime}\right|=|A Q|$.
|
| 73 |
+
|
| 74 |
+
## Lösungen zur 2. Auswahlklausur 2014/2015
|
| 75 |
+
|
| 76 |
+
## Aufgabe 1
|
| 77 |
+
|
| 78 |
+
Man bestimme alle Paare ( $x, y$ ) ganzer Zahlen, welche die Gleichung
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\sqrt[3]{7 x^{2}-13 x y+7 y^{2}}=|x-y|+1
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
erfüllen.
|
| 85 |
+
Lösung: Die Gleichung (1) ist symmetrisch in $x$ und $y$, so dass wir zunächst $x \geq y$ annehmen können und für $x \neq y$ zu jeder Lösung $(x, y)$ auch $(y, x)$ als Lösung erhalten. Mit
|
| 86 |
+
$d=x-y \geq 0$ folgt $\sqrt[3]{7 d^{2}+x y}=d+1$. Potenzieren liefert $x^{2}-d x+\left(-d^{3}+4 d^{2}-3 d-1\right)=0$ mit der Diskriminante $D=d^{2}-4\left(-d^{3}+4 d^{2}-3 d-1\right)=(d-2)^{2}(4 d+1) \geq 0$. Es ist also $x_{1 / 2}=\frac{d \pm(d-2) \sqrt{4 d+1}}{2}$. Für die Ganzzahligkeit von $x$ muss $4 d+1$ eine Quadratzahl sein, und zwar das Quadrat einer ungeraden Zahl. Der Ansatz $4 d+1=(2 m+1)^{2}$ mit $m \in\{0 ; 1 ; 2 ; \ldots\}$ liefert $d=m^{2}+m$, so dass sich $x_{1 / 2}=\frac{1}{2}\left[\left(m^{2}+m\right) \pm\left(m^{2}+m-2\right)(2 m+1)\right]$ ergibt. Dies führt zu $\left(x_{1}, y_{1}\right)=\left(m^{3}+2 m^{2}-m-1, m^{3}+m^{2}-2 m-1\right)$ und für $m \neq 1 \mathrm{zu}$ $\left(x_{2}, y_{2}\right)=\left(-m^{3}-m^{2}+2 m+1,-m^{3}-2 m^{2}+m+1\right)$ und den Lösungen $\left(y_{1}, x_{1}\right)$ bzw. $\left(y_{2}, x_{2}\right)$ für $m>0$. Eine Probe bestätigt, dass diese Paare tatsächlich Lösungen sind.
|
| 87 |
+
|
| 88 |
+
Hinweis: Die einfachen Spezialfälle wurden von den meisten Teilnehmern gefunden. Häufig wurde dann (vergeblich) versucht, mit Abschätzungen zu zeigen, dass es keine weiteren Lösungen gibt.
|
| 89 |
+
|
| 90 |
+
## Aufgabe 2
|
| 91 |
+
|
| 92 |
+
Es sei $A B C$ ein spitzwinkliges Dreieck mit dem Umkreis $k$ und dem Inkreismittelpunkt $I$. Die Orthogonale zu $C I$ durch I schneide die Seite $B C$ in $U$ und $k$ in $V$, wobei $V$ und $A$ auf verschiedenen Seiten von $B C$ liegen. Die Parallele zu $A I$ durch $U$ schneide $A V$ im Punkt $X$.
|
| 93 |
+
|
| 94 |
+
Man beweise: Wenn die Geraden $X I$ und $A I$ orthogonal zueinander sind, dann schneidet $X I$ die Seite $A C$ in ihrem Mittelpunkt $M$.
|
| 95 |
+
|
| 96 |
+
Lösung: In der Figur ist $M$ zunächst nur der Schnittpunkt von $X I$ und $A C . N$ ist der Schnittpunkt von $X U$ und $A B$ und $Y$ der Schnittpunkt von $X I$ und $A B$. Die halben Innenwinkel des Dreiecks $A B C$ sind mit $\alpha, \beta$ bzw. $\gamma$ bezeichnet. Wegen $\Varangle U I C=90^{\circ}$ ist $\Varangle C U I=\alpha+\beta$ und daher $\Varangle B N U=\Varangle B A I=\Varangle B I U=\alpha$, so dass die Punkte $B, U, I$ und $N$ auf einem Kreis liegen. Deshalb gilt $\overline{\Pi U}=\overline{I N}$ (Sehnen $\mathrm{zu} \beta$ ) und wegen $X \perp N U$ folgt $\overline{N X}=\overline{X U}$. Anwendung der Strahlensätze führt auf $\frac{\overline{V X}}{\overline{V A}}=\frac{\overline{X U}}{\overline{A I}}=\frac{\overline{N X}}{\overline{A I}}=\frac{\overline{Y X}}{\overline{Y I}}$, woraus $Y V \| A I$ folgt. Also ist auch $\Varangle B Y V=\alpha=\Varangle B N$, so
|
| 97 |
+
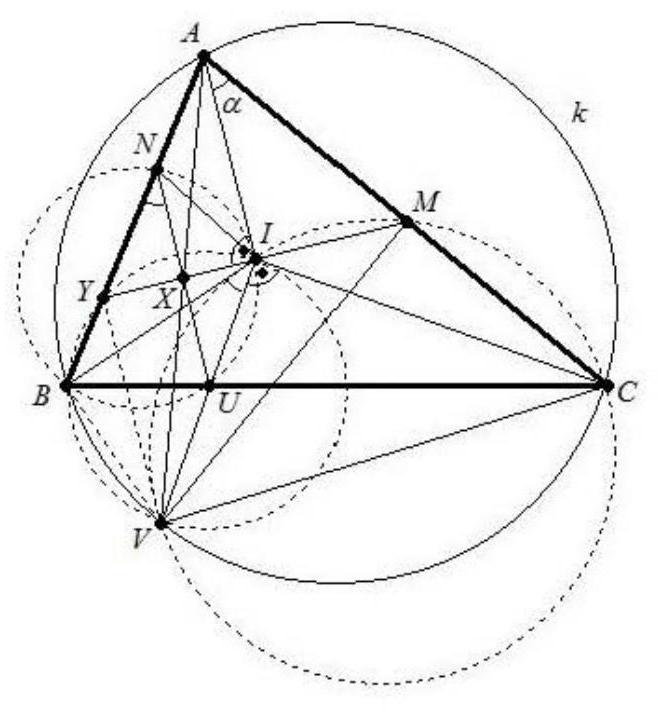
|
| 98 |
+
dass die Punkte $B, V, I$ und $Y$ auf einem Kreis
|
| 99 |
+
liegen. Daher ist $\Varangle V B I=\Varangle V Y I=90^{\circ}$. Da die Halbierenden von Innen- und Außenwinkel an einer Ecke im Dreieck stets orthogonal sind, ist $B V$ die Halbierende des Außenwinkels bei $B$. Im Sehnenviereck $A B V C$ (Umkreis von $A B C$ ) erkennen wir daher $\Varangle V A C=\Varangle V B C=\alpha+\gamma$ und $\Varangle A C V=180^{\circ}-\Varangle V B A=180^{\circ}-(\alpha+2 \beta+\gamma)=\alpha+\gamma$, also $\Varangle V A C=\Varangle A C V$. Das Dreieck $A V C$ ist somit gleichschenklig mit der Spitze $V$. Um nun zu zeigen, dass $M$ der Mittelpunkt von $A C$ ist, reicht der Nachweis von $\varangle V M C=90^{\circ}$. Dazu verwenden wir in den Sehnenvierecken $B V I Y$ und $A B V C$, dass $\Varangle V I M=180^{\circ}-\Varangle Y I V=\Varangle V B Y=\Varangle V B A=180^{\circ}-\Varangle A C V$ ist, so dass auch $V C M I$ ein Sehnenviereck ist. Dies liefert $\Varangle V M C=\Varangle V I C=90^{\circ}$.
|
| 100 |
+
|
| 101 |
+
Hinweis: Einige Teilnehmer haben eine Winkeljagd versucht, die jedoch ohne eine Jagd nach Sehnenvierecken erfolglos bleibt. Analytische Ansätze konnten nicht erfolgreich abgeschlossen werden.
|
| 102 |
+
|
| 103 |
+
## Aufgabe 3
|
| 104 |
+
|
| 105 |
+
Aus zwei 2x1-Dominosteinen kann man ein Tetromino konstruieren, indem man die beiden Dominosteine längs ihrer längeren Seiten so aneinanderlegt, dass der Mittelpunkt der längeren Seite des einen Dominosteins ein Eckpunkt des anderen Dominosteins ist. Dabei ergeben sich zwei hinsichtlich ihrer Orientierung verschiedene Typen von Tetrominos, die wir als $S$ - bzw. $Z$-Tetromino bezeichnen wollen.
|
| 106 |
+
$S$-Tetrominos:
|
| 107 |
+
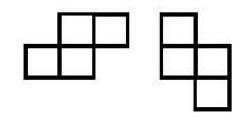
|
| 108 |
+
|
| 109 |
+
Z-Tetrominos:
|
| 110 |
+
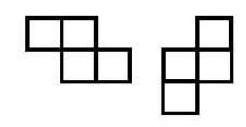
|
| 111 |
+
|
| 112 |
+
Ein Gitterpunktpolygon P ist eine einfach zusammenhängende Fläche, deren Randlinien nur auf Gitterlinien des ebenen ganzzahligen Koordinatengitters liegen. Eine Pflasterung von $P$ ist eine vollständige und überlappungsfreie Überdeckung von $P$ mit Flächenstücken, die auch nicht teilweise außerhalb von $P$ liegen.
|
| 113 |
+
|
| 114 |
+
Wir nehmen nun an, dass ein Gitterpunktpolygon $P$ nur mit $S$-Tetrominos gepflastert werden kann. Man beweise: Wenn auch eine Pflasterung von $P$ mit $S$ - und $Z$-Tetrominos möglich ist, dann ist die Anzahl der dabei verwendeten $Z$-Tetrominos stets gerade.
|
| 115 |
+
|
| 116 |
+
Lösung: Wir können annehmen, dass $P$ aus einem Teil der Einheitsquadrate des ganzzahligen Koordinatengitters besteht, die wie abgebildet eingefärbt sind. Unter dieser Färbung bedeckt jedes $S$-Tetromino eine gerade Anzahl schwarzer Quadrate und jedes $Z$-Tetromino eine ungerade Anzahl von diesen. Da $P$ vollständig mit $S$-Tetrominos gepflastert werden kann, enthält es eine gerade Anzahl schwarzer Quadrate. Wenn also eine Pflasterung mit $S$ - und $Z$-Tetrominos möglich ist, erfordert diese gerade Anzahl auch eine gerade Anzahl von Z-Tetrominos.
|
| 117 |
+

|
| 118 |
+
|
| 119 |
+
Hinweis: Es gibt weitere Färbungsansätze, z.B. mit zwei Färbungen. Das Argument, $P$ müsse vollständig in achsensymmetrische Teile zerlegbar sein, in denen dann zwei $S$-Tetrominos durch zwei $Z$-Tetrominos ersetzt werden können, ist wie alle Ansätze, die auf lokalen Eigenschaften von $P$ beruhen, nicht zwingend und deckt nur Spezialfälle $a b$.
|
| 120 |
+
|
Germany_TST/md/de-2016-loes_awkl_16.md
ADDED
|
@@ -0,0 +1,41 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 2. Auswahlklausur 2015/2016
|
| 2 |
+
|
| 3 |
+
## Aufgabe 1
|
| 4 |
+
|
| 5 |
+
Man bestimme alle positiven ganzen Zahlen $m$ mit folgender Eigenschaft:
|
| 6 |
+
Die Folge $a_{0}, a_{1}, a_{2}, \ldots$ mit $a_{0}=\frac{2 m+1}{2}$ und $a_{k+1}=a_{k}\left\lfloor a_{k}\right\rfloor$ für $k=0,1,2, \ldots$ enthält wenigstens eine ganze Zahl.
|
| 7 |
+
Hinweis: $\lfloor x\rfloor$ bezeichnet den größten ganzen Teil (integer-Funktion) von $x$.
|
| 8 |
+
Lösung: Es gilt $a_{0}=m+\frac{1}{2}$ und $a_{1}=a_{0}\left\lfloor a_{0}\right\rfloor=\left(m+\frac{1}{2}\right) \cdot m=m^{2}+\frac{m}{2}$. Dieser Ausdruck ist für gerades $m$ offensichtlich ganz, so dass hier die gesuchte Eigenschaft der Folge vorliegt.
|
| 9 |
+
Weiterhin gilt bei $m=1$, dass $a_{0}=\frac{3}{2},\left\lfloor a_{0}\right\rfloor=1$ und für $a_{k}=\frac{3}{2}$ stets auch $a_{k+1}=\frac{3}{2} \cdot 1=\frac{3}{2}$ ist. Hier gibt es also kein ganzzahliges Folgenglied.
|
| 10 |
+
Nun sei $m \geq 3$ ungerade. Es existiert die eindeutige Darstellung $m=2^{p} \cdot n_{0}+1$ mit $p \geq 1, n_{0}$ ungerade und $p, n_{0} \in \mathbb{N}$. Somit gilt $a_{0}=2^{p} n_{0}+\frac{3}{2}$, und für $a_{k}=2^{p} n_{k}+\frac{3}{2}$ ( $n_{k}$ ungerade) folgt $a_{k+1}=\left(2^{p} n_{k}+\frac{3}{2}\right)\left(2^{p} n_{k}+1\right)=2^{p-1}\left(2^{p+1} n_{k}^{2}+5 n_{k}\right)+\frac{3}{2}$, wobei die Klammer ungerade ist. Also existiert eine Darstellung $a_{k+1}=2^{p-1} n_{k+1}+\frac{3}{2}$ mit ungeradem $n_{k+1}$. Durch Erhöhen von $k$ um 1 wird also gleichzeitig $p$ um 1 vermindert, so dass $a_{k+p}=2^{0} n_{k+p}+\frac{3}{2}$ gilt und $\left\lfloor a_{k+p}\right\rfloor$ gerade ist. Dann ist $a_{k+p+1}$ eine ganze Zahl, und so liegt auch für jedes $m \geq 3$ die gesuchte Eigenschaft der Folge vor. Damit gehören alle positiven ganzen Zahlen außer 1 zur gesuchten Menge.
|
| 11 |
+
|
| 12 |
+
Hinweis: Das gelegentlich praktizierte Rechnen mit „gebrochenen Restklassen" modulo einer Zweierpotenz führte häufig zu Fehlern wie etwa der falschen Antwort, dass keine Zahlen mit Rest 1 mod 8 zur Menge gehören.
|
| 13 |
+
|
| 14 |
+
## Aufgabe 2
|
| 15 |
+
|
| 16 |
+
Man bestimme alle Funktionen $f: \mathbb{Z} \rightarrow \mathbb{Z}$, die für alle $x, y \in \mathbb{Z}$ die Gleichung $f(x-f(y))=f(f(x))-f(y)-1$
|
| 17 |
+
erfüllen.
|
| 18 |
+
|
| 19 |
+
Lösung: Die Gleichung (1) wird genau von den Funktionen $f_{1}: x \rightarrow-1$ und $f_{2}: x \rightarrow x+1$ erfüllt. Durch Einsetzen wird leicht bestätigt, dass beide Funktionen Lösungen sind.
|
| 20 |
+
Nun sei $f$ eine Funktion, die (1) für alle $x, y \in \mathbb{Z}$ erfüllt. Durch Einsetzen von $x=0$ und $y=f(0)$ erhalten wir mit $z=-f(f(0))$, dass $f(z)=-1$ ist. Einsetzen von $y=z$ in (1) führt auf $f(x+1)=f(f(x))$ für alle $x \in \mathbb{Z}$
|
| 21 |
+
Damit vereinfachen wir (1) zu $f(x-f(y))=f(x+1)-f(y)-1$
|
| 22 |
+
|
| 23 |
+
Mit $y=x$ in (3) und mit (2) ist $f(x+1)-f(x)=f(x-f(x))+1=f(f(x-1-f(x)))+1$.
|
| 24 |
+
Weil aus (3) folgt: $f(x-1-f(x))=f(x)-f(x)-1=-1$, vereinfacht sich dies zu $f(x+1)=f(x)+f(-1)+1=f(x)+c$ mit konstantem $c$. Daher ist $f$ linear und genügt dem Ansatz $f(x)=c x+b$ mit $b=f(0)$. Dies in (2) eingesetzt liefert $c x+c+b=c^{2} x+c b+b$ für alle $x \in \mathbb{Z}$. Für $x=0$ und $x=1$ erhalten wir $c+b=c b+b$ sowie $c^{2}=c$; daraus folgt $c=0$ oder $c=1$. Aus $c=1$ folgt $b=1$ und wir erhalten $f_{2}$; aus $c=0$ folgt, dass $f$ konstant ist, und mit (1) ergibt sich $b=-1$, also $f_{1}$. Damit ist alles gezeigt.
|
| 25 |
+
|
| 26 |
+
Hinweis: Oft wurden zu Beginn Einschränkungen vorgenommen (z.B. dass $x=f(y)$ ist, also zur Wertemenge gehört), die später „vergessen" wurden. Die Angabe $f: \mathbb{Z} \rightarrow \mathbb{Z}$ wurde gelegentlich so missverstanden, dass die Wertemenge alle ganzen Zahlen umfasst.
|
| 27 |
+
|
| 28 |
+
## Aufgabe 2
|
| 29 |
+
|
| 30 |
+
Es sei $A B C$ ein rechtwinkliges Dreieck mit $\varangle A C B=\gamma=90^{\circ}$. Ferner sei $H$ der Fußpunkt der Höhe von $C$ auf $A B$.
|
| 31 |
+
Nun wählen wir einen Punkt $D$ so im Inneren des Dreiecks $H B C$, dass $C H$ die Strecke $A D$ halbiert, und bezeichnen den Schnittpunkt von $C H$ und $B D$ mit $P$. Über der Strecke $B D$ als Durchmesser errichten wir denjenigen Halbkreis $k$, der von $B C$ geschnitten wird. Eine Gerade durch $P$ berührt $k$ im Punkt $Q$. Man beweise, dass sich die Geraden $C Q$ und $A D$ stets auf $k$ schneiden.
|
| 32 |
+
|
| 33 |
+
Lösung: Wie in der Figur sei $K$ der Fußpunkt des Lotes von $D$ auf $A B$ und $T$ der Schnittpunkt von $A D$ mit $k$. Wegen $\varangle A T B=\varangle A C B=90^{\circ}$ liegt $T$ auch auf dem Umkreis von $A B C$. Wegen $C H \| D K$ gilt $|A H|=|H K|$.
|
| 34 |
+
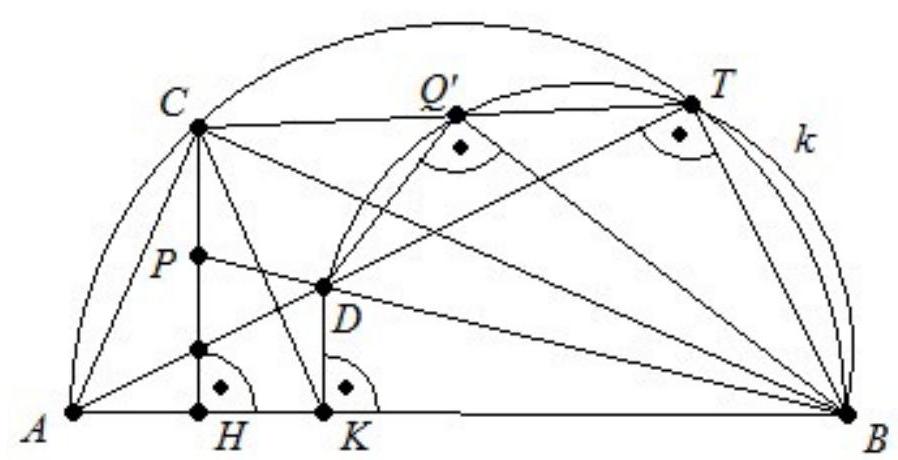
|
| 35 |
+
|
| 36 |
+
Um nachzuweisen, dass $C, Q$ und $T$ kollinear sind, betrachten wir den Schnittpunkt $Q^{\prime}$ von $C T$ mit $k$ und müssen nur zeigen, dass $P Q^{\prime} k$ berührt, bzw. dass $\varangle P Q^{\prime} D=\varangle Q^{\prime} B D$ ist.
|
| 37 |
+
Weil $B T Q^{\prime} D$ ein Sehnenviereck ist und die Dreiecke $A H C$ und $H K C$ kongruent sind, gilt
|
| 38 |
+
$\varangle Q^{\prime} B D=\varangle Q ' T D=\varangle C T A=\varangle C B A=\varangle A C H=\varangle H C K$. Also sind die rechtwinkligen Dreiecke $C H K$ und $B Q^{\prime} D$ ähnlich, woraus $|H K| /|C K|=\left|Q^{\prime} D\right| /|B D|$ folgt, also $|H K| \cdot|B D|=|C K| \cdot\left|Q^{\prime} D\right|$ (1). Wegen $P H \| D K$ gilt $|P D| /|B D|=|H K| /|B K|$, also $|P D| \cdot|B K|=|H K| \cdot|B D|$ (2). Der Vergleich von (1) und (2) führt auf $|P D| \cdot|B K|=|C K| \cdot\left|Q^{\prime} D\right|$ und somit $|P D| /\left|Q^{\prime} D\right|=|C K| /|B K|$. Deswegen und weil $\varangle C K A=\varangle K A C=\varangle B D Q^{\prime}$ ist, sind die Dreiecke $C K B$ und $P D Q^{\prime}$ ähnlich. Daher gilt $\varangle P Q^{\prime} D=\varangle C B A=\varangle Q^{\prime} B D$, was zu zeigen war.
|
| 39 |
+
|
| 40 |
+
Hinweis: Eine reine Winkeljagd führt nicht zu Ziel; allerdings gibt es andere Beweismöglichkeiten, wie etwa Ausnutzen einer geeigneten Drehstreckung mit Zentrum $B$.
|
| 41 |
+
|
Germany_TST/md/de-2017-loes_awkl_17.md
ADDED
|
@@ -0,0 +1,76 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2016/2017
|
| 2 |
+
|
| 3 |
+
1. Aufgabe. Gegeben seien positive ganze Zahlen $k$ und $n$ mit $n>k$. Unter einem Binärwort der Länge $n$ verstehen wir eine Folge aus $n$ Folgengliedern, die alle 0 oder 1 sind. Anja wählt unter allen möglichen Binärwörtern der Länge $n$ eines aus. Dann schreibt sie alle Binärwörter der Länge $n$, die sich von ihrem gewählten Wort an genau $k$ Stellen unterscheiden, an eine Tafel. Anschließend betritt Bernhard den Raum. Anja nennt ihm den Wert von $k$ und danach betrachtet er die Binärwörter an der Tafel. Er versucht nun das zu Beginn von Anja gewählte Binärwort zu erraten. Was ist (in Abhängigkeit von $k$ und $n$ ) die minimale Anzahl an Versuchen, die Bernhard benötigt um das Binärwort mit Sicherheit zu erraten?
|
| 4 |
+
|
| 5 |
+
Lösung. Die Antwort lautet: Falls $n \neq 2 k$ kann Bernhard das von Anja gewählte Wort stets im ersten Versuch erraten, im Fall $n=2 k$ braucht er zwei Versuche um das Wort mit Sicherheit zu erraten. Wir bezeichnen das von Anja zu Beginn gewählte Wort mit $u$.
|
| 6 |
+
|
| 7 |
+
Fall 1: $n \neq 2 k$. Es sei $1 \leq i \leq n$ beliebig. Von allen $\binom{n}{k}$ Wörtern an der Tafel stimmen genau $\binom{n-1}{k}$ an der $i$-ten Stelle mit $u$ überein und $\binom{n-1}{k-1}$ sind an der $i$-ten Stelle verschieden von $u$. Einfaches Nachrechnen zeigt, dass im Fall $n \neq 2 k$ auch $\binom{n-1}{k} \neq\binom{ n-1}{k-1}$ gilt, das heißt Bernhard kann durch das Betrachten der $i$-ten Stellen aller Wörter an der Tafel auf die $i$-te Stelle von $u$ schließen. Da dies für alle $i=1, \ldots, n$ funktioniert, kann Bernhard das von Anja zu Beginn gewählte Wort $u$ eindeutig bestimmen und errät es auf diese Weise im ersten Versuch. Fall $2: n=2 k$. Wir zeigen zunächst, dass Bernhard nicht eindeutig auf $u$ schließen kann, also möglicherweise mehr als einen Versuche benötigt. Angenommen, Anja hätte das (eindeutige) Binärwort $\bar{u}$ gewählt, dass sich an allen Stellen von ihrem tatsächlichen Wort $u$ unterscheidet. Ein beliebiges Binärwort der Länge $n$ stimmt genau dann in $k=n / 2$ Stellen mit $u$ überein, wenn es in $k=n / 2$ Stellen mit $\bar{u}$ übereinstimmt, das heißt Anja hätte in diesem Fall exakt die gleichen Binärwörter an die Tafel geschrieben. Dies bedeutet, dass Bernhard keine Möglichkeit hat zwischen $u$ und $\bar{u}$ zu unterscheiden und in seinem ersten Versuch Anjas Wort zu raten möglicherweise falsch liegt. Wir zeigen nun, dass Bernhard in zwei Versuchen stets Erfolg haben kann. Dazu genügt es zu beweisen, dass für jedes von $u$ und $\bar{u}$ verschiedene Binärwort $w$ der Länge $n$ die Menge aller Binärwörter der Länge $n$, die sich an genau $k=n / 2$ Stellen von $w$ unterscheiden, nicht identisch mit der Menge der Wörter an der Tafel ist. Dazu dürfen wir ohne Beschränkung der Allgemeinheit annehmen dass sich $w$ von $u$ an genau $a$ Stellen unterscheidet, wobei $0<a \leq k=n / 2$ (sonst betrachte $\bar{u}$ statt $u$ ). Dann können wir genau $k$ der übrigen $n-a \geq k$ Stellen abändern und erhalten ein Wort $w^{\prime}$, das sich an genau $k$ Stellen von $w$ unterscheidet, aber an $a+k>k$ Stellen von $u$, das heißt es steht nicht an der Tafel.
|
| 8 |
+
2. Aufgabe. Es sei $A B C D$ ein konvexes Viereck. Die Diagonale $B D$ halbiere den Winkel $\measuredangle C B A$. Der Umkreis des Dreiecks $A B C$ schneide die Strecken $\overline{C D}$ und $\overline{D A}$ in den inneren Punkten $P$ bzw. $Q$. Die durch den Punkt $D$ verlaufende Parallele zur Geraden $A C$ schneide die Geraden $B A$ und $B C$ in den Punkten $R$ bzw. $S$. Man beweise, dass die vier Punkte $P, Q, R$ und $S$ auf einem gemeinsamen Kreis liegen.
|
| 9 |
+
|
| 10 |
+
Lösung. Schritt 1: Wegen $\measuredangle B R D=\measuredangle B A C=\measuredangle B P C=\pi-\measuredangle D P B$ ist $B P D R$ ein Sehnenviereck. Analog zeigt man, dass auch $B S D Q$ ein Sehnenviereck ist. Schritt 2: Es sei $X$ definiert als der Schnittpunkt von $B D$ mit dem Umkreis des Dreiecks $A B C$. Dann gilt $\measuredangle D P X=\pi-\measuredangle X P C=\measuredangle C B X=1 / 2 \measuredangle C B A$. Da nach Schritt 1 auch $\measuredangle D P R=\measuredangle D B R=1 / 2 \measuredangle D B A$ gilt, liegt $X$ auf $P R$. Analog zeigt man, dass $X$ auch auf $Q S$ liegt. Schritt 3: Wir kombinieren die Erkenntnisse und rechnen (mithilfe des Sehnensatzes) $|P X| \cdot|X R|=|B X| \cdot|X D|=|Q X| \cdot|X S|$. Mit der Umkehrung des Sehnensatzes folgt nun die Behauptung.
|
| 11 |
+
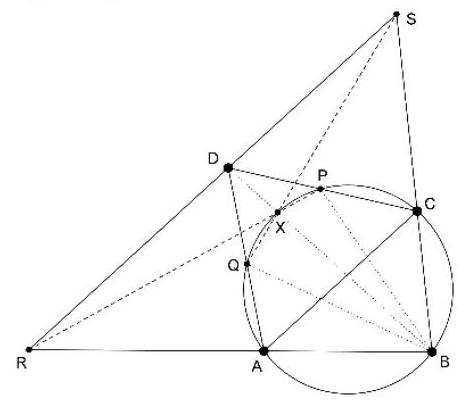
|
| 12 |
+
3. Aufgabe. Die Menge der positiven ganzen Zahlen sei mit $\mathbb{N}$ bezeichnet. Man bestimme alle Funktionen $f: \mathbb{N} \rightarrow \mathbb{N}$ mit der folgenden Eigenschaft: Für alle positiven ganzen Zahlen $m$ und $n$ ist die Zahl $f(m)+f(n)-m n$ von 0 verschieden und ist ein Teiler der Zahl $m f(m)+n f(n)$.
|
| 13 |
+
|
| 14 |
+
Lösung. Antwort: Es gibt genau eine Funktion, die die beschriebene Bedingung erfüllt, nämlich $f(k)=k^{2}$ für alle $k$. Zum Beweis sei $f$ wie verlangt. Schritt 1: Einsetzen von $m=n=1$ liefert $2 f(1)-1 \mid 2 f(1)$, also auch $2 f(1)-1 \mid 2 f(1)-(2 f(1)-1)=1$ und damit $2 f(1)-1=1$, also $f(1)=1$. Schritt 2: Von nun an stehe $p$ stets für eine Primzahl mit $p \geq 7$. Einsetzen von $m=n=p$ liefert $2 f(p)-p^{2} \mid 2 p f(p)$ und damit auch $2 f(p)-p^{2} \mid 2 p f(p)-p\left(2 f(p)-p^{2}\right)=p^{3}$, also
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
2 f(p)-p^{2} \in\left\{-p^{3},-p^{2},-p,-1,1, p, p^{2}, p^{3}\right\}
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
Da $f(p)>0$ folgt
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
f(p) \in\left\{\frac{p^{2}-p}{2}, \frac{p^{2}-1}{2}, \frac{p^{2}+1}{2}, \frac{p^{2}+p}{2}, p^{2}, \frac{p^{3}+p^{2}}{2}\right\} .
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
Schritt 3: Wir setzen $m=1, n=p$ und erhalten $f(p)+1-p \mid p f(p)+1$, also auch $f(p)+1-p \mid p f(p)+1-p(f(p)+1-p)=p^{2}-p+1$. Angenommen, es gilt $f(p) \neq p^{2}$. Dann folgt (beachte, dass $p^{2}-p+1$ ungerade ist) notwendigerweise $f(p)+1-p \leq 1 / 3\left(p^{2}-p+1\right)$. Nach Schritt 2 gilt jedoch $f(p) \geq\left(p^{2}-p\right) / 2$, es folgt also
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
\begin{aligned}
|
| 30 |
+
\frac{p^{2}-p}{2}+1-p & \leq \frac{p^{2}-p+1}{3} \\
|
| 31 |
+
3 p^{2}-3 p+6-6 p & \leq 2 p^{2}-2 p+1 \\
|
| 32 |
+
p^{2}+5 & \leq 7 p
|
| 33 |
+
\end{aligned}
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
was für $p \geq 7$ nicht der Fall ist. Also war die obige Annahme falsch und es muss $f(p)=p^{2}$ gelten. Schritt 4: Es sei $n \in \mathbb{N}$ beliebig. Wir setzen $m=p$ und erhalten $f(n)+p^{2}-p n \mid$ $p^{3}+n f(n)$, also auch $f(n)+p^{2}-p n \mid p^{3}+n f(n)-n\left(f(n)-p^{2}-p n\right)=p\left(p^{2}-p n+n^{2}\right)$. Für alle hinreichend großen Primzahlen $p$ ist $f(n)$ und damit auch die linke Seite des letzten Ausdrucks nicht durch $p$ teilbar, daher folgt $f(n)+p^{2}-p n \mid p^{2}-p n+n^{2}$ und somit auch $f(n)+p^{2}-p n \mid\left(f(n)+p^{2}-p n\right)-\left(p^{2}-p n+n^{2}\right)=f(n)-n^{2}$. Da die linke Seite beliebig groß werden kann (es gibt unendlich viele Primzahlen) folgt $f(n)-n^{2}=0$ und damit $f(n)=n^{2}$. Schritt 5: Die Probe bestätigt dass $f(k)=k^{2}$ für alle $k \in \mathbb{N}$ tatsächlich die Bedingung erfüllt: Es gilt $f(m)+f(n)-m n=m^{2}+n^{2}-m n \geq 2 m n-m n=m n>0$, und außerdem gilt $\left(m^{2}+n^{2}-m n\right)(m+n)=m^{3}+n^{3}=m f(m)+n f(n)$, das heißt $f(m)+f(n)-m n$ ist von 0 verschieden und ist ein Teiler der Zahl $m f(m)+n f(n)$.
|
| 37 |
+
|
| 38 |
+
## Aufgabe 1
|
| 39 |
+
|
| 40 |
+
Man bestimme die kleinste reelle Konstante $C$ mit folgender Eigenschaft:
|
| 41 |
+
Für fünf beliebige positive reelle Zahlen $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$, die nicht unbedingt verschieden sein müssen, lassen sich stets paarweise verschiedene Indizes $i, j, k, l$ finden, so dass
|
| 42 |
+
$\left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leq C$ gilt.
|
| 43 |
+
Lösung: Der gesuchte Wert ist $C=\frac{1}{2}$.
|
| 44 |
+
Zunächst beweisen wir, dass $C \leq \frac{1}{2}$ gilt. Dazu nehmen wir oBdA $a_{1} \leq a_{2} \leq a_{3} \leq a_{4} \leq a_{5}$ an und betrachten die fünf Brüche $\frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}}$. Nach dem Schubfachprinzip liegen in einem der Intervalle ]0, $\frac{1}{2}$ ] bzw. $\left.] \frac{1}{2}, 1\right]$ drei verschiedene dieser Brüche, wobei zwei von diesen in der Aufzählung direkt aufeinanderfolgen oder der erste und der letzte Bruch dabei sind. Jedenfalls ist die positive Differenz dieser beiden Brüche kleiner als $\frac{1}{2}$ und die vier beteiligten Indizes sind paarweise verschieden.
|
| 45 |
+
Nun zeigen wir, dass $C \geq \frac{1}{2}$ gilt. Dazu betrachten das Beispiel 1, 2, 2, 2 , $r$, wobei $r$ eine Riesenzahl sein soll. Mit diesen Zahlen lassen sich - der Größe nach geordnet - die Brüche $\frac{1}{r}, \frac{2}{r}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{r}{2}, \frac{r}{1}$ bilden, wobei nach der Aufgabenstellung $\frac{1}{r}$ und $\frac{2}{r}$ nicht gleichzeitig gewählt werden dürfen. Daher ist die kleinste positive Differenz gleich $\frac{1}{2}-\frac{2}{r}$, und dies nähert sich für $r \rightarrow \infty$ dem Wert $\frac{1}{2}$ von unten beliebig gut an. $\square$
|
| 46 |
+
|
| 47 |
+
## Aufgabe 2
|
| 48 |
+
|
| 49 |
+
Es sei $n$ eine positive ganze Zahl, die teilerfremd zu 6 ist. Wir färben die Ecken eines regulären $n$-Ecks so mit drei Farben, dass für jede Farbe die Anzahl der mit ihr gefärbten Ecken ungerade ist.
|
| 50 |
+
Man beweise, dass es dann stets ein gleichschenkliges Dreieck gibt, dessen Ecken zu den Ecken des $n$ Ecks gehören und alle verschieden gefärbt sind.
|
| 51 |
+
|
| 52 |
+
Lösung: Es seien $a_{1}, a_{2}, a_{3}$ die Anzahlen der gleichschenkligen Dreiecke, in deren Eckpunkten genau 1, 2 bzw. 3 Farben vorkommen. Wir nehmen an, dass $a_{3}=0$ gelte. Die Farben seien rot, grün und blau, wobei $r, g$ und $b$ die (ungerade) Anzahl der jeweils so gefärbten Ecken bezeichnet. Wir bestimmen nun auf zwei Arten die Anzahl $a$ der Paare ( $\Delta, v$ ), wobei $\Delta$ ein gleichschenkliges Dreieck mit mehr als einer Eckenfarbe und $v$ eine Seitenkante dieses Dreiecks ist, deren Endpunkte mit verschiedenen Farben belegt sind.
|
| 53 |
+
Wegen $a_{3}=0$ müssen die Eckpunkte eines solchen Dreiecks mit genau zwei Farben belegt sein, von denen eine zu zwei Ecken gehört, die jeweils Endpunkte einer Seitenkante $v$ sind. Also trägt jedes Dreieck zwei Paare bei und es ist $a=2 a_{2}$.
|
| 54 |
+
Zu je zwei Eckpunkten $A$ und $B$ gibt genau drei verschiedene Eckpunkte $C$, die mit $A$ und $B$ ein gleichschenkliges Dreieck bilden: entweder ist $A B=A C$ oder $A B=B C$ oder $A C=B C$. Dabei können keine dieser Möglichkeiten zusammenfallen, weil sonst $A B C$ gleichseitig und $n$ durch 3 teilbar wäre. $A C=B C$ existiert, weil $n$ ungerade ist und daher die Mittelsenkrechte von $A B$ durch genau einen weiteren Eckpunkt verläuft. Daher gilt, ausgehend von zwei verschieden gefärbten Eckpunkten $A$ und $B$, dass $a=3(r g+g b+b r)$ ist. Dieser Term ist nach Voraussetzung ungerade, im Widerspruch zu $a=2 a_{2}$. Daher muss $a_{3} \neq 0$ gelten.
|
| 55 |
+
|
| 56 |
+
[^0]
|
| 57 |
+
## Aufgabe 3
|
| 58 |
+
|
| 59 |
+
Es sei $A B C$ ein Dreieck mit $A B=A C \neq B C$. Ferner sei $I$ der Inkreismittelpunkt von $A B C$.
|
| 60 |
+
Die Gerade $B I$ schneidet $A C$ im Punkt $D$, und die Orthogonale zu $A C$ durch $D$ schneidet $A I$ im Punkt $E$. Man beweise, dass der Spiegelpunkt von $I$ bei Spiegelung an der Achse $A C$ auf dem Umkreis des Dreiecks BDE liegt.
|
| 61 |
+
|
| 62 |
+
Lösung: Zunächst beweisen wir (schon mit den zur Aufgabe passenden Bezeichnungen) folgendes Lemma: Die Mittelsenkrechte einer Seite $B I I^{\prime}$ und die Winkelhalbierende durch den dritten Eckpunkt $D$ schneiden sich auf dem Umkreis jedes nicht gleichschenkligen Dreiecks $B I^{\prime} D$. („Südpolsatz") Beweis des Lemmas: Es sei $M$ der Mittelpunkt des Umkreises von $B I^{\prime} D$ und $S$ der von $D$ verschiedene Schnittpunkt der Winkelhalbierenden mit dem Umkreis. Dann ist $\square B M I I^{\prime}$ als Mittelpunktswinkel doppelt so groß wie $\square B D I^{\prime}$ und $\square S D I^{\prime}$ halb so groß wie $\square B D I^{\prime}$. Da aber die Mittelsenkrechte von $B I^{\prime}$ beide Bögen des Umkreises zu dieser Sehne halbiert, muss sie durch $S$ gehen.
|
| 63 |
+
Korollar: Der andere Schnittpunkt der Mittelsenkrechten von $B I$ ' mit dem Umkreis sei $E$. Dann liegt nach dem Lemma $D$ auf dem Thaleskreis über $E S$ und es ist $\square E D S=90^{\circ}$ Somit ist $D E$ die äußere Winkelhalbierende von $\square B D I^{\prime}$. Die Umkehrung gilt ebenfalls: Wenn für den Punkt $E$ auf der äußeren Winkelhalbierenden von $\square B D I^{\prime}$ auch $B E=E I '$ gilt, dann liegt $E$ auf dem Umkreis von $B I^{\prime} D$.
|
| 64 |
+
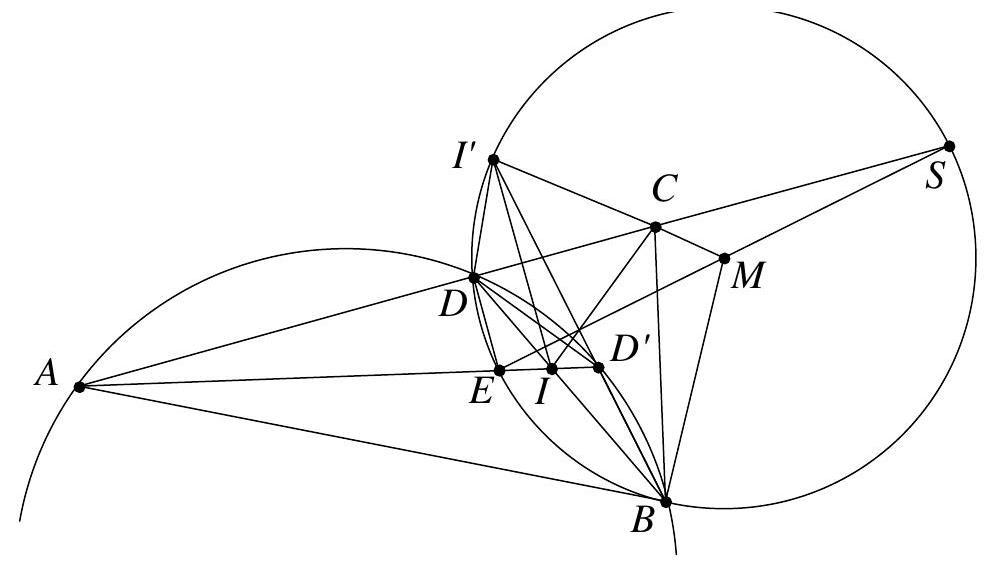
|
| 65 |
+
|
| 66 |
+
Für den Hauptbeweis bezeichnen wir den Spiegelpunkt von $I$ mit $I^{\prime}$ und den zweiten Schnittpunkt von $A I$ und dem Umkreis des Dreiecks $A B D$ mit $D^{\prime}$. Weil $A D^{\prime}$ die Winkelhalbierende von $\square B A D$ ist, liegt $D^{\prime}$ in der Mitte des Bogens $B D$ und so gilt $D D^{\prime}=B D^{\prime}=C D^{\prime}$.
|
| 67 |
+
Unter Verwendung des Umfangswinkelsatzes über der Sehne $A D$ sowie geeigneter Winkelhalbierender erhalten wir $\square D D^{\prime} E=\square D D^{\prime} A=\square D B A=\square C B I=\square I C B$. Weil $D^{\prime}$ wegen der gleichen Abstände der Umkreismittelpunkt des Dreiecks $B C D$ ist, gilt $\square E D D^{\prime}=90^{\circ}-\square D^{\prime} D C=\square C B D=\square C B I$, also sind wegen $\square C B I=\square I C B$ die Dreiecke $E D^{\prime} D$ und $I B C$ ähnlich. Daraus folgt $\frac{B C}{C I}=\frac{B C}{C I}=\frac{D D^{\prime}}{D^{\prime} E}=\frac{B D^{\prime}}{D^{\prime} E}$.
|
| 68 |
+
Außerdem gilt $\square I^{\prime} C B=\square A C B+\square I^{\prime} C A=\square A C B+\square A C I=\square A C B+\square C B D=\square B D A=\square B D^{\prime} E$, und daher sind die Dreiecke $B C I^{\prime}$ und $B D^{\prime} E$ ähnlich, ebenso sind $B C D^{\prime}$ und $B I^{\prime} E$ ähnliche Dreiecke, denn bei der Drehstreckung um $B$, die $B C I^{\prime}$ in $B D^{\prime} E$ überführt, geht $C D^{\prime}$ in $I^{\prime} E$ über.
|
| 69 |
+
Weil aber $B C D^{\prime}$ gleichschenklig ist, gilt auch $B E=E I^{\prime}$.
|
| 70 |
+
Nun ist $D E \perp A C$, und nach dem Korollar liegt $E$ auf dem Umkreis des Dreiecks $B I^{\prime} D$. .
|
| 71 |
+
|
| 72 |
+
Hinweis: Es gibt viele weitere Lösungswege zu diesem Problem, die jedoch alle nicht mit einer einfachen Winkeljagd auskommen. Sämtliche analytischen Lösungsansätze waren wegen der immer komplexer werdenden Terme zum Scheitern verurteilt. In der Skizze schneiden sich MI* und $D S$ in $C$; dies ist tatsächlich immer so.
|
| 73 |
+
|
| 74 |
+
|
| 75 |
+
[^0]: Hinweis: Viele Lösungsansätze über eine Prozedur, mit der man immer neue Punkte geeignet färbt, enthielten Lücken, weil Schleifen oder Mehrfachbelegungen nicht vollständig untersucht worden sind.
|
| 76 |
+
|
Germany_TST/md/de-2018-loes_awkl_18.md
ADDED
|
@@ -0,0 +1,115 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2017/2018
|
| 2 |
+
|
| 3 |
+
Aufgabe 1. Ein Rechteck $\mathcal{R}$ mit ungeraden ganzzahligen Seitenlängen ist in Rechtecke unterteilt, die alle ganzahlige Seitenlängen haben. Man beweise, dass für mindestens eines dieser Rechtecke die Abstände zu jeder der vier Seiten von $\mathcal{R}$ alle gerade oder alle ungerade sind.
|
| 4 |
+
|
| 5 |
+
Lösung. Wir unterteilen $\mathcal{R}$ in Einheitsquadrate und färben einige dieser Einheitsquadrate in rot oder blau ein, entsprechend der folgenden Illustration.
|
| 6 |
+
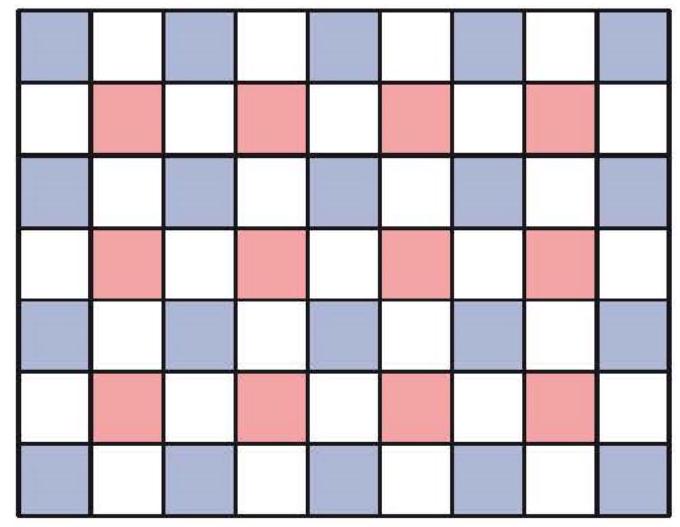
|
| 7 |
+
|
| 8 |
+
Da $\mathcal{R}$ laut Voraussetzung ungerade Seitenlängen hat, sind alle vier Eckfelder von $\mathcal{R}$ blau gefärbt, und es gibt insgesamt mehr gefäbte als ungefärbte Felder. Somit enthält auch mindestens eines der Rechtecke $\mathcal{R}_{1}, \ldots, \mathcal{R}_{k}$, in die $\mathcal{R}$ unterteilt wurde, mehr gefärbte als ungefärbte Felder, sei $\mathcal{R}_{i}$ ein solches. Dann hat $\mathcal{R}_{i}$ ungerade Seitenlängen und alle vier Eckfelder von $\mathcal{R}_{i}$ sind gefärbt. Daraus folgt, dass alle vier Eckfelder von $\mathcal{R}_{i}$ dieselbe Farbe tragen müssen. Falls sie blau sind, hat $\mathcal{R}_{i}$ gerade Abstände zu allen vier Seiten von $\mathcal{R}$; falls sie rot sind hat $\mathcal{R}_{i}$ ungerade Abstände zu allen vier Seiten von $\mathcal{R}$. In jedem Fall erfüllt $\mathcal{R}_{i}$ die geforderte Bedingung.
|
| 9 |
+
|
| 10 |
+
Aufgabe 2. Es sei eine positive ganze Zahl $d$ und eine Folge $\left(a_{i}\right)_{i=1,2,3, \ldots}$ positiver ganzer Zahlen gegeben. Wir nehmen an, dass folgende zwei Bedingungen erfüllt sind:
|
| 11 |
+
|
| 12 |
+
- Jede positive ganze Zahl taucht genau einmal in der Folge auf.
|
| 13 |
+
- Für alle Indizes $i \geq 10^{100}$ gilt $\left|a_{i+1}-a_{i}\right| \leq 2 d$.
|
| 14 |
+
|
| 15 |
+
Man beweise, dass unendlich viele Indizes $j$ existieren, für die $\left|a_{j}-j\right|<d$ gilt.
|
| 16 |
+
Lösung. Angenommen, die Behauptung wäre nicht erfüllt. Dann existiert ein Index $N>10^{100}$, sodass für alle $i \geq N$ entweder $a_{i} \leq i-d$ oder $a_{i} \geq i+d$ gilt. Im ersten Fall gilt wegen $i \geq N>10^{100}$ laut der zweiten Voraussetzung an die Folge auch
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
a_{i+1} \leq a_{i}+2 d \leq i-d+2 d=(i+1)+(d-1)
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
es muss also $a_{i+1} \leq(i+1)-d$ gelten. Induktiv folgt damit $a_{i} \leq j-d$ für alle $j \geq i$.
|
| 23 |
+
|
| 24 |
+
Damit haben wir gezeigt:
|
| 25 |
+
(A) Entweder es gilt $a_{i} \geq i+d$ für alle $i \geq N$, oder
|
| 26 |
+
(B) es existiert ein $M \geq N$, sodass $a_{i} \leq i-d$ für alle $i \geq M$ gilt.
|
| 27 |
+
|
| 28 |
+
Nehmen wir zunächst an, (A) sei erfüllt. Die Zahlen $1, \ldots, N$ müssen laut der ersten Voraussetzung an die Folge alle einmal in der Folge auftauchen. Nun gilt jedoch $a_{i} \geq i+d>i \geq N$ für alle $i \geq N$, das heißt es gibt nur die $N-1$ Folgenglieder $a_{1}, \ldots, a_{N-1}$, die einen dieser Werte annehmen können. Nach dem Schubfachprinzip ergibt sich ein Widerspruch.
|
| 29 |
+
Nehmen wir nun an, (B) sei erfüllt. Es sei $k=\max \left\{M, a_{1}, \ldots, a_{M}\right\}$. Dann sind die $k$ Folgenglieder $a_{1}, \ldots, a_{k}$ alle kleiner als $k$, denn für $i=1, \ldots M-1$ gilt $a_{i} \leq$ $\max \left\{a_{1}, \ldots, a_{M-1}\right\} \leq k$ und für $i=M, \ldots, k$ gilt $a_{i} \leq i-d<i \leq k$. Diese $k$ Zahlen liegen damit alle in der Menge $\{1,2, \ldots, k-1\}$. Nach dem Schubfachprinzip existieren daher zwei Indizes $1 \leq i<j \leq k$ mit $a_{i}=a_{j}$, was er ersten Voraussetzung an die Folge widerspricht.
|
| 30 |
+
Da wir in jedem Fall einen Widerspruch erhalten haben, gilt die Behauptung.
|
| 31 |
+
|
| 32 |
+
Aufgabe 3. Es sei $A B C$ ein Dreieck. Der dem Punkt $A$ gegenüberliegende Ankreis $\omega$ berühre die Strecke $\overline{B C}$ sowie die Strahlen $A C$ und $A B$ in den Punkten $D, E$ bzw. $F$. Der Umkreis des Dreiecks $A E F$ schneide die Gerade $B C$ in den Punkten $P$ und $Q$. Schließlich sei $M$ der Mittelpunkt der Strecke $\overline{A D}$. Man beweise, dass sich $\omega$ und der Umkreis des Dreiecks $M P Q$ berühren
|
| 33 |
+
|
| 34 |
+
Lösung. Es sei $J$ der Mittelpunkt des Ankreises $\omega$. Dann gilt $J E \perp A E$ und $J F \perp$ $A F$, der Thaleskreis $\Omega$ von $\overline{A J}$ verläuft also durch $E$ und $F$, und damit auch durch $P$ und $Q$. Der Strahl $A D$ schneide $\Omega$ und $\omega$ erneut in $N$ bzw. $T$.
|
| 35 |
+

|
| 36 |
+
|
| 37 |
+
Dann ist $J N$ die Lotgerade von $J$ auf $D T$, also ist $N$ der Mittelpunkt der Strecke $\overline{D T}$. Damit gilt laut dem Sehnensatz
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
|D M| \cdot|D T|=1 / 2 \cdot|D A| \cdot|D T|=|D A| \cdot|D N|=|D P| \cdot|D Q|
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
der Punkt $T$ liegt nach der Umkehrung des Sehnensatzes also auf dem Umkreis des Dreiecks $M P Q$. Wir betrachten nun den Bildpunkt von $N$ bei Inversion am Kreis $\omega$, dieser sei mit $Z$ bezeichnet. Da die Thaleskreise über $\overline{J D}$ und $\overline{J T}$ beide durch den Punkt $N$ verlaufen, liegt $Z$ auf den Bildern dieser Kreise, also den Tangenten durch $D$ und $T$ an $\omega$. Auf ersterer Geraden liegen auch $B, C, P$ und $Q$. Ferner liegt $N$ auf dem Kreis $\Omega$, der bei der betrachteten Inversion in die Gerade $E F$ übergeht, also liegt auch $Z$ auf der Geraden $E F$. Damit gilt nach dem Sekantensatz
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
|Z T|^{2}=|Z E| \cdot|Z F|=|Z P| \cdot|Z Q|,
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
nach der Umkehrung des Sekantensatzes tangiert $Z T$ daher auch den Umkreis des Dreiecks $M P Q$. Damit haben wir beweisen, dass sich dieser Kreis und $\omega$ im Punkt $T$ berühren.
|
| 50 |
+
|
| 51 |
+
## Lösungen zur 2. Auswahlklausur 2017/2018
|
| 52 |
+
|
| 53 |
+
## Aufgabe 1
|
| 54 |
+
|
| 55 |
+
Es seien $a_{1}, a_{2}, \ldots, a_{n}, k$ und $M$ positive ganze Zahlen mit den Eigenschaften
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}=k \quad \text { und } \quad a_{1} a_{2} \ldots a_{n}=M .
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Man beweise: Für $M>1$ hat das Polynom
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
P(x)=M(x+1)^{k}-\left(x+a_{1}\right)\left(x+a_{2}\right) \ldots\left(x+a_{n}\right)
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
keine positiven Lösungen.
|
| 68 |
+
Lösung: Wir zeigen $P(x)<0$ für alle $x>0$, also $M(x+1)^{k}<\left(x+a_{1}\right) \ldots\left(x+a_{n}\right) \Leftrightarrow$ $a_{1} a_{2} \ldots a_{n}(x+1)^{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}}<\left(x+a_{1}\right) \ldots\left(x+a_{n}\right) \Leftrightarrow \prod_{i=1}^{n} a_{i}(x+1)^{\frac{1}{a_{i}}}<\prod_{i=1}^{n}\left(x+a_{i}\right)$.
|
| 69 |
+
Dazu zeigen wir, dass für jedes $i\left((1 \leq i \leq n)\right.$ die Beziehung $a_{i}(x+1)^{\frac{1}{a_{i}}} \leq x+a_{i}(1)$ gilt und für wenigstens ein $i$ sogar $a_{i}(x+1)^{\frac{1}{a_{i}}}<x+a_{i}$ ist. Die Behauptung folgt dann durch Multiplikation für alle $i$.
|
| 70 |
+
Aus der AM-GM-Ungleichung für die Zahlen $x+1,1,1, \ldots, 1\left(a_{i}-1\right.$ Summanden 1$)$ folgt $\frac{x+a_{i}}{a_{i}} \geq \sqrt[a]{x+1}$, was nach Multiplikation mit $a_{i}$ gerade (1) ergibt. Das Gleichheitszeichen gilt genau für $a_{i}=1$, was nicht für alle $i$ sein kann, denn dann wäre $M=1$, im Widerspruch zur Voraussetzung $M>1$. Da für die gegebenen Werte alle Umformungen erlaubt sind, ist alles gezeigt.
|
| 71 |
+
|
| 72 |
+
Hinweis: Weitere Beweisansätze über die Bernoulli-Ungleichung, den binomischen Satz, die Jensensche Ungleichung oder Analysis sind möglich. Der Begriff „Lösung" in der Aufgabenstellung steht natürlich synonym zu „Nullstelle".
|
| 73 |
+
|
| 74 |
+
## Aufgabe 2
|
| 75 |
+
|
| 76 |
+
Es sei $A B C D E$ ein konvexes Fünfeck mit den Eigenschaften
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
\overline{A B}=\overline{B C}=\overline{C D}, \angle B A E=\angle D C B \text { und } \angle E D C=\angle C B A .
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
Man beweise, dass die Lotgerade von $E$ auf $B C$ durch den Schnittpunkt von $A C$ und $B D$ verläuft.
|
| 83 |
+
Lösung: Wegen der Voraussetzungen sind $\triangle A B C$ und $\triangle B C D$ gleichschenklig. Daher geht die Mittelsenkrechte zu $A C$ durch $B$ und die Mittelsenkrechte zu $B D$ durch $C$. Beide schneiden sich im Punkt $I$ (siehe Figur).
|
| 84 |
+
Wegen $B D \perp C I$ und $A C \perp B I$ schneiden sich $A C$ und $B D$ im Höhenschnittpunkt des Dreiecks $B C I$ und es folgt $I H \perp B C$. Wenn wir nun zeigen können, dass $E I \perp B C$ ist, folgt die Behauptung, weil es durch $I$ nur eine Orthogonale zu $B C$ geben kann. Weil $B I$ und $C I$ auch Winkelhalbierende von $\angle C B A$ bzw. $\angle D C B$ sind, folgt $\overline{I A}=\overline{I C}$ sowie $\overline{I B}=\overline{I D}$. Wegen $\overline{A B}=\overline{B C}=\overline{C D}$ sind die Dreiecke $A B I, B C I$ und $C D I$ kongruent. Daher ist $\angle B A I=\angle I C B=\frac{1}{2} \angle D C B=\frac{1}{2} \angle B A E$, so dass $I A$ Winkelhalbierende von $\angle B A E$ ist. Analog gilt, dass $I D$ Winkelhalbierende von $\angle E D C$ ist.
|
| 85 |
+
|
| 86 |
+
Die Verkettung der Achsenspiegelungen an $A I, B I, C I, D I$ und $E I$ ist eine Achsenspiegelung mit den Fixpunkten $E$ und $I$. Daher liegt $I$ auch auf der Winkelhalbierenden von $\angle A E D$.
|
| 87 |
+
Nun gilt $\angle A E D=540^{\circ}-2 \angle C B A-2 \angle B A E$, und damit folgt im Viereck $A B I E$ :
|
| 88 |
+
$\angle B I E=360^{\circ}-\angle B A E-\angle I B A-\angle A E I=360^{\circ}-\angle B A E-\frac{1}{2} \angle C B A-\left(270^{\circ}-\angle C B A-\angle B A E\right)$
|
| 89 |
+
$=90^{\circ}+\frac{1}{2} \angle C B A=90^{\circ}+\angle C B I$. Mit dem Außenwinkelsatz folgt $E I \perp B C$. ㅁ.
|
| 90 |
+
Hinweis: Es gibt andere Lösungswege über die Schnittpunkte der Verlängerungen geeigneter Seiten, mithilfe von
|
| 91 |
+
Trigonometrie oder (in der Regel sehr aufwändig) analytischer Geometrie. Fehler entstanden z.T. durch Verwendung der Behauptung im Beweis, etwa durch Nicht-Unterscheiden der Geraden $E T$ und IT.
|
| 92 |
+
|
| 93 |
+
## Aufgabe 3
|
| 94 |
+
|
| 95 |
+
Man bestimme alle ganzen Zahlen $n \geq 2$ mit der folgenden Eigenschaft:
|
| 96 |
+
Für beliebige, nicht notwendigerweise verschiedene ganze Zahlen $m_{1}, m_{2}, \ldots, m_{n}$, deren Summe nicht durch $n$ teilbar ist, existiert ein Index $i(1 \leq i \leq n)$, so dass keine der Zahlen
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
m_{i}, m_{i}+m_{i+1}, m_{i}+m_{i+1}+m_{i+2}, \ldots, m_{i}+m_{i+1}+\ldots+m_{i+n-1}
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
durch $n$ teilbar ist. (Dabei sei $m_{i}=m_{i-n}$ für $i>n$.)
|
| 103 |
+
Lösung: Bei den gesuchten Zahlen handelt es sich genau um die Primzahlen.
|
| 104 |
+
Teilbeweis 1: Keine Nichtprimzahl crfüllt allc Voraussctzungen.
|
| 105 |
+
Es sei $n=a \cdot b$ mit $1<a, b<n$ eine Zerlegung von $n$ in zwei echte Teiler. Wir wählen $m_{i}=a$ für $1 \leq i<n$ sowie $m_{n}=0$. Dann ist die Summe $m_{1}+m_{2}+\ldots+m_{n}=(n-1) a$ offensichtlich nicht durch $n$ teilbar, da beide Faktoren nicht durch $n$ teilbar sind.
|
| 106 |
+
Nun wählen wir zu einem beliebigen Index $i$ den Index $j=\left\{\begin{array}{ll}b & \text { für } 1 \leq i \leq n-b \\ b+1 & \text { für } n-b<i \leq n\end{array}\right.$ und erhalten $m_{i}+m_{i+1}+\ldots+m_{i+j-1}=a \cdot b=n \equiv 0 \bmod n$. Mit diesem Gegenbeispiel ist der Teilbeweis abgeschlossen.
|
| 107 |
+
|
| 108 |
+
Teilbeweis 2: Jede Primzahl erfüllt alle Voraussetzungen.
|
| 109 |
+
Es sei nun $n$ eine Primzahl. Für einen Widerspruchsbeweis nehmen wir an, dass es für die Zahlen $m_{1}, m_{2}, \ldots, m_{n}$, deren Summe nicht durch $n$ teilbar ist, zu jedem Index $i(1 \leq i \leq n)$ eine Zahl $j(1 \leq j \leq n)$ gibt, so dass die Summe $m_{l}+m_{i+1}+\ldots+m_{i+j-1}$ durch $n$ teilbar ist. Dabei gilt sogar $j \neq n$, denn die Summe aller $m_{i}$ ist nicht durch $n$ teilbar.
|
| 110 |
+
Nun konstruieren wir für $0 \leq k \leq n-1$ eine endliche Folge ganzer Zahlen $i_{0}, i_{1}, \ldots, i_{n}$ mit $i_{k+1}-i_{k} \leq n-1$ (1), indem wir $m_{i_{k}+1}+m_{i_{k}+2}+\ldots+m_{i_{k+1}} \equiv 0 \bmod n$ wählen. Der Startindex $i_{0}$ ist beliebig und der neue Index $i_{k+1}$ sei der jeweils kleinstmögliche nach $i_{k}$ beim zyklischen Weitergehen $\bmod n$.
|
| 111 |
+
Nach dem Schubfachprinzip gibt es in der Folge dieser $n+1$ Indizes zwei verschiedene Zahlen $i_{r}$ und $i_{s}$ mit $0 \leq r<s \leq n$, die $\bmod n$ kongruent sind. Mit ihnen gilt $\sum_{j=r}^{s-1}\left(m_{i_{j}+1}+m_{i_{j+2}}+\ldots+m_{i_{j+1}}\right) \equiv 0 \bmod n$, weil dies für jede Klammersumme gilt.
|
| 112 |
+
Andererseits folgt aus $i_{s} \equiv i_{r} \bmod n$, dass es eine positive ganze Zahl $d$ gibt mit $i_{s}-i_{r}=d \cdot n$. Wegen (1)
|
| 113 |
+
ist $i_{s}-i_{r} \leq(n-1) n$, so dass $d \leq n-1$ folgt. Dann kann $\sum_{j=r}^{s-1}\left(m_{i_{j}+1}+m_{i_{j+2}}+\ldots+m_{i_{j+1}}\right)=d\left(m_{1}+m_{2}+\ldots+m_{n}\right)$
|
| 114 |
+
aber kein Vielfaches von $n$ sein, denn $n$ ist prim und weder $d$ noch $m_{1}+m_{2}+\ldots+m_{n}$ sind Vielfache von $n$ - Widerspruch! $\square$
|
| 115 |
+
|
Germany_TST/md/de-2019-loes_awkl_19.md
ADDED
|
@@ -0,0 +1,145 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2018/2019
|
| 2 |
+
|
| 3 |
+
## Aufgabe 1
|
| 4 |
+
|
| 5 |
+
Die Menge aller positiver rationaler Zahlen sei mit $\mathbb{Q}^{+}$bezeichnet. Man bestimme alle Funktionen $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$mit der Eigenschaft $f\left(x^{2} f(y)^{2}\right)=f\left(x^{2}\right) f(y)\left(^{*}\right)$ für alle $x, y \in \mathbb{Q}^{+}$.
|
| 6 |
+
|
| 7 |
+
Lösung: Wir beginnen mit einigen für die Lösungsmenge wichtigen Eigenschaften der Grundmenge $\mathbb{Q}^{+}$. Bekanntlich liegt das Produkt $a b$ zweier Zahlen $a, b \in \mathbb{Q}^{+}$wieder in $\mathbb{Q}^{+}$, ebenso wie das Inverse $\frac{1}{a}$ zu jeder Zahl $a \in \mathbb{Q}^{+}$(was für $\sqrt{a}$ nicht immer erfüllt ist). Weil auch das neutrale Element 1 der (kommutativen) Multiplikation zu $\mathbb{Q}^{+}$gehört, bildet $\mathbb{Q}^{+}$bezüglich der Multiplikation eine kommutative (= abelsche) Gruppe. Jede nicht-leere Teilmenge $U$, für die mit $a, b \in U$ auch stets $\frac{a}{b} \in U$ gilt, ist eine (abelsche) Untergruppe von $\mathbb{Q}^{+}$, d.h. sie enthält die Zahl 1, jedes Produkt zweier ihrer Elemente und zu jeder ihrer Zahlen den Kehrwert. Ein Beispiel ist $D=\left\{3^{t} \mid t \in \mathbb{Z}\right\}$, die Menge aller Dreierpotenzen mit ganzzahligen Exponenten; triviale Beispiele sind $U=\{1\}$ sowie $U=\mathbb{Q}^{+}$.
|
| 8 |
+
Weiter wird zu einer Untergruppe $U$ von $\mathbb{Q}^{+}$und einer beliebigen Zahl $a \in \mathbb{Q}^{+}$die Menge $a U=\{a u \mid u \in U\}$ als Nebenklasse von $\mathbb{Q}^{+} / U$ mit dem Repräsentanten $a$ bezeichnet. Der Repräsentant einer Nebenklasse ist in der Regel nicht eindeutig bestimmt; ebenso sind die Nebenklassen in der Regel selber keine Gruppen. Ein Beispiel mit $a=2$ ist die Menge $2 D=\left\{2 \cdot 3^{t} \mid t \in \mathbb{Z}\right\}$, die z.B. auch den Repräsentanten 6 besitzt.
|
| 9 |
+
Nach diesen Vorbemerkungen können wir nun zunächst die Lösungsmenge beschreiben:
|
| 10 |
+
Es sei $U$ eine beliebige Untergruppe von $\mathbb{Q}^{+}$und $a_{1}, a_{2}, \ldots \in \mathbb{Q}^{+}$feste Repräsentanten der Nebenklassen von $\mathbb{Q}^{+} / U$. Ferner seien $u_{1}, u_{2}, \ldots$ Zahlen aus $U$, so dass jedem $a_{i}$ genau ein $u_{i}$ zugeordnet ist. Damit ergeben sich folgende Lösungen $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$:
|
| 11 |
+
|
| 12 |
+
$$
|
| 13 |
+
f(x)=\left\{\begin{array}{c}
|
| 14 |
+
r \cdot u_{i} \text { für } x=a_{i}^{2} \cdot r^{2} \text { mit } r \in U \\
|
| 15 |
+
u \text { beliebig } \in U \text { falls } x \text { kein Quadrat einer Zahl aus } \mathbb{Q}^{+} \text {ist }
|
| 16 |
+
\end{array}\right.
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Dabei kommen alle Lösungen durch die möglichen Untergruppen $U$ und die Auswahl der $u_{i}$ zustande, sowie durch beliebige Wahl von $u \in U$ (die $a_{i}$ sind für jedes $U$ fest).
|
| 20 |
+
Zum Beispiel ergibt sich Folgendes für die trivialen Untergruppen von $\mathbb{Q}^{+}$:
|
| 21 |
+
a) $U=\{1\}$ : Hier ist nur $r=u=1$ sowie $u_{i}=1$ möglich, so dass $f(x)=1$ für alle $x \in \mathbb{Q}^{+}$.
|
| 22 |
+
b) $U=\mathbb{Q}^{+}$: Hier ist $f(x)=a \sqrt{x}$ mit festem $a$, wenn $x$ eine Quadratzahl ist, sowie $f(x)$ beliebig aus $\mathbb{Q}^{+}$, wenn $x$ keine Quadratzahl ist.
|
| 23 |
+
Der Beweis erfolgt in zwei Schritten.
|
| 24 |
+
Schritt 1: Wir zeigen, dass die angegebenen Funktionen $f$ wohldefiniert sind und (*) erfüllen.
|
| 25 |
+
Jedes $t=x^{2}$ mit $x \in \mathbb{Q}^{+}$lässt sich nach der Definition der Nebenklassen eindeutig in der Form $t=a_{i}^{2} \cdot r^{2}$ mit $r \in U$ darstellen, und jedes Produkt $a_{i}^{2} \cdot r^{2}$ ist eine rationale Quadratzahl. Somit ist $f$ wohldefiniert. Aus der Definition folgt ferner, dass die Wertemenge $W_{f}$ von $f$ in $U$ liegt. Daher existiert für jedes $y \in \mathbb{Q}^{+}$ ein $u \in U$ mit $f(y)=u$. Weil für jedes $x \in \mathbb{Q}^{+}$wie oben bemerkt eine eindeutige Darstellung $x^{2}=a_{i}^{2} \cdot r^{2}$ existiert, folgt $f\left(x^{2} \cdot f(y)^{2}\right)=f\left(a_{i}^{2} r^{2} u^{2}\right)=f\left(a_{i}^{2}(r u)^{2}\right)=(r u) \cdot u_{i}=\left(r u_{i}\right) \cdot u=f\left(a_{i}^{2} r^{2}\right) f(y)=f\left(x^{2}\right) f(y)$, womit (*) erfüllt ist.
|
| 26 |
+
|
| 27 |
+
Schritt 2: Wir zeigen, dass keine weiteren Lösungen von (*) als die angegebenen existieren können.
|
| 28 |
+
Dazu sei $f$ eine Lösungsfunktion von $\left(^{*}\right)$ mit der Lösungsmenge $W_{f} \subseteq \mathbb{Q}^{+}$.
|
| 29 |
+
Wir setzen $y=1$ und $x=\frac{1}{f(1)}$ in $\left(^{*}\right)$ ein: $f\left(x^{2} f(y)^{2}\right)=f\left(\frac{f(1)^{2}}{f(1)^{2}}\right)=f(1)=f\left(x^{2}\right) f(1)$. Somit ist $1 \in W_{f}$.
|
| 30 |
+
Nun sei $z=\frac{1}{f(1)}$ fest (dies bedeutet nach dem oben Stehenden $f\left(z^{2}\right)=1$ ). Sei weiter $w \in W_{f}$ (dies bedeutet, dass es ein $u \in \mathbb{Q}^{+}$gibt mit $\left.f(u)=w\right)$. Wir setzen $y=u$ und $x=\frac{z}{f(y)}$ in (*) ein:
|
| 31 |
+
$f\left(x^{2} f(y)^{2}\right)=f\left(z^{2}\right)=1=f\left(x^{2}\right) \cdot w$, also $f\left(x^{2}\right)=\frac{1}{w}$. Somit liegt für jedes $w \in W_{f}$ auch $\frac{1}{w}$ in $W_{f}$.
|
| 32 |
+
Jetzt seien $v, w \in W_{f}$ (dies bedeutet, dass es $t, u \in \mathbb{Q}^{+}$gibt mit $f(t)=v$ und $\left.f(u)=w\right)$.
|
| 33 |
+
Wir setzen $x=z=\frac{1}{f(1)}$ und $y=u$ in (*) ein, bezeichnen $k=x \cdot f(y)$ und erhalten $f\left(k^{2}\right)=1 \cdot f(u)=w$.
|
| 34 |
+
Sodann setzen wir $x=k$ und $y=t$ neu in (*) ein: $f\left(x^{2} f(y)^{2}\right)=f\left(k^{2}\right) f(t)=w \cdot v$. Somit liegt für $v, w \in W_{f}$ auch stets das Produkt $v w$ in $W_{f}$.
|
| 35 |
+
Damit ist nachgewiesen, dass $W_{f}$ eine Untergruppe von $\mathbb{Q}^{+}$ist.
|
| 36 |
+
Seien nun $a_{1}, a_{2}, \ldots$ fest gewählte Repräsentanten der Nebenklassen von $\mathbb{Q}^{+} / W_{f}$ (wie in der Beschreibung der Lösungsmenge) und $r \in W_{f}$ beliebig mit $f(u)=r$. Wir setzen $x=a_{i}$ (für beliebiges $i$ ) und $y=u$ in (*) ein: $f\left(x^{2} f(y)^{2}\right)=f\left(a_{i}^{2} \cdot r^{2}\right)=f\left(a_{i}^{2}\right) f(u)=u_{i} \cdot r$ (wobei $f\left(a_{i}^{2}\right):=u_{i}$ gesetzt wird). Daraus ist ersichtlich, dass jede Lösungsfunktion $f$ tatsächlich die oben beschriebene Form haben muss. $\square$
|
| 37 |
+
|
| 38 |
+
Hinweis: Durch einen Übertragungsfehler ist diese Aufgabe schwerer geworden als beabsichtigt. Dieser Lösungsweg geht auf die Bearbeitung von Jonas Walter zurück, der als einziger Teilnehmer einen vollständigen Beweis angegeben hat. Die angemessene Berücksichtigung von $\mathbb{Q}^{+}$als Grundmenge (anstatt $\mathbb{R}^{+}$) gelang nur einzelnen Teilnehmern.
|
| 39 |
+
|
| 40 |
+
## Aufgabe 2
|
| 41 |
+
|
| 42 |
+
In einem gleichschenkligen Dreieck $A B C$ mit $|A B|=|A C|$ sei $M$ der Mittelpunkt von $B C$. Weiter sei $P$ ein Punkt, für den $P A$ parallel zu $B C$ ist und $|P B|<|P C|$ gilt. Ferner seien $X$ bzw. $Y$ je ein Punkt auf der Geraden $(P B)$ bzw. $(P C)$, so dass $B$ auf der Strecke $P X$ liegt, $C$ auf der Strecke $P Y$ liegt und $\measuredangle M X P=\measuredangle P Y M$ gilt. Man beweise, dass $A P X Y$ ein Sehnenviereck ist.
|
| 43 |
+
|
| 44 |
+
Lösung: Wir bezeichnen den Schnittpunkt von (AM) und der Senkrechten zu (PC) im Punkt $Y$ mit $Z$ und bemerken, dass $Z$ in der bezüglich $(B C)$ anderen Halbebene liegt wie $A$ und $P$.
|
| 45 |
+
Wegen $\measuredangle P A Z=\measuredangle P Y Z=90^{\circ}$ ist $A P Z Y$ ein
|
| 46 |
+
Sehnenviereck. Ebenso ist wegen $\measuredangle Z M C=\measuredangle C Y Z=90^{\circ}$ auch $C M Z Y$ ein
|
| 47 |
+
Sehnenviereck, woraus $\measuredangle C Z M=\measuredangle C Y M$ (1) folgt. Mit der Bedingung aus der Aufgabe ergibt sich $\measuredangle C Y M=\measuredangle M X B(2)$, und wegen der Achsensymmetrie zu $(A Z)$ ist $\measuredangle C Z M=\measuredangle M Z B$ (3). (1), (2) und (3) liefern $\measuredangle M X B=\measuredangle M Z B$. Also ist $B X Z M$ ebenfalls ein Sehnenviereck und es gilt $\measuredangle Z X B=180^{\circ}-\measuredangle B M Z=90^{\circ}$. Weil nun $\measuredangle Z X P=\measuredangle Z X B=90^{\circ}$ ist, liegt der Punkt $X$ auf dem
|
| 48 |
+
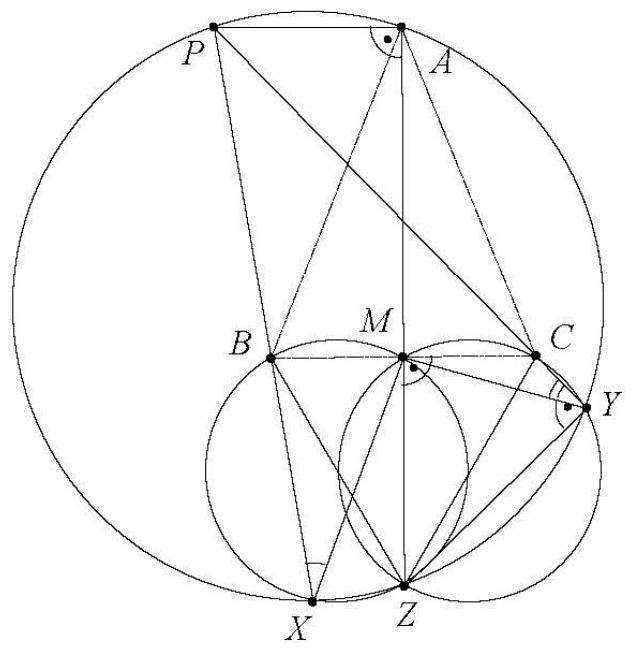
|
| 49 |
+
|
| 50 |
+
Umkreis des Sehnenvierecks $A P Z Y$. Somit bilden auch die vier Punkte $A, P, X$ und $Y$ ein Sehnenviereck. $\square$
|
| 51 |
+
|
| 52 |
+
Hinweis: Eine reine Winkeljagd führt hier nicht zum Ziel, ebenso wie Koordinatengeometrie. Dagegen gibt es weitere Lösungswege etwa über Inversion oder die Einführung anderer Hilfspunkte als Z.
|
| 53 |
+
|
| 54 |
+
## Aufgabe 3
|
| 55 |
+
|
| 56 |
+
Gegeben ist eine positive ganze Zahl $n$ und ein Spielbrett, das aus $n+1$ nebeneinander angeordneten quadratischen Feldern besteht, die von links nach rechts von 0 bis $n$ nummeriert sind. Zu Beginn des Spiels befinden $\operatorname{sich} n$ Spielsteine auf dem Feld Nr. 0 und die anderen Felder sind leer.
|
| 57 |
+
Ein geduldiger Spieler wählt nun für jeden Zug ein Feld mit $k \neq 0$ Steinen und rückt einen davon um höchstens $k$ Felder nach rechts. Dabei muss der Stein auf dem Spielbrett bleiben. Sein Ziel ist es, mit einer Folge solcher Züge alle $n$ Steine auf das Feld Nr. $n$ zu befördern.
|
| 58 |
+
Man beweise, dass der Spieler dieses Ziel nicht mit weniger als $\left\lceil\frac{n}{1}\right\rceil+\left\lceil\frac{n}{2}\right\rceil+\left\lceil\frac{n}{3}\right\rceil+\ldots+\left\lceil\frac{n}{n}\right\rceil$ Zügen erreichen kann. (Dabei bezeichnet $\lceil x\rceil$ die kleinste ganze Zahl, die nicht kleiner als $x$ ist.)
|
| 59 |
+
|
| 60 |
+
Lösung: Die Spielsteine sind ununterscheidbar und haben alle dasselbe Start- und Zielfeld. Daher kann der geduldige Spieler eine Vorschrift erfinden, die ihm angibt, welchen der Steine auf dem jeweils ausgewählten Feld er ziehen soll.
|
| 61 |
+
Eine mögliche Vorschrift erhält er, indem er die Steine fest von 1 bis $n$ nummeriert und in jedem Zug nach der Auswahl des Feldes den dort befindlichen Stein mit der höchsten Nummer bewegt.
|
| 62 |
+
Angenommen, er zieht auf diese Weise den Stein mit der Nummer $k(1 \leq k \leq n)$ nach rechts. Dann können auf dem dafür ausgewählten Feld nicht mehr als $k$ Steine gelegen haben, weil ihre Nummern höchstens gleich $k$ sind. Also wird Stein $k$ um jeweils höchstens $k$ Felder nach rechts bewegt. Weil er aber insgesamt um genau $n$ Felder bewegt wird, sind dafür wenigstens $\left\lceil\frac{n}{k}\right\rceil$ Züge erforderlich. Dies gilt für alle $k$ mit $1 \leq k \leq n$. Aufsummieren über $k$ liefert die Mindestanzahl der erforderlichen Spielzüge gemäß der Aufgabenstellung. $\square$
|
| 63 |
+
|
| 64 |
+
Hinweis: Ein Beweis mit vollständiger Induktion ist ebenso zum Scheitern verurteilt wie Betrachtungen scheinbar „optimaler" Strategien, deren Optimalität nur lokal einsichtig begründet werden kann.
|
| 65 |
+
Man kann zeigen, dass der genaue Wert des angegebenen Terms nur für $n=1,2,3,4,5,7$ erreicht werden kann.
|
| 66 |
+
|
| 67 |
+
## Lösungen zur 2. Auswahlklausur 2018/2019
|
| 68 |
+
|
| 69 |
+
Aufgabe 1. Finden Sie alle Paare $(a, b)$ positiver ganzer Zahlen, für die eine positive ganze Zahl $n$ existiert, sodass die Anzahl der Teiler von $n a$ und $n b$ identisch ist.
|
| 70 |
+
|
| 71 |
+
Lösung. Die gesuchten Paare sind jene, für die eine der drei Bedingungen $a=b, a \nmid b$ oder $b \nmid a$ erfüllt ist, also alle Paare positiver ganzer Zahlen mit Ausnahme solcher, für die eine der Zahlen $a, b$ ein echter Teiler der anderen ist.
|
| 72 |
+
Im gesamten Beweis werden wir die Anzahl aller Teiler einer positiven ganzen Zahl $m$ mit $\tau(m)$ bezeichnen. Zunächst ist klar, dass man im Fall $a=b$ ein beliebiges $n$ wählen kann. Ferner ist im Fall, dass $a$ ein echter Teiler von $b$ ist, für jede positive ganze Zahl $n$ die Zahl $n a$ ein echter Teiler von $n b$, die Menge ihrer Teiler ist damit eine echte Teilmenge der Menge der Teiler von $n b$, was $\tau(n a)<\tau(n b)$ impliziert. Der Fall $b \mid a, b<a$ wird analog behandelt.
|
| 73 |
+
Es bleibt zu zeigen, dass wir im Fall $a \nmid b, b \nmid a$ stets ein $n$ mit $\tau(n a)=\tau(n b)$ finden können. Dafür beweisen wir zunächts die folgende Aussage.
|
| 74 |
+
Lemma. Es seien $\alpha>\beta$ positive ganze Zahlen. Dann existiert für jede ganze Zahl $M>\beta$ eine positive ganze Zahl $\gamma$, sodass
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\frac{\alpha+\gamma+1}{\beta+\gamma+1}=1+\frac{1}{M}=\frac{M+1}{M} .
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
Beweis. Nach Umformen der ersten Gleichung erhält man $\gamma=M(\alpha-\beta)-(\beta+1) \geq 0$. Nun betrachten wir die Primfaktorzerlegung $a=\prod_{p} p^{\alpha_{p}}$ und $b=\prod_{p} p^{\beta_{p}}$ von $a$ und $b$. Es seien nun $p_{1}, \ldots p_{k}$ all jene Primzahlen $p$ mit $\alpha_{p}>\beta_{p}$ und $q_{1}, \ldots, q_{\ell}$ alle Primzahlen $q$ mit $\alpha_{q}<\beta_{q}$. Wegen $a \nmid b, b \nmid a$ sind $k$ und $\ell$ beide positiv. Es sei nun $X$ eine positive ganze Zahl, die größer als alle $\alpha_{p}$ und $\beta_{b}$ ist. Laut obigem Lemma können wir dann Zahlen $\gamma_{1}, \ldots, \gamma_{k}$ und $\gamma_{1}^{\prime}, \ldots, \gamma_{\ell}^{\prime}$ wählen, sodass
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\frac{\alpha_{p_{i}}+\gamma_{i}+1}{\beta_{p_{i}}+\gamma_{i}+1}=\frac{k X+i}{k X+i-1}, \quad \text { und } \quad \frac{\alpha_{q_{j}}+\gamma_{j}^{\prime}+1}{\beta_{q_{j}}+\gamma_{j}^{\prime}+1}=\frac{\ell X+j-1}{\ell X+j}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
für alle $1 \leq i \leq k$ und $1 \leq j \leq \ell$ gilt. Für $n=\left(\prod_{i=1}^{k} p_{i}^{\gamma_{i}}\right) \cdot\left(\prod_{j=1}^{\ell} q_{j}^{\gamma_{j}^{\prime}}\right)$ folgt nun mit Verwendung der allgemein bekannten Formel
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
\tau\left(\prod_{p} p^{\eta_{p}}\right)=\prod_{p}\left(\eta_{p}+1\right)
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
dass
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\frac{\tau(n a)}{\tau(n b)}=\left(\prod_{i=1}^{k} \frac{\alpha_{p_{i}}+\gamma_{i}+1}{\beta_{p_{i}}+\gamma_{i}+1}\right) \cdot\left(\prod_{j=1}^{\ell} \frac{\alpha_{q_{j}}+\gamma_{j}^{\prime}+1}{\beta_{q_{j}}+\gamma_{j}^{\prime}+1}\right)=\frac{k(X+1)}{k X} \cdot \frac{\ell X}{\ell(X+1)}=1
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
also ist $n$ wie behauptet.
|
| 99 |
+
|
| 100 |
+
Aufgabe 2. Entscheiden Sie, ob es eine Menge $M$ positiver ganzer Zahlen gibt, die folgende Eigenschaft hat: Für jede positive rationale Zahl $r<1$ existiert genau eine endliche Teilmenge $S$ von $M$, sodass $\sum_{s \in S} 1 / s=r$ gilt, das heißt die Summe der Kehrwerte aller Elemente von $S$ ist gleich $r$.
|
| 101 |
+
|
| 102 |
+
Lösung. Eine solche Menge existiert nicht, was wir mithilfe eines Widerpsruchsbeweises zeigen werden. Angenommen, $S$ hat die angegebene Eigenschaft. Offenbar ist $M$ dann unendlich, und wir dürfen ohne Beschränkung der Allgemeinheit annehmen, dass $1 \notin M$. Wir bezeichnen die Elemente von $M$ der Größe nach geordnet mit $m_{1}<m_{2}<m_{3}<\ldots$. Fall 1: Es gilt $m_{i} \geq 2 m_{i-1}$ für alle $i \geq 2$. Dann gilt $m_{i} \geq 2^{i-1} m_{1}$ für alle $i \geq 1$, und es folgt
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
r^{*}:=\sum_{i=1}^{\infty} \frac{1}{m_{i}} \leq \sum_{i=0}^{\infty} \frac{1}{2^{i} m_{1}}=\frac{2}{m_{1}},
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
das heißt falls $m_{1} \geq 3$ oder $m_{i}>2 m_{i-1}$ für mindestens ein $i$ erfüllt ist, dann gilt $r^{*}<1$. In diesem Fall erfüllt $M$ jedoch entgegen der Annahme nicht die im Aufgabentext angegebene Bedingung, falls $s \in\left(r^{*}, 1\right)$ gewählt wird. Somit muss $m_{1}=2$ und $m_{i}=2 m_{i-1}$ für alle $i$ gelten, also besteht $M$ genau aus den Zweierpotenzen größer als 1 . Da sich $1 / 3=\sum_{i=2}^{\infty} 2^{-i}$ aber nicht als endliche Summe von Kehrwerten von Zweierpotenzen schreiben lässt, ergibt sich auch in diesem Fall ein Widerspruch.
|
| 109 |
+
Fall 2: Es existiert ein $i>1$, sodass $m_{i}<2 m_{i-1}$. Wir betrachten
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
r:=\frac{1}{m_{i-1}}-\frac{1}{m_{i}}<\frac{1}{m_{i}} .
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Nach Annahme existiert eine endliche Teilmenge $S \subset M$, sodass $\sum_{s \in S} 1 / s=r$ gilt. Wegen $s<1 / m_{i}$ gilt $m_{i} \notin S$. Damit sind aber $S_{1}=S \cup\left\{m_{i}\right\}$ und $S_{2}=\left\{m_{i-1}\right\}$ zwei verschiedene endliche Teilmengen von $M$, sodass die Summen der Kehrwerte von $S_{1}$ und $S_{2}$ den Wert $1 / m_{i-1}$ ergeben, was ein Widerspruch ist.
|
| 116 |
+
|
| 117 |
+
Aufgabe 3. Wir betrachten ein Dreieck $A B C$ und einen Punkt $P$ in dessen Inneren. Die Spiegelpunkte von $P$ an den Seiten $\overline{B C}, \overline{C A}$ und $\overline{A B}$ seien mit $A_{1}, B_{1}$ und $C_{1}$ bezeichnet. Ferner sei $\Omega$ der Umkreis des Dreiecks $A_{1} B_{1} C_{1}$ und schließlich seien $A_{2}, B_{2}$ und $C_{2}$ die zweiten Schnittpunkte der Geraden $A_{1} P, B_{1} P$ und $C_{1} P$ mit $\Omega$. Beweisen Sie, dass sich die drei Geraden $A A_{2}, B B_{2}$ und $C C_{2}$ auf $\Omega$ schneiden.
|
| 118 |
+
|
| 119 |
+
Lösung. Wir arbeiten mit gerichteten Winkeln modulo $180^{\circ}$.
|
| 120 |
+
In dieser Skizze entspricht $T$ dem Punkt $P$.
|
| 121 |
+
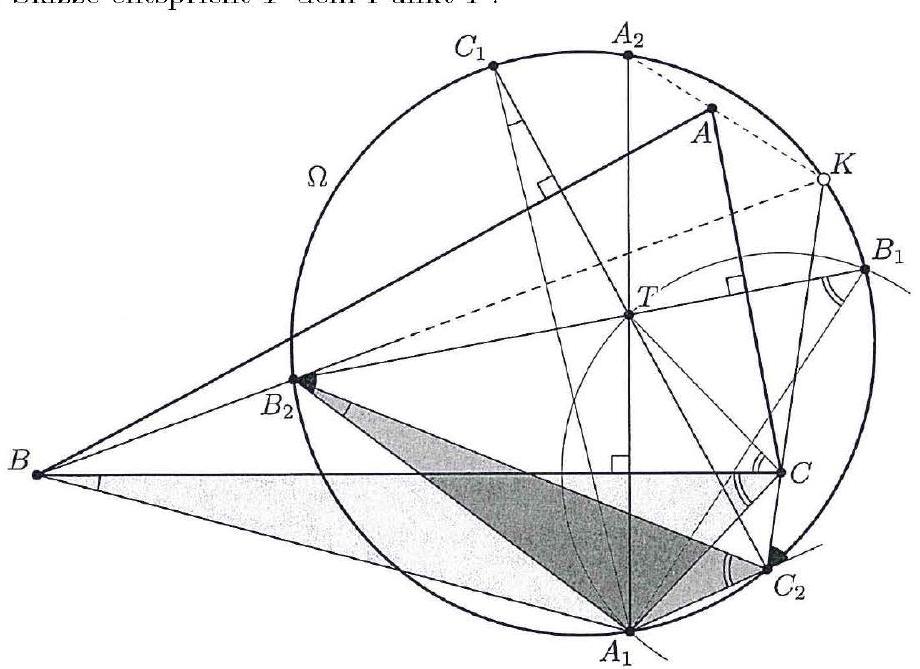
|
| 122 |
+
|
| 123 |
+
Schritt 1: Zunächst stellen wir fest, dass es sich bei $C A$ und $C B$ um die Mittelsenkrechten der Strecken $\overline{P B_{1}}$ und $\overline{P A_{1}}$ handelt, also ist $C$ der Umkreismittelpunkt des Dreiecks $P A_{1} B_{1}$ und es folgt
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\measuredangle A_{1} C B=\frac{1}{2} \measuredangle A_{1} C P=\measuredangle A_{1} B_{1} P=\measuredangle A_{1} B_{1} B_{2}=\measuredangle A_{1} C_{2} B_{2} .
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
Schritt 2: Analog wie in Schritt 1 folgt, dass $\measuredangle A_{1} B C=\measuredangle A_{1} B_{2} C_{2}$, also sind die Dreiecke $A_{1} B C$ und $A_{1} B_{2} C_{2}$ ähnlich.
|
| 130 |
+
|
| 131 |
+
Schritt 3: Unter Benutzung der soeben bewiesenen Ähnlichkeit folgt
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\measuredangle C A_{1} B=\measuredangle C_{2} A_{1} B_{2} \quad \text { und } \quad \frac{\left|\overline{A_{1} C}\right|}{\left|\overline{A_{1} B}\right|}=\frac{\left|\overline{A_{1} C_{2}}\right|}{\left|\overline{A_{1} B_{2}}\right|}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
und somit auch
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
\measuredangle B_{2} A_{1} B=\measuredangle C_{2} A_{1} C \quad \text { und } \quad \frac{\left|\overline{A_{1} B_{2}}\right|}{\left|\overline{A_{1} B}\right|}=\frac{\left|\overline{A_{1} C_{2}}\right|}{\left|\overline{A_{1} C}\right|}
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
also sind auch die Dreiecke $A_{1} B_{2} B$ und $A_{1} C_{2} C$ ähnlich.
|
| 144 |
+
Schritt 4: Es sei $K$ der Schnittpunkt von $C_{2} C$ mit $\Omega$. Dann gilt $180^{\circ}-\measuredangle A_{1} B_{2} K=$ $\measuredangle A_{1} C_{2} K=\measuredangle A_{1} C_{2} C=\measuredangle A_{1} B_{2} B$, also liegt $K$ auf der Geraden $B B_{2}$. Analog kann man zeigen, dass $K$ auch auf der Geraden $A A_{2}$ liegt, was den Beweis beendet.
|
| 145 |
+
|
Germany_TST/md/de-2020-loes_awkl_20.md
ADDED
|
@@ -0,0 +1,176 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Lösungen zur 1. Auswahlklausur 2019/2020
|
| 2 |
+
|
| 3 |
+
Aufgabe 1: Die reellen Zahlen $r_{1}, r_{2}, \ldots, r_{2019}$ erfüllen die Bedingungen
|
| 4 |
+
$r_{1}+r_{2}+\ldots+r_{2019}=0$ (1) sowie $r_{1}^{2}+r_{2}^{2}+\ldots+r_{2019}^{2}=1$ (2).
|
| 5 |
+
Es sei $a=\min \left(r_{1}, r_{2}, \ldots, r_{2019}\right)$ und $b=\max \left(r_{1}, r_{2}, \ldots, r_{2019}\right)$. Man beweise: $a b \leq \frac{-1}{2019}$.
|
| 6 |
+
|
| 7 |
+
1. Lösung: Weil wegen (2) die $r_{i}$ nicht alle 0 sein und wegen (1) nicht alle das gleiche
|
| 8 |
+
|
| 9 |
+
Vorzeichen haben können, gilt $b>0$ und $a<0$. Mit $P=\left\{i: u_{i}>0\right\}$ und $N=\left\{i: u_{i} \leq 0\right\}$
|
| 10 |
+
sowie $p=|P|$ und $n=|N|$ gilt $p+n=2019$ und aus (1) folgt
|
| 11 |
+
$0=\sum_{i=1}^{2019} u_{i}=\sum_{i \in P} u_{i}-\sum_{i \in N}\left|u_{i}\right|$, also $\sum_{i \in P} u_{i}=\sum_{i \in N}\left|u_{i}\right|$.
|
| 12 |
+
Damit können wir abschätzen: $\sum_{i \in P} u_{i}^{2} \leq \sum_{i \in P} b u_{i}=b \sum_{i \in N}\left|u_{i}\right| \leq b \sum_{i \in N}|a|=-n a b$ (3)
|
| 13 |
+
sowie $\quad \sum_{i \in N} u_{i}^{2} \leq \sum_{i \in N} a u_{i} \leq|a| \sum_{i \in N}\left|u_{i}\right|=|a| \sum_{i \in P} u_{i} \leq-p a b$ (4).
|
| 14 |
+
Es folgt $1=\sum_{i \epsilon P} u_{i}^{2}+\sum_{i \epsilon N} u_{i}^{2} \leq-(p+n) a b=-2019 a b$, und damit die Behauptung.
|
| 15 |
+
Anstelle von (3) und (4) ist eine Lösung über die AM-QM- bzw. die Cauchy-Schwarzsche Ungleichung möglich.
|
| 16 |
+
2. Lösung: Wiederum ausgehend von $b>0$ und $a<0$ betrachten wir die folgende konvexe Punktmenge $C$ in der $\mathrm{x}-\mathrm{y}$-Ebene:
|
| 17 |
+
(i) Der untere Rand von $C$ ist die Parabel $y=x^{2}$ im Bereich $a \leq x \leq b$.
|
| 18 |
+
(ii) Der obere Rand von $C$ ist die Gerade $g: y=(a+b) x-a b$ im Bereich $a \leq x \leq b$.
|
| 19 |
+
|
| 20 |
+
Jeder der Punkte ( $u_{i}, u_{i}^{2}$ ) liegt auf dem unteren Rand von $C$. Daher liegt der Schwerpunkt $S$ dieser 2019 Punkte, die mit gleicher Masse versehen seien, ebenfalls in C. Es gilt $S=\left(\frac{1}{2019} \sum_{i 1}^{2019} u_{i}, \frac{1}{2019} \sum_{i 1}^{2019} u_{i}^{2}\right)=\left(0, \frac{1}{2019}\right)$. Für $g$ gilt an der Stelle $x=0$, dass $y=-a b$ ist. $S$ darf nicht oberhalb der oberen Begrenzung liegen, woraus die Behauptung folgt.
|
| 21 |
+
3. Lösung: (Ein Ein-Zeilen-Beweis):
|
| 22 |
+
$0 \leq \sum_{i=1}^{2019}\left(r_{i}-a\right)\left(b-r_{i}\right)=\sum_{i=1}^{2019}\left(-r_{i}^{2}+(b+a) r_{i}-a b\right)=-1-2019 a b \Leftrightarrow a b \leq \frac{-1}{2019}$.
|
| 23 |
+
Hinweis: Häufig wurde mit einem „Schiebeargument" versucht, eine Lösung zu optimieren, bis die zu zeigende Ungleichung erfüllt war. Dabei traten oft Lücken auf.
|
| 24 |
+
|
| 25 |
+
Aufgabe 2: Gegeben sei ein Dreieck $A B C$. Ein Kreis $k$ geht durch $A$, schneidet die Seiten $\overline{A B}$ und $\overline{A C}$ nochmals in den Punkten $D$ bzw. $E$ und schneidet die Seite $\overline{B C}$ in den Punkten $F$ und $G$, wobei $F$ zwischen $B$ und $G$ liegt. Die Tangente an den Kreis durch $B, D$ und $F$ in $F$ und die Tangente an den Kreis durch $C, E$ und $G$ in $G$ schneiden sich in einem Punkt $T$. Wir nehmen an, dass $A \neq T$ gilt. Man beweise, dass die Geraden $A T$ und $B C$ parallel sind.
|
| 26 |
+
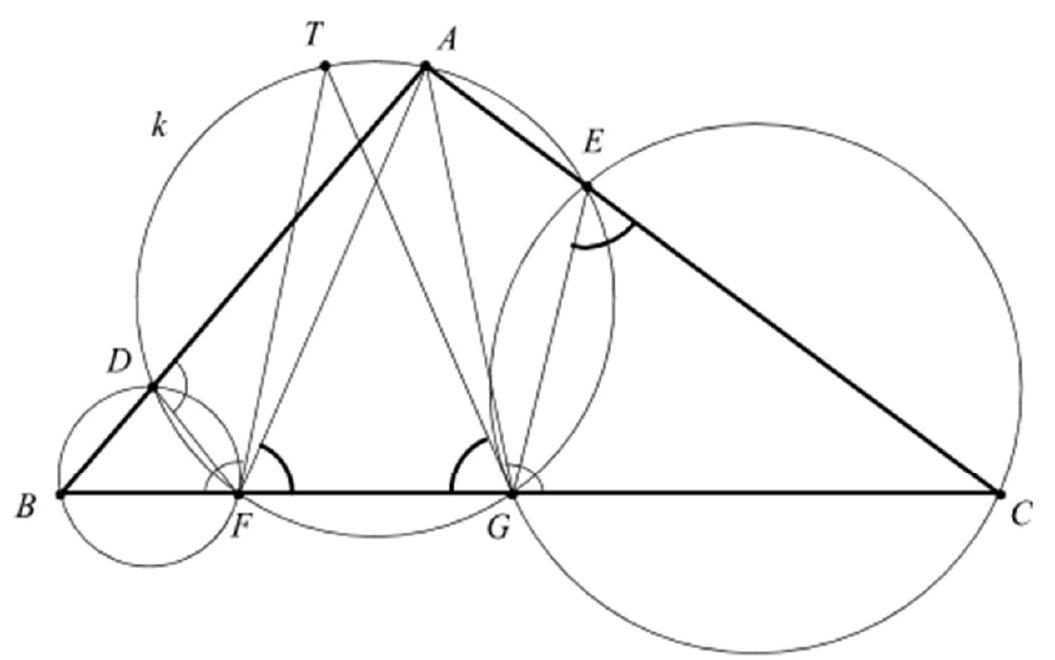
|
| 27 |
+
|
| 28 |
+
Lösung: Nach dem Sehnen-Tangentenwinkelsatz für die Sehne $\overline{F B}$ gilt (siehe Figur) $\angle T F B=180^{\circ}-\angle B D F=\angle F D A$. Im Sehnenviereck $A D F G$ gilt daher $\angle F D A=180^{\circ}-\angle A G F=\angle C G A$ (kleine Bögen), analog ist $\angle T G B=180^{\circ}-\angle C G T=\angle G E C$ und $\angle G E C=\angle C F A$ (Sehnenviereck $A F G E$, große Bögen). Also gilt $\angle T F B=\angle C G A$ (1), woraus $\angle G F T=\angle A G B$ folgt, und $\angle T G B=\angle C F A$ (2).
|
| 29 |
+
Damit sind die Dreiecke $A F G$ und $T F G$ nach wsw kongruent, somit ihre Höhen auf der gemeinsamen Seite $\overline{F G}$ gleich, woraus die Behauptung folgt.
|
| 30 |
+
Variante: Aus (1) und (2) folgt direkt, dass $\angle A F T=\angle A G T$ gilt. Dies bedeutet nach der Umkehrung des Satzes vom Sehnenviereck, dass $T$ auf $k$ liegt. Mit $\angle T A F=\angle T G F=\angle G F A$ folgt die Parallelität von $\overline{T A}$ und $\overline{F G}$.
|
| 31 |
+
Hinweis: Für einige Behauptungen ist eine Lagebetrachtung erforderlich, deren Fehlen einen Punktabzug zur Folge hatte.
|
| 32 |
+
|
| 33 |
+
Aufgabe 3: Es seien $m$ und $n$ zwei positive ganze Zahlen. Man beweise, dass die ganze Zahl $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil$ keine Quadratzahl ist.
|
| 34 |
+
(Dabei bezeichnet $\lceil x\rceil$ die kleinste ganze Zahl, die nicht kleiner als $x$ ist.)
|
| 35 |
+
Lösung: Für einen indirekten Beweis nehmen wir an, dass es ein $k \in \mathbb{N}$ gibt mit $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil=(m+k)^{2}$, d.h. $\left\lceil\frac{(2 m)^{2}}{n}\right\rceil=(2 m+k) k$. Offensichtlich ist $k \geq 1$. Also hat die Gleichung $\left\lceil\frac{c^{2}}{n}\right\rceil=(c+k) k(1)$ eine positive ganzzahlige Lösung $(c, k)$ mit geradem $c$. Ohne auf die Parität von $c$ zu achten, betrachten wir eine solche Lösung von (1) mit minimalem $k$. Aus $\frac{c^{2}}{n}>\left\lceil\frac{c^{2}}{n}\right\rceil-1=c k+k^{2}-1 \geq c k$ und $\frac{(c-k)(c+k)}{n}<\frac{c^{2}}{n} \leq\left\lceil\frac{c^{2}}{n}\right\rceil=(c+k) k$ entnehmen wir $c>n k>n-k$, so dass $c=k n+r$ mit geeignetem $0<r<k$ gilt. Dies in (1) eingesetzt liefert $\left\lceil\frac{c^{2}}{n}\right\rceil=\left\lceil\frac{(n k+r)^{2}}{n}\right\rceil=k^{2} n+2 k r+\left\lceil\frac{r^{2}}{n}\right\rceil$ und $(c+k) k=(k n+r+k) k=k^{2} n+2 k r+k(k-r)$, so dass $\left\lceil\frac{r^{2}}{n}\right\rceil=k(k-r)$ (2) folgt. Dies liefert eine andere positive ganzzahlige Lösung von (1) mit $c^{\prime}=r$ und $k^{\prime}=k-r<k$, was der Minimalität von $k$ widerspricht.
|
| 36 |
+
|
| 37 |
+
Variante: Es sei $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil=c^{2}$ für eine positive ganze Zahl $c>m$, woraus
|
| 38 |
+
$c^{2}-1<m^{2}+\frac{4 m^{2}}{n} \leq c^{2}$ und daraus $0 \leq c^{2} n-m^{2}(m+4)<n$ (3) folgt. Wir substituieren $d=c^{2} n-m^{2}(n+4), x=c+m$ und $y=c-m$, erhalten $c=\frac{x+y}{2}$ sowie $m=\frac{x-y}{2}$ und schreiben (3) damit um: $\left(\frac{x+y}{2}\right)^{2} n-\left(\frac{x-y}{2}\right)^{2}(n+4)=d$ bzw. $x^{2}-(n+2) x y+y^{2}+d=0$ mit $0 \leq d<n$. Wir wählen für festes $n$ und $d$ ein ganzzahliges Lösungspaar $(x, y)$, für das $x+y$ minimal ist. Wegen der Symmetrie von (4) können wir dabei $x \geq y \geq 1$ annehmen. Wie oben läst sich auch hier eine weitere Lösung $(z, y)$ finden, für die $z<x$ ist - Widerspruch!
|
| 39 |
+
Hinweis: Wer „Vieta jumping" kennt, kann auch diese Methode hier wunderbar anwenden. Diese Aufgabe war die schwerste der Klausur und wurde von keinem Teilnehmer vollständig gelöst. Relativ häufig auftretende Fehler: rationale Quadratzahlen wurden mit ganzen Quadratzahlen verwechselt, ebenso die obere mit der unteren Gaußklammer verwechselt, aus der Gaußklammer wurden Faktoren herausgezogen oder mit ihr wurde Restklassenrechnung betrieben.
|
| 40 |
+
|
| 41 |
+
## Lösungen zur 2. Auswahlklausur 2019/2020
|
| 42 |
+
|
| 43 |
+
Aufgabe 1. Ein Pirat möchte einen Schatz, bestehend aus 1000 Goldmünzen, die jeweils mindestens 1 g und zusammen genau 2 kg wiegen, in zwei Teile aufteilen, die in ihrer Masse jeweils um höchstens 1 g von 1 kg abweichen. Beweisen Sie, dass dies möglich ist.
|
| 44 |
+
|
| 45 |
+
1. Lösung (Vollständige Induktion). Die Massen der 1000 Münzen in Gramm, in aufsteigender Reihenfolge geordnet, seien mit $m_{1} \leq m_{2} \leq \cdots \leq m_{1000}$ bezeichnet. Wir beweisen nun zunächst mit vollständiger Induktion nach $\ell=1, \ldots, 1000$ die folgende Aussage.
|
| 46 |
+
Lemma. Für alle $1 \leq \ell \leq 1000$ und jede reelle Zahl $0 \leq x \leq 2+\sum_{i=1}^{\ell} m_{i}$ existiert eine (potentiell leere) Teilmenge $I \subset\{1,2, \ldots, \ell\}$, sodass $\sum_{i \in I} m_{i} \in[x-2, x]$ gilt.
|
| 47 |
+
|
| 48 |
+
Es gilt $x_{1} \leq 2000 / 1000=2$, also ist der Induktionsanfang $\ell=1$ klar: falls $x<2$, können wir $I=\emptyset$ wählen, ansonsten funktioniert $I=\{1\}$.
|
| 49 |
+
Für den Induktionsschritt $\left(\ell \rightarrow \ell+1\right.$, wobei $\ell \leq 999$ ) sehen wir, dass für $x \leq \sum_{i=1}^{\ell} m_{i}$ nichts zu zeigen ist. Da wir jede Menge $I$ durch $I \cup\{\ell+1\}$ ersetzen können, ist die Behauptung auch für $m_{\ell+1} \leq x \leq m_{\ell+1}+\sum_{i=1}^{\ell} m_{i}=\sum_{i=1}^{\ell+1} m_{i}$ erfüllt. Der Induktionssschritt ist also beendet, außer es gilt $2+\sum_{i=1}^{\ell} m_{i}<m_{\ell+1}$. In diesem Fall folgt $m_{i}>2+\ell$ für alle $\ell+1 \leq i \leq 1000$, was folgende Umgleichung impliziert.
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
2000=\sum_{i=1}^{1000} m_{i}=\sum_{i=1}^{\ell} m_{i}+\sum_{i=\ell+1}^{1000} m_{i}>\ell+(1000-\ell)(2+\ell)=2000+999 \ell-\ell^{2}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Damit folgt $\ell>999$, ein Widerspruch, was den Beweis des Lemmas abschließt.
|
| 56 |
+
Wir wenden das Lemma nun auf $\ell=1000$ und $x=1001$ an. Dadurch wird ersichtlich, dass eine Teilmenge $I \subset\{1,2, \ldots, 1000\}$ existiert, für die $\sum_{i \in I} x_{i} \in[999,1001]$ gilt. Wegen $\sum_{i=1}^{1000} m_{i}=$ 2000 gilt auch $\sum_{i \in\{1, \ldots, 1000\} \backslash I} x_{i} \in[999,1001]$, und die Aufteilung der Münzen, die der Zerlegung
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
\{1, \ldots, 1000\}=I \cup(\{1, \ldots, 1000\} \backslash I)
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
entspricht, erfüllt die Behauptung.
|
| 63 |
+
2. Lösung (Greedy-Algorithmus). Wir verwenden die gleiche Notation wie in der ersten Lösung. Der Pirat verteilt die Münzen nach folgendem Verfahren: Er legt alle Münzen, in absteigender Reihenfolge ihrer Massen (also beginnend mit der schwersten Münze mit Masse $m_{1000}$ ), nach und nach auf zwei Haufen $H_{1}$ und $H_{2}$, wobei er jede Münze auf denjenigen Haufen legt, der zu diesem Zeitpunkt leichter ist; bei eine Gleichgewicht wählt er einen beliebigen Haufen aus.
|
| 64 |
+
|
| 65 |
+
Wir behaupten, dass keiner der beiden Haufen jemals mehr als 1001 Gramm wiegt.
|
| 66 |
+
Angenommen, nach dem Hinzulegen der kten Münze mit Masse $m_{1001-k}$ ist doch einer der Haufen schwerer als 1001 Gramm. Vor diesem Schritt wogen beide Haufen zusammen $\sum_{i=1002-k}^{1000} m_{i}$
|
| 67 |
+
|
| 68 |
+
Gramm, und da die Münze auf den leichteren Haufen gelegt wurde, folgt
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
\begin{aligned}
|
| 72 |
+
m_{1001-k}+\frac{1}{2} \sum_{i=1002-k}^{1000} m_{i} & >1001 \\
|
| 73 |
+
m_{1001-k}+\frac{1}{2} \sum_{i=1}^{1000} m_{i} & >1001+\frac{1}{2} \sum_{i=1}^{1001-k} m_{i} \\
|
| 74 |
+
\frac{1}{2} m_{1001-k}+1000 & >1001+\frac{1}{2} \sum_{i=1}^{1000-k} m_{i} \\
|
| 75 |
+
m_{1001-k} & >2+\sum_{i=1}^{1000-k} m_{i} \geq 2+1000-k=1002-k
|
| 76 |
+
\end{aligned}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Damit folgt nun
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\begin{aligned}
|
| 83 |
+
2000=\sum_{i=1}^{1000} m_{i} & =\left(\sum_{i=1}^{1000-k} m_{i}\right)+\left(\sum_{i=1001-k}^{1000} m_{i}\right) \\
|
| 84 |
+
& \geq 1000-k+k \cdot m_{1001-k} \\
|
| 85 |
+
& >1000-k+k(1002-k)
|
| 86 |
+
\end{aligned}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
also folgt $f(k)=-k^{2}+1001 k-1000<0$, was wegen $f(k)=(k-1)(1000-k)$ und $1 \leq k \leq 1000$ jedoch ein Widerspruch ist.
|
| 90 |
+
|
| 91 |
+
Also stimmt die Behauptung, und auch nach dem Verteilen der leichtesten Münze mit Masse $m_{1}$ wiegen beide Haufen nicht mehr als 1001 Gramm. Da sie zusammen 2000 Gramm wiegen, muss damit jeder Haufen mindestens 999 Gramm wiegen, und wir haben eine Verteilung wie gefordert gefunden.
|
| 92 |
+
3. Lösung (Schubfachprinzip). Wir verwenden wieder die gleiche Notation wie in der ersten Lösung. Wegen $m_{1000} \geq 2>1$ gilt $m_{1}+\cdots+m_{999}<1999$, und die 1000 Summen
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
0, m_{1}, m_{1}+m_{2}, \ldots, m_{1}+m_{2}+\cdots+m_{999}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
liegen jeweils in genau einem der 1000 Schubfächer
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\begin{gathered}
|
| 102 |
+
{[0,1) \cup[1000,1001),} \\
|
| 103 |
+
{[1,2) \cup[1001,1002),} \\
|
| 104 |
+
\ldots, \\
|
| 105 |
+
{[998,999) \cup[1998,1999),} \\
|
| 106 |
+
{[999,1000)}
|
| 107 |
+
\end{gathered}
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Falls eine der Summen im letzten Schubfach $[999,1000)$ liegt, sind wir fertig, ansonsten liegen zwei Summen im gleichen Schubfach $[k, k+1) \cup[1000+k, 1001+k$ ) (für ein festes $0 \leq k \leq 998$ ). Da nach Voraussetzung $m_{i} \geq 1$ gilt, liegt eine der Summen im Intervall $[k, k+1)$ und die andere in $[1000+k, 1001+k)$, die Differenz $m_{i+1}+m_{i+2}+\cdots+m_{j}$ der beiden Summen liegt somit im Intervall $(999,1001)$ und liefert daher eine Verteilung wie gewünscht.
|
| 111 |
+
|
| 112 |
+
Aufgabe 2. Es seien ein Dreieck $A B C$ mit Umkreis $\Omega$ sowie Punkte $A_{1}, B_{1}$ und $C_{1}$ auf den Dreiecksseiten $\overline{B C}, \overline{C A}$ und $\overline{A B}$ gegeben, sodass die drei Geraden $A A_{1}, B B_{1}$ und $C C_{1}$ einen Punkt $P$ gemeinsam haben.
|
| 113 |
+
Es ist zu zeigen, dass höchstens zwei der drei Spiegelpunkte von $P$ bei Punktspiegelung an $A_{1}$, $B_{1}$, bzw. $C_{1}$ außerhalb von $\Omega$ liegen.
|
| 114 |
+
|
| 115 |
+
Lösung. Wegen $\measuredangle B P C+\measuredangle C P A+\measuredangle A P B=360^{\circ}=\left(180^{\circ}-\measuredangle B A C\right)+\left(180^{\circ}-\measuredangle C B A\right)+$ $\left(180^{\circ}-\measuredangle A C B\right)$ dürfen wir ohne Beschränkung der Allgemeinheit annehmen, dass $\measuredangle A P B \leq$ $180^{\circ}-\measuredangle A C B$ gilt. Da $P$ im Inneren des Dreiecks $A B C$ liegt, gilt $\angle A P B>\measuredangle A C B$, woraus $\measuredangle A P B \in\left[\measuredangle A C B, 180^{\circ}-\measuredangle A C B\right]$ und damit $\sin \measuredangle A P B \geq \sin \measuredangle A C B$ folgt.
|
| 116 |
+
Es seien $A_{2}, B_{2}$ und $C_{2}$ die im Aufgabentext beschriebenen Spiegelpunkte, sowie $A_{3}, B_{3}$ und $C_{3}$ die zweiten Schnittpunkte der Geraden $A P, B P$ und $C P$ mit $\Omega$. Wir werden nun beweisen, dass mindestens eines der Verhältnisse $\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|}$ und $\frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}$ nicht größer als 1 ist, woraus die Behauptung folgt.
|
| 117 |
+
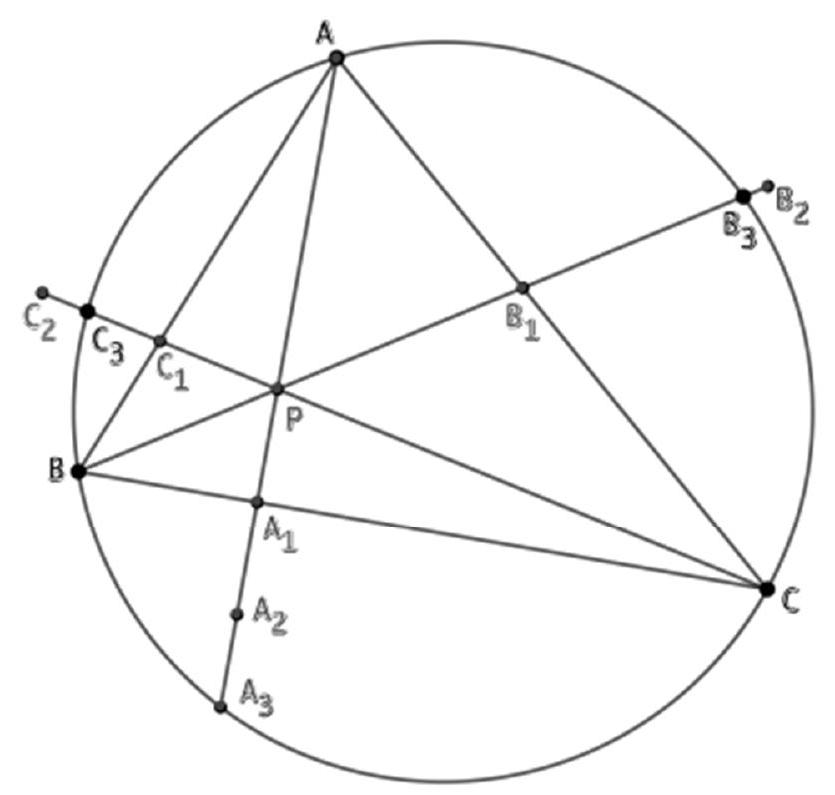
|
| 118 |
+
|
| 119 |
+
Dazu rechnen wir unter Ausnutzung des Sinussatzes,
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|}=\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} B}\right|} \cdot \frac{\left|\overline{A_{1} B}\right|}{\left|\overline{A_{1} A_{3}}\right|} \stackrel{(*)}{=} \frac{\sin \measuredangle C B P}{\sin \measuredangle A P B} \cdot \frac{\left|\overline{A_{1} A}\right|}{\left|\overline{A_{1} C}\right|}=\frac{\sin \measuredangle C B P}{\sin \measuredangle A P B} \cdot \frac{\sin \measuredangle A C B}{\sin \measuredangle P A C},
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
wobei wir im Schritt (*) die Gleichung $\left|\overline{A_{1} B}\right| \cdot\left|\overline{A_{1} C}\right|=\left|\overline{A_{1} A}\right| \cdot\left|\overline{A_{1} A_{3}}\right|$ verwendet haben, die aus dem Sehnensatz folgt. Analog zeigt man nun auch
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
\frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}=\frac{\sin \measuredangle P A C}{\sin \measuredangle A P B} \cdot \frac{\sin \measuredangle A C B}{\sin \measuredangle C B P},
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
und durch Multiplikation beider Gleichungen folgt schlieBlich
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|} \cdot \frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}=\frac{(\sin \measuredangle A C B)^{2}}{(\sin \measuredangle A P B)^{2}} \leq 1,
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
was die Behauptung impliziert.
|
| 138 |
+
Anmerkung: Viele der Teilnehmenden haben statt der eigentlich gestellten Aufgabe das (deutlich einfachere) Problem gelöst, in dem $P$ an den drei Seiten des Dreiecks statt an den Punkten $A_{1}, B_{1}$, und $C_{1}$ gespiegelt wird, und gezeigt, dass mindestens einer der resultierenden Spiegelpunkte nicht außerhalb des Dreiecks liegt.
|
| 139 |
+
|
| 140 |
+
Aufgabe 3. Es sei $\varepsilon>0$ gegeben. Zeigen Sie, dass es ganze Zahlen $a, b$ und $c$ gibt, die nicht alle 0 sind, sodass die Ungleichung $|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}|<\varepsilon$ erfüllt ist.
|
| 141 |
+
Beweisen Sie außerdem, dass in jedem Tripel $(a, b, c) \neq(0,0,0)$ ganzer Zahlen, für das diese Ungleichung gilt, mindestens einer der Absolutbeträge $|a|,|b|,|c|$ größer als $\varepsilon^{-1 / 3} / \sqrt{30}$ ist.
|
| 142 |
+
|
| 143 |
+
Lösung. Im ersten Beweis des ersten Teils bezeichnen wir für eine reelle Zahl $x$ sei $[x]$ die größte ganze Zahl, die nicht größer als $x$ ist (Gauß-Klammer), die Zahl $\langle x\rangle:=x-[x] \in[0,1)$ wird als als gebrochener Anteil von $x$ bezeichnet.
|
| 144 |
+
|
| 145 |
+
Wir wählen eine ganze Zahl $n>\sqrt{2} \varepsilon^{-1}$. Nach dem Schubfachprinzip existieren verschiedene Indizes $i, j \in\{0,1, d \ldots, n\}$, sodass $\langle i \sqrt{6}\rangle$ und $\langle j \sqrt{6}\rangle$ im gleichen der $n$ Intervalle
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\left[0, \frac{1}{n}\right),\left[\frac{1}{n}, \frac{2}{n}\right), \ldots,\left[\frac{n-1}{n}, 1\right)
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
liegen. Dann existiert eine ganze Zahl $a$, sodass $|a-(i \sqrt{6}-j \sqrt{6})|<1 / n$ gilt. Daraus folgt durch Multiplikation mit $\sqrt{2}$, für $b:=2(j-i)$, die Ungleichung $|a \sqrt{2}+b \sqrt{3}|<\sqrt{2} / n<\varepsilon$, was mit $c=0$ auf die Ungleichung im Aufgabentext führt.
|
| 152 |
+
Der zweite Beweis kommt ohne das Schubfachprinzip aus: Wegen $0<\sqrt{6}-2<1$ finden wir eine positive ganze Zahl $k$, sodass $X=(\sqrt{6}-2)^{k} \in(0, \varepsilon / \sqrt{3})$. Offenbar gibt es von 0 verschiedene ganze Zahlen $a_{0}, b_{0}$, sodass $X=a_{0} \sqrt{6}+b_{0}$. Wir setzen nun $a=3 a_{0}, b=b_{0}, c=0$, dann gilt $|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}|=\left|\sqrt{3}\left(a_{0} \sqrt{3} \sqrt{2}+b_{0}\right)\right|=\sqrt{3} X<\varepsilon$.
|
| 153 |
+
Anmerkung: es ist auch möglich, diesen Teil der Aufgabe in wenigen Zeilen aus dem Dirichletschen Approximationssatz oder dem Gitterpunktsatz von Minkowski herzuleiten. Bei der Korrektur wurde aber Wert darauf gelegt, dass diese Sätze genau zitiert wurden.
|
| 154 |
+
|
| 155 |
+
Für den (schwierigeren) zweiten Teil der Aufgabe nehmen wir an, dass $a, b$ und $c$ die Ungleichung erfüllen. Wir berechnen zunächst, dass es sich beim folgenden Ausdruck um eine ganze Zahl handelt.
|
| 156 |
+
|
| 157 |
+
$$
|
| 158 |
+
\begin{aligned}
|
| 159 |
+
Z & :=(a \sqrt{2}+b \sqrt{3}+c \sqrt{5})(a \sqrt{2}-b \sqrt{3}-c \sqrt{5})(a \sqrt{2}+b \sqrt{3}-c \sqrt{5})(a \sqrt{2}-b \sqrt{3}+c \sqrt{5}) \\
|
| 160 |
+
& =\left(2 a^{2}-\left(3 b^{2}+2 \sqrt{15} b c+5 c^{2}\right)\right)\left(2 a^{2}-\left(3 b^{2}-2 \sqrt{15} b c+5 c^{2}\right)\right) \\
|
| 161 |
+
& =\left(2 a^{2}-3 b^{2}-5 c^{2}\right)^{2}-60 b^{2} c^{2}
|
| 162 |
+
\end{aligned}
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Diese Zahl ist von 0 verschieden, denn ansonsten wäre 60 das Quadrat einer rationalen Zahl, was aufgrund der eindeutigen Primfaktorzerlegung positiver ganzer Zahlen aber nicht der Fall ist. Damit gilt $|Z| \geq 1$. Andererseits lässt sich $|Z|$ wie folgt nach oben abschätzen
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\begin{aligned}
|
| 169 |
+
|Z| & <|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}| \cdot(|a| \sqrt{2}+|b| \sqrt{3}+|c| \sqrt{5})^{3} \\
|
| 170 |
+
& <\varepsilon\left((2+3+5)^{\frac{1}{2}} \cdot\left(a^{2}+b^{2}+c^{2}\right)^{\frac{1}{2}}\right)^{3} \\
|
| 171 |
+
& <\left(\varepsilon^{1 / 3} \sqrt{10} \cdot \sqrt{3} \cdot \max (|a|,|b|,|c|)\right)^{3}
|
| 172 |
+
\end{aligned}
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
wobei wir im zweiten Schritt die Ungleichung von Cauchy-Schwarz verwendet haben. Nach Umstellung folgt die Behauptung.
|
| 176 |
+
|
Germany_TST/md/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.md
ADDED
|
@@ -0,0 +1,131 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade 2021
|
| 2 |
+
|
| 3 |
+
1.Auswahlklausur Beispiellosungen ( 17. Dezember 2020)
|
| 4 |
+
|
| 5 |
+
Aufgabe 1. Die Ecken eines regelmäßigen 100-Ecks $P$ seien so entweder rot oder blau gefärbt, dass jede Farbe mindestens 24 -mal vorkommt.
|
| 6 |
+
|
| 7 |
+
Beweisen Sie, dass es 24 paarweise disjunkte Vierecke $Q_{1}, Q_{2}, \ldots, Q_{24}$ gibt, deren Eckpunkte auch Ecken von $P$ sind, sodass jedes Viereck $Q_{i}$ entweder einen oder drei rote Eckpunkte hat.
|
| 8 |
+
|
| 9 |
+
Lösung. Wir zeigen per Induktion nach $n$ die folgende Aussage:
|
| 10 |
+
Wenn die Ecken eines konvexen $4 n$-Ecks $P$ so rot und blau gefärbt wurden, dass jede Farbe mindestens $(n-1)$-mal vorkommt, finden wir $(n-1)$ paarweise disjunkte Vierecke $Q_{1}, \ldots, Q_{n-1}$, deren Ecken auch Ecken von P sind.
|
| 11 |
+
Für $n=25$ erhalten wir die Behauptung aus der Aufgabenstellung.
|
| 12 |
+
Für $n=1$ ist nichts zu zeigen. Sei nun $n \geqslant 2$ und o.B.d.A. gebe es mindestens $2 n$ rote Ecken. Der Fall, dass die Ecken alternierend oder 2 -alternierend gefärbt sind, wird unten behandelt. Ansonsten muss es vier aufeinanderfolgende Ecken geben, unter denen nicht zwei rote und zwei blaue sind. Dann gibt es auch vier aufeinanderfolgende Ecken, unter denen mehr rote als blaue sind, denn andernfalls gäbe es weniger rote als blaue Ecken. Wähle solche vier Ecken aus: Wenn genau drei von ihnen rot sind, wählen wir das von den vier ausgewählten Ecken aufgespannte Viereck als $Q_{n-1}$. Die restlichen $4(n-1)$ Punkte bilden ein konvexes $4(n-1)$-Eck $P^{\prime}$, das $\mathrm{zu} Q_{n-1}$ disjunkt ist und auf das wir die Induktionsannahme anwenden können. Wenn hingegen alle vier der gewählten Ecken rot sind, gehen wir den Rand des $4 n$-Ecks entlang bis wir zum ersten Mal auf einen der mindestens $n-1>0$ blauen Punkte treffen und wenden das gleiche Argument wie im vorherigen Fall an.
|
| 13 |
+
|
| 14 |
+
Es bleiben noch die Fälle, dass die Ecken alternierend oder 2-alternierend gefärbt sind. Dafür gibt es verschiedene Konstruktionen. Wir betrachten zuerst den alternierenden Fall und bezeichnen die Ecken von $P$ mit $P_{1}, P_{2}, \ldots, P_{4 n}$, wobei o.B.d.A. $P_{1}$ blau sei. In diesem Fall gibt es (mindestens) zwei Konstruktionen (siehe folgende Skizzen).
|
| 15 |
+
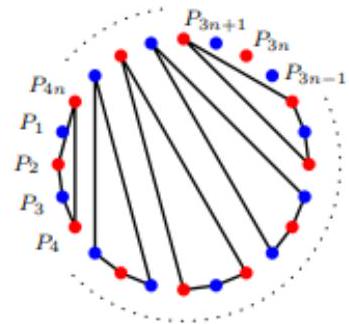
|
| 16 |
+
|
| 17 |
+
Variante 1
|
| 18 |
+
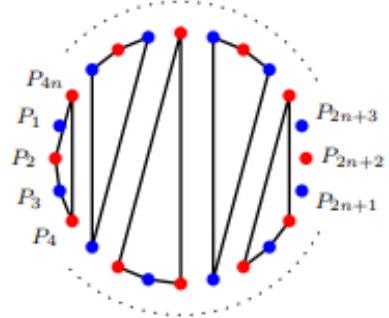
|
| 19 |
+
|
| 20 |
+
Variante 2
|
| 21 |
+
|
| 22 |
+
In Variante 1 beginnen wir mit dem Viereck $P_{2} P_{3} P_{4} P_{4 n}$ und gehen dann von $P_{4}$ aus gegen den Uhrzeigersinn in Dreierschritten und von $P_{4 n}$ aus im Uhrzeigersinn in Einerschritten weiter. Dabei bleiben genau
|
| 23 |
+
|
| 24 |
+
Bildung \& Begabung
|
| 25 |
+
wobei von jedem $a \in V$ genau eine Kante ausgeht, die in demjenigen eindeutig bestimmten $b \in V$ endet, sodass $b \equiv a^{2}+1(\bmod p)$ gilt. Man macht sich leicht klar, dass zwei verschiedene Inseln $p$-Landiens genau dann durch eine Brücke verbunden sind, wenn es die entsprechenden Zahlen in $G_{p}$ durch eine gerichtete Kante miteinander verbunden sind (egal in welcher Richtung). Die zu zeigende Behauptung ist also äquivalent dazu, dass $G_{p}$ als einfacher Graph, d.h. nach Vergessen der Orientierungen der Kanten und Weglassen von Schleifen ${ }^{1}$, nicht zusammenhängend ist.
|
| 26 |
+
|
| 27 |
+
Da jeder zusammenhängende einfache Graph mit $p$ Ecken mindestens $p-1$ Kanten haben muss, genügt es dafür zu zeigen, dass mindestens zwei der $p$ Kanten von $G_{p}$ Schleifen waren. Dazu können wir laut der Annahme an $p$ zunächst eine ganze Zahl $n$ finden, sodass $p \mid n^{2}-n+1$. O.B.d.A. dürfen wir sogar $n \in V$ annehmen. Dann gibt es in $G_{p}$ eine Kante, die von $n$ nach $n$ führt. Wegen $n^{\prime}=p-n+1 \in V$ und
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\left(n^{\prime}\right)^{2}-n^{\prime}+1 \equiv(1-n)^{2}-(1-n)+1 \equiv 1-2 n+n^{2}-1-n+1 \equiv n^{2}-n+1 \equiv 0(\bmod p),
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
liegt auch an der Ecke $n^{\prime}$ eine Schleife.
|
| 34 |
+
Um den Beweis zu beenden müssen wir noch nachweisen, dass $n \neq n^{\prime}$ gilt. Falls doch $n^{\prime}=n$, dann würde auch $p=2 n-1$ gelten, und damit wäre $4 n^{2}-4 n+1$ durch $p$ teilbar. Da aber auch $4 n^{2}-4 n+4$ durch $p$ teilbar ist, folgt schon $p=3$, was wir oben ausgeschlossen haben.
|
| 35 |
+
|
| 36 |
+
Aufgabe 3. Es sei $A B C D$ ein konvexes Parallelogramm, das bei $A$ spitzwinklig ist. Die Spiegelpunkte von $A$ an den Geraden $B C$ und $C D$ seien mit $P$ bzw. $Q$ bezeichnet. Außerdem schneidet die Gerade $B D$ die Strecken $\overline{A P}$ und $\overline{A Q}$ im Inneren in den Punkten $R$ bzw. $S$.
|
| 37 |
+
|
| 38 |
+
Beweisen Sie, dass sich die Umkreise der Dreiecke $B R P$ und $D Q S$ berühren.
|
| 39 |
+
|
| 40 |
+
Lösung. Wir betrachten den Spiegelpunkt $Z$ von $A$ bei Spiegelung an $B D$. Wir werden beweisen, dass sich die beiden in der Aufgabenstellung erwähnten Kreise in $Z$ berühren.
|
| 41 |
+
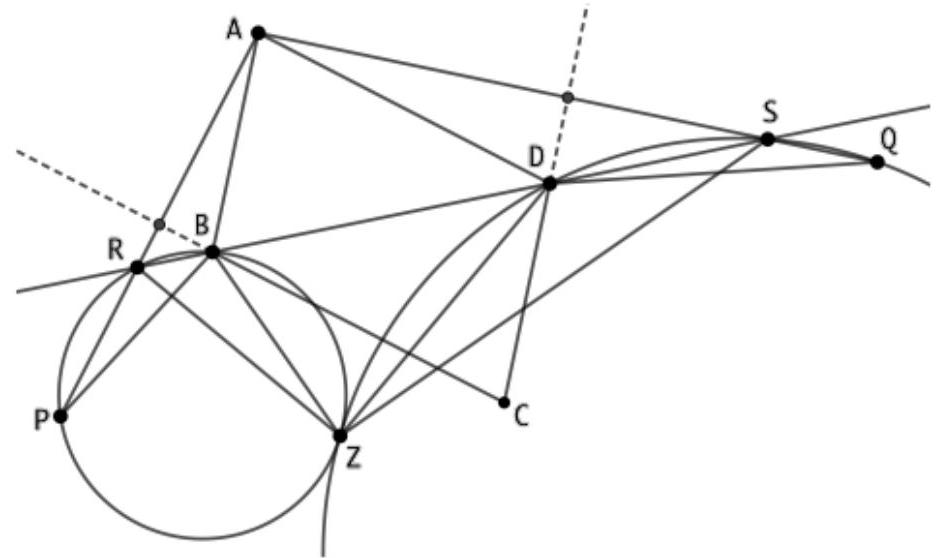
|
| 42 |
+
|
| 43 |
+
Zunächst ist wegen $\measuredangle B Z R=\measuredangle R A B=\measuredangle B P R$ und der Umkrehrung des Peripheriewinkelsatzes klar, dass $Z$ auf dem Umkreis $\omega_{1}$ von $B R P$ liegt. Analog zeigt man, dass $Z$ auch auf dem Umkreis $\omega_{2}$ von $D Q S$ liegt. Der Sehnen-Tangentenwinkel der Sehne $Z B$ von $\omega_{1}$ ist $\angle Z R B=\measuredangle B R A$. Da $A R$ auf $B C$ und damit auch auf $A D$ senkrecht steht, hat dieser Winkel die Größe $90^{\circ}-\angle A D B$. Analog zeigt man, dass der Sehnen-Tangentenwinkel der Sehne $Z D$ von $\omega_{2}$ gleich $90^{\circ}-\angle D B A$ ist. Die Summe dieser beiden Winkel beträgt nun $180^{\circ}-\measuredangle A D B-\angle D B A=\angle B A D=\angle D Z B$, was zeigt, dass die Tangenten an $\omega_{1}$ und $\omega_{2}$ im Punkt $Z$ übereinstimmen. Somit berühren sich beide Kreise wirklich.
|
| 44 |
+
|
| 45 |
+
[^0]
|
| 46 |
+
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade 2021
|
| 47 |
+
|
| 48 |
+
Beispiellösungen und Hinweise zur 2. Auswahlklausur
|
| 49 |
+
|
| 50 |
+
## Aufgabe 1
|
| 51 |
+
|
| 52 |
+
Beweisen Sie, dass es für jede beliebige nichtnegative ganze Zahl $z$ genau ein geordnetes Paar $(m, n)$ positiver ganzer Zahlen $m, n$ gibt, so dass $2 z=(m+n)^{2}-m-3 n$ (1) gilt.
|
| 53 |
+
|
| 54 |
+
## Erste Lösung:
|
| 55 |
+
|
| 56 |
+
Umformen von (1) ergibt $2 z=(m+n-1)^{2}+m-n-1=2 m-2+(m+n-1)(m+n-1-1)$, woraus $z+1=m+\frac{(m+n-1)(m+n-2)}{2}$ folgt. Wir setzen $m+n-1=k$ und erhalten $z+1=m+\frac{k(k-1)}{2}(2)$, wobei $0<m \leq k$ und $k \in \mathbb{Z}, k \geq 1$ gilt. Außerdem ist $\frac{k(k-1)}{2} \in \mathbb{Z}$.
|
| 57 |
+
Offensichtlich gibt es zu jeder positiven ganzen Zahl $z+1$ genau ein $k$ mit
|
| 58 |
+
$\frac{k(k-1)}{2}<z+1 \leq \frac{k(k-1)}{2}+k=\frac{(k+1) k}{2}$.
|
| 59 |
+
Dann sind auch $m=z+1-\frac{k(k-1)}{2}$ und $n=k+1-m$ eindeutig bestimmte positive ganze
|
| 60 |
+
Zahlen, so dass (2) eine eindeutige Darstellung jeder positiven ganzen Zahl $z+1$ und damit jeder nichtnegativen ganzen Zahl $z$ durch $m$ und $n$ liefert.
|
| 61 |
+
|
| 62 |
+
## Zweite Lösung:
|
| 63 |
+
|
| 64 |
+
Umformen von (1) ergibt $2 z=(m+n)(m+n-1)-2 n$. Wir bemerken, dass die rechte Seite stets gerade ist und setzen $m+n=k$. Für konstantes $k(k \geq 2)$ kann $n$ die Werte $1,2, \ldots, k-1$ annehmen, so dass die rechte Seite jeweils verschiedene gerade Zahlen von $k(k-1)-2$ bis $k(k-1)-2(k-1)=(k-1)(k-2)$ liefert. Für $k=2,3, \ldots$ entsteht so eine vollständige, disjunkte Zerlegung der Menge aller nichtnegativer gerader ganzer Zahlen. Die Zahl $2 z$ liegt daher in genau einem durch $k$ bestimmten Intervall an einer durch $n$ bestimmten Stelle, womit dafür auch $m$ eindeutig bestimmt ist. .
|
| 65 |
+
|
| 66 |
+
Hinweise: Der Beweis lässt sich auch mit vollständiger Induktion führen. Das Auftauchen der Dreieckszahlen $\frac{k(k-1)}{2}$ erlaubt eine schöne geometrische Darstellung der verschiedenen Intervalle, in denen $2 z$ liegen kann.
|
| 67 |
+
|
| 68 |
+
## Aufgabe 2
|
| 69 |
+
|
| 70 |
+
In einem gleichschenkligen Dreieck $A B C$ mit $\overline{B C}=\overline{C A}$ sei $D$ ein Punkt im Inneren der Seite $A B$, für den $\overline{A D}<\overline{D B}$ gilt. Weiter seien $P$ und $Q$ zwei Punkte im Inneren der Seiten $B C$ bzw. $C A$, so dass $\angle D P B=\angle A Q D=90^{\circ}$ gilt. Die Mittelsenkrechte von $P Q$ schneide $C Q$ im Punkt $E$, und die Umkreise der Dreiecke $A B C$ und $Q P C$ schneiden sich außer in $C$ in einem weiteren Punkt $F$.
|
| 71 |
+
Beweisen Sie: Wenn $P, E$ und $F$ kollinear sind, dann gilt $\angle A C B=90^{\circ}$.
|
| 72 |
+
|
| 73 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 74 |
+
|
| 75 |
+
Bildung \& Begabung
|
| 76 |
+
|
| 77 |
+
## Erste Lösung:
|
| 78 |
+
|
| 79 |
+
Wir bezeichnen die Mittelsenkrechte der Strecke $P Q$ mit $m$ und den Kreis $Q P C F$ mit $k$. Wegen $D P \perp B C$ und $D Q \perp A C$ liegt auch $D$ auf $k$ und $C D$ ist sogar Durchmesser von $k$. Die Strecken $Q E$ und $P E$ liegen symmetrisch zu $m$; gleichzeitig ist $m$ auch Symmetrieachse von $k$. Daher sind die Sehnen $C Q$ und $F P$ symmetrisch zu $m$, also auch $C$ und $F$ (nach
|
| 80 |
+
Voraussetzung sind $P, E$ und $F$ kollinear!). Somit stimmt die Mittelsenkrechte von $C F$ mit $m$ überein; es folgt, dass $m$ durch den Umkreismittelpunkt $O$ von $A B C$ verläuft.
|
| 81 |
+
Nun betrachten wir den Mittelpunkt $M$ der Strecke $A B$. Wegen $C M \perp D M$ liegt $M$ auch
|
| 82 |
+
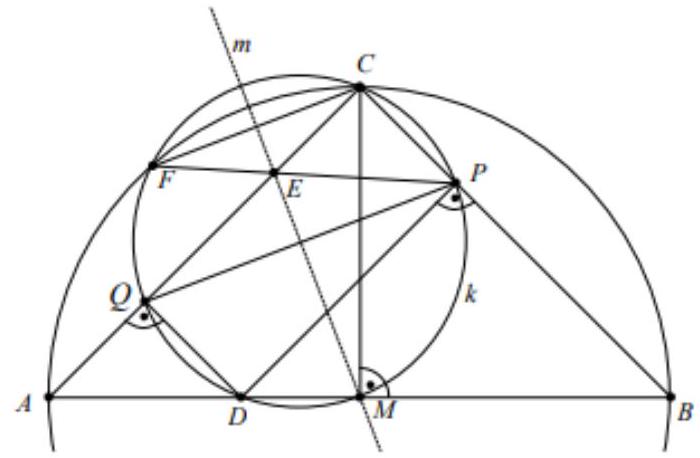
|
| 83 |
+
auf $k$. Wegen $\angle A C M=\angle M C B$ folgt aus dem Umfangswinkelsatz, dass die Sehnen $M P$ und $M Q$ von $k$ gleich lang sind. Damit ist aber gezeigt, dass $m$ durch $M$ verläuft. Da sowohl $O$ als auch $M$ auf $m$ und auf $C M$ liegen, folgt $O=M$ und damit $\angle A C B=90^{\circ}$.
|
| 84 |
+
|
| 85 |
+
## Zweite Lösung:
|
| 86 |
+
|
| 87 |
+
Wie in der ersten Lösung ausgeführt, stellen wir fest, dass die Punkte $P, C, F, Q, D$ und der Mittelpunkt $M$ von $A B$ auf dem Kreis $k$ mit Durchmesser $C D$ liegen, und dass die Mittelsenkrechte $m$ von $P Q$ durch $M$ verläuft.
|
| 88 |
+
Es sei $G$ der Schnittpunkt von $B F$ und $C M$ und wir bezeichnen $\alpha=\angle F B A$. Weil $E$ auf $m$ liegt, weil $P, E$ und $F$ kollinear sind,
|
| 89 |
+

|
| 90 |
+
und weil $C F A B$ und $C F Q P$ Sehnenvierecke sind, folgt $\angle P Q C=\angle P Q E=\angle E P Q=\angle F P Q=\angle F C Q=\angle F C A=\angle F B A=\alpha$.
|
| 91 |
+
Weiter gilt $\angle F E M=\angle F E Q+\angle Q E M=2 \alpha+\left(90^{\circ}-\alpha\right)=90^{\circ}+\alpha$. Ebenfalls mit Außenwinkeln gilt $\angle F G M=90^{\circ}+\alpha$; daher ist $M G E F$ ein Sehnenviereck.
|
| 92 |
+
Es folgt $\angle C G E=\angle M F E=\angle M F P=\angle M C P$. Also ist $G E \| B C$ und damit erhalten wir $\angle E A F=\angle C A F=\angle C B F=\angle E G F$, so dass $G E F A$ ebenfalls ein Sehnenviereck ist. Daraus folgt $\angle A C B=\angle A F B=\angle A F G=180^{\circ}-\angle G M A=90^{\circ}$, was zu zeigen war.
|
| 93 |
+
|
| 94 |
+
Hinweise: Es gilt auch die Umkehrung der zu beweisenden Aussage; daher ist auf die Unterscheidung von Voraussetzung und Behauptung zu achten, um Zirkelschlüsse zu vermeiden. Ein Beweis mit Strahlensatz ist ebenfalls möglich, dagegen führten Ansätze mit Drehstreckung (,„spiral similarity") nicht zum Ziel.
|
| 95 |
+
|
| 96 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 97 |
+
|
| 98 |
+
Bildung \& Begabung
|
| 99 |
+
|
| 100 |
+
## Aufgabe 3
|
| 101 |
+
|
| 102 |
+
Wir betrachten alle positiven reellen Zahlen $a, b, c, d$, für die $(a+c)(b+d)=a c+b d$ gilt.
|
| 103 |
+
Bestimmen Sie den kleinsten Wert, den $S=\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ annehmen kann.
|
| 104 |
+
|
| 105 |
+
## Erste Lösung:
|
| 106 |
+
|
| 107 |
+
Der kleinste mögliche Wert für $S$ ist 8 .
|
| 108 |
+
Um zu zeigen, dass stets $S \geq 8$ gilt, wenden wir zweimal die AM-GM-Ungleichung an:
|
| 109 |
+
$\left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geq 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geq 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8$.
|
| 110 |
+
An den Stellen der Ungleichungen gilt Gleichheit, wenn $a=c$ und $b=d$ ist. Damit lässt sich $(a+c)(b+d)=a c+b d$ umschreiben als $4 a b=a^{2}+b^{2}$. Auflösen nach $a$ liefert $a=b(2 \pm \sqrt{3})$ und damit eine mögliche Lösung $S=8$ für $b=d=1$ und $a=c=2+\sqrt{3}$.
|
| 111 |
+
|
| 112 |
+
## Zweite Lösung:
|
| 113 |
+
|
| 114 |
+
Die Verschiebung $(a, b, c, d) \rightarrow(b, c, d, a)$ ändert weder den Wert von $S$ noch die
|
| 115 |
+
Nebenbedingung. Daher können wir oBdA $a c \geq b d$ annehmen und setzen $t=\sqrt{\frac{a c}{b d}}$ mit $t \geq 1$.
|
| 116 |
+
Aus der Bedingung folgt $t^{2}+1=\frac{a c+b d}{b d}=(a+c)\left(\frac{1}{d}+\frac{1}{b}\right) \geq 2 \sqrt{a c} \cdot 2 \sqrt{\frac{1}{b d}}=4 t$, wobei im
|
| 117 |
+
vorletzten Schritt die AM-GM-Ungleichung verwendet wurde. Also gilt $t^{2}-4 t+1 \geq 0$ und daher $(t \geq 2+\sqrt{3} \vee t \leq 2-\sqrt{3})$, was wegen $t \geq 1$ auf $t \geq 2+\sqrt{3}$ führt.
|
| 118 |
+
Es ist $S=\left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geq 2 \sqrt{\frac{\alpha e}{b d}}+2 \sqrt{\frac{b d}{a c}}=2\left(t+\frac{1}{t}\right)$. Durch Ableiten sehen wir, dass für alle $t \geq 2+\sqrt{3}$ gilt: $S^{\prime}(t)=2-2 / t^{2} \geq 0$. Daher hat $S$ an der Stelle $t=2+\sqrt{3}$ ein Minimum und es folgt $S \geq 2\left(t+\frac{1}{t}\right) \geq 2\left(2+\sqrt{3}+\frac{1}{2+\sqrt{3}}\right)=2(2+\sqrt{3}+2-\sqrt{3})=8$.
|
| 119 |
+
Für $(a, b, c, d)=(1,2+\sqrt{3}, 1,2+\sqrt{3})$ ist sowohl
|
| 120 |
+
$(a+c)(b+d)=8+4 \sqrt{3}=1 \cdot 1+(2+\sqrt{3})(2+\sqrt{3})=a c+b d$ als auch
|
| 121 |
+
$S=\frac{1}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{1}+\frac{1}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{1}=2-\sqrt{3}+2+\sqrt{3}+2-\sqrt{3}+2+\sqrt{3}=8$.
|
| 122 |
+
Daher ist 8 der kleinste Wert von $S$. $\square$
|
| 123 |
+
Hinweise: Weitere Lösungen erreicht man über die Homogenität von $S$ und der
|
| 124 |
+
Nebenbedingung, die es erlaubt, etwa $a b c d=1$ oder $a=1$ oder $a+b+c+d=1$ zu setzen.
|
| 125 |
+
Nicht erlaubt sind jedoch Annahmen wie etwa $a \geq b \geq c \geq d$ oder andere, aus nicht gegebenen „Symmetriegründen" erschlossene Einschränkungen.
|
| 126 |
+
Auch mit der klassischen Methode zur Behandlung von Optimierungsproblemen mit
|
| 127 |
+
Nebenbedingungen, nämlich mit Lagrange-Multiplikatoren, ist eine, wenn auch aufwändige, Lösung dieser Aufgabe möglich.
|
| 128 |
+
|
| 129 |
+
|
| 130 |
+
[^0]: ${ }^{1}$ So werden Kanten bezeichnet, die im gleichen Eckpunkt beginnen und enden.
|
| 131 |
+
|
Germany_TST/md/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.md
ADDED
|
@@ -0,0 +1,220 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## BUNDESWEITE
|
| 2 |
+
|
| 3 |
+
MATHEMATIK-WETTBEWERBE
|
| 4 |
+
Bildung \& Begabung
|
| 5 |
+
|
| 6 |
+
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade 2022
|
| 7 |
+
|
| 8 |
+
## 1. Auswahlklausur Beispiellösungen " Stand: 31. Dezember 2021
|
| 9 |
+
|
| 10 |
+
Aufgabe 1. Der größte gemeinsame Teiler zweier positiver ganzer Zahlen $m$ und $n$ sei mit $\operatorname{ggT}(m, n)$ bezeichnet.
|
| 11 |
+
|
| 12 |
+
Es sei eine unendliche Menge $S$ positiver ganzer Zahlen gegeben, sodass es vier paarweise verschiedene Zahlen $v, w, x, y \in S$ gibt, für die $\operatorname{ggT}(v, w) \neq \operatorname{ggT}(x, y)$ gilt.
|
| 13 |
+
Beweisen Sie, dass es drei paarweise verschiedene Zahlen $a, b, c \in S$ gibt, für die $\operatorname{ggT}(a, b)=$ $\operatorname{ggT}(a, c) \neq \operatorname{ggT}(b, c)$ gilt.
|
| 14 |
+
|
| 15 |
+
Erste Lösung. Im folgenden nennen wir eine dreielementige Teilmenge $\{s, t, u\} \subset S$ ein ausgewogenes Dreieck, falls die Menge $\{\mathrm{ggT}(s, t), \operatorname{ggT}(s, u), \operatorname{ggT}(t, u)\}$ genau zwei verschiedene Elemente hat. Es ist zu zeigen, dass es ein ausgewogenes Dreieck gibt.
|
| 16 |
+
|
| 17 |
+
Lemma. Für paarweise verschiedene Zahlen $a, b, c, d \in S$, sodass $\operatorname{ggT}(a, b)=\operatorname{ggT}(a, c) \neq$ $\operatorname{ggT}(a, d)$ und $\operatorname{ggT}(b, d)=\operatorname{ggT}(c, d)$ gilt, enthält die Menge $\{a, b, c, d\}$ ein ausgewogenes Dreieck.
|
| 18 |
+
Beweis. Falls $\operatorname{ggT}(a, b)=\operatorname{ggT}(b, d)$, dann ist $\{a, b, d\}$ ein ausgewogenes Dreieck. Ansonsten gilt entweder $\operatorname{ggT}(a, d) \neq \operatorname{ggT}(a, b)$ oder $\operatorname{ggT}(a, d) \neq \operatorname{ggT}(b, d)$, also ist $\{a, b, c\}$ oder $\{b, c, d\}$ ein ausgewogenes Dreieck.
|
| 19 |
+
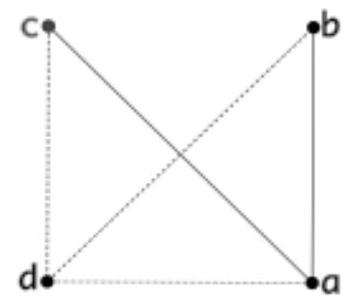
|
| 20 |
+
|
| 21 |
+
Für jedes Element $a \in S$ sei $S_{a}=\{\operatorname{ggT}(a, s) \mid s \in S, s \neq a\}$. Da diese Menge nur Teiler von $a$ enthält, ist sie endlich. Aus der Voraussetzung folgt, dass wir $a \in S$ so wählen können, dass $S_{a}$ mindestens zwei Elemente enthält, da ansonsten $\operatorname{ggT}(v, w)=\operatorname{ggT}(w, x)=\operatorname{ggT}(x, y)$ gelten würde.
|
| 22 |
+
|
| 23 |
+
Nach dem Schubfachprinzip finden wir eine unendliche Teilmenge $T \subset S$, sodass $\operatorname{ggT}(a, t)$ der gleiche Wert $g$ ist für alle $t \in T$. Nun wählen wir ein $d \in S \backslash(T \cup\{a\})$ sodass $\operatorname{ggT}(a, d) \neq g$, das wegen $\left|S_{a}\right|>1$ existieren muss. Da auch $S_{d}$ endlich ist, finden wir nach dem Schubfachprinzip zwei verschiedene Elemente $b, c \in T$ sodass $\operatorname{ggT}(b, d)=\operatorname{ggT}(c, d)$ gilt. Dann erfüllen $a, b, c, d$ die Voraussetzungen des Lemmas, also existiert in der Tat ein ausgewogenes Dreieck.
|
| 24 |
+
|
| 25 |
+
Zweite Lösung. Wir dürfen o.B.d.A. voraussetzen, dass keine ganze Zahl $g>1$ alle Zahlen aus $S$ teilt, da wir sonst die größte derartige Zahl $g$ wählen und $S$ durch die Menge $S^{\prime}=\{s / g \mid s \in S\}$ ersetzen könnten: Falls die Behauptung für $S^{\prime}$ gilt, dann auch für $S$.
|
| 26 |
+
|
| 27 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 28 |
+
|
| 29 |
+
Bildung \& Begabung
|
| 30 |
+
|
| 31 |
+
Angenommen für eine Primzahl $p$ wäre die Teilmenge $S_{p} \subset S$ aller durch $p$ teilbaren Zahlen unendlich groß, dann wählen wir $a \in S \backslash S_{p}$, was wegen der Vorüberlegung möglich ist. Da die Zahlen $\operatorname{ggT}(a, s)$ für $s \in S_{p}$ Teiler von $c$ sind, gibt es nach dem Schubfachprinzip verschiedene $b, c \in S_{p}$ mit $\operatorname{ggT}(a, b)=\operatorname{ggT}(a, c)$. Da $b, c$ beide durch $p$ teilbar sind, folgt auch $\operatorname{ggT}(b, c) \neq$ $\operatorname{ggT}(a, c)$, also die Behauptung.
|
| 32 |
+
|
| 33 |
+
Somit dürfen wir annehmen, dass jede Primzahl nur endlich viele Elemente aus $S$ teilt. Wegen der Voraussetzung finden wir nun aber Zahlen $b, c \in S$, die nicht teilerfremd sind. Es gibt nur endlich viele Primzahlen, die $b$ oder $c$ teilen, also enthält $S$ auch nur endlich viele Elemente, die nicht zu $b$ oder $c$ teilerfremd sind. Somit können wir wegen $|S|=\infty$ ein Element $a \in S$ wählen, dass zu $b$ und $c$ teilerfremd ist. Dann erfüllen $a, b, c$ die Behauptung.
|
| 34 |
+
|
| 35 |
+
Anmerkung: Es ist möglich, beliebig große endliche Mengen konstruieren, sodass die entsprechende Aussage nicht gilt, z.B. indem man für verschiedene Primzahlen $p_{1}, p_{2}, \ldots, p_{r}$ mit Produkt $N=p_{1} \cdots p_{r}$ die Menge $S=\left\{N / p_{i} \mid i=1, \ldots, r\right\}$ wählt. Dann sind ggT $(x, y), x, y \in S$ alle verschieden, also gilt die Voraussetzung, aber nicht die Behauptung aus der Aufgabe.
|
| 36 |
+
|
| 37 |
+
Aufgabe 2. Es sei $A B C D$ ein Parallelogramm mit $|A C|=|B C|$. Ein Punkt $P$ sei auf dem Strahl $A B$ gewählt, sodass $B$ zwischen $A$ und $P$ liegt. Der Umkreis des Dreiecks $A C D$ und die Strecke $P D$ haben außer dem Punkt $D$ noch den Punkt $Q$ gemeinsam. Der Umkreis des Dreiecks $A P Q$ und die Strecke $P C$ haben außer dem Punkt $P$ noch den Punkt $R$ gemeinsam.
|
| 38 |
+
|
| 39 |
+
Beweisen Sie, dass sich die drei Geraden $C D, A Q$ und $B R$ in einem Punkt schneiden.
|
| 40 |
+
Erste Lösung. Wir arbeiteten mit gerichteten Winkeln modulo 180 Grad. Zunächst erkennen wir, dass aus der Voraussetzung $|A C|=|B C|$ unmittelbar folgt, dass die Winkel $\angle B A C$, $\angle C B A, \angle D C A$ und $\angle A D C$ allesamt gleich groß sind.
|
| 41 |
+
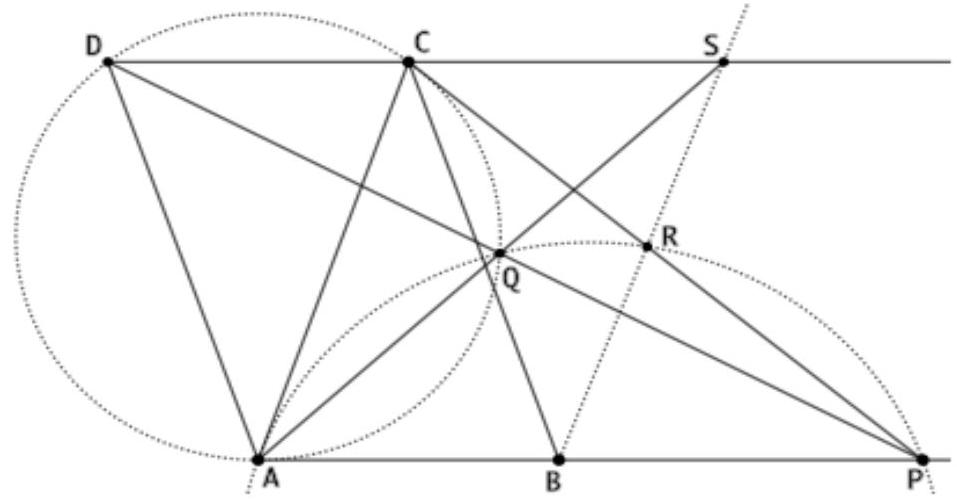
|
| 42 |
+
|
| 43 |
+
Es genügt zu zeigen, dass der Schnittpunkt $S$ der Geraden $A Q$ und $C D$ auf der Geraden $B R$ liegt. Wegen $\angle C S Q=\angle P A Q=\angle C R Q$ ist $C S R Q$ ein Sehnenviereck. Wegen $\angle C R A=180^{\circ}-$ $\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A$ ist auch $A B R C$ ein Sehnenviereck. Also gilt $\angle S R C=\angle S Q C=\angle A D C=\angle B A C=\angle B R P$, woraus in der Tat folgt, dass $P, R$ und $S$ auf einer Geraden liegen.
|
| 44 |
+
|
| 45 |
+
Zweite Lösung. Wie in der ersten Lösung zeigt man, dass $A B R C$ ein Sehnenviereck ist. Wir betrachten den Schnittpunkt $E$ der Geraden $A D$ und $B R$. Dann gilt $\angle E A P=\angle C B A=\angle B A C=$ $\measuredangle E R P$, also liegt $E$ auf dem Umkreis des Sehnenvierecks $A P R Q$.
|
| 46 |
+
|
| 47 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 48 |
+
|
| 49 |
+
Bildung \& Begabung
|
| 50 |
+
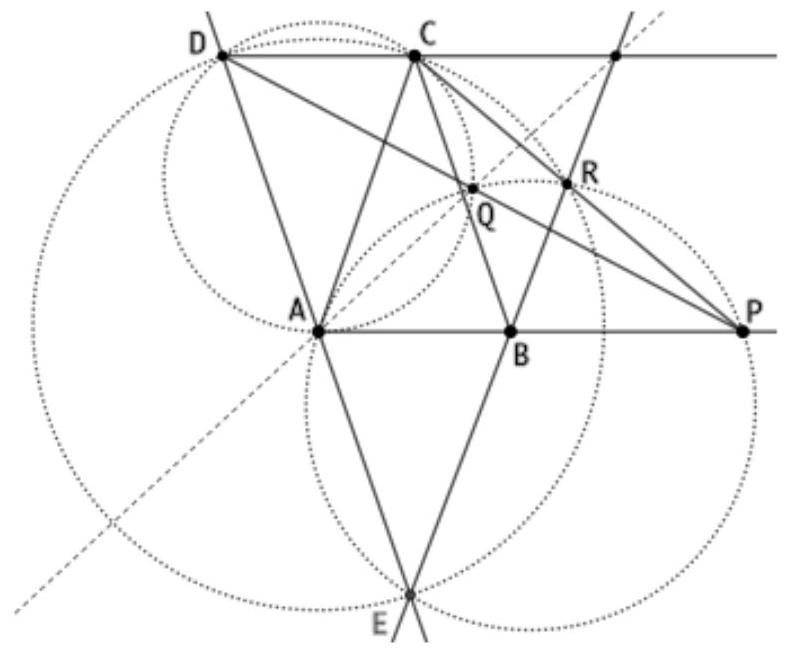
|
| 51 |
+
|
| 52 |
+
Nun gilt $\angle C E R=\angle A P R=180^{\circ}-\angle D C R$, also liegt $E$ auch auf dem Umkreis des Dreiecks $R C D$. Die paarweisen Potenzgeraden der Umkreise von $A C D, A P R$ und $R C D$ sind somit die Geraden $C D, A Q, R E=R B$, also schneiden sie sich in einem Punkt. Dies impliziert die Behauptung.
|
| 53 |
+
|
| 54 |
+
Dritte Lösung. Da $\angle Q A C=\measuredangle Q D C=\angle Q P A$ folgt mit der Umkehrung des Sehnen-Tangenten-Winkel-Satzes, dass die Gerade $A C$ den Umkreis des Sehnenvierecks $A P R Q$ tangiert. Wegen der Voraussetzung tangiert $A B$ auch den Umkreis des Sehnenvierecks $A Q C D$, also sind die Winkel $\angle A D Q$ und $\angle P A Q$ gleich groß. Damit folgt aber $\angle A C Q=\angle A D Q=\angle P A Q=\angle C R Q$, also tangiert $A C$ auch den Umkreis des Dreiecks $C Q R$.
|
| 55 |
+
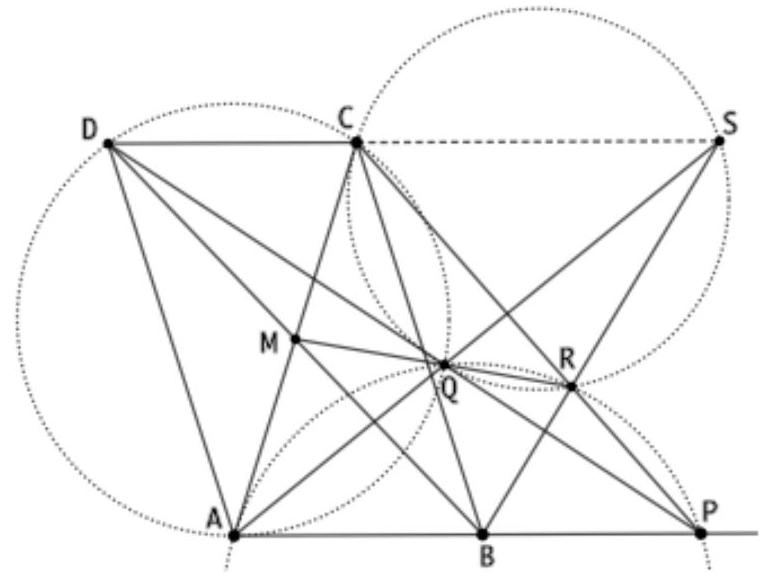
|
| 56 |
+
|
| 57 |
+
Der Schnittpunkt $M$ der Geraden $R Q$ und $A C$ erfüllt damit nach dem Sekanten-TangentenSatz $|M A|^{2}=|M Q| \cdot|M R|=|M C|^{2}$, also ist $M$ der Mittelpunkt der Strecke $A C$, also auch der Mittelpunkt der Strecke $B D$.
|
| 58 |
+
|
| 59 |
+
Der Satz von Pappos, angewandt auf die jeweils kollinearen Punkte $A, B, P$ und $R, Q, M$ impliziert nun, dass der Schnittpunkt $S$ der Geraden $A Q$ und $B R, C$ (als Schnittpunkt der Geraden $A M$ und $P R$ ), sowie $D$ (als Schnittpunkt der Geraden $B M$ und $P Q$ ) auf einer Geraden liegen, was der zu zeigenden Aussage entspricht.
|
| 60 |
+
|
| 61 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 62 |
+
|
| 63 |
+
Bildung \& Begabung
|
| 64 |
+
|
| 65 |
+
Aufgabe 3. Bestimmen Sie ${ }^{1}$ den kleinsten Wert, den der Ausdruck
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2022}}{2022}\right\rfloor
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
annehmen kann, wobei $a_{1}, a_{2}, \ldots, a_{2022} \geq 1$ reelle Zahlen sind, sodass $\left|a_{i}-a_{j}\right| \geq 1$ für alle $1 \leq i<j \leq 2022$ gilt.
|
| 72 |
+
Anmerkung: Für eine reelle Zahl $x$ bezeichnet $\lfloor x\rfloor$, genannt Gauß-Klammer von $x$, die größte ganze Zahl, die nicht größer als $x$ ist.
|
| 73 |
+
|
| 74 |
+
Lösung. Aus der Voraussetzung folgt, dass die kleinste der Zahlen $a_{1}, a_{2}, \ldots, a_{2022}$ mindestens 1, die zweitkleinste mindestens 2 ist, usw. bis zur 2022-ten, die mindestens 2022 sein muss. Wenn wir nun die Zahlen $a_{1}, \ldots, a_{2022}$ sukzessive der Größe nach durch $1,2, \ldots, 2022$ ersetzen, so wird die Summe aus dem Aufgabentext nicht größer. Wir sehen also, dass wir uns auf den Fall einschränken dürfen, dass $\left(a_{1}, a_{1}, \ldots, a_{2022}\right)$ paarweise verschiedene positive ganze Zahlen sind. Nun ersetzen wir 2022 durch eine beliebige positive ganze Zahl $k$ und behaupten, dass der kleinste Wert $s(k)$, den die Summe
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{k}}{k}\right\rfloor
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
annehmen kann, wenn $a_{1}, a_{1}, \ldots, a_{k}$ paarweise verschiedene positive ganze Zahlen sind, genau $\left\lfloor\log _{2}(k)\right\rfloor$ beträgt.
|
| 81 |
+
|
| 82 |
+
- Untere Schranke: Da $m$ offenbar monoton steigend ist, genügt es zu zeigen, dass $m\left(2^{t}\right) \geq t$ gilt. Der Fall $t=0$ ist klar, für $t>0$ verwenden wir vollständige Induktion und setzen daher $m\left(2^{t-1}\right) \geq t-1$ als bekannt voraus. Es seien $a_{1}, a_{1}, \ldots, a_{2}$ beliebige paarweise verschiedene positive ganze Zahlen. Dann ist das Maximum $a_{i}$ dieser Zahlen mindestens $2^{t}$. Falls $i>2^{t-1}$, so gilt nun
|
| 83 |
+
$\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t}}}{2^{t}}\right\rfloor \geq\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t-1}}}{2^{t-1}}\right\rfloor+\left\lfloor\frac{a_{i}}{i}\right\rfloor \geq m\left(2^{t-1}\right)+1=t-1+1=t$
|
| 84 |
+
Falls jedoch $i \leq 2^{t-1}$, so ist die Menge $X=\left\{1,2, \ldots, 2^{t-1}\right\} \backslash\left\{a_{1}, a_{2}, \ldots, a_{2^{t-1}}\right\}$ nicht leer. Sei $b \in X$ beliebig. Dann gilt $a_{i} \geq 2^{t}=2^{t-1}+2^{t-1} \geq b+i$, also gilt
|
| 85 |
+
$\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t}}}{2^{t}}\right\rfloor \geq\left\lfloor\frac{a_{1}}{1}\right\rfloor+\cdots+\left\lfloor\frac{b+i}{i}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t-1}}}{2^{t-1}}\right\rfloor+\geq m\left(2^{t-1}\right)+1=t-1+1=t$
|
| 86 |
+
- Obere Schranke: Wir setzen
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
a_{i}=\left\{\begin{array}{l}
|
| 90 |
+
i-1, \text { falls } i \text { keine Zweierpotenz ist, } \\
|
| 91 |
+
2^{s+1}-1, \text { falls } i=2^{s} .
|
| 92 |
+
\end{array}\right.
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
Dann sind $a_{1}, a_{2}, \ldots, a_{k}$ paarweise verschiedene positive ganze Zahlen und es gilt
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
\left\lfloor\frac{a_{i}}{i}\right\rfloor=\left\{\begin{array}{l}
|
| 99 |
+
0, \text { falls } i \text { keine Zweierpotenz ist, } \\
|
| 100 |
+
1 \text { andernfalls. }
|
| 101 |
+
\end{array}\right.
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
also folgt $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{k}}{k}\right\rfloor=\left\lfloor\log _{2}(k)\right\rfloor$.
|
| 105 |
+
Angewandt auf die konkrete Situation der Aufgabenstellung erhalten wir, dass der kleinste Wert, den die angegebene Summe annehmen kann, gleich $\left\lfloor\log _{2}(2022)\right\rfloor=11$ ist.
|
| 106 |
+
|
| 107 |
+
[^0]
|
| 108 |
+
## BUNDESWEITE
|
| 109 |
+
|
| 110 |
+
MATHEMATIK-WETTBEWERBE
|
| 111 |
+
Bildung \& Begabung
|
| 112 |
+
|
| 113 |
+
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade 2022
|
| 114 |
+
|
| 115 |
+
## Beispiellösungen und Hinweise zur 2. Auswahlklausur
|
| 116 |
+
|
| 117 |
+
## Aufgabe 1
|
| 118 |
+
|
| 119 |
+
Für eine feste positive ganze Zahl $m$ sei $A$ eine Teilmenge von $\left\{0,1,2, \ldots, 5^{m}\right\}$, die aus $4 m+$ Elementen besteht.
|
| 120 |
+
Beweisen Sie, dass es in $A$ stets drei Zahlen $a, b, c$ gibt, für die $a<b<c$ und $c+2 a>3 b$ gil
|
| 121 |
+
|
| 122 |
+
## Erste Lösung:
|
| 123 |
+
|
| 124 |
+
Wir nehmen an, dass es $4 m+2$ Elemente $x_{0}<x_{1}<\ldots<x_{4 m+1}$ aus $\left\{0,1,2, \ldots, 5^{m}\right\}$ gibt, für welche die Behauptung nicht erfullt ist. Dann gilt insbesondere $x_{4 m+1}+2 x_{i} \leq 3 x_{i+1}$ für alle $i=0,1, \ldots, 4 m-1$. Umformen ergibt $x_{4 m+1}-x_{i} \geq \frac{3}{2}\left(x_{4 m+1}-x_{i+1}\right)$.
|
| 125 |
+
Ein einfacher Induktionsschluss liefert daraus $x_{4 m+1}-x_{i} \geq\left(\frac{3}{2}\right)^{4 m-i}\left(x_{4 m+1}-x_{4 m}\right)$.
|
| 126 |
+
Hier führt nun $i=0$ auf $x_{4 m+1}-x_{0} \geq\left(\frac{1}{2}\right)^{4 m}\left(x_{4 m+1}-x_{4 m}\right)=\left(\frac{81}{16}\right)^{m}\left(x_{4 m+1}-x_{4 m}\right)>5^{m} \cdot 1$,
|
| 127 |
+
Widerspruch! ㅁ
|
| 128 |
+
|
| 129 |
+
## Zweite Lösung:
|
| 130 |
+
|
| 131 |
+
Wir bezeichnen das gröBte Element von $A$ mit $c$. Für $k=0, \ldots, 4 m-1$ definieren wir $A_{k}=\left\{x \in A \left\lvert\,\left(1-\left(\frac{2}{3}\right)^{k}\right) c \leq x<\left(1-\left(\frac{2}{3}\right)^{k+1}\right) c\right.\right\}$.
|
| 132 |
+
Wegen $\left(1-\left(\frac{2}{3}\right)^{4 m}\right) c=c-\left(\frac{16}{81}\right)^{m i n} c>c-\left(\frac{1}{5}\right)^{m!} c \geq c-1$ bilden die Mengen $A_{0}, A_{1}, \ldots, A_{4 m-1}$ eine Zerlegung von $A \backslash\{c\}$. Weil $A \backslash\{c\}$ aus $4 m+1$ Elementen besteht, muss nach dem Schubfachprinzip eine Menge $A_{k}$ existieren, die aus wenigstens zwei Elementen besteht. Wi bezeichnen zwei der Zahlen aus $A_{k}$ so mit $a$ und $b$, dass $a<b<c$ gilt. Dann ist $c+2 a \geq c+2\left(1-\left(\frac{2}{3}\right)^{k}\right) c=\left(3-2\left(\frac{2}{3}\right)^{k}\right) c=3\left(1-\left(\frac{2}{3}\right)^{k+1}\right) c>3 b$, wie verlangt. $\square$
|
| 133 |
+
|
| 134 |
+
Hinweise: Offensichtlich lässt sich in der Behauptung die Mächtigkeit von $A$ nicht auf $4 m+$ verkleinern, wie für $m=1$ das Beispiel $A=\{0,2,3,4,5\}$ zeigt. Ein gelegentlich auftretender Fehler bestand darin, die Elemente von $A$ zu manipulieren oder zu ersetzen, ohne dabei zu überprüfen, ob die daraus gezogenen Schlussfolgerungen für die ursprüngliche Menge $A$ gültig sind.
|
| 135 |
+
|
| 136 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 137 |
+
|
| 138 |
+
Bildung \& Begabung
|
| 139 |
+
|
| 140 |
+
## Aufgabe 2
|
| 141 |
+
|
| 142 |
+
Bestimmen Sie alle ganzen Zahlen $n \geq 1$, für die es ein Paar $(a, b)$ von positiven ganzen Zahlen mit folgenden Eigenschaften gibt:
|
| 143 |
+
i) Keine dritte Potenz einer Primzahl teilt $a^{2}+b+3$.
|
| 144 |
+
ii) Es gilt $\frac{a b+3 b+8}{a^{2}+b+3}=n$.
|
| 145 |
+
|
| 146 |
+
Antwort: Die einzige ganze Zahl mit diesen Eigenschaften ist $n=2$.
|
| 147 |
+
|
| 148 |
+
## Erste Lösung:
|
| 149 |
+
|
| 150 |
+
Es sei $p$ ein beliebiger Primfaktor von $a^{2}+b+3$ (ein solcher existiert, weil $a^{2}+b+3 \geq 5$ gilt). Dann ist $b \equiv-a^{2}-3 \bmod p$. Wegen der Ganzzahligkeit von $n$ muss $p$ aber auch ein Primfaktor von $a b+3 b+8$ sein. Somit gilt $0 \equiv a b+3 b+8 \equiv a\left(-a^{2}-3\right)+3\left(-a^{2}-3\right)+8 \equiv-a^{3}-3 a^{2}-3 a-1 \equiv-(a+1)^{3} \bmod p$, also muss $p$ auch ein Primfaktor von $a+1$ sein. Wegen $i$ ) kann $p$ in $a^{2}+b+3$ höchstens quadratisch vorkommen, also höchstens doppelt so oft wie in $a+1$. Weil das für jeden Primfaktor gilt, erhalten wir $a^{2}+b+3 \leq(a+1)^{2}$. Würde ein Primfaktor $p$ in $a^{2}+b+3$ dagegen höchstens einfach vorkommen, so hätten wir $a^{2}+b+3 \leq \frac{(a+1)^{2}}{p} \leq \frac{(a+1)^{2}}{2}$, im Widerspruch zu $\frac{(a+1)^{2}}{2} \leq a^{2}+1<a^{2}+4 \leq a^{2}+b+3$.
|
| 151 |
+
Also muss $a^{2}+b+3=(a+1)^{2}$ gelten. Folglich ist $b=2 a-2$ und damit $a b+3 b+8=a(2 a-2)+3(2 a-2)+8=2 a^{2}+4 a+2=2(a+1)^{2}$.
|
| 152 |
+
Somit ist $n=2$ die einzige mögliche Lösung. Das Beispiel $(a, b)=(2,2)$ mit $a^{2}+b+3=9$ zeigt, dass $n=2$ tatsächlich eine Lösung ist. ㅁ
|
| 153 |
+
|
| 154 |
+
## Zweite Lösung:
|
| 155 |
+
|
| 156 |
+
Wenn wir die Bedingung $i i)$ nach $b$ auflösen, erhalten wir $b=\frac{n a^{2}+3 n-8}{a+3-n}$.
|
| 157 |
+
Fall 1: $n=a+3$. Hier muss wegen $b \in \mathbb{Z}^{+}$auch der Zähler verschwinden, was nach Einsetzen $(a+1)^{3}=0$, also $a=-1$ liefert - ein Widerspruch zu $a \in \mathbb{Z}^{+}$.
|
| 158 |
+
Fall 2: $n \neq a+3$. Aus (1) folgt
|
| 159 |
+
$a^{2}+b+3=a^{2}+\frac{n a^{2}+3 n-8}{a+3-n}+3=\frac{a^{3}+3 a^{2}-n a^{2}+n a^{2}+3 n-8+3 a+9-3 n}{a+3-n}=\frac{(a+1)^{3}}{a+3-n}$.
|
| 160 |
+
Nun bezeichnen wir mit $v_{p}(z)$ die Häufigkeit, mit der ein Primfaktor $p$ in der Zahl $z \in \mathbb{Z}^{+}$ vorkommt. Gäbe es einen Primfaktor $p$ mit $v_{p}(a+1) \geq v_{p}(a+3-n)+1$, dann wäre nach (2) $v_{p}\left(a^{2}+b+3\right) \geq 2 v_{p}(a+3-n)+3 \geq 3$, was im Widerspruch zu $\left.i\right)$ steht. Also ist $v_{p}(a+1) \leq v_{p}(a+3-n)$, und somit ist $a+1$ ein Teiler von $a+3-n$. Aus (2) folgt noch $a+3-n>0$ und daher $a+1 \leq a+3-n$, also $n \leq 2$.
|
| 161 |
+
Für $n=1$ wäre dann $a+1 \mid a+2$, was für kein $a \in \mathbb{Z}^{+}$erfüllt ist. Also kann nur $n=2$ gelten, was mit dem Beispiel aus der ersten Lösung bestätigt wird. ㅁ
|
| 162 |
+
|
| 163 |
+
Hinweise: In der zweiten Lösung ist der Nachweis von $n<a+3$ unbedingt erforderlich.
|
| 164 |
+
|
| 165 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 166 |
+
|
| 167 |
+
Bildung \& Begabung
|
| 168 |
+
|
| 169 |
+
## Aufgabe 3
|
| 170 |
+
|
| 171 |
+
Für eine feste positive ganze Zahl $k$ sei $K$ die Menge aller Gitterpunkte $(x, y)$ in der Ebene, deren beide Koordinaten $x$ und $y$ nichtnegative ganze Zahlen kleiner als $2 k$ sind. Es gilt also $|K|=4 k^{2}$.
|
| 172 |
+
Eine Menge $V$ bestehe nun aus $k^{2}$ nicht-ausgearteten Vierecken mit folgenden Eigenschaften:
|
| 173 |
+
i) Die Ecken aller dieser Vierecke sind Elemente von $K$.
|
| 174 |
+
ii) Jeder Punkt in $K$ ist Eckpunkt von genau einem der Vierecke in $V$.
|
| 175 |
+
|
| 176 |
+
Bestimmen Sie den größtmöglichen Wert, den die Summe der Flächeninhalte aller $k^{2}$ Vierecke in $V$ annehmen kann.
|
| 177 |
+
|
| 178 |
+
Antwort: Der gröBtmögliche Wert der Flächensumme beträgt $S(k):=\frac{1}{3} k^{2}(2 k+1)(2 k-1)$.
|
| 179 |
+
Bezeichnungen: Der Flächeninhalt eines Polygons $X$ sei mit $[X]$ bezeichnet. Ein Viereck heiße legal, wenn alle seine Eckpunkte zu $K$ gehören. Weiter sei $O=\left(k-\frac{1}{2}, k-\frac{1}{2}\right)$ der Mittelpunkt von $K$. Ein legales Viereck heiße zentral, wenn es punktsymmetrisch mit $O$ als Mittelpunkt ist. Jede Menge $V$ von Vierecken, die die Bedingungen der Aufgabenstellung erfüllt, heiße akzeptabel. Für jede akzeptable Menge $V$ sei die Flächensumme ihrer Vierecke mit $S(V)$ bezeichnet.
|
| 180 |
+
|
| 181 |
+
## Erste Lösung:
|
| 182 |
+
|
| 183 |
+
Jeder Punkt aus $K$ ist Eckpunkt eines eindeutig definierten zentralen Quadrats. Daher ist die Menge $Q$ aller zentralen Quadrate akzeptabel. Wir zeigen $S(V) \leq S(Q)=S(k)$
|
| 184 |
+
woraus die Antwort folgt.
|
| 185 |
+
Wir benutzen das folgende
|
| 186 |
+
Lemma 1. Für jedes Viereck $V=A_{1} A_{2} A_{3} A_{4}$ und jeden beliebigen Punkt $O$ in der Ebene gilt
|
| 187 |
+
$[V] \leq \frac{1}{2} \sum_{i=1}^{4} O A_{i}^{2}$
|
| 188 |
+
wobei Gleichheit genau dann gilt, wenn $V$ ein Quadrat mit Mittelpunkt $O$ ist.
|
| 189 |
+
Beweis: Für $i=1, \ldots, 4$ und $A_{5}=A_{1}$ gilt $\left[O A_{i} A_{i+1}\right] \leq \frac{O A_{i} \cdot O A_{i+1}}{2} \leq \frac{O A_{i}^{2}+O A_{i+1}^{2}}{4}$. Daher gilt $[V] \leq \sum_{i=1}^{4}\left[O A_{i} A_{i+1}\right] \leq \frac{1}{4} \sum_{i=1}^{4}\left(O A_{i}^{2}+O A_{i+1}^{2}\right)=\frac{1}{2} \sum_{i=1}^{4} O A_{i}^{2}$, womit (2) bewiesen ist. In der Tat herrscht jeweils Gleichheit, wenn $V$ ein Quadrat mit Mittelpunkt $O$ ist. Nun betrachten wir eine beliebige akzeptable Menge $V$. Lemma 1 auf jedes Element von $V$ und jedes Element von $Q$ angewendet liefert $S(V) \leq \frac{1}{2} \sum_{A<K} O A^{2}=S(Q)$, womit die linke Seite von (1) bewiesen ist.
|
| 190 |
+
Nun berechnen wir $S(Q)=\frac{1}{2} \sum_{A c K} O A^{2}=\frac{1}{2} \sum_{i=0}^{2 k-1} \sum_{j=0}^{2 k-1}\left(\left(k-\frac{1}{2}-i\right)^{2}+\left(k-\frac{1}{2}-j\right)^{2}\right)$
|
| 191 |
+
$=\frac{1}{8} \cdot 4 \cdot 2 k \sum_{i=0}^{k-1}(2 k-2 i-1)^{2}=k \sum_{j=0}^{k-1}(2 j+1)^{2}=k\left(\sum_{j=1}^{2 k} j^{2}-\sum_{j=1}^{k}(2 j)^{2}\right)$
|
| 192 |
+
$=k\left(\frac{2 k(2 k+1)(4 k+1)}{6}-4 \cdot \frac{k(k+1)(2 k+1)}{6}\right)=\frac{k^{2}(2 k+1)(2 k-1)}{3}=S(k)$.
|
| 193 |
+
|
| 194 |
+
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
|
| 195 |
+
|
| 196 |
+
Bildung \& Begabung
|
| 197 |
+
|
| 198 |
+
## Zweite Lösung:
|
| 199 |
+
|
| 200 |
+
Für jedes Viereck $A B C D$ in einer akzeptablen Menge $V$ gilt
|
| 201 |
+
$[A B C D]=\frac{A C \cdot B D}{2} \cdot \sin \varphi \leq \frac{A C^{2}+B D^{2}}{4}$
|
| 202 |
+
mit $\varphi=\measuredangle(A C, B D)$. Wenden wir (3) auf alle Elemente von $V$ an, so erhalten wir $S(V) \leq \frac{1}{4} \sum_{i=1}^{2 k^{2}} A_{i} B_{i}^{2}$, wobei $\left(A_{1}, A_{2}, \ldots, A_{2 k^{2}}, B_{1}, B_{2}, \ldots, B_{2 k^{2}}\right)$ eine Permutation von $K$ ist.
|
| 203 |
+
Mit der Abkürzung $S:=\sum_{i=1}^{2 u^{2}} A_{i} B_{i}^{2}$ formulieren wir das folgende
|
| 204 |
+
Lemma 2. Der größtmögliche Wert von $S$ über alle Permutationen von $K$ beträgt $\frac{4}{3} k^{2}\left(4 k^{2}-1\right)$ und wird angenommen, wenn $A_{i}$ und $B_{i}$ für alle $i=1,2, \ldots, 2 k^{2}$ symmetrisch zu $O$ liegen.
|
| 205 |
+
Beweis: Es seien $A_{i}=\left(p_{i}, q_{i}\right)$ und $B_{i}=\left(r_{i}, s_{i}\right)$ für $i=1,2, \ldots, 2 k^{2}$. Dann ist
|
| 206 |
+
$S=\sum_{i=1}^{2 L^{2}}\left(p_{i}-r_{i}\right)^{2}+\sum_{i=1}^{2 L^{2}}\left(q_{i}-s_{i}\right)^{2}$. Mit der QM-AM-Ungleichung schätzen wir die erste Summe
|
| 207 |
+
$\mathrm{ab}: \sum_{i=1}^{2 k^{2}}\left(p_{i}-r_{i}\right)^{2}=\sum_{i=1}^{2 k^{2}}\left(2 p_{i}^{2}+2 r_{i}^{2}-\left(p_{i}+r_{i}\right)^{2}\right)=4 k \sum_{j=0}^{2 k-1} j^{2}-\sum_{i=1}^{2 k^{2}}\left(p_{i}+r_{i}\right)^{2}$
|
| 208 |
+
$\leq 4 k \sum_{j=0}^{2 k-1} j^{2}-\frac{1}{2 k^{2}}\left(\sum_{i=1}^{2 k^{2}}\left(p_{i}+r_{i}\right)\right)^{2}=4 k \sum_{j=0}^{2 k-1} j^{2}-\frac{1}{2 k^{2}}\left(2 k \cdot \sum_{j=0}^{2 k-1} j\right)^{2}$
|
| 209 |
+
$=4 k \cdot \frac{2 k(2 k-1)(4 k-1)}{6}-2 k^{2}(2 k-1)^{2}=\frac{2 k^{2}(2 k-1)(2 k+1)}{3}$, wobei Gleichheit genau dann
|
| 210 |
+
gilt, wenn $p_{i}+r_{i}=2 k-1$ für alle $i$ erfüllt ist. Da die zweite Summe völlig analog abgeschātzt werden kann, folgt $S \leq \frac{4}{3} k^{2}\left(4 k^{2}-1\right)$ mit Gleichheit bei $p_{i}+r_{i}=q_{i}+s_{i}=2 k-1$ für alle $i=1, \ldots, 2 k^{2}$, d.h. wenn $A_{i}$ und $B_{i}$ für alle $i=1,2, \ldots, 2 k^{2}$ symmetrisch zu $O$ liegen.
|
| 211 |
+
Mit dem Resultat aus Lemma 2 ergibt sich $S(V) \leq \frac{1}{4} \cdot \frac{4 k^{2}\left(4 k^{2}-1\right)}{3}=\frac{k^{2}(2 k-1)(2 k+1)}{3}$, wobei die Abschätzung für die Menge $Q$ scharf ist. ㅁ.
|
| 212 |
+
|
| 213 |
+
## Hinweise:
|
| 214 |
+
|
| 215 |
+
Das hăufig behauptete Ergebnis $S(k)=k^{4}$ ist falsch, weil es nicht auf der maximalen
|
| 216 |
+
Konfiguration beruht und nur für $k=1$ den korrekten Wert liefert. Die Formel von Pick ist bei dieser Aufgabe nicht zielführend, weil in der maximalen Konfiguration nicht alle Vierecke hinsichtlich der Aufteilung zwischen Rand- und inneren Gitterpunkten optimiert sind. Der größtmögliche Wert der Flächensumme bleibt derselbe, wenn man in der Aufgabenstellung „Vierecke" durch „Vielecke" ersetzt.
|
| 217 |
+
|
| 218 |
+
|
| 219 |
+
[^0]: ${ }^{1}$ Mit Beweis.
|
| 220 |
+
|
Germany_TST/raw/de-2000-aufgaben_awb_00.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:1bfcff517834094a47859374d0522e55fcebe576e40182504fbd79eb157eb8ed
|
| 3 |
+
size 22846
|
Germany_TST/raw/de-2001-aufgaben_awb_01.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:0a9104aefa7209a92d7821c650ef82e951f63eee035761a652dc8ddb923bbaba
|
| 3 |
+
size 21424
|
Germany_TST/raw/de-2002-loes_awkl1_02.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:f64bc924c2c66f59558a1828bcdda0b4dbdced837d65a911c45017f52060bbe6
|
| 3 |
+
size 29758
|
Germany_TST/raw/de-2002-loes_awkl2_02.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:fcc793fcd3f559719caa9bd052a7c0adad585bbb5b87a8a987484581efdc2508
|
| 3 |
+
size 38712
|
Germany_TST/raw/de-2003-loes_awkl1_03.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:5ceb7cdba8f5b1f631f7b9833888a48239ea2587d027ed5ba8ba40a3d35cd9c6
|
| 3 |
+
size 32780
|
Germany_TST/raw/de-2003-loes_awkl2_03.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:75a4a8324e7d83a47549c470e26afbb7e6f7cad311076591f6ed802afe062d24
|
| 3 |
+
size 67319
|
Germany_TST/raw/de-2004-loes_awkl1_04.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:2925e7d93f2a27db7a1cf356f02765e8e6f7460a26504fdae509b6fdaea1840d
|
| 3 |
+
size 44942
|
Germany_TST/raw/de-2004-loes_awkl2_04.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:85196f21d41841d59a66d939e61a023e19e1e7d7a12c548d8b7b980628cc5ec4
|
| 3 |
+
size 74606
|
Germany_TST/raw/de-2005-loes_awkl1_05.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:07d7891f7f70368f58a050305d2aadf75b35c95c33f1a44ce4d1f1cf7bd0207e
|
| 3 |
+
size 84501
|
Germany_TST/raw/de-2005-loes_awkl2_05.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:bd8286d738cd68898cd8672d0fe25c972d3ffa11c1d05cd5d4ec199ae7acf808
|
| 3 |
+
size 42148
|
Germany_TST/raw/de-2006-loes_awkl1_06.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:0b2a30c69cc5e18f1d92f00a66add8d11e4a82c3ba6508e5c5107b0439e11920
|
| 3 |
+
size 97641
|
Germany_TST/raw/de-2006-loes_awkl2_06.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:03db94798dab1e9af4566c2c98de14c8f2ca3da551e31156d6aa14fe6fa3de65
|
| 3 |
+
size 125420
|
Germany_TST/raw/de-2007-loes_awkl1_07.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:6882d65b64ce53513d93baf0a40c05e8ad205b91d8a3880ddb04c1137822c16f
|
| 3 |
+
size 97361
|
Germany_TST/raw/de-2007-loes_awkl2_07.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:7601666c5487e8b33088dbf1b53bc66add3c074169a45248164945b027bd87db
|
| 3 |
+
size 47374
|
Germany_TST/raw/de-2008-loes_awkl1_08.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:2cc2d7f52f05938892085e751a1116f2e76b62d23bb2bfb4964350580abdb0ac
|
| 3 |
+
size 95417
|