problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
2. How many natural numbers from 1 to 2017 have exactly three distinct natural divisors?
|
Answer: 14.
Solution: Only squares of prime numbers have exactly three divisors. Note that $47^{2}>2017$, so it is sufficient to consider the squares of prime numbers from 2 to 43. There are 14 of them.
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Petya is coming up with a password for his smartphone. The password consists of 4 decimal digits. Petya wants the password not to contain the digit 7, and at the same time, the password should have at least two (or more) identical digits. In how many ways can Petya do this?
|
# Answer 3537.
Solution: The total number of passwords not containing the digit 7 will be $9^{4}=6561$. Among these, 9x8x7x6=3024 consist of different digits. Therefore, the number of passwords containing identical digits is 6561-3024=3537 passwords.
|
3537
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the computer center, there are 200 computers, some of which (in pairs) are connected by cables, a total of 345 cables are used. We will call a "cluster" a set of computers such that a signal from any computer in this set can reach all the others via the cables. Initially, all computers formed one cluster. But one night, a malicious hacker cut several cables, resulting in 8 clusters. Find the maximum possible number of cables that were cut.
|
Answer: 153.
Solution: Let's try to imagine the problem this way: an evil hacker has cut all the wires. What is the minimum number of wires the admin needs to restore to end up with 8 clusters? Obviously, by adding a wire, the admin can reduce the number of clusters by one. This means that from 200 clusters, 8 can be obtained by restoring 192 wires. Therefore, the hacker could have cut a maximum of 153 wires.
## Variant 1-a
|
153
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the international StarCraft championship, 100 participants gathered. The game is played in a knockout format, meaning in each match, two players compete, the loser is eliminated from the tournament, and the winner remains. Find the maximum possible number of participants who won exactly two games?
|
Answer: 49
Solution: Each participant (except the winner) lost one game to someone. There are 99 such participants, so no more than 49 participants could have won 2 games (someone must lose 2 games to them).
We will show that there could be 49. Let's say №3 won against №1 and №2, №5 - against №3 and №4, ... №99 - against №97 and №98, and №100 won against №99. Then all participants with odd numbers (except the first) won exactly 2 games.
|
49
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On graph paper, a right-angled triangle with legs equal to 7 cells was drawn (see fig.). Then all the grid lines inside the triangle were outlined. What is the maximum number of triangles that can be found in this drawing?
|
Answer: 28 triangles
Solution: One of the sides of the triangle must go at an

angle, i.e., lie on the segment BC. If we fix some diagonal segment, the remaining vertex is uniquely determined. That is, we need to choose 2 points out of 8, which can be done in $7 \times 8 \backslash 2=28$ ways.
|
28
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all three-digit numbers $\overline{\Pi B \Gamma}$, consisting of distinct digits $\Pi, B$, and $\Gamma$, for which the equality $\overline{\Pi B \Gamma}=(\Pi+B+\Gamma) \times(\Pi+B+\Gamma+1)$ holds.
|
Answer: 156.
Solution: Note that П+В $\overline{\Pi В \Gamma}$ and (П + В + Г) should give the same remainder when divided by 9. This is only possible when $П+В+\Gamma$ is a multiple of 3. Note that $П+В+\Gamma=9$ - does not work, because (П + В + $\Gamma) \times(П+B+\Gamma+1)=90$-two-digit. By trying $12,15,18,21,24$, we get $\overline{\Pi В \Gamma}=$ $156=12 \times 13$.
## Variant 1-b
|
156
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many three-digit natural numbers have an even number of distinct natural divisors?
|
Answer: 878.
Solution: Note that only perfect squares have an odd number of divisors (for non-squares, divisors can be paired with their complements). There are 900 three-digit numbers in total. Among them, the perfect squares are $10^{2}, 11^{2}, \ldots, 31^{2}=961$ ( $32^{2}=1024-$ is a four-digit number). There are 22 of them, so the remaining 900-22 $=878$ are not squares.
|
878
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the international table tennis championship, 200 participants gathered. The game is played in a knockout format, i.e., in each match, two players participate, the loser is eliminated from the championship, and the winner remains. Find the maximum possible number of participants who won at least three matches.
|
Answer: 66.
Solution: Each participant (except the winner) lost one game to someone. There are 199 such participants, so no more than 66 participants could have won 3 games (someone must lose 3 games to them).
We will show that there could be 66 such participants. Let №4 win against №1,2,3; №7 - against №4,5,6,... №199 - against №196,197,198, and №200 win against №199. Then all participants with numbers giving a remainder of 1 when divided by 3 (except the first) won exactly 3 games.
|
66
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The turtle crawled out of its house and moved in a straight line at a constant speed of 5 m/hour. After an hour, it turned $90^{\circ}$ (right or left) and continued moving, then crawled for another hour, then turned $90^{\circ}$ (right or left) again... and so on. It crawled for 11 hours, turning $90^{\circ}$ at the end of each hour. What is the shortest distance from the house it could have been?
|
Answer 5 m.
Solution: We can consider a coordinate grid with nodes spaced 5 m apart. It is clear that the turtle crawls along

the nodes of this grid. The turtle cannot return to the initial position in 11 hours. However, it can be at a distance of 5 m - it is easy to construct an example.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Can you use the four arithmetic operations (and also parentheses) to write the number 2016 using the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 in sequence?
|
Answer: $1 \cdot 2 \cdot 3 \cdot(4+5) \cdot 6 \cdot 7 \cdot 8: 9=2016$.
|
2016
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Anya did not tell Misha how old she is, but she informed him that on each of her birthdays, her mother puts as many coins into the piggy bank as Anya is turning years old. Misha estimated that there are no fewer than 110 but no more than 130 coins in the piggy bank. How old is Anya?
|
Answer: 15. Solution. Either use the formula for the sum of an arithmetic progression: $110 \leq \frac{1+n}{2} n \leq 130$, or simply calculate the sum "brute force".
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many different right-angled triangles exist, one of the legs of which is equal to $\sqrt{2016}$, and the other leg and the hypotenuse are expressed as natural numbers
ANSWER: 12.
|
Solution. According to the condition $c^{2}-b^{2}=a^{2}=2016$, that is, $(c-b)(c+b)=2^{5} \cdot 3^{2} \cdot 7$. The system $\left\{\begin{array}{l}c-b=n, \\ c+b=k\end{array}\right.$ (here $n-$ is one of the divisors of the number 2016, and $k=\frac{2016}{n}$) has natural solutions $c=\frac{n+k}{2}, b=\frac{k-n}{2}$, if $n<k$ (that is, $n \leq 44$) and $n$ and $k$ are even.
Possible values of $n$: $2,2^{2}=4,2^{3}=8,2^{4}=16,2 \cdot 3=6,2^{2} \cdot 3=12,2^{3} \cdot 3=24$, $2 \cdot 7=14,2^{2} \cdot 7=28,2 \cdot 3^{2}=18,2^{2} \cdot 3^{2}=36,2 \cdot 3 \cdot 7=21$ - a total of 12 options.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The number $n+2015$ is divisible by 2016, and the number $n+2016$ is divisible by 2015. Find the smallest natural $n$ for which this is possible.
ANS: 4058209.
|
Solution. According to the condition $\left\{\begin{array}{l}n+2015=2016 m, \\ n+2016=2015 k .\end{array}\right.$ From this, $2016 m-2015 k=-1$. The solution of this equation in integers: $m=-1+2015 p, k=-1+2016 p$. Therefore, $n+2015=2016(-1+2015 p)=-2016+2016 \cdot 2015 p$, which means $n=-2015-2016+2016 \cdot 2015 p$. The smallest natural $n$ is $2016 \cdot 2015-2015-2016=2015^{2}-2016=4058209$.
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final stage tasks for the 2015/2016 academic year for 9th grade
|
4058209
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Kolya is twice as old as Olya was when Kolya was as old as Olya is now. And when Olya is as old as Kolya is now, their combined age will be 36 years. How old is Kolya now?
ANS: 16 years.
|
Solution: Let $x$ be Kolya's current age, $y$ be Olya's age. We can set up the system $\mathrm{x}=2(y-(x-y)) ; x+(x-y)+y+(x-y)=36$. Solving it: $x=16, y=12$.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many different right-angled triangles exist, one of the legs of which is equal to $\sqrt{1001}$, and the other leg and the hypotenuse are expressed as natural numbers
ANSWER: 4.
|
Solution: Let's write down the Pythagorean theorem: $a^{2}+1001=b^{2}$. From this, we get $(b-a)(b+a)=1001=7 \times 11 \times 13$. We can represent 1001 as the product of two factors $1 \times 1001=7 \times 143=11 \times 91=13 \times 77$ - the first factor must be smaller - there are 4 options in total.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the largest natural number that cannot be represented as the sum of two composite numbers.
OTBET: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. And odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we find that 11 cannot be represented in this way.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let $f(x)=x^{2}+p x+q$ where $p, q$ are some coefficients. By how much can the maximum value of the function $g(x)=|f(x)|$ differ from the minimum value of this function on the interval $[2 ; 6]$?
ANSWER: by 2.
|
Solution: For $f(x)=x^{2}+p x+q$ the difference between the maximum and the minimum value is at least 4 (this can be shown graphically). By choosing $q$,
we find that the maximum value of the modulus of the minimum differs by no more than 2. Example: $f(x)=(x-4)^{2}-2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many five-digit numbers of the form $\overline{a b 16 c}$ are divisible by 16? $(a, b, c-$ arbitrary digits, not necessarily different).
ANSWER: 90.
|
Solution: Note that the first digit does not affect divisibility, hence, a=1,..,9. On the other hand, divisibility by 8 implies that c=0 or 8. If c=0, then $b$ must be even, and if $c=8$ - odd. In both cases, we get 5 options, from which the total number is $9 *(5+5)=90$.
|
90
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Philatelist Andrey decided to distribute all his stamps equally into 3 envelopes, but it turned out that one stamp was extra. When he distributed them equally into 5 envelopes, 3 stamps were extra; finally, when he distributed them equally into 7 envelopes, 5 stamps remained. How many stamps does Andrey have in total, if it is known that recently he bought an additional album for them, which can hold 150 stamps, as such an old album was no longer sufficient
OTBET: 208.
|
Solution. If the desired number is $x$, then the number $x+2$ must be divisible by 3, 5, and 7, i.e., it has the form $3 \cdot 5 \cdot 7 \cdot p$. Therefore, $x=105 p-2$. Since by the condition $150<x \leq 300$, then $p=2$. Therefore, $x=208$.
|
208
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Solve the equation in natural numbers $2 n-\frac{1}{n^{5}}=3-\frac{2}{n}$
ANSWER: $n=1$.
|
Solution: $2 n=3-\frac{2}{n}+\frac{1}{n^{5}} \leq 3$, only $\mathrm{n}=1$ fits
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final Stage Tasks for the 2015/2016 Academic Year for 9th Grade
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the smallest natural number $N$ such that $N+2$ is divisible (without remainder) by 2, $N+3$ by 3, ..., $N+10$ by 10.
ANSWER: 2520.
|
Solution: Note that $N$ must be divisible by $2,3,4, \ldots, 10$, therefore, N= LCM $(2,3,4, . ., 10)=2^{3} \times 3^{2} \times 5 \times 7=2520$.
|
2520
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Captain Jack Sparrow found a cave with a pirate treasure. In it, there are 6 chests, and the treasure is only in one of them, while the other chests are home to venomous snakes, ready to attack anyone who disturbs their peace.
On the first chest, it says “The treasure is in the third chest.”
On the second, “The treasure is in me or in the first chest.”
On the third, “There is no treasure in me.”
On the fourth, “The treasure lies in a chest with an odd number.”
On the fifth, “There is no treasure in the second and sixth chests.”
On the sixth, “There is no treasure in the fourth chest.”
Help Jack find the treasure, knowing that exactly half of the inscriptions are true. In your answer, indicate the number of the chest with the treasure.
ANSWER: 2.
|
Solution: Let's create a $6 \times 6$ table. In the і-th row and ј-th column, we will place a cross if the і-th statement is true when the treasure is in the ј-th chest:
| | 1 | 2 | 3 | 4 | 5 | 6 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | | | X | | | |
| 2 | X | X | | | | |
| 3 | X | X | | X | X | X |
| 4 | X | | X | | X | |
| 5 | X | | X | X | X | |
| 6 | X | X | X | | X | X |
According to the problem, the column that fits is the one with exactly 3 crosses - i.e., the second.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $A B C D E F$ - a regular hexagon, point O - its center. How many different isosceles triangles with vertices at the specified seven points can be constructed? Triangles that differ only in the order of vertices are considered as
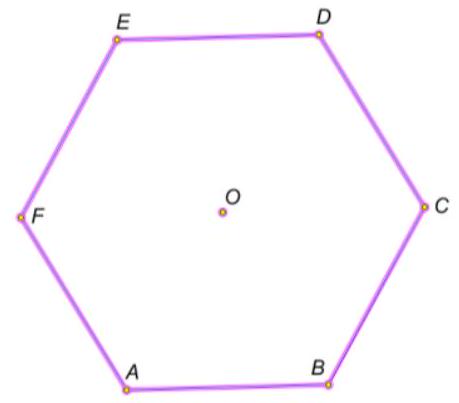
one triangle (for example, AOB and BOA).
ANSWER: 20.
|
Solution: First, consider the triangles that do not contain point O. These are two equilateral triangles and 6 triangles with an angle of $120^{\circ}$. With vertex $O$, there are 6 equilateral triangles and 6 triangles with an angle of $120^{\circ}$.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the largest natural number that cannot be represented as the sum of two composite numbers.
ANSWER: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. And odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we are convinced that 11 cannot be represented in this way.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $A B C D E F$ - a regular hexagon, point O - its center. How many different isosceles triangles with vertices at the specified seven points can be constructed? Triangles that differ only in the order of vertices are considered the same (for example, AOB and BOA).
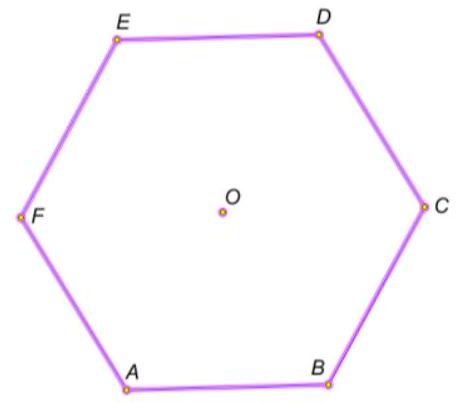
ANSWER: 20.
|
Solution: First, consider the triangles that do not contain point O. These are two equilateral triangles and 6 triangles with an angle of $120^{\circ}$. With vertex $O$, there are 6 equilateral triangles and 6 triangles with an angle of $120^{\circ}$.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. Given 2024 sets, each consisting of 44 elements. The union of any two of these sets contains 87 elements. How many elements does the union of all 2024 sets contain?
|
Answer: 87033.
II. Find the number of natural numbers $n$, not exceeding 500, for which the equation $x^{[x]}=n$ has a solution. Here $[x]$ is the greatest integer not exceeding $x$.
Solution. If $[x]=0$, then the solution is: $0 \leqslant x < 1$, and $n=1$.
If $[x]=1$, then the solution is: $1 \leqslant x < 2$, and $n=1$.
If $[x]=2$, then the solution is: $2 \leqslant x < 3$, and $n=4, 5, 6, 7, 8$.
If $[x]=3$, then the solution is: $3 \leqslant x < 4$, and $n=27, 28, \ldots, 63$.
If $[x]=4$, then the solution is: $4 \leqslant x < 5$, and $n=256, 257, \ldots, 500$.
Therefore, we get: $n=1,4,5,6,7,8,27,28, \ldots, 62,63,256,257, \ldots, 500$. In total, there are 288 numbers.
Answer: 288.
|
288
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Find the number of natural numbers $n$, not exceeding 3134, for which the equation $x^{[x]}=n$ has a solution. Here $[x]$ is the greatest integer not exceeding $x$.
|
Answer: 422.
III. Solve the inequality
$$
\frac{4^{-|x-2|}}{\sqrt{x^{2}-x-2}+2} \leqslant \frac{2^{1-|x|}}{\sqrt{x^{2}+6 x}+4}.
$$
In the answer, write the smallest root by absolute value, rounding it to two decimal places if necessary. If there are no solutions, then write the number 0.
Solution. Rewrite the inequality as
$$
\frac{4^{-|x-2|}}{\sqrt{(x+1)(x-2)}+2} \leqslant \frac{2^{-|x|}}{\sqrt{\left(\frac{x}{2}+3\right)\left(\frac{x}{2}\right)}+2}
$$
If we denote the left side by $f(x)$, then the right side is $f\left(\frac{x}{2}+2\right)$, and we get the inequality
$$
f(x) \leqslant f\left(\frac{x}{2}+2\right)
$$
Let's analyze the monotonicity. The domain of the original inequality is the set $(-\infty ;-6] \cup[2 ; \infty)$
On the set $x \leqslant-6$, both the left and right sides of the inequality are increasing, so we get $x \leqslant \frac{x}{2}+2$.
On the set $x \geqslant 2$, both the left and right sides of the inequality are decreasing, so we get $x \geqslant \frac{x}{2}+2$.
Since the solution to the inequality will be $x \in(-\infty ;-6] \cup[4 ; \infty)$, then $x=4$.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Between the pairs of solutions $(x, y)$ and $f(x, y)$ in this chain, there are no other solutions to the equation.
Suppose such a solution $(\alpha, \beta)$ does exist, then $(x, y)<(\alpha, \beta)<f(x, y)$. Apply the mapping $g$, which is the inverse of $f: g(x, y)=(3 x-2 y,-4 x+3 y)$, to all parts of this inequality. Perform this transformation enough times so that instead of $(x, y)$ we get the pair $(1,1)$, and instead of $f(x, y)$ we get the pair $(5,7)$. But then it would follow that there is another solution to the equation between the pairs $(1,1)$ and $(5,7)$, which is a contradiction.
Conclusion. The recursive sequence of pairs
$$
\left(x_{1}, y_{1}\right)=(1,1), \ldots,\left(x_{k}, y_{k}\right),\left(x_{k+1}, y_{k+1}\right)=\left(3 x_{k}+2 y_{k}, 4 x_{k}+3 y_{k}\right), \ldots
$$
exhausts the set of all natural solutions to the equation.
We find the first few pairs of this sequence:
$$
\begin{aligned}
& x_{2}=5, y_{2}=7, \quad x_{3}=29, y_{3}=41, \quad x_{4}=169, y_{4}=239, \\
& x_{5}=985, y_{5}=1393, \quad x_{6}=5741, y_{6}=8119, \ldots
\end{aligned}
$$
It is clear that only the pair $x_{5}=985, y_{5}=1393$ (and the corresponding values $k=492, n=696$) satisfy the conditions of the problem.
|
Answer: 696.
V-2. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 15-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is twice the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 1593, and Know-it-all lives in a room with a number greater than 200. Determine the room number where Don't-know-it lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Answer: 492.
V-3. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 25-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is twice the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 4591, and Know-it-all lives in a room with a number greater than 700. Determine the room number where Know-it-all lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Answer: 4059.
V-4. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 25-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is twice the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 4599, and Know-it-all lives in a room with a number greater than 700. Determine the room number where Don't-know-it lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Answer: 2870.
V-5. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 17-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is three times the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 1799, and Know-it-all lives in a room with a number greater than 200. Determine the room number where Know-it-all lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Solution. According to the problem, the room number of Don't-know-it $k$ and the room number of Know-it-all $n$ satisfy the relation $n^{2}+n=3\left(k^{2}+k\right)$. After the substitution $x=2 k+1, y=2 n+1$, this relation reduces to the form
$$
3 x^{2}-y^{2}=2
$$
The set of all natural solutions to the equation is exhausted by the following recursive sequence of pairs
$$
\left(x_{1}, y_{1}\right)=(1,1), \ldots,\left(x_{k}, y_{k}\right),\left(x_{k+1}, y_{k+1}\right)=\left(2 x_{k}+y_{k}, 3 x_{k}+2 y_{k}\right), \ldots
$$
We find the first few pairs of this sequence:
$$
\begin{aligned}
& x_{2}=3, y_{2}=5, \quad x_{3}=11, y_{3}=19, \quad x_{4}=41, y_{4}=71 \\
& x_{5}=153, y_{5}=265, \quad x_{6}=571, y_{6}=989, \quad x_{7}=2131, y_{7}=3691, \ldots
\end{aligned}
$$
Obviously, only the pair $x_{6}=571, y_{6}=989$ (and the corresponding values $k=285, n=494$) satisfy the conditions of the problem.
Answer: 494.
V-6. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 17-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is three times the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 1781, and Know-it-all lives in a room with a number greater than 200. Determine the room number where Don't-know-it lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Answer: 285.
V-7. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 17-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is three times the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 3791, and Know-it-all lives in a room with a number greater than 600. Determine the room number where Know-it-all lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Answer: 1845.
V-8. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 17-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is three times the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 3799, and Know-it-all lives in a room with a number greater than 600. Determine the room number where Don't-know-it lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Answer: 1065.
V-9. The summer vacation residents of Flower City, Know-it-all and Don't-know-it, spent in a large 17-story hotel by the sea. Know-it-all noticed that the sum of all room numbers from the first to his own, inclusive, is one and a half times the sum of all room numbers from the first to the one where Don't-know-it stayed, inclusive. All rooms in the hotel are numbered consecutively from 1 to 1799, and Know-it-all lives in a room with a number greater than 200. Determine the room number where Know-it-all lives.
If there are several room numbers, write their sum in the answer. If there are no such room numbers, write the number 0.
Solution. According to the problem, the room number of Don't-know-it $k$ and the room number of Know-it-all $n$ satisfy the relation $2\left(n^{2}+n\right)=3\left(k^{2}+k\right)$. After the substitution $x=2 k+1, y=2 n+1$, this relation reduces to the form
$$
3 x^{2}-2 y^{2}=1
$$
The set of all natural solutions to the equation is exhausted by the following recursive sequence of pairs
$$
\left(x_{1}, y_{1}\right)=(1,1), \ldots,\left(x_{k}, y_{k}\right),\left(x_{k+1}, y_{k+1}\right)=\left(5 x_{k}+4 y_{k}, 6 x_{k}+5 y_{k}\right), \ldots
$$
We find the first few pairs of this sequence:
$$
\begin{aligned}
& x_{2}=9, y_{2}=11, \quad x_{3}=89, y_{3}=109, \quad x_{4}=881, y_{4}=1079 \\
& x_{5}=8721, y_{5}=10681, \ldots
\end{aligned}
$$
Obviously, only the pair $x_{4}=881, y_{4}=1079$ (and the corresponding values $k=440, n=539$
|
539
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Place the numbers $1,2,3,4,5,6,7,8$ and 9 in the nine cells of the figure shown in the diagram, so that the sum of the numbers in each column, starting from the second, is 1 more than in the previous one. It is sufficient to find at least one such arrangement. In your answer, indicate the number in the first column.
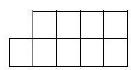
|
Answer: 7.
Solution: For now, we will not pay attention to the order of numbers in one column.
The sum of the given numbers is 45. Let $x$ be the number in the bottom-left cell. Then $5x + 10 = 45$, from which $x = 7$. Therefore, the sum of the numbers in the second column is $8 = 5 + 3 = 6 + 2$. If the second column contains 3 and 5, then the third column must contain 1 and 8, the fourth column must contain 6 and 4, and the last column must contain 2 and 9. If the second column contains 6 and 2, then the third column can contain 1 and 8 or 4 and 5. It can be shown that if the third column contains 1 and 8, it is impossible to select numbers for the fourth column. Therefore, the third column must contain 4 and 5, then the fourth column must contain 1 and 9, and the last column must contain 3 and 8. This results in 2 arrangements without considering the order of the numbers.
Notice that in each column (except the first), the numbers can be swapped, which gives 16 options for each arrangement. In the end, we get 32 options considering the order of the numbers in the columns.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A certain 4-digit number is a perfect square. If you remove the first digit from the left, it becomes a perfect cube, and if you remove the first 2 digits, it becomes a fourth power of an integer. Find this number.
|
Answer: 9216.
Solution: Only 16 and 81 are two-digit fourth powers. But 81 does not work, since no three-digit cube ends in $81\left(5^{3}=125,7^{3}=343,9^{3}=729\right)$. But 16 is the ending of $6^{3}=216$. Next, we look for a perfect square that ends in 216.
|
9216
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many natural numbers from 1 to 2015 inclusive have a sum of digits that is a multiple of 5?
|
Answer: 402.
Solution: Note that among ten numbers of the form $\overline{a 0}, \ldots, \overline{a 9}$, exactly two numbers have a sum of digits that is a multiple of five. Thus, among the numbers from 10 to 2009, there are exactly 200 such tens, and therefore, 400 such numbers. Considering also the numbers 5 and 2012, we get a total of 402 such numbers.
|
402
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Drop perpendiculars $D D_{1}, D D_{2}, D D_{3}$ from point $D$ to the planes $S B C$, $S A C$, and $S A B$ respectively. Let $D D_{1}=x, D D_{2}=y, D D_{3}=z$. According to the condition, we form the system of equations
$$
\left\{\begin{array}{l}
y^{2}+z^{2}=5 \\
x^{2}+z^{2}=13 \\
x^{2}+y^{2}=10
\end{array}\right.
$$

Fig. 6:
From here, we find $x=3, y=1, z=2$. Let the lengths of the edges $S A, S B$, and $S C$ be $a, b$, and $c$ respectively. Since points $A, B, C$, and $D$ lie in the same plane, the relation $\frac{3}{a}+\frac{1}{b}+\frac{2}{c}=1$ holds.
Using the inequality between the arithmetic mean and the geometric mean for three variables, we get:
$$
\begin{aligned}
& \frac{\frac{3}{a}+\frac{1}{b}+\frac{2}{c}}{3} \geqslant \sqrt[3]{\frac{3}{a} \cdot \frac{1}{b} \cdot \frac{2}{c}}=\sqrt[3]{\frac{6}{a b c}} \Longleftrightarrow \\
& \Longleftrightarrow 1=\left(\frac{3}{a}+\frac{1}{b}+\frac{2}{c}\right)^{3} \geqslant \frac{6 \cdot 27}{a b c} \Longleftrightarrow a b c \geqslant 6 \cdot 27
\end{aligned}
$$
with equality holding when $\frac{3}{a}=\frac{1}{b}=\frac{2}{c}=\frac{1}{3}$. The volume of the pyramid $V=\frac{a b c}{6}$, so $V \geqslant 27$. Equality holds when $a=9, b=3, c=6$.
|
Answer: 27.
Answer to option 17-2: 108.
Answer to option $17-3: 27$.
Answer to option $17-4: 108$.
[^0]: ${ }^{1}$ This equality can be proven by expressing $B C^{2}$ from two triangles $B A C$ and $B D C$ using the planimetric cosine theorem.
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x, y, z$ be the number of students in the categories of biology, physics, and chemistry, respectively. Then, according to the problem, we get the system of equations:
$$
\left\{\begin{array} { l }
{ 5 x = 2 ( y + z ) , } \\
{ 7 z = 3 ( x + y ) . }
\end{array} \Rightarrow \left\{\begin{array} { l }
{ 5 x - 2 y = 2 z , } \\
{ 3 x + 3 y = 7 z }
\end{array} \Rightarrow \left\{\begin{array}{l}
21 x=20 z \\
21 y=29 z
\end{array}\right.\right.\right.
$$
This means that the minimum values can only be: $x=20, y=29$, $z=21$.
|
Answer: 29. Answer to option: 4-2: 11.
#
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The solution can only exist if $a \in\left\{-\frac{\pi}{12}\right\} \cup\left(0 ; \frac{\pi}{12}\right]$, since otherwise the left side of the equation is either undefined or strictly positive. When $a=-\frac{\pi}{12}$, the equation becomes $2|x-16|=0$. Therefore, when $a=-\frac{\pi}{12}$, $x=16$. If $a \in\left(0 ; \frac{\pi}{12}\right]$, then $2^{\frac{1}{\sin ^{2}(2 a)}}>16$, and $2^{-4 \operatorname{tg}(3 a)}<1$. Therefore, the minimum value of the function $f(x)=\left|x-2^{\frac{1}{\sin ^{2}(2 a)}}\right|+\left|x-2^{-4 \operatorname{tg}(3 a)}\right|$ is not less than 15. On the other hand, the absolute value of the expression $g(a)=a\left(a+\frac{\pi}{12}\right)^{2}\left(a-\frac{\pi}{12}\right)$ on the half-interval $\left(0 ; \frac{\pi}{12}\right]$ is certainly no more than $1:|g(a)|<a\left(a+\frac{\pi}{12}\right)^{3}<1$.
Therefore, when $a \in\left(0 ; \frac{\pi}{12}\right]$, there are no solutions.
|
Answer: $x=16$ when $a=-\frac{\pi}{12}$. For other $a$, there are no solutions. Answer to option $5-2: x=-16$ when $a=\frac{\pi}{12}$. For other $a$, there are no solutions.
Lomonosov Moscow State University
## Olympiad "Conquer Sparrow Hills"
Option $6-1$ (Nizhny Novgorod)
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let's introduce the function $g(x)=f(x)+(x-2021)^{2}-4$. For this function, the conditions $g(2019)=g(2020)=g(2021)=g(2022)=g(2023)=0$ are satisfied, meaning that the function $g(x)$ has 5 roots. Since it is a polynomial of the 5th degree, it has no other roots. Therefore,
$$
g(x)=(x-2019)(x-2020)(x-2021)(x-2022)(x-2023),
$$
and
$$
f(x)=(x-2019)(x-2020)(x-2021)(x-2022)(x-2023)-(x-2021)^{2}+4
$$
Thus,
$$
f(2018)=(-1)(-2)(-3)(-4)(-5)-(-3)^{2}+4=-120-9+4=-125
$$
|
Answer: -125. Answer to option: 7-2: -115. 7-3: 115. 7-4: 125.
|
-125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest possible value of $\left|2015 m^{5}-2014 n^{4}\right|$, given that $m, n$ are natural numbers.
|
Answer: 0.
Solution: Let's find $N=2014^{x} \cdot 2015^{y}$ such that $m^{5}=2014^{x-1} \cdot 2015^{y}$ and $n^{4}=2014^{x} \cdot 2015^{y-1}$. For this, $x$ and $y-1$ must be multiples of 4, and $x-1$ and $y-5$ must be multiples of 5. For example, $x=16$ and $y=5$ work. Then, if we take $m=2014^{3} \cdot 2015$ and $n=2014^{4} \cdot 2015$, we get $\left|2015 m^{5}-2014 n^{4}\right|=0$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the largest three-digit number that is divisible by the sum of its digits and in which the first digit matches the third, but does not match the second.
|
Answer: 828.
Solution: Let this number be $\overline{a b a}=100 a+10 b+a$, where $a \neq b$. It must be divisible by $2 a+b$, so $101 a+10 b-10(2 a+b)=81 a$ is also divisible by $2 a+b$.
Since we need to find the largest such number, consider $a=9$. Then $81 a=729=3^{6}$, i.e., all divisors are powers of three, so $18+b=27$, from which $b=9$, which contradicts the condition $a \neq b$.
Now consider $a=8$. Then the number $81 a=648=2^{3} \cdot 3^{4}$ must be divisible by $16+b$ without a remainder, which is possible only when $b=2$ and $b=8$ (but the latter contradicts the condition $a \neq b$). Therefore, $a=8, b=2$.
|
828
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation in natural numbers
$$
a b c + a b + b c + a c + a + b + c = 164
$$
In your answer, specify the product $a b c$.
|
Answer: 80.
Solution: $(a+1) \times(b+1) \times(c+1)=a b c+a b+b c+a c+a+b+c+1=$ $165=3 \times 5 \times 11$, therefore, $a=2, b=4$ and $c=10$. Note that the solution is unique up to the permutation of $a, b$ and $c$, since $3,5,11$ are prime numbers.
## 2013/2014 Academic Year CRITERIA FOR DETERMINING WINNERS AND PRIZE WINNERS ${ }^{1}$
## of the school students' competition "CONQUER THE SPARROW MOUNTAINS!" IN MATHEMATICS
ELIMINATION STAGE
WINNER:
From 95 points inclusive and above.
PRIZE WINNER:
From
91
points to
94
points inclusive.
FINAL STAGE
WINNER (Diploma I degree):
From 90 points inclusive and above.
PRIZE WINNER (Diploma II degree):
From 75 points to 89 points inclusive.
PRIZE WINNER (Diploma III degree):
from 60 points to 74 points inclusive.[^0]
[^0]: ${ }^{1}$ Approved at the meeting of the jury of the school students' competition "Conquer the Sparrow Mountains!" in mathematics
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On the board in the laboratory, two numbers are written. Every day, the senior researcher Pyotr Ivanovich erases both numbers from the board and writes down their arithmetic mean and harmonic mean ${ }^{2}$. In the morning of the first day, the numbers 1 and 2 were written on the board.
Find the product of the numbers written on the board in the evening of the 2016th day.
|
# Solution:
The product of the numbers on the board does not change.
Indeed, $\frac{a+b}{2} \times \frac{2}{\frac{1}{a}+\frac{1}{b}}=a b$. Therefore, the desired product is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. In a certain company, there are 100 shareholders, and any 66 of them own no less than $50 \%$ of the company's shares. What is the largest percentage of all shares that one shareholder can own?
|
Solution. Let M be the shareholder owning the largest percentage of shares - x percent of shares. Divide the other 99 shareholders into three groups A, B, and
C, each with 33 shareholders. Let them own a, b, c percent of shares, respectively. Then
$$
2(100-x)=2(a+b+c)=(a+b)+(b+c)+(c+a) \geq 50+50+50
$$
That is, $x \leq 25$.
If each of the shareholders, except M, owns $\frac{75}{99}=\frac{25}{33} \%$ of the shares, then any 66 of them own exactly $50 \%$, and M owns exactly $25 \%$ of the shares.
Answer: $25 \%$ of the shares.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. A ticket to the Historical Museum costs 300 rubles for an adult and 60 rubles for a schoolchild, while pensioners can visit the museum for free. There is also a
"family ticket" for two adults and two children, which costs 650 rubles. What is the minimum amount in rubles that a family, including a father, a mother, a grandmother-pensioner, and four schoolchild children, should pay for visiting the museum?
|
Solution. All possible options are presented in the table.
| Grandmother | Father | Mother | 1st child | 1st child | 1st child | 1st child | Total cost, RUB |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| free | "adult" ticket 300 | "adult" ticket 300 | "child" 60 | "child" 60 | "child" 60 | "child" 60 | 840 |
| free | "family ticket" 650 | | | | "child" 60 | "child" 60 | 770 |
The minimum amount that a family, including a father, a mother, a grandmother-pensioner, and four school-age children, should pay for visiting the museum is 770 rubles.
Answer: 770 rubles
|
770
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. Is it possible to measure out exactly 4 liters of water into the larger of the two containers, using only a 3-liter and a 5-liter container, from a tap? If so, provide an example of how to do it.
|
Solution. You can, fill up 5 liters, pour 3 liters into the second container, then pour out this water, leaving 2 liters in the 5-liter container. Transfer these 2 liters to the 3-liter container. Fill the 5-liter container to the top and top up the second container (exactly 1 liter), then you will have 4 liters left in the first container. (There are other solutions as well)
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. When one of two integers was increased 1996 times, and the other was reduced 96 times, their sum did not change. What can their quotient be
|
Solution. Let the first number be x, and the second y. Then the equation $1996 x+\frac{y}{96}=x+y$ must hold, from which we find that 2016x=y. Therefore, their quotient is 2016 or $\frac{1}{2016}$.
Answer: 2016 or $\frac{1}{2016}$.
Criteria: Full solution - 7 points; correct answer without solution 1 point.
|
2016
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The function $f(x)$ is such that for all natural $n>1$ there exists a prime divisor $p$ of the number $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
It is known that $f(1001)=1$. What is $f(1002) ?$
|
Solution. Note that for any prime number p, the value $f(p)=f(1)-$ $f(p)$. Therefore, $f(p)=\frac{f(1)}{2}$ for any prime number. For prime numbers p and q, we get that either $\mathrm{f}(\mathrm{pq})=\mathrm{f}(\mathrm{p})-\mathrm{f}(\mathrm{q})=0$, or $\mathrm{f}(\mathrm{pq})=\mathrm{f}(\mathrm{q})-\mathrm{f}(\mathrm{p})=0$. For three prime numbers $\mathrm{p}, \mathrm{q}$, and $\mathrm{r}$, we get that $\mathrm{f}(\mathrm{pqr})=\mathrm{f}(\mathrm{pq})-\mathrm{f}(\mathrm{r})=-\mathrm{f}(\mathrm{r})=-\frac{\mathrm{f}(1)}{2}$ (the order of the prime numbers can be different). Then $f(1001)=f(7 \cdot 11 \cdot 13)=-\frac{f(1)}{2}=1$. But then $f(1002)=f(2 \cdot 3 \cdot 167)=-\frac{f(1)}{2}=1$.
Answer: 1.
Criteria: Full solution - 7 points. It is shown that $f(1)=-2$ or there is a proof that $f(p q)=0 - 2$ points.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a line, 3025 points are marked. The midpoints of every two of the marked points are painted green, blue, or red. Prove that the number of points painted in one of the colors on the line is at least 2016.
|
Solution. Let's start by considering three points. Obviously, for three points on a line, the midpoints of each pair of them are three different points. Consider the extreme point on the line. The midpoints between it and the two nearest points to it are two points that are not midpoints of any other points. If we remove this extreme point, the number of painted points will decrease by at least two. Next, we remove another extreme point. Then the number of painted points will decrease by at least two more. And so on until only three points remain. We get that the number of painted points is not less than \(3 + (n-3) \cdot 2 = 3 + 2n - 6 = 2n - 3\), where \(n\) is the number of marked points. In the case where there are 3025 points on the line, the number of midpoints marked is not less than \(3 \cdot 3025 - 3 = 6047\). This is possible if all marked points are located at equal distances from their neighbors. Suppose that the number of points of each color is no more than 2015. Then there should be no more than \(3 \cdot 2015 = 6045\) points, while the number of painted points is not less than 6047. Therefore, the number of points painted in one of the colors on the line is not less than 2016.
Criteria: Full solution - 7 points. Proved that the number of painted points is not less than 6047 - 4 points. Provided an example for 6047 painted points - 2 points. Proved that out of 6047 painted points, at least 2016 are painted in one color - 1 point.
|
2016
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. When one of two integers was increased 1996 times, and the other was reduced 96 times, their sum did not change. What can their quotient be?
|
Solution. Let the first number be x, and the second y. Then the equation $1996 x + \frac{y}{96} = x + y$ must hold, from which we find that $2016 x = y$. Therefore, their quotient is 2016 or $\frac{1}{2016}$.
Answer: 2016 or $\frac{1}{2016}$.
Criteria: Full solution - 7 points; correct answer without solution 1 point.
|
2016
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. At noon, a "Moskvich" left point A for point B. At the same time, "Zhiguli" left point B for point A on the same road. An hour later, the "Moskvich" was halfway between A and the "Zhiguli". When will it be halfway between the "Zhiguli" and B? (The speeds of the cars are constant and differ by less than a factor of two.)
|
Solution. Let the speeds of the "Moskvich" and "Zhiguli" be u and v, respectively. From the problem statement, it follows that if the speed of the "Moskvich" were $2 \mathrm{u}$, then its meeting with the "Zhiguli" (traveling at speed v) would occur one hour after the start of the journey. From this, it follows that if the speed of the "Zhiguli" were $\frac{v}{2}$, then their meeting with the "Moskvich" (traveling at speed u) would occur two hours after the start of the journey. This means that at this moment (2 PM), with the given (u and v) speeds, the "Moskvich" will be halfway between the "Zhiguli" and V.
Answer: at 2 PM.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. The faces of a cube are labeled with six different numbers from 6 to 11. The cube was rolled twice. The first time, the sum of the numbers on the four side faces was 36, the second time - 33. What number is written on the face opposite the one where the digit $10$ is written?
|
Solution: The sum of the numbers on all faces is
$$
6+7+8+9+10+11=51
$$
On the first roll, the sum of the numbers on the top and bottom faces is 51 $-36=15$, on the second roll $-51-33=18$. Therefore, the sum on the third pair of opposite faces is $51-15-18=18$. The sum of 18 can be obtained in two ways: $11+7$ or $10+8$. Therefore, on the pairs of faces with a sum of 18, 7 is opposite 11, and 8 is opposite 10.
## Answer: 8
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. Ostap Bender put new tires on the car "Gnu Antelope". It is known that the front tires of the car wear out after 25,000 km, while the rear tires wear out after 15,000 km (the tires are the same both in the front and in the rear, but the rear ones wear out more). After how many kilometers should Ostap Bender swap these tires to ensure that the "Gnu Antelope" travels the maximum possible distance? What is this distance?
|
Solution. Let Ostap Bender swap the tires after x kilometers. Then the rear tires have used up [x/15000] of their resource, and the front tires [x/25000]. After the swap, they can work for another
$$
25000 \cdot\left(1-\frac{x}{15000}\right) \text { and } 15000 \cdot\left(1-\frac{x}{25000}\right)
$$
kilometers, respectively. Thus, the total distance that can be traveled is no more than
$$
x+25000\left(1-\frac{x}{15000}\right)=25000-\frac{2}{3} x
$$
and no more than
$$
x+15000\left(1-\frac{x}{25000}\right)=15000+\frac{2}{5} x
$$
The maximum distance can be traveled if these expressions are equal (otherwise, either the first or the second set of tires will wear out earlier, since when the first expression increases, the second decreases and vice versa). Thus,
$$
25000-\frac{2}{3} x=15000+\frac{2}{5} x
$$
from which $10000=\frac{16}{15} x$, or $x=9375$.
Answer: The tires should be swapped after 9375 km, then a total of 18750 km can be traveled.
|
9375
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. To number the pages of a book, a total of 1392 digits were used. How many pages are in this book?
|
Solution. The first nine pages will require 9 digits, and for the next 90 pages, 2 digits are needed for each page, which means 2 * 90 digits are required. Let the book have x pages, then the pages with three digits will be x - 99, and the digits on them will be 3 * (x - 99). We get the equation: $9 + 2 \cdot 90 + 3 \cdot (x - 99) = 1392$, the solution to which is $x = 500$.
Answer: 500.
|
500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. There are 30 logs with lengths of 3 and 4 meters, the total length of which is 100 meters. How many cuts can be made to saw the logs into logs of 1 meter length? (Each cut saws exactly one log.)
#
|
# Solution.
First solution. Glue all the logs into one 100-meter log.
To divide it into 100 parts, 99 cuts are needed, 29 of which have already been made.
Second solution. If there were $m$ three-meter logs and $n$ four-meter logs,
then $m+n=30, 3m+4n=100$, from which $m=20, n=10$. Therefore, $20 \cdot 2 + 10 \cdot 3 = 70$ cuts are needed.
Answer. 70.
|
70
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. On the Island of Knights and Liars, knights always tell the truth, while liars always lie. One day, a traveler interviewed seven residents of the island.
- I am a knight, - said the first.
- Yes, he is a knight, - said the second.
- Among the first two, there are no less than 50% liars, - said the third.
- Among the first three, there are no less than 65% liars, - said the fourth.
- Among the first four, there are no less than 50% knights, - said the fifth.
- Among the first five, there are no less than 40% liars, - said the sixth.
- Among the first six, there are no less than 65% knights, - said the seventh.
Determine how many knights there are among them in reality.
|
Answer: 5.
Solution: Suppose the first inhabitant is a knight. Then the second is also a knight, while the third and fourth are liars. If, on the other hand, the first is a liar, then the second is also a liar, while the third and fourth are knights. In either case, among the first four, there are exactly two knights and two liars. Therefore, the statements of the fifth, sixth, and seventh inhabitants are true, i.e., they are knights.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Find all pairs of two-digit natural numbers for which the arithmetic mean is $25 / 24$ times greater than the geometric mean. In your answer, specify the largest of the arithmetic means for all such pairs.
|
Answer: 75.
Solution: Let $a, b$ be the required numbers (without loss of generality, we can assume that $a > b$) and let $\frac{a+b}{2}=25x$ and $\sqrt{ab}=24x$. Then $(\sqrt{a}+\sqrt{b})^2=a+b+2\sqrt{ab}=98x$ and $(\sqrt{a}-\sqrt{b})^2=$ $a+b-2\sqrt{ab}=2x$. From this, it follows that $\sqrt{a}+\sqrt{b}=7(\sqrt{a}-\sqrt{b})$. Therefore, $3\sqrt{a}=4\sqrt{b}$. Thus, $a:b=16:9$. Considering that $a$ and $b$ are two-digit numbers, the sum will be the largest for $a=16 \cdot 6=96, b=9 \cdot 6=54$. Their arithmetic mean is $\frac{96+54}{2}=75$.
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. All natural numbers from 1 to 2017 inclusive were written in a row. How many times was the digit 7 written?
|
Answer: 602.
Solution. First, consider the numbers from 1 to 2000. Then the digit 7 can be in the third position from the end: numbers of the form $7 * *$ or $17 * *$ - there are 200 such numbers. It can be in the second position: $* 7 *$ or $1 * 7 *$ - there are also 200 such numbers; or the last position: $* * 7$ or $1 * * 7$ - there are also 200 such numbers. In addition, there are 2007 and 2017 - two more 7s.
|
602
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. At the vertices of a cube, numbers $\pm 1$ are placed, and on its faces - numbers equal to the product of the numbers at the vertices of that face. Find all possible values that the sum of these 14 numbers can take. In your answer, specify their product.
|
Answer: -20160.
Solution. It is obvious that the maximum value of the sum is 14. Note that if we change the sign of one of the vertices, the sum of the numbers in the vertices will increase or decrease by 2. On the other hand, the signs of three faces will change. If their sum was $1, -1, 3, -3$, it will become $-1, 1, -3$, or 3, respectively, i.e., it will change by 2 or 6. It is clear that if we add two sums, the remainder when divided by 4 does not change. Therefore, we can obtain the numbers $10, 6, 2, -2$, $-6, -10$. The number -14, obviously, cannot be obtained, since this would require making all numbers equal to -1. For the other values, it is easy to construct corresponding examples.
|
-20160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. How many numbers from 1 to 1000 (inclusive) cannot be represented as the difference of two squares of integers
|
Answer: 250.
Solution. Note that any odd number $2n+1$ can be represented as $(n+1)^{2}-n^{2}$. Moreover, an even number that is a multiple of 4 can be represented as $4n=(n+1)^{2}-(n-1)^{2}$. The numbers of the form $4n+2$ remain. Note that a square can give remainders of 0 or 1 when divided by 4, so numbers of the form $4n+2$ cannot be obtained as the difference of squares. There is exactly one such number (of the form $4n+2$) in every set of four consecutive numbers, so the total number of such numbers from 1 to 1000 will be $1000 / 4 = 250$.
|
250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. The sequence is defined by the relations $a_{1}=1$,
$$
a_{2 n}=\left\{\begin{array}{ll}
a_{n}, & \text { if } n \text { is even, } \\
2 a_{n}, & \text { if } n \text { is odd; }
\end{array} \quad a_{2 n+1}= \begin{cases}2 a_{n}+1, & \text { if } n \text { is even, } \\
a_{n}, & \text { if } n \text { is odd. }\end{cases}\right.
$$
Find the smallest natural $n$ for which $a_{n}=a_{2017}$.
|
Answer: 5.
Solution: The given rules are easily interpreted in terms of the binary system: if $n$ ends in 0 and 1 is appended to the right, then 1 is appended to the right of $a_{n}$. If $n$ ends in 1 and 0 is appended, then 0 is appended to the right of $a_{n}$. In all other cases, $a_{n}$ does not change (when 0 is appended to 0 or 1 is appended to 1). Let's write the number 2017 in binary: $2017=11111100001_{2}$. It is easy to see that $a_{2017}=101_{2}=5_{10}$. By checking the first few values, we find $a_{5}=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. On the Island of Knights and Liars, knights always tell the truth, while liars always lie. One day, a traveler interviewed seven residents of the island.
- I am a knight, - said the first.
- Yes, he is a knight, - said the second.
- Among the first two, there are no less than 50% liars, - said the third.
- Among the first three, there are no less than 65% liars, - said the fourth.
- Among the first four, there are no less than 50% knights, - said the fifth.
- Among the first five, there are no less than 40% liars, - said the sixth.
- Among the first six, there are no less than 65% knights, - said the seventh.
Determine how many knights are among them in reality.
|
Answer: 5.
Solution: Suppose the first inhabitant is a knight. Then the second is also a knight, while the third and fourth are liars. If, on the other hand, the first is a liar, then the second is also a liar, while the third and fourth are knights. In either case, among the first four, there are exactly two knights and two liars. Therefore, the statements of the fifth, sixth, and seventh inhabitants are true, i.e., they are knights.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. How many four-digit numbers exist that contain the digit 9 in their notation, immediately followed by the digit 5?
|
Answer: 279.
Solution. For numbers of the form $95 * *$, the last two digits can be anything - there are $10 \cdot 10=100$ such numbers, and for numbers of the form $* 95 *$ and $* * 95$, the first digit cannot be 0, so there are $10 \cdot 9=90$ of each. The number 9595 was counted twice, so we get 279 numbers.
|
279
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. All natural numbers from 1 to 2017 inclusive were written in a row. How many times was the digit 7 written?
|
Answer: 602.
Solution. First, consider the numbers from 1 to 2000. Then the digit 7 can be in the third position from the end: numbers of the form $7 * *$ or $17 * *$ - there are 200 such numbers. It can be in the second position: $* 7 *$ or $1 * 7 *$ - there are also 200 such numbers; or the last position: $* * 7$ or $1 * * 7$ - there are also 200. In addition, there are 2007 and 2017 - two more 7s.
|
602
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. How many numbers from 1 to 1000 (inclusive) cannot be represented as the difference of two squares of integers
|
Answer: 250.
Solution. Note that any odd number $2 n+1$ can be represented as $(n+1)^{2}-n^{2}$. Moreover, an even number that is a multiple of 4 can be represented as $4 n=(n+1)^{2}-(n-1)^{2}$. The numbers of the form $4 n+2$ remain. Note that a square can give remainders of 0 or 1 when divided by 4, so numbers of the form $4 n+2$ cannot be obtained as the difference of squares. There is exactly one such number (of the form $4 n+2$) in every set of four consecutive numbers, so the total number of such numbers from 1 to 1000 will be $1000 / 4=250$.
|
250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Among all integer solutions of the equation $20 x+19 y=2019$, find the one for which the value of $|x-y|$ is minimal. In the answer, write the product $x y$.
|
Answer: 2623.
Solution. One of the solutions to the equation is the pair $x=100, y=1$. Therefore, the set of all integer solutions is $x=100-19 n, y=1+20 n, n \in \mathbb{Z}$. The absolute difference $|x-y|=$ $|100-19 n-1-20 n|=|99-39 n|$ is minimized when $n=3$, and the corresponding solution is $(x, y)=(43,61)$. We write the answer as $x y=43 \cdot 61=2623$.
|
2623
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. A teacher at a summer math camp took with him for the whole summer several shirts, several pairs of pants, several pairs of shoes, and two jackets. At each lesson, he wore pants, a shirt, and shoes, and he wore a jacket on some lessons. On any two lessons, at least one of the items of his clothing or shoes was different. It is known that if he had taken one more shirt, he could have conducted 18 more lessons; if he had taken one more pair of pants, he could have conducted 63 more lessons; if he had taken one more pair of shoes, he could have conducted 42 more lessons. What is the maximum number of lessons he could conduct under these conditions?
|
Answer: 126.
Solution: Let the teacher bring $x$ shirts, $y$ pairs of trousers, $z$ pairs of shoes, and 2 jackets. Then he can conduct $3 x y z$ lessons (the number 3 means: 2 lessons in each of the jackets and 1 lesson without a jacket). If he has one more shirt, the number of lessons will increase by $3 y z$. If he has one more pair of trousers, the number of lessons will increase by $3 x z$. If he has one more pair of shoes, the number of lessons will increase by $3 y z$. Thus, we get a system of three equations: $3 y z=18, 3 x z=63, 3 x y=42$. Therefore, $y z=6, x z=21, x y=14$, and thus $(x y z)^{2}=6 \cdot 21 \cdot 14, x y z=42$ (although it is not necessary, but we can calculate that $x=7, y=2, z=3$). The desired value: $3 x y z=126$.
Remark. There is a possible interpretation of the problem condition in which it is required to find the maximum number of lessons given that the teacher will take with him one more shirt, one more pair of trousers, and one more pair of shoes. The corresponding answer $3(x+1)(y+1)(z+1)=288$ is also considered correct.
|
126
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.4. A teacher at a summer math camp took with him for the whole summer several shirts, several pairs of pants, several pairs of shoes, and two jackets. At each lesson, he wore pants, a shirt, and shoes, and he wore a jacket on some lessons. On any two lessons, at least one of the items of his clothing or shoes was different. It is known that if he had taken one more shirt, he could have conducted 36 more lessons; if he had taken one more pair of pants, he could have conducted 72 more lessons; if he had taken one more pair of shoes, he could have conducted 54 more lessons. What is the maximum number of lessons he could conduct under these conditions?
|
Answer: 216.
Note. In versions $4.2,4.3,4.4$, answers $252,360,420$ respectively are also counted as correct.
|
216
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. It is known that $P(x)$ is a polynomial of degree 9 and $P(k)=2^{k}$ for all $k=1,2,3, \ldots, 10$. Find $P(12)$.
|
Answer: 4072.
Solution. Let $P(x)$ be a polynomial of degree $n$ and $P(k)=2^{k}$ for all $k=1,2,3, \ldots, n+1$. We will find $P(n+m+2), m=0,1, \ldots$. By the binomial theorem for any $k \in \mathbb{N}$ we have
$$
2^{k}=2 \cdot(1+1)^{k-1}=2 \sum_{i=0}^{k-1} C_{k-1}^{i}=2 \sum_{i=0}^{k-1} \frac{(k-1)(k-2) \ldots(k-i)}{i!}
$$
Note that the sum on the right side of this equation is a polynomial in $k$ of degree $k-1$, and if we add terms corresponding to $i=k, k+1, \ldots, n$, it will not change, since $(k-1)(k-2) \ldots(k-i)=0$ for $i \geqslant k$ (each such product contains a factor $(k-k)=0$). Therefore,
$$
2^{k}=2 \sum_{i=0}^{k-1} \frac{(k-1)(k-2) \ldots(k-i)}{i!}=2 \sum_{i=0}^{n} \frac{(k-1)(k-2) \ldots(k-i)}{i!} \quad \text { for } k \in \mathbb{N}, \quad n \geqslant k-1
$$
Consider the polynomial
$$
Q(x)=2 \sum_{i=0}^{n} \frac{(x-1)(x-2) \ldots(x-i)}{i!}
$$
This is a polynomial of degree $n$, and by the proven result, $Q(k)=2^{k}, k=1,2,3, \ldots, n+1$. Therefore, $P(x)=Q(x)$ as polynomials of degree $n$ that coincide at $n+1$ points.
Substituting $x=n+m+2(m \geqslant 0)$, we find
$$
P(n+m+2)=2 \sum_{i=0}^{n} C_{n+m+1}^{i}=2 \sum_{i=0}^{n+m+1} C_{n+m+1}^{i}-2 \sum_{i=n+1}^{n+m+1} C_{n+m+1}^{i}=2^{n+m+2}-2 \sum_{i=0}^{m} C_{n+m+1}^{i}
$$
(in the last equality, we again used the binomial theorem and the equality of binomial coefficients $\left.C_{n+m+1}^{i}=C_{n+m+1}^{n+m+1-i}\right)$. For $m=1$ we get
$$
P(n+3)=2^{n+3}-2-2(n+2)=2^{n+3}-2 n-6
$$
In particular, for the polynomial in the problem statement $n=9, P(12)=2^{12}-2 \cdot 9-6=4072$.
Another way to solve. A polynomial of degree $n$ is uniquely determined by its values at $n+1$ points $k=1,2,3, \ldots, n+1$. By direct substitution of these points, we verify that the condition of the problem is satisfied by the polynomial (Lagrange interpolation polynomial)
$$
\begin{aligned}
P(x)= & 2 \frac{(x-2)(x-3)(x-4) \ldots(x-(n+1))}{(1-2)(1-3)(1-4) \ldots(1-(n+1))}+2^{2} \frac{(x-1)(x-3)(x-4) \ldots(x-(n+1))}{(2-1)(2-3)(2-4) \ldots(2-(n+1))}+ \\
& +2^{3} \frac{(x-1)(x-2)(x-4) \ldots(x-(n+1))}{(3-1)(3-2)(3-4) \ldots(3-(n+1))}+\ldots+ \\
& +2^{n+1} \frac{(x-1)(x-2)(x-3) \ldots(x-n)}{(n+1-1)(n+1-2)(n+1-3) \ldots(n+1-n)}= \\
= & 2(-1)^{n} \frac{(x-2) \ldots(x-(n+1))}{n!}-2^{1} \frac{(x-1)(x-3) \ldots(x-(n+1))}{1!(n-1)!}+ \\
& \left.+2^{2} \frac{(x-1)(x-2)(x-4) \ldots(x-(n+1))}{2!(n-2)!}-\ldots+(-1)^{n} 2^{n} \frac{(x-1) \ldots(x-n)}{n!}\right) .
\end{aligned}
$$
Its value at the point $x=n+3$ is
$$
\begin{aligned}
P(n+3)= & 2(-1)^{n}\left(\frac{(n+1) n(n-1) \ldots 3 \cdot 2}{n!}-2^{1} \frac{(n+2) n(n-1) \ldots \cdot 3 \cdot 2}{1!(n-1)!}+\right. \\
& \left.+2^{2} \frac{(n+2)(n+1)(n-1) \ldots \cdot 3 \cdot 2}{2!(n-2)!}-\ldots+(-1)^{n} 2^{n} \frac{(n+2)(n+1) \ldots \cdot 4 \cdot 3}{n!}\right)= \\
= & \left.2(-1)^{n}(n+2)(n+1)\left(\frac{1}{n+2}-2^{1} C_{n}^{1} \cdot \frac{1}{n+1}+2^{2} C_{n}^{2} \cdot \frac{1}{n}+\ldots+(-1)^{n} 2^{n} C_{n}^{n} \cdot \frac{1}{2}\right)\right)= \\
= & 2(-1)^{n}(n+2)(n+1) \sum_{k=0}^{n}(-2)^{k} \frac{C_{n}^{k}}{n-k+2}=2(-1)^{n}(n+2)(n+1) S(1)
\end{aligned}
$$
where
$$
S(x)=\sum_{k=0}^{n} C_{n}^{k} \frac{(-2)^{k} x^{n-k+2}}{n-k+2}
$$
Since
$$
S^{\prime}(x)=\left(\sum_{k=0}^{n} C_{n}^{k} \frac{(-2)^{k} x^{n-k+2}}{n-k+2}\right)^{\prime}=\sum_{k=0}^{n} C_{n}^{k}(-2)^{k} x^{n-k+1}=x(x-2)^{n}=(x-2)^{n+1}+2(x-2)^{n}
$$
with the condition $S(0)=0$ we find $S(x)=\frac{(x-2)^{n+2}-(-2)^{n+2}}{n+2}+2 \frac{(x-2)^{n+1}-(-2)^{n+1}}{n+1}$. Therefore,
$$
\begin{aligned}
P(n+3) & =2(-1)^{n}(n+2)(n+1)\left(\frac{(-1)^{n+2}-(-2)^{n+2}}{n+2}+2 \frac{(-1)^{n+1}-(-2)^{n+1}}{n+1}\right)= \\
& =-2(n+1)(n+2)\left(\frac{2^{n+2}-1}{n+2}-\frac{2^{n+2}-2}{n+1}\right)=2\left(2^{n+2}-1\right)-2(n+2)=2^{n+3}-2 n-6
\end{aligned}
$$
|
4072
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The sequences $\left\{x_{n}\right\},\left\{y_{n}\right\}$ are defined by the conditions $x_{1}=11, y_{1}=7, x_{n+1}=3 x_{n}+2 y_{n}$, $y_{n+1}=4 x_{n}+3 y_{n}, n \in \mathbb{N}$. Find the remainder of the division of the number $y_{1855}^{2018}-2 x_{1855}^{2018}$ by 2018.
|
Answer: 1825.
Solution. For all $n \in \mathbb{N}$, the numbers $x_{n}$ and $y_{n}$ are odd. Notice that
$$
2 x_{n+1}^{2}-y_{n+1}^{2}=2\left(3 x_{n}+2 y_{n}\right)^{2}-\left(4 x_{n}+3 y_{n}\right)^{2}=2 x_{n}^{2}-y_{n}^{2}
$$
Therefore, $2 x_{n}^{2}-y_{n}^{2}=\ldots=2 x_{1}^{2}-y_{1}^{2}=242-49=193$.
Let $p=1009$. This number is odd and prime, so the number $\left(y_{n}^{2}-2 x_{n}^{2}\right)^{p}=(-193)^{p}$ gives the same remainder when divided by $2 p$, as $y_{n}^{2 p}-2^{p} x_{n}^{2 p}$, since all binomial coefficients $C_{p}^{1}, \ldots, C_{p}^{p-1}$ are divisible by $p$. Moreover, by Fermat's little theorem, $2^{p}$ gives a remainder of 2 when divided by $2 p=2018$ (and therefore the remainders of the numbers $y_{n}^{2 p}-2^{p} x_{n}^{2 p}$ and $y_{n}^{2 p}-2 x_{n}^{2 p}$ are the same), and $(-193)^{p}$ gives a remainder of $2018-193=1825$ when divided by $2 p=2018$.
|
1825
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many weeks can a year overlap? Assume that a year overlaps with a week if at least 6 and one day of this week falls within the given year.
|
Answer: On the 53rd 54th week. Solution. If there are 365 days in a year (a non-leap year), then since $365=52 \cdot 7+1$, there are no fewer than 53 weeks in a year. If it is a leap year, meaning there are 366 days in a year ( $366=52 \cdot 7+2$ ), there is a situation where the year starts with the last day of the week, followed by 52 full weeks, and then the first day of the following week - a total of 54 different weeks. If there are 55 (or more) weeks, then there must be no fewer than 53 full weeks, which is impossible, as $53 \cdot 7=371>366$.
|
54
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many numbers divisible by 4 and less than 1000 do not contain any of the digits $6,7,8,9$ or 0.
|
Answer: 31. Solution. According to the condition, these numbers consist only of the digits 1, 2, 3, 4, and 5. Out of such numbers, only one single-digit number is divisible by 4: 4. Among the two-digit numbers, the following are divisible by 4: $12, 24, 32, 44, 52$. If we prepend 1, 2, 3, 4, or 5 to all these two-digit numbers, they will also be divisible by 4. There will be no other three-digit numbers divisible by 4 (the rule for divisibility by 4). Therefore, the total number of such numbers is: $1 + 5 \cdot 6 = 31$.
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. In a right triangle $ABC$ with a right angle at $C$, the bisector $BD$ and the altitude $CH$ are drawn. A perpendicular $CK$ is dropped from vertex $C$ to the bisector $BD$. Find the angle $HCK$, if $BK: KD=3: 1$.
|
Answer: $30^{\circ}$.
Solution. Let $M$ be the midpoint of $B D$. Then $C M$ is the median of the right triangle $C B D$ and $C M=M B=M D$. In addition, $C K$ is the height and median of triangle $M C D$, so $M C=C D$ and triangle $C M D$ is equilateral. Then $\angle C D M=60^{\circ}$ and $\angle C B M=$ $\angle C B D=90^{\circ}-60^{\circ}=30^{\circ}$, therefore, $\angle C B A=2 \angle C B D=60^{\circ}$. Hence $\angle B C H=30^{\circ}$, $\angle H C K=90^{\circ}-30^{\circ}-30^{\circ}=30^{\circ}$.
Answer to variant 2: $30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Vanya thought of a two-digit number, then swapped its digits and multiplied the resulting number by itself. The result turned out to be four times larger than the number he thought of. What number did Vanya think of?
|
Answer: 81.
Solution. Let the intended number be $\overline{m n}=10 m+n$. Then $4 \overline{m n}=\overline{n m}^{2}$. Therefore, $\overline{n m}^{2}$ is divisible by 4, and $\overline{n m}$ is divisible by 2, so the digit $m$ is even (and not zero). Moreover, $\overline{m n}=\overline{n m}^{2}: 4=(\overline{n m}: 2)^{2}$, which means $\overline{m n}$ is a square of a natural number, starting with an even digit. Therefore, $\overline{m n}$ can be $25, 49, 64$ or 81. Checking shows that only the last one satisfies the condition.
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the lateral sides $AB$ and $BC$ of an isosceles triangle $ABC$, points $M$ and $N$ are marked such that $AM = MN = NC$. On the side $AC$, points $P$ and $Q$ are chosen such that $MQ \parallel BC$ and $NP \parallel AB$. It is known that $PQ = BM$. Find the angle $MQB$.
|
Answer: $36^{\circ}$. The answer can also be given in the form $\arccos \left(\frac{\sqrt{5}+1}{4}\right)$, etc.
Solution. Let $\angle A=\angle C=\alpha$, then by the property of parallel lines $\angle N P C=$ $\angle A Q M=\alpha$. It is not difficult to prove that $M N \| A C$ (through the similarity of triangles, or through the equality of distances from points $M, N$ to the line $A C$, or through the calculation of angles), therefore $\angle B M N=$ $\angle Q M N=\angle B N M=\angle M N P=\alpha$ and $A M N P$ is a rhombus, from which $A P=A M=M N$. (Seventh-graders can prove this equality through the equality $\triangle A M N=\Delta A P N$.)
First case. Suppose point $P$ lies on segment $A Q$. Then, taking into account the above, $\triangle A M Q=\triangle A P B$ by two sides and the angle between them, so $\angle A B P=\angle A Q M=\alpha$; similarly, $\angle Q B C=\angle C P N=\alpha$. $\angle B P Q=2 \alpha$ as an external angle for $\triangle A P B$, hence $\angle B P N=2 \alpha-\alpha=$ $\alpha$; similarly, $\angle M Q B=\alpha$. Since $\triangle A B Q$ is isosceles, $\angle A B Q=\angle A Q B=2 \alpha$, from which $\angle P B Q=\alpha$. By the theorem on the sum of angles in a triangle for $\triangle A B C$ we get $5 \alpha=180^{\circ}$, hence $\angle M Q B=\alpha=36^{\circ}$.
Second case. Suppose point $P$ lies on segment $C Q$. Then $M N=A P>P Q=B M$. In $\triangle B M N$ the larger angle lies opposite the larger side, so $\angle M B N=180^{\circ}-2 \alpha>\angle B N M=\alpha$, from which $\alphaA Q=A P-Q P=A M-Q P$, this means that $\angle A=\alpha>\angle A M Q=180^{\circ}-2 \alpha$, from which $\alpha>60^{\circ}$. The obtained contradiction shows that the second case is impossible.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. If the 200th day of some year is Sunday and the 100th day of the following year is also Sunday, then what day of the week was the 300th day of the previous year? Enter the number of this day of the week (if Monday, then 1, if Tuesday, then 2, etc.).
|
Answer. 1.
Solution. Between the $200-\mathrm{th}$ day of the year and the $100-\mathrm{th}$ day of the next year, there are either $165+100=265$ or $166+100=266$ days. The number 266 is divisible by 7, while the number $265-$ is not. Therefore, the current year has 366 days, meaning it is a leap year. Thus, the previous year was a common year. Therefore, between the $300-\mathrm{th}$ day of the previous year and the $200-\mathrm{th}$ day of the current year, there are $65+200=265$ days. Since $265=7 \cdot 37+6$, the number of days is 1 less than a multiple of 7. Therefore, it was a Monday.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. How many terms will there be if we expand the expression $\left(4 x^{3}+x^{-3}+2\right)^{2016}$ and combine like terms?
|
Answer: 4033.
Solution. In the resulting sum, there will be monomials of the form $k_{n} x^{3 n}$ for all integers $n \in[-2016 ; 2016]$ with positive coefficients $k_{n}$, i.e., a total of $2 \cdot 2016+1=4033$ terms.
|
4033
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. The function $f$ satisfies the equation $(x-1) f(x)+f\left(\frac{1}{x}\right)=\frac{1}{x-1}$ for each value of $x$, not equal to 0 and 1. Find $f\left(\frac{2016}{2017}\right)$.
|
Answer: 2017.
Solution. Substitute $\frac{1}{x}$ for $x$ in the equation. Together with the original equation, we get a system of two linear equations in terms of $f(x)$ and $f\left(\frac{1}{x}\right)$:
$$
\left\{\begin{array}{l}
(x-1) f(x)+f\left(\frac{1}{x}\right)=\frac{1}{x-1} \\
\left(\frac{1}{x}-1\right) f\left(\frac{1}{x}\right)+f(x)=\frac{x}{1-x}
\end{array}\right.
$$
Subtracting the first equation, multiplied by $\frac{1-x}{x}$, from the second equation, we get $\left(1+\frac{(1-x)^{2}}{x}\right) f(x)=\frac{x}{1-x}+\frac{1}{x}$, which simplifies to $\frac{x^{2}-x+1}{x} f(x)=\frac{x^{2}-x+1}{x(1-x)}$, or $f(x)=\frac{1}{1-x}$. Therefore, $f\left(\frac{2016}{2017}\right)=2017$.
|
2017
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. From point $A$ to point $B$, which are 10 km apart, a car departed at 7:00. After traveling $2 / 3$ of the distance, the car passed point $C$, from which a cyclist immediately set off for point $A$. As soon as the car arrived at $B$, a bus immediately departed from $B$ in the opposite direction and arrived at $A$ at 9:00. At what distance from $B$ did the bus catch up with the cyclist, if the cyclist arrived at point $A$ at 10:00 and the speed of each participant in the movement was constant?
|
Answer: 6.
Solution. Let's plot the graphs of the car's movement (segment $K L$), the bus's movement (segment $L M$), and the cyclist's movement (segment $N P$) on the axes $(t ; s)$, where $t$ is time (in hours) and $s$ is the distance (in kilometers) from point $A$. Let $Q$ be the intersection point of $L M$ and $N P$. According to the problem, $M K=2$ and $P M=1$. Draw $M G \| N Q, G \in K L$, then by Thales' theorem, $\frac{N G}{G K}=\frac{P M}{M K}=\frac{1}{2}$. Therefore, if $N G=2 x$, then $G K=4 x$, and $L N=3 x$. Hence (again by Thales' theorem) $\frac{L Q}{Q M}=\frac{L N}{N G}=\frac{3 x}{2 x}=\frac{3}{2}$. Therefore, the required distance is $\frac{3}{5} \cdot 10=6$ km.
Participants familiar with Menelaus' theorem can solve the problem as follows. Points $N, Q$, and $P$ lie on the same line, so $\frac{K N}{N L} \cdot \frac{L Q}{Q M} \cdot \frac{M P}{P K}=1$, or $\frac{2}{1} \cdot \frac{L Q}{Q M} \cdot \frac{1}{3}=1$. Therefore, $\frac{L Q}{Q M}=\frac{3}{2}$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Find the sum of all integers \( x \in [-3 ; 13] \) that satisfy the inequality
$$
\left(1-\operatorname{ctg}^{2} \frac{\pi x}{12}\right)\left(1-3 \operatorname{ctg}^{2} \frac{\pi x}{12}\right)\left(1-\operatorname{tg} \frac{\pi x}{6} \cdot \operatorname{ctg} \frac{\pi x}{4}\right) \leqslant 16
$$
|
Answer: 28.
Solution. Let $t=\frac{\pi x}{12}$, then the inequality takes the form
$$
\left(1-\operatorname{ctg}^{2} t\right)\left(1-3 \operatorname{ctg}^{2} t\right)(1-\operatorname{tg} 2 t \cdot \operatorname{ctg} 3 t) \leqslant 16
$$
Since
$$
\begin{gathered}
1-\operatorname{ctg}^{2} t=-\frac{\cos 2 t}{\sin ^{2} t}, \quad 1-3 \operatorname{ctg}^{2} t=\frac{\sin ^{2} t-3 \cos ^{2} t}{\sin ^{2} t}=\frac{4 \sin ^{2} t-3}{\sin ^{2} t}=-\frac{\sin 3 t}{\sin ^{3} t} \\
1-\operatorname{tg} 2 t \cdot \operatorname{ctg} 3 t=1-\frac{\sin 2 t \cdot \cos 3 t}{\cos 2 t \cdot \sin 3 t}=\frac{\sin t}{\cos 2 t \cdot \sin 3 t}
\end{gathered}
$$
the inequality reduces to $\frac{1}{\sin ^{4} t} \leqslant 16$, that is, $|\sin t| \geqslant \frac{1}{2}$. Therefore, $t \in\left[\frac{\pi}{6}+\pi n ; \frac{5 \pi}{6}+\pi n\right]$, $n \in \mathbb{Z}$. It is also necessary to take into account the conditions $\sin t \neq 0, \cos 2 t \neq 0, \sin 3 t \neq 0$. Thus, the points $\frac{\pi}{4}+\frac{\pi k}{2}$ and $\pm \frac{\pi}{3}+\pi k, k \in \mathbb{Z}$ need to be excluded from the obtained solution. Therefore, $x \in$ $[2+12 n ; 10+12 n], x \neq 3+6 n, x \neq \pm 4+12 n$. In the interval $[-3 ; 13]$, the numbers $-2,2,5,6,7$, 10 fall. Their sum is 28.
|
28
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find the smallest natural number $n$ for which the decimal representation of $n$ together with $n^{2}$ uses all the digits from 1 to 9 exactly once.
|
Answer: 567.
Solution: If $n \geqslant 1000$, then $n^{2} \geqslant 10^{6}$, so the decimal representations of $n$ and $n^{2}$ together contain at least 11 digits. If, however, $n \leqslant 316$, then $n^{2} \leqslant 99856$, and the decimal representations of $n$ and $n^{2}$ together contain no more than 8 digits. Therefore, $317 \leqslant n \leqslant 999$.
The sum of all digits from 1 to 9 is 45 and is divisible by 9, so $n+n^{2}$ is also divisible by 9. Since $n+n^{2}=n(n+1)$ is the product of two consecutive numbers, it is divisible by 9 only in two cases: 1) $n$ is divisible by 9; 2) $n+1$ is divisible by 9, i.e., $n$ has a remainder of 8 when divided by 9.
The first such numbers greater than 316 are 323 and 324. Therefore, the desired numbers lie in the arithmetic progressions $323+9 k$ and $324+9 k, k \in \mathbb{N}$. Moreover, the decimal representation of $n$ should not contain identical digits or the digit 0, and it should not end in 1, 5, or 6 (otherwise, its square would end in the same digit). Additionally, if $n$ contains the digit 4 and ends in 2 or 8, it is also not suitable, as then $n^{2}$ would end in 4. Taking this into account, we will sequentially list the remaining possible values of $n \geqslant 317$ in a table:
| $n$ | $n^{2}$ |
| :---: | :---: |
| 324 | 104976 |
| 359 | 128881 |
| 368 | 135424 |
| 369 | 136161 |
| $n$ | $n^{2}$ |
| :---: | :---: |
| 378 | 142884 |
| 387 | 149769 |
| 413 | 170569 |
| 423 | 178929 |
| $n$ | $n^{2}$ |
| :---: | :---: |
| 459 | 210681 |
| 467 | 218089 |
| 512 | 262144 |
| 513 | 263169 |
| $n$ | $n^{2}$ |
| :---: | :---: |
| 539 | 290521 |
| 549 | 301401 |
| 567 | 321489 |
| $\cdots$ | $\ldots$ |
Among the checked numbers, the first one that satisfies the condition of the problem is the number 567. Similarly, by checking possible values of $n \leqslant 999$ "from the end," the largest such number can be found, which is 854 (in this case, the search can be shortened by noting that for $n \geqslant 953$, the decimal representation of $n^{2} \geqslant 908209$ also contains the digit 9).
|
567
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find a two-digit number, the digits of which are different and the square of which is equal to the cube of the sum of its digits.
|
Answer: 27.
Solution: Let's write the condition as $\overline{A B}^{2}=(A+B)^{3}$. Note that the sum of the digits $(A+B)$ does not exceed 17, i.e., $\overline{A B}^{2} \leq 17^{3}$. Moreover, this number $\overline{A B}^{2}=n^{6}$, where $n$ is some natural number that does not exceed 4. However, 1 and 2 do not work because their cubes are single-digit numbers. Only 3 and 4 remain, and direct verification shows that $27^{2}=(2+7)^{3}=729$
|
27
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a circle, 100 points are marked, painted either red or blue. Some of the points are connected by segments, with each segment having one blue end and one red end. It is known that no two red points belong to the same number of segments. What is the maximum possible number of red points?
|
Answer: 50.
Solution: Take 50 red and 50 blue points. The first red point is not connected to any other, the second is connected to one blue, ..., the 50th is connected to 49 blues. Obviously, there cannot be more than 50 red points, because if there are 51 or more, then there are no more than 49 blues, hence the number of connection options is no more than 50, i.e., (by the pigeonhole principle) some two red points will belong to the same number of segments.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many diagonals in a regular 32-sided polygon are not parallel to any of its sides
|
Answer: 240.
Solution: In a 32-sided polygon, there are $32*(32-3)/2=464$ diagonals in total. We can divide the sides into 16 pairs of parallel sides. It is not hard to notice that if we fix a pair, i.e., 4 vertices, the remaining vertices can be connected in pairs by diagonals parallel to this pair. There will be a total of (32-4)/2 = 14 such diagonals. Therefore, the number of diagonals parallel to any side is $14 * 16=224$. The number of diagonals not parallel to any side is $464-224=240$.
|
240
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. For natural numbers $m$ and $n$, it is known that $3 n^{3}=5 m^{2}$. Find the smallest possible value of $m+n$.
|
Answer: 60.
Solution: Obviously, if $m, n$ contain prime factors other than 3 or 5, then they can be canceled out (and reduce $\mathrm{m}+\mathrm{n}$).
Let $n=3^{a} \cdot 5^{b}, m=3^{c} \cdot 5^{d}$. Then the condition implies that $3 a+1=2 c, 3 b=2 d+1$. The smallest possible values are: $a=1, b=1, c=2, d=1$, from which $n=15, m=45$.
|
60
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. On the Island of Misfortune, there live knights who always tell the truth, and liars who always lie. One day, a tourist met five inhabitants of the island and asked them: "How many liars are there among you?" The first answered: "One," the second answered: "Two," the third answered: "Three," the fourth answered: "Four," the fifth answered: "Five." How many liars were there in reality?
|
Answer: 4.
Solution: Among the islanders surveyed, exactly one is a knight, since they all gave different, and all possible answers. Then the remaining four are liars.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. On a grid paper, a square made up of several cells is shaded, with its sides lying on the grid lines. It is known that to get a larger square under the same condition, 47 more cells need to be shaded. Find the side length of the original square.
|
Answer: 23.
Solution. If the side of the original square was $n$, and the side of the obtained square became larger by $k$, then to obtain it, one needs to color $(n+k)^{2}-n^{2}=2 n k+k^{2}$ cells, i.e., $2 n k+k^{2}=47$. Therefore, $k$ is odd, and $k^{2}<47$, so $k \leqslant 5$. If $k=5$, then $10 n+25=47$, and $n$ is not an integer. If $k=3$, then $k=3$, then $6 n+9=47$, and again we get a non-integer $n$. If, however, $k=1$, then $2 n+1=47$, from which $n=23$.
|
23
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. At a sumo wrestling tournament, 20 sumo-tori (sumo wrestlers) arrived. After weighing, it was found that the average weight of the sumo-tori is 125 kg. What is the maximum possible number of wrestlers who weigh more than 131 kg, given that according to sumo rules, people weighing less than 90 kg cannot participate in the competition?
|
Answer: 17.
Solution: Let $n$ be the number of sumo-tori that weigh more than 131 kg. Their total weight is more than $131 n$ kg, and the total weight of the remaining ones is no less than $90(20-n)$. Therefore, $\frac{131 n+90(20-n)}{20}<125$, from which $41 n<35 \cdot 20$, i.e., $n<\frac{700}{41}=17 \frac{3}{41}$. The largest integer $n$ satisfying this condition is 17. If 17 sumo-tori weigh $131 \frac{3}{17}$ kg each, and the remaining 3 weigh 90 kg each, the conditions of the problem are met.
|
17
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Once, in a company, the following conversation took place:
- We must call Misha immediately! - exclaimed Vanya.
However, no one remembered Misha's phone number.
- I remember for sure that the last three digits of the phone number are consecutive natural numbers, - said Nastya.
- And I recall that the first five digits formed a palindrome, - noted Anton.
- Seven-digit numbers are not memorized as a whole; they are broken down into three groups: first three digits, and then two groups of two digits each. I think the three-digit number obtained in this way was divisible by 9 - remarked Nikita.
- That's right, - supported Mitya, - and there were three consecutive ones in the phone number.
- Only one of the two-digit numbers obtained by Nikita's method was prime, - added Sasha.
Help the guys restore Misha's phone number.
|
Answer: 7111765.
Solution. Note that three consecutive ones cannot stand at the beginning, as 111 is not divisible by 9. Therefore, among the first three digits, there is one that is different from one. If this is the second or third digit, then since the first five form a palindrome and the last three are consecutive natural numbers, there will be no three consecutive ones in the number. Therefore, the second, third, and fourth digits are ones, then the first and fifth are sevens. This means that the first two-digit number in the Nikitin partition is 17 (a prime number). The last three digits will be consecutive natural numbers if the second two-digit number is 89 or 65. But since 89 is a prime number, the only option left is 65. Therefore, the desired number is 7111765.
|
7111765
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. From one point on a circular track, a pedestrian and a cyclist started simultaneously in the same direction. The cyclist's speed is $55\%$ greater than the pedestrian's speed, and therefore the cyclist overtakes the pedestrian from time to time. At how many different points on the track will the overtakes occur?
|
Answer: 11.
Solution: Let's assume the length of the path is 55 (in some units), and the speeds of the pedestrian and the cyclist are $100 x$ and $155 x$. Then, the overtakes will occur every $1 / x$ units of time. During this time, the pedestrian covers 100 units, which means he will be 10 units away in the opposite direction from the start. This will happen at each overtake. At the 11th overtake, the pedestrian will have covered 1100 units and will be back at the starting point, after which the overtake points will start repeating.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. We will call a natural number interesting if all its digits, except the first and last, are less than the arithmetic mean of the two adjacent digits. Find the largest interesting number.
|
Answer: 96433469.
Solution. Let $a_{n}$ be the n-th digit of the desired number. By the condition, $a_{n}9$. Similarly, there cannot be four negative differences. Therefore, the maximum number of such differences can be 7, and the desired number is an eight-digit number. To make it the largest, the first digit should be 9, and the first differences between the digits should be as small as possible. If the differences are sequentially $3,2,1,0,-1,-2,-3$, then we get the answer: 96433469.
|
96433469
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Find the smallest natural solution of the inequality $2^{x}+2^{x+1}+\ldots+2^{x+2000}>2^{2017}$. Answer. 17.
|
Solution. The value $x=17$ is clearly a solution. If $x \leqslant 16$, then we have
$$
2^{x}+2^{x+1}+\ldots+2^{x+2000} \leqslant 2^{16}+2^{17}+\ldots+2^{2015}+2^{2016}<2^{2017}
$$
since this inequality reduces sequentially to the following: $2^{16}+2^{17}+\ldots+2^{2015}<$ $2^{2017}-2^{2016}=2^{2016}, 2^{16}+2^{17}+\ldots+2^{2014}<2^{2016}-2^{2015}=2^{2015}, \ldots, 2^{16}+2^{17}<2^{19}-2^{18}=2^{18}$, $2^{16}<2^{18}-2^{17}=2^{17}$, which is true.
|
17
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. First-grader Petya was laying out a contour of an equilateral triangle with the tokens he had, so that each of its sides, including the vertices, contained the same number of tokens. Then, with the same tokens, he managed to lay out the contour of a square in the same way. How many tokens does Petya have, if each side of the square contains 2 tokens less than each side of the triangle?
|
Answer: 24.
Solution. Let the side of the triangle contain $x$ chips, and the side of the square - $y$ chips. The total number of chips, counted in two ways, is $3 x-3=4 y-4$ (we account for the corner chips being counted twice). From the problem statement, it follows that $y=x-2$. Therefore, we get the equation $3(x-1)=4(x-3)$, from which $x=9$. Thus, the total number of chips is $3 \cdot 9-3=24$.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Petrov and Vasechkin were solving the same arithmetic problem. A certain number had to be divided by 2, multiplied by 7, and 1001 subtracted. Petrov performed all the operations correctly, while Vasechkin got everything mixed up: he divided by 8, squared the result, and also subtracted 1001. It is known that Petrov got a prime number. What number did Vasechkin get?
|
Answer: 295.
Solution. Note that the number 1001 is divisible by 7 without a remainder. This means that the number Petrov obtained must be divisible by 7. But it is a prime number, so Petrov got 7. Let's reverse the operations Petrov performed and find the original number: $\frac{7+1001}{7} \cdot 2=288$. Now, let's repeat Vasechkin's operations with it: $(288: 2)^{2}-1001=295$.
|
295
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The numbers from 1 to 8 are arranged at the vertices of a cube such that the sum of the numbers in any three vertices lying on the same face is at least 10. What is the smallest possible sum of the numbers at the vertices of one face?
|
Answer: 16.
Solution. Each face has a vertex where a number not less than 6 is placed. Indeed, otherwise, one of the triples of the remaining largest numbers $2,3,4,5$ would give a sum less than 10 (specifically, the triple $2,3,4$ with a sum of 9).
Consider a face containing the vertex where the number 6 is placed. Since the sum of the numbers in the other three vertices is not less than 10, the sum of all numbers in the vertices of this face is not less than 16.
An example of an arrangement where the smallest sum of numbers in the vertices of one face is 16 is shown in the figure: the sum of the numbers in the
front face is $2+3+5+6=16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On graph paper (the side of a cell is 1 cm) a rectangle is drawn, the sides of which lie on the grid lines, with one side being 5 cm shorter than the other. It turned out that it can be cut into several pieces along the grid lines and form a square from them. What can the side of this square be? Find all possible values.
#
|
# Answer: 6 cm.
Solution. Let the larger side of the rectangle be $k$ cm, $k>5$, and the side of the obtained square be $n$ cm. Then, from the equality of areas, we get $k(k-5)=n^{2}$. Note that $k^{2}-5k=k^{2}-6k+9=(k-3)^{2}$ for $k>9$. Therefore, $6 \leqslant k \leqslant 9$. For $k=6,7,8,9$, we get that $k(k-5)$ equals $6 \cdot 1=6, 7 \cdot 2=14, 8 \cdot 3=24, 9 \cdot 4=36$ respectively. Among these values, only the last one is a square of a natural number, and $n=6$. The rectangle $9 \times 4$ can be cut along the grid lines and assembled into a square $6 \times 6$ in many ways.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. All natural numbers, the sum of the digits of each of which is equal to 5, were arranged in ascending order. What number is in the 125th place?
Otvet: 41000.
|
Solution. Let's calculate the number of $n$-digit numbers, the sum of the digits of each of which is equal to 5, for each natural $n$. Subtract 1 from the leading digit, we get a number (which can now start with zero), the sum of the digits of which is equal to 4. Represent the digits of this number as cells, in each of which there is a number of balls equal to the digit in the corresponding place. Distributing 4 balls into $n$ cells is the same as placing $n-1$ partitions between 4 balls (there may be no balls between some partitions). This can be done in $C_{n+3}^{4}=\frac{(n+3)(n+2)(n+1) n}{24}$ ways, which is also the number of the sought $n$-digit numbers.
For $n=1,2,3,4,5$ we get respectively $C_{4}^{4}=1, C_{5}^{4}=5, C_{6}^{4}=15, C_{7}^{4}=35, C_{8}^{4}=70$, totaling 126 numbers. The number 50000, the largest five-digit number of this kind, stands at the 126th place. Therefore, the previous one, 41000, stands at the 125th place.
|
41000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Find the integer part of the number $a+\frac{9}{b}$, where $a$ and $b-$ are respectively the integer and fractional part of the number $\sqrt{76-42 \sqrt{3}}$.
|
Answer: 12.
Solution. The given number is $\sqrt{76-42 \sqrt{3}}=\sqrt{(7-3 \sqrt{3})^{2}}=7-3 \sqrt{3}=1+(6-3 \sqrt{3})$, where $6-3 \sqrt{3} \in(0 ; 1)$. Therefore, $a=1, b=6-3 \sqrt{3}$. Thus, $a+\frac{9}{b}=1+\frac{9}{6-3 \sqrt{3}}=1+\frac{3}{2-\sqrt{3}}=1+3(2+\sqrt{3})=7+3 \sqrt{3}$. Since $12<7+3 \sqrt{3}<13$, the integer part of the number $a+\frac{9}{b}$ is 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. For the sequence $\left\{a_{n}\right\}$, it is known that $a_{1}=1.5$ and $a_{n}=\frac{1}{n^{2}-1}$ for $n \in \mathbb{N}, n>1$. Are there such values of $n$ for which the sum of the first $n$ terms of this sequence differs from 2.25 by less than 0.01? If yes, find the smallest one.
|
Answer: yes, $n=100$.
Solution. The general formula for the terms of the sequence (except the first) can be written as $(n \geqslant 2)$:
$$
a_{n}=\frac{1}{n^{2}-1}=\frac{1}{2}\left(\frac{1}{n-1}-\frac{1}{n+1}\right)
$$
As a result, the sum of the first $n$ terms of the sequence, except the first, takes the form:
$$
\begin{aligned}
& \frac{1}{2}\left[\left(1-\frac{1}{3}\right)+\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\left(\frac{1}{4}-\frac{1}{6}\right)+\left(\frac{1}{5}-\frac{1}{7}\right)+\right. \\
& \left.\quad+\ldots+\left(\frac{1}{n-3}-\frac{1}{n-1}\right)+\left(\frac{1}{n-2}-\frac{1}{n}\right)+\left(\frac{1}{n-1}-\frac{1}{n+1}\right)\right]
\end{aligned}
$$
After simplifications, for the sum of the first $n$ terms of the sequence, we can write:
$$
S_{n}=1.5+\frac{1}{2}\left[1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}\right]=2.25-\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)
$$
Let $f(n)=\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)$. Then since $f(n)$ is decreasing and
$$
\begin{aligned}
f(100) & =\frac{1}{2}\left(\frac{1}{100}+\frac{1}{101}\right)\frac{1}{2}\left(\frac{1}{100}+\frac{1}{100}\right)=\frac{1}{100}
\end{aligned}
$$
the desired value of $n$ is 100.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. How many values of the parameter $a$ exist for which the equation
$$
4 a^{2}+3 x \lg x+3 \lg ^{2} x=13 a \lg x+a x
$$
has a unique solution
|
Answer: 2.
Solution. The given equation is equivalent to the equation $(3 \lg x-a)(x+\lg x-4 a)=0$, from which we have the system
$$
\left[\begin{array}{l}
\lg x=\frac{a}{3} \\
x+\lg x=4 a
\end{array}\right.
$$
Each equation in this system has a unique positive solution for any $a$, since the continuous functions $f_{1}(x)=\lg x$ and $f_{2}(x)=x+\lg x$ are strictly increasing on their domain $(0 ;+\infty)$ and take all possible values from $(-\infty ;+\infty)$. Therefore, it is necessary for these solutions to coincide. Then $x=11 a / 3, \lg x=a / 3$, hence, $10^{a / 3}=11 a / 3$. This equation has exactly two solutions due to the fact that the function $g(t)=10^{t}-11 t$ is strictly decreasing on $(-\infty ; \lg (11 \lg e)]$, strictly increasing on $[\lg (11 \lg e) ;+\infty)$, takes a negative value at the point $t=1$, and positive values at the points $t=0$ and $t=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Can non-negative integers be placed on the faces of two cubes so that when they are randomly thrown, the sum of the points showing can be equal to any divisor of the number 36? If this is possible, indicate the sum of all 12 numbers on the faces; if it is impossible - indicate 0.
|
Answer: The sum is 111. Solution. The numbers $1,2,3,4,5$ and 6 can be placed on the faces of one die, and $0,6,12,18,24,30$ on the faces of the other. Then the sum of the points rolled can be equal to any of the numbers from 1 to 36. The sum of the numbers on all faces is 111. This sum does not depend on how the dice are marked. Since the sum from 1 to 36 is 666, the average (expected value) is $666 / 36=18.5$. On the other hand, the average can be calculated for each die separately, resulting in $S_{1}+S_{2}=111$.
|
111
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all three-digit numbers $\overline{L O M}$, composed of distinct digits $L, O$ and $M$, for which the following equality holds:
$$
\overline{L O M}=(L+O+M)^{2}+L+O+M
$$
|
Answer: 156. Instructions. Let $x=L+O+M$. Then $\overline{L O M}=x(x+1)$. In this case, $x \geq 10$ (otherwise $x(x+1)<100)$ and $x \leq 24$ (the sum of digits does not exceed $9+8+7=24$). Therefore, $x \in[10 ; 24]$. From the relation $100 \cdot L+10 \cdot O+M=x^{2}+L+O+M$ it follows that $x^{2}=99 \cdot L+9 \cdot O$, which means $x$ is divisible by 3. It remains to substitute the values $12,15,18,21$ and 24 into $x(x+1)$ and check the sum of the digits of the resulting number. It matches $x$ only when $x=12$.
|
156
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Pete was given a new electric jigsaw for his birthday, with a function to count the length of the cuts made. To try out the gift, Pete took a square piece of plywood with a side of $50 \mathrm{cm}$ and cut it into squares with sides of 10 cm and squares with sides of 20 cm. How many squares in total were obtained, if the electric jigsaw shows a total length of cuts of 2 m $80 \mathrm{cm}$?
|
Answer: 16. Solution. Each protruding edge is part of the perimeter of two figures, in addition, the perimeter of the original square must be taken into account, from which we get that the total perimeter of the resulting small squares is $280 \cdot 2+200=760$. Now we can denote the number of squares through $x$ and $y$ respectively and solve the system $\left\{\begin{array}{c}10^{2}-x+20^{2}-y=50^{2}, \\ 4-10-x+4 \cdot 20-y=760,\end{array}\right.$, or follow the following reasoning. If all the squares had a side of 10, there would be $6 \mathbf{~} 25$ pieces, then the total perimeter would be $25 \cdot 40=1000$. If we replace four small squares $10 \times 10$ with a square $20 \times 20$, the perimeter will increase by $160-80=80 \mathrm{cm}$. To get 760 from 1000, this needs to be done 3 times. This means there will be 3 squares 20x20 and 13 squares 10x10 - a total of 16 squares.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many four-digit numbers exist that have the following properties: all digits of the number are even; the number is divisible by four, if the last digit is erased, the resulting three-digit number is not divisible by four?
|
Answer: 120. Solution. The last digit of the number must be divisible by 4 (that is, it can be 0, 4 or 8), and the second to last - not (2 or 6). In addition, the first digit is not zero. Therefore, we get $4 \cdot 5 \cdot 2 \cdot 3=120$ variants.
|
120
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.