problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
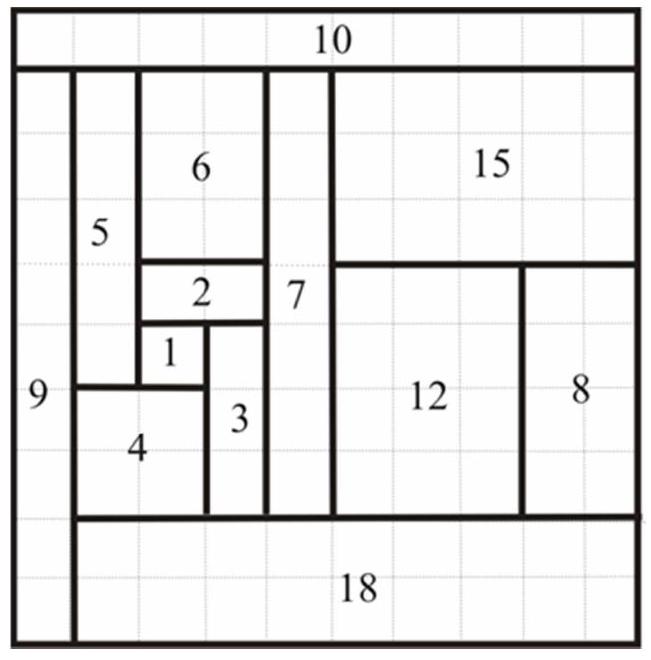
7. What is the minimum number of cells that need to be painted in a square with a side of 35 cells (a $35 \times 35$ square, with a total of 1225 cells), so that among any four of its cells forming a corner (an "L" shape), there is at least one painted cell.
#
|
# Solution.
You should color every 3rd cell diagonally (see the figure). Thus, $\left[\frac{N^{2}}{3}\right]$ cells will be colored. This is the minimum possible number, as within any $3 \times 3$ square, at least three cells need to be colored. $\left[\frac{35^{2}}{3}\right]=408$.

Answer: 408.
|
408
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find the sum of all integer values of c for which the equation $15|p-1|+|3 p-| p+c||=4$ has at least one root with respect to p
#
|
# Solution:
Consider the function $\mathfrak{1} \mathbb{R}=15|\mathrm{p}-1|+|3 \mathrm{p}-| \mathrm{p}+\mathrm{c}||-4 \mathrm{p}$. The coefficient of the first modulus in absolute value is greater than the sum of the other coefficients of $\mathrm{p}$. $15>4+1+3$. Therefore, on all intervals up to $\mathrm{p}=1$, the coefficient of the linear increment is negative, and after $\mathrm{p}=1$ it is positive. $\mathrm{P}=1$ is a point of minimum. For the equation $\mathrm{f}(\mathrm{p})=0$ to have at least one root, it is necessary and sufficient that the inequality:
$\mathrm{f}(1) \leq 0$
$\Rightarrow$ Let $|\mathrm{c}+1|=\mathrm{t} ;|3-\mathrm{t}|-4 \leq 0$
$(3-t)^{2}-4^{2} \geq 0$
$(7-t)(-1-t) \geq 0$
$\mathrm{t} \in[-1 ; 7]$
$|c+1| \leq 7$
Answer: -15.
|
-15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. It is known that the number of occurrences of a certain character in the text is from $10.5\%$ to $11\%$ of the length of the text (the length of the text is understood as the total number of characters in the text). Find the minimum possible length of the text.
#
|
# Solution:
Let the length of the text be L. Let a character appear in the text $x$ times. The problem can be reformulated as: find the smallest natural number $\mathrm{L}$, for which there exists a natural number $x$ such that $\frac{10.5}{100}19$ when $x \geq 3$.
Answer: 19.
## Solution variant № 2
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the arithmetic progression $\left(a_{n}\right)$, $a_{1}=1$, $d=3$.
Calculate $A=\frac{1}{\sqrt{a_{1}}+\sqrt{a_{2}}}+\frac{1}{\sqrt{a_{2}}+\sqrt{a_{3}}}+\ldots+\frac{1}{\sqrt{a_{1579}}+\sqrt{a_{1580}}}$.
In the answer, write the smallest integer greater than $A$.
|
Solution: We transform the expression by multiplying the numerator and denominator of each fraction by the expression conjugate to the denominator:
$$
\begin{aligned}
& A=\frac{1}{\sqrt{a_{1}}+\sqrt{a_{2}}}+\frac{1}{\sqrt{a_{2}}+\sqrt{a_{3}}}+\ldots+\frac{1}{\sqrt{a_{1579}}+\sqrt{a_{1580}}}= \\
& =\frac{\sqrt{a_{2}}-\sqrt{a_{1}}}{a_{2}-a_{1}}+\frac{\sqrt{a_{3}}-\sqrt{a_{2}}}{a_{3}-a_{2}}+\ldots+\frac{\sqrt{a_{1580}}-\sqrt{a_{1579}}}{a_{1580}-a_{1579}}=
\end{aligned}
$$
$=\frac{\sqrt{a_{2}}-\sqrt{a_{1}}}{d}+\frac{\sqrt{a_{3}}-\sqrt{a_{2}}}{d}+\ldots+\frac{\sqrt{a_{1580}}-\sqrt{a_{1579}}}{d}=$
$=\frac{\sqrt{a_{1580}}-\sqrt{a_{1}}}{d}=\frac{\sqrt{a_{1}+1579 d}-\sqrt{a_{1}}}{d}=\frac{\sqrt{1+1579 \cdot 3}-\sqrt{1}}{3}=\frac{\sqrt{4738}-1}{3}$
We estimate the value of $A: \quad 22<\frac{\sqrt{4738}-1}{3}<23$, and write the smallest integer greater than $A$ in the answer.
Answer: 23.
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In rectangle $A B C D$, $A B: A D=1: 2$. Point $M$ is the midpoint of $A B$, and point $K$ lies on $A D$ and divides it in the ratio $3: 1$ starting from point $A$. Find the sum of $\angle C A D$ and $\angle A K M$.
#
|
# Solution:
Complete the rectangle $A B C D$ to a square $A E F D$ with side $A D$.
$$
\begin{aligned}
& \text { Let } L \in E F, E L: L F=1: 3, \\
& \triangle M E L=\triangle A K M \Rightarrow \angle E M L=\angle A K M \\
& N \in F D, F N=N C, M R\|A D \Rightarrow M N\| A C \Rightarrow \\
& \Rightarrow \angle N M R=\angle C A D . \\
& \triangle E M L=\Delta L F N, M L=L N, \angle M L N=90^{\circ} \Rightarrow \\
& \Rightarrow \angle L M N=45^{\circ} \\
& \angle C A D+\angle A K M=\angle N M R+\angle E M L= \\
& =90^{\circ}-\angle L M N=90^{\circ}-45^{\circ}=45^{\circ} .
\end{aligned}
$$
Answer: 45.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are two lead-tin alloys. In the first alloy, the mass of lead is to the mass of tin as $1: 2$; in the second - as $2: 3$. How many grams of the first alloy are needed to obtain 22 g of a new alloy with the mass ratio of lead to tin being 4:7?
|
Solution. Let the first alloy contain x g of lead and 2x g of tin. In the second alloy, there are 2y g of lead and 3y g of tin. Then $k \cdot 3x + n \cdot 5y = 22 ; \frac{kx + n \cdot 2y}{k \cdot 2x + n \cdot 3y} = \frac{4}{7} ; \quad$ we need to find $k \cdot 3x$ and $5ny$. Let $ny = b ; kx = a \cdot \frac{a + 2b}{2a + 3b} = \frac{4}{7} ; 7a + 14b = 8a + 12b ; 2b = a$. Using the first equation $3a + 5b = 22 ; 11b = 22 ; b = 2 ; a = 4$. Therefore, $k \cdot 3x = 12 ; 5ny = 10$.
Answer: 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. What is the minimum number of cells that need to be painted in a square with a side of 35 cells (a total of $35 \times 35$ cells, which is 1225 cells in the square), so that from any unpainted cell it is impossible to move to another unpainted cell with a knight's move in chess?
|
# Solution.
Cells should be shaded in a checkerboard pattern. Thus, $\left[\frac{N^{2}}{2}\right]$ cells will be shaded. Since any "knight's move" lands on a cell of a different color, there is no move to a cell of the same color. A "knight's move" can traverse any square table (larger than $4 \times 4$) such that the knight visits each cell exactly once (see the 5x5 table). If these moves are numbered, it is clear that fewer than $\left[\frac{N^{2}}{2}\right]$ cells cannot be shaded because then there would necessarily be two consecutive unshaded cells in this sequence, i.e., a move from one to the other would be possible. The $35 \times 35$ table needs to be divided into 49 tables of $5 \times 5$, and numbered alternately, starting with the first $5 \times 5$ table. $\left[\frac{35^{2}}{2}\right]=612$.
| 21 | 16 | 5 | 10 | 23 | |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 6 | 11 | 22 | 17 | 4 | |
| 1 | 20 | 15 | 24 | 9 | 26 |
| 12 | 7 | 18 | 3 | 14 | |
| 19 | 2 | 13 | 8 | 25 | |
| | | | | | |
Answer: 612.
|
612
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A table consisting of 2019 rows and 2019 columns is filled with natural numbers from 1 to 2019 such that each row contains all numbers from 1 to 2019. Find the sum of the numbers on the diagonal that connects the top left and bottom right corners of the table, if the filling of the table is symmetric with respect to this diagonal.
#
|
# Solution:
We will show that all numbers from 1 to 2019 are present on the diagonal. Suppose the number $a \in\{1,2,3 \ldots, 2019\}$ is not on the diagonal. Then, due to the symmetry of the table, the number $a$ appears an even number of times. On the other hand, since the number $a$ appears once in each row, the total number of $a$ in the table is odd (2019). This is a contradiction.
There are 2019 cells on the diagonal, so each number from the set $\{1,2, \ldots 2019\}$ will appear exactly once on the diagonal. By calculating the sum of the arithmetic progression, we find the answer.
Answer: 2039190.
|
2039190
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate: $1^{2}-2^{2}+3^{2}-4^{2}+\ldots+2017^{2}$.
|
Solution: $1^{2}-2^{2}+3^{2}-4^{2}+\ldots+2017^{2}=$
$$
\begin{aligned}
& =\left(1^{2}-2^{2}\right)+\left(3^{2}-4^{2}\right)+\ldots+\left(2015^{2}-2016^{2}\right)+2017^{2}= \\
& =(1-2)(1+2)+(3-4)(3+4)+\ldots+(2015-2016)(2015+2016)+2017^{2}= \\
& =-(1+2)-(3+4)-\ldots-(2015+2016)+2017^{2}= \\
& =-(1+2+3+4+\ldots+2015+2016)+2017^{2}= \\
& =-\frac{1+2016}{2} \cdot 2016+2017^{2}=-2017 \cdot 1008+2017^{2}=2017 \cdot(2017-1008)= \\
& =2017 \cdot 1009=2035153
\end{aligned}
$$
Answer: 2035153.
|
2035153
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The train is traveling at a speed of 60 kilometers per hour, making stops every 48 kilometers. The duration of each stop, except the fifth, is 10 minutes, and the fifth stop is half an hour. How far has the train traveled if it departed at noon on September 29 and arrived at its destination on October 1 at 10:00 PM?
|
Solution: The train was on the way for 58 hours.
The train covers a section of 48 kilometers in $\frac{4}{5}$ of an hour.
Let the train make $N$ stops during its journey, then the time of its movement will be $\left(\frac{4}{5}+\frac{1}{6}\right)(N-1)+\left(\frac{4}{5}+\frac{1}{2}\right)+t=58$, where $t$ is the time to cover the last section of the path, which is more than 0 km but no more than 48 km, so $t \in\left(0 ; \frac{4}{5}\right]$. $\left(\frac{4}{5}+\frac{1}{6}\right)(N-1)+\left(\frac{4}{5}+\frac{1}{2}\right)+t=58$ $\frac{29}{30} N+\frac{1}{3}+t=58$ $t=57 \frac{2}{3}-\frac{29}{30} N$ $0<57 \frac{2}{3}-\frac{29}{30} N \leq \frac{4}{5}$ $56 \frac{13}{15} \leq \frac{29}{30} N<57 \frac{2}{3}$ $58 \frac{24}{29} \leq N<59 \frac{19}{29}$
We get that $\mathrm{N}=59, t=57 \frac{2}{3}-\frac{29}{30} \cdot 59=\frac{19}{30}$.
The distance covered by the train, $N \cdot 48+t \cdot 60=59 \cdot 48+\frac{19}{30} \cdot 60=2870$.
Answer: 2870 km.
|
2870
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Calculate $f(2)$, if $25 f\left(\frac{x}{1580}\right)+(3-\sqrt{34}) f\left(\frac{1580}{x}\right)=2017 x$. Round the answer to the nearest integer.
|
Solution: Let's make the substitution: $\mathrm{t}=\frac{x}{1580}$, then the equation will take the form:
$25 f(t)+(3-\sqrt{34}) f\left(\frac{1}{t}\right)=2017 \cdot 1580 \cdot t \quad(1)$,
substitute $\frac{1}{t}$ for $t$ in the equation, we get
$$
25 f\left(\frac{1}{t}\right)+(3-\sqrt{34}) f(t)=2017 \cdot 1580 \cdot \frac{1}{t}
$$
Solve the system of equations
$$
\begin{aligned}
& \left\{\begin{array}{l}
25 f(t)+(3-\sqrt{34}) f\left(\frac{1}{t}\right)=2017 \cdot 1580 \cdot t \\
25 f\left(\frac{1}{t}\right)+(3-\sqrt{34}) f(t)=2017 \cdot 1580 \cdot \frac{1}{t}
\end{array}\right. \\
& \left\{\begin{aligned}
25^{2} f(t)+25(3-\sqrt{34}) f\left(\frac{1}{t}\right) & =25 \cdot 2017 \cdot 1580 \cdot t \\
(3-\sqrt{34})^{2} f(t)+25(3-\sqrt{34}) f\left(\frac{1}{t}\right) & =2017 \cdot 1580 \cdot(3-\sqrt{34}) \cdot \frac{1}{t}^{, \text { then }}
\end{aligned}\right. \\
& \left(25^{2}-(3-\sqrt{34})^{2}\right) f(t)=25 \cdot 2017 \cdot 1580 \cdot t-2017 \cdot 1580 \cdot(3-\sqrt{34}) \cdot \frac{1}{t} \\
& f(t)=\frac{2017 \cdot 1580\left(25 t-(3-\sqrt{34}) \cdot \frac{1}{t}\right)}{\left(25^{2}-(3-\sqrt{34})^{2}\right)}, \text { then } \\
& f(2)=\frac{2017 \cdot 1580\left(50-(3-\sqrt{34}) \cdot \frac{1}{2}\right)}{\left(25^{2}-(3-\sqrt{34})^{2}\right)}=\frac{2017 \cdot 1580 \cdot(97+\sqrt{34})}{2 \cdot(582+6 \sqrt{34})}=\frac{2017 \cdot 1580}{2 \cdot 6} \\
& f(2)=\frac{2017 \cdot 395}{3}=265571 \frac{2}{3} \approx 265572
\end{aligned}
$$
Answer: 265572.
|
265572
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The number $\overline{6 x 62 y 4}$ is divisible by 11, and when divided by 9, it gives a remainder of 6. Find the remainder when this number is divided by $13 .(15$ points)
|
# Solution
By the divisibility rule for 11, we get
$((x+2+4)-(6+6+y)) \vdots 11$ or $(x-6-y) \vdots 11$
Let's find suitable options: $(0 ; 5)(1 ; 6)(2 ; 7)(3 ; 8)(4 ; 9)(6 ; 0)(7 ; 1)(8 ; 2)$ $(9 ; 3)$.
If the number $\overline{6 x 62 y 4}$ gives a remainder of 6 when divided by 9, then by the divisibility rule for 9 we get
$$
\begin{aligned}
& (6+x+6+2+y+4)-6: 9 \\
& \text { or }(12+x+y) \vdots 9
\end{aligned}
$$
The combination $(6 ; 0)$ fits, so the original number is 666204.
The remainder when this number is divided by 13 is 6.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Buratino, Karabas-Barabas, and Duremar are running along a path around a circular pond. They start simultaneously from the same point, with Buratino running in one direction and Karabas-Barabas and Duremar running in the opposite direction. Buratino runs three times faster than Duremar and four times faster than Karabas-Barabas. After Buratino meets Duremar, he meets Karabas-Barabas 150 meters further. What is the length of the path around the pond?
|
# Solution:
Let the length of the path be S.
Since Buratino runs three times faster than Duremar, by the time they meet, Buratino has run three-quarters of the circle ($3 / 4$ S), while Duremar has run one-quarter. Since Buratino runs four times faster than Karabas-Barabas, by the time they meet, Buratino has run four-fifths of the circle, while Karabas-Barabas has run one-fifth ($1 / 5$ S).
The distance between the meeting points is 150 meters. We get the equation:
$$
\begin{aligned}
& \frac{3}{4} S + 150 + \frac{1}{5} S = S \\
& S = 3000
\end{aligned}
$$
Answer: 3000 meters.
|
3000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At the same time, a cyclist leaves point $A$ for point $B$ at a speed of $15 \mathrm{km} / \mathrm{u}$, and a tourist leaves point $B$ for point $C$ at a speed of 5 km/h. After 1 hour and 24 minutes from the start of their journey, they were at the minimum distance from each other. Find the distance between the points if all three points are equidistant and connected by straight roads. (8 points)
|
Solution: Let $AB = BC = AC = S$. Denote the distance between the cyclist and the tourist as $r = r(t)$, where $t$ is the time from the start of the movement. Then, by the cosine theorem, we have: $r^{2} = (S - 15t)^{2} + (5t)^{2} - 5t(S - 15t)$. To find the time when the distance between the cyclist and the tourist was the smallest, we compute the derivative of the function $r^{2} = r^{2}(t)$:
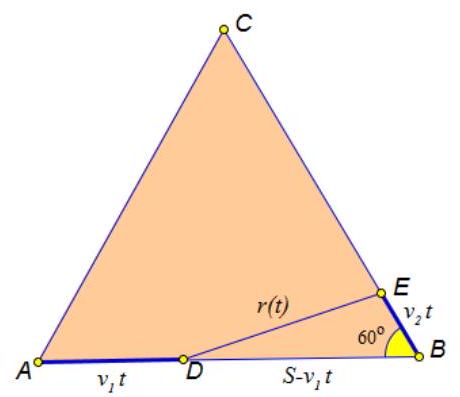
between the start and the movement.
$\left(r^{2}\right)^{\prime} = -2 \cdot 15(S - 15t) + 2 \cdot 25t - 5(S - 15t) + 15 \cdot 5t = -35S + 2(225 + 25 + 75)t = 0$.
Since the minimum value of the function $r^{2} = r^{2}(t)$ during the movement is achieved at $t = 1.4$, then $-35S + (225 + 25 + 75) \cdot 2.8 = 0$, and $S = 26$.
Answer: 26 km.
|
26
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the integers that belong to the set of values of the function $f(x)=\log _{3}(40 \cos 2 x+41)$ for $x \in[(5 / 3)(\operatorname{arctg}(1 / 5)) \cos (\pi-\arcsin (-0.8)) ; \operatorname{arctg} 3]$ (10 points)
|
Solution: Since $\cos (\pi-\arcsin (-0.8))=\cos (\pi+\arcsin 0.8)=-\cos (\arcsin 0.8)=-0.6$, then $x \in[(5 / 3)(\operatorname{arctg}(1 / 5)) \cos (\pi-\arcsin (-0.8)) ; \operatorname{arctg} 3]=[-\operatorname{arctg}(1 / 5) ; \operatorname{arctg} 3]$. $2 x \in[-2 \operatorname{arctg}(1 / 5) ; 2 \operatorname{arctg} 3]$. Since $\quad 0<\operatorname{arctg}(1 / 5)<\operatorname{arctg} 1=\pi / 4, \quad 0<2 \operatorname{arctg}(1 / 5)<\pi / 2$, $-\pi / 2<-2 \operatorname{arctg}(1 / 5)<0$, and also $\pi / 4<\operatorname{arctg} 3<\pi / 2, \pi / 2<2 \operatorname{arctg} 3<\pi$, then $\cos 2 x \in[\cos (2 \operatorname{arctg} 3) ; 1]$. Using the formula $\cos 2 \alpha=\frac{1-\operatorname{tg}^{2} \alpha}{1+\operatorname{tg}^{2} \alpha}$, we get $\cos (2 \operatorname{arctg} 3)=-0.8$, and $\cos 2 x \in[-0.8 ; 1]$. From this, we have $40 \cos 2 x+41 \in[9 ; 81]$, and $f(x)=\log _{3}(40 \cos 2 x+41) \in\left[\log _{3} 9 ; \log _{3} 81\right]=[2 ; 4]$.
The interval $[2 ; 4]$ is the range of the function $f(x)=\log _{3}(40 \cos 2 x+41)$ for $x \in[(5 / 3)(\operatorname{arctg}(1 / 5)) \cos (\pi-\arcsin (-0.8)) ; \operatorname{arctg} 3]$. The sum of the integers in the interval $[2 ; 4]$ is 9.
Answer: $E_{f}=[2 ; 4]$, the sum of the integers is 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the side $AC$ of triangle $ABC$, a circle is constructed with $AC$ as its diameter, which intersects sides $AB$ and $BC$ at points $D$ and $E$ respectively. The angle $EDC$ is $30^{\circ}$, $AE = \sqrt{3}$, and the area of triangle $DBE$ is to the area of triangle $ABC$ as $1:2$. Find the length of segment $BO$, where $O$ is the intersection point of segments $AE$ and $CD$.
|
# Solution:
1) $\angle E D C=\angle E A C=30^{\circ}$ (inscribed angles subtending the same arc);
2) $A C$ - diameter of the circle $\Rightarrow \triangle A E C$ - right triangle, $\angle A E C=90^{\circ}, \angle E C A=60^{\circ}$, $A C=\frac{A E}{\cos 30^{\circ}}=2, E C=A C \sin 30^{\circ}=1$
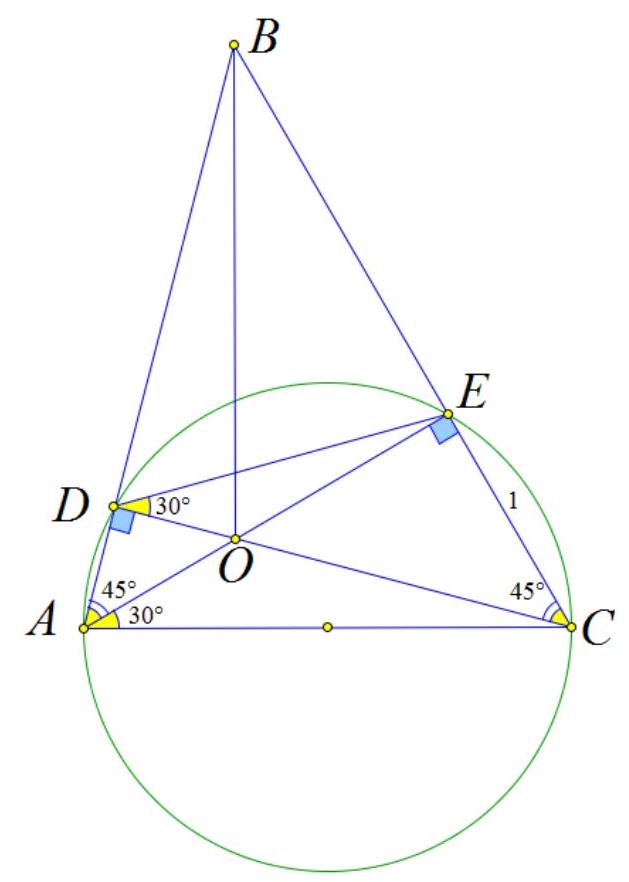
3) $\angle A D C=90^{\circ}, \angle E D C=30^{\circ} \Rightarrow \angle B D E=60^{\circ} \Rightarrow \triangle D B E \approx \triangle C B A \Rightarrow \frac{D E}{A C}=\frac{B D}{B C}=\frac{B E}{A B}=k$, $k^{2}=\frac{S_{D B E}}{S_{A B C}}=\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2}} \Rightarrow D E=\sqrt{2} ;$
4) $\triangle D E C$ - Law of Sines: $\frac{D E}{\sin (\angle D C E)}=\frac{E C}{\sin 30^{\circ}} \Rightarrow \frac{\sqrt{2}}{\sin (\angle D C E)}=2 \Rightarrow \sin (\angle D C E)=\frac{\sqrt{2}}{2}$ $\Rightarrow \angle D C E=45^{\circ} \Rightarrow \triangle E O C$ - isosceles right triangle, $E O=E C=1$;
5) $\angle D A E=45^{\circ} \Rightarrow \triangle A B E$ - isosceles right triangle, $B E=A E=\sqrt{3}$;
6) $\triangle B E O$ - right triangle $\Rightarrow B O^{2}=B E^{2}+E O^{2}$ (Pythagorean theorem) $\Rightarrow$ $B O^{2}=3+1=4 \Rightarrow B O=2$.
Answer: 2 .
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At the same time, a car departs from point $A$ to point $B$ at a speed of 80 km/h, and from point $B$ to point $C$ - a train at a speed of $50 \kappa м / ч$. After 7 hours of travel, they were at the shortest distance from each other. Find the distance between the points, if all three points are equidistant from each other and are connected by straight roads.
|
Solution: Let $AB = BC = AC = S$. Denote the distance between the car and the train as $r = r(t)$, where $t$ is the time from the start of the motion. Then, by the cosine theorem, we have: $r^{2} = (S - 80t)^{2} + (50t)^{2} - 50t(S - 80t)$. To find the time at which the distance between the car and the train was the smallest, we will compute the derivative of the function $r^{2} = r^{2}(t):$
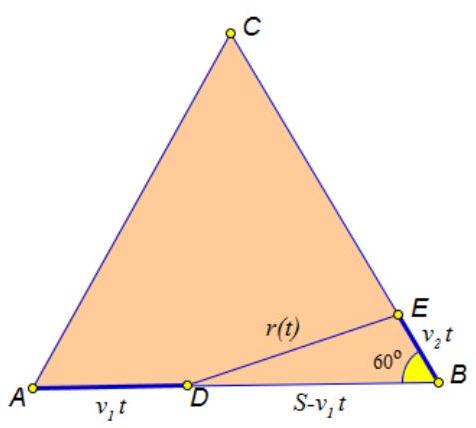
$\left(r^{2}\right)^{\prime} = -2 \cdot 80(S - 80t) + 2 \cdot 2500t - 50(S - 80t) + 80 \cdot 50t = -210S + 2(6400 + 2500 + 4000)t = 0$.
Since the function $r^{2} = r^{2}(t)$ takes its minimum value during the motion at $t = 7$, then $-105S + (6400 + 2500 + 4000) \cdot 7 = 0$, and $S = 860$.
Answer: $860 \kappa m$.
|
860
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the integers that belong to the set of values of the function $f(x)=\log _{3}(10 \cos 2 x+17)$ for $x \in[1,25(\operatorname{arctg} 0.25) \cos (\pi-\arcsin (-0.6)) ; \operatorname{arctg} 3] . \quad(10$ points $)$
|
# Solution:
Since $\quad$ $\cos (\pi-\arcsin (-0.6))=\cos (\pi+\arcsin 0.6)=-\cos (\arcsin 0.6)=-0.8, \quad$ then $x \in[1.25(\operatorname{arctg} 0.25) \cos (\pi-\arcsin (-0.6)) ; \operatorname{arctg} 3]=[-\operatorname{arctg} 0.25 ; \operatorname{arctg} 3] \quad$ Therefore, $2 x \in[-2 \operatorname{arctg} 0.25 ; 2 \operatorname{arctg} 3]$ Since $\quad 0<\operatorname{arctg} 0.25<\operatorname{arctg} 1=\pi / 4, \quad 0<2 \operatorname{arctg} 0.25<\pi / 2$, $-\pi / 2<-2 \operatorname{arctg} 0.25<0, \quad$ and $\quad \pi / 4<\operatorname{arctg} 3<\pi / 2, \quad \pi / 2<2 \operatorname{arctg} 3<\pi, \quad$ then $\cos 2 x \in[\cos (2 \operatorname{arctg} 3) ; 1] . \quad$ Using $\quad$ the formula $\cos 2 \alpha=\frac{1-\operatorname{tg}^{2} \alpha}{1+\operatorname{tg}^{2} \alpha}, \quad$ we get $\cos (2 \operatorname{arctg} 3)=-0.8, \quad$ and $\cos 2 x \in[-0.8 ; 1]$. From this, we have $10 \cos 2 x+17 \in[9 ; 27]$, and $f(x)=\log _{3}(10 \cos 2 x+17) \in\left[\log _{3} 9 ; \log _{3} 27\right]=[2 ; 3]$.
The interval $[2 ; 3]$ is the range of the function $f(x)=\log _{3}(10 \cos 2 x+17)$ for $x \in[1.25(\operatorname{arctg} 0.25) \cos (\pi-\arcsin (-0.6)) ; \operatorname{arctg} 3]$.
The sum of the integers in the interval $[2 ; 3]$ is 5.
Answer: $E_{f}=[2 ; 3]$, the sum of the integers is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the side $AC$ of triangle $ABC$, a circle is constructed with $AC$ as its diameter, which intersects sides $AB$ and $BC$ at points $D$ and $E$ respectively. The angle $EDC$ is $30^{\circ}$, $EC=1$, and the area of triangle $DBE$ is to the area of triangle $ABC$ as $1:2$. Find the length of segment $BO$, where $O$ is the intersection point of segments $AE$ and $CD$.
|
# Solution:
1) $\angle E D C=\angle E A C=30^{\circ}$ (inscribed angles subtending the same arc);
2) $A C$ - diameter of the circle $\Rightarrow \triangle A E C$ - right triangle, $\angle A E C=90^{\circ}, \angle E C A=60^{\circ}$,
$$
A C=\frac{E C}{\sin 30^{\circ}}=2, \quad A E=E C \operatorname{tg} 60^{\circ}=\sqrt{3}
$$
3) $\angle A D C=90^{\circ}, \angle E D C=30^{\circ} \Rightarrow \angle B D E=60^{\circ} \Rightarrow \triangle D B E \approx \triangle C B A \Rightarrow \frac{D E}{A C}=\frac{B D}{B C}=\frac{B E}{A B}=k$, $k^{2}=\frac{S_{D B E}}{S_{A B C}}=\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2}} \Rightarrow D E=\sqrt{2} ;$
4) $\triangle D E C$ - law of sines: $\frac{D E}{\sin (\angle D C E)}=\frac{E C}{\sin 30^{\circ}}$ $\Rightarrow \frac{\sqrt{2}}{\sin (\angle D C E)}=2 \Rightarrow \sin (\angle D C E)=\frac{\sqrt{2}}{2} \Rightarrow$ $\angle D C E=45^{\circ} \Rightarrow \triangle E O C$ - isosceles right triangle, $E O=E C=1$;
5) $\angle D A E=45^{\circ} \Rightarrow \triangle A B E$ - isosceles right triangle, $B E=A E=\sqrt{3}$;
6) $\triangle B E O$ - right triangle $\Rightarrow$ $B O^{2}=B E^{2}+E O^{2}($ Pythagorean theorem $) \Rightarrow$ $B O^{2}=3+1=4 \Rightarrow B O=2$.
Answer: 2 .
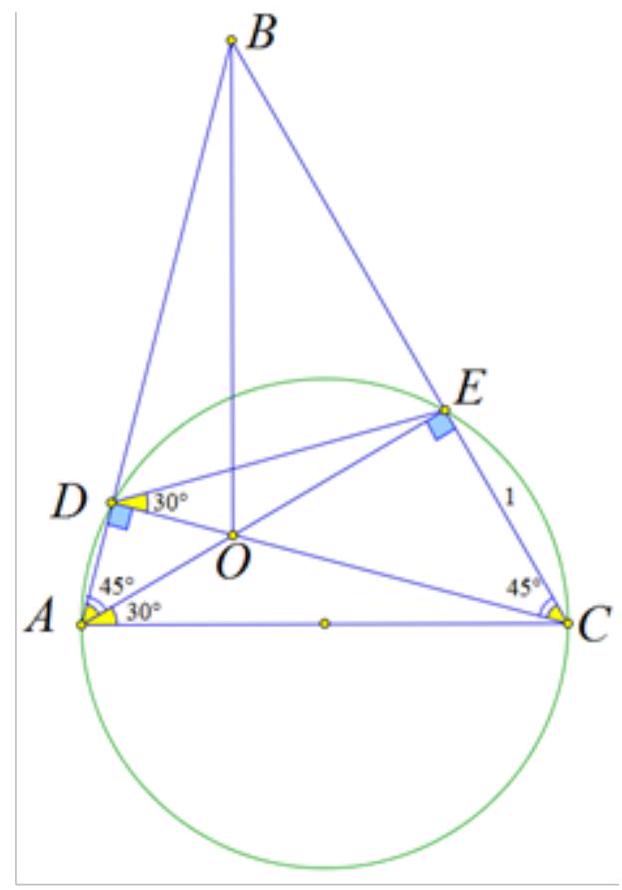
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At the same time, a car departs from point $A$ to point $B$ at a speed of $90 \mathrm{~km} / \mathrm{h}$, and from point $B$ to point $C$ - a train at a speed of $60 \mathrm{~km} /$ h. After 2 hours of travel, they found themselves at the minimum distance from each other. Find the distance between the points, if all three points are equidistant from each other and are connected by straight roads. (8 points)
|
Solution: Let $AB = BC = AC = S$. Denote the distance between the car and the train as $r = r(t)$, where $t$ is the time from the start of the motion. Then, by the cosine theorem, we have: $r^{2} = (S - 90t)^{2} + (60t)^{2} - 60t(S - 90t)$. To find the time at which the distance between the car and the train
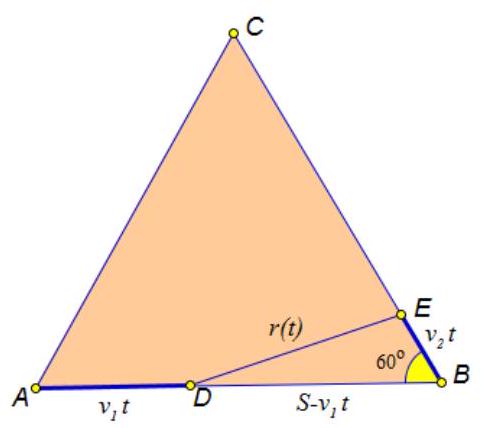
was the smallest, we will compute the derivative of the function $r^{2} = r^{2}(t):$
$\left(r^{2}\right)^{\prime} = -2 \cdot 90(S - 90t) + 2 \cdot 3600t - 60(S - 90t) + 90 \cdot 60t = -240S + 2(8100 + 3600 + 5400)t = 0$.
Since the function $r^{2} = r^{2}(t)$ takes its minimum value during the motion at $t = 2$, then $-120S + (8100 + 3600 + 5400) \cdot 2 = 0$, and $S = 285$.
Answer: 285 km.
|
285
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the integers that belong to the set of values of the function $f(x)=\log _{2}(5 \cos 2 x+11)$ for $x \in[1,25(\operatorname{arctg}(1 / 3)) \cos (\pi+\arcsin (-0.6)) ; \operatorname{arctg} 2] \quad$ (10 points)
|
# Solution:
Since $\quad$ $\cos (\pi+\arcsin (-0.6))=\cos (\pi-\arcsin 0.6)=-\cos (\arcsin 0.6)=-0.8, \quad$ then $x \in[1.25(\operatorname{arctg}(1 / 3)) \cos (\pi+\arcsin (-0.6)) ; \operatorname{arctg} 2]=[-\operatorname{arctg}(1 / 3) ; \operatorname{arctg} 2]$ Therefore, $2 x \in[-2 \operatorname{arctg}(1 / 3) ; 2 \operatorname{arctg} 2]$ Since $\quad 0<\operatorname{arctg}(1 / 3)<\operatorname{arctg} 1=\pi / 4, \quad 0<2 \operatorname{arctg}(1 / 3)<\pi / 2$, $-\pi / 2<-2 \operatorname{arctg}(1 / 3)<0, \quad$ and $\quad \pi / 4<\operatorname{arctg} 2<\pi / 2, \quad \pi / 2<2 \operatorname{arctg} 2<\pi, \quad$ then $\cos 2 x \in[\cos (2 \operatorname{arctg} 2) ; 1] . \quad$ Using the formula $\cos 2 \alpha=\frac{1-\operatorname{tg}^{2} \alpha}{1+\operatorname{tg}^{2} \alpha}, \quad$ we get $\cos (2 \operatorname{arctg} 2)=-0.6, \quad$ and $\quad \cos 2 x \in[-0.6 ; 1]$. From this, we have $5 \cos 2 x+11 \in[8 ; 16]$, and $f(x)=\log _{2}(5 \cos 2 x+11) \in\left[\log _{2} 8 ; \log _{2} 16\right]=[3 ; 4]$.
The interval $[3 ; 4]$ is the range of the function $f(x)=\log _{2}(5 \cos 2 x+11)$ for $x \in[1.25(\operatorname{arctg}(1 / 3)) \cos (\pi+\arcsin (-0.6)) ; \operatorname{arctg} 2]$.
The sum of the integers in the interval $[3 ; 4]$ is 7.
Answer: $E_{f}=[3 ; 4]$, the sum of the integers is 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the side $AC$ of triangle $ABC$, a circle is constructed with $AC$ as its diameter, which intersects sides $AB$ and $BC$ at points $D$ and $E$ respectively. The angle $EDC$ is $30^{\circ}$, the area of triangle $AEC$ is $\sqrt{3} / 2$, and the area of triangle $DBE$ is to the area of triangle $ABC$ as $1: 2$. Find the length of segment $BO$, where $O$ is the intersection point of segments $AE$ and $CD$.
|
Solution:
1) $\angle E D C=\angle E A C=30^{\circ}$ (inscribed angles subtending the same arc);
2) $A C$ - diameter of the circle $\Rightarrow \triangle A E C$ - right-angled, $\angle A E C=90^{\circ}, \angle E C A=60^{\circ}$, $A C=\frac{E C}{\sin 30^{\circ}}=2 E C, A E=E C \operatorname{tg} 60^{\circ}=\sqrt{3} E C ;$ $S_{A E C}=\frac{A E \cdot E C}{2}=\frac{\sqrt{3} E C^{2}}{2}=\frac{\sqrt{3}}{2} \Rightarrow E C=1$, $A C=2, A E=\sqrt{3} ;$
3) $\angle A D C=90^{\circ}, \angle E D C=30^{\circ} \Rightarrow \angle B D E=60^{\circ} \Rightarrow$ $\triangle D B E \approx \triangle C B A \Rightarrow \frac{D E}{A C}=\frac{B D}{B C}=\frac{B E}{A B}=k$, $k^{2}=\frac{S_{D B E}}{S_{A B C}}=\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2}} \Rightarrow D E=\sqrt{2} ;$
4) $\triangle D E C$ - law of sines: $\frac{D E}{\sin (\angle D C E)}=\frac{E C}{\sin 30^{\circ}}$
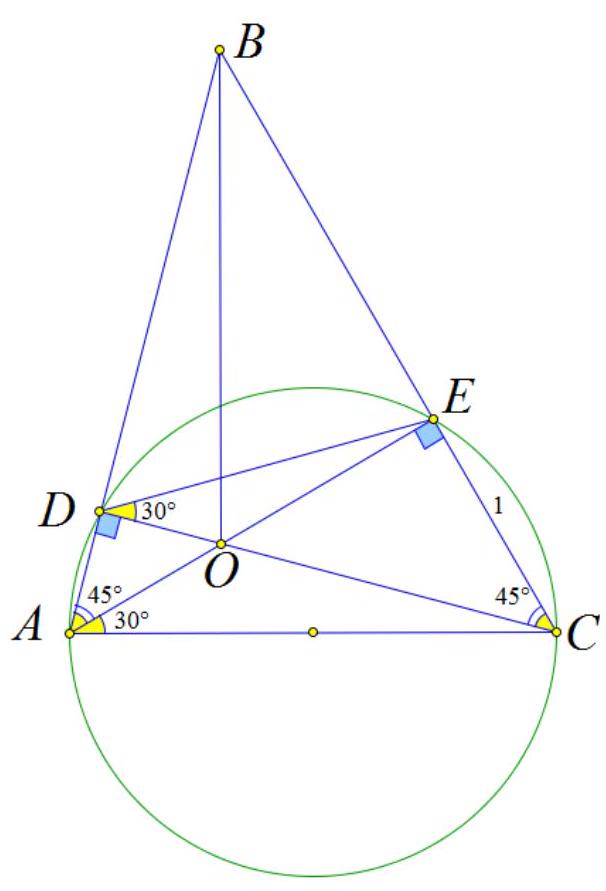
$\Rightarrow \frac{\sqrt{2}}{\sin (\angle D C E)}=2 \Rightarrow \sin (\angle D C E)=\frac{\sqrt{2}}{2} \Rightarrow \angle D C E=45^{\circ} \Rightarrow \triangle E O C$ - isosceles right-angled triangle, $E O=E C=1$;
5) $\angle D A E=45^{\circ} \Rightarrow \triangle A B E$ - isosceles right-angled triangle, $B E=A E=\sqrt{3}$
6) $\triangle B E O$ - right-angled triangle $\Rightarrow B O^{2}=B E^{2}+E O^{2}$ (Pythagorean theorem) $\Rightarrow$ $B O^{2}=3+1=4 \Rightarrow B O=2$.
Answer: 2
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For chemical experiments, two identical test tubes were taken, each containing 200 ml of a liquid substance. From the first test tube, $1 / 4$ of the content was poured out and the same amount of water was added, then this procedure was repeated 3 more times, each time pouring out a quarter of the content of the test tube and adding the same amount of water. A similar procedure was performed twice for the second test tube, each time pouring out a certain amount of the content of the test tube and adding the same amount of water. In the end, the concentration of the resulting mixtures in the first and second test tubes became related to each other as 9/16. Determine how much of the mixture was poured out each time from the second test tube.
(12 points)
|
Solution. The initial amount of the substance is $-V$. After pouring out $a$ part, the concentration of the substance in the test tube becomes $\frac{V-a}{V}$. After the second time, the concentration is $\left(\frac{V-a}{V}\right)^{2}$, and after the fourth time, it is $\left(\frac{V-a}{V}\right)^{4}$. Substituting the data from the problem, we get the ratio $\left(\frac{200-50}{200}\right)^{4}:\left(\frac{200-x}{200}\right)^{2}=\frac{9}{16}$, or $\left(\frac{3}{4}\right)^{4}:\left(\frac{200-x}{200}\right)^{2}=\frac{9}{16} \Rightarrow\left(\frac{3}{4}\right)^{2}:\left(\frac{200-x}{200}\right)^{2}=1 \Rightarrow \frac{200-x}{200}=\frac{3}{4} \Rightarrow x=50$
Answer: 50 ml.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $\quad \sqrt{x+\sqrt{x}-\frac{71}{16}}-\sqrt{x+\sqrt{x}-\frac{87}{16}}=\frac{1}{2}$.
|
Solution. Taking into account that $x$ is non-negative, we make the substitution $u=\sqrt{x+\sqrt{x}-\frac{71}{16}}, v=\sqrt{x+\sqrt{x}-\frac{87}{16}}, u \geq 0, v \geq 0$.
Then we obtain the system $\left\{\begin{array}{l}u-v=1 / 2, \\ u^{2}-v^{2}=1,\end{array} \Rightarrow\left\{\begin{array}{l}u-v=1 / 2, \\ u+v=2,\end{array} \Rightarrow\left\{\begin{array}{l}u=5 / 4, \\ v=3 / 4,\end{array} \Rightarrow\right.\right.\right.$ reverse substitution: $\left\{\begin{array}{l}x+\sqrt{x}-\frac{71}{16}=\frac{25}{16}, \\ x+\sqrt{x}-\frac{87}{16}=\frac{9}{16} .\end{array} \Rightarrow x+\sqrt{x}-6=0 \Rightarrow x=4\right.$.
## Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the maximum possible number of consecutive terms of an increasing geometric progression that can be three-digit natural numbers? Provide an example of such a sequence. (16 points)
|
Solution. Let the required members of the progression be $a_{0}, a_{1}, \ldots, a_{n}, a_{k}=a_{0} q^{k}$, the common ratio - an irreducible fraction $q=r / s, r>s$. Then $a_{0}=b s^{n}, a_{n}=b r^{n}, b \in \mathbb{N}$, since $r^{n}$ and $s^{n}$ are coprime. We obtain the restriction
$$
r^{n}<1000 / b, \quad s^{n} \geq 100 / b
$$
1) Let $r=2$, then $q=2 / 1, (2) \Longrightarrow n \leq 9$. For $n=9$ we have
$$
r=2, \quad s=1, \quad\left\{\begin{array}{c}
a_{0}=b \geq 100 \\
a_{n}=512 b<1000
\end{array} \Longrightarrow b=1\right.
$$
However, $a_{9}=512$ is not a valid solution since $a_{9} \geq 1000$ is required. Thus, $r=2$ is not useful.
2) Let $r=3$, then $q=3 / 2, (2) \Longrightarrow n \leq 5$. For $n=5$ we have
$$
r=3, \quad s=2, \quad\left\{\begin{array}{c}
a_{0}=32 b \geq 100 \\
a_{n}=243 b<1000
\end{array} \Longrightarrow b=4\right.
$$
3) Let $r \geq 4$, then ( 1$) \Longrightarrow n \leq 4$. The record $n=5$ cannot be broken.
Answer: 6. The only example: $128,192,288,432,648,972$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest natural number $m$, for which the expression $148^{n}+m \cdot 141^{n}$ is divisible by 2023 for any odd natural $n$. (16 points)
|
Solution. $2023=7 \cdot 289$, GCD $(7 ; 289)=1$. Since $n-$ is an odd number, then $148^{n}+m \cdot 141^{n}=(289-141)^{n}+m \cdot 141^{n}=289 l+(m-1) 141^{n}, l \in \square$. Then $(m-1) 141^{n}$ must be divisible by 289. Since 289 and 141 are coprime, then $m-1=289 k, k \in\{0\} \cup \square$. On the other hand $148^{n}+m \cdot 141^{n}=148^{n}+m \cdot(148-7)^{n}=7 p+(m+1) 148^{n}, p \in \square$. Since 7 and 148 are coprime, then $m+1=7 s, s \in \square$. Then $m=289 k+1$ and $m=7 s-1$, and $289 k+1=7 s-1$, $289 k+2=7 s, \quad 287 k+2 k+2=7 s, \quad 2 k+2=7(s-41 k)$. The number $(s-41 k)=2 q, q \in \square$, and $k=7 q-1, k \geq 6$. For $k=6$ we have $m=289 \cdot 6+1=1735$, and $s=248$.
Answer: 1735.
|
1735
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. $f(-x)=3(-x)^{3}-(-x)=-3 x^{3}+x=-\left(3 x^{3}-x\right)=-f(x)$ $g(-x)=f^{3}(-x)+f\left(\frac{1}{-x}\right)-8(-x)^{3}-\frac{2}{-x}=-f^{3}(x)-f\left(\frac{1}{x}\right)+8 x^{3}+\frac{2}{x}=-g(x)$
Therefore, $g$ is an odd function $\Rightarrow$ if $x_{0}$ is a root of the original equation, then $-x_{0}$ is also a root of the equation $\Rightarrow$ the sum of the roots is zero, if the roots exist
Check $\quad x=1: \quad f(1)=3 \cdot 1^{3}-1=2, \quad f\left(\frac{1}{1}\right)=f(1)=2, \quad$ substitute $\quad$ into the original equation:10=10 - correct $\Rightarrow x=1$ is a root $\Rightarrow$ the roots exist
|
Answer: 0.
Problem 8 (2nd version).
Find the sum of the roots of the equation $g^{3}(x)-g\left(\frac{1}{x}\right)=5 x^{3}+\frac{1}{x}$, where $g(x)=x^{3}+x$.
## Solution.
Consider the function $f(x)=g^{3}(x)-g\left(\frac{1}{x}\right)-5 x^{3}-\frac{1}{x}$, then the roots of the original equation are the roots of the equation $f(x)=0$.
Investigate the function $f$ for evenness:
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. $g(-x)=(-x)^{3}+(-x)=-x^{3}-x=-\left(x^{3}+x\right)=-g(x)$
$$
f(-x)=g^{3}(-x)-g\left(\frac{1}{-x}\right)-5(-x)^{3}-\frac{1}{-x}=-g^{3}(x)+g\left(\frac{1}{x}\right)+5 x^{3}+\frac{1}{x}=-f(x)
$$
Therefore, $f$ is an odd function $\Rightarrow$ if $x_{0}$ is a root of the original equation, then $-x_{0}$ is also a root of the equation $\Rightarrow$ the sum of the roots is zero, if the roots exist
Check $x=1: g(1)=1^{3}+1=2, g\left(\frac{1}{1}\right)=g(1)=2$, substitute into the original equation: $6=6$ - true $\Rightarrow x=1$ is a root $\Rightarrow$ the roots exist
|
# Answer: 0.
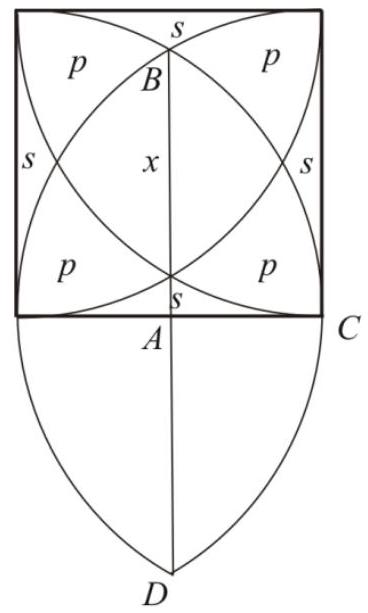
Task 9 (1st variant). In each vertex of an equilateral triangle with side $\sqrt{10}$, circles of radius $\sqrt{5}$ were constructed, the inner areas of which were painted gray, brown, and raspberry. Find the area of the gray-brown-raspberry region.
Solution. By symmetry, the areas of the figures formed by the intersection of the circles and the triangle are equal. The area of the entire triangle is $3 s+3 p+x=\frac{\sqrt{3}}{4} a^{2}=\frac{5 \sqrt{3}}{2}\left(a\right.$-side of the triangle), the area of a sector with an angle of $60^{\circ}$ is $s+2 p+x=\frac{\pi R^{2}}{6}=\frac{5 \pi}{6}$ ( $R$-radius of the circle). From the right triangle DEC we have
$D E=\sqrt{D C^{2}-E C^{2}}=\sqrt{R^{2}-\frac{a^{2}}{4}}=\frac{\sqrt{10}}{2}=E C$.
Therefore, triangle $\quad D E C$
is isosceles and $\angle D C E=45^{\circ}, \quad$ hence,
$\angle D C F=90^{\circ}$ and the area of the sector $D C F$ is
$S_{\text {secm }}=\frac{\pi R^{2}}{4}=\frac{5 \pi}{4}$.
Since the area of triangle $D C F$ is $S_{D C F}=\frac{1}{2} D F \cdot E C=\frac{5}{2}$, the area of the segment with arc
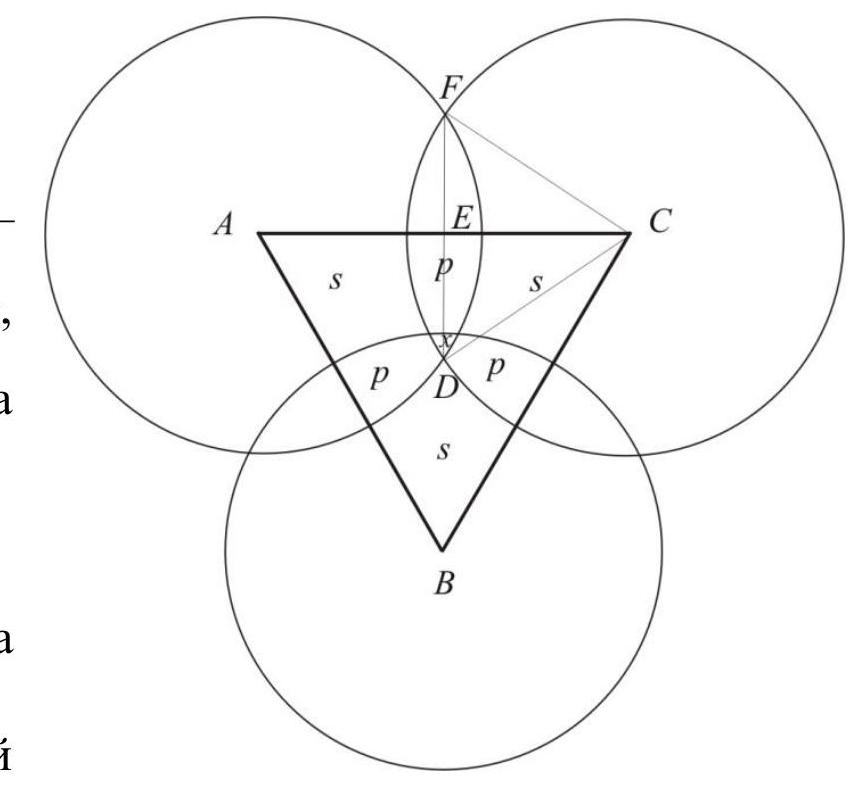
DF is $S_{\text {segm }}=\frac{5 \pi}{4}-\frac{5}{2}$.
Thus, we have the system of equations $\left\{\begin{array}{l}3 s+3 p+x=\frac{5 \sqrt{3}}{2} \\ s+2 p+x=\frac{5 \pi}{6} \\ p+x=\frac{5 \pi}{4}-\frac{5}{2}\end{array}\right.$, solving which, we find that $x=\frac{5 \pi}{4}-\frac{15}{2}+\frac{5 \sqrt{3}}{2}$.
Answer: $\frac{5 \pi}{4}-\frac{15}{2}+\frac{5 \sqrt{3}}{2}$.
Task 9 (2nd variant). In each vertex of a square with side $\sqrt{6}$, circles of radius $\sqrt{6}$ were constructed, the inner areas of which were painted in different colors: gray, brown, raspberry, and polka dot. Find the area of the region painted with all four colors.
Solution. The area of the square is $4 s+4 p+x=R^{2}=6(R$-radius of the circle), the area of a sector with an angle of $90^{\circ}$ is $2 s+3 p+x=\frac{\pi R^{2}}{4}=\frac{3 \pi}{2}$.
The area of the segment with arc $B D$ is the area of the sector with arc $B D$ minus the area of triangle $B C D$, so, $x+2 p+s=\frac{\pi R^{2}}{3}-\frac{1}{2} B D \cdot A C$, from which (considering that for triangle $A B C$ we have $A C=\frac{1}{2} B C$ )
$x+2 p+s=\frac{\pi R^{2}}{3}-\frac{\sqrt{3} R^{2}}{4}$.
We get the system of equations $\left\{\begin{array}{l}4 s+4 p+x=6 \\ 2 s+3 p+x=\frac{3 \pi}{2} \\ x+2 p+s=2 \pi-\frac{3 \sqrt{3}}{2}\end{array}\right.$, solving which, we find that $x=2 \pi-6 \sqrt{3}+6$.
Answer: $2 \pi-6 \sqrt{3}+6$.
Task 10 (1st variant). Given a triangle with sides $2 \sqrt{13}, 2 \sqrt{5}, 8$. On its sides, squares are constructed outward. Find the area of the triangle with vertices at the centers of these squares.
Solution. Let $A B C$ be the given triangle and $A B=2 \sqrt{13}, B C=2 \sqrt{5}, A C=8$. Let $K$, $M, N$ be the centers of the squares constructed on sides $A B, B C, A C$, respectively.
Then, by the cosine theorem for triangles $A K N$ (considering that the diagonals of the square form an angle of $45^{\circ}$ with the sides and $A K=\frac{A B}{\sqrt{2}}, A N=\frac{A C}{\sqrt{2}}$ ) we get
$$
\begin{aligned}
& K N^{2}=A K^{2}+A N^{2}-2 A K \cdot A N \cdot \cos \left(\angle A+\frac{\pi}{2}\right)= \\
& =A K^{2}+A N^{2}+2 A K \cdot A N \cdot \sin \angle A=
\end{aligned}
$$
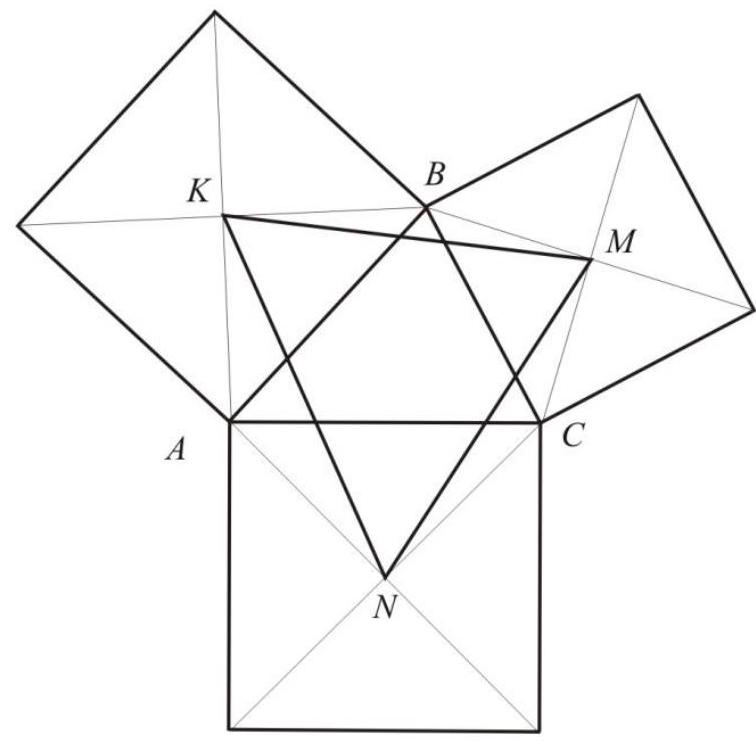
$$
=\frac{A B^{2}}{2}+\frac{A C^{2}}{2}+A B \cdot A C \cdot \sin \angle A=\frac{A B^{2}}{2}+\frac{A C^{2}}{2}+2 S_{A B C}
$$
Similarly, for triangles $B K M, C M N$ we get $K M^{2}=\frac{A B^{2}}{2}+\frac{B C^{2}}{2}+2 S_{A B C}$ and $N M^{2}=\frac{A C^{2}}{2}+\frac{B C^{2}}{2}+2 S_{A B C}$
We find the area of triangle $A B C$. We can calculate this area by first finding the height of the triangle (the height is 4), or by using Heron's formula, we get $S_{A B C}=16$.
Substituting the numerical values, we find, $K N^{2}=90, K M^{2}=68, N M^{2}=74$.
By Heron's formula for the area of a triangle through the squares of its sides, we have $S_{K M N}=\frac{1}{4} \sqrt{4 K M^{2} \cdot M N^{2}-\left(K M^{2}+M N^{2}-K N^{2}\right)^{2}}=33$.
Answer: 33.
Task 10 (2nd variant). Given a triangle with sides $2 \sqrt{13}, 2 \sqrt{5}, 8$. On its sides, squares are constructed inward. Find the area of the triangle with vertices at the centers of these squares.
Solution. Let $A B C$ be the given triangle and $A B=2 \sqrt{13}, B C=2 \sqrt{5}, A C=8$. Let $K$, $M, N$ be the centers of the squares constructed on sides $A B, B C, A C$, respectively.
Then, by the cosine theorem for triangles $A K N$ (considering that the diagonals of the square form an angle of $45^{\circ}$ with the sides and $\left.A K=\frac{A B}{\sqrt{2}}, A N=\frac{A C}{\sqrt{2}}\right)$ we get
$$
\begin{aligned}
& K N^{2}=A K^{2}+A N^{2}-2 A K \cdot A N \cdot \cos \left(\frac{\pi}{4}-\left(\angle A-\frac{\pi}{4}\right)\right)= \\
& =A K^{2}+A N^{2}-2 A K \cdot A N \cdot \sin \angle A= \\
& =\frac{A B^{2}}{2}+\frac{A C^{2}}{2}-A B \cdot A C \cdot \sin \angle A=\frac{A B^{2}}{2}+\frac{A C^{2}}{2}-2 S_{A B C}
\end{aligned}
$$
Similarly, for triangles $B K M, C M N$ we get $K M^{2}=\frac{A B^{2}}{2}+\frac{B C
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. In triangle $\mathrm{KLM}$ with angle $\mathrm{L}=120^{\circ}$, the angle bisectors LA and $\mathrm{KB}$ of angles KLM and LKM are drawn respectively. Find the measure of angle KBA.
|
# Solution.
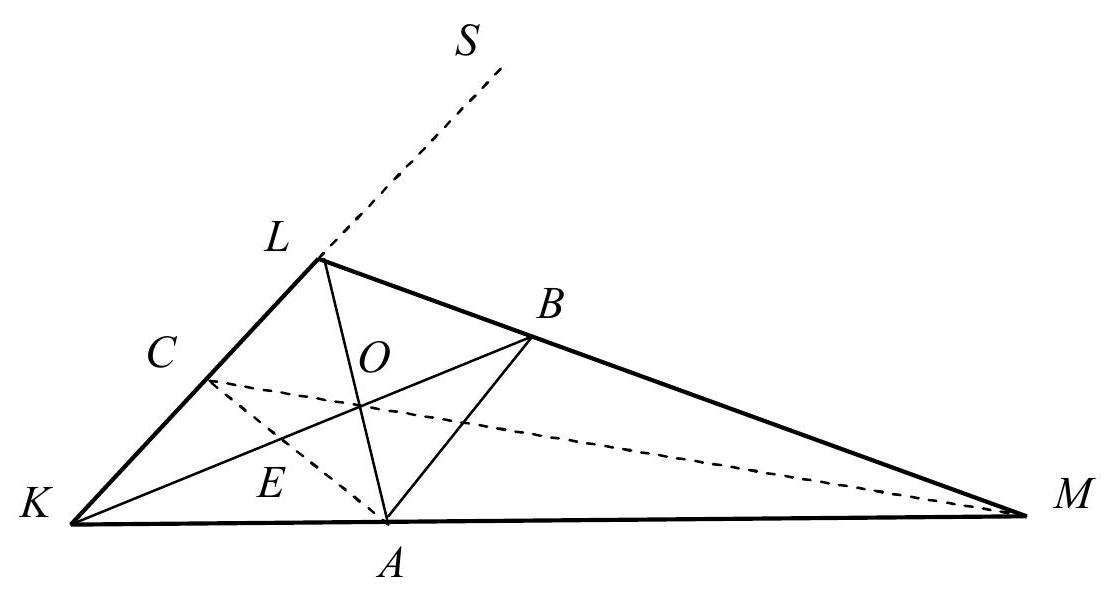
1). Let KS be the extension of KL beyond point L. Then LM is the bisector of angle MLS, since $\angle M L S = \angle M L A = \angle A L K = 60^{\circ}$. Point B is the intersection of the bisectors LM and KB of angles SLA and SKM, respectively $\Rightarrow$ the intersection of the bisectors of the external angles of triangle KLA $\Rightarrow \mathrm{AB}$ is the bisector of angle LAM.
2). Similarly, it can be proven that AC is the bisector of angle LAK, but angles LAM and LAK are adjacent $\Rightarrow \angle C A B = 90^{\circ}$.
3). In triangle KLA: E is the point of intersection of the bisectors $\Rightarrow$ $\angle K E A = \frac{1}{2} \angle K L A + 90^{\circ} = \frac{1}{2} 60^{\circ} + 90^{\circ} = 120^{\circ} \Rightarrow \angle B E A = 180^{\circ} - 120^{\circ} = 60^{\circ}$.
4). In triangle ВЕА: $\angle A = 90^{\circ} \Rightarrow \angle B = 180^{\circ} - 90^{\circ} - 60^{\circ} = 30^{\circ}$.
Answer: $\angle K B A = 30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A pedestrian left point $A$ for point $B$, and after some delay, a second pedestrian followed. When the first pedestrian had walked half the distance, the second had walked 15 km, and when the second pedestrian had walked half the distance, the first had walked 24 km. Both pedestrians arrived at point $B$ simultaneously. What is the distance between points $A$ and $B$?
|
# Solution:
Let $s$ be the distance between points $A$ and $B$, and $v_{1}, v_{2}$ be the speeds of the pedestrians. Then $\frac{s}{2 v_{1}}=\frac{s-15}{v_{2}}$ and $\frac{s-24}{v_{1}}=\frac{s}{2 v_{2}}$. From this, $\frac{s}{2(s-24)}=\frac{(s-15) \cdot 2}{s} ; s^{2}=4 s^{2}-4 \cdot 39 s+60 \cdot 24 ;$ $s^{2}-52 s+480=0 ; s_{1,2}=26 \pm 14 . s_{1}=40, s_{2}=12$ does not satisfy the conditions $s>15, s>24$.
Answer: 40 km.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. The base of the pyramid is a rectangle with sides $AB=24$ and $BC=30$, and the lateral edge of the pyramid $TA=16$ is perpendicular to the plane of the base. What is the minimum area that the section of the pyramid by a plane passing through the center of symmetry of the base $O$, the vertex of the pyramid, and a point $M$ lying on the side $BC$ can have? In this case, into what parts does point $M$ divide the edge $BC$?
|
# Solution:
Regardless of the position of point $M$ on side $B C$, the face $T A B$ is the orthogonal projection of the section $T M N$. The area of the section will be the smallest if the angle between the cutting plane and the face $T A B$ is the smallest. Since the cutting plane passes through the center of symmetry of the base $O$ and the vertex of the pyramid $T$, the segment $O T$ is the inclined line to the plane of the face $T A B$, and the smallest possible angle will be $\angle O T F$, where $O F \perp T A B, F \in A B$. The line of intersection of the cutting plane and the plane of the face $T A B \quad T K \perp T F$ and intersects the line $A B$ at point $K$. If the condition $T K \perp T F$ is not met, then $F T_{1}\operatorname{tg} \alpha, \cos \alpha_{1}\frac{S_{\triangle A T B}}{\cos \alpha}$.
The line passing through points $K$ and $O$ intersects the edge $A D$ at point $N$ and the edge $B C$ at point $M, \triangle N T M$ is the desired section.
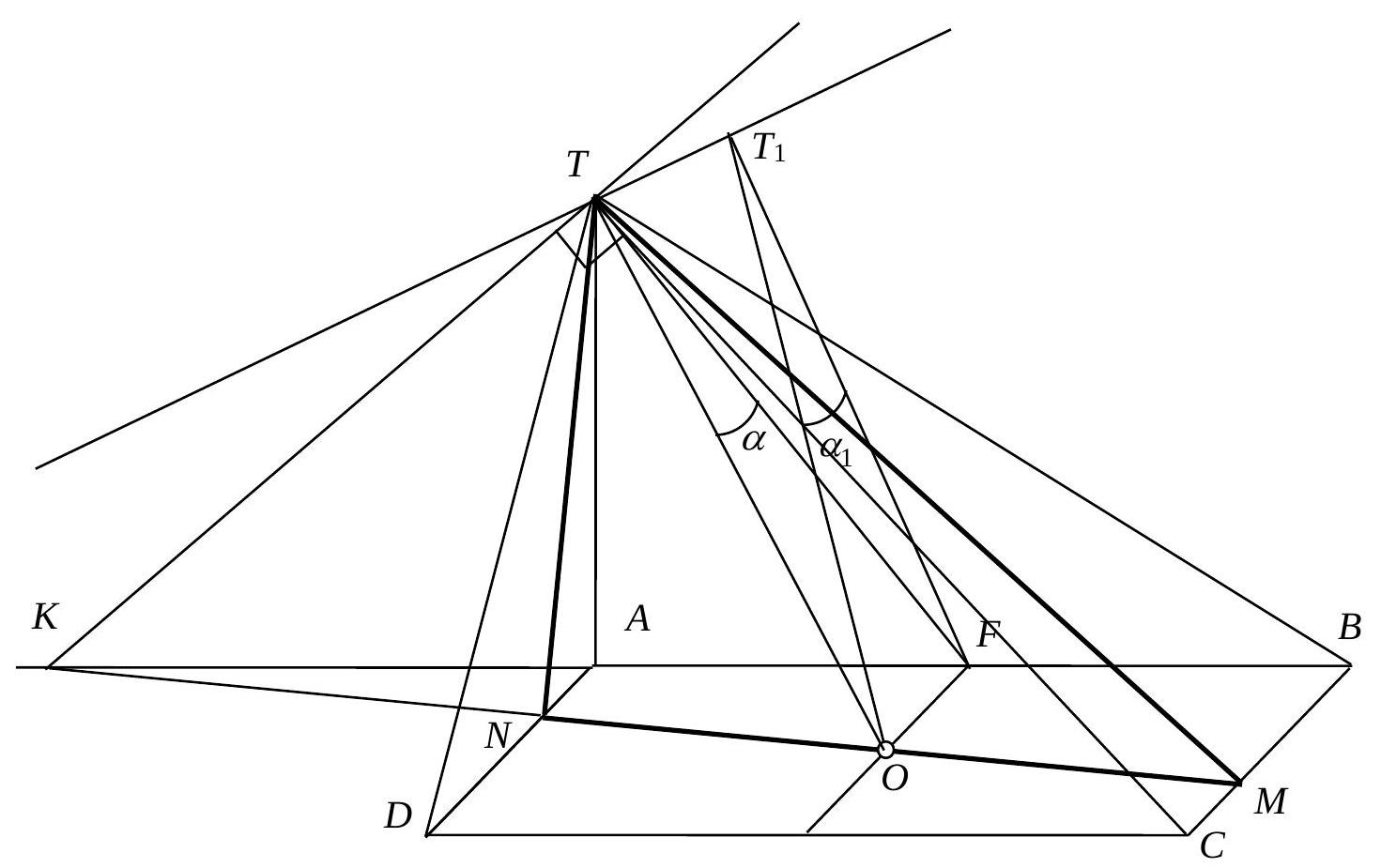
If we denote $\quad A B=a, B C=b, T A=c, \quad$ then $\quad T F=\sqrt{(a / 2)^{2}+c^{2}}$;
$T O=\sqrt{T F^{2}+O F^{2}}=\sqrt{(a / 2)^{2}+c^{2}+(b / 2)^{2}}=\sqrt{a^{2}+b^{2}+4 c^{2}} / 2, \quad \cos \angle O T F=\frac{T F}{T O}=\frac{\sqrt{a^{2}+4 c^{2}}}{\sqrt{a^{2}+b^{2}+4 c^{2}}}$.
$S_{\triangle N T M}=\frac{S_{\triangle A T B}}{\cos \alpha}=\frac{a c \sqrt{a^{2}+b^{2}+4 c^{2}}}{2 \sqrt{a^{2}+4 c^{2}}}=\frac{a c \sqrt{(a / 2)^{2}+(b / 2)^{2}+c^{2}}}{2 \sqrt{(a / 2)^{2}+c^{2}}}$.
In $\triangle K T F \angle K T F=90^{\circ}, A K=A T^{2} / A F=2 c^{2} / a . B K=A K+A B=\frac{2 c^{2}}{a}+a$.
Point $M$ divides the segment $B C$ in the ratio $\frac{B M}{M C}=\frac{B M}{A N}=\frac{B K}{A K}=\frac{a^{2}+2 c^{2}}{2 c^{2}}=1+\frac{1}{2} \frac{a^{2}}{c^{2}}$.
| $A B$ | $B C$ | $T A$ | $T F$ | $T O$ | $\cos \alpha$ | $S_{N T M}$ | $B M: M C$ | $B M$ | $M C$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 24 | 30 | 16 | 20 | 25 | $4 / 5$ | 240 | $17: 8$ | $102 / 5$ | $48 / 5$ |
First (qualifying) stage of the academic competition
"Step into the Future" School Olympiad in the subject of "Mathematics", autumn 2016
|
240
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two cyclists set off simultaneously from point A to point B. When the first cyclist had covered half the distance, the second cyclist still had 24 km to go, and when the second cyclist had covered half the distance, the first cyclist still had 15 km to go. Find the distance between points A and B.
|
# Solution:
Let $s$ be the distance between points $A$ and $B$, and $v_{1}, v_{2}$ be the speeds of the cyclists. Then $\frac{s}{2 v_{1}}=\frac{s-24}{v_{2}} \quad$ and $\quad \frac{s-15}{v_{1}}=\frac{s}{2 v_{2}} . \quad$ From this, $\quad \frac{s}{2(s-24)}=\frac{(s-15) \cdot 2}{s} ; \quad s^{2}=4 s^{2}-4 \cdot 39 s+60 \cdot 24 ;$ $s^{2}-52 s+480=0 ; s_{1,2}=26 \pm 14 . s_{1}=40, \quad s_{2}=12$ does not satisfy the conditions $s>15, s>24$.
Answer: 40 km.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two trucks were transporting fertilizers, making the same number of trips. It turned out that 4 tons less could be loaded onto the first truck and 3 tons less onto the second truck than planned, so each truck had to make 10 extra trips. As a result, the first truck transported 60 tons more than the second, as planned. How much fertilizer was loaded onto each truck and how many trips were made?
|
# Solution:
Let $x, y$ - capacity, $t-$ number of trips as planned.
$$
\left\{\begin{array}{l}
x t=(x-4)(t+10), \\
y t=(y-3)(t+10), \Leftrightarrow\left\{\begin{array} { l }
{ 1 0 x - 4 t = 4 0 } \\
{ \quad x t - y t = 6 0 }
\end{array} \quad \left\{\begin{array}{l}
10 y-3 t=30, \\
(x-y) t=60
\end{array} \Rightarrow 10(x-y)-t=10 \Rightarrow t^{2}+10 t-600=0\right.\right.
\end{array}\right.
$$
From here $t_{1}=20, t_{2}=-30-$ extraneous root; $x=12, y=9$. The first truck was loaded with 8 tons, the second with 6 tons, and 30 trips were completed.
Answer: 8 tons, 6 tons, 30 trips.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A batch of shoes, purchased for 180 thousand rubles, was sold in the first week at a price higher than the purchase price by $25 \%$, then the markup was reduced to $16 \%$ of the purchase price; and the entire batch of shoes was sold for $20 \%$ more than it was purchased for. For what amount was the shoes sold in the first week?
|
# Solution:
$x$ thousand rubles - the purchase cost of shoes sold in the first week, $y$ - the remainder.
$$
\left\{\begin{array} { c }
{ x + y = 180 } \\
{ 25 x + 16 y = 20 ( x + y ) ; }
\end{array} \left\{\begin{array} { c }
{ 5 x = 4 y , } \\
{ x + 5 / 4 x = 180 ; }
\end{array} \left\{\begin{array}{l}
x=80 \\
y=100
\end{array}\right.\right.\right.
$$
Revenue from sales in the first week is $80 \cdot 1.25=100$ thousand rubles.
Answer: 100 thousand rubles
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the greatest value that the sum of the first $n$ terms of the arithmetic progression $113,109,105, \ldots$ can take?
#
|
# Solution:
The sum of the first $n$ terms of an arithmetic progression $S_{n}$ takes its maximum value if $a_{n}>0$, and $a_{n+1} \leq 0$. Since $a_{n}=a_{1}+d(n-1)$, from the inequality $113-4(n-1)>0$ we find $n=[117 / 4]=29$.
Then $\max S_{n}=S_{29}=0.5 \cdot(113+113-4 \cdot 28) \cdot 29=1653$.
Answer: 1653.
|
1653
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the laboratory, there are flasks of two sizes (volume $V$ and volume $V / 2$) in a total of 100 pieces, with at least three flasks of each size. The lab assistant randomly selects three flasks in sequence, and fills the first one with an 80% salt solution, the second one with a 50% salt solution, and the third one with a 20% salt solution. Then he pours the contents of these three flasks into one dish and determines the percentage of salt in it. For what minimum number of large flasks $N$ will the event "the percentage of salt in the dish is between $45\%$ and $55\%$ inclusive" occur less frequently than the event "when two fair coins are tossed, one head and one tail appear (in any order)"? Justify your answer. (16 points)
|
Solution. If $N$ is the number of large flasks in the laboratory, $N=3,4, \ldots, 97$, then $n=100-N$ is the number of small flasks in the laboratory, $n=3,4, \ldots, 97$. For the event $A=\{$ the salt content in the dish is between $45 \%$ and $55 \%$ inclusive $\}$, it is necessary to find the smallest $N$ such that the probability $\mathrm{P}(A)45<N<55$. Therefore, $N_{\min }=46$.
Answer: when $N=46$.
|
46
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numerical sequence $\left\{a_{n}\right\}_{n=1}^{\infty}$ is defined such that $a_{1}=\log _{2}\left(\log _{2} f(2)\right), \quad a_{2}=$ $\log _{2}\left(\log _{2} f(f(2))\right), \ldots, a_{n}=\log _{2}(\log _{2} \underbrace{f(f(\ldots f}_{n}(2)))), \ldots$, where $f(x)=x^{x}$. Determine the index $n$ for which $a_{n}=2059+2^{2059}$.
(12 points)
|
# Solution.
If $\log _{2}\left(\log _{2} u\right)=t$, then $u=2^{2^{t}}, f(u)=\left(2^{2^{t}}\right)^{2^{2^{t}}}=2^{2^{t+2^{t}}}, \log _{2}\left(\log _{2} f(u)\right)=t+2^{t} . \quad$ If $u=2,2=2^{2^{t}}, t=0, a_{1}=\log _{2}\left(\log _{2} f(2)\right)=0+2^{0}=1$. If $u=f(2)$, then $t=\log _{2}\left(\log _{2} u\right)=$ 1 , and $a_{2}=\log _{2}\left(\log _{2} f(f(2))\right)=\log _{2}\left(\log _{2} f(u)\right)=t+2^{t}=1+2^{1}=3$. If $u=f(f(2))$, then $t=\log _{2}\left(\log _{2} u\right)=3$, and $a_{3}=\log _{2}\left(\log _{2} f(f(f(2)))\right)=\log _{2}\left(\log _{2} f(u)\right)=t+2^{t}=3+2^{3}=11$. If $u=f(f(f(2)))$, then $t=\log _{2}\left(\log _{2} u\right)=11$, and $a_{4}=\log _{2}\left(\log _{2} f(f(f(f(2))))\right)=\log _{2}\left(\log _{2} f(u)\right)=t+2^{t}=11+2^{11}=2059$. If $u=f(f(f(f(2))))$, then $t=\log _{2}\left(\log _{2} u\right)=2059$, and $a_{5}=\log _{2}\left(\log _{2} f(f(f(f(f(2)))))\right)=\log _{2}\left(\log _{2} f(u)\right)=2059+2^{2059}$.
## Answer: 5
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Clowns Plukha and Shmyaka have six pairs of valenki (traditional Russian felt boots) between them. Each pair of valenki is painted in a unique color, and the valenki in a pair are identical (they are not distinguished as left or right). In how many ways can both clowns be simultaneously wearing mismatched valenki? (16 points)
|
Solution. We can use valenki (traditional Russian felt boots) from two, three, or four pairs.
1) We choose two pairs of valenki $C_{6}^{2}=15$ ways. Each clown puts on one valenok from different pairs, choosing which one for which foot. This gives us $15 \cdot 2 \cdot 2=60$ ways.
2) We use three pairs of valenki. We choose one complete pair of valenki, and two other pairs from which we will take one valenok each. This can be done $6 \cdot C_{5}^{2}=60$ ways. Each clown puts on one valenok from the pair, choosing which foot to put it on. This can be done in 4 ways. Then each clown chooses one of the two different valenki in 2 ways. This gives us $60 \cdot 4 \cdot 2=480$ ways.
3) We use four pairs of valenki. We choose four pairs from which we will take one valenok each. This can be done $C_{6}^{4}=15$ ways. The four chosen valenki of different colors can be put on the four feet of the clowns in 4! ways. This gives us $15 \cdot 4! =360$ ways.
Finally, we have $60+480+360=900$.
## Answer: 900.
|
900
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. More and more countries are exploring space. The number of states that launch their satellites using their own launch vehicles is already 12. There are also countries that use the services of the main space powers to launch their satellites for economic purposes. Due to the increasing number of participants in space activities and the intensification of these activities, issues of ensuring the safety of space operations are arising. For example, NASA has approached the corporation "Energia" with a request to reduce the altitude of the ISS orbit.
a) Considering the Earth as a sphere with radius $R$, determine the maximum number of satellites that can simultaneously be in orbits around the Earth at the same height $H$ from its surface, such that the distance between the satellites is greater than $\sqrt{2}(R+H)$.
b) For the maximum number of satellites found, specify the coordinates of their possible locations in a coordinate system with the origin at the center of the Earth and the x-axis directed along the vector connecting the center of the Earth with one of the satellites. (20 points)
|
Solution. According to the condition, at the current moment, all satellites should be located on a sphere with radius $R+H$. Let $O$ be the center of the sphere, and its radius $R_{H}=R+H$. Denote the satellites by points $C_{i}, i=1, \ldots, n$. We need to determine the maximum value of $n$.
Let's find the distance $C_{i} C_{j}$, using the cosine theorem for triangle $O C_{i} C_{j}$.
$C_{i} C_{j}^{2}=O C_{i}^{2}+O C_{j}^{2}-2 O C_{i} \cdot O C_{j} \cdot \cos \left(\angle O C_{i}, O C_{j}\right)=2 R_{H}^{2}-2 R_{H}^{2} \cdot \cos \alpha=2 R_{H}^{2}(1-\cos \alpha)>2 R_{H}^{2}$,
Thus, $1-\cos \alpha>1 \Rightarrow \cos \alpha<0$, and the third axis is directed towards the nearest to $C_{3}\left(x_{3}, y_{3}, z_{3}\right)$, so that the z-coordinate is positive, i.e., $z_{3}>0$. Consider the scalar products of the vectors, noting that all of them are negative.
$\overrightarrow{O C_{1}} \cdot \overrightarrow{O C_{i}}=x_{i}, \quad i=\overline{2, n}, \quad \overrightarrow{O C_{2}} \cdot \overrightarrow{O C_{i}}=x_{2} x_{i}+y_{2} y_{i}, i=\overline{3, n}, \quad \overrightarrow{O C_{3}} \cdot \overrightarrow{O C_{i}}=x_{3} x_{i}+y_{3} y_{i}+z_{3} z_{i}, i=\overline{4, n}$.
Since $\cos \left(\angle O C_{i}, O C_{j}\right)<0$, the scalar products of the vectors are negative, and thus, $\quad x_{i}<0, i=\overline{2, n}, \quad$ meaning all $y_{i}<0, i=\overline{3, n}, \quad x_{3} x_{i}+y_{3} y_{i}+z_{3} z_{i}<0, i=\overline{4, n}$. Therefore, all $z_{i}<0, i=\overline{4, n}$. Thus, the coordinates of all vectors starting from $\overrightarrow{O C_{4}}$ will be negative. Consequently, the scalar product of vectors $\overrightarrow{O C_{4}}, \overrightarrow{O C_{5}}$ will be positive. We have reached a contradiction. The assumption of the existence of more than 4 satellites satisfying the required conditions is incorrect. Answer: 4 satellites.
b) 4 satellites are possible, for example, with coordinates that can be written as follows:
if the $o x$ axis is directed from the center of the sphere in the direction of one of the satellites, then the coordinates of this satellite will be $\left(R_{H}, 0,0\right)$, the other three satellites will be located on the plane $x=-R_{H} / 3$ and their coordinates will be respectively
$$
\left(-R_{H} / 3,0, r\right), \quad\left(-R_{H} / 3, \sqrt{3} r / 2,-r / 2\right), \quad\left(-R_{H} / 3,-\sqrt{3} r / 2,-r / 2\right)
$$
where $r=\sqrt{R_{H}^{2}-R_{H}^{2} / 9}=R_{H} \sqrt{8} / 3$.
These relationships are derived from considering the relationships between the elements of a regular
tetrahedron with side $a$. The height $H=\sqrt{a^{2}-\left(a \frac{\sqrt{3}}{2} \cdot \frac{2}{3}\right)^{2}}=a \sqrt{\frac{2}{3}} . \quad$ The radius $\quad$ of the sphere circumscribed around a regular tetrahedron is found from the similarity of triangles
$\frac{H}{a}=\frac{a}{2 R} \Rightarrow R=\frac{a^{2}}{2 \sqrt{\frac{2}{3}} a}=\frac{a \sqrt{3}}{2 \sqrt{2}} \Rightarrow \frac{H}{R}=\frac{\sqrt{\frac{2}{3}} a}{\frac{a \sqrt{3}}{2 \sqrt{2}}}=\frac{4}{3}$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. Option I.
The decimal representation of a natural number $N$ contains 1580 digits. Among these digits are threes, fives, and sevens, and no other digits. It is known that the number of sevens is 20 less than the number of threes. Find the remainder when the number $N$ is divided by 3.
|
Solution. Let $x$ be the number of threes in the number $N$. The sum of the digits of the number $N$ is $S=3 x+7(x-20)+5(1580-(2 x-20))=7860$.
The remainder of $S$ divided by 3 is equal to the remainder of $N$ divided by 3 and is 0.
Answer: 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. II variant.
The decimal representation of a 2015-digit natural number $N$ contains the digits 5, 6, 7 and no other digits. Find the remainder of the division of the number $N$ by 9, given that the number of fives in the representation of the number is 15 more than the number of sevens.
|
Solution. Let the number $N$ contain $x$ sevens. Then the sum of the digits of the number $N$ is $S=7x+5(x+15)+6(2015-(2x+15))=12075$.
$N \equiv S \equiv 6(\bmod 9)$.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. Option I.
Find the set of values of the parameter $a$, for which the sum of the cubes of the roots of the equation $x^{2}-a x+a+2=0$ is equal to -8.
#
|
# Solution.
1) $x_{1}^{3}+x_{2}^{3}=\left(x_{1}+x_{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}-3 x_{1} x_{2}\right)=a\left(a^{2}-3(a+2)\right)=a^{3}-3 a(a+2)$.
2) $a^{3}-3 a(a+2)=-8 \Leftrightarrow\left[\begin{array}{l}a=-2, \\ a=1, \\ a=4 .\end{array}\right.$
3) $D=a^{2}-4 a-8$.
For $a=-2 \quad D=4+8-8=4>0$, therefore, $a=-2$ is a solution.
For $a=1 \quad D=1-4-8<0$ - no roots; hence, $a=1$ is not a solution.
For $a=4 \quad D=16-16-8<0$, $a=4$ is also not a solution.
Answer: $\{-2\}$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. II variant.
Find the set of values of the parameter $a$, for which the sum of the cubes of the roots of the equation $x^{2}+a x+a+1=0$ is equal to 1.
|
# Solution.
1) $x_{1}^{3}+x_{2}^{3}=\left(x_{1}+x_{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}-3 x_{1} x_{2}\right)=-a\left(a^{2}-3(a+1)\right)=-a^{3}+3 a(a+1)$.
2) $-a^{3}+3 a(a+1)=1 \Leftrightarrow\left[\begin{array}{l}a=-1, \\ a=2 \pm \sqrt{3} \text {. }\end{array}\right.$
3) $D=a^{2}-4 a-4$.
For $a=-1 \quad D=1+4-4>0$, therefore, $a=-1$ is a solution.
For $a=2 \pm \sqrt{3} \quad D=7 \pm 4 \sqrt{3}-8 \mp 4 \sqrt{3}-4=-5<0$; hence, the values $a=2 \pm \sqrt{3}$ are not solutions.
Answer: $\{-1\}$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Option I.
Two different natural numbers are written on the board, the larger of which is 2015. It is allowed to replace one of the numbers with their arithmetic mean (if it is an integer). It is known that such an operation was performed 10 times. Find what numbers were originally written on the board.
|
Solution. After each iteration, the difference between the written numbers is halved. We get that the initial difference must be a multiple of $2^{10}=1024$. From this, we find the second number: $2015-1024=991$.
Answer: 991.
|
991
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. II variant.
Two different natural numbers are written on the board, the larger of which is 1580. It is allowed to replace one of the numbers with their arithmetic mean (if it is an integer). It is known that such an operation was performed 10 times. Find what numbers were originally written on the board.
|
Solution. After each iteration, the difference between the written numbers is halved. We get that the initial difference must be a multiple of $2^{10}=1024$. From this, we find the second number: $1580-1024=556$.
Answer: 556.
|
556
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. Option 1.
Given a triangle with sides 6, 8, and 10. Find the length of the shortest segment connecting points on the sides of the triangle and dividing it into two equal areas.
|
Solution. 1) Note that the given triangle is a right triangle: $6^{2}+8^{2}=10^{2}$.
2) Suppose first (and we will justify this later) that the ends of the desired segment $D E=t$ lie on the larger leg $A C=8$ and the hypotenuse $A B=10$ (see figure). Let $A D=x$, $A E=y, \angle B A C=\alpha$. Then
$S_{A D E}=\frac{1}{2} x y \sin \alpha=\frac{3}{10} x y$.
3) By the problem's condition $S_{A D E}=\frac{1}{2} S_{A B C}$,
$\frac{3}{10} x y=\frac{1}{2} \cdot \frac{1}{2} \cdot 6 \cdot 8$,
$x y=40$.
4) $\triangle A D E: t^{2}=x^{2}+y^{2}-2 x y \cos \alpha=$
$$
\begin{aligned}
& =x^{2}+y^{2}-2 \cdot 40 \cdot \frac{8}{10}= \\
& =x^{2}+y^{2}-64= \\
& =x^{2}+\frac{1600}{x^{2}}-64
\end{aligned}
$$
By the Cauchy-Schwarz inequality $t^{2} \geq 2 \sqrt{x^{2} \cdot \frac{1600}{x^{2}}}-64=16$.
The minimum value $t_{\min }=4$ is achieved when $x=y=\sqrt{40}=2 \sqrt{10}$.
5) In an isosceles triangle with base $t$ and vertex angle $\alpha$, the area is
$$
S=\frac{1}{2} t \cdot \frac{1}{2} t \operatorname{ctg} \frac{\alpha}{2}=\frac{1}{4} t^{2} \operatorname{ctg} \frac{\alpha}{2} .
$$
From this, $t=2 \sqrt{S \operatorname{tg} \frac{\alpha}{2}}$.
It is clear that for a fixed area $S$, as $\alpha$ increases, the base $t$ will also increase. Therefore, the found value $t_{\min }$, corresponding to the segment opposite the smallest of the three angles of the triangle, is indeed the desired one.
Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1.
A librarian at a physics and mathematics school noticed that if the number of geometry textbooks in the school library is increased by several (integer) times and the number of algebra textbooks is added to the resulting number, the total is 2015. If the number of algebra textbooks is increased by the same factor and the number of geometry textbooks is added to the resulting number, the total is 1580. How many algebra textbooks are in the library?
|
Solution. Let the number of geometry textbooks be $x$, and the number of algebra textbooks be $y$. We can set up the system
$$
\left\{\begin{array}{l}
x n+y=2015 \\
y n+x=1580
\end{array}\right.
$$
We can write an equivalent system, where the equations represent the sum and difference of the equations in the original system:
$\left\{\begin{array}{l}x(n+1)+y(n+1)=3595, \\ x(n-1)-y(n-1)=435\end{array} \Leftrightarrow\left\{\begin{array}{l}(x+y)(n+1)=5 \cdot 719, \\ (x-y)(n-1)=3 \cdot 5 \cdot 29 .\end{array}\right.\right.$
The factor $(n+1)$ of the number $5 \cdot 719$ must be 2 more than the factor $(n-1)$ of the number $3 \cdot 5 \cdot 29$. Clearly, this is only satisfied when $n=4$. Then
$$
\left\{\begin{array} { l }
{ x + y = 7 1 9 } \\
{ x - y = 1 4 5 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=432 \\
y=287
\end{array}\right.\right.
$$
Answer: 287.
|
287
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
One side of the parallelogram is $\sqrt{3}$ times larger than the other side. One diagonal of the parallelogram is $\sqrt{7}$ times larger than the other diagonal. How many times larger is one angle of the parallelogram than the other angle?
|
Solution. Let $x$ be the smaller side, then $\sqrt{3} x$ is the larger side. Let $y$ be the smaller diagonal, then $\sqrt{7} y$ is the larger diagonal. We have:
$2 x^{2}+2(\sqrt{3} x)^{2}=y^{2}+(\sqrt{7} y)^{2}$,
from which $x=y$.
We get: the acute angle of the parallelogram is $30^{\circ}$, the obtuse angle is $150^{\circ}$.
Answer: 5 times.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6.
A $10 \times 10$ square was cut into rectangles, the areas of which are different and expressed as natural numbers. What is the maximum number of rectangles that can be obtained?
|
Solution. The area of the square is 100. If we represent 100 as the sum of natural numbers, the number of addends will be the largest if the difference between the numbers is one. Let's take rectangles with areas of $1, 2, 3, 4, 5, 6, 7, 8, 9, 10$. Their total area is 55. Therefore, the sum of the areas of the remaining rectangles is 45.
Notice that if the area of a rectangle is greater than 10, it cannot be
a prime number, otherwise such a rectangle would have a side greater than 10 and would not fit into a $10 \times 10$ square. Composite numbers greater than ten are $12, 14, 15, 16, 18$, $19, \ldots$ Any four of them sum to a number greater than 45. Sums equal to 45 can be given, for example, by such three numbers: $12, 15, 18$ or $14, 15, 16$.
Thus, the number of rectangles is less than or equal to 13. An example of a possible arrangement for 13 rectangles is shown in the figure.
## Evaluation criteria for the correspondence round tasks for 9th grade
#
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From point $A$ to point $B$, which are 8 km apart, a tourist and a cyclist set out simultaneously. The cyclist, who took no less than half an hour to travel from $A$ to $B$, without stopping, turned back and started moving towards point $A$, increasing his speed by $25 \%$. After 10 minutes from his departure from point $B$, the cyclist met the tourist. Determine the greatest possible integer value of the tourist's speed (in km/h), and for this value of the tourist's speed, find the initial speed of the cyclist.
|
Solution: Let $x$ (km/h) be the speed of the tourist, $y$ (km/h) be the initial speed of the cyclist, and $t$ (h) be the time spent by the cyclist traveling from $A$ to $B$. Then
$$
\left\{\begin{array}{c}
x(t+1 / 6)+5 y / 24=8, \\
y t=8, \\
t \geq 0.5,
\end{array} \Rightarrow x(8 / y+1 / 6)+5 y / 24=8, \Rightarrow 5 y^{2}+(4 x-192) y+192 x=0\right.
$$
For the quadratic equation to have a solution, it is necessary that $D / 4=(2 x-96)^{2}-960 x \geq 0$. Therefore, $x^{2}-336 x+2304 \geq 0, D / 4=(72 \sqrt{5})^{2}$, $x \in(-\infty ; 168-72 \sqrt{5}] \cup[168+72 \sqrt{5} ;+\infty)$. Since by the condition $x \in \mathbb{N}$, and $x / 6<8$, i.e., $x<48$, then $x \in[1 ; 168-72 \sqrt{5}] \cap \mathbb{N}$. Using the estimate $2.23<\sqrt{5}<2.24$, we get the estimate $160<72 \sqrt{5}<161$, and $7<168-72 \sqrt{5}<8$. The largest possible integer value of the speed $x=7$. We find the initial speed of the cyclist when $x=7$ from the equation $5 y^{2}-164 y+192 \cdot 7=0, y_{1}=84 / 5$, $y_{2}=16$. Since $t \geq 0.5, \quad t=\frac{8}{y} \geq \frac{1}{2}$, and $y \leq 16$, then $y=16$.
Answer: 7 km/h, 16 km/h.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two numbers x and y satisfy the equation $280 x^{2}-61 x y+3 y^{2}-13=0$ and are the fourth and ninth terms, respectively, of a decreasing arithmetic progression consisting of integers. Find the common difference of this progression.
|
Solution: We factorize the expression $280 x^{2}-61 x y+3 y^{2}$. For $y \neq 0$, we have $y^{2}\left(280\left(\frac{x}{y}\right)^{2}-61\left(\frac{x}{y}\right)+3\right)=280 y^{2}\left(\frac{x}{y}-\frac{3}{40}\right)\left(\frac{x}{y}-\frac{1}{7}\right)=(40 x-3 y)(7 x-y)$. This formula is also valid for all real numbers $y$. According to the problem, the integers $x$ and $y$ satisfy the equation $(40 x-3 y)(7 x-y)=13$. The integers $40 x-3 y$ and $7 x-y$ are divisors of the number 13, and the following cases are possible:
$$
\left\{\begin{array} { c }
{ 4 0 x - 3 y = 1 3 , } \\
{ 7 x - y = 1 ; }
\end{array} \text { 2) } \left\{\begin{array} { c }
{ 4 0 x - 3 y = - 1 3 , } \\
{ 7 x - y = - 1 ; }
\end{array} \text { 3) } \left\{\begin{array} { c }
{ 4 0 x - 3 y = - 1 , } \\
{ 7 x - y = - 1 3 ; }
\end{array} \text { 4) } \left\{\begin{array}{c}
40 x-3 y=1, \\
7 x-y=13
\end{array}\right.\right.\right.\right.
$$
We solve each system using the method of addition. We multiply both sides of the second equation of the system by -3 and add it to the first:
$$
\left\{\begin{array} { l }
{ 1 9 x = 1 0 , } \\
{ 7 x - y = 1 ; }
\end{array} \text { 2) } \left\{\begin{array} { l }
{ 1 9 x = - 1 0 , } \\
{ 7 x - y = - 1 ; }
\end{array} \text { 3) } \left\{\begin{array} { c }
{ 1 9 x = 3 8 , } \\
{ 7 x - y = - 1 3 ; }
\end{array} \text { 4) } \left\{\begin{array}{l}
19 x=-38 \\
7 x-y=13
\end{array}\right.\right.\right.\right.
$$
Systems 1) and 2) do not have integer solutions. Since the progression is decreasing, we have $x < y$, which is satisfied by the solutions of system 4): $x=-2$, $y=-27$. Thus, $a_{4}=-2, a_{9}=-27$, or $a_{1}+3 d=-2, \quad a_{1}+8 d=-27$. From this, we get $d=-5$.
Answer: $d=-5$.
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From point $A$ to point $B$, which are 24 km apart, a pedestrian and a cyclist set out simultaneously. The cyclist, who spent no less than two hours on the journey from $A$ to $B$, without stopping, turned back and started moving towards point $A$ at a speed twice the initial speed. After 24 minutes from his departure from point $B$, the cyclist met the pedestrian. Determine the greatest possible integer value of the pedestrian's speed (in km/h), and for this value of the pedestrian's speed, find the initial speed of the cyclist.
|
Solution: Let $x$ (km/h) be the speed of the cyclist, $y$ (km/h) be the initial speed of the truck, and $t$ (h) be the time spent by the truck traveling from $A$ to $B$. Then
$$
\left\{\begin{array}{rl}
x(t+0.4)+0.8 y=24, \\
y t & =24, \\
t & \geq 2,
\end{array} \Rightarrow x(24 / y+0.4)+0.8 y=24, \Rightarrow 2 y^{2}+(x-60) y+60 x=0\right.
$$
For the quadratic equation to have a solution, it is necessary that $D=(x-60)^{2}-480 x \geq 0$. Therefore, $x^{2}-600 x+3600 \geq 0, D / 4=(120 \sqrt{6})^{2}$, and
$x \in(-\infty ; 300-120 \sqrt{6}] \cup[300+120 \sqrt{6} ;+\infty)$. Since by the condition $x \in \mathbb{N}$, and $0.2 x<12$, i.e., $x<60$, then $\quad x \in[1 ; 300-120 \sqrt{6}] \cap \mathbb{N}$. Using the estimate $2.44<\sqrt{6}<2.45$, we get the estimate $293<120 \sqrt{6}<294$, and $6<300-120 \sqrt{6}<7$. The largest possible integer value of the speed $x=6$. We find the initial speed of the truck when $x=6$ from the equation $2 y^{2}-54 y+360=0$, or $y^{2}-27 y+180=0, \quad y_{1}=12, \quad y_{2}=15$. Since $t \geq 2, \quad t=\frac{24}{y} \geq 2$, and $y \leq 12$, then $y=12$.
Answer: 6 km/h, 12 km/h.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two numbers \(x\) and \(y\) satisfy the equation \(26 x^{2} + 23 x y - 3 y^{2} - 19 = 0\) and are the sixth and eleventh terms, respectively, of a decreasing arithmetic progression consisting of integers. Find the common difference of this progression.
|
Solution: Factorize the expression $26 x^{2}+23 x y-3 y^{2}$. For $y \neq 0$, we have $y^{2}\left(26\left(\frac{x}{y}\right)^{2}+23\left(\frac{x}{y}\right)-3\right)=26 y^{2}\left(\frac{x}{y}+1\right)\left(\frac{x}{y}-\frac{3}{26}\right)=(x+y)(26 x-3 y)$. This formula is valid for all real numbers $y$. According to the problem, the integers $x$ and $y$ satisfy the equation $(x+y)(26 x-3 y)=19$. The integers $x+y$ and $26 x-3 y$ are divisors of the number 19, and the following cases are possible:
1) $\left\{\begin{array}{c}x+y=19 \\ 26 x-3 y=1\end{array}\right.$
2) $\left\{\begin{array}{c}x+y=-19 \\ 26 x-3 y=-1\end{array}\right.$
3) $\left\{\begin{array}{c}x+y=-1 \\ 26 x-3 y=-19\end{array}\right.$
4) $\left\{\begin{array}{c}x+y=1 \\ 26 x-3 y=19\end{array}\right.$
We solve each system by the method of addition. Multiply both sides of the first equation of the system by 3 and add to the second:
1) $\left\{\begin{array}{l}29 x=58 \\ x+y=19\end{array}\right.$
2) $\left\{\begin{array}{c}29 x=-58 \\ x+y=-19\end{array}\right.$
3) $\left\{\begin{array}{l}29 x=-22 \\ x+y=-1\end{array}\right.$
4) $\left\{\begin{array}{l}29 x=22, \\ x+y=1 .\end{array}\right.$
Systems 3) and 4) do not have integer solutions. Since the progression is decreasing, it follows that $x<y$, which is satisfied by the solutions of system 2): $x=-2$, $y=-17$. Thus, $a_{6}=-2, a_{11}=-17$, or $a_{1}+5 d=-2, a_{1}+10 d=-17$. From this, we get $d=-3$.
Answer: $d=-3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The production of ceramic items consists of 3 sequential stages: forming a ceramic item on a potter's wheel for 15 minutes, drying for 10 minutes, and firing for 30 minutes. It is required to produce 75 items. How should 13 masters be distributed between molders and firers to work on stages 1 and 3 respectively for the entire duration of the stage (drying does not require workers), to complete the work in the shortest time possible? In the answer, write the shortest time (in minutes) required to complete the entire job. Provide the answer as a number without indicating the unit. (5 points)
|
Solution. Molders - 4, decorators - 8. The thirteenth master can work at any stage, or not participate in the work at all. In this case, the working time is 325 minutes $\left(55+\left(\left[\frac{75}{4}\right]+1\right) \cdot 15=325\right)$. We will show that with other arrangements, the working time is longer. Suppose there are fewer than 4 molders (3, 2, or 1), then the time for molding is no less than 375 minutes. If there are fewer than 8 decorators, then the time for the third stage is no less than 330 minutes. Answer: 325
|
325
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all natural values of $n$ for which
$$
\cos \frac{2 \pi}{9}+\cos \frac{4 \pi}{9}+\cdots+\cos \frac{2 \pi n}{9}=\cos \frac{\pi}{9}, \text { and } \log _{2}^{2} n+45<\log _{2} 8 n^{13}
$$
In your answer, write the sum of the obtained values of $n$.
(6 points)
|
# Solution.
$$
\begin{aligned}
& \cos \frac{2 \pi}{9}+\cos \frac{4 \pi}{9}+\cdots+\cos \frac{2 \pi n}{9}=\cos \frac{\pi}{9} \quad \Leftrightarrow 2 \sin \frac{\pi}{9} \cos \frac{2 \pi}{9}+2 \sin \frac{\pi}{9} \cos \frac{4 \pi}{9}+\cdots+ \\
& 2 \sin \frac{\pi}{9} \cos \frac{2 \pi n}{9}=2 \sin \frac{\pi}{9} \cos \frac{\pi}{9} \Leftrightarrow
\end{aligned}
$$
$\sin \frac{3 \pi}{9}-\sin \frac{\pi}{9}+\sin \frac{5 \pi}{9}-\sin \frac{3 \pi}{9}+\cdots+\sin \frac{\pi}{9}(1+2 n)-\sin \frac{\pi}{9}(2 n-1)=\sin \frac{2 \pi}{9} \Leftrightarrow$ $\sin \frac{\pi}{9}(1+2 n)-\sin \frac{\pi}{9}=\sin \frac{2 \pi}{9} \Leftrightarrow \sin \frac{\pi}{9}(1+2 n)=\sin \frac{2 \pi}{9}+\sin \frac{\pi}{9} \Leftrightarrow \sin \frac{\pi}{9}(1+2 n)=$ $2 \sin \frac{\pi}{6} \cos \frac{\pi}{18} \Leftrightarrow \sin \frac{\pi}{9}(1+2 n)=\sin \frac{4 \pi}{9} \Leftrightarrow 2 \sin \left(\frac{\pi n}{9}-\frac{\pi}{6}\right) \cos \left(\frac{\pi n}{9}+\frac{5 \pi}{18}\right)=0 \Leftrightarrow \frac{\pi n}{9}-\frac{\pi}{6}=$ $\pi k, k \in \mathbb{Z}, \quad \frac{\pi n}{9}+\frac{5 \pi}{18}=\frac{\pi}{2}+\pi m, m \in \mathbb{Z}, \Leftrightarrow 2 n=3(6 k+1), k \in \mathbb{Z}, \quad n=2+$
$9 m, m \in \mathbb{Z}, m \geq 0$. Since $n$ is a natural number, the first relation does not hold (an even number cannot be equal to an odd number). Therefore, $n=2+9 m, m \in \mathbb{Z}, m \geq 0$.
Solve the inequality $\log _{2}^{2} n+45<\log _{2} 8 n^{13} \Leftrightarrow \log _{2}^{2} n-13 \log _{2} n+42<0$, $\Leftrightarrow$ $\left(\log _{2} n-6\right)\left(\log _{2} n-7\right)<0, \Leftrightarrow 2^{6}<n<2^{7}, \Leftrightarrow 64<2+9 m<128, m \in \mathbb{Z}, m \geq$ $0 \Leftrightarrow 6 \frac{8}{9}<m<14, m \in \mathbb{Z}, m \geq 0 \Leftrightarrow m=7,8,9,10,11,12,13 . S_{7}=\frac{65+119}{2}$. $7=644$.
## Answer: 644
|
644
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In how many ways can a bamboo trunk (a non-uniform natural material) 4 m long be sawn into three parts, the lengths of which are multiples of 1 dm, and from which a triangle can be formed?
(12 points)
|
Solution.
Let $A_{n}$ be the point on the trunk at a distance of $n$ dm from the base. We will saw at points $A_{p}$ and $A_{q}, p<q$. To satisfy the triangle inequality, it is necessary and sufficient that each part is no longer than 19 dm:
$$
p \leq 19, \quad 21 \leq q \leq p+19
$$
Thus, the number of ways to choose $p$ and $q$ will be
$$
\sum_{p=1}^{19}(p+19-20)=0+1+2+\ldots+18=\frac{18 \cdot 19}{2}=171
$$
## Answer: 171
|
171
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many solutions in natural numbers $x, y$ does the inequality $x / 76 + y / 71 < 1$ have?
(12 points)
|
# Solution.
All solutions lie in the rectangle
$$
\Pi=\{0<x<76 ; \quad 0<y<41\}
$$
We are interested in the number of integer points lying inside Π below its diagonal $x / 76 + y / 41=1$. There are no integer points on the diagonal itself, since 76 and 41 are coprime. So we get half the number of integer points inside Π:
$$
\frac{75 \cdot 40}{2}=1500
$$
Answer: 1500
|
1500
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Indicate the smallest value of the parameter $a$ for which the equation has at least one solution
$2 \sin \left(\pi-\frac{\pi x^{2}}{12}\right) \cos \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right)+1=a+2 \sin \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right) \cos \left(\frac{\pi x^{2}}{12}\right)$.
|
Solution.
Rewrite the equation as
$2 \sin \left(\pi-\frac{\pi x^{2}}{12}\right) \cos \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right)-2 \sin \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right) \cos \left(\pi-\frac{\pi x^{2}}{12}\right)=a-1$, or
$\sin \left(\pi-\frac{\pi x^{2}}{12}-\frac{\pi}{6} \sqrt{9-x^{2}}\right)=\frac{a-1}{2}$.
Consider the expression $t=\pi-\frac{\pi x^{2}}{12}-\frac{\pi}{6} \sqrt{9-x^{2}}$ separately, which can be rewritten as:
$$
\begin{gathered}
\pi-\frac{\pi x^{2}}{12}-\frac{\pi}{6} \sqrt{9-x^{2}}=\frac{\pi}{12}\left(12-x^{2}-2 \sqrt{9-x^{2}}\right)=\frac{\pi}{12}\left(9-x^{2}-2 \sqrt{9-x^{2}}+3\right) \\
=\frac{\pi}{12}\left(\left(\sqrt{9-x^{2}}-1\right)^{2}+2\right)
\end{gathered}
$$
Considering that the root takes values from 0 to 3, then $t \in\left[\frac{\pi}{6} ; \frac{\pi}{2}\right]$, so $\sin t \in$ $\left[\frac{1}{2} ; 1\right]$. Let's find the range in which the parameter varies: $\frac{1}{2} \leq \frac{a-1}{2} \leq 1 \Rightarrow 2 \leq a \leq 3$.
Answer: 2
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Rhombus $ABCD$ is the base of a pyramid with vertex $S$. All its lateral faces are inclined to the base plane at the same angle of $60^{\circ}$. Points $M, N, K$, and $L$ are the midpoints of the sides of rhombus $ABCD$. A rectangular parallelepiped is constructed on rectangle $MNKL$ as its base. The edges of the upper face of the parallelepiped (opposite to face $MNKL$) intersect the lateral edges of the pyramid $SABCD$ at points $F, P, R$, and $Q$, respectively. The volume of the polyhedron with vertices at points $M, N, K, L, F, P, R, Q$ is $12 \sqrt{3}$, and the radius of the circle inscribed in rhombus $ABCD$ is 2.4. Find the side of rhombus $ABCD$. (16 points)
|
Solution.
The height of the pyramid $SO = h$. The diagonals of the rhombus $AC = d_1, BD = d_2$.
The height of the parallelepiped is $h / 2$, and the sides of the base of the parallelepiped are $d_1 / 2$ and $d_2 / 2$.
The volume of the parallelepiped is
$$
V_{\Pi} = \frac{d_1}{2} \cdot \frac{d_2}{2} \cdot \frac{h}{2}
$$
The volume of the polyhedron is
$$
V_{\mathrm{M}} = V_{\Pi} - 4 \cdot \frac{1}{3} \cdot \frac{1}{2} \cdot \frac{d_1}{4} \cdot \frac{d_2}{4} \cdot \frac{h}{2} = \frac{d_1 d_2 h}{8} - \frac{d_1 d_2 h}{48} = \frac{5 d_1 d_2 h}{48}
$$
According to the condition $\frac{5 d_1 d_2 h}{48} = 12 \sqrt{3}$.
Since the radius of the circle inscribed in this rhombus is 2.4, and all lateral faces of the pyramid are inclined to the base plane at an angle of $60^{\circ}$, then $h = 2.4 \sqrt{3}$. Therefore,
$$
\frac{5 d_1 d_2 \cdot 2.4 \sqrt{3}}{48} = 12 \sqrt{3}, \text{ and } d_1 d_2 = 48
$$
Since $\quad S_{ABCD} = \frac{d_1 d_2}{2}, \quad$ and $S_{ABCD} = \frac{4 AB \cdot r_{\mathrm{B}}}{2} = 4.8 \cdot AB, \quad$ then $4.8 \cdot AB = 24 \Rightarrow AB = 5$.
## Answer: 5
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A workshop produces items of types $A$ and $B$. For one item of type $A$, 10 kg of steel and 23 kg of non-ferrous metals are used, and for one item of type $B-70$ kg of steel and 40 kg of non-ferrous metals are used. The profit from selling one item of type $A$ is 80 thousand rubles, and for type $B-100$ thousand rubles. The shift fund for steel is 700 kg, and for non-ferrous metals, it is 642 kg. How many items of types $A$ and $B$ should be produced per shift to maximize the profit from selling the items, given that resource consumption should not exceed the allocated shift funds? Write the maximum profit (in thousands of rubles) that can be obtained under these conditions. Provide the answer as a number without specifying the unit. $\quad$ (5 points)
|
Solution. Let $x$ be the number of items of type $A$, and $y$ be the number of items of type $B$. Then the profit per shift is calculated by the formula $D=80 x+100 y$, with the constraints $10 x+70 y \leq 700$, $23 x+40 y \leq 642$, and $x$ and $y$ are non-negative integers.
$10 x+70 y \leq 700 \quad \Leftrightarrow \quad y \leq 10-\frac{x}{7}, \quad 23 x+40 y \leq 642 \quad \Leftrightarrow \quad y \leq 16.05-\frac{23 x}{40}$.
The intersection point of the lines $x+7 y=70$ and $23 x+40 y=642$ is the point with coordinates $x=14, y=8$. In this case, $D=80 \cdot 14+100 \cdot 8=1920$, but when $x=\frac{642}{23}=27 \frac{21}{23}, y=0$, we have the maximum value of the function $D=80 x+100 y$ for non-negative $x$ and $y$ that satisfy the inequalities $10 x+70 y \leq 700, 23 x+40 y \leq 642$. This value is $2233 \frac{1}{23}$. Since $x$ and $y$ are integers, when $y=0, x=27$, the profit $D=2160$; when $y=1, x \leq \frac{602}{23}, x=26, D=2180$; when $y=2, x \leq \frac{562}{23}, x=24, D=2120$. Therefore, the maximum profit is 2180 thousand rubles, given the production of one item of type $A$ and 26 items of type $B$.
## Answer: 2180
|
2180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In how many ways can the number 210 be factored into the product of four natural numbers? The order of the factors does not matter.
$(12$ points)
|
# Solution.
Factorize 210 into a product of prime numbers: $2 \cdot 3 \cdot 5 \cdot 7$. Let's see how 4 prime
#### Abstract
divisors can be distributed among the desired factors
1) $4+0+0+0-1$ way.
2) $3+1+0+0-C_{4}^{3}=4$ ways.
3) $2+2+0+0-C_{4}^{2} / 2=3$ ways.
4) $2+1+1+0-C_{4}^{2}=6$ ways.
5) $1+1+1+1-1$ way.
Answer: 15.
## Answer: 15
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The sequence is defined recursively:
$x_{0}=0, x_{n+1}=\frac{\left(n^{2}+n+1\right) x_{n}+1}{n^{2}+n+1-x_{n}} . \quad$ Find $x_{8453}$. (12 points)
|
Solution.
$$
\text { We calculate } x_{1}=\frac{1}{1}=1, x_{2}=\frac{4}{2}=2, x_{3}=\frac{15}{5}=3 \text {, a hypothesis emerges: } x_{n}=n \text {. }
$$
Let's verify by induction:
$$
x_{n+1}=\frac{\left(n^{2}+n+1\right) n+1}{n^{2}+n+1-n}=\frac{n^{3}+n^{2}+n+1}{n^{2}+1}=n+1
$$
## Answer: 8453
|
8453
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the greatest area that a rectangle can have, the coordinates of whose vertices satisfy the equation $|y-x|=(y+x+1)(5-x-y)$, and whose sides are parallel to the lines $y=x$ and $y=-x$? Write the square of the found area in your answer. $\quad(12$ points $)$
#
|
# Solution.
Substitution: $x_{1}=x+y, y_{1}=y-x$. This substitution increases all dimensions by a factor of $\sqrt{2}$. We have $\left|y_{1}\right|=\left(x_{1}+1\right)\left(5-x_{1}\right), \quad S\left(x_{1}\right)=4\left(x_{1}-2\right)\left(x_{1}+1\right)\left(5-x_{1}\right), x_{1} \in(2 ; 5)$. $S^{\prime}\left(x_{1}\right)=4\left(\left(x_{1}+1\right)\left(5-x_{1}\right)+\left(x_{1}-2\right)\left(5-x_{1}\right)-\left(x_{1}-2\right)\left(x_{1}+1\right)\right)=$ $=-12\left(x_{1}^{2}-4 x_{1}+1\right)=-12\left(x_{1}-2-\sqrt{3}\right)\left(x_{1}-2+\sqrt{3}\right)=0$.
The maximum area is achieved at the point $x_{1}=2+\sqrt{3}$. In the coordinate system $\mathrm{Ox}_{1} \mathrm{y}_{1}$, the maximum area is
$$
S(2+\sqrt{3})=4 \sqrt{3}(3+\sqrt{3})(3-\sqrt{3})=24 \sqrt{3}
$$
In the original coordinate system, $S_{\max }=12 \sqrt{3}$. $\left(S_{\max }\right)^{2}=432$. Answer: 432
Answer: 432
|
432
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Specify the greatest value of the parameter $p$ for which the equation has at least one solution
$2 \cos \left(2 \pi-\frac{\pi x^{2}}{6}\right) \cos \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)-3=p-2 \sin \left(-\frac{\pi x^{2}}{6}\right) \cos \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)$. (16 points)
|
# Solution.
Let's rewrite the equation as
$$
\cos \left(2 \pi-\frac{\pi x^{2}}{6}\right) \cos \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)+\sin \left(2 \pi-\frac{\pi x^{2}}{6}\right) \sin \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)=\frac{p+3}{2} \text {, or }
$$
$\cos \left(2 \pi-\frac{\pi x^{2}}{6}-\frac{\pi}{3} \sqrt{9-x^{2}}\right)=\frac{p+3}{2}$.
Consider the expression $t=2 \pi-\frac{\pi x^{2}}{6}-\frac{\pi}{3} \sqrt{9-x^{2}}$ separately, which can be rewritten as:
$$
\begin{aligned}
2 \pi-\frac{\pi x^{2}}{6}- & \frac{\pi}{3} \sqrt{9-x^{2}}=\frac{\pi}{6}\left(12-x^{2}-2 \sqrt{9-x^{2}}\right)=\frac{\pi}{6}\left(9-x^{2}-2 \sqrt{9-x^{2}}+3\right) \\
= & \frac{\pi}{6}\left(\left(\sqrt{9-x^{2}}-1\right)^{2}+2\right)
\end{aligned}
$$
Considering that the root takes values from 0 to 3, then $t \in\left[\frac{\pi}{3} ; \pi\right]$, so $\cos t \in$ $\left[-1 ; \frac{1}{2}\right]$. Let's find the range in which the parameter varies: $-1 \leq \frac{p+3}{2} \leq \frac{1}{2} \Rightarrow-5 \leq p \leq-2$
## Answer: -2
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. The lateral face of a regular triangular pyramid $S A B C$ is inclined to the base plane $A B C$ at an angle $\alpha=\operatorname{arctg} \frac{3}{4}$. Points $M, N, K$ are the midpoints of the sides of the base $A B C$. Triangle $M N K$ is the lower base of a right prism. The edges of the upper base of the prism intersect the lateral edges of the pyramid $S A B C$ at points $F, P$, and $R$. The total surface area of the polyhedron with vertices at points $M, N, K, F, P, R$ is $53 \sqrt{3}$. Find the side of triangle $A B C$. (16 points)
|
# Solution.
The height of the pyramid $SO = h$. The side of the base of the pyramid $AC = a$.
The height of the prism is $3h/4$, and the sides of the base of the prism are $a/2$.
The area of triangle $MNK$:
$$
S_{MNK} = \frac{a^2 \sqrt{3}}{16}
$$
The area of triangle $FPR$:
$$
S_{FPR} = \frac{a^2 \sqrt{3}}{64}
$$
The area of triangle $MPN$:
$$
S_{MPN} = \frac{1}{2} \cdot \frac{a}{2} \cdot \frac{3h}{4}, \quad S_{MPN} = S_{NPK} = S_{KRM}
$$
The area of triangle $FPM: S_{FPN} = \frac{1}{2} \cdot \frac{a}{4} \cdot \sqrt{\frac{9h^2}{16} + \frac{3a^2}{64}}, \quad S_{FPN} = S_{PRK} = S_{RFM}$.
Since the radius of the circle inscribed in triangle $ABC$ is $\frac{a \sqrt{3}}{6}$, and all lateral faces of the pyramid are inclined to the base plane at an angle $\alpha = \operatorname{arctg} \frac{3}{4}$, then $h = \frac{a \sqrt{3}}{8}$.
According to the problem, the total surface area of the polyhedron with vertices at points $M, N, K, F, P, R$ is $53 \sqrt{3}$, i.e.,
$$
\begin{gathered}
S_{\mathrm{MH}} = S_{MNK} + S_{FPR} + 3 S_{MPN} + 3 S_{FPN} = \\
= \frac{a^2 \sqrt{3}}{16} + \frac{a^2 \sqrt{3}}{64} + \frac{9ah}{16} + \frac{3a}{8} \sqrt{\frac{9h^2}{16} + \frac{3a^2}{64}} = \\
= \frac{a^2 \sqrt{3}}{16} + \frac{a^2 \sqrt{3}}{64} + \frac{9a^2 \sqrt{3}}{128} \\
\quad + \frac{3a}{8} \sqrt{\frac{27a^2}{16 \cdot 64} + \frac{3a^2}{64}} = \\
= \frac{a^2 \sqrt{3}}{16} + \frac{a^2 \sqrt{3}}{64} + \frac{9a^2 \sqrt{3}}{128} + \frac{15a^2 \sqrt{3}}{256} \\
= \frac{53a^2 \sqrt{3}}{16^2} = 53 \sqrt{3}
\end{gathered}
$$
Therefore, $a = 16$.
Answer: 16
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Solution. Let the correct numbers in the table be $a, b, c$ and $d$. Consider the events
$$
A=\{\text { There is a cat }\} \text { and } B=\{\text { There is a dog }\} .
$$
| | There is a dog | There is no dog |
| :--- | :---: | :---: |
| There is a cat | $a$ | $b$ |
| There is no cat | $c$ | $d$ |
These events are independent if the proportion of "cat owners" among "dog owners" is the same as among "non-dog owners," i.e., the conditional probability of event $A$ given $B$ is equal to the probability of event $A$ given $\bar{B}: \mathrm{P}(A \mid B)=\mathrm{P}(A \mid \bar{B})$. We get ${ }^{1} \frac{a}{a+c}=\frac{b}{b+d}$, from which $a d=b c$.
Due to random variability in the data, this equality may not be exact, but it should hold at least approximately. Suppose that all numbers in the Scientist's report are correct except for $a$. Then $a$ is approximately (rounded to the nearest integer) $\frac{b c}{d}=\frac{1110 \cdot 978}{121} \approx 8972$, and the total number of respondents is approximately $8972+1110+978+121=11181$. This is much greater than the number of residents in the city, so this scenario is implausible.
Suppose now that the number $b$ is incorrect. In this case, $b \approx \frac{a d}{c}=\frac{765 \cdot 121}{978} \approx 95$, and the total number of respondents is approximately $765+95+978+121=1959$, which is much less than 3000. Similarly, if the number $c$ is incorrect, then $c \approx \frac{a d}{b}=\frac{765 \cdot 121}{1110} \approx 83$, and the total number of respondents is close to $765+1110+83+121=2079$, which is also too small.
If the incorrect number is $d$, then $d \approx \frac{b c}{a}=\frac{1110 \cdot 978}{765} \approx 1419$, and the total number of survey participants is approximately $765+1110+978+1419=4272$. This is possible.
|
Answer: approximately 4272 people.
Note. Instead of approximate equalities, estimates can be made using inequalities.
## Grading Criteria
| Solution is complete and correct | 2 points |
| :--- | :--- |
| Answer is correct, but there are no arguments showing that other options are implausible (for example, there is a guess about which number is incorrect) | 1 point |
| Solution is incorrect or missing | 0 points |
|
4272
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Solution. Let the correct numbers in the table be $a, b, c$ and $d$. Consider the events $A=\{$ Has a card $\}$ and $B=\{$ Makes online purchases $\}$. These events are independent if the proportion of cardholders among online shoppers is the same as among those who do not make online purchases, that is,
| | Has a card | No card |
| :--- | :---: | :---: |
| Buys online | $a$ | $b$ |
| Does not buy online | $c$ | $d$ |
the conditional probability of event $A$ given $B$ is equal to the probability of event $A$ given $\bar{B}: \mathrm{P}(A \mid B)=\mathrm{P}(A \mid \bar{B})$. We get $\frac{a}{a+b}=\frac{c}{c+d}$, from which $a d=b c$.
Due to random variability in the data, this equality may not be exact, but it should at least hold approximately. Suppose that all numbers in the Scientist's report are correct except for $a$. Then the number $a$ should approximately (rounded to the nearest integer) equal $\frac{b c}{d}=\frac{245 \cdot 1142}{535} \approx 523$, and the number of respondents will be approximately $523+1142+535+245=2445$. This is much greater than 2000. The assumption is implausible.
Suppose now that the incorrect number is $b$. Then $b \approx \frac{a d}{c}=\frac{81 \cdot 535}{1142} \approx 38$, and the total number of survey participants is close to $1142+535+81+38=1796$. This is possible.
If the incorrect number is $c$, then $c \approx \frac{a d}{b}=\frac{81 \cdot 535}{245} \approx 177$, and the approximate total number of respondents is $177+535+81+245=1038$. This is too small: according to the condition, the sample size is more than 1500 people.
If the incorrect number is $d$, then $d \approx \frac{c b}{a}=\frac{1142 \cdot 245}{81} \approx 3454$, and the total sample size is approximately $1142+245+81+3454=4922$. This is also implausible.
|
Answer: approximately 1796 people.
Note. Instead of approximate equalities, estimates can be made using inequalities.
## Grading Criteria
| Solution is complete and correct | 2 points |
| :--- | :--- |
| Answer is correct, but there are no arguments showing that other options are implausible (for example, there is a guess about which number is incorrect) | 1 point |
| Solution is incorrect or missing | 0 points |
|
1796
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. Minimum Sum (9th grade, 4 points). There are a lot of symmetric dice. They are thrown simultaneously. With some probability $p>0$, the sum of the points can be 2022. What is the smallest sum of points that can fall when these dice are thrown with the same probability $p$?
|
Answer: 337.
Solution. The distribution of the sum rolled on the dice is symmetric. To make the sum $S$ the smallest possible, the sum of 2022 should be the largest possible. This means that the sum of 2022 is achieved when sixes are rolled on all dice. Therefore, the total number of dice is $2022: 6=337$. The smallest sum of 337 is obtained if ones are rolled on all dice.
|
337
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (1b, 8-11) The probability that a purchased light bulb will work is 0.95. How many light bulbs need to be bought to ensure that with a probability of 0.99, there are at least 5 working ones among them?
|
# Solution.
Let's take 6 light bulbs. The probability that at least 5 of them will work is the sum of the probabilities that 5 will work and 1 will not, and that all 6 will work, i.e.,
$$
C_{6}^{5} \cdot 0.95^{5} \cdot 0.05 + C_{6}^{6} \cdot 0.95^{6} = 6 \cdot 0.95^{5} \cdot 0.05 + 0.95^{6} = 0.9672
$$
Let's take 7 light bulbs. The desired probability is
$$
\begin{aligned}
& C_{7}^{5} \cdot 0.95^{5} \cdot 0.05^{2} + C_{7}^{6} \cdot 0.95^{6} \cdot 0.05 + C_{7}^{7} \cdot 0.95^{7} = \\
= & 21 \cdot 0.95^{5} \cdot 0.05^{2} + 7 \cdot 0.95^{6} \cdot 0.05 + 0.95^{7} = 0.9962
\end{aligned}
$$
The minimum number of light bulbs required is 7.
Answer: 7.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (3b,9-11) In the conditions of a chess match, the winner is declared as the one who outperforms the opponent by two wins. Draws do not count. The probabilities of winning for the opponents are equal. The number of decisive games in such a match is a random variable. Find its mathematical expectation.
|
# Solution.
Let $\mathrm{X}$ be the number of successful games. At the beginning of the match, the difference in the number of wins between the two participants is zero. Let's list the possible cases of two successful games, denoting a win by the first participant as 1 and a win by the second participant as 2: $11, 12, 21, 22$. Two out of the four cases mean a win in the match, specifically, 11 and 22. The other two cases bring us back to the initial state with a zero difference in the number of wins. Thus, with a probability of $\frac{2}{4}=\frac{1}{2}$, the number of wins $X=2$ and with the same probability $X=2+\tilde{X}$ where $\tilde{X}$ is distributed the same as $X$. From this, we derive the equation for the expectation
$$
\begin{gathered}
\mathrm{M} X=2 \cdot \frac{1}{2}+(2+\mathrm{M} \tilde{X}) \cdot \frac{1}{2}=2 \cdot \frac{1}{2}+(2+\mathrm{M} X) \cdot \frac{1}{2} \\
\frac{1}{2} \mathrm{M} X=2 ; \mathrm{M} X=4
\end{gathered}
$$
Answer: 4.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. (4b, 8-11) In Anchuria, a checkers championship is being held in several rounds. The days and cities for the rounds are determined by a draw. According to the championship rules, no two rounds can take place in the same city, and no two rounds can take place on the same day. Among the fans, a lottery is organized: the main prize goes to the person who correctly guesses before the championship begins in which cities and on which days all the rounds will take place. If no one guesses correctly, the main prize will go to the championship organizing committee. There are eight cities in Anchuria, and the championship is allocated a total of eight days. How many rounds should the organizing committee schedule to have the highest probability of winning the main prize themselves?
|
# Solution.
In an $8 \times 8$ tour table, you need to select $k$ cells such that no more than one cell is chosen in any row or column. The value of $k$ should be chosen to maximize the number of combinations.
The number of combinations is given by $C_{8}^{k} A_{8}^{k}=\frac{8!\cdot 8!}{(8-k)!\cdot(8-k)!\cdot k!}$, where $C_{8}^{k}$ is the number of ways to choose $k$ cities from eight without regard to order, and $A_{8}^{k}$ is the number of ways to choose $k$ days from eight with regard to order, since each day must correspond to one of the cities. From the table
| $k$ | Number of Combinations |
| :---: | :---: |
| 0 | 1 |
| 1 | 64 |
| 2 | 1568 |
| 3 | 18816 |
| 4 | 117600 |
| 5 | 376320 |
| $\mathbf{6}$ | $\mathbf{5 6 4 4 8 0}$ |
| 7 | 322560 |
| 8 | 40320 |
it is clear that the maximum number of combinations occurs when $k=6$.
Answer: 6.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The King's Path (from 7th grade, 2 points). A chess king is on the a1 square of a chessboard and wants to move to the h8 square, moving right, up, or diagonally up-right. In how many ways can he do this?
|
Solution. Instead of letter designations for the columns, we use numerical ones. Then, instead of al, we can write $(1,1)$. Let $S_{m, n}$ be the number of ways to get from the cell $(1,1)$ to the cell $(m, n)$. We are interested in $S_{8,8}$.
Obviously, $S_{1, n}=1$ and $S_{m, 1}=1$ for all $m$ and $n$. In particular, we can consider that $S_{1,1}=1$, since the king can get to the cell $(1,1)$ in only one way: by standing in place and doing nothing.
If $m>1$ and $n>1$, then the cell $(m, n)$ can be reached only from one of the three cells $(m-1, n),(m, n-1)$, and $(m-1, n-1)$. This gives the recurrence relation $S_{m, n}=S_{m-1, n}+S_{m, n-1}+S_{m-1, n-1}$.
The calculations can be easily performed in Excel (Fig. 2).
| INDEX | | | $-x \vee f=C 5+C 6+D 6$ | | | | | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 4 | A | B | C | D | E | F | G | H | I |
| | 8 | 1 | 15 | 113 | 575 | 2241 | 7183 | 19825 | 48639 |
| | 7 | 1 | 13 | 85 | 377 | 1289 | 3653 | 8989 | 19825 |
| | 6 | 1 | 11 | 61 | 231 | 681 | 1683 | 3653 | 7183 |
| | 5 | 1 | 9 | 41 | 129 | 321 | 681 | 1289 | 2241 |
| | 4 | 1 | 7 | $=\mathrm{C} 5+$ | +D6 | 129 | 231 | 377 | 575 |
| | 3 | 1 | 5 | 13 | 25 | 41 | 61 | 85 | 113 |
| | 2 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| | | a | b | c | d | e | f | g | h |
Fig. 2. Solution to problem 8 in Excel
Answer: 48639.
|
48639
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Buratino the Statistician (from 7th grade, 2 points). Every month, Buratino plays in the "6 out of 45" lottery organized by Karabas-Barabas. In the lottery, there are 45 numbered balls, and in each draw, 6 random winning balls are drawn.
Buratino noticed that in each subsequent draw, there are no balls that appeared in the previous draw: in the second draw, there were no balls from the first, in the third draw, there were no balls from the second, and so on.
Buratino does not believe in events with a probability of less than 0.01. If such an event occurs, Buratino begins to suspect something is amiss. After which draw will Buratino start to suspect that Karabas-Barabas is cheating?
|
Solution. The probability that no numbers from the first draw will be repeated in the second draw is $a=\frac{39 \cdot 38 \cdot 37 \cdot \ldots \cdot 34}{45 \cdot 44 \cdot 43 \cdot \ldots 40}=0.40056 \ldots$, which is slightly more than 0.4. The probability that there will be no repetitions from the previous draw in both the second and third draws is the square of this number, that is, $a^{2}$. The probability of no repetitions in the draws from the second to the fourth is $a^{3}$, and so on. The fifth power of the number $a$ is greater than 0.01: $a^{5}>0.4^{5}=10^{-5} \cdot 2^{10}=0.01024$, while the sixth is already less: $a^{6}=0.0041 \ldots$. Therefore, Pinocchio can accuse Karabas-Barabas after this phenomenon repeats 6 times, that is, after the seventh draw.
## Answer: after the seventh.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Winter Camp. In the winter camp, Vanya and Grisha live in a room. Every evening they draw lots to decide who will turn off the light before going to bed: the switch is near the door, and the loser has to go to bed in complete darkness, bumping into chairs.
Usually, Vanya and Grisha draw lots without any complications, but this time Grisha came up with a special way to draw lots:
- Let's toss a coin. If an eagle (heads) comes up on any even throw, we stop tossing: I win. If a tail (tails) comes up on any odd throw, you win.
a) (from 8th grade, 2 points). What is the probability of Grisha winning?
b) (from 8th grade, 2 points). Find the expected number of coin tosses until the end of the draw.
|
Solution. a) Let's assume that heads in a coin toss give a one, and tails give a zero in the fractional part of a binary fraction. This results in some number $x$ represented by a binary fraction. For example, if the sequence of tosses starts with HTH, then the binary fraction is 0.101.
Obviously, $0 \leq x \leq 1$, and the probability of the event $0 \leq x \leq a$ is $a$ for any non-negative $a \leq 1$ (try to prove this rigorously).
It is easy to see that Grisha will win only if the sequence of tosses gives a number $x$ that is greater than
$$
0.10101010101 \ldots = 0 + \frac{1}{2} + \frac{0}{4} + \frac{1}{8} + \frac{0}{16} + \frac{1}{32} + \ldots = \frac{1}{2} \cdot \frac{1}{1 - 1/4} = \frac{2}{3}
$$
The probability of this is $\frac{1}{3}$. If the obtained fraction is less than $\frac{2}{3}$, Vanya wins. The event "exactly $\frac{2}{3}$" has a zero probability.
Another solution can be obtained by considering the first two tosses. Grisha wins only in the case of HH, and in the case of HT, no one wins, and the game starts again. Therefore, the probability of Grisha's win $p$ can be found from the equation
$$
p = \frac{1}{4} + \frac{1}{4} p, \text{ hence } p = \frac{1}{3}
$$
b) Let's call a successful toss one where the outcome is decided, i.e., heads on an even toss or tails on an odd toss. The probability of success on each individual toss is 0.5. Due to the independence of the tosses, the expected number of tosses is 2.
Answer: a) $1 / 3 ;$ b) 2.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. Happy Sums (from 8th grade, 4 points). In the "Happy Sum" lottery, there are $N$ balls numbered from 1 to $N$. During the main draw, 10 balls are randomly drawn. During the additional draw, 8 balls are randomly selected from the same set of balls. The sum of the numbers on the drawn balls in each draw is announced as the happy sum, and players who predicted this sum win a prize.
Can it be that events $A$ "the happy sum in the main draw is 63" and $B$ "the happy sum in the additional draw is 44" are equally likely? If yes, under what condition?
|
Solution. In the main draw, there are $C_{N}^{10}$ possible combinations, and in the additional draw, there are $C_{N}^{8}$ combinations. Let $S_{63,10}$ be the number of combinations in the first draw where the sum is 63. The addends are different natural numbers from 1 to $N$. If the smallest number is 2 or more, then the sum of all ten addends is no less than
$$
2+3+\ldots+11=\frac{2+11}{2} \cdot 10=13 \cdot 5=65
$$
Thus, the smallest number is 1. By removing one from each addend, i.e., subtracting 10 from the sum, we find that the remaining sum of 53 is obtained by nine different natural addends, each not exceeding the number $N$. In other words, the number of ways to get a sum of 63 with ten addends is the same as the number of ways to get a sum of 53 with nine addends: $S_{63,10}=S_{53,9}$.
Reasoning similarly, we get: $S_{63,10}=S_{53,9}=S_{44,8}$. Now we can find the ratio of probabilities:
$$
\frac{\mathrm{P}(B)}{\mathrm{P}(A)}=\frac{S_{44,8} \cdot C_{N}^{10}}{C_{N}^{8} \cdot S_{63,10}}=\frac{C_{N}^{10}}{C_{N}^{8}}=\frac{8!(N-8)!}{10!(N-10)!}=\frac{(N-8)(N-9)}{90}
$$
Let's find for which $N$ the obtained fraction equals one:
$$
\frac{(N-8)(N-9)}{90}=1 ; N^{2}-17 N-18=0, \text { from which } N=18
$$
Answer: This is possible if there are 18 balls in the lottery.
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In the village of Znoynoye, there are exactly 1000 residents, which exceeds the average population of villages in the valley by 90 people.
How many residents are there in the village of Raduzhny, which is also located in Sunny Valley?
|
Solution. Let $x$ be the total number of residents in all other villages except Znoynoye. Then the average population is
$$
\frac{1000+x}{10}=100+0.1 x=910, \text{ hence } x=8100
$$
Thus, the average population in 9 villages, except Znoynoye, is 900 people. If there are more than 900 residents in Raduzhny, there must be a village with fewer than 900 residents, but then the number of residents in Raduzhny would differ from the number of residents in Znoynoye by more than 100. This is a contradiction. Therefore, there are no more than 900 residents in Raduzhny. It is obvious that there are no fewer than 900 residents in Raduzhny. Thus, there are exactly 900 residents.
Answer: 900.
|
900
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.
|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Promotion. The store "Crocus and Cactus" announced a promotion: if a customer buys three items, the cheapest one of them is free. The customer took ten items, all of different prices: 100 rubles, 200 rubles, 300 rubles, and so on - the most expensive item cost 1000 rubles.
a) (from 6th grade. 1 point). What is the smallest amount the customer will pay if they arrange their purchases skillfully before the cashier?
b) (from 6th grade. 1 point). What is the largest amount the customer will pay if they arrange the purchases poorly?
c) (from 9th grade. 3 points). Find the expected value of the amount the customer will pay if they arrange the purchases randomly.
|
Solution. a) The cheapest item in each trio should be as expensive as possible. If the buyer distributes the purchases into trios as follows (indicating only the prices):
$(1000,900,800),(700,600,500),(400,300,200)$ and a separate item for $100 \mathrm{p}.$, then he will pay $1000+900+700+600+400+300+100=4000$ rubles.
b) The worst distribution is when the buyer gets the three cheapest items for free under the promotion, which are 100, 200, and 300 rubles. In this case, the buyer will pay 4900 rubles. For example, the distribution could be:
$(1000,900,100),(800,700,200),(600,500,300)$ and a separate item for $400 \mathrm{p}$.
c) Let's take an item priced at $100 k$ rubles ( $k=1,2, \ldots, 10)$. Introduce a random variable - the indicator $I_{k}$, which is 1 if the buyer did not have to pay for this item, and 0 if they did. Obviously, $I_{10}=I_{9}=0$.
In other cases, $I_{k}=1$ only if, along with the item priced at $100 k$, two of the $10-k$ more expensive items are in the same trio. Such a combination can be formed in $C_{10-k}^{2}$ ways. The probability of such a combination is $\frac{C_{10-k}^{2}}{C_{9}^{2}}=\frac{(10-k)(9-k)}{72}$. The number $C_{9}^{2}$ in the denominator of the fraction is the total number of ways to select two items from the remaining nine to form a trio with the item priced at $100 k$.
We get the distribution
$$
I_{k} \sim\left(\begin{array}{cc}
0 \\
-\frac{k^{2}-19 k+18}{72} & \frac{k^{2}-19 k+90}{72}
\end{array}\right)
$$
The expected value: $\mathrm{E} I_{k}=\frac{k^{2}-19 k+90}{72}$. The total amount the buyer will save is
$$
S=100 I_{1}+200 I_{2}+\ldots+1000 I_{10}=100\left(I_{1}+2 I_{2}+\ldots+8 I_{8}\right)=100 \sum_{k=1}^{8} k I_{k}
$$
Transitioning to expectations, we get:
$$
\begin{gathered}
\mathrm{E} S=100 \sum_{k=1}^{8} \frac{k\left(k^{2}-19 k+90\right)}{72}= \\
=100\left(\frac{72}{72}+2 \cdot \frac{56}{72}+3 \cdot \frac{42}{72}+4 \cdot \frac{30}{72}+5 \cdot \frac{20}{72}+6 \cdot \frac{12}{72}+7 \cdot \frac{6}{72}+8 \cdot \frac{2}{72}\right)=916 \frac{2}{3} .
\end{gathered}
$$
The expected savings have been found. Therefore, the expected amount to be paid is
$$
\left.\frac{100+1000}{2} \cdot 10-916 \frac{2}{3}=5500-916 \frac{2}{3}=4583 \frac{1}{3} \text { (rubles }\right),
$$
which is 4583 rubles and 33 kopecks.
Answer: a) 4000 rubles; b) 4900 rubles; c) 4583 rubles 33.
|
4583
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Stubborn Squares (from 7th grade. 2 points). Given 100 numbers. 2 was added to each of them. The sum of the squares of the numbers did not change. 2 was added to each of the resulting numbers again. How did the sum of the squares change now?
|
Solution. Let the given numbers be $x_{1}, x_{2}, \ldots, x_{100}$. By adding 2 to each number, we get the set $y_{j}=x_{j}+2$. Adding 2 again, we get the set $z_{j}=y_{j}+2=x_{j}+4$. However, the variances of all three sets are equal, that is,
$$
\overline{x^{2}}-\bar{x}^{2}=\overline{y^{2}}-\bar{y}^{2}=\overline{z^{2}}-\bar{z}^{2}
$$
By the condition, $\overline{x^{2}}=\overline{y^{2}}$ and, obviously, $\bar{y}=\bar{x}+2$. Therefore, $\bar{x}^{2}=(\bar{x}+2)^{2}$, from which $\bar{x}=-1$. Then $\bar{z}=-1+4=3$. Therefore,
$$
\overline{z^{2}}=\overline{x^{2}}+\bar{z}^{2}-\bar{x}^{2}=\overline{x^{2}}+9-1=\overline{x^{2}}+8
$$
Since there are 100 numbers in total, the sum of the squares has increased by $8 \cdot 100=800$.
Answer: the sum of the squares increased by 800.
|
800
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Magic Pen (recommended for 8th grade, 1 point). Katya correctly solves a problem with a probability of $4 / 5$, while the magic pen correctly solves a problem without Katya's help with a probability of $1 / 2$. In the test, there are 20 problems, and to get a B, one needs to solve at least 13 of them correctly. How many problems should Katya solve on her own, and how many should she entrust to the magic pen, so that the expected number of correct answers is at least 13?
|
Solution. Let $x$ be the number of examples Katya solves herself, and $20-x$ be the number of examples solved by the pen. Then the expected number of correctly solved problems is
$$
\frac{4}{5} x+\frac{1}{2}(20-x)=0.3 x+10
$$
From the inequality $0.3 x+10 \geq 13$ we get that $x \geq 10$. Therefore, Katya needs to try to solve at least 10 examples on her own.
Answer: at least 10 examples.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Retro Collection (recommended from 8th grade, 2 points). Vitya collects toy cars from the "Retro" series. The problem is that the total number of different models in the series is unknown - it is the biggest commercial secret, but it is known that different cars are produced in the same edition, and therefore it can be assumed that all models are uniformly and randomly distributed across different online stores.
On different websites, Vitya found several offers, but upon closer inspection, it turned out that among the offered cars, there were only 12 different ones. Vitya is almost convinced that there are only 12 cars in total and that further search is futile. But who knows?
How many more offers from other stores should Vitya consider to be convinced that there are only 12 models in the series? Vitya considers himself convinced of something if the probability of this event is higher than 0.99.
|
Solution. Let there be a series of $n \geq 13$ cars. The probability that among the next $k$ offers there will only be the 12 models that Vitya has already seen is
$$
\left(\frac{12}{n}\right)^{k} \leq\left(\frac{12}{13}\right)^{k}
$$
We form the inequality: $\left(\frac{12}{13}\right)^{k}\log _{12 / 13} 0.01=\frac{\ln 100}{\ln 13-\ln 12}=57.53 \ldots
$$
The smallest integer value of $k$ is 58.
Answer: 58.
Comment. The smallest integer solution to the inequality can be found without logarithms by trial and error using a calculator or computer.
|
58
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. New Year's Problem (recommended for 8th grade, 4 points). On the New Year's table, there are 4 glasses in a row: the first and third are filled with orange juice, while the second and fourth are empty. While waiting for guests, Vanya absent-mindedly and randomly pours the juice from one glass to another. In one move, she can take a full glass and pour all its contents into one of the two empty glasses.
Find the expected number of pourings after which, for the first time, everything will be the opposite: the first and third glasses will be empty, and the second and fourth will be full.
|
Solution. We will encode full glasses with the digit 1 and empty ones with the digit 0. We will construct a graph of possible pourings (Fig. 4). This graph turns out to be the graph of an octahedron. From each state to any adjacent one, one can move with a probability of $1 / 4$, and each edge is "traversable" in both directions.
From the initial state (1010) to the final state (0101), one can transition through any of the remaining four states. Let's identify these four intermediate states. We get a simpler graph with three vertices (Fig. 5).
For brevity, let's denote the initial and final states by $A$ and $C$, and all intermediate states by a single vertex $B$, without distinguishing between them. We will make the edges directed, showing all possible movements in the graph, except for the edge $C \rightarrow B$, which we do not need, since we are interested in the moment of the first arrival of the random process at vertex $C$. We will write the probabilities of the corresponding steps next to the edges. For example, the probability of the step $A \rightarrow B$ is 1, and the probability of the reverse step $B \rightarrow A$ is $1 / 4$. The probability of the step $B \rightarrow B$ is $1 / 2$.
Let $X$ be the random variable "the number of steps leading from A to C for the first time," and $Y$ "the number of steps leading from B to C for the first time."
It is clear that from $A$ one can only go to $B$, and after that, to reach vertex $C$, it will take $Y$ steps. Therefore,
$$
X=1+Y
$$
Fig. 4
Exiting from $B$, the process can go three ways, each of which we will invent an indicator for: let $I_{A}, I_{B}$, and $I_{C}$ be three random variables, each of which is 1 if the process transitions from point $B$ to $A, B$, or $C$ respectively, and 0 otherwise.
If the process from $B$ reaches the initial point $A$, then one step is spent and it will take another $X_{1}$ steps to reach $C$, and the quantities $X$ and $X_{1}$ are identically distributed. If the process from $B$ reaches $B$ again, then one step is spent, but nothing changes and it will take $Y_{1}$ steps to reach $C$, and the quantities $Y$ and $Y_{1}$ are identically distributed. Only in the case of transitioning to $C$ does the process end. We get the equation
$$
Y=I_{A}\left(1+X_{1}\right)+I_{B}\left(1+Y_{1}\right)+I_{C} \cdot 1
$$
The indicators $I_{A}, I_{B}$, and $I_{C}$ relate to the step taken from point $B$, while the quantities $X_{1}$ and $Y_{1}$ relate to subsequent steps. Therefore, the quantities $I_{A}$ and $X_{1}$ are independent, and $I_{B}$ and $Y_{1}$ are independent. Transitioning to mathematical expectations in equations (1) and (2), we get the system
$$
\left\{\begin{array}{l}
\mathrm{E} X=1+\mathrm{E} Y, \\
\mathrm{E} Y=\mathrm{E} I_{A} \cdot\left(1+\mathrm{E} X_{1}\right)+\mathrm{E} I_{B} \cdot\left(1+\mathrm{E} Y_{1}\right)+\mathrm{E} I_{C}
\end{array}\right.
$$
Let's find the mathematical expectations of the indicators:
$$
\mathrm{E} I_{A}=\mathrm{P}\left(I_{A}=1\right)=\mathrm{P}(B \rightarrow A)=\frac{1}{4}, \mathrm{E} I_{B}=\frac{1}{2} \text { and } \mathrm{E} I_{C}=\frac{1}{4} .
$$
Let $\mathrm{E} X=\mathrm{E} X_{1}=x$ and $\mathrm{E} Y=\mathrm{E} Y_{1}=y$. The system takes the form
$$
\left\{\begin{array}{l}
x=1+y \\
y=1+\frac{1}{4} x+\frac{1}{2} y,
\end{array}\right.
$$
Answer: 6.
Comment. The solution can be made more concise if we use the properties of conditional mathematical expectations.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. Messengers (recommended for 9th grade, 3 points). Once, the beautiful Queen Guinevere, while staying at her parental castle, asked King Arthur to send her 20 pearls. The roads are not safe, and Arthur, just in case, decided to send 40 pearls, with different messengers, ordering them to ride on different roads. Bandits may lie in wait for the messengers. The probability that each individual messenger will be robbed is $p$, independently of the chosen road and the fate of other messengers $(0<p<1)$.
The king is in a dilemma: should he send two messengers, giving each 20 pearls, send three messengers, giving one 20 and the other two 10 pearls each, or send four messengers, giving each 10 pearls? Which option should the king choose so that the queen has the highest probability of receiving at least 20 pearls?
|
Solution. The probability of not saving at least 20 pearls if there are two messengers:
$$
\mathrm{P}_{2}=p^{2}
$$
The probability of not saving at least 20 pearls if there are three messengers:
$$
\mathrm{P}_{3}=p^{3}+2 p^{2}(1-p)=p^{2}(2-p) .
$$
The probability of not saving at least 20 pearls if there are four messengers:
$$
\mathrm{P}_{4}=p^{4}+4 p^{3}(1-p)=p^{3}(4-3 p)
$$
Dividing all probabilities by \( p^{2} \), we get three functions:
$$
f_{2}=1, f_{3}=2-p, f_{4}=4 p-3 p^{2}
$$
Clearly, \( f_{2}<f_{3} \) for all \( p \in(0 ; 1) \) (Fig. 6), so the option with three messengers is inferior under any conditions. Let's compare \( f_{2} \) and \( f_{4} \):
$$
1<4 p-3 p^{2} ; 3 p^{2}-4 p+1<0, \text { hence } \frac{1}{3}<p<1
$$
Thus, when \( 0<p<\frac{1}{3} \), it is more advantageous to send four messengers, and when \( \frac{1}{3} \leq p<1 \) - two. In fact, when \( p=\frac{1}{3} \), two or four messengers will perform equally well, but why send four messengers if two are sufficient?
Answer: when \( 0<p<\frac{1}{3} \), it is more advantageous to send four messengers, and when \( \frac{1}{3} \leq p<1 \) - two.
Fig. 6.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. The Right Stars (from 8th grade, 3 points). Let natural numbers $k$ and $n$ be coprime, with $n \geq 5$ and $k < n / 2$. A proper $(n ; k)$-star is defined as a closed broken line that results from replacing every $k$ consecutive sides in a regular $n$-gon with a diagonal having the same endpoints. For example, the $(5 ; 2)$-star shown in the figure has 5 points of self-intersection, which are the bold points in the figure. How many self-intersections does the star $(2018 ; 25)$ have?
|
Solution. We will solve the problem in general for the $(n ; k)$-star. Let the vertices of the $n$-gon be denoted by $A_{0}, A_{1}$, and so on up to $A_{n-1}$. Take two consecutive segments of the star: $A_{0} A_{k}$ and $A_{1} A_{k+1}$. They intersect at a circle of radius $r_{1}$ with the center at the center of the $n$-gon. By rotating by $360\%$, we obtain another $n-1$ points lying on the same
circle. In total, there are $n$ points on this circle, located at the vertices of a smaller $n$-gon.
Now take the pair of segments $A_{0} A_{k}$ and $A_{2} A_{k+2}$. They have a common point on a circle of radius $r_{2} > r_{1}$. There are $n$ such points.
In the diagram, the case $k=3$ is shown: the intersection point of the segments $A_{0} A_{3}$ and $A_{1} A_{4}$ lies on a circle of radius $r_{1}$. On this same circle, the intersection point of the segments $A_{1} A_{4}$ and $A_{2} A_{5}$ is also located. The intersection point of the segments $A_{0} A_{4}$ and $A_{2} A_{5}$ lies on a larger circle of radius $r_{2}$.
Proceeding in this manner, we obtain a total of $k-1$ circles of different radii, each of which contains exactly $n$ intersection points. Therefore, no two points coincide. This way, all intersection points of the segments are enumerated, and there are a total of $n(k-1)$ of them.
For $n=2018, k=25$, we get that the number of self-intersections is $2018 \cdot 24 = 48432$.
Other solutions are possible, but in any case, it is necessary to explain why no two intersection points coincide.
Answer: 48432.
|
48432
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Target (from 8th grade, 2 points). A target is hanging on the wall, consisting of five zones: a central circle (the bullseye) and four colored rings (see figure). The width of each ring is equal to the radius of the bullseye. It is known that the number of points for hitting each zone is inversely proportional to the probability of hitting that zone, and that the bullseye is worth 315 points. How many points is a hit in the blue (second-to-last) zone worth?
|
Solution. Suppose, for definiteness, that the apple has a radius of 1. Then the blue zone is enclosed between circles with radii 3 and 4. The probability of hitting the blue zone relative to the probability of hitting the apple is the ratio of the areas of these zones:
$$
\frac{p_{g}}{p_{c}}=\frac{1}{4^{2}-3^{2}}=\frac{1}{7}
$$
Then the number of points \( x \) for the blue zone can be found from the proportion
$$
\frac{x}{315}=\frac{p_{g}}{p_{c}}=\frac{1}{7}
$$
from which \( x = 315 : 7 = 45 \).
Answer: 45.
## $\mathrm{XI}$ Internet Olympiad in Probability Theory and Statistics. Main (correspondence) round. $15.12 .77-21.01 .18$
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Lonely Cars. (From 9th grade, 4 points.) On a very long narrow highway, where overtaking is impossible, $n$ cars are driving in a random order, each with its own preferred speed. If a fast car catches up to a slower one, the fast car has to slow down and drive at the same speed as the slower one. Thus, the cars form groups. Find the expected number of "lonely" cars, that is, groups consisting of a single car.
|
Solution. Let $I_{k}$ be the indicator of the event "the $k$-th car in line is alone." For $k \leq n$, this event consists of the slowest car among the first $k+1$ cars being the last, and the second slowest being the second to last. The probability of this is $\frac{1}{(k+1) k}$. If $k=n$, then this event consists of the slowest car being the last (probability $\frac{1}{n}$).
The random variable $X$ "number of lonely cars" is equal to the sum of all indicators, therefore
$$
\begin{gathered}
\mathrm{E} X=\mathrm{E} I_{1}+\mathrm{E} I_{2}+\ldots+\mathrm{E} I_{n}=\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots .+\frac{1}{(n-1) n}+\frac{1}{n}= \\
=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\ldots+\frac{1}{n-1}-\frac{1}{n}+\frac{1}{n}=1
\end{gathered}
$$
Answer: 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The smallest set. (From 6th grade, 2 points) In a numerical set, the median is 3, the arithmetic mean is 5, and the only mode of the set is 6. What is the smallest number of numbers that can be in a set with the given properties?
|
Solution. It is clear that the number 6 appears at least twice in the set, and in addition, there are at least two more numbers.
If the set contains exactly four numbers $a, b, 6, 6$, then we can assume that $a \leq b \leq 3$ and, moreover, the sum of all numbers is 20, so $a+b=20-6-6=8$. Contradiction. The set cannot contain exactly four numbers.
If the set contains exactly five numbers, then the set has the form $a, b, 3, 6, 6$, where $a \leq b \leq 3$ and $a+b=25-6-6-3=10$. Contradiction. The set cannot consist of exactly five numbers.
A set of six numbers with the specified properties exists. For example, $-2, -1, 0, 6, 6, 21$.
## Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. How many airplanes? (11th grade, 8 points) The work of the Absent-Minded Scientist involves long business trips, and therefore he often flies on the same airline. This airline has many identical airplanes, and all of them have names. Since the Scientist does not fly every day or even every week, it can be assumed that each time he gets a random airplane. Out of curiosity and habit, the Absent-Minded Scientist records the name of the airplane he flies on each time. In his fifteenth flight, the Scientist found himself on board an airplane proudly named "Siméon Denis Poisson." After takeoff, the Scientist took out his notebook to record the name of the airplane and discovered that he had already flown on "Poisson" once before, and there were no other repetitions before that. Estimate the number of airplanes in the airline.
|
Solution. Consider the random variable $X$ "the ordinal number of the flight when the Scientist first gets a plane he has flown before". We will make a point estimate of the number of planes using the method of moments. For this, we need to solve the equation $\mathrm{E} X=15$ at least approximately.
Let's find $\mathrm{E} X$. Denote $n$ as the number of planes in the airline. Consider the event $A_{j}$ "there were no repetitions up to and including the $j$-th flight" $(j=1, \ldots, n)$. Let $I_{j}$ be the indicator of the event $A_{j}$. Then
$$
X=1+I_{1}+I_{2}+\ldots+I_{n}
$$
Let's find the expected values of the indicators.
$$
\mathrm{EI}_{j}=\mathrm{P}\left(A_{j}\right)=\frac{n(n-1)(n-2) \ldots(n-j+1)}{n^{j}}=\frac{n!}{(n-j)!\cdot n^{j}}
$$
Therefore,
$$
\mathrm{E} X=\mathrm{E}\left(1+I_{1}+I_{2}+\ldots+I_{n}\right)=\sum_{j=0}^{n} \frac{n!}{(n-j)!\cdot n^{j}}=\frac{n!}{n^{n}} \sum_{j=0}^{n} \frac{n^{n-j}}{(n-j)!}=\frac{n!}{n^{n}} \sum_{k=0}^{n} \frac{n^{k}}{k!}
$$
In the last transformation, we made the substitution $k=n-j$.
Consider the resulting sum separately:
$$
\sum_{k=0}^{n} \frac{n^{k}}{k!}=e^{n} \sum_{k=0}^{n} \frac{n^{k} e^{-n}}{k!}=e^{n} F(n)
$$
where $F(x)$ is the cumulative distribution function of the Poisson distribution with parameter $n$. The median of the Poisson distribution with an integer parameter $n$ is $n$. This means that
$$
F(n-1) \leq \frac{1}{2} \leq F(n)
$$
therefore
$$
F_{P}(n)=\sum_{k=0}^{n} \frac{n^{k} e^{-n}}{k!}=\frac{1}{2}+\theta \frac{n^{n} e^{-n}}{n!}
$$
where $0 \leq \theta \leq 1$. Setting $\theta=1 / 2$ for definiteness, we get:
$$
\mathrm{E} X=\frac{n!e^{n}}{n^{n}} F_{P}(n) \approx \frac{n!e^{n}}{n^{n}}\left(\frac{1}{2}+\frac{n^{n} e^{-n}}{2 n!}\right)=\frac{n!e^{n}}{2 n^{n}}+\frac{1}{2}
$$
Using Stirling's formula
$$
\mathrm{E} X \approx \frac{\sqrt{2 \pi n} \cdot n^{n} e^{n}}{2 n^{n} e^{n}}+\frac{1}{2}=\sqrt{\frac{\pi n}{2}}+\frac{1}{2}
$$
To find the estimate $x=\hat{n}$, solve the equation $\sqrt{\frac{\pi x}{2}}+\frac{1}{2}=15$. With rounding to the nearest integer, we get: $x \approx 134$.
Answer: approximately 134 (point estimate using the method of moments).
[^0]: ${ }^{1}$ English name - Stem-and-Leaf plot.
[^1]: ${ }^{2}$ The mode is the number that appears in the set more times than any other.
[^2]: ${ }^{3}$ It is believed that this problem was invented by Academician Andrei Dmitrievich Sakharov. I. F. Ginzburg. Academician A.D. Sakharov. Scientific works. Collection. - M.: AOZT "Izdatel'stvo TsentrKom", 1995.
[^3]: ${ }^{4}$ The number $e$ is also called Euler's number.
[^4]: ${ }^{5}$ The median of a random variable $X$ is a number $m$ such that $\mathrm{P}(X \leq m) \geq 0.5$ and $\mathrm{P}(X \geq m) \geq 0.5$. If the random variable has a finite density function $y=f(x)$, then the line $x=m$ divides the figure bounded by the x-axis and the density graph into two figures, each with an area of 0.5.
|
134
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Ministers in Anchuria. In the government cabinet of ministers in Anchuria, there are 100 ministers. Among them, there are crooks and honest ministers. It is known that among any ten ministers, at least one minister is a crook. What is the smallest number of crook ministers that can be in the cabinet?
|
Solution. There are no more than nine honest ministers, otherwise, a group of ten honest ministers would be found, which contradicts the condition. Therefore, the number of minister-cheats is no less than $100-9=91$.
Answer: 91.
|
91
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Patrick and Slippers. Every day, the dog Patrick gnaws one slipper from the existing supply in the house. With a probability of 0.5, Patrick wants to gnaw a left slipper, and with a probability of 0.5 - a right slipper. If the desired slipper is not available, Patrick gets upset. How many pairs of identical slippers need to be bought so that with a probability of at least 0.8, Patrick does not get upset for a whole week (7 days)?
|
Solution. It is clear that if 7 pairs are bought, Patrick will definitely have enough of the desired, even if he chooses only left slippers every day. The question is about the smallest number of slippers that need to be bought so that with a probability of 0.8 or higher, Patrick will not be disappointed. Probability theory often helps to solve a problem not with absolute certainty, but practically with certainty ${ }^{1}$, which is more important in real life.
Assume for definiteness that during the week Patrick will want to eat $S$ left and $7-S$ right slippers. We need to find such a $k$ that the inequality
$$
\mathrm{P}(S \leq k \cap 7-S \leq k) \geq 0.8
$$
holds. $k$ will be the required number of pairs. Rewrite the event in parentheses as:
$$
\mathrm{P}(7-k \leq S \leq k) \geq 0.8
$$
The probability on the left side of the inequality is equal to the sum
$$
C_{7}^{7-k} \frac{1}{2^{7}}+C_{7}^{8-k} \frac{1}{2^{7}}+\ldots+C_{7}^{k} \frac{1}{2^{7}}=\frac{1}{128} \cdot\left(C_{7}^{7-k}+C_{7}^{8-k}+\ldots+C_{7}^{k}\right)=\frac{1}{64} \cdot\left(C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k}\right)
$$
Then
$$
C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k} \geq 64 \cdot 0.8=51.2
$$
Considering that the left side is an integer, we need to find the smallest $k$ for which the inequality
$$
C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k} \geq 52
$$
holds.
Write out the 7th row of Pascal's triangle, starting from $C_{7}^{4}$:
| $C_{7}^{4}$ | $C_{7}^{5}$ | $C_{7}^{6}$ | $C_{7}^{7}$ |
| :---: | :---: | :---: | :---: |
| 35 | 21 | 7 | 1 |
The sum $C_{7}^{4}+C_{7}^{5}=35+21>52$, so the smallest $k$ is 5.
Answer: 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. For a procrastinator, the waiting time will increase by $a$ minutes.
Therefore, the total wasted time of all standing in the queue will decrease by $b-a$ minutes. We will thus swap people in pairs of "Procrastinator-Hurry" until we get a queue where all the hurries stand before all the procrastinators. In this queue, the wasted time will be minimal.
Let's find the total wasted time. The second person waits for the first, the third waits for the previous two, and so on.
The total time spent waiting for all the hurries in front to finish their operations is
$$
(a+2a+\ldots+(n-1)a)+m \cdot n a=a \cdot \frac{1+n-1}{2} \cdot(n-1)+m n a=a C_{n}^{2}+m n a
$$
Here, the term $m n a$ is the total time spent by all procrastinators waiting for all the hurries.
The total time spent waiting for the procrastinators in front to finish their operations is $b+2b+\ldots+(m-1)b=b C_{m}^{2}$.
The overall minimum waiting time for all customers is
$$
T_{\min }=a C_{n}^{2}+a m n+b C_{m}^{2}
$$
In our specific case, we get:
$$
1 \cdot C_{5}^{2}+1 \cdot 5 \cdot 3+5 \cdot C_{3}^{2}=10+15+15=40
$$[^3]
Similarly, it can be proven that the maximum wasted time will be if all procrastinators stand before all hurries. This time is
$$
T_{\max }=a C_{n}^{2}+b m n+b C_{m}^{2}
$$
With the numerical data from the problem, we get $1 \cdot C_{5}^{2}+5 \cdot 5 \cdot 3+5 \cdot C_{3}^{2}=10+75+15=100$.
b) Consider the $k$-th customer in the queue. Let $X_{k}$ be the number of procrastinators standing before him. Then $X_{k}=I_{1}+I_{2}+\ldots+I_{k-1}$, where the indicator $I_{j}$ takes the value 1 if the $j$-th customer is a procrastinator and 0 if the $j$-th customer is a hurry.
The $j$-th customer can be a procrastinator with probability $\frac{m}{m+n}$ and a hurry with probability $\frac{n}{m+n}$. Therefore, $\mathrm{E} I_{j}=0 \cdot \frac{n}{m+n}+1 \cdot \frac{m}{m+n}=\frac{m}{m+n}$.
Thus, $\mathrm{E} X_{k}=\frac{(k-1) m}{m+n}$.
Let $T_{k}$ be the waiting time of the $k$-th customer. We get:
$$
T_{k}=X_{k} b+\left(k-1-X_{k}\right) a=(b-a) X_{k}+a(k-1)
$$
Therefore,
$$
\mathrm{E} T_{k}=(b-a) \mathrm{E} X_{k}+a(k-1)=(b-a) \cdot \frac{(k-1) m}{m+n}+a(k-1)=\frac{b m+a n}{m+n} \cdot(k-1)
$$
Summing the obtained expression over all customers from 1 to $m+n$-th, we get the expected total wasted time:
$$
\begin{gathered}
\mathrm{E} T=\mathrm{E}\left(T_{1}+T_{2}+\ldots+T_{n}\right)=\frac{b m+a n}{m+n} \cdot(0+1+2+\ldots+(m+n-1))= \\
=\frac{(b m+a n)(n+m-1)}{2}=C_{n+m}^{2} \cdot \frac{b m+a n}{m+n}
\end{gathered}
$$
Substituting the known numbers from the condition: $C_{8}^{2} \cdot \frac{5 \cdot 3+1 \cdot 5}{8}=\frac{7 \cdot 20}{2}=70$.
|
Answer: a) 40 minutes and 100 minutes; b) 70 minutes.
Comment. The expected time turned out to be the arithmetic mean between the maximum and minimum possible. Try to prove the fact $\mathrm{E} T=\frac{T_{\min }+T_{\max }}{2}$ in general, that is, prove the combinatorial identity
$$
C_{n+m}^{2} \cdot \frac{b m+a n}{m+n}=a C_{n}^{2}+\frac{a+b}{2} m n+b C_{m}^{2}
$$
By the way, part b) could have been solved almost without calculations, by noting that each arrangement of slowpokes and hurries can be matched with a symmetrically equal and equally probable arrangement, and the sum of the waiting times for both arrangements will be equal to $a C_{n}^{2}+\frac{a+b}{2} \cdot m n+b C_{m}^{2}$. For this, it is convenient to use the graphical method (see the footnote above).
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Median. In a set of 100 numbers. If one number is removed, the median of the remaining numbers is 78. If another number is removed, the median of the remaining numbers is 66. Find the median of the entire set.
|
Solution. Arrange the numbers in ascending order. If we remove a number from the first half of the sequence (with a number up to 50), the median of the remaining numbers will be the $51-\mathrm{st}$ number in the sequence. If we remove a number from the second half, the median of the remaining numbers will be the number with the 50th position, but it is not greater than the 51st number. Therefore, the 50th number is 66, and the 51st number is 78. Thus, the median of the entire set is ${ }^{2}$ $\frac{66+78}{2}=72$.
Answer: 72.[^1]
|
72
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Traffic Light (from 10th grade. 2 points). A traffic light at a pedestrian crossing allows pedestrians to cross the street for one minute and prohibits crossing for two minutes. Find the average waiting time for the green light for a pedestrian who approaches the intersection.

|
Solution. With probability $\frac{1}{3}$, the pedestrian falls into the interval when the green light is on (event $G$), and therefore the conditional expected waiting time $T$ in this case is 0: $\mathrm{E}(T \mid G)=0$. With probability $\frac{2}{3}$, the pedestrian falls on the red signal and has to wait (event $\bar{G}$). In this case, the waiting time is uniformly distributed over the interval from 0 to 2 minutes, so the conditional expected value of $T$ given $\bar{G}$ is one minute: $\mathrm{E}(T \mid G)=\frac{0+2}{2}=1$ (min).
We get:
$$
\mathrm{E}(T)=\mathrm{E}(T \mid G) \cdot \mathrm{P}(G)+\mathrm{E}(T \mid \bar{G}) \cdot \mathrm{P}(\bar{G})=\frac{1}{3} \cdot 0+\frac{2}{3} \cdot 1=\frac{2}{3}(\text { min })
$$
Answer: 40 seconds.
|
40
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.
|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. There are 25 children in the class. Two are chosen at random for duty. The probability that both duty students will be boys is $\frac{3}{25}$. How many girls are in the class?
|
# Solution.
Let there be $n$ boys in the class, then the number of ways to choose two duty students from them is $\frac{n(n-1)}{2}$, the number of ways to choose two duty students from the entire class is $25 \cdot 24$. The ratio of the two obtained fractions, i.e., $\frac{n(n-1)}{25 \cdot 24}$. It is also equal to $\frac{3}{25}$ according to the condition. We get the quadratic equation $n^{2}-n-72=0$. Its roots are -8 and 9. Only the positive root fits us, i.e., there are 9 boys in the class, and, consequently, 16 girls.
Answer: 16.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. There are fewer than 30 people in the class. The probability that a randomly chosen girl is an excellent student is $\frac{3}{13}$, and the probability that a randomly chosen boy is an excellent student is $\frac{4}{11} \cdot$ How many excellent students are there in the class?
|
# Solution.
According to classical probability theory, the probability that a randomly chosen girl is an excellent student is equal to the ratio of the number of excellent girl students to the total number of girls in the class. Accordingly,
$$
\frac{3}{13}=\frac{\text { number of girls-excellent students }}{\text { number of girls }}
$$
Considering that the number of girls is a natural number, and that there are fewer than 30 people (and thus fewer than 30 girls) in the class, we find that there are either 13 girls (3 excellent students) or 26 (6 excellent students).
Applying the same reasoning to boys, we find that:
$$
\frac{4}{11}=\frac{\text { number of boys-excellent students }}{\text { number of boys }}
$$
In the class, there are either 11 boys (4 excellent students) or 22 (8 excellent students). Further, considering that there are fewer than 30 people in the class, we find that there are 13 girls (3 excellent students) and 11 boys (4 excellent students). Therefore, the number of excellent students is $3+4=7$.
Answer: 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. The figure shows a track scheme for karting. The start and finish are at point $A$, and the kart driver can make as many laps as they want, returning to the starting point.
The young driver Yura spends one minute on the path from $A$ to $B$ or back. Yura also spends one minute on the loop. The loop can only be driven counterclockwise (arrows indicate possible directions of movement). Yura does not turn back halfway and does not stop. The race duration is 10 minutes. Find the number of possible different routes (sequences of passing sections). #
|
# Solution.
Let $M_{n}$ be the number of all possible routes of duration $n$ minutes. Each such route consists of exactly $n$ segments (a segment is the segment $A B, B A$ or the loop $B B$).
Let $M_{n, A}$ be the number of such routes ending at $A$, and $M_{n, B}$ be the number of routes ending at $B$.
A point $B$ can be reached in one minute either from point $A$ or from point $B$, so $M_{n, B}=M_{n-1}$.
A point $A$ can be reached in one minute only from point $B$, so $M_{n, A}=M_{n-1, B}=M_{n-2}$. Therefore,
$$
M_{n, A}=M_{n-2}=M_{n-2, A}+M_{n-2, B}=M_{n-4}+M_{n-3}=M_{n-2, A}+M_{n-1, A}
$$
Additionally, note that $M_{1, A}=0, M_{2, A}=1$. Thus, the numbers $M_{n, A}$ form the sequence $0,1,1,2,3,5,8,13,21,34, \ldots$
The number $M_{10, A}$ is 34 - the ninth Fibonacci number ${ }^{1}$.
Answer: 34.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Disks (from 9th grade. 3 points). At a familiar factory, metal disks with a diameter of 1 m are cut out. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, there is a measurement error, and therefore the standard deviation of the radius is 10 mm. Engineer Sidorov believes that a stack of 100 disks will on average weigh 10000 kg. By how much is Engineer Sidorov mistaken?
|
Solution. Given $\mathrm{E} R=0.5 \mathrm{m}, \mathrm{D} R=10^{-4}$ (sq.m). Let's find the expected value of the area of one disk:
$$
\mathrm{ES}=\mathrm{E}\left(\pi R^{2}\right)=\pi \mathrm{E} R^{2}=\pi\left(D R+\mathrm{E}^{2} R\right)=\pi\left(10^{-4}+0.25\right)=0.2501 \pi
$$
Thus, the expected value of the mass of the disk is $\frac{0.2501 \pi}{0.25 \pi} \cdot 100=100.04$ kg. Therefore, a stack of 100 disks on average will weigh 10004 kg.
Answer: 4 kg.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. How many airplanes? (11th grade, 8 points) The work of the Absent-Minded Scientist involves long business trips, and therefore he often flies on the same airline. This airline has many identical airplanes, and all of them have names. Since the Scientist does not fly every day or even every week, it can be assumed that each time he gets a random airplane. Out of curiosity and habit, the Absent-Minded Scientist records the name of the airplane he flies on each time. In his fifteenth flight, the Scientist found himself on board an airplane proudly named "Siméon Denis Poisson." After takeoff, the Scientist took out his notebook to record the name of the airplane and discovered that he had already flown on the "Poisson" once before, and there were no other repetitions before that. Estimate the number of airplanes in the airline.
|
Solution. Consider the random variable $X$ "the ordinal number of the flight when the Scientist first gets a plane he has flown before". We will make a point estimate of the number of planes using the method of moments. For this, we need to solve the equation $\mathrm{E} X=15$ at least approximately.
Let's find $\mathrm{E} X$. Denote $n$ as the number of planes in the airline. Consider the event $A_{j}$ "there were no repetitions up to and including the $j$-th flight" $(j=1, \ldots, n)$. Let $I_{j}$ be the indicator of the event $A_{j}$. Then
$$
X=1+I_{1}+I_{2}+\ldots+I_{n}
$$
Let's find the expected values of the indicators.
$$
\mathrm{EI}_{j}=\mathrm{P}\left(A_{j}\right)=\frac{n(n-1)(n-2) \ldots(n-j+1)}{n^{j}}=\frac{n!}{(n-j)!\cdot n^{j}}
$$
Therefore,
$$
\mathrm{E} X=\mathrm{E}\left(1+I_{1}+I_{2}+\ldots+I_{n}\right)=\sum_{j=0}^{n} \frac{n!}{(n-j)!\cdot n^{j}}=\frac{n!}{n^{n}} \sum_{j=0}^{n} \frac{n^{n-j}}{(n-j)!}=\frac{n!}{n^{n}} \sum_{k=0}^{n} \frac{n^{k}}{k!}
$$
In the last transformation, we made the substitution $k=n-j$.
Consider the resulting sum separately:
$$
\sum_{k=0}^{n} \frac{n^{k}}{k!}=e^{n} \sum_{k=0}^{n} \frac{n^{k} e^{-n}}{k!}=e^{n} F(n)
$$
where $F(x)$ is the cumulative distribution function of the Poisson distribution with parameter $n$. The median of the Poisson distribution with an integer parameter $n$ is $n$. This means that
$$
F(n-1) \leq \frac{1}{2} \leq F(n)
$$
therefore
$$
F_{P}(n)=\sum_{k=0}^{n} \frac{n^{k} e^{-n}}{k!}=\frac{1}{2}+\theta \frac{n^{n} e^{-n}}{n!}
$$
where $0 \leq \theta \leq 1$. Setting $\theta=1 / 2$ for definiteness, we get:
$$
\mathrm{E} X=\frac{n!e^{n}}{n^{n}} F_{P}(n) \approx \frac{n!e^{n}}{n^{n}}\left(\frac{1}{2}+\frac{n^{n} e^{-n}}{2 n!}\right)=\frac{n!e^{n}}{2 n^{n}}+\frac{1}{2}
$$
Using Stirling's formula
$$
\mathrm{E} X \approx \frac{\sqrt{2 \pi n} \cdot n^{n} e^{n}}{2 n^{n} e^{n}}+\frac{1}{2}=\sqrt{\frac{\pi n}{2}}+\frac{1}{2}
$$
To find the estimate $x=\hat{n}$, solve the equation $\sqrt{\frac{\pi x}{2}}+\frac{1}{2}=15$. With rounding to the nearest integer, we get: $x \approx 134$.
Answer: approximately 134 (point estimate using the method of moments).
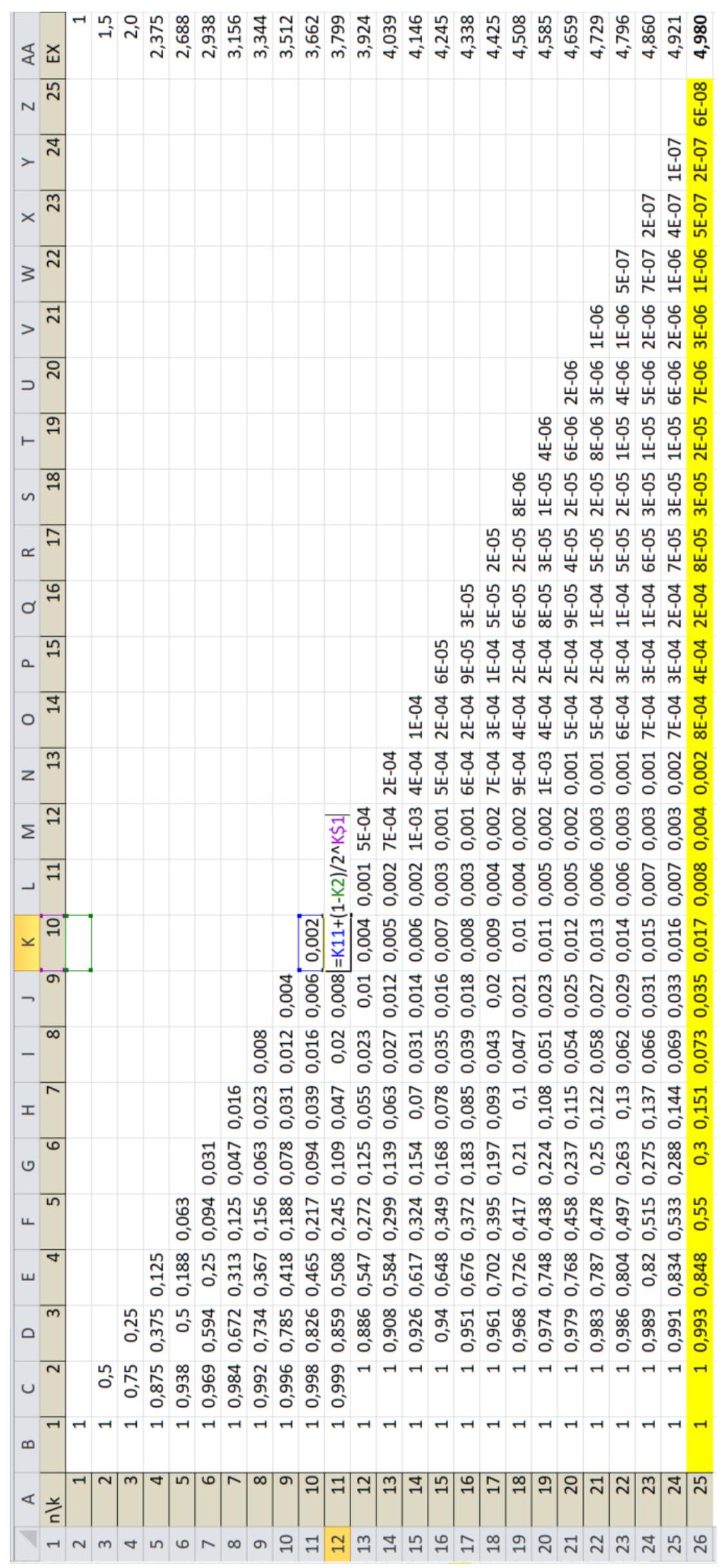
[^0]: ${ }^{1}$ English name - Stem-and-Leaf plot.
[^1]: ${ }^{2}$ The mode is the number that appears in the set more times than any other.
[^2]: ${ }^{3}$ It is believed that this problem was invented by Academician Andrei Dmitrievich Sakharov. I. F. Ginzburg. Academician A.D. Sakharov. Scientific works. Collection. - M.: AOZT "Izdatel'stvo TsentrKom", 1995.
[^3]: ${ }^{4}$ The number $e$ is also called Euler's number.
[^4]: ${ }^{5}$ The median of a random variable $X$ is a number $m$ such that $\mathrm{P}(X \leq m) \geq 0.5$ and $\mathrm{P}(X \geq m) \geq 0.5$. If the random variable has a finite density function $y=f(x)$, then the line $x=m$ divides the figure bounded by the x-axis and the density graph into two figures, each with an area of 0.5.
|
134
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. For a procrastinator, the waiting time will increase by $a$ minutes.
Therefore, the total wasted time of all standing in the queue will decrease by $b-a$ minutes. We will thus swap people in pairs of "Procrastinator-Hurry" until we get a queue where all the hurries stand before all the procrastinators. In this queue, the wasted time will be minimal.
Let's find the total wasted time. The second person waits for the first, the third waits for the previous two, and so on.
The total time spent waiting for all the hurries in front to complete their operations is
$$
(a+2a+\ldots+(n-1)a)+m \cdot n a=a \cdot \frac{1+n-1}{2} \cdot(n-1)+m n a=a C_{n}^{2}+m n a
$$
Here, the term $m n a$ is the total time spent by all procrastinators waiting for all the hurries.
The total time spent waiting for the procrastinators in front to complete their operations is $b+2b+\ldots+(m-1)b=b C_{m}^{2}$.
The overall minimum waiting time for all customers is
$$
T_{\min }=a C_{n}^{2}+a m n+b C_{m}^{2}
$$
In our specific case, we get:
$$
1 \cdot C_{5}^{2}+1 \cdot 5 \cdot 3+5 \cdot C_{3}^{2}=10+15+15=40
$$[^3]
Similarly, it can be proven that the maximum wasted time will be if all procrastinators stand before all hurries. This time is
$$
T_{\max }=a C_{n}^{2}+b m n+b C_{m}^{2}
$$
With the numerical data from the problem, we get $1 \cdot C_{5}^{2}+5 \cdot 5 \cdot 3+5 \cdot C_{3}^{2}=10+75+15=100$.
b) Consider the $k$-th customer in the queue. Let $X_{k}$ be the number of procrastinators standing before him. Then $X_{k}=I_{1}+I_{2}+\ldots+I_{k-1}$, where the indicator $I_{j}$ takes the value 1 if the $j$-th customer is a procrastinator and 0 if the $j$-th customer is a hurry.
The $j$-th customer can be a procrastinator with probability $\frac{m}{m+n}$ and a hurry with probability $\frac{n}{m+n}$. Therefore, $\mathrm{E} I_{j}=0 \cdot \frac{n}{m+n}+1 \cdot \frac{m}{m+n}=\frac{m}{m+n}$.
Thus, $\mathrm{E} X_{k}=\frac{(k-1) m}{m+n}$.
Let $T_{k}$ be the waiting time of the $k$-th customer. We get:
$$
T_{k}=X_{k} b+\left(k-1-X_{k}\right) a=(b-a) X_{k}+a(k-1)
$$
Therefore,
$$
\mathrm{E} T_{k}=(b-a) \mathrm{E} X_{k}+a(k-1)=(b-a) \cdot \frac{(k-1) m}{m+n}+a(k-1)=\frac{b m+a n}{m+n} \cdot(k-1)
$$
Summing the obtained expression over all customers from 1 to $m+n$-th, we get the expected total wasted time:
$$
\begin{gathered}
\mathrm{E} T=\mathrm{E}\left(T_{1}+T_{2}+\ldots+T_{n}\right)=\frac{b m+a n}{m+n} \cdot(0+1+2+\ldots+(m+n-1))= \\
=\frac{(b m+a n)(n+m-1)}{2}=C_{n+m}^{2} \cdot \frac{b m+a n}{m+n}
\end{gathered}
$$
Substituting the known numbers from the condition: $C_{8}^{2} \cdot \frac{5 \cdot 3+1 \cdot 5}{8}=\frac{7 \cdot 20}{2}=70$.
|
Answer: a) 40 minutes and 100 minutes; b) 70 minutes.
Comment. The expected time turned out to be the arithmetic mean between the maximum and minimum possible. Try to prove the fact $\mathrm{E} T=\frac{T_{\min }+T_{\max }}{2}$ in general, that is, prove the combinatorial identity
$$
C_{n+m}^{2} \cdot \frac{b m+a n}{m+n}=a C_{n}^{2}+\frac{a+b}{2} m n+b C_{m}^{2}
$$
By the way, part b) could have been solved almost without calculations, by noting that each arrangement of slowpokes and hurries can be matched with a symmetrically equal and equally probable arrangement, and the sum of the waiting times for both arrangements will be equal to $a C_{n}^{2}+\frac{a+b}{2} \cdot m n+b C_{m}^{2}$. For this, it is convenient to use the graphical method (see the footnote above).
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.