problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 9. (12 points)
Ivan, a full-time student, started working at his long-desired job on March 1 of the current year. In the first two months, during the probationary period, Ivan's salary was 20000 rubles. After the probationary period, the salary increased to 25000 rubles per month. In December, for exceeding the plan, Ivan was awarded a bonus of 10000 rubles. In addition, while studying in a full-time budget-funded graduate program, Ivan received a scholarship of 2800 rubles per month throughout the year. What amount of personal income tax should Ivan pay to the budget? (Provide the answer as a whole number, without spaces and units of measurement)
|
Answer: 32500.
## Comment
Solution: Personal Income Tax from salary $=(20000 \times 2+25000 \times 8+10000) \times 13\% = 32500$ rubles. The scholarship is not subject to Personal Income Tax.
|
32500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (8 points)
Lena receives 50,000 rubles per month and spends 45,000 rubles per month. She gets her salary on the 6th of each month. Lena has: a deposit in the bank $\mathrm{X}$ with a $1\%$ monthly interest rate with monthly capitalization and the possibility of topping up, but no withdrawals allowed, with the calculation day being the 6th of each month; a debit card, on which 6% of the minimum balance for the month is credited on the 6th of each month at an annual rate of $8\%$; a credit card with a payment due date of the 7th of each month and a limit of 100,000 rubles, with a $3\%$ fee for cash withdrawals or transfers.
Lena can pay all her expenses using her bank card. Describe the optimal strategy for Lena and calculate the annual income she can earn from her cooperation with the bank (in rubles).
|
Solution:
1) Of all the bank's products, the deposit brings Lena the highest income. She can use $50-45=5$ thousand rubles for savings, depositing them immediately after receiving her salary. Over a year, this will bring Lena $5000 * \frac{1.01 * (1.01^{12}-1)}{1.01-1} - 5000 * 12 \approx 4000$.
2) The remaining 45 thousand rubles per month cannot be deposited by Lena, as she will spend them during the month after receiving her salary, and the deposit does not allow withdrawals. Therefore, Lena needs to use the second most profitable instrument - a debit card with interest on the balance.
3) If Lena simply deposits the money into a debit card and uses it for payments, she will not gain any additional benefit, because by the end of the month, after receiving her salary, the balance on the card will be zero, and interest is calculated on the minimum balance.
4) To maximize her income, it is profitable for Lena to pay with a credit card and keep her salary on a debit card. This way, the minimum balance on the debit card will always be 45 thousand rubles, so over a year, this will bring Lena $45000 * 0.08 = 860$ rubles.
Let's describe Lena's strategy in detail: On the 6th of each month, after receiving her salary, she should deposit 5000 rubles into the deposit and 45000 rubles into the debit card. Then, on the 7th, pay off the credit card debt. All expenses during the month should be made using the credit card. Thus, Lena's annual income from cooperation with the bank will be $4000 + 860 = 4860$ rubles.
Criteria: description of the correct strategy - 4 points, calculation of income from the debit card - 2 points, correct formula for deposit income - 2 points.
|
4860
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (8 points)
Vasily is planning to graduate from the institute in a year. Only 270 out of 300 third-year students successfully pass their exams and complete their bachelor's degree. If Vasily ends up among the 30 expelled students, he will have to work with a monthly salary of 25,000 rubles. It is also known that every fifth graduate gets a job with a salary of 60,000 rubles per month, every tenth graduate earns 80,000 rubles per month, every twentieth graduate cannot find a job in their field and has an average salary of 25,000 rubles per month, while the salary of all others is 40,000 rubles.
When Vasily finished school, he could have chosen not to go to the institute but to work as a real estate assistant, as his friend Fyodor did. Fyodor's salary increases by 3,000 rubles each year. What is Vasily's expected salary? Whose salary will be higher in a year and by how much - Vasily's expected salary or Fyodor's actual salary, if Fyodor started working with a salary of 25,000 rubles at the same time Vasily enrolled in the institute?
Note: Bachelor's education lasts 4 years.
|
Solution:
Four years after graduating from school, Fedor will earn $25000 + 3000 * 4 = 37000$ rubles (2 points)
The expected salary of Vasily is the expected value of the salary Vasily can earn under all possible scenarios (2 points). It will be 270/300*(1/5*60 000 + 1/10*80 000 + 1/20*25 000 + (1 - 1/5 - 1/10 - 1/20) * 40000) + 30/300 * 25000 = 45025 rubles (4 points).
|
45025
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the store "Third is Not Excessive," there is a promotion: if a customer presents three items at the cash register, the cheapest of them is free. Ivan wants to buy 11 items costing $100, 200, 300, \ldots, 1100$ rubles. For what minimum amount of money can he buy these items?
|
Answer: 4800. It is clear that items should be listed in descending order of price, then the cost of the purchase will be $1100+1000+800+700+500+400+200+100=4800$ rubles.
|
4800
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A supermarket discount card that gives a $3 \%$ discount costs 100 rubles. Masha bought 4 cakes for 500 rubles each and fruits for 1600 rubles for her birthday. The seller at the cash register offered her to buy the discount card before the purchase. Should Masha agree?
1) no, they offer these cards to everyone
2) yes, of course, she should agree
3) it will not affect the cost of the purchase
|
Answer: 2. The cost of Masha's purchase is $4 * 500 + 1600 = 3600$. If Masha buys a discount card, she will spend $100 + 3600 * 0.97 = 3592$.
|
3592
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
7. Vanya decided to give Masha a bouquet of an odd number of flowers for her birthday, consisting of yellow and red tulips, so that the number of flowers of one color differs from the number of flowers of the other by exactly one. Yellow tulips cost 50 rubles each, and red ones cost 31 rubles. What is the largest number of tulips he can buy for Masha's birthday, spending no more than 600 rubles?
|
Answer: 15.
A bouquet with one more red tulip than yellow ones is cheaper than a bouquet with the same total number of flowers but one more yellow tulip. Therefore, Vanya should buy a bouquet with one more red tulip. The remaining flowers can be paired into red and yellow tulips, with each pair costing 81 rubles. Let's find the number of pairs of different colored tulips in the bouquet: $600: 81=7$ (remainder 33). Therefore, Vanya needs a bouquet with $7 * 2+1=$ 15 tulips.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. (8 points)
Irina Mikhailovna opened a foreign currency deposit in the "Western" Bank for an amount of $23,904 for a term of 1 year. The interest rate on the deposit was 5% per annum. Exactly 3 months later, the Bank of Russia revoked the license of the "Western" Bank. The official exchange rate on the date of the license revocation was 58 rubles and 15 kopecks per 1 dollar. All deposits of customers in the "Western" Bank were insured. What amount of the deposit should be returned to Irina Mikhailovna, taking into account the period during which the money was stored in the account?
a. 1,390,017 rubles and 60 kopecks;
b. 1,400,000 rubles;
c. 1,407,393 rubles;
d. $24,075.67.
|
Answer: $b$.
## Comment:
23904 USD $\times 58.15$ RUB $\times(1+5\% / 4)=1407393$ RUB. Since the Deposit Insurance Agency compensates deposits up to 1400000 RUB, this amount will be paid to Irina Mikhailovna.
|
1400000
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Problem 13. (8 points)
Dar'ya received a New Year's bonus of 60 thousand rubles, which she decided to save for a summer vacation. To prevent the money from losing value, the girl chose between two options for saving the money - to deposit the money at an interest rate of $8.6 \%$ annually for 6 months or to buy dollars and deposit them in a foreign currency deposit at an interest rate of $1.5 \%$ annually, also for 6 months. The bank's selling rate for dollars was 59.65 rubles, and the bank's buying rate for dollars was 56.65 rubles. Dar'ya chose the second option. After 6 months, Dar'ya withdrew the dollars from the foreign currency deposit, exchanged them for rubles, and went to a travel agency to purchase a tour package. The exchange rate on the day of the exchange operation was: the bank's selling rate for dollars was 58.95 rubles, and the bank's buying rate for dollars was 55.95 rubles. Determine the final financial result (profit or loss) from the operations performed by Dar'ya (rounding to the nearest whole number).
|
Answer: the loss incurred from the second option for placing funds is (rounded to the nearest whole number) $\underline{3300 \text{ RUB}}$
|
3300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. (8 points)
Anna Ivanovna bought a car from her neighbor last November for 300,000 rubles with an engine power of 250 hp, and in May she purchased a used rowing catamaran for 6 rubles. The transport tax rate is set at 75 rubles per 1 hp. How much transport tax should Anna Ivanovna pay? (Provide the answer as a whole number, without spaces or units of measurement.)
Answer: 3125.
## Comment:
|
Solution: transport tax $=250 \times 75 \times 2 / 12=3125$ rubles. A rowing catamaran is not a taxable object.
|
3125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. (8 points)
The earned salary of the citizen was 23,000 rubles per month from January to June inclusive, and 25,000 rubles from July to December. In August, the citizen, participating in a poetry competition, won a prize and was awarded an e-book worth 10,000 rubles. What amount of personal income tax needs to be paid to the budget? (Provide the answer as a whole number, without spaces or units of measurement.)
Answer: 39540.
## Comment:
|
Solution: Personal Income Tax from salary $=(23000 \times 6+25000 \times 6) \times 13\%=37440$ rubles.
Personal Income Tax from winnings $=(10000-4000) \times 35\%=2100$ rubles.
Total Personal Income Tax = 37440 rubles +2100 rubles$=39540$ rubles.
|
39540
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 14. (1 point)
Calculate the amount of personal income tax (NDFL) paid by Sergey for the past year, if he is a Russian resident and during this period had a stable income of 30000 rub./month and a one-time vacation bonus of 20000 rub. In the past year, Sergey sold a car he inherited two years ago for 250000 rub. and bought a land plot for building a residential house for 300000 rub. Sergey claimed all the tax deductions he was entitled to. (Provide the answer without spaces and units of measurement.)
|
Answer: 10400.
## Comment:
Solution: tax base $=30000 \times 12+20000+250000=630000$ rubles. The amount of the tax deduction $=250000+300000=550000$ rubles. The amount of personal income tax $=13 \% \times(630000-$ $550000)=10400$ rubles.
|
10400
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 20. (6 points)
Ivan Sergeyevich decided to raise quails. In a year, he sold 100 kg of poultry meat at a price of 500 rubles per kg, and also 20000 eggs at a price of 50 rubles per dozen. The expenses for the year amounted to 100000 rubles. What profit did Ivan Sergeyevich receive for this year? (Provide the answer as a whole number, without spaces and units of measurement.)
|
Answer: 50000.
Comment:
Solution: revenue $=100 \times 500 + 50 \times 20000 / 10 = 150000$ rubles. Profit $=$ revenue costs $=150000-100000=50000$ rubles.
|
50000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 21. (8 points)
Dmitry's parents decided to buy him a laptop for his birthday. They calculated that they could save the required amount in two ways. In the first case, they need to save one-tenth of their salary for six months. In the second case, they need to save half of their salary for one month, and then deposit it in the bank for ten months at $3\%$ per month (calculated using simple interest). In the first case, the money will be just enough for the laptop, while in the second case, after buying the laptop, there will be some money left, which will be enough to buy a computer desk for 2875 rubles. What is the mother's salary, if the father's salary is 30% higher? (Provide the answer as a whole number, without spaces or units of measurement.)
|
Answer: 25000.
## Comment:
Solution:
Mom's salary is $x$, then dad's salary is $1.3x$. We set up the equation:
$(x + 1.3x) / 10 \times 6 = (x + 1.3x) / 2 \times (1 + 0.03 \times 10) - 2875$
$1.38x = 1.495x - 2875$
$x = 25000$
|
25000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. When insuring property, the insurance amount cannot exceed its actual value (insurance value) at the time of concluding the insurance contract.
Insurance tariff - the rate of the insurance premium or the insurance premium (insurance premium) expressed in rubles, payable per unit of the insurance amount, which is usually 100 rubles. In simpler terms, it is the percentage of the insurance value of the property established by the insurance company within the framework of laws concerning insurance activities.
An underwriter of an insurance company is a person authorized by the insurance company to analyze, accept for insurance (reinsurance), and reject various types of risks, as well as classify the selected risks to obtain the optimal insurance premium for them.
Title insurance (title insurance) is protection against the risk of losing the right of ownership of real estate as a result of the transaction for the acquisition of real estate being declared invalid or illegal. A transaction can be declared invalid by a court in the following situations:
- the presence of unaccounted property interests of minors, heirs, persons serving time in places of deprivation of liberty;
- the discovery of errors or fraud in the current or previous transactions with the real estate;
- in the case of the incapacity of one of the parties to the transaction, etc.
The appraised value of the property is the final result of the appraisal study, calculated by a licensed appraiser.
The cadastral value of housing is the value of the real estate object established through state valuation, primarily for the calculation of taxes.
## Instruction:
In the event of a discrepancy between the insurance amount and the actual value of the property, the following consequences are established:
a) if the insurance amount is set below the actual value of the property in the Insurance Contract, the Insurer, in the event of an insurance case, compensates the Insured (Beneficiary) for the damage incurred within the limits of the insurance amount established by the Insurance Contract without applying the ratio of the insurance amount and the actual value of the property (first risk payment condition).
b) if the insurance amount specified in the Insurance Contract exceeds the actual value of the property, the Contract is void to the extent that the insurance amount exceeds the actual value of the property.
Gross insurance tariffs (title insurance)
| Group of insured objects | Number of previous transactions with the real estate object | Annual tariff |
| :--- | :--- | :---: |
| Apartments and parts of apartments, consisting of one or several isolated rooms, non-residential buildings | Primary market (one transaction) | 0.18 |
| Secondary market (no more than 3 transactions) | One transaction preceding the current transaction | 0.20 |
| No more than 3 transactions*** | | |
**** in the case of more than 3 transactions over the past 3 years preceding the current transaction, the tariff is agreed individually.
## List of corrective coefficients (title insurance)
| Factors | Coefficient |
| :--- | :---: |
| The presence in the history of the real estate object of one or more of the following facts: - a time gap of less than one year between two preceding (or between the current and the preceding) transfers of ownership of the real estate object; - the presence of lease transactions; - transfer of rights as a result of inheritance or gift; - transactions carried out by persons on the basis of a power of attorney; - more than 2 transfers of ownership of the real estate object. | |
| - the last transaction preceding the current one was more than 3 years ago | 1.2 |
| Absence of one of the necessary documents | 0.8 |
## MOSCOW OLYMPIAD OF SCHOOL STUDENTS IN FINANCIAL LITERACY FINAL STAGE $10-11$ GRADES 2nd variant Answers and solutions
## Problem 1
You are an underwriter of an insurance company. According to the instructions for title insurance (Appendix to this problem), based on the data provided below, you need to set the tariff and determine the amount of the insurance premium. Be sure to keep the glossary in front of you.
Data:
Insured Ostrozhnov Konstantin Petrovich is purchasing an apartment on the secondary market with the participation of credit funds. The loan amount secured by real estate is 20 million rubles. Konstantin Petrovich has a good credit history and easily obtained approval for such an amount. The appraised value of the apartment is 14,500,000 rubles, and the cadastral value is 15,000,000 rubles. The bank-lender requires Ostrozhnov to purchase a title insurance policy to protect its financial interests.
The seller - Ivanov G.L., born in 1952, is the sole owner of the apartment, which he purchased more than 5 years ago under a construction investment agreement. He is married, has adult children, and no one is registered in the apartment. At the time of purchasing the apartment, he was married. He provided all necessary documents except for certificates from the psychiatric and narcological dispensaries. He does not drive, does not have a driver's license, and is not subject to military service.
|
# Solution:
In accordance with the instruction, the base rate is $0.2\%$ of the insurance amount, apply a reducing factor for the absence of a change in ownership over the past 3 years $(0.8)$ and an increasing factor for the absence of certificates from the PND and ND $(1.3)$.
In total: $0.2 * 0.8 * 1.3=0.208\%$
The loan amount exceeds both the appraised and the cadastral value. Therefore, we choose the maximum value to minimize the difference between the loan amount (bank requirement) and the allowable amount by law - 15000000 and take it as the insurance amount. $15000000 * 0.00208=31200$
Answer: rate $0.208\%$, SP=31,200 rubles.
Maximum 20 points
Evaluation criteria:
2 points for each correctly found coefficient and 4 points in total for the correct explanation of the use of these coefficients (if there is a correct explanation of only one coefficient, only 1 point out of 4 is given, and if there is a correct explanation of only two coefficients, only 3 points out of 4 are given). In total, 10 points for this part of the correct solution.
2 points for the correct rate.
A total of 8 points for the correct insurance premium amount.
- Participants receive only 2 points if the insurance premium is calculated without arithmetic errors based on an incorrect appraised value of the apartment.
- Participants receive only 4 points if the insurance premium is correctly determined but lacks a complete correct justification for its application.
## Task 2
The following information is available for JSC «Total Trade».
The annual revenue of JSC «Total Trade» is 2,500,000 rubles (after VAT payment). It is known that the ratio of operating expenses to revenue is 3/5 annually. The authorized capital of JSC «Total Trade» consists of the nominal value of the company's shares acquired by shareholders and is eight times the minimum authorized capital of a public company established under Russian law. The authorized capital is made up of 1600 ordinary shares, $35\%$ of which belong to the general director.
|
31200
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In July, Volodya and Dima decided to start their own business producing non-carbonated bottled mineral water called "Dream," investing 1,500,000 rubles, and used these funds to purchase equipment for 500,000 rubles. The technical passport for this equipment indicates that the maximum production capacity is 100,000 bottles.
At the end of July, Dima and Volodya decided to launch a trial batch of water production and received 200 bottles, 5 of which were not full. In August, the equipment started operating at full capacity, and 15,000 bottles of water were produced. In the 20th of September, the equipment broke down and was idle for several days, but 12,300 bottles of water were produced over 20 days of this month.
In October, the friends decided to stop producing water, as it would not be in demand during the winter season, and decided to sell the equipment.
a) Determine the total depreciation of the equipment.
b) Determine the residual value of the equipment at the time of sale.
c) For what amount should the equipment be sold to achieve a profit of 10,000 rubles? (20 points)
|
# Answer:
a) The norm for 1 bottle of water = initial cost / maximum quantity: $500000 / 100000 = 5$ rubles;
- depreciation in July $5 \times 200 = 1000$ rubles;
- depreciation in March $15000 \times 5 = 75000$ rubles;
- depreciation in September $12300 \times 5 = 61500$ rubles, Total depreciation 137500 (6 points).
b) Residual value $-500000 - 137500 = 362500$ (4 points)
c) Sale amount - $362500 + 10000 = 372500$ (10 points)
- calculation errors were made, an incorrect numerical answer was given, a correct conclusion was made (2 points)
|
372500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Newlyweds Alexander and Natalia successfully got jobs at an advertising company in April. With their earnings, they want to buy new phones next month: phone "A" for Alexander, which costs 57,000 rubles, and phone "B" for Natalia, costing 37,000 rubles. Will they be able to do this, given the following data?
- Alexander's salary is 125,000 rubles.
- Natalia's salary is 61,000 rubles.
- They spend 17,000 rubles per month on utilities, transportation, and daily needs.
- They spend 15,000 rubles per month on loan repayment and maintenance.
- Cultural entertainment expenses per month (1 theater visit - 5,000 rubles, and 1 movie visit - 1,000 rubles - ticket price per person).
- Savings for a trip to Crimea - they save 20,000 rubles per month, planning to go in August.
- Dining out expenses for both on weekdays - 1,500 rubles, and on weekends - 3,000 rubles (20 weekdays and 10 weekends in a month).
a) Determine the total expenses.
b) Determine the net income.
c) Will the couple be able to buy the phones? Provide a detailed answer. (20 points)
|
Answer:
a) Total expenses: $17000+15000+12000+20000+30000+30000=$ $=124000$ (4 points);
b) Net income: $(125000+61000) \times 13 \% = 24180.186000 - 24180=$ $=161820$ (6 points);
c) Remaining funds: $161820-124000=37820$. The phone can only be bought for Natalia, and to buy a phone for Alexander, it is necessary to forego the trip to Crimea or postpone the trip to September and catch the off-peak season (10 points).
- calculation errors were made, an incorrect numerical answer was given, a correct conclusion was drawn (2 points)
|
37820
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let's say you have two bank cards for making purchases: a debit card and a credit card. Today, you decided to buy airline tickets for 20,000 rubles. If you pay for the purchase with a credit card (the credit limit allows it), you will have to return the money to the bank in $\mathrm{N}$ days to avoid going beyond the grace period, during which you can repay the credit for free. In this case, the bank will pay a cashback of $0.5 \%$ of the purchase amount after 1 month. If you pay for the purchase with a debit card (there is more than enough money on the card), you will receive a cashback of $1 \%$ of the purchase amount after 1 month. It is known that the annual interest rate on the average monthly balance of funds on the debit card is $6 \%$ per year (for simplicity, assume that each month has 30 days, interest on the card is paid at the end of each month, and interest earned on the balance is not capitalized). Determine the smallest number of days $\mathrm{N}$, under equal conditions, for which it is more profitable to pay for this purchase of airline tickets with a credit card. (15 points)
|
# Solution:
When paying by credit card, the amount of 20,000 rubles will be on your debit card for $\mathrm{N}$ days, which will earn you $\frac{6 \mathrm{~N}}{100 \cdot 12 \cdot 30} \cdot 20000$ rubles in interest on the remaining funds.
You will also receive $20000 \times 0.005 = 100$ rubles in cashback.
When paying by debit card, you will receive a cashback of 200 rubles after 1 month.
For it to be more profitable to pay for this purchase with a debit card, the inequality $\frac{6 N}{100 \cdot 12 \cdot 30} \cdot 20000 + 100 > 200$ must be satisfied.
This inequality holds if $\mathrm{N} > 30$. Therefore, the minimum number of days in the grace period, during which it is more profitable to pay for this purchase with a credit card, is 31 days.
Moscow Schoolchildren's Olympiad in Financial Literacy. 2017-2018 academic year. Final stage. $10-11$ grades. Variant 1
## Criteria:
Correctly accounted for the fact that interest is accrued on the average monthly balance of funds - up to 4 points.
Correctly calculated the cashback when paying with a credit card - up to 3 points.
Correctly calculated the cashback when paying with a debit card - up to 3 points.
Correctly formulated the inequality to find the required number of days - up to 3 points.
Obtained a correct and justified answer - up to 2 points
|
31
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Two friends, Arthur and Timur, with the support of their parents, decided to open several massage salons in Moscow. For this purpose, a business plan was drawn up, the economic indicators of which are presented below.
- Form of ownership - LLC
- Number of employees - no more than 50 people
- Planned revenues for the year:
- with their own funds, they purchased property and contributed it as a capital contribution, its market value is 7,000,000 rubles;
- planned revenue 120,000,000 rubles;
- advances received from a large company that will sign a contract for massage services for its employees 30,000,000 rubles.
- Planned monthly expenses:
- rental of massage rooms including utilities 770,000 rubles;
- expenses for the purchase of various oils 1,450,000 rubles;
- average salary for the entire staff 4,600,000 rubles;
- social insurance contributions paid on salaries 1,380,000 rubles;
- accounting services for all salons 340,000 rubles;
- advertising campaign 1,800,000 rubles;
- expenses for independent qualification assessment and retraining of personnel 800,000 rubles;
- other expenses (KKT maintenance, publication of reports in the media, office supplies) 650,000 rubles.
Which tax object would you recommend to the friends under the USN regime?
a) Revenues at a rate of $6 \%$;
b) Revenues minus expenses, at a rate of $15 \%$, or a minimum tax of $1 \%$ of revenues
c) Make the calculation, fill in the tables, and justify your answer. (20 points)
|
# Solution:
Reference information: Chapter 26.2, Part 2 of the Tax Code of the Russian Federation.
- Criteria applicable under the simplified tax system (STS) - Article 346.13;
- Taxable object - Article 346.14;
- Determination of income - Article 346.15;
- Determination of expenses - Article 346.16;
- Recognition of income and expenses - Article 346.17;
- Tax base and minimum tax - Article 346.18;
- Procedure for calculating the tax - Article 346.21
a) Income at a rate of 6%:
$120000000 + 30000000 = 150000000$ (2 points);
$150000000 \times 6\% = 9000000$ (2 points);
Reduction of the amount by 50% of the paid insurance contributions:
$1380000 \times 12$ months / $2 = 8280000$
To be paid to the budget at the end of the period:
$9000000 - 8280000 = 720000$ (4 points).
b) Income minus expenses at 15% or minimum tax at 1%:
Income 150000000
Expenses (770000 + 1450000 + 4600000 + 1380000 + 340000 + 1800000 + 800000 + 650000) $\times 12$ months = 141480000 (4 points);
Tax base: 150000000 - 141480000 = 8520000 (2 points);
Tax amount 8520000 * 0.15 = 1278000; (1 point);
Minimum tax amount - 150000000 * 1% = 1500000; (1 point);
Tax amount to be paid - 1500000 - 1278000 = 222000 (2 points).
c) Based on these indicators, it is more advantageous to use the income minus expenses method, as it is necessary to compare the calculated tax amount under options a) and b), using the cash method of determining the tax base (Article 346.17) (2 points for a justified answer).
| Indicators | Calculation for 6% |
| :--- | :--- |
| Income | 150000000 |
| Expenses | |
| Special calculation | 8280000 |
| Tax base | 150000000 |
| Tax amount | 9000000 |
| Tax amount to be paid to the budget | 720000 |
| Indicators | Calculation for 15% |
| :--- | :--- |
| Income | 150000000 |
| Expenses | 141480000 |
| Special calculation | |
| Tax base | 8520000 |
| Tax amount | 1278000 |
| Tax amount to be paid to the budget | 222000 |
| Indicators | Calculation for 1% |
| Income | 150000000 |
| Expenses | |
| Special calculation | |
| Tax base | 150000000 |
| Tax amount | 1500000 |
| Tax amount to be paid to the budget | |
|
222000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let's say you have two bank cards for making purchases: a debit card and a credit card. Today, at the beginning of the month, you decided to buy airline tickets for 12,000 rubles. If you pay for the purchase with a credit card (the credit limit allows it), you will have to return the money to the bank in $\mathrm{N}$ days to avoid going beyond the grace period, during which you can repay the credit for free. In this case, the bank will pay a cashback of $1 \%$ of the purchase amount after 1 month. If you pay for the purchase with a debit card (there is more than enough money on the card), you will receive a cashback of $2 \%$ of the purchase amount after 1 month. It is known that the annual interest rate on the average monthly balance of funds on the debit card is $6 \%$ per year (for simplicity, assume that each month has 30 days, interest on the card is paid at the end of each month, and interest earned on the balance is not capitalized). Determine the maximum number of days $\mathrm{N}$, under equal conditions, for which it is more profitable to pay for this purchase of airline tickets with a debit card. (15 points)
|
# Solution:
When paying by credit card, the amount of 12,000 rubles will be on your debit card for $\mathrm{N}$ days, which will earn you $\frac{6 \mathrm{~N}}{100 \cdot 12 \cdot 30} \cdot 12000$ rubles in interest on the remaining funds. Additionally, you will receive $12000 \times 0.01 = 120$ rubles in cashback.
When paying by debit card, you will receive a cashback of $12000 \times 0.02 = 240$ rubles after 1 month.
For it to be more profitable to pay for this purchase with a debit card, the inequality $\frac{6 N}{100 \times 2 \times 0} \geqslant 2000 + 120 < 240$ must be satisfied. This is true if N is 60. Therefore, the maximum number of days in the grace period, during which it is more profitable to pay for this purchase with a debit card, is 59 days.
Moscow Schoolchildren's Olympiad in Financial Literacy. 2017-2018 academic year.
Final stage. 10-11 grades. Variant 2
## Grading criteria:
Correctly accounted for the fact that interest is accrued on the average monthly balance of funds - up to 4 points.
Correctly calculated the cashback when paying with a credit card - up to 3 points.
Correctly calculated the cashback when paying with a debit card - up to 3 points.
Correctly formulated the inequality to find the required number of days - up to 3 points.
Obtained a correct and justified answer - up to 2 points
|
59
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Twin brothers, Anton Sergeyevich, a civil aviation pilot by profession, and Mikhail Sergeyevich, a neurologist, born on 05.06.1977, decided to go on vacation together and purchase a life and health insurance policy for 2,000,000 rubles. Anton Sergeyevich and Mikhail Sergeyevich had the same height - 187 cm and weight - 98 kg. Mikhail Sergeyevich decided to preliminarily calculate the cost of the policy on the insurance company's website. He looked at the rates and, without consulting and filling out the application, concluded that the cost of the insurance was the same for both brothers. Find the difference in the cost of the brothers' policies using the data in the appendix, given that insurers apply increasing coefficients for the insured person's belonging to a high-risk profession and excess weight (increased risk of cardiovascular diseases). (24 points)
Appendix: Body Mass Index (BMI) formula: BMI = weight (kg) / height^2 (m) (weight in kilograms must be divided by the square of the height, expressed in meters)
Increasing coefficients for BMI:
| BMI Range | 25-29 | 30-35 | 36-40 |
| :--- | :---: | :---: | :---: |
| Increasing Coefficient | 1 | 1.2 | 1.7 |
Increasing coefficient for occupation class:
pilot of civil aviation 1.5; neurologist 1.02
Basic rates:
| | basic rate age \ gender | | | | basic rate age \ gender | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Age | male | female | | Age | male | female |
| **31** | 0.21 | 0.12 | | **41** | 0.33 | 0.22 |
| **32** | 0.22 | 0.12 | | **42** | 0.35 | 0.24 |
| **33** | 0.22 | 0.14 | | **43** | 0.38 | 0.25 |
| **34** | 0.22 | 0.14 | | **44** | 0.41 | 0.25 |
| **35** | 0.24 | 0.15 | | **45** | 0.42 | 0.28 |
| **36** | 0.25 | 0.17 | | **46** | 0.5 | 0.32 |
| **37** | 0.26 | 0.18 | | **47** | 0.55 | 0.32 |
| **38** | 0.28 | 0.18 | | **48** | 0.61 | 0.4 |
| **39** | 0.3 | 0.2 | | **49** | 0.66 | 0.4 |
| **40** | 0.32 | 0.21 | | **50** | 0.74 | 0.43 |
|
# Solution:
Let's calculate the age. Both men are 40 years old. The base rate is $0.32\%$. By occupation class: Mikhail (doctor) $0.32\% \times 1.02 = 0.3264\%$.
Anton (pilot) $0.32\% \times 1.5 = 0.48\%$.
Calculate the BMI $= 98 / 1.87^2 = 98 / 3.4969 = $ (approximately) 28.025.
Find the increasing coefficient from the table. It is 1 (i.e., there is no increasing coefficient).
Apply the final rate: $2000000 \times 0.48\% = 9600$ (Anton) and $2000000 \times 0.3264\% = 6528$.
Answer: The difference in the cost of the insurance policies is 3072 rubles.
## Grading Criteria:
1) All calculation steps are correct, and the correct answer is obtained - 24 points
2) The logic of the calculation is correct (the increasing coefficients are correctly applied), but there is an arithmetic error in the final summation or percentage calculation - up to 20 points
3) The logic of the calculation is correct (the increasing coefficients are correctly applied), but the cost of the policy was calculated without considering that the base rate is expressed as a percentage - up to 12 points
4) The BMI scale is incorrectly determined, but all other calculations are correct - up to 6 points
5) The logic of applying the rates is violated, but the increasing coefficients are correctly found - up to 3 points
6) The logic of applying the rates is violated, and the data from the appendix is incorrectly found and other issues - **0** points
|
3072
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Anna and Ekaterina have opened a cosmetic salon in New Moscow. The enterprise applies the general taxation system. Ekaterina attended a seminar on taxation and learned about the Simplified System of Taxation (USNO). To avoid changing the document flow and control over financial and economic operations, the friends decided to compare the two taxation systems and choose the best one for the new year.
Financial indicators of the preceding year:
- Annual income of the cosmetic salon - 4,500,000 rubles;
- Monthly expenses of the cosmetic salon:
- Rent of premises - 60,000 rubles;
- Purchase of cosmetic products - 40,000 rubles;
- Wages of all employees - 120,000 rubles;
- Social insurance contributions on wages - 36,000 rubles;
- Advertising expenses - 15,000 rubles;
- Expenses for independent qualification assessment and retraining of personnel - 12,000 rubles;
- Other expenses (KKT maintenance, publication of reports in the media, expenses for office supplies) - 20,000 rubles;
- On average, no more than 45% of all expenses were paid in the tax period.
Help the girls with the following calculations:
a) Tax amount under the general taxation system (accrual method) - rate 20%;
b) Tax amount under the USNO - Income with a rate of 6%;
c) Income minus expenses with a rate of 15%, or a minimum tax of 1% of income;
d) Fill in the tables.
What recommendations would you give the girls? (20 points)
#
|
# Solution:
Reference information: Chapter 26.2, Chapter 25, Part 2 of the Tax Code of the Russian Federation.
- Criteria applicable under the simplified tax system (STS) - Article 346.13;
- Taxable object - Article 346.14;
- Determination of income - Article 346.15;
- Determination of expenses - Article 346.16;
- Recognition of income and expenses - Article 346.17;
- Tax base and minimum tax - Article 346.18;
- Calculation of tax - Article 346.21;
- Recognition of income under the accrual method - Article 271;
- Recognition of expenses under the accrual method - Article 272;
- Recognition of income and expenses under the cash method - Article 273.
a) Income at a rate of 6%:
$4500000 \times 6\% = 270000$; (2 points)
Reduction of the amount by 50% of the paid insurance contributions:
$36000 \times 12$ months / $2 = 216000$; paid - $45\% - 97200$;
By the end of the period to be paid to the budget:
$270000 - 97200 = 172800$; (4 points).
b) Income minus expenses 15% or minimum tax 1%:
Income 4500000;
Expenses $(60000 + 40000 + 120000 + 36000 + 15000 + 12000 + 20000) \times 12$ months = $3636000$; paid $45\% - 1636200$ (4 points);
Tax base: $4500000 - 1636200 = 2863800$ (2 points);
Tax amount: $2863800 \times 0.15 = 429570$; (2 points)
Minimum tax amount: $4500000 \times 1\% = 45000$; (1 point)
c) General tax system (GTS), accrual method, rate 20%:
Income - 4500000
Expenses - $(60000 + 40000 + 120000 + 36000 + 15000 + 12000 + 20000) \times 12$ months = $3636000$
Tax base: $4500000 - 3636000 = 864000$; (2 points)
Tax amount: $864000 \times 0.2 = 172800$ (1 point);
d) Comparison of tax amounts:
$6\% - 172800$
$15\% - 429570$
$20\% - 172800$.
Conclusion: It is possible to remain on the GTS or switch to the STS at 6%, if the revenue does not increase and the insurance contributions are fully paid. (2 points for a justified conclusion)
| Indicators | Calculation for 6% |
| :--- | :--- |
| Income | 4500000 |
| Expenses | |
| Special calculation | 97200 |
| Tax base | 4500000 |
| Tax amount | 270000 |
| Tax amount to be paid to the budget | 172800 |
| Indicators | Calculation for 15% |
| :--- | :--- |
| Income | 4500000 |
| Expenses | 3636000 |
| Special calculation | 163600 |
| Tax base | 2863800 |
| Tax amount | 429570 |
| Tax amount to be paid to the budget | 429570 |
Moscow School Olympiad in Financial Literacy. 2017-2018 academic year.
Final stage. 10-11 grades. Variant 2
| Indicators | Calculation for 1% |
| :--- | :--- |
| Income | 4500000 |
| Expenses | |
| Special calculation | |
| Tax base | 4500000 |
| Tax amount | 45000 |
| Tax amount to be paid to the budget | |
| Indicators | Calculation for 20% |
| :--- | :--- |
| Income | 4500000 |
| Expenses | 3636000 |
| Special calculation | |
| Tax base | 864000 |
| Tax amount | |
| Tax amount to be paid to the budget | 172800 |
|
172800
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. (8 points)
The earned salary of the citizen was 23,000 rubles per month from January to June inclusive, and 25,000 rubles from July to December. In August, the citizen, participating in a poetry contest, won a prize and was awarded an e-book worth 10,000 rubles. What amount of personal income tax needs to be paid to the budget? (Provide the answer as a whole number, without spaces or units of measurement.)
Answer: 39540.
## Comment:
|
Solution: Personal Income Tax from salary $=(23000 \times 6+25000 \times 6) \times 13\%=37440$ rubles.
Personal Income Tax from winnings $=(10000-4000) \times 35\%=2100$ rubles.
Total Personal Income Tax = 37440 rubles +2100 rubles$=39540$ rubles.
|
39540
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.
Every day after lunch, 7 half-eaten pieces of white bread are left on the desks of the second-grade students. If these pieces are put together, they make up half a loaf of bread. How many loaves of bread will the second-grade students save in 20 days if they do not leave these pieces? How much money will the school save on this in 20 days and 60 days if a loaf of bread costs 35 rubles? (Answer)
Suggest two topics for extracurricular activities for this class that involve fostering concepts of economic actions and thrift among students. (Answer)
|
Solution: 1. 0.5 (1/2) * 20 = 10 (loaves); 10 * 35 = 350 rubles; 2. 0.5 (1/2) * 60 = 30 (loaves); 30 * 35 = 1050 rubles.
Themes for extracurricular activities: "Young Economist," "Bread is the Head of Everything," "Saving and Frugality in Our School Canteen," "Journey to the School of the Frugal," "Frugality - the Main Source of Wealth," etc.
## Criteria:
20 points - for the correct answer with justifications, correct calculations, and 2 proposed themes for extracurricular activities
15 points - correct answer with justifications, 1 proposed theme for an extracurricular activity or general thematic areas.
10 points - for the correct answer without justifications, with calculations and one proposed extracurricular activity.
5 points - for the correct answer, but with calculation errors and one proposed extracurricular activity
3 points - incorrect answer and calculation, 2 proposed extracurricular activities
2 points - incorrect answer and calculation, 1 proposed extracurricular activity.
|
350
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Once, a god sent a little cheese to two ravens. The first raven received 100 g, from which part was taken by a fox. The piece of the second raven turned out to be twice as large as that of the first, but she managed to eat only half as much as the first raven. The portion of cheese that the fox got from the second raven turned out to be three times larger than from the first. How much cheese did the fox get in total?
|
Solution. Let the first crow eat $x$ grams of cheese. Then the fox received $100-x$ grams of cheese from the first crow. The second crow ate $\frac{x}{2}$ grams of cheese. From the second crow, the fox received $200-\frac{x}{2}$ grams of cheese. This was three times more, so: $200-\frac{x}{2}=3(100-x)$. Solution: $x=40$. The fox ate 240 grams.
|
240
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Four cars $A, B, C$, and $D$ start simultaneously from the same point on a circular track. $A$ and $B$ drive clockwise, while $C$ and $D$ drive counterclockwise. All cars move at constant (but pairwise different) speeds. Exactly 7 minutes after the start of the race, $A$ meets $C$ for the first time, and at the same moment, $B$ meets $D$ for the first time. After another 46 minutes, $A$ and $B$ meet for the first time. After how much time from the start of the race will $C$ and $D$ meet for the first time?
|
Solution. Since $A$ with $C$ and $B$ with $D$ meet every 7 minutes, their approach speeds are equal: $V_{A}+V_{C}=V_{B}+V_{D}$. In other words, the speeds of separation of $A, B$ and $C, D$ are equal: $V_{A}-V_{B}=V_{D}-V_{C}$. Therefore, since $A$ and $B$ meet for the first time at the 53rd minute, $C$ and $D$ will also meet for the first time at the 53rd minute.
Criteria. If 53 minutes is replaced with 46 - no more than 3 points. If the solution assumes that any of the speeds are equal - 1 point. Only the answer without explanation - 0 points.
|
53
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many solutions in natural numbers does the equation $(a+1)(b+1)(c+1)=2 a b c$ have?
|
Solution. Rewrite the equation as $(1+1 / a)(1+1 / b)(1+1 / c)=2$. Due to symmetry, it is sufficient to find all solutions with $a \leqslant b \leqslant c$. Then $(1+1 / a)^{3} \geqslant 2$, which means $a \leqslant(\sqrt[3]{2}-1)^{-1}<4$ and $a \in\{1,2,3\}$. In the case $a=1$, the inequality $2(1+1 / b)^{2} \geqslant 2$ holds, so there are no solutions. If $a=2$, then $\frac{3}{2}(1+1 / b)^{2} \geqslant 2$, which means $2 \leqslant b \leqslant\left(\frac{2 \sqrt{3}}{3}-1\right)^{-1}<7$. In this case, there are 3 solutions $(a, b, c)=(2,4,15),(2,5,9),(2,6,7)$ (for $b=2$ and $b=3$, the equation for $c$ has no solutions in natural numbers). Finally, if $a=3$, then $\frac{4}{3}(1+1 / b)^{2} \geqslant 2$, which means $3 \leqslant b \leqslant\left(\sqrt{\frac{3}{2}}-1\right)^{-1}<5$. This gives 2 more solutions $(a, b, c)=(3,3,8),(3,4,5)$. Taking into account permutations, there are a total of 27 solutions.
Criteria. If only part of the solutions is found, no more than 2 points are given.
|
27
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Marina needs to buy a notebook, a pen, a ruler, and a pencil to participate in the Olympiad. If she buys a notebook, a pencil, and a ruler, she will spend 47 tugriks. If she buys a notebook, a ruler, and a pen, she will spend 58 tugriks. If she buys only a pen and a pencil, she will spend 15 tugriks. How much money will she need for the entire set?
|
Solution. If Marina buys all three sets from the condition at once, she will spend $47+58+$ $15=120$ tugriks, and she will buy each item twice, so the full set of school supplies costs $120 / 2=60$ tugriks.
Criteria. Only the answer without explanation - 1 point. If in the solution they try to determine the cost of the pen and pencil (although it is not stated in the condition that the cost must be an integer) - 0 points.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There is a rectangular sheet, white on one side and gray on the other. It was folded as shown in the picture. The perimeter of the first rectangle is 20 more than the perimeter of the second rectangle. And the perimeter of the second rectangle is 16 more than the perimeter of the third rectangle. Find the perimeter of the original sheet.
|
Solution. From the figure, it can be seen that when folding, the perimeter of the rectangle decreases by twice the short side, so the short side of rectangle-1 is $20 / 2=10$, the short side of rectangle-2 is $16 / 2=8$. Therefore, the long side of rectangle-1 is 18, and the long side of the original sheet is 28. Thus, the perimeter is: $(28+18) \cdot 2=92$.
Criteria. An answer without justification or found by trial and error - 0 points.
|
92
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Egor wrote a number on the board and encrypted it according to the rules of letter puzzles (different letters correspond to different digits, the same letters correspond to the same digits). The result was the word "GUATEMALA". How many different numbers could Egor have initially written if his number was divisible by 25?
|
Solution. The number must be divisible by 25, so “$\lambda$A” equals 25, 50, or 75 (00 cannot be, as the letters are different). If “LA” equals 50, then for the other letters (“G”, “V”, “T”, “E”, “M”) there are $A_{8}^{5}$ options; otherwise, for the other letters there are $7 \cdot A_{7}^{4}$ options. In total, $8!/ 6 + 2 \cdot 7 \cdot 7!/ 6 = 18480$ ways.
Criteria. It is explicitly stated that the option 00 is not suitable for the letters “LA”, and all 3 cases are demonstrated - 3 points. If the 2 variants are further analyzed without errors, then another 4 points. If the answer is given as an expression not fully calculated - do not deduct points.
|
18480
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Four cars $A, B, C$, and $D$ start simultaneously from the same point on a circular track. $A$ and $B$ drive clockwise, while $C$ and $D$ drive counterclockwise. All cars move at constant (but pairwise different) speeds. Exactly 7 minutes after the start of the race, $A$ meets $C$ for the first time, and at the same moment, $B$ meets $D$ for the first time. After another 46 minutes, $A$ and $B$ meet for the first time. After how much time from the start of the race will $C$ and $D$ meet for the first time?
|
Solution. Since $A$ with $C$ and $B$ with $D$ meet every 7 minutes, their approach speeds are equal: $V_{A}+V_{C}=V_{B}+V_{D}$. In other words, the speeds of separation of $A, B$ and $C, D$ are equal: $V_{A}-V_{B}=V_{D}-V_{C}$. Therefore, since $A$ and $B$ meet for the first time at the 53rd minute, $C$ and $D$ will also meet for the first time at the 53rd minute.
Criteria. If 53 minutes is replaced with 46 - no more than 3 points. If the solution uses that any of the speeds are equal - 1 point. Only the answer without explanation - 0 points.

International Mathematical Olympiad
«Formula of Unity» / «The Third Millennium»
Year 2022/2023. Qualifying round
## Problems for grade R6
Each task is assessed at 7 points. Some problems have their own criteria (printed in gray).
|
53
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
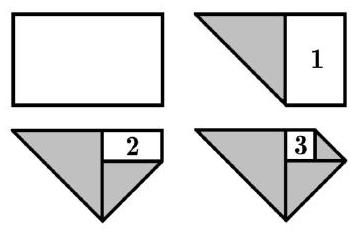
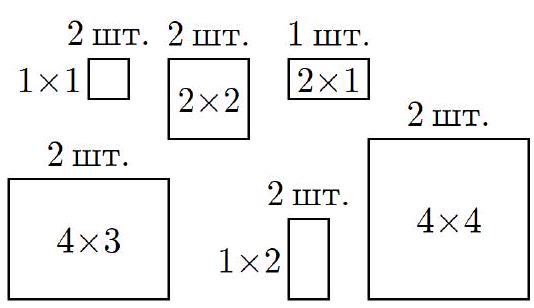
5. A few years ago, in the computer game "Minecraft," there were 11 different pictures (see the figure): one horizontal with dimensions $2 \times 1$, and two each with dimensions $1 \times 1$, $1 \times 2$ (vertical), $2 \times 2$, $4 \times 3$ (horizontal), and $4 \times 4$. In how many ways can all 11 pictures be placed on a rectangular wall that is 12 blocks long and 6 blocks high? The pictures should not overlap; they cannot be rotated.
(P. D. Mulyenko)
|
Answer: 16896.
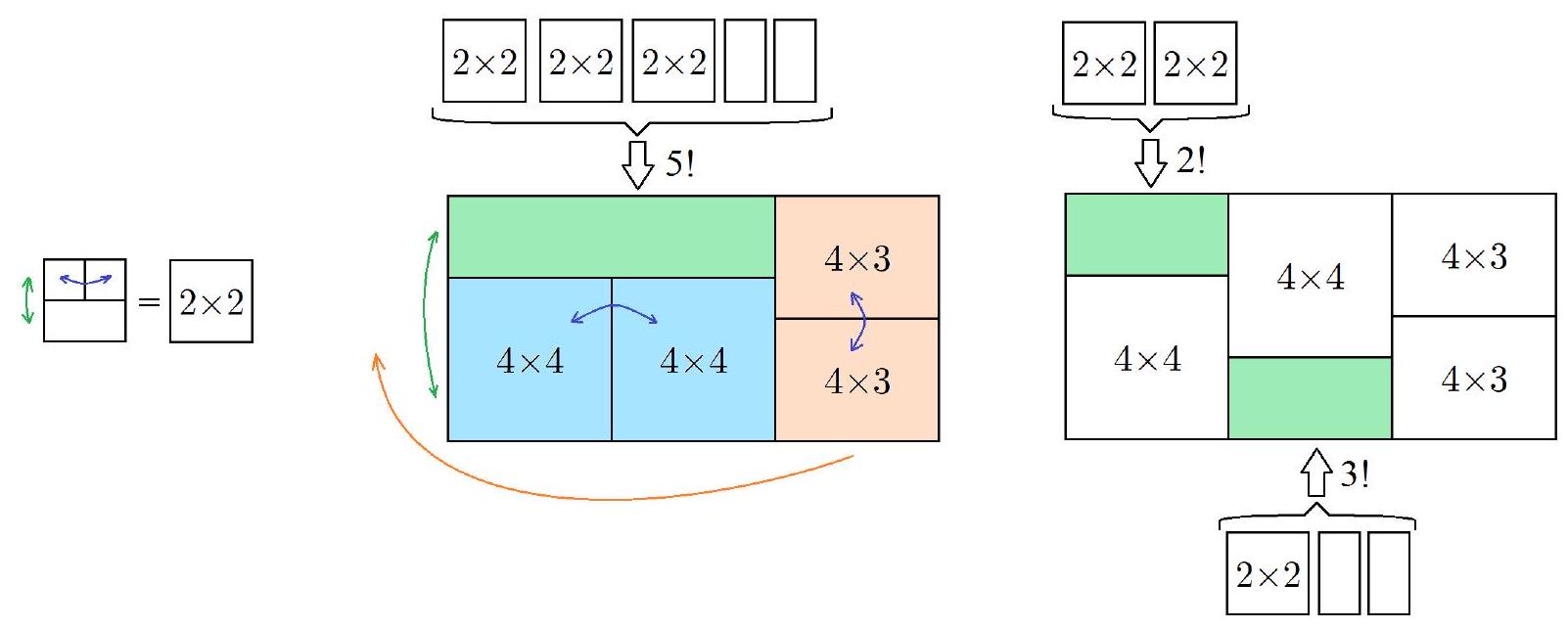
Solution. We will say that two pictures are in different columns if no block of the first picture is in the same column as any block of the second. It is clear that the $4 \times 4$ pictures are in different columns from each other and from the $4 \times 3$ pictures in any arrangement. Thus, the $4 \times 3$ pictures will necessarily be strictly one below the other. Both $4 \times 4$ pictures are pressed against the floor or ceiling, as at least 6 columns must have 2 free adjacent cells for the remaining pictures of height 2. There are $3 \cdot 2^{4}=48$ ways to place the 4-wide pictures (3 ways to choose the column with the $3 \times 3$ picture, $2^{2}$ ways to choose "floor/ceiling" in the other columns, 2 ways to permute the $4 \times 4$ pictures, and another 2 ways to permute the $4 \times 3$ pictures). Out of these, in 16 cases, a $8 \times 2$ empty area remains (there are 4 "degrees of freedom" with 2 options each, as shown by the colored arrows in the middle picture). In the remaining 32 cases, two separate $4 \times 2$ areas remain.
Note that in any case, the $1 \times 1$ pictures together with the $2 \times 1$ picture will form a $2 \times 2$ square, so they can be replaced by one glued picture (and the answer for the new set of pictures should be multiplied by 4 ways to unglue it).
If an $8 \times 2$ area remains, it needs to be filled with five vertical blocks in some order, for which there are $5!=120$ ways.
Consider the case where two $4 \times 2$ free areas remain. Then one area must be divided into two $2 \times 2$ pictures, and the other into one $2 \times 2$ picture and two $1 \times 2$ pictures. There are two ways to choose which area gets which, then 3 ways to choose which $2 \times 2$ picture (including the composite one) will be on the second area; after that, $2!$ ways to order the blocks for the first area and $3!$ for the second. In total, $2 \cdot 3 \cdot 6 \cdot 2=72$ ways.
In total, $4 \cdot(32 \cdot 72+16 \cdot 120)=16896$ variants.
Criteria. It is obtained that the three smallest pictures (two $1 \times 1$ and one $1 \times 2$) can only be placed together as a $2 \times 2$ square - 1 point.
It is obtained that the 4-wide pictures can be arranged in 48 ways - another 2 points (with an error in the calculation, ±1 point).
It is obtained that in the case of two "windows" $4 \times 2$, there are 72 ways to arrange the small pictures - another 2 points (with an error in the calculation, ±1 point).
It is obtained that in the case of a single $8 \times 2$ space, there are 120 ways to arrange the small pictures - another 2 points (with an error in the calculation, ±1 point).
|
16896
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In the Thrice-Tenth Kingdom, there are 17 islands, each inhabited by 119 people. The inhabitants of the kingdom are divided into two castes: knights, who always tell the truth, and liars, who always lie. During the census, each person was first asked: "Excluding you, are there an equal number of knights and liars on your island?". It turned out that on 7 islands, everyone answered "Yes", while on the others, everyone answered "No". Then each person was asked: "Is it true that, including you, there are fewer people of your caste than half the island's population?". This time, on some 7 islands, everyone answered "No", while on the others, everyone answered "Yes". How many liars are there in the kingdom?
(P. D. Mulyenko)
|
Answer: 1013.
## Solution.
1) Consider the first question. A "yes" answer would be given by either a knight on an island with exactly 60 knights, or a liar if the number of knights is different. A "no" answer would be given by either a liar on an island with 59 knights, or a knight if the number of knights is different. Therefore, on the 7 islands where everyone answered "yes" to the first question, the number of knights is either 60 or 0; on the other 10 islands, the number of knights is either 59 or 119.
2) For the second question, regardless of who answers, a "yes" answer indicates that the number of knights is less than half, and a "no" answer indicates that the number of liars is less than half. Therefore, on the 7 islands where everyone answered "no" to the second question, the number of knights is at least 60 (either 60 or 119); on the other 10 islands, the number of knights is no more than 59 (either 59 or 0).
3) Let $x$ be the number of islands with 60 knights, and $y$ be the number of islands with 59 knights; then (see point 1) on 7 - $x$ islands there are 0 knights, and on 10 - $y$ islands there are 119 knights. From point 2, we get: $x + (10 - y) = 7, y + (7 - x) = 10$. Both equations are equivalent to the equation $y - x = 3$.
4) Calculate the total number of knights:
$60 \cdot x + 59 \cdot y + (7 - x) \cdot 0 + (10 - y) \cdot 119 = 60x + 59(x + 3) + 119(7 - x) = 59 \cdot 3 + 119 \cdot 7 = 1010$.
Therefore, the number of liars is 1013.
Criteria. Correctly listed all possible numbers of knights and liars on each type of island - 2 points.
The problem is solved for the case where the 7 islands in the first and second questions are the same - 2 points. The problem is solved correctly, but the answer indicates the number of knights, not liars - 6 points.
|
1013
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find all real solutions to the system of equations
$$
\left\{\begin{array}{l}
\sqrt{x-997}+\sqrt{y-932}+\sqrt{z-796}=100 \\
\sqrt{x-1237}+\sqrt{y-1121}+\sqrt{3045-z}=90 \\
\sqrt{x-1621}+\sqrt{2805-y}+\sqrt{z-997}=80 \\
\sqrt{2102-x}+\sqrt{y-1237}+\sqrt{z-932}=70
\end{array}\right.
$$
(L. S. Korechkova, A. A. Tessler)
|
Answer: $x=y=z=2021$.
Solution. First, we prove that the solution is unique if it exists. Let $\left(x_{1}, y_{1}, z_{1}\right)$ and $\left(x_{2}, y_{2}, z_{2}\right)$ be two different solutions and, without loss of generality, $x_{1} \leqslant x_{2}$. Then there are four possible cases: $y_{1} \leqslant y_{2}$ and $z_{1} \leqslant z_{2}$ (with at least one of the three inequalities being strict); $y_{1} \leqslant y_{2}$ and $z_{1}>z_{2} ; y_{1}>y_{2}$ and $z_{1} \leqslant z_{2} ; y_{1}>y_{2}$ and $z_{1}>z_{2}$. Each case contradicts the corresponding equation due to monotonicity.
The solution itself can be found by assuming it is an integer and all roots are extracted as integers. For example, let $x=1621+a^{2}=1237+b^{2}$ for integers $a, b \geqslant 0$, then $(b+a)(b-a)=384$; if we try all possible values of $a$, it becomes clear that only $a=20$ allows the other roots to be extracted. Additionally, one can notice that some roots look similar (e.g., $\sqrt{x-997}$ and $\sqrt{z-997}$), so it is convenient to look for a solution where $x=y=z$. After this, the numbers 1121, 1621, 2102 can help guess the answer.
Criteria. 2 points for finding the solution (verifying the calculations that it fits or somehow motivating its discovery is not required); 5 points for proving uniqueness.
|
2021
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In each cell of a $10 \times 10$ table, a natural number was written. Then, each cell was shaded if the number written in it was less than one of its neighbors but greater than another neighbor. (Two numbers are called neighbors if they are in cells sharing a common side.) As a result, only two cells remained unshaded. What is the minimum possible sum of the numbers in these two cells?
|
Solution. Answer: 20. This value is achieved if the unshaded cells are in opposite corners and contain the numbers 1 and 19.
Evaluation.
1) The cells that contain the minimum and maximum numbers are definitely not shaded. This means that the minimum and maximum each appear exactly once, and they are in the unshaded cells. Let their values be $m$ and $M$ respectively.
2) If a cell contains the number $n$, then the length of the path from it to the minimum cell is no more than $n-1$. Indeed, from a cell, you can move to an adjacent cell with a number at least 1 less, and no later than after $n-1$ steps, we will definitely reach the cell with the minimum number.
Similarly, this is true "from the other side": if the number in a cell is less than the maximum by $k$, then the distance from that cell to the maximum is no more than $k$ steps.
3) We will prove that there is a corner cell for which the sum of the distances to the two unshaded cells is at least 18. (We will call the distance between cells the length of the shortest path between them.)
Indeed, let $(a, b)$ and $(c, d)$ be the coordinates of the unshaded cells. The sum of the distances from the first unshaded cell to the four corner cells is $(b-1+a-1)+(b-1+10-a)+(10-b+a-1)+(10-b+10-a)=36$. The same is true for the second unshaded cell, so the sum of all 8 distances from the corner cells to the unshaded cells is 72. Therefore, the sum of the distances from the unshaded cells to some one corner is at least 18.
4) Let the number in the corner cell found in point 3 be $x$. Then $M-m=(M-x)+(x-m)$ is no less than the sum of the lengths of the paths from the corner cell to the unshaded cells, which is at least 18. Since $m \geqslant 1$, then $M \geqslant 19$, from which $M+m \geqslant 20$.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many five-digit numbers are divisible by their last digit?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
2. The total number of five-digit numbers is $-99999-9999=90000$, and among them, there are an equal number of numbers ending in $0,1, \ldots, 9$, that is, 9000 numbers of each type.
Let $n_{i}$, where $i=0,1, \ldots, 9$, be the number of numbers ending in $i$ that are divisible by $i$. Then
$n_{0}=0$ (a number cannot be divisible by 0);
$n_{1}=9000$ (all numbers are divisible by 1);
$n_{2}=9000$ and $n_{5}=9000$ by the divisibility rules for 2 and 5.
Let's find $n_{3}$. The number $\overline{a b c d 3} \vdots 3$ if $\overline{a b c d 0} \vdots 3$, i.e., $10 \cdot \overline{a b c d}: 3$, which is equivalent to $\overline{a b c d}: 3$ (since 3 and 10 are coprime). Thus, we need to find the number of four-digit numbers divisible by 3. Since there are 9000 four-digit numbers and among any three consecutive numbers, exactly one is divisible by 3, then $n_{3}=9000: 3=3000$.
Similarly, $n_{9}$ is the number of four-digit numbers divisible by 9, i.e., $n_{9}=9000: 9=1000$. Similarly, $n_{7}$ is the number of four-digit numbers divisible by 7. The smallest of them is $7 \cdot 143=1001$, and the largest is $7 \cdot 1428=9996$, so $n_{7}=1428-143+1=1286$.
Now let's find $n_{4}$. The number $\overline{a b c d 4} \vdots 4 \Leftrightarrow 4+10 \cdot \overline{a b c d} \vdots 4 \Leftrightarrow 10 \cdot \overline{a b c d} \vdots 4 \Leftrightarrow 5 \cdot \overline{a b c d} \vdots 2 \Leftrightarrow \overline{a b c d} \vdots 2$. Therefore, $n_{4}$ is the number of even four-digit numbers, which is half of the total number of four-digit numbers. $n_{4}=9000 / 2=4500$.
Similarly, $\overline{a b c d 6}: 6 \Leftrightarrow \overline{a b c d 0} \vdots 6 \Leftrightarrow 10 \cdot \overline{a b c d}: 6 \Leftrightarrow 5 \cdot \overline{a b c d} \vdots 3 \Leftrightarrow \overline{a b c d} \vdots 3$, so $n_{6}=9000$ : $3=3000$.
$\overline{a b c d 8}: 8 \Leftrightarrow \overline{a b c d 0}: 8 \Leftrightarrow 10 \cdot \overline{a b c d}: 8 \Leftrightarrow 5 \cdot \overline{a b c d}: 4 \Leftrightarrow \overline{a b c d}: 4$, and $n_{8}=9000: 4=2250$.
The total number of the numbers of interest is
$n_{0}+n_{1}+n_{2}+\ldots+n_{9}=0+9000+9000+3000+4500+9000+3000+1286+2250+1000=42036$.
|
42036
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. In one move, you can either add one of its digits to the number or subtract one of its digits from the number (for example, from the number 142 you can get $142+2=144, 142-4=138$ and several other numbers).
a) Can you get the number 2021 from the number 2020 in several moves?
b) Can you get the number 2021 from the number 1000 in several moves?
|
Solution. a) Yes, for example, like this: $20 \mathbf{2 0} \rightarrow 20 \mathbf{1 8} \rightarrow \mathbf{2 0 1 9} \rightarrow 2021$.
b) Yes. For example, by adding the first digit (one), we can reach the number 2000; by adding the first digit (two), we can reach 2020; then see part a.
Criteria. Part a) 3 points, b) 4 points. In part (b), 1 point is given for progressing to 1999 (for example, for a "solution" of the form "from 1000, we add one at a time and there is the result 2021").
|
2021
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a rectangular grid 303 cells long and 202 cells wide, two diagonals were drawn and all cells through which they passed were painted. How many cells were painted?
(O. A. Pyayve, A. A. Tseler)

|
Solution. Mentally divide the large rectangle into $2 \times 3$ rectangles. (The central part of the rectangle is shown in the figure.)
Notice that each diagonal intersects 101 such rectangles (passing through their vertices), and in each of them, it passes through 4 cells. Thus, the two diagonals, it seems, pass through $404 \cdot 2 = 808$ cells. However, the central $2 \times 3$ rectangle is common to both diagonals, and in it, only 6 cells are shaded (not 8 as our calculation suggested).
Answer: 806 cells.
Criteria. The idea of dividing the rectangle into $2 \times 3$ rectangles or indicating that the diagonal passes through their nodes - at least 1 point (but for a "solution" like "in a $2 \times 3$ rectangle, the diagonals intersect 6 cells, so in a $202 \times 303$ rectangle, there will be 101 times more" - 0 points, as there is no idea of dividing into rectangles).
Missing the correction related to the center (i.e., the answer 808) - 3 points; the center is accounted for, but incorrectly - 4 points.
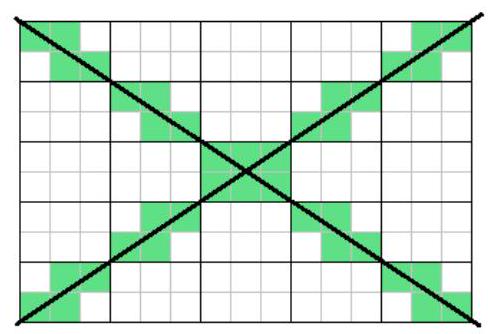
|
806
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are 28 students in the class. On March 8th, each boy gave each girl one flower - a tulip, a rose, or a daffodil. How many roses were given, if it is known that there were 4 times as many roses as daffodils, but 3 times fewer than tulips?
(A. A. Tesler)
|
Solution. Let the number of narcissus be $x$, then the number of roses is $4x$, and the number of tulips is $12x$, so the total number of flowers is $17x$. The number of flowers is the product of the number of boys and the number of girls. Since 17 is a prime number, one of these quantities must be divisible by 17, meaning it is 17 and 11. Therefore, $17x = 17 \cdot 11$, so $x = 11$, and the number of roses is $4x = 44$.
Answer: 44 roses.
Criteria. An incomplete enumerative solution - no more than 4 points. Only the answer - 1 point.
|
44
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Once, a god sent a little cheese to two ravens. The first raven received 100 g, from which a part was taken by a fox. The piece of the second raven turned out to be twice as large as that of the first, but she managed to eat only half as much as the first raven. The portion of cheese that the fox got from the second raven turned out to be three times larger than from the first. How much cheese did the fox get in total?
|
Solution. Let the first crow eat $x$ grams of cheese. Then the fox got $100-x$ grams of cheese from the first crow. The second crow ate ${ }_{2}^{x}$ grams of cheese. From the second crow, the fox received $200-\frac{x}{2}$ grams of cheese. This was three times more, so: $200-\frac{x}{2}=3(100-x)$. Solution: $x=40$. The fox ate 240 grams.
|
240
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Four cars $A, B, C$, and $D$ start simultaneously from the same point on a circular track. $A$ and $B$ drive clockwise, while $C$ and $D$ drive counterclockwise. All cars move at constant (but pairwise different) speeds. Exactly 7 minutes after the start of the race, $A$ meets $C$ for the first time, and at the same moment, $B$ meets $D$ for the first time. After another 46 minutes, $A$ and $B$ meet for the first time. After how much time from the start of the race will $C$ and $D$ meet for the first time?
|
Solution. Since $A$ with $C$ and $B$ with $D$ meet every 7 minutes, their approach speeds are equal: $V_{A}+V_{C}=V_{B}+V_{D}$. In other words, the speeds of separation of $A, B$ and $C, D$ are equal: $V_{A}-V_{B}=V_{D}-V_{C}$. Therefore, since $A$ and $B$ meet for the first time at the 53rd minute, $C$ and $D$ will also meet for the first time at the 53rd minute.
Criteria. If 53 minutes is replaced with 46 - no more than 3 points. If the solution assumes that any of the speeds are equal - 1 point. Only the answer without explanation - 0 points.
|
53
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Egor wrote a number on the board and encrypted it according to the rules of letter puzzles (different letters correspond to different digits, the same letters correspond to the same digits). The result was the word "GUATEMALA". How many different numbers could Egor have initially written if his number was divisible by 30?
|
Solution. The letter A must equal 0. The remaining 6 letters are non-zero digits with a sum that is a multiple of 3. Note that each remainder when divided by 3 appears three times. By enumeration, we find all sets of remainders whose sum is a multiple of three: 000111, 000222, 111222, 001122. We count the 6-element subsets of digits: the first three types have one each, and the last type has \(3^3 = 27\). Each of these can be permuted in \(6!\) ways. In total: \(30 \cdot 6! = 21600\).
Criteria. It is shown that “A” equals 0 - 1 point. Combinations of the remaining letters are found by enumeration - do not deduct, but if cases are lost - no more than 3 points. Error in calculations -1 point. The answer is given as an expression, not fully calculated - also -1 point.

International Mathematical Olympiad
«Formula of Unity» / «The Third Millennium»
Year 2022/2023. Qualifying round
## Problems for grade R8
Each task is assessed at 7 points. Some problems have their own criteria (printed in gray).
|
21600
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many ways are there to cut a $10 \times 10$ square into several rectangles along the grid lines such that the sum of their perimeters is 398? Ways that can be matched by rotation or flipping are considered different.
|
Solution: 180 ways.
If the entire square is cut into 100 unit squares, the sum of the perimeters will be $4 \times 100=400$. Therefore, we need to reduce this sum by 2, which is achieved by keeping one internal partition intact (in other words, the square is cut into 98 squares and 1 domino). There are a total of 180 internal partitions - 9 in each of the 10 rows and 9 in each of the 10 columns.
|
180
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A rectangle $11 \times 12$ is cut into several strips $1 \times 6$ and $1 \times 7$. What is the minimum total number of strips?
|
Solution. Answer: 20. The example is shown in the figure.
Evaluation: we will paint every seventh diagonal so that 20 cells are shaded (see figure). Each strip contains no more than one cell, so there are no fewer than 20 strips.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There is a rectangular sheet, white on one side and gray on the other. It was folded as shown in the picture. The perimeter of the first rectangle is 20 more than the perimeter of the second rectangle. And the perimeter of the second rectangle is 16 more than the perimeter of the third rectangle. Find the area of the original sheet.

|
Solution. From the figure, it can be seen that when folding, the perimeter of the rectangle decreases by twice the short side, so the short side of rectangle-1 is $20 / 2=10$, the short side of rectangle-2 is $16 / 2=8$. Therefore, the long side of rectangle-1 is 18, and the long side of the original sheet is 28. Thus, the area is: $28 \cdot 18=504$.
Criteria. If the perimeter is given instead of the area - 3 points. Any trial and error in selecting lengths (or the lengths of the numbered rectangles are simply stated without justification) - 0 points.
|
504
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Egor wrote a number on the board and encrypted it according to the rules of letter puzzles (different letters correspond to different digits, the same letters correspond to the same digits). The result was the word "GUATEMALA". How many different numbers could Egor have initially written if his number was divisible by 8?
|
Solution. For a number to be divisible by 8, "АЛА" must be divisible by 8, with "А" -
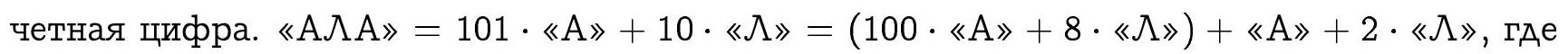
the expression in parentheses is clearly divisible by 8, so it is sufficient to require that ("А" + 2 * "Л") : 8. By enumeration, we find 11 options: (0,4), (0,8), (2,3), (2,7), (4,2), (4,6), (6,1), (6,5), (6,9), (8,0), (8,4). In three of them, where there is a zero, for the remaining five letters ("Г", "В", "Т", "Е", "М") there are \(A_{8}^{5} = 8!/3!\) options; in the other eight \(7 \cdot A_{7}^{4} = 7 \cdot 7!/3!\). In total: \(3 \cdot 8!/3! + 8 \cdot 7 \cdot 7!/3! = 67200\).
Criteria. The divisibility rule for 8 is formulated and it is explicitly stated that "А" is an even digit - 1 point. It is proven that "А" + 2 "Л" or 5 "А" + 10 "Л" is divisible by 8 - 3 points. For each
|
67200
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Four cars $A, B, C$, and $D$ start simultaneously from the same point on a circular track. $A$ and $B$ drive clockwise, while $C$ and $D$ drive counterclockwise. All cars move at constant (but pairwise different) speeds. Exactly 7 minutes after the start of the race, $A$ meets $C$ for the first time, and at the same moment, $B$ meets $D$ for the first time. After another 46 minutes, $A$ and $B$ meet for the first time. After how much time from the start of the race will all the cars meet for the first time?
|
Solution. $A$ and $C$ meet every 7 minutes, while $A$ and $B$ meet every 53 minutes. Therefore, all three will meet at a time that is a multiple of both 7 and 53, which is $7 \cdot 53 = 371$ minutes. At the same time, $B$ and $D$ also meet every 7 minutes, so on the 371st minute, car $D$ will be at the same point as the other three cars.
Criteria. If 53 minutes is replaced with 46 - no more than 3 points. If the solution assumes that any of the speeds are equal - 1 point. Only the answer without explanation - 0 points.
|
371
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Here is a problem from S. A. Rachinsky's problem book (late 19th century): "How many boards 6 arshins long and 6 vershoks wide are needed to cover the floor of a square room with a side of 12 arshins?" The answer to the problem is: 64 boards. Determine from these data how many vershoks are in an arshin.
|
Solution. The area of the room is $12 \cdot 12=144$ square arshins. Therefore, the area of each board is $144 / 64=2.25$ square arshins. Since the length of the board is 6 arshins, its width should be $2.25 / 6=3 / 8=6 / 16$ arshins. Thus, 6 vershoks make up $6 / 16$ arshins, meaning 1 vershok is $1 / 16$ arshin.
Another solution. Note that the total area of the boards covering the room does not depend on their arrangement. Therefore, we can assume that they lie in two rows, with 32 boards in each row. The length of each row is equal to the side of the room (12 arshins), and at the same time, it is 32 times greater than the width of the board (6 vershoks). Thus, 12 arshins are 32 times greater than 6 vershoks. Therefore, 6 arshins are 16 times greater than 6 vershoks, meaning an arshin is 16 times greater than a vershok.
Answer: there are 16 vershoks in an arshin.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a glade, two firs, each 30 meters tall, grow 20 meters apart from each other. The branches of the firs grow very densely, and among them are some that are directed straight towards each other, and the length of each branch is half the distance from it to the top. A spider can crawl up or down the trunk (strictly vertically), along the branches (strictly horizontally), or descend vertically down a web from one branch to another. What is the shortest distance the spider will have to crawl to get from the top of one fir to the top of the other?
|
Solution. From the diagram, it can be seen that the branches of the firs intersect at a height of no more than 10 meters from the ground. Indeed, at this height, the distance to the treetop is 20 meters, so the length of each branch is $20 / 2 = 10$ meters, and the total length of the branches of the two firs is equal to the distance between them. Therefore, the spider must descend to a height of 10 meters and then climb up. This means it has to overcome at least 40 meters vertically. Additionally, it needs to travel at least 20 meters horizontally. In total, its path will be at least 60 meters. Note that there are many paths of 60 meters (one of them is shown in black in the diagram).
There is another interpretation of the problem, where the path the spider traveled downward along the web is not counted (it falls rather than crawls). In this case, the answer is 40 meters (20 meters horizontally and 20 meters vertically).
|
60
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Nikita has a magic jar. If you put $n$ candies in the jar and close it for an hour, the number of candies inside will increase by the sum of the digits of $n$. For example, if there were 137 candies, it would become $137+1+3+7=148$. What is the maximum number of candies Nikita can get in 20 hours and 16 minutes, if he starts with one candy?
|
Solution. We need to strive to have as many candies as possible at the end of each hour. However, this does not mean that we should always put all the candies in the jar. The greatest sum of digits (i.e., the greatest increase in the number of candies) is achieved with a number where all digits (except the first) are nines.
1 hour: $1+1=2$
2 hour: $2+2=4$
3 hour: $4+4=8$
4 hour: $8+8=16$
5 hour: (put 9 candies) $16+9=25$
6 hour: (put 19 candies) $25+10=35$
7 hour: (put 29 candies) $35+11=46$
8 hour: (put 39 candies) $46+12=58$
9 hour: (put 49 candies) $58+13=71$
10 hour: (put 69 candies) $71+15=86$
11 hour: (put 79 candies) $86+16=102$
12 hour: (put 99 candies) $102+18=120$
13-17 hours: put 99 candies each hour, the number of candies increases by 18 each hour, resulting in $138,156,174,192,210$ candies.
18-20 hours: put 199 candies each hour, the number of candies increases by 19 each hour, resulting in $229,248,267$ candies.
In the remaining 16 minutes, it is impossible to gain anything.
Answer: 267 candies.
|
267
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many numbers from 1 to 999 without the digit "0" are written in the Roman numeral system exactly one symbol longer than in the decimal system?
(P. D. Mulyenko)
Reference. To write a number in Roman numerals, you need to break it down into place value addends, write each place value addend according to the table, and then write them sequentially from the largest to the smallest. For example, let's write the number 899. According to the table, $800 = \text{DCCC}$, $90 = \text{XC}$, $9 = \text{IX}$, we get DCCCXCIX.
| 1 I | $10 \text{X}$ | $100 \text{C}$ | $1000 \text{M}$ |
| :--- | :--- | :--- | :--- |
| $2 \text{II}$ | $20 \text{XX}$ | $200 \text{CC}$ | $2000 \text{MM}$ |
| 3 III | $30 \text{XXX}$ | $300 \text{CCC}$ | $3000 \text{MMM}$ |
| $4 \text{IV}$ | $40 \text{XL}$ | $400 \text{CD}$ | |
| 5 V | $50 \text{L}$ | $500 \text{D}$ | |
| $6 \text{VI}$ | $60 \text{LX}$ | $600 \text{DC}$ | |
| $7 \text{VII}$ | $70 \text{LXX}$ | $700 \text{DCC}$ | |
| $8 \text{VIII}$ | $80 \text{LXXX}$ | $800 \text{DCCC}$ | |
| 9 IX | $90 \text{XC}$ | $900 \text{CM}$ | |
|
Solution. Note that, regardless of the digit place and other digits of the number, a decimal digit $a$ is written as:
- one Roman numeral when $a=1$ and $a=5$,
- two Roman numerals when $a$ is $2,4,6,9$,
- three Roman numerals when $a=3$ and $a=7$,
- four Roman numerals when $a=8$.
Thus, in suitable numbers, only the digits 1, 5, and exactly one of the digits $2,4,6,9$ are used (otherwise, the total length of the record will be longer by more than one character). This means that 4 single-digit numbers, $4 \cdot 2 + 2 \cdot 4 = 16$ two-digit numbers, and $4 \cdot 2 \cdot 2 + 2 \cdot 4 \cdot 2 + 2 \cdot 2 \cdot 4 = 48$ three-digit numbers are suitable. In total, 68 numbers.
Criteria. Correct answer without justification - 2 points.
One of the above cases is missing or extra cases are considered - 0 points.
The condition about the absence of zero is incorrectly interpreted (for example, as "excluding zero," meaning that the length of the Roman record of the number should be one more than the number of non-zero digits - no more than 3 points.
|
68
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a spring math camp, between 50 and 70 children arrived. On Pi Day (March 14), they decided to give each other squares if they were just acquaintances, and circles if they were friends. Andrey calculated that each boy received 3 circles and 8 squares, while each girl received 2 squares and 9 circles. And Katya noticed that the total number of circles and squares given was the same. How many children arrived at the camp?
(P. D. Mulyenko)
|
Answer: 60.
Solution. Let the number of boys be $m$, and the number of girls be $-d$. Then $3 m + 9 d = 8 m + 2 d$ (the number of circles equals the number of squares). Transforming, we get $5 m = 7 d$, which means the number of boys and girls are in the ratio $7: 5$. Therefore, the total number of children is divisible by 12. Between 50 and 70, only the number 60 fits.
Criteria. Incorrectly understood condition (for example, that an equal number of gifts were given to boys and girls) 0 points.
Correct answer without explanation -2 points. Correct answer with verification -3 points.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many numbers from 1 to 999 are written in the Roman numeral system with the same number of symbols as in the decimal system?
(P. D. Mulyenko)
Reference. To write a number in Roman numerals, you need to break it down into place value addends, write each place value addend according to the table, and then write them sequentially from the largest to the smallest. For example, let's write the number 899. According to the table, $800 = \text{DCCC}$, $90 = \text{XC}$, $9 = \text{IX}$, we get DCCCXCIX.
| 1 I | $10 \text{X}$ | $100 \text{C}$ | $1000 \text{M}$ |
| :--- | :--- | :--- | :--- |
| $2 \text{II}$ | $20 \text{XX}$ | $200 \text{CC}$ | $2000 \text{MM}$ |
| 3 III | $30 \text{XXX}$ | $300 \text{CCC}$ | $3000 \text{MMM}$ |
| $4 \text{IV}$ | $40 \text{XL}$ | $400 \text{CD}$ | |
| 5 V | $50 \text{L}$ | $500 \text{D}$ | |
| 6 VI | $60 \text{LX}$ | $600 \text{DC}$ | |
| $7 \text{VII}$ | $70 \text{LXX}$ | $700 \text{DCC}$ | |
| 8 VIII | $80 \text{LXXX}$ | $800 \text{DCCC}$ | |
| $9 \text{IX}$ | $90 \text{XC}$ | $900 \text{CM}$ | |
| | | | |
|
Solution. Note that, regardless of the digit place and other digits of the number, a decimal digit a is written as:
- zero Roman numerals when $a=0$,
- one Roman numeral when $a=1$ and $a=5$,
- two Roman numerals when $a$ is $2,4,6,9$,
- three Roman numerals when $a=3$ and $a=7$,
- four Roman numerals when $a=8$.
Thus, for a number to meet the condition, it must:
1) either consist only of the digits 1 and 5,
2) or contain a pair of digits 0 and $x$, where $x$ is one of the digits $2,4,6$ or 9, and possibly one digit 1 or 5,
3) or consist of one digit 3 or 7 and two zeros.
There are a total of $2+2 \cdot 2+2 \cdot 2 \cdot 2=14$ numbers of the first type and 2 numbers of the third type (DCC and CCC). There are exactly 4 two-digit numbers of the second type, and 32 three-digit numbers $-2 \cdot 2 \cdot 4 \cdot 2=32$ (2 ways to place the digit "0", two ways to choose the position for the single-character digit, 4 ways to write the two-character digit, and 2 ways to write the single-character digit). In total, $14+$ $2+4+32=52$ numbers.
Criteria. Correct answer without justification - 2 points.
Each of the missing cases described above --2 points.
Arithmetic error in each of the cases --1 point.
|
52
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Milla and Zhena came up with a number each and wrote down all the natural divisors of their numbers on the board. Milla wrote down 10 numbers, Zhena wrote down 9 numbers, and the largest number written on the board twice is 50. How many different numbers are written on the board?
|
Solution. Note that a number written twice is a common divisor of the original numbers; the largest such number is their GCD. Therefore, all numbers written twice are divisors of the number 50, that is, the numbers $1,2,5,10,25,50$. Thus, among the listed numbers, exactly 6 are repeated, and the number of different numbers is $10+9-6=13$.
Criteria.
An example of a 7-point solution: "The numbers 1,2,5,10,25,50 are written twice, and all other numbers are written once; in total, there are 13 different numbers." That is, we do not require justification that non-divisors of the number 50 cannot repeat, or even an explicit mention of this fact. We do not need to prove that the number 50 has no other divisors. Providing an example confirming the existence of such numbers is not required.
Errors. It is stated that the number 50 has six divisors, but it is not explained why there are six - minus one point.
One divisor of the number 50 is not accounted for - minus one point, two divisors are not accounted for - minus two points, more than two are not accounted for - the problem is considered unsolved. Similarly for extra divisors.
The person thinks that "different numbers" are only those that appear once (then the answer is 7) — minus one point.
Progress. It is stated that the divisors of the number 50 are repeated, but the divisors are not counted or there are more than two errors in the count - 2 points. If the word "divisors" is missing (for example, "1 and 50 are repeated, so there are 17 different numbers") — 0 points.
Only the answer $13-1$ point.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On graph paper, a polygon with a perimeter of 36 is drawn, with its sides running along the grid lines. What is the maximum area it can have?
|
Solution. Consider the extreme verticals and horizontals. Moving from them inward does not allow reducing the perimeter, but it decreases the area. Therefore, the rectangle has the largest area. If A and B are the lengths of its sides, then A + B = 18.
By trying different rectangles with a perimeter of 36, such as (1,17), (2,16), etc., we find that the maximum value of the area AB is achieved when A = B = 9, and this area is 81.
## Criteria.
A complete solution consists of two parts: (1) proving that rectangles are better than other shapes and (2) proving that the best rectangle is a square.
If (1) is stated but not proven, the problem is not solved (max. 2 points). If (2) is stated but not proven, the problem is solved with a deficiency (5 points). As proof, it is sufficient to mention what needs to be tried.
Only the answer (or the answer with the indication that it is obtained for a square) — 1 point.
|
81
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The brothers found a treasure of gold and silver. They divided it so that each received 100 kg. The eldest received the most gold - 25 kg - and one eighth of all the silver. How much gold was in the treasure?
|
Solution. 1) The elder brother received 75 kg of silver, which is one-eighth of the total amount; therefore, the total mass of silver is 600 kg.
2) The others received more silver than the elder brother, i.e., each received more than 75 kg. If there are at least eight brothers, then in total they would receive more than 600 kg; therefore, there are no more than seven brothers.
3) But there must be at least seven of them, since the mass of the silver is 600 kg, which means the total mass of the treasure is more than 600 kg. Therefore, there are seven brothers.
4) The total mass of the treasure is 700 kg, so the mass of the gold is $700-600=100$ kg.
Criteria. The same as in problem 5.6.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Four cars $A, B, C$, and $D$ start simultaneously from the same point on a circular track. $A$ and $B$ drive clockwise, while $C$ and $D$ drive counterclockwise. All cars move at constant (but pairwise different) speeds. Exactly 7 minutes after the start of the race, $A$ meets $C$ for the first time, and at the same moment, $B$ meets $D$ for the first time. After another 46 minutes, $A$ and $B$ meet for the first time. After how much time from the start of the race will all the cars meet for the first time?
|
Solution. $A$ and $C$ meet every 7 minutes, while $A$ and $B$ meet every 53 minutes. Therefore, all three will meet at a time that is a multiple of both 7 and 53, which is $7 \cdot 53 = 371$ minutes. At the same time, $B$ and $D$ also meet every 7 minutes, so on the 371st minute, car $D$ will be at the same point as the other three cars.
Criteria. If 53 minutes is replaced with 46 - no more than 3 points. If the solution assumes that any of the speeds are equal - 1 point. Only the answer without explanation - 0 points.
|
371
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Let's call the efficiency of a natural number $n$ the fraction of all natural numbers from 1 to $n$ inclusive that have a common divisor with $n$ greater than 1. For example, the efficiency of the number 6 is $\frac{2}{3}$.
a) Does there exist a number with an efficiency greater than $80\%$? If so, find the smallest such number.
b) Does there exist a number with the maximum efficiency (i.e., not less than the efficiency of any other number)? If so, find the smallest such number.
|
Solution. Let's move on to studying inefficiency (1 minus efficiency). From the formula for Euler's function, it follows that it is equal to $\frac{p_{1}-1}{p_{1}} \cdot \ldots \frac{p_{k}-1}{p_{k}}$, where $p_{1}, \ldots, p_{k}$ are all distinct prime divisors of $n$. Then, by adding a new prime factor, we can increase the efficiency, so the answer in part (b) is "no".
The smallest number with an efficiency greater than $80 \%$ is $2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13=30030$. Its efficiency is $1-\frac{1}{2} \cdot \frac{2}{3} \cdot \frac{4}{5} \cdot \frac{6}{7} \cdot \frac{10}{11} \cdot \frac{12}{13} =\frac{809}{1001}$. We will prove that it is more efficient than all smaller numbers. Indeed, the presence of a prime factor with a power higher than the first does not affect the efficiency, so the sought number has all factors in the first power. If the factors are not consecutive primes, then by replacing one of the prime numbers with a smaller one, the efficiency will increase. Therefore, "efficiency records" can only be set by numbers of the form "the product of the first few primes"; but the efficiency of the number $2 \cdot 3 \cdot 5 \cdot 7 \cdot 11$ is too low.
Criteria. Part (a) is worth 5 points, part (b) - 2 points.
|
30030
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Since a syllable consists of two different letters, identical letters can only appear at the junction of syllables.
First, let's find the number of combinations of two syllables with a matching letter at the junction. Such syllables (in terms of the arrangement of vowels and consonants) are either AMMO $(3 \cdot 8 \cdot 3$ variants) or MAAN $(8 \cdot 3 \cdot 8$ variants), totaling 264 variants.
From each such combination, a funny word can be formed in two ways - by adding an arbitrary syllable either at the beginning or at the end. Since the language has 48 syllables $(8 \ldots 3=24$ syllables of the form MA and another 24 syllables of the form AM), each of these methods yields $264 \cdot 48$ words.
However, some words are counted twice. These are words where the letters at the junction of the first syllable with the second and the letters at the junction of the second with the third syllable match. Clearly, all such words have the form AMMOON or MAANNO, and their number is $3 \cdot 8 \cdot 3 \cdot 8 + 8 \cdot 3 \cdot 8 \cdot 3 = 2 \cdot 24^{2}$.
|
Answer: $2 \cdot 264 \cdot 48-2 \cdot 24^{2}=24192$ funny words.
|
24192
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a rectangular grid $20210 \times 1505$, two diagonals were drawn and all cells through which they passed were painted. How many cells were painted?
(O. A. Pyayve, A. A. Tessler)
|
Solution. This is a more complex version of problem 3 for 5th grade.

First, let's determine how many cells one diagonal crosses. Note that $20210=215$. $94,1505=215 \cdot 7$. Therefore, the diagonal passes through 215 rectangles of size $94 \times 7$. In each of these rectangles, it crosses 93 vertical and 6 horizontal grid lines (at non-coincident points), and 99 intersection points divide it into 100 segments, meaning it crosses 100 cells. In total, this results in 21500 cells.
Two diagonals should cross 43000 cells, but among these cells, there are overlapping ones (near the center of the rectangle) that are counted twice. Let's find out how many there are. The larger coordinate of the center is an integer, and the smaller one is a half-integer. The ratio of the sides of the rectangle is $94: 7$, so $x=\frac{1}{2} \cdot \frac{94}{7} \in (6 ; 7)$ (see the diagram). Therefore, the number of common cells is 14.
Answer: 42986.
Criteria. If the number of cells each diagonal crosses is correctly calculated but the overlap is not considered, -3 points. If, in addition to this, the "center" is considered but incorrectly, -4 points. If the GCD of the numbers is found without further progress, 1 point.
|
42986
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a plane, an equilateral triangle and three circles with centers at its vertices are drawn, and the radius of each circle is less than the height of the triangle. A point on the plane is painted yellow if it lies inside exactly one of the circles; green if inside exactly two; and blue if inside all three. It turns out that the yellow area is 1000, the green area is 100, and the blue area is 1. Find the area of the triangle. (P. D. Mulyenko)
|
Solution. The sum of the areas of the three circles is $1000+2 \cdot 100+3 \cdot 1=1203$; the sum of the areas of the three "lenses" is $100+3 \cdot 1=103$ (a "lens" is the intersection of two circles).
The area of the triangle is $S_{1}-S_{2}+S_{3}$, where
$S_{1}=1203 / 6-$ the sum of the areas of the three 60-degree sectors,
$S_{2}=103 / 2$ - the sum of the areas of the halves of the three "lenses" lying inside the triangle;
$S_{3}=1-$ the area of the blue region.
Indeed, with this calculation, each yellow region inside the triangle is counted 1 time, each green region: $2-1=1$ time, the blue region: $3-3+1=1$ time.
In total, we get $\frac{1203}{6}-\frac{103}{2}+1=\frac{1203-309+6}{6}=\frac{900}{6}=150$.
Answer: 150.
Criteria. Up to 3 points will be deducted for errors in the inclusion-exclusion formula.
|
150
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many five-digit numbers are roots of the equation $x=[\sqrt{x}+1][\sqrt{x}]$? The symbol $[a]$ denotes the integer part of the number $a$, that is, the greatest integer not exceeding $a$.
(0. A. Pyayve)
|
Solution. Let $n=[\sqrt{x}]$, then $[\sqrt{x}+1]=[\sqrt{x}]+1=n+1$, which means $x=n(n+1)$.
All numbers of the form $x=n(n+1)$ are suitable, since for them $n<\sqrt{x}<n+1$, meaning $[\sqrt{x}]$ is indeed equal to $n$.
It remains to count the five-digit numbers of this form. Note that 99$\cdot$100 $<10000<100 \cdot 101$, $315 \cdot 316<100000<316 \cdot 317$, so $x$ is a five-digit number for $n$ from 100 to 315 inclusive.
Answer: 216 numbers.
Criteria. No less than 3 points if the participant is looking for numbers of the form $n(n+1)$; no less than 4 points if he found the number 315 as the "upper bound".
5 points - the answer differs from the correct one by 1 in either direction.
6 points - the correct solution and answer, but with a vague explanation: for example, it is not proven (or even mentioned) that all numbers of the form $n(n+1)$ indeed fit.
|
216
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a rectangle of size $2021 \times 4300$. Inside it, there is a billiard ball. It is launched in a straight line, forming a $45^{\circ}$ angle with the sides of the rectangle. Upon reaching a side, the ball reflects at a $45^{\circ}$ angle; if the ball hits a corner, it exits along the same line it entered. (An example of the beginning of the ball's path is shown in the figure.)
a) Is it true for any point that if a ball is launched from it according to these rules, it will return to that point again?
b) Suppose that starting from some point $A$, the ball returns to it after some time. What is the maximum number of bounces off the sides it can make before returning to point $A$ for the first time?
(O. A. Plyve)
|
# Solution.
We will replicate the rectangle multiple times by reflecting it relative to its sides. In adjacent columns (rows), copies of the rectangle will be oriented differently, but when shifted by an even number of columns and an even number of rows, the orientation will match the initial one. Now, we can consider that when the ball touches the edge, it transitions to the next copy of the rectangle but continues along the same straight line. We are interested in the moment when the ball reaches one of the copies of the initial point.
a) Let's introduce a coordinate system such that one of the corners of the board has coordinates \((0,0)\), the horizontal side is shorter than the vertical side, and at the beginning of the ball's movement
both coordinates increase.
If the coordinates of the initial point are \(\left(x_{0}, y_{0}\right)\), then any point on the path has coordinates \(\left(x_{0}+a, y_{0}+a\right)\). A shift by \(a=\operatorname{LCM}(2021 \cdot 2, 4300 \cdot 2)\) along each coordinate brings us to a copy of the initial point, since we have moved an even number of sides of the rectangle in each direction.
b) Note that \(2021 = 43 \cdot 47\) and \(4300 = 43 \cdot 100\), so \(\operatorname{LCM}(2021 \cdot 2, 4300 \cdot 2) = 2 \cdot 43 \cdot 47 \cdot 100\). A shift by \(a = 2 \cdot 43 \cdot 47 \cdot 100\) along each coordinate corresponds to a shift of \(2 \cdot 100\) sides of length 2021 to the right and \(2 \cdot 47\) sides of length 4300 upwards. This means that a total shift of 294 rectangles to the right and upwards will bring us to a copy of the initial point. Each transition to the next rectangle corresponds to one bounce of the ball, so the coincidence will occur after 294 bounces.
Note that a coincidence with a copy of the initial point in a rectangle oriented as the initial one cannot occur earlier, since \(a\) must divide both \(2 \cdot 2021\) and \(2 \cdot 4300\). However, the number of bounces before the first coincidence can be less for one of the following two reasons:
- the trajectory passes through a corner (then two bounces "merge" into one);
- the ball hits the initial point in one of the copies oriented differently than the initial rectangle.
Let's provide an example where this does not happen: let \(x_{0} = \sqrt{3}\) and \(y_{0} = \sqrt{2}\). The trajectory will not pass through a corner, since for this \(x - y\) must be an integer, while it is always \(\sqrt{3} - \sqrt{2}\). Let's study the question of copies of the point in "reflected" rectangles. The coordinates of copies of the initial points always take the form \(\left(2021 k \pm x_{0}, 4300 l \pm y_{0}\right)\), where the choice of signs depends on the parity of \(k\) and \(l\), and in "reflected" rectangles at least one of the signs is minus. Suppose, for example, \(x_{0} + a = 2021 k - x_{0}\), then \((a + 2 \sqrt{2})\) is an integer. Depending on the sign in the second coordinate, we get that \(a\) or \((a + 2 \sqrt{3})\) is an integer, but this is impossible.
Answer: a) yes b) 294 bounces.
Criteria. Part a - 2 points, part b - 5 points. Correct answer to part b - 1 point.
|
294
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the country, there are 100 cities, and several non-stop air routes are in operation between them, such that one can travel from any city to any other, possibly with layovers. For each pair of cities, the minimum number of flights required to travel from one to the other was calculated. The transportation difficulty of the country is defined as the sum of the squares of these 4950 numbers. What is the maximum value that the transportation difficulty can take? The answer should be given as a number (in decimal notation).
|
Solution. First, we prove that the maximum transportation difficulty occurs when the cities are connected "in a chain."
Indeed, we can consider the graph as a tree (otherwise, we can remove some edges to leave a tree - the difficulty will increase). Choose the longest path in the tree. Suppose there are vertices not included in this path. Then among them, there is a pendant vertex $x$ (i.e., a vertex with only one edge leading to it). Let $y$ be the vertex on the longest path closest to $x$. Move the entire "branch" extending from $y$ and containing $x$ to the end of the longest path, the farthest from $y$. Note that as a result, the pairwise distances between the vertices within the "branch" do not change, nor do the distances between the vertices outside the branch. It is easy to see that for each vertex in the branch, the sum of the squares of the distances to all other vertices has increased. Indeed, if $k$ is the distance from some vertex $z$ in the branch to $y$, then the set of distances from $z$ to the vertices outside the branch (including $y$) was $k, k+1, k+1, k+2, k+2, \ldots, k+s, k+s, k+s+1, k+s+2, \ldots$, and it became $k, k+1, k+2, k+3, \ldots$

By such "re-hangings," we can bring the graph to the form of a chain, and the difficulty will always increase; hence, for the chain, it is maximal.
Now we calculate the difficulty for the "chain." The problem reduces to finding the sum $99 \cdot 1^{2} + 98 \cdot 2^{2} + 97 \cdot 3^{2} + \ldots + 1 \cdot 99^{2}$.
Let $S_{n}^{2} = 1^{2} + 2^{2} + \ldots + n^{2}$, $S_{n}^{3} = 1^{3} + 2^{3} + \ldots + n^{3}$. As is known, $S_{n}^{2} = \frac{n(n+1)(2n+1)}{6}$, $S_{n}^{3} = \left(\frac{n(n+1)}{2}\right)^{2}$ (this can be proven by induction).
Notice that the desired sum is equal to
$$
\begin{gathered}
100 \cdot \left(1^{2} + 2^{2} + \ldots + 99^{2}\right) - \left(1 \cdot 1^{2} + 2 \cdot 2^{2} + \ldots + 99 \cdot 99^{2}\right) = 100 S_{99}^{2} - S_{99}^{3} = \\
= 100 \cdot \frac{99 \cdot (99+1) \cdot (2 \cdot 99 + 1)}{6} - \left(\frac{99 \cdot (99+1)}{2}\right)^{2} = 32835000 - 24502500 = 8332500.
\end{gathered}
$$
|
8332500
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Marina needs to buy a notebook, a pen, a ruler, a pencil, and an eraser to participate in the Olympiad. If she buys a notebook, a pencil, and an eraser, she will spend 47 tugriks. If she buys a notebook, a ruler, and a pen, she will spend 58 tugriks. How much money will she need for the entire set, if the notebook costs 15 tugriks?
|
Solution. If Marina buys two sets from the condition, she will spend $47+58=105$ tugriks, but she will buy an extra notebook, so the full set of school supplies costs $105-15=90$ tugriks.
Criteria. Only the answer without explanation - 1 point. If in the solution they try to determine the cost of the pen and pencil (although it is not stated in the condition that the cost must necessarily be an integer) - 0 points.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. An accident has occurred in the reactor of a research spacecraft, and toxic substances are leaking from it. All corridors between rooms are equipped with airtight doors, but there is no time to close individual doors. However, the captain can still give the command "Close $N$ doors," after which the ship's artificial intelligence will close $N$ random doors. What is the smallest $N$ so that the entire crew can be guaranteed to survive in the lounge?
|
Solution. There are a total of 23 corridors on the spaceship. If no more than 21 doors are closed, then the corridors between the reactor and the right engine, and between the right engine and the lounge, may remain open, which means the crew will be in danger. Therefore, at least 22 doors must be closed.
Criteria. Correct answer without justification - 0 points. Error in counting the number of corridors - 4 points.

|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Egor wrote a number on the board and encrypted it according to the rules of letter puzzles (different letters correspond to different digits, the same letters correspond to the same digits). He got the word "GUATEMALA". How many different numbers could Egor have initially written if his number was divisible by 5?
|
Solution. The number must be divisible by 5, so the letter "A" is equal to 0 or 5. If it is equal to 0, then for the other letters ("G", "V", "T", "E", "M", "L") there are $A_{9}^{6}=9!/ 3$! options; if "A" is equal to 5, then for the other letters there are $8 \cdot A_{8}^{5}=8$!/3! options, since "G" cannot be zero. In total, $9!/ 6+8 \cdot 8!/ 6=114240$ ways.
Criteria. It is explicitly stated that for the letter "A" there are 2 options: 5 or $0-2$ points. If the two cases are further analyzed, that's another 5 points. If the answer is given as an expression not fully calculated to the end - do not deduct points.
|
114240
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Three cars $A, B$ and $C$ start simultaneously from the same point on a circular track. $A$ and $B$ drive clockwise, while $C$ drives counterclockwise. All cars move at constant (but pairwise distinct) speeds. Exactly 7 minutes after the start of the race, $A$ meets $C$ for the first time. After another 46 minutes, $A$ and $B$ meet for the first time. After how much time from the start of the race will all three cars meet for the first time?
|
Solution. $A$ and $C$ meet every 7 minutes, and $A$ and $B$ meet every 53 minutes. Therefore, all three will meet at a time that is a multiple of both 7 and 53, which is $7 \cdot 53=371$ minutes.
Criteria. If 53 minutes is replaced with 46 - 3 points. Solved by trial with lengths and speeds -1 point. Only the answer without explanation - 0 points.
|
371
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. There is a rectangular sheet, white on one side and gray on the other. It was folded as shown in the picture. The perimeter of the first rectangle is 20 more than the perimeter of the second rectangle. And the perimeter of the second rectangle is 16 more than the perimeter of the third rectangle. Find the perimeter of the original sheet.
|
Solution. From the figure, it can be seen that when folding, the perimeter of the rectangle decreases by twice the short side, so the short side of rectangle-1 is $20 / 2=10$, the short side of rectangle-2 is $16 / 2=8$. Therefore, the long side of rectangle-1 is 18, and the long side of the original sheet is 28. Thus, the perimeter is: $(28+18) \cdot 2=92$.
Criteria. An answer without justification or found by trial and error - 0 points.

International Mathematical Olympiad
«Formula of Unity» / «The Third Millennium»
Year 2022/2023. Qualifying round
## Problems for grade R5
Each task is assessed at 7 points. Some problems have their own criteria (printed in gray).
|
92
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Katya decided to calculate the sum of the cubes of all natural divisors of some natural number, and she got the result $M A T H$. But then she discovered that she had forgotten one of the divisors. Adding its cube, she got the correct result - MASS. Find the smallest possible value of the number $M A T H$. (MATH and $M A S S$ are four-digit numbers, where each digit is replaced by a letter, with the same digits replaced by the same letters, and different digits by different letters.)
|
Solution. Answer: 2017. The original natural number is $12 ; 12^{3}+6^{3}+4^{3}+2^{3}+1^{3}=$ 2017; if you add $3^{3}$, you get 2044.
We will prove that there are no smaller suitable numbers.
1) For any number less than 10, the sum of the cubes of all divisors, as is easily verified, is less than a thousand.
2) $10^{3}+5^{3}+2^{3}+1^{3}=1134$ and $11^{3}+1^{3}=1332$ cannot equal the number $M A S S$ (the last two digits are not equal).
3) For the number $12 M A S S=2044$; if you subtract a cube less than 27 from it, the result will be greater than 2017, and if a larger one, the result will already be less than 2000.
4) For $n \geqslant 13$ we get: $M A S S \geqslant n^{3} \geqslant 2197$, and therefore, $M A T H \geqslant 2100$.
|
2017
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are 28 students in the class. On March 8th, each boy gave each girl one flower - a tulip, a rose, or a daffodil. How many roses were given if it is known that there were 4 times as many roses as daffodils, but 10 times fewer than tulips? (A. A. Tesler)
|
Solution. This is a more complex version of problem 4 for 5th grade.
Let the number of narcissus be $x$, then the number of roses is $4x$, and the number of tulips is $40x$, so the total number of flowers is $45x$. The number of flowers is the product of the number of boys and the number of girls. If there are $m$ boys, then $m(28-m)$ is divisible by 45. Both factors cannot be divisible by 3, so one of them is divisible by 9, and the other by 5. The only option is $-18 \cdot 10$. Therefore, $45x = 180$, which means $x = 4$, and the required number of roses is $4x = 16$.
Answer: 16 roses.
Criteria. An incomplete enumerative solution - no more than 4 points.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Milla and Zhena came up with a number each and wrote down all the natural divisors of their numbers on the board. Milla wrote 10 numbers, Zhena - 9, and the number 6 was written twice. How many different numbers are on the board?
|
Solution. Since the number 6 is written twice, both original numbers (denote them as a and b) are divisible by 6.
If Vera's number has 10 divisors, then its factorization is either $p^{9}$ or $p^{1} \cdot q^{4}$ (where p and q are some prime numbers); the first is impossible since it is divisible by 6. Valya's number has 9 divisors, so its factorization is either $\mathrm{s}^{8}$ or $\mathrm{s}^{2} \mathrm{t}^{2}$; again, only the second is possible. In this case, the numbers p and q are 2 and 3 in some order, and the numbers $\mathrm{s}$ and $\mathrm{t}$ are also 2 and 3. It is easy to see that the GCD of such numbers is either $2 \cdot 3^{2}=18$ or $3 \cdot 2^{2}=12$, and in any case has $2 \cdot 3=6$ divisors. Therefore, among the listed numbers, exactly 6 are repeated, and the number of distinct numbers is $10+9-6=13$.
## Criteria.
A complete solution should include: (1) an indication of the form of the GCD factorization, with proof; (2) the calculation of the divisors of this GCD and the derivation of the answer, as in problem 7.1. Providing an example confirming the existence of such numbers is not required.
Errors. A person counts only the numbers that are written once (and gets the answer 7) — minus one point.
If the GCD factorization is correctly found but there are 1-2 errors in counting its divisors — deduct $1-2$ points.
Progress.
If the form of the GCD is correctly and justifiedly found, but then something goes wrong — 3 points can be given.
Reasonable attempts to determine the factorization of each of the original numbers — 1 point.
Incorrect but partially reasonable solutions.
"The numbers $1,2,3,6$ are written twice, so the number of different numbers is $10+9-4=15$ " — 1 point.
An example of suitable numbers is provided and the answer is found for it — 2 points.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On graph paper, a polygon with a perimeter of 2014 is drawn, with its sides running along the grid lines. What is the maximum area it can have?
|
Solution. First, consider the extreme verticals and horizontals. Moving from them inward does not allow reducing the perimeter, but it decreases the area. Therefore, the rectangle has the largest area. If A and B are the lengths of its sides, then $A + B = 1007$.
Now, among different rectangles with a perimeter of 2014, we need to find the rectangle with the largest value of the area $AB$. Since $4AB = (A + B)^2 - (A - B)^2 = 1007^2 - (A - B)^2$, to achieve the maximum value of the area $AB$, we need to choose A and B so that their difference is as small as possible. Since the sum of A and B is odd, they cannot be equal. Therefore, the smallest possible value of $A - B = 1$. Considering $A + B = 1007$, we find $A = 504, B = 503$, and $AB = \mathbf{253512}$.
## Criteria.
A complete solution consists of two parts: (1) proving that rectangles are better than other shapes and (2) proving that the best rectangle is a square.
If (1) is stated but not proven, the problem is not solved (max. 2 points). If (2) is stated but not proven, the problem is solved with a deficiency (5 points). As proof, the analysis of the quadratic function or a clear reference to the isoperimetric inequality is considered.
Only the answer (or the answer with the indication that it is obtained for a square) - 1 point.
|
253512
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. It is known that on Monday, the painter painted twice as slowly as on Tuesday, Wednesday, and Thursday, and on Friday - twice as fast as on these three days, but worked 6 hours instead of 8. On Friday, he painted 300 meters more of the fence than on Monday. How many meters of the fence did the painter paint from Monday to Friday?
|
Solution. Let's take $100 \%$ of the fence length that the painter painted on Tuesday, Wednesday, and Thursday. Then Monday accounts for $50 \%$, and Friday for $-150 \%$. Therefore, 300 meters of the fence correspond to $150 \% - 50 \% = 100 \%$. For the entire week (from Monday to Friday), it is $500 \%$, i.e., 1500 meters.
Criteria. According to general rules.
|
1500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of four-digit numbers in which all digits are different, the first digit is divisible by 2, and the sum of the first and last digits is divisible by 3.
|
Solution. The first digit can be 2, 4, 6, or 8. If the first is 2, the last can be 1, 4, 7; if the first is 4, the last can be 2, 5, 8; if the first is 6, the last can be 0, 3, (6 does not fit), 9; if the first is 8, the last can be 1, 4, 7. In total, there are 3 + 3 + 3 + 3 = 12 options for the first and last digits. For each of these options, there are 8 * 7 ways to choose the two middle digits. In total, 56 * 12 = 672 ways.
## Criteria.
Errors. Numbers of the form 6 ** 6 are incorrectly counted - two points are deducted.
Without explanation, it is stated that each first digit corresponds to three variants of the last - one point is deducted (this is not obvious, as it is only due to the impossibility of 6).
Numbers starting with zero are incorrectly counted - two points are deducted.
Arithmetic errors in the correct solution method - one point is deducted for each error.
Advancements. If it is written that the number of pairs (second digit, third digit) is not 7 * 8, but 9 * 9 or 8 * 8, etc., the problem is considered unsolved and no more than 2 points are given.
|
672
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Karlson bought several pancakes (25 rubles each) and several jars of honey (340 rubles each) at the buffet. When he told Little Man how much he spent at the buffet, Little Man was able to determine, based on this information alone, how many jars of honey and how many pancakes Karlson bought. Could this amount have exceeded 2000 rubles?
|
Solution. Could. For example, let's say Karlson spent $4 \cdot 340 + 25 \cdot 40 = 2360$ rubles. Suppose Karlson can make up this amount in some other way; for this, he should spend x rubles less on pancakes and x rubles more on honey (or vice versa). But then, for x rubles, he can buy both a whole number of pancakes and a whole number of pots of honey. This means that x is divisible by both 25 and 340. But the smallest such x is 1700; however, Karlson cannot spend 1700 rubles less on either honey or pancakes.
## Criteria.
Example of a correct solution (7 points). "Yes, it is possible, for example, if Karlson bought 4 jars of honey and 40 pancakes. The number of pancakes can only be changed by 68, and the number of jars of honey - only by 5, but neither is possible." In general, we do not require strict formulations - it is enough to demonstrate an intuitive understanding of what is happening.
Errors. An example is given of what Karlson could buy, but it is not explained why this quantity fits - we give 5 points.
Progress. The author tries to give an example and justify it in the correct way, but the example itself turns out to be unsuitable (for example, due to an arithmetic error) - we give 2 points.
Zero points: only for the answer "could"; for any attempts to prove that it could not.
|
2360
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The brothers found a treasure of gold and silver. They divided it so that each received 100 kg. The eldest received the most gold - 30 kg - and one fifth of all the silver. How much gold was in the treasure
|
Solution. 1) The elder brother received 70 kg of silver, which is one fifth of the total amount; therefore, the total mass of silver is 350 kg.
2) The others received more silver than the elder brother, i.e., each received more than 70 kg. If there are at least five brothers, then in total they would receive more than 350 kg; therefore, there are no more than four brothers.
3) But there must be at least four of them, since the mass of silver exceeds 300 kg. Therefore, there are four brothers.
4) The total mass of the treasure is 400 kg, so the mass of gold is 400-350=50 kg.
## Criteria.
If it is not proven (but simply assumed out of the blue) that there are exactly four brothers, the problem is not solved (no more than 3 points).
Errors. In addition to the correct answer, the participant suggests the variant "five brothers, each received 30 kg of gold" - deduct 1 point.
Progress. "The total mass of silver is 350 kg" - 1 point.
"Brothers are no more than four" with reasoning close to the correct one - 2 points.
Only an example is provided (without proving that the answer cannot be different) — 1 point.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given a right triangle $ABC$ with a right angle at $A$. On the leg $AC$, a point $D$ is marked such that $AD: DC = 1: 3$. Circles $\Gamma_{1}$ and $\Gamma_{2}$ are then constructed with centers at $A$ and $C$ respectively, passing through point $D$. $\Gamma_{2}$ intersects the hypotenuse at point $E$. Circle $\Gamma_{3}$ with center $B$ and radius $BE$ intersects $\Gamma_{1}$ inside the triangle at a point $F$ such that angle $AFB$ is a right angle. Find $BC$ if $AB = 5$.
(P. D. Mulyenko)
|
Answer: 13.
Solution. Let $AC = x$. Then $AD = x / 4, DC = CE = 3x / 4, BE = BC - CE = \sqrt{x^2 + 25} - 3x / 4$. According to the problem, $\angle AFB = 90^\circ$, so $AF^2 + FB^2 = AB^2$, which means $AD^2 + BE^2 = 25$. Expressing everything in terms of $x$ and simplifying, we get $13x = 12 \sqrt{x^2 + 25}$. Squaring both sides, we obtain $x^2 = 144$, so $x = 12$ and
$BC = 13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, points $A(0,0)$ and $B(1000,0)$ were marked, as well as points $C_{1}(1,1)$, $C_{2}(2,1), \ldots, C_{999}(999,1)$. Then all possible lines $A C_{i}$ and $B C_{i}(1 \leqslant i \leqslant 999)$ were drawn. How many integer-coordinate intersection points do all these lines have? (An integer-coordinate point is one where both coordinates are integers.)
(O. A. Pyayve)
|
Solution. Let $a_{n}$ and $b_{n}$ denote the lines passing through $A$ and $B$ respectively, as well as through a point on $l$ with an abscissa that is $n$ greater than the abscissa of $A$ (where $1 \leqslant n \leqslant 999$). The lines $a_{n}$ and $a_{m}$ for $n \neq m$ intersect at a non-integer point (between $A B$ and $l$). Finally, the lines $a_{n}$ and $b_{m}$ for $n \leqslant m$ intersect at a point at a distance $k$ from $A B$ such that $1000(k-1)=k(m-n)$ (it is an integer if and only if $k$ is an integer). Therefore, $k$ is a divisor of 1000, and conversely, for each divisor, the corresponding $m-n$ is an integer. For each of them, there are $\frac{1000}{k}-1$ suitable pairs $(n, m)$, so the answer is $1+2+4+8+5+10+20+40+25+50+100+200+125+$ $250+500+1000-16+2=2326$.
Criteria. 2 points - for the equation $1000(k-1)=k(m-n)$;
5 points - for the statement about $\frac{1000}{k}-1$ suitable pairs $(n, m)$ or something equivalent to it;
-1 point for a calculation error in the final step.
|
2326
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of five-digit numbers in which all digits are different, the first digit is divisible by 2, and the sum of the first and last digits is divisible by 3.
|
Solution. The first digit can be 2, 4, 6, or 8. If the first is 2, the last can be $1, 4, 7$; if the first is 4, the last can be $2, 5, 8$; if the first is 6, the last can be $0, 3, (6$ does not fit), 9; if the first is 8, the last can be $1, 4, 7$. In total, there are $3+3+3+3=13$ options for the first and last digits. For each of these options, there are $8 \cdot 7 \cdot 6=336$ ways to choose the two middle digits. In total, $336 \cdot 12=4032$ ways.
Criteria. The same as in 5.4.
|
4032
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of all roots of the equation:
$$
\begin{gathered}
\sqrt{2 x^{2}-2024 x+1023131}+\sqrt{3 x^{2}-2025 x+1023132}+\sqrt{4 x^{2}-2026 x+1023133}= \\
=\sqrt{x^{2}-x+1}+\sqrt{2 x^{2}-2 x+2}+\sqrt{3 x^{2}-3 x+3}
\end{gathered}
$$
(L. S. Korechkova)
|
Solution. Note that the radicands in the left part are obtained from the corresponding radicands in the right part by adding $x^{2}-2023 x+1023130=$ $(x-1010)(x-1013)$. Since all radicands are positive (it is sufficient to check for $x^{2}-x+1$ and for $\left.2 x^{2}-2024 x+1023131=2(x-506)^{2}+511059\right)$, the left part is less than the right part when $1010<x<1013$ and greater when $x \notin[1010,1013]$. Equality is achieved only at $x=1010$ and $x=1013$, so the answer is -2023.
Criteria. If the answer is found but it is not proven that there are no other roots of the equation, no more than 2 points.
|
-2023
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many solutions in natural numbers does the equation $(a+1)(b+1)(c+1)=2 a b c$ have?
|
Solution. Rewrite the equation as $(1+1 / a)(1+1 / b)(1+1 / c)=2$. Due to symmetry, it is sufficient to find all solutions with $a \leqslant b \leqslant c$. Then $(1+1 / a)^{3} \geqslant 2$, which means $a \leqslant(\sqrt[3]{2}-1)^{-1}<4$ and $a \in\{1,2,3\}$. In the case $a=1$, the inequality $2(1+1 / b)^{2} \geqslant 2$ holds, so there are no solutions. If $a=2$, then $\frac{3}{2}(1+1 / b)^{2} \geqslant 2$, which means $2 \leqslant b \leqslant\left(\frac{2 \sqrt{3}}{3}-1\right)^{-1}<7$. In this case, there are 3 solutions $(a, b, c)=(2,4,15),(2,5,9),(2,6,7)$ (for $b=2$ and $b=3$, the equation for $c$ has no solutions in natural numbers). Finally, if $a=3$, then $\frac{4}{3}(1+1 / b)^{2} \geqslant 2$, which means $3 \leqslant b \leqslant\left(\sqrt{\frac{3}{2}}-1\right)^{-1}<5$. This gives 2 more solutions $(a, b, c)=(3,3,8),(3,4,5)$. Taking into account permutations, there are a total of 27 solutions.
Criteria. If only part of the solutions is found, no more than 2 points are given.
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. $f(x)$ is a linear function, and the equation $f(f(x))=x+1$ has no solutions. Find all possible values of the quantity $f(f(f(f(f(2022)))))-f(f(f(2022)))-f(f(2022))$.
|
Solution. Let $f(x)=k x+b$, then $f(f(x))=k(k x+b)+b=k^{2} x+k b+b$. The equation can have no solutions only when $k^{2}=1$, that is, for functions $x+b$ or $-x+b$, so the answer is either $(2022+5 b)-(2022+3 b)-(2022+2 b)=-2022$, or $(-2022+b)-(-2022+b)-2022=-2022$.
Answer: -2022.
Criteria. Up to 2 points will be deducted for gaps in the proof that $k= \pm 1$.
|
-2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Let's call the efficiency of a natural number $n$ the fraction of all natural numbers from 1 to $n$ inclusive that have a common divisor with $n$ greater than 1. For example, the efficiency of the number 6 is $\frac{2}{3}$.
a) Does there exist a number with an efficiency greater than $80\%$? If so, find the smallest such number.
b) Does there exist a number with the maximum efficiency (i.e., not less than the efficiency of any other number)? If so, find the smallest such number.
|
Solution. Let's move on to studying inefficiency (1 minus efficiency). From the formula for Euler's function, it follows that it is equal to $\frac{p_{1}-1}{p_{1}} \cdot \ldots \frac{p_{k}-1}{p_{k}}$, where $p_{1}, \ldots, p_{k}$ are all distinct prime divisors of $n$. Then, by adding a new prime factor, we can increase the efficiency, so the answer in part (b) is "no".
The smallest number with an efficiency greater than $80\%$ is $2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 = 30030$. Its efficiency is $1 - \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{4}{5} \cdot \frac{6}{7} \cdot \frac{10}{11} \cdot \frac{12}{13} = \frac{809}{1001}$. We will prove that it is more efficient than all smaller numbers. Indeed, the presence of a prime factor with a power higher than one does not affect the efficiency, so the sought number has all factors in the first power. If the factors are not consecutive primes, then replacing one of the primes with a smaller one will increase the efficiency. Therefore, "efficiency records" can only be set by numbers of the form "the product of the first few primes"; but the efficiency of the number $2 \cdot 3 \cdot 5 \cdot 7 \cdot 11$ is too low.
Criteria. Part (a) is scored 5 points, part (b) - 2 points.

International Mathematical Olympiad
«Formula of Unity» / «The Third Millennium»
Year 2022/2023. Qualifying round
## Problems for grade R10
Each task is assessed at 7 points. Some problems have their own criteria (printed in gray).
|
30030
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A natural number $n$ is called cubish if $n^{3}+13 n-273$ is a cube of a natural number. Find the sum of all cubish numbers.
|
Solution. If $0<13n-273<13\cdot21$, so it remains to check all other numbers.
If $n=21$, then $13n-273=0$, so 21 is cubic. For $n-3n^{2}+3n-1$, the number $n$ will not be cubic (i.e., for $8<n<21$).
If $n=8$, then $13n-273=-169=-3\cdot8^{2}+3\cdot8-1$, so it is cubic. For $n \leqslant 5$, the expression $n^{3}+13n-273$ will be negative, so they are definitely not cubic. The numbers 6 and 7 are not cubic, which can be verified directly. In total, the answer is $8+21=29$.
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Pasha draws dots at the intersections of the lines on graph paper.
He likes it when four dots form a figure resembling a "kite," as shown on the right (the kite must be of this exact shape and size, but can be rotated). For example, the 10 dots shown in the second image form only two kites. Is it possible to draw a certain number of dots so that the number of kites is greater than the number of dots themselves?
|
Solution. For example, like this. Here there are 21 points and 24 snakes (6 snakes in each direction).
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a certain triangle, the sum of the tangents of the angles turned out to be 2016. Estimate (at least to the nearest degree) the magnitude of the largest of its angles.
|
Solution. One of the tangents must exceed 600. This is only possible for an angle very close to $90^{\circ}$. We will prove that it exceeds $89.5^{\circ}$. This is equivalent to the statement that $\operatorname{tg} 0.5^{\circ}>$ $1 / 600$.
Let's start with the equality $\sin 30^{\circ}=1 / 2$. Note that $\sin 2 x=2 \sin x \cos x$, so $\sin x=\frac{\sin 2 x}{2 \cos x}>\frac{\sin 2 x}{2}$ for acute angles. Therefore:
$\sin 32^{\circ}>1 / 2 ; \quad \sin 16^{\circ}>1 / 4 ; \quad \sin 8^{\circ}>1 / 8$
$\sin 4^{\circ}>1 / 16 ; \quad \sin 2^{\circ}>1 / 32 ; \quad \sin 1^{\circ}>1 / 64$
$\sin 0.5^{\circ}>1 / 128>1 / 600 ; \quad \operatorname{tg} 0.5^{\circ}>1 / 600$.
Thus, one of the angles of the triangle is in the interval from 89.5 to 90 degrees. Note that it may not be the largest; but in this case, the largest angle is less than $90.5^{\circ}$. Therefore, to the nearest degree, the largest angle is $90^{\circ}$ in any case.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Each cell of a $100 \times 100$ board is painted blue or white. We will call a cell balanced if among its neighbors there are an equal number of blue and white cells. What is the maximum number of balanced cells that can be on the board? (Cells are considered neighbors if they share a side.)
|
Solution. Cells lying on the border of the board but not in the corner cannot be equilibrium cells, since they have an odd number of neighbors (three). There are $4 \cdot 98=392$ such cells.
All other cells can be made equilibrium, for example, with a striped coloring (the first row is blue, the second row is white, the third row is blue, and so on). The number of these cells is $10000-392=9608$.
Answer: 9608.
|
9608
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a sheet of notebook paper, two rectangles are outlined. The first rectangle has a vertical side shorter than the horizontal side, while the second has the opposite. Find the maximum possible area of their common part, if each rectangle contains more than 2010 but less than 2020 cells.
|
Solution. The common part of these two rectangles (if it is non-empty) is a rectangle. Let's define the maximum possible lengths of its sides.
The vertical side of the first rectangle is shorter than the horizontal one, so it is less than $\sqrt{2020}$, which is less than 45; the same is true for the horizontal side of the second rectangle. At the same time, the sides of the intersection cannot exceed the corresponding sides of the original rectangles (but they can obviously be equal to them).
Let's find the greatest possible length of each of these sides. For this, we need to find the greatest number less than 45 that is a divisor of any number from 2011 to 2019 inclusive. It can be noted that none of the numbers $2011, \ldots, 2019$ are divisible by 44 (since $2024=45^{2}-1^{2}=$ $44 \cdot 46$ is divisible by 44), nor by 43 (since $2021=45^{2}-2^{2}=43 \cdot 48$ is divisible by 43). However, the number 2016 is divisible by 42 (since $2024=45^{2}-3^{2}=42 \cdot 48$), so the maximum possible length of each of the sides of the intersection is 42. Therefore, the maximum area of the intersection is $42^{2}=1764$. This value is achieved for rectangles $48 \times 42$ and $42 \times 48$, aligned, for example, by their top-left cells.
Answer: 1764.
|
1764
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the game "set," all possible four-digit numbers consisting of the digits $1,2,3$ (each digit appearing exactly once) are used. It is said that a triplet of numbers forms a set if, in each digit place, either all three numbers contain the same digit, or all three numbers contain different digits.
For example, the numbers 1232, 2213, 3221 form a set (in the first place, all three digits appear, in the second place, only the digit two appears, in the third place, all three digits appear, and in the fourth place, all three digits appear). The numbers $1123,2231,3311$ do not form a set (in the last place, two ones and a three appear).
How many sets exist in the game?
(Permuting the numbers does not create a new set: $1232,2213,3221$ and $2213,1232,3221$ are the same set.)
|
Solution. Note that for any two numbers, there exists exactly one set in which they occur. Indeed, the third number of this set is constructed as follows: in the positions where the first two numbers coincide, the third number has the same digit; in the position where the first two numbers differ, the third number gets the remaining digit. For example, for the numbers 1231 and 1223, the third in the set will be 1212.
Let's call an "ordered set" a set of three four-digit numbers with their order taken into account. In such a sequence, the first place can be occupied by any of the 81 numbers, the second by any of the 80 remaining; the third is exactly one (according to the principle described above). In total, there are $81 \cdot 80 \cdot 1$ ordered sets. Note that each unordered set $\{a, b, c\}$ corresponds to six ordered sets: $(a, b, c),(a, c, b),(b, a, c),(b, c, a),(c, a, b),(c, b, a)$. Therefore, there are six times fewer ordered sets.
Answer: $81 \cdot 80 / 6=1080$.
|
1080
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On a sheet of lined paper, two rectangles are outlined. The first rectangle has a vertical side shorter than the horizontal side, while the second has the opposite. Find the maximum possible area of their common part, if the first rectangle contains 2015 cells, and the second - 2016.
|
Solution. The common part of these two rectangles (if it is non-empty) is a rectangle. Let's determine the maximum possible lengths of its sides.
The vertical side of the first rectangle is shorter than the horizontal one, so it is less than $\sqrt{2015}$, which is less than 45; the same is true for the horizontal side of the second rectangle. At the same time, the sides of the intersection cannot exceed the corresponding sides of the original rectangles (but they can obviously be equal to them).
Note that $2015=5 \cdot 403=5 \cdot 13 \cdot 31 ; 2016=4 \cdot 504=4 \cdot 4 \cdot 126=4 \cdot 4 \cdot 2 \cdot 7 \cdot 9=2^{5} \cdot 3^{2} \cdot 7$.
Taking this into account, the vertical side is no more than 31, and the horizontal side is no more than 42 (these are the largest divisors of the numbers 2015 and 2016 that are less than 45). Therefore, the sides of the intersection do not exceed 31 and 42, and the area is no more than $31 \cdot 42=1302$. The case of equality is obviously achieved for rectangles $65 \times 31$ and $42 \times 48$, aligned, for example, by the top-left cells.
Answer: 1302.
|
1302
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A motorcyclist set out from point $A$ with an initial speed of 90 km/h, uniformly increasing his speed (that is, over equal time intervals, his speed increases by the same amount). After three hours, the motorcyclist arrived at point $B$, passing through $C$ along the way. After that, he turned around and, still uniformly increasing his speed, headed back. Two hours later, he passed point $C$ again at a speed of 110 km/h and continued on to $A$. Find the distance between points $A$ and $C$.
|
Solution. In 5 hours, the speed changed from 90 km/h to 110 km/h, so the acceleration is 4 km/h$^2$. From $A$ to $B$ the distance is
$$
90 \cdot 3+\frac{4}{2} \cdot 3^{2}=270+18=288(\text{km})
$$
from $B$ to $C-$
$$
110 \cdot 2-\frac{4}{2} \cdot 2^{2}=220-8=212(\text{km})
$$
And the required distance is 76 km.
|
76
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A natural number $n$ is called cubish if $n^{3}+13 n-273$ is a cube of a natural number. Find the sum of all cubish numbers.
|
Solution. If $021$, so it remains to check all other numbers.
If $n=21$, then $13 n-273=0$, so 21 is cubic. For $n-3 n^{2}+3 n-1$, the number $n$ will not be cubic (i.e., for $8<n<21)$
If $n=8$, then $13 n-273=-169=-3 \cdot 8^{2}+3 \cdot 8-1$, so it is cubic. For $n \leqslant 5$, the expression $n^{3}+13 n-273$ will be negative, so they are definitely not cubic. The numbers 6 and 7 are not cubic, which can be verified directly. In total, the answer is $8+21=29$.
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $a$ and $n$ be natural numbers, and it is known that $a^{n}-2014$ is a number with $2014$ digits. Find the smallest natural number $k$ such that $a$ cannot be a $k$-digit number.
|
Solution. Let $a$ be a $k$-digit number, then $10^{k-1} \leq a2013$, i.e., $k>45$.
We will check for $k$ starting from 46, whether the condition of the absence of an integer in the specified interval is met. We will find that
(for $k=46$) $2013 / 462013$ );
(for $k=47$) $2013 / 472013$ );
(for $k=48$) $2013 / 482013$ );
but (for $k=49$) $2013 / 49 > 41$ (since $\quad 41 \cdot 49 = 45^2 - 1^2 = 2025 - 16 < 2013$).
Thus, the interval $[2013 / 49, 2013 / 48)$ does not contain any integers, and for $k=49$, there are no suitable $n$.
## Answer: $\mathbf{k}=49$.
## Criteria.
The problem is complex, so don't be stingy with points for reasonable thoughts. Any answer in the vicinity of $\sqrt{2014}$, which is preceded by something reasonable, is worth points. A point is deducted for the absence of what is in small print.
|
49
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a certain language, there are 3 vowels and 5 consonants. A syllable can consist of any vowel and any consonant in any order, and a word can consist of any two syllables. How many words are there in this language?
|
1. The language has $3 \cdot 5=15$ syllables of the form "consonant+vowel" and the same number of syllables of the form "vowel+consonant", making a total of 30 different syllables. The total number of two-syllable words is $30 \cdot 30=900$
|
900
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Masha and Lena left home and went to the store for ice cream. Masha walked faster and got to the store in 12 minutes. Spending 2 minutes buying the ice cream, she headed back. After another 2 minutes, she met Lena. Walking a bit more, Masha finished her ice cream and, deciding to buy another one, turned around and went back to the store. As a result, Masha arrived at the store with Lena. How many minutes did Lena walk to the store?
|
3. Masha covers $1 / 6$ of the entire distance in 2 minutes, which means Lena covered $5 / 6$ of the distance by the time they met, and it took her 16 minutes. Therefore, $1 / 6$ of the distance takes Lena $16: 5=3 \frac{1}{5}$ minutes, i.e., 3 minutes and 12 seconds. For the entire distance, she would need 19 minutes and 12 seconds.
|
19
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a certain language, there are 5 vowels and 7 consonants. A syllable can consist of any vowel and any consonant in any order, and a word can consist of any two syllables. How many words are there in this language?
|
1. The language has $5 \cdot 7=35$ syllables of the form "consonant+vowel" and the same number of syllables of the form "vowel+consonant", making a total of 70 different syllables. The total number of two-syllable words is $70 \cdot 70=4900$.
|
4900
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given an isosceles triangle $A B C$, where $\angle A=30^{\circ}, A B=A C$. Point $D$ is the midpoint of $B C$. On segment $A D$, point $P$ is chosen, and on side $A B$, point $Q$ is chosen such that $P B=P Q$. What is the measure of angle $P Q C ?$ (S. S. Korechkova)
|
Answer: $15^{\circ}$.
Solution. Since $D$ is the midpoint of the base of the isosceles triangle, $A D$ is the median, bisector, and altitude of the triangle. Draw the segment $P C$. Since $\triangle P D B = \triangle P D C$ (by two sides and the right angle between them), $P C = P B = P Q$, meaning that all three triangles $\triangle P B C$, $\triangle P B Q$, and $\triangle P Q C$ are isosceles.
Notice that $\angle A B D = \angle A C B = (180^{\circ} - 30^{\circ}) : 2 = 75^{\circ}$. Let $\angle P B D = \angle P C D = \alpha$, then $\angle P B Q = \angle P Q B = 75^{\circ} - \alpha$, and $\angle P Q C = \angle P C Q = \beta$. The sum of the angles in triangle $\triangle Q C B$ is $2 \alpha + 2 \cdot (75^{\circ} - \alpha) + 2 \beta = 180^{\circ}$, from which $\beta = 15^{\circ}$.
Criteria. Correct answer without justification - 0 points.
Proven that $P B = P C = P Q - 3$ points.

|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A few years ago, in the computer game "Minecraft," there were 9 different pictures (see the figure): one horizontal picture measuring $2 \times 1$ and $4 \times 2$, one square picture measuring $2 \times 2$, and two each of pictures measuring $1 \times 1$, $4 \times 3$ (horizontal), and $4 \times 4$. In how many ways can all 9 pictures be placed on a rectangular wall measuring 12 blocks in length and 6 in height? The pictures should not overlap; they cannot be rotated.
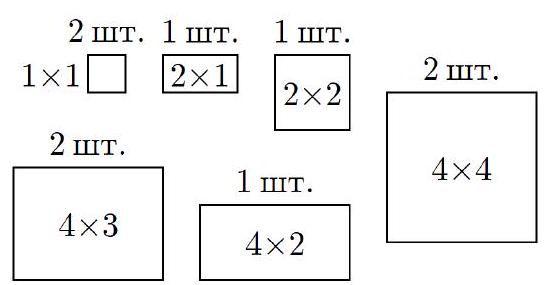
|
Answer: 896.
Solution. We will say that two paintings are in different columns if no block of the first painting is in the same column as any block of the second. It is clear that the $4 \times 4$ paintings are in different columns from each other and from the $4 \times 3$ paintings regardless of their placement. Thus, the $4 \times 3$ paintings will necessarily be strictly one below the other. The $4 \times 4$ paintings will be pressed against the floor or ceiling, as there must still be $4 \times 2$ and $2 \times 2$ paintings on the wall.
Consider the case where the $4 \times 2$ is strictly above or below one of the $4 \times 4$ paintings. It is clear that there are $3 \cdot 2^{2} \cdot 2^{3}=96$ ways to place all the paintings of width 4 (if we consider the small paintings as one $4 \times 2$ painting, we get 3 ways
| $4 \times 3$ | $4 \times 2$ | |
| :---: | :---: | :---: |
| | | |
| $4 \times 3$ | $4 \times 4$ | $4 \times 4$ |
to choose the column for the $4 \times 3$ paintings, $2^{2}$ ways to choose the attachment to the floor/ceiling in each of the other columns, and $2^{3}$ ways to swap paintings of the same size). The remaining paintings can be placed in $2^{3}=8$ ways in the remaining $4 \times 2$ wall space, as the $2 \times 2$ and $2 \times 1$ paintings must be in different columns.
Now let the $4 \times 2$ painting be above or below both $4 \times 4$ paintings. Since it and the $2 \times 2$ and $2 \times 1$ paintings must be in different columns, there are 16 ways to place all the paintings of width 4 (2 ways to choose the column for the $4 \times 3$, 2
| $4 \times 2$ | | | $4 \times 3$ |
| :---: | :---: | :---: | :---: | :---: |
| $4 \times 4$ | $4 \times 4$ | $4 \times 3$ | |
ways to choose "ceiling/floor" and $2^{2}=4$ ways to swap paintings of the same size). The remaining two $2 \times 2$ areas can be filled in 8 ways.
In total, $8 \cdot(96+16)=896$ options.
Criteria. It is shown that the three smallest paintings (two $1 \times 1$ and one $1 \times 2$) can only be placed together as a $2 \times 2$ square - 1 point.
Correct reasoning about the placement of the $4 \times 4$ and $4 \times 3$ paintings - another 2 points.
Any significant error in calculating the ways to place the paintings of width 4 (for example: not considering that the number of options in cases where the $4 \times 2$ painting is strictly below or above a $4 \times 4$ painting or below or above two of them, are different; or not considering that in cases where the $4 \times 4$ paintings are in adjacent columns, the number of remaining cases is different depending on their position (both above, both below, or one above and one below)) -2 points. Arithmetic error in counting cases - - -1 point.
|
896
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In each cell of a $100 \times 100$ table, a natural number was written. It turned out that each number is either greater than all its neighbors or less than all its neighbors. (Two numbers are called neighbors if they are in cells sharing a common side.) What is the smallest value that the sum of all the numbers can take?
|
Solution. Let's divide the board into dominoes. In each domino, the numbers are different, so their sum is at least $1+2=3$. Then the total sum of the numbers on the board is at least 15000. This estimate is achievable if we alternate ones and twos in a checkerboard pattern.
|
15000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the coordinate plane, an isosceles triangle $A B C$ was drawn: $A B=2016, B C=$ $A C=1533$, with vertices $A$ and $B$ lying on nodes on the same horizontal line. Determine how many nodes lie within the triangle $A B C$ (including nodes lying on the sides). A node is a point on the coordinate plane where both coordinates are integers.
|
Solution. Note that $1533^{2}-1008^{2}=(1533-1008)(1533+1008)=525 \cdot 2541=21 \cdot 25 \cdot 7 \cdot 363=$ $7 \cdot 3 \cdot 5^{2} \cdot 7 \cdot 3 \cdot 11^{2}=(7 \cdot 3 \cdot 5 \cdot 11)^{2}=1155^{2}$. Therefore, the height of the triangle is 1155.
We see that the GCD of 1155 and 1008 is 21. This means that there are 22 nodes (including the vertices) on the side, which divide it into 21 equal parts.
The further part of the solution is based on the fact that the triangle gradually transforms into a rectangle $1008 \times 1155$, the number of nodes in which is easy to calculate. This process is schematically shown in the figure. Let's denote the required number of nodes in the triangle by $T$.
1) Cut the triangle along the axis of symmetry into two halves (two right triangles) and consider each of them as a separate figure. The sum of the number of nodes in these halves is 1156 more than in the original triangle, that is, $T+1156$, since the nodes that were on the axis of symmetry have been duplicated.
2) Combine these two halves into a rectangle $1008 \times 1155$. The inner parts of the halves completely cover the rectangle, while 22 nodes, located in these halves, coincide. Therefore, the number of nodes in the rectangle is 22 less than in the two halves, that is, $T+1156-22$. At the same time, this number is obviously equal to $1009 \cdot 1156$. Thus, $T+1156-22=1009 \cdot 1156$; $T=1008 \cdot 1156+22=1156000+9248+22=1165270$.
Answer: 1165270 nodes.
|
1165270
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.