problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3.1. (12 points) The number
$$
\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+\ldots+\frac{2017}{2018!}
$$
was written as an irreducible fraction with natural numerator and denominator. Find the last two digits of the numerator.
|
Answer: 99.
Solution. We have
$\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+\ldots+\frac{2017}{2018!}=\left(1-\frac{1}{2!}\right)+\left(\frac{1}{2!}-\frac{1}{3!}\right)+\ldots+\left(\frac{1}{2017!}-\frac{1}{2018!}\right)=1-\frac{1}{2018!}=\frac{2018!-1}{2018!}$.
In the end, we obtained an irreducible fraction, and the last two digits of the number 2018! - 1 are two nines.
|
99
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. (12 points) The decreasing sequence $a, b, c$ is a geometric progression, and the sequence $19 a, \frac{124 b}{13}, \frac{c}{13}$ is an arithmetic progression. Find the common ratio of the geometric progression.
|
Answer: 247.
Solution. Let $b=a q, c=a q^{2}$. The properties of an arithmetic progression and the conditions of the problem lead to the equation $2 \cdot \frac{124 a q}{13}=19 a+\frac{a q^{2}}{13} \Leftrightarrow q^{2}-248 q+247=0$, from which $q=1$ or $q=247$. A decreasing geometric progression can only occur when $q=247$ (for example, if $a=-1$).
|
247
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. (12 points) Yura has unusual clocks with several minute hands moving in different directions. Yura calculated that the minute hands coincided in pairs exactly 54 times in one hour. What is the maximum number of minute hands that can be on Yura's clocks?
#
|
# Answer: 28.
Solution. Let two arrows coincide, then after 30 seconds they will coincide again. Therefore, the arrows in each such pair will coincide exactly 2 times per minute. Thus, if $n$ arrows move in one direction, and $m$ arrows move in the other, then $2 m n=54, m n=27$. Therefore, $n$ can be $1,3,9$ or 27. The largest sum $m+n$ is obtained when $n=1, m=27$ (or vice versa) and is equal to 28.
|
28
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. (12 points) In how many ways can eight of the nine digits $1,2,3,4,5,6$, 7,8 and 9 be placed in a $4 \times 2$ table (4 rows, 2 columns) so that the sum of the digits in each row, starting from the second, is 1 more than in the previous one?
|
# Answer: 64.
Solution. The sum of all nine numbers is 45. Let $x$ be the sum of the two numbers in the first row, and let $a$ be the one number out of the nine that we do not place in the figure. Then $x+x+1+x+2+x+3=45-a$, from which $4 x+a=39$. Since $a$ is an integer from 1 to 9, we get 2 possible cases: either $x=9, a=3$, or $x=8, a=7$.
If $a=3$, then we need to place the numbers $1,2,4,5,6,7,8,9$, and the sum of the numbers in the rows should be 9, 10, 11, and 12, respectively. Possible variants for the numbers in the first row: $9=1+8=2+7=4+5$.
If the first row contains 1 and 8, then the second row should contain 4 and 6, the third row 2 and 9, and the last row 5 and 7.
If the first row contains 2 and 7, then the second row should contain 1 and 9 (with other variants, it is impossible to select numbers for the third row), the third row 5 and 6, and the last row 4 and 8.
If the first row contains 4 and 5, then the second row can have 1 and 9 or 2 and 8. But in both cases, it is impossible to find numbers for the third row.
If $a=7$, then we need to place the numbers $1,2,3,4,5,6,8,9$, and the sum of the numbers in the rows should be 8, 9, 10, and 11, respectively. The sum of the numbers in the first row is $8=5+3=6+2$.
If the first row contains 3 and 5, then the second row should contain 1 and 8, the third row 6 and 4, and the last row 2 and 9.
If the first row contains 6 and 2, then the second row can contain 1 and 8 or 4 and 5. If they contain 1 and 8, it is impossible to select numbers for the next row. Therefore, they contain 4 and 5, then the next row contains 1 and 9, and the last row 3 and 8.
Thus, we have 4 variants of number placement without considering the order of numbers in the rows. Since the numbers in each row can be swapped, we get $2^{4}=16$ variants for each placement. In total, we get 64 variants.
|
64
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. (12 points) For different natural numbers $k, l, m, n$, it is known that there exist such three natural numbers $a, b, c$ that each of the numbers $k, l, m, n$ is a root of either the equation $a x^{2}-b x+c=0$, or the equation $c x^{2}-16 b x+256 a=0$. Find $k^{2}+l^{2}+m^{2}+n^{2}$.
|
Answer: 325.
Solution. If $k, l$ are the roots of the first equation, then the roots of the second equation are the numbers $m=\frac{16}{k}$, $n=\frac{16}{l}$. Therefore, the numbers $k, l, m, n$ are divisors of the number 16. The divisors of 16 are the numbers 1, 2, 4, 8, and 16, but the number 4 does not fit, as by the condition all numbers $k, l, m, n$ are distinct. Thus, $k^{2}+l^{2}+m^{2}+n^{2}=1^{2}+2^{2}+8^{2}+16^{2}=325$.
|
325
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Vanya thought of a two-digit number, then swapped its digits and multiplied the resulting number by itself. The result turned out to be four times larger than the number he thought of. What number did Vanya think of?
|
Answer: 81.
Solution. Let the intended number be $\overline{m n}=10 m+n$. Then $4 \overline{m n}=\overline{n m}^{2}$. Therefore, $\overline{n m}^{2}$ is divisible by 4, and $\overline{n m}$ is divisible by 2, so the digit $m$ is even (and not zero). Moreover, $\overline{m n}=\overline{n m}^{2}: 4=(\overline{n m}: 2)^{2}$, which means $\overline{m n}$ is a square of a natural number starting with an even digit. Therefore, $\overline{m n}$ can be 25, 49, 64, or 81. Checking shows that only the last one satisfies the condition.
|
81
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The Martian traffic light consists of six identical bulbs arranged in two horizontal rows (one above the other) with three bulbs in each. A rover driver in the fog can distinguish the number and relative position of the lit bulbs on the traffic light (for example, if two bulbs are lit, whether they are in the same horizontal row or in different rows, whether they are in the same vertical row, or in adjacent vertical rows, or in the two outer vertical rows). However, he cannot distinguish the unlit bulbs and the body of the traffic light. Therefore, if only one bulb is lit, it is impossible to determine which one of the six it is). How many signals of the Martian traffic light can the rover driver distinguish in the fog? If no bulb on the traffic light is lit, the driver cannot see it.
|
Answer: 44.
Solution. If two traffic light signals differ only by the shift of the lit bulbs, then the driver cannot distinguish them (and vice versa). Therefore, any signal can either be transformed by a shift to the left and/or up into an indistinguishable signal, which has at least one bulb lit in the top horizontal row and at least one in the left vertical row, or the signal already has this property. There are two cases.
|
44
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. (2 points) The average age of employees in a company consisting of 13 people is 35 years. After a new employee is hired, the average age of the employees becomes 34 years. Find the age of the new employee.
|
Answer: 21.
Solution. The sum of the employees' ages before the new hire was $13 \cdot 35$, and after the new employee was hired, the sum of the ages became $14 \cdot 34$. Therefore, the age of the new employee is $14 \cdot 34 - 13 \cdot 35 = 35 - 14 = 21$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. (12 points) An eraser, 3 pens, and 2 markers cost 240 rubles. Two erasers, 4 markers, and 5 pens cost 440 rubles. What is the total cost (in rubles) of 3 erasers, 4 pens, and 6 markers?
|
Answer: 520.
Solution. From the condition, it follows that 3 erasers, 8 pens, and 6 markers cost $440+240=680$ rubles. Moreover, 2 erasers, 6 pens, and 4 markers will cost $2 \cdot 240=480$ rubles. Therefore, one pen costs $480-440=40$ rubles. Then, 3 erasers, 4 pens, and 6 markers cost $680-4 \cdot 40=520$ rubles.
|
520
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. (12 points) In an acute-angled triangle $A B C$, angle $A$ is $35^{\circ}$, segments $B B_{1}$ and $C C_{1}$ are altitudes, points $B_{2}$ and $C_{2}$ are the midpoints of sides $A C$ and $A B$ respectively. Lines $B_{1} C_{2}$ and $C_{1} B_{2}$ intersect at point $K$. Find the measure (in degrees) of angle $B_{1} K B_{2}$.
|
# Answer: 75.
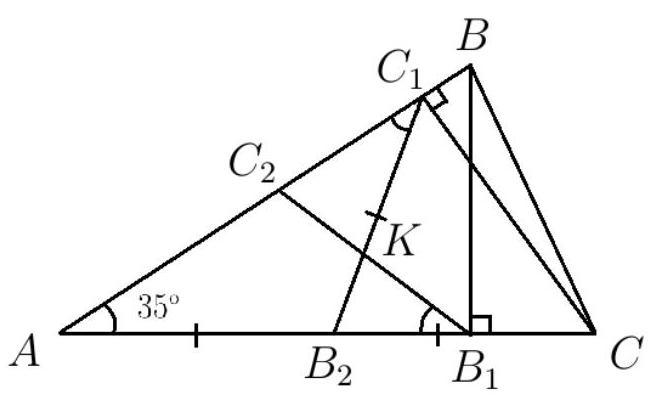
Solution. Note that angles $B$ and $C$ of triangle $ABC$ are greater than $\angle A=35^{\circ}$ (otherwise it would be an obtuse triangle), so point $C_{1}$ lies on side $AB$ between points $B$ and $C_{2}$, and point $B_{1}$ lies on side $AC$ between points $C$ and $B_{2}$. Therefore, the point $K$ of intersection of lines $B_{1} C_{2}$ and $C_{1} B_{2}$ lies inside the triangle. Since $C_{1} B_{2}$ is the median of the right triangle $C C_{1} A$, triangle $C_{1} B_{2} A$ is isosceles. Therefore, $\angle A B_{1} C_{2}=35^{\circ}$. Similarly, we get $\angle A C_{1} B_{2}=35^{\circ}$, from which $\angle A B_{2} C_{1}=180^{\circ}-2 \cdot 35^{\circ}=110^{\circ}$. Then $\angle B_{1} K B_{2}=\angle A B_{2} K-\angle A B_{1} K=110^{\circ}-35^{\circ}=75^{\circ}$.
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. (12 points) The equation $x^{2}+5 x+1=0$ has roots $x_{1}$ and $x_{2}$. Find the value of the expression
$$
\left(\frac{x_{1} \sqrt{6}}{1+x_{2}}\right)^{2}+\left(\frac{x_{2} \sqrt{6}}{1+x_{1}}\right)^{2}
$$
|
Answer: 220.
Solution. Since $x_{1}^{2}=-5 x_{1}-1$, then $\left(1+x_{1}\right)^{2}=1+2 x_{1}-5 x_{1}-1=-3 x_{1}$. Therefore,
$$
\begin{gathered}
\left(\frac{x_{1} \sqrt{6}}{1+x_{2}}\right)^{2}+\left(\frac{x_{2} \sqrt{6}}{1+x_{1}}\right)^{2}=6\left(\frac{-5 x_{1}-1}{-3 x_{2}}+\frac{-5 x_{2}-1}{-3 x_{1}}\right)=\frac{10\left(x_{1}^{2}+x_{2}^{2}\right)+2\left(x_{1}+x_{2}\right)}{x_{1} x_{2}}= \\
=\frac{10\left(x_{1}+x_{2}\right)^{2}-20 x_{1} x_{2}+2\left(x_{1}+x_{2}\right)}{x_{1} x_{2}}=\frac{10 \cdot 25-20-10}{1}=220
\end{gathered}
$$
|
220
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. (12 points) From point $A$ to point $B$, a bus and a cyclist departed simultaneously at 13:00. After arriving at point $B$, the bus, without stopping, headed back and met the cyclist at point $C$ at 13:10. Upon returning to point $A$, the bus again, without stopping, headed to point $B$ and caught up with the cyclist at point $D$, which is located $\frac{2}{3}$ km from point $C$. Find the speed of the bus (in km/h), if the distance between points $A$ and $B$ is 4 km, and the speeds of the bus and the cyclist are constant.
|
Answer: 40.
Solution. Let $v_{1}$ and $v_{2}$ be the speeds (in km/h) of the cyclist and the bus, respectively. By the time of the first meeting, they have collectively traveled $\frac{1}{6} v_{1}+\frac{1}{6} v_{2}=8$ km. Until the next meeting, the time that has passed is equal to $\frac{s_{0}}{v_{1}}=\frac{2 \cdot \frac{1}{6} v_{1}+s_{0}}{v_{2}}$ hours, where $s_{0}=\frac{1}{3}$ km. From this, we find $\frac{1}{4} v_{1}^{2}+v_{1}-24=0, v_{1}=8$ km/h (the second root is negative), $v_{2}=40 \text{km}/$ h.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. (14 points) Mitya is 11 years older than Shura. When Mitya was as old as Shura is now, he was twice as old as she was. How old is Mitya?
|
Answer: 33.
Solution. 11 years ago, Shura was half as old as she is now. So, she is 22 years old, and Mitya is 33.
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. (14 points) Represent the number $\frac{201920192019}{191719171917}$ as an irreducible fraction. In the answer, write down the denominator of the resulting fraction.
|
Answer: 639.
Solution. We have
$$
\frac{201920192019}{191719171917}=\frac{2019 \cdot 100010001}{1917 \cdot 100010001}=\frac{2019}{1917}=\frac{3 \cdot 673}{3 \cdot 639}=\frac{673}{639}
$$
Since $639=3^{2} \cdot 71$ and 673 is not divisible by 3 and 71, the resulting fraction is irreducible.
|
639
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. (14 points) How many six-digit numbers exist whose sum of digits equals 51?
|
Answer: 56.
Solution. Since the maximum sum of the digits of a six-digit number is $6 \cdot 9=54$, the sought numbers are $699999, 789999, 888999$, as well as all numbers obtained from them by rearranging the digits. The first of these numbers can form 6 six-digit numbers (the digit 6 can be in any of the 6 positions), the second can form $6 \cdot 5=30$ numbers (6 options for placing one of the digits 7, 8, and another 5 for the other), and the third can form $\frac{6 \cdot 5 \cdot 4}{1 \cdot 2 \cdot 3}=20$ numbers (6 options for one digit 8, another 5 options for the second, and 4 options for the third, but since these digits are the same, we have counted each number $1 \cdot 2 \cdot 3=6$ times). In total, $6+30+20=56$ numbers.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. (14 points) Find the smallest natural number whose representation contains 5 zeros and 7 ones, and the sum of the digits in the even positions is equal to the sum of the digits in the odd positions.
|
Answer: 1000001111131.
Solution. The number 7 is not divisible by 2, so the number cannot have exactly $5+7=12$ digits. Consider the case where the number has 13 digits. If the "new" digit is zero, we again get a contradiction. Therefore, the "new" digit must be at least 1. Thus, to find the smallest number, we choose it so that this digit is as far to the right in the number as possible. Let's try to find the desired number in the form 100000111111x. Equating the sums of the digits in the even and odd positions, we get the equation $4+x=3$, from which $x=1$, which is impossible. Let's check the number in the form $a=10000011111 x 1$. Calculating the sums of the digits in the even and odd positions, we get $5=2+x \Rightarrow x=3$. Therefore, the desired number is 1000001111131.
|
1000001111131
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2.
B-1.
At the time when a lion cub, who was 5 minutes away, set off for the watering hole, the second cub, having already quenched its thirst, started heading back along the same road at 1.5 times the speed of the first. At the same time, a tortoise, which was half an hour away, set off for the watering hole along the same road. After some time, all three met at one point and then continued on their way. How many minutes after the meeting did the tortoise reach the watering hole, given that all three moved at constant speeds?
|
Answer: 28
Solution. Let's take the entire path of the turtle as 1 and let $x$ be the speed of the 1st lion cub. Then the speed of the 2nd lion cub is $1.5x$, and the speed of the turtle is $1/30$. The entire path to the watering hole for the 1st lion cub is $5x$. Therefore, the meeting with the 2nd lion cub occurred after $5x/(x+1.5x)=2$ minutes from the start of the movement. The turtle also moved for the same amount of time before the meeting. The remaining distance was covered by the turtle in $30-2=28$ minutes.
## B-2
At the time when one lion cub, located 7.5 minutes away from the watering hole, set off for it, the second, having quenched his thirst, headed back along the same path at twice the speed of the first. At the same time, a turtle, located half an hour away from the watering hole, set off for it along the same path. After some time, all three met at one point and continued on their way. How many minutes after the meeting did the turtle reach the watering hole, given that all three moved at constant speeds?
Answer: 27.5
## B-3
At the time when one lion cub, located 7 minutes away from the watering hole, set off for it, the second, having quenched his thirst, headed back along the same path at 2.5 times the speed of the first. At the same time, a turtle, located half an hour away from the watering hole, set off for it along the same path. After some time, all three met at one point and continued on their way. How many minutes after the meeting did the turtle reach the watering hole, given that all three moved at constant speeds?
Answer: 28
## B-4
At the time when one lion cub, located 6 minutes away from the watering hole, set off for it, the second, having quenched his thirst, headed back along the same path at three times the speed of the first. At the same time, a turtle, located half an hour away from the watering hole, set off for it along the same path. After some time, all three met at one point and continued on their way. How many minutes after the meeting did the turtle reach the watering hole, given that all three moved at constant speeds?
Answer: 38.5
## Lomonosov School Olympiad in Mathematics
Preliminary stage $2020 / 21$ academic year for $5-6$ grades
## B-1
#
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
A square with a side of 75 mm was cut by two parallel cuts into three rectangles. It turned out that the perimeter of one of these rectangles is half the sum of the perimeters of the other two. What is this perimeter? Give your answer in centimeters.
|
# Answer: 20
Solution. For three rectangles, one of the sides is the same and equals 75 mm. The sum of the lengths of two such sides of one rectangle is half the sum of the lengths of all such sides of the other two. Therefore, the other side of the first rectangle is also half the sum of the other sides of the two other rectangles. Thus, it equals $75: 3=25$ mm, from which the perimeter of the first rectangle is $2 \cdot(25+75)=200$ mm $=20 \mathrm{cm}$.
## B-2
A square with a side of 105 mm was cut by two parallel cuts into three rectangles. It turned out that the perimeter of one of these rectangles is half the sum of the perimeters of the other two. What is this perimeter? Give your answer in centimeters.
Answer: 28
## B-3
A square with a side of 135 mm was cut by two parallel cuts into three rectangles. It turned out that the perimeter of one of these rectangles is half the sum of the perimeters of the other two. What is this perimeter? Give your answer in centimeters.
Answer: 36
## B-4
A square with a side of 165 mm was cut by two parallel cuts into three rectangles. It turned out that the perimeter of one of these rectangles is half the sum of the perimeters of the other two. What is this perimeter? Give your answer in centimeters.
Answer: 44
## Lomonosov School Olympiad in Mathematics
Preliminary stage $2020 / 21$ academic year for $5-6$ grades
## B-1
#
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
Find the smallest 12-digit natural number that is divisible by 36 and contains all 10 digits in its decimal representation.
|
Answer: 100023457896
Solution. The number is divisible by 4 and 9. Since the sum of ten digits is 45 (divisible by 9), two more digits should be added to these ten digits, the sum of which is 0, 9, or 18. Since we need the smallest number, we will add two digits 0 and place the number 10002345 at the beginning of the required number (this is the smallest possible "start" of the number). The remaining digits $6,7,8$ and 9 need to be arranged so that the number is divisible by 4. This means the last two digits should be 68, 76, or 96. The minimum is 7896.
## B-2
Find the smallest 13-digit natural number that is divisible by 75 and contains all 10 digits in its notation.
Answer: 1000023468975
Solution. The number is divisible by 3 and 25. The sum of ten digits is 45 (divisible by three), so the sum of the three additional digits in the number's notation should be $0,3,6, \ldots, 27$. The older the digit place, the smaller the digit it is better to put in it, so we will take three zeros and place the number 10000 at the beginning of the required number. To make the number divisible by 25, the last two digits should be 25, 50, or 75. The first two options use small digits, which are better placed in older places, so we choose 75 and get the answer: 1000023468975.
## B-3
Find the largest 12-digit natural number that is divisible by 36 and contains all 10 digits in its decimal notation.
Answer: 999876543120
The number is divisible by 4 and 9. Since the sum of ten digits is 45 (divisible by 9), two more digits should be added to these ten digits, the sum of which is 0, 9, or 18. The older the digit place, the larger the digit it is better to put in it, so we will add two nines to the ten digits and start the number as: 999.... For divisibility by 4, the last two digits should form a number divisible by 4: $00,04,08,12,16,20,24, \ldots, 96$. Of these options, 20 is the best because it leaves the larger digits for the older places (we have only one zero, so 00 is out). In the end, we get the number 999876543120.
## B-4
Find the largest 13-digit natural number that is divisible by 75 and contains all 10 digits in its notation.
Answer: 9999876432150
Solution. The number is divisible by 3 and 25. The sum of ten digits is 45 (divisible by three), so the sum of the three additional digits in the number's notation should be $0,3,6, \ldots, 27$. The older the digit place, the larger the digit it is better to put in it, so we will take three nines and start the number as: $9999 \ldots$. To make the number divisible by 25, the last two digits should be 25, 50, or 75. The five is used in any case, and it is best to choose 50 to leave the larger digits 7 and 2 for the older places. In the end, we get the number 9999876432150.
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary Stage 2020/21 academic year for 5-6 grades
#
|
100023457896
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5.
B-1
Chicks hatch on the night from Sunday to Monday. For two weeks, the chick sits with its beak open, the third week it silently grows feathers, and on the fourth week, it flies away from the nest. Last week, 20 chicks were sitting with their beaks open, and 14 were growing feathers, while this week, 15 were sitting with their beaks open and 11 were growing feathers. a) How many chicks were sitting with their beaks open two weeks ago? b) How many chicks will be growing feathers next week? In the answer, write the product of these numbers.
|
Answer: 225
Solution. In fact, the chicks should be divided into three categories: one-week-old, two-week-old, and three-week-old. With each new week, each chick moves to the next category. So, if 11 are feathering this week, then last week there were 11 two-week-olds, and, accordingly, 9 one-week-olds ( $9+11=20$ ). This means that this week there are 9 two-week-olds, and they will be feathering next week. Last week, there were 11 two-week-olds and 14 three-week-olds - which means that the week before last, there were 11 one-week-olds and 14 two-week-olds, and it was they who were opening their beaks. The answer is $9(11+14)$.
## B-2
In a workshop, wooden horses are made. A figurine is painted for two days, on the third day it is lacquered, and on the fourth day, it is shipped to the store. Today, 12 figurines are being painted, and 7 are being lacquered. Yesterday, 11 figurines were painted, and 10 were lacquered. a) How many figurines were painted the day before yesterday? b) How many figurines will be lacquered tomorrow? Write the product of these numbers as the answer.
Answer: 68
## B-3
In an enclosed area of the Universe, stars flare up. Each star shines brightly for two billion years, then glows dimly for a billion years, and then goes out completely. Today, in that area of the Universe, there are 7 bright and 12 dim stars, a billion years ago there were 16 bright and 8 dim. a) How many dim stars will you count there a billion years from now? b) How many bright stars were there two billion years ago? Write the product of the obtained numbers as the answer.
Answer: 80
## B-4
Every year, new models of phones appear on the market. In the first year after release, a model is considered the cutting edge of progress, in the second and third years, the model is downgraded to just "decent," and after that, it hopelessly becomes outdated. This year, there are 8 cutting-edge models and 11 decent ones. Last year, there were 4 cutting-edge models and 17 decent ones. a) How many models were at the cutting edge of progress by the standards of the year before last? b) How many decent models will there be next year? Write the product of the obtained numbers as the answer.
Answer: 84
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary stage $2020 / 21$ academic year for $5-6$ grades
## B-1
#
|
225
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6.
In the alphabet of the inhabitants of the magical planet ABV2020, there are only three letters: A, B, and V, from which all words are formed. In any word, two identical letters cannot be adjacent, and each of the three letters must be present in any word. For example, the words ABV, VABAVAB, and BVBVAB are permissible, while the words VAV, ABAAVA, and AVABBB are not. How many 20-letter words are there in the dictionary of this planet?
|
# Answer: 1572858
Solution. The first letter can be any of the three, and for each subsequent letter, there are two options. This results in $3 \cdot 2^{19}$ words. However, we need to subtract from this the words that are made up of only two letters, not three. There are 6 such words. Therefore, we get $3 \cdot 2^{19}-6=1572858$ different words.
## B-2
In the alphabet of the inhabitants of the magical planet ABV2020, there are only three letters: A, B, and V, from which all words are formed. In any word, two identical letters cannot be adjacent, and each of the three letters must be present in any word. For example, the words AVB, VAVAVA, BVVVBVA are valid, while the words VAV, ABAAVA, AVABB are not. How many 18-letter words are there in the dictionary of this planet?
Answer: 393210
## B-3
In the alphabet of the inhabitants of the magical planet ABV2020, there are only three letters: A, B, and V, from which all words are formed. In any word, two identical letters cannot be adjacent, and each of the three letters must be present in any word. For example, the words AVB, VAVAVA, BVVVBVA are valid, while the words VAV, ABAAVA, AVABB are not. How many 19-letter words are there in the dictionary of this planet?
Answer: 786426
## B-4
In the alphabet of the inhabitants of the magical planet ABV2020, there are only three letters: A, B, and V, from which all words are formed. In any word, two identical letters cannot be adjacent, and each of the three letters must be present in any word. For example, the words AVB, VAVAVA, BVVVBVA are valid, while the words VAV, ABAAVA, AVABB are not. How many 17-letter words are there in the dictionary of this planet?
Answer: 196602
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary stage $2020 / 21$ academic year for $5-6$ grades
## B-1
#
|
1572858
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 7.
Around a round table, 1001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turned out that next to each knight sits exactly one liar, and next to each liar there is a knight. What is the minimum number of knights that can sit at the table?
|
Answer: 502
Solution. From the condition, it follows that a knight cannot sit between two knights or two liars, and a liar cannot sit between two liars. Thus, when moving around the table, knights will be encountered in pairs, while liars will be encountered singly or in pairs. From this, it follows that each liar can be paired with a knight (and there will still be knights who have not been paired). Therefore, the number of knights at the table is more than half of the total number of people and is also an even number, i.e., at least 502.
An example seating arrangement of 502 knights and 499 liars that satisfies the condition: first, seat 248 groups of "knight, knight, liar, liar," then three more groups of "knight, knight, liar."
## B-2
At a round table, 2001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turns out that next to each knight sits exactly one liar, and next to each liar, there is a knight. What is the maximum number of liars that can sit at the table?
Answer: 999
## B-3
At a round table, 3001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turns out that next to each knight sits exactly one liar, and next to each liar, there is a knight. What is the minimum number of knights that can sit at the table?
Answer: 1502
## B-4
At a round table, 4001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turns out that next to each knight sits exactly one liar, and next to each liar, there is a knight. What is the maximum number of liars that can sit at the table?
Answer: 1999
|
502
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The numbers from 1 to 8 are arranged at the vertices of a cube such that the sum of the numbers in any three vertices lying on the same face is at least 10. What is the smallest possible sum of the numbers at the vertices of one face?
|
Answer: 16.
Solution. Each face has a vertex where a number not less than 6 is placed. Indeed, otherwise, one of the triples of the remaining largest numbers $2,3,4,5$ would give a sum less than 10 (specifically, the triple $2,3,4$ with a sum of 9).
Consider a face containing the vertex where the number 6 is placed. Since the sum of the numbers in the other three vertices is not less than 10, the sum of all numbers in the vertices of this face is not less than 16.
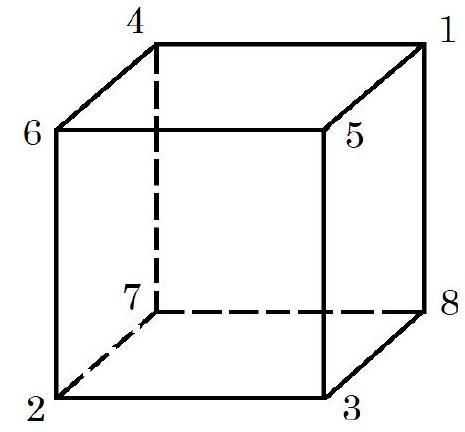
An example of an arrangement where the smallest sum of numbers in the vertices of one face is 16 is shown in the figure: the sum of the numbers in the front face is $2+3+5+6=16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. All natural numbers, the sum of the digits of each of which is equal to 5, were arranged in ascending order. What number is in the 125th place
|
Answer: 41000.
Solution. Let's calculate the number of $n$-digit numbers, the sum of the digits of each of which is equal to 5, for each natural $n$. Subtract 1 from the leading digit, we get a number (which can now start with zero), the sum of the digits of which is equal to 4. Represent the digits of this number as cells, in each of which there is a number of balls equal to the digit in the corresponding place. Distributing 4 balls into $n$ cells is the same as placing $n-1$ partitions between 4 balls (there may be no balls between some partitions). This can be done in $C_{n+3}^{4}=\frac{(n+3)(n+2)(n+1) n}{24}$ ways, which is also the number of the desired $n$-digit numbers.
For $n=1,2,3,4,5$, we get $C_{4}^{4}=1, C_{5}^{4}=5, C_{6}^{4}=15, C_{7}^{4}=35, C_{8}^{4}=70$, totaling 126 numbers. The 126th number is the largest five-digit such number, i.e., 50000. Therefore, the 125th number is the previous one - 41000.
|
41000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In "Dragon Poker," the deck has four suits. An Ace brings 1 point, a Jack -2 points, a Two $-2^{2}$, a Three $-2^{3}$, ..., a Ten $-2^{10}=1024$ points. Kings and Queens are absent. You can choose any number of cards from the deck. In how many ways can you score 2018 points?
|
Answer: $C_{2021}^{3}=1373734330$.
Solution. In any suit, you can score any number of points from 0 to 2047, and this can be done in a unique way. This can be done as follows: write down this number in binary and select the cards corresponding to the binary positions containing 1 (i.e., if there is a 1 in the $k$-th position, then you should take the card that brings $2^{k}$ points).
Thus, the problem reduces to partitioning the number 2018 into 4 non-negative integer addends. Reasoning similarly to the previous problem, we get the desired number of ways: $C_{2021}^{3}=1373734330$.
|
1373734330
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8.
Inside a convex $n$-gon, 100 points are placed such that no three of these $n+100$ points lie on the same line. The polygon is divided into triangles, each of whose vertices are 3 of the given $n+100$ points. For what maximum value of $n$ can there not be more than 300 triangles?
|
Answer: 102
Solution. If each point is a vertex of some triangle, then the sum of the angles of all the obtained triangles is $180^{\circ} \cdot(n-2)+360^{\circ} \cdot 100=180^{\circ} \cdot(n-2+200)=180^{\circ} \cdot(n+198)$. Therefore, $\frac{180^{\circ} \cdot(n+198)}{180^{\circ}}=n+198$ triangles are obtained. If one of the points does not participate in the cutting, there will be fewer triangles. Therefore, $n+198 \leqslant 300, n \leqslant 102$.
## B-2
Inside a convex 200-gon, $n$ points are placed such that no three of these $n+200$ points lie on the same line. The polygon is cut into triangles, the vertices of each of which are 3 of the given $n+200$ points. For what maximum value of $n$ can there not be more than 400 triangles?
Answer: 101
## B-3
Inside a convex $n$-gon, 200 points are placed such that no three of these $n+200$ points lie on the same line. The polygon is cut into triangles, the vertices of each of which are 3 of the given $n+200$ points. For what values of $n$ can there not be more than 600 triangles?
Answer: 202
## B-4
Inside a convex 100-gon, $n$ points are placed such that no three of these $n+100$ points lie on the same line. The polygon is cut into triangles, the vertices of each of which are 3 of the given $n+100$ points. For what values of $n$ can there not be more than 500 triangles?
Answer: 201
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary Stage 2020/21 academic year for $10-11$ grades
## B-1
|
102
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.
Given a polynomial $P(x)$ of degree 10 with the leading coefficient 1. The graph of $y=P(x)$ lies entirely above the $O x$ axis. The polynomial $-P(x)$ is factored into irreducible factors (i.e., polynomials that cannot be expressed as the product of two non-constant polynomials). It is known that at $x=2020$, all the obtained irreducible polynomials take the value -3. Find $P(2020)$.
|
Answer: 243
Solution. Note that since the graph of $y=P(x)$ is entirely above the $O x$ axis, the polynomial $P(x)$ has no real roots. This means that all irreducible polynomials in the factorization have degree 2, and their number is 5. Since the polynomial $-P(x)$ will have the same number of irreducible polynomials in its factorization, and all of them take the value -3 at the point $x=2020$, then $-P(2020)=(-3)^{5}=-243$. Hence, $P(2020)=243$.
## B-2
Given a polynomial $P(x)$ of degree 12 with the leading coefficient 1. The graph of $y=P(x)$ is entirely above the $O x$ axis. The polynomial $P(x)$ is factored into irreducible factors (i.e., polynomials that cannot be represented as a product of two non-constant polynomials). It is known that at $x=2020$ all the obtained irreducible polynomials take the value -3. Find $P(2020)$.
Answer: 729
## B-3
Given a polynomial $P(x)$ of degree 20 with the leading coefficient 1. The graph of $y=P(x)$ is entirely above the $O x$ axis. This polynomial is factored into irreducible factors (i.e., polynomials that cannot be represented as a product of two non-constant polynomials). It is known that at $x=2020$ all the obtained irreducible polynomials take the value 2. Find $P(2020)$.
Answer: 1024
## B-4
Given a polynomial $P(x)$ of degree 18 with the leading coefficient -1. The graph of $y=P(x)$ is entirely below the $O x$ axis. The polynomial $P(x)$ is factored into irreducible factors (i.e., polynomials that cannot be represented as a product of two non-constant polynomials). It is known that at $x=2020$ all the obtained irreducible polynomials take the value -2. Find $P(2020)$.
Answer: -512
## B-5
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-210 x+11000}{\sqrt[2021]{x^{2021}-420 x^{2020}}}>1
$$
Answer: 421
Solution. We will solve the problem in general, specifying the constraints on the parameters $a, b, c$: Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-(a+b) x+a b}{\sqrt[2021]{x^{2021}-c x^{2020}}}>1
$$
We assume that $a, b, c$ are natural numbers, $1 \leqslant a < b$, and $c \geqslant a+b$. For $x \leqslant a$, the numerator is non-positive, and the denominator is positive, so the left side of the inequality is non-positive. For $x \geqslant b$, the numerator is non-negative, and the denominator is positive, so the left side of the inequality is non-negative. For $a < x < b$, the numerator is positive, and the denominator is positive, so the left side of the inequality is positive. We need to find the smallest $x$ such that the left side of the inequality is greater than 1.
For $x = a$, the numerator is 0, and the denominator is positive, so the left side of the inequality is 0. For $x = b$, the numerator is 0, and the denominator is positive, so the left side of the inequality is 0. For $x = c$, the numerator is positive, and the denominator is positive, so the left side of the inequality is positive. We need to find the smallest $x$ such that the left side of the inequality is greater than 1.
For $x = c+1$, the numerator is positive, and the denominator is positive, so the left side of the inequality is positive. We need to check if the left side of the inequality is greater than 1.
The numerator is
$$
x^{2}-(a+b) x+a b = (x-a)(x-b)
$$
The denominator is
$$
\sqrt[2021]{x^{2021}-c x^{2020}} = x \sqrt[2021]{1 - \frac{c}{x}}
$$
For $x = c+1$, the denominator is
$$
(c+1) \sqrt[2021]{1 - \frac{c}{c+1}} = (c+1) \sqrt[2021]{\frac{1}{c+1}} = (c+1) \frac{1}{(c+1)^{1/2021}} = (c+1)^{1 - 1/2021}
$$
The left side of the inequality is
$$
\frac{(c+1-a)(c+1-b)}{(c+1)^{1 - 1/2021}}
$$
Since $c \geqslant a+b$, we have $c+1 > a+b$, so $(c+1-a)(c+1-b) > 1$. Since $(c+1)^{1 - 1/2021} < c+1$, we have
$$
\frac{(c+1-a)(c+1-b)}{(c+1)^{1 - 1/2021}} > 1
$$
Therefore, the smallest integer satisfying the inequality is $c+1$.
Answer: $c+1$
## B-6
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-171 x+7290}{\sqrt[2021]{x^{2021}-215 x^{2020}}}>1
$$
Answer: 216
## B-7
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-251 x+15730}{\sqrt[2021]{x^{2021}-374 x^{2020}}}>1
$$
Answer: 375
## B-8
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-294 x+21600}{\sqrt[2021]{x^{2021}-517 x^{2020}}}>1
$$
Answer: 518
## B-9
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-210 x+11000}{\sqrt[2021]{x^{2021}-425 x^{2020}}}>1
$$
Answer: 426
## B-10
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-171 x+2290}{\sqrt[2021]{x^{2021}-219 x^{2020}}}>1
$$
Answer: 220
## B-11
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-251 x+15730}{\sqrt[2021]{x^{2021}-379 x^{2020}}}>1
$$
Answer: 380
## B-12
Find the smallest integer satisfying the inequality
$$
\frac{x^{2}-294 x+21600}{\sqrt[2021]{x^{2021}-519 x^{2020}}}>1
$$
Answer: 520
## Lomonosov Olympiad for Schoolchildren
Preliminary Round 2020/21 academic year for $10-11$ grades
## B-1
#
|
243
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 10.
Set $A$ on the plane $O x y$ is defined by the equation $x^{2}+y^{2}=2 x+2 y+23$. Set $B$ on the same plane is defined by the equation $|x-1|+|y-1|=5$. Set $C$ is the intersection of sets $A$ and $B$. What is the maximum value that the product of the lengths of $n$ segments $X Y_{1} \cdot X Y_{2} \cdot X Y_{3} \cdot \ldots \cdot X Y_{n}$ can take, where point $X$ is an arbitrarily chosen point from set $A$, and points $Y_{1}, Y_{2}, Y_{3}, \ldots, Y_{n}$ are all elements of set $C$?
|
Answer: 1250
Solution. The set $A$ is $(x-1)^{2}+(y-1)^{2}=25$, which is a circle with center $(1 ; 1)$ and radius 5. The set $B$ is a square with vertices $(-4 ; 1),(1 ; 6),(6 ; 1),(1 ;-4)$. The center of the square is the point $(1 ; 1)$, the diagonals of the square are 10, and the sides are $5 \sqrt{2}$. The set $C$ consists of 4 points on the circle: $(-4 ; 1),(1 ; 6),(6 ; 1),(1 ;-4)$, which are also the vertices of the inscribed square. Let's denote them as $Y_{1}, Y_{2}, Y_{3}, Y_{4}$. If we now take a point $X$ on the arc $Y_{2} Y_{3}$ (for definiteness), denote the distance from $X$ to the line $Y_{1} Y_{2}$ as $a$, and note that $\angle Y_{2} X Y_{1}=\frac{\angle Y_{2} O Y_{1}}{2}=45^{\circ}$, then we get: $X Y_{1} \cdot X Y_{2}=\frac{X Y_{1} \cdot X Y_{2} \cdot 2 \sin 45^{\circ}}{2 \sin 45^{\circ}}=S_{X Y_{1} Y_{2}} \cdot \frac{2}{\sin 45^{\circ}}=\frac{Y_{1} Y_{2} \cdot a}{2} \cdot \frac{2 \cdot 2}{\sqrt{2}}=\frac{5 \sqrt{2} \cdot a}{2} \cdot \frac{4}{\sqrt{2}}=10 a$. Similarly, $X Y_{3} \cdot X Y_{4}=10(5 \sqrt{2}-a)$. Then $X Y_{1} \cdot X Y_{2} \cdot X Y_{3} \cdot X Y_{4}=100 a(5 \sqrt{2}-a)$. The maximum of this quadratic function is achieved at $a=\frac{5 \sqrt{2}}{2}$ and is equal to 1250. Note that this means that the point $X$ is at the midpoint of the arc $Y_{2} Y_{3}$ (or any of the other three arcs).
## B-2
The set $A$ on the plane $O x y$ is defined by the equation $x^{2}+y^{2}=2 x+2 y+14$. The set $B$ on the same plane is defined by the equation $|x-1|+|y-1|=4$. The set $C$ is the intersection of sets $A$ and $B$. What is the maximum value that the product of the lengths of $n$ segments $X Y_{1} \cdot X Y_{2} \cdot X Y_{3} \cdot \ldots \cdot X Y_{n}$ can take, where the point $X$ is an arbitrarily chosen point from set $A$, and the points $Y_{1}, Y_{2}, Y_{3}, \ldots, Y_{n}$ are all elements of set $C$.
Answer: 512
## B-3
The set $A$ on the plane $O x y$ is defined by the equation $x^{2}+y^{2}=2 x+2 y+7$. The set $B$ on the same plane is defined by the equation $|x-1|+|y-1|=3$. The set $C$ is the intersection of sets $A$ and $B$. What is the maximum value that the product of the lengths of $n$ segments $X Y_{1} \cdot X Y_{2} \cdot X Y_{3} \cdot \ldots \cdot X Y_{n}$ can take, where the point $X$ is an arbitrarily chosen point from set $A$, and the points $Y_{1}, Y_{2}, Y_{3}, \ldots, Y_{n}$ are all elements of set $C$.
Answer: 162
## B-4
The set $A$ on the plane $O x y$ is defined by the equation $x^{2}+y^{2}=2 x-2 y+34$. The set $B$ on the same plane is defined by the equation $|x-1|+|y+1|=6$. The set $C$ is the intersection of sets $A$ and $B$. What is the maximum value that the product of the lengths of $n$ segments $X Y_{1} \cdot X Y_{2} \cdot X Y_{3} \cdot \ldots \cdot X Y_{n}$ can take, where the point $X$ is an arbitrarily chosen point from set $A$, and the points $Y_{1}, Y_{2}, Y_{3}, \ldots, Y_{n}$ are all elements of set $C$.
Answer: 2592
|
1250
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. After treating the garden with a caterpillar control agent, the gardener noticed that from 12 blackcurrant bushes he was getting the same harvest as before from 15 bushes. By what percentage did the blackcurrant yield in the garden increase?
|
Answer: $25 \%$.
Solution. The yield from 12 bushes increased by $15 / 12=1.25$ times, which means the yield of currants increased by $25 \%$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the degree measure of angle $\angle A$, if its bisector forms an angle with one of its sides that is three times smaller than the angle adjacent to $\angle A$?
|
Answer: $72^{\circ}$.
Solution. Let $x$ be the degree measure of the angle formed by the angle bisector of $\angle A$ with one of its sides. Then the degree measure of the angle $\angle A$ is $2 x$, and the degree measure of the adjacent angle is $3 x$. Therefore, $2 x+3 x=180$, from which $x=36$ and $\angle A=72^{\circ}$.
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In "Dragon Poker," the deck has four suits. An Ace brings 1 point, a Jack -2 points, a Two $-2^{2}$, a Three $-2^{3}, \ldots$, a Ten $-2^{10}=1024$ points. Kings and Queens are absent. You can choose any number of cards from the deck. In how many ways can you score 2018 points?
|
Answer: $C_{2021}^{3}=1373734330$.
Solution. In any suit, you can score any number of points from 0 to 2047, and this can be done in a unique way. This can be done as follows: write down this number in binary and select the cards corresponding to the binary positions containing 1 (i.e., if there is a 1 in the $k$-th position, then you should take the card that brings $2^{k}$ points).
Thus, the problem reduces to partitioning the number 2018 into 4 non-negative integer addends. Reasoning similarly to the previous problem, we get the desired number of ways: $C_{2021}^{3}=1373734330$.
|
1373734330
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Calculate: $\frac{1 \cdot 2+2 \cdot 3+3 \cdot 4+\ldots+2013 \cdot 2014}{(1+2+3+\ldots+2014) \cdot \frac{1}{5}}$. If necessary, round the answer to the nearest hundredths.
|
Answer: 6710. Solution. Let's calculate the sum in the numerator: $\sum_{k=1}^{n} k(k+1)=\sum_{k=1}^{n} k^{2}+\sum_{k=1}^{n} k$ $=\frac{n(n+1)(2 n+1)}{6}+\frac{n(n+1)}{2}=\frac{n(n+1)(n+2)}{3}$. Here, the well-known formula for the sum of squares of natural numbers is used, which can be proven in various ways (these proofs can easily be found in literature).
Thus, the fraction specified in the condition is equal to $\frac{2013 \cdot 2014 \cdot 2015 \cdot 2 \cdot 5}{3 \cdot 2014 \cdot 2015}=\frac{2013 \cdot 10}{3}=6710$.
|
6710
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the sum of all integer values of $a$ belonging to the interval $[-10 ; 10]$, for each of which the double inequality $5 \leq x \leq 10$ implies the inequality $a x+3 a^{2}-12 a+12>a^{2} \sqrt{x-1}$.
|
Answer: -47. Solution. Let $t=\sqrt{x-1}$, then the original problem reduces to finding such values of $a$ for which the inequality $f(t) \equiv a t^{2}-a^{2} t+3 a^{2}-11 a+12>0$ holds for all $t \in[2 ; 3]$. This means that the minimum of the function $f(t)$ on the interval $2 \leq t \leq 3$ is positive.
If $a=0$, then $f(t) \equiv 12$. If $a \neq 0$, then there are two cases:
a) $\left\{\begin{array}{l}f\left(\frac{a}{2}\right)=-\frac{1}{4}(a-2)(a-4)(a-6)>0, \\ 2 \leq \frac{a}{2} \leq 3\end{array} \Leftrightarrow 40, \\ f(3)=2(6-a)>0\end{array} \Leftrightarrow a<3\right.$.
In the end, $a \in(-\infty ; 3) \cup(4 ; 6)$, and the sum of the sought values of $a$ on the interval $[-10 ; 10]$ is: $-10-9-8-\ldots-1+0+1+2+5=(-10-9-\ldots-6)-4-3=-47$.
|
-47
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. (14 points) Svetlana, Katya, Olya, Masha, and Tanya attend a math club, in which more than $60 \%$ of the students are boys. What is the smallest number of schoolchildren that can be in this club?
|
Answer: 13.
Solution. Let $M$ be the number of boys, $D$ be the number of girls in the club. Then $\frac{M}{M+D}>\frac{3}{5}$, hence $M>\frac{3}{2} D \geqslant \frac{15}{2}$. The minimum possible value of $M$ is 8, and the minimum possible value of $D$ is 5, making a total of 13 children.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. (14 points) Find all integer values that the fraction $\frac{8 n+157}{4 n+7}$ can take for natural $n$. In your answer, write the sum of the found values.
|
Answer: 18.
Solution. We have $\frac{8 n+157}{4 n+7}=2+\frac{143}{4 n+7}$. Since the divisors of the number 143 are only $1, 11, 13$, and 143, integer values of the fraction are obtained only when $n=1$ and $n=34$, which are 15 and 3, respectively, and their sum is 18.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. (14 points) A guard has detained a stranger and wants to drive him away. But the person caught said that he had made a bet with his friends for 100 coins that the guard would not drive him away (if the guard does, he has to pay his friends 100 coins, otherwise they pay him), and, deciding to bribe the guard, offered him to name a sum. What is the largest number of coins the guard can ask for so that the stranger, guided solely by his own profit, would definitely pay the guard?
|
Answer: 199.
Solution. If the guard asks for 199 coins, then by agreeing to give him this amount, the outsider will win the dispute and receive 100 coins. In total, he will lose 99 coins. If the outsider refuses, he will lose the dispute and lose 100 coins, which is less favorable (by 1 coin) for the one caught. If the guard demands 200, the outsider might refuse, as there is no difference in profit. If the guard demands more, it is more profitable for the outsider to refuse. The guard can ask for less, but the problem requires finding the largest amount. Thus, the answer is 199 coins.
|
199
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. (14 points) We will call a natural number a snail if its representation consists of the representations of three consecutive natural numbers, concatenated in some order: for example, 312 or 121413. Snail numbers can sometimes be squares of natural numbers: for example, $324=18^{2}$ or $576=24^{2}$. Find a four-digit snail number that is the square of some natural number.
|
Answer: 1089.
Solution. Note that a snail number can only be a four-digit number if the three numbers from which its record is formed are $8, 9, 10$ (numbers $7, 8, 9$ and smaller still form a three-digit number, while $9, 10, 11$ and larger - already form a number of no less than five digits). It remains to figure out the order of the selected numbers. The square of a natural number cannot end in 10 (there should be an even number of zeros or none at all). Also, a square cannot end in the digit 8. Therefore, the last digit must be 9. The remaining options are 8109 and 1089. Since $8109=90^{2}+9$ and $1089=33^{2}$, the only four-digit snail number that is a square is 1089.
|
1089
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. The sequence $\left\{x_{n}\right\}$ is defined by the conditions $x_{1}=20, x_{2}=17, x_{n+1}=x_{n}-x_{n-1}(n \geqslant 2)$. Find $x_{2018}$.
|
Answer: 17.
Solution: From the condition, it follows that $x_{n+3}=x_{n+2}-x_{n+1}=x_{n+1}-x_{n}-x_{n+1}=-x_{n}$, therefore $x_{n+6}=$ $-x_{n+3}=x_{n}$, i.e., the sequence is periodic with a period of 6. Since $2018=6 \cdot 336+2$, we get $x_{2018}=x_{2}=17$.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Philatelist Andrey decided to distribute all his stamps equally into 2 envelopes, but it turned out that one stamp was left over. When he distributed them equally into 3 envelopes, one stamp was again left over; when he distributed them equally into 5 envelopes, 3 stamps were left over; finally, when he tried to distribute them equally into 9 envelopes, 7 stamps were left over. How many stamps does Andrey have in total, if recently, to accommodate them all, he had to buy a second album for 150 stamps, as one such album was no longer sufficient?
|
Answer: 223.
Solution. If the desired number is $x$, then from the first sentence it follows that $x$ is odd, and from the rest it follows that the number $x+2$ must be divisible by 3, 5, and 9, i.e., has the form $5 \cdot 9 \cdot p$. Therefore, $x=45(2 k-1)-2=90 k-47$. According to the condition $150<x \leqslant 300$, so $k=3$. Therefore, $x=223$.
|
223
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Find the sum of the digits in the decimal representation of the integer part of the number $\sqrt{\underbrace{11 \ldots 11}_{2017} \underbrace{22 \ldots .22}_{2018} 5}$.
|
Answer: 6056 (the number from the condition of the problem is $\underbrace{33 \ldots 33}_{2017} 5$).
Solution. Since
$\underbrace{11 \ldots 11}_{2017} \underbrace{22 \ldots 22}_{2018} 5=\frac{10^{2017}-1}{9} \cdot 10^{2019}+\frac{10^{2018}-1}{9} \cdot 20+5=\frac{10^{4036}+10^{2019}+25}{9}=\left(\frac{10^{2018}+5}{3}\right)^{2}$,
the number from the condition of the problem is $\frac{10^{2018}+5}{3}=\overbrace{\frac{99 \ldots 99}{2018}+6}^{3}=\underbrace{33 \ldots 33}_{2018}+2=\underbrace{33 \ldots 3}_{2017} 5$, it is an integer, and the sum of its digits is $2017 \cdot 3+5=6056$.
|
6056
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. Find the sum of the digits in the decimal representation of the integer part of the number $\sqrt{\underbrace{11 \ldots 11}_{2018} \underbrace{55 \ldots 55}_{2017} 6}$.
|
Answer: 6055 (the number from the condition of the problem is $\underbrace{33 \ldots 33}_{2017} 4$ ).
|
6055
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. Find the sum of the digits in the decimal representation of the integer part of the number $\sqrt{\underbrace{44.44}_{2017} \underbrace{22 \ldots 22}_{2018}} 5$.
|
Answer: 12107 (the number from the condition of the problem is $\underbrace{66 \ldots 66}_{2017} 5$ ).
|
12107
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Find the sum of the digits in the decimal representation of the integer part of the number $\sqrt{\underbrace{44.44}_{2018} \underbrace{88 \ldots 88}_{2017} 9}$.
|
Answer: 12109 (the number from the condition of the problem is equal to $\underbrace{66 \ldots 66}_{2017} 7$ ).
|
12109
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Find all integer solutions of the equation $x \ln 27 \log _{13} e=27 \log _{13} y$. In your answer, specify the sum $x+y$ for the solution $(x, y)$, where $y$ is the smallest, exceeding 70.
|
Answer: 117.
Solution: The original equation is equivalent to the equation $\frac{x \ln 27}{\ln 13}=\frac{27 \ln y}{\ln 13} \Leftrightarrow x \ln 27=27 \ln y \Leftrightarrow$ $\ln 27^{x}=\ln y^{27} \Leftrightarrow 27^{x}=y^{27} \Leftrightarrow 3^{x}=y^{9}$, with $y \geqslant 1$, and thus $x \geqslant 0$. Since 3 is a prime number, either $y=1$ (then $x=0$), or $y$ is divisible by 3 and has no other prime divisors. Therefore, $y=3^{n}$, where $n \geqslant 0$. Hence, $x=9n$. Since $y>70$, then $n \geqslant 4$, the solution sought is: $(x, y)=(36,81)$. The answer is $x+y=117$.
|
117
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. Find the smallest 12-digit natural number that is divisible by 36 and contains each of the 10 digits at least once.
|
Answer: 100023457896.
Solution. The number must be divisible by 4 and by 9. Since the sum of ten different digits is 45, the sum of the two remaining digits must be 0, 9, or 18. We need the smallest number, so we add two digits 0 to the digits $0,1, \ldots, 9$ and place the digits 10002345 at the beginning of the desired number (this is the smallest possible "start" of the number). The remaining digits $6,7,8,9$ must ensure divisibility by 4. Therefore, the last two digits can be 76, 96, or 68. The smallest option: 7896.
|
100023457896
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. The sine of the dihedral angle at the lateral edge of a regular quadrilateral pyramid is $\frac{15}{17}$. Find the area of the lateral surface of the pyramid if the area of its diagonal section is $3 \sqrt{34}$.
|
Answer: 68.
Solution. Let the linear angle of the dihedral angle given in the problem be denoted as $\alpha$. This angle is always obtuse, so $\cos \alpha=-\frac{8}{17}$.
The projection of the lateral face onto the diagonal section is a triangle, the area of which is half the area of this section. Since the dihedral angle between the lateral face and the diagonal section is $\frac{\alpha}{2}$, we have $S_{\text {face }} \cdot \cos \frac{\alpha}{2}=\frac{1}{2} S_{\text {section }}$. Therefore, $S_{\text {lateral }}=4 \cdot \frac{S_{\text {section }}}{2 \cos \frac{\alpha}{2}}=\frac{2 \sqrt{2} S_{\text {section }}}{\sqrt{1+\cos \alpha}}=68$.
|
68
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. A batch of tablets from four different brands was delivered to a computer store. Among them, Lenovo, Samsung, and Huawei tablets made up less than a third, with Samsung tablets being 6 more than Lenovo. All other tablets were Apple iPads, and there were three times as many of them as Huawei. If the number of Lenovo tablets were tripled, and the number of Samsung and Huawei tablets remained the same (with the total number of all tablets unchanged), then there would be 59 Apple iPads. How many tablets were delivered to the store in total?
|
Answer: 94.
Solution. Let $n$ be the total number of tablets we are looking for, with $x$ being the number of Lenovo brand tablets, and $y$ being the number of Huawei brand tablets. Then the number of Samsung tablets is $x+6$, and the number of Apple iPad tablets is $n-2x-y-6=3y$. From the problem statement, we also have the equation $4x+y+6=n-59$. From these two equations, we find $x=\frac{3n-254}{14}$ and $y=\frac{n+53}{7}$. Since $x \geqslant 1$, we get $3n-254 \geqslant 14$, which leads to $n \geqslant \frac{268}{3}=89 \frac{1}{3}$. On the other hand, from the problem statement, we also have the inequality $2x+y+6<\frac{n}{3}$, which gives $\frac{33-254}{7}+\frac{n+53}{7}+6<\frac{n}{3}$, or $n<\frac{477}{5}=95 \frac{2}{5}$. Additionally, since $n+53$ is divisible by 7, the number $n$ gives a remainder of 3 when divided by 7. Among the integers from 90 to 95, there is only one such number, namely $n=94$.
|
94
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Solve the equation $x^{x+y}=y^{y-x}$ in natural numbers. In your answer, specify the sum $x+y$ for the solution $(x, y)$, where $y$ is the smallest, exceeding 1500.
|
Answer: 2744.
Solution. Let $y = t x$, where $t \in \mathbb{Q}$ for $x, y \in \mathbb{N}$. Then, substituting this into the equation, we find
$$
x = t^{\frac{t-1}{2}}, \quad y = t^{\frac{t+1}{2}}
$$
We will show that the number $t$ can only be an integer. Suppose the contrary: let $t$ be a rational number different from an integer, i.e., $t = \frac{p}{q}$, where the numbers $p$ and $q$ are coprime, $q \neq 1$. Then $y = \frac{p x}{q}$, and the equation becomes
$$
x^{x + \frac{p x}{q}} = \left(\frac{p x}{q}\right)^{\frac{p x}{q} - x} \Leftrightarrow x^{x q + p x} = \left(\frac{p x}{q}\right)^{p x - q x} \Leftrightarrow x^{x q} = p^{p x - x q} \cdot x^{-q x} \cdot q^{x(q - p)} \Leftrightarrow x^{2 q x} = \left(\frac{p}{q}\right)^{x(p - q)}
$$
In the last equation, the left side is always an integer, while the right side is not an integer. Contradiction.
Thus, $t \in \mathbb{N}$, so the numbers $x$ and $y$ will be natural only in the following two cases:
1) the number $t$ is odd: $t = 2k - 1$, then $x = (2k - 1)^{k - 1}, y = (2k - 1)^{k}, k \in \mathbb{N}$;
2) the number $t$ is a perfect square: $t = k^2$, then $x = k^{k^2 - 1}, y = k^{k^2 + 1}, k \in \mathbb{N}$.
We will summarize the obtained solutions in a table:
| $t$ | 1 | 3 | 4 | 5 | 7 | 9 | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $x$ | 1 | 3 | 8 | 25 | 343 | 6561 | $\ldots$ |
| $y$ | 1 | 9 | 32 | 125 | 2401 | 59049 | $\ldots$ |
The solution $(x, y)$, in which $y$ is the smallest, exceeding 1500, is $x = 343, y = 2401$, in which case $x + y = 2744$.
|
2744
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1.
In-1 Find $f(1)+f(2)+f(3)+\ldots+f(13)$, if $f(n)=4 n^{3}-6 n^{2}+4 n+13$.
|
Answer: 28743.
Solution. Since $f(n)=n^{4}-(n-1)^{4}+14$, then
$f(1)+f(2)+f(3)+\ldots+f(13)=1^{4}+2^{4}+\ldots+13^{4}-\left(0^{4}+1^{4}+\ldots+12^{4}\right)+14 \cdot 13=13^{4}+14 \cdot 13=28743$.
V-2 Find $f(1)+f(2)+f(3)+\ldots+f(11)$, if $f(n)=4 n^{3}+6 n^{2}+4 n+9$.
Answer: 20823.
V-3 Find $f(1)+f(2)+f(3)+\ldots+f(12)$, if $f(n)=4 n^{3}-6 n^{2}+4 n+7$.
Answer: 20832.
V-4 Find $f(1)+f(2)+f(3)+\ldots+f(14)$, if $f(n)=4 n^{3}+6 n^{2}+4 n+5$.
Answer: 50680.
V-5 Let $f(x)=x^{2}+10 x+20$. Solve the equation
$$
f(f(f(f(f(x)))))=0
$$
Answer: $-5 \pm \sqrt[32]{5}$.
Solution. Note that $f(x)=(x+5)^{2}-5$. Therefore, $f(f(x))=(x+5)^{4}-5, f(f(f(x)))=(x+5)^{8}-5, \ldots, f(f(f(f(f(x)))))=(x+5)^{32}-5=0$, from which $x=-5 \pm \sqrt[32]{5}$.
V-6 Let $f(x)=x^{2}+6 x+6$. Solve the equation
$$
f(f(f(f(f(x)))))=0
$$
Answer: $-3 \pm \sqrt[32]{3}$.
V-7 Let $f(x)=x^{2}+14 x+42$. Solve the equation
$$
f(f(f(f(x))))=0
$$
Answer: $-7 \pm \sqrt[16]{7}$.
V-8 Let $f(x)=x^{2}+18 x+72$. Solve the equation
$$
f(f(f(f(x))))=0
$$
Answer: $-9 \pm \sqrt[16]{9}=-9 \pm \sqrt[8]{3}$.
## Lomonosov Olympiad for Schoolchildren in Mathematics
Final Stage 2020/21 Academic Year for 10-11 Grades
#
|
28743
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
In-1 The numbers $a, b, c$ are such that each of the two equations $x^{2}+b x+a=0$ and $x^{2}+c x+a=1$ has two integer roots, and all these roots are less than (-1). Find the smallest value of $a$.
|
Answer: 15.
Solution. By Vieta's theorem, the product of the roots of the first equation is $a$, and the product of the roots of the second equation is $a-1$. Since the roots are integers and less than -1, their product is greater than 1, so each of the two consecutive numbers $a-1$ and $a$ is the product of two different integers greater than 1. Since the first odd number that is neither prime nor the square of a prime is 15, we get $a-1=14, a=15$. Then the roots of the first equation are -3 and -5 (in which case $b=8$), and the roots of the second equation are -2 and -7 (in which case $c=9$).
V-2 The numbers $a, b, c$ are such that each of the two equations $x^{2}+b x+a=0$ and $x^{2}+c x+a=-1$ has two integer roots, and all these roots are greater than 1. Find the smallest value of $a$.
Answer: 14.
V-3 The numbers $a, b, c$ are such that each of the two equations $x^{2}+b x+a=1$ and $x^{2}+c x+a=0$ has two integer roots, and all these roots are less than -1. Find the smallest value of $a$.
Answer: 15.
V-4 The numbers $a, b, c$ are such that each of the two equations $x^{2}+b x+a=-1$ and $x^{2}+c x+a=0$ has two integer roots, and all these roots are greater than 1. Find the smallest value of $a$.
Answer: 14.
V-5 How many different polynomials of the form $P(x)=x^{5}+A x^{4}+B x^{3}+C x^{2}+D x+E$, where $A, B, C, D, E$ are positive integers, exist for which $P(-1)=11, P(1)=21$?
Answer: 315.
Solution. Since $P(-1)=11$, we have $-1+A-B+C-D+E=11$; since $P(1)=21$, we have $1+A+B+C+D+E=21$. Therefore, $A+C+E=16, B+D=4$. The second of these two equations has 3 pairs of solutions in natural numbers, and the first equation has $C_{15}^{2}=\frac{15 \cdot 14}{2}=105$ solutions (arrange 16 "balls" in a row and divide them into three groups using two "partitions"). This corresponds to $3 \cdot 105=315$ different polynomials.
V-6 How many different polynomials of the form $P(x)=x^{5}+A x^{4}+B x^{3}+C x^{2}+D x+E$, where $A, B, C, D, E$ are positive integers, exist for which $P(-1)=8, P(1)=22$?
Answer: 455.
V-7 How many different polynomials of the form $P(x)=x^{5}+A x^{4}+B x^{3}+C x^{2}+D x+E$, where $A, B, C, D, E$ are positive integers, exist for which $P(-1)=9, P(1)=21$?
Answer: 364.
V-8 How many different polynomials of the form $P(x)=x^{5}+A x^{4}+B x^{3}+C x^{2}+D x+E$, where $A, B, C, D, E$ are positive integers, exist for which $P(-1)=10, P(1)=22$?
Answer: 420.
## Lomonosov Olympiad for Schoolchildren in Mathematics
Final Stage 2020/21 Academic Year for 10-11 Grades
#
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At Andrei's birthday, Yana was the last to arrive, giving him a ball, and Eduard was the second to last, giving him a calculator. Testing the calculator, Andrei noticed that the product of the total number of his gifts and the number of gifts he had before Eduard arrived is exactly 16 more than the product of his age and the number of gifts he had before Yana arrived. How many gifts does Andrei have?
|
Answer: 18. Solution. If $n$ is the number of gifts, and $a$ is Andrei's age, then $n(n-2)=a(n-1)$. From this, $a=\frac{n^{2}-2 n-16}{n-1}=n-1-\frac{17}{n-1}$. Therefore, $n-1=17, a=16$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In an equilateral triangle $ABC$, points $A_{1}$ and $A_{2}$ are chosen on side $BC$ such that $B A_{1}=A_{1} A_{2}=A_{2} C$. On side $AC$, a point $B_{1}$ is chosen such that $A B_{1}: B_{1}C=1: 2$. Find the sum of the angles $\angle A A_{1} B_{1}+\angle A A_{2} B_{1}$.
|
Answer: $30^{\circ}$. Solution. Since $A_{1} B_{1} \| A B$, then $\angle B A A_{1}=\angle A A_{1} B_{1}$. From symmetry, $\angle B A A_{1}=\angle C A A_{2}$. It remains to note that $\angle C B_{1} A_{2}=$ $\angle B_{1} A A_{2}+\angle A A_{2} B_{1}$ as an exterior angle in $\triangle A A_{2} B_{1}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. All natural numbers are divided into "good" and "bad" according to the following rules:
a) From any bad number, you can subtract some natural number not exceeding its half so that the resulting difference becomes "good".
b) From a "good" number, you cannot subtract no more than half of it so that it remains "good".
It is known that the number 1 is "good". Find the nearest "good" number to 2015.
|
Answer: 2047. Solution. Note that good numbers have the form $2^{n}-1$. Indeed, let a number have the form $M=2^{n}+k$, where $k=0,1, \ldots, 2^{n}-2$. Then from such a number, you can subtract $k+1 \leqslant \frac{1}{2}\left(2^{n}+k\right)=\frac{M}{2}$. On the other hand, from a number of the form $N=2^{n}-1$, you need to subtract at least $2^{n-1}$, which exceeds $\frac{N}{2}=2^{n-1}-\frac{1}{2}$. Therefore, the closest to 2015 will be the number $2047=2^{11}-1$
|
2047
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Calculate
$$
\frac{2 a b\left(a^{3}-b^{3}\right)}{a^{2}+a b+b^{2}}-\frac{(a-b)\left(a^{4}-b^{4}\right)}{a^{2}-b^{2}} \quad \text { for } \quad a=-1, \underbrace{5 \ldots 5}_{2010} 6, \quad b=5, \underbrace{4 \ldots 44}_{2011}
$$
Answer: 343.
|
Solution. Given $a$ and $b$, we get
$$
\begin{gathered}
\frac{2 a b\left(a^{3}-b^{3}\right)}{a^{2}+a b+b^{2}}-\frac{(a-b)\left(a^{4}-b^{4}\right)}{a^{2}-b^{2}}=2 a b(a-b)-(a-b)\left(a^{2}+b^{2}\right)= \\
\quad=-(a-b)\left(a^{2}-2 a b+b^{2}\right)=-(a-b)^{3}=-(-7)^{3}=343
\end{gathered}
$$
|
343
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the smallest natural number that is greater than the sum of its digits by 1755 (the year of the founding of Moscow University).
|
Answer: 1770.
Solution. From the condition, it follows that the desired number cannot consist of three or fewer digits. We will look for the smallest such number in the form $\overline{a b c d}$, where $a, b, c, d$ are digits, and $a \neq 0$. We will form the equation:
$$
\begin{gathered}
\overline{a b c d}=a+b+c+d+1755 \Leftrightarrow 1000 a+100 b+10 c+d=a+b+c+d+1755 \Leftrightarrow \\
\Leftrightarrow 999 a+99 b+9 c=1755 \Leftrightarrow 111 a+11 b+c=195
\end{gathered}
$$
From the last equation, we conclude that the only possible value for the digit $a$ is 1. Next, we get the equation $11 b+c=84$, which means the digit $b$ can only be 7. Finally, we need to find the value of $c=84-11 \cdot 7=7$. Therefore, the desired number is 1770, as it is the smallest among all numbers of the form $\overline{177 d}$.
|
1770
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.
Let $A(n)$ denote the greatest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9, A(64)=1$. Find the sum $A(111)+A(112)+\ldots+A(218)+A(219)$.
|
Answer: 12045
Solution. The largest odd divisors of any two of the given numbers cannot coincide, as numbers with the same largest odd divisors are either equal or differ by at least a factor of 2. Therefore, the largest odd divisors of the numbers $111, 112, \ldots, 218, 219$ are distinct. This means that the largest odd divisors of the numbers from $n+1$ to $2n$ are $n$ different odd numbers that do not exceed $2n$. Thus, these numbers are $1, 3, 5, \ldots, 2n-1$. If we add the number 220 to the set of numbers, the desired sum will be $1+3+5+\ldots+219-A(220)=\frac{1+219}{2} \cdot 110-55=110^2-55=12045$.
## B-2
Let $A(n)$ denote the largest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9$, $A(64)=1$. Find the sum $A(113)+A(114)+\ldots+A(222)+A(223)$.
Answer: 12537
## B-3
Let $A(n)$ denote the largest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9$, $A(64)=1$. Find the sum $A(115)+A(116)+\ldots+A(226)+A(227)$.
Answer: 12939
## B-4
Let $A(n)$ denote the largest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9$, $A(64)=1$. Find the sum $A(117)+A(118)+\ldots+A(230)+A(231)$.
Answer: 13427
|
12045
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Two circles touch each other internally at point K. A chord $AB$ of the larger circle touches the smaller circle at point $L$, and $AL=10$. Find $BL$, if $AK: BK=2: 5$.
|
Answer: $B L=25$.
Solution. Draw the chord $P Q$ and the common tangent $M N$ (see fig.), then
$$
\angle P Q K=\frac{1}{2} \smile P K=\angle P K M=\frac{1}{2} \smile A K=\angle A B K
$$
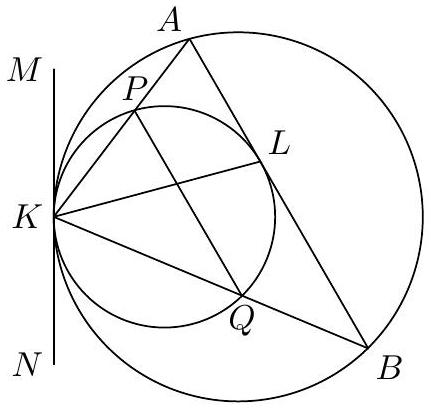
therefore $P Q \| A B$ and $\smile P L=\smile Q L$. Consequently, $\angle P K L=\angle Q K L$, i.e., $K L$ is the bisector of triangle $A K B$, from which we obtain
$$
\frac{A L}{B L}=\frac{A K}{B K}=\frac{2}{5} \Longrightarrow B L=10 \cdot \frac{5}{2}=25
$$
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. What is the smallest (same) number of pencils that need to be placed in each of 6 boxes so that in any 4 boxes there are pencils of any of 26 predefined colors (there are enough pencils available)?
|
Answer: 13.
Solution. On the one hand, pencils of each color should appear in at least three out of six boxes, since if pencils of a certain color are in no more than two boxes, then in the remaining boxes, which are at least four, there are no pencils of this color. Therefore, the total number of pencils should be no less than $3 \cdot 26$.
On the other hand, if we take 3 pencils of each of the 26 colors and arrange them so that no pencils of the same color are in the same box, then a pencil of any color will be found in any four boxes (since there are only two other boxes). The required arrangement of pencils can be achieved, for example, by dividing all the pencils into 3 groups of 26 pencils of all colors and distributing each group evenly (13 pencils) into two boxes.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
Masha tightly packed 165 identical balls into the shape of a regular triangular pyramid. How many balls are at the base?
|
Answer: 45
Solution. We will solve the problem in general for $\frac{1}{6} n(n+1)(n+2)$ balls. At the base of a triangular pyramid of height $n$ rows lies the $n$-th triangular number of balls $1+2+3+\ldots+n=\frac{1}{2} n(n+1)$. Then the total number of balls in the pyramid is $\sum_{k=1}^{n} \frac{k(k+1)}{2}=\frac{1}{6} n(n+1)(n+2)$. The problem can be solved by enumeration.
## B-2
Masha tightly packed 220 identical balls into a regular triangular pyramid. How many balls are at the base?
Answer: 55
## B-3
Masha tightly packed 286 identical balls into a regular triangular pyramid. How many balls are at the base?
Answer: 66
## B-4
Masha tightly packed 364 identical balls into a regular triangular pyramid. How many balls are at the base?
Answer: 78
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary Stage 2020/21 academic year for 9th grade
#
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6.
B-1
Find the minimum value of the expression $4 x+9 y+\frac{1}{x-4}+\frac{1}{y-5}$ given that $x>4$ and $y>5$.
|
Answer: 71
Solution. $4 x+9 y+\frac{1}{x-4}+\frac{1}{y-5}=4 x-16+\frac{4}{4 x-16}+9 y-45+\frac{9}{9 y-45}+61 \geq 2 \sqrt{4}+2 \sqrt{9}+61=$ 71 (inequality of means). Equality is achieved when $4 x-16=2,9 y-45=3$, that is, when $x=\frac{9}{2}, y=\frac{16}{3}$.
B-2
Find the minimum value of the expression $9 x+4 y+\frac{1}{x-3}+\frac{1}{y-4}$ given that $x>3$ and $y>4$.
Answer: 53
## B-3
Find the minimum value of the expression $4 x+9 y+\frac{1}{x-1}+\frac{1}{y-2}$ given that $x>1$ and $y>2$.
Answer: 32
## B-4
Find the minimum value of the expression $9 x+4 y+\frac{1}{x-5}+\frac{1}{y-6}$ given that $x>5$ and $y>6$.
Answer: 79
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary Stage 2020/21 Academic Year for 9th Grade
## B-1
#
|
71
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of the digits of the number $A$, if $A=2^{63} \cdot 4^{25} \cdot 5^{106}-2^{22} \cdot 4^{44} \cdot 5^{105}-1$. Answer: 959.
|
Solution. Since $2^{63} \cdot 4^{25} \cdot 5^{106}=2^{113} \cdot 5^{106}=2^{7} \cdot 10^{106}$ and $2^{22} \cdot 4^{44} \cdot 5^{105}=$ $2^{110} \cdot 5^{105}=2^{5} \cdot 10^{105}$, then $A+1=2^{7} \cdot 10^{106}-2^{5} \cdot 10^{105}=\left(2^{7} \cdot 10-2^{5}\right) \cdot 10^{105}=$ $1248 \cdot 10^{105}$. Therefore, the number $A$ is $1248 \cdot 10^{105}-1=1247 \underbrace{999 \ldots 999}_{105 \text { digits }}$, and the sum of its digits is $1+2+4+7+9 \cdot 105=959$.
|
959
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Each Kinder Surprise contains exactly 3 different gnomes, and there are 12 different types of gnomes in total. In the box, there are enough Kinder Surprises, and in any two of them, the triplets of gnomes are not the same. What is the minimum number of Kinder Surprises that need to be bought to ensure that after they are opened, there is at least one gnome of each of the 12 types?
|
Answer: 166.
Solution. From 11 different gnomes, a maximum of $C_{11}^{3}=\frac{11 \cdot 10 \cdot 9}{3 \cdot 2 \cdot 1}=165$ different Kinder can be formed, so if you take one more Kinder, there cannot be fewer than 12 different gnomes among them.
|
166
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that $m, n, k$ are distinct natural numbers greater than 1, the number $\log _{m} n$ is rational, and, moreover,
$$
k^{\sqrt{\log _{m} n}}=m^{\sqrt{\log _{n} k}}
$$
Find the minimum of the possible values of the sum $k+5 m+n$.
|
Answer: 278.
Solution. Transform the original equation, taking into account that the numbers $m, n, k$ are greater than 1 and the corresponding logarithms are positive:
$$
\begin{aligned}
& k \sqrt{\log _{m} n}=m \sqrt{\log _{n} k} \Leftrightarrow \log _{m} k \cdot \sqrt{\log _{m} n}=\sqrt{\log _{n} k} \Leftrightarrow \\
& \Leftrightarrow \log _{m} k \cdot \sqrt{\log _{m} n}=\sqrt{\frac{\log _{m} k}{\log _{m} n}} \Leftrightarrow \\
& \Leftrightarrow \sqrt{\log _{m} k} \cdot \log _{m} n=1 \Leftrightarrow \log _{m} k \cdot \log _{m}^{2} n=1
\end{aligned}
$$
By performing the substitution $k=n^{p}, m=n^{q}$, where $p \neq 0, q \neq 0$, we get
$$
\frac{p}{q} \cdot \frac{1}{q^{2}}=1 \Leftrightarrow p=q^{3}
$$
Thus, all triples $(k, m, n)$ that satisfy the condition of the problem have the form $\left(n^{q^{3}}, n^{q}, n\right)$.
It is clear that $q>0$ : otherwise, from the naturality of the number $n$ it follows that the number $n^{q}$ lies in the interval $(0 ; 1)$ and is not a natural number. The case $q=1$ contradicts the condition of the problem. If $q \in(0 ; 1)$, then $q=1 / r$, where $r>1$, and then the triple of natural numbers $\left(n^{q^{3}}, n^{q}, n\right)$ can be written in the form $\left(l, l^{r^{2}}, l^{r^{3}}\right)$ with a natural $l$. The sum $k+5 m+n$ for this triple will be greater than the same sum for the numbers in the triple $\left(l^{r^{3}}, l^{r}, l\right)$. Therefore, $q>1$.
For integer $q$, the triple of numbers with the minimum sum $k+5 m+n$ is obtained when $n=2, q=2$ : these are the numbers $k=2^{8}, m=2^{2}, n=2$, and for them the sum $k+5 m+n$ is 278. If $q$ is rational but not an integer, then for the number $n^{q^{3}}$ to be an integer, it is necessary that $n$ be at least the eighth power of an integer not less than 2, and, of course, the sum $n^{q^{3}}+5 n^{q}+n$ will be greater than 278 (since $n \geqslant 256$).
|
278
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. To guard the object, the client agreed with the guards on the following: all of them will indicate the time intervals of their proposed shifts with the only condition that their union should form a predetermined time interval set by the client, and he will choose any set of these intervals that also satisfies the same condition, and pay for the work at a rate of 300 rubles per hour for each guard. What is the longest time interval the client can set to ensure that he definitely stays within 90000 rubles?
|
6. $\frac{90000}{2 \cdot 300}=150 \text{h}$.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Find the sum of all integer values of $a$ from the interval $[-2012 ; 2013]$, for which the equation $(a-3) x^{2}+2(3-a) x+\frac{a-7}{a+2}=0$ has at least one solution.
|
Answer: 2011. Solution. When $a=3$ there are no solutions. For other $a$, it should be $\frac{D}{4}=(a-3)^{2}-\frac{(a-3)(a-7)}{a+2} \geq 0$. The last inequality (plus the condition $a \neq 3$) has the solution $a \in(-\infty ;-2) \bigcup\{1\} \cup(3 ;+\infty)$. The desired sum is: $-2012-2011-\ldots-5-4-3+1+4+5+\ldots 2013=-3+1+2013=2011$.
|
2011
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Among the numbers exceeding 2013, find the smallest even number $N$ for which the fraction $\frac{15 N-7}{22 N-5}$ is reducible.
|
Answer: 2144. Solution: The presence of a common factor in the numbers $15 N-7$ and $22 N-5$ implies that the same factor is present in the number $(22 N-5)-(15 N-7)=7 N+2$, and subsequently in the numbers $(15 N-7)-2 \cdot(7 N+2)=N-11,(7 N+2)-7 \cdot(N-11)=79$. Since 79 is a prime number, the fraction is reducible by 79, so $N-11=79 m, N=11+79 m$. Given that $N$ is even, we have $N=90+158 p$. The required value is achieved at $p=13$.
|
2144
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Find the area of the figure defined on the coordinate plane by the inequality $\sqrt{\arcsin \frac{x}{3}} \leq \sqrt{\arccos \frac{y}{3}} \cdot$ In your answer, specify the integer closest to the found value of the area.
|
Answer: 16. Solution. The domain of admissible values of the inequality is determined by the system $\left\{\begin{array}{l}\arcsin \frac{x}{3} \geq 0, \\ \arccos \frac{y}{3} \geq 0\end{array} \Leftrightarrow\left\{\begin{array}{c}0 \leq x \leq 3, \\ -3 \leq y \leq 3 .\end{array}\right.\right.$ If $-3 \leq y \leq 0$, then $\arccos \frac{y}{3} \geq \frac{\pi}{2} \geq \arcsin \frac{x}{3}$. Therefore, the entire square $\{0 \leq x \leq 3,-3 \leq y \leq 0\}$ with an area of 9 is included in the desired set.
On the remaining set $\{0 \leq x \leq 3,0 \leq y \leq 3\}$, the inequalities $0 \leq \arcsin \frac{x}{3} \leq \frac{\pi}{2}, 0 \leq \arccos \frac{y}{3} \leq \frac{\pi}{2}$ hold, and since the function $\sin t$ is increasing for $t \in\left[0 ; \frac{\pi}{2}\right]$, we obtain equivalent inequalities $\sin \left(\arcsin \frac{x}{3}\right) \leq \sin \left(\arccos \frac{y}{3}\right) \Leftrightarrow \frac{x}{3} \leq \sqrt{1-\left(\frac{y}{3}\right)^{2}} \Leftrightarrow x^{2}+y^{2} \leq 9$. Therefore, here the desired set includes a quarter circle, the area of which is $\frac{\pi \cdot 3^{2}}{4}$.
In total, the desired area is $9\left(1+\frac{\pi}{4}\right) \approx 16.069 \ldots$
|
16
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Given two different geometric progressions, the first terms of which are equal to 1, and the sum of the denominators is 3. Find the sum of the fifth terms of these progressions, if the sum of the sixth terms is 573. If the answer to the question is not unique, specify the sum of all possible values of the desired quantity.
|
Answer: 161. Solution. Let the denominators of the progressions be $p$ and $q$. According to the condition, we get: $\left\{\begin{array}{c}p+q=3, \\ p^{5}+q^{5}=573\end{array}\right.$. We need to find $p^{4}+q^{4}$. Denoting $p+q=a, p q=b$, we express:
$$
\begin{gathered}
p^{4}+q^{4}=\left((p+q)^{2}-2 p q\right)^{2}-2 p^{2} q^{2}=\left(a^{2}-2 b\right)^{2}-2 b^{2}=a^{4}-4 a^{2} b+2 b^{2} ; \\
p^{5}+q^{5}=(p+q)\left(p^{4}-p^{3} q+p^{2} q^{2}-p q^{3}+q^{4}\right)=(p+q)\left(p^{4}+q^{4}-p q\left(p^{2}+q^{2}\right)+p^{2} q^{2}\right) \\
=a\left(a^{4}-4 a^{2} b+2 b^{2}-b\left(a^{2}-2 b\right)+b^{2}\right)=a\left(a^{4}-5 a^{2} b+5 b^{2}\right) .
\end{gathered}
$$
$$
\text { According to the condition }\left\{\begin{array} { c }
{ a = 3 , } \\
{ a ( a ^ { 4 } - 5 a ^ { 2 } b + 5 b ^ { 2 } ) = 5 7 3 }
\end{array} \Leftrightarrow \left\{\begin{array} { c }
{ a = 3 , } \\
{ 8 1 - 4 5 b + 5 b ^ { 2 } = 1 9 1 }
\end{array} \Leftrightarrow \left\{\begin{array}{c}
a=3, \\
b^{2}-9 b-22=0
\end{array} .\right.\right.\right.
$$
From here, $b=11$ or $b=-2$. Since the system $\left\{\begin{array}{c}p+q=3, \\ p q=11\end{array}\right.$ has no solutions, then $b=-2$.
Therefore, $a=3$ and $b=-2$. Thus, $p^{4}+q^{4}=a^{4}-4 a^{2} b+2 b^{2}=81+72+8=161$.
|
161
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Chords $A A^{\prime}, B B^{\prime}$, and $C C^{\prime}$ of a sphere intersect at a common point $S$. Find the sum $S A^{\prime}+S B^{\prime}+S C^{\prime}$, if $A S=6, B S=3, C S=2$, and the volumes of pyramids $S A B C$ and $S A^{\prime} B^{\prime} C^{\prime}$ are in the ratio $2: 9$. If the answer is not an integer, round it to the hundredths.
|
Answer: 18. Solution. If $a, b, c$ are the given edges, $x, y, z$ are the corresponding extensions of these edges, and $k$ is the given ratio, then by the theorem of intersecting chords and the lemma on the ratio of volumes of pyramids with equal (vertical) trihedral angles at the vertex, we have: $\left\{\begin{array}{l}a x=b y=c z \\ a b c: x y z=k\end{array} \Rightarrow \sqrt[3]{a b c x y z}=\sqrt[3]{\frac{(a b c)^{2}}{k}} \Rightarrow x=\sqrt[3]{\frac{b^{2} c^{2}}{a k}}\right.$, from which we get $p=x+y+z=x\left(1+\frac{a}{b}+\frac{a}{c}\right)=\sqrt[3]{\frac{b^{2} c^{2}}{a k}}\left(1+\frac{a}{b}+\frac{a}{c}\right)$.
Here $a=6, b=3, c=2, k=\frac{2}{9} \Rightarrow p=\sqrt[3]{\frac{3^{2} \cdot 2^{2} \cdot 9}{6 \cdot 2}}\left(1+\frac{6}{3}+\frac{6}{2}\right)=18$.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the sum of all such integers $a \in[0 ; 400]$, for each of which the equation $x^{4}-6 x^{2}+4=\sin \frac{\pi a}{200}-2\left[x^{2}\right]$ has exactly six roots. Here the standard notation is used: $[t]$ - the integer part of the number $t$ (the greatest integer not exceeding $t$).
|
Answer: 60100. Solution. Let $b=\sin \frac{\pi a}{200}, t=x^{2}$. Using the equality $[t]=t-\{t\}$ (here $\{t\}$ is the fractional part of $t$), we get that the original equation is equivalent to the equation $t^{2}-6 t+4=b-2 t+2\{t\}$. Note that any positive $t$ corresponds to two different $x$, two different positive $t$ correspond to four different $x$, three different positive $t$ correspond to six different $x$, and so on.
Solve the equation:
$$
t^{2}-4 t+4=b+2\{t\}, b \in[-1 ; 1]
$$
Since the right-hand side of the equation belongs to the interval $[-1 ; 3)$, the left-hand side does not exceed this interval when $(t-2)^{2}<3$, i.e., when $t \in(2-\sqrt{3} ; 2+\sqrt{3})$.
Consider four cases:
1) Let $t \in(2-\sqrt{3} ; 1)$. Then $\{t\}=t$, and the original equation takes the form: $t^{2}-6 t+4=b$, from which $t_{1}^{ \pm}=3 \pm \sqrt{5+\sin b}$. Of these roots, only $t_{1}^{-}$ belongs to the interval $(2-\sqrt{3} ; 1)$ for $b \in(-1 ; 1]$.
2) Let $t \in[1 ; 2)$. Then $\{t\}=t-1$, and the original equation takes the form: $t^{2}-6 t+6=b$, from which $t_{2}^{ \pm}=3 \pm \sqrt{3+\sin b}$. Of these roots, only $t_{2}^{-}$ belongs to the interval $[1 ; 2)$ for any $b \in[-1 ; 1]$.
3) Let $t \in[2 ; 3)$. Then $\{t\}=t-2$, and the original equation takes the form: $t^{2}-6 t+8=b$, from which $t_{3}^{ \pm}=3 \pm \sqrt{1+\sin b}$. Of these roots, only $t_{3}^{-}$ belongs to the interval $[2 ; 3)$ for $b \in[-1 ; 0]$.
4) Let $t \in[3 ; 2+\sqrt{3})$. Then $\{t\}=t-3$, and the original equation takes the form: $t^{2}-6 t+10=b$, from which $(t-3)^{2}+(1-b)=0$. This equation has a unique solution $t_{4}=3$ for $b=1$ (recall that $b \in[-1 ; 1]$).
In the end, we get:
for $b=-1$ the equation (1) has one positive solution for $t$, namely $t_{2}^{-}$, from which the original equation has two different solutions for the variable $x$;
for $b \in(0 ; 1)$ the equation (1) has two different positive solutions for the variable $t$, namely $t_{1}^{-}, t_{2}^{-}$, from which the original equation has four different solutions for the variable $x$;
for $b \in(-1 ; 0] \cup\{1\}$ the equation (1) has three different positive solutions for the variable $t$, namely $t_{1}^{-}, t_{2}^{-}, t_{3}^{-}$ for $b \in(-1 ; 0]$ and $t_{1}^{-}, t_{2}^{-}, t_{4}$ for $b=1$, from which the original equation has six different solutions for the variable $x$.
Since $b=\sin \frac{\pi a}{200}$, then for $a \in[0 ; 400]$ we get that for $a \in\{0\} \bigcup\{100\} \bigcup[200 ; 300) \bigcup(300 ; 400]$ the original equation will have six solutions.
We get the answer: $0+100+(200+201+\ldots+400)-300=\frac{200+400}{2} \cdot 201-200=60100$.
|
60100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a box, there are a hundred colorful balls: 28 red, 20 green, 13 yellow, 19 blue, 11 white, and 9 black. What is the smallest number of balls that need to be pulled out without looking into the box to ensure that there are at least 15 balls of the same color among them?
|
Answer: 76. Solution. Worst-case scenario: 14 red, 14 green, 13 yellow, 14 blue, 11 white, and 9 black balls will be drawn - a total of 75 balls. The next ball will definitely be the 15th ball of one of the colors: either red, green, or blue.
Answer of variant 152: 109.
Answer of variant 153: 83.
Answer of variant 154: 98.
|
76
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Find the largest four-digit number in which all digits are different, and moreover, no two of them can be swapped to form a smaller number.
|
Answer: 7089.
Solution. If the digit 0 is not used, then the digits in each such number must be in ascending order, and the largest of such numbers is 6789. Since a number cannot start with zero, using 0, one can obtain additional suitable numbers where 0 is in the hundreds place, and the other digits are in ascending order. The largest of such numbers is 7089.
|
7089
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. On the board, all such natural numbers from 3 to 223 inclusive are written, which when divided by 4 leave a remainder of 3. Every minute, Borya erases any two of the written numbers and instead writes their sum, decreased by 2. In the end, only one number remains on the board. What can it be?
|
Answer: 6218.
Solution. Initially, the total number of written numbers is $224: 4=56$, and their sum is $(3+223) \cdot 56: 2=6328$. Every minute, the number of written numbers decreases by 1, and their sum decreases by 2. Therefore, one number will remain on the board after 55 minutes and will be equal to $6328-55 \cdot 2=6218$.
|
6218
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Masha has seven different dolls, which she arranges in six different doll houses so that each house has at least one doll. In how many ways can Masha do this? It is important which doll ends up in which house. It does not matter how the dolls are seated in the house where there are two of them.
|
Answer: 15120.
Solution. In each such seating arrangement, in one of the cabins there will be two dolls, and in the other cabins - one each. First, we choose which two dolls will sit in one cabin. This can be done in $7 \cdot 6: 2=21$ ways. Then we choose which cabin to seat these two dolls in. This can be done in 6 ways. Finally, we choose how to seat the remaining 5 dolls in the remaining 5 cabins. This can be done in $5!=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120$ ways. Therefore, the number of seating arrangements is $21 \cdot 6 \cdot 120=15120$.
|
15120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. It is known that $x+y+z=2016$ and $\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{1}{32}$. Find $\frac{z}{x+y}+\frac{x}{y+z}+\frac{y}{z+x}$
ANSWER: 60.
|
Solution: Add 1 to each fraction, we get $\frac{z}{x+y}+1+\frac{x}{y+z}+1+\frac{y}{z+x}+1=\frac{x+y+z}{x+y}+$ $\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}=2016 \cdot\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)=\frac{2016}{32}=63$.
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There are 5 identical buckets, each with a maximum capacity of some integer number of liters, and a 30-liter barrel containing an integer number of liters of water. The water from the barrel was distributed among the buckets, with the first bucket being half full, the second one-third full, the third one-quarter full, the fourth one-fifth full, and the fifth one-sixth full. How many liters of water were in the barrel?
ANSWER: 29.
|
The solution $-\frac{x}{2}+\frac{x}{3}+\frac{x}{4}+\frac{x}{5}+\frac{x}{6}=\frac{87 x}{60}=\frac{29 x}{20}$ will be an integer only when $x$ is a multiple of 20. But $x>20$ cannot be taken, as the sum will exceed 30 liters.
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two oligarchs, Alejandro and Maximilian, looted their country in 2012. It is known that Alejandro's wealth at the end of 2012 equals twice Maximilian's wealth at the end of 2011. And Maximilian's wealth at the end of 2012 is less than Alejandro's wealth at the end of 2011. Which is greater: Maximilian's wealth or the national wealth of the country?
|
Answer: Maximilian's state is greater.
Solution: Consider the table where $z, x-$ are the states of Alejandro and Maximilian in 2011:
| | 2011 | 2012 |
| :--- | :--- | :--- |
| $\mathrm{A}$ | $z$ | $2 x$ |
| $\mathrm{M}$ | $x$ | $y$ |
Then $N=(2 x+y)-(x+z)-$ are the national riches of the country. Subtracting $x$ from them, we get $N-x=y-z<0$, hence they are less than Maximilian's state. 2. In the Formula-2013 race, there are 2 drivers. The first driver completed 4 laps in the time it took the second driver to complete 3. Over the next three laps, due to fast driving, the first driver had to drive an additional 20 meters to the pit stop (without stopping). It is known that when the second driver completed 6 laps, the first driver completed 7.75 laps. Find the length of the lap. (The speeds of the drivers are constant.)
Answer: 80 meters.
Solution: If it were not for the pit stop, the first driver would have completed exactly 8 laps in the time it took the second driver to complete 6 laps. Therefore, the pit stop is exactly $\frac{1}{4}$ of a lap. Then the entire lap is 80 meters.
|
80
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Several boys and girls gathered around a round table. It is known that exactly for 7 girls, girls are sitting to their left, and for 12 - boys. It is also known that for $75\%$ of the boys, girls are sitting to their right. How many people are sitting at the table?
|
Answer: 35 people.
Solution: From the condition, it is clear that there are exactly 19 girls.
Note that the number of girls who have boys sitting to their left is equal to the number of boys who have girls sitting to their right. Thus, $75\%$ of the boys equals 12, i.e., there are 16 boys in total sitting at the table. Therefore, we get 19 girls + 16 boys $=35$ people.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the digits of the number $\underbrace{44 \ldots 4}_{2012 \text { times }} \cdot \underbrace{99 \ldots 9}_{2012 \text { times }}$
|
Answer: 18108.
Solution: Note that $\underbrace{4 \ldots 4}_{2012} \cdot \underbrace{9 \ldots 9}_{2012}=\underbrace{4 \ldots 4}_{2012} \underbrace{0 \ldots 0}_{2012}-\underbrace{4 \ldots 4}_{2012}=\underbrace{4 \ldots 4}_{2011} 3 \underbrace{5 \ldots 5}_{2011} 6$. The sum of the digits is $4 \cdot 2011+3+5 \cdot 2011+6=18108$.
|
18108
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. A trip in Moscow using the "Troyka" card in 2016 costs 32 rubles for one subway ride and 31 rubles for one trip on surface transport. What is the minimum total number of trips that can be made under these rates, spending exactly 5000 rubles?
|
Answer: 157.
Solution: If $x$ is the number of trips by surface transport and $y$ is the number of trips by subway, then we have $31x + 32y = 5000$, from which $32(x + y) = 5000 + x \geqslant 5000$. Therefore, $x + y \geqslant 5000 / 32 = 156 \frac{1}{4}$. The smallest integer value of $x + y$ is 157, which is achieved when $x = 24, y = 133$.
|
157
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Determine the number of natural divisors of the number $11!=1 \cdot 2 \cdot \ldots \cdot 10 \cdot 11$ that are multiples of three. Answer. 432.
|
Solution. The prime factorization of the given number is $11!=2^{8} \cdot 3^{4} \cdot 5^{2} \cdot 7 \cdot 11$. All multiples of three that are divisors of this number have the form $2^{\alpha} \cdot 3^{\beta} \cdot 5^{\gamma} \cdot 7^{\delta} \cdot 11^{\varphi}$, where $\alpha \in[0 ; 8], \beta \in[1 ; 4], \gamma \in[0 ; 2]$, $\delta \in[0 ; 1], \varphi \in[0 ; 1]$. The total number of such divisors is $(8+1) \cdot 4 \cdot(2+1)(1+1)(1+1)=432$.
|
432
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $-1,4,6,9,10,11,15,16,20,22$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: -4914 (numbers on the board: $-3,2,7,9,13$).
Solution. The sum of the numbers in the obtained set is 112. Each of the original five numbers appears 4 times in this sum. Therefore, the sum of the required numbers is $112: 4=28$. The sum of the two smallest numbers is -1, and the sum of the two largest numbers is 22. Therefore, the middle number (the third largest of the five) is $28-22-(-1)=7$. In the set given in the problem, the second number is equal to the sum of the first and third required numbers, from which the first number is $4-7=-3$, and the second is 2. Similarly, we obtain that the fourth number is 9, and the fifth is 13. Thus, the numbers on the board are $-3,2,7,9,13$, and their product is -4914.
|
-4914
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $3,8,9,16,17,17,18,22,23,31$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: 3360 (numbers on the board: $1,2,7,15,16$).
|
3360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $2,6,10,10,12,14,16,18,20,24$. Determine which numbers are written on the board. In your answer, write their product
|
Answer: -3003 (numbers on the board: $-1,3,7,11,13$ ).
|
-3003
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $6,9,10,13,13,14,17,17,20,21$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: 4320 (numbers on the board: $1,5,8,9,12$ ).
|
4320
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $-1,5,8,9,11,12,14,18,20,24$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: -2002 (numbers on the board: $-2,1,7,11,13$ ).
|
-2002
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.6. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $5,8,9,13,14,14,15,17,18,23$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: 4752 (numbers on the board: $2,3,6,11,12$).
|
4752
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.7. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $-1,2,6,7,8,11,13,14,16,20$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: -2970 (numbers on the board: $-3,2,5,9,11$).
|
-2970
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.8. On the board, there are 5 integers. By adding them in pairs, the following set of 10 numbers was obtained: $5,9,10,11,12,16,16,17,21,23$. Determine which numbers are written on the board. In your answer, write their product.
|
Answer: 5292 (numbers on the board: $2,3,7,9,14$).
|
5292
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In the expansion of the function $f(x)=\left(1+x-x^{2}\right)^{20}$ in powers of $x$, find the coefficient of $x^{3 n}$, where $n$ is equal to the sum of all coefficients of the expansion.
|
Answer: 760.
Solution. The expansion in powers of $x$ has the form $f(x)=\sum_{k=0}^{40} a_{k} x^{k}$. The sum of all coefficients is $\sum_{k=0}^{40} a_{k}=f(1)=1$. Therefore, we need to find the coefficient of $x^{3}$. We have:
$$
\begin{aligned}
f(x)=\left(\left(1-x^{2}\right)+x\right)^{20}=(1- & \left.x^{2}\right)^{20}+20\left(1-x^{2}\right)^{19} x+\frac{20 \cdot 19}{2}\left(1-x^{2}\right)^{18} x^{2}+ \\
& +\frac{20 \cdot 19 \cdot 18}{6}\left(1-x^{2}\right)^{17} x^{3}+\text { terms in which } x^{3} \text { does not appear. }
\end{aligned}
$$
In the first and third terms, $x^{3}$ does not appear. In the second term, $x^{3}$ appears with the coefficient $(-20) \cdot 19=-380$; in the fourth term, $x^{3}$ appears with the coefficient $\frac{20 \cdot 19 \cdot 18}{6}=1140$. Therefore, the coefficient of $x^{3}$ is $-380+1140=760$.
|
760
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find the smallest four-digit number that is not a multiple of 10 and has the following property: if the digits are reversed, the resulting number is a divisor of the original number, and the quotient is different from one.
Answer. 8712.
|
Solution. Let's find all four-digit numbers with the property specified in the problem. Let $\overline{a b c d}$ be the desired number, then $\overline{c b a d}$ is the number obtained from it by reversing the digits, $a, d \neq 0$. According to the condition, $\overline{a b c d}=k \cdot \overline{c b a d}$, where $k$ is a natural number, $k>1$. On one hand, we have $1000 k d k \cdot \overline{d c b a}=\overline{a b c d}>1000 a$, from which $k(d+1)>a, d>\frac{a}{k}-1$. Therefore, $d=\left[\frac{a}{k}\right]$, where $[x]$ denotes the integer part of the number $x$ (i.e., the smallest integer not exceeding $x$). Then $a \geqslant k$, otherwise $d=\left[\frac{a}{k}\right]=0$.
Notice also that the last digit of the number $a k$ must be equal to $d=\left[\frac{a}{k}\right]$. Let's create a table, in the cells of which for each pair $a$ and $k$ we will sequentially write the value $\left[\frac{a}{k}\right]$ (if it is different from zero) and the last digit of the number $a k$.
| $k \backslash a$ | 2 | 3 | | | 4 | | 5 | | | 6 | | 7 | | | 8 | | | 9 | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2 | 1 | 4 | 1 | 6 | 2 | 8 | 2 | 0 | 3 | 2 | 3 | 4 | 4 | 6 | 4 | 8 | | | |
| 3 | | | 1 | 9 | 1 | 2 | 1 | 5 | 2 | 8 | 2 | 1 | 2 | 4 | 3 | 7 | | | |
| 4 | | | | | 1 | 6 | 1 | 0 | 1 | 4 | 1 | 8 | 2 | 2 | 2 | 6 | | | |
| 5 | | | | | | 1 | 5 | 1 | 0 | 1 | 5 | 1 | 0 | 1 | 5 | | | | |
| 6 | | | | | | | | | 1 | 6 | 1 | 2 | 1 | 8 | 1 | 4 | | | |
| 7 | | | | | | | | | | 1 | 9 | 1 | 6 | 1 | 3 | | | | |
| 8 | | | | | | | | | | | | 1 | 4 | 1 | 2 | | | | |
| 9 | | | | | | | | | | | | | | | | 1 | 1 | | |
Here, the cells are highlighted where both digits are the same. Thus, the required condition can only be met in two cases: 1) $a=8, k=4$ (then $d=2$) and 2) $a=9, k=9$ (then $d=1$).
In the first case, for the digits $b$ and $c$, we get the equation
$$
8000+100 b+10 c+2=4 \cdot(2000+100 c+10 b+8) \Leftrightarrow 2 b=13 c+1
$$
If $c=0$, then $2 b=1$, which is impossible. For $c \geqslant 2$, we get $b=\frac{13 c+1}{2}>13$, which is also impossible. The only remaining option is $c=1, b=7$.
In the second case, for the digits $b$ and $c$, we get the equation
$$
9000+100 b+10 c+1=9 \cdot(1000+100 c+10 b+9) \quad \Leftrightarrow \quad b=89 c+8
$$
For $c \geqslant 1$, we have $b=89 c+8 \geqslant 97$, which is impossible. Therefore, in this case, $c=0, b=8$.
Thus, the numbers 8712 and 9801 possess the property specified in the problem.
|
8712
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. It is known that $x+y+z=2016$ and $\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{7}{224}$. Find $\frac{z}{x+y}+\frac{x}{y+z}+\frac{y}{z+x}$ ANSWER:60.
|
Solution: Add 1 to each fraction, we get $\frac{z}{x+y}+1+\frac{x}{y+z}+1+\frac{y}{z+x}+1=\frac{x+y+z}{x+y}+$ $\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}=2016 \cdot\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)=\frac{2016}{32}=63$.
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Construct on the plane the set of points whose coordinates satisfy the inequality $|3 x+4|+|4 y-3| \leq 12$. In your answer, specify the area of the resulting figure.
ANSWER: 24.
|
Solution: We will shift the coordinate axes by $-\frac{4}{3}$ along the Ox axis, and by $\frac{3}{4}$ along the Oy axis. In the new coordinates, the obtained figure is described by the inequality $|3 x|+|4 y| \leq 12$. It is not difficult to show that this will be a rhombus with diagonals of 6 and 8, therefore, its area is 24.
|
24
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the largest ten-digit number of the form $\overline{a_{9} a_{8} a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}}$, possessing the following property: the digit equal to $\mathrm{a}_{\mathrm{i}}$ appears in its representation exactly $\mathrm{a}_{9-\mathrm{i}}$ times (for example, the digit equal to $\mathrm{a}_{2}$ appears exactly $\mathrm{a}_{7}$ times).
ANSWER 8888228888.
|
Solution: We will divide all digits into pairs $a_{0}-a_{9}, \ldots, a_{4}-a_{5}$. We will prove that the digit 9 cannot be present in the given number. Suppose $a_{i}=9$, then the paired digit $a_{9-i}$ appears 9 times. If $a_{9-i} \neq 9$, then 9 appears only once, so we get a number consisting of one nine and nine ones, but then two ones would be in the same pair, which contradicts the condition. If $a_{9-i}=9$, then we get a number consisting of nine nines and one digit not equal to 9, and this digit would form a pair with a nine, which is also impossible.
Let's see if the number can contain 8. If it is paired with 8, then the number contains eight eights, forming pairs, the largest such number is 8888228888. If the paired digit is not 8, then the number contains 8 digits that are less than 8, i.e., it cannot start with four digits 8, so it is less than 8888228888.
|
8888228888
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. (2 points) On two bookshelves, there are mathematics books, with an equal number on each. If 5 books are moved from the first shelf to the second, then the second shelf will have twice as many books as the first. How many books are there in total on both shelves?
|
Answer: 30.
Solution. If $x$ is the number of books on both shelves, then $\frac{x}{3}+5=\frac{2 x}{3}-5$, from which $x=30$.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. (14 points) A team consisting of juniors and masters from the "Vimpel" sports society went to a shooting tournament. The average number of points scored by the juniors turned out to be 22, by the masters - 47, and the average number of points for the entire team - 41. What is the share (in percent) of masters in this team?
|
Answer: 76.
Solution. Let there be $x$ juniors and $y$ masters in the team. Then the total number of points scored by the team is $22x + 47y = 41(x + y)$, from which we find $19x = 6y$. Therefore, the proportion of masters is $\frac{y}{x+y} = \frac{19y}{19x + 19y} = \frac{19y}{25y} = 0.76$, i.e., $76\%$.
|
76
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. (14 points) Calculate $x^{3}+\frac{1}{x^{3}}$, given that $x+\frac{1}{x}=3$.
|
Answer: 18.
Solution. If $x+\frac{1}{x}=a$, then $a^{3}=\left(x+\frac{1}{x}\right)^{3}=x^{3}+3\left(x+\frac{1}{x}\right)+\frac{1}{x^{3}}$, from which $x^{3}+\frac{1}{x^{3}}=a^{3}-3 a=18$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. (14 points) An eraser, 3 pens, and 2 markers cost 240 rubles, while 2 erasers, 4 markers, and 5 pens cost 440 rubles. What is the total cost (in rubles) of 3 erasers, 4 pens, and 6 markers?
|
Answer: 520.
Solution. From the condition, it follows that 3 erasers, 8 pens, and 6 markers cost $440+240=680$ rubles. Moreover, 2 erasers, 6 pens, and 4 markers will cost $2 \cdot 240=480$ rubles. Therefore, one pen costs $480-440=40$ rubles. Then, 3 erasers, 4 pens, and 6 markers cost $680-4 \cdot 40=520$ rubles.
|
520
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. (14 points) In an acute-angled triangle $A B C$, angle $A$ is equal to $35^{\circ}$, segments $B B_{1}$ and $C C_{1}$ are altitudes, points $B_{2}$ and $C_{2}$ are the midpoints of sides $A C$ and $A B$ respectively. Lines $B_{1} C_{2}$ and $C_{1} B_{2}$ intersect at point $K$. Find the measure (in degrees) of angle $B_{1} K B_{2}$.
|
Answer: 75.
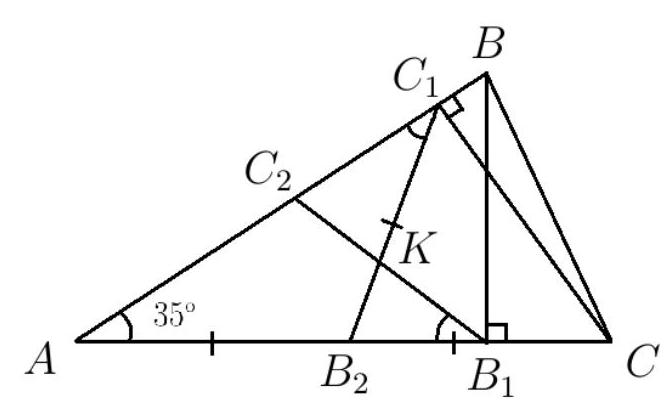
Solution. Note that angles $B$ and $C$ of triangle $ABC$ are greater than $\angle A=35^{\circ}$ (otherwise it would be an obtuse triangle), so point $C_{1}$ lies on side $AB$ between points $B$ and $C_{2}$, and point $B_{1}$ lies on side $AC$ between points $C$ and $B_{2}$. Therefore, the point $K$ of intersection of lines $B_{1} C_{2}$ and $C_{1} B_{2}$ lies inside the triangle. Since $C_{1} B_{2}$ is the median of the right triangle $C C_{1} A$, triangle $C_{1} B_{2} A$ is isosceles. Therefore, $\angle A B_{1} C_{2}=35^{\circ}$. Similarly, we get $\angle A C_{1} B_{2}=35^{\circ}$, from which $\angle A B_{2} C_{1}=180^{\circ}-2 \cdot 35^{\circ}=110^{\circ}$. Then $\angle B_{1} K B_{2}=\angle A B_{2} K-\angle A B_{1} K=110^{\circ}-35^{\circ}=75^{\circ}$.
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. (14 points) In a hut, several residents of the island gathered, some from the Ah tribe, and the rest from the Ukh tribe. The residents of the Ah tribe always tell the truth, while the residents of the Ukh tribe always lie. One of the residents said: "There are no more than 16 of us in the hut," and then added: "We are all from the Ukh tribe." Another said: "There are no more than 17 of us in the hut," and then noted: "Some of us are from the Ah tribe." The third said: "There are five of us in the hut," and, looking around, added: "There are no fewer than three residents of the Ukh tribe among us." How many residents from the Ah tribe are in the hut?
|
Answer: 15.
Solution. A resident of tribe Ah cannot say "we are all from tribe Ukh," so the first one is from tribe Ukh. Therefore, there are no fewer than 17 people in the hut. So the second one spoke the truth, i.e., he is from tribe Ah. Therefore, there are no more than 17 people in the hut. Thus, there are 17 people in the hut. The third one is from tribe Ukh, as he said there are five of them in total. But since he said there are no fewer than three residents from tribe Ukh, there are no more than two. Two have already been found (the third and the first), so there are exactly two. Then the number of residents from tribe Ah is 15.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.