title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
An approach with generator
|
random-point-in-non-overlapping-rectangles
| 0
| 1
|
# Intuition\nfirst of all, this is only one limit; Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.\n\nso, what we have to do is return all the points when user calls pick without duplication. actually, we don\'t need to use random function here to avoid duplication.\n\n# Approach\n- make generator for return value. this generator will make a point, which is never explored before by 2 for loop.\n- when a generator is done, let\'s move to next rectangle.\n- if we reach the last point, we can start with the first one.\n\n# Complexity\n- Time complexity: O(1)\n- Space complexity: O(1), but we need more space to keep a generator\n\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.curr = 0\n self.iter = self.generator(rects[0])\n\n def pick(self) -> List[int]:\n try:\n return next(self.iter)\n except:\n self.curr += 1\n if self.curr == len(self.rects):\n self.curr = 0\n\n self.iter = self.generator(self.rects[self.curr])\n return next(self.iter)\n \n def generator(self, rect):\n for i in range(rect[0], rect[2]+1):\n for j in range(rect[1], rect[3]+1):\n yield [i, j]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n```\n\nPlease correct me if this approach is wrong. thanks!
| 0
|
You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`.
| null |
An approach with generator
|
random-point-in-non-overlapping-rectangles
| 0
| 1
|
# Intuition\nfirst of all, this is only one limit; Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.\n\nso, what we have to do is return all the points when user calls pick without duplication. actually, we don\'t need to use random function here to avoid duplication.\n\n# Approach\n- make generator for return value. this generator will make a point, which is never explored before by 2 for loop.\n- when a generator is done, let\'s move to next rectangle.\n- if we reach the last point, we can start with the first one.\n\n# Complexity\n- Time complexity: O(1)\n- Space complexity: O(1), but we need more space to keep a generator\n\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.curr = 0\n self.iter = self.generator(rects[0])\n\n def pick(self) -> List[int]:\n try:\n return next(self.iter)\n except:\n self.curr += 1\n if self.curr == len(self.rects):\n self.curr = 0\n\n self.iter = self.generator(self.rects[self.curr])\n return next(self.iter)\n \n def generator(self, rect):\n for i in range(rect[0], rect[2]+1):\n for j in range(rect[1], rect[3]+1):\n yield [i, j]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n```\n\nPlease correct me if this approach is wrong. thanks!
| 0
|
You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104`
| null |
Python3 solution with random utility
|
random-point-in-non-overlapping-rectangles
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe key idea solve the problem is drawing uniform probility arrording to rect area and after that draw a point inside the choised rect uniformly\nwe cant utilize python3 random library choices, randint fo that job\nps. also we can use dev own\'s random choices: use binary-search and randint!\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. choice a rect with unfrom distrbution\n2. in that rect unformly draw a point\n\n\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self._areas,self._rects,self._indexs=[],rects,[]\n for i,(xl,yl,xr,yr) in enumerate(self._rects):\n self._areas.append((yr-yl+1)*(xr-xl+1)),self._indexs.append(i)\n \n def pick(self) -> List[int]:\n (xl,yl,xr,yr)=self._rects[random.choices(self._indexs,self._areas,k=1)[0]]\n return (random.randint(xl,xr),random.randint(yl,yr))\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n```
| 0
|
You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`.
| null |
Python3 solution with random utility
|
random-point-in-non-overlapping-rectangles
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe key idea solve the problem is drawing uniform probility arrording to rect area and after that draw a point inside the choised rect uniformly\nwe cant utilize python3 random library choices, randint fo that job\nps. also we can use dev own\'s random choices: use binary-search and randint!\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. choice a rect with unfrom distrbution\n2. in that rect unformly draw a point\n\n\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self._areas,self._rects,self._indexs=[],rects,[]\n for i,(xl,yl,xr,yr) in enumerate(self._rects):\n self._areas.append((yr-yl+1)*(xr-xl+1)),self._indexs.append(i)\n \n def pick(self) -> List[int]:\n (xl,yl,xr,yr)=self._rects[random.choices(self._indexs,self._areas,k=1)[0]]\n return (random.randint(xl,xr),random.randint(yl,yr))\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n```
| 0
|
You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104`
| null |
Weighted Selection of Rect + Generate point in selected Rect
|
random-point-in-non-overlapping-rectangles
| 0
| 1
|
```python\nfrom dataclasses import dataclass\nfrom functools import cached_property\nfrom itertools import accumulate\nfrom random import choices, randint\n\n\n@dataclass\nclass Rectangle:\n x: int\n y: int\n l: int\n b: int\n\n def generate(self) -> list[int]:\n return [\n self.x + randint(0, self.l),\n self.y + randint(0, self.b)\n ]\n\n @property\n def points(self) -> int:\n """\n :return: number of points inside and on boundary of the rectangle \n """\n return (self.l + 1) * (self.b + 1)\n\n\nclass Solution:\n def __init__(self, rects: list[list[int]]):\n self.rects = [Rectangle(x1, y1, x2 - x1, y2 - y1) for x1, y1, x2, y2 in rects]\n\n def pick(self) -> list[int]:\n return self.select_rect().generate()\n\n def select_rect(self) -> Rectangle:\n return choices(self.rects, cum_weights=self.cum_weights, k=1)[0]\n\n @cached_property\n def cum_weights(self) -> list[float]:\n rect_points = [r.points for r in self.rects]\n total_points = sum(rect_points)\n return list(accumulate(points / total_points for points in rect_points))\n```
| 0
|
You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`.
| null |
Weighted Selection of Rect + Generate point in selected Rect
|
random-point-in-non-overlapping-rectangles
| 0
| 1
|
```python\nfrom dataclasses import dataclass\nfrom functools import cached_property\nfrom itertools import accumulate\nfrom random import choices, randint\n\n\n@dataclass\nclass Rectangle:\n x: int\n y: int\n l: int\n b: int\n\n def generate(self) -> list[int]:\n return [\n self.x + randint(0, self.l),\n self.y + randint(0, self.b)\n ]\n\n @property\n def points(self) -> int:\n """\n :return: number of points inside and on boundary of the rectangle \n """\n return (self.l + 1) * (self.b + 1)\n\n\nclass Solution:\n def __init__(self, rects: list[list[int]]):\n self.rects = [Rectangle(x1, y1, x2 - x1, y2 - y1) for x1, y1, x2, y2 in rects]\n\n def pick(self) -> list[int]:\n return self.select_rect().generate()\n\n def select_rect(self) -> Rectangle:\n return choices(self.rects, cum_weights=self.cum_weights, k=1)[0]\n\n @cached_property\n def cum_weights(self) -> list[float]:\n rect_points = [r.points for r in self.rects]\n total_points = sum(rect_points)\n return list(accumulate(points / total_points for points in rect_points))\n```
| 0
|
You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104`
| null |
Solution
|
diagonal-traverse
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n vector<int> findDiagonalOrder(vector<vector<int>>& mat) {\n int N = mat.size();\n int M = mat[0].size();\n vector<int> answer;\n\n int x = 0; \n int sum = 0; \n int dir = -1;\n\n auto addToAnswer = [&]() {\n int y = sum - x;\n answer.push_back(mat[x][y]);\n };\n auto ok = [&](int x) {\n int y = sum - x;\n return x >= 0 && y >= 0 && x < N && y < M;\n };\n addToAnswer();\n while (sum != N + M - 2) {\n sum++;\n if ((dir == -1 && !ok(x)) || (dir == 1 && (ok(x + 1)))) {\n x++;\n }\n addToAnswer();\n dir = -dir;\n\n while (ok(x + dir)) {\n x += dir;\n addToAnswer();\n }\n }\n return answer; \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:\n r = 0\n c = 0 \n result = []\n m = len(mat)\n n = len(mat[0])\n\n direction = True\n\n for i in range(m * n):\n result.append(mat[r][c])\n\n if direction :\n \n if r== 0 and c!= n-1 :\n direction = False\n c+= 1 \n elif c == n-1 :\n direction = False\n r+= 1 \n else :\n r -= 1 \n c+= 1 \n\n else :\n if c== 0 and r!= m-1 :\n direction = True\n r+= 1 \n elif r == m-1 :\n direction = True\n c+= 1 \n else :\n c -= 1\n r+= 1 \n\n return result\n```\n\n```Java []\nclass Solution {\n public int[] findDiagonalOrder(int[][] mat) {\n if (mat.length < 0) \n return new int[] {};\n int m = mat.length;\n int n = mat[0].length;\n int[] dag = new int[m * n];\n int i = 0;\n int j = 0;\n int max = m * n;\n int count = 0;\n boolean dir = true;\n while (count < dag.length) {\n if (dir) {\n while (i >= 0 && j < n) {\n dag[count++] = mat[i][j];\n i--;\n j++;\n }\n i++;\n if (j >= n) { \n j = n - 1;\n i++;\n }\n } else {\n while (i < m && j >= 0) {\n dag[count++] = mat[i][j];\n i++;\n j--;\n }\n j++;\n if (i >= m) {\n i = m - 1;\n j++;\n }\n }\n dir = !dir;\n }\n return dag;\n }\n}\n```\n
| 1
|
Given an `m x n` matrix `mat`, return _an array of all the elements of the array in a diagonal order_.
**Example 1:**
**Input:** mat = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,4,7,5,3,6,8,9\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 104`
* `1 <= m * n <= 104`
* `-105 <= mat[i][j] <= 105`
| null |
Easy Python, NO DIRECTION CHECKING
|
diagonal-traverse
| 0
| 1
|
Hey guys, super easy solution here, with NO DIRECTION CHECKS!!!\nThe key here is to realize that the sum of indices on all diagonals are equal.\nFor example, in\n```\n[1,2,3]\n[4,5,6]\n[7,8,9]\n```\n2, 4 are on the same diagonal, and they share the index sum of 1. (2 is matrix[0][1] and 4 is in matrix[1][0]). 3,5,7 are on the same diagonal, and they share the sum of 2. (3 is matrix[0][2], 5 is matrix[1][1], and 7 is matrix [2][0]).\n\nSO, if you can loop through the matrix, store each element by the sum of its indices in a dictionary, you have a collection of all elements on shared diagonals. \n\nThe last part is easy, build your answer (a list) by elements on diagonals. To capture the \'zig zag\' or \'snake\' phenomena of this problem, simply reverse ever other diagonal level. So check if the level is divisible by 2. \n\n\n```\nclass Solution(object):\n def findDiagonalOrder(self, matrix):\n """\n :type matrix: List[List[int]]\n :rtype: List[int]\n """\n d={}\n\t\t#loop through matrix\n for i in range(len(matrix)):\n for j in range(len(matrix[i])):\n\t\t\t\t#if no entry in dictionary for sum of indices aka the diagonal, create one\n if i + j not in d:\n d[i+j] = [matrix[i][j]]\n else:\n\t\t\t\t#If you\'ve already passed over this diagonal, keep adding elements to it!\n d[i+j].append(matrix[i][j])\n\t\t# we\'re done with the pass, let\'s build our answer array\n ans= []\n\t\t#look at the diagonal and each diagonal\'s elements\n for entry in d.items():\n\t\t\t#each entry looks like (diagonal level (sum of indices), [elem1, elem2, elem3, ...])\n\t\t\t#snake time, look at the diagonal level\n if entry[0] % 2 == 0:\n\t\t\t\t#Here we append in reverse order because its an even numbered level/diagonal. \n [ans.append(x) for x in entry[1][::-1]]\n else:\n [ans.append(x) for x in entry[1]]\n return ans\n \n ```\n\t\t\t\t\nso 2 key facts:\n1. Diagonals are defined by the sum of indicies in a 2 dimensional array\n2. The snake phenomena can be achieved by reversing every other diagonal level, therefore check if divisible by 2\n\nLet me know if you need further explanation
| 1,086
|
Given an `m x n` matrix `mat`, return _an array of all the elements of the array in a diagonal order_.
**Example 1:**
**Input:** mat = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,4,7,5,3,6,8,9\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 104`
* `1 <= m * n <= 104`
* `-105 <= mat[i][j] <= 105`
| null |
Python Video Solution
|
diagonal-traverse
| 0
| 1
|
I have explained this in a [video](https://youtu.be/Njt7aZYq0wA).\n\n`row+col` for each element identifies which column it belongs to.\n\nWe can use this as a `diagonal_id` and store all elements corresponding to it in a HashMap.\n\nIf it is **even**, then we have to traverse the list in reverse order, else in forward order.\n\nIf this was helpful, please upvote, like the video and subscribe to the channel.\n\nCheers.\n\n```\nclass Solution:\n def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:\n \n R, C = len(mat), len(mat[0])\n \n diagonal_dict = defaultdict(list)\n \n for r in range(R):\n for c in range(C):\n diagonal_dict[r+c].append(mat[r][c])\n \n ans = []\n \n key = 0\n \n while key in diagonal_dict:\n if key%2: #odd\n ans.extend(diagonal_dict[key])\n else: #even\n ans.extend(diagonal_dict[key][::-1])\n \n key+=1\n \n return ans
| 3
|
Given an `m x n` matrix `mat`, return _an array of all the elements of the array in a diagonal order_.
**Example 1:**
**Input:** mat = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,4,7,5,3,6,8,9\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 104`
* `1 <= m * n <= 104`
* `-105 <= mat[i][j] <= 105`
| null |
Python solution
|
diagonal-traverse
| 0
| 1
|
```\nclass Solution:\n def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:\n M,N = len(mat), len(mat[0])\n diagonals = []\n \n # traverse first column\n for i in range(len(mat)):\n idx_i = i\n idx_j = 0\n diagonals.append([])\n while idx_i >= 0 and idx_j < N:\n diagonals[-1].append(mat[idx_i][idx_j])\n idx_i -= 1\n idx_j += 1\n \n # traverse last row\n for i in range(1, len(mat[-1])):\n idx_i = M-1\n idx_j = i\n diagonals.append([])\n while idx_j < N and idx_i>=0:\n diagonals[-1].append(mat[idx_i][idx_j])\n idx_i -= 1\n idx_j += 1\n \n # combine everything to answer\n answer = []\n for i, d in enumerate(diagonals):\n if i % 2 == 0:\n answer += d\n else:\n answer += d[::-1]\n return answer\n```
| 2
|
Given an `m x n` matrix `mat`, return _an array of all the elements of the array in a diagonal order_.
**Example 1:**
**Input:** mat = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,4,7,5,3,6,8,9\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 104`
* `1 <= m * n <= 104`
* `-105 <= mat[i][j] <= 105`
| null |
498: Time 97.90% and Space 98.87%, Solution with step by step explanation
|
diagonal-traverse
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize an empty list called result to store the elements in diagonal order.\n2. Get the dimensions of the matrix, m and n, and set the starting indices i and j to 0. Also initialize a variable direction to 0 to represent the up-right direction.\n3. Loop through each element in the matrix using a for loop that iterates m * n times. For each iteration, append the current element at index (i, j) to result. Then, check the current direction and update the indices accordingly:\n 1. If the current direction is up-right (direction == 0):\nIf we\'ve reached the right edge of the matrix (j == n - 1), change the direction to down-left (direction = 1) and move down to the next row (i += 1).\nIf we\'ve reached the top edge of the matrix (i == 0), change the direction to down-left (direction = 1) and move right to the next column (j += 1).\nOtherwise, move up one row and right one column (i -= 1 and j += 1).\n 2. If the current direction is down-left (direction == 1):\nIf we\'ve reached the bottom edge of the matrix (i == m - 1), change the direction to up-right (direction = 0) and move right to the next column (j += 1).\nIf we\'ve reached the left edge of the matrix (j == 0), change the direction to up-right (direction = 0) and move down to the next row (i += 1).\nOtherwise, move down one row and left one column (i += 1 and j -= 1).\n4. After the loop completes, return result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:\n # Step 1\n result = []\n # Step 2\n m, n = len(mat), len(mat[0])\n i = j = direction = 0\n \n # Step 3\n for _ in range(m * n):\n result.append(mat[i][j])\n \n if direction == 0: # Up-right direction\n if j == n - 1:\n direction = 1 # Change direction to down-left\n i += 1\n elif i == 0:\n direction = 1 # Change direction to down-left\n j += 1\n else:\n i -= 1\n j += 1\n else: # Down-left direction\n if i == m - 1:\n direction = 0 # Change direction to up-right\n j += 1\n elif j == 0:\n direction = 0 # Change direction to up-right\n i += 1\n else:\n i += 1\n j -= 1\n \n # Step 4\n return result\n\n```
| 6
|
Given an `m x n` matrix `mat`, return _an array of all the elements of the array in a diagonal order_.
**Example 1:**
**Input:** mat = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,4,7,5,3,6,8,9\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 104`
* `1 <= m * n <= 104`
* `-105 <= mat[i][j] <= 105`
| null |
✅Easy Python Code
|
keyboard-row
| 0
| 1
|
# Code\n```\nclass Solution:\n def findWords(self, words: List[str]) -> List[str]:\n row1 = list("qwertyuiop")\n row2 = list("asdfghjkl")\n row3 = list("zxcvbnm")\n\n ans = []\n\n for word in words:\n flag = 0\n temp = word\n word = word.lower()\n if word[0] in row1:\n res_row = row1\n elif word[0] in row2:\n res_row = row2\n else:\n res_row = row3\n for i in range(0, len(word)):\n if word[i] not in res_row:\n flag = 1\n break\n if flag == 0:\n ans.append(temp)\n\n return ans\n \n```
| 4
|
Given an array of strings `words`, return _the words that can be typed using letters of the alphabet on only one row of American keyboard like the image below_.
In the **American keyboard**:
* the first row consists of the characters `"qwertyuiop "`,
* the second row consists of the characters `"asdfghjkl "`, and
* the third row consists of the characters `"zxcvbnm "`.
**Example 1:**
**Input:** words = \[ "Hello ", "Alaska ", "Dad ", "Peace "\]
**Output:** \[ "Alaska ", "Dad "\]
**Example 2:**
**Input:** words = \[ "omk "\]
**Output:** \[\]
**Example 3:**
**Input:** words = \[ "adsdf ", "sfd "\]
**Output:** \[ "adsdf ", "sfd "\]
**Constraints:**
* `1 <= words.length <= 20`
* `1 <= words[i].length <= 100`
* `words[i]` consists of English letters (both lowercase and uppercase).
| null |
Solution
|
keyboard-row
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n vector<string> findWords(vector<string>& words) {\n static const vector<unordered_set<char>> rows{{\'q\', \'w\', \'e\', \'r\', \'t\', \'y\', \'u\', \'i\', \'o\', \'p\'},\n {\'a\', \'s\', \'d\', \'f\', \'g\', \'h\', \'j\', \'k\', \'l\'}, \n {\'z\', \'x\', \'c\', \'v\', \'b\' ,\'n\', \'m\'}};\n\n vector<string> result;\n for (const auto& word : words) {\n int k = 0;\n for (int i = 0; i < rows.size(); ++i) {\n if (rows[i].count(tolower(word[0]))) {\n k = i;\n break;\n }\n }\n result.emplace_back(word);\n for (const auto& c: word) {\n if (!rows[k].count(tolower(c))) {\n result.pop_back();\n break;\n }\n }\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findWords(self, words: List[str]) -> List[str]:\n l = list("qwertyuiop")\n l1 = list("asdfghjkl")\n l2 = list("zxcvbnm")\n k = []\n o,p,q = 0,0,0\n for i in words:\n m,n,x = i,i,i\n for j in m:\n if j.lower() in l:\n o += 1\n else:\n break\n \n if o == len(i):\n k.append(i)\n o = 0\n for a in n:\n if a.lower() in l1:\n \n p += 1\n \n else:\n break\n \n if p == len(i):\n k.append(i)\n p = 0\n for b in x:\n if b.lower() in l2:\n q += 1\n else:\n break\n \n if q == len(i):\n k.append(i)\n q = 0\n return k\n```\n\n```Java []\nclass Solution {\n private final Set<Character> row1 = Set.of(\'q\', \'w\', \'e\', \'r\', \'t\', \'y\', \'u\', \'i\', \'o\', \'p\');\n private final Set<Character> row2 = Set.of(\'a\', \'s\', \'d\', \'f\', \'g\', \'h\', \'j\', \'k\', \'l\');\n private final Set<Character> row3 = Set.of(\'z\', \'x\', \'c\', \'v\', \'b\', \'n\', \'m\');\n\n public String[] findWords(String[] words) {\n boolean[] mask = new boolean[words.length];\n Arrays.fill(mask, true);\n int stringArrSize = words.length;\n\n for(int j = 0; j < words.length; j++) {\n char firstCharacter = Character.toLowerCase(words[j].charAt(0));\n\n Set<Character> rowOfChoice;\n\n if (row1.contains(firstCharacter)) {\n rowOfChoice = row1;\n } else if (row2.contains(firstCharacter)) {\n rowOfChoice = row2;\n } else if (row3.contains(firstCharacter)) {\n rowOfChoice = row3;\n } else {\n return new String[0];\n }\n for(int i = 1; i < words[j].length(); i++) {\n char currentChar = Character.toLowerCase(words[j].charAt(i));\n if (!rowOfChoice.contains(currentChar)) {\n mask[j] = false;\n stringArrSize--;\n break;\n }\n }\n }\n String[] result = new String[stringArrSize];\n int resultIndex = 0;\n\n for(int i = 0; i < mask.length; i++) {\n if (mask[i]) {\n result[resultIndex++] = words[i];\n }\n }\n return result;\n }\n}\n```\n
| 2
|
Given an array of strings `words`, return _the words that can be typed using letters of the alphabet on only one row of American keyboard like the image below_.
In the **American keyboard**:
* the first row consists of the characters `"qwertyuiop "`,
* the second row consists of the characters `"asdfghjkl "`, and
* the third row consists of the characters `"zxcvbnm "`.
**Example 1:**
**Input:** words = \[ "Hello ", "Alaska ", "Dad ", "Peace "\]
**Output:** \[ "Alaska ", "Dad "\]
**Example 2:**
**Input:** words = \[ "omk "\]
**Output:** \[\]
**Example 3:**
**Input:** words = \[ "adsdf ", "sfd "\]
**Output:** \[ "adsdf ", "sfd "\]
**Constraints:**
* `1 <= words.length <= 20`
* `1 <= words[i].length <= 100`
* `words[i]` consists of English letters (both lowercase and uppercase).
| null |
Python easy solution no nested loop
|
keyboard-row
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findWords(self, words: List[str]) -> List[str]:\n l1="qwertyuiop"\n l2="asdfghjkl"\n l3="zxcvbnm"\n res=[]\n for word in words:\n w=word.lower()\n if len(set(l1+w))==len(l1) or len(set(l2+w))==len(l2) or len(set(l3+w))==len(l3) :\n res.append(word)\n return res\n\n\n \n```
| 26
|
Given an array of strings `words`, return _the words that can be typed using letters of the alphabet on only one row of American keyboard like the image below_.
In the **American keyboard**:
* the first row consists of the characters `"qwertyuiop "`,
* the second row consists of the characters `"asdfghjkl "`, and
* the third row consists of the characters `"zxcvbnm "`.
**Example 1:**
**Input:** words = \[ "Hello ", "Alaska ", "Dad ", "Peace "\]
**Output:** \[ "Alaska ", "Dad "\]
**Example 2:**
**Input:** words = \[ "omk "\]
**Output:** \[\]
**Example 3:**
**Input:** words = \[ "adsdf ", "sfd "\]
**Output:** \[ "adsdf ", "sfd "\]
**Constraints:**
* `1 <= words.length <= 20`
* `1 <= words[i].length <= 100`
* `words[i]` consists of English letters (both lowercase and uppercase).
| null |
Easy | Python Solution | Hashmap
|
keyboard-row
| 0
| 1
|
# Code\n```\nclass Solution:\n def findWords(self, words: List[str]) -> List[str]:\n hashmap = {}\n arr = [\'qwertyuiop\', \'asdfghjkl\', \'zxcvbnm\']\n\n for i in range(len(arr)):\n for j in arr[i]:\n hashmap[j] = i+1\n\n res = []\n\n for i in words:\n prev = 0\n flag = 1\n cp = i\n i = i.lower()\n \n for j in i:\n if prev == 0:\n prev = hashmap[j]\n else:\n if prev != hashmap[j]:\n flag = 0\n break\n if flag:\n res.append(cp)\n\n return res\n```\nDo upvote if you like the Solution :)
| 2
|
Given an array of strings `words`, return _the words that can be typed using letters of the alphabet on only one row of American keyboard like the image below_.
In the **American keyboard**:
* the first row consists of the characters `"qwertyuiop "`,
* the second row consists of the characters `"asdfghjkl "`, and
* the third row consists of the characters `"zxcvbnm "`.
**Example 1:**
**Input:** words = \[ "Hello ", "Alaska ", "Dad ", "Peace "\]
**Output:** \[ "Alaska ", "Dad "\]
**Example 2:**
**Input:** words = \[ "omk "\]
**Output:** \[\]
**Example 3:**
**Input:** words = \[ "adsdf ", "sfd "\]
**Output:** \[ "adsdf ", "sfd "\]
**Constraints:**
* `1 <= words.length <= 20`
* `1 <= words[i].length <= 100`
* `words[i]` consists of English letters (both lowercase and uppercase).
| null |
Python 3 || 2 lines for fun
|
keyboard-row
| 0
| 1
|
```\nrows = (set("qwertyuiop"), set("asdfghjkl"), set("zxcvbnm"))\n\nclass Solution:\n def findWords(self, words: list[str]) -> list[str]:\n \n return [w for w in words if any(set(w.lower()).issubset(row) for row in rows)]\n```
| 7
|
Given an array of strings `words`, return _the words that can be typed using letters of the alphabet on only one row of American keyboard like the image below_.
In the **American keyboard**:
* the first row consists of the characters `"qwertyuiop "`,
* the second row consists of the characters `"asdfghjkl "`, and
* the third row consists of the characters `"zxcvbnm "`.
**Example 1:**
**Input:** words = \[ "Hello ", "Alaska ", "Dad ", "Peace "\]
**Output:** \[ "Alaska ", "Dad "\]
**Example 2:**
**Input:** words = \[ "omk "\]
**Output:** \[\]
**Example 3:**
**Input:** words = \[ "adsdf ", "sfd "\]
**Output:** \[ "adsdf ", "sfd "\]
**Constraints:**
* `1 <= words.length <= 20`
* `1 <= words[i].length <= 100`
* `words[i]` consists of English letters (both lowercase and uppercase).
| null |
python 3 set
|
keyboard-row
| 0
| 1
|
```\nclass Solution:\n def findWords(self, words: List[str]) -> List[str]:\n #\n set1 = {\'q\',\'w\',\'e\',\'r\',\'t\',\'y\',\'u\',\'i\',\'o\',\'p\'}\n set2 = {\'a\',\'s\',\'d\',\'f\',\'g\',\'h\',\'j\',\'k\',\'l\'}\n set3 = {\'z\',\'x\',\'c\',\'v\',\'b\',\'n\',\'m\'}\n \n res = []\n for i in words:\n wordset = set(i.lower())\n if (wordset&set1 == wordset) or (wordset&set2 == wordset) or (wordset&set3 == wordset):\n res.append(i)\n return res\n```
| 33
|
Given an array of strings `words`, return _the words that can be typed using letters of the alphabet on only one row of American keyboard like the image below_.
In the **American keyboard**:
* the first row consists of the characters `"qwertyuiop "`,
* the second row consists of the characters `"asdfghjkl "`, and
* the third row consists of the characters `"zxcvbnm "`.
**Example 1:**
**Input:** words = \[ "Hello ", "Alaska ", "Dad ", "Peace "\]
**Output:** \[ "Alaska ", "Dad "\]
**Example 2:**
**Input:** words = \[ "omk "\]
**Output:** \[\]
**Example 3:**
**Input:** words = \[ "adsdf ", "sfd "\]
**Output:** \[ "adsdf ", "sfd "\]
**Constraints:**
* `1 <= words.length <= 20`
* `1 <= words[i].length <= 100`
* `words[i]` consists of English letters (both lowercase and uppercase).
| null |
✅ 99.87% 🏆 video walkthrough 🔥 optimal O(1) space solution
|
find-mode-in-binary-search-tree
| 0
| 1
|
https://youtu.be/A58XHd2Zo4M\n\nRecursion / DFS / BFS / Stack / Queue-based approaches **are NOT O(1) space**; **the cost to create the recursive callstack and/or data structures still has linear space complexity**. You can check for yourself by plugging in the code to https://pythontutor.com/ and seeing how the callstack blows up in recursive calls.\n\nHere is a true O(1) space solution walkthrough done via a Morris traversal. I recommend you watch the video as it\'s much easier to understand when you see the interactive visualization, and I also explain why it\'s necessary to do this\n\nPlease upvote if you found this helpful :)\n\nTime complexity: `O(N)`\nSpace complexity: `O(1)`\n\n```\nclass Solution:\n def findMode(self, root):\n curr_node = root\n result = []\n curr_streak = 0\n curr_num = float("inf")\n max_streak = 0\n\n while curr_node:\n if curr_node.left:\n neighbor = curr_node.left\n while neighbor.right is not None:\n neighbor = neighbor.right\n neighbor.right = curr_node\n \n tmp = curr_node.left\n curr_node.left = None\n curr_node = tmp\n else: \n # since we deleted the left pointer when we were done processing in the previous if-block, \n # we know that we only reach this else case \n # if we\'ve already processed this node. \n # Therefore, do the value processing here \n # and move to the right neighbor afterward\n if curr_node.val == curr_num:\n curr_streak += 1\n else:\n curr_streak = 0\n curr_num = curr_node.val\n \n if curr_streak == max_streak:\n result.append(curr_num)\n elif curr_streak > max_streak:\n max_streak = curr_streak\n result = [curr_num]\n \n curr_node = curr_node.right\n \n return result\n```
| 90
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
Single BT traversal with if else cases to get resultant array/list.
|
find-mode-in-binary-search-tree
| 0
| 1
|
# Intuition\n\n2 parts:\n1. Traversal through BST\n2. Finding element count and adding elements of highest count to a list (Note that there can be multiple elements with highest count)\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nInorder traversal using:\n- def inorder(root):\n if not root:\n return\n inorder(root.left)\n .... store/use value here : root.val ....\n inorder(root.right)\n\n inorder(root)\n\nNow we can use the ascending order of traversal to our advantage...\nDuring each traversal, keep track of the following:\n\n- val : current value\n- count : count of current value\n- maxc : maximum count\n\nWe can CLEAR and then append elements to result array for every new maxc (count > maxc) and append elements if maxcount is equal as well.\nThis way we can get all the elements of the same maximum count into the resultant array.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- The time complexity of the program is O(n), where n is the number of nodes in the binary tree. This is because the program performs an in-order traversal of the tree, visiting each node exactly once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- The space complexity of the program is O(h), where h is the height of the binary tree. In the worst case, the tree could be a skewed tree (i.e., a tree where every node has only one child), in which case pythe space complexity would be O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n\n self.count = 0 #count of concurrent elements\n self.maxc = 0 #maximum count is stored\n self.val = -999 #value of element\n res = [] #resultant array\n\n def order(root):\n if not root:\n return\n order(root.left)\n if self.val == root.val:\n self.count += 1\n else:\n self.count = 0\n self.val = root.val\n if self.maxc < self.count:\n res.clear()\n res.append(root.val)\n elif self.maxc == self.count:\n res.append(root.val)\n self.maxc = max(self.maxc, self.count)\n order(root.right)\n\n order(root)\n return res\n \n \n```
| 1
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
✅ 99.54% In-order Traversal Generator
|
find-mode-in-binary-search-tree
| 1
| 1
|
# Intuition\nWhen we are given a Binary Search Tree (BST) and asked about frequency or mode, the first thing that should come to mind is in-order traversal. This is because an in-order traversal of a BST gives a sorted sequence of its values. If we traverse the BST in-order, then same values will appear consecutively in the sequence. This makes it easy to count the occurrences of each value and determine the mode.\n\n# Live Coding + Logic\nhttps://youtu.be/h-3X7bUQsbo?si=nBLyZXQREsQUEaRe\n\n# Approach\n1. **In-order Traversal Generator**: We\'ll use an in-order traversal to traverse through the BST. Instead of doing the counting inside the recursive traversal, we use a generator to yield the values in-order.\n2. **Counting and Finding Modes**: As we iterate through the values returned from the in-order traversal, we keep track of the current number and its count. We compare it with the previous value:\n - If it\'s the same, we increment the count.\n - If it\'s different, we reset the count to 1 and update the current number.\n \n As we iterate, we keep track of the maximum count. If the count of a number equals the maximum count, we add it to the modes list. If it\'s greater than the maximum count, we reset the modes list and add the current number.\n\n# Complexity\n- **Time complexity**: $O(n)$. Each node is visited once in the in-order traversal, making the time complexity linear with respect to the number of nodes.\n- **Space complexity**: $O(n)$ in the worst case when storing the modes. However, if we exclude the space required for the output, the space complexity is $O(h)$, where $h$ is the height of the tree, because of the recursive stack. For a balanced BST, $h = \\log n$, but in the worst case (a skewed tree), $h = n$.\n\n# Code\n``` Python []\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n def in_order_traversal(node):\n nonlocal current_val, current_count, max_count, modes\n if not node:\n return\n \n in_order_traversal(node.left)\n \n current_count = current_count + 1 if node.val == current_val else 1\n current_val = node.val\n \n if current_count > max_count:\n max_count = current_count\n modes = [current_val]\n elif current_count == max_count:\n modes.append(current_val)\n \n in_order_traversal(node.right)\n \n current_val = None\n current_count = 0\n max_count = 0\n modes = []\n in_order_traversal(root)\n return modes\n```\n``` Go []\nfunc findMode(root *TreeNode) []int {\n var currentVal, currentCount, maxCount int\n var modes []int\n\n inOrderTraversal(root, ¤tVal, ¤tCount, &maxCount, &modes)\n\n return modes\n}\n\nfunc inOrderTraversal(node *TreeNode, currentVal, currentCount, maxCount *int, modes *[]int) {\n if node == nil {\n return\n }\n\n inOrderTraversal(node.Left, currentVal, currentCount, maxCount, modes)\n\n if node.Val == *currentVal {\n *currentCount++\n } else {\n *currentVal = node.Val\n *currentCount = 1\n }\n\n if *currentCount == *maxCount {\n *modes = append(*modes, *currentVal)\n } else if *currentCount > *maxCount {\n *maxCount = *currentCount\n *modes = []int{*currentVal}\n }\n\n inOrderTraversal(node.Right, currentVal, currentCount, maxCount, modes)\n}\n```\n``` Rust []\nuse std::rc::Rc;\nuse std::cell::RefCell;\n\nimpl Solution {\n pub fn find_mode(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {\n let mut current_val = 0;\n let mut current_count = 0;\n let mut max_count = 0;\n let mut modes = Vec::new();\n\n Self::in_order_traversal(&root, &mut current_val, &mut current_count, &mut max_count, &mut modes);\n\n modes\n }\n \n fn in_order_traversal(node: &Option<Rc<RefCell<TreeNode>>>, current_val: &mut i32, current_count: &mut i32, max_count: &mut i32, modes: &mut Vec<i32>) {\n if let Some(n) = node {\n let n = n.borrow();\n\n Self::in_order_traversal(&n.left, current_val, current_count, max_count, modes);\n\n *current_count = if n.val == *current_val { *current_count + 1 } else { 1 };\n *current_val = n.val;\n\n if *current_count == *max_count {\n modes.push(*current_val);\n } else if *current_count > *max_count {\n *max_count = *current_count;\n *modes = vec![*current_val];\n }\n\n Self::in_order_traversal(&n.right, current_val, current_count, max_count, modes);\n }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> findMode(TreeNode* root) {\n in_order_traversal(root);\n return modes;\n }\nprivate:\n int current_val = 0;\n int current_count = 0;\n int max_count = 0;\n std::vector<int> modes;\n\n void in_order_traversal(TreeNode* node) {\n if (!node) return;\n \n in_order_traversal(node->left);\n \n current_count = (node->val == current_val) ? current_count + 1 : 1;\n if (current_count == max_count) {\n modes.push_back(node->val);\n } else if (current_count > max_count) {\n max_count = current_count;\n modes = { node->val };\n }\n current_val = node->val;\n\n in_order_traversal(node->right);\n }\n};\n```\n``` Java []\nclass Solution {\n private int currentVal;\n private int currentCount = 0;\n private int maxCount = 0;\n private List<Integer> modes = new ArrayList<>();\n\n public int[] findMode(TreeNode root) {\n inOrderTraversal(root);\n int[] result = new int[modes.size()];\n for (int i = 0; i < modes.size(); i++) {\n result[i] = modes.get(i);\n }\n return result;\n }\n\n private void inOrderTraversal(TreeNode node) {\n if (node == null) return;\n\n inOrderTraversal(node.left);\n\n currentCount = (node.val == currentVal) ? currentCount + 1 : 1;\n if (currentCount == maxCount) {\n modes.add(node.val);\n } else if (currentCount > maxCount) {\n maxCount = currentCount;\n modes.clear();\n modes.add(node.val);\n }\n currentVal = node.val;\n\n inOrderTraversal(node.right);\n }\n}\n```\n``` C# []\npublic class Solution {\n private int? current_val = null;\n private int current_count = 0;\n private int max_count = 0;\n private List<int> modes = new List<int>();\n\n public int[] FindMode(TreeNode root) {\n in_order_traversal(root);\n return modes.ToArray();\n }\n\n private void in_order_traversal(TreeNode node) {\n if (node == null) return;\n\n in_order_traversal(node.left);\n\n current_count = (node.val == current_val) ? current_count + 1 : 1;\n if (current_count == max_count) {\n modes.Add(node.val);\n } else if (current_count > max_count) {\n max_count = current_count;\n modes.Clear();\n modes.Add(node.val);\n }\n current_val = node.val;\n\n in_order_traversal(node.right);\n }\n}\n```\n``` JavaScript []\n\nvar findMode = function(root) {\n let currentVal = null;\n let currentCount = 0;\n let maxCount = 0;\n let modes = [];\n\n function inOrderTraversal(node) {\n if (!node) return;\n\n inOrderTraversal(node.left);\n\n currentCount = (node.val === currentVal) ? currentCount + 1 : 1;\n if (currentCount === maxCount) {\n modes.push(node.val);\n } else if (currentCount > maxCount) {\n maxCount = currentCount;\n modes = [node.val];\n }\n currentVal = node.val;\n\n inOrderTraversal(node.right);\n }\n\n inOrderTraversal(root);\n return modes;\n};\n```\n``` PHP []\n\nclass Solution {\n private $currentVal;\n private $currentCount = 0;\n private $maxCount = 0;\n private $modes = [];\n\n /**\n * @param TreeNode $root\n * @return Integer[]\n */\n function findMode($root) {\n $this->inOrderTraversal($root);\n return $this->modes;\n }\n\n private function inOrderTraversal($node) {\n if ($node === null) return;\n\n $this->inOrderTraversal($node->left);\n\n $this->currentCount = ($node->val == $this->currentVal) ? $this->currentCount + 1 : 1;\n if ($this->currentCount == $this->maxCount) {\n $this->modes[] = $node->val;\n } else if ($this->currentCount > $this->maxCount) {\n $this->maxCount = $this->currentCount;\n $this->modes = [$node->val];\n }\n $this->currentVal = $node->val;\n\n $this->inOrderTraversal($node->right);\n }\n}\n```\n\n# Performance\n\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|------------|---------------------|-------------------|\n| Java | 0 | 43.7 |\n| Go | 6 | 6.0 |\n| Rust | 3 | 3.2 |\n| C++ | 10 | 24.4 |\n| PHP | 15 | 22.7 |\n| Python3 | 48 | 20.2 |\n| JavaScript | 68 | 48.4 |\n| C# | 140 | 46.3 |\n\n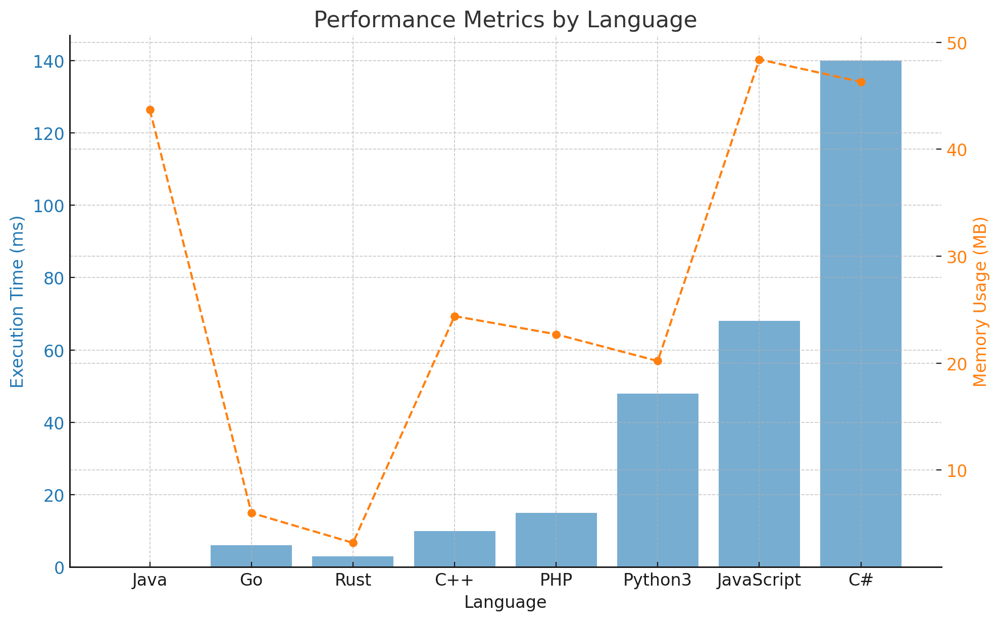\n\n\n# What did we learn?\n- The importance of in-order traversal in a BST when dealing with frequency or order-related questions.\n- How to effectively use Python\'s generator to make the code more Pythonic and readable.\n- The approach to count and find the mode by processing the nodes during the in-order traversal.
| 42
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
501. Find Mode in Binary Search Tree
|
find-mode-in-binary-search-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n res = []\n res_count = 0 \n curr = None\n curr_count = 0\n def traverse(node):\n if not node:\n return\n traverse(node.left)\n nonlocal res, res_count, curr, curr_count\n if node.val == curr:\n curr_count += 1\n else:\n curr = node.val\n curr_count = 1\n if curr_count > res_count:\n res = [curr]\n res_count = curr_count\n elif curr_count == res_count:\n res.append(node.val)\n traverse(node.right)\n traverse(root)\n return res\n```
| 1
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
Python || Easiest Solution
|
find-mode-in-binary-search-tree
| 0
| 1
|
# Intuition\nTo find the mode(s) in a binary search tree with duplicates, you can use an in-order traversal of the BST. \n\n# Approach\nDuring the traversal, you\'ll keep track of the current element and its count while comparing it with the previous element. If the count of the current element is greater than the count of the previous mode, you\'ll update the mode(s). If the count is equal to the count of the previous mode, you\'ll add the current element to the list of modes.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n def inorder_traversal(node):\n nonlocal prev_node , max_count,curr_count,modes\n if not node:\n return\n inorder_traversal(node.left)\n\n if node.val == prev_node:\n curr_count+=1\n else:\n curr_count=1\n if curr_count > max_count:\n max_count=curr_count\n modes=[node.val]\n elif curr_count==max_count:\n modes.append(node.val)\n prev_node=node.val\n inorder_traversal(node.right)\n \n prev_node=None\n max_count=0\n curr_count=0\n modes=[]\n inorder_traversal(root)\n return modes\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79**
| 1
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
Layman's Code in 🐍
|
find-mode-in-binary-search-tree
| 0
| 1
|
# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n # print(root)\n def treeToList(root):\n if not root:\n return []\n\n result = []\n \n def inorder(node):\n if node:\n inorder(node.left)\n result.append(node.val)\n inorder(node.right)\n inorder(root)\n return result\n a = treeToList(root)\n # print(a)\n return statistics.multimode(a)\n```
| 1
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
✅ Python3 | Recursion | 46ms | Beats 95% ✅
|
find-mode-in-binary-search-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nFirst we need to count every value in the tree, and then return a list of those that are tied for teh most occurences.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nRecursively traverse the tree, adding the value of each node to a Counter. Then we define an empty array, and iterate over every element in our Counter. For each element, if it occurred more times than those which we are saving so far, clear the list and save the new element. If it occurred the same number of times as those we are saving so far, then add the element to our list. Finally, if it occurred fewer times than those we are tracking then we disregard it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n$$O(n)$$, because every node in the tree must be traversed\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n$$O(n)$$, because in the worst case every element in the tree could be different, and ```counts``` could contain an entry for every val\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n counts = Counter()\n\n def recur(node):\n if not node:\n return\n counts[node.val] += 1\n recur(node.left)\n recur(node.right)\n\n recur(root)\n res = []\n maxCount = 0\n for i in counts:\n if counts[i] == maxCount:\n res.append(i)\n elif counts[i] > maxCount:\n maxCount = counts[i]\n res.clear()\n res.append(i)\n return res\n```
| 1
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
【Video】Give me 5 minutes - How we think about a solution - Why do we use inorder traversal?
|
find-mode-in-binary-search-tree
| 1
| 1
|
# Intuition\nTraverse ascending order.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/0i1Ze62pTuU\n\n\u25A0 Timeline of the video\n`0:04` Which traversal do you use for this question?\n`0:34` Properties of a Binary Search Tree\n`1:31` Key point of my solution code\n`3:09` How to write Inorder, Preorder, Postorder\n`4:08` Coding\n`7:13` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,908\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\nBefore I start to explain, seems like the follow up question says we can solve this question with $$O(1)$$ space, but in real interviews, Nobody will come up with the solution for 10 minutes, so I think $$O(n)$$ space is enough to pass the interview.\n\n### How we think about a solution\n\nWe know that we have 3 well known traversals. inorder, preorder and postorder.\n\n---\n\n\u25A0 Question\n\nWhich traversal do you use for this question?\n\n---\n\nThinking time...\n\n...\n\n...\n\n...\n\nMy answer is inorder.\n\n\n---\n\n\u2B50\uFE0F Points\n\nThe reason why `inorder` traversal is a good choice for this question is due to the properties of a Binary Search Tree (BST) and the fact that `inorder` traversal visits nodes in ascending order.\n\nProperties of a BST:\n\n1. A BST is a binary tree where each node has a value greater than all nodes in its left subtree and smaller than all nodes in its right subtree.\n\n2. `inorder` traversal of a BST visits the nodes in the tree in ascending order.\n\nFrom these properties, it follows that traversing a BST using `inorder` will make the same values appear consecutively, making it well-suited for finding the mode (most frequently occurring value). This is because the same values are consecutive, and you can update the count as you traverse, making it easy to identify the most frequently occurring value.\n\nThat\'s why `inorder` traversal aligns with the characteristics of a BST and is a suitable approach for efficiently finding the mode.\n\n---\n\n- How do you keep modes?\n\nSo now we decided to use inorder. I think the next question is "How do you keep modes?".\n\nThere is a possibility that we have multiple modes in BST, so we use `array` as a return values.\n\nWe don\'t know how many modes we have in BST, but at least we can say this.\n\n---\n\n\u2B50\uFE0F Points\n\nIf number of occurrence of current value is greater than current max occurrence count, we delete all previous modes and have only current value, because current value is the next max count. We don\'t need previous all numbers anymore.\n\n```\nmodes = [node.val]\n\nnode.val is current value\n```\n\nIf number of occurrence of current value is equal to current max occurrence count, we keep all previous modes and append current value, because the all values may be answers.\n\n```\nmodes.append(node.val)\n\nnode.val is current value\n```\n---\n\n- How to write inorder, preorder, postorder\n\nThis isn\'t directly related to this problem, but knowing how to write inorder, preorder, and postorder traversals might be helpful for other problems as well.\n\n```python []\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\ndef inorder(root):\n if not root:\n return []\n result = []\n result += inorder(root.left)\n result.append(root.val)\n result += inorder(root.right)\n return result\n\ndef preorder(root):\n if not root:\n return []\n result = []\n result.append(root.val)\n result += preorder(root.left)\n result += preorder(root.right)\n return result\n\ndef postorder(root):\n if not root:\n return []\n result = []\n result += postorder(root.left)\n result += postorder(root.right)\n result.append(root.val)\n return result\n```\n\nLet\'s focus on `result.append(root.val)`\n\n---\n\n\u2B50\uFE0F Points\n\nFor `Inorder`, we do something `between left and right`.\nFor `Preorder`, we do something `before left and right`.\nFor `Postorder`, we do something `after left and right`.\n\n---\n\nWe use inorder this time, so do the key point above between left and right.\nLet\'s see a real algorithm!\n\n\n### Algorithm Overview:\n\nThe algorithm finds the mode (the most frequently occurring value) in a binary search tree using an "inorder" traversal.\n\n### Detailed Explanation:\n\n1. Initialize an empty dictionary `counts` to store the count of each unique value in the tree. Initialize `max_count` to 0 to keep track of the maximum count, and initialize an empty list `modes` to store the modes.\n\n2. Define an `inorder` function that takes a `node` as its argument. This function performs an inorder traversal of the binary search tree.\n\n3. Inside the `inorder` function:\n - If the `node` is `None` (i.e., there are no more nodes to visit), return from the function.\n - Recursively call `inorder` on the left child of the current `node`, which explores the left subtree.\n \n4. Inside the `inorder` function (continued):\n - For the current `node`, update the `counts` dictionary to track the count of its value. If the value is not present in the dictionary, initialize its count to 1; otherwise, increment its count by 1.\n \n5. Inside the `inorder` function (continued):\n - Check if the count of the current `node`\'s value is greater than the `max_count`. If it is, update `max_count` to the new count, and set the `modes` list to contain only the current value (reset the modes list).\n \n6. Inside the `inorder` function (continued):\n - If the count of the current `node`\'s value is equal to the `max_count`, append the current value to the `modes` list (add it to the list of modes).\n \n7. Recursively call `inorder` on the right child of the current `node`, which explores the right subtree.\n\n8. Finally, call the `inorder` function on the `root` node to start the traversal of the binary search tree.\n\n9. Return the `modes` list, which contains the modes of the tree.\n\nIn summary, the algorithm uses an inorder traversal to count the occurrences of each value in the BST and keeps track of the maximum count and the modes as it traverses the tree. This approach efficiently finds the mode(s) in the given binary search tree.\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(N)$$\nN is the number of nodes in the binary search tree. This is because the algorithm performs an inorder traversal of the entire tree, visiting each node once.\n\n- Space complexity: $$O(N)$$\nIn the worst case (unbalanced tree), it is $$O(N)$$. Additionally, the algorithm uses space for the counts dictionary and the modes list, both of which have a space complexity of $$O(N)$$ in the worst case if all unique values in the tree are different.\n\nExample of unbalanced tree\n```\n1\n \\\n\u3000\u3000\u3000\u3000\u30002\n \\\n 3\n \\\n 4\n```\nNo left child. In this case, we return `[1,2,3,4]` which is $$O(N)$$.\n\n\n```python []\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n counts = {}\n max_count = 0\n modes = []\n\n def inorder(node):\n if not node:\n return\n inorder(node.left)\n\n nonlocal max_count, modes\n\n counts[node.val] = 1 + counts.get(node.val, 0)\n \n if counts[node.val] > max_count:\n max_count = counts[node.val]\n modes = [node.val]\n elif counts[node.val] == max_count:\n modes.append(node.val)\n\n inorder(node.right)\n\n inorder(root)\n\n return modes\n```\n```javascript []\nvar findMode = function(root) {\n const counts = {};\n let maxCount = 0;\n const modes = [];\n\n const inorder = function(node) {\n if (!node) {\n return;\n }\n\n inorder(node.left);\n\n const count = (counts[node.val] || 0) + 1;\n counts[node.val] = count;\n\n if (count > maxCount) {\n maxCount = count;\n modes.length = 0;\n modes.push(node.val);\n } else if (count === maxCount) {\n modes.push(node.val);\n }\n\n inorder(node.right);\n };\n\n inorder(root);\n\n return modes; \n};\n```\n```java []\nclass Solution {\n public int[] findMode(TreeNode root) {\n Map<Integer, Integer> counts = new HashMap<>();\n int[] maxCount = {0}; // Using an array to simulate nonlocal\n List<Integer> modes = new ArrayList<>();\n\n inorder(root, counts, maxCount, modes);\n\n int[] result = new int[modes.size()];\n for (int i = 0; i < modes.size(); i++) {\n result[i] = modes.get(i);\n }\n\n return result; \n }\n\n private void inorder(TreeNode node, Map<Integer, Integer> counts, int[] maxCount, List<Integer> modes) {\n if (node == null) {\n return;\n }\n\n inorder(node.left, counts, maxCount, modes);\n\n int count = counts.getOrDefault(node.val, 0) + 1;\n counts.put(node.val, count);\n\n if (count > maxCount[0]) {\n maxCount[0] = count;\n modes.clear();\n modes.add(node.val);\n } else if (count == maxCount[0]) {\n modes.add(node.val);\n }\n\n inorder(node.right, counts, maxCount, modes);\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> findMode(TreeNode* root) {\n unordered_map<int, int> counts;\n vector<int> modes;\n int maxCount = 0;\n\n inorder(root, counts, maxCount, modes);\n\n return modes; \n }\n\n void inorder(TreeNode* node, unordered_map<int, int>& counts, int& maxCount, vector<int>& modes) {\n if (node == nullptr) {\n return;\n }\n\n inorder(node->left, counts, maxCount, modes);\n\n int count = ++counts[node->val];\n\n if (count > maxCount) {\n maxCount = count;\n modes.clear();\n modes.push_back(node->val);\n } else if (count == maxCount) {\n modes.push_back(node->val);\n }\n\n inorder(node->right, counts, maxCount, modes);\n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-nodes-equal-to-average-of-subtree/solutions/4237404/video-give-me-10-minutes-how-we-think-about-a-solution-why-we-use-postorder-traversal/\n\nvideo\nhttps://youtu.be/MV6NpUXCfUU\n\n\u25A0 Timeline of the video\n`0:05` Which traversal do you use for this question?\n`1:55` How do you calculate information you need?\n`3:34` How to write Inorder, Preorder, Postorder\n`4:16` Coding\n`7:50` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-the-original-array-of-prefix-xor/solutions/4228796/video-give-me-5-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/ck4dJURKAlA\n\n\u25A0 Timeline of the video\n`0:05` Solution code with build-in function\n`0:06` quick recap of XOR calculation\n`0:28` Demonstrate how to solve the question\n`1:37` How you keep the original previous number\n`2:29` Continue to demonstrate how to solve the question\n`3:59` Coding\n`4:43` Time Complexity and Space Complexity
| 24
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
✅ Beats 95.48% 🔥 || Inorder Traversal 🚀
|
find-mode-in-binary-search-tree
| 1
| 1
|
\n\n# Intuition:\n**In this problem, we need to find the mode of the given BST. Mode is the element that occurs the most number of times in the given BST. We can solve this problem by using the inorder traversal of the BST. The inorder traversal of the BST gives us the elements in the sorted order. So, we can keep track of the previous element and the count of the current element. If the current element is equal to the previous element, we can increment the count. Otherwise, we can reset the count to 1. We can also keep track of the maximum count and the mode elements. If the current count is greater than the maximum count, we can reset the maximum count and the mode elements. If the current count is equal to the maximum count, we can append the current element to the mode elements. After the inorder traversal, we can return the mode elements.**\n\n# Algorithm:\n1. Initialize the mode elements, maximum count, previous element and the count of the previous element.\n2. Traverse the BST in the inorder fashion.\n3. If the previous element is None, set the previous element to the current element and set the count to 1.\n4. If the previous element is equal to the current element, increment the count.\n5. If the previous element is not equal to the current element, set the previous element to the current element and set the count to 1.\n6. If the count is greater than the maximum count, set the maximum count to the count and reset the mode elements to the current element.\n7. If the count is equal to the maximum count, append the current element to the mode elements.\n8. Return the mode elements.\n\n# Complexity Analysis:\n- Time Complexity: **O(N)**, where N is the number of nodes in the BST.\n- Space Complexity: **O(N)**, where N is the number of nodes in the BST.\n\n## Please UpVote \u2B06\uFE0F if this helps you\n\n# Code\n``` Python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n \n if root is None:\n return []\n \n self.mode = []\n self.max_count = 0\n self.prev = None\n self.count = 0\n \n self.inorder(root)\n \n return self.mode\n \n def inorder(self, root):\n \n if root is None:\n return\n \n self.inorder(root.left)\n \n if self.prev is None:\n self.prev = root.val\n self.count = 1\n elif self.prev == root.val:\n self.count += 1\n else:\n self.prev = root.val\n self.count = 1\n \n if self.count > self.max_count:\n self.max_count = self.count\n self.mode = [root.val]\n elif self.count == self.max_count:\n self.mode.append(root.val)\n \n self.inorder(root.right)\n```\n``` C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\nprivate:\n vector<int> mode;\n int max_count;\n int prev;\n int count;\n\npublic:\n vector<int> findMode(TreeNode* root) {\n if (root == NULL) {\n return mode;\n }\n\n mode.clear();\n max_count = 0;\n prev = -1;\n count = 0;\n\n inorder(root);\n\n return mode;\n }\n\n void inorder(TreeNode* root) {\n if (root == NULL) {\n return;\n }\n\n inorder(root->left);\n\n if (prev == -1) {\n prev = root->val;\n count = 1;\n } else if (prev == root->val) {\n count++;\n } else {\n prev = root->val;\n count = 1;\n }\n\n if (count > max_count) {\n max_count = count;\n mode = {root->val};\n } else if (count == max_count) {\n mode.push_back(root->val);\n }\n\n inorder(root->right);\n }\n};\n```\n``` Java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n private List<Integer> mode = new ArrayList<>();\n private int max_count = 0;\n private int prev = -1;\n private int count = 0;\n\n public int[] findMode(TreeNode root) {\n if (root == null) {\n return new int[0];\n }\n\n mode.clear();\n max_count = 0;\n prev = -1;\n count = 0;\n\n inorder(root);\n\n int[] result = new int[mode.size()];\n for (int i = 0; i < mode.size(); i++) {\n result[i] = mode.get(i);\n }\n\n return result;\n }\n\n private void inorder(TreeNode root) {\n if (root == null) {\n return;\n }\n\n inorder(root.left);\n\n if (prev == -1) {\n prev = root.val;\n count = 1;\n } else if (prev == root.val) {\n count++;\n } else {\n prev = root.val;\n count = 1;\n }\n\n if (count > max_count) {\n max_count = count;\n mode = new ArrayList<>();\n mode.add(root.val);\n } else if (count == max_count) {\n mode.add(root.val);\n }\n\n inorder(root.right);\n }\n}\n```\n``` JavaScript []\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @return {number[]}\n */\nvar findMode = function(root) {\n let mode = [];\n let maxCount = 0;\n let prev = -1;\n let count = 0;\n\n const inorder = function(node) {\n if (node === null) {\n return;\n }\n\n inorder(node.left);\n\n if (prev === -1) {\n prev = node.val;\n count = 1;\n } else if (prev === node.val) {\n count++;\n } else {\n prev = node.val;\n count = 1;\n }\n\n if (count > maxCount) {\n maxCount = count;\n mode = [node.val];\n } else if (count === maxCount) {\n mode.push(node.val);\n }\n\n inorder(node.right);\n };\n\n inorder(root);\n\n return mode;\n};\n```\n``` C# []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public int val;\n * public TreeNode left;\n * public TreeNode right;\n * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\npublic class Solution {\n List<int> mode = new List<int>();\n int maxCount = 0;\n int prev = -1;\n int count = 0;\n\n public int[] FindMode(TreeNode root) {\n InOrder(root);\n return mode.ToArray();\n }\n\n private void InOrder(TreeNode node) {\n if (node == null) return;\n\n InOrder(node.left);\n\n if (prev == -1) {\n prev = node.val;\n count = 1;\n } else if (prev == node.val) {\n count++;\n } else {\n prev = node.val;\n count = 1;\n }\n\n if (count > maxCount) {\n maxCount = count;\n mode.Clear();\n mode.Add(node.val);\n } else if (count == maxCount) {\n mode.Add(node.val);\n }\n\n InOrder(node.right);\n }\n}\n```\n``` TypeScript []\n/**\n * Definition for a binary tree node.\n * class TreeNode {\n * val: number\n * left: TreeNode | null\n * right: TreeNode | null\n * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n * }\n */\n\nfunction findMode(root: TreeNode | null): number[] {\n let mode: number[] = [];\n let maxCount = 0;\n let prev = -1;\n let count = 0;\n\n function inorder(node: TreeNode | null) {\n if (node === null) {\n return;\n }\n\n inorder(node.left);\n\n if (prev === -1) {\n prev = node.val;\n count = 1;\n } else if (prev === node.val) {\n count++;\n } else {\n prev = node.val;\n count = 1;\n }\n\n if (count > maxCount) {\n maxCount = count;\n mode = [node.val];\n } else if (count === maxCount) {\n mode.push(node.val);\n }\n\n inorder(node.right);\n }\n\n inorder(root);\n\n return mode;\n}\n```\n``` PHP []\n/**\n * Definition for a binary tree node.\n * class TreeNode {\n * public $val = null;\n * public $left = null;\n * public $right = null;\n * function __construct($val = 0, $left = null, $right = null) {\n * $this->val = $val;\n * $this->left = $left;\n * $this->right = $right;\n * }\n * }\n */\nclass Solution {\n\n /**\n * @param TreeNode $root\n * @return Integer[]\n */\n function findMode($root) {\n $this->mode = [];\n $this->maxCount = 0;\n $this->prev = null;\n $this->count = 0;\n \n $this->inOrder($root);\n \n return $this->mode;\n }\n \n function inOrder($node) {\n if ($node === null) {\n return;\n }\n\n $this->inOrder($node->left);\n\n if ($this->prev === null || $this->prev === $node->val) {\n $this->count++;\n } else {\n $this->count = 1;\n }\n\n if ($this->count > $this->maxCount) {\n $this->maxCount = $this->count;\n $this->mode = [$node->val];\n } elseif ($this->count === $this->maxCount) {\n $this->mode[] = $node->val;\n }\n\n $this->prev = $node->val;\n $this->inOrder($node->right);\n }\n}\n```\n``` Ruby []\n# Definition for a binary tree node.\n# class TreeNode\n# attr_accessor :val, :left, :right\n# def initialize(val = 0, left = nil, right = nil)\n# @val = val\n# @left = left\n# @right = right\n# end\n# end\n# @param {TreeNode} root\n# @return {Integer[]}\ndef find_mode(root)\n @mode = []\n @max_count = 0\n @prev = nil\n @count = 0\n \n in_order(root)\n \n return @mode\nend\n\ndef in_order(node)\n return if node.nil?\n\n in_order(node.left)\n\n if @prev.nil? || @prev == node.val\n @count += 1\n else\n @count = 1\n end\n\n if @count > @max_count\n @max_count = @count\n @mode = [node.val]\n elsif @count == @max_count\n @mode << node.val\n end\n\n @prev = node.val\n in_order(node.right)\nend\n```\n\n\n
| 16
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
EASIEST solution💯💯 || C++ || Java || Python || JavaScript || Python || Ruby
|
find-mode-in-binary-search-tree
| 1
| 1
|
\n```C++ []\nclass Solution {\npublic:\n unordered_map<int,int>mp;\n\n void isValid(TreeNode* root) {\n\n if(root==NULL) return;\n\n isValid(root->left);\n mp[root->val]++;\n isValid(root->right);\n\n }\n\n vector<int> findMode(TreeNode* root) {\n\n isValid(root);\n\n int maxi=0;\n for(auto it:mp){ //iterating in map\n if(it.second>maxi){ //it.second stores the frequency of elements\n maxi=it.second; // updating maxi variable with the highest frequency encountered\n }\n }\n vector<int>ans;\n for(auto it:mp){\n if(it.second==maxi){\n ans.push_back(it.first);\n }\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n private Map<Integer, Integer> mp = new HashMap<>();\n\n // Helper function to perform an in-order traversal and count the frequency of each value\n private void isValid(TreeNode root) {\n if (root == null) return;\n\n isValid(root.left); // Traverse left subtree\n mp.put(root.val, mp.getOrDefault(root.val, 0) + 1); // Update frequency count in the map\n isValid(root.right); // Traverse right subtree\n }\n\n // Main function to find the mode (most frequent elements)\n public int[] findMode(TreeNode root) {\n isValid(root); // Call the helper function to populate the frequency map\n\n int maxi = 0;\n // Find the maximum frequency encountered\n for (int value : mp.values()) {\n maxi = Math.max(maxi, value);\n }\n\n List<Integer> ans = new ArrayList<>();\n // Collect elements with the maximum frequency in the result list\n for (Map.Entry<Integer, Integer> entry : mp.entrySet()) {\n if (entry.getValue() == maxi) {\n ans.add(entry.getKey());\n }\n }\n\n // Convert the list to an array\n int[] result = new int[ans.size()];\n for (int i = 0; i < ans.size(); i++) {\n result[i] = ans.get(i);\n }\n\n return result;\n }\n}\n\n```\n```javascript []\nvar findMode = function(root) {\n // Initialize a Map to store the frequency of each value\n var frequencyMap = new Map();\n\n // Helper function to perform an in-order traversal and count the frequency of each value\n function isValid(node) {\n if (node === null) return;\n\n isValid(node.left); // Traverse left subtree\n frequencyMap.set(node.val, (frequencyMap.get(node.val) || 0) + 1); // Update frequency count in the map\n isValid(node.right); // Traverse right subtree\n }\n\n isValid(root); // Call the helper function to populate the frequency map\n\n let maxi = 0;\n // Find the maximum frequency encountered\n frequencyMap.forEach(value => {\n maxi = Math.max(maxi, value);\n });\n\n let ans = [];\n // Collect elements with the maximum frequency in the result list\n frequencyMap.forEach((value, key) => {\n if (value === maxi) {\n ans.push(key);\n }\n });\n\n return ans;\n};\n\n```\n\n```python []\nclass Solution:\n def __init__(self):\n self.mp = {}\n\n # Helper function to perform an in-order traversal and count the frequency of each value\n def isValid(self, root):\n if root is None:\n return\n\n self.isValid(root.left) # Traverse left subtree\n self.mp[root.val] = self.mp.get(root.val, 0) + 1 # Update frequency count in the dictionary\n self.isValid(root.right) # Traverse right subtree\n\n # Main function to find the mode (most frequent elements)\n def findMode(self, root):\n self.isValid(root) # Call the helper function to populate the frequency map\n\n maxi = 0\n # Find the maximum frequency encountered\n for value in self.mp.values():\n maxi = max(maxi, value)\n\n ans = []\n # Collect elements with the maximum frequency in the result list\n for key, value in self.mp.items():\n if value == maxi:\n ans.append(key)\n\n return ans\n\n```\n```ruby []\ndef find_mode(root)\n # Initialize a hash to store the frequency of each value\n frequency_map = {}\n\n # Helper function to perform an in-order traversal and count the frequency of each value\n def is_valid(node, frequency_map)\n return if node.nil?\n\n is_valid(node.left, frequency_map) # Traverse left subtree\n frequency_map[node.val] = (frequency_map[node.val] || 0) + 1 # Update frequency count in the hash\n is_valid(node.right, frequency_map) # Traverse right subtree\n end\n\n is_valid(root, frequency_map) # Call the helper function to populate the frequency map\n\n maxi = 0\n # Find the maximum frequency encountered\n frequency_map.each_value do |value|\n maxi = [maxi, value].max\n end\n\n ans = []\n # Collect elements with the maximum frequency in the result list\n frequency_map.each do |key, value|\n ans << key if value == maxi\n end\n\n ans\nend\n\n```\n
| 8
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
Python Clean O(1) Space
|
find-mode-in-binary-search-tree
| 0
| 1
|
```py\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n maxfreq = 0\n \n def dfs(node):\n if node:\n yield from dfs(node.left)\n yield node.val\n yield from dfs(node.right)\n \n for val, group in groupby(dfs(root)):\n freq = sum(1 for _ in group)\n maxfreq = max(maxfreq, freq)\n \n modes = []\n \n for val, group in groupby(dfs(root)):\n freq = sum(1 for _ in group)\n if freq == maxfreq:\n modes.append(val)\n \n return modes\n```
| 0
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
Really simple Python solution with explanation
|
find-mode-in-binary-search-tree
| 0
| 1
|
# Approach\n1. Get all the elements in the binary tree with `get_all`.\n2. Return the most common elements with `Counter.most_common()` + some filtering.\n\n# Code\n```\nfrom collections import Counter\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n ret = self.get_all(root)\n count_dict = Counter(ret).most_common()\n max_count = count_dict[0][1]\n return list(map(lambda y: y[0], filter(lambda x: x[1] == max_count, count_dict)))\n \n def get_all(self, root: Optional[TreeNode]) -> List[int]:\n ret = [root.val]\n if root.left:\n ret += self.get_all(root.left)\n if root.right:\n ret += self.get_all(root.right)\n return ret\n```
| 1
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
[Python3] Inorder traversal without HashMap
|
find-mode-in-binary-search-tree
| 0
| 1
|
```python3 []\nclass Solution:\n def findMode(self, root: Optional[TreeNode]) -> List[int]:\n res, prev, curStreak, maxStreak = [], None, 0, -1\n \n def dfs(node):\n if not node: return\n nonlocal prev, curStreak, maxStreak\n \n dfs(node.left)\n \n if node.val == prev:\n curStreak += 1\n else:\n prev = node.val\n curStreak = 1\n \n if curStreak == maxStreak:\n res.append(node.val)\n elif curStreak > maxStreak:\n res.clear()\n res.append(node.val)\n maxStreak = curStreak\n\n dfs(node.right)\n\n dfs(root)\n\n return res\n```
| 4
|
Given the `root` of a binary search tree (BST) with duplicates, return _all the [mode(s)](https://en.wikipedia.org/wiki/Mode_(statistics)) (i.e., the most frequently occurred element) in it_.
If the tree has more than one mode, return them in **any order**.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than or equal to** the node's key.
* The right subtree of a node contains only nodes with keys **greater than or equal to** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,null,2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
| null |
Day 54 || C++ || Priority_Queue || Easiest Beginner Friendly Sol
|
ipo
| 1
| 1
|
# Intuition of this Problem:\nThe problem asks us to maximize the total capital by selecting at most k distinct projects. We have a limited amount of initial capital, and each project has a minimum capital requirement and a pure profit. We need to choose the projects in such a way that we can complete at most k distinct projects, and the final maximized capital should be as high as possible.\n\nThe code uses a greedy approach to solve the problem. The basic idea is to sort the projects by the minimum capital required in ascending order. We start with the initial capital w and try to select k distinct projects from the sorted projects.(***Note : We sort the projects by their minimum capital required in ascending order because we want to consider the projects that we can afford with our current capital. By iterating over the sorted projects, we can ensure that we only consider the projects that have a minimum capital requirement less than or equal to our current capital.If we did not sort the projects, we would need to iterate over all the projects in each iteration to check if we can afford them. This would result in a time complexity of O(n^2) which is not efficient, especially if n is large.***)\n\nWe use a priority queue to store the profits of the available projects that we can start with the current capital. We also use a variable i to keep track of the next project that we can add to the priority queue.\n\nIn each iteration, we first add the profits of the available projects to the priority queue by iterating i until we find a project that requires more capital than our current capital. We then select the project with the highest profit from the priority queue, add its profit to our current capital, and remove it from the priority queue. If the priority queue is empty, we cannot select any more projects and break the loop.\n\nBy using a priority queue to select the project with the highest profit, we ensure that we select the most profitable project at each iteration. By iterating over the sorted projects, we ensure that we only consider the projects that we can afford with our current capital. By selecting at most k distinct projects, we ensure that we only select the most profitable projects that we can complete with our limited resources.\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create a vector of pairs "projects" to store the minimum capital required and pure profit of each project.\n2. Initialize a variable "n" to the size of the input "profits" vector.\n3. Sort the "projects" vector by the minimum capital required in ascending order.\n4. Initialize a variable "i" to 0 and a priority queue "maximizeCapital" to store the maximum profit we can get from a project.\n5. Loop k times and perform the following operations in each iteration:\n - a. While "i" is less than "n" and the minimum capital required for the project at index "i" is less than or equal to the current capital "w", push the profit of the project at index "i" to "maximizeCapital" and increment "i".\n - b. If "maximizeCapital" is empty, break out of the loop.\n - c. Add the maximum profit in "maximizeCapital" to "w" and pop it out of the priority queue.\n1. Return the final value of "w".\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n int n = profits.size();\n vector<pair<int, int>> projects(n);\n for (int i = 0; i < n; i++) {\n projects[i] = {capital[i], profits[i]};\n }\n //We sort the projects by their minimum capital required in ascending order because we want to consider the projects that we can afford with our current capital. By iterating over the sorted projects, we can ensure that we only consider the projects that have a minimum capital requirement less than or equal to our current capital.\n sort(projects.begin(), projects.end());\n int i = 0;\n priority_queue<int> maximizeCapital;\n while (k--) {\n //The condition projects[i].first <= w checks if the minimum capital requirement of the next project is less than or equal to our current capital w. If this condition is true, we can add the project to the priority queue because we have enough capital to start the project.\n //We use this condition to ensure that we only add the available projects that we can afford to the priority queue. By checking the minimum capital requirement of the next project before adding it to the priority queue, we can avoid adding projects that we cannot afford, and we can focus on selecting the most profitable project that we can afford with our current capital.\n //The loop while (i < n && projects[i].first <= w) runs until we add all the available projects that we can afford to the priority queue\n while (i < n && projects[i].first <= w) {\n maximizeCapital.push(projects[i].second);\n i++;\n }\n if (maximizeCapital.empty())\n break;\n w += maximizeCapital.top();\n maximizeCapital.pop();\n }\n return w;\n }\n};\n```\n```Java []\nclass Solution {\n public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {\n int n = profits.length;\n int[][] projects = new int[n][2];\n for (int i = 0; i < n; i++) {\n projects[i][0] = capital[i];\n projects[i][1] = profits[i];\n }\n Arrays.sort(projects, (a, b) -> Integer.compare(a[0], b[0]));\n int i = 0;\n PriorityQueue<Integer> maximizeCapital = new PriorityQueue<>(Collections.reverseOrder());\n while (k-- > 0) {\n while (i < n && projects[i][0] <= w) {\n maximizeCapital.offer(projects[i][1]);\n i++;\n }\n if (maximizeCapital.isEmpty()) {\n break;\n }\n w += maximizeCapital.poll();\n }\n return w;\n }\n}\n\n```\n```Python []\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n n = len(profits)\n projects = [(capital[i], profits[i]) for i in range(n)]\n projects.sort()\n i = 0\n maximizeCapital = []\n while k > 0:\n while i < n and projects[i][0] <= w:\n heapq.heappush(maximizeCapital, -projects[i][1])\n i += 1\n if not maximizeCapital:\n break\n w -= heapq.heappop(maximizeCapital)\n k -= 1\n return w\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(N log N + K log N) = O(N log N)**, where N is the number of projects and K is the number of projects that we can select. Sorting the "projects" vector takes O(N log N) time, and adding and removing elements from the priority queue takes O(log N) time. The while loop that adds the available projects to the priority queue runs at most N times, and the for loop that selects the projects to complete runs K times.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(N + N) = O(N)**, where N is the number of projects. The space is used to store the "projects" vector. The priority queue used in the solution has a maximum size of N,\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->
| 305
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
Python3 👍||⚡97/97 T/M beats, only 13 lines 🔥|| Two heap || Optimization Simple explain ||
|
ipo
| 0
| 1
|
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nYou need two heap to solve this problem.\nFirst heap is used to pick projects until appear a project can\'t do at k steps.\nSecend heap stored all be sorted profit of executable projects.\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n if w >= max(capital):\n return w + sum(nlargest(k, profits))\n cap_pro,executable_pro = [],[]\n for p,c in zip(profits,capital): heapq.heappush(cap_pro,(c,-p)) # sorted by capital\n for _ in range(k):\n while cap_pro: # add profit to executable_pro until \n cur_project = heapq.heappop(cap_pro) # capital of cur_project big than w\n if cur_project[0]>w:\n heapq.heappush(cap_pro,cur_project) # you need put it back to unexecutable heap \n break # because cap_pro be sorted so you can break.\n heapq.heappush(executable_pro,cur_project[1])\n if executable_pro: w += -heapq.heappop(executable_pro) # add the max profit of executable project \n return w\n\n\n```
| 1
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
[Python] sorting first, Daily Challenge Feb., Day 23
|
ipo
| 0
| 1
|
# Intuition\nit\'s hard to deal with profits and capital at same time, we can sort one of them and see if we can gain benefits from it.\n\nsince we only can do projects whose capital is lower than ours, it\'s intuitively that we can try to sort projects by capital.\n\nthen, we can iterate through all the projects whose capital is `<=` ours and choose one with maximum profits\n\napparently, we can use **Max Heap** to help us find maximum profit one.\n\nnow, our core logic is clear.\n\n1. sort project with capital\n2. throw all the projects whose capital is lower than or equal to our capital to max heap, and pick maximum profit one\n3. repeat second step until we choose at most `k` projects\n\n# Complexity\n- Time complexity:\n$$O(nlogn + klogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n n = len(profits)\n projects = []\n for i in range(n):\n projects.append((capital[i], profits[i]))\n projects.sort()\n\n currCap = w\n i = 0\n candidates = []\n while k:\n while i < n and projects[i][0] <= currCap:\n heapq.heappush(candidates, -projects[i][1])\n i += 1\n\n if candidates:\n currCap += -heapq.heappop(candidates)\n k -= 1\n return currCap\n```
| 1
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
Python Two Heaps
|
ipo
| 0
| 1
|
The strategy is greedy.\n1. Put all the profits you can pick with current w in a bag\n2. Pick the max profit from the bag\n```\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n \n heap1 = [(c, -p) for c, p in zip(capital, profits)]\n heap2 = []\n heapify(heap1)\n for _ in range(k):\n while heap1 and heap1[0][0] <= w:\n heappush(heap2, heappop(heap1)[1])\n w += -heappop(heap2) if heap2 else 0\n return w\n\n```
| 1
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
🚀Simplest Solution🚀 Beginner Friendly||🔥Priority Queue||🔥C++|| Python3🔥
|
ipo
| 0
| 1
|
# Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful\n```\n\n# Intuition\nExplanation\nThis code will first create a vector of pairs containing the capital and profits of each project. It will then sort this vector based on the capital required for each project. Then, it will use a priority queue to store the profits of the projects that can be completed with the available capital.\n\nThe code will then iterate k times and in each iteration, it will check for any projects that can be completed with the current capital and add their profits to the priority queue. It will then pop the top element from the priority queue (which will be the project with the highest profit) and add its profit to the current capital.\n\nFinally, the function will return the final capital after completing k projects.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Using Priority Queue\n Example\n k = 2, w = 0, profits = [1,2,3], capital = [0,1,1]\n \nExplanation: \nSince your initial capital is 0, you can only start the project indexed 0.\nAfter finishing it you will obtain profit 1 and your capital becomes 1.\nWith capital 1, you can either start the project indexed 1 or the project indexed 2.\nSo, we push both projext indexed 1 and the project indexed 2 into priority queue.\nSince you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital as it is at the **Top** of priority queue.\nTherefore, output the final maximized capital, which is 0 + 1 + 3 = 4.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: **O(n log n + k log n)**, where n is the number of projects. This is because the algorithm sorts the vector of pairs in O(n log n) time, and performs up to k iterations of a loop that may involve up to n operations (adding a potential profit to the max heap) and one pop operation on the max heap, which takes O(log n) time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n ^ 2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution\n{\npublic:\n int findMaximizedCapital(int k, int w, vector<int> &profits, vector<int> &capital)\n {\n int n = profits.size();\n vector<pair<int, int>> projects;\n for (int i = 0; i < n; i++)\n projects.push_back({capital[i], profits[i]});\n\n sort(projects.begin(), projects.end());\n priority_queue<int> pq;\n int i = 0, j = 0;\n while (k--)\n {\n while (i < n && projects[i].first <= w)\n {\n pq.push(projects[i++].second);\n }\n if (pq.empty())\n break;\n w += pq.top();\n pq.pop();\n }\n return w;\n }\n};\n```\n```python []\nimport heapq\n\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n n = len(profits)\n projects = [(capital[i], profits[i]) for i in range(n)]\n projects.sort()\n pq = []\n i = 0\n for _ in range(k):\n while i < n and projects[i][0] <= w:\n heapq.heappush(pq, -projects[i][1])\n i += 1\n if not pq:\n break\n w -= heapq.heappop(pq)\n return w\n```\n\n\n```\n Give a \uD83D\uDC4D. It motivates me alot\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/)
| 17
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
Python short and clean. Greedy. Two heaps (PriorityQueues).
|
ipo
| 0
| 1
|
# Approach\nTLDR; Same as [Official solution](https://leetcode.com/problems/ipo/solutions/2959870/ipo/), except another heap is used instead of sorting the projects.\n\n# Complexity\n- Time complexity: $$O(n * log(n))$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is the number of projects`.\n\n# Code\n```python\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: list[int], capital: list[int]) -> int:\n pool = list(zip(capital, profits)); heapify(pool)\n available = []\n\n cap = w\n for _ in range(k):\n while pool and pool[0][0] <= cap:\n _, p = heappop(pool)\n heappush(available, -p)\n if not available: break\n cap += -heappop(available)\n return cap\n\n\n```
| 2
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
🔥🔥🔥 Heap + Greedy Solution (Beats 99.69%) 🔥Python 3🔥
|
ipo
| 0
| 1
|
\n# Code\n```\nfrom heapq import heappush, heappop, nlargest\n\n\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n if w >= max(capital):\n return w + sum(nlargest(k, profits))\n \n projects = [[capital[i],profits[i]] for i in range(len(profits))]\n projects.sort(key=lambda x: x[0])\n \n heap = []\n \n for i in range(k):\n while projects and projects[0][0] <= w:\n heappush(heap, -1*projects.pop(0)[1])\n \n if not heap:\n break\n p = -heappop(heap)\n w += p\n return w\n```\n\n\n### If helpful, plz upvote :)
| 9
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
Clean Example🔥🔥|| Full Explanation✅|| Priority Queue✅|| C++|| Java|| Python3
|
ipo
| 1
| 1
|
# Intuition :\n- Here, We have to find maximum profit that can be achieved by selecting at most k projects to invest in, given an initial capital of W, a set of Profits and Capital requirements for each project.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- Here we are using two priority queues, a minHeap and a maxHeap. \n- The minHeap is used to keep track of all available projects sorted by their capital requirements in ascending order. \n- The maxHeap is used to keep track of all available projects that have capital requirements less than or equal to W, sorted by their profits in descending order.\n- Then iteratively select k projects to invest in, by removing projects from the minHeap and adding them to the maxHeap as long as their capital requirements are less than or equal to W. \n- Once k projects have been selected, terminate and return the total capital available, which is equal to the initial capital plus the sum of profits of the selected projects\n<!-- Describe your approach to solving the problem. -->\n\n# Explanation to Approach :\n- See, In this Problem you have a certain amount of money and a list of projects you can invest in. Each project requires some money to start and will give you a profit. You want to invest in the projects that will give you the most profit without running out of money.\n- So we are using two Priority Queues, one for all the projects sorted by their capital requirements and another for the projects you can currently invest in sorted by their profits. \n- Then go through the capital-sorted list and add any projects to the investable list that you can currently afford. \n- Do this until you have invested in the desired number of projects or you can\'t invest in any more.\n- Then return the total amount of money you have after investing in the projects.\n\n# Explanation with an Example :\n```\nSuppose you have $W = 50 to invest, and there are five projects available\nProject\t Capital Required\t Profit\n P1\t 10\t 25\n P2\t 20\t 30\n P3\t 30\t 10\n P4\t 40\t 50\n P5\t 50\t 5\n\nThe goal is to choose a maximum of k projects, given a budget of W, to maximize the profit.\n\nIf k is 3, then the optimal solution is to invest in projects P1, P2, and P4, which have a total capital requirement of 70 and a total profit of 105.\n\n```\n# Calling the findMaximizedCapital method with the following arguments:\n```\nint k = 3;\nint W = 50;\nint[] Profits = {25, 30, 10, 50, 5};\nint[] Capital = {10, 20, 30, 40, 50};\n\nSolution s = new Solution();\nint result = s.findMaximizedCapital(k, W, Profits, Capital);\n\n```\n# Here is how it will work with the above values :\n- Here\'s how the solution works:\n- The code initializes two priority queues, minHeap and maxHeap, and adds all the projects to the minHeap queue, which sorts the projects by their capital requirements in ascending order.\n- The code then iterates k times and selects the projects to invest in. In each iteration, the code checks the projects in minHeap and adds the projects that you can afford to maxHeap, which sorts the projects by their profits in descending order. \n- The code continues to add projects to maxHeap until all affordable projects have been added.\n- After adding projects to maxHeap, the code checks if maxHeap is empty, which means that there are no more affordable projects to invest in. If maxHeap is empty, the code breaks the loop and returns the current amount of money you have left.\n- If maxHeap is not empty, the code selects the project with the highest profit from maxHeap, invests in it, and updates the current amount of money you have left. It then removes the selected project from maxHeap.\n- The code repeats steps 2-4 until k projects have been selected or maxHeap is empty.\n- The code returns the current amount of money you have left, which represents the maximum profit that can be achieved by selecting at most k projects.\n- In this example, the code will iterate three times, selecting projects P1, P2, and P4 to invest in. After investing in these projects, you will have 105 left, which is the maximum profit that can be achieved by selecting at most 3 projects with an initial budget of $50.\n\n# Complexity :\n- Time complexity : O(nlogn)\n- Space complexity : O(n)\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n\n# Codes [C++ |Java |Python3] :\n```C++ []\nstruct T {\n int pro;\n int cap;\n T(int pro, int cap) : pro(pro), cap(cap) {}\n};\n\nclass Solution {\n public:\n int findMaximizedCapital(int k, int W, vector<int>& Profits,\n vector<int>& Capital) {\n auto compareC = [](const T& a, const T& b) { return a.cap > b.cap; };\n auto compareP = [](const T& a, const T& b) { return a.pro < b.pro; };\n priority_queue<T, vector<T>, decltype(compareC)> minHeap(compareC);\n priority_queue<T, vector<T>, decltype(compareP)> maxHeap(compareP);\n\n for (int i = 0; i < Capital.size(); ++i)\n minHeap.emplace(Profits[i], Capital[i]);\n\n while (k--) {\n while (!minHeap.empty() && minHeap.top().cap <= W)\n maxHeap.push(minHeap.top()), minHeap.pop();\n if (maxHeap.empty())\n break;\n W += maxHeap.top().pro, maxHeap.pop();\n }\n\n return W;\n }\n};\n```\n```Java []\nclass T {\n public int pro;\n public int cap;\n public T(int pro, int cap) {\n this.pro = pro;\n this.cap = cap;\n }\n}\n\nclass Solution \n{\n public int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) \n {\n Queue<T> minHeap = new PriorityQueue<>((a, b) -> a.cap - b.cap);\n Queue<T> maxHeap = new PriorityQueue<>((a, b) -> b.pro - a.pro);\n\n for (int i = 0; i < Capital.length; ++i)\n minHeap.offer(new T(Profits[i], Capital[i]));\n\n while (k-- > 0) {\n while (!minHeap.isEmpty() && minHeap.peek().cap <= W)\n maxHeap.offer(minHeap.poll());\n if (maxHeap.isEmpty())\n break;\n W += maxHeap.poll().pro;\n }\n\n return W;\n }\n}\n```\n```Python3 []\nimport heapq\nfrom typing import List\n\nclass T:\n def __init__(self, pro, cap):\n self.pro = pro\n self.cap = cap\n \n def __lt__(self, other):\n return self.cap < other.cap\n\nclass Solution:\n def findMaximizedCapital(self, k: int, W: int, Profits: List[int], Capital: List[int]) -> int:\n minHeap = []\n maxHeap = []\n\n for i in range(len(Capital)):\n heapq.heappush(minHeap, T(Profits[i], Capital[i]))\n\n while k > 0:\n while minHeap and minHeap[0].cap <= W:\n t = heapq.heappop(minHeap)\n heapq.heappush(maxHeap, (-t.pro, t.cap))\n if not maxHeap:\n break\n p, c = heapq.heappop(maxHeap)\n W -= p\n k -= 1\n\n return W\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n
| 35
|
Suppose LeetCode will start its **IPO** soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the **IPO**. Since it has limited resources, it can only finish at most `k` distinct projects before the **IPO**. Help LeetCode design the best way to maximize its total capital after finishing at most `k` distinct projects.
You are given `n` projects where the `ith` project has a pure profit `profits[i]` and a minimum capital of `capital[i]` is needed to start it.
Initially, you have `w` capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
Pick a list of **at most** `k` distinct projects from given projects to **maximize your final capital**, and return _the final maximized capital_.
The answer is guaranteed to fit in a 32-bit signed integer.
**Example 1:**
**Input:** k = 2, w = 0, profits = \[1,2,3\], capital = \[0,1,1\]
**Output:** 4
**Explanation:** Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
**Example 2:**
**Input:** k = 3, w = 0, profits = \[1,2,3\], capital = \[0,1,2\]
**Output:** 6
**Constraints:**
* `1 <= k <= 105`
* `0 <= w <= 109`
* `n == profits.length`
* `n == capital.length`
* `1 <= n <= 105`
* `0 <= profits[i] <= 104`
* `0 <= capital[i] <= 109`
| null |
Solution
|
next-greater-element-ii
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n stack<int> stk;\n vector<int> result(n);\n for(int i = 2 * n - 1; i >= 0; i--){\n while(!stk.empty() && stk.top() <= nums[i % n]) stk.pop();\n result[i % n] = stk.empty() ? -1 : stk.top();\n stk.push(nums[i % n]);\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n \n ans = [-1] * len(nums)\n stack = []\n \n for idx, num in enumerate(nums):\n \n while stack and nums[stack[-1]] < num:\n ans[stack.pop()] = num\n \n stack.append(idx)\n \n for num in nums:\n while stack and nums[stack[-1]] < num:\n ans[stack.pop()] = num\n \n return ans\n```\n\n```Java []\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int globalMax = Integer.MIN_VALUE;\n for (int i = 0; i < nums.length; i++) {\n globalMax = Math.max(globalMax, nums[i]);\n }\n int[] result = new int[nums.length];\n int nextMaxLast = nums[nums.length - 1];\n for (int i = 0; i < nums.length - 1; i++) {\n if (nums[i] > nums[nums.length - 1]) {\n nextMaxLast = nums[i];\n break;\n }\n }\n if (nextMaxLast == nums[nums.length - 1]) {\n result[nums.length - 1] = -1;\n } else {\n result[nums.length - 1] = nextMaxLast;\n }\n for (int i = nums.length - 2; i >= 0; i--) {\n if (nums[i] == globalMax) {\n result[i] = -1;\n } else if (nums[i + 1] > nums[i]) {\n result[i] = nums[i + 1];\n } else if (result[i + 1] > nums[i]) {\n result[i] = result[i + 1];\n } else {\n boolean hasFilled = false;\n for (int j = i + 2; j < result.length; j++) {\n if (result[j] > nums[i]) {\n result[i] = result[j];\n hasFilled = true;\n break;\n }\n }\n if (!hasFilled) {\n for (int j = 0; j < i; j++) {\n if (nums[j] > nums[i]) {\n result[i] = nums[j];\n break;\n }\n }\n }\n }\n }\n return result;\n }\n}\n```\n
| 1
|
Given a circular integer array `nums` (i.e., the next element of `nums[nums.length - 1]` is `nums[0]`), return _the **next greater number** for every element in_ `nums`.
The **next greater number** of a number `x` is the first greater number to its traversing-order next in the array, which means you could search circularly to find its next greater number. If it doesn't exist, return `-1` for this number.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[2,-1,2\]
Explanation: The first 1's next greater number is 2;
The number 2 can't find next greater number.
The second 1's next greater number needs to search circularly, which is also 2.
**Example 2:**
**Input:** nums = \[1,2,3,4,3\]
**Output:** \[2,3,4,-1,4\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
| null |
🔥[Python 3] Monotonic stack 2 traversal approaches
|
next-greater-element-ii
| 0
| 1
|
## Iteration from start to end:\n```python3\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack, L = [], len(nums)\n res = [-1] * L\n\n for i in range(L*2):\n idx = i % L\n while stack and nums[stack[-1]] < nums[idx]:\n res[stack.pop()] = nums[idx]\n stack.append(idx)\n return res\n```\n## Iteration from end to start:\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack, L = [], len(nums)\n res = [-1] * L\n\n for i in reversed(range(L * 2 - 1)):\n idx = i % L\n while stack and stack[-1] <= nums[idx]:\n stack.pop()\n res[idx] = stack[-1] if stack else -1\n stack.append(nums[idx])\n \n return res\n```\n\n
| 4
|
Given a circular integer array `nums` (i.e., the next element of `nums[nums.length - 1]` is `nums[0]`), return _the **next greater number** for every element in_ `nums`.
The **next greater number** of a number `x` is the first greater number to its traversing-order next in the array, which means you could search circularly to find its next greater number. If it doesn't exist, return `-1` for this number.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[2,-1,2\]
Explanation: The first 1's next greater number is 2;
The number 2 can't find next greater number.
The second 1's next greater number needs to search circularly, which is also 2.
**Example 2:**
**Input:** nums = \[1,2,3,4,3\]
**Output:** \[2,3,4,-1,4\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
| null |
Python Easy Solution
|
base-7
| 0
| 1
|
# Code\n```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n if num==0:\n return "0"\n res=""\n flg=0\n if num<0:\n flg=1\n num=abs(num)\n while(num>0):\n res+=str(num%7)\n num//=7\n if flg==1:\n res+="-"\n return res[::-1]\n```
| 1
|
Given an integer `num`, return _a string of its **base 7** representation_.
**Example 1:**
**Input:** num = 100
**Output:** "202"
**Example 2:**
**Input:** num = -7
**Output:** "-10"
**Constraints:**
* `-107 <= num <= 107`
| null |
✅✅✅ Faster than 98% | Easy to understand
|
base-7
| 0
| 1
|
```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n if num==0: return "0"\n a=\'\'\n if num<0:\n num=-num\n a = \'-\'\n base7 = \'\'\n while num>0:\n base7+=str(num%7)\n num = num//7\n return a+base7[::-1]\n```
| 1
|
Given an integer `num`, return _a string of its **base 7** representation_.
**Example 1:**
**Input:** num = 100
**Output:** "202"
**Example 2:**
**Input:** num = -7
**Output:** "-10"
**Constraints:**
* `-107 <= num <= 107`
| null |
Solution
|
base-7
| 1
| 1
|
```C++ []\nclass Solution {\n public:\n string convertToBase7(int num) {\n if (num < 0)\n return "-" + convertToBase7(-num);\n if (num < 7)\n return to_string(num);\n return convertToBase7(num / 7) + to_string(num % 7);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def convertToBase7(self, n: int) -> str:\n num, s = abs(n), \'\'\n while num:\n num, remain = divmod(num,7)\n s = str(remain) + s\n return "-" * (n < 0) + s or "0"\n```\n\n```Java []\nclass Solution {\n public String convertToBase7(int num) {\n return Integer.toString(num, 7);\n }\n}\n```\n
| 2
|
Given an integer `num`, return _a string of its **base 7** representation_.
**Example 1:**
**Input:** num = 100
**Output:** "202"
**Example 2:**
**Input:** num = -7
**Output:** "-10"
**Constraints:**
* `-107 <= num <= 107`
| null |
Python 3 || 7 lines, modular arithmetic || T/M: 100% / 84%
|
base-7
| 0
| 1
|
```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n\n if num == 0: return \'0\'\n\n ans, n = \'\', abs(num)\n\n while n:\n n, m = divmod(n,7)\n ans+=str(m)\n\n if num < 0: ans+= \'-\'\n\n return ans[::-1]\n```\n[https://leetcode.com/problems/base-7/submissions/587231651/](http://)\n\nI could be wrong, but I think that time complexity is *O*(log*N*) and space complexity is *O*(log*N*), in which *N* ~`num`.
| 4
|
Given an integer `num`, return _a string of its **base 7** representation_.
**Example 1:**
**Input:** num = 100
**Output:** "202"
**Example 2:**
**Input:** num = -7
**Output:** "-10"
**Constraints:**
* `-107 <= num <= 107`
| null |
504: Solution with step by step explanation
|
base-7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the input number is 0, return "0" in this case.\n2. Initialize a flag to keep track of whether the number is negative or not.\n3. Convert the input number to a positive integer if it\'s negative by taking the absolute value.\n4. Initialize an empty string variable to store the base 7 representation of the number.\n5. Loop until the input number becomes 0.\n6. At each iteration of the loop, compute the remainder when the input number is divided by 7.\n7. Add the remainder to the base 7 representation string variable.\n8. Update the input number to be the quotient when it\'s divided by 7.\n9. If the original input number was negative, add a \'-\' sign to the base 7 representation.\n10. Return the base 7 representation.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n # Handle the edge case where num is 0\n if num == 0:\n return "0"\n \n # Initialize a flag to keep track of whether num is negative or not\n is_negative = num < 0\n \n # Convert num to positive if it\'s negative\n if is_negative:\n num = -num\n \n # Initialize a variable to keep track of the base 7 representation\n base_7 = ""\n \n # Loop until num becomes 0\n while num > 0:\n # Compute the remainder when num is divided by 7\n remainder = num % 7\n \n # Add the remainder to the base 7 representation\n base_7 = str(remainder) + base_7\n \n # Update num to be the quotient when it\'s divided by 7\n num //= 7\n \n # If num was originally negative, add a \'-\' sign to the base 7 representation\n if is_negative:\n base_7 = \'-\' + base_7\n \n # Return the base 7 representation\n return base_7\n\n```
| 4
|
Given an integer `num`, return _a string of its **base 7** representation_.
**Example 1:**
**Input:** num = 100
**Output:** "202"
**Example 2:**
**Input:** num = -7
**Output:** "-10"
**Constraints:**
* `-107 <= num <= 107`
| null |
EFFICIENT PYTHON SOLUTION
|
base-7
| 0
| 1
|
Given an integer num, return a string of its base 7 representation.\n\n \n# Code\n```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n \n ans=""\n temp=num\n num = abs(num)\n while(num>0):\n ans+=str(num%7)\n num//=7\n neg_case="-"+ans[::-1]\n return ans[::-1] if temp>0 else "0" if temp==0 else neg_case\n\n```
| 2
|
Given an integer `num`, return _a string of its **base 7** representation_.
**Example 1:**
**Input:** num = 100
**Output:** "202"
**Example 2:**
**Input:** num = -7
**Output:** "-10"
**Constraints:**
* `-107 <= num <= 107`
| null |
python3 code
|
relative-ranks
| 0
| 1
|
\n\n# Approach\nThe approach of the code is to assign medals to the players based on their scores. The code first creates a copy of the scores list and then modifies it by replacing the top three scores with \'Gold Medal\', \'Silver Medal\', and \'Bronze Medal\'. The code then sorts the copy of the scores list in descending order and assigns ranks to the remaining scores. Finally, it returns the modified scores list with medals and ranks.\n\n\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n import copy\n w = copy.deepcopy(score)\n l=[]\n m = 0\n if(len(score)==1):\n c = max(score)\n for i in range(len(w)):\n if(w[i]==c):\n w[i] = \'Gold Medal\'\n return w\n elif(len(score)==2):\n c = max(score)\n for i in range(len(w)):\n if(w[i]==c):\n w[i] = \'Gold Medal\'\n score.remove(c) \n c = max(score)\n for i in range(len(w)):\n if(w[i]==c):\n w[i]= \'Silver Medal\'\n c = max(score) \n return w\n else:\n c = max(score)\n for i in range(len(w)):\n if(w[i]==c):\n w[i] = \'Gold Medal\'\n score.remove(c) \n c = max(score)\n for i in range(len(w)):\n if(w[i]==c):\n w[i]= \'Silver Medal\'\n score.remove(c) \n c = max(score)\n for i in range(len(w)):\n if(w[i]==c):\n w[i]=\'Bronze Medal\'\n score.remove(c)\n u = sorted([i for i in w if type(i)==int],reverse = True)\n for i in range(len(w)):\n if type(w[i])==int:\n r = u.index(w[i])+4\n w[i] = str(r)\n return w\n```
| 1
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
Readable Python solution
|
relative-ranks
| 0
| 1
|
\n\n# Code\n```\nclass Solution:\n def findRelativeRanks(self, nums: List[int]) -> List[str]:\n d = defaultdict(int)\n place = ["Gold Medal", "Silver Medal", "Bronze Medal"]\n n = len(nums)\n a = [" "]*n\n for i in range(n): d[nums[i]] = i\n nums.sort(reverse=True)\n\n for i in range(n):\n if i < 3:\n a[d[nums[i]]] = place[i] \n else:\n a[d[nums[i]]] = str(i+1)\n \n return a\n```
| 1
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
Solution
|
relative-ranks
| 1
| 1
|
```C++ []\nclass Solution {\n public:\n vector<string> findRelativeRanks(vector<int>& nums) {\n const int n = nums.size();\n vector<string> ans(n);\n vector<int> indices(n);\n\n iota(begin(indices), end(indices), 0);\n\n sort(begin(indices), end(indices),\n [&](const int a, const int b) { return nums[a] > nums[b]; });\n\n for (int i = 0; i < n; ++i)\n if (i == 0)\n ans[indices[0]] = "Gold Medal";\n else if (i == 1)\n ans[indices[1]] = "Silver Medal";\n else if (i == 2)\n ans[indices[2]] = "Bronze Medal";\n else\n ans[indices[i]] = to_string(i + 1);\n\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n d = {}\n score_o = score[:]\n\n score = sorted(score_o,reverse=True)\n for i, v in enumerate(score):\n d[v] = str(i + 1)\n ma = {"1": "Gold Medal", "2": "Silver Medal", "3": "Bronze Medal"}\n result = []\n for v in score_o:\n r = d[v]\n if r in ma:\n\n result.append(ma[r])\n else:\n result.append(d[v])\n return result\n```\n\n```Java []\nclass Solution {\n public String[] findRelativeRanks(int[] score) {\n int[] nums=score;\n String[] result = new String[nums.length];\n int max = 0;\n for (int i : nums) {\n if (i > max) max = i;\n }\n int[] hash = new int[max + 1];\n for (int i = 0; i < nums.length; i++) {\n hash[nums[i]] = i + 1;\n }\n int place = 1;\n for (int i = hash.length - 1; i >= 0; i--) {\n if (hash[i] != 0) {\n if (place == 1) {\n result[hash[i] - 1] = "Gold Medal";\n } else if (place == 2) {\n result[hash[i] - 1] = "Silver Medal";\n } else if (place == 3) {\n result[hash[i] - 1] = "Bronze Medal";\n } else {\n result[hash[i] - 1] = String.valueOf(place);\n }\n place++;\n }\n }\n return result;\n }\n}\n```\n
| 1
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
Simpler solution with explanation
|
relative-ranks
| 0
| 1
|
\n\n# Code\n```\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n score_positions = {score[i]: i for i in range(len(score))}\n \n # Sort the scores in descending order\n sorted_scores = sorted(score, reverse=True)\n \n # Create a dictionary to store the ranks\n ranks = {}\n \n # Assign ranks based on the sorted order\n for i in range(len(sorted_scores)):\n if i == 0:\n ranks[score_positions[sorted_scores[i]]] = "Gold Medal"\n elif i == 1:\n ranks[score_positions[sorted_scores[i]]] = "Silver Medal"\n elif i == 2:\n ranks[score_positions[sorted_scores[i]]] = "Bronze Medal"\n else:\n ranks[score_positions[sorted_scores[i]]] = str(i + 1)\n \n # Create the final result list based on the original order of scores\n result = [ranks[i] for i in range(len(score))]\n \n return result\n\n \n```
| 1
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
🔥 [Python 3] 2 solutions: Heap and Sort
|
relative-ranks
| 0
| 1
|
# Sorting:\n```\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n rank = ["Gold Medal", "Silver Medal", "Bronze Medal"] + list(map(str, range(4, len(score) + 1)))\n place = sorted(score, reverse = True)\n d = dict(zip(place, rank))\n\n return [d.get(s) for s in score]\n\n```\n# Heap:\n```\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n maxHeap = []\n for i, s in enumerate(score):\n heappush(maxHeap, (-s, i))\n \n res = [0] * len(score)\n place = 1\n while maxHeap:\n pos = heappop(maxHeap)[1]\n if place > 3:\n rank = str(place)\n elif place == 1:\n rank = "Gold Medal"\n elif place == 2:\n rank = "Silver Medal"\n elif place == 3:\n rank = "Bronze Medal"\n \n res[pos] = rank\n place +=1\n \n return res\n\n```
| 15
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
Python Elegant & Short | O(n*log(n)) time | Sorting
|
relative-ranks
| 0
| 1
|
\tclass Solution:\n\t\t"""\n\t\tTime: O(n*log(n))\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tMEDALS = {\n\t\t\t1: \'Gold Medal\',\n\t\t\t2: \'Silver Medal\',\n\t\t\t3: \'Bronze Medal\',\n\t\t}\n\n\t\tdef findRelativeRanks(self, nums: List[int]) -> List[str]:\n\t\t\tranks = {num: ind for ind, num in enumerate(sorted(nums, reverse=True), start=1)}\n\t\t\treturn [self._get_place(ranks[num]) for num in nums]\n\n\t\t@classmethod\n\t\tdef _get_place(cls, place: int) -> str:\n\t\t\treturn cls.MEDALS.get(place, str(place))\n
| 4
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
506: Time 99.42%, Solution with step by step explanation
|
relative-ranks
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function named findRelativeRanks that takes in an input list score and returns a list of strings as output.\n2. Create a copy of the input array and sort it in descending order, and store it in a new variable named sorted_scores.\n3. Create an empty dictionary named rank_dict to store the rank of each score.\n4. Loop through the sorted scores using the enumerate() function and assign ranks to each score in the rank_dict dictionary.\n5. If the index is 0, assign "Gold Medal" as the rank, if 1, assign "Silver Medal", if 2, assign "Bronze Medal", else assign a string of the rank as i+1.\n6. Create an empty list named result to store the results.\n7. Loop through the input array and append the rank of each score from the rank_dict dictionary to the result list.\n8. Return the result list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n # Create a copy of the input array and sort it in descending order\n sorted_scores = sorted(score, reverse=True)\n # Create a dictionary to store the rank of each score\n rank_dict = {}\n \n # Loop through the sorted scores and assign ranks\n for i, s in enumerate(sorted_scores):\n if i == 0:\n rank_dict[s] = "Gold Medal"\n elif i == 1:\n rank_dict[s] = "Silver Medal"\n elif i == 2:\n rank_dict[s] = "Bronze Medal"\n else:\n rank_dict[s] = str(i + 1)\n \n # Create a list to store the results\n result = []\n \n # Loop through the input array and append the rank of each score to the result list\n for s in score:\n result.append(rank_dict[s])\n \n # Return the result list\n return result\n\n```
| 8
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
solution using hashmap-->python3
|
relative-ranks
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRelativeRanks(self, score: List[int]) -> List[str]:\n sc=sorted(score,reverse=True)\n mapping={}\n for i in range(len(sc)):\n if i==0:\n mapping[sc[i]]="Gold Medal"\n elif i==1:\n mapping[sc[i]]="Silver Medal"\n elif i==2:\n mapping[sc[i]]="Bronze Medal"\n else:\n mapping[sc[i]]=str(i+1)\n res=[]\n for i in score:\n res.append(mapping[i])\n return res\n\n\n\n \n\n\n```
| 5
|
You are given an integer array `score` of size `n`, where `score[i]` is the score of the `ith` athlete in a competition. All the scores are guaranteed to be **unique**.
The athletes are **placed** based on their scores, where the `1st` place athlete has the highest score, the `2nd` place athlete has the `2nd` highest score, and so on. The placement of each athlete determines their rank:
* The `1st` place athlete's rank is `"Gold Medal "`.
* The `2nd` place athlete's rank is `"Silver Medal "`.
* The `3rd` place athlete's rank is `"Bronze Medal "`.
* For the `4th` place to the `nth` place athlete, their rank is their placement number (i.e., the `xth` place athlete's rank is `"x "`).
Return an array `answer` of size `n` where `answer[i]` is the **rank** of the `ith` athlete.
**Example 1:**
**Input:** score = \[5,4,3,2,1\]
**Output:** \[ "Gold Medal ", "Silver Medal ", "Bronze Medal ", "4 ", "5 "\]
**Explanation:** The placements are \[1st, 2nd, 3rd, 4th, 5th\].
**Example 2:**
**Input:** score = \[10,3,8,9,4\]
**Output:** \[ "Gold Medal ", "5 ", "Bronze Medal ", "Silver Medal ", "4 "\]
**Explanation:** The placements are \[1st, 5th, 3rd, 2nd, 4th\].
**Constraints:**
* `n == score.length`
* `1 <= n <= 104`
* `0 <= score[i] <= 106`
* All the values in `score` are **unique**.
| null |
The solution is in python3
|
perfect-number
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n if num == 1:\n return False\n \n sum = 1\n for i in range(2, int(num ** 0.5) + 1):\n if num % i == 0:\n sum += i + num //i\n \n return sum == num\n \n```
| 1
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
One Line of code Python-->Two Approaches
|
perfect-number
| 0
| 1
|
\n\n# 1. Only 5 perfect Number exist until 10^8\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n return num in [6,28,496,8128,33550336]\n//please upvote me it would encourage me alot\n\n```\n# 2. Rooting Approach [Accepted]\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n if num==1:\n return False\n count=1\n for i in range(2,int(num**0.5)+1):\n if num%i==0:\n count+=i+num//i\n return num==count\n\n//please upvote me it would encourage me alot\n\n\n```\n# please upvote me it would encourage me alot\n
| 34
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
507: Solution with step by step explanation
|
perfect-number
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the input number num is less than 2 (no even perfect number exists). If so, return False.\n2. Initialize the limit limit to the square root of num rounded up to the nearest integer, plus 1.\n3. Initialize the sum of divisors divisors_sum to 1, since 1 is always a divisor of num.\n4. Iterate through the prime numbers up to the limit limit. For each prime number i:\na. Check if i is a divisor of num by checking if num % i == 0.\nb. If i is a divisor of num, add it to divisors_sum.\nc. If num is not divisible by i, but is divisible by num // i, add num // i to divisors_sum.\n5. Check if num is equal to divisors_sum. If so, return True. Otherwise, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n # Check if num is less than 2 (no even perfect number exists)\n if num < 2:\n return False\n \n # Initialize the limit and the sum of divisors\n limit = int(num ** 0.5) + 1\n divisors_sum = 1\n \n # Iterate through the prime numbers up to the limit and calculate the sum of divisors\n for i in range(2, limit):\n if num % i == 0:\n divisors_sum += i\n if i != num // i:\n divisors_sum += num // i\n \n # Check if num is equal to the sum of divisors\n if divisors_sum == num:\n return True\n else:\n return False\n\n```
| 3
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
Solution
|
perfect-number
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n bool checkPerfectNumber(int num) {\n int sum = 1;\n for(int i = 2; i <= sqrt(num); ++i)\n if (num % i == 0) {\n sum += i + num/i;\n }\n if (sqrt(num)*sqrt(num)==num) sum -= sqrt(num);\n return sum==num;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n pefectnum = [6, 28, 496, 8128, 33550336]\n return num in pefectnum\n```\n\n```Java []\nclass Solution {\n public boolean checkPerfectNumber(int num) {\n return num == 6 || num == 28 ||\n num == 496 || num == 8128 || num == 33550336;\n }\n}\n```\n
| 2
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
Easy to understand
|
perfect-number
| 0
| 1
|
# Solution\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n if num==1: return False\n answer = 1\n i = 2\n while i*i<num:\n if num%i==0: answer+=i+num//i\n i+=1\n if i*i==num: answer+=i\n return answer==num\n```
| 2
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
Python simple solution fully explained
|
perfect-number
| 0
| 1
|
# Intuition\nThe intuition behind the solution is to iterate through all the numbers from 2 up to the square root of the given number. For each number, check if it is a divisor of the given number. If it is a divisor, add both the divisor and the quotient obtained by dividing the given number by the divisor to a running sum. Finally, compare the computed sum with the given number. If they are equal, the number is a perfect number; otherwise, it is not.\n\n# Approach\n1. Firstly, we have to check if the given number is **1**, cause \n```\n1 <= num <= 108\n```\n```\n if num == 1:\n return False\n```\nsince **1** cannot be a perfect number.\n\n---\n*A perfect number is defined as a positive integer that is equal to the sum of its proper divisors (excluding the number itself). Proper divisors are the positive divisors of a number excluding the number itself.\nThe number 1 only has one proper divisor, which is itself (1). Since the sum of proper divisors excluding the number itself is zero in the case of 1, it does not meet the criteria of a perfect number.*\n\n---\n2. Then, initialize a variable "ans" as 1 to store the running sum.\nIterate through all numbers from 2 up to the square root of the given number.\n```\nans = 1\n\nfor i in range(2, int(num**0.5) + 1):\n```\n\n---\n*The square root is often used as a mathematical shortcut when finding divisors because of a property related to factors. When we want to find the divisors of a number, we typically check for factors up to the square root of that number.\nTo understand why, consider that a factor of a number is a value that divides the number without leaving a remainder. For example, the factors of 12 are:*\n\n```\n1, 2, 3, 4, 6, and 12. \n```\n*Notice that the factors come in pairs:*\n\n```\n(1, 12), (2, 6), and (3, 4)\n```\n*In each pair, one number is smaller than the square root of 12 (which is approximately 3.46) and the other is larger. \nOnce we have exhausted all the factors smaller than the square root, we can determine the remaining factors by dividing the original number by each of these smaller factors.\nUsing this approach significantly reduces the number of divisions we need to perform, making it more efficient. If we continued checking for factors beyond the square root, it would be TLE (time limit exceeded).*\n\n---\n3. Check if the current number is a divisor of the given number.\nIf it is a divisor, add both the divisor and the quotient to the running sum.\n```\n if num % i == 0:\n ans += i + num // i\n```\n\n4. After the loop, compare the running sum with the given number.\nIf they are equal, return True (the number is a perfect number); otherwise, return False.\n```\nreturn ans == num\n```\n\n# Complexity\n- Time complexity:\nThe solution iterates up to the square root of the given number, which takes **O(sqrt(num))** iterations. \nSo, time complexity is **O(sqrt(num))**.\n\n- Space complexity:\nThe solution uses a constant amount of extra space. \nTherefore, the space complexity is **O(1)**.\n\n# Code (no comments)\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n if num == 1:\n return False\n\n ans = 1\n\n for i in range(2, int(num**0.5) + 1):\n \n if num % i == 0:\n ans += i + num // i\n\n return ans == num\n```\n\n# Code (with comments)\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n #If the given number is 1, return False since 1 cannot be a perfect number.\n if num == 1:\n return False\n\n #Initialize a variable "ans" as 1 to store the running sum.\n ans = 1\n\n #Iterate through all numbers from 2 up to the square root of the given number.\n for i in range(2, int(num**0.5) + 1):\n #Check if the current number is a divisor of the given number.\n if num % i == 0:\n #If it is a divisor, add both the divisor and the quotient to the running sum.\n ans += i + num // i\n #After the loop, compare the running sum with the given number. \n #If they are equal, return True (the number is a perfect number); otherwise, return False.\n return ans == num\n```
| 4
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
Python3 simple solution
|
perfect-number
| 0
| 1
|
```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n if num == 1:\n return False\n res = 1\n for i in range(2,int(num**0.5)+1):\n if num%i == 0:\n res += i + num//i\n return res == num\n```\n**If you like this solution, please upvote for this**
| 15
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
[Python] it's kinda cheating but anyway it works
|
perfect-number
| 0
| 1
|
# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkPerfectNumber(self, num: int) -> bool:\n pefectnum = [6, 28, 496, 8128, 33550336]\n return num in pefectnum\n\n```
| 4
|
A [**perfect number**](https://en.wikipedia.org/wiki/Perfect_number) is a **positive integer** that is equal to the sum of its **positive divisors**, excluding the number itself. A **divisor** of an integer `x` is an integer that can divide `x` evenly.
Given an integer `n`, return `true` _if_ `n` _is a perfect number, otherwise return_ `false`.
**Example 1:**
**Input:** num = 28
**Output:** true
**Explanation:** 28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, and 14 are all divisors of 28.
**Example 2:**
**Input:** num = 7
**Output:** false
**Constraints:**
* `1 <= num <= 108`
| null |
508: Solution with step by step explanation
|
most-frequent-subtree-sum
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a dictionary \'freq\' to store the frequency of each subtree sum.\n2. Define a helper function \'subtree_sum\' to calculate the subtree sum of a node. The function takes a node as input and returns the sum of values of all nodes in the subtree rooted at that node.\n3. Initialize the frequency of the subtree sum of the root to be 0.\n4. Calculate the subtree sum of the root by calling the \'subtree_sum\' function on the root node.\n5. Find the most frequent subtree sums by finding the maximum frequency of all the subtree sums in the \'freq\' dictionary.\n6. Return all the subtree sums that have the maximum frequency.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findFrequentTreeSum(self, root: Optional[TreeNode]) -> List[int]:\n # Define a dictionary to store the frequency of each subtree sum\n freq = Counter()\n \n # Define a helper function to calculate the subtree sum of a node\n def subtree_sum(node):\n if not node:\n return 0\n s = node.val + subtree_sum(node.left) + subtree_sum(node.right)\n freq[s] += 1\n return s\n \n # Calculate the subtree sum of each node in the tree\n subtree_sum(root)\n \n # Find the most frequent subtree sums\n max_freq = max(freq.values())\n return [s for s in freq if freq[s] == max_freq]\n\n```
| 2
|
Given the `root` of a binary tree, return the most frequent **subtree sum**. If there is a tie, return all the values with the highest frequency in any order.
The **subtree sum** of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
**Example 1:**
**Input:** root = \[5,2,-3\]
**Output:** \[2,-3,4\]
**Example 2:**
**Input:** root = \[5,2,-5\]
**Output:** \[2\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
| null |
Simple solution with Binary Tree in Python3
|
most-frequent-subtree-sum
| 0
| 1
|
# Intuition\nHere we have:\n- `root` as Binary Tree\n- our goal is to find **the most frequent** subtree sum\n\nThe algorithm is simple: traverse over tree, calculate subtree sum, store it into **HashMap** and extract **the most frequent**.\n\n# Approach\n1. declare `cache` and `maxFreq` to define max frequency of particular subtree sum\n2. define `dfs` to traverse over `root`, calculate `left` and `right` subtree sums and update `maxFreq`\n3. iterate over `cache` and push into `ans` vals, whose frequency is equal to `maxFreq`\n4. return `ans`\n\n# Complexityd\n- Time complexity: **O(N + K)**, to iterate over `root` and `cache`\n\n- Space complexity: **O(K)**, to store `cache`\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findFrequentTreeSum(self, root: Optional[TreeNode]) -> List[int]:\n cache = defaultdict(int)\n maxFreq = 0\n\n def dfs(node):\n nonlocal maxFreq\n\n if node:\n left = dfs(node.left)\n right = dfs(node.right)\n val = node.val + left + right\n cache[val] += 1\n maxFreq = max(maxFreq, cache[val])\n\n return val\n\n return 0\n\n dfs(root)\n ans = []\n\n for k, v in cache.items():\n if v == maxFreq: ans.append(k)\n\n return ans\n\n```
| 1
|
Given the `root` of a binary tree, return the most frequent **subtree sum**. If there is a tie, return all the values with the highest frequency in any order.
The **subtree sum** of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
**Example 1:**
**Input:** root = \[5,2,-3\]
**Output:** \[2,-3,4\]
**Example 2:**
**Input:** root = \[5,2,-5\]
**Output:** \[2\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
| null |
Python || DFS || Hashmap || Beats 98 %
|
most-frequent-subtree-sum
| 0
| 1
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nStore all the subtree sum using dfs then use a hashmap to count the occurance of all the sum then find the count which is the most frequent and the iterate through the values of hashmap and then use a result list to store the keys of the values which is equal to the most frequent sum. \n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(d+n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findFrequentTreeSum(self, root: Optional[TreeNode]) -> List[int]:\n\n res = []\n\n def dfs(root):\n if not root:\n return 0\n\n tot = root.val+dfs(root.left)+dfs(root.right)\n res.append(tot)\n return tot\n\n dfs(root)\n\n count = {}\n res2=[]\n\n for i in res:\n count[i] = 1 + count.get(i,0)\n\n maxi = max(count.values()) \n\n for j in count:\n if count[j]==maxi:\n res2.append(j)\n\n return res2 \n\n\n```
| 1
|
Given the `root` of a binary tree, return the most frequent **subtree sum**. If there is a tie, return all the values with the highest frequency in any order.
The **subtree sum** of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
**Example 1:**
**Input:** root = \[5,2,-3\]
**Output:** \[2,-3,4\]
**Example 2:**
**Input:** root = \[5,2,-5\]
**Output:** \[2\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
| null |
Solution
|
most-frequent-subtree-sum
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int dfs(TreeNode* root, unordered_map<int, int>& sums) {\n if(root == NULL) return 0;\n \n int sum = root->val;\n sum += dfs(root->left, sums);\n sum += dfs(root->right, sums);\n\n sums[sum]++;\n\n return sum;\n }\n vector<int> findFrequentTreeSum(TreeNode* root) {\n vector<int> ans;\n unordered_map<int, int> sums;\n int maxFreq = 0;\n dfs(root, sums);\n for(auto &it: sums) maxFreq = max(maxFreq, it.second);\n for(auto &it: sums) {\n if(it.second == maxFreq) ans.push_back(it.first);\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findFrequentTreeSum(self, root: Optional[TreeNode]) -> List[int]:\n HASH = {}\n def dfs(node):\n if not node: return 0\n total = node.val + dfs(node.left)+dfs(node.right)\n if total not in HASH: HASH[total] = 0\n HASH[total] += 1\n return total\n\n dfs(root)\n returnArr = []\n MAX = max(HASH.values())\n for key, val in HASH.items():\n if val == MAX: returnArr.append(key)\n\n return returnArr\n```\n\n```Java []\nclass Solution {\n\n int maxFrq = -1;\n List<Integer> arr = new ArrayList();\n\n public int[] findFrequentTreeSum(TreeNode root) {\n Map<Integer, Integer> map = new HashMap();\n helper(root, map);\n\n int[] res = new int [arr.size()];\n for(int i=0;i<arr.size();i++){\n res[i] = arr.get(i);\n }\n return res;\n }\n private int helper(TreeNode node, Map<Integer, Integer> map){\n if(node == null){\n return 0;\n }\n int sum = node.val + helper(node.left, map) + helper(node.right, map);\n map.put(sum, map.getOrDefault(sum, 0)+1);\n \n int frq = map.get(sum);\n if(frq == maxFrq){\n arr.add(sum);\n }else if(frq > maxFrq){\n arr.clear();\n arr.add(sum);\n maxFrq = frq;\n }\n return sum;\n }\n}\n```\n
| 1
|
Given the `root` of a binary tree, return the most frequent **subtree sum**. If there is a tie, return all the values with the highest frequency in any order.
The **subtree sum** of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
**Example 1:**
**Input:** root = \[5,2,-3\]
**Output:** \[2,-3,4\]
**Example 2:**
**Input:** root = \[5,2,-5\]
**Output:** \[2\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
| null |
Fast Python Recursive solution
|
most-frequent-subtree-sum
| 0
| 1
|
Hash map + DFS recursively.\n\n```python\nclass Solution:\n # 48 ms, 99%\n def findFrequentTreeSum(self, root: TreeNode) -> List[int]:\n if not root: return []\n \n D = collections.defaultdict(int)\n # DFS recursively\n\t\tdef cal_sum(node):\n if not node: return 0\n rv = node.val + cal_sum(node.left) + cal_sum(node.right)\n D[rv] += 1\n return rv\n \n cal_sum(root)\n mx = max(D.values())\n return [k for k, v in D.items() if v == mx] # return key if its val == max\n```\nI haven\'t tried but i expect DFS itertively would be much harder as you need to keep track of return_value. Let me know how you would do it iteratively.
| 12
|
Given the `root` of a binary tree, return the most frequent **subtree sum**. If there is a tie, return all the values with the highest frequency in any order.
The **subtree sum** of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
**Example 1:**
**Input:** root = \[5,2,-3\]
**Output:** \[2,-3,4\]
**Example 2:**
**Input:** root = \[5,2,-5\]
**Output:** \[2\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-105 <= Node.val <= 105`
| null |
Easy Solution ✅
|
fibonacci-number
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n current_val = 0\n next_val = 1\n if n == 0:\n return current_val\n elif n == 1:\n return next_val\n else:\n for i in range(2, n + 1):\n sum = current_val + next_val\n current_val = next_val\n next_val = sum\n\n return next_val\n\n \n```
| 2
|
The **Fibonacci numbers**, commonly denoted `F(n)` form a sequence, called the **Fibonacci sequence**, such that each number is the sum of the two preceding ones, starting from `0` and `1`. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given `n`, calculate `F(n)`.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** F(2) = F(1) + F(0) = 1 + 0 = 1.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:** F(3) = F(2) + F(1) = 1 + 1 = 2.
**Example 3:**
**Input:** n = 4
**Output:** 3
**Explanation:** F(4) = F(3) + F(2) = 2 + 1 = 3.
**Constraints:**
* `0 <= n <= 30`
| null |
Easy Solution ✅
|
fibonacci-number
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n current_val = 0\n next_val = 1\n if n == 0:\n return current_val\n elif n == 1:\n return next_val\n else:\n for i in range(2, n + 1):\n sum = current_val + next_val\n current_val = next_val\n next_val = sum\n\n return next_val\n\n \n```
| 2
|
Given an array of integers `arr`, return `true` if we can partition the array into three **non-empty** parts with equal sums.
Formally, we can partition the array if we can find indexes `i + 1 < j` with `(arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1])`
**Example 1:**
**Input:** arr = \[0,2,1,-6,6,-7,9,1,2,0,1\]
**Output:** true
**Explanation:** 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
**Example 2:**
**Input:** arr = \[0,2,1,-6,6,7,9,-1,2,0,1\]
**Output:** false
**Example 3:**
**Input:** arr = \[3,3,6,5,-2,2,5,1,-9,4\]
**Output:** true
**Explanation:** 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
**Constraints:**
* `3 <= arr.length <= 5 * 104`
* `-104 <= arr[i] <= 104`
| null |
Easy java solution ,c,c++,python
|
fibonacci-number
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int fib(int n) {\n int a=0;\n int b=1;\n if(n==0)\n return a;\n if(n==1)\n return b;\n if(n==2)\n return a+b;\n int c=a+b;\n for(int i=2;i<n;i++)\n {\n a=b;\n b=c;\n c=a+b;\n }\n return c;\n }\n}\n```
| 3
|
The **Fibonacci numbers**, commonly denoted `F(n)` form a sequence, called the **Fibonacci sequence**, such that each number is the sum of the two preceding ones, starting from `0` and `1`. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given `n`, calculate `F(n)`.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** F(2) = F(1) + F(0) = 1 + 0 = 1.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:** F(3) = F(2) + F(1) = 1 + 1 = 2.
**Example 3:**
**Input:** n = 4
**Output:** 3
**Explanation:** F(4) = F(3) + F(2) = 2 + 1 = 3.
**Constraints:**
* `0 <= n <= 30`
| null |
Easy java solution ,c,c++,python
|
fibonacci-number
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int fib(int n) {\n int a=0;\n int b=1;\n if(n==0)\n return a;\n if(n==1)\n return b;\n if(n==2)\n return a+b;\n int c=a+b;\n for(int i=2;i<n;i++)\n {\n a=b;\n b=c;\n c=a+b;\n }\n return c;\n }\n}\n```
| 3
|
Given an array of integers `arr`, return `true` if we can partition the array into three **non-empty** parts with equal sums.
Formally, we can partition the array if we can find indexes `i + 1 < j` with `(arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1])`
**Example 1:**
**Input:** arr = \[0,2,1,-6,6,-7,9,1,2,0,1\]
**Output:** true
**Explanation:** 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
**Example 2:**
**Input:** arr = \[0,2,1,-6,6,7,9,-1,2,0,1\]
**Output:** false
**Example 3:**
**Input:** arr = \[3,3,6,5,-2,2,5,1,-9,4\]
**Output:** true
**Explanation:** 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
**Constraints:**
* `3 <= arr.length <= 5 * 104`
* `-104 <= arr[i] <= 104`
| null |
Beats 100% | Easy To Understand | 0ms 🚀🔥
|
fibonacci-number
| 1
| 1
|
# Intuition\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Upvote if you find this helpful!!\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // Recursive Solution\n // TC -- O(2^N) and SC -- O(N)\n int fibRec(int n)\n {\n // 1. Base Case\n if(n == 1 or n == 0)\n return n;\n \n return fib(n - 1) + fib(n - 2);\n }\n\n // Using topDown Approach --> Recursion + Memoization\n // TC -- O(N + N) and SC -- O(N)\n int topDown(int n,vector<int>& dp)\n {\n // 1. Base Case\n if(n == 1 or n == 0)\n return n;\n // 2. Check if ans already exists\n if(dp[n] != -1)\n return dp[n];\n // 3. Store ans in dp array\n dp[n] = topDown(n - 1,dp) + topDown(n - 2,dp);\n // 4. Return dp array\n return dp[n];\n }\n\n // Using bottomUp Approach --> Tabulation Method [Iterative Way]\n // TC -- O(N) and SC -- O(N)\n int bottomUp(int n)\n {\n // 1. Create dp array\n vector<int> dp(n+1,-1);\n\n // 2. Base Case\n dp[0] = 0;\n if(n == 0) return dp[0];\n dp[1] = 1;\n if(n == 1) return dp[1];\n\n // 3.\n for(int i = 2; i <= n; i++)\n {\n dp[i] = dp[i-1] + dp[i-2];\n }\n\n return dp[n];\n }\n\n // Space Optimization\n // TC -- O(N) and SC -- O(1)\n int fibSpace(int n)\n {\n int prev2 = 0;\n int prev1 = 1;\n int curr;\n\n if(n <= 1) return n;\n\n for(int i = 2; i <= n; i++)\n {\n curr = prev1 + prev2;\n // Shifting\n prev2 = prev1;\n prev1 = curr;\n }\n return curr;\n }\n\n int fib(int n) {\n \n // 1. Create DP Array\n // vector<int> dp(n+1,-1);\n\n // return topDown(n,dp);\n\n // return bottomUp(n);\n\n return fibSpace(n);\n }\n};\n```
| 6
|
The **Fibonacci numbers**, commonly denoted `F(n)` form a sequence, called the **Fibonacci sequence**, such that each number is the sum of the two preceding ones, starting from `0` and `1`. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given `n`, calculate `F(n)`.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** F(2) = F(1) + F(0) = 1 + 0 = 1.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:** F(3) = F(2) + F(1) = 1 + 1 = 2.
**Example 3:**
**Input:** n = 4
**Output:** 3
**Explanation:** F(4) = F(3) + F(2) = 2 + 1 = 3.
**Constraints:**
* `0 <= n <= 30`
| null |
Beats 100% | Easy To Understand | 0ms 🚀🔥
|
fibonacci-number
| 1
| 1
|
# Intuition\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Upvote if you find this helpful!!\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // Recursive Solution\n // TC -- O(2^N) and SC -- O(N)\n int fibRec(int n)\n {\n // 1. Base Case\n if(n == 1 or n == 0)\n return n;\n \n return fib(n - 1) + fib(n - 2);\n }\n\n // Using topDown Approach --> Recursion + Memoization\n // TC -- O(N + N) and SC -- O(N)\n int topDown(int n,vector<int>& dp)\n {\n // 1. Base Case\n if(n == 1 or n == 0)\n return n;\n // 2. Check if ans already exists\n if(dp[n] != -1)\n return dp[n];\n // 3. Store ans in dp array\n dp[n] = topDown(n - 1,dp) + topDown(n - 2,dp);\n // 4. Return dp array\n return dp[n];\n }\n\n // Using bottomUp Approach --> Tabulation Method [Iterative Way]\n // TC -- O(N) and SC -- O(N)\n int bottomUp(int n)\n {\n // 1. Create dp array\n vector<int> dp(n+1,-1);\n\n // 2. Base Case\n dp[0] = 0;\n if(n == 0) return dp[0];\n dp[1] = 1;\n if(n == 1) return dp[1];\n\n // 3.\n for(int i = 2; i <= n; i++)\n {\n dp[i] = dp[i-1] + dp[i-2];\n }\n\n return dp[n];\n }\n\n // Space Optimization\n // TC -- O(N) and SC -- O(1)\n int fibSpace(int n)\n {\n int prev2 = 0;\n int prev1 = 1;\n int curr;\n\n if(n <= 1) return n;\n\n for(int i = 2; i <= n; i++)\n {\n curr = prev1 + prev2;\n // Shifting\n prev2 = prev1;\n prev1 = curr;\n }\n return curr;\n }\n\n int fib(int n) {\n \n // 1. Create DP Array\n // vector<int> dp(n+1,-1);\n\n // return topDown(n,dp);\n\n // return bottomUp(n);\n\n return fibSpace(n);\n }\n};\n```
| 6
|
Given an array of integers `arr`, return `true` if we can partition the array into three **non-empty** parts with equal sums.
Formally, we can partition the array if we can find indexes `i + 1 < j` with `(arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1])`
**Example 1:**
**Input:** arr = \[0,2,1,-6,6,-7,9,1,2,0,1\]
**Output:** true
**Explanation:** 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
**Example 2:**
**Input:** arr = \[0,2,1,-6,6,7,9,-1,2,0,1\]
**Output:** false
**Example 3:**
**Input:** arr = \[3,3,6,5,-2,2,5,1,-9,4\]
**Output:** true
**Explanation:** 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
**Constraints:**
* `3 <= arr.length <= 5 * 104`
* `-104 <= arr[i] <= 104`
| null |
🧩 [VIDEO] Fast Mastering the Fibonacci Sequence with Dynamic Programming Unraveled
|
fibonacci-number
| 1
| 1
|
# Intuition\nUpon reading this problem, my first thoughts were to use the concept of dynamic programming. The problem requires us to find the \'n-th\' Fibonacci number which is a classic example where dynamic programming can be utilized. The Fibonacci sequence has a special property where each number is the sum of the two numbers preceding it. Keeping this in mind, I thought of maintaining a list or an array to keep track of the Fibonacci numbers as they are calculated.\n\nhttps://youtu.be/2Du5GZbBiMs\n\n# Approach\nI started with the base cases where if \'n\' is 0 or 1, we return \'n\' directly. Then, I initialized an array with the first two Fibonacci numbers and filled the rest with zeros. A loop was then used to fill this array where for each number \'i\' from 2 to \'n\', \'fib_array[i]\' was set to the sum of the two preceding numbers. This adheres to the property of the Fibonacci sequence. Finally, the \'n-th\' Fibonacci number was returned by accessing \'fib_array[n]\'.\n\n# Complexity\n- Time complexity:\nThe time complexity of the solution is \\(O(n)\\), due to the single loop that iterates through the numbers from 2 to \'n\'.\n\n- Space complexity:\nThe space complexity of the solution is also \\(O(n)\\), as we are using an array of size \'n+1\' to store the Fibonacci numbers.\n\nThis code efficiently calculates the \'n-th\' Fibonacci number using dynamic programming. The approach taken here drastically reduces the time complexity from exponential in recursive solutions to linear in this case. It is a good example to understand the concept of dynamic programming.\n\n# Code\n```Python []\nclass Solution:\n def fib(self, n: int) -> int:\n if n <= 1: \n return n \n fib_array = [0, 1] + [0]*(n-1) \n for i in range(2, n+1): \n fib_array[i] = fib_array[i-1] + fib_array[i-2] \n return fib_array[n] \n``` \n``` C++ []\nclass Solution {\npublic:\n int fib(int n) {\n if (n <= 1) {\n return n;\n }\n vector<int> fib_array(n+1, 0);\n fib_array[1] = 1;\n for (int i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n }\n};\n```\n``` C# []\npublic class Solution {\n public int Fib(int n) {\n if (n <= 1) {\n return n;\n }\n int[] fib_array = new int[n+1];\n fib_array[1] = 1;\n for (int i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n }\n}\n```\n``` Java []\npublic class Solution {\n public int fib(int n) {\n if (n <= 1) {\n return n;\n }\n int[] fib_array = new int[n+1];\n fib_array[1] = 1;\n for (int i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar fib = function(n) {\n if (n <= 1) {\n return n;\n }\n let fib_array = new Array(n+1).fill(0);\n fib_array[1] = 1;\n for (let i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n};\n```
| 8
|
The **Fibonacci numbers**, commonly denoted `F(n)` form a sequence, called the **Fibonacci sequence**, such that each number is the sum of the two preceding ones, starting from `0` and `1`. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given `n`, calculate `F(n)`.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** F(2) = F(1) + F(0) = 1 + 0 = 1.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:** F(3) = F(2) + F(1) = 1 + 1 = 2.
**Example 3:**
**Input:** n = 4
**Output:** 3
**Explanation:** F(4) = F(3) + F(2) = 2 + 1 = 3.
**Constraints:**
* `0 <= n <= 30`
| null |
🧩 [VIDEO] Fast Mastering the Fibonacci Sequence with Dynamic Programming Unraveled
|
fibonacci-number
| 1
| 1
|
# Intuition\nUpon reading this problem, my first thoughts were to use the concept of dynamic programming. The problem requires us to find the \'n-th\' Fibonacci number which is a classic example where dynamic programming can be utilized. The Fibonacci sequence has a special property where each number is the sum of the two numbers preceding it. Keeping this in mind, I thought of maintaining a list or an array to keep track of the Fibonacci numbers as they are calculated.\n\nhttps://youtu.be/2Du5GZbBiMs\n\n# Approach\nI started with the base cases where if \'n\' is 0 or 1, we return \'n\' directly. Then, I initialized an array with the first two Fibonacci numbers and filled the rest with zeros. A loop was then used to fill this array where for each number \'i\' from 2 to \'n\', \'fib_array[i]\' was set to the sum of the two preceding numbers. This adheres to the property of the Fibonacci sequence. Finally, the \'n-th\' Fibonacci number was returned by accessing \'fib_array[n]\'.\n\n# Complexity\n- Time complexity:\nThe time complexity of the solution is \\(O(n)\\), due to the single loop that iterates through the numbers from 2 to \'n\'.\n\n- Space complexity:\nThe space complexity of the solution is also \\(O(n)\\), as we are using an array of size \'n+1\' to store the Fibonacci numbers.\n\nThis code efficiently calculates the \'n-th\' Fibonacci number using dynamic programming. The approach taken here drastically reduces the time complexity from exponential in recursive solutions to linear in this case. It is a good example to understand the concept of dynamic programming.\n\n# Code\n```Python []\nclass Solution:\n def fib(self, n: int) -> int:\n if n <= 1: \n return n \n fib_array = [0, 1] + [0]*(n-1) \n for i in range(2, n+1): \n fib_array[i] = fib_array[i-1] + fib_array[i-2] \n return fib_array[n] \n``` \n``` C++ []\nclass Solution {\npublic:\n int fib(int n) {\n if (n <= 1) {\n return n;\n }\n vector<int> fib_array(n+1, 0);\n fib_array[1] = 1;\n for (int i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n }\n};\n```\n``` C# []\npublic class Solution {\n public int Fib(int n) {\n if (n <= 1) {\n return n;\n }\n int[] fib_array = new int[n+1];\n fib_array[1] = 1;\n for (int i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n }\n}\n```\n``` Java []\npublic class Solution {\n public int fib(int n) {\n if (n <= 1) {\n return n;\n }\n int[] fib_array = new int[n+1];\n fib_array[1] = 1;\n for (int i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar fib = function(n) {\n if (n <= 1) {\n return n;\n }\n let fib_array = new Array(n+1).fill(0);\n fib_array[1] = 1;\n for (let i = 2; i <= n; i++) {\n fib_array[i] = fib_array[i-1] + fib_array[i-2];\n }\n return fib_array[n];\n};\n```
| 8
|
Given an array of integers `arr`, return `true` if we can partition the array into three **non-empty** parts with equal sums.
Formally, we can partition the array if we can find indexes `i + 1 < j` with `(arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1])`
**Example 1:**
**Input:** arr = \[0,2,1,-6,6,-7,9,1,2,0,1\]
**Output:** true
**Explanation:** 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
**Example 2:**
**Input:** arr = \[0,2,1,-6,6,7,9,-1,2,0,1\]
**Output:** false
**Example 3:**
**Input:** arr = \[3,3,6,5,-2,2,5,1,-9,4\]
**Output:** true
**Explanation:** 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
**Constraints:**
* `3 <= arr.length <= 5 * 104`
* `-104 <= arr[i] <= 104`
| null |
Python | Basic solution to Advanced ✅
|
fibonacci-number
| 0
| 1
|
# Solution #1 (Basic)\n\n# Intuition and Approach\nUsing standard recursion. For n > 1, Fn should return Fn-1 + Fn-2.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 2^n (Exponential complexity)\n- Space complexity: O(n) since maximum depth of the recursion tree is n.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n if(n<2):\n return n\n else:\n return self.fib(n-1)+self.fib(n-2)\n \n```\n# Solution #2\n\n# Intuition and Approach\nDuring standard recursion solution, we are computing the already computed values of fib. Since there are overlapping subproblems, we can create and store the fib values in an array.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n) (Linear complexity)\n- Space complexity: O(n) since we store the fib values in array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n if(n==0):\n return 0\n dp = [-1]*(n+1)\n dp[0] = 0\n dp[1] = 1\n for i in range(2,n+1):\n dp[i] = dp[i-1] + dp[i-2]\n return dp[n]\n\n```\n# Solution #3 (Optimised)\n\n# Intuition and Approach\nWe just to keep track of previous 2 fib values to compute the fib of a number. So if there is a way to keep track of those values in variables, we can complete this challenge in O(1) space. \'curr\' stores the final fib value to be returned. \'prev1\' stores the Fn-1 value, \'prev2\' keeps track of Fn-2 value.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n) (Linear complexity)\n- Space complexity: O(1) since we just use variables .\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n prev2 = 0\n prev1 = 1\n curr = 0\n\n if(n<2):\n return n\n else:\n for i in range(2,n+1):\n curr = prev1 + prev2\n prev2 = prev1\n prev1 = curr\n return curr\n\n```\n# Solution #4; O(1) solution using Math\n\n# Intuition and Approach\nWhen we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio "\u03C6" which is approximately 1.618034...\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n golden_ratio = (1 + 5 ** 0.5) / 2\n return int((golden_ratio ** n + 1) / 5 ** 0.5)\n\n```
| 4
|
The **Fibonacci numbers**, commonly denoted `F(n)` form a sequence, called the **Fibonacci sequence**, such that each number is the sum of the two preceding ones, starting from `0` and `1`. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given `n`, calculate `F(n)`.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** F(2) = F(1) + F(0) = 1 + 0 = 1.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:** F(3) = F(2) + F(1) = 1 + 1 = 2.
**Example 3:**
**Input:** n = 4
**Output:** 3
**Explanation:** F(4) = F(3) + F(2) = 2 + 1 = 3.
**Constraints:**
* `0 <= n <= 30`
| null |
Python | Basic solution to Advanced ✅
|
fibonacci-number
| 0
| 1
|
# Solution #1 (Basic)\n\n# Intuition and Approach\nUsing standard recursion. For n > 1, Fn should return Fn-1 + Fn-2.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 2^n (Exponential complexity)\n- Space complexity: O(n) since maximum depth of the recursion tree is n.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n if(n<2):\n return n\n else:\n return self.fib(n-1)+self.fib(n-2)\n \n```\n# Solution #2\n\n# Intuition and Approach\nDuring standard recursion solution, we are computing the already computed values of fib. Since there are overlapping subproblems, we can create and store the fib values in an array.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n) (Linear complexity)\n- Space complexity: O(n) since we store the fib values in array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n if(n==0):\n return 0\n dp = [-1]*(n+1)\n dp[0] = 0\n dp[1] = 1\n for i in range(2,n+1):\n dp[i] = dp[i-1] + dp[i-2]\n return dp[n]\n\n```\n# Solution #3 (Optimised)\n\n# Intuition and Approach\nWe just to keep track of previous 2 fib values to compute the fib of a number. So if there is a way to keep track of those values in variables, we can complete this challenge in O(1) space. \'curr\' stores the final fib value to be returned. \'prev1\' stores the Fn-1 value, \'prev2\' keeps track of Fn-2 value.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n) (Linear complexity)\n- Space complexity: O(1) since we just use variables .\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n prev2 = 0\n prev1 = 1\n curr = 0\n\n if(n<2):\n return n\n else:\n for i in range(2,n+1):\n curr = prev1 + prev2\n prev2 = prev1\n prev1 = curr\n return curr\n\n```\n# Solution #4; O(1) solution using Math\n\n# Intuition and Approach\nWhen we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio "\u03C6" which is approximately 1.618034...\n\n# Code\n```\nclass Solution:\n def fib(self, n: int) -> int:\n golden_ratio = (1 + 5 ** 0.5) / 2\n return int((golden_ratio ** n + 1) / 5 ** 0.5)\n\n```
| 4
|
Given an array of integers `arr`, return `true` if we can partition the array into three **non-empty** parts with equal sums.
Formally, we can partition the array if we can find indexes `i + 1 < j` with `(arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1])`
**Example 1:**
**Input:** arr = \[0,2,1,-6,6,-7,9,1,2,0,1\]
**Output:** true
**Explanation:** 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
**Example 2:**
**Input:** arr = \[0,2,1,-6,6,7,9,-1,2,0,1\]
**Output:** false
**Example 3:**
**Input:** arr = \[3,3,6,5,-2,2,5,1,-9,4\]
**Output:** true
**Explanation:** 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
**Constraints:**
* `3 <= arr.length <= 5 * 104`
* `-104 <= arr[i] <= 104`
| null |
Find bottom left tree value
|
find-bottom-left-tree-value
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n l=defaultdict(list)\n def bfs(root,h):\n if root is None:\n return\n l[h].append(root.val)\n bfs(root.left,h+1)\n bfs(root.right,h+1)\n bfs(root,0)\n return l[len(l)-1][0]\n```
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Solution
|
find-bottom-left-tree-value
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n void calculate(TreeNode* head,int level,int &maxlevel,int &ans){\n if(level>maxlevel){\n ans=head->val;\n maxlevel=level;\n }\n if(head->left){\n calculate(head->left,level+1,maxlevel,ans);\n }\n if(head->right){\n calculate(head->right,level+1,maxlevel,ans);\n }\n }\n int findBottomLeftValue(TreeNode* root) {\n int maxlevel=-1,ans=-1;\n calculate(root,0,maxlevel,ans);\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n def rec(node, level):\n if not node.left and not node.right:\n return node.val, level\n if node.left:\n leftnode, leftlevel = rec(node.left, level+1)\n else:\n leftnode, leftlevel = 0, float(\'-inf\')\n if node.right:\n rightnode, rightlevel = rec(node.right, level+1)\n else:\n rightnode, rightlevel = 0, float(\'-inf\')\n if rightlevel > leftlevel:\n return rightnode, rightlevel\n else:\n return leftnode, leftlevel\n ans, level = rec(root, 0)\n return ans\n```\n\n```Java []\nclass Solution {\n static int parent=-1;\n static int ans=0;\n public int findBottomLeftValue(TreeNode root) {\n help(root,0);\n int res=ans;ans=0;\n parent=-1;\n return res;\n }\n public static void help(TreeNode root,int level)\n {\n if(root==null)return ;\n if(level>parent){\n ans=root.val;\n parent=level;\n }\n help(root.left,level+1);\n help(root.right,level+1);\n }\n}\n```\n
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
python solution || Pre Order Traversal || Recursion || Easy to understand
|
find-bottom-left-tree-value
| 0
| 1
|
```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n self.leftmostelm = root.val\n self.depth = 0\n self.path = \'z\'\n self.find(root)\n return self.leftmostelm\n \n def find(self,root,s=\'r\',d=0):\n if root == None:\n return\n if self.depth < d or ( self.path > s):\n self.depth = d\n self.path = s\n self.leftmostelm = root.val\n self.find(root.left,s+\'l\',d+1)\n self.find(root.right,s+\'r\',d+1)\n```
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Solution Python Easy
|
find-bottom-left-tree-value
| 0
| 1
|
# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n q = [root]\n left_most = None\n while q:\n left_most = q[0]\n for _ in range(len(q)):\n curr = q.pop(0)\n if curr.left:\n q.append(curr.left)\n if curr.right:\n q.append(curr.right)\n\n return left_most.val\n\n \n \n\n\n\n \n```
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
BFS || DFS || Python || SOlution
|
find-bottom-left-tree-value
| 0
| 1
|
\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n ans = 0\n q = deque() \n q.append((root,0)) \n while q:\n node,level = q.popleft() \n ans = node.val\n if node.right:\n q.append((node.right,level+1)) \n if node.left:\n q.append((node.left,level+1)) \n return ans \n\n # if root:\n # if not root.left and not root.right:\n # return root.val \n # ans = [0] \n # max = [0] \n # def dfs(root , level):\n # if not root:\n # return; \n # if level>max[0]:\n # max[0] = level \n # ans[0] = root.val\n # dfs(root.left,level+1) \n # dfs(root.right,level+1) \n # dfs(root,0) \n # return ans[0]\n```
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Beats 95% with explanation
|
find-bottom-left-tree-value
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a queue within which we can iterate over the tree, while doing it, keep track of most left node, (because we prioritazing left over right), once we are done with whole tree, return the last element in answear, which is the left-most node\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n queue=deque([root])\n ans=[]\n while queue:\n curr=len(queue)\n ans.append(queue[0].val)\n for i in range(curr):\n node=queue.popleft()\n if node.left:\n queue.append(node.left)\n\n if node.right:\n queue.append(node.right)\n return ans[-1]\n```
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
513: Solution with step by step explanation
|
find-bottom-left-tree-value
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a queue with the root node.\n2. Initialize a variable to store the leftmost node value as the value of the root node.\n3. Perform level-order traversal using a while loop until the queue becomes empty.\n4. Get the number of nodes in the current level using the length of the queue.\n5. Traverse all the nodes in the current level using a for loop.\n6. Dequeue the front node from the queue.\n7. Update the leftmost node value if the current node is in the leftmost position of the current level.\n8. Enqueue the left and right child nodes of the current node (if they exist).\n9. After the while loop, return the leftmost node value found in the last level.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findBottomLeftValue(self, root: TreeNode) -> int:\n # Initialize a queue with the root node\n queue = deque([root])\n # Initialize a variable to store the leftmost node value\n leftmost_val = root.val\n \n # Perform level-order traversal\n while queue:\n # Get the number of nodes in the current level\n level_size = len(queue)\n \n # Traverse all the nodes in the current level\n for i in range(level_size):\n # Dequeue the front node from the queue\n node = queue.popleft()\n \n # Update the leftmost node value if the current node is in the leftmost position of the current level\n if i == 0:\n leftmost_val = node.val\n \n # Enqueue the left and right child nodes of the current node (if they exist)\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n # Return the leftmost node value found in the last level\n return leftmost_val\n\n```
| 7
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
python3 solution beats 96%
|
find-bottom-left-tree-value
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n if not root:\n return None\n q = []\n ans = []\n if root:\n q.append(root)\n while(q):\n node = q.pop(0)\n ans.append(node.val)\n if node.right:q.append(node.right)\n if node.left:q.append(node.left)\n return ans[-1]\n```
| 1
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Just do Level-Order -->Python solution
|
find-bottom-left-tree-value
| 0
| 1
|
\n# Code\n```\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n a = []\n\n def dfs(node, h):\n if not node: return\n if len(a) == h: a.append([])\n\n a[h].append(node.val)\n dfs(node.left, h+1)\n dfs(node.right, h+1)\n\n dfs(root, 0)\n\n return a[-1][0]\n```
| 2
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Pyhton3 BFS Solution || BGG
|
find-bottom-left-tree-value
| 0
| 1
|
```\nclass Solution:\n def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:\n q=[[root]]\n nodes=[]\n while q:\n nodes = q.pop(0)\n t=[]\n for n in nodes:\n if n.left:\n t.append(n.left)\n if n.right:\n t.append(n.right)\n if t:\n q.append(t)\n return nodes[0].val\n# Please upvote if you understand the solution
| 2
|
Given the `root` of a binary tree, return the leftmost value in the last row of the tree.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,2,3,4,null,5,6,null,null,7\]
**Output:** 7
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Solution
|
freedom-trail
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int dist(int size, int p, int t){\n return min(abs(t - p), size - abs(t - p));\n }\n int findRotateSteps(string ring, string key){\n int m[26][100] = {{0}};\n int cnt[26] = {0};\n int dp[100][100] = {{0}};\n\n const int rn = ring.size();\n const int kn = key.size();\n for(int i = 0; i < rn; ++i)\n m[ring[i]-\'a\'][cnt[ring[i]-\'a\']++] = i;\n\n for(int i = 0; i < cnt[key[0]-\'a\']; ++i){\n dp[0][m[key[0]-\'a\'][i]] = dist(rn, 0, m[key[0]-\'a\'][i]) + 1;\n }\n for(int i = 1; i < kn; ++i){\n for(int j = 0; j < cnt[key[i]-\'a\']; ++j){\n int mini = INT_MAX;\n for(int k = 0; k < cnt[key[i-1]-\'a\']; ++k){\n mini = min(mini, dp[i-1][m[key[i-1]-\'a\'][k]] + dist(rn, m[key[i]-\'a\'][j], m[key[i-1]-\'a\'][k]) + 1);\n }\n dp[i][m[key[i]-\'a\'][j]] = mini;\n }\n }\n int res = INT_MAX;\n for(int i = 0; i < cnt[key.back()-\'a\']; ++i){\n res = min(res, dp[kn-1][m[key[kn-1]-\'a\'][i]]);\n }\n return res;\n }\n};\n```\n\n```Python3 []\nimport bisect\nclass Solution:\n def findRotateSteps(self, ring: str, key: str) -> int:\n \n n = len(ring)\n ind_dict = defaultdict(list)\n for i, l in enumerate(ring):\n ind_dict[l].append(i)\n \n prev_arr = [0]\n prev_inds = [0]\n for l in key:\n inds = ind_dict[l]\n arr = [0] * len(inds)\n next_inds = [0] * len(inds)\n for i, ind in enumerate(inds):\n j = bisect.bisect(prev_inds, ind)\n if j == len(prev_inds):\n dist = min(prev_arr[-1] + ind - prev_inds[-1], prev_arr[0] + prev_inds[0] + n - ind)\n elif j == 0:\n dist = min(prev_arr[-1] + ind + n - prev_inds[-1], prev_arr[0] + prev_inds[0] - ind)\n else:\n dist = min(prev_arr[j - 1] + ind - prev_inds[j - 1], prev_arr[j] + prev_inds[j] - ind)\n arr[i] = dist\n prev_arr = arr\n prev_inds = inds\n return min(arr) + len(key)\n```\n\n```Java []\nclass Solution {\n public int findRotateSteps(String ring, String key) {\n char[] r=ring.toCharArray();\n List<Integer>[] p=new List[26];\n for(int i=0;i<r.length;i++) {\n int c=r[i]-\'a\';\n List<Integer> l=p[c];\n if(l==null) p[c]=l=new ArrayList<>();\n l.add(i);\n }\n return helper(0,0,p,key.toCharArray(),ring,new int[key.length()][r.length]);\n }\n int helper(int in, int pos, List<Integer>[] p, char[] k, String r, int[][] memo) {\n if(in==k.length) return 0;\n if(memo[in][pos]>0) return memo[in][pos]-1;\n int min=Integer.MAX_VALUE;\n for(int i: p[k[in]-\'a\']) {\n int m;\n if(i>=pos) m=Math.min(i-pos,pos+r.length()-i);\n else m=Math.min(pos-i,i+r.length()-pos);\n min=Math.min(min,m+helper(in+1,i,p,k,r,memo));\n }\n return (memo[in][pos]=min+2)-1;\n }\n}\n```\n
| 1
|
In the video game Fallout 4, the quest **"Road to Freedom "** requires players to reach a metal dial called the **"Freedom Trail Ring "** and use the dial to spell a specific keyword to open the door.
Given a string `ring` that represents the code engraved on the outer ring and another string `key` that represents the keyword that needs to be spelled, return _the minimum number of steps to spell all the characters in the keyword_.
Initially, the first character of the ring is aligned at the `"12:00 "` direction. You should spell all the characters in `key` one by one by rotating `ring` clockwise or anticlockwise to make each character of the string key aligned at the `"12:00 "` direction and then by pressing the center button.
At the stage of rotating the ring to spell the key character `key[i]`:
1. You can rotate the ring clockwise or anticlockwise by one place, which counts as **one step**. The final purpose of the rotation is to align one of `ring`'s characters at the `"12:00 "` direction, where this character must equal `key[i]`.
2. If the character `key[i]` has been aligned at the `"12:00 "` direction, press the center button to spell, which also counts as **one step**. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.
**Example 1:**
**Input:** ring = "godding ", key = "gd "
**Output:** 4
**Explanation:**
For the first key character 'g', since it is already in place, we just need 1 step to spell this character.
For the second key character 'd', we need to rotate the ring "godding " anticlockwise by two steps to make it become "ddinggo ".
Also, we need 1 more step for spelling.
So the final output is 4.
**Example 2:**
**Input:** ring = "godding ", key = "godding "
**Output:** 13
**Constraints:**
* `1 <= ring.length, key.length <= 100`
* `ring` and `key` consist of only lower case English letters.
* It is guaranteed that `key` could always be spelled by rotating `ring`.
| null |
514: Solution with step by step explanation
|
freedom-trail
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function dp(i, j) that takes two parameters:\ni: index of the character in the ring that is currently aligned with the "12:00" direction.\nj: index of the character in the key that needs to be spelled.\n2. If the current combination of i and j has already been computed and stored in the memoization dictionary, return its value.\n3. If j is equal to the length of the key, it means that all characters in the key have been spelled. Return 0 as there are no more steps needed.\n4. Initialize a variable ans to infinity.\n5. Loop through each character in the ring and check if it matches the character in the key at index j.\n6. If it is a match, calculate the number of steps needed to move the current character to the "12:00" direction using the formula:\ndelta: absolute difference between the current character\'s index and the index of the character that is aligned with the "12:00" direction.\nsteps: minimum of delta and len(ring) - delta, which represents the shortest number of steps needed to rotate the ring clockwise or anticlockwise to align the current character with the "12:00" direction.\n7. Recursively call dp with the next character in the key at index j+1 and the current character in the ring at index k.\n8. Update ans to the minimum of its current value and the sum of steps and the result of the recursive call to dp.\n9. Store the result in the memoization dictionary using the current combination of i and j as the key.\n10. Return ans as the minimum number of steps needed to spell all characters in the key starting from index j, plus the length of the key itself to account for the steps needed to press the center button.\n11. Call dp with initial values of i=0 and j=0 to solve the problem.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRotateSteps(self, ring: str, key: str) -> int:\n memo = {}\n def dp(i: int, j: int) -> int:\n if (i, j) in memo:\n return memo[(i, j)]\n if j == len(key):\n return 0\n ans = float(\'inf\')\n for k in range(len(ring)):\n if ring[k] == key[j]:\n delta = abs(k - i)\n steps = min(delta, len(ring) - delta)\n ans = min(ans, steps + dp(k, j+1))\n memo[(i, j)] = ans\n return ans\n return dp(0, 0) + len(key)\n\n```
| 4
|
In the video game Fallout 4, the quest **"Road to Freedom "** requires players to reach a metal dial called the **"Freedom Trail Ring "** and use the dial to spell a specific keyword to open the door.
Given a string `ring` that represents the code engraved on the outer ring and another string `key` that represents the keyword that needs to be spelled, return _the minimum number of steps to spell all the characters in the keyword_.
Initially, the first character of the ring is aligned at the `"12:00 "` direction. You should spell all the characters in `key` one by one by rotating `ring` clockwise or anticlockwise to make each character of the string key aligned at the `"12:00 "` direction and then by pressing the center button.
At the stage of rotating the ring to spell the key character `key[i]`:
1. You can rotate the ring clockwise or anticlockwise by one place, which counts as **one step**. The final purpose of the rotation is to align one of `ring`'s characters at the `"12:00 "` direction, where this character must equal `key[i]`.
2. If the character `key[i]` has been aligned at the `"12:00 "` direction, press the center button to spell, which also counts as **one step**. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.
**Example 1:**
**Input:** ring = "godding ", key = "gd "
**Output:** 4
**Explanation:**
For the first key character 'g', since it is already in place, we just need 1 step to spell this character.
For the second key character 'd', we need to rotate the ring "godding " anticlockwise by two steps to make it become "ddinggo ".
Also, we need 1 more step for spelling.
So the final output is 4.
**Example 2:**
**Input:** ring = "godding ", key = "godding "
**Output:** 13
**Constraints:**
* `1 <= ring.length, key.length <= 100`
* `ring` and `key` consist of only lower case English letters.
* It is guaranteed that `key` could always be spelled by rotating `ring`.
| null |
Python 3 || 8 lines, dfs, dict || T/M: 67% / 28%
|
freedom-trail
| 0
| 1
|
```\nclass Solution:\n def findRotateSteps(self, ring, key):\n \n rLen, kLen, d = len(ring), len(key), defaultdict(list)\n dist = lambda x,y : min((x-y)%rLen, (y-x)%rLen)\n\n for i, ch in enumerate(ring): d[ch].append(i)\n\n @lru_cache(None)\n def dfs(curr = 0,next = 0):\n\n if next >= kLen: return 0\n\n return min(dist(curr,k)+dfs(k,next+1) for k in d[key[next]])\n\n return dfs() + kLen\n```\n[https://leetcode.com/problems/freedom-trail/submissions/926131041/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*^3) and space complexity is *O*(*N*^2).\n
| 3
|
In the video game Fallout 4, the quest **"Road to Freedom "** requires players to reach a metal dial called the **"Freedom Trail Ring "** and use the dial to spell a specific keyword to open the door.
Given a string `ring` that represents the code engraved on the outer ring and another string `key` that represents the keyword that needs to be spelled, return _the minimum number of steps to spell all the characters in the keyword_.
Initially, the first character of the ring is aligned at the `"12:00 "` direction. You should spell all the characters in `key` one by one by rotating `ring` clockwise or anticlockwise to make each character of the string key aligned at the `"12:00 "` direction and then by pressing the center button.
At the stage of rotating the ring to spell the key character `key[i]`:
1. You can rotate the ring clockwise or anticlockwise by one place, which counts as **one step**. The final purpose of the rotation is to align one of `ring`'s characters at the `"12:00 "` direction, where this character must equal `key[i]`.
2. If the character `key[i]` has been aligned at the `"12:00 "` direction, press the center button to spell, which also counts as **one step**. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.
**Example 1:**
**Input:** ring = "godding ", key = "gd "
**Output:** 4
**Explanation:**
For the first key character 'g', since it is already in place, we just need 1 step to spell this character.
For the second key character 'd', we need to rotate the ring "godding " anticlockwise by two steps to make it become "ddinggo ".
Also, we need 1 more step for spelling.
So the final output is 4.
**Example 2:**
**Input:** ring = "godding ", key = "godding "
**Output:** 13
**Constraints:**
* `1 <= ring.length, key.length <= 100`
* `ring` and `key` consist of only lower case English letters.
* It is guaranteed that `key` could always be spelled by rotating `ring`.
| null |
Python3 with explanation
|
freedom-trail
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport collections\nimport sys\n\nclass Solution:\n def findRotateSteps(self, ring: str, key: str) -> int:\n # Store the positions of each character of ring in a dictionary\n pos = collections.defaultdict(list)\n for i, ch in enumerate(ring):\n pos[ch].append(i)\n \n # Initial dp table\n m, n = len(key), len(ring)\n dp = [[0]*n for _ in range(m)]\n min_val = sys.maxsize\n\n # For the first character in key, calculate the minimum steps directly\n for i in pos[key[0]]:\n dp[0][i] = min(i, n - i) + 1\n min_val = min(min_val, dp[0][i])\n\n for i in range(1, m):\n min_val = sys.maxsize\n for j in pos[key[i]]:\n dp[i][j] = min(dp[i - 1][k] + min(abs(j - k), n - abs(j - k)) for k in pos[key[i - 1]]) + 1\n min_val = min(min_val, dp[i][j])\n \n return min_val\n\n```
| 0
|
In the video game Fallout 4, the quest **"Road to Freedom "** requires players to reach a metal dial called the **"Freedom Trail Ring "** and use the dial to spell a specific keyword to open the door.
Given a string `ring` that represents the code engraved on the outer ring and another string `key` that represents the keyword that needs to be spelled, return _the minimum number of steps to spell all the characters in the keyword_.
Initially, the first character of the ring is aligned at the `"12:00 "` direction. You should spell all the characters in `key` one by one by rotating `ring` clockwise or anticlockwise to make each character of the string key aligned at the `"12:00 "` direction and then by pressing the center button.
At the stage of rotating the ring to spell the key character `key[i]`:
1. You can rotate the ring clockwise or anticlockwise by one place, which counts as **one step**. The final purpose of the rotation is to align one of `ring`'s characters at the `"12:00 "` direction, where this character must equal `key[i]`.
2. If the character `key[i]` has been aligned at the `"12:00 "` direction, press the center button to spell, which also counts as **one step**. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.
**Example 1:**
**Input:** ring = "godding ", key = "gd "
**Output:** 4
**Explanation:**
For the first key character 'g', since it is already in place, we just need 1 step to spell this character.
For the second key character 'd', we need to rotate the ring "godding " anticlockwise by two steps to make it become "ddinggo ".
Also, we need 1 more step for spelling.
So the final output is 4.
**Example 2:**
**Input:** ring = "godding ", key = "godding "
**Output:** 13
**Constraints:**
* `1 <= ring.length, key.length <= 100`
* `ring` and `key` consist of only lower case English letters.
* It is guaranteed that `key` could always be spelled by rotating `ring`.
| null |
Python solution beats 98.67%
|
freedom-trail
| 0
| 1
|
# Code\n```\nclass Solution:\n def findRotateSteps(self, ring: str, key: str) -> int:\n ln=len(ring)\n kln=len(key)\n def getSetp(id1,id2):\n d=abs(id1-id2)\n return min(d,ln-d)+1\n \n mp=defaultdict(list)\n for i,n in enumerate(ring):\n mp[n].append(i)\n for m in mp.values():\n m.sort()\n \n @cache\n def dps(id,ta)->int:\n c=key[ta]\n if ta==kln-1:\n if ring[id]==c:\n return 1\n elif len(mp[c])==1:\n return getSetp(id,mp[c][0])\n elif len(mp[c])==2:\n return min(getSetp(id,mp[c][0]),getSetp(id,mp[c][1]))\n else:\n n=bisect.bisect_left(mp[c],id)-1\n if n==-1 or n==len(mp[c])-1:\n return min(getSetp(id,mp[c][0]),getSetp(id,mp[c][-1]))\n else:\n return min(getSetp(id,mp[c][n]),getSetp(id,mp[c][n+1]))\n else:\n if ring[id]==c:\n return dps(id,ta+1)+1\n elif len(mp[c])==1:\n return getSetp(id,mp[c][0])+dps(mp[c][0],ta+1)\n elif len(mp[c])==2:\n return min(getSetp(id,mp[c][0])+dps(mp[c][0],ta+1),getSetp(id,mp[c][1])+dps(mp[c][1],ta+1))\n else:\n n=bisect.bisect_left(mp[c],id)-1\n if n==-1 or n==len(mp[c])-1:\n return min(getSetp(id,mp[c][0])+dps(mp[c][0],ta+1),getSetp(id,mp[c][-1])+dps(mp[c][-1],ta+1))\n else:\n return min(getSetp(id,mp[c][n])+dps(mp[c][n],ta+1),getSetp(id,mp[c][n+1])+dps(mp[c][n+1],ta+1))\n return dps(0,0)\n```
| 0
|
In the video game Fallout 4, the quest **"Road to Freedom "** requires players to reach a metal dial called the **"Freedom Trail Ring "** and use the dial to spell a specific keyword to open the door.
Given a string `ring` that represents the code engraved on the outer ring and another string `key` that represents the keyword that needs to be spelled, return _the minimum number of steps to spell all the characters in the keyword_.
Initially, the first character of the ring is aligned at the `"12:00 "` direction. You should spell all the characters in `key` one by one by rotating `ring` clockwise or anticlockwise to make each character of the string key aligned at the `"12:00 "` direction and then by pressing the center button.
At the stage of rotating the ring to spell the key character `key[i]`:
1. You can rotate the ring clockwise or anticlockwise by one place, which counts as **one step**. The final purpose of the rotation is to align one of `ring`'s characters at the `"12:00 "` direction, where this character must equal `key[i]`.
2. If the character `key[i]` has been aligned at the `"12:00 "` direction, press the center button to spell, which also counts as **one step**. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.
**Example 1:**
**Input:** ring = "godding ", key = "gd "
**Output:** 4
**Explanation:**
For the first key character 'g', since it is already in place, we just need 1 step to spell this character.
For the second key character 'd', we need to rotate the ring "godding " anticlockwise by two steps to make it become "ddinggo ".
Also, we need 1 more step for spelling.
So the final output is 4.
**Example 2:**
**Input:** ring = "godding ", key = "godding "
**Output:** 13
**Constraints:**
* `1 <= ring.length, key.length <= 100`
* `ring` and `key` consist of only lower case English letters.
* It is guaranteed that `key` could always be spelled by rotating `ring`.
| null |
Python DP, Beats 100%. Easy explained with comments.
|
freedom-trail
| 0
| 1
|
# Code\n```\nclass Solution:\n def findRotateSteps(self, ring: str, key: str) -> int:\n index = defaultdict(list)\n #Index Hashing\n for i in range(len(ring)):\n index[ring[i]].append(i)\n #DFS function + DP\n @lru_cache\n def dfs(r, k):\n if k == len(key):\n return 0\n ans = float("inf")\n for idx in index[key[k]]:\n clockwise_movement_cost = abs(idx - r) + 1\n anticlockwise_movement_cost = len(ring) - abs(idx - r) + 1\n ans = min(ans, min(clockwise_movement_cost, anticlockwise_movement_cost) + dfs(idx, k + 1))\n return ans\n #Invoking fn\n return dfs(0, 0)\n \n```
| 0
|
In the video game Fallout 4, the quest **"Road to Freedom "** requires players to reach a metal dial called the **"Freedom Trail Ring "** and use the dial to spell a specific keyword to open the door.
Given a string `ring` that represents the code engraved on the outer ring and another string `key` that represents the keyword that needs to be spelled, return _the minimum number of steps to spell all the characters in the keyword_.
Initially, the first character of the ring is aligned at the `"12:00 "` direction. You should spell all the characters in `key` one by one by rotating `ring` clockwise or anticlockwise to make each character of the string key aligned at the `"12:00 "` direction and then by pressing the center button.
At the stage of rotating the ring to spell the key character `key[i]`:
1. You can rotate the ring clockwise or anticlockwise by one place, which counts as **one step**. The final purpose of the rotation is to align one of `ring`'s characters at the `"12:00 "` direction, where this character must equal `key[i]`.
2. If the character `key[i]` has been aligned at the `"12:00 "` direction, press the center button to spell, which also counts as **one step**. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.
**Example 1:**
**Input:** ring = "godding ", key = "gd "
**Output:** 4
**Explanation:**
For the first key character 'g', since it is already in place, we just need 1 step to spell this character.
For the second key character 'd', we need to rotate the ring "godding " anticlockwise by two steps to make it become "ddinggo ".
Also, we need 1 more step for spelling.
So the final output is 4.
**Example 2:**
**Input:** ring = "godding ", key = "godding "
**Output:** 13
**Constraints:**
* `1 <= ring.length, key.length <= 100`
* `ring` and `key` consist of only lower case English letters.
* It is guaranteed that `key` could always be spelled by rotating `ring`.
| null |
✅☑[C++/Java/Python/JavaScript] || 3 Approaches || EXPLAINED🔥
|
find-largest-value-in-each-tree-row
| 1
| 1
|
# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (BFS)***\n1. The function takes a pointer to the root of a binary tree as input, represented by the `TreeNode` class. The goal is to find the largest values at each level of the tree.\n\n1. The function starts by checking if the `root` is a `nullptr` (i.e., an empty tree). If the tree is empty, it returns an empty vector, indicating that there are no largest values to find.\n\n1. If the tree is not empty, the function proceeds to find the largest values at each level.\n\n1. It initializes an empty vector `ans` to store the largest values and a `queue` queue for level-order traversal. The root node is pushed into the queue to start the traversal.\n\n1. The function enters a loop that continues until the queue is empty. Inside the loop, it processes one level of the tree at a time.\n\n1. For each level, it keeps track of the current level\'s length (the number of nodes in that level) and initializes `currMax` to the smallest possible integer value (`INT_MIN`) to find the largest value in that level.\n\n1. Another loop iterates through the nodes in the current level. It dequeues a node from the front of the queue and updates `currMax` if the value of the dequeued node is larger than the current maximum.\n\n1. For each dequeued node, if it has a left child, the left child is enqueued into the `queue`. If it has a right child, the right child is also enqueued.\n\n1. After processing all nodes in the current level, the largest value for that level (`currMax`) is added to the `ans` vector.\n\n1. The outer loop continues until all levels have been processed, and the `ans` vector contains the largest values for each level in the binary tree.\n\n1. Finally, the function returns the `ans` vector, which holds the largest values.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> largestValues(TreeNode* root) {\n if (root == nullptr) {\n return vector<int>{};\n }\n \n vector<int> ans;\n queue<TreeNode*> queue;\n queue.push(root);\n \n while (!queue.empty()) {\n int currentLength = queue.size();\n int currMax = INT_MIN;\n \n for (int i = 0; i < currentLength; i++) {\n TreeNode* node = queue.front();\n queue.pop();\n currMax = max(currMax, node->val);\n \n if (node->left) {\n queue.push(node->left);\n }\n \n if (node->right) {\n queue.push(node->right);\n }\n }\n \n ans.push_back(currMax);\n }\n \n return ans;\n }\n};\n\n```\n\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <limits.h>\n\n// Definition for a binary tree node.\nstruct TreeNode {\n int val;\n struct TreeNode* left;\n struct TreeNode* right;\n};\n\n// Definition for a queue node.\nstruct QueueNode {\n struct TreeNode* treeNode;\n struct QueueNode* next;\n};\n\n// Definition for a queue.\nstruct Queue {\n struct QueueNode* front;\n struct QueueNode* rear;\n};\n\n// Initialize a new queue.\nstruct Queue* createQueue() {\n struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));\n queue->front = queue->rear = NULL;\n return queue;\n}\n\n// Enqueue a tree node in the queue.\nvoid enqueue(struct Queue* queue, struct TreeNode* treeNode) {\n struct QueueNode* newNode = (struct QueueNode*)malloc(sizeof(struct QueueNode));\n newNode->treeNode = treeNode;\n newNode->next = NULL;\n \n if (queue->rear == NULL) {\n queue->front = queue->rear = newNode;\n return;\n }\n \n queue->rear->next = newNode;\n queue->rear = newNode;\n}\n\n// Dequeue a tree node from the queue.\nstruct TreeNode* dequeue(struct Queue* queue) {\n if (queue->front == NULL) {\n return NULL;\n }\n \n struct TreeNode* treeNode = queue->front->treeNode;\n struct QueueNode* temp = queue->front;\n queue->front = queue->front->next;\n \n if (queue->front == NULL) {\n queue->rear = NULL;\n }\n \n free(temp);\n return treeNode;\n}\n\nint* largestValues(struct TreeNode* root, int* returnSize) {\n if (root == NULL) {\n *returnSize = 0;\n return NULL;\n }\n\n // Initialize the answer array and queue for level-order traversal.\n int* ans = (int*)malloc(sizeof(int) * 1000);\n struct Queue* queue = createQueue();\n enqueue(queue, root);\n\n int idx = 0; // Index to track the current position in the answer array.\n\n while (queue->front != NULL) {\n int currentLength = 0;\n int currMax = INT_MIN;\n\n // Process nodes at the current level.\n for (currentLength = queue->front != NULL; currentLength > 0; currentLength--) {\n struct TreeNode* node = dequeue(queue);\n currMax = (node->val > currMax) ? node->val : currMax;\n\n // Enqueue left and right children if they exist.\n if (node->left != NULL) {\n enqueue(queue, node->left);\n }\n if (node->right != NULL) {\n enqueue(queue, node->right);\n }\n }\n\n // Store the maximum value in the answer array.\n ans[idx] = currMax;\n idx++;\n }\n\n // Set the return size and return the answer array.\n *returnSize = idx;\n return ans;\n}\n\nint main() {\n // Create a sample binary tree for testing.\n struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->val = 1;\n root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->left->val = 3;\n root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->left->left->val = 5;\n root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->left->right->val = 3;\n root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->right->val = 2;\n root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->right->right->val = 9;\n\n int returnSize;\n int* result = largestValues(root, &returnSize);\n\n printf("Largest values at each level: ");\n for (int i = 0; i < returnSize; i++) {\n printf("%d ", result[i]);\n }\n printf("\\n");\n\n return 0;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public List<Integer> largestValues(TreeNode root) {\n if (root == null) {\n return new ArrayList<Integer>();\n }\n \n List<Integer> ans = new ArrayList<Integer>();\n Queue<TreeNode> queue = new LinkedList<>();\n queue.add(root);\n \n while (!queue.isEmpty()) {\n int currentLength = queue.size();\n int currMax = Integer.MIN_VALUE;\n \n for (int i = 0; i < currentLength; i++) {\n TreeNode node = queue.remove();\n currMax = Math.max(currMax, node.val);\n \n if (node.left != null) {\n queue.add(node.left);\n }\n \n if (node.right != null) {\n queue.add(node.right);\n }\n }\n \n ans.add(currMax);\n }\n \n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n \n ans = []\n queue = deque([root])\n \n while queue:\n current_length = len(queue)\n curr_max = float("-inf")\n \n for _ in range(current_length):\n node = queue.popleft()\n curr_max = max(curr_max, node.val)\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n ans.append(curr_max)\n \n return ans\n\n```\n\n```javascript []\nfunction largestValues(root) {\n if (root === null) {\n return [];\n }\n \n const ans = [];\n const queue = [root];\n \n while (queue.length > 0) {\n const currentLength = queue.length;\n let currMax = -Infinity;\n \n for (let i = 0; i < currentLength; i++) {\n const node = queue.shift();\n currMax = Math.max(currMax, node.val);\n \n if (node.left) {\n queue.push(node.left);\n }\n \n if (node.right) {\n queue.push(node.right);\n }\n }\n \n ans.push(currMax);\n }\n \n return ans;\n}\n\n```\n\n\n---\n\n#### ***Approach 2 (DFS)***\n1. The `largestValues` function is the main entry point. It initializes an empty vector `ans` to store the largest values at each level and calls the `dfs` (depth-first search) function to traverse the binary tree.\n\n1. The `dfs` function is a recursive helper function. It takes two parameters: the current node and the depth of the current node.\n\n1. Inside the `dfs` function, it first checks if the current node is `nullptr`, indicating a leaf node or an empty subtree. If so, it returns without making any changes.\n\n1. If the depth is equal to the size of the `ans` vector, it means that we are at a new level in the tree. In this case, it pushes the value of the current node into the `ans` vector at the corresponding level.\n\n1. If the depth is not equal to the size of the `ans` vector, it means we have visited this level before. In this case, it updates the value at the corresponding level by taking the maximum of the existing value and the current node\'s value.\n\n1. The `dfs` function then makes two recursive calls to process the left and right children of the current node, incrementing the depth by 1 for each call.\n\n1. Once the `dfs` function completes its traversal, the `largestValues` function returns the `ans` vector, which contains the largest values at each level of the binary tree.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(h)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> ans;\n \n vector<int> largestValues(TreeNode* root) {\n dfs(root, 0);\n return ans;\n }\n \n void dfs(TreeNode* node, int depth) {\n if (node == nullptr) {\n return;\n }\n \n if (depth == ans.size()) {\n ans.push_back(node->val);\n } else {\n ans[depth] = max(ans[depth], node->val);\n }\n \n dfs(node->left, depth + 1);\n dfs(node->right, depth + 1);\n }\n};\n\n```\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\n// Definition for a binary tree node.\nstruct TreeNode {\n int val;\n struct TreeNode* left;\n struct TreeNode* right;\n};\n\nint* ans;\nint ansSize = 0;\n\nvoid dfs(struct TreeNode* node, int depth) {\n if (node == NULL) {\n return;\n }\n\n if (depth == ansSize) {\n ans = (int*)realloc(ans, (ansSize + 1) * sizeof(int));\n ans[ansSize++] = node->val;\n } else {\n ans[depth] = (ans[depth] > node->val) ? ans[depth] : node->val;\n }\n\n dfs(node->left, depth + 1);\n dfs(node->right, depth + 1);\n}\n\nint* largestValues(struct TreeNode* root, int* returnSize) {\n ans = NULL;\n ansSize = 0;\n dfs(root, 0);\n *returnSize = ansSize;\n return ans;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n List<Integer> ans;\n \n public List<Integer> largestValues(TreeNode root) {\n ans = new ArrayList<Integer>();\n dfs(root, 0);\n return ans;\n }\n \n public void dfs(TreeNode node, int depth) {\n if (node == null) {\n return;\n }\n \n if (depth == ans.size()) {\n ans.add(node.val);\n } else {\n ans.set(depth, Math.max(ans.get(depth), node.val));\n }\n \n dfs(node.left, depth + 1);\n dfs(node.right, depth + 1);\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n def dfs(node, depth):\n if not node:\n return\n \n if depth == len(ans):\n ans.append(node.val)\n else:\n ans[depth] = max(ans[depth], node.val)\n \n dfs(node.left, depth + 1)\n dfs(node.right, depth + 1)\n \n ans = []\n dfs(root, 0)\n return ans\n\n```\n\n```javascript []\n/**\n * Definition for a binary tree node.\n * function TreeNode(val) {\n * this.val = val;\n * this.left = this.right = null;\n * }\n */\n\n/**\n * @param {TreeNode} root\n * @return {number[]}\n */\nvar ans = [];\n\nvar largestValues = function(root) {\n dfs(root, 0);\n return ans;\n};\n\nvar dfs = function(node, depth) {\n if (node === null) {\n return;\n }\n\n if (depth === ans.length) {\n ans.push(node.val);\n } else {\n ans[depth] = Math.max(ans[depth], node.val);\n }\n\n dfs(node.left, depth + 1);\n dfs(node.right, depth + 1);\n};\n\n```\n\n\n---\n#### ***Approach 3 (DFS, Iterative)***\n1. The function `largestValues` takes the root of a binary tree as input and returns a vector of integers representing the largest values in each level.\n\n1. It checks if the root is `nullptr` (null). If the tree is empty, it returns an empty vector because there are no levels to process.\n\n1. It initializes an empty vector `ans` to store the largest values for each level.\n\n1. It uses a stack of pairs, where each pair contains a node from the tree and an integer representing its depth or level.\n\n1. It pushes the root node and level 0 into the stack as the starting point.\n\n1. It enters a loop that continues until the stack is empty. In each iteration:\n\n - It pops the top pair (node, depth) from the stack.\n\n - It checks if the `depth` is equal to the current size of the `ans` vector. If they are equal, this is the first node at this level, so it appends the node\'s value to the `ans` vector.\n\n - If the `depth` is not equal to the size of the `ans` vector, it means we\'ve already found a larger value for this level, so it compares the node\'s value with the existing value at that level and updates it if the current node\'s value is larger.\n\n - It then checks if the current node has left and right children. If it has a left child, it pushes that child into the stack with an increased depth. Similarly, if it has a right child, that child is pushed into the stack as well.\n\n1. The loop continues until all nodes at all levels are processed.\n\n1. Finally, it returns the `ans` vector, which contains the largest values for each level of the binary tree.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(h)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> largestValues(TreeNode* root) {\n if (root == nullptr) {\n return vector<int>{};\n }\n \n vector<int> ans;\n stack<pair<TreeNode*, int>> stack;\n stack.push(make_pair(root, 0));\n \n while (!stack.empty()) {\n pair<TreeNode*, int> pair = stack.top();\n stack.pop();\n TreeNode* node = pair.first;\n int depth = pair.second;\n \n if (depth == ans.size()) {\n ans.push_back(node->val);\n } else {\n ans[depth] = max(ans[depth], node->val);\n }\n \n if (node->left) {\n stack.push(make_pair(node->left, depth + 1));\n }\n \n if (node->right) {\n stack.push(make_pair(node->right, depth + 1));\n }\n }\n \n return ans;\n }\n};\n\n```\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n#include <stdbool.h>\n\nstruct TreeNode {\n int val;\n struct TreeNode *left;\n struct TreeNode *right;\n};\n\nstruct TreeNode* createNode(int val) {\n struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n newNode->val = val;\n newNode->left = NULL;\n newNode->right = NULL;\n return newNode;\n}\n\nstruct TreeNode* insert(struct TreeNode* root, int val) {\n if (root == NULL) {\n return createNode(val);\n }\n\n if (val < root->val) {\n root->left = insert(root->left, val);\n } else if (val > root->val) {\n root->right = insert(root->right, val);\n }\n\n return root;\n}\n\nvoid freeTree(struct TreeNode* root) {\n if (root == NULL) {\n return;\n }\n\n freeTree(root->left);\n freeTree(root->right);\n free(root);\n}\n\ntypedef struct TreeNode TreeNode;\n\nint* largestValues(TreeNode* root, int* returnSize) {\n if (root == NULL) {\n *returnSize = 0;\n return NULL;\n }\n\n int* ans = (int*)malloc(sizeof(int) * 10000);\n int depth = 0;\n\n struct {\n TreeNode* node;\n int depth;\n } stack[10000];\n int top = -1;\n\n stack[++top] = (struct { TreeNode* node; int depth; }) {root, 0};\n\n while (top >= 0) {\n TreeNode* node = stack[top].node;\n depth = stack[top].depth;\n top--;\n\n if (depth == *returnSize) {\n ans[depth] = node->val;\n (*returnSize)++;\n } else {\n ans[depth] = (ans[depth] > node->val) ? ans[depth] : node->val;\n }\n\n if (node->left != NULL) {\n stack[++top] = (struct { TreeNode* node; int depth; }) {node->left, depth + 1};\n }\n\n if (node->right != NULL) {\n stack[++top] = (struct { TreeNode* node; int depth; }) {node->right, depth + 1};\n }\n }\n\n return ans;\n}\n\nint main() {\n TreeNode* root = createNode(1);\n root->left = createNode(3);\n root->right = createNode(2);\n root->left->left = createNode(5);\n root->left->right = createNode(3);\n root->right->right = createNode(9);\n\n int returnSize = 0;\n int* largest = largestValues(root, &returnSize);\n\n printf("Largest values in each level: ");\n for (int i = 0; i < returnSize; i++) {\n printf("%d ", largest[i]);\n }\n\n free(largest);\n freeTree(root);\n\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public List<Integer> largestValues(TreeNode root) {\n if (root == null) {\n return new ArrayList<Integer>();\n }\n \n List<Integer> ans = new ArrayList<>();\n Stack<Pair<TreeNode, Integer>> stack = new Stack<>();\n stack.push(new Pair<>(root, 0));\n \n while (!stack.isEmpty()) {\n Pair<TreeNode, Integer> pair = stack.pop();\n TreeNode node = pair.getKey();\n int depth = pair.getValue();\n \n if (depth == ans.size()) {\n ans.add(node.val);\n } else {\n ans.set(depth, Math.max(ans.get(depth), node.val));\n }\n \n if (node.left != null) {\n stack.push(new Pair<>(node.left, depth + 1));\n }\n \n if (node.right != null) {\n stack.push(new Pair<>(node.right, depth + 1));\n }\n }\n \n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n \n ans = []\n stack = [(root, 0)]\n \n while stack:\n node, depth = stack.pop()\n if depth == len(ans):\n ans.append(node.val)\n else:\n ans[depth] = max(ans[depth], node.val)\n \n if node.left:\n stack.append((node.left, depth + 1))\n if node.right:\n stack.append((node.right, depth + 1))\n \n return ans\n\n```\n\n```javascript []\nvar largestValues = function(root) {\n if (root === null) {\n return [];\n }\n \n const ans = [];\n const stack = [[root, 0]];\n \n while (stack.length > 0) {\n const [node, depth] = stack.pop();\n \n if (depth === ans.length) {\n ans.push(node.val);\n } else {\n ans[depth] = Math.max(ans[depth], node.val);\n }\n \n if (node.left) {\n stack.push([node.left, depth + 1]);\n }\n \n if (node.right) {\n stack.push([node.right, depth + 1]);\n }\n }\n \n return ans;\n};\n\n```\n\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n---
| 4
|
Given the `root` of a binary tree, return _an array of the largest value in each row_ of the tree **(0-indexed)**.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** \[1,3,9\]
**Example 2:**
**Input:** root = \[1,2,3\]
**Output:** \[1,3\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
BFS Solution
|
find-largest-value-in-each-tree-row
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTraverse through each of the level uisng BFS and find the maximum value.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of calculating the height of the tree to store the result, we directly traverse the tree and find the solution in one traversal.\nEach element in the queue (used for BFS) consists of Node and the level the node is in. \nIf we reach a node with level that is not evaluated yet we append that into the queue.\nSo the elements of the same level will be checked with the value stored in result of that level. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n), where n is the number of nodes of tree. Each node is traversed only once\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n), Each node is stored in the queue and processed\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n # apply BFS\n result = []\n if root == None:\n return result\n \n process = [[root, 1]] # node and the level\n while len(process) > 0:\n front = process[0]\n node, level = front[0], front[1]\n process.pop(0)\n\n # based on the length check insert the node value\n if len(result) < level: # new level arrived\n result.append(node.val)\n else:\n result[level - 1] = max(result[level - 1], node.val)\n\n\n # insert the nodes in the process\n if node.left != None:\n process.append([node.left, level + 1])\n if node.right != None:\n process.append([node.right, level + 1])\n \n return result\n \n \n\n\n\n \n```
| 1
|
Given the `root` of a binary tree, return _an array of the largest value in each row_ of the tree **(0-indexed)**.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** \[1,3,9\]
**Example 2:**
**Input:** root = \[1,2,3\]
**Output:** \[1,3\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Python Solution using Queue and Map
|
find-largest-value-in-each-tree-row
| 0
| 1
|
\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\ndef max_from_rows(root):\n if not root:\n return\n \n queue = []\n queue.append(root)\n next_row = []\n max_ele_from_rows = []\n max_ele_from_rows.append(root.val)\n\n while queue:\n node = queue.pop(0)\n\n if node.left:\n next_row.append(node.left)\n\n if node.right:\n next_row.append(node.right)\n \n if not queue:\n queue, next_row = next_row, queue\n if queue:\n max_ele_from_rows.append(\n max(\n list(\n map(lambda x: x.val, queue)\n )\n )\n )\n return max_ele_from_rows\n \n\n\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n return max_from_rows(root)\n```
| 1
|
Given the `root` of a binary tree, return _an array of the largest value in each row_ of the tree **(0-indexed)**.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** \[1,3,9\]
**Example 2:**
**Input:** root = \[1,2,3\]
**Output:** \[1,3\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
✅ 98.68% BFS
|
find-largest-value-in-each-tree-row
| 1
| 1
|
# Intuition\nWhen presented with this problem, the immediate thought is to traverse through the tree level by level. This is because we need to determine the maximum value in each row. Level order traversal, also known as breadth-first search (BFS) for trees, is the ideal strategy for this. Using a queue, we can explore each level of the tree one by one and capture the maximum value for each.\n\n# Live Coding + Comments\nhttps://youtu.be/G4_vIA1eGA8?si=UBrPO5km7rbyQ5yJ\n\n# Approach\n1. **Initialization**: Begin with initializing a queue and adding the root node to it. This queue will help in level order traversal.\n2. **Level-wise Traversal**: As long as the queue is not empty, we keep on processing nodes. For each level, we will calculate its size (i.e., the number of nodes in the current level). This helps in segregating nodes of different levels.\n3. **Capture Maximum**: For each level, initialize a variable `max_val` with the smallest possible integer. As we process each node in the current level, we update `max_val` to be the maximum between the node\'s value and the current `max_val`.\n4. **Child Processing**: After processing a node, we add its left and right children (if they exist) to the queue for the next level\'s processing.\n5. **Result Update**: Once all nodes of a level are processed, the maximum value for that level (`max_val`) is added to the result list.\n\n# Complexity\n- **Time complexity**: $O(n)$. Each node is processed once, and the maximum value at each level is determined in constant time. So, the overall time taken is linear with respect to the number of nodes.\n \n- **Space complexity**: $O(n)$. In the worst case, the queue can hold all leaf nodes. In a balanced binary tree, the last level can have $n/2$ nodes. Thus, the space complexity is linear.\n\n# Code\n``` Python []\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n \n result = []\n queue = deque([root])\n \n while queue:\n curr_level_size = len(queue)\n max_val = float(\'-inf\')\n \n for _ in range(curr_level_size):\n node = queue.popleft()\n max_val = max(max_val, node.val)\n \n for child in [node.left, node.right]:\n if child:\n queue.append(child)\n \n result.append(max_val)\n \n return result\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> largestValues(TreeNode* root) {\n if (!root) return {};\n \n std::vector<int> result;\n std::queue<TreeNode*> queue;\n queue.push(root);\n \n while (!queue.empty()) {\n int curr_level_size = queue.size();\n int max_val = INT_MIN;\n \n for (int i = 0; i < curr_level_size; ++i) {\n TreeNode* node = queue.front();\n queue.pop();\n max_val = std::max(max_val, node->val);\n \n if (node->left) queue.push(node->left);\n if (node->right) queue.push(node->right);\n }\n \n result.push_back(max_val);\n }\n \n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<Integer> largestValues(TreeNode root) {\n if (root == null) return new ArrayList<>();\n \n List<Integer> result = new ArrayList<>();\n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root);\n \n while (!queue.isEmpty()) {\n int curr_level_size = queue.size();\n int max_val = Integer.MIN_VALUE;\n \n for (int i = 0; i < curr_level_size; i++) {\n TreeNode node = queue.poll();\n max_val = Math.max(max_val, node.val);\n \n if (node.left != null) queue.offer(node.left);\n if (node.right != null) queue.offer(node.right);\n }\n \n result.add(max_val);\n }\n \n return result;\n }\n}\n```\n``` Go []\nfunc largestValues(root *TreeNode) []int {\n if root == nil {\n return nil\n }\n \n var result []int\n queue := []*TreeNode{root}\n \n for len(queue) > 0 {\n curr_level_size := len(queue)\n max_val := ^(int(^uint(0) >> 1)) // Integer minimum\n \n for i := 0; i < curr_level_size; i++ {\n node := queue[0]\n queue = queue[1:]\n if node.Val > max_val {\n max_val = node.Val\n }\n \n if node.Left != nil {\n queue = append(queue, node.Left)\n }\n if node.Right != nil {\n queue = append(queue, node.Right)\n }\n }\n \n result = append(result, max_val)\n }\n \n return result\n}\n```\n``` JavaScript []\nfunction largestValues(root) {\n if (!root) return [];\n \n const result = [];\n const queue = [root];\n \n while (queue.length) {\n let curr_level_size = queue.length;\n let max_val = Number.MIN_SAFE_INTEGER;\n \n for (let i = 0; i < curr_level_size; i++) {\n const node = queue.shift();\n max_val = Math.max(max_val, node.val);\n \n if (node.left) queue.push(node.left);\n if (node.right) queue.push(node.right);\n }\n \n result.push(max_val);\n }\n \n return result;\n}\n```\n``` C# []\npublic class Solution {\n public IList<int> LargestValues(TreeNode root) {\n if (root == null) return new List<int>();\n \n List<int> result = new List<int>();\n Queue<TreeNode> queue = new Queue<TreeNode>();\n queue.Enqueue(root);\n \n while (queue.Count > 0) {\n int curr_level_size = queue.Count;\n int max_val = Int32.MinValue;\n \n for (int i = 0; i < curr_level_size; i++) {\n TreeNode node = queue.Dequeue();\n max_val = Math.Max(max_val, node.val);\n \n if (node.left != null) queue.Enqueue(node.left);\n if (node.right != null) queue.Enqueue(node.right);\n }\n \n result.Add(max_val);\n }\n \n return result;\n }\n}\n```\n``` PHP []\nclass Solution {\n function largestValues($root) {\n if (!$root) return [];\n \n $result = [];\n $queue = [$root];\n \n while (count($queue)) {\n $curr_level_size = count($queue);\n $max_val = PHP_INT_MIN;\n \n for ($i = 0; $i < $curr_level_size; $i++) {\n $node = array_shift($queue);\n $max_val = max($max_val, $node->val);\n \n if ($node->left) array_push($queue, $node->left);\n if ($node->right) array_push($queue, $node->right);\n }\n \n $result[] = $max_val;\n }\n \n return $result;\n }\n}\n```\n\n## Performance\n| Language | Execution Time (ms) | Memory (MB) |\n|------------|---------------------|-------------|\n| Java | 2 ms | 44.3 MB |\n| Go | 4 ms | 5.8 MB |\n| C++ | 15 ms | 22.5 MB |\n| PHP | 21 ms | 21.2 MB |\n| Python3 | 38 ms | 18.6 MB |\n| JavaScript | 64 ms | 46.9 MB |\n| C# | 140 ms | 44.9 MB |\n\n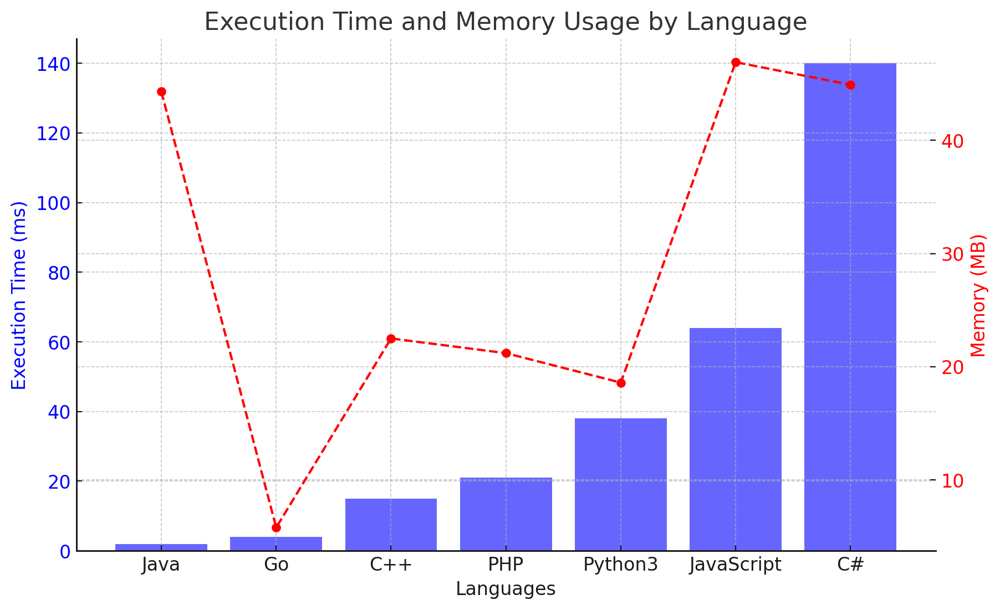\n\n\n# What have we learned?\nFrom this problem, we have reinforced the concept of level order traversal in trees. We also learned the importance of using a queue for BFS to traverse each level sequentially. By processing each level separately, we could easily compute the maximum value for each row. This problem is a good demonstration of how tree traversal techniques can be tailored to extract specific details from each level of a tree.\n\n# Why does it work?\nThis approach works because BFS ensures that all nodes at a particular depth (or level) are processed before moving on to nodes at the next depth. This ordering allows us to easily segregate nodes of different levels and compute the maximum value for each level separately.
| 48
|
Given the `root` of a binary tree, return _an array of the largest value in each row_ of the tree **(0-indexed)**.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** \[1,3,9\]
**Example 2:**
**Input:** root = \[1,2,3\]
**Output:** \[1,3\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Easiest Solution || Python
|
find-largest-value-in-each-tree-row
| 0
| 1
|
# Intuition\nVery easy approach by using BFS.\n\n# Approach\nAppending elements to queue by iterating through left and right childs of each element and poping and finding maximum at each level.\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(max_width)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n result =[]\n queue = [root]\n \n while queue:\n max_val=float(\'-inf\')\n for i in range(len(queue)):\n node = queue.pop(0)\n max_val = max(max_val,node.val)\n if node.right:\n queue.append(node.right)\n if node.left:\n queue.append(node.left)\n result.append(max_val)\n return result\n \n```\n# **PLEASE DO UPVOTE\uD83E\uDD79**
| 1
|
Given the `root` of a binary tree, return _an array of the largest value in each row_ of the tree **(0-indexed)**.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** \[1,3,9\]
**Example 2:**
**Input:** root = \[1,2,3\]
**Output:** \[1,3\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Python3 DFS approach
|
find-largest-value-in-each-tree-row
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI used a recursive approach to solve the question.In particular the dfs traversal.I started from the first node and traversed each node storing the maximum value on each level.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ since i am touching each node exactly once \n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ space used by the hash table \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom collections import defaultdict \nclass Solution:\n def largestValues(self, root: Optional[TreeNode]) -> List[int]:\n d = defaultdict()\n def dfs(root , level):\n if not root:\n return \n if level in d.keys():\n d[level] = max( d[level] , root.val )\n else:\n d[level] = root.val\n\n dfs(root.left , level+1)\n dfs(root.right , level+1)\n\n dfs(root , 0)\n return d.values()\n```
| 1
|
Given the `root` of a binary tree, return _an array of the largest value in each row_ of the tree **(0-indexed)**.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** \[1,3,9\]
**Example 2:**
**Input:** root = \[1,2,3\]
**Output:** \[1,3\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-231 <= Node.val <= 231 - 1`
| null |
Beats 98% of the users in Python3 in both Time and Space, O(n^2) solution Clean Short Code.
|
longest-palindromic-subsequence
| 0
| 1
|
# Intuition\n\n\n# Complexity\n- Time complexity:\n- O(n^2)\n\n- Space complexity:\n- O(n)\n\n# Code\n```\nclass Solution:\n def longestPalindromeSubseq(self, s: str) -> int:\n \n l=[0]*len(s)\n mo=1\n for i in range(len(s)):\n m=-1\n j=len(s)-1\n flag2=True\n k=i\n while(i<j):\n if s[i]==s[j] and flag2:\n if m<l[j]:\n flag2=False\n l[j]=m\n l[i]=m*(-1)\n k=j\n j=j-1\n continue\n if m==l[j]:\n m=l[j]-1\n flag2=True\n j=j-1\n if l[k]==l[k-1]*(-1):\n mo=max(mo,l[k]*(-1)*2)\n else:\n mo=max(mo,l[k]*(-1)*2+1)\n\n return mo\n\n\n\n```
| 1
|
Given a string `s`, find _the longest palindromic **subsequence**'s length in_ `s`.
A **subsequence** is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** s = "bbbab "
**Output:** 4
**Explanation:** One possible longest palindromic subsequence is "bbbb ".
**Example 2:**
**Input:** s = "cbbd "
**Output:** 2
**Explanation:** One possible longest palindromic subsequence is "bb ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists only of lowercase English letters.
| null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.