title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
554: Solution with step by step explanation
|
brick-wall
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create an empty dictionary called edge_counts.\n2. Loop through each row in the wall list:\na. Create a variable called edge_pos and set it to 0.\nb. Loop through each brick width in the current row up to the second to last brick (since the last brick cannot form an edge).\ni. Add the current brick width to edge_pos.\nii. Add 1 to the value in the edge_counts dictionary at the key of edge_pos, or add a new key-value pair with key edge_pos and value 1 if it doesn\'t exist.\n3. Return the difference between the length of the wall list and the maximum value in the edge_counts dictionary. If the edge_counts dictionary is empty, return the length of the wall list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def leastBricks(self, wall: List[List[int]]) -> int:\n edge_counts = {}\n for row in wall:\n edge_pos = 0\n for brick_width in row[:-1]:\n edge_pos += brick_width\n edge_counts[edge_pos] = edge_counts.get(edge_pos, 0) + 1\n return len(wall) - max(edge_counts.values(), default=0)\n\n```
| 5
|
There is a rectangular brick wall in front of you with `n` rows of bricks. The `ith` row has some number of bricks each of the same height (i.e., one unit) but they can be of different widths. The total width of each row is the same.
Draw a vertical line from the top to the bottom and cross the least bricks. If your line goes through the edge of a brick, then the brick is not considered as crossed. You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.
Given the 2D array `wall` that contains the information about the wall, return _the minimum number of crossed bricks after drawing such a vertical line_.
**Example 1:**
**Input:** wall = \[\[1,2,2,1\],\[3,1,2\],\[1,3,2\],\[2,4\],\[3,1,2\],\[1,3,1,1\]\]
**Output:** 2
**Example 2:**
**Input:** wall = \[\[1\],\[1\],\[1\]\]
**Output:** 3
**Constraints:**
* `n == wall.length`
* `1 <= n <= 104`
* `1 <= wall[i].length <= 104`
* `1 <= sum(wall[i].length) <= 2 * 104`
* `sum(wall[i])` is the same for each row `i`.
* `1 <= wall[i][j] <= 231 - 1`
| null |
Solution
|
brick-wall
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int leastBricks(vector<vector<int>>& wall) {\n int len = 0, n = wall.size();\n for(int i = 0; i < wall[0].size(); ++i){\n len += wall[0][i];\n }\n unordered_map<int, int> freq{};\n for(int i = 0; i < n; ++i){\n int cur = -1;\n for(int j = 0; j < wall[i].size() - 1; ++j){\n cur += wall[i][j];\n ++freq[cur];\n }\n }\n int ans = n;\n int m = 0;\n for(auto& a : freq){\n m = max(m, a.second);\n }\n return ans - m;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def leastBricks(self, wall: List[List[int]]) -> int:\n countGap = { 0 : 0 }\n\n for r in wall:\n total = 0\n for b in r[:-1]:\n total += b\n countGap[total] = 1 + countGap.get(total, 0)\n\n return len(wall) - max(countGap.values())\n```\n\n```Java []\nclass Solution {\n int best = 0;\n Map<Integer, Integer> freq = new HashMap<>();\n public int leastBricks(List<List<Integer>> wall) {\n for (int i = 0; i < wall.size(); i++)\n processRow(wall.get(i));\n return wall.size() - best;\n }\n public void processRow(List<Integer> row) {\n int rowSum = row.get(0);\n for (int j = 1; j < row.size(); j++) {\n int f = freq.getOrDefault(rowSum, 0) + 1;\n freq.put(rowSum, f);\n if (f > best) best = f;\n rowSum += row.get(j);\n } \n }\n}\n```\n
| 2
|
There is a rectangular brick wall in front of you with `n` rows of bricks. The `ith` row has some number of bricks each of the same height (i.e., one unit) but they can be of different widths. The total width of each row is the same.
Draw a vertical line from the top to the bottom and cross the least bricks. If your line goes through the edge of a brick, then the brick is not considered as crossed. You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.
Given the 2D array `wall` that contains the information about the wall, return _the minimum number of crossed bricks after drawing such a vertical line_.
**Example 1:**
**Input:** wall = \[\[1,2,2,1\],\[3,1,2\],\[1,3,2\],\[2,4\],\[3,1,2\],\[1,3,1,1\]\]
**Output:** 2
**Example 2:**
**Input:** wall = \[\[1\],\[1\],\[1\]\]
**Output:** 3
**Constraints:**
* `n == wall.length`
* `1 <= n <= 104`
* `1 <= wall[i].length <= 104`
* `1 <= sum(wall[i].length) <= 2 * 104`
* `sum(wall[i])` is the same for each row `i`.
* `1 <= wall[i][j] <= 231 - 1`
| null |
Python Elegant & Short | Prefix Sum
|
brick-wall
| 0
| 1
|
# Complexity\n- Time complexity: $$O(n * m)$$\n- Space complexity: $$O(m)$$\n\n# Code\n```\nclass Solution:\n def leastBricks(self, wall: List[List[int]]) -> int:\n n, m = len(wall), sum(wall[0])\n bricks = defaultdict(int)\n\n for row in wall:\n for acc in accumulate(row):\n bricks[acc] += 1\n\n return n - max((val for i, val in bricks.items() if 0 < i < m), default=0)\n```
| 2
|
There is a rectangular brick wall in front of you with `n` rows of bricks. The `ith` row has some number of bricks each of the same height (i.e., one unit) but they can be of different widths. The total width of each row is the same.
Draw a vertical line from the top to the bottom and cross the least bricks. If your line goes through the edge of a brick, then the brick is not considered as crossed. You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.
Given the 2D array `wall` that contains the information about the wall, return _the minimum number of crossed bricks after drawing such a vertical line_.
**Example 1:**
**Input:** wall = \[\[1,2,2,1\],\[3,1,2\],\[1,3,2\],\[2,4\],\[3,1,2\],\[1,3,1,1\]\]
**Output:** 2
**Example 2:**
**Input:** wall = \[\[1\],\[1\],\[1\]\]
**Output:** 3
**Constraints:**
* `n == wall.length`
* `1 <= n <= 104`
* `1 <= wall[i].length <= 104`
* `1 <= sum(wall[i].length) <= 2 * 104`
* `sum(wall[i])` is the same for each row `i`.
* `1 <= wall[i][j] <= 231 - 1`
| null |
Concise Python code - please downvote
|
brick-wall
| 0
| 1
|
\n# Code\n```\nclass Solution:\n def leastBricks(self, wall: List[List[int]]) -> int:\n counter = collections.Counter(\n (\n val \n for row in wall\n for val in itertools.accumulate(row)\n )\n )\n data = counter.most_common(2)\n return data[0][1] if len(data) == 1 else data[0][1] - data[1][1]\n\n \n \n \n```
| 0
|
There is a rectangular brick wall in front of you with `n` rows of bricks. The `ith` row has some number of bricks each of the same height (i.e., one unit) but they can be of different widths. The total width of each row is the same.
Draw a vertical line from the top to the bottom and cross the least bricks. If your line goes through the edge of a brick, then the brick is not considered as crossed. You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.
Given the 2D array `wall` that contains the information about the wall, return _the minimum number of crossed bricks after drawing such a vertical line_.
**Example 1:**
**Input:** wall = \[\[1,2,2,1\],\[3,1,2\],\[1,3,2\],\[2,4\],\[3,1,2\],\[1,3,1,1\]\]
**Output:** 2
**Example 2:**
**Input:** wall = \[\[1\],\[1\],\[1\]\]
**Output:** 3
**Constraints:**
* `n == wall.length`
* `1 <= n <= 104`
* `1 <= wall[i].length <= 104`
* `1 <= sum(wall[i].length) <= 2 * 104`
* `sum(wall[i])` is the same for each row `i`.
* `1 <= wall[i][j] <= 231 - 1`
| null |
Solution
|
next-greater-element-iii
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int nextGreaterElement(int n) {\n auto digits = to_string(n);\n nextPermutation(begin(digits), end(digits));\n auto result = stoll(digits);\n return (result > numeric_limits<int>::max() || result <= n) ? -1 : result;\n }\nprivate:\n template<typename BidiIt>\n bool nextPermutation(BidiIt begin, BidiIt end) {\n const auto rbegin = reverse_iterator<BidiIt>(end);\n const auto rend = reverse_iterator<BidiIt>(begin);\n \n auto pivot = next(rbegin);\n while (pivot != rend && *pivot >= *prev(pivot)) {\n ++pivot;\n }\n bool is_greater = true;\n if (pivot != rend) {\n auto change = find_if(rbegin, pivot, bind1st(less<int>(), *pivot));\n swap(*change, *pivot);\n } else {\n is_greater = false;\n }\n reverse(rbegin, pivot);\n return is_greater;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def nextGreaterElement(self, n: int) -> int:\n s = list(str(n))\n flag = False\n for i in range(len(s)-1, 0, -1):\n if s[i-1] < s[i]:\n j = -1\n while s[i-1] >= s[j]:\n j -= 1\n s[i-1], s[j] = s[j], s[i-1]\n s[i:] = sorted(s[i:])\n flag = True\n break\n m = int(\'\'.join(s))\n if m >= 2**31 or m < 1 or not flag: \n return -1\n else: \n return m\n```\n\n```Java []\nclass Solution {\n public int nextGreaterElement(int n) {\n String s = String.valueOf(n);\n int arr[] = new int[s.length()];\n int i=0;\n for(char c: s.toCharArray()) {\n arr[i++] = c - \'0\';\n }\n int index=-1;\n for(i=arr.length-1;i>0;i--) {\n if(arr[i-1]<arr[i]) {\n index = i-1;\n break;\n }\n }\n if(index == -1) return -1;\n for(i=arr.length-1;i>index;i--) {\n if (arr[i]>arr[index]) {\n int temp = arr[index];\n arr[index] = arr[i];\n arr[i] = temp;\n break;\n } \n }\n int l = index+1, r=arr.length-1;\n while(l<r) {\n int temp = arr[l];\n arr[l++] = arr[r];\n arr[r--] = temp;\n }\n int res = 0;\n for(i=0;i<arr.length;i++) {\n if ((Integer.MAX_VALUE-arr[i])/10<res) return -1;\n res = res*10 + arr[i];\n }\n return res;\n }\n}\n```\n
| 1
|
Given a positive integer `n`, find _the smallest integer which has exactly the same digits existing in the integer_ `n` _and is greater in value than_ `n`. If no such positive integer exists, return `-1`.
**Note** that the returned integer should fit in **32-bit integer**, if there is a valid answer but it does not fit in **32-bit integer**, return `-1`.
**Example 1:**
**Input:** n = 12
**Output:** 21
**Example 2:**
**Input:** n = 21
**Output:** -1
**Constraints:**
* `1 <= n <= 231 - 1`
| null |
Python || MinHeap || Binary search || O(NlogN) complexity solution
|
next-greater-element-iii
| 0
| 1
|
Runtime: 30 ms, faster than **94.94%** of Python3 online submissions for Next Greater Element III.\nMemory Usage: 13.9 MB, less than 26.34% of Python3 online submissions for Next Greater Element III.\n\n* First, I want to tell you this is **NOT** the optimal solution. The optimal solution should have a time complexity of O(N). \n* However, during interview, if you see this question, a heap+binary search solution **should be accepted by interviewer**. I think it is worthy to come up with a solution using topics that you are familiar with. For me, the topic is **Heap**.\n\nExplanation: \n1. Scanning from last element to first element\n2. If we meet any element that is smaller than the previous element, we record this location as switch_pos. Because this is the location where you should swap value with one of the element you have scanned.\n3. Using MinHeap to record all the values you have scanned (except for the switch_pos). Meanwhile, using binary search to determine which value should be swapped, among the scanned values.\n4. Do the swap, and re-concatenate the remaining values into the right order.\n\nHeap is my savior in a lot of questions. Even if they do not give the optimal time complexity, O(NlogN) is considered as acceptable in most cases.\n\n```\nclass Solution:\n def nextGreaterElement(self, n: int) -> int:\n import heapq\n import bisect\n \n MAX = 2**31-1\n \n n = str(n)\n n = [int(i) for i in n]\n switch_part = []\n minheap = []\n switch_pos = -1\n res = []\n for i in range(len(n)-1, -1, -1):\n if i<len(n)-1 and n[i] < n[i+1]:\n switch_pos = i\n break\n heapq.heappush(minheap, n[i])\n if switch_pos == -1: #No possible location to switch\n return -1\n \n for iterator in range(len(minheap)):\n switch_part.append(heapq.heappop(minheap))\n \n #find first number that is larger than target, then re-organize the remaining numbers from small to large\n target = n[switch_pos]\n k = bisect.bisect_right(switch_part, target)\n temp = n[switch_pos]\n n[switch_pos] = switch_part[k]\n switch_part[k] = temp\n \n i=0\n while i<=switch_pos:\n res.append(n[i])\n i+=1\n \n for i in switch_part:\n res+=[i]\n res = [str(i) for i in res]\n res = int(\'\'.join(res))\n if res > MAX:\n return -1\n else:\n return res\n```
| 0
|
Given a positive integer `n`, find _the smallest integer which has exactly the same digits existing in the integer_ `n` _and is greater in value than_ `n`. If no such positive integer exists, return `-1`.
**Note** that the returned integer should fit in **32-bit integer**, if there is a valid answer but it does not fit in **32-bit integer**, return `-1`.
**Example 1:**
**Input:** n = 12
**Output:** 21
**Example 2:**
**Input:** n = 21
**Output:** -1
**Constraints:**
* `1 <= n <= 231 - 1`
| null |
🔥[Python 3] Monotonic stack, with comments || beats 98%
|
next-greater-element-iii
| 0
| 1
|
```python3 []\nclass Solution:\n def nextGreaterElement(self, n: int) -> int:\n digits = list(map(int, str(n)))\n stack, L = [], len(digits)\n for i in reversed(range(L)):\n # because need to find smallest highest than n, need to work from the end\n # do, while not be found any number less than exists in the stack\n # stack is mono increasing, so on the top is always max number (compare with top)\n # for n = 230[2]41 the smallest highest value is 23041[2]\n # we need to find 2 on this step, 2 < 4 (top of the stack), stack = [1, 4]\n if not stack or digits[stack[-1]] <= digits[i]:\n stack.append(i)\n continue\n\n # find in the stack the index of the lowest biggest value than current digit, for 2 it\'s 4\n # stack is sorted in asc order => can be used binary search\n # notice, than in stack indexes, not values, so use lambda to compare values\n swapIndex = stack[bisect_right(stack, digits[i], key = lambda x: digits[x])]\n # after swap 2 with 4 we have [2, 3, 0, 4, [2], 1]\n digits[i], digits[swapIndex] = digits[swapIndex], digits[i]\n # sort all values after i index, in our case it\'s subarray [2, 1]\n # [2, 3, 0, 4, 1, 2] after sorting, but often part after index i will be already sorted\n digits[i+1:L] = sorted(digits[i+1:L])\n break\n # instead of comparison lenghts you can use flag and change it for True in else block\n # also check that final number less than 2**31, for example 2147483486 should return -1\n nextN = int(\'\'.join(map(str, digits)))\n \n return nextN if len(stack) < len(digits) and nextN < 2**31 else -1\n```\n```python []\nclass Solution:\n def nextGreaterElement(self, n: int) -> int:\n digits = list(map(int, str(n)))\n stack, L = [], len(digits)\n for i in reversed(range(L)):\n if not stack or digits[stack[-1]] <= digits[i]:\n stack.append(i)\n continue\n swapIndex = stack[bisect_right(stack, digits[i], key = lambda x: digits[x])]\n digits[i], digits[swapIndex] = digits[swapIndex], digits[i]\n digits[i+1:L] = sorted(digits[i+1:L])\n break\n\n nextN = int(\'\'.join(map(str, digits)))\n \n return nextN if len(stack) < len(digits) and nextN < 2**31 else -1\n```\n\n
| 5
|
Given a positive integer `n`, find _the smallest integer which has exactly the same digits existing in the integer_ `n` _and is greater in value than_ `n`. If no such positive integer exists, return `-1`.
**Note** that the returned integer should fit in **32-bit integer**, if there is a valid answer but it does not fit in **32-bit integer**, return `-1`.
**Example 1:**
**Input:** n = 12
**Output:** 21
**Example 2:**
**Input:** n = 21
**Output:** -1
**Constraints:**
* `1 <= n <= 231 - 1`
| null |
556: Solution with step by step explanation
|
next-greater-element-iii
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Convert the input number n into a list of digits.\n2. Traverse the list from right to left to find the first decreasing digit i-1.\n3. If there is no such digit, the input number is already the largest possible permutation, so return -1.\n4. Traverse the list again from right to left to find the smallest digit j greater than i-1.\n5. Swap i-1 with j.\n6. Reverse the sublist from i to the end of the list to obtain the smallest possible permutation greater than the original number.\n7. If the resulting permutation is greater than 2^31 - 1, return -1. Otherwise, return the permutation as an integer.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nextGreaterElement(self, n: int) -> int:\n nums = list(str(n))\n i = len(nums) - 1\n while i > 0 and nums[i-1] >= nums[i]:\n i -= 1\n if i == 0:\n return -1\n j = len(nums) - 1\n while j > i-1 and nums[j] <= nums[i-1]:\n j -= 1\n nums[i-1], nums[j] = nums[j], nums[i-1]\n nums[i:] = nums[i:][::-1]\n res = int(\'\'.join(nums))\n return res if res < 2**31 else -1\n\n```
| 6
|
Given a positive integer `n`, find _the smallest integer which has exactly the same digits existing in the integer_ `n` _and is greater in value than_ `n`. If no such positive integer exists, return `-1`.
**Note** that the returned integer should fit in **32-bit integer**, if there is a valid answer but it does not fit in **32-bit integer**, return `-1`.
**Example 1:**
**Input:** n = 12
**Output:** 21
**Example 2:**
**Input:** n = 21
**Output:** -1
**Constraints:**
* `1 <= n <= 231 - 1`
| null |
✅ 94.58% Split+Join & Two Pointers
|
reverse-words-in-a-string-iii
| 1
| 1
|
# Comprehensive Guide to Solving "Reverse Words in a String III"\n\n## Introduction & Problem Statement\n\nIn the "Reverse Words in a String III" problem, we are given a string `s`. The task is to reverse the order of characters in each word within a sentence while still preserving the whitespace and the initial word order. This problem is unique because instead of reversing the entire string or just the words\' order, we need to reverse the characters within each word.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **String Constraints**:\n - $$1 \\leq \\text{len}(s) \\leq 5 \\times 10^4$$\n - `s` contains printable ASCII characters.\n \n2. **Whitespace Preservation**: \n - We need to ensure that the spaces between words remain intact.\n\n3. **No Leading or Trailing Spaces**:\n - The input string does not contain any leading or trailing spaces.\n\n4. **Single Space Between Words**:\n - All words in the string `s` are separated by a single space.\n\n---\n\n## Live Coding & Comparing 2 Approaches\nhttps://youtu.be/2hlQrb6P4as?si=ZJ1rgtNj82eSHmQ5\n\n## Two Primary Strategies to Solve the Problem:\n\n## 1. Approach: Using Python\'s split and join methods\n\n### Key Data Structures:\n\n- **List Comprehension**: \n - Used to iterate over the words and reverse them.\n\n### Enhanced Breakdown:\n\n1. **Split the String**:\n - Use Python\'s `split()` method to split the string into individual words.\n \n2. **Reverse Each Word**:\n - Use list comprehension and the slicing method to reverse each word.\n \n3. **Join the Words**:\n - Join the reversed words back together with a single space between them using the `join()` method.\n\n### Complexity Analysis:\n\n**Time Complexity**: \n- $$O(n)$$, where $$n$$ is the length of the string `s`.\n\n**Space Complexity**: \n- $$O(n)$$, due to the extra space required for the list comprehension and the split string.\n\n# Code Split & Join\n``` Python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n return \' \'.join(word[::-1] for word in s.split())\n```\n``` JavaScript []\nvar reverseWords = function(s) {\n return s.split(\' \').map(word => word.split(\'\').reverse().join(\'\')).join(\' \');\n }\n```\n``` PHP []\nclass Solution {\n function reverseWords($s) {\n return implode(\' \', array_map(function($word) {\n return strrev($word);\n }, explode(\' \', $s)));\n }\n}\n```\n``` C# []\npublic class Solution {\n public string ReverseWords(string s) {\n return String.Join(" ", s.Split(\' \').Select(word => new string(word.Reverse().ToArray())));\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string reverseWords(std::string s) {\n std::istringstream stream(s);\n std::string word, result;\n \n while (stream >> word) {\n std::reverse(word.begin(), word.end());\n result += word + " ";\n }\n \n if (!result.empty()) {\n result.pop_back(); // Remove trailing space\n }\n \n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String reverseWords(String s) {\n String[] words = s.split(" ");\n StringBuilder result = new StringBuilder();\n \n for (String word : words) {\n result.append(new StringBuilder(word).reverse()).append(" ");\n }\n \n return result.toString().trim();\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn reverse_words(s: String) -> String {\n s.split_whitespace()\n .map(|word| word.chars().rev().collect::<String>())\n .collect::<Vec<String>>()\n .join(" ")\n }\n}\n```\n``` Go []\nimport (\n\t"strings"\n)\n\nfunc reverseWords(s string) string {\n\twords := strings.Split(s, " ")\n\tfor i, word := range words {\n\t\twords[i] = reverseString(word)\n\t}\n\treturn strings.Join(words, " ")\n}\n\nfunc reverseString(s string) string {\n\trunes := []rune(s)\n\tfor i, j := 0, len(runes)-1; i < j; i, j = i+1, j-1 {\n\t\trunes[i], runes[j] = runes[j], runes[i]\n\t}\n\treturn string(runes)\n}\n```\n\n\n---\n\n## 2. Approach: Two Pointers\n\n### Key Data Structures:\n\n- **List of Characters**: \n - Convert the string into a list of characters for in-place modifications.\n\n### Enhanced Breakdown:\n\n1. **Convert String to List**:\n - Convert the input string `s` to a list for easier in-place manipulation.\n \n2. **Initialize Start Pointer**:\n - Initialize the `start` pointer to 0.\n\n3. **Iterate through Characters**:\n - Traverse through the characters in the string using a loop.\n \n4. **Identify Word Boundaries**:\n - Identify the boundaries of each word using spaces or the end of the string.\n\n5. **Reverse the Word**:\n - Use two pointers, `start` and `end`, to reverse the characters within the identified word boundaries.\n\n6. **Return the Result**:\n - Convert the list of characters back to a string using `join()` and return the result.\n\n### Complexity Analysis:\n\n**Time Complexity**: \n- $$O(n)$$, where $$n$$ is the length of the string `s`.\n\n**Space Complexity**: \n- $$O(n)$$, because we convert the string into a list of characters.\n\n# Code Two Pointers\n``` Python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n s = list(s)\n start = 0\n\n for i in range(len(s)):\n if s[i] == \' \' or i == len(s) - 1:\n end = i\n if i == len(s) - 1 and s[i] != \' \':\n end += 1\n # Inline reverse logic\n while start < end:\n s[start], s[end - 1] = s[end - 1], s[start]\n start += 1\n end -= 1\n start = i + 1\n\n return \'\'.join(s)\n\n```\n``` Rust []\nimpl Solution {\n pub fn reverse_words(s: String) -> String {\n let mut chars: Vec<char> = s.chars().collect();\n let mut start = 0;\n\n for i in 0..chars.len() {\n if chars[i] == \' \' || i == chars.len() - 1 {\n let mut end = if i == chars.len() - 1 && chars[i] != \' \' { i + 1 } else { i };\n while start < end {\n chars.swap(start, end - 1);\n start += 1;\n end -= 1;\n }\n start = i + 1;\n }\n }\n\n chars.iter().collect()\n }\n}\n```\n``` Go []\nfunc reverseWords(s string) string {\n runes := []rune(s)\n start := 0\n\n for i := 0; i < len(runes); i++ {\n if runes[i] == \' \' || i == len(runes)-1 {\n end := i\n if i == len(runes)-1 && runes[i] != \' \' {\n end++\n }\n for start < end {\n runes[start], runes[end-1] = runes[end-1], runes[start]\n start++\n end--\n }\n start = i + 1\n }\n }\n\n return string(runes)\n}\n```\n``` C++ []\n#include <string>\n\nclass Solution {\npublic:\n std::string reverseWords(std::string s) {\n int start = 0;\n \n for (int i = 0; i < s.length(); i++) {\n if (s[i] == \' \' || i == s.length() - 1) {\n int end = (i == s.length() - 1 && s[i] != \' \') ? i + 1 : i;\n while (start < end) {\n std::swap(s[start], s[end - 1]);\n start++;\n end--;\n }\n start = i + 1;\n }\n }\n \n return s;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String reverseWords(String s) {\n char[] chars = s.toCharArray();\n int start = 0;\n \n for (int i = 0; i < chars.length; i++) {\n if (chars[i] == \' \' || i == chars.length - 1) {\n int end = (i == chars.length - 1 && chars[i] != \' \') ? i + 1 : i;\n while (start < end) {\n char temp = chars[start];\n chars[start] = chars[end - 1];\n chars[end - 1] = temp;\n start++;\n end--;\n }\n start = i + 1;\n }\n }\n \n return new String(chars);\n }\n}\n```\n``` C# []\npublic class Solution {\n public string ReverseWords(string s) {\n char[] chars = s.ToCharArray();\n int start = 0;\n \n for (int i = 0; i < chars.Length; i++) {\n if (chars[i] == \' \' || i == chars.Length - 1) {\n int end = (i == chars.Length - 1 && chars[i] != \' \') ? i + 1 : i;\n while (start < end) {\n char temp = chars[start];\n chars[start] = chars[end - 1];\n chars[end - 1] = temp;\n start++;\n end--;\n }\n start = i + 1;\n }\n }\n \n return new string(chars);\n }\n}\n```\n``` PHP []\nclass Solution {\n function reverseWords($s) {\n $chars = str_split($s);\n $start = 0;\n \n for ($i = 0; $i < count($chars); $i++) {\n if ($chars[$i] == \' \' || $i == count($chars) - 1) {\n $end = ($i == count($chars) - 1 && $chars[$i] != \' \') ? $i + 1 : $i;\n while ($start < $end) {\n list($chars[$start], $chars[$end - 1]) = array($chars[$end - 1], $chars[$start]);\n $start++;\n $end--;\n }\n $start = $i + 1;\n }\n }\n \n return implode(\'\', $chars);\n }\n}\n```\n``` JavaScript []\nvar reverseWords = function(s){\n let chars = [...s];\n let start = 0;\n\n for (let i = 0; i < chars.length; i++) {\n if (chars[i] === \' \' || i === chars.length - 1) {\n let end = (i === chars.length - 1 && chars[i] !== \' \') ? i + 1 : i;\n while (start < end) {\n [chars[start], chars[end - 1]] = [chars[end - 1], chars[start]];\n start++;\n end--;\n }\n start = i + 1;\n }\n }\n\n return chars.join(\'\');\n }\n```\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) | Method |\n|-----------|---------------------|-------------|---------|\n| Rust | 0 | 2.2 | Pointers|\n| Rust | 3 | 2.3 | Split |\n| Java | 4 | 44.3 | Pointers|\n| Java | 4 | 44.2 | Split |\n| PHP | 4 | 19.4 | Split |\n| C++ | 8 | 10.2 | Pointers|\n| Go | 9 | 7 | Split |\n| Go | 12 | 8.1 | Pointers|\n| C++ | 15 | 14.4 | Split |\n| PHP | 45 | 23 | Pointers|\n| JavaScript| 49 | 48.6 | Split |\n| JavaScript| 70 | 48.9 | Pointers|\n| C# | 75 | 45.1 | Pointers|\n| C# | 75 | 50.3 | Split |\n| Python3 | 34 | 17.1 | Split |\n| Python3 | 98 | 17 | Pointers|\n\n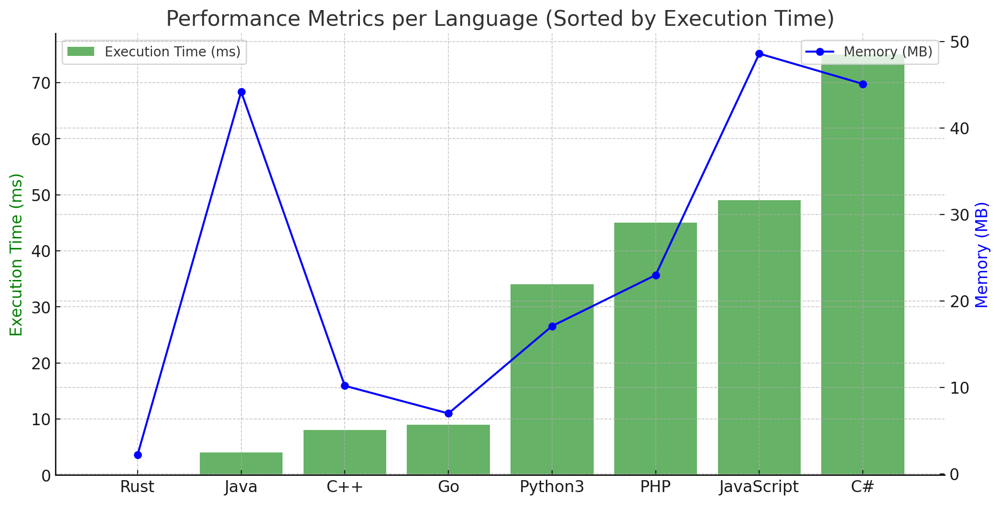\n\n\n## Conclusion\n\nThe problem "Reverse Words in a String III" tests our understanding of string manipulation and offers two distinct approaches to tackle it. Whether you prefer the elegance of Python\'s built-in methods or the manual control of the two-pointer approach, the key lies in accurately identifying word boundaries and efficiently reversing characters within those boundaries. Dive deep into these techniques, practice them, and enhance your string manipulation skills. Happy coding!
| 49
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
✅91.55%🔥Easy Solution🔥Reverse & Join
|
reverse-words-in-a-string-iii
| 1
| 1
|
# Problem\n##### The problem you\'re trying to solve is to reverse the order of characters in each word within a sentence while still preserving the original whitespace and the initial order of words.\n##### Here\'s an example to illustrate the problem:\n###### Input: "Let\'s take LeetCode contest"\n###### Output: "s\'teL ekat edoCteeL tsetnoc"\n\n##### In this example, you need to reverse the characters within each word, but the words themselves should remain in the same order, and the spaces should stay where they are.\n---\n# python Solution\n#### 1. s.split(): The input string s is first split into words using the default whitespace delimiter. This creates a list of words from the input string.\n\n#### 2. lambda word: word[::-1]: For each word in the list, a lambda function is applied to reverse the order of characters within the word. This is done using slicing with [::-1].\n\n#### 3. map(...): The map function applies the lambda function to each word in the list, effectively reversing the characters in each word.\n\n#### 4. \' \'.join(...): Finally, the reversed words are joined back together into a single string, with spaces between them, using the \' \'.join(...) method. This preserves the original whitespace and word order.\n\n#### So, when you call reverseWords with your input string, it returns the desired output with the words reversed while maintaining the original sentence structure.\n---\n# Code\n```python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n return \' \'.join(map(lambda word: word[::-1], s.split()))\n\n```\n```C# []\npublic class Solution\n{\n public string ReverseWords(string s)\n {\n string[] words = s.Split();\n string[] reversedWords = new string[words.Length];\n\n for (int i = 0; i < words.Length; i++)\n {\n char[] wordChars = words[i].ToCharArray();\n Array.Reverse(wordChars);\n reversedWords[i] = new string(wordChars);\n }\n\n return string.Join(" ", reversedWords);\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n stringstream ss(s);\n string temp,ans;\n while(ss>>temp){\n reverse(temp.begin(),temp.end());\n ans+= (temp+" ");\n }\n \n return ans.substr(0,ans.size()-1);\n }\n};\n```\n```C []\nvoid reverseWord(char *start, char *end) {\n char temp;\n while (start < end) {\n temp = *start;\n *start = *end;\n *end = temp;\n start++;\n end--;\n }\n}\n\nchar *reverseWords(char *s) {\n int length = strlen(s);\n char *start = s;\n \n for (int i = 0; i <= length; i++) {\n if (s[i] == \' \' || s[i] == \'\\0\') {\n reverseWord(start, &s[i - 1]);\n start = &s[i + 1];\n }\n }\n \n return s;\n}\n```\n```Java []\npublic class Solution {\n public String reverseWords(String s) {\n String[] words = s.split("\\\\s+"); \n StringBuilder reversed = new StringBuilder();\n for (String word : words) {\n StringBuilder reversedWord = new StringBuilder(word);\n reversedWord.reverse(); \n reversed.append(reversedWord).append(" "); \n }\n return reversed.toString().trim();\n }\n}\n```\n```javascript []\nvar reverseWords = function(s) {\n const words = s.split(\' \'); \n for (let i = 0; i < words.length; i++) {\n words[i] = words[i].split(\'\').reverse().join(\'\');\n }\n return words.join(\' \');\n};\n```\n```PHP []\nclass Solution {\n function reverseWords($s) {\n $words = explode(\' \', $s); \n foreach ($words as &$word) {\n $word = strrev($word);\n }\n return implode(\' \', $words);\n }\n}\n\n```\n```Go []\nfunc reverseWords(s string) string {\n words := strings.Fields(s) \n for i, word := range words {\n reversedWord := reverseString(word)\n words[i] = reversedWord\n }\n return strings.Join(words, " ")\n}\n\nfunc reverseString(s string) string {\n runes := []rune(s)\n left, right := 0, len(runes)-1\n for left < right {\n runes[left], runes[right] = runes[right], runes[left]\n left++\n right--\n }\n\n return string(runes)\n}\n```
| 124
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
98% - BEGINNER FRIENDLY ONE TRAVERSAL APPROACH IN c++/JAVA/PYTHON3(TIME-O(N) SPACE-O(1))
|
reverse-words-in-a-string-iii
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code provided is a C++ function named reverseWords that takes a string s as input and reverses the order of words in the string.\n\nHere\'s a breakdown of the code and its intuition:\n\n Initialization: Initialize variables i and j to 0. These will be used to keep track of the current word\'s start and end positions.\n\n Iteration through the string: Use a while loop to iterate through the string s character by character.\n\n If the current character is a space (\' \'), it means we have reached the end of a word. Reverse the characters from index i to j-1 (inclusive) to reverse the current word and update i to j+1 to start the next word.\n\n If we reach the end of the string (j == n-1), it means we have reached the end of the last word. Reverse the characters from index i to j (inclusive) to reverse the last word.\n\n Returning the modified string: Return the modified string s with the words reversed.\n\nThe code handles the reversal of words in the input string by finding word boundaries (spaces) and reversing the characters between those boundaries.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe provided code implements an algorithm to reverse the order of words in a given string. Here\'s the approach explained step by step:\n\n Initialization: Initialize variables i and j to 0. These variables will be used to mark the start and end positions of words in the string.\n\n Iterate Through the String: Use a while loop to iterate through the characters of the input string.\n\n a. If the current character is a space (\' \'), it indicates the end of a word. Reverse the characters from index i to j-1 to reverse the current word. Update i to j+1 to prepare for the next word.\n\n b. If we reach the end of the string (j == n-1), it means we have reached the end of the last word. Reverse the characters from index i to j to reverse the last word.\n\n Return the Modified String: Return the modified string s with the words reversed.\n\n Optimization for the Last Word: After the loop, reverse the last word (if any) separately.\n\n Reverse the Entire String: Reverse the entire string to obtain the final result with the words reversed in order.\n\nThe algorithm efficiently reverses the order of words in the input string by identifying word boundaries (spaces) and reversing the characters between those boundaries.\n\nThe key steps involve identifying word boundaries and reversing the words in the string, followed by reversing the entire string to get the final result with the words in reverse order.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\nThe time complexity is primarily determined by the operations performed in the while loop that iterates over the characters of the input string.\n\n Iterating Over Characters: The while loop iterates through each character in the input string once, so this takes O(n) time, where n is the length of the input string.\n\n Reversing Words: Inside the loop, reversing a word takes O(word_length) time for each word. However, the sum of the lengths of all words in the string is equal to the length of the string n. Therefore, the total time taken to reverse all words is also O(n).\n\n Reversing the Entire String: Reversing the entire string takes O(n) time.\n\nOverall, the dominant factor for time complexity is the iteration over characters, making the overall time complexity of the code O(n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\nThe space complexity of the code is determined by the space used for the input string s. Since no additional data structures or recursion are used, the space complexity is O(1).\n\n\n# code\n```c++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n int n = s.size();\n int i=0;\n int j = 0;\n while(j<n){\n if(s[j] == \' \'){\n reverse(s.begin() + i, s.begin() + j);\n i=j+1;\n }\n if(j == n-1) reverse(s.begin()+i,s.begin()+n);\n j++;\n }\n return s;\n }\n};\n```\n```java []\nimport java.util.*;\n\nclass Solution {\n public String reverseWords(String s) {\n int n = s.length();\n int i = 0;\n int j = 0;\n char[] charArray = s.toCharArray();\n while (j < n) {\n if (charArray[j] == \' \') {\n reverse(charArray, i, j);\n i = j + 1;\n }\n if (j == n - 1) reverse(charArray, i, n);\n j++;\n }\n return new String(charArray);\n }\n \n private void reverse(char[] arr, int start, int end) {\n while (start < end) {\n char temp = arr[start];\n arr[start] = arr[end];\n arr[end] = temp;\n start++;\n end--;\n }\n }\n}\n```\n\n```python3 []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n n = len(s)\n i = 0\n j = 0\n while j < n:\n if s[j] == \' \':\n s = s[:i] + s[i:j][::-1] + s[j:]\n i = j + 1\n if j == n - 1:\n s = s[:i] + s[i:j+1][::-1]\n j += 1\n return s\n```\n\n
| 1
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
NOOB CODE : Easy to Understand
|
reverse-words-in-a-string-iii
| 0
| 1
|
\n\n# Intuition\n1. Convert the sting to a list using split()\n2. Using for loop access each element of the list \n3. Reverse each element using basic string operation\n4. print the string \n# Approach\n1. `l = s.split()`: This line splits the input string `s` into a list of words. By default, `split()` splits the string on whitespace, so each element of the list `l` will be a word from the original string.\n\n2. `s = \'\'`: This line initializes an empty string `s` which will be used to build the reversed string.\n\n3. The for loop iterates over each word in the list `l`:\n - `for i in l:`\n\n4. Inside the loop, each word `i` is reversed using slicing with `[::-1]`. This effectively reverses the characters in each word.\n\n5. `s = s + \' \' + i[::-1]`: This line appends the reversed word to the `s` string, separated by a space. It builds the reversed string one word at a time.\n\n6. Finally, `return s[1:]` returns the `s` string starting from the second character to remove the leading space that was added in step 5. This is done because there is an extra space at the beginning of the `s` string due to the way words are concatenated in the loop.\n\nHere\'s an example of how you can use this `Solution` class:\n# Complexity\n- Time complexity:***O(n)***\n\n- Space complexity:***O(n)***\n\n# Code\n```\nclass Solution:\n def reverseWords(self, s: str) -> str:\n l=s.split()\n s=\'\'\n for i in l:\n s=s+\' \'+i[::-1]\n return(s[1:])\n```
| 2
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
Easy to Understand || Two Pointer ||C++ || Python || Java
|
reverse-words-in-a-string-iii
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nExplanation of Approach:\n\nThe given code takes a string s as input and reverses each word within the string while maintaining the order of the words. It uses two pointers, start and end, to identify words in the string. Here\'s a step-by-step explanation:\n\nInitialize start and end to 0.\n\nWhile \'start\' is less than the length of the string s, do the following:\n\na. Move \'end\' to the right while it\'s within the string bounds and not pointing to a space character, effectively finding the end of the current word.\n\nb. Reverse the characters in the word identified by the \'start\' and \'end\' pointers.\n\nc. Update \'start\' to be \'end + 1\' to move to the next word, and reset \'end\' to \'start\'.\n\nReturn the modified string.\n\n# Complexity\n- Time complexity:\nThe time complexity of this code is O(N), where N is the length of the input string s. This is because the code iterates through each character in the string exactly once.\n\n- Space complexity:\nThe space complexity is O(1) because the code uses only a constant amount of additional space regardless of the input string length.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n int start=0,end=0;\n while(start<s.length())\n {\n while(end<s.length() && s[end] != \' \')\n {\n end++;\n }\n reverse(s.begin()+start, s.begin()+end);\n start=end+1;\n end=start;\n } \n return s;\n }\n};\n```\n```python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n start, end = 0, 0\n s = list(s)\n while start < len(s):\n while end < len(s) and s[end] != \' \':\n end += 1\n s[start:end] = s[start:end][::-1]\n start = end + 1\n end = start\n return \'\'.join(s)\n\n```\n```Java []\nclass Solution {\n public String reverseWords(String s) {\n int start = 0, end = 0;\n char[] charArray = s.toCharArray();\n while (start < s.length()) {\n while (end < s.length() && charArray[end] != \' \') {\n end++;\n }\n reverse(charArray, start, end - 1);\n start = end + 1;\n end = start;\n }\n return new String(charArray);\n }\n \n private void reverse(char[] arr, int left, int right) {\n while (left < right) {\n char temp = arr[left];\n arr[left] = arr[right];\n arr[right] = temp;\n left++;\n right--;\n }\n }\n}\n\n```\n\n\n\n
| 6
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
Python 4 line code 96.68 % || 2 Approach
|
reverse-words-in-a-string-iii
| 0
| 1
|
**If you got help from this,... Plz Upvote .. it encourage me**\n\n# Code\n```\n<!-- 1st Approach Memory % is more -->\nclass Solution:\n def reverseWords(self, s: str) -> str:\n s = s.split(\' \')\n for i in range(len(s)):\n s[i] = s[i][::-1]\n return \' \'.join(s)\n\n\n# ===========================================================\n<!-- 2nd Approach Runtime % is More 96.68% -->\nclass Solution:\n def reverseWords(self, s: str) -> str:\n s = s.split(\' \')\n new = \'\'\n for word in s:\n new += word[::-1] + \' \'\n\n return new[:-1]\n\n```
| 5
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
💯Faster✅💯 Lesser✅4 Methods🔥Using Split and Join🔥Using a Stack🔥Two-Pointers Approach🔥
|
reverse-words-in-a-string-iii
| 1
| 1
|
# \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 4 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe "Reverse Words in a String III" problem is a common string manipulation problem often encountered in coding interviews and programming tasks. To solve this problem, you typically need to split the input string into individual words, reverse the characters within each word, and then join these reversed words back together with spaces in between. There are multiple ways to approach this problem, as demonstrated, and the choice of method depends on personal preference and programming language capabilities.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering four different methods to solve this problem:\n1. Using Split and Join\n2. Using a Stack\n3. Using Python Built-in Functions\n4. Two-Pointers Approach\n\n# 1. Using Split and Join: \n- Split the input string by spaces to obtain a list of words.\n- Iterate through the list of words and reverse each word.\n- Join the reversed words back into a single string with spaces between them.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n), where n is the length of the input string.\n\n- \uD83D\uDE80 Space Complexity: O(n) because we store the reversed words in a list.\n\n# Code\n```Python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n words = s.split()\n reversed_words = [word[::-1] for word in words]\n return \' \'.join(reversed_words)\n```\n```Java []\nclass Solution {\n public String reverseWords(String s) {\n String[] words = s.split(" ");\n StringBuilder result = new StringBuilder();\n for (String word : words) {\n StringBuilder reversedWord = new StringBuilder(word);\n reversedWord.reverse();\n result.append(reversedWord).append(" ");\n }\n return result.toString().trim();\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n stringstream ss(s);\n string word, result;\n while (ss >> word) {\n reverse(word.begin(), word.end());\n result += word + \' \';\n }\n result.pop_back(); // Remove the trailing space\n return result;\n }\n};\n\n```\n```C []\nvoid reverseWord(char *start, char *end) {\n while (start < end) {\n char temp = *start;\n *start = *end;\n *end = temp;\n start++;\n end--;\n }\n}\n\nchar *reverseWords(char *s) {\n int len = strlen(s);\n int start = 0;\n for (int end = 0; end <= len; end++) {\n if (s[end] == \' \' || s[end] == \'\\0\') {\n reverseWord(s + start, s + end - 1);\n start = end + 1;\n }\n }\n \n return s;\n}\n```\n# 2. Using Stack:\n- Initialize an empty stack.\n- Iterate through the characters of the input string.\n- Push characters onto the stack until a space is encountered.\n- When a space is encountered, pop characters from the stack and append them to the result string until the stack is empty.\n- Repeat steps 3-4 until the end of the string is reached.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n), where n is the length of the input string.\n\n- \uD83D\uDE80 Space Complexity: O(n) because we use a stack to store characters.\n\n# Code\n```Python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n stack = []\n result = []\n \n for char in s:\n if char != \' \':\n stack.append(char)\n else:\n while stack:\n result.append(stack.pop())\n result.append(\' \')\n \n while stack:\n result.append(stack.pop())\n \n return \'\'.join(result)\n```\n```Java []\nimport java.util.Stack;\n\nclass Solution {\n public String reverseWords(String s) {\n Stack<Character> stack = new Stack<>();\n StringBuilder result = new StringBuilder();\n \n for (char c : s.toCharArray()) {\n if (c != \' \') {\n stack.push(c);\n } else {\n while (!stack.isEmpty()) {\n result.append(stack.pop());\n }\n result.append(\' \');\n }\n }\n \n while (!stack.isEmpty()) {\n result.append(stack.pop());\n }\n \n return result.toString();\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n stack<char> st;\n string result = "";\n for (char c : s) {\n if (c != \' \') {\n st.push(c);\n } else {\n while (!st.empty()) {\n result += st.top();\n st.pop();\n }\n result += \' \';\n }\n }\n while (!st.empty()) {\n result += st.top();\n st.pop();\n }\n return result;\n }\n};\n\n```\n```C []\n//Soon i will add it\n```\n# 3. Using Python Built-in Functions:\n - Split the input string into words.\n - Use Python\'s built-in map and join functions to reverse each word and join them back together.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n), where n is the length of the input string.\n\n- \uD83D\uDE80 Space Complexity: O(n) because we split the string into a list of words.\n\n# Code\n```Python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n return \' \'.join(map(lambda word: word[::-1], s.split()))\n\n```\n```Java []\nclass Solution {\n public String reverseWords(String s) {\n String[] words = s.split(" ");\n StringBuilder result = new StringBuilder();\n for (String word : words) {\n StringBuilder reversedWord = new StringBuilder(word);\n result.append(reversedWord.reverse()).append(" ");\n }\n return result.toString().trim();\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n istringstream iss(s);\n string word, result;\n while (iss >> word) {\n reverse(word.begin(), word.end());\n result += word + \' \';\n }\n if (!result.empty()) {\n result.pop_back();\n }\n return result;\n }\n};\n```\n```C []\nvoid reverseString(char *str, int start, int end) {\n while (start < end) {\n char temp = str[start];\n str[start] = str[end];\n str[end] = temp;\n start++;\n end--;\n }\n}\n\nchar *reverseWords(char *s) {\n char *word;\n char *result = (char *)malloc(strlen(s) + 1);\n result[0] = \'\\0\';\n word = strtok(s, " ");\n while (word != NULL) {\n int len = strlen(word);\n reverseString(word, 0, len - 1);\n strcat(result, word);\n word = strtok(NULL, " ");\n if (word != NULL) {\n strcat(result, " ");\n }\n }\n return result;\n}\n\n```\n# 4. Two-Pointers Approach:\n - Convert the input string into a list of characters.\n - Initialize two pointers, one at the beginning of a word and one at the end of the word.\n - Reverse the characters between the two pointers.\n - Move the pointers to the next word and repeat until the end of the string is reached.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n), where n is the length of the input string.\n\n- \uD83D\uDE80 Space Complexity: O(n) because we convert the string into a list of characters.\n\n# Code\n```Python []\nclass Solution:\n def reverseWords(self, s: str) -> str:\n s = list(s)\n start = 0\n for end in range(len(s)):\n if s[end] == \' \':\n s[start:end] = reversed(s[start:end])\n start = end + 1\n s[start:] = reversed(s[start:])\n return \'\'.join(s)\n```\n```Java []\nclass Solution {\n public String reverseWords(String s) {\n char[] chars = s.toCharArray();\n int start = 0;\n for (int end = 0; end < chars.length; end++) {\n if (chars[end] == \' \') {\n reverse(chars, start, end - 1);\n start = end + 1;\n }\n }\n reverse(chars, start, chars.length - 1);\n return new String(chars);\n }\n \n private void reverse(char[] chars, int left, int right) {\n while (left < right) {\n char temp = chars[left];\n chars[left] = chars[right];\n chars[right] = temp;\n left++;\n right--;\n }\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string reverseWords(string s) {\n int start = 0;\n for (int end = 0; end < s.length(); ++end) {\n if (s[end] == \' \') {\n reverse(s.begin() + start, s.begin() + end);\n start = end + 1;\n }\n }\n reverse(s.begin() + start, s.end());\n return s;\n }\n};\n```\n```C []\nvoid reverseWord(char *start, char *end) {\n while (start < end) {\n char temp = *start;\n *start = *end;\n *end = temp;\n start++;\n end--;\n }\n}\n\nchar *reverseWords(char *s) {\n int len = strlen(s);\n int start = 0;\n for (int end = 0; end <= len; end++) {\n if (s[end] == \' \' || s[end] == \'\\0\') {\n reverseWord(s + start, s + end - 1);\n start = end + 1;\n }\n }\n return s;\n}\n```\n# \uD83C\uDFC6Conclusion: \nIn terms of efficiency, the most optimal approach among the four methods you\'ve presented would be the "Using Split and Join" method. Here\'s why:\n\n1. **Time Complexity**: All four methods have a time complexity of O(n), where n is the length of the input string. This means they all have similar linear time complexity.\n\n2. **Space Complexity**: In terms of space complexity, the "Using Split and Join" method also has an O(n) space complexity, just like the others. It stores the reversed words in a list. However, this space complexity is the same for all methods, so it doesn\'t provide a significant advantage or disadvantage compared to the others.\n\n3. **Simplicity**: The "Using Split and Join" method is generally considered more straightforward and easier to understand, especially in Python, due to the concise use of built-in functions. This simplicity can be an advantage, especially when writing maintainable and readable code.\n\nWhile all methods have similar time and space complexities, the choice of the most efficient method often depends on other factors, such as code readability, language constraints, and personal preferences. The "Using Split and Join" method is a good choice for its simplicity and ease of understanding, but the best approach may vary depending on the specific requirements of your project or the constraints of the programming environment you are working in.\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA
| 31
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
Python 1-liner. Functional programming.
|
reverse-words-in-a-string-iii
| 0
| 1
|
# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def reverseWords(self, s: str) -> str:\n return \' \'.join(w[::-1] for w in s.split(\' \'))\n\n\n```
| 1
|
Given a string `s`, reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
**Example 1:**
**Input:** s = "Let's take LeetCode contest"
**Output:** "s'teL ekat edoCteeL tsetnoc"
**Example 2:**
**Input:** s = "God Ding"
**Output:** "doG gniD"
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s` contains printable **ASCII** characters.
* `s` does not contain any leading or trailing spaces.
* There is **at least one** word in `s`.
* All the words in `s` are separated by a single space.
| null |
Solution
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n Node* intersect(Node* quadTree1, Node* quadTree2) {\n if(quadTree1 -> isLeaf)\n {\n if(quadTree1 -> val == 1) return quadTree1;\n return quadTree2;\n }\n if(quadTree2 -> isLeaf)\n {\n if(quadTree2 -> val == 1) return quadTree2;\n return quadTree1;\n }\n vector<Node*> arr;\n arr.push_back(intersect(quadTree1 -> topLeft, quadTree2 -> topLeft));\n arr.push_back(intersect(quadTree1 -> topRight, quadTree2 -> topRight));\n arr.push_back(intersect(quadTree1 -> bottomLeft, quadTree2 -> bottomLeft));\n arr.push_back(intersect(quadTree1 -> bottomRight, quadTree2 -> bottomRight));\n for(Node* node : arr)\n {\n if(!node -> isLeaf)\n {\n return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n }\n for(Node *node : arr)\n {\n if(!node -> val) return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n return new Node(true, true);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n if q1.isLeaf:\n return q1.val and q1 or q2\n elif q2.isLeaf:\n return q2.val and q2 or q1\n else:\n tLeft = self.intersect(q1.topLeft, q2.topLeft)\n tRight = self.intersect(q1.topRight, q2.topRight)\n bLeft = self.intersect(q1.bottomLeft, q2.bottomLeft)\n bRight = self.intersect(q1.bottomRight, q2.bottomRight)\n if tLeft.isLeaf and tRight.isLeaf and bLeft.isLeaf and bRight.isLeaf and tLeft.val == tRight.val == bLeft.val == bRight.val:\n node = Node(tLeft.val, True, None, None, None, None) \n else:\n node = Node(False, False, tLeft, tRight, bLeft, bRight)\n return node\n```\n\n```Java []\nclass Solution {\n public Node intersect(Node a, Node b) {\n if(a.isLeaf){\n return a.val ? a : b;\n }\n if(b.isLeaf){\n return b.val ? b : a;\n }\n a.topLeft = intersect(a.topLeft,b.topLeft);\n a.topRight = intersect(a.topRight,b.topRight);\n a.bottomLeft = intersect(a.bottomLeft,b.bottomLeft);\n a.bottomRight = intersect(a.bottomRight,b.bottomRight);\n\n if (a.topLeft.isLeaf && a.topRight.isLeaf \n && a.bottomLeft.isLeaf && a.bottomRight.isLeaf\n && a.topLeft.val == a.topRight.val \n && a.topRight.val == a.bottomLeft.val \n && a.bottomLeft.val == a.bottomRight.val) {\n return new Node(true,a.topLeft.val);\n }\n return a;\n }\n}\n```\n
| 1
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
Solution
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n Node* intersect(Node* quadTree1, Node* quadTree2) {\n if(quadTree1 -> isLeaf)\n {\n if(quadTree1 -> val == 1) return quadTree1;\n return quadTree2;\n }\n if(quadTree2 -> isLeaf)\n {\n if(quadTree2 -> val == 1) return quadTree2;\n return quadTree1;\n }\n vector<Node*> arr;\n arr.push_back(intersect(quadTree1 -> topLeft, quadTree2 -> topLeft));\n arr.push_back(intersect(quadTree1 -> topRight, quadTree2 -> topRight));\n arr.push_back(intersect(quadTree1 -> bottomLeft, quadTree2 -> bottomLeft));\n arr.push_back(intersect(quadTree1 -> bottomRight, quadTree2 -> bottomRight));\n for(Node* node : arr)\n {\n if(!node -> isLeaf)\n {\n return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n }\n for(Node *node : arr)\n {\n if(!node -> val) return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n return new Node(true, true);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n if q1.isLeaf:\n return q1.val and q1 or q2\n elif q2.isLeaf:\n return q2.val and q2 or q1\n else:\n tLeft = self.intersect(q1.topLeft, q2.topLeft)\n tRight = self.intersect(q1.topRight, q2.topRight)\n bLeft = self.intersect(q1.bottomLeft, q2.bottomLeft)\n bRight = self.intersect(q1.bottomRight, q2.bottomRight)\n if tLeft.isLeaf and tRight.isLeaf and bLeft.isLeaf and bRight.isLeaf and tLeft.val == tRight.val == bLeft.val == bRight.val:\n node = Node(tLeft.val, True, None, None, None, None) \n else:\n node = Node(False, False, tLeft, tRight, bLeft, bRight)\n return node\n```\n\n```Java []\nclass Solution {\n public Node intersect(Node a, Node b) {\n if(a.isLeaf){\n return a.val ? a : b;\n }\n if(b.isLeaf){\n return b.val ? b : a;\n }\n a.topLeft = intersect(a.topLeft,b.topLeft);\n a.topRight = intersect(a.topRight,b.topRight);\n a.bottomLeft = intersect(a.bottomLeft,b.bottomLeft);\n a.bottomRight = intersect(a.bottomRight,b.bottomRight);\n\n if (a.topLeft.isLeaf && a.topRight.isLeaf \n && a.bottomLeft.isLeaf && a.bottomRight.isLeaf\n && a.topLeft.val == a.topRight.val \n && a.topRight.val == a.bottomLeft.val \n && a.bottomLeft.val == a.bottomRight.val) {\n return new Node(true,a.topLeft.val);\n }\n return a;\n }\n}\n```\n
| 1
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
558: Time 99.4%, Solution with step by step explanation
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if either quadTree1 or quadTree2 is a leaf node. If quadTree1 is a leaf node, return quadTree1 if its value is True, else return quadTree2. If quadTree2 is a leaf node, return quadTree2 if its value is True, else return quadTree1.\n2. Recursively check the intersection of each child node of quadTree1 and quadTree2 by calling the intersect function on each of them. Store the return values in variables tl (top-left), tr (top-right), bl (bottom-left), and br (bottom-right).\n3. Check if all four child nodes (tl, tr, bl, br) are leaves and have the same value. If yes, create a new leaf node with the same value and return it.\n4. If any of the child nodes have a different value or are not leaf nodes, create a new internal node with the four child nodes as its children and return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n # If either of the trees is a leaf node, return the appropriate tree\n if quadTree1.isLeaf:\n return quadTree1 if quadTree1.val else quadTree2\n if quadTree2.isLeaf:\n return quadTree2 if quadTree2.val else quadTree1\n \n # Recursively check the intersection of each child node\n tl = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n tr = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bl = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n br = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n \n # If all four child nodes are leaves with the same value, return a new leaf node\n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and tl.val == tr.val == bl.val == br.val:\n return Node(tl.val, True, None, None, None, None)\n \n # Otherwise, return a new internal node with the four child nodes as children\n return Node(None, False, tl, tr, bl, br)\n\n```
| 3
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
558: Time 99.4%, Solution with step by step explanation
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if either quadTree1 or quadTree2 is a leaf node. If quadTree1 is a leaf node, return quadTree1 if its value is True, else return quadTree2. If quadTree2 is a leaf node, return quadTree2 if its value is True, else return quadTree1.\n2. Recursively check the intersection of each child node of quadTree1 and quadTree2 by calling the intersect function on each of them. Store the return values in variables tl (top-left), tr (top-right), bl (bottom-left), and br (bottom-right).\n3. Check if all four child nodes (tl, tr, bl, br) are leaves and have the same value. If yes, create a new leaf node with the same value and return it.\n4. If any of the child nodes have a different value or are not leaf nodes, create a new internal node with the four child nodes as its children and return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n # If either of the trees is a leaf node, return the appropriate tree\n if quadTree1.isLeaf:\n return quadTree1 if quadTree1.val else quadTree2\n if quadTree2.isLeaf:\n return quadTree2 if quadTree2.val else quadTree1\n \n # Recursively check the intersection of each child node\n tl = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n tr = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bl = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n br = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n \n # If all four child nodes are leaves with the same value, return a new leaf node\n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and tl.val == tr.val == bl.val == br.val:\n return Node(tl.val, True, None, None, None, None)\n \n # Otherwise, return a new internal node with the four child nodes as children\n return Node(None, False, tl, tr, bl, br)\n\n```
| 3
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
558. Logical OR of Two Binary Grids Represented as Quad-Trees
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n if q1.isLeaf:\n return q1.val and q1 or q2\n elif q2.isLeaf:\n return q2.val and q2 or q1\n else:\n tLeft = self.intersect(q1.topLeft, q2.topLeft)\n tRight = self.intersect(q1.topRight, q2.topRight)\n bLeft = self.intersect(q1.bottomLeft, q2.bottomLeft)\n bRight = self.intersect(q1.bottomRight, q2.bottomRight)\n if tLeft.isLeaf and tRight.isLeaf and bLeft.isLeaf and bRight.isLeaf and tLeft.val == tRight.val == bLeft.val == bRight.val:\n node = Node(tLeft.val, True, None, None, None, None) \n else:\n node = Node(False, False, tLeft, tRight, bLeft, bRight)\n return node\n```
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
558. Logical OR of Two Binary Grids Represented as Quad-Trees
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n if q1.isLeaf:\n return q1.val and q1 or q2\n elif q2.isLeaf:\n return q2.val and q2 or q1\n else:\n tLeft = self.intersect(q1.topLeft, q2.topLeft)\n tRight = self.intersect(q1.topRight, q2.topRight)\n bLeft = self.intersect(q1.bottomLeft, q2.bottomLeft)\n bRight = self.intersect(q1.bottomRight, q2.bottomRight)\n if tLeft.isLeaf and tRight.isLeaf and bLeft.isLeaf and bRight.isLeaf and tLeft.val == tRight.val == bLeft.val == bRight.val:\n node = Node(tLeft.val, True, None, None, None, None) \n else:\n node = Node(False, False, tLeft, tRight, bLeft, bRight)\n return node\n```
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
easy solution
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 1
| 1
|
\n\n# Code\n```java []\n/*\n// Definition for a QuadTree node.\nclass Node {\n public boolean val;\n public boolean isLeaf;\n public Node topLeft;\n public Node topRight;\n public Node bottomLeft;\n public Node bottomRight;\n\n public Node() {}\n\n public Node(boolean _val,boolean _isLeaf,Node _topLeft,Node _topRight,Node _bottomLeft,Node _bottomRight) {\n val = _val;\n isLeaf = _isLeaf;\n topLeft = _topLeft;\n topRight = _topRight;\n bottomLeft = _bottomLeft;\n bottomRight = _bottomRight;\n }\n};\n*/\n\nclass Solution {\n public Node intersect(Node a, Node b) {\n if(a.isLeaf){\n return a.val ? a : b;\n }\n if(b.isLeaf){\n return b.val ? b : a;\n }\n a.topLeft = intersect(a.topLeft,b.topLeft);\n a.topRight = intersect(a.topRight,b.topRight);\n a.bottomLeft = intersect(a.bottomLeft,b.bottomLeft);\n a.bottomRight = intersect(a.bottomRight,b.bottomRight);\n\n if (a.topLeft.isLeaf && a.topRight.isLeaf \n && a.bottomLeft.isLeaf && a.bottomRight.isLeaf\n && a.topLeft.val == a.topRight.val \n && a.topRight.val == a.bottomLeft.val \n && a.bottomLeft.val == a.bottomRight.val) {\n return new Node(true,a.topLeft.val);\n }\n return a;\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n Node* intersect(Node* quadTree1, Node* quadTree2) {\n if(quadTree1 -> isLeaf)\n {\n if(quadTree1 -> val == 1) return quadTree1;\n return quadTree2;\n }\n if(quadTree2 -> isLeaf)\n {\n if(quadTree2 -> val == 1) return quadTree2;\n return quadTree1;\n }\n vector<Node*> arr;\n arr.push_back(intersect(quadTree1 -> topLeft, quadTree2 -> topLeft));\n arr.push_back(intersect(quadTree1 -> topRight, quadTree2 -> topRight));\n arr.push_back(intersect(quadTree1 -> bottomLeft, quadTree2 -> bottomLeft));\n arr.push_back(intersect(quadTree1 -> bottomRight, quadTree2 -> bottomRight));\n for(Node* node : arr)\n {\n if(!node -> isLeaf)\n {\n return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n }\n for(Node *node : arr)\n {\n if(!node -> val) return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n return new Node(true, true);\n }\n};\n```\n```python3 []\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n if q1.isLeaf:\n return q1.val and q1 or q2\n elif q2.isLeaf:\n return q2.val and q2 or q1\n else:\n tLeft = self.intersect(q1.topLeft, q2.topLeft)\n tRight = self.intersect(q1.topRight, q2.topRight)\n bLeft = self.intersect(q1.bottomLeft, q2.bottomLeft)\n bRight = self.intersect(q1.bottomRight, q2.bottomRight)\n if tLeft.isLeaf and tRight.isLeaf and bLeft.isLeaf and bRight.isLeaf and tLeft.val == tRight.val == bLeft.val == bRight.val:\n node = Node(tLeft.val, True, None, None, None, None) \n else:\n node = Node(False, False, tLeft, tRight, bLeft, bRight)\n return node\n```\n\n
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
easy solution
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 1
| 1
|
\n\n# Code\n```java []\n/*\n// Definition for a QuadTree node.\nclass Node {\n public boolean val;\n public boolean isLeaf;\n public Node topLeft;\n public Node topRight;\n public Node bottomLeft;\n public Node bottomRight;\n\n public Node() {}\n\n public Node(boolean _val,boolean _isLeaf,Node _topLeft,Node _topRight,Node _bottomLeft,Node _bottomRight) {\n val = _val;\n isLeaf = _isLeaf;\n topLeft = _topLeft;\n topRight = _topRight;\n bottomLeft = _bottomLeft;\n bottomRight = _bottomRight;\n }\n};\n*/\n\nclass Solution {\n public Node intersect(Node a, Node b) {\n if(a.isLeaf){\n return a.val ? a : b;\n }\n if(b.isLeaf){\n return b.val ? b : a;\n }\n a.topLeft = intersect(a.topLeft,b.topLeft);\n a.topRight = intersect(a.topRight,b.topRight);\n a.bottomLeft = intersect(a.bottomLeft,b.bottomLeft);\n a.bottomRight = intersect(a.bottomRight,b.bottomRight);\n\n if (a.topLeft.isLeaf && a.topRight.isLeaf \n && a.bottomLeft.isLeaf && a.bottomRight.isLeaf\n && a.topLeft.val == a.topRight.val \n && a.topRight.val == a.bottomLeft.val \n && a.bottomLeft.val == a.bottomRight.val) {\n return new Node(true,a.topLeft.val);\n }\n return a;\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n Node* intersect(Node* quadTree1, Node* quadTree2) {\n if(quadTree1 -> isLeaf)\n {\n if(quadTree1 -> val == 1) return quadTree1;\n return quadTree2;\n }\n if(quadTree2 -> isLeaf)\n {\n if(quadTree2 -> val == 1) return quadTree2;\n return quadTree1;\n }\n vector<Node*> arr;\n arr.push_back(intersect(quadTree1 -> topLeft, quadTree2 -> topLeft));\n arr.push_back(intersect(quadTree1 -> topRight, quadTree2 -> topRight));\n arr.push_back(intersect(quadTree1 -> bottomLeft, quadTree2 -> bottomLeft));\n arr.push_back(intersect(quadTree1 -> bottomRight, quadTree2 -> bottomRight));\n for(Node* node : arr)\n {\n if(!node -> isLeaf)\n {\n return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n }\n for(Node *node : arr)\n {\n if(!node -> val) return new Node(\n true, false,\n arr[0], arr[1], arr[2], arr[3]\n );\n }\n return new Node(true, true);\n }\n};\n```\n```python3 []\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n if q1.isLeaf:\n return q1.val and q1 or q2\n elif q2.isLeaf:\n return q2.val and q2 or q1\n else:\n tLeft = self.intersect(q1.topLeft, q2.topLeft)\n tRight = self.intersect(q1.topRight, q2.topRight)\n bLeft = self.intersect(q1.bottomLeft, q2.bottomLeft)\n bRight = self.intersect(q1.bottomRight, q2.bottomRight)\n if tLeft.isLeaf and tRight.isLeaf and bLeft.isLeaf and bRight.isLeaf and tLeft.val == tRight.val == bLeft.val == bRight.val:\n node = Node(tLeft.val, True, None, None, None, None) \n else:\n node = Node(False, False, tLeft, tRight, bLeft, bRight)\n return node\n```\n\n
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
Python solution for Quadtree Intersection Problem
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\nThe problem statement asks to find the intersection of two quadtrees. A quadtree is a tree data structure in which each internal node has exactly four children: top left, top right, bottom left, and bottom right. Each leaf node represents a square region and has a boolean value. The quadtree is a recursive data structure, and hence we can use a recursive approach to solve this problem.\n# Approach\nWe can start by checking if either of the quad trees is empty, in which case we can simply return the other one. If both the quad trees are leaves, we merge them into a new node with the logical OR of their values. If one of the quad trees is a leaf and its value is True, we return it. We divide the quad trees into four sub-trees and recursively call the intersect function on these sub-trees. If all the sub-trees are leaves and have the same value, we merge them into a single node. Finally, we return the quad tree with the four sub-trees.\n\n\n# Complexity\n- Time complexity:\nSince we are visiting each node of the quad tree once, the time complexity of the algorithm is O(n), where n is the number of nodes in the quad tree.\n- Space complexity:\nThe space complexity of the algorithm is O(logn), where n is the number of nodes in the quad tree, because the maximum depth of the recursive call stack is logn.\n# Code\n```\n# Definition for a QuadTree node.\n# class Node:\n# def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n# self.val = val\n# self.isLeaf = isLeaf\n# self.topLeft = topLeft\n# self.topRight = topRight\n# self.bottomLeft = bottomLeft\n# self.bottomRight = bottomRight\n\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n \n # If either quad tree is empty, return the other one\n if not quadTree1:\n return quadTree2\n if not quadTree2:\n return quadTree1\n \n # If both quad trees are leaves, merge them\n if quadTree1.isLeaf and quadTree2.isLeaf:\n return Node(quadTree1.val or quadTree2.val, True, None, None, None, None)\n \n # If one of the quad trees is a leaf, and it\'s True, return it\n if quadTree1.isLeaf and quadTree1.val:\n return quadTree1\n if quadTree2.isLeaf and quadTree2.val:\n return quadTree2\n \n # Divide the quad trees into four sub-trees\n topLeft = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n topRight = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bottomLeft = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n bottomRight = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n \n # If all sub-trees are leaves and they have same values, merge them\n if topLeft.isLeaf and topRight.isLeaf and bottomLeft.isLeaf and bottomRight.isLeaf and \\\n topLeft.val == topRight.val == bottomLeft.val == bottomRight.val:\n return Node(topLeft.val, True, None, None, None, None)\n \n # Return the quad tree with the four sub-trees\n return Node(False, False, topLeft, topRight, bottomLeft, bottomRight)\n\n```
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
Python solution for Quadtree Intersection Problem
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\nThe problem statement asks to find the intersection of two quadtrees. A quadtree is a tree data structure in which each internal node has exactly four children: top left, top right, bottom left, and bottom right. Each leaf node represents a square region and has a boolean value. The quadtree is a recursive data structure, and hence we can use a recursive approach to solve this problem.\n# Approach\nWe can start by checking if either of the quad trees is empty, in which case we can simply return the other one. If both the quad trees are leaves, we merge them into a new node with the logical OR of their values. If one of the quad trees is a leaf and its value is True, we return it. We divide the quad trees into four sub-trees and recursively call the intersect function on these sub-trees. If all the sub-trees are leaves and have the same value, we merge them into a single node. Finally, we return the quad tree with the four sub-trees.\n\n\n# Complexity\n- Time complexity:\nSince we are visiting each node of the quad tree once, the time complexity of the algorithm is O(n), where n is the number of nodes in the quad tree.\n- Space complexity:\nThe space complexity of the algorithm is O(logn), where n is the number of nodes in the quad tree, because the maximum depth of the recursive call stack is logn.\n# Code\n```\n# Definition for a QuadTree node.\n# class Node:\n# def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n# self.val = val\n# self.isLeaf = isLeaf\n# self.topLeft = topLeft\n# self.topRight = topRight\n# self.bottomLeft = bottomLeft\n# self.bottomRight = bottomRight\n\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n \n # If either quad tree is empty, return the other one\n if not quadTree1:\n return quadTree2\n if not quadTree2:\n return quadTree1\n \n # If both quad trees are leaves, merge them\n if quadTree1.isLeaf and quadTree2.isLeaf:\n return Node(quadTree1.val or quadTree2.val, True, None, None, None, None)\n \n # If one of the quad trees is a leaf, and it\'s True, return it\n if quadTree1.isLeaf and quadTree1.val:\n return quadTree1\n if quadTree2.isLeaf and quadTree2.val:\n return quadTree2\n \n # Divide the quad trees into four sub-trees\n topLeft = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n topRight = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bottomLeft = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n bottomRight = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n \n # If all sub-trees are leaves and they have same values, merge them\n if topLeft.isLeaf and topRight.isLeaf and bottomLeft.isLeaf and bottomRight.isLeaf and \\\n topLeft.val == topRight.val == bottomLeft.val == bottomRight.val:\n return Node(topLeft.val, True, None, None, None, None)\n \n # Return the quad tree with the four sub-trees\n return Node(False, False, topLeft, topRight, bottomLeft, bottomRight)\n\n```
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
Python 3.10 match
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Approach\nRecursion\n\n# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n match (quadTree1,quadTree2):\n case (None,_)|(_,Node(isLeaf=1,val=1)):\n return quadTree2\n case (Node(isLeaf=1,val=1),_)|(_,None)|(Node(isLeaf=1),Node(isLeaf=1)):\n return quadTree1\n case _:\n topLeft = self.intersect(quadTree1.topLeft,quadTree2.topLeft)\n topRight = self.intersect(quadTree1.topRight,quadTree2.topRight)\n bottomLeft = self.intersect(quadTree1.bottomLeft,quadTree2.bottomLeft)\n bottomRight = self.intersect(quadTree1.bottomRight,quadTree2.bottomRight)\n if all([(n.isLeaf,n.val) == (1,topLeft.val) for n in [topLeft, topRight, bottomLeft, bottomRight]]):\n return Node(1,topLeft.val)\n else:\n return Node(1,0,topLeft, topRight, bottomLeft, bottomRight)\n```
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
Python 3.10 match
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Approach\nRecursion\n\n# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n match (quadTree1,quadTree2):\n case (None,_)|(_,Node(isLeaf=1,val=1)):\n return quadTree2\n case (Node(isLeaf=1,val=1),_)|(_,None)|(Node(isLeaf=1),Node(isLeaf=1)):\n return quadTree1\n case _:\n topLeft = self.intersect(quadTree1.topLeft,quadTree2.topLeft)\n topRight = self.intersect(quadTree1.topRight,quadTree2.topRight)\n bottomLeft = self.intersect(quadTree1.bottomLeft,quadTree2.bottomLeft)\n bottomRight = self.intersect(quadTree1.bottomRight,quadTree2.bottomRight)\n if all([(n.isLeaf,n.val) == (1,topLeft.val) for n in [topLeft, topRight, bottomLeft, bottomRight]]):\n return Node(1,topLeft.val)\n else:\n return Node(1,0,topLeft, topRight, bottomLeft, bottomRight)\n```
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
[Python] Recursion; Explained
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
We can recursively traverse each branch of the two trees.\n\nSince we are solving bitwise OR of the two trees, there are some special handling when we build a new node based on the return nodes from the children:\n(1) if this node is a leaf node, we can directly return this node if its value is 1 or the other node is its value is 0.\n(2) After we get the four children, if they all are leaf nodes and they all have the same value, we can create a new leaf node with the value.\n(3) If the four children are not leaf nodes, just build a new node and return it.\n\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n if quadTree1 is None:\n return quadTree2\n \n if quadTree2 is None:\n return quadTree1\n \n root = self.buildTree(quadTree1, quadTree2)\n \n return root\n \n def buildTree(self, t1, t2):\n if t1.isLeaf:\n if t1.val:\n return t1\n else:\n return t2\n \n if t2.isLeaf:\n if t2.val:\n return t2\n else:\n return t1\n \n # both nodes are not leaf\n tl = self.buildTree(t1.topLeft, t2.topLeft)\n tr = self.buildTree(t1.topRight, t2.topRight)\n bl = self.buildTree(t1.bottomLeft, t2.bottomLeft)\n br = self.buildTree(t1.bottomRight, t2.bottomRight)\n \n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf:\n if tl.val == tr.val == bl.val == br.val:\n new_node = Node(tl.val, True, None, None, None, None)\n else:\n new_node = Node(tl.val, False, tl, tr, bl, br)\n else:\n new_node = Node(tl.val, False, tl, tr, bl, br)\n \n return new_node\n```
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
[Python] Recursion; Explained
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
We can recursively traverse each branch of the two trees.\n\nSince we are solving bitwise OR of the two trees, there are some special handling when we build a new node based on the return nodes from the children:\n(1) if this node is a leaf node, we can directly return this node if its value is 1 or the other node is its value is 0.\n(2) After we get the four children, if they all are leaf nodes and they all have the same value, we can create a new leaf node with the value.\n(3) If the four children are not leaf nodes, just build a new node and return it.\n\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n if quadTree1 is None:\n return quadTree2\n \n if quadTree2 is None:\n return quadTree1\n \n root = self.buildTree(quadTree1, quadTree2)\n \n return root\n \n def buildTree(self, t1, t2):\n if t1.isLeaf:\n if t1.val:\n return t1\n else:\n return t2\n \n if t2.isLeaf:\n if t2.val:\n return t2\n else:\n return t1\n \n # both nodes are not leaf\n tl = self.buildTree(t1.topLeft, t2.topLeft)\n tr = self.buildTree(t1.topRight, t2.topRight)\n bl = self.buildTree(t1.bottomLeft, t2.bottomLeft)\n br = self.buildTree(t1.bottomRight, t2.bottomRight)\n \n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf:\n if tl.val == tr.val == bl.val == br.val:\n new_node = Node(tl.val, True, None, None, None, None)\n else:\n new_node = Node(tl.val, False, tl, tr, bl, br)\n else:\n new_node = Node(tl.val, False, tl, tr, bl, br)\n \n return new_node\n```
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
Python3 - Combine in place, then reconcile
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\nThis problem was more tedious than hard - child nodes should be in an array. Although, I did fail to simplify the output during the initial runthrough.\n\n# Code\n```\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n def rec(n1, n2):\n if n1.isLeaf and n2.isLeaf:\n n1.val = n1.val or n2.val\n elif (not n1.isLeaf) and not (n2.isLeaf):\n rec(n1.topLeft, n2.topLeft)\n rec(n1.topRight, n2.topRight)\n rec(n1.bottomLeft, n2.bottomLeft)\n rec(n1.bottomRight, n2.bottomRight)\n elif n1.isLeaf and n1.val or n2.isLeaf and n2.val:\n n1.isLeaf = True\n n1.val = True\n n1.topLeft = None\n n1.topRight = None\n n1.bottomLeft = None\n n1.bottomRight = None\n elif n1.isLeaf:\n n1.isLeaf = n2.isLeaf\n n1.val = n2.val\n n1.topLeft = n2.topLeft\n n1.topRight = n2.topRight\n n1.bottomLeft = n2.bottomLeft\n n1.bottomRight = n2.bottomRight\n\n rec(q1, q2)\n\n def color(n1):\n if n1.isLeaf:\n return n1.val\n items = set([color(n1.topLeft), color(n1.topRight), color(n1.bottomLeft), color(n1.bottomRight)])\n if len(items) > 1:\n return None\n item = items.pop()\n if item is None:\n return None\n n1.isLeaf = True\n n1.val = item\n n1.topLeft = None\n n1.topRight = None\n n1.bottomLeft = None\n n1.bottomRight = None\n\n return item\n \n color(q1)\n return q1\n\n```
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
Python3 - Combine in place, then reconcile
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Intuition\nThis problem was more tedious than hard - child nodes should be in an array. Although, I did fail to simplify the output during the initial runthrough.\n\n# Code\n```\nclass Solution:\n def intersect(self, q1: \'Node\', q2: \'Node\') -> \'Node\':\n def rec(n1, n2):\n if n1.isLeaf and n2.isLeaf:\n n1.val = n1.val or n2.val\n elif (not n1.isLeaf) and not (n2.isLeaf):\n rec(n1.topLeft, n2.topLeft)\n rec(n1.topRight, n2.topRight)\n rec(n1.bottomLeft, n2.bottomLeft)\n rec(n1.bottomRight, n2.bottomRight)\n elif n1.isLeaf and n1.val or n2.isLeaf and n2.val:\n n1.isLeaf = True\n n1.val = True\n n1.topLeft = None\n n1.topRight = None\n n1.bottomLeft = None\n n1.bottomRight = None\n elif n1.isLeaf:\n n1.isLeaf = n2.isLeaf\n n1.val = n2.val\n n1.topLeft = n2.topLeft\n n1.topRight = n2.topRight\n n1.bottomLeft = n2.bottomLeft\n n1.bottomRight = n2.bottomRight\n\n rec(q1, q2)\n\n def color(n1):\n if n1.isLeaf:\n return n1.val\n items = set([color(n1.topLeft), color(n1.topRight), color(n1.bottomLeft), color(n1.bottomRight)])\n if len(items) > 1:\n return None\n item = items.pop()\n if item is None:\n return None\n n1.isLeaf = True\n n1.val = item\n n1.topLeft = None\n n1.topRight = None\n n1.bottomLeft = None\n n1.bottomRight = None\n\n return item\n \n color(q1)\n return q1\n\n```
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
Python3 🐍 concise solution beats 99%
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n if quadTree1.isLeaf: return quadTree1 if quadTree1.val else quadTree2 # boundary condition \n if quadTree2.isLeaf: return quadTree2 if quadTree2.val else quadTree1 # boundary condition \n tl = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n tr = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bl = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n br = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and tl.val == tr.val == bl.val == br.val: \n return Node(tl.val, True, None, None, None, None)\n return Node(None, False, tl, tr, bl, br)\n```
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
Python3 🐍 concise solution beats 99%
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n if quadTree1.isLeaf: return quadTree1 if quadTree1.val else quadTree2 # boundary condition \n if quadTree2.isLeaf: return quadTree2 if quadTree2.val else quadTree1 # boundary condition \n tl = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n tr = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bl = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n br = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and tl.val == tr.val == bl.val == br.val: \n return Node(tl.val, True, None, None, None, None)\n return Node(None, False, tl, tr, bl, br)\n```
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
Python solution
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Approach\nThis problem is different from many other problems here. In reality we need to traverse both trees in parallel and construct the result tree. \nThe approach is defined as checking different cases:\n1. Two empty trees give an empty tree as the result (``None``)\n2. If one of the trees is empty - then result is a clone of the other tree\n3. If both trees are leaves - just perform logical ``or`` on their values and construct another leave node as the output\n4. If one of the trees is a leaf which is ``True``, then the other tree doesn\'t matter and we return a ``True`` leaf node\n5. Otherwise we deal with the general case and the recursion - joining each child subtree. A tricky thing here is that we could end up with all subtrees having ``True`` values - in this case we compress current node into a ``True`` leaf node. This will also be propagated bottom-up in the result tree.\n\n# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n\n if not quadTree1 and not quadTree2:\n return None\n\n if not quadTree1:\n return copy.deepcopy(quadTree2)\n\n if not quadTree2:\n return copy.deepcopy(quadTree1)\n\n if quadTree1.isLeaf and quadTree2.isLeaf:\n return Node(quadTree1.val or quadTree2.val, True, None, None, None, None)\n elif quadTree1.isLeaf and quadTree1.val or quadTree2.isLeaf and quadTree2.val:\n return Node(True, True, None, None, None, None)\n\n topLeft = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n topRight = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bottomLeft = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n bottomRight = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n\n if topLeft.isLeaf and topRight.isLeaf and bottomLeft.isLeaf and bottomRight.isLeaf and \\\n topLeft.val and topRight.val and bottomLeft.val and bottomRight.val:\n return Node(True, True, None, None, None, None)\n\n result = Node(False, False,\n topLeft,\n topRight,\n bottomLeft,\n bottomRight)\n\n return result\n```\n\n\nShall you have any questions or concerns please ask here, and upvote if you like the approach!
| 0
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
Python solution
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
# Approach\nThis problem is different from many other problems here. In reality we need to traverse both trees in parallel and construct the result tree. \nThe approach is defined as checking different cases:\n1. Two empty trees give an empty tree as the result (``None``)\n2. If one of the trees is empty - then result is a clone of the other tree\n3. If both trees are leaves - just perform logical ``or`` on their values and construct another leave node as the output\n4. If one of the trees is a leaf which is ``True``, then the other tree doesn\'t matter and we return a ``True`` leaf node\n5. Otherwise we deal with the general case and the recursion - joining each child subtree. A tricky thing here is that we could end up with all subtrees having ``True`` values - in this case we compress current node into a ``True`` leaf node. This will also be propagated bottom-up in the result tree.\n\n# Code\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n\n if not quadTree1 and not quadTree2:\n return None\n\n if not quadTree1:\n return copy.deepcopy(quadTree2)\n\n if not quadTree2:\n return copy.deepcopy(quadTree1)\n\n if quadTree1.isLeaf and quadTree2.isLeaf:\n return Node(quadTree1.val or quadTree2.val, True, None, None, None, None)\n elif quadTree1.isLeaf and quadTree1.val or quadTree2.isLeaf and quadTree2.val:\n return Node(True, True, None, None, None, None)\n\n topLeft = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n topRight = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bottomLeft = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n bottomRight = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n\n if topLeft.isLeaf and topRight.isLeaf and bottomLeft.isLeaf and bottomRight.isLeaf and \\\n topLeft.val and topRight.val and bottomLeft.val and bottomRight.val:\n return Node(True, True, None, None, None, None)\n\n result = Node(False, False,\n topLeft,\n topRight,\n bottomLeft,\n bottomRight)\n\n return result\n```\n\n\nShall you have any questions or concerns please ask here, and upvote if you like the approach!
| 0
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
[Python3] 9-line recursive (64ms 93.33%)
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n if quadTree1.isLeaf: return quadTree1 if quadTree1.val else quadTree2 # boundary condition \n if quadTree2.isLeaf: return quadTree2 if quadTree2.val else quadTree1 # boundary condition \n tl = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n tr = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bl = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n br = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and tl.val == tr.val == bl.val == br.val: \n return Node(tl.val, True, None, None, None, None)\n return Node(None, False, tl, tr, bl, br)\n```
| 2
|
A Binary Matrix is a matrix in which all the elements are either **0** or **1**.
Given `quadTree1` and `quadTree2`. `quadTree1` represents a `n * n` binary matrix and `quadTree2` represents another `n * n` binary matrix.
Return _a Quad-Tree_ representing the `n * n` binary matrix which is the result of **logical bitwise OR** of the two binary matrixes represented by `quadTree1` and `quadTree2`.
Notice that you can assign the value of a node to **True** or **False** when `isLeaf` is **False**, and both are **accepted** in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
* `isLeaf`: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
The input/output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** quadTree1 = \[\[0,1\],\[1,1\],\[1,1\],\[1,0\],\[1,0\]\]
, quadTree2 = \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Output:** \[\[0,0\],\[1,1\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
**Example 2:**
**Input:** quadTree1 = \[\[1,0\]\], quadTree2 = \[\[1,0\]\]
**Output:** \[\[1,0\]\]
**Explanation:** Each tree represents a binary matrix of size 1\*1. Each matrix contains only zero.
The resulting matrix is of size 1\*1 with also zero.
**Constraints:**
* `quadTree1` and `quadTree2` are both **valid** Quad-Trees each representing a `n * n` grid.
* `n == 2x` where `0 <= x <= 9`.
| null |
[Python3] 9-line recursive (64ms 93.33%)
|
logical-or-of-two-binary-grids-represented-as-quad-trees
| 0
| 1
|
\n```\nclass Solution:\n def intersect(self, quadTree1: \'Node\', quadTree2: \'Node\') -> \'Node\':\n if quadTree1.isLeaf: return quadTree1 if quadTree1.val else quadTree2 # boundary condition \n if quadTree2.isLeaf: return quadTree2 if quadTree2.val else quadTree1 # boundary condition \n tl = self.intersect(quadTree1.topLeft, quadTree2.topLeft)\n tr = self.intersect(quadTree1.topRight, quadTree2.topRight)\n bl = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)\n br = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)\n if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and tl.val == tr.val == bl.val == br.val: \n return Node(tl.val, True, None, None, None, None)\n return Node(None, False, tl, tr, bl, br)\n```
| 2
|
On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**.
| null |
[Python || O(N)]
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if root == None:\n return 0\n else:\n depth = 0\n nodes_queue = [root]\n next_nodes_queue = []\n while(nodes_queue):\n node_out = nodes_queue.pop(0)\n for child in node_out.children:\n next_nodes_queue.append(child)\n if nodes_queue == []:\n nodes_queue, next_nodes_queue = next_nodes_queue, nodes_queue\n depth += 1\n return depth\n```
| 1
|
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** 5
**Constraints:**
* The total number of nodes is in the range `[0, 104]`.
* The depth of the n-ary tree is less than or equal to `1000`.
| null |
[Python || O(N)]
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if root == None:\n return 0\n else:\n depth = 0\n nodes_queue = [root]\n next_nodes_queue = []\n while(nodes_queue):\n node_out = nodes_queue.pop(0)\n for child in node_out.children:\n next_nodes_queue.append(child)\n if nodes_queue == []:\n nodes_queue, next_nodes_queue = next_nodes_queue, nodes_queue\n depth += 1\n return depth\n```
| 1
|
You are given an integer array `stations` that represents the positions of the gas stations on the **x-axis**. You are also given an integer `k`.
You should add `k` new gas stations. You can add the stations anywhere on the **x-axis**, and not necessarily on an integer position.
Let `penalty()` be the maximum distance between **adjacent** gas stations after adding the `k` new stations.
Return _the smallest possible value of_ `penalty()`. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** stations = \[1,2,3,4,5,6,7,8,9,10\], k = 9
**Output:** 0.50000
**Example 2:**
**Input:** stations = \[23,24,36,39,46,56,57,65,84,98\], k = 1
**Output:** 14.00000
**Constraints:**
* `10 <= stations.length <= 2000`
* `0 <= stations[i] <= 108`
* `stations` is sorted in a **strictly increasing** order.
* `1 <= k <= 106`
| null |
6 lines awesome code
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if not root:\n return 0\n maxdepth=0\n for child in root.children:\n maxdepth=max(self.maxDepth(child),maxdepth)\n return maxdepth+1\n \n\n```
| 3
|
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** 5
**Constraints:**
* The total number of nodes is in the range `[0, 104]`.
* The depth of the n-ary tree is less than or equal to `1000`.
| null |
6 lines awesome code
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if not root:\n return 0\n maxdepth=0\n for child in root.children:\n maxdepth=max(self.maxDepth(child),maxdepth)\n return maxdepth+1\n \n\n```
| 3
|
You are given an integer array `stations` that represents the positions of the gas stations on the **x-axis**. You are also given an integer `k`.
You should add `k` new gas stations. You can add the stations anywhere on the **x-axis**, and not necessarily on an integer position.
Let `penalty()` be the maximum distance between **adjacent** gas stations after adding the `k` new stations.
Return _the smallest possible value of_ `penalty()`. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** stations = \[1,2,3,4,5,6,7,8,9,10\], k = 9
**Output:** 0.50000
**Example 2:**
**Input:** stations = \[23,24,36,39,46,56,57,65,84,98\], k = 1
**Output:** 14.00000
**Constraints:**
* `10 <= stations.length <= 2000`
* `0 <= stations[i] <= 108`
* `stations` is sorted in a **strictly increasing** order.
* `1 <= k <= 106`
| null |
559: Time 95.76%, Solution with step by step explanation
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the root node is None. If it is, return 0 as the maximum depth since there are no nodes in the tree.\n2. Create a variable called max_depth and set it to 0. This variable will keep track of the maximum depth of the tree.\n3. Iterate through each child node of the root node.\n4. Recursively call the maxDepth function on each child node to get the maximum depth of that subtree.\n5. Compare the maximum depth of the current subtree to the current max_depth variable. If the maximum depth is greater than max_depth, set max_depth to the maximum depth of the current subtree.\n6. Return max_depth plus 1, since we need to count the root node itself in the depth calculation.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a Node.\n# class Node:\n# def __init__(self, val=None, children=None):\n# self.val = val\n# self.children = children if children is not None else []\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if not root:\n return 0\n max_depth = 0\n for child in root.children:\n max_depth = max(max_depth, self.maxDepth(child))\n return max_depth + 1\n\n```
| 6
|
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** 5
**Constraints:**
* The total number of nodes is in the range `[0, 104]`.
* The depth of the n-ary tree is less than or equal to `1000`.
| null |
559: Time 95.76%, Solution with step by step explanation
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the root node is None. If it is, return 0 as the maximum depth since there are no nodes in the tree.\n2. Create a variable called max_depth and set it to 0. This variable will keep track of the maximum depth of the tree.\n3. Iterate through each child node of the root node.\n4. Recursively call the maxDepth function on each child node to get the maximum depth of that subtree.\n5. Compare the maximum depth of the current subtree to the current max_depth variable. If the maximum depth is greater than max_depth, set max_depth to the maximum depth of the current subtree.\n6. Return max_depth plus 1, since we need to count the root node itself in the depth calculation.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a Node.\n# class Node:\n# def __init__(self, val=None, children=None):\n# self.val = val\n# self.children = children if children is not None else []\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if not root:\n return 0\n max_depth = 0\n for child in root.children:\n max_depth = max(max_depth, self.maxDepth(child))\n return max_depth + 1\n\n```
| 6
|
You are given an integer array `stations` that represents the positions of the gas stations on the **x-axis**. You are also given an integer `k`.
You should add `k` new gas stations. You can add the stations anywhere on the **x-axis**, and not necessarily on an integer position.
Let `penalty()` be the maximum distance between **adjacent** gas stations after adding the `k` new stations.
Return _the smallest possible value of_ `penalty()`. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** stations = \[1,2,3,4,5,6,7,8,9,10\], k = 9
**Output:** 0.50000
**Example 2:**
**Input:** stations = \[23,24,36,39,46,56,57,65,84,98\], k = 1
**Output:** 14.00000
**Constraints:**
* `10 <= stations.length <= 2000`
* `0 <= stations[i] <= 108`
* `stations` is sorted in a **strictly increasing** order.
* `1 <= k <= 106`
| null |
[ Python ] Easy Solution | Faster than 94% submits
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
```\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n \n if not root : return 0\n \n if root.children :\n return 1 + max([self.maxDepth(x) for x in root.children])\n else :\n return 1 \n```
| 6
|
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** 5
**Constraints:**
* The total number of nodes is in the range `[0, 104]`.
* The depth of the n-ary tree is less than or equal to `1000`.
| null |
[ Python ] Easy Solution | Faster than 94% submits
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
```\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n \n if not root : return 0\n \n if root.children :\n return 1 + max([self.maxDepth(x) for x in root.children])\n else :\n return 1 \n```
| 6
|
You are given an integer array `stations` that represents the positions of the gas stations on the **x-axis**. You are also given an integer `k`.
You should add `k` new gas stations. You can add the stations anywhere on the **x-axis**, and not necessarily on an integer position.
Let `penalty()` be the maximum distance between **adjacent** gas stations after adding the `k` new stations.
Return _the smallest possible value of_ `penalty()`. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** stations = \[1,2,3,4,5,6,7,8,9,10\], k = 9
**Output:** 0.50000
**Example 2:**
**Input:** stations = \[23,24,36,39,46,56,57,65,84,98\], k = 1
**Output:** 14.00000
**Constraints:**
* `10 <= stations.length <= 2000`
* `0 <= stations[i] <= 108`
* `stations` is sorted in a **strictly increasing** order.
* `1 <= k <= 106`
| null |
PYTHON_(Simple BFS || Beats(TC : 99%))
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(V+E)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(|V|)$$\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if root==None:\n return 0\n que=Deque()\n que.append(root)\n count=0\n while(que):\n n=len(que)\n for _ in range(n):\n cur=que.popleft()\n for i in cur.children:\n que.append(i)\n count+=1\n return count\n```
| 1
|
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** 5
**Constraints:**
* The total number of nodes is in the range `[0, 104]`.
* The depth of the n-ary tree is less than or equal to `1000`.
| null |
PYTHON_(Simple BFS || Beats(TC : 99%))
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(V+E)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(|V|)$$\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if root==None:\n return 0\n que=Deque()\n que.append(root)\n count=0\n while(que):\n n=len(que)\n for _ in range(n):\n cur=que.popleft()\n for i in cur.children:\n que.append(i)\n count+=1\n return count\n```
| 1
|
You are given an integer array `stations` that represents the positions of the gas stations on the **x-axis**. You are also given an integer `k`.
You should add `k` new gas stations. You can add the stations anywhere on the **x-axis**, and not necessarily on an integer position.
Let `penalty()` be the maximum distance between **adjacent** gas stations after adding the `k` new stations.
Return _the smallest possible value of_ `penalty()`. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** stations = \[1,2,3,4,5,6,7,8,9,10\], k = 9
**Output:** 0.50000
**Example 2:**
**Input:** stations = \[23,24,36,39,46,56,57,65,84,98\], k = 1
**Output:** 14.00000
**Constraints:**
* `10 <= stations.length <= 2000`
* `0 <= stations[i] <= 108`
* `stations` is sorted in a **strictly increasing** order.
* `1 <= k <= 106`
| null |
Python BFS Iterative Beats 92%
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
```\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if not root:\n return 0\n \n nodes = deque()\n nodes.append((root, 1))\n maxx = 0\n while nodes:\n cur, val = nodes.popleft()\n maxx = val\n if cur.children:\n for child in cur.children:\n nodes.append((child, val+1))\n return maxx\n```
| 10
|
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** 5
**Constraints:**
* The total number of nodes is in the range `[0, 104]`.
* The depth of the n-ary tree is less than or equal to `1000`.
| null |
Python BFS Iterative Beats 92%
|
maximum-depth-of-n-ary-tree
| 0
| 1
|
```\nclass Solution:\n def maxDepth(self, root: \'Node\') -> int:\n if not root:\n return 0\n \n nodes = deque()\n nodes.append((root, 1))\n maxx = 0\n while nodes:\n cur, val = nodes.popleft()\n maxx = val\n if cur.children:\n for child in cur.children:\n nodes.append((child, val+1))\n return maxx\n```
| 10
|
You are given an integer array `stations` that represents the positions of the gas stations on the **x-axis**. You are also given an integer `k`.
You should add `k` new gas stations. You can add the stations anywhere on the **x-axis**, and not necessarily on an integer position.
Let `penalty()` be the maximum distance between **adjacent** gas stations after adding the `k` new stations.
Return _the smallest possible value of_ `penalty()`. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** stations = \[1,2,3,4,5,6,7,8,9,10\], k = 9
**Output:** 0.50000
**Example 2:**
**Input:** stations = \[23,24,36,39,46,56,57,65,84,98\], k = 1
**Output:** 14.00000
**Constraints:**
* `10 <= stations.length <= 2000`
* `0 <= stations[i] <= 108`
* `stations` is sorted in a **strictly increasing** order.
* `1 <= k <= 106`
| null |
[ Python ] ✅✅ Simple Python Solution Using PrefixSum and Dictionary 🔥✌
|
subarray-sum-equals-k
| 0
| 1
|
\n# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n\tclass Solution:\n\t\tdef subarraySum(self, nums: List[int], k: int) -> int:\n\n\t\t\tresult = 0 \n\t\t\tprefix_sum = 0\n\t\t\td = {0 : 1}\n\n\t\t\tfor num in nums:\n\t\t\t\n\t\t\t\tprefix_sum = prefix_sum + num\n\n\t\t\t\tif prefix_sum - k in d:\n\t\t\t\t\n\t\t\t\t\tresult = result + d[prefix_sum - k]\n\n\t\t\t\tif prefix_sum not in d:\n\t\t\t\t\n\t\t\t\t\td[prefix_sum] = 1\n\t\t\t\telse:\n\t\t\t\t\td[prefix_sum] = d[prefix_sum] + 1\n\n\t\t\treturn result\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D
| 304
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
[ Python ] ✅✅ Simple Python Solution Using PrefixSum and Dictionary 🔥✌
|
subarray-sum-equals-k
| 0
| 1
|
\n# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n\tclass Solution:\n\t\tdef subarraySum(self, nums: List[int], k: int) -> int:\n\n\t\t\tresult = 0 \n\t\t\tprefix_sum = 0\n\t\t\td = {0 : 1}\n\n\t\t\tfor num in nums:\n\t\t\t\n\t\t\t\tprefix_sum = prefix_sum + num\n\n\t\t\t\tif prefix_sum - k in d:\n\t\t\t\t\n\t\t\t\t\tresult = result + d[prefix_sum - k]\n\n\t\t\t\tif prefix_sum not in d:\n\t\t\t\t\n\t\t\t\t\td[prefix_sum] = 1\n\t\t\t\telse:\n\t\t\t\t\td[prefix_sum] = d[prefix_sum] + 1\n\n\t\t\treturn result\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D
| 304
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Python 3 Solution for Problem no. 560.
|
subarray-sum-equals-k
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing prefix sum and dictionary.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\tdef subarraySum(self, nums: List[int], k: int) -> int:\n\n\t\tres=0\n\t\tpresum=0\n\t\tdict1={0:1}\n\n\t\tfor i in nums:\n\t\t\tpresum = presum + i\n\n\t\t\tif (presum-k) in dict1:\n\t\t\t\tres = res + dict1[presum-k]\n\n\t\t\tif presum not in dict1:\n\t\t\t\tdict1[presum] = 1\n\t\t\telse:\n\t\t\t\tdict1[presum] = dict1[presum]+1\n\n\t\treturn res\n```
| 1
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Python 3 Solution for Problem no. 560.
|
subarray-sum-equals-k
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing prefix sum and dictionary.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\tdef subarraySum(self, nums: List[int], k: int) -> int:\n\n\t\tres=0\n\t\tpresum=0\n\t\tdict1={0:1}\n\n\t\tfor i in nums:\n\t\t\tpresum = presum + i\n\n\t\t\tif (presum-k) in dict1:\n\t\t\t\tres = res + dict1[presum-k]\n\n\t\t\tif presum not in dict1:\n\t\t\t\tdict1[presum] = 1\n\t\t\telse:\n\t\t\t\tdict1[presum] = dict1[presum]+1\n\n\t\treturn res\n```
| 1
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
✅☑[C++/C/Java/Python/JavaScript] || Easiest Approach So Far || Beats 100% || EXPLAINED🔥
|
subarray-sum-equals-k
| 1
| 1
|
# *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n\n# Approaches\n***(Also explained in the code)***\n1. **Initialize variables:**\n\n - `n` as the length of the input `nums` array.\n - `prefix` array to store prefix sums, where `prefix[i]` represents the sum of all elements from index 0 to `i` in `nums`.\n - Initialize `prefix[0]` with the value of `nums[0]` as the base case.\n \n1. **Calculate the prefix sums:**\n\n - Loop through `nums` starting from the second element.\n - For each element at index `i`, update `prefix[i]` by adding `nums[i]` to the previous prefix sum `prefix[i-1]`.\n - This step computes the prefix sums and stores them in the `prefix` array.\n1. Create an unordered map `mp` to keep track of prefix sums and their frequencies. Also, initialize `cnt` (count) to 0, which will store the total count of subarrays with the sum equal to `k`.\n\n1. **Loop through \'nums\' once more:**\n\n - At each step, check if `prefix[i]` is equal to `k`. If it is, increment `cnt` by 1. This handles subarrays that start from the beginning of `nums` and have a sum equal to `k`.\n1. Check if `mp` contains a key equal to `prefix[i] - k`:\n\n - If `mp` contains `prefix[i] - k`, it means that there exists a subarray with a sum of `k` ending at index `i` (i.e., a subarray whose sum from some previous index to `i` is `k`). In this case, increment `cnt` by the number of such subarrays stored in `mp[prefix[i] - k]`.\n1. Update the frequency of the current `prefix[i]` in the `mp` map.\n\n1. Continue this process for all elements in `nums`.\n\n1. Finally, return `cnt`, which represents the total count of subarrays with a sum equal to `k`.\n\n\n# Complexity\n- **Time complexity:**\n$$O(n)$$\n\n- **Space complexity:**\n$$O(n)$$\n\n#### **Code**\n```C++ []\nclass Solution {\npublic:\n int subarraySum(vector<int>& nums, int k) {\n int n = nums.size();\n int prefix[n];\n prefix[0] = nums[0];\n\n for(int i =1;i<n;i++){\n prefix[i] = nums[i] + prefix[i-1];\n }\n\n unordered_map<int,int>mp;\n int cnt=0;\n\n for(int i =0;i<n;i++){\n if(prefix[i]==k)cnt++;\n\n if(mp.find(prefix[i]-k) != mp.end()){\n cnt += mp[prefix[i]-k];\n }\n mp[prefix[i]]++;\n }\n return cnt;\n\n }\n};class Solution {\npublic:\n int subarraySum(vector<int>& nums, int k) {\n int n = nums.size();\n int prefix[n];\n prefix[0] = nums[0];\n\n for(int i =1;i<n;i++){\n prefix[i] = nums[i] + prefix[i-1];\n }\n\n unordered_map<int,int>mp;\n int cnt=0;\n\n for(int i =0;i<n;i++){\n if(prefix[i]==k)cnt++;\n\n if(mp.find(prefix[i]-k) != mp.end()){\n cnt += mp[prefix[i]-k];\n }\n mp[prefix[i]]++;\n }\n return cnt;\n\n }\n};\n```\n```C []\nint subarraySum(int nums[], int n, int k) {\n int prefix[n];\n prefix[0] = nums[0];\n\n for (int i = 1; i < n; i++) {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n\n int mp[100000] = {0}; // Assuming a maximum size, adjust if needed\n int cnt = 0;\n\n for (int i = 0; i < n; i++) {\n if (prefix[i] == k) {\n cnt++;\n }\n\n if (mp[prefix[i] - k]) {\n cnt += mp[prefix[i] - k];\n }\n mp[prefix[i]]++;\n }\n return cnt;\n}\n```\n```Java []\nimport java.util.HashMap;\n\nclass Solution {\n public int subarraySum(int[] nums, int k) {\n int n = nums.length;\n int[] prefix = new int[n];\n prefix[0] = nums[0];\n\n for (int i = 1; i < n; i++) {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n\n HashMap<Integer, Integer> mp = new HashMap<>();\n int cnt = 0;\n\n for (int i = 0; i < n; i++) {\n if (prefix[i] == k) cnt++;\n\n if (mp.containsKey(prefix[i] - k)) {\n cnt += mp.get(prefix[i] - k);\n }\n mp.put(prefix[i], mp.getOrDefault(prefix[i], 0) + 1);\n }\n return cnt;\n }\n}\n\n```\n```python []\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n n = len(nums)\n prefix = [0] * n\n prefix[0] = nums[0]\n\n for i in range(1, n):\n prefix[i] = nums[i] + prefix[i - 1]\n\n mp = {}\n cnt = 0\n\n for i in range(n):\n if prefix[i] == k:\n cnt += 1\n\n if prefix[i] - k in mp:\n cnt += mp[prefix[i] - k]\n mp[prefix[i]] = mp.get(prefix[i], 0) + 1\n\n return cnt\n\n```\n```javascript []\nvar subarraySum = function(nums, k) {\n const n = nums.length;\n const prefix = new Array(n).fill(0);\n prefix[0] = nums[0];\n\n for (let i = 1; i < n; i++) {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n\n const mp = new Map();\n let cnt = 0;\n\n for (let i = 0; i < n; i++) {\n if (prefix[i] === k) cnt++;\n\n if (mp.has(prefix[i] - k)) {\n cnt += mp.get(prefix[i] - k);\n }\n mp.set(prefix[i], mp.get(prefix[i]) ? mp.get(prefix[i]) + 1 : 1);\n }\n return cnt;\n};\n\n```\n\n#### ***Shorter Version:***\n\n```C++ []\nclass Solution {\npublic:\n \n\n int subarraySum(vector<int>& nums, int k) {\n unordered_map<int,int> map;\n \n int sum = 0, result = 0;\n map[sum] = 1;\n \n for (int n : nums) {\n sum += n;\n result += map[sum - k];\n map[sum]++;\n }\n \n return result;\n }\n\n \n};\n```\n```C []\nstruct HashMap {\n int* keys;\n int* values;\n int size;\n int capacity;\n};\n\nstruct HashMap* createHashMap() {\n struct HashMap* hashMap = (struct HashMap*)malloc(sizeof(struct HashMap));\n hashMap->size = 0;\n hashMap->capacity = 16; // Initial capacity, you can change this as needed\n hashMap->keys = (int*)malloc(sizeof(int) * hashMap->capacity);\n hashMap->values = (int*)malloc(sizeof(int) * hashMap->capacity);\n \n return hashMap;\n}\n\nint hashCode(struct HashMap* hashMap, int key) {\n return abs(key) % hashMap->capacity;\n}\n\nvoid resizeHashMap(struct HashMap* hashMap) {\n int newCapacity = hashMap->capacity * 2;\n int* newKeys = (int*)malloc(sizeof(int) * newCapacity);\n int* newValues = (int*)malloc(sizeof(int) * newCapacity);\n \n for (int i = 0; i < newCapacity; i++) {\n newKeys[i] = -1;\n newValues[i] = 0;\n }\n\n for (int i = 0; i < hashMap->capacity; i++) {\n if (hashMap->keys[i] != -1) {\n int newIndex = hashCode(hashMap, hashMap->keys[i]);\n\n while (newKeys[newIndex] != -1) {\n newIndex = (newIndex + 1) % newCapacity;\n }\n\n newKeys[newIndex] = hashMap->keys[i];\n newValues[newIndex] = hashMap->values[i];\n }\n }\n\n free(hashMap->keys);\n free(hashMap->values);\n hashMap->keys = newKeys;\n hashMap->values = newValues;\n hashMap->capacity = newCapacity;\n}\n\nvoid insert(struct HashMap* hashMap, int key, int value) {\n if (hashMap->size * 2 >= hashMap->capacity) {\n resizeHashMap(hashMap);\n }\n\n int index = hashCode(hashMap, key);\n\n while (hashMap->keys[index] != -1) {\n if (hashMap->keys[index] == key) {\n hashMap->values[index] = value;\n return;\n }\n index = (index + 1) % hashMap->capacity;\n }\n\n hashMap->keys[index] = key;\n hashMap->values[index] = value;\n hashMap->size++;\n}\n\nint search(struct HashMap* hashMap, int key) {\n int index = hashCode(hashMap, key);\n\n while (hashMap->keys[index] != -1) {\n if (hashMap->keys[index] == key) {\n return hashMap->values[index];\n }\n index = (index + 1) % hashMap->capacity;\n }\n\n return 0;\n}\n\nvoid freeHashMap(struct HashMap* hashMap) {\n free(hashMap->keys);\n free(hashMap->values);\n free(hashMap);\n}\n\nint subarraySum(int* nums, int numsSize, int k) {\n struct HashMap* hashMap = createHashMap();\n int sum = 0, count = 0;\n\n insert(hashMap, 0, 1);\n\n for (int i = 0; i < numsSize; i++) {\n sum += nums[i];\n count += search(hashMap, sum - k);\n insert(hashMap, sum, search(hashMap, sum) + 1);\n }\n\n freeHashMap(hashMap);\n \n return count;\n}\n```\n```Java []\nclass Solution {\n public int subarraySum(int[] nums, int k) {\n Map<Integer, Integer> map = new HashMap<>();\n int sum = 0, result = 0;\n map.put(0, 1);\n \n for (int n : nums) {\n sum += n;\n result += map.getOrDefault(sum - k, 0);\n map.put(sum, map.getOrDefault(sum, 0) + 1);\n }\n \n return result;\n }\n}\n```\n```python []\nclass Solution:\n def subarraySum(self, nums, k):\n map = {0: 1}\n sum = 0\n result = 0\n \n for n in nums:\n sum += n\n result += map.get(sum - k, 0)\n map[sum] = map.get(sum, 0) + 1\n \n return result\n\n```\n```javascript []\nvar subarraySum = function(nums, k) {\n let map = new Map();\n let sum = 0;\n let result = 0;\n map.set(0, 1);\n \n for (let n of nums) {\n sum += n;\n result += (map.get(sum - k) || 0);\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n \n return result;\n};\n\n```\n---\n\n# *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n\n---\n\n\n
| 8
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
✅☑[C++/C/Java/Python/JavaScript] || Easiest Approach So Far || Beats 100% || EXPLAINED🔥
|
subarray-sum-equals-k
| 1
| 1
|
# *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n\n# Approaches\n***(Also explained in the code)***\n1. **Initialize variables:**\n\n - `n` as the length of the input `nums` array.\n - `prefix` array to store prefix sums, where `prefix[i]` represents the sum of all elements from index 0 to `i` in `nums`.\n - Initialize `prefix[0]` with the value of `nums[0]` as the base case.\n \n1. **Calculate the prefix sums:**\n\n - Loop through `nums` starting from the second element.\n - For each element at index `i`, update `prefix[i]` by adding `nums[i]` to the previous prefix sum `prefix[i-1]`.\n - This step computes the prefix sums and stores them in the `prefix` array.\n1. Create an unordered map `mp` to keep track of prefix sums and their frequencies. Also, initialize `cnt` (count) to 0, which will store the total count of subarrays with the sum equal to `k`.\n\n1. **Loop through \'nums\' once more:**\n\n - At each step, check if `prefix[i]` is equal to `k`. If it is, increment `cnt` by 1. This handles subarrays that start from the beginning of `nums` and have a sum equal to `k`.\n1. Check if `mp` contains a key equal to `prefix[i] - k`:\n\n - If `mp` contains `prefix[i] - k`, it means that there exists a subarray with a sum of `k` ending at index `i` (i.e., a subarray whose sum from some previous index to `i` is `k`). In this case, increment `cnt` by the number of such subarrays stored in `mp[prefix[i] - k]`.\n1. Update the frequency of the current `prefix[i]` in the `mp` map.\n\n1. Continue this process for all elements in `nums`.\n\n1. Finally, return `cnt`, which represents the total count of subarrays with a sum equal to `k`.\n\n\n# Complexity\n- **Time complexity:**\n$$O(n)$$\n\n- **Space complexity:**\n$$O(n)$$\n\n#### **Code**\n```C++ []\nclass Solution {\npublic:\n int subarraySum(vector<int>& nums, int k) {\n int n = nums.size();\n int prefix[n];\n prefix[0] = nums[0];\n\n for(int i =1;i<n;i++){\n prefix[i] = nums[i] + prefix[i-1];\n }\n\n unordered_map<int,int>mp;\n int cnt=0;\n\n for(int i =0;i<n;i++){\n if(prefix[i]==k)cnt++;\n\n if(mp.find(prefix[i]-k) != mp.end()){\n cnt += mp[prefix[i]-k];\n }\n mp[prefix[i]]++;\n }\n return cnt;\n\n }\n};class Solution {\npublic:\n int subarraySum(vector<int>& nums, int k) {\n int n = nums.size();\n int prefix[n];\n prefix[0] = nums[0];\n\n for(int i =1;i<n;i++){\n prefix[i] = nums[i] + prefix[i-1];\n }\n\n unordered_map<int,int>mp;\n int cnt=0;\n\n for(int i =0;i<n;i++){\n if(prefix[i]==k)cnt++;\n\n if(mp.find(prefix[i]-k) != mp.end()){\n cnt += mp[prefix[i]-k];\n }\n mp[prefix[i]]++;\n }\n return cnt;\n\n }\n};\n```\n```C []\nint subarraySum(int nums[], int n, int k) {\n int prefix[n];\n prefix[0] = nums[0];\n\n for (int i = 1; i < n; i++) {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n\n int mp[100000] = {0}; // Assuming a maximum size, adjust if needed\n int cnt = 0;\n\n for (int i = 0; i < n; i++) {\n if (prefix[i] == k) {\n cnt++;\n }\n\n if (mp[prefix[i] - k]) {\n cnt += mp[prefix[i] - k];\n }\n mp[prefix[i]]++;\n }\n return cnt;\n}\n```\n```Java []\nimport java.util.HashMap;\n\nclass Solution {\n public int subarraySum(int[] nums, int k) {\n int n = nums.length;\n int[] prefix = new int[n];\n prefix[0] = nums[0];\n\n for (int i = 1; i < n; i++) {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n\n HashMap<Integer, Integer> mp = new HashMap<>();\n int cnt = 0;\n\n for (int i = 0; i < n; i++) {\n if (prefix[i] == k) cnt++;\n\n if (mp.containsKey(prefix[i] - k)) {\n cnt += mp.get(prefix[i] - k);\n }\n mp.put(prefix[i], mp.getOrDefault(prefix[i], 0) + 1);\n }\n return cnt;\n }\n}\n\n```\n```python []\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n n = len(nums)\n prefix = [0] * n\n prefix[0] = nums[0]\n\n for i in range(1, n):\n prefix[i] = nums[i] + prefix[i - 1]\n\n mp = {}\n cnt = 0\n\n for i in range(n):\n if prefix[i] == k:\n cnt += 1\n\n if prefix[i] - k in mp:\n cnt += mp[prefix[i] - k]\n mp[prefix[i]] = mp.get(prefix[i], 0) + 1\n\n return cnt\n\n```\n```javascript []\nvar subarraySum = function(nums, k) {\n const n = nums.length;\n const prefix = new Array(n).fill(0);\n prefix[0] = nums[0];\n\n for (let i = 1; i < n; i++) {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n\n const mp = new Map();\n let cnt = 0;\n\n for (let i = 0; i < n; i++) {\n if (prefix[i] === k) cnt++;\n\n if (mp.has(prefix[i] - k)) {\n cnt += mp.get(prefix[i] - k);\n }\n mp.set(prefix[i], mp.get(prefix[i]) ? mp.get(prefix[i]) + 1 : 1);\n }\n return cnt;\n};\n\n```\n\n#### ***Shorter Version:***\n\n```C++ []\nclass Solution {\npublic:\n \n\n int subarraySum(vector<int>& nums, int k) {\n unordered_map<int,int> map;\n \n int sum = 0, result = 0;\n map[sum] = 1;\n \n for (int n : nums) {\n sum += n;\n result += map[sum - k];\n map[sum]++;\n }\n \n return result;\n }\n\n \n};\n```\n```C []\nstruct HashMap {\n int* keys;\n int* values;\n int size;\n int capacity;\n};\n\nstruct HashMap* createHashMap() {\n struct HashMap* hashMap = (struct HashMap*)malloc(sizeof(struct HashMap));\n hashMap->size = 0;\n hashMap->capacity = 16; // Initial capacity, you can change this as needed\n hashMap->keys = (int*)malloc(sizeof(int) * hashMap->capacity);\n hashMap->values = (int*)malloc(sizeof(int) * hashMap->capacity);\n \n return hashMap;\n}\n\nint hashCode(struct HashMap* hashMap, int key) {\n return abs(key) % hashMap->capacity;\n}\n\nvoid resizeHashMap(struct HashMap* hashMap) {\n int newCapacity = hashMap->capacity * 2;\n int* newKeys = (int*)malloc(sizeof(int) * newCapacity);\n int* newValues = (int*)malloc(sizeof(int) * newCapacity);\n \n for (int i = 0; i < newCapacity; i++) {\n newKeys[i] = -1;\n newValues[i] = 0;\n }\n\n for (int i = 0; i < hashMap->capacity; i++) {\n if (hashMap->keys[i] != -1) {\n int newIndex = hashCode(hashMap, hashMap->keys[i]);\n\n while (newKeys[newIndex] != -1) {\n newIndex = (newIndex + 1) % newCapacity;\n }\n\n newKeys[newIndex] = hashMap->keys[i];\n newValues[newIndex] = hashMap->values[i];\n }\n }\n\n free(hashMap->keys);\n free(hashMap->values);\n hashMap->keys = newKeys;\n hashMap->values = newValues;\n hashMap->capacity = newCapacity;\n}\n\nvoid insert(struct HashMap* hashMap, int key, int value) {\n if (hashMap->size * 2 >= hashMap->capacity) {\n resizeHashMap(hashMap);\n }\n\n int index = hashCode(hashMap, key);\n\n while (hashMap->keys[index] != -1) {\n if (hashMap->keys[index] == key) {\n hashMap->values[index] = value;\n return;\n }\n index = (index + 1) % hashMap->capacity;\n }\n\n hashMap->keys[index] = key;\n hashMap->values[index] = value;\n hashMap->size++;\n}\n\nint search(struct HashMap* hashMap, int key) {\n int index = hashCode(hashMap, key);\n\n while (hashMap->keys[index] != -1) {\n if (hashMap->keys[index] == key) {\n return hashMap->values[index];\n }\n index = (index + 1) % hashMap->capacity;\n }\n\n return 0;\n}\n\nvoid freeHashMap(struct HashMap* hashMap) {\n free(hashMap->keys);\n free(hashMap->values);\n free(hashMap);\n}\n\nint subarraySum(int* nums, int numsSize, int k) {\n struct HashMap* hashMap = createHashMap();\n int sum = 0, count = 0;\n\n insert(hashMap, 0, 1);\n\n for (int i = 0; i < numsSize; i++) {\n sum += nums[i];\n count += search(hashMap, sum - k);\n insert(hashMap, sum, search(hashMap, sum) + 1);\n }\n\n freeHashMap(hashMap);\n \n return count;\n}\n```\n```Java []\nclass Solution {\n public int subarraySum(int[] nums, int k) {\n Map<Integer, Integer> map = new HashMap<>();\n int sum = 0, result = 0;\n map.put(0, 1);\n \n for (int n : nums) {\n sum += n;\n result += map.getOrDefault(sum - k, 0);\n map.put(sum, map.getOrDefault(sum, 0) + 1);\n }\n \n return result;\n }\n}\n```\n```python []\nclass Solution:\n def subarraySum(self, nums, k):\n map = {0: 1}\n sum = 0\n result = 0\n \n for n in nums:\n sum += n\n result += map.get(sum - k, 0)\n map[sum] = map.get(sum, 0) + 1\n \n return result\n\n```\n```javascript []\nvar subarraySum = function(nums, k) {\n let map = new Map();\n let sum = 0;\n let result = 0;\n map.set(0, 1);\n \n for (let n of nums) {\n sum += n;\n result += (map.get(sum - k) || 0);\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n \n return result;\n};\n\n```\n---\n\n# *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n\n---\n\n\n
| 8
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Easy python solution
|
subarray-sum-equals-k
| 0
| 1
|
# Code\n```\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n cnt=0\n dic={}\n for i in accumulate(nums):\n if i-k in dic:\n cnt+=dic[i-k]\n if i==k:cnt+=1\n if i in dic:dic[i]+=1\n else:dic[i]=1\n return cnt\n \n```
| 1
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Easy python solution
|
subarray-sum-equals-k
| 0
| 1
|
# Code\n```\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n cnt=0\n dic={}\n for i in accumulate(nums):\n if i-k in dic:\n cnt+=dic[i-k]\n if i==k:cnt+=1\n if i in dic:dic[i]+=1\n else:dic[i]=1\n return cnt\n \n```
| 1
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Simple Python solution with linear time complexity!! 🔥🔥
|
subarray-sum-equals-k
| 0
| 1
|
# Code\n```\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n res=0\n curSum=0\n prefixSums={0:1}\n\n for n in nums:\n curSum+=n\n diff=curSum-k\n res+=prefixSums.get(diff,0)\n prefixSums[curSum]=1+prefixSums.get(curSum,0)\n return res\n```
| 2
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Simple Python solution with linear time complexity!! 🔥🔥
|
subarray-sum-equals-k
| 0
| 1
|
# Code\n```\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n res=0\n curSum=0\n prefixSums={0:1}\n\n for n in nums:\n curSum+=n\n diff=curSum-k\n res+=prefixSums.get(diff,0)\n prefixSums[curSum]=1+prefixSums.get(curSum,0)\n return res\n```
| 2
|
Given an array of integers `nums` and an integer `k`, return _the total number of subarrays whose sum equals to_ `k`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1\], k = 2
**Output:** 2
**Example 2:**
**Input:** nums = \[1,2,3\], k = 3
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-1000 <= nums[i] <= 1000`
* `-107 <= k <= 107`
|
Will Brute force work here? Try to optimize it. Can we optimize it by using some extra space? What about storing sum frequencies in a hash table? Will it be useful? sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1.
Can we use this property to optimize it.
|
Solution with lil explanation
|
array-partition
| 0
| 1
|
\n```\nnums = [1,4,3,2]\n\nExplanation:\n------------ \nAll possible pairings (ignoring the ordering of elements) are:\n1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3\n2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3\n3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4\nSo the maximum possible sum is 4.\n\nNumber of pairs must be = nums.size() / 2 = 4 / 2 = 2\n\nSorted nums = [1,2,3,4] \nHere is 2 smaller number 1 and 2 & 2 larger number are 3 and 4.\nIf I pair like (1,3) (2,4) means if I put two smaller number in the 2 pair then\nI will end up having 1+2=3.\nBUT if I put two smaller number together then I will have a chance to pick a large number.\n(1,2) (3,4) -- 1 + 3 = 4.. This is the best way cause No matter what I pair a larger number\nwith another number, the another number will be smaller and will be picked means I can\nnever pick the 1st maximum value to sum but I can pick the 2nd Maximum value to\nsum by pairing the smallest values together. That\'s why we do sort first!\n```\n\n```python []\nclass Solution:\n def arrayPairSum(self, nums: List[int]) -> int:\n return sum(sorted(nums)[::2])\n```\n```CPP []\nclass Solution {\npublic:\n int arrayPairSum(vector<int>& nums) \n {\n sort(begin(nums),end(nums));\n int sum = 0;\n for(int i=0; i<nums.size(); i+=2) sum += nums[i];\n return sum;\n }\n};\n```\n``` Complexity []\nTime complexity : O(sort)\n\nSpace complexity : O(sort)\n```
| 1
|
Given an integer array `nums` of `2n` integers, group these integers into `n` pairs `(a1, b1), (a2, b2), ..., (an, bn)` such that the sum of `min(ai, bi)` for all `i` is **maximized**. Return _the maximized sum_.
**Example 1:**
**Input:** nums = \[1,4,3,2\]
**Output:** 4
**Explanation:** All possible pairings (ignoring the ordering of elements) are:
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
So the maximum possible sum is 4.
**Example 2:**
**Input:** nums = \[6,2,6,5,1,2\]
**Output:** 9
**Explanation:** The optimal pairing is (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9.
**Constraints:**
* `1 <= n <= 104`
* `nums.length == 2 * n`
* `-104 <= nums[i] <= 104`
|
Obviously, brute force won't help here. Think of something else, take some example like 1,2,3,4. How will you make pairs to get the result? There must be some pattern. Did you observe that- Minimum element gets add into the result in sacrifice of maximum element. Still won't able to find pairs? Sort the array and try to find the pattern.
|
2 One-liner 1 detailed Python3 Beat 97.4% 259ms
|
array-partition
| 0
| 1
|
\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n logn)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayPairSum(self, nums: List[int]) -> int:\n #1st Approach\n nums.sort()\n count = 0\n for i in range(0, len(nums),2):\n count += nums[i]\n return count\n\n\n #2nd Approach\n return sum(nums[i] for i in range(0, len(nums),2))\n\n #3rd Approach\n return sum(nums[0:len(nums):2])\n```
| 2
|
Given an integer array `nums` of `2n` integers, group these integers into `n` pairs `(a1, b1), (a2, b2), ..., (an, bn)` such that the sum of `min(ai, bi)` for all `i` is **maximized**. Return _the maximized sum_.
**Example 1:**
**Input:** nums = \[1,4,3,2\]
**Output:** 4
**Explanation:** All possible pairings (ignoring the ordering of elements) are:
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
So the maximum possible sum is 4.
**Example 2:**
**Input:** nums = \[6,2,6,5,1,2\]
**Output:** 9
**Explanation:** The optimal pairing is (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9.
**Constraints:**
* `1 <= n <= 104`
* `nums.length == 2 * n`
* `-104 <= nums[i] <= 104`
|
Obviously, brute force won't help here. Think of something else, take some example like 1,2,3,4. How will you make pairs to get the result? There must be some pattern. Did you observe that- Minimum element gets add into the result in sacrifice of maximum element. Still won't able to find pairs? Sort the array and try to find the pattern.
|
Algorithm and solution in python3
|
array-partition
| 0
| 1
|
The question states that we have to find the maximum sum obtained by taking minimum from **n** pairs. A pair can be formed from the elements of the list.\n\nHow to solve this:\n- **Sort** the list\n- **make a pair** starting from index 0\n- take **minimum** from each pair\n- **add** all the minimum obtained from the pairs\n\n**Logic and Working of the problem**:\nSuppose we have a list of **6** elements say ```[2,1,4,5,7,9]```\nFirst task is to pair them and thus we will have 3 pairs:\n```\n1. [1,2], [4,5], [7,9] Sum of their min : 1 + 4 + 7 = 12\n2. [1,2], [4,7], [5,9] Sum of thier min : 1 + 4 + 5 = 10\n3. [1,2], [4,9], [5,7] Sum of their min : 1 + 4 + 5 = 10\n4. [1,4], [2,5], [7,9] Sum of their min : 1 + 2 + 7 = 10\n5. [1,4], [2,7], [5,9] Sum of their min : 1 + 2 + 7 = 10\n6. [1,5], [2,4], [7,9] Sum of their min : 1 + 2 + 7 = 10\n7. [1,4], [2,9], [5,7] Sum of their min : 1 + 2 + 5 = 8\n8. [1,7], [2,4], [5,9] Sum of their min : 1 + 2 + 5 = 8\n9. [1,9], [2,4], [5,7] Sum of their min : 1 + 2 + 5 = 8\n10. [1,5], [2,7], [4,9] Sum of their min : 1 + 2 + 4 = 7\n11. [1,7], [2,5], [4,9] Sum of their min : 1 + 2 + 4 = 7\n12. [1,7], [2,9], [4,5] Sum of their min : 1 + 2 + 4 = 7\n13. [1,5], [2,9], [4,7] Sum of their min : 1 + 2 + 4 = 7\n14. [1,9], [2,5], [4,7] Sum of their min : 1 + 2 + 4 = 7\n15. [1,9], [2,7], [4,5] Sum of their min : 1 + 2 + 4 = 7\n```\n\nFrom the above pair and their sum we can conclude that the maximum sum is obtained from the pair which are obtained after sorting. Hence the answer to the above problem will be **12** which is obtained from the pairs ```[1,2], [4,5], [7,9]```\n\nOne solution can be\n\n```py\nclass Solution:\n def arrayPairSum(self, nums: List[int]) -> int:\n nums.sort()\n sum_ = 0\n for i in range(0,len(nums),2):\n sum_ += nums[i]\n return sum_\n\n# Time : 356 ms\n# Memory : 16.7 M\n \n```\n\nAnother solution can be:\n```py\nclass Solution:\n def arrayPairSum(self, nums: List[int]) -> int:\n return sum(sorted(nums)[::2])\n \n# Time : 332 ms\n# Memory : 16.5 M\n```\n\nPlease upvote this post if you like the solution, and I will keep on posting well commented solutions.\n\nCurrently I am using private repository for the solutions of Leetcode, but very soon I will make the repo public, so if you want to connect with me\nGItHub : https://github.com/ramanaditya\nLinkedIn : https://www.linkedin.com/in/ramanaditya/\nTwitter : https://twitter.com/_adityaraman\nWebsite : https://ramanaditya.github.io/
| 59
|
Given an integer array `nums` of `2n` integers, group these integers into `n` pairs `(a1, b1), (a2, b2), ..., (an, bn)` such that the sum of `min(ai, bi)` for all `i` is **maximized**. Return _the maximized sum_.
**Example 1:**
**Input:** nums = \[1,4,3,2\]
**Output:** 4
**Explanation:** All possible pairings (ignoring the ordering of elements) are:
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
So the maximum possible sum is 4.
**Example 2:**
**Input:** nums = \[6,2,6,5,1,2\]
**Output:** 9
**Explanation:** The optimal pairing is (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9.
**Constraints:**
* `1 <= n <= 104`
* `nums.length == 2 * n`
* `-104 <= nums[i] <= 104`
|
Obviously, brute force won't help here. Think of something else, take some example like 1,2,3,4. How will you make pairs to get the result? There must be some pattern. Did you observe that- Minimum element gets add into the result in sacrifice of maximum element. Still won't able to find pairs? Sort the array and try to find the pattern.
|
563: Time 93.99%, Solution with step by step explanation
|
binary-tree-tilt
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Set the "total_tilt" attribute to 0 as we will be incrementally adding to this as we calculate the tilt of each node.\n2. Define a helper function called "calculate_tilt" that takes in a node and returns an integer representing the sum of the node\'s left and right subtrees and the node\'s value.\n3. In the "calculate_tilt" function, check if the node is None. If it is, return 0 as there is no subtree to sum.\n4. Recursively call the "calculate_tilt" function on the node\'s left and right children, storing the results in the "left_sum" and "right_sum" variables.\n5. Calculate the tilt of the current node by taking the absolute difference between the left_sum and right_sum.\n6. Increment the total_tilt by the current node\'s tilt.\n7. Return the sum of the left_sum, right_sum, and node\'s value.\n8. Call the "calculate_tilt" function on the root node to recursively calculate the tilt of every node in the binary tree.\n9. Return the total_tilt as the result of the "findTilt" method.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTilt(self, root: Optional[TreeNode]) -> int:\n self.total_tilt = 0\n \n def calculate_tilt(node):\n if not node:\n return 0\n \n left_sum = calculate_tilt(node.left)\n right_sum = calculate_tilt(node.right)\n tilt = abs(left_sum - right_sum)\n \n self.total_tilt += tilt\n \n return left_sum + right_sum + node.val\n \n calculate_tilt(root)\n return self.total_tilt\n\n```
| 6
|
Given the `root` of a binary tree, return _the sum of every tree node's **tilt**._
The **tilt** of a tree node is the **absolute difference** between the sum of all left subtree node **values** and all right subtree node **values**. If a node does not have a left child, then the sum of the left subtree node **values** is treated as `0`. The rule is similar if the node does not have a right child.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 1
**Explanation:**
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1
**Example 2:**
**Input:** root = \[4,2,9,3,5,null,7\]
**Output:** 15
**Explanation:**
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
**Example 3:**
**Input:** root = \[21,7,14,1,1,2,2,3,3\]
**Output:** 9
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
|
Don't think too much, this is an easy problem. Take some small tree as an example. Can a parent node use the values of its child nodes? How will you implement it? May be recursion and tree traversal can help you in implementing. What about postorder traversal, using values of left and right childs?
|
Solution
|
binary-tree-tilt
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\nint sum=0;\n int findTilt(TreeNode* root) {\n fun(root);\n return sum;\n }\n int fun(TreeNode* root){\n if(root==NULL){\n return 0;\n }\n int left=fun(root->left);\n int right=fun(root->right);\n\n sum=sum+abs(left-right);\n return root->val+left+right;\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def findTilt(self, root: Optional[TreeNode]) -> int:\n\n self.res = 0\n def f(root):\n \n if not root:\n return 0\n\n l = f(root.left)\n r = f(root.right)\n\n self.res += abs(l - r)\n\n return root.val + l + r\n\n f(root)\n\n return self.res\n```\n\n```Java []\nclass Solution {\n int sum = 0;\n public int dfs(TreeNode root){\n if( root == null) return 0;\n int left = dfs(root.left);\n int right = dfs(root.right);\n int res = left+right+root.val;\n sum+=Math.abs(left-right);\n root.val = Math.abs(left-right);\n return res;\n }\n public int dfs2(TreeNode root){\n if( root == null) return 0;\n return root.val+dfs2(root.left)+dfs2(root.right);\n }\n public int findTilt(TreeNode root) {\n dfs(root);\n return sum;\n }\n}\n```\n
| 3
|
Given the `root` of a binary tree, return _the sum of every tree node's **tilt**._
The **tilt** of a tree node is the **absolute difference** between the sum of all left subtree node **values** and all right subtree node **values**. If a node does not have a left child, then the sum of the left subtree node **values** is treated as `0`. The rule is similar if the node does not have a right child.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 1
**Explanation:**
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1
**Example 2:**
**Input:** root = \[4,2,9,3,5,null,7\]
**Output:** 15
**Explanation:**
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
**Example 3:**
**Input:** root = \[21,7,14,1,1,2,2,3,3\]
**Output:** 9
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
|
Don't think too much, this is an easy problem. Take some small tree as an example. Can a parent node use the values of its child nodes? How will you implement it? May be recursion and tree traversal can help you in implementing. What about postorder traversal, using values of left and right childs?
|
Recursive solution Python
|
binary-tree-tilt
| 0
| 1
|
Time complexity: O(N) because you need to check for every element once\nSpace complexity: O(N) because of the recursion stack\n\n```\nclass Solution:\n def findTilt(self, root: Optional[TreeNode]) -> int:\n def rec(node):\n nonlocal res\n if not node:\n return 0\n left_sum = rec(node.left)\n right_sum = rec(node.right)\n res += abs(left_sum - right_sum)\n \n return left_sum + node.val + right_sum\n \n res = 0\n rec(root)\n return res\n```
| 3
|
Given the `root` of a binary tree, return _the sum of every tree node's **tilt**._
The **tilt** of a tree node is the **absolute difference** between the sum of all left subtree node **values** and all right subtree node **values**. If a node does not have a left child, then the sum of the left subtree node **values** is treated as `0`. The rule is similar if the node does not have a right child.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 1
**Explanation:**
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1
**Example 2:**
**Input:** root = \[4,2,9,3,5,null,7\]
**Output:** 15
**Explanation:**
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
**Example 3:**
**Input:** root = \[21,7,14,1,1,2,2,3,3\]
**Output:** 9
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
|
Don't think too much, this is an easy problem. Take some small tree as an example. Can a parent node use the values of its child nodes? How will you implement it? May be recursion and tree traversal can help you in implementing. What about postorder traversal, using values of left and right childs?
|
---Explained ---Easy code in python3 with constant Time ----
|
find-the-closest-palindrome
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nYou have to check 7 tests.Check minimum absolute difference and return the element with minimum difference\n- For example we have 100000\n1. (10^(len))+1 , i.e(100001)\n2. (10^(len))-1 , i.e(99999)\n3. (10^(len-1))+1 , i.e(10001)\n4. (10^(len-1))-1 , i.e(99999)\n5. Make palindrome with suffix , i.e (100001)\n6. Add 1 to the suffix and make palindrome , i.e(101101)\n7. Subtract 1 to the suffix and make palindrome , i.e(9999)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nearestPalindromic(self, n: str) -> str:\n if len(n)==1:\n return str(int(n)-1)\n tests=[]\n tests.append(10**(len(n)-1)+1)\n tests.append(10**(len(n))+1)\n tests.append(10**(len(n)-1)-1)\n tests.append(10**(len(n))-1)\n if len(n)%2==0:\n tests.append(int(n[:len(n)//2]+n[:len(n)//2][::-1]))\n x=str(int(n[:len(n)//2])-1)\n tests.append(int(x+x[::-1]))\n y=str(int(n[:len(n)//2])+1)\n tests.append(int(y+y[::-1]))\n else:\n tests.append(int(n[:len(n)//2]+n[:len(n)//2+1][::-1]))\n x=str(int(n[:1+len(n)//2])-1)\n tests.append(int(x+x[::-1][1:]))\n y=str(int(n[:1+len(n)//2])+1)\n tests.append(int(y+y[::-1][1:]))\n n=int(n)\n ans=0\n mini=float("inf")\n for i in tests:\n if abs(i-n)<mini and i!=n:\n mini=abs(i-n)\n ans=i\n elif abs(i-n)==mini and ans>i:\n ans=i\n return str(ans)\n```
| 12
|
Given a string `n` representing an integer, return _the closest integer (not including itself), which is a palindrome_. If there is a tie, return _**the smaller one**_.
The closest is defined as the absolute difference minimized between two integers.
**Example 1:**
**Input:** n = "123 "
**Output:** "121 "
**Example 2:**
**Input:** n = "1 "
**Output:** "0 "
**Explanation:** 0 and 2 are the closest palindromes but we return the smallest which is 0.
**Constraints:**
* `1 <= n.length <= 18`
* `n` consists of only digits.
* `n` does not have leading zeros.
* `n` is representing an integer in the range `[1, 1018 - 1]`.
|
Will brute force work for this problem? Think of something else. Take some examples like 1234, 999,1000, etc and check their closest palindromes. How many different cases are possible? Do we have to consider only left half or right half of the string or both? Try to find the closest palindrome of these numbers- 12932, 99800, 12120. Did you observe something?
|
Python 3 || 8 lines, w/ comments || T/M: 86% / 83%
|
find-the-closest-palindrome
| 0
| 1
|
```\nclass Solution:\n def nearestPalindromic(self, n: str) -> str:\n\n k = len(n)\n cands = {str(c:=pow(10,k)+1), str((c-1)//10-1)} # The two edge-case candidates\n # (e.g: "10001" and "999" \n # for any 4-digit n)\n\n pref = (str(int(n[:(k + 1)//2])+i) for i in (-1,0,1)) # left sides of the remaining\n # three candidates \n for left in pref:\n rght = left[-2::-1] if k%2 else left[::-1] # complete these three candidates \n cands.add(left + rght) # with their right sides\n\n cands.discard(n) # n is prohibited from candidacy\n\n return min(cands, key=lambda x: # return the winner\n (abs(int(x) - int(n)), int(x))\n```\n[https://leetcode.com/problems/find-the-closest-palindrome/submissions/987372472/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*K*) and space complexity is *O*(1), in which *K* ~`len(n)` (the number of digits in `n`).
| 5
|
Given a string `n` representing an integer, return _the closest integer (not including itself), which is a palindrome_. If there is a tie, return _**the smaller one**_.
The closest is defined as the absolute difference minimized between two integers.
**Example 1:**
**Input:** n = "123 "
**Output:** "121 "
**Example 2:**
**Input:** n = "1 "
**Output:** "0 "
**Explanation:** 0 and 2 are the closest palindromes but we return the smallest which is 0.
**Constraints:**
* `1 <= n.length <= 18`
* `n` consists of only digits.
* `n` does not have leading zeros.
* `n` is representing an integer in the range `[1, 1018 - 1]`.
|
Will brute force work for this problem? Think of something else. Take some examples like 1234, 999,1000, etc and check their closest palindromes. How many different cases are possible? Do we have to consider only left half or right half of the string or both? Try to find the closest palindrome of these numbers- 12932, 99800, 12120. Did you observe something?
|
Beats 99%.A very unique approach.O(n) time complexity
|
find-the-closest-palindrome
| 0
| 1
|
# Intuition\nDone with checking 7 conditions\n# Approach\n1.first we\'ll check 10**n+1,10**n-1,10**(n-1)-1,10**(n-1)+1.4 are done\n2.Then,we\'ll make a palindrome of half of given n+inverse of n e.g. "123" = "121".5 is done\n3.now we\'ll check last two conditions half of given (n+1) + inverse of (n+1) and (n-1) + inverse of (n-1).Last two are also done.\n\n# Complexity\nO(n) time only\n- Space complexity:\nUnder 17 mb\n\n# Code\n```\nclass Solution:\n def nearestPalindromic(self, n: str) -> str:\n y=int(n)\n x=len(n)\n ls,mid=[10**(x)+1,10**(x)-1,10**(x-1)+1,10**(x-1)-1],x//2\n if x%2==1:\n e=int(n[:mid+1])\n ls.append(int(n[:mid]+n[mid]+(n[:mid][::-1])))\n ls.append(int(str(e+1)+(str(e+1)[::-1][1:])))\n ls.append(int(str(e-1)+(str(e-1)[::-1][1:])))\n else:\n e=int(n[:mid])\n ls.append(int(n[:mid]+(n[:mid][::-1])))\n ls.append(int(str(e+1)+(str(e+1)[::-1])))\n ls.append(int(str(e-1)+(str(e-1)[::-1])))\n diff=float(inf)\n j=0\n for i in range(len(ls)):\n s=abs(ls[i]-y)\n if s<diff and s!=0:\n diff=s\n j=i\n if s==diff and ls[i]<ls[j]:\n j=i\n return str(ls[j])\n\n```
| 3
|
Given a string `n` representing an integer, return _the closest integer (not including itself), which is a palindrome_. If there is a tie, return _**the smaller one**_.
The closest is defined as the absolute difference minimized between two integers.
**Example 1:**
**Input:** n = "123 "
**Output:** "121 "
**Example 2:**
**Input:** n = "1 "
**Output:** "0 "
**Explanation:** 0 and 2 are the closest palindromes but we return the smallest which is 0.
**Constraints:**
* `1 <= n.length <= 18`
* `n` consists of only digits.
* `n` does not have leading zeros.
* `n` is representing an integer in the range `[1, 1018 - 1]`.
|
Will brute force work for this problem? Think of something else. Take some examples like 1234, 999,1000, etc and check their closest palindromes. How many different cases are possible? Do we have to consider only left half or right half of the string or both? Try to find the closest palindrome of these numbers- 12932, 99800, 12120. Did you observe something?
|
Only 5 Cases to Consider: Concise implementation in Python with Full Explanation
|
find-the-closest-palindrome
| 0
| 1
|
The implementation can be annoying for handling the carry and the borrow at the boundary. To make easy, we reduce all the cases into 5 possibilities only. Taking the number 1234 as an example, we find the closest one from the following candidates: \n\n1. 1221 # Case 1: the palindrome with the same first-half to [12]34; Skip this case for the input that is also a palindrome like 1221. \n2. 1111 # Case 2: the palindrome with the closest first-halt smaller than [12]34\n3. 1331 # Case 3: the palindrome with the closest first-halt greater than [12]34\n4. 999 # Case 4: the greatest palindrome with one less digit than 1234\n5. 10001 # Case 5: the smallest palindrome with one more digit than 1234\n\n```\nclass Solution:\n def find_next_palindrome(self, n, additive):\n l = len(n)\n if l == 0:\n return 0\n first_half = str(int(n[:l // 2 + l % 2]) + additive)\n return int(first_half + first_half[(-1 - l%2)::-1])\n \n def nearestPalindromic(self, n: str) -> str:\n m = int(n)\n candidates = [self.find_next_palindrome(n, additive) for additive in range(-1, 2)] # Cases 1, 2, and 3\n candidates.append(self.find_next_palindrome("9"*(len(n)-1), 0)) # Case 4\n candidates.append(self.find_next_palindrome("1" + "0"*len(n), 0)) # Case 5\n\n ans = None\n for t in candidates:\n if t == m:\n continue\n if ans is None or abs(ans - m) > abs(t - m) or (abs(ans - m) == abs(t - m) and t < m):\n ans = t\n return str(ans)\n \n
| 7
|
Given a string `n` representing an integer, return _the closest integer (not including itself), which is a palindrome_. If there is a tie, return _**the smaller one**_.
The closest is defined as the absolute difference minimized between two integers.
**Example 1:**
**Input:** n = "123 "
**Output:** "121 "
**Example 2:**
**Input:** n = "1 "
**Output:** "0 "
**Explanation:** 0 and 2 are the closest palindromes but we return the smallest which is 0.
**Constraints:**
* `1 <= n.length <= 18`
* `n` consists of only digits.
* `n` does not have leading zeros.
* `n` is representing an integer in the range `[1, 1018 - 1]`.
|
Will brute force work for this problem? Think of something else. Take some examples like 1234, 999,1000, etc and check their closest palindromes. How many different cases are possible? Do we have to consider only left half or right half of the string or both? Try to find the closest palindrome of these numbers- 12932, 99800, 12120. Did you observe something?
|
[Python] 3 lines with comments || Case by Case
|
find-the-closest-palindrome
| 0
| 1
|
It took couple of WA before getting AC, edge cases are really annoying... \n\n# Code\n```\nclass Solution:\n """\n what are the possible candidates for answer? \n Main case: \n 1. reflection 12345: 12321 (+1)\n edge cases:\n 2. 4 digits: 999 1001 9999 10001 (+4)\n 3. 1283? currently it will map to 1221 which is wrong so need to modify middle digit before building reflection (+2)\n """\n def nearestPalindromic(self, n: str) -> str:\n if(len(n)==1): return str(int(n)-1)\n def build(x): return x[:(len(x)+1)//2] + x[:len(x)//2][::-1]\n cands = [build(n),str(10**(len(n)-1)-1),str(10**(len(n)-1)+1),str(10**(len(n))-1),str(10**(len(n))+1),build(str(int(n)-(10**((len(n))//2 )))),build(str(int(n)+(10**((len(n))//2 ))))]\n vals = [(abs(int(n)-int(x)),int(x)) for x in cands if x!=n]\n return str(min(vals)[1])\n```
| 1
|
Given a string `n` representing an integer, return _the closest integer (not including itself), which is a palindrome_. If there is a tie, return _**the smaller one**_.
The closest is defined as the absolute difference minimized between two integers.
**Example 1:**
**Input:** n = "123 "
**Output:** "121 "
**Example 2:**
**Input:** n = "1 "
**Output:** "0 "
**Explanation:** 0 and 2 are the closest palindromes but we return the smallest which is 0.
**Constraints:**
* `1 <= n.length <= 18`
* `n` consists of only digits.
* `n` does not have leading zeros.
* `n` is representing an integer in the range `[1, 1018 - 1]`.
|
Will brute force work for this problem? Think of something else. Take some examples like 1234, 999,1000, etc and check their closest palindromes. How many different cases are possible? Do we have to consider only left half or right half of the string or both? Try to find the closest palindrome of these numbers- 12932, 99800, 12120. Did you observe something?
|
Solution
|
find-the-closest-palindrome
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n string nearestPalindromic(string n) {\n if(n.length()==1)\n return to_string(stoi(n)-1);\n \n int d = n.length();\n vector<long> candidates;\n candidates.push_back(pow(10,d-1)-1);\n candidates.push_back(pow(10,d)+1);\n\n int mid = (d+1)/2;\n long prefix = stol(n.substr(0,mid));\n vector<long> v = {prefix,prefix+1, prefix-1};\n for(long i : v)\n {\n string postfix = to_string(i);\n if(d%2!=0)\n postfix.pop_back();\n reverse(postfix.begin(), postfix.end());\n string c = to_string(i)+postfix;\n candidates.push_back(stol(c));\n }\n long mindiff = LONG_MAX;\n long result;\n long num = stol(n);\n for(int i=0;i<5;i++)\n {\n if(candidates[i]!=num && abs(candidates[i]-num)<mindiff)\n {\n mindiff = abs(candidates[i]-num);\n result = candidates[i];\n }\n else if(abs(candidates[i]-num)==mindiff)\n result = min(result, candidates[i]);\n }\n return to_string(result);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def nearestPalindromic(self, n: str) -> str:\n k = len(n)\n candidates = set((str(10 ** k + 1), str(10 ** (k - 1) - 1)))\n prefix = int(n[:(k + 1) // 2])\n for num in map(str, (prefix - 1, prefix, prefix + 1)):\n suffix = num if k % 2 == 0 else num[:-1]\n candidates.add(num + suffix[::-1])\n candidates.discard(n)\n return min(candidates, key=lambda x: (abs(int(x) - int(n)), int(x)))\n```\n\n```Java []\nclass Solution {\n public String nearestPalindromic(String n) {\n if (Long.parseLong(n) == 1) { return "0"; }\n char[] arr = n.toCharArray();\n int mid = arr.length / 2;\n \n return getClosestPalindrome(arr, mid - (1 - arr.length % 2), mid); \n }\n String getNextPalindromeForPalindromeNumber(String palinString, int beforeMid, int afterMid) {\n int carry = 1;\n char[] num = palinString.toCharArray();\n \n while (beforeMid >= 0) {\n int number = (num[beforeMid] - \'0\');\n number += carry;\n num[beforeMid] = (char)(number % 10 + \'0\');\n num[afterMid] = (char)(number % 10 + \'0\');;\n carry = number / 10;\n beforeMid--;\n afterMid++;\n }\n if (carry == 1) {\n char[] numNew = new char[num.length + 1];\n Arrays.fill(numNew, \'0\');\n numNew[numNew.length - 1] = \'1\';\n numNew[0] = \'1\';\n return new String(numNew);\n } else {\n return new String(num);\n }\n }\n String getPrevPalindromeForPalindromeNumber(String palinString, int beforeMid, int afterMid) {\n int carry = 1;\n char[] num = palinString.toCharArray();\n \n while (beforeMid >= 0) {\n int number = (num[beforeMid] - \'0\');\n number = (number == 0 && carry == 1) ? 10 : number;\n number -= carry;\n num[beforeMid] = (char)(number + \'0\');\n num[afterMid] = (char)(number + \'0\');;\n carry = (number == 9 && carry == 1) ? 1 : 0;\n beforeMid--;\n afterMid++;\n }\n if (num[0] == \'0\') {\n char[] numNew = new char[num.length - 1];\n Arrays.fill(numNew, \'9\');\n return new String(numNew);\n } else {\n return new String(num);\n }\n }\n String getClosestPalindrome(char[] num, int beforeMid, int afterMid) {\n Long originalNum = Long.parseLong(new String(num));\n \n while (beforeMid >= 0) {\n if (num[beforeMid] != num[afterMid]) {\n if (num[beforeMid] > num[afterMid]) {\n num[afterMid] = num[beforeMid];\n } else {\n num[afterMid] = num[beforeMid];\n }\n }\n beforeMid--;\n afterMid++;\n }\n String palinString = new String(num);\n Long palinNum = Long.parseLong(palinString);\n \n String prevPalinString = null;\n String nextPalinString = null;\n if (palinNum.equals(originalNum)) {\n prevPalinString = getPrevPalindromeForPalindromeNumber(palinString, (num.length / 2) - (1 - num.length % 2), num.length / 2);\n nextPalinString = getNextPalindromeForPalindromeNumber(palinString, (num.length / 2) - (1 - num.length % 2), num.length / 2);\n } else if (palinNum < originalNum) {\n prevPalinString = palinString;\n nextPalinString = getNextPalindromeForPalindromeNumber(palinString, (num.length / 2) - (1 - num.length % 2), num.length / 2);\n } else {\n prevPalinString = getPrevPalindromeForPalindromeNumber(palinString, (num.length / 2) - (1 - num.length % 2), num.length / 2); \n nextPalinString = palinString;\n }\n Long prevPalinNum = Long.parseLong(prevPalinString);\n Long nextPalinNum = Long.parseLong(nextPalinString);\n\n if ((originalNum - prevPalinNum) <= (nextPalinNum - originalNum)) {\n return prevPalinString; \n } else {\n return nextPalinString;\n }\n }\n}\n```\n
| 2
|
Given a string `n` representing an integer, return _the closest integer (not including itself), which is a palindrome_. If there is a tie, return _**the smaller one**_.
The closest is defined as the absolute difference minimized between two integers.
**Example 1:**
**Input:** n = "123 "
**Output:** "121 "
**Example 2:**
**Input:** n = "1 "
**Output:** "0 "
**Explanation:** 0 and 2 are the closest palindromes but we return the smallest which is 0.
**Constraints:**
* `1 <= n.length <= 18`
* `n` consists of only digits.
* `n` does not have leading zeros.
* `n` is representing an integer in the range `[1, 1018 - 1]`.
|
Will brute force work for this problem? Think of something else. Take some examples like 1234, 999,1000, etc and check their closest palindromes. How many different cases are possible? Do we have to consider only left half or right half of the string or both? Try to find the closest palindrome of these numbers- 12932, 99800, 12120. Did you observe something?
|
565: Time 90.23%, Solution with step by step explanation
|
array-nesting
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nInitialize a boolean visited list of size n, where visited[i] indicates if nums[i] has been visited or not.\nInitialize a variable max_length to zero, which will be used to store the maximum length of any set.\nIterate over all elements of nums using a for loop with loop variable i:\nCheck if nums[i] has already been visited, by checking if visited[i] is True. If it has been visited, skip to the next iteration of the loop.\nIf nums[i] has not been visited, initialize a variable length to zero.\nSet a variable j to i, which is the starting index of the current set.\nEnter a while loop that runs until nums[j] has already been visited:\nMark nums[j] as visited by setting visited[j] to True.\nSet j to nums[j], which is the index of the next element in the current set.\nIncrement length by one.\nIf the length of the current set is greater than max_length, update max_length to the length of the current set.\nReturn max_length.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def arrayNesting(self, nums: List[int]) -> int:\n visited = [False] * len(nums) # mark if a number is visited\n max_length = 0\n \n for i in range(len(nums)):\n if visited[i]: # if already visited, skip\n continue\n \n length = 0\n j = i\n while not visited[j]:\n visited[j] = True # mark as visited\n j = nums[j] # move to next element in set\n length += 1\n \n max_length = max(max_length, length) # update max_length\n \n return max_length\n\n```
| 2
|
You are given an integer array `nums` of length `n` where `nums` is a permutation of the numbers in the range `[0, n - 1]`.
You should build a set `s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... }` subjected to the following rule:
* The first element in `s[k]` starts with the selection of the element `nums[k]` of `index = k`.
* The next element in `s[k]` should be `nums[nums[k]]`, and then `nums[nums[nums[k]]]`, and so on.
* We stop adding right before a duplicate element occurs in `s[k]`.
Return _the longest length of a set_ `s[k]`.
**Example 1:**
**Input:** nums = \[5,4,0,3,1,6,2\]
**Output:** 4
**Explanation:**
nums\[0\] = 5, nums\[1\] = 4, nums\[2\] = 0, nums\[3\] = 3, nums\[4\] = 1, nums\[5\] = 6, nums\[6\] = 2.
One of the longest sets s\[k\]:
s\[0\] = {nums\[0\], nums\[5\], nums\[6\], nums\[2\]} = {5, 6, 2, 0}
**Example 2:**
**Input:** nums = \[0,1,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length`
* All the values of `nums` are **unique**.
| null |
CLEAN & SHORT PYTHON, O(N) TIME, O(N) SPACE
|
array-nesting
| 0
| 1
|
* If the number is not present in the global set, then calculate the respective set for that number,\n* Else just continue because that number will yeild an already visited set ( and that will not make any difference to the result).\n```\nclass Solution:\n def arrayNesting(self, nums: List[int]) -> int:\n res, l = 0, len(nums)\n globalSet = set()\n for k in range(l):\n if k not in globalSet:\n currLength, currSet, val = 0, set(), k\n while True:\n if nums[val] in currSet: break\n currSet.add(nums[val])\n globalSet.add(nums[val])\n currLength, val = currLength + 1, nums[val]\n res = max(res, currLength) \n return res\n```
| 7
|
You are given an integer array `nums` of length `n` where `nums` is a permutation of the numbers in the range `[0, n - 1]`.
You should build a set `s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... }` subjected to the following rule:
* The first element in `s[k]` starts with the selection of the element `nums[k]` of `index = k`.
* The next element in `s[k]` should be `nums[nums[k]]`, and then `nums[nums[nums[k]]]`, and so on.
* We stop adding right before a duplicate element occurs in `s[k]`.
Return _the longest length of a set_ `s[k]`.
**Example 1:**
**Input:** nums = \[5,4,0,3,1,6,2\]
**Output:** 4
**Explanation:**
nums\[0\] = 5, nums\[1\] = 4, nums\[2\] = 0, nums\[3\] = 3, nums\[4\] = 1, nums\[5\] = 6, nums\[6\] = 2.
One of the longest sets s\[k\]:
s\[0\] = {nums\[0\], nums\[5\], nums\[6\], nums\[2\]} = {5, 6, 2, 0}
**Example 2:**
**Input:** nums = \[0,1,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length`
* All the values of `nums` are **unique**.
| null |
Solution
|
array-nesting
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int arrayNesting(vector<int>& nums) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n\n int maxLen = 1;\n for (int i = 0; i < nums.size(); ++i) {\n if (nums[i] == i) continue;\n int currLen = 1;\n while (nums[i] != i) {\n int next_i = nums[i];\n nums[i] = nums[next_i];\n nums[next_i] = next_i;\n currLen++;\n }\n maxLen = max(maxLen, currLen);\n }\n return maxLen;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def arrayNesting(self, nums: List[int]) -> int:\n ans = 0\n for x in nums:\n if x == -1: continue\n cnt = 0\n while nums[x] != -1:\n cnt += 1\n nums[x], x = -1, nums[x]\n ans = max(ans, cnt)\n \n return ans\n```\n\n```Java []\nclass Solution {\n public int arrayNesting(int[] nums) {\n int res = 0;\n for (int i = 0; i < nums.length; i++) {\n if (nums[i] != Integer.MAX_VALUE) {\n int start = nums[i], count = 0;\n while (nums[start] != Integer.MAX_VALUE) {\n int temp = start;\n start = nums[start];\n count++;\n nums[temp] = Integer.MAX_VALUE;\n }\n res = Math.max(res, count);\n }\n }\n return res;\n }\n}\n```\n
| 2
|
You are given an integer array `nums` of length `n` where `nums` is a permutation of the numbers in the range `[0, n - 1]`.
You should build a set `s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... }` subjected to the following rule:
* The first element in `s[k]` starts with the selection of the element `nums[k]` of `index = k`.
* The next element in `s[k]` should be `nums[nums[k]]`, and then `nums[nums[nums[k]]]`, and so on.
* We stop adding right before a duplicate element occurs in `s[k]`.
Return _the longest length of a set_ `s[k]`.
**Example 1:**
**Input:** nums = \[5,4,0,3,1,6,2\]
**Output:** 4
**Explanation:**
nums\[0\] = 5, nums\[1\] = 4, nums\[2\] = 0, nums\[3\] = 3, nums\[4\] = 1, nums\[5\] = 6, nums\[6\] = 2.
One of the longest sets s\[k\]:
s\[0\] = {nums\[0\], nums\[5\], nums\[6\], nums\[2\]} = {5, 6, 2, 0}
**Example 2:**
**Input:** nums = \[0,1,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length`
* All the values of `nums` are **unique**.
| null |
Python3 | Strongly Connected Components
|
array-nesting
| 0
| 1
|
# Intuition\nThe array $\\mathrm{nums}$ can be modelled as a graph where there\'s a *directed edge* from $i$ to $\\mathrm{nums}[i]$, for $0 \\le i < n$. Once the situation is modelled as a graph, all that is left to do is finding the strongly connected components and returning the size of the largest one.\n\n# Approach\nTo find the strongly connected components, I used a slightly modified version of Kosaraju\'s algorithm, which is a depth-first algorithm for finding the strongly connected components of a graph in linear time. Once this is done, every node will be mapped to its corresponding component in the $\\mathrm{components}$ array, and a frequency dictionary is set up, and we return the frequency of the mode(s) (the most commonly occuring element(s)).\n\n# Complexity\n- Time complexity: $\\mathcal{O}(n)$\n\n- Space complexity: $\\mathcal{O}(n)$\n\n# Code\n```Python3 []\nclass Solution:\n def arrayNesting(self, nums: List[int]) -> int:\n graph = defaultdict(list)\n n = len(nums)\n for i in range(n):\n graph[i].append(nums[i])\n \n v = set()\n pseudo_topsort = []\n components = [-1] * n\n def visit(node):\n if node in v: return\n v.add(node)\n for k in graph[node]:\n visit(k)\n pseudo_topsort.append(node)\n def assign(node,parent):\n if components[node] != -1: return\n components[node] = parent\n for k in graph[node]:\n assign(k,parent)\n for i in range(n):\n visit(i)\n for i in pseudo_topsort:\n assign(i,i)\n counts = defaultdict(int)\n for i in components:\n counts[i] += 1\n return max(counts.values())\n \n```
| 0
|
You are given an integer array `nums` of length `n` where `nums` is a permutation of the numbers in the range `[0, n - 1]`.
You should build a set `s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... }` subjected to the following rule:
* The first element in `s[k]` starts with the selection of the element `nums[k]` of `index = k`.
* The next element in `s[k]` should be `nums[nums[k]]`, and then `nums[nums[nums[k]]]`, and so on.
* We stop adding right before a duplicate element occurs in `s[k]`.
Return _the longest length of a set_ `s[k]`.
**Example 1:**
**Input:** nums = \[5,4,0,3,1,6,2\]
**Output:** 4
**Explanation:**
nums\[0\] = 5, nums\[1\] = 4, nums\[2\] = 0, nums\[3\] = 3, nums\[4\] = 1, nums\[5\] = 6, nums\[6\] = 2.
One of the longest sets s\[k\]:
s\[0\] = {nums\[0\], nums\[5\], nums\[6\], nums\[2\]} = {5, 6, 2, 0}
**Example 2:**
**Input:** nums = \[0,1,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length`
* All the values of `nums` are **unique**.
| null |
Python || O(1) Space Solution
|
array-nesting
| 0
| 1
|
```\nVISITED = -1\n\n\nclass Solution:\n def arrayNesting(self, A: list[int]) -> int:\n # return self.simple_solution(A)\n return self.space_efficient_solution(A)\n\n @staticmethod\n def simple_solution(A: list[int]) -> int:\n n = len(A)\n\n is_visited = [False] * n\n\n def dfs(i: int) -> int:\n output = 0\n\n while not is_visited[i]:\n is_visited[i], i = True, A[i]\n output += 1\n\n return output\n\n return max(dfs(i) for i in range(n) if not is_visited[i])\n\n @staticmethod\n def space_efficient_solution(A: list[int]) -> int:\n n = len(A)\n\n output = 0\n\n for i in range(n):\n loop = 0\n\n A[i], v = VISITED, A[i]\n\n while v != VISITED:\n A[v], v = VISITED, A[v]\n loop += 1\n\n output = max(output, loop)\n\n return output\n```
| 0
|
You are given an integer array `nums` of length `n` where `nums` is a permutation of the numbers in the range `[0, n - 1]`.
You should build a set `s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... }` subjected to the following rule:
* The first element in `s[k]` starts with the selection of the element `nums[k]` of `index = k`.
* The next element in `s[k]` should be `nums[nums[k]]`, and then `nums[nums[nums[k]]]`, and so on.
* We stop adding right before a duplicate element occurs in `s[k]`.
Return _the longest length of a set_ `s[k]`.
**Example 1:**
**Input:** nums = \[5,4,0,3,1,6,2\]
**Output:** 4
**Explanation:**
nums\[0\] = 5, nums\[1\] = 4, nums\[2\] = 0, nums\[3\] = 3, nums\[4\] = 1, nums\[5\] = 6, nums\[6\] = 2.
One of the longest sets s\[k\]:
s\[0\] = {nums\[0\], nums\[5\], nums\[6\], nums\[2\]} = {5, 6, 2, 0}
**Example 2:**
**Input:** nums = \[0,1,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length`
* All the values of `nums` are **unique**.
| null |
[Python] Intuitive + Direct for Beginners with Illustrations
|
reshape-the-matrix
| 0
| 1
|
Given a matrix `mat` of 3 rows * 4 columns, \nwe want reshape it into 2 rows (`r = 2`) * 6 columns(`c = 6`): \n```\n[[0, 1, 2, 3],\n [4, 5, 6, 7], -> [[0, 1, 2, 3, 4, 5],\n [8, 9, 10, 11]] [6, 7, 8, 9, 10, 11]]\n```\n**Step 1:** Flatten the given matrix `mat` to a 1-D list `flatten` for easier visualizations and calculations for future steps\n```\nflatten = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]\n```\n**Step 2:** Check whether the total number of given elements `len(flatten)` and the new shape `r * c` matches (i.e. whether "*given parameters is possible and legal*")\n```\nr = 2, c = 6\nr * c = 12\n```\n**Step 3:** Rearrange all elements in 1-D list `flatten` into the `new_mat` according to given number of row `r` and given number of columns `c`\n```\nflatten = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]\n```\n\nreshaping: \n```\n [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]\nrow_index: 0\t\t\t| c0 c1 c2 c3 c4 c5 |\nrow_index: 1 \t\t\t | c0 c1 c2 c3 c4 c5 |\n\nindex in flatten: [row_index * c : row_index * c + c])\n\n\t\t\t [0*6 : 0*6 + 6], \n\t\t\t\t\t\t\t\t\t\t [1*6 : 1*6+6]\n\t\t\t\t\t\t\t\t\t\t\t\t \n [0 : 6], \n\t\t\t\t\t\t\t\t\t\t [6 : 12]\n```\n- **iteration 0**:` row_index` **0**\n```\nflatten[0 : 6] -> [0, 1, 2, 3, 4, 5]\n\nappending:\nnew_mat = [[0, 1, 2, 3, 4, 5]]\n```\n- **iteration 1**: `row_index` **1**\n```\nflatten[6 : 12] -> [6, 7, 8, 9, 10, 11]\n\nappending:\nnew_mat = [[0, 1, 2, 3, 4, 5],\n [6, 7, 8, 9, 10, 11]]\n```\n\n\n\n___________________________\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n flatten = []\n new_mat = []\n for row in mat:\n for num in row:\n flatten.append(num)\n \n if r * c != len(flatten): # when given parameters is NOT possible and legal\n return mat\n else:\n for row_index in range(r):\n new_mat.append(flatten[row_index * c : row_index * c + c])\n return new_mat\n```\n\n________________________________________________________________________\n\nAs a total beginner, I am writing these all out to help myself, and hopefully also help anyone out there who is like me at the same time.\n\nPlease upvote\u2B06\uFE0F if you find this helpful or worth-reading for beginners in anyway. \nYour upvote is much more than just supportive to me. \uD83D\uDE33\uD83E\uDD13\uD83E\uDD70\n\nIf you find this is not helpful, needs improvement, or is questionable, would you please leave a quick comment below to point out the problem before you decide to downvote? It will be very helpful for me (maybe also others) to learn as a beginner.\n\nThank you very much either way \uD83E\uDD13.\n
| 130
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
[Python] Intuitive + Direct for Beginners with Illustrations
|
reshape-the-matrix
| 0
| 1
|
Given a matrix `mat` of 3 rows * 4 columns, \nwe want reshape it into 2 rows (`r = 2`) * 6 columns(`c = 6`): \n```\n[[0, 1, 2, 3],\n [4, 5, 6, 7], -> [[0, 1, 2, 3, 4, 5],\n [8, 9, 10, 11]] [6, 7, 8, 9, 10, 11]]\n```\n**Step 1:** Flatten the given matrix `mat` to a 1-D list `flatten` for easier visualizations and calculations for future steps\n```\nflatten = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]\n```\n**Step 2:** Check whether the total number of given elements `len(flatten)` and the new shape `r * c` matches (i.e. whether "*given parameters is possible and legal*")\n```\nr = 2, c = 6\nr * c = 12\n```\n**Step 3:** Rearrange all elements in 1-D list `flatten` into the `new_mat` according to given number of row `r` and given number of columns `c`\n```\nflatten = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]\n```\n\nreshaping: \n```\n [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]\nrow_index: 0\t\t\t| c0 c1 c2 c3 c4 c5 |\nrow_index: 1 \t\t\t | c0 c1 c2 c3 c4 c5 |\n\nindex in flatten: [row_index * c : row_index * c + c])\n\n\t\t\t [0*6 : 0*6 + 6], \n\t\t\t\t\t\t\t\t\t\t [1*6 : 1*6+6]\n\t\t\t\t\t\t\t\t\t\t\t\t \n [0 : 6], \n\t\t\t\t\t\t\t\t\t\t [6 : 12]\n```\n- **iteration 0**:` row_index` **0**\n```\nflatten[0 : 6] -> [0, 1, 2, 3, 4, 5]\n\nappending:\nnew_mat = [[0, 1, 2, 3, 4, 5]]\n```\n- **iteration 1**: `row_index` **1**\n```\nflatten[6 : 12] -> [6, 7, 8, 9, 10, 11]\n\nappending:\nnew_mat = [[0, 1, 2, 3, 4, 5],\n [6, 7, 8, 9, 10, 11]]\n```\n\n\n\n___________________________\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n flatten = []\n new_mat = []\n for row in mat:\n for num in row:\n flatten.append(num)\n \n if r * c != len(flatten): # when given parameters is NOT possible and legal\n return mat\n else:\n for row_index in range(r):\n new_mat.append(flatten[row_index * c : row_index * c + c])\n return new_mat\n```\n\n________________________________________________________________________\n\nAs a total beginner, I am writing these all out to help myself, and hopefully also help anyone out there who is like me at the same time.\n\nPlease upvote\u2B06\uFE0F if you find this helpful or worth-reading for beginners in anyway. \nYour upvote is much more than just supportive to me. \uD83D\uDE33\uD83E\uDD13\uD83E\uDD70\n\nIf you find this is not helpful, needs improvement, or is questionable, would you please leave a quick comment below to point out the problem before you decide to downvote? It will be very helpful for me (maybe also others) to learn as a beginner.\n\nThank you very much either way \uD83E\uDD13.\n
| 130
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
easy solution || Reshape the Matrix
|
reshape-the-matrix
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n temp=[]\n result=[]\n for i in mat:\n for j in i:\n temp.append(j)\n if r*c!=len(temp):\n return mat\n else:\n for i in range(r):\n result.append(temp[i*c:i*c+c])\n return result\n\n \n```
| 1
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
easy solution || Reshape the Matrix
|
reshape-the-matrix
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n temp=[]\n result=[]\n for i in mat:\n for j in i:\n temp.append(j)\n if r*c!=len(temp):\n return mat\n else:\n for i in range(r):\n result.append(temp[i*c:i*c+c])\n return result\n\n \n```
| 1
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
[Python] - Clean & Simple - O(m*n) Solution
|
reshape-the-matrix
| 0
| 1
|
# Complexity\n- Time complexity: $$O(m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n m = len(mat)\n n = len(mat[0])\n\n if m * n != r * c :\n return mat \n\n cnt = 0\n ans = []\n row = []\n for i in range(m):\n for j in range(n):\n row.append(mat[i][j])\n cnt+=1\n if cnt == c:\n ans.append(row)\n row = []\n cnt = 0\n return ans\n```\n## Numpy:\n```\nimport numpy as np\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n try:\n return np.reshape(mat, (r, c)).tolist()\n except:\n return mat\n```
| 6
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
[Python] - Clean & Simple - O(m*n) Solution
|
reshape-the-matrix
| 0
| 1
|
# Complexity\n- Time complexity: $$O(m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n m = len(mat)\n n = len(mat[0])\n\n if m * n != r * c :\n return mat \n\n cnt = 0\n ans = []\n row = []\n for i in range(m):\n for j in range(n):\n row.append(mat[i][j])\n cnt+=1\n if cnt == c:\n ans.append(row)\n row = []\n cnt = 0\n return ans\n```\n## Numpy:\n```\nimport numpy as np\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n try:\n return np.reshape(mat, (r, c)).tolist()\n except:\n return mat\n```
| 6
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
566: Solution with step by step explanation
|
reshape-the-matrix
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, check if it is possible to reshape the matrix by comparing the product of the number of rows and columns of the original matrix with the product of the number of rows and columns of the desired reshaped matrix. If they are not equal, return the original matrix.\n2. Create a new matrix of size r x c using nested list comprehension.\n3. Traverse the original matrix in row-major order using a single index that starts at 0.\n4. For each element in the new matrix, calculate its row and column indices in the original matrix using integer division and modulo operations on the index, and then fill in the corresponding value from the original matrix.\n5. Increment the index by 1 for each iteration.\n6. Return the new matrix.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n # Check if it is possible to reshape the matrix\n m, n = len(mat), len(mat[0])\n if m * n != r * c:\n return mat\n \n # Create a new matrix of size r x c\n new_mat = [[0] * c for _ in range(r)]\n \n # Traverse the original matrix in row-major order\n index = 0\n for i in range(r):\n for j in range(c):\n # Fill in the values of the new matrix\n row, col = divmod(index, n)\n new_mat[i][j] = mat[row][col]\n index += 1\n \n return new_mat\n\n```
| 5
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
566: Solution with step by step explanation
|
reshape-the-matrix
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, check if it is possible to reshape the matrix by comparing the product of the number of rows and columns of the original matrix with the product of the number of rows and columns of the desired reshaped matrix. If they are not equal, return the original matrix.\n2. Create a new matrix of size r x c using nested list comprehension.\n3. Traverse the original matrix in row-major order using a single index that starts at 0.\n4. For each element in the new matrix, calculate its row and column indices in the original matrix using integer division and modulo operations on the index, and then fill in the corresponding value from the original matrix.\n5. Increment the index by 1 for each iteration.\n6. Return the new matrix.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n # Check if it is possible to reshape the matrix\n m, n = len(mat), len(mat[0])\n if m * n != r * c:\n return mat\n \n # Create a new matrix of size r x c\n new_mat = [[0] * c for _ in range(r)]\n \n # Traverse the original matrix in row-major order\n index = 0\n for i in range(r):\n for j in range(c):\n # Fill in the values of the new matrix\n row, col = divmod(index, n)\n new_mat[i][j] = mat[row][col]\n index += 1\n \n return new_mat\n\n```
| 5
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
Python solution for beginner|| easy & explained
|
reshape-the-matrix
| 0
| 1
|
# Complexity\n- Time complexity:\nO(r*c) \n\n- Dont use "[[0]* col] * row" for new matrix. This cannot be mutated for each cell since it only creates a single object for each row.\n- [i//c] gives the row number and [i%c] gives the coloum number \n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n\n if not mat or r*c != len(mat) * len(mat[0]):\n return mat\n \n l = [[0 for _ in range(c)] for _ in range(r)]\n\n n=len(mat[0])\n\n i=0\n while i < r*c:\n l[i//c][i%c] = mat[i//n][i%n] \n i+=1\n return l
| 3
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
Python solution for beginner|| easy & explained
|
reshape-the-matrix
| 0
| 1
|
# Complexity\n- Time complexity:\nO(r*c) \n\n- Dont use "[[0]* col] * row" for new matrix. This cannot be mutated for each cell since it only creates a single object for each row.\n- [i//c] gives the row number and [i%c] gives the coloum number \n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n\n if not mat or r*c != len(mat) * len(mat[0]):\n return mat\n \n l = [[0 for _ in range(c)] for _ in range(r)]\n\n n=len(mat[0])\n\n i=0\n while i < r*c:\n l[i//c][i%c] = mat[i//n][i%n] \n i+=1\n return l
| 3
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
6 Lines of Code ----> python
|
reshape-the-matrix
| 0
| 1
|
\n# please upvote me it would encourage me alot\n\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n list1,matrix=list(chain.from_iterable(mat)),[]\n if len(mat)*len(mat[0])!=r*c:\n return mat\n for i in range(0,len(list1),c):\n matrix.append(list1[i:i+c])\n return matrix\n \n```\n# please upvote me it would encourage me alot\n
| 10
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
6 Lines of Code ----> python
|
reshape-the-matrix
| 0
| 1
|
\n# please upvote me it would encourage me alot\n\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n list1,matrix=list(chain.from_iterable(mat)),[]\n if len(mat)*len(mat[0])!=r*c:\n return mat\n for i in range(0,len(list1),c):\n matrix.append(list1[i:i+c])\n return matrix\n \n```\n# please upvote me it would encourage me alot\n
| 10
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
Very Easy || 100% || Fully Explained || Java, C++, Python, JavaScript, Python3
|
reshape-the-matrix
| 1
| 1
|
# **Java Solution:**\n```\n// Runtime: 1 ms, faster than 92.33% of Java online submissions for Reshape the Matrix.\n// Time Complexity : O(r*c)\n// Space Complexity : O(r*c)\nclass Solution {\n public int[][] matrixReshape(int[][] mat, int r, int c) {\n // If transformation doesn\'t occur, return mat...\n if (mat.length * mat[0].length != r * c) {\n return mat;\n }\n // Otherwise create a output matrix and fill the cells...\n int[][] output = new int[r][c];\n // Traverse the matrix through the loop... \n for (int idx = 0; idx < r * c; idx++) {\n // idx % c will give us the current column number...\n // idx / c will give us how many rows we have completely filled...\n output[idx/c][idx % c] = mat[idx / mat[0].length][idx % mat[0].length];\n }\n return output; // Return the output matrix...\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Time Complexity : O(r*c)\n// Space Complexity : O(r*c)\nclass Solution {\npublic:\n vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {\n // If transformation doesn\'t occur, return mat...\n if (mat.size() * mat[0].size() != r * c) {\n return mat;\n }\n // Otherwise create a output matrix and fill the cells...\n vector<vector<int>> output(r, vector<int>(c));\n // Traverse the matrix through the loop... \n for (int idx = 0; idx < r * c; idx++) {\n // idx % c will give us the current column number...\n // idx / c will give us how many rows we have completely filled...\n output[idx/c][idx % c] = mat[idx / mat[0].size()][idx % mat[0].size()];\n }\n return output; // Return the output matrix...\n }\n};\n```\n\n# **Python/Python3 Solution:**\n```\n# Time Complexity : O(r*c)\n# Space Complexity : O(r*c)\nclass Solution(object):\n def matrixReshape(self, mat, r, c):\n # Base case...\n if not mat: return mat\n # If transformation doesn\'t occur, return mat...\n if len(mat) * len(mat[0]) != r * c:\n return mat\n # Otherwise create a output matrix and fill the cells...\n output = [[0 for i in range(c)] for i in range(r)]\n idx = 0\n # Traverse the matrix through the loop... \n while idx < r * c:\n # idx % c will give us the current column number...\n # idx / c will give us how many rows we have completely filled...\n output[idx // c][ idx % c] = mat[idx // len(mat[0])][idx % len(mat[0])]\n idx += 1\n return output # Return the output matrix...\n```\n \n# **JavaScript Solution:**\n```\n// Time Complexity : O(r*c)\n// Space Complexity : O(r*c)\nvar matrixReshape = function(mat, r, c) {\n // If transformation doesn\'t occur, return mat...\n if (mat.length * mat[0].length != r * c) {\n return mat;\n }\n // Otherwise create a output matrix and fill the cells...\n const output = new Array(r).fill(0).map(() => new Array(c).fill(0));\n // Traverse the matrix through the loop... \n for (let idx = 0; idx < r * c; idx++) {\n // idx % c will give us the current column number...\n // idx / c will give us how many rows we have completely filled...\n output[Math.floor(idx/c)][idx % c] = mat[Math.floor(idx / mat[0].length)][idx % mat[0].length];\n }\n return output; // Return the output matrix...\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...**
| 35
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
Very Easy || 100% || Fully Explained || Java, C++, Python, JavaScript, Python3
|
reshape-the-matrix
| 1
| 1
|
# **Java Solution:**\n```\n// Runtime: 1 ms, faster than 92.33% of Java online submissions for Reshape the Matrix.\n// Time Complexity : O(r*c)\n// Space Complexity : O(r*c)\nclass Solution {\n public int[][] matrixReshape(int[][] mat, int r, int c) {\n // If transformation doesn\'t occur, return mat...\n if (mat.length * mat[0].length != r * c) {\n return mat;\n }\n // Otherwise create a output matrix and fill the cells...\n int[][] output = new int[r][c];\n // Traverse the matrix through the loop... \n for (int idx = 0; idx < r * c; idx++) {\n // idx % c will give us the current column number...\n // idx / c will give us how many rows we have completely filled...\n output[idx/c][idx % c] = mat[idx / mat[0].length][idx % mat[0].length];\n }\n return output; // Return the output matrix...\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Time Complexity : O(r*c)\n// Space Complexity : O(r*c)\nclass Solution {\npublic:\n vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {\n // If transformation doesn\'t occur, return mat...\n if (mat.size() * mat[0].size() != r * c) {\n return mat;\n }\n // Otherwise create a output matrix and fill the cells...\n vector<vector<int>> output(r, vector<int>(c));\n // Traverse the matrix through the loop... \n for (int idx = 0; idx < r * c; idx++) {\n // idx % c will give us the current column number...\n // idx / c will give us how many rows we have completely filled...\n output[idx/c][idx % c] = mat[idx / mat[0].size()][idx % mat[0].size()];\n }\n return output; // Return the output matrix...\n }\n};\n```\n\n# **Python/Python3 Solution:**\n```\n# Time Complexity : O(r*c)\n# Space Complexity : O(r*c)\nclass Solution(object):\n def matrixReshape(self, mat, r, c):\n # Base case...\n if not mat: return mat\n # If transformation doesn\'t occur, return mat...\n if len(mat) * len(mat[0]) != r * c:\n return mat\n # Otherwise create a output matrix and fill the cells...\n output = [[0 for i in range(c)] for i in range(r)]\n idx = 0\n # Traverse the matrix through the loop... \n while idx < r * c:\n # idx % c will give us the current column number...\n # idx / c will give us how many rows we have completely filled...\n output[idx // c][ idx % c] = mat[idx // len(mat[0])][idx % len(mat[0])]\n idx += 1\n return output # Return the output matrix...\n```\n \n# **JavaScript Solution:**\n```\n// Time Complexity : O(r*c)\n// Space Complexity : O(r*c)\nvar matrixReshape = function(mat, r, c) {\n // If transformation doesn\'t occur, return mat...\n if (mat.length * mat[0].length != r * c) {\n return mat;\n }\n // Otherwise create a output matrix and fill the cells...\n const output = new Array(r).fill(0).map(() => new Array(c).fill(0));\n // Traverse the matrix through the loop... \n for (let idx = 0; idx < r * c; idx++) {\n // idx % c will give us the current column number...\n // idx / c will give us how many rows we have completely filled...\n output[Math.floor(idx/c)][idx % c] = mat[Math.floor(idx / mat[0].length)][idx % mat[0].length];\n }\n return output; // Return the output matrix...\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...**
| 35
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
Best python solution easy to understand!!!
|
reshape-the-matrix
| 0
| 1
|
\n# Approach\n<!-- Describe your approach to solving the problem. --> First we should check if it is possible to reshape the given matrix to asked one. Then we make one dimensional array from given matrix (flat). After, we add the subarrays which are defined by dividing the flat array into c, r times .\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n if r*c!=len(mat)*len(mat[0]):\n return mat\n flat,ans=[],[]\n for i in mat:\n flat+=i\n for i in range(r):\n ans+=[flat[i*c:i*c+c]]\n return ans\n \n```
| 7
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
Best python solution easy to understand!!!
|
reshape-the-matrix
| 0
| 1
|
\n# Approach\n<!-- Describe your approach to solving the problem. --> First we should check if it is possible to reshape the given matrix to asked one. Then we make one dimensional array from given matrix (flat). After, we add the subarrays which are defined by dividing the flat array into c, r times .\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:\n if r*c!=len(mat)*len(mat[0]):\n return mat\n flat,ans=[],[]\n for i in mat:\n flat+=i\n for i in range(r):\n ans+=[flat[i*c:i*c+c]]\n return ans\n \n```
| 7
|
In MATLAB, there is a handy function called `reshape` which can reshape an `m x n` matrix into a new one with a different size `r x c` keeping its original data.
You are given an `m x n` matrix `mat` and two integers `r` and `c` representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the `reshape` operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
**Example 1:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 1, c = 4
**Output:** \[\[1,2,3,4\]\]
**Example 2:**
**Input:** mat = \[\[1,2\],\[3,4\]\], r = 2, c = 4
**Output:** \[\[1,2\],\[3,4\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `-1000 <= mat[i][j] <= 1000`
* `1 <= r, c <= 300`
|
Do you know how 2d matrix is stored in 1d memory? Try to map 2-dimensions into one. M[i][j]=M[n*i+j] , where n is the number of cols.
This is the one way of converting 2-d indices into one 1-d index.
Now, how will you convert 1-d index into 2-d indices? Try to use division and modulus to convert 1-d index into 2-d indices. M[i] => M[i/n][i%n] Will it result in right mapping? Take some example and check this formula.
|
✔️ [Python3] SLIDING WINDOW OPTIMIZED ( ❝̆ ·̫̮ ❝̆ )✧, Explained
|
permutation-in-string
| 0
| 1
|
**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe only thing we care about any particular substring in `s2` is having the same number of characters as in the `s1`. So we create a hashmap with the count of every character in the string `s1`. Then we slide a window over the string `s2` and decrease the counter for characters that occurred in the window. As soon as all counters in the hashmap get to zero that means we encountered the permutation.\n\nTime: **O(n)** - linear for window sliding and counter\nSpace: **O(1)** - conctant for dictionary with the maximum 26 pairs (English alphabet)\n\n```\ndef checkInclusion(self, s1: str, s2: str) -> bool:\n\tcntr, w = Counter(s1), len(s1) \n\n\tfor i in range(len(s2)):\n\t\tif s2[i] in cntr: \n\t\t\tcntr[s2[i]] -= 1\n\t\tif i >= w and s2[i-w] in cntr: \n\t\t\tcntr[s2[i-w]] += 1\n\n\t\tif all([cntr[i] == 0 for i in cntr]): # see optimized code below\n\t\t\treturn True\n\n\treturn False\n```\n\n### Optimized:\nWe can use an auxiliary variable to count a number of characters whose frequency gets to zero during window sliding. That helps us to avoid iterating over the hashmap for every cycle tick to check whether frequencies turned into zero.\n```\ndef checkInclusion(self, s1: str, s2: str) -> bool:\n\tcntr, w, match = Counter(s1), len(s1), 0 \n\n\tfor i in range(len(s2)):\n\t\tif s2[i] in cntr:\n\t\t\tif not cntr[s2[i]]: match -= 1\n\t\t\tcntr[s2[i]] -= 1\n\t\t\tif not cntr[s2[i]]: match += 1\n\n\t\tif i >= w and s2[i-w] in cntr:\n\t\t\tif not cntr[s2[i-w]]: match -= 1\n\t\t\tcntr[s2[i-w]] += 1\n\t\t\tif not cntr[s2[i-w]]: match += 1\n\n\t\tif match == len(cntr):\n\t\t\treturn True\n\n\treturn False\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**
| 245
|
Given two strings `s1` and `s2`, return `true` _if_ `s2` _contains a permutation of_ `s1`_, or_ `false` _otherwise_.
In other words, return `true` if one of `s1`'s permutations is the substring of `s2`.
**Example 1:**
**Input:** s1 = "ab ", s2 = "eidbaooo "
**Output:** true
**Explanation:** s2 contains one permutation of s1 ( "ba ").
**Example 2:**
**Input:** s1 = "ab ", s2 = "eidboaoo "
**Output:** false
**Constraints:**
* `1 <= s1.length, s2.length <= 104`
* `s1` and `s2` consist of lowercase English letters.
|
Obviously, brute force will result in TLE. Think of something else. How will you check whether one string is a permutation of another string? One way is to sort the string and then compare. But, Is there a better way? If one string is a permutation of another string then they must one common metric. What is that? Both strings must have same character frequencies, if one is permutation of another. Which data structure should be used to store frequencies? What about hash table? An array of size 26?
|
Solution
|
permutation-in-string
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n bool checkInclusion(string s1, string s2) {\n vector<int>s1hash(26,0);\n vector<int>s2hash(26,0);\n if(s1.size()>s2.size())\n return 0;\n\n int left=0,right=0;\n while(right<s1.size())\n {\n s1hash[s1[right]-\'a\']++;\n s2hash[s2[right]-\'a\']++;\n right++;\n }\n if(s1hash==s2hash)\n return 1;\n\n while(right<s2.size())\n {\n s2hash[s2[left]-\'a\']--;\n s2hash[s2[right]-\'a\']++;\n if(s1hash==s2hash)\n return 1;\n right++; \n left++; \n } \n return 0;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n \n def checkInclusion(self, s1: str, s2: str) -> bool:\n target = {c: 0 for c in string.ascii_lowercase}\n window = {c: 0 for c in string.ascii_lowercase}\n n = len(s1)\n for c in s1:\n target[c] += 1\n for c in s2[:n]:\n window[c] += 1\n for i in range(n, len(s2)):\n if window == target:\n return True\n window[s2[i-n]] -= 1\n window[s2[i]] += 1\n return window == target\n```\n\n```Java []\nclass Solution {\n public boolean checkInclusion(String s1, String s2) {\n if (s2.length() < s1.length()) return false;\n int[] arr = new int[26];\n for (int i = 0; i < s1.length(); i++) {\n arr[s1.charAt(i) - \'a\']++;\n }\n int i = 0;\n int j = 0;\n for (; j < s1.length(); j++) {\n arr[s2.charAt(j) - \'a\']--;\n }\n j--;\n if (isEmpty(arr)) return true;\n while (j < s2.length()) {\n arr[s2.charAt(i) - \'a\']++;\n i++;\n j++;\n if (j < s2.length()) arr[s2.charAt(j) - \'a\']--;\n if (isEmpty(arr)) return true;\n }\n return isEmpty(arr);\n }\n public boolean isEmpty(int[] arr) {\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] != 0) return false;\n }\n return true;\n }\n}\n```\n
| 1
|
Given two strings `s1` and `s2`, return `true` _if_ `s2` _contains a permutation of_ `s1`_, or_ `false` _otherwise_.
In other words, return `true` if one of `s1`'s permutations is the substring of `s2`.
**Example 1:**
**Input:** s1 = "ab ", s2 = "eidbaooo "
**Output:** true
**Explanation:** s2 contains one permutation of s1 ( "ba ").
**Example 2:**
**Input:** s1 = "ab ", s2 = "eidboaoo "
**Output:** false
**Constraints:**
* `1 <= s1.length, s2.length <= 104`
* `s1` and `s2` consist of lowercase English letters.
|
Obviously, brute force will result in TLE. Think of something else. How will you check whether one string is a permutation of another string? One way is to sort the string and then compare. But, Is there a better way? If one string is a permutation of another string then they must one common metric. What is that? Both strings must have same character frequencies, if one is permutation of another. Which data structure should be used to store frequencies? What about hash table? An array of size 26?
|
Best Explained Solution
|
permutation-in-string
| 1
| 1
|
\n```\nclass Solution {\n fun checkInclusion(s1: String, s2: String): Boolean {\n if (s1.length > s2.length) return false\n val s1map = IntArray(26)\n val s2map = IntArray(26)\n for (i in s1.indices) {\n s1map[s1[i] - \'a\']++\n s2map[s2[i] - \'a\']++\n }\n for (i in 0 until s2.length - s1.length) {\n if (matches(s1map, s2map)) return true\n s2map[s2[i + s1.length] - \'a\']++\n s2map[s2[i] - \'a\']--\n }\n return matches(s1map, s2map)\n }\n\n private fun matches(s1map: IntArray, s2map: IntArray): Boolean {\n for (i in 0..25) {\n if (s1map[i] != s2map[i]) return false\n }\n return true\n }\n}\n```
| 1
|
Given two strings `s1` and `s2`, return `true` _if_ `s2` _contains a permutation of_ `s1`_, or_ `false` _otherwise_.
In other words, return `true` if one of `s1`'s permutations is the substring of `s2`.
**Example 1:**
**Input:** s1 = "ab ", s2 = "eidbaooo "
**Output:** true
**Explanation:** s2 contains one permutation of s1 ( "ba ").
**Example 2:**
**Input:** s1 = "ab ", s2 = "eidboaoo "
**Output:** false
**Constraints:**
* `1 <= s1.length, s2.length <= 104`
* `s1` and `s2` consist of lowercase English letters.
|
Obviously, brute force will result in TLE. Think of something else. How will you check whether one string is a permutation of another string? One way is to sort the string and then compare. But, Is there a better way? If one string is a permutation of another string then they must one common metric. What is that? Both strings must have same character frequencies, if one is permutation of another. Which data structure should be used to store frequencies? What about hash table? An array of size 26?
|
Best of C++, Java, Python
|
permutation-in-string
| 1
| 1
|
# Complexity\n- Time complexity: $$O(n + m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$ \n`target` and `pending` are of fixed size regardless of input strings\' lengths.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool checkInclusion(string s1, string s2) {\n vector<int> target(26), pending(26);\n for (auto c: s1) {\n target[c - \'a\']++;\n }\n\n int begin = 0, end = 0, n = s2.length(), m = s1.length();\n char c;\n while (end < n) {\n c = s2[end];\n pending[c - \'a\']++;\n while (pending[c - \'a\'] > target[c - \'a\']) {\n pending[s2[begin++] - \'a\']--;\n }\n end += 1;\n if (end - begin == m) return true;\n }\n\n return false;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean checkInclusion(String s1, String s) {\n int[] target = new int[26];\n for (char c: s1.toCharArray()) {\n target[c - \'a\']++;\n }\n int[] pending = new int[26];\n\n int begin = 0, end = 0, n = s.length(), m = s1.length();\n char c;\n\n while (end < n) {\n c = s.charAt(end);\n pending[c - \'a\']++;\n while (pending[c - \'a\'] > target[c - \'a\']) {\n pending[s.charAt(begin++) - \'a\']--;\n }\n end++;\n if (end - begin == m) return true;\n }\n\n return false;\n }\n}\n```\n```Python []\nclass Solution:\n def checkInclusion(self, s1: str, s2: str) -> bool:\n target = [0] * 26\n pending = [0] * 26\n for c in s1:\n target[ord(c) - ord(\'a\')] += 1\n begin, end, n, m = 0, 0, len(s2), len(s1)\n while end < n:\n c = s2[end]\n pending[ord(c) - ord(\'a\')] += 1\n while pending[ord(c) - ord(\'a\')] > target[ord(c) - ord(\'a\')]:\n pending[ord(s2[begin]) - ord(\'a\')] -= 1\n begin += 1\n end += 1\n if end - begin == m:\n return True\n return False\n```
| 1
|
Given two strings `s1` and `s2`, return `true` _if_ `s2` _contains a permutation of_ `s1`_, or_ `false` _otherwise_.
In other words, return `true` if one of `s1`'s permutations is the substring of `s2`.
**Example 1:**
**Input:** s1 = "ab ", s2 = "eidbaooo "
**Output:** true
**Explanation:** s2 contains one permutation of s1 ( "ba ").
**Example 2:**
**Input:** s1 = "ab ", s2 = "eidboaoo "
**Output:** false
**Constraints:**
* `1 <= s1.length, s2.length <= 104`
* `s1` and `s2` consist of lowercase English letters.
|
Obviously, brute force will result in TLE. Think of something else. How will you check whether one string is a permutation of another string? One way is to sort the string and then compare. But, Is there a better way? If one string is a permutation of another string then they must one common metric. What is that? Both strings must have same character frequencies, if one is permutation of another. Which data structure should be used to store frequencies? What about hash table? An array of size 26?
|
Python3 sort solution
|
permutation-in-string
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkInclusion(self, s1: str, s2: str) -> bool:\n checker = \'\'.join(sorted(s1))\n \n for i in range(len(s2) - len(s1)+1):\n temp = \'\'.join(sorted(s2[i:i+len(s1)]))\n if temp == checker:\n return True\n return False\n\n```
| 1
|
Given two strings `s1` and `s2`, return `true` _if_ `s2` _contains a permutation of_ `s1`_, or_ `false` _otherwise_.
In other words, return `true` if one of `s1`'s permutations is the substring of `s2`.
**Example 1:**
**Input:** s1 = "ab ", s2 = "eidbaooo "
**Output:** true
**Explanation:** s2 contains one permutation of s1 ( "ba ").
**Example 2:**
**Input:** s1 = "ab ", s2 = "eidboaoo "
**Output:** false
**Constraints:**
* `1 <= s1.length, s2.length <= 104`
* `s1` and `s2` consist of lowercase English letters.
|
Obviously, brute force will result in TLE. Think of something else. How will you check whether one string is a permutation of another string? One way is to sort the string and then compare. But, Is there a better way? If one string is a permutation of another string then they must one common metric. What is that? Both strings must have same character frequencies, if one is permutation of another. Which data structure should be used to store frequencies? What about hash table? An array of size 26?
|
BFS✅| PYTHON ✅| O(N * M)| ✅
|
subtree-of-another-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSolving the problem requires you to iterate over the tree and check each node against the predetermined subRoot to see if the tree contains the subRoot. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we will use BFS (Breadth-First Search) to check all the nodes closest to the root. Every time we iterate over a node, we will start a process that compares the current node to the subRoot. This process, which we will call "compare", will recursively check each of our node\'s children against each of the subRoot\'s children, returning true if they are all the same, or false if they are not.\n# Complexity\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Time complexity: O(n * m)\n - n is the number of nodes in the root tree.\n - m is the number of nodes in the subRoot tree.\n\n# Code\n```\nfrom collections import deque\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:\n\n queue = deque([root])\n def compare(main, sub):\n if not main and not sub:\n return True\n if not main or not sub or main.val != sub.val:\n return False\n return compare(main.left, sub.left) and compare(main.right, sub.right)\n\n while queue:\n for i in range(len(queue)):\n node = queue.popleft()\n if node:\n if compare(node, subRoot):\n return True\n queue.append(node.left)\n queue.append(node.right)\n \n return False\n```
| 1
|
Given the roots of two binary trees `root` and `subRoot`, return `true` if there is a subtree of `root` with the same structure and node values of `subRoot` and `false` otherwise.
A subtree of a binary tree `tree` is a tree that consists of a node in `tree` and all of this node's descendants. The tree `tree` could also be considered as a subtree of itself.
**Example 1:**
**Input:** root = \[3,4,5,1,2\], subRoot = \[4,1,2\]
**Output:** true
**Example 2:**
**Input:** root = \[3,4,5,1,2,null,null,null,null,0\], subRoot = \[4,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in the `root` tree is in the range `[1, 2000]`.
* The number of nodes in the `subRoot` tree is in the range `[1, 1000]`.
* `-104 <= root.val <= 104`
* `-104 <= subRoot.val <= 104`
|
Which approach is better here- recursive or iterative? If recursive approach is better, can you write recursive function with its parameters? Two trees s and t are said to be identical if their root values are same and their left and right subtrees are identical. Can you write this in form of recursive formulae? Recursive formulae can be:
isIdentical(s,t)= s.val==t.val AND isIdentical(s.left,t.left) AND isIdentical(s.right,t.right)
|
BFS✅| PYTHON ✅| O(N * M)| ✅
|
subtree-of-another-tree
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSolving the problem requires you to iterate over the tree and check each node against the predetermined subRoot to see if the tree contains the subRoot. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we will use BFS (Breadth-First Search) to check all the nodes closest to the root. Every time we iterate over a node, we will start a process that compares the current node to the subRoot. This process, which we will call "compare", will recursively check each of our node\'s children against each of the subRoot\'s children, returning true if they are all the same, or false if they are not.\n# Complexity\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Time complexity: O(n * m)\n - n is the number of nodes in the root tree.\n - m is the number of nodes in the subRoot tree.\n\n# Code\n```\nfrom collections import deque\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:\n\n queue = deque([root])\n def compare(main, sub):\n if not main and not sub:\n return True\n if not main or not sub or main.val != sub.val:\n return False\n return compare(main.left, sub.left) and compare(main.right, sub.right)\n\n while queue:\n for i in range(len(queue)):\n node = queue.popleft()\n if node:\n if compare(node, subRoot):\n return True\n queue.append(node.left)\n queue.append(node.right)\n \n return False\n```
| 1
|
Given the roots of two binary trees `root` and `subRoot`, return `true` if there is a subtree of `root` with the same structure and node values of `subRoot` and `false` otherwise.
A subtree of a binary tree `tree` is a tree that consists of a node in `tree` and all of this node's descendants. The tree `tree` could also be considered as a subtree of itself.
**Example 1:**
**Input:** root = \[3,4,5,1,2\], subRoot = \[4,1,2\]
**Output:** true
**Example 2:**
**Input:** root = \[3,4,5,1,2,null,null,null,null,0\], subRoot = \[4,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in the `root` tree is in the range `[1, 2000]`.
* The number of nodes in the `subRoot` tree is in the range `[1, 1000]`.
* `-104 <= root.val <= 104`
* `-104 <= subRoot.val <= 104`
|
Which approach is better here- recursive or iterative? If recursive approach is better, can you write recursive function with its parameters? Two trees s and t are said to be identical if their root values are same and their left and right subtrees are identical. Can you write this in form of recursive formulae? Recursive formulae can be:
isIdentical(s,t)= s.val==t.val AND isIdentical(s.left,t.left) AND isIdentical(s.right,t.right)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.